Author: Сергиенко А.Б.
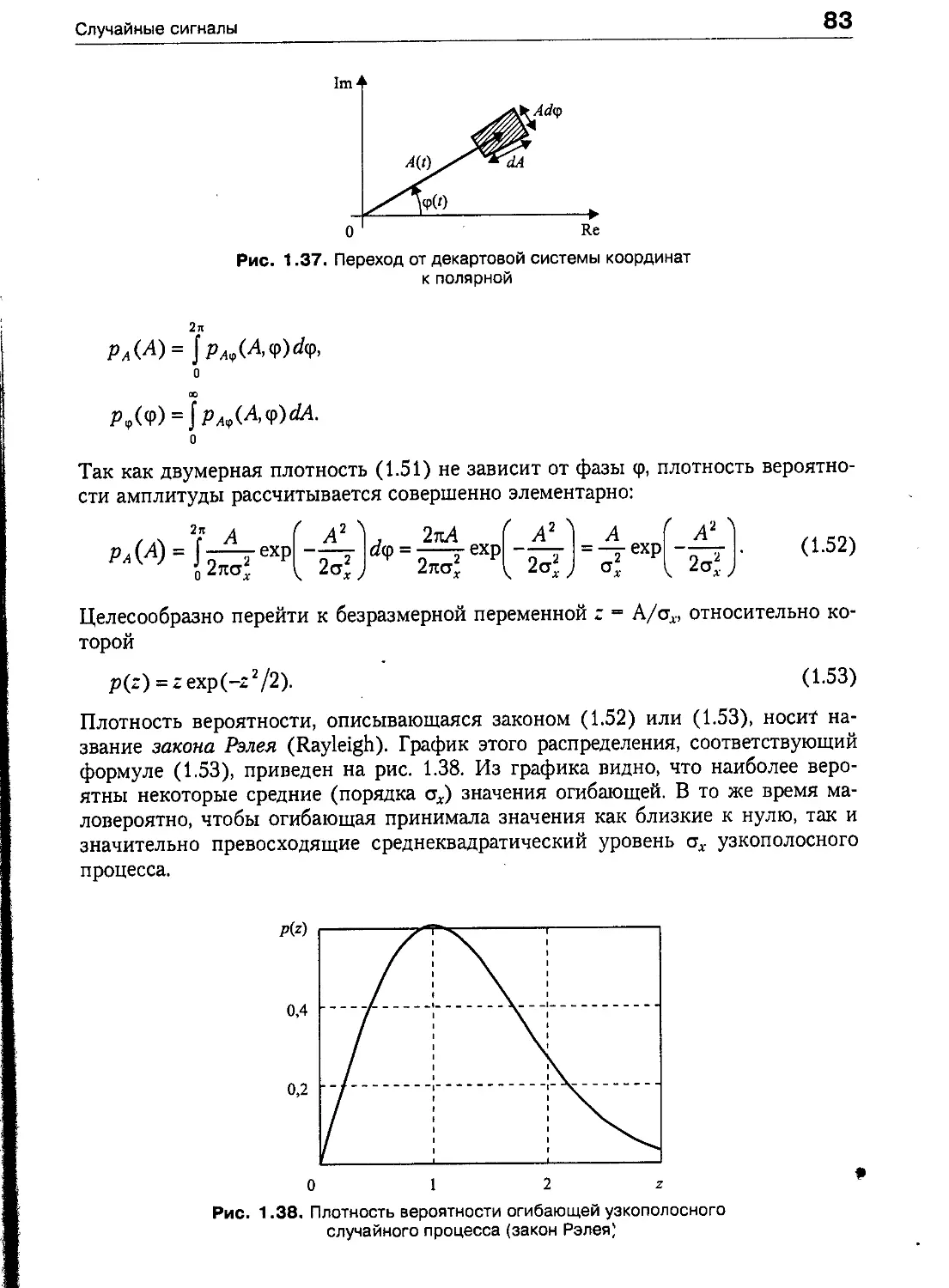
Tags: электротехника кибернетика учебник для вузов цифровые устройства основы теории дискретных сигналов и систем методы спектрального анализа фильтрация дискретных сигналов алгоритмы синтеза дискретных фильтров влияние эффектов квантования конечная точность вычислений методы модуляции
ISBN: 5-318-00666-3
Year: 2002
А. Б. Сергиенко
ЦИФРОВАЯ
ОБРАБОТКА СИГНАЛОВ
/ДЛЯ ВУЗОВ
а
• для студентов
и преподавателей
высших учебных
• фундаментальный
курс, охватывающий
основные разделы
цифровой обработки
сигналов
• сочетание теоретических
сведений и практических
А. Б. Сергиенко
ЦИФРОВАЯ
ОБРАБОТКА СИГНАЛОВ
Допущено Министерством образования Российской Федерации
в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению подготовки дипломированных специалистов
«Информатика и вычислительная техника»
Москва ■ Санкт-Петербург • Нижний Новгород • Воронеж
Ростов-на-Дону ■ Екатеринбург • Самара
Киев ■ Харьков • Минск
2002
ББК 32.811.3я7
УДК 621.391.26@75)
С32
Федеральная целевая программа «Культура России»
подпрограмма «Поддержка полиграфии и книгоиздания России»
Рецензенты:
Еркович С. П., доктор физико-математических наук, профессор
Московского Государственного технического университета (МГТУ) им. Н. Э. Баумана
Ревунков Г. И., кандидат технических наук, доцент
Московского Государственного технического университета (МГТУ) им. Н. Э. Баумана
С32 Цифровая обработка сигналов / А. Б. Сергиенко — СПб.: Питер, 2002. — 608 с: ил.
ISBN 5-318-00666-3
Учебник представляет собой базовый курс по цифровой обработке сигналов. В нем изложены
основы теории дискретных сигналов и систем, рассмотрены методы спектрального анализа и
фильтрации дискретных сигналов, алгоритмы синтеза дискретных фильтров, влияние эффектов
квантования и конечной точности вычислений на работу цифровых устройств, а также методы
модуляции, применяемые для передачи цифровой информации. Вводные главы посвящены основам
анализа сигналов и теории аналоговых систем. Материал изложен так, чтобы наглядно продемон-
продемонстрировать сущность алгоритмов, их взаимосвязь и области применения.
Теоретические сведения сопровождаются примерами реализации обсуждаемых алгоритмов
с помощью системы MATLAB и ее пакетов расширения Signal Processing, Communications и Filter
Design.
Книга допущена в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению подготовки дипломированных специалистов «Информатика и вы-
вычислительная техника», преподавателей, научных работников, программистов, а также всех, кто
интересуется компьютерной обработкой сигналов и иных данных.
ББК 32.611.3я7
УДК 621.391.26@75)
ISBN 5-318-00666-3 © ЗАО Издательский дом «Питер», 2002
Краткое содержание
Введение 13
Глава 1. Основы анализа сигналов 17
Глава 2. Аналоговые системы 87
Глава 3. Дискретные сигналы 127
Глава 4. Дискретные системы 189
Глава 5. Спектральный анализ 249
Глава 6. Проектирование дискретных фильтров 313
Глава 7. Эффекты квантования в цифровых системах 373
Глава 8. Модуляция и демодуляция 426
Приложение А. Основы работы с MATLAB 508
Приложение Б. Обзор функций MATLAB 557
Приложение В. Компоненты MATLAB 568
Приложение Г. Программа SPTool 574
Литература 585
Алфавитный указатель 586
Содержание
Введение 13
Структура книги 14
Чего нет е этой книге 16
Благодарности 16
От издательства 16
Глава 1. Основы анализа сигналов 17
Классификация сигналов 18
Энергия и мощность сигнала 21
Ряд Фурье 22
Синусно-косинусная форма 23
Вещественная форма 24
Комплексная форма 24
Примеры разложения сигналов в ряд Фурье 25
Преобразование Фурье 31
Примеры расчета преобразования Фурье 34
Свойства преобразования Фурье 42
Фурье-анализ неинтегрируемых сигналов 47
Корреляционный анализ 50
Корреляционная функция 50
Взаимная корреляционная функция 52
Связь между корреляционными функциями и спектрами сигналов 53
Энергетические расчеты в спектральной области 54
Комплексная огибающая 55
Преобразование Гильберта 56
Спектр аналитического сигнала 58
Случайные сигналы 60
Ансамбль реализаций 60
Модели случайных процессов 60
Вероятностные характеристики случайных процессов 63
Корреляционные функции случайных процессов 68
Стационарные и эргодические случайные процессы 71
Содержание
Спектральные характеристики случайных процессов 74
Теорема Винера—Хинчина 76
Узкополосный случайный процесс 80
Глава 2. Аналоговые системы 87
Классификация систем 87
Характеристики линейных систем 88
Импульсная характеристика 88
Переходная характеристика 89
Условие физической реализуемости 89
Комплексный коэффициент передачи 89
Коэффициент передачи по мощности 90
Фазовая и групповая задержка 90
Взаимный спектр выходного и входного сигналов 90
Взаимная корреляция между входом и выходом 91
Преобразование случайного процесса в линейной системе 91
Спектральная плотность мощности 91
Корреляционная функция 92
Дисперсия 92
Плотность вероятности 92
Частный случай белого шума 92
Способы описания линейных систем 93
Дифференциальное уравнение 93
Функция передачи 93
Нули и полюсы 94
Полюсы и вычеты 94
Пространство состояний 96
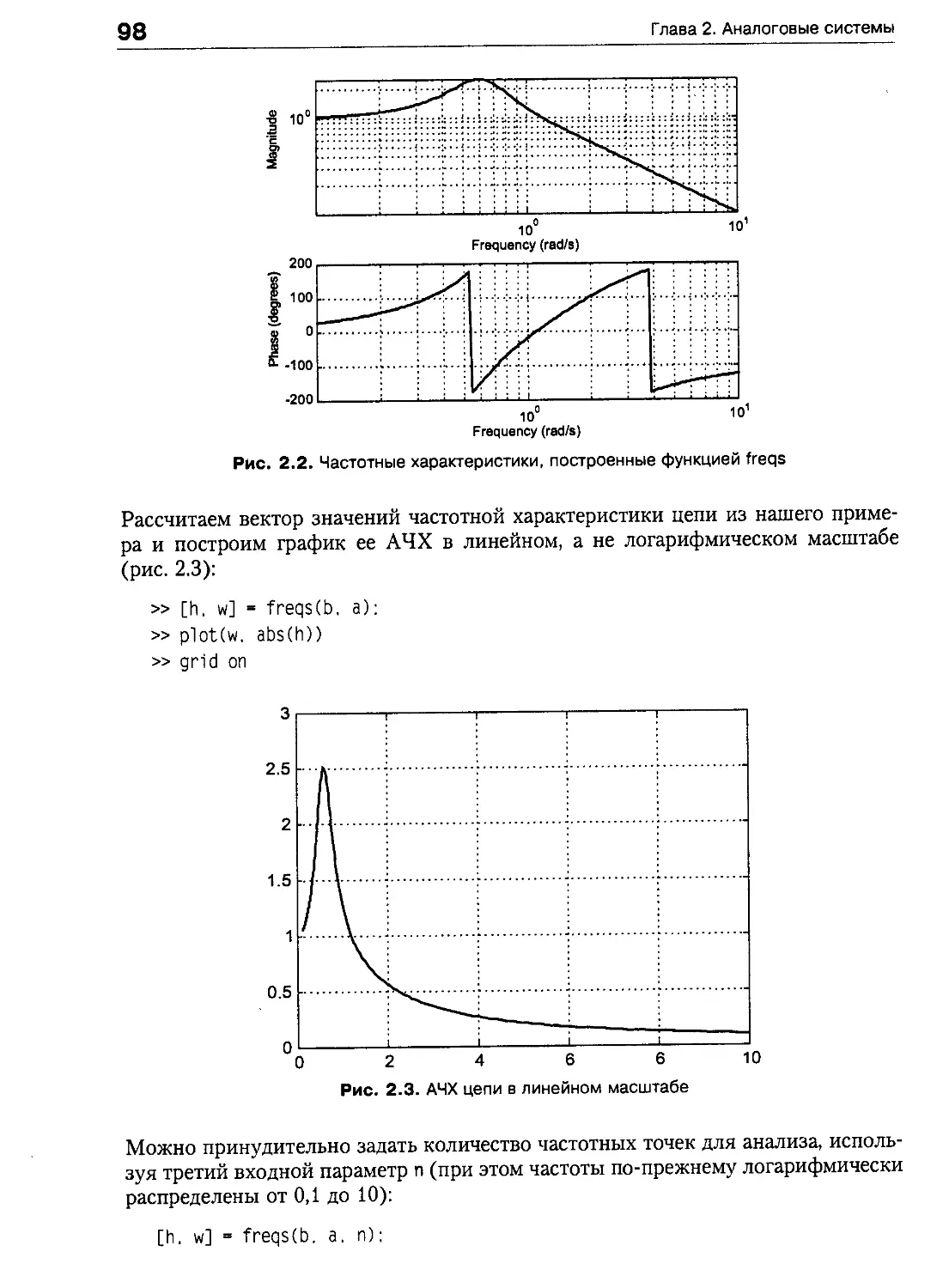
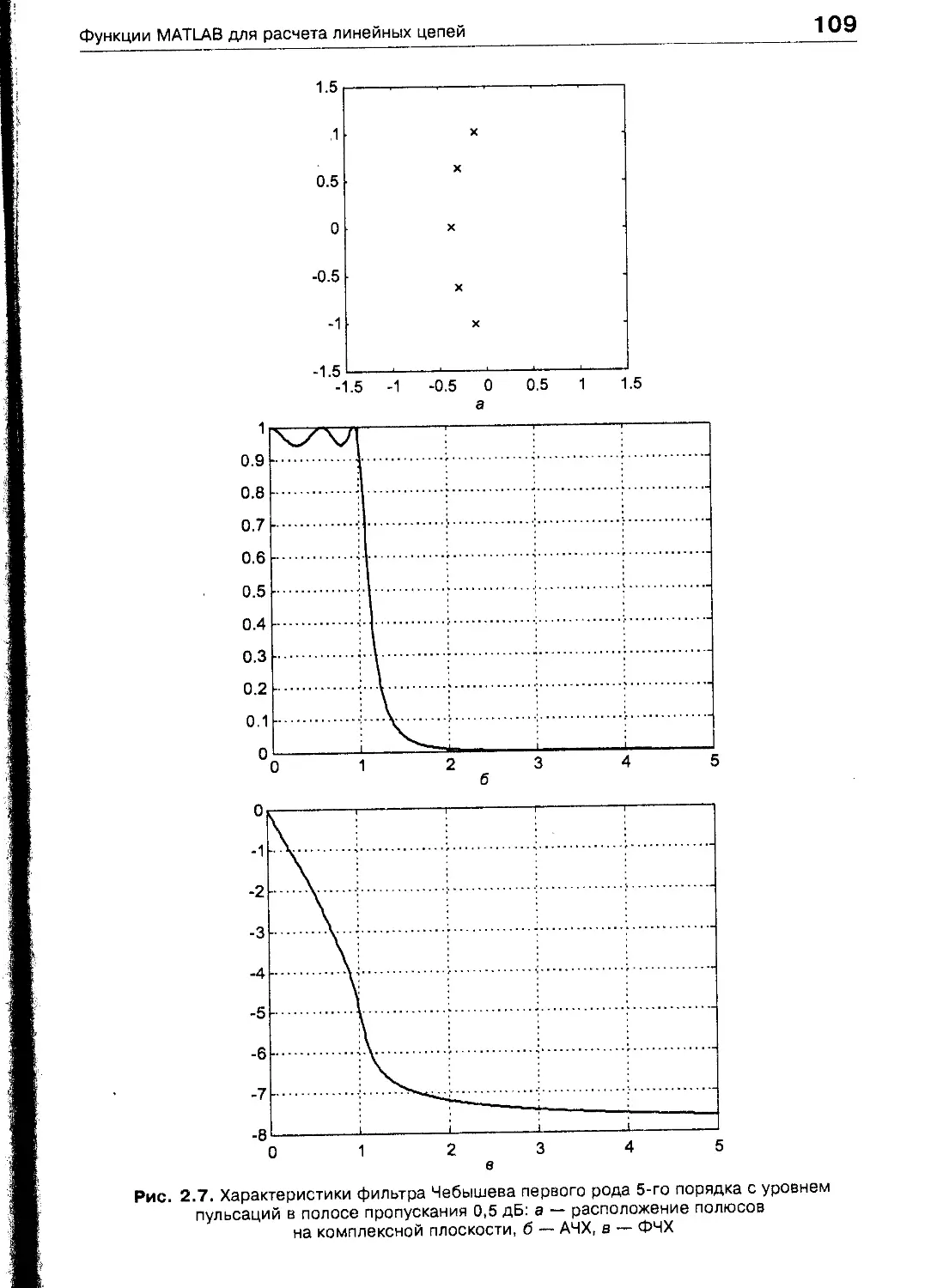
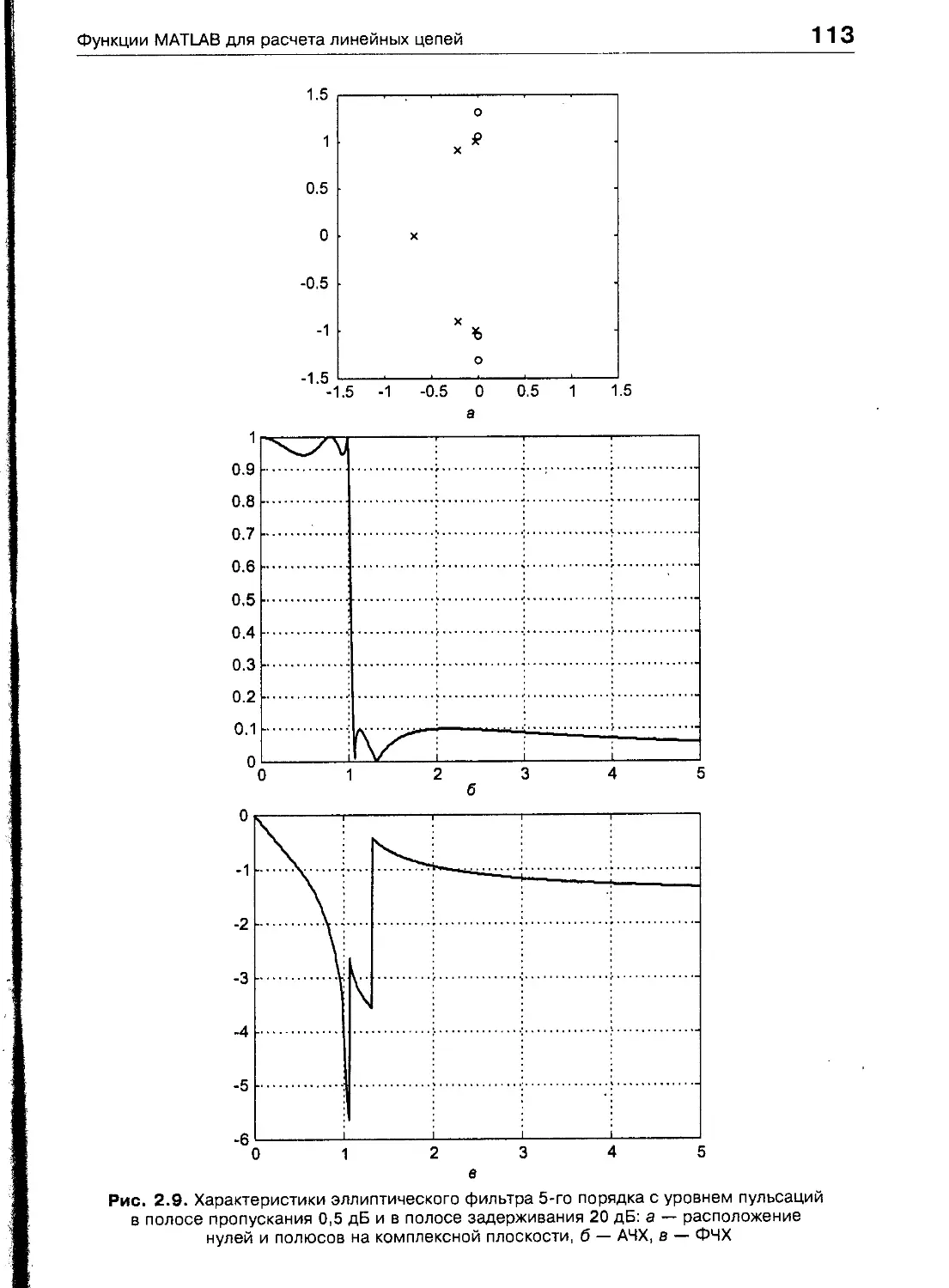
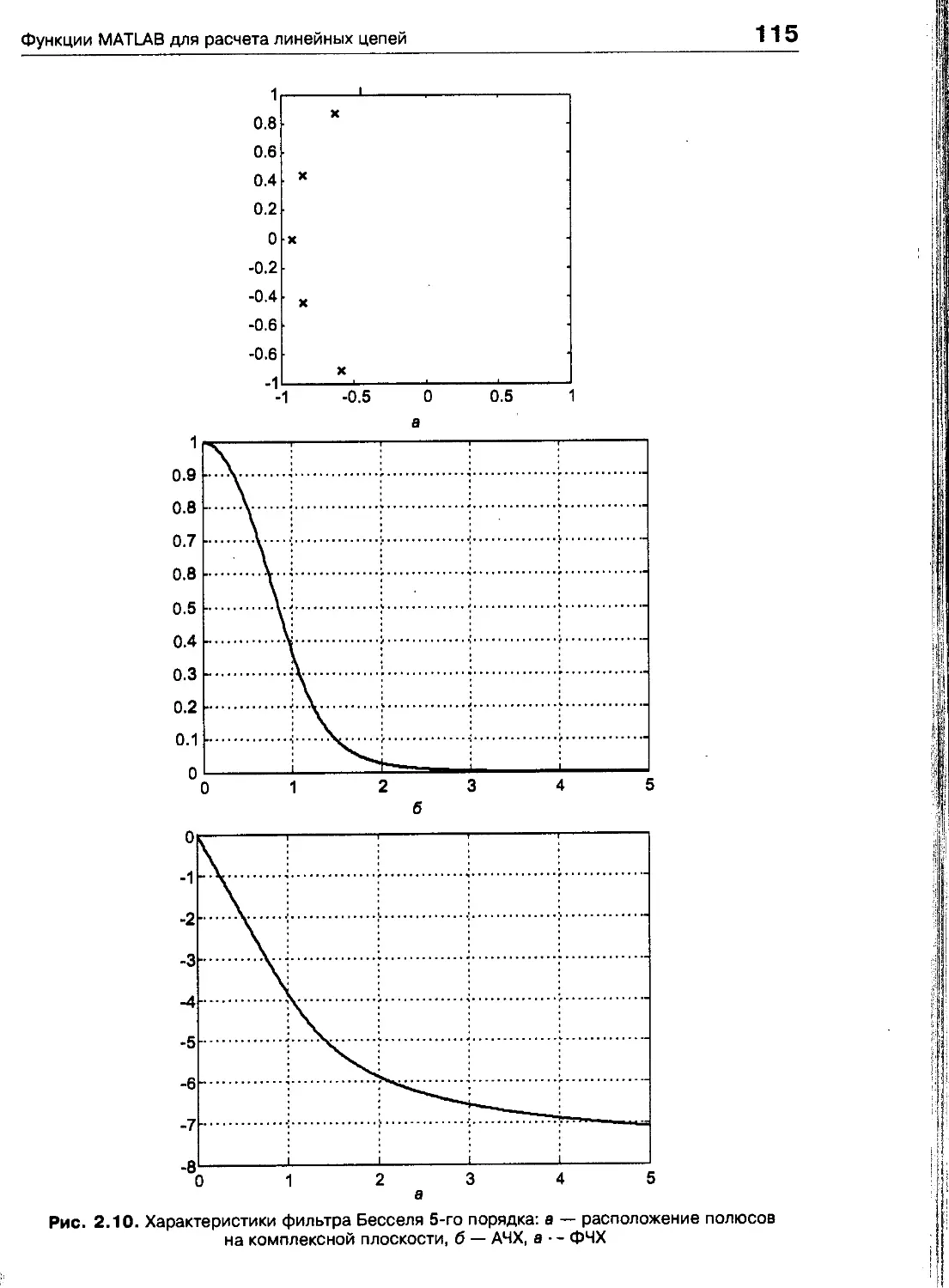
Функции MATLAB для расчета линейных цепей 97
Расчет частотных характеристик 97
Построение графиков фазочастотных характеристик 99
Преобразование способов описания линейных цепей 100
Расчет аналоговых фильтров-прототипов 104
Преобразования фильтров-прототипов 116
Расчет аналоговых фильтров 120
Выбор порядка фильтра 121
Расчет групповой задержки 123
Глава 3. Дискретные сигналы 127
Аналоговые, дискретные и цифровые сигналы 127
Аналого-цифровое и цифро-аналоговое преобразование 129
Частота Найквиста 129
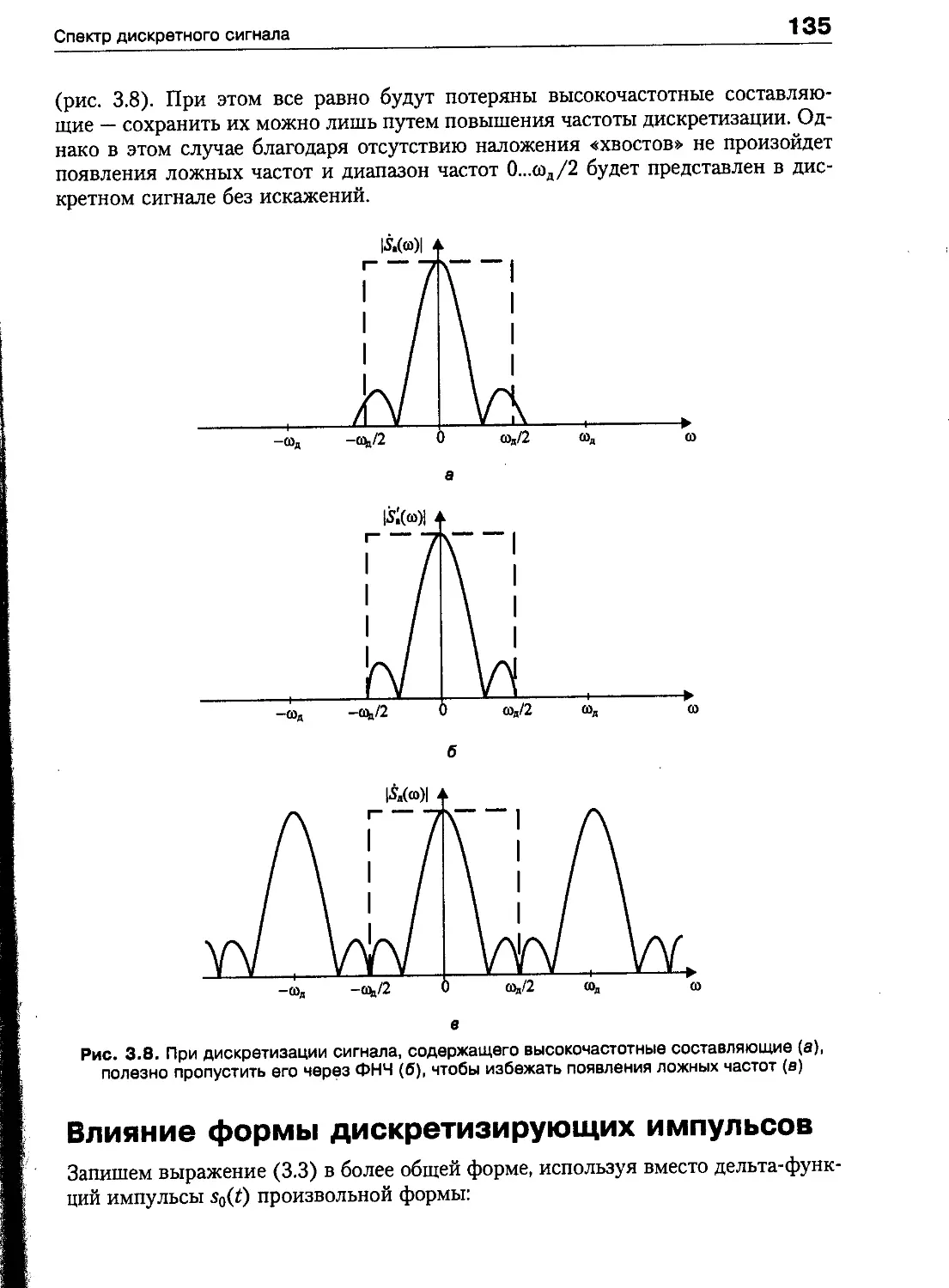
Спектр дискретного сигнала 131
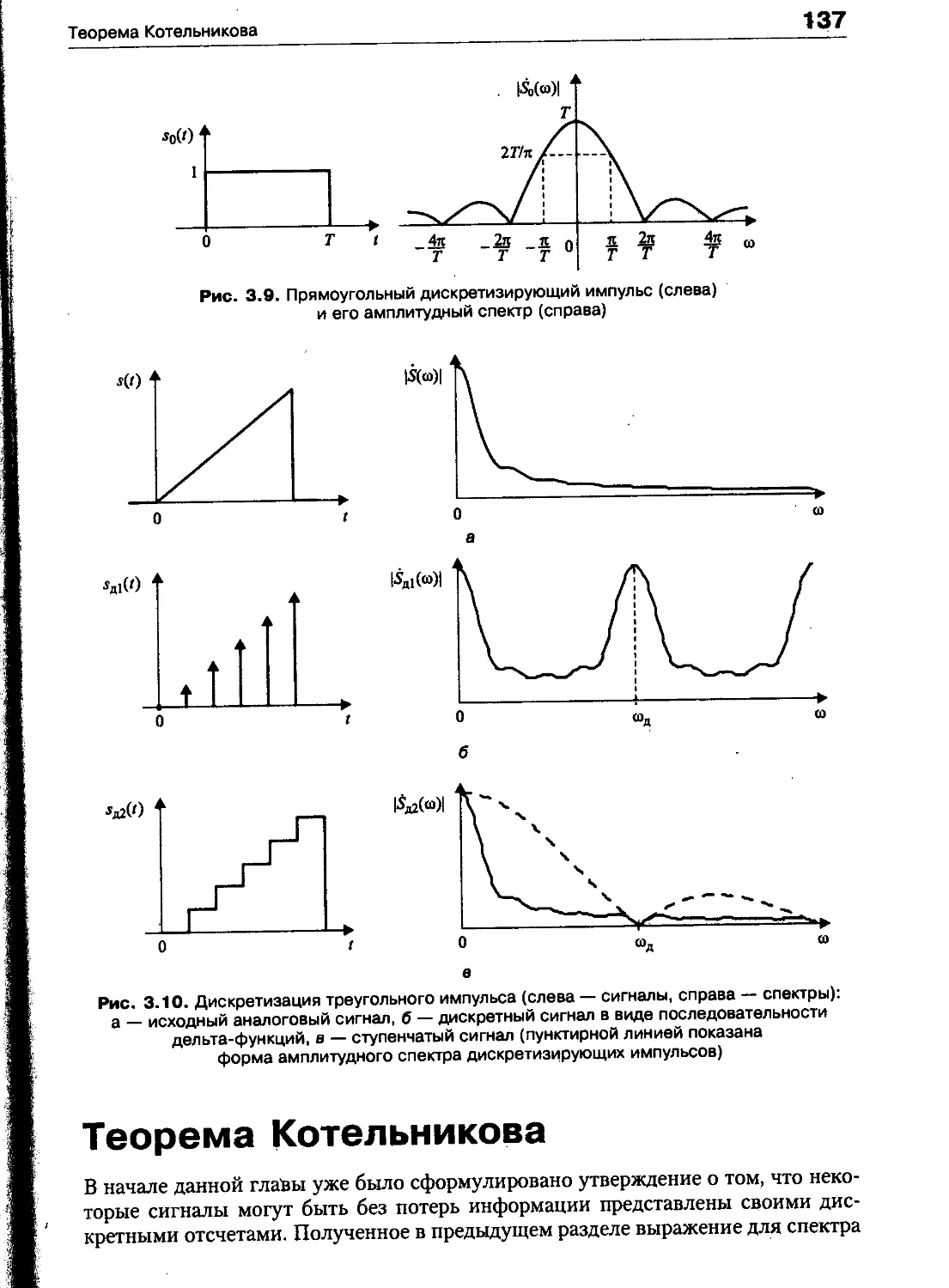
Влияние формы дискретизирующих импульсов 135
6 Содержание
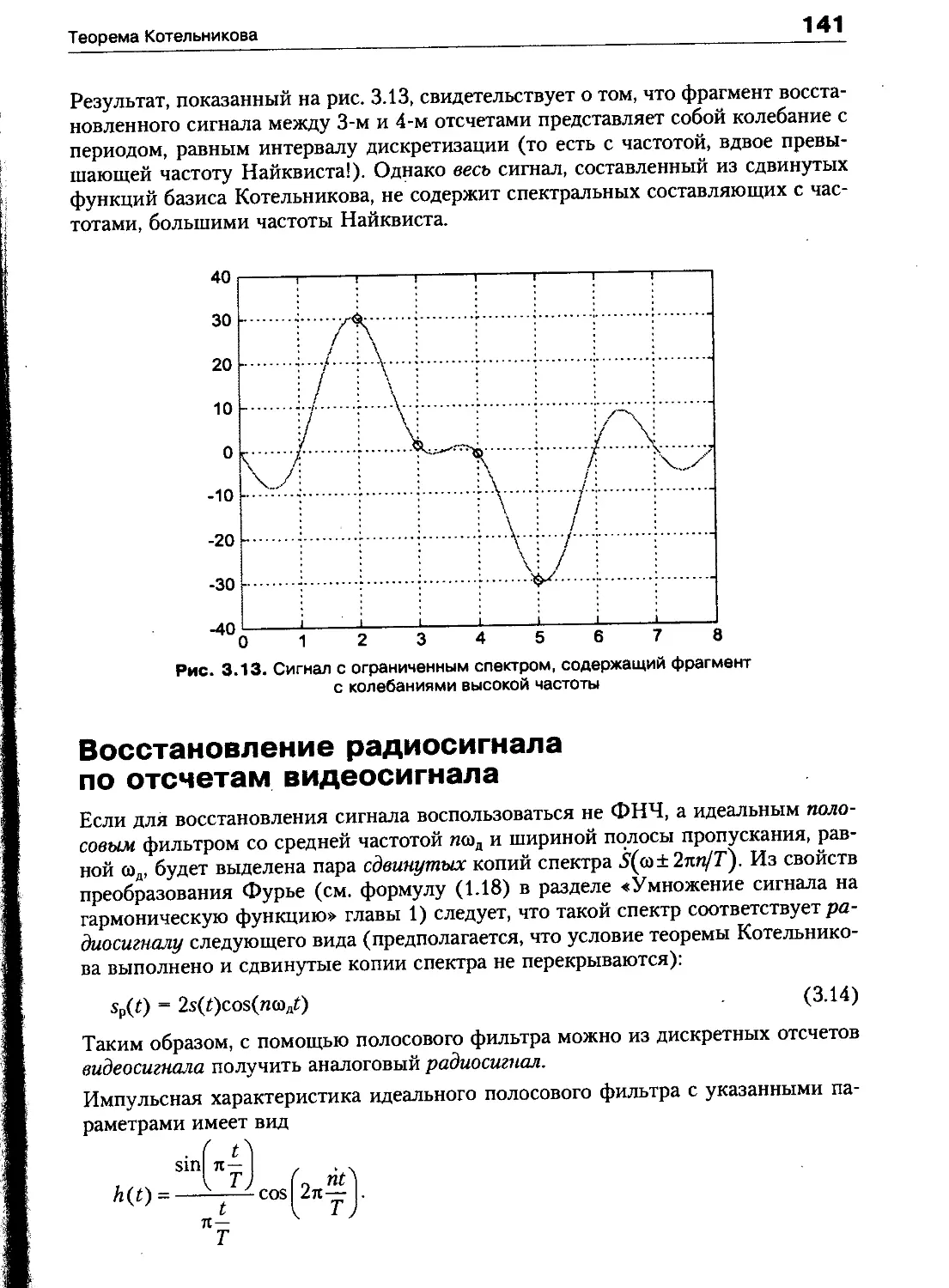
Теорема Котельникова 137
Восстановление радиосигнала по отсчетам видеосигнала 141
Квадратурная дискретизация узкополосных сигналов 142
Z-преобразование 143
Примеры вычисления z-преобразования 144
Связь z-преобразования с преобразованиями Лапласа и Фурье 145
Свойства z-преобразования 146
Обратное z-преобразование 147
Дискретные случайные сигналы 148
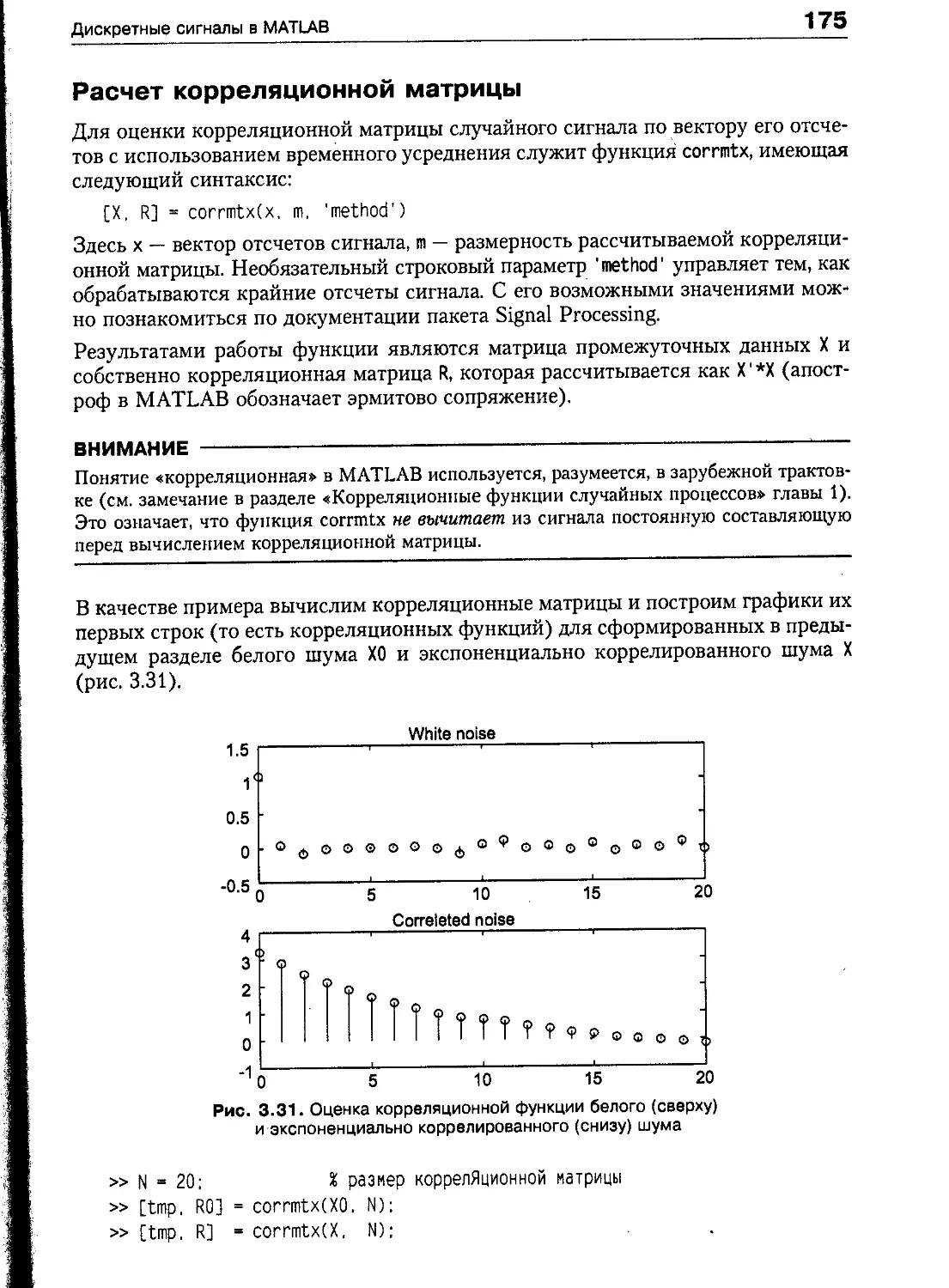
Корреляционная матрица 149
Дискретный белый шум 150
Дискретные сигналы в MATLAB 150
Расчет временных функций 151
Функции генерации одиночных импульсов 155
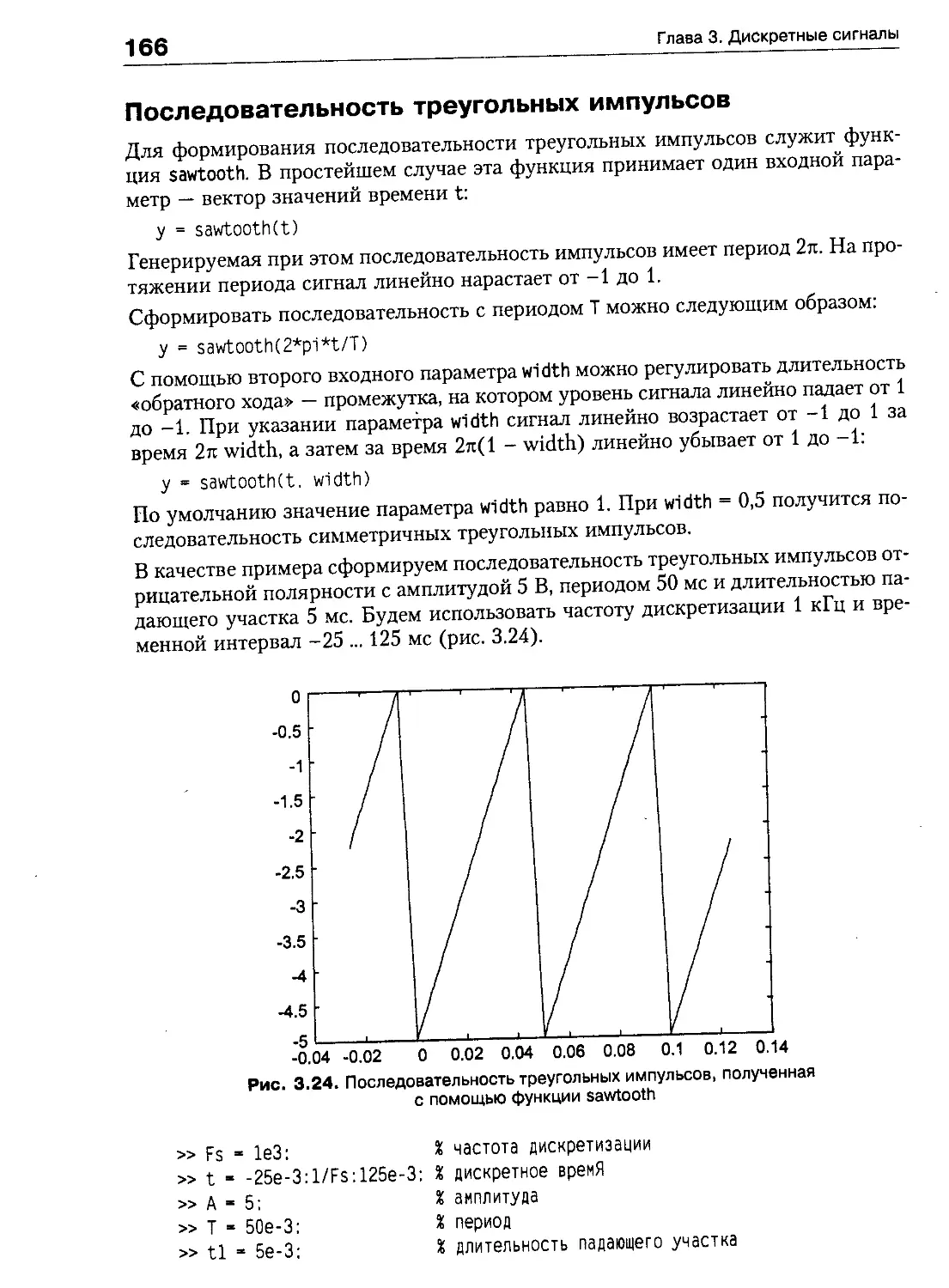
Генерация последовательности импульсов 161
Функции генерации периодических сигналов 164
Генерация сигнала с меняющейся частотой 168
Формирование случайных сигналов 172
Получение данных из внешних источников 178
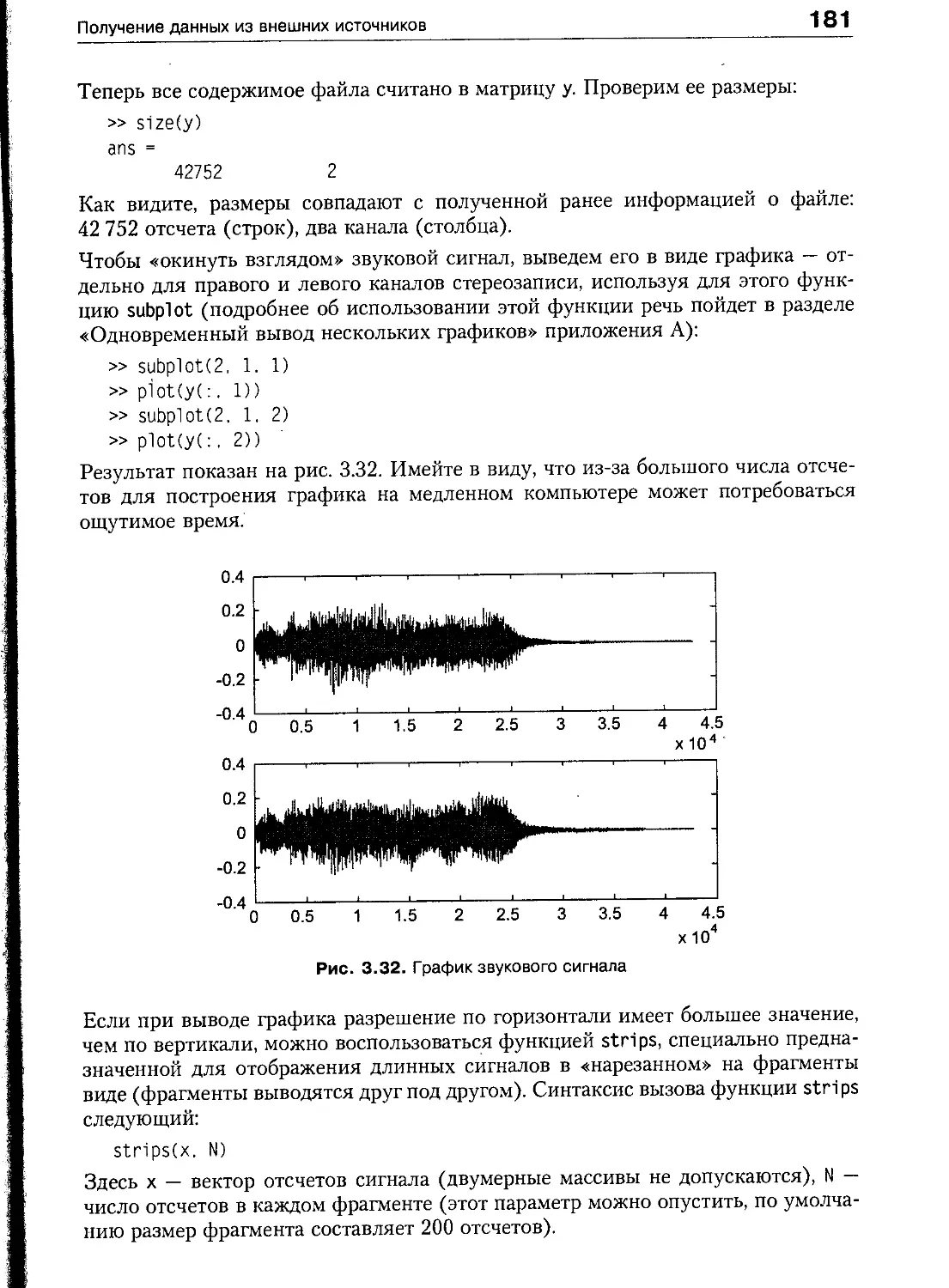
Чтение wav-файлов 178
Запись wav-файлов 182
Воспроизведение звука 183
Запись звука 185
Готовые записи сигналов 185
Пакет расширения Data Acquisition 186
Глава 4. Дискретные системы 189
Сущность линейной дискретной обработки 189
Способы описания дискретных систем 193
Импульсная характеристика 193
Функция передачи 195
Нули и полюсы 196
Полюсы и вычеты 198
Пространство состояний v 200
Преобразование случайного сигнала в дискретной системе 200
Рекурсивные и нерекурсивные дискретные фильтры . 202
Нерекурсивные фильтры 202
Рекурсивные фильтры 205
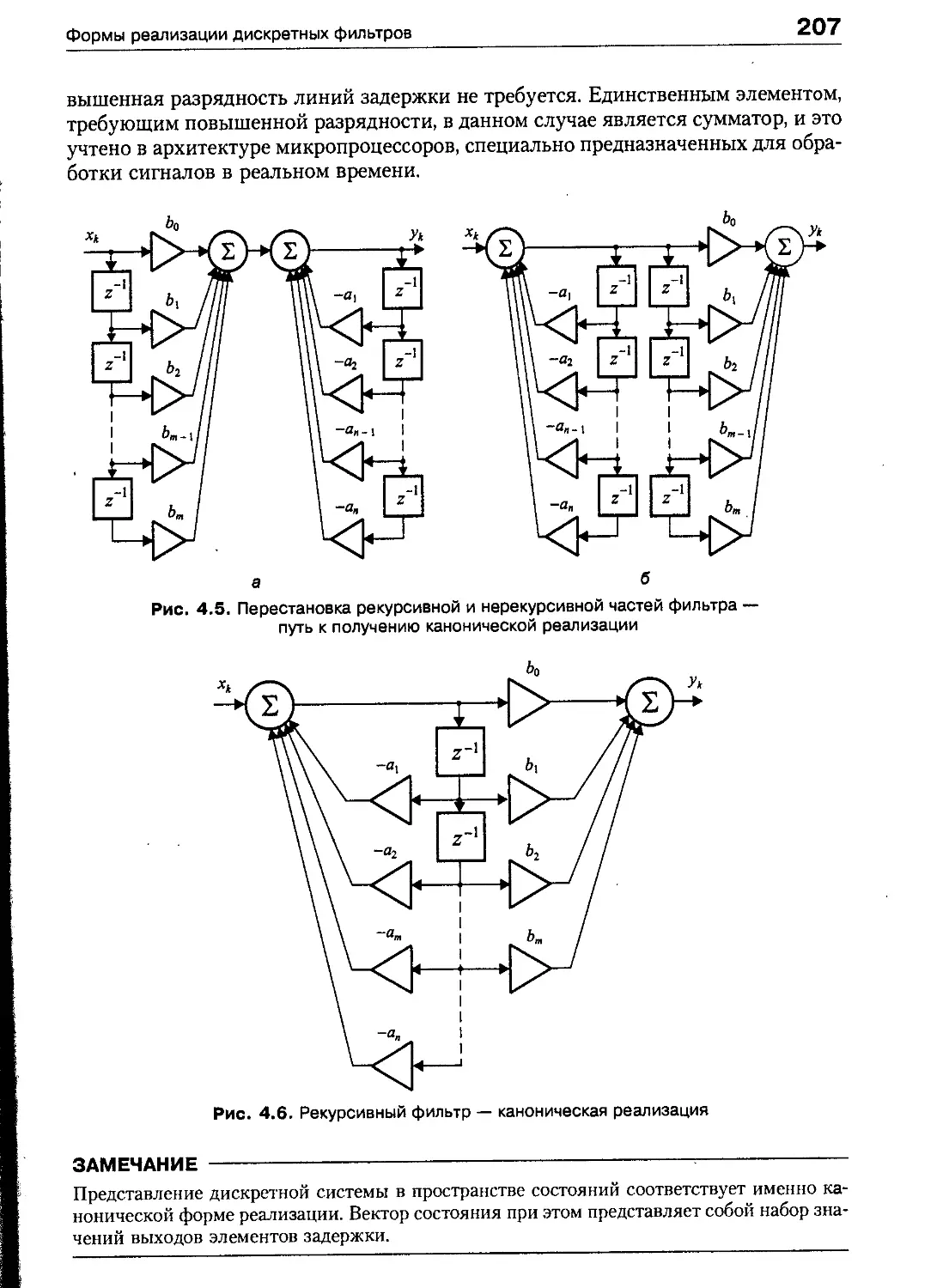
Формы реализации дискретных фильтров 206
Каноническая форма 206
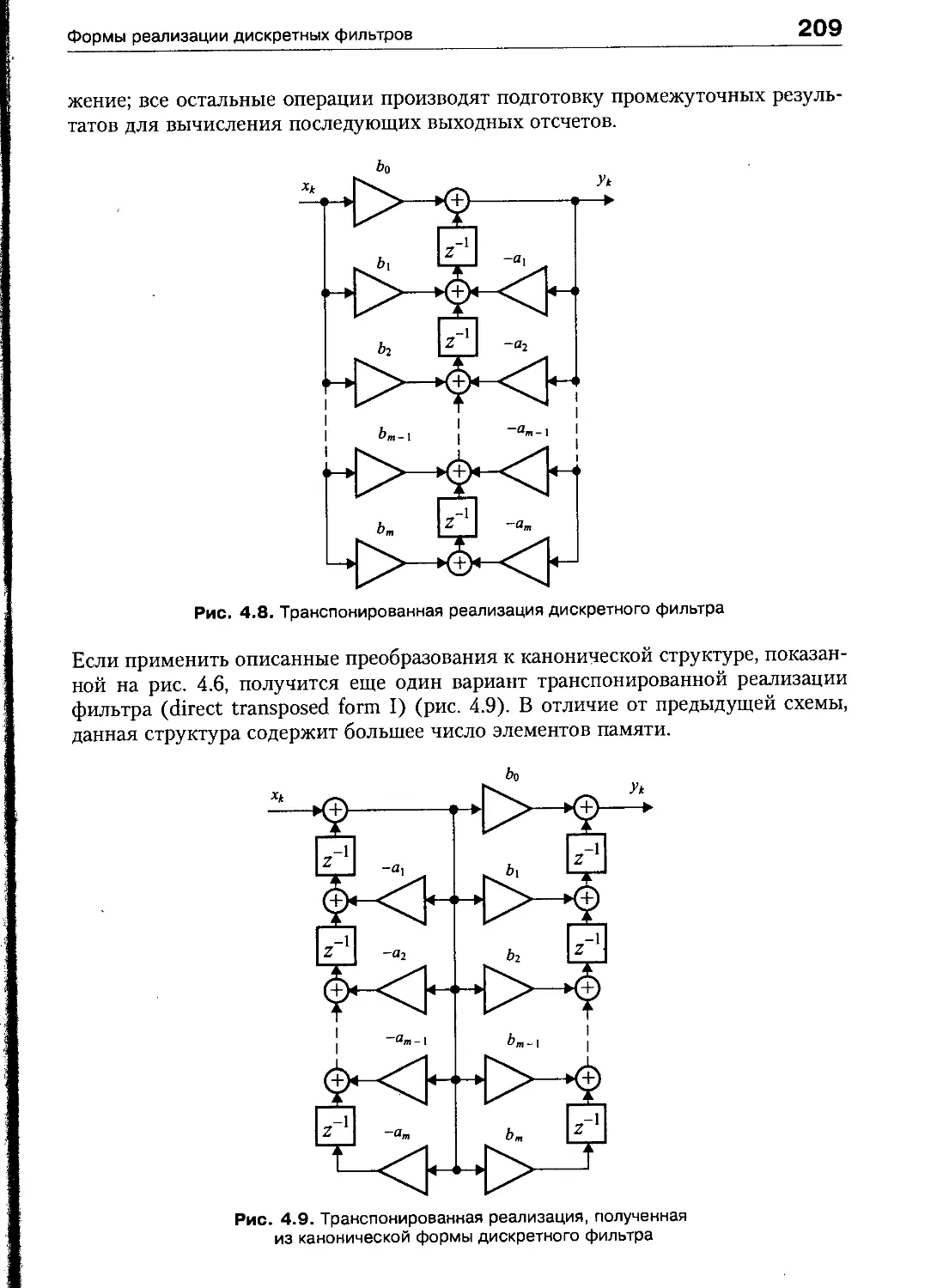
Транспонированная форма 208
Содержание
Последовательная (каскадная) форма 210
Параллельная форма 210
Дискретная фильтрация в MATLAB 211
Дискретная свертка 212
Обращение свертки 212
Функция дискретной фильтрации 213
Доступ к внутреннему состоянию фильтра 214
Компенсация фазового сдвига 215
Расчет импульсной характеристики 216
Расчет частотной характеристики 217
Расчет групповой задержки дискретной системы 219
Отображение нулей и полюсов фильтра 222
Свертка как матричное умножение 223
Преобразование способов описания дискретных фильтров 224
Изменение частоты дискретизации 230
Прореживание 231
Интерполяция 235
Передискретизация 237
Некоторые идеализированные фильтры 240
Дискретное преобразование Гильберта 240
Идеальный дифференцирующий фильтр 244
Визуализатор фильтров 247
Глава 5. Спектральный анализ 249
Дискретное преобразование Фурье 250
Свойства дискретного преобразования Фурье 251
Восстановление непрерывного сигнала с помощью ДПФ 253
Матрица ДПФ 254
Связь ДПФ и спектра дискретного сигнала 254
Алгоритм быстрого преобразования Фурье 256
БПФ с прореживанием по времени 256
БПФ с прореживанием по частоте 258
Основание алгоритма БПФ 260
Выводы 261
Взаимосвязь ДПФ и фильтрации 262
ДПФ как дискретная фильтрация 262
Дискретная фильтрация с помощью ДПФ 265
Растекание спектра 270
Весовые функции 273
Спектр дискретного случайного процесса 274
8 Содержание
Непараметрические методы 275
Периодограмма 275
Метод Узлча 276
Параметрические методы 277
Авторегрессионная модель 277
Метод MUSIC 282
Метод EV 284
Функции спектрального анализа в MATLAB 284
Прямое и обратное ДПФ 285
Функция fftshift 286
Матрица ДПФ 287
Блочная фильтрация в частотной области 287
Окна 287
Функции непараметрического спектрального анализа 298
Параметрический спектральный анализ в MATLAB 305
Реализация метода MUSIC 308
Функции peig и rooteig ■ 311
Глава 6. Проектирование дискретных фильтров 313
Синтез рекурсивных фильтров по аналоговому прототипу 313
Метод билинейного z-преобразования 314
Метод инвариантной импульсной характеристики 315
Прямые методы синтеза 317
Оптимальные методы 318
Субоптимальные методы 319
Субоптимальный синтез нерекурсивных фильтров 320
Синтез с использованием окон 320
Фильтры с косинусоидальным сглаживанием АЧХ 324
Синтез дискретных фильтров в MATLAB 328
Функции, использующие билинейное z-преобразование 329
Функция impinvar 335
Функции прямого синтеза рекурсивных фильтров 336
Функции синтеза с использованием окон 340
Функции расчета ФНЧ с косинусоидальным сглаживанием 344
Функция расчета рекурсивного фильтра Гильберта 348
Функции минимизации среднеквадратической ошибки 349
Реализация метода Ремеза 355
Функции пакета Filter Design 362
Графическая среда для синтеза и анализа фильтров 367
Содержание 9
Глава 7. Эффекты квантования в цифровых системах 373
Форматы представления чисел 374
Представление отрицательных чисел 374
Формат с фиксированной запятой 375
Формат с плавающей запятой 377
Процесс квантования 380
Шум квантования . . .' 380
Неравномерное квантование 382
Эффекты квантования в цифровых фильтрах 383
Квантование коэффициентов цифровых фильтров 383
Масштабирование коэффициентов цифровых фильтров 386
Переполнение разрядной сетки в процессе вычислений 388
Округление промежуточных результатов вычислений 391
Предельные циклы 393
Учет эффектов конечной точности вычислений в MATLAB 395
Функции квантования 396
Функции пакета расширения Filter Design 399
Квантователи 400
Квантованные фильтры 408
Анализ предельных циклов 417
Расширение программы fdatool 418
Квантованное БПФ 421
Глава 8. Модуляция и демодуляция 426
Амплитудная модуляция 427
Однотональная AM 429
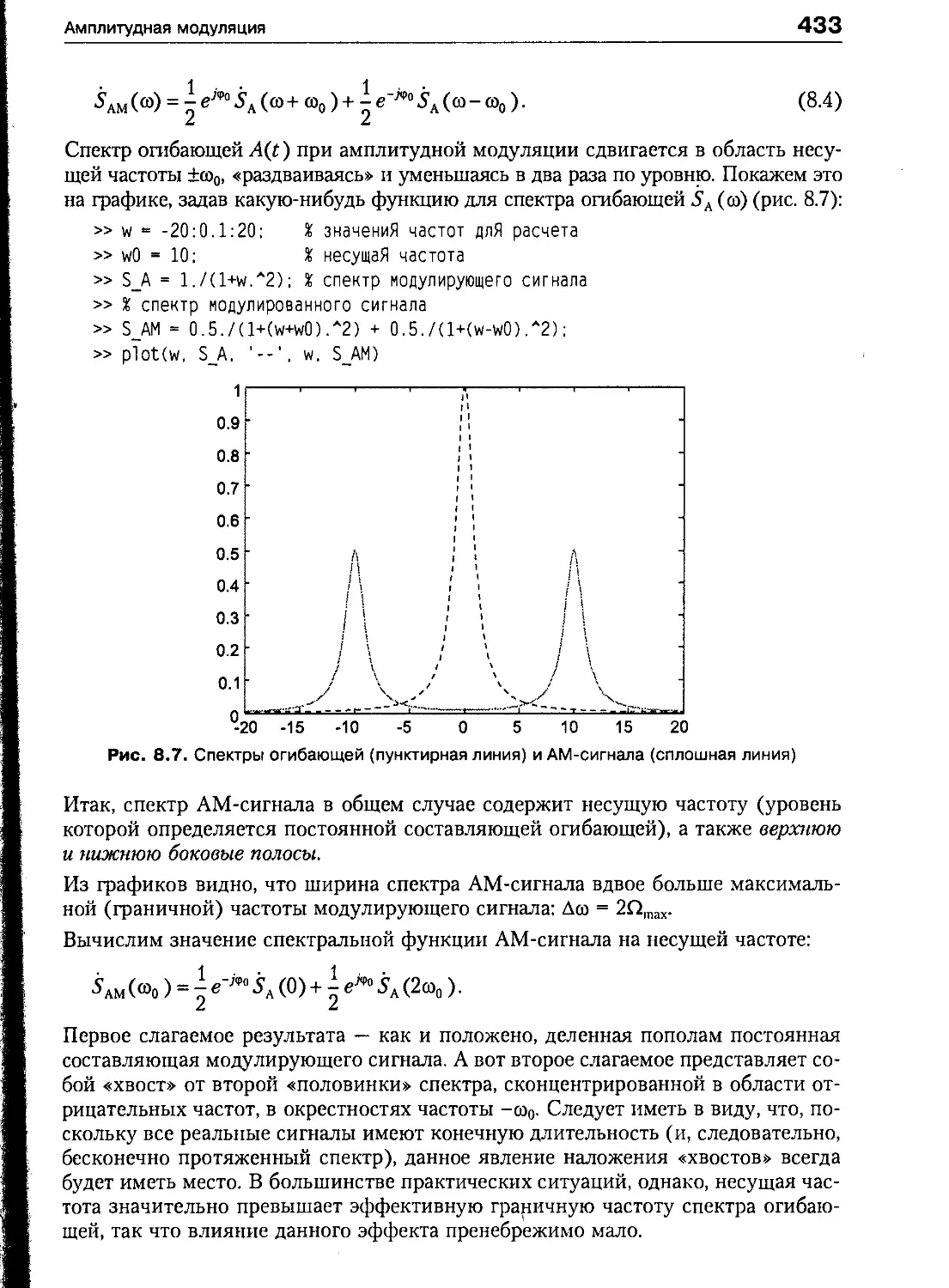
АМ-сигнал в Общем случае 432
Энергетические соотношения в АМ-сигнапе 434
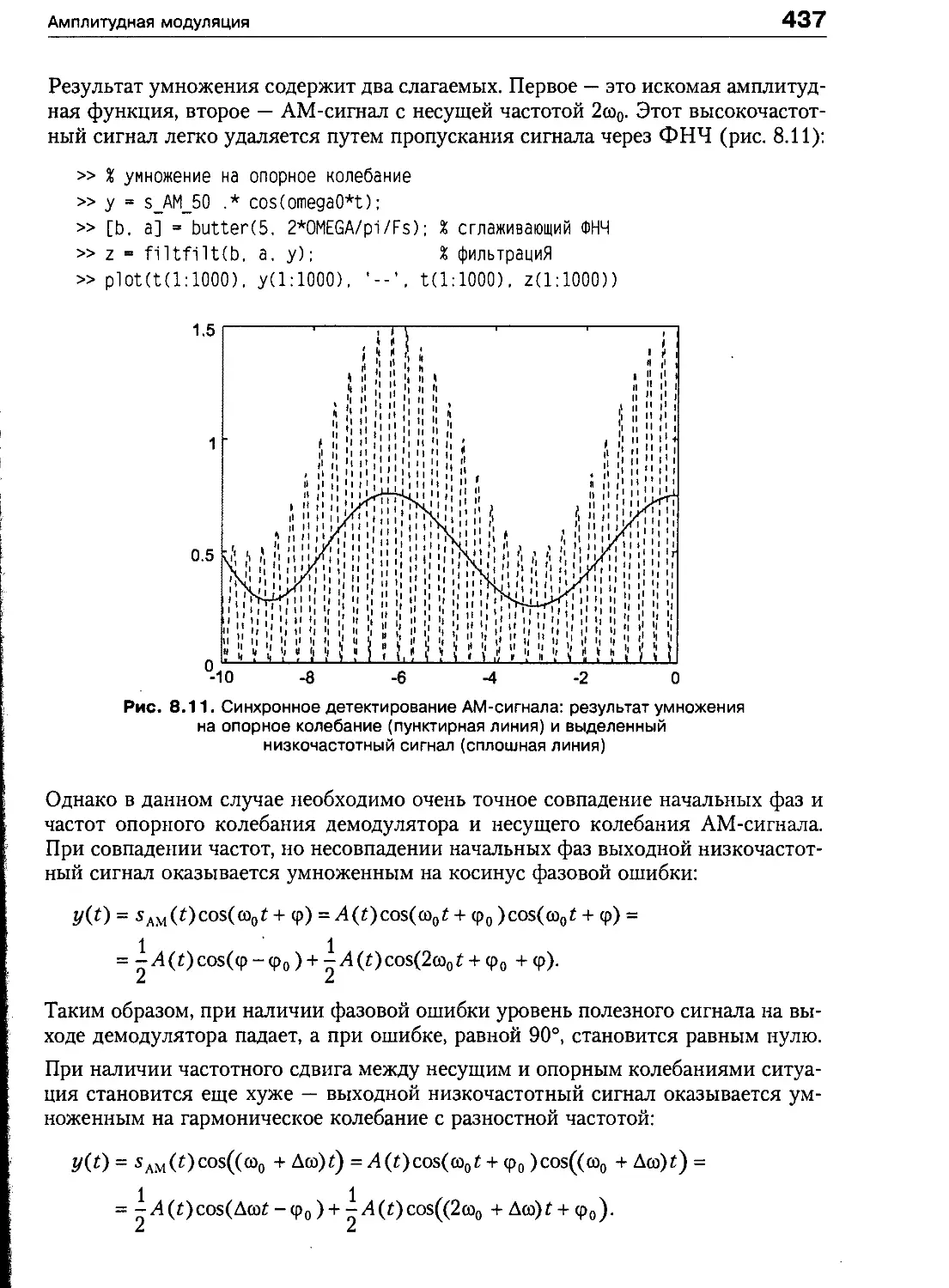
Демодуляция AM 436
Разновидности амплитудной модуляции 438
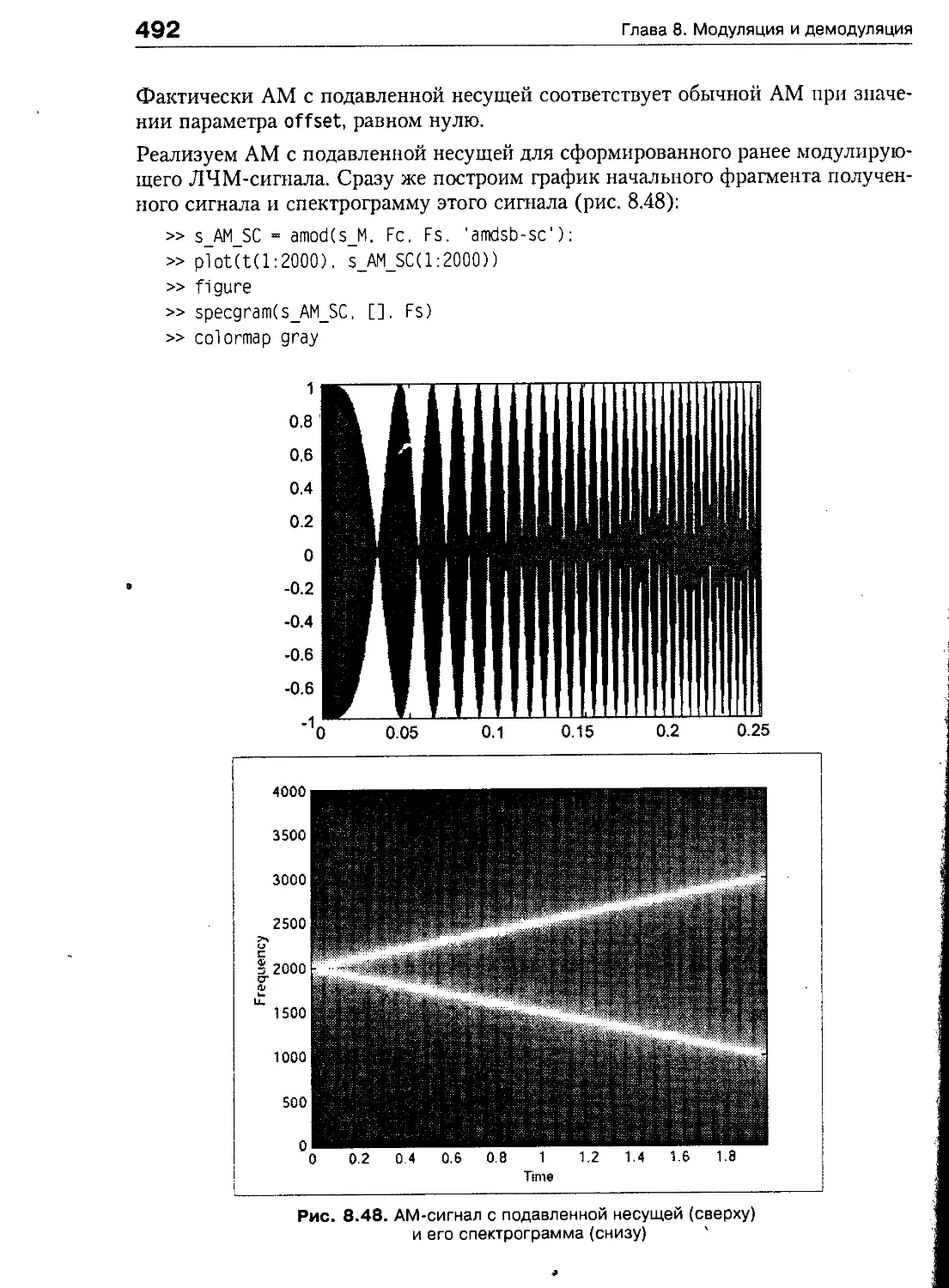
AM с подавленной несущей 438
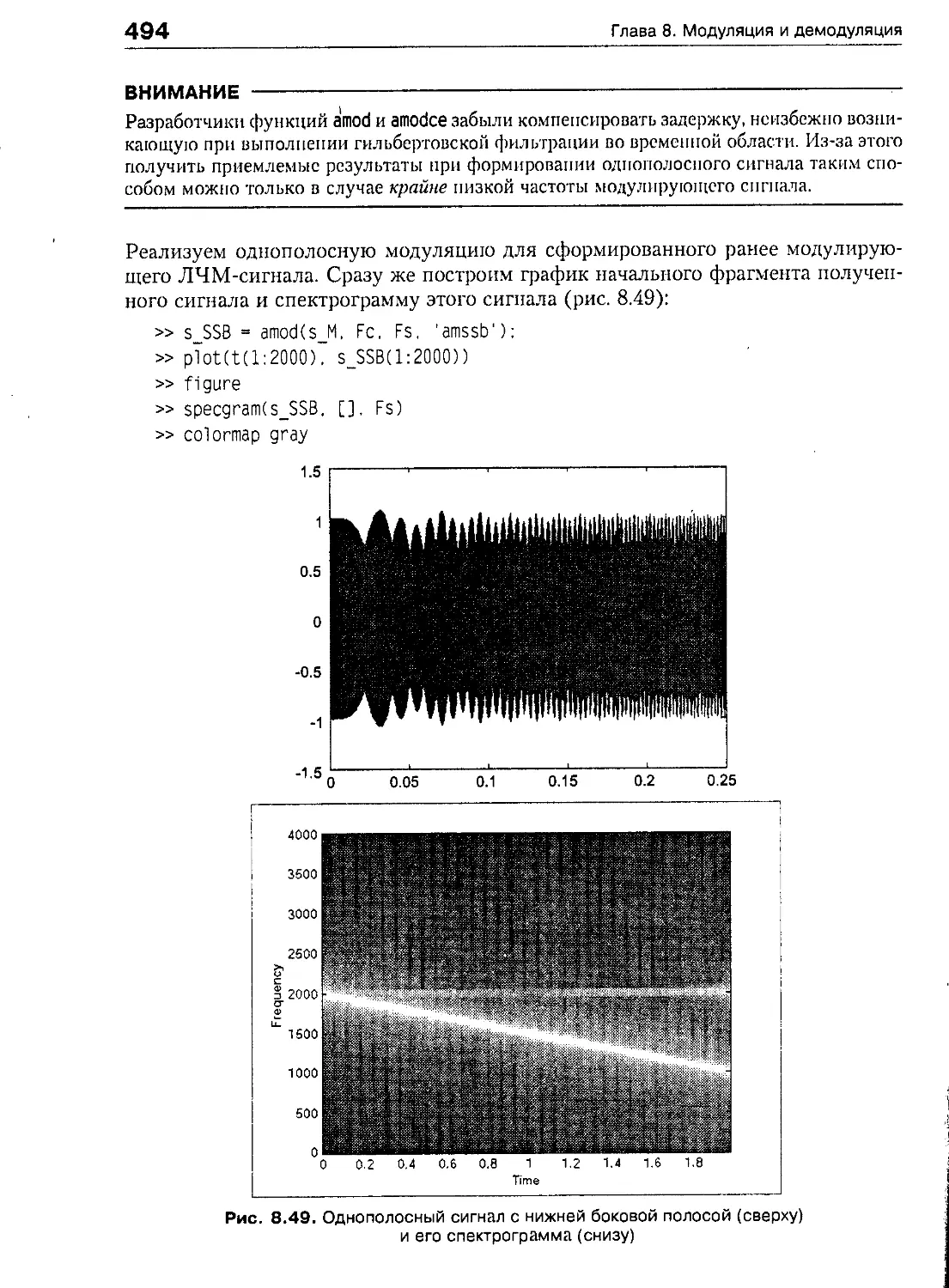
Однополосная модуляция 439
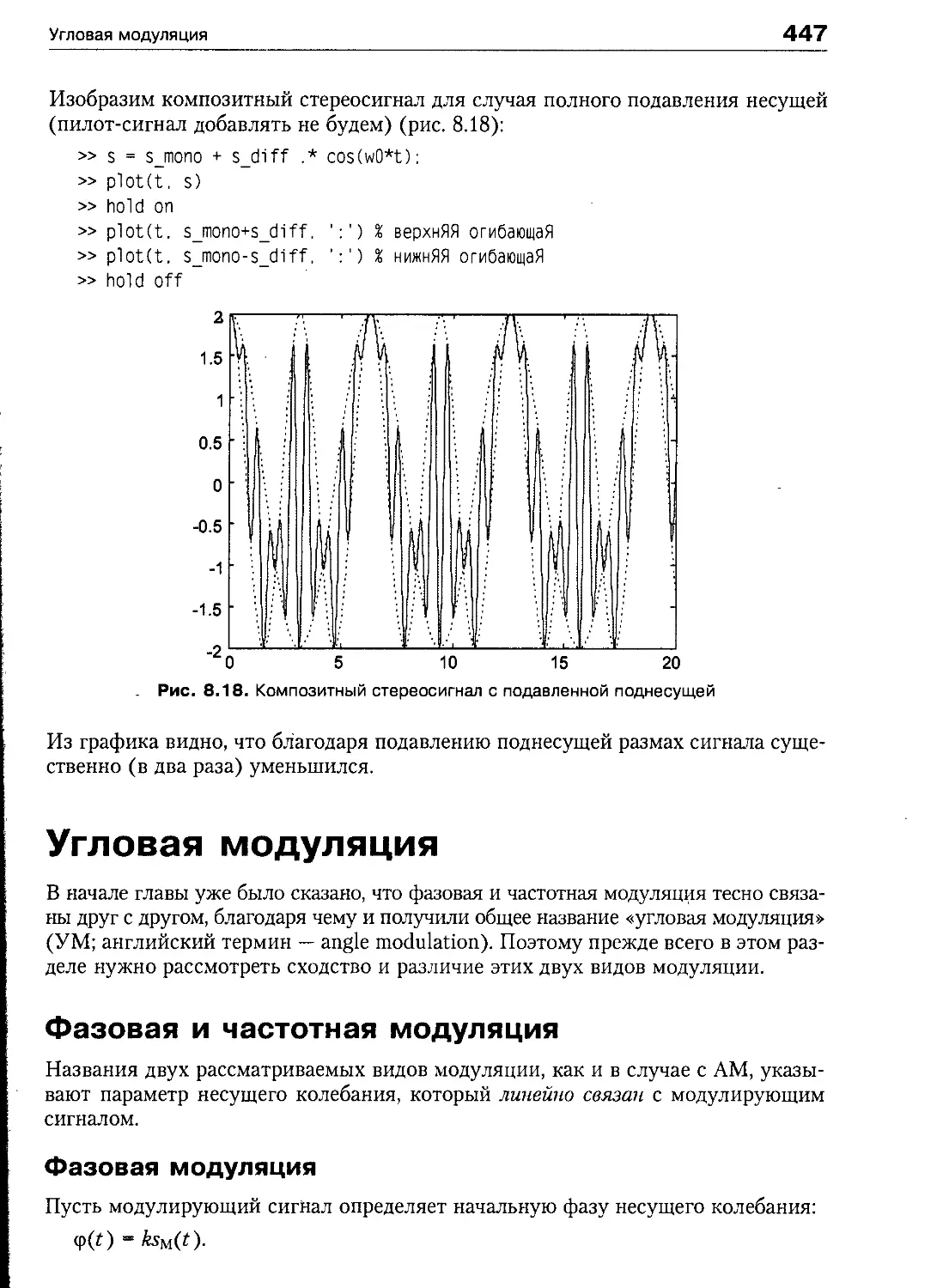
Полярная модуляция 444
Угловая модуляция 447
Фазовая и частотная модуляция 447
Гармоническая угловая модуляция 449
Спектр сигнала с гармонической угловой модуляцией 451
Ширина спектра сигнала с гармонической УМ 454
Демодуляция УМ 456
Квадратурная модуляция 458
Спектр сигнала с квадратурной модуляцией 459
Демодуляция сигнала с квадратурной модуляцией 459
10 Содержание
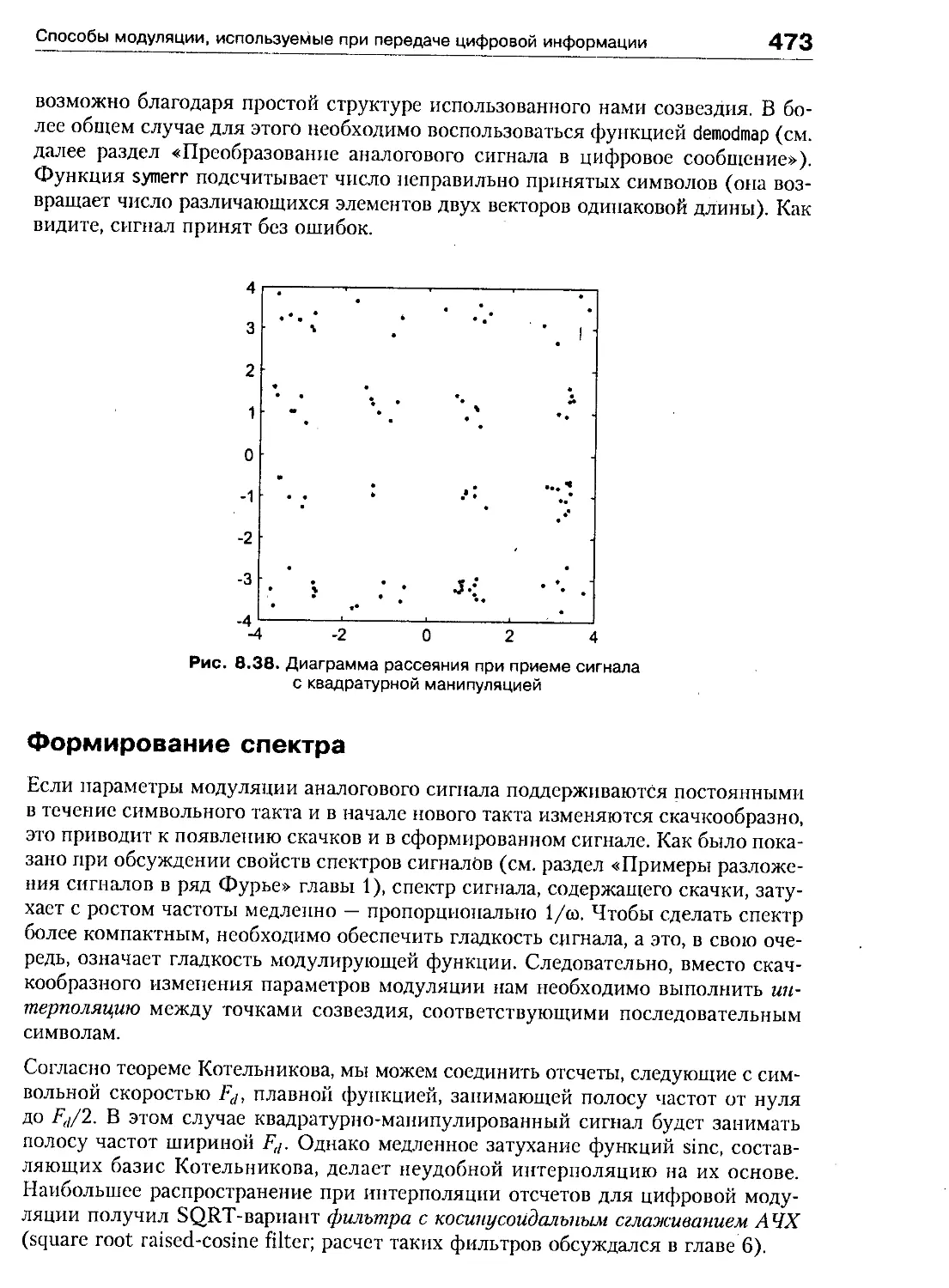
Способы модуляции, используемые при передаче цифровой информации . . 461
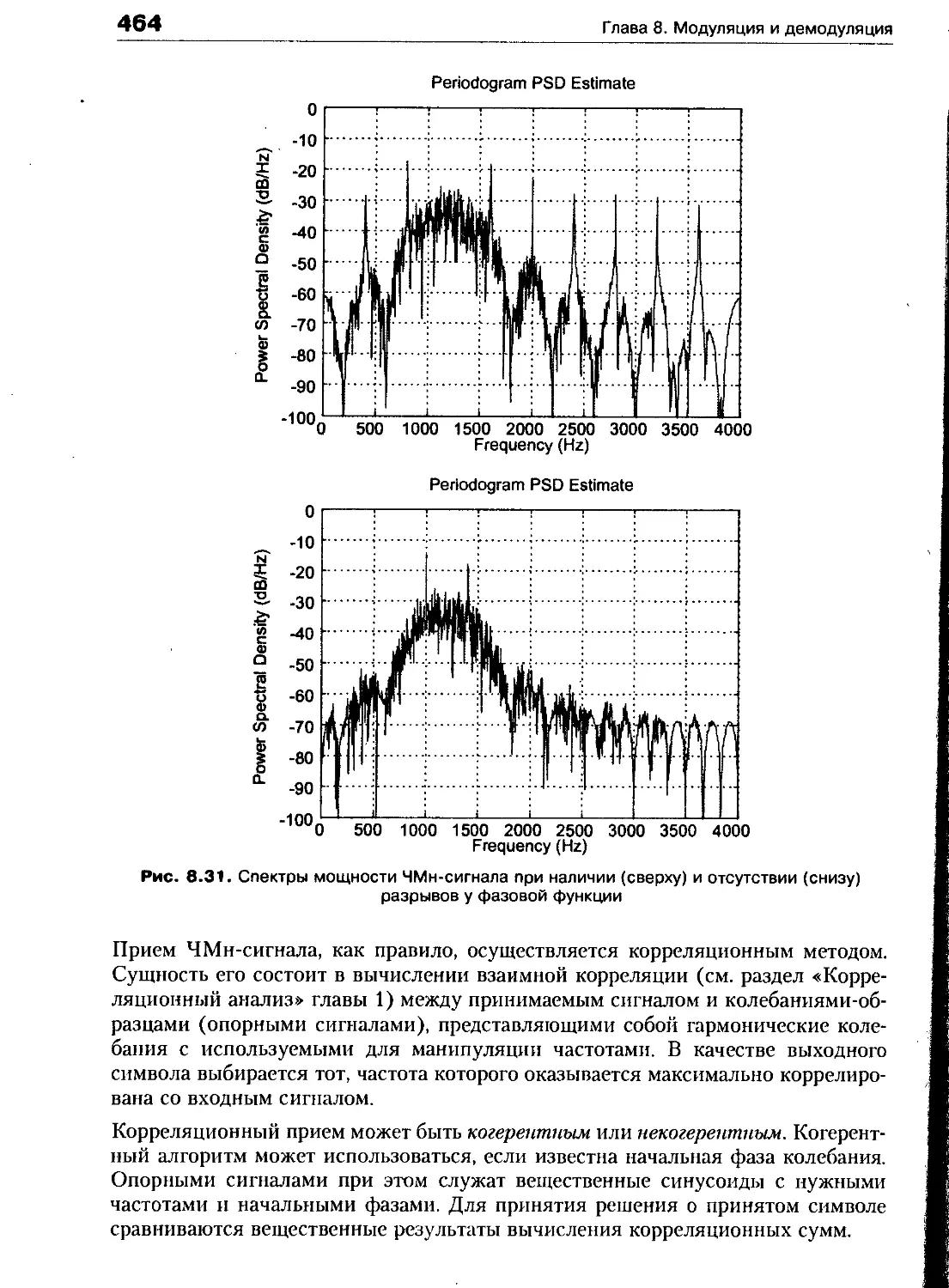
Частотная манипуляция : 462
Амплитудная манипуляция 466
Фазовая манипуляция 467
Квадратурная манипуляция 467
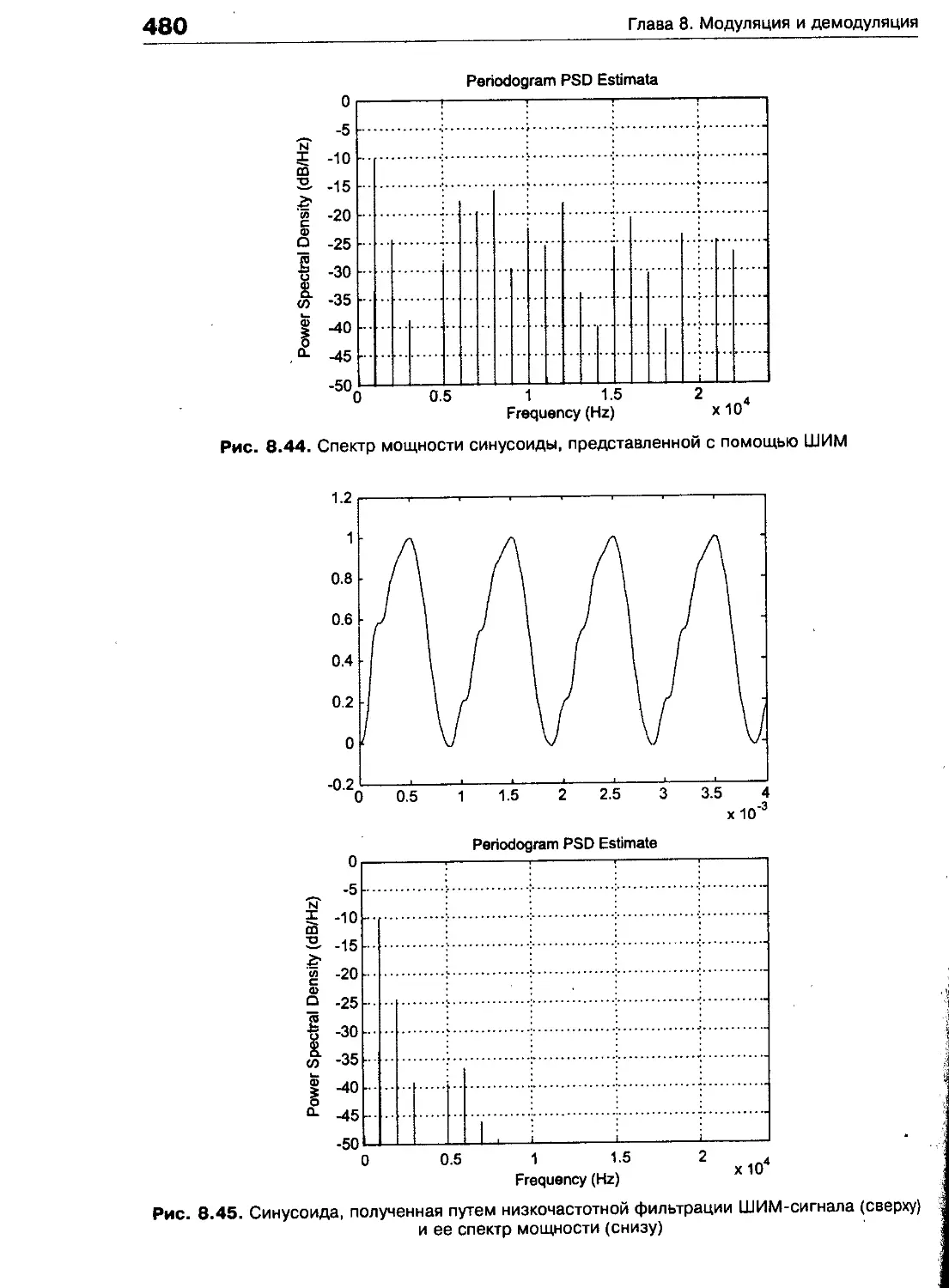
Широтно-импульсная модуляция 477
Функции модуляции и демодуляции пакета Signal Processing 481
Амплитудная модуляция 482
AM с подавленной несущей 483
Однополосная модуляция 483
Фазовая модуляция 484
Частотная модуляция 484
Квадратурная модуляция 485
Широтно-импульсная модуляция 486
Время-импульсная модуляция 486
Функции модуляции и демодуляции пакета Communications 487
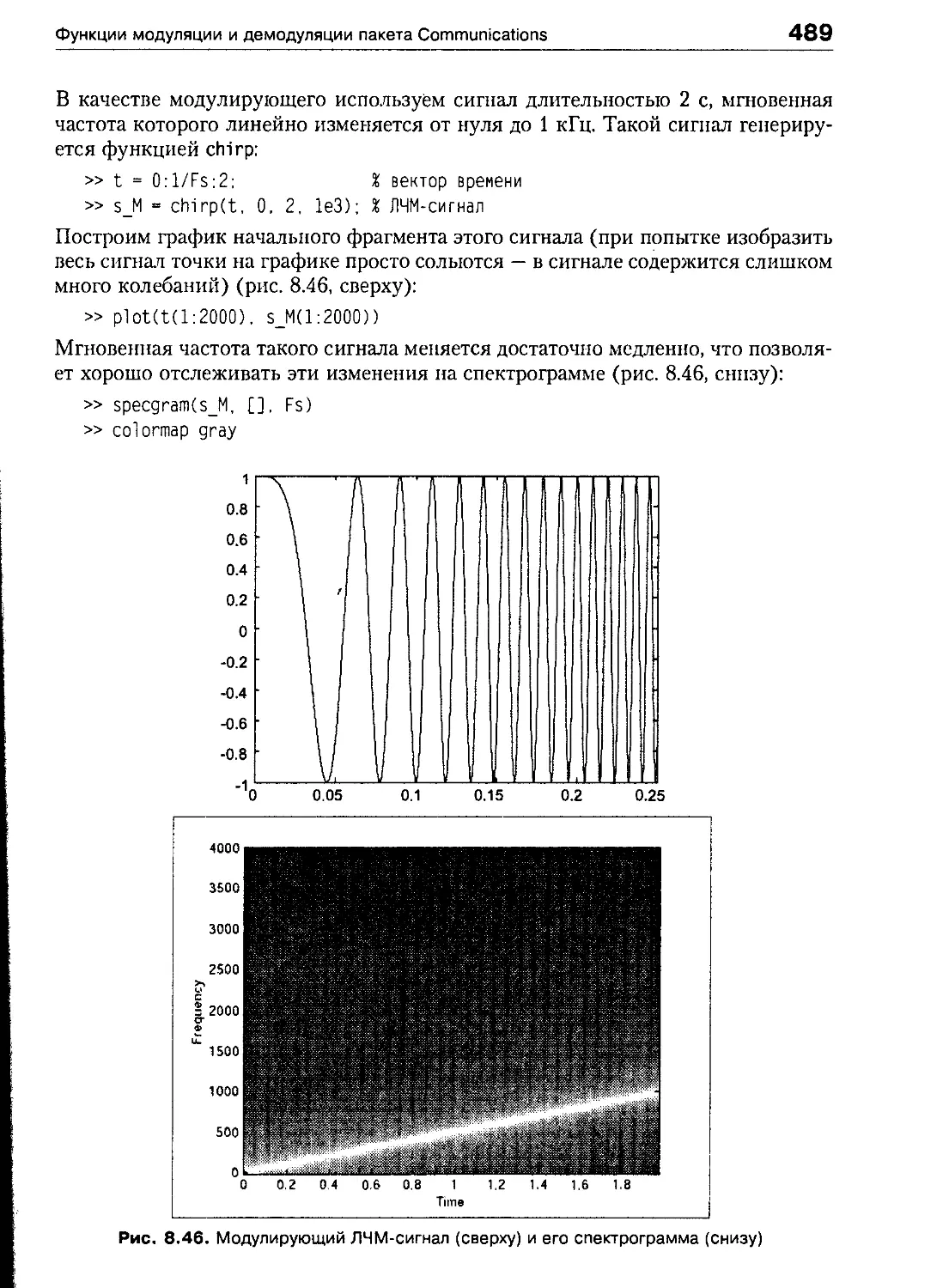
Аналоговая модуляция в пакете Communications 488
Цифровая модуляция в пакете Communications 499
Приложение А. Основы работы с MATLAB 508
Установка 508
Работав интерактивном режиме 510
Справочная система 515
Интерфейс главного окна 517
Массивы 518
Другие типы данных 521
Многомерные массивы 521
Строки 522
Структуры 523
Массивы ячеек 523
Программирование 524
Программы и функции 525
Редактор/отладчик М-файлов 526
Создание функций 526
Путь поиска . . ■ 527
Логические условия 528
Условный оператор .'....' 528
Оператор выбора 529
Циклы 529
Функции с переменным числом параметров 531
Ввод и вывод данных 532
Содержание 1 1
Работа с отладчиком 533
Оптимизация MATLAB-программ 534
MATLAB и русский язык 542
Графика 542
Двумерная графика 542
Трехмерная графика 545
Настройка внешнего вида графиков 549
Одновременный вывод нескольких графиков 553
Дальнейшее использование графиков 555
Дополнительные источники информации 556
Приложение Б. Обзор функций MATLAB 557
Audio 557
Datafun 557
Datatypes 559
Demos 559
Elfun 559
Elmat 560
Funfun 562
General 562
Graph2d 562
Graph3d 562
Graphics 563
lofun 563
Lang 563
Matfun 564
Ops 564
Polyfun 564
Sparfun 565
Specfun 565
Specgraph 566
Strfun 566
Timefun 567
Uitools 567
Verctrl 567
Winfun ' 567
Приложение В. Компоненты MATLAB 568
MATLAB 568
Пакеты расширения MATLAB 569
Математика и анализ 569
Экспорт и импорт данных 569
12 Содержание
Обработка сигналов и изображений 570
Разработка систем управления 570
Финансовое моделирование и анализ 571
Simulink , 571
Наборы блоков Simulink 573
Приложение Г. Программа SPTool 574
Загрузка сигнала 575
Просмотр графика сигнала 576
Спектральный анализ сигнала 577
Расчет фильтра 578
Просмотр характеристик фильтра 579
фильтрация сигнала 580
Сохранение результатов работы 582
Литература 583
Алфавитный указатель 586
Введение
Цифровая обработка сигналов как направление развития науки и техники заро-
зародилась в 1950-х годах и поначалу представляла собой довольно экзотическую
отрасль радиоэлектроники, практическая ценность которой была далеко не оче-
очевидной. Однако за прошедшие пятьдесят лет благодаря успехам микроэлектро-
микроэлектроники системы цифровой обработки сигналов не только воплотились в реальность,
но и вошли в нашу повседневную жизнь в виде CD- и DVD-проигрывателей, мо-
модемов, сотовых телефонов и многого другого. Более того, в некоторых приклад-
прикладных областях цифровая обработка сигналов стала вытеснять «традиционную»
(аналоговую). В значительной мере это произошло в аудиотехнике, интенсивно
идет процесс перехода телевизионного вещания на цифровую основу.
Бурное развитие цифровых технологий во многом изменило как смысл самого
понятия «радиотехника», так и требования, предъявляемые к подготовке специа-
специалистов в этой области, сделав необходимыми новые знания и умения.
Для приобретения знаний нужна соответствующая литература, однако выбор
книг, содержащих информацию о цифровой обработке сигналов, весьма невелик.
Учебники и учебные пособия по курсу «Радиотехнические цепи и сигналы» и
родственным дисциплинам, такие как [1-4], содержат лишь минимальные сведе-
сведения о теории дискретных сигналов и фильтров. Фундаментальные труды [7, 8]
изданы давно и в настоящее время малодоступны. С момента издания книги [10]
тоже прошло более десяти лет, и она охватывает только вопросы, связанные со
спектральным анализом. Начавшие появляться в последнее время книги, посвя-
посвященные цифровым сигнальным процессорам (например, [11]), уделяют больше
внимания архитектуре процессоров и средствам разработки программ для них,
нежели теоретическим вопросам и алгоритмам.
Данная книга является попыткой хотя бы частично восполнить этот пробел, рас-
рассмотрев теоретические основы базовых алгоритмов цифровой обработки сигна-
сигналов, продемонстрировав их сущность, взаимосвязь и области применения.
В качестве средства создания иллюстрационных примеров выбрана система
MATLAB®, созданная фирмой The MathWorks, Inc. и являющаяся мировым стан-
стандартом в области научных и технических расчетов. Базовая библиотека MATLAB,
а также пакеты расширения Signal Processing, Filter Design и Communications
14 Введение
содержат большое количество функций, позволяющих легко и быстро осуществ-
осуществлять разнообразные расчеты, связанные с цифровой обработкой сигналов. Для
читателей, незнакомых с этой системой, в приложении А приводится краткое
описание принципов работы с ней.
Книга предназначена для широкого круга читателей — студентов, преподава-
преподавателей, научных работников, программистов и вообще всех, кто интересуется
компьютерной обработкой сигналов и иных данных. Требуемая для понимания
материала математическая подготовка соответствует примерно первому курсу
технического вуза.
Структура книги
Книга состоит из восьми глав и четырех приложений. Первые две главы, «Осно-
«Основы анализа сигналов» и «Аналоговые системы», являются вводными и посвяще-
посвящены не цифровым, а аналоговым сигналам и системам. Поскольку методы анализа
цифровых и аналоговых сигналов и систем тесно связаны друг с другом, хоро-
хорошее понимание обсуждаемых здесь вопросов необходимо для освоения материа-
материала последующих глав.
В главе 3, «Дискретные сигналы», рассматриваются принципы математического
описания и анализа числовых последовательностей, которые и являются дис-
дискретными сигналами. Здесь же обсуждается разница между понятиями аналого-
аналоговых, дискретных и цифровых сигналов.
В главе 4, «Дискретные системы», изложены принципы линейной обработки дис-
дискретных сигналов (дискретной фильтрации), рассмотрены способы описания
дискретных систем и формы их реализации.
Глава 5, «Спектральный анализ», как явствует из ее названия, посвящена вопро-
вопросам спектрального анализа дискретных сигналов. Здесь рассматриваются дис-
дискретное преобразование Фурье и быстрые алгоритмы его вычисления, способы
реализации фильтрации в частотной области, а также непараметрические и па-
параметрические методы оценивания спектра дискретного случайного процесса.
В главе 6, «Проектирование дискретных фильтров», рассматриваются методы
синтеза дискретных фильтров, то есть способы расчета дискретных систем, удов-
удовлетворяющих заданным требованиям. Обсуждаются как методы, связанные с ис-
использованием аналоговых фильтров-прототипов, так и прямые методы, основан-
основанные на использовании численных алгоритмов оптимизации.
Глава 7, «Эффекты квантования в цифровых системах», посвящена эффектам,
возникающим при практической реализации алгоритмов цифровой обработки
сигналов из-за конечной точности представления чисел в вычислительных уст-
устройствах. Здесь рассматриваются такие вопросы, как шум квантования, округ-
округление коэффициентов и промежуточных результатов вычислений в цифровых
фильтрах, возможности возникновения переполнения при вычислениях, а также
предельные циклы.
Наконец, в главе 8, «Модуляция и демодуляция», речь идет о способах преобра-
преобразования сигналов для их передачи по каналам связи. Рассматриваются методы
Введение 15
модуляции, используемые для передачи как аналоговых сигналов (амплитудная,
угловая и квадратурная модуляция), так и цифровой информации (амплитуд-
(амплитудная, частотная, фазовая и квадратурная манипуляция).
Три из четырех приложений посвящены системе MATLAB. В приложении А из-
изложены основы работы с MATLAB, приложение Б содержит краткий обзор базо-
базовой библиотеки функций MATLAB, а в приложении В перечислены компоненты
MATLAB.
В приложении Г приводится описание графической среды SPTool (Signal Pro-
Processing Tool), имеющейся в одном из рассматриваемых в книге пакетов расшире-
расширения MATLAB — Signal Processing Toolbox. Эта программа позволяет просматривать
графики сигналов, производить спектральный анализ, рассчитывать дискретные
фильтры и осуществлять фильтрацию сигнала. Данные операции относятся к те-
тематике глав 3-6, поэтому, чтобы не разбивать описание программы SPTool на
несколько частей, соответствующая информация помещена в отдельное прило-
приложение.
Во всех главах, начиная со второй, важное место отводится описанию функций
MATLAB, реализующих рассматриваемые алгоритмы. Как правило, в первой
половине главы содержится теоретическая информация, а вторая половина по-
посвящена соответствующим средствам MATLAB. При этом демонстрационные
примеры в теоретической части реализованы в основном с помощью общемате-
общематематических функций MATLAB, без использования специализированных средств
обработки сигналов. Это сделано для того, чтобы более наглядно продемонстри-
продемонстрировать внутреннюю сущность реализуемых алгоритмов. Однако упомянутое раз-
разделение материала не является абсолютным — иллюстрации, необходимые при
изложении теоретических вопросов, не всегда удается получить без специальных
средств MATLAB, а при описании функций MATLAB иногда возникает необ-
необходимость привести дополнительные теоретические сведения. Таким образом,
теоретическая и «компьютерная» части глав книги дополняют друг друга, пре-
предоставляя читателю возможность взглянуть на обсуждаемые вопросы с разных
точек зрения.
В книге много иллюстраций, полученных с помощью MATLAB, при этом во всех
случаях приводится и соответствующий программный код. Разумеется, при опи-
описании многих функций MATLAB также демонстрируется их использование. Та-
Таким образом, книга содержит множество примеров реализации алгоритмов обра-
обработки сигналов средствами MATLAB, так что заинтересованный читатель сможет
освоить эту систему и использовать ее для решения собственных задач.
Следующее необходимое замечание касается терминологии. Наука и техника ин-
интернациональны по самой своей природе, и бурное развитие информационных
технологий лишь сделало это еще более очевидным. Поэтому любому, кто зани-
занимается обработкой сигналов, приходится иметь дело со множеством зарубежных,
и прежде всего англоязычных, источников информации. Помимо собственно вла-
владения английским языком это требует знания терминологии, которая не всегда
соответствует принятой в отечественной литературе. Чтобы облегчить читателю
работу с англоязычной литературой, при введении новых понятий в книге при-
приводятся соответствующие английские термины.
16 Введение
Чего нет в этой книге
Книга является базовым курсом по цифровой обработке сигналов, поэтому в ней
обсуждаются фундаментальные положения и отсутствуют разделы, касающиеся
более сложных вопросов, таких как адаптивные фильтры, решетчатые фильтры,
вейвлет-анализ, спектральный анализ высокого порядка, двумерная обработка сиг-
сигналов, помехоустойчивое кодирование и т. д. Задача книги — лишь подготовить
читателя к восприятию этих актуальных и современных тем.
Не является данная книга и справочником по рассматриваемым пакетам расши-
расширения MATLAB, хотя в ней описана большая часть функций пакетов Signal Pro-
Processing и Filter Design и значительная часть функций пакета Communications. Сле-
Следует иметь в виду, что при описании некоторых функций MATLAB приведены
не все, а лишь наиболее употребительные способы их вызова. Наиболее полную
информацию о функциях можно получить лишь из документации MATLAB и
пакетов расширения.
Благодарности
Прежде всего хотелось бы поблагодарить самых близких мне людей — жену
Юлию и сына Андрея — за терпение и понимание, проявленное ими на протяже-
протяжении долгих месяцев. И конечно, никто не смог бы сверстать эту книгу лучше,
чем Юля.
Этот проект не был бы возможен без поддержки издательства «Питер», и прежде
всего, главного редактора Екатерины Строгановой и заведующего компьютерной
редакцией Ильи Корнеева. Огромная благодарность также корректору Виктории
Листовой и вообще всем сотрудникам издательства, принявшим участие в под-
подготовке и выпуске книги.
Особой благодарности заслуживает фирма The MathWorks, Inc. — за создание
замечательной компьютерной системы MATLAB и за предоставление в распоря-
распоряжение автора последних версий MATLAB и описываемых в книге пакетов рас-
расширения.
От издательства
Ваши замечания, предложения, вопросы отправляйте по адресу электронной поч-
почты comp@piter.com (издательство «Питер», компьютерная редакция). Мы будем
рады узнать ваше мнение!
Подробную информацию о наших книгах вы найдете на web-сайте издательства
http://www. piter.com.
ГЛАВА 1 Основы анализа
сигналов
Анализ — один из ключевых компонентов обработки сигналов. Его теоретиче-
теоретические основы рассматриваются в большом числе книг — от учебников и учебных
пособий по курсу «Радиотехнические цепи и сигналы» [1-4] до фундаменталь-
фундаментальных монографий, таких как [5]. В данной главе будут приведены основополагаю-
основополагающие понятия и методы анализа сигналов.
Эта глава является вводной и в ней рассматриваются аналоговые сигналы, а не
дискретные или цифровые. Однако методы анализа аналоговых и дискретных
сигналов тесно взаимосвязаны, поэтому полноценное освоение изложенного здесь
материала необходимо для глубокого понимания главы 3, посвященной дискрет-
дискретным сигналам. Глава получилась весьма объемной, поскольку в ней вводится и
обсуждается большое количество базовых понятий. Средства MATLAB в данной
главе используются в основном для построения графиков.
Основной целью анализа является сравнение сигналов друг с другом для выяв-
выявления их сходства и различия. Можно выделить три основных составляющих
анализа сигналов:
Q измерение числовых параметров сигналов. К таким параметрам прежде всего
относятся энергия, средняя мощность и среднеквадратическое значение, а речь
об их расчете пойдет в разделе «Энергия и мощность сигнала»;
О разложение сигнала на элементарные составляющие для их рассмотрения по
отдельности либо для сравнения свойств различных сигналов. Такое разло-
разложение производится с использованием рядов и интегральных преобразова-
преобразований, важнейшими среди которых являются ряд Фурье и преобразование Фу-
Фурье. Им будут посвящены одноименные разделы;
О количественное измерение степени «похожести» различных сигналов. Такое
измерение производится с применением аппарата корреляционного анализа,
который будет рассмотрен в соответствующем разделе.
18 Глава 1. Основы анализа сигналов
Классификация сигналов
Прежде чем приступать к рассмотрению задач анализа сигналов, выделим неко-
некоторые классы сигналов, которые будут часто встречаться нам в дальнейшем. Это
необходимо по двум причинам. Во-первых, проверка принадлежности сигнала к
конкретному классу сама по себе является процедурой анализа. Во-вторых, для
представления и анализа сигналов разных классов зачастую приходится исполь-
использовать разные средства и подходы.
Итак, что же такое сигнал? В наиболее общей формулировке это зависимость
одной величины от другой (то есть с математической точки зрения сигнал явля-
является функцией). Чаще всего рассматриваются зависимости от времени, хотя это
не обязательно. Например, в системах оптической обработки информации си-
сигналом может являться зависимость интенсивности света от пространственных
координат. Физическая природа сигнала может быть весьма различной. Очень
часто это напряжение, несколько реже — ток, возможны и многие другие физи-
физические величины.
В данной книге подразумевается (если иное не оговорено специально), что сиг-
сигнал представляет собой зависимость напряжения от времени.
А теперь обратимся к собственно классификации.
В зависимости от того, известен ли нам сигнал точно, различают детерминиро-
детерминированные и случайные сигналы. Детерминированный сигнал полностью известен —
его значение в любой момент времени можно определить точно. Случайный же
сигнал в любой момент времени представляет собой случайную величину, кото-
которая принимает конкретные значения с некоторой вероятностью. Специфические
свойства случайных сигналов будут рассмотрены в конце данной главы, а осно-
основы анализа сигналов мы будем обсуждать применительно к сигналам детермини-
детерминированным.
Следующий важный класс сигналов — сигналы с интегрируемым квадратом. Еще
их называют сигналами с ограниченной энергией (почему, станет ясно из раздела
«Энергия и мощность сигнала»). Для таких сигналов s(t) выполняется соотно-
соотношение
Многие важные соотношения теории сигналов получены в предположении о ко-
конечности энергии анализируемых сигналов. Если это условие не выполняется,
приходится менять подходы к решению задачи (см., например, определения по-
понятия корреляционной функции для сигналов с конечной и бесконечной энер-
энергией в разделе «Корреляционная функция») или прибегать к использованию
аппарата обобщенных функций (см. раздел «Фурье-анализ неинтегрируемых
сигналов»).
Еще один признак классификации сигналов, существенно влияющий на методы
их анализа, — периодичность. Для периодического сигнала с периодом Т выпол-
выполняется соотношение
s(t + пТ) = s(t) при любом t,
Классификация сигналов 19
где п — произвольное целое число. Если величина Г является периодом сигнала s(t),
топериодами для него будут и кратные ей значения: 2Т, ЗТ и т. д. Как правило, го-
говоря о периоде сигнала, имеют в виду минимальный из возможных периодов.
Величина, обратная периоду, называется частотой повторения сигнала: / = 1/Г.
В теории сигналов также часто используется понятие круговой частоты со = 2я/,
измеряемой в радианах в секунду.
Очевидно, что любой периодический сигнал (за исключением сигнала, тождест-
тождественно равного нулю) имеет бесконечную энергию.
Следующий класс — сигналы конечной длительности (их еще называют финит-
финитными сигналами). Такие сигналы отличны от нуля только на ограниченном про-
промежутке времени. Иногда говорят, что сигнал существует на конечном времен-
временном интервале.
Очевидно, что сигнал конечной длительности будет иметь и конечную энергию —
если только он не содержит разрывов второго рода (с уходящими в бесконеч-
бесконечность ветвями функции).
Перейдем к более узким классам сигналов. Очень важную роль в технике обра-
обработки сигналов играют гармонические колебания, которые в самом общем виде
записываются следующим образом:
s(t) = A cos(co£ + ф).
Гармонический сигнал полностью определяется тремя числовыми параметрами:
амплитудой А, частотой со и начальной фазой ср.
Гармонический сигнал является одним из широко распространенных тестовых
сигналов, применяющихся для анализа характеристик цепей. Кроме него к тес-
тестовым относятся еще две очень важные в радиотехнике функции: дельта-функ-
дельта-функция и функция единичного скачка.
Дельта-функция 8(t), или функция Дирака, представляет собой бесконечно уз-
узкий импульс с бесконечной амплитудой, расположенный при нулевом значении
аргумента функции. «Площадь» импульса тем не менее равна единице:
Г о, t ф о,
= 1.
]b{t)dt
Разумеется, сигнал в виде дельта-функции невозможно реализовать физически,
однако эта функция очень важна для теоретического анализа сигналов и систем.
На графиках дельта-функция обычно изображается жирной стрелкой, высота ко-
которой пропорциональна множителю, стоящему перед дельта-функцией (рис. 1.1).
Одно из важных свойств дельта-функции — так называемое фильтрующее свой-
свойство. Оно состоит в том, что если дельта-функция присутствует под интегралом
в качестве множителя, то результат интегрирования будет равен значению осталь-
остального подынтегрального выражения в той точке, где сосредоточен дельта-импульс:
]f(tM(t-to)dt = f(to). A.1)
20 Глава 1. Основы анализа сигналов
t
►
О ' 1 t
Рис. 1.1. График сигнала s(t) = b(t) + 2б(( - 1)
Пределы интегрирования в A.1) не обязательно должны быть бесконечными, глав-
главное, чтобы в интервал интегрирования попадало значение t0; в противном случае
интеграл будет равен нулю.
Из того факта, что интеграл от дельта-функции дает безразмерную единицу, сле-
следует, что размерность самой дельта-функции обратна размерности ее аргумента.
Например, дельта-функция времени имеет размерность 1/с, то есть размерность
частоты.
Функция единичного скачка a(t), она же функция Хевисайда, она же функция вклю-
включения, равна нулю для отрицательных значений аргумента и единице — для по-
положительных. При нулевом значении аргумента функцию считают либо неопре-
неопределенной, либо равной 1/2:
A.2)
В MATLAB данную функцию можно смоделировать с помощью оператора срав-
сравнения, возвращающего значение 0 или 1:
у = (х >= 0);
Отличие такой реализации функции включения от формулы A.2) состоит толь-
только в том, что при нулевом значении аргумента результат равен единице; впро-
впрочем, в большинстве случаев это отличие несущественно.
График функции единичного скачка приведен на рис. 1.2.
a(t) I
1
0
t
Рис. 1.2. Функция единичного скачка
Функцию единичного скачка удобно использовать при создании математиче-
математических выражений для сигналов конечной длительности. Простейшим примером
Энергия и мощность сигнала 21
является формирование прямоугольного импульса с амплитудой А и длительно-
длительностью Г:
s(t) = A(a(t) - a(t - Г)).
Вообще, любую кусочно-заданную зависимость можно записать в виде единого
математического выражения с помощью функции единичного скачка.
Энергия и мощность сигнала
В начале этой главы в качестве одной из составляющих анализа сигналов было
названо измерение их количественных параметров. На практике очень часто ис-
используются такие параметры, как энергия и мощность сигнала. Их определения,
принятые в теории сигналов, отличаются от обычных, а потому требуют некото-
некоторых комментариев.
Начнем с обычных, «физических» понятий мощности и энергии. Если к резисто-
резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся
в резисторе мощность будет равна
p.SL.
R
За время Т в этом резисторе выделится тепловая энергия, равная
г и2т
R
Пусть теперь к тому же резистору приложено не постоянное напряжение, а сиг-
сигнал s(t). Рассеивающаяся в резисторе мощность при этом тоже будет зависеть от
времени, то есть в данном случае речь идет о мгновенной мощности (instanta-
(instantaneous power):
s\t)
P(t) =
R
Чтобы вычислить выделяющуюся за время Т энергию, мгновенную мощность
необходимо проинтегрировать:
Можно ввести также понятие средней мощности (average power) за заданный
промежуток времени, разделив энергию на длительность временного интервала:
ср т R
Во все приведенные формулы входит сопротивление нагрузки R. Однако, если
энергия и мощность интересуют нас не как физические величины, а как средство
сравнения различных сигналов, этот параметр можно из формул исключить
(принять R = 1). Тогда мы получим определения энергии, мгновенной мощности
и средней мощности, принятые в теории сигналов:
22 Глава 1. Основы анализа сигналов
1 о
E = \s\t)dt,
о
Pit) = s\t),
A.3)
«Мощность» здесь имеет размерность В2, а «энергия» — В2 • с.
ЗАМЕЧАНИЕ
Данные параметры иногда называют удельной мощностью и энергией, чтобы подчеркнуть
подразумеваемое при этом единичное значение сопротивления нагрузки.
Энергия сигнала может быть конечной или бесконечной. Например, любой сиг-
сигнал конечной длительности будет иметь конечную энергию (если только он не
содержит дельта-функций или ветвей, уходящих в бесконечность). А любой пе-
периодический сигнал, напротив, имеет бесконечную энергию.
Если энергия сигнала бесконечна, можно определить его среднюю мощность на
всей временной оси. Для этого нужно воспользоваться формулой A.3) и выпол-
выполнить предельный переход, устремив интервал усреднения в бесконечность:
Рср =1™^ \s\t)dt. A.4)
-И° 1 -Г/2
Квадратный корень из средней мощности дает среднеквадратическое (действую-
(действующее) значение сигнала (английский термин — root mean square, RMS):
J1 772
liml \s\t)dt.
1 -Г/2
J1 7
liml \s\t)dt. A.5)
Для периодического сигнала с периодом Г предельный переход в формулах A.4)
и A.5) выполнять не обязательно — достаточно выполнить усреднение по пе-
периоду.
Ряд Фурье
Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом
они представляются в виде суммы гармонических функций либо комплексных
экспонент с частотами, образующими арифметическую прогрессию. Для того
чтобы такое разложение существовало, фрагмент сигнала длительностью в один
период должен удовлетворять условиям Дирихле:
□ не должно быть разрывов второго рода (с уходящими в бесконечность ветвя-
ветвями функции);
□ число разрывов первого рода (скачков) должно быть конечным;
Ряд Фурье 23
□ число экстремумов должно быть конечным (в качестве примера функции, ко-
которая на конечном интервале имеет бесконечное число экстремумов, можно
привести sin(l/r) в окрестности нуля).
В зависимости от конкретной формы базисных функций различают несколько
форм записи ряда Фурье.
ЗАМЕЧАНИЕ
Ряд Фурье может быть применен для представления не только периодических сигналов,
но и сигналов конечной длительности. При этом оговаривается временной интервал, для
которого строится ряд Фурье, а в остальные моменты времени сигнал считается равным
нулю. Для расчета коэффициентов ряда такой подход фактически означает периодическое
продолжение сигнала за границами рассматриваемого интервала.
Синусно-косинусная форма
В этом варианте ряд Фурье имеет следующий вид:
s(t) = ^- + £(а4 cos(*ca,O + bk япОЦО) A.6)
2 4 = 1
Здесь со! = 2n/T — круговая частота, соответствующая периоду повторения сиг-
сигнала, равному Т. Входящие в формулу кратные ей частоты 1гщ называются гар-
гармониками; гармоники нумеруются в соответствии с индексом k; частота со* = ^cot
называется k-vi гармоникой сигнала. Коэффициенты ряда ak и bk рассчитываются
по формулам:
2 г/2
ак =- Js
J -Г/2
2 г/2
\
2 /
bk = — \ s(t)sat(ka\t)dt.
l -Г/2
Константа а0 рассчитывается по общей формуле для ак. Ради этой общности и
введена несколько странная на первый взгляд форма записи постоянного слагае-
слагаемого (с делением на два). Само же это слагаемое представляет собой среднее
значение сигнала на периоде:
Л * -Г/2
ЗАМЕЧАНИЕ
Пределы интегрирования не обязательно должны быть такими, как в приведенных выше
формулах (от -Г/2 до Т/2). Интегрирование может производиться по любому интервалу
длиной Т — результат от этого не изменится. Конкретные пределы выбираются из сообра-
соображений удобства вычислений; например, может оказаться удобнее выполнять интегрирова-
интегрирование от 0 до Г или от -Т до 0.
Если s(t) является четной функцией, то все bk будут равны нулю и в формуле
ряда Фурье будут присутствовать только косинусные слагаемые. Если 5@ явля-
24 Глава 1. Основы анализа сигналов
ется нечетной функцией, равны нулю будут, наоборот, косинусные коэффициен-
коэффициенты щи в формуле останутся лишь синусные слагаемые.
Вещественная форма
Некоторое неудобство синусно-косинусной формы ряда Фурье состоит в том,
что для каждого значения индекса суммирования k (то есть для каждой гармони-
гармоники с частотой k&x) в формуле фигурируют два слагаемых — синус и косинус.
Воспользовавшись формулами тригонометрических преобразований, сумму этих
двух слагаемых можно трансформировать в косинус той же частоты с иной ам-
амплитудой и некоторой начальной фазой:
A.7)
*=i
Если s(t) является четной функцией, фазы ср4 могут принимать только значе-
значения 0 и л, а если s(t) — функция нечетная, то возможные значения для фазы рав-
равны ±71/2.
Комплексная форма
Данная форма представления ряда Фурье является, пожалуй, наиболее употре-
употребимой в радиотехнике. Она получается из вещественной формы представлением
косинуса в виде полусуммы комплексных экспонент (такое представление выте-
вытекает из формулы Эйлера е'х = cos х +j sin х):
cos x =-(e'x + е~'х).
Применив данное преобразование к вещественной форме ряда Фурье, получим
суммы комплексных экспонент с положительными и отрицательными показате-
показателями:
*@ = ^Г + Z ^Г(ехР(.М* + М ) + ехр(-;£со, t - jq>k )).
I 4=1 ^
А теперь будем трактовать экспоненты со знаком «минус» в показателе как чле-
члены ряда с отрицательными номерами. В рамках этого же общего подхода посто-
постоянное слагаемое ао/2 станет членом ряда с нулевым номером. В результате полу-
получится комплексная форма записи ряда Фурье:
s(t)= ±Ске-}к°«. A.8)
* —=0
Комплексные коэффициенты ряда связаны с амплитудами Ак и фазами ф4, фигу-
фигурирующими в вещественной форме записи ряда Фурье.A.7), следующими не-
несложными соотношениями:
= 2\Ck
Ряд Фурье
25
Несложно выглядят и формулы связи с коэффициентами ак и Ък синусно-коси-
нусной формы ряда Фурье A.6):
ак =
Ьк =-2Im(Ct).
Отсюда сразу же следует и формула непосредственного расчета коэффициентов
Ск ряда Фурье в комплексной форме:
с -1 щ
A.9)
Если s(t) является четной функцией, коэффициенты ряда Ск будут чисто веще-
вещественными, а если s(t) — функция нечетная, коэффициенты ряда окажутся чис-
чисто мнимыми.
Совокупность амплитуд гармоник ряда Фурье часто называют амплитудным
спектром, а совокупность их фаз — фазовым спектром. Эти понятия не следует
путать с амплитудно- и фазочастотными характеристиками, которые относятся
не к сигналам, а к цепям.
Если анализируемый сигнал s(t) является вещественным, то его амплитудный
и фазовый спектры обладают симметрией:
А_к =Ак, ф_4
С -С'
Примеры разложения сигналов в ряд Фурье
В данном разделе мы применим ряд Фурье для анализа конкретных сигналов.
Последовательность прямоугольных импульсов
Первым рассматриваемым сигналом будет последовательность прямоугольных
импульсов с амплитудой А, длительностью т и периодом повторения Т. Начало
отсчета времени примем расположенным в середине импульса (рис. 1.3).
-т/2
О т/2
Рис. 1.3. Периодическая последовательность прямоугольных импульсов
26 Глава 1. Основы анализа сигналов
Данный сигнал является четной функцией, поэтому для его представления удоб-
удобнее использовать синусно-косинусную форму ряда Фурье — в ней будут присут-
присутствовать только косинусные слагаемые а*, равные
2 т/2 / o_Z> Л о л
ак= — Acos\ t\dt = —s
Tj/2 [Т ) nk
Внимательно рассматривая полученную формулу, можно заметить, что длитель-
длительность импульсов и период их следования входят в нее не обособленно, а исклю-
исключительно в виде отношения. Этот параметр — отношение периода к длитель-
длительности импульсов — называют скважностью последовательности импульсов и
обозначают буквой q: q = Г/т. Введем этот параметр в полученную формулу для
коэффициентов ряда Фурье, а затем приведем формулу к виду
nk
nk
, . sinl
2^sin[^ = M_L^. (U0)
ЗАМЕЧАНИЕ
В зарубежной литературе вместо скважности используется обратная величина, называе-
называемая коэффициентом заполнения (duty cycle) и равная т/Г.
При такой форме записи становится хорошо видно, чему равно значение посто-
постоянного слагаемого ряда: поскольку при х -> 0 sin(^r)/^: -> 1, то
а0 _А_Ах
Теперь можно записать и само представление последовательности прямоуголь-
прямоугольных импульсов в виде ряда Фурье:
А ^2А . (nk) Bя4 Л
q fank [q J { T )
Амплитуды гармонических слагаемых ряда зависят от номера гармоники по за-
закону sin(^r)/^: (рис. 1.4).
График функции sin(^r)/^: имеет лепестковый характер. Говоря о ширине этих
лепестков, следует подчеркнуть, что для графиков дискретных спектров перио-
периодических сигналов возможны два варианта градуировки горизонтальной оси —
в номерах гармоник и в частотах. На рис. 1.4 градуировка оси соответствует но-
номерам гармоник, а частотные параметры спектра нанесены на график с помощью
размерных линий.
Итак, ширина лепестков, измеренная в количестве гармоник, равна скважности
последовательности (при k - nq имеем sm(nk/q) - 0, если п * 0). Отсюда следу-
следует важное свойство спектра последовательности прямоугольных импульсов —
в нем отсутствуют (имеют нулевые амплитуды) гармоники с номерами, кратны-
кратными скважности.
Ряд Фурье
27
Ах/Т ,
4 2я
22L
Т
Ткл''
Ы
-9 0 1? it
Рис. 1.4. Коэффициенты ряда Фурье для последовательности
прямоугольных импульсов
Расстояние по частоте между соседними гармониками равно частоте следования
импульсов — 2п/Т. Ширина лепестков спектра, измеренная в единицах частоты,
равна 2тс/т, то есть обратно пропорциональна длительности импульсов. Это, как
мы увидим далее, проявление общего закона — чем короче сигнал, тем шире его
спектр.
Меандр
Важным частным случаем предыдущего сигнала является меандр — последова-
последовательность прямоугольных импульсов со скважностью, равной двум, когда дли-
длительности импульсов и промежутков между ними становятся равными (рис. 1.5).
-3774
-774
774
3774
►
Рис. 1.5. Меандр
Подставив q - 2 в формулу A.10), получим
аь =А
sin(nk/2)
nk/2
k=0,
k =2тп,
А,
О,
2Л
nk'
—-, k = 4m-i.
nk
Здесь m — произвольное целое число.
28 Глава 1. Основы анализа сигналов
Таким образом, в спектре меандра присутствуют только нечетные гармоники.
Это согласуется с общим правилом, приведенным выше. Представление меандра
в виде ряда Фурье с учетом этого может быть записано следующим образом:
_ А 2А( BяЛ 1 (о2яЛ 1 (к2пЛ ^
s(t) = — + — cos —м--cos 3—t +-cos 5 —1\- ... .
2 n{ [Т ) 3 { T ) 5 { T ) )
Гармонические составляющие, из которых складывается меандр, имеют ампли-
амплитуды, обратно пропорциональные номерам гармоник, и чередующиеся знаки.
Покажем на примере меандра, как складывается заданный сигнал из отдельных
гармоник (рис. 1.6):
» N = 8: % число ненулевых гармоник
» t = -1:0.01:1: % вектор моментов времени
» А = 1: % амплитуда
» Т = 1; % период
» nh = A:N)*2-1: % номера ненулевых гармоник
» % строки - гармоники
» harmonics = cosB*pi*nh'*t/T):
» Am = 2/pi./nh: % амплитуды гармоник
» AmB:2:end) = -AmB:2:end): % чередование знаков
» si = harmonics .* repmatCAm'. 1. length(t)):
» % строки - частичные суммы гармоник
» s2 = cumsum(sl):
» for k=l:N, subplotD. 2. k). plotCt. s2(k.:)). end
Вообще, последовательность прямоугольных импульсов плохо подходит для пред-
представления рядом Фурье — она содержит скачки, а сумма любого числа гармони-
гармонических составляющих с любыми амплитудами всегда будет непрерывной функ-
функцией. Поэтому поведение ряда Фурье в окрестностях разрывов представляет
особый интерес. На графиках рис. 1.6 хорошо видно, что в окрестности точки
разрыва суммирование ряда Фурье дает наклонный участок, причем крутизна
наклона возрастает с ростом числа суммируемых гармоник. В самой точке раз-
разрыва ряд Фурье сходится к полусумме правого и левого пределов:
s'(t0) = -( lim s(t)+ lim s(
2V«i-« t-*4+o
Здесь s{t) — исходный сигнал, s '{t) — сумма ряда Фурье для него.
На примыкающих к разрыву участках сумма ряда Фурье дает заметные пульса-
пульсации, причем на графиках рис. 1.6 заметно, что амплитуда этих пульсаций не
уменьшается с ростом числа суммируемых гармоник — пульсации лишь сжима-
сжимаются по горизонтали, приближаясь к точке разрыва. Это явление, присущее ря-
рядам Фурье для любых сигналов с разрывами первого рода (скачками), называет-
называется эффектом Гиббса. Можно показать, что амплитуда первого (самого большого)
выброса составляет примерно 9 % от величины скачка.
Ряд Фурье
29
1
0.5
0
-0.5
-1
t у
-1
о
Рис. 1.6. Промежуточные стадии суммирования ряда Фурье для меандра
Пилообразный сигнал
Следующий сигнал, который мы рассмотрим, — пилообразный (рис. 1.7). В пре-
пределах периода он описывается линейной функцией:
Данный сигнал является нечетной функцией, поэтому его ряд Фурье в синусно-
косинусной форме A.6) будет содержать только синусные слагаемые:
30
Глава 1. Основы анализа сигналов
7
Х
-Г -Т/2
О Г/2
Рис. 1.7. Пилообразный сигнал
Сам ряд Фурье для пилообразного сигнала выглядит следующим образом:
,.ч 2А( . BяЛ 1 . @2яЛ 1 . Го2яЛ 1 . Г,2яЛ
s(t) = — sin —t --sin 2 — t +-sin 3—t --sin 4—1\+...
n{ [Т J 2 { T J 3 { T J 4 { T J
У рассмотренных выше спектров прямоугольного и пилообразного периодиче-
периодических сигналов есть одна общая черта — амплитуды гармоник с ростом их номе-
номеров убывают пропорционально k. У следующего сигнала скорость затухания
спектра будет иной, а почему, мы обсудим после расчета коэффициентов ряда
Фурье для него.
Последовательность треугольных импульсов
Очередной сигнал, для которого мы получим разложение в ряд Фурье, представ-
представляет собой периодическую последовательность треугольных импульсов. Строго
говоря, импульсы в предыдущем сигнале тоже были треугольными, но в данном
случае они будут иметь не пилообразную, а симметричную форму (рис. 1.8):
s(t) = A\ 1-4
\t-kT\
Л Л
у™.
Рис. 1.8. Последовательность треугольных импульсов
Вычислим коэффициенты ряда Фурье (сигнал является четной функцией, по-
поэтому в синусно-косинусной форме ряда Фурье A.6) будут присутствовать толь-
только косинусные слагаемые):
Преобразование Фурье , 31
Как и в случае меандра, здесь присутствуют только нечетные гармоники. Сам
ряд Фурье имеет следующий вид:
яМ \~Т ) "W I ~T J ~5^ I ~~Т )
Как видите, в отличие от последовательностей прямоугольных и пилообразных
импульсов, для треугольного периодического сигнала амплитуды гармоник убы-
убывают пропорционально второй степени номеров гармоник к. Это проявление об-
общего правила, гласящего, что скорость убывания спектра зависит от степени
гладкости сигнала. Прямоугольный и пилообразный сигналы имеют разрывы
первого рода (скачки), и в их спектрах присутствует множитель 1/k. Треуголь-
Треугольный сигнал является непрерывной функцией (но ее первая производная содер-
содержит разрывы), и амплитуды гармоник его ряда Фурье содержат множитель 1/k .
Экстраполировав эту зависимость, получим следующее правило: если N — номер
последней непрерывной производной сигнала, то спектр этого сигнала будет
убывать со скоростью 1/k . Предельным случаем является гармонический сиг-
сигнал, дифференцировать который без потери непрерывности можно бесконечно.
Согласно общему правилу, это даст бесконечную скорость убывания спектра,
что вполне соответствует действительности (ряд Фурье для гармонического сиг-
сигнала содержит только одну гармонику).
Преобразование Фурье
Преобразование Фурье (Fourier transform) является инструментом спектрально-
спектрального анализа непериодических сигналов. Впрочем, чуть позже мы увидим, что его
можно применять и к сигналам периодическим, но это потребует использования
аппарата обобщенных функций.
Для наглядной иллюстрации перехода от ряда Фурье к преобразованию Фурье
часто используется не вполне строгий математически, но зато понятный подход.
Представим себе периодическую последовательность импульсов произвольно-
произвольного вида и сформируем ряд Фурье для нее. Затем, не меняя формы одиночных
импульсов, увеличим период их повторения (заполнив промежутки нулевым
значением) и снова рассчитаем коэффициенты ряда Фурье. Формула A.9) для
расчета коэффициентов ряда показывает, что нам придется вычислить тот же
самый интеграл, но для более тесно расположенных частот со* = k(o{. Изменение
пределов интегрирования не играет роли — ведь на добавившемся между им-
импульсами пространстве сигнал имеет нулевое значение. Единственное дополни-
дополнительное изменение будет состоять в уменьшении общего уровня гармоник из-за
деления результата интегрирования на увеличившийся период Т.
На рис. 1.9 описанные изменения иллюстрируются на примере двукратного уве-
увеличения периода следования прямоугольных импульсов. Обратите внимание на
32
Глава 1. Основы анализа сигналов
то, что горизонтальная ось спектральных графиков проградуирована в значени-
значениях частот, а не номеров гармоник.
А
к
X
0
А
^ * 1
X
/
Тч/
\/\ \\
23
km
2п
т
Рис. 1.9. Изменение спектра последовательности импульсов
при двукратном увеличении периода их следования
Итак, с ростом периода следования импульсов гармоники располагаются ближе
друг к другу по частоте, а общий уровень спектральных составляющих становит-
становится все меньше. При этом вид вычисляемого интеграла A.9) не меняется.
Наконец, если устремить период к бесконечности (превратив тем самым перио-
периодическую последовательность в одиночный импульс), гармоники спектра будут
плотно занимать всю частотную ось, а их амплитуды упадут до нуля (станут бес-
бесконечно малыми). Однако взаимное соотношение между уровнями гармоник ос-
остается неизменным и определяется все тем же интегралом A.9). Поэтому при
спектральном анализе непериодических сигналов формула для расчета коэффи-
коэффициентов комплексного ряда Фурье модифицируется следующим образом:
□' частота перестает быть дискретно меняющейся и становится непрерывным
параметром преобразования (то есть &a>i в формуле A.9) заменяется на ю);
□ удаляется множитель 1/Т;
□ результатом вычислений вместо нумерованных коэффициентов ряда С* явля-
является функция частоты 5(ю) — спектральная функция сигнала s(t). Иногда ее
называют также спектральной плотностью.
В результате перечисленных модификаций формула A.9) превращается в фор-
формулу прямого преобразования Фурье:
A.11)
Преобразование Фурье 33
В формуле самого ряда Фурье суммирование, естественно, заменяется интегри-
интегрированием (и, кроме того, перед интегралом появляется деление на 2л). Получаю-
Получающееся выражение называется обратным преобразованием Фурье:
\S((o)eMdco A.12)
ЗАМЕЧАНИЕ
Если использовать не круговую частоту ю, а обычную частоту/- (о/Bя), формулы прямо-
прямого и обратного преобразования Фурье становятся еще более симметричными, отличаясь
лишь знаком в показателе экспоненты:
Чтобы преобразование Фурье было применимо, сигнал должен удовлетворять
следующим требованиям:
Q должны выполняться условия Дирихле (см. раздел «Ряд Фурье»);
Q сигнал должен быть абсолютно интегрируемым. Это означает, что интеграл
от его модуля должен быть конечной величиной:
00
j\s(t)\dt<oo.
Однако с привлечением математического аппарата обобщенных функций воз-
возможно выполнение Фурье-анализа и для некоторых сигналов, не удовлетворяю-
удовлетворяющих этим требованиям (речь об этом пойдет далее, в разделе «Фурье-анализ не-
интегрируемых сигналов»).
Если анализируемый сигнал s(t) — вещественная функция, то соответствующая
спектральная функция 5((о) является «сопряженно-симметричной» относитель-
относительно нулевой частоты. Это означает, что значения спектральной функции на часто-
частотах со и -со являются комплексно-сопряженными по отношению друг к другу:
Если s(t) — четная функция, то, как и в случае ряда Фурье, спектр будет чисто
вещественным (и, следовательно, будет являться четной функцией). Если, на-
напротив, s(t) — функция нечетная, то спектральная функция 5(ю) будет чисто
мнимой (и нечетной).
Модуль спектральной функции часто называют амплитудным спектром, а ее ар-
аргумент — фазовым спектром. Легко показать, что для вещественного сигнала ам-
амплитудный спектр является четной, а фазовый — нечетной функцией частоты:
34
Глава 1. Основы, анализа сигналов
Примеры расчета спектральных функций конкретных сигналов и соответствую-
соответствующие графики будут приведены далее.
Итак, преобразование Фурье A.11) ставит в соответствие сигналу, заданному во
времени, его спектральную функцию. При этом осуществляется переход из вре-
временной области в частотную. Преобразование Фурье является взаимно-одно-
взаимно-однозначным, поэтому представление сигнала в частотной области (спектральная
функция) содержит ровно столько же информации, сколько и исходный сигнал,
заданный во временной области.
Примеры расчета преобразования Фурье
В этом разделе будут рассмотрены примеры расчета преобразования Фурье для
некоторых сигналов, часто встречающихся при решении различных задач.
Прямоугольный импульс
Начнем с прямоугольного импульса, центрированного относительно начала от-
отсчета времени (рис. 1.10):
5@ =
А М<т/2,
О, И>т/2.
-т/2 0 т/2 t
Рис. 1.10. Прямоугольный импульс
Вычисляем спектральную функцию:
со
2
сот/2
Как видите, спектр представляет собой функцию вида sin(x)/x (рис. 1.11). Ам-
Амплитудный спектр имеет лепестковый характер, и ширина лепестков равна 2я/т,
то есть обратно пропорциональна длительности импульса. Значение спектраль-
спектральной функции на нулевой частоте равно площади импульса — Ах. Спектральная
функция является вещественной, поэтому фазовый спектр принимает лишь два
значения — 0 и я, в зависимости от знака функции sin(x)/x. Значения фазы л
и -я неразличимы, разные знаки для фазового спектра при со > 0 и со < 0 исполь-
использованы лишь с целью представить его в виде нечетной функции.
Теперь посмотрим, что изменится после сдвига импульса во времени. Пусть им-
импульс начинается в нулевой момент времени (рис. 1.12):
Преобразование Фурье
35
5@ =
[Л
lo,
/
0 < t < -с,
t < 0, г >
Ах ,
V
(
\
)
т.
\,
V
2s
т
4тс
т
Ч
—- ш
-тс ■
2S
т
0
' (
is 6
Т 1
1.13)
s
СО
Рис. 1.11. Амплитудный (слева) и фазовый (справа) спектры прямоугольного импульса
О т
Рис. 1.12. Прямоугольный импульс, задержанный во времени
Вычисляем преобразование Фурье и строим графики амплитудного и фазового
спектров (рис. 1.13):
A.14)
ККК
23
6п
Рис. 1.13. Амплитудный (слева) и фазовый (справа) спектры
задержанного прямоугольного импульса
ЗАМЕЧАНИЕ
Этот пример демонстрирует проявление свойства преобразования Фурье, касающегося
изменения спектра при сдвиге сигнала во времени. Это свойство в общем виде будет рас-
рассмотрено далее, в разделе «Свойства преобразования Фурье».
36
Глава 1. Основы анализа сигналов
Из формулы A.14) и графиков рис. 1.13 видно, что после сдвига импульса во
времени его амплитудный спектр остался прежним, а фазовый приобрел сдвиг,
линейно зависящий от частоты.
Строго говоря, спектр данного сигнала простирается до бесконечности, лишь по-
постепенно затухая. Поэтому вводят понятие эффективной ширины спектра. Как
видно из графиков, спектр имеет лепестковый характер и ширина главного лепе-
лепестка равна 2л/т. При лепестковом характере спектра за эффективную ширину
спектра можно принять ширину главного лепестка. Из графиков видно, что она
составляет 2л/т, то есть обратно пропорциональна длительности импульса. Это
общее соотношение: чем короче сигнал, тем шире его спектр. Произведение же
эффективных значений длительности сигнала и ширины его спектра (оно назы-
называется базой сигнала) остается равным некоторой константе, зависящей от кон-
конкретного способа определения этих параметров. В нашем примере это произве-
произведение, очевидно, равно 2гс. Вообще, для сигналов простой формы (не имеющих
сложной внутриимпульсной структуры) величина базы независимо от способа
определения эффективных значений длительности и ширины спектра составля-
составляет несколько единиц.
Длительность сигнала и ширина его спектра подчиняются соотношению неопре-
неопределенности, гласящему, что произведение этих параметров (база сигнала) не мо-
может быть меньше единицы. Ограничений максимального значения базы сигаала
не существует. Отсюда следует, что можно сформировать сигнал большой дли-
длительности, одновременно имеющий и широкий спектр (такие сигналы называют
широкополосными, или сложными, или сигналами с большой базой). А вот корот-
короткий сигнал с узким спектром, согласно соотношению неопределенности, сущест-
существовать не может.
Несимметричный треугольный импульс
Далее рассмотрим несимметричный треугольный импульс (рис. 1.14):
t<Q, t>T.
О Т I
Рис. 1.14. Несимметричный треугольный импульс
Рассчитываем спектр и строим графики (рис. 1.15):
А А А
л\ /\ —УсоУ* ^* —пат
(»2Г (»2 Г 7<ю
Преобразование Фурье
37
АТ/2
АТПО
/
1
1
1
1
\
\
\
\
\
V.,
-- _
я-8я -6я -4п -2
4п 6п
Рис. 1.15. Амплитудный (слева) и фазовый (справа) спектры
несимметричного треугольного импульса
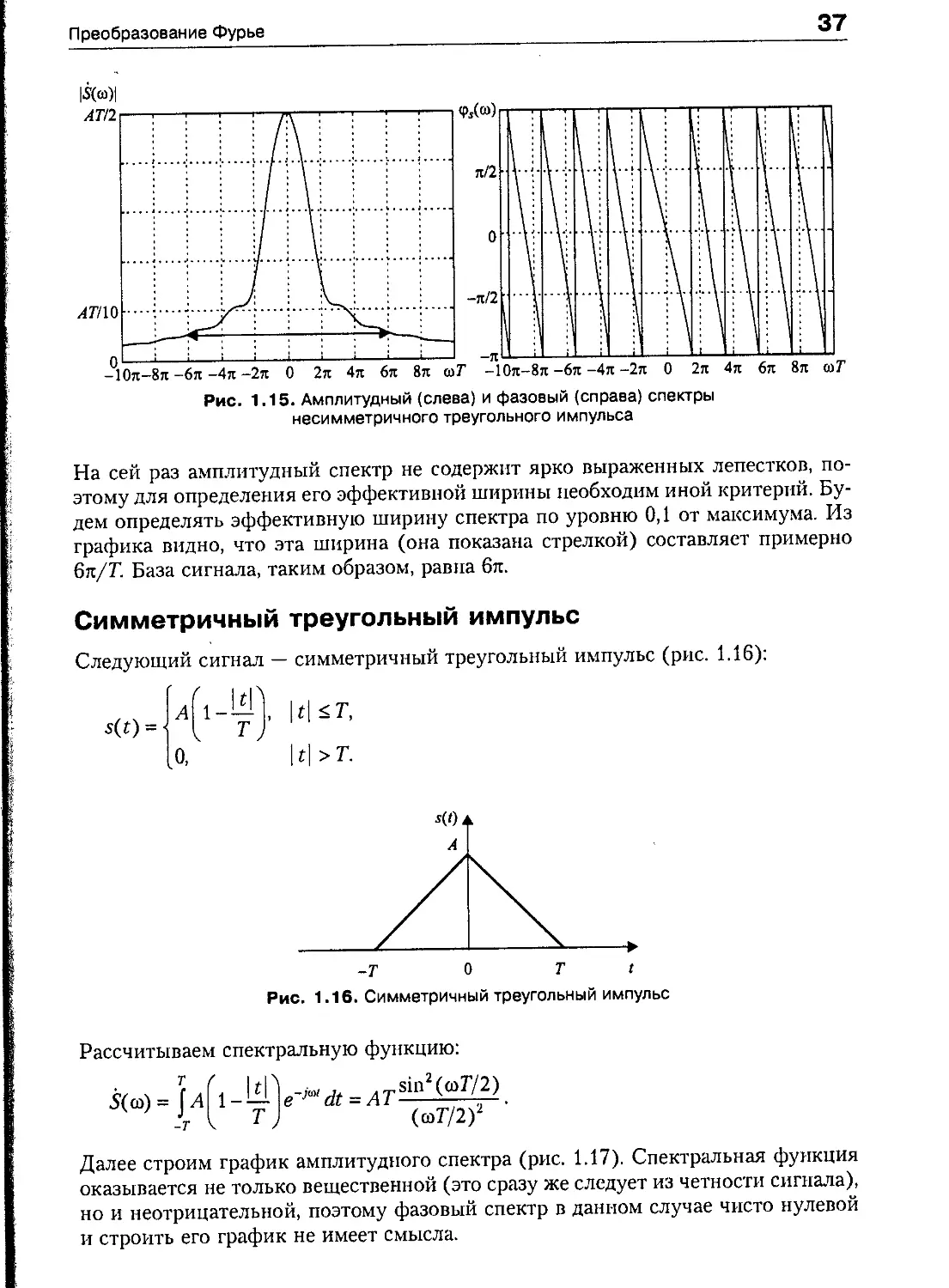
На сей раз амплитудный спектр не содержит ярко выраженных лепестков, по-
поэтому для определения его эффективной ширины необходим иной критерий. Бу-
Будем определять эффективную ширину спектра по уровню 0,1 от максимума. Из
графика видно, что эта ширина (она показана стрелкой) составляет примерно
бк/Т. База сигнала, таким образом, равна 6л.
Симметричный треугольный импульс
Следующий сигнал — симметричный треугольный импульс (рис. 1.16):
о,
-Т 0 Т t
Рис. 1.16. Симметричный треугольный импульс
Рассчитываем спектральную функцию:
-г
(соГ/2J
Далее строим график амплитудного спектра (рис. 1.17). Спектральная функция
оказывается не только вещественной (это сразу же следует из четности сигнала),
но и неотрицательной, поэтому фазовый спектр в данном случае чисто нулевой
и строить его график не имеет смысла.
38
Глава 1. Основы анализа сигналов
S(co)
Л1
АТ/2
АТПО
п
—— -.—
/
/
1
1
1
1
1
У
\
\
V
\
\
\
V
V
V
-Зп -2п -к 0 п 2л соГ
Рис. 1.17. Амплитудный спектр симметричного треугольного импульса
Из фафика видно, что спектр опять имеет лепестковую структуру и ширина глав-
главного лепестка составляет 2п/Т, как и в случае прямоугольного импульса. Однако
длительность сигнала в данном случае вдвое больше BГ), и база оказывается
равной 4л.
Далее перейдем от сигналов конечной длительности к бесконечно протяженным
сигналам. '
Односторонний экспоненциальный импульс
Первым из сигналов бесконечной длительности будет рассмотрен односторон-
односторонний экспоненциальный импульс (рис. 1.18):
6@ =
Ае~
0,
о l/e г
Рис. 1.18. Односторонний экспоненциальный импульс
Рассчитываем преобразование Фурье:
А
Далее строим графики амплитудного и фазового спектров (рис. 1.19).
Преобразование Фурьа
39
Ala
Alia
А/Юа
О
>
/
\
\
\
\
/
f
\
\
\
\
\
V
\
S
ч
к—
я/4
-
\
\
Л
\
——
-10 -8 -6 -4 -2 0
-я/4
-я/2
6 8 ю/а -10 -8-6-4-2 0 2 4 6 8 ю/а
Рис. 1.19. Амплитудный (слава) и фазовый (справа) спактры
одностороннаго экспонанциального импульса
Двусторонний экспоненциальный импульс
Теперь пусть экспоненциальный импульс будет двусторонним (симметричным,
рис. 1.20):
о I/a t
Рис. 1.20. Двусторонний экспоненциальный импульс
1А1а
Ala
I
I 1
—*
у
1
I
г
1
1
/
f
\
1
1
\
4
4
1
A 15a
0
-10 -8-6-4-202468 ю/а
Рис. 1.21. Амплитудный спактр двустороннаго экспонанциального импульса
40
Глава 1. Основы анализа сигналов
Рассчитываем преобразование Фурье:
2Ло
5(ш) = f
L
-iM dt =
„ ,
« + со2
Спектр в данном случае чисто вещественный, поэтому строить график фазового
спектра нет смысла (рис. 1.21).
Гауссов импульс
Следующий очень важный сигнал — гауссов импульс (рис. 1.22). Как и преды-
предыдущий, он имеет бесконечную протяженность в обоих направлениях временной
оси:
s(t) = Ae-aV.
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
п
!
1
/
г
/.
/
у
/
/
7
/
г
\
\
\
\
\
\
1
у
\
\
\
\
V
-3 -2-10 1
Рис. 1.22. Гауссов импульс
at
Вычисляем спектр:
00
j(co) = I Ae e at =
Поскольку сигнал является четной функцией, его спектр чисто вещественный.
Поэтому строим график только для амплитудного спектра (рис. 1.23).
Важным свойством гауссова импульса является то, что его спектр тоже описыва-
описывается гауссовой функцией.
Гауссов импульс имеет бесконечную протяженность как во временной, так и в
частотной области. Определим его эффективную длительность и ширину спек-
спектра по уровню 1/е от максимума: т = 2/а, Дсо ■= 2а. База сигнала, таким образом,
равна четырем.
Преобразование Фурье
41
S(co)
Ayfn
Ala
1
/
У
г
/
/
■■■/
/
\
\
\
\
\
\
\
A 15a
0
-4-2 0 2 4 co/o
Рис. 1.23. Амплитудный спектр гауссова импульса
Сигнал вида sin(x)/x
Следующий пример призван продемонстрировать дуальность преобразования
Фурье. Если сравнить формулы прямого и обратного преобразования Фурье,
можно заметить, что они отличаются друг от друга лишь знаком в показателе
комплексной экспоненты-и множителем перед интегралом. Отсюда следует, что
если четной функции времени /(£) соответствует спектральная функция g(co)
(она будет также четной), то функции времени g(t) будет соответствовать спек-
спектральная функция 2л/((о). Проверим это на конкретном примере. В начале этого
раздела мы выяснили, что прямоугольному импульсу соответствует спектраль-
спектральная функция вида sin((o)/co. Теперь же рассмотрим временной сигнал вида
sin(t)/t и проверим, будет ли его спектральная функция прямоугольной.
Итак, задаем временной сигнал (используем параметр Т для обозначения полу-
полупериода функции sin) (рис. 1.24):
5@ = А
sin(nt/T)
nt/T
Рассчитываем спектр и строим график (рис. 1.25):
L
,
nt/T
2л
sin (o+ — \t + sin со— \t
{ T) { TJ
dt =
sinl <o+— \t
-4Н-
sin со— \t
2л _■> t
42
Глава 1. Основы анализа сигналов
s{t)IA
0.8
0.6
0.4
0.2
О
-0.2
-0.4
Л
L
V
/
1
/
\
\
......
\
\
J
У
Л
ЧУ
-5 -4-3-2-10 1 2 3
Рис. 1.24. Сигнал вида sin(at)/(at)
tIT
-п/Т 0 я/Г со
Рис. 1.25. Сигнал вида sin(at)/(at) имеет прямоугольный спектр
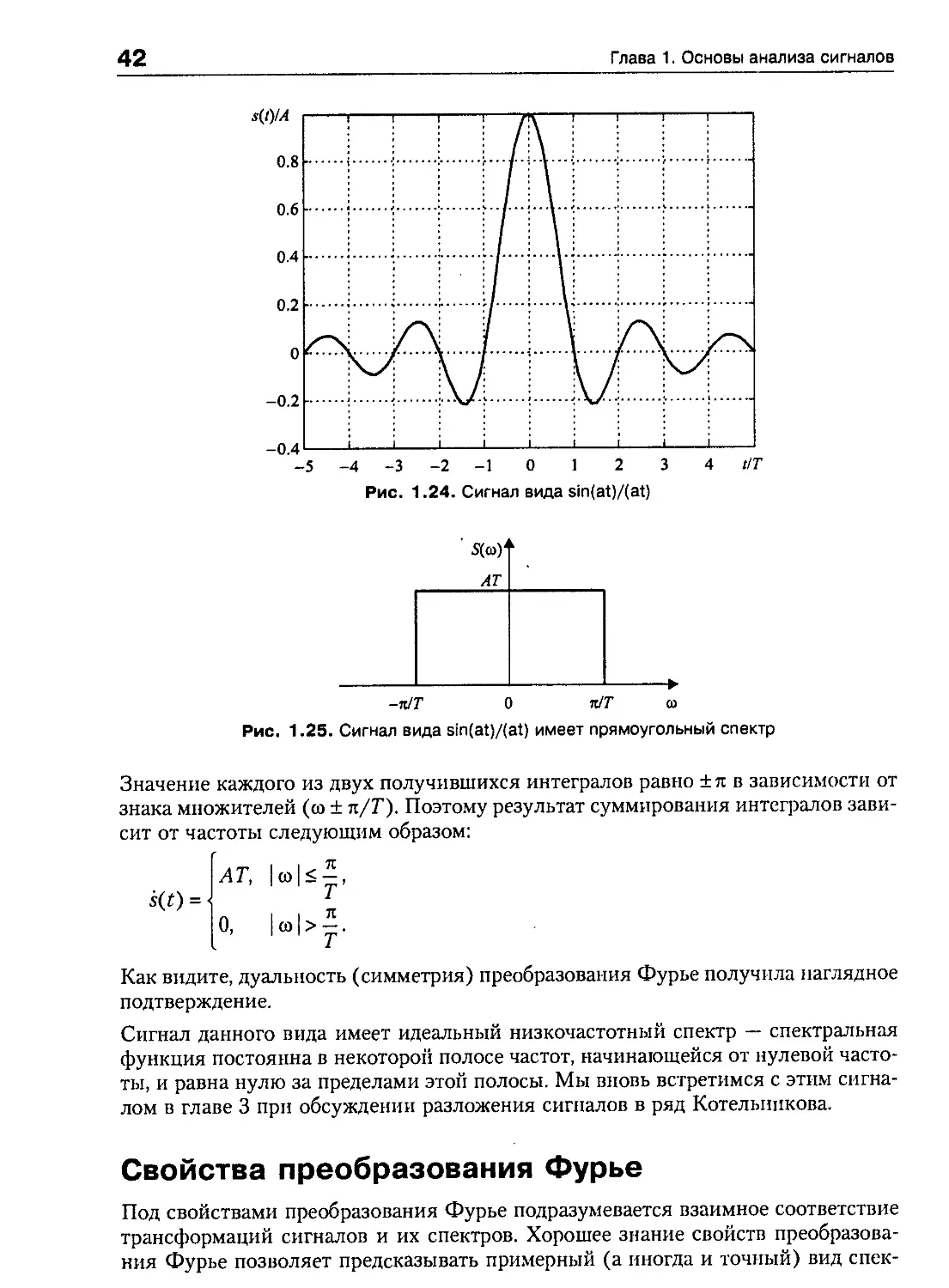
Значение каждого из двух получившихся интегралов равно ± п в зависимости от
знака множителей (со ± я/Г). Поэтому результат суммирования интегралов зави-
зависит от частоты следующим образом:
AT,
О,
со
г
Как видите, дуальность (симметрия) преобразования Фурье получила наглядное
подтверждение.
Сигнал данного вида имеет идеальный низкочастотный спектр — спектральная
функция постоянна в некоторой полосе частот, начинающейся от нулевой часто-
частоты, и равна нулю за пределами этой полосы. Мы вновь встретимся с этим сигна-
сигналом в главе 3 при обсуждении разложения сигналов в ряд Котелышкова.
Свойства преобразования Фурье
Под свойствами преобразования Фурье подразумевается взаимное соответствие
трансформаций сигналов и их спектров. Хорошее знание свойств преобразова-
преобразования Фурье позволяет предсказывать примерный (а иногда и точный) вид спек-
Преобразование Фурье 43
тра анализируемого сигнала и таким образом контролировать правдоподобность
результата, выдаваемого компьютером.
В этом разделе мы будем рассматривать два абстрактных сигнала, f(t) и g(t),
и считать, что их спектральные функции равны /(со) и G(co).
Линейность
Преобразование Фурье является линейным интегральным преобразованием. Смысл
свойства линейности можно сформулировать так: спектр суммы равен сумме
спектров. Говоря математическим языком, линейная комбинация сигналов име-
имеет спектр в виде такой же (с теми же коэффициентами) линейной комбинации
их спектральных функций:
если s(t) = сс/(?) + pg(O, то 5(со) = af(co) + pG(co).
Задержка
А теперь посмотрим, как сказывается на спектральной функции задержка сигна-
сигнала во времени. Итак, пусть т — время задержки:
тогда спектральная функция изменится следующим образом:
5(со)= ]f{t-x)e4'atdt= ]/{t-x)e-Mt-'l)d(t-z)e-Jm =F(ro)e^.
-X -ao
Результат показывает, что спектр исходного сигнала оказался умноженным на
комплексную экспоненту вида е'-'сот. Таким образом, амплитудный спектр сигна-
сигнала не меняется (ведь модуль такой комплексной экспоненты равен 1; к тому же
здравый смысл подсказывает, что соотношение между амплитудами спектраль-
спектральных составляющих из-за сдвига сигнала во времени измениться не должно). Фа-
Фазовый спектр приобретает дополнительное слагаемое -сот, линейно зависящее от
частоты.
ЗАМЕЧАНИЕ
Если в результате какого-либо преобразования сигнала его спектр умножается на некото-
некоторую функцию, не зависящую от преобразуемого сигнала, это означает, что данное преобра-
преобразование может быть выполнено линейной системой с постоянными параметрами. Речь
о системах данного класса пойдет в главе 2.
Изменение масштаба оси времени
Рассматривая конкретные примеры, мы уже познали на практике общее прави-
правило: чем короче сигнал, тем шире его спектр. Теперь взглянем на это правило со
строгих теоретических позиций. Если изменить длительность сигнала f{t), со-
сохраняя его форму, то новый сигнал s(t) следует записать как
= Rat).
44 Глава 1. Основы анализа сигналов
При |а| > 1 сигнал сжимается, при |а| < 1 — растягивается. Если а < О, дополни-
дополнительно происходит зеркальное отражение сигнала относительно вертикальной оси.
Посмотрим, как такое преобразование сказывается на спектре:
00 Л 00 • W 4 / \
5(со) = J f(at) е'м Л = - f f(at) ё'~~а d(at) = - F - .
Итак, изменение длительности сигнала приводит к изменению ширины спектра
в противоположную сторону (аргумент t на а умножается, а со делится) в сочета-
сочетании с увеличением (при растяжении, а < 1) или уменьшением (при сжатии,
а > 1) уровня спектральных составляющих.
Полученная формула справедлива для а > 0. При а < 0 использованная замена
переменной t -> at вызовет перестановку пределов интегрирования и, как следст-
следствие, изменение знака у результата:
5(ш) = -->(-!, а<0
а {а)
Объединяя оба случая, можно записать
В частном случае а - -1 полученная формула дает следующее:
Итак, зеркальное отражение сигнала относительно начала отсчета времени при-
приводит к зеркальному отражению спектра относительно нулевой частоты. Для ве-
вещественного сигнала это соответствует комплексному сопряжению спектра.
ЗАМЕЧАНИЕ
В данном случае результат не сводится к умножению исходного спектра на некоторую
функцию. В соответствии с предыдущим замечанием это означает, что изменение длитель-
длительности сигнала не может быть осуществлено линейной системой с постоянными парамет-
параметрами.
Дифференцирование сигнала
Посмотрим, как влияет на спектр дифференцирование сигнала во временной
области. Для этого нам придется воспользоваться определением понятия произ-
производной:
1ш/ .
dt e-° e
Применим к этому выражению преобразование Фурье:
ад -
е->0 р е->0
-00 Ь
Е->0
Преобразование Фурье 45
Спектр производной получается путем умножения исходного сигнала на ju>.
Таким образом, при дифференцировании низкие частоты ослабляются, а высо-
высокие усиливаются. Фазовый спектр сигнала сдвигается на 90° для положитель-
положительных частот и на - 90° для отрицательных.
Множитель ja называют оператором дифференцирования сигнала в частотной
области.
Интегрирование сигнала
Интегрирование, как известно, является операцией, обратной дифференцирова-
дифференцированию. Поэтому, исходя из результатов, полученных в предыдущем разделе, каза-
казалось бы, можно ожидать следующий результат:
Однако все не так просто. Детальный анализ, выполненный, например, в [1], по-
показывает, что эта формула справедлива лишь для сигналов, не содержащих по-
постоянной составляющей, у которых
В общем же случае результат должен содержать дополнительное слагаемое в виде
дельта-функции на нулевой частоте. Множитель перед дельта-функцией пропор-
пропорционален постоянной составляющей сигнала: \
t:F@)8((o). A.15)
Итак, при интегрировании исходного сигнала высокие частоты ослабляются, а
низкие усиливаются. Фазовый спектр сигнала смещается на -90° для положи-
положительных частот и на 90° для отрицательных. Множитель l/О'оо) называют опера-
оператором интегрирования в частотной области.
Спектр свертки сигналов
Свертка сигналов является очень часто используемой в радиотехнике интеграль-
интегральной операцией, поскольку она описывает, в частности, прохождение сигнала че-
через линейную систему с постоянными параметрами (подробнее это будет обсуж-
обсуждаться в главе 2):
s(t)=]f(t)g(t-t>)dt.
-со
Подвергнем такую конструкцию преобразованию Фурье:
W= J ]f(f)g(t-t')dt'e-Jatdt =
■ A.16)
= \f(? )e-**' \g(t - t')e-tai('-'">d(t -1' )dt' =
46 Глава 1. Основы анализа сигналов
Полученный результат очень важен, он часто используется на практике: спектр
свертки равен произведению спектров.
Спектр произведения сигналов
Дуальность преобразования Фурье и соотношение A.16), полученное в преды-
предыдущем разделе, позволяют легко предугадать результат. Однако все-таки полу-
получим его:
тогда
ЗД = ]f(tW)e-**dt = ] fj- ]F^)eJa'rd(Ag(t)e-iatdt =
-» -Д*я-« J A.17)
= J_ jF(cy)fg(t)e^<"""')tA drt = —
Как и следовало ожидать, спектр произведения представляет собой свертку
спектров. Единственной дополнительной тонкостью является множитель 1/Bя)
перед интегралом свертки.
ЗАМЕЧАНИЕ
При выводе соотношения A.17) мы представили сигнал/(t) с помощью обратного преоб-
преобразования Фурье A.12) от его спектральной функции.
Умножение сигнала на гармоническую функцию
Умножим исходный сигнал, спектр которого нам известен, на гармоническую
функцию:
5@ - /(О cos(w0£ + фо).
Посмотрим, что произошло со спектром сигнала:
5(ш)=
J/(t)e>oe''<m"WoK* +
]f(t)eedt A.18)
-ос * -оо
= - е™ F(ro - ш0) + - е'т F(co + ш0).
Как видите, спектр «раздвоился» — распался на два слагаемых вдвое меньшего
уровня (множитель 1/2), смещенных на ш0 вправо (ш - ш0) и влево (со + ш0) по
оси частот. Кроме того, при каждом слагаемом имеется множитель, учитываю-
учитывающий начальную фазу гармонического колебания. С практическим применением
этого свойства мы столкнемся в главе 8 при обсуждении свойств сигналов с амп-
амплитудной модуляцией.
Преобразование Фурье 47
Связь преобразования Фурье
и коэффициентов ряда Фурье
Пусть s(t) — сигнал конечной длительности, а 5(со) — его спектральная функция.
Получим на основе s(t) периодический сигнал, взяв период повторения Г не
меньше длительности сигнала:
5,@= ts(t-kT).
Сравнивая формулы A.11) для расчета преобразования Фурье сигнала s(t) и A.9)
для расчета коэффициентов ряда Фурье сигнала sr(t), можно заметить, что эти
формулы предполагают вычисление одного и того же интеграла. Различие состо-
состоит в том, что для расчета коэффициентов ряда Фурье в подынтегральное выра-
выражение подставляются не произвольные, а дискретные значения частоты щ ■= 2nk/T
и, кроме того, результат интегрирования делится на период сигнала Г.
Таким образом, между спектральной функцией 5(со) одиночного импульса и ко-
коэффициентами Ск ряда Фурье для периодической последовательности таких им-
импульсов существует простая связь:
ЗАМЕЧАНИЕ
Данная формула справедлива и в том случае, еслн период повторения импульсов меньше
их длительности (то есть если соседние импульсы периодической последовательности пе-
перекрываются).
Фурье-анализ неинтегрируемых сигналов
При введении понятия преобразования Фурье были указаны условия его приме-
применимости: выполнение условий Дирихле и абсолютная интегрируемость сигнала.
Однако в ряде случаев можно применить преобразование Фурье и к сигналам,
этим условиям не удовлетворяющим, и получить при этом вполне осмысленный
и практически полезный результат.
Итак, в данном разделе мы воспользуемся преобразованием Фурье для спек-
спектрального анализа таких сигналов, к которым оно формально неприменимо.
Дельта-функция
Прежде всего вычислим преобразование Фурье для сигнала в виде дельта-функ-
дельта-функции (о ее свойствах шла речь в разделе «Классификация сигналов», и фильтрую-
фильтрующее свойство A.1) нам сейчас как раз понадобится):
Спектр дельта-функции представляет собой константу, то есть является равно-
равномерным в бесконечной полосе частот. Это вполне согласуется с общим соотно-
48 Глава 1. Основы анализа сигналов
шепнем между длительностью сигнала и шириной его спектра: дельта-импульс
имеет бесконечно малую длительность, а его спектр бесконечно широк.
Из полученного результата следует, что дельта-функцию можно записать в виде
обратного преобразования Фурье следующим образом:
5@ = — ]eiatd(o. A.19)
Это полезное соотношение мы используем при анализе следующего сигнала.
Постоянный во времени сигнал (константа)
Поскольку мы уже знаем, что спектром дельта-функции является константа, бла-
благодаря дуальности преобразования Фурье можно сразу же сказать, что спектром
константы (s(t) = А) будет дельта-функция частоты. Проверим это, воспользо-
воспользовавшись только что полученным соотношением A.19):
5(со) = \Ае-м dt=2nA 5(co).
Наши предположения полиостью подтвердились. Здесь опять хорошо прослежи-
прослеживается обратная пропорциональность между длительностью сигнала и шириной
его спектра: бесконечно протяженный сигнал имеет бесконечно узкий спектр.
Функция единичного скачка
Функция единичного скачка A.2) (см. раздел «Классификация сигналов») пред-
представляет собой интеграл от дельта-функции, поэтому, в соответствии со свойст-
свойствами преобразования Фурье (см. предыдущий раздел), мы получаем
5(со)= [(О"^Л 8()
Поскольку дельта-функция имеет ненулевую (равную 1) постоянную состав-
составляющую, то в полном соответствии с формулой A.15), приведенной для данного
случая в разделе «Свойства преобразования Фурье», в спектре появляется до-
дополнительное слагаемое в виде дельта-функции на нулевой частоте.
Гармонический сигнал
Рассчитаем спектр гармонического сигнала общего вида:
s(t) - A cos(co0£ + ф) •
Для расчета спектральной функции представим косинус в виде полусуммы ком-
комплексных экспонент и воспользуемся формулой A.19):
S(eo) = JAcos((o0t + <p0)e-imtdt= \A- — e'jmt dt =
= J deMe-y(—o)^+ J Ae-me-H»+»»)t£ = A.20)
-x
—да
co- co0) + Ane'm 5(co+ co0).
Преобразование Фурье 49
Результат, как видим, представляет собой пару дельта-функций, расположенных
на частотах ±со0. Множители при них отражают амплитуду и начальную фазу (то
есть комплексную амплитуду ) гармонического сигнала.
ЗАМЕЧАНИЕ
Тот же результат можно было бы получить, применив к спектру постоянного во времени
сигнала свойство преобразования Фурье A.18), касающееся умножения сигнала на гармо-
гармоническую функцию.
Комплексная экспонента
Впервые в этой книге мы рассматриваем сигнал, не являющийся вещественным:
s(t) = А
Результат вычисления его спектра легко предугадать: только что рассмотренный
гармонический сигнал дал спектральную функцию в виде двух дельта-функций,
а косинус с помощью формулы Эйлера можно представить в виде полусуммы
двух комплексных экспонент. Значит, спектром комплексной экспоненты долж-
должна являться одиночная дельта-функция:
5(со) = j Аем>'e-jat dt = 2Ляб(со-со0). A.21)
Результат, как видите, не обманул наших ожиданий. Обратите внимание на то,
что поскольку сигнал не является вещественным, его спектр теряет свойство
симметрии.
На первый взгляд, польза от рассмотрения комплексных сигналов невелика. Од-
Однако они оказываются очень удобным средством для анализа модулированных
сигналов, особенно когда у них одновременно меняются и амплитуда, и началь-
начальная фаза. С такими сигналами нам предстоит встретиться в разделе «Комплекс-
«Комплексная огибающая» далее в этой главе.
Произвольный периодический сигнал
Как мы уже знаем, периодический сигнал с периодом Т может быть представлен
в виде ряда Фурье A.8):
» . А
s(t)= Y,Cke T .
После вычисления спектров гармонического сигнала A.20) и комплексной экс-
экспоненты A.21) читателю уже должно быть ясно, что спектральная функция та-
такого сигнала представляет собой набор дельта-функций, расположенных на час-
частотах гармоник ряда Фурье:
5(со) =
*—°
Множители при дельта-функциях равны соответствующим коэффициентам ряда
Фурье Ck, умноженным на 2я.
50 Глава 1. Основы анализа сигналов
Корреляционный анализ
Корреляционный анализ наряду со спектральным играет большую роль в теории
сигналов. Говоря кратко, его смысл состоит в количественном измерении степе-
степени сходства различных сигналов. Для этого служат корреляционные функции, с
рассмотрения которых мы и начнем этот раздел.
Корреляционная функция
Корреляционная функция (КФ; английский термин — correlation function, CF)
детерминированного сигнала с конечной энергией представляет собой интеграл
(в бесконечных пределах) от произведения двух копий сигнала, сдвинутых друг
относительно друга на время т:
Bs(T)=]s(t)s(t~T)dt.
-00
Корреляционная функция показывает степень сходства между сигналом и его
сдвинутой копией — чем больше значение корреляционной функции, тем это
сходство сильнее. Кроме того, корреляционная функция обладает следующими
свойствами:
1. Значение КФ при т - 0 равно энергии сигнала, то есть интегралу от его квад-
квадрата:
2. КФ является четной функцией своего аргумента т:
В,(т) - В,(-т).
3. Значение КФ при т = О является максимально возможным значением:
вд * Д<@).
4. С ростом абсолютного значения т КФ сигнала с конечной энергией затухает:
lim 5,(т) = 0.
5. Если сигнал s(t) не содержит особенностей в виде дельта-функций, его КФ не
может иметь разрывов (то есть обязана быть непрерывной функцией).
6. Если сигнал — напряжение, то размерность его КФ равна В2 • с.
В качестве примера вычислим КФ прямоугольного импульса A.13), показанного
ранее на рис. 1.12:
□ при 0 < т < Г
}
□ при-Г<т < О
В,(х) = JA2dt--
о
Корреляционный анализ
51
а при |т| > т
ад = о.
Объединяя результаты, можно записать
График КФ прямоугольного импульса показан на рис. 1.26.
-Т 0 Г т
Рис. 1.26. Корреляционная функция прямоугольного импульса
В случае периодического сигнала (и вообще любого сигнала с бесконечной энер-
энергией) воспользоваться приведенным определением не удастся. Поэтому КФ пе-
периодического сигнала с периодом Т вычисляют, усредняя произведение сдвину-
сдвинутых копий в пределах одного периода:
Т/2
1 '
-Т/2
Набор свойств такой КФ несколько меняется.
1. Значение при т = 0 равно не энергии, а средней мощности анализируемого
сигнала:
1 Т/2
± ]
1 -Т/2
2. Свойство четности сохраняется: Д,(-т) = Д<(т).
3. Значение КФ при т = 0 по-прежнему является максимально возможным:
ад й в,@).
4. КФ периодического сигнала является периодической функцией с тем же пе-
периодом, что и сам сигнал: Д,(т + Г) = Д,(т).
5. Если сигнал не содержит дельта-функций, его КФ будет непрерывной функ-
функцией.
6. Размерность КФ периодического сигнала — квадрат размерности сигнала (В2,
если сигнал — напряжение).
В качестве примера вычислим КФ гармонического сигнала с частотой соо:
s(t) — A cos(coo£ + фо)-
52 Глава 1. Основы анализа сигналов
Вычисляем корреляционный интеграл, учитывая, что период такого сигнала ра-
равен 2п/соо:
со я'<"° А2
Bs(x) = — f Л cos(co0t + 90)/1cos(go0(£-i) + фо)й£ = — cos((a0x).
2п -*/«>о 2
Как видите, КФ гармонического сигнала тоже является гармонической функци-
функцией. Еще очень важен тот факт, что полученный результат не зависит от началь-
начальной фазы гармонического сигнала (параметр ф в полученное выражение не во-
вошел). Это проявление общего свойства всех КФ, о котором пойдет речь далее в
разделе «Связь между корреляционными функциями и спектрами сигналов».
Взаимная корреляционная функция
Если КФ показывает степень сходства между сдвинутыми копиями одного и
того же сигнала, то взаимная корреляционная функция (ВКФ; английский тер-
термин — cross-correlation function, CCF) позволяет измерить аналогичную величи-
величину для сдвинутых экземпляров двух разных сигналов.
Общий вид формулы КФ сохраняется, но под интегралом стоит произведение
двух разных сигналов, один из которых задержан на время г.
B12(x)=]s{(t)s2(t-x)dt.
ЗАМЕЧАНИЕ
Очевидно, что КФ является частным случаем ВКФ, когда оба сигнала одинаковы:
s2(t) - s(t).
В качестве примера вычислим ВКФ прямоугольиого и треугольного импульсов
(см. рис. 1.12 и 1.14):
[О, t<O,t>T, |д( t<Oi(>r.
□ при 0 < х < Т
□ при -Г<т<0
Т
□ при |х| > Т
Корреляционный анализ
53
Объединяя результаты, можно записать
[А2
2Т
А^_
2Т
О,
(Г-тJ, 0<т<Г,
(Г2-т2), -Г<т<0,
I т| > Т.
График полученной ВКФ представлен на рис. 1.27.
-Г О Г х
Рис. 1.27. ВКФ прямоугольного и треугольного импульсов
Свойства ВКФ несколько отличаются от свойств КФ:
1. |512(т)| < ^EtE2, где £i и £г — энергии сигналов S\(t) и s2(t).
2. В\2(~х) = 52i(x), то есть изменение знака т равносильно взаимной перестанов-
перестановке сигналов.
3. Значение ВКФ при т = 0 ничем не выделяется; максимум может быть распо-
расположен в любом месте оси т.
4. С ростом абсолютного значения т ВКФ сигналов с конечной энергией зату-
затухает:
lim А,(т) = 0.
ui->« 12V '
5. Если сигналы S\(£) и 5г@ не содержат особенностей в виде дельта-функций, их
ВКФ не может иметь разрывов (то есть обязана быть непрерывной функцией).
6. Если сигналы — напряжение, то размерность их ВКФ равна В2 • с.
Для периодических сигналов понятие ВКФ обычно не применяется, хотя оно мо-
может быть введено в случае, если сигналы st(t) и s2(t) имеют одинаковый период.
Связь между корреляционными функциями
и спектрами сигналов
Поскольку как корреляционные функции, так и спектры являются интегральны-
интегральными преобразованиями анализируемых сигналов, логично предположить, что эти
характеристики как-то связаны друг с другом. Для выявления этой связи под-
54 Глава 1. Основы анализа сигналов
вергнем взаимную корреляционную функцию преобразованию Фурье, считая,
что сигналы s,(£) и s2(t) имеют спектральные функции 5;(co) и 52(со):
= J
Полученный результат очень прост: ВКФ связана преобразованием Фурье с так
называемым взаимным спектром сигналов. Взаимный спектр 512(со)для сигналов
s,@ и s2(t) представляет собой произведение их спектральных функций, одна из
которых подвергнута комплексному сопряжению:
512(co) = 5((co)S2(co). A.22)
Отсюда можно сделать очень важный вывод: если спектры сигналов не перекры-
перекрываются, то их взаимный спектр равен нулю на всех частотах, а значит, равна
нулю и их ВКФ при любых временных сдвигах т. Таким образом, сигналы с непе-
неперекрывающимися спектрами являются некоррелированными.
Приняв s{(t) = s2@ = s(t), получаем аналогичный результат для КФ:
= J
-оо -оо
= ]s(t)e-Jat]s(t-x)eMt-x)d(t-x)dt= A.23)
= 5(соM*(со) = |
Итак, КФ сигнала связана преобразованием Фурье с квадратом модуля спектраль-
спектральной функции, или с энергетическим спектром сигнала.
Отсюда следует еще один важный факт: КФ сигнала не зависит от его фазового
спектра. Следовательно, сигналы, амплитудные спектры которых одинаковы,
а фазовые различаются, будут иметь одинаковую КФ. Еще одно следствие за-
заключается в том, что по КФ нельзя восстановить исходный сигнал (опять же из-
за утраты информации о фазе).
Энергетические расчеты
в спектральной области
В разделе «Связь между корреляционными функциями и спектрами сигналов»
мы показали, что ВКФ двух сигналов связана преобразованием Фурье с их вза-
взаимным спектром. Запишем эту связь в виде формулы обратного преобразования
Фурье:
Теперь подставим в эту формулу значение т = 0 и раскроем выражения для ВКФ
и взаимного спектра. Получится соотношение, именуемое теоремой Рэлея:
Комплексная огибающая 55
Если теперь принять сигналы одинаковыми (s^t) = s2(t) = s(t)), получится соот-
соотношение, позволяющее вычислять энергию сигнала как во временной, так и в
частотной области и называемое равенством Парсеваля:
Е= js2(t)dt = — J|5(co)|2</co. A.24)
Последнее, на чем следует остановиться в этом разделе, — это вычисление сред-
средней мощности периодического сигнала по коэффициентам его ряда Фурье. За-
Запишем периодический сигнал s(t) в виде ряда Фурье в комплексной форме A.8):
А теперь применим к этому выражению формулу для расчета средней мощности
за период:
г f l dt.
I k =—oo m =-oo q
Промежуток О...Гсоответствует целому числу периодов стоящей под интегралом
комплексной экспоненты, поэтому интеграл будет равен нулю при всех k *■ -m.
При k = -m экспонента становится константой, и интеграл будет равен Г:
*—«
Результат оказывается очень простым: средняя мощность периодического сигна-
сигнала равна сумме квадратов модулей коэффициентов его ряда Фурье.
Комплексная огибающая
В различных системах передачи информации часто применяются узкополосные
сигналы, спектр которых сосредоточен в окрестности некоторой частоты со„. При
анализе таких сигналов удобно пользоваться понятиями комплексной огибающей,
амплитудной огибающей и фазовой функции сигнала. Эти понятия и будут рас-
рассмотрены в данном разделе.
Рассмотрим сигнал, представленный в виде колебаний с частотой со0, у которых
меняются во времени как амплитуда, так и начальная фаза:
5@ = A(t) cos(co0£ + ф@). A.25)
Множитель A(t) называется амплитудной огибающей, а начальная фаза ср(£) —
фазовой функцией сигнала s(t). Весь аргумент функции cos называют полной фа-
фазой сигнала:
56 Глава 1. Основы анализа сигналов
Сигнал A.25) можно представить как вещественную часть комплексной функ-
функции, заменив косинус комплексной экспонентой:
В комплексном выражении, стоящем под функцией Re, можно выделить два мно-
множителя: exp(jco0t) представляет немодулированное несущее колебание и является
быстро меняющимся, a A(t) exp(jcp(£)) меняется, как правило, значительно мед-
медленнее и содержит информацию об амплитудной огибающей и начальной фазе
одновременно. Этот медленно меняющийся множитель и называется комплекс-
комплексной огибающей сигнала:
ЗАМЕЧАНИЕ
Комплексная огибающая, объединяя и себе информацию об амплитуде и фазе сигнала, яв-
является обобщением понятия комплексной амплитуды, широко используемого в теоретиче-
теоретической электротехнике.
Рассмотрим теперь другую задачу — представим произвольный сигнал s(t) в фор-
форме A.25), то есть выделим его амплитудную огибающую и фазовую функцию.
Ясно, что способов сделать это бесконечно много, поскольку мы хотим одной
функции s(t) поставить в соответствие набор из двух функций A(t) и ф(£). Одна-
Однако искомое представление должно удовлетворять нескольким очевидным огра-
ограничениям. В частности, для гармонического сигнала искомая процедура должна
давать в результате постоянные амплитуду и начальную фазу. Кроме того, ра-
разумно потребовать, что фазовая функция не должна меняться при умножении
сигнала на произвольный постоянный множитель. С учетом этих требований
способ выделения амплитудной огибающей и фазовой функции из произвольно-
произвольного сигнала оказывается единственным: такое выделение производится с помо-
помощью преобразования Гильберта, речь о котором пойдет в следующем разделе.
ЗАМЕЧАНИЕ
Подробное и интересное обсуждение данной проблемы можно найти в [6]. Вообще, с этой
замечательной книгой, рассказывающей о различных парадоксах и заблуждениях, связан-
связанных с теорией связи, должен познакомиться каждый, кто занимается обработкой сигналов,
радиотехникой или телекоммуникациями.
Преобразование Гильберта
Для выделения амплитуды и фазы произвольный сигнал s(t) представляется кап
вещественная часть комплексного сигнала sa@ (он называется аиалитическил
сигналом):
Вещественная часть аналитического сигнала, естественно, должна совпадать '
исходным сигналом s(t). Мнимая же часть s±(t) называется сопряженным сигна
лом или квадратурным дополнением:
sa(t) = s(t) + j sx(t).
Комплексная огибающая 57
Сопряженный сигнал получается из исходного с помощью преобразования Гиль-
Гильберта. Вычисляется преобразование Гильберта следующим образом:
s±(t) = -]^,dt'. A.26)
Данный интеграл представляет собой свертку сигнала s(t) и функции i/{nt). Это
означает, что преобразование Гильберта может быть выполнено линейной систе-
системой с постоянными параметрами (такие системы будут описаны в главе 2; забе-
забегая вперед, скажем, что система, осуществляющая преобразование Гильберта,
является физически нереализуемой, поскольку ее импульсная характеристика
имеет бесконечную протяженность в обоих направлениях временной оси). Из
этого, в свою очередь, следует, что мы можем определить частотную характери-
характеристику преобразования Гильберта:
Г;, со<0,
К±(а) = J—в'** dt = 0, со = 0, A.27)
"°nt {-j, со>0.
Итак, АЧХ преобразования Гильберта равна единице всюду, кроме нулевой час-
частоты, то есть преобразование Гильберта не меняет амплитудных соотношений в
спектре сигнала, лишь удаляя из него постоянную составляющую. Фазы всех
спектральных составляющих в области положительных частот уменьшаются на
90°, в области отрицательных частот — увеличиваются на 90°.
Таким образом, устройство, осуществляющее преобразование Гильберта, должно
представлять собой идеальный фазовращатель, вносящий на всех частотах фазо-
фазовый сдвиг, равный 90°.
Очевидно, что обратное преобразование Гильберта должно вносить такой же фа-
фазовый сдвиг, но с обратным знаком, опять же при сохранении амплитудных со-
соотношений в спектре преобразуемого сигнала. Математически это будет выгля-
выглядеть так:
К> (со) =
Сравнение этой формулы с коэффициентом передачи прямого преобразования
Гильберта A.27) показывает, что
Следовательно, формулы обратного и прямого преобразований Гильберта разли-
различаются лишь знаком:
n-it-t'
58 Глава 1. Основы анализа сигналов
Спектр аналитического сигнала
Ранее уже было сказано, что аналитический сигнал получается путем добав-
добавления к вещественному сигналу s(t) мнимой части в виде его преобразования
Гильберта:
Теперь вычислим спектр аналитического сигнала, учитывая, что преобразование
Гильберта является линейным и его коэффициент передачи определяется фор-
формулой A.27):
ГО, со<0,
5а (со) = 5(«о) + А(со) = 5(«о)A + jK^oS)) = | 5@), со = 0,
[25(ю), со > 0.
Полученный результат довольно любопытен. В области положительных частот
спектры вещественного сигнала и добавленной мнимой части (с учетом допол-
дополнительного 90-градуспого фазового сдвига, вносимого множителем;') складыва-
складываются, давая удвоенный результат. В области же отрицательных частот эти спек-
спектры оказываются противофазными и взаимно уничтожаются. В результате спектр
аналитического сигнала оказывается односторонним (рис. 1.28, а, б).
Итак, чтобы для произвольного сигнала определить амплитудную огибающую и
фазовую функцию, необходимо прежде всего сформировать аналитический сиг-
сигнал, получив его мнимую часть с помощью преобразования Гильберта. Далее ам-
амплитудная огибающая находится как модуль аналитического сигнала:
Полная фаза представляет собой аргумент комплексного аналитического сиг-
сигнала:
Чтобы получить начальную фазу сигнала, нужно выделить из полной фазы ли-
линейное слагаемое а>0£. Для этого, в свою очередь, нужно знать значение централь-
центральной частоты сз0. После этого можно будет получить начальную фазу и комплекс-
комплексную огибающую:
Спектр комплексной огибающей представляет собой сдвинутый на со0 спектр
аналитического сигнала:
В общем случае спектр комплексной огибающей не является симметричным от-
относительно нулевой частоты (рис. 1.28, в).
Выбор центральной частоты сз0. вообще говоря, является произвольным. Для
узкополосных сигналов существует «разумное» значение со0, при использовании
которого оказывается наиболее простой аналитическая запись комплексной оги-
огибающей. Например, для гармонического сигнала
s(t) = A cos(m + ф)
Комплексная огибающая
59
аналитический сигнал имеет вид
sa(t) - А ехр(;Ш +;'ф).
Амплитудная огибающая равна А, полная фаза — Clt + ср. В общем случае, выбрав
произвольное значение «средней» частоты соо, мы получаем начальную фазу
ф@ - (П - шо) t + ф
и комплексную огибающую
Am(t) - A exp(j(fi - шо)г
-щ
о
а
со
О
б
->
со
Рис. 1.28. Амплитудные спектры вещественного сигнала (а), соответствующего ему
аналитического сигнала (б) и его комплексной огибающей (а)
Если выбранная «средняя» частота со0 будет совпадать с частотой гармоническо-
гармонического сигнала (со0 = О), комплексная огибающая станет константой:
Am(t) - А ехр (jcp).
Метод замены исходных функций их комплексными огибающими для анализа
прохождения сигналов через различные цепи называется методом низкочастот-
низкочастотного эквивалента. При этом принципиально то, что все комплексные огибающие
должны вычисляться относительно одной и той же центральной частоты со0, даже
если ее значение для некоторых сигналов будет выглядеть «неестественным».
60 Глава 1. Основы анализа сигналов
В целом же следует помнить, что понятие комплексной огибающей имеет смысл
только при указании частоты а>0, относительно которой эта комплексная огибаю-
огибающая вычислена.
Случайные сигналы
В отличие от детерминированных сигналов, форму которых мы знаем точно, мгно-
мгновенные значения случайных сигналов заранее не известны и могут быть предска-
предсказаны лишь с некоторой вероятностью, меньшей единицы. Характеристики таких
сигналов являются статистическими, то есть имеют вероятностный вид.
В радиотехнике существует два основных класса сигналов, нуждающихся в веро-
вероятностном описании. Во-первых, это шумы — хаотически изменяющиеся во вре-
времени электромагнитные колебания, возникающие в разнообразных физических
системах из-за беспорядочного движения носителей заряда. Во-вторых, случай-
случайными являются все сигналы, несущие информацию, поэтому для описания зако-
закономерностей, присущих осмысленным сообщениям, также прибегают к вероят-
вероятностным моделям.
Ансамбль реализаций
Математическая модель изменяющегося во времени случайного сигнала называ-
называется случайным процессом. По определению, случайный процесс X(t) — это
функция особого вида, характеризующаяся тем, что значения, принимаемые ею
в любой момент времени t, являются случайными величинами.
ЗАМЕЧАНИЕ
В технической литературе термины «случайный сигнал» и «случайный процесс» часто ис-
используются как синонимы.
До регистрации (до приема) случайный сигнал следует рассматривать именно
как случайный процесс, представляющий собой совокупность {ансамбль) функ-
функций времени xt(t), подчиняющихся некоторой общей для них статистической
закономерности. Одна из этих функций, ставшая полиостью известной после
приема сообщения, называется реализацией случайного процесса. Эта реализа-
реализация является уже не случайной, а детерминированной функцией времени. На
рис. 1.29 приведен пример нескольких реализаций случайного процесса.
Модели случайных процессов
Для анализа свойств и характеристик случайного процесса, а также различных
его преобразований необходимо задать математическую модель случайного про-
процесса. Такая модель может представлять собой описание возможных реализаций
случайного процесса в сочетании с указанием относительной частоты их появле-
появления. Приведем несколько примеров моделей случайных процессов, задаваемых
таким образом.
Случайные сигналы
61
\JVM/U. Л.
. Лч , / А\д Лл а ,
Рис. 1.29. Реализации случайного процесса
Гармонический сигнал со случайной начальной фазой
Во многих практических задачах используется модель случайного процесса, реа-
реализации которого представляют собой гармонические колебания с известными
(детерминированными) амплитудой и частотой, но случайной начальной фазой.
Таким образом, реализация рассматриваемого случайного процесса может быть
записана как
x(t) = A cos(cuo£ + ф).
где А — амплитуда (детерминированная), со0 — частота (детерминированная) и
Ф — случайная начальная фаза, которая в большинстве практически интересных
случаев может считаться равномерно распределенной на интервале О...2я, то есть
имеющей следующую плотность вероятности:
-, 0<ф<2я,
ГС
[О, в остальных случаях.
Графики нескольких реализаций данного случайного процесса, представляющие
собой синусоиды, смещенные друг относительно друга по временной оси, пока-
показаны на рис. 1.30.
Как видите, конкретный вид реализации процесса в данном случае определяется
значением всего лишь одной случайной величины — начальной фазы.
ЗАМЕЧАНИЕ
Случайные процессы, конкретный вид реализаций которых определяется значениями ко-
конечного числа параметров (случайных величин), иногда называют квазидетерминировап-
иыми случайными процессами.
62
Глава 1. Основы анализа сигналов
*(')
Рис. 1.30. Реализации гармонического сигнала со случайной начальной фазой
Случайный телеграфный сигнал
Таким сигналом в [5] назван случайный процесс, реализации которого принима-
принимают значения +1 и — 1, причем перепады уровня происходят в случайные моменты
времени и число N перепадов уровня, происходящих за время т, является слу-
случайной величиной с дискретным распределением вероятности, описываемым за-
законом Пуассона:
A.28)
Здесь X — неотрицательный параметр, определяющий среднюю частоту возник-
возникновения перепадов уровня.
ЗАМЕЧАНИЕ
Напомним, что прописной буквой Р обозначается вероятность некоторого события, ука-
указываемого в скобках. В формуле A.28) P(N, т) — это вероятность того, что за время т прои-
произойдет N перепадов уровня сигнала.
Скачки уровня происходят в случайные моменты времени tk, поэтому аналити-
аналитически записать формулу для отдельной реализации данного случайного процес-
процесса оказывается весьма затруднительно, а изобразить ее график можно лишь
условно (рис. 1.31).
-1
Рис. 1.31. Реализация случайного телеграфного сигнала
В данном случае конкретная реализация задается бесконечным множеством слу-
случайных величин — моментов перепадов уровня 4. а характеристики случайного
процесса определяются статистическими свойствами этих случайных величин.
Итак, полное описание случайного процесса дает его ансамбль реализаций. Одна-
Однако для решения практических задач часто достаточно более простых характеры-
Случайные сигналы 63
стик, выражающихся в виде числовых параметров и детерминированных функ-
функций. Об этом пойдет речь далее.
Вероятностные характеристики
случайных процессов
Пусть X(t) — случайный процесс, заданный ансамблем реализаций {x^t), x2(t),...,
xk{t), ...}. Выбрав произвольный момент времени tu зафиксируем значения, при-
принимаемые всеми реализациями: {х^), x2{t\) xk{t{), ...} (см. рис. 1.29). Сово-
Совокупность этих значений образует одномерное сечение случайного процесса и пред-
представляет собой случайную величину X(tt). Напомним кратко основные характе-
характеристики случайных величин, отметив при этом, что для одномерных сечений
случайных процессов они в общем случае зависят от выбранного момента време-
времени £,.
Функциональные характеристики
Функция распределения вероятности (cumulative distribution function, CDF),
обозначаемая как F(x, t{), равна вероятности того, что в момент времени tt значе-
значение случайного процесса не превосходит х:
F(x, tj) является неубывающей функцией, значения которой лежат в диапазоне
О < F{x, t\)<\. Для предельных значений х выполняются следующие соотноше-
соотношения: F(-oo, £,) = 0 и F(oo, £,) - 1.
Вероятность попадания значения случайного процесса в интервал {а, Ь] равна
разности значений функции распределения на концах этого интервала:
Р(а < X(ti) йЬ)- F(b, tt) - F(a, t,).
Одномерная плотность вероятности (probability density function, PDF) обозна-
обозначается p(x, t{) и представляет собой производную от функции распределения:
p(x,t1) =
dF(x,tx)
chc '
Произведениер{х, tt) dx равно вероятности попадания значения случайного про-
процесса X{t{) в бесконечно малый интервал шириной dx в окрестности х:
откуда следует, что плотность вероятности является неотрицательной функцией:
р(х, tj) > 0. Чтобы рассчитать вероятность попадания значения X{t{) в произ-
произвольный интервал [а, Ь], необходимо вычислить следующий интеграл:
ь
Так как случайная величина обязательно принимает какое-нибудь значение, долж-
должно выполняться условие нормировки:
64 Глава 1. Основы анализа сигналов
jp(x,ti)dx = Р(-оо <Х(£,) < да) = 1. A.29)
Зная плотность вероятности, можно рассчитать и функцию распределения: „
F(x,tx)=)p{x,t,)dx. A.30)
-со
Числовые характеристики
Знание одномерной плотности вероятности р(х, t{) позволяет произвести стати-
статистическое усреднение как самой величины Х(^), так и любой функции от нее.
Под статистическим усреднением (ensemble averaging) подразумевается усред-
усреднение по множеству (по ансамблю реализаций) в каком-либо сечении процесса,
то есть в фиксированный момент времени.
Для практических приложений наибольшее значение имеют следующие пара-
параметры случайного процесса:
□ математическое ожидание (mean value), которое служит теоретической оцен-
оценкой среднего взвешенного значения случайного процесса в момент времени t:
mx(t) = M{X(t)} = ]xp(x,t)dx; A.31)
ЗАМЕЧАНИЕ
Во многих практических задачах приходится вычислять математическое ожидание неко-
некоторой функции/от случайной величины х, имеющей плотность вероятности рх(х). Такое
вычисление выполняется по следующей несложной формуле:
M{f(x)}=]f(x)px(x)dx. A.32)
— аз
Формула для математического ожидания A.31) является частным случаем A.32) при
/СО - х.
□ дисперсия (variance), характеризующая среднюю мощность отклонений слу-
случайного процесса от его среднего значения mx{t), называемых флуктуациями
(fluctuation):
Dx(t) = M{[X(t)-mx(t)f}=M{X\t)}-mlx(t)=]x2p(x,t)dx-ml(t); A.33)
□ среднее квадратическое отклонение (standard deviation), представляющее со-
собой квадратный корень из дисперсии и служащее амплитудной мерой разбро-
разброса значений случайного процесса в момент времени t относительно математи-
математического ожидания:
- 0,@ = 4ЩГ) = ^M{[X(t)-mx(t)f} =^M{X2(t)}-m2x(t) . A.34)
ЗАМЕЧАНИЕ :
Дисперсия случайной величины X часто обозначается как а2.
Случайные сигналы
65
Равномерное распределение
Одним из часто используемых на практике законов распределения случай-
случайных величин является равномерное распределение (uniform distribution). При
этом плотность вероятности является константой на некотором интервале [а, Ь]
(рис. 1.32, слева). Величина этой константы, согласно условию нормировки
A.29), должна быть равна 1/F - а):
а<х
Ь-а
О, х < а, х > Ь.
Рис. 1.32. Плотность вероятности (слева) и функция распределения (справа)
случайной величины с равномерным распределением
Функция распределения, согласно A.30), на интервале [а, Ь] линейно возрастает
от 0 до 1 (см. рис. 1.32, справа):
о,
X
Ь
1,
-а
t
-а
х •
а г
х :
<а,
ix<
>Ь.
ь,
Математическое ожидание, как и предсказывает интуиция, равно середине ин-
интервала возможных значений случайной величины:
т..
1
а + Ь
Ь-а
ЗАМЕЧАНИЕ
Если функция плотности вероятности имеет симметричный вид, то значение математиче-
математического ожидания всегда совпадает с центром симметрии.
Для расчета дисперсии необходимо сначала определить средний квадрат:
4 2 1 j b3 -a3 a2 +ab + Ь2
Ь-а З(Ь-а) 3
Теперь можно рассчитать дисперсию согласно A.33):
а2+аЬ + Ь2 (а + Ь\2 _ (Ь-аJ
12
66
Глава 1. Основы анализа сигналов
Итак, дисперсия равна одной двенадцатой квадрата ширины интервала. Среднее
квадратическое значение, естественно, оказывается пропорциональным этой ши-
ширине:
_ _ /тг -ъ~а
Нормальное распределение
Нормальный (гауссов) закон распределения случайных величин (normal distri-
distribution, Gaussian distribution) очень удобен для анализа и часто встречается на
практике, особенно он характерен для помех канала связи. Одномерная плот-
плотность вероятности нормальной случайной величины определяется выражением
р{х) = ■
1
ехр -
(x-mxf
2al
A.35)
где тх и о/ — соответственно математическое ожидание и дисперсия процесса.
На рис. 1.33 приведен график плотности вероятности нормальной случайной ве-
величины, построенный согласно A.35) при тх = 0 и о, = 1.
-3-2-10 1 2 л
Рис. 1.33. Плотность вероятности случайной величины с нормальным распределением
Функция распределения для закона Гаусса, к сожалению, не выражается через
элементарные функции. В отечественной литературе принято выражать ее через
так называемый интеграл вероятности:
., . ) 1 { (х1J
dx\
A.36)
Для нормального закона с математическим ожиданием тх и дисперсией и2х
функция распределения выражается через интеграл вероятности следующим об-
образом:
F(x) = Ф
В зарубежной литературе большее распространение получила так называемая
функция ошибок (error function) erf:
Случайные сигналы 67
erf (x) = ~J e-'2 dt. A.37)
VJtJ
Связь между функцией ошибок A.37) и интегралом вероятности A.36) выража-
выражается с помощью линейных преобразований аргументов функций и их резуль-
результатов:
erf(x) = 2O(W2)-l,
2 2 {J2
Функция распределения для нормального закона с математическим ожиданием
тх и дисперсией о2х выражается через функцию ошибок A.37) следующим обра-
образом:
1 1 Jx-тЛ
2 0 /о
ЗАМЕЧАНИЕ
В MATLAB имеется функция erf, реализующая формулу A.37). Есть также функция erfc,
возвращающая значение 1 - erf (х), и обратная функция erfinv.
Непосредственно вычислять функциональные характеристики нормального закона рас-
распределения можно с помощью функций normpdf (плотность вероятности), normcdf (функ-
(функция распределения) и norminv (обратная функция распределения), входящих в пакет
Statistics:
у = normpdf(х. m, sigma);
у = normcdf(x, m, sigma);
х = norminv(y, m, sigma):
Здесь т — математическое ожидание, sigma — среднее квадратическое отклонение.
Широкое распространение нормального закона распределения в природе объяс-
объясняется тем, что при суммировании достаточно большого числа равномощных
статистически независимых случайных величин, имеющих произвольные плот-
плотности распределения вероятности, плотность распределения суммы стремится к
нормальной. Это положение носит название центральной предельной теоремы.
Весьма полезным для математического анализа свойством нормального распре-
распределения является то, что из некоррелированности гауссовых случайных величин
следует их статистическая независимость (о разнице между этими понятиями
см. далее в разделе «Корреляционные функции случайных процессов»).
Одномерная плотность вероятности и связанные с ней числовые характеристики
позволяют получить важную информацию о свойствах случайного процесса. Од-
Однако для решения многих задач таких сведений недостаточно, так как они дают
вероятностное представление о случайном процессе X(t) только в отдельные мо-
моменты и ничего1 не говорят о том, как он изменяется во времени. Для описания
его временных характеристик необходимо использовать корреляционную функ-
функцию или привлечь для этого спектральные характеристики случайного процесса.
Упомянутые способы описания случайных процессов будут рассмотрены далее.
68 Глава 1. Основы анализа сигналов
Корреляционные функции случайных процессов
Как отмечалось в разделе «Вероятностные характеристики случайных процес-
процессов», одномерной плотности вероятности недостаточно для описания поведения
случайного процесса во времени. Гораздо больше сведений можно получить, рас-
располагая двумя сечениями случайного процесса в произвольные моменты време-
времени t{ и t2 (см. рис. 1.29). Совокупность этих двух сечений образует двумерную
случайную величину {X(£t), X(t2)}, которая описывается двумерной плотностью
вероятностир(х{, х2, tlt t2). Произведение р{хь х2, t\, t2)dx\dx2 представляет собой
вероятность того, что реализация случайного процесса X(t) в момент времени t{
попадает в бесконечно малый интервал шириной dx\ в окрестности хи а в мо-
момент времени t2 — в бесконечно малый интервал шириной dx2 в окрестности х2.
Естественным обобщением является n-мерное сечение случайного процесса, при-
приводящее к и-мерной плотности вероятности р{х\, х2 х„, tb t2, ..., tn). При п -> <ю
такая функция является исчерпывающей вероятностной характеристикой слу-
случайного процесса.
Описание свойств случайных процессов с помощью многомерных плотностей ве-
вероятности высокой размерности может быть весьма подробным, однако на этом
пути часто встречаются серьезные математические трудности. К счастью, многие
задачи, связанные с описанием случайных сигналов, удается решить на основе
двумерной плотности вероятности.
В частности, задание двумерной плотности вероятности р(хь хъ tu t2) позволяет
определить важную характеристику случайного процесса — его ковариационную
функцию
Согласно этому определению, ковариационная функция случайного процесса
X(t) представляет собой статистически усредненное произведение значений слу-
случайной функции X(t) в моменты времени tx и t2.
Для каждой реализации случайного процесса произведение x(tx)x(t2) является
некоторым числом. Совокупность реализаций образует множество случайных
чисел, распределение которых характеризуется двумерной плотностью вероят-
вероятности р(хь х2, tb t2). Если эта плотность вероятности известна, операция усредне-
усреднения по множеству осуществляется по формуле
00 X
Kx(tvt2)= J \xix1p{xvx1,tvt2)dxidx2-
-00 -00
Часто при анализе случайных процессов основной интерес представляет их флук-
туационная составляющая. В таких случаях применяется корреляционная функ-
функция, представляющая собой статистически усредненное произведение значений
центрированной случайной функции X(t) - mx(t) в моменты времени t\ и t2:
Случайные сигналы 69
Rx(tl,t2) = M{[x(tl)-m3c(ti)][x(t2)-mx(t2)]} =
оо -~
= J
-00 -00
= Kx(tl,t2)-mx(tl)mt(t2).
Корреляционная функция характеризует степень статистической связи тех значе-
значений случайного процесса, которые наблюдаются при t = tx и t = t2. При tx = t2 = t
последнее выражение соответствует определению дисперсии случайного процес-
процесса X(t) (см. формулу A.33)). Следовательно, при совмещении сечений функция
корреляции равна дисперсии:
р //■ /\ — Т£ (+ ~t\ т (/"\ — ТЛ (~t"\ ( \ *\$£\
ЗАМЕЧАНИЕ
Так сложилось, что в иностранной литературе используется обратная терминология —
Kx{t\, ti) называется корреляционной (correlation), a Rx(t\, t2) ковариационной функцией
(covariance). Во избежание недоразумений об этом следует помнить при работе с зарубеж-
зарубежными источниками. Впрочем, при анализе центрированных (имеющих нулевое математи-
математическое ожидание) случайных процессов корреляционная и ковариационная функции
совпадают.
В качестве примера рассчитаем корреляционную функцию гармонического сиг-
сигнала со случайной равномерно распределенной начальной фазой (см. раздел
«Модели случайных процессов» ранее в этой главе).
Можно легко убедиться, что данный случайный процесс является центрирован-
центрированным, то есть его математическое ожидание не зависит от времени и равно нулю:
оо 2гс л
ф)—г/ф = О. A.39)
2л
Поэтому ковариационная и корреляционная функции данного процесса совпа-
совпадают и могут быть найдены следующим образом (поскольку реализации данно-
данного случайного процесса представляют собой функции, зависящие от одной слу-
случайной величины, для усреднения произведения нет необходимости прибегать
к двумерной плотности вероятности — достаточно воспользоваться формулой
A.32), позволяющей произвести усреднение произвольной функции от случай-
случайной величины):
00
ДЛ*1>*2) = Кх(*1'*г)= Ix(ti)x(t2)pv(<p)dy =
-00
2it л
= Ji4cos(co0^ + ф)Лсоз(со0г2 + ф)—с/ф =
о 2л
2тг I { 2
9 2 ^\
f - cos(co0 (£j + t2) + 2ф)г/ф + f - cos(co0 (tj -12 ))<&p
о2 о2 ;
Здесь в первом слагаемом интегрирование производится по двум периодам функ-
функции cos, поэтому данный интеграл равен нулю. Во втором слагаемом подынте-
70 Глава 1. Основы анализа сигналов
тральная функция не зависит от переменной интегрирования ср, так что резуль-
результат интегрирования равен произведению подынтегрального выражения и длины
промежутка интегрирования, равной 2л. Окончательно получаем
Rx(tvt2) = Kx(tvt2) = ~cos((o0(ti-t2)). A.40)
Как видите, корреляционная функция данного случайного процесса гармониче-
гармонически зависит от расстояния между анализируемыми моментами времени. При
совпадении моментов времени tx и t2 мы получаем величину дисперсии случай-
случайного процесса:
Dx{t) = Rx(t,t)~- . . A-41)
Некоррелированность и статистическая независимость
Если совместно рассматривать две случайные величины Хх и Х2, между ними мо-
может существовать либо не существовать статистическая связь. Отсутствие та-
такой связи означает, что плотность вероятности одной случайной величины не за-
зависит от того, какое значение принимает другая случайная величина. Двумерная
плотность вероятности при этом представляет собой произведение одномерных
плотностей:
i, х2) = pi(xi) рг(х2).
Это условие называется условием статистической независимости.
При наличии статистической связи между случайными величинами статистиче-
статистические свойства каждой из них зависят от значения, принимаемого другой случай-
случайной величиной. Эта связь может быть сильной или слабой, линейной или нели-
нелинейной. Мерой линейной статистической связи между случайными величинами
является коэффициент корреляции:
_ M{XlX2}-M{X1}M{X2}
" ЩхЩЩ~-
Можно показать, что ri2\ < 1. Предельные значения ±1 достигаются, если реали-
реализации случайных величин жестко связаны линейным соотношением х2 ~ ах\ + Ь,
где а и Ь — некоторые константы. Знак коэффициента корреляции при этом сов-
совпадает со знаком множителя а.
Равенство коэффициента корреляции нулю свидетельствует об отсутствии ли-
линейной статистической связи между случайными величинами (при этом говорят
об их некоррелированности). Как видно из A.42), при этом математическое ожи-
ожидание произведения случайных величин равно произведению их математиче-
математических ожиданий:
M{XtX2) - M{Xj} М{Х2).
Легко показать, что из статистической независимости следует некоррелирован-
некоррелированность случайных величин. Обратное утверждение в общем случае неверно — не-
некоррелированные случайные величины могут быть зависимыми.
Случайные сигналы 71
ЗАМЕЧАНИЕ
Классическим примером этого является пара случайных величин Х\ = cos ф и Хг = sin q>, где
Ф — случайная величина, равномерно распределенная на интервале 0... 2я. Очевидно, что Xi
и Х2 зависят друг от друга; однако их коэффициент корреляции оказывается равным нулю.
Стационарные и эргодические
случайные процессы
В общем случае, как уже говорилось, вероятностные и корреляционные характе-
характеристики случайных процессов зависят от одного или нескольких моментов вре-
времени, в которые эти характеристики определяются. Однако существует класс
случайных процессов, у которых зависимость характеристик от времени отсутст-
отсутствует. Кроме того, для некоторых случайных процессов не обязательно произво-
производить усреднение по ансамблю реализаций — можно ограничиться рассмотрением
одной реализации и ее усреднением во времени.
Такие случайные процессы и будут рассматриваться в данном разделе.
Стационарные случайные процессы
Так принято называть случайные процессы, статистические характеристики ко-
которых одинаковы во всех временных сечениях.
Говорят, что случайный процесс строго стационарен (или стационарен в узком
смысле), если его многомерная плотность вероятности р(хи х2, ..., х„, tb t2, ..., tn)
произвольной размерности п не изменяется при одновременном сдвиге всех вре-
временных сечений tlt t2, ..., tn вдоль оси времени на одинаковую величину х:
р(хи х2,..., х„, t\, t2,..., tn) = р{хъ х2 х„, ti+x, t2+x,..., tn + x) при любом х.
Если же ограничить требования тем, чтобы от временного сдвига не зависели
лишь одномерная и двумерная плотности вероятности, то такой случайный про-
процесс будет стационарен в широком смысле. Понятно, что из стационарности в уз-
узком смысле следует стационарность в широком смысле, но не наоборот.
Для стационарного случайного процесса математическое ожидание и дисперсия
не зависят от времени, а корреляционная функция зависит не от самих моментов
времени, а только от интервала между ними х = t2 - t{.
Rx{tu t2) - Rx{t2 - to - Rx{x).
По этой причине при записи статистических параметров стационарного случай-
случайного процесса можно опускать обозначения фиксированных моментов времени:
тх, Dx, Kx(x), Rx(r).
Легко убедиться, что корреляционная функция стационарного случайного про-
процесса является четной:
Кроме того, абсолютные значения этой функции при любых х не превышают ее
значения при т = 0 (напомним, что это значение равно дисперсии случайного
процесса):
\Rx(x)\<Rx@) = Dx.
72 Глава 1. Основы анализа сигналов
Часто удобно использовать коэффициент корреляции (его также называют нор-
нормированной корреляционной функцией)
Для коэффициента корреляции выполняются соотношения гх@) = 1, \гх(х)\ < 1
и гх(-х) = гх(т).
Функции Rx(i) и гх(х) характеризуют связь (корреляцию) между значения-
значениями X(t), разделенными промежутком т. Чем медленнее убывают эти функции с
ростом абсолютного значения т, тем больше промежуток, в течение которого на-
наблюдается статистическая связь между мгновенными значениями случайного
процесса, и тем медленнее, плавнее изменяются во времени его реализации.
Легко видеть, что гармонический случайный процесс со случайной начальной
фазой (см. раздел «Модели случайных процессов» и вычисление характеристик
этого процесса в разделе «Корреляционные функции случайных процессов»)
является стационарным в широком смысле. Действительно, зависящие от одно-
одномерной плотности вероятности математическое ожидание A.39) и дисперсия
A.41) не зависят от времени, а корреляционная функция A.40), зависящая от
двумерной плотности вероятности, зависит лишь от интервала между рассмат-
рассматриваемыми моментами времени:
A.43)
Коэффициент корреляции такого случайного процесса равен
r,<j) = -~ = cos(c»0t).
ЗАМЕЧАНИЕ '■
Здесь следует отметить, что стационарным будет любой случайный процесс, реализации
которого являются периодическими функциями, идентичными по форме и различающи-
различающимися лишь «начальной фазой», то есть положением начала отсчета времени в пределах пе-
периода. При этом принципиальной является равномерность распределения начальной
фразы в пределах периода. Действительно, пусть у гармонического процесса начальная
фаза равномерно распределена в пределах половины окружности — на интервале 0...я. Ма-
Математическое ожидание процесса в этом случае будет равно
+ ф)-б/ф = Sm^ta° ■
-оо О Я 71
Результат вычислений показывает, что математическое ожидание процесса зависит от
времени, следовательно, он не является стационарным.
Эргодические случайные процессы
Дальнейшее упрощение анализа случайных процессов достигается при исполь-
использовании условия эргодичности процесса. Стационарный случайный процесс
называется эргодическим (ergodic), если при определении любых его статисти-
Случайные сигналы 73
ческих характеристик усреднение по множеству (ансамблю) реализаций эквива-
эквивалентно усреднению по времени (time averaging) одной, теоретически бесконечно
длинной, реализации.
Обозначив усреднение по времени угловыми скобками, можно записать следую-
следующие выражения, позволяющие вычислить важнейшие статистические характе-
характеристики эргодического случайного процесса по его единственной реализации
x(t) (еще раз обращаем внимание на то, что эргодический случайный процесс
обязательно является и стационарным, но не наоборот):
* Т/2
= \im± \x(t)dt
1 Г/2
1 -Г/2
Dx = ([x(t)-mxf) = limffx\t)dt-mx
Дх(т) = {[x{t) - mx ][x(t - t) - mx ]) = (x(t)x(t - т)) -ml =
| Г/2
= lim- \x{t)x{t-x)dt-m2x.
1 -T/2
Математическое ожидание эргодического случайного процесса равно постоян-
постоянной составляющей любой его реализации, а дисперсия имеет наглядный физиче-
физический смысл мощности флуктуационной составляющей.
Достаточным условием эргодичности случайного процесса, стационарного в ши-
широком смысле, является стремление к нулю его корреляционной функции с рос-
ростом временного сдвига т:
НтДГт) = 0. A.44)
При экспериментальном исследовании случайных процессов доступно, как пра-
правило, наблюдение одной реализации сигнала, а не всего ансамбля. Если изу-
изучаемый процесс является эргодическим, то его реализация достаточной длины
является «типичным» представителем статистического ансамбля. Согласно при-
приведенным выше формулам по этой единственной реализации можно определить
математическое ожидание, дисперсию и корреляционную функцию эргодическо-
эргодического случайного процесса. На практике интегрирование выполняется, естественно,
не в бесконечных пределах, а на конечном интервале, длина которого должна
быть тем больше, чем выше требования к точности результатов измерения.
В качестве примера проверим эргодичность гармонического процесса со случай-
случайной начальной фазой (стационарность такого процесса была проверена ранее).
Его корреляционная функция A.43) с ростом т не стремится к нулю, так что
условие A.44) не выполняется. Однако это лишь достаточное, но не необхо-
необходимое условие, поэтому его невыполнение еще не означает неэргодичности про-
процесса. Проверим эргодичность согласно определению, вычислив усредненные по
времени параметры:
со ^ш°
271
74 Глава 1. Основы анализа сигналов
со я''Шо
2
со
~t)-тх]) - — \Л2 cos(co0i + (p)cos(co0(£-T)
2Я -я/о.0
л2
= —сов(<а0т) = Яг(т).
ЗАМЕЧАНИЕ
Тот факт, что реализации рассматриваемого процесса являются периодическими функ-
функциями, позволяет упростить вычисления, заменив усреднение по бесконечному (в преде-
пределе) промежутку времени усреднением по одному периоду, равному в данном случае 2п/щ.
Итак, параметры, вычисленные усреднением по времени, совпали с параметра-
параметрами, полученными ранее путем статистического усреднения. Следовательно, гар-
гармонический случайный процесс со случайной начальной фазой является эргоди-
ческим.
ЗАМЕЧАНИЕ
Здесь также следует отметить, что любой случайный процесс, реализации которого яв-
являются периодическими функциями, идентичными по форме и различающимися лишь
равномерно распределенной в пределах периода «начальной фазой», будет не только ста-
стационарным, но и эргодическим.
Спектральные характеристики
случайных процессов
Каждая отдельно взятая реализация случайного процесса представляет собой де-
детерминированную функцию, и к ней можно применить преобразование Фурье.
При этом различные реализации будут, естественно, иметь различные спектры.
Нас же интересуют статистически усредненные характеристики случайных про-
процессов. Попытаемся найти среднее значение спектральной плотности случайно-
случайного процесса (горизонтальной чертой здесь и далее обозначается операция стати-
статистического усреднения по ансамблю реализаций):
5х(со) = \x{t)e4aitdt = \x{t)e-i0*dt = \mx{t)e4°* dt.
-00 -00 -00
Как видите, усредненная спектральная плотность случайного процесса представ-
представляет собой спектр его детерминированной составляющей (математического ожи-
ожидания). Для центрированных процессов mx(t) = 0 и 5j.(co)=0. Таким образом,
усредненное значение спектральной плотности не несет никакой информации о
флуктуационной, то есть собственно случайной, составляющей случайного про-
процесса. Это говорит о том, что фазы спектральных составляющих в различных
реализациях процесса случайны и независимы.
Случайные сигналы 75
Можно, однако, рассмотреть спектральную плотность мощности случайного
процесса, поскольку мощность не зависит от соотношения фаз спектральных со-
составляющих.
Рассмотрим центрированный случайный процесс и выделим из его ансамбля ка-
какую-либо реализацию x(t), ограничив ее длительность конечным интервалом
времени [-Г/2; Т/2]. Применив затем к этой реализации прямое преобразование
Фурье, найдем ее спектральную плотность ХТ(а>). Энергию Ет рассматриваемого
отрезка реализации согласно равенству Парсеваля A.24) можно вычислить как
Т/2 , оо -
Ет = J x\t)dt = — fXr(©) afco.
-т/2 2тг_оо
Разделив эту энергию на Г, получим среднюю мощность РТ реализации на дан-
данном временном интервале:
J
Г
-б/со.
При увеличении длительности промежутка времени Г энергия отрезка реализа-
реализации неограниченно возрастает, а средняя мощность стремится к некоторому пре-
пределу. Совершив предельный переход Г -» оо, получим
*r(a»f л 1
(ХЧО)=~ Jlim
где функция
W(a>) = lim— A.45)
представляет собой спектральную плотность средней мощности рассматривае-
рассматриваемой реализации.
ЗАМЕЧАНИЕ
Часто говорят «спектральная плотность мощности» или «спектр мощности». Английский
термин — power spectral density, PSD.
В общем случае спектральную плотность мощности W(co) необходимо усреднить
по множеству реализаций. Однако, если ограничиться рассмотрением эргодиче-
ских процессов, можно считать, что найденная по одной реализации (то есть пу-
путем усреднения по времени) функция W(co) характеризует весь процесс в целом.
Так как мы рассматриваем центрированный эргодический случайный процесс,
средняя мощность любой его реализации равна дисперсии процесса. Таким об-
образом,
Dx =—\W(a)d(o. A.46)
T6 Глава 1. Основы анализа сигналов
W(a>) — вещественная функция, она не содержит информации о фазах спектраль-
спектральных составляющих и не позволяет восстановить отдельные реализации случай-
случайного процесса. Кроме того, из определения спектральной плотности A.45) оче-
очевидно, что W(a>) является неотрицательной и четной функцией частоты.
ЗАМЕЧАНИЕ
Здесь не приводится примеров расчета спектра случайного процесса согласно приведенно-
приведенному определению, поскольку такого рода расчет редко необходим на практике. Как прави-
правило, вычисление спектра случайного процесса производится на основе его корреляционной
функции с помощью теоремы Винера—Хинчина, речь о которой пойдет в следующем раз-
разделе.
Теорема Винера—Хинчина
Как распределение спектральной плотности мощности, так и вид корреляцион-
корреляционной функции связаны со скоростью изменения случайного процесса во времени.
Найдем связь между этими двумя характеристиками.
Как известно, корреляционная функция детерминированного сигнала связана
преобразованием Фурье с его энергетическим спектром. Применим это свойство
к отрезку реализации случайного процесса длительностью Г:
Г/2 . ос, .
J x(t)x(t-x)dt = — JXr(ffl) ejmd<s>.
-т/2 2л_ж
Разделим обе части этого равенства на Г и устремим Г к бесконечности:
1 т'2 1 ■? |-Хг(о>)| .
limi; J x(t)x(t-x)dt = ± J lim1 ' e*"(fa. A.47)
Если считать рассматриваемый процесс эргодическим, то в левой части послед-
последнего равенства стоит корреляционная функция процесса, полученная путем
усреднения по времени. В правой части под интегралом содержится выражение
A.45) для спектральной плотности мощности случайного процесса. С учетом
этого
Д(т) = — Jw{<o)e*"dv. A.48)
ЗАМЕЧАНИЕ
В случае неэргодического процесса к обеим частям равенства A.47) необходимо дополни-
дополнительно применить усреднение по ансамблю реализаций, что приведет к тому же самому
результату.
Таким образом, корреляционная функция случайного процесса и его спектраль-
спектральная плотность мощности связаны друг с другом преобразованием Фурье. Это со-
соотношение носит название теоремы Винера—Хинчина.
Случайные сигналы 77
Так как и R(x), и W(<o) являются четными вещественными функциями, можно
отказаться от комплексной формы записи преобразования Фурье и перейти к
полубесконечным пределам интегрирования:
Д(-с) = 1 lw@3)cos((x)z)d(u,
"о
СО
W((o) = 2 J #(т) cos (ют) Л.
Очень часто используемая модель случайного процесса оказывается такова, что
воспользоваться непосредственно определением A.45) для расчета спектраль-
спектральной плотности мощности не представляется возможным. Если при этом удается
вычислить корреляционную функцию, получить спектральную информацию по-
позволяет теорема Винера—Хинчина.
В качестве примера рассмотрим случайный телеграфный сигнал (см. раздел
«Модели случайных процессов»). Поскольку скачки уровня происходят в слу-
случайные моменты времени, для данного случайного процесса затруднительно
даже изобразить график отдельной реализации, не говоря уже о расчете спектра
ее ограниченного во времени фрагмента.
Однако рассчитать корреляционную функцию для данного процесса оказывает-
оказывается совсем несложно. Действительно, произведение значений случайного процес-
процесса, разнесенных во времени на т, может быть равно +1 (если эти значения имеют
одинаковый знак) или -1 (если знаки противоположны). Но совпадение знаков
означает, что за интервал х произошло четное количество перепадов уровня,
а несовпадение знаков соответствует нечетному количеству перепадов. Итак, что-
чтобы найти вероятности для двух возможных значений произведения x(t) x(t - т),
нужно просуммировать значения, даваемые формулой A.28) отдельно для чет-
четных и нечетных N:
1 *Го B* + 1)!
~2 ~б ~2~2б
Полученные результаты позволяют рассчитать среднее значение произведения
x(t) x(t - т):
Итак, корреляционная функция данного случайного процесса экспоненциально
затухает с ростом абсолютного значения х. Теперь с помощью теоремы Вине-
Винера—Хинчина можно найти спектральную плотность мощности:
78 Глава 1. Основы анализа сигналов
= J ДДтК^т = f e-2XM e-*
Интервал корреляции
Случайные процессы, встречающиеся в задачах обработки сигналов и изучаемые
в радиотехнике, часто обладают следующим свойством: их функция корреляции
стремится к нулю с увеличением временного сдвига х (напомним, что это явля-
является достаточным условием эргодичности процесса). Чем быстрее убывает функ-
функция /?(т), тем слабее оказывается статистическая связь между мгновенными зна-
значениями случайного сигнала в два несовпадающих момента времени.
Числовой характеристикой, служащей для оценки «скорости изменения» реали-
реализаций случайного процесса, является интервал корреляции тк, определяемый
как
Если известна информация о поведении какой-либо реализации случайного про-
процесса «в прошлом», то возможен вероятностный прогноз случайного процесса на
время порядка хк.
Эффективная ширина спектра
Пусть исследуемый случайный процесс характеризуется спектром плотности
мощности W(co), имеющим максимальное значение Wmax. Заменим мысленно
данный случайный процесс другим, у которого спектральная плотность мощно-
мощности постоянна и равна Wmw в пределах некоторой полосы частот, выбираемой из
условия равенства дисперсий (то есть средних мощностей) обоих процессов.
Ширина этой полосы частот называется эффективной шириной спектра случай-
случайного процесса:
Эффективную ширину спектра случайного процесса можно определить и други-
другими способами, например исходя из условия уменьшения значений спектра мощ-
мощности на границе этого частотного интервала до уровня 0,1 Wmax. В любом случае
величины тк и АсоЭф связаны известным из свойств преобразования Фурье соот-
соотношением неопределенности
хк - 2л.
Для иллюстрации этого соотношения на рис. 1.34 в центре приведены примеры
реализаций двух случайных процессов, слева — корреляционные функции этих
процессов, а справа — их спектры плотности средней мощности.
Случайные сигналы
79
Рис. 1.34. Взаимосвязь между видом реализаций случайных процессов (слева),
их корреляционными функции (в центре) и спектрами (справа)
Белый шум
В радиотехнике белым шумом (white noise) называют стационарный случайный
процесс, спектральная плотность мощности которого постоянна на всех частотах:
W(co) - Wo - const.
Согласно теореме Винера—Хинчина, корреляционная функция белого шума пред-
представляет собой дельта-функцию:
то есть равна нулю всюду, кроме точки т - 0. Дисперсия белого шума бесконечно
велика.
В несовпадающие моменты времени значения белого шума некоррелированы —
как бы ни был мал интервал т, сигнал за это время может измениться на любую
величину.
Белый шум является абстрактной математической моделью и физически суще-
существовать не может. Это объясняется прежде всего бесконечностью его дисперсии
(то есть средней мощности). Однако в тех случаях, когда полоса пропускания
исследуемой системы существенно уже эффективной ширины спектра шума, ко-
который на нее воздействует, можно для упрощения анализа приближенно заме-
заменить реальный случайный процесс белым шумом.
ЗАМЕЧАНИЕ
Отметим еще раз, что вероятностные и корреляционные (или спектральные) характе-
характеристики случайного процесса — это совершенно разные и не связанные между собой
функции. Так, например, нормальный случайный процесс может иметь разнообразную
спектральную плотность мощности, а белый шум — произвольную функцию распределе-
распределения. Единственная «точка соприкосновения» вероятностных и корреляционных харак-
характеристик — это возможность расчета дисперсии случайного процесса как на основе
одномерной плотности вероятности (формула A.33)), так и исходя из корреляционной
функции (формула A.38)).
80 Глава 1. Основы анализа сигналов
Узкополосный случайный процесс
Важную роль в радиотехнике играет особый класс случайных процессов, спектр
которых сосредоточен в относительно узкой полосе вблизи некоторой частоты со0.
Рассмотрим статистические свойства таких процессов.
Итак, пусть x(t) — случайный процесс, спектр плотности мощности которого
W,.(co) имеет узкополосный характер (рис. 1.35). Будем также считать этот слу-
случайный процесс стационарным, нормальным и центрированным.
О а>о со
Рис. 1.35. Спектральная плотность мощности узкополосного случайного процесса
Согласно теореме Винера—Хинчина (см. формулу A.48)), корреляционная функ-
функция и спектральная плотность мощности случайного процесса связаны друг с
другом преобразованием Фурье. Узкополосный характер спектра Wx(a>) говорит
о том, что корреляционная функция Rx(x) имеет вид узкополосного радиосиг-
радиосигнала:
Rx(x) - Д0(т) cos [со0т + сро(т)],
где R0(x) и Фо(т) — медленно (по сравнению с cos (со0т)) меняющиеся функции.
Узкополосный спектр и осциллирующий характер корреляционной функции озна-
означают, что отдельные реализации узкополосного случайного процесса представ-
представляют собой квазигармонические колебания:
x(t) - A(t) cos [co0t + cp(OL
у которых как огибающая A(t), так и начальная фаза ср(£) являются случайными
функциями, медленно (по сравнению с cos (co0£)) изменяющимися во времени.
Для того чтобы определить статистические параметры огибающей и начальной
фазы, рассмотрим комплексный аналитический сигнал Z{t), соответствующий ве-
вещественному случайному процессу x(t) (см. раздел «Комплексная огибающая»
ранее в этой главе):
где xx(t) — сопряженный случайный процесс, реализации которого связаны с
реализациями процесса х(£) преобразованием Гильберта (см. ранее раздел «Пре-
«Преобразование Гильберта»):
]^df. A.49)
В том же разделе было показано, что с помощью сопряженного сигнала можно
определить мгновенные значения огибающей и полной фазы узкополосного сиг-
сигнала:
Случайные сигналы 81
A(t) = \Z(t)\ =
Urctg[x(t)/x(t)] + n, x(t)<0.
Рассмотрим статистические свойства сопряженного процесса. Во-первых, опре-
определим его математическое ожидание, применив усреднение к формуле A.49) и
затем поменяв усреднение и интегрирование местами:
t-? J ni t-f
Результат равен нулю, так как процесс x(t) является центрированным.
Далее, поскольку процесс x(t) нормальный, а преобразование Гильберта являет-
является линейным интегральным преобразованием, то нормальным будет и сопряжен-
сопряженный процесс xx(t).
Из свойств преобразования Гильберта (см. ранее раздел «Преобразование Гиль-
Гильберта», формула A.27)) следует, что спектры конкретных реализаций процессов
x{t) и xx(t) связаны следующим образом:
ю>0,
ю = 0,
ю<0,
откуда видно, что энергетические спектры реализаций процессов х{€) и xx(t) сов-
совпадают, а следовательно, совпадают и спектральные плотности мощности этих
процессов: WXi(a>) = Wx(ai). Корреляционные функции связаны со спектрами
плотности мощности обратным преобразованием Фурье, поэтому они тоже рав-
ны:ДХ1(т) = ДДт).
Нам осталось выяснить, имеется ли статистическая связь между процессами x(t)
и хх(£). Ограничимся при этом расчетом корреляции между ними в совпадающие
моменты времени, то есть вычислим Rxr @)
Далее, как и ранее, внесем операцию статистического усреднения под знак инте-
интеграла, а затем используем замену переменной т = t - ?:
1 яЛ t-f ni t-f ni x
Результат интегрирования равен нулю, так как Дд(т) является четной функцией,
а все подынтегральное выражение, следовательно, — нечетной. Таким образом,
процессы x(t) и xx(t) в совпадающие моменты времени некоррелированы. По-
Поскольку они, кроме того, являются нормальными, то из некоррелированности
следует статистическая независимость.
82
Глава 1. Основы анализа сигналов
Огибающая и полная фаза
узкополосного случайного процесса
Мгновенное значение комплексного случайного процесса Z{t) можно графиче-
графически изобразить в виде вектора на комплексной плоскости (рис. 1.36). Проекции
этого вектора на оси Re и Im равны мгновенным значениям процессов x(t) и
xjjt) соответственно. Эти мгновенные значения статистически независимы и
имеют нормальные распределения с нулевым средним и одинаковыми диспер-
дисперсиями (равенство дисперсий следует из равенства корреляционных функций).
Поэтому совместная плотность вероятности процессов x(t) и xx(t) равна произ-
произведению их одномерных плотностей вероятности, каждая из которых имеет вид
A.35):
1 ( х2 +х2}
x\ —j-i I A.50)
у 2 )
2ах
х@ Re
Рис. 1.36. Комплексный случайный процесс
в виде вектора на комплексной плоскости
Для определения статистических свойств огибающей и фазы необходимо пе-
перейти в выражении A.50) от декартовой (х,хх) к полярной системе коорди-
координат (А, ф) (см. рис. 1.36) и определить совместную плотность вероятности
р,4ф(Л, ф). Связь между этими двумя системами координат выражается следую-
следующими формулами:
х = A cos ф,
xL =
Кроме того, вероятность попадания в бесконечно малую область в окрестности
каждой точки комплексной плоскости при смене системы координат должна,
очевидно, остаться неизменной. Площадь такой бесконечно малой области в
декартовых координатах выражается как dxdxL, а в полярных — как A dA й?ф
(рис. 1.37). Таким образом, получаем
pxx±(.x,x1)dxdxx = pXXi(
Отсюда видно, что искомая плотность вероятности выражается как
А ( А2
exp -—-
\ 2ах
A.51)
Чтобы найти одномерные плотности вероятности для огибающей и фазы, нужно
проинтегрировать двумерную плотность A.51) по «лишним» координатам:
Случайные сигналы
83
Im4
Re
Рис. 1.37. Переход от декартовой системы координат
к полярной
2л
Рл(А) =
Так как двумерная плотность A.51) не зависит от фазы <р, плотность вероятно-
вероятности амплитуды рассчитывается совершенно элементарно:
A.52)
Целесообразно перейти к безразмерной переменной z - А/ах, относительно ко-
которой
p(z) = zexp(-z2/2). A.53)
Плотность вероятности, описывающаяся законом A.52) или A.53), носи? на-
название закона Рэлея (Rayleigh). График этого распределения, соответствующий
формуле A.53), приведен на рис. 1.38. Из графика видно, что наиболее веро-
вероятны некоторые средние (порядка ах) значения огибающей. В то же время ма-
маловероятно, чтобы огибающая принимала значения как близкие к нулю, так и
значительно превосходящие среднеквадратический уровень оЛ. узкополосного
процесса.
0,4
0,2
/
/
^ч '
\
V--
\
\
Рис. 1.38. Плотность вероятности огибающей узкополосного
случайного процесса (закон Рэлея;
84 Глава 1. Основы анализа сигналов
ЗАМЕЧАНИЕ
Для работы с законом распределения Рэлея в статистическом пакете расширения
MATLAB (Statistics Toolbox) имеются следующие функции: raylrnd (генерация случай-
случайных чисел, распределенных по закону Рэлея), raylpdf (расчет плотности вероятности),
raylcdf (расчет функции распределения), raylinv (расчет обратной функции распределе-
распределения) и raylstat (расчет математического ожидания и дисперсии).
Формула A.52) позволяет известным способом (см. раздел «Вероятностные ха-
характеристики случайных процессов») вычислить среднее значение и дисперсию
огибающей:
_*O2 = 2-- oj«0,429o2r.
Чтобы найти плотность вероятности фазы, необходимо проинтегрировать выра-
выражение A.51) по А:
f л2 \ л
A.54)
то есть фаза имеет равномерное распределение на интервале [0, 2п]. Физически
это означает отсутствие какого-либо преимущественного значения полной фазы
у отдельных реализаций узкополосного случайного процесса.
Из A.51), A.52) и A.54) видно, что
следовательно, амплитуда и полная фаза узкополосного случайного процесса
в один и тот же момент времени являются статистически независимыми.
Узкополосный случайный процесс при наличии
детерминированной составляющей
Рассмотрим теперь ситуацию, когда к узкополосному шуму добавлен узкополос-
узкополосный детерминированный сигнал. Комплексный случайный процесс в данном
случае будет иметь следующий вид:
Z(t) = s(t) + js±(t) + x(t) + jx±(t).
Изображение мгновенного значения Z(t) на комплексной плоскости будет отли-
отличаться от рис. 1.36 наличием детерминированного вектора s{t) (рис. 1.39).
Совместная плотность вероятности вещественной и мнимой частей этого комп-
комплексного процесса будет отличаться от A.50) наличием смещений для х и xL,
равных s(t) и sx(t) соответственно:
Случайные сигналы
85
ехр "
(X-S(t)J+(X±-S±(t)J
Z(t)
z@ Re
Рис. 1.39. Комплексный случайный процесс в виде вектора
на комплексной плоскости при наличии
детерминированной составляющей
Переход от декартовой системы координат к полярной, аналогичный рассмот-
рассмотренному ранее (см. A.51) и рис. 1.37), дает следующее:
= Apxi(Acos
А (
Ф) =
2тга
•j-exp
2а
SJax=0
/А
/ sm
/
X ^
/
SJax=5
/ ^
/
N.
0,6
0,4
0,2
0 2 4 6 8 A/ax
Рис. 1.40. Плотность вероятности огибающей узкополосного случайного процесса
при наличии детерминированной составляющей (закон Рэлея—Раиса)
Интегрирование этой двумерной плотности по фазе ф дает одномерную плот-
плотность вероятности для амплитуды данного случайного процесса (промежуточ-
(промежуточные выкладки опущены):
Ра (А) = J Рл<р (А
А ( Л2+5,2
A.55)
где Sm =^js2(t) + s^(t) — амплитудная огибающая детерминированного сигна-
сигнала в данный момент времени, /0 — модифицированная функция Бесселя первого
86 Глава 1. Основы анализа сигналов
рода нулевого порядка. Плотность вероятности A.55) носит название закона
распределения Рэлея—Раиса. На рис. 1.40 показаны графики данной плотности
вероятности, соответствующие разным отношениям сигнал/шум, то есть разным
значениям Sm/<jx. При Sm = 0 из A.55) получается плотность вероятности, соот-
соответствующая закону Рэлея A.53). При Sm/ax » 1, как видно из графиков, рас-
распределение огибающей приближается к нормальному закону.
ЗАМЕЧАНИЕ
Для расчета плотности вероятности закона Рэлея—Раиса с помощью MATLAB придется
непосредственно воспользоваться формулой A.55), поскольку пакет расширения Statis-
Statistics не содержит специальных средств для этого. Функция распределения закона Рэлея—
Раиса выражается через так называемую Q-функцию Маркума. Для ее расчета в пакете
расширения Communications имеется функция marcumq.
ГЛАВА 2 Аналоговые
системы
Данная глава, так же как и предыдущая, посвящена не цифровой, а аналоговой
обработке сигналов. Ее цель — дать читателю представление о характеристиках
и способах описания аналоговых систем. Понимание этих вопросов необходимо
для более глубокого восприятия теории дискретных систем, поскольку многие
методы анализа аналоговых и дискретных систем находятся в тесном родстве.
Кроме того, в основе ряда методов проектирования дискретных фильтров лежит
использование аналоговых прототипов, поэтому квалифицированное примене-
применение этих методов также требует знакомства с теорией аналоговых систем.
Итак, данная глава носит обзорный характер, чем и объясняются сжатое изло-
изложение и отсутствие конкретных примеров анализа прохождения сигналов через
аналоговые системы.
ЗАМЕЧАНИЕ
Положения, приводимые в данной главе, в литературе часто называют теорией линейных
цепей с постоянными параметрами (см., например, [1, 2]). В данной книге используется
термин «система», чтобы подчеркнуть высокоуровневый характер рассмотрения — систе-
система описывается только своими числовыми и функциональными характеристиками, без
привлечения конкретных принципиальных схем.
Классификация систем
Системы, используемые для преобразования сигналов, имеют самые разнообраз-
разнообразные физические характеристики и могут классифицироваться по различным при-
признакам.
Важнейшим классификационным признаком является линейность или нели-
нелинейность системы. Линейными называются системы, для которых выполняется
принцип суперпозиции: реакция на сумму сигналов равна сумме реакций на эти
сигналы, поданные на вход по отдельности. Системы, для которых принцип су-
суперпозиции не выполняется, называются нелинейными.
88 Глава 2. Аналоговые системы
Следующим критерием классификации систем является постоянство или непо-
непостоянство их характеристик во времени. Если произвольная задержка подавае-
подаваемого на вход сигнала приводит лишь к такой же задержке выходного сигнала, не
меняя его формы, система называется стационарной, или системой с постоянны-
постоянными параметрами. В противном случае система называется нестационарной, па-
параметрической или системой с переменными параметрами.
Два указанных способа классификации делят системы на четыре класса. В дан-
данной книге речь пойдет только о линейных стационарных системах.
Характеристики линейных систем
Для рассматриваемых в этой главе линейных систем с постоянными параметра-
параметрами справедливы принципы суперпозиции и стационарности. Это сильно упро-
упрощает анализ прохождения сигналов через такие системы, позволяя использовать
для этого различные характеристики, речь о которых пойдет в данном разделе.
Импульсная характеристика
Линейность и стационарность позволяют легко найти реакцию системы на лю-
любой входной сигнал, зная всего одну функцию — реакцию системы на поданную
на вход дельта-функцию. Эта реакция называется импульсной характеристикой
системы и обозначается h(t).
Любой сигнал может быть представлен в виде свертки самого себя с дельта-
функцией (см. фильтрующее свойство дельта-функции A.1) в разделе «Класси-
«Классификация сигналов» главы 1):
Линейная система преобразует относительно переменной t все функции, входя-
входящие в это выражение. Входной сигнал sBX(t) при этом превращается в выходной
сигнал sDbIX(£), а дельта-функция 8(£ -1') — в импульсную характеристику h{t-t').
Функция sm(t') от t не зависит и поэтому остается без изменений. В результате
получается формула, показывающая, что выходной сигнал линейной системы с
постоянными параметрами равен свертке выходного сигнала и импульсной ха-
характеристики системы:
]f)df. B.1)
ЗАМЕЧАНИЕ
Если входной и выходной сигналы системы имеют одинаковую размерность, то импульс-
импульсная характеристика, как и дельта-функция времени, имеет размерность частоты.
Формирование выходного сигнала можно пояснить следующим образом. Беско-
Бесконечно малый «кусочек» входного сигнала sm(?) шириной dt' порождает на выхо-
Характеристики линейных систем
89
де отклик, представляющий собой импульсную характеристику, умноженную на
sBX{t')dt' и задержанную по времени на V, то есть sex(t')h(t-t')dt' (рис. 2.1).
Чтобы получить значение выходного сигнала в момент времени t, нужно сло-
сложить вклады от всех этих бесконечно малых «кусочков», то есть выполнить ин-
интегрирование по V, что и дает приведенную выше формулу свертки B.1)
Рис. 2.1. Формирование выходной реакции цепи
Переходная характеристика
Переходной характеристикой называют реакцию системы на поданную на вход
функцию единичного скачка. Обозначается переходная характеристика как g(t).
Поскольку дельта-функция — это производная от единичного скачка, импульс-
импульсная и переходная характеристики связаны друг с другом операциями дифферен-
дифференцирования и интегрирования:
g(t)=\h(t')dt'.
Условие физической реализуемости
Любая физически реализуемая система обладает свойством причинности — вы-
выходная реакция не может возникнуть раньше входного сигала. Отсюда следует,
что для физически реализуемой системы импульсная и переходная характери-
характеристики должны быть равны нулю при t < 0.
ЗАМЕЧАНИЕ
Под физической реализуемостью здесь понимается только выполнение свойства причин-
причинности, а не возможность создать систему в каком-нибудь конкретном виде. Дополнитель-
Дополнительные требования, которым должны удовлетворять характеристики систем, реализуемых в
виде цепей с сосредоточенными параметрами, будут рассмотрены в этой главе далее, в раз-
разделе «Способы описания линейных систем».
Комплексный коэффициент передачи
Выходной сигнал линейной системы, как было показано выше, представляет со-
собой свертку входного сигнала и импульсной характеристики. Преобразование
Фурье от свертки дает произведение спектров сворачиваемых сигналов, так что
90 Глава 2. Аналоговые системы
в частотной области прохождение сигнала через линейную систему описывается
очень просто:
Здесь К(и>) — преобразование Фурье импульсной характеристики системы:
= ]h{t)e'M dt.
Эта функция называется комплексным коэффициентом передачи системы, а ее
модуль и фаза — соответственно амплитудно-частотной (АЧХ) и фазочастотной
(ФЧХ) характеристиками системы.
Значение К(со) показывает, как изменяется при прохождении через систему комп-
комплексная амплитуда синусоиды с частотой со. АЧХ показывает, во сколько раз
изменится амплитуда синусоиды, а ФЧХ — каков будет полученный ею фазо-
фазовый сдвиг.
Коэффициент передачи по мощности
Мощность гармонического сигнала пропорциональна квадрату его амплитуды
и не зависит от его фазы. Поэтому коэффициент передачи по мощности равен
квадрату модуля комплексного коэффициента передачи, то есть квадрату АЧХ:
Фазовая и групповая задержка
При преобразовании сигнала линейной системой различают два вида задержки.
Фазовая задержка (phase delay) на частоте со — это задержка гармонического ко-
колебания с частотой со, проходящего через систему. Значение фазовой задержки
равно фазовому сдвигу, вносимому системой, деленному на частоту гармониче-
гармонического колебания, с обратным знаком:
Тф(СО) = -фК(С0)/С0.
Групповая задержка (group delay) на частоте со — это задержка огибающей узко-
полосного сигнала со средней частотой со. Групповая задержка равна производ-
производной от ФЧХ системы с обратным знаком:
тГр = -dq>K(a>)/da>. B.2)
Пример, поясняющий разницу между фазовой и групповой задержкой, будет при-
приведен применительно к дискретным системам (см. далее раздел «Расчет группо-
групповой задержки дискретной системы» главы 4).
Взаимный спектр выходного
и входного сигналов
Взаимный спек'р выходного и входного сигналов линейной системы легко най-
найти, исходя из определения взаимного спектра A.22) (см. раздел «Связь между
корреляционными функциями и спектрами сигналов» главы 1):
Преобразование случайного процесса в линейной системе 91
., . . . 2 .
вых вхС00) =''выхС'О/^вхС03) = ^вхСсО/^С^/^вхСС0) = ''вхС03) Л (СО). (^-3)
Отсюда следует, что комплексный коэффициент передачи системы равен отно-
отношению взаимного спектра выходного и входного сигналов к энергетическому
спектру входного сигнала:
ЗАМЕЧАНИЕ :
Аналогичная формула, связывающая коэффициент передачи со спектрами случайных сиг-
сигналов, имеет большое значение для идентификации систем, то есть оценки комплексного
коэффициента передачи по результатам совместного наблюдения входного и выходного
сигналов.
Взаимная корреляция между входом и выходом
Применив обратное преобразование Фурье к формуле B.3), получим выражение
для ВКФ выходного и входного сигналов (используем при этом формулу A.23)
из раздела «Связь между корреляционными функциями и спектрами сигналов»
главы 1):
Итак, ВКФ выходного и входного сигналов линейной системы представляет со-
собой свертку КФ входного сигнала с импульсной характеристикой системы.
Преобразование случайного
процесса в линейной системе
Как говорилось в главе 1, случайный процесс представляет собой ансамбль реа-
реализаций. Каждая отдельная реализация является детерминированным сигналом,
и ее преобразование линейной системой анализируется с помощью формул, при-
приведенных в этой главе ранее. В данном же разделе будет рассмотрено именно
преобразование статистических характеристик случайного процесса. При этом
подразумевается стационарный случайный процесс с нулевым математическим
ожиданием.
Спектральная плотность мощности
Поскольку спектром случайного процесса считается спектр его мощности^ он
преобразуется в линейной системе пропорционально коэффициенту передачи по
мощности:
Wm (со) = WttX (со)*мощ(со) = Wm (со) ВД 2. B.4)
92 Глава 2. Аналоговые системы
Корреляционная функция
Согласно теореме Винера—Хинчина, корреляционная функция случайного про-
процесса связана с его спектром преобразованием Фурье (см. раздел «Теорема Ви-
Винера—Хинчина» главы 1). Применение преобразования Фурье к формуле B.4)
дает свертку:
„(т')ВА(т-с')Л'. B.5)
Здесь Bh(x) — результат обратного преобразования Фурье от коэффициента пе-
передачи по мощности | К((я)\2. Согласно разделу «Связь между корреляционными
функциями и спектрами сигналов» главы 1, это преобразование дает корреляци-
корреляционную функцию импульсной характеристики системы:
Bh(x)=}h(t)h(t-x)dt.
Дисперсия
Дисперсия случайного процесса равна значению его корреляционной функции
при т = 0. Подстановка этой величины в формулу B.5) для выходной корреляци-
корреляционной функции дает
А™ = *выХ@) = |Явх(ОЯ„(т')Л'- B.6)
Можно рассчитать дисперсию и в частотной области (см. формулу A.46) в раз-
разделе «Спектральные характеристики случайных процессов» главы 1). Восполь-
Воспользовавшись приведенной выше формулой B.4) для выходного спектра, получаем:
d^ B.7)
Плотность вероятности
В общем случае плотность вероятности случайного процесса на выходе линей-
линейной системы не поддается расчету простыми средствами. Исключение состав-
составляет частный случай нормального случайного процесса, поскольку нормальное
распределение остается нормальным при любых линейных преобразованиях.
Поэтому нормальный случайный процесс с нулевым средним значением после
прохождения через линейную систему сохранит свою нормальность и нулевое
математическое ожидание, а его дисперсия может быть рассчитана по одной из
формул B.6), B.7) предыдущего раздела.
Частный случай белого шума
Если входной случайный процесс является белым шумом (см. раздел «Теорема
Винера—Хинчина» главы 1), все приведенные ранее формулы существенно упро-
упрощаются:
Способы описания линейных систем
93
оо ггг оо «
= W0Bh@) = Wo Jh\t)dt = -S- J |*T(co)| dco
£tt\i
Способы описания линейных систем
В данном разделе рассматриваются различные эквивалентные способы пред-
представления характеристик линейных систем, реализуемых в виде цепей с сосредо-
сосредоточенными параметрами. Понимание сущности этих вариантов представления и
способов перехода от одного представления к другому важно для правильного
использования соответствующих функций MATLAB.
Дифференциальное уравнение
Связь между входным и выходным сигналами линейной цепи с сосредоточенны-
сосредоточенными параметрами может быть выражена в виде дифференциального уравнения
(ДУ) вида
dny d"-ly d"-2i
+ а . — + а „ —-Г...-ГЫ.
dt
а„
dt"
а„ .
п 2
dy
а, — + aoy(t) =
dt
dmx
dtm
dt
m'2
, dx , _
b, — + bnx(t).
' dt °
B.8)
Здесь x(t) — входной сигнал, y(t) — выходной сигнал, а, и bt — постоянные
коэффициенты. Таким образом, цепь описывается наборами коэффициентов {а,)
и {*,-}.
Должно выполняться неравенство т < п, то есть максимальный порядок про-
производной входного сигнала не может превышать максимального порядка произ-
производной выходного сигнала. Это связано с невозможностью реализации операции
«чистого» дифференцирования аналоговой цепью. Значение п называется по-
порядком цепи.
Если задать конкретный вид входного сигнала x(t), получится линейное неодно-
неоднородное дифференциальное уравнение с постоянными коэффициентами. Решение
этого ДУ дает выходной сигнал y(t).
Функция передачи
Если применить к обеим частям приведенного в предыдущем разделе ДУ B.8)
преобразование Лапласа, получится выражение для операторного коэффициен-
коэффициента передачи, или функции передачи цепи (transfer function):
94 Глава 2. Аналоговые системы
Щс)_Ьа5а +bm_lsm-i+bm,2sm-2+...+ bls + b0 _ B9)
ans" +an.1s"~1 +an.2s" +...+ 0^ + 0^
Здесь а,- и bt — те же постоянные коэффициенты, что и в приведенном ранее ДУ.
ЗАМЕЧАНИЕ
Преобразование Лапласа [1-3] можно рассматривать как обобщение преобразования Фу-
Фурье, при котором частота может принимать комплексные значения. Рассчитывается пря-
прямое преобразование Лапласа как F(s) = 1.а/(()е~лси (сравните эту формулу с формулой
прямого преобразования Фурье A.11)). В этой главе для нас важно только то, что преоб-
преобразование Лапласа является линейным и при дифференцировании сигнала во времени его
преобразование Лапласа умножается на комплексную частоту s.
Комплексный коэффициент передачи получается из функции передачи B.9) пу-
путем подстановки s = jco:
ад =
а„0'со)" -ha^O'co)" +an.2(jco)
)"
Нули и полюсы
Разложив числитель и знаменатель функции передачи B.9) на множители, мы
получим функцию передачи в следующем виде:
(s-pn )(s -р„_,)E ~рп_2 )...(s~Pi)'
Здесь k - bm/an — коэффициент усиления (gain), г,- — нули функции передачи
(zero), pi — полюсы функции передачи (pole). В точках нулей Я(г,) - 0, а в точках
полюсов H(pi) -4 00.
В данном случае цепь описывается набором параметров {r,}, {pt}, k.
Нули функции передачи могут быть вещественными либо составлять комплекс-
комплексно-сопряженные пары. То же относится и к полюсам. Коэффициент усиления
всегда вещественный.
Полюсы и вычеты
Еще одним способом преобразования дробно-рациональной функции передачи
B.9) является ее представление в виде суммы простых дробей. При отсутствии
кратных корней у знаменателя такое представление имеет следующий вид:
H(s) = —^— + Г"-' + Г"'2 +... + —^— + С0. B.10)
*-Р„ s-Pn-i s-Pn-2 s~Pi
Здесь pi — полюсы функции передачи, а числа г; называются вычетами. Со — це-
целая часть функции передачи, отличная от нуля только в случае равенства степе-
степеней полиномов числителя и знаменателя.
В данном случае цепь описывается набором параметров {г,}, {р,}, Со.
Способы описания линейных систем 95
Полюсы функции передачи могут быть вещественными либо составлять комп-
комплексно-сопряженные пары. Вычеты, соответствующие комплексно-сопряжен-
комплексно-сопряженным полюсам, также являются комплексно-сопряженными.
При наличии кратных полюсов функции передачи разложение на простые дроби
становится сложнее. Каждый от-кратный полюс pt дает т слагаемых следующего
вида:
■+...+ —— . B.11)
s-Pi (s-PiY (s-PiY
Расчет импульсной характеристики
Представление функции передачи в виде суммы простых дробей позволяет вы-
вычислить импульсную характеристику системы, поскольку каждое слагаемое
функции передачи вида rj(s - pt) соответствует слагаемому импульсной харак-
характеристики вида
r,ent,t7>0.
Пара комплексно-сопряженных полюсов дает пару слагаемых импульсной ха-
характеристики в виде комплексно-сопряженных экспонент. Сумма таких слагае-
слагаемых представляет собой синусоиду с экспоненциально меняющейся амплитудой:
г, ехр(р,О + г; ехр(р'О = 2Re[r, exp(ptt)] =
= 2Re[| rj exp(;arg(r, ))exp(Re(pi)t)exp(jlm(pi )t)] =
= 2|rjexp (Re (p,) t) cos (Im(jo;) t + arg(r,)).
Здесь arg(r,) — фаза комплексного числа г,.
Что касается кратных полюсов, то от-кратный полюс р\ даст в выражении для им-
импульсной характеристики т слагаемых следующего вида:
г„е"' +r,2te"" +г,3 уер" +...+ rta j
Устойчивость линейных систем
Система называется устойчивой, если при нулевом входном сигнале выходной
сигнал затухает при любых начальных условиях:
Это требование равносильно требованию затухания импульсной характеристики:
ШпА(£)=0.
£->оо
В предыдущем разделе было показано, что импульсная характеристика системы
в общем случае содержит слагаемые вида
г —ePit
где pt — полюсы функции передачи системы, г,- — соответствующие им вычеты,
к — целые числа в диапазоне от нуля до значения, на единицу меньшего кратно-
кратности полюса Pj.
96
Глава 2. Аналоговые системы
Такие слагаемые при t —» со затухают, если вещественная часть полюса pt являет-
является отрицательной:
Re(p,-)<0.
Отсюда получаем общее условие: линейная система является устойчивой тогда
и только тогда, когда полюсы ее функции передачи лежат в левой комплексной по-
полуплоскости.
Пространство состояний
Еще одним способом описания линейной цепи является ее представление в про-
пространстве состояний (state space). При этом состояние цепи описывается векто-
вектором состояния s(t), а собственные колебания цепи и ее реакция на входной сиг-
сигнал x(t) характеризуются следующим образом:
B.12)
Если размерность вектора состояния s(t) равна N (s(t) — вектор-столбец), а вход-
входной x{t) и выходной y{t) сигналы являются скалярными, то размерность пара-
параметров в этих формулах будет следующей: А — матрица N х N,3 — столбец N х 1,
С — строка 1 х N, D — скаляр. Если входной и/или выходной сигналы являются
векторными, размерность параметров соответствующим образом изменяется.
Описанием цепи в данном случае является набор параметров А, В, С, D.
От представления цепи в пространстве состояний можно легко перейти к функ-
функции передачи цепи. Если применить преобразование Лапласа к уравнениям
состояния B.12), а затем выразить из них операторный коэффициент передачи,
получится следующее:
Я(«) = D - С(А - sI^B. B.13)
Здесь I — единичная матрица N х N.
Обратное преобразование выполняется следующим образом. Прежде всего, если
степени числителя и знаменателя функции передачи совпадают, из дроби выде-
выделяется целая часть, которая становится значением параметра D (если степень
числителя меньше степени знаменателя, то D = 0).
Далее оставшаяся после выделения целой части дробь, степень числителя кото-
которой (т) гарантированно меньше степени знаменателя (и), преобразуется в пара-
параметры А, В и С следующим образом:
А =
С =
—а
„_Jan -a
1
0
0
... 0 Ьп
п-2/ап ■
0
1
0
.. -ajan
0
0
1
• ь{ ьл
-ао/а
0
0
0
в =
B.14)
Функции MATLAB для расчета линейных цепей 97
Функции MATLAB для расчета
линейных цепей
MATLAB и его пакеты расширения ориентированы прежде всего на цифровую
обработку сигналов, поэтому функции, связанные с расчетом аналоговых цепей,
рассматриваются как вспомогательные. В основном они предназначены для вы-
вызова из других функций, использующих аналоговые прототипы при синтезе циф-
цифровых фильтров. Однако и сами по себе эти функции могут быть весьма полезны.
Большая часть рассматриваемых в данном разделе функций относится к пакету
Signal Processing.
Расчет частотных характеристик
Как уже говорилось, для расчета комплексного коэффициента передачи необхо-
необходимо подставить в функцию передачи мнимый аргумент: s = /со. Соответствую-
Соответствующие расчеты выполняются с помощью функции freqs. В простейшем виде она
имеет следующий синтаксис:
freqs(b. a);
Здесь b и а — векторы коэффициентов полиномов, соответственно числителя и
знаменателя функции передачи. Коэффициенты следуют в порядке убывания
степеней, заканчивая постоянным слагаемым.
Для расчета характеристики по умолчанию выбирается 200 частот, логарифми-
логарифмически равномерно распределенных в диапазоне от 0,1 до 10.
При отсутствии выходных параметров функция freqs строит графики АЧХ и
ФЧХ. АЧХ выводится в логарифмическом масштабе (но без пересчета в деци-
децибелы), ФЧХ — в градусах.
Пусть анализируемая цепь имеет функцию передачи
s* -3s3 + As2 -2s + f ■
Строим ее АЧХ и ФЧХ (рис. 2.2):
» b = [1 3 3 1];
» а = [1 -3 4 -2 1];
» freqs(b. a)
Чтобы вместо построения графика получить вектор рассчитанных значений
комплексного коэффициента передачи, нужно присвоить результат, возвращае-
возвращаемый функцией freqs, какой-либо переменной:
h = freqs(b. a):
При этом не стоит забывать про точку с запятой в конце строки, которая позво-
позволит подавить вывод рассчитанного вектора на экран.
Если использовать второй выходной параметр, то в нем функция возвратит век-
вектор частот, для которых рассчитаны значения импульсной характеристики:
[h. w] = freqs(b. a);
98
Глава 2. Аналоговые системы
200
100
О
-100
-200
10"
Frequency (rad/s)
10"
Frequency (rad/s)
101
.
t
/^
ii!
101
Рис. 2.2. Частотные характеристики, построенные функцией freqs
Рассчитаем вектор значений частотной характеристики цепи из нашего приме-
примера и построим график ее АЧХ в линейном, а не логарифмическом масштабе
(рис. 2.3):
» [h. w] = freqsCb. a):
» plot(w, abs(h))
» grid on
2.5
2
1.5
1
0.5
Л
\
—
2 4 6 6
Рис. 2.З. АЧХ цепи в линейном масштабе
10
Можно принудительно задать количество частотных точек для анализа, исполь-
используя третий входной параметр п (при этом частоты по-прежнему логарифмически
распределены от ОД до 10):
[h. w] = freqsCb. a. n):
Функции MATLAB для расчета линейных цепей 99
Наконец, можно принудительно задать частоты для анализа — также с помощью
третьего входного параметра, которым в данном случае является вектор круго-
круговых частот w. Признаком, отличающим данную ситуацию от предыдущей, явля-
является векторный характер третьего выходного параметра. Возвращать значения
частот в данном случае не имеет смысла:
h - freqs(b, a, w);
ЗАМЕЧАНИЕ
Для дискретных линейных систем, функция передачи которых задана в виде отношения
полиномов в z-области, аналогичные расчеты и построения выполняются функцией freqz
(см. главу 4).
Построение графиков фазочастотных
характеристик
Как видно из рис. 2.2, ФЧХ цепи содержит большое количество разрывов (скач-
(скачков). Те из них, величины которых равны 180°, действительно являются скач-
скачками ФЧХ, а остальные, величина которых составляет 360°, являются «фиктив-
«фиктивными». Они возникают только из-за того, что результаты вычисления фазы
комплексного числа всегда лежат в диапазоне +180°. Наличие этих многочислен-
многочисленных скачков затрудняет восприятие истинной формы ФЧХ и маскирует скачки
«настоящие».
Избавиться от лишних разрывов позволяет функция unwrap, которая ищет в пе-
переданном ей векторе скачки между соседними элементами, превышающие задан-
заданную пороговую величину (по умолчанию равную я), и сдвигает соответствую-
соответствующие фрагменты вектора на +2л нужное число раз.
Продемонстрируем действие функции unwrap, построив график ФЧХ для цепи
из примера предыдущего раздела (рис. 2.4):
» [h. w] = freqs(b. a);
» % ФЧХ
» phi = angie(h);
» % устранение скачков
» phi = unwrap(phi):
» % отображаем в градусах
» plot(w. phi*180/pi)
» grid on •
Сравнение графиков ФЧХ на рис. 2.2 и 2.4 наглядно демонстрирует сущность
функции unwrap.
При необходимости можно задать порог обнаружения скачков, указав его в каче-
качестве второго аргумента функции unwrap:
у = unwrapU, threshold);
100
Глава 2. Аналоговые системы
/
/
I
■ ■" /
/
/
/
,—■ —
600
500
400
300
200
100
0 2 4 6 8 10
Рис. 2.4. ФЧХ цепи с устраненными скачками на 360°
Преобразование способов описания
линейных цепей
В теоретической части данной главы было рассмотрено несколько эквивалент-
эквивалентных способов описания линейных цепей. В пакете Signal Processing имеется ряд
функций, предназначенных для преобразования описаний из одной формы в
другую. Имена этих функций имеют вид хх2уу, где хх — обозначение исходной
формы описания, а уу — обозначение целевой формы описания цепи.
ЗАМЕЧАНИЕ
По-английски цифра «2» (two) произносится сходно с частицей «to», служащей, среди
прочего, для указания на конечную цель или результат какого-либо процесса. Поэтому
цифра «2» традиционно используется в середине идентификаторов функций, осуществ-
осуществляющих различные преобразования.
Формы описания цепей в именах функций обозначаются следующим образом:
□ tf — коэффициенты полиномов числителя и знаменателя функции передачи
(transfer function);
О zp — нули и полюсы (zeros and poles);
О ss — описание в пространстве состояний (state-space).
Необходимость в преобразовании описаний часто возникает из-за того, что функ-
функции расчета цепей (такие как рассматриваемые далее функции расчета фильт-
фильтров-прототипов) дают результат в одной форме, а функция, например, построения
частотной характеристики требует задания входных параметров в другой форме.
Далее кратко рассматриваются конкретные функции преобразования описаний це-
цепей. Для входных и выходных параметров используются следующие обозначения:
О функция передачи:
Ob — вектор-строка коэффициентов (в порядке убывания степеней) числи-
числителя функции передачи;
Функции MATLAB для расчета линейных цепей 101
О а — вектор-строка коэффициентов (в порядке убывания степеней) знаме-
знаменателя функции передачи;
□ нули и полюсы:
О z — вектор нулей (столбец);
О р — вектор полюсов (столбец);
О к — коэффициент усиления (скаляр);
□ пространство состояний:
О А — квадратная матрица связи вектора состояния и его производной;
О В —вектор-столбец связи входного сигнала и производной вектора состояния;
О С — вектор-строка связи выходного сигнала и вектора состояния;
О D — скалярный коэффициент связи выходного и входного сигналов.
ЗАМЕЧАНИЕ
Размерности параметром указаны для случая цепи с одним входом и одним выходом.
Функции преобразования могут обрабатывать описания ценен с несколькими выходными
сигналами (с векторным выходом). В этом случае размерности параметров соответствую-
соответствующим образом изменяются.
Функция tf2zp
Функция tf2zp преобразует наборы коэффициентов полиномов числителя и зна-
знаменателя функции передачи в векторы нулей и полюсов, рассчитывая также зна-
значение общего коэффициента усиления:
[z, p. k] = tf2zp(b. a):
Преобразование производится путем вычисления корней полиномов числителя
и знаменателя функции передачи с помощью функции roots. Коэффициент уси-
усиления к рассчитывается как отношение ЬA)/аA).
Функция zp2tf
Функция zp2tf является обратной но отношению к функции tf2zp: она осущест-
осуществляет преобразование коэффициента усиления, а также векторов нулей и полю-
полюсов функции передачи в коэффициенты полиномов ее числителя и знаменателя:
[b. a] = zp2tf(z. p. к):
Преобразование производится с помощью функции poly, предназначенной для
вычисления коэффициентов полинома по заданным его корням. В завершение
вектор коэффициентов числителя умножается на к.
Функция tf2ss
Функция tf2ss преобразует наборы коэффициентов полиномов числителя и зна-
знаменателя функции передачи в параметры представления цепи в пространстве со-
состояний:
[А. В. С. D] = tf2ss(b. a);
Преобразование производится согласно формулам B.14), приведенным в этой
главе ранее, в разделе «Пространство состояний».
102 Глава 2. Аналоговые системы
Функция ss2tf
Функция ss2tf является обратной по отношению к функции tf2ss: она преобра-
преобразует параметры пространства состояний в коэффициенты полиномов функции
передачи цепи:
[b, a] = ss2tf(A. В. С, D);
Преобразование производится согласно формуле B.13), приведенной в этой гла-
главе ранее, в разделе «Пространство состояний».
Функция zp2ss
Функция zp2ss преобразует нули, полюсы и коэффициент усиления цепи в ее
параметры пространства состояний:
[А. В, С. D] = zp2ss(z. p. к);
Преобразование производится путем последовательного вызова функций zp2tf и
tf2ss.
Функция ss2zp
Функция ss2zp является обратной по отношению к функции zp2ss, преобразуя
параметры пространства состояний в нули, полюсы и коэффициент усиления
цепи:
[z. p, k] = ss2zp(A. В. С. D);
Полюсы системы являются собственными числами матрицы А и вычисляются с
помощью функции eig. Нули являются конечными решениями обобщенной за-
задачи нахождения собственных чисел и рассчитываются следующим образом:
z = eigCCA B;C D]. diag([ones(l.n) 0]));
Функция residue
Идентификатор последней функции, позволяющей преобразовывать описания
линейных цепей, выпадает из общего ряда. Это связано с тем, что данное преоб-
преобразование не является специфическим для обработки сигналов — оно сводится к
разложению дробно-рациональной функции на простейшие дроби и часто при-
применяется в математике. По этой же причине данная функция относится не к па-
пакету Signal Processing, а к базовой библиотеке MATLAB.
Преобразование функции передачи, заданной в виде коэффициентов полиномов
числителя и знаменателя, в сумму простых дробей производится с помощью функ-
функции residue. Она же осуществляет и обратное преобразование; нужное направле-
направление преобразования выбирается в зависимости от числа входных параметров.
При двух входных параметрах производится разложение функции передачи на
простые дроби:
[г, р, к] «= residue(b, a)
Здесь b и а — коэффициенты полиномов числителя и знаменателя функции пе-
передачи соответственно. Выходные параметры — векторы-столбцу полюсов (р) и
соответствующих им вычетов (г), а также строка коэффициентов целой части к.
Функции MATLAB для расчета линейных цепей
103
Разложение производится согласно формулам B.10) и B.11), приведенным ра-
ранее в разделе «Полюсы и вычеты», включая случай наличия кратных полюсов.
При использовании трех входных параметров функция residue производит пре-
преобразование вычетов, полюсов и коэффициентов целой части в коэффициенты
числителя и знаменателя функции передачи, то есть осуществляет суммирова-
суммирование простых дробей:
[b, a] = residue(r, p, к)
В качестве примера разложим на простые дроби функцию передачи вида
ж <\ -
п \ь) 4
» Ь = [1
» а = [1
» [г. р,
г =
2.0000
2.0000
-4.0000
5.0000
Р =
-1.0000
-1.0000
-1.0000
-1.0000
52 -25 + 2
+ 453 +752 +65 + 2
-2 2];
4 7 6 2];
к] - residue(b, a)
+ 2.0000i
- 2.00001
+ 1.00001
- 1.00001
к
Результаты преобразования показывают, что данная система имеет двукратный
полюс, равный -1, и пару комплексно-сопряженных полюсов, равных -1 ±j. По-
Поскольку степень полинома числителя меньше, чем степень полинома знаменате-
знаменателя, целая часть их отношения равна нулю, и в параметре к функция возвращает
пустую матрицу. Рассчитанные значения вычетов позволяют записать представ-
представление функции передачи в виде суммы простых дробей (с учетом наличия крат-
кратного полюса):
;2 ^ 2-;2 4 ^ 5
#(«) = ■ ■ ■
5 + 1-j 5 + 1 + j 5 + 1 E + 1)
Произведем с помощью функции residue обратное преобразование вычетов и по-
полюсов в коэффициенты полиномов числителя и знаменателя функции передачи:
[Ы, al] = residue(r, p, k)
Ы =
-0.0000 1.0000 -2.0000 2.0000
al =
1.0000 4.0000 7.0000 б.0000 2.0000
Полученные значения совпадают с исходными. Знак «минус» при нулевом зна-
значении bid) обусловлен вычислительными погрешностями — после обратного
1 04 Глава 2. Аналоговые системы
преобразования получается не ровно нуль, а малое отрицательное число (при-
(примерно -4-105).
ВНИМАНИЕ
Вычислительная задача разложения дробно-рациональной функции на простые дроби
плохо обусловлена. Это означает, что если функция передачи имеет полюсы, близкие к
кратным, то малые вариации исходных данных могут приводить к большим погрешно-
погрешностям вычисления полюсов и вычетов. В таких случаях документация MATLAB рекомен-
рекомендует использовать описание системы в виде нулей и полюсов либо в пространстве
состояний.
Расчет аналоговых фильтров-прототипов
Одной из часто возникающих на практике задач является создание фильтров,
пропускающих сигналы в определенной полосе частот и задерживающих осталь-
остальные частоты. При этом различают:
□ фильтры нижних частот (ФНЧ; английский термин — low-pass filter), про-
пропускающие частоты, меньшие некоторой частоты среза соо;
□ фильтры верхних частот (ФВЧ; английский термин — high-pass filter), про-
пропускающие частоты, большие некоторой частоты среза юо;
□ полосовые фильтры (ПФ; английский термин — band-pass filter), пропускаю-
пропускающие частоты в некотором диапазоне coi... 002 (они могут также характеризо-
характеризоваться средней частотой ©о = (ffl| + юг)/2 и шириной полосы пропускания
До = а?. - coi);
□ режекторные фильтры (другие возможные названия — заграждающий фильтр,
фильтр-пробка, полосно-задерживающий фильтр; английский термин — band-
stop filter), пропускающие на выход все частоты, кроме лежащих в некотором
диапазоне coi... св2 (они тоже могут характеризоваться средней частотой юо =
- (оо| + ю2)/2 и шириной полосы задерживания Аса - оог - ©|).
Идеальная форма АЧХ фильтров этих четырех типов показана на рис. 2.5.
Однако такая идеальная (прямоугольная) форма АЧХ не может быть физически
реализована. Поэтому в теории аналоговых фильтров разработан ряд методов
аппроксимации прямоугольных АЧХ. Функции, реализующие эти методы, будут
рассмотрены ниже.
Кроме того, рассчитав ФНЧ, можно несложными преобразованиями изменить
его частоту среза, превратить его в ФВЧ, полосовой либо режекторный фильтр с
заданными параметрами. Поэтому расчет аналогового фильтра начинается с рас-
расчета так называемого фильтра-прототипа, представляющего собой ФНЧ с час-
частотой среза, равной 1 рад/с. Далее применяются функции преобразования часто-
частоты среза и преобразования типов фильтров, которые также будут рассмотрены
ниже.
Все функции MATLAB для расчета аналоговых прототипов возвращают векто-
векторы-столбцы нулей и полюсов функции передачи, а также значение коэффициен-
коэффициента усиления.
Функции MATLAB для расчета линейных цепей
105
ЩУ
со0
со0
ФНЧ
ФВЧ
Щ)
ЩУ
С02
СО-) С02 СО U »1
Полосовой фильтр Режекторный фильтр
Рис. 2.5. АЧХ фильтров различного типа
ВНИМАНИЕ
При сравнении результатов использования фильтров различного типа в какой-либо сис-
системе обработки сигналов следует помнить о том, что частота среза для разных фильтров
определяется по-разному. Подробная информация об этом приводится в следующих раз-
разделах, посвященных конкретным фильтрам. Немного забегая вперед, скажем, что для
фильтра Баттерворта частота среза определяется по уровню l/>/2, для фильтра Чебышсва
первого рода и эллиптического фильтра — по уровню пульсаций в полосе пропускания,
для фильтра Чебышева второго рода — по уровню пульсаций в полосе задерживания. На-
Наконец, для фильтра Бесселя само понятие частоты среза яиляется весьма условным.
Фильтр Баттерворта
Функция передачи фильтра-прототипа Баттерворта (Butterworth filter) не имеет
нулей, а ее полюсы равномерно расположены на s-плоскости в левой половине
окружности единичного радиуса (см. далее рис. 2.6, а).
Благодаря такому размещению полюсов формула для АЧХ фильтра Баттерворта
оказывается очень простой:
где со0 — частота среза (для фильтра-прототипа она равна 1 рад/с), п — порядок
фильтра.
106
Глава 2. Аналоговые системы
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-1.5
-1.5 -1
I
\
\
о
-1
-2
-3
-4
-5
-6
-7
-8
\
L
\
^^Ss^.
■—_
п,
—
Рис. 2.6. Характеристики фильтра Баттерворта 5-го порядка: а — расположение полюсов
на комплексной плоскости, б — АЧХ, а — ФЧХ
Функции MATLAB для расчета линейных цепей 107
Коэффициент передачи на нулевой частоте равен 1, а на частоте среза независи-
независимо от порядка фильтра составляет l/V2 « 0,707 * -3 дБ. При со -> оо АЧХ стре-
стремится к нулю.
АЧХ фильтра Баттерворта (см. рис. 2.6, б) является максимально плоской при
со - 0 и со -> оо. Это означает, что в данных точках равны нулю 2га - 1 производ-
производных АЧХ по частоте.
В целом АЧХ монотонно спадает от единицы до нуля при изменении частоты от
нуля до бесконечности.
В MATLAB расчет аналогового фильтра-прототипа Баттерворта производится с
помощью функции buttap:
[z. p. k] = buttap(n):
Входной целочисленный параметр п — это порядок фильтра.
На рис. 2.6 показано расположение полюсов фильтра Баттерворта 5-го порядка
на комплексной плоскости, а также его АЧХ и ФЧХ:
» [z, p, k] = buttapE); % нули и полюсы прототипа
» plot(p. 'x') % график расположения полюсов
» axis equal
» axis([-1.5 1.5 -1.5 1.5])
» w = 0:0.01:5:
» [b, a] = zp2tf(z, p, k); % коэффициенты функции передачи
» h = freqs(b, a, w); % комплексный коэффициент передачи
» figure
» plot(w, abs(h)), grid % график АЧХ
» figure
» plot(w. unwrap(angle(h))), grid % график ФЧХ
ВНИМАНИЕ
Прописная буква «Я» в одном из комментариев только что приведенного листинга — не
опечатка. К сожалению, шестая версия MATLAB не позволяет использовать строчную
русскую букву «я» в комментариях и строковых константах (см. также раздел «MATLAB
и русский язык» приложения А).
Фильтр Чебышева первого рода
Функция передачи фильтра Чебышева первого рода (Chebyshev type I filter) также
не имеет нулей, а ее полюсы расположены в левой половине эллипса на s-плос-
кости (см. далее рис. 2.7, а).
АЧХ фильтра Чебышева первого рода описывается следующим образом:
1
Здесь со0 — частота среза, Т„(х) — полином Чебышева и-го порядка, п — порядок
фильтра, е — параметр, определяющий величину пульсаций АЧХ в полосе про-
пропускания.
108 Глава 2. Аналоговые системы
Полином Чебышева Т„(х) при \х\ < 1 колеблется в диапазоне -1... + 1, а при |лг| > 1
неограниченно возрастает по абсолютной величине. Поэтому АЧХ фильтра Че-
Чебышева первого рода в полосе пропускания (при jcoj < coo) колеблется между зна-
значениями 1/-V1+ е2 и 1, а вне полосы пропускания (при |со| > со0) монотонно зату-
затухает до нуля (см. далее рис. 2.7, б).
Коэффициент передачи на нулевой частоте равен 1 при нечетном порядке
фильтра и l/лД + е2 — при четном. На частоте среза коэффициент передачи
фильтра равен 1/л/1 + е2, то есть уровню пульсаций АЧХ в полосе пропускания.
При со —> со АЧХ стремится к нулю.
По сравнению с фильтром Баттерворта того же порядка фильтр Чебышева обес-
обеспечивает более крутой спад АЧХ в области перехода от полосы пропускания
к полосе задерживания.
Значение параметра е и уровень пульсаций Rp (в децибелах) связаны хледую-
щим образом:
Rp = 20 lg(Vl + £2) = Ю lg(l + е2) дБ,
При со -> со АЧХ фильтра Чебышева первого рода является максимально пло-
плоской.
В MATLAB фильтр-прототип Чебышева первого рода рассчитывается с помо-
помощью функции cheblap:
[z, p, k] = cheblap(n. Rp)
Здесь п — порядок фильтра, Rp — уровень пульсации в полосе пропускания (в де-
децибелах).
На рис. 2.7 показано расположение на комплексной плоскости полюсов фильтра
Чебышева первого рода 5-го порядка с уровнем пульсаций 0,5 дБ, а также его
АЧХ и ФЧХ:
>> [z. p, k] = cheblapE. 0.5): % нули и полюсы прототипа
» plot(p, 'x') % график оасположениЯ полюсов
» axis equal
» axis([-1.5 1.5 -1.5 1.5])
» w = 0:0.01:5:
» [b. a] = zp2tf(z. p. Ю: % коэффициенты функции передачи
» h = freqs(b, a. w): % комплексный коэффициент передачи
» figure
» % график АЧХ
» plot(w. abs(h)), grid
» figure
» % график ФЧХ
» plot(w, unwrap(angle(h))). grid
Функции MATLAB для расчета линейных цепей
109
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
о
x-/vl
I
\
\
\
\
\
\
>^
-^*^
—■ —
^—■
1 —"
1
Рис. 2.7. Характеристики фильтра Чебышева первого рода 5-го порядка с уровнем
пульсаций в полосе пропускания 0,5 дБ: а — расположение полюсов
на комплексной плоскости, б — АЧХ, в — ФЧХ
110 Глава 2. Аналоговые системы
Фильтр Чебышева второго рода
Функция передачи фильтра Чебышева второго рода (Chebyshev type II filter),
в отличие от предыдущих случаев, имеет и нули, и полюсы (рис. 2.8, а). Она
связана с функцией передачи фильтра Чебышева первого рода следующим обра-
образом:
H2(s) - I - Hi(l/s).
Здесь #i(s) и H2(s) — функции передачи фильтров-прототипов Чебышева перво-
первого и второго рода соответственно.
Полюсы функции передачи фильтров-прототипов Чебышева первого и второго
рода (ри и p2i соответственно) связаны друг с другом соотношением
По этой причине фильтры Чебышева второго рода называют еще инверсными
фильтрами Чебышева (inverse Chebyshev filter).
АЧХ фильтра Чебышева второго рода описывается следующим образом:
J
Здесь соо — частота среза, Т„(х) — полином Чебышева и-го порядка, п — порядок
фильтра, е — параметр, определяющий величину пульсаций АЧХ в полосе задер-
задерживания.
В результате указанного выше преобразования функции передачи АЧХ фильтра
Чебышева второго рода ведет себя следующим образом: в полосе пропускания
она монотонно затухает, а в полосе задерживания колеблется между нулем и
значением l/Vl + е2 (рис. 2.8, б).
ВНИМАНИЕ
Частотой среза фильтра Чебышева второго рода считается не конец полосы пропускания,
а начало полосы задерживания.
Коэффициент передачи фильтра на нулевой частоте равен 1, на частоте среза —
заданному уровню пульсаций в полосе задерживания. При со -> оо коэффициент
передачи равен нулю при нечетном порядке фильтра и уровню пульсаций — при
четном.
Значение параметра е и уровень пульсаций Rs (в децибелах) связаны следующим
образом:
R, = 20 lg(Vl + e2) = 10 lg(l + е2) дБ,
При со = 0 АЧХ фильтра Чебышева второго рода является максимально плоской.
Функции MATLAB для расчета линейных цепей
111
1
0.9
0.8
0.7
0.8
0.5
0.4
0.3
0.2
0.1
0
1
0.5
О
-0.5
-1
-1.5
-2
-2.Е--
-3
-3.5
-4
-4.5
V
\
\
\
\
\
V
N
К
"—-—
Рис, 2.8. Характеристики фильтра Чебышева второго рода 5-го порядка с уровнем
пульсаций в полосе задерживания 20 дБ: а — расположение нулей и полюсов
на комплексной плоскости, б — АЧХ, в — ФЧХ
112 Глава 2. Аналоговые системы
В MATLAB фильтр-прототип Чебышева второго рода рассчитывается с помо-
помощью функции cheb2ap:
[z. p, k] = cheb2ap(n. Rs)
Здесь п — порядок фильтра, Rs — уровень пульсаций в полосе задерживания (в де-
децибелах).
На рис. 2.8 показано расположение на комплексной плоскости полюсов фильтра
Чебышева второго рода 5-го порядка с уровнем пульсаций 20 дБ, а также его
АЧХ и ФЧХ:
» [z. p. k] = cheb2apE, 20); % нули и полюсы прототипа
» plot(p, 'x') % график расположения полюсов
» hold on
» plot(z. 'о') % график расположения нулей
» hold off
» axis equal
» axis([-2 2 -2 2])
» w = 0:0.01:5;
» [b. a] = zp2tf(z, p, k); % коэффициенты функции передачи
» h = freqs(b. a, w); % комплексный коэффициент передачи
» figure
» plot(w. abs(h)). grid % график АЧХ
» figure
» plot(w, unwrap(angle(h))). grid % график ФЧХ
Эллиптический фильтр
Эллиптические фильтры (фильтры Кауэра; английские термины — elliptic filter,
Cauer filter) в некотором смысле объединяют в себе свойства.фильтров Чебыше-
Чебышева первого и второго рода, поскольку АЧХ эллиптического фильтра имеет пуль-
пульсации заданной величины как в полосе пропускания, так и в полосе задержи-
задерживания (рис. 2.9, б). За счет этого удается обеспечить максимально возможную
(при фиксированном порядке фильтра) крутизну ската АЧХ, то есть переходной
зоны между полосами пропускания и.задерживания.
Функция передачи эллинтического фильтра имеет как полюсы, так и нули. Нули,
как и в случае фильтра Чебышева второго рода, являются чисто мнимыми и об-
образуют комплексно-сопряженные пары (рис. 2.9, а). Количество нулей функ-
функции передачи равно максимальному четному числу, не превосходящему порядка
фильтра.
АЧХ эллиптического фильтра описывается следующей формулой:
Здесь щ — частота среза, п — порядок фильтра, R,,(...) — рациональная функция
Чебышева и-го порядка, е и L — параметры, определяющие величину пульсаций
в полосах пропускания и задерживания.
Функции MATLAB для расчета линейных цепей
113
-1.5 -1 -0.5 0 0.5 1 1.5
0.9 •■
0.8
0.7
0.6
0.5 ■
0.4
0.3
0.2
0.1 Ь
-1
-2
-3
-5
-6
\
I
VJ
\-
1
Рис. 2.9. Характеристики эллиптического фильтра 5-го порядка с уровнем пульсаций
в полосе пропускания 0,5 дБ и в полосе задерживания 20 дБ: а — расположение
нулей и полюсов на комплексной плоскости, б — АЧХ, в — ФЧХ
114 Глава 2. Аналоговые системы
В MATLAB эллиптический фильтр-прототип рассчитывается с помощью функ-
функции ellipap:
[z, p, k] = ellipap(n, Rp. Rs)
Здесь n — порядок фильтра, Rp — уровень пульсаций в полосе пропускания, Rs —
уровень пульсаций в полосе задерживания. Уровни пульсаций указываются в де-
децибелах.
На рис. 2.9 показано расположение на комплексной плоскости нулей и полюсов
эллиптического фильтра 5-го порядка с уровнем пульсаций 0,5 дБ в полосе про-
пропускания и 20 дБ в полосе задерживания, а также его АЧХ и ФЧХ:
» [z. p. k] = ellipapE. 0.5. 20): % нули и полюсы прототипа
» plot(p, 'x') % график расположения полюсов
» hold on
» plot(z, 'о') % график расположения нулей
» hold off
» axis equal
» axis([-1.5 1.5 -1.5 1.5])
» w - 0:0.01:5;
» [b. a] = zp2tf(z, p. k); % коэффициенты функции передачи
» h - freqs(b. a, w); % комплексный коэффициент передачи
» figure
» plot(w, abs(h)), grid % график АЧХ
» figure
» plot(w, unwrap(angle(h))), grid % график ФЧХ
Фильтр Бесселя
В отличие от фильтров предыдущих типов, фильтры Бесселя (Bessel filter) не
аппроксимируют прямоугольную АЧХ — их АЧХ (рис. 2.10, б) по форме близка
к гауссовой кривой (точнее, стремится к ней с ростом порядка фильтра). Прак-
Практическая ценность фильтров Бесселя определяется тем, что для них зависимость
группового времени задержки от частоты является максимально гладкой в точке
со - 0 и групповая задержка очень мало меняется в полосе пропускания.
Функция передачи фильтра Бесселя имеет только полюсы, лежащие на окруж-
окружности с центром в положительной области вещественной оси (рис. 2.10, а). Сама
функция передачи имеет следующий вид:
k = 0
Коэффициенты полинома знаменателя рассчитываются по следующей формуле:
k ~2"-kk\(n-k)\'
Функции MATLAB для расчета линейных цепей
115
-1
-0.5
0.5
0.9 ■■
0.8 -
0.7 •■
0.8 ■■
0.5
0.4 ••
0.3 -
0.2
0.1
0
\
у
\
\
— I
-1 ••
-2
-3
-4
-5
-6
-7
-8
\
Рис. 2.10. Характеристики фильтра Бесселя 5-го порядка: а — расположение полюсов
на комплексной плоскости, б — АЧХ, а • - ФЧХ
116 Глава 2. Аналоговые системы
В MATLAB фильтр-прототип Бесселя рассчитывается с помощью функции
bessel ар:
[z. p. k] = besselap(n)
Здесь п — порядок фильтра.
На рис. 2.10 показано расположение на комплексной плоскости нулей и полюсов
фильтра Бесселя 5-го порядка, а также его АЧХ и ФЧХ:
» [z. p. k] = besselapE): % нули и полюсы прототипа
» plot(p. 'x') % график расположения нулей
» axis equal
» axis([-l 1 -1 1])
» w = 0:0.01:5;
» [b. a] = zp2tf(z. p. k); % коэффициенты функции передачи
» h = freqs(b, a, w): % комплексный коэффициент передачи
» figure
» plot(w, abs(h)). grid % график АЧХ
» figure
» plot(w, unwrap(angle(h))). grid % график ФЧХ
Преобразования фильтров-прототипов
Следующий этап после расчета фильтра-прототипа — его преобразование с це-
целью получения фильтра заданного вида с требуемыми частотами среза. Для этого
используются приведенные ниже четыре функции MATLAB. Принцип составле-
составления их имен следующий: сначала идет сокращение 1 р, означающее, что исходным
фильтром является ФНЧ (low-pass), потом следует символ преобразования 2 и в
конце стоит обозначение типа результирующего фильтра:
□ 1р21р — изменение частоты среза ФНЧ (low-pass);
□ Ip2hp — преобразование ФНЧ в ФВЧ (high-pass);
Q Ip2bp — преобразование ФНЧ в полосовой фильтр (band-pass);
Q Ip2bs — преобразование ФНЧ в режекторный фильтр (band-stop).
Все эти функции могут преобразовывать фильтры, заданные двумя способами —
в виде коэффициентов полиномов числителя и знаменателя функции передачи
либо в пространстве состояний. Различаются эти два варианта по числу входных
и выходных параметров.
Изменение частоты среза ФНЧ
Изменение частоты среза ФНЧ-прототипа сводится к простому масштабирова-
масштабированию частотной оси и выполняется путем следующей замены переменной 5 в вы-
выражении для функции передачи:
s
s —> ,
со,,
Функции MATLAB для расчета линейных цепей 117
где а>о — требуемая частота среза ФНЧ. Такое преобразование производится
функцией 1р21р:
[Ы. al] = Ip21p(b. a. wO)
[Al. Bl. Cl. Dl] = lp21p(A, B. C. D. wO)
Входными параметрами функции являются описание фильтра (в виде коэффи-
коэффициентов полиномов числителя и знаменателя функции передачи — Ь, а, или
в пространстве состояний — А, В, С, D) и требуемая частота среза wO.
Возвращаемый результат — пересчитанные параметры фильтра.
Преобразование ФНЧ в ФВЧ
Преобразование ФНЧ-прототипа в ФВЧ требует инверсии частотной оси и вы-
выполняется путем следующей замены переменной s в выражении для функции пе-
передачи:
со,
s ->
s
'о
где а>о — требуемая частота среза ФВЧ. Такое преобразование производится
функцией Ip2hp:
[bl. al] = Ip2hp(b. a. wO)
[Al. Bl. Cl. Dl] = lp2hp(A. B. C, D. wO)
Входными параметрами функции являются описание фильтра (в виде коэффи-
коэффициентов полиномов числителя и знаменателя функции передачи — Ь, а или в
пространстве состояний — А, В, С, D) и требуемая частота среза wO.
Возвращаемый результат — пересчитанные параметры фильтра.
Преобразование ФНЧ в полосовой фильтр
Преобразование ФНЧ-прототина в полосовой фильтр требует более сложной
трансформации частотной оси, чем в предыдущих случаях. Так, нулевая и беско-
бесконечная частоты должны преобразовываться в бесконечное значение на частот-
частотной оси ФНЧ-прототипа (там, где его коэффициент передачи стремится к
нулю). Частоты, соответствующие краям требуемой полосы пропускания, долж-
должны после преобразования давать значения ±1, равные частоте среза ФНЧ-прото-
ФНЧ-прототипа. Наконец, преобразование должно выполняться с помощью дробно-рацио-
дробно-рациональной функции, чтобы сохранить дробно-рациональную структуру функции
передачи.
Перечисленным требованиям удовлетворяет следующая замена переменной s:
S/Ч
где оз0 = д/о^соз, Q = ©о/(ю2 ~ Ю1)> оз( и оз2 — соответственно нижняя и верхняя
границы полосы пропускания фильтра.
118 Глава 2. Аналоговые системы
Такое преобразование выполняется функцией 1 р2Ьр:
[Ы. al] = Ip2bp(b, a. wO, Bw)
[Al. Bl, Cl, Dl] = lp2bp(A. В, С D. wO. Bw)
Входными параметрами функции являются описание фильтра (в виде коэффи-
коэффициентов полиномов числителя и знаменателя функции передачи — Ь, а или в
пространстве состояний — А, В, С, D), средняя частота wO и ширина Bw полосы про-
пропускания фильтра (в радианах в секунду).
ВНИМАНИЕ
Обратите внимание на то, что средняя частота полосы пропускания — это среднее геомет-
геометрическое, а не среднее арифметическое частот среза: wO=sqrt(wl*w2). Полоса пропускания
рассчитывается без особенностей: Bw=w2-wl.
Возвращаемый результат — пересчитанные параметры фильтра.
Рассчитаем в качестве примера полосовой фильтр Чебышева первого рода 5-го
порядка с полосой пропускания от 1 кГц до 9 кГц и уровнем пульсаций в полосе
пропускания 3 дБ:
» [z, p, k] = cheblapE, 3); % ФНЧ-прототип
» [b. a] = zp2tf(z. p. к): % функция передачи
» fl = 1еЗ: * % нижнЯЯ частота среза
» f2 = 9еЗ: % верхняя частота среза
» wO = 2 * pi * sqrtCfl * f2): % средняя частота
» Bw = 2 * pi * (f2 - f1): % полоса пропускания
» [b. a] = Ip2bp(b. a, wO. Bw): % полосовой фильтр
» f = 0:1:20еЗ; % вектор частот длЯ расчета
» h = freqs(b. a, 2*pi*f): % частотная характеристика
» plot(f/1000, abs(h)), grid % график АЧХ
» axis tight
» figure
» plot(f/1000, unwrap(angle(h))). grid % график ФЧХ -
Построенные графики АЧХ и ФЧХ приведены на рис. 2.11. Обратите внимание
на то, что характеристики фильтра несимметричны — они сжаты слева и растя-
растянуты справа. Если проанализировать формулу замены переменной, использо-
использованную для преобразования ФНЧ в полосовой фильтр, окажется, что частоты,
на которых коэффициент передачи имеет одинаковые значения, связаны соотно-
соотношением ю,ю2 = raj;. Поэтому графики станут симметричными, если использовать
логарифмический масштаб по оси частот.
Асимметрия частотных характеристик проявляется тем сильнее, чем больше от-
отношение граничных частот полосы пропускания фильтра. Именно по этой при-
причине в рассмотренном примере специально использованы столь сильно (в 9 раз)
различающиеся частоты среза.
Функции MATLAB для расчета линейных цепей
119
ю
15
20
Рис. 2.11. При большом отношении граничных частот полосы пропускания
полосового фильтра отчетливо наблюдается асимметрия частотных
характеристик (сверху — АЧХ, снизу — ФЧХ)
Преобразование ФНЧ в режекторный фильтр
Для преобразования ФНЧ-прототипа в режекторный фильтр трансформация
частотной оси должна быть обратной по отношению к предыдущему случаю. Ну-
Нулевая и бесконечная частоты должны преобразовываться в нулевое значение на
частотной оси ФНЧ-прототипа (там, где коэффициент передачи велик). Часто-
Частоты, соответствующие краям требуемой полосы задерживания, должны после
преобразования давать значения ±1, равные частоте среза ФНЧ-прототипа. Кро-
Кроме того, некоторое значение частоты в полосе задерживания должно преобра-
преобразовываться в бесконечность (там, где коэффициент передачи ФНЧ-прототипа
стремится к нулю). Наконец, преобразование должно выполняться с помощью
дробно-рациональной функции, чтобы сохранить дробно-рациональную струк-
структуру функции передачи.
120 Глава 2. Аналоговые системы
Перечисленным требованиям удовлетворяет следующая замена переменной s:
Q(E/co0J+l)'
где со0 = -y/cujCO2, Q = соо/(со2 - cot), co( и со2 — соответственно нижняя и верхняя
границы полосы задерживания фильтра.
Такое преобразование выполняется функцией Ip2bs:
[Ы. al] = Ip2bs(b, a, wO, Bw)
[Al, Bl, Cl, Dl] = lp2bs(A, B, C, D, wO, Bw)
Входными параметрами функции являются описание фильтра (в виде коэффи-
коэффициентов полиномов числителя и знаменателя функции передачи — Ь, а или в
пространстве состояний — А, В, С, D), средняя частота wO и ширина Bw полосы за-
задерживания фильтра (в радианах в секунду).
Возвращаемый результат — пересчитанные параметры фильтра.
Все сказанное выше применительно к полосовым фильтрам о связи средней час-
частоты с частотами среза и об асимметрии характеристик справедливо и для ре-
жекторных фильтров.
Расчет аналоговых фильтров
Как уже говорилось, для расчета аналогового фильтра необходимо выполнить
две основные операции: рассчитать ФНЧ-прототип и преобразовать его к нуж-
нужному типу фильтра с заданными частотами среза. Требуемая последовательность
действий оформлена в виде следующих функций MATLAB:
□ butter(n, wO, type, 's') —расчет фильтров Баттерворта;
□ chebyKn, Rp, wO, type, 's') —расчет фильтров Чебышева первого рода;
□ cheby2(n, Rs, wO, type, 's') — расчет фильтров Чебышева второго рода;
□ ellip(n, Rp, Rs, wO, type, 's')—расчет эллиптических фильтров;
□ besse1f(n, wO, type) — расчет фильтров Бесселя.
Параметры всех функций задаются одинаково, поэтому обсуждать функции по
отдельности не будем.
Перечисленные функции, за исключением функции besself, позволяют рассчи-
рассчитывать как аналоговые, так и дискретные фильтры. Признаком аналогового рас-
расчета служит строка ' s', использованная в качестве последнего входного парамет-
параметра. Об использовании этих функций для расчета дискретных фильтров речь
пойдет в главе 6.
Параметры n, Rp, Rs (их состав зависит от типа фильтра) — это параметры фильт-
фильтра-прототипа: п — порядок фильтра, Rp — уровень пульсаций в полосе пропуска-
пропускания (в децибелах), Rs — уровень пульсаций в полосе задерживания (в децибелах).
Более подробное описание этих параметров было приведено ранее, в разделах,
посвященных фильтрам-прототипам.
Функции MATLAB для расчета линейных цепей 121
Параметры wO и type используются совместно для задания типа фильтра и значе-
значений его частот среза (в радианах в секунду):
□ ФНЧ: wO — скаляр, параметр type отсутствует;
□ ФВЧ: wO — скаляр, type='high';
□ полосовой фильтр: wO — двухэлементный вектор частот среза [wl w2], пара-
параметр type отсутствует;
□ режекторный фильтр: wO — двухэлементный вектор частот среза [wl w2],
type-'stop1.
ВНИМАНИЕ
Следует подчеркнуть, что в данных функциях нри разработке полосовых и режекторпых
фильтров в качестве параметров задаются именно частоты среза, а не средняя частота
и полоса пропускания, как в функциях преобразования фильтров-прототипов.
В зависимости от того, сколько выходных параметров указано при вызове, функ-
функции могут возвращать результаты расчета в виде коэффициентов полиномов
числителя и знаменателя функции передачи (два выходных параметра), нулей и
полюсов (три выходных параметра) либо параметров пространства состояний
(четыре выходных параметра):
[Ь, а] = ...
[z. р. к] = ...
[А, В. С, D] = ...
С учетом всего сказанного перечислим действия, выполняемые функциями рас-
расчета аналоговых фильтров:
1. Производится расчет фильтра-прототипа с заданными параметрами АЧХ.
2. Полученные нули и полюсы преобразуются в параметры пространства со-
состояний.
3. Производится преобразование фильтра-прототипа к требуемому типу с за-
заданными частотами среза.
4. Выполняется преобразование описания фильтра к заданному при вызове
виду.
Выбор порядка фильтра
Рассмотренные выше функции расчета фильтров требуют задания в качестве
входных параметров порядка фильтра и его частоты среза. При этом понятие
частоты среза для фильтров разных типов определяется по-разному. Однако ис-
исходными данными при разработке фильтров, как правило, являются другие па-
параметры: частотные границы полос пропускания (сор) и задерживания (cov), а так-
также допустимая неравномерность АЧХ в полосе пропускания (Rp) и минимально
необходимое затухание в полосе задерживания (Rs) (рис. 2.12). Серые области на
рисунке демонстрируют допуски, в которые должна укладываться АЧХ фильтра
в полосах пропускания и задерживания.
122
Глава 2. Аналоговые системы
*р\\
7ХМ
ФНЧ
ФВЧ
i \
Rs /\
0
О
copB) ca,B) ю
Полосовой фильтр Режекторный фильтр
Рис. 2.12. Задание исходных параметров для расчета ФНЧ, ФВЧ, полосовых
и режекторных фильтров
Выбрать минимально необходимый порядок фильтра позволяют следующие од-
однотипные функции пакета Signal Processing:
[п. Wn] = buttord (Wp. Ws. Rp. Rs, 's')
[n. Wn] = cheblord (Wp. Ws, Rp, Rs. 's')
[n, Wn] = cheb2ord (Wp, Ws. Rp, Rs, 's')
[n, Wn] = eiiipord (Wp, Ws, Rp. Rs. 's')
ЗАМЕЧАНИЕ
Данные функции позволяют выбирать порядок как для аналоговых, так и для дискретных
фильтров. Последний параметр V является признаком аналогового расчета. Использова-
Использование этих функций для определения требуемого порядка дискретных фильтров обсуждает-
обсуждается в разделе «Функции выбора порядка фильтров» главы 6.
Входной параметр Rp — допустимый уровень пульсаций в полосе пропускания
(в децибелах), Rs — минимально необходимое затухание в полосе задерживания
(в децибелах). Параметры Wp и Ws задают границы полос пропускания и задержи-
задерживания, способ задания этих параметров зависит от типа проектируемого фильтра:
Q ФНЧ: Wp и Ws — числа, при этом должно выполняться неравенство Wp < Ws;
Q ФВЧ: Wp и Ws — числа, при этом должно выполняться неравенство Wp > Ws;
□ полосовой фильтр: Wp и Ws — двухэлементные векторы, при этом должны вы-
выполняться неравенства Ws(l) < Wp(l) < WpB) < WsB);
□ режекторный фильтр: Wp и Ws — двухэлементные векторы, при этом должны
выполняться неравенства Wp(l) < Ws(l) < WsB) < WpB).
Функции MATLAB для расчета линейных цепей 123
Значения параметров Wp и Ws были обозначены на рис. 2.12 как сор и cos соответст-
соответственно.
Выходными параметрами являются минимально необходимый для выполне-
выполнения заданных требований порядок фильтра п и частота среза фильтра Wn. Эти па-
параметры должны затем использоваться при вызове функции расчета фильтра.
Возврат значения Wn избавляет пользователя от забот, связанных с тем, что при
расчете разных фильтров понятие частоты среза имеет разный смысл. Для эл-
эллиптических фильтров и фильтров Чебышева первого рода Wn = Wp, для фильт-
фильтров Чебышева второго рода Wn = Ws, а для фильтров Баттерворта значение Wn (на-
(напомним, что оно определяет частоту среза по уровню 3 дБ) зависит от заданного
уровня пульсаций Rp следующим образом:
га„ =■
Поскольку порядок фильтра — величина целочисленная, то обычно оказывается,
что фильтр минимально необходимого порядка обеспечивает некоторый запас
по исходным параметрам. Этот запас можно использовать по-разному — либо
сделать пульсации в полосе пропускания точно равными заданным, но увели-
увеличить затухание в полосе задерживания, либо точно выдержать заданное затуха-
затухание в полосе задерживания, уменьшив при этом пульсации в полосе пропус-
пропускания. Для эллиптических фильтров возможен еще один вариант — сужение
переходной зоны за счет расширения полосы задерживания. Поведение функций
выбора порядка фильтра в этом аспекте определяется тем, что при расчете
фильтра должны будут использоваться те же параметры пульсаций Rp и Rs, что и
при выборе порядка фильтра. Поэтому для фильтров Баттерворта и Чебышева
первого рода будет увеличиваться затухание в полосе задерживания, для фильт-
фильтров Чебышева второго рода — уменьшаться пульсации в полосе пропускания,
а для эллиптических фильтров — расширяться полоса задерживания.
Расчет групповой задержки
В MATLAB нет функции, позволяющей вычислять групповую задержку для ана-
аналоговых систем (функция grpdelay предназначена только для дискретных сис-
систем; речь о ней пойдет в разделе «Расчет групповой задержки дискретной систе-
системы» главы 4). Поэтому в качестве небольшого примера рассмотрим возможную
реализацию такой функции. Назовем ее, скажем, grp_del.
Прежде всего следует определиться с входными и выходными параметрами. Пусть
функция получает векторы коэффициентов b и а полиномов числителя и знаме-
знаменателя функции передачи, а также вектор значений круговой частоты w для рас-
расчета групповой задержки. Возвращаемый результат tau — вектор рассчитанных
значений групповой задержки. Итак, функция будет использоваться следующим
образом:
tau = grp_de1(b, a, w)
Теперь нужно разобраться с алгоритмом работы функции, то есть получить фор-
формулы, по которым будут выполняться вычисления. Для этого вспомним, что
функция передачи выражается в виде отношения двух полиномов и что при
1 24 Глава 2. Аналоговые системы
делении комплексных чисел их фазы вычитаются. Если все это учесть в опреде-
определении групповой задержки (см. формулу B.2) в разделе «Фазовая и групповая
задержка»), получим следующее:
, ч d Л()(о) d .. . . d
* Ф О) = -г arg "БтЧ = У аг8 Л(-^" ТГ
аю 5(уш) аю аю
Фаза комплексного числа равна арктангенсу отношения мнимой и веществен-
вещественной частей (добавление константы ±п не имеет значения, так как оно не повлия-
повлияет на результат дифференцирования по со):
. . d 1тЛ(;'ю) d . imB(jco)
х.... (ю) = — arctg ^—^ arctg ^—^.
" doc ЯеЛОш) dec ReB(j(o)
Наконец, дифференцирование арктангенса дроби дает следующее:
Re A(j(u)—Im A(jd) - 1тЛ(;ю)—Re A(jai)
x /s drodra
B.15)
Re B(;co) A Im B( jco) - Im B( jco)—Re B(;<a)
Поскольку числитель и знаменатель функции передачи являются полиномами
относительно переменной s -jco, выделение вещественной и мнимой частей, так
же как и дифференцирование, сводится к простым манипуляциям с векторами
коэффициентов полиномов. Комментарии на этот счет приводятся непосредст-
непосредственно в листинге функции:
function tau = grpjjeKb, a, w)
% размещаем коэффициенты в порЯдке возрастания степеней
b = fliplr(b):
а = fliplr(a);
% выравниваем длины векторов
[b. a] = eqtflength(b. a);
% выделяем вещественную часть числителя
Вг = Ь:
BrB:2:end) =0; % только четные степени
BrC:4:end) = -BrC:4:end); % через раз - знак "минус"
% выделяем мнимую часть числителя
Bi = b;
BiС1:2:end) = 0; % только нечетные степени
BiD:4:end) = -BiD:4:end): % через раз - знак "минус"
% выделЯем вещественную часть знаменателя
Аг = а:
ArB:2:end) =0; % только четные степени
ArC:4:end) = -ArC:4:end): % через раз - знак "минус"
% выделЯем мнимую часть знаменателя
Функции MATLAB для расчета линейных цепей 1 25
Ai = а:
Ai(l:2:end) =0; % только нечетные степени
AiD:4:end) = -AiD:4:end): % через раз - знак "минус"
% размещаем коэффициенты в порЯдке убывания степеней
Ar=fliplr(Ar):
Ai=fliplr(Ai);
Br-fliplr(Br):
Bi-fliplr(Bi):
% вычисляем знаменатели слагаемых
den_B = conv(Br. Br) + conv(Bi. Bi);
den_A - conv(Ar, Ar) + conv(Ai, Ai);
% вычисляем числители слагаемых
[num_B. tmp] = polyder(Bi, Br);
[num_A, tmp] - polyder(Ai. Ar):
% вычисляем групповую задержку
tau = -polyval(num_B, w)./polyval(den_B. w) + ...
polyval(num_A, w)./polyval(den_A, w);
Этот программный код в точности реализует формулу B.15). Приведем ряд до-
дополнительных комментариев. Переворачивание векторов-строк «задом наперед»
с помощью функции fl ipl г производится исключительно для удобства выделения
вещественных и мнимых частей — отсчитывать коэффициенты при этом проще
от начала вектора, чем от конца. Функция eqtflength выравнивает длины пере-
переданных ей векторов, дополняя более короткий из них нулями в конце. Функция
polyder, вызванная с двумя входными и выходными параметрами, вычисляет
производную отношения двух полиномов, возвращая коэффициенты числителя
и знаменателя результата. Нас в данном случае интересует только первый вы-
выходной параметр, поскольку числители слагаемых в B.15) совпадают с числите-
числителями производных от дробей Im B(ja)/Re B(ja) и Im A(ja)/Re A(ja). Умноже-
Умножение полиномов эквивалентно свертке векторов их коэффициентов, выполняемой
с помощью функции conv (см. раздел «Дискретная свертка» главы 4). Для вычис-
вычисления значений полиномов в заданных точках используется функция pol yval.
Мы реализовали лишь простейший вариант — вычисление групповой задержки
в заданных частотных точках. В принципе функцию можно расширить, реализо-
реализовав возможности, аналогичные тем, которыми обладает функция freqs: вывод
графика при отсутствии выходных параметров, задание вектора частот по умол-
умолчанию и т. д. Заинтересованный читатель может сделать это, изучив исходный
код функции freqs (файл MATLABR12\Toolbox\Signal\Signal\freqs.m).
В качестве примера применения разработанной функции (не забудьте сохранить
ее в виде файла с именем grp_del.m) построим с ее помощью графики зависимо-
зависимости групповой задержки от частоты для двух рассмотренных ранее фильтров-
прототипов — Чебышева первого рода и Бесселя (рис. 2.13):
» % фильтр Чебышева первого рода
» [z, p. k] = cheblapE. 0.5): % нули и полюсы прототипа
» [b. a] » zp2tf(z. p, к): % коэффициенты функции передачи
» w = 0:0.01:5;
» tau = grp_del(b. a. w); % групповая задержка
126
Глава 2. Аналоговые системы
» plot(w, tau), grid
» % фильтр Бесселя
» [z, р. к] - besselapE):
» [b, a] = zp2tf(z, p, k);
» w = 0:0.01:5;
» tau = grp_del(b, a, w);
» figure
» plot(w, tau), grid
% график групповой задержки
% нули и полюсы прототипа
% коэффициенты функции передачи
% групповая задержка
% график групповой задержки
4
3.5
3
2.5
2
1.5
1
0.5
О
Рис. 2.13. Частотная зависимость групповой задержки для фильтров Чебышева
первого рода (сверху) и Бесселя (снизу)
Результаты расчетов показывают, что частотная зависимость групповой задерж-
задержки для фильтра Чебышева первого рода имеет весьма изрезанный вид, а анало-
аналогичный параметр для фильтра Бесселя, как и было отмечено при рассмотрении
соответствующего фильтра-прототипа, в полосе пропускания практически не
меняется.
\
\
\
\
\
7*"»<
,
ГЛАВА 3 Дискретные
сигналы
После двух вводных глав, посвященных основам теории сигналов и линейных
систем, мы наконец приступаем к рассмотрению вопросов, непосредственно свя-
связанных с предметом данной книги — цифровой обработкой сигналов.
Сущность цифровой обработки состоит в том, что физический сигнал (напряже-
(напряжение, ток и т. д.) преобразуется в последовательность чисел, которая затем подвер-
подвергается математическим преобразованиям в вычислительном устройстве. Транс-
Трансформированный цифровой сигнал (последовательность чисел) при необходимости
может быть преобразован обратно в напряжение или ток.
В данной главе будут рассмотрены принципы математического описания и ана-
анализа дискретных сигналов. Но прежде всего следует пояснить некоторые терми-
терминологические тонкости, которые, возможно, уже были замечены внимательным
читателем: в названии книги упоминается цифровая обработка сигналов, а дан-
данная глава посвящена дискретным сигналам. С обсуждения разницы между этими
понятиями мы и начнем.
Аналоговые, дискретные
и цифровые сигналы
Исходный физический сигнал является непрерывной функцией времени. Такие
сигналы, определенные во все моменты времени, называют аналоговыми (analog).
Последовательность чисел, представляющая сигнал при цифровой обработке,
является дискретным рядом (discrete series) и не может полностью соответство-
соответствовать аналоговому сигналу. Числа, составляющие последовательность, являются
значениями сигнала в отдельные (дискретные) моменты времени и называются
отсчетами сигнала (samples). Как правило, отсчеты берутся через равные про-
промежутки времени Г, называемые периодом дискретизации (или интервалом, ша-
шагом дискретизации — sample time). Величина, обратная периоду дискретизации,
128
Глава 3. Дискретные сигналы
называется частотой дискретизации (sampling frequency): /д = \/Т. Соответст-
Соответствующая ей круговая частота определяется следующим образом: шд = 2п/Т.
Ясно, что в общем случае представление сигнала набором дискретных отсчетов
приводит к потере информации, так как мы ничего не знаем о поведении сигнала
в промежутках между отсчетами. Однако, как будет показано далее в разделе
«Теорема Котелыгакова», существует класс аналоговых сигналов, для которых
такой потери информации не происходит и которые могут быть точно восста-
восстановлены по значениям своих дискретных отсчетов.
Процесс преобразования аналогового сигнала в последовательность от счетов на-
называется дискретизацией (sampling), а результат такого преобразования — дис-
дискретным ситалом.
При обработке сигнала в вычислительных устройствах его отсчеты представля-
представляются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследст-
Вследствие этого отсчеты могут принимать лишь конечное множество значений и, сле-
следовательно, при представлении сигнала неизбежно происходит его округление.
Процесс преобразования отсчетов сигнала в числа называется квантованием по
уровню (quantization), а возникающие при этом ошибки округления — ошибками
(или шумами) квантования (quantization error, quantization noise).
Сигнал, дискретный во времени, но не квантованный но уровню, называется дис-
дискретным (discrete-time) сигналом. Сигнал, дискретный во времени и квантован-
квантованный по уровню, называют цифровым (digital) сигналом. Сигналы, квантованные
по уровню, но непрерывные во времени, на практике встречаются редко. Раз-
Разницу между аналоговыми, дискретными и цифровыми сигналами иллюстрирует
рис. 3.1.
0 2 4 6
Рис. 3.1. Аналоговый (слева), дискретный (в центре) и цифровой (справа) сигналы
10
Вычислительные устройства; предназначенные для обработки сигналов, могут
оперировать только цифровыми сигналами. Существуют также устройства, по-
построенные в основном на базе аналоговой схемотехники, которые работают с
дискретными сигналами, представленными в виде импульсов различной ампли-
амплитуды или длительности. Чтобы подчеркнуть отсутствие квантования по уровню,
такие устройства иногда называют дискретно-аналоговыми (ДАУ).
В большей части книги речь пойдет о дискретных сигналах и методах их обра-
обработки, поскольку эффекты, связанные с квантованием по уровню, в большинстве
случаев не будут приниматься во внимание. Однако этим эффектам, а также
другим проблемам, связанным с конечной точностью представления чисел в вы-
вычислительных устройствах, специально посвящена глава 7.
Аналого-цифровое и цифро-аналоговое преобразование
129
Аналого-цифровое и цифро-
аналоговое преобразование
Обобщенная структура системы цифровой обработки сигналов приведена на
рис. 3.2. На вход поступает аналоговый сигнал sax(t). Его временная дискретиза-
дискретизация и квантование по уровню производятся в аналого-цифровом преобразовате-
преобразователе (АЦП; английский термин — Analog-to-Digital Converter, ADC). Вообще эти
два процесса — дискретизация и квантование — являются независимыми друг от
друга, но они, как правило, выполняются внутри одной микросхемы. Выходным
сигналом АЦП является последовательность чисел, поступающая в цифровой
процессор ЦП, выполняющий требуемую обработку. Процессор осуществляет
различные математические операции над входными отсчетами; ранее получен-
полученные отсчеты и промежуточные результаты могут сохраняться в памяти процес-
процессора для использования в последующих вычислениях. Результатом работы про-
процессора является новая последовательность чисел, представляющих собой отсчеты
выходного сигнала. Аналоговый выходной сигнал smM(t) восстанавливается по
этой последовательности чисел с помощью цифро-аналогового преобразователя
(ЦАП; английский термин — Digital-to-Analog Converter, DAC). Напряжение на
выходе ЦАП имеет ступенчатую форму (это также показано на рис. 3.2); при не-
необходимости оно может быть преобразовано в плавно меняющийся выходной
сигнал с помощью сглаживающего фильтра Ф.
АЦП
ЦАП
Ф
{хо,хих2, ...}
ъ ■■■}
Рис. 3.2. Структурная схема системы цифровой обработки сигналов
Устройства, реализуемые с помощью структуры типа рис. 3.2, могут иметь са-
самый разнообразный характер. В цифровой форме можно создавать фильтры,
анализаторы спектра, нелинейные преобразователи сигналов и многое другое.
ЗАМЕЧАНИЕ :
Использование входных и выходных сигналов в аналоговой форме (и, следовательно, на-
наличие АЦП и ЦАП) не всегда является необходимым. Так, при реализации цифрового ге-
генератора сигналов не нужен входной аналоговый сигнал, а ЦАП может отсутствовать,
если конечный результат необходим только в цифровой форме.
Частота Найквиста
Гармонический сигнал может быть адекватно представлен дискретными отсчета-
отсчетами, если его частота не превышает половины частоты дискретизации (эта часто-
130
Глава 3. Дискретные сигналы
та называется частотой Найквиста (Nyquist frequency) — fN - /д/2 ~ 1/B2");
<bn - сйд/2 - л/Т). Происхождение этого ограничения поясняет рис. 3.3. В зави-
зависимости от соотношения между частотой дискретизируемого гармонического
сигнала и частотой Найквиста возможны три случая.
1. Если частота гармонического сигнала меньше частоты Найквиста, дискретные
отсчеты позволяют правильно восстановить аналоговый сигнал (рис. 3.3, а).
2. Если частота гармонического сигнала равна частоте Найквиста, то дискрет-
дискретные отсчеты позволяют восстановить аналоговый гармонический сигнал с
той же частотой, но амплитуда и фаза восстановленного сигнала (он показан
пунктирной линией) могут быть искажены (рис. 3.3, б). В худшем случае все
дискретные отсчеты синусоиды могут оказаться равными нулю.
3. Если частота гармонического сигнала больше частоты Найквиста, восстанов-
восстановленный по дискретным отсчетам аналоговый сигнал (как и в предыдущем слу-
случае, он показан пунктирной линией) будет также гармоническим, но с иной
частотой (рис. 3.3, в). Данный эффект носит название появления ложных час-
частот (aliasing), мы продолжим его рассмотрение в следующем разделе «Спектр
дискретного сигнала».
Рис. 3.3. Дискретизация гармонических сигналов с разной частотой
ЗАМЕЧАНИЕ
Эффекты, связанные с дискретизацией периодических процессов, наглядно проявляются
при кино- и видеосъемке вращающихся объектов (таких, например, как колеса автомоби-
автомобилей). Из-за недостаточно высокой частоты дискретизации (частоты смены кадров) быстро
вращающееся колесо может выглядеть неподвижным либо медленно поворачивающимся
(причем в любую сторону).
Спектр диокретного сигнала 131
Спектр дискретного сигнала
Преобразование Фурье позволяет вычислить спектральную плотность сигнала,
представляющего собой функцию (как правило, времени либо пространственных
координат). Дискретный же сигнал является последовательностью чисел, поэто-
поэтому для анализа его спектра обычными-(аналоговыми) средствами необходимо
сопоставить этой последовательности некоторую функцию.
Традиционным способом такого сопоставления является представление отсче-
отсчетов в виде дельта-функций с соответствующими множителями и задержками.
Для последовательности отсчетов {x(k)} получится следующий сигнал:
5@= ix(k)b(t-k). C.1)
* —00
Преобразование Фурье линейно, спектр дельта-функции равен единице, а за-
задержка сигнала во времени приводит к умножению спектра на комплексную экс-
экспоненту. Все это (см. раздел «Свойства преобразования Фурье» главы 1) позво-
позволяет сразу же записать спектр дискретного сигнала:
ад =£*(*)*-**: C.2)
Из этой формулы видно главное свойство спектра любого дискретного сигнала:
спектр является периодическим, и его период в данном случае равен 2я (то есть
круговой частоте дискретизации, поскольку, составляя сигнал из дельта-функ-
дельта-функций, мы выбрали единичный интервал между ними, что дает <вд » 2я):
5(ю±2я) =
Следует также обратить внимание на размерность спектральной функции дис-
дискретного сигнала: она совпадает с размерностью отсчетов. Это связано с тем, что
дельта-функции времени, из которых был составлен сигнал C.1), имеют размер-
размерность частоты (см. раздел «Классификация сигналов» главы 1).
Формула C.2) позволяет вычислить спектральную функцию по известным от-
отсчетам x(k). При конечном числе ненулевых отсчетов этот расчет несложен; он
может быть выполнен с помощью функции MATLAB freqz (подробнее об этой
функции см. раздел «Расчет частотной характеристики» главы 4).
Теперь рассмотрим несколько иную задачу. Пусть значения х (k) являются от-
отсчетами аналогового сигнала s(t), взятыми с периодом Т:
x(k)-s(kT).
Выясним, как в этом случае спектр дискретного сигнала C.2) связан со спектром
аналогового сигнала S(a>).
Итак, мы рассматриваем дискрепгизированный сигнал в виде последовательности
дельта-функций, «взвешенной» значениями отсчетов s(kT) аналогового сигна-
сигнала s(t) (рис. 3.4):
| C.3)
132
Глава 3. Дискретные сигналы
fflk
0 TIT t
Рис. 3.4. Дискретизированный сигнал в виде последовательности дельта-функций
ЗАМЕЧАНИЕ
Термин «дискретизированный» в данном контексте подчеркивает, что последователь-
последовательность отсчетов получена именно в результате дискретизации аналогового сигнала.
Так как функция b(t - kT) равна нулю всюду, кроме момента t = kT, можно заме-
заменить в выражении C.3) константы s (kT) на исходный непрерывный сигнал s(t):
C.4)
Далее заметим, что сумма, входящая в выражение C.4), является периодическим
сигналом, а потому может быть представлена в виде ряда Фурье. Коэффициенты
этого ряда, согласно A.9), равны
C.5)
-Г/2
В формуле C.5) было учтено, что в интервал интегрирования (-Т/2, Т/2) попа-
попадает только одна дельта-функция, соответствующая k — 0.
Таким образом, периодическая последовательность дельта-функций может быть
представлена в виде комплексного ряда Фурье A.8):
« Л ГГ.
C.6)
г„е„
где ш„ - 2пп/Т. Подставив C.6) в C.4), получим
Умножение сигнала на ехр(/ш„£) соответствует сдвигу спектральной функции
на со„, поэтому спектр дискретизированного сигнала можно записать следующим
образом:
C.7)
Таким образом, спектр дискретизированного сигнала представляет собой беско-
бесконечный ряд сдвинутых копий спектра исходного непрерывного сигнала s(t)
(рис. 3.5). Расстояние по частоте между соседними копиями спектра равно час-
частоте дискретизации сод - 2п/Т.
Следует также отметить, что из-за наличия в формуле C.7) множителя \/Т
спектр дискретизированного сигнала имеет размерность, совпадающую с размер-
Спектр дискретного сигнала
133
ностью сигнала (как уже говорилось, это связано с тем, что функция 5(£) имеет
размерность частоты).
№,(«)! +
-Шд/2 0 шд/2
Рис. 3.5. Спектр дискретизированного сигнала
Характер спектра дискретизированного сигнала еще раз демонстрирует частот-
частотно-временную дуальность преобразования Фурье:
□ периодический сигнал -> дискретный спектр;
□ периодический спектр -» дискретный сигнал.
В начале данного раздела мы получили формулу C.2), позволяющую рассчитать
спектр последовательности отсчетов {x(k)}, никак не связывая эти отсчеты с ана-
аналоговым сигналом. Только что полученная формула C.7) предполагает, что от-
отсчеты {x(k)} получены путем дискретизации аналогового сигнала s(t), и показы-
показывает связь между спектрами дискретизированного и аналогового сигналов. Следует
подчеркнуть, что эти две формулы дают одинаковый результат.
Отсюда следует еще один важный факт. Соединить отсчеты {x(k)} для получе-
получения аналогового сигнала можно произвольным образом. В каждом случае анало-
аналоговый сигнал будет, разумеется, иметь свой спектр. Однако результат суммиро-
суммирования сдвинутых копий спектров по формуле C.7) всегда будет одним и тем же,
поскольку определяется только значениями дискретных отсчетов {x(k)} = {s(kT)}
и формулой C.2).
Рисунок 3.5 наглядно демонстрирует и способ восстановления непрерывного
сигнала по дискретным отсчетам. Для этого необходимо пропустить дискретный
сигнал через идеальный фильтр нижних частот (ФНЧ) с частотой среза, рав-
равной половине частоты дискретизации. АЧХ такого фильтра показана на рис. 3.5
пунктиром.
Очевидно, что точное восстановление сигнала возможно, если сдвинутые копии
спектра не перекрываются. Из рис. 3.5 видно, что для этого необходимо, чтобы
частота дискретизации как минимум в два раза превышала верхнюю граничную
частоту в спектре сигнала:
2сов.
C.8)
Спектральное представление дискретного сигнала позволяет объяснить появле-
появление ложных частот (aliasing), речь о которых шла в разделе «Частота Найкви-
ста» этой главы. Пусть дискретизации подвергается гармонический сигнал с час-
134
Глава 3. Дискретные сигналы
тотой шо> превышающей частоту Найквиста, но меньшей частоты дискретизации.
Спектр такого сигнала показан на рис. 3.6 сверху. Сдвинутые копии спектра,
возникающие при дискретизации, создают попадающие в полосу восстановления
(от нуля до частоты Найквиста) спектральные составляющие с частотой ид - ю0
(рис. 3.6, снизу). Спектры, получающиеся после дискретизации гармонических
сигналов с частотами ш0 и <°д ~ ио> оказываются идентичными. Данный рисунок
иллюстрирует в частотной области процесс дискретизации гармонического сиг-
сигнала, показанный ранее на рис. 3.3.
-Шд -СОо
СОо
-2сод+соо -сод
сод-с
Рис. 3.6. Спектры аналоговой (сверху) и дискретизированной (снизу) синусоиды
с частотой, превышающей частоту Найквиста
В случае произвольного сигнала, если условие C.8) не выполняется, сдвинутые
копии спектра будут накладываться друг на друга, что приведет к неизбежным
искажениям при восстановлении непрерывного сигнала (рис. 3.7).
|Sa(co)|
Рис. 3.7. Перекрытие сдвинутых копий спектра при недостаточно высокой
частоте дискретизации
Эти искажения вызваны тем, что спектральные составляющие сигнала с частота-
частотами, превышающими частоту Найквиста, равную шд/2, не могут быть восстанов-
восстановлены правильно — вместо этого они вызывают наложение «хвостов» соседних
сдвинутых копий спектра и появление ложных частот.
Если подлежащий дискретизации сигнал может содержать спектральные состав-
составляющие с частотами, превышающими частоту Найквиста, полезно предвари-
предварительно пропустить его через ФНЧ с частотой среза, равной частоте Найквиста
Спектр дискретного сигнала
135
(рис. 3.8). При этом все равно будут потеряны высокочастотные составляю-
составляющие — сохранить их можно лишь путем повышения частоты дискретизации. Од-
Однако в этом случае благодаря отсутствию наложения «хвостов» не произойдет
появления ложных частот и диапазон частот 0...сод/2 будет представлен в дис-
дискретном сигнале без искажений.
№(»)! ♦
№.(ео)| А
Рис. 3.8. При дискретизации сигнала, содержащего высокочастотные составляющие (а),
полезно пропустить его через ФНЧ (б), чтобы избежать появления ложных частот (в)
Влияние формы дискретизирующих импульсов
Запишем выражение C.3) в более общей форме, используя вместо дельта-функ-
дельта-функций импульсы so(t) произвольной формы:
136 Глава 3. Дискретные сигналы
2> C.9)
Получить выражение для спектральной функции сигнала C.9) будет проще все-
всего, если рассмотреть этот сигнал как результат прохождения последовательности
дельта-функций C.3) через линейную стационарную систему с импульсной ха-
характеристикой so(t). Действительно, при этом каждая из дельта-функций в C.3)
будет порождать на выходе цепи сигнал so(t) с соответствующими временной за-
задержкой и амплитудным множителем, так что в результате получится именно
выражение C.9).
Поскольку при прохождении сигнала через линейную систему с постоянными
параметрами его спектр умножается на комплексный коэффициент передачи этой
системы (см. главу 2), спектр сигнала C.9) будет отличаться от выражения C.7)
лишь дополнительным множителем — спектром импульса so(t):
(З.Ю)
Итак, отличие формы дискретизирующих импульсов от дельта-функций вызы-
вызывает мультипликативные искажения спектра дискретного сигнала. Спектральная
функция импульса, имеющего конечную энергию, затухает с ростом частоты, по-
поэтому возникающие при дискретизации сдвинутые копии спектра сигнала s(t)
оказываются ослабленными.
Рассмотрим важный с практической точки зрения случай, когда so(t) представ-
представляет собой прямоугольный импульс с единичной амплитудой и длительностью,
равной периоду дискретизации (рис. 3.9, слева). В данном случае дискретный
сигнал приобретает ступенчатую форму, что характерно для сигнала на выходе
ЦАП перед сглаживающим фильтром (см. рис. 3.2). Искажения спектра при этом
описываются множителем 50 (со) следующего вида:
График модуля функции 50 (со) приведен на рис. 3.9 справа. Спад амплитудного
спектра на частоте Найквиста, равной л/Т, составляет
= 2а _
|50@)| я/2 п
В качестве примера на рис. 3.10 приведены результаты дискретизации треуголь-
треугольного импульса дельта-функциями и рассмотренными прямоугольными импуль-
импульсами.
Из графиков видно, что ЦАП сам по себе является фильтром нижних частот, од-
однако с весьма невысокой степенью подавления сдвинутых копий спектра. Кроме
того, поскольку АЧХ такого фильтра весьма далека от прямоугольной, он обла-
обладает сильной неравномерностью в полосе пропускания и заметно ослабляет вы-
высокочастотные составляющие сигнала (на частоте Найквиста ослабление состав-
составляет почти 4 дБ).
Теорема Котельникова
г 37
Рис. 3.9. Прямоугольный дискретизирующий импульс (слева)
и его амплитудный спектр (справа)
*(«) t
*Д1« t
Рис. 3.10. Дискретизация треугольного импульса (слева — сигналы, справа — спектры):
а — исходный аналоговый сигнал, б — дискретный сигнал в виде последовательности
дельта-функций, в — ступенчатый сигнал (пунктирной линией показана
форма амплитудного спектра дискретизирующих импульсов)
Теорема Котельникова
В начале данной главы уже было сформулировано утверждение о том, что неко-
некоторые сигналы могут быть без потерь информации представлены своими дис-
дискретными отсчетами. Полученное в предыдущем разделе выражение для спектра
138
Глава 3. Дискретные сигналы
дискретизированного сигнала позволяет выделить тот класс сигналов, для кото-
которых это возможно, и описать способ такого восстановления.
Согласно C.7), спектр дискретизированного сигнала представляет собой сумму
сдвинутых копий спектра исходного сигнала, при этом шаг сдвига равен частоте
дискретизации сод. Из рис. 3.5 видно, что если в спектре аналогового сигнала не
содержится составляющих с частотами, превышающими частоту Найквиста (сод/2),
то сдвинутые копии спектра не будут перекрываться. В этом случае использова-
использование идеального ФНЧ с прямоугольной АЧХ позволит выделить исходную (не-
(несдвинутую) копию спектра, сосредоточенную в окрестностях нулевой частоты,
и, таким образом, в точности восстановить исходный аналоговый сигнал.
АЧХ идеального ФНЧ, восстанавливающего аналоговый сигнал, приведена на
рис. 3.11 слева. Коэффициент передачи в полосе пропускания равен Т, а не еди-
единице, чтобы компенсировать множитель 1/Ув формуле C.7). С помощью обратного
преобразования Фурье найдем импульсную характеристику фильтра (рис. 3.11
справа):
sin| я—
T
C.11)
-к/Т
А@
-гт -т
гт
Рис. 3.11. Амплитудно-частотная (слева) и импульсная (справа) характеристики
идеального восстанавливающего фильтра
Дискретизированный сигнал C.3) представляет собой сумму дельта-функций.
При прохождении такого сигнала через восстанавливающий ФНЧ каждая дель-
дельта-функция породит на выходе соответствующим образом сдвинутую и масшта-
масштабированную копию импульсной характеристики фильтра. Выходной сигнал
(в точности соответствующий исходному аналоговому сигналу), таким образом,
будет представлять собой сумму сдвинутых и умноженных на отсчеты сигнала
копий импульсных характеристик идеального ФНЧ C.11):
sin я
s(t)=
t-kT
*=-»
t-kT
C.12)
Подводя итог всему сказанному, сформулируем теорему Котельникова: любой
сигнал s(t), спектр которого не содержит составляющих с частотами выше неко-
некоторого значения сов = 2я/в, может быть без потерь информации представлен свои-
Теорема Котельникова 139
ми дискретными отсчетами {s(kT)}, взятыми с интервалом Г, удовлетворяющим
следующему неравенству:
t<-L = JL. (злз)
2/в ©в
Восстановление исходного непрерывного сигнала s(t) по набору его дискретных
отсчетов {s(kT)} производится по формуле C.12).
ЗАМЕЧАНИЕ
В зарубежных источниках данная теорема называется теоремой Найквиста (Nyquist
theorem) или теоремой дискретизации (sampling theorem).
Формула C.12) представляет собой разложение сигнала s(t) в ряд по системе
функций {фк(ОЬ называемой базисом Котельникова:
. ( t-kT
sin я
t-kT '
тс
Г
Формирование непрерывного сигнала по его дискретным отсчетам поясняет
рис. 3.12. Пунктиром показаны графики отдельных слагаемых формулы C.12),
сплошной линией — восстановленный сигнал. Ниже приводится код MATLAB,
использованный при построении рисунка:
» t = -2:0.01:6: % времЯ длЯ восстановленного сигнала
» td = -2:6; % номера отсчетов
»s= [0 0432100 0]; % дискретный сигнал
» d = [td' s']; % данные длЯ функции pulstran
» у - pulstran(t. d, 'sine'): % восстановленный сигнал
» plot(td, s, 'о', t. у) % график восстановленного сигнала
» hold on % выводим графики отдельных sine-импульсов
» for k=l:length(s), plot(t. s(k)*sinc(t-td(k)). ':'), end
» hold off
ЗАМЕЧАНИЕ
При построении рис. 3.12 была использована функция pulstran. Она позволяет сформи-
сформировать сигнал в виде суммы конечного числа импульсов произвольной формы с заданны-
заданными задержками и множителями, что делает ее очень удобной при построении графиков
сигналов, восстановленных по дискретным отсчетам согласно теореме Котельникова. Эта
функция будет подробно рассмотрена далее, в разделе «Генерация последовательности
импульсов» этой главы.
Рисунок 3.12 наглядно демонстрирует главное свойство сигнала с ограниченным
спектром — его бесконечность во времени. Хотя отличны от нуля лишь несколь-
несколько отсчетов показанного сигнала, аналоговый сигнал оказывается бесконечно ко-
колеблющимся — между нулевыми отсчетами (на рисунке это отсчеты с номерами
-2, -1, 4, 5, 6) его значения отличны от нуля. Эти колебания нигде не заканчива-
заканчиваются, хотя их амплитуда стремится к нулю.
140
Глава 3. Дискретные сигналы
-2-1 0 1 2 3 4 5 6
Рис. 3.12. Восстановление непрерывного сигнала по его дискретным отсчетам
Иногда можно встретить примерно следующее «объяснение» сущности теоре-
теоремы Котельникова: «если брать отсчеты достаточно часто, в промежутках между
ними сигнал с ограниченными спектром не успеет сильно измениться, и мы смо-
сможем точно восстановить его». Такая трактовка является принципиально непра-
неправильной. Замечательное обсуждение этого вопроса содержится в [6], здесь же ог-
ограничимся краткими пояснениями и одним примером.
Когда мы говорим об ограниченной полосе частот сигнала, имеется в виду спек-
спектральная функция всего сигнала, имеющего бесконечную длительность. При этом
мгновенные спектры отдельных фрагментов сигнала могут содержать сколь угод-
угодно высокие частоты.
ЗАМЕЧАНИЕ
Под мгновенным спектром подразумевается спектральная функция «вырезанного» из сиг-
сигнала фрагмента конечной длительности.
В частности, в отдельном промежутке между соседними отсчетами сигнал с ог-
ограниченным спектром может иметь сколь угодно сложную форму, например
произвольное число раз менять знак.
В качестве примера восстановим по формуле C.12) непрерывный сигнал на ос-
основе последовательности, содержащей четыре ненулевых отсчета: ..., О, 0, 30, 1,
-1, -30, 0, 0,... (рис. 3.13):
» t = 0:0.01:8: ■
» td - 2:5;
» s = [30 1 -1 -30];
» d = [td1 s']:
» у = pulstrand, d.
» plotdd. s. 'o'. t
» grid
X времЯ длЯ восстановленного сигнала
X номера ненулевых отсчетов
X дискретный сигнал
X данные длЯ функции pulstran
'sine'): X восстановленный сигнал
У)
Теорема Котельникова
141
Результат, показанный на рис. 3.13, свидетельствует о том, что фрагмент восста-
восстановленного сигнала между 3-м и 4-м отсчетами представляет собой колебание с
периодом, равным интервалу дискретизации (то есть с частотой, вдвое превы-
превышающей частоту Найквиста!). Однако весь сигнал, составленный из сдвинутых
функций базиса Котельникова, не содержит спектральных составляющих с час-
частотами, большими частоты Найквиста.
40
30
20
10
0
-10
-20
-30
-40
Рис. 3.13. Сигнал с ограниченным спектром, содержащий фрагмент
с колебаниями высокой частоты
г-
(
J
1
\
\
\
\
\
\
V
\
..\
\
\
\
\
„ .Si
j
j
1
1
I
J
Восстановление радиосигнала
no отсчетам видеосигнала
Если для восстановления сигнала воспользоваться не ФНЧ, а идеальным поло-
полосовым фильтром со средней частотой исод и шириной полосы пропускания, рав-
равной сод, будет выделена пара сдвинутых копий спектра 5(со±2яя/Г). Из свойств
преобразования Фурье (см. формулу A.18) в разделе «Умножение сигнала на
гармоническую функцию» главы 1) следует, что такой спектр соответствует ра-
радиосигналу следующего вида (предполагается, что условие теоремы Котельнико-
Котельникова выполнено и сдвинутые копии спектра не перекрываются):
sp@ = 2s(t)cos(ti(uat) . C.14)
Таким образом, с помощью полосового фильтра можно из дискретных отсчетов
видеосигнала получить аналоговый радиосигнал.
Импульсная характеристика идеального полосового фильтра с указанными па-
параметрами имеет вид
t
sin л—
I T
t
я—
T
cosl2n—
142 Глава 3. Дискретные сигналы
Поэтому во временной области формирование радиосигнала по отсчетам видео-
видеосигнала описывается следующим образом:
. ( t-кТЛ
sin я I
5@= £ s(kT)—i JLJ.cashn—l C.15)
*=-» _t-RT \ T)
ЗАМЕЧАНИЕ
В формулах C.14) и C.15) имеется множитель со5(яоод£), что свидетельствует о чисто амп-
амплитудной модуляции получаемого радиосигнала. Подробнее о модуляции речь пойдет
в главе 8.
Квадратурная дискретизация
узкополосных сигналов
Пусть дискретизации необходимо подвергнуть узкополосный сигнал, который
в общем случае может иметь как амплитудную, так и угловую модуляцию:
S(t)-A(t) COS
где со0 — несущая частота, A(t) и <р(£) — законы амплитудной и фазовой модуля-
модуляции соответственно, представляющие собой медленно (по сравнению с cos(co0t))
меняющиеся функции.
Частоту дискретизации для такого сигнала можно выбрать исходя непосред-
непосредственно из теоремы Котельникова, при этом она должна быть не меньше, чем
со0 + Асо, где Асо — ширина спектра сигнала s(t). Однако возможен другой вари-
вариант (правда, требующий предварительной обработки сигнала) — квадратурная
дискретизация.
Запишем аналитический сигнал для s(t) (аналитический сигнал был рассмотрен
в разделе «Комплексная огибающая» главы 1):
s(t) = A(t)eMt)eia<".
Информация, переносимая сигналом, заключена в его комплексной огибающей
A(t) = A(t)eMt).
Спектр этого комплексного сигнала занимает полосу частот -Асо/2...Асо/2. По-
Поэтому, согласно теореме Котельникова, минимально допустимая частота дискре-
дискретизации для этого сигнала равна Дсо, что значительно меньше, чем в случае прямой
дискретизации. Однако отсчеты такого сигнала, естественно, будут комплексными.
Рассмотрим способ реализации квадратурной дискретизации (рис. 3.14). Вход-
Входной сигнал умножается на колебания двух генераторов (гетеродинов, heterodyne)
с частотой со0, сдвинутые по фазе друг относительно друга на 90° — cos со0£ и
sin aot. Результат каждого из умножений содержит две составляющие — низко-
низкочастотную и высокочастотную (на частоте 2со0):
Z-преобразование
143
s(t)cos(u0t = A(t)cos(p0t + (p(£))cosco0t =
| 1 A(t)cosBa>0t
ФНЧ
SUlfflg/
Рис. 3.14. Квадратурная дискретизация
Таким образом, для получения вещественной и мнимой частей комплексной оги-
огибающей сигнала нужно после перемножения пропустить результаты через фильт-
фильтры нижних частот, чтобы устранить вторую гармонику несущей. Полученные в
результате сигналы, пропорциональные ReA(t) и lmA(t), подвергаются дискре-
дискретизации с частотой не ниже, чем
Асо „
2 Асо
ЗАМЕЧАНИЕ :
Данная процедура сдвига спектра сигнала путем умножения его на опорное гармоническое
колебание с последующим вьвделением нужных спектральных составляющих с помощью
фильтра называется гетеродинированием (heterodyning).
Рассмотренная схема получила широкое распространение при обработке радио-
радиосигналов. Квадратурное гетеродинирование просто и дешево реализуется ана-
аналоговыми средствами, цифровая часть благодаря низкой частоте дискретизации
также оказывается сравнительно несложной.
Z-преобразование
Удобным способом анализа дискретных последовательностей является z-преоб-
z-преобразование (r-transform). Смысл его заключается в том, что последовательности
144 Глава 3. Дискретные сигналы
чисел {x(k)} ставится в соответствие функция комплексной переменной z, опре-
определяемая следующим образом:
X(z)= f>(£)z"\ C.16)
k = — 00
Разумеется, функция X(z) определена только для тех значений z, при которых
ряд C.16) сходится.
Z-преобразование играет для дискретных сигналов и систем такую же роль, как
преобразование Лапласа — для аналоговых. Определяющим при этом являет-
является тот факт, что, как мы увидим в главе 4, z-преобразование импульсной харак-
характеристики дискретной системы является дробно-рациональной функцией пере-
переменной z.
Примеры вычисления z-преобразования
Вычислим r-преобразование для некоторых часто встречающихся на практике
дискретных сигналов.
Единичная импульсная функция
Единичная импульсная функция является дискретным аналогом дельта-функ-
дельта-функции (см. раздел «Классификация сигналов» главы 1) и представляет собой оди-
одиночный отсчет с единичным значением:
t 4=0,
О, £*0.
Расчет его z-преобразования не представляет сложности:
Функция X0(z) сходится на всей комплексной плоскости.
Единичный скачок
Дискретный единичный скачок по смыслу полностью соответствует своему ана-
аналоговому прообразу (см. раздел «Классификация сигналов» главы 1):
Используя определение г-преобразования C.16), получаем
X(z)= ±x(k)z~k =£l Г*. C.18)
Ряд C.18) является суммой бесконечной геометрической прогрессии с первым
членом l-z"° = 1 и знаменателем z'x. Как известно, такой ряд сходится при
|z~'| < 1, то есть при | z \ > 1, и его сумма равна
Z-преобразование 145
C.19)
1 -с
ЗАМЕЧАНИЕ «
Можно записать результат и в виде X(z) = z/(z - 1), но в теории г-преобразования принято
использовать отрицательные степени z.
Дискретная экспоненциальная функция
Дискретная экспоненциальная функция определяется следующим образом:
О, k<0,
[ak, k>0.
Для вычисления z-преобразования нужно вычислить сумму следующего ряда:
со со
Как и в предыдущем случае, этот ряд представляет собой сумму геометрической
прогрессии. Первый член равен 1, знаменатель равен аг'х. Таким образом, ряд
сходится при \az'l\ < 1, то есть при \z\ > \a\, а его сумма равна
X(z) = ~-1. C.20)
i-az
Дискретная затухающая синусоида
Последняя из рассматриваемых здесь дискретных последовательностей представ-
представляет собой отсчеты синусоиды с произвольными частотой и начальной фазой и
экспоненциально меняющейся амплитудой:
x{k) = ак cos(©& + ф).
Для вычисления z-преобразования можно представить косинус по формуле Эй-
Эйлера в виде полусуммы двух комплексных экспонент, а потом воспользоваться
уже готовым результатом C.20):
_ cos(p-acos(co-(p)z~'
\-2acos{<u)z-1 +z-2
Так же как и в случае дискретной экспоненты, ряд сходится при |г| > \а\.
Связь z-преобразования с преобразованиями
Лапласа и Фурье
Дискретное z-преобразование очень просто связано с преобразованиями Лапла-
Лапласа и Фурье. Рассмотрим последовательность, определенную при k > 0, и сопоста-
сопоставим ей временной сигнал в виде набора дельта-функций:
f C.21)
146 Глава 3. Дискретные сигналы
где Т — интервал дискретизации. Преобразование Лапласа для сигнала C.21)
равно:
о*-° *=°
Воспользовавшись фильтрующим свойством дельта-функции (см. формулу A.1)
в разделе «Классификация сигналов» главы 1), получим
*-0
Эта формула переходит в формулу C.16), определяющую г-преобразование,
если выполнить подстановку z — ерТ.
Таким образом, взаимное соответствие между r-преобразованием X(z) и преоб-
преобразованием Лапласа 5(р) описывается следующим образом:
Похожими формулами описывается и связь r-преобразования X(z) с преобразо-
преобразованием Фурье 5(со) (заметим, что при рассмотрении этой связи нет необходимо-
необходимости считать последовательность односторонней):
) C.22)
Свойства z-преобразования
Тесная связь r-преобразования с преобразованиями Фурье и Лапласа обуслов-
обусловливает и подобие свойств этих преобразований. Однако имеется и некоторая спе-
специфика, возникающая из-за дискретного характера рассматриваемых сигналов.
Линейность
Z-преобразование, согласно определению C.16), является линейной комбинацией
отсчетов последовательности, поэтому оно подчиняется принципу суперпозиции:
если {*,(*)} <-> X{(z) и {x2(k)} ++ X2(z),
то {a Xi(k) + Ъ x2(k)} <r> aXi(z) + bX2(z).
Задержка
Если z-преобразование последовательности {x(k)} равно X(z), то г-преобразо-
г-преобразование последовательности, задержанной на k0 тактов (y(k) - x(k - k0)), будет
иметь вид
Z-преобразование
147
(z)= ±y(k)
z-k =
Таким образом, при задержке последовательности на kQ тактов необходимо ум-
умножить ее z-преобразование на z~*°. Множитель z~*° является оператором за-
задержки дискретной последовательности на k0 тактов.
Свертка
Свертка двух бесконечных дискретных последовательностей {xi(k)} и {x2(k)} опре-
определяется следующим образом:
Вычислим z-преобразование для последовательности {y(k)}:
Y(z) = У г
*—оГ
00
_ у1
00 I 00
—00 l П—00
C.23)
Итак, свертке дискретных последовательностей соответствует произведение их
z-преобразований.
ЗАМЕЧАНИЕ
Рассматриваемая здесь свертка бесконечных дискретных последовательностей называется
линейной сверткой; ее не следует путать с круговой сверткой периодических последователь-
последовательностей, речь о которой пойдет при описании свойств дискретного преобразования Фурье
в главе 5.
Обратное z-преобразование
Соответствие между дискретной последовательностью чисел и ее z-преобразова-
нием является взаимно-однозначным. Формула перехода от z-преобразования к
последовательности чисел называется обратным z-преобразованием и формаль-
формально записывается следующим образом:
C.24)
148 Глава 3. Дискретные сигналы
Интеграл в C.24) берется по произвольному замкнутому контуру, расположен-
расположенному в области сходимости функции X(z) и охватывающему все ее полюсы.
Практическое вычисление обратного r-преобразования чаще производится пу-
путем разложения функции X(z) на простые дроби. Поясним это на несложном
примере. Пусть
2 2
Представим X(z) в виде суммы простых дробей:
X(z) = 1— , = —Ц- \—. C.25)
1И 1 l
Из сравнения слагаемых C.25) с примерами z-преобразований C.19) и C.20)
видно, что первое слагаемое соответствует скачку с амплитудой, равной 2, а вто-
второе — дискретной показательной функции —2~ , k > 0. Итак, искомая последова-
последовательность имеет вид
О, k<0.
Дискретные случайные сигналы
Когда дискретизации подвергается случайный процесс, получаемая последова-
последовательность отсчетов будет зависеть от конкретной реализации дискретизируемого
процесса, и, следовательно, она должна анализироваться статистическими мето-
методами.
Что касается одномерной плотности вероятности и связанных с ней статистиче-
статистических характеристик, здесь нет никаких отличий от случая аналогового сигнала —
просто возможные одномерные сечения случайного процесса соответствуют мо-
моментам дискретизации: ^ = kT, и поэтому для привязки статистических парамет-
параметров ко времени можно использовать номер отсчета: рх(х, k), mx(k) и т. д.
Двумерные сечения дискретного случайного процесса также могут браться толь-
только в моменты дискретизации: tx = kT, t2"nT. Поэтому двумерная плотность веро-
вероятности и связанные с ней характеристики случайного процесса зависят от двух
номеров отсчетов k n n: px(xu x2, k, n), Rx(k, n) и т. д.
В случае стационарного в широком смысле случайного процесса одномерные ха-
характеристики не зависят от момента времени (номера отсчета), а двумерные за-
зависят лишь от промежутка между моментами времени (в дискретном случае —
от разности номеров отсчетов Ak = k - п):
рх(х, k) = рх(х),
mx(k) = тх,
Дискретные случайные сигналы
149
рх(хи хъ к, п) = рх(хи х2, Ak),
Rx{k, n) = Rx{Ak).
Таким образом, для стационарного дискретного случайного процесса корреляци-
корреляционная функция является дискретной, то есть представляет собой последователь-
последовательность чисел {Rx(Ak)}.
Для вещественного случайного процесса Rx{k, п) = Rx{n, k), а если процесс еще
и стационарный, то Rx{-k) = Rx(k).
Корреляционная матрица
Во многих задачах необходимо рассматривать конечный во времени фрагмент
случайного процесса длиной N отсчетов. В этом случае корреляционная функ-
функция Rx{k,ri) может быть представлена в виде матрицы, называемой корреляцион-
корреляционной матрицей случайного процесса (для простоты будем считать, что случайный
процесс имеет нулевое математическое ожидание):
Rx=[Rx(k,n)] =
х@)хф)
хA)хф)
x(O)x(N-l)
x(N)x@) x(N)x(i) ...
Чертой сверху здесь обозначено усреднение по ансамблю реализаций.
Если процесс нестационарный, все элементы матрицы могут быть различными.
В случае стационарного процесса корреляционная матрица полностью определя-
определяется своими первыми строкой и столбцом, поскольку вдоль всех диагоналей, па-
параллельных главной, стоят одинаковые элементы:
RAO)
RAO)
RX(N-2) ЯДЛГ-1)"
RAN-3) RAN~2)
Rx(-N + 2) Rx(-N + 3)
Rx(-N + 1) Rx(-N + 2)
RA0)
RAO)
ЗАМЕЧАНИЕ
Матрицы, обладающие таким свойством, называются матрицами Теплица (Toeplitz mat-
matrix). В MATLAB сгенерировать матрицу Теплица по первым строке и столбцу позволяет
функция toeplitz.
В случае вещественного случайного процесса, как уже отмечалось, Rx(-k) = Rx(k),
и корреляционная матрица становится симметричной:
150 Глава 3. Дискретные сигналы
R, =
RA0)
ад)
RAN-2)
RAN-1)
ад ...
RAO) ...
RAN-3) ...
RAN-2) ...
RAN-2)
RAN-3)
RAO)
ад)
RAN-i)
RAN-2)
ад)
RAO) .
C.26)
Важным свойством матриц вида C.26) является то, что они всегда являются
неотрицательно определенными, то есть все их собственные числа вещественны
и неотрицательны.
Дискретный белый шум
Так называется стационарный дискретный случайный процесс, отсчеты которо-
которого некоррелированы друг с другом:
о, д**о.
В отличие от случая аналогового белого шума, дисперсия дискретного белого
шума не является бесконечной, а потому такой шум является физически реали-
реализуемым.
Корреляционная матрица дискретного белого шума будет, очевидно, иметь диа-
диагональную структуру:
R,-D,I,
где I — единичная матрица.
Дискретные сигналы в MATLAB
Дискретный сигнал представляет собой последовательность чисел, а потому в
MATLAB он представляется в виде вектора. Если необходимо реализовать мно-
многоканальную обработку сигналов, для этого удобно использовать второе измере-
измерение, представив набор сигналов в виде матрицы. Многоканальная обработка
поддерживается многими функциями MATLAB.
Если сигнал одномерный, то в большинстве случаев функции MATLAB пра-
правильно обработают его при любой ориентации вектора — как в виде строки, так
и в виде столбца. Однако в многоканальном случае, когда входной сигнал пред-
представлен в виде матрицы, обработка производится по столбцам.
Таким образом, столбцы матрицы трактуются как сигналы разных каналов,
а строки — как отдельные векторные отсчеты многоканального сигнала. Для из-
избежания путаницы рекомендуется и в одноканальном случае задавать сигналы
в виде столбцов.
Отсчеты дискретного сигнала могут быть получены двумя путями. Первый ва-
вариант — расчет значений сигнала {моделирование сигнала), второй — получение
Дискретные сигналы в MATLAB 151
сигнала извне путем считывания его записи. Работу с записями сигналов в виде
wav-файлов мы рассмотрим ближе к концу главы, а сейчас обсудим моделирова-
моделирование сигналов.
Расчет временных функций
Аналоговый сигнал, как уже говорилось, с математической точки зрения пред-
представляет собой функцию (как правило — функцию времени), и при его дискретиза-
дискретизации мы получаем отсчеты, являющиеся значениями этой функции, вычисленны-
вычисленными в дискретные моменты времени. Поэтому для расчета дискретизированного
сигнала необходимо прежде всего сформировать вектор дискретных значений
времени. Для этого удобно задать значение частоты дискретизации Fs (sampling
frequency) и использовать обратную величину в качестве шага временного ряда:
» Fs = 8еЗ; % частота дискретизации 8 кГц
» t = 0:1/Fs:1; % одна секунда дискретных значений времени
» t = t'; % преобразуем строку в столбец
Сформировав вектор опорных значений времени, можно вычислять значения сиг-
сигнала, используя этот вектор в соответствующих формулах. Большинство мате-
математических функций MATLAB обрабатывают векторный аргумент поэлементно,
так что с этим проблем не возникает. Однако следует помнить о том, что опера-
операции умножения, деления и возведения в степень в MATLAB имеют матричный
смысл, поэтому при расчете одномерных функций времени следует использовать
поэлементные версии этих операций (.*, ./и .л). Приведем несколько примеров:
» А = 2; % амплитуда - два вольта
» fO = 1еЗ; % частота - 1 кГц
» phi = pi/4: % начальная фаза - 45°
» si = А * cosB*pi*fO*t + phi); % гармонический сигнал
» alpha = 1еЗ: % скорость затухания
» s2 = exp(-alpha*t) .* si; % затухающая синусоида
Для визуализации дискретных сигналов могут использоваться различные гра-
графические средства MATLAB в зависимости от конкретной ситуации. Часто
вполне допустимым является соединение дискретных отсчетов линиями, то есть
построение графика с помощью функции plot (рис. 3.15, а). При этом хорошо
видна общая форма сигнала (фактически в этом случае мы получаем график
аналогового сигнала, полученного путем линейной интерполяции), но незамет-
незаметны отсчетные точки. Если необходимо отобразить именно их, можно отказаться
от соединения точек линиями (рис. 3.15, б). N
Помимо функции plot существуют другие графические функции, специально
предназначенные для отображения дискретных последовательностей. Функция
stem изображает сигнал в виде «стебельков» (рис. 3.15, в), а функция stairs —
в ступенчатом виде (рис. 3.15, г). В последнем случае изображается аналоговый
сигнал с кусочно-постоянной интерполяцией (интерполяцией нулевого поряд-
порядка). Такой сигнал получается на выходе ЦАП при отсутствии сглаживающего
фильтра. Вот последовательность команд MATLAB, при помощи которой был
получен рис. 3.15:
152
Глава 3. Дискретные сигналы
» subp1otB, 2, 1); plot(s2(l:100))
» subp!otB. 2.. 2); p1ot(s2(l:100), '.'
» subp1otB, 2, 3); stem(s2A:100))
» subp!otB. 2. 4): stairs(s2(l:100))
1.5
1
0.5
О
-0.5
-1
40 eo
a
20
40
60
100
80
в г
Рис. 3.15. Различные формы представления графиков дискретного сигнала
ЗАМЕЧАНИЕ
Еще один способ визуализации сигналов обеспечивает функция strips. Она будет рассмот-
рассмотрена далее, в разделе «Чтение wav-файлов» этой главы.
Горизонтальная ось на приведенных графиках проградуирована в номерах отсче-
отсчетов. Чтобы показать на этой оси значения времени, при вызове графических
функций следует использовать два параметра, передав в первом из них соответ-
соответствующий временной вектор, например так:
plot(t(l:100). 52A:100))
Если необходимо сгенерировать многоканальный сигнал, каналы которого опи-
описываются одной и той же формулой, но с разными числовыми значениями пара-
параметров, для этого можно эффективно использовать средства матричных операций
MATLAB. Простейший пример — генерация набора синусоид с заданными час-
частотами (в приводимом ниже коде используется вектор t, сформированный ранее):
» f = [600 800 1000 1200 1400]; % вектор частот (строка!)
» s3 = cosB*pi*t*f); % пятиканальный сигнал
Дискретные сигналы в MATLAB
153
Здесь столбец значений времени t умножается на строку частот f. В результате
получается матрица, содержащая все необходимые значения произведения вре-
времени и частоты. Далее эта матрица подвергается поэлементным преобразовани-
преобразованиям (умножение на 2л и вычисление косинуса). Результат вычислений показан на
рис. 3.16:
» plot(t(l:100),
хЮ"
Рис. 3.16. Многоканальный сигнал
ЗАМЕЧАНИЕ
Напомним, что при визуализации матрицы функция plot строит графики именно по
столбцам.
Если вычисление значений сигнала производится однократно, необходимые вы-
вычисления можно выполнить в ходе интерактивного сеанса работы либо описать в
тексте MATLAB-программы. Если же в ходе решения задачи необходимо по-
повторно обращаться к вычислениям, целесообразно оформить их в виде функции
(см. раздел «Программирование» приложения А). При этом следует иметь в
виду, что для использования многочисленных эффективных численных алгорит-
алгоритмов, реализованных в MATLAB, функция для расчета значений сигнала должна
быть способна принимать векторный аргумент, содержащий набор значений вре-
времени.
Кусочные зависимости
Довольно часто возникает необходимость моделирования отсчетов сигнала, ко-
который для разных интервалов времени описывается разными формулами. Про-
Простейший случай такого рода — моделирование импульсов конечной длительно-
длительности, значения которых описываются одной или несколькими формулами в пре-
пределах заданного интервала, а в остальное время равны нулю.
154 • Глава 3. Дискретные сигналы
В MATLAB возможно несколько способов задания кусочных функций. Первый
вариант — воспользоваться тем, что операции сравнения возвращают 1 при вы-
выполнении неравенства и 0 в противном случае, причем в случае векторного аргу-
аргумента возвращается вектор результатов сравнения. Зададим таким образом од-
односторонний экспоненциальный импульс (см. рис. 1.18):
s - А * exp(-alpha * t) .* (t >= 0);
Прямоугольный импульс, центрированный относительно начала отсчета време-
времени (см. рис. 1.10):
s = А * (abs(t) <= Т/2):
Несимметричный треугольный импульс (см. рис. 1.14):
S = А * t / Т .* (t >= 0) .* (t <= Т);
В приведенных примерах следует обратить внимание на использование операто-
оператора .* для поэлементного перемножения векторов.
Недостаток данного способа состоит в том, что значения сигнала сначала вычис-
вычисляются по заданной формуле для всех значений аргумента и лишь затем «выре-
«вырезается» нужная область. Помимо возрастания времени вычислений это может
привести к выдаче сообщения об ошибке, например, если при вычислении экс-
экспоненты в первом из приведенных примеров для большого отрицательного зна-
значения аргумента t произойдет переполнение.
Второй способ — выполнять вычисления только для тех моментов времени, для
которых это действительно необходимо. Выделение набора элементов вектора t,
для которых выполняется заданное условие, производится с помощью функции
find. В этом случае следует принять во внимание два аспекта:
□ необходимо заранее, до вычислений, создать вектор сигнала такого же разме-
размера, как вектор моментов времени t (обычно этот вектор заполняют нулями);
□ поскольку набор номеров элементов вектора t, для которых выполняются нуж-
нужные условия, придется использовать два раза, целесообразно сохранить этот
набор в переменной.
Покажем, как данным способом генерируются те же три кусочно-заданных сиг-
сигнала.
Односторонний экспоненциальный импульс:
% заполняем вектор сигнала нулями
s = zeros(size(t)):
% находим номера неотрицательных элементов вектора t
inds - findCt >= 0);
% рассчитываем сигнал только в нужных точках
s(inds) = А * exp(-alpha * t(inds));
Прямоугольный видеоимпульс (поскольку для расчета значений такого импуль-
импульса не требуется вычислений с вектором t, переменную inds можно не создавать —
она понадобилась бы лишь один раз):
s - zeros(size(t));
s(find(abs(t) <- Т/2)) - А;
Дискретные сигналы в MATLAB 155
Несимметричный треугольный импульс:
s - zeros(size(t));
inds = findUt >- 0) & (t <= T)):
s(inds) = A * t(inds) / T;
Как видите, команд в данном случае нужно больше, но зато при этом не будет
выполняться лишних вычислений и не появятся упомянутые выше сообщения
об ошибках.
Функции генерации одиночных импульсов
В пакете Signal Processing имеется ряд функций, генерирующих часто встречаю-
встречающиеся на практике непериодические сигналы:
□ rectpul s — прямоугольный импульс;
□ tripuls — треугольный импульс;
□ sine — импульс вида sin(nt)/(nt);
□ gauspul s — радиоимпульс с гауссовой огибающей;
□ pul stran — последовательность из конечного числа импульсов произвольной
формы.
Далее эти функции рассматриваются более подробно.
Прямоугольный импульс
Для формирования одиночного прямоугольного импульса с единичной амплиту-
амплитудой служит функция rectpul s:
у = rectpuls(t. width)
Здесь t — вектор значений времени, width — ширина (длительность) импульса.
Возвращаемый результат у — вектор рассчитанных значений сигнала, определяе-
определяемых по следующей формуле:
и _
Параметр width можно опустить, при этом его значение по умолчанию равно 1
и функция rectpul s производит результат, соответствующий математической
функции rect.
В качестве примера сформируем пару разнополярных прямоугольных импуль-
импульсов с амплитудой 5 В и длительностью 20 мс каждый, расположенных справа и
слева от начала отсчета времени. Частоту дискретизации выберем равной 1 кГц.
Результат показан на рис. 3.17:
» Fs - 1еЗ: % частота дискретизации
» t - -40e-3:l/Fs:40e-3; % дискретное время
» Т - 20е-3; % длительность импульсов
156
Глава 3. Дискретные сигналы
» А = 5: % амплитуда
» s = -А * rectpuls(t+T/2. T) + А * rectpuls(t-T/2. T):
» plotCt. s)
» ylim([-6 б])
ь
4
2
0
-2
-4
-R
■
-
-
-
-
-0.04 -0.03 -0.02 -0.01 0 0.01 0.02 0.03 0.04
Рис. 3.17. Сигнал, сформированный с использованием функции rectpuls
Треугольный импульс
Для формирования одиночного треугольного импульса с единичной амплитудой
служит функция tripuls:
у = tripuls(t. width, skew)
Здесь t — вектор значений времени, width — ширина (длительность) импульса,
skew — коэффициент асимметрии импульса, определяющий положение его вер-
шины. Пик импульса расположен при t = width*skew/2. Параметр skew должен ле-
лежать в диапазоне от -1 до 1.
Возвращаемый результат у — вектор рассчитанных значений сигнала, определяе-
определяемых по следующей формуле:
2t + width
width (skew +1)
It- width
width width • skew
2~~ < 2 '
width-skew _ , width
width(skew -1)'
0,
Параметры skew или skew и width можно опустить, при этом используются их зна-
значения по умолчанию: skew = 0 (симметричный импульс) и width = 1.
В качестве примера сформируем симметричный трапециевидный импульс с амп-
амплитудой 10 В и размерами верхнего и нижнего оснований 20 и 60 мс соот-
Дискретные сигналы в MATLAB
157
ветственно. Частоту дискретизации выберем равной 1 кГц. Результат показан на
рис. 3.18:
» Fs = 1еЗ: % частота дискретизации
» t = -50e-3:l/Fs:50e-3: % дискретное времЯ
» А = 10; % амплитуда
» Т1 = 20е-3; % верхнее основание
» Т2 = б0е-3; % нижнее основание
» s = A*(T2*tripuls(t, T2) - Tl*tripuls(t,
» plot(t, s)
-0.05 0 0.05
Рис. 3.18. Сигнал, сформированный с использованием функции tripuls
Импульс с ограниченной полосой частот
Для формирования сигнала, имеющего прямоугольный, то есть ограниченный
по частоте спектр, служит функция si nc:
у = sinc(t)
Единственным входным параметром является вектор значений времени t.
Возвращаемый результат у — вектор рассчитанных значений сигнала, определяе-
определяемых по следующей формуле:
sin(nx)
У=-
пх
ВНИМАНИЕ
В отечественной литературе под функцией sine чаще всего понимается выражение
sin(x)/x — без умножения аргумента на л. Средствами MATLAB такая функция может
быть рассчитана как sinc(x/pi).
Спектральная функция сигнала, генерируемого функцией sine, имеет прямо-
прямоугольный вид:
158
Глава 3. Дискретные сигналы
1, | Сй | < ТС,
О, | ю | > тс.
В качестве примера построим с помощью функции sine график амплитудного
спектра очень короткого радиоимпульса, на длительности которого укладывает-
укладывается лишь один период синусоидального заполнения. Согласно свойствам преоб-
преобразования Фурье (см. главу 1) спектр такого сигнала должен представлять собой
сумму двух спектров прямоугольного импульса, сдвинутых на величину частоты
заполнения в сторону положительных и отрицательных частот. Спектр прямо-
прямоугольного импульса, в свою очередь, описывается именно функцией sine (см. фор-
формулу A.14) в разделе «Примеры расчета преобразования Фурье» главы 1). Ре-
Результат показан на рис. 3.19.
50
Рис. 3.19. Короткий радиоимпульс (сверху) и его амплитудный спектр (снизу),
построенный с помощью функции sine
Fs
t
fO
T
s
f
- Ie3;
- -O.l:l/Fs:O
- 10;
- 1/fO:
- rectpuisCt.
- -50:50;
1-
T)
Дискретные сигналы в MATLAB 159
% частота дискретизации
% дискретное времЯ
% частота заполнения
% длительность радиоимпульса
.* cosB*pi*fO*t); % радиоимпульс
% вектор частот длЯ расчета спектра
» sp = Т/2 * (sinc((f-fO)*T) + sinc((f+fO)*T));
» plot(t. s) % график сигнала
» yl1m([-l.l 1.1])
» figure
» plot(f, abs(sp)) % график амплитудного спектра
Как видите, из-за наложения друг на друга «хвостов» функции sine спектр ока-
оказывается существенно несимметричным относительно частоты заполнения ра-
радиоимпульса. Более подробно этот эффект будет обсуждаться в главе 8, посвя-
посвященной модуляции.
Гауссов радиоимпульс
Для формирования одиночного радиоимпульса с гауссовой огибающей и единич-
единичной амплитудой служит функция gauspul s:
у = gauspu1s(t. fc, bw, bwr)
Здесь t — вектор значений времени, fc — несущая частота в герцах, bw — относи-
относительная ширина спектра (ширина спектра, деленная на несущую частоту), bwr —
уровень (в децибелах), по которому производится измерение ширины спектра.
Возвращаемый результат у — вектор рассчитанных значений сигнала, определяе-
определяемых по следующей формуле:
у - exp(-a f2) cosB7t/cO- C-27)
Коэффициент а управляет длительностью импульса и, соответственно, шириной
его спектра. Сигнал C.27) имеет спектральную функцию, равную (см. раздел
«Примеры расчета преобразования Фурье» главы 1)
(ш+2я/е)М ( (со-2 Y
Если /с » Va, то можно пренебречь наложением «хвостов» сдвинутых копий
спектра. Тогда параметр а связан с относительной шириной спектра и уровнем
(в децибелах), по которому она определяется, следующим образом:
а_ 5B7t/c-bwJ
bwr-lnlO
Параметры bwr, bw и fс можно опустить, при этом используются их значения по
умолчанию: bwr - -6 дБ, bw - 0,5 и fc = 1000 Гц.
При вызове функции gauspuls можно использовать от одного до трех выходных
параметров:
[у, yq. ye] = gauspuls(...)
160
Глава 3. Дискретные сигналы
Во втором выходном параметре yq функция возвращает квадратурное (quadra-
(quadrature ) дополнение для рассчитанного радиоимпульса у. Вектор yq отличается от век-
вектора у фазовым сдвигом несущего колебания на 90° (подробнее о понятии квад-
квадратурного дополнения речь шла в разделе «Преобразование Гильберта» главы 1).
В третьем выходном параметре уе функция возвращает огибающую (envelope)
сформированного радиоимпульса. Вектор уе представляет собой первый множи-
множитель формулы C.27) (отсутствует умножение на косинус).
В качестве примера сформируем гауссов радиоимпульс с несущей частотой
4 кГц и относительной шириной спектра 10 %, измеренной по уровню -20 дБ,
а затем построим график его спектра, чтобы убедиться в правильности расчетов.
Частоту дискретизации примем равной 16 кГц. Результат показан на рис. 3.20.
-100 ■
-150
-200
0.01
1000 2000 3000 4000 5000 6000 7000 8000
Рис. 3.20. Гауссов радиоимпульс, сформированный функцией gauspuls (сверху),
и его амплитудный спектр (снизу)
Дискретные сигналы в MATLAB 161
» Fs = 1беЗ; % частота дискретизации
» t = -10e-3:l/Fs:10e-3; % дискретное время
» Fc = 4еЗ: % несущая частота
» bw = 0.1: % относительная ширина спектра
» bwr = -20: % уровень измерения ширины спектра
» s = gauspulsCt. Fc, bw, bwr):
» Nfft = 2xnextpow2(length(s)):
» sp = fft(s, Nfft): % спектр
» sp_dB = 20*loglO(abs(sp)): % амплитудный спектр в децибелах
» f = @:Nfft-1)/Nfft*Fs: % вектор частот спектра
» plot(t, s) % график сигнала
» figure
» % график амплитудного спектра
» plot(f(l:Nfft/2), sp_dB(l:Nfft/2))
» % максимальный уровень спектра в децибелах
» sp_max_db = 20*1oglO(max(abs(sp))):
» edges = Fc * [l-bw/2 l+bw/2]: % граничные частоты
» % отображаем заданные при расчете границы спектра
» hold on
» plotCedges. sp_max_db([l l])+bwr. 'о')
» hold off
Из графика спектра (см. рис. 3.20 снизу) видно, что заданные при вызове функ-
функции gauspul s параметры спектра выдержаны точно.
Наконец, у функции gauspul s есть еще один вариант использования — она позво-
яет рассчитать время, за которое огибающая гауссового импульса упадет до за-
заданного уровня относительно максимума. При этом вместо вектора значений
времени в качестве первого входного параметра используется строка 'cutoff:
tc = gauspuls('cutoff'. fc, bw, bwr. tpe)
Входные параметры fc, bw и bwr имеют тот же смысл, что и раньше, a tpe — уро-
уровень огибающей (в децибелах относительно максимума), момент достижения ко-
которого нужно определить.
Возвращаемый результат tc — момент достижения огибающей уровня tpe (то
есть полуширина импульса, измеренная по уровню tpe).
В качестве примера рассчитаем время, за которое огибающая сформированного в
предыдущем примере импульса уменьшается на 6 дБ (примерно в два раза):
» gauspulsC 'cutoff'. Fc, bw., bwr. -6)
ans =
0.0020
Полученный результат соответствует графику сигнала, приведенному выше на
рис. 3.20.
Генерация последовательности импульсов
Функция pul stran служит для генерации конечной последовательности импуль-
;ов (pulse train) одинаковой формы с произвольно задаваемыми задержками
162 Глава 3. Дискретные сигналы
и уровнями. Сами импульсы могут задаваться одним из двух способов: именем
функции, генерирующей импульс, либо уже рассчитанным вектором отсчетов.
Если импульсы задаются именем генерирующей функции, функция pul stran вы-
вызывается следующим образом:
у - pulstrarHt. d. 'func', pi, p2, ...)
Здесь t — вектор значений времени, d — вектор задержек, 'func1 — имя функции,
генерирующей одиночный импульс. В качестве этой функции могут исполь-
использоваться, например, rectpuis, tripuls, gauspuls, а также любые другие функции
.(в том числе и «самодельные»), принимающие в качестве первого входного пара-
параметра вектор моментов времени и возвращающие вектор рассчитанных отсчетов
сигнала. Оставшиеся параметры pi, р2, ... — дополнительные, они передаются
функции func при ее вызове.
Таким образом, функция pul stran в данном варианте использования генерирует
выходной сигнал следующим образом:
у = func(t-dd), pi, р2, ...) + ...
func(t-dB). pi. р2. ...) + ...
func(t-dC). pi. р2, ...) + ...
Если d — двухстолбцовая матрица, то первый столбец трактуется как задержки
импульсов, а второй — как их уровни. При этом выходной сигнал формирует-
формируется так:
у = d(l.l) * func(t-dA.2). pi, p2. ...) + ...
dB,l) * func(t-dB,2), pi, p2, ...) + ...
dC.1) * func(t-dC,2). pi. p2, ...) + ...
В качестве примера сформируем последовательность из пяти симметричных
треугольных импульсов, интервалы между которыми линейно увеличиваются,
а амплитуды экспоненциально уменьшаются. Частоту дискретизации выберем
равной 1 кГц. Длительность импульса — 20 мс. Результат показан на рис. 3.21:
» Fs » 1еЗ; % частота дискретизации
» t = 0:1/Fs:0.5: % дискретное времЯ
» tau = 20е-3; % длительность импульса
» d - [20 80 160 260 380]' * 1е-3: % задержки импульсов
» d(:,2) = 0.8.А@:4)': % амплитуды импульсов
» у - pulstrarUt, d. 'tripuls'. tau):
» plot(t, у)
Если для генерации одиночного импульса нет готовой функции, можно рас-
рассчитать вектор отсчетов импульса, а затем использовать второй вариант вызова
функции pul stran:
у = pulstranCt. d, p, fs, 'method')
Смысл входных параметров t и d тот же, что и раньше. Вектор р должен содер-
содержать отсчеты одиночного импульса, а параметр f s указывает частоту дискретиза-
Дискретные сигналы в MATLAB
163
ции, использованную при расчете этого вектора. Считается, что первый отсчет
из вектора р соответствует нулевому моменту времени.
Рис. 3.21. Последовательность треугольных импульсов, сформированная
с помощью функции pulstran
Поскольку частота fs может не совпадать с шагом значений вектора t (в принци-
принципе они даже не обязаны представлять собой равномерную последовательность)
и задержки из вектора d тоже не обязательно кратны этому шагу, для пересчета
задержанных импульсов к сетке моментов времени t в общем случае необходимо
использование интерполяции. Метод интерполяции может быть явно задан с по-
помощью строкового параметра ' method'. Возможны все методы, поддерживаемые
функцией interpl: 'nearest', 'linear', 'spline', 'pchip', 'cubic' и 'v5cubic'.
Параметры fs и 'method' при вызове могут опускаться, в этом случае использу-
используются их значения по умолчанию: f s - 1 и ' method' ■ ' 1 i near'.
В качестве примера сформируем последовательность из шести импульсов, имею-
имеющих форму одного периода функции sin2. Пусть длительность импульса равна
60 мс, а частота его дискретизации — 400 Гц. Расстояние между центрами им-
импульсов будет одинаковым и равным 64 мс, а частота дискретизации выходного
сигнала — 1 кГц. Импульсы будут экспоненциально затухать с ростом номера.
Результат показан на рис. 3.22.
» % генерируем вектор отсчетов одиночного импульса
» FsO = 400; % частота дискретизации импульса
»- tau = 60е-3; % длительность импульса
» to = 0:1/FsO:tau: % дискретное время для импульса
» sO = sin(pi*tO/tau).*2; % вектор отсчетов импульса
» % генерируем последовательность импульсов
» Fs = 1еЗ; % частота дискретизации последовательности
» t = 0:1/Fs:0.5: % дискретное времЯ для последовательности
» d ■ A:6)' * 64е-3; % задержки импульсов
164
Глава 3. Дискретные сигналы
» d(:,2) = 0.6.Л@:5)'; % амплитуды импульсов
» % последовательность импульсов
» у = puistrantt. d. sO. FsO):
» p!ot(t. у)
'О 0.1 0.2 0.3 0.4 0.5
Рис. 3.22. Последовательность импульсов, сформированная функцией pulstran
из вектора отсчетов одиночного импульса
Функции генерации периодических сигналов
Эти функции, входящие в пакет Signal Processing, позволяют формировать от-
отсчеты периодических сигналов различной формы:
□ square — последовательность прямоугольных импульсов;
□ sawtooth — последовательность треугольных импульсов;
□ diric — функция Дирихле (периодическая sine-функция).
Последняя рассматриваемая в данном разделе функция chi гр генерирует не пе-
периодический сигнал, а колебания с меняющейся частотой.
Далее эти функции рассматриваются более подробно.
Последовательность прямоугольных импульсов
Для формирования последовательности прямоугольных импульсов служит функ-
функция square. В простейшем случае эта функция принимает один входной пара-
параметр — вектор значений времени t:
у = square(t)
Генерируемая при этом последовательность импульсов имеет период 2п и скваж-
скважность 2 (то есть длительность импульса равна половине периода). Последова-
Последовательность является двуполярной — сигнал принимает значения -1 и 1.
Сформировать последовательность с периодом Т можно следующим образом:
у = squareB*pi*t/T)
Дискретные сигналы в MATLAB
165
С помощью второго входного параметра duty можно регулировать скважность
получаемой последовательности. Однако этот параметр задает не саму скваж-
скважность, а обратную ей величину — коэффициент заполнения (в процентах), то есть
отношение длительности импульса к периоду:
у = squared, duty)
По умолчанию значение параметра duty равно 50, то есть генерируется меандр.
ВНИМАНИЕ
Обратите внимание на то, что значение параметра duty задается именно в процентах, а не
в дробных единицах.
В качестве примера сформируем последовательность однополярных прямоуголь-
прямоугольных импульсов с амплитудой 3 В, частотой следования 50 Гц и длительностью
5 мс. Будем использовать частоту дискретизации 1 кГц и временной интервал
-10... 50 мс (рис. 3.23):
» Fs = 1еЗ: % частота дискретизации
» t = -10e-3:l/Fs:50e-3; % дискретное времЯ
» А = 3:
» fO = 50;
» tau = 5е-3:
» s = (squareB*pi*t*fO, f0*tau*100)
» plot(t. s)
» ylim([0 5])
% амплитуда
% частота следования импульсов
% длительность импульсов
1) * А/2;
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
-
-
■
■
•
-0.01 0 0.01 0.02 0.03 0.04 0.05
Рис. 3.23. Последовательность прямоугольных импульсов,
полученная с помощью функции square
ЗАМЕЧАНИЕ
На рис. 3.23 видно, что импульсы имеют неодинаковую ширину. Поскольку длительность
импульса в данном случае равна ровно пяти интервалам дискретизации E мс х 1 кГц - 5),
из-за погрешностей представления значений времени в компьютере каждый импульс мо-
может быть представлен либо пятью, либо шестью ненулевыми отсчетами.
166
Глава 3. Дискретные сигналы
Последовательность треугольных импульсов
Для формирования последовательности треугольных импульсов служит функ-
функция sawtooth. В простейшем случае эта функция принимает один входной пара-
параметр — вектор значений времени t:
у = sawtooth(t)
Генерируемая при этом последовательность импульсов имеет период 2ти. На про-
протяжении периода сигнал линейно нарастает от -1 до 1.
Сформировать последовательность с периодом Т можно следующим образом:
у = sawtoothB*pi*t/T)
С помощью второго входного параметра width можно регулировать длительность
«обратного хода» — промежутка, на котором уровень сигнала линейно падает от 1
до -1. При указании параметра width сигнал линейно возрастает от -1 до 1 за
время 2л width, а затем за время 2яA - width) линейно убывает от 1 до -1:
у = sawtooth(t, width)
По умолчанию значение параметра width равно 1. При width = 0,5 получится по-
последовательность симметричных треугольных импульсов.
В качестве примера сформируем последовательность треугольных импульсов от-
отрицательной полярности с амплитудой 5 В, периодом 50 мс и длительностью па-
падающего участка 5 мс. Будем использовать частоту дискретизации 1 кГц и вре-
временной интервал -25 ... 125 мс (рис. 3.24).
-0.04 -0.02 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14
Рис. 3.24. Последовательность треугольных импульсов, полученная
с помощью функции sawtooth
» Fs - 1еЗ:
» t - -25e-3:l/Fs-.125e-3:
» А - 5:
» Т « 50е-3;
» tl - 5е-3;
% частота дискретизации
% дискретное время
% амплитуда
% период
% длительность падающего участка
Дискретные сигналы в MATLAB 167
» s = (sawtoothB*pi*t/T, 1-tl/T) - 1) * А/2:
» plot(t. s)
Функция Дирихле
Функция Дирихле описывается формулой
п sin (ж/2)
где п — целое положительное число.
Функция имеет пульсирующий вид: пульсации максимального уровня располо-
расположены при х - 2nk, значение функции в этих точках равно (-1)*(п" Ч Между эти-
этими главными пульсациями расположены пульсации меньшего уровня. При не-
нечетном п все главные пульсации имеют положительную полярность, и период
функции равен 2я. При четном п полярность главных пульсаций чередуется,
и период функции оказывается вдвое больше — 4л.
Для расчета функции Дирихле в MATLAB служит функция diric. Синтаксис ее
вызова следующий:
у = diric(x. n)
Назначение входных параметров х и п соответствует приведенной выше фор-
формуле.
Функцию Дирихле называют еще периодической sine-функцией (о функции sine
речь шла в этой главе ранее, в разделе «Импульс с ограниченной полосой час-
частот»). При нечетном п это действительно так, и функцию Дирихле можно пред-
представить следующим образом:
(ft
diric,, (ж) = £ sine n\—-k
При четном п функция Дирихле является суммой сдвинутых во времени sine-
функций с чередующимися знаками:
00 (ft
diricn(x) = X И)* sine я —
Поскольку функция sine имеет равномерный спектр в полосе частот от нуля
до я, представление функции Дирихле в виде ряда Фурье (такое представление
легко получить с помощью формулы, приведенной в разделе «Связь преобразо-
преобразования Фурье и коэффициентов ряда Фурье» главы 1) имеет очень простой вид —
количество гармонических слагаемых конечно, а их амплитуды одинаковы:
□ при нечетном п
ч 1 2 , v 2 /о ч 2 (и-1
^) = - + -cos(x) + -cosB^)+ ... + -cos х
п п п п \ 2
□ при четном п
2-^-2-Щ+... + и^:
(х\ 2
cos — +-cos
я \2) п
168
Глава 3. Дискретные сигналы
В качестве примера построим графики функции Дирихле при нечетном и чет-
четном значениях п (и = 7 и п - 8, рис. 3.25):
» х = 0:0.01:15:
» plot(x, diric(x. 7))
» grid on
» titleCn = 7')
» figure
» plot(x. diric(x, 8))
» grid on
» titleCn = 8')
'0 5 10 15
Рис. 3.25. Функция Дирихле нечетного (сверху) и четного (снизу) порядка
Генерация сигнала с меняющейся частотой
Функция chi гр предназначена для генерации колебаний с единичной амплиту-
амплитудой, мгновенная частота которых меняется по заданному закону:
Дискретные сигналы в MATLAB 169
у = chirp(t. fO. tl. fl, 'method', phi)
Здесь t — вектор значений времени, phi — начальная фаза колебания. Осталь-
Остальные параметры определяют закон изменения частоты.
ЗАМЕЧАНИЕ
Подробнее понятие мгновенной частоты будет обсуждаться в разделе «Угловая модуля-
модуляция» главы 8.
Строковый параметр 'method' определяет тип зависимости мгновенной частоты
от времени — 'linear', 'quadratic' или 'logarithmic'. Числовые параметры fO, tl
и f 1 создают опорные точки для расчетов: в нулевой момент времени мгновенная
частота равна fO, а в момент времени tl она равна fl.
Математически закон изменения мгновенной частоты выглядит следующим об-
образом:
□ 'linear':
/о + Р*. где p = AzA;
□ 'quadratic':
fo + №2, где
□ 'logarithmic' на деле противоречит своему названию — зависимость мгновен-
мгновенной частоты от времени при этом не логарифмическая, а экспоненциальная:
где
ЗАМЕЧАНИЕ
Диапазон значений времени в векторе t может не включать в себя значений 0 и tl.
Параметры phi и 'method' при вызове функции можно опускать, тогда будут ис-
использованы их значения по умолчанию: phi = 0 и 'method' ж 'linear'.
Ограничение сигнала по длительности не производится, колебания генерируют-
генерируются для всех значений времени, переданных функции в векторе t.
В качестве примера сформируем три сигнала, определенных на промежутке
О ... 1 с и имеющих разные законы изменения мгновенной частоты. В нулевой мо-
момент времени все сигналы имеют мгновенную частоту 1 кГц, а в момент време-
времени 1 с — 2 кГц. Частоту дискретизации выберем равной 8 кГц:
» Fs = 8еЗ: % частота дискретизации
» t = O:l/Fs:l; % дискретное времЯ
» fO = 1еЗ:
» tl - 1:
» fl = 2еЗ;
» si = chirp(t. fO. tl. fl, 'linear'):
» s2 = chirp(t, fO, tl. fl, 'quadratic'):
170
Глава 3. Дискретные сигналы
» s3 = chirp(t, fO. tl, fl. 'logarithmic');
» specgram(sl, [], Fs)
» title('linear')
» colormap gray
» figure
» specgram(s2, []. Fs)
» title('quadratic')
» colormap gray
» figure
» specgram(s3, [], Fs)
» titleClogarithmic')
» colormap gray
На рис. 3.26-3.28 показаны спектрограммы сформированных сигналов, наглядно
демонстрирующие характер изменения мгновенной частоты при различных зна-
значениях параметра 'method1. Обратите внимание на то, что значения мгновенной
частоты при t = 0 и t = 1 для всех трех сигналов совпадают.
ЗАМЕЧАНИЕ
Функция specgram строит спектрограмму, то есть зависимость мгновенного амплитудно-
амплитудного спектра сигнала от времени. Величина модуля спектральной функции отображается
цветом в координатах «время — частота». Подробнее о функции specgram будет рассказа-
рассказано в главе 5. Команда colormap gray устанавливает для графиков палитру оттенков серого
цвета; в противном случае при черно-белом воспроизведении цветных спектрограмм зави-
зависимость оттенка от уровня амплитудного спектра оказалась бы немонотонной.
0.1 0.2 0.3 0.4 0 5 0.5 0.7 0.8 0.S
• 'Тем
Рис. 3.26. Спектрограмма сигнала, сформированного функцией chirp
при линейном законе изменения мгновенной частоты
Дискретные сигналы в MATLAB
171
quadratic
0.1 0 2 0.3 0.4 0.5 0.6 0.7 0 8 OS
Рис. 3.27. Спектрограмма сигнала, сформированного функцией chirp
при квадратичном законе изменения мгновенной частоты
logarithmic
8.1 0,2 ' 0.3 0.4 0.5
'" Time
0,7 ' 0.8 0.9
Рис. 3.28. Спектрограмма сигнала, сформированного функцией chirp
при экспоненциальном законе изменения мгновенной частоты
172 Глава 3. Дискретные сигналы
Формирование случайных сигналов
Для генерации случайных чисел в MATLAB служат функции rand (равномерное
распределение) и randn (нормальное распределение), а также средства пакета
расширения Statistics, которые поддерживают множество разных законов рас-
распределения вероятности. В данном разделе мы кратко рассмотрим формирова-
формирование дискретных случайных сигналов с заданным распределением вероятности и
корреляционными свойствами.
Реализация заданного закона
распределения вероятности
Как уже говорилось, средства генерации случайных чисел с различными закона-
законами распределения вероятности имеются в пакете Statistics. Справочная инфор-
информация об этом пакете имеется, например, в книге [13], здесь же мы рассмотрим
лишь общий способ получения случайных чисел с заданной функцией распреде-
распределения на основе равномерно распределенных случайных чисел.
Пусть X — случайная величина, равномерно распределенная на интервале 0...1
(см. раздел «Равномерное распределение» главы 1). Для получения случайной
величины У, имеющей функцию распределения Fy(y), случайную величину X не-
необходимо подвергнуть следующему нелинейному преобразованию:
y=fy(-1)(X), C.28)
где Fj~{) — функция, обратная по отношению к Fy(y).
Действительно, при таком расчете вероятность того, что Y не превышает значе-
значения у, равна
Но X имеет равномерное распределение, поэтому
P(X<Fy(y)) =
Таким образом,
то есть У действительно имеет требуемую функцию распределения.
ВНИМАНИЕ
С теоретической точки зрения рассмотренный подход является универсальным, однако на
практике он может оказаться неудобным, поскольку обратные функции распределения
для многих законов (например, для нормального) не выражаются через элементарные
функции. В таких случаях приходится использовать более изощренные методики.
Формулу C.28) можно обобщить на случай произвольного преобразования
функции распределения. Если случайная величина X имеет функцию распреде-
распределения Fx(x), а нужно получить случайную величину Ус функцией распределе-
распределения Fy (у), искомое преобразование следует записать следующим образом:
Дискретные сигналы в MATLAB
173
Преобразование FX(X) делает распределение случайной величины равномерным,
а преобразование F^'n(...) формирует случайную величину с заданным распре-
распределением вероятности.
В качестве примера сгенерируем по формуле C.28) случайные числа с рэлеев-
ским законом распределения A.52). Функция распределения для закона Рэлея
получается интегрированием его плотности вероятности:
и
х
Обратная функция будет иметь вид
Генерируем равномерно распределенные случайные числа с помощью функции
rand, производим их преобразование по формуле C.29) и строим гистограмму
с помощью функции hist (рис. 3.29):
» N - 10000: % количество чисел
» sigma =1; % параметр рэлеевского закона
» X = randd, N): % равномерное распределение
» Y = sigma * sqrt(-2 * logd - X)); % закон РзлеЯ
» histCY. 25) % гистограмма по 25 интервалам
1200
"О 0.5 1 1.5 2 2.5 3 3.5 4 4.5
Рис. 3.29. Гистограмма случайных чисел с рэлеевским распределением
Полученная гистограмма показывает хорошее соответствие с графиком рэлеев-
ской плотности вероятности, показанным ранее на рис. 1.38.
Реализация заданной корреляционной функции
Поскольку корреляционная функция случайного сигнала взаимно-однозначно
связана с его спектром (см. раздел «Теорема Винера—Хинчина» главы 1), для
формирования сигнала с заданной КФ можно взять отсчеты белого шума и про-
пропустить их через фильтр с соответствующей АЧХ (ФЧХ фильтра не имеет зна-
174
Глава 3. Дискретные сигналы
чения, поскольку к случайным процессам неприменимо понятие фазового спек-
спектра). О теории работы дискретных фильтров речь пойдет в главе 4, а о методах
их расчета — в главе 6. Здесь же мы, несколько забегая вперед и используя мате-
материал последующих глав, рассмотрим лишь один пример, сформировав сигнал
с экспоненциальной функцией корреляции:
< 1. C.30)
Для формирования сигнала с такой КФ необходимо пропустить белый шум че-
через дискретный фильтр, корреляционная функция импульсной характеристики
которого имеет вид C.30). Этому требованию удовлетворяет импульсная харак-
характеристика вида
k>0.
Такая характеристика соответствует рекурсивному фильтру первого порядка с
коэффициентом обратной связи, равным а. Требуемую фильтрацию осуществим
с помощью функции filter (она также будет рассмотрена в главе 4):
» ХО = randnd, 1000); % независимые нормальные отсчеты
» а * 0.9; % параметр экспоненциальной корреляции
» sigma = 2; % среднеквадратическое значение результата
» X - fiHer(sigma*sqrt(l-aA2), [I -a]. X0); * фильтрация
» subplotB, 1. 1)
» plot(X0(l:200)) % график белого шума
» title('White noise')
» subplotB. 1. 2)
» plot(X(l:200)) % график коррелированного шума
»' title('Correlated noise')
Графики белого шума и экспоненциально коррелированного сигнала показаны
на рис. 3.30. Хорошо видно, что коррелированный шум сильно сглажен по срав-
сравнению с белым шумом.
White noise
О
Рис
50 100 150 200
3.30. Белый (сверху) и коррелированный (снизу) шум
Дискретные сигналы в MATLAB
175
Расчет корреляционной матрицы
Для оценки корреляционной матрицы случайного сигнала по вектору его отсче-
отсчетов с использованием временного усреднения служит функция corrmtx, имеющая
следующий синтаксис:
[X, R] - corrmtx(x, m. 'method')
Здесь х — вектор отсчетов сигнала, m — размерность рассчитываемой корреляци-
корреляционной матрицы. Необязательный строковый параметр 'method' управляет тем, как
обрабатываются крайние отсчеты сигнала. С его возможными значениями мож-
можно познакомиться по документации пакета Signal Processing.
Результатами работы функции являются матрица промежуточных данных X и
собственно корреляционная матрица R, которая рассчитывается как X' *Х (апост-
(апостроф в MATLAB обозначает эрмитово сопряжение).
ВНИМАНИЕ
Понятие «корреляционная» в MATLAB используется, разумеется, в зарубежной трактов-
трактовке (см. замечание в разделе «Корреляционные функции случайных процессов» главы 1).
Это означает, что функция corrmtx не вычитает из сигнала постоянную составляющую
перед вычислением корреляционной матрицы.
В качестве примера вычислим корреляционные матрицы и построим графики их
первых строк (то есть корреляционных функций) для сформированных в преды-
предыдущем разделе белого шума ХО и экспоненциально коррелированного шума X
(рис. 3.31).
White noise
10
15
Рис. 3.31. Оценка корреляционной функции белого (сверху)
и экспоненциально коррелированного (снизу) шума
» N = 20: % размер корреляционной матрицы
» [tmp. R0] = corrmtx(X0. N):
» Сtmp. R] = corrmtx(X, N); .
176 Глава 3. Дискретные сигналы
» к = 0-.N; % индексы КФ
» subp1otB, 1, 1)
» % график КФ белого шума
» stem(k, R0(l,-.))
» title('White noise')
» subp1otB. 1, 2)
» % график КФ коррелированного шума
» stem(k. R(l.:))
» title('Correlated noise')
Из графиков видно, что отсчеты белого шума действительно некоррелированы,
а отсчеты фильтрованного шума действительно дают требуемую экспоненциаль-
экспоненциальную функцию корреляции.
Генерация дискретного нормального белого шума
Дискретный белый шум с нормальным распределением можно сгенерировать
с помощью функции randn, имеющей следующий синтаксис:
X = randn(m, n)
В результате вызова функции генерируется массив X, содержащий m строк и
п столбцов псевдослучайных чисел, имеющих нормальное распределение с нуле-
нулевым математическим ожиданием и единичной дисперсией.
Параметр п при вызове можно опустить, по умолчанию используется значение
п = ш, то есть генерируется квадратная матрица.
В задачах, связанных с обработкой сигналов, для генерации дискретного нор-
нормального белого шума удобнее использовать функцию wgn (white Gaussian noise)
пакета Communications, поскольку она позволяет в явном виде задавать уровень
генерируемого шума. Синтаксис вызова функции следующий:
у = wgn(m. n. p. imp. state, 'powertype', 'outputtype');
Здесь тип — как и ранее, размеры генерируемой матрицы, ар — мощность гене-
генерируемого шума в единицах, задаваемых параметром 'powertype' (по умолчанию —
в децибелах). Остальные параметры являются необязательными и имеют значе-
значения по умолчанию.
Параметр imp задает импеданс нагрузки в омах (предполагается, что генерируют-
генерируются отсчеты случайного напряжения на этой нагрузке). По умолчанию использу-
используется импеданс нагрузки, равный 1 Ом.
Целочисленный параметр state позволяет принудительно задавать начальное со-
состояние генератора гауссовских случайных чисел MATLAB (функция randn). По
умолчанию используется текущее состояние.
Строковый параметр 'powertype1 задает единицы измерения мощности, исполь-
использованные при указании параметра р. Возможны следующие значения:
□ 'dB' — мощность р задается в децибелах, значению 0 дБ соответствует еди-
единичная дисперсия (если использован параметр imp, дисперсия равна imp*2);
Дискретные сигналы в MATLAB 177
□ ' dBra' — мощность р задается в децибелах, значению 0 дБ соответствует диспер-
дисперсия, равная 10~3 (если использован параметр imp, дисперсия равна imp^2/1000);
□ ' 1 inear' — мощность р задается в ваттах, дисперсия генерируемого шума рав-
равна p*imp.
Строковый параметр 'outputtype' позволяет задавать генерацию вещественного
или комплексного шума. Возможны значения ' real' (вещественный шум; гене-
генерируется по умолчанию) и 'complex' (комплексный шум). Если генерируется
комплексный шум, его вещественная и мнимая части имеют мощности р/2.
Добавление белого шума к сигналу
, В том же пакете Communications имеется еще одна полезная функция, работаю-
работающая с нормальным белым шумом. Это функция" awgn, реализующая канал связи
с аддитивным белым гауссовым шумом (additive white Gaussian noise channel,
AWGN channel), то есть добавляющая к сигналу белый шум с заданным уров-
уровнем. Синтаксис вызова функции следующий:
у = awgn(x, snr, sigpower. state, 'powertype');
Здесь х — вектор отсчетов сигнала. Скаляр snr задает отношение сигнал/шум в
единицах, задаваемых параметром 'powertype' (по умолчанию — в децибелах).
Остальные параметры являются необязательными и имеют значения по умол-
умолчанию.
Параметр sigpower указывает мощность сигнала х в единицах, задаваемых пара-
параметром 'powertype' (по умолчанию — в децибелах). По умолчанию предполагает-
предполагается, что мощность сигнала равна 0 дБ. Параметр sigpower может также принимать
строковое значение 'measured', при этом мощность сигнала автоматически изме-
измеряется.
Целочисленный параметр state позволяет принудительно задавать начальное со-
состояние генератора гауссовских случайных чисел MATLAB (функция randn). По
умолчанию используется текущее состояние.
Строковый параметр ' powertype' задает единицы измерения мощности, исполь-
использованные при указании параметров snr и sigpower. Возможны следующие зна-
значения:
□ ' dB' — мощность сигнала и отношение сигнал/шум задаются в децибелах;
□ 'linear' '— мощность сигнала задается в ваттах, отношение сигнал/шум —
в разах.
При расчете мощности сигнала предполагается, что значения вектора х представ-
представляют собой отсчеты напряжения на нагрузке с импедансом 1 Ом.
Результатом работы является вектор «зашумленных» отсчетов у. Если значения х
являются вещественными, функция awgn добавляет вещественный шум, если ком-
комплексными — комплексный.
178 Глава 3. Дискретные сигналы
Получение данных
из внешних источников
Преобразование аналогового сигнала в цифровой и обратно — это процессы, ко-
которые выполняются аппаратными средствами. MATLAB же, будучи программ-
программным продуктом, может лишь взаимодействовать с соответствующим оборудова-
оборудованием (такое взаимодействие осуществляется, например, с помощью пакета Data
Acquisition). Кроме того, в MATLAB предусмотрены средства для воспроизведе-
воспроизведения и записи звука, а также для работы со звуковыми файлами формата wav.
В данном разделе мы подробно рассмотрим считывание и запись wav-файлов,
а также воспроизведение звука. Детально рассматривать вопросы взаимодейст-
взаимодействия с оборудованием ввода/вывода данных из-за ограниченного объема книги не
представляется возможным, поэтому в конце главы будет приведен лишь крат-
краткий обзор возможностей и демонстрационных примеров пакета Data Acquisition.
Чтение wav-файлов
Для считывания wav-файлов в MATLAB используется функция wavread. В про-
простейшем случае она может быть использована следующим образом:
у = wavreadC filename');
Здесь f i 1 ename — имя звукового файла (расширение .wav указывать не обязатель-
обязательно). В имя файла необходимо включить полный путь, за исключением тех случа-
случаев, когда файл находится в текущем (для MATLAB) каталоге или в одном из ка-
каталогов, входящих в список поиска MATLAB.
В результате вызова функции в переменную у будет помещено все содержимое
указанного файла. Строки матрицы у соответствуют отсчетам сигнала, столб-
столбцы — каналам, которых в wav-файле может быть несколько.
ВНИМАНИЕ
Прежде чем вызывать функцию wavread в простейшей форме, подумайте, хватит ли ваше-
вашему компьютеру ресурсов, чтобы считать wav-файл в память целиком. Ведь всего одна ми-
минута стереозаписи звука, сделанной с CD-качеством (частота дискретизации 44,1 кГц),
содержит 60 с х 44 100 Гц х 2 канала - 5 292 000 отсчетов. MATLAB представит эти отсче-
отсчеты в формате с плавающей запятой, затратив на каждый отсчет 8 байт (формат double).
Таким образом, одна минута звука займет в памяти 42 336 000 байт (примерно 40 Мбайт).
А ведь звуковые файлы бывают и длиннее...
ЗАМЕЧАНИЕ
Приведенная строка вызова функции вовсе не случайно оканчивается точкой с запятой.
Этот символ подавляет вывод результатов на экран. Если его убрать, вы увидите бегущие
по экрану ряды чисел — все содержимое матрицы у. Как правило, вывод этой информации
не представляет интереса. Если вы все-таки забыли поставить в конце строки точку с запя-
запятой, ничего страшного. Просто прервите вывод, нажав клавиши Ctrl+C. Сама команда в
этот момент уже выполнена, матрица у сформирована — вы прерываете только вывод ин-
информации на экран.
Получение данных из внешних источников 179
В звуковых файлах отсчеты сигнала представлены целыми числами, лежащими
в диапазоне -128...+127 (8 бит на отсчет) либо -32 768...+32 767 A6 бит на от-
отсчет). MATLAB нормирует эти значения, приводя их к диапазону -1...+1.
Помимо собственно отсчетов сигнала, в wav-файлах хранится еще и служебная
информация о частоте дискретизации, количестве бит на отсчет и т. п. Узнать
частоту дискретизации можно, используя при вызове функции второй выходной
параметр:
[у. Fs] = wavreadCfilename'):
При этом переменная Fs получает значение, равное частоте дискретизации в гер-
герцах.
Чтобы узнать, сколько уровней сигнала содержится в звуковом файле (точнее,
число бит на отсчет), необходимо добавить третий выходной параметр:
[у, Fs, bits] - wavread('filename'):
Еще два параметра, которые часто хочется знать заранее, — это число отсчетов и
каналов записи. Для получения данной информации нужно вызвать функцию
wavread с двумя входными параметрами. Первый — это по-прежнему имя файла,
вторым же должна быть текстовая строка 'size':
wavesize - wavread('filename', 'size')-,
В отличие от предыдущих вариантов вызова функции, в данном случае не про-
производится считывания самих звуковых данных. Из wav-файла лишь извлекается
служебная информация, которая возвращается в виде двухэлементного вектора-
строки (в приведенном примере — wavesize). Первый элемент вектора содержит
число отсчетов, второй — число каналов.
Наконец, имеется и важнейшая возможность считывания данных из wav-файла
не целиком, а отдельными фрагментами (без этого нельзя было бы работать с
большими файлами). Для этого также используется второй входной параметр
функции wavread. Если этот параметр является числом, будет считано соответст-
соответствующее количество отсчетов (начиная с первого):
у - wavread('filename', N):
Если же нужный фрагмент расположен не в начале файла, придется указать его
начало и конец. В этом случае второй входной параметр функции wavread должен
представлять собой двухэлементный вектор:
у = wavread('filename', [nl n2]):
В результате в переменную у будут считаны отсчеты с номерами от nl до п2
включительно (нумерация отсчетов, как и элементов матриц в MATLAB, начи-
начинается с единицы). При этом считываются все каналы звукозаписи. Возможно-
Возможности считывания информации из отдельных каналов не предусмотрено.
СОВЕТ :
Как видите, получить информацию о частоте дискретизации и числе бит на отсчет можно
только одновременно со считыванием звуковых данных. Если необходимо получить эту
информацию заранее, до основной работы со звуком, можно считать всего один отсчет:
[у, Fs. bits] = wavread('filename'. 1):
180 Глава 3. Дискретные сигналы
Рассмотрим работу с wav-файлами на конкретном примере. Возьмем для этого
бодрый аккорд tada.wav, входящий в стандартный набор звуков Windows.
Прежде всего узнаем число отсчетов и каналов:
» wavesize = wavread('c:\windows\media\tada'. 'size')
wavesize =
42752 2
Как видим, эта стереозапись B канала) содержит 42 752 отсчета.
ЗАМЕЧАНИЕ ft
*
В рассматриваемых примерах используется файл tada.wav, входящий в состав Windows 98.
В Windows 95 этот файл был монофоническим (одноканальным) и имел меньшую частоту
дискретизации. Только что приведенный вызов функции wavread вернет для него вектор
[27459 1] B7 459 отсчетов и один канал).
Далее извлекаем информацию о частоте дискретизации и числе бит на отсчет:
» [у, Fs, bits] = wavread('c:\windows\media\tada', 1)
У =
О О
Fs =
22050
bits =
16
Полученные результаты очевидны — частота дискретизации 22,05 кГц, исполь-
используется 16 бит на отсчет F5 536 уровней сигнала). «В нагрузку» мы получили
значения первого отсчета из обоих каналов (вектор у ).
Теперь мы можем узнать о файле кое-что еще, например определить продолжи-
продолжительность звучания. Для этого нужно разделить число отсчетов (первый элемент
полученного ранее вектора wavesize) на частоту дискретизации Fs:
» wavesize(l)/Fs
ans =
1.9389
Результат — длительность звука в секундах.
Чтобы узнать, сколько памяти потребуется MATLAB для хранения всей записи,
нужно перемножить число отсчетов и число каналов, а затем увеличить резуль-
результат еще в 8 раз. Можно сразу же поделить полученное значение на 1024, чтобы
получить ответ в килобайтах, или на 10242,,если ожидаемое число лучше изме-
измерять мегабайтами:
» prod(wavesize)*8/1024
ans =
668
Расход памяти оказывается вполне умеренным F68 Кбайт), так что мы можем
позволить себе считать файл в память целиком (не забудьте про точку с запятой
в конце строки):
» у = wavread('c:\windows\media\tada'):
Получение данных из внешних источников
181
Теперь все содержимое файла считано в матрицу у. Проверим ее размеры:
» size(y)
ans =
42752 2
Как видите, размеры совпадают с полученной ранее информацией о файле:
42 752 отсчета (строк), два канала (столбца).
Чтобы «окинуть взглядом» звуковой сигнал, выведем его в виде графика — от-
отдельно для правого и левого каналов стереозаписи, используя для этого функ-
функцию subplot (подробнее об использовании этой функции речь пойдет в разделе
«Одновременный вывод нескольких графиков» приложения А):
» subplotB. 1. 1)
» piot(y(:. 1))
» subplotB, 1. 2)
» plot(y(:, 2))
Результат показан на рис. 3.32. Имейте в виду, что из-за большого числа отсче-
отсчетов для построения графика на медленном компьютере может потребоваться
ощутимое время.
-0.4
-0.4
0.5 1 1.5
Рис. 3.32. График звукового сигнала
хЮ
Если при выводе графика разрешение по горизонтали имеет большее значение,
чем по вертикали, можно воспользоваться функцией stri ps, специально предна-
предназначенной для отображения длинных сигналов в «нарезанном» на фрагменты
виде (фрагменты выводятся друг под другом). Синтаксис вызова функции stri ps
следующий:
strips(x. N)
Здесь х — вектор отсчетов сигнала (двумерные массивы не допускаются), N —
число отсчетов в каждом фрагменте (этот параметр можно опустить, по умолча-
умолчанию размер фрагмента составляет 200 отсчетов).
182
Глава 3. Дискретные сигналы
В качестве примера выведем с помощью функции strips график первого (лево-
(левого) канала сигнала tada.wav (рис. 3.33):
» strips(y(:.l), 10000)
10000
20000
30000
40000 "
0 2000 4000 6000 8000 10000
Рис. 3.33. График сигнала, выведенный с помощью функции strips
Над помещенным в переменную MATLAB звуковым сигналом можно выпол-
выполнять любые преобразования, а затем воспроизвести полученный звук или сохра-
сохранить его в виде нового wav-файла. Обо всем этом пойдет речь в нескольких
следующих разделах. Можно также сохранить сигнал на диске как переменную
MATLAB (в виде МАТ-файла) — см. раздел «Ввод и вывод данных» приложе-
приложения А.
Функция wavread не является встроенной — она целиком написана на языке
MATLAB с использованием средств работы с двоичными файлами. Если вас ин-
интересует структура wav-файлов и организация их считывания, попробуйте разо-
разобраться в тексте функции wavread — файл wavread.m расположен в каталоге
MATLABR12\TOOLBOX\MATLAB\AUDIO.
MATLAB умеет работать только с несжатыми wav-файлами (формат РСМ). При
попытке считать файл, в котором использован какой-либо из методов сжатия
информации, будет выдано сообщение «Data compression format (...) is not
supported».
ЗАМЕЧАНИЕ
В MATLAB имеется также функция auread, которая позволяет считывать звуковые файлы
формата AU, используемого в основном на UNIX-платформах NeXT и SUN.
Запись wav-файлов
Чтобы записать вектор (или матрицу) на диск в виде wav-файла, используется
функция wavwri te:
wavwrite(y, Fs. N. 'filename')
Получение данных из внешних источников 183
Здесь у — записываемые данные (вектор для монофонической записи, двух-
двухстолбцовая матрица — для создания стереофайла), Fs — частота дискретизации в
герцах, N — число бит на отсчет (8 или 16), 'filename' — имя создаваемого файла.
Выходных параметров у данной функции нет.
Параметры N и Fs можно опускать, при этом используются значения по умолча-
умолчанию — N = 16 и Fs = 8000:
wavwrite(y. Fs. 'filename')
wavwrite(y, 'filename')
Записываемые данные должны быть вещественными и лежать в диапазоне -1...1.
Значения, выходящие из этого диапазона, будут «обрезаны» и сделаны равны-
равными ±1.
ЗАМЕЧАНИЕ
В MATLAB имеется также функция auwrite, которая позволяет записывать звуковые фай-
файлы в формате AU, используемом в основном на UNIX-платформах NeXT и SUN.
Воспроизведение звука
Если ваш компьютер оборудован звуковой картой, то, помимо работы с wav-
файлами, вы имеете и возможность воспроизведения векторов и матриц в зву-
звуковом виде. Для этого имеются целых три функции — sound, soundsc и wavplay.
В простейшем случае все три функции вызываются одинаково и обеспечивают
воспроизведение вектора у (или двухстолбцовой матрицы — для стереозвука),
содержащего отсчеты сигнала, с заданной частотой дискретизации Fs (в герцах):
sound(y, Fs)
soundsc(y, Fs)
wavplay(у, Fs)
Различие между этими функциями заключается в предоставляемых ими допол-
дополнительных возможностях.
Функция sound
Функция sound обеспечивает воспроизведение сигнала с заданными частотой
дискретизации и числом уровней (бит на отсчет):
sound(y, Fs. bits)
Здесь у — вектор или двухстолбцовая матрица отсчетов сигнала, Fs — частота
дискретизации в герцах, bits — число бит на отсчет (8 или 16).
Параметры bits и Fs можно опускать, при этом будут использоваться их значе-
значения по умолчанию! Fs ■ 8192 и bits = 16.
Воспроизводимые данные у должны быть вещественными и лежать в диапазо-
диапазоне -1...1. Значения, выходящие из этого диапазона, «обрезаются» и делаются
равными ±1.
Выходных параметров у функции нет. После вызова она передает вектор у зву-
звуковой карте для воспроизведения и сразу же, не дожидаясь окончания звука,
возвращает управление командной строке MATLAB.
184 Глава 3. Дискретные сигналы
Если следующая команда sound будет использована до окончания предыдущего
звука, будет выдано сообщение об ошибке «Unable to open sound device» (Невоз-
(Невозможно открыть звуковое устройство).
Функция soundsc
Функция soundsc (sound scaled) отличается от функции sound лишь тем, что про-
производит предварительное масштабирование отсчетов сигнала. Для управления
масштабированием добавляется четвертый входной параметр s_lim:
soundsc(y. Fs. bits, sjirn)
Здесь входные параметры у, Fs, bits имеют то же назначение, что и для функции
sound. Параметр s_lim должен быть двухэлементным вектором [s_1ow s_high],
он задает диапазон значений, который будет линейно преобразован к интервалу
—1...1. Преобразование, таким образом, производится по формуле
/(,ow high)
У= -_ —•
5 high 5low
При si im = [-1 1] функция soundsc эквивалентна функции sound.
Параметры si im, bits и Fs при вызове можно опускать, при этом используются
их значения по умолчанию: Fs = 8192, bits = 16 и slim = [min(y) max(y)]. Значе-
Значение по умолчанию для s_lim обеспечивает точное приведение полного диапазона
значений сигнала к интервалу -1...1.
Функция wavplay
Наконец, третья функция, предназначенная для воспроизведения звука, имеет
имя wavpl ay:
wavplay(у. Fs. 'mode')
Входные параметры у и Fs имеют тот же смысл, что и у предыдущих функций,
а параметр 'mode' управляет режимом воспроизведения. Этот параметр может
принимать два значения:
□ 'sync' — синхронный режим, означающий, что функция вернет управление
интерпретатору MATLAB только после окончания звука;
□ 'async' — асинхронный режим, при котором функция передает данные для
воспроизведения звуковым драйверам Windows и сразу же возвращает управ-
управление системе MATLAB, не дожидаясь окончания звука.
Параметры 'mode' и Fs при вызове можно опускать, при этом используются их
значения по умолчанию: Fs = 11025 и 'mode' = 'async'.
Синхронный режим позволяет организовать в MATLAB-программе выдачу не-
нескольких звуков подряд, не заботясь о расчете и соблюдении временных интер-
интервалов между соответствующими командами. В асинхронном же режиме можно
одновременно с воспроизведением звука продолжать выполнение программы.
К сожалению, при этом нет возможности программным путем проверить, закон-
закончилось ли воспроизведение звука.
Получение данных из внешних источников
185
ЗАМЕЧАНИЕ
Такая программная проверка будет возможна, если для воспроизведения звука воспользо-
воспользоваться средствами пакета Data Acquisition (краткая информация о его возможностях при-
приводится далее).
Запись звука
Функция wavrecord позволяет записать звук в переменную MATLAB с помощью
звуковой карты компьютера:
у = wavrecord(n, Fs, ch, 'dtype')
Здесь n — число записываемых отсчетов, Fs — частота дискретизации в герцах,
ch — число каналов записи, ' dtype' — тип записываемых данных.
Возвращаемый результат у — матрица, каждый столбец которой соответствует
одному каналу записи. При стереозаписи первый столбец — левый канал, вто-
второй — правый.
Для параметра ' dtype' возможны следующие значения:
О 'double' — 16-битовая запись, данные масштабируются к диапазону -1...1 и
представляются в 8-байтовом формате с плавающей запятой;
Q 'single' — 16-битовая запись, данные масштабируются к диапазону -1...1 и
представляются в 4-байтовом формате с плавающей запятой;
Q 'intl6' — 16-битовая запись, данные представляются в двухбайтовом цело-
целочисленном формате (диапазон -32 768...32 767);
О 'uint8' — 8-битовая запись, данные представляются в однобайтовом беззна-
беззнаковом целочисленном формате (диапазон 0...255, нулевому напряжению на
входе соответствует значение 1128);
Входные параметры 'dtype', ch и Fs можно опускать, при этом будут использо-
использоваться их значения по умолчанию: Fs = 11025, ch = 1, 'dtype' = 'double'.
Готовые записи сигналов
В разделе Audio базовой библиотеки MATLAB и в пакете расширения Signal
Processing имеется несколько готовых записей сигналов, сохраненных в виде
МАТ-файлов. Эти сигналы используются в качестве исходных данных в приме-
примерах, приводимых в документации, и демонстрационных программах. Возможно,
вам они пригодятся для тестирования собственных программ и алгоритмов. Све-
Сведения об имеющихся сигналах приведены в табл. 3.1.
Таблица 3.1
Имя файла
chirp.mat
. Записи сигналов, имеющиеся в MATLAB
Пакет
MATLAB
Имя пере-
переменной
У
Размер
13 129 A,6 с)
Частота
дискрети-
дискретизации, Гц
8192
Характер звука
Импульсы с меняю-
меняющейся частотой
Продолжение
186
Глава 3. Дискретные сигналы
Таблица 3.1 {продолжение)
Имя файла
gong.mat
handel.mat
laughter.mat
spiat.mat
train.mat
mtlb.mat
vcosig.mat
Пакет
MATLAB
MATLAB
MATLAB
MATLAB
MATLAB
SP
SP
Имя пере-
переменной
У
У
У
У
У
mtlb
vcosig
Размер
42 028 E,1 с)
73 ИЗ (8,9 с)
52 634 F,4 с)
10 001 A,2 с)
12 880 A,5 с)
4001 @,54 с)
19 661 B,4 с)
Частота
дискрети-
дискретизации, Гц
8192
8192
8192
8192
8192
7418
8192
Характер звука
Удар гонга
Хор
Смех
Тон с меняющейся
частотой, затем звук
удара
Гудок поезда
Произнесенное слово
«MATLAB»
Данный сигнал имеет
очень забавную
спектрограмму
Пакет расширения Data Acquisition
Пакет расширения Data Acquisition позволяет непосредственно из MATLAB ра-
работать с оборудованием аналогового и цифрового ввода/вывода данных. В ком-
комплект поставки входят драйверы для следующих устройств:
□ звуковых карт, поддерживаемых операционной системой Windows;
□ плат фирмы National Instruments серий Е и 1200;
□ плат фирмы ComputerBoards;
□ VXI-модулей Е1432А/ЗЗА/34А фирмы Agilent Technologies.
Разработать драйверы для других устройств можно с помощью Data Acquisition
Toolbox Adaptor Kit; дополнительную информацию можно получить на сайте фир-
фирмы The MathWorks, Inc. по адресу http://www.mathworks.com/products/daq/.
Пакет Data Acquisition (разумеется, в сочетании с перечисленным оборудовани-
оборудованием) предоставляет следующие возможности:
□ аналоговый ввод и вывод информации в реальном масштабе времени, вклю-
включая возможность одновременного выполнения аналого-цифрового и цифро-
аналогового преобразований;
□ цифровой ввод и вывод информации в реальном масштабе времени;
□ запись вводимых данных на диск либо их загрузка непосредственно в пере-
переменную MATLAB;
Q буферизацию данных для осуществления ввода в фоновом режиме;
□ триггеры, управляемые программно или аппаратно генерируемыми события-
событиями (это дает возможность осуществлять синхронизацию — например, запус-
Получение данных из внешних источников
187
кать процесс аналогового ввода при достижении входным сигналом некото-
некоторого уровня).
Подробно рассматривать пакет Data Acquisition в рамках данной книги не пред-
представляется возможным, поэтому покажем лишь пример его использования в
двух демонстрационных программах, поставляемых в составе пакета.
Первая программа реализует осциллограф, позволяя просматривать графики сиг-
сигналов, получаемых от имеющихся в системе устройств ввода данных. Данная про-
программа может быть вызвана из командной строки (ее имя — daqscope ) либо из
окна демонстрационных программ MATLAB (команда меню Help ► Demos, раз-
раздел Toolboxes/Data Acquisition, программа Example Oscilloscope).
Вид окна осциллографа приведен на рис. 3.34. Подходящего источника сигнала
под рукой не оказалось, поэтому наблюдаются шумы и наводки, поступающие на
линейный вход левого канала звуковой карты компьютера. Из графика видно,
что основной период наводок равен 20 мс — это означает, что их главным источ-
источником является питающая сеть, напряжение которой имеет частоту 50 Гц. Уро-
Уровень наводок составляет примерно 11 мВ, поэтому для того, чтобы их увидеть на
графике, понадобилось перевести переключатель вертикального масштаба в по-
положение Autoset (при этом у выводимой слева оцифровки вертикальной оси ока-
оказались «за кадром» знак «минус», ноль и десятичная точка).
-,:5 An Example Oscilloscope
ВНИЗ
Г SampteRato
<"" Vglfe/Div
4410
Рис. 3.34. Осциллограф — демонстрационный пример пакета Data Acquisition
Второй пример — генератор сигналов различной формы. Имя программы для
вызова из командной строки — daqfcngen. При использовании окна демонстра-
демонстрационных программ MATLAB после вызова команды меню Help ► Demos необхо-
188
Глава 3. Дискретные сигналы
димо выбрать раздел Toolboxes/Data Acquisition и программу Example Function
Generator).
Вид окна генератора приведен на рис. 3.35. В списке, расположенном в левой
части окна над полем графика, выбирается тип генерируемого сигнала:
□ Sine — гармонический сигн^р;
□ Sine — периодическая sine-функция (функция Дирихле);
□ Square — последовательность прямоугольных импульсов;
□ Triangle — последовательность симметричных треугольных импульсов;
□ Sawtooth — последовательность пилообразных импульсов;
□ Random — случайный сигнал;
□ Chirp — колебания с плавно меняющейся частотой.
•ф An Example Function Geneiatoi
-' " ^i....;wi..;.at --
Channeli (Left!
Channel (Right)
Chirp
Рис. 3.35. Функциональный генератор — демонстрационный пример пакета Data Acquisition
Набор параметров, настраиваемых в нижней части окна, зависит от выбранного
типа сигнала.
ГЛАВА 4 Дискретные
системы
Теоретические сведения, приводимые в данной главе, в литературе довольно часто
фигурируют под заголовками «Дискретные фильтры», «Принципы цифровой
фильтрации» и т. п. (см., например, [1, 2, 4]). В принципе «дискретная система»
и «дискретный фильтр» — это одно и то же, однако понятие «фильтр», созна-
сознательно или подсознательно, довольно тесно связывается с системами, которые
одни частоты пропускают, а другие задерживают (см. рис. 2.5 в главе 2, где были
показаны идеализированные АЧХ фильтров такого рода). Такой подход может
создать ложное, ограниченное представление о назначении и возможностях дис-
дискретных линейных систем, которые способны выполнять и иные задачи, нежели
выделение из сигнала определенной полосы частот. По этой причине в названии
данной главы использован термин «дискретные системы». Однако в тексте гла-
главы слова «фильтр» и «система» будут использоваться как синонимы.
ЗАМЕЧАНИЕ
Далее, в главе 6, где пойдет речь о расчете (синтезе) систем, реализующих заданные (во
многих случаях действительно полосовые) частотные характеристики, будет употреблять-
употребляться исключительно слово «фильтр».
Сущность линейной
дискретной обработки
Вообще, дискретный фильтр — это произвольная система обработки дискретно-
дискретного сигнала, обладающая свойствами линейности и стационарности. Под этими
свойствами понимается то же, что и в аналоговом случае (см. раздел «Классифи-
«Классификация систем» главы 2): линейность означает, что выходная реакция на сумму
сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельно-
отдельности, а стационарность — что задержка входного сигнала приводит лишь к такой
же задержке выходного сигнала, не меняя его формы.
190
Глава 4. Дискретные системы
ЗАМЕЧАНИЕ
Существуют и фильтры с переменными параметрами, не обладающие свойством стацио-
стационарности. Это, например, адаптивные фильтры, меняющие свои параметры в зависимости
от статистических свойств входного сигнала. Рассмотрение таких систем выходит за рам-
рамки данной книги. Дополнительную информацию можно найти в [18, 19]. Кроме того,
несколько функций, реализующих алгоритмы адаптивной фильтрации, добавлено в по-
последнюю B.1) версию пакета Filter Design.
Любой фильтр обладает определенной частотной характеристикой. Чтобы она
была нетривиальной, то есть чтобы коэффициент передачи фильтра на разных
частотах был разным, выходной сигнал фильтра y(k) должен зависеть от не-
нескольких отсчетов входного сигнала x(k). Таким образом, дискретный фильтр
должен обладать памятью.
Чтобы обеспечить линейность и стационарность, производимые фильтром мате-
математические операции должны ограничиваться сложением и умножением на кон-
константы.
Рассмотрим простейший пример. Пусть выходной сигнал фильтра равен сумме
двух последних отсчетов входного сигнала:
y(k) =x(k) + хф~ 1).
Убедимся в том, что эта система по-разному пропускает на выход сигналы раз-
разных частот. Для начала подадим на вход фильтра серию одинаковых отсчетов
(то есть сигнал нулевой частоты):
Вход
1
1
1
1
...
Выход
...
1 + 1-2
1 + 1-2
1 + 1-2
Как видите, уровень постоянного сигнала фильтр увеличил в два раза. Теперь
подадим на вход отсчеты, одинаковые по модулю, но с чередующимися знаками
(то есть отсчеты гармонического сигнала с частотой Найквиста):
Вход
...
1
-1
Выход
...
-1 + 1 = 0
Сущность линейной дискретной обработки
191
Вход
1
-1
...
Выход
1+(-1)-0
-1 + 1=0
В отличие от постоянного сигнала, сигнал с частотой Найквиста на выход про-
просто не прошел. Далее попробуем что-нибудь промежуточное, например сигнал с
частотой, равной половине частоты Найквиста:
Вход
1
0
-1
0
1
0
-1
Выход
...
0+1-1
-1 +0--1
0 + (-1)--1
1+0-1
0+1-1
-1+0--1
На выходе в данном случае получаются отсчеты синусоиды, имеющей в л/2 раз
большую амплитуду и некоторый фазовый сдвиг по сравнению со входным сиг-
сигналом. Рассмотренный пример представляет собой простейший случай нерекур-
нерекурсивного фильтра. Такие фильтры суммируют некоторое число входных отсчетов,
умножая их при этом на постоянные весовые коэффициенты.
Теперь заметим, что помимо выходных отсчетов мы можем использовать для
вычислений и ранее рассчитанные значения выходного сигнала. Попробуем про-
просто суммировать входной отсчет и предыдущий выходной отсчет:
y{k) -*(*) + y(k - 1).
Подаем на вход постоянный сигнал (начальное состояние фильтра считаем ну-
нулевым):
Вход
1
1
Выход
1 + 0=1
1 + 1 = 2
192
Глава 4. Дискретные системы
Вход
1
1
Выход
1 + 2 = 3
1+3 = 4
Так, очевидно, будет продолжаться и далее — выходной сигнал будет линейно
нарастать, что рано или поздно приведет к переполнению разрядной сетки вы-
вычислительного устройства. Это сразу же демонстрирует нам главную отличи-
отличительную черту фильтров, использующих при вычислениях предыдущие отсчеты
выходного сигнала (их называют рекурсивными фильтрами) — из-за наличия об-
обратных связей они могут быть неустойчивыми.
Попробуем уменьшить влияние обратной связи, разделив предыдущий отсчет
выходного сигнала на 2:
y{k) = *(*) + 0,5 y{k - 1).
Снова подаем на вход постоянный сигнал:
Вход
1
1
1
1
1
Выход
1 +0,5-0 = 1
1 + 0,5-1 = 1,5
1 + 0,5-1,5= 1,75
1 +0,5-1,75 = 1,875
1 +0,5 -1,875 = 1,9375
Как видим, ситуация радикально изменилась — теперь выходной сигнал с умень-
уменьшающейся скоростью стремится к значению 2. Таким образом, переходный про-
процесс в фильтре является бесконечным. Это еще одна отличительная черта рекур-
рекурсивных фильтров.
Итак, рекурсивные фильтры суммируют при расчетах не только входные, но и
некоторое количество предыдущих выходных отсчетов сигнала, умножая их при
этом на постоянные весовые коэффициенты.
В общем случае дискретный фильтр суммирует (с весовыми коэффициентами)
некоторое количество входных отсчетов (включая последний) и некоторое коли-
количество предыдущих выходных отсчетов:
y{k) = b0 x(k) + bt x(k - 1) + ... + bm x(k - m) -
- a{y(k- 1) - a2 y(k - 2) - ... - an y(k - n),
где uj и fe; — вещественные коэффициенты.
D.1)
Способы описания дискретных систем 193
Данная формула называется алгоритмом дискретной фильтрации. Если по-ино-
по-иному сгруппировать слагаемые, чтобы с одной стороны от знака равенства были
только входные отсчеты, а с другой — только выходные, получим форму записи,
называемую разностным уравнением:
y(k) + a, y(k -\) + a2 y(k - 2) + ... + ап y(k - п) =
- h x(k) + bi x(k - 1) + ... + bmx(k - m). D.2)
ВНИМАНИЕ
Между отечественными и зарубежными источниками существуют расхождения в обозна-
обозначениях коэффициентов при описании дискретных систем. В зарубежных публикациях ко-
коэффициенты а, относятся к отсчетам выходного сигнала, а коэффициенты Ъ, — к отсчетам
входного сигнала. В отечественной литературе (см., например, [1, 2, 4]) все наоборот — ко-
коэффициенты а, относятся к отсчетам входного сигнала, а 6, — выходного. В данной книге,
демонстрирующей идеи и алгоритмы обработки сигналов с помощью системы MATLAB,
ради уменьшения возможности путаницы принят вариант обозначений, соответствующий
документации MATLAB.
Структура разностного уравнения похожа на структуру дифференциального
уравнения аналоговой линейной системы (см. формулу B.10) в разделе «Спосо-
«Способы описания линейных систем» главы 2), только вместо операции дифферен-
дифференцирования в формуле фигурируют задержки дискретных последовательностей.
Как мы увидим далее, этим определяется и общность подходов к описанию ана-
аналоговых и дискретных систем. Однако весьма существенным является то, что в
дискретной системе не существует каких-либо принципиальных ограничений на
соотношение между тип— количествами входных и выходных отсчетов, ис-
используемых при вычислениях.
Способы описания
дискретных систем
Дискретные системы, как и аналоговые, могут описываться различными спосо-
способами. Благодаря сходству свойств z-преобразования со свойствами преобразова-
преобразований Лапласа и Фурье способы описания аналоговых и дискретных систем в ос-
основном похожи друг на друга.
Кроме того, практически каждый способ описания дискретной системы соответ-
соответствует определенной структурной схеме из числа рассмотренных в разделе «Фор-
«Формы реализации дискретных фильтров».
Импульсная характеристика
В случае линейных систем с постоянными параметрами для анализа прохожде-
прохождения любого сигнала достаточно знать результат прохождения элементарного им-
импульса в виде дельта-функции. Для дискретных систем также можно ввести в
рассмотрение единичную импульсную функцию xo(k) (см. раздел «Примеры вы-
вычисления z-преобразования» и формулу C.17) в главе 3).
194
Глава 4. Дискретные системы
Выходная реакция на единичный импульс xo(k) называется импульсной характе-
характеристикой дискретной системы и обозначается h(k).
Исходные сигналы
т
Т
I
0 12 к
х(к): | 1 | 3 | 2 | k
Процедура вычисления
0 1 2 3
2 | 3 | 4
* = 0: х(т):
А@-ж): [7
Ч2
1
1
3|2
A(l-m):
hB-m):
Л(З-т):
hD-m):
к = 5:
АE - т):
х(т):
|4|з
1
2
3
1
2
м
х(т):
I4
1
3
3
2
2
1
>-(!)= 1-2+3-1 = 5
1-3 + 3-2 + 2-1 = 11
x(m):
1
4
3
3
2
2
2 1
>-D) = 3-4 + 2-3 = 18
3 2 1
Результат
Л
0 12 3 4 5 *
у(к): | l| 5|ll|l7|l8T8i
Рис. 4.1. Вычисление дискретной свертки
Способы описания дискретных систем 195
Как и в случае линейных систем с постоянными параметрами, знание импульс-
импульсной характеристики позволяет проанализировать прохождение через дискретную
систему любого сигнала. Действительно, прежде всего заметим, что произволь-
произвольный сигнал {x(k)} можно представить в виде линейной комбинации единичных
отсчетов:
оо
x(k)=
Выходной сигнал, исходя из линейности и стационарности рассматриваемой
системы, должен представлять собой линейную комбинацию импульсных харак-
характеристик:
y(k) = £х(т)Л(*-те). D.3)
Выражение D.3) называется дискретной сверткой (точнее, дискретной линейной
сверткой — ее не следует путать с круговой сверткой, которая будет рассматри-
рассматриваться далее, при обсуждении свойств дискретного преобразования Фурье в гла-
главе 5). Для физически реализуемой системы h(k) - 0 при k < О, поэтому верхний
предел суммирования в формуле D.3) можно заменить на к
y(k) = £,х(т)к(к-т).
т=-эо
Это означает, что система при вычислении очередного отсчета может опериро-
оперировать только прошлыми значениями входного сигнала и еще ничего не знает о бу-
будущих.
Пример вычисления дискретной свертки, подробно иллюстрирующий выполняе-
выполняемые при этом математические операции, приведен на рис. 4.1.
Функция передачи
Применим рассмотренное в главе 3 r-преобразование к уравнению дискретной
фильтрации D.3). Так как это уравнение представляет собой дискретную сверт-
свертку, то, согласно свойствам ^-преобразования (см. формулу C.23)), результатом
будет являться произведение г-преобразований:
У(г) = X(z) Н(г). D.4)
Входящая в D.4) функция H(z), равная отношению r-преобразований выходно-
выходного и входного сигналов и представляющая собой z-преобразование импульсной
характеристики системы, называется функцией передачи (transfer function) или
системной функцией дискретной системы:
^\ ±k. D.5)
Применив z-преобразование к обеим частям разностного уравнения D.2), получим
У(г)A + ci г + a2 z~2 + ... + в„ z"n) -
- X(z)(b0 + bi г + b2 z-2 + ... + bm z~m).
196 Глава 4. Дискретные системы
Отсюда легко получить вид функции передачи:
Таким образом, функция передачи физически реализуемой дискретной системы
может быть представлена в виде отношения полиномов по отрицательным сте-
степеням переменной z.
Частотная характеристика
Чтобы получить комплексный коэффициент передачи (частотную характерис-
характеристику) дискретной системы, воспользуемся формулой C.22) (см. раздел «Z-npe-
образование» главы 3), описывающей связь ^-преобразования и преобразования
Фурье:
**r. D.7)
Из D.7) видно, что частотная характеристика дискретной системы, так же как и
спектры дискретизированных сигналов (см. формулу C.2) в главе 3), является
периодической функцией частоты с периодом, равным частоте дискретиза-
дискретизации юд = 2п/Т.
Нули и полюсы
Так же как и в аналоговом случае, разложив числитель и знаменатель функции
передачи на множители, мы получим функцию передачи в следующем виде:
Здесь k = b0 — коэффициент усиления (gain), г, — нули функции передачи (zero),
Pi — полюсы функции передачи (pole). В точках нулей Я(г,) = 0, а в точках по-
полюсов H(pi) —> оо. Некоторая специфика формулы разложения связана лишь с
тем, что при записи функции передачи дискретной системы используются отри-
отрицательные степени переменной z.
В данном случае дискретная система описывается набором параметров {г,}, {р,}, к
Нули функции передачи могут быть вещественными либо составлять комплекс-
комплексно-сопряженные пары. То же относится и к полюсам. Коэффициент усиления
всегда вещественный.
Представление дискретной системы в виде наборов нулей и полюсов соответст-
соответствует последовательной форме ее реализации (см. раздел «Формы реализации
дискретных фильтров» далее в этой главе).
Всепропускающие фильтры
Всепропускающими (allpass) называют фильтры, АЧХ которых равна единице
на всех частотах. Такие фильтры изменяют только фазы спектральных состав-
Способы описания дискретных систем 197
ляющих входного сигнала и могут использоваться, например, для линеаризации
ФЧХ дискретных систем (то есть для выравнивания групповой задержки, вно-
вносимой системой).
Представление функции передачи дискретной системы в виде разложения на
множители позволяет легко получить условия, при выполнении которых рекур-
рекурсивный фильтр будет всепропускающим. Рассмотрим функцию передачи фильт-
фильтра первого порядка, имеющего один полюс р1 и один нуль z{.
\-pxz
Квадрат АЧХ такого фильтра равен
\к(со)\2 = H(ejaT)H'(ejaT) = k2 A
(l
-z\e*°T
D.8)
Мы хотим, чтобы квадрат АЧХ был равен единице на всех частотах. Для этого
необходимо, чтобы коэффициенты при всех степенях е;ш в числителе и знамена-
знаменателе D.8) были одинаковы:
k\\ + nz,*) = I +plpl*,
Из этих уравнений легко получить следующее (тривиальное решение k = 1 и
Z\ = pi нас не интересует):
4?\ =\PiV D9>
Рх
Понятно, что если включить последовательно произвольное количество фильт-
фильтров, удовлетворяющих D.9), то АЧХ системы в целом будет по-прежнему равна
единице на всех частотах. Таким образом мы получаем условия, при которых
фильтр является всепропускающим:
□ число нулей равно числу полюсов;
□ значения нулей являются обратными и комплексно-сопряженными по отно-
отношению к полюсам;
□ коэффициент усиления k равен произведению модулей полюсов фильтра.
Убедимся в справедливости сказанного, рассчитав АЧХ и ФЧХ фильтра, удов-
удовлетворяющего указанным условиям (рис. 4.2):
» р = [0.5+0.5i;0.5-0.5i;-0.7]; % полюсы фильтра
» z = 1./conj(p): % нули фильтра
» k = prod(abs(p)); % коэффициент усиления
» [b. a] = zp2tf(z. p. k); % функция передачи
» freqz(b. a) % частотные характеристики
198
Глава 4. Дискретные системы
m
|0.5
I
-0.5 -
-1
0 0
Nc
_
2 0
irmalized Fr
*\
4 0
equency (>
6 0
я rad/samp
1 ——
8 1
le)
|-400
a.
-600
0 0.2 0.4 0.6 0.6 1
Normalized Frequency (хтс rad/sample)
Рис. 4.2. АЧХ и ФЧХ всепропускающего фильтра
Как видите, фильтр имеет единичную АЧХ @ дБ) и нелинейную ФЧХ. Регули-
Регулируя количество и расположение полюсов, можно получить ФЧХ весьма сложной
формы.
ЗАМЕЧАНИЕ
В пакете Filter Design имеется функция iirgrpdelay, позволяющая рассчитывать всепро-
пускающие фильтры с заданной зависимостью групповой задержки от частоты (см. раздел
«Функции пакета Filter Design» главы 6).
Полюсы и вычеты
Идея представления дробно-рациональной функции передачи в виде суммы про-
простых дробей была рассмотрена в главе 2 применительно к аналоговым системам.
В дискретном случае такое представление имеет несколько иной вид и при от-
отсутствии кратных корней у знаменателя может быть записано следующим образом:
*
D.10)
Здесь, как и в аналоговом случае, р,- и г,- — полюсы функции передачи и соответ-
соответствующие им вычеты. Поскольку на соотношение степеней полиномов числите-
числителя и знаменателя в дискретном случае не накладывается никаких ограничений,
целая часть функции передачи, представленная коэффициентами kit может со-
содержать не только константу.
В данном случае цепь описывается набором параметров {г,}, {р;}, {&,-}.
Полюсы функции передачи могут быть вещественными либо составлять комп-
комплексно-сопряженные пары. Вычеты, соответствующие комплексно-сопряженным
полюсам, также являются комплексно-сопряженными.
Если полюс Pi имеет кратность т, то в разложении на простые дроби он порож-
порождает т слагаемых следующего вида:
Способы описания дискретных систем 199
+ -+т.—*Ьтг- D.11)
Представление дискретной системы в виде наборов полюсов и вычетов соответ-
соответствует параллельной форме ее реализации (см. раздел «Формы реализации дис-
дискретных фильтров» далее в этой главе).
Расчет импульсной характеристики
Представление функции передачи в виде суммы простых дробей позволяет вы-
вычислить импульсную характеристику системы, поскольку каждое слагаемое функ-
функции передачи вида г,/A - р,2 '), согласно формуле C.20), соответствует экспо-
экспоненциальному слагаемому импульсной характеристики вида
пр?, k>0.
Пара комплексно-сопряженных полюсов дает пару слагаемых импульсной харак-
характеристики в виде комплексно-сопряженных экспонент. Сумма таких слагаемых
представляет собой синусоиду с экспоненциально меняющейся амплитудой:
ri(Pi)" +г'(р]У = 2 Re [rf (р, )" ] = 2 Re П ^ i ■ | p, I" exp(j(argrf + n argp,))] =
= 2\ri\-\pi\" cos(nargp, +argrf).
Здесь arg г, и arg pt — фазы комплексных чисел г, и pt.
Что касается кратных полюсов, то m-кратный полюс р,- даст в выражении для им-
импульсной характеристики m слагаемых следующего вида:
А0Р) + A{k рк +A2k2pk +...+ Am_ik""lp^, k > 0.
Коэффициенты Aj представляют собой рациональные дроби и для каждой кон-
конкретной кратности k могут быть рассчитаны индивидуально. Вот несколько кон-
конкретных примеров:
Л '" k)pk, k>0,
0-*-)'
кго.
Устойчивость дискретных систем
При отсутствии входного сигнала в дискретной системе могут существовать сво-
свободные колебания. Их вид зависит от начальных условий, то есть значений, хра-
хранящихся в элементах памяти системы в момент отключения входного сигнала.
Система называется устойчивой, если при любых начальных условиях свобод-
свободные колебания являются затухающими, то есть если при x{k) = 0
\imy(k) = 0.
200 Глава 4. Дискретные системы
Любой сигнал на выходе линейной стационарной системы представляет собой
линейную комбинацию ее задержанных во времени импульсных характеристик.
Поэтому для затухания свободных колебаний необходимо, чтобы была затухаю-
затухающей импульсная характеристика системы h{k):
В предыдущем разделе было показано, что импульсная характеристика системы
в общем случае содержит слагаемые вида
А р? k",
где Pi — полюсы функции передачи системы, п — неотрицательные целые числа,
меньшие кратности полюса р„ А — некая константа.
Такие слагаемые при k -» qo затухают, если полюс р{ по модулю меньше единицы:
Ы < 1.
Теперь мы можем окончательно сформулировать условие устойчивости: чтобы
дискретная система была устойчива, полюсы ее функции передачи должны нахо-
находиться на комплексной плоскости внутри круга единичного радиуса.
Пространство состояний
Сущность представления дискретной системы в пространстве состояний та же,
что и в аналоговом случае, — имеется вектор параметров, описывающих внут-
внутреннее состояние системы, и две формулы, согласно которым производится из-
изменение этого состояния и формирование выходного сигнала в зависимости от
текущего состояния и входного сигнала:
s(* + 1) - As(*) + Bx(k),
y{k) - Cs(*) + Dx{k).
Здесь s{k) — вектор состояния, x{k) и y(k) — соответственно отсчеты входного и
выходного сигналов, А, В, С и D — параметры, описывающие систему. Если х и
у — скалярные сигналы и размерность вектора состояния равна N, то размер-
размерность параметров будет следующей: А — матрица NxN, В — столбец N* 1, С —
строка 1 x-N, D — скаляр. Если входной и/или выходной сигналы являются век-
векторными, размерность матриц соответствующим образом изменяется.
Представление дискретной системы в пространстве состояний соответствует ка-
канонической форме ее реализации (см. раздел «Каноническая форма» далее в
этой главе).
Преобразование случайного сигнала
в дискретной системе
Пусть на вход дискретной системы с импульсной характеристикой h(k) поступа-
поступает дискретный стационарный центрированный случайный процесс {x{k)} с кор-
корреляционной функцией Rx(&k). Найдем корреляционную функцию выходного
Преобразование случайного сигнала в дискретной системе 201
случайного процесса. Для этого воспользуемся определением корреляционной
функции (см. раздел «Дискретные случайные сигналы» главы 3) и формулой
D.3), описывающей преобразование сигнала, осуществляемое системой:
щ =-оо П2~—те
Преобразуем произведение сумм в двойную сумму, воспользуемся линейностью
операции статистического усреднения и заметим, что х(щ )х(п2 ) = Rx{n2 ~ п\ )'•
00 _CO_
Ry(Ak)= £
И]=-сол2=-со D.12)
= I 1/гг(я,-я2)А(*-я1)А(*-
П| = — oo П'2 = — оо
Произведем замену второго индекса суммирования: т = Пг - щ. С учетом этого
формула D.12) принимает вид
00 00
D.13)
—»—
Внутренняя сумма в D.13) представляет собой корреляционную функцию им-
импульсной характеристики системы:
Таким образом, окончательно получаем, что корреляционная функция случай-
случайного сигнала на выходе системы представляет собой свертку корреляционной
функции входного шума и корреляционной функции импульсной характеристи-
характеристики системы:
Ry(Ak)= ±Rx(m)Bh(Ak-m). D.14)
ЗАМЕЧАНИЕ
Полученная формула является дискретным аналогом формулы B.7), описывающей пре-
преобразование корреляционной функции аналогового шума в линейной цепи.
Дисперсия выходного случайного процесса может быть рассчитана как
Dy=Ry@)=fjRx(m)Bh(m).
П=-оо
В этой формуле учтена четность функции Bh(m).
Если входной случайный процесс является дискретным белым шумом, формула
D.14) упрощается:
Ry(Ak) = Dx Bh(Ak).
202 Глава 4. Дискретные системы
Дисперсия выходного шума при этом составляет
Таким образом, при воздействии на вход системы дискретного белого шума дис-
дисперсия выходного сигнала пропорциональна сумме квадратов отсчетов импульс-
импульсной характеристики системы.
Рекурсивные и нерекурсивные
дискретные фильтры
В начале главы, рассматривая идею обработки сигнала дискретной линейной сис-
системой, мы уже ввели понятия нерекурсивных и рекурсивных фильтров. Настало
время вернуться к этому вопросу и обсудить его более обстоятельно. Для этого мы
рассмотрим структурные схемы устройств, реализующих уравнение D.1), в об-
общем виде описывающее процесс обработки сигнала дискретной системой.
Нерекурсивные фильтры
Прежде всего следует отметить, что в общем случае при вычислении очередного
выходного отсчета y(k) используется информация двух типов: некоторое коли-
количество отсчетов входного сигнала и некоторое количество предыдущих отсчетов
выходного сигнала. Ясно, что хотя бы один отсчет входного сигнала должен уча-
участвовать в вычислениях; в противном случае выходной сигнал не будет зависеть
от входного. В противоположность этому, предыдущие отсчеты выходного сиг-
сигнала могут и не использоваться. Уравнение фильтрации D.1) в этом случае при-
приобретает следующий вид:
^Ъгх(к-1). D.15)
Количество используемых предыдущих отсчетов т называется порядком фильтра.
Структурная схема, реализующая алгоритм D.15), приведена на рис. 4.3. Неко-
Некоторое количество предыдущих отсчетов входного сигнала хранится в ячейках па-
памяти, которые образуют дискретную линию задержки. Эти отсчеты умножаются
на коэффициенты 6, и суммируются, формируя выходной отсчет y(k).
ЗАМЕЧАНИЕ
Согласно свойствам z-преобразования (см. раздел «Z-преобразование» главы 3), задержка
дискретной последовательности на один такт соответствует умножению ее г-преобразова-
ния на z~{. Поэтому элементы памяти, осуществляющие такую задержку, обозначены на
структурной схеме как «z"'».
Так как при вычислениях не используются предыдущие отсчеты выходного сиг-
сигнала, в схеме отсутствуют обратные связи. Поэтому такие фильтры называют-
называются нерекурсивными (nonrecursive). Применяется также термин «трансверсальный
фильтр» (от английского transversal — поперечный).
Рекурсивные и нерекурсивные дискретные фильтры
203
Хк
Хк-,
Рис. 4.3. Нерекурсивный фильтр
Импульсная характеристика нерекурсивного фильтра определяется очень про-
просто. Подставим в уравнение D.15) единичный импульс xo(k) в качестве входного
сигнала:
Но отсчет xo(k - i) равен нулю для всех k, кроме k - i, когда этот отсчет равен
единице. Поэтому мы получаем очень простой результат:
то есть коэффициенты й, являются отсчетами импульсной характеристики фильт-
фильтра. Это можно наглядно пояснить с помощью рис. 4.3. При подаче на вход еди-
единичного импульса он будет перемещаться по линии задержки, умножаться на ко-
коэффициенты b0, bb b2, ... и проходить на выход устройства (ведь все остальные
входные сигналы сумматора при этом равны нулю). Очевидно, что в реальном
устройстве линия задержки содержит конечное число элементов, поэтому им-
импульсная характеристика нерекурсивного фильтра также является конечной по
длительности. Это обусловило еще одно название таких фильтров — фильтры
с конечной импульсной характеристикой (КИХ-фильтры; английский термин —
finite impulse response, FIR).
ЗАМЕЧАНИЕ
Вследствие отсутствия обратных связей любой нерекурсивный фильтр является устойчи-
устойчивым — ведь каковы бы ни были начальные условия (то есть отсчеты, хранящиеся в линии
задержки), при отсутствии сигнала на входе (x(k) = 0) выходной сигнал (свободные коле-
колебания) будет отличен от нуля в течение не более чем т тактов, необходимых для очистки
линии задержки.
204
Глава 4. Дискретные системы
Простота анализа и реализации, а также наглядная связь коэффициентов фильт-
фильтра с отсчетами его импульсной характеристики и абсолютная устойчивость при-
привели к тому, что нерекурсивные фильтры широко применяются на практике.
Однако для получения хороших частотных характеристик (например, полосо-
полосовых фильтров с высокой прямоугольностью АЧХ) необходимы нерекурсивные
фильтры высокого порядка — до нескольких сотен и даже тысяч.
Симметричные фильтры
Очень важное значение имеет тот факт, что нерекурсивные фильтры позволяют
легко обеспечить линейную ФЧХ, а значит, постоянные (не зависящие от часто-
частоты) групповую и фазовую задержки. Для этого необходима лишь симметрия им-
импульсной характеристики. Эта симметрия может быть двух типов:
□ четная симметрия (even symmetry): bk = b^-k Для всех k = О, 1 N;
□ нечетная симметрия (odd symmetry): bk = -Ьы-k для всех k = 0, 1, ..., N.
ЗАМЕЧАНИЕ
Иногда под симметричными подразумевают только характеристики с четной симметрией,
а для нечетной симметрии используют термин «антисимметричные».
Групповая задержка для симметричных фильтров не зависит от частоты и равна
N/2 отсчетов.
При четном N и нечетной симметрии импульсной характеристики, очевидно, ее
средний отсчет должен быть равен нулю: bN/2 - 0. Кроме того, четность или не-
нечетность порядка фильтра и наличие того или иного типа симметрии накладыва-
накладывают определенные ограничения на коэффициенты передачи фильтра на нулевой
частоте и на частоте Найквиста. Эти ограничения легко получить из условий
симметрии и формулы D.7) для комплексного коэффициента передачи фильтра.
Сочетание четности порядка фильтра и типа симметрии дает четыре типа сим-
симметричных фильтров, перечисленных в табл. 4.1 вместе с указанными ограниче-
ограничениями значений АЧХ. Приведенные в таблице номера типов часто используются
в зарубежной литературе.
Таблица 4.1. Типы симметричных фильтров
Тип
I
II
III
IV
Порядок фильтра
Четный
Нечетный
Четный
Нечетный
Тип симметрии
Четная
Четная
Нечетная
Нечетная
К@)
Любой
Любой
0
0
К(с0д/2)
Любой
0
0
Любой
Рекурсивные и нерекурсивные дискретные фильтры
205
Рекурсивные фильтры
Если уравнение фильтрации имеет общий вид D.1), то есть содержит как вход-
входные, так и выходные отсчеты, для реализации такого фильтра в схему, приведен-
приведенную на рис. 4.3, необходимо добавить вторую линию задержки — для хранения
выходных отсчетов y(k - i). Получающаяся при этом структура показана на
рис. 4.4.
Ук
Ук-п*\
Ук-п
Рис. 4.4. Рекурсивный фильтр — прямая реализация
Так как при вычислениях используются предыдущие отсчеты выходного сигна-
сигнала, в схеме присутствуют обратные связи. Поэтому такие фильтры называют ре-
рекурсивными (recursive).
ЗАМЕЧАНИЕ
Количество предыдущих входных и выходных отсчетов, используемых для вычислений,
может не совпадать. В таком случае порядком фильтра считается максимальное из чи-
чисел тип.
Импульсная характеристика рекурсивного фильтра рассчитывается значительно
сложнее, чем для нерекурсивного. Рассмотрим формирование лишь нескольких
первых ее отсчетов. При поступлении на вход единичного импульса он умножа-
умножается на Ьо и проходит на выход. Таким образом,
Далее входной единичный импульс попадает во входную линию задержки, а вы-
выходной отсчет, равный Ьо, — в выходную линию задержки. В результате второй
отсчет импульсной характеристики будет формироваться как
206 Глава 4. Дискретные системы
Продолжив рассмотрение перемещения входного единичного импульса вдоль
входной линии задержки и заполнения выходными отсчетами выходной линии
задержки, можно получить
/гB) - Ь2 + а2 /г@) + d /гA) - b2 + b0 а2 + fli(fci + b0 a{) -
= Ъ2 + Ь\ п\ + bo a2 + bo fli2.
Видно, что по мере того, как выходная линия задержки заполняется отсчетами им-
импульсной характеристики, сложность аналитических формул быстро возрастает.
Наличие в схеме обратных связей позволяет получить бесконечную импульсную
характеристику, поэтому рекурсивные фильтры называют также фильтрами с бес-
бесконечной импульсной характеристикой (БИХ-фильтрами; английский термин —
infinite impulse response, IIR). По этой же причине рекурсивные фильтры могут
быть неустойчивыми.
Формы реализации
дискретных фильтров
Структурная схема, показанная ранее на рис. 4.4, называется прямой формой реа-
реализации рекурсивного фильтра (direct form I) и не является единственно воз-
возможной. Рассмотрим еще несколько вариантов.
Каноническая форма
Разделим общий сумматор в схеме рис. 4.4 на два отдельных — для рекурсивной
и нерекурсивной частей фильтра (рис. 4.5, а). В результате получаем два после-
последовательно соединенных фильтра, один из которых является нерекурсивным,
а другой, напротив, содержит только рекурсивную часть. Так как результат по-
последовательного прохождения сигнала через ряд линейных стационарных уст-
устройств не зависит от последовательности их соединения, мы можем поменять
местами две «половинки» нашего фильтра (рис. 4.5, б). Теперь остается заме-
заметить, что в обе линии задержки подается один и тот же сигнал, поэтому они бу-
будут содержать одинаковые наборы отсчетов. Это позволяет объединить линии
задержки. Полученная в результате схема изображена на рис. 4.6, она называется
канонической формой реализации рекурсивного фильтра (canonic form или direct
form II).
С теоретической точки зрения эти варианты эквивалентны. Однако при практи-
практической реализации необходимо обратить внимание на ряд особенностей, прису-
присущих этим схемам. С одной стороны, при канонической реализации используется
общая линия задержки, что уменьшает число необходимых ячеек памяти. Одна-
Однако при этом абсолютные величины отсчетов, «бегающих» в линии задержки, мо-
могут существенно превосходить амплитуду входного и выходного сигналов. Это
приводит к необходимости увеличивать разрядность представления чисел в ли-
линии задержки по сравнению с разрядностью входного и выходного сигналов, что
усложняет реализацию устройства. При прямой реализации в линиях задержки
хранятся непосредственно отсчеты входного и выходного сигналов, то есть по-
Формы реализации дискретных фильтров
207
вышенная разрядность линий задержки не требуется. Единственным элементом,
требующим повышенной разрядности, в данном случае является сумматор, и это
учтено в архитектуре микропроцессоров, специально предназначенных для обра-
обработки сигналов в реальном времени.
Рис. 4.5. Перестановка рекурсивной и нерекурсивной частей фильтра —
путь к получению канонической реализации
Рис. 4.6. Рекурсивный фильтр — каноническая реализация
ЗАМЕЧАНИЕ
Представление дискретной системы в пространстве состояний соответствует именно ка-
канонической форме реализации. Вектор состояния при этом представляет собой набор зна-
значений выходов элементов задержки.
208
Глава 4. Дискретные системы
Транспонированная форма
Поменяем в схеме рис. 4.3 последовательность выполнения операций умноже-
умножения и задержки, используя в каждой ветви отдельную линию задержки на нуж-
нужное количество тактов. Разделим также общий сумматор на несколько двух-
входовых сумматоров. Получившаяся структура показана на рис. 4.7. Теперь,
рассмотрев любую пару соседних сумматоров, можно заметить, что суммируе-
суммируемые ими сигналы претерпевают некоторую общую задержку. Это дает возмож-
возможность поменять местами операции суммирования и задержки. Получившаяся схе-
схема, показанная на рис. 4.8, называется транспонированной реализацией дискрет-
дискретного фильтра (direct transposed form II).
i>—¥
-1
-2
-m + l
z~m
Рис. 4.7. Изменение последовательности выполнения операций умножения и задержки —
путь к получению транспонированной реализации фильтра
ЗАМЕЧАНИЕ
Разумеется, в транспонированной форме может быть реализован и нерекурсивный фильтр.
Для этого в структурной схеме рис. 4.8 необходимо удалить все ветви с коэффициента-
коэффициентами Ь\, кроме Ьо.
Транспонированная схема позволяет эффективно распараллелить вычисления и
потому применяется при реализации дискретных фильтров в виде специализи-
специализированных интегральных схем. Действительно, при реализации фильтра в форме
рис. 4.3 или рис 4.4 можно одновременно выполнять все операции умножения, но
для получения выходного результата необходимо дождаться окончания выпол-
выполнения всех операций сложения. В транспонированной же схеме, помимо умноже-
умножения, можно одновременно выполнять и все операции сложения, поскольку они
являются независимыми (то есть не используют в качестве суммируемых вели-
величин результаты других сложений). Как видно из схемы рис. 4.8, собственно для
расчета выходного сигнала необходимо выполнить одно умножение и одно ело-
Формы реализации дискретных фильтров
209
жение; все остальные операции производят подготовку промежуточных резуль-
результатов для вычисления последующих выходных отсчетов.
Рис. 4.8. Транспонированная реализация дискретного фильтра
Если применить описанные преобразования к канонической структуре, показан-
показанной на рис. 4.6, получится еще один вариант транспонированной реализации
фильтра (direct transposed form I) (рис. 4.9). В отличие от предыдущей схемы,
данная структура содержит большее число элементов памяти.
Ук
Рис. 4.9. Транспонированная реализация, полученная
из канонической формы дискретного фильтра
210
Глава 4. Дискретные системы
Последовательная (каскадная) форма
В разделе «Нули и полюсы» было показано, что числитель и знаменатель функ-
функции передачи физически реализуемого дискретного фильтра можно разложить
на линейные (относительно г) множители. Перемножение функций передачи
соответствует последовательному (каскадному) включению соответствующих
фильтров, поэтому такое представление дает реализацию фильтра в виде после-
последовательно включенных фильтров 1-го порядка (при этом некоторые из них мо-
могут иметь комплексные коэффициенты) либо фильтров 1-го и 2-го порядка с ве-
вещественными коэффициентами.
Рассмотрим конкретный пример, задавшись численными значениями коэффи-
коэффициентов фильтра:
„, , 0,0985 +0,29561-' + 0,2956 г'2 + 0,0985Г3
H(Z) =
1-0.5772Г-1 +0,4218r -0,0563Г3
0,0985A + г~1)A + 2г'1 +z'2)
A-0,1584г-1)A-0,4188г-1+0,3554г-2)
D.16)
ЗАМЕЧАНИЕ
Данный фильтр является фильтром Баттерворта 3-го порядка с частотой среза, равной
1/5 частоты дискретизации, синтезированным методом билинейного z-преобразования
(о данном методе синтеза дискретных фильтров речь пойдет в главе 6).
Структурная схема получившейся последовательной реализации фильтра пред-
представлена на рис. 4.10.
0,0985
z
\
\ 0,4188
\ ^\
\
\ -0,3554
-1
z
-1
z
Рис. 4.10. Последовательная реализация дискретного фильтра
Последовательная реализация часто используется на практике, поскольку она по-
позволяет ослабить нежелательные эффекты, связанные с ошибками округления [8].
Такие эффекты обсуждаются в главе 7.
Параллельная форма
Еще один способ преобразования функции передачи физически реализуемого
фильтра — представление ее в виде суммы простейших дробей. Об этом уже шла
Дискретная фильтрация в MATLAB
211
речь в разделе «Полюсы и вычеты» (см. формулу D.10)). Каждое из слагаемых
при таком представлении соответствует функции передачи рекурсивного фильт-
фильтра 1-го порядка (возможно, с комплексными коэффициентам) либо 1-го или 2-го
порядка (если используется представление в виде суммы простейших дробей толь-
только с вещественными коэффициентами). Сама операция сложения эквивалентна па-
параллельному соединению этих фильтров с суммированием выходных результатов.
Рассмотрим конкретный пример, используя ту же функцию передачи D.16), что
и раньше:
0,0985 +0,2956 z"' + 0,2956z'2 + 0,0985;-*
H(z) =
1-0,5772;"' + 0,4218; -0,0563; ~3
50777 -1,229 + 0,3798;-'
= -1,7502 +
1-0,1584;'' 1-0,4188;''+0,3554;
I--2
Структурная схема получившейся параллельной реализации фильтра представ-
представлена на рис. 4.11. Постоянному слагаемому соответствует верхняя ветвь струк-
структурной схемы, содержащая только умножитель.
-1,7502
Рис. 4.11. Параллельная реализация дискретного фильтра
Дискретная фильтрация в MATLAB
В данном разделе рассматриваются средства MATLAB, предназначенные для
выполнения дискретной фильтрации и анализа параметров дискретных фильт-
фильтров. Следует отметить, что сфера применения технологий дискретной фильтра-
212 Глава 4. Дискретные системы
ции в настоящее время не ограничивается обработкой сигналов — это техноло-
технологии обработки любых данных. Данный факт нашел свое отражение и в том, что в
MATLAB базовые функции дискретной фильтрации не относятся к пакету рас-
расширения Signal Processing, а являются встроенными в ядро программы.
Помимо многочисленных функций расчета параметров дискретных фильтров в
составе пакета Signal Processing имеется программа fdatool (Filter Design & Ana-
Analysis Tool) — графическая среда для анализа дискретных фильтров. Эта программа
позволяет не только анализировать, но и рассчитывать (синтезировать) фильтры
с заданными свойствами, поэтому она будет описана в главе 6, посвященной про-
проектированию дискретных фильтров.
Дискретная свертка
Дискретная свертка, являющаяся основой алгоритма дискретной фильтрации,
в MATLAB вычисляется с помощью функции conv:
z = conv(x. у);
Вычислим с помощью функции conv свертку тех же числовых последовательно-
последовательностей, что рассматривались в качестве примера при пояснении идеи дискретной
свертки в разделе «Импульсная характеристика»:
» х = [1 3 2];
» h = [1 2 3 4];
» у = conv(x. h)
У =
1 5 11 17 18 8
Результат, разумеется, соответствует тому, что было получено ранее (см. рис. 4.1).
Длина выходного вектора равна length(x)+length(y)-l.
Обращение свертки
Зная результат свертки и один из сворачиваемых векторов, можно найти второй.
Если перейти к r-преобразованиям векторов, данная операция (она называется
обращением свертки — deconvolution) сводится к делению полиномов. В MATLAB
эта операция реализуется с помощью функции deconv, имеющей следующий син-
синтаксис:
[q. r] = deconv(b. a)
Здесь b — результат свертки (коэффициенты полинома-числителя), а — один из
сворачиваемых векторов (коэффициенты полинома-знаменателя).
Выходные параметры имеют следующий смысл: q — результат деления полино-
полиномов (частное; quotient), то есть искомый второй вектор свертки, г — остаток
(remainder) от деления полиномов (если вектор b действительно является сверт-
сверткой вектора а с чем-нибудь, остаток от деления будет нулевым).
В общем случае исходные данные b и а связаны с результатами расчета следую-
следующим образом:
b = conv(q, a) + г
Дискретная фильтрация в MATLAB 213
Продемонстрируем использование функции deconv, взяв данные из предыдущего
примера:
» [q. г] = deconv(у, h)
q =
1 3 2
г =
0 0 0 0 0 0
Поскольку вектор у был получен в результате свертки, мы получили исходный
сигнал (см. вектор х в предыдущем примере) и нулевой остаток.
Функция дискретной фильтрации
Основная функция, реализующая дискретную фильтрацию в MATLAB, носит имя
filter. В простейшем виде она имеет следующий синтаксис:
у = filterCb, a, x):
Здесь b — вектор коэффициентов нерекурсивной части фильтра (числителя функ-
функции передачи), а — вектор коэффициентов рекурсивной части фильтра (знаме-
(знаменателя функции передачи), х — входной сигнал.
Возвращаемой величиной является вектор отсчетов выходного сигнала фильтра.
Если первый элемент вектора а не равен 1, значения векторов b и а нормируют-
нормируются — делятся на аA).
Между функциями f i I ter и conv есть два основных различия. Во-первых, функ-
функция conv требует задания импульсной характеристики фильтра в виде вектора,
поэтому данная импульсная характеристика должна иметь конечную длину. Фак-
Фактически это означает, что с помощью функции conv можно реализовать только
нерекурсивный фильтр. Функция filter позволяет задавать как нерекурсивные,
так и рекурсивные фильтры, реализуя в том числе и бесконечные импульсные
характеристики. Во-вторых, функция filter возвращает результат, длина кото-
которого равна длине входного сигнала: это, как мы увидим чуть ниже, позволяет ор-
организовать блочную обработку сигнала.
Повторим пример, рассмотренный выше при описании функции conv, на сей раз
реализовав расчеты с помощью функции filter. Поскольку мы используем непо-
непосредственно импульсную характеристику фильтра, она должна быть передана
функции в качестве вектора b коэффициентов нерекурсивной части фильтра.
Вектор а рекурсивной части фильтра в этом случае представляет собой скаляр,
равный единице:
» у = filterCh, 1, х)
У =
1 5 11
Как видите, результат фильтрации совпадает с полученными в предыдущем раз-
разделе значениями. Однако теперь вектор z не содержит затухающего «хвоста». Дело
в том, что функция conv предполагала завершенность входного сигнала, а функ-
функция filter позволяет при необходимости продолжить его обработку, подавая на
вход фильтра новые отсчеты (см. далее раздел «Доступ к внутреннему состоя-
состоянию фильтра»).
214 Глава 4. Дискретные системы
Чтобы получить результат, полностью совпадающий с тем, что дает функция conv,
можно дополнить вектор х соответствующим количеством нулей:
» у = filter(h. 1, [х 0 0 0])
У =
1 5 11 17 18 8
Входной сигнал х может быть матрицей. При этом ее столбцы фильтруются не-
независимо.
Доступ к внутреннему состоянию фильтра
Функция f i I ter позволяет задавать и считывать внутреннее состояние дискрет-
дискретного фильтра. Для этого используются дополнительные входной и выходной па-
параметры:
[у. z2] = filter(b. a. x, zl):
Здесь zl — начальное внутреннее состояние фильтра (входной параметр), z2 —
конечное внутреннее состояние фильтра (выходной параметр).
По умолчанию предполагается нулевое внутреннее состояние фильтра.
Чтобы понимать, что именно представляет собой вектор внутреннего состояния
фильтра, нужно знать, как организованы вычисления в функции f i I ter. Данная
функция реализует рекурсивный дискретный фильтр в транспонированной фор-
форме (direct transposed form II, см. рис. 4.8).
Возможность доступа к внутреннему состоянию фильтра позволяет при необхо-
необходимости реализовать обработку сигнала по частям:
% 1-й блок данных
[y(l:N). z] = filterCb, a. x(l:N));
% 2-й блок данных
[y(N+l:2*N). z] = filterCb. a, x(N+l:2*N), z):
Если текущее внутреннее состояние фильтра не известно, но известны предыду-
предыдущие отсчеты входного и выходного сигналов, состояние фильтра можно полу-
получить с помощью функции fПtic («ic» обозначает начальное состояние — initial
conditions):
z = filticCb, а, у, х);
Здесь b и а — параметры фильтра, у — предыдущие значения выходного сигнала,
х — предыдущие значения входного сигнала.
Предыдущие значения сигналов задаются в обратном порядке: первые элементы
векторов х и у — это последние значения входного и выходного сигналов, вторые
элементы — предпоследние значения и т. д.
Число элементов векторов х и у, необходимое для расчетов, на единицу меньше
длин векторов b и а соответственно. При недостаточной длине векторов х и/или у
они дополняются нулями, при чрезмерной длине лишние элементы игнорируют-
игнорируются. Вектор х может не задаваться, тогда он считается заполненным нулями.
Возвращаемый функцией результат — вектор-столбец внутреннего состояния
фильтра.
Дискретная фильтрация в MATLAB 215
Компенсация фазового сдвига
При фильтрации сигналов в ряде случаев возникает требование сохранения фа-
фазовых соотношений в исходом сигнале. Для этого требуется фильтр с линейной
ФЧХ или, что то же самое, с постоянной (не зависящей от частоты) фазовой за-
задержкой.
Как говорилось в разделе «Симметричные фильтры», для получения линейной
ФЧХ фильтр должен иметь симметричную импульсную характеристику. Поэтому
линейную ФЧХ несложно реализовать в нерекурсивном фильтре — для этого
нужна только симметрия набора коэффициентов фильтра: bt = bm _ t или bt = -bm _;.
Из симметрии импульсной характеристики фильтра и соображений его физиче-
физической реализуемости следует конечность импульсной характеристики. Поэтому
рекурсивные фильтры, обладающие бесконечной импульсной характеристикой,
принципиально не могут иметь линейную ФЧХ.
Однако при обработке сигнала не в реальном масштабе времени можно обойти
ограничение физической реализуемости и использовать фильтр, для которого не
выполняется условие причинности.
ЗАМЕЧАНИЕ
Еще один, менее шокирующий подход к данной ситуации можно сформулировать так.
Нам известен весь входной сигнал, и мы знаем, что он уже закончился, то есть на вход
фильтра в дальнейшем будут поступать только нулевые значения. Поэтому можно счи-
считать, что условие причинности по-прежнему соблюдается, но фильтр вносит очень боль-
большую задержку, превышающую длительность всего входного сигнала.
Для реализации фильтрации с нулевым фазовым сдвигом в MATLAB предна-
предназначена функция filtfiit. Ее название символизирует смысл выполняемых ею
действий: сначала входной сигнал фильтруется как обычно, а затем производит-
производится второй проход фильтрации, при котором сигнал обрабатывается от конца
к началу. Если заданный в качестве параметров функции фильтр имеет функцию
передачи Я(г), импульсную характеристику h(k) и АЧХ К(а>), то фильтр, экви-
эквивалентный двум проходам обработки сигнала, будет иметь функцию передачи
H(z)H(z~l), АЧХ \К((£>)\2 и нулевую ФЧХ. Импульсная характеристика представ-
представляет собой корреляционную функцию исходной импульсной характеристики:
h'(k)= ^h(m)h(m-k), -x<k<oo.
Синтаксис вызова функции filtfilt такой же, как для функции filter:
у.= filtfilt(b. а. х)
Приведем пример, демонстрирующий компенсацию фазового сдвига с помощью
функции filtfilt. Создадим сигнал в виде прямоугольного импульса, дополнен-
дополненного с обеих сторон нулями:
» s = [zerosE0, 1): onesdOO. 1): zerosE0. 1)]:
В качестве фильтра используем ФНЧ Чебышева первого рода с достаточно
сильными пульсациями АЧХ в полосе пропускания C дБ) и низкой часто-
216
Глава 4. Дискретные системы
той среза @,05 частоты Найквиста), чтобы выходной импульс был заметно ис-
искажен:
» [b, a] = chebylE. 3. 0.05);
Обрабатываем сигнал с помощью функций filter и filtfilt и строим графики
входного и выходных сигналов (рис. 4.12):
» si = filter(b, a. s):
» s2 = filtfilt(b. a. s);
» plot(s)
» hold on
» plot(sl. '--■)
» plot(s2. '-.')
» hold off
1.2
1
0.8
0.6
0.4
0.2
0
-0.2
.' / »
i '
1
1
f
/
i
1
1
I
/
\
\
\
\
\
\
\
\
\
x \
\
\ \
i \
\
\ У -
_, • Г " ""
-• \
0
50
100
150
200
Рис. 4.12. Входной сигнал (сплошная линия), результат обычной фильтрации
(пунктирная линия) и фильтрации с компенсацией фазового сдвига
(штрихпунктирная линия)
На рисунке хорошо видно, что при фильтрации обычным ФНЧ сигнал приобре-
приобретает существенную задержку по времени. После повторной фильтрации в обрат-
обратном направлении эта задержка компенсируется. Форма сигнала при втором про-
проходе фильтрации также несколько изменяется, поскольку суммарное действие
двух ФНЧ эквивалентно двукратному увеличению порядка фильтра.
Расчет импульсной характеристики
Чтобы получить импульсную характеристику, необходимо подать на вход фильт-
фильтра единичный отсчет, дополненный некоторым количеством нулей:
filter(b, a. [I zerosd. N)])
Для удобства такой расчет реализован в функции impz, которая к тому же обла-
обладает рядом дополнительных возможностей.
Дискретная фильтрация в MATLAB
217
В простейшем виде синтаксис вызова функции impz следующий:
h = impz(b. a);
Входные параметры b и а — коэффициенты полиномов числителя и знаменателя
функции передачи соответственно.
Возвращаемое значение h — вектор отсчетов импульсной характеристики. Число
рассчитываемых отсчетов выбирается автоматически и зависит от поведения им-
импульсной характеристики. Более подробную информацию об этом можно найти
в документации пакета Signal Processing.
Чтобы явно задать число рассчитываемых отсчетов импульсной характеристики,
следует использовать третий входной параметр п:
h = impz(b, a, n);
Теперь обратимся к выходным параметрам функции. В приведенных выше вари-
вариантах использовался один выходной параметр — вектор отсчетов импульсной ха-
характеристики. Если выходные параметры отсутствуют, функция impz строит гра-
график импульсной характеристики с использованием графической функции stem.
Построим график импульсной характеристики фильтра Баттерворта 5-го поряд-
порядка с частотой среза, равной 0,1 частоты дискретизации (рис. 4.13):
» [b, a] = butterE. 0.2);
» impz(b, a)
0.25
10
20
30
40
50
Рис. 4.13. График импульсной характеристики, построенный функцией impz
Расчет частотной характеристики
Частотная характеристика дискретного фильтра рассчитывается с помощью функ-
функции freqz, которая очень похожа на функцию freqs, выполняющую аналогичные
расчеты для аналоговых цепей.
В простейшем виде функция freqz используется следующим образом:
freqz(b, a)
218
Глава 4. Дискретные системы
Входные параметры b и а — векторы коэффициентов полиномов числителя и зна-
знаменателя функции передачи фильтра.
При расчете используются нормированные значения частот, измеряемые в ра-
радианах на отсчет (при такой нормировке частота дискретизации равна 2л, а час-
частота Найквиста — я). По умолчанию выбирается 512 частотных точек, равномер-
равномерно распределенных в диапазоне 0...Л.
При отсутствии выходных параметров функция freqz строит графики АЧХ (в де-
децибелах) и ФЧХ (в градусах) фильтра.
Построим графики частотных характеристик фильтра, использованного при де-
демонстрации дискретной свертки, но добавим к этому фильтру рекурсивную
ветвь с коэффициентом передачи 0,1. Результат показан на рис. 4.14:
» b = [1 2 3 4]:
» а = [1 -0.1];
» freqz(b. a)
ш
2.
(Л
25
20
i 15
? 10
5
0
-200
-400
-600
0 0.2 0.4 0.1
Normalized Frequency (>
"
>?г>^^
3 0.8 1
тс rad/sample)
1
0.2 0.4 0.6 0.8
Normalized Frequency (хтс rad/sample)
Рис. 4.14. Частотная характеристика дискретного фильтра, построенная функцией freqz
Если при вызове функции указаны выходные параметры, построение графика не
производится:
[h. w] - freqz(b. a):
В векторе h возвращаются рассчитанные значения комплексного коэффициента
передачи, а в векторе W — использованные при расчете значения нормированных
частот.
Чтобы задать количество частотных точек для расчета, используется третий
входной параметр п (частоты при этом по-прежнему равномерно распределяют-
распределяются в диапазоне 0...л ):
freqz(b. а. п):
Можно заставить функцию freqz использовать ряд частот, равномерно распреде-
распределенных на интервале О...2л, то есть вплоть до частоты дискретизации. Это может
Дискретная фильтрация в MATLAB 219
быть необходимо при анализе фильтров с комплексными коэффициентами, час-
частотные характеристики которых не являются симметричными. Такое указа-
указание дается функции f reqz с помощью четвертого входного параметра — строки
'whole':
freqz(b. a. n, 'whole');
Наконец, можно задать вектор нормированных круговых частот w для расчета
частотной характеристики:
h = freqz(b, a, w);
Использование второго выходного параметра в этом случае не имеет смысла, по-
поскольку вектор частот задан на входе.
ЗАМЕЧАНИЕ ;
При выводе графиков ФЧХ фильтров функция freqz применяет к вектору рассчитанных
фазовых сдвигов функцию unwrap, чтобы устранить «фиктивные» разрывы, о которых
шла речь в разделе «Построение графиков фазочастотных характеристик» главы 2.
Задание вектора частот
Для некоторого повышения удобства задания вектора частот при расчете частот-
частотных характеристик служит функция f reqspace. Эта функция очень проста и име-
имеет следующий синтаксис вызова:
у = freqspace(n)
Возвращаемый вектор f содержит значения, не превосходящие частоту Найкви-
ста и нормированные к этой частоте. При этом подразумевается, что на п равных
частей делится частотный диапазон от нуля до частоты дискретизации (после
нормировки к частоте Найквиста она равна двум). Значения частот в векторе f
рассчитываются как 0:2/п:1, так что этот вектор содержит Лоог(п/2+1) элементов.
При необходимости сформировать набор значений в диапазоне от нуля до двух
(то есть до частоты дискретизации) следует использовать второй входной пара-
параметр — строку ' whol e':
у * freqspace(n. 'whole')
При этом вектор у содержит п элементов и рассчитывается так:
у = @:п-1)*2/п
Расчет групповой задержки
дискретной системы
Для вычисления групповой задержки дискретного фильтра в MATLAB служит
функция grpdel ay. В простейшем виде она вызывается так:
grpdelay(b. a)
Здесь b и а — векторы коэффициентов числителя и знаменателя передаточной
функции фильтра соответственно.
Дополнительные входные параметры используются точно так же, как и для рас-
рассмотренной ранее функции расчета частотной характеристики freqz.
220 Глава 4. Дискретные системы
При отсутствии выходных параметров функция grpdel ay строит график зависи-
зависимости группового времени задержки от частоты. При указании одного выходно-
выходного параметра функция возвращает вектор рассчитанных значений групповой
задержки. При использовании двух выходных параметров во втором из них воз-
возвращается вектор использованных при расчете значений частот (второй выход-
выходной параметр можно использовать, если частоты для расчета не задаются прину-
принудительно среди входных параметров):
tau = grpdelay(b. a. ...):
[tau. w] = grpdelay(b, a. ...):
Как было сказано в разделе «Фазовая и групповая задержка» главы 2, при про-
прохождении узкополосного сигнала через линейную систему его огибающая и не-
несущее колебание приобретают разные задержки. Задержка несущей — это фазо-
фазовая задержка, а задержка огибающей — групповая задержка. Продемонстрируем
это на несложном примере, показав заодно и использование функции grpdel ay.
Сформируем сигнал в виде радиоимпульса с треугольной огибающей. Обратите
внимание на фазу несущего колебания — максимум огибающей совпадает с мак-
максимумом внутреннего заполнения (рис. 4.15, сверху):
» Fs = 1000: X частота дискретизации
» t = -1:1/Fs:1.5: % вектор значений времени
» Fc = 5: % несущая частота
» А = A - abs(t)).*(abs(t)<=l); % огибающая сигнала
» s = A.*cosB*pi*Fc*t): % входной радиоимпульс
Далее пропускаем этот сигнал через фильтр нижних частот Баттерворта с часто-
частотой среза, равной несущей частоте сигнала, синтезированный методом билиней-
билинейного z-преобразования (подробнее об этом и других методах проектирования
дискретных фильтров см. далее главу 6).
» [b, a] = butterE. Fc*2/Fs); % фильтр нижних частот
» si = filter(b. a. s): % выходной сигнал фильтра
» plotCt. s)
» figure
» plotCt. si)
На рис. 4.15 снизу показан график выходного сигнала фильтра. На рисунке хо-
хорошо видно, что максимумы огибающей и несущего колебания больше не совпа-
совпадают — между ними возникает временной сдвиг.
Посмотрим теперь, как это согласуется с величинами фазовой и групповой за-
задержки:
» f = 0.01:0.01:10: * % частоты длЯ расчета (в герцах)
» h = freqz(b, a. f. Fs): % частотная характеристика
» tau_phase = -unwrap(angle(h))/2/pi./f; % фазовая задержка
» tau_group = grpdelay(b. a. f. Fs)/Fs: % групповая задержка
» piot(f. tau_phase. ':', f. tau_group. '-')
» ylim([0 0.2])
» xlabelCFrequency, Hz')
» ylabeK'Delay. s')
» legend('Phase delay', 'Group delay')
» grid on
Дискретная фильтрация в MATLAB
221
.
-0.8.
-0.5
0.5
1.5
Рис. 4.15. Входной (сверху) и выходной (снизу) сигналы полосового фильтра
демонстрируют разницу между групповой и фазовой задержками
0.2
0.18
0.16
0.14
0.12
0.1
0.08
0.06
0.04
0.02
0
....
У
V
р
•\
\
\
hase delay
roup delay
4 6
Frequency, Hz
10
Рис. 4.16. Фазовая (пунктирная линия) и групповая (сплошная линия) задержки,
вносимые фильтром нижних частот
222
Глава 4. Дискретные системы
Построенные графики фазовой (пунктирная линия) и групповой (сплошная ли-
линия) задержек показаны на рис. 4.16. Видно, что на частоте 5 Гц, равной несущей
частоте нашего сигнала, эти задержки существенно различаются.
Таким образом, мы наглядно продемонстрировали эффект сдвига огибающей от-
относительно несущей, вызванный различием между фазовой и групповой задерж-
задержками.
Отображение нулей и полюсов фильтра
Для отображения нулей и полюсов функции передачи фильтра на комплексной
плоскости предназначена функция zpl ane:
zp1ane(z. p)
zplaneCb, a)
Входными параметрами являются векторы-столбцы нулей и полюсов (z. p) либо
векторы-стярокм коэффициентов полиномов числителя и знаменателя функции
передачи (Ь, а). Различение этих двух случаев производится именно по ориента-
ориентации передаваемых функции векторов.
Поскольку функция просто вычисляет (при необходимости) и отображает корни
полиномов на комплексной плоскости, она может использоваться как для дис-
дискретных (z-шюскость), так и для аналоговых (s-плоскость) фильтров. Единст-
Единственным неудобством может быть отображение единичной окружности, несуще-
несущественной для аналоговых фильтров.
В качестве примера покажем расположение на комплексной плоскости нулей
и полюсов дискретного эллиптического фильтра нижних частот 5-го порядка с
уровнем пульсаций 1 дБ в полосе пропускания и затуханием 40 дБ в полосе за-
задерживания при частоте среза, равной 0,2 частоты Найквиста (рис. 4.17).
» [b. a] = ellipE, 1. 40, 0.2);
» zplaneCb. a)
ш
Q.
е-
га
с
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
о.
х-
X '.
X
Х-'
0
..О'
-1
-0.5
0
Real Part
0.5
Рис. 4.17. Нули и полюсы эллиптического фильтра, выведенные функцией zplane
Дискретная фильтрация в MATLAB
223
Нули функции передачи отображаются кружочками, полюсы — крестиками.
ЗАМЕЧАНИЕ
Аналоговые эллиптические фильтры рассматривались в главе 2. Дискретный фильтр в
данном примере рассчитан по аналоговому прототипу методом билинейного г-преобразо-
вания, которое будет обсуждаться в главе 6. ,
При необходимости можно получить дескрипторы созданных функцией графи-
графических объектов, используя выходные параметры:
[hz, hp, ht] = zpianeC.)
Здесь hz — вектор дескрипторов нулей, hp — вектор дескрипторов полюсов, ht —
вектор дескрипторов осей, единичной окружности и текстовых объектов.
Свертка как матричное умножение
Дискретная свертка D.3) представляет собой сумму поэлементных произведе-
произведений, поэтому при конечной длине импульсной характеристики эту операцию
можно представить как скалярное произведение двух векторов. Одним вектором
при этом служит импульсная характеристика фильтра, а другим — набор отсче-
отсчетов входного сигнала и(&), определяемый как
u(k) -
), x(k - 1), x(k - 2), ..., x(k - N)].
Считая импульсную характеристику вектором-столбцом, выражение для &-го от-
отсчета выходного сигнала можно записать следующим образом:
При расчете разных отсчетов выходного сигнала используются соответствующие
векторы и(&). Для получения всего выходного сигнала отдельные строки u(k)
организуются в матрицу
U =
хф)
x(i)
хB)
0
хф)
хA)
0
0
хф) ...
0
0
0
x(N) x(N-l) x(N-2)
x(N + 1) x(N) x(N -1)
x(M) x(M-l) x(M-2)
0 x(M) x(M-l)
0 0 x(M)
0
0
0
хф)
x(M-N)
x(M-N + l)
x(M-N + 2)
x(M)
224 Глава 4. Дискретные системы
Эта матрица называется матрицей свертки (convolution matrix), а выходной сиг-
сигнал фильтра может быть получен путем матрично-векторного умножения:
У = U h.
Вычисление матрицы свертки в MATLAB производится с помощью функции
convmtx, имеющей следующий синтаксис:
U = convmtx(x, n)
Здесь х — вектор отсчетов сигнала, п — размерность свертки (длина второго уча-
участвующего в свертке вектора).
Результатом работы функции является матрица свертки U. Ее размер зависит от
ориентации вектора х:
□ если х — столбец, то матрица U имеет length(x) + п - 1 строк и п столбцов;
□ если х — строка, то матрица U имеет п строк и length(x) + n - 1 столбцов.
Нерекурсивный фильтр с импульсной характеристикой h с помощью матрично-
матричного умножения может быть реализован следующим образом:
у = convmtx(x. length(h)) * h % х. у и h - столбцы
у = h * convmtx(x, length(h)) % х. у и h - строки
Однако такой вариант требует значительно большего расхода памяти, чем при
использовании функций conv и filter. Поэтому функцию convmtx следует ис-
использовать только для реализации каких-либо специфических алгоритмов обра-
обработки сигналов.
Приведем пример формирования матрицы свертки:
» h = [1 2 3 4];
» convmtx(h. 4)
ans =
1
0
0
0
2
1
0
0
3
2
1
0
4
3
2
1
0
4
3
2
0
0
4
3
0
0
0
4
Как видите, по краям, там, где при фильтрации формируются «хвосты» сигнала,
недостающие входные данные дополняются нулями.
ЗАМЕЧАНИЕ
Формирование матрицы свертки производится с помощью функции toeplitz.
Преобразование способов описания
дискретных фильтров
Преобразование описаний дискретных фильтров между тремя вариантами — ко-
коэффициентами полиномов числителя и знаменателя функции передачи, набора-
наборами нулей и полюсов и параметрами пространства состояний — выполняется теми
же шестью функциями, что и для аналоговых цепей (см. раздел «Преобразова-
«Преобразование способов описания линейных цепей» главы 2). Единственная особенность их
Дискретная фильтрация в MATLAB 225
использования в дискретном случае состоит в том, что векторы b и а, содер-
содержащие коэффициенты полиномов числителя и знаменателя функции передачи,
должны иметь одинаковую длину. Поэтому для удобства преобразования описа-
описаний дискретных фильтров в пакете Signal Processing имеется функция eqtflength,
дополняющая нулями в конце более короткий из переданных ей двух векторов:
[Ы. al] = eqtfiengthCb, a);
Что касается разложения на простые дроби, здесь преобразование дискретной
системы несколько отличается от аналогового случая, поэтому для этого преду-
предусмотрена специальная функция reziduez.
Наконец, для дискретных систем имеет большое практическое значение после-
последовательная, или каскадная, реализация, когда система представляется в виде
последовательного соединения секций второго порядка (second order sections).
Для преобразования описания дискретной системы в эту форму и из нее служат
функции sos2ss, sos2tf, sos2zp, ss2sos, zp2sos и tf2sos.
Кратко напомним имена и синтаксис функций преобразования, общих для ана-
аналоговых и дискретных систем:
□ преобразование коэффициентов полиномов числителя и знаменателя функ-
функции передачи в нули, полюсы и коэффициент усиления:
[z, р, k] = tf2zp(b, a):
□ преобразование нулей, полюсов и коэффициента усиления в коэффициенты
полиномов числителя и знаменателя функции передачи: ,
[b, a] = zp2tf(z, p, к);
□ преобразование коэффициентов полиномов числителя и знаменателя функ-
функции передачи в параметры пространства состояний:
[А, В, С, D] = tf2ss(b, a);
□ преобразование параметров пространства состояний в коэффициенты поли-
полиномов числителя и знаменателя функции передачи:
[b, a] = ss2tf(A. В, С, D);
□ преобразование параметров пространства состояний в нули, полюсы и коэф-
коэффициент усиления:
[z. p, k] = ss2zp(A. В, С. D):
□ преобразование нулей, полюсов и коэффициента усиления в параметры про-
пространства состояний:
[А, В, С. D] = zp2ss(z. p, к):
Далее переходим к описанию функций преобразования, специфических для дис-
дискретных систем.
Разложение на простые дроби
Функция reziduez обеспечивает преобразование функции передачи дискретного
фильтра в сумму простейших дробей и обратно (см. ранее в этой главе раздел
«Полюсы и вычеты»). Ее отличие от функции residue, которая осуществляет
226 Глава 4. Дискретные системы
такое преобразование для аналоговых систем, состоит в форме представления
простейших дробей. Для уяснения разницы между функциями residue и residuez
полезно сравнить используемые ими формулы разложения. Для функции
residue это формула B.12) (см. главу 2), для функции residuez — формула D.10).
Как уже говорилось, функция residuez может выполнять преобразование в обе
стороны. Требуемый тип преобразования определяется количеством выходных
параметров:
[г, p. k] - residuezCb. a)
[b, a] - residuez(r, p, к)
Здесь b и а — векторы коэффициентов полиномов числителя и знаменателя функ-
функции передачи соответственно, г — вектор вычетов, р — вектор полюсов, к — век-
вектор коэффициентов целой части функции передачи.
Разложение функции передачи фильтра на простые дроби соответствует парал-
параллельной реализации фильтра (см. раздел «Параллельная форма»). Каждой про-
простой дроби соответствует рекурсивный фильтр первого порядка; выходные сиг-
сигналы этих фильтров суммируются.
В качестве примера разложим на простые дроби функцию передачи фильтра
Баттерворта 3-го порядка, параллельная реализация которого была показана ра-
ранее на рис. 4.11:
» [b, a] = butterO, 0.4)
b -
0.0985 0.2956 0.2956 0.0985
а -
1.0000 -0.5772 0.4218 -0.0563
» [г, р, k] = residuezCb. a)
г =
-0.6145 - 0.1096т
-0.6145 + 0.1096i
3.0777
Р =
0.2094 + 0.55821
0.2094 - 0.5582т
0.1584
к =
-1.7502
Как видите, постоянное слагаемое и вещественный полюс с вычетом соответст-
соответствуют двум верхним ветвям схемы на рис. 4.11. Для пар комплексно-сопряжен-
комплексно-сопряженных полюсов и вычетов такое сравнение выполнить сложнее, ведь на рисунке
они были скомбинированы в секцию второго порядка с вещественными коэффи-
коэффициентами. Чтобы получить коэффициенты этой секции, выполним с помощью
функции residuez обратное преобразование, задав в качестве входных парамет-
параметров только эти пары полюсов и вычетов:
» [Ы. al] = residuez(r(l:2). p(l:2), [])
Ы =
-1.2290 0.3798
Дискретная фильтрация в MATLAB 227
al =
1.0000 -0.4189 0.3554
Теперь видно, что результат объединения комплексно-сопряженных пар полю-
полюсов и вычетов соответствует секции второго порядка, показанной на рис. 4.11.
ЗАМЕЧАНИЕ
Хотя в последнем расчете не нужно было задавать целую часть функции передачи, нам
пришлось указать соответствующий параметр в виде пустой матрицы. Без этого функция
residuez не поймет, что мы хотим осуществить преобразование полюсов и вычетов в коэф-
коэффициенты числителя и знаменателя функции передачи, а не наоборот.
Функции, работающие с секциями второго порядка
В разделе «Последовательная (каскадная) форма» мы уже говорили, что разбие-
разбиение структуры фильтра на последовательно включенные блоки часто использу-
используется на практике. В том, что это действительно уменьшает проблемы, связанные
с конечной точностью вычислений, нам предстоит убедиться в главе 7, а пока
рассмотрим функции MATLAB, работающие с таким представлением дискрет-
дискретных систем.
Казалось бы, для создания последовательной реализации системы достаточно
рассчитать ее нули и полюсы, после чего представить систему в виде каскадно
включенных звеньев первого порядка. Однако часть этих звеньев (или все) мо-
может оказаться с комплексными коэффициентами. По этой причине при каскад-
каскадной реализации вещественных фильтров их делят на секции второго порядка
(second-order sections). При этом пары комплексно-сопряженных нулей и полю-
полюсов объединяются и образуют каскады второго порядка. Легко убедиться, что для
расчета выходного сигнала вещественного фильтра второго порядка необходимо
выполнить меньше операций, чем для расчета выходного сигнала двух последо-
последовательно соединенных комплексных фильтров первого порядка.
В пакете Signal Processing имеется шесть функций, осуществляющих преобразо-
преобразование описания дискретной системы между набором секций второго порядка и
другими формами описания. Имена этих функций построены так же, как и име-
имена других функций преобразования описаний систем; аббревиатура последова-
последовательной формы — sos (second-order sections):
□ преобразование секций второго порядка в коэффициенты полиномов числи-
числителя и знаменателя функции передачи:
[b, a] = sos2tf(sos, g)
□ преобразование секций второго порядка в нули, полюсы и коэффициент уси-
усиления:
[z. p. k] = sos2zp(sos, g)
□ преобразование секций второго порядка в параметры пространства состояний:
[А. В. С. D] = sos2ss(sos. g)
□ преобразование коэффициентов полиномов числителя и знаменателя функ-
функции передачи в секции второго порядка:
[sos. g] = tf2sos(b. a, 'order', 'scale')
228 Глава 4. Дискретные системы
□ преобразование нулей, полюсов и коэффициента усиления в секции второго
порядка:'
[sos, g] = zp2sos(z, p, k, 'order', 'scale')
□ преобразование параметров пространства состояний в секции второго порядка:
[sos, g] = ss2sos(A, В, С, D, 'order', 'scale')
Набор секций второго порядка представляется с помощью 6-столбцовой матри-
матрицы sos, каждая строка которой соответствует одной секции и устроена следую-
следующим образом:
[bo b\ Ъг 1 а\ аг].
Такой строке соответствует функция передачи вида
Параметр g — дополнительный множитель (gain), добавляемый к функции пере-
передачи, составленной из секций второго порядка. Этот параметр при вызове может
опускаться, для входного параметра д это означает использование значения по
умолчанию д = 1, а для выходного — учет этого коэффициента в первой секции
фильтра.
Преобразование описания из набора секций второго порядка в какую-либо дру-
другую форму является однозначным, а обратное — нет. Ведь можно разными спо-
способами группировать нули и полюсы для формирования секций, менять порядок
включения секций и по-разному распределять коэффициент усиления между
ними (например, если у одной секции все коэффициенты bt в одинаковое число
раз увеличить, а у другой — во столько же раз уменьшить, общая функция пере-
передачи фильтра останется без изменений).
Группировка нулей и полюсов функциями xx2sos выполняется следующим обра-
образом. Прежде всего выделяются комплексно-сопряженные пары нулей и полюсов.
Эти пары образуют числители и знаменатели секций, причем для каждой секции
выбирается пара нулей, расположенных ближе всего к паре полюсов секции. Для
вещественных полюсов и нулей применяется аналогичный подход, при этом
группируются в пары полюсы, максимально близкие по модулю.
Последовательностью включения секций можно управлять с помощью входного
параметра 'order', имеющегося у функций xx2sos. Этот параметр определяет ре-
режим сортировки строк матрицы sos и может принимать одно из двух значений:
□ 'up' — строки матрицы sos расположены в порядке приближения полюсов
секций к единичной окружности (этот вариант принят по умолчанию);
□ ' down' — строки матрицы sos расположены в порядке удаления полюсов сек-
секций от единичной окружности.
Наконец, входной параметр 'scale', имеющийся у функций xx2sos, управляет
распределением коэффициента усиления между секциями фильтра и множите-
множителе: 1 д. Этот параметр может принимать одно из трех значений:
Дискретная фильтрация в MATLAB 229
□ 'попе' — никакого дополнительного масштабирования не производится, во
всех секциях Ьа = 1, а необходимый коэффициент усиления формируется с
помощью общего множителя g (этот вариант принят по умолчанию);
□ 'inf' — масштабирование коэффициентов 6; производится исходя из ^-нор-
^-нормы АЧХ секций (£оо-норма равна максимальному значению функции);
□ 'two' — масштабирование коэффициентов Ь\ производится исходя из 1г-нор-
мы АЧХ секций (£2-норма равна корню квадратному из интеграла от квадра-
квадрата модуля функции).
ЗАМЕЧАНИЕ
Подробнее о масштабировании последовательно включенных секций можно прочитать в [8].
Естественно, масштабирование и порядок включения секций не влияют на об-
общую функцию передачи фильтра. Однако при практической реализации фильт-
фильтра с использованием вычислений с фиксированной запятой эти вещи обязатель-
обязательно следует принимать во внимание. Эффектам, связанным с конечной точностью
вычислений, посвящена глава 7, здесь же приведем лишь два соображения, упо-
упоминаемых в документации MATLAB применительно к функциям xx2sos:
□ при 'order' = 'up' и 'scale' = 'inf минимизируется вероятность переполне-
переполнения в процессе промежуточных вычислений;
□ при ' order' = ' down' и ' seal e' - ' two' минимизируется пиковое значение шума
округления.
В качестве иллюстрации выполним разложение на секции второго порядка для
фильтра, использованного для примера в разделе «Последовательная (каскадная)
форма» (напомним, что это был фильтр Баттерворта 3-го порядка с частотой
среза, равной 0,4 частоты Найквиста, синтезированный методом билинейного
г-преобразования):
» [Ь, а] = butterC. 0.4)
b =
0.0985 0.2956 0.2956 0.0985
а =
1.0000 -0.5772 0.4218 -0.0563
» [sos, g] = tf2sos(b. a)
SOS =
1.0000 1.0000 0 1.0000 -0.1584 0
1.0000 2.0000 1.0000 1.0000 -0.4189 0.3554
g -
0.0985
Полученный результат соответствует приведенному ранее на рис. 4.10. Проде-
Продемонстрируем теперь варианты масштабирования и расположения секций, упо-
упомянутые выше:
» [sos. g] = tf2sos(b. a, 'up', 'inf')
SOS =
0.3919 0.3919 0 1.0000 -0.1584 0
0.2987 0.5975 0.2987 1.0000 -0.4189 0.3554
230 Глава 4. Дискретные системы
0.8416
Как видите, изменились только коэффициенты нерекурсивных частей секций (пер-
(первые три столбца матрицы sos) и коэффициент усиления д.
А теперь испытаем второй вариант масштабирования и расположения:
» [sos. g] = tf2sos(b. a, 'down', 'two')
sos =
0.3185 0.6370 0.3185 1.0000 -0.4189 0.3554
0.3480 0.3480 0 1.0000 -0.1584 0
9 =
0.8889
Теперь секции поменялись местами, а их коэффициенты усиления несколько из-
изменились.
ЗАМЕЧАНИЕ
В MATLAB можно непосредственно осуществлять обработку сигнала фильтром, пред-
представленным в виде секций второго порядка, не преобразуя описание фильтра к стандартной
форме функции передачи. Для этого служит функция sosfilt, вызываемая следующим об-
образом: у = sosfilt(sos, x). Здесь sos — описание фильтра в рассмотренном выше формате,
х и у — соответственно входной и выходной сигналы.
Изменение частоты дискретизации
При решении различных задач обработки сигналов приходится увеличивать или
уменьшать частоту дискретизации сигналов. Это необходимо, например, для со-
согласования различных стандартов хранения и передачи дискретной информации.
Классическим примером является преобразование аудиозаписей между форма-
форматами компакт-дисков (частота дискретизации 44,1 кГц) и цифровой магнитной
записи R-DAT (частота дискретизации 48 кГц).
Приведенный пример не относится к самым простым, поскольку коэффициент
изменения частоты дискретизации не является целым числом. В зависимости от
значения этого коэффициента выделяют следующие варианты:
□ интерполяция (interpolation) — повышение частоты дискретизации в целое
число раз;
□ прореживание (decimation) — понижение частоты дискретизации в целое чис-
число раз;
□ передискретизация (resampling) — изменение частоты дискретизации в про-
• извольное (в общем случае дробное) число раз.
Рассмотрим алгоритмы реализации этих вариантов изменения частоты дискре-
дискретизации более подробно.
Изменение частоты дискретизации
231
Прореживание
Казалось бы, ломать — не строить, и для понижения частоты дискретизации
в N раз достаточно взять из исходной последовательности каждый N-й отсчет.
В принципе это так и есть, однако для предупреждения возможных побочных
эффектов следует принять некоторые меры.
Дело в том, что процесс прореживания по сути сводится к дискретизации дис-
дискретного сигнала. При этом имеют место все эффекты, упомянутые в разделе
«Спектр дискретного сигнала» главы 3, в том числе и появление ложных частот
(aliasing, рис. 4.18):
» к = 0:20;
» t = 0:0.01:20;
» si = cosB*pi*t/4);
» sdl = cosB*pi*k/4);
» Dec = 3;
» sd2 = sdl(l:Dec:end);
» s2 = cosB*pi*t/12);
» subplotd, 2, 1)
» stem(k, sdl): hold on;
» subplotd, 2, 2)
X дискретное время
% аналоговое время
% аналоговый сигнал
% дискретный сигнал
% коэффициент прореживания
% прореженный сигнал
% ложный сигнал
plot(t. si, '--■); hold off
stem(k(l:Dec:end), sd2); hold on; plot(t, s2. '--'); hold off
I
\
1
\
/
1
i
i
j
\
1
r
i
20
10
15
20
Рис. 4
Появление ложных частот при прореживании дискретного сигнала
Таким образом, если в спектре исходного (прореживаемого) сигнала содержатся
частоты, превышающие половину новой частоты дискретизации (то есть новую
частоту Найквиста), это приведет к появлению в спектре выходного сигнала
ложных частотных составляющих.
Для устранения этого нежелательного эффекта следует, как и при дискретиза-
дискретизации аналогового сигнала, предварительно пропустить сигнал через ФНЧ с час-
частотой среза, равной новой частоте Найквиста.
Чтобы сохранить фазовые соотношения во входном сигнале, следует использо-
использовать нерекурсивный фильтр с линейной ФЧХ. Использование нерекурсивного
232 Глава 4. Дискретные системы
фильтра позволяет весьма эффективно организовать вычисления — поскольку
нас интересует только каждый JV-й отсчет выходного сигнала, остальные отсчеты
можно и не вычислять. При этом можно считать, что сигнал «заталкивается» в
линию задержки фильтра порциями по N отсчетов. Если использовать рекурсив-
рекурсивный фильтр, такой экономии добиться не удастся — из-за наличия обратных
связей придется вычислять весь выходной сигнал фильтра и только потом отбра-
отбрасывать лишние отсчеты.
В MATLAB прореживание выполняется с помощью функции decimate. Синтак-
Синтаксис ее вызова следующий:
у - decimate(x, г)
Здесь х — входной сигнал, г — целочисленный коэффициент понижения частоты
дискретизации. Выходной параметр у — прореженный сигнал.
В качестве предварительного фильтра по умолчанию используется ФНЧ Чебы-
шева первого рода 8-го порядка с уровнем пульсаций в полосе пропускания 0,05 дБ
и частотой среза, равной 0,8 новой (после прореживания) частоты Найквиста.
Для устранения фазовых искажений применяется двунаправленная обработка
входного сигнала с помощью функции filtfilt (см. раздел «Компенсация фазо-
фазового сдвига»). Поэтому в конечном счете порядок фильтра удваивается.
Можно задать порядок фильтра Чебышева, используя для этого третий число-
числовой входной параметр:
у = decimate(x. г. п)
При этом не рекомендуется использовать п > 13.
Если в качестве третьего входного параметра использовать строку 'fir1, будет
использован нерекурсивный фильтр 30-го порядка, рассчитанный с помощью
функции firl (см. раздел «Функции синтеза с использованием окон» главы 6):
у - decimate(x, r, 'fir')
Данный нерекурсивный фильтр имеет линейную ФЧХ, поэтому производить дву-
двунаправленную фильтрацию нет необходимости. Это позволяет уменьшить рас-
расход памяти при выполнении операции прореживания.
Наконец, при использовании четырех входных параметров можно задать поря-
порядок нерекурсивного фильтра:
у - decimate(x, г. n, 'fir')
Для демонстрации прореживания сформируем сигнал, мгновенная частота кото-
которого меняется по гармоническому закону от нуля до частоты Найквиста и обрат-
обратно в течение одной секунды (рис. 4.19):
» Fs - ЮОеЗ;
» t - O:l/Fs:l:
» s - cosB*pi*t*Fs/4-Fs/4*sinB*pi*t));
» specgram(s, [], Fs)
» colormap gray
Изменение частоты дискретизации 233
ЗАМЕЧАНИЕ
О понятии мгновенной частоты речь пойдет в разделе «Угловая модуляция» главы 8.
Функция specgram, которая показывает цветом зависимость мгновенного амплитудного
спектра от времени, будет рассмотрена в главе 5.
0.1 0.2 0.3 0.4 0.S 0.6 0.7 0.8 0.9
ТЪпе
Рис. 4.19. Спектрограмма прореживаемого сигнала
На спектрограмме сигнала видно, что в его спектре содержатся частоты, которые
после прореживания с любым коэффициентом будут превышать новую частоту
Найквиста, что неминуемо должно вызвать появление ложных частот.
Убедимся в этом, понизив частоту дискретизации в два раза путем выборки каж-
каждого второго отсчета (рис. 4.20):
» si - s(l:2:end); % прореженный сигнал
» specgram(sl. []. Fs/2)
» color-map gray
Теперь выполним прореживание с предварительной фильтрацией, воспользовав-
воспользовавшись для этого функцией decimate (рис. 4.21):
» s2 = decimate(s. 2): % прореженный сигнал
» specgram(s2. []. Fs/2)
» coiormap gray
Графики показывают, что при прореживании с предварительной фильтрацией
оказалась удалена середина сигнала, содержащая высокие частоты. Однако в
данном случае не произошло появления ложных частот.
234
Глава 4. Дискретные системы
О 0.1 0.2 0.3 0.4 0.S 0.6 0.7 0.8 0.9
Рис. 4.20. Прореживание без предварительной фильтрации
создает ложные частоты
О 0.1 0.2 0.3 0.4 0.5 О.Ь 0 7 0 8 0.9
Рис. 4.21. Предварительная фильтрация позволяет устранить ложные частоты
при прореживании сигнала
Изменение частоты дискретизации
235
Интерполяция
При интерполяции нам необходимо повысить частоту дискретизации в N раз, то
есть «растянуть» входной сигнал, а образовавшиеся промежутки между отсчета-
отсчетами чем-то заполнить.
Подобно тому как прореживание сводится к дискретизации дискретного сигна-
сигнала, процесс интерполяции оказывается подобным процессу восстановления не-
непрерывного сигнала, только происходящему в дискретной области.
Исходный сигнал имеет периодический спектр, повторяющийся с частотой дис-
дискретизации /д (рис. 4.22, а). Прежде всего мы «растягиваем» этот сигнал, добав-
добавляя между его отсчетами по N - 1 нулей. При этом частота дискретизации сиг-
сигнала станет равна Nfa, но период повторения спектра останется прежним — /д
(рис. 4.22, б). Теперь необходимо пропустить полученный сигнал через ФНЧ с
частотой среза/д/2 (его идеализированная АЧХ показана на рис. 4.22, б). В ре-
результате фильтрации получится интерполированный сигнал, у которого частота
дискретизации равна Nf&, а спектр в полосе частот от нуля до/д/2 остался преж-
прежним (рис. 4.22, е).
AL
Nfa f
а
Рис. 4.22. Спектры сигналов в процессе интерполяции
Nfn
Для сохранения фазовых соотношений во входном сигнале следует использовать
нерекурсивный фильтр с линейной ФЧХ. Поскольку в линии задержки фильтра
в каждый момент содержится большое количество нулевых отсчетов и положе-
положения этих отсчетов на каждом шаге заранее известны, при реализации алгоритма
236 Глава 4. Дискретные системы
можно сэкономить время вычислений, игнорируя арифметические операции с
этими отсчетами.
В MATLAB интерполяция выполняется с помощью функции interp. Синтаксис
ее вызова следующий:
у = interp(x. г)
Здесь х — входной сигнал, г — целочисленный коэффициент повышения частоты
дискретизации. Выходной параметр у — интерполированный сигнал.
Для интерполяции используется нерекурсивный фильтр с линейной ФЧХ, пере-
перекрывающий целое число межотсчетных интервалов. По умолчанию порядок
фильтра равен 8*г, то есть фильтр в каждый момент использует 8 отсчетов вход-
входного сигнала. Частота среза фильтра по умолчанию равна половине исходной
частоты Найквиста.
ВНИМАНИЕ
Обратите внимание на то, что по умолчанию функция interp считает полосу частот вход-
входного сигнала ограниченной половиной частоты Найквиста.
Используя третий и четвертый входной параметры, можно управлять длиной
фильтра и его частотой среза:
у = interp(x, г, 1, alpha)
Здесь 1 — половина количества отсчетов, используемых для интерполяции (дли-
(длина фильтра равна 2*г*1 + 1), alpha — нормированная частота среза фильтра (зна-
(значение 1 соответствует частоте Найквиста). По умолчанию 1 = 4 и alpha = 0.5.
При указании двух выходных параметров во втором из них функция возвращает
коэффициенты фильтра, использованного для интерполяции:
[у. b] = interpL.)
Рассмотрим пример интерполяции, сформировав для этого 13 отсчетов, прини-
принимающих значения ±1, и дополнив их с каждой стороны пятью нулями (рис. 4.23):
» х=[0 0 0 0 0 11111-1-111-11-110 0 0 0 0];
» % повышаем частоту дискретизации в пЯть раз
» у = interp(x. 5);
» % график интерполированного сигнала - сплошная линия
» plot(@:length(y)-l), у)
» % график исходного сигнала - кружочки
» hold on
» plot(@:length(x)-l)*5, x, 'о')
» hold off
Обратите внимание на большие выбросы, сформированные между отсчетами с
одинаковыми значениями в процессе интерполяции. Эти выбросы обусловлены
именно ограничением полосы частот выходного сигнала. Если соединить исход-
исходные отсчеты «более плавно выглядящей» кривой, спектр полученного сигнала
окажется шире. Таким образом, мы получили еще одно подтверждение факта,
упоминавшегося при обсуждении теоремы Котельникова в главе 3: ограничен-
Изменение частоты дискретизации
237
ность полосы частот, занимаемой сигналом, вовсе не означает малости измене-
изменения значений сигнала между отсчетами.
-0.5
-1
-1.5
0 20 40 60 80 100 120
Рис. 4.23. Исходный (кружочки) и интерполированный (сплошная линия) сигналы
при пятикратном повышении частоты дискретизации
ЗАМЕЧАНИЕ —
Данный сигнал называется 13-элементным кодом Баркера. Главным свойством кодов Бар-
Баркера является вид их корреляционной функции, представляющей собой узкий высокий
пик, окруженный треугольными лепестками малого уровня. Коды Баркера имеют макси-
максимально возможное для бинарных (то есть принимающих два значения) сигналов отноше-
отношение высоты центрального пика корреляционной функции к уровню ее боковых лепестков.
Это отношение равно числу отсчетов сигнала и в данном примере составляет 13.
Передискретизация
Если частоту дискретизации необходимо изменить в нецелое число раз, но это
число раз является рациональной дробью, используется процедура передискре-
передискретизации (resampling).
Передискретизация является сочетанием интерполяции и прореживания. Если
исходную частоту дискретизации необходимо умножить на p/q, сначала выпол-
выполняется интерполяция с коэффициентом р, а затем прореживание с коэффициен-
коэффициентом q. Поэтому в принципе данную операцию можно осуществить средствами
MATLAB следующим образом:
у = decimate(interp(x. p), q)
Однако в этом случае будет выполняться много лишних операций, которые мо-
могут быть устранены при оптимальной организации вычислений.
Рассмотрим последовательность действий, выполняемых при последовательном
осуществлении интерполяции и прореживания.
238 Глава 4. Дискретные системы
1. Между отсчетами входного сигнала вставляется по (р - 1) нулей.
2. Полученный сигнал пропускается через ФНЧ с частотой среза/д/2.
3. Полученный сигнал пропускается через ФНЧ с частотой среза (/лр/#)/2.
4. Из полученного сигнала выбирается каждый q-й отсчет.
Шаги 1 и 2 относятся к процессу интерполяции, 3 и 4 — к процессу прореживания.
Первое, что можно заметить, — это последовательное пропускание сигнала через
два ФНЧ с разными частотами среза. Очевидно, что фильтр с большей частотой
среза является избыточным. Поэтому можно оставить только один фильтр с мень-
меньшей частотой среза. При повышении частоты дискретизации эта частота среза
равна частоте Найквиста входного сигнала, при понижении — частоте Найкви-
ста выходного сигнала.
Вторая модификация та же, что рассматривалась ранее при обсуждении процесса
прореживания. Поскольку нас интересует лишь каждый q-й отсчет фильтрован-
фильтрованного сигнала, нет смысла выполнять фильтрующие вычисления для всех отсче-
отсчетов. Наконец, как и в случае интерполяции, в линии задержки фильтра в каждый
момент содержится большое количество нулевых отсчетов, которые можно игно-
игнорировать при вычислениях.
С учетом сказанного последовательность действий передискретизации будет вы-
выглядеть следующим образом.
1. Между отсчетами входного сигнала вставляется по (р - 1) нулей.
2. Полученный сигнал порциями по q отсчетов «заталкивается» в ФНЧ с часто-
частотой среза, равной/д/2 ■ min(l, p/q). Результаты фильтрации для этих порций
являются отсчетами сигнала с частотой дискретизации fnp/q. При фильтра-
фильтрации игнорируются арифметические операции с отсчетами, имеющими нуле-
нулевые значения.
Данный алгоритм (он называется полифазным — polyphase) минимизирует чис-
число вычислительных операций и широко используется на практике [9].
В МATLAB для выполнения передискретизации используется функция resampl e.
Синтаксис ее вызова следующий:
у = resample(x. p. q)
Здесь х — входной сигнал, р и q — числитель и знаменатель дробного коэффици-
коэффициента изменения частоты дискретизации. Выходной параметр у — передискрети-
зированный сигнал.
В качестве фильтра используется нерекурсивный ФНЧ, рассчитанный с помо-
помощью функции firl s с использованием окна Кайзера.,
ЗАМЕЧАНИЕ
Подробнее об использовании функции firls для синтеза фильтров с линейной ФЧХ речь
пойдет в главе 6; окно Кайзера, наряду с другими весовыми функциями, будет рассмотре-
рассмотрено в главе 5.
Ядром функции resample является функция upfirdn (upsampling, FIR filtering and
downsampling), которая и выполняет приведенную выше последовательность дей-
Изменение частоты дискретизации
239
ствий. Эта функция реализована в машинных кодах (в виде DLL-файла) для до-
достижения максимальной производительности. Функцию upfirdn можно исполь-
использовать в тех случаях, когда необходимо задать конкретный ФНЧ. Синтаксис вы-
вызова функции upf i rdn следующий:
у = upfirdn(x. h, p. q)
Здесь х — входной сигнал, p/q — коэффициент изменения частоты дискретизации,
h — импульсная характеристика нерекурсивного ФНЧ. Выходной параметр у —
передискретизированный сигнал.
Для осуществления блочной обработки сигнала имеется вариант синтаксиса с до-
доступом к внутреннему состоянию фильтра:
[у. z2] - upfirdn(x, h, p, q, zl)
Здесь zl — начальное состояние фильтра, z2 — его конечное состояние. Длина
вектора zl должна быть на единицу меньше длины импульсной характеристики
фильтра h. Использование начального и конечного состояний фильтра для орга-
организации блочной фильтрации обсуждалось в разделе «Доступ к внутреннему со-
состоянию фильтра».
Если один из параметров х и h является матрицей, эта матрица рассматривается
как многоканальный сигнал или фильтр (каждый столбец матрицы соответству-
соответствует одному каналу). Если оба параметра х и h являются матрицами с одинаковым
числом столбцов, при обработке каждого сигнала используется свой фильтр.
Выходной сигнал у во всех этих случаях является матрицей с тем же числом
столбцов.
В качестве примера увеличим в 5/4 раз частоту кусочно-линейного сигнала,
представляющего собой набор отсчетов со значениями
{4, 5, 6, 7, 8, 9, 10, 6, 5, 4, 3, 2}.
Результат показан на рис. 4.24.
11
ю
9
8
7
6
5
4
3
2
1
■ о»
о
о
х
х°
X
о
о
X
о
X
о
в
о
X
о „
о
■
-
_
-
X
о
10
12
Рис. 4.24. Исходный (крестики) и передискретизированный (кружочки) сигналы
при повышении частоты дискретизации в 5/4 раз
240 Глава 4. Дискретные системы
» х = [4:10 6:-1:2]:
» у = resample(x. 5, 4):
» % график исходного сигнала - крестики
» plot@:length(xbl, x, 'х')
» % график передискретизированного сигнала - кружочки
» hold on
» plot(@:length(y)-l)*4/5. у. 'о')
» hold off
На рис. 4.24 видно, что новые отсчеты действительно интерполируют исходный
сигнал, однако наблюдается и эффект Гиббса (см. раздел «Примеры разложения
сигналов в ряд Фурье» главы 1), хотя в данном случае он выражен слабо, по-
поскольку частота дискретизации меняется незначительно.
Некоторые идеализированные
фильтры
В данном разделе мы рассмотрим частотные и импульсные характеристики иде-
идеальных фильтров, осуществляющих над дискретным сигналом преобразование
Гильберта и дифференцирование. Эти фильтры являются нереализуемыми,
поскольку их функции передачи не выражаются в виде рациональных дробей,
а импульсная характеристика является бесконечной в обоих направлениях. Од-
Однако знание того, как выглядят идеализированные характеристики, полезно для
понимания принципов синтеза фильтров, аппроксимирующих данные преобра-
преобразования (этот вопрос будет рассмотрен в главе 6).
Дискретное преобразование Гильберта
Все сказанное в разделе «Комплексная огибающая» главы 1 о преобразовании
Гильберта относилось к аналоговым сигналам. В дискретном случае указанные
спектральные соотношения должны выполняться в рабочей полосе частот (то
есть от нуля до частоты Найквиста). Таким образом, частотная характеристика
дискретного преобразования Гильберта имеет следующий вид:
, < со < &со.,
-
0, ю = -сод
для всех целочисленных k. Графики АЧХ и ФЧХ дискретного преобразования
Гильберта показаны на рис. 4.25.
Для нахождения импульсной характеристики можно, например, выделить сред-
средний участок спектра (для |<в| й я/Т), вычислить обратное преобразование Фурье
Некоторые идеализированные фильтры
241
и взять дискретные отсчеты результата. Обратное преобразование Фурье будет
равно
№>)!
-•—►
шд/2
я/2
-Щ./2
-я/2
Шд/2
—О
.25. АЧХ (сверху) и ФЧХ (снизу) дискретного преобразования Гильберта
Рис. 4
Дискретизируем это выражение с шагом Т = 2тг/сод (можно легко показать, что
предел при t -> 0 равен 0). Кроме того, значения /z(&) необходимо умножить на Г,
поскольку в формуле C.7), дающей связь между спектрами аналогового и дис-
кретизированного сигналов, имеется множитель 1/7". В конечном счете получаем
следующее:
{0, k четно,
2 и
—, к нечетно.
nk
Как и для аналогового случая, импульсная характеристика получилась физиче-
физически нереализуемой — она является бесконечно протяженной в обоих направле-
направлениях. Ее график показан на рис. 4.26.
» к = -20:20;
» h = 2 /,pi ./ к .* mod(k, 2):
» h(find(—к)) = 0: % убираем Inf из-за деления на ноль
» stem(k, h)
Поскольку фильтр оказывается физически нереализуемым, осуществить дискрет-
дискретное преобразование Гильберта можно лишь приближенно. Простое усечение им-
импульсной характеристики во времени приводит к нежелательным эффектам,
связанным с явлением Гиббса. Поэтому фильтры, приближенно реализующие
преобразование Гильберта, приходится аппроксимировать с применением более
сложных алгоритмов. Речь о них пойдет в разделе «Реализация метода Ремеза»
главы 6.
242
Глава 4. Дискретные системы
<
G
>
)
it
о 1 © 1 ©I©Т©т©т©т©т©Ф<
0.8
0.6
0.4
0.2
0<
-0.2
-0.4
-0.6
' '6-20 -15 -10 -5 0 5 10 15 20
Рис. 4.26. Импульсная характеристика дискретного преобразования Гильберта
Для иллюстрации искажений частотных характеристик, возникающих при усе-
усечении импульсной характеристики во времени, построим график АЧХ фрагмен-
фрагмента импульсной характеристики, приведенного выше на рис. 4.26 (симметрия ис-
используемого фрагмента импульсной характеристики является принципиальной
для сохранения линейной ФЧХ фильтра). Результаты показаны на рис. 4.27 (на
горизонтальной оси графика отложены нормированные значения частоты, такие,
что частота Найквиста равна единице).
» [hh. f] = freqz(h, 1, 'whole');
» plot(f/pi. abs(hh)), grid
» xlabeK'Normalized Frequency')
» ylabeK'Magnitude')
1.4
1.2
1
0.8
0.6
0.4
0.2
0 0.5 1 1.5 2
Normalized Frequency
Рис. 4.27. Искажения, возникающие при усечении импульсной характеристики
преобразования Гильберта
Л
л/vaAJ-I
/vvvy
Л
Д.Л.д./\/\
и х/ vv\
Л
/•VVV'u
Некоторые идеализированные фильтры 243
На рис. 4.27 хорошо заметны выбросы АЧХ вблизи частот, кратных частоте Найк-
виста. Величина максимального выброса составляет примерно 18 % от номиналь-
номинального коэффициента передачи (это согласуется с тем, что говорилось в главе 1
применительно к разложению меандра в ряд Фурье — в данном случае коэффи-
коэффициент передачи меняется скачком от -j до_/, так что величина скачка равна двум,
и выброс составляет 9 % от величины этого скачка).
Для уменьшения пульсаций АЧХ при синтезе фильтров, выполняющих преобразо-
преобразование Гильберта, задают переходные полосы вблизи нулевой частоты и частоты
Найквиста. Коэффициент передачи фильтра в этих полосах считается неопре-
неопределенным, и оптимизация производится только в оставшейся (рабочей) полосе
частот.
Функция Hilbert
В М ATLAB для формирования аналитического сигнала служит функция hi I bert.
Синтаксис ее вызова более чем прост:
у = hi Ibert(x)
Здесь х — входной вещественный сигнал (если х — матрица, отдельные столбцы
обрабатываются независимо), у — сформированный комплексный аналитический
сигнал.
ВНИМАНИЕ
Вопреки своему названию, функция hilbert осуществляет не преобразование Гильберта,
а именно формирование аналитического сигнала. Преобразование Гильберта с помощью
этой функции можно реализовать, взяв мнимую часть результата: imag(hilbert(x)).
Формирование аналитического сигнала функцией hi!bert производится в час-
частотной области. Вычисляется дискретное преобразование Фурье (оно будет рас-
рассмотрено в главе 5) входного сигнала, далее обнуляется половина спектра (то
есть создается односторонний спектр аналитического сигнала) и, наконец, про-
производится обратное преобразование Фурье.
В качестве второго аргумента можно указать желаемую размерность дискретно-
дискретного преобразования Фурье:
у = hi Ibert(x, n)
При этом входные данные х усекаются или дополняются нулями до заданного
размера.
ЗАМЕЧАНИЕ
Как указывалось ранее, преобразование Гильберта физически нереализуемо. Однако это
ограничение можно обойти, если известны (точнее, считаются известными) будущие зна-
значения сигнала. Например, мы можем считать, что сигнал закончился (то есть все его буду-
будущие значения равны нулю). Именно это и предполагается в функции hilbert.
В качестве примера вычислим аналитический сигнал для функции Дирихле
9-го порядка (рис. 4.28):
244
Глава 4. Дискретные системы
» t = 0:0.01:4*pi; % рассматриваем два периода функции
» х = diric(t. 9):
» у = hilbert(x):
» plot(t, real(у), t, imag(y). '--')
Рис. 4.28. Функция Дирихле (сплошная линия) и ее преобразование Гильберта
(пунктирная линия)
На графике видно, что вблизи тех мест, где исходный сигнал имеет экстремумы,
его преобразование Гильберта пересекает ось абсцисс, и наоборот.
Идеальный дифференцирующий фильтр
В разделе «Свойства преобразования Фурье» главы 1 было показано, что при
дифференцировании сигнала по времени его спектральная функция умножается
на ./со. В дискретной дифференцирующей системе это соотношение должно вы-
выполняться в полосе частот от нуля до частоты Найквиста. Таким образом, час-
частотная характеристика идеального дискретного дифференцирующего фильтра
имеет вид
Я© *а>д).
со-£сод
0,
со-£сод
со
со
для всех целочисленных к. Графики АЧХ и ФЧХ идеального дискретного диф-
дифференцирующего фильтра показаны на рис. 4.29.
Для нахождения импульсной характеристики поступим так же, как ранее при
обсуждении дискретного преобразования Гильберта. Обратное преобразование
Фурье от среднего участка спектра (для |со| < сОд/2 = ж/Т) будет равно
(
-sin
I
I 2
Некоторые идеализированные фильтры
245
л/2
-Шд/2 О
о-
Шд/2
-л/2
Рис. 4.29. АЧХ (сверху) и ФЧХ (снизу) идеального дискретного
дифференцирующего фильтра
После дискретизации и умножения на Т получаем следующее:
ГО, 4=0,
kT
Разумеется, импульсная характеристика получилась физически нереализуемой —
она является бесконечно протяженной в обоих направлениях. Кроме того, им-
импульсная характеристика не является безразмерной — из-за деления на Т она
имеет размерность частоты. Причиной является тот факт, что дифференцирова-
дифференцирование аналоговой функции меняет ее размерность. Построим график импульсной
характеристики идеального дискретного дифференцирующего фильтра, считая
период дискретизации равным единице (рис. 4.30):
» к = -20:20:
» h = (-1).Ак ./ к:
» % убираем Inf из-за деления на ноль
» h(find(-k)) = 0:
» stemCk, h)
Поскольку фильтр оказывается физически нереализуемым, осуществить диффе-
дифференцирование дискретного сигнала можно лишь приближенно. Простое усече-
усечение импульсной характеристики во времени приводит к нежелательным эффек-
эффектам, связанным с явлением Гиббса. Поэтому фильтры, приближенно реализующие
дифференцирование, приходится аппроксимировать с применением более слож-
сложных алгоритмов. Они будут обсуждаться в разделе «Реализация метода Ремеза»
главы 6.
246
Глава 4. Дискретные системы
Рис. 4.30. Импульсная характеристика идеального дискретного
дифференцирующего фильтра
Для иллюстрации искажений частотных характеристик, возникающих при про-
простом усечении импульсной характеристики во времени, построим график АЧХ
фрагмента импульсной характеристики, приведенного выше на рис. 4.30 (сим-
(симметрия используемого фрагмента импульсной характеристики является прин-
принципиальной для сохранения линейной ФЧХ фильтра). Результаты показаны на
•рис. 4.31.
» [hh. f] = freqz(h. 1, 'whole');
» plot(f/pi, abs(hh)). grid
» xlabeK'Normalized Frequency')
» ylabeK'Magnitude')
4
3.5
3
1.5
1
0.5
0
0.5 1 1.5
Normalized Frequency
Рис. 4.31. Искажения АЧХ, возникающие при усечении импульсной характеристики
идеального дифференцирующего фильтра
На рис. 4.31 хорошо заметны пульсации АЧХ, усиливающиеся при приближе-
приближении к частоте Найквиста. Для уменьшения этих пульсаций при синтезе диффе-
Визуализатор фильтров
247
рейдирующих фильтров применяют те же подходы, что и для фильтров, выпол-
выполняющих преобразование Гильберта, — задают переходные полосы вблизи нулевой
частоты и частоты Найквиста, считают коэффициент передачи фильтра в этих
полосах неопределенным и производят оптимизацию только в оставшейся (ра-
(рабочей) полосе частот.
Визуализатор фильтров
В последней E.1) версии пакета Signal Processing появилась функция fvtool (Filter
Visualization Tool), предназначенная для визуализации характеристик дискрет-
дискретных фильтров. Синтаксис вызова этой функции следующий:
fvtool(b, a)
Здесь b и а — коэффициенты полиномов числителя и знаменателя функции пе-
передачи соответственно.
Можно вызвать функцию fvtool для одновременного просмотра характеристик
нескольких фильтров, в этом случае следует указать в списке входных парамет-
параметров несколько пар векторов:
fvtool(Ы. al. Ь2. а2, ...)
В качестве примера вызовем функцию fvtool для просмотра характеристик того
же фильтра, что использовался ранее, при описании функции freqz (см. рис. 4.14).
Ф Filtei Visualization Tool - Gioup Delay
У
r~~
/
/
I
(
1
1 ™
\
\
f
/
02
Sampbs
Рис. 4.32. Просмотр характеристик дискретного фильтра с помощью функции fvtool
248 Глава 4. Дискретные системы
» Ь = [1 2 3 4];
» а - [1 -0.1];
» fvtooKb. a)
Появится окно, показанное на рис. 4.32. Выбор отображаемой характеристики
производится с помощью кнопок панели инструментов. На рис. 4.32 представлен
график частотной зависимости групповой задержки анализируемого фильтра.
Интерфейс окна просмотра характеристик фильтра аналогичен интерфейсу про-
программы расчета и анализа фильтров FDATool, которая будет рассмотрена в гла-
главе 6.
ГЛАВА 5 Спектральный
анализ
В главе 3 было показано, что при дискретизации аналогового сигнала его спектр
становится периодическим с периодом повторения, равным частоте дискретиза-
дискретизации. Однако одного только этого соотношения оказывается недостаточно для ре-
решения всех практических задач спектрального анализа. Во-первых, в качестве
исходных данных выступает именно последовательность дискретных отсчетов,
а не аналоговый сигнал. Во-вторых, в большинстве случаев анализируемые сиг-
сигналы являются случайными процессами, что требует выполнения какого-либо
усреднения при расчете их спектров. Кроме того, в ряде случаев нам известна
некоторая дополнительная информация об анализируемом сигнале, и эту инфор-
информацию желательно учесть в спектральном анализе.
Обо всех этих аспектах спектрального анализа и пойдет речь в данной главе.
Прежде всего мы рассмотрим дискретное преобразование Фурье (ДПФ) — раз-
разновидность преобразования Фурье, специально предназначенную для работы с
дискретными сигналами. Далее обсудим идеи, лежащие в основе алгоритмов бы-
быстрого преобразования Фурье, позволяющих значительно ускорить вычисления.
Дискретное преобразование Фурье, по возможности вычисляемое быстрыми мето-
методами, лежит в основе различных технологий спектрального анализа, предназна-
предназначенных для исследования случайных процессов. Дело в том, что если анализи-
анализируемый сигнал представляет собой случайный процесс, то простое вычисление
его ДПФ обычно не представляет большого интереса, так как в результате полу-
получается лишь спектр единственной реализации процесса. Поэтому для спектраль-
спектрального анализа случайных сигналов необходимо использовать усреднение спектра.
Такие методы, в которых используется только информация, извлеченная из са-
самого входного сигнала, называются непараметрическими (nonparametric).
Другой класс методов предполагает наличие некоторой статистической модели
случайного сигнала. Процесс спектрального анализа в данном случае включает в
себя определение параметров этой модели, и потому такие методы называются
параметрическими (parametric). Используется также термин «модельный спек-
спектральный анализ» (Model-Based Spectrum Analysis, MBSA).
250 Глава 5. Спектральный анализ
В MATLAB имеются функции, реализующие разнообразные методы спектраль-
спектрального анализа, — как параметрические, так и непараметрические. Все они будут
рассмотрены в этой главе.
Дискретное преобразование Фурье
В разделе «Спектр дискретного сигнала» главы 3 мы проанализировали явле-
явления, происходящие со спектром при дискретизации сигнала. Рассмотрим теперь,
что представляет собой спектр дискретного периодического сигнала.
Итак, пусть последовательность отсчетов {x(k)} является периодической с перио-
периодом N:
x(k + N) = x(k) для любого k.
Такая последовательность полностью описывается конечным набором чисел, в ка-
качестве которого можно взять произвольный фрагмент длиной N, например {x(k),
k = 0, 1,..., N- 1}. Поставленный в соответствие этой по следовательности сигнал
из смещенных по времени дельта-функций:
s(t)= ±x(kM(t-kT) E.1)
также, разумеется, будет периодическим с минимальным периодом N Т.
Так как сигнал E.1) является, дискретным, его спектр должен быть периоди-
периодическим с периодом 2п/Т. Так как этот сигнал является также и периодическим,
его спектр должен быть дискретным с расстоянием между гармониками, рав-
равным 2n/(NT).
Итак, периодический дискретный сигнал имеет периодический дискретный спектр,
который также описывается конечным набором из N чисел (один период спектра
содержит y-1'jjf = N гармоник).
Рассмотрим процедуру вычисления спектра периодического дискретного сигна-
сигнала. Так как сигнал периодический, будем раскладывать его в ряд Фурье. Коэф-
Коэффициенты Х{п) этого ряда, согласно общей формуле A.9), равны
* NT л NT N-\
о о 4 = 0
JV-1 NT > jv-1
^L^k)\b{t-kT)e-^tdt = ^-YJx{k)e-^kT = E.2)
4=0 о M* *=0
1 «=? ... ( .2nnk\
= > x(«)exp -j .
NT fa Pl J N )
Таким образом, формула для вычисления комплексных амплитуд гармоник пред-
представляет собой линейную комбинацию отсчетов сигнала.
В выражении E.2) реальный масштаб времени фигурирует только в множите-
множителе 1/Т перед опспатором суммирования. При рассмотрении дискретных последо-
последовательностей обычно оперируют номерами отсчетов и спектральных гармоник
без привязки к действительному масштабу времени и частоты. Поэтому мно-
Дискретное преобразование Фурье 251
житель 1/Гиз E.2) удаляют, то есть считают частоту дискретизации равной еди-
единице. Удаляют обычно и множитель 1/N (об этом см. замечание ниже). Полу-
Получившееся выражение называется дискретным преобразованием Фурье (ДПФ;
английский термин — Discrete Fourier Transform, DFT):
X(n) = 2>(
Существует и обратное дискретное преобразование Фурье. Переход от дискрет-
дискретного спектра к временным отсчетам сигнала выражается следующей формулой:
E-4>
Это выражение отличается от формулы прямого ДПФ E.3) лишь знаком в пока-
показателе комплексной экспоненты и наличием множителя 1/N перед оператором
суммирования.
ЗАМЕЧАНИЕ
В размещении множителя 1/N в формулах E.3) и E.4) нет полного единства. В большин-
большинстве источников, среди которых [1,4, 8], а также в математических пакетах компьютерных
программ (в том числе и в MATLAB) этот множитель фигурирует в формуле обратного
ДПФ E.4) (этот вариант принят и в данной книге). В то же время в учебнике [2] этот мно-
множитель включен в формулу прямого ДПФ E.3).
Свойства дискретного преобразования Фурье
В целом свойства ДПФ аналогичны свойствам непрерывного преобразования
Фурье (см. главу 1), однако дискретный характер анализируемого сигнала прив-
привносит некоторую специфику.
Линейность
Из формулы E.3) очевидно, что ДПФ является линейным, то есть если последо-
последовательностям {x{k)) и {y(k)) с одним и тем же периодом N соответствуют наборы
гармоник Х{п) и Y{ri), то последовательности {ax{k) + by(k)} будет соответствовать
спектр аХ(п)+ bY(n).
Задержка
Если задержать исходную последовательность'на один такт (y(k) - x{k - 1)), то,
согласно E.3), спектр необходимо умножить на exp(-j2nn/N):
Поскольку мы считаем последовательность {x(k)} периодической, рассматривае-
рассматриваемый здесь сдвиг является циклическим: г/@) - х{~\) = x(N - 1).
252 Глава 5. Спектральный анализ
Симметрия
Как уже отмечалось, спектр дискретного периодического сигнала является пе-
периодическим. Кроме того, сохраняется и свойство симметрии, которым обладает
спектр непрерывного вещественного сигнала E(-со) = 5* (со)). Поэтому
X(N-n) = X(-n) = X\n). E.5)
Гармоника с нулевым номером (постоянная составляющая), как видно из E.3),
представляет собой сумму отсчетов последовательности на одном периоде:
Х@) = ]£>(*)•
Если N четно, то амплитуда гармоники с номером ЛГ/2 является суммой отсчетов
с чередующимися знаками:
.+*(JV-2)-x(N~ 1) -
Согласно E.5), спектр является «сопряженно-симметричным» относительно ЛГ/2,
то есть содержит ровно такое же количество информации, что и сам сигнал. В са-
самом деле, исходная последовательность представляется набором из N вещест-
вещественных чисел. Спектр же представляется набором из ЛГ/2 (вторая половина вза-
взаимно-однозначно связана с первой) комплексных чисел, каждое из которых с
информационной точки зрения эквивалентно двум вещественным. Если же ис-
исходная последовательность {x(k)} не является вещественной, симметрия спектра
отсутствует и Л^ комплексным отсчетам во временной области соответствует ЛГ
комплексных отсчетов в спектральной области.
с
ДПФ произведения последовательностей
Возьмем две последовательности отсчетов {Xi(k)} и {x2(k)} одинаковой длины ЛГ
и вычислим результат их поэлементного умножения:
y(k) = Xi(k) x2(k).
Если применить к этой формуле прямое ДПФ, получится следующее выра-
выражение:
Пп) = ^Х,{г)Х2{п-1). E.7)
ЗАМЕЧАНИЕ
При выполнении вычислений по формуле E.7) могут понадобиться значения X2(i) с но-
номерами i, выходящими за рамки диапазона 0...N- 1. В этом случае следует воспользовать-
воспользоваться свойством периодичности спектра: X2(i) = X2(i ± ЛГ).
Это выражение представляет собой круговую свертку спектров Х,(г) и Х2 (г). Итак,
как и для непрерывного преобразования Фурье, спектр произведения является
сверткой спектров.
При п - 0 из E.7) получается дискретный аналог теоремы Рэлея (см. раздел «Энер-
«Энергетические расчеты в спектральной области» главы 1):
N-l
I40)=5>i(*
k=0
1 ЛГ-1 .
■ /■X-2\K) —— А-Л,
N ,--o
1 N-l
(i)X2(-i) = ±ld
Дискретное преобразование Фурье 253
■(О- E-8)
При выводе формулы E.8) были использованы соотношения E.5) и E.6).
Если, кроме того, последовательности {x{(k)} и {x2(k)} совпадают, то есть Xi(k) =
- x2(k) - x(k) для всех k - 0... N - 1, из E.8) получается дискретный аналог ра-
равенства Парсеваля (см. раздел «Энергетические расчеты в спектральной облас-
области» главы 1 и формулу A.24)):
N-l 1 N-l, ,о
Круговая свертка
Так как мы рассматриваем периодические последовательности, то и суммирова-
суммирование при вычислении свертки таких последовательностей следует производить по
одному периоду. Такую операцию называют круговой сверткой:
N-l N-l
n(h\ — N ' v ( j'W (h i\ — 7 y t'i\v ((h i\ тлл W\ (^\ Q*\
if\t*/ — / лл^yt}лпук if — / длj^t)л2\\ /А1^*-*^ /• \ /
/=0 i=0
ЗАМЕЧАНИЕ
В этой формуле выражение (k - г) mod N означает взятие (k - i) по модулю N, то есть вы-
вычисление остатка от деления (k - i) на N.
Подставив выражение E.9) в E.3), легко убедиться, что круговая свертка пе-
периодических временных последовательностей соответствует перемножению их
спектров:
У(п) = Х,(п)Х2(п). E.10)
ЗАМЕЧАНИЕ
Круговую свертку периодических последовательностей не следует путать с линейной сверт-
сверткой D.3), являющейся основой алгоритма дискретной фильтрации.
Восстановление непрерывного сигнала
с помощью ДПФ
Являясь по своей сути спектром дискретного периодического сигнала, дискрет-
дискретное преобразование Фурье позволяет легко восстановить непрерывный периоди-
периодический сигнал, занимающий ограниченную полосу частот. Для этого в формуле
обратного ДПФ E.4) необходимо заменить дискретный параметр (номер отсче-
отсчета k) на непрерывный — нормированное время t/T, где Т — период дискретиза-
дискретизации:
Eл1)
254
Глава 5. Спектральный анализ
Следует обратить внимание на еще одно отличие этого соотношения от форму-
формулы E.4): диапазон индексов суммирования смещен вниз на N/2 (при четном N;
при нечетном N суммирование производится от п = - (N - 1)/2 до (N - 1)/2).
Это необходимо, чтобы получить аналоговый сигнал, занимающий полосу час-
частот от 0 до п/Т. Коэффициенты Х(п) с отрицательными номерами могут быть по-
получены из соотношения симметрии E.5).
Результат восстановления непрерывного периодического сигнала с помощью
ДПФ, разумеется, совпадает с результатами, получаемыми при использовании
ряда Котельникова C.12). Однако использование ДПФ в данном случае оказы-
оказывается более предпочтительным, так как ряд Котельникова для периодического
сигнала содержит бесконечное число слагаемых, а формула E.11) — конечное.
Матрица ДПФ
ДПФ является линейным преобразованием, трансформирующим вектор времен-
временных отсчетов в вектор такой же длины, содержащий отсчеты спектральные. Та-
Такое преобразование может быть реализовано [5] как умножение некоторой квад-
квадратной матрицы на входной вектор-столбец:
У = Ах,
где А — матрица преобразования. В случае ДПФ эта матрица имеет вид
ADFT -
1
,2л
An
,6л
1
.4л
,8л
.12л
1
1
1
1
1 e
Общая формула для элемента матрицы, расположенного в п-м столбце т-й стро-
строки, выглядит так:
Г(т1)(?г1I 1 < m < N, l<n<N.
1
,6л
,12л
18л
e>N :
-j~3(N-l)
N
о
• . С
.. е
.. е
.. е
1
-j^(AT-l)
,2л
г!
N
2я
Вычисление ДПФ путем умножения матрицы на вектор полностью соответству-
соответствует формуле E.3). Этот метод требует большого количества вычислительных опе-
операций, поэтому на практике вместо него применяются быстрые алгоритмы, рас-
рассматриваемые далее.
Связь ДПФ и спектра дискретного сигнала
Имея один и тот же конечный набор чисел, можно рассчитать либо спектраль-
спектральную функцию этого дискретного сигнала по формуле C.2), либо его ДПФ по
формуле E.3). Разумеется, возникает вопрос о том, как связаны друг с 'другом
Дискретное преобразование Фурье
255
эти два спектральных представления, полученные на основе одних и тех же от-
отсчетов сигнала.
Сравнение формул C.2) и E.3) показывает, что ДПФ представляет собой просто
дискретные отсчеты спектральной функции дискретного сигнала, соответст-
соответствующие частотам со„ - (олп/№
—1 = $(«>_—\ E.12)
NT) { д NJ V '
По этой причине значения ДПФ иногда называют спектральными отсчетами.
Из соотношения E.12) следует еще один важный вывод: если добавить к конеч-
конечному набору отсчетов некоторое количество нулей, спектральная функция дис-
дискретного сигнала, естественно, не изменится, но ДПФ даст большее число спек-
спектральных отсчетов, соответствующих частотам, более тесно расположенным в ин-
интервале от нуля до частоты дискретизации.
Поясним сказанное на простом примере, вычислив ДПФ для отсчетов прямо-
прямоугольного импульса при разном количестве концевых нулей (рис. 5.1):
xl = [ones(8.
yl = fft(xl):
1);
zeros(8,l)]:
х2 = [xl; zerosA6.1)];
y2 = fft(x2);
subplotB, 2,
xlim([.O 31])
subplotB, 2.
subplotB, 2,
xlim([0 31])
subplotB. 2.
1).
2),
3),
4)
stem@:15, xl)
stem(@:15)/16, abs(yl))
stem@:31, x2)
* 16 отсчетов
% ДПФ сигнала xl
% добавляем 16 нулей
% ДПФ сигнала х2
% график сигнала xl
% модуль ДПФ сигнала xl
% график сигнала х2
stem(@:31)/32, abs(y2))
% модуль ДПФ сигнала х2
0.8
0.6
0.4
0.2
n <-
see
е—. .
OOOOQOOO ' *-
0.8
0.6
0.4
I
10
20
30
ООЗОСОООСХХХХВСХХХХЮСООФФ
10
20
30
8?
6
4
2
Т ? ? ? т Т
0.2 0.4 0.6 0.8
Рис. 5.1. Повышение спектрального разрешения ДПФ при дополнении сигнала нулями:
сверху — исходный сигнал и модуль его ДПФ, снизу — сигнал, дополненный 16 нулями,
и модуль его ДПФ
256 Глава 5. Спектральный анализ
Горизонтальные оси на спектральных графиках проградуированы в долях часто-
частоты дискретизации. Из рис. 5.1 видно, что после увеличения длины сигнала вдвое
за счет добавления нулевых отсчетов результат ДПФ стал содержать вдвое боль-
больше значений, соответствующих в два раза чаще расположенным частотам. Таким
образом, дополнение сигнала нулями позволяет повысить спектральное разре-
разрешение при вычислении ДПФ.
Алгоритм быстрого
преобразования Фурье
Для вычисления одного коэффициента ДПФ по формуле E.3) необходимо вы-
выполнить N комплексных умножений и сложений. Таким образом, расчет всего
ДПФ, содержащего N коэффициентов, потребует N2 пар операций «умножение-
сложение». Число операций возрастает пропорционально квадрату размерности
ДПФ. Однако, если ./V не является простым числом и может быть разложено на
множители, процесс вычислений можно ускорить, разделив анализируемый набор
отсчетов на части, вычислив их ДПФ и объединив результаты. Такие способы вы-
вычисления ДПФ называются быстрым преобразованием Фурье (БПФ; английский
термин — Fast Fourier Transform, FFT) и повсеместно используются на практике.
При реализации БПФ возможно несколько вариантов организации вычислений
в зависимости от способа деления последовательности отсчетов на части {проре-
{прореживание по времени либо по частоте) и от того, на сколько фрагментов произво-
производится разбиение последовательности на каждом шаге {основание БПФ).
БПФ с прореживанием по времени
Рассмотрим идею БПФ с прореживанием по времени (decimation in time, DIT) на
примере деления набора отсчетов пополам.
Итак, пусть N — четное число. Выделим в формуле E.3) два слагаемых, соответ-
соответствующих элементам исходной последовательности с четными и нечетными но-
номерами:
#/2-1 _ .2д2тк Л'/2-1 _ .2лBт+1)л
Х(п) = £ хBт)е''~1Г + £ хBт+\)е' N .
Введем обозначения у(т) = хBт) и z{m) = хBт+1), а также вынесем из второй
суммы общий множитель e'j2nn/K:
JV/'M .2 ятя ,2яп лу2-1 j2nmn
Х(п)=±у(т)е т +е~' " £ z(m)e m . E.13)
Две суммы в E.13) представляют собой ДПФ последовательностей {у(т)} (от-
(отсчеты с четными номерами) и {z(m)} (отсчеты с нечетными номерами). Каждое
из этих ДПФ имеет размерность N/2. Таким образом,
_ 2ля
~'~r E.14)
Алгоритм быстрого преобразования Фурье
257
где Y(n) и Z(n) — ДПФ соответственно последовательностей отсчетов с четными
и нечетными номерами:
-;-
.2тшл
N/2-l
m=0
N/2-l
m-0
Так как ДПФ размерности N/2 дает лишь N/2 спектральных коэффициентов,
непосредственно использовать формулу E.14) можно только при 0 < п < N/2.
Для остальных п (N/2 < п < N) следует воспользоваться периодичностью спек-
спектра дискретного сигнала (и, соответственно, периодичностью результатов ДПФ):
С учетом этого при п > N/2 формула E.14) представляется в виде
-J~J N
E.15)
Процесс вычисления 8-точечного ДПФ путем разбиения его на два 4-точечных
ДПФ иллюстрируется на рис. 5.2.
Рис. 5.2. Вычисление 8-точечного ДПФ с помощью двух 4-точечных ДПФ
Блоки, выполняющие на рис. 5.2 объединение результатов двух ДПФ, требуют
дополнительных комментариев. Каждый такой блок имеет два входных и два
выходных сигнала. Один из входных сигналов умножается на комплексную экс-
экспоненту wk, после чего суммируется со вторым входным сигналом и вычитается
258
Глава 5. Спектральный анализ
из него, формируя таким образом два выходных сигнала. Это соответствует реа-
реализации формул E.14) и E.15). Данная операция получила название «бабочки»
(butterfly). Расшифровка ее структуры представлена на рис. 5.3.
Z{k)
Рис. 5.3. Условное обозначение «бабочки» БПФ с прореживанием по времени (слева)
и ее структурная схема (справа)
Оценим количество операций, необходимое для вычисления ДПФ указанным спо-
способом. Каждое из двух ДПФ половинной размерности требует N2/4 операций.
Кроме того, при вычислении окончательных результатов каждый спектральный
коэффициент Z(n) умножается на экспоненциальный комплексный множитель.
Это добавляет еще JV/2 операций. Итого получается 2 N2/4 + JV/2 = N(N + l)/2, что
почти вдвое меньше, чем при вычислении ДПФ прямым способом.
Если JV/2 тоже является четным числом (то есть если N делится на 4), можно
продолжить описанную процедуру, выразив результат через четыре ДПФ раз-
размерности JV/4. Это позволяет еще больше сократить число требуемых вычисли-
вычислительных операций.
ЗАМЕЧАНИЕ
Делить исходную последовательность можно на любое количество частей. Таким образом,
приведенный алгоритм позволяет уменьшить число операций в случае любого N, не яв-
являющегося простым числом. Степень ускорения вычислений зависит от числа фрагментов
последовательности и является максимальной при делении на две части, как в рассмот-
рассмотренном примере.
Наибольшая степень ускорения вычислений может быть достигнута при N - 2*,
в этом случае деление последовательностей на две части можно продолжать до
тех пор, пока не получатся двухэлементные последовательности, ДПФ которых
рассчитывается вообще без использования операций умножения (достаточно
вычислить сумму и разность двух отсчетов). Число требуемых при этом пар опе-
операций «умножение — сложение» можно оценить как N log2(iV). Таким образом,
вычислительные затраты по сравнению с непосредственным использованием фор-
формулы E.3) уменьшаются в JV/log2(iV) раз. При больших JV это отношение стано-
становится весьма велико (например, 1024/log2A024) - 102,4, то есть при N = 1024
достигается более чем 100-кратное ускорение).
БПФ с прореживанием по частоте
Формулы прямого и обратного ДПФ E.3) и E.4) отличаются только знаком в
показателе экспоненты и множителем перед суммой. Поэтому можно получить
еще один вариант алгоритма БПФ, выполнив преобразования, показанные на
схеме рис. 5.2, в обратном порядке. Этот способ вычислений называется проре-
Алгоритм быстрого преобразования Фурье 259
живанием по частоте (decimation in frequency, DIF). Покажем, как получить опи-
описание этого метода на основе формулы прямого ДПФ E.3).
Разделим исходную последовательность {x(k)} на две следующие друг за другом
половины (как и в предыдущем случае, N должно быть четным числом):
N12-1 12птп N12-1 \Т .2x(m*N/2)n
Х(п)= %x(m)eJ N + 1 £'
Из второй суммы можно выделить множитель
.2n(N/2)n
Этот множитель равен 1 или -1 в зависимости от четности номера вычисляемо-
вычисляемого спектрального отсчета п, поэтому дальше рассматриваем четные и нечетные п
по отдельности. После выделения множителя ±1 комплексные экспоненты в обе-
обеих суммах становятся одинаковыми, поэтому выносим их за скобки, объединяя
две суммы:
XBk) = jT, \х(тп) + х(тп+—) е ,
»ol 2 )
м/') \ / ~ »v \ .2ктпк 2iwi
m»0 V ^ /
Фигурирующие здесь суммы представляют собой ДПФ суммы и разности поло-
половин исходной последовательности, при этом разность перед вычислением ДПФ
умножается на комплексные экспоненты exp(-j2nm/N). Каждое из двух исполь-
используемых здесь ДПФ имеет размерность N/2.
Итак, при прореживании по частоте вычисления организуются следующим об-
образом:
1. Из исходной последовательности {x(k)} длиной Дополучаются две последова-
последовательности {у(тп)} и {z(m)} длиной N/2 согласно следующим формулам:
y(m)=x(m) + x\ m + -
2. ДПФ последовательности {y(m)} дает спектральные отсчеты с четными номе-
номерами, ДПФ последовательности {z(m)} — с нечетными:
N12-1 -jiazi
= ВД= £ y(m)e m ,
ет=0
JV72— I -j
-1) = Z(&)= £ z(tri)e N/2 .
Все сказанное в предыдущем разделе о возможности деления последователь-
последовательности на иное, отличное от двух, число частей и об уменьшении числа опера-
260
Глава 5. Спектральный анализ
ций, требуемых для расчетов, относится и к алгоритму с прореживанием по час-
частоте.
Процесс вычисления 8-точечного ДПФ путем разбиения его на два 4-точечных
ДПФ с прореживанием по частоте показан на рис. 5.4.
Рис. 5.4. Вычисление 8-точечного ДПФ с помощью двух 4-точечных ДПФ
путем прореживания по частоте •
Поскольку комплексный экспоненциальный множитель в данном алгоритме при-
применяется к результату вычитания двух сигналов, «бабочка» БПФ с прорежива-
прореживанием по частоте имеет несколько иную структурную схему (рис. 5.5).
x(m)
z(m)
Рис. 5.5. Условное обозначение «бабочки» БПФ с прореживанием по частоте (слева)
и ее структурная схема (справа)
ЗАМЕЧАНИЕ
Для получения алгоритма обратного БПФ достаточно поменять в приведенных формулах
знак в показателях комплексных экспонент и добавить на выходе (или на входе) деление
на два (в более общем случае — на используемый коэффициент прореживания).
ЗАМЕЧАНИЕ
Возможен также обобщенный подход к рассмотрению алгоритмов БПФ с прореживанием
по времени и по частоте. Его описание можно найти в [7, 8].
Основание алгоритма БПФ
В названиях алгоритмов БПФ можно встретить слово «RADIX» («основание» —
в математическом смысле). Следующее после него число обозначает число фраг-
Алгоритм быстрого преобразования Фурье 261
ментов, на которое разбивается сигнал на каждом этапе прореживания (а также
минимальный размер «кусочков» входного вектора, который достигается в ре-
результате его последовательных разбиений).
В алгоритмах «RADIX-2» размер анализируемой последовательности должен
быть равен степени двойки, а ее половинное деление производится вплоть до по-
получения двухэлементных последовательностей. Вычисление их ДПФ не требует
операций умножения — два спектральных отсчета представляют собой .сумму и
разность отсчетов временных:
В алгоритмах «RADIX-4» количество отсчетов сигнала должно быть равно сте-
степени четверки, при каждом прореживании сигнал делится на четыре фрагмента,
а последней стадией деления являются четырехэлементные последовательности.
При вычислении их ДПФ умножение производится только на ±j, а такое умно-
умножение сводится к взаимной перестановке вещественной и мнимой частей комп-
комплексного числа с изменением знака у одной из них:
Хф) = хф) + хA) + хB) + хC),
ХB) = хф) - хA) + хB) -хC),
= хф) + j хA) - хB) - j x(
В [8] показано, что использование основания 4 позволяет ощутимо уменьшить
число выполняемых умножений.
Выводы
Наибольшее ускорение вычислений благодаря алгоритму БПФ достигается при
длине анализируемого вектора, равной степени двойки. При разложении длины
вектора на иные множители ускорение также возможно, хотя и не столь значи-
значительное. Если длина вектора — простое число, вычисление спектра может быть
выполнено только по прямой формуле ДПФ.
Пример, демонстрирующий зависимость числа вычислительных операций от
размерности БПФ, будет приведен далее, при описании функции fft в разделе
«Функции спектрального анализа в MATLAB».
Завершая краткое рассмотрение идеи БПФ, необходимо отметить следующее:
□ БПФ не является приближенным алгоритмом; при отсутствии вычислитель-
вычислительных погрешностей он даст точно такой же результат, что и исходная формула
ДПФ E.3). Ускорение достигается исключительно за счет оптимальной орга-
организации вычислений;
□ применение БПФ имеет смысл, если число элементов в анализируемой по-
последовательности является степенью числа 2. Как уже отмечалось, некоторое
ускорение вычислений возможно и при разложении N на другие множители,
однако это ускорение не столь велико, как при N ~ 2 ;
262 Глава 5. Спектральный анализ
□ алгоритм БПФ предназначен для одновременного расчета всех спектральных
отсчетов Х(п). Если же необходимо получить эти отсчеты лишь для некото-
некоторых п, может оказаться предпочтительнее прямая формула ДПФ или рас-
рассматриваемый далее алгоритм Герцеля.
Взаимосвязь ДПФ и фильтрации
К данному моменту мы уже познакомились с понятиями дискретной фильтра-
фильтрации и дискретного преобразования Фурье, однако пока что эти понятия обсуж-
обсуждались по отдельности. В данном разделе рассматривается, как они связаны друг
с другом, причем связь эта оказывается двусторонней — ДПФ можно предста-
представить как обработку сигнала набором фильтров, а дискретную фильтрацию мож-
можно организовать с помощью ДПФ, что позволяет значительно уменьшить число
вычислительных операций за счет использования алгоритмов БПФ.
ДПФ как дискретная фильтрация
Рассмотрев принципы дискретной фильтрации и познакомившись с дискретным
преобразованием Фурье, можно заметить, что формулы, описывающие эти два
процесса, весьма схожи — в обоих случаях они представляют собой линейную ком-
комбинацию отсчетов входного сигнала. Это говорит о том, что ДПФ можно трактовать
как обработку сигнала фильтром с соответствующей импульсной характеристикой.
Эту импульсную характеристику можно получить, если заметить, что е}2т = 1 при
целочисленном и, и с учетом этого записать формулу прямого ДПФ E.3) в виде
Преобразованная таким способом формула ДТ1Ф представляет собой дискрет-
дискретную свертку D.3), то есть N-й отсчет результата обработки входного сигнала
х (k) фильтром, импульсная характеристика которого равна
*-0, 1 2V-1.
Разумеется, импульсная характеристика для каждого частотного отсчета ДПФ
своя; чтобы подчеркнуть это, в ее обозначении использован индекс п.
Определим частотную характеристику такого фильтра. Для этого, как было по-
показано в разделе «Способы описания дискретных систем» главы 4, сначала необ-
необходимо получить функцию передачи:
z-N
^J;-1 -I
Взаимосвязь ДПФ и фильтрации
263
ЗАМЕЧАНИЕ
Для расчета функции передачи использована формула суммы конечной геометрической
прогрессии:
4=0
q-\
Для расчета частотной характеристики используем подстановку z = е'аТ:
АЧХ такого фильтра после несложных тригонометрических преобразований мож-
можно записать следующим образом:
. соЛТ
sin
sin тиЛГ-
sin- соГ
2l N
sin
со.
E.17)
п
где со„ = — (
Результат показывает, что АЧХ фильтра описывается рассмотренной в разделе
«Функции генерации периодических сигналов» главы 3 функцией Дирихле:
К(ю) - diricjv (со - со„).
На рис. 5.6 показан график АЧХ одного из каналов ДПФ при ЛГ= 8 (градуировка
частотной оси выполнена в номерах каналов). Пунктирной линией на этом ри-
рисунке изображена АЧХ соседнего частотного канала:
» N = 8:
» w - 0:0.1:N:
» plot(w. abs(diric((w-3)/N*2*pi. N)))
» hold on
» plot(w. abs(diric((w-4)/N*2*pi. N)). '--')
» hold off
Как видно из графиков, АЧХ фильтра, реализуемого при вычислении ДПФ,
имеет большой уровень боковых лепестков — примерно 1/(NsinCn/BN))). При
N » 1 это выражение стремится к 2/(Зтг)« 0,2 « -13,5 дБ. Для уменьшения уров-
уровня боковых лепестков используют весовые функции, или окна (см. в этой главе
далее).
264
Глава 5. Спектральный анализ
12 3 4 5 6 7
Рис. 5.6. АЧХ частотных каналов ДПФ
Алгоритм Герцеля
Функция передачи отдельного канала ДПФ, записанная в форме E.16), соответ-
соответствует рекурсивному фильтру N-ro порядка. Поэтому вычисление отдельного
спектрального отсчета можно реализовать с помощью такого фильтра. Если не-
необходимо вычислить лишь некоторые отсчеты ДПФ, данный алгоритм может
оказаться предпочтительнее, чем использование БПФ, принципиально ориенти-
ориентированного на получение всех спектральных отсчетов.
Однако для удобства практического использования формулу E.16) можно моди-
модифицировать. Прежде всего заметим, что слагаемое -z'N в числителе выполняет
лишь роль «ограничителя», заставляя импульсную характеристику закончиться,
достигнув длины N отсчетов. Такой фильтр вычисляет отсчет мгновенного спектра
сигнала, все время используя последние N отсчетов входного сигнала. Если же мы
будем обрабатывать сигнал порциями по N отсчетов, перед каждой порцией об-
обнуляя состояние фильтра, то конечность длины импульсной характеристики не
будет иметь значения. В этом случае можно удалить слагаемое -z~N из числителя
функции передачи, получив таким образом рекурсивный фильтр первого порядка:
ti /-\ _
" l-exp(j2nn/N)z'r
Следующее изменение связано с тем, что коэффициент обратной связи в единст-
единственной рекурсивной ветви данного фильтра является комплексным. Поэтому при
обработке каждого входного отсчета необходимо выполнить четыре веществен-
вещественных умножения и столько же вещественных сложений. Число операций можно
сократить, умножив числитель и знаменатель функции передачи на A - е~'2л "/Nz~l),
перейдя за счет этого к фильтру второго порядка:
l-exp(-j2nn/N)z-i l
n{z) =
l-2cosBnn/N)z^ +z-2
Рекурсивная часть получившегося фильтра имеет вещественные коэффициенты,
к тому же коэффициент при z'2 равен единице. Поэтому при обработке каждого
Взаимосвязь ДПФ и фильтрации
265
входного отсчета в рекурсивной ветви фильтра необходимо выполнить всего
одно вещественное умножение и два вещественных сложения.
В рекурсивной ветви фильтра комплексные коэффициенты исчезли, но они, ес-
естественно, появились в числителе функции передачи, то есть в нерекурсивной
части фильтра. Однако если реализовать фильтр в канонической форме (см.
рис. 4.6 в главе 4), то расчеты будут выполняться сначала в рекурсивной ветви,
а затем в нерекурсивной. Поскольку нас интересует только конечный результат
вычисления спектрального отсчета, комплексное умножение и сложение в нере-
нерекурсивной ветви должны быть выполнены только один раз — для получения
окончательного результата.
Полученная структура фильтра показана на рис. 5.7. Данный способ вычисления
отдельного спектрального отсчета называется алгоритмом Герцеля (Hoertzel) [7].
Рис. 5.7. Алгоритм Герцеля
Для вычисления спектрального отсчета по алгоритму Герцеля требуется N + 4 ве-
вещественных умножений и 2N + 3 вещественных сложений. Если число вычис-
вычисляемых спектральных отсчетов невелико, этот алгоритм оказывается эффектив-
эффективнее, чем расчет всех спектральных отсчетов с помощью БПФ.
Дискретная фильтрация с помощью ДПФ
Ранее в этой главе мы представили ДПФ как дискретную фильтрацию. Теперь
же займемся обратной задачей — реализацией фильтрации с помощью ДПФ.
Рассматривая свойства ДПФ, мы видели, что перемножение дискретных спек-
спектров соответствует круговой свертке периодических последовательностей, в то
время как выходной сигнал дискретного фильтра представляет собой линейную
свертку последовательностей конечной длины — входного сигнала и импульс-
импульсной характеристики фильтра (см. раздел «Способы описания дискретных сис-
систем» главы 4). Однако с помощью ДПФ можно получить и линейную свертку,
для этого необходимо добавить к каждой из сворачиваемых последовательно-
последовательностей нулевые отсчеты в количестве, не меньшем, чем длина второй последова-
последовательности минус единица. Длины двух последовательностей после этого должны
стать одинаковыми и равными как минимум длине линейной свертки исходных
последовательностей.
Круговая свертка таких дополненных нулями последовательностей совпадает
с линейной сверткой исходных последовательностей.
266
Глава 5. Спектральный анализ
Поясним сказанное на простом примере. Пусть сворачиваемые последовательно-
последовательности состоят из четырех элементов:
*i-{l,2,4,8}HJf2-{2,3,4,5}.
Линейная свертка этих последовательностей рассчитывается согласно формуле
D.3). Процесс расчета показан на рис. 5.8, сверху.
Исходные сигналы
ф|4
g
4
5
3
4
1
2
1
3
4
8
2
2
4
g
LI
1
5
1
2
4
2
5
4
3
4
4
g
2
g
3
* M3|4|5|
Вычисление линейной свертки
Я0) = 1-2 = 2
jKl)= 1-3 + 2-2 = 7
у{2)= 1-4 + 2-3 +4-2= lg
у{У)= 1-5 + 2-4 + 4-3 + 8-2 = 41
уD) = 2-5 + 4-4 + g-3 = 50
12 4
4 3 2
1
2
2
5
4
4
g
3
1
3
2
2
4
5
g
4
1
4
2
3
4
2
g
5
1
5
2
4
4
3
g
2
Вычисление круговой свертки
Я0)= 1-2+ 2-5+ 4-4 +g-3 = 52
Я1)=1 3+2-2 + 4-5 + 8-4 = 59
><2> = 1-4 + 2-3 + 4-2 + 8-5 = 58
Я3)= 1-5 + 2-4 + 4-3 + 8-2 = 41
Результат
2 | 7 | 18|41 150 1521401
Результвт
159 |58 | 411.
Рис. 5.8. Расчет линейной (сверху) и круговой (снизу) свертки
дискретных последовательностей
Взаимосвязь ДПФ и фильтрации
267
Круговая свертка этих же последовательностей рассчитывается по формуле E.9).
Процесс расчета показан на рис. 5.8, снизу. Результат, как видите, совсем другой.
Но если мы дополним каждую из последовательностей тремя нулями, чтобы их
длины стали равны семи (это длина их линейной свертки), и вычислим круго-
круговую свертку еще раз, то получим результат линейной свертки, приведенный
ранее (рис. 5.9).
Исходные сигналы
': Г1 Г2!
°Т° 1 *2'- |21 з[ 4 [7] о|о I о]
Вычисление круговой свертки
1
2
2
0
4
0
8
0
0
5
0
4
0
3
1
3
2
2
4
0
8
0
0
0
0
5
0
4
у@)=1-2
уA)= 1-3 + 2-2 = 7
1
4
2
3
4
2
8
0
0
0
0
0
0
5
1
5
2
4
4
3
8
2
0
0
0
0
0
0
1
0
2
5
4
4
8
3
0
2
0
0
0
0
1
0
2
0
4
5
8
4
0
3
0
2
0
0
у{Л) = 2-5 + 4-4 + 8-3 = 50
уE) = 4-5 + 8-4 = 52
Результат
1
0
2
0
4
0
8
5
0
4
0
3
0
2
Т\1
Рис. 5.9. Круговая свертка последовательностей, дополненных нулями, совпадает
с их линейной сверткой
Поскольку ДПФ линейной свертки равно произведению ДПФ сворачиваемых
последовательностей, мы получаем следующий алгоритм фильтрации в частот-
частотной области.
1. Последовательность отсчетов входного сигнала и импульсная характеристика
фильтра дополняются нулями так, чтобы длины последовательностей стали
равными и не меньшими, чем сумма длин исходных последовательностей ми-
минус единица.
2. Вычисляются ДПФ дополненных нулями последовательностей.
268 Глава 5. Спектральный анализ
3. Вычисленные ДПФ поэлементно перемножаются.
4. Вычисляется обратное ДПФ от результата перемножения.
Реализуем обычную линейную свертку и приведенный алгоритм средствами
MATLAB. Сначала задаем исходные последовательности:
» xl - [1 2 4 8]:
» х2 = [2 3 4 5];
Теперь вычислим линейную свертку, чтобы затем было с чем сравнивать резуль-
результаты фильтрации с помощью ДПФ:
» у - conv(xl. x2)
У =
2 7 18 41 50 52 40
Далее реализуем рассмотренный алгоритм (забегая вперед, скажем, что ДПФ в
MATLAB вычисляется по быстрому алгоритму с помощью функции fft; описа-
описание данной функции будет приведено в этой главе далее). Дополнять векторы
нулями в явном виде не обязательно — это сделает функция fft при принуди-
принудительном задании размерности преобразования:
» XI = fft(xl. 8):
» Х2 = fft(x2, 8):
» Y = XI .* Х2;
» y_fft = ifft(Y)
y_fft =
Columns 1 through 6
2.0000 7.0000 18.0000 41.0000 50.0000 52.0000
Columns 7 through 8
40.0000 0.0000
Как видите, результат в точности соответствует полученному выше.
Количество нулей, добавляемых к последовательностям, может быть больше ми-
минимально необходимого — при этом лишь появится соответствующее число крае-
краевых нулей в вычисленной свертке (именно это было проделано в только что при-
приведенном примере). Таким образом, мы всегда можем выбрать количество нулей
таким, чтобы длина получившейся последовательности была равна степени двой-
двойки, и использовать эффективный алгоритм БПФ. Это дает возможность сущест-
существенно сократить число операций по сравнению с вычислением свертки обычным
методом.
Недостатком описанного метода фильтрации является то, что входной сигнал об-
обрабатывается сразу целиком, то есть расчеты можно начать только по окончании
входного сигнала. Однако на практике в большинстве случаев необходимо обра-
обрабатывать отсчеты входного сигнала по мере их поступления.
Возможным решением проблемы является блочная, или секционная, обработка вход-
входного сигнала. При этом последовательность входных отсчетов делится на блоки
(секции) заданного размера, и эти блоки подвергаются фильтрации в частотной
области по отдельности. При выборе размера блока необходимо реализовать ком-
компромисс между числом операций (чем больше размер блока, тем эффективнее
Взаимосвязь ДПФ и фильтрации 269
использование алгоритма БПФ) и задержкой получения выходного сигнала (чем
меньше размер блока, тем меньше эта задержка).
При использовании блочной фильтрации необходимо разобраться в идее объ-
объединения выходных сигналов, полученных при обработке отдельных блоков.
Рассмотрим ее на конкретном примере.
Пусть входной сигнал х и импульсная характеристика фильтра h имеют следую-
следующий вид:
» h - [1 4 2];
» х = [123454332211];
Прежде всего вычислим линейную свертку, чтобы знать, что должно получиться:
» у = conv(x. h)
V -
Columns I through 10
1 6 13 20 27 32 29 23 20 16
Columns 11 through 14
13 9 6 2
Теперь разобьем входной сигнал на два блока по 6 отсчетов и обработаем их по
отдельности:
» xl = хA:6):
» х2 = xG:end):
» yl = conv(xl, h)
VI =
1 6 13 20 27 32 26 8
'» у2 = conv(x2. h)
У2 =
3 15 20 16 13 9 6 2
Анализируя полученные результаты, мы заметим, что первые шесть отсчетов век-
вектора yl совпадают с первыми шестью элементами полного выходного сигнала у.
Последние шесть отсчетов вектора у2, в свою очередь, совпадают с шестью по-
последними элементами полного выходного сигнала у. Оставшиеся два «средних»
элемента G-й и 8-й) вектора у могут быть получены суммированием двух по-
последних элементов вектора yl с двумя первыми элементами вектора у2.
» y_add = [yl(l:6) у1G:8)+у2A:2) y2C:end)]
y_add =
Columns 1 through 10
1 6 13 20 27 32 29 23 20 16
Columns 11 through 14
13 9 6 2
Результат совпадает с полученным ранее. Итак, в общем случае фильтрация ор-
организуется следующим образом.
1. Входной сигнал разбивается на блоки длиной N отсчетов.
2. Каждый блок фильтруется независимо. Длина выходного сигнала составля-
составляет N + М - 1 отсчетов, где М — длина импульсной характеристики фильтра.
270 Глава 5. Спектральный анализ
Для повышения эффективности фильтрация осуществляется в частотной об-
области с использованием БПФ.
3. Блоки выходного сигнала объединяются, при этом их крайние М - 1 отсчетов
перекрываются и суммируются.
Данный алгоритм называется методом перекрытия с суммированием (overlap-add).
Другой возможный вариант — перекрытие с накоплением (overlap-save). При этом
входной сигнал разбивается на блоки, перекрывающиеся по краям на М - 1 от-
отсчетов, а у выходного сигнала для каждого блока отбрасываются крайние «хво-
«хвосты» по М - 1 отсчетов с каждой стороны. После этого выходные блоки объеди-
объединяются без перекрытия.
Растекание спектра
Как уже говорилось, при ДПФ предполагается, что последовательность отсчетов
анализируемого сигнала является периодически продолженной вперед и назад
во времени. При этом, если значения начальных и конечных отсчетов сигнала
сильно различаются, при периодическом повторении на стыках сегментов возни-
возникают скачки, из-за которых спектр сигнала расширяется.
Это явление, называемое растеканием спектра (spectrum leakage), можно нагляд-
наглядно проиллюстрировать на простейшем примере вычисления спектра дискретно-
дискретного гармонического сигнала
s(k) - A cos(akT + ф). E.18)
Если анализируемая последовательность содержит целое число периодов гармо-
гармонического сигнала (то есть если отношение NaT/Bn) является целым числом),
то периодически продолженный сигнал представляет собой гармонические коле-
колебания (без скачков), а подстановка E.18) в формулу ДПФ E.3) показывает, что
вычисленное ДПФ содержит лишь два спектральных отсчета, отличных от нуля:
О, в остальных случах.
Таким образом, аналогично спектру непрерывного гармонического сигнала, ДПФ
отличается от нуля всего для двух значений п. Однако если отношение МоГ/Bя)
не является целым числом, спектр оказывается значительно более богатым. Это-
Этому можно дать простое объяснение: ведь в данном случае периодически продол-
продолженная последовательность уже не может являться набором отсчетов непрерыв-
непрерывной синусоиды. Поэтому, в полном соответствии со свойствами преобразования
Фурье, в спектре появляются дополнительные составляющие.
Построим графики дискретных сигналов, содержащих по 16 отсчетов гармони-
гармонических сигналов с периодами, равными 4 отсчетам (периодически продолжен-
продолженный сигнал является периодическим, рис. 5.10 сверху) и 6 отсчетам (периоди-
Взаимосвязь ДПФ и фильтрации
271
чески продолженный сигнал содержит скачки, рис. 5.10 снизу), и покажем вид
модуля их ДПФ:
% времЯ длЯ дискретных сигналов
% времЯ длЯ аналоговых сигналов
% период первого сигнала - 4 отсчета
% период второго сигнала - б. отсчетов
» td = 0:15;
» ta = 0:0.1:16:
» Tl = 4:
» Т2 = 6:
» xld = cosB*pi*td/Tl);
» xla = cosB*pi*ta/Tl);
» yl - fft(xld):
» x2d = cosB*pi*td/T2);
» x2a = cosB*pi*ta/T2);
» у2 = fft(x2d):
» subplotB. 2. 1)
» stem(td, xld)
» hold on
» plot(ta, xla, '--')
» hold off
» xlim([0 16])
» subplotB, 2, 2)
» stenHtd, abs(yl))
» subplotB. 2. 3)
» stem(td. x2d)
» hold on
» plottta, x2a, '--')
» hold off
» xlim([0 16])
» subplotB, 2, 4)
stem(td, abs(y2))
% дискретный сигнал
% аналоговый сигнал
% ДПФ
% дискретный сигнал
% аналоговый сигнал
% ДПФ
% график дискретного сигнала
% график аналогового сигнала
% график спектра
% график дискретного сигнала
% график аналогового сигнала
% график спектра ■
1
0.5
О
-0.5
-1
\ /
\ 1
V
\
1
\
\
Ф
\
I
I
\
Ф
1
t
\
1
\ ' I
\ ,
^ i
\ i
\ i ■
Ф | Ф
8
8
4
2
п t
10
15
0
10
10
15
<
> <
10
15
Рис. 5.10; Дискретное преобразование Фурье для целого (сверху) и нецелого (снизу)
числа периодов гармонического сигнала (слева — исходные последовательности,
справа — модули их ДПФ)
Необходимо подчеркнуть, что причиной растекания спектра является именно
периодическое продолжение анализируемого сигнала. Спектр одиночного фраг-
272 Глава 5. Спектральный анализ
мента дискретной синусоиды, в соответствии с тем, что говорилось в главе 3, яв-
является периодической непрерывной функцией частоты. Эта функция имеет ле-
лепестковую структуру независимо от того, целое или нецелое число периодов ук-
укладывается в анализируемом сегменте. Однако дискретный ряд частот, на
которых вычисляется ДПФ, может быть по-разному расположен относительно
лепестков спектральной функции. В случае целого числа периодов все анализи-
анализируемые частоты (кроме двух) попадают как раз на границы между лепестками.
При нецелом числе периодов такого не происходит. Для иллюстрации этого
факта построим графики периодически продолженных сигналов, а также моду-
модулей их ДПФ и непрерывных амплитудных спектров одиночных фрагментов си-
синусоиды (рис. 5.11):
» td_m = [[td-16. td. td+1633;
» xldjn = [xld, xld, xld]; % продолженный сигнал xld
» x2d_m = [x2d. x2d. x2d]; % продолженный сигнал x2d
» % спектры одиночных сигналов xld и x2d
» [hi. wl] = freqz(xld. 1, [], 16, 'whole'):
» [h2, w2] = freqz(x2d. 1. [], 16, 'whole');
» subplotB. 2, 1)
» stem(td_m, xldjn) % график продолженного сигнала xld
» hold on
» % график продолженного сигнала xla
» plot(ta-16, xla, 'b--'. ta. xla, 'b--', ta+16, xla. 'b--')
» hold off
» xlim([-16 32])
» subplotB, 2, 2)
» stem(td, abs(yl)) % график модуля ДПФ сигнала xld
» hold on
» plot(wl, abs(hl), '--') % спектр одиночного сигнала xld
» xlim([0 16])
» hold off
» subplotB, 2. 3)
» stem(td_m, x2d_m) % график продолженного сигнала x2d
» hold on
» % график продолженного сигнала х2а
» plot(ta-16, x2a, 'b--', ta, x2a. 'b--'. ta+16, x2a, 'b--')
» hold off
» xlim([-16 32])
» subplotB. 2, 4)
» stem(td, abs(y2)) % график модуля ДПФ сигнала x2d
» hold on
» plot(w2, abs(h2). '--') % спектр одиночного сигнала x2d
» xlim([0 16])
» hold off
Возможна еще одна трактовка причины растекания спектра. В этом случае мы не
считаем анализируемый сигнал периодически продолженным, а предполагаем,
что все содержащиеся в нем гармонические компоненты существуют и за преде-
Взаимосвязь ДПФ и фильтрации
273
лами анализируемого фрагмента. Спектр такого сигнала представляет собой на-
набор дельта-функций, а растекание спектра при ДПФ можно объяснить наличием
боковых лепестков у АЧХ фильтров, соответствующих отдельным частотным
каналам ДПФ (см. раздел «ДПФ как дискретная фильтрация», формулу E.17) и
рис. 5.6).
10
15
Рис. 5.11. Происхождение растекания спектра: слева — периодически продолженные
сигналы, справа — амплитудные спектры одиночных сигналов (пунктирные линии)
и модули ДПФ (кружочки)
ЗАМЕЧАНИЕ :
Аналогичные проблемы, связанные с наличием боковых лепестков у АЧХ фильтров, соот-
соответствующих отдельным частотным каналам ДПФ, возникают при использовании ДПФ
для синтеза дискретных фильтров (см. далее раздел «Синтез с использованием окон» гла-
главы 6).
Весовые функции
Для уменьшения растекания спектра при ДПФ применяются весовые функции
(weighting functions), которые также называют окнами (window). В этом случае
перед расчетом ДПФ сигнал умножается на весовую функцию w(k), которая
должна спадать к краям сегмента. Формула прямого ДПФ E.3) при использова-
использовании весовых функций принимает следующий вид:
ЛГ-1 ,-2та*
Роль весовой функции в этой формуле можно рассматривать с различных точек
зрения. Сначала проанализируем ситуацию во временной области. Если мы ис-
используем весовую функцию, которая имеет максимум в середине (при k = N/2) и
плавно спадает к краям (kz=0nk = N- 1), то это приведет к ослаблению эффек-
эффектов, связанных с возникновением скачков сигнала при периодическом повторе-
повторении анализируемой конечной последовательности, и, таким образом, к уменьше-
уменьшению растекания спектра.
274 Глава 5. Спектральный анализ
Аналогичный вывод можно сделать, рассмотрев влияние весовой функции в час-
частотной области. Умножение сигнала на весовую функцию соответствует свертке
спектров сигнала и весовой функции (см. раздел «Свойства дискретного преоб-
преобразования Фурье»). Это приводит к тому, что пики, содержащиеся в спектре сиг-
сигнала, несколько расширяются. Однако при этом становится возможно умень-
уменьшить уровень боковых лепестков спектральной функции, что и является целью
применения весовых функций.
Если трактовать ДПФ как фильтрацию, при использовании весовой функции
w(k) получаются частотные характеристики фильтров следующего вида:
Выбирая весовую функцию w{k) определенным образом, можно уменьшить уро-
уровень боковых лепестков частотой характеристики фильтров, соответствующих
отдельным каналам ДПФ. Естественно, платой за это является расширение цен-
центрального лепестка частотной характеристики.
Спектр дискретного
случайного процесса
Все сказанное в этой главе до сих пор относилось к детерминированным сигна-
сигналам, теперь же мы переходим к рассмотрению спектров дискретных случайных
процессов.
Для определения спектральных характеристик дискретного случайного процесса
используем тот же подход, что и в аналоговом случае (см. раздел «Спектральные
характеристики случайных процессов» главы 1 и формулу A.45)) — будем ус-
усреднять спектр мощности:
W(co)=lim:
1
-jmkT
k'-n
2
E.19)
Черта сверху обозначает здесь усреднение по ансамблю реализаций. Если про-
процесс эргодический, спектр мощности для всех реализаций является одинаковым
и выполнять усреднение по ансамблю не обязательно.
Выполнять вычисления непосредственно по формуле E.19) неудобно, поэтому
попробуем привести ее к более приемлемому виду. Для этого раскроем выраже-
выражение для квадрата модуля:
1
W(a) = lim
*--«
Непараметрические методы
275
Суммируемые слагаемые зависят от разности индексов суммирования knm, по-
поэтому можно преобразовать двойную сумму в одиночную:
I
Поскольку при любом /
lim
= 1,
2и +
окончательно получаем
E.20)
Выражение E.20) представляет собой дискретный аналог теоремы Винера—Хин-
чина: спектр дискретного случайного процесса является преобразованием Фурье
от его корреляционной функции.
Непараметрические методы
При использовании непараметрических методов расчета спектра случайного
процесса используется только информация, заключенная в отсчетах сигнала, без
каких-либо дополнительных предположений. Мы кратко рассмотрим два таких
метода — периодограмму и метод Уэлча (Welch). Примеры реализации данных
методов спектрального анализа будут приведены далее, при описании соответст-
соответствующих функций MATLAB.
Периодограмма
Этим довольно странно звучащим термином — периодограмма (periodogram) —
называется оценка спектральной плотности мощности, полученная по N отсче-
отсчетам одной реализации случайного процесса согласно определению E.19) (есте-
(естественно, не путем взятия предела, а усреднением конечного числа слагаемых).
Таким образом, периодограмма рассчитывается по следующей формуле:
,-jahT
6-0
E.21)
Деление на частоту дискретизации /д необходимо для получения оценки спек-
спектральной плотности мощности аналогового случайного процесса, восстановлен-
восстановленного по отсчетам x(k) (ведь в формуле C.7), связывающей спектры аналогового
и дискретизированного сигналов, имеется множитель 1/Г).
Если при расчете спектра используется весовая функция (окно) с коэффициен-
коэффициентами w{k), формула E.21) слегка модифицируется — вместо числа отсчетов Nb
знаменателе должна стоять сумма квадратов модулей коэффициентов окна. По-
Полученная оценка спектра мощности называется модифицированной периодограм-
периодограммой (modified periodogram):
276 Глава 5. Спектральный анализ
JV-1
1
E.22)
В [10] показано, что периодограмма не является состоятельной оценкой спек-
спектральной плотности мощности, поскольку дисперсия такой оценки сравнима с
квадратом ее математического ожидания. С ростом числа используемых отсче-
отсчетов значения периодограммы начинают все быстрее флуктуировать.
Метод Уэлча
При вычислении периодограммы по длинному фрагменту случайного сигнала она
оказывается весьма изрезанной (см. далее пример вычисления периодограммы в
разделе, посвященном описанию функции periodogram — рис. 5.24). Для умень-
уменьшения этой изрезанности необходимо применить какое-либо усреднение. Дань-
елл (Daniell) предложил сглаживать быстрые флуктуации выборочного спектра
путем усреднения по соседним частотам спектра. Данный метод, называемый
периодограммой Даньелла, сводится к вычислению свертки периодограммы со
сглаживающей функцией. В методе Бартлетта (Bartlett) анализируемый сигнал
делится на неперекрывающиеся сегменты, для каждого сегмента вычисляется
периодограмма и затем эти периодограммы усредняются. Если корреляционная
функция сигнала на длительности сегмента затухает до пренебрежимо малых
значений, то периодограммы отдельных сегментов можно считать независимы-
независимыми. В этом случае дисперсия периодограммы Бартлетта обратно пропорциональ-
пропорциональна числу используемых сегментов, однако с ростом числа сегментов при фик-
фиксированном общем числе отсчетов сигнала падает спектральное разрешение (за
счет того, что сегменты становятся короче).
Уэлч (Welch) внес в метод Бартлетта два усовершенствования: использование
весовой функции и разбиение сигнала на перекрывающиеся фрагменты. Приме-
Применение весовой функции позволяет ослабить растекание спектра и уменьшить
смещение получаемой оценки спектра плотности мощности ценой незначитель-
незначительного ухудшения разрешающей способности. Перекрытие сегментов введено для
того, чтобы увеличить их число и уменьшить дисперсию оценки.
Итак, вычисления при использовании метода Уэлча (он называется еще методом
усреднения модифицированных периодограмм — averaged modified periodogram
method) организуются следующим образом:
1. Вектор отсчетов сигнала делится на перекрывающиеся сегменты. Как прави-
правило, на практике используется перекрытие на 50 %. Строго говоря, оптималь-
оптимальная степень перекрытия зависит от используемой весовой функции. В [10]
приводятся данные о том, что для гауссовских случайных процессов при ис-
использовании окна Ханна минимальная дисперсия оценки спектра плотности
мощности получается при перекрытии сегментов на 65 %.
2. Каждый сегмент умножается на используемую весовую функцию.
3. Для взвешенных сегментов вычисляются модифицированные периодограммы.
4. Периодограммы всех сегментов усредняются.
Параметрические методы
277
Так же как и для периодограммы Бартлетта, дисперсия оценки, получаемой мето-
методом Уэлча, уменьшается примерно пропорционально числу сегментов. Благода-
Благодаря перекрытию в методе Уэлча используется больше сегментов, поэтому диспер-
дисперсия оценки спектра плотности мощности оказывается меньше, чем для метода
Бартлетта.
Метод Уэлча, согласно [10], является наиболее популярным периодограммным
методом спектрального анализа.
Параметрические методы
Использование параметрических методов подразумевает наличие некоторой ма-
математической модели анализируемого случайного процесса. Спектральный ана-
анализ сводится в данном случае к решению оптимизационной задачи, то есть поиску
таких параметров модели, при которых она наиболее близка к реально наблю-
наблюдаемому сигналу.
Мы рассмотрим два параметрических метода: авторегрессионный и MUSIC
(Multiple Signal Classification).
Авторегрессионная модель
Среди возможных параметрических методов спектрального анализа наибольшее
распространение получили методы, основанные на авторегрессионной (Autore-
gressive, AR) модели формирования сигнала. Это обусловлено простотой моде-
модели, удобством расчетов на ее основе и тем, что данная модель хорошо соответст-
соответствует многим реальным задачам.
Согласно авторегрессионной модели, сигнал {x(k)} формируется путем пропуска-
пропускания дискретного белого шума {n(k)} через «чисто рекурсивный» фильтр N-ro по-
порядка (рис. 5.12).
Рис. 5.12. Авторегрессионная модель формирования сигнала
278
Глава 5. Спектральный анализ
ЗАМЕЧАНИЕ
Помимо авторегрессионной существуют и другие модели формирования сигнала путем
пропускания белого шума через формирующий фильтр. Так, в МА-модели (Moving
Average, «скользящее среднее») для этого используется нерекурсивный фильтр, а в
ARMA-модели (Autoregressive Moving Average) — фильтр общего вида, содержащий ре-
рекурсивную и нерекурсивную ветви.
Спектральная плотность мощности такого сигнала пропорциональна квадрату
модуля коэффициента функции передачи фильтра:
1
/л |1-<
E.23)
Таким образом, данный метод спектрального анализа сводится к определению
коэффициентов модели {а,} заданного порядка N, оценке мощности белого шума
а„2 и расчету спектральной плотности мощности по формуле E.23).
Для определения коэффициентов модели производится минимизация ошибки
линейного предсказания сигнала. Сущность этого метода состоит в следующем.
Сигнал {x(k)} пропускается через нерекурсивный фильтр с коэффициентами
{1, -Ьь -Ь2, ..., -bN} (рис. 5.13).
х(к)
Ошибка
предсказания
Предсказанное
значение
Рис. 5.13. Линейное предсказание сигнала
Взвешенную сумму предыдущих отсчетов входного сигнала называют линейным
предсказанием (linear prediction) следующего входного отсчета, а выходной сиг-
сигнал рассматриваемого фильтра, то есть разность между истинным и предсказан-
предсказанным значением отсчета, — ошибкой предсказания (prediction error).
Z-преобразование ошибки предсказания с учетом модели формирования сигнала
{x(k)} можно записать следующим образом:
-...-bNz'N
-1
-a
.-2
-...-a,
„-N '
Параметрические методы 279
Отношение двух полиномов можно в общем случае записать в виде бесконечно-
бесконечного полинома по отрицательным степеням переменной г, причем целая часть это-
этого отношения в данном случае, очевидно, равна единице:
Y(z) = N(z) (I + hit'1 + h2z + ...).
Сам выходной сигнал будет представлять собой результат преобразования бело-
белого шума {n(k)} эквивалентным фильтром {h{k))\
y(k) = n(k) + hin(k - 1) + h2n(k - 2) + ...
Поскольку отсчеты белого шума являются независимыми, дисперсия сигнала {y(k)}
рассчитывается согласно следующей формуле:
а2 - а„2 A + hi2 + h22 + ...).
Отсюда видно, что а2 > а2 и равенство достигается, только когда /г,- = 0 для
всех г. Это возможно, если наборы коэффициентов {а,) и {bt) совпадают.
Таким образом, коэффициенты фильтра, минимизирующего дисперсию (или
среднеквадратическое значение) ошибки предсказания, совпадают с коэффици-
коэффициентами авторегрессионной модели формирования сигнала.
Теперь обратимся к собственно процедуре расчета коэффициентов предсказы-
предсказывающего фильтра по отсчетам сигнала {x(k)}. Ошибка предсказания определяет-
определяется как
= x(k)-b1x(k-\)-b2x(k-2)-...-bNx(k-N) =
Нам нужно подобрать коэффициенты Ьт, обеспечивающие минимальное средне-
среднеквадратическое значение уф). Возведем y(k) в квадрат:
т~\
Теперь усредняем это по ансамблю реализаций, чтобы получить средний квадрат
(считаем случайный процесс x(k) центрированным, поэтому математическое
ожидание у{к) также равно нулю, а средний квадрат равен дисперсии):
т=\ т=\ п = [
Усредненные попарные произведения, входящие в это выражение, дают значе-
значения корреляционной функции входного сигнала:
x(k)x(k-m) = Rx(m),
х (k - m)x (k - n) - Rx (m - n).
280 Глава 5. Спектральный анализ
С учетом этих обозначений средний квадрат сигнала {у(к)} можно записать сле-
следующим образом:
°l = °l -2tbmRx(m)+ t tbmbnRx(m-n). E.24)
т=\ т~\ п = \
Дифференцирование этого выражения по bk дает
да2,
Таким образом, для нахождения коэффициентов линейного предсказания необ-
необходимо решить систему линейных уравнений
tbmRx(m-k) = Rx(k), А - 1, 2,.... М
Можно записать эту систему в матричном виде:
R, Ь = р.
Здесь R,. — корреляционная матрица сигнала {x{k)} (см. раздел «Дискретные
случайные сигналы» главы 3), b — столбец коэффициентов Ьт, р — столбец зна-
значений корреляционной функции Rx(k) для к от 1 до N.
Теперь можно записать искомое решение:
b = R/1 р. E.25)
Подстановка найденного вектора b в формулу E.24) дает минимально возмож-
возможное значение среднего квадрата ошибки предсказания:
(^)mta=^-pTR*p. E-26)
ЗАМЕЧАНИЕ :
В приведенных выкладках предполагалось, что сигнал {x(k)} вещественный. Это было сде-
сделано лишь для упрощения изложения материала и не является принципиальным. В ком-
комплексном случае формула E.25) не меняется, а операцию транспонирования в E.26)
следует заменить эрмитовым сопряжением (сочетанием транспонирования с комплекс-
комплексным сопряжением). Кроме того, при вычислении корреляционной функции комплексного
сигнала один из перемножаемых сигналов подвергается комплексному сопряжению.
На практике мы не знаем истинной корреляционной функции исследуемого сиг-
сигнала, поэтому для минимизации ошибки предсказания используются оценки КФ,
полученные путем временного усреднения. Был разработан целый ряд методов
авторегрессионного анализа, отличающихся в основном подходом к обработке
краевых эффектов (то есть к способу вовлечения в вычисления тех краевых от-
отсчетов сигнала, для которых при вычислении КФ не оказывается сдвинутой пары).
Это метод Берга (Burg), ковариационный метод, модифицированный ковариа-
ковариационный метод, авторегрессионный метод Юла—Уолкера (Yule—Walker) и не-
некоторые другие. Подробные теоретические сведения об этих методах можно найти
в [10], здесь же отметим лишь то, что при анализе длинных последовательно-
последовательностей отсчетов все методы дают практически одинаковые результаты, различия
начинают проявляться в случае коротких сигналов. Достоинства и недостатки
Параметрические методы
281
методов авторегрессионного спектрального анализа, реализованных в MATLAB,
кратко перечислены в табл. 5.1.
Таблица 5.1. Характеристики авторегрессионных методов спектрального анализа
Метод
Берга
Ковариационный
Модифициро-
Модифицированный
ковариационный
Юла—Уолкера
Достоинства
Высокая разрешающая способ-
способность при анализе коротких
сигналов
Гарантированная стабильность
рассчитанного формирующего
фильтра
Большая (по сравнению с мето-
методом Юла—Уолкера) разрешаю-
разрешающая способность при анализе
коротких сигналов
Возможность оценки частот для
сигнала, представляющего со-
собой сумму «чистых» синусоид
Высокая разрешающая способ-
способность при анализе коротких
сигналов
Возможность оценки частот для
сигнала, представляющего со-
собой сумму «чистых» синусоид
Отсутствие расщепления спек-
спектральных пиков
Хорошие результаты при анали-
анализе длинных сигналов
Гарантированная стабильность
рассчитанного формирующего
фильтра
Недостатки
Положения спектральных пи-
пиков сильно зависят от началь-
начальных фаз синусоид
При большом порядке модели
может наблюдаться расщепле-
расщепление спектральных пиков
При анализе суммы синусоид с
шумом получаются смещенные
спектральные пики
Рассчитанный формирующий
фильтр может оказаться неста-
нестабильным
При анализе суммы синусоид с
шумом получаются смещенные
спектральные пики
Положения спектральных пи-
пиков в некоторой степени зави-
зависят от начальных фаз синусоид
Рассчитанный формирующий
фильтр может оказаться неста-
нестабильным
При анализе суммы синусоид с
шумом получаются слегка сме-
смещенные спектральные пики
Плохие результаты при анализе
коротких сигналов
При анализе суммы синусоид с
шумом получаются смещенные
спектральные пики
Авторегрессионные методы анализа спектра больше всего подходят для сигна-
сигналов, действительно являющихся авторегрессионными процессами. Вообще, хо-
хорошие результаты эти методы дают тогда, когда спектр анализируемого сигнала
имеет четко выраженные пики. В частности, к таким сигналам относится сумма
нескольких синусоид с шумом.
При использовании авторегрессионных методов важно правильно выбрать поря-
порядок авторегрессионной модели — он должен быть в два раза больше числа сину-
синусоидальных колебаний, которые предположительно содержатся в анализируемом
сигнале.
282 Глава 5. Спектральный анализ
Пример, демонстрирующий влияние порядка модели на результаты расчетов,
будет приведен далее, при описании функций авторегрессионного спектрального
анализа, имеющихся в MATLAB.
Помимо спектрального анализа техника линейного предсказания широко исполь-
используется для кодирования звуковых сигналов. При этом звук делится на фрагмен-
фрагменты (кадры) и вместо самих отсчетов звука для каждого кадра передаются только
коэффициенты авторегрессионной модели формирования звука, что позволяет
во много раз уменьшить требуемую скорость передачи данных. Такая техноло-
технология используется, например, в сотовых телефонных сетях GSM и в радиотелефо-
радиотелефонах стандарта DECT.
Формула E.25) имеет очень важное значение, и сфера ее использования далеко
не ограничивается расчетом коэффициентов линейного предсказания, Рассмат-
Рассматривая нашу частную задачу, мы получили формулу оптимального фильтра Ви-
Винера, который позволяет сделать входной сигнал максимально близким (в смыс-
смысле среднеквадратической ошибки) к заданному образцу. При этом R* в формуле
E.25) — это по-прежнему корреляционная матрица входного сигнала, ар — век-
вектор взаимных корреляций между желаемым (образцовым) значением выходного
сигнала фильтра и входными отсчетами, используемыми при вычислениях (это,
как обычно, текущий отсчет и некоторое количество предыдущих).
Метод MUSIC
Метод MUSIC (Multiple Signal Classification) предназначен для спектрального
анализа сигналов, представляющих собой сумму нескольких синусоид (точнее,
в общем случае — нескольких комплексных экспонент) с белым шумом. Целью
спектрального анализа подобных сигналов, как правило, является не расчет спек-
спектра как такового, а определение частот и уровней (амплитуд или мощностей)
гармонических составляющих. Метод MUSIC предназначен именно для этого,
поэтому получаемая с его помощью зависимость уровня сигнала от частоты на-
называется псевдоспектром (pseudospectrum).
В основе метода лежит анализ собственных чисел и собственных векторов кор-
корреляционной матрицы сигнала. Подробное математическое обоснование можно
найти в [10], ниже приводятся лишь базовые идеи.
Итак, пусть сигнал представляет собой сумму М комплексных экспонент, началь-
начальные фазы которых случайны, с белым шумом:
exp(jcomW4jcpm). E.27)
m=l
Здесь n(k) — отсчеты дискретного белого шума, Ат, сот и cpm — соответственно
амплитуды, частоты и начальные фазы комплексных экспонент, содержащихся в
сигнале, Т — период дискретизации. Начальные фазы cpm — независимые случай-
случайные величины, равномерно распределенные на интервале О...2я.
ЗАМЕЧАНИЕ
Каждая вещественная синусоидальная составляющая сигнала может быть представлена
как сумма двух комплексных экспонент с помощью формулы Эйлера.
Параметрические методы
283
Корреляционная функция такого сигнала будет иметь следующий вид:
м
E.28)
m=i ■
Здесь xo(k) — единичная импульсная функция C.17), равная 1 при k = 0 и 0 в ос-
остальных случаях, ст„2 — дисперсия шума n(k).
Далее из отсчетов корреляционной функции формируется корреляционная мат-
матрица размера Nх N, причем размер матрицы должен превышать число комплекс-
комплексных экспонент: N> M.
Анализируя собственные числа и собственные векторы такой корреляционной
матрицы, можно показать, что наименьшее собственное число равно а2п, и оно
имеет кратность N - М. Остальные М собственных чисел превышают а2п, а их
конкретные значения зависят от амплитуд и частот комплексных экспонент.
Собственные векторы, соответствующие М наибольшим собственным числам, пред-
представляют собой линейные комбинации комплексных экспонент, содержащихся в
сигнале. Множество всех таких линейных комбинаций называют сигнальным под-
подпространством (signal subspace), а упомянутые собственные векторы образуют
базис в этом подпространстве.
Оставшиеся N — М собственных векторов ортогональны всем комплексным экс-
экспонентам, содержащимся в сигнале. Эти векторы образуют базис шумового под-
подпространства (noise subspace).
Спектр комплексной экспоненты, рассчитанный аналитически, представляет со-
собой дельта-функцию, расположенную на соответствующей частоте. Чтобы полу-
получить бесконечные выбросы на частотах сот, псевдоспектр при использовании ме-
метода MUSIC рассчитывается следующим образом:
W(co) = - -. E.29)
i
N-i
„-jismT
Здесь vk(ri) — и-й элемент k-vo собственного вектора корреляционной матрицы.
Векторы пронумерованы по убыванию соответствующих им собственных чисел.
Таким образом, внешняя сумма по k от М + 1 до N задает участие в вычислениях
только шумовых собственных векторов. Внутренняя сумма представляет собой
вычисление спектра собственного вектора на частоте со. Шумовые собствен-
собственные векторы ортогональны всем комплексным экспонентам с частотами сот, со-
содержащимся в сигнале. Поэтому при со = сога все внутренние суммы равны нулю,
и W(co) -> оо. ,
Сами частоты сога можно получить, приравняв к нулю знаменатель формулы E.29):
N N-\ . 2
k=M+\ n = 0
Раскроем квадрат модуля, превратив его в двойную сумму:
£
N-\ N-\
Z I
E.30)
284 Глава 5. Спектральный анализ
Теперь видно, что левая часть полученного выражения в конечном счете представ-
представляет собой полином относительно е~;шГ степени 2N - 2. Те корни этого полинома,
которые лежат на единичной окружности, равны ехр(-_/'ютГ), и для расчета час-
частот остается вычислить аргументы этих комплексных чисел и разделить их на Т.
Все сказанное до сих пор относилось к идеализированной модели сигнала E.27) и
аналитически полученной корреляционной функции E.28). В реальных ситуаци-
ситуациях, когда сигнал не вполне соответствует модели E.27), а его корреляционная
функция оценивается по результатам измерений (к тому же зачастую без воз-
возможности усреднения по нескольким наблюдениям), результаты оказываются не-
несколько иными — пики в E.29) будут иметь конечную высоту, а корни полинома
E.30) не будут лежать строго на единичной окружности. Однако если сигнал бли-
близок к предполагаемой модели, метод MUSIC дает хорошие результаты. Для расче-
расчета частот выбираются корни полинома E.30), ближайшие к единичной окружности.
Метод EV
Близким родственником MUSIC является метод анализа собственных векторов
(eigenvectors, EV). Его отличие состоит лишь в том, что в формулах E.29) и E.30)
при суммировании по k используются весовые коэффициенты, обратно пропор-
пропорциональные соответствующим собственным числам. Таким образом, формула для
псевдоспектра принимает вид:
г, E.31)
*=Л/+1
у ЛГ-1
1 = 0
a-janT
а уравнение, которое необходимо решить для оценки значений частот, оказыва-
оказывается следующим:
I ^-II^(«)^(/)e-M"-')r=0. E.32)
k = M+l А,£ „ = о /=0
В этих формулах кк — собственное число, соответствующее &-му собственному
вектору v*.
В [10] приводятся сведения о том, что при заданном значении порядка М метод
EV порождает меньше ложных спектральных пиков, чем MUSIC, и, как правило,
лучше передает форму спектра шума.
Еще раз подчеркнем, что псевдоспектры E.29) и E.31) не являются оценками
истинного спектра плотности мощности, а представляют собой лишь спектраль-
спектральные псевдооценки, позволяющие оценивать частоты синусоидальных или узко-
узкополосных составляющих сигнала с разрешением, несколько превосходящим раз-
разрешение авторегрессионных методов.
Функции спектрального анализа
в MATLAB
Для выполнения спектрального анализа в MATLAB имеется большое число функ-
функций, реализующих разнообразные методы — от обычного ДПФ до MUSIC.
Функции спектрального анализа в MATLAB 285
Прямое и обратное ДПФ
Для выполнения прямого и обратного ДПФ в MATLAB служат функции fft и if ft:
□ у - fft(x) — вычисляет прямое ДПФ для вектора х; если х — матрица, преоб-
преобразование производится для каждого ее столбца по отдельности;
□ у = fft(x, N) — предварительно приводит исходные данные к размеру N, уре-
урезая их или дополняя нулями;
□ х = ifft(y) и х = ifft(y, N) — аналогичные варианты вызова для функции об-
обратного ДПФ.
Функции fft и i fft входят в базовую библиотеку MATLAB. Вычисления орга-
организованы так, что реализуется максимально возможное для каждой длины ис-
исходного вектора ускорение вычислений: длина вектора (число строк в матрице) х
раскладывается на простые множители, число этих множителей соответствует
количеству ступеней БПФ, а сами множители определяют коэффициенты про-
прореживания на разных ступенях БПФ.
Продемонстрируем зависимость числа вычислительных операций от размерности
БПФ. Создадим вектор из 128 случайных чисел (на всякий случай — комплекс-
комплексных, чтобы лишить MATLAB возможности что-либо сэкономить на отсутствии
мнимой части у исходных данных; впрочем, при использовании алгоритмов БПФ
такая экономия очень мала).
ВНИМАНИЕ
Приводимый ниже пример работает только в младших версиях MATLAB — до,5.x включи-
включительно. Дело в том, что в версии 6 было обновлено ядро MATLAB и функция flops, подсчи-
подсчитывавшая число выполненных арифметических операций, более не поддерживается.
N =128:
х = randn(N. 1) + i * randnCN. 1):
for k=l:N
flops(O): % В MATLAB 6 это не работает!
у = fft(x. k);
flop(k) = flops: % В MATLAB б это не работает!
end
plot(flop)
hold on
plot((l:N).*8. ':')
plot((l:N).*log2(l:N)*6, ':')
hold off
Полученный график (рис. 5.14) настолько показателен, что не привести этот при-
пример было бы совершенно непростительно, несмотря на то, что он не работает в
последних версиях MATLAB.
Кроме собственно зависимости числа операций от размерности БПФ на графике
показаны также верхняя и нижняя границы. Верхняя линия — это число операций,
соответствующее прямой формуле ДПФ и равное 8JV2 (множитель 8 возникает
из-за того, что функция flops подсчитывает вещественные операции). Нижняя
286
Глава 5. Спектральный анализ
линия — число операций, соответствующее максимальному ускорению вычисле-
вычислений и равное 6N\og2(N) (множитель 6 также возникает из-за подсчета функцией
flops вещественных операций). Хорошо видно, что график числа операций при
БПФ касается верхней границы, если N — простое число, и касается нижней гра-
границы, если N — степень двойки.
хЮ4
О 20 40 60 60 100 120 140
Рис. 5.14. Зависимость числа арифметических операций от размерности БПФ
Функция fftshift
Элементы вектора, возвращаемого функцией fft, соответствуют частотам, равно-
равномерно распределенным в диапазоне от нуля и почти до частоты дискретизации.
Первый элемент, таким образом, соответствует нулевой частоте, а последний —
частоте, меньшей частоты дискретизации на/д/iV, где N— размер входного и выход-
выходного векторов. При выводе спектральных графиков иногда желательно, чтобы
нулевая частота находилась в центре, а диапазон отображаемых частот прости-
простирался от -/д/2 до/д/2. Сделать это позволяет функция fftshift, которая меняет
местами половины переданного ей вектора:
у = fftshift(x)
Продемонстрируем действие функции fftshift на примере двух коротких векто-
векторов четной и нечетной длины:
» fftshift([l 2 3 4])
ans =
3 4 12
» fftshift([l 2 3 4 5])
ans =
4 5 12 3
Функции спектрального анализа в MATLAB 287
Как видите, в случае четной длины действительно происходит перестановка по-
половин входного вектора (при этом первый элемент результирующего вектора
соответствует частоте Найквиста). В случае нечетной длины перестановка вы-
выполняется так, чтобы первый элемент, соответствующий нулевой частоте, стал
средним элементом результирующего вектора.
Разумеется, функцию fftshift можно использовать не только для вывода спек-
спектральных графиков, но и в других случаях, когда требуется поменять местами
половины вектора.
Матрица ДПФ
В MATLAB расчет матрицы прямого ДПФ реализуется с помощью функции
dftmtx. Синтаксис ее вызова следующий:
А = dftmtx(n)
Здесь п — размерность ДПФ.
Матрица обратного ДПФ отличается от матрицы прямого ДПФ комплексным
сопряжением и делением на N, поэтому она может быть получена следующим
образом:
A_inv = conj(dftmtx(n))/n
Блочная фильтрация в частотной области
Для реализации блочной фильтрации с помощью БПФ в MATLAB использует-
используется функция fftfilt, имеющая следующий синтаксис:
у = fftfiltCh. х. п)
Здесь h — импульсная характеристика фильтра, х — входной сигнал, п — размер-
размерность БПФ (точнее, размерность БПФ при задании этого параметра определяет-
определяется так: Nf ft - 2*nextpow2(n), то есть п округляется вверх до степени двойки).
Выходной параметр у — результат фильтрации.
Третий входной параметр п при вызове можно опускать, тогда размерность БПФ
будет выбираться автоматически, исходя из максимальной эффективности вы-
вычислений (минимального числа операций).
Окна
MATLAB содержит (в пакете Signal Processing) целый ряд стандартных весо-
весовых функций. Они возвращают векторы отсчетов, которые могут использоваться
в качестве одного из параметров разнообразных функций непараметрического
спектрального анализа.
Все рассматриваемые ниже функции принимают в качестве параметра требуе-
требуемую длину вектора (п), которая должна быть целым положительным числом, и
возвращают вектор-столбец w. При п=1 все функции возвращают значение 1.
Амплитудный спектр весовой функции соответствует частотной характеристике
нулевого канала ДПФ при использовании данной весовой функции. При рас-
288 Глава 5. Спектральный анализ
смотрении конкретных функций графики их амплитудных спектров будут стро-
строиться в логарифмическом масштабе для п = 16. Чтобы обеспечить на нулевой
частоте значение спектральной функции, равное единице @ дБ), перед вычисле-
вычислением спектра весовые функции нормируются — делятся на сумму своих отсчетов.
Графики спектров будут строиться функцией f reqz (см. раздел*«Расчет частотной
характеристики» главы 4). Поскольку фазовый спектр для всех весовых функ-
функций линейно зависит от частоты, его графики не представляют интереса и пото-
потому не приводятся. Для повышения наглядности частотная ось градуируется в
номерах каналов ДПФ, для этого при вызове функции f reqz указана частота дис-
дискретизации, равная длине окна.
Прямоугольное окно
Функция boxcar, реализующая «прямоугольное окно», введена в MATLAB лишь
для полноты набора весовых функций, поскольку она соответствует отсутствию
взвешивания:
w = Ьохсаг(п)
Возвращаемый вектор заполнен единицами: w = ones(n.l).
Приводить график данной весовой функции не имеет смысла, а ее амплитудный
спектр (смещенный по горизонтали) для п = 8 был показан ранее на рис. 5.6.
Треугольное окно
Функция triang реализует треугольное окно:
w = triang(n)
Отсчеты треугольного окна рассчитываются по следующей формуле:
2k л ,, я + 1
w(k) =
w(k) =
n+\ 2
для нечетного п,
n + 1
n
— -, - + \<k<n
2
для четного п.
При нечетном п треугольное окно является симметричным, его крайние значе-
значения (при k " 1 и k = п) равны 2/{п + 1), а в середине окна (при k = (п + 1)/2)
достигается единичное значение.
При четном п треугольное окно является несимметричным, его можно предста-
представить как отсчеты симметричного треугольного импульса, который начинается
при k = 0,5 и заканчивается при k = п + 1. Вершина импульса расположена при
к = /г/2 + 0,75, а его амплитуда равна 1 + 1/Bп). При k = п/2 + 1 отсчет окна име-
имеет единичное значение.
На рис. 5.15 приведены графики треугольного окна и его амплитудного спектра
при п = 16:
Функции спектрального анализа в MATLAB
289
» w = triangA6):
» w = w/sum(w);
» plot(w)
» figure
» [h. f] = freqz(w, 1, []. 16):
» plot(f. 20*loglO(abs(h)))
» ylim([-80 0])
» grid on
0.12
0.08
0.06
0.04
0.02
0 12345678
Рис. 5.15. Треугольное окно (сверху) и его амплитудный спектр (снизу)
Уровень первого бокового лепестка составляет -26,5 дБ.
Окно Бартлетта
Функция bartlett реализует окно Бартлетта:
w = bartlett(n)
290
Глава 5. Спектральный анализ
Окно Бартлетта, по сути, тоже является треугольным, но рассчитывается не-
несколько иначе:
w(k) =
{ n-i
w(k) =
n-i
2{n-k)
n-i
n+i
n-i
2(n-k) n + i
для нечетного п,
<k<n
для четного п.
-+i<k<n
2
8 10 12 14 16
О
-10
-20 -
-30 ■
-40
-50
-60
-70
АП
0 12 3 4 5 6 7 8
Рис. 5.16. Окно Бартлетта (сверху) и его амплитудный спектр (снизу)
л
\
1
/■
— ■/• ■
/
д
л/
1
\
л
\
д
\
( \
Функции спектрального анализа в MATLAB 291
В отличие от треугольного окна, значения окна Бартлетта по краям (при k m 1 и
k = п) равны нулю. Кроме того, независимо от четности п оно является симмет-
симметричным. Окно Бартлетта представляет собой отсчеты симметричного треуголь-
треугольного импульса, который начинается при k = 1, заканчивается при k = n и имеет
единичную амплитуду. Максимум значения этого импульса достигается при
к = и/2, поэтому при нечетном п окно Бартлетта не достигает единичного значе-
значения в середине.
При нечетном п ненулевые отсчеты окна Бартлетта совпадают с отсчетами тре-
треугольного окна длины п - 2.
На рис. 5.16 приведены графики окна Бартлетта и его амплитудного спектра при
п = 16:
» w = bartlettA6);
» w = w/sum(w);
» plot(w)
» figure
» [h. f] = freqz(w. 1. []. 16):
» plot(f. 20*loglO(abs(h)))
» ylim([-80 0])
» grid on
Уровень первого бокового лепестка, как и в случае треугольного окна, составля-
составляет -26,5 дБ.
Окно Ханна
Функция hann реализует окно Ханна (по аналогии с рассматриваемым далее ок-
окном Хэмминга его часто ошибочно называют окном Хэшшпга; даже соответст-
соответствующая функция в предыдущей версии пакета Signal Processing имела имя
hanning):
w = hann(n. 'sflag')
Строковый параметр 'sflag' позволяет выбрать режим расчета окна. При значе-
значении 'symmetric', принятом по умолчанию, генерируется симметричное окно, для
которого w(k) = w(n + 1 - k). При значении 'periodic' создается слегка несим-
несимметричное окно, синусоидальные компоненты которого будут аккуратно стыко-
стыковаться при соединении нескольких экземпляров окна.
В симметричном случае отсчеты окна Ханна рассчитываются по формуле
/;. if. f_ k-l
w(k) = -\ 1-cos 2к
Для периодического варианта п - 1 в знаменателе формулы заменяется на п (воз-
(возможна и иная трактовка: выполняется расчет по приведенной формуле для окна
длиной п + 1, а затем последний элемент отбрасывается).
На рис. 5.17 приведены графики окна Ханна и его амплитудного спектра при
и- 16:
» w - hannA6):
» w = w/sum(w):
292
Глава 5, Спектральный анализ
» plot(w)
» figure
» [h. f] = freqz(w. 1. []. 16):
» plot(f. 20*loglO(abs(h)))
» ylim([-80 0])
» grid on
Уровень первого бокового лепестка составляет -31,5 дБ.
6 8 10 12 14 16
-10
-20
-30
-40
-50
-60
-70
'800 1234567 8
Рис. 5.17. Окно Ханна (сверху) и его амплитудный спектр (снизу)
>
\
I
\г\
\
\ -
I
I
\ ^
V
I
Окно Хэмминга
Функция hamming реализует окно Хэмминга:
w = hamming(n, 'sflag')
Функции спектрального анализа в MATLAB
293
Строковый параметр 'sflag' позволяет выбрать режим расчета окна. При значе-
значении 'symmetric', принятом по умолчанию, генерируется симметричное окно, для
которого w(k) " w(n + 1 - к). При значении 'periodic' создается слегка несим-
несимметричное окно, синусоидальные компоненты которого будут аккуратно стыко-
стыковаться при соединении нескольких экземпляров окна.
В симметричном случае отсчеты окна Хэмминга рассчитываются по формуле
Bn
V. и-1
Для периодического варианта п - 1 в знаменателе формулы заменяется на п (воз-
(возможна и иная трактовка: выполняется расчет по приведенной формуле для окна
длиной п + 1, а затем последний элемент отбрасывается).
0 12345678
Рис. 5.18. Окно Хэмминга (сверху) и его амплитудный спектр (сверху)
294 Глава 5. Спектральный анализ
На рис. 5.18 приведены графики окна Хэмминга и его амплитудного спектра при
я- 16:
» w = hammingA6);
» w = w/sum(w);
» plot(w)
» figure
» [h. f] = freqz(w, 1, []. 16);
» plot(f. 20*loglO(abs(h)))
» ylim([-80 0])
» grid on
Уровень первого бокового лепестка в данном примере составляет -40 дБ; с рос-
ростом п этот уровень уменьшается до -43 дБ.
Окно Блэкмена
Функция Ы ackman реализует окно Блэкмена:
w = blackman(n, 'sflag')
Строковый параметр 'sflag' позволяет выбрать режим расчета окна. При значе-
значении 'symmetric', принятом по умолчанию, генерируется симметричное окно, для
которого w(k) - w(n + 1 - k). При значении 'periodic' создается слегка несим-
несимметричное окно, синусоидальные компоненты которого будут аккуратно стыко-
стыковаться при соединении нескольких экземпляров окна.
В симметричном случае отсчеты окна Блэкмена рассчитываются по формуле
w(k) = 0,42-0,5cosf2л—| + 0,08cos[ 4л—
^ п-\) К п-\
Для периодического варианта п - 1 в знаменателе формулы заменяется на п
(возможна и иная трактовка: выполняется расчет по приведенной формуле для
окна длиной п + 1, а затем последний элемент отбрасывается).
На рис. 5.19 приведены графики окна Блэкмена и его амплитудного спектра при
и = 16:
» w = blackmanA6);
» w = w/sum(w);
» plot(w)
» figure
» [h. f] = freqz(w. 1, []. 16):
» plot(f. 20*loglO(abs(h)))
» ylim([-100 0])
» grid on
Уровень первого бокового лепестка составляет -58 дБ. Окно Блэкмена имеет не-
несколько более широкий главный лепесток и меньший уровень боковых лепест-
лепестков по сравнению с окнами Ханна и Хэмминга той же длины.
Функции спектрального анализа в MATLAB
295
о
-10
-20
-30
-40
-50
-60
-70
-80
-90
-100
012345678
Рис. 5.19. Окно Блэкмена (сверху) и его амплитудный спектр (снизу)
Окно Кайзера
Функция kaiser реализует окно Кайзера:
w - kaiser(n. beta)
Здесь beta — параметр окна (см. формулу ниже).
Отсчеты окна Кайзера рассчитываются по формуле
\
S.
\
\
\
-
I/
If
\ г-
\i
\г
w(k) =
1, 2 п.
Здесь /() — модифицированная функция Бесселя первого рода нулевого порядка.
Чем больше р, тем больше доля энергии, сосредоточенная в главном лепестке
спектра (и тем шире этот главный лепесток), и тем меньше уровень боковых ле-
лепестков. На практике используются значения р от 4 до 9.
296
Глава 5. Спектральный анализ
8 10 12 14 16
;;%
\ ^
\
V
\
\ /->
\\l
■'
V 1
1 ■••,!■
||
1 ■ ■ • -|Г ■
1. '
t.'
1
1 1
< 1
II
■;
1
Л
.......J........
/ и i
l' I1 I
:! }• 1
о
-10
-20
-30
-40
-50
-60
-70
-80
-90
-100
012345678
Рис. 5.20. Окно Кайзера (сверху) и его амплитудный спектр (снизу)
для р = 4 (сплошные линии) и р = 9 (пунктирные линии)
На рис. 5.20 приведены графики окна Кайзера и его амплитудного спектра при
п = 16 для двух указанных крайних значений р:
» wl = kaiserA6. 4);
» w2 = kaiserA6. 9);
» wl = wl/sum(wl):
» w2 = w2/sum(w2):
» plot(wl); hold on; plot(w2. '--'): hold off
» figure
» [hi. f] = freqz(wl. 1. []. 16);
» h2 = freqz(w2. 1. [], 16):
» plotCf, 20*loglO(abs(hl)))
» hold on
» plotCf. 20*loglO(abs(h2)). '--')
» hold off
Функции спектрального анализа в MATLAB
297
» ylim([-100 0])
» grid on
Из графиков видно, что при р - 4 главный лепесток имеет ширину 1,75 (за еди-
единицу принято расстояние между соседними каналами частотного анализа), а уро-
уровень боковых лепестков составляет -32,5 дБ. При р = 9 главный лепесток расши-
расширяется примерно до 3,2, а уровень боковых лепестков падает до -66 дБ.
Окно Чебышева
Функция chebwin реализует окно Чебышева:
w = chebwin(n, beta)
Здесь beta — степень подавления боковых лепестков в децибелах (см. формулу
ниже).
10 12
14 16
\
\
\
V
!
L
|
А
I
А
А
I \
-ю -
-20 "
-30 "
■40 -
-50
-60
012345676
Рис. 5.21. Окно Чебышева (сверху) и его амплитудный спектр (снизу)
для уровня боковых лепестков -40 дБ
298 Глава 5. Спектральный анализ
Для окна Чебышева все боковые лепестки имеют одинаковый, заданный при
расчете окна уровень. Отсчеты окна Чебышева рассчитываются путем вычисле-
вычисления обратного преобразования Фурье от его частотной характеристики:
cos (w-l)arccos n—
*, ч I I aJ) ,Га
5(со) = -, где а = ch
ch((n-l)arch(a)) ^ п-\
Здесь р — степень подавления боковых лепестков в децибелах, п — требуемое ко-
количество отсчетов окна.
На рис. 5.21 приведены графики окна Чебышева и его амплитудного спектра при
п = 16 для уровня боковых лепестков -40 дБ:
» w = chebwinA6, 40):
» w = w/sum(w);
» plot(w)
» figure
» [h, f] = freqz(w. 1, []. 16):
» plot(f. 20*loglO(abs(h)))
» ylim([-60 0])
» grid on
Как обычно, с уменьшением уровня боковых лепестков главный лепесток рас-
расширяется.
Новые весовые функции в Signal Processing Toolbox 5.1
В последней E.1) версии пакета Signal Processing появилось еще несколько весо-
весовых функций:
□ barthannwin — окно Бартлетта—Ханна (линейная комбинация окон Бартлетта
и Ханна);
□ blackmanharris — окно Блэкмена—Харриса (в отличие от окна Блэкмена, сум-
суммируется не два, а три косинусоидальных слагаемых);
□ bohmanwin — окно Бомена (свертка двух одинаковых косинусоидальных им-
импульсов);
□ gausswin — гауссово окно;
□ nuttalwin — версия окна Блэкмена—Харриса, предложенная Наттоллом (слег-
(слегка отличаются весовые коэффициенты при суммировании косинусондальных
слагаемых);
□ tukeywin — окно Тьюки (прямоугольник с косинусоидально сглаженными края-
краями; при крайних допустимых значениях коэффициента сглаживания получа-
получаются прямоугольное окно и окно Ханна).
Функции непараметрического
спектрального анализа
В данном разделе будут рассмотрены три функции, осуществляющие спектраль-
спектральный анализ сигнала без использования дополнительной информации:
Функции спектрального анализа в MATLAB
299
□ specgram — вычисление мгновенного спектра сигнала;
□ periodogram — вычисление спектральной плотности мощности одной реализа-
реализации случайного сигнала;
□ pweich — оценка спектральной плотности мощности случайного процесса ме-
методом усреднения модифицированных периодограмм.
Для демонстрации работы многих функций спектрального анализа будет исполь-
использоваться дискретный случайный процесс с экспоненциальной функцией корре-
корреляции. Формирование такого процесса было рассмотрено в разделе «Формиро-
«Формирование случайных сигналов» главы 3, поэтому соответствующие строки листингов
далее будут приводиться без комментариев.
Чтобы в дальнейшем было с чем сравнивать получаемые результаты, построим
теоретический спектр плотности мощности данного сигнала. Поскольку он явля-
является авторегрессионным процессом первого порядка, его спектр можно рассчи-
рассчитать по формуле E.23), положив в ней N = 1. Коэффициент alt как и в примере
главы 3, принимаем равным 0,9, а частоту дискретизации /д и дисперсию белого
шума а2п считаем равными единице. Функции спектрального анализа пакета Signal
Processing для вещественного сигнала рассчитывают односторонний спектр плот-
плотности мощности, поэтому умножим результат вычислений по формуле E.23) на
два. Строим график спектра плотности мощности (рис. 5.22):
» Т = 1; % период дискретизации
» var_n = 1; % дисперсия белого шума
» а 1 = 0.9: % параметр экспоненциальной корреляции
» f = 1inspaceCO. 1/B*Т), 100): % вектор значений частот
» % рассчитываем спектр плотности мощности
» Р = 2 * var_n * Т ./ absd - al * exp(-i*2*pi*f*T)) .Л2:
» psdplotCP. f. 'Hz')
&
25
20
15
10
5
о •
-5
\
0.1
0.2 0.3
Frequency (Hz)
0.4
0.5
Рис. 5.22. Спектр плотности мощности экспоненциально коррелированного
дискретного случайного процесса
300 Глава 5. Спектральный анализ
Спектрограмма
Спектрограммой (spectrogram ) сигнала называется его мгновенный спектр, зави-
зависящий от времени. Для вычисления спектрограммы вектор сигнала разбивает-
разбивается на сегменты (возможно, с перекрытием). Для каждого сегмента вычисляется
спектр с помощью функции fft. Набор спектров всех сегментов и образует спек-
спектрограмму.
Для вычисления спектрограммы служит функция specgram:
В - specgramU, Nf ft. Fs. window, numoverlap)
Здесь x — вектор сигнала (сигнал не может быть многоканальным), Nfft — ис-
используемая размерность дискретного преобразования Фурье, Fs — частота дис-
дискретизации в герцах, window — вектор отсчетов весовой функции (размер этого
вектора определяет размер сегментов, на которые разбивается анализируемый
сигнал), numoverl ар — величина перекрытия соседних сегментов (в отсчетах).
Обязательным входным параметром является только вектор значений сигнала х,
остальные параметры имеют значения по умолчанию, которые используются,
если в качестве параметра указана пустая матрица ([]) или если несколько по-
последних параметров при вызове опущены:
a Nfft = minB56. length(x));
□ Fs = 2;
□ window = hann(nfft. 'periodic');
□ numoverlap = length(window)/2.
Выходной параметр В — матрица, столбцы которой являются комплексными спек-
спектрами отдельных сегментов сигнала. Если входной вектор х является веществен-
вещественным, спектр вычисляется только для положительных частот и возвращаемая
матрица В содержит Nfft/2+l (для четного Nfft) или (Nfft+l)/2 (для нечетного
Nfft) строк. В случае комплексного анализируемого вектора х спектр не обладает
симметрией, и возвращаемая матрица В содержит Nfft строк.
При отсутствии выходных параметров функция specgram строит графическое
изображение спектрограммы в координатах «время — частота», отображая зна-
значения амплитудного спектра с помощью цвета (для этого используется функция
imagesc):
specgramL.)
Примеры использования функции specgram уже приводились в главах 3 и 4 (см.
рис. 3.26 и рис. 4.19-4.21). Поэтому здесь мы покажем, какой забавный вид мо-
может иметь спектрограмма сигнала, сформированного из нескольких импульсов
с меняющейся частотой. Запись такого сигнала содержится в файле vcosig.mat,
входящем в состав пакета Signal Processing. В этом же файле хранится и значе-
значение частоты дискретизации этого сигнала (переменная Fs). Формируем спектро-
спектрограмму (рис. 5.23):
» load vcosig
» specgram(vcosig. [], Fs)
Функции спектрального анализа в MATLAB
301
Рис. 5.23. Пример использования функции specgram
ВНИМАНИЕ
Для отображения спектрограммы используется цветовая палитра jet, так что минимально-
минимальному уровню амплитудного спектра соответствует темно-синий цвет, максимальному — тем-
темно-красный. Переход от синего к красному происходит через оттенки голубого, зеленого и
желтого. В результате при черно-белой печати заиисимость оттенка графика от уровня спек-
спектра оказывается немонотонной. Для правильной передачи уровня спектра в черно-белом
виде следует установить для рисунка палитру оттенков серого командой colormap gray.
В данном примере этого не сделано только потому, что «рожица» выглядит выразительнее
именно после преобразования исходных цветов рисунка в оттенки серого, а не при исполь-
использовании серой палитры для вывода спектрограммы.
Расчет периодограммы
Для вычисления периодограммы в MATLAB предназначена функция periodogram.
Синтаксис ее вызова следующий:
[Рхх. f] = periodogram(x. window. Nfft, Fs, 'range')
Единственным обязательным входным параметром является х — вектор отсчетов
сигнала. Остальные параметры имеют значения по умолчанию, которые исполь-
используются, если в качестве параметра указана пустая матрица [] или если некоторое
количество параметров (начиная с последнего) опущены при вызове.
Вектор window должен содержать коэффициенты используемого окна (при этом
вычисляется модифицированная периодограмма по формуле E.22)). По умолча-
умолчанию используется прямоугольное окно, то есть периодограмма вычисляется по
формуле E.21).
302
Глава 5. Спектральный анализ
Параметр Nfft задает размерность БПФ, используемого для вычисления перио-
периодограммы. По умолчанию этот параметр равен maxB56, 2Anextpow2(length(x))).
Входной сигнал, умноженный на окно, приводится к размеру Nfft (обрезается
либо дополняется нулями).
Параметр Fs — частота дискретизации в герцах. Эта величина используется в
формулах E.21) и E.22), а также для оцифровки графика и расчета возвращае-
возвращаемого вектора частот f. Значение по умолчанию равно 2тс.
Строковый параметр 'range' определяет частотный диапазон для возвращаемого
вектора Рхх. Возможны два значения:
□ 'twosided' — векторы Рхх и f имеют длину Nfft и соответствуют полному диа-
диапазону частот O...Fs. Этот вариант используется по умолчанию, если х содер-
содержит комплексные отсчеты;
□ 'onesided' — векторы Рхх и f имеют длину ceil((Nfft + 1)/2) и соответствуют
половинному диапазону частот O...Fs/2. Этот вариант используется по умол-
умолчанию в случае вещественного вектора х.
Параметр 'range' может быть указан в списке параметров в любом месте после
wi ndow.
Возвращаемые параметры: Рхх — вектор значений спектральной плотности мощ-
мощности, f — вектор значений частот, использованных для расчета. Шаг между со-
соседними элементами этого вектора равен Fs/Nfft, первый элемент равен нулю.
Если выходные параметры при вызове не указаны, функция строит график спек-
спектральной плотности с помощью функции psdplot.
Periodogram PSD Estimate
30
I" 20
£■ 10
5 о
I -20
-30
0.1
0.2 0.3
Frequency (Hz)
0.4
0.5
Рис. 5.24. Периодограмма экспоненциально коррелированного случайного процесса,
полученная с помощью функции periodogram
В качестве примера оценим спектр плотности мощности экспоненциально кор-
коррелированного случайного процесса (рис. 5.24):
Функции спектрального анализа в MATLAB 303
» % формирование случайного сигнала
» ХО = randnd. 1000):
» а = 0.9;
» X - filterd, [1 -а], ХО):
» % оценка спектра плотности мощности
» periodogram(X, [], [], 1)
Как видите, хотя общий ход графика совпадает с аналитически построенным
спектром данного случайного процесса (см. рис. 5.22), периодограмма оказыва-
оказывается сильно изрезанной, что полностью соответствует теоретическим сведениям,
приведенным ранее в разделе «Непараметрические методы».
Реализация метода Уэлча
Функция pwel ch предназначена для определения спектра мощности случайного
сигнала методом Уэлча (методом усреднения модифицированных периодограмм —
averaged modified periodogram method). Синтаксис вызова функции следующий:
[Рхх. f] = pwe1ch(x, Nwin, Noverlap, Nfft, Fs, 'range')
Единственным обязательным входным параметром является х — вектор отсчетов
анализируемого сигнала. Все остальные параметры имеют значения по умолча-
умолчанию, которые используются, если при вызове в качестве параметра указана пус-
пустая матрица ([]) или если несколько последних параметров опущено.
Параметр Nwi n управляет выбором окна, используемого для анализа. Если Nwi n —
число, используется окно Хэмминга указанной длины, если вектор, то данный
вектор используется в качестве окна. По умолчанию используется окно Хэм-
Хэмминга, длина которого выбирается так, чтобы с учетом заданного перекрытия
(см. ниже) сигнал оказался разделенным на 8 фрагментов.
Параметр Noverl ар задает (в отсчетах) перекрытие соседних фрагментов сигнала,
для которых вычисляются периодограммы. По умолчанию перекрытие равно по-
половине длины окна.
Параметр Nfft задает размерность БПФ, используемого для вычисления перио-
периодограммы. По умолчанию Nfft ■ maxB56, 2*nextpow2(Nwin)), где Nwin — длина фраг-
фрагмента сигнала (длина используемого окна).
Параметр Fs указывает частоту дискретизации сигнала. Это значение использу-
используется для нормировки рассчитанного спектра мощности, а также при расчете воз-
возвращаемого вектора f и для оцифровки графика. По умолчанию значение этого
параметра равно 2л.
Строковый параметр ' range' определяет частотный диапазон для возвращаемого
вектора Рхх. Возможны два значения:
□ 'twosided' — векторы Рхх и f имеют длину Nfft и соответствуют полному диа-
диапазону частот O...Fs. Этот вариант используется по умолчанию, если х содер-
содержит комплексные отсчеты;
□ 'onesided' — векторы Рхх и f имеют длину ceil ((Nfft + D/2) и соответствуют
половинному диапазону частот O...Fs/2. Этот вариант используется по умол-
умолчанию в случае вещественного вектора х.
304
Глава 5. Спектральный анализ
Параметр ' range' может быть указан в списке параметров в любом месте после
Noverlap.
Возвращаемые параметры: Рхх — вектор значений спектральной плотности мощ-
мощности, f — вектор значений частот, использованных для расчета. Шаг между со-
соседними элементами этого вектора равен Fs/Nfft, первый элемент равен нулю.
Если выходные параметры при вызове не указаны, функция строит график спек-
спектральной плотности мощности с помощью функции psdpl ot.
Расчет спектра производится следующим образом. Анализируемый сигнал х де-
делится на перекрывающиеся фрагменты согласно параметрам Nwin и Noverlap. Для
каждого фрагмента вычисляется модифицированная периодограмма с использо-
использованием заданных окна и размерности БПФ (см. раздел «Расчет периодограммы»
в этой главе). Полученный набор модифицированных периодограмм усредняет-
усредняется, и результат делится на Fs.
В качестве примера оценим спектр плотности мощности экспоненциально кор-
коррелированного случайного процесса (рис. 5.25):
» % формирование случайного сигнала
» ХО = randnCl. 1000):
» а - 0.9:
» X - filterd. [1 -а]. ХО):
» % оценка спектра плотности мощности
» pwelchCX. []. []. []. 1)
Welch PSD Estimate
25
nT 20
S 15
10
-10
Л
4
4
V
Л
An
0.1
0.2 0.3
Frequency (Hz)
0.4
0.5
Рис. 5.25. Оценка спектра плотности мощности, полученная
с помощью функции pwelch
Как видите, по сравнению с периодограммой, показанной ранее на рис. 5.24, спектр
значительно меньше изрезан и приближается к теоретическому спектру данного
процесса (см. рис. 5.22).
Функции спектрального анализа в MATLAB 305
ВНИМАНИЕ
В предыдущих версиях 4.x пакета Signal Processing, поставлявшихся с версиями MATLAB 5.x,
данный метод спектрального анализа был реализован с помощью функции psd. Она сохра-
сохранена и в нынешней, пятой версии пакета Signal Processing, но считается устаревшей, по-
поэтому использовать ее не рекомендуется.
Функция построения графика спектра мощности
Функция psdplot предназначена для построения графика спектральной плотно-
плотности мощности. В частности, она используется для этого всеми функциями спек-
спектрального анализа, если при их вызове не указаны выходные параметры. Син-
Синтаксис вызова функции psdplot следующий:
psdplot(Pxx, f, 'units', 'yscale'. 'title')
Здесь Рхх — вектор значений спектральной плотности мощности (данный пара-
параметр может быть матрицей, в таком случае выводится несколько графиков, соот-
соответствующих отдельным столбцам этой матрицы), f — вектор той же длины, что
и Рхх, содержащий значения частот, которым соответствуют значения спектраль-
спектральной плотности мощности.
Остальные параметры являются необязательными. Параметр 'units' задает под-
подпись для оси частот — 'rad/sample' (радиан/отсчет, этот вариант использует-
используется по умолчанию) или 'Hz'. Параметр 'yscale' управляет режимом построе-
построения графика. Принятое по умолчанию значение 'db' задает вывод мощности в
децибелах, то есть в логарифмическом масштабе. Линейный масштаб использу-
используется при значении 'linear'. Наконец, параметр 'title' — строка заголовка для
графика.
Параметрический спектральный анализ
в MATLAB
В данном разделе будет рассмотрено семейство функций, осуществляющих спек-
спектральный анализ с использованием авторегрессионных моделей, а также несколь-
несколько функций, реализующих методы MUSIC и EV.
Работа с авторегрессионными моделями
В MATLAB реализовано несколько методов анализа спектра на основе авто-
авторегрессионной модели формирования сигнала. Эти методы отличаются друг
от друга способом оценивания коэффициентов авторегрессионной модели. Каж-
Каждому методу соответствуют две функции — функция вычисления коэффици-
коэффициентов модели и функция собственно спектрального анализа. Функция спек-
спектрального анализа вызывает функцию расчета коэффициентов модели, а затем
производит вычисление спектра по формуле E.23). Имена функций сведены в
табл. 5.2.
Синтаксис вызова функций для разных методов анализа совершенно одинаков,
поэтому рассматривать функции по отдельности не имеет смысла.
306
Глава 5. Спектральный анализ
Таблица 5.2. Функции авторегрессионных моделей
Назввние методе
Ковариационный метод
Модифицированный
ковариационный метод
Метод Берга
Авторегрессионный метод
Юла—Уолкера
Функция рвсчетв
коэффициентов модели
arcov
armcov
arburg
aryule
Функция спектрвльного
внвлизв
pcov
pmcov
pburg
pyulear
Функции расчета коэффициентов
авторегрессионных моделей
Синтаксис вызова функций, выполняющих оценивание коэффициентов авторег-
авторегрессионных моделей формирования сигнала, приведен ниже:
[а, е] = агххх(х, р)
Здесь агххх — имя одной из функций, перечисленных во втором столбце
табл. 5.2.
Входные параметры: х — вектор отсчетов сигнала, р — порядок авторегрессион-
авторегрессионной модели.
Выходные параметры: а — вектор коэффициентов модели (это полный вектор
знаменателя функции передачи формирующего фильтра, его длина равна р + 1,
а первый элемент равен 1), е — оценка дисперсии белого шума, возбуждающего
фильтр.
В качестве примера оценим параметры авторегрессионной модели для экспонен-
экспоненциально коррелированного шума (такой шум является авторегрессионным про-
процессом первого порядка, поэтому задаем р = 1):
» % формирование случайного сигнала
» ХО = randnd, 1000):
» а = 0.9:
» X = filterd. [I -a], X0):
» % оценка параметров авторегрессионной модели
» [аа. е] = arburg(X, 1)
аа =
1.0000 -0.9107
е =
0.8904
Как видите, оценка коэффициента обратной связи весьма близка к истинной.
Оценка дисперсии белого шума, возбуждающего авторегрессионный формирова-
формирователь, для данной реализации процесса оказывается несколько заниженной.
Функции спектрального анализа в MATLAB 307
Функции авторегрессионного спектрального анализа
Синтаксис вызова функций, производящих расчет спектра мощности на основе
авторегрессионной модели формирования сигнала, приведен ниже:
[Рхх, f] = рххх(х, р, Nfft, Fs, 'range')
Здесь рххх — имя одной из функций, перечисленных в последнем столбце табл. 5.2.
Обязательные входные параметры: х — вектор отсчетов сигнала, р — порядок ав-
торегрессиониой модели. Остальные входные параметры имеют значения по умол-
умолчанию, которые используются, если параметр представляет собой пустую матри-
матрицу ([]) или отсутствует.
Параметр Nfft задает число частотных точек для расчета спектра. По умолчанию
его значение равно 256. Параметр Fs — частота дискретизации входного сигнала
(используется при расчете возвращаемого вектора частот f и для оцифровки го-
горизонтальной оси графика). Значение по умолчанию — 2л Гц.
Строковый параметр 'range' определяет частотный диапазон для возвращаемого
вектора Рхх. Возможны два значения:
□ 'twosided' — векторы Рхх и f имеют длину Nfft и соответствуют полному диа-
диапазону частот O...FS. Этот вариант используется по умолчанию, если х содер-
содержит комплексные отсчеты;
Q 'onesided' — векторы Рхх и f имеют длину ceil ((Nfft + l)/2) и соответствуют
половинному диапазону частот 0...FS/2. Этот вариант используется по умол-
умолчанию в случае вещественного вектора х.
Параметр ' range' может быть указан в любом месте списка параметров после р.
Возвращаемые параметры: Рхх — вектор значений спектральной плотности мощ-
мощности, f — вектор значений частот, использованных для расчета. Шаг между со-
соседними элементами этого вектора равен Fs/Nfft, первый элемент равен нулю.
Если выходные параметры при вызове не указаны, функции строят график спек-
спектральной плотности с помощью функции psdpiot.
В качестве примера выполним спектральный анализ экспоненциально корре-
коррелированного случайного сигнала. Такой сигнал является авторегрессионным
процессом первого порядка, поэтому мы продемонстрируем влияние порядка
авторегрессионной модели на получаемые результаты, построив оценки спектра
(рис. 5.26) для р = 1 (оптимальный порядок модели) и р = 20 (избыточный по-
порядок):
» % формирование случайного сигнала
» ХО = randnd. 1000):
» а = 0.9;
» X = filterd. [1 -а]. ХО):
» % оценка спектра плотности мощности
» pburgCX, 1, [], 1) % порЯдок модели оптимален
» figure
» pburg(X, 20, []. 1) % порЯдок модели избыточен
308
Глава 5. Спектральный анализ
Burg PSD Estimate
N
m
H
га
a.
i
25
20
15
10
-5
-10,
25
20
15
10
5
0
-5
-10,
\
-———
0.1 0.2 0.3
Frequency (Hz)
Burg PSD Estimate
0.1
0.2 0.3
Frequency (Hz)
0.4
0.4
0.5
Л
\
r/\
r\
0.5
Рис. 5.26. Результаты авторегрессионного спектрального анализа
при оптимальном (сверху) и избыточном (снизу) порядке модели
Из графиков видно, что при оптимальном порядке модели (рис. 5.26, сверху)
спектр практически совпадает с теоретическими результатами (см. рис. 5.22),
а при избыточном (см. рис. 5.26, снизу) в спектре начинают возникать ложные
флуктуации.
Реализация метода MUSIC
Функция pmusic реализует расчет псевдоспектра путем анализа собственных чи-
чисел и собственных векторов корреляционной матрицы сигнала (метод MUSIC).
Синтаксис вызова функции pmusic следующий:
[s. f. v. е] = pmusic(x. p. Nfft. Fs. Nwin. Noverlap. 'range')
Функции спектрального анализа в MATLAB 309
У функции много входных параметров, однако обязательными являются только
х и р. В простейшем случае х — это вектор отсчетов сигнала, ар — целое число,
задающее размерность сигнального подпространства. Однако смысл этих пара-
параметров может быть и несколько иным, о чем речь пойдет чуть ниже.
Формирование корреляционной матрицы
Данный метод расчета спектра основан на анализе корреляционной матрицы сиг-
сигнала, поэтому прежде всего необходимо определить эту матрицу. Если х — век-
вектор отсчетов сигнала, формированием корреляционной матрицы управляют па-
параметры Nwin и Noverlap. Параметр Nwin может быть числом, обозначающим раз-
размер прямоугольного окна, или вектором, содержащим коэффициенты окна. Сигнал
делится на фрагменты в соответствии с длиной окна (равной Nwin или length(Nwin)),
при этом перекрытие соседних фрагментов составляет Noverlap отсчетов.
По умолчанию используется прямоугольное окно, размер которого в два раза пре-
превышает заданную размерность сигнального подпространства. Перекрытие фраг-
фрагментов по умолчанию на единицу меньше размера окна (то есть соседние фраг-
фрагменты сигнала сдвинуты друг относительно друга на один отсчет).
Кроме вектора, входной параметр х может быть матрицей, содержащей несколь-
несколько реализаций (наблюдений) случайного процесса. При этом каждая строка
матрицы соответствует отдельной реализации. Корреляционная матрица в этом
случае рассчитывается как х'*х. Параметр Noverlap игнорируется, так же как и
числовой параметр Nwin. Если Nwin задан в виде вектора, его длина должна быть
равна числу столбцов в матрице х (при этом каждая реализация сигнала поэле-
поэлементно умножается на вектор коэффициентов окна перед вычислением корреля-
корреляционной матрицы).
Наконец, в качестве х можно подставить уже готовую корреляционную матрицу
(в этом случае параметр х должен удовлетворять свойствам корреляционной
матрицы — быть квадратной эрмитовой, то есть обладающей комплексно-сопря-
комплексно-сопряженной симметрией, матрицей Теплица). Чтобы использовать такой вариант,
в число входных параметров необходимо включить строку 'согг' (в любом месте
списка параметров после размерности сигнального подпространства р). Парамет-
Параметры Nwin и Noverlap в данном случае игнорируются.
Управление размером сигнального подпространства
Как уже говорилось, в простейшем случае размерность сигнального подпростран-
подпространства задается числом р. Однако функция pmusic позволяет использовать более
гибкий способ разделения собственного пространства корреляционной матрицы
на сигнальное и шумовое подпространства. Для этого параметр р должен быть
двухэлементным вектором. Значение рA) задает максимально допустимый пре-
предел размерности сигнального подпространства, а значение рB), — пороговый уро-
уровень для собственных чисел, соответствующих сигнальному подпространству.
Если X.min — минимальное собственное число корреляционной матрицы, то собст-
собственные числа, меньшие чем XminpB), будут отнесены к шумовым компонентам,
а собственные числа, превышающие этот порог, — к сигнальным компонентам.
Чтобы использовать этот режим, длина окна должна быть не меньше, чем рA).
310 Глава 5. Спектральный анализ
Значение рA) может быть равно бесконечности (Inf), при этом необходимо яв-
явное задание параметра Nwin, поскольку использование значения по умолчанию
оказывается невозможным.
Управление расчетом псевдоспектра
Параметр Nfft задает число точек для расчета псевдоспектра. Значение по умол-
умолчанию — 256. Частота дискретизации Fs используется для расчета возвращаемо-
возвращаемого вектора f и для вывода графика. Ее значение по умолчанию равно 2тг. Нако-
Наконец, строковый параметр 'range' задает диапазон частот анализа. Этот параметр
может принимать одно из двух значений:
□ 'whole' — длина возвращаемых векторов s и f равна Nf ft, расчет проводится
для всего частотного диапазона O...FS. Этот вариант принят по умолчанию для
случая, когда х содержит комплексные элементы;
□ 'half — длина возвращаемых векторов s и f равна cei1((Nfft+l)/2), расчет
проводится для половинного частотного диапазона O...Fs/2. Этот вариант при-
принят по умолчанию для вещественного сигнала х.
Выходные параметры
Возвращаемые функцией pmusic результаты имеют следующий смысл:
□ s — вектор рассчитанных значений псевдоспектра;
□ f — вектор частот, которым соответствуют значения в векторе s;
□ v — собственные векторы корреляционной матрицы, соответствующие шумо-
шумовому подпространству;
□ е — собственные числа корреляционной матрицы, соответствующие шумово-
шумовому подпространству.
Функция rootmusic
Если функция pmusic дает вектор рассчитанных значений псевдоспектра, то функ-
функция rootmusic, используя тот же метод анализа MUSIC, извлекает из корреляци-
корреляционной матрицы сигнала несколько иную информацию — частоты содержащихся
в сигнале комплексных экспонент и соответствующие им мощности.
Синтаксис вызова функции следующий:
[f. pow] = rootmusic(x. p, Fs, 'согг')
Все входные параметры имеют тот же смысл, что и для функции pmusic.
Результатами работы функции являются векторы частот f и соответствующих
им мощностей pow. Длина вектора f равна размерности сигнального подпростран-
подпространства. Размер вектора pow зависит от того, вещественным или комплексным явля-
является анализируемый сигнал х. Если сигнал х комплексный, длина вектора pow
равна длине вектора f, а если вещественный, то она вдвое меньше.
Пример использования
В качестве примера применения функций pmusic и rootmusic сформируем сигнал,
состоящий из трех синусоид разного уровня, смешанных с белым шумом, а затем
Функции спектрального анализа в MATLAB
311
частота дискретизации
частоты, содержащиеся в сигнале
выведем график его псевдоспектра (рис. 5.27) и оценим частоты гармонических
составляющих:
» Fs = 1000:
» fl = 50:
» f2 = 120:
» f3 = 300:
» t = 0:1/Fs:1: % дискретное времЯ
» % анализируемый сигнал
» s = 2*cosB*pi*fl*t) + 5*sinB*pi*f2*t) - 0.5*cosB*pi*f3*t):
» s = awgn(s. 10, 'measured'): % отношение С/Ш = 10 дБ
» pmusic(s, 6. []. Fs) % график псевдоспектра
» rootmusic(s. 6, Fs) % оценка частот
ans =
120.0306
-120.0306
49.8887
296.9443
-296.9443
30
25
20
15
10
5
О
-5
-10
-15
MUSIC Pseudospectrum
г
/V
.. i
/
\
\
...\
\
/
\
\
100
400
500
200 300
Frequency (Hz)
Рис. 5.27. Оценка псевдоспектра, полученная с помощью функции pmusic
Как видите, частоты оценены довольно точно, а график демонстрирует четкие
пики.
I
Функции peig и rooteig
Функции peig и rooteig аналогичны функциям pmusic и rootmusic соответственно.
Отличие состоит в том, что ими реализуется метод EV и расчеты производятся
по формулам E.31) и E.32), где при суммировании используются весовые коэф-
312 Глава 5. Спектральный анализ
фициенты, обратно пропорциональные «шумовым» собственным числам корре-
корреляционной матрицы сигнала. Синтаксис вызова функций следующий:
[s. f. v. e] = peig(x, p, Nfft, Fs, Nwin, Noverlap. 'range')
[f. pow] = rooteig(x, p. Fs, 'corr')
Все входные и выходные параметры соответствуют описаниям, приведенным вы-
выше для функций pmusic и rootmusic.
ГЛАВА 6 Проектирование
дискретных
фильтров
Под проектированием (или синтезом) цифрового фильтра понимается выбор
таких наборов коэффициентов {а,} и {6,}, при которых характеристики получаю-
получающегося фильтра удовлетворяют заданным требованиям. Строго говоря, в задачу
проектирования входит и выбор подходящей структуры фильтра (см. раздел
«Формы реализации дискретных фильтров» главы 4) с учетом конечной точ-
точности вычислений. Это особенно актуально при реализации фильтров «в желе-
железе» — с использованием специализированных БИС или цифровых сигнальных
процессоров. Эффекты, связанные с конечной точностью вычислений, будут об-
обсуждаться в главе 7, здесь же речь пойдет только о методах синтеза цифровых
фильтров, то есть способах получения значений {а,} и {bt}.
Методы синтеза цифровых фильтров можно классифицировать по различным
признакам:
□ по типу получаемого фильтра:
О методы синтеза рекурсивных фильтров;
О методы синтеза нерекурсивных фильтров;
□ по наличию аналогового прототипа:
О методы синтеза с использованием аналогового прототипа;
О прямые {без использования аналогового прототипа) методы синтеза.
Синтез рекурсивных фильтров
по аналоговому прототипу
При синтезе дискретного фильтра по аналоговому прототипу необходимо реали-
реализовать переход из s-области в z-область, то есть преобразовать функцию переда-
передачи аналогового фильтра H(s) в функцию передачи дискретного фильтра H(z).
Получающийся дискретный фильтр не может быть полностью идентичен анало-
314 Глава 6. Проектирование дискретных фильтров
говому по сбоим характеристикам — хотя бы потому, что частотные характеристи-
характеристики дискретного фильтра являются периодическими. Можно говорить только об
определенном соответствии характеристик аналогового и дискретного фильтров.
В данном разделе мы рассмотрим два метода синтеза рекурсивных дискретных
фильтров по аналоговым прототипам:
□ метод билинейного ^-преобразования;
□ метод инвариантной импульсной характеристики.
Поскольку теория аппроксимации идеальных АЧХ аналоговыми средствами хо-
хорошо развита (см. раздел «Расчет аналоговых фильтров-прототипов» главы 2),
методы синтеза дискретных фильтров по аналоговым прототипам получили ши-
широкое распространение.
Метод билинейного z-преобразования
Данный метод позволяет синтезировать рекурсивный дискретный фильтр по час-
частотной характеристике аналогового прототипа.
Функция передачи аналоговой цепи с сосредоточенными параметрами представ-
представляет собой дробно-рациональную функцию переменной s. Чтобы получить функ-
функцию передачи дискретного фильтра, необходимо перейти из s-области в ^-область,
причем дробно-рациональный характер функции должен сохраниться (см. раз-
раздел «Функция передачи» главы 4). Поэтому замена для переменной s должна
представлять собой также дробно-рациональную функцию переменной г. Чтобы
частотные характеристики аналогового и дискретного фильтров были связаны
простой зависимостью, искомая замена переменной должна отображать мнимую
ось в s-области па единичную окружность в r-области. В этом случае частотные
характеристики аналогового и дискретного фильтров будут связаны лишь транс-
трансформацией частотной оси и никаких искажений «по вертикали» не будет.
Простейшей из функций, удовлетворяющих перечисленным требованиям, явля-
является билинейное z-преобразование (bilinear transformation):
5=£^_1=2/л1-Ц.. F.1)
Частотные характеристики аналогового Ка (со) и дискретного Хл((о) фильтров, как
уже было сказано, связаны друг с другом лишь трансформацией частотной оси:
ш
На низких частотах, когда соГ « 1, тангенс примерно равен своему аргументу,
так что
2 (аТ} - ,
— tg — « со, если со 1 « 1.
Синтез рекурсивных фильтров по аналоговому прототипу
315
Поэтому в области низких частот частотные характеристики аналогового и дис-
дискретного фильтров почти совпадают. Далее, по мере ускорения роста функции
тангенса, частотная характеристика дискретного фильтра все сильнее сжимается
по горизонтали (по сравнению с аналоговым прототипом) и на частоте Найкви-
ста, равной п/Т, достигает значения, которое частотная характеристика аналого-
аналогового фильтра имела бы на бесконечной частоте (рис. 6.1).
Шд/2 со
Рис. 6.1. Трансформация частотной оси при билинейном z-преобразовании
При билинейном ^-преобразовании левая половина 5-плоскости отображается
внутрь единичной окружности на z-плоскости, поэтому синтез по устойчивому
аналоговому прототипу даст гарантированно устойчивый дискретный фильтр
(см. раздел «Полюсы и вычеты» в главах 2 и 4, где шла речь об условиях устой-
устойчивости соответственно аналоговых и дискретных систем).
Для получения дискретного фильтра с заданными частотами среза необходимо
скорректировать частоты среза аналогового прототипа, чтобы компенсировать
искажения частотной оси. Так, для синтеза дискретного ФНЧ с частотой сре-
среза а>од аналоговый фильтр-прототип должен иметь частоту среза со0а, связанную
с оHд следующим образом:
">0а =^<
(б.з,
Метод инвариантной импульсной
характеристики
Метод инвариантной импульсной характеристики (impulse invariance) позволяет
синтезировать рекурсивный дискретный фильтр путем дискретизации импульс-
импульсной характеристики аналогового прототипа.
Как говорилось в разделе «Полюсы и вычеты» главы 2, импульсная характери-
характеристика аналоговой цепи с сосредоточенными параметрами может быть представ-
представлена в виде суммы экспоненциальных слагаемых
316 Глава 6. Проектирование дискретных фильтров
и (при наличии кратных полюсов) слагаемых вида
h2(t) -At" epl.
Каждое из этих слагаемых может быть дискретизировано и воспроизведено в
дискретном виде. Экспоненциальные слагаемые вида hx(t) после дискретизации
дают последовательность отсчетов
h(k)-AekpT. F.4)
Z-преобразование этой последовательности равно (см. раздел «Примеры вычис-
вычисления z-преобразования» главы 3)
Я, (г) = ЛA + e"V + e2"Tz'2 + e3"V3 +...) = ■ Л
1-e'V1
Такая функция передачи соответствует дискретному рекурсивному фильтру 1-го по-
порядка.
Теперь займемся слагаемыми вида h2(t), соответствующими кратным полюсам.
Такое слагаемое дает после дискретизации последовательность отсчетов
h2(k)=A (kT)"ekpT.
Z-преобразование этой последовательности можно легко рассчитать, если заме-
заметить, что она представляет собой я-ю производную по р от последовательно-
последовательности F.4):
BТ)" е2V2
Такая функция передачи, получаемая после вычисления я-й производной, соот-
соответствует дискретному рекурсивному фильтру я-го порядка.
Выполнив указанные преобразования для всех слагаемых, мы получим дискрет-
дискретный фильтр, импульсная характеристика которого представляет собой дискрети-
зированную версию импульсной характеристики аналогового прототипа.
Частотная характеристика получаемого фильтра связана с частотной характери-
характеристикой аналогового прототипа точно так же, как спектр дискретизированного
сигнала связан со спектром сигнала аналогового — периодическим повторением
(см. раздел «Спектр дискретного сигнала» главы 3). Поэтому для получения хо-
хороших результатов при таком методе синтеза коэффициент передачи аналогово-
аналогового прототипа должен быть пренебрежимо малым на частотах, превышающих час-
частоту Найквиста. Отсюда следует также, что этот метод подходит для создания
ФНЧ и полосовых фильтров, но непригоден для синтеза ФВЧ и режекторных
фильтров.
В качестве примера синтезируем методом инвариантной импульсной характерна
стики ФНЧ Чебышева 2-го порядка с частотой среза 10 кГц, причем специально
выберем недостаточно высокую частоту дискретизации D8 кГц), чтобы хорошо
видеть эффекты, связанные с наложением сдвинутых копий спектра (рис. 6.2):
» fO = ЮеЗ; % частота среза
» [b, a] = chebylB, 3, fO*2*pi, 's'); Ж' аналоговый фильтр
Прямые методы синтеза
317
» Fs = 48еЗ:
» [bz. az] = impinvar(b. a,
» % ЧХ дискретного фильтра
» [hz, wz] = freqz(bz. az.
» % ЧХ аналогового фильтра
» h = freqs(b. a. 2*pi*wz);
» plot(wz. abs(h). ':')
» hold on
» plot(wz. abs(hz))
» hold off
» xlabelС Frequency (Hz)')
» yiabeK 'Magnitude')
» xlim([0 Fs])
» grid on
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
Fs);
% частота дискретизации
% дискретный фильтр
[]. Fs, 'whole'):
a)
CD
Я
/ \
\
/
/
/
)
/
\
\
t
V
0.5 1 1.5
3.5
4.5
2 2.5 3
Frequency (Hz) x104
Рис. 6.2. АЧХ аналогового прототипа (пунктир) и дискретного фильтра (сплошная линия),
синтезированного методом инвариантной импульсной характеристики
На рисунке хорошо видно, что из-за недостаточно высокой частоты дискретиза-
дискретизации коэффициент передачи аналогового фильтра на частоте Найквиста недоста-
недостаточно мал, что обусловливает заметные искажения формы АЧХ синтезированного
дискретного фильтра. Повышение частоты дискретизации позволяет сделать эти
искажения пренебрежимо малыми.
Прямые методы синтеза
Название «прямые методы» означает, что в данном случае не используется ана-
аналоговый прототип. Исходными данными для синтеза служат какие-либо пара-
параметры фильтра (чаще всего — его АЧХ), которые могут задаваться, вообще гово-
говоря, произвольно.
318 Глава 6. Проектирование дискретных фильтров
Прямые методы синтеза можно разделить на две категории:
□ оптимальные методы, в которых численными итерационными методами
ищется минимум заданной функции качества;
□ субоптимальпые методы, не дающие в точности оптимального решения, но по-
позволяющие значительно упростить вычисления по сравнению с оптимальными
методами. Как правило, эти методы используют специфику решаемой задачи, на-
например дробно-рациональный вид функции передачи рекурсивного фильтра или
экспоненциальный вид отдельных слагаемых его импульсной характеристики.
Оптимальные методы
Чаще всего отправной точкой при расчете фильтра служит его желаемая частот-
частотная характеристика — либо АЧХ (когда фазовые характеристики не важны), либо
комплексный коэффициент передачи. В качестве минимизируемой меры откло-
отклонения характеристики фильтра от заданной в общем случае используется р-нор-
ма ошибки. Такая норма Lv для функции f{x), определенной на интервале от а
до Ь, рассчитывается следующим образом:
Lp(f)M\f(x)\»dx) .
Чаще всего используются два значения р: р = 2 и р = оо. При р = 2 норма L2 про-
пропорциональна среднеквадратическому значению функции. При р -> оо норма 1Ж
дает максимальное (по модулю) значение функции, достигаемое на рассматри-
рассматриваемом интервале.
Поскольку корень р-й степени при любом р является монотонно возрастающей
функцией, при расчете минимизируемой величины его можно не вычислять.
Если при синтезе фильтра нас интересует только его АЧХ, р-норма ошибки е (со)
рассчитывается следующим образом:
ы"
Ln(e)= jz<v(a)D((o)~\k(a)\\ da, F.5)
о
где £>(со) — желаемая АЧХ, | К(а)\ — АЧХ фильтра, да(со) — неотрицательная ве-
вещественная весовая функция. Использование весовой функции позволяет при-
придать разную значимость различным участкам частотной оси. В частности, это
дает возможность задать переходные зоны, поведение АЧХ в которых не имеет
значения. В этих зонах значение весовой функции должно быть нулевым.
Если необходимо аппроксимировать заданную частотную зависимость комплекс-
комплексного коэффициента передачи, норма ошибки аппроксимации рассчитывается так:
Lp(e)= iw((u)\b((x>)-k((u)\'d(x>. F.6)
О
i
Здесь £>(&) — желаемая комплексная частотная характеристика, К(ю) — частот-
частотная характеристика реального фильтра.
В большинстве случаев задача минимизации функции F.5) или F.6) не имеет
аналитического решения. Исключение составляет синтез нерекурсивного фильт-
фильтра при р - 2, когда рассматриваемая оптимизационная задача приводит к систе-
Прямые методы синтеза 319
ме линейных уравнений относительно коэффициентов фильтра. При этом если
весовая функция не используется (то есть если да(со) = 1), то коэффициенты фильт-
фильтра представляют собой коэффициенты разложения желаемой частотной характе-
характеристики в ряд Фурье. Однако минимизация среднеквадратической ошибки при-
приводит к появлению больших выбросов АЧХ при попытке аппроксимировать ее
скачкообразное изменение. Это связано с явлением Гиббса, которое рассматри-
рассматривалось в' главе 1 при обсуждении рядов Фурье.
В общем случае задача, как уже говорилось, не имеет аналитического решения и
поэтому должна решаться итерационными численными методами. Для уменьше-
уменьшения влияния эффекта Гиббса при этом может использоваться наложение огра-
ограничений на предельное абсолютное отклонение частотной характеристики от
заданной. Узнать подробнее о численных методах оптимизации, в том числе с ог-
ограничениями, можно, например, из книги [17].
При р - оо рассматриваемая норма ошибки равна максимальному абсолютному
отклонению характеристики от заданной. Минимизация этой нормы соответст-
соответствует минимаксной аппроксимации (minimax approximation) и дает фильтры с
равномерными пульсациями АЧХ (equiripple filter). Для минимаксного синтеза
нерекурсивных фильтров используется метод чебышевской аппроксимации с ис-
использованием алгоритма многократной замены Ремеза, соответствующий алго-
алгоритм расчета применительно к синтезу дискретных фильтров разработан Парк-
сом (Т. W. Parks) и Мак-Клелланом (J. H. McClellan). Узнать о данном алгорит-
алгоритме подробнее можно, например, из книги [8].
Субоптимальные методы
Как уже говорилось, субоптимальные методы позволяют упростить вычисления
за счет учета специфики решаемой задачи. При этом, в частности, может исполь-
использоваться тот факт, что коэффициенты числителя функции передачи фильтра ли-
линейно связаны с его комплексной частотной характеристикой и потому влияют
на ее форму значительно слабее, чем коэффициенты знаменателя.
Кроме того, для поиска коэффициентов знаменателя часто используются методы
авторегрессионного анализа (см. раздел «Авторегрессионная модель» главы 5).
Вот перечень субоптимальных методов синтеза, реализованных в MATLAB (па-
(пакет Signal Processing):
Q метод, основанный на решении системы уравнений Юла—Уолкера (Yule-
Walker) для поиска коэффициентов знаменателя функции передачи фильтра;
Q метод идентификации частотной характеристики, в котором минимизируется
норма разности между числителем функции передачи и произведением желае-
желаемой частотной характеристики и знаменателя функции передачи фильтра;
Q аппроксимация заданной импульсной характеристики с помощью метода экс-
экспоненциального оценивания Прони (данный алгоритм был разработан Гаспаром
Рише (бароном де Прони) в 1795 г. для подгонки экспоненциальной модели
под экспериментальные данные при исследовании физических свойств газов);
320 Глава 6. Проектирование дискретных фильтров
□ метод, основанный на использовании весовых функций (окон). Данный алго-
алгоритм будет подробно рассмотрен далее, в разделе «Синтез с использованием
окон»;
□ синтез ФНЧ с косинусоидальным сглаживанием АЧХ является частным слу-
случаем использования окон; данный метод также будет подробно рассмотрен
далее (см. раздел «Фильтры с косинусоидальным сглаживанием АЧХ»).
Дополнительные сведения о конкретных субоптимальных методах будут приве-
приведены далее, при описании соответствующих функций MATLAB.
Субоптимальный синтез
нерекурсивных фильтров
В данном разделе будет подробно рассмотрена общая идея синтеза нерекурсив-
нерекурсивных фильтров с использованием окон, а также частный случай, связанный с при-
применением конкретного окна и приводящий к фильтрам с косинусоидальным
сглаживанием АЧХ.
Синтез с использованием окон
Данный метод предназначен для синтеза нерекурсивных фильтров. Идея его
очень проста. Прежде всего мы задаем желаемый комплексный коэффициент пе-
передачи в виде непрерывной функции, определенной в диапазоне частот от нуля
до частоты Найквиста (если синтезируется вещественный фильтр) или до часто-
частоты дискретизации (если проектируется комплексный фильтр). Обратное преоб-
преобразование Фурье этой характеристики, вычисленное с учетом ее периодического
характера, даст бесконечную в обе стороны последовательность отсчетов им-
импульсной характеристики. Для получения реализуемого нерекурсивного фильт-
фильтра заданного порядка эта последовательность усекается — из нее выбирается
центральный фрагмент нужной длины.
Простое усечение последовательности отсчетов импульсной характеристики со-
соответствует использованию прямоугольного окна. Из-за усечения первоначально
заданная частотная характеристика искажается — она сворачивается со спектром
окна. В результате появляются переходные полосы между областями пропускания
и задерживания, наблюдаются колебания коэффициента передачи в полосах про-
пропускания, а в полосах задерживания АЧХ приобретает лепестковый характер.
Для ослабления перечисленных эффектов и прежде всего для уменьшения уров-
уровня лепестков в полосах задерживания усеченная импульсная характеристика
умножается на весовую функцию (окно), плавно спадающую к краям.
Мы уже говорили о весовых функциях применительно к спектральному анализу
(см. раздел «Весовые функции» главы 5) и видели, что различные используемые
на практике окна имеют разный уровень боковых лепестков. Однако величина
боковых лепестков собственного спектра окна не совпадает с величиной лепест-
лепестков АЧХ фильтра, синтезированного с применением данного окна. Убедимся в
этом на простом примере, используя различные окна для синтеза нерекурсивно-
нерекурсивного ФНЧ 32-го порядка с частотой среза, равной 1/4 от частоты Найквиста.
Субоптимальный синтез нерекурсивных фильтров
321
Прежде всего рассчитываем бесконечную импульсную характеристику. Обрат-
Обратное преобразование Фурье от интересующей нас АЧХ (ФЧХ считаем нулевой)
дает следующее:
4 я А/4
—00 < k < 00.
F.7)
Для получения фильтра 32-го порядка выбираем 33 отсчета этой импульсной
характеристики, расположенных симметрично относительно нуля, то есть исполь-
используем k — -16...16. Выбор симметричного фрагмента бесконечной импульсной
характеристики позволяет получить фильтр с линейной ФЧХ и, следователь-
следовательно, постоянной групповой задержкой, равной (в отсчетах) половине порядка
фильтра.
Рис. 6.3. Импульсная характеристика (сверху) и АЧХ (снизу) ФНЧ,
синтезированного с использованием прямоугольного окна
322
Глава 6. Проектирование дискретных фильтров
Урезав импульсную характеристику, мы фактически использовали прямоуголь-
прямоугольное окно. Построим графики импульсной характеристики полученного фильтра
и его АЧХ (рис. 6.3).
» к = (-16:16)':
» b = sinc(k/4)/4:
» impz(b) % график импульсной характеристики
» figure
» [h. f] = freqz(b. 1. []. 2):
» plot(f. 20*1oglO(abs(h))) % график АЧХ в децибелах
» ylim([-50 10])
» grid on
Из графика АЧХ видно, что уровень боковых лепестков составляет -21 дБ, а их
ширина равна 1/32 от частоты дискретизации.
Рис. 6.4. Импульсная характеристика (сверху) и АЧХ (снизу) ФНЧ,
синтезированного с использованием окна Хэмминга
Субоптимальный синтез нерекурсивных фильтров
323
Теперь воспользуемся какой-либо весовой функцией, например окном Хэммии-
га, которое используется по умолчанию при синтезе фильтров данным методом в
MATLAB (функции firl и fir2). Результаты показаны на рис. 6.4.
% график импульсной характеристики
» Ы - b .* hammingC3):
» impz(bl)
» figure
» [hi. f] = freqz(bl, 1, []. 2):
» plot(f. 20*loglO(abs(hl))) % график АЧХ в децибелах
» ylim([-80 10])
» grid on
Как видите, уровень лепестков в полосе задерживания упал примерно до -52 дБ
за счет некоторого расширения полосы пропускания.
Сведения об уровне лепестков, достигаемом при синтезе ФНЧ с использованием
разных окон, сведены в табл. 6.1. Результаты получены с помощью MATLAB при
синтезе фильтра 256-го порядка с частотой среза, равной 1/4 от частоты Найк-
виста. Уровень лепестков в некоторой степени зависит от порядка фильтра и
его частоты среза, поэтому данные, приводимые в различных литературных
источниках, могут несколько различаться. Этот эффект мы только что наблюдали:
АЧХ, приведенная на рис. 6.4, имеет уровень боковых лепестков -52 дБ (фильтр
32-го порядка), а в табл. 6.1 для окна Хэмминга указана величина -53,6 дБ
(фильтр 256-го порядка).
Таблица 6.1. Уровень боковых лепестков при синтезе ФНЧ с окнами разного типа
Тип окна
Прямоугольное
Треугольное
Бартлетта
Ханна
Хэмминга
Блэкмена
Кайзера при р = 4
Кайзера при р = 9
Чебышсва при Р = 40 дБ
Чебышева при Р - 60 дБ
Чебышева при р - 80 дБ
Уровень боковых лепестков, дБ
-21,0
-26,5
-26,5
-44,0 ч^
-53,6
-75,3
-45,2
-90,5
-51,0
-71,6
-92,4
В случае окон Кайзера и Чебышева результаты зависят от дополнительных па-
параметров этих окон. Для окна Кайзера есть эмпирическая формула, связываю-
324 Глава 6. Проектирование дискретных фильтров
щая параметр р с уровнем подавления боковых лепестков а (в децибелах) при
синтезе ФНЧ (см., например, документацию пакета Signal Processing):
[О, а<21
р = |о,5842(а-21)°'4+0,07886(а-21), 21<а<50, F.8)
[0,1102 (а-8,7), а>50.
Из табл. 6.1 видно, что использование весовых функций позволяет достигнуть
подавления боковых лепестков, превышающего 90 дБ. Однако следует помнить
о том, что уменьшение уровня боковых лепестков неизбежно приводит к расши-
расширению переходной зоны между полосами пропускания и задерживания. Поэтому
выбирать весовую функцию следует исходя из требований, предъявляемых к па-
параметрам фильтра.
Фильтры с косинусоидальным
сглаживанием АЧХ
Строго говоря, расчет фильтров с косинусоидальным сглаживанием АЧХ следует
отнести к категории методов, основанных на весовых функциях. Однако мы рас-
рассматриваем эти фильтры отдельно по следующим двум причинам. Во-первых, они
получили широкое распространение в телекоммуникационных системах (в част-
частности, для формирования спектра при квадратурной манипуляции). Во-вторых,
и это главное, данный частный метод удобно рассматривать с несколько иной
точки зрения, чем использование окон вообще, а умение видеть различные трак-
трактовки одной и той же проблемы является важнейшим качеством современного
специалиста в любой области.
Итак, пусть нам необходимо синтезировать ФНЧ с заданной частотой среза. Об1
суждая использование окон, мы видели, что обратное преобразование Фурье от
идеальной прямоугольной АЧХ дает отсчеты бесконечной в обе стороны импульс-
импульсной характеристики вида sm(ak)/(ak) (см. формулу F.7)). Далее было показано,
что простое усечение этой бесконечной импульсной характеристики плохо ска-
сказывается на АЧХ, поэтому необходимо использовать весовые функции. На сей
раз задумаемся, от чего может зависеть степень проявления нежелательных эф-
эффектов при усечении бесконечных характеристик. Очевидный ответ — от скоро-
скорости убывания отсчетов характеристики. Исходный вариант F.7), соответствую-
соответствующий прямоугольной АЧХ, убывает пропорционально k. Это связано с наличием
разрывов (скачков) у АЧХ (см. раздел «Примеры разложения сигналов в ряд
Фурье» главы 1. Там идет речь о связи скорости убывания спектра с количест-
количеством непрерывных производных у сигнала, но благодаря дуальности прямого и
обратного преобразований Фурье те же соотношения выполняются и в другую
сторону).
Итак, увеличив скорость затухания импульсной характеристики, можно надеять-
надеяться, что ее усечение скажется на виде АЧХ не столь катастрофически. Для уско-
ускорения затухания необходимо изменить синтезируемую АЧХ так, чтобы она не
содержала разрывов. В этом разделе мы рассматриваем косинусоидалыюе сгла-
сглаживание, при котором в переходной зоне от полосы пропускания к полосе задер-
Субоптимальный синтез нерекурсивных фильтров
325
живания АЧХ представляет собой половину периода косинуса. Такой фильтр
называется фильтром с косинусоидалъпым сглаживанием АЧХ (raised cosine filter)
и для аналогового случая описывается в частотной области следующим образом
(рис. 6.5):
<со0A-сх),
со
1 1 . I n со - con
sin - '—! -
2 2 1,2 acoA
0,
со0A-а) <|со | < сооA+ а),
со | > со()A + а).
F.9)
Функция cos
-ш0 0 шоA-а) Шо шоA+а) т
Рис. 6.5. АЧХ фильтра с косинусоидальным сглаживанием
Параметр а называется коэффициентом сглаживания (rolloff factor), он равен по-
половине ширины переходной зоны, нормированной к частоте среза. При а = 0
фильтр превращается в идеальный ФНЧ с прямоугольной АЧХ, при а = 1 АЧХ
перестает содержать плоский участок в полосе пропускания.
Чтобы понять, как выглядит импульсная характеристика такого фильтра, заме-
заметим, что его АЧХ может быть получена как сьертка идеальной прямоугольной
АЧХ с функцией в виде половины периода косинуса (рис. 6.6 слева), математи-
математически описываемой следующим образом:
I со | < асо0,
I со > асо„.
Ща)
w(t)
-аш0
аш0
In
Зтг
Рис. 6.6. Весовая функция косинусоидального сглаживания в частотной (слева)
и временной (справа) областях
326 Глава 6. Проектирование дискретных фильтров
Такой спектр соответствует временному сигналу
... 1 а? тс2 (п а) ,ш, , cos(aa>0t)
w(t) = — cos \eJm'dm = —-~. F.10)
Свертка спектров соответствует перемножению функций времени, так что полу-
полученное выражение, по сути дела, описывает весовую функцию. Ее график пока-
показан на рис. 6.6 справа.
При aa>0£ = ±тс/2 формула F.10) дает неопределенность вида 0/0. Вычисление
предела показывает, что значение весовой функции в этих точках равно тс/4:
lim w{t) = —.
t-+±n/Ba.oi0) 4
С учетом всего сказанного получаем выражение для импульсной характеристи-
характеристики ФНЧ с косинусоидальным сглаживанием АЧХ:
Использованный способ сглаживания делает непрерывной не только саму АЧХ,
но и ее первую производную, поэтому полученная импульсная характеристика
фильтра убывает пропорционально t3.
Проверим, как будет выглядеть АЧХ дискретного фильтра с косинусоидальным
сглаживанием после усечения импульсной характеристики. Пусть частота среза
составляет 1/8 от частоты дискретизации A/4 от частоты Найквиста). Тогда в
F.11) нужно подставить дискретные значения
,_, 2тс , 2тс , nk
t = kT = — k k = •
шд 8ю0 4ю0
С учетом этого
(ank) . (nk) (ank) . (nk
cos sin — cos sin —
^ 4 J {A J 1 I 4 J {A
71 л (akJ IE* 4 (ap2
1 — I / 1 —
I 2 J 4 I 2
Будем использовать коэффициент сглаживания a = 0,25 и рассчитаем фильтр
32-го порядка, взяв k в диапазоне -16...16 (рис. 6.7):
» к - -16:16:
» alpha = 0.25: % коэффициент сглаживания
» w = cos(alpha*pi*k/4) ./ A - (a1pha*k/2).*2):
» w(isinf(w)) - pi/4: % устранение неопределенности
» b = w .* sinc(k/4) / 4:
» impz(b) % график импульсной характеристики
» figure
» [h. f] - freqz(b. 1. []. 2):
» plot(f. 20*loglO(abs(h))) % график АЧХ в децибелах
Субоптимальный синтез нерекурсивных фильтров
327
» ylim([-60 10])
» grid on
и.з
0.25
0.2
0.15
0.1
0.05
0'
f\ ЛС
•
-
-
-
-
жТТч*-
10
15
20
25
30
0.2
0.4
0.6 0.8 1
Рис. 6.7. Импульсная (сверху) и частотная (снизу) характеристики дискретного фильтра
с косинусоидальным сглаживанием АЧХ
Сравнение рис. 6.7 и 6.3, где были приведены результаты простого усечения им-
импульсной характеристики идеального ФНЧ, показывает, что импульсная харак-
характеристика фильтра с косинусоидальным сглаживанием затухает быстрее, а уро-
уровень боковых лепестков АЧХ уменьшился более чем на 10 дБ (до -33,3 дБ) без
заметного расширения полосы пропускания. Пульсации коэффициента передачи
в полосе пропускания в данном случае тоже оказываются слабее.
SQRT-вариант
Фильтры с косииусоидальным сглаживанием АЧХ, как уже говорилось, часто
используются в системах связи для формирования спектра сигнала. При этом
иногда используется идея «распределения» этого фильтра между передатчиком
328
Глава 6. Проектирование дискретных фильтров
и приемником. Тогда на передающей и приемной сторонах используются одина-
одинаковые фильтры, АЧХ которых показана на рис. 6.8 и представляет собой квад-
квадратный корень из формулы F.9):
1,
cos
О,
| со
со
<со0A-а),
-со0A-а))|, сооA-а)<|со| <со0A + а),
со | > со0A + а).
0,707
2асоо
^Функция cos
—wq 0 too(l-a) coq озоA+а) со
Рис. 6.8. АЧХ SQRT-варианта ФНЧ с косинусоидальным сглаживанием
Импульсная характеристика такого фильтра описывается следующей формулой:
4асо„
пг -Dасо0О2
cos((l + а)соог)
sin((l-g)co0f)
4асо0 t/n
F.12)
Фильтр такого типа называется SQRT-вариантом срильтра с косинусоидальиьш
сглаживанием АЧХ (square root raised cosine filter).
Синтез дискретных фильтров
в MATLAB
В MATLAB имеется более двадцати функций синтеза дискретных фильтров. Боль-
Большая их часть сосредоточена в пакете Signal Processing, три функции расчета кон-
конкретных фильтров имеются в пакете Communications, наконец, несколько редко
используемых на практике методов добавляет специализированный пакет Filter
Design.
Общие сведения о функциях расчета фильтров представлены в табл. 6.2. В столб-
столбце «Пакет» используются следующие обозначения:
□ SP — Signal Processing;
□ Comm — Communications;
□ FD - Filter Design.
Кроме перечисленных функций в пакете Signal Processing имеется программа
FDATool (Filter Design and Analysis Tool), реализующая графический интерфейс
для расчета фильтров и просмотра их характеристик.
Синтез дискретных фильтров в MATLAB 329
Функции, использующие
билинейное z-преобразование
В пакете Signal Processing имеется функция bilinear, позволяющая синтезиро-
синтезировать дискретный фильтр методом билинейного r-преобразования но произволь-
произвольному аналоговому прототипу. Кроме того, имеются готовые функции расчета
фильтров Баттерворта, Чебышева первого и второго рода, а также эллиптиче-
эллиптических фильтров (фильтров Кауэра). Свойства этих аналоговых прототипов были
описаны в главе 2, там же были рассмотрены функции MATLAB для расчета
аналоговых вариантов данных фильтров. При расчете дискретных фильтров ис-
используются те же самые функции, только без последнего параметра 's'; кроме
того, частоты среза задаются нормированными к частоте Найквиста. Аналогич-
Аналогичное «двойное назначение» имеют и функции выбора порядка фильтра (см. раз-
раздел «Выбор порядка фильтра» главы 2).
В принципе сказанного должно быть достаточно, чтобы читатель смог восполь-
воспользоваться функциями синтеза дискретных фильтров, обратившись к материалу
главы 2. Однако, чтобы сосредоточить информацию о синтезе дискретных фильт-
фильтров в одном месте, кратко повторим синтаксис вызова функций и описание их
параметров.
Функции синтеза стандартных фильтров
Функции, о которых здесь пойдет речь, выполняют расчет дискретных ФНЧ, ФВЧ,
полосовых и режекторных фильтров по аналоговым прототипам Баттерворта,
Чебышева (первого и второго рода) и Кауэра методом билинейного z-преобразо-
вания. Требуемая при этом последовательность действий оформлена в виде сле-
следующих функций MATLAB:
□ butter(n, wO, type) — расчет фильтров Баттерворта;
Q chebyKn. Rp, wO, type) — расчет фильтров Чебышева первого рода;
Q cheby2(n, Rs, wO, type) — расчет фильтров Чебышева второго рода;
Q eTlip(n, Rp, Rs, wO, type) — расчет эллиптических фильтров (фильтров Кау-
Кауэра).
Параметры всех функций задаются одинаково, поэтому обсуждать функции по
отдельности не будем.
Перечисленные функции позволяют рассчитывать как дискретные, так и анало-
аналоговые фильтры. Признаком дискретного расчета служит отсутствие строки ' s' в
конце списка входных параметров. Использование этих функций для расчета
аналоговых фильтров было рассмотрено в разделе «Расчет аналоговых фильт-
фильтров» главы 2.
Параметры n, Rp, Rs (их состав зависит от типа фильтра) — это параметры фильт-
фильтра-прототипа: п — порядок фильтра, Rp — уровень пульсаций АЧХ в полосе про-
пропускания (в децибелах), Rs — уровень пульсаций АЧХ в полосе задерживания (в де-
децибелах). Более подробное описание этих параметров было приведено в разде-
разделах главы 2, посвященных фильтрам-прототипам.
Таблица 6.2
Функция
butter
chebyl
cheby2
ellip
bilinear
inipinvar
yulewalk
invfreqz
prony
firl
fir2
firls
fircls
. Функции синтеза дискретных фильтров
Пакет
SP
SP
SP
SP
SP
SP
SP
SP
SP
SP
SP
SP
SP
Тип фильтра
Рекурсивный
Рекурсивный
Рекурсивный
Рекурсивный
Рекурсивный
Рекурсивный
Рекурсивный
Рекурсивный
Рекурсивный
Нерекурсивный
Нерекурсивный
Нерекурсивный
Нерекурсивный
АЧХ
Баттерворта
Чебышева первого рода
Чебышева второго рода
Кауэра (эллиптическая)
Произвольный аналоговый
прототип
Произвольный аналоговый
прототип
Кусочно-линейная
Произвольная
Синтез по заданной
импульсной
характеристике
Многополоспая
Кусочно-линейная
Кусочно-линейная
с переходными полосами
Кусочно-постоянная
Метод синтеза
Билинейное ^-преобразование
Билинейное ^-преобразование
Билинейное г-преобразование
Билинейное г-иреобразование
Билинейное г-прсобразование
Инвариантное преобразование импульсной
характеристики
Авторегрсссиоииый метод
Минимизация разности между числителем
функции передачи н произведением ее знаме-
знаменателя и желаемой ЧХ
Экспоненциальная аппроксимация Пронн
Обратное преобразование Фурье
с использованием окон
Обратное преобразование Фурье
с использованием окоп
Минимизация средпеквадратической ошибки
Минимизация среднеквадратической ошибки
с ограничением максимального отклонения
Функция
firclsl
firrcos
intfilt
remez
cremez
rcosfir
rcosiir
hilbiir
grenez
firipnorm
iirgrpdelay
i i rlpnorm
iiripnormc
Пакет
SP
SP
SP
SP
SP
Comm
Comm
Comm
FD
FD
FD
FD
FD
Тип фильтра
Нерекурсивный
Нерекурсивный
Нерекурсивный
Нерекурсивный
Нерекурсивный (в том числе
с нелинейной ФЧХ и комп-
комплексными коэффициентами)
Нерекурсивный
Рекурсивный
Рекурсивный
Нерекурсивный
Нерекурсивный
Рекурсивный
Рекурсивный
Рекурсивный
АЧХ
ФНЧ, ФВЧ
ФНЧ
ФНЧ
Кусоч но-л инейная
с переходными полосами
Кусочно-линейная
с переходными полосами
ФНЧ
ФНЧ
Фильтр Гильберта
Кусочно-линейная
с переходными полосами
Кусочно-линейная
с переходными полосами
Синтез по заданной
групповой задержке
Кусочно-линейная
с переходными полосами
Кусоч но-л иней ная
с переходными полосами
Метод синтеза
Минимизация среднеквадратической ошибки
с ограничением максимального отклонения
Косинусоидальное сглаживание
Минимаксная аппроксимация
Минимаксная аппроксимация
Минимаксная аппроксимация
Косинусоидальное сглаживание
Разложение по сингулярным числам матрицы
Ганкеля, заполненной отсчетами импульсной
характеристики
Разложение по сингулярным числам матрицы
Гапкеля, заполненной отсчетами импульсной
характеристики
Минимаксная аппроксимация
Минимизация р-нормы ошибки
Минимизация р-нормы ошибки
Минимизация р-нормы ошибки
Минимизация р-нормы ошибки с
ограничением модулей полюсов фильтра
332 Глава 6. Проектирование дискретных фильтров
Параметры wO и type используются совместно для задания типа фильтра и значе-
значений его частот среза (нормированных к частоте Найквиста):
□ ФНЧ: wO — скаляр, параметр type отсутствует;
□ ФВЧ: wO — скаляр, type='high';
□ полосовой фильтр: wO — двухэлементный вектор частот среза [wl w2], пара-
параметр type отсутствует;
□ режекторный фильтр: wO — двухэлементный вектор частот среза [wl w2],
type='stop'.
В зависимости от того, сколько выходных параметров указано при вызове, функ-
функции могут возвращать результаты расчета в виде коэффициентов полиномов
числителя и знаменателя функции передачи (два выходных параметра), нулей и
полюсов (три выходных параметра) либо параметров пространства состояний
(четыре выходных параметра):
[а. Ь] - ...
[z, р, к] - ...
[А. В. С, D] = ...
С учетом всего сказанного перечислим действия, выполняемые функциями при
расчете дискретных фильтров:
1. Производится расчет фильтра-прототипа с заданными параметрами АЧХ.
2. Полученные нули и полюсы преобразуются в параметры пространства состоя-
состояний.
3. Производится преобразование фильтра-прототипа к требуемому типу с задан-
заданными частотами среза (частоты среза при этом корректируются по формуле
F.3)).
4. С помощью функции bilinear аналоговый фильтр преобразуется в дискрет-
дискретный.
5. Выполняется преобразование описания фильтра к виду, заданному при вызо-
вызове функции.
Функции выбора порядка фильтров
Рассмотренные выше функции расчета фильтров требуют задания в качестве
входных параметров порядка фильтра и его частоты среза. При этом понятие
частоты среза для фильтров разных типов определяется по-разному. Однако ис-
исходными данными при разработке фильтров, как правило, являются другие па-
параметры: частотные границы полос пропускания и задерживания, а также допус-
допустимая неравномерность АЧХ в полосе пропускания и минимально необходимое
затухание в полосе задерживания (см. рис. 2.12 в разделе «Выбор порядка фильт-
фильтра» главы 2).
Выбрать минимально необходимый порядок фильтра позволяют следующие од-
однотипные функции пакета Signal Processing:
[п. Wn] = buttord(Wp. Ws, Rp, Rs)
[n. Wn] = cheblord(Wp. Ws. Rp. Rs)
Синтез дискретных фильтров в MATLAB 333
[п. Wn] = cheb2ord(Wp. Ws, Rp, Rs)
[n, wn] = ellipord(Wp, Ws, Rp, Rs)
ЗАМЕЧАНИЕ
Данные функции позволяют выбирать порядок как для дискретных, так и для аналоговых
фильтров. Признаком дискретного расчета является отсутствие строки У в конце списка
входных параметров. Использование этих функций для определения требуемого порядка
аналоговых фильтров обсуждалось в разделе «Выбор порядка фильтра» главы 2.
Входной параметр Rp — допустимый уровень пульсаций в полосе пропускания
(в децибелах), Rs — минимально необходимое затухание в полосе задерживания
(в децибелах). Параметры Wp и Ws задают границы полос пропускания и задержи-
задерживания (нормированные к частоте Найквиста), способ задания этих параметров
зависит от типа проектируемого фильтра:
щ
□ ФНЧ: Wp и Ws — числа, при этом должно выполняться неравенство Wp < Ws;
□ ФВЧ: Wp и Ws — числа, при этом должно выполняться неравенство Wp > Ws;
□ полосовой фильтр: Wp и Ws — двухэлементные векторы, при этом должны вы-
выполняться неравенства Ws(l) < Wp(l) < WpB) < WsB);
□ режекториый фильтр: Wp и Ws — двухэлементные векторы, при этом должны
выполняться неравенства Wp(l) < Ws(l) < WsB) < WpB).
Выходными параметрами являются минимально необходимый для выполнения
заданных требований порядок фильтра п и частота среза фильтра Wn (нормиро-
(нормированная к частоте Найквиста). Эти параметры должны затем использоваться при
вызове функции расчета фильтра. Возврат значения Wn избавляет пользователя
от забот, связанных с тем, что при расчете разных фильтров понятие частоты
среза имеет разный смысл.
Поскольку порядок фильтра — величина целочисленная, то обычно оказывается,
что фильтр минимально необходимого порядка обеспечивает некоторый запас
по исходным параметрам. Функции выбора порядка фильтра при дискретном
варианте расчета используют этот запас точно так же, как в аналоговом случае
(см. раздел «Выбор порядка фильтра» главы 2): для фильтров Баттерворта и Че-
бышева первого рода будет увеличиваться затухание в полосе задерживания, для
фильтров Чебышева второго рода — уменьшаться пульсации в полосе пропуска-
пропускания, а для эллиптических фильтров — расширяться полоса задерживания.
В качестве примера зададим очень жесткие требования к АЧХ фильтра нижних
частот — узкую переходную полосу, малые пульсации в полосе пропускания и
большое затухание в полосе задерживания — и посмотрим, каким окажется ми-
минимальный порядок для фильтров четырех стандартных типов:
» Wp = 0.2: % конец полосы пропускания
» Ws = 0.21: % начало полосы задерживания
» Rp = 1: % пульсации АЧХ в полосе пропускания (дБ)
» Rs = 60: % затухание в полосе задержи-ваниЯ (дБ)
» [п. Wn] = buttord(Wp, Ws. Rp. Rs)
n =
145
334 Глава 6. Проектирование дискретных фильтров
Wn =
0.2009
» [п. Wn] = cheblord(Wp. Ws. Rp. Rs)
n =
26
Wn =
0.2000
» [n.Wn] = cheb2ord(Wp. Ws, Rp. Rs)
n =
26
Wn =
0.2095
» [n. Wn] = elliporcKWp. Ws, Rp, Rs)
n = *
10
Wn =
0.2000
Результаты показывают, что для фильтра Баттерворта требуется очень большой
порядок, порядок фильтров Чебышева обоих типов более чем в пять раз меньше
и, наконец, минимальный порядок требуется при синтезе эллиптического фильтра.
Функция bilinear
Функция bilinear предназначена для синтеза дискретных фильтров по произ-
произвольным аналоговым прототипам методом билинейного ^-преобразования. Она
может преобразовывать заданные различными способами аналоговые описания
систем в дискретные и поэтому имеет три варианта синтаксиса:
[bz, az] = bilinear(b. a. Fs. Fp)
[zz. pz. kz] = bilineaKz. p. k, Fs, Fp)
[Az. Bz, Cz, Dz] = bilinear(A. В, С D. Fs, Fp)
Здесь b и а — коэффициенты полиномов числителя и знаменателя функции пе-
передачи аналогового прототипа, z, р и к — нули, полюсы и коэффициент усиления
аналогового прототипа, А, В, С и D — параметры пространства состояний для ана-
аналогового прототипа. Аналогичные идентификаторы с буквой z в конце обознача-
обозначают соответствующие параметры синтезированной дискретной системы.
Функция различает способы задания описания аналогового прототипа по размеру
переданных параметров. Если два первых входных параметра — векторы-строки,
они считаются коэффициентами полиномов числителя и знаменателя функции
передачи. Если два первых входных параметра — векторы-столбцы, они счита-
считаются нулями и полюсами функции передачи. Если первый входной параметр —
матрица, значит, аналоговый прототип задан в пространстве состояний.
ВНИМАНИЕ
Аналоговый прототип при использовании функции bilinear должен быть физически реа-
реализуемым, то есть степень полинома числителя функции передав не должна превышать
степень полинома ее знаменателя.
Синтез дискретных фильтров в MATLAB
335
Параметр Fs задает частоту дискретизации в герцах. Последний входной пара-
параметр — Fp — является необязательным. При его отсутствии билинейное г-преоб-
разование выполняется по формуле F.1), а трансформация частотной оси опи-
описывается соотношением F.2) (см. ранее в этой главе раздел «Метод билинейного
z-преобразования»).
Если при вызове использован параметр Fp, то он задает частоту (в герцах), на ко-
которой комплексные коэффициенты передачи аналоговой и дискретной систем
будут совпадать. Для этого производится предварительное масштабирование
частотной оси в s-области, в результате чего используемая при билинейном
г-преобразовании подстановка принимает вид
s =■
2F.
1-г
.-1
1 + Г
Трансформация частотной оси при этом выглядит следующим образом:
то есть комплексный коэффициент передачи аналоговой системы на частоте /а
будет совпадать с комплексным коэффициентом передачи дискретной системы
на частоте/д. Из формул видно, что если/а = Fp, то и/д = Fp. На низких частотах
/а и /д связаны приблизительно линейно:
/.-/.■
'F,
tg 71
F.
при/д« Fp.
Функция impinvar
Функция impinvar предназначена для синтеза дискретных фильтров по произ-
произвольным аналоговым прототипам методом инвариантной импульсной характе-
характеристики. Синтаксис вызова функции следующий:
[bz, az] = impinvar(b. a, Fs. tol)
Входные параметры Ь и а — коэффициенты числителя и знаменателя функции
передачи аналогового прототипа, Fs — частота дискретизации (по умолчанию ее
значение равно 1 Гц).
336 Глава 6. Проектирование дискретных фильтров
Параметр to! задает относительный порог обнаружения кратных полюсов. Два
близко расположенных полюса считаются совпадающими, если расстояние меж-
между ними, деленное на больший из их модулей, меньше to!.
Выходные параметры bz и az — коэффициенты числителя и знаменателя функ-
функции передачи для синтезированного дискретного фильтра.
В соответствии с теорией, изложенной ранее в этой главе в разделе «Метод ин-
инвариантной импульсной характеристики», функция impinvar при синтезе фильт-
фильтра производит следующие действия:
1. Функция передачи аналогового прототипа представляется в виде суммы про-
простых дробей.
2. Найденные полюсы р трансформируются в exp(p/Fs).
3. Функция передачи из суммы простейших дробей преобразуется обратно в дроб-
дробно-рациональный вид.
Функции прямого синтеза
рекурсивных фильтров
В этом разделе будут рассмотрены функции yulewalk, invfreqz и ргопу, реализую-
реализующие алгоритмы прямого синтеза рекурсивных фильтров, перечисленные ранее в
разделе «Субоитимальные методы».
Функция yulewalk
Функция yulewalk предназначена для синтеза рекурсивных фильтров по задан-
заданной кусочно-линейной АЧХ. При этом производится минимизация среднеквад-
ратической ошибки во временной области. Синтаксис вызова функции следую-
следующий:
[b, a] = yulewalk(n, f. m)
Здесь n — порядок рассчитываемого фильтра (возвращаемые векторы b и а будут
иметь длину п + 1).
Параметры f и m должны быть векторами одинаковой длины, они совместно оп-
определяют желаемую АЧХ синтезируемого фильтра. Вектор f содержит значения
частот, нормированные к частоте Найквиста, а вектор m — соответствующие этим
частотам значения АЧХ. В промежутках между заданными точками АЧХ интер-
интерполируется по линейному закону. Частоты в векторе f должны образовывать
неубывающую последовательность, кроме того, должны выполняться равенства
f(l) = 0 и f(end) = 1. Вывести график синтезируемой АЧХ можно командой
plot(f. m).
ВНИМАНИЕ
Частоты в пекторе f могут дублироваться, что дает возможность задать скачкообразное из-
изменение АЧХ. Однако задавать такие скачки при синтезе рекурсивных фильтров не реко-
рекомендуется.
Синтез дискретных фильтров в MATLAB 337
Результатами работы функции являются векторы b и а коэффициентов полино-
полиномов числителя и знаменателя функции передачи рекурсивного фильтра. Длина
этих векторов равна п + 1.
Расчет фильтра выполняется следующим образом. Сначала определяется поли-
полином знаменателя, при этом числитель функции передачи считается равным еди-
единице и задача оптимизации сводится к решению модифицированной системы
уравнений Юла—Уолкера (отсчеты корреляционной функции определяются пу-
путем обратного ДПФ от квадрата модуля АЧХ). Затем оптимизируется полином
числителя, чтобы улучшить приближение к заданным характеристикам.
Функция invfreqz
Функция invfreqz, как следует из ее названия, является обратной по отношению
к функции freqz (см. раздел «Расчет частотной характеристики» главы 4). Это
значит, что она позволяет получить коэффициенты полиномов числителя и зна-
знаменателя функции передачи рекурсивного дискретного фильтра по значениям
его комплексного коэффициента передачи. Таким образом, функция invfreqz мо-
может использоваться для синтеза рекурсивных фильтров, причем, в отличие от
многих других функций синтеза, здесь в качестве желаемого результата задается
не АЧХ, а комплексная частотная характеристика (то есть АЧХ вместе с ФЧХ).
Синтаксис вызова функции следующий:
[b, a] = invfreqz(h. w. nb. na. wt, iter. tol. 'trace')
Здесь w — вектор частот, ah — вектор соответствующих им значений комплекс-
комплексного коэффициента передачи. Параметры w и h должны быть векторами одинако-
одинаковой длины. Частоты в векторе w должны лежать в диапазоне от 0 до л, значение л
соответствует частоте Найквиста.
ВНИМАНИЕ
Нормировка частот, используемая в функции invfreqz, отличается от варианта, принятого
почти во всех других функциях обработки сигналов, поэтому стоит повторить еще раз:
частота Найквиста в данном случае равна к, а не единице.
Частотная характеристика синтезируемого фильтра сравнивается с заданной
только в указанных дискретных частотных точках; никакой интерполяции не
производится.
При указанном выше способе вызова частотная характеристика считается сим-
симметричной и рассчитывается фильтр с вещественными коэффициентами. Чтобы
синтезировать фильтр с комплексными коэффициентами, необходимо после па-
параметра w поставить дополнительный параметр в виде строки ' compl ex':
[b. a] = invfreqzCh. w. 'complex'. ...)
В этом случае элементы вектора w могут лежать в диапазоне от -л до л.
Параметры nb и па задают степени полиномов числителя и знаменателя функции
передачи фильтра.
Остальные параметры функции являются необязательными и имеют значения
по умолчанию. Вектор wt должен иметь такой же размер, как векторы h и w.
338 Главв 6. Проектирование дискретных фильтров
Он задает весовые коэффициенты для расчета ошибки. По умолчанию все час-
частотные точки имеют одинаковый вес.
Оставшиеся три входных параметра имеют отношение лишь к одному из двух
возможных алгоритмов расчета, так что само их наличие или отсутствие управ-
управляет выбором алгоритма.
Если параметры iter, tol и 'trace' отсутствуют, то функция минимизирует ошиб-
ошибку, рассчитываемую следующим образом:
f h(k)A(w(k))-B(w(k))\2. F.13)
Здесь N -- количество элементов в векторах w, h и wt, aA(zt>(k)) и Б(да(&)) — спек-
спектры векторов, составленных из коэффициентов полиномов числителя и знамена-
знаменателя функции передачи фильтра, вычисленные на k-й частоте из вектора w:
A(w(k)) = "^a(n)e-Hn-^h\ B(w(k)) = "^Ъ{п)еЧ{п-Х)хе{к). F.14)
л = 1 n = l
Подстановка F.14) в F.13) и приравнивание к нулю частных производных по
Ь(п) и а{п) дает систему линейных уравнений относительно коэффициентов фильт-
фильтра. Эта система решается соответствующими средствами MATLAB (оператор \).
Разумеется, критерий F.13) не минимизирует отклонение частотной характери-
характеристики фильтра от заданной. Однако он приводит к несложной задаче решения
системы линейных уравнений и дает точное решение, если векторы h и w дейст-
действительно описывают фильтр, имеющий nb нулей и па полюсов.
Другой алгоритм — это «честный» поиск фильтра, дающего минимальную взве-
взвешенную квадратическую ошибку воспроизведения заданной частотной характе-
характеристики. Минимизируемая ошибка рассчитывается при этом следующим образом:
4=1
h(k)-
B(w{k))
A(w(k))
F.15)
В данном случае дифференцирование критерия е по коэффициентам фильтра
дает систему нелинейных уравнений, поэтому найти аналитическое решение не
удается и оптимизация производится численным итерационным методом.
Признаком расчета по второму алгоритму является наличие входного параметра
iter, задающего число итераций. Необходимое количество итераций зависит от
параметров синтезируемого фильтра. Можно начать со значения 20, увеличивая
его, если заданная точность не будет достигнута.
Параметр tol задает критерий остановки итерационного алгоритма. Если вели-
величина нормы градиента целевой функции F.15) становится меньше tol, решение
считается найденным. По умолчанию значение tol равно 0,01.
Наконец, при указании параметра 'trace' функция выводит информацию о ходе
итерационной оптимизации.
Результатом работы функции являются векторы b и а коэффициентов полино-
полиномов числителя и знаменателя функции передачи синтезированного рекурсивно-
рекурсивного фильтра. Размеры этих векторов составляют nb + 1 и па + 1 соответственно.
Синтез дискретных фильтров в MATLAB
339
Функция ргопу
Функция ргопу позволяет синтезировать рекурсивный фильтр по заданной им-
импульсной характеристике. Синтаксис вызова функции следующий:
[b. a] = prony(h. nb, na)
Здесь h — вектор отсчетов синтезируемой импульсной характеристики, nb и па —
порядки полиномов числителя и знаменателя функции передачи рекурсивного
фильтра соответственно.
Возвращаемые результаты — векторы b и а коэффициентов полиномов числите-
числителя и знаменателя функции передачи синтезированного рекурсивного фильтра.
Длина вектора b равна nb+1, длина вектора а — па+1.
Расчет фильтра производится следующим образом. Сначала определяется знаме-
знаменатель функции передачи с помощью ковариационного метода анализа авторег-
авторегрессионных моделей. Затем находится такой полином числителя, чтобы первые
nb+1 отсчетов импульсной характеристики получившегося фильтра в точности
совпадали с соответствующим фрагментом вектора п. Устойчивость рассчитан-
рассчитанного фильтра не гарантируется, однако данный метод может дать точные резуль-
результаты, если отсчеты в векторе h действительно представляют собой начало им-
импульсной характеристики, рекурсивного фильтра с числителем и знаменателем
порядков nb и па.
В качестве примера попытаемся синтезировать рекурсивный фильтр 5-го поряд-
порядка с конечной импульсной характеристикой треугольного вида. Чтобы умень-
уменьшить «хвост» после окончания заданного фрагмента, дополним задаваемую им-
импульсную характеристику некоторым количеством нулей. Результат синтеза
(импульсная характеристика полученного фильтра) показан на рис. 6.9.
» h - [123454321 zerosd. 9K:
» [b, a] = prony(h, 5, 5):
» impz(b. a)
4 ■
3 "
-1
■ \
\
^
<
)
)
1
(
t
i
i
i. :
10
15
20
Рис. 6.9. Результаты аппроксимации треугольной импульсной характеристики
в рекурсивном виде с помощью функции ргопу
340 Глава 6. Проектирование дискретных фильтров
Из графика видно, что результаты получены весьма неплохие — затухающий
«хвост» оказался небольшим.
ЗАМЕЧАНИЕ '-
Если при вызове функции ргопу указать порядок числителя, на единицу меньший числа
ненулевых отсчетов заданной импульсной характеристики (в пашем примере — 8) пли
превышающий это значение, будет снитезиронан нерекурсивный фильтр, точно воспроиз-
воспроизводящий заданную импульсную характеристику.
Функции синтеза с использованием окон
Общая идея синтеза нерекурсивных фильтров с использованием окон была рас-
рассмотрена ранее, в разделе «Субоптимальпый синтез нерекурсивных фильтров».
В пакете Signal Processing имеется две функции, реализующие данный метод.
Различия между ними состоят в типе аппроксимируемой АЧХ — функция firl
предназначена для синтеза многополосных фильтров, АЧХ которых в заданных
частотных точках скачкообразно меняется, принимая значения 0 или 1, а функ-
функция fi г2 допускает задание произвольной кусочно-линейной АЧХ. Кроме того,
в том же пакете Signal Processing имеется функция kaiserord, предназначенная
для выбора порядка фильтра, который при синтезе с применением окна Кайзера
будет удовлетворять заданным требованиям.
Функция firl
Функция firl позволяет рассчитывать нерекурсивные гюлосно-пропускающие
фильтры с линейной ФЧХ, в том числе многополосные (multiband), методом об-
обратного преобразования Фурье с использованием окон. Синтаксис вызова функ-
функции следующий:
b = firl(n. Wn. 'ftype'. window, 'normalization')
Здесь п — порядок рассчитываемого фильтра (его импульсная характеристика
будет содержать п + 1 ненулевых отсчетов).
Параметры Wn и 'ftype' (который может отсутствовать) совместно определяют
тип синтезируемого фильтра и его частоту (частоты) среза. Частоты среза зада-
задаются нормированными к частоте Найквиста (то есть их значения должны ле-
лежать в диапазоне 0...1, величина 1 соответствует половине частоты дискретиза-
дискретизации). Значения этих параметров зависят от типа фильтра:
□ ФНЧ: Wn — частота среза, параметр 'ftype' отсутствует;
□ ФВЧ: Wn — частота среза, 'ftype' = 'high';
□ полосовой фильтр: Wn = [wl w2], где wl и w2 — границы полосы пропускания,
параметр 'ftype' отсутствует;
Q режекторный фильтр: Wn = [wl w2], где wl и w2 — границы полосы задержива-
задерживания, 'ftype' = 'stop';
Q многополосный фильтр, пропускающий низкие частоты: Wn = [wl w2 ... wn], где
wi — границы полос пропускания, упорядоченные по возрастанию, 'ftype' =
= ' DC -1'. Такой фильтр будет иметь полосы пропускания O...wl, w2...w3 и т. д.;
Синтез дискретных фильтров в MATLAB 341
□ многополосный фильтр, задерживающий низкие частоты: Wn = [wl w2 ... wn], где
wi — границы полос пропускания, упорядоченные по возрастанию, ' ftype' =
= 'DC-0'. Такой фильтр будет иметь полосы пропускания wl...w2, w3...w4 и т. д.
ЗАМЕЧАНИЕ
Обозначения 'DC-0' и 'DC-Г расшифровываются следующим образом: DC обозначает по-
постоянный ток (direct current), то есть нулевую частоту, а 0 или 1 — коэффициент передачи
синтезируемого фильтра на пулевой частоте.
Для ФВЧ и режекторных фильтров, а также многополосных фильтров с ненуле-
ненулевым коэффициентом передачи на частоте Найквиста возможен только четный
порядок. Если задать нечетное п, будет рассчитан фильтр на единицу большего
порядка.
Параметр wi ndow задает используемое при синтезе окно. Это должен быть вектор-
столбец, содержащий п + 1 элементов. По умолчанию используется окно Хэм-
минга, рассчитываемое путем вызова функции hamming(n+l).
Строковый параметр 'normalization' управляет нормировкой (масштабировани-
(масштабированием) рассчитанной импульсной характеристики фильтра. По умолчанию исполь-
используется значение 'scale', при.котором импульсная характеристика нормируется
так, чтобы обеспечить единичное значение @ дБ) коэффициента передачи в цен-
центре полосы пропускания (для многополосных фильтров — в центре самой низ-
низкочастотной полосы пропускания). Второе возможное значение параметра —
'noscale', в этом случае нормировка не производится.
Результатом работы функции является вектор Ь коэффициентов нерекурсивного
фильтра. Рассчитанный фильтр имеет линейную ФЧХ и вносит групповую за-
задержку, независимо от частоты равную п/2 отсчетов. Расчет фильтра выполняет-
выполняется следующим образом: обратное преобразование Фурье от заданной идеальной
АЧХ дает бесконечный набор отсчетов импульсной характеристики. Этот набор
симметрично усекается до п + 1 отсчетов и для ослабления эффектов усечения
умножается на используемое окно. Если задана нормировка, определяется мо-
модуль коэффициента передачи получившегося фильтра в центре полосы пропус-
пропускания, и коэффициенты фильтра делятся на это значение.
Функция fir2
Функция fi г2, так же как и firl, предназначена для синтеза нерекурсивных
фильтров с линейной ФЧХ методом обратного преобразования Фурье с исполь-
использованием окон. Отличие заключается в том, что при синтезе можно задать про-
произвольную кусочно-линейную АЧХ. Синтаксис вызова функции следующий:
b = fir2(n, f, гл. Npt, lap. window)
Здесь п — порядок рассчитываемого фильтра (его импульсная характеристика
будет содержать п + 1 ненулевых отсчетов).
Параметры f и m должны быть векторами одинаковой длины, они совместно оп-
определяют желаемую АЧХ синтезируемого фильтра. Вектор f содержит значения
частот, нормированные к частоте Найквиста, а вектор m — соответствующие этим
частотам значения АЧХ. В промежутках между заданными точками АЧХ интер-
342 Глава 6. Проектирование дискретных фильтров
полируется по линейному закону. Частоты в векторе f должны образовывать
неубывающую последовательность, кроме того, должны выполняться равенства
f A) = 0 и f (end) = 1. Частоты могут дублироваться, что дает возможность задать
скачкообразное изменение АЧХ. Вывести график синтезируемой АЧХ можно
командой plotCf, m).
Для фильтров, коэффициент передачи которых на частоте Найквиста не равен
нулю, возможен только четный порядок. Если задать нечетное п, будет рассчитан
фильтр на единицу большего порядка.
Остальные параметры функции являются необязательными. Параметр Npt зада-
задает число точек, используемое при интерполяции заданной АЧХ. По умолчанию
его значение равно 512.
Параметр 1 ар задает ширину переходных зон вокруг скачков. При интерполяции
АЧХ в этих зонах вместо скачка будет сформирован линейный переход. Ширина
зон измеряется в точках интерполяции и по умолчанию равна 25.
Параметр wi ndow задает используемое при синтезе окно. Это должен быть вектор-
столбец, содержащий п + 1 элементов. По умолчанию используется окно Хэм-
минга, рассчитываемое путем вызова функции hamming(n+1).
Результатом работы функции является вектор b коэффициентов нерекурсивного
фильтра. Рассчитанный фильтр имеет линейную ФЧХ и вносит групповую за-
задержку, независимо от частоты равную и/2 отсчетов. Расчет фильтра выполняет-
выполняется следующим образом: заданная АЧХ кусочно-линейно интерполируется на
равномерную сетку из Npt точек, обратное ДПФ дает импульсную характеристи-
характеристику, она симметрично усекается до п + 1 отсчетов и для ослабления эффектов усе-
усечения умножается на используемое окно.
ЗАМЕЧАНИЕ
Число точек интерполяции должно быть не меньше длины синтезируемого фильтра. По-
Поэтому при расчете фильтров порядка 512 и более значение параметра Npt, принятое по
умолчанию, оказывается недостаточным и его необходимо задать явно.
Функция kaiserord
Функция kaiserord предназначена для определения порядка фильтра, удовлетво-
удовлетворяющего заданным требованиям, при синтезе функцией firl с использованием
окна Кайзера. Функция имеет два варианта синтаксиса:
[п. wn. beta, ftype] = kaiserord(f. a. dev. Fs)
с =-kaiserord(f, a. dev, Fs. 'cell')
Во втором варианте синтаксиса возвращаемый массив ячеек с содержит полный
набор параметров для вызова функции firl.
Параметры f и а совместно задают кусочно-постоянную АЧХ. В векторе f долж-
должна содержаться возрастающая последовательность значений частот. Вектор а
задает постоянные значения АЧХ для полос, ограниченных парами частот из
вектора f, при этом первая полоса начинается от нулевой частоты, а последняя
заканчивается на частоте Найквиста:
:
Синтез дискретных фильтров в MATLAB 343
□ в полосе от нуля до f(l) АЧХ равна аA);
□ в полосе от f(l) до fB) АЧХ не определена;
□ в полосе от f B) до f C) АЧХ равна аB);
□ в полосе от fC) до fD) АЧХ не определена;
□ так продолжается до конца векторов f и а;
□ в полосе от f(end-l) до f(end) АЧХ не определена;
□ в полосе от f (end) до Fs/2 АЧХ равна a(end).
Таким образом, длина вектора f должна быть равна length(a)*2-2.
Поскольку функция формирует исходные данные для функции firl, в векторе а
могут содержаться только значения 0 и 1.
Параметр dev должен быть вектором той же длины, что и а, содержащим вещест-
вещественные положительные числа. Он задает максимально допустимую ошибку вос-
воспроизведения кусочно-постоянной АЧХ для отдельных частотных полос. Ошиб-
Ошибка задается как абсолютная погрешность АЧХ.
Параметр Fs задает частоту дискретизации и является необязательным. При его
использовании следует указывать в векторе' f не нормированные, а исходные
значения частот в тех же единицах, что и Fs. По умолчанию частота дискретиза-
дискретизации считается равной двум, так что частота Найквиста равна единице.
Результатами работы функции являются порядок фильтра п, вектор нормиро-
нормированных частот среза wn, параметр окна Кайзера beta и указатель типа фильтра
ftype. Эти параметры затем должны использоваться при вызове функции firl
следующим образом:
b = firKn. wn, kaiser(n+l. beta), ftype. 'noscale')
Если использован второй вариант вызова функции kaiserord, вызывать функцию
f i rl следует так:
b = firl(c{l}, с{2}. с{3}. с{4}. с{5})
Функция kaiserord использует эмпирические формулы для расчета параметров.
Так, параметр окна Кайзера beta определяется по формуле F.8) (см. ранее в этой
главе раздел «Синтез с использованием окон»). Порядок фильтра п оценивается
по следующей формуле:
_ а-7,95
2,285 Доо"
Здесь а — степень подавления боковых лепестков АЧХ в децибелах, а Дсо — нор-
нормированная ширина самой узкой переходной полосы с неопределенной АЧХ.
Функция основана на простых прикидочных формулах и поэтому может давать
неточные результаты, особенно если в заданной АЧХ имеются частоты среза,
близкие к нулю или частоте Найквиста, или если задано слишком слабое по-
подавление боковых лепестков (в векторе dev есть элементы, превышающие 0,1).
Поэтому после синтеза фильтра функцией firl следует проверить его АЧХ с по-
помощью функции f reqz и при необходимости попробовать точнее подобрать поря-
порядок фильтра вручную.
344 Глава 6. Проектирование дискретных фильтров
Функции расчета ФНЧ с косинусоидальным
сглаживанием
Функции для расчета ФНЧ с косинусоидальным сглаживанием АЧХ имеются в
двух пакетах расширения MATLAB — Signal Processing (функция firrcos) и
Communications (функция rcosine и две вызываемые ею функции более низкого
уровня rcosfir и rcosiir). Сравнивая их, следует отметить, что функция firrcos
из пакета Signal Processing имеет более общий характер, тогда как функции па-
пакета Communications приспособлены для решения конкретной задачи — интер-
интерполяции сигнала с целью формирования спектра при квадратурной манипуля-
манипуляции. Этим обусловлен ряд ограничений на параметры фильтра (на каждый
лепесток импульсной характеристики должно приходиться целое число интерва-
интервалов дискретизации, на длине нерекурсивного фильтра должно укладываться це-
целое число лепестков и т. п.). В функции firrcos ограничения такого рода отсутст-
отсутствуют. Зато пакет Communications дает возможность аппроксимировать данный
фильтр в рекурсивном виде (функция rcosiir).
Еще одно различие между функцией firrcos и функциями rcosfir и rcosiir за-
заключается в используемой нормировке. Функция firrcos рассчитывает фильтр,
коэффициент передачи которого в полосе пропускания равен единице, а функ-
функции пакета Communications делают равной единице высоту пика импульсной ха-
характеристики.
Подводя итог, скажем, что выбор функции для расчета фильтра в конкретной
ситуации следует производить из соображений удобства задания параметров.
А теперь перейдем к описанию конкретных функций.
Функция firrcos
Функция firrcos (пакет Signal Processing) предназначена для расчета нерекур-
нерекурсивного ФНЧ с косинусоидальным сглаживанием АЧХ. Синтаксис ее вызова
следующий:
b = firrcosCn, FO. df, Fs, 'transition', 'type', delay, window)
Здесь п — порядок рассчитываемого фильтра (его импульсная характеристика
будет содержать п + 1 ненулевых отсчетов), F0 — частота среза, Fs — частота дис-
дискретизации (F0 и Fs должны быть заданы в одних и тех же единицах).
Параметр df задает ширину переходной зоны между полосами пропускания и за-
задерживания. Это может делаться двумя способами в зависимости от значения
параметра 'transition':
□ при 'transition' = 'bandwidth' параметр df задает ширину переходной зоны в
единицах частоты (при этом должны выполняться неравенства df < 2*F0 и
F0+df/2 < Fs/2). Этот вариант принят по умолчанию;
□ при 'transition' = 'rolloff параметр df задает коэффициент сглаживания АЧХ,
обозначенный в формулах F.9) и F.11) как а. Значение параметра df в этом
случае должно лежать в диапазоне 0...1.
Входные параметры, начиная с Fs, являются необязательными и имеют значения
по умолчанию, которые используются, если при вызове в качестве параметра
Синтез дискретных фильтров в MATLAB 345
указана пустая матрица ([]) или если несколько последних параметров опущено.
Частота дискретизации Fs по умолчанию считается равной двум, так что частота
Найквиста равна единице.
Строковый параметр 'type' задает тип синтезируемого фильтра. При принятом
по умолчанию варианте 'normal' рассчитывается обычный ФНЧ с косинусои-
дальным сглаживанием по формуле F.11). Если 'type' = 'sqrt', рассчитывается
SQRT-вариант данного фильтра по формуле F.12).
Параметр del ay задает вносимую фильтром задержку (то есть место расположе-
расположения пика импульсной характеристики). Задержка измеряется в отсчетах и долж-
должна быть целым числом в диапазоне от нуля до п + 1. По умолчанию принято зна-
значение Лоог((п + 1) / 2).
Параметр window позволяет использовать при синтезе фильтра дополнительную
весовую функцию (см. ранее раздел этой главы «Синтез с использованием окон»).
Это должен быть вектор-столбец длиной п + 1. По умолчанию весовая функция
не используется (то есть применяется прямоугольное окно).
Результатом работы функции является вектор b коэффициентов нерекурсивного
фильтра.
Функция rcosine
Функция rcosine пакета Communications позволяет рассчитывать ФНЧ с коси-
пусоидальпым сглаживанием АЧХ в нерекурсивном и рекурсивном виде. Для
этого она вызывает две другие функции более низкого уровня — rcosfir и rcosiir,
которые мы рассмотрим далее. Синтаксис вызова функции следующий:
[b. a] = rcosine(Fd, Fs. 'type', г. delay, tol)
Обязательными параметрами здесь являются только Fs и Fd. Использованная в
этой функции система задания параметров отражает основное назначение дан-
данных фильтров, которые в системах связи широко используются для интерполя-
интерполяции сигнала при цифровой модуляции. Параметр Fd — это символьная скорость
(то есть частота дискретизации до интерполяции), a Fs — частота дискретизации
выходного сигнала. Отношение Fs/Fd должно быть положительным целым чис-
числом. Оно равно числу отсчетов, приходящихся на один лепесток импульсной ха-
характеристики фильтра.
Остальные входные параметры являются необязательными и имеют значения по
умолчанию, которые используются, если при вызове в качестве параметра указа-
указана пустая матрица ([]) или если несколько последних параметров опущено.
Строковый параметр 'type' задает тип рассчитываемого фильтра. Возможны сле-
следующие варианты:
□ 'default' или 'fir/normal' — рассчитывается нерекурсивный ФНЧ с косину-
соидальным сглаживанием. Этот вариант принят по умолчанию;
□ 'iir' или 'iir/normaV — рассчитывается рекурсивный ФНЧ, аппроксимирую-
аппроксимирующий АЧХ с косинусоидальным сглаживанием;
□ 'sqrt' или 'fir/sqrt' — рассчитывается SQRT-вариант нерекурсивного ФНЧ
с косинусоидальным сглаживанием;
346 Глава 6. Проектирование дискретных фильтров
□ ' iir/sqrt' — рассчитывается SQRT-вариаит рекурсивного ФНЧ с косинусои-
дальным сглаживанием.
Параметр г задает коэффициент сглаживания АЧХ. По умолчанию используется
значение 0,5.
Параметр delay задает вносимую фильтром задержку, то есть положение пика
импульсной характеристики. Величина задержки измеряется в символьных так-
тактах (то есть в лепестках импульсной характеристики) и должна быть целым
положительным числом. По умолчанию задержка раина трем тактам (в секун-
секундах - 3/Fd).
Порядок нерекурсивного фильтра определяется требованием линейности ФЧХ
и, следовательно, симметрии импульсной характеристики. Таким образом, пик
импульсной характеристики должен находиться в ее середине, и длительность
импульсной характеристики составляет 2*de1 ay символьных тактов. Порядок
фильтра получается равным 2*de1ay*Fs/Fd.
В случае рекурсивного фильтра его порядок можно задать явно с помощью пара-
параметра to!, указав для него целое положительное значение. Если to! меньше еди-
единицы, этот параметр задает относительную погрешность синтеза рекурсивного
фильтра, а порядок фильтра при этом выбирается автоматически. По умолчанию
используется значение 0,01. При расчете нерекурсивных фильтров параметр to!
игнорируется.
Возвращаемыми результатами являются векторы коэффициентов полиномов чис-
числителя b и знаменателя а функции передачи рассчитанного фильтра. Если рас-
рассчитывался нерекурсивный фильтр, знаменатель а содержит один элемент, рав-
равный единице.
Функция rcosfir
Функция rcosfir вызывается функцией rcosine для расчета нерекурсивного
фильтра с косинусоидальным сглаживанием АЧХ. Синтаксис вызова функции
следующий:
[b, Ts] = rcosfir(R. n_T. rate. T. 'type')
Здесь R — коэффициент сглаживания АЧХ. Это единственный обязательный па-
параметр функции.
Остальные входные параметры являются необязательными и имеют значения по
умолчанию, которые используются, если при вызове в качестве параметра указа-
указана пустая матрица ([]) или если несколько последних параметров опущено.
Параметр п_Т задает протяженность импульсной характеристики и вносимую
фильтром задержку. Он может быть числом или двухэлементным вектором.
Элементы вектора указывают число символьных тактов до и после пика. Если
п_Т — число, оно задает одинаковое количество символьных тактов до и после
пика импульсной характеристики. По умолчанию этот параметр равен трем.
Параметр rate за. чет коэффициент интерполяции, то есть число отсчетов импульс-
импульсной характеристики, приходящееся на один ее лепесток (с параметрами, исполь-
используемыми в функции rcosine, это соотносится следующим образом: rate = Fs/Fd).
Синтез дискретных фильтров в MATLAB
347
Этот параметр должен быть целым положительным числом. По умолчанию ко-
коэффициент интерполяции равен 5.
ЗАМЕЧАНИЕ
Первый элемент вектора п_Т может быть положительным или отрицательным. Его знак не
влияет на расчет, а число лепестков импульсной характеристики слева от пика определя-
определяется модулем этого элемента.
Параметр Т, по умолчанию равный единице, задает длительность символьного
такта (эта величина является обратной по отношению к используемому в функции
rcosine параметру Fd). Значение этого параметра не влияет на рассчитываемую
импульсную характеристику, от него зависит только возвращаемая величина Ts.
Строковый параметр ' type' определяет тип рассчитываемого фильтра. По умол-
умолчанию используется вариант ' normal', соответствующий обычному косинусоидаль-
ному сглаживанию. Чтобы рассчитать SQRT-вариант фильтра, необходимо за-
задать для этого параметра значение ' sqrt'.
Результатами расчета являются вектор коэффициентов импульсной характери-
характеристики фильтра b и величина периода дискретизации выходного сигнала филь-
фильтра Ts. Порядок фильтра равен rate*(n_TB)+abs(n_T(l))); длина вектора b на еди-
единицу больше. Период дискретизации выходного сигнала равен T/rate.
При отсутствии выходных параметров функция выводит графики импульсной
характеристики и АЧХ рассчитанного фильтра. При этом с помощью дополни-
дополнительного строкового параметра 'color' можно задать цвет и тип линии, анало-
аналогично тому, как это делается в функции plot (см. раздел «Настройка внешнего
вида графиков» приложения А):
rcosfir(R. n_T, rate. T. 'type', 'color')
Параметр 'color' обязательно должен быть шестым по счету, так что опускать
предыдущие параметры нельзя; для использования значений по умолчанию сле-
следует задавать пустые матрицы ([]).
Для расчета фильтра функция rcosfi г вызывает функцию firrcos, предваритель-
предварительно преобразовав значения входных параметров к нужному виду.
Функция rcosiir
Функция rcosiir вызывается функцией rcosine для расчета рекурсивного фильт-
фильтра с косинусоидальным сглаживанием АЧХ. Синтаксис вызова функции сле-
следующий:
[b.'a. Ts] = rcosiir(R. delay, rate, Т. tol, 'type')
Здесь R — коэффициент сглаживания АЧХ. Это единственный обязательный па-
параметр функции.
Остальные входные параметры являются необязательными и имеют значения по
умолчанию, которые используются, если при вызове в качестве параметра указа-
указана пустая матрица ([]) или если несколько последних параметров опущено.
Параметр delay задает вносимую фильтром задержку, то есть положение пика
импульсной характеристики. Величина задержки измеряется в символьных так-
348 Глава 6. Проектирование дискретных фильтров
тах (то есть в лепестках импульсной характеристики) и должна быть целым по-
положительным числом. По умолчанию задержка равна трем тактам C*Т секунд).
Параметр rate задает коэффициент интерполяции, то есть число отсчетов импульс-
импульсной характеристики, приходящееся на один ее лепесток (с параметрами, исполь-
используемыми в функции rcosine, это соотносится следующим образом: rate = Fs/Fd).
Этот параметр должен быть целым положительным числом. По умолчанию ко-
коэффициент интерполяции равен 5.
Параметр Т, по умолчанию равный единице, задает длительность символьного
такта (эта величина является обратной по отношению к используемому в функ-
функции rcosine параметру Fd). Значение этого параметра не влияет на рассчитывае-
рассчитываемую импульсную характеристику, оно используется только при расчете возвра-
возвращаемой величины Ts и выводе графиков (см. далее).
Параметр tol определяет порядок синтезируемого фильтра. Указав целое поло-
положительное число, можно задать порядок фильтра в явном виде. Если в качестве
tol указано значение, меньшее единицы, оно задает относительную погрешность
аппроксимации. При этом чем меньше tol, тем больше порядок фильтра.
Строковый параметр 'type' определяет тип рассчитываемого фильтра. По умол-
умолчанию используется вариант 'normal', соответствующий обычному косинусои-
дальному сглаживанию. Чтобы рассчитать SQRT-вариант фильтра, необходимо
задать для этого параметра значение 'sqrt'.
Результатами расчета являются векторы коэффициентов полиномов числите-
числителя b и знаменателя а функции передачи фильтра, а также величина периода дис-
дискретизации выходного сигнала фильтра Ts. Этот период равен T/rate.
При отсутствии выходных параметров функция выводит графики импульсной
характеристики и АЧХ рассчитанного фильтра. При этом с помощью дополни-
дополнительного строкового параметра 'color' можно задать цвет и тип линии, анало-
аналогично тому, как это делается в функции plot (см. раздел «Настройка внешнего
вида графиков» приложения А):
rcosiir(R, delay, rate, T, tol, 'type', 'color')
Параметр ' col or' обязательно должен быть седьмым по счету, так что опускать
предыдущие параметры нельзя; для использования значений по умолчанию сле-
следует задавать пустые матрицы ([]).
Полученный в результате расчета рекурсивный фильтр приближенно аппрок-
аппроксимирует импульсную характеристику, соответствующую косинусоидалыюму
сглаживанию АЧХ. Точность аппроксимации возрастает при увеличении вноси-
вносимой фильтром задержки (параметр delay).
Функция расчета рекурсивного
фильтра Гильберта
Расчет рекурсивного фильтра, аппроксимирующего преобразование Гильберта,
можно выполнить с помощью входящей в состав пакета Communications функ-
функции hilbiir, имеющей следующий синтаксис вызова:
[num. den] = hilbiir(ts, dly. bandwidth, tol):
Синтез дискретных фильтров в MATLAB 349
Все входные параметры функции являются необязательными и имеют значения
по умолчанию. Параметр ts задает интервал дискретизации входного сигнала
фильтра. По умолчанию используется значение 2/7 с.
Параметр сПу задает вносимую фильтром групповую задержку. Ее значение долж-
должно как минимум в несколько раз превышать величину периода дискретизации ts.
Рекомендуется также выбирать соотношение между этими двумя параметрами
так, чтобы значение dly было равно полуцелому числу интервалов ts (то есть
rem(dly.ts) - ts/2). Например, можно взять ts равным 2*dly/N, где N — положи-
положительное нечетное целое число. По умолчанию групповая задержка равна ts*7/2.
Параметр bandwidth задает предполагаемую полосу частот входного сигнала, по-
позволяя функции использовать дополнительный фильтр-компенсатор, чтобы в по-
полосе частот сигнала приблизить коэффициент передачи синтезированного фильт-
фильтра к идеальному. Если значение bandwidth равно нулю или превосходит l/B*ts),
то компенсатор не используется.
Если параметр to! превышает единицу, он задает порядок рассчитываемого фильт-
фильтра (по умолчанию — 4). Если to! < 1, значение этого параметра задает допуск,
используемый при синтезе фильтра методом разложения по сингулярным чис-
числам. По умолчанию этот допуск равен 0,05.
Результатами работы являются векторы коэффициентов числителя num и знаме-
знаменателя den функции передачи рекурсивного фильтра. Функцию можно вызвать с
четырьмя выходными параметрами, тогда будут возвращены параметры фильтра
в пространстве состояний:
[А. В. С. D] = hilbiirC...):
При отсутствии выходных параметров функция строит графики импульсных ха-
характеристик синтезированного и идеального фильтров Гильберта.
Расчет фильтра производится следующим образом. Сначала рассчитывается им-
импульсная характеристика идеального фильтра Гильберта с заданной групповой
задержкой. Затем выполняется аппроксимация этой импульсной характеристики
методом разложения соответствующей матрицы Ганкеля по сингулярным числам.
Функции минимизации
среднеквадратической ошибки
В пакете Signal Processing имеется три функции, реализующие синтез нерекур-
нерекурсивных фильтров по критерию минимального квадратического отклонения АЧХ
от заданной. Функция firls аппроксимирует произвольную кусочно-линейную
АЧХ с переходными (незаданными) полосами. Остальные две функции выпол-
выполняют оптимизацию с ограничением максимального абсолютного отклонения АЧХ
от зада!шой. Функция f i rcl s реализует произвольную кусочно-постоянную АЧХ,
а функция firclsl предназначена для синтеза ФНЧ и ФВЧ.
Функция firls
Функция firls предназначена для синтеза нерекурсивных фильтров с линейной
ФЧХ по критерию минимальной среднеквадратической ошибки воспроизведе-
350 Глава 6. Проектирование дискретных фильтров
ния заданной АЧХ в заданном наборе частотных полос. При этом ошибка в раз-
разных частотных полосах может учитываться с разными весовыми коэффициента-
коэффициентами. Синтаксис вызова функции следующий:
b = firisCn. f. a. w. 'ftype')
Здесь п — порядок рассчитываемого фильтра (его импульсная характеристика
будет содержать п + 1 ненулспых отсчетов).
Параметры f на должны быть векторами одинаковой четной длины, они совме-
совместно определяют желаемую АЧХ синтезируемого фильтра. Вектор f содержит
значения частот, нормированные к частоте Найквиста, а вектор а — соответст-
соответствующие этим частотам значения АЧХ. В промежутках между заданными точка-
точками АЧХ интерполируется по линейному закону. Частоты в векторе f должны об-
образовывать неубывающую последовательность, однако, в отличие от функций
f i г2 и yulewalk, ограничений на первый и последний элементы вектора f не на-
накладывается.
Синтезируемая АЧХ определяется с помощью векторов f и а следующим образом:
□ в полосах частот orfBk - 1) до/B&) АЧХ линейно меняется от aBk - 1) до
aBk). Здесь k — целые числа от единицы до половины длины векторов f и а;
□ в полосах частот от fBk) д.о/Bк +1) АЧХ считается не заданной и в процес-
процессе синтеза может оказаться произвольной.
Вывести график синтезируемой АЧХ можно следующей командой:
» plot(reshape(f.2.1ength(f)/2). reshapeCa.2.length(a)/2). 'b')
ЗАМЕЧАНИЕ
Если не задать синий цвет линий принудительно с помощью строки Ъ', отдельные линей-
линейные фрагменты будут выводиться разными цветами.
Для фильтров, коэффициент передачи которых на частоте Найквиста не равен
нулю, возможен только четный порядок. Если задать нечетное п, будет рассчитан
фильтр на единицу большего порядка.
Остальные параметры функции являются необязательными. Параметр w задает
весовые коэффициенты для оптимизируемых частотных полос. Этот параметр
должен быть вектором, длина которого вдвое меньше, чем длина векторов f и а,
и содержать неотрицательные вещественные числа. В тех частотных полосах, ко-
которым приписаны большие весовые коэффициенты, будет обеспечена меньшая
ошибка воспроизведения заданной АЧХ. По умолчанию все весовые коэффици-
коэффициенты считаются одинаковыми.
При отсутствии параметра 'ftype' производится расчет фильтров с симметрич-
симметричной импульсной характеристикой, для которой b(k) = b(n + 2 - k). Если исполь-
использовать параметр 'ftype', становится возможным синтезировать фильтры с анти-
антисимметричной импульсной характеристикой, когда b(k) = -b(n + 2 - k). Данный
параметр может принимать одно из двух строковых значений:
□ 'hilbert' — синтезируется фильтр с антисимметричной импульсной характе-
характеристикой. Название данного режима объясняется тем, что такую характери-
Синтез дискретных фильтров в MATLAB
351
стику, в частности, должен иметь фильтр, реализующий преобразование Гиль-
Гильберта (см. раздел «Дискретное преобразование Гильберта» главы 4);
□ 'differentiator' — синтезируется фильтр с антисимметричной импульсной ха-
характеристикой и, кроме того, при расчете взвешенной ошибки дополнительно
используется весовой множитель I//2. В результате ошибка воспроизведения
АЧХ на низких частотах будет намного меньше, чем на высоких. При синте-
синтезе дифференцирующего фильтра, АЧХ которого пропорциональна частоте
(см. раздел «Свойства преобразования Фурье» главы 1), это означает мини-
минимизацию относительной ошибки воспроизведения заданной АЧХ.
Результатом работы функции является вектор b коэффициентов нерекурсивного
фильтра. Рассчитанный фильтр имеет линейную ФЧХ и вносит групповую за-
задержку, независимо от частоты равную и/2 отсчетов.
Расчет фильтра производится следующим образом. Минимизация взвешенной
среднеквадратической ошибки воспроизведения заданной АЧХ приводит к систе-
системе линейных уравнений относительно коэффициентов фильтра. Порядок систе-
системы с учетом симметрии коэффициентов составляет примерно и/2. Составленная
система решается с помощью оператора левого матричного деления \. В процес-
процессе решения возможна выдача предупреждения «Matrix is close to singular or badly
scaled» (матрица близка к сингулярной или плохо масштабирована). Это, как
правило, означает неудачное сочетание порядка фильтра и заданной АЧХ. Воз-
Возвращаемые результаты могут быть ненадежными, поэтому необходимо прове-
проверить их, рассчитав частотную характеристику с помощью функции f reqz (впро-
(впрочем, это полезно сделать в любом случае).
1
0.8
0.6
0.4
0.2
^->. /Л
\
\ ■
i
\
:
1
""I ;"
\ '
1 :
\ ,
\/\
0.2
0.4
0.6
0.8
Рис. 6.10. АЧХ ФНЧ, синтезированного путем минимизации
среднеквадратической ошибки с помощью функции firls
В качестве примера синтезируем данным методом ФНЧ 32-го порядка с норми-
нормированной частотой среза, равной 0,2, и началом полосы задерживания на норми-
нормированной частоте 0,25. График АЧХ полученного фильтра приведен на рис. 6.10.
352 Глава 6. Проектирование дискретных фильтров
» f = [0 0.2 0.25 1]:
» а = [1 1 0 0]:
» b= firlsC2, f. a);
» [h. w] = freqz(b);
» plot(w/pi, abs(h)) % график АЧХ
» grid on
» ylimCEO 1.1])
На рисунке хорошо видны проявления эффекта Гиббса, неизбежно возникающе-
возникающего при минимизации среднеквадратической ошибки — амплитуда максимальных
выбросов АЧХ составляет примерно 0,05. Далее мы синтезируем фильтр с таки-
такими же исходными данными еще несколькими методами, чтобы оценить разницу
результатов синтеза.
Функция fircls
Функция fircls предназначена для синтеза нерекурсивных фильтров с линей-
линейной ФЧХ путем минимизации среднеквадратической ошибки воспроизведения
заданной кусочно-постоянной АЧХ с ограничением предельно допустимых от-
отклонений от нее (constrained least square). Синтаксис вызова функции следую-
следующий:
b = ficr1s(n, f. amp. up. To. 'design_flag')
Здесь п — порядок рассчитываемого фильтра (его импульсная характеристика
будет содержать п + 1 ненулевых отсчетов).
Векторы f и amp совместно определяют желаемую АЧХ синтезируемого фильтра.
Вектор f содержит значения частот, нормированные к частоте Найквиста. Эти
частоты должны образовывать возрастающую последовательность, кроме того,
должны выполняться равенства f(l) = 0 и f(end) = 1. Длина вектора amp должна
быть на единицу меньше, чем длина вектора f. Элементы вектора amp задают ку-
кусочно-постоянную АЧХ (в диапазоне частот от f (к) до f (к + 1) постоянное зна-
значение АЧХ равно атр(к)). Вывести график синтезируемой АЧХ можно следую-
следующей командой:
» stairsCf. [amp(:):amp(end)])
Для фильтров, коэффициент передачи которых на частоте Найквиста не равен
нулю, возможен только четный порядок. Если задать нечетное п, будет рассчитан
фильтр на единицу большего порядка.
Векторы up и То задают верхнюю и нижнюю допустимые границы для значений
АЧХ синтезируемого фильтра. Эти векторы должны иметь такой же размер, как
и вектор amp. Используемый критерий оптимизации можно сформулировать сле-
следующим образом: ищутся коэффициенты фильтра заданного порядка, которые
дают АЧХ, лежащую между То и up и имеющую при этом минимальное средне-
квадратическое отклонение от amp.
Строковый параметр 'designflag' является необязательным, он позволяет управ-
управлять выводом информации о ходе поиска решения (по умолчанию зта информа-
информация не выводится). Возможны три значения данного параметра:
Синтез дискретных фильтров в MATLAB
353
Q 'trace' — текстовый вывод величины ошибки для каждой итерации;
Q 'plots' — на каждой итерации выводится набор графиков: общий вид АЧХ
и крупным планом все отдельные полосы частот;
Q 'both' — одновременный вывод текста и графиков.
Результатом работы функции является вектор b коэффициентов нерекурсивного
фильтра. Рассчитанный фильтр имеет линейную ФЧХ и вносит групповую за-
задержку, независимо от частоты равную и/2 отсчетов.
Расчет фильтра осуществляется численным итерационным методом оптимиза-
оптимизации с ограничениями.
В качестве примера синтезируем ФНЧ с теми же параметрами, что и в примере
для функции firls (см. рис. 6.10), задав ограничение отклонения АЧХ от желае-
желаемой, равное 0,02 (напомним, что амплитуда максимальных выбросов АЧХ при
минимизации среднеквадратической ошибки без ограничений составила при-
примерно 0,05). Функция fircls осуществляет аппроксимацию кусочно-постоянной
АЧХ, не позволяя задавать переходные полосы, поэтому зададим для границы
между полосами пропускания и задерживания значение 0,225, равное середине
переходной полосы из примера для функции firls. График АЧХ полученного
фильтра приведен на рис. 6.11:
» f = [0 0.225 1]:
» а = [1 0]:
» 1о = [0.98 -0.02]: % минимальный коэффициент передачи
» up = [1.02 0.02]; % максимальный коэффициент передачи
» b - firclsC2. f. a. up. lo):
» [h. w] = freqz(b):
» plot(w/pi. abs(h)) % график АЧХ
» grid on
» ylimCCO 1.1])
1
0.8
0.6
0.4
0.2
\
\
\
I
T
\
...I
\
0.2
0.4
0.6
0.8
Рис. 6.11. АЧХ ФНЧ, синтезированного путем минимизации среднеквадратической ошибки
с ограничением минимального отклонения с помощью функции fircls
354 Глава 6. Проектирование дискретных фильтров
Сравнение АЧХ на рис. 6.10 и 6.11 показывает, что во втором случае амплитуда
пульсаций действительно уменьшилась до заданного уровня 0,02, по при этом
расширилась переходная полоса, ширину которой функция fircis выбирает ав-
автоматически.
Функция firclsi
Функция fircisl — это специализированная версия функции fircis, предназна-
предназначенная для синтеза ФНЧ и ФВЧ с линейной ФЧХ путем минимизации средне-
квадратической ошибки воспроизведения идеальной частотной характеристики
с ограничением предельно допустимых отклонений от нее (constrained least square).
Кроме того, функция дает возможность более гибкого задания допустимых от-
отклонений АЧХ в полосах пропускания и задерживания, а также учета ошибки в
этих полосах с разным весом. Синтаксис вызова функции следующий:
b = ficrisKn. wO, dp. ds. 'ftype')
Здесь п — порядок рассчитываемого фильтра (его импульсная характеристика
будет содержать п + 1 ненулевых отсчетов).
Параметр wO задает частоту среза, как обычно, нормированную к частоте Найквиста.
Параметры dp и ds задают допустимые абсолютные уровни пульсаций в полосах
пропускания (passband) и задерживания (stopband) соответственно. В полосе
пропускания фильтр должен иметь коэффициент передачи, лежащий в пределах
1 ± dp, а в полосе задерживания — в пределах ±ds (здесь имеется в виду не АЧХ,
а вещественная частотная характеристика, получающаяся после компенсации
вносимой фильтром задержки, поэтому возможны и отрицательные значения).
При отсутствии параметра 'ftype' синтезируется ФНЧ, при 'ftype' = 'high' —
ФВЧ. Для ФВЧ, поскольку их коэффициент передачи на частоте Найквиста не
равен нулю, возможен только четный порядок. Если задать нечетное п, будет рас-
рассчитан фильтр на единицу большего порядка.
Между ds и 'ftype' могут находиться дополнительные параметры, причем их на-
назначение меняется в зависимости от их количества, поэтому данные варианты
синтаксиса мы рассматриваем отдельно. Первый такой вариант выглядит сле-
следующим образом:
b = ficrisKn. wO. dp. ds. wt. 'ftype')
Появившийся здесь параметр wt указывает нормированную частоту, за которой
должно удовлетворяться ограничение dp или ds. Это облегчает работу функции,
позволяя образовать переходную зону между полосами пропускания и задержи-
задерживания. Как именно формируется переходная зона, зависит от соотношения меж-
между wt и wO и от типа синтезируемого фильтра:
□ если синтезируется ФНЧ:
О wt < wO: коэффициент передачи лежит в пределах 1 ± dp при 0 < со < wt;
О wt > wO: коэффициент передачи лежит в пределах ±ds при wt < со < 1;
□ если синтезируется ФВЧ:
О wt < wO: коэффициент передачи лежит в пределах ±ds при 0 < со < wt;
О wt > wO: коэффициент передачи лежит в пределах 1 ± dp при wt < со < 1.
Синтез дискретных фильтров в MATLAB 355
Следующий вариант синтаксиса содержит три дополнительных параметра:
b - firclsHn. wO. dp. ds. wp. ws, k. 'ftype')
В этом случае можно задать соотношение между ошибками воспроизведения
АЧХ в полосах пропускания и задерживания. Это соотношение задается пара-
параметром к, а параметры wp и ws указывают границы полос пропускания и задержи-
задерживания для расчета соотношения ошибок:
□ при синтезе ФНЧ должны выполняться неравенства wp < wO < ws, a k рассчи-
рассчитывается по формуле
\\A(a)\2 da
□ при синтезе ФВЧ должны выполняться неравенства ws < wO < wp, а к рассчи-
рассчитывается по формуле
||Л(со)-1|2Жо
j\A(a>)\2 dm
о
Здесь Л(со) — АЧХ синтезированного фильтра, а частоты считаются нормиро-
нормированными к частоте Найквиста.
Наконец, в любом варианте синтаксиса в конец списка параметров можно доба-
добавить строковый параметр 'design_flag':
b = ficrlsK.... 'design_flag')
Этот параметр позволяет управлять выводом информации о ходе поиска реше-
решения (по умолчанию эта информация не выводится). Возможны три значения
данного параметра:
Q 'trace' — текстовый вывод величины ошибки для каждой итерации;
Q 'plots' — на каждой итерации выводится набор графиков: общий вид АЧХ
и крупным планом все отдельные полосы частот;
Q ' both' — одновременный вывод текста и графиков.
Результатом работы функции является вектор b коэффициентов нерекурсивного
фильтра. Рассчитанный фильтр имеет линейную ФЧХ и вносит групповую за-
задержку, независимо от частоты равную п/2 отсчетов.
Расчет фильтра осуществляется численным итерационным методом оптимиза-
оптимизации с ограничениями.
Реализация метода Ремеза
Как говорилось ранее в разделе «Прямые методы синтеза», метод Ремеза предна-
предназначен для синтеза нерекурсивных фильтров путем минимаксной аппроксима-
356 Глава 6. Проектирование дискретных фильтров
ции заданной АЧХ. В настоящее время в MATLAB имеется три функции, реали-
реализующие данный метод и несколько различающиеся по своим возможностям. Две
из них, remez и cremez, находятся в пакете Signal Processing, а третья, gremez (она
является наиболее обобщенным вариантом), — в пакете Filter Design. Кроме того,
в пакете Signal Processing имеется функция remezord, предназначенная для оцен-
оценки порядка фильтра, который при синтезе методом Ремеза будет удовлетворять
заданным требованиям.
Функция remez
Функция remez предназначена для синтеза нерекурсивных фильтров с линейной
ФЧХ и кусочно-линейной АЧХ с возможными зонами неопределенности. Воз-
Возможно также задание произвольной формы АЧХ с помощью функции пользова-
пользователя (см. далее). Синтаксис вызова функции следующий:
[b. delta, opt] = remez(n. f. a. w. 'ftype'. {lgrid})
Здесь п — порядок рассчитываемого фильтра (его импульсная характеристика
будет содержать п + 1 ненулевых отсчетов).
Параметры f и а должны быть векторами одинаковой четной длины, они совме-
совместно определяют желаемую АЧХ синтезируемого фильтра. Вектор f содержит
значения частот, нормированные к частоте Найквиста, а вектор а — соответст-
соответствующие этим частотам значения АЧХ. В промежутках между заданными точками
АЧХ интерполируется по линейному закону. Частоты в векторе f должны обра-
образовывать строго возрастающую последовательность (повторяющиеся элементы
не допускаются).
Синтезируемая АЧХ определяется с помощью векторов f и а следующим обра-
образом:
□ в полосах частот от fBk - 1) до/B&) АЧХ линейно меняется от aBk - 1) до
aBk). Здесь k — целые числа от единицы до половины длины векторов f и а;
□ в полосах частот от f{2k) до/B& +1) АЧХ считается не заданной и в процес-
процессе синтеза может оказаться произвольной.
Вывести график синтезируемой АЧХ можно следующей командой:
» plot(reshape(f. 2. length(f)/2), reshape(a. 2. length(a)/2). 'b')
ЗАМЕЧАНИЕ
Если не задать синий цвет линий принудительно с помощью строки Ъ', отдельные линей-
линейные фрагменты будут выводиться разными цветами.
Для фильтров, коэффициент передачи которых на частоте Найквиста не равен
нулю, возможен только четный порядок. Если задать нечетное п, будет рассчитай
фильтр на единицу большего порядка.
Остальные параметры функции являются необязательными. Параметр w задает
весовые коэффициенты для оптимизируемых частотных полос. Этот параметр
должен быть вектором, длина которого вдвое меньше, чем длина векторов f и а,
и содержать неотрицательные вещественные числа. В тех частотных полосах,
Синтез дискретных фильтров в MATLAB 357
которым приписаны большие весовые коэффициенты, будет обеспечена мень-
меньшая ошибка воспроизведения заданной АЧХ. По умолчанию все весовые коэф-
коэффициенты считаются одинаковыми.
При отсутствии параметра 'ftype' производится расчет фильтров с симметрич-
симметричной импульсной характеристикой, для которой b{k) = b(n + 2 - k). Если исполь-
использовать параметр 'ftype', становится возможным синтезировать фильтры с анти-
антисимметричной импульсной характеристикой, когда h(k) = -h(n + 2 - /г). Данный
параметр может принимать одно из двух строковых значений:
□ ' hi I bert' — синтезируется фильтр с антисимметричной импульсной характе-
характеристикой. Название данного режима объясняется тем, что такую характери-
характеристику, в частности, должен иметь фильтр, реализующий преобразование
Гильберта (см. раздел «Дискретное преобразование Гильберта» главы 4);
□ 'differentiator' — синтезируется фильтр с антисимметричной импульсной ха-
характеристикой и, кроме того, при расчете взвешенной ошибки дополнительно
используется весовой множитель 1//. В результате ошибка воспроизведения
АЧХ на низких частотах будет намного меньше, чем на высоких. При синте-
синтезе дифференцирующего фильтра, АЧХ которого пропорциональна частоте
(см. раздел «Свойства преобразования Фурье» главы 1), это означает мини-
минимизацию относительной ошибки воспроизведения заданной АЧХ.
ЗАМЕЧАНИЕ
Обратите внимание на то, что в режиме 'differentiator' функциями remez и firls использу-
используются разные дополнительные весовые функции — 1//и 1/у соответственно. Это объясня-
объясняется различием используемых критериев оптимизации — функция remez минимизирует
максимальное отклонение АЧХ от заданной (ошибка линейно связана с АЧХ), а функция
firls минимизирует ошибку, связь которой с АЧХ является квадратичной.
Параметр {Igrid}, хотя и является целым положительным числом, должен быть
задан в виде одноэлементного массива ячеек (то есть в фигурных скобках). Этот
параметр регулирует плотность сетки частот, которая используется при расчете
АЧХ фильтра с целью измерения величины пульсаций. Число точек сетки при-
приблизительно равно 1grid*n/B*bw), где bw — суммарная полоса пропускания фильт-
фильтра, нормированная к частоте Найквиста. Увеличение параметра Igrid может сде-
сделать пульсации более равномерными, но приведет к увеличению времени расчета.
По умолчанию значение параметра Igrid равно 16.
Главным результатом работы функции является вектор b коэффициентов нере-
нерекурсивного фильтра. Рассчитанный фильтр имеет линейную ФЧХ и вносит груп-
групповую задержку, независимо от частоты равную и/2 отсчетов. Кроме того, можно
получить дополнительную информацию о результатах синтеза с помощью пара-
параметров del ta и opt.
Выходной параметр del ta содержит величину пульсаций АЧХ полученного фильт-
фильтра (то есть значение максимального отклонения АЧХ от заданной).
Выходной параметр opt представляет собой структуру со следующими полями:
□ opt.fgrid — вектор сетки частот, использованной при синтезе;
□ opt.des — значения заданной АЧХ для частот из opt.fgrid;
358 Глава 6. Проектирование дискретных фильтров
□ opt.wt — весовые коэффициенты для частот из opt.fgrid;
□ opt.H — получившаяся комплексная частотная характеристика фильтра для
частот из opt.fgrid;
□ opt.erroi— ошибка воспроизведения заданной частотной характеристики для
частот из opt.fgrid;
□ opt.iextr — номера элементов вектора opt.fgrid, соответствующих экстре-
экстремальным частотам (частотам, на которых отклонение АЧХ от заданной мак-
максимально);
□ opt.fextr — вектор значений экстремальных частот.
Основная часть алгоритма синтеза реализована в машинных кодах (в виде DLL-
файла) на основе FORTRAN-программы, листинг которой приведен, например,
в [8].
В процессе расчета может быть выдано сообщение о том, что алгоритм не схо-
сходится (возможно, из-за ошибок округления):
-- Failure to Converge --
Probable cause is machine rounding error.
В этом случае следует обязательно проверить результаты синтеза, рассчитав АЧХ
полученного фильтра с помощью функции freqz. Впрочем, такой контроль поле-
полезен всегда.
Задание пользовательской функции расчета АЧХ
Если АЧХ, которую необходимо синтезировать, не является кусочно-линейной,
можно воспользоваться другим вариантом синтаксиса функции remez:
[b. delta, opt] = remez(n. f. 'fresp'. w. 'ftype'. {Igrid})
Здесь ' fresp1 — имя функции, рассчитывающей желаемую АЧХ. Остальные па-
параметры имеют то же назначение, что и ранее. Функция fresp должна вызывать-
вызываться следующим образом:
[dh. dw] = fresp(n. f. gf. w)
Входные параметры n, f и w здесь те же, что используются при вызове функции
remez, а вектор gf — сетка частот, сформированная функцией remez исходя из зна-
значений параметров n, f и Igrid.
Функция fresp должна вычислить значения АЧХ dh и весовых -коэффициен-
-коэффициентов dw для частот из вектора gf. Остальные входные параметры (n, f и w) в прин-
принципе при расчете могут не использоваться. Их передача в функцию fresp позво-
позволяет реализовать дополнительную гибкость.
При необходимости можно организовать передачу в функцию fresp дополни-
дополнительных параметров. Для этого при вызове функции remez необходимо взять имя
функции расчета АЧХ вместе с ее дополнительными параметрами в фигурные
скобки:
... = remez(n. f. {'fresp'. pi. p2 ...}. w, 'ftype'. {Igrid})
Функция fresp при этом будет вызвана так:
[dh. dw] = fresp(n, f. gf, w. pi. p2 ...)
Синтез дискретных фильтров в MATLAB
359
В каталоге toolbox\signal\signal\private (содержимое данного каталога доступно
только функциям пакета Signal Processing) имеется несколько готовых функций
расчета АЧХ, которые можно использовать в качестве параметров при вызове
remez и cremez. Так, функция remezfrf реализует кусочно-линейную интерполя-
интерполяцию АЧХ и используется по умолчанию функцией remez. Данная функция вызы-
вызывается следующим образом: {'remezfrf , а}. Здесь а — вектор значений АЧХ, со-
соответствующих частотам из вектора f. Таким образом, приведенный ранее первый
вариант синтаксиса вызова функции remez на самом деле трансформируется так:
... = remez(n. f, {'remezfrf. a}, w, ' f type'. {1 grid})
Другие функции этого семейства имеют следующие имена: all pass, lowpass, highpass,
bandpass, bandstop, multiband, invsinc, hilbfilt, differentiator. Справку об их ис-
использовании можно получить в командной строке MATLAB, введя команду
» help рпуа1е/имя_функции
Текст перечисленных функций можно использовать в качестве образца при на-
написании собственных функций расчета АЧХ.
Пример использования
В качестве примера синтезируем методом Ремеза ФНЧ с теми же параметрами,
что и при демонстрации использования функций firls и fircls (см. рис. 6.10 и
6.11). График АЧХ полученного фильтра представлен на рис. 6.12.
» f = [0 0.2 0.25 1]:
» а = [1 1 0 0]:
» b = remezC2. f. a):
» [h, w] = freqz(b):
» plot(w/pi, abs(h)) % график АЧХ
» grid on
» ylimCCO 1.1])
0.8
0.6 ■
0.4
0.2 "
s
\
\f V V
/w
0.2
0.4
0.6
0.8
Рис. 6.12. АЧХ ФНЧ, синтезированного путем минимаксной аппроксимации
с помощью функции remez
360 Глава 6. Проектирование дискретных фильтров
Сравнение АЧХ на рис. 6.10-6.12 показывает, что пульсации АЧХ получились
больше, чем при минимизации среднеквадратической ошибки (их амплитуда
составляет примерно 0,085). Однако фильтр, синтезированный методом Ремеза,
дает минимальную ширину переходной полосы (равномерный характер пульса-
пульсаций в полосах пропускания и задерживания строго выдержан, тогда как при ми-
минимизации среднеквадратической ошибки АЧХ далеко отходит от заданных зна-
значений при приближении к переходной зоне). Если задать границы переходной
зоны такими, какими они оказались в действительности при использовании функ-
функции fircls (примерно от 0,175 до 0,275, см. рис. 6.11), синтез методом Ремеза
даст такие же или меньшие пульсации. Убедимся в этом, не выводя график АЧХ,
а проверив значение второго выходного параметра функции remez:
» f = [0 0.175 0.275 1];
» а = [1 1 0 0];
» [b, d] = remezC2, f. a);
» disp(d) % вывод амплитуды пульсаций
0.0176
Как видите, в данном случае пульсации действительно оказались несколько мень-
меньше, чем при минимизации среднеквадратической ошибки с ограничением макси-
максимального отклонения.
Функция cremez
Функция cremez является расширенным вариантом функции remez, имеющим
следующие отличия:
□ ФЧХ фильтра ие обязательно должна быть линейной;
□ можно синтезировать фильтры с комплексными коэффициентами;
□ тип симметрии импульсной характеристики задается в явном виде, а не кос-
косвенно;
□ в алгоритм расчета добавлена вторая стадия, уточняющая решение, найден-
найденное методом Ремеза;
□ имеется некоторое количество предопределенных функций расчета АЧХ.
Синтаксис вызова функции следующий:
[b. delta, opt] = cremez(n. f. a. w. {Igrid}. ...
'sym'. 'skip_stage2'. 'debug')
или
[b, delta, opt] = cremez(n. f, {'fresp', pi, p2 ...}. ...
w, {Igrid}, 'sym'. 'skip_stage2', 'debug')
Выходные и почти все входные параметры совпадают с параметрами функции
remez, рассмотренной ранее. Поэтому остановимся только на имеющихся разли-
различиях.
Частоты в векторе f должны лежать в диапазоне -1...1. Возможность задавать
поведение АЧХ в области отрицательных частот позволяет рассчитывать фильт-
фильтры с комплексными коэффициентами.
Синтез дискретных фильтров в MATLAB 361
Число точек частотной сетки, регулируемое параметром {lgrid}, ориентировочно
равно 2*nextpow2(lgrid*n). По умолчанию значение lgrid равно 25.
Строковый параметр 'sym' позволяет управлять симметрией импульсной харак-
характеристики. Возможны следующие четыре значения:
Q ' попе' — ограничений симметрии не накладывается;
Q 'even' — четная симметрия импульсной характеристики: b(k) = b(n + 2 - k);
Q 'odd' — нечетная симметрия импульсной характеристики: b(k) - -b(n + 2 - k);
□ ' real' — комплексно-сопряженная симметрия импульсной характеристики:
b(k) - b'(n + 2 - k) (этот вариант позволяет получить фильтр с линейной
ФЧХ и несимметричной относительно нулевой частоты АЧХ).
Использование отрицательных частот в векторе f возможно только при 'sym' -
- 'none' пли 'real'.
При указании в списке параметров строки 'skip_stage2' отключается вторая ста-
стадия алгоритма (она выполняется, если оптимальное решение не найдено стан-
стандартным методом Ремеза). Это может повысить скорость расчетов за счет умень-
уменьшения точности.
Последний входной параметр 'debug' управляет выдачей сообщений о ходе опти-
оптимизации. Возможны следующие строковые значения:
□ ' off' — сообщения не выводятся (этот вариант используется по умолчанию);
Q 'trace' — выводятся текстовые сообщения;
□ 'plots' — выводятся графики;
Q ' both' — выводятся текстовые сообщения и графики.
Функция remezord
Функция remezord предназначена для оценки требуемого при синтезе методом
Ремеза порядка многополосного нерекурсивного фильтра с заданной величиной
пульсаций АЧХ. Синтаксис вызова функции следующий:
[п. fo. ao. w] = remezord(f. a, dev, Fs)
Параметры f и а совместно задают кусочно-постоянную АЧХ. В векторе f долж-
должна содержаться возрастающая последовательность значений частот. Вектор а за-
задает постоянные значения АЧХ для полос, ограниченных парами частот из век-
вектора f, при этом первая полоса начинается от нулевой частоты, а последняя
заканчивается на частоте Найквиста:
□ в полосе частот от нуля до f(l) АЧХ равна аA);
□ в полосе частот от f A) до f B) АЧХ не определена;
□ в полосе частот от fB) до fC) АЧХ равна аB);
□ в полосе частот от fC) до fD) АЧХ не определена;
□ так продолжается до конца векторов f и а;
О в полосе частот от f(end-l) до f(end) АЧХ не определена;
□ в полосе частот от f (end) до Fs/2 АЧХ равна a(end).
362 Глава 6. Проектирование дискретных фильтров
Таким образом, длина вектора f должна быть равна length(a)*2-2.
Параметр dev должен быть вектором той же длины, что и а, содержащим вещест-
вещественные положительные числа. Он задает максимально допустимую ошибку вос-
воспроизведения кусочно-постоянной АЧХ для отдельных частотных полос. Ошиб-
Ошибка задается как абсолютная погрешность АЧХ.
Параметр Fs задает частоту дискретизации и является необязательным. При его
использовании следует указывать в векторе f не нормированные, а исходные зна-
значения частот в тех же единицах, что и Fs. По умолчанию частота дискретизации
считается равной двум, так что частота Найквиста равна единице.
Результатами работы функции являются порядок фильтра п и векторы fо, ао и w,
которые предназначены для использования при вызове функции remez:
b = remez(n, fo. ao, w)
Результаты работы функции могут быть неточными, если у заданной АЧХ
имеются частоты среза, близкие к нулю или частоте Найквиста. Кроме того,
в любом случае оценка порядка фильтра, производимая функцией remezord,
является приближенной, поэтому если синтезированный фильтр не удовлетво-
удовлетворяет заданным требованиям, необходимо более точно подобрать порядок фильт-
фильтра вручную.
ЗАМЕЧАНИЕ
Механизм автоматического подбора минимально необходимого порядка фильтра встроен
в функцию gremcz пакета Filter Design (см. далее).
Функции пакета Filter Design
Пакет Filter Design содержит пять функций, предназначенных для синтеза дис-
дискретных фильтров. Это функция gremez, представляющая собой еще один расши-
расширенный вариант метода Ремеза, и четыре функции, минимизирующие р-норму
ошибки при произвольном р.
Функция gremez
Функция gremez, входящая в пакет Filter Design, обладает расширенными воз-
возможностями по сравнению с функциями remez и cremez. Основными из этих рас-
расширений являются следующие:
□ возможность автоматического подбора порядка фильтра;
□ возможность задания ограничений величины пульсаций для отдельных час-
частотных полос;
□ возможность описания особых точек АЧХ;
□ большее количество информации, возвращаемой в структуре opt;
□ возможность группировки частотных полос для расчета нескольких отдель-
отдельных ошибок аппроксимации.
Синтез дискретных фильтров в MATLAB 363
Новые поля структуры opt
В простейшем варианте синтаксис вызова функции gremez такой же, как у функ-
функции remez:
[b, error, opt] = gremez(n, f. a, w)
[b, error, opt] = gremez(n, f. a, 'hilbert')
[b. error, opt] = gremez(n, f. a. 'differentiator')
При таком способе вызова работа функции ничем не отличается от того, что де-
делает функция remez, разве что в информационной структуре opt присутствует ряд
дополнительных полей:
□ opt.order — порядок синтезированного фильтра;
□ opt.edgeCheck — результаты проверки аномалий в переходных зонах (см. да-
далее). Это вектор, содержащий по одному элементу на каждую частотную по-
полосу. Возможны следующие значения элементов вектора: 1 — все в порядке,
О — обнаружена аномалия, -1 — проверка не выполнялась;
□ opt.iterations — число выполненных итераций;
□ opt.evals — число вычислений целевой функции.
Поддерживается и вариант синтаксиса с задаваемой пользователем функцией рас-
расчета АЧХ:
[b, error, opt] = gremez(n. f. {'fresp', pi. p2 ...}, w)
По умолчанию в качестве fresp используется функция remezfrf2, расположенная
в каталоге toolbox\filterdesign\filterdesign\private и реализующая расчет кусочно-
линейной АЧХ.
Подбор порядка фильтра
Для реализации автоматического подбора порядка фильтра при заданной вели-
величине пульсаций АЧХ функция gremez вызывается следующим образом:
[b. error, opt] = gremezCm'. f. a. r)
Вместо порядка фильтра указывается строковый параметр 'т\ который может
принимать одно из трех следующих значений:
□ 'minorder' — подбирается минимальный порядок фильтра, при котором от-
отклонения АЧХ от заданной лежат в допустимых пределах;
□ 'mineven' — подбирается минимально возможный четный порядок фильтра,
при котором отклонения АЧХ от заданной лежат в допустимых пределах;
□ 'minodd' — подбирается минимально возможный нечетный порядок фильтра,
при котором отклонения АЧХ от заданной лежат в допустимых пределах.
Параметр г — вектор допустимых абсолютных значений пульсаций АЧХ для от-
отдельных частотных полос. Его длина должна быть в два раза меньше длины век-
вектора f.
Начальное приближение ni для подбора порядка фильтра можно указать сле-
следующим образом:
[b. error, opt] = gremez({'m'. ni}. f. a, r)
364 Глава 6. Проектирование дискретных фильтров
Такое указание начального значения порядка фильтра является обязательным в
тех случаях, когда нельзя использовать функцию remezord (например, при расче-
расчете дифференцирующих фильтров и преобразователей Гильберта).
Принудительное ограничение величины пульсаций
Чтобы задать ограничения величины пульсаций АЧХ в некоторых полосах час-
частот, функцию gremez нужно вызывать следующим образом:
[b. error, opt] = gremez(n. f. a, w. c)
Сами ограничения пульсаций задаются в векторе весовых коэффициентов w,
а параметр с определяет, какие из элементов вектора w являются весами, а ка-
какие — ограничениями. Параметр с должен представлять собой массив ячеек с
числом элементов, равным длине вектора w. Каждый элемент с{к} может прини-
принимать одно из двух строковых значений:
□ ' с' — &-й элемент вектора w трактуется как предельно допустимая величина
(constraint) пульсаций АЧХ для k-й полосы частот;
□ V — &-й элемент вектора w трактуется как весовой коэффициент (weight)
для k-й полосы частот.
Необходимо, чтобы хотя бы одна частотная полоса не имела ограничения на ве-
величину пульсаций. Поэтому массив ячеек с должен содержать хотя бы один эле-
элемент, равный 'W.
Использование независимых ошибок аппроксимации
Чтобы независимо минимизировать величину пульсаций АЧХ в разных полосах
частот, функция gremez вызывается следующим образом:
[b. error, opt] = gremez(n. f. a, w, e)
Параметр е определяет, как группируются частотные полосы для расчета неза-
независимых ошибок аппроксимации. Этот параметр представляет собой массив яче-
ячеек с числом элементов, равным длине вектора w. Каждый элемент е{к} должен
быть строкой вида 'е#', где # — целое положительное число. Это означает, что
k-я полоса частот принимает участие в расчете ошибки аппроксимации с номе-
номером #.
В данном режиме функция gremez пытается независимо минимизировать от-
отклонение АЧХ от заданной в нескольких полосах частот. В результате получа-
получается фильтр, пульсации АЧХ которого равномерны в каждой группе частот-
частотных полос, формирующих общую ошибку аппроксимации, но для разных групп
полос пульсации будут разными. Таким образом можно, например, синтезиро-
синтезировать фильтр, в полосе пропускания которого пульсации АЧХ будут меньше, чем
в полосе задерживания. В результате иногда могут получаться фильтры, имею-
имеющие очень узкие переходные зоны между полосами пропускания и задержива-
задерживания.
По умолчанию параметр е имеет значение {'el', 'el', 'el', ...}, то есть все час-
частотные полосы формируют одну общую ошибку аппроксимации АЧХ.
Синтез дискретных фильтров в MATLAB 365
Описание особых точек АЧХ
Для описания особых точек АЧХ фильтра используется массив ячеек s, число
элементов в котором должно быть равно длине векторов f и а:
[b. error, opt] = gremez(n. f. a. s)
Элементами массива s являются односимвольные строки, имеющие следующее
значение:
□ "п1 — обычная точка АЧХ (normal point);
□ 's' — «точечная» полоса (single-point band);
□ Т — коэффициент передачи синтезированного фильтра на данной частоте
должен быть точно равен заданному (forced frequency point);
□ ' i' — коэффициент передачи на данной частоте не определен (indeterminate
frequency point; такую точку можно использовать на границе вплотную при-
примыкающих друг к другу частотных полос).
Указание дополнительных свойств синтезируемого фильтра
Для синтеза фильтра, обладающего некоторыми дополнительными свойствами,
в конце списка параметров функции gremez могут использоваться следующие
строковые значения:
□ 'I1, '2','3' или '4' — синтезируется фильтр соответствующего типа (см.
табл. 4.1 в разделе «Симметричные фильтры» главы 4);
□ 'minphase' или 'maxphase' — синтезируется соответственно минимально-фазо-
минимально-фазовый фильтр (все нули функции передачи лежат на z-плоскости внутри еди-
единичной окружности или на ней) или максимально-фазовый фильтр (все нули
функции передачи лежат на r-плоскости снаружи единичной окружности или
на ней);
□ ' check' — выполняется проверка наличия аномалий в переходных зонах и при
их обнаружении выдается соответствующее предупреждение. Информация
об обнаруженных аномалиях возвращается также в поле edgeChedc структуры
opt (см. выше).
Функции, использующие р-норму ошибки
Перечисленные ниже функции выполняют прямой синтез фильтров путем ми-
минимизации р-нормы ошибки воспроизведения заданной характеристики (АЧХ
или групповой задержки):
□ firlpnorm — расчет нерекурсивного фильтра по заданной АЧХ:
[Ь, егг] = firlpnorm(n.f.edges.a.w,p.dens.ЬО)
□ iirlpnorm — расчет рекурсивного фильтра по заданной АЧХ:
[b. a. err] = iirlpnorm(n.d.f.edges.a.w.p.dens.bO.aO)
□ i i rl pnormc — расчет рекурсивного фильтра по заданной АЧХ с ограничением
модуля полюсов:
[Ь.а.егг] = i i rlpnormc(n.d.f.edges,a.w.radius,p.dens,bO.aO)
366 Глава 6. Проектирование дискретных фильтров
□ i i rgrpdel ay — расчет всепропускающего (см. раздел «Нули и полюсы» главы 4)
рекурсивного фильтра по заданной зависимости групповой задержки от час-
частоты:
[Ь,а.tau]=iirgrpdelay(n,f,edges,gd,w,radi us.p,dens,aO.tau)
Параметры всех этих функций задаются одинаково и имеют следующий смысл:
□ п — порядок числителя функции передачи фильтра;
□ d — порядок знаменателя функции передачи фильтра;
□ f — вектор частот для задания частотной характеристики фильтра (вектор
должен содержать возрастающую последовательность значений, нормирован-
нормированных к частоте Найквиста, причем должны выполняться равенства f(l) = 0 и
f(end) = 1);
□ а — вектор значений АЧХ для частот из вектора f (используется кусочно-ли-
кусочно-линейная интерполяция);
□ gd — вектор значений групповой задержки, измеряемой в отсчетах, для частот
из вектора f (используется кусочно-линейная интерполяция);
□ edges — вектор четной длины, задающий границы частотных полос, в проме-
промежутках между которыми АЧХ считается незаданной. Таким образом, АЧХ
считается заданной в полосах edges(l)...edgesB), edgesC)...edgesD) и т. д. и не-
неопределенной в полосах O...edges(l), edgesB)...edgesC) и т. д. Вектор edges дол-
должен содержать значения частот, имеющиеся в векторе f.
Приведенные ниже параметры являются необязательными и имеют значения по
умолчанию:
□ w — вектор весовых коэффициентов. Он должен иметь такой же размер, как
векторы f, а и gd, и содержать неотрицательные вещественные числа. По умол-
умолчанию все элементы этого вектора равны единице;
□ radius — предельно допустимая величина модулей полюсов синтезируемого
фильтра. По умолчанию используется значение 0,999999;
□ р — двухэлементный вектор вида [pmin ртах], указывающий границы для
параметра р используемой при расчете нормы ошибки. Элементы вектора
должны быть целыми положительными четными числами. По умолчанию
используется значение [2 128], что дает результаты, близкие к минимаксной
оптимизации. Возможно также значение 'inspect', при этом оптимизация не
производится и функция выдает используемое ею начальное приближение;
□ dens — плотность частотной сетки, используемой функцией для расчета оши-
ошибок. Число точек сетки равно dens*(n+l). По умолчанию используется значе-
значение dens = 20;
□ Ь0 — начальное приближение для числителя функции передачи фильтра;
□ аО — начальное приближение для знаменателя функции передачи фильтра;
□ tau — дополнительное смещение групповой задержки, используемое функци-
функцией ii rgrpdel ay для того, чтобы сделать заданную групповую задержку неотри-
неотрицательной на всех частотах (всепропускающие фильтры могут иметь только
положительную групповую задержку). По умолчанию tau = max(gd).
Синтез дискретных фильтров в MATLAB
367
Результатами работы функций являются векторы b и а коэффициентов полино-
полиномов числителя и знаменателя функции передачи фильтра, а также достигнутое
минимальное значение р-нормы ошибки егг. Функция iirgrpdelay может также
возвращать дополнительное смещение групповой задержки tau, использованное
при синтезе.
Графическая среда для синтеза
и анализа фильтров
В пакете Signal Processing имеется две графических среды, позволяющих рассчи-
рассчитывать и анализировать дискретные фильтры. Это новая среда FDATool (Filter
Design & Analysis Tool) и блок работы с фильтрами, входящий в более старую
универсальную среду SPTool. В программе FDATool поддерживается больше
методов синтеза; пожалуй, единственная возможность, имеющаяся в SPTool и
отсутствующая в FDATool, — это ручное графическое редактирование располо-
расположения нулей и полюсов функции передачи фильтра.
Далее в этой главе описываются возможности фафического интерфейса FDATool.
Краткий обзор средств программы SPTool будет приведен в приложении Г.
Для запуска программы расчета фильтров необходимо набрать ее имя в команд-
командной строке MATLAB:
» fdatool
После этого появится окно программы, показанное на рис. 6.13.
3» ft* J>« b«M Jwtali
,;6 s» н a' ^ >■- saass л □ -••• в ti
Siabte V«
Btmtuik)
Mag. (dB)
I 1
t'
0
T
с * -
Г B«jkJmsi
Г Bar»)**.
«" » ]3ull«.
win
tfe
Sjl Qusnln
zi
- f
WmH 4 if nf
^ ь« -* jJ
ii
j 48C0O
| 96O0
M»rrrinrip*iD*w(T4itnfit
иЛ jd8 ^J
«MU- j 1
Рис. 6.13. Интерфейс программы fdatool
368 Глава 6. Проектирование дискретных фильтров
Большая часть команд меню программы fdatool дублирует действия, выполняе-
выполняемые с помощью элементов графического интерфейса, поэтому отдельно обсуж-
обсуждать структуру меню мы не будем. Однако следует отметить, что многим опера-
операциям сопоставлены клавиатурные комбинации, узнать которые можно, заглянув
именно в меню.
Расчет фильтра
Расчет фильтра начинается с задания требуемых параметров на вкладке Design
Filter (см. рис. 6.13). Тип синтезируемой АЧХ выбирается с помощью переключа-
переключателя Filter Туре. Возможны следующие варианты: Lowpass (ФНЧ), Highpass (ФВЧ),
Bandpass (полосовой фильтр), Bandstop (режекторный фильтр). Выбор пятого,
самого нижнего, положения переключателя позволяет использовать раскрываю-
раскрывающийся список, в котором перечислены более сложные варианты: Differentiator
(дифференцирующий фильтр), Hilbert Transformer (преобразователь Гильберта),
Multiband (многополосный фильтр), Arbitrary Magnitude (произвольная АЧХ) и
Arbitrary Group Delay (произвольная групповая задержка).
Выбрав категорию синтезируемой АЧХ, следует выбрать тип синтезируемого
фильтра, установив переключатель, расположенный в разделе Design Method,
в положение MR (рекурсивный) или FIR (нерекурсивный). Каждому положению
переключателя соответствует список возможных методов синтеза. Состав этого
списка меняется в зависимости от выбранного типа АЧХ. Например, при синтезе
фильтра с произвольной зависимостью групповой задержки от частоты (Arbitrary
Group Delay) переключатель автоматически установится в положение IIR, а в спи-
списке будет доступен всего один метод — метод минимизации р-нормы ошибки
(Constrained Least Pth Norm). В случае синтеза АЧХ четырех простейших типов
набор возможных методов синтеза значительно шире:
□ нерекурсивные фильтры (FIR). Здесь доступны следующие методы:
О Equiripple — синтез фильтров с равномерными пульсациями АЧХ методом
Ремеза;
О Least-Squares — минимизация среднеквадратического отклонения АЧХ от
заданной;
О Window — синтез с использованием весовых функций (окон);
□ рекурсивные фильтры (HR). Здесь доступны четыре варианта синтеза по раз-
различным аналоговым прототипам методом билинейного г-преобразоваиия:
О Butterworth — синтез фильтра Баттерворта;
О Chebyshev Type I — синтез фильтра Чебышева первого рода;
О Chebyshev Type II — синтез фильтра Чебышева второго рода;
О Elliptic — синтез эллиптического фильтра.
ЗАМЕЧАНИЕ
Набор доступных методов синтеза зависит от того, установлен ли пакет Filter Design.
Далее необходимо выбрать порядок фильтра в разделе Filter Order. Во многих
случаях помимо явного указания порядка в поле ввода Specify order возможен
Синтез дискретных фильтров в MATLAB 369
автоматический выбор порядка путем установки переключателя в положение
Minimum order.
Наконец, необходимо задать числовые параметры этой АЧХ в разделах Fre-
Frequency Specifications и Magnitude Specifications (при выборе типа АЧХ из допол-
дополнительного раскрывающегося списка эти два раздела объединяются под общим
названием Frequency and Magnitude Specifications). Содержимое этих областей окна
меняется в зависимости от выбранного типа АЧХ. На рис. 6.13 показаны поля
ввода параметров, соответствующие синтезу ФНЧ. При заполнении полей ввода
можно ссылаться на переменные, существующие в данный момент в рабочей об-
области памяти MATLAB.
ЗАМЕЧАНИЕ
Подробное описание способов задания разнообразных АЧХ вы можете найти в разделах
этой главы, посвященных функциям синтеза фильтров. Параметры, задаваемые в fdatool,
как правило, передаются в функцию, реализующую выбранный метод синтеза, без допол-
дополнительных преобразований.
Числовые параметры, которые необходимо задать, иллюстрируются графиком,
выводимым в разделе Filter Specifications. Вид этого графика также меняется в за-
зависимости от выбранного типа АЧХ, на рис. 6.13 он соответствует синтезу ФНЧ.
Выбрав метод синтеза и задав характеристики фильтра, щелкните па располо-
расположенной в нижней части окна кнопке Design Filter. Программа fdatool вызовет нуж-
нужную функцию синтеза, передав ей указанные вами спецификации фильтра.
ЗАМЕЧАНИЕ
Если установлен пакет Filter Design, в программе fdatool можно установить флажок Turn
quantization on, чтобы сделать доступной вкладку Set Quantization Parameters, позволяю-
позволяющую задавать параметры квантования коэффициентов фильтра. Об эффектах квантова-
квантования и об использовании этой вкладки речь пойдет далее, в главе 7.
Просмотр характеристик фильтра
После выполнения расчета фильтра в разделе Current Filter Information окна про-
программы fdatool появится информация о завершении вычислений (Source: Desig-
Designed). Теперь можно просматривать характеристики получившегося фильтра, что-
чтобы проверить, соответствует ли он нашим требованиям.
Выбор графика для просмотра производится с помощью кнопок панели инстру-
инструментов, показанных на рис. 6.14, или следующих команд меню Analysis:
□ Filter Specifications — вывод графика, поясняющего задание параметров АЧХ;
□ Magnitude Response — вывод графика АЧХ;
□ Phase Response — вывод графика ФЧХ;
□ Magnitude and Phase — одновременный вывод графиков АЧХ и ФЧХ;
□ Group Delay — вывод графика частотной зависимости групповой задержки;
□ Impulse Response — вывод графика импульсной характеристики;
370 Глава 6. Проектирование дискретных фильтров
□ Step Response — вывод графика переходной характеристики;
□ Pole/Zero Plot — вывод графика расположения нулей и полюсов на г-плоскости;
□ View Filter Coefficients — просмотр коэффициентов фильтра. Выводимое здесь
представление фильтра зависит от выбранной формы реализации (см. далее).
Magnitude Response Group Delay Pole/Zero Plot
Filter Specifications
Filter Coefficients
Phase Response
Step Response
Magnitude and Phase Response Impulse Response
Рис. 6.14. Панель инструментов программы fdatool
Когда на экран выведен какой-либо из графиков, можно использовать кнопки
Zoom In и Zoom Out панели инструментов для управления масштабом отображе-
отображения. Щелкнув на кнопке Zoom In, нужно затем щелкнуть в той точке графика, ко-
которая должна оказаться в центре увеличенного изображения. При включенном
режиме Zoom Out щелчок на точке графика аналогичным образом уменьшает мас-
масштаб отображения. Правая кнопка мыши в этих двух режимах выполняет проти-
противоположное действие (в режиме Zoom In уменьшает масштаб, в режиме Zoom Out —
увеличивает).
Сохранение результатов работы
Чтобы сохранить результаты текущего сеанса работы с программой fdatool, щелк-
щелкните на кнопке Save session панели инструментов или воспользуйтесь одноимен-
одноименной командой меню File. В этом меню есть также команда Save session As, позво-
позволяющая сохранить сеанс под новым именем. Файлы сохраненных сеансов рабо-
работы имеют расширение fda.
Загрузить сохраненный сеанс можно с помощью кнопки Open Session панели ин-
инструментов или одноименной команды меню File.
Разумеется, ценность программы fdatool была бы невелика, если бы в ней не было
средств экспорта коэффициентов рассчитанного фильтра для использования в
MATLAB или других программах. Экспорт описания фильтра производится с
помощью команды Export меню File или комбинации клавиш Ctrl+E. После выбо-
выбора команды появляется окно экспорта, показанное на рис. 6.15.
Раскрывающийся список Export To позволяет выбрать способ экспорта:
□ Workspace — данные передаются непосредственно в рабочую область памяти
MATLAB;
□ Text-file — коэффициенты фильтра записываются в текстовый файл. Формат
этого файла совпадает с форматом представления информации о коэффици-
коэффициентах фильтра в окне программы fdatool;
□ MAT-file — информация о фильтре сохраняется в виде МАТ-файла, который
затем можно будет загрузить в MATLAB командой load.
Синтез дискретных фильтров в MATLAB
371
■} Export
[Workspa
Numwatt»; \
jDen
Г" Ovetwtite «swung variables
Рис. 6.15. Окно экспорта описания фильтра
В разделе Variable Names задаются имена переменных для хранения векторов и
матриц, описывающих фильтр. Состав полей ввода зависит от формы реализа-
реализации фильтра (см. далее). При записи информации в текстовый файл эти поля
ввода недоступны.
При экспорте в рабочую область памяти MATLAB доступен также флажок Over-
Overwrite existing variables. Если он установлен, то при наличии в памяти MATLAB
переменных, имена которых совпадают с теми, что указаны в окне экспорта, их
значения будут заменены новыми. Если флажок снят, то попытка экспортиро-
экспортировать данные в уже существующую переменную вызовет появление сообщения об
ошибке.
Задав все необходимые параметры, щелкните на кнопке ОК для выполнения экс-
экспорта данных. При экспорте в файл будет запрошено имя создаваемого файла.
Импорт описания фильтра
Программу fdatool можно использовать не только для расчета фильтров с задан-
заданными параметрами, но и для анализа характеристик уже рассчитанных фильт-
фильтров. Для этого используется режим импорта описания фильтра, выбираемый с
помощью команды Import Filter меню Filter. При включении этого режима вкладка
Design Filter заменяется на вкладку Import Filter, показанную на рис. 6.16.
Под импортом в программе fdatool подразумевается получение готовых век-
векторов и матриц, описывающих фильтр. Можно ввести эти векторы и матрицы
вручную (используя синтаксис MATLAB) или сослаться на идентификаторы пе-
переменных, существующих в данный момент в рабочей области памяти MATLAB
и хранящих описание фильтра. Эти векторы или имена переменных задаются в
полях ввода, состав которых зависит от выбранной формы описания фильтра (фор-
(форма выбирается с. помощью раскрывающегося списка Filter Structure). На рис. 6.16
выбрана прямая форма реализации фильтра, поэтому предлагается ввести векто-
векторы коэффициентов полиномов числителя (поле Numerator) и знаменателя (поле
Denominator) функции передачи.
В разделе Sampling Frequency задается частота дискретизации — она использует-
используется для оцифровки частотных осей графиков. Единица измерения частоты выби-
372
Глава 6. Проектирование дискретных фильтров
рается из списка Units, а само значение вводится в поле Fs. По умолчанию выбра-
выбраны нормированные частоты, при этом частота Найквиста равна единице.
Import FiRm
Sal 0 jwreatoh Pamelas
L Г to Coftaann
tD e-'l re II1 ar'C'i^d
j^j Nimtnbr
||0028 00530071
JilCOT 2 026 2148
005300281
115Э0 27Э1
Clgy |
Jn*i
Fr
t<
S»ci>y t>«ооа'пвл»dnsiitbi«taliabwdelred»theMAtLAS Мики»»
Рис. 6.16. Вкладка Import Filter
Задав каким-либо способом описание фильтра, щелкните на кнопке Import Filter,
расположенной в нижней части окна программы, и выводимый в данный момент
график будет перерисован в соответствии с результатами анализа импортиро-
импортированного фильтра.
Теперь можно просматривать графики характеристик импортированного фильт-
фильтра, как было описано выше. Для возврата в режим расчета фильтров используй-
используйте команду Design Filter меню Filter.
ГЛАВА 7 Эффекты
квантования
в цифровых
системах
В разделе «Аналоговые, дискретные и цифровые сигналы» главы 3 мы обсужда-
обсуждали разницу между дискретными и цифровыми сигналами. До сих пор, строго го-
говоря, речь шла о дискретных сигналах и системах, поскольку отсчеты сигналов
и коэффициенты фильтров считались представленными точно (без погрешно-
погрешностей). В данной главе мы займемся именно цифровыми сигналами и системами,
рассмотрев эффекты, возникающие вследствие конечной точности представле-
представления отсчетов сигналов и параметров систем в вычислительных устройствах.
Теоретический анализ вопросов, связанных с конечной точностью представления
чисел в цифровых системах, весьма непрост. В данной главе мы лишь рассмот-
рассмотрим основные источники погрешностей и познакомимся со средствами MATLAB,
позволяющими производить квантование сигналов и анализировать эффекты кван-
квантования в алгоритмах цифровой обработки сигналов. Читатель, которого заинте-
заинтересуют более подробные теоретические построения, может обратиться к фунда-
фундаментальному труду [8].
Эффекты, связанные с конечной разрядностью представления чисел, можно раз-
разделить на следующие категории:
□ шум квантования, возникающий при аналого-цифровом преобразовании;
□ искажения характеристик, происходящие при квантовании коэффициентов
цифровых фильтров;
□ переполнение разрядной сетки в процессе вычислений;
□ округление промежуточных результатов вычислений.
Далее мы рассмотрим эти категории подробнее. Но сначала поговорим о спосо-
способах представления чисел в вычислительных устройствах.
374 Глава 7. Эффекты квантования в цифровых системах
Форматы представления чисел
Форматы представления дробных чисел в вычислительных устройствах можно
разделить на две группы: форматы с фиксированной запятой (fixed point) и фор-
форматы с плавающей запятой (floating point). В дополнение к этому существует не-
несколько способов представления отрицательных чисел.
Представление отрицательных чисел
Для представления знака числа обычно используется старший двоичный разряд,
при этом возможно несколько способов:
□ прямой код: 0 в старшем разряде соответствует положительным числам, 1 —
отрицательным. Остальные разряды представляют модуль числа. В таком коде
удобно осуществлять операции умножения (модули чисел перемножаются,
а знаковые разряды складываются по модулю два), но неудобно реализо-
вывать сложение. Кроме того, некоторые проблемы создает наличие двух
представлений нуля — «положительного» и «отрицательного»;
□ дополнительный код: 0 в старшем разряде соответствует положительным чис-
числам, 1 — отрицательным. Неотрицательные числа представляются без ка-
каких-либо особенностей, а для превращения положительного числа в рав-
равное ему по модулю отрицательное необходимо инвертировать все разряды
двоичного представления (включая знаковый) и к получившемуся двоично-
двоичному числу прибавить единицу. В дополнительном коде удобно выполнять опе-
операции сложения (числа со знаком складываются точно так же, как беззна-
беззнаковые);
□ обратный код: 0 в старшем разряде соответствует положительным числам,
1 — отрицательным. Неотрицательные числа представляются без каких-либо
особенностей, а превращение положительного числа в равное ему по модулю
отрицательное производится путем простой инверсии всех разрядов двоично-
двоичного представления (включая знаковый);
□ смещенный код: трактовка знакового разряда здесь противоположна предыду-
предыдущим вариантам — 1 означает положительное число, а 0 — отрицательное. Пред-
Представления чисел получаются путем прибавления к ним константы 2'v - 1, где
N — число двоичных разрядов (не считая знакового).
В табл. 7.1 описанные варианты поясняются на примере 8-разрядных целых
чисел.
Наибольшее распространение для представления целых чисел и чисел с фикси-
фиксированной запятой получил дополнительный код. Прямой код используется для
представления мантиссы, а смещенный код — для представления порядка чисел
в формате с плавающей запятой (см. далее).
Форматы представления чисел
375
Таблица 7.1.
Беззнаковое
значение
0
1
126
127
128
129
254
255
Способы представления чисел со знаком
Двоичное
представление
00000000
00000001
01111110
01111111
10000000
10000001
...
11111110
11111111
Значение
Прямой
код
0
1
126
127
-0
-1
-126
-127
Дополнитель-
Дополнительный код
0
1
126
127
-128
-127
-2
-1
со знаком
Обратный
код
0
1
126
127
-127
-126
-1
Смещенный
код
-127
-126
-1
0
1
2
127
128
Формат с фиксированной запятой
Название «формат с фиксированной запятой» означает, что в двоичном пред-
представлении дробного числа для хранения его целой и дробной частей отведено
фиксированное число разрядов. Иными словами, запятая, разделяющая целую и
дробную части в двоичном представлении числа, находится на фиксированном
месте.
Часто формат с фиксированной запятой обозначают парой целых чисел: ММ
В большинстве случаев (об одном из исключений будет сказано далее) М обо-
обозначает число разрядов целой части числа (включая знак), a JV — число разрядов
дробной части. Этот способ обозначения широко распространен в литературе по
цифровой обработке сигналов.
В качестве примера рассмотрим формат 1.15, часто применяемый для представ-
представления чисел в цифровых сигнальных процессорах. Как следует из обозначения,
целая часть числа содержит только один разряд — знаковый. Поэтому числа, ко-
которые можно представить в этом формате, по модулю не превосходят единицы.
Пятнадцать разрядов после запятой обеспечивают дискретность представления,
равную 25 - 1/32768 « 3 • 10~5. Для представления отрицательных чисел ис-
используется дополнительный код (см. ранее раздел «Представление отрицатель-
отрицательных чисел»). Более детально данный формат иллюстрируется в табл. 7.2.
Приведенная таблица наглядно демонстрирует два важных факта, характеризую-
характеризующих форматы с фиксированной запятой. Во-первых, сравнение столбцов «Целое
число в дополнительном коде» и «Число в формате 1.15» показывает, что фор-
формат с фиксированной запятой, по сути дела, означает просто договоренность
376
Глава 7. Эффекты квантования в цифровых системах
делить целые числа на постоянный коэффициент, равный 2N (N — число разря-
разрядов дробной части). В нашем примере этот коэффициент равен 32 768.
Таблица 7.2. Формат с фиксированной запятой 1.15
Двоичное
представление
0000 0000 0000 0000
0000 0000 0000 0001
0000 0000 0000 0010
0111 1111 1111 1110
0111 1111 1111 1111
1000 0000 0000 0000
1000 0000 0000 0001'
1111 1111 1111 1110
1111 1111 1111 1111
Шестнвдцвтерич-
ное представление
0000
0001
0002
7FFE
7FFF
8000
8001
FFFE
FFFF
Целое число
в дополнительном коде
0
1
2
...
32 766
32 767
-32 768
-32 767
...
-2
-1
Число в формвте
1.15
0
1
32768
2
32768
32766
32768
32767
32768
32767
32768
...
2
32768
1
32768
Во-вторых, из таблицы видно, что значение -1 в данном формате представить
можно, а +1 — нет (максимальное положительное число равно 32767/32768»
« 0,9999695). Это общее свойство форматов с фиксированной запятой — макси-
максимальное по модулю отрицательное число равно -2м ~ \ а максимальное положи-
тельное «не дотягивает» до 2м'' на 2~N.
ВНИМАНИЕ
В языках программирования высокого уровня часто применяется другая трактовка перво-
первого из пары чисел M.N, обозначающих формат с фиксированной запятой, — М обозначает не
число разрядов целой части, а общее число двоичных разрядов, используемое для пред-
представления чисел. Такой подход используется и в MATLAB. В частности, в объектах-кваи-
товатслях, создаваемых средствами пакета Filter Design (о них пойдет речь далее в этой
главе), рассмотренный формат 1.15 задается с помощью двухэлементного вектора [16 15).
Достоинствами формата с фиксированной запятой являются равномерность кван-
квантования и простота реализации арифметических операций; главный недостаток —
Форматы представления чисел 377
ограниченный динамический диапазон. Динамическим диапазоном называют от-
отношение между самым большим и самым малым по модулю (но отличным от
нуля) числами, которые можно представить с помощью данного формата. Для
формата с фиксированной запятой это отношение равно 2м'1 - 1.
Формат с плавающей запятой
Числа в формате с плавающей запятой (иногда его называют еще экспоненциаль-
экспоненциальным форматом или научной нотацией) представляются в виде
x-f-Г,
где/— мантисса (mantissa), a e — порядок (exponent). Обычно мантисса пред-
представляется в формате с фиксированной запятой, а порядок является целым чис-
числом.
Поскольку в экспоненциальной форме записи числа присутствуют два парамет-
параметра, такое представление оказывается неоднозначным. Приведем простой пример:
2=2-2° =1-2* =--22 =...
2
Чтобы устранить эту неоднозначность, принято ограничивать диапазон допусти-
допустимых значений мантиссы, например, так: 0,5 < |/| < 1, или так: 1 < |/| < 2 (этот ва-
вариант используется наиболее часто). Процедура приведения мантиссы к допус-
допустимому диапазону называется нормализацией, а экспоненциальная запись числа,
удовлетворяющая указанным ограничениям, — нормализованной экспоненциаль-
экспоненциальной формой.
Нормализация мантиссы позволяет сэкономить один разряд в ее двоичном пред-
представлении. Действительно, если нормализованная мантисса лежит в диапазоне
[0,5, If, то ее двоичная запись имеет вид «0,1...», а если для нормализации ис-
используется диапазон [1, 2[, двоичная запись будет выглядеть как «1,...». В обоих
случаях заранее известно, что первый значащий разряд равен единице, поэтому
его можно не хранить. Иногда это называется использованием неявного старше-
старшего бита.
Для представления отрицательных чисел необходимо обеспечить возможность
представления отрицательных значений мантиссы. Как правило, для этого ис-
используется прямой код (см. ранее раздел «Представление отрицательных чисел»),
то есть модуль мантиссы и знаковый бит хранятся независимо.
Использование строго нормализованной мантиссы делает невозможным пред-
представление нулевого значения в формате с плавающей запятой. Поэтому исполь-
используется специальное соглашение о том, что число, содержащее нули во всех раз-
разрядах мантиссы и порядка, считается нулем. Знаковый разряд при этом может
иметь любое значение. Таким образом, имеется два представления нуля — «по-
«положительный нуль» и «отрицательный нуль». Об этом уже говорилось ранее в
разделе «Представление отрицательных чисел».
Чтобы использование данного соглашения для представления нуля не привело
к возникновению «дырки» в наборе представимых чисел, нулевое представле-
представление порядка должно соответствовать не нулевому, а минимально возможному
378
Глава 7. Эффекты квантования в цифровых системах
(то есть отрицательному) его значению. Поэтому для представления порядка чи-
чисел с плавающей запятой используется смещенный код (см. ранее раздел «Пред-
«Представление отрицательных чисел»).
ЗАМЕЧАНИЕ
Если бы порядок хранился, например, в дополнительном коде, число, имеющие нули во
всех разрядах мантиссы и порядка, формально равнялось бы единице, и замена его на нуль
привела бы к невозможности представления единичного значения, что явно неприемлемо.
Итак, для представления нулевого значения в формате с плавающей запятой ман-
мантисса неминуемо должна быть деиормализованиой. Однако если использовать
денормализованную мантиссу только для представления нуля, малые по модулю
числа, представимые в данном формате, оказываются расположены неравномер-
неравномерно — вокруг нуля появляется «мертвая зона», размер которой существенно пре-
превышает расстояние между ближайшими к нулю представимыми числами.
Чтобы решить эту проблему и сделать расположение представимых чисел вбли-
вблизи нуля равномерным, применяют следующее соглашение о денормализации: если
все разряды порядка имеют нулевые значения, то величина порядка увеличи-
увеличивается на единицу, а мантисса считается депормализованпой, то есть содержащей
в неявном старшем бите нуль, а не единицу. Это позволяет расширить возмож-
возможности представления малых по модулю чисел. Фактически в данном случае мы
увеличиваем диапазон возможных отрицательных порядков за счет сокращения
числа значащих цифр мантиссы.
Поясним сказанное на примере, рассмотрев 6-битовый формат с плавающей за-
запятой, в котором отведено 2 бита для хранения порядка и 3 — для хранения ман-
мантиссы. Биты двоичного представления числа, таким образом, имеют следующее
назначение:
seemmm
Здесь s — знаковый бит, е — биты порядка, m — биты мантиссы. Рассчитаем и по-
покажем на графике (рис. 7.1) все числа, которые можно представить в данном
формате без использования и с использованием денормализации мантиссы для
малых чисел. Соответствующие вычисления можно осуществить с помощью сле-
следующей MATLAB-программы:
X первый вариант - денормализациЯ только длЯ нулЯ
for k = 0:63
s = 1 - 2 * bitgetCk. 6):
е = bi2de(bitget(k. 4:5))
in = 1 + bitand(k. 7) / 8;
if -bitand(k. 31)
f(k+l)=O;
else
f(k+l)=s*m*BAe);
end
end
subplotB. 1. 1)
% перебор всех возможных представлений
X знаковый множитель
X порЯдок
X мантисса
X нуль - особый случай
Форматы представления чисел
379
plot(f. f*0, '.')
% второй вариант - денормализациЯ длЯ малых по модулю чисел
for к = 0:63 % перебор всех возможных представлений
s = 1 - 2 * bitget(k. 6); % знаковый множитель
е = bi2de(bitget(k, 4:5)); X смещенный порЯдок
if e
X обычный случай - нормализуем мантиссу
е = е-1: X истинный порЯдок
m = 1 + bitand(k, 7) / 8: X нормализованная мантисса
else
% нули в поле порЯдка - не нормализуем мантиссу
m = bitand(k. 7) / 8; X денормализованнаЯ мантисса
end
f(k+l)=s*m*BAe);
end
subplotB. 1. 2)
plot(f. f*0, '.')
1
0
1
1
0
1
1
3 -6
r
-4
-2
1
I
0
1
1
1
2
i
1
i
4
i
i
6 8
1
■18
-6
-2
О
Рис. 7.1. Числа, представимые в 6-битовом формате с плавающей запятой
без использования (сверху) и с использованием (снизу) соглашения
о денормализации мантиссы для малых чисел
Сравнение двух графиков рис. 7.1 наглядно демонстрирует, как денормалызация
мантиссы влияет на возможности представления малых по модулю чисел.
ЗАМЕЧАНИЕ
В приведенном листинге использованы следующие функции MATLAB: bitget — возвра-
возвращает биты с заданными номерами из двоичного представления целого неотрицательного
числа; bitand — выполняет побитовую логическую операцию «И» над неотрицательными
целыми числами; bi2de — преобразует вектор, состоящий из нулей и единиц, трактуя его
как запись числа в двоичной системе счисления.
В заключение данного разделе приведем сведения о форматах с плавающей за-
запятой, поддерживаемых процессорами персональных компьютеров:
Q формат с одинарной точностью (single в языке Pascal, float в языке С) —
32 бита, включающие знаковый разряд, 8 бит порядка и 23 бита мантиссы;
Q формат с двойной точностью (doubi e в языках Pascal и С) — 64 бита, включаю-
включающие знаковый разряд, 11 бит порядка и 52 бита мантиссы. Это основной фор-
формат хранения данных в MATLAB;
380 Глава 7. Эффекты квантования в цифровых системах
□ формат с расширенной точностью (extended в языке Pascal, long double в язы-
языке С) — 80 бит, включающих знаковый разряд, 15 бит порядка и 64 бита ман-
мантиссы. В отличие от двух предыдущих форматов, здесь не используется неяв-
неявный старший бит мантиссы.
Формат с плавающей запятой за счет экспоненциального представления чисел
обладает существенно большим динамическим диапазоном, чем формат с фикси-
фиксированной запятой при той же длине слова. Однако платой за это является нерав-
неравномерность квантования и повышенная сложность реализации арифметических
операций.
Процесс квантования
Как уже отмечалось в главе 3, квантованием называется процесс преобразования
истинных значений отсчетов сигнала в двоичные числа, имеющие конечное чис-
число разрядов. Там же было введено понятие шума квантования. В данном разделе
мы обсудим шум квантования несколько подробнее, а также рассмотрим идею
неравномерного квантования.
Шум квантования
Как было отмечено в разделе «Аналоговые, дискретные и цифровые сигналы»
главы 3, при представлении отсчетов дискретного сигнала в виде чисел с ограни-
ограниченной разрядностью происходит их округление. Разность между исходным и
округленным значениями называется шумом квантования.
Анализ вопросов, связанных с шумами квантования и ошибками округления
в цифровых системах обработки сигналов, весьма сложен (см., например, [8]).
В данном разделе будет представлено лишь несколько положений общего харак-
характера.
В качестве иллюстрации процесса квантования на рис. 7.2 показаны (без дискре-
дискретизации по времени) гармонический сигнал s(t), результат его квантования sK(t)
и возникающий при этом шум e(t) = s(t) - sK(t). Очевидно, что значения шума
квантования лежат в следующих пределах:
-^<е(о<-,
2 2
где Д — расстояние между соседними уровнями квантования, то есть разность
между ближайшими возможными значениями квантованного сигнала.
В большинстве случаев можно считать e(t) случайным процессом, имеющим
равномерное распределение вероятности в указанных пределах. Такой случай-
случайный процесс имеет нулевое среднее значение и дисперсию, равную Д2/12.
После дискретизации шум квантования представляет собой последовательность
чисел e(kT), образующую дискретный случайный процесс (см. раздел «Дискрет-
«Дискретные случайные сигналы» главы 3). Во многих случаях отсчеты этой последова-
последовательности можно считать некоррелированными друг с другом.
Процесс квантования
381
A A
e(t)
о i /
Рис. 7.2. Процесс квантования гармонического сигнала
ЗАМЕЧАНИЕ
На рис. 7.2 предполагалось, что при квантовании производится округление значений уровня
сигнала. В реальных АЦП вместо этого может использоваться усечение, то есть округление
в сторону меньшего значения. В этом случае шум квантования лежит в диапазоне 0...Д, его
среднее значение равно Д/2, а дисперсия, как и в случае округления, составляет Д2/12.
В качестве примера рассчитаем отношение сигнал/шум (signal-to-noise ratio, SNR)
при квантовании гармонического сигнала. Пусть квантованию подвергается гар-
гармонический сигнал с амплитудой А. Определим отношение сигнал/шум, разде-
разделив эту амплитуду на средиеквадратическое значение шума квантования:
где N = 2А/А — число уровней квантования, укладывающихся в размахе сигнала.
АЦП, имеющий q двоичных разрядов, обеспечивает N = 2q уровней квантования.
Если размах сигнала соответствует полному рабочему диапазону АЦП, то отно-
отношение сигнал/шум равно
С/Ш=2"л/3.
Если выразить этот результат в децибелах, получится простая формула, показы-
показывающая связь между числом двоичных разрядов, используемых для представле-
представления отсчетов сигналов, и максимально достижимым в этом случае отношением
сигнал/шум:
С/ШлБ =
382 Глава 7. Эффекты квантования в цифровых системах
Неравномерное квантование
Равномерное квантование, о котором шла речь до сих пор, гарантирует, что раз-
размах шума квантования не будет превосходить величины шага квантования (за
исключением тех случаев, когда значение входного сигнала выходит за допусти-
допустимые пределы). Однако если потребовать минимизации среднеквадратического
значения шума квантования, оптимальный набор уровней квантования будет за-
зависеть от статистических свойств сигнала, а именно от плотности вероятности
его мгновенных значений.
В этом случае интуитивно ясно, что уровни квантования должны располагаться
плотнее друг к другу в областях тех значений, которые сигнал принимает с боль-
большей вероятностью.
Идея неравномерного квантования в общем случае формулируется следующим
образом: диапазон возможных значений сигнала делится на N зон квантования
а0... аь п\ ... а2,..., ajV_ i... aN. Зонам квантования сопоставлены квантованные зна-
значения bk e \ak_ i, ак]. Если входной сигнал попадает в диапазон а*_ j... ak, его кван-
квантованное значение принимается равным bk.
Итак, пусть сигнал имеет плотность вероятности р(х) и мы хотим осуществить
его JV-уровневое квантование так, чтобы сделать нулевым среднее значение и ми-
минимизировать дисперсию шума квантования. Среднее значение ошибки кванто-
квантования е будет равно
Л' "е л' "г _ л'
е = Х \{x-bk)p{x)dx = x-2_,bk \p{x)dx=x-2_,bhPk,
где х — математическое ожидание сигнала х, a Pk — вероятность попадания сиг-
сигнала в £-ю зону квантования.
Средний квадрат ошибки рассчитывается как
= £ \{х -bkf p{x)dx = х~*
Приравнивание к нулю частных производных этого выражения по а^ и Ьк дает
следующие соотношения для оптимальных параметров квантования:
Г
xp(x)dx и
*"'
. . .
p(x)dx
11 \\
( }
Данные формулы при известной плотности вероятности р(х) дают систему не-
нелинейных уравнений относительно ац и Ьк. Аналитическое решение этой системы
даже для несложных функций р(х) оказывается весьма непростым и его в боль-
большинстве случаев приходится искать численными методами.
ЗАМЕЧАНИЕ
Выполнение условий G.1) автоматически обеспечивает и нулевое среднее значение шума
квантования.
Эффекты квантования в цифровых фильтрах
383
Если формула для плотности вероятности сигнала неизвестна, но имеется «ти-
«типичный» набор его отсчетов, можно произвести оптимизацию параметров кван-
квантования по этому тестовому набору. Поиск оптимальных значений а^ и Ь^ в этом
случае производится численным итерационным методом (см. далее в этой главе
описание функций MATLAB quantiz и lloyds).
Неравномерное квантование применяется, например, в современных цифровых
телефонных сетях. Малые значения речевого сигнала более вероятны, чем боль-
большие, поэтому используется нелинейное преобразование сигнала, когда диапазон
значений, при равномерном квантовании представляемый 12 двоичными раз-
разрядами D096 уровней), квантуется на 256 (8 двоичных разрядов) неравномерно
расположенных уровней согласно Рекомендации ITU-T G.711. Зависимость уров-
уровня квантования от его номера представляет собой кусочно-линейную аппрокси-
аппроксимацию экспоненциального закона. В цифровых каналах связи передаются 8-раз-
8-разрядные номера уровней квантования, а при цифро-аналоговом преобразовании
они конвертируются в 12-разрядные значения соответствующих им уровней сиг-
сигнала.
Эффекты квантования
в цифровых фильтрах
Шум квантования — не единственная проблема, связанная с конечной разрядно-
разрядностью используемых чисел. Так, неизбежное округление разнообразных коэффи-
коэффициентов, используемых в алгоритмах цифровой обработки сигналов, приводит
к тому, что параметры фильтров и других устройств отличаются от желаемых,
причем возможны ситуации, когда эти отличия весьма существенны. Кроме того,
из-за округления промежуточных результатов может происходить накопление вы-
вычислительных погрешностей, также искажающих конечный результат. Эти эф-
эффекты будут рассмотрены в данном разделе.
Квантование коэффициентов
цифровых фильтров
До сих пор, рассматривая характеристики дискретных фильтров, мы получали
коэффициенты фильтров некоторыми расчетными методами и считали, что они
представлены точно. Однако при практической реализации фильтров почти не-
неизбежно возникает необходимость округления их коэффициентов. При исполь-
использовании цифровых сигнальных процессоров это связано с поддерживаемыми ими
форматами представления чисел, при создании программ обработки сигналов для
персональных компьютеров — со стремлением повысить быстродействие.
Из-за округления коэффициентов характеристики фильтра претерпевают иска-
искажения, величина которых зависит не только от погрешности представления ко-
коэффициентов, но и от исходных параметров фильтра и формы его построения
(см. раздел «Формы реализации дискретных фильтров» главы 4).
384
Глава 7. Эффекты квантования в цифровых системах
В нерекурсивных фильтрах коэффициенты равны отсчетам импульсной характе-
характеристики и линейно связаны с комплексным коэффициентом передачи. Поэтому
малые искажения коэффициентов приводят к малым искажениям частотных ха-
характеристик и проблемы, связанные с округлением коэффициентов, проявляют-
проявляются редко. Однако, если фильтр должен иметь очень крутой спад АЧХ между по-
полосами пропускания и задерживания, округление коэффициентов все же может
привести к заметным искажениям частотных характеристик.
Убедимся в этом на простом примере. Синтезируем методом Ремеза ФНЧ 256-го
порядка с полосой пропускания, простирающейся до 0,2, и полосой задержива-
задерживания, начинающейся от 0,21 (указаны частоты, нормированные к частоте Найкви-
ста). Затем округлим коэффициенты фильтра с точностью до 1/256, оставив в
них 8 двоичных разрядов после запятой, и построим графики АЧХ до и после
округления (рис. 7.3):
» b = remezB56. [О 0.2 0.21 1]. [1 1 0 0]);
» bq = round(b*256)/256; % округление
» [h. f] = freqz(b);
» hq = freqz(bq):
» subplotd, 2.1)
» plot(f/pi. abs(h))
» subplotd. 2. 2)
» plot(f/pi. abs(hq))
1.4
1.2
1VWWWWW
0.8
0.6
0.4
0.2
u0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1
Рис. 7.З. АЧХ нерекурсивного ФНЧ до (слева) и после (справа) округления коэффициентов
Как видите, ничего особенно страшного не произошло — лишь увеличился раз-
размах пульсаций АЧХ. Естественно, в любом случае следует обязательно про-
проконтролировать параметры фильтра после округления коэффициентов, чтобы
проверить, удовлетворяет ли квантованный фильтр предъявляемым к нему тре-
требованиям.
Значительно серьезнее сказывается округление коэффициентов на характери-
характеристиках рекурсивных фильтров, поскольку коэффициенты знаменателя функции
передачи связаны с импульсной и частотными характеристиками нелинейно. Как
правило, наибольшие искажения происходят в тех случаях, когда АЧХ фильтра
Эффекты квантования в цифровых фильтрах
385
имеет крутые скаты в переходных зонах между полосами пропускания и задер-
задерживания.
Приведем пример, иллюстрирующий сказанное. Рассчитаем эллиптический ФНЧ
6-го порядка, имеющий частоту среза, составляющую 0,2 от частоты Найквиста,
пульсации в полосе пропускания, равные 1 дБ, и уровень пульсаций в полосе за-
задерживания, равный -40 дБ. Напомним, что из всех фильтров, синтезируемых
по аналоговым прототипам, именно эллиптические фильтры дают максимальную
крутизну спада АЧХ при переходе от полосы пропускания к полосе задержива-
задерживания. Далее округляем коэффициенты фильтра точно так же, как это делалось в
предыдущем примере, и строим графики АЧХ фильтра до и после округления
(рис. 7.4):
» [b. a] = ellipF. 1. 40, 0.2); % исходный фильтр
» bq = round(b*256)/256; % округление числителя
» aq = round(a*256)/256; % округление знаменателя
» [h. f] = freqz(b. a); % ЧХ исходного фильтра
» hq = freqz(bq. aq); % ЧХ округленного фильтра
» plotCf/pi. abs(h). f/pi. abs(hq). '--')
0.6
0.8
Рис. 7.4. АЧХ рекурсивного фильтра до (сплошная линия) и после (пунктирная линия)
округления коэффициентов
В данном случае АЧХ изменилась просто катастрофически: в несколько раз уве-
увеличилась амплитуда пульсаций коэффициента передачи в полосе пропускания,
скат АЧХ стал заметно более пологим, в полосе задерживания исчезли две точки
с нулевым коэффициентом передачи.
Теперь посмотрим, что изменится, если мы представим исходный фильтр по-
другому — в виде трех последовательно включенных секций второго порядка.
В данном случае разница между АЧХ исходного и квантованного фильтра на-
настолько мала, что визуально она не проявляется. Поэтому вместо графиков са-
самих АЧХ построим график их разности (рис. 7.5):
» sos = tf2sos(b, a); % секции 2-го порЯдка
» sos_q = round(sos*256)/256; % округление коэффициентов
386
Глава 7. Эффекты квантования в цифровых системах
» [b_sos_q. a_sos_q] .- sos2tf(sos):
» [h. f] = freqz(b, a):
» h_sos_q = freqz(b_sos_q, a_sos_q):
» plot(f/pi. abs(h)-abs(h sos q))
0.4
0.6
0.8
Рис. 7.5. Разность двух АЧХ, полученных до и после округления коэффициентов
рекурсивного фильтра, представленного в виде секций 2-го порядка
Рисунок 7.5 показывает, что отклонение АЧХ квантованного фильтра от исход-
исходной не превосходит 310~!2, то есть весьма невелико. Таким образом, при пред-
представлении фильтра в виде последовательно включенных секций второго порядка
округление коэффициентов влияет на характеристики фильтра значительно сла-
слабее, чем при прямой форме реализации.
Данный пример демонстрирует общую закономерность, впервые установленную
Кайзером [8]: параметры любого фильтра с резким изменением частотной харак-
характеристики в переходной полосе, реализованного в прямой форме, крайне чувст-
чувствительны к значениям коэффициентов фильтра.
Существует два основных подхода к анализу и синтезу фильтров с квантован-
квантованными коэффициентами. Можно рассматривать погрешности представления ко-
коэффициентов как случайные величины и, задав статистическое описание этих
погрешностей, оценить среднеквадратическое отклонение частотной характерис-
характеристики от исходной. Второй подход заключается в использовании прямой оп-
оптимизации квантованных коэффициентов с целью достижения минимального
(в смысле среднеквадратической ошибки или максимального модуля разности)
отклонения АЧХ от заданной. Более подробную информацию об этом можно
найти в [8].
Масштабирование коэффициентов
цифровых фильтров
При разработке систем, работающих в реальном масштабе времени, для ускоре-
ускорения вычислений часто используется формат с фиксированной запятой. В этом
Эффекты квантования в цифровых фильтрах 387
случае может оказаться, что значения некоторых коэффициентов фильтров вы-
выходят за пределы диапазона, представимого в выбранном формате. Для решения
данной проблемы прибегают к масштабированию фильтров. Наиболее часто ко-
коэффициенты приводят к диапазону [-1, 1].
Рассмотрим сущность масштабирования на несложном примере. Рассчитаем эл-
эллиптический ФНЧ 4-го порядка с частотой среза, равной 20 % от частоты Найк-
виста, пульсациями в полосе пропускания 1 дБ и подавлением сигнала в полосе
задерживания 60 дБ:
» [b, a] = ellipD, 1, 60, 0.2)
b -
0.0059 0.0053 0.0096 0.0053 0.0059
а »
1.0000 -3.0477 3.8240 -2.2926 0.5523
Как видите, максимальное (по модулю) значение коэффициентов фильтра со-
составляет 3,824. Запишем для данного фильтра алгоритм фильтрации (см. форму-
формулу D.1) в разделе «Сущность линейной дискретной обработки» главы 4), а затем
разделим и умножим правую часть формулы на 4 (в качестве коэффициента масш-
масштабирования удобно выбирать степень двойки):
у (к) = 0,0059х(Л) + 0,0053л:(Л -1) + 0,0096 x(k - 2) + 0,0053л:(Л - 3) +
+ 0,0059х(& - 4) + 3,0477 y(k -1) -3,8240y(k -2) +
+ 2,2926 y(k - 3) - 0,5523 y(k - 4) =
= 4@,0015 я:(£) + 0,0013я:(£ -1) +0,0024 x(k -2) +
+ 0,0013.г(Л - 3) + 0,0015 x(k - 4) + 0,7619г/(Л -1) -
В полученной формуле алгоритма фильтрации значения коэффициентов по мо-
модулю не превышают единицы, а для сохранения результата неизменным понадо-
понадобилось умножение выходного сигнала на коэффициент масштабирования. Ис-
Исходный и масштабированный варианты структурной схемы показаны на рис. 7.6.
Итак, при масштабировании цифрового фильтра все его коэффициенты делятся
на одну и ту же константу, и на нее же умножается рассчитанный выходной сиг-
сигнал. В качестве масштабирующего множителя удобно выбирать степень двойки,
поскольку умножение на степень двойки в формате с фиксированной запятой
сводится к поразрядному сдвигу двоичного представления числа влево.
Если фильтр высокого порядка реализуется «целиком» (без разделения его на
последовательно включенные секции), диапазон абсолютных значений коэффи-
коэффициентов фильтра может быть весьма широк. При представлении коэффициентов
в формате с фиксированной запятой оказывается, что самые маленькие (по мо-
модулю) коэффициенты могут из-за округления потерять несколько значащих цифр.
Это приводит к искажению характеристик фильтра, порой весьма существенному,
особенно в рекурсивных фильтрах. Данный эффект мы уже обсуждали в преды-
предыдущем разделе. Там же мы видели, что реализация фильтра в виде последова-
последовательно включенных секций второго порядка значительно ослабляет эти искаже-
искажения. Это происходит из-за того, что в каждой отдельно взятой секции второго
порядка разброс абсолютных значений коэффициентов оказывается значитель-
388
Глава 7. Эффекты квантования в цифровых системах
но меньше, чем у фильтра в целом, особенно если при разбиении на секции груп-
группировать ближайшие друг к другу пары нулей и полюсов.
0,0059
3,0477
-3,8240^,
2,2926.
-0,5523.
4—
♦—
4—
i
Z~
Z
-1
z~
Ук
Рис. 7.6. Фильтр 4-го порядка (сверху) подвергается масштабированию
с коэффициентом 4 (снизу)
Переполнение разрядной сетки
в процессе вычислений
В процессе вычисления выходного сигнала фильтра производится множество
операций умножения и сложения. При этом промежуточные результаты вычис-
Эффекты квантования в цифровых фильтрах 389
лении могут значительно превосходить окончательное значение и вызвать пере-
переполнение разрядной сетки вычислительного устройства.
В качестве примера посмотрим, каких значений достигают промежуточные ре-
результаты вычислений при обработке синусоидального сигнала фильтром нижних
частот Баттерворта 4-го порядка, реализованным в прямой форме (см. рис. 4.4 в
главе 4). Чтобы получить доступ к промежуточным результатам вычислений, нам
придется вместо использования функции filter реализовать фильтр вручную.
Приведенная ниже MATLAB-программа рассчитывает фильтр методом билиней-
билинейного r-преобразования, а затем пропускает через него синусоидальный сигнал,
сохраняя при этом в массиве state всю историю работы единственного суммато-
сумматора, имеющегося в данной схеме фильтра:
Fs = 8еЗ; % частота дискретизации
t = 0:1/Fs:0.01: % дискретное времЯ
F0 = 1еЗ: % частота сигнала
s = sinB*pi*F0*t); % входной сигнал
N = 4; % порЯдок фильтра
[b, a] = butter(N. F0/Fs*2); % частота среза равна частоте сигнала
dx = zerosd, N+l): % линиЯ задержки длЯ входного сигнала
dy = zerosd, N+l): % линиЯ задержки длЯ выходного сигнала
m = 1;
state = zerosd, 2*N*length(s)):
у = zerosd, length(t)):
for k = l:length(t) % цикл по отсчетам входного сигнала
y(k) =0; % начальное состояние сумматора
dx = [s(k) dx(l:N)]; % новое состояние линии задержки
for n = 1:N+1 % цикл по нерекурсивной ветви
У(Ю = у(к) + b(n) * dx(n):
state(m) = y(k); % текущее состояние сумматора
m = m + 1:
end
for n = 2:N+l % цикл по рекурсивной ветви
y(k) = y(k) - a(n) * dy(n):
state(m) = y(k): % текущее состояние сумматора
m = m + 1;
end
dyB:N+l) = [y(k) dyB:N)]: % новое состояние линии задержки
end
plot(t. s, t, у, '--') % входной и выходной сигналы
figure
plot(state) % промежуточные состояния сумматора
Входной и выходной сигналы фильтра показаны на рис. 7.7 сверху, а промежу-
промежуточные результаты суммирования — снизу. Из графиков видно, что промежуточ-
промежуточные значения достигают ±1,3 и превосходят амплитуду как входного, так и вы-
выходного сигналов. Это может привести к переполнениям в арифметическом
устройстве и искажениям в выходном сигнале.
При реализации фильтра в канонической форме (см. рис. 4.6 в главе 4) вычис-
вычисления выполняются сначала в рекурсивной ветви, а затем в нерекурсивной.
390
Глава 7. Эффекты квантования в цифровых системах
При этом уровень сигнала, отсчеты которого хранятся в единственной линии за-
задержки фильтра, может значительно превышать амплитуды входного и выходно-
выходного сигналов.
1
0.8
0.8
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0.002 0.004 0.006 0.008 0.01
-0.5
-1
-1.5
100 200 300 400
600 700 800
Рис. 7.7. Входной и выходной сигналы ФНЧ Баттерворта (сверху)
и промежуточные результаты суммирования (снизу)
Продемонстрируем это, рассмотрев тот же фильтр Баттерворта 4-го порядка, ко-
который использовался в предыдущем примере. Сигнал, хранящийся в линии за-
задержки при канонической реализации фильтра, получается в результате обра-
обработки входного сигнала «чисто рекурсивным» фильтром, в нерекурсивной ветви
которого не используется задержанных отсчетов. Для оценки уровня этого сиг-
сигнала достаточно рассчитать АЧХ рекурсивной части фильтра (рис. 7.8):
» [b. a] = butterD. 1/4); % расчет фильтра
» [b. f] = freqzd. a, [], 2); % АЧХ рекурсивной ветви
Эффекты квантования в цифровых фильтрах
391
:» plot(f. abs(h))
» grid on
% график АЧХ
v
V
\
у
1 у
\
\
\
.—
8
7 ■
6 ■
5 "
4 ■
3 ■
2 "
1 ■
О 0.2 0.4 0.6 0.8 1
Рис. 7.8. АЧХ рекурсивной части ФНЧ Баттерворта 4-го порядка
В данном случае для возникновения переполнений оказывается еще больше воз-
возможностей, чем в предыдущем, — как видно из графика, коэффициент передачи
рекурсивной части фильтра может достигать семи. Это означает, что промежу-
промежуточные результаты вычислений для канонической формы реализации фильтра
могут в семь раз превосходить амплитуду входного сигнала!
Приведенные примеры показывают, что переполнения в процессе вычислений
могут стать серьезной проблемой при реализации алгоритмов цифровой обра-
обработки сигналов. Уменьшить вероятность переполнений можно, используя для
хранения чисел формат с плавающей запятой, обладающий большим динамиче-
динамическим диапазоном, однако в этом случае возрастает сложность реализации ариф-
арифметических операций. В любом случае разработанная система обработки сигна-
сигналов должна тщательно тестироваться для обнаружения потенциальных проблем,
связанных с конечной точностью вычислений. Такое тестирование можно реали-
реализовать, например, с помощью средств пакета Filter Design, рассматриваемых да-
далее в этой главе.
Округление промежуточных результатов
вычислений
При реализации различных алгоритмов обработки сигналов в процессе вычисле-
вычислений формируется множество промежуточных результатов. Формат хранения
этих результатов зачастую вынуждает округлять их, что приводит к появлению
дополнительных погрешностей. Операции, при которых появляются эти по-
погрешности, зависят от способа представления чисел, используемого в вычисли-
вычислительном устройстве.
392 Глава 7. Эффекты квантования в цифровых системах
При использовании арифметики с фиксированной запятой операции сложения
и вычитания не приводят к необходимости округления результатов — они могут
вызвать лишь переполнение. Действительно, ведь количество знаков после запя-
запятой у результата сложения двух чисел, представленных в формате с фиксирован-
фиксированной запятой, такое же, как было у слагаемых (слева суммируемые числа записа-
записаны в двоичной системе счисления, справа — в десятичной):
10.1100 2,75
+ +
01.0101 1.3125
100.0001 4.0625
В данном примере суммируемые числа имели по 4 двоичных разряда после за-
запятой и столько же разрядов после запятой необходимо для представления их
суммы.
А вот для представления целой части суммы нужно три разряда, тогда как для
слагаемых было достаточно двух. Поэтому, если для представления целой части
чисел используется два разряда, в данном случае возникнет переполнение.
В отличие от сложения умножение чисел с фиксированной запятой приводит к
увеличению числа значащих цифр результата (по сравнению с сомножителями)
и, следовательно, к необходимости округления. Перемножим те же два числа, ко-
которые использовались в примере сложения:
10.1100 2.75
X X
01.0101 1.3125
10
11.
10
1011
1100
1001
1100
00
1100
3.609375
Результат умножения в данном примере имеет 6 значащих цифр после запятой.
Если для представления результата используется тот же формат, что и для со-
сомножителей, придется производить округление:
11.10011100 а 11.1010 3.609375 « 3.625
Если для представления чисел используется формат с плавающей запятой, все
сказанное об умножении сохраняет силу. Впрочем, если результат умножения по
модулю не превосходит единицы, использование формата с плавающей запятой
даст большую точность, поскольку не будут зря тратиться разряды для представ-
представления незначащих нулей слева.
Однако операции сложения в формате с плавающей запятой тоже могут приво-
приводить к потере точности. Пусть рассматриваемые нами два числа представлены в
формате с плавающей запятой, использующем 6 разрядов для хранения дробной
части нормализованной мантиссы (мантисса и порядок записаны в двоичной
системе счисления):
Эффекты квантования в цифровых фильтрах 393
10,1100 - 0.101100 • 210
01.0101 - 0.101010 ■ 201
Представим результат сложения тоже в экспоненциальном формате:
0.1О1100 • 210 + 0.101010 • 201 = 0.1000001 • 211
Как видите, для точного представления результата шести значащих цифр ман-
мантиссы оказалось мало, а значит, придется выполнять округление. В данном слу-
случае, когда погрешность округления в обе стороны одинакова, возможно исполь-
использование различных подходов. Выберем, например, округление в большую сторону:
0.1000001 ■ 211 « 0.100001 ■ 2П 4.0625 * 4.125
В результате при сложении чисел с плавающей запятой может не выполняться
свойство ассоциативности — результат суммирования нескольких чисел может
зависеть от последовательности выполнения сложений. При обучении програм-
программированию обычно дается рекомендация складывать числа, начиная с меньших
(по модулю) и заканчивая самыми большими. Однако при реализации алгорит-
алгоритмов цифровой обработки сигналов мы, как правило, лишены возможности про-
произвольно менять последовательность суммирования (хотя бы потому, что для
сортировки слагаемых потребуется дополнительное время).
Для статистического анализа ошибок округления в структурную схему фильтра
вводятся эквивалентные источники шума, добавляемого к результатам умноже-
умножения и (при использовании арифметики с плавающей запятой) сложения. Более
подробную информацию об этом можно найти в [8].
Примеры моделирования ошибок округления в цифровом фильтре и при расче-
расчете БПФ будут приведены далее в этой главе, при описании функций qfilt и qfft
пакета Filter Design.
Предельные циклы
Ошибки округления при вычислениях в цифровых фильтрах могут приводить к
еще одной очень серьезной неприятности — появлению так называемых предель-
предельных циклов (limit cycle), когда вроде бы устойчивый фильтр начинает демонстри-
демонстрировать неустойчивое поведение.
Поясним это явление на простейшем примере, взятом из [8]. Пусть имеется ре-
рекурсивный фильтр первого порядка, описываемый разностным уравнением
Единственный полюс функции передачи данного фильтра, равный 0,95, нахо-
находится внутри единичной окружности, что свидетельствует об устойчивости
фильтра. Пусть входной сигнал отсутствует (x(k) = 0), а внутреннее состояние
фильтра, которое в данном случае представляется единственным числом г/@),
равно 13. При точных вычислениях сигнал на выходе фильтра экспоненциально
затухает:
г/A) = 0,95 г/@) = 0,95 ■ 13 = 12,35,
г/B) - 0,95 г/A) = 0,95 • 12,35 = 11,7325,
г/C) = 0,95 г/B) - 0,95 ■ 11,7325 = 11,145875,
394 Глава 7. Эффекты квантования в цифровых системах
уD) = 0,95 уC) = 0,95 • 11,145875 - 10,58858125,
г/E) = 0,95 г/D) = 0,95 • 10,58858125 - 10,0591521875, ;
А теперь будем считать, что в ячейке памяти фильтра значение хранится в цело-
целочисленном формате и после выполнения умножения используется округление
(будем обозначать его квадратными скобками). Выходной сигнал радикально из-
изменится:
уA) - [0,95 у@)] - [0,95 • 13] = [12,35] = 12,
уB) - [0,95 уA)] = [0,95 • 12] - [11,4] = И,
г/C) = [0,95 г/B)] = [0,95 • 11] - [10,45] = 10,
г/D) = [0,95 z/C)] = [0,95 • 10] = [9,5] = 10,
г/E) - [0,95 уD)] = [0,95 • 10] = [9,5] - 10,
Итак, выходной сигнал фильтра «залипает» на значении 10 и далее не меняется.
Это и есть простейший случай предельного цикла (с периодом, равным единице).
Если в разностном уравнении фильтра изменить знак у коэффициента 0,95, мы
получим предельный цикл с периодом, равным двум, в виде чередования значе-
значений 10 и -10. В фильтрах более высокого порядка могут возникать предельные
циклы с разным периодом.
Различают две разновидности предельных циклов:
□ «зернистые» (granular) предельные циклы возникают, когда значения внут-
внутреннего состояния фильтра при отсутствии входного сигнала затухают, но из-
за ошибок округления не доходят до нуля. Именно такой цикл наблюдается в
приведенном примере;
□ «переполняющие» (overflow) предельные циклы имеют место в том случае,
когда из-за вычислительных погрешностей значения внутреннего состояния
фильтра при отсутствии входного сигнала не затухают, а возрастают, вызывая
переполнение.
Для анализа возможностей возникновения предельных циклов используется по-
понятие эффективных значений коэффициентов знаменателя функции передачи
фильтра. Под эффективным значением коэффициента понимается отношение
округленного результата умножения к использованному в качестве множителя
значению внутреннего состояния фильтра. Эффективное значение коэффициента
будет разным для разных значений состояния. Если для какого-то внутреннего со-
состояния фильтра набор эффективных значений коэффициентов дает полюс функ-
функции передачи, расположенный на единичной окружности, это означает, что даннбе
внутреннее состояние при отсутствии входного сигнала дает предельный цикл.
В нашем примере эффективное значение единственного коэффициента фильтра
равно
_ [Q,95y(ft -1)]
т y(k-\)
Учет эффектов конечной точности вычислений в MATLAB
395
Построим график значений ao^t для целочисленных значений y{k - 1), лежащих
в диапазоне от -20 до 20 (рис. 7.9):
» у = -20:20;
» y(find(-y))=[]: % удалЯем нулевое значение
» a_eff = round@.95*y)./y:
» plot(у. a_eff. '.')
» ylim([0.9 1.1])
» xlabeH'y(k-D')
» ylabeK'aJeff}')
Рис. 7.9. Зависимость эффективного значения коэффициента рекурсивного фильтра
первого порядка от внутреннего состояния фильтра
Как видите, если y(k - 1) лежит в диапазоне от -10 до 10, значение атщ, стано-
становится равным единице, а фильтр оказывается на границе устойчивости (полюс
функции передачи лежит на единичной окружности), что и приводит к появле-
появлению предельного цикла.
В приведенном примере анализ предельных циклов оказывается очень простым,
поскольку внутреннее состояние фильтра описывается единственным числом.
Для фильтров, степень знаменателя функции передачи которых превышает еди-
единицу, анализ базируется на тех же принципах, но оказывается более сложным.
Для выполнения такого анализа в пакете Filter Design имеется специальная
функция limitcycle, которую мы рассмотрим далее в этой главе.
Учет эффектов конечной точности
вычислений в MATLAB
В пакетах расширения MATLAB имеется ряд средств для учета эффектов, свя-
связанных с конечной точностью представления чисел в вычислительных системах.
К таким средствам относятся функции, реализующие равномерное и неравно-
396 - Глава 7. Эффекты квантования в цифровых системах
мерное квантование, а также объекты квантователей, квантованных фильтров
и квантованных БПФ.
Функции квантования
Функции квантования имеются в двух пакетах расширения MATLAB. В пакете
Signal Processing содержатся функции uencode и udecode, осуществляющие равно-
равномерное (буква «и» в именах функций означает «uniform» — равномерный) кван-
квантование и восстановление сигнала. Пакет Communications предоставляет в рас-
распоряжение пользователя более гибкую функцию неравномерного квантования
quantiz, а также функцию lloyds, предназначенную для оптимизации параметров
неравномерного квантования по тестовому набору данных.
Функция uencode
Функция uencode осуществляет равномерное квантование входного сигнала. Син-
Синтаксис вызова функции следующий:
у = uencode(x. n. v. 'signflag')
Здесь х — массив неквантованных отсчетов входного сигнала (числа с плаваю-
плавающей запятой), п — число двоичных разрядов, используемое для представления
квантованных значений, которое может лежать в диапазоне от 2 до 32.
Остальные входные параметры являются необязательными. Параметр v задает
предельное абсолютное значение квантуемого сигнала. По умолчанию этот пара-
параметр равен 1, так что уровни квантования перекрывают диапазон -1...1.
Результатом работы функции является массив у, содержащий целые числа — но-
номера уровней квантования, соответствующих отсчетам из массива х. Размеры
массивов х и у совпадают.
Способ нумерации уровней квантования определяется последним входным па-
параметром 'signflag', который может принимать одно из двух строковых значе-
значений:
□ 'unsigned' — в массиве у содержатся целые числа от 0 до 2" - 1 (этот вариант
принят по умолчанию);
□ 'signed' — в массиве у содержатся целые числа от -2й ~] до 2п'х - 1.
MATLAB хранит выходной массив у в одном из целочисленных форматов дан-
данных согласно следующей таблице.
Число разрядов п
2...8
9...16
17...32
'signflag'
uint8
uintl6
uint32
Тип
= 'unsigned'
выходных двнных
'signflag' = 'signed'
int8
intl6
int32
Учет эффектов конечной точности вычислений в MATLAB
397
Если значения входного сигнала выходят за пределы диапазона -v...v, происхо-
происходит насыщение (saturation): значениям, меньшим ~v, соответствует минимально
возможное значение у @ или -2"), а значениям, превышающим v, — макси-
максимально возможное B" - 1 или 2"~' - 1).
Обратное преобразование номеров уровней квантования в квантованные значе-
значения производится рассматриваемой далее функцией udecode.
Функция udecode
Функция udecode является обратной по отношению к uencode — она превращает
номера уровней квантования в соответствующие квантованные значения. Син-
Синтаксис вызова функции следующий:
х = udecode(y, n, v, 'saturatemode')
Смысл параметров х, у, п и v здесь тот же, что и для функции uencode.
Строковый параметр 'saturatemode' определяет поведение функции в случае, если
в массиве у обнаруживаются значения, представленные большим числом двоич-
двоичных разрядов, чем указано в параметре п;
□ 'saturate' (насыщение; этот вариант принят по умолчанию) — при выходе зна-
значений у из допустимого диапазона для их представления в массиве х исполь-
используются крайние (минимальный и максимальный) уровни квантования;
□ 'wrap' (перенос) — при выходе значений у из допустимого диапазона «лиш-
«лишние» старшие разряды просто игнорируются, что эквивалентно смещению но-
номеров уровней квантования иа 2" (возможно, неоднократному).
1
0.8
0.6
0.4
0.2
о
-0.2
-0.4
-0.6
-0.8
-1
0
Рис. 7.
10
15
20
10. Квантованный сигнал, восстановленный при недостаточном числе уровней
квантования: слева — режим насыщения, справа — режим переноса
В качестве примера использования функций uencode и udecode произведем кван-
квантование синусоидального сигнала, а затем при восстановлении квантованных
значений уменьшим число двоичных разрядов, чтобы продемонстрировать влия-
влияние параметра 'saturatemode1 (рис, 7.10):
» t = 0:0.1:20:
» s = 0.75 * cos(t);
398 Глава 7. Эффекты квантования в цифровых системах
» у = uencode(s. 5. 1. 'signed'); % 32 уровня квантования
» % при восстановлении используем 16 уровней квантования
» xl = udecode(y. 4. 1, 'saturate'): % режим насыщения
» х2 = udecode(y. 4. 1, 'wrap'); % режим переноса
» subplotd. 2. 1)
» plot(t. xl)
» subplotd, 2, 2)
» plotCt. x2)
Функция quantiz
Функция quantiz реализует неравномерное квантование сигнала, описанное в этой
главе ранее. Синтаксис вызова функции следующий:
[index, quants, distor] = quantiz(sig. partition, codebook)
Здесь sig — вектор отсчетов сигнала, partition — вектор границ зон квантования
(в разделе «Неравномерное квантование» для этих границ использовалось обо-
обозначение ак), codebook — вектор уровней квантования. Длина этого вектора долж-
должна на единицу превосходить длину вектора partition.
Выходные параметры i ndex и quants имеют такие же размеры, как и вектор сигна-
сигнала, и содержат соответственно индексы и значения квантованного сигнала. Ре-
Результат i ndex определяется следующим образом:
□ если sig(k) < partition(l), то index(k) = 0;
□ если partition(m) < sig(k) < partition(im-l), то index(k) = m;
□ если sig(k) > partition(end), то index(k) = length(partition).
Результат quants содержит квантованные значения входного сигнала и рассчиты-
рассчитывается как codebook(index+l). Таким образом, величина codebook(l) задает уровень
квантования для всех значений сигнала, меньших, чем partitiond), величина
codebook(m) соответствует зоне квантования partition(m-l)...partition(m), а послед-
последнее значение codebook(end) будет использоваться в качестве уровня квантования
для всех значений сигнала, превышающих partition(end).
Третий выходной параметр distor содержит значение среднего квадрата ошибки
квантования.
Если выходные параметры quants я distor не используются, входной параметр
codebook при вызове функции можно опустить.
Функция lloyds
Функция lloyds осуществляет оптимизацию параметров неравномерного кван-
квантования, основываясь на тестовом сигнале, являющемся «типичным представи-
представителем» тех данных, которые будут затем подвергаться квантованию. Синтаксис
вызова функции следующий:
[partition, codebook. distor] = ...
lloyds(x, initcodebook. tol, plotflag)
Здесь x — тестовый сигнал, который должен быть достаточно длинным, чтобы по
нему можно было оценить плотность вероятности отсчетов, initcodebook — на-
Функции пакета расширения Filter Design 399
чальное приближение для набора уровней квантования. Этот параметр может
также быть не вектором, а числом, в таком случае он задает лишь количество
уровней квантования, а начальное приближение выбирается автоматически.
Оставшиеся два входных параметра являются необязательными и при вызове
могут быть опущены.
Параметр tol позволяет управлять критерием завершения итерационного алго-
алгоритма поиска оптимального решения. Если относительное изменение среднего
квадрата ошибки на очередной итерации оказывается меньше tol, решение счи-
считается найденным. По умолчанию значение параметра tol равно 10.
При использовании параметра plotflag функция выводит график тестового сиг-
сигнала, показывая горизонтальными линиями зеленого цвета подобранные уровни
квантования, а линиями красного цвета — границы зон квантования. Значение
параметра plotflag может быть любым — важен лишь факт его наличия или от-
отсутствия.
Результаты работы функции — выходные параметры partition, codebook и distor —
имеют тот же смысл, что и для функции quantiz.
Функции пакета расширения
Filter Design
В пакете расширения Filter Design реализованы квантователи, а также алгорит-
алгоритмы фильтрации и БПФ, использующие представление чисел (в том числе и про-
промежуточных результатов вычислений) в заданных форматах. Прежде чем пере-
переходить к описанию конкретных функций, необходимо сказать несколько общих
слов об их устройстве.
Дело в том, что квантователи, фильтры и блоки вычисления БПФ реализованы
в пакете Filter Design в виде объектов, имеющих некоторый набор свойств, а обыч-
обычные функции filter, fft и некоторые другие расширены таким образом, что они
могут принимать такие объекты в качестве одного из параметров.
Упомянутые объекты сначала нужно создать. Это делается с помощью функции-
коиструктора. Например, для квантованного фильтра роль конструктора вы-
выполняет функция qfi 11. В простейшем варианте конструктор может вызываться
без параметров:
» hq = qfilt;
При этом будет создан объект квантованного фильтра с именем hq, все свойства
которого принимают значения по умолчанию. Для установки нужных значений
свойств используется функция set:
» set(hq, 'name', value);
Здесь hq — идентификатор объекта, 'name' — строка с именем свойства, value —
задаваемое для него значение.
Считать значение свойства можно с помощью функции get:
» value = get(hq. 'name')
400 Глава 7. Эффекты квантования в цифровых системах
Смысл параметров hq и 'name' здесь тот же, что и для функции set, а результат
value содержит текущее значение запрашиваемого свойства.
Свойства объектов доступны также через синтаксис обращения к полям струк-
структуры:
hq.name = value; % присваивание значения
value - hq.name; % считывание значения
Конструктор объекта может вызываться с параметрами, задающими значения
свойств сразу же при создании объекта. Подробнее речь об этом пойдет при опи-
описании конкретных функций и объектов.
ЗАМЕЧАНИЕ
Имена свойств нечувствительны к регистру символов. Более того, при обращении к ним
можно использовать лишь несколько начальных символов имени — необходимо только,
чтобы этот начальный фрагмент однозначно идентифицировал свойство. Так, обратиться
к свойству QuantizedCoefficients объекта квантованного фильтра можно, указав строку
'quantizedcoefficients' или всего одну букву 'q' (других свойств на эту букву данный объект
не имеет).
После создания объекта и настройки его свойств объект можно использовать,
указывая его в качестве параметров различных функций. Например, для выпол-
выполнения обработки сигнала квантованным фильтром уже знакомая нам функция
filter используется следующим образом:
у = filter(hq, x)
Как видите, вместо двух векторов коэффициентов в списке параметров фигури-
фигурирует объект квантованного фильтра.
В пакете Filter Design имеется множество функций, предназначенных для работы
с объектами. Некоторые из них просто позволяют получать значения отдельных
свойств более удобным путем, чем с помощью функции get, другие производят
более специфические действия. Например, с помощью функции qreport можно
получить статистическую информацию, накопленную объектом, — число выпол-
выполненных операций, количество возникших переполнении и т. п.
Далее перейдем к рассмотрению конкретных функций и объектов.
Квантователи
Для создания объекта квантователя служит функция quantizer. У данного объек-
объекта немного свойств, причем числовым является только одно из них, а все строко-
строковые свойства имеют уникальные значения. Это позволяет вызывать конструктор
объекта, указывая только значения свойств и опуская их имена:
q = quantizer(valuel. value2. ...)
При этом не обязательно перечислять значения всех свойств — те из них, ко-
которые не заданы при вызове функции, сохранят значения, принятые по умол-
умолчанию.
Функции пакета расширения Filter Design
401
Разумеется, возможен и полный вариант вызова, когда указываются и имена,
и значения свойств:
q = quantizer ('namel'. vaiuel, 'name2', va!ue2. ...)
Здесь ' namel', ' name2' и т. д. — имена свойств, a val uel, val ue2 и т. д. — соответст-
соответствующие значения.
Список свойств квантованного фильтра приведен в табл. 7.3. Как уже говори-
говорилось, считывать и задавать значения этих свойств можно с помощью функций
get и set соответственно.
Таблица 7.3. Свойства объекта квантователя
Имя свойства
Мах
Min
Mode
Noperations
Noverf1ows
Nunderf1ows
RoundMode
Описание
Максимальное значение входного (неквантовапного) сигнала,
зафиксированное за время работы квантователя (только для чтения)
Минимальное значение входного (неквантованного) сигнала,
зафиксированное за время работы квантователя (только для чтения)
Тип квантователя:
' doubl e' — квантователь с плавающей запятой, стандартный
64-битовый формат double. Все остальные параметры
в данном случае игнорируются;
'float' — квантователь с плавающей запятой;
'fixed' — квантователь с фиксированной запятой (этот вариант
принят по умолчанию);
'single' — квантователь с плавающей запятой, стандартный
32-битовый формат single. Все остальные параметры
в данном случае игнорируются;
'ufixed' — беззнаковый квантователь с фиксированной запятой
Количество выполненных операций кпантовання (только для чтения)
Число переполнений, зафиксированное за время работы квантователя
(только для чтения)
Число случаев потери значимости (когда ненулевой входной сигнал
в результате квантования округляется до нуля; используется также
термин «антипереполненис»), зафиксированное за время работы
квантователя (только для чтения)
Режим округления:
1 cei 1' — округление вверх;
'convergent' — округление к ближайшему целому значению, в случае
равенства расстояний выбирается четное значение;
'fix' — округление к нулю;
'floor' — округление вниз (этот вариант принят по умолчанию);
'round' — округление к ближайшему целому значению, в случае
равенства расстояний выбирается значение, большее по модулю
Продолжение
402 Глава 7. Эффекты квантования в цифровых системах
Таблица 7.3 (продолжение) . '
Имя свойстве
OverfiowMode
Format
Описвние
Реакция на переполнение (только для формата с фиксированной
запятой):
1 saturate' — при переполнении происходит насыщение (этот вариант
принят по умолчанию);
'wrap' — при переполнении игнорируются «лишние» старшие разряды
Двухэлементный вектор, первый элемент которого задает общее число
двоичных разрядов, используемое для представления квантованных
чисел. Второй элемент вектора для квантователей с фиксированной
запятой (Mode ■ 'fixed' или 'ufixed') указывает число разрядов
дробной части, а для квантователей с плавающей запятой
(Mode = ' f 1 oat') — число разрядов; используемое для представления
порядка. Значение по умолчанию равно [16 15]
Значения свойств Max, Min, Noperations, Noverflows и Nunderflows, предоставляющих
статистическую информацию и доступных только для чтения, обновляются при
каждом выполнении операции квантования (функция quantize, см. далее) и об-
обнуляются при выполнении функции reset.
Операция квантования выполняется с помощью функции quantize. Синтаксис ее
вызова следующий:
у = quantize(q. x)
Здесь q — объект квантователя, ах — массив значений входного сигнала. Резуль-
Результатом работы является массив квантованных значений у. Размеры массивов х и у
одинаковы.
Можно вызывать функцию quantize для квантования нескольких переменных
одновременно:
[yl. у2, ...] = quantized, xl, х2. ...)
Здесь yl — результат квантования xl, у2 — результат квантования х2 и т. д.
Как отмечалось в разделе «Формат с фиксированной запятой», диапазон пред-
ставимых в таком формате чисел является несимметричным. В частности, если
целая часть содержит единственный знаковый разряд, оказывается невозмож-
невозможным точно представить значение +1. Для решения этой проблемы в пакете Filter
Design имеются функция unitquantize и объект unitquantizer.
Функция unitquantize вызывается точно так же, как и функция quantize:
у = unitquantize(q, x) , ■
[yl. у2. ...] = unitquantize(q, xl. x2. ...)
Работа этой функции отличается от функции quantize лишь в одном аспекте: зна-
значения, близкие к единице (точнее, отстоящие от нее не более чем на eps, где eps —
точность представления чисел в квантователе, см. далее), при квантовании ста-
становятся равными единице.
Функции пакета расширения Filter Design
403
Чтобы пояснить разницу между функциями quantize и unitquantize, приведем
простой пример. Создадим квантователь с фиксированной запятой, использую-
использующий один разряд для целой части и 7 — для дробной:
» q = quantizer('fixed', [8 7]):
Теперь произведем квантование единичного значения с помощью данного кван-
квантователя и функций quantize и unitquantize:
» quantize(q. 1)
Warning: 1 overflow.
> In ...design\quantization\@quantizer\quantize.m at line 88
ans = ■■
0.9922. ■ . ■ . .
» unitquantize(q. 1) '
ans =
1 . , - ,■ ,
При использовании функции quantize было выдано предупреждение о произо-
произошедшем переполнении (строка с длинным путем к М-файлу функции quantize
в приведенном листинге сокращена), а квантованное значение оказалось мень-
меньше единицы (оно равно максимальному числу, нредставимому в используемом
нами формате 1.7). При использовании же функции unitquantize переполнения
не происходит, а результат квантования оказывается равен единице.
Той же цели — обеспечению точного представления единичных значений — слу-
служит и объект unitquantizer. Он полностью аналогичен объекту quantizer, но для
него не нужно явно вызывать функцию unitquantize — это будет сделано автома-
автоматически при обычном квантовании.
ВНИМАНИЕ
Перечисленные трюки с квантованием единичных значений становятся возможны исклю-
исключительно благодаря тому, что MATLAB использует для представления всех дробных чи-
чисел (как неквантованных, так и квантованных) формат с плавающей запятой double. При
реализации алгоритмов обработки сигнала «в железе» или па языках высокого уровня с
использованием целочисленной арифметики точно представить непредставимые значе-
значения, естественно, не удастся. Зачем же,тогда пакет Filter Design содержит такие средства?
Дело в том, что объекты квантователей предназначены прежде всего для использования в
составе квантованных фильтров и БПФ, которые будут рассматриваться далее. При ре-
реальной обработке сигналов этими устройствами проблему с единичными значениями
можно обойти, проигнорировав операции умножения отсчетов сигнала на коэффициенты,
равные единице. В MATLAB же при установке режима оптимизации умножений (свойст-
(свойство OptimizeUnityGains, см. далее) для коэффициентов фильтров и БПФ используются
квантователи типа unitquantizer. Это позволяет не модифицировать общий алгоритм вы-
вычислений.
Для иллюстрации сказанного создадим объект unitquantizer с теми же парамет-
параметрами, как у квантователя в предыдущем примере, и выполним квантование еди-
единичного значения:
404 Глава 7. Эффекты квантования в цифровых системах
» uq = unitquantizer('fixed'. [8 7]);
» quantize(uq. 1)
ans =
1
Как видите, переполнения не произошло, а результат равен единице.
Помимо функций quantize и unitquantize с объектами квантователей могут рабо-
работать следующие функций:
□ ql = copyobj(q) — создает независимую копию объекта квантователя с теми же
значениями свойств, что у исходного объекта q;
ВНИМАНИЕ
Программная реализация обычной операции присваивания объектов в MATLAB (ql = q)
сводится к копированию указателя, так что в результате оба идентификатора ссылаются
на одну и ту же область памяти. Функция же copyobj создает новый объект и копирует в
него все значения свойств оригинала.
□ х = denormalmax(q) — для квантователей с плавающей запятой возвращает зна-
значение наибольшего денормализованиого положительного квантованного чис-
числа. Для квантователей с фиксированной запятой возвращает eps(q);
□ х = denormaimin(q) — для квантователей с плавающей запятой возвращает зна-
значение наименьшего депормализоваипого положительного квантованного чис-
числа. Для квантователей с фиксированной запятой возвращает eps(q);
□ disp(q) — выводит на экран свойства объекта;
□ е = eps(q) — возвращает относительную точность представления чисел в кван-
квантователе q. Под точностью представления подразумевается минимальное чис-
число, при добавлении которого к единице результат квантования будет отли-
отличаться от единицы;
□ b = exponentbias(q) — возвращает смещение, используемое в квантователе с
плавающей запятой при представлении порядка квантованных чисел. В слу-
случае формата с фиксированной занятой результат всегда равен нулю;
□ е = exponent!ength(q) — возвращает число двоичных разрядов, используемое в
квантователе с плавающей запятой для представления порядка квантованных
чисел. В случае формата с фиксированной запятой результат всегда равен нулю;
□ etnax = exponentmax(q) — если в квантователе используется формат с плаваю-
плавающей запятой, возвращает максимальное значение порядка квантованных чи-
чисел. В случае формата с фиксированной запятой результат всегда равен нулю;
□ etnin = exponentmin(q) — если в квантователе используется формат с плаваю-
плавающей запятой, возвращает минимальное значение порядка квантованных чи-
чисел. В случае формата с фиксированной запятой результат всегда равен нулю;
□ f = fraction!ength(q) — возвращает количество разрядов дробной части кван-
квантованных чисел;
□ х = hex2num(q, h) — преобразование строки h, трактуемой как шестнадпатерич-
ная запись внутреннего представления квантованного числа в квантователе q,
в число х;
Функции пакета расширения Filter Design 405
□ х = max(q) — возвращает значение свойства Мах;
□ х = min(q) — возвращает значение свойства Min;
□ n = noperations(q) — возвращает значение свойства Noperations;
□ n = noverflows(q) — возвращает значение свойства Noverflows;
□ h = num2hex(q. x) — преобразование числа х в строку h, представляющую собой
шестиадцатеричную запись квантованного числа, в соответствии с форматом,
используемым квантователем q;
□ n = nunderflows(q) — возвращает значение свойства Nunderflows;
□ qreport(q) — выводит на экран статистическую информацию о работе кванто-
квантователя (максимальное и минимальное значения входного сигнала, число пе-
переполнений и случаев потери значимости, а также количество выполненных
квантований);
□ s = qreport(q) — возвращает ту же информацию в полях структуры s;
□ г = range(q) — возвращает двухэлементный вектор, содержащий минимальное
и максимальное значения выходного квантованного сигнала для квантовате-
квантователя q; ч
□ [a. b] = range(q) — возвращает минимальное и максимальное значения вы-
выходного квантованного сигнала для квантователя q в виде двух отдельных пе-
переменных а (минимальное значение) и b (максимальное значение);
□ х = realmax(q) — возвращает наибольшее положительное квантованное число;
□ х = realmin(q) — возвращает наименьшее положительное нормализованное кван-
квантованное число;
□ reset(q) — сбрасывает в исходное состояние значения свойств квантователя q,
связанных со сбором статистической информации (Max, Min, Noperations, Nover-
Noverflows и Nunderflows);
□ s = tostring(q) — возвращает строку вызова функции quantizer, в результате
выполнения которой будет создан объект, совпадающий с объектом q;
□ w = wordlength(q) — возвращает общее число двоичных разрядов, используе-
используемое квантователем для представления квантованных чисел.
В качестве примера использования функций quantizer и quantize создадим объ-
объекты квантователей с фиксированной и плавающей запятой, а затем построим
для них графики характеристик квантования, то есть зависимости выходного
(квантованного) сигнала от входного (неквантованного).
Чтобы на этих графиках был хорошо виден ступенчатый характер зависимостей,
число уровней квантования должно быть небольшим, поэтому будем использо-
использовать длину слова, равную шести двоичным разрядам.
В квантователе с фиксированной запятой дробная часть будет содержать пять
разрядов. Для обработки переполнений зададим режим насыщения, а всем ос-
остальным свойствам оставим значения по умолчанию:
» q_fixed = quantizer^'fixed'. [6 5]. 'saturate')
q_fixed =
406 Глава 7. Эффекты квантования в цифровых системах
Mode = fixed
RoundMode = floor
OverflowMode = saturate
Format = [6 5]
Max = reset
Min = reset
NOverflows = 0
NUnderflows = 0
NOperations = 0
Построим график характеристики квантования (рис. 7.11 сверху), выбрав такой
диапазон значений входного сигнала, чтобы вызвать переполнение квантователя.
Для автоматического определения этого диапазона используем функцию real max:
» x_max=2*realmax(q_fixed):
» х = linspace(-xjnax. xjnax, 1000):
» у = quantize(q_fixed. x):
Warning: 484 overflows.
> In ...design\quantization\@quantizer\quantize.m at line 88
» plot(x, y)
Теперь изменим режим обработки переполнения, чтобы вместо насыщения про-
происходило отбрасывание «лишних» старших разрядов. Затем снова построим ха-
характеристику квантования (рис. 7.11 снизу):
» q_fixed.overflowmode = 'wrap':
» у = quantize(q_fixed, x):
Warning: 484 overflows.
> In ...design\quantization\@quantizer\quantize.m at line 88
» plot(x. y)
Графики на рис. 7.11 наглядно иллюстрируют сущность различий между режи-
режимами обработки переполнений 'saturate' и 'wrap'.
В квантователе с плавающей запятой используем три разряда для хранения по-
порядка. Значения остальных свойств оставим установленными по умолчанию:
» q_float = quantizer^ 'float'. [6 3])
q_float =
Mode = float
RoundMode = floor
Format = [6 .3]
Max = reset
Min = reset
NOverflows = 0
NUnderflows = 0
NOperations = 0
Функции пакета расширения Filter Design
407
-2
-1.5
-1
-0.5
0.5
1
Рис. 7.11. Характеристика квантования для квантователя с фиксированной запятой:
сверху — при переполнении происходит насыщение, снизу — при переполнении
отбрасываются старшие разряды
Теперь строим характеристику квантования так же, как и раньше (рис. 7.12):
» x_max=1.2*realmax(q_float):
» х = linspace(-xjnax. xjnax. 1000):
» у = quantize(q_f1 oat. x):
Warning: 168 overflows.
> In ...design\quantization\@quantizer\quantize.m at line 88
» plot(x. y)
408
Глава 7. Эффекты квантования в цифровых системах
0 -15 -10 -5 0 5 10 15 20
Рис. 7.12. Характеристика квантования для квантователя с плавающей запятой
Сравнение характеристик квантования на рис. 7.11 и 7.12 наглядно демонстри-
демонстрирует особенности квантователей с фиксированной и плавающей запятой.
Квантованные фильтры
Для создания объекта квантованного фильтра служит функция qf i 11. В простей-
простейшем случае она может вызываться без входных параметров, но для фильтра это
не имеет особого смысла — ведь нам в любом случае необходимо задать форму
реализации и коэффициенты. Поэтому основным вариантом синтаксиса являет-
является следующий:
hq = qfi11С'structure'. {coef})
Здесь ' structure' — строковый параметр, задающий форму реализации фильтра,
a {coef} — массив ячеек, содержащий исходные (неквантованпые) коэффициен-
коэффициенты фильтра. Способ задания коэффициентов зависит от выбранной формы реа-
реализации фильтра, соответствующая информация сведена в табл. 7.4. .
ЗАМЕЧАНИЕ
Возможны также следующие варианты для параметра structure', соответствующие ре- ■
шетчатым фильтрам, не рассматриваемым в данной книге: 'latticear', 'latticema', 'latti- ■;
cearma', 'latticeca' и 'latticecapc'. Ознакомиться со способами задания коэффициентов |
фильтра для этих форм реализации можно но документации пакета Filter Design. i
Для задания свойств объекта (их список будет приведен ниже) можно указывать
при вызове функции qfilt дополнительные параметры в виде пар «имя свойст-
свойства — значение свойства»:
hq = qf i It С 'structure'. {coeff}, 'namel', valuel, 'name2'. value2. ...)
Здесь 'namel', 'name2' и т. д. — имена свойств, a valuel, va1ue2 и т. д. — соответст-
соответствующие значения.
Таблица 7.4. Возможные формы реализации квантованных фильтров и способы задания коэффициентов для них
Значение параметра
'structure'
'dfl'
"dflf
'df2'
'df2t'
'fir'
"firf
'symmetricfir'
'antisymmetricfir'
' statespace'
Форма реализации фильтра
Direct Form I (прямая форма, см. рис. 4.4)
Direct Form I Transposed (транспонированная
форма, см. рис. 4.9)
Direct Form II (каноническая форма,
см. рис. 4.6)
Direct Form II Transposed (транспонированная
форма, см. рис. 4.8)
FIR (прямая форма нерекурсивного фильтра,
см. рис. 4.3)
FIR Transposed (транспонированная форма
нерекурсивного фильтра)
Symmetric FIR (нерекурсивный фильтр С
четной симметрией, см. табл. 4.1, типы I и II)
Antisymmetric FIR (нерекурсивный фильтр с
нечетной симметрией, см. табл. 4.1, типы III
и IV)
Реализация в пространстве состояний
Способ задания коэффициентов
{coef} = {b, а}, то есть параметр {coef} должен быть массивом
ячеек, содержащим два вектора, задающие коэффициенты
полиномов числителя и знаменателя функции передачи фильтра
То же, что для 'dfl'
То же, что для 'dfl'
То же, что для 'dfl'
{coef} = {b}, то есть параметр {coef} должен быть массивом
ячеек, содержащим единственный вектор b отсчетов
импульсной характеристики фильтра
То же, что для 'fir'
То же, что для 'fir', но вектор b должен удовлетворять
условиям четной симметрии: b(k) = b(length(b)+l-k)
То же, что для 'fir', по вектор b должен удовлетворять
условиям нечетной симметрии: b(k) = -b(length(b)+l-k).
Если длина вектора нечетная, то средний элемент должен
быть нулевым: b(Oength(b)+l)/2) = 0
{coef} = {А, В, С, D}, то есть параметр {coef} должен
содержать четыре ячейки с параметрами описания фильтра
в пространстве состояний (см. раздел «Пространство
состояний» главы 4)
410 Глава 7. Эффекты квантования в цифровых системах
Особо отметим еще один вариант вызова, позволяющий задать общий формат
квантования для всех величин в фильтре. Для этого в списке параметров нужно
задать значение свойства'quantizer':
hq = qfilt(.... 'quantizer', [M N]. ...)
В результате для всех величин будет использован формат с фиксированной за-
запятой с длиной слова М бит и N битами после запятой.
Список свойств квантованного фильтра приведен в табл. 7.5. Как уже говори-
говорилось, считывать и задавать значения этих свойств можно с помощью функций
get и set соответственно.
Обработка сигнала квантованным фильтром осуществляется, как уже было ска-
сказано, с помощью функции filter:
[у. zo. s. z. v] = filter(hq. x, zi)
Здесь hq — объект квантованного фильтра, х — входной сигнал, zi — начальное
состояние фильтра (этот параметр является необязательным).
Результатами работы функции являются выходной сигнал у, конечное внутрен-
внутреннее состояние фильтра zo и три параметра, позволяющие получить информацию
о «внутренней жизни» фильтра в процессе работы:
□ s — структура, содержащая информацию о работе квантователей (она созда-
создается функцией qreport, см. далее);
□ z — массив ячеек, содержащий историю изменений внутренних состояний
для всех секций фильтра. Ячейка к соответствует k-\i секции фильтра, а со-
содержимое ячейки представляет собой матрицу, каждый столбец которой дает
внутреннее состояние k-й секции в соответствующий момент времени. Так,
начальное состояние k-й секции равно z{k}(:, 1), а конечное — z{k}(: .end);
□ v — массив ячеек, содержащий количество переполнений, произошедших в
каждой секции фильтра на каждом временном шаге. Ячейка к соответствует
k-й секции фильтра и содержит вектор, значения которого показывают коли-
количество переполнений в данной секции на разных временных тактах.
Помимо функции filter пакет Filter Design расширяет реализации функций
freqz, impz и zplane, так что они тоже могут вместо двух векторов а и b принимать
на входе объект квантованного фильтра для расчета или отображения его соот-
соответствующих характеристик: . .
freqz(hq, ...)
impz(hq. ...)
zplaneChq. ...)
Кроме перечисленных функций с объектами квантованных фильтров могут ра-
работать следующие функции: .■.•.-,,
□ hql = convert (hq, 'newstruct') — производит преобразование формы реализа-
реализации квантованного фильтра. Новая форма задается параметром 'newstruct';
□ hql = copyobj(hq) — создает независимую копию объекта квантованного фильт-
фильтра с теми же значениями свойств, что у исходного объекта hq (см. приведенный
ранее комментарий к одноименной функции для объектов квантователей);
Функции пакета расширения Filter Design
411
Таблица 7.5. Свойства объекта квантованного фильтра
Имя свойстве
CoefficientFormat
FilterStructure
InputFormat
NumberOfSections
MultiplicandFormat
OptimizeUnityGains
OutputFormat
ProductFormat
Quanti zedCoeff1cients
ReferenceCoeff1ci ents
SealeValues
StatesPerSectiori
SumFormat
Описание
Объект quantizer, задающий формат квантования
коэффициентов фильтра
Форма реализации фильтра (см. табл. 7.4)
Объект quantizer, задающий формат квантования входного
сигнала
Число каскадно включенных секций фильтра (только для
чтения)
Объект quantizer, задающий формат квантования чисел,
умножаемых на коэффициенты фильтра
Это свойство не отображается в явном виде при выводе инфор-
информации об объекте на экран, поскольку ему не соответствует
поле структуры объекта. Однако значение этого свойства можно
считывать и задавать (возможные варианты — 'on' и принятое
по умолчанию 'off'). Если установлено состояние 'on', при
вычислениях будут исключены умножения на коэффициенты,
равные единице. Кроме того, при этом для квантования
коэффициентов фильтра вместо объекта quanti zer будет
использован объект unitquantizer, что позволяет точно пред-
представлять единичные значения
Объект quantizer, задающий формат квантования выходного
сигнала
Объект quantizer, задающий формат квантования результатов
операций умножения
Коэффициенты фильтра после квантования (только для
чтения)
Исходные (до квантования) коэффициенты фильтра
Коэффициенты масштабирования входных и выходных сигна-
сигналов секций фильтра. Это свойство может быть скаляром (тогда
на заданный коэффициент умножается только входной сигнал
фильтра) либо вектором с числом элементов, на единицу пре-
превышающим число секций фильтра. В последнем случае первый
элемент вектора задает коэффициент масштабирования для
входного сигнала, последующие значения используются для
масштабирования сигнала между секциями, а последний коэф-
коэффициент применяется к выходному сигналу фильтра
Число элементов памяти (задержек) в каждой секции фильтра
(только для чтения)
Объект quantizer, задающий формат квантования результатов
операций сложения
412 Глава 7. Эффекты квантования в цифровых системах
□ disp(hq) — выводит на экран свойства объекта;
□ eps(hq) — выводит на экран относительную точность представления чисел в
квантованном фильтре;
□ flag = i sail pass (hq) — возвращает 1, если фильтр hq имеет всепропускающие
секции, и 0 в противном случае;
□ flag = i sail pass (hq. k) — возвращает 1, если k-я секция фильтра hq является
всепропускающей, и 0 в противном случае;
□ flag = isfir(hq) — возвращает 1, если фильтр hq является нерекурсивным,
и 0 в противном случае;
□ flag = isfir(hq, k) — возвращает 1, если k-я секция фильтра hq является нере-
нерекурсивной, и 0 в противном случае;
□ flag = islinphase(hq) — возвращает 1, если фильтр hq имеет хотя бы одну сек-
секцию с линейной ФЧХ, и 0 в противном случае;
□ flag = islinphaseChq. k) — возвращает 1, если k-я секция фильтра hq имеет ли-
линейную ФЧХ, и 0 в противном случае;
□ flag = ismaxphase(hq) — возвращает 1, если фильтр hq имеет хотя бы одну мак-
максимально-фазовую секцию (все нули функции передачи которой лежат на
комплексной плоскости вне единичной окружности или на ней), и 0 в против-
противном случае;
□ flag = ismaxphase(hq, k) — возвращает 1, если k-я секция фильтра hq является
максимально-фазовой, и 0 в противном случае;
□ flag = isminphase(hq) — возвращает 1, если фильтр hq имеет хотя бы одну ми-
минимально-фазовую секцию (все нули функции передачи которой лежат на ком-
комплексной плоскости внутри единичной окружности или на ней), и 0 в про-
противном случае;
□ flag = isminphase(hq, k) — возвращает 1, если k-я секция фильтра hq является
минимально-фазовой, и 0 в противном случае;
□ flag = isreal(hq) — возвращает 1, если все исходные коэффициенты фильт-
фильтра hq являются вещественными, и 0 в противном случае;
□ flag = issos(hq) — возвращает 1, если фильтр hq составлен из секций второ-
второго порядка, то есть если порядок любой его секции не превосходит двух, и О
в противном случае;
□ flag = isstable(hq) — возвращает 1, если фильтр hq является устойчивым, и О
в противном случае;
□ flag = isstable(hq. k) — возвращает 1, если k-я секция фильтра hq является
устойчивой, и 0 в противном случае;
□ limitcycle — функция анализа предельных циклов в квантованных фильтрах.
Она будет подробно рассмотрена далее;
□ nl m — функция оценки частотной характеристики квантованного фильтра шу-
шумовым методом (noise loading method, NLM). Рассмотрение этого метода вы-
выходит за рамки тематики данной книги;
□ noperations(hq) — выводит на экран сведения о числе операций квантования,
выполненных различными квантователями квантованного фильтра hq;
Функции пакета расширения Filter Design
413
□ hql = normal ize(hq) — нормализация коэффициентов квантованного фильтра.
Возвращаемый объект квантованного фильтра hql имеет коэффициенты, по
модулю не превосходящие единицу. Нормализация производится путем деле-
деления всех коэффициентов на одно и то же число, равное степени двойки. Если
фильтр составлен из последовательно включенных секций, нормализация для
каждой секции выполняется независимо. Нормализации не могут подвергать-
подвергаться фильтры, реализованные в пространстве состояний (state-space), и решет-
решетчатые (lattice) фильтры;
□ noverflows(hq) — выводит на экран сведения о числе переполнений, возник-
возникших при выполнении операций квантования различными квантователями кван-
квантованного фильтра hq;
□ num2bin(hq) — отображает квантованные коэффициенты фильтра в виде дво-
двоичных строк (то есть строк, содержащих символы ' 0' и ' 1');
□ с - num2bin(hq) — возвращает массив ячеек, содержащий значения квантован-
квантованных коэффициентов фильтра в виде двоичных строк;
□ num2hex(hq) — отображает квантованные коэффициенты фильтра в виде шест-
надцатеричных строк (то есть строк, содержащих символы '0'...'9' и 'A'...'F');
□ с = num2hex(hq) — возвращает массив ячеек, содержащий значения квантован-
квантованных коэффициентов фильтра в виде шестнадцатеричных строк;
□ num2int(hq) — отображает квантованные коэффициенты фильтра в виде целых
чисел;
□ с = num2int(hq) — возвращает массив ячеек, содержащий значения квантован-
квантованных коэффициентов фильтра в виде целых чисел;
□ ns = numberofsections(hq) — возвращает число секций квантованного фильт-
фильтра hq;
□ opt = optimizeunitygains(hq) — возвращает значение свойства Opti mi zellnityGains;
□ n = order(hq) — возвращает порядок фильтра;
□ n - order(hq, k) — возвращает порядок k-й секции фильтра;
□ [bq. aq, br, ar] = qfiH2tf(hq) — расчет функции передачи квантованного
фильтра. Выходные параметры bq и aq содержат значения коэффициентов по-
полиномов числителя и знаменателя функции передачи квантованного фильт-
фильтра, a br и аг — аналогичные коэффициенты для исходного фильтра;
□ [cq, cr] = qfilt2tf(hq, 'sections') — возвращает массивы ячеек, содержащие
функции передачи отдельных секций квантованного (cq) и исходного (сг)
фильтров. Поясним структуру возвращаемых массивов ячеек на примере мас-
массива cq: cq = {{bql.aql}, {bq2.aq2}....}, где bql и aql — коэффициенты полино-
полиномов числителя и знаменателя функции передачи первой секции фильтра, bq2
и aq2 — то же для второй секции и т. д.;
□ qreport(q) — выводит на экран статистическую информацию о работе кванто-
квантователей, входящих в состав фильтра (максимальное и минимальное значения
входного сигнала, число переполнений и случаев потери значимости, а также
количество выполненных квантований);
□ s = qreport(q) — возвращает ту же информацию в полях структуры s;
414 Глава 7. Эффекты квантования в цифровых системах
□ range(hq) — отображает сведения о минимальных и максимальных значениях
выходного квантованного сигнала для квантователей, входящих в состав объ-
объекта квантованного фильтра hq;
□ [Rl, R2, ...] = range(hq, Tl, T2, ...) — возвращает двухэлементные векторы Rl, R2
и т. д., содержащие минимальные и максимальные значения выходного кван-
квантованного сигнала для квантователей, входящих в состав объекта кванто-
квантованного фильтра hq и указанных входными строковыми параметрами Tl, T2
и т. д. Возможные значения этих параметров — 'coefficient', ' input', 'output',
'multiplicand', 'product' и 'sum';
□ reset (hq) — сбрасывает в исходное состояние значения свойств, связанных со
сбором статистической информации (Max, Min, Noperations, Noverflows и Nunder-
flows), для всех квантователей, входящих в состав квантованного фильтра hq;
□ s = scalevalues(hq) — возвращает значение свойства ScaieValues;
□ hql » setbits(hq, format) — задает значение свойства Format для всех квантова-
квантователей, входящих в состав квантованного фильтра hq;
□ hql » sos(hq, order, scale) — преобразование квантованного фильтра hq в на-
набор последовательно включенных секций второго порядка (объект hql). Смысл
необязательных параметров order и scale тот же, что и для функции tf2sos
(см. раздел «Преобразование способов описания дискретных фильтров» гла-
главы 4);
□ s = tostring(hq) — возвращает строку вызова функции qfilt, в результате вы-
выполнения которой будет создан объект, совпадающий с объектом hq.
В качестве примера рассчитаем эллиптический Ф.НЧ 5-го порядка, создадим для
него объект квантованного фильтра и произведем с помощью этого фильтра об-
обработку последовательности прямоугольных импульсов.
Пусть ФНЧ имеет частоту среза, равную 20 % от частоты Найквиста, пульсации
АЧХ в полосе пропускания 1 дБ и ослабление в полосе задерживания 40 дБ:
» [b. a] = ellipE. 1. 40. 0.2)
b =
0.0153 -0.0221 0.0154. 0.0154 -0.0221 0.0153
а = !
1.0000 -3.^043 6.5819 -5.8940 2.7935 -0.5599
Как видите, ряд коэффициентов фильтра по модулю превышает единицу. Чтобы
использовать параметры квантователей по умолчанию, коэффициенты фильтра
необходимо привести к диапазону [-1, 1]. Поэтому при создании объекта кван-
квантованного фильтра мы разделим векторы b и а на 8:
» hq = qfi1t('df2t'. {b/8. a/8})
hq =
Quantized Direct form II transposed filter !
Numerator . :
QuantizedCoefficientsjl} ReferenceCoefficients{l}
A) 0.001922607421875 0.001915044555875759
B) -0.002746582031250 -0.002760232429165185 ' . '. -•
Функции пакета расширения Filter Design
415
C) 0.001922607421875
D) 0.001922607421875
E) -0.002746582031250
F) 0.001922607421875
Denominator
QuantizedCoefficients{2}
A) 0.125000000000000
B) -0.488037109375000
C) 0.822753906250000
D) -0.736755371093750
E) 0.349182128906250
F) -0.069976806640625
FilterStructure = df2t
ScaieVaiues - [1]
NumberOfSections - 1
StatesPerSection - [5]
CoefficientFormat - quantizer^
InputFormat - quantizer^
OutputFormat - quantizer(
MultipiicandFormat = quantizer(
ProductForraat - quantizer^
SumFormat = quantizer(
0.001923857337327012
0.001923857337327022
-0.002760232429165193
0.001915044555875762
ReferenceCoeffi с i ents{2}
0.125000000000000000
-0.488037284420594630
0.822741734035389300
-0.736744248400267980
0.349188852654597430
-0.069991714941048944
fixed', 'round', 'saturate', [16 15])
fixed', 'floor', 'saturate'. [16 15])
fixed', 'floor', 'saturate', [16 15])
fixed', 'floor', 'saturate'. [16 15])
fixed', 'floor', 'saturate', [32 30])
fixed', 'floor', 'saturate'. [32 30])
Мы использовали стандартную для MATLAB форму реализации фильтра — Direct
Form II Transposed (см. рис. 4.8 в главе 4).
Теперь построим графики АЧХ и ФЧХ квантованного фильтра. Для этого вос-
воспользуемся функцией freqz (рис. 7.13):
» freqz(hq)
Quantized response
Reference response
0.2 0.4 0.6 0.8
Normalized Frequency (хтс rad/sampla)
0.2 0.4 0.6 0.8
Normalized Frequency (xn rad/sample)
Рис. 7.13. АЧХ и ФЧХ каантоаанного эллиптического ФНЧ 5-го порядка
416 Глава 7. Эффекты квантования в цифровых системах
На графиках зеленым цветом выводятся характеристики исходного фильтра,
а синим — квантованного. Однако в данном случае благодаря выполненному
нами масштабированию коэффициентов (делению их на 8) и довольно высокой
A5 двоичных разрядов после запятой) точности их квантованного представле-
представления разница характеристик практически незаметна.
Далее создаем входной сигнал в виде нескольких двуполярных прямоугольных
импульсов с амплитудой 0,8:
» х = 0.8 * [ones(l.lOO) -ones(l.lOO) ones(l.lOO)];
Чтобы пропустить этот сигнал через исходный (неквантованный) фильтр, вос-
воспользуемся функцией fi I ter:
» у = filter(b. a. x);
Та же функция используется и для обработки сигнала квантованным фильтром:
» y_q = filter(hq. x):
Warning: 173 overflows in QFILT/FILTER.
> In ...\filterdesign\quantization\@qfilt\filter.m at line 241
Max Min NOverflows NUnderflows NOperations
Coefficient
Input
Output
Multiplicand
Product
Sum
0.8227
0.8
1
2
6.498-
1.194
-0.7367
-0.8
-1
-2
-6.515
-1.303
0
0
0
1056
173
0
0
0
0
0
0
0
12
300
300
4200
4200
3300
Наконец, строим графики выходного сигнала для исходного (рис. 7.14 сверху) и
квантованного (рис. 7.14 снизу) фильтров:
» plot(y)
» figure
» plot(y_q)
Сравнение верхнего и нижнего графиков на рис. 7.14 показывает, что, хотя абсо-
абсолютные значения сигнала на выходе исходного фильтра не превосходят едини-
единицы, выходной сигнал квантованного фильтра похож на исходный только в те-
течение первой половины периода, а после этого квантованный фильтр, как
говорится, «идет вразнос». Это происходит из-за того, что при промежуточных
вычислениях (а точнее, как свидетельствует выдаваемая статистическая инфор-
информация, при квантовании результатов умножения) происходит большое число пе-
переполнений. Таким образом, предельная амплитуда правильно обрабатываемой
последовательности прямоугольных импульсов должна быть ощутимо меньше
единицы (в данном конкретном примере переполнения исчезают при амплитуде
прямоугольных импульсов, равной 0,78). Альтернативой уменьшению уровня
входного сигнала является использование квантователей с более высокой верх-
верхней границей диапазона представимых чисел.
Функции пакета расширения Filter Design
417
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
'1 0 50 100 150 200 250 300
Рис. 7.14. Выходной сигнал неквантованного (сверху) и квантованного (снизу) фильтров
| Д 111
Анализ предельных циклов
Для проверки возможности возникновения предельных циклов в квантованном
фильтре служит функция limitcycle. Синтаксис ее вызова следующий:
[LCtype, Zi. Period. Seq. Ovf, Trial. Section] = ...
limitcycle(hq, N. L. Stop. Disp)
Единственным обязательным входным параметром здесь является hq — объект
квантованного фильтра. Остальные входные параметры имеют значения по умол-
умолчанию.
Сущность работы функции limitcycle состоит в задании случайных начальных
состояний фильтра и анализе его поведения при нулевом входном сигнале. Чис-
Число испытаний задается параметром N и по умолчанию равно 20.
Параметр L задает продолжительность анализа (длительность нулевого входного
сигнала). По умолчанию поведение фильтра анализируется в течение 100 отсчетов.
418 Глава 7. Эффекты квантования в цифровых системах
Строковый параметр Stop позволяет управлять критерием остановки работы функ-
функции. Возможны следующие значения:
□ 'попе' — независимо от обнаружения предельных циклов выполняются все
N испытаний;
□ 'granular' — остановка работы производится при обнаружении «зернистого»
предельного цикла;
□ 'overflow' — остановка работы производится при обнаружении «переполняю-
«переполняющего» предельного цикла;
□ 'either' — остановка работы производится при обнаружении предельного
цикла любого типа (этот вариант используется по умолчанию).
Наконец, если параметр D1sp не равен нулю, в процессе работы после каждого ис-
испытания выводятся текстовые сообщения о результатах. При обнаружении пре-
предельного цикла и отсутствии выходных параметров сообщение выводится в лю-
любом случае, вне зависимости от значения параметра Di sp.
Функция может возвращать большое количество выходных параметров, содер-
содержащих информацию о результатах анализа:
□ LCtype — строка, показывающая тип обнаруженного предельного цикла и рав-
равная 'granular', 'overflow' или 'none';
□ Zi — вектор начального состояния фильтра, вызвавшего предельный цикл;
□ Period — период предельного цикла;
□ Seq — последовательность внутренних состояний фильтра в предельном цик-
цикле. Каждый столбец матрицы Seq соответствует внутреннему состоянию фильт-
фильтра в очередной момент времени;
□ Ovf — массив ячеек, в котором ячейка {к} содержит целочисленный вектор,
показывающий число переполнений, произошедших в k-й секции фильтра на
всех тактах предельного цикла;
□ Trial — номер испытания, на котором обнаружен предельный цикл;
□ Section — номер секции фильтра, в которой обнаружен предельный цикл.
Если в процессе работы функции было найдено несколько предельных циклов,
возвращаются сведения о последнем из них. Если циклов не обнаружено, воз-
возвращаются просто параметры последнего испытания.
Расширение программы fdatool
Пакет Filter Design расширяет графическую среду расчета и анализа фильтров
fdatool, добавляя в нее возможность описания и анализа квантованных фильтров.
Для выполнения квантования фильтра необходимо установить флажок Turn quan-
quantization on и перейти на вкладку Set Quantization Parameters, показанную на рис. 7.15.
В левой части вкладки расположена кнопка Show filter structures. Щелчок на ней
открывает окно, показанное на рис. 7.16. Оно содержит раскрывающийся список
возможных форм реализации квантованного фильтра (см. табл. 7.4) и блок-схе-
блок-схему, которая меняется в соответствии с выбранной формой.
Функции пакета расширения Filter Design
419
tool [unfilled Idd "I
3*f>
_Cw**f tar Wbmmw» . . .
tfmtoala*
tstwtdeuoun 1
Пне"
■0*/ «
-«MM*», , .
0
% -SO
«-108
1 OS
"' ' Y '
Qd?-tl2«r
1 t 5
Frequenty Dj)
- I
i
2
no* *j
OumUwli*» - Ио&г - Fcundmwie -
ЗРГЗП^~1
~J
tJ I i*
|'«= ZJ
i -»= ZJ
1 9i.ee
3 П ■--■'
Рис. 7.15. Вкладка задания параметров квантования фильтра
» S*
а»
qEixti dll ЛЬ *}
<Jf1
(Direct Form I)
f ■""" *i
kttl
л ■•<■'?
»CW
Рис. 7.16. Окно блок-схем возможных форм реализации квантованного фильтра
420 Глава 7. Эффекты квантования в цифровых системах
ВНИМАНИЕ
Необходимо подчеркнуть, что в данном окне лишь демонстрируются блок-схемы для воз-
возможных форм реализации фильтров. Реальный выбор формы реализации производится
в окне, появляющемся после щелчка на кнопке Convert structure.
В левой верхней части вкладки Set Quantization Parameters находится кнопка
Scale transfer-fen coeffs <= 1. Щелчок на этой кнопке производит автоматическое
масштабирование коэффициентов фильтра так, чтобы их абсолютные значения
не превышали единицы (см. ранее в этой главе раздел «Масштабирование коэф-
коэффициентов цифровых фильтров», а также описание функции normalize). При
этом синхронно меняется и содержимое расположенного ниже поля ввода Input/
output scaling. В этом поле задаются коэффициенты масштабирования сигналов в
квантованном фильтре (см. выше описание свойства ScaleValues в табл. 7.5).
Большую часть вкладки занимают шесть групп элементов настройки параметров
квантователей. Подписи к группам очевидным образом соответствуют именам
свойств объекта квантованного фильтра (см. табл. 7.5). Каждая группа содержит
следующие элементы управления (подробные комментарии о смысле задавае-
задаваемых ими параметров квантователей были приведены в табл. 7.3, где перечислены
свойства объектов квантователей):
□ раскрывающийся список Quantizer type позволяет задать класс объекта кван-
квантователя — quantizer или unitquantizer;
□ раскрывающийся список Mode позволяет задавать тип квантователя — с фик-
фиксированной (fixed) или плавающей (float) запятой. Есть также два предопре-
предопределенных варианта квантователей с плавающей запятой — double и single;
□ раскрывающийся список Round mode позволяет задавать режим округления
при квантовании — ceil, convergent, fix, floor или round;
□ раскрывающийся список Overflow mode позволяет задавать режим обработки
переполнений при квантовании — saturate или wrap;
□ поле ввода Format предназначено для указания двухэлементного вектора, за-
задающего общее число двоичных разрядов квантованных значений и число
разрядов дробной части (в случае фиксированной запятой) или число разря-
разрядов порядка (для квантователей с плавающей запятой).
После задания всех параметров квантования необходимо щелкнуть на кнопке Apply,
в результате будут рассчитаны характеристики квантованного фильтра. На гра-
графиках характеристики исходного фильтра выводятся синим цветом, а кванто-
квантованного — зеленым.
ЗАМЕЧАНИЕ
На рассчитываемые частотные и временные характеристики фильтра влияет только фор-
формат квантования коэффициентов (Coefficient Format). Остальные параметры квантова-
квантования имеет смысл настраивать только в том случае, если квантованный фильтр планируется
экспортировать из программы fdatool.
Функции пакета расширения Filter Design 421
Квантованный фильтр можно экспортировать из программы fdatool обычным спо-
способом — с помощью команды Export меню File. Данные экспортируются в виде
объекта квантованного фильтра, описанного ранее. Таким образом, среда fdatool
предоставляет графический интерфейс для настройки свойств объекта кванто-
квантованного фильтра.
Квантованное БПФ
Для создания объекта квантованного БПФ служит функция qfft. В простейшем
случае она может вызываться без входных параметров, но поскольку обычно
требуется выполнять БПФ заданной размерности, удобнее всего задавать раз-
размерность БПФ сразу же при создании объекта. Для этого нужно использовать в
качестве параметров функции-конструктора строку 'length' и значение размер-
размерности:
f - qfftClength'. N)
Здесь N — размерность БПФ.
Для задания свойств объекта (их список будет приведен ниже) можно указывать
при вызове функции qfft параметры в виде пар «имя свойства — значение свой-
свойства»:
f = qfftCnamel'. valuel. 'name2', value2. ...)
Здесь 'namel', 'name2' и т. д. — имена свойств, a valuel, value2 и т. д. — соответст-
соответствующие значения.
Особо отметим еще один вариант вызова, позволяющий задать общий формат
квантования для всех величин при вычислении БПФ. Для этого в списке пара-
параметров нужно задать значение свойства 'quantizer':
f - qfft(..., 'quantizer1. [M N]. ...)
В результате для всех величин будет использован формат с фиксированной за-
запятой с длиной слова М бит и N битами после запятой.
Список свойств квантованного БПФ приведен в табл. 7.6. Как уже говорилось,
считывать и задавать значения этих свойств можно с помощью функций get и
set соответственно.
Вычисление квантованного БПФ осуществляется с помощью функций fft (пря-
(прямое БПФ) и ifft (обратное БПФ). Отличие от обычного варианта использова-
использования этих функций состоит в том, что в начало списка параметров добавляется
объект квантованного БПФ:
у - fft(f. х)
х - ifft(f. у)
Здесь f — объект квантованного БПФ, х — сигнал во временной области, у — сиг-
сигнал в частотной области.
Если размерность неквантованного БПФ в MATLAB подстраивается под длину
сигнала, то в случае квантованного БПФ все наоборот — сигнал дополняется ну-
нулями или усекается, чтобы его длина стала равна размерности БПФ.
Таблица 7.6. Свойства объекта квантованного БПФ
Имя свойства
CoefficientFormat
InputFormat
Length
NumberOfSections
MultipiicandFormat
Optimi zellni tyGai ns
OutputFormat
ProductFormat
Radix
ScaieVaiues
SumFormat
Описание
Объект quantizer, задающий формат квантования коэффициентов (twiddle factors), используемых
при вычислении БПФ
Объект quantizer, задающий формат квантования входного сигнала
Размерность БПФ. Она должна являться степенью основания БПФ (см. ниже описание
свойства Radix). Значение по умолчанию равно 16
Число ступеней БПФ, равное 1og2(Length)/Log2(Radix) (только для чтения)
Объект quantizer, задающий формат квантования чисел, умножаемых на коэффициенты БПФ
Это свойство не отображается в явном виде при выводе информации об объекте на экран,
поскольку ему не соответствует поле структуры объекта. Однако значение этого свойства можно
считывать и задавать (возможные варианты — ' on' и принятое по умолчанию ' off'). Если
установлено состояние 'on', при вычислениях будут исключены умножения на коэффициенты,
равные единице. Кроме того, при этом для квантования коэффициентов вместо объекта
quantizer будет использован объект unitquantizer, что позволяет точно представлять
единичные значения
Объект quantizer, задающий формат квантования выходного сигнала
Объект quantizer, задающий формат квантования результатов операций умножения
Основание БПФ, которое может быть равно 2 (по умолчанию) или 4
Коэффициенты масштабирования сигналов. Значение этого свойства может быть либо числом
(масштабируется только входной сигнал), либо вектором длиной NumberOfSections
(масштабируется входной сигнал каждой ступени БПФ)
Объект quantizer, задающий формат квантования результатов операций сложения
Функции пакета расширения Filter Design 423
Помимо функций fft и if ft с объектами квантованных БПФ могут работать сле-
следующие функции:
□ fl = copyobj(f) — создает независимую копию объекта квантованного БПФ
с теми же значениями свойств, что у исходного объекта f (см. приведенный
ранее комментарий к одноименной функции для объектов квантователей);
□ disp(f) — выводит на экран свойства объекта;
□ eps(f) — выводит на экран относительную точность представления чисел
в объекте квантованного БПФ;
□ n = length(f) — возвращает размерность БПФ (значение свойства Length);
□ noperations(f) — выводит на экран сведения о числе операций квантования,
выполненных различными квантователями объекта квантованного БПФ f;
□ noverflows(f) — выводит на экран сведения о числе переполнений, возникших
при выполнении операций квантования различными квантователями объекта
квантованного БПФ f;
□ opt = optimizeunitygains(f) — возвращает значение свойства OptimizeUnityGains;
□ qreport(f) — выводит на экран статистическую информацию о работе кванто-
квантователей, входящих в состав объекта квантованного БПФ (максимальное и ми-
минимальное значения входного сигнала, число переполнений и случаев потери
значимости, а также количество выполненных квантований);
□ s - qreport(f) — возвращает ту же информацию в полях структуры s;
□ г = radix(f) — возвращает основание БПФ (значение свойства Radix);
□ range(f) — отображает сведения о минимальных и максимальных значениях
выходного квантованного сигнала для квантователей, входящих в состав объ-
объекта квантованного БПФ f;
□ [Rl, R2, ...] = range(f, Tl, Т2, ...) — возвращает двухэлементные векторы Rl, R2
и т. д., содержащие минимальные и максимальные значения выходного кван-
квантованного сигнала для квантователей, входящих в состав объекта квантован-
квантованного БПФ f и указанных входными строковыми параметрами Tl, T2 и т. д.
Возможные значения этих параметров — 'coefficient', 'input', 'output',
'multiplicand', 'product' и 'sum';
□ reset(hq) — сбрасывает в исходное состояние значения свойств, связанных со
сбором статистической информации (Max, Min, Noperations, Noverflows и Nunder-
flows), для всех квантователей, входящих в состав объекта квантованного
БПФТ;
□ s = tostring(f) — возвращает строку вызова функции qfft, в результате вы-
выполнения которой будет создан объект, совпадающий с объектом f;
□ w = twiddles(f) — возвращает квантованные значения коэффициентов (ком-
(комплексных экспонент), используемых объектом f при вычислении БПФ.
В качестве примера создадим объект квантованного БПФ размерности 256 и за-
затем вычислим спектр синусоидального сигнала с помощью обычной функции
fft и с помощью квантованного объекта.
При создании объекта необходимо задать только размерность БПФ, для всех ос-
остальных свойств мы оставляем значения по умолчанию:
424 Глава 7. Эффекты квантования в цифровых системах
» f - qfftClength', 256)
f -
Radix = 2
Length = 256
CoefficientFormat = quantizerC'fixed'. 'round', 'saturate'. [16 15])
InputFormat = quantizerCfixed'. 'floor', 'saturate'. [16 15])
OutputFormat - quantizer^' fixed'. 'floor', 'saturate', [16 15])
MultiplicandFormat = quantizerC'fixed'. 'floor1, 'saturate'. [16 15])
ProductFormat = quantizerCfixed'. 'floor1, 'saturate', [32 30])
SumFormat - quantizerC'fixed'. 'floor', 'saturate'. [32 30])
NumberOfSections = 8
ScaleValues = [1]
Пусть обрабатываемый сигнал имеет такую частоту, что анализируемый фраг-
фрагмент B56 отсчетов) содержит нецелое число периодов:
» t = 0:255: % дискретное времЯ
» % период сигнала равен 7
» s - l/32*cosB*pi*t/7):
Теперь рассчитываем два варианта спектра: с помощью обычного (вектор sp) и
квантованного (вектор sp_q) БПФ и выводим графики их модулей (рис. 7.17):
» sp = fft(s): % обычное БПФ
» % квантованное БПФ
» sp_q = fft(f. s):
Warning: 14 overflows in quantized fft.
> In ...\quantization\@qfft\private\privfft.m at line 132
In ...\filterdesign\quantization\@qfft\fft.m at line 31
Max Min NOverflows NUnderflows NOperations
Coefficient 1 -1 8
Input 0.03125 -0.02816 0
4
6
0
4
Output 2
Multiplicand 1.408
Product 0.7433
Sum 2.174
» plot(t. abs(sp));
» figure
» plot(t, abs(sp q))
-1
-0.
-2
-2
.408
7883
.174
7
0
0
29
0
0
510
256
512
8192
4096
10240
Сравнение верхнего и нижнего графиков на рис. 7.17 показывает, что переполне-
переполнения, о которых сообщил при вычислениях объект f, весьма существенно искази-
исказили результаты расчета — в спектре появились ложные составляющие. Это свиде-
свидетельствует о необходимости либо уменьшить уровень входного сигнала (в данном
случае, чтобы избавиться от переполнений, необходимо уменьшить амплитуду
гармонического сигнала с 1/32 до 1/128), либо использовать в объекте f кванто-
квантователи с большей верхней границей диапазона представимых чисел.
Функции пакета расширения Filter Design
425
2.5
1.5
300
Рис. 7.17. Результаты вычисления спектра синусоидального сигнала с помощью
обычного (сверху) и квантованного (снизу) БПФ
ГЛАВА 8 Модуляция
и демодуляция
При создании систем передачи информации в большинстве случаев оказывается,
что спектр исходного сигнала, подлежащего передаче, сосредоточен отнюдь не на
тех частотах, которые эффективно пропускает имеющийся канал связи. Кроме
того, очень часто необходимо в одном и том же канале связи передавать несколь-
несколько сигналов одновременно. Одним из способов решения этой задачи является
использование частотного разделения каналов, при котором разные сигналы за-
занимают неперекрывающиеся полосы частот.
Далее, во многих случаях требуется, чтобы передаваемый сигнал был узкополос-
узкополосным. Это означает, что эффективная ширина спектра намного меньше его цен-
центральной частоты:
А/«/о-
Перечисленные причины приводят к необходимости такой трансформации ис-
исходного сигнала, чтобы требования, предъявляемые к занимаемой сигналом по-
полосе частот, были выполнены, а сам исходный сигнал можно было восстановить.
Решение указанной проблемы достигается при использовании модуляции (mo-
(modulation), сущность которой заключается в следующем. Формируется некоторое
колебание (чаще всего гармоническое), называемое несущим колебанием или
просто несущей (carrier), и какой-либо из параметров этого колебания изменяет-
изменяется во времени пропорционально исходному сигналу. Исходный сигнал называют
модулирующим (modulating signal), а результирующее колебание с изменяющи-
изменяющимися во времени параметрами — модулированным сигналом (modulated signal).
Обратный процесс — выделение модулирующего сигнала из модулированного
колебания — называется демодуляцией (demodulation).
Запишем (в очередной раз) гармонический сигнал общего вида:
s(t) = A cos(coo t + фо).
У данного сигнала есть три параметра: амплитуда А, частота со0 и начальная фа-
фаза ф0. Каждый из них можно связать с модулирующим сигналом, получив таким
образом три основных вида модуляции: амплитудную, частотную и фазовую. Как
мы увидим далее, частотная и фазовая модуляция очень тесно взаимосвязаны,
Амплитудная модуляция 427
поскольку обе они влияют на аргумент функции cos. Поэтому эти два вида моду-
модуляции имеют общее название — угловая модуляция.
В современных системах передачи цифровой информации также получила рас-
распространение квадратурная модуляция, при которой одновременно изменяются
амплитуда и фаза сигнала.
Все упомянутые виды модуляции будут более подробно рассмотрены в следую-
следующих разделах.
В MATLAB функции, реализующие процедуры модуляции и демодуляции, име-
имеются в двух пакетах расширения — Signal Processing и Communications. Возмож-
Возможности этих пакетов несколько различаются — как по набору реализованных
методов модуляции/демодуляции, так и по степени контроля над параметрами
модулированного сигнала.
В процессе изложения теоретического материала демонстрационные примеры
будут реализовываться с помощью базовых функций MATLAB, без использова-
использования специальных средств модуляции/демодуляции из упомянутых пакетов. Это
позволит читателю лучше понять сущность рассматриваемых методов и алго-
алгоритмов.
Амплитудная модуляция
Как явствует из названия, при амплитудной модуляции (AM; английский тер-
термин — amplitude modulation, AM) в соответствии с модулирующим сигналом из-
изменяется амплитуда несущего колебания:
5ам@ = A{t) cos(co0£ + Фо)-
Однако если амплитуду A(t) просто сделать прямо пропорциональной модули-
модулирующему сигналу, возможно возникновение следующей проблемы. Как правило,
модулирующий сигнал является двуполярным (знакопеременным). Рассмотрим,
например, такой сигнал (рис. 8.1, сверху):
sM@ = 3 cosBtc t) - sinFrc t + л/4).
Если мы непосредственно используем его в качестве амплитудной функции A(t),
получится следующее (рис. 8.1, снизу):
» t = -1:0.01:1;
» s_M = 3 * cosB*pi*t) - sinF*pi*t+pi/4);
» Fc = 10; % несущая частота
» s_AM = s_M .* cosB*pi*Fc*t):
» subplotB, 1, 1)
» plot(t, s_M)
» grid on
» subplotB, 1, 2)
» plot(t. s_AM, t, abs(s_M), '--')
» grid on
428
Глава 8. Модуляция и демодуляция
-0.5
0.5
Рис. 8.1. Умножение двуполярного модулирующего сигнала (сверху) на несущее колебание
дает неправильную амплитудную огибающую (снизу)
Из нижнего графика на рис. 8.1 видно, что амплитудная огибающая, которая бу-
будет выделена в процессе демодуляции, в данном случае оказывается неправиль-
неправильной — она соответствует модулю исходного сигнала.
Поэтому при реализации AM к модулирующему сигналу предварительно добав-
добавляют постоянную составляющую, чтобы сделать его однополярным:
A(t) = Ао + ksM(t).
Для нашего примера достаточно будет постоянной составляющей, равной четы-
четырем (рис. 8.2):
» s_AM = D + s_M) .* cosB*pi*Fc*t):
» plottt. s_AM, t, 4+s_M. '--')
» grid on
Рис. 8.2. Добавление постоянной составляющей
делает модулирующий сигнал однополярным
Амплитудная модуляция 429
Теперь форма амплитудной огибающей соответствует модулирующему сигналу
с точностью до постоянной составляющей, которая легко может быть удалена
после демодуляции.
Итак, окончательно можно записать АМ-сигнал в следующем виде:
«ам@ = (Ло + *sm(O) cos(cM + Фо). (8.1)
Однотональная AM
Для понимания сути амплитудной модуляции и спектральной структуры АМ-
сигнала полезно подробнее рассмотреть частный случай, когда модулирующий
сигнал является гармоническим:
Ам cos(Q t + Фо).
«am(O = (Л + Лм cos(Q t + Фо)) cos(cM + Фо). (8.2)
Отношение между амплитудами модулирующего сигнала Лм и несущего колеба-
колебания Ло называется коэффициентом модуляции или глубиной модуляции:
С учетом этого можно записать
«ам(О = ЛоA + т cos(Q t + Фо)) cos(co0t + фо).
На рис. 8.3 показан вид однотонального АМ-сигнала при разных значениях ко-
коэффициента модуляции.
» Fs =100: % частота дискретизации
» t = -10:1/Fs: 10: % дискретное вренЯ
» omegaO =10: % несущая частота
» OMEGA =1; % частота модулирующего сигнала
» s_AM_0 = cos(omega0 * t):
» s_AM_50 = (l+0.5*cos(OMEGA*t)) .* cos(omega0 * t):
?•> s_AM_100 = A+ cos(OMEGA*t)) .* cos(omega0 * t):
» subplotC. 1. 1)
» plot(t. s_AM_0) % модуляция отсутствует
» subplotC, 1, 2)
» plot(t. s_AM_50) % глубина модуляции 50^
» subplotC. 1. 3)
» plot(t. s__AM_100) % глубина модуляции 100U
Очевидно, что максимальное значение огибающей однотонального АМ-сигнала
достигается тогда, когда оба косинуса равны 1:
Лтах -Л A +т).
Минимальное значение огибающей соответствует тем моментам, когда косинус
модулирующего сигнала равен -1:
Лт]„ - Л A -т).
430
Глава 8. Модуляция и демодуляция
-10 -5 0 5 10
Рис. 8.3. Однотональный АМ-сигнап: сверху — т = 0 (немодулированная несущая),
в центре — т = 0,5, снизу — т = 1
Отсюда следует формула, позволяющая вычислить коэффициент модуляции т
по результатам измерения (например, с помощью осциллографа) максимальной
и минимальной амплитуд сигнала:
А
-А,
Аих + Aiiin
Обычно коэффициент модуляции должен лежать в диапазоне 0...1. При т > 1
имеет место перемодуляция; подстановка таких значений в приведенную форму-
формулу дает результат, показанный на рис. 8.4.
» А_АМ_150 = 1 + 1.5 * cos(OMEGA*t);
» s_AM_150 = A_AM_150 .* cos(omegaO * t):
» plot(t. s_AM_150, t. abs(A_AM_150), '--')
2.5
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-2.5
-10 -5 0 5 10
Рис. 8.4. Однотональный АМ-сигнал в случае перемодуляции (т = 1,5)
Амплитудная модуляция
431
Как уже указывалось, амплитудная огибающая при перемодуляции искажается.
Однако, как мы увидим далее, и этот режим может быть полезен на практике.
Теперь займемся анализом спектрального состава такого колебания. Для этого
сначала раскроем скобки в выражении для однотонального АМ-сигнала, а затем
выполним тригонометрические преобразования:
«ам(О = Ао cos(&0t + ф0) + A0mcos(Qt + Фо)cos(co0£ + ср0) =
= А0
• COS ((
co0
+ ф0).
(8.3)
-Фо).
Результат преобразования показывает, что однотональный АМ-сигнал состоит
из трех гармонических составляющих, одна из которых представляет собой несу-
несущее колебание с частотой со0, а две оставшихся (их называют боковыми частота-
частотами) отстоят от него вверх и вниз по частоте на величину Q. Амплитуда несущего
колебания равна Ао и не зависит от уровня модулирующего сигнала. Амплитуды
боковых частот, равные А0т/2, напротив, пропорциональны коэффициенту мо-
модуляции.
Для верхней боковой частоты начальные фазы несущей и модулирующего сигна-
сигнала складываются, а для нижней — вычитаются.
Амплитудный и фазовый спектры однотонального АМ-сигнала показаны на
рис. 8.5.
а 4
1
1
со0 — О to0 to0 + Г2 to
Ф А
Фо
Фо-
Фо Т
jLL
со0-Г2
Рис. 8.5. Амплитудный (а) и фазовый (б) спектры однотонального АМ-сигнала
ЗАМЕЧАНИЕ
Следует подчеркнуть, что в общем случае полученное представление однотонального АМ-
сигнала не является его разложением в ряд Фурье. Такое представление в виде суммы гар-
гармонических функций может рассматриваться как ряд Фурье только в том случае, когда
для всех трех частот спектральных составляющих существует общий делитель. Это воз-
возможно, если отношение coo/Q является рациональной дробью.
432
Глава 8. Модуляция и демодуляция
Из графиков видно, что ширина спектра однотонального АМ-сигнала в два раза
превышает частоту модулирующего сигнала: Дсо « 2С1.
Чтобы понять, как из трех гармонических составляющих с постоянной амплиту-
амплитудой складывается сигнал с меняющейся амплитудой, создадим векторную диа-
диаграмму. Для этого представим каждое из трех гармонических колебаний как ве-
вещественную часть комплексной экспоненты:
Построим векторную диаграмму, демонстрирующую суммирование этих состав-
составляющих (рис. 8.6).
ImA
О Re
Рис. 8.6. Векторная диаграмма формирования однотонального АМ-сигнала
При сложении колебаний с разными частотами постоянно меняются их взаим-
взаимные фазовые соотношения. Векторы боковых частот вращаются в разные сто-
стороны с угловой скоростью Q относительно вектора несущего колебания. В ре-
результате колебания боковых частот оказываются то синфазными с несущим
колебанием, увеличивая его амплитуду, то противофазными с ним (тогда ампли-
амплитуда сигнала уменьшается). Наконец, вектор несущей частоты вращается с угло-
угловой скоростью со0. Значение АМ-сигнала определяется проекцией результирую-
результирующего вектора на вещественную (горизонтальную) ось.
АМ-сигнал в общем случае
Формула, связывающая спектр АМ-сигнала со спектром модулирующего сигна-
сигнала, нами уже была получена (см. в главе 1 свойство преобразования Фурье
A.18), касающееся умножения сигнала на гармоническую функцию). Действи-
Действительно, ведь АМ-сигнал — это и есть результат умножения модулирующего сиг-
сигнала (с добавленной постоянной составляющей) на гармоническое несущее ко-
колебание.
Повторим, слегка изменив обозначения, полученную ранее формулу A.18):
Амплитудная модуляция
433
>-ю0). (8.4)
i i
Спектр огабающей A(t) при амплитудной модуляции сдвигается в область несу-
несущей частоты ±соо, «раздваиваясь» и уменьшаясь в два раза по уровню. Покажем это
на графике, задав какую-нибудь функцию для спектра огибающей 5Л (ю) (рис. 8.7):
» w = -20:0.1:20; % значения частот длЯ расчета
» wO = 10; % несущая частота
» S_A = l./(l+w.*2); % спектр модулирующего сигнала
» % спектр модулированного сигнала
» S_AM = 0.5./(l+(w+v/0).A2) + 0.5./(l+(w-w0).A2):
» pTot(w, S_A. '--'. w. S_AM)
°20 -15 -10 -5 0 5 10 15 20
Рис. 8.7. Спектры огибающей (пунктирная линия) и АМ-сигнала (сплошная линия)
Итак, спектр АМ-сигнала в общем случае содержит несущую частоту (уровень
которой определяется постоянной составляющей огибающей), а также верхнюю
и нижнюю боковые полосы.
Из графиков видно, что ширина спектра АМ-сигнала вдвое больше максималь-
максимальной (граничной) частоты модулирующего сигнала: Аю = 2О,пах.
Вычислим значение спектральной функции АМ-сигнала на несущей частоте:
Первое слагаемое результата — как и положено, деленная пополам постоянная
составляющая модулирующего сигнала. А вот второе слагаемое представляет со-
собой «хвост» от второй «половинки» спектра, сконцентрированной в области от-
отрицательных частот, в окрестностях частоты -ю0. Следует иметь в виду, что, по-
поскольку все реальные сигналы имеют конечную длительность (и, следовательно,
бесконечно протяженный спектр), данное явление наложения «хвостов» всегда
будет иметь место. В большинстве практических ситуаций, однако, несущая час-
частота значительно превышает эффективную граничную частоту спектра огибаю-
огибающей, так что влияние данного эффекта пренебрежимо мало.
434
Глава 8. Модуляция и демодуляция
Графически проиллюстрируем наложение «хвостов» сдвинутых копий спектра,
уменьшив в рассмотренном ранее примере несущую частоту (рис. 8.8):
» w = -5:0.1:5; % значения частот длЯ расчета
» wO = 2: % несущая частота
» S_A = l./(l+w.A2); % спектр модулирующего сигнала
» % спектр модулированного сигнала
» S_AM = 0.5./(l+(w+w0).A2) + 0.5./(l+(w-w0).A2);
» plot(w. S_A. '--'. w. S_AM)
1
0.9
0.8 \
07 [
0.6 I"
Ц
0.4 Г
0.3 Г
i
0.2 h
0.1k
/■\
\
°-5 О о
Рис. 8.8. При недостаточно высокой несущей частоте спектр АМ-сигнала (сплошная линия)
может быть существенно несимметричным относительно несущей частоты
из-за наложения «хвостов»
Энергетические соотношения в АМ-сигнале
В этом разделе нам вновь придется вернуться к рассмотрению однотонального
АМ-сигнала (8.2), чтобы выяснить, как распределяется мощность в его спектре.
Для начала определим пиковую мощность однотонального АМ-сигнала. Как ука-
указывалось ранее, его максимальная амплитуда равна ЛоA + т), следовательно,
пиковая мощность составляет
Теперь займемся средней мощностью. Как говорилось ранее, АМ-сигнал в об-
общем случае не является периодическим, поэтому для расчета средней мощности
необходимо применить предельный переход согласно формуле A.4):
Рсп =lim- \s2(t)dt =
1
lim—
Т/2
dt =
-Т/2
Амплитудная модуляция
435
ЗАМЕЧАНИЕ
Тот же результат можно получить и без вычисления интеграла. Достаточно вспомнить,
что мощность гармонического колебания с амплитудой А равна А2/2 и что гармонические
колебания разных частот являются некоррелированными, а потому их мощности можно
складывать. Далее остается только применить все сказанное к представлению однотональ-
однотонального АМ-сигнала в виде суммы гармонических составляющих (см. формулу (8.3) и
рис. 8.5).
Первое слагаемое не зависит от коэффициента модуляции и представляет собой
мощность немодулированной несущей. Полезная мощность, заключенная в бо-
боковых частотах, представлена вторым слагаемым.
Введем в рассмотрение коэффициент полезного действия (КПД) амплитудной
модуляции, определив его как отношение мощности боковых частот к общей сред-
средней мощности сигнала:
Лам =■
Л2 —
т
т2 +2
Построим график зависимости КПД от коэффициента модуляции т (рис. 8.9):
» m = 0:0.01:1:
» eta = m.A2./(m.A2+2):
» plot(m, eta)
» xlabel('m')
» y1abel('\eta_{AM}')
О 0.2 0.4 0.6 0.6 1
m
Рис. 8.9. Зависимость КПД от коэффициента амплитудной модуляции
Результаты неутешительные — даже при максимально допустимом значении ко-
коэффициента модуляции (т = 1) КПД составляет лишь 33 %, то есть две трети
436
Глава 8. Модуляция и демодуляция
мощности тратится на передачу бесполезной в информационном отношении не-
несущей.
Исторически AM была первым практически освоенным видом модуляции. Од-
Однако низкий КПД и ширина спектра, вдвое превышающая ширину спектра
модулирующего сигнала, привели к тому, что сфера применения AM стала до-
довольно узкой. В настоящее время AM применяется для радиовещания на срав-
сравнительно низких частотах (в диапазонах длинных, средних и коротких воли) и
для передачи изображения в телевизионном вещании.
Демодуляция AM
Демодуляция АМ-сигнала может быть выполнена несколькими способами. Про-
Простейший путь — имитировать работу аналогового двухполупериодного детекто-
детектора. Мы вычисляем модуль входного АМ-сигнала, а затем сглаживаем получив-
получившиеся однополярные косинусоидальные импульсы, пропуская их через ФНЧ
(рис. 8.10):
» у = abs(s_AM_50); % модуль АМ-сигнала
» [b. a] = butterE. 2*0MEGA/pi/Fs): % сглаживающий ФНЧ
» z = filtfilt(b. а, у): % фильтрация
» plot(t(l:1000). уA:1000), '--'. t(l:1000), z(l:1000))
1.5
0.5 Г
" i
Ik
a
-10
-6
-2
Рис. 8.10. Двухполупериодное детектирование АМ-сигнала: однополярные импульсы
(пунктирная линия) и результат их сглаживания (сплошная линия)
Данный способ, очевидно, не будет работать правильно в случае перемодуляции.
Следующий метод — так называемое синхронное детектирование, суть которого
состоит в умножении частоты сигнала на опорное колебание с несущей частотой:
2/@ = *am(Ocos(co0£ + ф0 ) = A(t)cos2(aot + ф0) =
1 1 (8-5)
-A(t) cosBco01 + 2Фо).
Амплитудная модуляция
437
Результат умножения содержит два слагаемых. Первое — это искомая амплитуд-
амплитудная функция, второе — АМ-сигнал с несущей частотой 2со0. Этот высокочастот-
высокочастотный сигнал легко удаляется путем пропускания сигнала через ФНЧ (рис. 8.11):
» % умножение на опорное колебание
» у = s_AM_50 .* cos(omegaO*t);
» [b, a] = butterE. 2*0MEGA/pi/Fs); % сглаживающий ФНЧ
» z = filtfilKb. а. у); % фильтрация
» plOt(t(l:1000), y(l:1000), '--', t(l:1000), z(l:1000))
-2
Рис. 8.11. Синхронное детектирование АМ-сигнала: результат умножения
на опорное колебание (пунктирная линия) и выделенный
низкочастотный сигнал (сплошная линия)
Однако в данном случае необходимо очень точное совпадение начальных фаз и
частот опорного колебания демодулятора и несущего колебания АМ-сигнала.
При совпадении частот, но несовпадении начальных фаз выходной низкочастот-
низкочастотный сигнал оказывается умноженным на косинус фазовой ошибки:
ф).
= sAM(t)cos(co0t + ф) = A(t)cos((o0t + ф0 )cos(co0*: + ср) =
= -Л(£)со5(ф-ф0) + -
Таким образом, при наличии фазовой ошибки уровень полезного сигнала на вы-
выходе демодулятора падает, а при ошибке, равной 90°, становится равным нулю.
При наличии частотного сдвига между несущим и опорным колебаниями ситуа-
ситуация становится еще хуже — выходной низкочастотный сигнал оказывается ум-
умноженным на гармоническое колебание с разностной частотой:
y{t) = sAM(£)cos((co0 + Aa)t) =
= -4(Ocos(Affl£-(p0) + -
ф0 )cos((co0
438
Глава 8. Модуляция и демодуляция
В результате выходной сигнал будет пульсировать с частотой Дох Это явление
называется биениями (beat), а разность частот Аю — частотой биений (beat fre-
frequency).
Для поддержания частотной и фазовой синхронизации между несущим и опор-
опорным колебаниями используются следящие системы фазовой автоподстройки час-
частоты (ФАПЧ), рассмотрение которых выходит за рамки тематики данной книги.
Достоинством синхронного детектирования является то, что оно позволяет пра-
правильно демодулировать сигнал даже в случае перемодуляции (ведь формула (8.5)
не перестает быть верной в случае знакопеременной функции A(t)).
Разновидности амплитудной
модуляции
Попытки улучшить характеристики AM привели к разработке нескольких ее мо-
модификаций, которые и будут рассмотрены в данном разделе.
AM с подавленной несущей
Первое, что приходит в голову при размышлении на тему повышения КПД амп-
амплитудной модуляции, — это идея удалить бесполезное несущее колебание, все-
таки отказавшись от добавления постоянной составляющей к модулирующему
сигналу. Такой способ называется AM с подавленной несущей (АМ-ПН, англий-
английский термин — amplitude modulation with suppressed carrier, AM-SC):
s(t) = sM(t) cos((o0t + (po)-
0
Рис.
2 4 6 8 10
8.12. Однотональная AM с подавленной несущей
Построим график такого сигнала при однотональной модуляции (рис. 8.12).
Разновидности амплитудной модуляции
439
» t = 0:0.01:10; % дискретное времЯ
» omegaO = 20: % несущая частота
» OMEGA =1; % частота модулирующего сигнала
» s_M = cos(OMEGA*t); % модулирующий сигнал
» s_AM_SC = s_M .* cos(omega0*t): % АМ-ПН сигнал
» plot(t, s_AM_SC)
Энергетический выигрыш при этом, конечно, велик (согласно введенному нами
определению, КПД становится равным 100 %).
Ширина спектра АМ-сигнала с подавленной несущей такая же, как в случае
обычной AM (ведь подавлена средняя (несущая) частота, а боковые частоты ос-
остались на месте).
Таким образом, AM с подавленной несущей обладает определенными преимуще-
преимуществами по сравнению с обычной AM. Однако этот способ модуляции не получил
широкого распространения, и связано это с проблемами, возникающими при де-
демодуляции сигнала.
Демодуляция AM с подавленной несущей
Как было указано в разделе «Демодуляция AM», формула (8.5) справедлива
как для однополярной, так и для знакопеременной амплитудной функции A(t).
Поэтому демодуляция AM с подавленной несущей может выполняться путем
синхронного детектирования. При этом сохраняет силу все сказанное о необхо-
необходимости точного соответствия частот и начальных фаз несущего и опорного ко-
колебаний.
Для облегчения правильного восстановления несущей иногда применяют сле-
следующий прием. На передающей стороне несущее колебание подавляется не пол-
полностью. Его «остаток» с небольшой амплитудой (он называется пилот-сигналом)
используют для синхронизации частоты и фазы несущего колебания на прием-
приемной стороне.
Однополосная модуляция
Рассмотренная в предыдущем разделе двухполосная AM с подавленной несущей
имеет преимущества перед обычной AM только в энергетическом смысле — за
счет устранения несущего колебания. Ширина же спектра при этом остается рав-
равной удвоенной частоте модулирующего сигнала.
Однако можно легко заметить, что спектры двух боковых полос АМ-сигнала яв-
являются зеркальным отражением друг друга, то есть они несут одну и ту же ин-
информацию. Поэтому одну из боковых полос можно удалить. Получающаяся мо-
модуляция называется однополосной (английский термин — single side band, SSB).
В зависимости от того, какая боковая полоса сохраняется, говорят об однополос-
однополосной модуляции с использованием верхней или нижней боковой полосы. Форми-
Формирование однополосного сигнала проще всего пояснить, приведя несколько спек-
спектральных графиков (рис. 8.13).
440
Глава 8. Модуляция и демодуляция
О
а
О
б
соо
-«о
соо
Рис. 8.13. Однополосная модуляция: а — спектр модулирующего сигнала,
б — спектр однополосного сигнала с верхней боковой полосой,
в — то же с нижней боковой полосой
По сути дела, при однополосной модуляции происходит просто сдвиг спектра
сигнала в окрестности частоты несущего колебания. В отличие от AM каждая
«половинка» спектра смещается в своем направлении: область положительных
частот — к со0, а область отрицательных частот — к -ю0.
Очевидно, что ширина спектра одиополосного сигнала равна ширине спектра
модулирующего сигнала. Таким образом, спектр однополосного сигнала оказы-
оказывается в два раза уже, чем при обычной AM.
В отличие от предыдущих случаев здесь нам не удастся простыми средствами
выразить связь между модулированным и модулирующим сигналами. Чтобы сде-
сделать это, придется воспользоваться преобразованием Гильберта и понятием ана-
аналитического сигнала (см. раздел «Комплексная огибающая» главы 1).
Итак, прежде всего мы формируем из модулирующего сигнала аналитический
сигнал, имеющий односторонний спектр. Умножение этого сигнала на ехр (joHt)
сдвигает его односторонний спектр на ю0 вправо (вверх по частоте), формируя
односторонний спектр однополосного сигнала с верхней боковой полосой. Нако-
Наконец, чтобы перейти от аналитического сигнала обратно к вещественному, нужно
взять вещественную часть. Формирование сигнала с нижней боковой полосой
описывается аналогично, только умножать аналитический сигнал нужно на
ехр (-j<£>o t) (тогда его спектр сдвинется влево, в область отрицательных частот,
Разновидности амплитудной модуляции 441
и займет положение нижней боковой полосы). Теперь осталось записать все ска-
сказанное математически:
= x(t)cos aot T ^(
Знак «минус» в окончательной формуле соответствует выделению верхней боко-
боковой полосы, «плюс» — нижней.
Итак, однополосный сигнал можно представить как сумму двух АМ-сигналов,
несущие колебания которых имеют одну и ту же частоту, но сдвинуты по фазе
друг относительно друга на 90°. Амплитудными функциями этих АМ-сигналов
являются модулирующий сигнал и его квадратурное дополнение. В зависимости
от того, складываются эти два АМ-сигнала или вычитаются (а точнее, какая из
двух несущих опережает другую по фазе), формируется однополоспый сигнал с
верхней или нижней боковой полосой.
Амплитудная огибающая однополосного сигнала нисколько не похожа на моду-
модулирующий низкочастотный сигнал. Проверим это на конкретном примере. Слу-
Случай гармонической модуляции на сей раз рассматривать не будем — он слишком
прост (синусоида с частотой Q при однополосной модуляции превратится в си-
синусоиду с частотой со0 ± Q; выбор знака определяется тем, какая используется
боковая полоса). Возьмем модулирующий сигнал, состоящий из двух гармоник
(рис. 8.14):
» Fs = 1000; % частота дискретизации
» t = 0:1/Fs:1: % дискретное времЯ
» Fc = 25: % несущая частота
», f1 = 5: % первая частота модуляции
» f2 - 10: % вторая частота модуляции
»
» % модулирующий сигнал
» s_M = cosB*pi*fl*t) + cosB*pi*f2*t);
» % SSB-сигнал с верхней боковой полосой
» S_SSB_U = cosB*p1*(Fc+fl)*t) + cosB*p1*(Fc+f2)*t);
» % SSB-сигнал с нижней боковой полосой
» s_SSB_L = cosB*p1*(Fc-fl)*t) + cosB*pi*(Fc-f2)*t);
» subplotO. 1, 1)
» plot(t, s_M)
» ylabel('s_{M}(t)')
» titleC'Modulating Signal')
» subplotO, 1, 2)
» plot(t, s SSB_U)
» ylabeK'sJSSB U}(t)')
» titleCSSB Signal with Upper Side Band1)
» subplotO, 1, 3)
» plot(t, s SSB L)
» ylabeK'sJSSB L}(t)')
» titleCSSB Signal with Lower Side Band')
442
Глава 8. Модуляция и демодуляция
Modulating Signal
SSB Signal with Upper Side Band
SSB Signal with Lower Side Band
Рис. 8.14. Однополосная модуляция: сверху — модулирующий сигнал, в центре — сигнал
с верхней боковой полосой, снизу — сигнал с нижней боковой полосой
Однополосная модуляция с различным уровнем несущего колебания — от пол-
полного подавления до полного сохранения — нашла широкое применение в техни-
технике профессиональной радиосвязи.
Демодуляция однополосного сигнала
Несмотря на то что визуально (на графике) однополосный сигнал сильно отли-
отличается от обычного АМ-сигнала, его демодуляция возможна тем же методом
синхронного детектирования — путем умножения на опорное колебание:
y(t) = sSSB(t) cos ()
= -
Результат умножения (рис. 8.15, сверху) содержит два слагаемых. Первое — это
модулирующий сигнал, второе — однополосный сигнал на удвоенной несу-
несущей 2ю0- Остается лишь выделить модулирующий сигнал с помощью ФНЧ
(рис. 8.15, снизу):
» % умножение на опорное колебание
» у = s_SSB_U .* cosB*pi*Fc*t);
» [b, a] = batterE, Fc/Fs*2); % сглаживающий ФНЧ
» z = filtfiitCb. а. у); % фильтрация
» subplotB, 1. 1)
-x(t)cos2(£>0t±-x1(t)sin2(£>Qt.
Разновидности амплитудной модуляции
443
» plot(t. у)
» subp1otB. 1.
» plotCt. z)
2)
0.8
0.8
1
Рис. 8.15. Демодуляция однополосного сигнала, показанного на рис. 8.14:
сверху — результат умножения на несущее колебание,
снизу — отфильтрованный демодулированный сигнал
Эффекты, возникающие при наличии частотного или фазового сдвига у опорно-
опорного колебания, в случае однополосного сигнала проявляются не так, как при де-
демодуляции AM. Сначала рассмотрим ситуацию, когда есть только фазовый сдвиг,
а ошибка по частоте отсутствует:
y{t) = sSSB(t)cos((aQt + ф) = (x(t)cos aot ± xx(t)sin<£iot) cos(co0£ + ф) =
= X(t)COS (£lot COS((Dor + (p)±X±(t)sin<£l0tCOS((£l0t + ф) =
= - (x(t) cos <p±x±(t) simp) + -(x(£)cosBco0r
ф)).
Низкочастотная составляющая в этом случае представляет собой линейную ком-
комбинацию модулирующего сигнала x(t) и его квадратурного дополнения xx(t).
Со спектральной точки зрения это означает фазовый сдвиг всех частотных со-
составляющих сигнала на ф. Форма сигнала, разумеется, при этом искажается.
Приемлемы ли такие искажения, зависит от характера передаваемого сигнала.
Если однополосная модуляция используется для передачи звукового сигнала,
фазовые искажения несущественны, поскольку ухо человека нечувствительно к
фазовым соотношениям в акустическом сигнале.
Пусть теперь опорное колебание имеет частоту со0 + Дсо. Чтобы получить результат
умножения, достаточно подставить в предыдущую формулу значение ф = Aat:
= -(x(t)cos(Ac£>t)±x1(t)sin(A(ut)) +
SB(Ocos((co0
--(x(Ocos(Bco0 +Aa,)t)±xx(t)sin(B(u0 +Aw)t)).
444 Глава 8. Модуляция и демодуляция
Низкочастотная составляющая здесь фактически представляет собой однопо-
однополосный сигнал с несущей частотой Асо. С частотной точки зрения это означает
сдвиг спектра модулирующего сигнала на Асо. Это, разумеется, значительно бо-
более серьезные искажения, чем в предыдущем случае. Скажем, при передаче му-
музыки искажения такого рода совершенно неприемлемы. При передаче же речево-
речевого сигнала (а профессиональная радиосвязь — это основная сфера применения
однополосной модуляции) сдвиг спектра приводит к искажению тембра голоса,
но разборчивость речи сохраняется при величине сдвига до нескольких десят-
десятков, а для опытного оператора — до нескольких сотен герц.
Полярная модуляция
То, что мы рассмотрим в этом разделе, не является отдельным видом модуляции.
Это скорее демонстрация применения амплитудной модуляции для решения кон-
конкретной технической задачи. Речь пойдет о том, как реализуется стереофониче-
стереофоническое радиовещание в УКВ-диапазоне.
Для осуществления стереовещания необходимо передавать два сигнала sL(t) и
sR(t) (левого и правого каналов) одновременно. В то же время при разработке
системы такого вещания накладывается еще и требование совместимости с уже
имеющимися монофоническими приемниками. Поэтому для стереовещания мо-
модифицируется низкочастотный модулирующий сигнал, который поступает на
вход модулятора передатчика (в передатчике используется угловая модуляция,
которая будет рассмотрена далее). Низкочастотная составляющая модулирую-
модулирующего сигнала, лежащая в звуковом диапазоне, для совместимости с монофониче-
монофоническими приемниками должна представлять собой монофонический сигнал, то
есть сумму сигналов левого и правого каналов:-
Smono(O = si(O + Sr(C).
В области более высоких (ультразвуковых) частот модулирующего сигнала с по-
помощью амплитудной модуляции передается дополнительный сигнал, позволяю-
позволяющий впоследствии выделить из полученной смеси сигналы sL(t) и sR(t) по от-
отдельности. Поскольку монофонический сигнал — это сумма двух каналов, этим
дополнительным компонентом, позволяющим восстановить исходные сигналы
двух каналов, естественно выбрать их разность:
Рассмотрим конкретный пример, задав для правого и левого каналов гармониче-
гармонические сигналы разных частот:
Si(t) " Al COS(QiOi
suit) - AR zos(SlRt).
Графики сигналов sL{t), sR{t), %ono(O и sdiff(O Для данного случая показаны
на рис. 8.16.
» t - 0:0.01:20; % дискретное времЯ
» w L - 1: % частота сигнала левого канала
» w_R =2; % частота сигнала правого канала
» s L = cos(w L*t): % сигнал левого канала
Разновидности амплитудной модуляции
445
» s_R = cos(w_R*t);
» s_mono = s_L + s_R:
» s_diff = s_L - s_R;
» subplotB.~2. 1)"
» plot(t. s_L)
» titleCLeft channel
» subplotB. 2. 2)
» plottt. s_R)
» title('Right channel')
» subplotB. 2. 3)
» plot(t. s_mono)
» titleCSJMONO}1)
» subplotB. 2. 4)
» plotCt. s_diff)
» titleCSJDIFF}')
Left channel
% сигнал правого канала
% монофонический сигнал
% разностный сигнал
')
Right channel
Рис. 8.16. Сверху: сигналы левого и правого каналов,
снизу: суммарный и разностный сигналы
Складывая и вычитая сигналы sMONO(£ ) и sDIFF (t), можно восстановить сигналы
левого и правого каналов:
5@ + Spiff (О
Монофонический сигнал, как уже было сказано, для совместимости должен пе-
передаваться как есть, а разностный сигнал модулирует несущую частоту, располо-
расположенную несколько выше звукового диапазона частот (ее называют подпесущей
(subcarrier), поскольку весь сигнал, о формировании которого идет речь, затем
используется для угловой модуляции несущего колебания радиопередатчика):
5 (О = SMONO(£ ) + (А0 + 5D[FF (t)) COS(C001).
Построим график получающегося сигнала (рис. 8.17):
» wO = 10: % поднесущаЯ частота
» АО = 2: % смещение длЯ разностного сигнала
446
Глава 8. Модуляция и демодуляция
» % композитный стереосигнал
» s = s_mono + (АО + s_diff) .* cos(wO*t):
» plotCt. s)
» hold on
» plotCt. s_mono+AO+s_diff, '--') % верхняя огибающая
» plotCt. s_mono-AO-s_diff. '--') % нижняя огибающая
» hold off
5 10 15
Рис. 8.17. Композитный стереосигнал
20
Получающийся сигнал (его называют композитным стереосигналом), как видно
из рисунка, благодаря наличию низкочастотной составляющей обладает интерес-
интересным свойством: его верхняя и нижняя (положительная и отрицательная) оги-
огибающие не совпадают. Более того, каждая из них с точностью до постоянной со-
составляющей соответствует сигналу одного из стереоканалов: верхняя (положи-
(положительная) огибающая — это левый канал, а нижняя (отрицательная) — правый.
Такая структура сигнала позволяет легко выделить из него сигналы стереока-
стереоканалов.
Однако в показанном на рис. 8.17 виде сигнал для передачи не используется.
Дело в том, что из-за наличия несущего колебания размах сигнала (разность ме-
между его максимальным и минимальным значениями) сильно увеличивается по
сравнению с монофоническим сигналом, что нежелательно. Поэтому несущее
колебание частично или полностью подавляют, так что разностный сигнал пере-
передается в режиме перемодуляции.
ЗАМЕЧАНИЕ
Отечественный стандарт, согласно которому ведется радиовещание в диапазоне 65-74 МГц,
предусматривает частичное подавление поднесущей частоты, равной 31,25 кГц. Зарубеж-
Зарубежный стандарт, используемый в диапазоне 88-108 МГц, специфицирует полное подавление
поднесущей частоты, равной 38 кГц. При этом для обеспечения возможности правильного
восстановления поднесущего колебания в стереодекодере приемника в состав сигнала вво-
вводится пилот-сигнал на половинной частоте поднесущей A9 кГц).
Угловая модуляция
447
Изобразим композитный стереосигнал для случая полного подавления несущей
(пилот-сигнал добавлять не будем) (рис. 8.18):
» s = sjnono + s_diff .* cos(wO*t);
» plot(t. s)
» hold on
» plot(t. s_mono+s_diff, '-.')% верхняя огибающая
» plot(t. s_mono-s_diff, ':') % нижнЯЯ огибающая
» hold off
■О 5 10 15 20
- Рис. 8.18. Композитный стереосигнал с подавленной поднесущей
Из графика видно, что благодаря подавлению поднесущей размах сигнала суще-
существенно (в два раза) уменьшился.
Угловая модуляция
В начале главы уже было сказано, что фазовая и частотная модуляция тесно связа-
связаны друг с другом, благодаря чему и получили общее название «угловая модуляция»
(УМ; английский термин — angle modulation). Поэтому прежде всего в этом раз-
разделе нужно рассмотреть сходство и различие этих двух видов модуляции.
Фазовая и частотная модуляция
Названия двух рассматриваемых видов модуляции, как и в случае с AM, указы-
указывают параметр несущего колебания, который линейно связан с модулирующим
сигналом.
Фазовая модуляция
Пусть модулирующий сигнал определяет начальную фазу несущего колебания:
Ф(О = ksM(t).
448 Глава 8. Модуляция и демодуляция
Тогда мы получаем сигнал с фазовой модуляцией (ФМ; английский термин —
phase modulation, PM):
= A cos(co0t + ksu(t)). (8.7)
Весь аргумент функции cos, взятый целиком, называется полной фазой коле-
колебания:
4»(t) = co0t + faM(O-
Круговая частота колебания по определению представляет собой скорость изме-
изменения начальной фазы. Подобно тому как в случае неравномерного движения
вводится понятие мгновенной скорости (равной производной от координаты по
времени), для колебаний с угловой модуляцией вводится понятие мгновенной
частоты (instantaneous frequency), равной производной от полной фазы по вре-
времени:
,dsu
at at
Итак, в случае фазовой модуляции изменяется не только начальная фаза, но
и мгновенная частота колебания.
Соответственно, полная фаза может быть найдена путем интегрирования мгно-
мгновенной частоты:
Частотная модуляция
Теперь мы можем ввести понятие частотной модуляции (ЧМ; английский тер-
термин — frequency modulation, FM), при которой модулирующий сигнал линейно
связан с мгновенной частотой колебания:
Добавка в виде константы со0 необходима для того, чтобы сделать колебание вы-
высокочастотным.
Полная фаза находится, как уже говорилось, путем интегрирования:
%. (8.8)
Здесь ф0 — произвольная постоянная интегрирования.
Наконец, сам ЧМ-сигнал имеет следующий вид:
«чм(О = А cos (юог + Ц ^(f )dt> + Фо) •
Как видим, начальная фаза колебания при частотной модуляции претерпевае!
изменения, пропорциональные интегралу от модулирующего сигнала:
Таким образом, частотная и фазовая модуляции оказываются взаимосвязанньг
ми: если изменяется начальная фаза колебания, изменяется и его мгновения*
Угловая модуляция
449
частота, и наоборот. По этой причине два этих вида модуляции и объединяют
под общим названием «угловая модуляция».
Из сказанного можно сделать несколько выводов:
1. По форме колебания с угловой модуляцией нельзя определить, ФМ это или
ЧМ. Для этого необходимо знать еще и модулирующий сигнал.
2. Если пропустить модулирующий сигнал через идеальное дифференцирующее
устройство, а затем подать его на частотный модулятор, получится фазовая
модуляция (верхняя ветвь на рис. 8.19).
3. Если пропустить модулирующий сигнал через идеальное интегрирующее уст-
устройство, а затем подать его на фазовый модулятор, получится частотная мо-
модуляция (нижняя ветвь на рис. 8.19).
ФМ-сигнал
ЧМ-сигнал
Рис. 8.19. Взаимосвязь фазовой и частотной модуляции
В заключение данного раздела приведем сводную таблицу, показывающую, как
связаны с модулирующим сигналом различные характеристики модулированно-
модулированного колебания при фазовой и частотной модуляции.
d
dt
J
Частотный
модулятор
Фазовый
модулятор
Параметр
Начальная фаза
Полная фаза
Мгновенная частота
ФМ
Ф(О - ksM(t)
Ч»(О - (Orf + *Sm(O
со(О = со0 + *^М
at
ЧМ
4>it) = kjsu(f)df+if>0
xV(t) = aot+kjsM(t)de+if>o
a(t) = шо + bM(t)
Гармоническая угловая модуляция
Аналогично тому, как мы это делали для амплитудной модуляции, рассмотрим
случай гармонического модулирующего сигнала. Начальная фаза колебания из-
изменяется при этом по гармоническому закону:
ф@ = Psin(m)-
Коэффициент р называется индексом угловой модуляции (modulation index). Он
определяет интенсивность колебаний начальной фазы.
Полная фаза получится путем добавления линейного слагаемого щ t:
450
Глава 8. Модуляция и демодуляция
Наконец, сам сигнал с гармонической УМ:
s(t) - A cos(co01 + р sin(D t)).
Как уже говорилось, при изменении начальной фазы изменяется и мгновенная
частота:
<o(*)^ <do +pnc
at
В данном случае мгновенная частота меняется также по гармоническому закону.
Как видно из полученной формулы, ее максимальное отклонение от среднего зна-
значения соо составляет рп. Эта величина называется девиацией частоты (frequency
deviation) и обозначается со,/. Таким образом, мы получили важную формулу, по-
показывающую, что индекс угловой модуляции равен отношению девиации часто-
частоты к частоте модулирующего сигнала:
Итак, при гармонической УМ и начальная фаза, и мгновенная частота меняются
по гармоническому закону. Различия между частотной и фазовой модуляцией
начинают проявляться при изменении частоты модулирующего сигнала С1.
При ФМ индекс р является характеристическим параметром модуляции и от час-
частоты модулирующего сигнала не зависит. Девиация частоты оказывается прямо
пропорциональной С1:
р = const,
corf = р П .
При ЧМ характеристическим параметром, не зависящим от частоты модулирую-
модулирующего сигнала, является девиация частоты со,/. Индекс модуляции в этом случае
оказывается обратно пропорциональным П:
со,/ - const,
,
Зависимости индекса модуляции и девиации частоты от частоты модулирующе-
модулирующего сигнала в случае ФМ и ЧМ представлены на рис. 8.20.
ЧМ
ФМ
п
Рис. 8.20. Зависимость индекса модуляции (слева) и девиации частоты (справа)
от частоты гармонического модулирующего сигнала при ФМ и ЧМ
Угловая модуляция 451
Спектр сигнала с гармонической
угловой модуляцией
В данном разделе мы сначала получим точное выражение для спектра радиосиг-
радиосигнала с гармонической УМ, а затем рассмотрим его приближенный вариант, спра-
справедливый для малых индексов модуляции (р « 1).
Для расчета спектрального представления сигнала с гармонической УМ мы пре-
прежде всего представим сигнал в виде вещественной части комплексной экспо-
экспоненты:
- Re (А ехр(;сэог + ;<Ро + ;Psin(Q t + Фо)))
- Re (Л expOo* +; Фо) ехр(;р sin(Q t + Фо))).
Теперь воспользуемся представлением выражения expO'psin x) в виде ряда Фу-
Фурье:
(8.9)
к—с
Здесь ,/*(р) — функция Бесселя 1-го рода порядка k от аргумента р.
Используя представление (8.9), можно записать
syM(O = Re
= Л £/,(p)cos((co0
4—оо
Как видите, спектр сигнала содержит бесконечное количество составляющих с
частотами ш0 + kCl, k = 0, ±1, ±2,... . Амплитуда &-й составляющей равна AJk(fi),
то есть пропорциональна функции Бесселя &-го порядка, аргументом которой
является индекс модуляции р.
Функции Бесселя имеют колебательный характер (графики нескольких из них
приведены на рис. 8.21), поэтому спектр при удалении от несущей частоты ш0
спадает немонотонно. Для примера на рис. 8.22 приведены спектрограммы, соот-
соответствующие р - 1, 10 и 100. Ца рисунке предполагается, что ш0» Г2, так что на-
наличием «хвостов», заползающих из области отрицательных частот, можно пре-
пренебречь:
» % построение графиков функций БесселЯ
» х = 0:0.01:10: ■
» figure
» hold on \■'■■"
» for k = 0:5. plot(x. besselj(k. x)), end
» hold off
» grid on
» xlabeK 'x')
» ylabel('J_{k}(x)[)
45?
Глава 8. Модуляция и демодуляция
0.5
-0.5
...../....у
(^
\ А
10
Рис. 8.21. Функции Бесселя
» % спектрограммы УМ-сигналов с разным индексом модулЯции
» subplotC, 1, 1)
» к = -10:10:
» stem(k. abs(besselj(k. D). '.')
» subplotC. 1. 2)
» к = -20:20:
» stem(k. abs(besselj(k, 10)). '.')
» subplotC. 1. 3)
» к = -150:150:
» stem(k. abs(besselj(k. 100)), '.')
0.5
-10
0.4
0.2
I, .
-5
10
...ill
?
1
r
!
Ill "
Рис. 8.22. Амплитудный спектр сигнала с гармонической УМ при индексе модуляции,
равном 1 (сверху), 10 (в центре) и 100 (снизу)
Угловая модуляция 453
Теперь приближенно рассмотрим частный случай малого индекса модуляции
(р « 1). Начнем с того, что применим к сигналу с гармонической УМ тригоно-
тригонометрические преобразования, чтобы раскрыть косинус суммы:
sy\i(t) = A cos(co0£ + <ро) cos(p sin(fi t + Фо)) -
- A sin(coo£ + фо) sin(p sin(Q t + Фо)).
Поскольку мы считаем, что р « 1, можно приближенно принять, что
cos(p sin(fi£ + O0))« I,
sin(p sin(fi t + Фо)) * p sin(fi t + Фо).
С учетом этого
5уМ@ ~ A cos(co0£ + фо) - A sin(co0£ + фо) Р sin(fi t + Фо).
Остается представить последнее слагаемое в виде полуразностй косинусов:
Аи
^-cos((co0 +П)г + фо +Ф0) +
^ Фо -Фо).
Полученный результат сильно напоминает полученное ранее представление (8.3)
для АМ-сигнала с гармонической модуляцией — тоже три составляющих с теми
же частотами, да и амплитуды их рассчитываются аналогично (только вместо
коэффициента амплитудной модуляции т в формуле фигурирует индекс угло-
угловой модуляции р). Однако есть не слишком бросающееся в глаза, но тем не ме-
менее принципиальное отличие, превращающее амплитудную модуляцию в уг-
угловую — знак «минус» перед одним из слагаемых, соответствующих боковым
частотам. Почему этот знак оказывается столь важным, мы увидим чуть ниже,
при создании векторной диаграммы, а пока отметим главное: чтобы превратить
сигнал с гармонической AM в сигнал с гармонической УМ, достаточно изменить
на 180° начальную фазу одной из боковых частот.
ЗАМЕЧАНИЕ
Еще один способ превратить AM о УМ — изменить фазу составляющей с несущей часто-
частотой на 90°. В том, почему это именно так, читателю предлагается разобраться самостоя-
самостоятельно.
Амплитудный и фазовый спектры сигнала с УМ при малом индексе модуляции
(ее еще называют узкополосной УМ) показаны на рис. 8.23 (пунктирная линия
демонстрирует фазу верхней боковой частоты для случая AM).
Теперь построим векторную диаграмму аналогично тому, как мы делали это для
гармонической AM. Поскольку спектральные представления сигналов с гармо-
гармонической AM и УМ различаются лишь знаком перед одним из слагаемых, под-
подробно комментировать построение иллюстрации, показанной на рис. 8.24, нет
необходимости. Скажем только, что для большей наглядности при построении
выбрано довольно большое значение индекса модуляции (р = 0,5).
454
Глава 8. Модуляция и демодуляция
<в0 - П (о0 щ + С1
Ф А
Фо-
ФО
ф0 Т ;
Т I т
ф0 + Фо - Я
0 - Q
ш0 + Q
Рис. 8.23. Амплитудный и фазовый спектры сигнала с гармонической УМ при р
Im ▲
I
О Re
Рис. 8.24. Векторная диаграмма сигнала с гармонической УМ
ЗАМЕЧАНИЕ
Из векторной диаграммы видно, что при показанном сложении векторов меняется не
только начальная фаза, но и амплитуда результирующего вектора. Это связано с тем, что
формула, но которой производится построение диаграммы, является приближенной. За-
Заинтересованный читатель может выполнить точный расчет амплитудной огибающей и
фазовой функции данного сигнала, воспользовавшись преобразованием Гильберта (см. раз-
раздел «Комплексная огибающая» главы 1).
Ширина спектра сигнала с гармонической УМ
При малом индексе модуляции, когда можно использовать только что рассмот-
рассмотренное приближенное спектральное представление, ширину спектра можно, оче-
очевидно, принять равной 2О. (то же имело место в случае АМ-сигнала). Сложнее
оценить эффективную ширину спектра в случае большого индекса модуляции р.
(В случае УМ речь идет именно об эффективной ширине спектра, поскольку
спектр, строго говоря, содержит бесконечное число составляющих.)
Угловая модуляция
455
При фиксированном аргументе р функции Бесселя затухают с ростом (по моду-
модулю) их порядка к. Попробуем на глаз оценить, как соотносятся индекс модуля-
модуляции р и номер функции Бесселя к, начиная с которого абсолютные величины
функций Бесселя становятся пренебрежимо малыми. Для этого построим линии
равного уровня для функций Бесселя в координатах (Р, k) при изменении р и k
от 0 до 40 (рис. 8.25):
» N = 40: % предельное значение beta и к
» for к = 0:N. х(к+1.:) = BesselJCk. 0:N);
» contourf@:N. 0:N. x, [-1:0.1:1])
end
» xiabel('\beta'
» ylabel('к')
» coiorbar
» colormap gray
Рис. 8.25. Зависимость функций Бесселя от аргумента р и порядка к
Из графика видно, что с ростом порядка k при фиксированном аргументе р функ-
функции Бесселя затухают. Обычно считают, и рисунок это подтверждает, что при
оценке эффективной ширины спектра в. случае Р » 1 можно пренебречь состав-
составляющими с номерами, по абсолютной величине превосходящими индекс угло-
угловой модуляции р. Таким образом, остаются составляющие, для которых \к\ < р, и
эффективная ширина спектра оказывается равной
С учетом приведенного выше соотношения, определяющего индекс угловой мо-
модуляции как отношение между девиацией частоты и частотой модулирующего
456 Глава 8. Модуляция и демодуляция
сигнала, эффективная ширина спектра оказывается равной удвоенной девиации
частоты:
Итак, в зависимости от значения индекса модуляции р можно привести две фор-
формулы для расчета эффективной ширины спектра УМ-сигнала:
Q при р « 1 ширина спектра равна удвоенной частоте модулирующего сигнала:
ДсОэфф = 2Q;
Q при р » 1 ширина спектра равна удвоенной девиации частоты: Дсо-к|И|, = 2со,/.
В отличие от AM, в случае угловой модуляции получить аналитическое выраже-
выражение для спектра при произвольном модулирующем сигнале не удается. Даже по-
попытка рассмотреть двухтональный модулирующий сигнал делает аналитические
выкладки намного сложнее, чем при гармонической модуляции.
Демодуляция УМ
Как и в случае AM, демодуляция УМ-сигнала может выполняться различными
способами. Наиболее радикальный подход — вычислить аналитический сигнал
(см. раздел «Комплексная огибающая» главы 1) и выделить его фазовую функ-
функцию. Дальнейшие действия зависят от вида угловой модуляции. Для демодуляции
ФМ из фазовой функции вычитается линейное слагаемое со0£, соответствующее
немодулировашюй несущей. В случае ЧМ фазовая функция дифференцируется,
а из результата вычитается константа «о (рис. 8.26):
» Fs =100: % частота дискретизации
» t = 0:1/Fs:3: % дискретное времЯ ^
» % сигнал с гармонической УМ
» beta = pi; % индекс модулЯции
» Fc = 10: % несущая частота
» F = 1: % частота модулЯции
» s = cosB*pi*Fc*t + beta*sinB*pi*F*t)):
» у = hilbert(s): % аналитический сигнал
» phi = unwrap(angle(y)): % фазоваЯ функция
» z_pm = phi - 2*pi*Fc*t: % демодулЯциЯ ФМ
» z_fm = diff(phi)*Fs - 2*pi*Fc: % демодулЯциЯ ЧМ
» plotCt. z_pm, t(l:end-l). z_fm. '--')
ЗАМЕЧАНИЕ
В приведенном коде вычисление производной от полной фазы по времени аппроксимиру-
аппроксимируется конечными разностями — diff(phi)*Fs.
Недостатком данного метода является обработка всего входного сигнала сразу
с использованием преобразования Гильберта. Для реализации демодуляции в
реальном масштабе времени необходима последовательная обработка поступаю-
поступающих отсчетов входного сигнала. Это можно реализовать, используя для получе-
получения аналитического сигнала приближенную гильбертовскую фильтрацию во
Угловая модуляция
457
временной области (синтез нерекурсивных и рекурсивных фильтров Гильберта
был рассмотрен в главе 6).
-20
0.5
1.5
2.5
Рис. 8.26. Результаты фазовой (сплошная линия) и частотной (пунктирная линия)
демодуляции сигнала с гармонической УМ
Еще одной альтернативой, пригодной для реализации в реальном масштабе вре-
времени, является квадратурная обработка. При этом входной сигнал умножается
на два опорных колебания, сдвиг по фазе между которыми составляет 90°:
- syM(f )cosoHf =
A A
= -cos(p(£) + -c
cp(O)cosa>0£ =
A A
= --sinq>@ + -sinBcV + ф(О).
Каждый из результатов умножения содержит два слагаемых. Одно из них — низ-
низкочастотное (косинус или синус начальной фазы), другое — высокочастотное
(УМ-сигнал с несущей частотой 2а>0). Низкочастотные составляющие выделя-
выделяются с помощью ФНЧ:
у', (О = А/2 cosФ(О,
Дальнейшие действия, так же как и раньше, зависят от вида угловой модуляции.
Для демодуляции ФМ нам необходимо вычислить фазу полученной пары квад-
квадратурных составляющих:
А
А
;s
А
458
Глава 8. Модуляция и демодуляция
Для демодуляции ЧМ полученную фазовую функцию необходимо продиффе-
продифференцировать:
х
ЧМ*
dt
dt
jy'Q(t)) =
/i (О
Структурная схема получившегося демодулятора показана на рис. 8.27.
ф(/) Демодуляция ФМ
da>
iL Демодуляция ЧМ
Рис. 8.27. Квадратурная обработка сигнала с угловой модуляцией
Достоинством данной схемы является то, что при высокой несущей частоте
входные блоки (генератор опорного колебания и умножители) могут быть вы-
выполнены в аналоговом виде (см. раздел «Квадратурная дискретизация узкопо-
узкополосных сигналов» главы 3).
Еще одним способом демодуляции сигналов с УМ является использование сле-
следящих систем ФАПЧ. Рассмотрение таких систем выходит за рамки тематики
данной книги.
Квадратурная модуляция
В предыдущих разделах мы рассмотрели случаи, когда амплитуда и начальная
фаза гармонического колебания подвергались модуляции по отдельности. Одна-
Однако можно изменять эти два параметра одновременно, получив за счет этого воз-
возможность передавать два сигнала сразу:
5@ = A(t) cos((u0t + Ф(О)- •■•;
Такую модуляцию можно было бы назвать амплитудпо-фазо13рц.О!Д,щко два мо-
модулирующих сигнала оказываются в данном случае «неравноправными», так как
они модулируют существенно разные параметры несущего колебания. Можно
сделать ситуацию более «симметричной», слегка преобразовав форму представ-
представления рассматриваемого сигнала. Для начала раскроем косинус суммы:
5@ = Л@ cos(cooO cos ф@ ~ ^@ sin(cooO sin
Квадратурная модуляция 459
Теперь сигнал оказался представленным в виде суммы двух АМ-колебаний. Их
несущие — cos(co0t) и sin(a>0£) — сдвинуты по фазе на 90° друг относительно дру-
друга, а амплитудные функции равны A(t) cos ф(£) и -A(t) sin ф(О- Обозначим эти
амплитудные функции как a(t) и b(t) и используем их в качестве новой пары мо-
модулирующих сигналов (вместо амплитуды и начальной фазы):
5@ = a(t) cos(cooO + bit) sin((BoO. (8.10)
Такое представление рассматриваемого сигнала называется квадратурным (quad-
(quadrature), а данный способ модуляции — квадратурной модуляцией (КАМ, англий-
английский термин — quadrature amplitude modulation, QAM). Модулирующие сигналы
при этом оказываются совершенно равноправными.
ЗАМЕЧАНИЕ
Следует подчеркнуть, что квадратурная модуляция и амплитудно-фазовая модуляция —
это разные представления одного и того же сигнала. Различие между ними состоит только
в том, как пара модулирующих сигналов управляет параметрами результирующего коле-
колебания.
Спектр сигнала с квадратурной модуляцией
В случае амплитудно-фазового представления сигнала записать аналитическое
выражение для спектра не представляется возможным. А вот для квадратурного
представления получить спектральную функцию не составляет труда.
Поскольку КАМ-сигнал представляет собой сумму двух АМ-сигиалов, мы мо-
можем воспользоваться формулой (8.4) и сразу же записать
5(ю) = -Л(со+ со0) + -Л(со-со0 )--;5(со+ со0) + -;5(со-со0).
Итак, аналогично тому, что происходит при амплитудной модуляции, спектры
модулирующих сигналов «раздваиваются» и «переезжают» в окрестности частоты
несущей ±со0. Если спектры модулирующих сигналов a(t) vib{t) занимают одну
и ту же полосу частот (как обычно и бывает), то они будут перекрываться и по-
после сдвига в область несущей частоты. Однако при этом спектр, соответствую-
соответствующий синусной несущей, дополнительно умножается на ±j. Именно это дает воз-
возможность разделить квадратурные составляющие нри приеме сигнала.
Демодуляция сигнала с квадратурной
модуляцией
Как и другие разновидности AM, квадратурно-модулированный сигнал может
быть демодулирован путем умножения на опорное колебание. Однако поскольку
КАМ-сигнал представляет собой сумму двух АМ-сигналов, то и опорных коле-
колебаний должно быть два — со сдвигом фаз на 90°:
460
Глава 8. Модуляция и демодуляция
У|(О = sKAM(t )cos <o0t = (a(Ocos mot + b(t) sinwot) cos &ot =
11 1
= -a(t) + -a(t)cos2(o0t + -b(t) sin2co0£,
22 2 (8.11)
yQ(t) = sKAM(t)s\nwot = ( b)
= -b(t) + -a(t
Результат каждого умножения содержит три слагаемых. Одно из них является
низкочастотным и представляет собой модулирующую функцию a(t) или b(t) с
уменьиЛенным вдвое уровнем. Остальные два слагаемых образуют. КАМ*сйгашл с
несущей частотой 2ю0- Поэтому полезные составляющие легко выделяются пу-
путем пропусканий результатов умножения через ФНЧ. Структура демодулятора
показана на рис. 8.28, а.
— b(t) cos2(o0t.
ФНЯ
ЯЙ
ФНЧ
COS(O0(
ФНЧ
Ua(t)+jb{t))
ехр(/ю0О
sin щ!
а б
Рис. 8.28. Демодуляция КАМ-сигнала в вещественном (а) и комплексном (б) представлении
Если не ограничиваться вещественными сигналами, можно представить демоду-
демодуляцию КАМ несколько проще. При этом требуется всего один канал, а опорным
колебанием служит комплексная экспонента exp(/eo0t):
= (a(t )cos a>ot + b(t )sm<o0t)exp(jw0t) =
у (t) = sKAM(t
(a(t) + jb(t)) +
Результат комплексного умножения содержит низкочастотное слагаемое, пред-
представляющее обе модулирующие функции, и высокочастотное комплексное сла-
слагаемое, содержащее множитель ехр(/2ооо£). Низкочастотное слагаемое, как обычно,
выделяется с помощью ФНЧ. Структура комплексного варианта демодулятора
показана на рис. 8.28, б. Вещественная и мнимая части комплексного выходного
сигнала соответствуют двум выходным сигналам вещественного демодулятора.
При демодуляции очень важно точное соблюдение частоты и начальной фазы
опорного колебания. При наличии фазовой ошибки Дф на выходах демодулятора
будут получены линейные комбинации модулирующих функций:
Re((a@ +jb(t)) ехрО'Дф)) = a(t) cos Дф - b(t) sin Дф,
Im((o@ + jb(t)) ехр(_/Дф)) = a(t) sin Дф + b(t) cos Дф.
Способы модуляции, используемые при передаче цифровой информации 461
При наличии ошибки по частоте фазовый сдвиг линейно меняется во времени,
так что достаточно подставить в предыдущую формулу Дер = А<й£
Re((a(O + jb(t)) ехр(уДюО) = «(О cos Дю£ - b(t) sin
Im((a(O +jb(t)) expO'Aort)) = a(t) sin Aat + b{t) cos
Таким образом, выходные сигналы демодулятора оказываются промодулирова-
ны по амплитуде частотой биений.
Способы модуляции, используемые
при передаче цифровой информации
В настоящее время все большая часть информации, передаваемой по разнообраз-
разнообразным каналам связи, существует в цифровом виде. Это означает, что передаче под-
подлежит не непрерывный (аналоговый) модулирующий сигнал, а последователь-
последовательность целых*чисел щ, пи п2,..., которые могут принимать значенияиз некоторого
фиксированного конечного множества. Эти числа, называемые символами (symbol),
поступают от источника информации с периодом Г, а частота, соответствующая
этому периоду, называется символьной скоростью (symbol rate):/r = 1/Т.
ЗАМЕЧАНИЕ
Часто используемым на практике вариантом является двоичная (binary) последовательность
символов, когда каждое из чисел п, может принимать одно из двух значений — 0 или 1.
Последовательность передаваемых символов является, очевидно, дискретным сиг-
сигналом. Поскольку символы принимают значения из конечного множества, этот
сигнал фактически является и квантованным, то есть, согласно определениям,
введенным в разделе «Аналоговые, дискретные и цифровые сигналы» главы 3,
его можно назвать цифровым сигналом. Далее в этой главе будут рассматривать-
рассматриваться вопросы, связанные с преобразованием этого цифрового сигнала в аналого-
аналоговый модулированный сигнал.
Типичный подход при осуществлении передачи дискретной последовательности
символов состоит в следующем. Каждому из возможных значений символа со-
сопоставляется некоторый набор параметров несущего колебания. Эти параметры
поддерживаются постоянными в течение интервала Г, то есть до прихода сле-
следующего символа. Фактически это означает преобразование последовательности
чисел {nk} в ступенчатый сигнал sn(t) с использованием кусочно-постоянной ин-
интерполяции:
5„(О =/(«*). kT<t<(k+\)T.
Здесь/— некоторая функция преобразования. Полученный сигнал sn(t) далее
используется в качестве модулирующего сигнала обычным способом.
Такой способ модуляции, когда параметры несущего колебания меняются скачко-
скачкообразно, называется манипуляцией (keying). В зависимости от того, какие именно
параметры изменяются, различают амплитудную (АМи), фазовую (ФМн), час-
частотную (ЧМн) и квадратурную (КАМн) манипуляцию. Кроме того, при передаче
462
Глава 8. Модуляция и демодуляция
цифровой информации может использоваться несущее колебание, отличное по
форме от гармонического. Так, при использовании в качестве несущего колебания
последовательности прямоугольных импульсов возможны амплитудно-импульсная
(АИМ), широтно-импульсная (ШИМ) и время-импульсная (ВИМ) модуляция.
Частотная манипуляция
При частотной манипуляции (ЧМн; английский термин -*- frequency shift keying,
FSK) каждому возможному значению передаваемого символа сопоставляется
своя частота. В течение каждого символьного интервала передается гармониче-
гармоническое колебание с частотой, соответствующей текущему символу.
В качестве примера сформируем 2-позиционный (бинарный) ЧМн-сигиал, в ко-
котором возможным значениям символов 0 и 1 соответствуют частоты 1000 и
1400 Гц. Символьная скорость будет равна 400 символам п секунду, а частота
дискретизации — 8 кГц (рис. 8.29):
» bits = [01001 randintd, 95)]; % цифровое сообщение
» N - length(bits):
» Fd - 400:
» FsFd - 20:
» Fs = Fd * FsFd:
» f - [1000 1400]:
» t = (O:FsFd-l)/Fs:
» sO = cosB*pi*t'*f);
» s_fsk = s0(:. bits+1):
» s_fsk = s_fsk(:):
» td = (O:N*FsFd-l)/FsFd
% длина сообщения
% символьная скорость
% отношение Fs/Fd
% частота дискретизации
% частоты манипуляции
% дискретное время длЯ одной посылки
% столбцы - отсчеты посылок 0 и 1
% каждый столбец - один символ
% "растягиваем" сигнал в один столбец
% время длЯ графика - в символах
% число символов, выводимых на график
» Ng - 5:
» plot(td(l:Ng*FsFd+l), s_fsk(l:Ng*FsFd+D)
» xlabeK 'Symbols')
» ylabeK'sJFSK}1)
» ylim([-l.l 1.1])
1
0.5
О
-0.5
-1
2 3
Symbols
Рис. 8.29. Частотно-манипулированный сигнал
ЗАМЕЧАНИЕ
Первые пять бит сообщения задаются принудительно, чтобы на выводимом фрагменте
графика обязательно были представлены и нулевые, и единичные биты. Полный же сиг-
сигнал должен быть достаточно длинным и случайным — это необходимо для последующего
спектрального анализа. Поэтому остаток 100-битового сообщения формируется с помо-
помощью функции randint из пакета Communications, генерирующей случайные целые числа.
Способы модуляции, используемые при передаче цифровой информации
463
Поскольку мы формировали каждую посылку независимо, сформированный сиг-
сигнал содержит скачки — это хорошо видно на графике. В разделе «Примеры раз-
разложения сигналов в ряд Фурье» главы 1 было показано, что чем более гладким
является сигнал, тем быстрее убывает его спектр. Поэтому можно попытаться
сделать спектр ЧМн-сигнала компактнее, изменив способ формирования так,
чтобы устранить скачки.
Такой способ формирования сигнала называется частотной манипуляцией с не-
непрерывной фазовой функцией (continuous phase frequency shift keying, CPFSK).
При этом формируется линейно меняющаяся полная фаза колебания, а пере-
передаваемые символы управляют скоростью ее изменения. (Можно сказать и так:
передаваемые символы переключают значение мгновенной частоты; эта частота
интегрируется, давая непрерывную фазовую функцию; косинус такой полной
фазы тоже будет непрерывной функцией.) Сформируем указанным способом
ЧМн-сигнал с теми же параметрами, что и в предыдущем примере (рис. 8.30):
» pps - 2*pi*f/Fs: % сдвиг фазы на один отсчет
» si - repmat(pps. FsFd. 1): % столбцы - сдвиги длЯ 0 и 1
» d_cpfsk = sl(:, bits+1): % каждый столбец - один символ
» d_cpfsk - d_cpfsk(:): % "растягиваем" в один столбец
» phi_cpfsk - cumsum(d_cpfsk): % интегрируем фазовые сдвиги
» s_cpfsk = cos(phi_cpfsk): % ЧМн-сигнал
» pTot(td(l:Ng*FsFd-l). s_cpfsk(l:Ng*FsFd-D)
» xlabel('Symbols')
» ylabeK'sJCPFSK}1)
» ylim([-l.l 1.1])
0 1 2 3 4 5
Symbols
Рис. 8.30. ЧМн-сигнал с непрерывной фазовой функцией
Как видите, скачки исчезли. Теперь сравним спектры мощности при двух вари-
вариантах формирования ЧМн-сигнала (рис. 8.31):
» periodogram(s_fsk, []. []. Fs)
» yl1m([-W0 0])
» figure
» periodogram(s_cpfsk. []. []. Fs)
» ylim([-100 0]7
Сравнение верхнего и нижнего графиков рис. 8.31 показывает, что при наличии
скачков фазы в спектре присутствуют ярко выраженные пики на частотах, крат-
кратных символьной скорости 400 Гц. У сигнала с непрерывной фазовой функцией
такие пики отсутствуют, и спектр в целом получился более компактным.
464
Глава 8. Модуляция и демодуляция
Periodogram PSD Estimate
i
Q.
со
-Л
1
I
1
1
1
L.
JliUn
Щ
' 1
1 .
1 1
41
1
I
■■[■■
■■■■[•■
i
j
111/A
1
.i
i\
■
П
H
1
1
I i i * i
500 1000 1500 2000 2500 3000 3500 4000
Frequency (Hz)
Periodogram PSD Estimate
0
-10
-20
-30
-40
-50
-60
-70
-80
-90
-100,
111
!
1
1.
..bkUtl-
. aw
..И.
П
hi
1
m
i
HI
500
1000 1500 2000 2500 3000 3500 4000
Frequency (Hz)
Рис. 8.31. Спектры мощности ЧМн-сигнала при наличии (сверху) и отсутствии (снизу)
разрывов у фазовой функции
Прием ЧМн-сигнала, как правило, осуществляется корреляционным методом.
Сущность его состоит в вычислении взаимной корреляции (см. раздел «Корре-
«Корреляционный анализ» главы 1) между принимаемым сигналом и колебаниями-об-
колебаниями-образцами (опорными сигналами), представляющими собой гармонические коле-
колебания с используемыми для манипуляции частотами. В качестве выходного
символа выбирается тот, частота которого оказывается максимально коррелиро-
вана со входным сигналом.
Корреляционный прием может быть когерентным или некогерентпым. Когерент-
Когерентный алгоритм может использоваться, если известна начальная фаза колебания.
Опорными сигналами при этом служат вещественные синусоиды с нужными
частотами и начальными фазами. Для принятия решения о принятом символе
сравниваются вещественные результаты вычисления корреляционных сумм.
Способы модуляции, используемые при передаче цифровой информации 465
На практике, однако, начальная фаза, как правило, неизвестна. В таких случаях
применяют некогерентный корреляционный прием, при котором опорные сиг-
сигналы представляют собой комплексные экспоненты с нужными частотами. Для
принятия решения о принятом символе сравниваются модули комплексных ре-
результатов вычисления корреляционных сумм. Модуль комплексной ВКФ не за-
зависит от начальных фаз сигналов, однако помехоустойчивость такого алгоритма
несколько хуже, чем в случае когерентного приема.
Реализуем когерентную демодуляцию для первого варианта формирования ЧМн-
сигнала (с разрывами начальной фазы). В этом случае начальные фазы всех по-
посылок одинаковы, что сильно упрощает когерентную демодуляцию (хотя это не
означает, что для ЧМн-сигнала с непрерывной начальной фазой когерентная де-
демодуляция невозможна — просто она реализуется сложнее):
» у - reshape(s_fsk. FsFd. N): % каждый столбец - один символ
» z - sO' * у; % 1-Я строка -'корреляции с "О". 2-Я - с "
» х = zB,:) > z(l.:); % решения о принятых символах
» symerrCbits. x) % число ошибок приема
ans =
О
В этом коде использованы скалярные переменные и матрица опорных колеба-
колебаний sO из примера формирования ЧМн-сигнала. Как видите, сигнал принят без
ошибок.
Теперь демодулируем сигнал с непрерывной начальной фазой некогерентным
методом:
» у - reshape(s_cpfsk, FsFd. N); % каждый столбец - символ
» sO_exp = exp(i*2*pi*t'*f); % столбцы - опорные сигналы
» z - sO_exp.' * у; % корреляции с "О" (строка 1) и с " B)
» х = abs(zB,:)) > abs(z(l.:)): % решения о принятых символах
» symerrCbits. х) % число ошибок приема
ans =
О
Ошибок и в этом случае нет.
Минимальная частотная манипуляция
Для повышения помехоустойчивости ЧМн желательно, чтобы посылки, соответ-
соответствующие разным символам, были некоррелированы (см. раздел «Корреляцион-
«Корреляционный анализ» главы 1). Считая начальные фазы посылок нулевыми, ЧМн-сигна-
лы для символов 0 и 1 можно записать так:
so(t) - A cos (aot, О й t < Т,
5i@ = A cos ©it, 0 < t < Т.
Их ВКФ при нулевом временном сдвиге равна
~ „ч. г , *. , *. , д^г , A2 sin(oo, + (£>ЛТ A2 sin(oo, -a>n)T
BmW)=\s0(t)Si(t)dt = A2\cos(u0tcos^tdt = ---±-±-^- + — к * °; .
о о 2(Ю1+ юо) 2@0,-00,,)
466
Глава 8. Модуляция и демодуляция
Если (coj + щ)Т» 1, то первое слагаемое значительно меньше второго и им мож-
можно пренебречь:
В01@).
-со0)Г
2(со,-со0)
Это значение равно нулю при (@( - со0)Г = nk, где k — целое число, не равное
нулю. Таким образом, минимальное значение расстояния между частотами ма-
манипуляции, при котором посылки, соответствующие разным символам, оказыва-
оказываются некоррелированными, составляет
AcOmin = ~ ' A/min =2J=~2'
(8.12)
где /т — символьная скорость,,
Двухпозиционная (бинарная) ЧМн, частоты которой выбраны согласно (8.12),
получила название минимальной частотной манипуляции (МЧМн, английский
термин — minimum shift keying, MSK).
Амплитудная манипуляция
Как будет показано далее, амплитудная манипуляция (АМн; английский термин -
amplitude shift keying, ASK), при которой скачкообразно меняется амплитуда не-
несущего колебания, является частным случаем квадратурной манипуляции. Поэто-
Поэтому здесь мы только построим в качестве примера график АМн-сигиала (рис. 8.32).
0 12 3 4
Рис. 8.32. Сигнал с амплитудной манипуляцией
» sy - [1 3 2 4 1];
» Fd - 1:
» Fc - 4;
» FsFd = 40:
% передаваемые символы
% символьная скорость
% несущая частота
% отношение Fs/Fd
Способы модуляции, используемые при передаче цифровой информации
467
» Fs - Fd * FsFd; % частота дискретизации
» t = (O:length(sy)*FsFd-l)/Fs; % дискретное время
» % формируем АМн-сигнал
» s_ask = sy(floor(Fd*t)+l) .* cosB*pi*Fc*t):
» plotCt. s_ask)
Фазовая манипуляция
Фазовая манипуляция (ФМн; английский термин — phase shift keying, PSK),
при которой скачкообразно меняется фаза несущего колебания, тоже является
частным случаем квадратурной манипуляции.
На практике фазовая манипуляция используется при небольшом числе возмож-
возможных значений начальной фазы — как правило, 2, 4 или 8. Кроме того, при приеме
сигнала сложно измерить абсолютное значение начальной фазы; значительно
проще определить относительный фазовый сдвиг между двумя соседними сим-
символами. Поэтому обычно используется фазоразпостпая манипуляция (синони-
(синонимы — дифференциальная фазовая манипуляция, относительная фазовая мани-
манипуляция; английский термин — differential phase shift keying, DPSK).
Построим график сигнала с 4-позиционной фазовой манипуляцией (р'йс. 8.33):
» sy = [0 2 1 3 0];
» Fd = 1;
» FC = 4;
» FsFd - 40;
» FS = Fd * FsFd;
» t = (O:length(sy)*FsFd-l)/Fs
» % формируем ФМн-сигнал
» s_psk = cosB*pi*Fc*t + pi/2*sy(floor(Fd*t)+U);
» plotCt. s_psk)
» xlabelCSymbols')
» ylabeK's {PSK}')
» ylim([-l.l 1.1])
% передаваемые символы
% символьная скорость
% несущая частота
% отношение Fs/Fd
% частота дискретизации
% дискретное время
v
О 1 2 3 4 5
Symbols
Рис. 8.33. Сигнал с 4-позиционной фазовой манипуляцией
Квадратурная манипуляция
При квадратурной манипуляции (КАМн; английский термин — quadrature am-
amplitude shift keying, QASK) каждому из возможных значений дискретного симво-
символа С,, ставится в соответствие пара величин — амплитуды синфазной и квадра-
468
Глава 8. Модуляция и демодуляция
турной составляющих либо, что эквивалентно, амплитуда и начальная фаза не-
несущего колебания:
Ск -> {ак, b/t), s(t) = ак cos юо£ + bk sin юо£, kT< t < (k
или
Ск -> (ЛА, щ), s(t) = Ак cos(m0t + щ), kT<t<(k
Параметры аналогового колебания, сопоставленные дискретному символу Ск,
удобно представлять в виде комплексного числа в алгебраической {ак + jbk) или
экспоненциальной (Л* ехр(/ф*)) форме. Совокупность этих комплексных чисел
для всех возможных значений дискретного символа называется сигнальным со-
созвездием (constellation).
ЗАМЕЧАНИЕ
В отечественной литературе также используется громоздкий и не слишком наглядный
термин «сишально-кодовая конструкция» (СКК). В данной книге сделан выбор в пользу
более выразительного и запоминающегося слова «созвездие».
При представлении дискретного символа комплексным числом Ск сигнал с квад-
квадратурной манипуляцией можно записать следующим образом:
s(t) = Re(Ck ехр(->со00)- kT<t<(k+
На практике используются созвездия, содержащие от четырех точек до несколь-
нескольких тысяч. На рис. 8.34 показаны некоторые созвездия, используемые модемами,
предназначенными для передачи данных по телефонным линиям.
• •
• •
i
■ .•■..•.:•.:::::
" —:::::::::
:::::::::::::: >
:::..:::::::•.•
Рис. 8.34. Примеры созвездий, используемых при квадратурной манипуляции:
а — 16 точек (протокол V.32, скорость 9600 бит/с), 6—128 точек
^протокол V.32bis, скорость 14 400 бит/с), в — 640 точек
(протокол V.34, скорость 28 800 бит/с)
График сигнала с квадратурной манипуляций"! оказывается не очень наглядным
из-за смешанного (амплитудно-фазового) характера модуляции. Изменения амп-
амплитуды и фазы при переходе от символа к символу могут быть небольшими и
плохо заметными на графике.
Способы модуляции, используемые при передаче цифровой информации
469
Построим тем не менее график сигнала, сформированного с использованием 16-
точечного «квадратного» созвездия, показанного выше на рис. 8.34, а. Поскольку
нас сейчас не интересует конкретный способ связи дискретных символов и точек
созвездия, мы просто создадим векторы амплитуд синфазной и квадратурной
составляющих, значения которых случайно выбраны из набора {-3, -1, 1, 3}
(рис. 8.35):
% число символов
% случайные целые числа 0...3
% преобразуем к требуемому набору
% символьная скорость
% несущая частота
% число отсчетов на один символ
% частота дискретизации
» N = 1000:
» aa = rand-intd. N. 4):
» bb = randintd. N. 4):
» al = 2*aa-3:
» bl = 2*bb-3:
» Fd = 2400:
» Fc = 1800:
» FsFd = 4:
» Fs. = Fd * FsFd:
» % дублируем каждый отсчет FsFd раз
» al = repmat(al, FsFd. 1):
» al = al(:):
» bl = repmat(bl. FsFd. 1):
» bl = bl(:):
» % формируем аналоговый сигнал
» t = (O:N*FsFd-l)/Fs: % дискретное времЯ
» t = t': % превращаем строку в столбец
» s_qaskl6 = al .* cosB*pi*Fc*t) + bl .* sinB*pi*Fc*t);
» plot(t(l:100). s_qaskl6A:100))
'0 0.002 0.004 0.006 0.008 0.01 0.012
Рис. 8.35. Сигнал с 16-позиционной квадратурной манипуляцией
Параметры сформированного сигнала (структура созвездия, значения символь-
символьной скорости и несущей частоты) соответствуют модему, передающему данные со
скоростью 9600 бит/с в соответствии с Рекомендацией ITU-T V.32. Прослушаем
470
Глава 8. Модуляция и демодуляция
сигнал, используя для этого функцию soundsc, чтобы не заботиться о приведении
сигнала к диапазону уровней -1...1:
» soundsc(repmat(s_qaskl6, 10. 1). Fs)
ЗАМЕЧАНИЕ
Функция repmat использована здесь, чтобы повторить сформированный сигнал десять
раз — иначе звук окажется слишком коротким.
Если вы когда-нибудь слышали шуршащий звук модема, то должны заметить,
что в сформированном нами сигнале что-то не так. Действительно, на практике
при осуществлении квадратурной манипуляции выполняется еще одна опера-
операция, которую мы пока пропустили. Речь о ней пойдет далее, в разделе «Форми-
«Формирование спектра».
При квадратурной манипуляции могут меняться и амплитуда, и начальная фаза
несущего колебания, поэтому амплитудная и фазовая манипуляция являются ча-
частными случаями квадратурной — нужно лишь использовать соответствующие
созвездия. Выведем графики этих созвездий с помощью функции modmap (она бу-
будет рассмотрена далее, в разделе «Преобразование цифрового сигнала в аналого-
аналоговые параметры модуляции»). Результат показан на рис. 8.36.
» subplotd. 2. 1)
» modmapCask'. 8)
» subplotd. 2. 2)
» modmap('psk'. 8)
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.8
-0.8
-1
ASK constellation
+ + + + + + ♦♦
•
-1
-0.5 0 0.5
In-phase component
ASK/PSK Constellation
Рис. 8.38. Созвездия, соответствующие 8-позиционной амплитудной (слева)
и фазовой (справа) манипуляции
ЗАМЕЧАНИЕ
Функции цифровой модуляции пакета Communications при реализации амплитудной ма-
манипуляции используют как положительные, так и отрицательные амплитудные множи-
множители, допуская, таким образом, .скачки фазы несущей на 180°. Это видно из графика
созвездия амплитудной манипуляции, приведенного на рис. 8.36 слева.
Способы модуляции, используемые при передаче цифровой информации
471
Помехоустойчивость
За счет использования двумерного характера гармонического несущего коле-
колебания (под двумерностью здесь понимается наличие двух параметров, которые
можно независимо изменять) квадратурная манипуляция обеспечивает боль-
большую помехоустойчивость (то есть меньшую вероятность ошибки)", чём АМп и
ФМн. Не вдаваясь в подробности, скажем, что помехоустойчивость тем выше,
чем больше расстояние d между ближайшими точками созвездия на комплекс-
комплексной плоскости. При этом для корректности сравнения разных созвездий у них
должны быть одинаковыми, помимо числа точек, среднеквадратические ампли-
амплитуды:
Сравним для примера помехоустойчивость 16-позициопных амплитудной, фазо-
фазовой и квадратурной манипуляций (рис. 8.37).
d ■.
+
+
ч
1'
+
+
■<
. d
> 4
*■ 4
Рис. 8.37. Сравнение помехоустойчивости 16-позиционной амплитудной (слева),
фазовой (в центре) и квадратурной (справа) манипуляции
Результаты расчетов минимального расстояния между точками, среднеквадрати-
ческого уровня сигналов, а также межточечного расстояния, нормированного к
этому уровню, сведены в табл. 8.1.
Таблица 8.1. Сравнение помехоустойчивости разных видов манипуляции
Вид манипуляции
АМн
ФМн
КАМн
Минимальное
межточечное
расстояние, dmin
—-0,1333
10
2 sinf—I a 0,39
U6J
Среднеквадратиче-
ский уровень
сигнала, а
^ « 0,6146
15
1
^«0,745
Нормированное
расстояние, dm,n/a
-i, •* 0v2.169-
2sinf—) «0,39- , .
-== а 0,63
л/5
472 Глава 8. Модуляция и демодуляция
Анализ данных из таблицы показывает, что квадратурная манипуляция обеспе-
обеспечивает максимальное межточечное расстояние, нормированное к среднеквадра-
тическому уровню сигнала.
Демодуляция
Дёмодулируется сигнал с квадратурной манипуляцией так же, как и в случае
аналоговой квадратурной модуляции — сигнал умножается на два несущих ко-
колебания, сдвинутых по фазе друг относительно друга на 90°, а результаты умно-
умножения пропускаются через ФНЧ (см. ранее рис. 8.28 в разделе «Демодуляция
сигнала с квадратурной модуляцией»). На выходе этих ФНЧ будут получены
аналоговые сигналы синфазной и квадратурной составляющих. Далее эти сигна-
сигналы дискретизируются с частотой, равной символьной скорости. Пары отсчетов
синфазной и квадратурной составляющих образуют комплексное число, и бли-
ближайшая к этому числу точка используемого созвездия (а точнее — соответствую-
соответствующий этой точке информационный символ) выдается в качестве выходного ре-
результата.
Реализуем описанный алгоритм демодуляции для сформированного ранее сиг-
сигнала s_qaskl6. Приведенный ниже код реализует квадратурную демодуляцию, дис-
дискретизацию полученного сигнала с символьной частотой (для этого из вектора у
выбираются элементы с шагом Fs/Fd), вывод графика расположения принятых
точек на комплексной плоскости (такой график называется диаграммой рассея-
рассеяния — scatter plot, рнс. 8.38), выбор ближайших координат точек из использован-
использованного созвездия и сравнение полученных синфазных а2 и квадратурных Ь2 ампли-
амплитуд с исходными амплитудами аа и Ыэ:
» % умножение на комплексное опорное колебание
» у = s_qaskl6 .* exp(j*2*pi*Fc*t) * 2; ; '
» [b. a] = butterB, Fd*2/Fs); % сглаживающий ФНЧ
» у = filtfilt(b. а. у): % фильтрация
» z = yC:FsFd:end): % дискретизация с символьной частотой
» plot(z. '.') % вывод диаграммы рассеЯниЯ
» axis square
» а2 = round((real(z)+3)/2): % оценка синфазной амплитуды
» a2(find(a2<0)) = 0;
» a2(find(a2>3)) = 3;
» Ь2 = round((imag(z)+3)/2): % оценка квадратурной амплитуды
» b2(find(b2<0)) = 0;
» b2(find(b2>3)) = 3;
» symerrCaa'. а2) % число ошибок по синфазной амплитуде
ans =
0 ' "
» symerr(bb', Ь2) % число ошибок по квадратурной амплитуде
ans =
О
Функция округления round в этом коде применена для поиска точки используе-
используемого созвездия, наиболее близкой к принятому отсчету сигнала. Такое решение
Способы модуляции, используемые при передаче цифровой информации
473
возможно благодаря простой структуре использованного нами созвездия. В бо-
более общем случае для этого необходимо воспользоваться функцией demodmap (см.
далее раздел «Преобразование аналогового сигнала в цифровое сообщение»).
Функция symerr подсчитывает число неправильно принятых символов (она воз-
возвращает число различающихся элементов двух векторов одинаковой длины). Как
видите, сигнал принят без ошибок.
Рис. 8.38. Диаграмма рассеяния при приеме сигнала
с квадратурной манипуляцией
Формирование спектра
Если параметры модуляции аналогового сигнала поддерживаются постоянными
в течение символьного такта и в начале нового такта изменяются скачкообразно,
это приводит к появлению скачков и в сформированном сигнале. Как было пока-
показано при обсуждении свойств спектров сигналов (см. раздел «Примеры разложе-
разложения сигналов в ряд Фурье» главы 1), спектр сигнала, содержащего скачки, зату-
затухает с ростом частоты медленно — пропорционально 1/со. Чтобы сделать спектр
более компактным, необходимо обеспечить гладкость сигнала, а это, в свою оче-
очередь, означает гладкость модулирующей функции. Следовательно, вместо скач-
скачкообразного изменения параметров модуляции нам необходимо выполнить ин-
интерполяцию между точками созвездия, соответствующими последовательным
символам.
Согласно теореме Котельникова, мы можем соединить отсчеты, следующие с сим-
символьной скоростью Fd, плавной функцией, занимающей полосу частот от нуля
до F(//2. В этом случае квадратурно-манипулированный сигнал будет занимать
полосу частот шириной F,/. Однако медленное затухание функций sine, состав-
составляющих базис Котельникова, делает неудобной интерполяцию на их основе.
Наибольшее распространение при интерполяции отсчетов для цифровой моду-
модуляции получил SQRT-вариант фильтра с косинусоидалъпым сглаживанием АЧХ
(square root raised-cosine filter; расчет таких фильтров обсуждался в главе 6).
474
Глава 8. Модуляция и демодуляция
Фильтр, используемый для интерполяции, определяет форму спектра КАМн-
сигиала, поэтому его называют формирующим фильтром (shaping filter), а сам
процесс интерполяции — формировшшем спектра (spectral shaping).
Скачкообразное изменение параметров модуляции можно рассматривать как ис-
использование формирующего фильтра с прямоугольной импульсной характери-
характеристикой, длительность которой равна символьному интервалу.
Повторим формирование 16-позициоиного квадратурно-манипулироваиного сиг-
сигнала (см. рис. 8.35), используя на сей раз формирующий фильтр с косинусои-
дальным сглаживанием АЧХ (рис. 8.39):
» % используем сформированные ранее векторы амплитуд аа и bb
» als = 2*aa-3; % преобразуем к требуемому набору
» bis = 2*bb-3;
» als = rcosf1t(als. Fd, Fs, 'sqrt');
» bis = rcosflt(bls. Fd, Fs, 'sqrt'):
» % формируем сигнал с квадратурной манипуляцией
» t = @:1ength(als)-1)/Fs: % дискретное времЯ
» t = t'; % превращаем строку в столбец
» s_qaskl6s = als .* cosB*pi*Fc*t) + bis .* sinB*pi*Fc*t);
» plot(t(l:100). s_qaskl6s(l:100))
0.002 0.004 0.006 0.008 0.01 0,012
Рис. 8.39. Сигнал с 16-позиционной квадратурной манипуляцией
при использовании формирования спектра
Прослушаем и этот сигнал, снова используя функцию soundsc:
» soundsc(repmat(s_qaskl6s. 10. 1). Fs)
Звук стал больше похож на тот, что прризводится модемом, — все дело именно в
формировании спектра.
Сравним спектры мощности сигналов s_qaskl6 и s_qaskl6s, чтобы наглядно пока-
показать влияние формирующего фильтра (рис. 8.40).
Способы модуляции, используемые при передаче цифровой информации
475
» [PI, f] = pwelch(s_qaskl6. [], [], []. Fs):
» Р2 = pwelch(s_qaskl6s. []. []. [], Fs):
» psdplot([Pl P2], f, 'Hz')
500 1000 1500 2000 2500 3000 3500 4000 4500
Frequency (Hz)
Рис. 8.40. Спектры плотности мощности сигналов с квадратурной манипуляцией
при отсутствии (верхний график) и наличии (нижний график)
формирующего фильтра
Из графиков видно, что при использовании формирующего фильтра спектр сиг-
сигнала оказывается значительно компактнее.
При приеме такого сигнала в качестве ФНЧ необходимо использовать такой же
фильтр, как для формирования спектра. Последовательное использование двух
SQRT-фильтров с косинусоидальным сглаживанием дает результирующую им-
импульсную характеристику вида F.6) (см. рис. 6.7), равную нулю в точках, сдви-
сдвинутых на целое число символов относительно пика. Это позволяет при правиль-
правильном выборе моментов взятия отсчетов устранить помехи от соседних символов
(так называемую межсимволъпую интерференцию, МСИ; английский термин —
intersymbol interference, ISI):
» % умножение на комплексное опорное колебание
» у = s_qaskl6s .* exp(j*2*pi*Fc*t) * 2;
» b = rcosine(Fd. Fs. 'sqrt'); % сглаживающий ФНЧ
» у = filterCb. 1, у); % фильтрация
» % подготовка данных длЯ глазковой диаграммы
» у_еуе = reshape(y, FsFd. length(y)/FsFd);
» у_еуе - [0 y_eye(end,l:end-l): y_eye]:
» % вывод глазковой диаграммы
» subplotB, 1. 1)
» plot@:FsFd, real(y_eye), 'b')
» title ('Eye diagram')
» subplotB. 1. 2)
» plotCO:FsFd. imag(y_eye), 'b')
476 Глава 8. Модуляция и демодуляция
» xlabelС Offset (samples)')
» % выбор моментов взЯтиЯ отсчетов
» offset = 1;
» % дискретизация с символьной частотой
» z = y(offset:FsFd:end);
» z(l:6) = []; % удаление начального «хвоста»
» figure
» plot(z. '.') % вывод диаграммы рассеЯниЯ
» axis square
» а2 = round((real(z)+3)/2); % оценка синфазной амплитуды
» a2(find(a2<0)) = 0:
» a2(find(a2>3)) = 3:
» Ь2 = round((imag(z)+3)/2): % оценка квадратурной амплитуды
» b2(find(b,2<0)) = 0:
» b2(find(b2>3)) = 3;
» symerr(aa', a2) % число ошибок по синфазной амплитуде
arts =
0
» symerr(bb'. Ь2) % число ошибок по квадратурной амплитуде
arts =
0
На рис. 8.41 сверху показана глазковая диаграмма (eye diagram) для данного сиг-
сигнала. Глазковая диаграмма представляет собой «осциллограмму» сигнала, постро-
построенную при длительности «прямого хода развертки», равной одному символьно-
символьному такту, и бесконечном «времени послесвечения экрана». В точках оптималь-
оптимальной дискретизации линии на такой диаграмме образуют узкие пучки, свободное
пространство между которыми по форме напоминает раскрытый глаз. В дан-
данном случае видно, что выбирать элементы из вектора у нужно начиная с перво-
первого. Поскольку сигнал является комплексным, приведены отдельные графики для
его вещественной и мнимой частей. На рис. 8.41 снизу приведена диаграмма
рассеяния, полученная при приеме данного сигнала. Благодаря использованию
согласованных друг с другом фильтров на передающей и приемной сторонах
разброс точек оказывается значительно меньше, чем на приведенном ранее
рис. 8.38.
При прохождении сигнала через канал связи, обладающий частотной диспер-
дисперсией, то есть вносящий разную групповую задержку на разных частотах, сим-
символы оказываются «размазанными» во времени и «наползают» друг на друга.
В этом случае устранить межсимвольную интерференцию полностью не удается.
Чтобы минимизировать ее, используют адаптивные фильтры, параметры ко-
которых автоматически подстраиваются под характеристики обрабатываемого сиг-
сигнала. Рассмотрение таких фильтров выходит за рамки тематики данной книги.
Информацию о них можно найти, например, в [18, 19], а также в документации
последней B.1) версии пакета Filter Design — в эту версию пакета добавле-
добавлены функции, реализующие несколько распространенных алгоритмов адаптивной
фильтрации.
Способы модуляции, используемые при передаче цифровой информации
477
Eye diagram
О 0.5 1 1.5 2 2.5 3 3.5 4
0.5
1.5 2 2.5
Offset (samples)
4
3
2
1
0
-1
-2
-3
•
•
• к » ■
• • »
■
* * • •
■
♦ • If
-4
-2
Рис. 8.41. Глазковая диаграмма (сверху) и диаграмма рассеяния (снизу),
полученные при приеме сигнала с квадратурной манипуляцией
Широтно-импульсная модуляция
При широтно-импульсной модуляции (ШИМ; английский термин — pulse width
modulation, PWM) в качестве несущего колебания используется периодическая
последовательность прямоугольных импульсов, а ннформационным параметром,
связанным с дискретным модулирующим сигналом, является длительность этих
импульсов (рис. 8.42).
Периодическая последовательность прямоугольных импульсов одинаковой дли-
длительности имеет постоянную составляющую, обратно пропорциональную скваж-
скважности импульсов, то есть прямо пропорциональную их длительности (см. раздел
«Примеры разложения сигналов в ряд Фурье» главы 1). Пропустив импульсы
через ФНЧ с частотой среза, значительно меньшей, чем частота следования им-
импульсов, эту постоянную составляющую можно легко выделить, получив посто-
постоянное напряжение. Если длительность импульсов будет различной, ФНЧ выделит
478
Глава 8. Модуляция и демодуляция
медленно меняющееся напряжение, отслеживающее закон изменения длитель-
длительности импульсов. Таким образом, с помощью ШИМ можно создать несложный
ЦЛП: значения отсчетов сигнала кодируются длительностью импульсов, а ФНЧ
преобразует импульсную последовательность в плавно меняющийся сигнал.
ЗАМЕЧАНИЕ
Именно такие ЦАП используются, например, для реализации настройки па каналы, регу-
регулировок громкости, яркости и т. и, в большинстве современных телевизоров: команды от
кнопок управления меняют скважность импульсов, вырабатываемых управляющим про-
процессором, а сглаживающие цени формируют из этих импульсов постоянные напряжения,
управляющие аналоговыми цепями.
IT
ЪТ
4Г
^шим(')
5Г
4—
О ■ Т IT ЪТ 4Т 5Г t
Рис. 8.42. Широтно-импульсная модуляция
Число уровней напряжения, формируемых таким ЦАП, определяется числом
возможных длительностей импульсов. Если импульсы формируются в цифро-
цифровом виде, шаг изменения длительности определяется частотой дискретизации
импульсной последовательности. Отношение этой частоты к частоте дискретиза-
дискретизации формируемого сигнала даст возможное число уровней.
Например, если мы захотим поэкспериментировать с ШИМ, используя звуко-
звуковую карту компьютера, нам окажется доступно всего шесть уровней (максималь-
(максимальная частота дискретизации, обеспечиваемая звуковой картой, — 48 кГц; мини-
минимально приемлемая частота дискретизации звукового сигнала — 8 кГц; получаем
48/8 = 6 уровней). Для реальной работы, конечно, маловато, а для эксперимен-
экспериментов подойдет.
Попробуем сформировать таким путем синусоиду:
»' N = 6: % число уровней
» Fs = 8еЗ:
» FsO = Fs * N:
» fO = 1еЗ:
» t = O:l/Fs:l;
» tO = (O:length(t)*N-l)/FsO;
% частота дискретизации сигнала
% частота дискретизации импульсов
% частота синусоиды
% одна секунда дискретного времени
% дискретное время импульсов
Способы модуляции, используемые при передаче цифровой информации
479
» s - sinB*pi*fO*t): % отсчеты дискретной синусоиды
» sq = round((s+l)*N/2); % квантованные отсчеты
» s_pwm = zerosCN. length(t)): % заготовка длЯ ШИМ-сигнала
» for k-l:N. s_pwm(k, find(sq>=k)) = 1; end
» s_pwm = s_pwm(:); % "растягиваем" матрицу в один столбец
В приведенном коде следует обратить внимание на цикл for, с помощью которо-
которого формируется ШИМ-сигнал. Мы сначала создаем шестистрочную матрицу, за-
заполненную нулями, а затем построчно формируем ее содержимое, в цикле срав-
сравнивая отсчеты сигнала с постепенно увеличивающимся порогом и записывая
единицы в те столбцы, где отсчеты сигнала превышают порог или равны ему.
Посмотрим, как выглядят исходные отсчеты синусоиды и соответствующий
ШИМ-сигнал (рис. 8.43):
» subplotB. 1. 1)
» stem(t(l:33). sq(l:33))
» subplotB. 1, 2)
» stairs(tO(l:193). s_pwmA:193))
» ylim([-0.1 1.1])
6
<
о
>
>
(
> (
u
<
)
)
<
<
> <
1
>
>
<
>
(
) (
u
(
1
>
<
I
(
1 О
и
0 0.5 1 1.5 2 2.5 3 3.5 ,4
x10
A
0.8-
0.6-
0.4-
0.2-
0 •
1
-
-
0 0.5 1 1.5 2 2.5 3 3.5 ,4
x 10
Рис. 8.43. Отсчеты синусоиды (сверху) и соответствующий им ШИМ-сигнал (снизу)
Теперь взглянем на спектр ШИМ-сигнала (рис. 8.44):
» periodogram(s_pwm. [], []. FsO):
» y1im([-50 0])
Как видите, наиболее интенсивная спектральная составляющая (не считая со-
составляющей с нулевой частотой) действительно имеет частоту исходной сину-
синусоиды — 1 кГц. Выделим ее, пропустив ШИМ-сигнал через ФНЧ с частотой сре-
среза, равной частоте Найквиста, то есть 4 кГц (рис. 8.45):
» [b. a] - butterE. Fs/FsO):
» s_filtered = fi1ter(b. a. s_pwm);
» plot(tO(l:193). s_filtered(l;193))
» figure: periodogram(s_filtered.[].[].FsO):ylim([-50 0])
480
Глава 8. Модуляция и демодуляция
О
-5
"Я"
5 -10
2. -15
« -20
0 -25
1 0
<П -35
I °
. °- -45
-50
Periodogram PSD Estimata
...
0.5
1 1.5
Frequency (Hz)
хЮ*
Рис. 8.44. Спектр мощности синусоиды, представленной с помощью ШИМ
2- -15 -
|
-20
i
1 -30
<п -35
| -40
£ -45
-50
0.5
1 1.5 2 2.5 3
Periodogram PSD Estimate
0.5
1 1.5
Frequency (Hz)
3.5
хЮ
...
...
...
■
Рис. 8.45. Синусоида, полученная путем низкочастотной фильтрации ШИМ-сигнала (сверху)
и ее спектр мощности (снизу)
Функции модуляции и демодуляции пакета Signal Processing 481
Результат, как видите, действительно напоминает синусоиду, хотя оставшиеся
искажения хорошо заметны на глаз — шести уровней квантования все-таки явно
маловато. Желающие могут послушать, как звучат ШИМ-сигнал и выделенная
из него низкочастотная составляющая:
» wavplay(s_pwm. FsO) % ШИМ-сигнал
» wavplay(s_fiItered. FsO) % восстановленная синусоида
Тональный сигнал хорошо прослушивается в обоих случаях, но в фильтрован-
фильтрованном сигнале он, естественно, звучит значительно чище.
Функции модуляции и демодуляции
пакета Signal Processing
В пакете Signal Processing модуляция и демодуляция реализуются с помощью
всего двух функций — modul ate и demod соответственно. Используемый вид моду-
модуляции указывается в качестве одного из входных параметров этих функций.
В общем виде синтаксис вызова функций modulate и demod выглядит так:
[у, t] = modulate(x. Fc, Fs. 'method', opt)
x = demod(y, Fc. Fs. 'method', opt)
Здесь x — вектор отсчетов модулирующего сигнала, у — вектор отсчетов модули-
модулированного сигнала, Fc — несущая частота, Fs — частота дискретизации, ' method' —
вид модуляции. Назначение дополнительного параметра opt зависит от вида мо-
модуляции и для конкретных случаев будет рассмотрено ниже.
Второй выходной параметр t, возвращаемый функцией modulate, — это вектор
моментов времени, использованный для расчетов. Он определяется следующим
образом:
t = (@:1ength(y)-l)/Fs)':
Обе функции могут обрабатывать многоканальные сигналы, в этом случае х и у
являются матрицами, обработка которых производится, как обычно, по столб-
столбцам.
Параметры opt и 'method' при вызове функций можно опускать. В качестве вида
модуляции в случае отсутствия параметра ' method' подразумевается AM с подав-
подавленной несущей. Используемое по умолчанию значение параметра opt зависит
от вида модуляции.
ВНИМАНИЕ
Следует отметить, что функция демодуляции demod, входящая в пакет Signal Processing,
носит демонстрационный характер и будет хорошо работать только с «чистым» сигналом
(желательно — сформированным именно с помощью функции modulate). Причиной явля-
является упрощенный характер реализованных алгоритмов и невозможность управления их
параметрами (например, начальной фазой опорного колебания при демодуляции различ-
различных видов AM). В этом смысле более приспособленными к реальному миру являются
функции демодуляции из пакета Communications.
482 Глава 8. Модуляция и демодуляция
Для получения хороших результатов следует выбирать достаточно высокое от-
отношение Fs/Fc. Для аналоговых видов модуляции (все разновидности AM и УМ,
а также квадратурная модуляция) достаточным является Fs/Fc = 4. Для ШИМ и
ВИМ это отношение определяет число представимых уровней сигнала и потому
должно быть существенно больше.
А теперь перейдем к рассмотрению использования функций modulate и demod для
реализации конкретных видов модуляции.
Амплитудная модуляция
Для реализации амплитудной модуляции параметр ' method' должен иметь значе-
значение 'amdsb-tc'. Расшифровка аббревиатуры следующая:
□ am — амплитудная модуляция (amplitude modulation);
□ dsb — две боковые полосы (double side band);
□ tc — передача несущей (transmitted carrier).
Параметр opt задает уровень смодулированной несущей, поэтому дадим ему бо-
более осмысленное обозначение АО:
[у, t] = modu1ate(x, Fc. Fs, 'amdsb-tc'. АО)
x = demod(y. Fc. Fs, 'amdsb-tc', АО)
Модуляция реализуется почти по формуле (8.1):
у = (х - АО) .* cosB*pi*Fc*t)
Значение по умолчанию для параметра АО равно min(min(x)). Это обеспечивает
однополярность амплитудного множителя (х-АО). Двукратное применение функ-
функции mi n обеспечивает правильный выбор постоянного смещения в случае много-
многоканального сигнала.
ВНИМАНИЕ
Обратите внимание на то, что величина АО не прибавляется к модулирующему сигналу х,
а вычитается из него. Поэтому при задании параметра АО вручную его значение должно
быть отрицательным, если модулирующий сигнал является двуполярным.
При демодуляции входной сигнал прежде всего умножается на опорное колеба-
колебание:
х = у .* cosB*pi*Fc*t):
Низкочастотная составляющая выделяется с помощью ФНЧ с частотой среза,
равной несущей частоте. Чтобы фильтрация не вносила сдвига по времени, она
осуществляется с помощью функции filtfilt (см. раздел «Компенсация фазово-
фазового сдвига» главы 4). В качестве ФНЧ используется фильтр Баттерворта 5-го по-
порядка:
[b. a] = butterE. Fc*2/Fs):
х = filtfilt(b. а, х);ы
Наконец, из демодулированного сигнала вычитается уровень несущей АО:
х = х - АО:
Функции модуляции и демодуляции пакета Signal Processing 483
По умолчанию значение параметра АО в функции demod равно нулю.
ВНИМАНИЕ
Поскольку и при модуляции, и при демодуляции параметр ЛО фигурирует со знаком «ми-
«минус», для правильного удаления постоянного смещения из демодулиропанного сигнала
уровни несущей, задаваемые при модуляции и демодуляции, должны иметь разные злаки
и соотноситься друг с другом как соответственно АО и -АО/2, Деление па 2 необходимо
из-за того, что после умножения ла опорное колебание и нлзкочастотной фильтрации вы-
выделенный полезный сигнал имеет вдвое меньший уровень, чем исходный модулирующий
сигнал (см. формулу (8.5)).
Если значение параметра АО при модуляции слишком велико (больше, чем
min(min(x))), амплитудный множитель перестает быть однополярным, то есть
возникает перемодуляция (см. рис. 8.4). Демодуляция такого сигнала осуществ-
осуществляется правильно.
Векторы (матрицы) х и у в случае AM имеют одинаковые размеры.
AM с подавленной несущей
Для реализации AM с подавленной несущей параметр 'method' должен иметь зна-
значение 'amdsb-sc' или просто 'am'. Это значение параметра 'method' принято по
умолчанию. Первая часть аббревиатуры вида модуляции расшифровывается так
же, как в случае обычной AM, a sc означает подавленную несущую (suppressed
carrier):
[у. t] = modulate(x. Fc, Fs. 'amdsb-sc')
x = demod(y, Fc. Fs. 'amdsb-sc')
AM с подавленной несущей получается из обычной AM, реализация которой была
рассмотрена в предыдущем разделе, при АО = 0. Входной параметр opt в случае
AM с подавленной несущей не используется. Демодуляция осуществляется так
же, как для обычной AM (с учетом нулевого значения параметра АО).
Векторы (матрицы) х и у в случае AM с подавленной несущей имеют одинако-
одинаковые размеры.
Однополосная модуляция
Для реализации однополосной модуляции параметр 'method' должен иметь зна-
значение ' amssb'. В этой аббревиатуре ssb означает одну боковую полосу (single side
band). Параметр opt для данного вида модуляции не используется:
[у. t] = modulate(x. Fc. Fs. 'amssb1)
x = demod(у. Fc. Fs. 'amssb')
Формирование однополосного сигнала производится по формуле (8.6):
у = х .* cosB*pi*Fc*t) + imag(hilbert(x)) .* sinB*pi*Fc*t)
При этом результирующий сигнал содержит нижнюю боковую полосу. Форми-
Формирование сигнала с верхней боковой полосой официально не предусмотрено, но
функцию можно легко «обмануть», задав отрицательное значение для несущей
484 Глава 8. Модуляция и демодуляция
частоты Fc. Согласно формуле (8.6), благодаря нечетности функции sin это при-
приведет к смене выделяемой боковой полосы.
Демодуляция однополосного сигнала производится функцией demod точно так же,
как и демодуляция других разновидностей AM — модулированный сигнал умно-
умножается на опорное колебание, а затем пропускается через ФНЧ.
Векторы (матрицы) х и у в случае однополосиой модуляции имеют одинаковые
размеры.
Фазовая модуляция
Для реализации фазовой модуляции параметр 'method' должен иметь значение
'рт'. Параметр opt задает интенсивность флуктуации начальной фазы, поэтому
дадим ему обозначение beta (буква р использовалась ранее для обозначения ин-
индекса угловой модуляции):
[у, t] = modulate(x. Fc, Fs, 'pm'. beta)
x = demod(y, Fc. Fs. 'pm'. beta)
Формирование сигнала с фазовой модуляцией производится по формуле (8.7):
у = cosB*pi*Fc*t + beta*x)
По умолчанию величина параметра beta выбирается так, чтобы максимальное
положительное отклонение фазы было равно л:
beta = pi/max(max(x))
Отклонение фазы в отрицательную сторону зависит от минимального значения
модулирующего сигнала и может быть любым. Двукратное применение функ-
функции max обеспечивает правильный выбор интенсивности флуктуации фазы в слу-
случае многоканального сигнала.
Демодуляция ФМ-сигнала производится путем формирования аналитического
сигнала с помощью функции hilbert, сдвига его спектра в область нулевых час-
частот путем умножения на exp(-j2nFct) и выделения фазового угла. В завершение
результат делится на параметр beta:
х = angle(hilbert(y) .* exp(-i*2*pi*Fc*t)) / beta:
При демодуляции параметр beta по умолчанию равен единице.
Векторы (матрицы) х и у в случае фазовой модуляции имеют одинаковые раз-
размеры.
Частотная модуляция
Для реализации частотной модуляции параметр 'method' должен иметь значение
'fm'. Параметр opt задает интенсивность флуктуации мгновенной частоты, по-
поэтому дадим ему обозначение dw:
[у. t] = modulate(x. Fc. Fs, 'fm', dw)
x = demod(y, Fc, Fs, 'fm', dw)
Начальная фаза при ЧМ пропорциональна интегралу от модулирующего сигна-
сигнала (см. раздел «Фазовая и частотная модуляция» и формулу (8.8)). Интегриро-
Функции модуляции и демодуляции пакета Signal Processing 485
вание производится с помощью функции cumsum (данная функция вычисляет
частичные суммы элементов вектора; это соответствует численному интегриро-
интегрированию методом прямоугольников):
у = cosB*pi*Fc*t + dw*cumsum(x))
По умолчанию величина параметра dw выбирается так, чтобы максимальное по-
положительное отклонение мгновенной частоты было равно Fc:
dw = Fc/Fs * 2*pi/max(max(x))
Отклонение мгновенной частоты в отрицательную сторону зависит от минималь-
минимального значения модулирующего сигнала и может быть любым. Двукратное при-
применение функции max обеспечивает правильный выбор интенсивности флуктуа-
флуктуации мгновенной частоты в случае многоканального сигнала.
Демодуляция ЧМ-сигнала производится путем формирования аналитического сиг-
сигнала с помощью функции hilbert, сдвига его спектра в область нулевых частот
путем умножения на ехр(-^'27г/>0 и выделения фазового угла. Далее фаза диф-
дифференцируется с помощью функции cliff, а результат делится на параметр dw:
х = diff(unwrap(angle(hilbert(y) .* exp(-i*2*pi*Fc*t)))) / dw:
При демодуляции параметр dw по умолчанию равен единице.
Векторы (матрицы) х и у в случае частотной модуляции имеют одинаковые раз-
размеры.
Квадратурная модуляция
Для реализации квадратурной модуляции параметр 'method' должен иметь зна-
значение ' qam'. Параметр х в данном случае является синфазным модулирующим
сигналом, а параметр opt — квадратурным. Дадим этим параметрам обозначения
x_i (синфазная составляющая, in-phase) и x_q (квадратурная составляющая,
quadrature):
[у, t] = modulate(x_i, Fc, Fs. 'qam', x_q)
[x_i, x_q] = demod(y, Fc, Fs, 'qam')
Синтаксис вызова функции демодуляции является исключением из общего пра-
правила — используются два выходных параметра.
Формирование сигнала с квадратурной модуляцией производится по форму-
формуле (8.10):
у = x_i .* cosB*pi*Fc*t) + x_q .* sinB*pi*Fc*t)
Векторы (матрицы) x_i и x_q должны иметь одинаковые размеры. Тот же размер
будет иметь и сформированный сигнал у.
Демодуляция сигнала с квадратурной модуляцией производится так же, как
в случае AM, только используются два опорных колебания, сдвинутых по фазе
на 90° друг относительно друга:
x_i = 2 * у .* cosB*pi*Fc*t);
x_q = 2 * у .* sinB*pi*Fc*t):
[b, a] = butterE, Fc*2/Fs):
486 Глава 8. Модуляция и демодуляция
x_i = filtfilt(b. a. x_i):
x_q = filtfilt(b, a. x_q):
Дополнительный параметр opt при демодуляции не используется.
Широтно-импульсная модуляция
Для реализации широтно-импульсной модуляции параметр 'method' должен иметь
значение ' pwm'. При отсутствии дополнительного параметра opt формируемые им-
импульсы выравниваются влево, то есть начало импульса совпадает с началом вре-
временного такта.
Под несущей частотой Fc в данном случае понимается частота следования им-
импульсов, а параметр Fs представляет частоту дискретизации сформированного
сигнала. Это отношение определяет возможное число уровней сигнала, предста-
вимое с помощью ШИМ (см. ранее раздел «Способы модуляции, используемые
при передаче цифровой информации»):
[у, t] = modulate(x, Fc. Fs, 'pwm')
x = demod(y, Fc, Fs, 'pwm')
Выходной сигнал у содержит в Fs/Fc раз больше отсчетов, чем модулирующий
сигнал х.
При использовании в качестве параметра opt текстовой строки 'centered' им-
импульсы центрируются относительно начала временных тактов. Для демодуляции
ШИМ-сигнала, сформированного в таком режиме, тоже нужно указать данный
параметр:
[у, t] = modulate(x, Fc, Fs, 'pwm', 'centered')
x = demod(y, Fc. Fs. 'pwm', 'centered')
Отсчеты модулирующего сигнала в векторе х должны лежать в диапазоне 0...1,
они задают длину формируемых импульсов в долях периода следования им-
импульсов.
Время-импульсная модуляция
Время-импульсная модуляция (ВИМ; английский термин — pulse time modula-
modulation, РТМ) не рассматривалась в теоретическом разделе данной главы. Моду-
Модулированный сигнал при использовании ВИМ представляет собой неравномер-
неравномерную последовательность импульсов фиксированной длительности. Смещения,им-
Смещения,импульсов относительно моментов начала тактовых интервалов пропорциональны
модулирующему сигналу. Таким образом, информационным параметром ВИМ-
сигнала является временное положение импульсов в пределах тактовых интер-
интервалов.
Для реализации время-импульсной модуляции параметр ' method' должен иметь
значение ' ptm', Под несущей частотой Fc в данном случае понимается величина,
обратная длительности тактового интервала, а параметр Fs представляет частоту
дискретизации сформированного сигнала. Это отношение определяет возмож-
возможное число уровней сигнала, представимое с помощью ВИМ.
Функции модуляции и демодуляции пакета Communications 487
Параметр opt в данном случае задает длительность формируемых импульсов,
нормированную к длительности тактового интервала. Дадим этому параметру
обозначение tau:
[у. t] = modulate(x. Fc. Fs. 'ptm'. tau)
x = democKy. Fc. Fs. 'ptm')
Выходной сигнал у содержит в Fs/Fc раз больше отсчетов, чем модулирующий
сигнал х.
По умолчанию значение параметра tau равно 0,1.
Отсчеты модулирующего сигнала в векторе х должны лежать в диапазоне 0...1,
они задают относительно положение формируемых импульсов в пределах такто-
тактовых интервалов.
Для получения хороших результатов должно выполняться соотношение
tau*Fs/Fc » 1, то есть длительность формируемых импульсов, измеренная в от-
отсчетах, должна быть существенно больше единицы. В противном случае погреш-
погрешности из-за округления положения импульсов оказываются слишком велики.
При демодуляции дополнительный параметр tau не используется. Для правиль-
правильной демодуляции необходимо, чтобы соседние импульсы не перекрывались (пе-
(перекрытие может возникнуть при модуляции, если за отсчетом модулирующего
сигнала, близким к 1, следует отсчет, близкий к 0).
Функции модуляции и демодуляции
пакета Communications
В пакете расширения Communications содержится ряд функций, относящихся к
задачам модуляции и демодуляции. Они позволяют осуществлять аналоговую и
цифровую модуляцию с использованием различных видов модуляции, давая ре-
результат в виде набора отсчетов вещественного модулирующего сигнала либо его
комплексной огибающей. В документации пакета эти два варианта обозначаются
соответственно терминами «passband» (полосовой сигнал) и «baseband» (низко-
(низкочастотный сигнал).
Для осуществления собственно модуляции и демодуляции служат следующие
функции (способ модуляции указывается при вызове в качестве одного из пара-
параметров):
□ amod — аналоговая модуляция (вещественный результат);
□ amodce — аналоговая модуляция (комплексная огибающая);
□ ademod >-— аналоговая демодуляция (вещественный входной сигнал);
□ ademodce — аналоговая демодуляция (вход — комплексная огибающая);
□ dmod — цифровая модуляция (вещественный результат);
□ dmodce — цифровая модуляция (комплексная огибающая);
□ ddemod — цифровая демодуляция (вещественный входной сигнал);
□ ddemodce — цифровая демодуляция (вход — комплексная огибающая).
488 Глава 8. Модуляция и демодуляция
Имена этих функций будет легко запомнить, если понять, как они формируются:
□ первая буква а или d обозначает соответственно аналоговую (analog) или циф-
цифровую (digital) модуляцию/демодуляцию;
□ далее следует mod для модуляции или demod для демодуляции;
□ буквы се в конце идентификатора обозначают, что функция возвращает (для
модуляции) или принимает на входе (для демодуляции) комплексную оги-
огибающую сигнала (complex envelope).
Аналоговая модуляция
в пакете Communications
При описании синтаксиса вызова рассматриваемых ниже функций аналоговой
модуляции и демодуляции используются следующие общие параметры:
□ х — модулирующий сигнал. Если х — вектор, он может быть как строкой, так
и столбцом. Если х — матрица, каждый ее столбец обрабатывается независи-
независимо, что позволяет осуществлять многоканальную обработку сигнала. Несколь-
Несколько по-иному х задается в случае квадратурной модуляции, об этом будет ска-
сказано отдельно;
□ у — модулированный сигнал;
□ z — демодулированный сигнал;
□ Fs — частота дискретизации модулированного сигнала. При аналоговой моду-
модуляции она же является и частотой дискретизации модулирующего сигнала.
Этот параметр может быть задан в виде двухэлементного вектора [Fs phase],
в этом случае второй элемент задает начальную фазу несущего колебания
(в радианах). По умолчанию начальная фаза равна нулю;
□ Fc — несущая частота. Для функций, работающих с комплексной огибающей,
этот параметр не используется, поскольку комплексная огибающая вычисля-
вычисляется именно относительно несущей частоты;
□ num и den — соответственно числитель и знаменатель передаточной функ-
функции фильтра, используемого для фильтрации выходного сигнала в функциях
демодуляции. Если не указывать эти параметры, в функции ademodce фильт-
фильтрация просто не производится, а в функции ademod по умолчанию использует-
используется фильтр Баттерворта 5-го порядка с частотой среза, равной несущей час-
частоте.
При рассмотрении теоретических основ различных видов модуляции было при-
приведено достаточное количество временных зависимостей, поэтому при рассмот-
рассмотрении функций MATLAB мы будем приводить в основном спектрограммы
сигналов, хорошо демонстрирующие разницу между различными способами мо-
модуляции.
Для рассматриваемых ниже примеров будем использовать частоту дискретиза-
дискретизации 8 кГц и несущую частоту 2 кГц:
» Fs - 8еЗ:
» Fc = 2еЗ:
Функции модуляции и демодуляции пакета Communications
489
В качестве модулирующего используем сигнал длительностью 2 с, мгновенная
частота которого линейно изменяется от нуля до 1 кГц. Такой сигнал генериру-
генерируется функцией chirp:
» t = 0:1/Fs:2: % вектор времени
» s_M = chirpCt. 0. 2, 1еЗ); % ЛЧМ-сигнал
Построим график начального фрагмента этого сигнала (при попытке изобразить
весь сигнал точки на графике просто сольются — в сигнале содержится слишком
много колебаний) (рис. 8.46, сверху):
» plot(t(l:2000). s_M(l:2000))
Мгновенная частота такого сигнала меняется достаточно медленно, что позволя-
позволяет хорошо отслеживать эти изменения на спектрограмме (рис. 8.46, снизу):
» specgram(s_M, []. Fs)
» color-map gray
0.05
0.1
0.15
0.2
0.25
4000 щ
35001
3000 К
2500 В
§2000 В
" 1
и. Ж
1500 В
юоо щ
ш
500 R
0 к
с
ш
1
1
р
0 2
■lIHHHiHIilMHHIiHiH
^tiiifeilHglllliilii
"' ' • °2 * '■■ '^Ш&Ш
0 4 Qi< 0 8 1 12 14 10 18
Time
Рис. 8.46. Модулирующий ЛЧМ-сигнал (сверху) и его спектрограмма (снизу)
490 Глава 8. Модуляция и демодуляция
Амплитудная модуляция
Амплитудная модуляция производится перечисленными выше функциями при
указании в них параметра типа модуляции 'amdsb-tc'. Здесь am означает ампли-
амплитудную модуляцию (amplitude modulation), dsb — наличие обеих боковых полос
(double side band), tc — сохранение несущего колебания (transmitted carrier). Син-
Синтаксис вызова функций имеет следующий вид:
у = amod(x, Fc. Fs, 'amdsb-tc'. offset):
у = amodce(x. Fs. 'amdsb-tc'. offset):
Необязательный параметр offset — постоянная составляющая, добавляемая к мо-
модулирующему сигналу перед умножением его на несущее колебание. По умолча-
умолчанию значение этого параметра равно -min(min(x)), то есть выбирается минимально
возможная одинаковая для всех каналов постоянная составляющая, обеспечи-
обеспечивающая однополярность амплитудного множителя.
Если заданная величина параметра offset недостаточна для однополярности ам-
амплитудного множителя, формируется сигнал с перемодуляцией.
Реализуем амплитудную модуляцию для сформированного ранее модулирующе-
модулирующего ЛЧМ-сигнала. Сразу же построим график начального фрагмента полученного
АМ-сигиала и спектрограмму этого сигнала (рис. 8.47):
» s_AM = amod(s_M. Fc, Fs, 'amdsb-tc');
» plot(t(l:2000), s_AM(l:2000))
» figure
» specgram(s_AM. []. Fs)
» colormap gray
На спектрограмме АМ-сигнала хорошо видны несущее колебание и две боковые
полосы.
При использовании функции amodce результирующая комплексная огибающая
представляет собой модулирующий сигнал с добавлением смещения offset, ум-
умноженный затем на фазовый множитель ехр(-j*phase).
Демодуляция АМ-сигнала производится с помощью функций ademod и ademodce:
z = ademod (у, Fc, Fs, 'amdsb-tc'. offset, num. den);
z = ademod(y, Fc. Fs, 'amdsb-tc/costas', offset, num. den);
z = ademodce (y, Fs. 'amdsb-tc', offset, num. den):
z = ademodce(y, Fs, 'amdsb-tc/costas', offset, num. den):
Если метод демодуляции указан как 'amdsb-tc', входной сигнал у умножается на
несущее колебание, при этом очень важна правильность фазы несущего колеба-
колебания (о способе задания начальной фазы говорилось выше, при перечислении об:
щих параметров функций модуляции/демодуляции). Если указан метод ' amdsb-
tc/costas', применяется демодуляция с использованием системы фазовой авто- '
подстройки Частоты (ФАПЧ), правильная начальная фаза в этом случае уста-
устанавливается автоматически.
Оба способа демодуляции позволяют правильно обрабатывать и сигнал с пере-
перемодуляцией.
Функции модуляции и демодуляции пакета Communications
491
Параметр offset — это константа, вычитаемая из полученных значений ампли-
амплитудной огибающей. По умолчанию он выбирается таким, чтобы постоянная со-
составляющая демодулированного сигнала была равна нулю.
О 0.2 0.1 0,6 0.8 1 1.2 1.4 1.6 1.8
Рис. 8.47. АМ-сигнал (сверху) и его спектрограмма (снизу)
AM с подавленной несущей
AM с подавленной несущей и ее демодуляция реализуются перечисленными выше
функциями при указании в них режима 'amdsb-sc' (расшифровка аналогична пре-
предыдущему случаю, за исключением окончания sc, обозначающего подавленную
несущую — suppressed carrier). Синтаксис вызова функций модуляции следующий:
у = amod(x, Fc, Fs, 'amdsb-sc');
у = amodce(x, Fs, 'amdsb-sc');
492
Глава 8. Модуляция и демодуляция
Фактически AM с подавленной несущей соответствует обычной AM при значе-
значении параметра offset, равном нулю.
Реализуем AM с подавленной несущей для сформированного ранее модулирую-
модулирующего ЛЧМ-сигнала. Сразу же построим график начального фрагмента получен-
полученного сигнала и спектрограмму этого сигнала (рис. 8.48):
» s_AM_SC - amod(s_M. Fc, Fs. 'amdsb-sc');
» plot(t(l:2000). s_AM_SCA:2000))
» figure
» specgram(s_AM_SC, [], Fs)
» colormap gray
Рис. 8.48. АМ-сигнал с подавленной несущей (сверху)
и его спектрограмма (снизу)
Функции модуляции и демодуляции пакета Communications 493
Из рис. 8.47 и 8.48 хорошо видно, что спектрограмма АМ-сигнала с подавленной
несущей отличается от спектрограммы обычного АМ-сигнала только отсутстви-
отсутствием несущего колебания.
При использовании функции amodce результирующая комплексная огибающая
представляет собой модулирующий сигнал, умноженный на фазовый множитель
exp(-j*phase), представляющий начальную фазу несущего колебания.
Демодуляция АМ-сигнала с подавленной несущей производится с помощью
функций ademod и ademodce:
z = ademocKy. Fc, Fs, 'amdsb-sc'. num. den):
z = ademod(y, Fc, Fs, 'amdsb-sc/costas', num, den);
z = ademodce(y, Fs, 'amdsb-sc'. num. den);
z = ademodce(y, Fs, 'amdsb-sc/costas'. num. den);
Если метод демодуляции указан как 'amdsb-sc', входной сигнал у умножается на
несущее колебание, при этом очень важна правильность фазы несущего колеба-
колебания (о способе задания начальной фазы говорилось выше, при перечислении об-
общих параметров функций модуляции/демодуляции). Если указан метод ' amdsbsc/
costas', применяется демодуляция с использованием системы фазовой автопод-
автоподстройки частоты (ФАПЧ), правильная начальная фаза в этом случае устанавли-
устанавливается автоматически.
Однополосная модуляция
Однополосная модуляция производится перечисленными выше функциями при
указании в них параметра типа модуляции ' amssb'. Здесь am расшифровывается
как и раньше, a ssb означает наличие только одной боковой полосы (single side
band). Синтаксис вызова функций модуляции позволяет использовать несколь-
несколько способов формирования однополосного сигнала. Кроме того, возможности
функций amod и amodce, а также задание их параметров несколько различаются.
По умолчанию используется формирование сигнала с помощью преобразования
Гильберта, выполняемого в частотной области:
у = amod(x, Fc. Fs. 'amssb'):
у = amodce(x. Fs. 'amssb');
Можно выполнить формирование сигнала с помощью преобразования Гильбер-
Гильберта, выполняемого во временной области с использованием стандартного фильтра
Гильберта (этот фильтр рассчитывается с помощью функции hilbiir следующим
образом: [num,den]=hilbiir(l/Fs)):
у = amod(x. Fc, Fs, 'amssb', hilbertflag):
у = amodce(x, Fs, 'amssb/time'):
Параметр hilbertflag, используемый для функции amod, может принимать произ-
произвольное значение.
Наконец, пользователь может с помощью параметров num и den задать свой фильтр
для выполнения преобразования Гильберта во временной области:
у = amod(x, Fc. Fs, 'amssb', num, den);
у = amodce(x, Fs, 'amssb/time', num, den):
494
Глава 8. Модуляция и демодуляция
ВНИМАНИЕ
Разработчики функций amod и amodce забыли компенсировать задержку, неизбежно возни-
возникающую при выполнении гильбертовской фильтрации во временной области. Из-за этого
получить приемлемые результаты при формировании одпополосного сигнала таким спо-
способом можно только в случае крайне низкой частоты модулирующего сигнала.
Реализуем однополосную модуляцию для сформированного ранее модулирую-
модулирующего ЛЧМ-сигнала. Сразу же построим график начального фрагмента получен-
полученного сигнала и спектрограмму этого сигнала (рис. 8.49):
» s_SSB = amod(s_M, Fc. Fs. 'amssb'):
» p1ot(t(l:2000). s_SSB(l:2000))
» figure
» specgram(s_SSB. []. Fs)
» eolormap gray
0.05
0.1 0.15 0.2 0.25
Рис. 8.49. Однополосный сигнал с нижней боковой полосой (сверху)
и его спектрограмма (снизу)
Функции модуляции и демодуляции пакета Communications
495
На спектрограмме однополосного сигнала хорошо видно отсутствие верхней бо-
боковой полосы; правда, наблюдаются и неподавленные остатки несущего коле-
колебания.
По умолчанию функции amod и amodce формируют сигнал с нижней боковой по-
полосой. Для функции amodce формирование сигнала с верхней боковой полосой не
предусмотрено. Согласно документации пакета Communications, функция amod
должна давать сигнал с верхней боковой полосой при указании режима модуля-
модуляции 'amssb/up'. Однако из-за ошибки в М-файле amod.m функция отказывается
обрабатывать такое значение параметра (это относится по крайней мере к верси-
версиям 2.0 и 2.0.1 пакета Communications). Решить эту проблему можно, передав
функции отрицательное значение несущей частоты (рис. 8.50):
» s_SSB_UP = amod(s_M, -Fc, Fs. 'amssb');
» specgram(s_SSB_UP. []. Fs)
» eolormap gray
Рис. 8.50. Спектрограмма однополосного сигнала с верхней боковой полосой
Спектрограмма наглядно показывает, что в данном случае в сигнале действи-
действительно сохранена только верхняя боковая полоса.
Демодуляция однополосного сигнала производится с помощью функций ademod
и ademodce:
z - ademod(y. Fc, Fs, 'amssb1, num. den);
z - ademodce(y.'Fs. 'amssb', num. den);
При демодуляции входной сигнал у умножается на несущее колебание, при этом
фаза несущей, в отличие от случая AM при наличии двух боковых полос, не
влияет на уровень демодулированного сигнала, а определяет только его фазовый
сдвиг.
496 Глава 8. Модуляция и демодуляция
Квадратурная модуляция
Квадратурная модуляция производится перечисленными выше функциями при
указании в них параметра типа модуляции 'qam' (quadrature amplitude modula-
modulation). Синтаксис вызова функций имеет следующий вид:
у = amod(x, Fc, Fs. 'qam');
у = amodce(x. Fs, 'qam'):
В отличие от других видов модуляции, в данном случае входной сигнал х должен
быть матрицей с четным числом столбцов. Столбцы с нечетными номерами зада-
задают амплитуды синфазных составляющих, столбцы с четными номерами — амп-
амплитуды квадратурных составляющих модулирующих сигналов. Модулирован-
Модулированный сигнал у представляет собой матрицу с числом столбцов вдвое меньшим,
чем у модулирующего сигнала х.
Демодуляция квадратурно-модулированного сигнала производится с помощью
функций ademod и ademodce:
z = ademod(у, Fc. Fs. 'qam'. num. den):
z = ademodce(y. Fs. 'qam'. num. den):
Демодулированный сигнал z представляет собой матрицу с числом столбцов вдвое
большим, чем у входного модулированного сигнала у. Столбцы с нечетными но-
номерами содержат амплитуды синфазных составляющих, столбцы с четными но-
номерами — амплитуды квадратурных составляющих демодулированиых сигналов.
Фазовая модуляция
Фазовая модуляция производится перечисленными выше функциями при ука-
указании в них параметра типа модуляции 'pm' (phase modulation). Синтаксис вызо-
вызова функций имеет следующий вид:
у = amod(x. Fc. Fs. 'pm'. deviation):
у = amodce(x. Fs. 'pm', devation);
Необязательный параметр deviation — константа, на которую умножается моду-
модулирующий сигнал перед использованием его в качестве начальной фазы несуще-
несущего колебания. По умолчанию значение этого параметра равно единице.
Реализуем фазовую модуляцию для сформированного ранее модулирующего
ЛЧМ-сигпала. Сразу же построим спектрограмму этого сигнала (рис. 8.51):
» s_PM = amod(s_M, Fc. Fs. 'pm'):
» specgram(s_PM. [], Fs)
» colormap gray
На спектрограмме ФМ-сигнала хорошо видны несущее колебание и множество
боковых частот. Согласно формулам, приведенным ранее в разделе «Спектр сиг-
сигнала с гармонической угловой модуляцией», амплитуды спектральных состав-
составляющих пропорциональны функциям Бесселя. «Отражения» спектральных ли-
линий от верхнего и нижнего краев спектрограммы связаны с появлением ложных
частот (aliasing, подробнее см. разделы «Аналоговые, дискретные и цифровые
сигналы» и «Спектр дискретного сигнала» главы 3).
Функции Модуляции и демодуляции пакета Communications
497
Frequency
4000 МШ
збооИНДа
3000 ИДИИ
ни
2°°°L; :-
юоо^^Н
sooBnH
оНН
0 0.2
■
1
и
ш
т
ш
1
■
0.4
вЯкЖ
0.6 0.8 1
Ttnte
1.2 1.4 1.6 1.3
Рис. 8.51. Спектрограмма ФМ-сигнала
При использовании функции amodce результирующая комплексная огибающая
представляет собой комплексную экспоненту
exp(i*deviation*x + i*phase)
Демодуляция ФМ-сигнала производится с помощью функций ademod и ademodce:
z = ademod(у. Fc. Fs. 'pm1, num. den, vcoconst);
z = ademodce(y, Fs, 'pm'. num. den, vcoconst);
Демодуляция выполняется с использованием системы ФАПЧ, необязательный
параметр vcoconst задает чувствительность генератора, управляемого напряже-
напряжением (в герцах на вольт). По умолчанию значение этого параметра равно 1.
Частотная модуляция
Частотная модуляция производится перечисленными выше функциями при ука-
указании в них параметра типа модуляции 'fm' (frequency modulation). Синтаксис
вызова функций имеет следующий вид:
у = amod(x, Fc, fs, 'fm', deviation);
у = amodce(x. Fs, 'fm', devation);
Необязательный параметр deviation — константа, на которую умножается моду-
модулирующий сигнал перед использованием его в качестве отклонения мгновенной
частоты от несущей частоты. По умолчанию значение этого параметра равно
единице.
При формировании ЧМ-сигнала модулирующий сигнал приближенно интегри-
интегрируется с помощью функции cumsum, а затем используется в качестве начальной
фазы несущего колебания. Коэффициенты масштабирования выбраны.так, что при
отсутствии параметра deviation модулирующий сигнал х задает отклонение мгно-
мгновенной частоты сигнала в тех же единицах, в которых заданы параметры Fc и Fs.
498
Глава 8. Модуляция и демодуляция
Реализуем частотную модуляцию для сформированного ранее модулирующего
ЛЧМ-сигнала, задав максимальное отклонение мгновенной частоты равным
500 Гц (поскольку амплитуда модулирующего сигнала равна единице, параметр
deviation следует задать равным 500). Сразу же построим спектрограмму полу-
полученного сигнала (рис. 8.52):
» s_FM = amod(s_M. Fc, Fs. 'fm'. 500):
» specgram(s_FM. []. Fs)
» colormap gray
О 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.
Рис. 8.52. Спектрограмма ЧМ-сигнала
На спектрограмме ЧМ-сигнала, как и в случае ФМ (см. рис. 8.51), хорошо видны
несущее колебание и множество боковых частот. Однако имеются и отличия:
сначала, пока частота модулирующего сигнала низкая, индекс модуляции велик
(напомним, что при ЧМ индекс угловой модуляции меняется обратно пропор-
пропорционально частоте модулирующего сигнала), и мы наблюдаем большое количе-
количество боковых частот — белое пятно в левой части графика имеет значительно
большую высоту, чем в случае ФМ. По мере роста частоты модулирующего сиг-
сигнала индекс модуляции падает и количество значимых боковых частот уменьша-
уменьшается. В результате в правой части графика спектр визуально не отличается от
случая ФМ.
При использовании функции amodce результирующая комплексная огибающая
представляет собой комплексную экспоненту
exp(i*2*pi*deviation*cumsum(x)/Fs + i*phase)
Демодуляция ЧМ-сигнала производится с помощью функций ademod и ademodce:
z = ademod(у. Fc. Fs. 'fm'. num. den. vcoconst):
z = ademodce(y, Fs, 'fm'. num. den. vcoconst):
Функции модуляции и демодуляции пакета Communications 499
Демодуляция выполняется с использованием системы ФАПЧ, необязательный
параметр vcoconst задает чувствительность генератора, управляемого напряже-
напряжением (в герцах на вольт). По умолчанию значение этого параметра равно 1.
Цифровая модуляция в пакете Communications
При описании синтаксиса вызова рассматриваемых ниже функций цифровой моду-
модуляции и демодуляции используются те же общие параметры Fs (частота дискрети-
дискретизации) и Fc (несущая частота), что были рассмотрены в начале раздела «Аналого-
«Аналоговая модуляция в пакете Communications». Кроме того, используется специфичный
для цифровой модуляции параметр Fd, представляющий частоту следования сим-
символов. Отношение Fs/Fd должно быть положительным целым числом. Параметр Fd
может быть двухэлементным вектором, в этом случае собственно символьная ско-
скорость задается его первым элементом Fd(l), а второй элемент FdB) представляет
собой смещение (offset), используемое при дискретизации сигнала после аналого-
аналоговой демодуляции. По умолчанию величина этого смещения равна нулю. Более
подробно об использовании параметра смещения см. далее в описании функции
demodmap (раздел «Преобразование аналогового сигнала в цифровое сообщение»).
Амплитудная манипуляция
Для реализации амплитудной манипуляции параметр 'method' должен иметь зна-
значение 'ask':
у = dmod(x, Fc. Fd, Fs. 'ask'. M)
у = dmodce(x, Fd, Fs, 'ask', M)
Здесь М — число уровней, используемых при манипуляции. Входной сигнал х дол-
должен содержать целые числа в диапазоне 0...М- 1. Этим числам сопоставляются
амплитудные множители, равномерно распределенные в диапазоне -1...1, то есть
разность между соседними значениями составляет 2/(М - 1). Входному симво-
символу 0 соответствует амплитудный множитель 1, символ (М- 1) отображается в
амплитудный множитель, равный -1.
В качестве примера на рис. 8.53 показано сигнальное созвездие для 8-позицион-
ной АМн:
» modmap('ask', 8)
Демодуляция по умолчанию производится путем умножения входного сигнала
на опорное колебание:
z = ddemod(y. Fc. Fd, Fs, 'ask', M. num. den)
z = ddemodce(y, Fd, Fs, 'ask'. M. num. den)
Если для параметра 'method' указать значение 'ask/costas', для демодуляции бу-
будет использован алгоритм Костаса (система ФАПЧ):
z = ddemod(y, Fc. Fd, Fs, 'ask/costas1. M, num. den)
z = ddemodce(y, Fd, Fs, 'ask/costas ', M, num. den)
Чтобы использовать ФНЧ для выделения низкочастотной составляющей сигна-
сигнала после аналогового демодулятора, следует задать коэффициенты полиномов
числителя и знаменателя функции передачи фильтра в дополнительных вход-
пых параметрах num и den. По умолчанию ФНЧ не используется.
500
Глава 8. Модуляция и демодуляция
ASK constellation
-1 -0.5
Рис. 8.53. Сигнальное созвездие 8-позиционной амплитудной манипуляции
О 0.5
In-phase component
Квадратурная манипуляция
Функции пакета Communications позволяют осуществлять квадратурную мани-
манипуляцию с использованием созвездий различных типов. Мы подробно рассмот-
рассмотрим только наиболее гибкий вариант, когда созвездие задается пользователем
и может быть произвольным (о других режимах см. замечание в конце раздела).
В этом случае параметр 'method' должен иметь значение 'qask/arb'. Аббревиа-
Аббревиатура arb означает произвольное (arbitrary) созвездие. Оно задается с помощью
двух векторов map_i и map_q:
у = dmod(x, Fc. Fd, Fs. 'qask/arb'. map_i. map_q)
у = dmodce(x, Fd. Fs. 'qask/arb', map_i. map_q)
z = ddemod(y, Fc, Fd, Fs, 'qask/arb'. map_i, map_q. num. den)
z = ddemodce(y. Fd. Fs. 'qask/arb'. map_i, map_q, num. den)
Для Аппозиционной КАМн векторы map_i и mapq должны иметь длину А/. Эти
векторы задают синфазные и квадратурные амплитуды (вещественные и мни-
мнимые части) сигнальных Посылок. Таким образом, k-й отсчет входного сигнала
отображается в точку на комплексной плоскости, равную
map_i(x(k)+l) + j*map_q(x(k)+l)
Отобразить используемое созвездие на экране можно с помощью функции plot:
plot(map_i, map_q, '.')
или с помощью функции modmap (она дополнительно нанесет на график несколь-
несколько поясняющих надписей):
modmap('qask/arb'. map_i. map_q)
Амплитуды и фазы посылок поддерживаются постоянными на протяжении так-
тактовых интервалов и при переходе от такта к такту изменяются скачкообразно.
Использование интерполирующих фильтров для формирования спектра не пре-
предусмотрено.
Решить проблему формирования спектра можно следующим образом. Сначала с
помощью функции modmap производится отображение входных символов в сип-
Функции модуляции и демодуляции пакета Communications 501
фазные и квадратурные амплитуды точек созвездия при одинаковых значениях
Fd и Fs (чтобы не менялась частота дискретизации сигнала). Впрочем, для такого
отображения использовать функцию modmap не обязательно — достаточно задать
созвездие в виде вектора комплексных чисел тар и произвести следующее преоб-
преобразование:
xjnapped = map(x+l)
Полученный сигнал (двухканальный вещественный или одноканальный комплекс-
комплексный) подвергается интерполяции с нужным коэффициентом Fs/Fd с помощью
функций rcosflt или interp. Наконец, полученный интерполированный сигнал
используется для аналоговой квадратурной модуляции.
Демодуляция в этом случае может осуществляться как обычно, однако необхо-
необходим тщательный подбор (или автоподстройка) параметра offset, передаваемого
в функцию demodmap.
Чтобы использовать ФНЧ для выделения низкочастотной составляющей сигна-
сигнала после аналогового демодулятора, следует задать коэффициенты полиномов
числителя и знаменателя функции передачи фильтра в дополнительных вход-
входных параметрах num и den. По умолчанию ФНЧ не используется.
ЗАМЕЧАНИЕ
Рассматриваемые функции пакета Communications поддерживают также квадратурную
манипуляцию с «квадратными» (режим 'qask') и «концентрическими» (режим 'qask/cir')
созвездиями. Эти варианты можно использовать в демонстрационных целях, но они плохо
подходят для моделирования реальных систем — даже если требуемое созвездие является
«квадратным» (а в «концентрическом» формате можно, в принципе, представить произ-
произвольное созвездие), функции не дают возможности задать нужное соответствие между
символами и точками созвездия, тогда как в режиме 'qask/arb' это делается без труда. Если
вы все-таки решите использовать эти созвездия, ознакомьтесь с их формированием по до-
документации пакета Communications. Вывести эти созвездия на экран можно с помощью
функций qaskcnco(M) («квадратное») и apkconst(numsig, amp, phs, 'n') («концентриче-
(«концентрическое»).
Фазовая манипуляция
Для реализации фазовой манипуляции параметр 'method' должен иметь значе-
значение 'psk':
у = dmod(x, Fc, Fd. Fs, 'psk', M)
у = dmodce(x, Fd, Fs, 'psk', M)
Здесь М — число градаций начальной фазы, используемых при манипуляции.
Входной сигнал х должен содержать целые числа в диапазоне 0... М - 1. Этим
числам сопоставляются начальные фазы, равномерно распределенные в диапа-
диапазоне 0 ... 2п(М - 1)/М, то есть разность между соседними значениями составля-
составляет 2п/М. Входному символу 0 соответствует нулевая начальная фаза, символ
(М - 1) отображается в начальную фазу, равную 2п(М - 1)/М.
В качестве примера на рис. 8.54 показано сигнальное созвездие для 8-позицион-
ной ФМн:
» modmap('psk'. 8)
502
Глава 8. Модуляция и демодуляция
ASK/PSK Constellation
Рис. 8.54. Сигнальное созвездие 8-позиционной фазовой манипуляции
Демодуляция ФМн производится так же, как для квадратурной манипуляции,
с использованием соответствующего созвездия. Синтаксис вызова функций де-
демодуляции следующий:
г = ddemod(y, Fc, Fd, Fs, 'psk'. M, num. den)
z = ddemodce(y, Fd, Fs, 'psk', M, num, den)
Чтобы использовать ФНЧ для выделения низкочастотной составляющей сигна-
сигнала после аналогового демодулятора, следует задать коэффициенты полиномов
числителя и знаменателя функции передачи фильтра в дополнительных вход-
входных параметрах num и den. По умолчанию ФНЧ не используется.
Частотная манипуляция
Для реализации частотной манипуляции параметр 'method' должен иметь значе-
значение 'fsk':
у = dmod(x. Fc, Fd, Fs. 'fsk'. M, tone)
у = dmodce(x. Fd, Fs. 'fsk', M, tone)
Здесь М — число частот, используемых при манипуляции. Входной сигнал х дол-
должен содержать целые числа в диапазоне 0 ... М - 1. Этим числам сопоставляют-
сопоставляются частоты, равномерно распределенные с шагом tone вокруг центральной часто-
частоты Fc. Таким образом, входному символу 0 соответствует частота Fc - (M-l)*tone/2,
символу (М - 1) — частота Fc + (M-l)*tone/2.
Входной параметр tone при вызове можно опускать, его значение по умолчанию
равно Fd.
В качестве примера на рис. 8.55 показано сигнальное созвездие (при ЧМн
под созвездием подразумевается набор частотных сдвигов относительно мини-
минимальной частоты) для 8-позиционной ЧМн при разносе соседних частот, рав-
равном 300 Гц:
» modmap('fsk', 8, 300)
Функции модуляции и демодуляции пакета Communications
503
FSK constellation
500
1000 1500
Frequency (Hz)
2000
Рис. 8.55. Частотные сдвиги при 8-позиционной частотной манипуляции
с разносом частот, равным 300 Гц
Демодуляция по умолчанию производится корреляционным когерентным ме-
методом:
z = ddemod(y. Fc. Fd, Fs. 'fsk'. M, tone)
z = ddemodce(y. Fd. Fs. 'fsk', M, tone)
Если для параметра 'method' указать значение 'fsk/noncoherence', для демоду-
демодуляции будет использован корреляционный некогерентный (квадратурный) алго-
алгоритм:
z = ddemod(y. Fc. Fd. Fs. 'fsk/noncoherence', M. tone)
z = ddemodce(y. Fd. Fs. 'fsk/noncoherence'. M, tone)
Минимальная частотная манипуляция
Для реализации минимальной частотной манипуляции (МЧМ) параметр 'method'
должен иметь значение 'msk'. Дополнительные входные параметры в этом случае
не используются:
у = dmod(x. Fc. Fd. Fs, 'msk')
у = dmodce(x. Fd. Fs. 'msk')
Минимальная частотная манипуляция — это ЧМп с разносом частот нуля и еди-
единицы, равным половине символьной скорости (Fd/2). Как говорилось в разделе
«Способы модуляции, используемые при передаче цифровой информации», сиг-
сигналы, соответствующие нулю и единице, при этом оказываются некоррелирован-
некоррелированными. Входному символу 0 соответствует частота Fc - Fd/4, символу 1 — частота
Fc + Fd/4.
Таким образом, режим 'msk' эквивалентен ЧМн ('fsk') при М = 2 и tone = Fd/2:
у = dmod(x. Fc. Fd. Fs, 'fsk1, 2. Fd/2)
у = dmodce(x, Fd. Fs, 'fsk'. 2. Fd/2)
z = ddemod(y, Fc. Fd. Fs, 'fsk', 2, Fd/2)
z = ddemodce(y. Fd, Fs, 'fsk1. 2. Fd/2)
504 Глава 8. Модуляция и демодуляция
Демодуляция, как и в общем случае ЧМн, может производиться когерентным
и некогерентным методом:
z = ddemod(y, Fc, Fd, Fs. 'msk')
z = ddemod(y. Fc. Fd. Fs, 'msk/noncoherence')
z = ddemodce(y. Fd. Fs. 'msk')
z = ddemodce(y, Fd. Fs. 'msk/noncoherence')
Преобразование цифрового сигнала
в аналоговые параметры модуляции
В разделе «Способы модуляции, используемые при передаче цифровой инфор-
информации» уже говорилось, что главная идея цифровой модуляции состоит в том,
что каждому возможному значению передаваемого символа ставятся в соответ-
соответствие некоторые параметры аналогового несущего колебания. Такое преобразо-
преобразование выполняется функцией modmap, которая к тому же повышает частоту дис-
дискретизации сигнала, повторяя каждую рассчитанную аналоговую точку Fs/Fd раз.
Синтаксис вызова функции nrodmap следующий:
x_mapped = modmap(x, Fd. Fs, 'method', ...)
Все параметры здесь имеют тот же смысл, что и в рассмотренных выше функци-
функциях цифровой модуляции/демодуляции.
Кроме собственно преобразования, функция modmap может выводить изображе-
изображение используемого сигнального созвездия (используемые частотные сдвиги от-
относительно несущей — для ЧМ и МЧМ, точки на комплексной плоскости — для
остальных видов манипуляции). Синтаксис вызова функции при этом следую-
следующий:
modmap( 'method', ...)
Здесь ' method' — строка вида модуляции, на месте многоточия должны стоять те
же параметры, что и при обычном вызове для данного метода. Исключением яв-
является МЧМ — для отображения частотных сдвигов необходимо указать сим-
символьную скорость:
modmap('msk'. Fd)
Мы уже использовали функцию modmap для отображения созвездий при рассмот-
рассмотрении функций цифровой модуляции.
Преобразование аналогового сигнала
в цифровое сообщение
При приеме сигнала с цифровой модуляцией, за исключением режима ЧМн,
производится сначала аналоговая демодуляция, а затем преобразование отсчетов
аналогового демодулированного сигнала в цифровое сообщение. Такое преобра-
преобразование производится функцией demodmap, имеющей следующий синтаксис вы-
вызова:
х = demodmap(y, [Fd offset], Fs, 'method'. ...)
Здесь у — отсчеты входного аналогового сигнала, имеющего частоту дискретиза-
дискретизации Fs, Fd — символьная скорость (частота дискретизации цифрового сигнала;
отношение Fs/Fd должно быть положительным целым числом), offset — смеще-
Функции модуляции и демодуляции пакета Communications 505
ние отсчетиых точек (см. ниже), ' method' — вид манипуляции. Возможные виды
манипуляции и соответствующие им дополнительные параметры, которые долж-
должны стоять на месте многоточия, такие же, как для функций цифровой модуля-
модуляции, рассмотренных выше.
Функция demodmap выполняет две отдельных операции — понижение частоты дис-
дискретизации в Fs/Fd раз и собственно преобразование отсчетов в цифровое сооб-
сообщение.
Понижение частоты дискретизации производится просто путем выборки отсче-
отсчетов с шагом Fs/Fd. Задержка моментов взятия отсчетов относительно начала так-
такта задается с помощью параметра offset. Итак, прореживание осуществляется
следующим образом:
у = у(offset : Fs/Fd : end):
Параметр offset при вызове может опускаться, тогда его значение считается рав-
равным нулю.
Далее для каждого отсчета прореженного сигнала ищется ближайшая точка ис-
используемого в данном режиме созвездия. Символы, соответствующие найден-
найденным точкам, возвращаются в векторе х.
Построение диаграммы рассеяния
Для построения диаграммы рассеяния (см. ранее рис. 8.38 и 8.41, а также ком-
комментарии к ним) предназначена функция scatterplot, имеющая следующий син-
синтаксис вызова:
h = scatterptot(x, n, offset, piotstring, h):
Обязательным параметром является только входной сигнал х. Интерпретация мас-
массива х зависит от размера массива и наличия у него мнимой части:
□ если х — вещественная двухстолбцовая матрица, функция scatterplot интер-
интерпретирует первый столбец как синфазную, а второй — как квадратурную со-
составляющую;
□ если х — комплексный вектор, функция scatterpi ot интерпретирует его веще-
вещественную часть как синфазную, а мнимую — как квадратурную составляю-
составляющую;
□ если х — вещественный вектор, функция scatterplot интерпретирует его как
вещественный сигнал (то есть в данном случае квадратурная составляющая
равна нулю).
Остальные входные параметры являются необязательными и имеют значения по
умолчанию. Параметр п задает число отсчетов на символьный такт (примени-
(применительно к обозначениям, использованным ранее, оно равно Fs/Fd). При построении
диаграммы используется только каждый n-й отсчет сигнала, то есть предвари-
предварительно выполняется прореживание сигнала х с коэффициентом п. По умолчанию
значение параметра п равно единице.
Параметр offset задает смещение, используемое при прореживании. При по-
построении диаграммы используется каждый n-й отсчет сигнала х, начиная с отсче-
отсчета с номером (offset+1). Значение параметра offset должно быть целым числом,
506 Глава 8. Модуляция и демодуляция
лежащим в диапазоне от 0 до п-1. По умолчанию значение параметра offset рав-
равно нулю.
Строковый параметр plotstring задает символы точек, тип линии и цвет для диа-
диаграммы. Формат и назначение элементов строки те же самые, что используются
в функции plot (см. далее раздел «Настройка внешнего вида графиков» прило-
приложения А). По умолчанию диаграмма выводится точками синего цвета.
При указании входного параметра h вместо создания нового графического окна
диаграмма выводится в существующем окне с дескриптором h. Параметр h дол-
должен быть дескриптором графического окна, ранее созданного функцией scatterplot.
Имеющаяся в этом окне диаграмма стирается. Для вывода нескольких сигналов
в одном окне можно использовать команду hold on.
Выходным параметром h является дескриптор графического окна, содержащего
диаграмму.
В случае вещественной двухстолбповой матрицы х диаграмма рассеяния форми-
формируется функцией scatterplot следующим образом:
plot(x(offset+l:n:end.l), x(offset+l:n:end,2). plotstring)
Если х — комплексный вектор, формирование диаграммы рассеяния описывает-
описывается так:
plot(real (x(offset+l:n:end)), imag(x(offset+l:n:end)). plotstring)
Наконец, в случае вещественного вектора х диаграмма строится так:
plot(x(offset+l:n:end). O*x(offset+l:n:end). plotstring)
Использование диаграмм рассеяния иллюстрируется демонстрационной програм-
программой scattereyedemo, имеющейся в составе пакета Communications,
Построение глазковой диаграммы
Для построения глазковой диаграммы (см. ранее рис. 8.41 и комментарии к нему)
предназначена функция eyediagram, имеющая следующий синтаксис вызова:
h = eyediagram(x. n. period, offset, plotstring. h):
Обязательными параметрами являются входной сигнал х и число отсчетов на
символьный такт п (применительно к обозначениям, использованным ранее, оно
равно Fs/Fd), Интерпретация массива х и число выводимых диаграмм зависят от
размера массива и наличия у него мнимой части:
□ если х — вещественная двухстолбцовая матрица, функция eyediagram интер-
интерпретирует первый столбец как синфазную, а второй — как квадратурную
составляющую. Диаграммы для двух составляющих выводятся в отдельных
системах координат в общем графическом окне;
□ если х — комплексный вектор, функция eyediagram интерпретирует его веще-
вещественную часть как синфазную, а мнимую — как квадратурную составляю-
составляющую. Диаграммы для двух составляющих выводятся в отдельных системах
координат в общем графическом окне;
□ если х — веь >ственный вектор, функция eyediagram интерпретирует его как
вещественный сигнал. Графическое окно в данном случае содержит единст-
единственную диаграмму.
Функции модуляции и демодуляции пакета Communications 507
Остальные входные параметры являются необязательными и имеют значения по
умолчанию. Параметр period задает длительность символьного такта. Это значе-
значение используется для оцифровки горизонтальной оси, крайние значения кото-
которой считаются равными -period/2 и period/2. По умолчанию значение параметра
period равно единице.
Параметр offset задает горизонтальное смещение графика. Функция предпола-
предполагает, что значениям времени, кратным длительности символьного такта period,
соответствуют отсчет сигнала с номером offset+1 и следующие за ним с шагом п.
Значение параметра offset должно быть неотрицательным целым числом, лежа-
лежащим в диапазоне от 0 до п-1. По умолчанию значение параметра offset равно
нулю.
Строковый параметр plotstring задает символы точек, тип линии и цвет для гра-
графика. Формат и назначение элементов строки те же самые, что используются в
функции plot (см. далее раздел «Настройка внешнего вида графиков» приложе-
приложения А). По умолчанию, как обычно, графики выводятся сплошными линиями
синего цвета.
При указании входного параметра h вместо создания нового графического окна
график выводится в существующем окне с дескриптором h. Параметр h должен
быть дескриптором графического окна, ранее созданного функцией eyedi agram.
ВНИМАНИЕ
Вывод диаграмм для нескольких сигналов в одном окне нельзя реализовать с помощью ко-
команды hold on.
Выходным параметром h является дескриптор графического окна, содержащего
диаграмму.
Использование глазковых диаграмм иллюстрируется демонстрационной програм-
программой scattereyedemo, имеющейся в составе пакета Communications.
Приложение А
Основы работы
с MATLAB
Система MATLAB (сокращение от MATrix LABoratory — матричная лаборато-
лаборатория) появилась в 1984 г. и за прошедшие более чем пятнадцать лет стала миро-
мировым стандартом в области научных и технических расчетов. Основная причина
этой популярности, вероятно, кроется в том, что MATLAB дал инженерам и уче-
ученым именно то, что им было нужно, — возможность с непревзойденной легкостью
применять к произвольным данным, представленным в виде векторов и матриц,
разнообразнейшие численные алгоритмы. Удобный язык программирования,
в котором благодаря матричной ориентации системы значительно уменьшилась
необходимость в циклах, еще больше расширил сферу применения MATLAB.
В данном приложении приведены основные сведения о работе с MATLAB. Этой
информации достаточно для того, чтобы познакомиться с системой и затем про-
продолжить осваивать ее самостоятельно. За более подробными сведениями обра-
обращайтесь к книгам, целиком посвященным MATLAB (таким как [12]), а также,
разумеется, к справочной системе и документации. Надеюсь также, что некото-
некоторую помощь в освоении MATLAB окажут многочисленные примеры расчетов,
имеющиеся во всех главах книги.
Информация, приводимая в данном приложении, соответствует версии MATLAB 6.O.
Установка
Прежде всего следует сказать несколько слов о системных требованиях. В целом
можно сказать, что если на вашем компьютере работает система Windows 95/98/
ME/NT/2000, то должен работать и MATLAB. Тип процессора и объем опера-
оперативной памяти влияют только на быстродействие. Размер необходимого диско-
дискового пространства сильно варьируется в зависимости от состава устанавливае-
устанавливаемых компонентов — от 138 Мбайт (только ядро MATLAB без документации) до
817 Мбайт (полная установка с документацией). Комплект, минимально необхо-
необходимый для работы с данной книгой (MATLAB плюс три пакета расширения),
требует 212 Мбайт с документацией или 150 Мбайт без нее.
Установка
509
ВНИМАНИЕ
Версии MATLAB до 6.0 включительно ие работают на компьютерах с процессором Intel
Pentium 4. Эта проблема решена в версии 6.1. В то же время с процессорами фирмы AMD
(К5, Кб, Athlon, Duron и т. д.) MATLAB работает нормально.
Кроме того, имеются сообщения о проблемах, возникающих при попытках использования
предыдущих версий MATLAB (до 5.3 включительно) с последними версиями операцион-
операционной системы (Windows 2000 и ХР).
Если вам приходилось устанавливать программное обеспечение в системе Win-
Windows, установка MATLAB не должна вызвать сложностей. Прокомментируем
лишь один этап, связанный с выбором устанавливаемых компонентов (рис. А.1).
jCSmatlabR12
1683M
' -Г l
<~ I
3, Sdrot Imguage of deeumentato.
1S0M
62 И
Рис. А.1. Выбор устанавливаемых компонентов MATLAB
В первом из четырех разделов этого окна предлагается выбрать папку для уста-
установки MATLAB. Дополнительных комментариев этот раздел не требует.
Трехпозиционный переключатель в разделе 2 управляет установкой HTML-до-
HTML-документации (она занимает весь второй диск дистрибутива MATLAB). При выбо-
выборе варианта Install products and documentation документация устанавливается на
жесткий диск компьютера. Если переключатель установлен в положение Install
products only, документация устанавливаться не будет. При этом в среде MATLAB
будет по-прежнему доступна справочная информация, встроенная в функции и
вызываемая из командной строки, а для просмотра HTML-документации при-
придется вставить CD-ROM (документация на нем хранится в несжатом виде). Тре-
Третий вариант, Install documentation only, предлагает установить только документа-
документацию и в большинстве случаев не представляет интереса.
510
Приложение А. Основы работы с MATLAB
Поскольку большинство российских пользователей вряд ли заинтересует воз-
возможность установить документацию MATLAB на японском языке, на раздел 3
можно вообще не обращать внимания.
Наконец, в разделе 4 перечислены компоненты системы, включая большое коли-
количество пакетов расширения (toolbox). Для работы с рассматриваемыми в книге
примерами необходимо установить собственно MATLAB, а также три его пакета
расширения — Signal Processing Toolbox, Communications Toolbox и Filter Design
Toolbox. Остальные компоненты при работе с книгой не понадобятся, так что
можете выбирать их, руконодствуясь собственными профессиональными инте-
интересами и объемом свободного места на диске. Список компонентов с очень крат-
краткими описаниями их назначения приведен в приложении В.
Работа в интерактивном режиме
После запуска MATLAB на экране появится окно, показанное на рис. А.2.
MATLAB — интерактивная диалоговая система, поэтому большая часть ее глав-
главного окна предназначена для ввода команд и вывода результатов. Эта область
называется командным окном — Command Window.
4&MATUB
^Conouunications Toolbox
^\Data Accfuisition Toolbox
^Filter Design Toolbox
^Motorola DSP Developer's Kit
^Optimization Toolbox
^\Signal Processing Toolbox
^System Identification Toolbox
^Wavelet Toolbox
*% SimulirJi
Оо Coiumunications Blockset
•Bv ПЧ? Pilnrkvr
I * taunch Раз
help ode
sqrt(C03(pi/12)A2 ■
x - 1 0.5:5
x • 2
exp(x)
exp(x)/x
x * x
exp(x) ./ x
x . * x
у - x1
To get started, select Ш1АВ Help" Crom the Help menu.
sqct(cos(pi/12)'-2 + 1)
ens -
1.3903
> x - 1:0.5:5
Colimns 1 through 7
1.0000 1.5000 2.0000 2.5000 3.0000 3.5000
Colimns 8 through 9
4.5000 5.0000
■> x • 2
ana -
23456789 10
> exp(x)
ans -
Columns 1 through 7
iL
tmto
Рис. А.2. Главное окно MATLAB
Работа в интерактивном режиме 511
Попробуем вычислить значение какого-нибудь выражения:
» sqrt(cos(pi/12)A2 + 1)
ans =
1.3903
Итак, MATLAB может работать как очень большой и мощный калькулятор, вы-
вычисляя значения математических выражений. При этом арифметические опера-
операции записываются традиционно, для возведения в степень используется знак А,
порядком вычислений можно управлять с помощью круглых скобок, и в круг-
круглых же скобках записываются аргументы вызываемых функций (в данном при-
примере используются функции косинуса cos и квадратного корня sqrt).
На рис. А.2 показано, как выглядят вводимые команды и выводимые результаты
в окне MATLAB. При представлении результатов в книге пустые строки удале-
удалены для экономии места.
Поскольку мы не присвоили результат вычислений никакой переменной,
MATLAB автоматически создал для него переменную с именем ans и показал ее
значение.
Однако главная ценность MATLAB состоит в возможности одновременно опе-
оперировать несколькими значениями. Введем следующую команду:
» х = 1:0.5:5
х =
Columns I through 7
1.0000 1.5000 2.0000 2.5000 3.0000 3.5000 4.0000
Columns 8 through 9
4.5000 5.0000
Мы создали переменную х, которая представляет собой вектор-строку, содержа-
содержащую 9 элементов. Стоящее справа от знака равенства выражение генерирует
арифметическую прогрессию, первый член которой равен 1, разность между со-
соседними элементами равна 0,5, а последний член не превосходит 5.
ЗАМЕЧАНИЕ
Имена переменных MATLAB чувствительны к регистру символов, так что X и X — это две
разные переменные. Однако имена функций к регистру не чувствительны, поскольку фак-
фактически являются именами файлов (см. далее раздел «Создание функций»).
Над полученным вектором можно выполнять математические операции:
» х * 2
ans =
23456789 10
Можно применять к векторам математические функции:
» ехр(х)
ans -
Columns I through 7
2.7183 4.4817 7.3891 12.1825 20.0855 33.1155 54.5982
Columns 8 through 9
90.0171 148.4132
512 Приложение А. Основы работы с MATLAB
Но вычисление следующего выражения дает неожиданный результат:
» ехр(х)/х
ans =
16.6289
А этот пример вообще вызовет появление сообщения об ошибке:
» X * X
??? Error using ==> *
■ Inner matrix dimensions must agree.
Дело в том, что операции умножения, деления и возведения в степень в MATLAB
выполняются не поэлементно, а по правилам матричных операций. Матричные
правила запрещают умножение строки на строку, поэтому выдано сообщение о
несовместимости размеров перемножаемых матриц.
ЗАМЕЧАНИЕ
Несовместимость размеров матриц — вероятно, одна из наиболее часто встречающихся
ошибок. Есть две главных причины се возникновения. Во-первых, может оказаться непра-
неправильной ориентация какого-нибудь из используемых в выражении массивов (пример —
попытка сложить вектор-строку и вектор-столбец). Во-вторых, какой-нибудь из промежу-
промежуточных результатов, с вашей точки зрения являющийся числом (скаляром), может на
самом деле оказаться матрицей — скажем, из-за ускользнувших от вашего внимания тон-
тонкостей работы вызываемой функции или из-за каких-то особенностей обрабатываемых
данных.
Чтобы произвести поэлементные действия, к знаку операции необходимо доба-
добавить точку спереди (.*, ./ или .Л). Теперь мы можем получить желаемые резуль-
результаты, переписав два последних примера:
» ехр(х) ./ х
ans =
Columns I through 7
■2.7183 2.9878 3.6945 4.8730 6.6952 9.4616 13.6495
Columns 8 through 9
20.0038 29.6826
» x .* x
ans =
Columns 1 through 7
1.0000 2.2500 4.0000 6.2500 9.0000 12.2500 16.0000
Columns 8 through 9
20.2500 25.0000
Чтобы продемонстрировать именно матричное умножение, создадим второй век-
вектор, причем не строку, а столбец:
» у = х' '
У =
1.0000
1.5000
2.0000
Работа в интерактивном режиме 513
2.5000
3.0000
3.5000
4.0000
4.5000
5.0000
Апостроф в MATLAB обозначает эрмитово сопряжение — сочетание транспони-
транспонирования с комплексным сопряжением. В данном случае вектор х вещественный,
поэтому комплексное сопряжение ничего не меняет. Для выполнения транспо-
транспонирования без комплексного сопряжения к апострофу необходимо добавить точ-
ку(-').
Теперь у нас есть вектор-строка х и вектор-столбец у, размерности которых по-
позволяют перемножать их, причем в любом порядке:
» x * у
ans =
96
» у * х
ans =
Columns 1
1.0000
1.5000
2.0000
2.5000
3.0000
3.5000
4.0000
4.5000
5.0000
Columns 8
4.5000
6.7500
9.0000
11.2500
13.5000
15.7500
18.0000
20.2500
22.5000
through 7
1.5000
2.2500
3.0000
3.7500
4.5000
5.2500
6.0000
6.7500
7.5000
through 9
5.0000
7.5000
10.0000
12.5000
15.0000
17.5000
20.0000
22.5000
25.0000
2.
3.
4.
5.
6.
7.
8.
9.
10.
0000
0000
0000
0000
0000
0000
0000
0000
0000
2.
3.
5.
6.
7.
8.
10.
11.
12.
5000
7500
0000
2500
5000
7500
0000
2500
5000
3.
4.
6.
7.
9.
.10.
12.
13.
15.
0000
5000
0000
5000
0000
5000
0000
5000
0000
3
5
7
8
10
12
14
15
17
.5000
.2500
.0000
.7500
.5000
.2500
.0000
.7500
.5000
4
6
8
10
12
14
16
18
20
.0000
.0000
.0000
.0000
.0000
.0000
.0000
.0000
.0000
В соответствии с правилами матричных операций при умножении строки на
столбец получилось число, а при умножении столбца на строку — квадратная
матрица.
Векторы и матрицы можно формировать и из отдельных элементов, при этом
элементы в строке разделяются пробелами или запятыми, между строками ста-
ставится точка с запятой, а все в целом ограничивается квадратными скобками:
514 Приложение А. Основы работы с MATLAB
» М = [1 2:3.4]
М =
1 2
3 4
Точка с запятой имеет и еще одно важное применение — размещенная в конце
строки, она подавляет вывод результата вычислений на экран:
» М2 = М * М;
Узнать значение переменной можно, просто нведя ее имя:
» М2
М2 =
7 10
15 22
И в заключение первого знакомства приведем несложный пример, связанный с
тематикой книги — обработкой сигналов. Для начала зададим частоту дискрети-
дискретизации Fs равной 8 кГц:
» Fs = 8еЗ:
Теперь сформируем вектор значений времени, охватывающих с этой частотой
дискретизации интервал длиной в одну секунду:
» t = 0:1/Fs:I:
Рассчитаем для этих моментов времени значения периодической последователь-
последовательности двуполярных прямоугольных импульсов с частотой следования fO, равной
50 Гц. Для этого вычислим значения синусоиды нужной частоты и применим к
ним знаковую функцию sign:
» fO = 50:
» s = sign(sinB*pi*fO*t)):
Теперь подготовим фильтр для обработки нашего сигнала. Пусть это будет ФНЧ
Баттерворта 4-го порядка с частотой среза f 1, равной 200 Гц. Такой фильтр рас-
рассчитывается с помощью функции butter из пакета расширения Signal Processing:
>;
>;
b
а
> fl
• [b.
=
= 200
. a] =
1.Oe-003
0
1
.0312
.0000
butterD.
*
0.1250
-3.5897
fl*2/Fs)
0
4.
1874
8513
0
ГЧ)
.1250
.9241
0
0
.0312
.6630
Здесь мы впервые сталкиваемся с интересной особенностью MATLAB: в отли-
отличие от большинства языков программирования, функции MATLAB могут воз-
возвращать несколько результатов (в данном примере это векторы b и а — коэффи-
коэффициенты полиномов числителя и знаменателя функции передачи рассчитанного
фильтра).
Работа в интерактивном режиме
515
ЗАМЕЧАНИЕ
Выходные параметры функции перечисляются через запятую в квадратных скобках. При
использовании такой функции в составе математического выражения значением функции
является первый из списка возвращаемых сю результатов.
Теперь можно обработать сигнал s фильтром, описываемым векторами b и а. Для
этого предназначена функция filter:
» s2 = filterCb, a. s);
Наконец, взглянем на полученные результаты, выведя графики первых 200 зна-
значений входного и выходного сигналов с помощью функции plot:
» plot(tC:200), s(l:200). tCl:200). s2Cl:200), ':')
Результирующий график, который выводится в отдельном окне, называемом
графическим окном (figure window), показан на рис. А.З. Подробнее о функции
plot будет рассказано далее, в разделе «Графика» данного приложения.
I tiguio No. 1
£w>
.mail Z.oas \gmdov
1 5-
0.5
-0.5
-1 S ■
/ ...U.v^.
0.005 0 01 0 015 002 0 C25
Рис. А.З. Графики входного (сплошная линия) и выходного (пунктирная линия) сигналов
дискретного фильтра
Справочная система
В MATLAB имеется два уровня справочной системы: встроенная справка и
HTML-документация.
Встроенная справка доступна всегда, даже в том случае, если вы отказались от
установки документации (см. ранее раздел «Установка»), поскольку ее текст рас-
516
Приложение А. Основы работы с MATLAB
положен непосредственно в файлах функций MATLAB. Для получения справки
о конкретной функции необходимо ввести команду help имя_функции, например:
» help Iog2
L0G2 Base 2 logarithm and dissect floating point number.
Y = L0G2(X) is the base 2 logarithm of the elements of X.
[F.E] = L0G2(X) for each element of the real array X, returns an
array F of real numbers, usually in the range 0.5 <= abs(F) < 1.
and an array E of integers, so that X = F .* 2.ЛЕ. Any zeros in X
produce F = 0 and E = 0. This corresponds to the ANSI С function
frexpO and the IEEE floating point standard function logbO.
See also LOG. LOGIC P0W2, NEXTP0W2, REALMAX, REALMIN.
Для просмотра HTML-документации выберите одну из первых четырех команд
меню Help (Full Product Family Help, MATLAB Help, Using the Desktop или Using the
Command Window) или введите команду helpdesk. Появится окно, показанное на
рис. А.4.
iorj2 ■ ' '
logarithm
base ten
basehvo
complex [1]
complex [2]
matrix (natural)
natural
of beta function (natural)
of gamma function (na...
plotting
logarithm analysis with a...
logarithmically spaced ve
logfile startup option
LogFileName
Logging
data to memory
<i f
MATLAB - ftJO
MATLA8 - Rt,
MATLAB - R^ _
MATLAB ■ R<<-
MATLAB■ Rf
MATLAB■ R(
MATLAB- Rs
MATLAB ■ Rt
MATLAB - RS,
MATLAB ■ Rs
MATLAB- Re
MATLAB - Mi
MATLAB - R<
MATLAB - DS,
DataAcquis
Data Acquis
DataAcquis *
* ♦,
| MATLAB Function Reference Iog2 J*_ ^^_^^^
MATLAB Function Reference' '', ' ', ' Э ff
Iog2
Base 2 logarithm and dissect floating point numbers into exponent and mantissa
Syntax
[F,E] • log2(X)
Description
Y - log2(X) computes the base 2 logarithm of the elements of X.
[F,E] - iog2{X) returns arrays Fand E. Argument T is an array of real values,
usualty in the range o.s< abs(F) < l.Forreal X. r satisfies the equation x -
f.*2.ae. Argument E is an array of integers that, for real X, satisfy the equation X ■
Г.'2.АЕ.
Remarks
This function corresponds to the ANSI С function f rexp о and the IEEE floating point
standard function iogb().Anyzerosin x produce f = о and E • o.
Examples
zf-
Рис. А.4. Просмотр HTML-документации
В левой части окна имеется раздел Help Navigator с четырьмя вкладками —
Contents (содержание), Index (указатель), Search (поиск) и Favorites (избранное).
Работа в интерактивном режиме
517
На рис. А.4 показано, как с помощью указателя найдена справка по той же функ-
функции 1од2. Как видите, HTML-документация содержит больше информации, чем
встроенная справка.
На втором диске дистрибутива MATLAB имеется также документация в форма-
формате PDF. Она не устанавливается на жесткий диск компьютера, а ее текст полно-
полностью совпадает с HTML-версией (к сожалению, дублируются и иногда встре-
встречающиеся в документации ошибки). Назначение PDF-варианта документации —
обеспечить удобство распечатывания.
Интерфейс главного окна
Говоря об интерфейсе главного окна MATLAB, следует сразу отметить главное —
MATLAB был и остается системой командной строки, и все элементы интерфей-
интерфейса, которыми он обзавелся в пятой и особенно в шестой версии, являются лишь
средством «мышиного» доступа к некоторым командам. Однако по-прежнему
абсолютно все необходимые операции можно выполнять из командной строки.
На приведенном ранее рис. А.2 слева от командного окна видны еще два окна,
каждое из которых, в свою очередь, имеет две вкладки. На рис. А.2 видны вклад-
вкладки Launch Pad и Command History, а оставшиеся вкладки Workspace и Current
Directory в отцепленном от командного окна виде представлены на рис. А.5.
В* £» 'Mm Уе
Sub
Щи
Ци2
СШ
ffla
gpans
fflb
H"
ffltl
ffl»
Ш'2
fflt
|§х
ШУ
%'$ww* ' -,,!
■■■■
■■■
8..-Г-Т-—Tj
j 31 zt
ilxl
12x2
2x2
1x5
9x9
1x5
1x1
lxl
ilxSOOl
: 1X8001
ilxSOGl
1x9
9x1
is
i32
32
i40
40
■8
is
64008
164008
64008
72
72
! Clas. j
idouble array i
idouble ar
idouble' ar
idouble ar
idouble ar
jdouble ar
idouble ar
idouble ar
idouble ar
jdouble ar
idouble ar
,double ar
double ar
T* s ~ "°'IV
cay
cay i
ay I
ay •
cay j
ay i.
ay I
■•У i
4 i
•У !
ay
ay
] С aacei-b.^ l-ik
1 ill file» _^
DBulldError.n
^1 dsp_book. spt
OlrcocCount.i
Эехр_согг.в
'.;J £1304. tic
3group_ilel.ii
S^p.del.s
Sl"d_di££.B
9lnd_dl££l.s
Sl°d_di££2.s
1 J.
l?lie Tn
И-£11е
И-£11е
H-£ile
H-£lle
И-£11е
И-£11е
И-£11е
И-£11е
H-£lle
И-£11е
И-£Ие
' '**! к
е j Last Kodid
10:45
04:23
10:52
08:29
10:43
U:08
03:49
10:37
11:53
09:29
11:53
02:44
04:02
•
Ed.'ueaecipUen
•
subplot[2r 1,1.
первий вариант ч ^
yll»([-0.1 0.2].
разкешаек коз44 .ч
з-:оиагеB*р1*Г
ЛИ »j
Рис. А.5. Вкладки Workspace (слева) и Current Directory (справа)
Очень удобным новшеством шестой версии MATLAB стала вкладка Command
History. Здесь представлен список вводившихся команд, причем этот список ох-
охватывает не только текущий сеанс работы, но и предыдущие. Команды из списка
можно повторно выполнять (двойным щелчком мыши) либо перетаскивать в ко-
командную строку для редактирования.
Еще один способ доступа к предыдущим использованным командам — их «пере-
«перелистывание» в командной строке с помощью клавиш Т и 4-.. ,
518 Приложение А. Основы работы с MATLAB
Вкладка Workspace демонстрирует содержимое рабочей области памяти MATLAB.
Здесь представлены имена переменных (Name), их размер в элементах (Size),
число занимаемых байтов памяти (Bytes) и тип данных (Class). Двойной щелчок
на имени переменной вызывает визуальный редактор массивов — Array Editor.
Вкладка Launch Pad показывает список установленных компонентов MATLAB и
предоставляет удобный доступ к их документации, демонстрационным приме-
примерам и специализированным графическим средам.
Вкладка Current Directory позволяет работать с файлами текущего каталога — от-
открывать их для редактирования, переименовывать, удалять, запускать MATLAB-
нрограммы.
Что касается панели инструментов главного окна MATLAB (см. рис. А.2), отметим
лишь раскрывающийся список Current Directory, в котором перечислены исполь-
использовавшиеся рабочие каталоги. При работе с несколькими MATLAB-ироектами
этот список дает возможность удобного переключения между ними. Выбрать но-
новый рабочий каталог позволяет кнопка с многоточием, расположенная справа от
списка.
Массивы
В этом разделе мы познакомимся с массивами — основными типами данных
MATLAB. Как уже говорилось, название системы MATLAB расшифровывается
как «MATrix LABoratory». Для простоты можно считать, что все, с чем опериру-
оперирует MATLAB, является массивами, состоящими из комплексных чисел, вещест-
вещественная и мнимая части которых представлены в 8-байтовом формате double.
Даже обычное число (скаляр) с точки зрения MATLAB представляет собой мат-
матрицу размера 1x1.
MATLAB — интерпретирующая система, поэтому массивы не нужно как-то спе-
специально описывать. Размер массива может меняться в ходе работы — если вы
присвоите значение элементу массива, указав индекс, превышающий текущий
размер, MATLAB увеличит массив, дополнив его нулями. Уменьшить текущий
размер массива можно только принудительно, удалив часть его элементов.
ВНИМАНИЕ
При каждом изменении размера массива MATLAB заиоио выделяет для него блок памяти.
О том, к каким неприятностям это может принести, будет рассказано в разделе «Оптими-
«Оптимизация MATLAB-ирограмм».
Посмотрим, как меняется размер массива в процессе работы, набрав в главном
окне MATLAB несколько команд.
Для начала создадим числовую переменную:
» х = 5
х =
5
Массивы 519
Как указывалось выше, даже такая переменная х трактуется системой как мас-
массив. Убедимся в этом с помощью функции size, возвращающей вектор, содержа-
содержащий количество строк и столбцов массива:
» size(x)
ans =
1 1
ЗАМЕЧАНИЕ
Кроме функции size, возвращающей вектор размеров массива по всем измерениям, имеет-
имеется функция length, позволяющая определить максимальный из размеров массива. Особен-
Особенно она удобна при определении длины одномерных векторов.
Итак, с точки зрения MATLAB х — это массив 1x1. Сделаем эту переменную
«настоящим» массивом, присвоив значение, скажем, элементу, расположенному
в пятом столбце четвертой строки:
» хD, 5) - 6
х =
5
0
0
0
ЗАМЕЧАНИЕ
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
6
Нумерация .элементов массивов в MATLAB начинается с. единицы, как это принято при за-
записи матриц в математике, а не с нуля, как, скажем, в языках программирования C/C++.
При обращении к элементу массива индексы указываются через запятую в круглых скобках.
Как видите, переменная х стала массивом размером 4x5:
» size(x)
ans *
4 5
При попытке обратиться к элементу с индексами, выходящими за текущий раз-
размер массива, разумеется, выдается сообщение об ошибке:
» хB. 7)
??? Index exceeds matrix dimensions.
Чтобы уменьшить размер массива, нужно удалить из него некоторое количество
строк или столбцов. Для этого нужно просто присвоить соответствующему фраг-
фрагменту массива «пустое» значение ([]):
» хB. :) = []
X —
5
0
0
0
0
0
0
0
0
0
0
0
0
0
б
Здесь мы использовали и качестве второго индекса символ двоеточия (:), что оз-
означает «все элементы массива вдоль данной размерности». Таким образом, мы
A =
17
23
4
10
11
24
5
6
12
18
1
7
13
19
25
8
14
20
21
CNJ
520 Приложение А. Основы работы с MATLAB
получили доступ не к одному элементу массива, а к целому фрагменту. Возмож-
Возможность работы с фрагментами массивов, имеющаяся в MATLAB, отсутствует в
большинстве языков программирования, поэтому ее стоит обсудить подробнее.
Для использования в дальнейших примерах сформируем квадратную матрицу А
размером 5x5 — «магический квадрат»:
» А = magicE)
15
16
22
3
9
Для начала выделим из этого массива прямоугольный блок, простирающийся от
второй до третьей строки и от второго до четвертого столбца:
» АB:3. 2:4)
ans =
5 7 14
6 13 ■ 20
Таким образом можно выделить из массива произвольный прямоугольный блок.
Если выделяемый блок по одному из измерений совпадает с размером исходного
массива, вместо задания диапазона индексов можно указать просто двоеточие
(мы уже сталкивались с этим при удалении фрагмента массива):
» АC:4, :)
ans =
4 6 13 20 22
10 12 19 21 3
Некоторые отступления от общего синтаксиса возможны и тогда, когда выделяе-
выделяемый фрагмент «упирается» в границу массива справа или снизу. В этом случае
для обозначения последнего (максимального) возможного значения индекса по
какой-либо размерности можно использовать ключевое слово end. Это значение
можно использовать и при вычислении индексов. Например, выделим из масси-
массива А блок размером 2x3, расположенный в правом нижнем углу:
» A(end-l:end. end-2:end)
ans =
19 21 3
25 2 9
Выделяемый фрагмент не обязательно должен быть сплошным. Выделим из
массива А второй и четвертый элементы первой и последней строк:
» A([l end]. [2 4])
ans =
24 8
18 2
Наконец, для выделения из массива абсолютно произвольного набора элементов
придется прибегнуть к обращению по линейному (то есть одномерному) индек-
Другие типы данных 521
су. Элементы двумерных массивов при этом нумеруются по столбцам. Выделим
из массива А элементы, лежанию на кросс-диагонали:
» А([5 9 13 17 21])
ans =
11 12 13 14 15
Для автоматического формирования одномерных индексов из двумерных пред-
предназначена функция sub2ind. Применим ее для получения одномерных индексов
элементов массива А, лежащих на его кросс-диагонали:
» х = 1:5:' % номера столбцов
» у = 5:-1:1: % номера строк
» ind = sub2ind(size(A). у, х)
ind =
5 9 13 17 21
Полученные значения фрагментов массивов можно не только сохранять в виде
новых переменных, с ними можно производить вычисления, так сказать, «на мес-
месте». В качестве примера увеличим в два раза значения элементов первого столб-
столбца массива А:
» А(:, 1) = А(:. 1)*2
А =
34
46
8
20
22
24
5
6
12
18
1
7
13
19
25
8
14
20
21
2
15
16
22
3
9
Мы рассмотрели лишь основные приемы работы с массивами в MATLAB. Име-
Имеется еще множество функций, реализующих преобразования массивов, матрич-
матричные операции и т. д. Часть этих функций перечислена в приложении Б, а более
подробная информация содержится в справочной системе и документации.
Другие типы данных
Помимо одномерных векторов и двумерных матриц MATLAB поддерживает ряд
других типов данных. К ним относятся многомерные массивы, строки, структу-
структуры, массивы ячеек, а также объекты. Подробное рассмотрение реализации объ-
объектно-ориентированных концепций в MATLAB выходит за рамки этого краткого
описания, хотя минимальные сведения о работе с объектами приведены в главе 7
при обсуждении функций пакета Filter Design. Остальные перечисленные типы
данных рассматриваются ниже.
Многомерные массивы
Многомерные массивы являются естественным обобщением двумерных масси-
массивов. Для обращения к их элементам используется необходимое число индексов,
однако заполнять многомерный массив числами и выражениями приходится по
частям, так как синтаксис MATLAB позволяет записывать поэлементное содер-
522 Приложение А. Основы работы с MATLAB
жимое только для одно- и двумерных массивов. В качестве примера создадим
трехмерный массив размером 2x2x2:
» х(:.:,!) = [1 2:3 4]: X первый «слой»
» х(:,:,2) = [5 6:7 8]: % второй «слой»
» х
х(:,:.1) =
1 2
3 4
х(:.:.2) =
5 6
7 8
Как видите, вывод значений многомерного массива MATLAB тоже осуществля-
осуществляет по «слоям».
Многие функции MATLAB, ориентированные на работу с векторами, при полу-
получении входного параметра в виде двумерного массива обрабатывают его столб-
столбцы независимо. При использовании в качестве параметра многомерного массива
такая обработка будет вестись вдоль первого измерения, размер массива вдоль
которого не равен единице. Например, для созданного в приведенном примере
трехмерного массива были бы независимо обработаны двухэлементные векторы
х(: ,1.1), х(: .2,1), х(: ,1,2) и х(: ,2,2). Кроме того, многие такие функции позво-
позволяют явно указать, вдоль какой размерности следует выбирать векторы из мно-
многомерного массива. Соответствующий параметр в документации обычно обо-
обозначается идентификатором DIM. В качестве примера можно привести функции
быстрого преобразования Фурье fft и if ft, имеющие следующий вариант син-
синтаксиса: у = fft(x, N. DIM) и х = ifftCy. N, DIM).
Имеются и функции, специально предназначенные для обработки многомерных
данных. Обычно идентификаторы таких функции отличаются от имен их одно-
одномерных родственников добавленной в конце буквой <<п>>. Примером опять-таки
могут служить функции быстрого преобразования Фурье, у которых имеются
многомерные варианты fftn и Ifftn.
Строки
Для задания строковых констант используются апострофы:
» si = 'Digital';
» s2 = 'Signal':
» s3 = 'Processing':
С точки зрения MATLAB строки представляют собой массивы символов. Поэто-
Поэтому, например, операция соединения (конкатенации) строк выполняется не с по-
помощью оператора сложения, а с использованием синтаксиса горизонтального со-
соединения матриц:
» S4 = [si ' ' s2 ' ' s3]
s4 =
Digital Signal Processing
Основные функции работы со строками перечислены в разделе «Strfun» прило-
приложения Б.
Другие типы данных 523
Структуры
Структуры (structure) позволяют объединить в одной переменной разнородные
данные (поля — field) и осуществлять доступ к ним по именам. В языке С соот-
соответствующий тип данных тоже называется структурой, а в языке Pascal — запи-
записью (record).
В MATLAB для создания структуры не требуется специальных объявлений —
достаточно присвоить значение какому-либо полю. Имена полей указываются
после имени неременной через точку. Например, для хранения информации, из-
извлеченной из wav-файла, можно использовать следующую структуру:
» w.name = 'c:\windows\media\tada.wav'; % имЯ файла
» w.Fs = 22050; % частота дискретизации
» w.bits = 16: % число бит на отсчет
» w.channels =2: % число каналов
» w.samples = 42752; % число отсчетов
» w.data = wavread(w.name); % двумерный массив отсчетов
MATLAB показывает значения переменных-структур следующим образом:
» w
W =
name: ' с: \wi ndows\medi aUada. wav'
Fs; 22050
bits: 16
channels: 2
samples: 42752
data: [42752x2 double]
Значения полей, имеющих короткие представления, выводятся полностью, а для
больших массивов указываются только размеры и тип данных.
Можно создавать и массивы структур, для этого, как обычно, используются ин-
индексы. Превратим переменную w в двухэлементный массив структур:
» wB).name = 'c:\windows\media\chord.wav'
w =
1x2 struct array with fields:
name
Fs
bits
channels
samples
data
Для массивов структур MATLAB показывает только размеры массива и список
полей.
Массивы ячеек
Массивы ячеек (cell array), так же как и структуры, позволяют объединить в
одной переменной разнородные данные. Однако обращение к этим данным про-
524 Приложение А. Основы работы с MATLAB
изводится не по именам полей, а по числовым индексам. Чтобы отличить мас-
массив ячеек от обычного массива, его индексы записываются не в круглых скоб-
скобках, а в фигурных. В качестве примера представим ту же информацию из wav-
файла, которую мы использовали при рассмотрении структур, в виде массива
ячеек:
» w{l} = 'c:\windows\media\tada.wav'; % имЯ файла
» w{2} = 22050; % частота дискретизации
» w{3} =16; % число бит на отсчет
» w{4} =2; % число каналов
» w{5} = 42752; % число отсчетов
» w{6} = wavread(w{l}): % двумерный массив отсчетов
Приведенный пример не имеет особого практического смысла — в данном слу-
случае значительно удобнее был бы доступ по именам полей. Однако массивы ячеек
удобны в тех случаях, когда нужно создать массив из векторов разной длины
или матриц разного размера. Примером может служить хранение в массиве яче-
ячеек информации о фильтре, составленном из последовательно включенных сек-
секций разного порядка.
MATLAB показывает содержимое массивов ячеек следующим образом:
» w
W =
Columns I through 5
[1x25 char] [22050] [16] [2] [42752]
Columns 6 through б
[42752x2 double]
Как и в случае структур, значения элементов, имеющих короткие представления,
выводятся полностью, а для больших массивов указываются только размеры и
тип данных. В данном случае «слишком длинной» для вывода оказалась и тек-
текстовая строка.
Программирование
Интерактивная работа с MATLAB в режиме командной строки очень удобна при
освоении системы и при необходимости поэкспериментировать, чтобы испытать
разные подходы к анализу и обработке имеющихся данных. Однако по мере при-
приобретения опыта, а также при решении конкретной задачи вы заметите, что очень
часто набираете одни и те же последовательности команд. Это означает, что на-
настало время превратить такие последовательности в программы (сценарии) и функ-
функции MATLAB.
Эти программы и функции представляют собой текстовые (ASCII) файлы с рас-
расширением .т, в которых записаны команды и операторы MATLAB. В принципе
такие файлы могут создаваться и модифицироваться с помощью любого ASCII-
редактора, но, начиная с версии 5, в MATLAB появился свой редактор, обеспе-
обеспечивающий, в частности, цветовое выделение синтаксических элементов языка,
а также интегрированный с отладчиком. О работе с редактором речь пойдет
Программирование 525
далее, а сначала следует рассмотреть различия между программами и функция-
функциями MATLAB.
Программы и функции
Как уже говорилось, текстовые файлы; содержащие операторы MATLAB, могут
быть двух типов: программы (script; иногда используется дословный перевод —
«сценарий» ) и функции (function). Между ними имеются следующие различия:
□ функции имеют заголовок function, а программы — заголовок script или во-
вовсе не имеют заголовка;
□ функции могут принимать входные параметры и возвращать результаты вы-
вычислений, а программы — нет;
□ программы используют рабочую область памяти среды MATLAB, а каждая
функция при вызове создает свою собственную рабочую область памяти и об-
общается с внешним миром только через параметры и глобальные переменные
(см. далее);
□ функции могут вызываться из программ и других функций, а программу мож-
можно запустить только вручную, набрав ее имя в командной строке MATLAB.
Итак, как уже было сказано, программы и функции MATLAB представляют со-
собой текстовые файлы с записью команд, операторов п вызовов функций MATLAB.
В этих файлах могут содержаться любые команды MATLAB, в том числе те, кото-
которые обычно не применяются в командной строке (операторы циклов, условные
операторы и т. п.; использование этих средств в командной строке возможно, но
приводит к необходимости набирать много текста, так что удобнее оказывается
сохранять такие фрагменты в виде файлов программ).
В одной строке можно записывать несколько операторов. Для их разделения сле-
следует использовать точку с запятой (если необходимо подавить вывод результа-
результатов вычислений в командное окно) или запятую (если этот вывод нужно разре-
разрешить).
Длинные строки для улучшения читаемости программы можно делить на части.
Признаком того, что запись оператора продолжается па следующей строке, явля-
являются три точки в конце строки. Удобно использовать эту возможность, напри-
например, для более наглядной записи поэлементно заданной матрицы:
М = [a b с d: ...
b b с d: ...
с с с d: ...
d d d d];
Хорошая программа невозможна без комментариев. Для обозначения коммента-
комментариев в MATLAB используется знак X — комментарием считается часть строки
справа от него. Средства создания многострочных комментариев в MATLAB не
предусмотрены. При необходимости закомментировать большой фрагмент тек-
текста или, наоборот, снять с него знаки комментария можно воспользоваться соот-
соответственно командами Comment и Uncomment меню Text редактора/отладчика
(см. далее).
526
Приложение А. Основы работы с MATLAB
Редактор/отладчик М-файлов
Для запуска редактора/отладчика М-файлов необходимо создать новый М-файл
или открыть существующий. Для этого используются команды New > M-file и
Open меню File главного окна MATLAB или соответствующие кнопки панели ин-
инструментов. Окно редактора/отладчика показано на рис. А.6.
!?> C:\mailebR12\woik\clo>e:t.m
£fc £* iww lent Uobuu Вчфзоши W«i JgiMtot» t
0 С*- в # h У,Й •« -^ I*'/»1 j'D
' fl
< -4
r
У
-.
,fkm
funtrion у ■ closest(A, x)
[tmp, ind] ■ min(ubs(A - x));
у - A(ind);
A\<* . ','...
1'-/ Г. X
14 Pv JO f>;ju
•
Рис. А.6. Редактор/отладчик М-файлов
Функции редактирования и работы с файлами, обеспечиваемые редактором/от-
редактором/отладчиком М-файлов, являются типичными для текстовых редакторов, поэто-
поэтому мы не будем обсуждать их. Из специфических возможностей следует отме-
отметить цветоиое выделение синтаксических элементов языка программирования
MATLAB, а также команды меню- Text, позволяющие закомментировать выде-
выделенный фрагмент текста (Comment), убрать знаки комментария (Uncomment),
проверить соответствие правых и левых скобок (Balance Delimiters), а также авто-
автоматически отформатировать левый край выделенного фрагмента текста (Smart
Indent).
Правая часть панели инструментов содержит кнопки управления отладчиком.
Эти функции редактора/отладчика будут рассмотрены далее, в разделе «Работа
с отладчиком».
Создание функций
Текст М-файла функции должен начинаться с заголовка function, имеющего сле-
следующий вид:
function [yl. у2. ...] = fname(xl. x2. ...)
Здесь fname — имя функции, xl, х2 и т. д. — входные параметры, yl, у2 и т. д. — вы-
выходные параметры. Входные и/пли выходные параметры могут отсутствовать.
На самом деле имя функции определяется не строкой fname, а именем, под кото-
которым сохранен М-файл. По этой же причине имена функций, в отличие от имен
переменных, не чувствительны к регистру символов.
В качестве примера создадим функцию closest, которая будет принимать два
входных параметра, вектор и число, и выбирать из вектора значение, максималь-
Программирование 527
но близкое ко второму (числовому) параметру. Для этого, открыв окно редакто-
редактора/отладчика командой меню File ► New ► M-file, введите следующий текст:
function у = closest(A. x)
% Выбор из массива А элемента, ближайшего к х
[tmp, ind] = min(abs(A - х));
у - A(ind):
Введя текст, сохраните файл под именем closest.m.
Теперь кратко прокомментируем этот программный код. Первая строка — это за-
заголовок функции, составленный согласно приведенному ранее шаблону. Вторая
строка, являющаяся комментарием, — это встроенная справка об использовании
нашей функции. По команде help fname и командное окно выводятся строки ком-
комментария, расположенные в файле fname.m непосредственно после заголовка
функции. Проверим это:
» help closest
Выбор из массива А элемента, ближайшего к х -
Таким образом, создавать встроенную справку для собственных функций совсем
несложно.
Далее с помощью функции min определяется номер интересующего нас элемента,
и в последней строке выходному параметру у присваивается значение этого эле-
элемента.
Переменные ind и tmp, создаваемые внутри функции, являются локальными. Они
создаются внутри функции и уничтожаются при завершении ее работы. Если
переменные с такими же именами существовали в рабочей области памяти
MATLAB до вызова функции, их значения не изменятся.
Функция общается с внешним миром только через свои параметры и глобальные
переменные. Чтобы объявить переменную х глобальной, необходимо использо-
использовать в головной программе и во всех функциях, которые должны иметь доступ к
данной переменной, следующую директиву:
global х
Возврат из функции производится по достижении конца ее файла. Для досроч-
досрочного возврата можно использовать оператор return. В любом случае результата-
результатами работы функции являются значения, которые выходные параметры имели на
момент возврата.
Путь поиска
Для того чтобы программа или функция была доступна из среды MATLAB, сис-
система должна быть способна найти соответствующий М-файл. Поиск файлов осу-
осуществляется следующим образом: сначала просматривается текущий рабочий
каталог (его имя показано и панели инструментов главного окна, см. рис. А.2),
а затем каталоги, входящие в путь поиска (MATLAB search path ). Когда поль-
пользователь начинает создавать собственные М-файлы, встает вопрос о том, где их
целесообразно размещать. На этот счет можно дать следующую рекомендацию:
файлы, относящиеся к разным проектам, следует размещать в отдельных катало-
528 Приложение А. Основы работы с MATLAB
гах, пе добавляя эти каталоги в путь поиска. Выпадающий список Current Directory
панели инструментов главного окна обеспечивает удобство перемещения между
каталогами разных проектов. Если же в процессе работы у вас начинает фор-
формироваться собственная библиотека функций, используемых сразу в нескольких
проектах, имеет смысл собрать их в один каталог и добавить его имя в путь поис-
поиска (для вызова редактора пути поиска используется команда Set Path меню File
главного окна MATLAB). Тогда эти функции будут доступны в любой момент,
вне зависимости от того, какой каталог является текущим.
Логические условия
В качестве логических условий в условных операторах и циклах while (см. далее)
могут использоваться числовые скалярные значения. При этом нулевое значение
трактуется как «ложь» (false), а любое ненулевое — как «истина» (true).
Кроме того, для формирования условий часто используются операторы сравне-
сравнения = (равно), -= (не равно), < (меньше), > (больше), <= (меньше или равно), >=
(больше или равно). Следует иметь в виду, что для массивов они производят по-
поэлементное сравнение, возвращая массив такого же размера, как сравниваемые
аргументы. Результирующий массив содержит единицы там, где сравнение эле-
элементов дало выполнение условия, и нули там, где условие сравнения выполнено
не было.
Для формирования логических условий полезны также следующие функции:
□ all(x) — возвращает 1, если все элементы х отличны от нуля;
□ апу(х) — возвращает 1, если хотя бы один элемент х отличен от нуля;
□ isequaKx, у) — возвращает 1, если значения х и у совпадают. В отличие от
конструкции all(x=y), использование данной функции не приведет к ошиб-
ошибке, если размеры х и у не совпадают;
□ isempty(x) — возвращает 1, если х является пустой матрицей (то есть имеет
размер 0x0).
Имеется еще довольно много функций проверки разнообразных условий, имена
которых имеют вид i s.... За более подробной информацией обратитесь к справоч-
справочной системе.
Условный оператор
Условный оператор в MATLAB реализуется с помощью ключевых слов if, else
и end:
if cond
% ветвь, выполняемая, если cond истинно
else
% ветвь, выполняемая, если cond ложно
end
Программирование
529
Здесь cond — проверяемое значение (см. ранее раздел «Логические условия»).
Для оператора if, вложенного в ветвь else другого (внешнего) оператора if, есть
сокращенная форма записи с использованием ключевого слова el sei f:
if condl
% ветвь, выполняемая, если condl истинно
el seif cond2
% ветвь, выполняемая, если condl ложно, a cond2 истинно
else
% ветвь, выполняемая, если condl и cond2 ложны
end
Аналогичным образом можно использовать eiseif несколько раз.
Оператор выбора
Если в условном операторе выбирается одна из двух возможных альтернатив, то
оператор выбора реализует разветвление программы на несколько путей. Выбор
конкретного пути зависит от значения заданной переменной. Запись операто-
оператора выбора в MATLAB производится с помощью ключевых слов switch, case,
otherwise и end:
switch x
case xl
% ветвь, выполняемая, если х равно xl
case x2
% ветвь, выполняемая, если х равно х2
otherwise
% ветвь, выполняемая, если все условия case не соблюдаются
end
При выполнения оператора switch значение х поочередно сравнивается с xl, х2
и т. д. При обнаружении первого совпадения выполняются операторы соответст-
соответствующей ветви, после чего производится выход из оператора выбора. Таким обра-
образом, в отличие от аналогичного оператора языка С, «проваливания» на следую-
следующую ветвь не происходит и операторы break в конце каждой ветви в MATLAB не
нужны.
Циклы
Для реализации циклов в MATLAB имеется два оператора — for и whi I e. В опе-
операторе for переменная-счетчик цикла поочередно принимает значения элемен-
элементов некоторого вектора:
530 Приложение А. Основы работы с MATLAB
for к = х
% тело цикла
end
Операторы, входящие в тело цикла, будут выполняться при значении перемен-
переменной к, равном хA), затем хB) и т. д. до x(end). После завершения цикла значение к
остается равным x(end).
Разумеется, чаще всего в цикле for используется последовательный перебор це-
целочисленных значений счетчика цикла:
for k = 1:N
Однако ири пеобходимости можно использовать дробное значение шага
for k = -1:0.01:1
или перебор произвольных значений:
for к = [1 10 pi 9 lnC)]
ВНИМАНИЕ
Изучая программирование, люди, как правило, приобретают привычку использовать в ка-
качестве счетчиком циклов переменные с именами i и j, В MATLAB это чревато неприятно-
неприятностями, поскольку по умолчанию эти переменные имеют значение мнимой единицы.
Использование переменной i или j одновременно в качестве счетчика цикла и в качестве
мнимой единицы — это те «грабли», на которые рано пли поздно наступают очень многие
пользователи MATLAB. Чтобы избежать неприятностей, необходимо выработать новые
привычки. Здесь есть несколько вариантов. Во-первых, можно просто избегать использо-
использования имен i и j в качестве счетчиков. Во-вторых, можно в качестве мнимом единицы ис-
использовал, не переменную i (j), а константу li (lj). В третьих, можио приучить себя
использовать двухбуквеппые имена счетчиков: И, jj и т. д.
Второй тин циклов реализуется с помощью оператора while. Тедо цикла выполня-
выполняется, пока условие cond остается истинным (то есть значение cond отлично от нуля):
while cond
% тело цикла
end
Если cond изначально имеет нулевое значение, тело цикла не будет выполнено
пи разу.
Чтобы реализовать досрочное завершение цикла, используется оператор break.
Разумеется, он должен применяться в сочетании с условным оператором, напри-
например так:
for k = 1:N
% первая половина тела цикла
% проверка дополнительного условия завершения
if cond
break
end
Программирование 531
% вторая половина тела цикла
end
Оператор break можно использовать для реализации циклов с проверкой усло-
условия завершения не в начале (как делает оператор while), а в произвольном месте
цикла. Для этого с помощью оператора while создается «вечный» цикл, а его за-
завершение произво/штся оператором break:
while I % «вечный» цикл
% первая половина тела цикла
% проверка условия завершения
if cond
break
end
% вторая половина тела цикла
end
Кроме оператора break для управления выполнением программы внутри цикла
имеется оператор continue. Размещенный внутри цикла for или while, этот опера-
оператор передает управление на проверку условия завершения цикла, пропуская при
этом оставшийся фрагмент тела цикла. Это позволяет сделать код более нагляд-
наглядным, избежав использования длинного оператора i f.
Функции с переменным числом параметров
При вызове функции можно использовать меньшее количество входных и вы-
выходных параметров, чем указано в заголовке функции. При этом рассчитанные
функцией «лишние» выходные параметры просто игнорируются. Что касается
неуказанных входных параметров, то функция выдаст сообщение об ошибке, ко-
когда попытается обратиться к одному из них. Однако внутри функции доступны
сведения об использованном при вызове числе входных и выходных параметров,
что позволяет в зависимости от этого управлять алгоритмом работы функции.
Число переданных входных параметров можно узнать с помощью функции nargin,
а число ожидаемых выходных параметров — с помощью функции nargout. В про-
простейшем случае функция nargin может использоваться для задания входным па-
параметрам значений по умолчанию:
function у = nargin_demo(x. N. mu. fid)
if nargin < 4
fid = 1:
end
if nargin < 3
mu = 0.2:
end
if nargin < 2
N = 256;
end
532 Приложение А. Основы работы с MATLAB
При вызове такой функции можно опускать один, два или три последних вход-
входных параметра, аналогично тому, как это позволяют делать язык C++ и послед-
последние версии языка Object Pascal:
у = nargin_demo(x, N, mu, fid) % полный вариант
у = nargin_demo(x, N, mu)
у = nargin_demo(x. N)
у = nargin_demo(x)
Вместо опущенных параметров будут использованы заданные в тексте функции
значения по умолчанию.
Аналогичным образом можно использовать и функцию nargout — например, что-
чтобы сэкономить время, не вычисляя незатребованные выходные величины. Мож-
Можно использовать функции nargin и nargout и для более серьезного управления ло-
логикой работы — скажем, менять используемый алгоритм в зависимости от числа
входных и выходных параметров.
Ввод и вывод данных
Как мы уже знаем, простейшим способом вывода значения переменной в команд-
командное окно MATLAB является указание ее имени без точки с запятой. Аналогич-
Аналогичное действие производит функция disp(name), отличие заключается только в том,
что на экран не будет выводиться идентификатор переменной name.
Форматированный вывод
Чтобы выводить в командное окно информацию в более аккуратном виде, следу-
следует воспользоваться функциями форматированного вывода. Это функции sprintf
(формирование строковой переменной с форматированным текстом) и fprintf
(вывод форматированного текста в поток вывода). Синтаксис обеих функций
очень схож и практически не отличается от синтаксиса соответствующих функ-
функций языка С. Поэтому кратко рассмотрим лишь функцию fprintf:
fprintf (fid. 'format', xl. x2....)
Здесь fid — числовой идентификатор потока вывода. При нулевом значении вы-
вывод не производится, значение 1 соответствует стандартному потоку вывода (вы-
(вывод в командное окно), значение 2 — стандартному потоку вывода сообщений об
ошибках (по умолчанию это тоже вывод в командное окно). Для записи инфор-
информации в файл в качестве fid необходимо использовать значение, полученное от
функции fopen при открытии файла (работа с файловыми потоками в данном
приложении не рассматривается). Данный параметр можно опустить, тогда по
умолчанию вывод будет производиться в командное окно.
Строковый параметр ' format' задает формат вывода. Эта строка должна содер-
содержать фиксированный выводимый текст и спецификаторы формата, на место
которых будут подставлены значения переменных xl, х2 и т. д. Спецификато-
Спецификаторы формата начинаются со знака X, за которым следуют цифры, задающие число
символов для вывода, и буква, определяющая тип формата. Полная информация
о возможных спецификаторах формата имеется в HTML-справке, здесь же при-
приведем лишь несколько конкретных примеров:
Программирование 533
□ %d — вывод целого числа, количество позиций выбирается автоматически;
□ *.3f — вывод числа в формате с фиксированной запятой, после запятой выво-
выводится три десятичных знака, количество позиций для целой части выбирает-
выбирается автоматически;
□ Я-15.3е — вывод числа в экспоненциальном формате, мантисса имеет три де-
десятичных знака после запятой, поле вывода занимает 15 символов, текст вы-
выравнивается по левому краю поля.
Для вывода специальных символов можно использовать комбинации \п (перс-
вод строки), \г (возврат каретки), \t (табуляция), \Ь (забой), \\ (обратная косая
черта), XX (символ процента), '' (одиночный апостроф).
Теперь используем перечисленные спецификаторы и некоторые из символов:
» п = 15;
» егг = 128.3567:
» value = 1234567890;
» fprintfd. 'Шаг %d, ошибка S.3f \nx"= S-15.3e м'. n, err, value)
Шаг 15. ошибка 128.357
x'= 1.235e+009 м
Сохранение и загрузка значений переменных
MATLAB позволяет сохранять переменные в виде МАТ-файлов (они имеют рас-
расширение .mat), которые затем могут быть снова загружены. Для сохранения все-
всего содержимого рабочей области памяти используется команда
» save filename
Все существующие в данный момент переменные будут записаны в расположен-
расположенный в текущем каталоге файл filename.mat.
Чтобы сохранить значения только некоторых переменных, следует указать их
имена после имени файла:
» save filename x у asd ...
В файл filename.mat будут записаны только значения переменных х, у, asd и т. д.
Загрузка сохраненных переменных производится командой 1 oad:
» load filename
Файл filename.mat должен быть доступен, то есть он должен находиться в теку-
текущем каталоге или в одном из каталогов, внесенных в список для поиска файлов
(см. ранее раздел «Путь поиска»).
Работа с отладчиком
Отладочные средства собраны в правой части панели инструментов ркна редак-
редактора/отладчика (рис. А.7), а также в меню Debug и Breakpoints.
Кнопки панели инструментов имеют следующее назначение:
□ Set/clear breakpoint — установка или сброс точки прерывания в текущей строке;
□ Clear all breakpoints — сброс всех точек прерывания;
534 Приложение А. Основы работы с MATLAB
□ Step — выполнение одной строки программы, при этом вызов функции счи-
считается одним оператором и заход внутрь вызываемой функции не произво-
производится;
□ Step in — выполнение одной строки программы с заходом внутрь вызываемых
функций;
□ Step out — выполнение оставшейся части текущей функции, остановка про-
программы производится после возврата из функции;
□ Continue — продолжение выполнения программы;
□ Exit Debug Mode — завершение отладки;
□ Stack — этот раскрывающийся список позволяет переключаться между рабо-
рабочими пространствами MATLAB и вызванных функций.
Clear all breakpoints Exit Debug Mode
Set/clear breakpoint
Continue Stack
Step Step out
Step in
Рис. А.7. Отладочные средства панели инструментов окна редактора/отладчика
При остановке программы в отладочном режиме (в установленной точке преры-
прерывания или при пошаговом выполнении) в главном окне появляется отладочная
подсказка К». При этом становятся доступными рабочие области памяти всех
вызванных в данный момент функций. По умолчанию текущей является рабочая
область памяти последней вызванной функции. Переключаться между рабочими
областями памяти всего стека функций можно с помощью раскрывающегося
списка Stack панели отладочных инструментов (см. рис. А.7). Такой же список
имеется в панели инструментов вкладки Workspace (см. рис. А.5). Область памя-
памяти среды MATLAB фигурирует в списке под именем Base.
Кроме того, узнать значение переменной можно, задержав указатель мыши на ее
идентификаторе в окне редактора/отладчика. Появится всплывающая подсказ-
подсказка, отображающая значение переменной. Этот способ имеет смысл применять
только для скалярных переменных и массивов небольшого размера, поскольку
для больших массивов отображается только часть содержимого либо только раз-
размер и тип данных.
Оптимизация MATLAB-программ
Под оптимизацией в данном случае подразумевается повышение скорости рабо-
работы функций и программ. В MATLAB применимы все или почти все общие прие-
приемы оптимизации программ (типа вынесения из цикла наружу всех вычислений,
не зависящих от счетчика цикла). Однако у MATLAB имеется и некоторая спе-
специфика, которую следует учитывать при оптимизации кода. Об этой специфике
и пойдет речь в данном разделе.
Программирование 535
При необходимости повысить быстродействие MATLAB-программы следует учи-
учитывать два аспекта:
□ MATLAB — интерпретирующая, а не компилирующая система;
□ функции векторпо-матричпых операции встроены в ядро системы и выпол-
выполняются предельно быстро.
Самая общая рекомендация, которая дается практически в любой книге, посвя-
посвященной MATLAB, — стараться избегать использования циклов, заменяя их век-
торно-матричными операциями и поэлементными операциями над массивами.
Приведем^ простейший пример, вычислив 10 000 значений функции sin двумя
способами — с помощью цикла и путем выполнения поэлементной операции над
вектором. Хронометраж будем вести с помощью функции tic и toe. Первая из
них фиксирует начало отсчета времени, а вторая выводит на экран время (в се-
секундах), прошедшее после tic. Вот соответствующий программный код:
» X вычисления в цикле
» % длЯ чистоты эксперимента уничтожаем все переменные
» clear all
» tic
» for k = 1:10000. x(k) = sin(k): end
» toe
elapsed_time =
3.7900
» X векторная операция
» % длЯ-чистоты эксперимента уничтожаем все переменные
» clear all
» tic
» х = sinC1:10000):
» toe
elapsed_time =
0.0500
Как видите, отказ от использования цикла ускорил вычисления примерно в
75 раз!
ЗАМЕЧАНИЕ
Время выполнения фрагмента программы может зависеть от того, существуют используе-
используемые переменные или их приходится создавать (см. далее обсуждение вопросов, связанных
с выделением памяти). Поэтому для повышения чистоты эксперимента в приведенном
листинге перед началом расчетов псе имеющиеся переменные уничтожаются командой
clear all. Эту команду можно также использовать для выборочного уничтожения перемен-
переменных — в этом случае вместо слова all необходимо указать имена стираемых переменных,
разделяя их пробелами: clear x у z....
Однако пе следует воспринимать данный совет как абсолютную догму. Не все
алгоритмы хорошо поддаются векторизации, и иногда попытка искусственно
свести алгоритм к последовательности матричных операций может потребовать
создания промежуточных матриц большого размера. Необходимость выделения
536 Приложение А. Основы работы с MATLAB
памяти для хранения этих матриц может свести на нет преимущества отказа от
циклов.
Итак, без циклов все-таки обойтись не удается, но при необходимости их ис-
использования следует обратить внимание еще на один аспект — выделение па-
памяти для хранения переменных. Язык программирования MATLAB, являясь
интерпретируемым языком сверхвысокого уровня, скрывает от пользователя
операции, связанные с выделением и освобождением памяти. В результате мы
чаще всего даже не задумываемся над тем, что в действительности происходит
при выполнении простейшего (с точки зрения пользователя) оператора при-
присваивания. Рассмотрим небольшой пример:
for k = 1:N
% какие-нибудь вычисления
х(Ю = ...
end
Если переменная х не,существовала до начала цикла, то при каждом проходе
цикла происходит увеличение числа элементов в ней. В результате при каждом
выполнении оператора присваивания система должна проделать следующее:
□ выделить память под переменную х нового размера;
□ скопировать туда старое содержимое переменной;
□ освободить память, отведенную ранее под хранение старого значения х;
□ наконец, выполнить собственно оператор присваивания для х(к).
Операции выделения и освобождения памяти выполняются довольно медленно,
поэтому необходимость проделывать их при каждом проходе цикла может силь-
сильно замедлить работу программы, особенно если наращиваемые массивы имеют
большой размер и если в цикле их используется несколько.
В качестве примера будем в цикле заполнять два вектора случайными гауссовы-
гауссовыми числами, выводя на экран время, потребовавшееся для добавления каждых
1000 элементов:
» clear all % для чистоты эксперимента
» tic
» for k = 1:1е4
»
»
»
»
»
»
»
» end
1000:
2000:
3000:
4000:
x(k) = randn:
y(k) = randn:
if rem(k. le3)==0
t=toc:
fprintfd. '%
tic
end
0.060 seconds
0.270 seconds
0.330 seconds
0.500 seconds
%d: %.3f seconds\n'. k. t)
Программирование 537
5000: 0.770 seconds
6000: 1.040 seconds
7000: 1.210 seconds
8000: 1.430 seconds
9000: 1.590 seconds
10000: 1.810 seconds
Как видите, по мере роста размера массивов скорость работы сильно падает —
для добавления последней тысячи элементов понадобилось в 30 раз больше вре-
времени, чем для первой!
Решением этой проблемы является предварительное выделение памяти под за-
заполняемые в цикле массивы. Для этого необходимо создать переменную нужно-
нужного размера, скажем, с помощью функции zeros, формирующий массив, заполнен-
заполненный нулями. Модифицируем предыдущий пример:
» clear all % длЯ чистоты эксперимента
» х = zerosd. 1е4); % создаем массивы
» у = zerosd. 1е4); % заранее
» tic
» for k = 1:1е4
» x(k) = randn:
» y(k) = randn:
» if rem(k. le3)==0
» t=toc:
» fprintfd. '%ti: *.3f seconds\n'. k. t)
» tic
» end
» end
1000: 0.060 seconds
2000: 0.000 seconds
3000: 0.000 seconds
4000: 0.050 seconds
5000: 0.000 seconds
6000: 0.000 seconds
7000: 0.060 seconds
8000: 0.000 seconds
9000: 0.000 seconds
10000: 0.050 seconds
Результат налицо: работа цикла проходит равномерно, не замедляясь.
ЗАМЕЧАНИЕ
Функция сое измеряет время дискретными порциями, размер которых лежит между 50
й 60 мс. Этим и объясняются нулевые значения, несколько раз полученные при выполне-
выполнении последнего примера.
При использовании оператора while число проходов цикла заранее не известно.
Поэтому не известен и итоговый размер наращиваемых в таком цикле массивов.
В этой ситуации можно применить компромиссный подход, увеличивая массивы
538 Приложение А. Основы работы с MATLAB
внутри цикла, но не при каждом проходе, а изредка, зато большими кусками. По-
Получается код наподобие следующего:
sizejncr = 10000: % дискретность приращениЯ
х = zerosd. sizejncr); % создание массивов
у = zerosd. sizejncr):
k = 1: % счетчик элементов
while cond
% проверяем, не исчерпана ли текущая длина массивов
if k>length(x)
% выделяем дополнительную памЯть
х = [х zerosd. sizejncr)];
у = ty zerosd. sizejncr)];
end
% какие-нибудь вычисления
x(k) = ...
у(Ю - ... ' ■
k = k+1: % увеличиваем значение счетчика
end
% после завершения цикла удалЯем нулевые «хвосты»
x(k:end) = []:
y(k:end) = [];
Данный подход позволяет существенно ускорить вычисления, если число прохо-
проходов цикла заранее не известно.
До сих пор мы измеряли время выполнения фрагментов программы с помощью
функций tic и toe. Они весьма полезны, но в MATLAB имеется и более серьез-
серьезный хронометрирующий инструмент — утилита профилирования, вызываемая
командой
profile on
В качестве примера создадим несколько вариантов функции ind_diff, вычисляю-
вычисляющей квадратную матрицу, значения элементов которой равны разности их ин-
индексов: Ay = i - j. Единственным входным параметром является размер N созда-
создаваемой матрицы.
Первая версия кода будет наиболее прямолинейной — с использованием двух
вложенных циклов:
function у = ind_diff(N)
for k = 1:N
for 1 = 1:N
y(k.l) = k - 1:
end
end
Сохраняем текст функции в виде файла ind_diff.m, включаем профилирование
и вызываем фу* ':цию:
» profile on
» у = ind_diffA00):
Программирование
539
Для вывода результатов профилирования используется следующая команда:
» profile report
MATLAB сгенерирует отчет в HTML-формате и покажет его в установленном
в системе web-браузере (рис. А.8).
Ж MATLAO Profile) Report ■ Netscape
£*> £d« yim £« £{M»unicator
4 * а л ^ M
tefc ч >i . RtiMd Home S««th Netscape
-*
I Me WCI/WINDOWS/TEMP/lp0806?6 biml
MATLAB Profile Report: Summary
Report generated 19-Ja»-2OO2 23:08:07
Total recorded time: 7.58 s
Number of M-functions: 2
Clock precision: 0.050 s
Function List
JNuna frimr' iciiilii jTime/ciiii Self dim Location
inci axtt J7 58 100 0%: I {' 7 58 |758[1OOO%' ~sH.gbi>b 4i»unt *itt
[piotilc jo00 0 0% I
0 00 0 001 0 0% ~
O.t l'l«l4l . с -tftP ( I l_J_) 111
Рис. А.8. Итоговый отчет о профилировании
В итоговом отчете показаны общее время профилирования, число вызванных
функций и время, затраченное на их выполнение. В данном случае кроме самой
функции profile вызывалась только наша функция ind_diff. Чтобы получить
подробную информацию о результатах профилирования этой функции, необхо-
необходимо щелкнуть на ее имени в таблице. После перехода по гиперссылке откроется
страница детализированной информации (рис. А.9).
Наибольший интерес здесь представляют выведенные под таблицей отдельные
строки листинга функции, рядом с которыми показано абсолютное (в секундах)
и относительное (в процентах) время их выполнения.
Проанализируем полученные результаты. Некоторое время потрачено на обслу-
обслуживание циклов (строки 5 и 6), но основные затраты G1 %) пришлись на опера-
оператор присваивания (строка 4).
Воспользуемся данным ранее советом и заранее выделим память под создавае-
создаваемый массив:
function у = ind_diff(N)
у = zeros(N, N);
540
Приложение А. Основы работы с MATLAB
for к = 1:N
for I = 1:N
У(к,1) = к - 1;
end
end
* MATLAB F'nililei Repoil - Netscape
1гГ
Hen»
- Netscape' ,
Loel»to'jlile///CWINDQWS/TEMP/tp080676 html
MATLAB Profile Report: Function Details
i.na_ditt С ■:\f.&v,latifl2\\Ki£\ft liid d-j.ff.ni
Time: 7.58 s A00.0%)
Calls; 1
Self time: 7.58 s A00.0%)
Function: jfinte
ina diff G.58 i
[
Parent fimctioiu:
none
Child {unctions:
ИО1М
"Cills JTbtte/caU
j 1 j 7J8
100% of the total time in this function was spent on the following lines1.
3: for 1 - 1:H
S.41 714 4: у (к, 1) - к - 1;
2.11 28t s: eiid
0.06 It 6: end
profile С';\ИАТЦВШ2\г1>о1)ао>;\п!аЧаЬ\депега1\ profile.и
Tune 0 00 s @.0%)
Рис. А.9. Отчет о результатах профилирования — детальная информация
о вызываемых функциях
Сохраняем новую версию и снова включаем профилирование (команда profile
report выключает режим профилирования):
» profile on
» у = ind_diffC00);
» profile report
Программирование
541
Сгенерированный детальный отчет показан на рис. А. 10. Как видите, время, за-
затрачиваемое на выполнение присваивания внутри цикла, существенно уменьши-
уменьшилось. Завершаем работу с утилитой профилирования:
» profile off
Ш MATLAB Profile) Report - Netscape
lto.Wa/WINDOWS/TEMP/lp5428S8.hlml
Jruti' tj< n J 'ЫлI;
MATLAB Profile Report: Function Details
3~ ' b'crk''' net
Time 6 65 s A00 0%)
Calls 1
Self tone 6 65 s A00 0%)
Function: [Time 'Ca
Parent functions:
none
СЫЫ functions:
none
Us Time/call'
1 665
-•
100% of the total time in this function was spent on the following lines:
3: for It - 1:N
O.O6 14 4: for 1 - 1:N
3.87 SBH 5: y(fc,l) - fc - 1;
2.72 41* 6: end
7: end
mnflle
I
- A
Рис. А. 10. Результаты профилирования оптимизированного кода
ЗАМЕЧАНИЕ
Приведенные варианты кода были рассмотрены лишь с целью продемонстрировать про-
профилирование. Время выполнения данной функции можно еще сильнее уменьшить, отка-
отказавшись от циклов вовсе. Если вам действительно нужно создать такую матрицу, следует
заметить, что вдоль ее диагоналей, параллельных главной, стоят одинаковые числа, и вос-
воспользоваться функцией toeplitz:
у = toeplitz@:N-l. -(O:N-D);
Это, пожалуй, наиболее быстрый способ.
542 Приложение А. Основы работы с MATLAB
MATLAB и русский язык
Поскольку разработчики системы MATLAB не предусматривали работы с ки-
кириллицей, при попытке использования русского языка в MATLAB возникает
ряд проблем. Конкретный набор возможных неприятностей зависит от конкрет-
конкретных версий MATLAB и операционной системы, поэтому перечислим здесь лишь
несколько вещей, характерных для шестой версии MATLAB. Во-первых, в ком-
комментариях и текстовых константах нельзя использовать строчную букву «я» (это
вообще довольно типичная беда программ, написанных на языке С). Именно по
этой причине в комментариях к листингам в данной книге везде используется
прописная буква «Я». Во-вторых, при наборе в командной строке строчной рус-
русской буквы «с» происходит переход на следующую строку, причем уже набран-
набранная строка не выполняется и не запоминается. В-третьих, при попытке исполь-
использовать русский текст в надписях на графиках иногда возникают проблемы с
кодировкой выбираемого MATLAB шрифта. Впрочем, последнюю проблему, как
правило, удается решить, изменив настройки, используемые для вывода надпи-
надписей по умолчанию.
Графика
Говоря о графических средствах MATLAB, прежде всего нужно отметить сле-
следующее. MATLAB — матричная программа, и ее графические команды могут
лишь разнообразными способами визуализировать векторы и матрицы. На прак-
практике это означает, что точки, соответствующие элементам векторов и матриц,
могут соединяться лишь прямыми линиями — никакого сглаживания или интер-
интерполяции производиться не будет. Если вы хотите, чтобы график выглядел более
плавным, позаботьтесь о том, чтобы в визуализируемом массиве было больше
точек. Если строится график функции, уменьшите шаг между соседними значе-
значениями ее аргумента. Если необходимо сгладить экспериментально полученные
данные, для которых получить дополнительные точки затруднительно, следует
воспользоваться функциями интерполяции (interp*, spline, pchip, griddata*) или
аппроксимации (polyfit; кроме того, имеется графический интерфейс аппрокси-
аппроксимации, вызываемый командой Basic Fitting из меню Tools графических окон). За
более подробными сведениями обратитесь к документации MATLAB.
Двумерная графика
Основным средством двумерной графики является функция plot. Наиболее ти-
типичный вариант ее использования выглядит следующим образом:
plotCx. у)
Здесь х и у — векторы одинаковой длины, задающие соответствующие коорди-
координаты точек, выводимых на график. По умолчанию точки соединяются сплош-
сплошными линиями синего цвета. Тип и цвет линий и символов точек можно из-
изменить, об этом будет рассказано далее, в разделе «Настройка внешнего вида
графиков».
Графика
543
В качестве примера построим график функции у = sin(nx)/(;u"), которая в
MATLAB имеет имя sine (рис. А. 11):
» х = -10:0.1:10: % значения координаты х
» у = sinc(x): % значения координаты у
» plotCx. у)
i Figure No. I
0,8 ■
0,6 ■ ■
0,4
Ok
•0,4
1
. - Л |
--V/ V \/ \ |
1A /\/w-
Рис. А.11. График, построенный функцией plot
Если на экране еще не было графиков, функция plot создаст графическое окно.
Если на экране уже имелись графические окна, график будет выведен в текущее
окно — то, которое последним выводилось на передний план. О том, как можно
создать несколько графических окон, будет рассказано далее, в разделе «Одно-
«Одновременны]! вывод нескольких графиков».
ЗАМЕЧАНИЕ
Можно использовать функцию plot с одним аргументом — plot(y). В этом случае вектор у
задает вертикальные координаты точек, а по горизонтали откладываются номера элемен-
элементов вектора.
Панель управления графического окна
В верхней части графического окна расположена панель инструментов (рис. А. 12),
кнопки которой выполняют следующие функции:
□ New Figure — создает новое графическое окно;
□ Open File — позволяет создать новое графическое окно, загрузив в него ранее
сохраненный график;
544 Приложение А. Основы работы с MATLAB
Save Figure Zoom In
Open File
New Figure
Print Figure
Zoom Out
Rotate 3D
Ш
i
Edit Plot
r
Insert Line
Insert Text Insert Arrow
Рис. А. 12. Панель инструментов графического окна
□ Save Figure — позволяет сохранить графическое окно в виде файла с расшире-
расширением .fig (к сожалению, в окне сохранения файла это расширение не добавля-
добавляется к имени автоматически — его приходится вводить вручную). Сохраняе-
Сохраняемый файл представляет собой МАТ-файл (см. ранее раздел «Ввод и вывод
данных»), в котором записаны массивы данных, представленных на графике,
а также все параметры настройки графического окна. Сохраненный fig-файл
впоследствии можно загрузить с помощью кнопки Open File, воссоздав запи-
записанный график;
□ Print Figure — позволяет распечатать содержимое графического окна;
□ Edit Plot — включает режим редактирования графика. В этом режиме можно
выделять элементы графика мышью и настраивать их свойства;
□ Insert Text — включает режим интерактивного размещения текста на графике;
□ Insert Arrow — включает режим рисования стрелок на графике;
□ Insert Line — включает режим рисования линий на графике;
□ Zoom In — включает режим увеличения масштаба. В этом режиме щелчок
левой кнопкой мыши в области графика увеличивает масштаб отображения,
правой — уменьшает;
□ Zoom Out — включает режим уменьшения масштаба. В этом режиме щелчок
левой кнопкой мыши в области графика уменьшает масштаб отображения,
правой — увеличивает;
□ Rotate 3D — включает режим настройки точки обзора. В этом режиме пере-
перемещение указателя мыши в области графика при нажатой левой кнопке мыши
приводит к повороту габаритного параллелепипеда трехмерного графика. Ис-
Использование данного режима для двумерных графиков не имеет особого
смысла.
Команды меню графического окна в основном совпадают с кнопками панели ин-
инструментов. Отметим лишь несколько команд, представляющих особый интерес:
□ File ► Export — позволяет сохранить график в виде файла одного из поддержи-
поддерживаемых графических форматов;
□ Tools ► Basic Fitting — выводит окно настройки аппроксимации, с помощью ко-
которого можно подобрать подходящую аппроксимирующую кривую для пред-
представленных на графике данных;
□ Tools ► Data Statistics — выводит окно просмотра статистической информации
о представленных на графике данных.
Графика 545
ВНИМАНИЕ
График MATLAB является векторным графическим объектом, для превращения которого
в экранные пикселы может понадобиться проделать значительный объем вычислений.
При перетаскивании окна размер графика не меняется, так что нет необходимости пере-
пересчитывать его заново — Windows лишь перемещает растровый образ окна. Если же вы ме-
меняете размер окна, разворачивая его, перетаскивая его границы или используя команду
Размер системного меню окна, все вычисления, необходимые для построения растрового
образа графика, системе придется проделать заново. Поэтому перерисовка графика после
изменения размеров его окна потребует столько же времени, сколько и первоначальное
построение. Имейте это в виду, если ваш график содержит большое количество элементов.
Ситуация усугубляется, если в Windows установлен режим отображения содержимого
окна при перетаскивании (соответствующий флажок расположен на вкладке Эффекты
окна свойств экрана). При этом система попытается отследить перетаскивание границы
окна, непрерывно перерисовывая график. В случае сложного графика это может привести
к весьма существенному торможению работы.
Другие разновидности двумерных графиков
Кроме функции plot есть еще целый ряд функций с аналогичным синтаксисом,
позволяющих получить друкие разновидности двумерных графиков. Ниже пере-
перечислены только некоторые из этих функций, наиболее полезные в инженерных и
научных приложениях:
□ semilogx(x. у) — график с логарифмическим масштабом по оси х;
□ semilogy(x, у) — график с логарифмическим масштабом по оси у;
□ loglog(x, у) — график с логарифмическим масштабом по обеим осям;
□ plotyyCxl. yl. х2. у2) — вывод зависимостей yl от xl и у2 от х2 с раздельной
оцифровкой вертикальных осей (для первого графика оцифровка вертикаль-
вертикальной оси наносится слева, для второго — справа);
□ stem(x, у) — график в виде «стебельков»;
□ stairs(x. у) — график в виде ступенчатой линии;
□ polar(phi, г) — график в полярных координатах (phi — угловые координаты
точек в радианах, г — соответствующие им радиусы).
Трехмерная графика
В MATLAB имеется функция с именем plot3, но, вопреки ожиданиям, основным
средством трехмерной графики является вовсе не она. Дело в том, что функция
plot3(x. у, z) является просто трехмерным аналогом функции plot, то есть она
позволяет построить линию в трехмерном пространстве по координатам точек,
задаваемым векторами х, у и z. На практике гораздо чаще бывает необходимо
строить графики функций двух переменных в виде поверхностей или линий рав-
равного уровня.
Для построения трехмерных поверхностей служит функция surf, имеющая сле-
следующий синтаксис:
surf(X, Y, Z)
546 Приложение А. Основы работы с MATLAB
Здесь X, Y и Z — двумерные массивы одинакового размера. Функция строит по-
поверхность, состоящую из четырехугольных ячеек. Координаты углов каждой ячей-
ячейки задаются, значениями четырех соседних элементов массивов X, Y и Z с индекса-
индексами (i, j), (i, j+1), (i+l, j) и (i+l, j+1). Цвет ячеек (точнее, индекс цвета в текущей
палитре) по умолчанию меняется пропорционально координате z.
Из способа задания параметров для функции surf видно, что ее возможности не
ограничиваются построением двухкоординатных функциональных зависимостей.
Действительно, функция surf позволяет строить произвольные трехмерные по-
поверхности. Однако эта гибкость несколько усложняет построение обычных гра-
графиков функций двух переменных.
Чтобы построить график функционально заданной поверхности z - f(x, у), мас-
массивы X и Y, передаваемые функции surf, должны задавать сетку (как правило,
равномерную). Значения массива Z рассчитываются по формуле функциональ-
функциональной зависимости с использованием поэлементных операций над массивами X и Y.
Массивы X и Y в данном случае удобнее всего формировать с помощью специаль-
специальной функции meshgrid, имеющей следующий синтаксис:
[X. Y] = meshgrid(x. у)
Здесь х и у — векторы, задающие наборы значений х- и г/-координат. Формируе-
Формируемые массивы X и Y имеют length(y) строк и length(x) столбцов. Строки массива X
являются копиями вектора х, а столбцы массива Y — копиями вектора у. Чтобы
пояснить работу функции meshgrid, передадим ей два целочисленных вектора:
» [X, Y] = meshgnd(l:5. -3:3)
1
1
1
1
1
1
1
-3
CM
-1
0
1
CM
3
CM
CM
CM
CM
CM
CM
2
-3
-2
-1
0
1
CM
3
3
3
3
3
3
3
3
-3
CM
-1
0
1
2
3
4
4
4
4
4
4
4
-3
CM
-1
0
1
2
3
5
5
5
5
5
5
5
-3
IV)
-1
0
1
2
3
В качестве примера построим график функции
\х2 +у2
V0 О
•v _i_ tit
х +у
при изменении х и у от -5 до 5 с шагом 0,2 (рис. А. 13):
» х = -5:0.2:5:
» [X. Y] = meshgrid(x):
Графика
547
» Z = sinc(sqrt(X.~2+Y.~2));
» surf(X, Y, Z)
» colormap gray
hi Figure No. 1
F.le £tf Uch
'1
I
■0 5*1.
5
,r-ert Iocs ffiirioow {jep
3 ^ A /" / & & ~
•6 -5
Рис. А. 13. Трехмерная поверхность, построенная с помощью функции surf
ЗАМЕЧАНИЕ
В приведенном фрагменте кода функция meshgrid используется с одним входным пара-
параметром. Это сокращенный вариант вызова, эквивалентный meshgrid(x, x).
Для построения графика функции двух переменных в виде линий равного уров-
уровня служит функция contour, имеющая- следующий синтаксис:
[с. h] = contouKX, Y, Z. V)
Здесь Z — двумерный массив, содержащий значения функции, а параметры X и Y
могут быть как массивами, полученными от функции meshgrid (см. выше), так и
векторами координат, передаваемыми функции meshgrid. При отсутствии этих пара-
параметров в качестве координат используются номера строк и столбцов матрицы 1.
Параметр V может быть числом (тогда он задает количество выводимых линий
уровня) или вектором (тогда этот параметр трактуется как набор значений
функции для построения линий равного уровня). При отсутствии данного пара-
параметра значения уровня выбираются автоматически.
Возвращаемыми результатами с и h являются структуры данных, которые необ-
необходимо передать другой функции, clabel, для нанесения оцифровки на линии
уровня:
clabeKc. h)
548
Приложение А. Основы работы с MATLAB
В качестве примера построим линии уровня для функции peaks. Это демонстра-
демонстрационная функция трехмерной графики MATLAB, генерирующая поверхность с
несколькими пиками и впадинами. Нанесем также на линии уровня оцифровку с
помощью функции clabel (рис. А.14):
» [с. h] = contour(peaks):
» clabel(с. h)
»> Fiuine No. 1
fife £dit )&m inm Tools
'10 Ф S3 Ш ] ^ A /"
45
40
< 35
„ 30
- .2$
' 2I?
,1S
. г -
/~2-^\'* '
y" ! „■■',■
I "^
о, , ,
'■;■
v 4 1
11A
5 10 15 20 2S 30 S5
45
Рис. А. 14. Линии равного уровня, построенные с помощью функции contour,
с оцифровкой, нанесенной функцией clabel
Другие разновидности трехмерных графиков
Кроме функций surf и contour есть еще целый ряд функций с аналогичным син-
синтаксисом, позволяющих получить другие разновидности трехмерных графиков.
Ниже перечислены только некоторые из этих функций, наиболее полезные в ин-
инженерных и научных приложениях:
□ surfc(X, Y, Z) — комбинация функций surf и contour. Линии равного уровня
выводятся на нижней координатной плоскости;
□ mesh(X, Y. Z) — построение поверхности в виде сетки с окрашенными ребрами
и незакрашенными четырехугольными ячейками;
□ meshc(X, Y. Z) — комбинация функций mesh и contour. Линии равного уровня
выводятся на нижней координатной плоскости;
□ meshz(X. Y, Z) — то же, что mesh, но с краев построенной сетчатой поверхности
вниз спадает «занавес»;
Графика 549
□ waterfall (X, Y. Z) — то же, что mesh, ио ребра, разделяющие ячейки, проводят-
проводятся только вдоль оси х. В результате объемное тело выглядит «нарезанным на
ломтики»;
□ stem3(X, Y, Z) — вывод трехмерного графика в виде «стебельков», начинаю-
начинающихся при z = 0 в точках, задаваемых массивами X и Y. Высота «стебельков»
определяется массивом Z;
□ contourf(X. Y. Z) — то же, что contour, ио пространство между линиями равно-
равного уровня окрашено в различные цвета в зависимости от значений Z;
□ contour3(X. Y, Z) — то же, что contour, но линии равного уровня рисуются не в
одной плоскости, а при соответствующих значениях z-координаты;
□ pcolor(X, Y. Z) — строит двумерный график, представляющий собой сетку из
четырехугольных ячеек, координаты вершин которых задаются массивами X
и Y. Ячейки закрашены цветами, определяемыми значениями элементов мас-
массива Z. Тот же результат можно получить, если для поверхности, построенной
функцией surf, установить точку обзора точно сверху.
Настройка внешнего вида графиков
В большинстве случаев параметры оформления графиков, выбираемые по умол-
умолчанию, оказываются вполне приемлемыми. Однако иногда для повышения выра-
выразительности изображения возникает необходимость изменить тип и цвет линий,
нанести на график поясняющие надписи и т. п. В данном разделе кратко рас-
рассматриваются соответствующие средства MATLAB.
Настройка линий и точек
Соединение точек графика отрезками синего цвета — не единственный вариант
отображения. MATLAB позволяет управлять цветом графика, типом линии и
способом отображения точек данных. Для этого используется дополнительный
параметр команд pi ot, stem и т. п. Этот параметр представляет собой текстовую
строку ' Li neSpec', символы которой и указывают нужные режимы:
plot(x. у, 'LineSpec')
Список возможных символов и их значения приведены в табл. А.1.
Таблица А. 1. Символы управления линиями и точками графиков
Символ
Назначение
Управление цветом
b
с
9
к
Синий (по умолчанию) — Blue
Голубой — Cyan
Зеленый — Green
Черный — ЫасК
Продолжение
550
Приложение А. Основы работы с MATLAB
Таблица А.1 {продолжение)
Символ
m
г
w
У
Назначение
Фиолетовый — Magenta
Красный — Red
Белый — White
Желтый — Yellow
| Управление типом линии
-•
Непрерывная (по умолчанию)
Пунктирная, длинный штрих
Пунктирная, короткий штрих
Штрихпуиктирная
Управление маркерами точек данных
+
*
0
X
S
d
Р
h
V
А
<
>
Точка (но умолчанию)
Знак «плюс»
Звездочка
Кружок
Крестик
Квадрат — Square
Ромб — Diamond
Пятиконечная зиезда — Pentagram
Шестиконечная звезда — Hexagram
Треугольник острием вниз
Треугольник острием вверх
Треугольник острием влево
Треугольник острием вправо
Перечисленные в таблице символы можно комбинировать. К примеру, строка ' -. dr'
задаст вывод точек графика ромбиками (d), а соединяющих точки линий — штрих-
пунктиром (-.). И точки, и линии при этом будут красного цвета (г).
Функции оформления графиков
Только что рассмотренные параметры управления точками и линиями задаются
непосредственно при выводе графика функцией pi ot или одной из ей подобных.
Графика 551
Кроме того, существует еще целый ряд функций, которые вызываются уже после
построения, графика и меняют его внешний вид. Эти функции воздействуют
только на текущий график (то есть график в текущем графическим окне и, если
использовалась команда subplot, в текущей клетке этого окна). Ниже приведен
список наиболее важных из этих функций:
□ axis — настройка координатных осей. Вот некоторые способы использования
этой функции (обратите внимание на то, что не все перечисленные режимы
являются взаимоисключающими):
О axis([xmin xmax ymin ymax]) — настройка предельных значений осей для дву-
двумерного графика;
О axis([xmin xmax ymin ymax zmin zmax]) — настройка предельных значений
осей для трехмерного графика;
О axis auto — автоматический выбор пределов (этот режим установлен по
умолчанию);
О axis tight — предельные значения.осей в точности соответствуют диапазо-
диапазонам изменения данных;
О axis equal — для всех осей графика устанавливается одинаковый масштаб;
О axis image — то же, что комбинация axis equal и axis tight;
О axis square — делает длину осей одинаковой (а область графика — квадрат-
квадратной);
О axis normal — отменяет действие режимов axis square и axis equal;
О axis off — отключает отображение осей вместе с оцифровкой, подписями
и фоном графика;
О axis on — включает отображение осей, их оцифровки, подписей, а также
фона графика;
□ grid — включение (grid on) и выключение (grid off) отображения линий
сетки;
□ box — включение (box on) и выключение (box off) отображения обрамляющего
график прямоугольника или параллелепипеда;
□ legendCstringl', 'string2', 'string3', ...)—добавление аннотации («леген-
(«легенды») к графику. Каждая из строк-параметров задает аннотацию для одной из
выведенных на график зависимостей;
□ title('text') — добавление заголовка к графику;
□ xlabel ('text') — добавление подписи к оси х;
□ ylabel ('text') — добавление подписи к оси у;
□ zlabel ('text') — добавление подписи к оси ?,
□ text(x, у, 'string') или text(x. у, z, 'string') — размещение строки 'string'
в точке двумерного или трехмерного графика с указанными координатами;
□ xlim([xmin xmax]) — задание пределов по оси х;
□ ylim([ymin ymax]) — задание пределов по оси у;
□ zlim([zmin zmax]) — задание пределов по оси г.
552
Приложение А. Основы работы с MATLAB
В качестве примера повторим вывод графика, показанного ранее на рис. А.11,
штрихпунктирной линией. Кроме того, добавим сетку, подписи к осям, «леген-
«легенду» и заголовок. Результат показан на рис. А.15.
» х = -10:0.1:10: % значения координаты х
» у - sinc(x): % значения координаты у
» plot(x. у, '-.')
» grid on % добавляем сетку
» xlabei('x') % подпись оси х
» ylabeK 'sinc(x)') % подпись оси у
» legendC'sine function') % аннотация
» % заголовок графика
» title('Plot of function sinc(x)=sin(\pi x)/(\pi x)')
"A Figure No- 1
Ptef of runction *inc{jt)»a.in(*x)/<» x>
0.6
г"
Я 0.2
о
•о.г
-0.4,
•-•-'-у-]
I
I
)
I
Г'
I
Л I
,\ , , ,
........т- Г-
\ I
S
I
- - ■ sine function
!
-^ --------
1
1
1 Л Л
'. ' ^ 7
Рис. А.15. График с настроенными параметрами отображения линий,
подписями осей, «легендой» и заголовком
Обратите внимание на то, что последовательность символов \pi, использованная
в аргументе функции title, на рис. А.15 превратилась в греческую букву п. Ана-
Аналогичным образом при использовании функций title, xlabel, ylabel, legend и т. п.
можно получить и другие специальные символы. Дело в том, что MATLAB рас-
распознает в выводимых на график текстовых строках некоторые команды языка
ТеХ. Это команды вывода греческих букв (\alpha, \beta и т. д. для строчных букв
и \Gamma, \Delta и т. д. для прописных, не совпадающих по начертанию с англий-
английскими), вывода математических символов (\infty для со, \leq для <, \geq для >,
\рт для ± и т. п.), форматирования нижних и верхних индексов (соответственно
_{...} и *{...}), а также управления начертанием шрифта (\bf — полужирный, \1t —
Графика ' 553
курсив, \sl — наклонный, \rm — обычный). За более подробной информацией
о форматировании выводимого на график текста обратитесь к документации
MATLAB.
ЗАМЕЧАНИЕ
ТеХ — это непревзойденная по своим возможностям система подготовки текстов, содер-
содержащих математические формулы. ТеХ не является визуальной системой — это скорее
язык программирования. Чтобы продемонстрировать идею, приведем маленький при-
пример — вы набираете во входном файле, скажем, $\gamma=\sqrt{\alphaA2+\betaA2}$ и по-
получаете на печати у = ^[а2 + р2- Подумайте — может быть, это лучше, чем щелкать мышью
в Equation Editor? Подробнее узнать о ТеХ можно, например, из книги [16].
Одновременный вывод нескольких графиков
Вывести на экран несколько графиков одновременно можно по-разному — в раз-
разных графических окнах, в разных областях одного окна или же в общих осях ко-
координат. В зависимости от этого используются различные средства MATLAB.
Чтобы вывести несколько графиков в разных графических окнах, нужно создать
эти графические окна с помощью функции figure или команды меню File ►
New ► Figure главного окна MATLAB (в меню графических окон есть более ко-
короткий вариант — команда File ► New Figure). После создания нового окна оно
становится текущим, и последующий графический вывод направляется именно
в него.
ЗАМЕЧАНИЕ
Сделать конкретное графическое окно текущим можно, выведя его на передний план и за-
затем переключившись в командное окно MATLAB.
Приведенные ниже команды создадут два графика в разных окнах:
» plotCxl, yl)
» figure
» plot(x2. y2)
Для вывода нескольких графиков в разных областях одного окна используется
команда subplot, имеющая следующий синтаксис:
subplot(Rows, Cols, N)
В результате графическое окно будет разбито на клетки в виде матрицы, имею-
имеющей Rows строк и Cols столбцов, и N-я клетка (в отличие от нумерации элементов
в матрицах, нумерация клеток ведется по строкам) становится текущей.
Приведенные ниже команды создают четыре графика, располагая их в одном гра-
графическом окне в две строки и два столбца (рис. А.16):
» t = 0:0.01:10:
» subplotB, 2, 1)
» plot(t. sin(t))
» subplotB, 2, 2)
» plot(t. cos(t))
554
Приложение А. Основы работы с MATLAB
» subplotB, 2. 3)
» plot(t. t.*2+l)
» subplotB, 2. 4)
» plot(t. l./(t.*2+D)
i Figure No. 1
£fc Ed* y«w iw«* Iw*
[Q «id! * A
OS
0
\
\
/
/
/
/
\
\
\
\
\
10
Рис. А. 16. Результат использования команды subplot
Наконец, вывести несколько графиков в общих осях тоже можно разными спо-
способами. Во-первых, если параметр функции plot, задающий значения координа-
координаты у, является матрицей, то строятся отдельные графики для каждого столбца
матрицы, например:
» х = @:0.1:10)':
» plot(x. [sin(x) cos(x)])
Во-вторых, при вызове функции plot можно перечислить несколько пар значе-
значений х- и г/-координат:
plotCxl. yl, х2. у2, ...)
При этом для каждой пары (xi, yi) будет построен свой график. Поэтому тот же
результат, что и в предыдущем примере, можно получить и таким образом:
» plotCx. sin(x), x. cos(x))
В-третьих, можно использовать команду hold on, включающую режим сохране-
сохранения содержимого текущих координатных осей при выводе в них новых графи-
графиков. Тогда новые команды pi ot будут строить графики поверх имеющихся, не за-
затирая их. Для выключения этого режима используется команда hold off.
Перепишем наш пример еще раз, используя команды hold:
Графика 555
» plotCx. sin(x))
» hold on
» plotCx, cos(x))
» hold off
Дальнейшее использование графиков
Содержимое графического окна можно распечатать, используя следующие ко-
команды меню File: Page Setup, Print Setup, Print Preview и Print. Печать в MATLAB
выполняется так же, как в других Windows-приложениях, поэтому подробно
рассматривать этот процесс мы не будем.
Печатать графики непосредственно из MATLAB проходится редко, гораздо чаще
необходимо использовать их в документах, создаваемых, например, в Microsoft
Word. Для этого необходимо скопировать изображение в буфер обмена коман-
командой Edit ► Copy Figure меню графического окна.
Однако для получения желаемого результата необходимо настроить параметры
копирования с помощью команды Edit ► Copy Options меню графического окна.
После ее вызова откроется соответствующий раздел окна Preferences. В нем име-
имеется два трехпозиционных переключателя и один флажок. Переключатель Clip-
Clipboard format позволяет выбирать следующие варианты:
О Metafile (may lose information) — в буфер помещается векторный образ окна;
□ Preserve information (metafile if possible) — MATLAB выбирает растровый или
векторный вариант по своему усмотрению, в зависимости от сложности изо-
изображения;
□ Bitmap — в буфер помещается растровый образ окна.
Векторное изображение можно масштабировать без потери качества и редакти-
редактировать в соответствующих программах (CorelDRAW, Adobe Illustrator и т. п.).
При копировании растрового образа неизбежно происходит потеря информации,
однако прорисовка и печать растрового рисунка может оказаться быстрее, чем в
случае сложного векторного изображения. В большинстве случаев целесообраз-
целесообразно выбирать вариант Preserve information (metafile if possible).
Переключатель Figure background color управляет копированием фона графиче-
графического окна:
□ Use figure color — копируется фоновый прямоугольник того же цвета, что на
экране (по умолчанию — серый);
□ Force white background — копируется фоновый прямоугольник белого цвета;
□ transparent background — изображение копируется без фонового прямоуголь-
прямоугольника.
Наиболее целесообразный вариант — Transparent background.
Наконец, флажок Match figure screen size управляет размером копируемого изо-
изображения. Если флажок установлен, копируемое изображение будет иметь такие
же размеры, как на экране. Если флажок снят, размер копируемого изображения
определяется настройками, сделанными в окне Page Setup.
556 Приложение А. Основы работы с MATLAB
ЗАМЕЧАНИЕ
Помимо копирования в буфер обмена изображения могут выводиться на печать и записы-
записываться в файлы различных графических форматов с помощью команды print. Она имеет
большое количество дополнительных ключей, ознакомиться с назначением которых мож-
можно по документации MATLAB.
Дополнительные источники
информации
В этом приложении были представлены лишь основные приемы использования
MATLAB. Далее,- в приложении Б, будет приведен краткий обзор функций ба-
базовой библиотеки MATLAB, а в приложении В — список компонентов системы.
За дополнительной информацией следует обращаться к справочной системе,
документации и книгам о MATLAB, которых издано уже немало. Кроме того,
на сайте фирмы-производителя www.mathworks.com можно найти информацию
о последних версиях программных продуктов, документацию, а также коллек-
коллекцию М-файлов, разработанных пользователями MATLAB. Возможно, вам удаст-
удастся найти в этой коллекции что-нибудь полезное для решения стоящих перед
вами задач.
Форум по MATLAB (англоязычный, разумеется) в иерархии телеконферен-
телеконференций USENET имеет имя comp.soft-sys.matlab. Через Web он доступен по адресу
newsreader.mathworks.com.
Компания Softline (www.softline.ru) — официальный дилер фирмы Mathworks в
России — поддерживает сайт www.matlab.ru, на котором имеются информацион-
информационные материалы (на русском языке) по MATLAB и некоторым пакетам расшире-
расширения. Там же организован и форум отечественных пользователей MATLAB.
Приложение Б
Обзор функций
MATLAB
В данном приложении будет дан краткий обзор функций, входящих в базовую
библиотеку MATLAB. Этих функций слишком много, чтобы можно было при-
привести хотя бы краткое описание для каждой из них. Поэтому ниже приводится
лишь список тематических разделов с краткой их характеристикой. Для некото-
некоторых разделов перечислены также важнейшие функции. За более подробным
описанием следует обращаться к справочной системе и документации MATLAB.
Разделы перечислены в алфавитном порядке имен их каталогов, а не в порядке
значимости. Получить справку по конкретному разделу можно, набрав в команд-
командной строке следующий текст:
» help имя_раздела
В результате будет выведен список функций данного раздела с краткими ком-
комментариями по их назначению.
Audio
В данном разделе содержатся функции работы со звуковой картой компьютера.
Важнейшие из этих функций были рассмотрены в разделе «Получение данных
из внешних источников» главы 3.
Datafun
В этом разделе сосредоточены разнообразные функции анализа данных. Боль-
Большинство из них ориентировано на работу с векторным аргументом; матрицы об-
обрабатываются по столбцам. Вот список важнейших функций:
□ Базовые операции:
О max — вычисление наибольшего элемента и его индекса;
О mi n — вычисление наименьшего элемента и его индекса;
558 Приложение Б. Обзор функций MATLAB
О mean — среднее значение;
О std — оценка среднеквадратического отклонения;
О var — оценка дисперсии;
О sort — сортировка элементов по возрастанию;
О sortrows — сортировка строк матрицы по возрастанию;
О sum — сумма элементов;
О prod — произведение элементов;
О hist — расчет и вывод гистограммы;
О trapz — численное интегрирование методом трапеций;
О cumsum — расчет частичных сумм элементов (численное интегрирование
методом прямоугольников);
О cumprod — расчет частичных произведений элементов.
□ Конечные разности:
О diff — вычисление разностей между соседними элементами;
О gradient — аппроксимация градиента;
О del 2 — дискретный лапласиан.
□ Корреляция:
О corrcoef — коэффициент взаимной корреляции;.
О cov — ковариационная матрица;
О subspace — расчет угла между векторами.
□ Фильтрация и свертка:
О filter — одномерная дискретная фильтрация;
О filter2 — двумерная дискретная фильтрация;
О conv — свертка (умножение полиномов);
О conv2 — двумерная свертка;
О convn — многомерная свертка;
О deconv — обращение свертки (деление полиномов);
О detrend — удаление линейного тренда.
□ Преобразование Фурье:
О fft — одномерное прямое дискретное преобразование Фурье;
О fft2 — двумерное прямое дискретное преобразование Фурье;
О fftn — многомерное прямое днскретное преобразование Фурье;
О if ft — одномерное обратное дискретное преобразование Фурье:
О ifft2 — двумерное обратное днскретное преобразование Фурье;
О ifftn — многомерное обратное дискретное преобразование Фурье;
О fftshift — перестановка половин вектора пли квадрантов матрицы;
О ifftshift — перестановка, обратная по отношению к fftshift.
Bfun 559
Datatypes
В этом разделе сосредоточены средства поддержки типов данных MATLAB.
Demos
В данном разделе собраны демонстрационные примеры.
Elfun
Как явствует из названия раздела, в нем содержатся файлы, реализующие эле-
элементарные математические функции. В большинстве случаев эти функции
встроены в ядро системы, так что в М-файлах содержится только текст справки.
□ Тригонометрические функции:
О sin — синус;
О sinh — гиперболический синус;
О asin — арксинус;
О asinh — гиперболический арксинус;
О cos — косинус;
О cosh — гиперболический косинус;
О acos — арккосинус;
О acosh — гиперболический арккосинус;
О tan — тангенс;
О tanh — гиперболический тангенс;
О atan — арктангенс;
О atan2 — вычисление угловой координаты точки по паре ее декартовых ко-
координат;
О atanh — гиперболический арктангенс;
О sec — секанс;
О seen — гиперболический секанс;
О asec — арксеканс;
О asech — гиперболический арксеканс;
О esc — косеканс;
О csch — гиперболический косеканс;
О acsc — арккосеканс;
О acsch — гиперболический арккосеканс;
О cot — котангенс;
О coth — гиперболический котангенс;
560 Приложение Б. Обзор функций MATLAB
О acot — арккотангенс;
О acoth — гиперболический арккотангенс.
Q Экспоненциальные функции:
О ехр — экспонента;
О 1 од — натуральный логарифм;
О 1 одЮ — десятичный логарифм;
О 1 од2 — двоичный логарифм, а также выделение порядка и мантиссы числа;
О pow2 — функция 2Л, а также «сборка» числа из мантиссы и порядка;
О sqrt — квадратный корень;-
О nextpow2 — ближайшая «сверху» степень двойки.
□ Функции для работы с комплексными числами:
О abs — модуль;
О angle — аргумент (фаза) комплексного числа;
О compi ex — «сборка» комплексного числа из вещественной и мнимой частей;
О conj — комплексное сопряжение;
О imag — мнимая часть комплексного числа;
О real — вещественная часть комплексного числа;
О unwrap — устранение скачков фазы (подробнее см. раздел «Построение гра-
графиков фазочастотных характеристик» главы 2);
О isreal — проверка вещественности массива;
О cpixpair — сортировка чисел по комплексно-сопряженным парам.
Q Округление и остаток:
О fix — округление в сторону нуля;
О floor — округление вниз;
О ceil — округление вверх;
О round — округление к ближайшему целому числу;
О mod — взятие по модулю (остаток со знаком);
О геш — остаток от деления;
О sign — знаковая функция.
Elmat
В данном разделе собраны функции элементарных матричных операций.
Q Создание элементарных матриц:
О zeros — матрица, заполненная нулями;
О ones — матрица, заполненная единицами;
О eye — единичная матрица;
О repmat — дублирование матрицы «мозаикой»;
Elmat 561
О rand — генерация случайных чисел с равномерным распределением;
О randn — генерация случайных чисел с нормальным распределением;
О linspace — генерация арифметической прогрессии;
О logspace — генерация геометрической прогрессии;
О freqspace — генерация вектора частот для анализа частотных характери-
характеристик;
О meshgrid — генерация массивов координат для построения трехмерных гра-
графиков.
□ Информационные функции:
О size — размер массива;
О length — длина вектора;
О ndims — число размерностей массива;
О disp — вывод значения переменной;
О isempty — проверка на «пустоту»;
О isequal — проверка массивов на равенство;
О isnumeric — проверка, является ли массив числовым;
О islogical — проверка, является ли массив логическим;
О logical — преобразование числовых величин в логические.
□ Преобразования матриц:
О reshape — изменение размеров матрицы при сохранении числа элементов;
О diag — создание диагональных матриц и выделение вектора диагональных
элементов матрицы;
О blkdiag — создание блочно-диагональной матрицы;
О tril — выделение нижнего треугольного блока матрицы;
О triu — выделение верхнего треугольного блока матрицы;
О fliplr — зеркальное отражение матрицы относительно вертикальной оси;
О fl ipud — зеркальное отражение матрицы относительно горизонтальной оси;
О flipdim — зеркальное отражение многомерного массива относительно ука-
указанной размерности;
О rot90 — поворот матрицы на 90°;
О find — индексы ненулевых элементов;
О end — последний индекс вдоль данной размерности;
О sub2ind — преобразование набора индексов в линейный индекс;
О ind2sub — преобразование линейного индекса в набор индексов.
□ Специальные переменные и константы:
О ans — результат последней операции;
О eps — относительная точность вычислений с плавающей запятой;
О real max — максимально возможное число с плавающей запятой;
О real mi n — минимально возможное число с плавающей запятой;
562 Приложение Б. Обзор функций MATLAB
О pi — число я;
О 1, j — мнимая единица;
О inf — бесконечность;
О NaN — нечисловое значение (Not-a-Number);
О isnan — проверка на NaN;
О isinf — проверка на бесконечность значения;
О isfinite — проверка на конечность значения.
Funfun
В данном разделе собраны функции поиска минимумов и нулей функций, чис-
численного интегрирования, а также численного решения дифференциальных урав-
уравнений. Все эти операции требуют создания М-файла функции, с которой будет
вестись работа, поэтому данный раздел и получил такое имя — «Function func-
functions». Вот важнейшие функции этого раздела:
□ fzero — решение нелинейных уравнений;
□ fminsearch — многомерная нелинейная минимизация без ограничений;
□ fmi nbnd — скалярная нелинейная минимизация с ограничениями;
□ quad, quadl — численное интегрирование;
□ dbl quad — численное вычисление двойного интеграла;
□ ode45, ode23, odell3, ode23t, odel5s, ode23s, ode23tb — различные методы числен-
численного решения дифференциальных уравнений.
General
Данный раздел содержит функции общего назначения. Сюда относятся команды
работы со справочной системой, управления рабочей областью памяти, откры-
открытия и сохранения файлов, настройки пути поиска файлов, управления команд-
командным окном, средства вызова команд операционной системы, а также отладочные
средства.
Graph2d
В данном разделе содержатся средства двумерной графики. Важнейшие из них
были рассмотрены в разделе «Двумерная графика» приложения А.
Graph3d
В данном разделе содержатся средства трехмерной графики. Важнейшие из них
были рассмотрены в разделе «Трехмерная графика» приложения А.
г Lang 563
Graphics
В этом разделе собраны средства поддержки дескрипторпой графики (Handle
Graphics®) MATLAB. Вкратце се идею можно описать следующим образом. Все
графические функции, такие как figure, plot и прочие, могут возвращать резуль-
тат — число или несколько чисел, являющихся дескрипторами (handle) создап-
ных функцией графических объектов — графических окон, координатных осей,
графиков и т. д. Эти дескрипторы используются для получения программного
доступа к графическим объектам и их свойствам. Более подробное описание де-
скрипторной графики выходит за рамки тематики данной книги. За необходи-
необходимой информацией обратитесь к справочной системе MATLAB и книге «Using
MATLAB Graphics», поставляемой в составе документации.
lofun
К данной категории относятся средства файлового ввода/вывода. Важнейшие
функции работы с файлами были рассмотрены в разделе «Ввод и вывод данных»
приложения А, а работа со звуковыми файлами подробно описана в разделе
«Получение данных из внешних источников» главы 3.
Lang
В данном разделе собраны конструкции языка программирования MATLAB. Ос-
Основные элементы языка были описаны в разделе «Программирование» приложе-
приложения А. Из того, что не вошло в этот раздел, отметим следующее:
□ try и catch — операторы для обработки исключительных ситуаций (exception);
□ eval('S') — вычисление MATLAB-выражепия, заданного в виде строкового
входного параметра 'S';
□ fevaH'F', xl, х2, ...) —вычисление функции, имя которой задано строковым
входным параметром 'F', с передачей ей входных параметров xl, х2 и т, д.;
□ global — определение глобальной переменной;
□ persistent — определение локальной переменной функции, значение которой
сохраняется при следующем вызове функции;
□ exist — проверка существования переменной или функции;
□ isglobal — проверка глобальности переменной;
□ disp — вывод значения переменной в командное окно MATLAB;
□ fprintf — запись форматированных данных в поток вывода;
□ sprintf — запись форматированных данных в строку;
□ input — запрос на ввод значения переменной пользователем;
□ pause — приостановка работы программы.
564 Приложение Б. Обзор функций MATLAB
Matfun
В данном разделе собраны матричные функции линейной алгебры. Отметим лишь
важнейшие из них:
□ norm — норма матрицы или вектора;
□ rank — ранг матрицы;
□ det — определитель матрицы;
□ trace — след матрицы (сумма диагональных элементов);
□ \ и / — решение систем линейных уравнений (матричное деление);
□ inv — обращение матрицы;
□ eig — расчет собственных чисел и собственных векторов матрицы;
□ svd — разложение по сингулярным числам;
□ poly — характеристический полином матрицы;
□ ехрш — матричная экспонента;
□ login — матричный логарифм;
□ sqrtm — матричный квадратный корень.
Ops
Данный раздел посвящен операторам и символам, имеющим для MATLAB спе-
специальное значение. Поскольку поддержка этих базовых возможностей встроена
в ядро системы, в каталоге Ops в основном содержится лишь справочная инфор-
информация. Исключением, в частности, являются функции работы с битовыми пред-
представлениями неотрицательных целых чисел:
□ bitand — побитовое «И»;
□ bitemp — побитовое «НЕ»;
□ bitor — побитовое «ИЛИ»;
□ bitmax — максимальное целое число, которое можно точно представить в ис-
используемом MATLAB формате с плавающей запятой. Для платформы PC это
значение равно 253 - 1;
□ bitxor — побитовое «исключающее ИЛИ»;
□ bitset — установка бита с заданным номером в заданное значение;
□ bitget — считывание значения бита с заданным номером;
□ bitshift — побитовый сдвиг на заданное число разрядов.
Polyfun
В данном разделе собраны функции интерполяции и работы с полиномами. Пе-
Перечислим лишь наиболее важные для задач обработки сигналов функции работы
с полиномами:
Specfun , 565
□ roots — поиск корней полинома;
□ poly — расчет коэффициентов полинома по его корням;
□ polyval — вычисление значения полинома в заданной точке;
□ polyvalm — вычисление значения полинома от матричного аргумента;
□ residue — представление дробно-рациональной функции в виде суммы про-
простых дробей (эта функция была рассмотрена в разделе «Преобразование спо-
способов описания линейных цепей» главы 2);
□ polyfit — полиномиальная аппроксимация данных;
□ polyder — дифференцирование полиномоп, их произведений и отношений;
□ polyint — интегрирование полиномов;
□ conv — умножение полиномов;
□ deconv — деление полиномов.
Sparfun
В некоторых предметных областях приходится иметь дело с матрицами очень
большого размера, у которых отлична от нуля лишь малая часть элементов. Та-
Такие матрицы называются разреженными (sparse). На хранение нулевых элемен-
элементов и выполнение математических операций с ними впустую тратится много ре-
ресурсов компьютера. В данном разделе собраны функции, позволяющие хранить
матрицы и выполнять матричные операции непосредственно в разреженном
виде, то есть хранить только значения и индексы ненулевых элементов матриц.
В задачах обработки сигналов такие матрицы практически не встречаются, по-
поэтому конкретные функции данного раздела здесь не перечисляются.
Specfun
Как явствует из названия, в этом разделе находятся специальные математиче-
математические функции. Вот важнейшие из них:
□ airy — функции Эйри;
□ bessel j, bessely, besselh, besseli, besselk — функции Бесселя;
□ beta, betainc, betaln — бета-функция, неполная бета-функция и логарифм бе-
бета-функции;
□ el I i p j — эллиптические функции Якоби;
□ ellipke — полный эллиптический интеграл;
□ erf — функция ошибок;
□ erfc — дополнительная функция ошибок;
□ erfcx — масштабированная дополнительная функция ошибок;
□ erfinv — обратная функция ошибок;
□ expint — интегральная экспонента;
□ gamma, gammainc, gammaln — гамма-функция, неполная гамма-функция и лога-
логарифм гамма-функции;
566 Приложение Б. Обзор функций MATLAB
□ 1 egendre — присоединенная функция Лежандра;
□ cross — векторное произведение;
□ dot — скалярное произведение векторов;
□ factor — разложение натурального числа на простые множители;
□ isprime — проверка, является ли натуральное число простым;
□ primes — генерация простых чисел;
□ gcd — наибольший общий делитель;
□ 1 cm — наименьшее общее кратное;
□ rat — рациональная аппроксимация;
□ factorial — факториал.
Specgraph
В данном разделе собраны специализированные графические функции. Сюда от-
относятся разнообразные диаграммы (area, bar, barh, pie и др.), рассмотренные
нами ранее функции stem, stairs, contour и contourf, а также многие другие. Осо-
Особый интерес представляют функции, имена которых начинаются с букв ez (от
«easy» — «легкий») — ezplot, ezpolar, ezcontour, ezcontourf, ezgraph3, ezmesh, ezmeshc,
ezp1ot3, ezsurf и ezsurfc. Они позволяют строить графики соответствующих ти-
типов (см. раздел «Графика» приложения А), задавая не массивы даных, а строки,
в которых записаны формулы для вычислений. Также в данном разделе имеются
функции чтения и записи графических файлов, трехмерной визуализации и ани-
анимации.
Strfun
К данному разделу относятся функции работы со строками (см. раздел «Стро-
«Строки» приложения А). Важнейшими из них являются следующие:
□ Ы anks — создание строки, заполненной пробелами;
□ deblank — удаление концевых пробелов из строки;
□ strcat — соединение строк;
□ strcmp — сравнение строк;
□ strncmp — сравнение первых N символов строк;
□ strcmpi — сравнение строк без учета регистра символов;
□ strncmpi — сравнение первых N символов строк без учета регистра символов;
□ findstr — поиск одной строки внутри другой;
□ upper — преобразование строки к верхнему регистру;
□ 1 ower — преобразование строки к нижнему регистру;
□ num2str — преобразование числа в строку;
□ int2str — преобразование целого числа в строку;
Winfun 567
□ str2doubl e — преобразование строки в число в формате doubl e;
□ str2num — преобразолание матрицы строк в числовой массив;
□ sprintf — запись форматированных данных в строку;
□ hex2dec — преобразование шестнадцатеричной строки в целое число;
□ dec2hex — преобразование целого числа в шестнадцатеричную строку;
□ bin2dec — преобразование двоичной строки в целое число;
□ dec2bin — преобразование целого числа в двоичную строку.
Timefun
В данном разделе собраны функции работы с датами и временем. Важнейшими
из них являются следующие:
□ now — текущие дата и время в виде числа;
□ date — текущая дата;
□ el ock — текущие дата и время в виде вектора;
□ tic — запуск таймера;
□ toe — остановка таймера;
□ pause — приостановка работы программы на заданное время.
Uitools
MATLAB позволяет создавать программы, имеющие графический пользова-
пользовательский интерфейс. В данном разделе библиотеки собраны средства, обеспечи-
обеспечивающие соответствующие функции. Вопросы создания пользовательского интер-
интерфейса выходят далеко за рамки тематики данной книги, скажем лишь, что запуск
конструктора форм производится функцией guide. За дополнительной информа-
информацией обратитесь к справочной системе и документации MATLAB.
Verctrl
Функции данного раздела обеспечивают взаимодействие MATLAB с системами
контроля версий файлов (version control system, VCS).
Winfun
В данном разделе собраны функции взаимодействия MATLAB с операционной
системой Windows через интерфейсы DDE и ActiveX. Работу с ActiveX демон-
демонстрируют два примера: mwsamp (создаиие элемента управления ActiveX) и sampev
(создание обработчика события для сервера ActiveX; эта функция используется
примером mwsamp).
Приложение В
Компоненты
MATLAB
MATLAB — сложная система, и она постоянно развивается, приобретая все но-
новые возможности. Главная сила MATLAB — это многочисленные пакеты расши-
расширения, ориентированные на решение задач в различных предметных областях.
В данном приложении перечислены компоненты MATLAB и приведены их
краткие описания.
Набор поставляемых фирмой Math Works компонентов постоянно пополняется.
Приводимый ниже список показывает состояние на январь 2002 г. Разделение
компонентов на категории соответствует предлагаемому фирмой MathWorks.
MATLAB
Помимо собственно ядра MATLAB в состав системы входит целый ряд компо-
компонентов, предоставляющих дополнительные возможности:
□ MATLAB — ядро системы MATLAB («язык технических вычислений», как
называют свой продукт разработчики);
□ MATLAB Compiler — средство преобразования М-файлов в программный код
на языке C/C++;
□ MATLAB C/C++ Graphics Library — библиотека графических функций
MATLAB для использования в программах на C/C++;
□ MATLAB C/C++ Math Library — библиотека математических функций
MATLAB для использования в программах на C/C++;
□ MATLAB Excel Builder — средство создания модулей расширения для Mic-
Microsoft Excel;
□ MATLAB Report Generator — средство создания документации для
MATLAB-приложений и данных;
□ MATLAB Runtime Server — средство преобразования MATLAB-приложе-
MATLAB-приложений в автономные программные продукты;
Пакеты расширения MATLAB 569
□ MATLAB Web Server — средство разработки и распространения MATLAB-
приложений, запускаемых через Интернет;
□ MatrixVB — интерфейс для вызова функций MATLAB из Microsoft Visual
Basic.
Пакеты расширения MATLAB
Пакеты расширения MATLAB (toolbox) представляют собой наборы функций,
объединенные общей тематикой и ориентированные на решение задач конкрет-
конкретной предметной области.
Математика и анализ
□ Curve Fitting Toolbox — функции аппроксимации;
□ Optimization Toolbox — функции, реализующие разнообразные численные
методы оптимизации, в том числе при наличии линейных и нелинейных огра-
ограничений [13];
□ Statistics Toolbox — функции статистического моделирования и проверки
гипотез [13];
□ Neural Network Toolbox — функции моделирования и анализа нейронных
сетей [13];
□ Symbolic/Extended Symbolic Math Toolbox — реализация аналитических
j расчетов с использованием ядра программы Maple [13];
1 □ Partial Differential Equation Toolbox — решение дифференциальных уравне-
I иий в частных производных;
| □ PLS_Toolbox — анализ и моделирование временной динамики химических
I процессов методом частичных наименьших квадратов (Partial Least Squares,
j PLS);
□ Mapping Toolbox — пакет расширения для визуализации географических
карт и работы с другой географической информацией;
□ Spline Toolbox — функции кусочно-полиномиальной (сплайновой) аппрок-
аппроксимации и интерполяции;
□ Structural Dynamics Toolbox — анализ колебаний и вибраций в механиче-
механических системах методом конечных элементов;
□ Virtual Reality Toolbox — средство создания виртуальных трехмерных моде-
моделей, управляемых из среды MATLAB или Simulink, на основе языка VRML.
Экспорт и импорт данных
□ Data Acquisition Toolbox — средство взаимодействия с оборудованием ана-
аналогового и цифрового ввода/вывода данных;
□ Instrument Control Toolbox — средство взаимодействия MATLAB с совре-
современной измерительной аппаратурой через протоколы GPIB и VISA;
570 Приложение В. Компоненты MATLAB
□ Database Toolbox — средство обмена данными с реляционными базами данных;
□ Excel Link — средство взаимодействия MATLAB с Microsoft Excel;
□ Portable Graph Object — средство, позволяющее экспортировать графики
MATLAB в Microsoft Word в виде объектов ActiveX, обеспечивающих воз-
возможность настройки параметров графика.
Обработка сигналов и изображений
□ Signal Processing Toolbox — функции анализа и обработки сигналов;
□ Image Processing Toolbox — функции анализа и обработки изображений;
□ Communications Toolbox — функции анализа и моделирования систем связи;
□ Frequency Domain System Identification Toolbox — функции идентификации
линейных динамических систем в частотной области [14];
□ System Identification Toolbox — функции идентификации линейных динами-
динамических систем, то есть создания их математических моделей на основе изме-
измеренных входных и выходных сигналов [14];
□ Wavelet Toolbox — функции анализа, очистки от шума и компрессии сигна-
сигналов и изображений с использованием вейвлет-алгоритмов;
□ Filter Design Toolbox — функции анализа и синтеза фильтров, в том числе
с учетом эффектов квантования и арифметики с фиксированной запятой;
□ Motorola DSP Developer's Kit — функции моделирования и тестирования
кода для цифровых сигнальных процессоров серий 56300 и 56600 фирмы
Motorola;
□ Developer's Kit for Texas Instruments™ DSP — функции моделирования
и тестирования кода для цифровых сигнальных процессоров фирмы Texas
Instruments.
Разработка систем управления
□ Control System Toolbox — функции моделирования и анализа систем автома-
автоматического управления (систем с обратной связью) [14];
□ Fuzzy Logic Toolbox — функции моделирования и анализа систем с нечеткой
логикой [13];
□ Robust Control Toolbox — функции моделирования и анализа систем управ-
управления, устойчивых по отношению к случайным воздействиям;
□ u-Analysis and Synthesis Toolbox — функции моделирования и анализа сис-
систем управления со многими переменными при наличии неопределенности
модели;
□ LMI Control Toolbox — функции моделирования и анализа устойчивых сис-
систем управления с использованием методов оптимизации выпуклых функций;
□ Model Predictive Control Toolbox — функции моделирования и анализа сис-
систем управления с большим числом входных и выходных параметров при на-
наличии ограничений;
Simulink 571
□ Polynomial Toolbox — функции, реализующие современные полиномиальные
методы применительно к системам управления;
□ QFT Frequency Domain Control Design Toolbox — функции моделирования
и анализа устойчивых систем управления в частотной области с использова-
использованием теории количественных обратных связей (Quantitative Feedback Theory).
Финансовое моделирование и анализ
□ Financial Toolbox — функции для моделирования финансовых данных и раз-
разработки алгоритмов финансового анализа;
□ Financial Time Series Toolbox — функции для анализа финансовых данных
методом временных рядов;
□ GARCH Toolbox — функции анализа изменчивости финансовых рынков с ис-
использованием одномерных GARCH-моделей;
□ Financial Derivatives Toolbox — функции анализа и моделирования процент-
процентных ставок и рисков;
□ Datafeed Toolbox — средство получения финансовых данных от поставщиков
информации в реальном времени.
Simulink
С технической точки зрения Simulink® является расширением MATLAB, од-
однако он предоставляет столько новых возможностей, что его следует рассмат-
рассматривать как отдельный программный продукт. Simulink — это графическая среда
моделирования аналоговых и дискретных систем. Моделирование производится
путем перетаскивания блоков из окон библиотек в окно создаваемой модели и
настройки связей между ними. Большое число имеющихся библиотек позво-
позволяет моделировать самые разнообразные электрические, механические, гидрав-
гидравлические и другие системы. После создания модели можно запустить процесс
моделирования. Simulink создаст систему дифференциальных уравнений, опи-
описывающих модель, и начнет выполнять ее решение численным методом. В каче-
качестве примера на рис. В. 1 показана модель системы подавления шума с помощью
адаптивного фильтра (это один из демонстрационных примеров набора блоков
DSP Blockset). Кроме окна модели на рисунке видны окна трехканального ос-
осциллографа, анализатора спектра и графика импульсной характеристики фильтра.
В процессе моделирования графики постоянно обновляются. Подробнее о систе-
системе Simulink можно прочитать в книгах [13, 15].
Simulink в настоящее время представляет собой весьма сложную систему, со-
'■ стоящую из нескольких отдельно устанавливаемых компонентов:
□ Simulink — ядро системы Simulink, среда моделирования систем непрерывно-
непрерывного и дискретного времени;
\ □ Simulink Performance Tools — средства, упрощающие работу с большими Simu-
\ link-моделями и позволяющие выполнять их оптимизацию;
i
572
Приложение В. Компоненты MATLAB
\Л imtdemo/Fiftei
■>;;.;.
•-.'■':■. А
* '■•'■ ■
■■ -; л - ♦ .
■■'Г «Л:"«й
Тар*
^ .-*
Г* :
.:....'.. ,'j
: /
' 1 \
'. * i
'■ 1 '.
! ' "' ■/
: ■;' \ , *
: ■' *"' ■
|
:
■"'*>:■■
-J.
■■■■
'■'
i \
; У Т
; \ ■
'■■ V
■ \
: \
" \
: \
й 5 0
т\
Рис. В.1. Simulink-модель и окна графиков, динамически обновляемых
в процессе моделирования
□ Stateflow® — средство моделирования систем, управляемых событиями [14];
□ Stateflow Coder — средство генерации С-кода на основе диаграмм Stateflow;
□ Real-Time Windows Target — среда моделирования, обеспечивающая выпол-
выполнение моделей Simulink и Stateflow на персональном компьютере в реальном
времени (с частотой дискретизации до 10 кГц);
□ Real-Time Workshop® — средство генерации С-кода на основе Simulink-мо-
делей [14];
□ Real-Time Workshop Embedded Coder — средство генерации высококачест-
высококачественного исходного кода для встраиваемых систем;
□ Real-Time Workshop Ada Coder — средство генерации кода Ada 95 и Ada 83
на основе Simulink-моделей;
□ хРС Target — средство быстрого прототипирования приложений реального
времени, использующих стандартные аппаратные средства персональных ком-
компьютеров;
Наборы блоков Simulink 573
□ хРС Target Embedded Option — средство создания и распространения при-
приложений реального времени, использующих стандартные аппаратные средст-
средства персональных компьютеров;
□ Simulink Report Generator — средство создания документации для моделей
Simulink и Stateflow;
□ Requirements Management Interface — средство связывания набора формаль-
формальных технических требований с моделями Simulink, М-файлами и диаграмма-
диаграммами Stateflow;
□ SimMechanics — средства моделирования механических систем.
Наборы блоков Simulink
Наборы блоков Simulink (blockset) представляют собой тематические библиоте-
библиотеки, ориентированные на конкретные предметные области:
□ CDMA Reference Blockset — блоки для моделирования систем мобильной
телефонии IS-95A;
□ Communications Blockset — блоки для моделирования систем связи [14];
□ Dials & Gauges Blockset — набор графических блоков измерительных прибо-
приборов для отображения сигналов и параметров моделирования;
□ DSP Blockset — блоки для моделирования систем цифровой обработки сиг-
сигналов;
□ Fixed-Point Blockset — блоки для моделирования арифметики с фиксиро-
фиксированной запятой;
□ Nonlinear Control Design Blockset — блоки для моделирования нелинейных
систем управления [14];
□ Power System Blockset — блоки для моделирования энергетических сис-
систем [14].
Приложение Г
Программа SPTool
Программа SPTool (Signal Processing Tool) предоставляет в распоряжение поль-
пользователя графическую среду для просмотра графиков сигналов и их спектров,
расчета и анализа фильтров, а также фильтрации сигналов. Перечисленные дей-
действия относятся к тематике разных глав дайной книги, поэтому описание про-
программы SPTool размещено в приложении.
Для запуска программы SPTool необходимо набрать ее имя в командной строке
MATLAB:
» sptool
Появится основное окно программы, показанное на рис. ГЛ.
J SPIool itailup ipt
m Ed* Window
Siena).
chirp [vector]
train [vector]
Нф
d
. Filtet*
PZIp (imported]
FIRbp [design]
zl
-'* - ■ - %■ ч.
chiipse [auto]
Uainse Mo]
d
View
Рис. Г.1. Программа SPTool — главное окно
В трех списках этого окна перечислены загруженные в программу SPTool сигна-
сигналы (Signals), фильтры (Filters) и спектры (Spectra). Расположенные под списка-
списками кнопки позволяют выполнять различные операции, большинство из которых
мы рассмотрим далее.
Загрузка сигнала
575
Типичный набор действий, выполняемых с помощью программы SPTool, вклю-
включает в себя следующие операции:
□ загрузка сигнала;
□ просмотр графика сигнала;
□ спектральный анализ сигнала;
О расчет фильтра;
□ фильтрация сигнала.
Далее мы кратко рассмотрим выполнение всех перечисленных процедур.
Загрузка сигнала
Для загрузки сигнала в меню File главного окна программы SPTool необходимо
выбрать команду Import. Появится окно Import to SPTool, показанное на рис. Г.2.
Sour»
С FtamOtA
>, ■ ,Г v
I—Wwkipes*
■ impottAi: j Signal
JgaussT
Рис. Г.2. Программа SPTool — окно импорта данных
Переключатель Source позволяет указать место хранения загружаемого сигна-
сигнала — рабочую область MATLAB (From Workspace) или МАТ-файл (From Disk).
Во втором случае становится доступным поле ввода MAT-file Name, в которое
нужно ввести вручную или с помощью кнопки Browse имя нужного МАТ-файла.
В списке Workspace Contents перечислены переменные, имеющиеся в рабочей па-
памяти MATLAB в данный момент. Если в качестве источника был выбран МАТ-
файл, этот список будет называться File Contents и перечислять переменные, со-
сохраненные в выбранном файле.
В раскрывающемся списке Import As выберите вариант Signal. Остальные два ва-
варианта, Filter и Spectrum, позволяют импортировать описания фильтров и уже
рассчитанных спектров для просмотра и анализа.
576
Приложение Г. Программа SPTool
Выберите в списке переменную, содержащую отсчеты загружаемого сигнала,
и щелкните на кнопке -->, расположенной рядом с полем ввода Data. Можно
также вручную ввести в это поле идентификатор переменной.
В поле ввода Sampling Frequency по умолчанию находится значение 1. Его можно
отредактировать вручную, а можно импортировать, введя идентификатор пере-
переменной или выбрав его в списке и щелкнув на нижней кнопке -->.
Наконец, в поле ввода Name можно отредактировать имя, под которым данный
сигнал будет фигурировать в программе SPTool. Сделав это, щелкните на кноп-
кнопке ОК. Импортированный сигнал появится в списке Signals основного окна про-
программы (см. рис. Г.1).
Просмотр графика сигнала
Для просмотра графика сигнала выберите его в списке Signals (см. рис. Г.1) и
щелкните на кнопке View, расположенной под этим списком. Появится окно Sig-
Signal Browser, показанное на рис. Г.З.
■A Signal Biimsei
File
' 4-! U
gauss A001x1 real Fs-1000)
0Д
Time
a. an
Рис. Г.З. Программа SPTool — окно просмотра сигналов
В данном окне выводятся два графика. Нижний, с надписью Раппег, показывает
панораму всего сигнала. Верхний график первоначально тоже отображает весь
сигнал, но масштаб отображения можно увеличить, и тогда верхний график бу-
будет показывать лишь фрагмент сигнала, а положение этого фрагмента на общей
панораме демонстрируется с помощью прямоугольника на нижнем графике. Этот
прямоугольник можно перетаскивать мышью, меняя тем самым участок обзора.
Спектральный анализ сигнала
577
Кнопки панели инструментов окна Signal Browser позволяют распечатывать гра-
график сигнала, воспроизводить сигнал с помощью звуковой карты компьютера,
управлять масштабом отображения, выбирать нужный канал в случае многока-
многоканального сигнала и задавать нужный режим отображения маркеров.
На график можно нанести два маркера, позволяющие производить над сигналом
количественные измерения. Маркеры перетаскиваются с помощью мыши, а ин-
информация о помеченных ими отсчетах сигнала выводится в нижней части окна.
Можно экспортировать эту информацию в рабочую область памяти MATLAB в
виде структуры — для этого служит команда Export меню Markers.
Спектральный анализ сигнала
Для анализа спектра сигнала, загруженного в программу SPTool, выберите нуж-
нужный сигнал в списке Signals главного окна программы (см. рис. Г.1) и щелкните
на кнопке Create, расположенной под списком Spectra. Появится окно Spectrum
Viewer, показанное на рис. Г.4.
] riwtt hom
° d
-50
100
150
•win
л
■A
/ \
I
i
I
PSD
I
I
i
i
I
0 SO 100 150 200 250 300 3S0 490 450 500
Frequency
К -136.8918
Рис. Г.4. Программа SPTool — окно спектрального анализа
В левой части окна выбирается метод спектрального анализа и настраиваются
его параметры. За более подробной информацией о сущности различных мето-
методов и имеющихся у них параметрах обратитесь к материалу главы 5.
Раскрывающийся список, в котором первоначально выведена строка Inherit from,
позволяет скопировать полный набор настроек анализатора спектра из другого
расчета, представленного в списке Spectra основного окна программы.
Произведя настройку параметров анализа, щелкните на кнопке Apply. Будет рас-
рассчитана оценка спектра сигнала и выведен соответствующий график. Кнопки
578
Приложение Г. Программа SPTool
панели инструментов позволяют выполнять те же операции, что были перечисле-
перечислены выше применительно к просмотру графиков сигналов. При просмотре спек-
спектра также возможно использование маркеров.
Расчет фильтра
Для расчета дискретного фильтра щелкните на кнопке New Design, расположен-
расположенной под списком Filters в главном окне программы SPTool (см. рис. Г.1). Можно
также изменить параметры уже рассчитанного фильтра, выбрав его в списке
Filters и щелкнув на кнопке Edit Design. В любом из перечисленных случаев по-
появится окно Filter Designer, показанное на рис. Г.5.
fit )&dm Htfe
Filer
Sanding Fieguanc7 A^ga-em
Specifications
Г Minimum Ode
ыр?
F*f J125
Г" Aulo Design
I
10
Frequency Response
■v-;--
i J-:±T±-;Th-J
•40
0 IOC- 200
Frequency
500
Pansand-
Actual Rs 1315
Рис. Г.5. Программа SPTool — окно расчета фильтров
В раскрывающемся списке Algorithm выбирается метод расчета, а в разделе Spe-
Specifications задаются параметры синтезируемого фильтра. За более подробной ин-
информацией о методах синтеза дискретных фильтров обратитесь к материалу гла-
главы 6.
Выбрав метод расчета и задав параметры фильтра, щелкните на кнопке Apply для
выполнения синтеза. В центре окна будет выведен график АЧХ получившегося
фильтра, а в разделе Measurements показаны его параметры.
Кнопки панели инструментов позволяют управлять масштабом отображения
графика. Кроме того, можно вывести график АЧХ в полосе пропускания круп-
крупным планом, а также наложить на АЧХ график одного из спектров, перечислен-
перечисленных в списке Spectra основного окна программы.
Просмотр характеристик фильтра
579
Возможности программы SPTool по синтезу фильтров существенно ограничены
по сравнению с программой FDATool, описанной в главе 6. Единственная воз-
возможность, имеющаяся в SPTool и отсутствующая в FDATool, — это прямое ре-
редактирование расположения нулей и полюсов фильтра. Для такого редактирова-
редактирования выберите в списке Algorithm последнюю строку — Pole/Zero Editor. Окно Filter
Designer примет вид, показанный на рис. Г.6.
Рис. Г.6. Программа SPTool — редактирование расположения нулей и полюсов фильтра
В этом режиме редактирования фильтра можно перемещать нули и полюсы мы-
мышью, добавлять и удалять их, автоматически формировать из них комплексно-
сопряженные пары.
ЗАМЕЧАНИЕ
Поскольку в окне Filter Designer при редактировании нулей и полюсов не выводится гра-
график АЧХ фильтра, при использовании данного режима следует одновременно с окном
Filter Designer открыть и рассматриваемое далее окно Filter Viewer. При редактировании
фильтра в окне Filter Designer его характеристики, отображаемые в окне Filter Viewer, бу-
будут синхронно обновляться. Вообще окна программы SPTool не являются модальными, то
есть можно открыть любое их количество и свободно переключаться между ними.
Просмотр характеристик фильтра
Для просмотра характеристик фильтра, загруженного в программу SPTool, вы-
выберите его в списке Filters основного окна программы (см. рис. Г.1) и щелкните
580
Приложение Г. Программа SPTool
на кнопке View, расположенной под этим списком. Появится окно Filter Viewer,
показанное на рис. Г.7.
ftTtao
(PHt ,
1 degrees
3E ♦
las'
P anptoflewenw'
P Stepflwpon»
$«*,- <
< flrew
Rang*
-
Help
N4 4» j
J
J
1
2
1
°<
0
) 100
p
i N
100
.
,. J
M«lu*1 «■)
Magmtiide
200 300
Frequency
hese (degree.
Л P J .N
200 300
Frequency
_ ч ;.o
a
"■ A ~
400
.-: ,n
400
■
M«
500
j'
500
«ker: «
f
•io
0
0 гк
-05
0
| - Л5 ^
■
Zeroi & Poles
t * )■
-2 'o" 2
Real
Impulse Response
о oi о сг о.оз
Tune
l»4^ l>* ' "•
0 01 0 02 0 03
Tune
«lit 1 3529349
Рис. Г.7. Программа SPTool — просмотр характеристик фильтра
В левой части окна Filter Viewer расположена группа флажков Plots для выбора
состава отображаемых графиков. В разделе Frequency Axis можно выбрать час-
частотный диапазон для просмотра характеристик и задать тип шкалы частот — ли-
линейный или логарифмический.
Кнопки панели инструментов позволяют управлять режимом отображения и вы-
выводом маркеров для текущего графика, оси которого выделяются красным цве-
цветом. Информация о маркерах, как обычно, выводится в нижней части окна.
Фильтрация сигнала
Для пропускания сигнала через фильтр необходимо выбрать сигнал и фильтр
соответственно в списках Signals и Filters основного окна программы (см.
рис. Г.1), а затем щелкнуть на кнопке Apply, расположенной под списком Filters.
Появится окно Apply Filter, показанное на рис. Г.8.
Единственным доступным полем ввода в этом окне является поле Output Signal,
в котором нужно задать имя для выходного сигнала. В раскрывающемся списке
Algorithm можно выбрать функцию MATLAB для осуществления фильтрации —
filter, filtfilt или fftfilt (см. главу 4). Выполнив эти действия, щелкните на
кнопке ОК. Будет рассчитан выходной сигнал, который появится под указанным
именем в списке Signals основного окна программы.
Фильтрация сигнала
581
"^
Siuss_i,iie,«j
Cane* j
OK
Рис. Г.8. Программа SPTool — окно применения фильтра
Просмотреть график выходного сигнала и выполнить анализ его спектра можно
описанными ранее способами. Для одновременного просмотра графиков входно-
входного и выходного сигналов нужно выбрать их оба в списке Signals основного окна
программы (для этого при щелчке на выбираемом сигнале необходимо, как это
принято в Windows, нажать клавишу Ctrl) и щелкнуть на кнопке View. В открыв-
открывшемся окне Signal Browser будут показаны графики обоих выбранных сигналов
(рис. Г.9).
Д /W /ft -'Л ;
Рис. Г.9. Программа SPTool — одновременный просмотр графиков входного и выходного
сигналов фильтра
ЗАМЕЧАНИЕ
Аналогичным образом можно просматривать несколько спектров или характеристики не-
нескольких фильтров одновременно.
582
Приложение Г. Программа SPTool
Сохранение результатов работы
Сеанс работы с программой SPTool можно сохранить с помощью команды Save
Session или Save Session As из меню File основного окна программы. Файлы сеан-
сеансов имеют расширение spt. Загрузить сохраненный сеанс можно командой Open
Session того же меню File.
Кроме того, можно экспортировать сигналы, фильтры и спектры в виде структур
данных. Для этого используется команда Export из меню File основного окна про-
программы SPTool. После выбора данной команды появится окно Export from SPTool,
показанное на рис. Г. 10.
} Export hom SPTool
<
$
ЕЦМ<Ш..| и.ппя.и,,, , ■
Signal chizp [v«c«ot]
Signal: «z«in [victti]
nit.i: LSlp [J..ijn)
3p*e«zwn: jnelb»* [*u«o]
Ensort юО* I
E»pc«!toWotj.spsc< j
Рис. Г.1О. Программа SPTool — окно экспорта данных
В списке, занимающем левую часть этого окна, необходимо выбрать экспорти-
экспортируемые объекты. Щелчок на кнопке Export to Workspace произведет экспорт соот-
соответствующих структур данных в рабочую область памяти MATLAB, а для их за-
записи в МАТ-файл необходимо воспользоваться кнопкой Export to Disk.
Информацию о составе экспортируемых структур данных можно получить из
справочной системы пакета Signal Processing.
Литература
Я решил несколько отойти от традиции, согласно которой список литературы
должен выглядеть как монотонный и безликий перечень. Вместо этого я разбил
список на несколько групп и дал комментарии к каждой группе, постаравшись
пояснить, с какой целью включена в список каждая книга и какую пользу смо-
сможет извлечь из нее читатель.
В список литературы помещались только источники, доступные читателю, по-
поэтому в нем отсутствуют зарубежные издания (имеется лишь единственное ого-
оговоренное исключение).
Радиотехника
К этой группе относятся книги, посвященные преимущественно теоретической
радиотехнике. В них можно найти более глубокое теоретическое обоснование
материала глав 1-2. [1] и [2] — это последние из нескольких изданий двух клас-
классических учебников по курсу «Радиотехнические цепи и сигналы». Двухтомный
курс лекций [3] представляет зарубежный подход к этим вопросам. Книга [4] —
учебное пособие на ту же тему, в составлении которого принимал участие и ав-
автор данной книги. Монография [5] — фундаментальный курс по теории сигна-
сигналов, где подробно изложены принципы построения пространства сигналов и ре-
решения оптимизационных задач в этом пространстве. Наконец, [6] — поистине
великолепная книга, помогающая пытливо и непредвзято взглянуть на некото-
некоторые вопросы теории связи и информации, получив при этом весьма неожидан-
неожиданные на первый взгляд результаты. В общем, эту книгу должен прочесть каждый,
кто собирается серьезно заниматься обработкой сигналов или телекоммуника-
телекоммуникациями.
1. Гоноровский И. С, Демин М. П. Радиотехнические цепи и сигналы: Учебник
для вузов. — М.: Радио и связь, 1994.
2. Баскаков С. И. Радиотехнические цепи и сигналы: Учебник для вузов по спец.
«Радиотехника». — М.: Высш. шк., 2000.
3. Сиберт У. М. Цепи, сигналы, системы: В 2 ч. / Пер. с англ. — М.: Мир, 1988.
584 Литература
4. Иванов М.Т., Сергиенко А. Б., Ушаков В. Н. Теоретические основы радиотехни-
радиотехники. Учебное пособие / Под ред. В. Н. Ушакова. — М.: Высш. шк., 2002.
5. Френке Л. Теория сигналов / Пер. с англ.; Под ред. Д. Е. Вакмана. — М.: Сов.
радио, 1974.
6. Финк Л. М. Сигналы, помехи, ошибки... Заметки о некоторых неожиданно-
неожиданностях, парадоксах и заблуждениях в теории связи. 2-е изд., перераб. и доп. —
М.: Радио и связь, 1984.
Цифровая обработка сигналов
К данной группе относятся книги, речь в которых идет о собственно цифровой
обработке сигналов. К сожалению, их немного, и изданы они по большей части
довольно давно. [7] и [8] — два классических труда по цифровой обработке сигна-
сигналов. В них подробно изложена теория дискретных сигналов, дискретной фильт-
фильтрации и дискретного спектрального анализа. Несмотря на свой солидный возраст,
эти книги не потеряли актуальности — разве что главы, посвященные аппарат-
аппаратной реализации цифровой обработки сигналов, сейчас могут вызвать лишь нос-
ностальгическую улыбку... Об их непреходящей ценности свидетельствует и тот факт,
что обе книги [7, 8] включены в список литературы к курсу «Discrete-Time Signal
Processing», читаемому в MIT (Massachusetts Institute of Technology, Массачу-
сетский технологический институт — одно из ведущих высших учебных заведе-
заведений мира в области радиотехники, телекоммуникаций и вычислительной техни-
техники). Книга [9], хотя и издана в США, может быть доступна читателю. Дело в том,
что она входила в комплект документации, поставлявшейся фирмой Analog De-
Devices, Inc. вместе с учебно-демонстрационными платами на цифровых сигналь-
сигнальных процессорах ADSP218x. Кроме того, эта книга в PDF-формате имеется на
CD-ROM с информационными материалами, бесплатно распространяемом фир-
фирмой Analog Devices. На этом диске содержится еще несколько книг, посвящен-
посвященных базовым понятиям цифровой обработки сигналов. Книга [10] посвящена циф-
цифровому спектральному анализу, в ней можно найти подробное теоретическое
обоснование вопросов, обсуждавшихся в главе 5. Наконец, в книге [11] описаны
как некоторые алгоритмы цифровой обработки сигналов, так и вопросы, связан-
связанные с реализацией этих алгоритмов на специализированных цифровых сигналь-
сигнальных процессорах.
7. Голд Б., Рэйдер Ч. Цифровая обработка сигналов / Пер. с англ.; Под ред.
А. М. Трахтмана. — М.: Сов. радио, 1973, 368 с.
8. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов /
Пер. с англ.; Под ред. Ю. И. Александрова. — М.: Мир, 1978.
9. Digital Signal Processing Applications Using the ADSP-2100 Family. — Prentice
Hall, Englewood Cliffs, 1992.
10. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с
англ. - М.: Мир, 1990.
11. Куприянов М. С, Матюшкин Б. Д. Цифровая обработка сигналов: процессоры,
алгоритмы, средства проектирования. — СПб.: Политехника, 1999.
Разное 585
MATLAB
В данную группу собраны книги, посвященные системе MATLAB. За последнее
время таких книг издано несколько десятков, поэтому ограничимся лишь не-
несколькими названиями. Книга [12] — учебный курс по последней, шестой версии
MATLAB. Справочник [13] посвящен пакетам расширения MATLAB, имеющим
общематематический характер. Для обработки сигналов из этих пакетов наи-
наиболее интересны Statistics (Статистика) и Neural Networks (Нейронные сети).
В справочнике [14], среди прочих, кратко описан пакет Communications. Учеб-
Учебный курс [15] посвящен Simulink — расширению MATLAB, предназначенному
для моделирования динамических систем (см. приложение В). Наконец, книга
[16] содержит описания системы численных расчетов MATLAB, системы анали-
аналитических вычислений Maple и системы верстки текстов с математическими фор-
формулами LaTeX.
12. Дьяконов В. П. MATLAB 6: Учебный курс. - СПб.: Питер, 2002.
13. Дьяконов В., Круглое В. Математические пакеты расширения MATLAB: Спе-
Специальный справочник. — СПб.: Питер, 2001.
14. Дьяконов В., Круглое В. MATLAB. Анализ, идентификация и моделирование
систем: Специальный справочник. — СПб.: Питер, 2002.
15. Гультяев А. Визуальное моделирование в среде MATLAB: Учебный курс. —
СПб: Питер, 2000.
16. Говорухин В. #., Цибулин В. Г. Компьютер в математическом исследовании:
Учебный курс. - СПб.: Питер, 2001.
Разное
К данной группе отнесены книги, не попадающие в предыдущие категории. Кни-
Книга [17] посвящена численным методам оптимизации, которые могут исполь-
использоваться, в частности, при прямом синтезе дискретных фильтров (см. главу 6).
В книгах [18] и [19] рассматриваются адаптивные фильтры, параметры которых
автоматически подстраиваются в соответствии со статистическими свойствами
обрабатываемых сигналов. Такие фильтры сейчас повсеместно применяются в
разнообразных системах обработки сигналов.
17. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация / Пер. с англ. — М.:
Мир, 1985.
18. Адаптивные фильтры / Пер. с англ.; Под ред. К. Ф. Н. Коуэна и П. М. Гран-
Гранта. - М.: Мир, 1988.
19. Уидроу Б., Стирнз С. Д. Адаптивная обработка сигналов. — М.: Радио и связь,
1989.
Алфавитный указатель
' (апостроф), эрмитово сопряжение, 513
< (меньше), 528
% (знак процента), 525
( ) (круглые скобки), 519
, (запятая), 513, 525
.*, поэлементное умножение, 512
.', транспонирование, 513
... (три точки), 525
./, поэлементное деление, 512
.Л, поэлементное возведение в степень, 512
: (двоеточие), 519-520
: (точка с запятой), 513-514, 525
{} (фигурные скобки), 524
— (не равно), 528
= (меньше или равно), 528
-= (равно), 528
< (меньше), 528
> (больше), 528
>= (больше или равно), 528
ц-Analysis and Synthesis Toolbox, 571
A
ADC, 129
additive white Gaussian noise channel, 177
ademod, функция, 487
AM с подавленной несущей, 493
амплитудная модуляция, 490
квадратурная модуляция, 496
однополосиая модуляция, 495
фазовая модуляция, 497
частотная модуляция, 498
ademodce, функция, 487
AM с подавленной несущей, 493
амплитудная модуляция, 490
квадратурная модуляция, 496
однополосиая модуляция, 495
фазовая модуляция, 497
частотная модуляция, 498
aliasing, 130, 133, 231
all, функция, 528
allpass filter, 196
AM, 427
amod, функция, 487
AM с подавленной несущей, 491
амплитудная модуляция, 490
квадратурная модуляция, 496
однополосная модуляция, 493
фазовая модуляция, 49G
частотная модуляция, 497
amodce, функция, 487
AM с подавленной несущей, 491
амплитудная модуляция, 490
квадратурная модуляция, 496
однополосиая модуляция, 493
фазовая модуляция, 496
частотная модуляция, 497
amplitude modulation, 427
with suppressed carrier, 438
amplitude shift keying, 466
AM-SC, 438
analog, 127
Analog-to-Digital Converter, 129
Analysis, меню, 369
angle modulation, 447
ans, переменная, 511
any, функция, 528
Apply Filter, окно, 581
Apply, кнопка, 420
AR model, 277
arburg, функция, 305
arcov, функция, 305
ARMA model, 278
armcov, функция, 305
Array Editor, 518
aryule, функция, 305
ASK, 466
aurcad, функция, 182
Алфавитный указатель
587
autoregressive model, 277
Autoregressive Moving Average, 278
auwrite, функция, 183
averaged modified periodogram method, 276
AWGN channel, 177
awgn, функция, 177
axis, функция, 551
В
band-pass filter, 104
band-stop filter, 104
Bartlett, 276
bartlett, функция, 289
beat, 438
besselap, функция, 116
besself, функция, 120
bi2de, функция, 379
bilinear transformation, 314
bilinear, функция, 334
binary, 461
bitand, функция, 379
bitget, функция, 379
blackman, функция, 294
blockset, 574
box, функция, 551
boxcar, функция, 288
break, ключевое слово, 530
buttap, функция, 107
butter, функция, 120, 329
butterfly, 258
buttord, функция, 122, 332
С
canonic form, 206
carrier, 426
case, ключевое слово, 529
CDMA Reference Blockset, 574
cell array, 523
cheblap, функция, 108
cheblord, функция, 122, 332
cheb2ap, функция, 112
cheb2ord, функция, 122, 333
chebwin, функция, 297
chebyl, функция, 120, 329
cheby2, функция, 120, 329
chirp, функция, 168
clabel, функция, 547
clear, команда, 535
colormap, функция, 170, 301
Command History, вкладка, 517
Command Window, 510
Communications Blockset, 574
Communications Toolbox, 571
constellation, 468
constrained least square, 352, 354
continue, ключевое слово, 531
continuous phase frequency shift keying, 463
contour, функция, 547
contour3, функция, 549
contourf, функция, 549
Control System Toolbox, 571
conv, функция, 125, 212
Convert structure, кнопка, 420
convert, функция, 410
convmtx, функция, 224
convolution matrix, 224
copyobj, функция, 404, 410, 423
correlation, 69
correlation function, 50
covariance, 69
CPFSK, 463
cremez, функция, 360
cross-correlation function, 52
cumulative distribution function, 63
Current Directory,
вкладка, 518
список, 518, 528
Curve Fitting Toolbox, 570
D
DAC, 129
Daniell, 276
daqfcngen, демонстрационная
программа, 187
daqscope, демонстрационная
программа, 187
Data Acquisition Toolbox, 186, 570
Database Toolbox, 571
Datafeed Toolbox, 572
ddemod, функция, 487
амплитудная манипуляция, 499
квадратурная манипуляция, 500
минимальная частотная
манипуляция, 504
фазовая манипуляция, 502
частотная манипуляция, 503
ddemodce, функция, 487
амплитудная манипуляция, 499
квадратурная манипуляция, 500
минимальная частотная
манипуляция, 504
фазовая манипуляция, 502
частотная манипуляция, 503
decimate, функция, 232
588
Алфавитный указатель
decimation, 230
in frequency, 259
in time, 256
deconv, функция, 212
deconvolution, 212
DECT, 282
demod, функция, 481
AM с подавленной несущей, 483
амплитудная модуляция, 482
время-импульсная
модуляция, 486
квадратурная модуляция, 485
однополосная модуляция, 483
фазовая модуляция, 484
частотная модуляция, 484
широтно-импульсная модуляция, 486
demodmap, функция, 504
demodulation, 426
Denominator, поле ввода, 371
denormalmax, функция, 404
denormalmin, функция, 404
Design Filter,
вкладка, 368
кнопка, 369
команда меню, 372
переключатель, 368
Developer's Kit
for Texas Instruments™ DSP, 571
DFT, 251
dftmtx, функция, 287
Dials & Gauges Blockset, 574
DIF, 259 ,
differential phase shift keying, 467
digital, 128
Digital-to-Analog Converter, 129
direct form I, 206
direct form II, 206
direct transposed form I, 209
direct transposed form II, 208, 214
diric, функция, 167
Discrete Fourier Transform, 251
discrete series, 127
discrete-time, 128
disp, функция, 404, 412, 423, 532
DIT, 256
dmod, функция, 487
амплитудная манипуляция, 499
квадратурная манипуляция, 500
минимальная частотная
манипуляция, 503
фазовая манипуляция, 501
частотная манипуляция, 502
dmodce, функция, 487
амплитудная манипуляция, 499
квадратурная манипуляция, 500
минимальная частотная манипуляция,
503
фазовая манипуляция, 501
частотная манипуляция, 502
double, 379
DPSK, 467
DSP Blockset, 574
Е
eigenvectors, 284
ellip, функция, 120, 329
ellipap, функция, 114
ellipord, функция, 122, 333
else, ключевое слово, 528
elseif, ключевое слово, 529
end, ключевое слово
максимальное значение индекса, 520
оператор for, 529
оператор while, 530
оператор выбора, 529
условный оператор, 528
ensemble averaging, 64
envelope, 160
eps, функция, 404, 412, 423
eqtflength, функция, 125, 225
equiripple filter, 319
erf, функция, 67
erfc, функция, 67
erfinv, функция, 67
ergodic, 72
error function, 66
EV, 284
even symmetry, 204
Excel Link, 571
exponent, 377
exponentbias, функция, 404
exponentlength, функция, 404
exponentmax, функция, 404
exponentmin, функция, 404
Export from SPTool, окно, 583
Export To, список, 370
Export, команда меню, 370
extended, 380
eye diagram, 476
eyediagram, функция, 506
Fast Fourier Transform, 256
fda, расширение файлов, 370
Алфавитный указатель
589
FDATool, среда для расчета фильтров, 367
анализ фильтра, 369 v
импорт фильтра, 371
квантование фильтров, 418
синтез фильтра, 368
сохранение результатов, 370
FFT, 256
fft, функция, 285, 399, 421, 522
fftfilt, функция, 287, 581
fftn, функция, 522
fftshift, функция, 286
field, 523
figure window, 515
figure, функция, 553
File, меню, 370
Filter Design Toolbox, 571
Filter Designer, окно, 579
Filter Order, раздел, 368
Filter Specifications, график, 369
Filter Specifications, команда меню, 369
Filter Structure, список, 371
Filter Type, переключатель, 368
Filter Viewer, окно, 581
Filter, меню, 371-372
filter, функция, 213, 399-400, 410, 581
filtfilt, функция, 215, 232, 581
filtic, функция, 214
Financial Derivatives Toolbox, 572
Financial Time Series Toolbox, 572
Financial Toolbox, 572
find, функция, 154
finite impulse response, 203
FIR filter, 203
firl, функция, 340
fir2, функция, 341
fircls, функция, 352
firclsl, функция, 354
firlpnorm, функция, 365
fills, функция, 238, 349
firrcos, функция, 344
fixed point, 374
Fixed-Point Blockset, 574
fliplr, функция, 125
float, 379
floating point, 374
flops, функция, 285
fluctuation, 64
FM, 448
for, ключевое слово, 529
Format, поле ввода, 420
Fourier transform, 31
fprintf, функция, 532
fractionlength, функция, 404
freqs, функция, 97
freqspace, функция, 219
Frequency and Magnitude Specifications,
раздел, 369
frequency deviation, 450
Frequency Domain System Identification
Toolbox, 571
frequency modulation, 448
frequency shift keying, 462
Frequency Specifications, раздел, 369
freqz, функция, 217, 288, 410
Fs, поле ввода, 372
FSK, 462
function, 525
ключевое слово, 526
Fuzzy Logic Toolbox, 571
G
gain, 94, 196, 228
GARCH Toolbox, 572
gauspuls, функция, 159
Gaussian distribution, 66
get, функция, 399
granular limit cycle, 394
gremez, функция, 362
grid, функция, 551
group delay, 90
Group Delay, команда меню, 369
grpdelay, функция, 219
GSM, 282
H
hamming, функция, 292
hann, функция, 291
help, команда, 516, 527
Help, меню, 516
helpdesk, команда, 516
heterodyne, 142
heterodyning, 143
hex2num, функция, 404
high-pass filter, 104
hilbert, функция, 243, 484
hilbiir, функция, 348
hist, функция, 173
Hoertzel, 265
I
if, ключевое слово, 528
ifft, функция, 285, 421, 522
ifftn, функция, 522
IIR filter, 206
590
Алфавитный уквзатель
iirgrpdelay, функция, 366
iirlpnorm, функция, 365
iirlpnormc, функция, 365
imag, функция, 243
Image Processing Toolbox, 571
imagesc, функция, 300
impinvar, функция, 335
Import Filter,
вкладка, 371
кнопка, 372
комадна меню, 371
Import to SPTool, окно, 576
impulse invariance, 315
Impulse Response, команда меню, 369
impz, функция, 216, 410
infinite impulse response, 206
initial conditions, 214
Input/output scaling, поле ввода, 420
instantaneous frequency, 448
Instrument Control Toolbox, 570
interp, функция, 236
interpolation, 230
polyphase algorithm, 238
intersymbol interference, 475
inverse Chebyshev filter, 110
invfreqz, функция, 337
isallpass, функция, 412
isempty, функция, 528
isequal, функция, 528
isfir, функция, 412
ISI, 475
islinphase, функция, 412
ismaxphase, функция, 412
isminphase, функция, 412
isreal, функция, 412
issos, функция, 412
isstable, функция, 412
К
kaiser, функция, 295
kaiserord, функция, 342
keying, 461
Launch Pad, вкладка, 518
leakage, 270
legend, функция, 551
length, функция, 423, 519
limit cycle, 393
limitcycle, функция, 412, 417
linear prediction, 278
lloyds, функция, 398
LMI Control Toolbox, 571
load, команда, 533
loglog, функция, 545
long double, 380
low-pass filter, 104
Ip2bp, функция, 118
Ip2bs, функция, 120
Ip2hp, функция, 117
1р21р, функция, 117
M
MA model, 278
Magnitude and Phase, команда меню, 369
Magnitude Response, команда меню, 369
Magnitude Specifications, раздел, 369
mantissa, 377
Mapping Toolbox, 570
marcumq, функция, 85
MATLAB
C/C++ Graphics Library, 569
C/C++ Math Library, 569
Compiler, 569
Excel Builder, 569
Report Generator, 569
Runtime Server, 569
Web Server, 570
графика, 542
двумерная, 542
копирование графиков, 555
настройка оформления, 549
панель инструментов
графического окна, 543
трехмерная, 545
интерактивный режим, 510
интерфейс главного окна, 517
использование русского языка, 542
командное окно, 510
компоненты, 569
переменные, 511
глобальные, 527
локальные, 527
подавление вывода результата, 514
поэлементные операции, 512
программирование, 524
ввод и вывод данных, 532
запись нескольких операторов
в строке, 525
комментарии, 525
логические условия, 528
оператор выбора, 529
оптимизация программ, 534
отладка, 533
Алфавитный указатель
591
MATLAB (продолжение)
программы, 525
профилирование, 538
разрыв длинных строк, 525
редактор/отладчик М-файлов, 526
сценарии, 525
условный оператор, 528
функции,525-526
циклы, 529
путь поиска файлов, 527
системные требования, 508
справочная система, 515
HTML-документация, 516
PDF-документация, 517
встроенная справка, 515
типы данных
массивы, 518
массивы ячеек, 523
многомерные массивы, 521
нумерация элементов, 519
строки, 522
структуры, 523
установка, 509
ядро, 569
MatrixVB, 570
МАТ-файлы, 185, 533
max, функция, 405
MBSA, 249
McClcllanJ. H., 319
mean value, 64
mesh, функция, 548
meshc, функция, 548
meshgrid, функция, 546
meshz, функция, 548
min, функция, 405
minimax approximation, 319
Minimum order, переключатель, 369
minimum shift keying, 466
Mode, список, 420
Mode] Predictive Control Toolbox, 571
Model-Based Spectrum Analysis, 249
modified periodogram, 275
modmap, функция, 504
modulate, функция, 481
AM с подавленной несущей, 483
амплитудная модуляция, 482
время-импульсная модуляция, 486
квадратурная модуляция, 485
однополосная модуляция, 483
фазовая модуляция, 484
частотная модуляция, 484
широтно-импульсная модуляция, 486
modulated signal, 426
modulating signal, 426
modulation, 426
index, 449
Motorola DSP Developer's Kit, 571
Moving Average, 278
MSK, 466
multiband filter, 340
Multiple Signal Classification, 282
MUSIC, 282
оценка частот, 283
N
nargin, функция, 531
nargout, функция, 531
Neural Network Toolbox, 570
nlm, функция, 412
noise subspace, 283
Nonlinear Control Design
Blockset, 574
nonparametric spectrum
analysis, 249
nonrecursive filter, 202
noperations, функция, 405, 412, 423
normal distribution,,66
normalize, функция, 413
normedf, функция, 67
norminv, функция, 67
normpdf, функция, 67
noverflows, функция, 405, 413, 423
nuin2bin, функция, 413
num2hex, функция, 405, 413
num2int, функция, 413
numberofsections, функция, 413
Numerator, поле ввода, 371
nunderflows, функция, 405
Nyquist frequency, 130
Nyquist theorem, 139
О
odd symmetry, 204
Open Session, кнопка, 370
Optimization Toolbox, 570
optimizeunitygains, функция, 413, 423
order, функция, 413
otherwise, ключевое слово, 529
overflow limit cycle, 394
Overflow mode, список, 420
overlap-add, 270
overlap-save, 270
Overwrite Existing Variables,
флажок, 371
592
Алфавитный указатель
parametric spectrum analysis, 249
Parks Т. W., 319
Partial Differential Equation
Toolbox, 570
pburg, функция, 305
pcolor, функция, 549
pcov, функция, 305
PDF, 63
peig, функция, 311
periodogram, 275
periodogram, функция, 301
phase
delay, 90
modulation, 448
Phase Response, команда меню, 369
phase shift keying, 467
plot, функция, 151, 153, 542
plot3, функция, 545
plotyy, функция, 545
PLS_Toolbox, 570
PM, 448
pmcov, функция, 305
pmusic, функция, 308
polar, функция, 545
pole, 94, 196
Pole/Zero Plot, команда меню, 370
poly, функция, 101
polyder, функция, 125
Polynomial Toolbox, 572
polyphase algorithm, 238
polyval, функция, 125
Portable Graph Object, 571
power spectral density, 75
Power System Blockset, 574
prediction error, 278
print, функция, 556
probability density function, 63
profile, команда, 538
prony, функция, 339
psd, функция, 305
psdplot, функция, 305
pseudospectrum, 282
PSK, 467
PTM, 486
pulse
time modulation, 486
train, 161
width modulation, 477
pulstran, функция, 161
pwelch, функция, 303
PWM, 477
pyulear, функция, 305
р-норма, 318, 365
Q
QAM, 459
QASK, 467
qfft, функция, 421
свойства объекта, 421
qfilt, функция, 408
свойства объекта, 410
структура фильтра, 408
qfilt2tf, функция, 413
QFT Frequency Domain Control Design
Toolbox, 572
qreport, функция, 400, 405, 413, 423
quadrature, 160
amplitude modulation, 459
amplitude shift keying, 467
quantiz, функция, 398
quantization, 128
error, 128
noise, 128
quantize, функция, 402
Quantizer type, список, 420
quantizer, функция, 400
свойства объекта, 401
quotient, 212
R
RADIX, 260
radix, функция, 423
raised cosine filter, 325
square root, 328
rand, функция, 172-173
randint, функция, 462
randn, функция, 172, 176
range, функция, 405, 414, 423
raylcdf, функция, 84
Rayleigh, 83
raylinv, функция, 84
raylpdf, функция, 84
raylrnd, функция, 84
raylstat, функция, 84
rcosfir, функция, 346
rcosiir, функция, 347
rcosine, функция, 345
realmax, функция, 405
realmin, функция, 405
Real-Time Windows Target, 573
Real-Time Workshop, 573
Ada Coder, 573
Embedded Coder, 573
Алфавитный указатель
593
rectpuls, функция, 155
recursive filter, 205
remainder, 212
remez, функция, 356
remezord, функция, 361
repmat, функция, 470
Requirements Management Interface, 574
resample, функция, 238
resampling, 230, 237
reset, функция, 405, 414, 423
residue, функция, 102
return, ключевое слово, 527
reziduez, функция, 225
Robust Control Toolbox, 571
rolloff factor, 325
rooteig, функция, 311
rootmusic, функция, 310
roots, функция, 101
Round mode, список, 420
round, функция, 472
sample time, 127
samples, 127
sampling, 128
frequency, 127, 151
theorem, 139
Sampling Frequency, раздел, 371
saturation, 397
Save session, кнопка, 370
Save session As, команда меню, 370
save, команда, 533
sawtooth, функция, 166
Scale transfer-fcn coeffs-1, кнопка, 420
scale values, функция, 414
scatter plot, 472
scattereyedemo, демонстрационная
программа, 506-507
scatterplot, функция, 505
script, 525
search path, 527
second-order sections, 227
semilogx, функция, 545
semilogy, функция, 545
set, функция, 399
Set Quantization Parameters,
вкладка, 369, 418
setbits, функция, 414
shaping filter, 474'
Show filter structures, кнопка, 418
Signal Browser, окно, 577, 582
Signal Processing Tool, программа, 575
Signal Processing Toolbox, 571
signal subspace, 283
signal-to-noise ratio, 381
SimMechanics, 574
Simulink, 572
Performance Tools, 572
Report Generator, 574
Simulink, ядро, 572
sine, функция, 157
single, 379
single side band, 439
size, функция, 519
SNR, 381
sos, функция, 414
sos2ss, функция, 227
sos2tf, функция, 227
sos2zp, функция, 227
sosfilt, функция, 230
sound, функция, 183
soundsc, функция, 184, 470
specgram, функция, 170, 300
Specify order, поле ввода, 368
spectral shaping, 474
spectrogram, 300
spectrum leakage, 270
Spectrum Viewer, окно, 578
Spline Toolbox, 570
sprintf, функция, 532
SPTool, программа, 575
импорт данных, 576
просмотр графика сигнала, 577
просмотр характеристик фильтра, 580
расчет фильтров, 579
сохранение и загрузка сеанса, 583
спектральный анализ, 578
фильтрация сигнала, 581
экспорт данных, 583
square root raised-cosine filter, 328, 473
square, функция, 164
ss2sos, функция, 228
ss2tf, функция, 102, 225
ss2zp, функция, 102, 225
SSB,439
stairs, функция, 151, 545
standard deviation, 64
state space, 96
Stateflow, 573
Coder, 573
Statistics Toolbox, 172, 570
stem, функция, 151, 217, 545
stem3, функция, 549
Step Response, команда меню, 370
594
Алфавитный указатель
strips, функция, 181
Structural Dynamics Toolbox, 570
structure, 523
sub2ind, функция, 521
subcarrier, 445
subplot, функция, 181, 553
surf, функция, 545
surfc, функция, 548
switch, ключевое слово, 529
symbol, 461
symbol rate, 461
Symbolic/Extended Symbolic Math
Toolbox, 570
symerr, функция, 473
System Identification Toolbox, 571
5-плоскость, 222
T
TeX, 553
text, функция, 551
tf2sos, функция, 227
tf2ss, функция, 101, 225
tf2zp, функция, 101, 225
tic, функция, 535
time averaging, 73
title, функция, 551
toe, функция, 535
Toeplitz matrix, 149
toeplitz, функция, 149, 224
toolbox, 510
tostring, функция, 405, 414, 423
transfer function, 93, 195
transversal filter, 202
triang, функция, 288
tripuls, функция, 156
Turn quantization on,
флажок, 369, 418
twiddles, функция, 423
и
udecode, функция, 397
uencode, функция, 396
uniform distribution, 65
unitquantize, функция, 402
unitquantizer, функция, 403
Units, список, 372
unwrap, функция, 99, 219
upfirdn, функция, 238
Variable names, раздел, 371
variance, 64
View Filter Coefficients, команда меню, 370
Virtual Reality Toolbox, 570
w
Walker, 319
waterfall, функция, 549
Wavelet Toolbox, 571
wavplay, функция, 184
wavread, функция, 178
wavrecord, функция, 185
wavwrite, функция, 182
wav-файлы, 178
weighting functions, 273
Welch, 276
method, 276
wgn, функция, 176
while, ключевое слово, 530
white Gaussian noise, 176
white noise, 79
window, 273
wordlength, функция, 405
Workspace, вкладка, 518
xlabel, функция, 551
xlim, функция, 551
xPC Target, 573
Embedded Option, 574
ylabel, функция, 551
ylim, функция, 551
Yule, 319
yulewalk, функция, 336
z
z-преобразование
обратное, 147
свойства, линейность, 146
связь с другими преобразованиями, 145
zero, 94, 196
zeros, функция, 537
zlabel, функция, 551
zlim, функция, 551
Zoom In, кнопка, 370
Zoom Out, команда, 370
zp2sos, функция, 228
zp2ss, функция, 102, 225
zp2tf, функция, 101, 225
zplane, функция, 222, 410
z-transform, 143
г-плоскость, 222
Алфавитный указатель
595
z-преобразовапие, 143
свойства
задержка, 146
свертка, 147
абсолютная интегрируемость, 33
авторегрессионная модель, 277
линейное предсказание, 278
спектр сигнала, 278
формирование сигнала, 277
адаптивные фильтры,476
аддитивный белый гауссов шум, 177
алгоритм
Герцеля, 265
дискретной фильтрации, 193
Ремеза, 319
AM, 427
АМн, 466
амплитуда, 19, 427
комплексная, 49, 56
амплитудная
манипуляция, 466, 470
амплитудная модуляция, 427
демодуляция, 436
КПД, 435
мощность, 434
однотональная, 429
векторная диаграмма, 432
спектр, 431
ширина спектра, 432
перемодуляция, 430
с подавленной несущей, 438
спектр, 433
амплитудная огибающая, 55, 58, 428
амплитудно-частотная
характеристика, 90
амплитудный спектр, 25, 33
АМ-ПН, 438
анализ
корреляционный, 50
сигналов, 17
аналитический сигнал, 56, 440, 456
спектр, 58
аналого-цифровой
преобразователь, 129
ансамбль реализаций, 60
аппроксимация АЧХ, 104
АЦП, 129, 381
АЧХ, 90, 97, 104, 173
крутизна ската, 112
максимально плоская, 107-108, НО
Б
бабочка, 258, 260
база сигнала, 36
базис Котельникова, 139
белый шум, 79
дискретный, 150
преобразование в линейной
системе, 92
биения, 438, 461
билинейное z-преобразование, 314, 334
БИХ-фильтры, 206
блочная обработка, 268
боковые полосы, 433
боковые частоты, 431
БПФ, 256
квантованное, 421
обратное, 260
основание, 260
прореживание
по времени, 256
по частоте, 259
число операций, 258, 285
быстрое преобразование Фурье, 256
В
вектор, 150
вектор состояния, 200, 207
вектор-строка, 511
верхняя боковая полоса, 439
весовые функции, 273, 287, 320
взаимный спектр, 54, 90
ВИМ, 486
восстановление
радиосигнала, 141
непрерывного сигнала, 133, 139
временная область, 34
время-импульсная модуляция, 486
выбор порядка фильтра, 332
для метода Ремеза, 361
вычеты, 94, 198
гармоники, 23
генерация
импульсов, 155
периодических сигналов, 164
последовательности импульсов, 161
программа daqfengen, 187
сигнала с меняющейся частотой, 168
гетеродин, 142
гетеродиннроваиие, 143
гистограмма, 173
596
Алфавитный указатель
глазковая диаграмма, 476, 506
глубина модуляции, 429
графическое окно, 515
групповая задержка, 90, 114, 321, 366
для симметричных фильтров, ,204
расчет для аналоговых систем, 123
двоичная последовательность, 461
девиация частоты, 450
действующее значение, 22
дельта-функция, 19, 88
спектр, 47
фильтрующее свойство, 19, 146
демодуляция, 426
AM, 436
с подавленной несущей, 439
КАМ, 459
квадратурной манипуляции, 472
однополосного сигнала, 442
УМ, 456
ФМ, 456-457
ЧМ, 456, 458
ЧМн, 464
диаграмма рассеяния, 472, 505
динамический диапазон, 377
дискретизация, 128
дискретного сигнала, 231
квадратурная, 142
дискретная
синусоида, 145
экспоненциальная функция, 145
дискретно-аналоговые устройства, 128
дискретное преобразование Фурье, 251
дискретный единичный скачок, 144
дисперсия, 64, 69, 75
выходного сигнала линейной
системы, 92
дифференциальное уравнение линейной
системы, 93
дополнительный код, 374-375
ДПФ, 251
единичная импульсная функция, 144
единичный скачок, дискретный, 144
задержка
групповая, 90, 219
фазовая, 90
записи сигналов, 185
запятая
плавающая, 377
фиксированная, 375
звук
воспроизведение, 183
запись, 185
И
импульс
гауссов, 40
конечная последовательность, 161
прямоугольный, 34, 154-155
задержанный, 34
трапециевидный, 156
треугольный, 156
несимметричный, 36, 154-155
симметричный, 37
экспоненциальный
двусторонний, 39
односторонний, 38, 154
импульсная характеристика, 315
аналоговой системы, 88
расчет, 95
дискретной системы, 194, 216
расчет, 199
индекс угловой модуляции, 449
интеграл
вероятности, 66
интервал
дискретизации, 127
корреляции, 78
интерполяция, 163, 230, 235, 473
искажения мультипликативные, 136
К
КАМ, 459
КАМн, 467
квадратурная
дискретизация, 142
манипуляция, 467
демодуляция, 472
помехоустойчивость, 471
спектр мощности, 474
формирование спектра, 473
модуляция, 459
обработка сигнала, 457
квадратурное дополнение, 56, 160
квантование, 128, 380
в цифровых фильтрах, 383
гармонического сигнала, 380
отношение сигнал/шум, 381
зоны, 382
Алфавитный указатель
597
квантование (продолжение)
квантованные значения, 382
неравномерное, 382, 398
уровни, 380
характеристика квантования, 405
шум, 380
квантованные значения, 382
КИХ-фильтры, 203
классификация сигналов, 18
ковариационная функция, 68-69
код Баркера, 237
колебания квазигармонические, 80
командное окно, 510
комментарии, 525
комплексная
амплитуда, 49, 56
огибающая, 56, 58
экспонента, спектр, 49
комплексный коэффициент
передачи, 90, 196
композитный стереосигнал, 446
константа, спектр, 48
конструктор, 399
корреляционная матрица, 149
белого шума, 150
неотрицательная
определенность, 150
корреляционная функция, 50, 68-69
взаимная, 52
выходного и входного
сигналов, 91
импульсной характеристики, 92
интервал корреляции, 78
коэффициент корреляции, 72
нормированная, 72
периодического сигнала, 51
связь со спектрами сигналов, 53
корреляционный анализ, 50
косинусоидальное сглаживание
АЧХ, 324, 344
коэффициент сглаживания, 325
коэффициент
заполнения, 165
корреляции, 70
модуляции, 429
передачи, 90
сглаживания, 325
усиления, 94, 196
Л
лепестки спектра, 26, 34
линейное предсказание, 278
линейность, 87, 189
линия задержки, 202
ложные частоты, 130, 133, 231
м
манипуляция, 461
амплитудная, 466, 470
квадратурная, 467
фазовая, 467, 470
частотная, 462
мантисса, 377
денормализованная, 378
нормализация, 377
массив ячеек, 523
массивы, 518
масштабирование коэффициентов
фильтров, 387
математическое ожидание, 64
матрица, 150
единичная, 150
собственные числа, 150
Теплица, 149
мгновенная частота, 448
меандр, 27
межсимвольная интерференция, 475
метод
инвариантной импульсной
характеристики, 315, 335
низкочастотного эквивалента, 59
Прони, 319
усреднения модифицированных
периодограмм, 276
Уэлча, 276
Юла-Уолкера, 319
минимаксная аппроксимация, 319
минимизация р-нормы
ошибки, 365
многополосные фильтры, 340
моделирование сигналов, 151
модельный спектральный
анализ, 249
модулированный сигнал, 426
модулирующий сигнал, 426
модуляция, 426
амплитудная, 142, 427
квадратурная, 459
однополосная, 439
угловая, 142, 427, 447
фазовая, 448
цифровая, 461
частотная, 448
широтно-импульсная, 477
598
Алфавитный указатель
мощность, 21
мгновенная, 21
средняя, 21, 51
случайного процесса, 75
МСИ, 475
мультипликативные искажения, 136
МЧМн, 466
н
насыщение, 397
научная нотация, 377
начальная фаза, 19, 58
независимость статистическая, 67
некоррелированность, 67, 150
нелинейность, 87
иепараметрический спектральный
анализ, 249
нестационарность, 88
несущая, 426
несущее колебание, 426
нижняя боковая полоса, 439
низкочастотный эквивалент, 59
нули функции
передачи, 94, 196, 222
О
обратный код, 374
объект, 399
огибающая, 90, 160, 428
амплитудная, 55, 58
комплексная, 56, 58
однополосная модуляция, 439
демодуляция, 442
окно, 273, 287, 320
Бартлетта, 289
Блэкмена, 294
Кайзера, 238, 295, 342
прямоугольное, 288
треугольное, 288
Ханна, 291
Хэмминга, 292, 323, 341-342
Чебышева, 297
округление, 380
коэффициентов фильтров, 383.
промежуточных результатов, 391
оператор
дифференцирования, 45
интегрирования, 45
операции поэлементные, 151
опорное колебание, 436
остаток, 212
отношение сигнал/шум, 381
отсчеты, 127, 178
комплексные, 142
спектральные, 255
ошибка предсказания, 278
ошибки квантования, 128
п
пакет расширения, 510
параллельные вычисления, 208
параметрические системы, 88
параметрический спектральный
анализ, 249
передискретизация, 230, 237
полифазный алгоритм, 238
перекрытие
с накоплением, 270
с суммированием, 270
перемодуляция, 430, 446, 483
переполнение, 389
переходная характеристика, 89
период дискретизации, 127
периодическое продолжение
сигнала, 23
периодограмма, 275
Бартлетта, 276
Даньелла, 276
модифицированная, 275
пилот-сигнал, 439, 446
плавающая запятая, 377
плотность вероятности, 382
выходного сигнала линейной
системы, 92
двумерная, 68
многомерная, 68
одномерная, 63
поднесущая, 445
поле структуры, 523
полином Чебышева, 110
полиномы, деление, 212
полифазный алгоритм, 238
полная фаза, 55, 58, 448
полоса
задерживания, 104
пропускания, 104
полосовой фильтр
идеальный, 141
получение данных из внешних
источников, 178
полюсы функции передачи, 94, 96, 196,
198, 222
кратные, 95
полярная модуляция, 444
Алфавитный указатель
599
порядок
линейной цепи, 93
фильтра, 202, 205
числа, 377
последовательность импульсов
меандр, 27
пилообразных, 29, 188
прямоугольных, 25, 164, 188
треугольных, 30, 166, 188
постоянная составляющая, 73
постоянный во времени сигнал,
спектр, 48
поэлементные операции, 151
предельный цикл, 393
разновидности, 394
преобразование Гильберта, 57, 80, 440
дискретное, 240, 351, 357
преобразование Лапласа, 94, 96
связь с z-преобразованием, 146
преобразование Фурье, 31
быстрое, 256
дискретное, 251
быстрые алгоритмы, 256
восстановление непрерывного
сигнала, 253
матрица преобразования, 254
свойства, 251
связь со спектральной
функцией, 255
спектральное разрешение, 256
эквивалентный фильтр, 262
дуальность, 41, 133
задержка, 43
обратное, 33
примеры расчета, 34
прямое, 32
свойства, 42
дифференцирование, 44
изменение масштаба оси
времени, 44
интегрирование, 45
линейность, 43
произведение, 46
свертка, 45
умножение на гармоническую
функцию, 46
связь с z-нреобразованием, 146
связь с рядом Фурье, 47
причинность, 89, 215
проектирование цифровых
фильтров, 313
Прони, 319
прореживание, 230-231, 256
по времени, 256
по частоте, 259
пространство состояний, 200, 207
простые дроби, 94
простые сигналы, 36
прототип аналоговый, 313
прямой код, 374, 377
прямые методы синтеза цифровых
фильтров, 317
псевдоспектр, 282, 284
пульсации АЧХ, 107, 110, 112
равномерные, 319
ПФ, 104
равенство Парсеваля, 55
дискретное, 253
радиоимпульс, 158
гауссов, 159
разностное уравнение, 193
распределение вероятности
гауссово, 66
нормальное, 66
Пуассона, 62
равномерное, 65, 380
Рэлея, 83
генерация случайных
чисел, 173
функция распределения, 173
Рэлея—Раиса, 85
растекание спектра, 270
реализация случайного процесса, 60
редактор массивов, 518
Рише, Гаспар, 319
русский язык в MATLAB, 542
ряд Котельннкова, 254
ряд Фурье, 22, 451
в точках разрыва, 28
вещественный, 24
вычисление мощности сигнала, 55
комплексный, 24
примеры разложения сигналов, 25
связь с преобразованием Фурье, 47
синусио-косипусный, 23
частичные суммы, 28
С
свертка, 88, 91-92
дискретная, 212
линейная, 147, 195
матрица свертки, 224
600
Алфавитный указатель
свертка (продолжение)
представление в виде скалярного
произведения, 223
круговая, 252-253, 265
линейная, 265
обращение, 212
свободные колебания, 199
свойства объектов, 399
секции второго порядка, 227
секционная обработка, 268
сигнал, 18
аналитический, 56, 142, 243, 440, 456
аналоговый, 127
гармонический, 19, 188
дискретный, 270
со случайной начальной
фазой, 61
спектр, 48
детерминированный, 18
дискретизированный, 131, 138
дискретный, 128 "*
случайный, 148
конечной длительности, 19
многоканальный, 150, 152
модулированный, 426
модулирующий, 426
периодический, 18
спектр; 49
простой, 36
с большой базой, 36
с меняющейся частотой, 188
с ограниченной
полосой частот, 157
энергией, 18
сложный, 36
случайный, 18, 60, 188
сопряженный, 56
физический, 127
финитный, 19
цифровой, 128, 461
широкополосный, 36
сигнал/шум, 381
сигнальное подпространство, 283
сигнально-кодовая конструкция, 468
символ, 461
символьная скорость, 461
синтез цифровых фильтров, 313
билинейное z-преобразование, 314
классификация методов, 313
метод инвариантной импульсной
характеристики, 315
метод Ремеза, 355
синтез цифровых фильтров (продолжение)
прямые методы, 317
оптимальные, 318
субоптимальные, 319
с использованием окон, 320, 340
функции MATLAB, 328
синхронное детектирование, 436, 439
системная функция, 195
системы
аналоговые, 87
дискретные
способы описания, 193
устойчивость, 199
физическая реализуемость, 196
классификация, 87
с переменными параметрами, 88
с постоянными параметрами, 88
физическая реализуемость, 89
системы линейные, 87
комплексный коэффициент
передачи, 94
преобразование
детерминированных сигналов, 88
случайных процессов, 91
способы описания, 93
дифференциальное
уравнение, 93
нули и полюсы, 94
операторный коэффициент
передачи, 93
полюсы и вычеты, 94
пространство состояний, 96
функция передачи, 93
устойчивость, 95-96
характеристики, 88
скважность, 26, 165, 477
СКК, 468
скорость затухания спектра, 30-31
сложные сигналы, 36
случайные величины, 63
генерация, 172
двумерные, 68
коэффициент корреляции, 70
независимость, 67, 70
некоррелированность, 67, 70
статистическая связь, 70
случайный процесс, 60
вероятностные характеристики
двумерные, 68
многомерные, 68
одномерные, 63
вещественный, 149
Алфавитный указатель
601
случайный процесс (продолжение)
дискретный, 148, 380
корреляционная матрица, 149
дисперсия, 64
интервал корреляции, 78
квазидетерминированный, 61
ковариационная функция, 68
корреляционная функция, 68
математическое ожидание, 64
модели, 60
плотность вероятности, одномерная, 63
реализация, 60
сечение, одномерное, 63
спектр мощности, 75
спектральные характеристики, 74
среднее квадратическое
отклонение, 64
стационарный, 71, 148
коэффициент корреляции, 72
узкополосный, 80
огибающая, 83, 85
при наличии детерминированной
составляющей, 84
фаза, 84
функция распределения
вероятности, 63
центрированный, 68
экспоненциально
коррелированный, 299
эргодический, 72
смещенный код, 374, 378
созвездие, 468
соотношение неопределенности, 36
сопряженный сигнал, 56
спектр, 25
взаимный, 54
дискретизированного сигнала, 132
влияние формы импульсов, 135
размерность, 132
дискретного сигнала, 131, 271
периодического, 250
дискретного случайного процесса, 274
мгновенный, 300
мощности, 75
односторонний,. 58
растекание, 270
симметрия, 33
скорость затухания, 30-31
ширина эффективная, 36, 78
энергетический, 54
спектральная плотность, 32
средней мощности, 75
спектральная функция, 32
спектральный анализ
модельный, 249
непараметрические методы, 275
метод Уэлча, 276
периодограмма, 275
непараметрический, 249
параметрические методы, 249, 277
EV, 284
MUSIC, 282
авторегрессионные, 277
спектрограмма, 300
среднее квадратическое отклонение, 64
среднеквадратическое значение, 22
средняя мощность, 51
статистическая независимость, 67
статистическое усреднение, 64
стационарность, 71, 88, 189
стереовещание, 444
стереосигнал композитный, 446
строки, 522
структура, 523
т
теорема
Винера—Хинчина, 76
дискретная, 275
дискретизации, 139
Котельникова, 138
Найквиста, 139
Рэлея, 54
дискретная, 252
У
угловая модуляция, 427, 447
гармоническая, 449
векторная диаграмма, 453
девиация частоты, 450
индекс, 449
спектр, 451
ширина спектра, 454
демодуляция, 456
узкополосность, 426
уровни квантования, 380
усечение, 381
условия
устойчивости, 96
Дирихле, 22
усреднение
по времени, 73
статистическое, 64
устойчивость, 95
602
Алфавитный указатель
Ф
фаза
начальная, 58
полная, 55, 58, 448
фазовая
автоподстройка частоты, 438
задержка, 90
манипуляция, 467, 470
дифференциальная, 467
относительная, 467
фазоразностная, 467
модуляция, 448
демодуляция, 456-457
функция, 55
фазовращатель, 57
фазовый спектр, 25, 33, 54
фазочастотная характеристика, 90
ФАПЧ, 438, 458
физическая реализуемость, 89
фиксированная запятая, 375
фильтр
адаптивный, 190, 476
антисимметричный, 204
Баттерворта, 105, 120, 482
Бесселя, 114, 120
групповая задежка, 125
верхних частот, 104
Винера, 282
внутреннее состояние, 214
всепропускающии, 196, 366
выбор порядка, 121
дискретный, 213
блочный в частотной области, 268
внутреннее состояние, 239
преобразование способов
описания, 224
реализация в частотной
области, 265
устойчивость, 395
форма реализации, 206
частотная характеристика, 217
дифференцирующий, 351, 357
заграждающий, 104
Кауэра, 112
максимально-фазовый, 365
минимально-фазовый, 365
мпогополосный, 340
начальное состояние, 214
нерекурсивный, 191, 202
импульсная характеристика, 203
нижних частот, 104
полосно-задерживающий, 104
фильтр (продолжение)
полосовой, 104
идеальный, 141
пробка, 104
прототип, 104, 313
преобразование, 116
режекторный, 104
рекурсивный, 192, 205
импульсная характеристика, 205
с бесконечной импульсной
характеристикой, 206
с конечной импульсной
характеристикой, 203
с косииусоидальным сглаживанием
АЧХ, 324, 344
SQRT-вариант, 328, 473
с переменными параметрами, 190
симметричный, 204, 215
трансверсальный, 202
цифровой
масштабирование, 387
предельный цикл, 393
Чебышева
второго рода, НО, 120
групповая заде5кка, 125
первого рода, 107, 120
эллиптический, 112, 120
флуктуации, 64, 68, 73-74
ФМ, 448
ФМн, 467
ФНЧ, 104
идеальный, 138
форма реализации дискретного фильтра
каноническая, 206, 210
каскадная, 210, 227
параллельная, 211, 226
последовательная, 210, 227
прямая, 206
транспонированная, 208
форматы представления чисел, 374
отрицательных, 374
с плавающей запятой, 377
неявный старший бит, 377
нормализованный, 377
с двойной точностью, 379
с одинарной точностью, 379
с расширений точностью, 380
соглашение
о денормализации, 378
с фиксированной запятой, 375
формирование спектра, 474
формирующий фильтр, 474
Алфавитный указатель
603
функция
Бесселя, 451
включения, 20
Дирака, см. дельта-функция, 19
Дирихле, 167, 188
единичного скачка, 20, 89
спектр, 48
кусочно-заданная, 154
ошибок, 66
передачи, 195
распределения вероятности, 63
преобразование, 172
с переменным числом
параметров, 531
фазовая, 55
Хевисайда, 20
Чебышева, рациональная, 112
ФЧХ, 90, 97
линейная, 215
х, ц
характеристика квантования, 405
ЦАП, 129, 136, 151
ШИМ-реализация, 478
центральная предельная теорема, 67
центральная частота, 58
цифро-аналоговый
преобразователь, 129
ч
частное, 212
частота, 19
биений, 438
дискретизации, 127, 151, 179
мгновенная, 168, 448
Найквиста, 130
средняя, 104
среза, 104
центральная, 58
частотная дисперсия, 476
частотная манипуляция, 462
демодуляция, 464
когерентная, 464
некогерентная, 465
минимальная, 465
с непрерывной фазовой
функцией, 463
частотная модуляция, 448
демодуляция, 456, 458
частотная область, 34
частотная характеристика, 196
частотное разделение каналов, 426
частоты ложные, 130, 133
чебышевская аппроксимация, 319
ЧМ, 448
ЧМн, 462
ш
шаг дискретизации, 127
ШИМ, 477
широкополосные сигналы, 36
широтно-импульсная модуляция, 477
шум, 60
белый, 79
коррелированный, 174, 176
шум квантования, 128, 380
размах, 382
шумовое подпространство, 283
э,я
экспоненциальный формат, 377
энергетический спектр, 54
энергия, 21, 50, 53
случайного процесса, 75
эргодичность, 72
эффект Гиббса, 28, 319
эффективная ширина спектра, 36, 78
ячейка памяти, 202
Сергиенко Александр Борисович
Цифровая обработка сигналов
Главный редактор Е. Строганова
Заведующий редакцией И. Корнеев
Литературный редактор Е. Бочкарева
Художник Н. Биржаков
Корректор В. Листова
Верстка Ю. Сергиенко
Лицензия ИД № 05784 от 07.09.2001.
Подписано в печать 01.07.02. Формат 70х100'/16.
Усл. п. л. 49,02. Тираж 4500 экз. Заказ № 806. '
ООО «Питер Принт».
196105, Санкт-Петербург, ул. Благодатная, 67в.
Налоговая льгота - общероссийский классификатор продукции
ОК 005-93, том 2; 953005 - литература учебная.
Отпечатано с готовых диапозитивов в ФГУП «Печатный двор» им. А. М. Горького
Министерства РФ по делам печати, телерадиовещания и средств массовых коммуникаций.
197110, Санкт-Петербург, Чкаловский пр., 15.
А. Б. Сергиенко
ЦИФРОВАЯ
ОБРАБОТКА СИГНАЛОВ
| УЧЕБНИК /ДЛЯ ВУЗОВ |
Базовый курс для студентов высших
учебных заведений.
Задача этой книги — познакомить читателя
алгоритмами цифровой обработки
сигналов. Материал изложен так, чтобы
наглядно продемонстрировать сущность
алгоритмов, их взаимосвязь и области
Теоретические сведения сопровождаются
гримерами реализации обсуждаемых
алгоритмов с помощью системы MATLAB
и ее пакетов расширения Signal Processing,
Communications и Filter Design.
Книга предназначена для широкой
читательской аудитории — студентов,
преподавателей, научных работников,
программистов, а также всех,
кто интересуется компьютерной
обработкой сигналов и иных данных.
■ППТЕР*