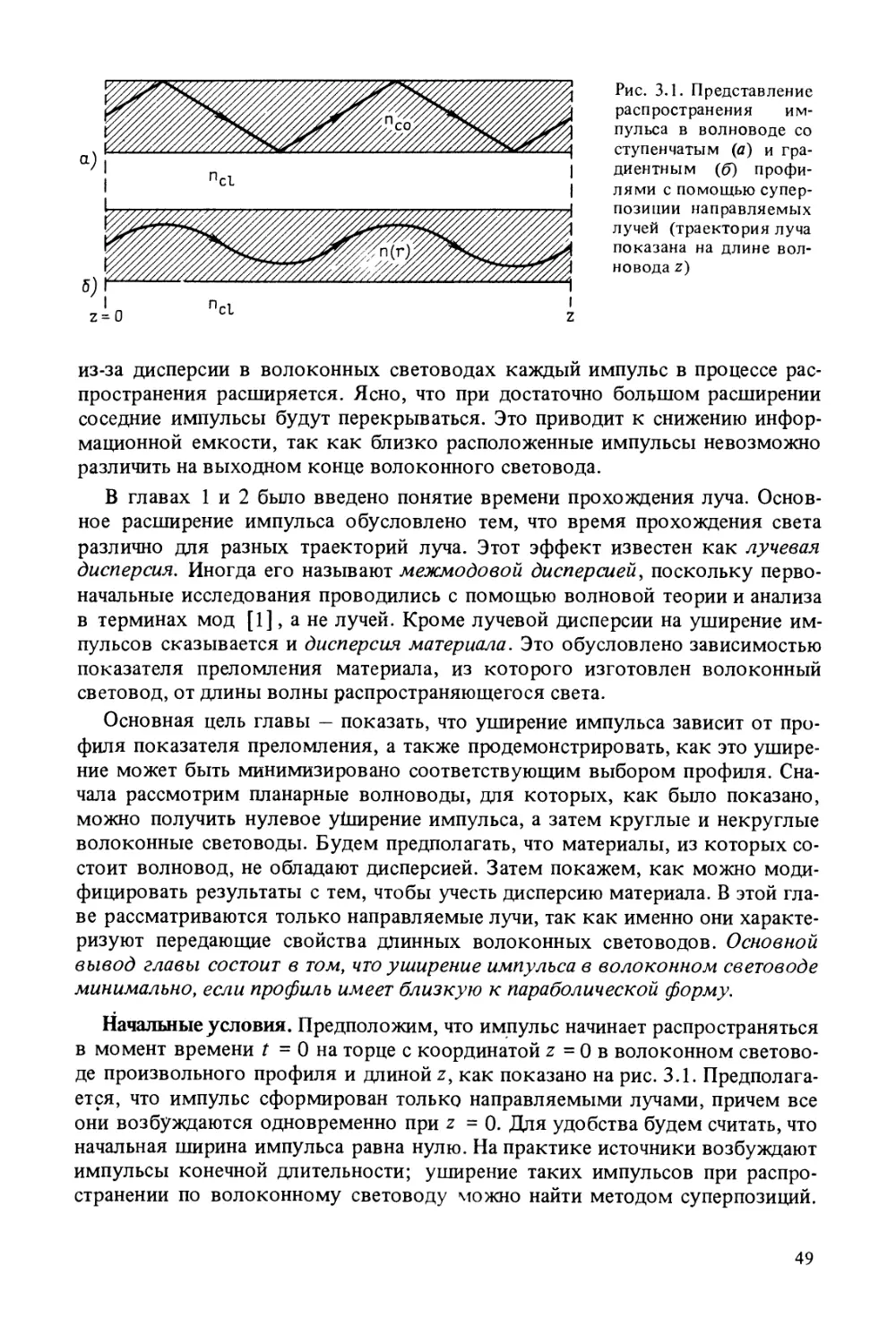
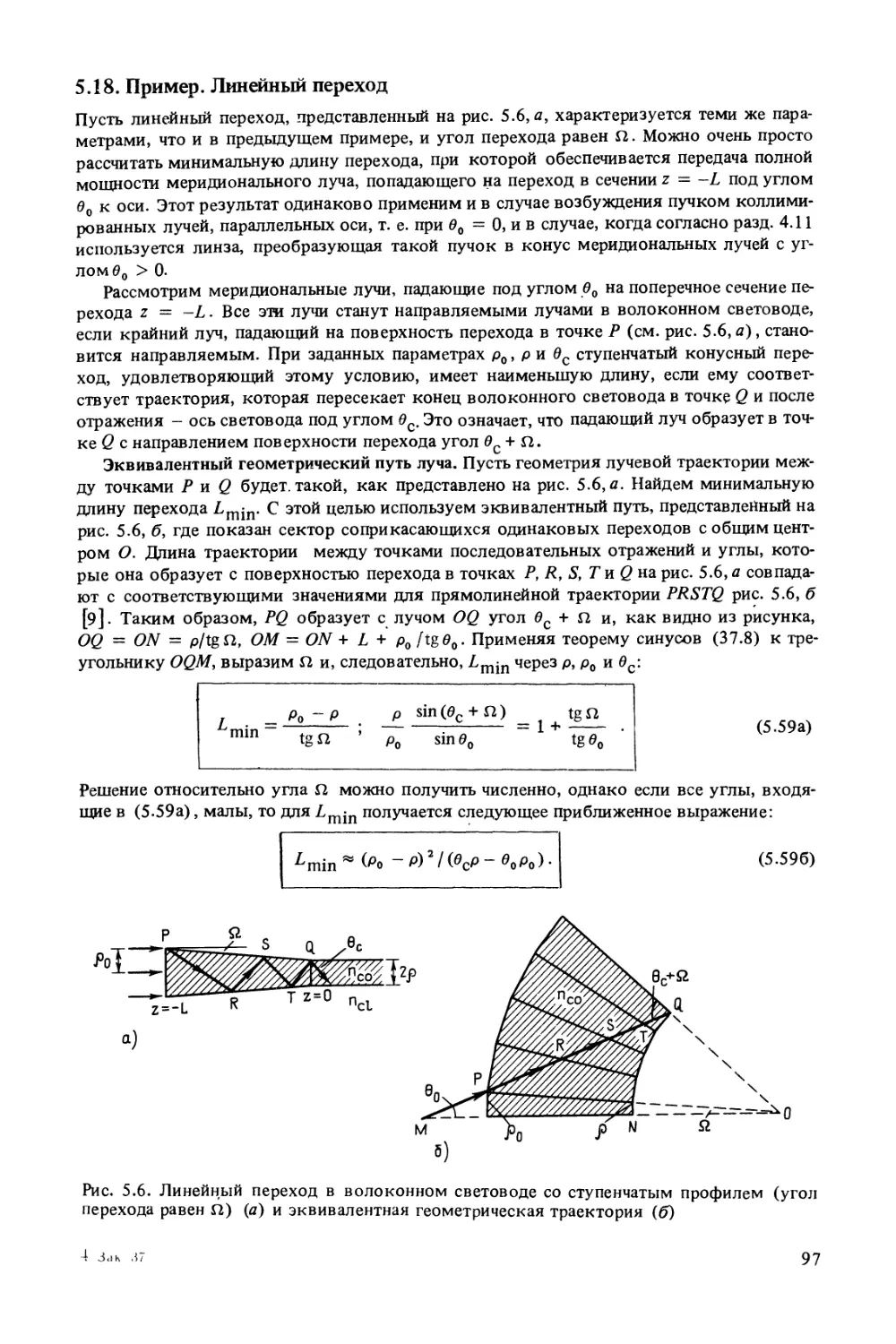
Author: Снайдер А. Лав Дж.
Tags: электротехника наука и знание в целом науковедение организация умственного труда физика оптические волноводы
Year: 1987
Text
Теория оптических волноводов
Теория
оптических
волноводов
Таблица I
Лучевые параметры
Числовая апертура |
{л2(г)-л*}1/2 Локальная числовая апертура >
С п2 Р/2 0Jr) = sin’4 1 п (г)) = cos’1 I — 1 1 "(О J Локальный критический угол скольжения
ОАг) Угол между траекторией луча и осью
Ъ(г) Угол между проекцией траектории на поперечное сечение световода и азимутальной осью
а(г) Угол между траекторией и радиальным направлением
/Г = n(r)cos 0z(r) Осевой инвариант
г Т= — и(г) sin 0z(r) cos 0ф(г) Р Азимутальный инвариант
Гк Радиус внутренней каустики
гч> Радиус каустики точек поворота
г - р1 Радиус каустики излучения
1 Zp_ N Полупериод траектории луча, отсчитываемый вдоль оси световода
N = - 2р Число отражений, или точек поворота на единице длины световода
ч Геометрическая длина пути луча на полупериоде траектории
Lo Оптическая длина пути луча на полупериоде траектории
С V =* • п(г) Локальная скорость света
t Время прохождения луча
Таблица I
Параметры волновода или световода
л(х,у) or л(г) Профиль показателя преломления
л2(х,у) = п^{1 -2bf(x,y)} л2(г) = «£,{1 -2A/V)} Представление профиля
an Групповой показатель
Л . "со-”2! ... sin20c 2"t ' 2 Параметр высоты профиля
3 '«Л О Q II Т?|"е8 1 1 с *35 II <х>° Критический угол скольжения
«со (/'0) Максимальное значение показателя преломления в сердцевине
nd =пм(1-2Д),/2 (/=1) Однородный показатель преломления оболочки
S=l-/ Форма профиля
П= 1 (1-/)с1Л= хал ^oc Объем профиля
Неограниченное поперечное сечение
Поперечное сечение сердцевины
p Радиус сердцевины (для градиентных световодов - полуширина)
к Длина волны в свободном пространстве
2л _ V 2 рпю(2Д)1;2 Волновое число в свободном пространстве
V = М"«-л21)‘/2 = <срп^(2Д)1/2 = kpnco sin 0С Волноводный, или волоконный параметр
"со = па ог Д < 1 д "со~"с1 "со / п2 \1/2 / И . \ = (2А)1/2 = ( 1--4 ) ^cos-Ч -М \ </ \лсо/ Приближение слабонаправляющего волновода, или параксиальное при ближение
Теория
а снайдер оптических
ДЖ. лав ВОЛНОВОДОВ
Optical
Waveguide
Theory
ALLAN W. SNYDER
JOHN D. LOVE
Institute of Advanced Studies
Australian National University
Canberra, Australia
LONDON NEW YORK
Chapman and Hall
А.СНАЙДЕР
Дж. ЛАВ
Теория
оптических
волноводов
Перевод с английского
под редакцией
Е.М.Дианова и В. В. Ш-евченко
@
Москва
« Радио и связь» 1987
Scan AAW
УДК 621.372.8.029.7:001
Снайдер А., Лав Дж. Теория оптических волноводов: Пер. с англ. - Радио и связь,
1987. - 656 с.: ил.
Книга австралийских ученых является фундаментальным трудом по теории опти-
ческих волноводов как передающей среды для оптических систем связи и передачи ин-
формации. В ней проведен анализ физических явлений и процессов в оптических волно-
водах, в первую очередь в волоконных световодах, и рассмотрены методы расчета ос-
новных параметров как самих волноводов, так и направляемых ими волн (мод).
Книга состоит из трех частей.
В ч. I на основе лучевого подхода проанализированы многомодовые оптические
волноводы: рассмотрены волоконные световоды со ступенчатым и градиентным профи-
лями показателя преломления и распространение в них направляемых лучей, проанали-
зированы процессы распространения импульсов, влияние на них условий возбуждения
источниками и дисперсии материала волоконные световодов, исследованы нерегуляр-
ности и изгибы световодов, рассмотрены вытекающие лучи и связанные с ними потери.
В ч. И изложена теория электромагнитных волн применительно к маломодовым и
одномодовым оптическим волноводам; даны основы скалярного приближения теории
мод в слабонаправляющих волоконных световодах и векторное уточнение этой теории
для тех случаев, когда важны поляризационные эффекты; исследованы световоды с
круглым и некруглым сечениями, рассмотрены вопросы определения и достижения
одномодового режима работы волоконных световодов, возбуждения и гауссовой ап-
проксимации основных мод, включая расчет их параметров методами теории возмуще-
ний, проведен анализ условий распространения волн в нерегулярных световодах и вли-
яния микроизгибов на основе теории связанных волн, исследованы проблемы соедине-
ния световодов, разработки направленных ответвителей и др.
В ч. III дано физико-математическое обоснование анализа, проведенного в ч. I и II.
В ней рассмотрены основные положения теории электромагнитных волн: уравнения
Максвелла, теорема взаимности, метод функций Грина, а также связь между волновым
и лучевым методами описания мод в волноводах. Приведен ряд важных математичес-
ких формул, используемых при изложении основного материала.
Для научных работников.
Табл. 43. Ил. 160. Библиогр. 364 назв.
Переводчики: А. Б. Грудинин, В. Б. Сулимов, С. Я. Фельд, О. Е. Шушпанов
Редакция переводной литературы
_ 2402040000-200
046 (01)-87
© 1983 Allan W. Snyder and John D. Love
© Перевод на русский язык, предисловие редакторов пере-
вода, примечания переводчиков и редакторов, дополнитель-
ный список литературы. Издательство ’’Радио и связь”, 1987
ПРЕДИСЛОВИЕ АВТОРОВ К РУССКОМУ ИЗДАНИЮ
Нам чрезвычайно приятно, что книга ’’Теория оптических
волноводов” станет доступна теперь и советскому читате-
лю и послужит основой лучшего взаимопонимания при
последующих исследованиях и публикациях на двух язы-
ках. В наши намерения входило подготовить достаточно
исчерпывающий и глубокий материал по данному пред-
мету, что и было подтверждено успехом английского
издания книги. Кроме исправления опечаток текст пол-
ностью сохранен.
Дж. Лав
А. Снайдер
ПРЕДИСЛОВИЕ РЕДАКТОРОВ ПЕРЕВОДА
В современной теории оптических волноводов используются как методы гео-
метрической оптики, применимые к многомодовым волоконным светово-
дам, так и волновые методы прикладной электродинамики, используемые в
основном при анализе маломодовых и одномодовых волоконных светово-
дов, а также волноводов интегральной оптики. Изложенная в данной книге
теория отражает оба указанных подхода. При этом следует отметить, что
описанная в книге волновая методика частично повторяет, частично развива-
ет ряд положений общей электродинамической теории регулярных и нерегу-
лярных волноводов, включая теорию связанных волн на основе обобщенных
телеграфных уравнений [Д1, Д2], метода поперечных сечений [ДЗ — Д5] и
метода, основанного на использовании формул сдвига [Д6, Д7].
Книга содержит в основном все результаты, полученные по теории воло-
конных световодов к моменту выхода английского издания. Исключением
являются результаты по статистически нерегулярным волоконным светово-
дам, которые слабо отражены в книге. В литературе на русском языке эти
результаты имеются кроме переводных изданий [Д8, Д9] в монографиях
[ДЮ, Д11 ]. В книге не уделено также достаточного внимания такой актуаль-
ной теме, как поляризационные и когерентные свойства излучения в одномо-
довых и многомодовых световодах. Этот пробел читатели могут восполнить,
ознакомившись, например, с работами [Д12 — Д15].
Авторы книги — известные специалисты в области волоконной оптики.
Член Австралийской академии наук проф. А. Снайдер и д-р Дж. Лав, а также
сотрудники Института перспективных исследований при Австралийском на-
циональном университете в Канберре, работающие под руководством проф.
А. Снайдера, внесли существенный вклад в теорию оптических волноводов,
в первую очередь в теорию волоконных световодов. Их работы широко из-
вестны. .Они составляют основу книги. Вместе с включенными в нее важны-
ми результатами других авторов книга представляет собой фундаменталь-
ный труд по теории оптических волноводов. Она написана в такой форме,
что ею могут пользоваться не только специалисты, но и студенты старших
курсов и аспиранты, специализирующиеся в области оптической связи и пере-
дачи информации.
При переводе в книге исправлены некоторые неточности и опечатки,
включая те, на которые указали авторы книги.
Е. М. Дианов
В. В. Шевченко
6
ПРЕДИСЛОВИЕ
Цель данной монографии — попытаться дать глубокое и полное изложение
теории оптических волноводов. Мы постарались выявить фундаментальные
физические процессы, подчеркнуть некоторые принципиальные моменты и
провести математический анализ явлений. В книге имеются довольно обшир-
ные дополнительные разделы, восполняющие недостающий математический
материал и обеспечивающие достаточно полное и строгое математическое
описание. Для облегчения понимания в каждой главе акцент делается глав-
ным образом на одной какой-либо идее, поэтому главы относительно корот-
кие. Для иллюстрации применения теории рассмотрены полные решения бо-
лее 150 задач. Благодаря простоте изложения и многочисленным примерам
книга доступна для студентов. Многие вопросы изложены впервые, однако,
что важнее, весь материал собран воедино. Книга позволяет читателю по-
нять основные идеи с помощью наиболее простых методов. Для этого потре-
бовалось, чтобы материал в целом устоялся, поэтому текст совершенствовал-
ся в течение последних 10 лет.
СТРУКТУРА КНИГИ
Книга разбита на три части. В первой представлены методы анализа распро-
странения света в многомодовых оптических волноводах, применяемые в
геометрической оптике. Во второй рассмотрена волновая теория, причем
основное внимание уделено волноводам, в которых может распространять-
ся одна или несколько мод. Для таких волноводов методы, предложенные
в первой части, неприменимы. В третьей содержатся дополнительные разде-
лы по физико-математическим методам, позволяющим в основном дать опи-
сание физических явлений в волноводах, о которых шла речь в первых двух
частях. Можно читать вторую часть, не читая первой, однако, делать это не ре-
комендуется. Кроме того, хотя и не обязательно читать все главы по поряд-
ку, целесообразно подробно ознакомиться, по крайней мере, с темами каж-
дой из них. Пояснения по этому и другим вопросам даны во введениях к
первой и второй частям.
ЛИТЕРАТУРА
В тексте цитируется литература, с которой мы наиболее знакомы и которая
может помочь в понимании изучаемого предмета. Пока еще не было предпри-
нято попыток оценить вклад каждого автора публикаций по рассматривае-
мым вопросам, поэтому даны ссылки в основном на оригинальные работы,
посвященные новым и важным методам теории оптических волноводов.
7
РЕКОМЕНДАЦИИ ЧИТАТЕЛЮ
Поскольку основная цель книги — провести исчерпывающее рассмотрение
теории оптических волноводов, то для полноты изложения авторы намерен-
но расположили все разделы в логическом порядке. Однако для читателей,
интересующихся конкретными вопросами, чтение всех глав необязательно.
Для облегчения выборочного чтения в книге даются соответствующие пояс-
нения. В частности, при первом чтении для понимания существа вопроса до-
статочно ознакомиться лишь с некоторыми главами. Таким образом, для не-
большого 30-часового лекционного курса, рассчитанного на 10 недель, мо-
гут быть рекомендованы главы 1,3, 5, 6 и 10 из первой части и главы 11,
12, 13, 14, 15, 19 и 20 из второй части. При этом исключается в основном ма-
териал, касающийся потерь на излучение.
БЛАГОДАРНОСТИ
В заключение мы хотим выразить благодарности д-ру К. Паску, нашему кол-
леге и ближайшему сотруднику, который дал много ценных рекомендаций
по всем вопросам, и д-ру А. Анкиевичу, оказавшему помощь по проверке
математических выкладок. В течение нескольких лет существенный вклад
своими вопросами и критическими замечаниями, а также ценными резуль-
татами исследований внесли многие наши бывшие студенты. Особенно нам
хочется поблагодарить д-ров К. Ф. Баррела, М. К. Кэмпбелла, Д. Д. Карпен-
тера, К. Д. Хасси, П. Д. Макинтайера, Р. А. Сэмата, И. А. Уайта, К. Уинклера
и У. Р. Янга, а также наших нынешних студентов Р. Д. Блэка, Ф. Рюла и
И. Скиннера. Перепечатка окончательного варианта рукописи была осуще-
ствлена Д. Алекс и П. Уоллей, подготовка иллюстраций была выполнена
С. Смит.
Ч А С Т Ь I. ЛУЧЕВОЙ АНАЛИЗ МНОГОМОДОВЫХ
ОПТИЧЕСКИХ ВОЛНОВОДОВ
ВВЕДЕНИЕ
Оптические волноводы - это диэлектрические структуры, по которым мо-
жет распространяться электромагнитная энергия в видимой и инфракрасной
областях спектра. Реальные волноводы, используемые в оптической связи,
представляют собой гибкие волокна из прозрачных диэлектрических мате-
риалов. Поперечное сечение таких волоконных световодов имеет размеры,
сравнимые с размерами человеческого волоса, и обычно состоит из трех
областей, как показано на рис. 1.1. Центральная область — сердцевина — окру-
жена оболочкой, которая, в свою очередь, окружена защитным покрытием.
В области сердцевины показатель преломления п может быть постоянным
или изменяться по сечению, показатель преломления оболочки обычно по-
стоянен по сечению. Два случая, соответствующие ступенчатому и градиент-
ному профилям показателя преломления, иллюстрируются на рис. 1.1. Для
обеспечения направляющих свойств необходимо, чтобы показатель прелом-
ления сердцевины хотя бы в части сечения превосходил показатель прелом-
ления оболочки. В большинстве применений основная доля передаваемой
энергии распространяется в сердцевине и лишь малая ее часть — по оболоч-
ке. Покрытие практически полностью оптически изолировано от сердцеви-
ны, поэтому мы обычно будем пренебрегать его влиянием и при анализе для
простоты будем предполагать, что оболочка снаружи не ограничена.
Многомодовые и одномодовые волноводы. Оптические волноводы можно
условно разделить на две группы — многомодовые (с относительно больши-
ми поперечными размерами сердцевины) и одномодовые ( с относительно
малыми поперечными размерами сердцевины). Такое разделение обсужда-
ется в разд. 10.3 и гл. 11, 12. Для многомодовых волноводов справедливо
условие (2тгр/Х) (п20 - п2})1/2 >> 1, где р — характерный размер сердцеви-
ны, например радиус сердцевины волоконного световода, X — длина волны
света в свободном пространстве, — максимальное значение показателя
преломления сердцевины, а ис1 — показатель преломления оболочки. Они рас-
смотрены в ч. I, тогда как ч. II посвящена в основном одномодовым и мало-
модовым волноводам. Типичные области значений параметров волоконных
световодов, используемых для дальней связи, представлены на рис. 1.1 [1].
С вопросами их применения можно ознакомиться в работах [2, 3].
Лучевой подход. Распространение электромагнитных волн по оптическим
волноводам может быть описано строго с помощью уравнений Максвелла.
Однако хорошо известно, что классическая геометрическая оптика дает
приближенное описание распространения света в среде, где показатель пре-
ломления слабо изменяется на расстояниях порядка длины волны света. Это
условие обычно выполняется для многомодовых оптических волноводов,
используемых в системах связи. Таким образом, наиболее прямой и нагляд-
9
Покрытие
Оболочка
СерЭцебана
Многомобобый
болоконный сбетобоб
12,5мкм<р< ЮОмкм
0,8 мкм< X < 1,6 мкм
0,01 < А < 0,03
Обномобобый
волоконный, сбетобоб
Zmkm<p<5мкм
0,8мкм< Л < 1,6мкм
0,003 < А < 0,01
ж
Рис. 1.1. Обозначения, профили показателя преломления и области значений параметров
для типичных оптических волокон (р - радиус сердцевины, X - длина волны света в
в свободном пространстве Д - (1 - /2 [1]
ный способ описания распространения света в многомодовых волноводах —
с помощью лучей, распространяющихся по сердцевине. Поэтому первые пять
глав основываются только на классической геометрической оптике. Читате-
ли, интересующиеся решениями уравнений Максвелла применительно к клас-
сической геометрической оптике, могут обратиться к началу гл. 35.
Волновые эффекты. Согласно классической геометрической оптике пре-
небрежем всеми волновыми эффектами. Как будет показано в гл. 10, это
справедливо для многомодовых волноводов, однако в некоторых исключи-
тельных ситуациях подобные эффекты накапливаются экспоненциально с
расстоянием вдоль светового луча. В таких случаях их необходимо учиты-
вать, так как в волноводах большой протяженности они оказывают суще-
ственное влияние на распространение света. Примеры таких ситуаций, а так-
же потери мощности на излучение, поглощение в оболочке и излучение на
изгибах рассмотрены в гл. 6 - 9. В каждом таком случае будем модифициро-
вать классическую геометрическую оптику на основе концепции локальных
плоских волн.
Описание с помощью мод. Существует альтернативный подход к описанию
распространения света в многомодовых волноводах, основанный на корот-
коволновом приближении для электромагнитных волн, распространяющихся
в оптических волноводах. Он дает те же результаты, что и классическая гео-
метрическая оптика, однако это требует выполнения дополнительных алге-
10
браических преобразований. Этот подход описан в гл. 36 и может рассматри-
ваться как пример получения результатов из решений уравнений Максвелла
в пределе малых длин волн.
Уширение импульсов. Наибольший практический интерес с точки зрения
использования волоконных световодов для линий связи большой протяжен-
ности представляет явление уширения распространяющихся по ним импуль-
сов. В случае идеальных многомодовых волоконных световодов уширение
импульсов может быть легко описано с помощью классической геометри-
ческой оптики, как показано в гл. 3. Для изучения вопросов, связанных толь-
ко с уширением импульсов, можно ограничиться гл. 3 и некоторыми резуль-
татами гл. 1. Однако цели первой части значительно обширнее — заложить
основы для всеобъемлющего рассмотрения оптических волноводов с при-
влечением геометрической оптики. Это позволяет полнее учесть послед-
ствия отклонений от идеализированных условий, характерных для практики.
ГЛАВА 1. НАПРАВЛЯЕМЫЕ ЛУЧИ В ПЛАНАРНЫХ ВОЛНОВОДАХ
Лучевой анализ многомодовых оптических волноводов проведем для про-
стейшей диэлектрической структуры — планарного волновода, или плоского
слоя, на примере которого проиллюстрируем основные принципы теории.
К тому же эта структура широко используется в интегральной оптике. По-
скольку анализ направляющих свойств волновода можно провести, исполь-
зуя суперпозицию лучевых траекторий, то необходимо детально изучить их
поведение. В этой главе будем исследовать траектории лучей в планарных
волноводах, особое внимание уделяя направляемым лучам, которые в
волноводах из непоглощающих материалов распространяются без потерь
энергии и, таким образом, могут передаваться на достаточно большие рас-
стояния.
1.1. Планарные волноводы
Структура планарного волновода представлена на рис. 1.1. Типичные волно-
воды этого класса состоят из световедущего слоя — сердцевины — толщиной
2р, расположенного между двумя слоями оболочки. Как уже отмечалось во
введении, для простоты мы предполагаем, что слои оболочки имеют беско-
нечную толщину. Плоскости х = ±р являются границами раздела сердцеви-
на — оболочка. Так как волновод простирается неограниченно во всех на-
правлениях, ортогональных к оси х, то структура является двумерной. Ось
z расположена вдоль средней линии между границами раздела. Тогда по-
казатель преломления п (х) в сердцевине может быть либо постоянным по
сечению, либо изменяющимся в поперечном направлении. В оболочке показа-
тель преломления обычно постоянен по сечению и равен ис1. При этом пока-
затель преломления сердцевины должен превосходить яс1 для обеспечения
направляющих свойств волновода. Далее в этой главе будем предполагать,
что профиль не изменяется вдоль осиг, т. е. волновод обладает трансляцион-
11
Рис. 1.1. Обозначения и система координат, используемые при описании планарных вол-
новодов. Изображен градиентный профиль — переменный в сердцевине и постоянный в
оболочке, которая предполагается неограниченной
Рис. 1.2. Прямолинейное распространение луча между противоположными границами
сердцевины в планарном волноводе со ступенчатым профилем
ной инвариантностью, или ”цилиндрической” симметрией*. Параметры пред-
ставленного на рис. 1.1 волновода и длина волны света X в свободном прост-
ранстве могут быть объединены в один безразмерный параметр V, называе-
мый волноводным параметром, или волноводной частотой. Пусть nCQ — мак-
симальное значение п(х), которое не обязательно совпадает со значением
п (0) на оси волновода, тогда Vопределяется следующим образом:
И=^р(п2 -и2,)1/2.
X со сг
(1-1)
Альтернативная форма представления V дана в табл. I (см. форзац). Луче-
вой подход применим только к многомодовым волноводам, т. е. волново-
дам, удовлетворяющим условию V> > 1 (см. гл. 10 и 36).
ПЛАНАРНЫЕ ВОЛНОВОДЫ СО СТУПЕНЧАТЫМ ПРОФИЛЕМ
В обозначениях рис. 1.2 профиль показателя преломления планарного волно-
вода со ступенчатым профилем может быть записан в виде
п(х) =ПСО, —р<х<р; п(х) =па,\х\>р, (1.2)
* Слово ’’цилиндрическая” взято здесь в кавычки, так как оно относится к волокон-
ному световоду, а здесь рассматривается плоский волновод. - Прим. ред.
12
где «со и ис1 — константы и ис0 > «с1. Теперь покажем, как Построить луче-
вые траектории в сердцевине с помощью закона Спелля. Одна из наиболее
важных задач — определение условий, при которых луч является направля-
емым, т. е. распространяется вдоль непоглощающего волновода без потерь
мощности.
1.2. Построение лучевых траекторий
В волноводе со ступенчатым профилем (рис. 1.2) свет распространяется в
сердцевине по прямым линиям. Если луч выходит из точки Р на одной грани-
це раздела под углом 0Z к оси волновода, то он пересекает вторую границу
раздела в точке Q, как показано на рисунке. Причем ситуация в точке Q эк-
вивалентна падению луча на границу раздела двух полупространств, заполнен-
ных средами с показателями преломления пс0 и ис1 (см. рис. 1.3). Отражение
в этом случае подчиняется закону Спелля [1, 2]. Обычно этот закон записы-
вается для углов, образуемых лучами с нормалью QN, как это показано
в разд. 35.2, здесь будем использовать углы скольжения 0Z. Преимущество
такого выбора станет очевидным в гл. 2 при классификации лучевых траек-
торий в волоконных световодах. Таким образом, в терминах углов скольже-
ния падающий луч в точке Q испытывает полное внутреннее отражение, если
О < 0Z < 0С, а при выполнении условия 0С ^z < я/2 он частично отражается
и частично преломляется; здесь вс - критический угол скольжения,опреде-
ляемый следующим соотношением:
(1.3)
В первом случае, как видно из рис. 1.3, а, отраженный луч распространяет-
ся под тем же углом к поверхности раздела, что и падающий. Во втором слу-
чае (рис. 1.3, б) луч раздваивается: часть мощности отражается под углом
0Z, а другая часть преломляется и распространяется в оболочке под углом
к поверхности раздела согласно закону Спелля
/?cocos0z =flcicos0t. (1.4)
Рис. 1.3. Отражение от плоской границы раздела полупространств с показателями пре-
ломления псо и пс\.
а — полное внутреннее отражение; б — частичное отражение и преломление
13
Рис. 1.4. Зигзагообразные траектории направляемых (я) и рефрагируюших лучей (6) в
сердцевине планарного волновода со ступенчатым профилем показателя преломления
Только в случае полного внутреннего отражения мощность луча сохраняется,
т. е. энергия, распространяющаяся по лучевой траектории, полностью возвра-
щается в область сердцевины.
Лучевая траектория. Луч, отраженный от границы раздела, возвращает-
ся в область сердцевины под углом 0Z как при частичном, так и при полном
внутреннем отражении. Повторяя эту процедуру последовательно, можно
построить зигзагообразные пути световых лучей, или траектории, изображен-
ные на рис. 1.4. Траектория (а) соответствует лучу, который каждый раз ис-
пытывает полное внутреннее отражение. Такие лучи оказываются направля-
емыми, так как их траектории полностью расположены внутри сердцевины.
Траектория (5) соответствует лучу, который каждый раз испытывает лишь
частичное отражение. Такие лучи называются рефрагирующими. Все лучи мо-
гут быть классифицированы в соответствии со значением угла в7 следующим
образом:
(1.5а)
(1.56)
Поскольку после каждого отражения вся мощность направляемых лучей
полностью возвращается в область сердцевины, такие лучи могут распростра-
няться на неограниченные расстояния без затухания. Рефрагирующие же лучи
теряют часть своей мощности при каждом отражении и поэтому затухают в
процессе распространения. Этот случай будет рассмотрен в гл. 7.
направляемые лучи: O<0Z<0C;
рефрагирующие лучи: 0с < 0z < *
1.3. Лучевой инвариант
Периодический характер лучевой траектории на рис. 1.4 является следстви-
ем транслЯ-Ционной инвариантности волновода и позволяет ввести лучевой
инвариант /3, который постоянен вдоль пути распространения луча и характе-
ризует его направление в любой точке поперечного сечения сердцевины. Для
ступенчатых волноводов инвариантность выражается уравнением (1.4), по-
этому /3 определим так:
@ = nco^s3z -^C\cos6t. (1.6)
14
Хотя для ступенчатых волноводов указанное соотношение тривиально и
не дает каких-либо преимуществ, в случае градиентных профилей введение
лучевого инварианта существенно упрощает описание лучевой траектории,
как будет показано в разд. 1.7. Зависимость между лучевым инвариантом и
направлением распространения позволяет классифицировать лучи в соот-
ветствии со значением их инварианта /3. Из (1.5) получаем следующие соот-
ношения:
(1.7а)
(1-76)
направляемые лучи: 77С1 < @ псо ’
рефрагирующие лучи: 0 < (3 <лсГ
1.4. Лучевые параметры
Удобно ввести параметры, характеризующие путь распространения луча в
целом, поскольку они являются более важными, чем параметры, описываю-
щие пространственное положение лучевой траектории. Совместно с лучевым
инвариантом эти параметры будут часто использованы в последующих гла-
вах. Лучевая траектория на рис. 1.5 полностью определяется, если задан угол
0Z. Определим длину пути Lp между последовательными отражениями луча
как расстояние между точками Р и Q. Она будет использована при рассмотре-
нии затухания в гл. 6. Из соображений геометрии
2р 2рпсо
Р sin0z ^2 -(руп ’
где 3 определяется соотношением (1.6). Для определения в дальнейшем вре-
мени прохождения луча введем оптическую длину пути LQf которая в одно-
родной среде определяется как произведение длины пути на показатель пре-
ломления. Соответственно
_ 2рлсо 2рп2со
О "«СО^р - sinpz - (л2о _ £2)1/2 • (1-9)
При рассмотрении затухания будет часто использоваться полупериод траекто-
рии луча zp, который представляет собой расстояние между точками после-
довательных отражений, измеренное вдоль оси волновода,
Zp = tg0z
= Zpcos0z =
Рис. 1.5. Длина пути £р и полупериод zp
траектории луча, распространяющегося в
сердцевине планарного волновода со сту-
пенчатым профилем показателя прелом-
ления
(1-10)
2рР
(«со - 02)1'2
15
Таблица I. I. Лучевые параметры в планарных волноводах
Профиль п2 (х) Полупериод лучевой траектории zp= 1/N Длина пути Lp Оптическая длина пути Lo Время прохождения луча t
Ступенчатый «ch |*|>Р 2р? ой-?2)1'2 2р«со (л^-?2)*'2 2Р«» (и^-?2),/2 с?
Г радиентный п2(х); |х| < р «I;1*1> р _ f *р- dx n(x)dx Г^р n2(x)dx CZP
дТх,Р{«2(*)-л,/2 J-X,p{"2(*)-Р2}1'2 J-^p{n2(*)-?2},/2
Параболи- ческий 44)’} *Р? n„s/(2A) 2pf3«eo . ? 1 4 I ? "J Д< 1 ^й+?| 2 1? J Ml N 83 I'5»
Г иперболи- ческий секансный п^, sech2 | яр Т(2Д) A Vco n | N 83
Усеченный степенной 4-2лГ}; _|*|_<_р «ей 1*1 > Р ч/ФОЛр / Р Г «"соУД \*.р/ Г(1/«+1/2) {«+2}tao Д« 1 Исо f лсо . 1 4T2VT+d 2 «co f "co.^?l c(<j + 2)C? n№)
Д = COS0х:ступенчатый профиль 7= и(х) COS 0t(x) = n(xtp): градиентный профиль « 1 к 1 II <1 ГЧ
Примечание. Полупериод, длина пути и оптическая длина пути указаны между точками последовательных отражений, или точками по-
ворота, а время прохождения определяется на длине волновода 2. Количество отражений, или точек поворота, на единицу длины N =
= 1/2р, р — полуширина сердцевины, или масштабный параметр профиля. Каустика определяется из условия п (х) = Д.
Количество отражений N на единицу длины волновода обратно пропорцио-
нально полупериоду траектории луча. Следовательно,
Из этих определений следует, что в произвольной точке на расстоянии z от
начала волновода длина пути, оптическая длина пути и количество отражений
определяются соответственно выражениями:
zpLV' zpL°> г ZP • (1.12)
Для удобства все эти параметры сведены в табл. 1.1.
1.5. Время прохождения луча
Наиболее важной величиной, необходимой для описания процесса уширения
импульса, является время прохождения луча t. Это время, в течение которо-
го луч распространяется на расстояние z вдоль волновода по зигзагообразной
траектории, показанной на рис. 1.4. Скорость света вдоль лучевой траектории
Ug=c/«CO> (1ЛЗ)
где с — скорость света в вакууме, «со — показатель преломления сердцеви-
ны. При этом время прохождения луча в соответствии с соотношениями
(1.6) — (1.12) определяется следующим образом:
____z _ z _ z ”со _ £ ”со
г = £ «7 Zp 6- Ср С COS0Z
следовательно, чем больше 0Z, тем больше время прохождения луча.
Дисперсия материала. Учтем дисперсию материала, являющуюся следстви-
ем зависимости показателя преломления от длины волны света X, т. е. исо =
= псо (X). Это требует более сложного анализа, основанного на представлении
лучей локально-плоскими волнами. В разд. 35.3 будет показана справедли-
вость такого подхода. Луч распространяется с групповой скоростью ug, ко-
торая в недиспергирующей среде определяется соотношением (1.13), а при на-
личии дисперсии материала выражается в более сложной форме [3]
( dnCOW I"1
yg=c|wco(M ----J . (1.15)
Удобно ввести групповой показатель преломления п& следующим образом:
^пл(Х)
«g=«co(X)-X^^-> (1-16)
в этом случае время прохождения луча определяется выражением
17
z ng _ z_ ngn^o
C COS0Z C /3
(1.17)
и является функцией Oz и X.
ПЛАНАРНЫЕ ВОЛНОВОДЫ С ГРАДИЕНТНЫМ ПРОФИЛЕМ
Описание распространения лучей в волноводах со ступенчатым профилем
легко обобщается на волноводы с градиентным профилем. Для простоты
будем рассматривать профили, подобные изображенному на рис. 1.1, у кото-
рого градиентной является только сердцевина. Однако полученные резуль-
таты легко обобщаются на профили с градиентной оболочкой.
1.6. Построение лучевых траекторий
Если профиль показателя преломления градиентный, траектория луча опре-
деляется уравнением эйконала, или лучевым уравнением с функцией профи-
ля «(г) [1,2]
<ii8>
где s — расстояние, отсчитываемое вдоль траектории луча, г — радиус-вектор
точки на ней (см. рис. 1.6). Это уравнение можно рассматривать как обоб-
щение закона Спелля и получить различными методами [4]. Градиентный
профиль можно представить как предельный случай структуры, состоящей
из множества тонких однородных слоев. Последовательное применение за-
кона Спелля (1.4) к каждому слою дает в пределе уравнение (1.18). С дру-
гой стороны, оно может быть получено с помощью принципа наименьшего
времени, а также предельного перехода X -> 0 из уравнений Максвелла, где
X — длина волны [1, 2]. Если п — постоянно, V п = 0, то лучевые траекто-
рии превращаются в прямые линии; в противном случае V и описывает кри-
визну лучевой траектории в плоскости, где лежит N п.
Составляющие лучевого уравнения. В случае планарного волновода про-
филь показателя преломления п (х) зависит только от координаты х, поэто-
му каждая точка (х, z) лучевой траектории определяется с помощью двух
(х-го и z-ro) компонентов уравнения (1.18) :
О’)
Рис. 1.6. Расстояние s вдоль траектории луча
до точки Р в среде с изменяющимся показа-
телем преломления п (х), описываемое радиу-
сом-вектором г = (х, z) (Gz(x) - угол между
касательной к траектории и осью z, элемент
ds направлен вдоль траектории и имеет ком-
поненты dx и dz)
18
ncl
a)
Рис. 1.7. Траектории луча в планарном волноводе с градиентным профилем при х > 0:
а - луч проходит через точку поворота возвращается к оси, б — луч достигает гра-
ницы раздела и уходит из волновода
Для выяснения физического смысла этих уравнений введем угол 0Z (х), об-
разующийся между касательной к траектории луча и осью волновода (см.
рис. 1.6). Тогда можно записать
^=sin0z(x); -g-=eos0z(x). (1.20)
Второе уравнение (1.19) можно проинтегрировать, при этом получится со-
отношение
h(x)cos0z(x) = «(O)cos0z (0), (1.21)
справедливое при всех х. Оно является обобщением закона Спелля (1.4)
для градиентных сред. При этом п (х) cos0z (х) постоянно вдоль траектории
луча. Для конкретного профиля траектория луча однозначно определяется
начальным углом 0Z (0).
Каустика точек поворота. Из уравнения (1.21) следует, что если и(х)
уменьшается при удалении от оси волновода, то внутри сердцевины суще-
ствует граница, на которой 0Z (х) = 0. Причем положение этой границы опре-
деляется значением 0Z (0). За ней луч распространяться не может. Указанную
границу будем называть точкой поворота xtp, которая определяется из
условия
fl(xtp) =h(O)cos0z (0); 0<xtp<p. (1.22)
Из сопоставления понятия кривизны лучевой траектории с понятием точки
поворота видно, что траектория луча подобна траектории на рис. 1.7, а, если
уравнение (1.22) имеет решение, и траектории на рис. 1.7, б, если оно не име-
ет решения. В первом случае луч непрерывно поворачивается и возвращается
к оси, во втором случае луч достигает границы сердцевины и, преломляясь,
выходит наружу. Так как профиль непрерывен вблизи границы раздела, то
угол падения равен углу преломления, 0t = 0Z (р). Штриховая линия, соот-
ветствующая х =xtp, представляет собой геометрическое место точек пово-
рота для всех лучей с одинаковым значением 0Z (0), которое часто называют
лучевой каустикой, или каустикой точек поворота.
Характеристики траектории луча. Траекторию луча в волноводе можно
построить повторением отрезков траектории, изображенной на рис. 1.7, а.
Если профиль показателя преломления симметричный, т. е. п(-х) = п(х),
то траектория имеет вид синусоиды (рис. 1.8). Она никогда не достигает
границы раздела сердцевина - оболочка, что исключает потери мощности.
19
ncl
Рис. 1.8. Синусоидальная траектория направляемого луча в сердцевине планарного вол-
новода с градиентным профилем
Такие лучи являются направляемыми. Луч, траектория которого достигает
границы раздела, теряет свою мощность и называется рефрагирующим по
аналогии с соответствующими лучами в волноводе со ступенчатым профи;
лем. Траектория луча, касающаяся границы раздела сердцевины с оболоч-
кой, разделяет области, заполненные траекториями лучей каждого из ука-
занных типов. Для граничной траектории xtp = р. Обозначая соответствую-
щее этой траектории значение 0Z (0) через 0С(О), из (1.22) получаем
cos0c(O) = и(р)/п(0) =«с1/иСо> (1-23)
предполагая, что п (0) = лсо — максимальное значение п (х). Таким образом,
лучи в волноводе с градиентным профилем могут быть классифицированы
в соответствии со значением 0Z (0) :
направляемые лучи: 0 < 0Z (0) < 0С (0),
рефрагирующие лучи: 0С (0) < 0Z (0) < я/2.
(1.24а)
(1.246)
Решение уравнения (1.19) для лучевых траекторий рассматривается в разд. 1.8.
1.7. Лучевой инвариант
В разд. 1.3 было введено понятие лучевого инварианта 3- В случае градиент-
ного профиля с учетом (1.20) и (1.21) он определяется следующим выра-
жением [5]:
0 =n(x)cos0z (х) =и(х)-^-. (1.25)
Следовательно, Р постоянен вдоль траектории и определяет направление лу-
ча в любой ее точке, а также положение точки поворотах^. Так как в точке
поворота 0Z (х) = 0, то __
w(*tp)=0> (Г26)
и между и /3 существует взаимно однозначное соответствие. Классифи-
кация лучей в соответствии с (1.24) может быть проведена также и относи-
тельно (3. При х = 0 и 0Z (0) = 0С(О) из уравнения (1.25) с учетом (1.23) сле-
дует, что (3 = пс\. Таким образом,
направляемые лучи: псХ < (3 < исо, (1.27а)
рефрагирующие лучи: 0 < (3 < «с1, (1.276)
где «со ~ максимальное значение п (х).
20
1.8. Лучевые параметры
Удобно ввести параметры, характеризующие распространение луча в волно-
воде с градиентным профилем, которые будут использованы в последующих
главах. К ним относятся, в частности, параметры, введенные в разд. 1.4 для
волноводов со ступенчатым профилем, которые легко обобщаются на волно-
воды с градиентным профилем. Хотя.процесс обобщения можно упростить,
получив предварительно явное решение систем уравнений (1.19) для траек-
тории луча, однако на практике очень редко используют зависимость харак-
теристик луча вдоль траектории. Заменяя в первом уравнении (1-19) ds на
dz из (1.25), после соответствующих преобразований получаем
d2x _ 1 dn2 (х)
^^"2 dx *
Полагая cPx/dz2 =xdx/dx, где x' = dx/dz, после интегрирования имеем
^^={«2(х)-|32}1/2, (1.29)
так как dx/dz = 0 и п (х) = j3 при х = xtp. Второе интегрирование дает
z(x) = (3 f
о
________dx_______
{п2 (х) - (32} 1/2
(1.30)
где z = 0 при х = 0. Это выражение является точным для траектории направ-
ляемых лучей при 0 < х <xtp и для рефрагирующих лучей при 0 < х < р.
Параметры траектории луча находятся с помощью рис. 1.9, на котором
представлен отрезок траектории направляемого луча между следующими
друг за другом точками поворота Р и Q, отстоящими на расстоянии, равном
полупериоду Zp и измеренном вдоль оси волновода. Длина пути £р и опти-
ческая длина пути £0 определяются интегралами по траектории:
е Q
Lp=fds; Lo= f n{x)ds, (1.31)
P P
где s - расстояние вдоль траектории. Заменяя ds на dz из (1.25) и dz на dx
из (1.29), получаем
£ = /Р n(x)dx______________ . = XtP п2 (x)dx
-*tp {п2(х) -02} 1/2 ’ ° Jtp {н2 (х) - 0 2 } 1/2
Полупериод траектории луча можно получить из (1.30) в виде
(1.32)
(1.33)
4 {и2(х)-ё2р'2 •
Рис. 1.9. Полупериод траектории направляе-
мого луча zp в сердцевине планарного волно-
вода с градиентным профилем (длина пути
Lp измеряется вдоль траектории между точ-
ками Р и Q)
21
Отсюда определяется и количество точек поворота траектории луча на едини-
цу длины волновода N = l/zp. В случае симметричного профиля интеграл вы-
числяется для 0 <х <xtp, а результат удваивается.
Локальный критический угол скольжения. Для наглядности в случае рас-
смотрения волноводов с градиентным профилем удобно ввести дополнитель-
ный параметр. В разд. 1.2 отмечалось, что в любой точке поперечного сечения
сердцевины волновода со ступенчатым профилем все направляемые лучи
распространяются под углами к оси волновода, значения которых лежат в
интервале 0 < 0Z < 0С, где 6С — критический угол скольжения. Однако для
волноводов с градиентным профилем область значений углов 0Z (х) направ-
ляемых лучей изменяется в зависимости от положения луча в поперечном
сечении. На оси указанная область определяется (1.24а), а на границе серд-
цевины направляемых лучей нет*. Соответственно определим локальный
критический угол скольжения 0с (х), как
П. f Лс1 ) 1/2
=7^ sin9««= V ~ 7^77 <L34>
В результате интервал углов направляемых лучей в точке с координатой х
определяется следующим образом:
O<0Z (х) <0с(х); 0<х<р. (1.35)
При х = 0 (1.35) сводится к (1.24а), а прих = р 0z(x) = 0. Все указанные вы-
ше параметры, а также время прохождения луча, рассматриваемое в следую-
щем разделе, представлены в табл. 1.1.
1.9. Время прохождения луча
Время прохождения луча в волноводах с градиентным профилем определяет-
ся интегралом вдоль искривленной траектории луча (см. рис. 1.8). Локаль-
ная скорость света непрерывно изменяется по закону с/п (х), где с — ско-
рость света в свободном пространстве и п (х) — профиль показателя прелом-
ления. Итак, время прохождения луча на расстояние z вдоль оси волновода
определяется интегральным выражением
t = -i- fn (х) ds = -U fn2 (x) dz. . (1.36)
c cp
Оно получено с помощью уравнения (1.25). Здесь интегрирование выполня-
ется вдоль кривой х = x(z). Этот интеграл не имеет простого представле-
ния, но его можно аппроксимировать. Из (1.31) следует, что время про-
хождения луча на расстояние, равное полупериоду траектории z состав-
ляет Ljc, где Lo — оптическая длина пути. Таким образом, если z точно
кратно полупериоду траектории, то время прохождения луча можно пред-
ставить выражением
r=zZ0/(czp). (1.37)
* Точнее говоря, на границе сердцевины все направляемые лучи имеют 6С (р) = 0, т.е.
они параллельны оси волновода. - Прим. ред.
22
В общем случае z не кратно zp, однако при z >> zp выражение (1.37) мо-
жет служить достаточно точным приближением для (1.36).
Выравнивание времени прохождения. В волноводах с градиентным профи-
лем происходит выравнивание времени прохождения для различных лучей,
что легко объяснить. Так как п (х) уменьшается при удалении от оси, то чем
дальше от оси распространяется луч, тем больше локальная скорость света
с/п (х). Такое увеличение скорости частично компенсирует увеличение дли-
ны пути неосевых лучей. В разд. 1.12 будет показано, что в случае гипербо-
лического секансного профиля происходит полное выравнивание.
Дисперсия материала. Рассмотрение влияния дисперсии материала на груп-
повую скорость, проведенное в разд. 1.5, может быть легко обобщено на слу-
чай градиентных сред. При этом профиль п (х) в первом интеграле правой
части (1.36) необходимо заменить групповым показателем ng. Следовательно,
г (х, X)*; ng =п(х, X)-Х-|у (х, X). (1.38а)
Далее, повторяя рассуждения , используемые при выводе (1.37) из (1.36),
получаем
t _ z_
xtp ng (x, X)n (x, X)
Xtp {n2 (x, X) -02} 1/2
dx.
(1.386)
Таким образом, заменяет оптическую длину пути Lo в (1.37).
СЛАБОНАПРАВЛЯЮЩИЕ ВОЛНОВОДЫ
Оптические волноводы, используемые в технике связи, обычно являются сла-
бонаправляющими, т. е. перепад между максимумом и минимумом показа-
теля преломления в поперечном сечении мал и обычно не превосходит 1 % от
максимального значения. В ч. II будут часто использоваться вытекающие от-
сюда преимущества, так как это позволяет значительно упростить алгебра-
ические выражения и решать задачи, которые в общем случае не могут быть
решены аналитически. Здесь рассматриваются некоторые особенности такого
приближения применительно к лучевому анализу.
1.10. Параксиальное приближение
Если максимальное и минимальное значения показателя преломления близ-
ки, то из (1.3) и (1.23) следует, что критические углы скольжения 0С и 0С (0)
малы и справедливо следующее соотношение:
s in 0С ~ 0С * (1 - « С1/«СО)1/2 (1 -39)
аналогичное соотношение получается для 0С(О). Таким образом, интервал
углов направляемых лучей в (1.5а) и (1.24а) мал, и любой направляемый
луч распространяется почти параллельно оси. Такое приближение называет-
ся параксиальным.
Параксиальное приближение не_приводит к упрощению уравнений (1.19),
поскольку, как видно из (130), 0 — константа, а и(х) принимает значения,
уменьшающиеся вплоть до /3. Однако оно позволяет упростить выражения
23
для длины пути Zp в (1.32) при использовании указанной ниже аппроксима-
ции. Профиль может быть описан следующим образом:
П2 (х) =п2о {1 -2Д/(х)},
(1-40)
где псо — максимальное значение показателя преломления, f(x) — неотрица-
тельная функция, а Д — константа, определяемая с учетом (1.3) соотношением
2Д = 1 -п2а/п2о =sin20c. (1.41)
В однородной оболочке п (х) = лс1, а/(х) = 1. Такое определение Д предпола-
гает выполнение условия Д < < 1 в приближении слабонаправляющего вол-
новода, т. е. условия nCQ «с1. Таким образом, в низшем порядке прибли-
жения величина Д представляет собой относительный перепад между исо и
лс1,т. е.
Л "со - пс1
Д ~ 2 %-----П------’ "со или 0С<< 1, (1.42)
со
и характеризует относительную высоту профиля, поэтому параметр Д будем
называть параметром высоты профиля. При Д/(х) << 1 из (1.40) получа-
ем приближенное соотношение
п(х) {1-А/М}, (1.43)
которое будет использовано при определении Zp ниже.
ГРАДИЕНТНЫЕ ПРОФИЛИ, ДОПУСКАЮЩИЕ АНАЛИТИЧЕСКИЕ РЕШЕНИЯ
Для иллюстрации использования полученных результатов в случае волново-
дов с градиентным профилем рассмотрим примеры профилей, допускающих
аналитические решения для всех или части представляющих интерес коли-
чественных параметров траектории луча, в том числе в слабонаправляющих
волноводах. Наиболее важные из таких параметров представлены в табл. 1.1.
1.11. Пример. Параболический профиль
В качестве первого примера рассмотрим бесконечный параболический профиль, соот-
ветствующий на рис. 1.10 сплошной кривой q = 2 и пунктирному продолжению, кото-
рый определяется выражением
п2 (х) = п2со (1 - 2 А (х/р) 2 } ; —оо<х<оо, (1.44)
где р - эффективная ширина профиля. С одной стороны, показатель преломления не-
прерывно изменяется в бесконечных пределах (профиль является нереальным), так
как п2 (х) — «> при х ± °°. С другой стороны, этот профиль является одним из про-
стейших для понимания процессов распространения, поэтому будем его использовать
как составной элемент при анализе волноводов параболического профиля с однородной
оболочкой (см. разд. 1.13). Так как профиль является бесконечным, то каждая траек-
тория луча имеет точку поворота на конечном расстоянии от оси, определяемо^ соот-
ношением (1.26)
(n^o-?)v2 _ sinez(0) ez(0)
*tp~±P nco^ ±PsinM0) X±P *C(0)’
Рис. 1.10. Графики степенных
профилей (1.59) при различ-
ных значениях q. Усеченный
параболический профиль со-
ответствует q = 2, ступенча-
тый профиль — q =«>. Гипер-
болический секансный про-
филь (1.51) изображен штри-
ховой линией. Пунктирная
линия неограниченно продол-
жает профиль, соответствую-
щий q = 2 в сердцевине,
до параболического профиля
(1.44)
где последнее выражение справедливо в параксиальном приближении. Таким образом,
чем больше угол 0Z (0) или чем меньше 0,тем дальше от оси расположена точка поворо-
та. Поскольку не существует лучевых траекторий, являющихся решениями уравнения
(1.30), расположенных за точками поворота, то все лучи являются направляемыми, а
инвариант 0 направляемых лучей удовлетворяет условию
0<£<исо. (1.46)
Подставляя (1.45) в уравнение (1.30) и используя замену переменных х = xtpsinw,
получаем интеграл по аргументу w, который легко вычисляется. Итак, траектория луча
определяется соотношениями
j z I 1 тгрв
X = Xtp sin \ 7г —У; Z = - = -~=- , (1-47)
I PJ р N исоЖ
где z - полупериод траектории луча, вычисленный аналогичным образом с помощью
(1.33). Используя ту же замену переменных, из (1.32) можно вычислить оптическую
длину пути
£o = zp('7co+?2)/(2?), (1.48)
тогда как геометрическая длина пути £р выражается через полный эллиптический ин-
теграл 2-го рода Е(у) согласно соотношению (37.103). Однако в приближении слабо-
направляющего волновода (1.43) при Д < < 1 можно получить упрощенное выражение
ЛР = Р(1)1/2Г(2Д—} j-j3”C°-- +— I (1-49)
Р д рг 4 I Д «со J
Наконец, время прохождения луча (1.37) определяется непосредственно из соотноше-
ний (1.47), (1.48) как
t = Z(02 +п|0)/(2сД).
(1.50)
По сравнению с выражением (1.14) для ступенчатого профиля время прохождения луча
в волноводе с градиентным профилем частично выравнивается по причинам, указанным
в разд. 1.9.
1.12. Пример. Гиперболический секансный профиль
Указанный профиль характеризуется изменением показателя преломления в бесконеч-
ной области поперечного сечения, описываемым штриховой линией на рис. 1.10, и опре-
деляется следующим выражением:
п2 (х) = п2С0 sch2 ( ^2Д х/р); < х < *>. (1-51)
25
Так как п (х) О при х -* ± то и в этом случае все лучи будут направляемыми, а луче-
вой инвариант удовлетворяет соотношению (1.46). Подставляя функцию профиля в
уравнение (1.26), получаем положение точки поворота
xtp = P(2A)'v’arch(nc0/©. (1-52)
Замена переменной ( V 2Д х/р) = ('’сО//32 - 1)V2 sin w в (1.30) дает интеграл по w, ко-
торый легко вычисляется. В результате уравнение траектории луча имеет вид
х ) sin( г_) I; г 1 = . (1.53)
х/2Д [ р ZP J Р N
Аналогичным образом из (1.31) определяется полупериод траектории. С помощью та-
кой же замены переменных в интеграле для оптической длины пути (1.32) получим но-
вое выражение, которое можно получить, используя (37.112):
^о = ^cozp* (1«54)
Таким образом, полупериод траектории луча и оптическая длина пути не зависят от 0 и,
следовательно, от наклона траектории в точке пересечения с осью волновода. Для опре-
деления длины пути необходимо использовать указанную выше замену в сочетании с
преобразованием w = я/2 - в, что позволяет получить для соответствующего интеграла
выражение, пропорциональное полной эллиптической функции К (у) 1-го рода, опреде-
ляемой с помощью (37.103):
2 "со “ 02
>• (1-55)
"со
Для приближения слабонаправляющего волновода, исключая Д/(х) из равенств (1.40),
(1.43), с точностью до Д получаем
П (X) « {п2с0 +п2 (х)} / (2«со); д<<1. (1.56)
Далее из уравнений (1.32), (1.33) имеем
^р « (wcozp+^)/<2^co) = *р(? +"со)/<2Д). (1.57)
Выражение для времени прохождения луча определяется из уравнения (1.37) с учетом
(1.54) и (1.53):
t=znCQ/c. (1.58)
Итак, оно одинаково для всех лучей и равно времени прохождения луча, распространя-
ющегося по оси волновода [б].
1.13. Пример. Усеченный степенной профиль
В качестве последнего примера рассмотрим усеченный степенной профиль, определяе-
мый соотношениями [7]
п2 (х) = п2С0 [1 - 2Д Ix/pl^J; -рСхСр, (1.59а)
= Пс1 = псо I1 ~ 2Д]; |х| >р, (1.596)
где q - положительная константа. Таким профилям соответствуют сплошные кривые на
рис. 1.10. Ступенчатый профиль соответствует пределу при q -**>,а усеченный параболи-
ческий профиль - q = 2. В случае степенных профилей диапазон значений (3 для направ-
ляемых лучей определяется условием (1.27а). С учетом этого ограничения все резуль-
таты разд. 1.11 для параболического профиля применимы к усеченному параболическо-
му профилю, так как оба профиля (1.44) и (1.59а) идентичные области сердцевины, а
лучевые параметры для направляемых лучей не зависят от свойств оболочки. Подстав-
ляя (1.59а) в (1.26), найдем положение точки поворота для произвольного q
26
n2co~02 1 W_ ( sin 6z(0) 12/? ( 8Z (0) 1 yq
%tp ( 2и*0Д J “ “P{ sin6c(0) J “±P[ 0C(O)
(1.60)
Последнее выражение справедливо в параксиальном приближении. Не существует обще-
го решения уравнения лучевой траектории (1.30), однако для некоторых значений q
оно может быть получено, например, при q = 2 траектория определяется соотношением
(1.47). Здесь не будут рассматриваться другие существующие решения. Полупериод
траектории луча может быть выражен аналитически для любых q. С помощью подста-
новки w = (x/xtp)2 интеграл (1.33) можно представить в виде бета-функции (см.
(37.104)), через гамма-функцию (37.105) можно представить полупериод:
z = - = I ___Г (1/?) ,
Р N ?<Д> nco{xtpj г(1/? + 1/2) ‘ (1‘ ’
Применяя ту же подстановку в интеграле (1.32), с помощью рекуррентной формулы
для гамма-функции (37.106а) найдем
(1.62)
Интеграл в (1.32) может быть вычислен строго только для некоторых значений q, на-
пример, q = 2. Однако в параксиальном приближении (1.43) выражение для можно
получить по аналогии с £0 [5] в виде
(1.63)
с точностью до членов порядка Д. Наконец, время прохождения луча (1.37) определяет-
ся с помощью (1.62) [5]:
Таким образом, разброс значений времени прохождения различных лучей уменьшается
при q^»2 (см. разд. 1.9).
НЕСИММЕТРИЧНЫЕ ВОЛНОВОДЫ
В этой главе исследовано распространение лучей в планарных волноводах в
предположении, что профиль показателя преломления симметричный, т. е.
п (-х) = п (х). Однако изложенные методы построения траекторий лучей при-
менимы для анализа волноводов с несимметричным профилем. Единствен-
ное существенное отличие заключается в том, что в случае симметричного
профиля для определения полной траектории достаточно рассчитать путь лу-
ча только на полупериоде, в то время как для построения траектории луча в
несимметричном волноводе необходимо знать путь луча на полном периоде
траектории. Параметры траектории для несимметричного профиля опреде-
ляются с помощью соответствующей модификации выражений для сим-
метричных волноводов.
ГЛАВА 2. НАПРАВЛЯЕМЫЕ ЛУЧИ В ВОЛОКОННЫХ СВЕТОВОДАХ
В гл. 1 были даны основы лучевого анализа планарных волноводов. Здесь мы
проведем анализ волоконных световодов, которые используются в высоко-
информативных линиях связи большой протяженности. Когда речь идет о
траектории лучей, единственное различие между планарными и волоконными
световодами заключается во введении в последнем случае третьего измере-
ния. Итак, хотя основные понятия остаются теми же, что и в гл. 1, анализ и
результирующие выражения в общем случае усложняются, что обусловлено
геометрией волоконных световодов. Тем не менее один из важных результа-
тов настоящей главы заключается в том, что время прохождения луча в во-
локонном световоде со ступенчатым и усеченным степенным профилями
показателя преломления для круглого и некруглого поперечных сечений
совпадает с временем прохождения луча в планарных волноводах соответ-
ствующего профиля. Если это существенное упрощение принять без доказа-
тельств, то можно непосредственно переходить к изучению уширения импуль-
сов в таких волоконных световодах (см. гл. 3), опуская при первом чтении
материал данной главы.
Большая часть главы посвящена классификации лучей и построению их
траекторий в волоконных световодах круглого сечения с симметричным
профилем. Помимо этого рассматриваются некруглые волокна, так как по-
перечное сечение реальных волоконных световодов может отличаться от
,круглого и иметь, например, эллиптическую форму. Поскольку большая
часть материала этой главы аналогична материалу гл. 1, но применительно
к другой геометрии световодов, то будет полезно сравнить результаты со-
ответствующих разделов.
2.1. Волоконные световоды с круглым сечением
Волоконный световод рассматриваемого типа представлен на рис. 2.1. Если
не оговорено особо, то предполагается, что сердцевина с круглым сечением
радиуса р окружена оболочкой, которую для простоты будем считать неогра-
ниченной. Граница между сердцевиной и оболочкой представляет собой ци-
линдрическую поверхность г = р. В пределах сердцевины осесимметричный
Рис. 2.1. Обозначения, используемые при описании круглых волоконных световодов.
Декартовы координаты х, у, z и цилиндрические полярные координаты г, р, z ориентиро-
ваны так, что ось z направлена вдоль оси световода. Изображен градиентный профиль —
переменный в сердцевине и постоянный в оболочке, которая считается неограниченной
28
профиль показателя преломления п(г) является либо постоянным, либо
изменяется, а в оболочке он имеет постоянное значение
Безразмерный параметр V (1.1) применим также и для волоконных све-
товодов и называется в этом случае волоконным параметром. Итак,
Г = 2^<ЛСО-«С1)1/2.
(2.1)
где пс0 - максимальное значение п(г), р - радиус сердцевины, X - длина
волны света в свободном пространстве. Величину (п2о - «^1)1/2 часто назы-
вают числовой апертурой световода, а выражение [п2 (г) - «^}1/2 — ло-
кальной числовой апертурой. Развитая здесь лучевая теория применима толь-
ко к многомодовым волоконным световодам с V> > 1 (см. гл. 10 и 36).
ВОЛОКОННЫЕ СВЕТОВОДЫ СО СТУПЕНЧАТЫМ ПРОФИЛЕМ
В обозначениях рис. 2.1 показатель преломления волоконного световода со
ступенчатым профилем можно записать в виде:
я(0=ясо’ 0О<р; /1(г)=пс1, р<г<°°, (2.2)
где nCQ > пс\. Определим теперь траекторию луча внутри сердцевины.
2.2. Построение лучевых траекторий
Траекторию луча в сердцевине можно построить, обобщая методы разд. 1.2.
Между точками отражений луч распространяется по прямой линии, а направ-
ление луча после отражения определяется законом Снелля. Таким образом,
падающий и отраженный лучи и нормаль в точке отражения лежат в одной
плоскости, а углы падения и отражения (образуемые направлением луча с
нормалью) равны между собой. В результате траектория луча приобретает
вид, представленный на рис. 2.2.
Рис. 2.2. Траектории лучей и их проекции на поперечное сечение в сердцевине волокон-
ного световода со ступенчатым профилем:
а — зигзагообразная траектория меридионального луча и б - спиралеобразная траекто-
рия косого луча
29
Меридиональные и косые лучи. Удобно провести разграничение между
лучами, пересекающими ось волокна между точками отражений и называе-
мыми меридиональными, и лучами, никогда не пересекающими ось волок-
на, называемыми косыми лучами. Из рис. 2.2, а видно, что меридиональные
лучи лежат в плоскости, проходящей через ос£ световода, в полосе шириной
2р. В результате эти лучи обладают такими же свойствами, что и лучи соот-
ветствующего планарного волновода, а выражения из табл. 1.1 применимы
к меридиональным лучам волоконных световодов, если декартову коорди-
нату х заменить цилиндрической полярной координатой г (см. рис. 2.1). Косые
лучи распространяются по спиралеобразной траектории, проекция которой
на поперечное сечение волокна представляет собой правильный многоуголь-
ник (в общем случае незамкнутый), как показано на рис. 2.2, б. Точки в се-
редине отрезков траектории между последующими отражениями лежат на
цилиндрической поверхности с радиусом ric, называемой внутренней кау-
стикой.
Будем характеризовать меридиональные лучи углом 6Z , образованным лу-
чом и осью z (см. разд. 1.2). Соответственно диапазон углов 07 для направ-
ляемых и рефрагирующих лучей будет определяться условием (1.5), в кото-
ром для ступенчатого профиля (2.2) сохраняется определение критического
угла скольжения 0С (1.3).
Из рис. 2.2, б видно, что для задания траектории косого луча кроме угла
наклона 6Z необходимо знать второй угол, характеризующий скос луча. Опре-
делим 0^ как угол в плоскости сечения сердцевины между касательной к гра-
нице раздела и проекцией траектории луча, как показано на рис. 2.2, б. Из
геометрических соображений следует, что угол 0^ одинаков при всех отра-
жениях.
Направляющие углы. Углы 6^ и 0Z являются сферическими полярными уг-
лами, отсчитываемыми от осевого направления PQ на рис. 2.3, на этом же ри-
сунке показан угол а между падающим или отраженным лучами и нормалью.
С помощью проекций находим соотно-
Q —Л/ X r k \ 1 7 Ж. \ । шение между тремя направляющими углами cosa = sin0z sin0^. (2.3) Рис. 2.3. Углы для описания отражения луча, падающего в точку Р на границе сердцевины волоконного световода со ступенчатым про- филем. Углы падения и отражения, отсчиты- ваемые от нормали PN, равны а. Падающий и отраженный лучи образуют угол 0Z с осевым направлением PQ и угол 0^ (в сечении свето- вода) между касательной РТ и проекцией тра- ектории луча (PR для отраженного луча)
30
Радиус rjc внутренней каустики на рис. 2.2, б определяется соотношением
ric=pcos^ (2.4)
и зависит, таким образом, только от угла скоса. Для меридиональных лучей
= тг/2 иг,с =0.
Классификация лучей. Согласно закону Снелля (см. разд. 35.2) в точке
Р (см. рис. 2.3) луч будет преломляться при а < aCi где ас - критический
угол падения, определяемый выражением
sin Qc —/?с|/^со ~ cos ^с, (2.5)
и испытывать полное внутреннее отражение при а > ас. Таким образом, мож-
но предположить, что все лучи с а > ас являются направляемыми, однако в
действительности только некоторые лучи, удовлетворяющие этому условию,
будут направляемыми. Это связано с тем, что закон Снелля справедлив для
отражения от плоской поверхности, поверхность же волокна искривлена.
Как будет показано в разд. 2.7, для того чтобы луч был направляемым, не-
обходимо выполнение условия 0 < 0z <0с независимо от значения угла в.
Указанное условие получено из уравнения лучевой траектории и совпадает
с (1.5а) для планарных волноводов. Однако в случае волоконных светово-
дов оно ограничивает конус углов в каждой точке сечения волокна и имеет
силу как для меридиональных, так и для косых лучей. Косые лучи, которые
не принадлежат ни к_направляемым, ни к рефрагирующим лучам, образуют
третий класс - туннелирующие лучи [1] (см. разд. 2.7). Все ненаправляемые
лучи, т. е. туннелирующие и рефрагирующие, называются вытекающими
лучами.
Суммируя сказанное, отметим, что лучи в волоконных световодах со сту-
пенчатым профилем могут быть классифицированы в соответствии со значе-
ниями углов 0z, 0^ и а:
(2.6а)
(2.66)
(2.6в)
где ас и 0с определены с помощью (2.5). Все углы показаны на рис. 2.3.
2.3. Лучевые инварианты
На основе геометрических соображений в предыдущем разделе показано,
что углы 0z и 6^ постоянны вдоль выбранной траектории луча. Удобно вве-
сти два инварианта, выраженные через указанные углы;. Первый инвариант
Р идентичен введенному в (1.6) и выражает факт наличия трансляционной
инвариантности световода вдоль его оси. Второй инвариант Z, связанный с
углом скоса О, выражает азимутальную симметрию волоконного световода.
Определим инвариант I в соответствии с выражением (2.17) для градиентно-
го профиля. Итак,
направляемые лучи: 0 (7Z < ис,
рефрагирующиелучи: 0 <а<ас,
туннелирующие лучи: 0С < 0z < у
я
3-«cocos0z; Z = flcosin0z cosfl^,
02 + Z2 =«20 sin2 a,
(2.7а)
(2.76)
31
Таблица 2.1. Лучевые параметры в волоконных световодах
Профиль п2 (г) Полупериод лучевой траектории zp= 1/N Длина пути L P Оптическая длина пути Lq Время прохождения луча t
Ступенчатый nJ,; 0 < г < р nJ; р < г < оо 2pjg(p)112 2pnmg(p)111 g(p) = nl.-T1 -I7 2pn2mg(p)tl2 cT
Г радиентный л2(г); 0 г р "J; р sg г < оо frtp dr g(r)-- p₽n(r)dr _1гк£(гГ/2 = n2(r)-7P -~Pp2/г2 ppn2(r)dr _J_rK^±'2_ z CZP
Параболи - ческий 4-ЧУ} *pf n«V(2A) Zp f^nco . 7 1 <17 "J Д«1 ^k.N Ms3- 2 с J )
2 Зак
Окончание табл. 2.1
Профиль п2 (г) Пол у период лучевой траектории zp = 1/N Длина пути Lp Оптическая длина пути Lq Время прохождения луча t
Усеченный степенной i 8 1 V еч ^-1 * 1 V | V/ Е О| Е 1 Только при q = 2 см. выше, для 1 = 0 см. табл. 1.1 +д w со J Д<1 Z С 1 _2е_ L^ + 2/^ (4 + 2) C# Р) Z "со L"co , -Д 1 С (<? + 2) (/р "со J
Несимметри- чный сте - пенной "«{1 -2Д/(х,у)} Г X F V /= - + ^ г L Рх Ру J — оо < х, у < оо Луш гвая траектория не периоди 1чна 2 "«> с (</ + 2) Г J "J
75 л ~г • л л ступенчатый Р = "оо cos et ; Т= nrosin 0, cos в/ профипь -г- градиентный Д = n(r)cos02(r); Т= n(r)sin02(r)cosO„(r): профиль
Примечание. Полупериод, длина пути и оптическая длина пути определяются между последовательными отражениями или точками по-
ворота, а время прохождения определяется на длине волокна Z. Количество отражений или точек поворота на единицу длины волокна
N ~ 1/Zp, р — радиус сердцевины или масштабный параметр профиля. Как так и определяются из условия g(r) = 0.
причем последнее соотношение вытекает из (2.3). Для меридиональных лу-
чей I = 0, а для косых I > 0. Лучи могут бь/ть классифицированы с помощью
этих инвариантов. Из уравнений (2.5) - (2.7) следует, что независимо от
значения I лучи являются направляемыми, если ис1 < 0 < исо, и вытекающи-
ми, если 0 < 3 < ис1- Разделение вытекающих лучей на туннелирующие и
рефрагирующие производится в соответствии со значением I по следующему
критерию,который легко проверить:
направляемые лучи: пс\ < 3 < ис0,
рефрагирующиелучи: 0<32+/2<^2Ь
туннелирующие лучи: п2с\ < /З2 + 12 < n2CQ и 0 < /3 < ис1.
(2.8а)
(2.86)
(2.8в)
При фиксированном значении (3 для направляемых лучей значение I нахо
дится в диапазоне 0 < / < п20 - /32 .
2.4. Лучевые параметры
Лучевые параметры, введенные в разд. 1.4, легко обобщаются при описании
траекторий косых лучей (см. рис. 2.2, б). С помощью углов 0z и 0^ (рис. 2.3)
и лучевых инвариантов (2.7) длина пути L между точками Р и Q может
быть записана, исходя из геометрических соображений, так:
sin 0 (п2 п 2 1 2 ч 1/2
Ар = 2р = 2рпс0 -Leo g----------L2_
Р sin0z С° n2o-02
(2-9)
Отсюда непосредственно следует выражение для оптической длины пути
sin0 _ (и20 - /З2 - / 2)1/2
А: “«со^р ~2рнсо sjn0 “2рисо ~2 (2.10)
z ПСО — р
Полупериод zp траектории луча и количество отражений на единицу длины
волокна Доопределяются с помощью соотношений
Z
р
-^=ApCos0z =2р
sin^
tg^z
Сп2 -В2 _ Г2 А 1/2
= 2р? ( со Р }
п со |32
(2.И)
Суммарная длина пути, оптическая длина пути и количество отражений на
длине z волоконного световода определяются в соответствии с (1.12). Для
удобства эти параметры включены в табл. 2.1.
2.5. Время прохождения луча
В разд. 1.5 время прохождения луча t было определено как время распро-
странения луча на расстояние z вдоль волновода. Для волоконных светово-
дов со ступенчатым профилем из (1.14), (2.10) и (2.11) получим
. __z_ Lo _ z «СО =z «jo
zp c c cos0z c p
где (3 - лучевой инвариант (2.7). Таким образом, время прохождения луча
не зависит от угла скоса, а определяется только значением угла 0Z. Так как
34
соотношение (2.12) идентично (1.14), изучение распространения импульсов
в волоконных световодах не сложнее, чем в планарных волноводах со сту-
пенчатым профилем (см. гл. 3). С учетом влияния дисперсии материала
время про хождения^ луча определяется выражением (1.17). Для удобства
все определения, связанные с описанием процесса распространения света в
волоконных световодах и планарных волноводах со ступенчатым профилем,
представлены в табл. 2.1.
ВОЛОКОННЫЕ СВЕТОВОДЫ С ГРАДИЕНТНЫМ ПРОФИЛЕМ
Распространим лучевой анализ волокон со ступенчатым профилем на волок-
на с градиентной сердцевиной. Такое рассмотрение может быть обобщено и
на профили с бесконечным поперечным сечением.
2.6. Построение лучевых траекторий и лучевые инварианты
Исходным пунктом анализа является уравнение траектории луча (1.18) для
градиентных сред достаточно общего вида. В разд. 35.4 будет показано, что
для осесимметричного профиля показателя преломления п(г) (рис. 2.1) ра-
диальная, азимутальная и продольная компоненты лучевого уравнения соот-
ветственно имеют вид [2]
w , (2.I3a)
ds [ v 7 ds J v 7 ds7 dr 9 v 7
=0) (2.i36)
as ( ds ) r ds ds
4-W)44=0, (2.13b)
ds ( v ds J 7
где s — расстояние вдоль траектории, г, z — цилиндрические полярные ко-
ординаты, определенные на рис. 2.1. Для облегчения физической интерпрета-
ции этих уравнений обобщим определения углов 0Z , 0^ и а, представленных
на рис. 2.3. Итак, в точке г 0z (г) представляет собой угол между осью волок-
на и касательной к траектории луча в этой точке, 0 (г) - угол между проек-
цией касательной к траектории луча в поперечном сечении и нормалью к ра-
диусу, проведенному в исходную точку (см. рис. 2.4, в). Если-а (г) опреде-
лить как угол между касательной к траектории и радиусом, проведенным в
исходную точку, то по аналогии с (2.3) все указанные выше углы в каждой
точке траектории связаны между собой соотношением
cos а (г) = sin 0z (г) sin 0^ (г). (2.14)
С помощью разложения получим
cos о (г); ^=cos0z(r), (2.15а)
~ sin ez (Г) cos (г), (2.156)
причем последнее соотношение вытекает из тождества ds2 = dr2 + г2 dip2 +
+ dz2.
2*
35
Рис. 2.4. Траектории меридионального (а) и ко-
сого (б) лучей и их проекции на сечение сердце-
вины в волоконном световоде с градиентным
профилем и угол (г) между проекцией траек-
тории и азимутальным направлением (в)
Лучевые инварианты. Интегрируя уравнение (2.1 Зв), получаем лучевой
инвариант для волокон с градиентным профилем
— dz
P=n(r) ~^=n(r) COS0z(r).
(2.16)
Это выражение идентично выражению (1.25) для градиентных планарных
волноводов и выражает трансляционную инвариантность световодов. Умно-
жая (2.136) на г2 и интегрируя, получаем второй инвариант, представленный
в безразмерной форме [3]
1 = Г Sin вг C0S ’
р as р
(2.17)
где р — радиус сердцевины. Наличие этого инварианта обусловлено осесим^
метричностью профиля. Исключая 0Z (г) из выражений для инвариантов 3
и Г, можно связать угол скоса 0 (г) непосредственно с функцией профиля:
cos^ W = Г 7....2 Г (2Л8)
г [П2 (г) - Р2 } 1/2
Заметим, что (г) = тт/2 для меридиональных лучей (/ =0). Теперь ясно,
почему I для ступенчатого профиля имеет вид (2.7) — в этом случае выра-
жение для I совпадаете (2.17) при г =рип(г) = исо.
36
Характеристики лучевой траектории. Общая форма лучевых траекторий
может быть получена из соответствующих траекторий в градиентном планар-
ном волноводе (рис. 1.8) и траекторий в волоконных световодах со ступен-
чатым профилем (рис. 2.2). Траектории, расположенные в пределах сердце-
вины, имеют характерный вид, показанный на рис. 2.4. Меридиональные лу-
чи лежат в одной плоскости и пересекают ось волоконного световода между
соседними точками поворота. Эти лучи идентичны лучам в градиентных пла-
нарных волноводах. Поэтому выражения в табл. 1.1 применимы и для мери-
диональных лучей в волоконных световодах, если декартову координату х
заменить радиальной координатой г. Косые лучи распространяются по спи-
ралевидной траектории (рис. 2.4, б) и попеременно касаются цилиндричес-
ких поверхностей г = ric и г = rtp, являющихся соответственно внутренней
каустикой и каустикой точек поворота. Из определения очевидно, что на обе-
их каустиках 0^ (г) = 0. Таким образом, для данного профиля из (2.18)
следует, что ric и rtp являются корнями функции
g(f) = п2 (г) - З2 -12 -£- = 0. (2.19)
Для меридиональных лучей I = 0 и ric = 0.
2.7. Классификация лучей
Простой способ классификации лучей в градиентных волоконных светово-
дах основан на использовании лучевого уравнения для определения интер-
вала значений радиальной координаты г, при котором могут распространять-
ся лучи. Для этого радиальную компоненту лучевого уравнения (2.13а) на-
до выразить в виде соотношения между г и z. С помощью (2.16) ds заменя-
ют на dz и подставляют d<p/ds из (2.17). В результате получается уравнение
Р £ 4 , (2.20)
которое можно проинтегрировать, положив d2r/dz2 = г dr /dr, где г = dr/dz.
При этом получим
.02 ($z)2=Z(r) =п2(г) -02 -I2 ,
(2.21)
так как dr/dz = 0 и g (rtp) = 0 при г = rtp. Отсюда сразу же следует, что рас-
сматриваемые лучевые траектории могут существовать только тогда, когда
правая часть (2.21) неотрицательна. Этот критерий определяет диапазон зна-
чений г для данного профиля. Таким образом, для идентификации лучей со-
вершенно необязательно определять их траекторию.
Направляемые и рефрагирующие лучи. Для простоты предположим, что
п(г) монотонно уменьшается от максимального значения псо на оси до мини-
мального на поверхности сердцевины, совпадающего с показателем прелом-
ления оболочки, т. е. п(р) - ис1 (см. рис. 2.1). Рефрагирующий луч должен
пересекать поверхность сердцевины, что предполагает выполнение неравен-
ства g(p) > 0. В терминах уравнения (2.21) это требование эквивалентно
37
Рис. 2.5. Качественная картина особенностей поведения функции g(r) (2.21) для типич-
ного волоконного световода с градиентным профилем. Лучи распространяются только
при g(f) > 0, область их распространения обозначена жирной линией на оси г [3]
выполнению условия 0 < /З2 + 12 < п2^ В этом случае в области сердцеви-
ны существует только один корень ric функции g (г), что иллюстрируется
рис. 2.5, в. Луч будет направляемым, если везде в оболочке g(r) < О; из
(2.21) видно, что это приводит к требованию ис1 < (3 < псо, которое идентич-
но условию (1.27а) для планарных волноводов. Траектории косых направля-
емых лучей соответствуют области значений г между корнями ric и rtp функ-
ции g(r), как показано на рис. 2.5, а, а траектории меридиональных лучей
расположены между осью световода и корнем rtp, как показано на рис. 2.5,
Туннелирующие лучи. Приведенные выше рассуждения не касались обла-
сти значений /Ти Г, удовлетворяющих одновременно условиям
(3<пс\ и п2сХ<$2 +12 (2.22)
и соответственно не относящихся ни к направляемым, ни к рефрагирующим
лучам. Эта область значений инвариантов соответствует классу так называе-
мых туннелирующих лучей. Такое их название связано с тем, что они проса-
чиваются в оболочку через барьер конечной толщины, т. е. туннелируют [1],
что аналогично механизму нарушения полного внутреннего отражения [4].
Для обоснования этого явления укажем, что из (2.21) при выполнении усло-
вия (2.22) следует неравенство g(r) < 0. Однако при исследовании поведе-
ния функции g (г) в оболочке обнаруживается, что g (г) становится положи-
тельной при всех г, превышающих некоторое значение rrad, определяемое из
условия g (rrad) = 0. Следовательно,
38
Рис. 2.6. Траектория туннелирующего луча в волоконном световоде с градиентным
профилем, касающаяся каустики точек поворота в сердцевине в точке Р (а) (излучение
происходит в точке Q оболочки и распространяется вдоль QR по касательной к радиа-
ционной-каустике) и ее проекция на поперечное сечение волоконного световода (б)
rrad=Pl /(«cl-^2)1/2>
(2.23)
и цилиндрическая поверхность радиуса rrad является каустикой излучения.
Из второго условия (2.22) вытекает, что rrad > р. Другими словами, в обо-
лочке существуют лучевые траектории, уходящие за поверхность г = rrad, а
так как показатель преломления оболочки постоянен, то они являются пря-
мыми линиями. Траектории в сердцевине и оболочке разделены областью
rtp < г < rrad, в которой лучи не распространяются. Для наглядности рас-
смотрим поведение функции g(r) (рис. 2.5, г), а также отрезки траекторий
туннелирующих лучей в градиентном световоде, изображенные в двух сече-
ниях на рис. 2.6. На последнем рисунке показано также положение начала
траектории луча в оболочке на каустике излучения относительно точки по-
ворота траектории в сердцевине. Лучевое уравнение не дает никакой инфор-
мации о физическом механизме, связывающем две области, в которых рас-
положена траектория туннелирующего луча. Однако на рис. 2.6 предполага-
ется, что часть мощности, распространяющейся в сердцевине, ’’вытекает” в
оболочку вследствие туннельного эффекта, аналогичного нарушению полно-
го внутреннего отражения. Это предположение будет подтверждено в гл. 7.
Вывод. Можно получить классификацию лучей (2.8) и для световодов со
ступенчатым профилем, поскольку она является частным случаем классифи-
кации лучей в световодах с градиентным профилем (ступенчатый профиль
можно- рассматривать как предельный случай градиентного профиля, в кото-
ром все изменения показателя преломления происходят на границе сердце-
вины) . Следовательно, лучи в световодах с оболочкой являются направля-
емыми_при лс1 < псо и вытекающими при 0 < Р < ис1 независимо от зна-
чения /. В то же время разделение вытекающих лучей на рефрагирующие и
туннелирующие существенно зависит от значения I. Итак [3],
39
Рис. 2.7. Схематическое представление областей лучей в волоконных световодах круг-
лого сечения относительно инвариантов Д' и 7 для ступенчатого профиля (2.8) (а) и усе-
ченного степенного профиля (2.43) (б) [3] . Заштрихованные области соответствуют
туннелирующим (ТЛ) и рефрагирующим лучам (РЛ); незаштрихованные области -
направляемым лучам (НЛ)
направляемые лучи: пс1<0^псо>
рефрагирующие лучи: 0</32+/2<л2с1,
туннелирующие лучи: 0min < /3 < ис1 и п2с1 - 02 < 12 < /^ах (0),
(2.24а)
(2.246)
(2.24в)
где 0min и Zmax (/3) для_ туннелирующих лучей зависят от формы профиля.
При заданном значении (3 для направляемых лучей значение I лежит в преде-
лах 0 < I < /тах (Р). Указанные области изображены на рис. 2.7, а для свето-
водов со ступенчатым профилем (2.8)_и на рис. 2.7, б для световодов с усе-
ченным степенным профилем (2.43), /тах(Р) определяется соотношением
(4.53), a Pmin — (8.10).
2.8. Лучевые параметры
Любой луч в градиентном волоконном световоде характеризуется инвариан-
тами (3 и I. В последующих главах для большинства применений знание луче-
вой траектории не обязательно — достаточно знание только лучевых парамет-
ров. Интеграл лучевого уравнения (2.13а) записывается в виде (2.21), пов-
торное интегрирование приводит к выражениям
z = zo +3 f „Z.ai/2 ; g(r) =n2 (r) -fi2 -I2 K-, (2.25)
ra g vJ r
где (r0, z0) — фиксированная точка траектории и для направляемых лучей
удовлетворяет условию ric < r0 < rtp, гДе ric и rtp ~ к0Рни g(г). Длина пу-
ти £р и оптическая длина пути Lo измеряются вдоль траектории луча (см.
рис. 2.4) между последовательно расположенными точками Р и Q, в которых
траектория касается каустики точек поворота. Из симметрии следует, что в
средней точке полупериода траектория или касается внутренней каустики в
40
случае косых лучей, или пересекает ось в случае меридиональных лучей. Сле-
довательно,
Q Q
L =fds; Lo=fn(r)ds, (2.26)
Р Р Р
где интегрирование выполняется вдоль траектории луча. С помощью (2.16)
заменим ds на dz и с помощью (2.21) dz на dr. Таким образом,
r^n^dr =2r^n^r)dr
р 4 gw175* ° 4glry12 ’ (2-27^
где^(г) определяется соотношением (2.25). Полупериод zp траектории, яв-
ляющийся расстоянием вдоль оси между точками Р и Q (см. рис. 2.4), можно
записать в виде
1 Q dr
ZP= (2.28)
p ric
где N — количество точек поворота на единицу длины световода. В вышепри-
веденных выражениях предполагается, что для меридиональных лучен / = О
и ric = 0. Все эти выражения, а также выражение для времени прохождения
луча (см. след, разд.) приведены в табл. 2.1.
Локальный критический угол скольжения. В разд. 1.8 было введено поня-
тие локального критического угла скольжения вс(х) для градиентных планар-
ных волноводов. По аналогии для волоконных световодов определим 6с(г)
через профиль показателя преломления:
л пс\ л f Пс1 1 1/2
cos0cW = 7^. smW = р• <2-29)
Диапазон значений 0Z (г) для направляемых лучей в точке с радиусом г со-
ставляет
O<0z(r) <0с(г); 0<г<р. (2.30)
На границе сердцевины отсутствует область направляемых лучей, т. е. 0С (р) =
= 0. На оси волоконного световода эта область соответствует 0 < 0Z (0) <
< 0С(О) при условии, что л(0) = псо, и совпадает с областью значений 0z
(2.6а) для световода со ступенчатым профилем.
2.9. Время прохождения луча
Время прохождения луча t на расстояние z вдоль волоконного световода по
аналогии с (1.36) определяется с учетом (2.16) следующим образом:
t = ^fn(r)ds = -^-fn2 (r)dz, (2,31)
c CP о
где интегрирование во втором интеграле выполняется вдоль траектории г =
= r(z). Из разд. 1.9 следует, что время прохождения луча в волоконных све-
товодах можно представить в той же форме, что и в планарных волноводах.
Таким образом, при z > > zp из (1.37) следует, что
Г = z£o/(czp),
(2.32)
41
где Lo - оптическая длина пути согласно (2.27), a z - полупериод траекто-
рии (2.28). Для учета дисперсии материала в первом интеграле (2.31) необ-
ходимо заменить п(г) на групповой показатель /ig. По аналогии с (1.38)
получим
t = (г, X)ds- Hg(r,X) =n(r,X~) (2.33a)
c b 0Л
а выражения, соответствующие (1.386), запишутся в виде
_ z
с Zp ’ 7>т — 2 f z ч i/2 dr, т Г-С g(r,X)l/2 (2.336)
причем g(r, X) определяется в соответствии с (2.25), где п(г) заменено на
п (г, X).
Подчеркнем, что в общем случае время прохождения луча зависит как от
(Т, так и от / и совпадает с соответствующим выражением для планарного
волновода только в случае меридиональных лучей. Однако, как будет пока-
зано ниже, для определенных профилей, например,_ддя ступенчатого и усечен-
ного степенного время прохождения не зависит от Z и соответственно от угла
скоса. Справедливым остается также утверждение, сделанное в разд. 1.9 о
том, что в случае градиентного профиля происходит выравнивание времени
прохождения различных лучей по сравнению со ступенчатым профилем. Од-
нако в отличие от планарных волноводов для волоконных световодов не из-
вестен такой профиль, для которого происходило бы полное выравнивание
времени прохождения всех лучей.
ГРАДИЕНТНЫЕ ПРОФИЛИ, ДОПУСКАЮЩИЕ АНАЛИТИЧЕСКИЕ РЕШЕНИЯ
Рассмотрим волоконные световоды с градиентными профилями, для ко-
торых могут быть получены аналитические выражения для всех или хотя
бы для части лучевых параметров. Для простоты при определении длины пу-
ти воспользуемся параксиальным приближением (см. разд. 1.10). Получен-
ные результаты представлены в табл. 2.1.
2.10. Пример. Параболический профиль
Рассмотрим сначала бесконечный параболический профиль, описываемый соотношением
"ЧП ="сО{1-2Д('7р)2} ; 0<г<°°, (2.34)
где А определяется согласно (1.41), ар- масштабный параметр, характеризующий эф-
фективную ширину профиля. Как уже отмечалось в разд. 1.11, такой профиль является
нереальным, но тем не менее полезен для понимания процесса распространения света,
так как в этом случае фактически для всех лучевых параметров получаются простые вы-
ражения. Все лучи, удовлетворяющие условию (1.46), являются направляемыми. Под-
ставляя (2.34) в (2.19) и решая результирующее биквадратное уравнение, получаем
следующие выражения соответственно для радиусов внутренней каустики и каустики
точек поворота:
Г‘с=2^Т7Г И"со-^) - [("со-?)2 -8A/4J1'2} (2.35а)
42
rtP~ 2псУ,/2
Полагая z = 0 при г = г*с и раскладывая подынтегральное выражение в (2.25) с учетом
(2.35) на множители, получаем
, rtp
г = —Pl_____ f
«со>лд 4 ('V'1)
co
- 8д7’«со]1Л }'п
rdr
(г3 - л? )1/3
1С
(2.356)
(2.36)
Это табличный интеграл, который в соответствии с (37.121) после соответствующих
преобразований можно записать в виде
ic+ rtp 'ф-'к 2z "со'/2д
~2— --------2-- cos(— }
г
(2.37)
Проекция такой траектории на поперечное сечение представляет собой эллипс. Полупе-
риод zp лучевой траектории из (2.28) равен отсчитываемому вдоль оси расстоянию меж-
ду последовательно расположенными точками траектории, в которых г = rtp, что соот-
ветствует увеличению аргумента косинуса в (2.37) на 2тг. Следовательно,
Zp — 1/)V = nppl(nсо V2A), (2.38)
где TV - количество точек поворота на единицу длины световода. Оптическая длина пу-
ти Lq получается подстановкой выражения (2.34) во второй интеграл (2.27). По анало-
гии с (2.36) с учетом (2.38) получим
_ лсо 7 г3 dr______
° Д Zp р ric (^р-г2)1'3 (Г2 - г?с)
Табличный интеграл вычисляется в соответствии с (37.122). С помощью (2.35) и (2.38)
его можно записать в виде
= +Лсо)/(23)- <2-4°)
Первый же интеграл в (2.27), определяющий длину пути, в общем случае не может быть
вычислен, но его можно оценить в параксиальном приближении. При А < < 1 можно
записать л (г) в виде (1.43) и по аналогии с (2.39) получим
nco V 24 *р г3 dr
P
(2.39)
ric ('•?р-г’),/а (г2 -г?с:
(2.41a)
z ( Зп „
_ Р j СО + (3
j3 лсо
При этом использованы соотношения (2.35), (2.38) и (37.122). Наконец, время t про-
хождения луча, определяемое (2.32), находится непосредственно из (2.40):
(2.416)
t = z(p + n3o)/(2cj3).
(2.42)
Это выражение идентично аналогичному выражению (1.50) для планарного волновода.
2.11. Пример. Усеченный степенной профиль
Усеченный степенной профиль определяется следующим образом:
п3 (г) = л’о[1 - 2А (г/р)^]; 0
(2.43а)
= лс1 = "Job ~2Д]; р<г<
(2.436)
43
где q - положительная константа. Частные случаи этого профиля представлены на
рис. 1.10, где координату х следует заменить на г. Диапазон значений 0, соответствую-
щих направляемым лучам, определяется условием (2.24а). Для произвольных косых
лучей с Г > 0 только время прохождения луча может быть выражено в простой явной
форме. Лучевые параметры для меридиональных лучей приведены в табл. 1.1, причем
во всех выражениях необходимо заменить х на г. Как отмечалось в разд. 1.13, резуль-
таты для параболического профиля применимы и в случае усеченного параболического
профиля, так как лучевые параметры для направляемых лучей не зависят от*наличия
оболочки. Для того чтобы определить время прохождения лучей, подставим (2.43а) в
выражение для ошической длины пути (2.27) и, выполняя необходимые преобразова-
ния, получаем
"со 4n2 A tp rq
L = -S2-Z_______££_ f ---------dr,
/3 p Pq ''ic £<ГГ/2
s (Г) = n2co-F - Г - 1n2co^C-)q,
(2.44a)
(2.446)
где Zp - полупериод траектории (2.28). Для вычисления интеграла используем особен-
ности степенного профиля. Взятие интеграла в (2.44а) по частям дает
rjP ёРг ( Л-' 2 )
/ . / g(rV-dr = f | ^ОА Ur, (2.45)
так как g (г) = 0 при г = гjc и г — rtp. Перегруппировка членов и подстановка (2.446)
приводит к следующему выражению:
rtp ] г л
1 = 1 + / ~Г77Г [ё1 ~п1о+ 2)"сод f dr. (2.46)
ric g И) P
В результате из (2.28) получаем соотношение
^^г = Р^О^со-РЧ 2
ric g (Г)1/2 2(<? + 2)п2оД^ 2р’
(2.47)
которое позволяет записать выражение (2.44а) для LQ в явном виде. Подставляя LQ в
(2.32), окончательно получаем [3]
_ z Wco ( ^со + 20 1
" с “(772Г + «со Г
(2.48)
что полностью совпадает с аналогичным выражением (1.64) для планарного волновода.
ВОЛОКОННЫЕ СВЕТОВОДЫ С НЕКРУГЛЫМ СЕЧЕНИЕМ
До сих пор в этой главе рассматривались только волоконные световоды с
круглым сечением. Однако в реальных случаях форма поперечного сечения
может существенно отличаться от круглой, например в случае эллиптических
световодов. Поэтому обобщим анализ для световодов с некруглыми сечения-
ми и неосесимметричными профилями показателя преломления. Лучевые ме-
тоды можно применять для анализа волоконных световодов с любой формой
поперечного сечения при единственном условии, что они являются многомо-
довыми. Лучевые траектории в круглых волоконных световодах могут быть
44
описаны с помощью лучевых инвариантов /3 и /, выражающих трансляцион-
ную и азимутальную симметрию. Некруглые волокна обладают только
трансляционной симметрией, поэтому их лучевой анализ в общем случае
сложнее, чем у круглых. Более того, в некруглых световодах могут распро-
страняться лучи нового класса (в дополнение к направляемым, рефрагирую-
щим и туннелирующим), которые называются туннелирующими-рефрагиру-
ющими лучами [5]. Эти лучи являются вытекающими, они теряют мощность
за счет туннелирования при последовательных отражениях или при прохож-
дении точек поворота, а также частично или полностью высвечиваются в обо-
лочку за счет преломления.
2.12. Лучевые уравнения
Лучевое уравнение (1.18) можно разложить на декартовые составляющие
(см. рис. 2.1). Они имеют вид
(2.49а)
г ds [ ds ) ду
П(х,у)^\ =0, (2.496)
-у- J П (X, у) — I = -&L
ds | v ds J
_d_
ds
где 5 - расстояние вдоль траектории, а п (х, у) - функция профиля. Из по-
следнего уравнения можно получить лучевой инвариант (39 который в рас-
сматриваемом случае определяется следующим образом:
__ » /77
3 = л (х, у) --- = п (х, у) cos 0Z (х, у), (2.50)
где 0Z (х, у) — угол между осью световода и касательной к траектории; х =
= x(z), у = y(z) — текущие координаты точек траектории. Исключая из
(2.49а) ds с помощью выражения для 3, получаем следующие уравнения лу-
чевой траектории:
2(р ^х = дп2(х,у) 2в2 -2- = д”2 (х'
dz2 дх ’ dz2 by
(2.51)
Записывая ds2 =dx2 + dy2 + dz2 и подставляя в (2.50), получаем соотношение
dx_\2 + /4У v = п2 (х> У) _ 1
dz’ 'dz’ jp
(2.52)
справедливое на лучевой траектории. Это первый интеграл для лучевых урав-
нений. Если л(х, у) имеет в оболочке постоянное значение ис1, то из (2.52)
следует, что в оболочке отсутствуют лучевые траектории при /3 > пс1, т. е.
лучи являются направляемыми. Далее, если ncQ - максимальное значение
п(х, у) в сердцевине, то уравнение (2.52) показывает, что 3 не может превы-
шать лС(?. Соответственно значение инварианта (3 для направляемых лучей ле-
жит в интервале лс1 < (3 < пс0, и он не зависит ни от формы профиля, ни от
геометрии поперечного сечения волоконного световода.
45
Время прохождения луча. Локальная скорость света равна с/п(х, у), поэ-
тому время прохождения луча на расстояние z вдоль световода определяется
интегралом по траектории:
1 1 z t = -^fn(x,y)ds = —J n2 (x, y)dz, C C@ 0 (2.53)
где второй интеграл получен с помощью (2.50), а х = х (z) и у =у (z) .
2.13. Пример. Профиль, описываемый однородной функцией
Рассмотрим волоконный световод с некруглым сечением и профилем, описываемым
произвольной однородной функцией f(x, у) в виде
л2 (х, У) = «со {1 “ 2Д/(х> 1 5 -°° < х, у < (2.54а)
Однородная функция степени q обладает следующим свойством: если а - константа, то
f (ах, ay} = a9f(x, у); х (Э//Эх) + у (д//Эу) = qf. (2.546)
Примером такого профиля может служить класс степенных профилей некруглого сече-
ния, рассмотренный в [5]:
п2(х,у) = л2со|1 -2Д[|-£-|р+ (2-55)
I х Ру )
где р - параметр формы профиля, а рх, ру - масштабные длины. Указанный класс вклю-
чает степенные профили (2.43а) круглых волоконных световодов, при этом рх — ру —
= Р, р = 2, а. г2 = х2 + у2. Для произвольной однородной функции интеграл в выраже-
нии (2.53) для времени прохождения луча может быть вычислен точно. Для этого пе-
рейдем к интегрированию по радиусу г = (х2 +у2)1/2 в цилиндрических координатах.
Взяв вторую производную по z от этого выражения и подставив (2.51), (2.52) и (2.54),
получим
02 d2r2 = 2 {п1 (х, у) -j?2} - 2«е0 Д-J у) + у—(х, у)>, (2.56а)
dz ( ОХ ду J
=. (<7 + 2) и2 (х, у) - qn2c0 - 2р. (2.566)
После интегрирования по z левая часть имеет вид р [dr2/dz]$ ,и по сравнению с членами
в правой части, линейными по z, ею можно пренебречь, если z достаточно велико. Пра-
вая часть содержит интегральное выражение (2.53) для времени прохождения и, выпол-
няя соответствующие преобразования, получаем выражение в виде [5]
z wco ( wco /3
Г = F7TT q + 2--------
d+ 2 ( $ Псо
(2.57)
которое идентично выражению (2.48) в случае усеченного степенного профиля в круг-
лых волоконных световодах , а также выражению (2.12) для ступенчатого профиля при
q 00. Таким образом, основной результат заключается в том, что время прохождения
луча в случае профиля, описываемого однородной функцией, не зависит от формы сече-
ния и угла скоса луча.
46
2.14. Пример. Профиль, описываемый функцией с разделяющимися
переменными
Функцию профиля с разделяющимися переменными можно представить в виде [б]
п1 (х, у) = п2с0 (1 - 2 А [/(х) + g(y) ] ], -оо < х, у < оо, (2.58)
где f (х) и g(y) - соответственно функции х и у. Лучевое уравнение (2.51) в случае
таких профилей распадается на два обыкновенных дифференциальных уравнения, ко-
торые можно записать в виде
dx{dz> ™ dx •
(2.59)
где Г2 = «со x/2A //3. После интегрирования и соответствующих преобразований полу-
чим для лучевой траектории следующее выражение:
z = - f ---------—----------- = Г f---------—-------------, (2.60)
П {/(xtp)-/(%)} 1/2 ПУо {g(ytp) ~g(y)} ',г
при этом предполагается, что в сечении z = 0 луч проходит через точку х0, у0. Коорди-
наты точек поворота xtp и уtp определяются начальным направлением луча.
Характеристики лучевой траектории. Для заданной траектории каустика точек пово-
рота образует поверхность, проходящую через точки xtp и ytp, на которой dx/dz = 0 и
dy/dz — 0. Если предположить, что f (х) и g (у) являются возрастающими функциями,
тогда п (х, у) уменьшается при удалении от оси, а каустика точек поворота имеет в сече-
нии вид прямоугольника со сторонами 2*tp и 2ytp, как показано на рис. 2.8, а. В общем
случае проекция траектории на поперечное сечение по мере распространения луча каса-
ется всех точек контура прямоугольника и заполняет весь прямоугольник, если пред-
положить, что волоконный световод имеет бесконечную длину. Подставляя первый ин-
теграл уравнения (2.59) в (2.52), после преобразований получаем соотношение
02 =n20'l -2A[/(xtp) +^Otp)]}, (2.61)
которое с учетом (2.58) показывает, что углы прямоугольника должны лежать на кон-
туре, вдоль которого показатель преломления постоянен и который определяется урав-
нением п(х, у) = 0. Указанный контур изображен на рис. 2.8, а и является огибающей
всех возможных прямоугольных каустик лучевых траекторий, удовлетворяющих соот-
ношению (2.61) и соответствующих различным начальным условиям, но одному и тому
же значению 0.
Классификация лучей. Рассмотрим теперь усеченные профили, у которых п (х, у)
имеет постоянное значение пс| вне границы раздела. Предположим, что п (х, у) имеет
Рис. 2.8. Прямоугольные каустики точек поворота направляемых (а) и туннелируюших-
рефрагирующих лучей (0 [5] в волоконных световодах с функцией профиля с разде-
ляющимися переменными (2.58)
47
максимум, равный лсо при х = у — 0. Как было показано в разд. 2.12, направляемые
лучи имеют инварианты в интервале пс| < 0 <исо, соответствующие прямоугольникам
с огибающими, лежащими между границей раздела 0 = ис1 и осью 0 = nQQ. Для направ-
ляемых лучей каждая прямоугольная каустика полностью расположена внутри сердце-
вины. Для остальных (вытекающих) лучей, у которых 0 < 0 < исЬ внутри сердцевины
может находиться только часть каждой прямоугольной каустики. Пример такой ситуа-
ции изображен на рис. 2.8, б. Типичная лучевая траектория касается каустики последо-
вательно в точках Рх, Р2, Р3 и Р4. В заштрихованной области между каустикой и грани-
цей сердцевины лучи не распространяются, но так как 0 < я^из уравнения (2.52) сле-
дует, что они могут распространяться в оболочке. Поэтому при отражениях в точках Рг,
Р2, Р3 и Р4 энергия будет теряться из-за туннелирования (см. разд. 2.7). После отраже-
ния в точке Р4 луч пересекает границу сердцевины и уходит в оболочку, т. е. преломля-
ется. Следовательно, здесь мы сталкиваемся с новым типом лучей, которые либо тунне-
лируют, либо преломляются в различных точках траектории. Такие лучи называются
туннелирующими-рефрагирующими [5] и могут распространяться только в некруглых
волоконных световодах.
2.15. Пример. Параболический эллиптический профиль
В этом случае волоконный световод имеет профиль следующего вида:
п2(х,у) = и’о (1 -2Д(^- + ^-)к (2.62)
I Ргх Ру )
где рх и ру - длины большой и малой полуосей эллипса, а контуры с постоянным значе-
нием показателя преломления есть эллипсы с одинаковым эксцентриситетом е, опреде-
ляемым соотношением е — (1 - P^/pJ) 1/2. Такой профиль одновременно является при-
мером профиля, описываемого однородной функцией, соответствующего уравнению
(2.55) при р - q = 2, а также примером профиля, описываемого функцией с разделяю-
щимися переменными, соответствующего уравнению (2.58), где f (х) = х2 /pxng(y) =
= у2/ру. Следовательно, время прохождения луча определяется соотношением (2.57),
а лучевые уравнения (2.59) можно записать в виде
d2x _ _ SI2 d2y _
dz2
(2.63)
где П = п 2^/0. Эти уравнения являются гармоническими и имеют следующие ре-
шения [5, 6 ]:
х = (х|р-х2)1/2 sin (ш/рх) +х0 cos(Hz/px), (2.64а)
У = Otp “ У о)1 /2 sin + у О cos (^z/py)> (2.646)
где х0, у0 - координаты траектории луча в сечении z = 0, a ±xtp, ±ytp - координаты
каустик точек поворота. Как легко показать, в такой форме выражения (2.64) удовлет-
воряют условиям (2.52) и (2.61). В случае произвольного эксцентриситета лучевые тра-
ектории полностью заполняют область, ограниченную прямоугольной каустикой (см.
рис. 2.8,6), причем, когда Ру/рх - рациональная дробь, т. е. тпрх = пру, где т и п - це-
лые числа, проекция траектории представляет собой фигуру Лиссажу. При рх = ру — р
эти траектории вырождаются в эллипсы в поперечном сечении круглого волоконного
световода (см. разд. 2.10).
Г Л А В А 3. УШИРЕНИЕ ИМПУЛЬСОВ
Передача информации по волоконным световодам обычно осуществляется с
помощью передачи последовательности импульсов световой энергии. Однако
48
Рис. 3.1. Представление
распространения им-
пульса в волноводе со
ступенчатым (а) и гра-
диентным (0 профи-
лями с помощью супер-
позиции направляемых
лучей (траектория луча
показана на длине вол-
новода z)
из-за дисперсии в волоконных световодах каждый импульс в процессе рас-
пространения расширяется. Ясно, что при достаточно большом расширении
соседние импульсы будут перекрываться. Это приводит к снижению инфор-
мационной емкости, так как близко расположенные импульсы невозможно
различить на выходном конце волоконного световода.
В главах 1 и 2 было введено понятие времени прохождения луча. Основ-
ное расширение импульса обусловлено тем, что время прохождения света
различно для разных траекторий луча. Этот эффект известен как лучевая
дисперсия. Иногда его называют межмодовой дисперсией, поскольку перво-
начальные исследования проводились с помощью волновой теории и анализа
в терминах мод [1], а не лучей. Кроме лучевой дисперсии на уширение им-
пульсов сказывается и дисперсия материала. Это обусловлено зависимостью
показателя преломления материала, из которого изготовлен волоконный
световод, от длины волны распространяющегося света.
Основная цель главы — показать, что уширение импульса зависит от про-
филя показателя преломления, а также продемонстрировать, как это ушире-
ние может быть минимизировано соответствующим выбором профиля. Сна-
чала рассмотрим планарные волноводы, для которых, как было показано,
можно получить нулевое уйпирение импульса, а затем круглые и некруглые
волоконные световоды. Будем предполагать, что материалы, из которых со-
стоит волновод, не обладают дисперсией. Затем покажем, как можно моди-
фицировать результаты с тем, чтобы учесть дисперсию материала. В этой гла-
ве рассматриваются только направляемые лучи, так как именно они характе-
ризуют передающие свойства длинных волоконных световодов. Основной
вывод главы состоит в том, что уширение импульса в волоконном световоде
минимально, если профиль имеет близкую к параболической форму.
Начальные условия. Предположим, что импульс начинает распространяться
в момент времени t = 0 на торце с координатой z = 0 в волоконном светово-
де произвольного профиля и длиной z, как показано на рис. 3.1. Предполага-
ется, что импульс сформирован только направляемыми лучами, причем все
они возбуждаются одновременно при z = 0. Для удобства будем считать, что
начальная ширина импульса равна нулю. На практике источники возбуждают
импульсы конечной длительности; уширение таких импульсов при распро-
странении по волоконному световоду можно найти методом суперпозиций.
49
3. ЛУЧЕВАЯ ДИСПЕРСИЯ В ПЛАНАРНЫХ ВОЛНОВОДАХ
Простейшими структурами для вычисления дисперсии являются планар-
ные волноводы, рассмотренные в гл. 1. Начнем исследование волноводов со
ступенчатым профилем, а потом перейдем к волноводам с градиентным
профилем.
3.1. Ступенчатый профиль
Как было показано на рис. 1.4, а, направляемые лучи распространяются по
зигзагообразной траектории в сердцевине под углом 0Z к оси волновода. Ин-
тервал значений углов 0Z для направляемых лучей в соответствии с (1.5а)
О < 0Z < 0С, где 0С — критический угол скольжения, определенный в табл. I.
Время прохождения луча t (1.14) изменяется обратно пропорционально
cos0z. Следовательно, минимальное время прохождения rmin соответствует
0Z = 0, т. е. лучам, распространяющимся параллельно оси, а максимальное
время прохождения Гтах соответствует 0Z = вс. Итак,
t . = L.n • t = — = — —— (3 1)
min c co> fmax c COS 0C C nci ’
где nco и ис1 - показатели преломления сердцевины и оболочки, z — длина
волновода, с — скорость света в свободном пространстве. Таким образом,
уширение импульса, или лучевая дисперсия, rd во временных координатах
есть разность максимального и минимального времен прохождения, которая
определяется соотношением
с л )
^^max-^in=7"co -7П -1 =|"со {(1-2Д)-1/2 -1} (3.2)
через высоту профиля показателя преломления, определенную в табл. I. При
увеличении длины волновода импульс уширяется в большей степени. Для
слабонаправляющих волноводов, у которых исо & псЬ из (1.42) следует
'd *z«coA/c*z«co0c2/2^
(3.3)
так как Д, вс < < 1. Следовательно, дисперсию можно уменьшить, снижая пе-
репад показателей преломления. Это одна из причин того, что реальные вол-
новоды имеют малые значения Д или, что эквивалентно, 0с.
Пространственное уширение. Альтернативный путь рассмотрения диспер-
сии заключается в том, что ее характеризуют значением пространственного
уширения zd импульса по мере его распространения. Это расстояние между
передним фронтом импульса, распространяющимся со скоростью с/п^ и
его задним фронтом, распространяющимся со скоростью cnc]/n2CQ. Итак, че-
рез время t уширение достигает величины
Z Ct I 1 _ cI I Ct A — —
d ^co [ wco J ^co ^co
где указанные приближенные равенства справедливы для слабонаправляю-
щих волноводов в случае параксиальных лучей. Очевидно, что пространствен-
ное уширение растет с увеличением длины волновода. В заключение отметим,
50
что описание уширения импульса с помощью соотношения (3.2) является
простейшим среди существующих, в том числе и с помощью среднеквадра-
тической ширины импульсного отклика (см. разд. 4.20) .
3.2. Усеченный степенной профиль
Уширение импульса, соответствующее ступенчатому профилю, можно умень-
шить, создавая плавное изменение показателя преломления в сердцевине.
Как следует из (1.13), скорость света вдоль траектории равна с/п(х), где
п(х) — профиль показателя преломления в сердцевине. Поэтому чем меньше
показатель преломления, тем больше скорость света. Если сделать так, чтобы
лучи, траектории которых больше удалены от оси, проходили через области
с меньшим показателем преломления, то можно выровнять время их про-
хождения для различных траекторий. Как показано в разд. 1.12, такая схе-
ма компенсации позволяет полностью это сделать для всех лучей в планар-
ном волноводе с гиперболическим секансным профилем {2]. Однако в во-
локонных световодах с таким же профилем выравнивание времени про-
хождения происходит только для меридиональных лучей, нс неизвестна
форма профиля, позволяющая полностью выровнять время прохождения
как меридиональных, так и косых лучей. Соответственно усеченные степен-
ные профили, для которых время прохождения не зависит от угла скоса лу-
ча [1, 3, 4], как было показано в общем случае в разд. 2.13, представляют
большой практический интерес для волоконных световодов.
Оптимальный профиль. Усеченные степенные профили для планарных вол-
новодов задаются соотношением (1.59) и иллюстрируются рис. 1.10. Теперь
определим, какой из этих профилей (т. е. при каком значении #•) обеспечива-
ет минимальное уширение импульса. В отличие от волноводов со ступенча-
тым профилем в случае градиентного профиля и синусоидальной траектории
(см. рис. 1.8) только из геометрических соображений нельзя определить,
какая из траекторий соответствует максимальному и минимальному време-
ни прохождения луча. Выражение для времени прохождения направляемых
лучей, приведенное также в табл. 1.1, зависящее от лучевого инварианта /3
и показателя профиля q, имеет вид
+ »с1<в<"ео- (3.5)
*2 • I LJ LU j
Если построить график t((3) для произвольного q, то получится характер-
ная кривая параболической формы _(рис. 3.2). Минимум времени прохож-
дения для данного q достигается при (3 = (Зт. Дифференцируя, найдем
г(?т) =1’ТГГисо; 0т = ф1/2исо- (з.б)
Следует рассмотреть три случая, так как (Зт не всегда находится в интервале
значений /3 (3.5), соответствующих направляемым лучам. Максимальное и
минимальное время прохождения ZLmax и ?min для каждого случая определя-
ются соответственно из (3.1), а ширина импульса задается соотношениями
^d ~ ^max ~ ^min ” (wcl) ~ ? (Дсо) > # ==^ 2, (3.7а)
51
f Z(«ri) - r(Pm) 1
'd = 'max-'min=supj C\ J 2 - 4Л < q < 2,
|/(«co) -f(0m)J
= r(«co)-Hwcl); 0<<7<2-44
(3-76)
(3.7b)
(3.7г)
для соответствующих значений q; символ sup — указывает, что выбирают
большее из двух выражений. Значение q = ^opt, минимизирующее время ZLd,
может быть определено либо формальным дифференцированием, либо с по-
мощью следующих простых рассуждений. Используя для Ц|3) выражения
(3.5) и (3.6), легко убедиться, что увеличивается с ростом q в (3.7а) и
(3.76) и с'уменьшением q в (3.7в) и (3.7г). Минимальное значение ZLd соот-
ветствует случаю, когда (3.76) и (3.7в) совпадают, это достигается при [3, 4]
<?oPt = 2(l — 2Д)1/2 ^=2-2Д ~2-02,
чему соответствует минимальное значение уширения импульса:
d с «со + лс1 со с 8 со с 32 со’
(3-8)
(3-9)
Приближенные равенства в (3.8) и (3.9) справедливы для параксиальных лу-
чей в слабонаправляющих волноводах. Видно, что оптимальный профиль бли-
зок к параболическому. При этом ширина импульса существенно меньше,
чем в случае ступенчатого профиля, так как в выражении для rd появляется
коэффициент Д/8, или #с2/16 (сравните с (3.3)). Поскольку l/rd является од-
ной из характеристик информационной емкости волноводов, то для опти-
мального профиля она в 8/Д, или 16/02 раз больше, чем для ступенчатого
профиля. Построим график для rd (3.7) в виде зависимости нормированно-
го времени ctJznCQ от q для Д = 0,01, или 0С 0,14 (сплошная кривая на
рис. 3.3). При q = ^opt на кривой расположена точка острого минимума, что
свидетельствует о чрезвычайной чувствительности лучевой дисперсии к ма-
лым вариациям q вблизи q^v Например, при q = gopt ± Д ширина импульса
возрастает почти в 10 раз. Для сравнения на рисунке представлена нормиро-
ванная ширина импульса для ступенчатого профиля (q = 00) с тем же значе-
нием Д.
ЛУЧЕВАЯ ДИСПЕРСИЯ В ВОЛОКОННЫХ СВЕТОВОДАХ
Уширение импульсов в волоконных световодах исследуется точно так же,
как и в случае планарных волноводов. Некоторые усложнения связаны с тем,
что при рассмотрении волоконных световодов помимо меридиональных не-
обходимо учитывать еще и косые лучи. В гл. 2 было показано, что меридио-
нальные лучи обладают теми же свойствами, что и лучи в планарных волно-
водах и, следовательно, имеют то же время прохождения, тогда как для ко-
сых лучей оно зависит в общем случае от обоих лучевых инвариантов (3 и
/. Однако из табл. 2.1 видно, что время прохождения для косых лучей в во-
локонных световодах со ступенчатым и усеченным степенным профилями не
зависит от I и поэтому совпадает со временем прохождения меридиональных
52
.Рис. 3.3. Зависимость нормированной ширины импульса ct^/znco (3.7) от q для усечен-
ных степенных профилей (сплошная линия); горизонтальная линия (q = °°) соответ-
ствует зависимости (3.2) для ступенчатого профиля; штриховая линия — аналогичной
зависимости при наличии дисперсии материала, при этом значение показателя степени
оптимального профиля изменяется от ?opt « 1,98 до ?opt + bq « 2,26 для случая сла-
бонаправляющего волновода. Для всех трех кривых А = 0,01, или #с « 0,14
лучей. Следовательно, лучевая дисперсия в волоконных световодах со сту-
пенчатым профилем определяется тем же самым выражением, что и в случае
планарных волноводов со ступенчатым профилем, т. е. соотношениями
(3.2) и (3.3). Точно так же оптимальный показатель профиля и минималь-
ное уширение импульса для волоконных световодов с усеченным степенным
профилем определяются с помощью соответствующих выражений для пла-
нарных волноводов (3.8) и (3.9).
Из разд. 3.2 ясно, что в планарных волноводах с гиперболическим секанс-
ным профилем лучевая дисперсия отсутствует. Однако в волоконных свето-
водах того же профиля она уже не равна нулю. Не известен профиль, кото-
рый обеспечивал бы нулевую дисперсию и для косых, и для меридиональ-
ных лучей.
3.3. Некруглые волоконные световоды
В разд. 2.13 было показано, что время прохождения луча в волоконных све-
товодах со ступенчатым профилем не зависит от геометрии поперечного сече-
ния. Следовательно, выражения (3.2) и (3.3) описывают лучевую дисперсию
в волоконных световодах со ступенчатым профилем и произвольной формой
поперечного сечения. В разд. 2.13 также было определено, что время прохож-
дения луча в некруглых волоконных световодах с усеченным степенным про-
филем (2.55) и с симметричным усеченным степенным профилем (см.
табл. 2.1) идентично, т. е. зависит только от 0. Таким образом, выражения
(3.8) и (3.9) определяют оптимальный профиль и минимальное уширение
импульса и для некруглых профилей [5], в том числе для усеченного парабо-
53
лического профиля в волоконных световодах с эллиптическим сечением.
Другими словами, лучевая дисперсия в волоконных световодах со ступен-
чатым профилем произвольного поперечного сечения и некруглых с усечен-
ным степенным профилем определяется соответствующими выражениями
для планарных волноводов.
ДИСПЕРСИЯ МАТЕРИАЛА И ДИСПЕРСИЯ ПРОФИЛЯ
В данной главе при анализе уширения импульсов предполагалось, что среды,
образующие волновод, не имеют дисперсии. Рассмотрим эффекты, связан-
ные с дисперсией материалов, образующих волновод. Хотя дисперсия мате-
риала сама по себе обычно мала, в разд. 3.8 будет показано, что при наличии
лучевой дисперсии она может оказывать существенное воздействие на ушире-
ние импульсов.
3.4. Дисперсия материала
Номинально монохроматический источник света с длиной волны X имеет в
действительности конечную ширину линии 6Х. В то же время реальные вол-
новоды состоят из материалов, обладающих дисперсией. Дисперсия описыва-
ется с помощью вариаций (обычно очень малых) функции профиля показа-
теля преломления при изменении длины волны, например, п = п (г, X) для
круглых волоконных световодов. Следовательно, лучи, следующие по оди-
наковым траекториям, но возбуждаемые на различных длинах волн, будут
распространяться с различными скоростями. При этом уширение импульса
происходит совсем не так, как в случае лучевой дисперсии. В этом можно
убедиться на простом примере. Рассмотрим лучи, распространяющиеся па-
раллельно оси на расстояние z в волноводе со ступенчатым профилем, имею-
щем показатель преломления сердцевины «С0(Х). Время прохождения луча
с длиной воЛны X задается соотношением (1.17) в терминах группового
индекса^ (1.16). При 0Z =0 /3 = псо и, следовательно,
(3-10)
с I и A j
Так как 5Х << X, ширина импульса приближенно может быть выражена
в виде
. I dt ica _zX nco(X) hiiA
gylSX-— I—---------- I6X, (3.11)
и уширение импульса пропорционально второй производной [6]. В реальных
ситуациях это уширение мало по сравнению с дисперсией профиля, обсужда-
емой ниже.
3.5. Дисперсия профиля
Рассмотрим теперь, как лучевая дисперсия и дисперсия материала влияют на
уширение импульсов. Для описания комбинации двух указанных эффектов
удобно использовать понятие дисперсия профиля [3]. Неожиданным явля-
ется тот факт, что на уширение импульса дисперсия материала существенно
влияет даже тогда, когда вторая производная Э2лг/ЭX2 равна нулю. Это обус-
54
ловлено тем, что компонента JA/JX первой производной Эи/ЭХ играет реша-
ющую роль во взаимодействии двух форм дисперсии, как будет показано в
примере (см. разд. 3.8). Сначала рассмотрим специфическую зависимость
профиля от длины волны. Хотя в последующих разделах мы проиллюстриру-
ем причины дисперсии профиля на примере оптических волоконных свето-
водов, поскольку они представляют наибольший практический интерес, это
может быть сделано и на примере планарных волноводов.
3.6. Линейная дисперсия
Экспериментально установлено, что если материалы, из которых изготовле-
ны волоконные световоды, обладают дисперсией, то для описания профиля в
первом приближении спраьэдлива следующая модель [7, 8] :
и2(г,Х) =и2со(Х) {1 — 2А(Х)/(г)}, (3.12)
в которой функция профиля f (г) не зависит от длины волны. Такое прибли-
жение иногда называют линейной дисперсией потому, что в слабонаправляю-
щем волноводе (А << 1) групповой показатель'является линейной функ-
цией п. Если в (2.33а) положить п & псо (X) {1 - А(Х)/(г)} , то сразу же
получаем
ng =а(Х)п + Ь(Х), (3.13)
где а и b — функции только X. Поясним эту модель на примерах.
3.7. Пример. Волоконный световод со ступенчатым профилем
Показатели преломления сердцевины и оболочки в волоконных световодах со ступенча-
тым профилем равны соответственно «С0(Х) и hcj(X) в случае диспергирующих матери-
алов. В разд. 2.5 было показано, что время прохождения луча в этом случае идентично
соответствующему выражению (1.17) для планарных волноводов, содержащему груп-
повой показатель (1.16). По аналогии с выводом, проведенным в разд. 3.1, для выраже-
ния уширения импульса получим
z ( "со<А> 1 г х !
-ф1А -1’ <3141)
|. (3.146)
где приближенные равенства справедливы в случае слабонаправляющего волново-
да, когда Д(Х) « 1 - «С1 (X)/псо (X) << 1. Первый член в квадратных скобках (3.146)
описывает лучевую дисперсию, а второй член - дисперсию материала.
3.8. Пример. Волоконные световоды с усеченным степенным профилем
Из (3.12) следует, что при наличии дисперсии материала, чтобы удовлетворить крите-
рию линейной дисперсии, такие профили должны иметь следующую форму:
п’ (г, К) = л20(Х) |1 -2Д(Х) (^•),|; ос Г Ср, (3.15а)
= «cl<x) =п’0(Х) {1 -2Д(Х)}; р<г <оо, (3.156)
где показатель степени q не зависит от X. Время прохождения луча в этом случае опреде-
ляется соотношением (2.336). Подставив (3.15а) в выражение для группового показа-
теля (2.33а), представим выражение для Lm в (2.336) в виде
55
"а"со(А> Зр (r/p)q
— Z zp - 2na«co(X) Д (X) (2 - p) J 2 dr,
e rlc g (r)
(3.16)
где 0, Zp, rtp, rjc и g (г) зависят от X, что становится очевидным при замене п (г) нап(г, X)
в соответствующих определениях. Групповой показатель п& на оси и параметр внеосе-
вой дисперсии материала р являются функциями только длины волны и определяются
следующим образом:
d"coW
"а — псо (^ —
„ _ __X d Д (X)
Р п^ АХ ~(Г\
(3.17)
Интеграл в (3.16) легко вычисляется в соответствии с (2.47) и, подставляя (3.16) в
(2.336), найдем время прохождения луча
с а + 2 )(/7 + ^) п +(2 р) г J ис1 (М < 0 71 со (X).
v ( .р со j
(3.18)
Таким образом, время прохождения луча не зависит от угла сцоса и совпадает с соот-
ветствующим выражением для планарного волновода в линейном приближении для дис-
персии материала. Подразумевается, что р в этих выражениях мало.
Оптимальный профиль. Профиль, который минимизирует уширение импульса, может
быть получен из (3.18) с помощью процедуры, описанной в разд. 3.2. Итак, минималь-
ное время прохождения луча и соответствующий лучевой инвариант представим в виде
— 7 я П + (7 I 1z 2
= ё77^-<р-М),/2(2-р)1/2; = Исо. (3.19)
Легко показать
зом:
[4], что оптимальный профиль q = # определяется следующим обра-
Qopt=2(l -2Д)1'2 - р{ 1 + (1 -2Д)1/2} «2(1 -р) - Д(2-р),
(3.20)
а соответствующее минимальное уширение равно
_ Z ("со -"d2)2 Z Д2 Z ес4
fd-F Псо + лсГ "а~"а7^-~"а?ЗГ’
(3.21)
где исо = исо (X), ис1 — ис1(х), а приближенные равенства справедливы в случае слабо-
направляющего волновода, или, что эквивалентно, для параксиальных лучей. Таким
образом, хотя минимум уширения импульса не зависит от р, он изменяется с длиной
волны благодаря зависимости Д и «а от X.
Чувствительность дисперсии к отклонению параметров профиля от оптимального
значения. Небольшой сдвиг оптимального показателя профиля от q t до d?Opt из-за
дисперсии профиля может быть найден из (3.8) и (3.20) в приближении слабонаправля-
ющего волновода и приближенно равен &7Opt = -2р. Хотя сдвиг 5%pt мал, тем не ме-
нее он оказывает существенное воздействие на дисперсию импульсов. Вычислим луче-
вую дисперсию = tmax - tmjn из (3.18) по аналогии с (3.7) и построим график зави-
симости нормированной ширины импульса ct^/zn^ от q, полагая р = -0,14 и А- = 0,01
[4] (штриховая кривая на рис. 3.3). Сплошная кривая построена без учета дисперсии
56
материала (р = 0). Таким образом, влияние дисперсии профиля проявляется в сдвиге
провала (острого минимума), соответствующего оптимальному профилю, на расстоя-
ние 5%pt> как показано на рисунке. Однако ширина импульса при переходе от сплош-
ной кривой к штриховой в окрестности q = <70р{ изменяется почти на два порядка.
На практике часто выполняется условие |р| > > Д, в этом случае согласно (3.20) при
нахождении оптимального профиля дисперсия профиля преобладает над лучевой дис-
персией.
3.9. Нелинейная дисперсия
Если профиль п (г, X) не удовлетворяет условию линейности дисперсии
(3.13), то имеет место нелинейная дисперсия. Член с разделяющимися пере-
менными 2Д(Х)/(г) в (3.12) заменяется при этом членом F(X, г), который
не может быть записан в таком виде, как, например, для усеченного сте-
пенного профиля (3.15) при зависимости показателя профиля от длины вол-
ны. В этом случае определение оптимального профиля с помощью аналити-
ческих методов фактически невозможно. Однако при некоторых упроща-
ющих предположениях относительно формы функциональной зависимости
времени прохождения луча можно сформулировать задачу иным образом,
допускающим ее решение.
В разд. 3.8 указывалось, что в случае линейной дисперсии время прохож-
дения (3.18) для усеченных степенных профилей находится в достаточно
простой зависимости от инварианта 0, что, в свою очередь, дает непосред-
ственно выражение для оптимального профиля (3.20). Если дисперсия не-
линейная, то будем предполагать, что время прохождения луча по-прежнему
имеет ту же функциональную зависимость от /3, т. е.
г(з-22)
с ( р "со J
где А и В не зависят от /3. Если А и В заданы, то оптимальный профиль может
быть легко определен. Задача состоит в том, чтобы найти профиль, для кото-
рого время прохождения луча удовлетворяет соотношению (3.22). Такие
профили позволяют обеспечить достаточную гибкость при конструировании
волоконных световодов. Подробный вывод приведен в [9,10], где показа-
но, что (3.22) справедливо, если F (X, г) удовлетворяет условию
4г tD"7ir4r ~2(D-1)f = 0' ,3?J|
где да определено в (3.17), a D — произвольная функция длины волны. Об-
щее решение этого уравнения имеет вид
Х=^-ехр{-/^. (3.24)
В особом случае, когда функция G есть просто степень аргумента, т. е. G =
= Х^+2, где q — константа, переменные в F(X, г) разделяются, что дает ряд
степенных профилей с линейной дисперсией, подобных (3.15). Альтернатив-
ный метод решения уравнения (3.23) предполагает разложение F в степенной
ряд по г/р для каждой длины волны [11]. Эти решения могут быть использо-
ваны для улучшения дисперсионных характеристик волоконных световодов.
57
ГЛАВА 4. ВОЗБУЖДЕНИЕ ВОЛОКОННЫХ СВЕТОВОДОВ И ФОРМА
ИМПУЛЬСА
В предыдущих главах уширение импульсов было описано с помощью макси-
мально допустимого временнбго разброса ^тах - ^т|п. Теперь* исследуем
уширение импульсов более детально, изучив формы импульса после прохож-
дения через волоконный световод, т. е. распределение энергии в импульсе,
или импульсный отклик. Получим форму импульса в момент времени t,
считая, что вначале импульс имел нулевую ширину. Затем, используя сверт-
ку, можно определить отклик импульса произвольной начальной формы. При
анализе будем рассматривать только направляемые лучи, так как именно они
характеризуют передаточные свойства длинных волоконных световодов.
Многомодовые волоконные световоды обычно возбуждают диффузными
источниками. Для таких источников импульсный отклик в случае ступенча-
того или усеченного параболического профилей практически имеет форму
прямоугольника с основанием ^тах - ^т|П. Поэтому максимальный времен-
ной разброс для таких профилей довольно точно определяет импульсный от-
клик. Тем не менее необходимо подчеркнуть, что форма импульса чрезвы-
чайно чувствительна к малым отклонениям формы профиля от параболи-
ческой.
Для определения формы импульса необходимо исследовать характеристи-
ки возбуждающего излучения и передающую способность волоконных све-
товодов. В соответствии с этим рассмотрим, каким образом различные ис-
точники возбуждают сердцевину волоконного световода и как излучаемая
мощность распределяется между различными направляемыми лучами. Мате-
риал этой главы необходим для рассмотрения импульсных откликов в ко-
ротких волоконных световодах, в которых значительная доля мощности пе-
реносится вытекающими лучами, и влияния поглощения в сердцевине и обо-
лочке волоконного световода, приводящего к искажению импульсного от-
клика (гл. 6, 8).
Лучевые трубки. В гл. 1 и 2 обсуждались характеристики индивидуальных
лучевых траекторий. В этой главе рассматривается распределение мощности
по различным лучевым направлениям. Так как мощность отдельного луча не
определена, целесообразно ввести понятие лучевой трубки, т. е. трубки лу-
чей с бесконечно малым поперечным сечением, в пределах которой все лучи
распространяются в одном и том же направлении_или, что эквивалентно, име-
ют одинаковые значения лучевых инвариантов Р и Т. Трубки для волокон-
ных световодов со ступенчатым и градиентным профилями иллюстрируются
рис. 4.1. Это понятие представляет собой лучевую аналогию трубки потока
мощности в электромагнитной теории [1] и более подробно обсуждается в
разд. 35.3. Поток световой мощности параллелен направлению луча; полный
поток внутри трубки постоянен вдоль ее длины. В дальнейшем везде в ч. I
при рассмотрении вопросов, связанных с мощностью, будем под словом
’"луч" понимать лучевую трубку.
ИСТОЧНИКИ ИЗЛУЧЕНИЯ
Источник характеризуется распределением мощности по всем направле-
ниям лучей от каждого элементами его поверхности. Например, источник на
58
Рис. 4.1. Лучевые труб-
ки в волоконных све-
товодах со ступенча-
тым (а) и градиент-
ным (б) профилями
пс1
ПС1
Рис. 4.2. Качественное представление элементарной площадки источника dA, испуска-
ющей лучи в телесном углес?Г внутри конуса с половинным углом при вершине 0S
Рис. 4.3. Поперечные сечения пучков:
а - диффузного, и ли'ламбертова; б — коллимированного
рис. 4.2 испускает лучи внутри конуса с половинным углом при вершине
0s. Свет, испускаемый под углом 0о к нормали, имеет интенсивность 1(0о) в
единичном телесном угле и на единичной площади поверхности источника.
Таким образом, элемент излучаемой мощности определяется следующим
образом:
dP = I(Q0)drdA, O<0o<0s; dP = 0, 0S<0O<-^. (4.1)
где dr — элемент телесного угла, изображенный на рисунке. Теперь опреде-
лим два типа источников, которые будут использоваться в ч. I.
4.1. Диффузный, или ламбертов источник
Диффузный, или ламбертов источник [2] характеризуется тем, что каждый
элемент площади dA поверхности источника испускает лучи во всех направ-
лениях, т. е. 0S = я/2 в выражении (4.1). Поперечное сечение такого источни-
ка схематически представлено на рис. 4.3, а. Это наиболее типичные для прак-
тики источники, они хорошо моделируют светоизлучающие диоды (СИД).
Распределение интенсивности в этом случае имеет вид [2]
/(0О) =/ocos0o; О<0о<у, (4.2)
где Iq — константа. Однако СИД могут быть и неоднородно излучающими со
спадающим к краям источника распределением интенсивности. В этом слу-
59
чае /0 зависит от цилиндрической радиальной координаты г, отсчитываемой
от центра источника, который считается осесимметричным, и может быть ап-
проксимирована гауссовым распределением
/0 (г) = а ехр (-от21р}), (4.3)
где ps — радиус источника, А, а — положительные константы.
Частично диффузный источник. Если лучи, испускаемые источником,
удовлетворяют условию 0 < < 0S < тг/2, как показано на рис. 4.2, то такой
источник называется частично диффузным источником.
4.2. Коллимированный пучок
Источники с конечными поперечными размерами, излучающие только в на-
правлении оси, как показано на рис. 4.3, бу формируют коллимированный
пучок. Каждый бесконечно малый элемент dA поверхности источника излу-
чает свет в направлении #s = 0 (см. рис. 4.2). Для однородного пучка интен-
сивность в (4.1) постоянна по сечению пучка и равна /0- Такой пучок аппрок-
симирует излучение, генерируемое лазером.
ПРОХОЖДЕНИЕ ИЗЛУЧЕНИЯ ЧЕРЕЗ ТОРЕЦ ВОЛОКОННОГО СВЕТОВОДА
Рассмотрим поведение лучей при распространении от источника через вход-
ной торец в сердцевину световода. Если показатель преломления среды и0,
окружающей источник, отличается от показателя преломления сердцевины,
то необходимо учитывать как изменение направления лучей из-за преломле-
ния, так и потери мощности за счет отражений.
4.3. Отражение и преломление
Предположим, что источник расположен в однородной среде с показателем
преломления и, кроме того, он достаточно велик, так что полностью осве-
щает, по крайней мере, торец сердцевины волоконного световода, как это
обычно и бывает в реальных ситуациях. Луч от источника падает на входной
торец z = 0 в точке Q (рис. 4.4) и образует угол 0о с нормалью QN, или осью.
Полярные координаты точки Q на торце световода — г и (относительно
"cl
Рис. 4.4, Отражение и прелом-
ление лучей от источника в
точке Q на торце волокон-
ного световода. Полярные ко-
ординаты гиф определяют
положение точки Q, а проек-
ция траектории луча на торец
световода составляет угол Оф
с азимутальной осью в точ-
ке Q
60
оси х). Рассматриваются только лучи, падающие на торец сердцевины; лучи,
падающие на торец оболочки, не могут стать направляемыми в сердцевине.
Закон Снелля. Для удобства предположим, что п0 < где однородный
показатель преломления ис1 является минимальным значением функции про-
филя п(г) волоконного световода. Это условие обычно выполняется, так
как наиболее распространенной средой, в которой расположен источник,
является воздух, для которого п0 = 1. При этом падающий луч (см. рис. 4.4)
частично отражается под углом 0О и при любом значении угла 0очастично пре-
ломляется, проходя в сердцевину. Угол преломления 0Z (г) между нормалью
QN и касательной QR к лучевой траектории в сердцевине световода в точке
z = 0 связан с углом 0Q законом Снелля
п0 sin0o = n(r) sin0z (г); О<0о<у- (4.4)
При подстановке (4.4) в (2.16) начальное положение и направление траекто-
рии в сердцевине определяют лучевой инвариант 0. Из закона Снелля также
следует, что угол скоса луча относительно оси при пересечении входного тор-
ца световода сохраняется, так как возбуждающий луч источника, луч, рас-
пространяющийся в световоде, и нормаль компланарны. Если 0^ угол между
проекцией падающего луча на торец световода и азимутальной осью (см.
рис. 4.4), то второй лучевой инвариант I для траектории в сердцевине полу-
чается подстановкой (4.4) в (2.17) при 0^ (г) = 0^. Следовательно,
р = {п2 (г) - «о sin20О} 1/2 ; I = ^-«0 sin0О cos0^,
(4.5)
и каждый луч определяет значение инвариантов, описывающих продолжение
траектории луча в сердцевине волоконного световода.
Максимальный угол падения. Определим 0т (г) как максимальное значе-
ние угла 0О (см. рис. 4.4), при котором луч от источника может распростра-
няться в сердцевине как направляемый. Интервал значений 0Z (г) для направ-
ляемых лучей задается неравенством (2.30) в предположении, что п (г) моно-
тонно спадает при удалении от оси к границе сердцевины. Полагая 0О = 0т (г)
в (4.4), получим для 0т (г) соотношение
«о sin ет (г) = п (г) sin ес (г) = [ п2 (г) - п2с} } 1/2
(4-6)
где 0с(г) - критический угол скольжения, определяемый (2.29). В случае
ступенчатого профиля п (г) заменяется на «с0, а 0С (г) на 0С. Для параксиаль-
ного приближения 0С (г) « 1, поэтому 0m (г) ъ п (r)0c (г)/и0 •
4.4. Прохождение мощности
Показатель преломления п0 среды, окружающей источник, обычно отличает-
ся от показателя преломления сердцевины, следовательно, не вся мощность
источника может быть введена в сердцевину. Однако, как будет показано,
на практике не более 4 % мощности источника отражается от входного тор-
ца, поэтому этим эффектом обычно пренебрегают. Если световод имеет сту-
пенчатый профиль, то доля мощности Г, вводимой в сердцевину, определяет-
61
ся с помощью классических формул Френеля для коэффициентов отражения
от плоской границы раздела диэлектриков. В случае многомодовых светово-
дов электромагнитные поля в любой достаточно малой области входного
торца подобны полям плоских волн (см. разд. 35.3). Для простоты ограни-
чимся параксиальным приближением, когда направляемые лучи распростра-
няются практически параллельно оси световода, т. е. нормально к его торцу.
Доля мощности, вводимой в сердцевину при 0о 0, определяется первым
выражением в (35.21), если пс| заменить на п0. Следовательно [3],
Г = 4п0«со/(«о+«со)2- (4-7)
Этот результат приближенно справедлив также и для волоконных светово-
дов с градиентным профилем, так как n(r) & пс0. На практике ис0 ^1,5,
«о ~ 1 и, таким образом, не менее 96 % мощности источника вводится в серд-
цевину. Далее будем пренебрегать этими малыми потерями, но их можно
учесть заменой интенсивности/(0О) в (4.1) на77(0о).
ДИФФУЗНОЕ ВОЗБУЖДЕНИЕ
Теперь можно вычислить мощность направляемых лучей при облучении све-
товода диффузным источником. В этом разделе будут определены полная
мощность источника, полная мощность направляемых лучей и распределение
мощности по радиусу в поперечном сечении. В следующих разделах будет по-
казано, как получить распределение мощности по направляемым лучам.
Пусть источник, изображенный на рис. 4.3, а, находится напротив торца воло-
конного световода (см. рис. 4.4), причем его поверхность покрывает, по
крайней мере, торец сердцевины. Только часть поверхности источника, соот-
ветствующая сечению сердцевины, может возбудить направляемые лучи, по-
этому не будем рассматривать влияние участков поверхности источника вне
указанной области. Возбуждение лучей источником рассматривается в гл. 8.
Элемент мощности dP, излучаемой в телесном угле dV с площади dA ис-
точника в среде ’с показателем преломления w0, определяется соотношения-
ми (4.1) и (4.2). На рис. 4.4 углы 00,0 являются сферическими полярными
углами, отсчитываемыми от нормали (W, а г и — полярные координаты от-
носительно оси световода. Итак [4 — 6],
dP = IQ со8 0обМб?Г; dA=rdrd<p\ dV = sin 0об/0о^^, (4.8)
где направления лучей от источника удовлетворяют условиям 0 < 0О < тг/2,
О < 0,- < 2тг, а координаты точек на торце лежат в интервалах 0 < г < р\ 0 <
<S^27T.
4.5. Полная мощность источника
Полная мощность PXqV излучаемая источником во всех направлениях и по
всей площади сечения сердцевины (см. рис. 4.4), определяется интегрирова-
нием dP в (4.8) по всему диапазону значений каждой из четырех указанных
выше переменных. Соответственно [6]
Р 2л 7г/2 2л
Aot = ^r f f f /or sin0Ocos 0od0 . (4.9a)
0 0 0 0
62
Предполагается, что интенсивность зависит только от г; выполняя далее ин-
тегрирование, получим
р
Ptot = 2тг2 f rlodr. (4.96)
О
Для однородного освещения /0 = const и, таким образом,
’tot = я2р2/0.
(4.Ю)
Лишь часть полной мощности источника расходуется на возбуждение направ-
ляемых лучей, остальная - на возбуждение вытекающих лучей (см. гл. 8).
Обозначим мощность источника, переносимую всеми направляющими луча-
ми, через РЬ1., тогда эффективность возбуждения источника определяется
соотношением
&=PbAt = WA)-
(4.11)
в котором не учитываются малые потери мощности*за счет отражения от тор-
ца. Этот вопрос рассматривался в разд. 4.4. Можно предвидеть, что в слабо-
направляющих световодах эффективность & будет мала из-за малой области
направлений, соответствующих направляемым лучам.
4.6. Полная мощность направляемых лучей
Мощность направляемых лучей РЬг можно определить интегрированием
(4.8) по всей области значений координат г и угла 0 определенной ниже
соотношения (4.8) . Область значений 0О соответствует направляемым лучам
в световоде, т. е. 0 < 0о' ^m(r), где угол 0m(r) определен в разд. 4.3. Сле-
довательно,
2я р 2я
Pbr = /0 f rdr fdO f sm0ocosM0o- (4.12)
oo o^o
Подставляя 0m (г) из (4.6), после интегрирования получим
/о р
Pbr = 2я2 ~ frS(r)dr, S (г) = п2 (г) - п2с1,
По о
(4.13)
где S (г) — квадрат локальной числовой апертуры. Помимо коэффициента
я7о/«о, связанного с интенсивностью источника и средой вокруг него,РЬг за-
висит также и от объема профиля П, определяемого как объем тела, полу-
ченного вращением кривой профиля вокруг оси световода. Таким образом,
т р р Г )
РЬг=я-^-Л; ^ = 2тг f rS(r)dr = 2nfr \п2 (г) -n2Adr. (4.14)
«о о о L J
Непосредственным следствием этого результата является то, что при облуче-
нии диффузным источником световодов с одинаковым объемом профиля
полные мощности направляемых лучей одинаковы. Кроме того, из (4.13)
63
следует, что плотность мощности направляемых лучей на единицу площади
поперечного сечения в точке с радиусом г пропорциональна квадрату локаль-
ной числовой апертуры. Если обозначить ее через Р(г), то получим
Р(г) =тг-2-5(г); Pbr = / P(r)dA,
по Лео
(4-15)
где Лсо — площадь поперечного сечения сердцевины. Приведем примеры.
4.7. Пример. Ступенчатый и усеченный степенной профили
Полная мощность направляемых лучей, возбуждаемых в волоконном световоде со сту-
пенчатым профилем, может быть получена, если в (4.13) положить п (г) = nQQ, т. е.
РЬг = 2/0 (7трисо/и0)2 Д = /0 (яр«со/«0 ) 2 sin2 0С, (4.16)
где использованы соотношения, приведенные в списке обозначений. Таким образом,
Р^г пропорциональна квадрату числовой апертуры, которая является мерой световос-
приимчивости световода. Из (4.11) и (4.16) эффективность возбуждения
8 = 2(исо/п0)2Д - (nco/n0)’sin’9c « (псо/по)202. (4.17)
Приближенное равенство справедливо для слабонаправляющего волновода, когда на-
правляемые лучи переносят лишь малую часть мощности источника, поскольку 0 с < < 1.
Если в качестве п (г) в (4.13) подставить усеченный степенной профиль из табл. 2.1.
то полная мощность направляемых лучей при диффузном возбуждении может быть
легко определена [б]:
р --^-1
°br — q + 2 7о
(яр"со)2 . .
----------sin20p,
(яр«со)г Я
д_ Я +
(4.18)
п
а соответствующее (4.17)
2q "со
выражение
Я
эффективности источника принимает вид
-----------------£
(4.19)
Для
л ' ^СО • 2
Д = —у-------sin2 ег
? + 2 „з с Я + 2 п.
Таким образом, и Р^г, и & в последнем случае меньше соответствующих значений для
ступенчатого профиля в q/(q + 2) раз. В частности, световоды с усеченным параболи-
ческим профилем (q = 2) передают только половину мощности направляемых лучей в
световоде со ступенчатым профилем (q = 00).
Профили равного объема. Усеченный степенной профиль, определенный в табл. 2.1,
имеет объем, отличающийся от объема ступенчатого профиля. Однако их можно выров-
нять, изменяя радиус сердцевины для каждой формы профиля. Соответственно заменив
р на ре, подставив п (г) в (4.14) и приравняв П объему тгр2 (п*о - и2р для ступенчатого
профиля, получим
Р(.= {(<7 + 2)/<?} ,/2р.
(4.20)
Полная мощность направляемых лучей в световодах с модифицированным усеченным
степенным профилем выражается с помощью (4.18), где р следует заменить на pQ. Если
затем подставить в него полученное выше выражение для ре, то подтвердится вывод,
сделанный в разд. 4.6: при диффузном возбуждении в световоде с модифицированным
усеченным степенным профилем передается та же мощность, что и в световоде со сту-
пенчатым профилем.
64
4.8. Неоднородное возбуждение
До сих пор полагалось, что интенсивность /0 излучения равномерно распреде-
лена по поверхности источника. Теперь исследуем влияние неоднородности
распределения интенсивности в диффузном источнике на полную мощность
направляемых лучей, используя гауссово распределение интенсивности (4.3)
[6]. Полная мощность, излучаемая источником, находится подстановкой
(4.3) в (4.96) прир8 = р:
Ptot = тг2р2 Л (1 — е“а)/а. (4.21)
Если световод имеет ступенчатый профиль, полная мощность направляемых
лучей определяется выражением (4.12), где То заменяется на Л, а множитель
ехр(—ог2/р2) вводится в подынтегральное выражение интеграла по радиусу.
Вычисляя интегралы, получим
(4.22)
«О «0
и, следовательно, эффективность возбуждения
р н2
<? _ Ьг _ О СО А СО 2 л> /л
----2—5-Д = —5 sm20c. (4-23)
rtot л0 по
что совпадает с выражением (4.17) для однородного источника.
Волоконные световоды с усеченным параболическим профилем. Такой
профиль соответствует усеченному степенному профилю при q = 2 и пред-
ставлен в табл. 2.1. Выражения для полной мощности направляемых лучей
и эффективности возбуящения можно получить аналогично случаю ступен-
чатого профиля:
(7грлгп)2 1 п2 ё~а + а — 1
Ры = 24 -g-0 - е \а ~ 1 А; & = 2 -------— Д. (4.24)
«о а2 п20 а(1—е )
Эффективность источника минимальна при а ->0, что соответствует однород-
ному источнику, и удваивается при а -> «>, когда лучи возбуждаются только
в центре входного сечения. Хотя эффективность возрастает с увеличением
неоднородности, мощность направляемых лучей уменьшается и становится
пренебрежимо малой при а -> °°*.
ВОЗБУЖДЕНИЕ КОЛЛИМИРОВАННЫМ ПУЧКОМ
Рассмотрим источник (см. разд. 4.2), который расположен таким образом,
что облучает световод коллимированным пучком под углом 0Q к его оси,
как показано на рис. 4.5. Коллимированный пучок является хорошей ап-
проксимацией излучения лазера. Он также позволяет описать диффузное
возбуждение, которое можно рассматривать как суперпозицию пучков, рас-
пространяющихся под разными углами. Только часть пучка, падающая на
сердцевину, может возбуждать направляемые лучи, поэтому не будем учиты-
вать лучи, падающие на оболочку. Ясно, что если пучок распространяется под
достаточно большим углом к оси, то он не сможет возбудить направляемые
* Этот результат связан с неудачным выбором модели источника (4.3), для которой
полная мощность излучения стремится к нулю при а->°° согласно (4.21). - Прим. ред.
3 Зак 37 65
Рис. 4.5. Коллимированный пучок, падающий
под углом 0О к оси световода параллельно
плоскости х, z
лучи. Действительно, направляемые лучи возбуждаются только в том случае,
если Bq не превышает максимального значения 0m(r) (4.6) в сердцевине. Рас-
смотрим примеры.
4.9. Пример. Ступенчатый профиль
Максимально допустимый угол падения для направляемых лучей 0т определяется с по-
мощью (4.6) при п (г) = исо, т. е. sin0m = («со/«0) sin0C’ и угол 0т одинаков по всему
сечению сердцевины. Следовательно, направляемые лучи будут возбуждены, если 0 <
< &Q < 0т, и не возбуждены, если 0О > 0т. Если пучок имеет равномерно распределен-
ную мощность Pj на единице площади поперечного сечения, то полная падающая мощ-
ность равна Ptot = 7rpaPjCos0o. Соответственно полная мощность направляемых лучей
и эффективность источника (4.11) равны
Р-Р - )^P2picoseo'>
ГЬГ ^tOt ] 0;
( 1о < 0О < 0т»
[0; ет< е„ <я/2.
(4.25)
Здесь не учитываются малые потери мощности из-за отражения на входном торце. Для
слабонаправляющих световодов с 0С < < 1 диапазон углов пучка для возбуждения на-
правляемых лучей будет мал.
4.10. Пример. Градиентные профили
В волоконных световодах с градиентным профилем, монотонно спадающим при удале-
нии от оси к поверхности сердцевины, максимально допустимый угод падения, при ко-
тором еще возбуждаются направляемые лучи (0m(r) из (4.6)), уменьшается от своего
максимального значения на оси sin0m(O) = (w co/w0) sin 0С до 0т(р) = 0 на границе серд-
цевины. При этом п (г) уменьшается от исо до иср Соответственно если 0О > 0т(О), то
направляемые лучи не возбуждаются, а при 0 < 0О < 0т(О) возбуждаются в пределах
окружности с радиусом rbr, где - корень уравнения 0О = 0m(rbr)- Рассчитывая в ка-
честве примера усеченный степенной профиль из табл. 2.1, получаем из (4.6) [7]
гЬг= р{1 - («osin0o/«cosin6’cr } 1/<?; 0 <<?0 <0т(О). (4.26)
Вне области значений возбуждаются только вытекающие лучи (эта ситуация рас-
смотрена в гл. 8). Если 0О = 0, то пучок направлен вдоль оси и направляемые лучи
возбуждаются в пределах всего сечения сердцевины и распространяются параллельно
оси световода. Если пучок имеет равномерно распределенную мощность на единице
сечения, то полная мощность направляемых лучей и эффективность источника (4.11)
определяются соотношениями
/> = J’rrbrpicoseo; _ o<0„<em,
bl I 0; 0; 0m<0o<n/2,
где множитель cos0o учитывает направление пучка.
(4.27)
66
ВОЗБУЖДЕНИЕ С ПОМОЩЬЮ ЛИНЗЫ
На практике площадь поперечного сечения источника может существенно
превосходить размеры сердцевины волоконного световода. Если располо-
жить такой источник напротив входного торца световода, то свет, попадаю-
щий в оболочку, не сможет возбудить направляемых лучей, и поэтому эф-
фективность возбуждения (4.11) будет тем меньше, чем больше размеры
источника. Если источник имеет сильнонаправленное излучение, как в случае
коллимированного пучка, то можно повысить эффективность возбуждения,
располагая линзу между световодом и источником. В то же время, как по-
казано в разд. 4.14, использование линз не может улучшить эффективность
возбуждения в случае диффузного источника.
4.11. Коллимированный пучок
Рассмотрим источник, испускающий коллимированный пучок с радиусом
Гц. Он может быть сфокусирован на торец световода в точке О, расположен-
ной на оси, введением тонкой линзы с радиусом, равным радиусу пучка, и
фокусным расстоянием / (рис. 4.6,а). Источник возбуждает только направ-
ляемые лучи, если угол фокусирования пучка линзой 0d в точке Q не пре-
восходит максимально допустимого угла падения 0т (0), определенного в
(4.6). Предполагая для простоты, что профиль является ступенчатым и пола-
гая п (0) = пс0, имеем 0m(O) = arcs in { (лсо/и0) sin 0С}. Подставляя 0d из со-
отношения rd = /tg 0d в неравенство 0d < 0m(O) и преобразуя результат с уче-
том (37.7), найдем, что фокусное расстояние должно превышать некое ми-
нимальное значение
r {(п0/псоу -sin20c}1/2 _ п0 rd
" d sin^c ~ "со 0С ’
(4.28)
Приближенное равенство справедливо в случае слабонаправляющих светово-
дов, для которых 0С << 1. Наличие линзы увеличивает мощность, возбужда-
ющую направляемые лучи, и соответственно эффективность источника в
(rd/p)2 Раз по сравнению со случаем непосредственного возбуждения свето-
вода тем же источником. Другими словами, вся мощность источника идет на
возбуждение направляемых лучей, если выполняется условие (4.28). Из сим-
Рис. 4.6. Соосные линзы, фокусирующие на торец световода осевой коллимированный
(а) и косой коллимированный (б) пучки
3s
67
метрии возбуждения видно, что в рассмотренном случае в точке Q возбужда-
ются только меридиональные лучи.
4.12. Пример. Распределение интенсивности
Полезно знать угловое распределение интенсивности в среде, в которой в точке Q рас-
положен источник (см. рис. 4.6, а). Это распределение может быть использовано, напри-
мер, для вычисления импульсного отклика (см. конец главы). Если пучок имеет равно-
мерно распределенную мощность на единице площади поперечного сечения, то мощ-
ность dP, падающая в точку Q под углами от 0О до 0О + d60, проходит сквозь кольцевую
область с длиной окружности 27r/tg0o и шириной tf(/tg0o) = (fleas* 60)de0 в плоскости
линзы. Следовательно,
• </P=2?rPi/!(tg0o/cos20o)</0o. (4.29)
Из симметрии следует, что интенсивность I света в единице телесного угла равна (1 /2тг) X
X dP/deQ. Если ввести пространственную зависимость интенсивности на торце в поляр-
ных координатах (см. рис. 4.4), то
р.
1=-^—f-, 0<ео <0 ; ц = o,0d<0o < 5- (4.30)
COS3 0О u
где 8 - дельта-функция Дирака. При малых значениях интенсивность практически не
зависит от 0О в пределах угла 0д.
4.13. Пример. Косое падение пучка
В этом случае коллимированный пучок составляет с осью волоконного световода угол
$s, как показано на рис. 4.6, б, а фокальная точка Q смещена вдоль оси х на расстояние
rs — Му При этом предполагается, что направление пучка параллельно плоскости х, z.
В сердцевине возбуждаются как меридиональные, так и косые лучи, и все эти лучи
являются направляемыми, если максимальный угол падения для луча PQ на рис. 4.6, б
не превосходит 0m(r) (4.6). Если световод имеет ступенчатый профиль, то 0m(r) =
= arcsin {(л?со/л20 ) sin 0С} и можно, как и при выводе (4.28), показать, что фокусное
расстояние для слабонаправляющих световодов должно удовлетворять условию
Гл С 0 'I
J i _ - s
WCO 0С [ псо )
0С< < 1.
(4.31)
Ясно, что es < («СО/«О)0С- Другими словами, не все лучи в точке Q направляются све-
товодом.
Распределение интенсивности. Распределение интенсивности по торцу волоконного
световода в среде, окружающей источник, имеет вид подобный (4.30), потому что плот-
ность мощности равномерно распределена по поверхности линзы. Заменим Pj HaPjCOs0s,
где Pj - мощность, проходящая через единицу поперечного сечения пучка, а Ь(г}1г на
6 (г - rs)/rs, т. е. осуществим сдвиг точки Q от г = 0 до г = rs вдоль оси х (см. рис. 4.4).
Асимметрия лучевого распределения относительно нормали в точке Q на рис. 4.6, б
означает, что верхний предел для 0О не зависит от полярного угла (см. рис. 4.4). Сле-
довательно, распределение интенсивности имеет вид
6(r-r) /’PjCoses
1 - -----------, где 0 < 0О < 0d (у>) (4.32а)
27lTs COS30o
и равно нулю, если 0д (^) удовлетворяет соотношению
/tg 0d(v>) = (г2-г2sin’,р)1/2 -rscos^, (4.326)
которое также следует из геометрии.
68
4.14. Диффузный источник
Пусть диффузный источник радиуса расположен на расстоянии f qt воло-
конного световода, как показано на рис. 4.7, а. Каждая точка на поверхно-
сти источника испускает световые лучи во всех возможных направлениях.
Когда эти лучи достигают плоскости входного торца световода z = 0, диапа-
зон направлений лучей в каждой точке этой плоскости уменьшается. Иначе
говоря, диффузный источник конечного размера (рис. 4.7, а) можно заме-
нить частично диффузным источником неограниченной протяженности, не-
посредственно примыкающим к торцу световода (рис. 4.7, б).
Введение тонкой линзы между диффузным источником и световодом мо-
дифицирует распределение интенсивности при z = 0. Ясно, что, выбирая лин-
зу с радиусом, равным радиусу источника, а фокусное расстояние, равным
расстоянию между источником и световодом, можно сконцентрировать мощ-
ность на входном торце световода вблизи оси, если линзу расположить вплот-
ную к источнику, как на рис. 4.8. Если фокусное расстояние велико по срав-
нению с радиусами сердцевины и источника, то угол фокусирования пуч-
Рис. 4.7. Диффузный источник конечного радиуса г , расположенный на расстоянии f от
торца световода (а), эквивалентный частично диффузному источнику неограниченной
протяженности, непосредственно примыкающему к торцу световода (6)
Рис. 4.8. Линза, распо-
ложенная на оси свето-
вода вплотную к диф-
фузному или частично
диффузному источнику
и фокусирующая пучок
на торец светодиода
69
ка линзой Од мал и распределение интенсивности по сечению сердцевины яв-
ляется почти равномерным. Точность этого приближения оценивается в сле-
дующем разделе в предположении, что свет, испускаемый источником, мож-
но представить в виде суперпозиции коллимированных пучков.
Оптимальная мощность направляемых лучей. С точки зрения оптимиза-
ции мощности направляемых лучей фокусное расстояние линзы и соответ-
ственно расстояние между источником и световодом выбирается так, чтобы
при ступенчатом профиле угол фокусирования пучка линзой 0d на торце
сердцевины был равен максимальному углу падения для направляемых лу-
чей. Для слабонаправляющего световода это условие с учетом (4.6) имеет
вид
6d = M0) - ("Со/”оЖ; 0С«1- (4-33)
Мощность источника, расходуемая на возбуящение направляемых лучей, в
этом приближении представляет собой произведение телесного угла фокуси-
рования пучка линзой 7г0ц в каждой точке поверхности раздела, площади се-
чения сердцевины яр2 и интенсивности источника (4.2), которая имеет прак-
тически постоянное .значение /0, поскольку угол 0О мал. Таким образом, из
(4.33) получаем выражение
= Л) (яр«со/«о ) 2 9с, (4.34)
которое идентично соответствующему выражению в (4.16) для 0С << 1.
Итак, линза не может повысить эффективность возбуждения направляемых
лучей диффузным источником,
4.15. Пример. Распределение интенсивности
Определим распределение интенсивности по сечению сердцевины для ситуации, изобра-
женной на рис. 4.8, что позволит оценить точность приближенного выражения для пол-
ной мощности направляемых лучей, полученного в предыдущем разделе. Заменим диф-
фузный источник эквивалентной осесимметричной суперпозицией коллимированных
пучков, направления распространения которых задаются сферическими полярными уг-
лами в и отсчитываемыми соответственно от оси световода и азимутальной оси, при-
чем 0 < 0 < 7г/2 и 0 < < 2тг. Плотность мощности Рр проходящей через единицу площа-
ди поперечного сечения пучка в интервале углов от в до в + d0 и от до + d<p, полу-
ченная из (4.8), имеет вид
P^ed<p = I0 sin е cos Oded#. (4.35)
В разд. 4.13 было показано, что угловая зависимость распределения интенсивно-
сти / по сечению световода для конкретного пучка, падающего под углом 6$ к линзе,
определяется вторым сомножителем в (4.32а), т. e./2PjCOs0s/cos30o, гдеР|СО8 0§ - плот-
ность мощности пучка. Далее заменим Pjcos0s правой частью равенства (4.35) и для/
получим
Irdrdip — 10р (sin0cos0/cos30o)d0(Z^. (4.36)
Из геометрических соображений следует, что каждый пучок фокусируется на торце
световода на расстоянии г = f tg 0 от оси. Дифференцируя это выражение и подставляя
в (4.36) вместо 6 его выражение через г и /, имеем
1=dhr 9г : 0 с • (4-37)
При больших углах 0О / = 0, а 0ц (^) - определяется с помощью (4.326) при замене rs
на г. Если полная мощность, падающая на торец световода, равна полной мощности на-
70
правляемых лучей, то, интегрируя выражение (4.37) по углам падения луча 0О, 0^ и по
поперечному сечению световода, после непосредственного вычисления интегралов по-
лучаем
Р 2rr 2 я
Pb = Jr<lr f d^p f J Ide = Io -5—75- • (4-38>
U 0 0 0 0 f +J
Для f >> p знаменатель можно заменить на/2, при r^/f « 0^, где 0d - угол фокусирова-
ния линзой. С учетом (4.33) для слабонаправляющих световодов выражение (4.38) сво-
дится к (4.34).
‘4.16. Частично диффузный источник
В предыдущих пяти разделах было показано, что использование линзы, с
одной стороны, может повысить эффективность возбуждения волоконного
световода коллимированным пучком, а, с другой стороны, оказывается не-
эффективным в случае диффузного источника. Из сопоставления этих фак-
тов и представления диффузного источника в виде суперпозиции коллимиро-
ванных пучков видно, что эффективность частично диффузного источника
может быть повышена применением линзы. Это иллюстрируется рис. 4.8.
Пусть волоконный световод со ступенчатым профилем является слабона-
правляющим, т. е. 0С << 1, а фокусное расстояние линзы f>>p, так что
угол стягивания 0d ~ rjf мал и (как и интенсивность) практически равно-
мерно распределен по сечению световода.
При этих условиях максимум мощности направляемых лучей достигает-
ся, когда 0d удовлетворяет (4.33), т. е. 0d « (^со/ло)^с» и весь свет от исто4’
ника падает на торец сердцевины в области/0S <<р, где 0S - максимальный
угол между направлением лучей, испускаемых источником, и осью светово-
да. Комбинируя эти два условия, получим, что вся мощность источника рас-
ходуется на возбуждение направляемых мод, если 0S < (р/га) (лсо/ло)^с- Та-
ким образом, максимум мощности направляемых лучей увеличивается в
(rd/P)2 Раз по сравнению со случаем непосредственного расположения источ-
ника перед торцом световода.
РАСПРЕДЕЛЕНИЕ МОЩНОСТИ ПО НАПРАВЛЯЕМЫМ ЛУЧАМ
В разд. 4.6 было показано, как определить полную мощность направляемых
лучей и радиальное распределение их мощности в сердцевине световода при
возбуждении его однородным диффузным источником, непосредственно
прилегающим к торцу. Определим распределение мощности источника по
направляемым лучам. Оно может быть соответствующим образом описано
в терминах лучевых инвариантов, если функцию распределения F(0,1 ) опре-
делить следующим образом [6] :
F(j3,1)-— мощность всех направляемых лучей с инвариантами, изме-
няющимися в интервалах от ? до (3 + d{3 и от I до I + dl.
(4.39)
Вычисление импульсного отклика в этой и последующей главах значительно
упрощается при использовании этой функции распределения.
71
4.17. Вывод функции распределения
Исходным при выводе является выражение для полной мощности направля-
емых лучей в случае однородного диффузного источника (4.12). Произведем
интегрирование по tp и заменим угловые переменные 0О, на инварианты
0, I с помощью (4.5). Хотя оси переменных (3 и I неортогональны, однако
при использовании их в качестве переменных интегрирования соответствую-
щий якобиан/ дает правильное преобразование. Таким образом, из (37.129)
получим
= JL 1 Р ________________1 . = „2 _ Q2 _Т2 Л
д(0,1) «о sin 60 cos 0О r g (г)i/2 ’ О О г2
(4.40)
и, следовательно, (4.12) можно заменить на
т Р п(г) _ _ jt
/>br»8w^- У W / (4.41а)
по о лс1 о Ку)
{п2(г) -ё2} 1/2, (4.416)
где верхний и нижний пределы по (3 равны соответственно нулевому ^макси-
мальному значениям 0о для направляемых лучей. Те же пределы по I равны
0^ = 0 и 0^ = 7г/2 соответственно, а коэффициент 4 учитывает полный диапа-
зон значений 0^ в (4.12). ____
Преобразование интегралов. Для того чтобы определить F(J3,1), необхо-
димо выполнить интегрирование по г во внутренних интегралах по (3 и I
(4.41). Поменяем порядок интегрирования по г и (3, при этом получим
т «со _ _ г(Д) Тт<г>& ,Г
^Ьг = 8яр^- f Pd0 f dr f n(r(P))=P, (4.42)
no ncl о о #(r)
где пределы интегрирования взяты согласно рис. 4.9, я, на котором дано из-
менение показателя преломления от его значения на оси до значения ис1 на
границе. Области интегриривания по двум переменным на рисунке заштрихо-
ваны. Верхний предел п(г) при интегрировании по 0 в (4.41) заменяется
Рис. 4.9. Области интегрирования (заштрихованные) в плоскости (3,г (а) и в плоскости
1,г (б)
72
верхним пределом г((3) при интегрировании по г в (4.42), где г ((3) является
решением уравнения п(г (0)) = (3 в случае градиентного профиля и г ((3) = р
в случае ступенчатого профиля. Теперь поменяем порядок интегрирования
по г и I и получим
т со _
РЪт=^Р-^- f d@
"° "cl
^max^ _ [ _ rtp j
(4.43)
где пределы интегрирования определяются с помощью рис. 4.9, б. Из поясне-
ний к (4.41) и (4.42) следует, что верхние пределы интегралов по г и I в
(4.42) равны при g(r) = 0. График кривой g(f) =0 имеет характерную фор-
му, показанную на рис._4.9, б, так что 7=0 при г = 0 и г = г(/3). Верхний
предел в интеграле по 7 в (4.42) определяет как верхний, так и нижний
пределы интегрирования по г в (4.43) (на пересечении горизонтальной ли-
нии с кривой g(r) = 0, т. е. на внутренней каустике ric и на каустике точек
поворота Гф,_как следует из (2.19)). Итак, верхний предел интегрирования
по 7 в (4.43) 7тах (|3) есть максимальное значение 7 на кривой g(r) = 0. Не-
посредственное дифференцирование дает
Лпах (?) = {«2 (rm) - ?2} 1/2 (rm/p), (4.44а)
где rm — зйачение г , являющееся решением уравнения
2 {п2 <rm) - ?2 } = ~rm (dnl (О/dr) г (4.446)
m
Выражение в фигурных скобках в (4.43) совпадает с выражением для полу-
периода лучевой траектории (см. табл. 2.1). Учитывая определение функции
распределения (4.39), из (4.43) получим [7]
F(/3,/) = (4тгр/о/по)2р.
(4.45а)
Таким образом, функция распределения для мощности направляемых лу-
чей пропорциональна полупериоду лучевой траектории. Примеры даны в
разд. 4.19.
Нормированная функция распределения. Удобно ввести нормированную
функцию распределения F(/3,7), соответствующую единичной полной мощ-
ности_возбуждаемых в световоде направляемых лучей. Она равна отношению
F(/3,7) (4.45а) и Рьг (4.14), следовательно,
F(p,l) = 4ргр/П,
(4.456)
где £2 — объем профиля, определенный в (4.14).
4.18. Функция распределения, зависящая только от /3
При нахождении импульсного отклика рассмотрим в качестве примера сту-
пенчатый и усеченный степенной профили, для которых время прохождения
луча не зависит от угла скоса или значения 7. Удобно ввести функцию распре-
деления G(0), зависящую только от /3, которая представляет собой интеграл
73
от ^(0, /) по I во всем диапазоне значений /, т. е. G(j3) Д' — мощность* пе-
реносимая всеми_ лучами с инвариантом 0 в диапазоне от Д до Д + d0. Для
определения G(0) в явном виде не требуется знания F(0, Т) и соответ-
ственно zp. Это полезно в случае усеченных степенных профилей, так как
Zp выражается аналитически только для параболического профиля. Из (4.42)
получим
dl
g(r)i/2
G(0) = 8np-^-0 f dr f
^0 0 о
Произведем замену переменной l на w, где I = Tm (r, Д) sin w;_ заметим так-
же, что с учетом (4.40) и (4.41) можно положить g (г) = { (г, 0) —I2 } р2 fr2 .
После интегрирования получаем
(4.46)
G(0) = (2тт2/о/«о)|3г2 (0); n(r(0)) = 0.
(4.47a)
Нормированная функция распределения G((3 ), соответствующая единичной
полной мощности, определяется по аналогии с (4.456) :
G(0) = 2я0г2 (jj)/n,
(4.476)
где Q - объем профиля (4.14) ; r(0) = p для ступенчатого профиля.
(4.49)
4.19. Пример. Ступенчатый и усеченный степенной профили
Полу период лучевой траектории для волоконного световода со ступенчатым профилем
представлен в табл. 2.1, а объем профиля, определенный в (4.14), П = яр2 (п20 - и2р.
Соответственно функции распределения (4.45) для такого профиля имеют вид
70 («’со-?2 -72)1/3 - - 8 0("со-Г2)1'2
F(ft I) = W -----------; F (0,1) = } , г ,----— • (4.48)
«S «со - я ("го - "с1> («со - 0 )
Аналогично с учетом г(р)= р функция распределения (4.47) имеет вид
Л _ - _ 2?
wma2 G^ = -—тг •
"о "со “"cl
Диапазон значений ft и Т для направляемых лучей определен в (2.8а).
Для усеченных степенных профилей в табл. 2.1 не существует общего выражения для
полупериода лучевой траектории при произвольном значении показателя q, и функция
распределения F(ft /) не может быть выражена в явном виде (заисключением парабо-
лического профиля (q = 2)), однако функция G (0) может быть определена в явной
форме. Из (4.47а) и (4.14) вытекает
Ко-ft2 1 VQ
'•(ft) = P(-Y2-z—>
("со ""cl J
что, в свою очередь, приводит к
"? 1"со-"с1 J 4 "со — "cl l"ro-"cl J
n =яр2 7Tr("co-”cl)’
I/ -г
(4.50)
Диапазон значений 0 для направляемых лучей указан в (2.24а).
74
(4.51)
Усеченный параболический профиль. Выражение для полупериода приведено в
табл. 2.1, откуда с учетом (4.45) и (4.50) получим выражения, которые не зависят от
угла скоса:
F(p,l)= 4^рг —-------------
по ("со - "с1>
8Д
("со~ "cl)3'1'
(4.52)
=
Диапазон инвариантов для косых лучей. В разд. 2.7 было показано, что направляе-
мые лучи' в световодах с оболочкой имеют значения инварианта 0, лежащие в интерва-
ле (2.24а). Соответствующий диапазон значений I задается неравенствами 0 < I <
< fmax(0)’ где верхний предел определяется (4.44). Для ступенчатого профиля rm =
= Р и 7тах(0)= (лсо ~ )1/2, с другой стороны, для усеченных степенных профилей пос-
ле подстановки соответствующего выражения из табл. 2.1 в (4.44) получим выражения
2
РЬ + 2
"co-g1 | !/<?.
"co-"cl J
^тах(^) <?'1
2
"со-"с1
1/<7 ( "’0- 3 (<? + 2)/2<7
( Q +2 J
(4.53)
которые переходят в выражения для волоконных световодов со ступенчатым профи-
лем при q ->00.
ИМПУЛЬСНЫЙ отклик
В предыдущей главе уширение импульса описывалось с помощью разности
между временем прохождения самого быстрого и самого медленного из рас-
пространяющихся лучей, т. е. ^тах - rmin. Та^ое описание очень удобно, так
как определяет верхнюю границу уширения импульса для произвольного ис-
точника излучения. Если форма импульса близка к прямоугольной, то доста-
точно знать ширину импульса, чтобы описать его. Если форма импульса силь-
но отличается от прямоугольной, то необходима информация о распределе-
нии мощности в пределах длительности импульса, или импульсный отклик.
Далее покажем, как получить это распределение для произвольного источни-
ка, и рассмотрим конкретные примеры. Сначала обсудим класс профилей,
у которых время прохождения луча зависит только от инварианта 3, а затем
произвольные профили, Для которых оно зависит от обоих инвариантов.
Остановимся кратко на воздействии дисперсии материала.
4.20. Время прохождения луча, зависящее только от 0
Как и в гл. 3, будем рассматривать импульсы, имеющие на входе световода
нулевую ширину и конечную мощность. Такие импульсы описывают с помо-
щью дельта-функции Дирака. Отклик на произвольный входной импульс ко-
нечной длительности может быть определен с использованием свертки.
Вывод выражения для импульсного отклика. Импульсный отклик описы-
вает распределение мощности в импульсе на выходном торце световода как
функцию времени прохождения t и обозначается Q(t). Тогда выходная мощ-
ность в интервале времени от t до t + dt равна Q(t)dt. Для простоты будем
предполагать, что полная мощность импульса равна единице, т. е.
^тах
f Q(t)dt=\, (4.54)
^min
где ^тах и ^min “ время прохождения соответственно самого медленного и
самого быстрого из распространяющихся лучей. Для профилей, рассматрива-
75
емых в примерах, оно не зависит от угла скоса или от I. Следовательно, все
лучи с одинаковым значением /3 достигают выходного торца световода од-
новременно через время t ((3 ). Мощность этих лучей описывается с помощью
нормированной функции распределения G((3 ) (см. разд. 4.18). Соответствен-
но на выходе световода мощность лучей, для которых инвариант (3 изменяет-
ся от (3 до /3 + d/З, равна G((3)d(3, где разброс d/З соответствует разбросу вре-
мени прохождения dt. Таким образом, получим [6]
2(0 =G(0)|J0/Jd, (4.55)
где введен знак модуля, так как Q(t) по определению положительна. Правая
часть может быть_выражена через t, для чего соотношение_для времени про-
хождения t = t (@) необходимо разрешить относительно (3 в виде 0 = (3 (t).
Если время прохождения одинаково для двух или более значений (3, то пра-
вая часть будет_состоять из двух или более слагаемых, соответствующих
этим значениям (3.
Средняя квадратическая ширина о. В ней содержится информация о рас-
пределении мощности в импульсе. Она полезна, если импульс непрямоуголь-
ный и не может быть адекватно описан своей шириной. Для того чтобы оце-
нить а, определим Rm как т-й момент импульсного отклика, тогда из (4.55)
следует [6]
?тах - п со
Rm= f tmQ(f)dt = f tm(0)G(0)d0, (4.56)
?min n cl
и Ro = 1 в результате нормировки (4.54). Первый момент Ri определяет
среднее время прохождения Г, усредненное с весовой функцией распределе-
ния мощности в импульсе. Средняя квадратическая ширина определяется че-
рез первый и второй моменты:
7 = Ri; (R2-R21)1/2. (4.57)
Рассмотрим теперь конкретный пример с диффузным возбуждением.
4.21. Пример. Ступенчатый профиль
Время прохождения лучей в волоконном световоде со ступенчатым профилем, выра-
женное через 0, приведено в табл. 2.1, откуда после преобразования выражения t (р) =
= znco/^c^ получим
0(0 = zn’0/(cr). (4.58)
Функция распределения G((3) при диффузном возбуждении определяется выражением
(4.49), а импульсный отклик - выражением (4.55). Следовательно,
Q (,) = ------«2^2- ?-*
с2г3 С213
rmin rmax-
(4.59)
Вне этого интервала Q = 0, a rmjn и ?тах определяются соотношениями (3.1). Следует
отметить, что приближенное равенство справедливо в случае слабонаправляющих свето-
водов. Хотя величина Q (Г) обратно пропорциональна третьей степени времени про-
76
хождения, реальное отличие на концах интервала на практике очень мало. Например,
при исо = 1,45, ис1 = 1,44 иг - 1 км 6(0 изменяется от 3,01 X 107 до 2,95 X 107 с"1
при увеличении t от rmjn до Гтах. Следовательно, импульсный отклик в волоконном
световоде со ступенчатым профилем имеет практически прямоугольную форму. Сред-
нее время прохождения в (4.57)
7 - * 2”СО = 1 (t +t х _ “СО (”СО-"С1)2
С"со + "с1 2 таХ 2с "С1 "СО + ИС1
(4.60)
откуда следует, что t немного ближе к rmjn, чем к Гтах. Видно, что преобладание в пере-
носимой мощности для более быстрых лучей, распространяющихся под меньшими угла-
ми 0Z, незначительно. Для слабонаправляющих световодов средняя квадратическая ши-
рина а (4.57), как легко показать, приблизительно равна (?max - 7mjn)/ \/Т2.
4.22. Пример. Усеченные степенные профили
Время прохождения t = t (0) для лучей в световодах с усеченным степенным профилем
приведено в табл. 2.1. Обращая это соотношение, получаем выражение
<7 + 2
МО =Л4~-
ct j гct Я + 2 ]2 Яг
z ± ) Ь 4 J 2 со
(4.61)
из которого следует, что для каждого значения г существуют два различных значения 0.
В случае диффузного возбуждения подставим G (0) из (4.51) в (4.55). Тогда импульс-
ный отклик будет определяться членом [б]
2(0 = у
(<? + 2)г
<7«сод
03(t)
1<?"со - (О I
[ Исо - (Г) ] 2/q
(4.62)
если учитывать только одно значение 0(Г), и суммой двух подобных членов (по одно-
му для каждого значения 0 (г)), если учитываются оба значения 0 (г). Диапазон значений
t и количество значений 0 (Г) зависят от q и определяются с помощью (3.7). Вне указан-
ного диапазона функция Q(t) равна нулю. Качественно форма импульсного отклика
для всех значений q представлена на рис. 4.10. Для реальных значений и «с| импульс-
ный отклик в световоде с усеченным параболическим профилем имеет практически пря-
моугольную форму. Если значение q не равно 2, то форма импульсного отклика сильно
отличается от прямоугольной. В частности, когда q = <7Opt (оптимальный профиль (3.8),
минимизирующий полную ширину импульса), импульсный отклик неограниченно воз-
растает при t -> 7mjn. Полная мощность в импульсе остается конечной. Для усеченного
параболического профиля среднее время прохождения (4.57) в приближении слабона-
правляющего волновода 0С < < 1 определяется соотношением
t (znCQlc) (1 + 0c/i6) — (7max + Тпнп)/2, (4.63)
справедливым с точностью до членов порядка 0*, что может быть проверено с помощью
(3.5) и (3.7). Средняя квадратическая ширина о = (rmax ~ ^mjn) / \Z12.
Рис. 4.10. Импульсный отклик (4.62) как функция времени прохождения t для различ-
ных показателей степени q усеченных степенных профилей [6]. Для оптимального про-
филя <7opt = 2 - 2Д « 2 - (?’
77
4.23. Время прохождения луча, зависящее от обоих инвариантов
Время прохождения луча при произвольном профиле зависит в общем слу-
чае от обоих инвариантов, т. е. t = t ((3 ,1). Таким образом, лучи с различны-
ми значениями /3 и I могут иметь одинаковое время прохождения t. На
рис. 4.11, я им соответствует контур t (0 ,7) = t в координатной плоскости
0, I. Лучам с временем прохождения t + dt соответствует контур t((3,1) =
= t + dt. Отсюда следует, что полная мощность, достигающая выходного тор-
ца световода за время от t до t + dt, переносится лучами, соответствующими
области dA, заключенной между_ двумя контурами. Используя нормирован-
ную функцию распределения F(0, I ) для направляемых лучей, введенную в
разд. 4.17, получим
Q (Г) dt = ff F(0,7) dPdl. (4.64)
dA
Аналитически Q(t) находится делением правой части на dt и переходом к
пределу при dt -> 0.
Вычисление импульсного отклика. Фактически для всех профилей, пред-
ставляющих практический интерес, интеграл в (4.64) нельзя представить в
достаточно простом виде. Поэтому функция Q(t) определяется числен-
но и удобнее использовать несколько иной подход [8]. Вместо того что-
бы _определить контур с постоянным временем прохождения, плоскость
0± / делится сеткой на малые прямоугольные области _со_ сторонами dfi и
dl, как показано на рис. 4.11,5. Мощность F(0, l}d$dl лучей, располо-
женных в пределах прямоугольника, зависит от среднего времени прохожде-
ния r(0c, 7С), которое определяется в центре прямоугольника. Весь ин-
тервал rmax - rmin делится на большое количество отрезков. Ясно, что
7(0С, Iс) находится на одном из этих отрезков. Тогда мощность, соответству-
ющую t (0С, I с), будем соотносить со всем этим отрезком. Повторяя эту
процедуру для всех прямоугольников, аппроксимируем импульсный отклик
распределением накопленной мощности в пределах каждого отрезка. При
этом чем меньше размеры прямоугольников и отрезков, тем точнее аппрок-
симация Q(t). Этот способ подробно рассмотрен в работе [8].
Рис. 4.11. Контур, соответствующий одинаковому времени прохождения лучей (а) и сет-
ка для вычисления импульсного отклика (б), показанные в плоскости Z (3
78
4.24. Дисперсия материала
Учет дисперсии материала достигается простой модификацией выражений
для импульсного отклика, представленных в разд. 4.21 и 4.22. Из разд. 3.7
следует, что в случае ступенчатого профиля Q(t) по-прежнему пропорцио-
нально 1/Г3, как и в (4.59), хотя Q(t) и диапазон значений t изменяются при
учете зависимостей исо, ис1 и Д от длины волны. Подобное заключение спра-
ведливо также и для усеченных степенных профилей (соответствующие ре-
зультаты приведены в работе [6]).
ГЛАВА 5. НЕРЕГУЛЯРНЫЕ ВОЛОКОННЫЕ СВЕТОВОДЫ
В первых четырех главах предполагалось, что оптические волноводы явля-
ются регулярными, т. е. однородными вдоль оси. Профили показателя пре-
ломления и поперечные сечения у них не изменяются вдоль длины. Однако в
действительности из-за несовершенства технологии изготовления и внешних
воздействий это не так. Даже у идеально непоглощающего волоконного све-
товода, изготовленного из оптически прозрачных материалов, имеются ес-
тественные неоднородности, обусловленные молекулярным строением мате-
рии. В этой главе будут рассмотрены нерегулярные волоконные световоды,
у которых профили показателя преломления и поперечные сечения изменя-
ются по длине. Иногда нерегулярности вводят намеренно для того, чтобы до-
биться требуемых характеристик по расширению импульса. Их вносят в та-
кие устройства, как конусные волоконные переходы или фоконы.
Цель этой главы состоит в том, чтобы исследовать влияние нерегулярно-
стей, в частности, на уширение импульса. Важный для практики результат
состоит в том, что уширение импульса может быть уменьшено за счет введе-
ния нерегулярностей, однако это всегда достигается ценой потерь мощности
импульса из-за излучения из волоконного световода. Здесь будет развита
простая теория, позволяющая исследовать световоды, параметры которых
медленно изменяются с длиной* и которые часто встречаются на практике.
Кроме того, будут исследованы фокусирующие свойства нерегулярных во-
локонных световодов, например волоконных переходов.
Различают два типа нерегулярностей. Первый тип — это непрерывные мак-
роскопические нерегулярности, например изменение радиуса сердцевины.
В этом случае световая мощность, переносимая направляемыми лучами, при
распространении лучей остается постоянной, хотя нерегулярности и изменя-
ют их траектории. Второй тип — это малые скачкообразные нерегулярности,
например отдельные очень маленькие рассеиватели. В этом случае световая
мощность, переносимая направляемым лучом, падающим на рассеиватель,
перераспределяется между лучами, имеющими всевозможные направления.
Эти две ситуации будут рассмотрены с применением различных методов. Ес-
ли волоконные световоды являются достаточно длинными, то для описания
случайно распределенных вдоль них нерегулярностей могут быть использова-
ны приближенные статистические модели, а это приводит к тому, что выводы
в обоих указанных ситуациях оказываются сходными.
* Изменяются мало на длине порядка длины волны света. - Прим. ред.
79
Рис. 5.1. Волоконный световод со ступенча-
тым профилем показателя преломления, серд-
цевина которого имеет переменный радиус
(полупериод Zp (z) траектории направляе-
мых лучей изменяется вдоль оси)
НЕПРЕРЫВНО ИЗМЕНЯЮЩИЕСЯ НЕРЕГУЛЯРНОСТИ
Сначала будут рассмотрены волоконные световоды, нерегулярности которых
непрерывно зависят от продольной координаты z.
На рис. 5.1 в качестве простого примера приведен волоконный световод
со ступенчатым профилем, у которого радиус сердцевины p(z) является
функцией z. Траектория направляемого луча остается зигзагообразной, од-
нако ее полупериод, равный расстоянию между проекциями на ось двух по-
следовательных точек отражения, не является постоянным. Непрерывный
характер нерегулярности обеспечивает сохранение мощности, переносимой
лучом вдоль измененного пути, который может значительно отличаться от
лучевой траектории в регулярном волоконном световоде. Для того чтобы
лучевой анализ был справедлив, радиус сердцевины должен медленно изме-
няться на расстояниях порядка длины световой волны, однако его изменение
может быть совершенно произвольным на полупериоде лучевой траектории.
5.1. Время прохождения луча
Пусть круглый волоконный световод имеет профиль показателя преломле-
ния л (г, z). Локальная скорость света составляет c/n(r, z), поэтому время
прохождения лучом участка световода длиной z равно
* с
r=l/n(r,z)dS=l/^-^- =
С v СJ COS вг (Г, Z) • С 0 (Z)
(5.1)
где ds — дифференциал траектории луча и
_ ^2
0 (Z) = и (г, z) cos ег (г, Z) =п (г, Z) —
(5-2)
— лучевая функция, определенная по аналогии с лучевым инвариантом (2.16).
Здесь 0Z (г, z) — угол между касательной в точке траектории и направлени-
ем оси.
Следует подчеркнуть, что интегралы в (5.1) нужно брать вдоль траекто-
рии г = г (z). Если волоконный световод изменяется по длине, выполнить
это достаточно сложно: лучевая функция не является более инвариантом,
т. е. 0(z) ^=0(0), как в случае регулярного волоконного световода, и нельзя
использовать метод вычисления времени прохождения, примененный в
разд. 2.9. Для нахождения 0 (z) обратимся к уравнениям лучевой траектории.
80
5.2. Уравнения лучевой траектории
Если в уравнении (1.18) и во всех выражениях разд. 35.4 заменить п(г) на
и (г, z), то получим соответственно радиальную, азимутальную и аксиаль-
ную составляющие уравнения лучевой траектории
d f z ч dr ) z ч z Эл (г, z) ч
А=о, (5.3б)
ds I 4 7 ds J г ds ds k 7
d f z 4 dz ] bn (r, z) _ 4
n(r,z)—> = —, (5.3b)
ds ( v 7 ds J dz v 7
где s — длина траектории, (r, z) — цилиндрические полярные координаты
(см. рис. 2.1).
Лучевая функция. Исключая ds из соотношений (5.2) и (5.Зв), получим
уравнение для лучевой функции (3 (z)
d(32(z) bn2 (г, z) I
dz ~ bz
(5.4)
где r (z) вычисляется вдоль лучевой траектории. Решение этого уравнения
имеет вид
jP0=pW(/^l|t.,B4,
(5-5)
где 0 (0) — исходное значение (3 (z) в начале волоконного световода. Инте-
грирование выполняется вдоль лучевой траектории. Нахождение этой траек-
тории усложняется из-за изменения профиля показателя преломления вдоль
волоконного световода.
Лучевой инвариант Z . Вследствие круговой симметрии волоконного све-
товода в каждом сечении z существует инвариант I, соответствующий азиму-
тальному направлению. Для того чтобы найти Z, умножим (5.36) наг2 и про-
интегрируем. Отсюда
Z = -f-T- п (г, = п (г, z) sin 0Z (г, z) cos 0^ (r, z).
p(0) 4 7 ds p(0) v 7 zv 7 7
(5.6)
Здесь 0^ (г, z) — угол между азимутальным направлением и касательной к
проекции лучевой траектории на поперечное сечение волоконного световода.
Инвариант?, не зависит ни от г, ни от z. Благодаря тому, что выражение (5.6)
содержит р (0), Z оказывается безразмерным и при п (г, z) = п (г) и р (0) = р
сводится к инварианту однородного световода (2.17).
_ Лучевая траектория. Для нахождения времени прохождения луча (5.1) и
(3 (z) (5.5) требуется знание лучевой траектории г = г (z). Ее можно постро-
ить, используя уравнение (5.3а), в котором с помощью быражения (5.6)
dip/ds исключена.
81
5.3. Пример. Волоконный световод со ступенчатым профилем и продольно
изменяющимся показателем преломления сердцевины
Для того чтобы определить время прохождения луча в произвольном нерегулярном во-
локонном световоде, необходимо иметь явное выражение для лучевой траектории г =
= г (z). Исключением является световод со ступенчатым профилем, сердцевина которо-
го имеет постоянный радиус. В этом случае нет необходимости знать траекторию. Пока-
затель преломления п (z) зависит только от z и, следовательно, частная производная в
уравнении (5.4) становится полной. Решение этого уравнения имеет вид
01 (z) = ё2 (0) + пг (z) - п1 (0). (5.7а)
Используя угол 0z (z) , который траектория образует с осью волоконного световода, и
определение (5.2) , преобразуем (5.7а) :
п (z) sin fy(z) = п (0) sin % (0). (5.76)
Если подставить выражение для 0(z) в уравнение (5.1) и положить и (г, z) = n(z), то
время прохождения задается простым интегралом по z
J_ / __________пг (z)dz____________
~ о [«’(Z) + Д2(0) -и2 (О)]1'2
и не зависит от лучевой траектории, не считая ее начального направления.
СЛУЧАЙНЫЕ НЕРЕГУЛЯРНОСТИ
В общем случае аналитического выражения для времени прохождения луча
получить не удается, однако для волоконных световодов со случайными и
медленно изменяющимися нерегулярностями существуют два интересных
для практики случая, когда применимы приближенные методы, которые об-
суждаются в этом и следующих разделах. Если нерегулярности световода
случайно распределены по его длине, то для нахождения времени прохожде-
ния луча с помощью (5,1) нужно знать только некоторые средние статисти-
ческие значения лучевой траектории г = г (z) и соответствующей лучевой
функции /3 (z) (5.2). Для этого, вообще говоря, нужно решить лучевые
уравнения, использовав статистические методы, однако для волоконного
световода со ступенчатым профилем в этом нет необходимости. Например,
изменение радиуса сердцевины можно моделировать, используя в выраже-
нии (5.1) случайную переменную 0z(z) при условии постоянства n(r, z) =
= исо. Согласно соотношению (5.76) изменения показателя преломления
сердцевины п (z) моделируются той же случайной переменной. Среднее вре-
мя прохождения луча и среднее квадратическое отклонение относительно не-
го можно затем рассчитать, применяя к (5.1) стандартные статистические
методы. Как будет показано, в случае некоррелированных нерегулярностей
простое физическое рассуждение обеспечивает необходимое понимание.
5.4. Уменьшение уширения импульса
Рассмотрим волоконный световод длиной z, в котором распределение нере-
гулярностей является достаточно случайным, так что корреляции между
направлением луча в начале и в конце световода не существует. Предполо-
жим далее, что световод возбуждается диффузным источником, рассмотрен-
82
ным в разд. 4.1, и возбуждаются все направляемые лучи. При этом после
достаточно большого числа полупериодов каждая лучевая траектория бу-
дет иметь все возможные направления или, иначе говоря, принимать все
возможные значения (3 (z). Следовательно, время прохождения для каждого
направляемого луча, возбуждаемого источником, примерно равняется сред-
нему времени прохождения. Оно пропорционально длине волоконного свето-
вода z поскольку, как показано в разд. 2.5 и 2.9, времена прохождения для
всех лучевых направлений пропорциональны z. Вследствие случайной приро-
ды нерегулярностей флуктуации времени прохождения луча относительно
этого среднего значения, измеряемые средним квадратическим отклонением,
или дисперсией, как известно из статистики [1], пропорциональны квадрат-
ному корню из среднего времени прохождения и, следовательно, пропорцио-
нальны z1/2. В гл. 3 было показано, что в отсутствие нерегулярностей ушире-
ние импульса пропорционально длине волоконного световода z. Таким обра-
зом, при введении случайных нерегулярностей импульс уширяется с расстоя-
нием в раз медленнее, если волоконный световод является достаточно
длинным и статистическая ситуация реализуется [1]. Этот результат остает-
ся в силе в том случае, если нерегулярности являются достаточно большими,
так что луч может_иметь все направления направляемых лучей или прини-
мать все значения (3 (z) при прохождении через световод. Например, для све-
товода со ступенчатым профилем размер нерегулярности должен быть доста-
точным, чтобы случайным образом изменить направление луча на угол 0С9
где вс — критический угол скольжения. Как показано в разд. 5.7, зависи-
мость вида z1/2 не имеет места для медленно изменяющихся волоконных све-
товодов, в которых на полупериоде луча происходит лишь небольшое изме-
нение (3 (z). В таких случаях направление каждого выходящего луча корре-
лировано с направлением входящего луча, поскольку средняя флуктуация
на нерегулярностях равна нулю.
Платой за уменьшение уширения импульса [2] является то, что часть
мощности направляемых лучей неизбежно теряется на излучение. Это про-
исходит потому, что изменение j3(z) на полупериоде луча может быть до-
статочным для того, чтобы превратить направляемый луч в туннелирующий
или дифрагирующий (см. разд. 2.7). Потери на излучение меньше, когда не-
регулярности приводят к изменениям направлений луча преимущественно в
прямом направлении, т. е. в сторону больших значений (3 (z).
МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ВОЛОКОННЫЕ СВЕТОВОДЫ
Рассмотрим второй важный для практики случай, когда можно приближен-
но оценить время прохождения. Пусть изменения параметров вдоль све-
товода являются настолько медленными, что профиль показателя преломле-
ния оказывается по существу постоянным, т. е. независящим от z, на рассто-
яниях zp, равных полупериоду луча, так что z^\bn(r, z)fbz\ << 1. Пример
медленно изменяющегося волоконного световода приведен на рис. 5.2. Не-
регулярности могут быть достаточно большими, например, в случае конусо-
образного волоконного световода, у которого радиус сердцевины на одном
конце может во много раз отличаться от радиуса на другом конце, хотя угол
конусности поцсюду мал.
83
Рис. 5.2. Волоконный световод со ступенчатым профилем. Показатели преломления
сердцевины и оболочки волокна постоянны, а радиус сердцевины p(z) мало изменяется
на полупериоде лучевой
траектории (z)
Рис. 5.3. Плавно изменяющийся волоконный световод (радиус сердцевины p(z) и про-
филь показателя преломления n(r, z) медленно изменяются вдоль оси z) (а) и его
приближенная модель, составленная из набора однородных участков (для ясности из-
менения параметров световода преувеличены; в пределах каждого участка радиус серд-
цевины и профиль показателя преломления не зависят otz) (d)
Приближенная модель. Если условия медленного изменения выполнены,
то можно построить приближенную модель нерегулярного волоконного све-
товода, разбивая его, как показано на рис. 5.3, на ряд регулярных участков.
Каждый участок имеет длину zp (z), равную полу периоду траектории луча, и
для удобства считается, что радиус p(z) и профиль показателя преломления
и (г, z) участка совпадают с соответствующими значениями в его средней
точке.
5.5. Время прохождения луча
Время прохождения для нерегулярного волоконного световода (рис. 5.3, а)
равно сумме времен прохождения для каждого из регулярных участков
(рис. 5.3, б). Если rp(z) - время прохождения однородного участка длины
zp (z), то, используя выражение (2.32), имеем
Zp(z) = Z0(z)/c, (5.9)
где с — скорость света в свободном пространстве, LQ (z) — длина оптического
пути, которая по аналогии с (2.27) имеет вид
io(z)=2 ; g(r,z) =и2(г, z) -p2(z)--Т2-^/^,(5.10)
S\r, z) г
84
где z — средняя точка сечения, Р (z) — определяется выражением (5.5), 7 -
инвариант (5.6) и р(0) — радиус сердцевины в начале волоконного светово-
да. Ясно, что при выполнении интегрирования z остается фиксированным.
Сумму значений t (z) можно приближенно заменить интегралом, если поло-
жить zp (z) — dz. Тогда полное время прохождения составляет
1 1
t=- f
с о
ZP(Z)
dz,
(5.11)
где Zp (z) — задается выражением, аналогичным (2.28), через функцию
g(r, z) из (5.10) npnz, соответствующем средней точке:
rtp(z) ,
z’<2) ’W) (5Л2)
По сравнению с (5.1) последнее выражение для t оказывается значительно
проще, поскольку нет необходимости интегрировать вдоль лучевой траекто-
рии в нерегулярном волоконном световоде, а требуется знать только ее па-
раметры.
Характерные масштабы. Физическим рассуждениям, которые позволили
получить выражение (5.11), можно поставить в соответствие более строгий
математический вывод. Из рис. 5.2 видно, что лучевые траектории в медлен-
но изменяющихся волоконных световодах характеризуются двумя масшта-
бами — быстрым и медленным. Быстрый масштаб равен лучевому полупе-
риоду zp(z), а медленный масштаб характеризует нерегулярность, которая
существенна только на расстояниях, больших полупериода. Изменение про-
филя показателя преломления в радиальном направлении оказывается го-
раздо более быстрым, чем в продольном, так что выполняется условие
| bn/br | > > | bn/bz |. Поэтому при выводе выражения (5.11) быстрое измене-
ние направления траектории усредняется по лучевому полупериоду, в преде-
лах которого волоконный световод рассматривается как аксиально регуляр-
ный. Математически это эквивалентно замене подынтегрального выражения
в (5.1) его средним значением по полупериоду. Таким образом,
п2 (г, z) >
?(Z)
1
0(z)zp(z)
Z + zp(z)/2
f n2(T(t),z)di;,
z - Zp(z)/2
(5.13)
где для ясности использована переменная f, чтобы различать аксиальное рас-
стояние в локально регулярном волоконном световоде и расстояние z вдоль
нерегулярного световода. Важно понимать, что интегрирование выполняется
вдоль лучевой траектории регулярного волоконного световода*. Расстояние
этой траектории от оси световода быстро изменяется с изменением f. Про-
филь же с изменением z медленно меняется. Иными словами, величину z и
в пределах интегрирования, и в подынтегральном выражении в правой части
(5.13) следует считать постоянной при интегрировании. Если, кроме того, по
* Такой вспомогательный регулярный волновод называется также волноводом срав-
нения. - Прим. ред.
85
аналогии с выражением (2.21) положить (z) =dr/g(r,z)1/2 и использовать
соотношение (5.10), то снова получим подынтегральное выражение (5.11).
Уравнение для лучевой функции. Как видно из выражений (5.10) и (5.12),
величины Lq (z) и zp (z) зависят от (3 (z). Поэтому, чтобы оценить время про-
хождения луча с помощью выражения (5.11), нужно знать решение уравне-
ния (5.4). Задаваемое соотношением (5.5) оно предполагает, что известна
лучевая траектория. Однако если учесть, что волоконный световод является
медленно меняющимся, то правую часть выражения (5.4) можно усреднить
по полупериоду (обоснование уже было дано ниже выражения (5.13)). Та-
ким образом [3, 4],
d(32 (z) _ ди2 (г, z)
dz bz
(5.14)
где среднее значение определяется, как в выражении (5.13). В разд. 5.10 при-
водится альтернативный метод нахождения 0 (z).
5.6. Пример. Усеченный степенной профиль
Проиллюстрируем применение полученных выше результатов, рассмотрев волоконные
световоды, у которых параметры р, Д и ис0 усеченного степенного профиля медленно
изменяются вдоль световода, а показатель степени q фиксирован. Такие профили зада-
ются соотношениями
л2 (г, z) = «^(z) {1 - 2Д (z) [r/p(z)]<?}; 0<r<p(z), (5.15а)
= ”cl = nco<z> {1 -2А(*)}; p(z)<r<~. (5.156)
Отношение Zo (z) Jz получается из отношения Lo /z или ct/z, Приведенного в табл. 2.1,
при замене 0 на 0(z) и исо на исо(г). Поэтому выражение (5.11) для времени прохож-
дения луча принимает вид
Г “ c(q + 2)
/ f и2 (z) )
/ < Ч-~--------- + 2/3(z) > dz.
о I 0(z) J
(5.16)
Чтобы найти 0(z), с помощью (5.15) получим, что в сердцевине
az dz (fl с0 dz (fl
Использование выражения (5.13) позволяет показать, что на лучевом полупериоде
(5.17)
/ а , , , 7.» (z) 1
--~г
Подставляя (5.17) и (5.18) в уравнение (5.14), получим для обыкновенное диффе-
ренциальное уравнение первого порядка, решение которого имеет вид [4]
(z) + qn3C0 (z) I.
(5.18)
"со GO - У (2) = n2CQ(z) -и3с1(г)
р(0)? , 2/ (<? + 2)
”со<0) - ”cl(0)
(5.19)
86
Это выражение дает, в частности, значение j?(z) для усеченного параболического профи-
ля при q = 2 и для ступенчатого профиля при q = 00. Подставляя в последнем случае
вместо j3(z) его выражение (5.2), после преобразований имеем соотношение
nco(z)p<z) sin<9z (z) = "co(°)P(0) sin<9z(0), (5.20)
которое является обобщением. (5.76) для переменного радиуса сердцевины р (z).
5.7. Малые нерегулярности
На практике нерегулярности волоконных световодов, как правило, малый,
кроме того, являются медленно меняющимися. При этом определения вре-
мени прохождения луча и, следовательно, уширения импульса значительно
упрощаются. Прежде чем рассматривать специфичные характеристики малых
нерегулярностей, напомним, что, как показано в разд. 5.4, если такие измене-
ния являются случайными и медленно изменяющимися, то ширина импульса
не может расти как z1/2. Такой рост предполагает, что направление каждого
выходящего луча на конце волоконного световода некоррелировано с на-
правлением входящего луча в начале световода, а это несовместимо с предпо-
ложением о медленном изменении параметров волоконного световода на
лучевом периоде. В самом деле, решение уравнения (5.14) для (3 (z) и адиа-
батический инвариант (см. разд. 5.10) явно показывают корреляцию между
направлениями луча в начале и конце волоконного световода независимо от
характера изменений световода, если они медленно изменяющиеся.
В гл. 3 было показано, что в регулярном волоконном световоде ушире-
ние импульса пропорционально расстоянию z вдоль волокна. Влияние, кото-
рое медленная нерегулярность может оказать на этот результат, состоит в
том, что изменяется множитель перед z и, кроме того, изменяется форма им-
пульса, и вследствие излучения уменьшается его мощность. Это будет рас-
смотрено в разд. 5.13. Однако, как будет показано ниже, эти эффекты, как
правило, малы, если изменения параметров световода малы.
Разложение лучевой функции. Предположим, что приближенное решение
уравнения (5.14) можно получить, разлагая (3 (z) по степеням малой без-
размерной величины к (z), которая пропорциональна величине нерегулярно-
сти. По причинам, которые будут разъяснены ниже, сохраним в этом разло-
жении члены до второго порядка:
0(z) = 0(0) + 0^(z) + 02k2(z), (5.21)
где 0(0) — значение 0(z) в начале волоконного световода, а /3! и 02 не зави-
сят от z. Эти коэффициенты определяются итерированием уравнения (5.14).
Для нулевого порядка малой величины k(z) правая часть уравнения (5.14)
равна нулю. Это соответствует тому, что в регулярном световоде 0 (z) = 0 (0).
Для того чтобы получить поправку первого порядка 0Ь нужно в уравнении
(5.14) приравнять члены порядка к(z) и проинтегрировать
(г) ' Л (0) = °' (5'22)
Процедура усреднения была разъяснена выше при получении выражения
(5.13) и выполняется с точностью до членов порядка k(z), причем в уравне-
87
нии лучевой траектории /3 (z) приближенно заменяется на (3 (0). Подобным
образом рассчитывается и поправка второго порядка.
Время прохождения луча. В медленно изменяющемся волоконном свето-
воде оно определяется выражением (5.11), в котором аналогично (5.21)
можно разложить £0 (z) и z?(z) по степеням k(z) . Подставляя эти разложе-
ния в выражение (5.11), с точностью до членов второго порядка получим
t =tn + AK + Вк2 9 (5.23)
где tu — время проховдения луча для регулярного волоконного световода с
13 (z) = (3 (0) ; коэффициенты А, В не зависят от z, но содержат параметры све-
товода и лучевой траектории. Среднее значение к(г) и усредненное по длине
волоконного световода значение к2 (z) определяются формулами
к =2 f K(z)dz; к2 = 2 f к2 (z)dz. (5.24)
z о z о
Ясно, что всегда можно выбрать параметры регулярного волоконного свето-
вода таким образом, чтобы среднее значение неоднородностей на длине све-
товода равнялось нулю. Тогда поправка времени прохождения луча имеет
второй порядок малости, т. е. в выражении (5.23) коэффициент А -0.
Уширение импульса. Поправка к времени прохождения луча, вызванная
неоднородностями волоконного световода, мала, однако ширина импульса
в слабонаправляющем волокне, как было показано в гл. 3, тоже мала. На-
пример, в соответствии с выражением (3.9) минимальная ширина импульса
для оптимального усеченного степенного профиля пропорциональна Д2, или
О с. Влияние дисперсии материала на уширение импульса было исследовано в
разд. 3.8; здесь рассматривается влияние малых нерегулярностей на мини-
мальную ширину импульса.
5.8. Пример. Малые изменения радиуса сердцевины
Рассмотрим волоконный световод с усеченным степенным профилем, приведенным
в табл. 2.1, у которого радиус сердцевины изменяется незначительно. Таким обра-
зом, пусть
p(z) = р0 + 6p(z); |6p(z)|< <р0, (5.25)
где р0 - радиус сердцевины регулярного волоконного световода, у которого 6р = 0.
Среднее значение 5р определяется первым из соотношений (5.24), причем k(z) =
= 8p(z)lpQ. Для того чтобы найти члены разложения (5.21) при 0(z) и k(z) = 8p(z)/p0,
можно либо использовать итеративную процедуру, в основе которой лежит соотношение
(5.22), либо разложить точное решение уравнения (5.19), в результате чего получим
Ч___ "со - (0) в =- 3q+2 в_________%-
Я + 2 Д(0) ’ 2' 2(4 + 2) 2Д(0)
(5.26)
Подставив эти соотношения в выражение (5.16), где nco(z) заменено на имеем
t-t +zd^-- п- + (2?2(0) -<7»^)^?(0)
1 zu 2 ’ и ~ --------------------Z-------------- ’ (5.27)
р0 (<7 + 2)/?’ (0)
поскольку 6р — 0. Время прохождения луча для регулярного волоконного световода
приведено в табл. 2.1 при (3 = (3(0) и р = р0, а величина 8р 2 /р2 определяется вторым со-
отношением из (5.24) прик(г) = 6p(z)/p0.
88
Уширение импульса. Уширение импульса в регулярных волоконных световодах с
усеченным степенным профилем рассмотрено в разд. 3.2. Если повторить анализ, ис-
пользуя время прохождения луча, задаваемое для нерегулярного световода выражением
(5.27), то окажется, что rm|n имеет место приблизительно при 0(z) = 0т (0т задано со-
отношением (3.6)), a fmax - при 0(z) = пс\. При оптимальном показателе степени (3.8)
выражение для уширения импульса (3.9) в слабонаправляющих световодах модифици-
руется вследствие присутствия небольших нерегулярностей и принимает вид [4]
rmax~fmin^d {1 + 8 (6?2/р2)}; q = <7opt * 2 - в2. (5.28)
Следовательно, увеличение ширины импульса зависит только от амплитуды нерегуляр-
ностей и не зависит от их пространственной частоты. Лучше всего это можно проиллю-
стрировать, рассматривая волоконный световод с синусоидально изменяющимся радиу-
сом сердцевины
6p(z) = 6pmcos(z/zs); Spm < < р„, (5.29)
где zs - пространственный период. Подстановка (5.29) в выражение (5.28) в предполо-
жении, что z > > z , дает
rmax ~ rmin + (5Рт/ро) }• (5.30)
Таким образом, в случае оптимального профиля изменение радиуса сердцевины на 10 %
приводит к увеличению ширины импульса только на 4 %.
5.9. Пример. Малые изменения показателя степени
Теперь рассмотрим волоконный световод с усеченным степенным профилем показателя
преломления (см. табл. 2.1). Пусть вдоль волоконного световода медленно изменяется
только показатель степени q (z) [3 — 5 ] - Изменение q относительно некоторого средне-
го значения qQ мало и можно считать, что
<7 (z) = <70 + 6<7 (z); l«<7 (z)/?0 I < < 1, (5-31)
где qQ выбирается так, чтобы Sq (z) имела нулевое среднее значение при усреднении по
длине волоконного световода, т. е. bq = 0. В этом случае точное решение уравнения
(5.14) неизвестно и должно быть найдено итеративным методом, рассмотренным в
разд. 5.7. В результате итераций определяются коэффициенты в (5.21) при степенях
k(z) = 6q (z)!q0. Аналогично выражению (5.16) для времени прохождения луча имеем
t = f—i— f ( 2co. | dz
c о <?(z)+2 I ?(Z) "co J
(5.32)
Подставляя сюда выражения (5.21) и (5.31) и учитывая, что 8q = 0, получаем с точно-
стью до второго порядка результат [4], аналогичный (5.27):
(5.33)
t = tu + (С3 +ДС4)6<72,
где С3 и С4 - безразмерные константы, зависящие от 0(0), исо и q0.
Эффективный показатель степени. Если волоконный световод является слабонаправ-
ляющим и характеризуется достаточно малым изменением профиля, то членом ДС4 в
выражении (5.33) можно пренебречь по сравнению с С3. Это эквивалентно предположе-
нию, что 0(z) = 0(0) в уравнении лучевой траектории при итерировании уравнения
(5.14) для всех порядков относительно 8q (z). Если сделать это предположение относи-
тельно выражения (5.32) и ввести эффективный показатель степени qe, определенный
В [3],
1 _ j_ л dz
~ 2 О 2 + 7(2) ’
то для времени прохождения луча получаем
z "со f 2j?(0) "со I
С 2+qe { "со е( ’ 3(0) Г
(5.34)
(5.35)
89
По виду это выражение совпадает с выражением для времени прохождения луча в регу-
лярном волоконном световоде, приведенным в табл. 2.1, если положить 0 = 0(0) и за-
менить q на qQ. Таким образом, небольшое изменение показателя степени профиля в
медленно изменяющемся слабонаправляющем волоконном световоде эквивалентно пе-
реходу к регулярному световоду с другим показателем степени профиля. Если подста-
вить (5.31) в (5.34), то с точностью до второго порядка получим
Qe= - 6V/(2+<70), (5.36)
поскольку 6^=0. Следовательно, на ширину импульса влияет только амплитуда изме-
нения q (z). Если предположить, что bq (z) имеет синусоидальный закон изменения
6?(z) = 6<7mcos(z/zs); 5<7m< <q0, (5.37)
где 8qm - максимальное значение 8q (z), то получим [4]
<7е =«о -Ит/2^о+2), (5.38)
при условии, ЧТО Z > > Zs.
Уширение импульса. В разд. 3.2 было показано, что минимальная ширина импульса
в регулярном волоконном световоде с усеченным степенным профилем чрезвычайно
чувствительна к малым изменениям показателя степени относительно оптимального зна-
чения. Выражение для оценки влияния нерегулярностей показателя степени на опти-
мальный профиль можно получить, подставив <7ор{ из соотношения (3.8) в выражение
(5.36). Поскольку волоконный световод по предположению является слабонаправля-
ющим, эффективный показатель степени
qQ «2 - 2Д - ^q2/4 «2 - О2 - bq2 /4. (5.39)
Отклонение показателя степени на ± Д относительно q = <?Opt вызывает согласно рис. 3.3
десятикратное увеличение ширины импульса. Следовательно, если ^q2 = 4Д, то происхо-
дит такое же увеличение ширины. С другой стороны, если волоконный световод харак-
теризуется медленными изменениями показателя степени, то с учетом соотношения
(5.39) их влияние можно компенсировать. Иными словами, если значение bq2 задано,
то профиль с показателем q = 2 - 2Д + bq2 /4 характеризуется минимальным ушире-
нием импульса. Более того, с уменьшением относительной высоты профиля Д ушире-
ние импульса оказывается более чувствительным к нерегулярностям. Оно зависит толь-
ко от нерегулярностей и не зависит от их пространственного распределения при усло-
вии, что они являются медленно изменяющимися. Заметим, наконец, что уширение им-
пульса оказывается чувствительнее к небольшим парциальным изменениям показателя
степени профиля, чем к эквивалентным парциальным изменениям радиуса сердцевины,
рассмотренным в предыдущем примере.
5.10. Адиабатический инвариант
Рассмотрим альтернативный способ описания медленно изменяющихся во-
локонных световодов, основанный на представлениях из других областей
физики.
Если световод является регулярным, построить лучевую траекторию до-
статочно просто, поскольку 13 и I ^постоянны вдоль нее. Если он является не-
регулярным, то для инварианта I имеется выражение (5.6), справедливое
при условии, что световод сохраняет осевую симметрию, однако для инва-
рианта /3~, вообще говоря, не существует эквивалентного обобщения. Но если
световод изменяется мало на лучевом полупериоде, то существует параметр,
который остается постоянным вдоль его длины и который упрощает нахож-
дение характеристик лучевой траектории. Назовем этот параметр адиабати-
ческим инвариантом. Изменения могут быть произвольно большими при
единственном условии, что это происходит на расстояниях, больших лучево-
90
го полупериода. Например, отношение радиусов сердцевины на концах ко-
нусообразного волоконного световода велико, хотя угол конусности всю-
ду мал.
Для того чтобы получить этот инвариант, напомним, что лучевые траекто-
рии в медленно изменяющихся волоконных световодах, как было показано
в разд. 5.5, характеризуются малым масштабом, равным полупериоду zp (z),
и масштабом нерегулярностей, который велик по сравнению с zp (z). Опера-
ция усреднения уравнений (5.3) лучевой траектории по полупериоду позво-
ляет исключить быстрые изменения вдоль траектории. Это приводит к соот-
ношениям, которые описывают медленные изменения, вызванные нерегу-
лярностями, например, можно сравнить точное выражение (5.6), уравнение
(5.14) и уравнение, соответствующее усредненному уравнению (5.3а). С по-
мощью этих соотношений можно показать, что вдоль траектории остается
почти постоянным параметр
/= f n(r,z)^-dr. (5.40)
Zp(z) ds
Здесь ds — элемент траектории и интегрирование выполняется по полупери-
оду траектории, причем явная зависимость величин п(г, z) и zp (z) от z не
учитывается. Это хорошо известный результат классической механики, где
I называют адиабатическим инвариантом [6]. Во многих работах [7, 8] лу-
чевое распространение рассматривается методами классической механики.
Используя выражение (5.2) и очевидное обобщение соотношения (2.21) на
медленно изменяющиеся волоконные световоды, можно получить выраже-
ние для / в более удобной форме
_ rtp(Z) , rtp(z) f л2 /Пч Л
Z=20(z) f dr_dr =2 J -J2 P_I01_?2(2)l 1/2^
ric(z) dz ric(z) ( r J
(5.41)
где /*jc (z) и Гф (z) — положения внутренней каустики и каустики точек пово-
рота. Этот инвариант полностью определяется инвариантом 0 (z). При инте-
грировании явная зависимость п (г, z), 0 (z), ric (z) и (z) от z не учитыва-
ется. Продемонстрируем полезность этого результата на простых примерах.
5.11. Пример. Ступенчатый профиль
Если нерегулярный волоконный световод имеет ступенчатый профиль, то показатель
преломления сердцевины п (z) зависит только от z и верхний предел интегрирования в
выражении (5.41) заменяется на радиус сердцевины p(z). Если при этом траектория об-
разует с осью угол 0z (z), то с помощью соотношения (5.2) получаем
p(z) ( 72оЧ0)'1
/=2 f I”2 (z) sin30z(z)----> dr, (5.42)
'ic^ I r J
где = Ip(0)/ {n(z) sin0z(z)}. Заменив переменную г на х - r/r^z), получим
_ P(Z)>(Z)
Z=2Zp(0) f ------------———dx. (5.43)
91
Поскольку I является инвариантом для круглого волоконного световода, из этого сле-
дует, что p(z) lr[c(z) - тоже инвариант и
n(z)p(z) sin0z(z) = и(0)р(0) sin0z(O). (5.44)
Это выражение было подучено непосредственно из уравнений лучевой траектории (5.20).
Напомним, что этот результат применим только к лучам, у которых полупериод мал по
сравнению с расстоянием вдоль световода, на котором происходит значительное измене-
ние показателя преломления или радиуса сердцевины. Следовательно, лучи, для кото-
рых 0Z (z) s 0, исключаются, поскольку z^(z) -> °° при 0Z (z) ->0. Этот результат иден-
тичен закону синусов Аббе в геометрической оптике [7, 9]. Если подставить (5.44) в
(5.2), то для (3(z) получим явное выражение
0(z) = {«’(z) - [я2 (0) - Д2 (0) ]р2 (0)/р2 (z)} v2, (5.45)
где 0(0) = п (0) cos0z (0). Если радиус сердцевины является однородным, т. е. p(z) =
= р(0), то выражения (5.45) и (5.44) переходят в соотношения (5.7а) и (5.76) соот-
ветственно, которые являются точными и получены непосредственно из соотношения
(5.4) для 0(z).
Малые нерегулярности. Для световода с малыми отклонениями от первоначальных
значений показателя преломления и радиуса можно положить
«(z) = п (0) + 5n(z); p(z) = p(0)-+5p(z), (5.46)
где 15л (z) | < < n (0) и 15p(z)| < < p(0). Подставляя (5.46) в (5.45) и сохраняя только
члены низших порядков, получаем
п (0) п2 (0) - (З2 (0)
/?(z) = 0(0) +tA2 5«(z) +——^-^-5p(z). (5>47)
0(0) 0(0) р(0)
Из этого выражения видно, что если волоконный световод является слабонаправляю-
щим, т. е. 0(0) = п (0), то малые изменения показателя преломления сердцевины гораз-
до сильнее влияют на 0 (z), чем эквивалентные изменения ее радиуса р (z).
5.12. Пример. Усеченные степенные профили
Рассмотрим теперь волоконные световоды с усеченными степенными профилями. Эти
профили имеют вид, задаваемый выражением (5.15), причем «со, Аир зависят от z,
а значение показателя степени q будем считать постоянным. Подставляя (5.15) в выра-
жение (5.41), имеем
rtp<z> f /з 2 q ) U2
/=2 f i "co<z) -02<г)--------------24(z)p’o(z)dr. (5.48)
Г]С(г) I r p(z) )
Сделаем замену переменной г на х и введем параметр h (z):
r= __________2.___________А(г)= 2Д(г)и*0(г)____________ (5 49)
{и’0(г)-/32(г)} 1/2 ’ Р(г)Ч'{40(г)-^2(Z)} « + 2>/2
Тогда выражение для инварианта принимает более простой вид
Xfn(z) г
1=2 J - -—-j - h (Z)xq | dx, (5.50)
xic(z) I x J
где xic(z) = (hco(z) “ P2(z) } y2 ric(z) (аналогичная зависимость имеет место для
xtp (z)) • Поскольку xic_(z) и xtp (z) являются корнями подынтегрального выражения,
они зависят только от 7р(0), h (z) и q. Следовательно, инвариант I является функцией
92
этих трех величин, но поскольку I является инвариантом, a q постоянна по предположе-
нию, то h (z) также должен быть инвариантом. Преобразуя уравнение h (z) = h (0) с
учетом (5.49), снова получаем выражение (5.19).
Медленно изменяющийся показатель степени. Если теперь предположить, что пока-
затель степени q изменяется вдоль оси z, то можно получить инвариант для меридио-
нальных лучей. Положим в выражении (5.50) I ='Xjc(z) — 0,ig = q (z) и сделаем заме-
ну переменной и = h {z)x^z^ , так что х = xtp(z) соответствует и = 1. Получающийся
в результате интеграл можно вычцслить, используя соотношения (37.104) и (37.105),
и получить инвариант
1 r(l + l/?(z)) 1 Г(1 + 1/?(0))
h(z)1/q(Z) Г (3/2 + 1/<7 (z)) й(0)1/<г(О) Г (3/2 +(0)) ’ J
где h(z) определен (5.49) при q = q (z).
5.13. Потери на излучение
В регулярном волоконном световоде луч, который является направляемым
в начале световода, остается направляемым вдоль всей его длины. В нерегу-
лярном же световоде луч, который первоначально был направляемым, мо-
жет на части траектории стать вытекающим и потерять мощность из-за излу-
чения, если изменение параметра З(^), задаваемого (5.2), оказывается до-
статочно большим. В противном случае он остается направляемым по всей
длине волоконного световода даже при условии изменения 3 (z). Здесь будет
приведена простая оценка верхней границы потерь, вызванных излучением.
Верхняя граница потерь на излучение. Рассмотрим нерегулярный воло-
конный световод, у которого показатель преломления оболочки «с1 постоя-
нен, а радиус сердцевины р (z) и профиль ее показателя преломления п (г, z)
произвольно меняются на длине световода. Согласно (2.24а) лучи, которые
оказываются направляемыми в начале световода, удовлетворяют соотноше-
нию ис1 < |3(0) < исо(0), где лсо(2) ~ максимальное значение показателя
преломления сердцевины в сечении z. Впоследствии значение параметра
3 (z) для некоторых из этих лучей станет таким, что 3 (z) < hcj и, как показа-
но на рис. 5.4, они будут излучать мощность на части траектории. Фактичес-
кие потери мощности для отдельных лучей рассматриваются в гл. 7. Здесь
будет дана оценка верхней границы этих потерь, получаемая в предположе-
нии, что теряется вся мощность лучей, которые становятся вытекающими.
Предположим для простоты, что волоконный световод возбуждается диф-
фузным источником. Тогда полная начальная мощность направляемых лу-
чей РЬг дается выражением (4.13), в котором р и п(г) заменены на р(0) и
п (г, 0). Пусть РЬг — это полная мощность лучей, которые остаются направля-
емыми на всей длине световода, т. е. для них при любых z @(z) > ис1. Тогда
максимальная мощность, которая может быть- потеряна на излучение, со-
ставляет
Л-ad А>г А)г- (5.52)
Для_того чтобы определить РЬг, необходимо знать, каким образом изменяет-
ся 3 (z) вдоль волоконного световода. Если предположить, что волоконный
93
Рис. 5.4. Волоконные световоды со ступенчатым и градиентным профилями, у которых
радиус сердцевины и профиль показателя преломления изменяются с длиной:
а, б — луч остается направляемым; в, г — на части траектории направляемый луч стано-
вится вытекающим
световод является медленно изменяющимся, то можно использовать резуль-
таты предыдущих разделов. Найдем теперь значение Prad для волоконных
световодов, у которых медленно изменяется только радиус сердцевины.
5.14. Пример. Ступенчатый волоконный световод с изменяющимся радиусом
сердцевины
Рассмотрим ступенчатый волоконный световод, у которого показатели преломления
оболочки и сердцевины составляют соответственно и ис0 и радиус сердцевины p(z)
является медленно изменяющимся. Угол 0Z (z), который луч образует с направлением
оси в сечении z, связан с начальным значением угла 0Z (0) соотношением (5.44), в кото-
ром ^co(z) = исо(0) = исо. Луч, который первоначально является направляемым, мо-
жет стать вытекающим, только если радиус сердцевины станет меньше своего пер-
воначального значения р(0). Если наименьший на длине световода радиус сердцевины
составляет Pmjn и zm — координата соответствующего сечения, то направление луча в
сечении задается выражением
Sinez(zm) = {p(O)/pmjn} sinez(0). (5.53)
Следовательно, аналогично соотношению (2.6а) луч является направляемым на всей
длине волоконного световода, если 0Z (zm) < 0С, где значение 0С задается выражением
(2.5). Таким образом, на выходе световода этому условию удовлетворяют только те
лучи, для которых
0 <sinPz(0) < {Pmin/P(0)} sinPc. (5.54)
Для того чтобы рассчитать заметим, что полная мощность направляемых лучей при
возбуждении световода диффузным источником (4.25) изменяется пропорционально
квадрату радиуса сердцевины. Следовательно, значение пропорционально Р^щ и
максимальная доля полной первоначальной мощности направляемых лучей, которая мо-
жет быть потеряна на излучение, составляет
94
^rad/Ли 1 ^min^ (0)
(5.55)
где Pracj задается выражением (5.52), и приближение справедливо, если pm|n « р (0).
5.15. Пример. Световод с усеченным степенным профилем и изменяющимся
радиусом сердцевины
Рассмотрим теперь волоконные световоды с усеченным степенным профилем (см.
табл. 2.1), у которых медленно изменяется только радиус сердцевины p(z). Если ради-
ус сердцевины минимален в сечении zm, то 0(zm) и 0(0) связаны с p(z) = pmin уравне-
нием (5.19). Луч всюду является направляемым, если 0(zm) > «С1 и на входном тор-
це световода 0 (0) удовлетворяет условиям
«со[1-2Д{Рпйп/Р(0)} 2<г/(<7 + 2)] < (0) <и2о(0). (5.56)
Для того чтобы найти P^r, заметим, что полная мощность направляемых лучей, возбуж-
денных диффузным источником, задается выражением (4.18) и также, как в случае во-
локонного световода со ступенчатым профилем, пропорциональна квадрату радиуса
сердцевины. Следовательно, доля первоначальной излучаемой мощности направляемых
лучей задается выражением (5.55) и не зависит от показателя степени q, т. е. не зависит
от формы профиля.
КОНУСНЫЕ ПЕРЕХОДЫ И ФОКУСИРОВКА СВЕТА
Часто бывает необходимо принимать с максимальной эффективностью свет
от источника или волоконного световода с относительно большим размером
поперечного сечения световодом меньшего поперечного сечения. Использо-
вание линз для этой цели рассматривалось в гл. 4. Здесь будет исследована
возможность концентрировать световую мощность с помощью конусооб-
разных волоконных переходов, например таких, как показано на рис. 5.5.
Сначала покажем, как, используя лучевые траектории, можно просто и точ-
но рассчитать фокусирующие свойства линейного и параболического воло-
конных переходов с произвольным углом конусности. Поскольку весьма
часто конусность мала, т. е. локальный угол конусности мал, для описания
фокусирующих свойств в остальном произвольных конусных переходов мож-
но воспользоваться приближенным лучевым инвариантом (см. разд. 5.11).
Рис. 5.5. Конусные переходы в световоде со ступенчатым профилем:
a-плавный медленно изменяющийся, возбуждаемый диффузным источником; ^-парабо-
лический, возбуждаемый пучком лучей, параллельных оси световода
95
Непосредственное сравнение результатов в случае линейных переходов поз-
волит оценить точность приближения, которое основано на предположении,
что изменения являются медленными. Для более простой иллюстрации ис-
пользуемых идей, будем рассматривать только переходы между волоконны-
ми световодами со ступенчатыми профилями и считать, что у соединяемых
световодов показатели преломления сердцевин и оболочек одинаковые.
5.16. Возбуждение коллимированным пучком
Когда радиус сердцевины конусного перехода меняется по длине произ-
вольным образом, предположение о медленном изменении оказывается не-
справедливым и требуется нахождение точной траектории каждого луча.
Поэтому проще всего рассмотреть только меридиональные лучи. Пусть ко-
нусный переход возбуждается коллимированным пучком лучей, радиус ко-
торого Ро равен радиусу начала перехода. Цель состоит в том, чтобы при за-
данных радиусах на концах перехода и заданном критическом угле 0С присое-
диняемого волоконного световода определить минимальную длину перехода,
при которой вся мощность, падающая на переход, преобразуется в светово-
де в направляемые лучи.
5.17. Пример. Параболический переход
Пусть коллимированный пучок лучей, параллельных оси, падает на ступенчатый парабо-
лический конусный переход в сечении z = — L (см. рис. 5.5, б), где радиус сердцевины
равен р0. Ступенчатый световод с сердцевиной радиусом р примыкает к концу перехода
в сечении z = 0. Для простоты считаем, что показатели преломления сердцевины свето-
вода, конусного перехода и среды источника одинаковы и равны п а показатели пре-
ломления оболочки волоконного световода и оболочки перехода одинаковы и равны
иср Каждый параллельный оси луч отражается от параболической границы раздела так,
что углы падения и отражения относительно касательной к границе равны. Хорошо из-
вестно, что все лучи, отраженные от параболической поверхности, проходят через ее фо-
кус F, как показано на рисунке. Более того, угол, который отраженный луч образует
с осью, увеличивается по мере смещения точки отражения к концу перехода. Таким об-
разом, при заданных р0, р и 0С, определенных на рис. 5.5, б, минимальная длина перехо-
да £mjn, при которой вся световая мощность, попадающая на переход, возбуждает толь-
ко направляемые лучи волоконного световода, определяется из условия: луч, отражен-
ный в точке Q, должен образовывать с осью волоконного световода угол 0С в соответ-
ствии с соотношением (2.6а). Тогда из закона Снелля следует, что угол между падаю-
щим лучом и касательной к границе сердцевины в точке Q равен 0с/2. Просто показать,
что граница перехода (см. рис. 5.5, б) относительно оси задается уравнением
х2 = р2 - (р$ - р2) (z/Z.); -Л <z < 0. (5.57)
Если потребовать, чтобы в сечении z = 0 выполнялось условие dx/dz = -tg(0c/2), то
I - р0 ~р2 1 _ Ро - Р2 (5.58)
тт 2р tg(0c/2) ^с
Приближенный результат применим, когда волоконный световод является слабонаправ-
ляющим, т. е. 0С < < 1.
96
5.18. Пример. Линейный переход
Пусть линейный переход, представленный на рис. 5.6, а, характеризуется теми же пара-
метрами, что и в предыдущем примере, и угол перехода равен П. Можно очень просто
рассчитать минимальную длину перехода, при которой обеспечивается передача полной
мощности меридионального луча, попадающего на переход в сечении z = -L под углом
0О к оси. Этот результат одинаково применим и в случае возбуждения пучком коллими-
рованных лучей, параллельных оси, т. е. при 0О = 0, и в случае, когда согласно разд. 4.11
используется линза, преобразующая такой пучок в конус меридиональных лучей с уг-
лом 0О > 0.
Рассмотрим меридиональные лучи, падающие под углом 0О на поперечное сечение пе-
рехода z = —L. Все эти лучи станут направляемыми лучами в волоконном световоде,
если крайний луч, падающий на поверхность перехода в точке Р (см. рис. 5.6, а), стано-
вится направляемым. При заданных параметрах р0, р и 0С ступенчатый конусный пере-
ход, удовлетворяющий этому условию, имеет наименьшую длину, если ему соответ-
ствует траектория, которая пересекает конец волоконного световода в точке Q и после
отражения - ось световода под углом 0С. Это означает, что падающий луч образует в точ-
ке С с направлением поверхности перехода угол 0С + П.
Эквивалентный геометрический путь луча. Пусть геометрия лучевой траектории меж-
ду точками Р и Q будет, такой, как представлено на рис. 5.6, а. Найдем минимальную
длину перехода £mjn. С этой целью используем эквивалентный путь, представленный на
рис. 5.6, б, где показан сектор соприкасающихся одинаковых переходов с общим цент-
ром О. Длина траектории между точками последовательных отражений и углы, кото-
рые она образует с поверхностью перехода в точках Р, R, S, Т и Q на рис. 5.6, а совпада-
ют с соответствующими значениями для прямолинейной траектории PRSTQ рис. 5.6, б
[9]. Таким образом, PQ образует с лучом OQ угол 0С + П и, как видно из рисунка,
OQ = ON = p/tg П, ОМ = ON + L + p0 /tg0o. Применяя теорему синусов (37.8) к тре-
угольнику OQM, выразим П и, следовательно, £min через р, р0 и 0С:
Ро ~~ Р . Р sin(0c + n) _ * tgn
tg D p0 sin 0O tg 0O
(5.59a)
Решение относительно угла n можно получить численно, однако если все углы, входя-
щие в (5.59а), малы, то для получается следующее приближенное выражение:
£min^^o -Р)2/(0СР-0ОРО)- (5-596)
Рис. 5.6. Линейный переход в волоконном световоде со ступенчатым профилем (угол
перехода равен П) (а) и эквивалентная геометрическая траектория (б)
4 За к 37
97
В случае коллимированного пучка лучей, параллельных оси, 0О = 0, и из выражений
(5.58) и (5.596) видно, что минимальная длина параболического перехода больше, чем
у соответствующего линейного перехода в (р0 + р) / (р0 — р) раз при условии, что угол
конусности мал и волоконный световод является слабонаправляющим.
5.19. Возбуждение диффузным источником
Точный лучевой анализ переходов произвольной формы оказывается слож-
ным, особенно в том случае, когда возбуждаются как меридиональные, так
и косые лучи. Однако если конусность перехода является достаточно малой,
т. е. локальный угол конусности невелик, то можно обойти эти трудности,
воспользовавшись приближенным инвариантом, выведенным ранее в этой
главе. Для того чтобы продемонстрировать это, допустим, что диффузный
источник радиуса р0, равного начальному радиусу перехода, состыкован со
ступенчатым конусным переходом, изображенном на рис. 5.5, а. Радиус пере-
хода уменьшается до р на расстоянии L, где к нему пристыкован ступенчатый
волоконный световод с сердцевиной радиуса р. Пусть для простоты среда
источника, сердцевины перехода и волоконного световода имеют одинако-
вые показатели преломления псо и, аналогично, показатели преломления
оболочки ис1.
Рассмотрим возбуждаемый источником луч, который образует угол 0z (z)
с осью перехода в сечении z; Этот луч будет направляемым, если он удовлет-
воряет условию 0z (0) < 0с, где z = 0 соответствует концу перехода. Если ра-
диус конусного перехода р (z) монотонно уменьшается с ростом z, то интер-
вал направлений лучей в начальном сечении перехода z = —L, для которого
лучи остаются направляемыми, удовлетворяет условию 0 < 0Z (—L) < 0О • Ес-
ли конусность перехода является малой, то эти величины связаны соотноше-
нием (5.20), и так как показатель преломления сердцевины постоянен, на-
правления лучей удовлетворяют условию
Po’sin0o = P(Z) sin0z (z) = psin0c. (5.60)
Соответственно связь между полной мощностью направляемых лучей, входя-
щих в волоконный световод, РЬ1. и полной мощностью РЬг лучей внутри ин-
тервала углов 0 < 0Z (—Z) < 0С в начале перехода по аналогии с (5.55) опре-
деляется выражением
Ли = (Р2/Ро)РЬг-
(5.61)
Поскольку согласно (4.16) полная мощность направляемых лучей пропор-
циональна площади сердцевины, а р2/ро — отношение площадей сечений серд-
цевины и источника, ясно, что никаких преимуществ расположения источни-
ка в схеме рис. 5.5,а по сравнению с непосредственным соединением свето-
вода с источником нет. Следовательно, если источник возбуждает лучи, на-
правления которых выходят за пределы интервала лучей, направляемых
волоконным световодом, то невозможно увеличить их мощность возбуж-
дения использованием перехода. Это аналогично выводу, сделанному в
разд. 4.14 при рассмотрении применения линзы для фокусирования мощно-
сти диффузного источника.
98
Частично диффузный источник. Рассмотрим переход, представленный да
рис. 5.5, а, когда диффузный источник заменен на частично диффузный,
который излучает свет только в пределах интервала углов О <0Z (— L) <0S.
Если 0S не превышает 0о, задаваемого соотношением (5.60), то вся мощ-
ность источника преобразуется в направляемые лучи и по сравнению со слу-
чаем, когда источник располагается в непосредственной близости от воло-
конного световода, использование перехода позволяет увеличить полную
мощность направляемых лучей в Ро/р2 раз. Этот вывод соответствует резуль-
татам разд. 4.16 для линзы и частично диффузного источника.
Конус с произвольным углом перехода. Выводы, сделанные выше, были
получены при рассмотрении конусного перехода с малым углом. Однако до-
пустимы более общие утверждения относительно конусных переходов с про-
извольно изменяющимся радиусом. С этой целью вместо утомительной про-
цедуры исследования траекторий каждого из лучей в переходе рассматрива-
ется целое семейство лучей, возбуждаемых источником [10]. Можно пока-
зать, что вместо соотношения (5.60) получается неравенство posin0o
< psin0c. Иными словами, выражение (5.61) дает верхний предел для фоку-
сировки света.
5.20. Точность приближения для перехода с медленным изменением радиуса
Приближенный лучевой инвариант для волоконного перехода с медленно из-
меняющимся радиусом сердцевины выражается соотношением (5.60). Это
соотношение является точным при условии, что изменение радиуса перехода
6p(z) в пределах локального лучевого полупериода мало. Если и переход, и
волоконный световод являются слабонаправляющими, то 0Z << 1, и, обоб-
щая выражение для zp (см. табл. 2.1) на случай медленно изменяющихся
волоконных световодов, получаем, что для меридиональных лучей zp (z) &
& 2р (z)/0z (z). Для локального угла конусности перехода £1 (z) условие мед-
ленного изменения эквивалентно требованию
S2(z) ~6p(z)/zp(z) <<p(z)/zp(z) s«z/2.
(5.62a)
Следовательно, для того чтобы соотношение (5.60) было точным всюду на
переходе, лучевой угол должен значительно превосходить угол конусности
перехода. Более того, хотя соотношение (5.60) не позволяет определить ми-
нимальную длину перехода Zmin, она может быть качественно оценена реше-
нием уравнения (5.62а) для каждого значения z. Этот критерий применим к
задаче о диффузном источнике, рассмотренном в предыдущем разделе.
Линейный конусный переход. Можно оценить точность полученного в пре-
дыдущем разделе выражения (5.60) для линейного конусного перехода.
В случае перехода минимальной длины (5.596) для меридиональных лучей
с помощью (5.59а) получаем
2(f2/0c) = 2{р — (0о/0с)Ро}/(Ро -Р). (5.626)
Если Ро » Р, то £2 << 0с/2 независимо от значения 0О. Это качественно со-
гласуется с выражением (5.62а), когда 0Z (z) = 0С. Однако если р0 > р, то
0О — 0 и соотношение (5.62а) не выполняется.
99
4-
Рис. 5.7. Рассеяние мощности направляемого луча в сердцевине (д) и угловые направле-
ния падающего (на рассеиватель) и рассеянного лучей относительно оси световода со
ступенчатым профилем (6)
РЕЗКИЕ НЕРЕГУЛЯРНОСТИ И РАССЕИВАТЕЛИ
Обратимся теперь к рассмотрению нерегулярностей, связанных с разрывами
или скачкообразным изменением среды в регулярном цилиндрическом воло-
конном световоде, сосредоточившись на влиянии малых изолированных рас-
сеивателей, расположенных по всей длине сердцевины. Предполагается, что
размеры каждого из рассеивателей малы по сравнению с длиной волны света.
Когда направляемый луч падает на один из таких рассеивателей, его мощ-
ность перераспределяется, вообще говоря, по всем направлениям, как пока-
зано на рис. 5.7, а для волоконного световода со ступенчатым профилем. До-
ля падающей мощности, рассеиваемая в определенном направлении, зависит
от природы рассеивателя. Некоторая часть мощности будет рассеяна в выте-
кающие лучи, остальная перераспределяется между направляемыми луча-
ми. Поскольку этот процесс происходит на каждом рассеивателе, ясно, что
первоначальное распределение мощности будет изменяться вдоль волокон-
ного световода и некоторая ее часть будет потеряна из-за излучения. Очевид-
но, что это изменение происходит тем быстрее, чем больше плотность рас-
сеивателей.
Когда рассеиватели распределены вдоль длины волоконного световода
случайным образом, каждый луч на выходе волоконного световода не кор-
релирован с каждым лучом на его входе. Это как раз те условия, которые,
как обсуждалось в разд. 5.4, приводят к тому, что уширение импульса про-
исходит пропорционально z1/2. Цель этого раздела состоит в том, чтобы полу-
чить уравнение, которое описывает распределение интенсивности света между
различными лучевыми направлениями [11]. Как будет показано в разд. 5.22,
такое уравнение сводится к уравнению диффузии для случая, когда рассея-
ние направлено преимущественно в’ прямом направлении вдоль световода.
5.21. Распределение мощности направляемых лучей
Сначала рассмотрим перераспределение мощности луча при его падении на
изолированный рассеиватель, затем выведем интегральное уравнение распре-
деления мощности направляемых лучей в волоконном световоде с большим
количеством рассеивателей. Для простоты предполагается, что волоконные
световоды имеют ступенчатый профиль, однако вывод легко обобщается на
волоконные световоды с градиентным профилем [11].
100
Сечение рассеяния. Пусть луч падает на изолированный рассеиватель S
(см. рис. 5.7,6). Обычно рассеяние описывают с помощью дифференциаль-
ного сечения рассеяния ad, которое определяет распределение рассеянной
мощности при падении на рассеиватель плоской волны [12]. Для того чтобы
описать ad воспользуемся понятием луча как локально плоской волны (см.
разд. 35.3). Рассмотрим локально плоскую волну, связанную с падающим
лучом (см. рис. 5.7, 6), как часть бесконечной плоской волны, распространя-
ющейся в том же направлении. Таким образом, можно положить
> (5.63)
где Ps — мощность, рассеиваемая в единице телесного угла, а/\ — мощность,
падающая на единицу площади. Направление падающего луча, как показано
на рис. 5.7, 6, определяется углами 0^ и вг относительно азимутального и ак-
сиального направлений, а каждое направление рассеяния — углами и 0z.
Поскольку ad зависит от угла между падающим и рассеивающимися лучами,
то ad = ad (в^ — (%, и, кроме того, имеется зависимость от простран-
ственного распределения интенсивности падающего света и его изменения с
длиной волны X.
Распределение интенсивности. По аналогии с соотношением (4.1) опреде-
лим функцию распределения интенсивности I(s) как лучевую мощность, от-
несенную к единице телесного угла лучевых направлений и к единице площа-
ди поперечного сечения сердцевины. Поэтому мощность, падающая на едини-
цу площади рассеивателя, изображенного на рис. 5.7, 6, составляет 7s/cos0z,
где 0z _ уГол между направлениями падающего луча и оси. Мощность, рассеи-
ваемая в лучи с направлениями 0^, 0Z9 составляет adZs/cos0z. Если плотность
рассеивателей на единицу объема равна 7V, то в объеме с длиной dz и попереч-
ным сечением dA находится NdAdz рассеивателей. Полная мощность, рассеи-
ваемая в лучи с направляющими углами 0^, 0Z, составляет в единице телесно-
го угла
NdzdA
(5.64)
vz
Уравнение переноса излучения. Пусть /(0^, 0Zi z) - полная мощность в
единице телесного угла всех лучей, имеющих в поперечном сечении сердце-
вины с координатой z углы 0^, 0Z. Тогда I и /s связаны соотношением
Р 277
1(0* = frdr f dpis (r, z, 0 0Z), (5.65)
0 0
где г и (/? — полярные координаты в поперечном сечении световода. Уравне-
ние для I можно получить, если рассмотреть составляющие изменения мощ-
ности на длине dz. Во-первых, часть мощности лучей с направлением 0^, 0z
рассеивается во все направления 0^, 0Z, в том числе в направляемые, туннели-
рующие и рефрагирующие лучи. Связанное с этим изменение мощности dPs
составляет
ЛЛ77 277 , 77 , , ,
°tot= f(5.66)
COS(7Z 0 0
По определению полное поперечное сечение atot не зависит от 0^ и 0^, а по
предположению ad не зависит от местоположения. Во-вторых, часть мощно-
сти, распространяющейся в направлении 0^, 0z, увеличивается за счет мощно-
101
сти, рассеиваемой в этом направлении. Пренебрегая вкладом вытекающих
лучей, оценим вклад направляемых лучей, у которых интервал изменения
в? удовлетворяет соотношению (2.6а). Интегрируя (5.64) по поперечному
сечению, получим приращение мощности
27Г
dP =Ndz f dd^ f I(ep,ei,Z)od^-e ez-ez) tgW. (5.67)
0 0
Изменение I равно сумме dPs и JPg. Если волоконный световод является сла-
оонаправляющим, т. е. 0Z, 0Z << 1, то Iудовлетворяет интегро-дифференци-
альному уравнению [ 11 ]
^-+7VototZ = 7V/cZ0; f /ad0'< (5.68)
o o
где /(0^, 0Z, 0) — значение I на входе волоконного световода. Полная мощ-
ность направляемых лучей в любом сечении является решением уравнения
(5.68) в
2п 5
= f^0z. (5.69)
о 0
Распространение импульса. При выводе уравнения (5.68) предполагалось,
что режим возбуждения является установившимся во времени. Для того
чтобы описать распространение импульса, необходимо учесть зависимость
/от времени. Для этого достаточно заменить в (5.68) частную производную
d/dz на полную производную d/dz с учетом соотношения (2.12) :
- JL + _JL = Л- + —!2со— Л_ г5 7qa
dz dz dz dt dz ccos0z bt ‘ \ )
Тогда вместо (5.68) получим [И]
+ +Natotl=N2f de' f Iod6'd0' (5.71)
dz ccos0z bt tot о %
В появлении перед производной по времени множителя (cos 0Z)~1 нет ничего
удивительного, поскольку, как было показано в разд. 3.1, именно такая за-
висимость от 0Z вызывает дисперсию. Рассмотрим примеры.
5.22. Пример. Диффузионное уравнение
Здесь будет рассмотрено влияние рассеивателей, которые рассеивают мощность преиму-
щественно в направлениях, близких к направлению падающего луча (см. рис. 5.7, б).
Тогда фактически вся мощность направляемых лучей перераспределяется между ними,
за исключением пренебрежимо малой части полной мощности, которая теряется на из-
лучение от направляемых лучей, распространяющихся под углами 0Z « 0С. Пусть х -
угол между направлениями падающего 0^, 0Z и рассеяного 0^, 0Z лучей, тогда дифферен-
циальное сечение рассеяния сг^(х) имеет вид узкого пика, сосредоточенного в окрест-
ности х = О.,Эту зависимость можно описать гауссовым распределением
а = а0 ехр(—6 X2) ; Ь>>1, (5.72)
где а0 и b - константы. Из геометрических соображений
cosx = cos^cos0z + sin0Zsin0Zcos(0^ - 0p , (5.73)
102
uk чю в окрестности х - О для слабонаправляющего волоконного света получаем
приближенное соотношение
х3 * (0Z -0z)2 + (5.74)
В связи с тем, что о имеет вид узкого пика в окрестности 0Z = oz, 0^ - можно без
заметной потери точности заменить интервал интегрирования по 6'^ и О'? на бесконеч-
ный интервал °0). Тогда уравнение (5.71) можно переписать следующим образом:
17+ 7777ё~ 17 = Уа»_£ % Л ехр(~6х ’!/(0^ *) ^)} W
(5.75)
Запишем члены в фигурных скобках в виде
+ {Z(0v,>0i,z)-/(0ip)02,z)}
и разложим их в окрестности 0^ и 0Z в ряд Тейлора по степеням 6^ - 6^ и O'z - Под-
ставляя затем выражения (5.74) для х и используя интегралы (37.126) с точностью до
членов порядка Zr2, получаем
э/ t И со Э/ _ Л_1_ ЭУ + +_2_ Э/ |
9z ccos07 bt (0? 90s Э03 07 be, Г
k. L <р L L с j
nNa0
где D —-----—. Следовательно, / удовлетворяет уравнению диффузии, причем коэффи-
4Ь2
циент диффузии D постоянен и пропорционален плотности рассеивателей. Это же урав-
нение при I, не зависящем от 0^, было получено при описании многомодовых волокон-
ных световодов методом уравнений связанных мощностей при связи соседних мод в
слабонаправляюших волоконных световодах [13]. Из этого уравнения можно получить
зависимость среднеквадратической ширины импульса вида z1/2 для установившегося
режима при z -> <». Детальное рассмотрение этого вопроса проводится в [14].
5.23. Пример. Рэлеевское рассеяние
Ранее уже было введено понятие идеального волоконного световода, в котором не'1’
поглощения и каких-либо неоднородностей. Однако на практике волоконные светово-
ды делают из материалов, которые являются слабо поглощающими. Кроме того, моле-
кулярная структура материала вызывает рэлеевское, или дипольное рассеяние. Рассмот-
рим распространение света в волоконном световоде со ступенчатым профилем, прене-
брегая поглощением, чтобы выделить только эффект рэлеевского рассеяния [15]. Для
слабонаправляющего волоконного световода дифференциальное сечение рассеяния <j&
и полное сечение atot имеют вид [16]
<7d(x) = к(1 +cds2x); crtot = 167ТК-/3; к < < 1, (5.77)
где угол х связан с лучевыми направлениями соотношением (5.73). Константа к задает
полную рассеивающуюся мощность и включает зависимость от длины волны света вида
А"4. Поскольку к < ad < 2к, ясно, что рассеяние близко к изотропному. В частности,
для всех направляемых лучей ad « 2к. Таким'образом, в выражении (5.71) можно про-
интегрировать зависимость от 0^, вводя функцию
27Т
G (»z. z, t) = вг, z, (5-78)
0
Выполняя интегрирование в предположении, что 0Z, О? < < 1, получаем
d (7 «гл d G Зек г'
+ —25 + aG = — f G(0' z, t)e‘de' (5.79)
dz------------------------------------------------------------ccos0z dt-' 4 q z z Z’
103
Рис. 5.8. Зависимость импульсного отклика
(5.83) от t при Го = zhco/c и 0С = 0,1 [15]
где а = Если задан вид G при z = 0,
можно получить решение этого уравнения
при малых а и 0Z методом итераций.
Пучок, параллельный оси. Пусть при z =
= 0 импульс представляет собой однород-
ный коллимированный пучок лучей, параллельных оси световода, с единичной полной
мощностью. Используя выражения (5.69) и (5.78), получаем
G(0z,O,f) = 6(r)6(0z)/0z; Pbr(0) = 1, (5.80)
где 6 - дельта-функция Дирака. Решение уравнения (5.79) низшего порядка сосответ-
ствует а — 0. Следовательно,
G (0Z, z, f) = 8 (t — znCQjc) 6 (0Z) /#z- (5.81)
Иными словами, если пренебречь рассеянием, то импульс распространяется вдоль воло-
конного световода без затухания и искажения со скоростью c/nQQ. В первом приближе-
нии можно рассмотреть эффекты рассеяния раздельно для двух членов уравнения (5.79),
связанных с а. Член aG в левой части уравнения вызывает общее ослабление G за счет
умножения на exp (~oz), а член в правой части соответствует дисперсии. Его вклад мож-
но найти, подставляя значение G из выражения (5.81), умноженное на exp (-az), и инте-
грируя относительно z при t = wcoz/ccos0z. Объединив оба эффекта, получим с точно-
стью до первого порядка
_ Г znco 6 (0Z) 3a г cos0z )
G(ez,z,t) = -----I exp (-az) (5.82)
(. c 6Z 4 Wco 1 - COS0Z J
при (znCQ/c) < t < (znCQ/c COS0Z); вне этого интервала G = 0. Первый член в фигурных
скобках соответствует неискаженному импульсу, второй - распространению рассеянной
мощности, а общее ослабление вызвано потерями в вытекающие лучи. В этом описании
игнорируется вторичное рассеяние этих лучей в направляемые.
Затухание мощности импульса. Импульсный отклик равен интегралу от G по всем
лучевым направлениям. Учитывая ограничения, при которых справедливо выражение
(5.82), и условие 0С < < 1, получаем для импульсного отклика на интервале {znCG/c') <
< z < (z«co/ccos0z)
Q
Q(z,t)= f Gezdez as exp (-az) Js(f - —ln(-^-)l, (5.83)
0m I 2 "co °m )
где cos^h = zn^ct и 0m a - znCQjct)1/2 . График функции Q(z, t) приведен на
рис. 5.8. Наконец, находим мощность импульсаPbr(z), интегрируя импульсный отклик
по времени
Pbr(z) = (5.84)
О
Однако проще заменить Q(z, t) выражением (5.83) и изменить порядок интегрирова-
ния. Тогда получаем
вс zwco/ccos0z г 3a 'j
Pbr(z) = fezdez f Gdt= b+-^0c2 z > exp (-az), (5.85)
0 znco/c ( » )
где в низшем порядке член в фигурных скобках выражения (5.82) умножен на ширину
импульса (z«co/c)(l/cos0z - 1). Таким образом, результат справедлив только в том слу-
чае, если z не слишком велико.
104
Итак, влияние Рэлеевских рассеивателей на импульс, который вначале состоял из лу-
чей, параллельных оси световода, сводится к перераспределению мощности между все-
ми направляемыми лучами и искажению импульса вследствие дисперсии. Одновремен-
но мощность импульса теряется на излучение. Потери мощности существенны всякий
раз, когда существенно уширение импульса.
ГЛАВА 6. ПОГЛОЩЕНИЕ В МАТЕРИАЛЕ
До сих пор при лучевом анализе предполагалось, что волоконные световоды
являются непоглощающими и, следовательно, направляемые лучи будут рас-
пространяться по бесконечно длинному регулярному световоду неограничен-
но. Однако материалы, из которых изготовляются сердцевина и оболочка
волоконных световодов для систем связи, являются поглощающими. Поэто-
му при распространении направляемого луча в волоконном световоде его
мощность постепенно уменьшается вследствие поглощения, и при достаточ-
но большой его длине поглотится практически вся первоначальная мощность.
Цель этой главы — рассчитать это затухание и определить его влияние на фор-
му импульса.
Потери мощности, вызванные поглощением в сердцевине, имеют инте-
гральный эффект на каждой лучевой траектории и, таким образом, могут
быть учтены в рамках классической геометрической оптики. Иное дело поте-
ри мощности из-за поглощения в оболочке — их нельзя определить непосред-
ственно, поскольку они имеют место вне лучевой траектории там, где мощ-
ность луча равняется нулю. Следовательно, для описания этих потерь нужен
другой механизм. Поглощение мощности света вне лучевой траектории — это
дифракционное или волновое явление, так как оно зависит от длины волны
света в сердцевине, и поэтому его необходимо ввести в лучевое описание.
Основа последующего анализа состоит в использовании метода ключевых
задач, который включает: 1) сохранение траекторий геометрической оптики;
2) описание затухания мощности луча вдоль траектории с помощью коэффи-
циента затухания [1,2].
Для волоконных световодов, параметры которых представляют практи-
ческий интерес, поглощение в материале в основном проявляется в затуха-
нии мощности импульса и одновременном небольшом изменении формы им-
пульса. Изменение формы импульса вызвано тем, что лучи с большими угла-
ми наклона к оси волоконного световода со ступенчатым профилем или с
точками поворота луча, лежащими ближе к границе в волоконном световоде
с градиентным профилем, теряют в оболочке относительно большую долю
своей мощности.
6.1. Поглощающая среда и затухание
Когда диэлектрический материал является поглощающим, математически
удобно описывать поглощение, приписывая показателю преломления мате-
риала в каждой точке мнимую составляющую. Следовательно, если матери-
ал является слабо поглощающим, то
n(r) =п (г) + п*(г)«пг(г), (6.1)
105
где верхние индексы г и i обозначают действительную и мнимую части.
В этой главе будут рассмотрены только аксиально симметричные волокон-
ные световоды, так что пг (г) и иг’(г) являются функциями радиуса цилин-
дрического поперечного сечения или константами. Будем пользоваться также
энергетическим коэффициентом поглощения мощности а (г), который по
определению равен мощности, поглощенной на единице длины траектории:
а (г ) = 4тт? (г ) /X = 2кп* (г ), (6.2)
где X — длина волны в свободном пространстве. Для каждого фиксированно-
го значения г этот коэффициент совпадает с коэффициентом затухания мощ-
ности при распространении плоской волны в неограниченной однородной сре-
де с однородным показателем преломления (6.1). Это можно проверить,
подставив п = пг + ш* в выражение (35.1а). Тогда, используя выражение для
плотности мощности (35.2), получим множитель, характеризующий затуха-
ние ехр (—2и*кг).
Коэффициент затухания мощности. Для того чтобы onncaib затухание,
введем функцию P(z), которая равна мощности, передаваемой внутри узкой
лучевой трубки, рассмотренной в начале гл. 4 и изображенной на рис. 4.1.
Введем еще коэффициент затухания мощности
7rz)=--J-^l
4 ’ P(z) dz ’
где dP(z) — изменение лучевой мощности вследствие поглощения на длине
световода dz. Следовательно, y(z) — это скорость, с которой теряется мощ-
ность на единице длины. Решение уравнения дает мощность в любом сече-
нии через начальную мощность Р(0) для случаев, когда коэффициент затуха-
ния мощности изменяется вдоль волоконного световода:
(6.3)
P(z) =Р(0)ехр|~/y(z)<fe
I о
(6.4а)
и когда коэффициент затухания мощности постоянен:
P(z) =Р(0) exp {-yz}. (6.46)
Первое выражение удобно для медленно изменяющихся или изогнутых по-
глощающих волоконных световодов.
ПОГЛОЩЕНИЕ В СЕРДЦЕВИНЕ
Рассмотрим сначала волоконные световоды, которые имеют поглощающую
сердцевину и непоглощающую оболочку. В этом случае коэффициент погло-
щения мощности в сердцевине асо (г) связан с п*(г) соотношением (6.2), а в
оболочке он равен нулю. Мощность, которая поглощается на длине лучевой
траектории ds, можно получить, используя определение асо(г). Ее можно
также выразить через расстояние dz вдоль оси световода, воспользовавшись
лучевым инвариантом р (2.16), если заменить п(г) mnr (г). Итак,
-dP(z) = ас0 (r)P(z)ds = {асс (r)n' (г )P(z)/0}dz, (6.5)
106
где величины r - r (s) и z = z (s), входящие в среднее выражение, вычисляют-
ся вдоль лучевой траектории, это же относится к величине г = г(z) в выра-
жении справа. Сравнивая соотношения (6.3) и (6.5), получаем коэффици-
ент затухания мощности за счет поглощения в сердцевине
7со (z) = “со (г)«Г (Г)1Р< (6.6)
где г =r(z) вычисляется вдоль траектории. Из соотношений (6.3) и (6.5) выра-
жение для лучевой мощности в сечении z волоконного световода имеет вид
P(z) =Р(0) ехр < - 4 J “со (r)nr(r)dz [ = Р(0) exp I - f a (r)ds к (6.7)
( Р о ) I о J
где интегралы вычисляются вдоль лучевой траектории.
Цилиндрическая симметрия. Коэффициент поглощения мощности асо (г)
не изменяется вдоль волоконного световода с цилиндрической симметрией.
Поэтому, если z велико по сравнению с лучевым полупериодом z можно
получить достаточно точные оценки для интегралов в выражении (6.7), ис-
пользуя рассуждения разд. 1.9. В результате получаем
1 Zp
P(z) = P(0) exp(-7coz); 7C0 = “co = z J “co (л) ds>
P 0
(6.8)
где постоянная усо - это эффективный коэффициент затухания мощности,
который по определению равен среднему значению коэффициента поглоще-
ния мощности асо> рассчитанному на полупериоде лучевой траектории.
6.2. Пример. Сердцевина с однородным поглощением
Если коэффициент поглощения мощности является однородным, т. е. асо (г) = ас0, то
коэффициент затухания мощности (6.6) оказывается пропорциональным действитель-
ной части профиля показателя преломления. Выражение для лучевой мощности с учетом
(6.8) имеет вид
P(z) - Р(0) exp { -ас0 (£p/zp)z}, (6.9)
где Zp - длина пути (2-26). Для ступенчатого профиля из табл. 2.1 получаем, что -
= l/cos0z и, следовательно,
P(z) = Р(0) exp {~acoz/cos0z } ; = 2bi£o, (6.10)
где ez - наклон лучевой траектории к оси. Таким образом, хотя коэффициент затуха-
ния мощности не зависит от скоса лучей, затухание увеличивается с ростом 0Z. Поэтому
направляемые лучи, распространяющиеся под углом, близким к критическому углу 0С,
испытывают наибольшее затухание.
Усеченные степенные профили. В приближении слабонаправляющего волоконного
световода значения отношения в случае, усеченных степенных профилей приведе-
ны в табл. 2.1. Если положить п = лг(г) + ШсО, где пг(г) - профиль и (г), заданный в
табл. 2.1, и - константа, тогда [3]
Г г 0 1 (
P(z) =Р(0) ехр<- -52- [(<? + 1) ^2- +-—]О; е < < 1, (6.11)
I <? + 2 0 <о J
где асо = 2кп^ и nrCQ - значение пг(г) на оси. Это выражение переходит в выражение
(6.10) для волоконного световода со ступенчатым профилем, когда q -►00, и тоже не за-
висит от скоса лучей. Просто проверить, что наибольшее затухание имеет место на траек-
тории, которая достигает границы, т. е. 0 = ис1 = nrCG (1 - 2Д)1/2.
107
6.3. Пример. Сердцевина с неоднородным поглощением
В общем случае, когда асо (г) меняется по сечению сердцевины, интеграл в соотношении
(6.8) нужно оценивать численно. Однако в одном интересном для практики случае ре-
шение можно получить в аналитическом виде [4]. Это случай, когда коэффициент по-
глощения мощности пропорционален действительной части функции профиля, т. е.
“coW =“co(0)«z'(H/nJo> (6.12)
где «со ~ значение пг (г} на оси. Интеграл в (6.8) пропорционален оптической длине пу-
ти Lq (2.26). Таким образом, в случае усеченных степенных профилей из табл. 2.1 по-
лучаем
P(z) = Р(0) ехр(- ас°<0) +2 ]Д (6-13)
[ ? + 2 0 «'со J
Второй случай, когда можно получить аналитическое решение, соответствует изменению
коэффициента поглощения мощности обратно пропорционально функции профиля, т. е.
acoW = оссо(0) nr (Q)/nr (г). (6.14)
Подставляя это выражение в (6.8) и используя инвариант 0 (2.16) с учетом пг (г), пере-
ходим к интегрированию вдоль z и получаем, что интеграл пропорционален лучевому
пол у пери оду. Следовательно,
P(z) =Р(0) ехр{~асо(0)>/(0)г/Д}; (6.15)
и затухание не зависит от функции профиля.
ПОГЛОЩЕНИЕ В ОБОЛОЧКЕ
В отличие от случая поглощающей сердцевины потери мощности, вызванные
поглощением в оболочке, нельзя непосредственно описать с помощью геоме-
трической оптики. Эти потери имеют место вне лучевой траектории и явля-
ются поэтому дифракционным, или волновым эффектом, зависящим от дли-
ны волны света в сердцевине. Это первый случай, когда конкурируют волно-
вой эффект и лучевая мощность. Можно сохранить лучевые траектории гео-
метрической оптики и предположить, что луч теряет мощность только в точ-
ках отражения или поворота. Тогда скорость, с которой теряется мощность,
зависит просто от расстояния вдоль световода между точками отражения или
поворота или от плотности расположения таких точек. Найдем долю мощно-
сти луча, которая теряется в каждой точке отражения или поворота, рассма-
тривая луч как локальную плоскую волну. Тогда, используя теорию локаль-
ных плоских волн, можно непосредственно получить выражение для потерь
мощности в волоконных световодах со ступенчатым и градиентным профиля-
ми [1, 2]. В первом случае оно совпадает с выражением, впервые получен-
ным Френелем для отражения плоской волны от плоской поверхности [5].
Если выражение для потерь мощности в точке отражения или поворота из-
вестно, то для расчета затухания лучевой мощности вдоль волоконного све-
товода, вызванного поглощением в оболочке, нужно знать только расстояние
между точками отражения или поворота или плотность их расположения, ко-
торые находятся методами геометрической оптики.
6.4. Спадающие поля
Чтобы понять механизм возникновения потерь за счет поглощения оболоч-
ки, будем рассматривать луч в окрестности точки отражения или поворо-
108
Рис. 6.1. Экспоненциальные зависимости амплитуды электрического поля |Е| заграни-
цей сердцевины волоконного световода со ступенчатым профилем (а) и за каустикой
точек поворота волоконного световода с градиентным профилем (б)
та как плоскую волну. Обоснование такого рассмотрения обсуждается в
разд. 35.3. В области вне лучевой траектории, т. е. за границей сердцевина-
оболочка в волоконном световоде со ступенчатым профилем и за точкой по-
ворота в волоконном световоде с градиентным профилем, поля, соответству-
ющие локальным плоским волнам, становятся спадающими и уменьшаются
экспоненциально с увеличением расстояния от оси. Это уменьшение оказы-
вается очень быстрым фактически для всех лучей и описывается экспонен-
той, показатель которой обратно пропорционален длине волны X в сердце-
вине (см., например, выражения (35.22а) и (35.32в) для волоконных свето-
водов со ступенчатым и градиентным профилями). Качественные картины по-
лей приведены на рис. 6.1. В рамках классической геометрической оптики
(X = 0) вне лучевой траектории поля отсутствуют.
6.5. Коэффициент прохождения мощности
В случае конечной длины волны света X часть мощности спадающих полей
теряется в поглощающей оболочке. Это, в свою очередь, приводит к поте-
рям мощности луча. Она сосредоточена в узких лучевых трубках (см. начало
гл. 4) и потери ее в них могут иметь место только в точках отражения или
поворота, т. е. там, где в трубке есть резкие разрывы или ее поперечное сече-
ние равно нулю. Потери в этих точках выражаются через коэффициент про-
хождения мощности Т, который известен также как коэффициент потерь,
определяемый безразмерным отношением
р„
г=1-^, (6.16)
где Pi — мощность падающего луча; рг — мощность отраженного луча. Други-
ми словами, через границу раздела сердцевины и оболочки или точку поворо-
та в спадающие поля переходит часть лучевой мощности Т, которая погло-
щается в оболочке. Это схематически показано на рис. 6.2.
Коэффициент затухания мощности ус1 за счет поглощения в оболочке на-
ходится либо как среднее значение Т на лучевом полупериоде zp, равном рас-
стоянию между соседними точками отражения или поворота, либо как сум-
марные потери в ТУтаких точках на единичной длине световода. В любом слу-
чае
109
Рис. 6.2. Часть лучевой мощности направляемого луча Т (волнистые линии), поглощае-
мая в оболочке в точках отражения для световода со ступенчатым профилем (а) и в
точках поворота для световода с градиентным профилем (6)
7С1 = 77zp =7V7’. (6.17)
В цилиндрическом симметричном световоде коэффициент затухания мощно-
сти является константой, он связан с лучевой мощностью соотношением
(6.3), где у заменяется на ус1. Если Р(0) — лучевая мощность в начале свето-
вода, то
P(z) =Р(0) ехр(—ус1и). (6.18)
Для расчета ус1 воспользуемся выражениями для лучевого полупериода и ко-
эффициента передачи мощности (см. гл. 2 и разд. 35.13). Ниже будут приве-
дены примеры. В большинстве интересных для практики случаях показатель
преломления оболочки является однородным, поэтому считаем, что он по-
стоянен: ис1 = Тогда коэффициент поглощения мощности в оболоч-
ке ас1 тоже постоянен и по аналогии с выражением (6.2)
ас1 = 4яи^/Х = 2^!, (6.19)
где X — длина волны в свободном пространстве. Дальнейшее упрощение воз-
можно в том случае, если предположить, что поглощение мало, т. е. «пгсу.
6.6. Пример. Ступенчатый профиль
Рассмотрим волоконный световод со ступенчатым профилем, непоглощающая сердцеви-
на которого имеет радиус р и показатель преломления «с0, а оболочка является погло-
щающей, и ее показатель преломления п с| = Если значения ^со и пгсу произволь-
ны, поглощение мощности зависит от поляризации луча (т. е. вектор электрического или
магнитного поля при этом описывается локальной плоской волной (см. разд. 35.3)).
Когда волоконный световод является слабонаправляющим, т. е. nQQ — п^, этой зависи-
мостью можно пренебречь. Простая формула для коэффициента прохождения мощности
получена при этих условиях в разд. 35.13. Если в выражении (35.52) положить п1^ =
= 0, то получим
ПО
(6.20)
2 “cl
я/2 — a
{^- (я/2-a)’}1'3 ’
вС knc\
где Q!c| - коэффициент поглощения мощности (6.19), 0C = { 1 - (wcp2/wco) 12 “
критический угол скольжения и а - угол между лучевой траекторией и нормалью
рис. 2.3. Это выражение является предельной формой коэффициента прохождения
Френеля (35.24) при отражении от плоской границы между неограниченными однород-
ными средами с показателями преломления nQQ и wcj [5]. Оно зависит только от значе-
ния а независимо от того, является лучевая траектория косой или меридиональной, и
считается точным при условии, что значение угла я/2 — а не слишком близко к 0С.
В приближении слабонаправляющего волоконного световода 0с < < 1, и, следовательно,
выражение (6.20) охватывает узкую область направляемых лучей, удовлетворяющих
условию тг/2 - 6С < а < тг/2. Заметим, наконец, что при X -> 0 или к = 2я/Х т. е. при
переходе к классической геометрической оптике, Т 0. Это подтверждает, что погло-
щение в оболочке - эффект, который зависит от длины волны.
Коэффициент затухания мощности. Для того чтобы получить коэффициент затуха-
ния мощности, подставим (6.20) и (2.11) для в выражение (6.17). Выразим угол a
в числителе и знаменателе (6.20) через углы 0Z и 0^, используя соотношение (2.3) и по-
лагая, что тг/2 - а = sin (тг/2 - a) cosa. Кроме того, используя определение волновод-
ного параметра И, представим к в виде к = V/(pncQs\n 0С) ~ И/(рл^0с), поскольку
0С < < 1 и nCQ Тогда для коэффициента затухания мощности получим
C1 V {1 - (0z/ec)5sin^} -'3 ’
(6.21)
Этот результат является точным для всех направляемых лучей, за исключением тех,
направления которых близки к 0Z = 0С и 0^ = я/2. При фиксированном значении 0Z за-
тухание максимально, когда луч является меридиональным, т. е. 0^ =• тг/2, и уменьша-
ется с увеличением скоса луча. Хотя в световоде заданной длины косой луч испытыва-
ет большее число отражений чем меридиональный, это компенсируется меньшим значе-
нием коэффициента прохождения для косых лучей.
6.7. Градиентные профили
Рассмотрим теперь волоконный световод с градиентным профилем, непогло-
щающая сердцевина которого имеет радиус р и профиль показателя прелом-
ления и (г), а окружающая ее однородная оболочка имеет профиль показа-
теля преломления мс1 = nr^ + Предположим также для простоты, что
м(0) — максимальное значение функции профиля, которое обозначим через
мсо, и что световод является слабонаправляющим, т. е. nCQ пгсХ. Коэффици-
ент прохождения мощности при этих условиях получен в разд. 35.13, и выра-
жение (35.51) позволяет представить
Г=-^----=—--------------exo f—2к f [/3 2 + Z 2 ~—n2(r)]1/2dr\
2к 02+Z2 - (п'с1)2 Р1 4 r J
(6.22)
через лучевые инварианты (3 и I из табл. 2.1, определяющие траекторию на-
правляемого луча, и радиус каустики точек поворота который соответ-
111
ствует наибольшему отклонению траектории от оси волоконного световода.
Это выражение справедливо для всех направляемых лучей, за исключением
тех немногих лучей, у которых точки поворота фактически совпадают с гра-
ницей сердцевины, т. е. rtp р, или (02 + I 2 )1/2 пгс\. Ясно, что за счет экс-
поненциального множителя в (6.22) (сравните с (6.20)) для большинства
лучей волоконных световодов с градиентным профилем часть мощности, те-
ряемой в оболочке, оказывается гораздо меньше, чем для лучей волоконных
световодов со ступенчатым профилем с такими же значениями 0 и 7. Это
объясняется тем, что ахмплитуда спадающего поля быстро уменьшается на
интервале между точкой поворота и границей сердцевины, что и вызывает
появление экспоненциального множителя. Только те лучи, у которых точки
поворота расположены очень близко к границе сердцевины, т. е. % р, име-
ют потери на поглощение, сравнимые с потерями лучей волоконного светово-
да со ступенчатым профилем. Коэффициент затухания мощности можно по-
лучить из соотношения (6.17), используя общее выражение для лучевого по-
лупериода волоконных световодов с градиентным профилем (2.28) .
Линейное приближение. Выражение для коэффициента прохождения
(6.22) оказывается неоправданно сложным для лучей, которые испытывают
значительные потери мощности на конечных расстояниях. Для них точки по-
ворота расположены вблизи границы сердцевины и интеграл в выражении
(6.22) можно оценить приближенно, раскладывая выражение в квадратных
скобках аргумента экспоненты в ряд Тейлора в окрестности точки г - и
сохраняя затем только член низшего порядка. Таким образом,
+ _n2{r) ~ (,_rtp) (6.23)
поскольку Гф р, и, подставляя в (6.22), получаем выражение
^CL _______^СО_______ ( 4, г _ fo2 (Г) I ?т211/2П rtpa/ J
2fc + 72 _ (nri)2 ехР| злР1 Р dr \p-2l ] (1--г) j,
(6.24)
в котором нужно знать только производную профиля показателя преломле-
ния на границе сердцевины.
6.8. Пример. Усеченный параболический профиль
Для того чтобы определить коэффициент прохождения (6.22) волоконного световода с
усеченным параболическим профилем, заданным в табл. 2.1, напомним, что согласно
(2.19) радиусы внутренней каустики и каустики точек поворота являются корнями
подынтегрального выражения, которое, следовательно, можно представить в виде
(«со0с/^) - '2р),/2/г’ (6-25)
где rjc и определены соотношениями (2.35) через лучевые инварианты. С помощью
интеграла (37.123) получаем, что
Т'ГГ.Г <6.26.)
112
(6.266)
где£ выражается через нормированные радиусы а — г^1р нЬ = г^с/р
. -у а2 + b2 [ 1 + р3 а + b
g = (1 -fl2)1'2 (1 -ft2)1'5-----ln(p+p_) -flftlnj 1+p., -——
и p± = {(1 - fl2)1/2 + (1 - ft2)1/2 } / (fl ± ft). При приближении каустики точек поворота
к границе сердцевины это выражение переходит в (6.24) для линейного приближения, а
(6.266) в выражение
4 ч/Т ( I J rtp 3/2
g = 11 - (—ц-)Ч1/2 а
3 I wco0c J р
(6.27)
которое приемлемо во многих практических случаях.
Коэффициент затухания мощности. Используя выражение для лучевого полуперио-
да, заданное в табл. 2.1, и соотношения (6.17) и (6.26а), представим коэффициент зату-
хания мощности в виде
у , = С ”со_____________________
C1 2К „р р* + 72 -
exp (- Vg),
(6.28)
где V « крпсоОс и 0С « {1 - (л£1)3 /исо }1/2 • Выражение для g, пригодное для решения
конкретной задачи, получается с помощью соотношений (6.266) или (6.27).
6.9. Пример. Волоконные световоды с усеченными степенными профилями
Для волоконных световодов с усеченными степенными-профилями (см. табл. 2.1) нель-
зя получить аналитические выражения для коэффициента прохождения (6.22), исклю-
чая световоды с параболическим профилем. Однако в пределах линейного приближения
Т задается выражением (6.24) , в котором член - pdn2 (г) /dr |р заменяется на Цп2сое& где
вс = (2Д)1/3 для слабонаправляющего световода. Кроме того, лучевой полупериод
определен точно только для параболического профиля.
Предельный переход к ступенчатому профилю. В пределе при q -+ °° усеченные сте-
пенные профили переходят в ступенчатые, однако это несправедливо для коэффициен-
тов, описываемых выражениями (6.24) и (6.20). Для того чтобы продемонстрировать
это, подставим функции этих профилей в соотношение (2.19) и найдем rtp. Если поло-
жить Гф = р(1 - е) и сохранить только члены с линейной зависимостью от е , то. пола-
гая п2С0 (1 - 2Д) = (n£i) 2, просто показать, что
J g2 + И - (^1)2
р 2(^О</Д-Г)
(6.29)
Таким образом, rtp р, когда q -> «> при заданных значениях Д и Т, а экспоненциальный
множитель в выражении (6.24) стремится к единице. Из соотношения (2.7а) видно, что
остальные множители в выражении (6.24) не переходят в выражение (6.20), причиной
чего, как обсуждалось в разд. 35.11, является способ вывода. При расчете коэффициен-
тов прохождения для градиентных профилей были использованы результаты, получен-
ные для локальной плоской волны. При этом предполагалось, что профиль медленно из-
меняется на расстояниях порядка длины волны. По мере увеличения q профили рис. 1.10
становятся все круче, это условие перестает выполняться и коэффициенты прохождения
перестают быть точными.
СУММАРНОЕ ПОГЛОЩЕНИЕ В СЕРДЦЕВИНЕ И ОБОЛОЧКЕ
Когда материалы сердцевины и оболочки волоконного световода одновре-
менно являются поглощающими, коэффициент затухания мощности луча у
113
равен сумме коэффициентов поглощения в сердцевине и оболочке. Следо-
вательно,
y(z) =7co + 7cb
(6.30)
и лучевая мощность определяется соотношением (6.4). Это является оправ-
данным потому, что коэффициенты затухания вычислялись на длине светово-
да dz. Коэффициент затухания усо был определен ранее в этой главе с исполь-
зованием лучевой траектории и геометрической оптики. Коэффициент затуха-
ния ус| выражается через коэффициент прохождения мощности Т для погло-
щающей оболочки в предположении, что сердцевина является непоглощающей.
ВЛИЯНИЕ ПОГЛОЩЕНИЯ НА ФОРМУ ИМПУЛЬСА
Если волоконный световод является малопоглощающим. то поглощение лу-
чевой мощности не оказывает никакого влияния на времена прохождения
лучей, так что ширина импульса, как показано в гл. 3, не меняется. Однако
форма импульса или импульсный отклик, введенный в гл. 4 и описывающий
распределение мощности внутри импульса, изменяется. Если волоконный све-
товод является слабонаправляющим и имеется небольшое изменение погло-
щения в сердцевине, то независимо от профиля все направляемые лучи при
распространении на расстояние z, как следует из выражения (6.10) при
0Z << 1, испытывают-приблизительно одинаковое затухание ехр(—acoz).
Следовательно, поглощение в сердцевине не оказывает заметного влияния
на форму импульса, хотя полная мощность импульса уменьшается прибли-
зительно как ехр(—acoz) [3].
Поглощение в оболочке. Затухание из-за поглощения в оболочке, как бы-
ло показано в разд. 6.6 и 6.7, чувствительно к конкретной форме лучевой
траектории. Для лучей, удовлетворяющих условию = 0 или (3 = псо, соот-
ветственно в волоконных световодах со ступенчатым или градиентным про-
филем затухание очень мало, ио оно быстро увеличивается при 0z 0с или
(3 -> пс1. Увеличение оказывается наиболее существенным для меридиональ-
ных лучей. Если импульс возбуждается диффузным источником, то при ма-
лых значениях 0z каждый направляемый луч первоначально переносит при-
мерно одинаковую мощность. Однако по мере того как импульс распростра-
няется и диспергирует, различные скорости затухания вызывают изменение
его формы. Как будет показано ниже в примерах, наименьшим затуханием
характеризуются лучи с 0 % 0 или (3 = nCQi наибольшим — лучи с 0z = вс
или (3 « ис1. Пока поглощение в оболочке не является настолько сильным,
что теряется фактически вся мощность импульса, эффективное уменьшение
среднеквадратической ширины импульса оказывается несущественным по
сравнению с его уширением вследствие лучевой дисперсии. По указанным
причинам в последующих примерах не будем рассматривать поглощение в
сердцевине и исследуем влияние поглощающей оболочки.
6.10. Пример. Ступенчатый профиль
Рассмотрим слабонаправляющий волоконный световод со ступенчатым профилем и
поглощающей оболочкой, которая согласно (6.19) характеризуется однородным коэф-
114
Рис. 6.3. Нормированные импульсные отклики для волоконного световода с поглоща-
ющей оболочкой и параметрами V = 70, Д = 0,01 и пх = 1,5 при различных значениях
”cl2/p [6]:
а — ступенчатый профиль; б — усеченный параболический профиль
фициентом поглощения мощности аср Диффузный источник возбуждает импульс в се-
чении z = 0. Если acj = 0, то, как следует из соотношения (4.55), импульсный отклик
Q(t} зависит только от инварианта /3, или, что то же самое, от угла 0Z, поскольку время
прохождения луча не зависит от его скоса. Если ас| > 0, то коэффициент затухания мощ-
ности 7ci для каждого из лучей импульса определяется выражением (6.21) и зависит от
обоих углов, или от обоих инвариантов Д и Z (2.7а). Поэтому импульсный отклик теперь
определяется выражением (4.64), где функция распределения F(0, 7) имеет множитель
ехр(~7с1^), который учитывает поглощение [б]. Поскольку время прохождения не за-
висит от 7, согласно замечанию, приведенному ниже соотношения (4.64), получаем, что
। । Lnax(^ .______
Q(f) = -г- f /?(|3,/)exp(-7clz)d/, (6.31)
' at 1 о
где функция распределения/^/?, 7) задается выражением (4.48) и ^гпах(^)= (лсо ~ ? ) 1/2>
зависимость /?=/?(?) - выражением (4.58) и интервал значений Г, для которых Q (t)
отлична от нуля, - соотношением (4.59). Полная мощность импульса в сечении z
пcl ^тах(^) Л
Pbr(z)= J f F(/?,7)exp(-7ciz)dZ, (6.32)
nco 0
или, что то же самое, равна интегралу от Q (г) по интервалу < t < rmaX.
Интегралы в выражении (6.31) берутся численно [б]. На рис. 6.3, а приведены им-
пульсные отклики для волоконного световода с параметрами V = 70, «со = 1,5 и Д =
115
= 0,01. При увеличении мнимой части показателя преломления оболочки лучи, кото-
рые распространяются медленнее, т. е. под большими углами к оси световода, теряют
больше мощности. Среднеквадратическая ширина импульса существенно уменьшает-
ся только в тех случаях, когда либо велико п1с^ либо световод имеет большую длину,
так что имеет место значительное уменьшение полной мощности импульса.
6.11. Пример. Усеченный параболический профиль
Можно повторить вывод из предыдущего примера для сердцевины с усеченным парабо-
лическим профилем, приведенным в табл. 2.1. Импульсный отклик и полная мощность
задаются выражениями (6.31) и (6.32), но/ (0, Т), 7cj и g теперь определяются соот-
ветственно выражениями (4.52), (6.28) и (6.27). Верхний предел интегрирования
^тах® задается выражением (4.53) при q = 2 и 0=0(0 из выражения (4.61).
Интеграл в выражении (6.31) оценивается численно [б]. На рис. 6.3, б приведены
нормированные импульсные отклики для волоконных световодов с такими же значе-
ниями параметров, как и для ступенчатого профиля. Наиболее медленно распространя-
ющиеся лучи испытывают наибольшее затухание, но в сравнении со ступенчатым профи-
лем потери мощности при одинаковых значениях z и п1с^ оказываются гораздо меньше.
Это объясняется тем, что значительное затухание испытывают только те лучи, у кото-
рых точки поворота расположены близко к границе сердцевины, тогда как в волокон-
ном световоде со ступенчатым профилем все лучи доходят до нее.
ГЛАВА 7. ВЫТЕКАЮЩИЕ ЛУЧИ
До сих пор лучевое описание распространения света в основном относилось
к направляемым лучам, которые без потерь переносят мощность по непогло-
щающим оптическим волноводам, и предполагалось, что потери мощности
на излучение соответствуют рефрагирующим и туннелирующим лучам. В этой
главе будут описаны физические механизмы, приводящие к потерям мощно-
сти из-за рефракции и туннелирования, и выведены выражения для скорости
затухания мощности.
В гл. 1 и 2 указывалось, что согласно закону Спелля и уравнению лучевой
траектории некоторые лучи в сердцевине волновода будут испытывать пре-
ломление на границе сердцевины и оболочки. Эти лучи называются рефраги-
рующими. Кроме того, из лучевого уравнения следует, что в сердцевине во-
локонного световода существуют другие лучи, которые имеют еще и соот-
ветствующие участки траектории в оболочке, начинающиеся на конечном
радиальном расстоянии от границы сердцевины и простирающиеся неограни-
ченно. Эти лучи называются туннелирующими [1,2]. Кроме них существуют
еще туннелирующие-рефрагирующие лучи, которые распространяются в не-
круглых волоконных световодах [3]. Эти три типа лучей имеют более об-
щий термин — вытекающие лучи, поскольку, как следует из геометрической
оптики, каждый из них будет частично ’’вытекать”, т. е. терять некоторую
часть мощности за счет радиального распространения. Однако геометричес-
кая оптика не позволяет оценить скорость затухания мощности.
Потери на излучение — это волновое явление, поэтому их нельзя вычис-
лить с помощью геометрической оптики. Таким образом, снова возникает
ситуация, сходная с ситуацией в гл. 6, когда в лучевое рассмотрение приш-
лось вводить волновые эффекты для того, чтобы исследовать влияние погло-
116
щения в оболочке. Поэтому будем следовать подходу гл. 6: сохраним луче-
вые траектории и предположим, что потери мощности на излучение имеют
место только в точках отражения или поворота. Тогда скорость затухания
мощности зависит только от расстояния между точками отражения или пово-
рота вдоль волоконного световода или плотности их расположения. Часть
мощности луча, которая теряется в каждой точке отражения или поворота,
найдем, рассматривая луч локально как плоскую волну. Тогда, прменяя тео-
рию локальных плоских волн, несложно вывести выражения для потерь на
излучение в волноводах со ступенчатым и градиентным профилями [4, 5].
В случае планарных волноводов со ступенчатым профилем выражение для
потерь на излучение, связанных с отражением рефрагирующего луча от гра-
ницы сердцевины, совпадает с выражением, которое было впервые выведено
Френелем для преломления плоских волн на плоской границе [6]. Вывод вы-
ражения для определения потерь в точках отражения или поворота методами
теории локальных плоских волн приведен в гл. 35. При заданном значении
этих потерь для расчета затухания мощности луча вдоль волновода требует-
ся знать только расстояние между точками отражения или поворота или плот-
ность их расположения, которые определяются методами геометрической
оптики.
Если волоконные световоды возбуждаются источниками, излучающими
свет в широком диапазоне углов, как например диффузный источник (см.
разд. 4.1), то в них распространяются как направляемые, так и вытекающие
лучи. При достаточном удалении от источника каждый из вытекающих лучей
потеряет за счет излучения практически всю свою мощность и почти всю ос-
тавшуюся в волоконном световоде мощность будут переносить направляе-
мые лучи. Однако при умеренном расстоянии значительный вклад в общую
световую мощность могут внести вытекающие лучи (в случае круглых све-
товодов это главным образом туннелирующие лучи). Эта глава является под-
готовительной к следующей главе. В ней будет показано, что рефрагирующие
и туннелирующие-рефрагирующие лучи затухают очень быстро, однако тун-
нелирующие лучи могут иметь сколь угодно малые скорости затухания и
вести себя почти как направляемые лучи, когда параметр Vдостаточно велик.
РЕФРАГИРУЮЩИЕ ЛУЧИ
В гл. 1 и 2 рефрагирующие лучи в сердцевинах планарных волноводов и круг-
лых волоконных световодов были отождествлены. Важной особенностью
таких лучей является раздвоение траектории в каждой-точке отражения от
границы сердцевина—оболочка. Здесь будет рассмотрено влияние этого эф-
фекта на поток мощности вдоль траектории. Для пояснения используемых
идей сначала рассмотрим простейшие примеры.
7.1. Планарный волновод со ступенчатым профилем
Траектории рефрагирующих лучей рассмотрены в разд. 1.2 на примере пла-
нарного волноводоа со ступенчатым профилем, сердцевина и оболочка кото-
рого имеют показатели преломления nCQ и ис1 и полуширина сердцевины рав-
на р (см. рис. 1.4,6). Раздвоение траекторий происходит в каждой точке
отражения: одна ее часть возвращается обратно в сердцевину, а другая пере-
117
ходит в оболочку. Это же происходит со световой мощностью, причем мощ-
ность, уходящая в оболочку, теряется как излучение из волновода. Эти поте-
ри удобно описывать коэффициентом прохождения мощности Г, или коэф-
фициентом потерь, который определяется соотношением
<7Л)
где р. — мощность в падающем луче, р* — мощность в отраженном луче. Та-
ким образом, при каждом отражении теряется часть мощности, равная Т.
Коэффициент затухания лучевой мощности у находится либо усреднением
Т по лучевому полупериоду zp между последовательными отражениями, ли-
бо суммированием потерь при N отражениях на единицу длины волоконного
световода. В любом случае получаем [7]
7 = = NT,
zp
(7.2)
и лучевая мощность в сечении z в предположении, что у - константа, по ана-
логии с разд. 6.1 задается выражением (6.46)
P(z) = Р(0) exp(-yz).
(7.3)
Коэффициент прохождения мощности. Коэффициент прохождения мощно-
сти Т получен при рассмотрении луча в виде локальной плоской волны (часть
бесконечной плоской волны, падающей на плоскую границу раздела неогра-
ниченных сред, у которых показатели преломления совпадают с показателя-
ми преломления сердцевины и оболочки волновода исо, ис1 (см. рис. 1.38).
В приближении слабонаправляющего световода, когда исо = hcj, коэффици-
ент прохождения не зависит от поляризации и получен в разд. 35.6. Из выра-
жения (35.20) имеем [7]
= 4sin0z(sin20z - sin2 ее)1/2 ,7 ..
{sin 0Z + (sin2 0Z - sin2 0C)1/2}2 ’ '
где 0z — угол между лучом и направлением оси, а 0С - критический угол
скольжения. Это выражение остается в силе для всех рефрагирующих лучей с
< Я/2-
Коэффициент затухания мощности. Лучевой полупериод zp для рефраги-
рующих лучей дается выражением (1.10), которое использовалось для на-
правляемых лучей. Подставляя (7.4) в соотношение (7.2), получаем выраже-
ние для коэффициента затухания мощности
_ 2sin2 0Z (sin2 0z - sin2 0C) 1/2
7 pcos 0Z {sin 0Z + (sin2 0Z -- sin2 0C)1/2} 2
(7.5)
118
Если 0Z тг/2, затухание становится сколь угодно большим, а если 0z ~+вС9
оно может быть сколь угодно малым. Другими словами, если 0z достаточно
близко к 6С, то рефрагирующий луч может распространяться вдоль планарно-
го волновода на большие расстояния, прежде чем большая часть его мощно-
сти потеряется на излучение.
7.2. Планарные волноводы с градиентным профилем
Рассмотрим планарный волновод с градиентным профилем, у которого про-
филь показателя преломления п (х) монотонно уменьшается при переходе от
оси к границе сердцевины и имеет постоянное значение «с1 = п(р) в оболоч-
ке. В разд. 1.6 было показано, что рефрагирующий луч имеет типичную тра-
екторию, приведенную на рис. 1.7, б, Таким образом, вся лучевая мощность
передается через границу, и коэффициент прохождения мощности Т = 1. Этот
вывод основан на классической геометрической оптике, которая предполага-
ет, что длина волны равна нулю. Однако при конечной длине волны света X
не вся лучевая мощность передается через границу — часть мощности падаю-
щего луча отражается обратно в сердцевину вследствие скачкообразного
изменения производной функции профиля показателя преломления на грани-
це сердцевины от dn (x)ldx до нуля при х = р. Это иллюстрируется рис. 7.1, а,
на котором показаны падающий, отраженный и проходящий лучи, образую-
щие с границей раздела один и тот же угол 0t. Аналогично траектории на
рис. 1.8, траектория рефрагирующего луча в волноводе имеет характерный
вид, показанный на рис. 7.1, б. Коэффициент прохождения мощности через
границу сердцевины получен в разд. 35.9. В приближении слабо направляю-
щего волновода с учетом (35.36) получим выражение [8]:
Т= 1/
1 + (-----------JS---------
k8^w^sin30t '
1 __ (___К-.Ч2 ____L__
^8Ди31 sin60t’
(7.6а)
(7.66)
которое справедливо для всех углов преломления при условии, что 0t не
слишком близко к 0t = 0. Производная оценивается на границе раздела со
стороны сердцевины, и выражение (7.66) имеет силу, когда второй член мал
по сравнению с единицей.
Рис. 7.1. Траектории лучей в планарном волноводе с градиентным профилем:
а — падающего, проходящего и отраженного на изломе профиля показателя преломле-
ния; б — рефрагирующего в волноводе
119
Рис.7.2. Коэффициент прохождения мощности Т:
а — для рефрагирующих лучей в планарном волноводе с оболочкой параболического
профиля и параметрами р = 50 мкм, X — 1 мкм, Д = 0,0056, «со ~ 1,504, Ос = 0,106 и
V = 50 (кривая (7) получена в [в], а кривая (2) рассчитана по выражению (7.6);
задается в градусах; лучи пересекают ось под углом 0Z (0) и являются направляемыми
при условии, что 0 < #z(0) < в; б - для косых вытекающих лучей при I = 0,032 в во-
локонном световоде с оболочкой параболического профиля и теми же параметрами
(кривая (7) получена в [в], кривая (2) рассчитана по выражениям (7.6) и (7.9), а кри-
вая (3) — по выражению (7.18) ; угол 0^ задается в градусах; штриховая линия соот-
ветствует значению 0 = (Ц2С| — I 2 )V2, и справа от нее лучи являются рефрагирующими,
а слева — туннелирующими). Для значений /^соответствующих меридиональным лучам
(/ — 0), справедливы кривые (я)
б) (ЛСО~Р)/ "со
Усеченный параболический профиль. Из табл. 2.1 следует, что для воло-
конного световода с таким профилем к = ФДи^/р. Кривая (2) на рис. 7.2, а
соответствует Т, рассчитанному согласно выражению (7.6а), в зависимости
от угла 6t и угла 6Z (0), который траектория образует с осью волоконного
световода (см. рис. 7.1,а). Для сравнения приведена кривая (1) для малых
значений 0t [8]. Ясно, что Т = 1 справедливо для всех направлений проходя-
щих через границу лучей, за исключением очень малых значений 0^, Наобо-
рот, преломленный луч с достаточно малым значением 0t, или (3 < «с1, может
распространиться вдоль плоского волновода с градиентным профилем на
большое расстояние, прежде чем большая часть его мощности будет потеря-
на на излучение. Лучевой полупериод для рефрагирующих лучей находится
из выражения (1.33), в котором пределы интегрирования, как следует из
рис. 7.1, б, заменяются на ± р. Тогда коэффициент затухания можно полу-
чить из выражений (7.2) и (7.6).
7.3. Волоконный световод со ступенчатым профилем
В планарных волноводах с профилями, рассмотренными в двух предыдущих
разделах, могут распространяться только направляемые и рефрагирующие
лучи. Однако, как показано в разд. 2.7, в волоконных световодах с профи-
лями такого же вида существуют еще и туннелирующие лучи. Здесь будут по-
лучены выражения для затухания рефрагирующих лучей в волоконных све-
товодах (туннелирующие лучи будут рассмотрены позже). Указанные выра-
120
жения являются простым обобщением соответствующих выражений для пла-
нарного волновода, которые были приведены выше и справедливы как для
косых, так и для меридиональных лучей.
На рис. 2.3 показан косой рефрагирующий луч, который падает на криво-
линейную границу сердцевины волоконного световода со ступенчатым про-
филем и образует угол а с нормалью. Если а лежит в интервале, задаваемом
выражением (2.66), то соответствующий луч является рефрагирующим. Яс-
но, что, если радиус сердцевины р велик по сравнению с длиной волны света
в сердцевине Х/лСо> то криволинейная граница будет для луча локально плос-
кой. Тогда из разд. 7.1 следует, что коэффициент прохождения Т совпадает
с классическим коэффициентом Френеля (35.50). Преломленный луч образу-
ет с нормалью угол л/2 — 0t, где зависит от угла а в законе Снелля и от
углов 0^ и 0Z (2.3). Следовательно,
hc1cos 0t = исо sin a; sin 0t (sin2 0Z sin2 0^ - 0*)1/2, (7.7)
где nCQ ис1 и 0C = (1 — «с1/лсо)1/2 << 1 в предположении слабонаправля-
ющего волоконного световода. Подставляя эти выражения в соотношение
(35.50), с помощью (7.2) и (2.11) получаем коэффициент затухания мощ-
ности
2sin20z (sin20zsin2%,-02)1/2___________
Р cos {sin s’n + (sin2 0Z sin2 Q? — 02)1/2} 2
Для меридиональных лучей (0^> = л/2) это соотношение переходит в выра-
жение (7.4) для планарного волновода. Более строгий анализ, в котором
принимается во внимание кривизна поверхности, показывает, что.приведен-
ные выше выражения с высокой точностью справедливы для всех направле-
ний рефрагирующих лучей за исключением тех, которые очень близки к
критическому углу ас = л/2 — 0С [9].
7.4. Волоконные световоды с градиентным профилем
Коэффициент прохождения рефрагирующего луча для косых лучей воло-
конных световодов с градиентным профилем в пределах приближения ло-
кальной плоской волны дается выражением (7.6), в котором 0t = л/2 — а и
а — угол между падающим, отраженным или проходящим лучами и нормалью
к границе сердцевины. Из выражений (2.14), (2.16) и (2.17) получаем
«clsin0t = (ис1 - ?2 ~72) 1/2 > (7.9)
где Р и I — лучевые_инварианты; ис1 — показатель преломления однород-
ной оболочки. Если I = 0, то снова получается соотношение для плоского
волновода, а именно Р = ис1 cos 0t.
Усеченный параболический профиль. На рис. 7.2, б приведен график Т
как функции 0t, который получен в результате подстановки (7.9) в выра-
жение (7.6) и расчета значения Т для косого луча с инвариантом Т = 0,032
в волоконном световоде с усеченным параболическим профилем, парамет-
ры которого совпадают с параметрами профиля дня кривых на рис. 7.2, а.
121
Кривая (2) соответствует не слишком малому 0t. Кривая (1) для малых
значений 0t получена в [8]. Коэффициент затухания мощности определяет-
ся из соотношений (7.6), (7.2) и выражения (2.28) для лучевого полупе-
риода при замене предела интегрирования rtp на р.
Косые и меридиональные лучи. Из соотношения (7.8) и из рис. 7.2 сле-
дует, что при -> 0 коэффициент прохождения Т 0 только для меридио-
нальных лучей. Для каждого косого луча Т стремится к конечному преде-
лу при -> О'и, следовательно, фактически все косые рефрагирующие лучи
очень быстро теряют мощность при распространении. Поскольку меридио-
нальные лучи составляют незначительную часть рефрагирующих лучей, мож-
но сделать вывод, что вообще вся мощность рефрагирующих лучей быстро
теряется на очень коротких участках волоконного световода [10]. Значи-
тельный вклад в полную лучевую мощность на больших длинах световода
могут вносить туннелирующие лучи, которые рассматриваются ниже.
ТУННЕЛИРУЮЩИЕ ЛУЧИ
В разд. 2.7 из уравнения лучевой траектории геометрической оптики было
найдено, что в сердцевине круглого волоконного световода существуют лу-
чи, имеющие в оболочке соответствующие участки траектории, начинающи-
еся на конечном радиальном расстоянии от границы сердцевины и простира-
ющиеся неограниченно. Это предполагает потери мощности на излучение;
такие лучи называются туннелирующими, поскольку их мощность туннели-
рует из сердцевины в оболочку [1,2]. В планарных волноводах с профиля-
ми показателя преломления, рассмотренными в гл. 1, туннелирующие лу-
чи не существуют. Механизм появления потерь на излучение в результате
туннелирования является одной из форм нарушения полного внутреннего
отражения [И], вызванного в данном случае кривизной границы сердце-
вины и оболочки. Здесь будут описаны физические свойства этих лучей и
получено выражение для коэффициента затухания их мощности [5, 12, 13].
7.5. Волоконные световоды с градиентным профилем
В разд. 2.7 рассматривались траектории туннелирующих лучей для свето-
водов с монотонным градиентным профилем, минимальное значение кото-
рого ис1 соответствовало показателю преломления оболочки и максималь-
ное значение показателя преломления сердцевины псо находилось на оси.
На рис. 7.3, а показана часть траектории узкой трубки идентичных туннели-
рующих лучей. Каждый луч касается каустики точек поворота, имеющей
радиус Гф, где Гф — наибольший корень уравнения (2.19). Траектории про-
должаются в оболочке, начинаясь на каустике излучения, радиус которой
задается соотношением (2.23). Поскольку оболочка является однородной,
траектория, как показано на рисунке, оказывается прямой линией, являю-
щейся касательной к каустике.
Туннелирующий луч теряет мощность всякий раз, когда он касается каус-
тики точек поворота. При этом теряемая мощность достигает каустики из-
лучения и излучается наружу вдоль траектории в оболочке (рис. 7.3,а).
В области между двумя каустиками поле локальной плоской волны, свя-
занной с туннелирующим лучом, является затухающим. Через затушеван-
122
Рис. 7.3. Туннелирующие лучи:
а — в волоконном световоде с градиентным профилем (каустика точек поворота имеет
радиальную координату г = граница сердцевины г — р и каустика излучения г =
= rrad); б - в волоконном световоде со ступенчатым профилем (граница сердцевины
имеет координату г — р, и каустика излучения г = rrad)
ную область между штриховыми линиями рис. 7.3, а, которая соединяет
границы лучевых трубок, оно передает мощность от точки касания к каусти-
ке излучения. Поскольку между каустиками свет увидеть нельзя, говорят
о процессе передачи как об электромагнитном туннелировании, или просто
о туннелировании. В планарных волноводах с такой же формой профиля
(монотонно убывающей от оси к границе) туннелирующих лучей не суще-
ствует. Таким образом, туннелирование в волоконном световоде обуслов-
лено только кривизной границы таких профилей, в том числе и ступенчато-
го. Тем не менее при соответствующем выборе профиля туннелирующие
лучи распространяются и в планарных волноводах. Примером такого вол-
новода является многослойный планарный волновод, рассмотренный в [14].
Классификация вытекающих лучей. Диапазон значений лучевых инвари-
антов для туннелирующих лучей задается соотношением (2.24в), которое
справедливо как для градиентных, так и для ступенчатых профилей, моно-
тонно убывающих от оси к границе сердцевины
3min Р <"cl и «cl С / 2 ^^тах(З), (7.10)
где и /тах(3) зависят от профиля. Меридиональные лучи (I = 0) не
удовлетворяют обоим условиям, так что любой туннелирующий луч должен
быть косым.
Альтернативный способ задания этих условий, который позволяет дать
их простое физическое истолкование, состоит в том, чтобы рассмотреть со-
ответствующие значения радиуса каустики излучения rrad- Из
(2.23) имеем rrad = рТ/ (n2d - р2)1/2.
соотношения
(7.П)
Несложно показать, что - р при 02 + / 2 и rrad ->°° при
Таким образом, для каждого туннелирующего луча значение rrad находится
на интервале р < rrad < ©о, в пределе, когда rrad неограниченно возрастает,
в оболочке не существует его траектории, и туннелирующий луч становит-
ся направляемым. Когда rrad -> р, траектория в оболочке начинается на гра-
нице сердцевины, и, как видно из уравнения (2.19), р, так что тунне-
лирующий луч становится рефрагирующим. Классификация типов лучей в
соответствии со значениями и rrad приведена в табл. 7.1.
Таблица 7.1. Классификация типов лучей в соответствии со значениями
радиуса каустики излучения в оболочке rrad и радиуса каустики точек пово-
рота rtp для волоконных световодов со ступенчатым и градиентным профи-
лями
Тип луча г tp г rad
Ступенчатый Г радиентный
Направляемый Р о < Пр < р 00
Т уннелирующий Р О^г*<р Р < 'rad < °0
Рефрагирующий Р р р
Поворот проходящего луча. Согласно закону Снелля, когда луч прелом-
ляется на границе раздела, падающий, преломленный лучи и нормаль лежат
в одной плоскости. Однако это несправедливо для туннелирующих лучей.
Если определить плоскость падения на рис. 7.3, а как плоскость, содержа-
щую нормаль, или радиальное направление, и касательную к лучевой траек-
тории в точке поворота, то преломленный в оболочку луч не лежит в этой
плоскости [9]. Для того чтобы определить направление траектории в обо-
лочке, напомним, что азимутальный угол 0^ (г), определенный соотношени-
ем (2.14), равен нулю на двух каустиках, приведенных на рис. 7.3, а, по-
скольку лучевые траектории перпендикулярны к нормали. Плоскость па-
дения и преломленный луч образуют с осью соответственно углы 0Z (Гф) и
0z(rrad)- Взяв отношение инвариантов (2.16) и (2.17), получаем уравне-
ние, которому удовлетворяют эти углы:
J- = r-f Wtp) = Wrad) • (7.12)
Все туннелирующие лучи являются косыми (/ ф 0) и rrad > rtp. Следова-
тельно, 0Z (rrad) < 0Z (rtp), и прошедший луч поворачивается по направле-
нию к оси световода на угол 0Z (гф) - 0Z (rrad), причем из уравнения (7.12)
получаем
t8 (вг(гф) - вг(гиа)) . (7.13)
Р 1 + Р ' rad'tp
В случае предельного перехода к рефрагирующему лучу rrad -> и угол по-
ворота равен нулю, в то время как в случае предельного перехода к направ-
ляемому лучу rrad ->00, 0z (rrad) ->0, так что угол поворота в точности равен
0Z Оф). Таким образом, при достаточно больших значениях rrad направление
преломленного луча фактически параллельно оси волоконного световода.
7.6. Волоконный световод со ступенчатым профилем
Траектории туннелирующего луча в волоконном световоде со ступенчатым
профилем, у которого сердцевина и оболочка имеют показатели преломле-
ния исо и ис1 соответственно, рассмотрены в разд. 2.2. Часть траектории из
124
N
Рис. 7.4. Классификация лучей в волоконном световоде со ступенчатым профилем в со-
ответствии с углом падения на границу сердцевины
узкой трубки туннелирующих лучей приведена на рис. 7.3, б. Единственное
ее отличие от траектории в волоконных световодах с градиентным профи-
лем состоит в том, что траектория в сердцевине отражается от ее границы, а
не от точки поворота. Следовательно, поля локальных плоских волн явля-
ются спадающими в области между г = р и г = rrad.
Классификация вытекающих лучей. Интервал значений инвариантов для
вытекающих лучей задан соотношением (2.8). Интервалы углов для направ-
ляемых, рефрагирующих и туннелирующих лучей, заданные соотношением
(2.6), проиллюстрирует рис. 7.4. В точке Р на изогнутой границе сердцеви-
ны направляемые лучи занимают телесный угол, ограниченный полукону -
сом, ось которого проходит через точку Р и параллельна направлению оси
z, а угол при вершине 0С является критическим углом скольжения. Рефра-
гирующие лучи занимают телесный угол в пределах второго полуконуса с
углом при вершине ас = л/2 — 0С, ось которого NP направлена вдоль норма-
ли, или радиального направления. Два полуконуса касаются общей образу-
ющей, и направления туннелирующих лучей занимают телесный угол между
конусами, как показано на рисунке. Классификация типов лучей по значе-
нию rrad совпадает с классификацией для волоконных световодов с гради-
ентным профилем в табл. 7.1 при замене на р.
Поворот преломленного луча. Туннелирующие лучи волоконных свето-
водов со ступенчатым профилем испытывают поворот (см. разд. 7.5) . Тра-
ектория луча в оболочке поворачивается от плоскости падения падающего
луча и нормали в направлении к оси. На каустике излучения 0Z (rrad) зада-
ется выражением (7.12), и в точке отражения на границе сердцевины /3 =
= ncocos 0Z. Используя выражение (7.11) для rrad, можно получить выраже-
ния для угла поворота
х, 10 -0 (г Й = ("со ~^2) 1/2 - (»cl-ff2)1/2 S’ z7 14ч
tg{0Z ^rad)} р + („2(_ 02)1/2 („2o_ 02)1/2 0’ <7-14)
который не зависит от скоса луча. В случае предельного перехода к рефра-
гирующим лучам 0 2 + 7 2 -> п2с1 и 0Z (rrad) -> 0Z (р), где jT = hc1cos 0z (p). Тог-
да разность между 0Z и 0Z (р) согласуется с условием компланарности пада-
125
ющего и преломленного лучей и нормали, т. е. с законом Спелля. В случае
предельного перехода /3 -> ис1 угол поворота равен 3Z, Следовательно, при
г rad >> Р направление излучения практически параллельно оси волоконно-
го световода.
7.7. Затухание туннелирующих лучей
Мощность туннелирующего луча P(z) в сечении волоконного световода z
связана с коэффициентом затухания мощности у соотношением (7.3), ко-
торый через коэффициент прохождения и лучевой полупериод определяется
выражением (7.2). Коэффициент прохождения определяет долю мощности
падающего луча, которая передается через область затухания, как показано
на рис. 7.3. В отличие от рефрагирующих лучей полупериод zp задается теми
же выражениями, что и для направляемых лучей в табл. 2.1, и значения (3 ле-
жат в интервале, определенном соотношением (2.24в), а не (2.24а). Выра-
жения для коэффициента прохождения выводятся в гл. 35 с использованием
приближения локальной плоской волны. Теперь рассмотрим примеры.
7.8. Пример. Градиентные профили
Рассмотрим слабонаправляющие волоконные световоды, у которых профили показате-
ля преломления монотонно уменьшаются от максимального значения на оси до по-
казателя преломления однородной оболочки «с| на границе сердцевины. В пределах
приближения локальной плоской волны коэффициент прохождения для туннелирую-
щих лучей задается выражением (35.45) [5, 12, 13]
f rad 2
Т= exp\-2к f \р2 +V — п2
rtp г’
(г)} 1,2dr >, (7.15)
где к = 2тг/Х, длина волны в свободном пространстве равна X, и лучевые инварианты
определены в табл. 2.1. Радиус сердцевины равен р, радиальная координата каустики то-
чек поворота является наибольшим корнем уравнения (2.19) , и каустика излучения за-
дается выражением (2.23). Это выражение справедливо при условии, что rtp и rrad не
слишком близки друг к другу. По мере того, как увеличивается ширина области затуха-
ния ггад - гtp на рис. 7.3, я, значение Т очень быстро уменьшается и стремится к нулю
при гга(| -> оо. Таким образом, как указывалось в конце разд. 7.4, туннелирующие лучи
могут внести значительный вклад в полную лучевую мощность на больших расстояниях.
Слаботуннелирующие лучи. Лучи, которые имеют очень маленькие значения коэф-
фициента прохождения, известны под названием слаботуннелирующих лучей и в соот-
ветствии с обсуждением, которое было проведено выше, имеют значения ггац 00 или
3 < «с1 согласно соотношению (2.23). Таким образом, каустика излучения находит-
ся гораздо дальше от границы сердцевины, чем каустика точек поворота, т. е. гга^ -
- Р >> Р - rtp. В этом случае нижний предел интегрирования rtp в выражения (7.15)
для Т можно приближенно заменить на р и получить правильное выражение для всех
слаботуннелирующих лучей. Поскольку в оболочке п (г) = то с помощью соотноше-
ния (37.118) получаем явное выражение
Т = exp j-2*pZ [In {р + (р2 - 1) 1/2} - J)1;i ]
_ rrad _ ________Z_____
P P («cl-32)1/2
(7.16a)
(7.166)
126
Этот результат не зависит от профиля показателя преломления в сердцевине, поскольку
получен для лучевых инвариантов, определяющих траекторию в сердцевине.
Линейное приближение. Большинство туннелирующих лучей имеют каустики точек
поворота и каустики излучения, которые находятся недалеко от границы сердцевины,
т. е. rtp « р, rra j р. Тогда можно использовать разложение в окрестности границы серд-
цевины, линеаризуя аргумент квадратного корня в подынтегральном выражении соот-
ношения (7.15) при г < ри г > р соответственно. Это сделано в разд. 35.12 при получе-
нии выражения (35.49а) для Г [5] через производную профиля показателя преломле-
ния на границе со стороны сердцевины:
( 2, ’«’"с! (72+/?2-и2])3'2 ) = 1 dn2 (г) I
0^,-2/’ nci(n^-P) Г К -«2С1 dr Ь-
(7.17)
Лучи, удовлетворяющие условию rtp ^ггац, имеют значительно большие коэффициенты
прохождения, чем слабовытекающие лучи, описанные выше.
Какой бы из приведенных выше способов ни использовался при выводе коэффици-
ента прохождения, коэффициент затухания мощности получается из соотношения (7.2),
где лучевой полу период определяется выражением (2.28) для градиентых профилей.
7.9. Пример. Усеченный параболический профиль
Для усеченного параболического профиля из табл. 2.1, используя (7.15), можно полу-
чить коэффициент прохождения в аналитическом виде. Вклад оболочки в значение ин-
теграла (аргумента экспоненты), т. е. на интервале р < г < rrad, получается из выраже-
ния (7.16) и вклад сердцевины, т. е. на интервале rtp < г < р, - из экспоненты выраже-
ния (6.26). Таким образом, Т можно представить в виде
Т= exp {-kpin^ej. + 27/,)}, (7.18а)
где I, и 12 - функции нормированных радиусов каустик а = rtp /р, Ъ = гЛр нр = г^/р,
которые определяются соотношениями:
I, = (1 -а2)1/2(1 -62)!/2 _а +Ь in(d+O -gdln)1+^. -+-. L (7.186)
2 [1 + а_ я - о J
12 = 1п{р+ (р2 - I)1'2} - (рг - 1рп/р, (7.18в)
где d± = {(1 — а2)1/2 + (1 - Z>2) 1/2} / (а ± Ь). Радиусы каустик в сердцевине выража-
ются через лучевые инварианты соотношением (2.35), и радиус каустики в оболочке за-
дается выражением (7.16)/ На рис. 7.2, б кривая (3) - это график Т как функции 1 -
- ?/«со для косых туннелирующих лучей при 7 = 0,033. Вертикальная штриховая ли-
ния - граница между туннелирующими и рефрагирующими лучами при rrad = ~ р
или Д = (h£i - 72) 1/2. Тогда 0 превышает это значение, коэффициент прохождения быст-
ро уменьшается, однако вблизи этого значения выражение (7.18) теряет силу. Соответ-
ствующие значения Т в последнем случае задаются кривой (1), которая получена в [8].
Лучевой полупериод, приведенный в табл. 2.1, выражения (7.18) и (7.2) позволяют
получить коэффициент затухания мощности.
7.10. Пример. Ступенчатый профиль
Коэффициент прохождения для туннелирующих лучей в слабонаправляющем волокон-
ном световоде со ступенчатым профилем, показатели преломления сердцевины и обо-
лочки которого равны «со и лс|, выводится в разделе 35.12 в приближении локальной
плоской волны. Таким образом, имеем выражение [9, 14]
127
f rad na
T = |7f lexp <-2# f (02 + I2 —
( P r
(7.19a)
где rrad задается выражением (7.16) и Tf - аналитическое продолжение классического
коэффициента прохождения Френеля для области значений углов, меньших критическо-
го угла скольжения 0С (см. рис. 1.3, б), т. е. в область лучей, которые были бы направ-
ляемыми в плоском волноводе. Используя лучевые инварианты, запишем выражение
(35.46в)
4 _ _
^f1 = -Z2)1/2(02 + Z2 -и2])1'2, (7.196)
псо Яс1
где интервалы значений 0 и I для туннелирующих лучей приведены в (2.8в). Множитель
I Tf | учитывает скачок профиля на границе сердцевины, а экспоненциальный множитель
обусловлен спадающим полем в области между границей сердцевины и каустикой из-
лучения. Интеграл в экспоненте оценивается с использованием выражения (37.118), так
что получается аналитическое выражение для коэффициента прохождения
Т= |Tf|exp {~2k.pl [1п{р+ (р2 -I)1'2} - (р2 - 1)*'2/р]},
(7.20)
где р - задается выражением (7.166). Это выражение является неточным только для
тех лучей, у которых каустики расположены очень близко к границе сердцевины.
Следует отметить, что выражение (7.19) не может быть выведено из выражения
(7.15) для градиентного профиля при -> р. Как разъяснялось в разд. 6.9, вывод с ис-
пользованием локальной плоской волны требует, чтобы профиль показателя преломле-
ния очень медленно изменялся на расстоянии, равном длине волны света. Если профиль
становится круче и приближается к ступенчатому, то это условие нарушается и выраже-
ние (7.15) не является точным [15].
Линейное приближение. Для тех туннелирующих лучей, у которых каустики излуче-
ния расположены не слишком далеко от границы сердцевины, можно получить более
простое приближенное выражение для коэффициента прохождения, линеаризуя аргу-
мент квадратного корня в подынтегральном выражении соотношения (7.19а). Это пре-
образование проделано в разд. 35.12 при получении выражения (35.496)
, . С 2 (?2 + /2 -«cl)3/2 1
Т = | Tf lexp j- jkp-(7.21)
где значение |7^| определено соотношением (7.196).
7.11. Переход от туннелирующих к рефрагирующим лучам
Коэффициенты прохождения, заданные выражениями (7.15) и (7.19), при-
менимы ко всем туннелирующим лучам в волоконных световодах с гради-
ентным и ступенчатым профилями за исключением предельного случая,
когда туннелирующий луч становится рефрагирующим, т. е. когда rrad р,
В этом предельном случае значение коэффициента прохождения относитель-
но велико по сравнению с его значением для туннелирующих лучей, близ-
ких к направляемым лучам, т. е. при rrad -> <». Следовательно, для опреде-
ленных задач возбуждения, затрагивающих все или почти все направления
вытекающих лучей, предположение, что соотношения (7.15) и (7.19) име-
ют силу для всех туннелирующих лучей, вносит ничтожно малую ошибку в
128
вычисление полной лучевой мощности в сечениях, расположенных достаточ-
но далеко от источника вдоль оси волоконного световода. Оно принимает-
ся в следующей главе, в которой обсуждается пространственно-неустано-
вившийся режим.
Для случаев, когда это предположение не может быть принято, для коэф-
фициента прохождения получены выражения, справедливые в промежуточ-
ной области между туннелирующими и рефрагирующими лучами [4, 8].
Значения Т (кривая_(1)) приведены на рис. 7.2,5 для косых вытекающих
лучей с параметром I = 0,033 в волоконном световоде с усеченным парабо-
лическим профилем. Слева от вертикальной штриховой линии кривая соот-
ветствует туннелирующим лучам и совпадает при увеличении 0 с кривой,
полученной на основе выражения (7.18) для локальной плоской волны [8].
Подобным образом, справа от вертикальной штриховой линии кривая со-
ответствует рефрагирующим лучам и совпадает при уменьшении 0 с выра-
жением (7.6), полученным с помощью локальной плоской волны. Подоб-
ные переходы имеют место для косых вытекающих лучей в волоконном
световоде со ступенчатым профилем [16].
7.12. Универсальные коэффициенты прохождения
Ранее были представлены выражения, полученные на основе метода локаль-
ных плоских волн, для коэффициентов прохождения рефрагирующих и тун-
нелирующих лучей в волоконных световодах со ступенчатым и градиент-
ным профилями, а в предыдущем разделе было показано, что для перехода
от одного к другому требуется третье выражение. Описание* затухания вы-
текающего луча не только позволяет понять физические различия между
рефрагирующими и туннелирующими лучами, но и приводит к простейшей
формуле для Т. Наоборот, можно использовать метод равномерного прибли-
жения [17] и вывести единственную формулу для Т, справедливую для
всех вытекающих лучей (рефрагирующих и туннелирующих) и. обеспечи-
вающую взаимосвязь между ними. Эта формула, хотя и не является прос-
той, как приведенные выше выражения, чрезвычайно полезна для вычисле-
ния. Ее вывод для волоконных световодов с градиентным и ступенчатым
профилями приведен в [16].
НЕКРУГЛЫЕ И НЕРЕГУЛЯРНЫЕ ВОЛОКОННЫЕ СВЕТОВОДЫ
До сих пор в этой главе рассматривались вытекающие лучи только в пла-
нарных волноводах и круглых волоконных световодах. Здесь анализ будет
распространен на вытекающие лучи в некруглых волокнах, например эл-
липтических и нерегулярных волоконных световодах, в частности изогну-
тых. В гл. 2 было показано, что в некруглых волоконных световодах появ-
ляются туннелирующие-рефрагирующие лучи, когда луч теряет мощность
как за счет туннелирования в точках поворота вдоль своей траектории, так
и за счет преломления на границе. Ниже показано, что понятие вытекающих
лучей применимо к этим более общим волноводам при условии, что коэф-
фициент прохождения зависит только от локальной геометрии. Получены
формулы для коэффициентов прохождения туннелирующих лучей, завися-
щие только от двух главных радиусов кривизны каустики точек поворота
или границы сердцевины.
129
5 Зак 37
7.13. Локальные коэффициенты прохождения мощности
Лучевой анализ многомодовых волоконных световодов (безотносительно
к свойствам их симметрии или регулярности) предполагает, что лучевую
траекторию вдоль волоконного световода можно проследить и что каждый
раз, когда траектория, на которой теряется лучевая мощность, отражается
от каустики или границы сердцевины, можно ввести коэффициент прохож-
дения, позволяющий рассчитать часть падающей мощности, излучаемой на-
ружу. Лучевая траектория определяется направлением локального волно-
вого вектора, как показано в разд. 35.3, и поэтому естественно, что коэф-
фициент прохождения зависит только от локальной геометрии. Это удов-
летворяется в планарных волноводах и круглых волоконных световодах,
потому что коэффициент прохождения имеет одно и то же значение всюду
на границе сердцевины или на каустике точек поворота. Существует также
ряд некруглых профилей с таким свойством [18]. Ясно, что в случае про-
извольного поперечного сечения, если радиус кривизны границы сердцеви-
ны или каустики точек поворота велик по сравнению с длиной волны све-
та и если каустика излучения находится не слишком далеко от границы серд-
цевины, то коэффициент прохождения будет зависеть только от локальной
геометрии. Если каустика излучения находится очень далеко от границы
сердцевины, то коэффициент прохождения будет зависеть от геометрии
всего поперечного сечения сердцевины и за исключением упомянутых выше
случаев не будет локальным. Только туннелирующие вытекающие лучи,
характеризующиеся малыми коэффициентами затухания, имеют каустики
излучения, расположенные очень далеко от границы сердцевины. Следова-
тельно, для многих практических задач потери на излучение из волоконных
световодов произвольных поперечных сечений могут быть описаны с помо-
щью коэффициентов прохождения вытекающих лучей. Ниже приводятся
эти локальные коэффициенты прохождения.
7.14. Границы сёрдцевины и каустики произвольной кривизны
В соответствии с проведенным выше обсуждением потери мощности выте-
кающего луча в некруглых и нерегулярных волоконных световодах описы-
ваются локальными коэффициентами прохождения для границ и каустик
точек поворота произвольной кривизны при условии, что кривизна вели-
ка по сравнению с длиной волны и каустика излучения расположена не
слишком далеко от границы сердцевины. Эти коэффициенты могут быть
формально получены разложением полей в окрестности границы или каус-
тики точек поворота [4, 19]. Однако для многих практически важных за-
дач достаточно знать коэффициенты прохождения только для туннелирую-
щих лучей. Эти коэффициенты можно найти либо из более общих резуль-
татов [4, 19], либо интуитивно обобщением коэффициентов для туннели-
рующих лучей в круглых волоконных световодах. Последний подход ис-
пользован в разд. 35.14.
Там показано, что зависимость коэффициентов прохождения от локаль-
ной геометрии круглого волоконного световода сводится только к зависи-
мости от радиуса кривизны р в плоскости падения луча, т. е. радиуса кри-
визны границы сердцевины или каустики точек поворота в плоскости,
130
Рис. 7.5. Траектории лучей:
а — отраженного от произвольно изогнутой границы между однородными средами с по-
казателями преломления л?с0 и иср б — касающегося произвольно изогнутой поверхно-
сти каустики точек поворота п = п (г^) в градиентной среде
определяемой лучевой траекторией или касательной к ней и нормалью. За-
тем утверждается, что локальные коэффициенты прохождения для грани-
цы сердцевины или каустики точек поворота произвольной кривизны име-
ют такую же функциональную зависимость от р, как и в круглом волокон-
ном световоде. В этих случаях р зависит от двух главных радиусов кривиз-
ны, а не от одного, как в случае круглого волоконного световода.
Отражение на границе сердцевины. Ступенчатый профиль. Рассмотрим
границу произвольной кривизны между средами с однородными показа-
телями преломления т?со и т?с1, показанную на рис. 7.5,а. Декартовы оси
Ру и Pz лежат в плоскости, касающейся границы в точке Р, и ортогональны
к нормальному или радиальному направлению. Их ориентация такова, что
два главных радиуса кривизны ру и pz лежат соответственно в плоскостях
гу и rz. Локальный коэффициент прохождения для туннелирующего луча,
падающего под углом а к радиальному направлению, получен в разд. 35.14.
Из соотношений (35.53) и (35.54) получаем [4]
(sin2 а — sin2ap)3/2
-----------............
(7.22а)
где Tf — аналитическое продолжение коэффициента прохождения Френеля
I | = 4cosa(sin2a - sin2ac) 1/2/cos2 ас. (7.226)
Критический угол ас = arcsin(«cl/«co), и радиус кривизны в плоскости па-
дения в точке Р дается выражением
р = pypz sin2 а/ (ру cos2 6Z + pz cos2 0y), (7.22в)
где Оу и 0z — углы между направлением падающего луча и соответствен-
но осями Ру и Pz на рис. 7.5, а. Выражение для Т имеет силу при условии
kpnCQ >> l/cos3a [4,20].
Отражение от каустики. Градиентная среда. Каустика точек поворота
произвольной кривизны изображена на рис. 7.5, она определяется по-
верхностью п - п (г^), где rtp - радиальное положение точек поворота. Пред-
положим, что точка поворота расположена не слишком далеко от пересече-
ния радиальной оси с границей г = р, за которой профиль показателя пре-
ломления является однородным, т. е. п = я(р) = п р Касательная к лучевой
траектории в точке Р лежит в плоскости, касающейся траектории в той же
точке, и образует с осями у и z соответственно углы я/2 — 0z и 0Z. Остальные
обозначения на рисунке совпадают с обозначениями рис. 7.5, а. Локальный
коэффициент прохождения задается выражением (35.55) [19]
Т = ехп / коп гП (rtp) 11 з/2 I
Т ехр^--крпс} ^_2 [ -1]
(7.23а)
где ’’наклон” профиля показателя преломления к на границе и радиус кри-
визны в плоскости падения р, определяемый выражением (35.36) :
K=_l_ У?Ук I _ • Z =_______________. (7 236)
n2ci dr и-p-’ р pycos20z + pzsin20z )
Выражение для Т имеет силу при условии kpnCQ >> 1 [19].
ПОГЛОЩАЮЩИЕ ВОЛОКОННЫЕ СВЕТОВОДЫ
Когда вытекающий луч распространяется вдоль поглощающего волоконного
световода, то ясно, что полное затухание является суммой коэффициентов
затухания мощности за счет поглощения в сердцевине, оболочке и потерь на
излучение. Если их обозначить соответственно ус0, ус1 и то мощность луча
в сечении z волоконного световода задается выражением [21]
P(z) = Р(0) exp (-7Z); у = ?со + yd + 7^ (7.24)
где Tjj. обозначает коэффициент затухания, заданный выражением (7.3); за-
висимость поглощения в сердцевине и в оболочке от коэффициентов усо и
ус1 рассмотрена в гл. 6. Локальный коэффициент прохождения мощности для
поглощающей оболочки и границы сердцевины произвольной кривизны мож-
но получить тем же способом, что и при выводе формулы (7.22) [22].
ГЛАВА 8. ПРОСТРАНСТВЕННО-ЯЕУСТАНОВИВШИЙСЯ РЕЖИМ
Главное внимание в первых шести главах было уделено изучению поведения
направляемых лучей, которые в непоглощающих волоконных световодах
распространяются без потерь мощности и дают полное описание распростра-
нения света на достаточно больших расстояниях от источника, когда вытека-
ющие лучи теряют фактически всю свою мощность. Такой режим называют
пространствешю-у становившимся. В этой главе рассматривается промежу-
точная область, лежащая между источником и началом пространственно-
установившегося режима, где распространение света характеризуется про-
странственно-неустановившимся режимом.
132
8.1. Пространственно-неу становившийся и пространственному становившийся
режимы
Рассмотрим идеальный непоглощающий волоконный световод произвольно-
го поперечного сечения и с произвольным профилем показателя преломле-
ния. Пусть входной торец световода возбуждается источником, как показа-
но на рис. 8.1. Вообще говоря, источник возбуждает и направляемые, и выте-
кающие лучи. Направляемые лучи переносят световую мощность вдоль воло-
конного световода без потерь на неограниченное расстояние. При распростра-
нении каждого вытекающего луча его мощность экспоненциально затухает
в соответствии с выражением (7.3), так что их полная мощность очень быст-
ро уменьшается за счет излучения при удалении от источника, как схемати-
чески показано на рис. 8.1. На достаточно большом расстоянии от начала све-
товода полная мощность вытекающих лучей может быть сколь угодно ма-
лой, но полностью она излучится из сердцевины только при z -> <». Однако
для практических целей удобно разделить волоконный световод сечением
z - z0 на две такие области, что при z >zQ мощность вытекающих лучей ока-
зывается пренебрежимо малой по сравнению с полной мощностью направля-
емых лучей. Распространение света в области z0 <z <<» фактически соответ-
ствует пространственно-установившемуся режиму и точно описывается с по-
мощью только направляемых лучей. Область 0 < z < z0 соответствует про-
странственно-неустановившемуся режиму, где распространение описывается
как направляемыми, так и вытекающими лучами.
Сначала будет найдена мощность вытекающих лучей в волоконных свето-
водах, возбуждаемых диффузным источником. Будет показано, что про-
странственно-неустановившийся режим просто и точно описывается един-
ственным безразмерным параметром, который содержит все количественные
физические характеристики. Этот же параметр будет использован для описа-
ния влияния вытекающих лучей на дисперсию импульса. Затем будет пока-
Рис. 8.1. Иллюстрация зависимости потерь на излучение от длины волоконного свето-
вода. Более темные области соответствуют большей интенсивности света и более жир-
ные стрелки - большим потерям на излучение
133
зано, как с помощью вытекающих лучей можно объяснить явление черной
полосы в волоконных световодах со ступенчатым профилем и похожее яв-
ление в волоконных световодах с градиентным профилем. Вслед за крат-
ким обсуждением влияния вытекающих лучей на распространение света в
асимметричных волоконных световодах будет рассмотрена взаимосвязь по-
терь на излучение и поглощение.
Протяженность области пространственно-неустановившегося режима. Глав-
ная цель первых одиннадцати разделов главы состоит в том, чтобы опреде-
лить эффективную длину, или протяженность области неустановившегося
режима, а также форму импульса. Поскольку выводы являются одновремен-
но и простыми, и важными, они будут предварительно кратко изложены
здесь для того, чтобы показать перспективу их получения, а также для удоб-
ства ссылок.
Пространственно-неустановившийся режим в волоконных световодах
определяется главным образом направляемыми и туннелирующими лучами,
поскольку рефрагирующие лучи очень быстро затухают [1, 2]. Таким обра-
зом, кроме области вблизи источника полная световая мощность в сечении
z сердцевины волоконного световода складывается из мощности направля-
емых лучей РЬг и мощности туннелирующих лучей ^tr(z). Если источник яв-
ляется диффузным, то эти мощности в начале слабонаправляющего волокон-
ного световода со ступенчатым профилем примерно одинаковы, т. е. РЬг «
« (0) [3], а в случае световода с усеченным параболическим профилем
Pbr-3PtI(0) [4].
В разд. 4 21 и 4.22 было показано, что форма импульсного отклика в во-
локонных световодах со ступенчатым и усеченным параболическим профиля-
ми является фактически прямоугольной. Этот вывод имеет силу только в
пространственно-установившемся режиме. В пространственно-неустановив-
шемся режиме мощность туннелирующих лучей проявляется в виде ’’хвоста”
к импульсу. Мощность в ’’хвосте” велика вблизи источника, но становится
пренебрежимо малой в начале области пространственно-установившегося ре-
жима [5].
Протяженность области пространственно-неустановившегося режима z0 за-
висит от длины волны или, что то же самое, от волоконного параметра V,
поскольку затухание туннелирующих лучей зависит от длины волны. Пола-
гая, что z0 - это сечение волоконного световода, в котором мощность тун-
нелирующих лучей уменьшается на 90%, получаем оценку для zQ при диф-
фузном возбуждении волоконного световода со ступенчатым профилем и
сердцевиной радиуса р (см. разд. 8.8) [6, 7]
z0 « (р/20с)ехр(К/2), (8.1а)
где параметры V и 0с были определены ранее. В случае типичного многомо-
дового волоконного световода с р = 25 мкм, 0с = 0,14 и И = 30, z0 300 м,
а при V < 10 область неустановившегося режима занимает всего лишь не-
сколько сантиметров. В разд. 8.9 будет показано, что для волоконного свето-
вода с усеченным параболическим профилем получается следующее выраже-
ние [6, 7]:
z0 (яр/0с)ехр(К/2),
(8.16)
134
так что область неустановившегося режима оказывается в 2л раз протяжен-
нее, чем для волоконного световода со ступенчатым профилем.
ИЗЛУЧЕНИЕ ИЗ ВОЛОКОННЫХ СВЕТОВОДОВ, ВОЗБУЖДАЕМЫХ ДИФФУЗНЫМ
ИСТОЧНИКОМ
В разд. 4.6 и 4.17 было рассмотрено возбуждение волоконных световодов,
освещаемых диффузным источником. Во внимание принималась мощность
направляемых лучей. Здесь будут рассмотрены мощность вытекающих лучей
и ее изменения вдоль волоконного световода. Для удобства волоконные све-
товоды со ступенчатым и градиентным профилями рассматриваются отдельно.
8.2. Возбуждение вытекающих лучей в волоконных световодах со ступенча-
тым профилем
Диффузный источник (см. рис. 4.3, а) облучает входной торец волоконного
световода со ступенчатым профилем, изображенный на рис. 4.4, возбуждая
всевозможные лучи — туннелирующие, рефрагирующие, а также направляе-
мые. Для того чтобы рассчитать мощность возбуждаемых туннелирующих
лучей, нужно сначала найти функцию распределения.
Функция распределения. В разд. 4.17 с помощью определения (4.39) была
введена функция распределения F(0,1), которая описывает мощность, пере-
носимую направляемыми лучами, и было показано, что при диффузном воз-
буждении она пропорциональна лучевому полупериоду в соответствии с
выражением (4.45а). Таким образом, F((3, I) зависит только от лучевой
траектории в сердцевине. Поскольку туннелирующие лучи отличаются от
направляемых только своим поведением в оболочке, можно заключить, что
функция распределения для туннелирующих лучей имеет такой же вид. Если
повторить рассуждения разд. 4.17, этот результат можно получить формаль-
но, исходя из соотношения (4.41), в котором пределы интегрирования по
/3 и I заменены на те, которые приведены ниже в выражениях (8.46) . Таким
образом, для волоконного световода со ступенчатым профилем с помощью
выражения (4.48) получим
, = 8тгр2/р J3 (и2о - Р2 -I2)1'2
} «о и2со - Р2
(8.2а)
Выражение (2.8в) задает интервалы значений инвариантов для туннелирую-
щих лучей
0<?<ис1; («d-^2)!/2 < (п20-Р2)1'2,
(8.26)
где иС0’И ис1 — показатели преломления сердцевины и оболочки соответ-
ственно.
Часто оказывается полезным проинтегрировать функцию распределения
по параметру скоса луча, т. е. по I ..В разд. 4.18 была введена функция_рас-
пределения G(/3 ), которая по определению равна интегралу функции F((3 , / )
135
на интервале значений I . Для направляемых лучей G(/3) задается выражени-
ем (4.47а), а для того чтобы получить такую функцию в случае туннелирую-
щих лучей, проинтегрируем выражение (8.2а) на интервале изменения I , за-
данном в соотношении (8.26). Выполняя подстановку / = (п2С0 - 02)1/2sinw
и интегрируя, получаем функцию
С(?) м -1
° t V 1 СО /
fl2y/2
(8.3)
где 0<р <лс1.
Инварианты и распределение мощности на входном торце. Интервал зна-
чений инвариантов направляемых лучей в каждой точке входного торца во-
локонного световода со_ступенчатым профилем не зависит от положения точ-
ки и составляет «с1 < /3 < «с0. Однако в случае туннелирующих лучей этот
интервал изменяется по сечению торца и его можно получить, если найти
мощность Р(г) всех возбуждаемых туннелирующих лучей в каждой точке
входного торца. Напомним, что соотношение (4.41) задает полную мощность
направляемых лучей и, следовательно, в силу симметрии, мощность направ-
ляемых лучей, возбуждаемых в каждой точке входного торца, задается пра-
вой частью выражения (4.41а), в которой опущено интегрирование по радиу-
су и добавлен множитель 1/2ттг. По аналогии Р(г) задается таким_же_выраже-
нием, в котором верхний и нижний пределы интегрирования по /3 и I опреде-
лены в выражении (2.24в) . Следовательно,
/о Р "С1 1^Г’^
f М f
0 0imn<r> («с1-?2)1/г
dl
g(f) ’
(8.4а)
где g(r) и I m (г, /3) определены соответственно выражениями (4.40) и
(4.416), в которых п (г) заменено на псо. Поскольку нижний предел при ин-
тегрировании по I не может превышать верхний, интеграл по (3 имеет ниж-
ний предел 0mjn (г) > 0, который равен значению (3, когда пределы интегри-
рования по 7 одинаковы. Следовательно, интервалы значений инвариантов
для туннелирующих лучей с радиальной координатой г, как можно прове-
рить, удовлетворяют условиям
0тш(О<0 <«cb («2с1-|32)1/2</ (8.46)
0min 0 = max |0,-^-_r2 C0
(8.4b)
Схематически эти области представлены на рис. 8.2: а — 0min(r) = 0 и б -
0min (г) > 0. Незаштрихованные области соответствуют инвариантам направ-
ляемых лучей, а заштрихованные области — инвариантам рефрагирующих и
туннелирующих лучей. Эти области являются подмножеством областей, ука-
занных на рис. 2.7, а для всего волоконного световода.
Рефрагирующие лучи. В гл. 7 было показано, что рефрагирующие лучи так
быстро затухают, что их вклад в полную световую мощность существен толь-
ко в непосредственной близости от источника. Поэтому при определении
пространственно-неустановившегося режима можно пренебречь их присут-
136
Рис. 8.2. Области возможных значений инвариантов для направляемых (НЛ), туннели-
рующих (ТЛ) и рефрагирующих (РЛ) лучей в точках с координатой г в сечении воло-
конного световода со ступенчатым профилем, возбуждаемого диффузным источником:
а) г > рпс}/пс0 и f min(r) = 0; б) г < рпс]/псо и 0min(r) > 0
ствием в сечениях волоконного световода, отстоящих достаточно далеко от
источника. Количественный анализ, основанный на подобном подходе, пол-
ностью это оправдывает [8].
Первоначальная мощность туннелирующих лучей. Для того чтобы найти
полную мощность туннелирующих лучей (0), возбуждаемых на входном
торце волоконного световода, проинтегрируем выражение (8.3) в интервале
0 < Р < лс1. Интегрирование упрощается, если второй член в фигурных скоб-
ках проинтегрировать по частям, чтобы избавиться от арксинуса и затем
объединить результат с третьим членом. Подстановка0 =ис1(1 — w2)1/2 сво-
дит интеграл к виду (37.116). Если пронормировать результат относительно
полной мощности направляемых лучей (4.16), то
Лг(°)
9 2 л cos20P
= 1 - Ctg^c + - . on
7Г с 7Г С sin20c
1,
1--|-^; 0с
Зя с
(8.56)
где sin0c = {1 — «cl/^coJ 1/2 • В приближении слабонаправляющего волокон-
ного световода мощности направляемых и туннелирующих лучей в нулевом
порядке по 6С равны. Однако, как следует из выражения (4.19), полная мощ-
ность направляемых и туннелирующих лучей в 02 меньше, чем полная мощ-
ность, излучаемая источником. Следовательно, по существу вся мощность
диффузного источника затрачивается на возбуждение рефрагирующих лучей,
которые излучаются из сердцевины на очень коротких расстояниях вдоль во-
локонного световода.
8.3. Пространственно-неустановившийся режим для волоконных световодов
со ступенчатым профилем
Протяженность области пространственно-неустановившегося режима зависит
от изменения полной лучевой мощности вдоль волоконного световода. По
137
Рис. 8.3. Характеристики переходного режима:
а — относительная суммарная мощность направляемых и туннелирующих лучей, остаю-
щаяся в волоконном световоде со ступенчатым профилем, возбуждаемым диффузным
источником; б — зависимость распределения мощности направляемых (НЛ) и туннели-
рующих (ТЛ) лучей от параметра G((3) - обозначение нормированной функции
G(?)n’/(2rrsp’/0«co) со
причинам, указанным выше, пренебрежем рефрагирующими лучами и опре-
делим Ps (z) как сумму мощности направляемых и туннелирующих лучей в
сечении z. Мощность направляемых лучей постоянна вдоль непоглощающего
волоконного световода, следовательно,
ps(z) -pbr + ptI(*); Л(0) -Л,г + Лг(0). (8.6)
Значение отношения Ps (z) /Ps (0) определяет потери на излучение и протяжен-
ность области пространственно-неустановившегося режима. Для того чтобы
получить полную мощность туннелирующих лучей в сечении z, проинтегриру-
ем произведение множителя, описывающего затухание, и функции распреде-
ления, заданной выражением (8.2а), на интервале значений инвариантов
(8.26). Таким образом,
"cl _("со~ё2)1/2
Р (z) = f d$ f F(3 J)exp {-7(3,/)z} di, (8.7)
о (n2cl-p2)1/2
где коэффициент затухания, заданный выражением (7.2), равняется отноше-
нию коэффициента прохождения (7.20) и лучевого полупериода из табл. 2.1.
Результаты численного интегрирования приведены на рис. 8.3, а в виде зави-
симостей отношения Ps(z)/Ps(0) (8.6) от нормированного расстояния zip
вдоль оси волоконного световода при различных значениях волоконного па-
раметра V и 0С - 0,1 [9]. Для облегчения интерпретации этих кривых на
рис. 8.3, б приведены первоначальные распределения мощности направляе-
мых и туннелирующих лучей от отношения 3/^со при том же значении вс.
Использованы ^задаваемые выражениями (4.49) и (8.3) нормированные опре-
деления ПцС(А)1 (2тг2р210псо). При уменьшении/Гот значения ясо мощность
направляемых лучей остается фактически постоянной, а мощность туннели-
рующих лучей, т. е. лучей с 3 < ис1> образующих с осью волоконного све-
товода большие углы 0Z, быстро уменьшается. Кроме того, при увеличении
6Z увеличивается коэффициент затухания. Это означает, что лучи с меньшими
значениями 0z переносят большую часть мощности туннелирующих лучей и
138
имеют наименьшее затухание. В классической геометрической оптике при
X -+ 0 или V -+ 00 затухания нет; этому случаю соответствует горизонтальная
линия V = °° на рис. 8.3, а. При увеличении X или уменьшении V полная лу-
чевая мощность в заданном сечении z уменьшается, а при z ->«> остается толь-
ко мощность направляемых лучей. В этом предельном случае с помощью вы-
ражений (8.5) и (8.6) при условии 0с << 1 получаем
Ps(0) 2 Зтг с’
z -><».
(8.8)
Область пространственно-неустановившегося режима может иметь значитель-
ную протяженность для больших значений V, прежде чем будет достигнуто
это предельное значение. Иными словами, если V велико, то для описания
распространения даже в длинных волоконных световодах одних направляе-
мых лучей недостаточно.
8.4. Возбуждение вытекающих лучей в волоконных световодах с градиент-
ным профилем
Здесь будут рассмотрены волоконные световоды с усеченными градиентны-
ми профилями показателя преломления и, как и в разд. 8.3, рефрагирующие
лучи не рассматриваются. Напомним, что согласно разд. 2.7 интервалы значе-
ний инвариантов для туннелирующих лучей зависят от профиля и задаются
выражением (2.24в) . Верхний предел для I в случае усеченных степенных про-
филей (см. табл. 2.1) был получен в разд. 4.19 и задается выражением (4.53)
Т - „1/2 ( 2 1 * ( »co-g2 1 Й +
f | q + 2 J
(8-9)
В разд. 8.2 было показано, что минимальное значение Р получается при при-
равнивании нижнего и верхнего пределов I, откуда
с о; + (8.юа)
[«С1 - (<7/2) (п2С0 - п2с1) ] 1/2 ; П2о с „21(? + 2)/<7 (8.Юб)
Для применяемых на практике полоконных световодов «с0 « псу и q = 2, по-
этому обычно выполняется соотношение (8.106), что и предполагается в даль-
нейшем. Распределение типов лучей в плоскости 0 ,Т приведено на рис. 2.7, б.
Начальная мощность туннелирующих лучей. Интервалы значений инвари-
антов для туннелирующих лучей в каждой точке входного торца волоконно-
го световода задаются соотношениями (8.46), где по аналогии с выражени-
ем (8.4в) для волоконного световода с градиентным профилем
fain (0 = max |0> r2 I J p fa fa = f (r) - fa } 1/2 • (8.11)
Мощность возбуждаемых туннелирующих лучей в каждой точке определяет-
ся выражением (8.4а), в котором в качестве пределов интегрирования ис-
пользованы значения pmin (г) и I т (г, ft) .
Функция распределения. В разд. 4.19 было показано, что функция распре-
деления мощности F(jJ, I ) как направляемых, так и туннелирующих лучей
для волоконного световода с усеченным параболическим профилем имеет
вид (4.52)
= 4тт2р2 . (8.12a)
«0 0co-«d)
Если проинтегрировать эту функцию на интервале (и^ — 02)1/z < 7 <
< Zmax (0 ) > используя выражение (8.9) при q =_2, то получим распределение
мощности туннелирующих лучей на интервале 0min < 0 <ис1, соответствую-
щее распределению (8.3) для волоконного световода со ступенчатым про-
филем: _
G(P) К,-?2 -2(»2со-»2с1)1/2(»2с1-?2)1/2} •
"о «со “ "cl
(8.126)
Начальная мощность туннелирующих лучей. Полная мощность туннелиру-
ющих лучей, возбуждаемых на входном торце, получается интегрированием
распределения (8.126) на интервале /3, причем 0min задается выражением
(8.106) при q = 2. Если пронормировать результат относительно полной мощ-
ности направляемых лучей (4.18) при q = 2, то получим
Аг (о) /Аг = 1/з.
(8.13)
Таким образом, используя этот результат и выражения (4.16), (4.18) и (8.56),
заключаем, что в приближении слабонаправляющего волновода диффузный
источник возбуждает в волоконном световоде со ступенчатым профилем
направляемые и туннелирующие лучи, мощности которых соответственно в
два и шесть раз больше, чем в волоконном световоде с параболическим про-
филем.
Усеченные степенные профили. Можно найти отношение первоначальной
мощности туннелирующих лучей к мощности направляемых лучей для воло-
конного световода с усеченным степенным профилем (см. табл. 2.1) [4]
АДФ _ q + 2 (<7 + 4 _ /—Г [ (<? + 2)/2] |
РЪг я (<7 + 2 V Г[(<? + 3)/2] J’ <•
где РЬг — задается выражением (4.18) и Г — гамма-функция, определяемая
выражением (37.104). Это отношение монотонно возрастает от 0,288 при
q = 1 до 0,333 при q = 2 и 0,370 при q = 3. Подчеркнем, что формула (8.5а)
для волоконного световода со ступенчатым профилем не является пределом
выражения (8.14) при q -► °°, поскольку в (8.14) предполагается, что 0min >
> 0, а для ступенчатого профиля 0min = 0.
8.5. Пространственно-неустановившийся режим для волоконных световодов
с усеченным параболическим профилем
Ситуация в этом случае аналогична той, которая рассмотрена в разд. 8.3, ес-
ли заменить ступенчатый профиль на усеченный параболический. Полная
мощность туннелирующих лучей задается выражением (8.7), в кото-
ром распределение F(|3,1 ) определяется выражением (8.12а), верхний ^пре-
дел при интегрировании по I и нижний предел при интегрировании по /3 за-
менены соответственно на Zmax (0) (8.9) и 0min (8.106). Коэффициент зату-
хания у(1391) равен отношению коэффициента прохождения (7.18) и лучево-
140
Рис. 8.4. Относительная суммарная мощность Pg(z) 1,0
направляемых и туннелирующих лучей, оста- Ps(0)
ющаяся в волоконном световоде с усеченным
параболическим профилем, который возбуж- 0,9
дается диффузным источником
0,8
0 10z 104 106 108
Т./?
го полупериода (см. табл. 2.1). На рис. 8.4 приведены результаты численно-
го расчета с использованием (8.7) и (8.6) отношения Ps(z)/Ps(0) как функ-
ции нормированного расстояния z/p при различных значениях волноводно-
го параметра V и 0с = 0, 1 [10]. Каждая из кривых стремится к значению
0,75 при zip -+<*>, и отклонение от результата классической геометрической
оптики в заданном сечении увеличивается с уменьшением V. При достаточно
больших значениях V пространственно-неустановившийся режим может су-
ществовать на больших расстояниях. Таким образом, кривые на рис. 8.3, а
и 8.4 имеют одинаковый вид, хотя для волоконного световода с усеченным
параболическим профилем отношение мощностей туннелирующих лучей
Лг(2)/Лг(0) уменьшается медленнее. Это согласуется с тем фактом, что в
волоконных световодах с градиентным профилем коэффициент затухания
для лучей, у которых точки поворота расположены достаточно далеко от гра-
ницы сердцевины, оказывается значительно меньше, чем в волоконных све-
товодах со ступенчатым профилем, где каждый луч достигает границы серд-
цевины.
ОБОБЩЕННЫЕ ПАРАМЕТРЫ
Если распространить рассмотрение пространственно-неустановившегося ре-
жима, проведенное в разд. 8.3 и 8.5, на произвольные источники излучения и
профили волоконных световодов, то полная мощность туннелирующих лу-
чей всегда будет задаваться двойным интегралом, отличающимся от (8.7)
только пределами интегрирования. Следовательно, пространственно-неуста-
новивший ся режим зависит от трех безразмерных параметров, связанных с
волоконным световодом: нормированного расстояния вдоль световода z/p,
волоконного параметра V и критического угла скольжения 0С. Для каждого
набора этих параметров двойной интеграл необходимо оценивать численно.
Однако можно вывести приближенное выражение для той начальной мощно-
сти туннелирующих лучей, которая остается в сердцевине в сечении z и зави-
сит только от одного параметра, называемого обобщенным параметром G.
Это простая комбинация величин z/p, V и 0С) которая определяется профи-
лем показателя преломления и может быть получена при качественном рас-
смотрении коэффициентов затухания туннелирующих лучей.
Затухание мощности туннелирующих лучей. В сечении z волоконного све-
товода начальная мощность каждого туннелирующего луча согласно выраже-
нию (7.3) уменьшается в ехр(—yz) раз, где у — коэффициент затухания мощ-
ности. Произведение yz для каждого луча зависит как от параметров воло-
конного световода р, 0С, К, так и от лучевых инвариантов j3,1. Если для не-
141
которого луча yz >> 1, то фактически вся его мощность теряется на излу-
чение, наоборот, если yz << 1, то первоначальная мощность остается почти
неизменной вдоль волоконного световода. Иными словами, затухание явля-
ется практически бесконечным или нулевым в соответствующих случаях.
Будем считать, что мощность каждого туннелирующего луча либо прибли-
женно равняется нулю, если yz 1, либо равняется первоначальному значе-
нию, если yz 1. Граница соответствует yz = 1, и это приводит к комбина-
ции параметров волоконного световода, которая определена как обобщен-
ный параметр. Точное граничное значение yz можно получить, если предста-
вить yz в безразмерном виде, как будет показано в следующих примерах.
8.6. Обобщенный параметр для волоконных световодов со ступенчатым
профилем
Согласно выражению (7.3^ затухание мощности туннелирующих лучей зави-
сит от произведения y(j3, I )z, где коэффициент затухания равен отношению
коэффициента прохождения Т и лучевого полупериода z Для ступенчатого
профиля значение последнего приведено в табл. 2.1, а для Т воспользуемся
линейным приближением (7.21), которое справедливо для всех лучей, кро-
ме слаботуннелирующих. Если выразить к через параметр V, то получим
у(в nz = псо-ё2 (Р2^2-^!)172 f IV № + 1г-п2сУ'2 1
р 0 «со-лс1 Р1 3 (n2cl-02)(n2co-n2cl)1/2 J
(8.15)
Преобразуем это выражение так, чтобы множитель перед экспонентой не за-
висел от V, z или р и был безразмерным. Тогда изменение у(0,1 )z будет
полностью определяться экспоненциальным множителем
"со ”co~ff2 (g~2 +Z2 -»cl)1/2 у
Р nlo ~ пс1 («?о ~ п cl) 1/2
X (exp < G —
(g2 + Р -^)3/2 1 V
(«с1-?2)(исо-пс1)1/2 )
где обобщенный параметр G определяется соотношением [6, 7]
G = 4- In S 2<эс- к
V р J
(8.16)
(8.17)
Здесь 0С % (1 — n2c]/n'1CQ)vl в приближении слабонаправляющего волоконно-
го световода.
Когда волоконный световод является многомодовым, можно сделать ко-
личественные оценки величины y(j3, Z)z. Если туннелирующий луч имеет та-
кие параметры Р и I, что аргумент экспоненты в выражении (8.16) положи-
телен, то произведение у(0, Z)z будет очень большим почти для всех таких
лучей, поскольку V» 1. Аппроксимируем большое затухание, полагая, что
у (Р, I )z = ©о. Наоборот, если параметры^ и Z таковы, что аргумент экспонен-
ты отрицательный, то произведение у(0, Z)z оказывается чрезвычайно ма-
лым почти для всех таких лучей. Для того чтобы аппроксимировать очень
142
малые затухания, полагаем у(0, l)z =0. Иными словами, при заданныхz/p,
V и 0С, а, следовательно G, каждому туннелирующему лучу в зависимости
от значений /3 и I (соответственно положительного или отрицательного аргу-
мента экспоненты в выражении (8.16)) приписывается либо бесконечное,
либо нулевое затухание. Граница между этими двумя классами лучей опре-
деляется из условия равенства нулю аргумента экспоненты, т. е.
ЗС(л2, -02)(ИсО -«d)1/2 =2(02 +72 -«21)3/2, (8.18)
где /3 и I находятся в интервалах (2.8в), соответствующих туннелирующим
лучам.
8.7. Обобщенный параметр для волоконных световодов с градиентным
профилем
Получим обобщенный параметр волоконного световода с градиентным про-
филем, который является простейшим примером световода с усеченным па-
раболическим профилем. Коэффициент затухания равен отношению коэф-
фициента прохождения Т к лучевому полупериоду zp (см. табл. 2.1). Исполь-
зуя для Т приближенное выражение (7.16) и выражая к через V с помощью
приведенного выше соотношения, получаем
2 И/
("co-"cl)1/2
(1п{р+ (р2 -1)1/2} —)
(8.19)
где р = I / (и^ — /32) 1/2 и 2Д = 0С в приближении слабонаправляющего во-
локонного световода. Преобразуя это выражение подобно (8.16), получаем
[ехр|(7- (In\р + (р2 - D1/2} - )!• ] V,
Р V vZco ncl) ” )
(8.20)
где обобщенный параметр G определяется соотношением [6, 7]
с’т‘”Кч}' (8'21)
и 0с = (1 — ^cl/^co) 1/2 • Классификация туннелирующих лучей в зависимости
от их затухания (практически бесконечного или нулевого) соответствует рас-
суждениям, проведенным после выражения_(8.17). Граница между этими
двумя классами определяется значениями /3 и I, которые удовлетворяют
уравнению
С(йсо -«С1)1/2 = 2/ {1п[р + (р2 - 1)1/2] ~(р2 - 1)1/2/р] (8.22)
и находятся в пределах интервалов (2.24в) для туннелирующих лучей.
Усеченные степенные профили. Для остальных усеченных степенных про-
филей, приведенных в табл. 2.1, обобщенный параметр нельзя получить так
легко, поскольку не существует простого выражения для лучевого полупери-
ода. Однако, аппроксимируя соответствующим образом лучевой полупериод
и используя коэффициент прохождения (7.16), можно показать [7], что
143
G,“-Fln{A^ W- (8'23)
Это выражение переходит в (8.21) для параболического профиля при q = 2.
Теперь рассмотрим примеры использования обобщенных параметров.
8.8. Пример. Диффузное возбуадение волоконных световодов со ступен-
чатым профилем
Здесь будет повторено рассмотрение пространственно-неустановившегося режима,
проведенное в разд. 8.3, с использованием обобщенного параметра, полученного в
разд. 8.6. Полная мощность туннелирующих лучей задается выражением (8.7), где те-
перь учитываются только лучи с эффективно нулевым затуханием. Значения (3 и 7 для
них должны удовлетворять условиям (2.8в) и гарантировать, что правая сторона урав-
нения (8.18) не меньше левой. Следовательно,
Z (^) <Z </тах<3> = <"со - 1/2; 0g <0 (8-24а)
где 7(3) обозначает решение уравнения (8.18) и 3g находится из условия 7 (3) =
= 7тях (0) • Отсюда
них
( о ) 1/2 ( 0 2 7 )
% = "со J1 - вс С1 + - "со I1 ~ y-d + (8.246)
поскольку вс < < 1. Подынтегральное выражение в (8.7) равняется нулю, если /3 и
7 не удовлетворяют условиям (8.24а) при yz = 0. Если выполнить нормирование от-
носительно начальной мощности туннелирующих лучей (0), приблизительно равной
мощности направляемых лучей (4.16) при 0С < < 1, и подставить в качестве функ-
ции распределения (4.48), то
= 8 1 fC1 mrX
Ptr(0) я "со ~ "cl 3g "со ~ 7(3)
(8.25)
Выполним интегрирование по I, положив 7 - (п^0 - З2) 1 /2 sin s. Тогда удобно провести
замену переменной 3 на и, где п^0 - З2 — u2 (п 20 - w2j) , и в результате интеграл оказы-
вается только функцией G:
Р (z) Л
—- = — f и {arccos w(u) - w(u) [1 - w2(w)]1/2 } du,
я 1
(8.26a)
где
“g=l1+4F( ; 1 h2 - 1 + (^-(u2 - 1))2'4 . (8.266)
I ) u I 2 I
На рис. 8.5, а приведены результаты расчета этого интеграла как функции G (сплош-
ная кривая). Отношение полной мощности в сечении z к полной начальной мощности
получается из выражений (8.6) и (4.16) и представлено на рис. 8.5, б сплошной кри-
вой. Непосредственный расчет этого же отношения с помощью (8.7) для ряда значе-
ний z/р, V и вс дает точки, которые лежат на или вблизи штриховой кривой. Относи-
тельно малое расхождение двух кривых подтверждает точность метода обобщенного
параметра [б, 7].
Протяженность области пространственно-неустановившегося режима. Теперь в со-
ответствии с обсуждением, проведенным в разд. 8Д, можно рассчитать протяженность
области пространственно-неустановившегося режима. Если принять во внимание, что
она начинается там, где мощность туннелирующих лучей уменьшается до 0,1 от перво-
начального значения, то из рис. 8.5, а видно, что при этом G s 0,5. Тогда, используя
144
Рис. 8.5. Зависимость относительной мощности лучей, остающихся в волоконном свето-
воде, от параметра G:
а — мощность туннелирующих лучей в световоде со ступенчатым (сплошная кривая) и
усеченным параболическим (штриховая кривая) профилями; источник возбуждения —
диффузный; б — суммарная мощность направляемых и туннелирующих лучей: точный
численный результат (сплошная кривая), результат, полученный методом обобщенного
параметра (штриховая кривая)
(8.17), можно связать G и протяженность области пространственно-неустановившего-
ся режима и получить
z0 « (р/2<9с)ехр(Г/2),
(8.27)
что совпадает с (8.1а) .
8.9. Пример. Диффузное возбуждение волоконных световодов с усеченным
параболическим профилем
Используем обобщенный параметр (8.21) для повторного рассмотрения простран-
ственно-неустановившегося режима. Оно подобно вычислению, которое проведено в
разд. 8.8. Значения 0и7 лежат в интервалах (8.24а), однако /тах (?) задается выраже-
нием (8.9) при q = 2, I (?) обозначает решение уравнения (8.22) и ?g - наименьшее
значение ?, удовлетворяющее уравнению 7 (?) = 7тах (?). Начальная мощность тунне-
лирующих лучей определяется выражением (8.13), и функция распределения F((3,1)-
выражением (4.52). По аналогии с (8.25)
Лг(^) = 24
Лг<°) ("co-"cl)3/2
pg ’ v
Полезно сделать замену переменных (3,7 на и и w, где
получаем
п cl ^тах®
f Ш _f dl • (8-28)
Тогда (8.28) можно представить как функцию только параметра G:
Р (z) Wg (1+^)/2 ё
= 12 (du f = +3u|-12 f w(u)du, (8.296)
Лг(0) о Н«) 8 g О
где w (и) является решением преобразованного уравнения (8.22), т. е.
G = 2w(w)ln [w(w) + {w2(u) - и] 1/2 ] - w(w)lnw - 2 {w2 (и) - и} 1/2, (8.30а)
145
и Wg является решением этого уравнения при I (р) = Iтах(Ю или w - (1 + Mg)/2. Та-
ким образом,
2G = 2и„ - 2 - (1 + u„) Inw . (8.306)
fe о b
Результаты численного расчета этого интеграла приведены на рис. 8.5, б (штриховая
кривая). Если отношение полной мощности в сечении z к полной начальной мощно-
сти вычисляется на оеновании выражений (8.6) и (4.18) при q = 2, то для реальных
значений G ошибка по сравнению с точным решением (8.7) составляет 1 - 2 % [7].
Протяженность области пространственно-неустановившегося режима. Для того что-
бы рассчитать протяженность области пространственно-неустановившегося режима, до-
пустим, как и для ступенчатого профиля, что область пространственно-установившегося
режима начинается там, где мощность туннелирующих лучей уменьшается до 0,1 от сво-
его начального значения. Согласно рис. 8.5, я это соответствует G 0,5. Тогда, исполь-
зуя (8.21), получаем
I I
| z0 (7гр/ас)ехр(Г/2). j (8.31)
Таким образом, область пространственно-неустановившегося режима в волоконном све-
товоде с усеченным параболическим профилем в 2тг раз протяженнее чем в ступенчатом,
что следует из (8.16) .
В настоящем и предыдущем разделах было показано, что использование обобщенных
параметров значительно упрощает описание пространственно-неустановившегося режи-
ма при возбуждении волоконного световода диффузным источником. Подобное упро-
щение имеет место при использовании обобщенного параметра для описания простран-
ственно-неустановившегося режима в волоконных световодах, возбуждаемых колли-
мированным пучком [11].
УШИРЕНИЕ ИМПУЛЬСА
В гл. 3 уширение импульса анализировалось с точки зрения изменения време-
ни прохождения лучей, распространяющихся под различными углами к на-
правлению оси 0Z (г) . Анализ был ограничен направляемыми лучами, для ко-
торых 0 < 0z (г) < 0с(г), где 0с(г) — локальный критический угол (2.29).
Однако предполагалось, что источник возбуждения диффузный и возбужда-
ет вытекающие лучи, которые распространяются под углами вс (г) < 0z (г) <
< я/2. Время прохождения t для вытекающих лучей, распространяющихся
в плоскости поперечного сечения (0Z (г) = я/2), бесконечно. Таким образом,
с учетом вытекающих лучей лучевая дисперсия становится много больше
дисперсии, обусловленной одними направляемыми лучами. Но большинство
вытекающих лучей, которые распространяются при больших значениях 0Z (г),
очень быстро затухают и практически не могут быть обнаружены в волокон-
ном световоде значительной длины. Поскольку увеличение дисперсии по
сравнению с обусловленной направляемыми лучами почти целиком связано
с этими лучами, ясно, что эффективное увеличение ширины импульса из-за
вытекающих лучей оказывается гораздо меньше.
Можно оценить изменение лучевой дисперсии за счет вытекающих лучей,
используя обобщенный параметр G (см. разд. 8.6 и 8.7), чтобы классифици-
ровать лучи в соответствии с эффективным затуханием (бесконечным или
нулевым). Сначала будут рассмотрены волоконные световоды со ступенча-
тым профилем, а затем со степенным профилем; наибольшее влияние оказы-
вается в случае оптимального профиля (3.8).
146
8.10. Пример. Лучевая дисперсия в волоконных световодах со ступенчатым
профилем
Дисперсия, вызванная направляемыми лучами, в слабонаправляющих волоконных све-
товодах «со ступенчатым профилем задается выражением (3.3). Если включить в рас-
смотрение вытекающие лучи, то следует учитывать только туннелирующие лучи с прак-
тически нулевым затуханием. Поскольку время прохождения не зависит от угла скоса
лучей, т. е. от 7, то это эквивалентно изменению нижнего предела интегрирования по
0ис] на j3g (8-246) . Таким образом, разность между временем прохождения самого быст-
рого (осевого) направляемого луча (0 = п ) и самого медленного туннелирующего
луча (0 — 0g) составляет согласно табл. 2.1 [7] при Д < < 1
Z 2 I 1
rd- f"coL
1 pg
J-
"co J co
_2_(, "со
3G} ~ с 2
2_ U
3GI с
(8.32)
и сводится к (3.3) при G -> <». С учетом выражения для G (fi.XT) из (8.32)
просто оценить влияние вытекающих лучей на ширину импульса при заданных
НИЯХ z/p, V И 0С-
Форма импульса. Хотя туннелирующие лучи могут значительно увеличить ширину
импульса, исследование распределения мощности в импульсе или импульсного отклика
показывает, что в применяемых на практике волоконных световодах туннелирующими
лучами переносится очень малая мощность. Для того чтобы показать это, повторим про-
цедуру определения импульсного отклика Q (t) с помощью функции распределения
G(0) (см. разд. 4.20). Для направляемых лучей функция G© задается выражением
(4.476), а для туннелирующих лучей с практически нулевым затуханием она пропорци-
ональна правой части выражения (8.25) без интеграла по 0. Поскольку G (0) непрерывна
при 0 — п2, то для туннелирующих лучей
0
можно
значе-
G (?) — — ~~—5— {arccos w(tz) - w(u) [1 -w2(u)l1/3
я «со - «cl
где w (и) определена выражением (8.26), 0а - (8.246) и и = (и* -02)1/2/(и2 -«ri)1/J
"cP (8.33)
Рис. 8.6. Зависимость нормированного импульсного отклика Q(t) = Q(t)/Q(t0) от нор-
мированного времени прохождения (t - при различных значениях обобщенного
параметра G (при G = - °° учитывается вклад всех туннелирующих лучей, при G =
= оо _ только направляемых лучей) :
— znco(nco ~ ncl^cncl’ ~ znwJC (волоконный световод со ступенчатым профи-
лем) ; б) ~ z("co - "cp/“c"cl» Zo = ZJ?co/c (волоконный световод с усеченным парабо-
лическим профилем)
147
Заменим, используя (4.58), 0 на t и подставим в (4.55). На рис. 8.6, а приведены резуль-
таты расчетов нормированного отношения Q(t) /Q(t0) от (t - tQ)/t^, где tQ = znCQ/c и
= znco (nco ~ "clH^cl ~ ширина импульса направляемых лучей согласно (3.2). При
увеличении G уменьшается и ширина импульса, и часть мощности импульса, переноси-
мая туннелирущими лучами. При G — -<» мощность переносится всеми туннелирующи-
ми лучами, а при (л = °° - только направляемыми лучами.
8.11. Пример. Лучевая дисперсия в волоконных световодах с усеченным па-
раболическим профилем
Влияние туннелирующих лучей на уширение импульса и импульсный отклик в волокон-
ных световодах с усеченным степенным профилем можно количественно оценить, пов-
торяя выкладки предыдущего раздела. Простым примером является усеченный парабо-
лический профиль, для которого эффективное уширение импульса легко получить с
помощью табл. 2.1 [5]:
rd = f(?g) -Г(лсо) ~|^A41+«g)2 ^-(l+«g)44> (8.34)
где Д < < 1. Здесь G, ug и ^определяются выражениями (8.21), (8.29а), (8.306).Ес-
ли G -> °°, то Ug -> 0, и^ц переходит в (3.7а). Парис. 8.7 приведена нормированная диспер-
сия 2(7^/(z Д2лсо). В области реальных значений 0,3 < G < 0,5 наблюдается уширение
импульса примерно на 20 %.
Оптимальный профиль. Для оптимального профиля с показателем степени
(3.8) эффективное уширение импульса получается из уравнения (3.7) и табл. 2.1 [5] :
'd = 'G?g) ~H0m) -|-^-A2(l+2Ug)2 ~ |-^-(l + 2«g)20c\ (8.35)
где pm - задается соотношением (3.6). Поскольку 40pt « 2, использованы значения
fig и G для параболического профиля. Это справедливо, так как согласно выражению
(8.23) G слабо зависит от q. Нормированная дисперсия Setj/(zДаисо) приведена на
рис. 8.7 (штриховая кривая). Видно, что вытекающие лучи вызывают ее увеличение на
40... 50 %. Ясно, что в случае оптимального профиля они вызывают максимальное
уширение импульса вследствие быстрого изменения ширины импульса в окрестности
%pt (см. рис. 3.3).
Импульсный отклик. Используя метод, примененный в предыдущем разделе, можно
найти импульсный отклик для волоконного световода с усеченным параболическим
профилем. Результаты приведены на рис. 8.6, б [5]. В этом случае часть мощности им-
Рис. 8.7. Зависимость ширины импульса t j, норми-
рованной относительно ширины импульса направ-
ляемых лучей, от обобщенного параметра G. Сплош-
ная кривая соответствует волоконному световоду
с усеченным параболическим профилем (Fj =
— 2ct д/z А* п ), штриховая - с оптимальным про-
филем (fd = Sct^/z^2nco)
148
пульса,содержащаяся в туннелирующих лучах, оказывается гораздо меньшей, чем в во-
локонном световоде со ступенчатым профилем. Это согласуется с тем фактом, что в во-
локонном световоде с параболическим профилем диффузный источник, как было пока-
зано в разд. 8.4, возбуждает туннелирующие лучи, мощность которых составляет лишь
треть мощности направляемых лучей.
НЕКРУГЛЫЕ ВОЛОКОННЫЕ СВЕТОВОДЫ
Область пространственно-неустановившегося режима в некруглых волокон-
ных световодах можно определить, суммируя мощность вытекающих лучей
в каждом сечении z, однако, вообще говоря, анализ при этом очень услож-
няется. Траектории более не имеют периода, как в осесимметричном свето-
воде, так что, в частности, лучевой пол у период будет изменяться от отраже-
ния к отражению. В гл. 2 было показано, что в некруглом волоконном све-
товоде вытекающий луч может быть либо туннелирующим, либо рефрагиру-
ющим, либо туннелирующим-рефрагирующим лучом. Последний при отраже-
ниях от каустики точек поворота или границы сердцевины ведет себя или
как туннелирующий, или как рефрагирующий луч. В тех волоконных свето-
водах, где возбуждаются только рефрагирующие или туннелирующие-рефра-
гирующие лучи, область пространственно-неустановившегося режима будет
совсем короткой по сравнению с круглым волоконным световодом вслед-
ствие потерь большой части лучевой мощности при каждом отражении.
Коэффициент прохождения мощности Т будет, как правило, изменяться
вдоль траектории вытекающего луча. Поэтому удобно ввести средний коэф-
фициент затухания у с тем, чтобы мощность P(z) вытекающего луча умень-
шалась в соответствии с уравнением P(z) = P(0)exp(—yz). Если через
обозначить часть лучевой мощности, теряющейся при z-м отражении, а через
zpi - соответствующий полупериод, то у = Поскольку Т\ зависит от
параметров траектории и профиля показателя преломления волоконного све-
товода в окрестности каустики или границы сердцевины, будем пользовать-
ся локальными коэффициентами прохождения, введенными в разд. 7.14.
Существует общий класс некруглых световодов с градиентным профилем,
в которых часть мощности, теряемой при каждом отражении, не изменяется,
т. е. Т оказывается постоянным для данной лучевой траектории [12] .Тогда
коэффициент затухания мощности задается выражением T/<z >, где <zp> —
среднее значение лучевого полупериода вдоль волоконного световода.
Если асимметрия незначительна, анализ иногда можно упростить, рассмат-
ривая некруглый волоконный световод как круглый g малым возмущением.
Таким образом, например, можно заменить лучевой инвариант I круглого
волоконного световода на приближенный инвариант I (z), который очень
медленно изменяется вдоль некруглого волокна. Пространственно-неустано-
вившийся режим в эллиптическом волоконном световоде с усеченным пара-
болическим профилем может быть определен в пределах этого приближения
(см. [13]).
РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ НА КОНЦЕ ВОЛОКОННОГО СВЕТОВОДА
Если волоконный световод возбуждается диффузным источником, то свето-
вая мощность в его начале распределяется между всеми направляемыми и
149
Рис. 8.8. Наблюдение удаленным наблюдате-
лем О пучка лучей, выходящих под углом 0О
из волоконного световода, который возбуж-
дается диффузным источником 5
вытекающими лучами — как туннелирующими, так и рефрагирующими.
Мощность каждого из направляемых лучей остается постоянной вдоль воло-
конного световода, однако каждый вытекающий луч при распространении
излучает мощность. Здесь будет рассмотрено распределение интенсивности
света после того, как он выходит из дальнего конца волоконного световода
и наблюдается удаленным наблюдателем.
Под углом Oq к оси волоконного световода (рис. 8.8) наблюдатель видит
эллиптический пучок параллельных лучей, исходящих из поперечного сече-
ния сердцевины. Если пренебречь небольшими потерями на отражение от кон-
ца волоконного световода, то лучи этого пучка, соответствующие направля-
емым, будут иметь такую же интенсивность, как и в начале. Однако лучи,
соответствующие вытекающим, будут иметь меньшую интенсивность. Поэто-
му наблюдатель на конце волоконного световода увидит структуру светлых
и темных областей. Форма этой структуры зависит от профиля показателя
преломления волоконного световода, его длины и значения 60. Нет необходи-
мости определять затухание каждого вытекающего луча — достаточно оце-
нить распределение лучей по сердцевине. Рассмотрим простые примеры.
8.12. Пример. Волоконный световод со ступенчатым профилем
В разд. 4.9 была определена связь между углом падения 0О коллимированного пучка на
волоконный световод со ступенчатым профилем и типами лучей, которые возбуждают-
ся в сердцевине. Ясно, что эта связь не изменится, если направление распространения
каждого луча, составляющего пучок, изменить на противоположное. Это показано на
рис. 8.8 при п (г) = пс0, и можно использовать результаты разд. 4.9. Таким образом, ес-
ли 0 < 0О < %, где п0 sin 0m = псо sin 0С и sin 0С = {1-м*\/п30} 1/3, то каждый луч выхо-
дящего пучка является направляемым, и все поперечное сечение сердцевины наблюда-
тель видит ярко освещенным (см. рис. 8.9, а). Если 0т < 0О < я/2, то каждый луч пучка
является вытекающим. Граница между туннелирующими и рефрагирующими лучами
(2.24) соответствует /З3 + Т2 = п^. Если подставить выражения для инвариантов (2.16)
и (2.17) при п (г) = 0Z (г) = 0Z и выполнить преобразования, то получим
sin3 0С
sin3 0Z
Напомним, что 0^ (г) - угол между проекцией траектории на поперечное сечение и ази-
мутальным направлением (см. рис. 2.4, в). Таким образом, уравнение (8.36) определя-
ет две прямые линии, расположенные на расстоянии 2р{1 — sin3 0c/sin2 0Z }1/2 друг от
друга, как показано на рис. 8.9, б. Линии параллельны плоскости, определяемой осью
волоконного световода и направлением пучка. Область между ними соответствует реф-
рагируюшим лучам, и две области по обе стороны - туннелирующим лучам. Поскольку
рефрагирующие лучи имеют коэффициенты затухания, которые в среднем гораздо боль-
ше, чем у туннелирующих лучей, то, если только волоконный световод не слишком длин-
ный, наблюдатель будет видеть область между двумя линиями гораздо более темной,
150
— COS0 (г) = J 1
р V )
(8.36)
ncosin0z = Wosin0(
Рис. 8.9. Структура интенсивности свече-
ния выходного торца волоконного све-
товода со ступенчатым профилем:
а — светлый круг соответствует направ-
ляемым лучам; б — темная полоса со-
ответствует рефрагирующим лучам, за-
штрихованные области — туннелирую-
щим лучам
поскольку фактически вся мощность рефрагирующих лучей идет на излучение. Однако
туннелирующие лучи в среднем потеряют малую часть своей мощности, и две соседние
области наблюдатель будет видеть почти равномерно и относительно ярко освещенны-
ми. Границы между светлыми и темными областями не будут резкими, так как тунне-
лирующие и рефрагирующие лучи в окрестности 02 + Р = и2р или а - ас, имеют почти
одинаковые коэффициенты затухания. Этот эффект известен как явление черной поло-
сы [14, 15]. При увеличении длины волоконного световода интенсивность туннелирую-
щих лучей уменьшается, и в конце концов весь торец будет казаться темным.
8.13. Пример. Волоконные световоды с усеченным степенным профилем
Повторяя рассуждения, приведенные в начале предыдущего раздела, можно использо-
вать результаты разд. 4.10 при определении структуры пучка на рис. 8.8, когда воло-
конный световод имеет усеченный степенной профиль, определенный в табл. 2.1. Если
6т (0) < 0О < я/2, где 0т (0) = % и определено выше, то пучок не содержит направля-
емых лучей, а если 0 < Оо < 0т(О), то в круге радиусом гЬг (4.26) на выходном торце
волоконного световода находятся только направляемые лучи. Если пренебречь эллип-
тичностью пучка, которая обусловлена наблюдением торца под острым углом, то наблю-
датель будет видеть яркую область внутри окружностей, выделенных на рис. 8.10
штриховкой. Граница между туннелирующими и рефрагирующими лучами задается в
соответствии с выражением (2.24) уравнением /32 + Т2 = н2р Если подставить выраже-
Рис. 8.10. Зависимость структуры интенсивности свечения торца волоконного светово-
да с усеченным степенным профилем от показателя степени q и угла наблюдения 0О.
Черные области соответствуют рефрагирующим, заштрихованные - туннелирующим,
а светлые области внутри штриховых окружностей - направляемым лучам
151
ния для инвариантов (2.16) и (2.17) и функцию профиля, то с помощью соотношения
п (г) sin 0z (г) = w0sin<90 найдем [11]
г я
у
sin20n . и2sin2вп
-----Г- (t-)2cos20 (г) +-^------1 = 0.
"£о-«с1 р псо~пс1
(8.37)
Для параболического профиля (q = 2) эта кривая является эллипсом. При q < 2 и 0 <
< <90 < % она определяет границу между черными областями, соответствующими рефра-
гирующим лучам, и заштрихованными областями, соответствующими туннелирующим
лучам (см. рис. 8.10). Допустим, что длина волоконного световода является не слиш-
ком большой, так что, как объяснено в предыдущем разделе, существует резкое отли-
чие между средними интенсивностями рефрагирующих и туннелирующих лучей и между
интенсивностями направляемых и средними интенсивностями туннелирующих лучей.
Если <9т < 0О < я/2 и q < 2, то уравнение (8.37) не имеет решения, и пучок содержит
лишь рефрагирующие лучи, соответствующие черным областям. При q > 2 пучок содер-
жит как туннелирующие, так и рефрагирующие лучи, если значение 0О не превышает
значения решения уравнения [11]
2«?sins0o = <7 («со -«сР- (8.38)
Когда уравнение (8.37) не имеет решения, пучок содержит только рефрагирующие лучи.
ПОТЕРИ НА ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ
До сих пор в этой главе предполагалось, что волоконный световод является
непоглощающим и что все потери мощности связаны исключительно с излу-
чением вытекающих лучей. Теперь будет рассмотрено суммарное действие
потерь, вызванных излучением и поглощением в материале. Наиболее важ-
ным результатом является то, что пространственно-установившегося режима
более не существует, поскольку каждый направляемый луч теряет при рас-
пространении мощность. При достаточно длинном волоконном световоде
любая мощность, которая не была потеряна на излучение, в конце концов бу-
дет поглощена.
Мощность в каждом луче спадает как ехр(—yz), где z — расстояние вдоль
волоконного световода и у — коэффициент затухания мощности. Для направ-
ляемых лучей у = 7С0 +'ус? где усо и ус1 - коэффициенты затухания за счет
поглощения в сердцевине и оболочке, и для вытекающих лучей у = усо + ус1 +
+ у1г, где 71г — коэффициент затухания вытекающих лучей. Пренебрежем реф-
рагирующими лучами, поскольку они быстро затухают. Это эквивалентно
предположению, что у^ = <». Полную лучевую мощность в сечении z волокон-
ного световода Ps (z) найдем’ интегрируя функцию распределения (4.45а) с
весом, равным множителю, характеризующему затухание по всем лучевым
направлениям. Следовательно,
"со _7тах(Й)
Ps(z)=/6?/3 / F()3,/ )ехр(—yz)d/, (8.39)
о о
где /тах (0) задается выражением (2.24). Теперь рассмотрим примеры, ког-
да в качестве возбудителя используется диффузный источник.
8.14. Пример. Волоконный световод со ступенчатым профилем
В волоконном световоде со ступенчатым профилем коэффициент затухания туннелиру-
ющих лучей задается отношением коэффициента прохождения (7.19) к лучевому полу-
периоду (см. табл. 2.1). Если предположить, что коэффициенты поглощения в сердце-
152
Рис. 8.11. Относительная суммарная мощность направляемых и туннелирующих лучей,
остающаяся в поглощающем волоконном световоде со ступенчатым (а) и усеченным
параболическим (б) профилями, возбуждаемом диффузным источником. Верхняя кри-
вая на рис. 8.11, а при 7tr = 0 соответствует нулевому затуханию туннелирующих лу-
чей, нижние кривые на обоих рисунках - нулевой мощности туннелирующих лучей.
Штриховые кривые построены для непоглощающего волоконного световода
вине и оболочке асо и аср то соответствующие коэффициенты затухания задаются выра-
жениями (6.10) и (6.21), где углы 6Z и 6^ связаны с 0 и 7 соотношениями (2.7). Отно-
шения Ps(z) /Ps(0), получающиеся в результате численного интегрирования уравнения
(8.39), приведены на рис. 8.11, а (средняя кривая) для V = 70, 0с - 0,1, р = 70 мкм,
асо ~ 5 дБ/км и acj =50 дБ/км [16]. Лучевая мощность спадает до нуля на расстоянии
приблизительно 4 км. При расчете верхней кривой считалось, что потерь на излучение
нет. Это эквивалентно 7^ = 0 в уравнении (8.39). Штриховые кривые соответствуют
непоглощающему волоконному световоду (в уравнении (8.39) 7Ю = 7cj = 0). Нижняя
кривая относится только к направляемым лучам, т. е. Ps(z) = (z).
8.15. Пример. Волоконный световод с усеченным параболическим профилем
В волоконном световоде с усеченным параболическим профилем коэффициент затуха-
ния туннелирующих лучей 7^ задается отношением (7.18) к лучевому полупериоду
Zp (см. табл. 2.1). Пусть сердцевина является непоглощающей, а оболочка - поглощаю-
щей, тогда 7ci определяется выражениями (6.28) и (6.266). На рис. 8.11, б приведены
результаты численного интегрирования уравнения (8.39) для волоконного световода
при V = 50, 0С = 0,14 и aci = 100 дБ/км [10]. Кривые подобны кривым для ступен-
чатого профиля, однако влияние поглощения в оболочке сильно ослаблено, поскольку у
большинства лучевых траекторий точки поворота расположены достаточно далеко от
границы сердцевины.
ГЛАВА 9. ИЗГИБЫ
В этой главе изучаются потери на излучение из оптических волноводов, вы-
званные изгибами. Как будет показано с помощью уравнения лучевых траек-
торий, в изогнутых волноводах не существует направляемых лучей. Соответ-
ственно каждый луч является вытекающим и излучает мощность за счет тун-
153
копирования или рефракции (см. гл. 7). Иными словами, полное внутреннее
отражение, которое имеет место в прямолинейном волноводе, нарушается
вследствие изгиба. При вычислении потерь на излучение будем использовать
геометрическую оптику для определения траектории вытекающего луча
внутри сердцевины изогнутого волновода и соответствующий коэффициент
прохождения мощности при определении потерь в точках поворота или от-
ражения [1]. Полные потери на излучение равны сумме потерь вдоль всех
траекторий вытекающих лучей [2]. Для применяемых на практике многомо-
довых волноводов потери на изгибе пренебрежимо малы, поскольку радиус
изгиба, как правило, чрезвычайно велик по сравнению с размерами серд-
цевины [3,4].
В изогнутых планарных волноводах потери на излучение обусловлены вы-
текающими лучами, которые являются либо туннелирующими, либо рефра-
гирующими. При определении потерь на участках, достаточно удаленных от
начала изгиба, достаточно рассмотреть только туннелирующие лучи. Анализ
упрощается благодаря тому, что распространение лучей вдоль изогнутого
плоского волновода идентично их распространению в поперечном сечении
круглого волновода. Поэтому коэффициенты прохождения являются просто
частными случаями аналогичных коэффициентов для волоконных светово-
дов [5].
Изогнутый волоконный световод можно представить себе как сегмент
кольца или тора, а траектории вытекающих лучей соответствуют траектори-
ям рефрагирующих либо туннелирующих, либо туннелирующих-рефрагиру-
ющих лучей. По сравнению с изогнутыми планарными волноводами опреде-
ление потерь на излучение в волоконных световодах требует построения лу-
чевой траектории в сердцевине более сложной геометрии и использования
локальных коэффициентов прохождения для границ сердцевины или каус-
тик точек поворота, определяемых двумя радиусами кривизны, как это об-
суждалось в разд. 7.13 и 7.14. Это аналогично определению потерь на излу-
чение в некруглых волоконных световодах (см. гл. 8).
При рассмотрении планарных волноводов сначала будет показано, что
все лучи являются вытекающими. Затем будут найдены их траектории и
затухание.
ИЗОГНУТЫЕ ПЛАНАРНЫЕ ВОЛНОВОДЫ
Показанный на рис. 9.1 планарный волновод имеет прямолинейный участок
длиной J, переходящий к изогнутому участку с постоянным радиусом изги-
ба R. Диффузный источник S возбуждает в сечении z волновода все направ-
ляемые и рефрагирующие лучи. Пусть длина d достаточно велика, так что
имеет место пространственно-установившийся режим. Тогда на изгибе следу-
ет рассматривать только те лучи, которые на прямолинейном участке волно-
вода являются направляемыми. Любой луч, являющийся на прямолинейном
участке вытекающим, на изогнутом участке имеет гораздо большее затуха-
ние, и им можно пренебречь.
9.1. Классификация лучей на изгибе
Здесь будет показано, что все лучи в изогнутом планарном волноводе явля-
ются вытекающими независимо от профиля показателя преломления. Рас-
154
Ч ф=о
Рис. 9.1. Диффузный источник 5, возбуждающий торен прямолинейного участка планар-
ного волновода или волоконного световода, который переходит в изгиб с радиусом R
(длина прямолинейного участка - d, полуширина или радиус сердцевины - р)
Рис. 9.2. Лучевые траектории на изгибе планарного волновода со ступенчатым профилем
(д) и зависимость относительной мощности, остающейся в волноводе, от длины изгиба
при V = 50 и вс = 0,1 (б)
смотрим изгиб как часть круглого волоконного световода, ось которого
ортогональна плоскости изгиба и проходит через точку С (см. рис. 9.1). Име-
ются две границы: при г = R ± р, где г — радиус в цилиндрических коорди-
натах с центром в точке С, и предполагается, что форма профиля показателя
преломления сердцевины не изменяется при изгибе, т. е. п (г) = п(х),г = х +
+ R. Вследствие азимутальной симметрии каждый луч следует по изогнутой
синусоподобной траектории. Если сердцевина является градиентной, то траек-
тория имеет характерный вид, показанный на рис. 9.1, а если она однородна,
то траектория имеет зигзагообразную или многоугольную форму, показан-
ную на рис. 9.2, а. Эти траектории лежат в поперечном сечении воображаемо-
го волоконного световода и, следовательно, продольный лучевой инвариант
{$ удовлетворяет условию |Т= 0 для каждого луча.
155
Лучевой инвариант для изгиба. Для каждой траектории в изгибе существу-
ет инвариант I ь. По аналогии с выражением (2.17) положим 0Z (г) = я/2 и
определим
Tb = {rl (R + р)} п (г) cos (R), (9.1)
где R + р — радиус наружной границы и 0^ (г) — угол между касательной к
траектории и азимутальным направление^ (см. рис. 9.1). Свяжем/ь с инва-
риантом 3S прямолинейного волновода (|3 в табл. 1.1) через функцию про-
филя п (х) и угол между касательной к траектории и направлением оси 0Z (х).
В начале изгиба 0Z (х) = 0^ (г0), где г0 — значение г при = 0, так что в пря-
молинейном волноводе
=«(x)cos0z (х) =w(r0)cos^(r0)- . (9.2)
Если сравнить выражения (9.2) и (9.1) при г = г0, то получим для изгцба
7b = Ы(Я + р)} 3S- (9.3)
В прямоугольном волноводе инварианты направляемых лучей удовлетворя-
ют условию ис1 < Ps < пс0. Следовательно, для любого профиля значения
/ь ограничены условием
nci(R - р)/(R + р) <ть <«со> (9-4)
поскольку R — р <г0 <Р + р.
Каустика излучения на изгибе. Для туннелирующего луча на изгибе поло-
жение каустики излучения rrad и траектории в оболочке показаны на рис. 9.1.
Значение rrad задается выражением (2.23) при 3 = 0,Z = /ь и замене р наR + р:
г^ = (Я + р)Ть/лс1. (9.5)
Поскольку согласно (9.4) /ь конечно, rrad должна быть конечной, и поэто-
му каждый луч на изгибе является вытекающим. Туннелирующие лучи име-
ют rrad >R + р, а рефрагирующие лучи rrad = R + р. На изгибе с малой кривиз-
ной фактически все лучи являются туннелирующими.
9.2. Затухание световой мощности
Каждый луч на изгибе излучает мощность за счет либо туннелирования, либо
рефрагирования. Для того чтобы определить затухание мощности каждого
луча, воспользуемся описанием, приведенным в разд. 7.1, заменив z на угло-
вую координату (см. рис. 9.1). Если Р(<р) — мощность в сечении и у —
коэффициент затухания мощности, тогда по аналогии с (7.3) имеем
P(ip) = Р(0) exp (—?</>), (9.6)
где Р(0) — мощность направляемого луча в прямолинейном волноводе. Для
того чтобы установить связь между у и коэффициентом прохождения мощно-
сти (7.1), определим <рр как угловое расстояние между последовательными
точками поворотов или отражений, в которых теряется мощность (на рис. 9.1.
<рр - угол между лучами СР и CQ). Тогда по аналогии с (7.2) имеем
7 = Т/<рр. (9.7)
Для того чтобы найти полную лучевую мощность Р(<р) в сечении изгиба,
проинтегрируем выражение (9.6) по всем лучевым направлениям и по попе-
156
речному сечению сердцевины. Если предположить, что волновод является
слабонаправляющим, то начальная мощность Р(0) на прямолинейном участ-
ке волновода фактически одинакова для всех лучей. Тогда по аналогии с
(4.12) в предположении, что геометрия волновода является плоской и лучи
затухают, имеем
R+P ос(г)
GO = Р(0) f dr f exp (—y<p) d6z, (9.8)
R-p
где вс(г) << 1 — локальный критический угол скольжения (2.29), отнесен-
ный к центру кривизны. Поскольку Т и зависят от профиля показателя
преломления, рассмотрим характерные примеры.
9.3. Пример. Ступенчатый профиль
В изогнутом ступенчатом планарном волноводе лучевые траектории являются отрезка-
ми прямых линий, соединяющими точки отражения от внутренней и внешней границ,
как показано на рис. 9-2, а. Траектория 1 отражается попеременно от внутренней и внеш-
ней границ, а траектория 2 - только от внешней границы, такой луч называется лучом
"шепчущей галереи" [б]. Для любой траектории инвариант (9.1) сводится к
/ь = «Cocos^ = {(R ~ р)/(-R + ncQcose^> (9-9)
где и 0^ - углы между траекторией и касательной к наружной или внутренней грани-
цам соответственно. Следовательно, лучи шепчущей галереи удовлетворяют условию
cos0^> (R-p)l(R+p). (9.10)
Поскольку на практике R > > р, то лишь некоторые лучи, близкие к 0^ = 0, удовлетво-
ряют этому условию. Границу между туннелирующими и рефрагирующими лучами на
изгибе найдем, подставляя (9.9) в (9.5), откуда
''rad/ + Р) = (”co/”cl>cosV <9Л1>
На основании разд. 9.1 заключаем, что если > ес, где вс = arccos {п^/п^ - крити-
ческий угол скольжения, то луч рефрагирует на внешней границе, и если 0^ < 0С, то он
туннелирует. На внутренней границе имеет место рефракции, если 0^ > 0С; мощность не
теряется, если 0^ < 0С, так как для падающего луча граница является выпуклой [5].
Поскольку в соответствии с выражением (9.9) 0' < 0 , то лишь некоторые лучи рефра-
гируют на одной из двух или на обеих границах. Это те направляемые лучи прямолиней-
ного волновода, для которых 0Z близко к 0С. Таким образом, фактически все лучи на
изгибе являются туннелирующими и теряют мощность только на наружной границе.
Затухание мощности. Для того чтобы описать потери из-за туннелирования, использу-
ем коэффициент прохождения мощности (7.20) при 0 = 0 и 7 = 7b = nCQcos0 . При рас-
чете потерь за счет рефракции используем выражение (7.4) для классического коэффи-
циента Френеля, заменив 0Z на 0^ или 0^ соответственно для наружной и внутренней гра-
ниц. Угол ^р, используемый в выражении (9.7), для траекторий 7 и 2 рис. 9.2, а задается
соответственно соотношениями .
*р = 2%-9; = (9Л2)
если лучи теряют мощность только на наружной границе. Для лучей, которые рефраги-
руют на внутренней границе, = 0^ - 0^. Если R>> р, то из выражения (9.9) получа-
ем, что 0^ - 0^ « 2pl0 R> и угол, при котором траектория 7 переходит в траекторию 2,
составляет 0 « 2 (р/7?)1/2. Угол 0^ связан с углом 0Z в прямолинейном волноводе соот-
ношениями (9-2), (9.3) и (9.9), откуда
cos^ = rocos0z/(7? +р). (9.13)
157
Поскольку R - р < r0 <Л + p, заключаем, что 0^ > 0z. Даже если 0z < < 1, 0^ может
быть много больше, чем 0z. Только когда R/р -► «>, можно предположить, что 0^ е^.
Используя факты, приведенные выше, вычислим коэффициент затухания мощности
(9.7) и с помощью выражения (9.8) при 0С (г) = 0С полную мощность. Зависимость оста-
ющейся мощности от нормированного расстояния z /р = R^/p вдоль оси изогнутого вол-
новода приведена на рис. 9.2, б для V = 50 и 0с = — 0,1 [2, 3]. При уменьшении
нормированного радиуса кривизны Л/р мощность теряется быстрее. Каждая из кривых
имеет один и тот же характер поведения. В начале существует переходная область с
быстрыми потерями мощности, обусловленными рефрагирующими и туннелирующими
лучами с наибольшими коэффициентами затухания. Затем кривые переходят по суще-
ству в прямые, соответствующие области пространственно-установившегося режима,
где мощность экспоненциально уменьшается с ростом zip. Эта область соответствует
только туннелирующим лучам. Кроме того, при фиксированном значении V потери рас-
тут при уменьшении 0с. Наиболее важно, однако, то, что при используемых на практике
радиусах изгиба, удовлетворяющих соотношению Rlp> 103 .потери пренебрежимо малы.
9.4. Пример. Усеченный параболический профиль
Рассмотрим снова рис. 9.1. Прямолинейный волновод имеет усеченный параболический
профиль, заданный в табл. 1.1, а на изгибе - профиль показателя преломления сердце-
вины относительно оси С, определенный выражением
и2(г) =и’о {1-2Д(г-/?)3/р2). (9.14)
Каждой траектории соответствует инвариант (9.1), который соотношением (9.3)
связан с инвариантом 0S соответствующей траектории направляемого луча на прямоли-
нейном участке. _
Из выражения (9.1) ясно, что если < wcp то траектория доходит до наружной гра-
ницы изгиба и преломляется. Однако существует лишь незначительное количество та-
ких траекторий, для которых 0$ ~ «с1. Каждый туннелирующий луч имеет характерную
траекторию, показанную на рис. 9.3, а. и значение его инварианта изменяется в диапазо-
не ис1 < <«со- Эта траектория образует угол 6^ (г) с азимутальным или z-направлени-
ем и лежит между внутренней каустикой и каустикой точек поворота с радиусами г-с
и rtp относительно центра изгиба С. Если подставить выражение (9.14) в (9.1) и поло-
жить (г) = 0, то найдем, что и rtp являются корнями квадратного уравнения
(Л+р)27^г2л2 (г). (9.15)
Рис. 9.3. Лучевая траектория на изгибе планарного волновода с усеченным параболи-
ческим профилем (а) и зависимость относительной мощности, остающейся в волноводе,
от длины изгиба при Е=5Ои0с=О,1 (б)
158
По сравнению с прямолинейным волноводом влияние изгиба проявляется в смещении
каустик по направлению к внешней границе (см. рис. 9.3, а).
Затухание мощности. Пусть рефрагирующий луч теряет всю мощность, когда он
достигает границы, т. е. Т - 1. Туннелирующие лучи теряют мощность только на каусти-
ке точек поворота потому, что внутренняя каустика является выпуклой для лучевой
траектории. Достаточно высокая точность определения затухания обеспечивается в том
случае, если для коэффициента прохождения использовать линейное приближение (7.17),
в котором Д — 0, 1 = 7^ и р заменено на R + р. Подставляя выражение для профиля по-
казателя преломления (9-14), получаем
f ? 7? р 7* )
Г =ехрЛ^/ЦЯ+р) (-£- ~ l)3/3/d --7Г1-------(916)
I з n’j R+p J
где 2Д = 02. При определении углового расстояния между последовательными на-
ружными точками поворота на рис. 9.3,а заметим, что если R >> р, то соответствую-
щее расстояние вдоль оси в прямолинейном волноводе приблизительно задается удвоен-
ным лучевым полупериодом г?. Заменив в выражении для (см. табл. 2.1) 0 на 7^ и
использовав соотношение R<рр = 2zp, получим
«Рр ~ 2itplbIR (п^ - и2с1)1/2. (9.17)
Коэффициент затухания мощности для каждого луча получается из выражения (9.7), а
полная остающаяся мощность рассчитывается из выражения (9.8) после замены пере-
менной 0Z на 0 = п (х) cos0z. На рис. 9.3, б показаны кривые зависимости остающейся
мощности от нормированного расстояния z Ip = Rip Ip вдоль изогнутой оси волновода
при V = 50 и 0С = (2Д)1/2 = 0,1 [2, 4]. Характер поведения этих кривых напоминает
характер поведения кривых на рис. 9.2, б для волновода со ступенчатым профилем. Од-
нако при заданном радиусе изгиба потери в случае параболического профиля оказыва-
ются больше. Это связано с тем, что каустика точек поворота смещается по направле-
нию к наружной границе (см. рис. 9.3, я) . Вследствие этого потери становятся больше и
сравнимы с потерями для соответствующей траектории (при таком же значении Э в
прямолинейном волноводе (см. рис. 9.3, б); в последнем случае угол распространения
луча в световоде увеличивается от 0Z до 0^. Вывод: потери на изгибе в применяемых на
практике волноводах оказываются пренебрежимо малыми.
ИЗОГНУТЫЕ ВОЛОКОННЫЕ СВЕТОВОДЫ
Как указывалось в начале этой главы, идея нахождения потерь на изгибе пла-
нарных волноводов и волоконных световодов одинакова. Конечно, существу-
ет усложнение геометрии, связанное с еще одним измерением, и лучи в изог-
нутом световоде, вообще говоря, имеют трехмерные спиралевидные траек-
тории. Более важно однако то, что каждый луч касается или отражается от
поверхностей, которые теперь определяются двумя радиусами кривизны, и
при этом в соответствии с разд. 7.14 требуются более общие выражения для
потерь.
Классификация лучей. Изогнутый волоконный световод, показанный на
рис. 9.4, можно представить как сегмент кольца или тора. Меридиональные
лучи распространяются в плоскости изгиба, определяемой изогнутой осью
волоконного световода и центром кривизны С, и идентичны лучам на изги-
бе планарного волновода. В частности, они распространяются вдоль траекто-
рий с постоянными пол у периодами. Все остальные лучи являются косыми и
вследствии асимметрии, вносимой изгибом, распространяются вдоль траек-
торий с переменными пол у периодами, как показано на рис. 9.4.
159
Рис. 9.4. Траектория косого луча с переменным полупе-
риодом на участке изогнутого волоконного световода
Затухание световой мощности. Как было по-
казано на примере изогнутых планарных волно-
п водов, все лучи в изогнутых волоконных свето-
с водах являются вытекающими. Меридиональные
f /\ ] лучи оказываются либо туннелирующими, либо
рефрагирующими, а косые лучи теряют мощность
в последовательных точках отражения или пово-
рота за счет либо туннелирования, либо рефрагирования. Последние аналогии
ны туннелирующим-рефрагирующим лучам в некруглых волоконных свето-
водах, рассмотренных в разд. 2.14. Пусть, как и в случае, показанном на
рис. 9.1, диффузный источник возбуждает достаточно длинный прямолиней-
ный участок волоконного световода, так что в начале изгиба достигается про-
странственно-установившийся режим. Анализ лучевых траекторий на изогну-
том участке зависит от профиля показателя преломления. Если профиль яв-
ляется ступенчатым, то на участках между последовательными отражениями
траектория задается отрезками прямых линий, а координаты точек отраже-
ния являются решениями кубического уравнения или уравнения четвертого
порядка; если профиль является усеченным параболическим, то использует-
ся параксиальное приближение [2]. Граница и каустика точек поворота яв-
ляются кривыми поверхностями. Они определяются двумя главными радиу-
сами кривизны, которые зависят как от радиуса сердцевины р, так и от ра-
диуса изгиба R. При этих условиях можно пользоваться локальными коэф-
фициентами прохождения (см. разд. 7.14) каждый раз, когда луч теряет
мощность вследствие туннелирования. Если мощность теряется за счет ре-
фракции, будем использовать для ступенчатого профиля коэффициент Фре-
неля (35.50), а для усеченного параболического профиля считать, что мощ-
ность теряется полностью, т. е. Т - 1.
По аналогии с выражением (9.8) полная мощность в любом сечении изо-
гнутого участка задается четырехкратным интегралом от мощности в каж-
дом луче по поперечному сечению и по всем направлениям вытекающих лу-
чей. Вычисление этого интеграла усложнено тем, что в отличие от меридио-
нальных лучей коэффициент затухания для косого луча изменяется вдоль
его траектории. Это означает, что для правильного определения затухания не-
обходимо найти всю траекторию.
9.5. Пример. Ступенчатый и усеченный параболический профили
Вычисление лучевой мощности в изогнутых волоконных световодах с такими профиля-
ми основывается на описанной выше методике. Здесь будут представлены результаты
(более подробно см. например, [2]). На рис. 9.5 представлены графики отношения
мощностей Ps(z)/Ps(0) от нормированного расстояния z/p вдоль изогнутой оси воло-
конного световода для ступенчатого профиля (я) и усеченного параболического профи-
ля (6). Здесь Ps (0) обозначает полную мощность направляемых лучей на прямолиней-
ном участке. В обоих случаях V — 50 и 0с = 0,1 и Rip соответствуют значениям для изо-
гнутых планарных волноводов (см. рис. 9.2, б и 9.3, б). Качественный характер кривых
160
Рис. 9.5. Зависимость относительной мощности, остающейся в волоконном световоде,
от длины изогнутого участка при V = 50 и 0С = 0,1 для ступенчатого (а') и для усечен-
ного параболического (б) профилей
на рис. 9.5 тот же, что и у кривых для планарных волноводов, однако потери мощности
в пространственно-неустановившемся режиме не так велики, поскольку только неко-
торые лучи с траекториями вблизи меридиональной плоскости имеют большие потери.
За областью пространственно-неустановившегося режима затухания мощности больше
чем для планарного волновода. Это связано с тем, что косые лучи могут,проходить че-
рез области большого затухания, хотя первоначально могли иметь малое затухание. Од-
нако так же, как и для планарных волноводов, потери мощности в изогнутых волокон-
ных световодах при используемых на практике значениях радиусов изгиба пренебрежи-
мо малы.
ГЛАВА 10. ДИФРАКЦИОННЫЕ ЯВЛЕНИЯ
В первых пяти главах при описании распространения света в оптических вол-
новодах использовалась только геометрическая оптика и поэтому игнориро-
вались все явления, которые зависят от длины волны, В этой главе будет по-
казано, что такое описание является точным для волноводов со сравнитель-
но большим поперечным сечением сердцевины, т. е. для многомодовых вол-
новодов с V >> 1. Однако в случае волноводов с относительно малыми раз-
мерами сердцевины и малыми значениями V для описания распространения
света требуется подход, основанный на теории электромагнитных волн (см.
ч. II). Наша цель состоит в том, чтобы объяснить с физической точки зрения
несостоятельность анализа с помощью геометрической оптики при малых V
и предсказать новые свойства света при его распространении. Главное пред-
положение всех предшествующих глав состоит в том, что световая мощность
переносится вдоль лучевых траекторий, определяемых соответствующим
уравнением. Любое отклонение потока мощности от лучевой траектории
обусловлено только волновой природой света, т. е. конечной длиной волны
[1]. В этой главе влияние волновых эффектов на распространение света бу-
дет исследовано на простейших возможных моделях. Сначала напомним, что
отклонение потока мощности от лучевой траектории часто оказывается нич-
6 Зак 37
161
тожно малым в многомодовых волноводах, применяемых на практике, и им
можно пренебречь, как это было сделано в гл. 1-5. Однако при рассмотре-
нии потерь, обусловленных поглощением в оболочке или кривизной оси вол-
новода, волновыми эффектами пренебречь нельзя, несмотря на их слабое
проявление, поскольку они лежат в основе механизмов затухания мощности.
В гл. 6 — 9 такие волновые эффекты были учтены с помощью использования
коэффициента прохождения, который был выведен с привлечением теории
локальных плоских волн, но лучевые траектории были сохранены. Э1а гла-
ва посвящена главным образом рассмотрению ошибки, вызванной исполь-
зованием лучевой траектории и неучтенной во всех предыдущих главах.
Сначала будет качественно показано, что вследствие дифракции невозмож-
но удержать свет только внутри сердцевины волновода с любым конечным
значением V. Таким образом, свет должен распространяться как внутри серд-
цевины, так и внутри оболочки, если он должен быть направляемым. Эта си-
туация не описывается классической геометрической оптикой. Используя
планарный волновод со ступенчатым профилем, можно достаточно просто
показать, как дифракция изменяет классическую лучевую картину распро-
странения света. Для начала кратко рассмотрим дифракцию пучка света, рас-
пространяющегося в свободном пространстве, поскольку это является осно-
вой анализа.
ДИФРАКЦИЯ ПУЧКА СВЕТА
При описании с помощью геометрической оптики можно было бы ожидать,
что ограниченный пучок параллельных лучей распространяется в однородной
среде на неограниченное расстояние, не расширяясь. Однако из-за дифракции
оказывается, что чем уже пучок, тем больше диапазон направлений лучей, его
образующих и, следовательно, тем больше он расширяется при своем распро-
странении. Это одна из причин, почему для передачи на большое расстояние
необходима направляющая структура — оптический волновод. Для того что-
бы количественно оценить это расширение, дадим краткий обзор основных
свойств дифракции пучка, дополнив его простыми примерами.
10.1. Однородные и гауссовы пучки
Для того чтобы описать дифракцию пучка, разложим его электрическое поле
на составляющие плоские волны, выполняя двумерное преобразование
Фурье (см. разд. 36.3). Дифракция, или расширение, пучка вызывается тем,
что эти составляющие плоские волны, или лучи, распространяются в различ-
ных направлениях. Это аналогично дифракции на апертуре, площадь которой
равна поперечному сечению пучка [2, 3]. В качестве примеров рассмотрим
однородный и гауссов пучки круглого поперечного сечения, которые распро-
страняются в z -направлении в среде с однородным показателем преломления
п. Поля пучков являются монохроматическими с длиной волны в свободном
пространстве. Зависимость амплитуды осесимметричного электрического по-
ля Е(г) от цилиндрической координаты г приведена в табл. 10.1, где я не-
произвольные масштабные длины. Амплитуда дифракционной структуры
А (и) является двумерным преобразованием Фурье функции Е (г) и нормиру-
ется к единице для волн, распространяющихся вдоль оси (и = 0), где и опи-
162
сывает наклон дифракционных волн к оси z под углом 0Z. Это преобразова-
ние часто называется преобразованием Ханкеля, таблицы для которого даны
в [4].
Таблица 10.1. Поля пучков и их Фурье-преобразования
Гауссов пучок Однородный пучок
£(г) ехр( — (г/а)2) u*' V <л V/ Д О U -Г сГ
Л (и) ехр { — (иа/2)2} 2Jt(urs)
2яи . л и = — sin 0z Л(и)= f E(r)J0(ur)rdr 1 f E(r)rdr Jo 1 Jo
Примечание. Амплитуда электрического поля Е(г) и амплитуда дифрак-
ционной структуры?! (и) \ Jo и Jx — функции Бесселя.
Преобразование пучка. Преобразование гауссова пучка является гауссо-
вым по форме, а преобразование однородного пучка дает цилиндрический
аналог функции sinх/х. Полезно также заметить, что интенсивность А2 (и)
дифракционной структуры однородного пучка является почти гауссовой
для значений ws, меньших чем первый нуль функции (urs) , и поэтому мо-
жет быть представлена в виде
А2 (и) ехр(-0,28 (ws) 2) . (10.1)
Наоборот, гауссов пучок с а % 0,75rs имеет почти такую же интенсивность
дифракционной структуры, как однородный пучок радиуса rs. Этот случай
иллюстрирует рис. 10.1. Ясно, что функция Л2 (и) является также почти гаус-
совой для пучков различных сглаженных профилей, промежуточных между
однородным и гауссовым, например заданных выражением (15.9), поэтому,
результаты и выводы, полученные для гауссова пучка широко применимы.
Характеристическая угловая ширина пучка. Полезно при описании интен-
сивности дифракционной картины ввести малую угловую ширину 0d в на-
правлении угла 0Z. Свяжем ее с соответствующим значением переменной
преобразования Md, для которой амплитуда дифракционной структуры
уменьшается в 1/е раз относительно своего максимального значения, т. е.
A (Md) = 1/е. Это дает
и d ~ 2/л; 0d X/ (ш) (10.2а)
для гауссова пучка и
~ 2,7/rs; 0d ~ 0,43X/flrs (10.26)
для гауссова приближения (10.1) однородного пучка. При уменьшении ха-
рактеристического радиуса пучка rs увеличивается 0d, и световое пятно рас-
163
6:
Рис. 10.1. Амплитуда электрического поля Е(г) и интенсивность дифракционной струк-
туры/!2^) для гауссова (а) иоднородного (б) пучков. Штриховая кривая соответству-
ет приближенному описанию однородного пучка гауссовым пучком (10.1). Величина
определена в (10.2)
ширяется быстрее в процессе своего распространения в z -направлении. Если
через rs(z) обозначить характеристический радиус пучка на расстоянии z
вдоль пучка, то в соответствии с геометрией он зависит линейно от з, т. е.
'sCO =rs(0) +z6d.
10.2. Удержание света волоконным световодом
Теперь можно осмыслить роль дифракции при распространении света вдоль
волоконных световодов с относительно малыми значениями К, используя
качественные соображения, основанные на дифракции пучка и направляемых
лучах. Рассмотрим слабонаправляющий волоконный световод, который име-
ет сердцевину радиуса р и произвольный профиль показателя преломления.
Допустим, что электрическое поле является х-поляризованным, его ампли-
туда Е(г) зависит от радиуса г и имеет гауссову форму, приведенную на
рис. 10.1, а. Интенсивность света S в поперечном сечении волоконного свето-
вода тоже имеет гауссову зависимость, поскольку она пропорциональна
Е2 (г). Таким образом, электрическое поле волоконного световода является
электрическим полем гауссова пучка, рассмотренного в предыдущем разде-
ле. Это дает нам возможность определить масштабную длину а из табл. 10.1,
которая позволяет характеризовать концентрацию направляемого света в
пределах сердцевины волоконного световода. В разд. 10.1 было показано,
что пучок имеет присущую ему угловую ширину 0d, вызванную дифракцией.
Поэтому ясно, что самый узкий пучок, который сохраняет распределение ин-
тенсивности света вдоль волоконного световода, имеет дифракционное рас-
ширение, равное критическому углу скольжения 0С, поскольку все лучи, рас-
пространяющиеся в пределах этого угла, являются направляемыми. Следова-
тельно, используя (10.2а), заключаем, что
0d=0c; л = Х/тги0с, (10.3)
где 0С было определено выше, а однородный показатель преломления п ^nCQ4
В частном случае, когда значение а совпадает с радиусом сердцевины р, ис-
пользуя определение К, получаем V = 2.
164
Хотя приведенные выше рассуждения являются только качественными,
они важны, поскольку показывают, что при распространении света имеет
место равновесие между расширением направлений лучей из-за дифракции и
удержанием лучей за счет градиента профиля показателя преломления. Мерой
этого равновесия является волоконный параметр. Если в формуле V -
= крпс0 (2Д)1/2 положить р =а и подставйть соотношения (10.2а), то получим
Г = 20с/0а. (10.4)
Следовательно, для многомодовых волоконных световодов, у которых
V » 1, имеем 0d << 0С, и дифракция играет незначительную роль при рас-
пространении света. Однако для волоконных световодов, у которых V < 2,
0d > 0С, и дифракция оказывает основное влияние на распространение света.
Это позволяет объяснить, почему невозможно концентрировать световую
мощность внутри волоконных световодов малого радиуса, т. е. с р << я,
где а задается выражением (10.3).
10.3. Применимость геометрической оптики
Рассмотрение, проведенное выше, дает возможность оценить случай, когда
использование геометрической оптики для анализа распространения света в
оптических волноводах имеет силу. В классических случаях, например при
построении хода лучей через линзу, требуется только постоянство профиля
показателя преломления п на расстоянии, равном длине волны света в среде.
Для оптического волновода это условие выполняется при р >> Х/и, где р —
радиус сердцевины и X — длина волны света в свободном пространстве. Од-
нако вследствие дифракции при рассмотрении оптических волноводов этого
условия недостаточно; как будет показано ниже, для того чтобы применить
геометрическую оптику, необходимо дополнительное требование — оптичес-
кий волновод должен быть многомодовым с параметром V » 1. По опре-
делению V = 27гр«со0с/Х; ясно, что рпСО/Х может быть сколь угодно большим,
однако V может оказаться малым, если достаточно мало 0с, Например, ти-
пичный о дно модовый волоконный световод с V = 2,4 и @с = 0,01 имеет
pnCQl\ - 38, тем не менее применение геометрической оптики, например для
расчета дисперсии импульса, как это сделано в гл. 3, привело бы к весьма не-
точным результатам.
Дифракционное ограничение. В соответствии с геометрической оптикой
весь направляемый свет распространяется по траекториям направляемых лу-
чей и, следовательно, весь сосредоточен внутри сердцевины волоконного све-
товода, Однако вследствие дифракции, если свет занимает область радиуса
р, это вызывает угловое расширение с характеристической шириной 0d, кото-
рая согласно (10.2а) пропорциональна XlpnQQ. Очевидно геометрическая оп-
тика является плохим приближением, если ширина 0d не оказывается малой
по сравнению с угловой шириной всего пучка направляемых лучей (2.6а),
т. е. если не выполняется условие 0d << 0С. Учитывая это условие и выраже-
ние (10.4), получаем требование V>> 1.
Распространение в оболочке. Проведенное выше рассмотрение дает осно-
вание ожидать, что световая мощность должна проникать глубоко в оболоч-
ку волоконного световода с малым значением параметра V, поскольку угло-
вое расширение, вызванное дифракцией, увеличивается при уменьшении ши-
165
рины пучка. Это противоречит положению геометрической оптики, что мощ-
ность полностью сосредоточена внутри сердцевины. Дифракция является так-
же причиной неприменимости геометрической оптики и в более известных
примерах: в фокусе линзы и на каустиках, ограничивающих лучевые траек-
тории в волоконных световодах.
ВЛИЯНИЕ ДИФРАКЦИИ НА ПОЛНОЕ ВНУТРЕННЕЕ ОТРАЖЕНИЕ
Рассмотрим теперь планарный волновод со ступенчатым профилем, чтобы
дать количественный пример влияния дифракции на анализ методами класси-
ческой геометрической оптики при малых значениях волноводного парамет-
ра V. В гл. 1. было показано, что лучевые траектории направляемых лучей в
сердцевине такого волновода являются зигзагообразными (см. рис. 1.4, я),
и лучи испытывают полное внутреннее отражение на границах сердцевины и
оболочки. Пересмотрим теперь эту интерпретацию, более подробно рассмот-
рев механизм полного внутреннего отражения на плоской границе с тем, что-
бы лучше понять физику механизма проникновения световой мощности
внутрь материала оболочки. Это дает возможность показать, каким обра-
зом дифракционные эффекты могут быть описаны совместно с лучевой
картиной.
Полное внутреннее отражение. Когда плоская волна испытывает полное
внутреннее отражение на плоской границе между двумя полубесконечными
однородными диэлектрическими средами (рис. 10.2), в менее плотной сре-
де устанавливается спадающее поле, и отраженная волна по фазе отличает-
ся от падающей. Воспользуемся формулами, приведенными в разд. 35.6.
Рис. 10.2. Полное внутреннее отражение плоской
волны от плоской границы раздела между полу-
бесконечными средами с показателями преломле-
ния т?со и т?с). Если ис1 «ис0, фазовый сдвиг прак-
тически не зависит от направления вектора Е, т. е.
от поляризации
Рис. 10.3. Сдвиг луча при отражении от границы сердцевина-оболочка:
а — схематическое изображение лучевой траектории в оболочке; б — продольный сдвиг
пучка zy ось которого образует угол 0О с границей раздела сердцевина—оболочка; в —
сдвиг пучка, падающего на границу раздела под углом 0О = 0С, равен его ширине в
z-направлении. Показатели преломления граничащих сред составляют т?с0 и т?с| < лс0
166
В лучевом анализе в первых девяти главах фаза не учитывалась и предпола-
галось, что мощность передается только вдоль траекторий внутри более
плотной среды. Однако некоторая часть мощности луча переносится спада-
ющим полем, так что ’’полное” внутреннее отражение можно более точно
описать с помощью лучевой траектории, схематически показанной на
рис. 10.3,которая проходит через оболочку. Здесь предполагается, что
длина волны конечна, в то время как для траектории на рис. 10.2, я X = 0,
и она построена на основании закона Снелля. Исследуем теперь подробнее
этот вопрос, рассматривая влияние дифракционных эффектов на полное
внутреннее отражение.
10.4. Продольный сдвиг
Плоская волна считается бесконечно протяженной и поэтому не дает точно-
го описания потока мощности вдоль луча, занимающего лишь конечную об-
ласть пространства. По этой причине рассмотрим поток мощности в пучке,
который отражается от плоской диэлектрической границы (см. рис. 10.3, б).
В разд. 10.1 было показано, что пучок является суперпозицией континуума
плоских волн. Если 0z — угол между направлением распространения одной
из таких волн и границей, то зависимость амплитуды падающего и отражен-
ного электрических полей от z можно представить согласно разд. 35.6 в виде
Ei(z) =Лехр(10г); ET(z) =Лехр($г + 1Ф (0Z)), (10.5)
где А - константа, (3 = 2тсо cos 0Z/X; X - длина волны пучка в свободном
пространстве. Изменение фазы Ф(0г) при отражении зависит, вообще го-
воря, от поляризации поля, но если nCQ ncif то зависимость о.т поля-
ризации незначительная и выражается формулой Ф = —2arctg[(sin20c —
- sin20z)1/2/#sin0z], где# = 1 (вектор Е параллелен границе) и# =Л2с]/Л1с0
(вектор Н параллелен границе). Поскольку Ф(0г) является функцией 0Z,
плоские волны, формирующие пучок, испытывают при отражении разные
фазовые сдвиги. Суммируя отраженные волны, получим поле отраженного
пучка, которое отличается от поля падающего пучка. Теперь покажем, что
пучок при отражении сдвигается.
Определение продольного сдвига. Если падающий пучок образует с грани-
цей угол 0О, то, как следует из разд. 10.1, пучок характеризуется малой
угловой шириной относительно угла 30 для волн, составляющих пучок.
Таким образом, можно было бы разложить Ф(0г) по степеням 0z -0о,но
удобнее это сделать по степеням /3 — (30, где /30 = 2tt«cocos 0О/Х. Следова-
тельно, в первом приближении
ф(0) *М0о) + (Р-Зо)ФЧЗо), (10.6)
где Ф'(0О) означает производную дФ(/3) /д/3 в точке |30. Если подставить
это выражение в (10.5), получим поле отраженного пучка
Лг(и) =Cexp{i/3[z+Ф'(|3о)]}, (10.7)
где С — константа, не зависящая от (3. Тогда можно интерпретировать член
ФЧЗо), как сдвиг zs положения отраженного пучка (см. рис. 10.3, б). Если
исо а? ис1, то должно выполняться условие 0О << 1, чтобы имело место
полное внутреннее отражение. Дифференцируя выражение для Ф, находим,
что
167
ЭФ I 2 1
Э0 к кпсо0о (0С2-0О2)1/2
(10.8)
где к = 2я/Х и 0С - {1 — «с1/лсо )1/2 • Этот сдвиг часто называют сдвигом
Гооса-Генхена. В [5] приведен обзор многих работ из обширной литерату-
ры, посвященной этому вопросу, более поздние исследования содержатся
в [6 — 10]. На оптических частотах этот сдвиг очень мал, за исключением слу-
чая падения лучей под углом 0О = 0С. При этом падающий пучок проникает
глубоко в менее плотную среду.
Интерпретация с точки зрения потока мощности. Приведенный вывод ос-
новывается на рассмотрении фазы, и из него непосредственно не следует,
что сдвиг вызван распространением световой мощности внутри менее плот-
ной среды. Исчерпывающее доказательство требует более веских доводов
[6 — 10]. Для того чтобы показать связь между сдвигом и потоком мощно-
сти, рассмотрим ограниченный участок плоской волны шириной zssin0o> па-
дающей под углом 0Q к границе (см. рис. 10.3, в). Благодаря сдвигу падаю-
щая и отраженная волны не перекрываются и, следовательно, вся мощность
в отраженной волне должна ’’перетекать” из менее плотной среды в более
плотную. В самом деле, просто показать, что полный поток мощности в z-на-
правлении в менее плотной среде полностью совпадает с мощностью в пада-
ющей и отраженной волнах, если 0о & 0с. С использованием обозначений
разд. 35.6 последняя выражается формулой (zs/2)\А |2ис0 (б0/д0)1/2, а пер-
вая равна интегралу от (Ф2/2)ис1(бо/до)1/2 из выражения (35.22а) по интер-
валу 0 < х < °°. Используя соотношение между А и С (35.226) и приближе-
ния (sin20c — sin20o)1/2 << 0Q и 0о ^с, можно проверить приведенный вы-
ше результат.
10.5. Время прохождения продольного сдвига
Определим время прохождения пучком продольного сдвига z$. Концепция
времени прохождения подразумевает, что рассматривается пучок, существу-
ющий лишь конечный промежуток времени. Это соответствует концепции
сдвига, согласно которой используются пучки конечной протяженности или
пучки, неоднородные в пространстве. Следовательно, пучок не может быть
монохроматическим, а имеет малую полосу частот 6^ относительно цент-
ральной частоты са0. Фазовая функция Ф(0г) зависит от частоты вследствие
соотношения (3 - 2ttmcocos 0Z/X. Если выразить X через са, используя вы-
ражение Хсо = 27гс, где с — скорость света в свободном пространстве, то 0 =
= сапсоcos 0z/c. Разложим Ф(са) в окрестности соо и с учетом членов первого
порядка малости получим
Ф(са) =Ф(са0) + (са-сао)Ф'(сао), (10.9)
где Ф'(с^о) обозначает производную ЭФ(са)/Эсо в точке со0- Поле пучка не
явно зависит от времени [ехр(—io#)], и по аналогии с (10.7) изменение во
времени поля отраженного пучка может быть представлено в виде
£r(f)=Z)exp {ica[Ф'(са0) (10.10)
168
где D — константа, не зависящая от со. Теперь отождествляем Ф'(со0) с вре-
менем прохождения ts. Подставляя для Ф выражение
Ф = -2 ar ct g
(sin20c — sin2 0Z)1/2
g sin0z
g = 1, если E вектор параллелен поверхности, g = «с1/лсо» если вектор па-
раллелен поверхности, в котором 0z можно выразить через 0 и со, и учиты-
вая, что в0, вс << 1, получаем [9]
= ЭФ I
С
ZsCOS в0,
(10.11)
где zs определяется выражением (10.8).
Интересно заметить, что явное выражение для времени прохождения
(10.11) может быть найдено непосредственно с помощью теории плоской вол-
ны. Если рассмотреть плоскую волну, падающую, как показано на рис. 10.2,
то скорость распространения мощности параллельно границе на рис. 10.3, за-
дается направленной вдоль z групповой скоростью =dGj[d$ =e/(«cocos 0О),
поскольку $ = co«cocos во/с. Следовательно, ts -zjv^ в соответствии с урав-
нением (10.11).
В этом и предшествующем разделах предполагалось, что среда не имеет
дисперсии. Если ее учесть, то nQQ и ис1 будут зависеть от со. Сдвиг zs задается
выражением (10.8) при условии, что будет принято во внимание изменение
«со и вс с частотой. Однако время прохождения необходимо вычислять зано-
во, начиная с производной ЭФ(со0)/Эсо0 в выражении (10.11) [9].
Краткие выводы. Взятые вместе выражения (10.8) и (10.11) описывают
влияние дифракции на траекторию и время прохождения луча, испытываю-
щего полное внутреннее отражение на плоской границе диэлектрика. Физи-
ческим источником сдвига является распространение света в менее плотной
среде. Теперь используем этот результат, полученный при рассмотрении паде-
ния плоской волны на единственную границу раздела сред, при Изучении вли-
яния дифракции на распространение луча в планарных волноводах.
10.6. Продольный сдвиг в планарных волноводах
В гл. 1 распространение света в планарных волноводах со ступенчатым про-
филем было описано с точки зрения направляемых лучей, распространяю-
щихся по зигзагообразным траекториям и испытывающих полное внутрен-
нее отражение на каждой границе. Здесь будет показано, каким образом
это описание модифицируется для волноводов с малым V при учете продоль-
ного сдвига. Если при каждом отражении вдоль траектории направляемого
луча учесть продольный сдвиг zs, то траектория, приведенная на рис. 1.4, я,
превратится в траекторию, показанную на рис. 10.4, а.
Время прохождения луча. Если tg0 — время прохождения расстояния z
вдоль волновода, полученное согласно геометрической оптике, то из выра-
жения (1.14) имеем ^g0 = znCQ/c cos 0Z. Время прохождения такого же рассто-
яния с учетом сдвига можно найти, рассматривая полупериод PQR (см.
169
Рис. 10.4. Продольный сдвиг лучевой траектории zs в планарном волноводе со ступенча-
тым профилем (л), эквивалентный увеличению полуширины сердцевины до значения
эффективной полуширины peff (б)
рис. 10.4,а). Время прохождения участка PQR задается формулой + ts,
где = 2pnCQ/c sin 0Z — время прохождения отрезка PQ и ts - время прохож-
дения сдвига zs. Полупериод равен zp + zs, где zp — согласно геометрической
оптике полупериод (1.10) . Предполагая, что z >> + zs, можно воспользо-
ваться аргументацией, приведенной ниже выражения (1.36), и получить
[9]
t =z(rp + rs)/(zp + zs). (10.12)
Подставляя сюда выражения (10.8) и (10.11) при 0О и преобразуя, име-
ем [11]
f 0z ]
r 's°V ~ 1 + r (10,13)
где 0Z 0c « 1. Иными словами, следствием продольного сдвига является
то, что время прохождения луча уменьшается по сравнению с временем, опре-
деленным согласно геометрической оптике, т. е. чем меньше значение V, тем
меньше t. С другой стороны, для волноводов с большим значением V оно
значительно отличается только*у лучей с 0Z % 0с, Однако на практике лишь
малая часть полной мощности источника переносится лучами, для которых
0Z 0С? так что ПРИ определении ширины импульса геометрическая оптика
обеспечивает достаточно хорошее приближение для волноводов с большим
значением К
Явления, связанные с потерями. В гл. 6 — 9 было учтено влияние потерь
мощности из сердцевины, вызванных поглощением в оболочке и излучени-
ем, с помощью коэффициента прохождения мощности Т, который был полу-
чен на основе теории локальной плоской волны. В случае поглощения в обо-
лочке это — хорошо известный коэффициент прохождения Френеля при пол-
ном внутреннем отражении плоской волны от границы поглощающего диэ-
лектрика (см. разд. 35.7). Таким образом, в Т уже учтено присутствие свето-
вой мощности в оболочке. Однако ранее не был принят во внимание сдвиг zs
лучевой траектории, связанный с механизмом проникновения света из сердце-
вины в оболочку. В разд. 36.10 доказывается существование этой связи с
помощью простых аргументов, обусловленных затуханием мощности. Сдвиг
оказывает такое же воздействие, как и уменьшение количества отражений.
Поэтому для анализа удобно сохранить зигзагообразную траекторию и учесть
влияние продольного сдвига, заменив полуширину сердцевины р на эффек-
тивную полуширину peff. Из рис. 10.4, б и [8,9] очевидно, что
170
-£eff. _ j 2s. tg0 = j __________1_______
p 2p 18 z K(1-^/0C2)1/2
(10.14)
где 0Z — угол между лучевой траекторией и осью волновода, V = £рисо0с и
zs определяется из выражения (10.8) при 0О = 6Z « 1.
Эффективная полуширина. Таким образом, влияние продольного сдвига
на потери в оболочке эквивалентно увеличению ширины волновода. Подстав-
ляя в выражения для затухания мощности, полученные в гл. 6 — 9, peff вмес-
то р, найдем, что исходные формулы, в которых продольный сдвиг игнори-
руется, завышают потери. Например, для того чтобы оценить влияние про-
дольного сдвига на поглощение в оболочке, заменим V на Vp ^1р в выраже-
нии (6.21), полагая 6^ = тг/2, так что выражение применимо к планарному
волноводу. Тогда оказывается, что результирующее значение для коэффици-
ента затухания мощности ус1 приближается к ас1, если V уменьшается при
0Z % ®с’ где ас1 ~ коэффициент затухания плоской волны в среде с потерями.
Если пренебречь продольным сдвигом, то, как следует из выражения (6.21),
7С1 00• Таким образом, выражение для поглощения в оболочке является
очень неточным для волноводов с малым V. Из (10.14) также ясно, что про-
дольный сдвиг сказывается при V » 1 только на лучах, имеющих 0Z ~ 0С.
На практике эти лучи обычно переносят незначительную часть полной мощно-
сти источника, и поэтому ими можно пренебречь.
В заключение подчеркнем, что продольный сдвиг не является единствен-
ным проявлением дифракции в планарном волноводе со ступенчатым профи-
лем. Недостаточно учитывать только его для описания распространения света
в волноводах с малым значением V. Для того чтобы лучше отличать электро-
магнитную теорию от лучевых методов, исследуем другое дифракционное
явление.
10.7. Предпочтительные лучевые направления
При анализе с помощью геометрической оптики возбуждения планарного
волновода источником предполагается, что могут возбуждаться любые на-
правляемые лучи, направления которых принадлежат континууму (1.5а).
Однако вследствие дифракции возбуждаются только лучи с определенными
предпочтительными направлениями*. Если V достаточно мало, то существует
только одно предпочтительное направление, и все направляемые лучи имеют
одно и то же время прохождения. Если же V велико, количество предпочти-
тельных направлений лучей становится достаточно большим, так что его мож-
но приближенно принять за континуум.
Условия согласования. Явление дифракции, которое вызывает появление
предпочтительных лучевых направлений, — это условие согласования фаз ло-
кальных плоских волн, образующих эту траекторию; оно является результа-
том симметрии волновода, т. е. его трансляционной инвариантности относи-
тельно продольной оси. Поэтому появление предпочтительных направлений
* Здесь правильнее сказать: вследствие интерференции. - Прим. ред.
171
филем, содержащий полный
Рис. 10.5. Участок траектории направляемого лу-
ча в планарном волноводе со ступенчатым про-
лучевой период 2z
Р
лучей является следствием геометрии всего волновода, в отличие от продоль-
ного сдвига, являющегося локальным явлением и проявляющегося в измене-
нии фазы при полном внутреннем отражении.
Для определения предпочтительных лучевых направлений в планарном
волноводе со ступенчатым профилем следует представить лучи как локаль-
ные плоские волны, распространяющиеся по зигзагообразным траекториям
(см. рис. 10.5), и рассмотреть их фазы на полном лучевом периоде 2zp [12,13].
На пути ABCD изменение фазы обусловлено двумя составляющими. Первая
определяется произведением длины пути 4p/sin0z и волнового числа кп со,
а вторая — изменением фазы в точках В и С за счет полного внутреннего от-
ражения от границ, которое задается величиной Ф. Инвариантность волново-
да относительно продольного сдвига означает, что изменение фазы, вызван-
ное тем, что z-составляющая вектора локальной плоской волны в точке А
смещается параллельно оси волновода на расстоянии 2zp в точку £>,*т. е. зна-
чение (Ъгс0 cos 0Z) (2zp), должно быть равно изменению фазы вдоль траекто-
рии с точностью до целого числа 2я. Отсюда
4fcp«co/sin07 + 2Ф = 'Ikzti cos 07 + 2тти, (10.15)
• VxJ 1 Lt Ly Lt ' X Z
где n = 0, ± 1, ... Подставим вместо его выражение из табл. 1.1 и вместо
Ф его представление, приведенное на стр. 169, и предположим, что волновод
является слабонаправляющим (g ъ 1). Тогда
{sin2 0С - sin2 0Z} 1/2 = sin 0Z tg( V sin 0Z/sin 0C) , (10.16)
если n — нуль или четное целое, и похожее выражение, если п — нечетное це-
лое. Важно отметить, что только лучи определенных направлений, соответ-
ствующих решениям приведенного выше уравнения относительно 0Z, могут
переносить мощность. При V < я/2 возможна только одно такое направле-
ние. В разд. 36.7 показано, каким образом получить предпочтительные направ-
ления лучей для волноводов более общего вида.
ДИФРАКЦИОННЫЕ ЭФФЕКТЫ В ПРОИЗВОЛЬНЫХ ВОЛНОВОДАХ
Были указаны эффекты проявления дифракции при распространении луча
в планарном волноводе со ступенчатым профилем — продольный сдвиг и на-
личие предпочтительных направлений лучей. Из проведенного анализа ясно,
что если V уменьшается, значительная часть мощности распространяется в
оболочке, и поэтому поведение лучей не соответствует их локальности, а
именно локальность использовалась в гл. 1 — 9. С использованием двух диф-
ракционных явлений в лучевой картине были введены точные выражения
для планарного волновода со ступенчатым профилем. Если, кроме того,
учесть дифракцию на источнике, то можно найти распределение мощности
172
между предпочтительными направляемыми лучами. Поля в таком волноводе
точно задаются суперпозицией полей уже двух плоских волн, как показано
в разд. 36.1. Поэтому неудивительно, что лучевые методы могут быть просто
модифицированы и позволяют получить точные результаты, соответствую-
щие теории электромагнитных волн*. Однако все волноводы должны быть
многомодовыми с V » 1 для того, чтобы можно было использовать луче-
вые методы или методы локальной плоской волны. Другими словами, неод-
нородность среды сердцевины и ограниченность поперечного сечения серд-
цевины вызывают дополнительные дифракционные эффекты, которые в об-
щем случае не просто учесть, если V мало. При этом можно применить кон-
цепции продольного сдвига и предпочтительного направления лучей к любо-
му волноводу, но известно, что такие волноводы хорошо описываются мето-
дами, данными в гл. 1 — 9. В общем же случае методы, данные в ч. II книги,
более подходят для волноводов с малыми значениями V.
♦ Правильнее сказать: результаты, соответствующие волновой теории. - Прим. ред.
173
Ч А С Т Ь II. ВОЛНОВОЙ АНАЛИЗ
ОПТИЧЕСКИХ ВОЛНОВОДОВ
ВВЕДЕНИЕ
В ч. I распространение света в оптических волноводах было рассмотрено в
рамках классической геометрической оптики, а обобщенные коэффициенты
Френеля позволили учесть потери из-за поглощения в оболочке и излучения,
вызванные спадающим полем в оболочке. В то же время в гл. 10 было отме-
чено, что это рассмотрение применимо только к многомодовым волноводам
с волноводным параметром V » 1. Часть II посвящена волновому анализу
оптических волноводов, основанному на решении уравнений Максвелла, ко-
торые в общем случае могут быть решены либо методом собственных функ-
ций (метод мод), либо методом функций Грина. В данной части используют-
ся оба метода, но в основном первый. В этом методе, который применим так-
же к металлическим волноводам [1 —3], электромагнитное поле представ-
ляется суммой решений уравнений Максвелла для среды без источников.
В методе функций Грина вначале определяется поле от элементарного дипо-
ля, находящегося в произвольной точке, а затем с использованием линейной
суперпозиции полей от совокупности диполей определяется поле для задан-
ного источника. Такой подход, использующийся в теории антенн [2, 3], весь-
ма полезен при определении потерь на излучение в оптических волноводах,
как это будет показано ниже в гл. 21 и 23.
Пространственно-неуст^новившийся и пространственно-установившийся
режимы. В идеальном (непоглощающем) волноводе без потерь распростра-
няется только часть полной мощности источника. Остальная часть излучает-
ся. Мощность, распространяющуюся без потерь, удобно представить классом
мод, число которых конечно и которые называются направляемыми модами,
аналогичными направляемым лучам в ч. I. Излучаемую мощность можно
представить различными способами в зависимости от характера решаемой
задачи.
На достаточно большом расстоянии от источника излучения поле внутри
сердцевины волновода формируется главным образом направляемыми мода-
ми, в то время как часть исходной мощности теряется на излучение на началь-
ном участке волновода. Поле в области волновода вблизи источника соответ-
ствует так называемому пространственно-неустановившемуся (нестационар-
ному) режиму, а вдали от источника — пространственно-установившемуся
(стационарному) режиму. Это схематически представлено на рис. II. 1 и для
многомодовых волноводов рассмотрено в гл. 8. Там же было показано, что
протяженность области пространственно-неустановившегося режима может
составлять километры для многомодовых световодов и менее сантиметра
для одномодовых.
Основные моды. В ч. II основное внимание уделяется одномодовым вол-
новодам, в которых распространяется только одна направляемая мода, назы-
174
Рис. IL1. Качественное представление излучения из волновода, возбужденного источни-
ком, расположенным на его входном торце. Стрелками показан поток мощности поля
излучения. Более темная область соответствует более высокой плотности мощности в
сердцевине
ваемая основной, поскольку они представляют значительный практический
интерес как для систем оптической связи [4 — 6], так и для изучения меха-
низма зрения животных [7, 8]. Чтобы в дальнейшем не возникало путаницы,
заранее оговоримся, что под „о дно модовым волноводом” понимается такой,
в котором основная мода может распространяться в двух состояниях поля-
ризации. При этом прилагательное ’’направляемая” опускается.
Историческая справка. Хотя первое теоретическое исследование оптичес-
ких волокон* было проведено Хондросом и Дебаем в 1910 г. [9], интерес к
световодам возник только в конце шестидесятых — начале семидесятых го-
дов, когда стало технически возможным получение высоко прозрачных мате-
риалов. Изготовление волоконных световодов, способных передавать инфор-
мацию на десятки километров, стимулировало быстрое развитие методов те-
оретического анализа их волноводных свойств. Дело в том, что решения урав-
нений Максвелла, позволяющие точно определить волноводные характерис-
тики, можно получить лишь численными методами. Ситуация значительно
упрощается, если принять во внимание физические соображения, касающиеся
малых изменений показателя преломления в радиальном направлении воло-
конных световодов, предназначенных для системы дальней связи. Это снача-
ла приводит к введению приближения слабонаправляющих волноводов и поз-
воляет заменить уравнения Максвелла скалярным волновым уравнением, а
затем — к гауссову приближению, которое дает возможность довольно легко
получить аналитические выражения фактически для всех характеристик рас-
пространения волны в волоконном световоде с произвольным профилем по-
казателя преломления. Поэтому значительное место в ч. II уделено выводу и
применениям этих приближений.
Чтобы лучше понять природу и границы применимости различных исполь-
зуемых приближений в гл. 11 изложены основные свойства направляемых
* Правильнее сказать: диэлектрических волноводов. - Прим. ред.
175
мод оптических волноводов. В гл. 12 рассмотрены некоторые типы волново-
дов, для которых могут быть получены точные аналитические решения урав-
нений Максвелла. Затем в гл. 13 — 19 излагаются приближенные методы на-
хождения характеристик мод волноводов различных типов. Глава 20 посвя-
щена возбуждению волноводов, а в гл. 21 — 26 исследуются поля излучения
волноводов. В гл. 27 и 28 рассмотрена связь мод внутри одного волоконно-
го световода, а в гл. 29 — перекрестное взаимодействие между несколькими
световодами. Кроме того, необходимо обратить внимание на ч. III книги, в
которой приведены дополнительные сведения, необходимые при выводе
многих выражений ч. II.
ГЛАВА 11. ОСНОВНЫЕ СВОЙСТВА МОД
Распространение света в непоглощающем оптическом волноводе в случае, ес-
ли источник возбуждения находится достаточно далеко, т. е. достигнут про-
странственно-установившийся режим, наиболее удобно описывать, используя
направляемые моды волновода. Направляемые моды — это решения уравне-
ний Максвелла для среды без источников. Подобно колебательным мод м
натянутой мембраны они образуются при резонансе в поперечном сечении
волновода. В пространственно-установившемся режиме направляемые моды
являются основой для описания распространения света, так как поле волно-
вода можно разложить по полям этих мод.
В этой главе рассматриваются основные свойства направляемых мод иде-
ального волновода (однородного по длине и выполненного из непоглощаю-
щего диэлектрика). Вывод получаемых результатов из уравнений Максвелла
приведен в гл. 30 и 31. Многие определения и допущения, введенные в этой
главе, используются в дальнейшем. Несмотря на то, что глубокое понимание
на данном этапе не является необходимым, перед дальнейшим чтением целе-
сообразно ознакомиться с гл. 11, 30 и 31, так как материал, изложенный в
них, неоднократно используется.
ВОЛНОВОЙ АНАЛИЗ РАСПРОСТРАНЕНИЯ СВЕТА
Рассмотрим волновод, схематически изображенный на рис. 11.1, а. Заштрихо-
ванная область обозначает сердцевину с поперечным сечением произвольной
формы. Сердцевина окружена оболочкой, которая считается неограниченной.
Поверхность между сердцевиной и оболочкой называется границей и распо-
ложена на расстоянии р(х, у) от оси волновода. Для описания волновода вве-
дем декартову систему координат, в которой ось z совпадает с осью волно-
вода. Изменение показателя преломления по сечению волновода характери-
зуется его профилем п (х, у), который является действительной величиной,
поскольку волновод предполагается непоглощающим.
Все профили, рассматриваемые в этой книге, можно разбить на два класса.
Первый класс — это профили, имеющие постоянный показатель преломления
в оболочке иС1 и произвольно изменяющейся в сердцевине, как это показано
на рис. 11.1,6. Такие профили характеризуются скачкообразным изменени-
ем показателя преломления или его производной на границе сердцевина -
176
Рис. 11.1. Обозначения и оси координат для описания свойств оптических волноводов
(а) и пример градиентного профиля п (х, у), показатель преломления которого изменя-
ется в сердцевине и остается неизменным в оболочке, предполагаемой неограничен-
ной (б)
оболочка. Второй класс, примером которого может служить неограниченный
параболический профиль, — это профили, показатель преломления которых
плавно меняется по бесконечному поперечному сечению. Поскольку в таких
волноводах не существует четкой границы между сердцевиной и оболочкой,
то под р будем понимать характерный радиус профиля, в пределах которого
показатель преломления изменяется в определенное число раз. Определим
ис0 — максимальный показатель преломления сердцевины;
«с1 — однородный показатель преломления оболочки,
(11-1)
где условие исо >ис1 обеспечивает направляющие свойства волоконного све-
товода.
Разложение полей. Электрический и магнитный векторы поля Е(х, у, z) и
Н(х, у, z) можно представить в виде двух частей, первая из которых соответ-
ствует мощности, направляемой волноводом без затухания, вторая — излуча-
емой мощности. Направляемая мощность представляет собой конечную сум-
му мощностей направляемых мод, являющихся решениями уравнений Макс-
велла для волновода без источников. Электромагнитные моды могут рас-
сматриваться как поперечный резонанс полей в волноводе аналогично нор-
мальным колебательным модам мембраны, закрепленной на краях. Следует,
однако, иметь в виду, что если мембрана имеет бесконечное число направля-
емых мод, то волновод может поддерживать только конечное их число. Поэ-
тому можно положить
E(x,y,z) = £aJEj(x,y,z) + £a_jE_/x,y,z) + Erad(x,y,z), (11.2а)
Н (х, у, z) = £ Н; (х, у, z) + £ а _; Н _, (х, у, z) + Н rad (х, у, z), (11.26)
j J
где j = 1, 2, . . . , М. Первое суммирование проводится по всем впер ед-рас-
пространяющимся модам, т. е. в положительном направлении оси z, второе
суммирование — по всем назад-распространяющимся модам, т. е. в отрица-
177
тельном направлении оси z (см. рис. 11.1,а). Индексы ”rad” означают поле
излучения. Постоянные и я-j — это амплитуды моды, зависящие от источ-
ника возбуждения. Поле /-й вперед- и назад-распространяющихся мод описы-
вается векторами EpHj и Е_рН_^ соответственно. Одинаковые амплитуды мод
обоих разложений (11.2) являются свойством уравнений Максвелла (30.1).
Рассмотрим свойства направляемых мод и их полей. Все результаты полу-
чены из уравнений Максвелла (см. гл. 30 и 31).
11.1. Постоянная распространения и фазовая скорость
Цилиндрическая симметрия, или трансляционная инвариантность волново-
да, позволяет осуществить разделение переменных и представить поле мо-
ды в виде
Ej (х, у, z) = ej (х, у) exp (i0jz);
Hj (х, У, z) = hj (х, у) exp (i|3j z),
(11.3)
где величина j3j называется постоянной распространения, или собственным
значением /-й моды. В общем случае постоянные распространения различных
мод различны.
Везде в дальнейшем подразумевается, что временная зависимость полей
выражается множителем ехр(—icoZ), где со — угловая частота. Если учесть эту
временную зависимость, то поле моды изменяется как exp(ij3jZ — и,
следовательно, каждая мода распространяется с фазовой скоростью =
- (jj/Py Чтобы различать моды с одинаковыми постоянными распростране-
ния, но распространяющиеся в разные стороны, будем следовать правилу,
которое по отношению к уравнению (11.2) действует следующим образом:
а} - вперед-распространяющаяся мода и 0j > 0; (11.4а)
а_ - - назад-распространяющаяся мода и . = — (3- <0, (11.46)
/=1,2...М, 'J
где М общее число вперед- или назад-распространяющихся мод. Поэтому фа-
зовая скорость, например U&, удовлетворяет соотношению
= = О1-5)
J P-j
Величины j3j на данной частоте определяются из характеристического уравне-
ния, которое является условием согласования, или поперечного резонанса, и
получено в предположении, что решения уравнения Максвелла для среды без
источников: 1) ограничены; 2) достаточно быстро стремятся к нулю в бес-
конечности; 3) удовлетворяют всем граничным условиям. Характеристи-
ческое уравнение приведено в разд. 11.13, а конкретные примеры в следу-
ющей главе.
178
11.2. Свойства симметрии составляющих поля
В дальнейшем будут часто использоваться соотношения для полей вперед- и
назад-распространяющихся мод. Они могут быть получены разложением по-
лей (11.3) на поперечную и продольную составляющие, которые обозначим
индексами t и z соответственно. В результате имеем
Ej = ej (х, у) exp (i 0jZ) = [е^ (х, у) + ezj (х, у) i ] exp (-i^z); (11.6а)
Hj = hj (х, у) exp(i0jZ) = [h^ (х, у) + ftzj(x, у) z] exp (ifyz), (11.66)
где z — единичный вектор, параллельный оси волновода (см. рис. 11.1,а).
В соответствии с условием (11.4) вперед- и назад-распространяющимся мо-
ды с одинаковыми постоянными распространения имеют индексы / и -/ со-
ответственно (/ > 0). В разд. 30.5 показано, что поля этих мод можно связать
двумя способами. В данной книге будем придерживаться способа, выражае-
мого соотношением (30.116), а именно
e-j etj ezj^ h-j \j+ ^zjz; - Pj.
(И.7)
Это справедливо и для волноводов с поглощением, в которых показатель
преломления п (х, у) является комплексной величиной. Такие волноводы бу-
дут рассмотрены ниже.
11.3. Поля непоглощающих волноводов
Если волновод непоглощающий, т. е. показатель преломления п (х, у} являет-
ся действительной величиной, то, как показано в разд. 30.4, среди возмож-
ных составляющих поля для каждой направляемой моды всегда можно выб-
рать такие, которые удовлетворяют условию
etj, htJ- — действительные функции;
ezj, hzj — мнимые функции,
(11-8)
где индексы t и z относятся соответственно к поперечным и продольным со-
ставляющим поля. Такое представление помогает упростить физическую ин-
терпретацию многих результатов. Поскольку часто приходится использовать
комплексно-сопряженные поля мод, то используя (11.7) и (11.8), для непо-
глощающего волновода получаем
е* =e-j =etj-«Zj£;
h^-h-j =htj-^f; 0* = -0_.=^,
(П-9)
где/ > 0 и знак * означает комплексное сопряжение.
179
11.4. Соотношения ортогональности и нормировка
При определении амплитуд полей направляемых мод в разложении (11.2)
необходимо учитывать соотношение ортогональности, которое является след-
ствием теоремы взаимности уравнений Максвелла (разд. 31.1). Согласно ему
в непоглощающем волноводе поля /-й и к-й вперед-распространяющихся мод
подчиняются векторному условию ортогональности (31.14), а именно
f е, х hp idA = f е* х Ь • idA= 0; /=# к,
А Л К J
(11-10)
где А — площадь бесконечного поперечного сечения, * — знак комплексно-
го сопряжения и z - единичный вектор, параллельный оси волновода. Отме-
тим, что в результате подынтегральное выражение содержит только попереч-
ные составляющие поля. Если одна или обе моды являются назад-распростра-
няющимися, то для получения соотношения ортогональности нужно выра-
зить поля e_j, h_j, e_k и h_k через параметры вперед-распространяющейся мо-
ды, используя соответствующие уравнения. Моды непоглощающего волново-
да также подчиняются условию ортогональности в несопряженной форме
(11.14), однако сопряженная форма более удобна для получения количест-
венной оценки мощности моды, как это будет показано в разд. 11.7.
В разд. 31.3 отмечается, что любая направляемая мода ортогональна полю
излучения в уравнении (11.2). Следовательно,
(11-11)
| f е- х h*'zdA |. (11.12)
где j > 0 и индексы ”rad” означают поле излучения.
Определим нормировку моды TVj непоглощающего волновода следующим
образом:
Поскольку модуль обеспечивает положительное TVj для всех мод, то из (11.7)
и (11.12) HMeeMALj =7Vj. Используя условие ортогональности (11.10) и нор-
мировку для двух вперео-распростраНяющихся мод, получаем [1]
у f ej X h* • idA = 1 f e* x hj • zcU =
TVj, если/ =k;
0, если/ ^k,
(11.13)
где /, к > 0. Если обе или одна из мод назад-распространяющиеся, необходи-
мо, используя уравнение (11.7), выразить поля мод через соответствующие
поля вперед-распространяющейся моды и затем подставить их в уравнение
(11.12).
180
Волноводы с поглощением. Наиболее общая форма условия ортогонально-
сти, справедливая как для поглощающих, так и непоглощающих волноводов,
имеет вид (31.16), а именно
f е- х hk • zdA = f ek x h: • idA = 0; j Ф k. (11.14)
Нормировка и ортогональность с полем излучения выражаются формулами
(11.11) и (11.13) без комплексного сопряжения.Следует,однако, отметить,
что, как будет показано ниже, сопряженные соотношения (11.13) приблизи-
тельно справедливы и для слабопоглощающей среды.
11.5. Ортонормальные моды
В ряде случаев удобно использовать поля мод, имеющие единичную норми-
ровку. Моды, удовлетворяющие этому условию, называются ортонормаль-
ными модами и получаются из мод с произвольной нормировкой заменой
®j =ej/V^; Ц = lij/vQV?,
e-j =e_j/x<^; h_j =h_j/V^’> (11-15)
для вперед- и назад-распространяющихся мод соответственно. Условие орто-
гональности для двух вперед-распространяющихся ортонормальных мод име-
ет вид
, х ~ х 1 А - fl, если/ =&;
If в: х h* ‘ TdA = - f е* х к • zdA = <
2a3 k 2 Л k J (.0, если/
(11.16)
Поля вперед- и назад-распространяющихся ортонормальных мод связаны со-
отношением (11.7), в котором над каждой составляющей поля стоит знак
л, а соотношение ортогональности назад-распространяющихся ортонормаль-
ных мод получается так же, как это описано в разд. 11.4.
ЭНЕРГИЯ И МОЩНОСТЬ
Направляемое поле переносит мощность излучения вдоль волновода. Часть
этой энергии запасена в поле каждой направляемой моды, которая также пе-
реносит часть полной мощности. Зная энергию и мощность в каждой моде,
можно получить полную запасенную энергию и мощность, переносимую
вдоль волновода.
11.6. Запасенные электрическая и магнитная энергии
Рассмотрим непоглощающий волновод с недиспергирующим показателем
преломления, т. е. п (х, у) — действительная, не зависящая от длины волны
функция. Пусть и ~ усредненные по времени электрическая и маг-
181
нитная энергии на единице длины волновода для /-й вперед-распространяю-
щейся моды, определенные как
*ej = | l*jl2e0 f «2lej|2^; = ||<Zj|2M0 f lhj|2A4, (11.17)
ЛОО
где a-} — амплитуды мод, Аж — бесконечное поперечное сечение, |ej |2 =
= • е*, п — профиль показателя преломления и е0, д0 — диэлектрическая и
магнитная проницаемости вакуума. Запасенную энергию для/-й назад-распро-
страняющейся моды можно получить из выражения (11.17), если в соответ-
ствии с формулами (11.7) и (11.9) заменить^ ная-j. В разд. 31.5 показано,
что запасенные энергии равны
^=*;j + *hj=2#'ej, (И-18)
где #j — полная запасенная энергия на единице длины волновода.
Если волновод является диспергирующим, то магнитная проницаемость
и диэлектрическая постоянная зависят от длины волны X, т. е. е = е(Х), р =
= д (X). В этом случае полная запасенная энергия на единице длины равна [2]
») = -т|а1|2У {">lei|2 £Ф + "ч12 dx^\dA- <11Л9)
При выводе этого выражения предполагалось, что волновод является непо-
глощающим и тем самым игнорировалась зависимость между дисперсией и
поглощением, которая выражается соотношением Крамерса — Кронига [2].
Однако учет относительно малого поглощения дает весьма малые поправки
к выражению (11.19).
11.7. Поток мощности
В общем случае в возбужденном оптическом волноводе мощность перено-
сят все моды. Эффективность возбуждения каждой отдельной моды зави-
сит от природы источника и будет рассматриваться в гл. 20 и 21. В непогло-
щающем волноводе мощность переносится вдоль его оси и для /-й моды рас-
пределена по бесконечному поперечному сечению с плотностью, или интенсив-
ностью 5j, которая определяется усредненным по времени вектором Пойн-
тинга. Из уравнений (11.3) и (11.8) имеем
5j = A|aj|2Re(EjxH*-i)=l|aj|2ejxh*-i> (11.20)
где — амплитуда моды, a Re означает действительную часть величины. Пол-
ная мощность каждой моды находится после интегрирования Sj по всему7 по-
перечному сечению Аж. Для /-й вперед- и назад-распространяющихся мод,
используя соотношения (11.9), находим, что
pj=4|aj|2 J ej x hj,idA’
Л ОС
P_j =- 1 kJ2 f ej x h: -zdA.
2 л J J
(11.21a)
(11.216)
182
Таким образом Pj > 0 представляет собой мощность, переносимую в поло-
жительном направлении оси z (см. рис. 11.1, а), и ZLj < 0 - мощность, пере-
носимую в отрицательном направлении оси z. Используя условие нормиров-
ки (11.12), имеем
Р. =|aj|2^j; =-la-jl2^,
(11.22а)
а для ортонормальных мод на основании (11.16) получаем
Pj=l«jl2; P_j =-1%12- (п.226)
11.8. Часть мощности моды в сердцевине
Различные распределения показателей преломления в сердцевине и в оболоч-
ке (см. рис. 11.1, а) вызывают существенно различное поведение полей в
этих областях. Однако довольно часто удается подробно проанализировать
их, исследуя часть мощности моды, распространяющуюся в сердцевине. Опре-
деляя параметр как
мощность моды, переносимая по сердцевине
полная мощность моды * ‘ '
и используя выражение (11.21) для непоглощающего волновода, имеем
- f е: х h* • idA
J ± / ef х h* • idA
(11.24)
где Л co — площадь поперечного сечения сердцевины и Аж — площадь беско-
нечного поперечного сечения. Это выражение также справедливо и для слабо-
поглощающих волноводов, которые будут рассмотрены ниже.
11.9. Полная переносимая мощность
Определим Ptot как усредненную по времени полную мощность, переноси-
мую вдоль волновода в положительном направлении оси z (см. рис. 11.1, я).
Используя выражение (11.2) для полных полей и интегрируя вектор Пойн-
тинга по бесконечному поперечному сечению Аж , получаем
Ptot = 1 Re f Е х Н* • idA. (11.25)
А оо
Ее можно представить в виде суммы мощности направляемого поля и мощ-
ности поля излучения, т. е.
Л = я- (11.26)
tot bd rad v
183
Подставляя уравнение (11.2) и (11.3) в (11.25), используя условие ортого-
нальности (11.13) иопределение мощности моды (И.21),выражение (11.26)
для непоглощающего волновода можно записать в виде
м мм
pbd= 2 +<Р = 2 |ajR- 2 Ny
j=1 J /=1 /=1 J
(11.27)
где «j и a__y — амплитуды /-й вперед- и назад-распространяющихся мод, TVj —
нормировка (11.12). Таким образом, полная направляемая мощность, пере-
носимая в положительном направлении оси z, равна разности мощности всех
вперед-распространяющихся мод и мощности всех назад-распространяющих-
ся мод. В любом сечении волновода мощность поля излучения Prad есть раз-
но сть между Ptot и Pbd. га
11.10. Часть полной мощности в сердцевине
Выражение (11.25) для полной мощности Ptot представляет собой сумму
полной мощности в сердцевине Рсо и полной мощности в оболочке, причем
jPco=4Re(7 Е х Н* • IdA). (11.28)
лсо
Для областей волновода, расположенных достаточно далеко от любых источ-
ников возбуждения, поле излучения в сердцевине мало и полная мощность
поля в сердцейине определяется направляемыми модами в разложении (11.2).
Однако поскольку направляемые моды не являются ортогональными в лю-
бом конечном поперечном сечении, выражение для PQQ весьма сложно. Чтобы
продемонстрировать это, рассмотрим случай, когда возбуждены только впе-
ред-распространяющиеся моды непоглощающего волоконного световода.
Подставляя (11.2) в (11.28) и используя (11.3) , получаем
Лю =4 22ajakexp[i(0j -/3k)z] / ^xh^'idA, (11.29)
2 i k Лс0
где /, k > 0. Перегруппировка членов и использование определений (11.21а)
и (11.24) дает выражение
РСО = 2 Vji + I 2 2 ajak ехр ~ ^k)z] $ ejXh*-zcM, (11.30)
со 7 2 лсо J К
которое имеет простую физическую интерпретацию. В первом члене сумми-
руются мощности, переносимые по сердцевине каждой модой. Второй член
обусловлен интерференцией между различными модами из-за их неортого-
нальности в сердцевине, однако во многих практически важных случаях он
мал и его можно опустить [11.3].
ГРУППОВАЯ СКОРОСТЬ
Мощность моды переносится вдоль волновода с групповой скоростью U&
которую следует отличать от фазовой скорости (11.5), определяющей ско-
184
рость распространения волнового фронта вдоль волоконного световода
[11.7]. Групповая скорость определяется как
тт -
я х2
(11.31)
где со — угловая частота, входящая во временную зависимость поля exp (—iatf),
X — длина волны в вакууме и — постоянная распространения /-й моды.
Групповую скорость можно определить, дифференцируя по частоте характе-
ристическое уравнение и подставляя величину Р- . С другой стороны, если по-
ля мод известны, то как будет показано в разд. 31.6, выражение для группо-
вой скорости в случае непоглощающего волновода с магнитной проницаемо-
стью р имеет вид
— f е, х h*‘ idA
2 л J J
Лоо
-------------------------------------------------------
(X2/4) f [во I ej |2 (и2/X) + I hj |2 ^(M/X) ]dA
Aqq
(11.32)
Это выражение учитывает дисперсию материала, т. е. зависимость п и д от X,
и не учитывает поглощение. Для волновода без дисперсии материала уравне-
ние (11.32) можно заменить уравнением (31.31) , т. е.
(c|3j/2) f ejXh^idA
А„ J
kj2 f n2 ej x h* • idA
(11.33)
Сравнение числителя и знаменателя в выражении (11.32) с (11.19) и (11.21)
показывает, что групповую скорость можно представить в виде
C/gj=^j/*j, (11.34)
где /j — мощность, переносимая модой, a — полная запасенная энергия на
единице длины волновода.
11.11. Групповая задержка
Обычно на практике [4, 5] вместо групповой скорости используют вре-
мя групповой задержки на единицу длины волновода
7j=l%. (11.35)
Групповая задержка в волноводе длиной z дает среднее время распростране-
ния tj. Из уравнения (11.31) имеем
t=-^—=ZT = z = -z*L_
j Ugi j z du 2nc d\
(11.36)
185
где с — скорость света в вакууме. Для мод, распространяющихся в многомо-
довом волноводе, Zj равно времени распространения луча Г, введенного в
гл. 3, как показано в разд. 36.9.
УШИРЕНИЕ ИМПУЛЬСА
Во время распространения импульса света по волноводу ряд причин вызыва-
ет искажение его формы. Первой является различная групповая задержка
мод (аналогично времени распространения разных лучей в гл. 3). Поэтому,
если импульс света формируется более чем одной модой, во время распро-
странения по волноводу он будет уширяться. Этот процесс называется меж-
модовой дисперсией и для многомодовых волноводов был проанализиро-
ван в гл. 3 методами классической геометрической оптики. В круглом изо-
тропном одномодовом волоконном световоде межмодовая дисперсия рав-
на нулю, т. к. в этом исключительном случае обе основные моды, как будет
видно из (11.51), имеют одинаковые групповые задержки.
Второй причиной уширения импульса является малая, но конечная спект-
ральная ширина источника излучения. Она важна вследствие зависимости
групповой задержки каждой моды от длины волны — это и зависимость по-
казателя преломления от длины волны (дисперсия материала) и зависимость
характеристик распространения моды от X (волноводная дисперсия). Ушире-
ние импульса в этом случае называется внутримодовой дисперсией. Домини-
рующей, как правило, является дисперсия материала [5, 6].
11.12. Уширение импульса в одномодовых волоконных световодах
В гл. 3 говорилось об уширении импульса в многомодовых волоконных све-
товодах. Рассмотрим теперь одномодовый волоконный световод и предпо-
ложим, что обе основные моды имеют одинаковое среднее время распростра-
нения, т. е. волоконный световод является круглым. Поскольку присутству-
ет только внутримодовая дисперсия, то уширение импульса является след-
ствием разброса среднего времени распространения ЬЦ из-за конечной спект-
ральной ширины источника излучения 5 со или 6Х. Поэтому из уравнения
(11.36) имеем
cP|3j , </2|3j d/3.
6“=~s p'1^-
Вклад волноводной дисперсии и дисперсии материала вб^ в общем случае
определить трудно [5, 6]. Поэтому каждую составляющую внутримодовой
дисперсии исследовать отдельно можно только при определенных предпо-
ложениях.
Дисперсия материала. Чтобы исследовать дисперсию материала абстраги-
руемся от волноводных свойств волоконного световода и представим моду
в виде плоской волны, распространяющейся в направлении оси z, для кото-
рой j3j = 2яи(Х)/Х и показатель преломления пространственно однороден.
Используя выражение (11.36), находим, что
"Е='"ОТ-^. (11.38)
186
где n& - групповой показатель преломления, введенный в разд. 1.5. Из этого
выражения следует, что уширение импульса равно
^=~Zc^^ (П-39)
и зависит только от второй производной h.
Волноводная дисперсия. Вклад волноводной дисперсии в уширение им-
пульса можно найти из уравнения (11.37) предположив, что п не зависит от
X. Вид выражения для б/g зависит от профиля показателя преломления. Ни-
же в разд. 11.20 волноводная дисперсия будет выражена через более удобные
параметры моды.
СВОЙСТВА ПОЛЕЙ МОД
Электрическое и магнитное поля Ej и Hj направляемых мод являются реше-
ниями уравнений Максвелла для среды без источников (30.1) или, что экви-
валентно, векторных волновых уравнений (30.14). Однако сложность этих
уравнений определяется векторным лапласианом V2 ? который в произволь-
ной системе координат связывает компоненты волновых векторов. Ситуа-
ция существенно упростится, если компоненты векторов Ej и Hj связать с
декартовой системой координат, что приведет к замене векторного лапласи-
ана V2 скалярным V2. Кроме того, трансляционная инвариантность поля
(11.3) приводит к дальнейшему упрощению векторного волнового уравне-
ния, как показано в разд. 30.7. Из уравнения (30.18) имеем
<У2+пЧ2 -Ppej = - (Vt + ip.i) (etj -Vtln«2);
(yi + пЧ2 -0?)h. =-(?tlnn2) x [(Vt + i/3jZ) x hj],
(11.40а)
(11.406)
где 0j - постоянная распространения,п=п(х,у) — профиль показателя пре-
ломления, к = 2тт/Х — волновое число в вакууме и X — длина волны в ваку-
уме. Как отмечено в гл. 30, если не оговорено особо, то магнитная проница-
емость равна своему значению в вакууме д0 • Соотношение между п, к, \ и
другими величинами приведено в табл. I. Временна'я зависимость полей пред-
полагается в виде ехр(— iatf) ,где со —угловая частота света. Выражения для
поперечной составляющей лапласиана V2 и векторного оператора приведе-
ны в табл. 30.1. Необходимо подчеркнуть, что поля имеют декартовы состав-
ляющие, т. е.
ej=exji + eyjy + ezj£; (п 41)
bj =/zxjx + Ayjy + /iZjZ,
где х, у, z — единичные векторы, параллельные осям на рис. 11.1, а, а про-
странственные зависимости этих компонент могут быть выражены в любой
системе координат с цилиндрической симметрией. Поэтому, например, урав-
нения для компонент поля планарного волновода (30.21) и круглого воло-
конного световода (30.23), полученные из уравнения (11.41), имеют раз-
ный вид.
187
11.13. Характеристическое уравнение
Векторные волновые уравнения являются фактически уравнениями Макс-
велла для волновода с произвольным профилем показателя преломления.
Они содержат всю информацию, необходимую для определения простран-
ственных зависимостей полей волновода при условии, что поля мод везде
ограничены и при достаточно большом удалении от оси волновода спадают
до нуля. Электрическое и магнитное поля могут быть определены и другим
путем из решений тех же уравнений в областях, где профиль показателя пре-
ломления изменяется непрерывно, и при выполнении граничных условий
уравнения Максвелла в любой точке разрыва. В любом случае, для определе-
ния постоянной распространения моды 0j необходимо выполнение условия
согласования полей, что приводит к характеристическому уравнению. В каче-
стве решения характеристического уравнения постоянная распространения
является явной функцией поля моды. Для непоглощающего волоконного
световода уравнение (31.23) дает
J H2ej х h**
’ (lh42)
Аж J
где Лоо — площадь бесконечного поперечного сечения и | е> |2 = ej • е*. По-
скольку поля мод неявно зависят от j3j, то выражение (11.42) является ин-
тегральной формой характеристического уравнения для волновода с произ-
вольным профилем.
11.14. Решение, выраженное через продольные составляющие поля
Если известны продольные составляющие поля, то нет необходимости решать
векторное волновое уравнение для поперечных составляющих ej и hj, по-
скольку, как показано в разд. 30.3, они связаны между собой соотношени-
ем (30.6):
etj =—;-----г [0j - (i^-)1/2ki X Vtfcz];
4 n2k2 -0? J J e0 ‘ z
= n2k2-&2 № + ф1/2kn2 i x Vtez,
(11.43а)
(11.436)
где п = п(х, у) ,к = 27г/Х, е0 и д0 — диэлектрическая и магнитная проницаемо-
сти в вакууме. В разд. 30.8 показано, что продольные составляющие поля
удовлетворяют уравнениям для связанных амплитуд (30.25)
(V^ + Pj)ezj --pi- Vtezj • vtln n2 = - (^-)1/2 z • (Vt/izj x Vt In n2).
(11.44a)
„2 e kn2Q-
' <vfti * vt 1"»’)
1 (11.446)
где Pj = n2k2 - 02 и n = n (x, y).
188
11.15. Взаимодействие составляющих поля
В уравнениях (11.40) и (11.44) выражения, содержащие Vt In и2, описывают
взаимодействие различных составляющих поля. Эти члены описывают, как
это будет показано ниже, поляризационные явления, обусловленные волно-
водной структурой, и значительно усложняют получение аналитического ре-
шения. Они же являются математическим обоснованием гибридной природы
полей мод, обсуждаемой в следующем разделе. Прежде чем исследовать об-
щий случай, рассмотрим волновод со ступенчатым профилем показателя
преломления.
Волновод со ступенчатым профилем показателя преломления и скалярное
волновое уравнение. Для волновода со ступенчатым профилем (п = nCQ в
сердцевине и п = лс1 в оболочке) все члены, содержащие Vt In п2 в уравнени-
ях (11.40) и (11.44), исчезают в сердцевине и в оболочке, но не на границе
сердцевины с оболочкой. Следовательно, каждая декартова составляющая
поля в уравнении (11.40) удовлетворяет упрощенному уравнению внутри
сердцевины и оболочки, т. е.
(V? + „2fc2 -0?)ezj=O. (11.45)
Это уравнение иногда называют скалярным волновым уравнением. Однако в
этой книге компоненты поля являются решениями скалярного волнового
уравнения только в том случае, если они удовлетворяют уравнению (11.45)
для всех х и у, включая и границу, и, следовательно, являются непрерывны-
ми, и имеют везде непрерывные первые производные (см. разд. 33.1). Оче-
видно, что для любых декартовых компонент поля ej ступенчатого волново-
да с произвольной формой поперечного сечения эти условия не выполняются,
поскольку члены с Vt In п2 не равны нулю на границе. Поэтому, чтобы полу-
чить решение для ezj, справедливое в любой точке поперечного сечения зало-
жим граничные условия уравнений Максвелла на решения уравнения (11.45),
полученные для сердцевины и оболочки. Аналогично получаются решения и
для hzy Можно получить решения уравнения (11.44), и не отбрасывая члены
содержащих Vt In п2. В этом случае поперечные компоненты получаются из
соотношений (11.43).
Отличительной особенностью ступенчатого профиля является возможность
аналитического решения векторного волнового уравнения для некоторых
форм поперечного сечения волновода с учетом членов, содержащих Vtlnw2,
но без конкретизации их вида. Можно рассматривать ступенчатый профиль
как особый случай градиентного, в котором градиент проявляется лишь на
границе сердцевины с оболочкой. Поэтому ступенчатый профиль оказывает
наибольшее влияние на поляризацию поля.
ТЕ-моды. Существуют два особых случая, когда члены содержащие Vt 1пи2
не появляются в векторном волновом уравнении для поперечных компонент
поля. Это происходит для мод с ezj = 0 в планарных волноводах и в волокон-
ных световодах для мод с круговой симметрией, называемых TF-модами.
В этих двух специальных случаях, поперечное электрическое поле eZJ- везде
удовлетворяет скалярному волновому уравнению (см. разд. 33.1).
189
11.16. Гибридная природа полей мод
Исходя из физических соображений, изложенных в предыдущем разделе, ис-
следуем некоторые свойства полей мод. Рассмотрим металлический волно-
вод, состоящий из идеально проводящей оболочки и однородной сердцеви-
ны, выполненной из диэлектрика, так что в сердцевине Vtlnn2 = 0. Уравне-
ния для продольных компонент поля (11.44) сведутся к однородным урав-
нениям (11.45) для ezj и /zzj. Легко заметить, что моды такого волновода
представляют собой две линейно независимые системы [7]. Для одной си-
стемы мод продольная составляющая магнитного вектора равна нулю в лю-
бой точке поперечного сечения, и такие моды называются поперечно-магнит-
ными (ТМ), для другой — продольные составляющие электрического векто-
ра равны нулю, и моды называются поперечно-электрическими (ТЕ). В опти-
ческих волноводах ненулевые члены, содержащие Vtlnn2 в уравнении
(11.44), связывают ezj и h7], и уравнения, в общем случае не могут быть
разделены. А поскольку ни е • = 0, ни Zzzj = 0 не являются решениями, то и
ТЕ- и ТМ-моды не являются в общем случае модами оптического волновода.
Поэтому моды оптических волноводов в общем случае гибридные и содер-
жат продольные составляющие как электрического, так и магнитного векто-
ров. Они называются НЕ- или ЕН-модами [8]. В некоторых случаях в зависи-
мости от геометрии поперечного сечения и формы профиля показателя пре-
ломления правая часть в уравнении (11.44) равна нулю, и ряд мод оптичес-
ких волноводов является либо чисто ТЕ-, либо чисто ТМ-модами. Простей-
шим примером таких структур является планарный волновод. Другим при-
мером служат осесимметричные поля круглых волоконных световодов. За
исключением тривиального случая бесконечной однородной среды поля мод
никогда не являются ТЕМ-волнами, у которых в любой точке ezj = 7zzj = 0.
Физический смысл ТЕ- и ТМ-мод. В планарном волноводе ТЕ- и ТМ-модам
соответствуют два возможных состояния поляризации электромагнитного
поля. Это является следствием полного внутреннего отражения плоской вол-
ны от границы двух однородных полубесконечных диэлектрических сред,
как это показано на рис. 10.2. Фаза отраженной волны отличается от фазы
падающей и зависит от того, какой из векторов — электрический или маг-
нитный - параллелен границе, но в любом случае направление одного из них
не изменяется, так что либо ezj = 0, либо Zzzj = 0, и ТЕ- и ТМ-моды не смеши-
ваются. Таким образом, физической причиной различия между ТЕ- и ТМ-мо-
дами в планарном волноводе является зависимость коэффициента отражения
плоской волны от поляризации. Эду же зависимость отражают члены в век-
торном волновом уравнении, содержащие Vt In п2. Подобное качественное
рассмотрение можно провести и обобщить для среды с градиентным профи-
лем показателя преломления, только в этом случае необходимо использо-
вать понятия локальных плоских волн (см. разд. 35.3) .
В круглых волоконных световодах ТЕ- и ТМ-моды с полями, имеющими
круговую симметрию, распространяются таким же образом, как и в планар-
ных волноводах, поскольку их электрический и магнитный векторы парал-
лельны границе между сердцевиной и оболочкой. С точки зрения локальных
плоских волн или лучей только для меридиональных лучей (пересекающих
ось волновода) при каждом отражении ezj = 0 или AZJ = 0. Поэтому только
меридиональные лучи могут быть представлены ТЕ- или ТМ-модами кругло-
190
Рис. 11.2. Вектор электрического поля е:
а. — в волоконных световодах со ступенчатым ;урофилем показателя преломления для
меридиональных лучей, параллельный фиксированному направлению; б — для косых
лучей, изменяющий направление при каждом отражении; в — в волоконных световодах
с параболическим профилем, непрерывно изменяющий направление вдоль траектории
косого луча
го волновода (см. рис. 11.2,а). Это также согласуется с тем, что поля этих
мод в векторном волновом уравнении не зависят друг от друга. Хотя такое
описание не совсем строго для одномодовых и маломодовых волноводов,
тем не менее оно дает качественно правильную картину.
Физический смысл гибридных мод. Используем понятие локальных плос-
ких волн для определения природы гибридных мод в круглом волоконном
световоде. Рассмотрим траекторию луча в нем. В общем случае луч распро-
страняется по винтовой или косой траектории как в ступенчатых, так и в
градиентных волоконных световодах, как показано на рис. 11.2,5 и 11.2,в.
Если, учитывая понятие локальной плоской волны, следовать за направле-
нием электрического вектора вдоль косого луча, то становится понятным
невозможность выполнения условий eZJ - 0 или hL] = 0 на всем его пути, по-
скольку направление электрического или магнитного вектора зависит от про-
дольной координаты. Следовательно, в случае косого луча происходит пере-
мешивание ТЕ- и ТМ-поляризаций при каждом отражении, т. е. поле моды
содержит составляющие электрического и магнитного векторов и является
гибридной модой и, наоборот, ЕН- и НЕ-моды формируются из косых лучей.
Вращение электрического вектора в векторном волновом уравнении
(35.8) описывает член, содержащий Vtlnw2. Очевидно, что чем меньше
Vt In п2, тем больше аксиальный период, на котором луч совершает полный
191
оборот. Следовательно, какой бы малой ни была величина Vtln«2, электри-
ческий вектор все равно повернется на 360°. Именно этому явлению гибрид-
ные моды и обязаны своим возникновением.
Резюмируя сказанное, отметим, что поляризационные свойства волновод-
ной структуры обусловлены геометрией ее поперечного сечения и профилем
показателя преломления и в векторном волновом уравнении (11.40) описы-
ваются членами, содержащими Vtln«2, которые вызывают появление гиб-
ридных мод. Отбрасывание этих членов ведет к игнорированию поляризаци-
онных свойств волноводной структуры и к скалярному волновому уравне-
нию.
11.17. Постоянная распространения
Значение постоянной распространения j3j для каждой направляемой моды на-
ходится из характеристического уравнения, рассмотренного в разд. 11.13.
Для данной длины волны в вакууме X и профиля показателя преломления
п (х, у) возможны только определенные значения, диапазон изменения кото-
рых можно найти из следующих физических соображений. По определению
направляемая мода в непоглощающем волноводе распространяется без зату-
хания, поэтому j3j — действительная величина. Профиль показателя прелом-
ления удовлетворяет условию исо > и (х, у) > ис1, где псо и «с1- максималь-
ное и минимальное значения показателя преломления. Поэтому минималь-
ная фазовая скорость волны равна минимальной фазовой скорости света в
волноводе, т. е. c/nCQ. С другой стороны, хотя максимальная фазовая ско-
рость моды и может превышать фазовую скорость в оболочке, однако это
приведет к потере мощности излучения. Следовательно, фазовая скорость
направляемой моды ограничена этими пределами. Используя уравнение
(11.5) и соотношения из табл. 1, получим, что независимо от геометрии по-
перечного сечения и профиля показателя преломления
(11.46)
где к = 2я/Х.
ВОЛНОВОДНЫЕ ПАРАМЕТРЫ И ПАРАМЕТРЫ МОД
Поля мод волновода зависят от всех физических величин волновода, т. е.
от параметров, описывающих профиль показателя преломления и геометрию
поперечного сечения, а также от частоты или длины волны источника возбуж-
дения. С помощью их определим два безразмерных параметра. Первый — вол-
новодный параметр (нормированная частота)
(П-47)
куда входят максимальный и минимальный показатели преломления ис0 и
ис1 (см. рис. 11.1,6)', длина волны в вакууме X и характерный линейный раз-
192
мер поперечного сечения сердцевины р (радиус сердцевины световода или
полуширина планарного волновода). Второй - параметр высоты профиля
А = | (1 -«с1/«со)-
(11.48)
Эквивалентные обозначения V и Д даны в табл. I.
Волновод называется многомодовым, если V » 1 и распространяется
большое количество направляемых мод. В противоположном предельном
случае, если V достаточно мало, т. е. может распространяться только основ-
ная мода в двух состояниях поляризации, волновод называется одномодо-
вым. Например, для круглого волоконного световода со ступенчатым про-
филем, как это показано в разд. 12.9, одномодовый режим реализуется при
Г <2,405.
Электрическое поле моды волновода с. данным поперечным сечением и
формой профиля может быть нормировано таким образом, что в качестве
параметров будет содержать только величины К Дир, т. е. = ej(K Д,р).
Магнитное поле будет иметь ту же параметрическую зависимость за исключе-
нием множителя ис0 (бо/Мо)1/2 > который получается из первого уравнения
Максвелла (30.1а) при нормировке оператора V х. Дополнительные пара-
метры потребуются при учете изменений поперечного сечения (например,
эксцентриситета эллипса поперечного сечения в эллиптических волноводах)
и формы профиля (например,' параметра профиля в степенном профиле
(1-59)).
Параметры мод. При решении характеристического уравнения удобнее
оперировать безразмерными параметрами мод, чем ненормированной посто-
янной распространения. Поэтому, чтобы упростить описание полей мод, вве-
дем безразмерные параметры Щ и для сердцевины и оболочки
Ц = р(к2п2С0 -0?)1/2;
[^=Р(/3- - ^2«с1)1/2 >
(11.49)
где к = 2тг/Х, исо -- максимальный показатель преломления сердцевины и
т?с1 — показатель преломления однородной оболочки. Под р понимается ха-
рактерный размер сердцевины (полуширина или радиус). Очевидно, что для
направляемых мод непоглощающего волновода U- и Wj являются действи-
тельными величинами. Из выражения (11.47) видно, что волноводный и мо-
довые параметры связаны между собой соотношением
V2 = и?+ W2,
J J
(11.50)
а пределы изменения постоянной распространения направляемых мод в вы-
ражении (11.46) эквивалентны условиям:
0 < t/j < Г; 0 < FVj < V
(11.51)
7 Зак 37
193
для данного значения К По определению основными являются моды с двумя
наименьшими значениями £/ или, что эквивалентно, имеющие две наиболь-
шие постоянные распространения, которые при данном V удовлетворяют
характеристическому уравнению. В волоконном световоде они равны.
Предельный случай малых V. Из выражения (11.47) следует, что V -+ 0 при
X -> о°. Поэтому при V = 0 имеем электростатический предел для векторного
волнового уравнения (11.40а) . При этом V х etJ = 0, V • (w2etJ) = Ои поэто-
му etj можно выразить через такую скалярную функцию Ф (х, у), что
72Ф + • Vtlnw2 = 0; etJ=Vt^. (11.52)
В случае однородной оболочки уравнение для Ф переходит в уравнение
Лапласа.
11.18. Частота отсечки моды
Минимально возможное значение постоянной распространения направляемой
моды в выражении (11.46) = кпсХ называется частотой отсечки моды, или
просто отсечкой. Она может быть определена через безразмерные параметры
моды (11.49) и (11.50)
^ = 0. (11.53)
Основные моды всех типов волноводов, рассматриваемых в данной книге,
имеют отсечку при V = 0. При отсечке фазовая скорость моды равна фазо-
вой скорости плоской волны в неограниченной среде с показателем прелом-
ления ис1, но при этом следует иметь в виду, что за исключением специаль-
ных случаев, поля мод не являются ТЕМ-волнами. Вообще говоря, даже при
отсечке значительная часть мощности моды распространяется по сердцеви-
не, т. е. в уравнении (11.24) ф 0, что приводит к отличию фазовой скоро-
сти от групповой. Ниже отсечки моды являются вытекающими и распростра-
няются с потерями (см. гл. 24). Если оболочка однородная, то правая часть
векторного волнового уравнения (11.40а) равна нулю, и условие отсечки
j3j - кпс\ приводит левую часть к уравнению Лапласа
V2ej =0, (11.54)
где оператор V2 определен в табл. 30.1. В круглых волоконных световодах
поперечное электрическое поле основной моды однородно в оболочке, что со-
ответствует аксиально симметричному граничному решению этого уравнения.
Мода вдали от отсечки. Это справедливо, если V >> или ~ ^псо>
что приводит к условию
Е->оо. (11.55)
В этом случае вся мощность моды сосредоточена вокруг области с макси-
мальным показателем преломления сердцевины п nCQ. Для волоконных
световодов с оболочкой она целиком находится в сердцевине.
11.19. Число направляемых мод
Точное количество направляемых мод волновода может быть найдено в ре-
зультате подсчета всех дискретных решений характеристического уравнения.
В общем случае это довольно трудоемкая процедура, но для многомодовых
волноводов, для которых V» 1, можно получить простые выражения, при-
веденные в разд. 36.12 и 36.13.
194
11.20. Параметр искажения
Уширение импульса вследствие волноводной дисперсии обсуждалось в
разд. 11.12. Выразим теперь уширение импульса 6Л в уравнении (11.37) че-
рез волноводный параметр V и параметр моды Для этого запишем это
уравнение, используя определение групповой скорости моды (11.31)
, v dv• v dv yi d2pi
foJ &J
Из выражения (11.31) также следует, что
с_________dV = с (V2 — 2 Ду)1/2
gJ исо(2Д)1/2 c?(p0j) «со V-Ду'
(11.57)
где у = 1/? и штрих означает дифференцирование по И Подставляя теперь вы-
ражение (11.57) в (11.56) , получаем
5t. = 2-|^ ВУД8ы =-2--^ОУД8Л,
1 с со с X
(11.58)
где D - D(V, Д) — безразмерный параметр искажения, определяемый соот-
ношением
ПП7 \\ 1 _ _1_______d , с у _ со ч
( ’ ) (2Д)1/2 dV2 2псод dV (ugj) (Н.59а)
_ Д(2.уу" -у'2) - (И2/' -2Уу' + 2у)
2CV2 — 2Ду)3/2
Таким образом, уширение импульса, обусловленное волноводной дисперсией,
характеризуется произведением £>ИД. На практике, как правило, частота или
длина волны источника излучения заданы, а р и Д являются параметрами
структуры.
В табл. I даны физические величины и волноводные параметры, определя-
ющие распространение света в волноводе и параметры направляемых мод.
В табл. 11.1 даны характеристики направляемых мод.
11.21. Связь с лучевым инвариантом
В части I лучевой анализ был использован для решения задачи распростране-
ния света в многомодовом волноводе с профилем показателя преломления,
плавно изменяющимся на расстоянии, равном длине волны света. Очевидно,
что эту же задачу можно решить волновым методом, используя моды волно-
вода, рассмотренные в этой главе, что и показано в гл. 36, где демонстри-
руется эквивалентность обоих подходов. Поскольку в ч. II достаточно часто
упоминаются результаты, полученные в ч. I, то представляется полезным свя-
зать параметры моды с инвариантами луча. В многомодовом волноводе по-
стоянная распространения моды /3j и продольный лучевой инвариант 0 (36.2)
связаны соотношением
0 = Х^/2л, (11.60)
7*
195
Таблица 11.1. Свойства направляемых мод
Электрическое поле моды E(*,y,z) = {et(x,y) + zez(x,y)} ехр(i^z)
Магнитное поле моды H(x,y,z) = {h1(x,>) + z/iz(x,})[exp(i0z)
Условие ортогональности eyxhf -zd4 = e;xh/zd4 = 0
Нормировка N = z exh*-zd4 2 k
Ортонормальные моды Л e £ h e=N172’ h = /vr75‘
Плотность мощности, или интенсивность S = j|a|2 exh*-z
Мощность моды P = j|a|2 | exh*-zd/i * А»
Мощность моды в сердцевине 1 1 exh*"2d4 2 J. 4 = j f“ exh*-zdA
Фазовая скорость 1 n2|el2d4 w 1 Vp - « = f P n2exh*-zd>l
Групповая скорость (среда без дисперсии) exh*-zdA V ®° f n2|e|2d4 *
Параметр искажения 1 d2(p£) ( ’ (2Д)1'2 d Г2
Примечание. Индекс моды / опущен, если в выражение входят характеристики одной
моды. Волновод считается непоглощающим, т. е. в качестве е^., могут быть взяты дей-
ствительные функции, тогда ez, hz будут мнимыми. Амплитудный коэффициент моды
а определяется выражениями (11-2).
где X — длина волны света в вакууме. Отметим, что эта связь не зависит от
профиля показателя преломления волновода. В случае ступенчатого профиля
196
можно выразить и параметры моды U-} и Wj через угол между траекторией
луча и осью волновода 0z, как это сделано в табл. 36.1 (при этом индекс /
опущен). Другие соотношения для круглых волоконных световодов рас-
сматриваются в разд. 36.2.
ВОЛНОВОДЫ С ПОГЛОЩЕНИЕМ
Если волновод изготовлен из материала с поглощением, то при распростра-
нении мода теряет часть своей мощности. Математически процесс поглоще-
ния описывается мнимой добавкой к диэлектрической проницаемости мате-
риала или показателю преломления, как это видно из табл. 11.2. Поскольку
теперь профиль показателя преломления комплексный, то комплексными
являются и постоянная распространения, и волноводные, и модовые парамет-
ры. Поэтому использовать результаты разд. 11.3 нельзя, так как там все по-
перечные поля были действительными.
Таблица 11.2. Основные выражения, описывающие распространение волн в по-
глощающих волноводах
Комплексный профиль показателя преломления е(х,у) = е'(х, у) + й?(х, у); п(х,у) = nr(x,y) + mi(x,}') ef = e0{(«r)2-(«')2}; «‘ = 2£onrn'
Параметры мод p = + Ц = UJ + iUj; Wj = И?-НИ?
Поля мод Ej = е/х,у) exp(i£jz)exp( -0]z); Н7 = hj(x,y)exp($Jz)exp( -0’z)
Мощность МГД Pj(z) = Pj(O)exp(-V); Ъ = 2Д!
Коэффициент затухания мощности ъ = 24 -) — у I J a J
Примечание. Индексы г и i обозначают действительную и мнимую части, Re -
действительную часть. Для с лабопоглощающих волноводов поля в выражении для
7 могут быть аппроксимированы полями непоглощающего волновода.
11.22. Затухание мощности
Множитель ехр(—где ^является мнимой частью постоянной распростра-
нения, описывает затухание полей мод (табл. 11.2). Если обозначить мощ-
ность моды на расстоянии z от начала волновода через Zj (z), то, подставляя
выражение для полей в уравнение (11.21а), получим выражение для потерь
мощности через коэффициент затухания мощности г и начальную мощность
Pj(O).
197
Однородная среда. Сначала рассмотрим тривиальный случай бесконечной
однородной среды с постоянным показателем преломления п = п1 + ini.
ле моды, временная зависимость которого неявно выражается множителем
ехр(—ко?), является полем плоской волны, распространяющейся в направле-
нии оси z с постоянной распространения 0j = кп1 + ikn\ где к = 2я/Х. Очевид-
но, что амплитуда поля уменьшается пропорционально ехр(—kn[z), и поэто:
му коэффициент затухания мощности равен ?j = = 2кп\ Величина 2кп'
есть коэффициент поглощения мощности а, введенный ранее в выражении
(6.2), и поэтому в данном случае ?j = а.
Неоднородная среда. Труднее определить коэффициент затухания мощно-
сти в волноводе, состоящем из материалов с произвольными коэффициента-
ми поглощения. Эта задача может быть решена двумя способами. Первый
заключается в получении характеристического уравнения для волновода с
поглощением и нахождении комплексных корней этого уравнения, которые
соответствуют постоянным распространения направляемых мод. Следует
подчеркнуть, что таким способом задача решается только численно. Второй
способ, который используется ниже, заключается в выражении коэффициен-
та затухания мощности через поля мод (как это сделано в уравнении (11.42)
для постоянной распространения в непоглощающих волноводах) .
Поглощенную мощность dP^ на длине волновода dz можно найти через
усредненный по времени вектор Пойтинга (см. разд. 30.9). Она определяет-
ся выражением (30.28), где вектор Е заменен амплитудой моды ^jEj. Если
под V понимать объем волновода между сечениями z и z + dz, то
dP =-fc(6o/Mo)1/2ltfjl2cfe f zZn’lE;|2Л4, (11.61)
J J J
где Ам — площадь бесконечного поперечного сечения. С другой стороны,
дифференцируя выражение для мощности в табл. 11.2, имеем
dP> = -rdP-j (0) ехр(-у). (11.62)
Учитывая для мощности модыР: (0) выражение (11.21а), а для Ej выраже-
ние в табл. 11.2 и приравнивая уравнения (11.61) и (11.62), получаем коэф-
фициент поглощения мощности
J nTn \tA2dA
7j ' Re( / е. 'х h*-zcL4) ’
Аж J J
(11.63)
где Re означает действительную часть выражения, (*) - комплексное сопря-
жение иг — единичный вектор, параллельный оси волновода. Остальные па-
раметры определены в табл. 1. Подчеркнем, что поля в выражении (11.63)
получаем для поглощающего волновода.
Слабое поглощение. Если волновод имеет небольшое поглощение, что
обычно выполняется на практике, то, используя различные приближения,
можно получить явные выражения-для коэффициента ослабления мощности.
В одном случае мнимая часть постоянной распространения определяется из
характеристического уравнения поглощающего волновода, при этом она,
198
как и ранее, представляется в виде /3 = /3? + 1/3]', а отношение /3-//3j раскладыва-
ется в ряд и учитываются лишь линейные члены. Во втором случае произво-
дится замена ej и hj в (11.63) соответствующими функциями для непогло-
щающего волновода. Фактически такое приближение можно использовать
во всех расчетах характеристик слабопоглощающих волноводов при усло-
вии, что в выражения для полей Ej и FL введен множитель ехр(—P-z), а в
выражение для мощности моды — коэффициент ослабления exp(-7jZ), как
это проделано в табл. 11.2. Некоторые характеристики слабопоглощающих
волноводов будут рассмотрены в гл. 13 и 18.
АНИЗОТРОПНЫЕ ВОЛНОВОДЫ
До сих пор рассматривались свойства волноводов, изготовленных из изо-
тропного материала. Рассмотрим теперь волноводы, изготовленные из анизо-
тропного материала. Сначала опишем распространение плоской волны в нео-
граниченной однородной анизотропной среде, а затем рассмотрим моды ани-
зотропного волновода.
11.23. Однородная анизотропная среда
Основное свойство изотропной среды заключается в том, что вектор Е сов-
падает по направлению с вектором электрического смещения еои2 Е, иными
словами, показатель преломления среды не зависит от направления вектора
Е, а плоская волна может распространяться в любом направлении с любым
и неизменным состоянием поляризации. Поэтому в общем случае распростра-
нение в каждом направлении может быть описано двумя линейно поляризо-
ванными плоскими волнами, векторы электрического поля, которых орто-
гональны друг другу, но в пространстве ориентированы произвольным
образом.
Анизотропный материал состоит из пространственно-ориентированных
молекул и тем самым обладает рядом свойств, присущих кристаллическим
материалам [2, 9, 10]. В частности, вектор смещения в общем случае не па-
раллелен вектору Е, т. е. показатель преломления зависит от его направле-
ния. Кристалл имеет три взаимно ортогональных главных оси, характеризу-
емые тем, что если электрический вектор параллелен любой из них, то век-
тор смещения параллелен полю. В этом случае описание распространения
света не сложнее, чем в изотропной среде, за исключением того, что необхо-
димо ввести три величины п, соответствующих вектору смещения D = eon2 Е,
если вектор Е параллелен оси х, D = 60h2E, если вектор Е параллелен оси у,
и D = еом2Е, если вектор Е параллелен оси z. Однако если вектор Е не парал-
лелен одной из главных осей, то
£>x=eon^x; Dy=eon2Ey-, Dz=eon2zEz, (11.64)
и вектор D уже не является параллельным вектору Е, а описание распростра-
нения света значительно усложняется. Так, в частности, для каждого направ-
ления распространения существует только два разрешения состояния поляри-
зации плоской волны, а моды такой среды подобны модам кристаллической
среды. Каждая мода может быть представлена линейно поляризованной
плоской волной. Разрешенные состояния поляризации и постоянные распро-
199
странения этих двух мод могут быть найдены при решении трех однородных
линейных уравнений относительно Е^Е и Ezi которые можно записать в ви-
де [2, 9]
j32 [Е - (к • Е)к] =к2п2 • Е =к2 (пхЕхх + пуЕуу + n2zEzi), (11.65)
где к — единичный вектор, параллельный направлению распространения
плоской волны, к — волновое число, определенное в табл. 1, и х, у, z — еди-
ничные векторы, параллельные декартовым, или главным осям. Свойствами
решения уравнения (11.65) являются компланарность векторов k, D и Е,
различные направления потока мощности и волнового вектора к, к и в об-
щем случае зависимость величины постоянной распространения 0, по крайней
мере, для одного из разрешенных направлений от направления распростра-
нения волны.
Плоская волна, распространяющаяся вдоль одной из осей. Описание рас-
пространения света существенно упрощается в некоторых частных случаях.
Например, если направление распространения совпадает с осью z, то одна раз-
решенная (собственная) мода является поляризованной вдоль оси х плоской
волной в среде с показателем преломления п = пх, а другая разрешенная мо-
да — поляризэванной вдоль оси у плоской волной в среде с показателем пре-
ломления п = пу. Если пх = пу, то кристалл называется одноосным, а если
nx^ny ^nz ~ двуосным.
11.24. Анизотропные волноводы
Основные уравнения, описывающие распространение света в анизотропных
волноводах, приведены в разд. 30.10. Найти их решения в общем случае зна-
чительно труднее, чем для соответствующих уравнений для изотропных вол-
новодов. Из приведенных выше рассуждений становится ясным, что если три
главные оси диэлектрического материала не совпадают с геометрическими
осями волновода, изображенного на рис. 11.1, а, то моды волновода являют-
ся очень сложными. Если совпадают две оси, то ТМ-моды анизотропного
планарного волновода с показателями преломления пх, пу. и nz являются
простым обобщением мод соответствующего изотропного планарного волно-
вода, в то время как ТЕ-моды идентичны модам изотропного планарного
волновода с показателем преломлениям =му, который остается неизменным
вдоль оси у. Этот вопрос будет обсуждаться ниже в разд. 12.19. По аналогии
с модами планарного волновода моды одноосного волоконного световода
с показателями преломления пх = пу являются также простым обобщением
мод изотропного волоконного световода и более подробно рассматриваются
в разд. 12.20. Отметим, однако, что моды двуосного кристаллического воло-
конного световода с пх Ф пу Ф nz не могут быть представлены в аналити-
ческом виде и это не удивительно, поскольку анизотропия нарушает круго-
вую симметрию профиля показателя преломления.
Постоянная распространения. Диапазон значений постоянной распределе-
ния j3j для направляемых мод анизотропных волноводов с оболочкой можно
получить, обобщая соображения разд. 11.17 относительно изотропных волно-
водов. В частности, если предположить, что то постоянная распро-
странения направляемых мод должна удовлетворять условию > кп*\, в
противном случае часть поля моды, поляризованной вдоль осих, будет излу-
200
чаться вследствие фазовой скорости, превосходящей фазовую скорость поля-
ризованной вдоль оси х плоской волнь! в оболочке. Если показатели прелом-
ления в оболочке для света, поляризованного вдоль осей х и у, обозначить
соответственно через и лс1» т0 обобщение формулы (11.46) на случай ани-
зотропного волновода в предположении, что п*о > пУо и и* > дает
(11.66)
где п*о — максимальный показатель преломления сердцевины для света, по-
ляризованного вдоль оси х. В общем случае нижнее значение 0j определяется
наибольшей из величин п^ и пусХ, а верхнее значение зависит от наибольшей
из величин п*о и пуо.
При выводе соотношения (11.66) предполагалось, что поля мод имеют
х- и у-составляющие. В случае планарного анизотропного волновода попереч-
ные поля мод могут быть, как это показано в разд. 12.19, поляризованными
либо вдоль оси х, либо вдоль оси у. Другими словами, х- и у-поляризованные
моды таких волноводов не взаимодействуют между собой, и постоянная
распространения х-поляризованной моды подчиняется условию (11.66). Для
постоянной распространения у'-поляризованной моды справедливо то же ус-
ловие при замене индексах на у.
Слабонаправляющие анизотропные волноводы. Если показатели прелом-
ления сердцевины и оболочки волновода приблизительно одинаковые незави-
симо от направления вектора Е, то такие волноводы называются слабона-
правляющими. В таких случаях направляемые моды можно представить в ви-
де плоских волн, распространяющихся почти вдоль оси волновода. Это упро-
щает выражения для характеристик распространения, что можно было пред-
видеть из обсуждения в конце разд. 11.23. Моды таких структур рассматри-
ваются в гл. 13, здесь же подчеркнем, что несмотря на то, что волновод явля-
ется слабонаправляющим, анизотропия может существенно изменить харак-
теристики распространяющегося света.
Волноводы со слабой анизотропией. Волноводы, являющиеся почти изо-
тропными, могут быть исследованы методами теории возмущений (см.
гл. 18) . Свойства слабонаправляющих волноводов обсуждаются в разд. 18.9,
а свойства волноводов с произвольными профилями показателя преломле-
ния — в разд. 18.21.
ГЛАВА 12. ВОЛНОВОДЫ, ДЛЯ КОТОРЫХ УРАВНЕНИЯ МАКСВЕЛЛА
ИМЕЮТ ТОЧНЫЕ РЕШЕНИЯ
В предыдущей главе были рассмотрены основные свойства направляемых
мод оптических волноводов. В этой главе продемонстрируем эти свойства на
примерах тех немногих типов волноводов, для которых уравнения Максвел-
ла имеют точные решения. Основная цель данной главы — получить аналити-
ческие выражения для векторных полей мод, которые, как это отмечалось
в разд. 11.16, содержат всю информацию о поляризационных свойствах вол-
201
новодов. Особое внимание уделим основным модам, так как именно они мо-
гут распространяться в одномодовых волноводах. Поскольку здесь рассмат-
риваются отдельные моды, то индекс в выражениях для их полей можно опу-
стить. Поля мод в выражении (11.3) можно теперь представить как
Е(х,у, z) = е(х, у) exp(ij3z) ; Н(х; у; z) = h(х, у)exp(i0z) , (12.1)
где 3 -- постоянная распространения. Компоненты поля являются решениями
однородных векторных уравнений (30.14)
(У^+пЧ2 - 02)е = —(Vt + i/Jz)et *Vtln/?2, (12.2а)
(Vt2+«2A:2 -/32)h = [(Vt + ipi) xh] X AJnn2, (12.26)
где n = n (x, у) — профиль показателя преломления, к - 2тг/Х и X — длина вол-
ны в вакууме. Индекс t означает поперечные компоненты, az — единичный
вектор, параллельный оси z. Векторные операторы Vt2 и Vt определены выра-
жениями (37.38) и (37.33) соответственно. Для планарных волноводов и
волоконных световодов с круговой симметрией будут использоваться урав-
нения составляющих поля (30.21) и (30.15). Рассмотрение начнем со ступен-
чатого профиля показателя преломления, так как, во-первых, это важный
для практики случай, а во-вторых, при этом можно попутать точные аналити-
ческие решения уравнений Максвелла.
12.1. Волноводы со ступенчатым профилем показателя преломления
Волноводы со ступенчатым профилем представляют собой сердцевину с по-
казателем преломления исо, окруженную бесконечной оболочкой с показа-
телем преломления ис1. Таким образом, изменение показателя преломления
на границе сердцевины с оболочкой происходит скачком. Такой профиль по-
казателя преломления позволяет получить точные аналитические выражения
для полей мод как планарных волноводов, так и эллиптических волоконных
световодов и волоконных световодов с круговой симметрией.
Решение векторного волнового уравнения. Общий подход к нахождению
полей в волноводах со ступенчатым профилем заключается в решении век-
торных волновых уравнений (12.2) для сердцевины и оболочки, т. е. для об-
ластей с Vt In и2 = 0, и использовании граничных условий уравнений Макс-
велла при определении амплитуд полей. Такой подход уже обсуждался в
разд. 11.15, где было подчеркнуто, что члены, содержащие Vt In и2, входят в
граничные условия. Уравнение (12.2) необходимо решить только для про-
дольных компонент поля, поскольку поперечные компоненты находятся
тогда из соотношения (11.43). Таким образом, уравнения для продоль-
ных компонент поля внутри сердцевины и оболочки имеют вид уравнения
(11.45), т.е.
(У2 + иЧ2 - 02)Ф = О, (12.3)
где под Ф подразумевается ег или /zz, а оператор V2 определен в табл. 30.1.
Граничные условия уравнений Максвелла (30.1) подразумевают непрерыв-
ность h и тангенциальной компоненты е на границе и ограниченность поля в
любой точке поперечного сечения волоконного световода. Решение уравне-
ний находится с точностью до постоянного множителя, являющегося ампли-
202
тудой моды tfj, который определяется либо источником возбуждения, либо
условиями нормировки.
ПЛАНАРНЫЕ ВОЛНОВОДЫ СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ
ПРЕЛОМЛЕНИЯ
Простейшим примером ступенчатого волновода является симметричный пла-
нарный волновод (рис. 12.1) с профилем
п(х) =исо> 1*1 <р;
п(х) =ис1, р<|х| <оо, (12.4)
где р — полуширина сердцевины. Такая структура является двумерной, и при
соответствующей ориентации декартовых осей (см. рис. 12.1) поле зависит
только отх и у, т. е.
Е(х, у) = e(x)exp(ij3z); Н(х, у) = h (х) exp (ij3z) . (12.5)
Рис. 12.1. Сечение планарного волновода,
размеры которого в направлении осей у и z
неограничены. Волновод имеет полуширину
сердцевины р и профиль показателя прелом-
ления п (х). Ось z совпадает с осью волново-
да, расположенной посередине между верх-
ней и нижней границами сердцевины с обо-
лочкой
Параметры волновода и длина волны источника возбуждения X заключены в
волноводном параметре Кив параметре высоты профиля Д, определение ко-
торых дано в табл. I.
12.2. Поля мод
Найдем поля мод, следуя соображениям, изложенным в разд. 12.1. Подстав-
ляя выражение (12.4) в (12.3) и используя табл. 30.1, получаем
(р2 + ^)Ф = 0; 0<|х|<р,
ах
(Р2-^Г -И/2)Ф = 0; р<|х|<°°,
(12.6а)
(12.66)
где параметры мод U и W определены выражением (11.49), а под Ф понима-
ется ez или hz. Решения имеют вид sin(t/x/p) или cos(UJp) в сердцевине и
ехр (—И/|х |/р) в оболочке. В разд. 11.6 было объяснено, почему моды пла-
нарного волновода являются ТЕ-модами с ez = 0 или ТМ-модами с hz = 0.
В любом случае, продольная компонента поля непрерывна на границе и пред-
ставляется в форме, данной в табл. 12.1. Ненулевые поперечные компоненты,
поля определяются из уравнения (30.8) - Непрерывность hx или hy в точке
х = ±р приводит к характеристическому уравнению в табл. 12.2, которое ис-
пользуется также для определения амплитуды составляющих поля в табл. 12.1.
203
Таблица 12.1. Составляющие полей мод планарного волновода со ступенчатым профилем показателя преломления
h2
Сердце- вина Оболочка Сердцевина Оболочка Сердцевина Оболочка
Четная ТЕ cos(C/X) cost/ ехр(->Г|Х|) ехр(-ИО />А0 y,2cos(UX) к\До J cosU _£Ло¥'2 ехр(-Ж|Х|) Адо/ ехр(-И') A1 '2 sin(UX) кр \До / sin ‘’♦'ЛоУ'2 X ехр(->F|X|) kp\pj |Х| exp(-IF)
Нечетная ТЕ sin(UX) sin U X ехр(-И'|Х|) |Х| ехр<-Ж) Д/е0\|/2яп(С/Х) к \Яо / sin /?/еоу;2 X ехр(-И'|Х|) k\pj |Х| exp(-JF) iW7eoy<2cos(UXj кр \Яо / cos L7 'И7«о А*'2 ехр( -H'lХ|) кр\Ро/ ехр(-1Г)
ех = е, = = 0
Л, ег
Сердце* вина Оболочка Сердцевина Оболочка Сердцевина Оболочка
Четная ТМ cosWX) cos U п^, ехр(->Г|Х|) "d ехр(-И') кп^ /g0 V12 cos(C/X) Р \pQ / cos U fcn^/eo у '2 ехр(-Н'|У|) /» \Яо/ exp(->F) sin(UX) рр n£| sin U -^Пгт X ехр(-1Г|%|) рр л2 |Х| exp(-»F)
Нечетная ТМ sin(UX) sin U X ехр(-И'М) п2 |Х| .expt-JF) knw(eo У /2 яМ*7*) Р \pQJ sin U кп2ю Zs» у11 X exp(-»F|X|) 0 |Х| exp(-W) -ilTn^cos(UX) рр п2! COS и -i>Tn^exp(-tF|X|) pfi exp(-W)
е, = hx = h, = О
Примечание. Оси координат изображены на рис. 12.1, X = х/р, где р — полуширина сердцевины. Показатели преломления сердце-
вины и оболочки равны Псо и«с] соответственно, а остальные параметры определены в табл. 1.
Предположим, что внутри сердцевины еу = 1 или ех = 1 при х = р. Поперечное
электрическое поле четной и нечетной мод является четной или нечетной
Таблица 12.2. Свойства мод планарных волноводов со ступенчатым профилем по-
казателя преломления (а) и асимптотические выражения для U (б)
а)
Четные ТЕ-моды Нечетные ТЕ-моды Четные ТМ-моды Нечетные ТМ-моды
Характерис- тическое уравнение W = U Un и >У= -U cot U = пj С Un С nLw= -4dUcotU
Нормировка N _рр(ео\1'2 Г2 2к \д0) U2 W 20 U/ 1 "с4! и2 nc2! U2W\
Мощность в сердцевине и2 П - 1 ~ r2(l+iy) ! "«"d^2 nMncl’/2 + <H/J+'IXl/2
Г рупповая скорость с 0 1 V* * 1 “2Д(1-Ч)
Число направ- ляемых мод Mh= Int<—> I n J
б)
ТЕ^. -моды ТМ^. -моды
Отсечка и = г, W = 0 С! II 7 к>Га
Вблизи отсечки и * И, W * 0 е: j с: 11 1 п 1 d 1 1 т । 1 х—С 1 ~ 1 з 1 - 1 1 С! 1 С! ; « 1 ?? 1 । 1 । 83*|с?* 1 । 1 1 [ V । II о 1 >9 1 1 1 1 1
Г = И7 = оо п 1/= 0+1)2
Вдали от отсечки W> 1 G'<'+,|i{'-77T} ^U + l)"}1 „«Д:} 2 1 Лс1 'псо J
г, Л Диапазон одномодового режима 0 < V < — 2
Примечание. Характеристики мод N, т] и Vg рассчитаны на основании табл. 11.1, и
и Пс1 ~ показатели преломления сердцевины и оболочки, остальные параметры опреде-
лены в табл. I.
205
функцией х. В непоглощающем волноводе nQQ и /?с1 — действительные вели-
чины и поля мод подчиняются условию (11.8), т. е. ez, hz — мнимые функ-
ции, а ех, еу, hx и hy — действительные. Полная пространственная зависи-
мость полей следует из выражения (12.5) .
В следующем разделе будет показано, что U зависит от V или от К и Д.
Поэтому если вместо 0 и «со/пс1 подставить безразмерные величины из
табл. 1, то параметрическая зависимость электрического поля в табл. 12.1 бу-
дет включать только независимые параметры И, Д и р, т. е. е = е(И, Д, р) ана-
логично выражению (11.48). Магнитное поле за исключением множителя
исо (ео/до) зависит от тех же параметров.
Альтернативный подход. Вывод выражений для полей мод через продоль-
ные компоненты, данный в предыдущем разделе, основан на том, что про-
дольные компоненты поля в векторном волновом уравнении для ступенча-
того волновода не связаны между собой, как это отмечалось в разд. 11.15. Од-
нако в ряде частных случаев поля ТЕ и ТМ мод планарных волноводов мож-
но найти, решая уравнения непосредственно для компонент поля еу и Лу,
как это будет продемонстрировано в разд. 12.14 и 12.15.
12.3. Постоянные распространения
Как было отмечено выше, характеристические уравнения получаются из ус-
ловия непрерывности тангенциальных составляющих поля. Существует четы-
ре характеристических уравнения, соответствующих четным и нечетным ТЕ-
и ТМ-модам. Эти уравнения приведены в табл. 12.2. Решение каждого уравне-
ния позволяет найти U, а затем, используя соотношения из табл. 1, постоян-
ную распространения р. Значение р лежит в пределах, удовлетворяющих ус-
ловию направляемых мод < р < кпс0.
Характеристическое уравнение является трансцендентным и может быть
решено только численно. На рис. 12.2 представлена зависимость (/(К) для
первых восьми мод волновода при А = 0,32. Чтобы подчеркнуть различие ре-
шений для ТЕ- и ТМ-мод, выбрана относительно большая разница показате-
лей преломления сердцевины и оболочки. Четные и нечетные значения индек-
са / относятся к четным или нечетным TEj- и TMj-модам, причем / увеличива-
ется с ростом U.
Рис. 12.2. Численные решения
характеристических уравне-
ний из табл. 12.2, а для
первых восьми мод. Значения
вдоль штриховой прямой со-
ответствуют значениям U на
частоте отсечки
206
Параметры моды на частоте отсечки и при V = °°. Значения Uпри отсечке
(см. разд. 11.18) находятся подстановкой U = V в каждое характеристичес-
кое уравнение. Из табл. 12.2 видно, что U = как для ТЕр так и TMj-мод.
Поскольку основные ТЕ0- и ТМ0-моды отсечки не имеют, то волновод явля-
ется одно модовым в диапазоне 0 < V < тг/2, в котором могут распространять-
ся только эти две моды. При V -> 00 волноводный параметр U -+ (/ + 1) тг/2.
Таким образом, для всех мод U увеличивается на тг/2 при увеличении V от
значения отсечки до бесконечности. Все эти результаты представлены в
табл. 12.2.
Параметры моды вблизи и вдали от частоты отсечки. Приближенные вы-
•ражения для Uвблизи и вдали от отсечки приведены в табл. 12.2. В первом
случае U раскладывается в ряд по степеням (И - /я/2) и в характеристи-
ческом уравнении приравниваются коэффициенты при одинаковых степе-
нях разложения. Во-втором случае характеристические уравнения дифферен-
цируются [1 ], например, для четных ТЕ-мод
= ___________1________ П27)
dV V 1 + (V2 - Ц2)1'2
и поскольку V » U, U в знаменателе опускается, что дает интегрируемую
функцию. Результат приведен в табл. 12.2. Сравнение приближенных и точ-
ных результатов показывает, что относительная ошибка растет вблизи часто-
ты отсечки при росте V и вдали от частоты отсечки при уменьшении И Для
ТЕ0-мод ошибка обоих приближений составляет 10,4% при V = 0,72, а для
ТМ0-мод - 25,2 % при V = 1,26.
12.4. Свойства мод
Подставляя выражения для полей мод из табл. 12.1 в табл. 11.1, получаем
выражения для N, ц и vg в табл. 12.2. Интегралы по поверхности в табл. 11.1
для планарных волноводов сводятся к однократным интегралам по попереч-
ной координате х с пределами ±°°. Как будет показано ниже, параметры т? и
vg отражают волноводные свойства структуры.
ТМ-моды. Если в характеристическом уравнении для ТМ-мод в табл. 12.2
W и «со/лс1 выразить через безразмерные волноводные параметры V и Д, то
U будет зависеть от обоих. Поляризационные свойства волновода обусловле-
ны зависимостью U от Д, т. е. членами, содержащими Vt In п2 в уравнении
(12.2) (или, как отмечалось в разд. 11.16, зависимостью коэффициента от-
ражения плоской волны от ее состояния поляризации на границе планарно-
го волновода). Она усиливается с ростом Д.
ТЕ-моды. Если в характеристическом уравнении для ТЕ-мод в табл. 12.2
выразить И7 через К то параметр моды будет зависеть только от Vи не будет
зависеть от Д, т. е. от поляризации волны, как и предсказывалось в разд. 11.15,
и поэтому в уравнениях (30.216) и (30.21г) для компонент еу и Лх соответ-
ственно члены, содержащие Vt In п2, отсутствуют. Следовательно, попереч-
ные компоненты поля удовлетворяют скалярному волновому уравнению
в любой точке поперечного сечения волновода, включая границу. В разд. 33.1
показано, что любое решение скалярного волнового уравнения должно быть
непрерывным в любой точке поперечного сечения и иметь непрерывную пер-
207
вую производную. Используя это свойство, можно получить характеристи-
ческое уравнение для ТЕ-мод непосредственно из уравнения (12.3) без уче-
та граничных условий уравнений Максвелла. Продольные компоненты поля
удовлетворяют уравнениям (30.21в) и (30.21е),в которых члены, содержа-
щие Vt In п2, отсутствуют везде, за исключением точек на границе, и поэтому
ez и hz не являются решениями скалярного волнового уравнения.
Параметры моды вблизи и вдали от частоты отсечки. По мере приближе-
ния U к своему значению при отсечке W -*0 и /3 -»kncl. Из табл. 12.2 следует,
что 7? —> 0, т. е. вся мощность моды распространяется в оболочке, а и -+с/пс],
т. е. групповая скорость моды стремится к скорости света в оболочке. Более
того, из табл. 12.1 следует, что ez -* 0, hz -> 0, так что моды вблизи частоты
отсечки являются ТЕМ-модами. Необходимо подчеркнуть, что условие??-*О
и превращение полей в ТЕМ для всех мод при отсечке является спецификой
только планарных волноводов.
Вдали от отсечки, где W -> V -+<*> и /3 -> кпс0, ?? -> 1, a vp -> с/пс0. Это означа-
ет, что вся мощность моды сосредоточена в сердцевине, а групповая скорость
равна скорости света в сердцевине.
Число мод. Полное число направляемых модМЬт, которые могут распро-
страняться в планарном волноводе, наиболее просто находится подсчетом ре-
шений характеристического уравнения. Поскольку значения U при отсечке
кратны я/2 (см. рис. 12.2) и каждая мода может существовать в двух состо-
яниях поляризации, то общее число мод Mbm =Int(4E/?r), где Int означает
наибольшее целое, не превосходящее 4Р/я. Таким образом, число мод зави-
сит только от К
12.5. Слабонаправляющие волноводы
Волновод называется слабонаправляющим, если показатели преломления
«со и «сЬ приблизительно равны или, что эквивалентно, если параметр высо-
ты профиля мал, т. е. Д << 1. Это приводит к слабой зависимости Uот Д
для ТМ-мод в характеристическом уравнении в табл. 12.2. Кроме того, об-
ласть значений постоянной распространения направляемых мод становится
очень узкой bzcl < /3 < кп с0 и {3 кпсо % И/р(2Д)1/2. Очевидно также, что
продольные составляющие поля из табл. 12.1 в Д"1/2 раз меньше поперечных
составляющих и, следовательно, поля мод слабонаправляющих волноводов
являются почти ТЕМ-волнами со слабой зависимостью от его поляризацион-
ных свойств.
12.6. Разложение полей мод по плоским волнам
Поле каждой моды в сердцевине планарного волновода со ступенчатым про-
филем может быть точно разложено по двум системам плоских волн (см.
разд. 36.1). Каждая плоская волна или луч распространяются под углом к
оси 0Z, удовлетворяющем условию направляемых лучей 0 < 0z < 0с, где 3 =
= кпсо cos 3Z и 0С = arcsin(l - f?2j/«20) — предельный угол скольжения. Если
волновод слабонаправляющий, то /3 kncQf и лучи являются параксиальны-
ми, т. е. 3Z << 1. Дискретные значения /3 соответствуют преимущественным
направлениям лучей (см. разд. 10.7).
208
Время распространения мод и лучей. Из выражения (11.36) следует, что
время распространения моды t в волноводе длиной z равно t ~z/v^ Обозна-
чим соответствующее время распространения луча, определенное в табл. 1.1,
через ^g0. Подставляя выражение для групповой скорости из табл. 12.2 и ис-
пользуя соотношение между постоянной распространения 3 и лучевым инва-
риантом 3 в табл. 36.1, получаем
r = rgo[l — 2Д(1 -т?)].
(12.8)
Таким образом, время распространения моды и луча равны лишь при д 1.
Это условие выполняется только для лучей, соответствующих модам вдали
от частоты отсечки, т. е. когда V >> Uили 0z << вс. Поэтому для произ-
вольного значения 0Z определение времени распространения луча с помощью
rgo является некорректным из-за пренебрежения дифракционными эффекта-
ми, рассмотренными в гл. 10. Однако планарный волновод со ступенчатым
профилем представляет собой тот частный случай, в котором все дифракци-
онные эффекты могут быть точно учтены введением продольного сдвига
луча при отражении и выделением преимущественных направлений распро-
странения. Это было проделано в разд. 10.6, а для лучей, или локальных
плоских длин, поляризованных в у-направлении (см. рис. 10.2) было получе-
но модифицированное выражение для времени распространения луча (10.13).
Если, используя табл. 36.1, выразить 0z и вс через параметры U, Ии IVи под-
ставить т? для ТЕ-моды из табл. 12.2, то выяснится, что выражения (10.13) и
(12.8) идентичны даже при 6Z « вс. Эти же выводы справедливы для ТМ-мод
и локальных плоских-волн с вектором магнитного поля, параллельным оси
у (см. рис. 10.2).
Поглощение в материале. Если материал сердцевины и оболочки волново-
да является слабопоглощающим, то при учете продольного сдвига луча коэф-
фициент потерь мощности луча (6.3) идентичен коэффициенту потерь мощ-
ности моды в табл. 11.2. Подробный анализ представлен в разд. 36.10.
Характеристическое уравнение. Как показано в разд. 36.7, характеристи-
ческое уравнение в табл. 12.2 можно получить непосредственно из траекто-
рии плоской волны в сердцевине волновода, рассчитывая полный фазовый
сдвиг вдоль нее и при отражениях и принимая во внимание простое условие
согласования.
12.7. Асимметричные и многослойные волноводы
До сих пор рассматривались симметричные планарные волноводы. Однако
уравнение (12.6) легко обобщить на случай асимметричного волновода, у
которого показатель преломления постоянный, но различный в областях
х > р и х < — р (см. рис. 12.1) [2]. Подобным образом находятся решения и
для многослойных волноводов, в которых дополнительные слои расположе-
ны параллельно плоскости х = 0. Поля мод в таких волноводах являются ре-
шениями уравнений (12.6) для каждого слоя, а тангенциальные составляю-
щие поля ’’сшиты” на каждой границе.
209
ВОЛОКОННЫЕ СВЕТОВОДЫ СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ
ПРЕЛОМЛЕНИЯ
Волоконный световод со ступенчатым профилем показателя преломления
схематически изображен на рис. 12.3. Эта структура имеет круговую симмет-
рию и профиль показателя преломления
л (г) ~пс' Q<r<p-
у со- Р, (J2.9)
п(г) =ис,; р <Г < °°,
где р — радиус сердцевины. Поля мод в общем случае зависят от всех трех
цилиндрических координат и могут быть записаны в виде
E(r, <p,z) = e(r, <p)exp(i0z);
Н (г, z) = h (г, <р) exp (i|3z). 1 J
Рис. 12.3. Сечение волоконного световода с кру-
говой симметрией, размеры которого в направ-
лении осей г и z неограничены. Радиус серд-
цевины - р и профиль показателя преломле-
ния — п (г). Ось z совпадает с осью симметрии
Параметры волоконного световода и длина волны источника излучения опре-
деляют волноводный парахметр (нормированную частоту световода) V и па-
раметр высоты профиля Д, выражения для которых приведены в табл. I.
12.8. Поля мод
Найдем поля мод, следуя соображениям, изложенным в разд. 12.1. Подста-
вив выражение (12.9) в уравнение (12.3) и использовав табл. 30.1, опреде-
лим, что если под Ф понимать ez или hz, то Ф является решением уравнений
('"дЯ2' + Я Ия + Я2 +и2)^ = 0- 0<£<1, (12.11а)
1 _L + -L -Ц------И/2)ф = 0;
ЭЯ2 Я дЯ R2 д*2 }
(12.116)
1 < R < °°,
где нормированный радиус R = г/р, a Un W определены в табл. I. Решения,
ограниченные в любой точке поперечного сечения, имеют вид Jv (UR)cos
или (UR) sin v<p в сердцевине и Kv (IVA) cos v<p или Kv (И7?) sin v<p в оболочке,
где v — положительное целое число или нуль, Jv — функция Бесселя первого
рода (37.62), Kv — модифицированная функция Бесселя второго рода
(37.66). В разд. 11.16 объяснялось, почему моды световода при линейной
комбинации ТЕ- и ТМ-мод в общем случае являются гибридными. Гибридные
моды имеют как ez, так и hz компоненты и называются НЕ- и ЕН-модами.
Функциональная зависимость полей этих мод одинакова, но, как показано в
210
следующем разделе, значения модового параметра U для них разные. Чтобы
получить выражение для поля моды, необходимо в первую очередь выбрать
продольные составляющие, являющиеся непрерывными на границе, т. е.
JV(UR) JAUR)
(12.12а)
л К (WR) . х 1 „ KV(WR)
еъ ~ А (щ) 4 (^) ’ “ В к (ц/) Sv (<Р) > 1 < /^ < °°, (12.126)
где А и В - постоянные, а/р ngp определены в табл. 12.3,а. Поперечные ком-
поненты находятся из уравнения (30.9) . Налагая условие непрерывности ази-
мутальных компонент поля в точке R = 1, можно определить отношение Л/В и
получить характеристическое уравнение для ЕН- и НЕ-мод (см. табл. 12.4,а).
Можно положить А = 1, однако, как отмечается в разд. 12.11, Л удобнее вы-
бирать из соображений согласования с результатами анализа слабонаправля-
ющих волноводов. Поля мод представлены в табл. 12.3, а. Четные и нечет-
ные моды имеют радиальные составляющие электрического поля (четные
или нечетные функции . Для осесимметричных ТЕ- и ТМ-мод составля-
ющие поля приведены в табл. 12.3, б, а характеристическое уравнение в
табл. 12.4,а. Обозначения даны в табл. 12.3,я. Если световод непоглощающий,
то 71со и пс1 являются действительными величинами и поля мод подчиняются
соотношению (11.8), т. е. ez и hz — мнимые величины, ет, е hT, — дей-
ствительные. Повторив рассуждения, приведенные в разд. 12.2, можно сде-
лать вывод о том, что электрическое поле е в табл. 12.3 параметрически за-
висит от К Д и р, а магнитное поле h, кроме того, — еще и от множителя
«со(ео/^о)1/2 •
12.9. Постоянные распространения
Как отмечалось выше, характеристическое уравнение для четных и нечетных
НЕрт-, ЕНрт-, ТМОт- и ТЕ0т-мод может быть получено из условия непре-
рывности тангенциальных компонент поля. Каждой моде присваивается два
индекса, первый из которых v означает порядок, а второй гп — номер корня
характеристического уравнения. Корни нумеруются таким образом, чтобы
т = 1 соответствовал корню с наименьшим значением Uили, что эквивалент-
но, с наибольшим значением 0 для данного v. Увеличение номера т приводит
к увеличению U. Значения 0 для всех мод лежат внутри интервала < /3 <
< кпсо. Повторив рассуждения разд. 12.4, выясним, что для ЕНрт и НЕрт -мод
величина U зависит от К Ди р, для ТМ0т-мод - отри Ди для ТЕот-мод -
только от v. Кроме того, поперечные компоненты полей ТЕ0т-мод удовлет-
воряют скалярному волновому уравнению в любой точке поперечного сече-
ния волоконного световода, в том числе и на границе. Иными словами, ТЕ-мо-
ды круглого световода в полярной системе координат эквивалентны ТЕ-мо-
дам планарного волновода в декартовой.
211
Таблица 12.3. Составляющие поля НЕрт-и ЕНрт- (д) и ТЕОт- и ТМ0т-мод (б) волоконного световода со ступенчатым профилем по-
казателя преломления
а)
Составляющие Сердцевина Оболочка
вг aiJ,_AUR) + a2J,+ AUR) JAU) 7,1 ' Ua^K'.AWRy-a^AWR) w kv(H9 }
еУ alJ„-l(UR)—a2J,+ l(UR) ~ j.m - e-m UaiK,.,(fFR) + a2K,+ l(^R) t 4 W К.(И') 9'
ez pP jau) M ' pP kaw) 7,1
hr Ao Y'2 kn2m a3J,.t(UR)-atJ, + AUR) \Mo / P JAU) 9A /e<>Y/2 kn2aU a3K,_AWR) + a6K, + AWR) t. \pj P KAW)
h<f _(e<>\il2kn2aa3J,-AUR) + a<Jv + AUR) \pJ p JAU) Ш) _ Ao V'2 kn^ U asK,-AWR)-a6K,+AWR) [pj p W KAW) Л’
_.AoY/2 uf2 jaur) .. 'W kp JAU) ,(Eo\ll2UF2 KAWR) 'U/ kp KAW) 9Л
fcos(v«p) f {sin(vv’) ’ { — sin(v^) четные моды fU^\2bt + (l-2A)b2 p . V ) “ V ’ f2 = l / V \2 v
COS(v^) нечетные моды ^1Л»7 bi+Ьг
01 = (Fi-D. (F.-D 2 ’ 2 (F.-1+2A) ; -5= 2 . . 1 p,->(V) MdU)} * 2U( MU) MU) J
а2 = (Fi + П (F. + l) - 2 ; «< = 2 (F,+ 1—2A) ; a6= 2 2 2W( K*(W) KAW) J
б) ТЕ-моды ТМ-моды
Составляющие Сердцевина Оболочка
-MUR) MU) -KdWR)
KV^pMUR) к MU) fepY12 P Ki(WR) W к K^)
h2 /ерУ'2 U MUR) ‘[pj kp MU) /^y12^ K0{l¥R) kp Kt(W)
Ct II Ct II II О
Составляющие Сердцевина Оболочка
JAUR) n2aKt{WR) n2dKi(WR)
MU)
iU Jq(UR) pP MU) -in2m WK0(WR) л2 pP KJfF)
АЛ1'2 kn^MUR) U/ P MU) /eo\1/2 kn^MlWR) \pj p Kt(W)
e* = hr = h2 = 0
Примечание. Оси координат изображены на рис. 12.3, R = г/р, где р — радиус сердцевины. Показатели преломления сердцевины и обо-
лочки равны исо и ис| соответственно, остальные параметры определены в табл. I.
Рис. 12.4. Численное решение характеристических уравнений из табл. 12.4, а для первых
двенадцати мод. Штриховая прямая соответствует значениям V на частоте отсечки,
штриховая кривая - решению для основной моды в волоконном световоде при исо «
Характеристическое уравнение является трансцендентным и может быть
решено только численно. На рис. 12.4 представлены зависимости U(И) для
ряда мод волоконного световода при Д = 0,32. Относительно большое значе-
ние Д взято для того, чтобы подчеркнуть различие в решениях для разных
мод. Штриховой линией показано решение для НЕ1Гмоды в случае Д = 0
(«со =«С1)-
Параметры моды вблизи частоты отсечки и при V = 00. Следуя рассужде-
ниям разд. 11.18, получаем, что значение U при отсечке находится подстанов-
кой U = Vf W = 0 в каждое характеристическое уравнение в табл. 12.4, а. Ис-
пользуя асимптотическое выражение (37.86) дляЛ'р(И/) при W 0, получа-
ем неявные выражения для (7»на частоте отсечки (табл. 12.4, 6}. Четные и не-
четные НЕ n-моды являются основными модами волоконного световода, так
как имеют наименьшее значение Uпри любом И и не имеют отсечки. При ко-
нечном значении V ТЕог и ТМ01-моды имеют наименьшую отсечку, которая
определяется первым нулем функции Бесселя Jo, т. е. U* 2,405. Таким об-
разом, волоконный световод является одномодовым, если 0 < V < 2,405.
При V асимптотическое выражение (37.88) дляЛ’ДИ') при приво-
дит к неявным значениям Uвдали от отсечки (см. табл. 12.4, б), Как следует
из рис. 12.4 Uрастет монотонно с ростом И
Выражения для параметров моды вблизи и вдали от частоты отсечки.
Приближения для U вблизи и вдали от частоты отсечки могут быть получены
в частности для основных мод, которые важны для одномодовых волокон-
ных световодов. Следуя методам, описанным в разд. 12.3, можно вывести
характеристическое уравнение, взяв dU/dV из характеристического уравне-
ния для НЕц-моды в табл. 12.4, я, которое дает выражения для параметров
мода вдали [3] и вблизи частоты отсечки [4], приведенные в табл. 12.4, в.
214
Таблица 12.4. Характеристические уравнения волоконного световода со ступенча-
тым профилем показателя преломления (а), предельные значения параметра моды U
(б), основные моды (в)
а)
HEvmu ЕНУт“моды Альтернатив- ная форма put/) jau) пга K'AW) I _ / у)? у / V у lUJAU) WKAWtflUJAU) n^WKAW)) \fcncJ pwj = P2F2
ТЕд^-моды JAU)- кино и j0(U) И'Ко(И')
ТМОи- моды n^JAU) UJ0(U) И'Ко(И')
б)
Мода Отсечка JP = 0, U = V V = w= 00
TE0. TMOm J0(U) = o Л((/) = о
НЕ1я J>(l/) = 0 J<AU) = о
EHVW JAU) = 0 J,+ 1(t/) = O
HE„ (v > 1) U J,.2(U) _ -2Д (v-i)J,.AU) ~ 1-2Д J,-i(t/) = O
Диапазон одномодового режима Q < V < 2.405
в;
ш J-1+Д-Wl 1
, r _ . _ _ f 1 4- Л1 U » 2.405 exp< — > 1
Примечание. Параметры определены в табл. 1, «со и ис1 - показатели преломления
сердцевины и оболочки соответственно.
215
Подобные выражения можно получить и для других мод [3, 4]. Сравнение
приближенных значений для НЕц-моды с точными показывает, что относи-
тельная ошибка аппроксимации вблизи отсечки растет с ростом К а для ап-
проксимации вдали от отсечки растет по мере уменьшения V. При V = 1,4
ошибка в каждом случае равна 8,1 %,
12.10. Свойства мод
Подставляя выражения для полей мод из табл. 12.3 в табл. 11.1, пол учим выра-
жения для Sz, N, tj и Vg в табл. 12.5. Элементарная площадь dA = p2RdRdip,
интегралы от функций Бесселя и рекуррентные соотношения приведены в
гл. 37. На рис. 12.5 приведены зависимости т?(Е) для первых двенадцати
мод волоконного световода с теми же параметрами, что и на рис. 12.4. Штри-
ховой линией представлена зависимость для НЕц-моды при Д = 0 («со = «cl).
Поляризация полей мод. В любой точке поперечного сечения волоконно-
го световода поле моды может быть представлено как линейно поляризован-
ное, но поскольку оно зависит от координаты точки, то направление вектора
электрического поля меняется по поперечному сечению, что иллюстрируется
на рис. 12.6. Для аксиально-симметричных мод линии напряженности элект-
рического поля являются либо окружностями (ТЕот-моды), либо радиаль-
ными прямыми (ТМот-моды).
Пространственное распределение интенсивности моды. Интенсивность
5Z ЕН- и НЕ-мод в табл. 12.5 изменяется как по радиусу, так и по углу. 5Z —
осесимметрична только для ТЕ- и ТМ-мод, как показано на рис. 12.7 для
случая ТЕог и ТМ0рмод. Более темная область соответствует большей интен-
сивности, которая достигает максимума при UR % 1,8 и равна Нулю на оси.
Поле моды вблизи и вдали от частоты отсечки. В отличие от мод планарно-
го волновода только некоторые моды волоконного световода при отсечке
не переносят мощность по сердцевине, т. е. ?? = 0, что иллюстрируется рис. 12.5.
Рис. 12.5. Зависимость мощности, распространяющейся по сердцевине, для каждой из
двенадцати мод от V. Штриховая кривая соответствует основным модам при «с0 «
~"с1
216
Рис. 12.6. Направления векторов электрического и магнитного полей (соответственно
сплошные и штриховые линии) мод низших порядков в поперечном сечении волокон-
ного световода со ступенчатым профилем показателя преломления при мс0
Рис. 12.7. Качественное представление распределения интенсивности по поперечному
сечению волоконного световода со ступенчатым профилем для ТЕ01- и ТМ01-мод, облада-
ющих осевой симметрией. Более темная область соответствует большей интенсивности
К ним относятся ТЕОт-, ТМот-, НЕ1т и НЕ2т-моды, для всех остальных мод
при отсечке ?? > 0. Поэтому, как следует из табл. 12.5, только моды с т? = 0
при отсечке имеют групповую скорость, равную скорости света в оболочке
с/псХ. Для остальных мод ug < с/п^.
217
218
Таблица 12.5. Свойства мод волоконного световода со ступенчатым профилем показателя преломления
Сердцевина Оболочка
S, ТЕОт |а|2 /е0 jf(VR) 2 W к Ы2 Ao Y'2 A 2 W к Kl(W)
тмОп |д|2 /«о V11 кп^ Jl(UR) 2 \м0/ Р Jf(U) н2 y 12 кп^ 2 \д0/ ₽(1 -2Д) Kt(W)
EHvm и HEvn 2 \До/ 0J;(U) { + а2а47?+1(С'Л) + 1~^‘F2 Л-!(UR)J„+1(l/R)cos(2v<₽)| Ы2 /£0 \1/2 kn2 U2 ( Лмо) PK^hK-‘(M/R) + a2a6R2v+I(fyR) 1-2A-F,F2 , ) ± j—~1 К«-' (И'Л)К‘ +1 (И'Л) cos(2v?) >
К = *со+*с1 ТЕ0„ *со яр2 /Ч Y'2 ёУ1 JqWWiM] 2 \pj О J Nd -пр2 Ao Y'2 Mj _K0(tF)K2(»F) 1 2 VpoJ H K2(fn j
тмОм 2 UJ Р 1 Ji(V) J -пр2 /co Y'2 kn2№ f K0(W)K2(W)\ 2 W /?(l-2A)t K2(W) J
ЕНут и HEvm яр2/ео\‘'2 кп2т г fj2 (Ш -J,(U)J,-2(U)}+a2a4{J2,+ i(U) -Jv(U)Jv+2(U)}] -7tp2AoY/2 кП№ Г fvl IU7\ 2 PK2(W)fV2 -K,(»F)Kv.2(»r)} + a2a6{K?+I(fF) -K,(W)K, + 2(W)}-i
п Все Nm + Na
vt Все с 0 1 п2ак 1 — 2Д(1 -П)
мЬт Dm (У2) Int< — >; ( 2 J
Примечание. Все параметры определены в табл. 12.3, а и табл. I и рассчитаны на основании табл 11.1. Знаки ”+’
ным и нечетным модам, R = r/p, Q — амплитуда моды, и — показатели преломления сердцевины и оболочки.
и ” относятся к чет-
Таблица 12.6. Разложение Тейлора полей четной моды НЕП слабонаправляющего волоконного световода со ступенчатым профилем
показателя преломления
Сердцевина Оболочка
ёх J0(UR) J0(U) KqQFR) Ко(й')
0 0
^.l2U MUR) -21/2i- cos У Jo(U) -21/2i , cos V K0(w\
0 0
po A1'2 J0(UR) Лс°\Яо/ Jo(U) /ЕрХ1'2 K0(WR) П<”\ц0) K0(w)
,1/2. Ao\,/2UJ1(UR) . -2 4J иЛ1й”" ZeoY^^K^R) . -2 4J
р(1) С X 4^(jo(UR) + ^J^UR)+J2(UR)c°s2j. Jo4J) ( U ) С 2Л ) 5 TrT^Uo^Rb-^K^RbKHH^ct^ ) (. W )
р(1) СУ - 1>UUsin2 2 Jo(U) k<Aw)
Сердцевина Оболочка
£>(3/2) - 7777-; ] Ji (UR) + U»>R J0(UR) kos ч> V •'О \U J I * J 21/2iTF f U2 ) Ii!7A-7T2 -W»>RKo(WR) cos^
hi*» 1 /% V'2 ft/2 - „Л JiiUR) , MJ k‘+™ и® ln f6°Y/2|2^2|H>IF<4K2(^)Sin2T 2 “UJ \v2+ww f k0(w) 1
1И /Er. 12 ( -w -i—— ) {UU^JotURj + lU^RJAUR) (2V2 \ ) + 1 -^ + UU(lnj2(UR)cos2‘P> n (E \1/2 (/ — <|2-И,И,(,)ко(И'К) + 2И,,1,«К1(И/К) 2Ко(^)\До7 p. /2JK2 \ - ) -H -р- + Н'И/(1) Jk2(H'R)cos2¥’>
h<3'2» 7^2 in f p \1/2 ~ -T7Zr(— ) —77-{UJ1(UR)-RJ0(UR)}sin^ •'оШ) \Mo / * 2 1/2in /p f - ) —I —^{»'Kl(W'R)-RK0(W'K)>sm¥> Ko(jr)Vo/ V I J
Характеристическое уравнение Поправки к параметрам мод = IF-^2; l/2+IF2 = Г2; Fx ~ - 1 + + F2 «-1 + bUUa> JoiU) K0(JF) I K2j 2
= fFa,= _^W. = v2 клиО’ у2 Ki(>r)’
Примечание. Разложение проведено в (12.13) по степеням А1/2 вплоть до кубических членов R — г}р. Параметры определены в табл. I.
Вдали от отсечки все моды концентрируют свою мощность в сердцевине,
т. е. т? -> 1, если V -> <», и, следовательно, групповая скорость мод стремится
к скорости света в сердцевине с/иС0.
Число мод. Подсчитать число решений для направляемых мод волоконно-
го световода Afbm труднее, чем для планарного волновода, поскольку корни
характеристических уравнений в табл. 12.4, а расположены неравномерно.
Однако, как показано в разд. 36.13, в многомодовом волоконном светово-
де при V» 1 это можно сделать с помощью выражения Afbm =Int(V2/2).
Здесь под Int понимается наименьшее целое число, превышающее К2/2.
12.11. Слабонаправляющие волоконные световоды
Световод является слабонаправляющим, если псо % пс1, или, что эквивалент-
но, если Д << 1. При этих условиях /3 & &исо, и решения характеристичес-
ких уравнений в табл. 12.4, а фактически не зависят от Д, т. е. являются не-
чувствительными к поляризационным свойствам световода. Выражая волно-
вое число к через V, имеем 0 « К/р(2Д)1/2, что в совокупности с Д << 1
и табл. 12.3 дает |et| >> |ez |, |ht| >> |/zz|. Следовательно, моды таких све-
товодов являются почти ТЕМ-волнами.
Разложение точных выражений для полей мод. В ряде случаев полезно
знать первые несколько членов разложения полей мод при Д << 1. В качест-
ве иллюстрации рассмотрим основные моды, поскольку они важны для од-
номодовых световодов. Математическая сторона разложения подробно осве-
щена в разд. 32.1, а свойства поля и значения параметров основной моды сла-
бонаправляющего световода — в гл. 13 и 14, поэтому здесь приведем лишь
результаты. Разлагая по степеням Д1/2 и учитывая три члена для поля четной
НЕ1Гмоды, имеем
е = ?хх + Д1/2ер/2)£ + Д(е^ х + у) + Д^2^3/2)^; (12.13а)
h =Ауу +Д1/2/г(1/2)£ +у) + Д3/2/?(з/2)£, (12.136)
где х, у и z — единичные векторы, параллельные осям на рис. 12.3, знак ~ оз-
начает слабонаправляемые (нулевого порядка) поля, индекс вверху — сте-
пень Д. Цилиндрические и декартовы координаты связаны между собой со-
отношением (37.49). Коэффициенты при каждой степени Д в табл. 12.6 по-
лучены разложением точных выражений для полей мод в табл. 12.3, я, при-
чем разложение параметров мод ограничено линейным членом, т. е.
£/={/+Д{7(1); W = W + ДИ/(1), (12.14)
где U и W — определены в табл. I. Если эти разложения подставить в характе-
ристическое уравнение в табл. 12.4 и приравнять коэффициенты при одина-
ковых степенях Д, то получим характеристическое уравнение для U и 1Р и
выражения для UW и в табл. 12.6. Соотношения (37.72) и (37.73)
устанавливают связь между функциями Бесселя. Нормировка точных выра-
жений для полей в табл. 12.6 осуществлена таким образом, чтобы на границе
сердцевины с оболочкой ех = 1.
222
12.12. Разложение полей мод по плоским волнам
В отличие от планарного волновода, в котором поле может быть разложено
по двум наборам плоских волн, поле в сердцевине волоконного световода,
как показано в разд. 36.2, может быть представлено суперпозицией бесконеч-
ного числа плоских волн. Однако в многомодовом волоконном световоде
моды высших порядков, для которых U» 1 или р>> 1 (см. табл. 12.3),
могут быть достаточно точно аппроксимированы суммой плоских волн,
распространяющихся в четырех направлениях. Каждая плоская волна, или
луч, распространяется под углом 6Z к оси волоконного световода, где /3 =
= fcnco cos 0Z, а проекция волнового вектора на поперечное сечение составляет с
азимутальным направлением угол (см. рис. 12.3), причем v = knCQr sin 0Z x
x cosfl^. Углы, под которым могут распространяться направляемые лучи,
определяются выражением (2.6а), где вс = arcsin(l - ^cl/^co)172 ~ крити-
ческий угол скольжения. Соотношения между параметрами мод, углами лу-
чей и лучевыми инвариантами даны в табл. 36.1. В слабонаправляющих воло-
конных световодах (3 = knCQi а лучи являются параксиальными, т. е. 0Z « 1.
Дискретные значения (3 соответствуют преимущественным направлениям
лучей, рассмотренным в разд. 10.7.
Времена распространения'мод и лучей. Выражения для групповой скорости
в табл. 12.5 и 12.2 идентичны и, следовательно, время распространения моды
t = z/vg на длине z волоконного световода идентично соответствующему вы-
ражению для планарного волновода. Поскольку времена распространения лу-
чей в планарном волноводе fgo в табл. 1.1 и табл. 2.1 также одинаковые, то
в световоде t и fgo связаны выражением (12.8) и только при 0z << 0с (см.
разд. 12.6). Для углов 0z ъ вс они различаются вследствие того, что rgo не
учитывает дифракционные эффекты. В световоде они не могут быть учтены
введением продольного сдвига при отражении (см. гл. 10). Имеются и до-
полнительные дифракционные эффекты, связанные с кривизной границы
световода, так как т? зависит от азимутального числа р.
Характеристические уравнения. В разд. 36.7 показано, как получить харак-
теристические уравнения для мод высших порядков многомодового воло-
конного световода, используя условие согласования фаз вдоль траектории
каждой плоской волны. Эти уравнения являются предельными случаями для
характеристических уравнений высоких порядков в табл. 12.4, а.
12.13. Многослойные и эллиптические волоконные световоды
Анализ волоконных световодов со ступенчатым профилем может быть без
труда обобщен на многослойные волоконные световоды с неизменным пока-
зателем преломления в каждом слое, например на трехслойные Петипа, в ко-
торых промежуточный слой имеет наименьший показатель преломления [6].
Поля мод и характеристические уравнения таких структур получаются из со-
ответствующих решений уравнений (12.11) в каждом слое при условии, что
тангенциальные компоненты полей непрерывны на каждой границе.
Методы, изложенные в разд. 12.1, могут быть использованы для вывода
выражений для полей мод и характеристических уравнений волоконных све-
товодов с эллиптической формой поперечного сечения сердцевины, причем
эксцентриситет эллипса может быть произвольным. К сожалению, понять фи-
223
зическую картину, обусловленную эллиптичностью, трудно, поскольку поля
мод выражаются через бесконечные суммы функций Матье [7].
ВОЛНОВОДЫ С ГРАДИЕНТНЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
Существует всего лишь несколько градиентных профилей показателя пре-
ломления, которые позволяют получить точные аналитические решения урав-
нений Максвелла для полей мод, и большинство из них не представляет ни-
какого практического интереса. Получаемые решения обычно нельзя выра-
зить через простые функции, однако они полезны при проверке численных и
приближенных решений. Ниже в примерах для ряда градиентных профилей
будет дан краткий вывод характеристических уравнений и выражений для
полей мод. Поскольку продольные компоненты поля в области, где имеется
градиент показателя преломления, связаны между собой, то подход, изло-
женный в разд. 12.1, является некорректным, и поэтому для получения ис-
комых выражений используется векторное волновое уравнение (30.14).
Примеры даны для довольно большого числа профилей показателя прелом-
ления, когда для полей мод существуют аналитические решения, но они не
охватывают всех профилей.
12.14. Пример. ТЕ-моды планарного волновода с градиентным профилем по-
казателя преломления
Предположим, что планарный волновод, изображенный на рис. 12.1, имеет профиль по-
казателя преломления п (х) и поля мод мбжно представить в виде (12.5). В этом случае
согласованные решения уравнений Максвелла имеют вид выражений (30.5), в которых
ех ~ ez ~ ^у = 0- Эти решения являются ТЕ-модами, а еу удовлетворяет уравнению
(30.216). Если профиль показателя преломления представить в общем виде
п3(Х) = «Jo П - 2Д/(Х)]. Х=х/р, (12.15)
где f(X) > 0, и затем подставить в уравнение (30.216), то с учетом определений из
табл. 1 имеем
[^7 + U* - Г/(Х)]еу= 0 (12.16)
и, следовательно, еу является решением скалярного волнового уравнения. Остальные
компоненты поля могут быть определены с помощью (30.5) как
h = -(-^-)1/2Л? • h - - 1-^-11/2 ± (12 17)
х (Мо) ИУ’ z W к dx ' °
В табл. 12.7 приведены профили показателя преломления, которые приводят к аналити-
ческим решениям для еу и соответствующим характеристическим уравнениям. Каждый
профиль является четной функцией х и изображен на рис. 12.8. Параметр р характеризу-
ет поперечный размер профиля, поскольку для форм профиля от (а) до (е) четко опре-
деленной границы между сердцевиной и оболочкой нет. Для таких профилей волновод-
ный параметр равен V = к рп ^(2^) 1/2, а характеристическое уравнение получается из
условий ограниченности еу в любой точке поперечного сечения и непрерывности еу и
dey/dx в точке х = 0. Отметим, что профили (а), (д) и (г) физически нереализуемы, по-
скольку для первых двух п2 (х) -> при х -> ±°° и для третьего при х -* ±тг/2. Если V
достаточно велико, то мощность моды в основном сосредоточена вблизи оси волновода
и влиянием периферии профиля (|х| » р} можно пренебречь.
В волноводах с неограниченным параболическим профилем (а) поле в табл. 12.7 выра-
жается через полиномы Эрмита Нп порядкам >0 [8], которые являются решением урав-
224
Рис. 12.8. Профили показателя преломления (см. табл. 12.7 — 12.9) как функции по-
перечной координаты х (для планарных волноводов) или радиуса г (для волоконных
световодов), где р — полуширина или радиус сердцевины
нения (12.16), если провести замену переменных w = XVх12 и еу = exp (-vv2 /2)g (w).
Четные и нечетные моды соответствуют четным и нечетным значениям п. Основная мода
имеет наибольшее значение 0 (и — 0), и из табл. 1 имеем
еу = exp (- VX2 /2); U - К1/а.
(12.18)
Выражения (37.107) описывают явно полиномы Эрмита низших порядков. В случае гм-
перболического тангенсного профиля (б) преобразование И' = th X в уравнении (12.15)
приводит к уравнению Лежандра. Поля мод выражаются через функции Лежандра
pn-s Где индекс 5 не обязательно должен быть целым числом, а четные и нечетные зна-
чения п соответствуют четным и нечетным модам [9]. В случае экспоненциального про-
филя (в) преобразованием- = Иехр(—IJTI) в уравнении (12.16) приводит к уравнению
Бесселя и еу описывается функцией Бесселя первого рода J порядок которой р неяв-
но определяется непрерывностью поля в точке х = 0 [8]. Лишь тангенсный профиль (г)
имеет конечные размеры поперечного сечения. Легко проверить, что в этом случае реше-
ние уравнения (12.16) можно представить в виде ряда [10]. Для основной моды (п =
= 0) имеем
ey=cosflX; U = ах'2
(12.19)
Преобразование vv = (V2X - U2) в уравнении (12.16) в случае линейного профиля (д)
приводит к уравнению Эйри, и еу выражается через функции Эйри первого рода Ai [11].
Поля мод в волноводах с обратным, квадратичным профилем (е)выражаются через мо-
дифицированные функции Бесселя второго рода чисто мнимого порядка K-w [12]. Эти
функции являются решениями уравнений, подобных уравнению Бесселя, получаемых
подстановкой w = (1 + X) IV и еу - Wx/2g(w) в уравнение (12.16), где W = (V2 - U2)1/2.
И, наконец, усеченный параболический профиль (ж) представляет собой пример слож-
ного профиля, в котором показатель преломления изменяется по параболическому за-
кону (а) в сердцевине и остается неизменным и равным ис] в оболочке. Поэтому в та-
ком профиле показатель преломления на границе не испытывает скачка. Преобразова-
ние w = XVxr2 иеу = exp(-w2/2)g(w) в уравнении (12.16) для сердцевины приводит к
выражениям для полей четных и нечетных мод через конфлюэнтные гипергеометричес-
кие функции, обозначаемые соответственно Me(w2) и Mo(w2) [13]. В оболочке еу
пропорциональна exp(-HW). Подобным образом из профилей табл. 12.7 могут быть
сконструированы и другие сложные профили.
8 Зак 37
225
226
Таблица 12.7. ТЕ-моды осесимметричных планарных волноводов с градиентным профилем показателя преломления
Профиль пг (X) Электрическое поле еу Характеристическое уравнение
а <{1~2ДХ2} VX2I2)H„(XV111) и = (2n + 1)1/2 Г1'2
б И^{ 1 — 2Д tanh2X} PT’(tanh X); s = {(4Г2 + I)1'2 - 1}/2 U = { И2 — (s —л)2}1'2
в <{1-2Д[1 —ехр(—2|Х|)]} ^„(Kexpf — |Х|}) четная (Х/|Х|)7,(Иехр{-|Х|}) нечетная 1 Jp( V) = 0 четная| 1 L/ = (К2—р2)1/2 Jp( V) — 0 нечетная
г и^{1 — 2Д tan2X} — л/2 X л/2 " [ четная т = 0 cose X У Ci sin2 X l i = m । и, i четная Ci + 2 (и—i)(w + i + 2a)i нечетная тя=1 Ci (i+l)(i + 2) | n, i нечетные и = {(п + а)2 — К2}1'2 а = {(4И2 + I)1'2 + 1}/2
Д л^{1-2Д|Х|} Ai({|X|K2 - 1/2}/И4'3) четная (Х/| X |)Ai({| X | V2 - U1}/К4'3) нечетная Ai'( — L/2/K4/3) = 0 четная Ai( — (У2/К4/3) = 0 нечетная
е "41 Ч1 (1+и)2]} Fl'2Kn(WF) четная (X/|A'|)F*'2K1V(H'F) нечетная ! K„(W)= -2(FK',V(H') четная ] v2 = И2 —1/4 “I Klv(lF) = O нечетная 1 F=1+|X|
ж п^{1 -2ДХ2} 0<|Х| $ 1 1 |Х| < оо ехр( - Г Х2/2)Ме( VX2)/MC( К) четная ехр( - ИХ2/2)МО(ИХ2)/МО( V) нечетная ехр( — И^{(Х| — 1} - Г/2) четная (Х/|Х|)ехр(—ЙК{|Х| — 1} — V/2) нечетная 21И;(И-Ме(Г)= -W четная Мс(УХг) = м(-~ + - \, УХ2] \ 4 И 42 / 2Мф( И) + MQ( И) = —ИИ нечетная /и2 1 1 \ МО(ИХ2)=М — + -, УХ2 \4г 4 2 /
Примечание. Параметры определены в табл. I. Штрих обозначает дифференцирование по аргументу, X = х/р, ncQ и «с1 - показатели
преломления сердцевины и оболочки. Обозначения ’’четная” и ’’нечетная” относятся к модам, у которых составляющая еу является чет-
ной или нечетной функцией х. В профиле (б) п - положительное целое число или нуль, в профиле (в) индекс р не обязательно целое чис-
ло. В профилях (Д), (г) и (б) все моды являются направляемыми.
12.15. Пример. ТМ-моды планарных волноводов с градиентным профилем
показателя преломления
Вторая система совместных решений уравнений Максвелла (30.5) для планарных вол-
новодов в случае еу = hx = /?7 = 0 представляет собой ТМ-моды. Тогда уравнение
(30.21 д) для hy в безразмерных переменных можно записать в виде
^-^ЛЛЭ]ЙУ=О, (12.20)
где п = п (X), X ~ х/р и f (X} определяется формулой (12.15). Один из методов реше-
ния этого уравнения заключается в том, что сначала производится преобразование Лу =
= п (X)g (X), что дает [12]
Если затем ввести условие
-p-<fe’=4’ (12-22)
где А является постоянной величиной, то уравнение (12.21) будет идентично уравнению
(12.16) при замене U2 + А на (72. Поскольку ez является непрерывной функцией, то из
уравнения (30.56) следует, что Лу и dhyfdx непрерывны в любой точке поперечного се-
чения. Кроме ступенчатого существуют еще три профиля, удовлетворяющие условию
(12.22), позволяющие получить аналитические решения уравнения (12.21) и поддержи-
вающие направляемые моды. Эти профили изображены на рис. 12.8 и представлены в
табл. 12.8 совместно с выражениями для Луи соответствующими характеристическими
уравнениями. Профили (з), (и) и (к) являются частными случаями профилем (б), (в)
и (е) в табл. 12.7 соответственно, если положить 2Д = 1 и V = крп^. Остальные ком-
поненты поля могут быть получены из (12.5), а именно
j dh «г
(Мо/^о) к^~НУ’ ег = (Мо/ео)1/2 dx , (12.23)
и выражение (12.5) дает полную информацию о пространственной зависимости каждой
ТМ-моды.
Профили из табл. 12.8 удовлетворяют условию п (х) -+ 0 при |Х1 ->°°. Величина Л на-
ходится подстановкой выражения для каждого профиля в формулу (12.22). Решение
уравнения (12.21) для профилей (з), (и) или (к) получается по аналогии с решением
(12-16) для профилей (б), (в) или (е) соответственно в табл. 12.7.
12.16. Пример. ТЕ-моды волоконных световодов с градиентным профилем
показателя преломления
Предположим, что волоконный световод с круговой симметрией, изображенный на
рис. 12.3, имеет профиль показателя преломления п (г), а поля мод можно представить
в виде (12.10). Согласованные решения векторного волнового уравнения могут быть
получены из уравнений (30.15) при условии, что поля мод не зависят от и ет = ez =
= = 0. Эти решения соответствуют ТЕ-модам, и является решением уравнения
(30.156), которое в нормированной форме имеет вид
^OTl.,-0, <12.24)
где R =г/ри профиль показателя преломления представляется в виде
п1 (R) =л£о[1 -2Д/(Ю]. (12.25)
228
Таблица 12.8. ТМ-моды симметричных планарных волноводов с градиентным профилем показателя преломления
Профиль п2 (X) Магнитное поле hy Характеристическое уравнение
3 sech2 X sech ХР", ’’(tanh X); s = {(4 V2 +1)112 -1 }/2 l/ = {P + l-(n-s)2},/2
и "мехр(-2|х|) ехр( — |X|)J,(Fexp{-|Х|}) четная {(Х/|Х|)ехр(-|Х|)}7(>(Гехр{-|Х|})нечетж Jp(V)= -VJ'r(V) четная I — — 1 U = (V2 + l-p2)'12 |я^( Ю = о нечетная । . I
к Псо (1+|х|)2 f */2К,,(>Р£) четная (X/\X\)F~ll2Kn(WF) нечетная 1 Ki,(JF)= -ЗИ'КгДИ') четная 1 v2=K2-l/4 1 Kj,(»F) = 0 нечетная | F = 1 +1X |
Примечание. Штрих обозначает дифференцирование по аргументу, X = х/р, ncQ и ис] — показатели преломления сердцевины и обо-
лочки. Обозначения ’’четная” и ’’нечетная” относятся к модам, у которых компонента е* является четной или нечетной функцией х,
V = крп , Ц/ = /Зр, остальные параметры определены в табл. 1. В профиле (з) п является положительным целым числом или нулем,
в профиле (и) индекс р не обязательно целое число.
229
Таким образом, удовлетворяет скалярному волновому уравнению, а остальные ком-
поненты поля могут быть получены с помощью соотношений (30.5)
йг = -(ео/мо),л
Лг=-(ео/Мо),'’^7
(12.26)
На рис. 12.8 изображены профили, приводящие к аналитическим решениям уравнения
(12.24), а в табл. 12.9 приведены выражения для формы профиля, для е^ и соответству-
ющие характеристические уравнения.
Для неограниченного параболического профиля (л) преобразование w = 7?К1/2 и
е^ = ^exp(-wa/2)g(w) в уравнении (12.24) приводит к уравнению, решения которого
выражаются через обобщенные полиномы ЛагерраЛ^1) порядкам > 0 [13]. Световоды
с профилем (м), называемым обратным квадратичным, имеют сердцевину с неизмен-
ным показателем преломления и оболочку, в которой показатель преломления изменя-
ется обратно пропорционально квадрату радиуса. Поле в сердцевине выражается через
функции Бесселя первого рода и первого порядка Jx, а поле в оболочке - через моди-
фицированную функцию Бесселя второго рода чисто мнимого порядка Следующий
обратный линейный профиль (н) в сердцевине идентичен профилю (м), однако в обо-
лочке с ростом радиуса показатель преломления уменьшается линейно. Поле в оболоч-
ке выражается через функции Уиттекера х [14]. И, наконец, последний параболи-
ческий профиль (о) в сердцевине идентичен профилю (л), но в оболочке показатель пре-
ломления остается неизменным и равным на границе показателю преломления сердце-
вины. Поле в сердцевине выражается через функции Уиттекера [13], а поле в обо-
лочке - через модифицированную функцию Бесселя второго родаК\. В разд. 12.18 бу-
дут рассмотрены ТЕ-моды световода с профилем (н).
12.17. Пример. ТМ-моды волоконных световодов с градиентным профилем
показателя преломления
Уравнения (30.15) имеют и вторую систему решений, которая не зависит от азимуталь-
ной координаты у. Этими решениями являются ТМ-моды, для которых е^ = hT = hz =
= 0, и является решением уравнения (30.15д). В нормированной форме это уравне-
ние имеет вид
+ = (12.27)
где п = n(R), R = г/р и функция/(У?) определяется выражением (12.25). Поскольку
ez является непрерывной функцией, то из (ЗО.5в) следует, что и dh^dr являются
также непрерывными функциями. Остальные компоненты поля определяются с помо-
щью выражений (30.5)
= (Мо/во),/а^у-^; ez=7 (Мо/е.)1Я^г (12.28)
Для решения уравнения (12.27) используем подход, изложенный в разд. 12.15, и поло-
жим = п (R)g(R). Отсюда
+ R Jr ~ ~R* +^-V4(.R) +p(R)]g = 0, (12.29а)
где
<‘22’”
230
Таблица 12.9. ТЕ-моды осесимметричных волоконных световодов с градиентным профилем показателя преломления
Профиль и2(Л) Электрическое поле Характеристическое уравнение
л п*о{1- 2&R2} Яехр(-ИК2/2)£»’(ГК2) и = 2(n+1)1/2К1;2
м 1 3 3 7 1 ° N) । /Л %, 1 * * Л 1/Л м I 1 — т! V 1 1 1 1 Л(1/К)/Л((7) K|y(lFR)/Kj,(JF) JJU) Kiv(JF) v2 = Г2 - 1
н 1 1 -1 8 V/ v к. 1 * V/ 1 V/ о 1 - г. 8 ’ 81 ix s: | s: 1 i Jl(UR)/Jl(U) R-'^AW/W^Mp) Л (U) PPW,^(2Pp) 2 V =
о и^{1- 2ДЯ2}; O«R<1 п2 = л^{1-2Д}; R21 M^VR1)/ RM..„(И K^Rj/K^W) M'AV) KQ(W) 2 V— •д — v K,(Fr) к= (/2/4И;д = 1/2
Примечание. Штрих обозначает дифференцирование по аргументу, R = r/p, wco и — показатели преломления сердцевины и оболоч-
ки. В профиле (л) п является положительным целым числом или нулем.
В частном случае степенных профилей показателя преломления
и3(Я) = «co^; р(Я) =-ч7(4 + <?)/4Я3, (12.30)
и уравнение (12.29а) становится скалярным волновым уравнением (12.24), в котором
член 1/R2 заменен на — (2 + q) 2 /4R2. Аналитические решения, соответствующие направ-
ляемым модам, существуют при q = — 2 или q = —1. Обратные квадратичные профили
будут обсуждаться в следующем разделе, и профиль с q = — 1 описывает изменение по-
казателя преломления в оболочке профиля (н) на рис. 12.8. В сердцевине поля выра-
жаются через функции Бесселя первого рода Jx (UR). В оболочке U2 -
= (kpn^yiR - (дЗ)2, и преобразование w = 2p&R, g = y/R112 приводит
(12.29) к уравнению Уиттекера с решениями W*, [13]. Таким образом,
, Л (UR)
j,(U) ;
. _ 1/2 (2gr)
* ЛЙ/к,1/2(2^ ’ 1<Л<°°’
где к = p£2«£q/20, а характеристическое уравнение имеет вид
К7(Я) =
уравнение
(12.31а)
UJ0(U) ^к, 1/2 (2/М)
------- — 2а Р----—1------.
где штрих означает дифференцирование по аргументу.
(12.316)
12.18. Пример. Гибридные моды волоконного световода с градиентным про-
филем показателя преломления
Предположим, что волоконный световод имеет профиль показателя преломления, изо-
бражаемый кривой (н) на рис. 12.8. Показатель преломления в сердцевине равен исо и
не зависит от радиальной координаты, а в оболочке уменьшается обратно пропорцио-
нально квадрату радиуса, т. е.
n2(R)=n2co; 0<Я<1;
(12.32)
п2 (R) = n2CQ/R2, 1 < оо,
где R = г/р. Поля каждой моды световода с таким профилем можно представить анали-
тически [15]. Рассматривая азимутальные компоненты векторного волнового уравне-
ния (30.156) и (30.15д), находим, что в области 1 < R < °° эти уравнения не содержат
члены с ет и Лг соответственно. Если азимутальные составляющие поля представить в
виде
G(A)gp(^); h^= (12.33)
где функции fv и gv определены в табл. 12.3, а, то уравнения (30.156) и (30.15д) можно
свести к обыкновенным безразмерным дифференциальным уравнениям
(+ i +~pi02)G=0; (12-34а)
[ +1 + = °’ (12-34б)
где V = pknCQ. Решения, ограниченные при R можно представить в виде
^(р^)
Л — (---X----
* *ip(p0)
_ D ^iq <Р#О
(12.35)
232
где С, D - постоянные величины, р - (Ё2 -р2 -1)1/2, q = (V2 - р2) 1/2 и Лф, - мо-
дифицированные функции Бесселя второго рода чисто мнимого порядка (37.67). Ос-
тальные компоненты поля выражаются только через и h^, в чем можно убедиться,
если вывести пару уравнений, подобных (30.6) [15]. К этому же выводу можно прийти,
если уравнения Максвелла для среды без источников (ЗОЛ) подставить в (30.15). В ре-
зультате имеем
Ъ = ф[(Мо /во) inp20kRF - V ;
к (Л1\
(12.36а)
ez = —~~ [(мо/ео)12 Рк~^ ~ 00pG] ;
к и/\
— Гг dF ~ !L у2Г1.
к 1 4r (м0} к v G]’
(12.366)
где G = СЛ-ф (pfsR) IKip (р/3), F = ОК~Щ (P0R) /tfiq (p/J) и к = V2 - v2.
Продольные компоненты полей еъ и в сердцевине определяются выражением
(12.12а), а остальные - выражением (30.9). Условие непрерывности четырех тангенци-
альных составляющих на границе' (R = 1) дает для ТЕОт- и ТМ0т-мод соответственно
характеристические уравнения
„^iq^
U-------- = рв-------- ;
J, (If) A'iq
, (12.37а)
J0(M Kip(P^
U •------ = 1 + р/3------- j
Л (Щ л\р(рЮ
(£^)4p/351(^
й lw/ciq(M)
JV(U)
JV(U) P& K4(p0) J
Kip 4 (G) п г _
>0—-----------и —--------1 = [ V2 - V2 - р202 +
A-ip(P/3) 4(G)J 1
J'(U) r Aj'(p/3) 1
v2 ~ + UfaT\ t1 + P0 ] [
•'у (Ю a- (p/0 J
1 (12.376)
для HEprn- и ЕНргп-мод, где штрих обозначает дифференцирование по аргументу. Отме-
тим, что физически более реальными являются трехслойные световоды, состоящие из
однородной (имеющей постоянный показатель преломления) сердцевины, однородной
оболочки и области между ними, в которой показатель преломления изменяется обрат-
но пропорционально квадрату радиуса. Свойства таких структур рассмотрены, напри-
мер, в [15].
АНИЗОТРОПНЫЕ ВОЛНОВОДЫ
В этой части главы рассматриваются волноводы, состоящие из анизотропных
материалов. Общий подход к анализу таких волноводов был изложен в кон-
це гл. 11. Здесь дается количественная оценка параметров таких волноводов
на примере анизотропного планарного волновода [16, 17] и одноосного во-
локонного световода со ступенчатым профилем показателя преломления
[18]. Поскольку эти результаты подобны результатам для соответствующих
233
Таблица 12.10. Составляющие полей мод анизотропного планарного волновода со ступенчатым профилем показателя преломления
h, h2
Сердцевина Оболочка Сердцевина Оболочка Сердцевина Оболочка
Четная ТЕ cos(l7X) cos 17 ехр(-1Г|Х|) exp(-FF) ^/toY^costUX) 1с\Яо/ cosl7 i/%Y'*eitp(->*'i*i) *\Яо/ exp(-FF) 3*7У'2 sin(l7X) pk\p<J sin 17 У'2 X exp(-H'|X|) pk\po) |X| expf-FF)
Нечетная ТЕ sin(UX) sin U X ехр(-У|Х|) |X| exp( —W) р/срХ'^япШХ) k\p<J sin 17 Р(ч\',г X exp(-y|X|) *\/W 1*1 exp(-FF) M'/cl,Y'2cos(UX) pk\i^J cos 17 Д»7гоу'Дехр(-»Н*|) pk\n<J exp(-FF)
ех = е, = = 0
ex e2
Сердцевина Оболочка Сердцевина Оболочка Сердцевина Оболочка
Четная TM COSCKqq 17X) cospc^l/) /ио>У exp( —Kd(F|X|) \"d/ exp( — KdW) 2 cos^t/X) COStKatU) kln^)2 M A*/2 exp(-xd»F|X|) 0 exp(-Kd^) [n^\2 sinjK^UX) P0 {"dJ sin^U) -»>FA2 X exp(-Kd»F|X|) Pfi V»d/ |X| exp(-KdFF)
Нечетная ТМ sin^l/X) smCx^U) i — i —* |Х| «р(-к1|И'|Х|) ехр(-МП К^/ЧУ'2 Д \Мо/ sinQ^t/X) ыпОСд, U) Ця^/ЧА1'2 ехр(-кС|Нл|Х|) Д W ехр(- кс1ИО -Wcos(KmUX} pfi \ла/ cos^U) / л^ У ехр( - KrflF | X |) \ла/ exp(-xdJF)
*. = *, = *, = 0 = = Лео nd
ТЕ-мода и = pttknj»)2-Л2]1'2 »K = p[P2-(knj)2)1'2 v = (U> +»'*)><* = kptln’,)2 -(nJ)2]1'2
ТМ-мода и = р[(*л«)2-02],/2 W’ = p[/»2-(b3)2]’'2 V = (U1 +W2)'12 = кр[(п^2-(п^2У'2
Примечание. Приведенные выражения аналогичны соотношениям, приведенным в табл. 12.1 для изотропного волновода. Обозначения
сохранены за тем исключением, что показатель преломления теперь зависит от ориентации вектора электрического поля, а параметры U,
W и V различны для ТЕ- и ТМ-мод. Поля нормированы таким образом, что на границе (х = р) е — 1 или е — 1. Показатели преломле-
— У х
ния сердцевины и оболочки — И лср
изотропных волноводов, полученным ранее в этой главе, то предполагается,
что аналогичен и вывод соотношений для компонент полей, характеристик
мод и характеристических уравнений (табл. 12.1 — 12.4) .
Показатели преломления сердцевины и оболочки анизотропного волново-
да зависят от направления, или поляризации, вектора электрического поля Е.
Если предположить, что главные оси параллельны осям волновода, то имеем
Направление век- тора Е Поляризация вдоль оси X : Поляризация Поляризация
вдоль оси у вдоль оси z
Показатель прелом- ления сердцевины пх "со "со "со
Показатель прелом- „X пУ Z
ления оболочки "cl ”с1 rtcl
где ось z совпадает с осью волновода, а плоскость х, у — с поперечным сече-
нием волновода. Для волноводов со ступенчатым профилем все показатели
преломления являются постоянными.
12.19. Планарный волновод со ступенчатым профилем показателя
преломления
Предположим, что планарный волновод, изображенный на рис. 12.1, имеет
ступенчатый профиль и изготовлен из анизотропного материала. Поля явля-
ются либо ТЕ-, либо ТМ-модами при условии, что главные оси параллельны
осям декартовых координат (см. разд. 30.11) .
ТЕ-моды. В разд; 30.11 показано, что поля ТЕ-мод находятся из решения
скалярного волнового уравнения (30.22а) для е а остальные компоненты
полей связаны с еу соотношениями (30.33). Поскольку выражения для по-
лей изотропного волновода могут быть получены аналогичным образом из
уравнений (12.16) и (12.17), как это отмечалось в разд. 12.2 и 12.14, то поля
анизотропного и изотропного волноводов по форме идентичны, если во всех
выражениях псо и ис1 заменить на nyCQ и В результате получим выражения
для полей ТЕ-мод, представленные в табл. 12.10, где U, V и W определены че-
рез п^о и пу{. Выражения для мод в табл. 12.11 идентичны своему ’’изотроп-
ному аналогу” из табл. 12.2, что можно легко проверить, если выражения
для полей из табл. 12.10 подставить в формулы дляТУ и т? из табл. 11.1. Груп-
повая скорость находится из (31.31) при замене «2et на п2 ° et = и2ехх +
+ у.
ТМ-моды. Выражения для полей мод получаются из решения уравнения
(30.326) для hy и уравнения (30.33). Компоненты полей представлены в
табл. 12.10, где Ut V и W определены теперь через n*Q) п^0, и п^. Отличие
от выражений для ТМ-мод из табл. 12.1 обусловлено изменениями показате-
ля преломления, что становится очевидным, если сравнить уравнения (30.32)
и (30.33) соответственное (12.20) и (12.23). Характеристические уравнения
в табл. 12.11 являются следствием условия непрерывности компонент ez и
hy на границе сердцевины с оболочкой, а остальные выражения, за исключе-
236
Таблица 12.11. Свойства мод анизотропного планарного волновода со ступенчатым профилем показателя преломления
Четные ТМ-моды Нечетные ТМ-моды Четные ТМ-моды Нечетные ТМ-моды
Характеристическое уравнение W = и tg и ,^= -U ctg(/ уЛсоЛсо / Х^о^со/
Нормировка Pp(eo\l'2(v\2i+w 2k\pJ \u) W _ pk(nx№)2 /ер V/2 f (W \2 /г&иЦ2 V2 (п*о)21 2Д \До/ 1 W/\ncl"cl/ nclncl J
Мощность в сердцевине . V1 И2(1+»Г) ! {(»^)2/"с|"с|}^2 1/2И'+ (n^n^/n^nj)2 JF3 + ((п^)2/п*|П^)И2
Г рупповая скорость С Р 1 (и^)2 к 1-2Д/1-Г/) С Р 1 Vg ~ (и^)2 к 1 — 2ДХ(1 -п)
Параметр высоты профиля \r,co / К О ( и 8 J 1 II <г гч
Примечание. Характеристические уравнения и характеристики мод рассчитаны на основании табл. 11.1.Они аналогичны соотношениям
из табл; 12.2 для изотропного волновода. Выражение для групповой скорости получено из (31.31),в котором п2е^ заменена на п2 • et =
= пхехх + пуеуУ' Показатели преломления сердцевины и оболочки - %оияс|.
нием выражения для групповой скорости, которая рассчитывается по моди-
фицированной формуле (31.31), получаются из табл. 11.1.
Слабонаправляющие волноводы. Если анизотропный волновод является
слабонаправляющим, все шесть показателей преломления в (12.38) прибли-
зительно равны и в табл. 12.10 ксо~ кс1 ~ 1. Поэтому единственное суще-
ственное различие между ТЕ- и ТМ-модами заключается в определении пара-
метра И В первом случае V зависит от (и^о)2 - (и^)2, а во втором - от
(и*о)2 - (п^)2. Более того, поля ТЕ- и ТМ-мод могут быть выражены через
известные поля ТЕ-мод изотропного волновода простой заменой псо, ис1 на
пЪ или пг} соответственно.
V U VI VVI VI
12.20. Одноосный волоконный световод со ступенчатым профилем показа-
теля преломления
Предположим теперь, что волоконный световод, изображенный на рис. 12.3,
имеет ступенчатый профиль показателя преломления, изготовлен из анизо-
тропных материалов, является одноосным (см. разд. 30.12) и имеет следую-
щие параметры:
Направление векто- ра Е Поляризация вдоль оси х или у Поляризация вдоль оси z
Показатель прелом- ления сердцевины со "со "со пм
Показатель прелом- ления оболочки t X у «И — П cl — п cl
где все показатели преломления являются постоянными величинами и <
< «со» пс\ < «со'- Если эти параметры подставить в (30.34) , то уравнения для
продольных компонент поля можно представить в виде, аналогичном (12.11)
для изотропного световода (см. табл. 12.12). Волноводные и модовые пара-
метры определены в этой же таблице вверху справа. В разд. 30.13 показано,
что если компоненты е7 и известны, то поперечные компоненты поля на-
ходятся с помощью уравнений (30.9) при р = (knto)2 - (З2 в сердцевине и
р = (Ч\)2 — £2 в оболочке. Таким образом, методы формирования мод анизо-
тропного и изотропного волноводов идентичны, но свойства мод различаются.
Характеристическое уравнение. Условие непрерывности тангенциальных
составляющих поля , h^t еъ и /zz на границе сердцевины с оболочкой (г =
= р) приводит к характеристическому уравнению в табл. 12.12. Изучение его
решений показывает, что в отличие от изотропного в анизотропном светово-
де невозможно различить НЕ- и ЕН-моды. В общем случае моды анизотроп-
ного световода могут иметь любую комбинацию ТЕ- и ТМ-составляющих,
за исключением мод с индексом v = 0, которые являются чистыми ТЕ- или
ТМ-модами [18]. Этот вывод подтверждается исследованием частот от-
сечки мод.
Частота отсечки. При отсечке U=V=VcnW = 0 (см. разд. 11.18). Величи-
ны Vc приведены в табл. 12.12 для каждого индекса и и совпадают с анало-
гичными величинами в табл. 12.4 для изотропного световода при ксо = кс| =
238
Таблица 12.12. Одноосный волоконный световод со ступенчатым профилем показателя преломления
Продольные компоненты поля
Сердцевина(О г р) Оболочка (р г < оо)
(p2V2 +к^,и2)е2 =0 (p2V2 + U2)hz = 0 (p2V2-K21»K2)e2 = 0 (p2V2-W2)h2 = 0
Параметры мод и световода
и = р{(Ко)2 - Л*'2 = р{р2 - (kn',)2}12
V = (U2 +^2)‘ '2 = кр{ (п^)2 - (л',)2} *'2
Кео = </< Ксо = ”d/nd
Характеристическое уравнение
1 J'su) 1 к;(ир
U J,(U)W К,(И7)
KCOJ'V(U) ка /п{ДК',(ка№)
U JV(U)
Отсечка
V = 0 J0(U) = 0 (ТЕ-мода) Л)(*со^) — 0 (ТМ-мода)
V - 1 Л(1/) = 0 Л(Ксо1/) = 0
V ^2 \ncl / ‘U-D 'I'C»U>J-|U|-0
239
Примечание. Параметры, не определенные в этой таблице, приведены в табл. 1. Штрих обозначает дифференцирование по аргументу,
п со и «с1 ~ показатели преломления сердцевины и оболочки.
= 1. Для первых ТЕ- и ТМ-мод частоты отсечки равны Vc = 2,405 и Vc =
= 2,405 (^ci/^co) соответственно. Моды с индексом и = 1 расщепляются ана-
логичным образом, а моды с индексом v > 2 уже не расщепляются, т. е. явно-
го различия 1йежду НЕ- й ЕН-модами в анизотропном волноводе не суще-
ствует (сравните с табл. 12.4).
ГЛАВА 13. СЛАБОНАПРАВЛЯЮЩИЕ ВОЛНОВОДЫ
В гл. 11 были рассмотрены основные свойства мод оптических волноводов,
векторные поля которых являются решениями уравнений Максвелла для
среды без источников, или однородного векторного волнового уравнения.
Однако, как показано в гл. 12, точные аналитические решения уравнений
Максвелла могут быть получены лишь для некоторых известных профилей
показателя преломления, из которых, по-видимому, только ступенчатый
представляет практический интерес. Даже для этого относительно простого
профиля получение выражений для векторных полей мод является весьма
трудоемкой задачей. Цель данной главы — дать основы приближенного мето-
да [1,2], основанного на предположении о малом изтиенении показателя пре-
ломления в поперечном сечении волоконных световодов, используемых в
системах передачи информации на дальние расстояния, т. е. А << 1, где А —
параметр высоты профиля в уравнении (11.48). Его простота заключена в
решении не векторного волнового уравнения, а скалярного.
Оптические волноводы с А << 1 или псо % ис1, называются слабонаправ-
ляющими. Такое название не должно вводить в заблуждение, поскольку при
А << 1 могут быть обеспечены как сильная направляемость волн, так и до-
статочная концентрация излучения в сердцевине. Моды слабонаправляющих
оптических волноводов впервые были выведены для волоконных светово-
дов со ступенчатым профилем [2], а понятие ’’слабая направляемость” было
затем дано в [3]. Подробнее свойства таких структур рассмотрены в [4].
Позже теория была обобщена на волноводы с произвольным поперечным се-
чением [1].
13.1. Поляризационные явления, обусловленные волноводной структурой
Для оценки используемых приближений рассмотрим сначала в качестве до-
бавления к разд. 11.16 некоторые аспекты распространения излучения.
Однородная среда. Предположим, что волновод состоит из неограничен-
ной однородной среды с показателем преломления исо, т. е. является эффек-
тивным ’’свободным пространством”. Поля мод находятся из уравнений
Максвелла и являются поперечными электромагнитными или ТЕМ-волнами,
распространяющимися в направлении оси 2, параллельной оси волновода.
Таким образом, постоянная распространения равна (3 = Ъ?со, продольные
компоненты равны ez = hz = 0, а для поперечных компонент электрического
и магнитного полей справедливо соотношение
ht= (-?“),/2«cozxet>
(13.1)
240
где z — единичный вектор, параллельный оси волновода, а е0 и д0 опреде-
лены в табл. 1. Поскольку постоянная распространения не зависит от ориен-
тации вектора et, то волновод не обладает поляризационными свойствами.
Очевидно, что в этом тривиальном случае каждая декартова составляющая
векторов et или ht подчиняется скалярному волновому уравнению в любой
точке пространства, так как в однородной среде правая часть уравнения
(11.10) равна нулю.
Неоднородная среда. Рассмотрим теперь волновод с профилем показате-
ля преломления п = п (х, у). В этом случае постоянная распространения зави-
сит от ориентации вектора электрического поля, и моды уже не являются
ТЕМ-волнами. В общем случае поля мод являются решениями не скалярных,
а векторных волновых уравнений (11.40), в которых волноводные поляри-
зационные эффекты описываются членами, содержащими Vt In п1. Исключе-
ниями являются ТЕ-моды планарных волноводов и волоконных световодов,
рассмотренные в разд. 12.14 и 12.16. Простым примером, иллюстрирующим
зависимость параметров распространения от поляризации, обусловленную
волноводной структурой, является волновод с плоской границей раздела
между однородными средами с показателями преломления «со и псХ. Если
плоская волна падает на границу раздела из среды с показателем преломле-
ния псо (см. рис. 10.2) и подвергается полному внутреннему отражению,
фазы падающей и отраженной волн отличаются, а с ростом («со - пс1) эта
разница увеличивается. Это объясняет различие между ТЕ- и ТМ-модами в
ступенчатых волноводах, рассмотренных в разд. 11.16. Иными словами, вол-
новодная структура обусловливает поляризационные эффекты, с которыми
связано появление членов, содержащих Vtlnn2 в векторном волновом
уравнении.
С другой стороны, в приведенном выше примере вариации изменения фа-
зы в зависимости от поляризации плоской волны электрического поля ма-
лы, если мала разница между псо и пс1, хотя падающая волна и испытывает
полное внутреннее отражение. Таким образом, если показатели преломления
приблизительно равны, падающая волна испытывает полное внутреннее от-
ражение, но по отношению к поляризации среда является фактически одно-
родной. Далее, как показано в разд. 35.6, поля, образованные при отражении
плоской волны, являются решением скалярного волнового уравнения. Поэ-
тому можно ожидать, что этому же уравнению будут подчиняться и поля мод
волновода с произвольным профилем показателя преломления при условии,
что параметр высоты профиля волновода мал, т. е. Д « 1 или пс0 % ис1.
Покажем теперь, как находить поля мод слабонаправляющих волноводов,
используя приведенную выше физическую аргументацию. Выражения для по-
лей мод могут быть формально получены, как показано в гл. 32, из уравне-
ний Максвелла методом возмущений.
МОДЫ СЛАБОНАПРАВЛЯЮЩИХ ВОЛНОВОДОВ
Напомним, что согласно выражению (11.6) электрическое и магнитное поля
волноводов можно представить в виде
Е(х, у, z) =е(х, jr)exp(i0z) = [et + zez)exp(ij3z) ; (13.2а)
Н(х, у, z) = h(x, j/)exp(ij3z) = (ht + ihz) exp(ij3z) , (13.26)
241
где р — постоянная распространения, а индексы t и z означают соответствен-
но поперечную и продольную компоненты. Индекс моды опущен, поскольку
в этой главе рассматриваются только отдельные моды. Волновод, представ-
ленный на рис. 11.1, а, имеет максимальный показатель преломления псо и
показатель преломления оболочки пс1. Если псо ~ пс1, то из определения па-
раметра высоты профиля, данного в табл. 1, следует
Д=1л _ "с! ч ~ "со - Ис1
2 «с0 ~ "со
(13.3)
Профиль показателя преломления удобно записать следующим образом:
п2 (х,у) =И*О[1 -2ДГ(х,.у)],
(13.4)
где / = 0 для максимального показателя преломления и / = 1 в оболочке.
13.2. Аппроксимация мод ТЕМ-волнами
С учетом (11.46) постоянные распространения направляемых мод ограниче-
ны интервалом
кпс1<(}<кпс0. (13.5)
Поскольку в слабонаправляющих волноводах он очень узкий, то для всех
направляемых мод можно положить
0 « Ллс0 * Ллс1. (13.6)
Следовательно, моды должны быть почти ТЕМ-волнами, у которых ez & О,
hz « 0, а поперечные компоненты поля приближенно подчиняются соотноше-
нию (13.1). Поэтому, зная et, можно полностью определить поле моды.
13.3. Пространственная зависимость полей мод
Выше было показано, что моды слабонаправляющих волноводов являются
почти ТЕМ-волнами с полями е ~ et, h ht и ht связано с et соотношением
(13.1). При точном анализе для нахождения пространственной зависимости
et (х’ У) необходимо решить уравнение Максвелла, или векторное волновое
уравнение (11.40а). Однако при Д << 1 поляризационные эффекты, обус-
ловленные волноводной структурой, малы, и декартовы компоненты векто-
ра et могут быть аппроксимированы решениями скалярного волнового урав-
нения. Основой такого подхода в разд» 13.1 служило то, что при Д << 1
волновод является фактически однородным и нечувствительным к поляри-
зационным эффектам. Как было показано в разд. 11.16, эти эффекты опреде-
ляются членом, содержащим Vtlnn2 в векторном волновом уравнении, а
поэтому пренебрежение ими эквивалентно отсутствию подобных членов в
уравнении (11.40а). Таким образом, если обозначить
et (х, у) = ех (х, у) х + еу (х, у) у,
(13.7)
242
где х и у — единичные векторы, параллельные декартовым осям координат на
рис. 11.1, я, а Ф обозначает ех или еу. Тогда Ф является решением уравнения
[Vt2 + к2 п2 (х, у) - /32 ] Ф = 0,
(13.8)
где к = 2тг/Х, X - длина волны в вакууме; оператор Vt2 определен в табл. 30.1.
Хотя декартовы компоненты вектора et удовлетворяют уравнению (13.8),
их пространственная зависимость может быть определена в любой цилиндри-
ческой системе координат, например, в цилиндрических полярных координа-
тах et = et (г, (оператор Vt2 приведен в табл. 30.1) .
Необходимо подчеркнуть, что в уравнении (13.8) означает постоянную
распространения скалярного волнового уравнения в отличие от точной посто-
янной распространения /3 для векторного волнового уравнения. В разд. 33.1
показано, что условие непрерывности любого решения скалярного волново-
го уравнения и его первой производной в любой точке сечения волновода в
совокупности с требованием ограниченности Ф приводит к характеристи-
ческому уравнению, позволяющему определить разрешенные значения ,
Несмотря на то, что уравнения (13.7) и (13.8) определяют пространствен-
ную зависимость et (х, у), они не дают информации о поляризации волны,
т. е. о направлении вектора поля. Оно может быть определено либо из поля-
ризационных свойств волновода, либо из соображений симметрии.
ВЕКТОРНЫЕ СВОЙСТВА ПОЛЕЙ МОД
Ранее было установлено, что моды слабонаправляющих волноводов являют-
ся почти ТЕМ-волнами и пространственная зависимость et (х, у) находится
из скалярного волнового уравнения. Осталось только определить направле-
ние вектора et (х, у) как функцию поперечной координаты. В общем случае
функция et (х, у) включает в себя как составляющую ех (х, у) , так и еу (х, у).
Конкретная комбинация определяется поляризационными свойствами вол-
новода (профилем показателя преломления) и обычно может быть определе-
на из свойств симметрии поперечного сечения волновода. Если пренебречь
поляризационными свойствами волновода, то справедливой будет любая ли-
нейная комбинация, но, как будет показано ниже, это часто приводит к боль-
шим ошибкам.
Сначала рассмотрим основные моды, а затем моды высших порядков.
Подобно точной постоянной распространения (3 скалярная постоянная рас-
пространения больше для основных мод. Для удобства все волноводы раз-
делим на два типа: волоконные световоды с круглым поперечным сечением
и волноводы с поперечным сечением произвольной формы.
13.4. Основные и НЕ1т-моды круглых волоконных световодов
Основные и НЕ1т-моды волоконных световодов с круглым поперечным се-
чением находятся из скалярного волнового уравнения, не содержащего ази-
мутальной переменной. Следовательно, Ф в уравнении (13.8) зависит только
от радиальной координаты г. Поскольку в круглом поперечном сечении не
существует преимущественных осей симметрии, то в этом случае поперечное
243
электрическое поле может быть направлено вдоль любого из произвольной
пары ортогональных направлений. Если эту пару направлений обозначить ося-
ми х и у, как на рис. 12.3, то существуют две основные, или НЕп-моды, по-
перечное электрическое поле одной из которых параллельно х-направлению,
а другой - у-направлению. Из соображений симметрии следует, что скаляр-
ные постоянные распространения каждой пары мод равны. Принимая во вни-
мание все сказанное, из уравнений (13.1) и (13.2) получаем [1,2]:
для мод, поляризованных
вдоль оси х:
Ех = Eo(f)exp(i0 z);
Ну = (“77“)
для мод, поляризованных
вдоль оси у:
Еу = Fo(r) exp(i0z);
Мо
(13.9а)
(13.96)
где Fo (г) — осесимметричное решение уравнения (13.8), а остальные состав-
ляющие поля малы. Примеры будут даны в следующей главе, здесь же под-
черкнем, что описание полей (13.9) является чисто скалярным и не содержит
информации о поляризационных свойствах волоконного световода, и в этом
смысле основные и НЕ 1т-моды световодов являются необычными. Все ос-
тальные моды, как будет показано в разд. 13.7, содержат некоторую инфор-
мацию о поляризации.
£Р-обозначение для основных мод. Основные моды слабонаправляющих
круглых волоконных световодов иногда называют £Р0гМОдами [3], а не
НЕп-модами. Этим стремятся подчеркнуть однонаправленность поляризации
полей мод, т. е. что они являются плоскими или однородно поляризованными.
13.5. Основные моды волноводов с поперечным сечением произвольной
формы
Если поперечное сечение некруглое, то поперечное электрическое поле везде
параллельно одному из двух ортогональных направлений, которые обозначим
через х0 и у0 и назовем оптическими осями поперечного сечения волновода.
Во многих случаях оптические оси очевидны из симметрии поперечного се-
чения, например, они параллельны большой и малой оси волновода с эллип-
тическим сечением и параллельны осям х и у планарного волновода на
рис. 12.1. Всю информацию об оптических осях дают члены векторного вол-
нового уравнения (11.40), содержащие Vtlnn2. Вследствие малых вариаций
профиля показателя преломления слабонаправляющих волноводов эти чле-
ны малы и в тех случаях, когда направления осей х0 и у о не могут быть опре-
делены из общих соображений, их можно найти методами возмущений. Этот
вопрос обсуждается в разд. 32.5. Для удобства будем предполагать, что оси
х и у расположены вдоль х0- и у0-направлений.
По определению для основных мод решение уравнения (13.8) Ф имеет
наибольшую постоянную распространения (3. Далее, если в круглом волокон-
ном световоде существуют две моды, являющиеся решением этого уравне-
ния, одна из. которых поляризована вдоль оси х, а другая — вдоль оси у, и
скалярные постоянные распространения этих мод равны, то для волновода
с некруглым поперечным сечением точные постоянные распространения этих
мод |3Х и Зу будут различны. Эта разница обусловлена поляризационными
244
свойствами, или двойным лучепреломлением волновода, что подтвержда-
ется членами, содержащими Vt In и2 в уравнении (11.40). В этом смысле рас-
пространение волн в некрутлых волноводах подобно распространению волн
в анизотропной среде (см. гл. 12). Небольшая разность (Зх - 0у дает интер-
ференцию, или биения, между полями двух мод. Более того, время распро-
странения двух основных мод становится различным, в результате чего в од-
номодовых волноводах дополнительно уширяется импульс (наряду с ушире-
нием вследствие дисперсии материала и волноводной дисперсии, рассмотрен-
ных в разд. 11.12). Поэтому очевидно, что постоянную распространения каж-
дой моды необходимо знать с большей точностью, по сравнению с той, кото-
рую дает решение скалярного волнового уравнения. Поляризационные свой-
ства волновода дают небольшие поправки 8(3Х и 8ру к постоянной распро-
странения Р каждой моды, как будет показано в следующем разделе. Прини-
мая это во внимание, из уравнений (13.1) и (13.2) получаем для мод [1],
поляризованных вдоль оси х: поляризованных вдоль оси у:
Ех = Ф(х, X)exp[i(j3 + 6j3x)z]; Еу = Ф (х, у} exp [i(0 + 6j3y)z]; (13.10а)
ЯУ= O1/2«co^x; = _(-g-)1/2nco£ (13.106)
где Ф(х, j>) является решением уравнения (13.8) для наибольшей величины
0, а все другие компоненты поля малы. Напомним, что по предположению
оси х и у параллельны оптическим осям поперечного сечения волновода.
Примеры будут даны в гл. 16.
13.6. Поляризационные поправки к скалярной постоянной распространения
Если принимать во внимание влияние поляризационных свойств волновода
на постоянную распространения, то необходимо учесть поправку 60 к ска-
лярной постоянной распространения £?. Чтобы определить точное значение,
следует решить векторное волновое уравнение. Однако в слабонаправляю-
щих волноводах член, содержащий Vt In п2 в правой части уравнения (11.40а),
мал, поэтому удобнее воспользоваться методом возмущений, изложенным
в разд. 32.4. Из выражения (32.24) имеем
р (24) 3/2 / <Vt ’ et) et ‘ vt Ж У) dA
Л ‘
(13.11)
где Д << 1 — параметр высоты профиля показателя преломления, К-волно-
водный параметр, Аж — площадь бесконечного поперечного сечения и/(х, у) —
изменяющаяся часть профиля в выражении (13.4). Для ступенчатого профи-
ля показателя преломления Vt/(x, у) является 6-функцией на границе серд-
цевины с оболочкой и 60 можно получить из выражения (32.26), а именно
п(2Д)3/2
5^ »----——fz(Vt • et)et • ndl/ f e?tdA.
A OQ
(13.12)
245
Контур интегрирования I проходит вдоль границы между сердцевиной и обо-
лочкой, а п - внешняя нормаль к нему в поперечном сечении волновода.
Поляризационные поправки 60х и 60у в выражениях (13.10) для некруг-
лых волноводов могут быть найдены из уравнения (13.11), где et = Ф(х, ^)х
и et = Ф (х, у) у, а х и у - это единичные векторы.
13.7. Моды высших порядков круглых волоконных световодов
Рассмотрим теперь высшие моды волоконных световодов с круговой сим-
метрией поперечного сечения и профиля показателя преломления. Если выра-
зить Vt2 в цилиндрических координатах г, у, как это сделано в табл. 30.1, то
уравнение (13.8) будет иметь два решения для каждой величины (Т, а имен-
но: Ф = FL(r)cosZ(£ и Ф = Fx(f) sin Z^, где Z - положительное целое число, а
FL(r) — решение уравнения в табл. 13.1. Вследствие симметрии любая пара
ортогональных осей х и у может быть выбрана в качестве оптических осей
поперечного сечения световода. Кроме того, из симметрии следует, что суще-
ствует четыре возможных направления et> зависящих от конкретной ком-
бинации двух решений скалярного волнового уравнения (13.7) [1, 2] (см.
разд. 32.7). Поэтому для каждого Z > 0 существует четыре моды, поля кото-
рых описываются выражениями в табл. 13.1. Эти комбинации могут быть по-
лучены и без учета симметрии с помощью формальных методов, изложенных
в разд. 32.6. Обычно такое представление et является самым простым из воз-
можных (объяснение см. в разд. 32.8) .
Эти четыре моды имеют одинаковые скалярные постоянные распростране-
ния 0 и различные точные постоянные распространения, что можно было
ожидать из-за симметрии [1], а также из рассмотрения световода со ступен-
чатым профилем показателя преломления, рассмотренного в гл. 12. Таким
образом, поскольку моды высших порядков круглого световода аналогич-
ны основным модам волноводов с произвольным поперечным сечением, то
по причинам, изложенным в разд. 13.5, поляризационные свойства световода
необходимо учитывать введением небольшой поправки 8(3i к ft для каждой
моды. Для z-й моды в табл. 13.1 она дается выражением (13.11), где et =eti,
а интегралы приведены в табл. 14.1. В следующей главе будут приведены
примеры мод слабонаправляющих круглых световодов.
£Р-обозначение для мод с индексом Z > 1. В отличие от основных и всех
мод с индексом Z = 0 поля мод с индексом Z > 1 не являются линейно поля-
ризованными. Более того, вследствие поляризационных свойств световода,
направление поля зависит от координаты точки в поперечном сечении, что
следует из табл. 13.1. Поэтому ZP-обозначение в данном случае,неприменимо.
Однако если пренебречь поляризационными свойствами световода и считать,
что все четыре моды имеют одинаковую постоянную распространения (Т, т. е.
= 0, то направление поля будет неизменным по поперечному сечению и
его можно представить линейно поляризованной волной, например, etl =
= F^(r) cos Z^x или etl = /^(r) exp (±iffy) x. Тем не менее необходимо подчерк-
нуть, что такое описание полей мод может в общем случае привести к значи-
тельным ошибкам (см. разд. 14.7). Это не относится к многомодовому све-
товоду, в котором поляризационные эффекты индивидуальных мод усредня-
ются, и распространение излучения непосредственно описывается методами
классической геометрической оптики, изложенной в ч. I.
246
Таблица 13.1. Поля направляемых мод слабонаправляющих волноводов
Е (х, у, z) = е (х, у) exp {i (0 + 60)z} е(х,у) * et(x,y) H(x,y,z) = h(x,y}exp{i(ji + 6P)z} h(x, у) « Ц (х, у) = ( — ) nco г хе, (х, у) \ До /
{Vf+k2n2(x,y)-p2}e{ = 0 к = 2п/Х п2(х,у) = п^{1 -2Д/(х,у)}
1PV ’ 1 ’!dA
Поперечное сечение прризвольной формы
е„ = Тх е,2 = Ту {V2+ к2п2 (х, у) - р2} 'Р = 0
Круглое поперечное сечение
etl = F|(r){cos(/¥>)x-sin(/¥’)y}
«ts = F|(r){sin(Mx + cos(MJ}
*i2 = F|(r){cos(/<₽)S + sin(My}
e,4 = F|(r){sin-cos(/</>)y}
d2 1 d
dr2 r dr
Jc2n2(r)-^ - 02
F, = 0
Почти круглое поперечное сечение
«ti = Fi(r){cos(lv)* + a_ sin(/<p)y}
et3 = F,(r){sin(/<p)x + a+cos(/<p)y
a± = Л±(1+Л2)1/2
et2 = F|(r){cos(/<p)x + a+sin(/<p)y}
et4 = Fj(r){sin(/<p)x-+-Л-cos(/<p)y}
л = (Л-До)/(^1-%)
Примечание. Вид функций поля зависит от формы поперечного сечения волновода
Векторные операторы определены в табл. 30.1, а параметры — в табло I.
247
13.8. Моды высших порядков волноводов с поперечным сечением произволь-
ной формы
Моды высших порядков волноводов с произвольным поперечным сечением
составляются из каждой пары решений уравнения (13.8) Фе(х, у) и Фо (х, у)
и соответствующих этим решениям скалярных постоянных распространения
/3 е и (30. Поперечное электрическое поле этих мод поляризовано вдоль тех
же оптических осей, что и поле основных мод (см. разд. 13.5). Таким обра-
зом, имеются две пзры мод высших порядков, поля которых описываются
выражением (13.10), где под и Ф (х,у) необходимо понимать (3 е и Фе(х,у)
для одной пары мод, и Фо (х, у) — для другой. Поляризационные поправ-
ки к постоянной распространения 60хе, д(3Х0, 8[Зуе и 8(Зуо можно получить
из выражения (13.11), если вместо et подставить соответствующее выраже-
ние для поля.
13.9. Моды высших порядков почти круглых волоконных световодов
Несмотря на то, что выражения для поперечного электрического поля мод
высших порядков в световодах с круглым и произвольным поперечным се-
чениями в табл. 13.1 сильно различаются, очевидно, что должна существовать
некоторая переходная область, в которой почти круглые световоды начина-
ют обладать свойствами идеально круглых. Поэтому приведенное описание
полей высших мод применимо для существенно некруглого сечения. Од-
нако положение существенно меняется, если световод является слабонаправ-
ляющим. В этом случае даже небольшая асимметрия формы поперечного се-
чения световода приводит к деформации полей мод. Другими словами, од-
нородная поляризация полей мод нарушается, если поперечное сечение све-
товода не является действительно круглым. Следовательно, при достаточно
малых Д поля мод почти круглых световодов описываются выражениями,
полученными для волноводов с поперечным сечением произвольной формы.
Если Д и асимметрия (т. е. эксцентриситет поперечного сечения световода с
малой эллиптичностью) одного порядка, то существует конкуренция между
эффектами, обусловленными слабонаправляющими свойствами световода и
его некруглым сечением. Поэтому представляется необходимым описать по-
ля мод в таком промежуточном случае.
Обычно пространственные изменения полей мод в световодах с небольшой
асимметрией и круглых подобны, при этом поля поляризованы вдоль осей,
которые можно считать оптическими осями круглого световода. Если осе-
си мметричность поперечного сечения нарушается, то поперечное электричес-
кое поле уже не описывается точно симметричной или несимметричной сос-
тавляющими в табл. 13.1 для круглого поперечного сечения и может быть
представлено в более общей форме (табл. 13.1 внизу), где постоянные а±
(пока неизвестные) в пределе дают выражения для двух частных случаев.
В первом случае, когда а± = ±1, выражения для полей мод сводятся к точ-
ным выражениям для круглого световода, а при а >> а_ или а_ >> а* —
с некоторым приближением к выражениям для полей мод волновода с про-
извольным поперечным сечением, рассмотренным в разд. 13.8. Формулы для
коэффициентов а± получены в разд. 32.9 методом возмущений и для удоб-
ства выражены через безразмерный параметр Л =^е - ^o/53i — 6j32, характе-
248
ризующий отношение эффектов нециркулярности поляризации круглого све-
товода. Примеры, относящиеся к обсуждаемой здесь переходной области, и
количественная оценка даны в гл. 16 и 18.
СВОЙСТВА МОД СЛАБОНАПРАВЛЯЮЩИХ ВОЛНОВОДОВ
Модам слабонаправляющих волноводов свойственны фундаментальные свой-
ства мод, рассмотренных в гл. И. Вследствие того, что поля мод можно
приближенно представить ТЕМ-волнами, этим свойствам легко придать про-
стую форму (см. табл. 13.2). В первом столбце даны выражения поперечно-
го электрического поля et, которые применимы для любого слабонаправля-
ющего волновода. Выражения во втором столбце относятся к волноводам с
существенно круглым поперечным сечением, поэтому et можно заменить од-
ним из двух соответствующих выражений из табл. 13.1. В третьем столбце
представлены выражения для круглых волноводов, в которых et заменено
одной из четырех линейных комбинаций etj для волноводов с круглым
поперечным сечением из табл. 13.1. Следует подчеркнуть, что выражения в
табл. 13.2 справедливы для всех мод.
Первые шесть выражений в первом столбце получены подстановкой выра-
жений для полей из табл. 13.1 в соответствующие выражения в табл. 11.1.
Они могут быть получены и другим способом — непосредственно из скаляр-
ного волнового уравнения с использованием методов, описанных в гл. 33,
при замене Ф на et. Примером тому может служить доказательство ортого-
нальности полей мод (см. разд. 33.2). Остальные выражения (за исключени-
ем параметра искажения) не могут быть получены подобной простой подста-
новкой, поскольку при выводе выражений для полей мод высших порядков
требуется введение поправок, хотя они и не входят явно в конечные форму-
лы. Выражения для постоянной распространения моды и ее групповой скоро-
сти проще получить из скалярного волнового уравнения (см. разд. 33.3 и
33.4 соответственно). Формула для V2 вытекает из определения (13.14), а
выражения для профиля показателя преломления из примечания к табл. 13.2.
Выражение для dU/dV получено параллельно с выводом формулы для груп-
повой скорости (см. разд. 33.4). Согласно условию в разд. 11.3 для гарантии
того, что поперечные поля мод в непоглощающем волноводе являются дей-
ствительными функциями Ф и F^(r) считаются действительными.
13.10. Зависимость поглощения от поляризации
В разделе 11.22 было показано, что при распространении по поглощающему
волноводу мода теряет свою мощность, а коэффициент затухания зависит от
мнимой части постоянной распространения. Приближение слабонаправляю-
щих волноводов применимо и к поглощающим волноводам при условии, что
как действительная, так и мнимая части профиля показателя преломления
иг (х, у) ип'(х, у) незначительно меняются по поперечному сечению волново-
да. Скалярная постоянная распространения является комплексной величи-
ной и ее действительная и мнимая части определяются в общем случае чис-
ленным решением характеристического уравнения, полученного из скалярно-
го волнового уравнения. Однако на практике, как правило, поглощение
очень мало и коэффициент затухания мощности можно определить из выра-
249
Таблица 13.2. Свойства направляемых мод слабонаправляющих вол-
новодов
Произвольный профиль
Профиль показателя преломления п^{1 -2Д/(х,у)}
Ортогональность
Нормировка N 2 \pJ
Интенсивность, или плотность мощности S И’тСгГ*.2 2 \До/
Мощность моды р и /г \1/2 Г И’т(^) 1 2 \Яо/ Ja.
Часть мощности в сердцевине J е^ёЛ j J е^ёЛ ^со
Коэффициент затухания мощности 2/с Г л'е^ёЛ / Г е^ёЛ •м, / «М,
Постоянная распространения д2
1 е^ёЛ
Параметр моды йг f {fy1t^+(pVt9^2+(pVt*y)1\dA *^00
Полезная производная du dV Y) f 1 f «?d-4 u 1 Ja„
Групповая скорость с» Cp f , / f _ _ — е^ёЛ / .и’е^ёЛ * <4. 1 Ja*
Параметр искажения D d2 (U2\ dV2\2v)
Примечание. Параметры определены в табл. 1. Амплитуды мода зада-
ются условиями возбуждения, Лсо— поперечное сечение сердцевины. Пред-
полагается, что в|,Фи являются действительными функциями в непо-
250
Волновод с поперечным сечением произвольной формы Круглый волоконный световод
и^,{1-2Д/(х,у)} »£>{! -2Д/(Л)}
Г T;TkdX = 0 <4Х I Fjy> Ff“ Л ал = 0 Jo
f Ч-2аЛ 2 W J,. /ел\1/2 f® ЛР2М~" ) F/RdK \До/ Jo
2 \Яо/ 2 \До/
«нал 2 U/ L. ’VIla|24»(—) f F2 RdR \^/ Jo
1 ч*2 ал / | ч*2 ал f1 1 f® F? RdR / FfRdR Jo /Jo
2k j rf^AA^ Ч»2 ал 2k Гибкая/ Гл?лал Jo ' Jo
Г {(*лЧ,)2-(?,ч*)2}ал •Ь. Jo I \ил / \ л / J
| ч<2ал p2 1 Fl2лaл Jo
[ {№ч'2 + (р?,ч')2}ал f® (/dF \2 / I2 \ ") £ О
Г ч*2 ал pFfKdR Jo
X 1 /ч»2ал / Г ч«2ал и Ja. 1 Ja. и Г® / Г® -T fFfRdR / Fl RAR U Jo /Jo
yf ч'2ал/| п2ч<2ал * J-*. 1 Ja. R С00 1 f® C7 Fl RAR / n2FlRAR * Jo /Jo
а2 /и2\ ar2^2rj a2 /t/2\ AF2\2v)
глощающих волноводах и приближенно действительными в волноводах
с поглощением, если л1 < < п1 ^псо- «Функции Фи /^являются решения-
ми уравнений из табл. 13.1, a Fp) и F.K обозначают различные решения
I и
скалярного волнового уравнения с одинаковым индексом I. Векторные
операторы даны в табл. 30.1.
251
жений в табл. 13.2, считая Ф решением уравнения (13.8) для непоглощающе-
го волновода.
В разд. 13.6 была получена поляризационная поправка 8(3 к скалярной
постоянной распространения (3. В поглощающем волноводе как поле моды
et, так и функция профиля показателя преломления f являются комплекс-
ными величинами, и поэтому, как следует из выражения (13*11), 8(3 также
является комплексной величиной. Мнимая часть 8(3 обычно значительно
меньше действительной, однако она может дать существенное затухание мощ-
ности моды на большой длине волновода. В этом единственном случае et
не может рассматриваться как приблизительно действительная функция, по-
скольку отношение мнимой части к действительной у et и f почти одинако-
вое. В общем случае для 8(3Т и 8(3* необходимо рассчитывать два разных ин-
теграла, однако существуют два частных случая, в которых возможны неко-
торые упрощения.
Если действительная и мнимая части п(х, у) имеют одинаковые простран-
ственные зависимости, т. е. п^п1 = const, то Vt In п2 = Vt ln(«r) 2. Следователь-
но, если для непоглощающего волновода с профилем показателя преломле-
ния пт(х, у) известна 8(3, то для поглощающего волновода она определяется
тем же выражением при замене /Т на + i/Т*, как это следует из выраже-
ния (13.11).
В случае волновода со ступенчатым профилем показателя преломления 8(3
можно выразить через интеграл (13.12). При любых мнимой и действитель-
ной частях показателей преломления сердцевины и оболочки, как показано
в разд. 32.4, действительная и мнимая части 8(3 пропорциональны отношению
интегралов в выражении (13.12), где et - комплексная величина.
13.11. Поляризационные поправки высших порядков
В предыдущих разделах было показано, что моды слабонаправляющих вол-
новодов являются почти ТЕМ-волнами с поперечными составляющими et и
ht. Однако в точные выражения для полей мод входят и продольные компо-
ненты. В слабонаправляющих волноводах эти компоненты очень малы и мо-
гут быть приближенно выражены через et и ht. Из разложений (32.15) имеем
ez ^j£?A)1/2 (pV. ,et). ^..i(2A).1/2 (pVt.ht). (13.13)
Эти составляющие поля малы и используются очень редко, а в случаях, ког-
да они начинают сказываться, и точность поперечных составляющих поля
должна превосходить точность выражений в табл. 13.1, ее можно повысить,
если в разложении полей мод по малому параметру Д учитывать члены более
высокого порядка (см. разд. 32.2), однако это значительно усложняет вы-
ражения.
Групповая скорость и параметр искажения. Выражения в табл. 13.2 для
групповой скорости и параметра искажения получены из решений скалярно-
го волнового уравнения. Используя поляризационную поправку 8(3 к скаляр-
ной постоянной распространения, для этих выражений можно получить по-
25 2
правки высших порядков. Наиболее просто это сделать с помощью парамет-
ра моды U, который связан со скалярной постоянной распространения за-
висимостью
£/=р(АЛ?со-02)1/2. (13.14)
Если 8U — поляризационная поправка к /7, то точные параметр моды U и
постоянная распространения /3 достаточно хорошо аппроксимируются выра-
жениями
0^0+80, (13.15)
а поправки, как показано в разд. 32.2, связаны соотношением (32.11 б), т. е.
dU= _ [pV/и (2Д)1/2 ] др. (13.16)
Чтобы получить выражение для групповой скорости, разложим правый член
(11.57) в ряд по степеням Д вплоть до квадратичного, опустив индекс моды,
и подставим выражение (13.15) для U, учитывая согласно (13.11) и (13.16),
что порядки величин dUn Д равны. В результате имеем
и =Ug + 5ug; ug = -^-(1 + Ду), (13.17а)
псо
S С Л2 г 1 и и4 „ d ,U
—Д=^+-Л_ —
J и2
y = (13л7б)
Соответствующее разложение для параметра искажения можно получить из
второго выражения (11.59а) для D. Учитывая члены, линейные относитель-
но Д, получаем
- - d2 U2 х
D=D+6D; D
(13.18)
Д d , о пс(.
где у определяется выражением (13.176).
АНИЗОТРОПНЫЕ СЛАБОНАПРАВЛЯЮЩИЕ ВОЛНОВОДЫ
Обобщим теперь теорию, изложенную в этой главе, на одномодовые волново-
ды, выполненные из анизотропного материала (см. разд. 11.23). Такие вол-
новоды имеют не только различные практические применения [5], но и явля-
ются моделью, описывающей механизм зрения животных [6, 7]. Вначале бу-
дут рассмотрены характеристики распространения волноводов, анизотропия
которых обусловлена исключительно геометрией, т. е. волноводов со струк-
турной анизотропией. Затем рассмотрим те поляризационные эффекты, кото-
рые вызваны анизотропией материала. Основное внимание будет уделено
волноводам с сильной анизотропией материала, поскольку свойства волно-
водов со слабой анизотропией могут быть проанализированы непосредствен-
но с помощью метода возмущений и рассмотрены в разд. 18.9.
253
Структурная анизотропия. В изотропном одномодовом волноводе рас-
пространяются две основные ортогонально-поляризованные моды, постоян-
ные распространения которых в случае отличия формы поперечного сечения
волновода от круглой разные. Это обусловлено геометрией поперечного се-
чения волновода, т. е. структурной анизотропией. Чем больше отклонение
поперечного сечения от осесимметричного, тем больше структурная анизо-
тропия. Поэтому она максимальна для планарных волноводов со ступенча-
тым профилем показателя преломления. Физический механизм ее заключает-
ся в зависимости коэффициента полного внутреннего отражения волны от
состояния поляризации (см. рис. 10.2) и проявляется в поляризационной за-
висимости продольного сдвига. Такой поляризационной зависимостью, рас-
смотренной в гл. 10, пренебрегаем, поскольку в данном случае рассматрива-
ются только слабонаправляющие волноводы.
Большая разность показателей преломления. В случае, когда показатель
преломления сердцевины «со значительно превосходит показатель преломле-
ния оболочки ис1, т. е. «с]/исо 0, или А -> 1/2, структурная анизотропия
сильно влияет на распространение излучения в планарных волноводах. Для
примера рассмотрим две основные моды планарного волновода со ступен-
чатым профилем показателя преломления — первые четные ТЕ- и ТМ-моды.
Часть мощности, переносимая в сердцевине, т? для обеих поляризаций опре-
деляется выражением в табл. 12.2. При V = 1,55 и любом значении А 80%
мощности ТЕ-моды распространяется в сердцевине, в то время как мощ-
ность ТМ-моды зависит от А и падает до нуля при А -> 1/2. Так, например,
при А 0,495 в сердцевине распространяется всего 10% мощности ТМ-мо-
ды. В противоположном случае, когда разность показателей преломления ма-
ла, обе основные моды переносят по сердцевине примерно одинаковую мощ-
ность, так при А 0,05 различие составляет всего 1 %. Таким образом,
структурная анизотропия несущественна в слабонаправляющих волноводах
и проявляется в небольшом различии постоянных распространения мод
(см. разд. 13.5). С другой стороны, анизотропия материала, как будет пока-
зано, может значительно повлиять на характеристики распространения слабо-
направляющих волноводов.
Анизотропия материала. Рассмотрим волновод из анизотропного, напри-
мер из кристаллического, материала. Некоторые свойства такого волновода
были рассмотрены в разд. 11.23. Для простоты предположим, что три глав-
ные оси диэлектрической среды параллельны трем геометрическим осям изо-
тропного волновода. В общем случае пространственное распределение профи-
ля показателя преломления различно для каждого направления поляризации.
Для света, поляризованного вдоль оси х, волновод характеризуется профи-
лем показателя преломления пх (х, у) и связанными с ним параметрами Ах
и Кх, а для света, поляризованного вдоль оси у, — соответственно параметра-
ми пу (х, у), Ах и Кх, где
2ДХ = 1 - («с1/«со)2; 2ДУ = 1 - («с1/«с0)2;
(13.19)
их = крп'со (2ДХ)1/2; Vy = крпу0 (2Ду)1/2.
Эти параметры являются обобщением определений, данных в табл. 1 для изо-
тропного волновода. Таким образом, п*0 и п?0 — максимальные значения по-
254
казателя преломления сердцевины, а п§ и - показателя преломления
оболочки.
1342. Моды анизотропных волноводов
Обобщим теперь теорию, изложенную в предыдущих разделах этой главы, на
слабонаправляющие анизотропные волноводы, у которых n*Q nyQ «
«ср Во-первых, напомним, что две аксиально-направленных (вдоль осиг)
моды неограниченной однородно-анизотропной среды являются ТЕМ-волна-
ми, причем если декартовы оси координат совпадают с главными осями ани-
зотропией среды, то одна волна поляризована вдоль оси х, а другая вдоль оси
у (см. разд. 11.23). Во-вторых, в разд. 13.2 было показано, что моды слабо-
направляющего изотропного волновода также являются распространяющи-
мися в z -направлении ТЕМ-волнами, а из разд. 13.4 и 13.5 следует, что одна
из основных мод поляризована вдоль оси х, а другая вдоль оси у, где х и
у — оптические оси поперечного сечения волнрвода. Примерами оптических
осей могут служить большая и малая оси эллипса поперечного сечения волно-
вода или любая пара ортогональных осей круглого волновода.
Круглые анизотропные волоконные световоды. Интуитивно ясно, что ос-
новные моды круглого анизотропного световода должны быть поляризова-
ны вдоль главных осей х и у. Следовательно, анизотропия нарушает геомет-
рическую циркулярную симметрию световода, а это эквивалентно случаю
световода с некруглым поперечным сечением, рассмотренному в разд. 13.5.
Поэтому относительно моды, поляризованной вдоль оси х, световод характе-
ризуется параметрами пх (х, у) , Дх и Кх, а относительно моды, поляризован-
ной вдоль оси у, — параметрами пу(х, у), Ду и Ку, что иллюстрируется на
рис. 13.1. В приближении слабонаправляющего волновода моды аппрокси-
мируются ТЕМ-волнами и поэтому не зависят от аксиального распределения
профиля показателя преломления п? (х, у). Таким образом, результаты, по-
лученные для изотропного слабонаправляющего световода, справедливы и
для анизотропного световода при условии, что величины п (х, у), псо, ис1 и
а) б)
Рис. 13.1. Два примера анизотропных волоконных световодов, каждый из которых для
света, поляризованного вдоль оси х, описывается профилем показателя преломления
пх, а для света, поляризованного вдоль оси у, - профилем пу
255
Д заменены соответствующими выражениями (13.19), а декартовы оси х
и у параллельная главным осям анизотропного диэлектрического материала.
В качестве примера приведем выражения для полей основных мод, поляризо-
ванных соответственно вдоль осей х и у и полученных из соотношений (13.9):
(0 ехР <Ж2); ну = Ъ (0 ехР (i^y2);
(13.20)
где Фх, |3Х и Фу, (Зу являются фундаментальными решениями скалярного
волнового уравнения (13.8), в котором п заменено на«х и пу соответствен-
но. За исключением некоторых частных случаев [8] выражения для полей
мод высших порядков имеют вид (13.20) , поскольку, как отмечалось выше,
анизотропия нарушает циркулярную симметрию поперечного сечения свето-
вода. Однако если анизотропия материала достаточно слаба, т. е. «Х(х, у)
~ «у (х, у), то поля мод Высших порядков могут быть описаны соответству-
ющими выражениями, полученными для случая почти круглого световода
в разд. 13.9.
Поляризационные поправки. Небольшую поляризационную поправку к
скалярной постоянной распространения (39 обусловленную структурной ани-
зотропией, можно получить из выражения (13.11). Для круглого изотропно-
го световода они одинаковые для двух основных мод, т. е. 50х = 8ру. По-
правки справедливы не только для изотропного, но и для анизотропного
световода, параметры которого (13.19) зависят от поляризации волны, по-
скольку разностью \5(3Х - 8|3у | можно пренебречь ввиду ее малости по срав-
нению с разностью постоянных распространения |/Зх - 0у| слабонаправляю-
щего световода (13.20).
Математический вывод. Полученные выше результаты, основанные на ин-
туитивных представлениях, могут быть получены методом возмущений, рас-
смотренных в разд. 32.6. Используя векторное волновое уравнение (30.31)
для вектора электрического поля Е, можно доказать, что упрощенная форма
этого уравнения (30.35), приведенная в разд. 30.13, справедлива для полей
мод слабонаправляющего анизотропного волновода. Таким образом, пос-
кольку уравнение (30.35) по форме идентично своему аналогу для изотроп-
ного волновода, все результаты, полученные в этом случае методом возму-
щений справедливы и для анизотропного волновода при условии, что про-
филь показателя преломления заменяется на соответствующие состояния
поляризации волны величины пх или пу.
Поперечное сечение произвольной формы. Если главные оси анизотропно-
го материала параллельны оптическим осям световода с поперечным сечени-
ем произвольной формы, то интуитивно ясно, что фундаментальные моды
поляризованы вдоль этих осей. Эта ситуация аналогична рассмотренной выше
для круглого световода за тем исключением, что Фх (г) в выражении (13.20)
необходимо заменить на Фх(х, у), а Фу(г) - на Фу(х, у). Таким образом,
все результаты, полученные для слабонаправляющих изотропных волново-
дов,применимы к слабонаправляющим анизотропным волноводам при соот-
ветствующей замене параметров (см. выше) .
256
Мы пренебрегли малыми поляризационными поправками (13.11) к ffx
и 0у, поскольку для изотропного волновода с нециркулярным поперечным
сечением $х Ф (Зу. Это приближение является довольно точным при условии,
что порядок величины анизотропии материала больше величины А 3/2, обус-
ловленной волноводной структурой. Выражения для полей мод высших по-
рядков имеют такой же вид, как и для основных мод, за исключением слу-
чая почти круглого световода (см. разд. 13.9).
13.13. Одномодовые однополяризационные волоконные световоды
При обсуждении структурной анизотропии было показано, что для суще-
ственного различия характеристик распространения двух основных мод не-
обходимо, чтобы показатель преломления сердцевины был незначительно
больше показателя преломления оболочки. Покажем теперь, что относитель-
но небольшая анизотропия материала может сильно изменить характеристики
распространения и привести к возможности существования лишь одного из
двух состояний поляризации основной моды, в результате чего световод ста-
новится действительно одномодовым.
Рассмотрим круглый световод со ступенчатым профилем показателя пре-
ломления. На рис. 13.1, б показан профиль показателя преломления пх для
волны, поляризованной вдоль оси х. Предположим, что величина Vx такова,
что моды высших порядков распространяться не могут. Таким образом,
источник поляризованного вдоль оси х излучения будет возбуждать основ-
ную моду, поле которой 7ГХ определяется выражением (13.20). Чтобы мода,
поляризованная вдоль оси у, не возбуждалась, необходимо подобрать такой
профиль показателя преломления пу9чтобы свет, поляризованный в направ-
лении оси волноводом не направлялся. Наиболее прямой путь — это вырав-
нять показатели преломления сердцевины и оболочки, т. е. обеспечить Ду = 0.
Существует и другой способ, который будет рассмотрен ниже.
ИЗЛУЧЕНИЕ ЧЕРЕЗ ВЫТЕКАЮЩИЕ МОДЫ В АНИЗОТРОПНЫХ СВЕТОВОДАХ
При описании свойств анизотропных световодов предполагалось, что состоя-
ние поляризации мод не зависят друг от друга. Такой подход справедлив
только для однородно поляризованных полей мод, имеющих место лишь в
планарных волноводах, как отмечалось в разд. 11.15 и 11.16. Из разд. 12.11
следует, что даже в изотропном слабонаправляющем волоконном световоде
мода, поляризованная вдоль оси х9 имеет очень маленькую, порядка А,
^-составляющую, а мода, поляризованная вдоль оси — х-составляющую та-
кого же порядка. Таким образом, мощность, распространяющаяся в х-поля-
ризованной моде, ’’чувствует” профиль показателя преломления пу. Други-
ми словами, между модами существует слабая связь. Покажем теперь, что
у-поляризованная мода на рис. 13.1,а будет терять мощность на излучение,
если двойное лучепреломление будет достаточно большим. Это можно было
предвидеть еще в разд. 11.24 при определении минимального значения /3 для
мод, являющихся направляемыми в анизотропных световодах.
13.14. Одномодовые однополяризационные световоды на вытекающих модах
Рассмотрим световод, профиль показателя преломления которого показан
на рис. 13.1, а. На основании изложенного в разд. 11.24 известно, что любая
257
9 Зак 37
мода будет терять мощность на излучение при (3 < кп^ Q3 имеет мнимую
часть). Поэтому j^-поляризованная мода на рис. 13.1,а при распространении
будет ’’вытекать” [9], если двойное лучепреломление слишком велико, что-
бы обеспечить /Зу < кп*\. При выполнении последнего условия часть ^-поляри-
зованной моды ’’чувствует” показатель преломления оболочки п^9 значение
которого больше Ру/к, и поэтому условия направляемое™ излучения не вы-
полняются. Количественная оценка потерь на вытекание может быть получе-
на из векторного волнового уравнения (30.31), которое в данном случае
можно решать методом возмущений, поскольку мнимая часть £Гу мала, а
световод — слабонаправляющий [10]. Таким образом, при определенных
длине световода и коэффициенте потерь на вытекание, световод на рис. 13.1, а
является фактически одномодовым о дно поляризационным волноводом
[9,11].
Следуя рассуждениям, изложенным выше и в разд. 11.24, можно также
предсказать, что мода, поляризованная вдоль оси х, в волноводе с профилем
показателя преломления, на рис. 13.1, б будет вытекающей, если показатель
преломления однородного профиля пу будет значительно большей^, так что
Рх < &ncl-
ГЛАВА 14. ВОЛОКОННЫЕ СВЕТОВОДЫ КРУГЛОГО ПОПЕРЕЧНОГО
СЕЧЕНИЯ
В предыдущей главе было показано, каким образом из решений скалярного
волнового уравнения получают выражения для полей мод слабонаправляю-
щих волноводов. В этой главе рассматриваются свойства полей мод волокон-
ных световодов круглого поперечного сечения и для некоторых конкретных
профилей показателя преломления с аксиальной симметрией дается аналити-
ческое решение скалярного волнового уравнения. Основное внимание уделя-
ется одномодовым световодам и свойствам основных мод НЕИ. Одно из
важнейших свойств широкого класса одномодовых световодов со степен-
ным законом изменения профиля показателя преломления в сердцевине
заключается в том, что как распределение мощности основной моды по по-
перечному сечению, так и максимальное значение волноводного параметра
V в основном зависят от ’’объема” профиля показателя преломления, про-
порционального интегралу от распределения показателя преломления по по-
перечному сечению сердцевины, и малочувствительны к его форме. С другой
стороны, дисперсия импульса в одномодовых световодах, наоборот, зависит
главным образом от формы профиля показателя преломления и малочув-
ствительна к объему профиля.
НАПРАВЛЯЕМЫЕ МОДЫ КРУГЛЫХ ВОЛОКОННЫХ СВЕТОВОДОВ
На рис. 14.1 представлен круглый волоконный световод и оси декартовых
и цилиндрических координат, используемые при описании полей мод. Про-
филь показателя преломления представим в виде
”2(Д) ="со[1 -2A/W; А=г/Р, (14.1)
где псо — максимальный показатель преломления, a f(R) — функция изме-
нения показателя преломления. Радиальная координата г нормирована на р,
258
Рис.14.1. Волоконный световод с круго-
вой симметрией и неограниченными раз-
мерами вдоль осей г w z. Радиус сердце-
вины световода равен р, нормированный
радиус равен R = г/р, а показатель пре-
ломления в сечении световода изменя-
ется по закону п (г)
т. е. на радиус сердцевины, если оболочка имеет постоянный показатель пре-
ломления, либо характерный размер поперечного сечения световода, если яв-
ной границы между сердцевиной и оболочкой нет. Параметр высоты профиля
или относительная разность показателей преломления А в слабонаправляю-
щих световодах значительно меньше единицы. Поэтому из соотношения
(11.48) для световодов с постоянным показателем преломления оболочки
имеем
"со
(14.2)
14.1. Структура полей мод
В главе 13 было показано, что поля мод слабонаправляющих световодов в
наиболее общей форме можно представить следующим образом:
Е ~ et (х, j)exp[i(0 +60)z]; Н ht (х, j) exp [i(0 + 3j3)z]; (14.3a)
ht ~ «co(eo/Mo)'/2z x et. (14.36)
В круглом световоде структура вектора et с физической точки зрения рас-
сматривалась в разд. 13.4 и 13.7, а с точки зрения теории возмущений [1] —
в разд. 32.6 и 32.7, где было показано, что для нахождения et необходимо ре-
шить скалярное волновое уравнение (13.8) . Для круглых световодов опера-
тор Vt1 2 определен в табл. 30.1 и решения можно представить в виде Ф =
= /*\(г) cosfy? и Ф = /д(г) sin где Z = 0, 1, . . . , а /д(г) является решением
обыкновенного дифференциального уравнения
1^- + Г IF +k2n2(r) -yr -0W) =°- (14.4а)
Переходя к более удобным безразмерным величинам, подставляя выраже-
ние {14.Q для п (R) ,R=r/pu используя определения волноводных парамет-
ров U и V из табл. I, получаем
1 z7 72 ~
[dR^ + + C72-rV^)].Fl(A)=°; R=r/p. (14.46)
259
9*
Таблица 14.1. Поля мод слабонаправляющих круглых волоконных световодов
i Мода к.
Основные НЕц“ и НЕ1|И (/ = 0)-моды
1 Четная НЕ1т xF0 /Р \1/2 / £0 \ псо — УГо ХДо /
3 Нечетная НЕ1М уТо /р \1/2 1 ео \ _М т xF° ХДо /
Моды высших порядков (Z> 1)
1 Четная НЕ|+1,„ {xcos(/^ — ysin/pjF, /e \1/2 лсс I ~ ) {x sin + у cos /<p} F, \До/
2 тмОт (/ = 1) {х cos + у sin } Fj /р \l/2 Ze0 1 t Л . Л x „ — n^l — 1 {x sin <p - у cos «pJFj X До/
2 Четная ЕН,-, „ (/> 1) {xcos/«P + y sin/«p}F, /е0\1/2 — лсо 1 — 1 {x sin /<р — у cos I v} Ft XMo /
3 Нечетная НЕ/+1Ж {xsin/p + ycos/p}F, /fi0\1/2 -Meo 1 — ) {xcos/^-y sin/^}F/ X До /
4 ТЕОж 0=1) {x sin <p — у cos <P} Fj /е \1/2 лс»( “ I {x cos 4-у sin <p}Fj хДо/
4 Нечетная EH,_,.m (/>1) {x sin/«p — у cos/<p}F/ I — ) {x cos /«p + у sin /<p} F, ХДо/
260
ezi h.t
Основные НЕц и НЕ1т (/ = 0) -моды
. (2Д)1/2 1———G0COS¥> / «0 \1/2(2Д)1/2 „ . ,nco(._ I v Go sin V> \Mo / y l,
(2А)1/2 „ . i —-— Go sm /ЧХ1'2 (2Д)1/2 _ ) v G0cos¥> \Mo / y II
Моды высших порядков
(2Д)1/2 i у Gr cos(/+l)^ \MO / y Il-Il
. (2Д)1/2 . 1 v G* 0 2(11 + 11)
(2Д)1/2 x i ——— G* cos(/-1)v \MO / y Ii+Ii
(2Д),/2 i—y-Gi sin(/+l)¥> /р \l/2 рдй/2 Wco( ) IZ G| cos(/+l)¥> \ До / y Ii-h
0 /е0У/2(2А),/2г + “L / V G* 0
(2Д)1/2 i~y— G| sin(/—l)v? \M0 / y h+Il
(2A)3/2 1 , , _/(2Д)3/2 2 1 RFI (dFt/dRMdf/dRjdR / Г RFfdR Jo /Jo | Ff(df/dR)dR | RFfdR Jo / Jo
Примечание. Индексы t и z обозначают поперечную и продольную составляющие.
Единичные векторы х, у и z параллельны декартовым осям (см. рис. 14.1). Параметры
определены в табл. I.
261
Условие непрерывности и dFy/dR по поперечному сечению световода при-
водит, как это показано в разд. 33.1, к характеристическому уравнению для
постоянной распространения j? каждой моды.
По известным решениям FV(R) можно определить поля (см. разд. 13.4
и 13.7 и табл. 13.1). В табл. 14.1 приведены выражения для полей мод круг-
лого световода; обозначения мод соответствуют принятым в разд. 11.16.
В левой части таблицы приведены выражения для и htj, а в правой — ма-
лые поправки, обусловленные поляризационными эффектами световодной
структуры. Поправки 8/3i в выражениях (14.3а) существенны для всех
НЕ1т-мод по причинам, указанным в разд. 13.4 и 13.7. Они получены подста-
новкой eti из табл. 14.1 в выражение для 6j3j в табл. 13.1 и заменой dA на
p2RdRd^p. Продольные компоненты поля ezi, hzi определены из выражений
(13.13). По причинам, отмеченным в разд. 13.11, они используются очень
редко и приведены для полноты изложения.
14.2. Основные и НЕ1т (Z = 0)-моды
Свойства двух основных НЕц-мод и всех пар НЕ1т-мод обсуждались в
разд. 13.4. Направление электрического вектора, или поляризации попереч-
ного электромагнитного поля, параллельно одной из произвольно выбран-
ной пары ортогональных осей поперечного сечения световода [1]. Это озна-
чает, что эти моды однородно поляризованы. Для удобства будем считать,
что одна из них поляризована вдоль оси х, а другая — вдоль оси у (см.
рис. 14.1). Все они соответствуют одному и тому же решению скалярного
волнового уравнения (14.4) при I = 0. Выражения для поперечных полей мод
(13.9), повторенные в табл. 14.1, не учитывают поляризационных свойств
световода. Поскольку в ряде случаев удобно использовать составляющие
поля не в декартовой, а в полярной системе координат, то в табл. 14.1 слева
внизу записаны выражения, позволяющие переходить от одной системы к
другой. Напомним также, что решению уравнения (14.4) для основной моды
соответствует максимальное значение р или минимальное значение U для
направляемых мод, а поправка 6)3 одинакова как для четных, так и для не-
четных мод.
14.3. Моды высших порядков (/ > 1)
Структура мод высших порядков (Z > 1) из табл. 14.1 обсуждалась в
разд. 13.7. Для каждого I > 1 существует четыре моды. В крайнем левом
столбце в табл. 14.1 стоят значения i для соответствующих полей из
табл. 13.1. Эти моды не являются однородно поляризованными, т. е. направ-
ление вектора зависит от его положения в поперечном сечении световода.
Моды обозначаются в соответствии с их гибридной природой и согласуются
с обозначениями точных мод в гл. 12, что можно проверить, рассмотрев вы-
ражения для поперечных компонент поля в световоде со ступенчатым профи-
лем показателя преломления в табл. 12.3 при Д -> 0 [2]. Моды НЕ1т, о ко-
торых шла речь в предыдущем разделе, являются частным случаем мод
НЕ1+1,т пРи/ = °-
Следует отметить, что если для каждого I > 1 две из четырех мод имеют
различные поправки 8/3^ то при Z = 1 в общем случае четыре моды имеют три
262
различные поправки 6j3p По этой причине выражения для полей мод нельзя
представить в более простом виде, чем в табл. 14.1, например в виде цирку-
лярно поляризованных полей, рассмотренных в разд. 32.8.
Кратко резюмируя все изложенное в этих двух разделах, подчеркнем,
что выражения для полных полей мод и постоянных распространения мод с
учетом поляризационных поправок для всех направляемых мод слабонаправ-
ляющих круглых световодов могут быть получены из табл. 14.1. Конкрет-
ный вид выражений зависит от профиля показателя преломления и определя-
ется решением уравнения (14.4) Ft(A).
14.4. Пример. Неограниченный параболический профиль показателя
преломления
В качестве первого примера рассмотрим световод с профилем показателя преломления
вида [14.3]
и2 (Я) =и£о(1 - 2ДЯ3); R — r/p (14.5)
(кривая к на рис. 12.8). Как было показано в разд. 12.16, точные аналитические реше-
ния уравнений Максвелла известны только для ТЕ-мод. Однако в рамках приближения
слабонаправляющего волновода для всех мод существуют аналитические решения ска-
лярного волнового уравнения, из которых можно получить простые выражения для по-
лей и постоянных распространения мод, а также исследовать интересующие свойства
мод. Эти решения также лежат в основе гауссова приближения, рассмотренного в гл. 15.
Необходимо отметить, что, с одной стороны, параболический профиль физически нереа-
лизуем, поскольку и2 (/?)-> при R -> °°, а, с другой стороны, приближение слабона-
правляющего волновода дает достаточную точность только при малых R, удовлетворя-
ющих условию п (R) « и (0). Поэтому рассмотрение будет корректным, если поле каж-
дой моды сосредоточено внутри или вблизи области с радиусом р, а Д < < 1. Оба этих
ограничения обсуждаются ниже. С увеличением области сосредоточения поля моды вли-
яние поляризационных эффектов световода растет, и точность приближения слабона-
правляющего волновода падает.
Поля мод. Если в уравнении (14.4) положить / — R2 и произвести замену перемен-
ных w = VR2 и F{(R) = gi(w)R^exp (-ViVR2), то получим уравнение [3]
Решением, обеспечивающим ограничение, накладываемое на F^являются обобщенные
полиномы Лагерра где I и т - индексы моды в табл. 14.1. Общее выражение
для F^n конкретные выражения для'основной и ряда мод низших порядков представ-
лены в табл. 14.2, в которой полные выражения для полей мод получены подстановкой
в табл. 14.1.
Постоянная распространения и поляризационные поправки. Решая уравнение (14.6),
одновременно получаем характеристическое уравнение, дающее величину а следова-
тельно, и скалярную постоянную распространения (3, явно выраженные через I, т и V
в табл. 14.2. Поскольку ни для одной моды не существует частоты отсечки, то при про-
извольном значении V распространяются все моды. Кроме того, при R -* °°? п2 (Я) -> -*>
моды излучения отсутствуют, и полный набор мод состоит только из направляемых мод.
Поляризационная поправка 60* в табл. 14.2 находится подстановкой / = R2 в инте-
грал в табл. 14.1. Используя интегрирование по частям в числителе выражения для Ц ,
получаем Ц = - (2A) 3/2/2рК a I2 = -IIх. Заметим, что 60 = 0 как для ТЕ-, так и для
ТМ-мод. Таким образом, в этом случае для четырех мод, определяемых одним и тем же
решением Е^при I > 1, существуют лишь два различных значения поправки 60^ Однако,
как легко показать из уравнения (32.22), поправки к 0 следующего порядка малости
263
Таблица 14.2. Моды волоконного световода с неограниченным параболическим профилем показателя преломления
n2(R)^n£>{l-2AR2}; Л=^; И- крпт(2&У'2 Выражения для мод высших порядков
Основные моды (1 = 0, т = 1) Моды высших порядков (/ >0, m > 1) / т F,(R) и
Радиальная зависимость Fo = ехр( —j ИЛ2) Go = -ИЛехр(-|ИЛ2) F, = R'LJJ-! (ИЛ^ехрС -1 ИЛ2) 0 2 (1-ИЛ2)ехр(-1ИЛ2) (6 И)1'2
0 3 (1 -2 ИЛ2 + j И2Л4)ехр( - j ИЛ2) (10И)1'2
Характерис- тическое уравнение U = (2И)1'2 U = {2V(2m + l-1)}1/2
1 1 Лехр( —|ИЛ2) (4И)1/2
Постоянная распростра- нения - v ( 4др'2 Р р(2Д)1/2 J V J v ( 4Д 11/2 ^-p(2A)1/2{1 И(2т + /
1 2 Л(2—ИЛ2)ехр(-| ИЛ2) (8 И)1'2
Поправка к постоянной распростра- нения । < to и и 11 L QQ. ’О <O <5/?,=<5/?з = -ltl(2A)3'2 ^2 = а/?4 = ^1(2Д)2'2 2p V 1 3 Л(3-ЗИЛ2 + |И2Л4)х ехр( —|ИЛ2) (12 И)1'2
2 1 Л2ехр(-{ ИЛ2) (6 И)1'2
Свойства основной моды 2 2 Л2(3-ИЛ2Цхр(-1ИЛ2) (10И)1'2
2 \р J V с с Д2 4Д »f = —, ^f=-4—-у; D = 0, ^=--у лсо 1 лсо V V 2 3 Л2(6—4ИЛ2 + |И2Л4)х ехр( —|ИЛ2) (14И),/2
1 1 Л'ехр(-|ИЛ2) {2И(/+1)},/2
Примечание. Векторные поля мод находятся подстановкой в выражения табл. 14.1. Параметры определены в табл. I.
для ТМ-мод имеют порядок (2Д)5/2, а для ТЕ-мод равны нулю, поскольку в последнем
случае /^является точным решением скалярного волнового уравнения.
Основные моды (/ = 0, т = 1). Поперечные поля основных мод имеют гауссову
зависимость от радиальной координаты, как это следует из табл. 14.1 и 14.2. Подстав-
ляя решение FQ в табл. 13.2, получим простые выражения для основных параметров
моды. Часть мощности в сердцевине т? растет с увеличением V и падает с уменьшением р
вследствие рассмотренных в гл. 10 дифракционных эффектов. Распространенней уши-
рение импульса рассматривалось в гл. 11. Приведенные в табл. 14.2 выражения для
групповой скорости показывают, что в рамках приближения слабонаправляющего вол-
новода групповая скорость моды близка к скорости светаjb среде с показателем пре-
ломления nCQ. Поскольку скалярный параметр искажения D из табл. 13.2 равен нулю,
то волноводная дисперсия является эффектом более высокого порядка. Если учесть
поляризационную поправку 6 U. то из соотношений (13.17) и (13.18) получим поправки
6Vg и 8D (см. табл. 14.2) .
Условие, при котором волновод является слабонаправляющим. Как отмечалось в
начале этого примера, поля мод в рамках приближения слабонаправляющего волновода
являются хорошей аппроксимацией точных полей мод только при выполнении некото-
рых условий, основным из которых является условие Д < < 1. Из него следует, как по-
казано в разд. 13.2, /3 « кпсо, а подстановка 0 и V из табл. 14.2 приводит к условию
V > > 4Д для основных мод. Таким образом, при этом ограничении выражения для по-
лей основных мод будут справедливы в областях, где переносится основная часть
мощности.
Поляризационные поправки к полям мод. Выражения для поперечных компонент
поля основных мод в табл. 14.1 не содержат членов, описывающих поляризационные
эффекты световода. Они учитываются в поправках более высоких порядков, получае-
мых разложением в ряд (см. разд. 32.1). Поправка второго порядка к поперечной ком-
поненте электрического поля является решением уравнения в табл. 32.1. Если положить
f = R2, а вместо et подставить etl или et3 из табл. 14.1 и принять U, из
табл. 14.2, то легко показать, что решениями для полей второго порядка будут
г ДЯ2ехр(-ЙИЯ2) cos и гД/?3ехр(-ЙКЯ3) sin (14.7)
соответственно для четной и нечетной основных мод, где г - единичный вектор в ради-
альном направлении. Эта поля являются гипотетически малыми поправками к etl и et3,
и поэтому они существенны только при R < < Д-1/3. Указанное ограничение является
следствием физической нереализуемости данного профиля показателя преломления.
14.5. Пример. Неограниченный степенной профиль показателя преломления
Распределение показателя преломления в таких профилях подчиняется закону
п2 (Я) =и£о(1 - 2ДЯЧ), о <<?<“>; R = r/p, (14.8)
где q - постоянная величина, ар- такой характерный радиус, что, если 7? = 1, п {R} =
= мср На рис. 14.2, а показаны зависимости показателя преломления от радиальной ко-
ординаты при разных q, в том числе для параболического профиля (q = 2), рассмотрен-
ного в предыдущем разделе. Очевидно, что при q -> 0 «(/?)= пс1, т. е. выражение (14.8)
описывает однородную среду, а при q -> °° форма профиля приближается к ступенчатой.
При любом значении q профиль показателя преломления является физически нереализу-
емым, поскольку л3 (R) -►-«>, если R -> Поэтому, как показано выше, приближение
слабонаправляющего волновода справедливо для достаточно больших значений парамет-
ра световода К Если в уравнении (14.4) положить / = Я4, то аналитических решений
для Fj не существует, за исключением случая q = 2.
Постоянная распространения. С использованием масштабного преобразования в
разд. 33.6 показано, что для мод с индексом I = 0 параметр U может быть выражен ана-
литически. Из выражения (33.27) имеем для всех НЕ1т-мод [4]
255
Рис. 14.2. Зависимости показателя преломления от радиальной координаты в светово-
дах с неограниченным степенным профилем (14.8) (д), параметра моды U (14.9) и па-
раметра искажения D (14.11) от нормированной частоты для основной моды (б и в)
~= q/q + 2 = + 2 9
L 2Г(1/<?) J УЧ) ’ 1 ’
где Г - гамма-функция (37.104), т - индекс моды в табл. 14.1, а скалярная постоян-
ная распространения /3 связана с U соотношением, представленным в табл. I.
Групповая скорость и волноводная дисперсия. Мода переносит мощность с опреде-
ленной групповой скоростью. Подставляя выражение (14.9) в (13.17), получаем
V — [1 + д^—— —^-7--- ], (14.10)
S "со 1 2+<? j/2q/q + 2 J ' '
где с - скорость света в вакууме, a G (q) определено выражением (14.9). Волноводная
дисперсия описывается в табл. 13.2 параметром искажения. Подставляя выражение
(14.9), имеем
-^G’(^(3q+2)/(4+2). (14Л1)
В световодах с параболическим профилем показателя преломления волноводная дис-
персия первого порядка равна нулю. Поправки более высоких порядков отличны от
нуля, о чем было сказано в предыдущем разделе.
Условие, при котором световод является слабонаправляющим. Точность приближе-
ния слабонаправляющего волновода для неограниченного параболического профиля по-
казателя преломления была рассмотрена в разд. 14.4. Используя условие (3 ™кпсо, из
выражения (14.9) и табл. 14.2 получим, что при V > > {G (q) Д1/2} Q + световоды с
266
неограниченным степенным профилем показателя преломления являются слабона-
правляюшцми. ~ _
Основные моды. На рис. 14.2, б и 14.2, в представлены зависимости t/и В от парамет-
ра V при различных q для основных мод (Z = 0, т = 1), построенные на основании вы-
ражений (14.9) и (14.11) соответственно. На рис. 14.2, в приведена зависимость G (q).
ВОЛОКОННЫЕ СВЕТОВОДЫ СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ
ПРЕЛОМЛЕНИЯ
Рассмотрим теперь профиль показателя преломления, представляющий
наибольший практический интерес. Световоды со ступенчатым профилем
показателя преломления имеют однородные сердцевину и оболочку, так что
профиль можно представить в виде
n(R) = «со или/ = 0; 0<Я<1, (14.12а)
n(R) =ис1 или/ = 1; 1<^<°°, (14.126)
где R = г/р, р — радиус сердцевины. Предполагается, что псо ~ яс1, или Д « 1,
т. е. световод является слабонаправляющим. Малое изменение показателя
преломления означает отсутствие ограничений на значение параметра V в
отличие от неограниченных профилей показателя преломления в предыду-
щих двух разделах. Выражения для полей мод могут быть найдены либо из
точных выражений, полученных в гл. 12, предельным переходом Д О (см.
разд. 12.11 [2]), либо из решения скалярного волнового уравнения в гл. 13.
В этой главе используется последний подход [1], а в дальнейшем с целью
еще большего упрощения описания свойств таких световодов будут исполь-
зованы приближенные методы.
14.6. Основные и HElm (Z = 0)-моды
Решение уравнения (14.4) Fo (7?) для Z = О дает радиальную зависимость по-
ля основных и НЕ1т-мод. Подставляя / из (14.12) и нормируя решения та-
ким образом, чтобы Fq = 1 при R = 1, находим
Fo (Я) О<я<1; Fo (R) , 1 < оо (14.13)
J0(U) K0(W)
где JQ — функция Бесселя первого рода, KQ — модифицированная функция
Бесселя второго рода. Скалярные параметры моды и и W для сердцевины и
оболочки определены в табл. I и связаны с параметрами световода соотно-
шениями
И2 = t72 + IV2; V = kp(n2co-n2cl)1/2} (14.14)
где к = 2я/Х, а X — длина волны в вакууме. Компоненты поля находятся под-
становкой выражений (14.13) в табл. 14.1. Поскольку в дальнейшем будут
часто использоваться выражения для компонент поля световода со ступен-
чатым профилем показателя преломления, они приведены в табл. 14.3.
Постоянные распространения и поляризационные поправки. Из условия
непрерывности решения Fo уравнения (14.4) и его первой производной
267
Таблица 14.3. Основные и НЕ1т-моды слабонаправляющего светово-
да со ступенчатым профилем показателя преломления
Четная Нечетная
Поперечные компоненты = Ео h, = Псо) — ) Ео \Яо / II Ji- ll 1 £7? о*5
Продольные компоненты <2А)‘'2 е, = ।—— Go cos <f> . . /ЧУ'2(2Д)’'2 . *> = ‘«со ( — j —у— Go smy e, = i!^CoSinv ^ = - Co cos *
Г 'о(УЯ) 0<R<1 ° J„(O)' 0 * R * K0(WR) - K„(^) ’ 1 * R < 00 “«<«
Характерис- тическое уравнение t/2+’p=,/2: у-*2-*»®
Диапазон одномодового режима о < V < 2.405
Постоянная распространения V ( и2)1'2 * р(2Д)|/2 Г 2ДГ2}
Поляризацион- ные поправки (2Д)2'2 U^WKoiW] Л„ С/Й'/С0(Й>) if= 2р Р К,(ИТ W'4K>K1(r)
Производная параметра моды dt) Ко(й')| dV
Нормировка х^Поо/соУ'2 И K?QF) 2 U7 о1
Интенсивность Со, II я? 8Я OW
Часть мощности в сердцевине - Ко(И>)1 “ 'й (U7 + к?(^) J
Групповая скорость ..Ж
Параметр искажения - (й2 A t/2-JF2 , FF2-U2 . За J D = 2 Р ’>2’ + ° ” +2^ ‘J
Примечание. Параметры определены в табл. I. Мощность моды равна
\а | *N, где а — амплитуда моды.
268
Таблица 14.4. Численные значения параметров основной моды волоконных свето-
водов со ступенчатым профилем показателя преломления
V и W т (-У"'- \£о/ п N еоР’ п А \ с ) D dU dV fpd р
4.00 1.907 3.516 0.370 8.890 0.949 -0.1262 -0.0123 0.106 1.293
3.95 1.902 3.462 0.372 8.749 0.948 -0.1274 -0.0122 0.108 1.297
3.90 1.896 3.408 0.374 8.610 0.946 -0.1286 -0.0120 0.110 1.301
3.85 1.890 3.354 0.376 8.472 0.944 -0.1298 -0.0119 0.113 1.306
3.80 1.885 3.300 0.378 8.335 0.943 -0.1310 -0.0117 0.116 1.310
3.75 1.879 3.245 0.378 8.200 0.941 -0.1320 -0.0115 0.119 1.315
3.70 1.873 3.191 0.380 8.067 0.939 -0.1322 -0.0112 0.122 1.319
3.65 1.867 3.137 0.382 7.935 0.936 -0.1344 -0.0109 0.124 1.325
3.60 1.860 3.082 0.384 7.806 0.934 -0.1354 -0.0106 0.127 1.330
3.55 1.854 3.027 0.386 7.678 0.932 . -0.1364 -0.0101 0.131 1.335
3.50 1.847 2.973 0.388 7.552 0.929 -0.1374 -0.0097 0.134 1.341
3.45 1.841 2.918 0.390 7.427 0.927 -0.1384 -0.0091 0.137 1.347
3.40 1.834 2.863 0.390 7.304 0.924 -0.1392 -0.0085 0.141 1.352
3.35 1.827 2.808 0.392 7.184 0.921 -0.1400 -0.0078 0.144 1.359
3.30 1.819 2.753 0.394 7.064 0.918 -0.1408 -0.0070 0.148 1.365
3.25 1.812 2.698 0.394 6.947 0.915 -0.1414 -0.0061 0.152 1.372
3.20 1.804 2.643 0.396 6.832 0.912 -0.1420 -0.0051 0.156 1.378
3.15 1.796 2.588 0.398 6.719 0.909 -0.1424 -0.0040 0.160 1.386
3.10 1.788 2.532 0.398 6.607 0.905 -0.1428 -0.0027 0.165 1.394
3.05 1.780 2.477 0.400 6.498 0.901 -0.1430 -0.0013 0.169 1.401
3.00 1.771 2.421 0.400 6.390 0.897 -0.1432 -0.0002 0.174 1.409
2.95 1.762 2.366 0.402 6.286 0.893 -0.1430 0.0020 0.179 1.418
2.90 1.753 2.310 0.402 6.183 0.889 -0.1426 0.0039 0.184 1.427
2.85 1.744 2.254 0.402 6.082 0.884 -0.1422 0.0061 0.190 1.436
2.80 1.734 2.198 0.402 5.984 0.879 -0.1414 0.0085 0.196 1.446
2.75 1.724 2.143 0.402 5.889 0.874 -0.1404 0.0112 0.202 1.456
2.70 1.714 2.086 0.402 5.795 0.868 -0.1392 0.0142 0.208 1.467
2.65 1.704 2.030 0.402 5.700 0.862 -0.1376 0.0176 0.215 1.578
2.60 1.693 1.973 0.402 5.613 0.856 -0.1356 0.0213 0.221 1.490
2.55 1.681 1.917 0.400 5.532 0.849 -0.1332 0.0253 0.229 1.503
2.50 1.670 1.860 0.400 5.446 0.842 -0.1306 0.0300 0.236 1.516
2.45 1.658 1.804 0.398 5.367 0.835 -0.1274 0.0350 0.244 1.530
2.40 1.645 1.748 0.396 5.295 0.827 -0.1236 0.0406 0.253 1.544
2.35 1.633 1.690 0.394 5.218 0.818 -0.1192 0.0470 0.262 1.561
2.30 1.619 1.634 0.392 5.153 0.809 -0.1142 0.0539 0.271 1.577
2.25 1.605 1.577 0.390 5.090 0.800 -0.1084 0.0616 0.281 1.595
2.20 1.591 1.519 0.386 5.028 0.789 -0.1018 0.0703 0.291 1.614
2.15 1.576 1.462 0.382 4.974 0.779 -0.0944 0.0798 0.302 1.635
2.10 1.561 1.405 0.380 4.922 0.767 -0.0858 0.0906 0.314 1.657
2.05 1.545 1.347 0.374 4.877 0.754 -0.0762 0.103 0.326 1.681
2.00 1.528 1.290 0.368 4.841 0.741 -0.0652 0.116 0.339 1.706
1.95 1.511 1.233 0.362 4.808 0.726 -0.0530 0.130 0.353 1.733
1.90 1.493 1.175 0.354 4.785 0.711 -0.0392 0.147 0.368 1.764
1.85 1.474 1.118 0.346 4.771 0.694 -0.0236 0.164 0.384 1.796
1.80 1.454 1.061 0.338 4.768 0.677 — 0.0064 0.184 0.400 1.832
1.75 1.434 1.003 0.328 4.773 0.658 0.0134 0.207 0.418 1.871
269
Окончание табл. 14.4
V и W 3U poY'2 N \Ео / ПСОР2 П Д \ с / D аг р
1.70 1.413 0.945 0.318 4.793 0.637 0.0354 0.231 0.437 1.915
1.65 1.390 0.889 0.308 4.831 0.616 0.0594 0.257 0.456 1.962
1.60 1.367 0.832 0.294 4.885 0.592 0.0868 0.287 0.478 2.016
1.55 1.343 0.774 0.280 4.962 0.566 0.1176 0.320 0.501 2.077
1.50 1.317 0.718 0.266 5.068 0.539 0.1508 0.354 0.525 2.145
1.45 1.290 0.662 0.250 5.207 0.510 0.1882 0.392 0.551 2.222
1.40 1.262 0.606 0.234 5.389 0.479 0.230 0.432 0.578 2.311
1.35 1.232 0.552 0.216 5.623 0.447 0.274 0.473 0.606 2.475
1.30 1.201 0.498 0.1970 5.931 0.411 0.324 0.517 0.637 2.531
1.25 1.168 0.445 0.1776 6.327 0.375 0.376 0.558 0.669 2.672
1.20 1.134 0.393 0.1564 6 865 0.336 0.436 0.500 0.703 2.840
1.15 1.098 0.342 0.1354 7.582 0.296 0.498 0.635 0.738 3.048
1.10 1.060 0.294 0.1146 8.549 0.255 0.562 0.662 0.773 3.297
1.05 1.021 0.245 0.0924 10.01 0.211 0.632 0.678 0.811 3.635
Примечание. Выражения для этих характеристик приведены в табл. 14.3 (за исключе-
нием глубины проникновения поля в оболочку, которая пояснена в (14.18) .
dFQ/dR при R = 1 с использованием рекуррентных соотношений (37.75) по-
лучаем характеристическое уравнение
Jo(£7) K0(W) ’
(14.15)
где $ связано с U соотношением (14.14). Оно определяет значение V для
каждой НЕ 1т-моды, которая может распространяться при данном V. Наи-
меньшее значение V соответствует основным модам НЕп, а увеличение TJ —
увеличению индекса моды тп. Постоянная распространения моды 0 связана
с U соотношением, приведенном в табл. 14.3. Поскольку уравнение (14.15)
является трансцендентным, то оно может быть решено только численно. Для
основной моды в табл. 14.4 даны значения при изменении V от 1,05 до
4, а на рис. 14.3, а показана зависимость V (К).
Поляризационная поправка к скалярной постоянной распространения, вы-
раженная в интегральной форме через Ц, приведена в табл. 14.1. В числителе
Л подынтегральное выражение содержит производную профиля показателя
преломления df/dR, которая для ступенчатого профиля показателя прелом-
ления в соответствии с соотношением (32.13) равна дельта-функции Дира-
ка 6 (R — 1). Интеграл, стоящий в знаменателе, приведен в табл. 14.6, полу-
ченные выражения для 60 и bU — в табл. 14.3. На рис. 14.3, б показана зависи-
мость отношения bUI&V от величины V для основной моды. Оно имеет мак-
симум ~ 0,24 при V & 2,25. Сравнение скорректированного параметра моды
U + bUс точным решением характеристического уравнения для основной мо-
ды из табл. 12.4 показывает, что максимальная относительная ошибка соот-
270
Рис. 14.3. Характеристики основной моды в волоконном световоде со ступенчатым
профилем: ~ ~
а — параметр моды U, часть мощности в сердцевине т] и глубина проникновения поля в
оболочку б — нормированная поляризационная поправка SU/kU; в — нормирован-
ное распределение интенсивности; — нормированная групповая скорость (левая ось
ординат) и параметр искажения D (правая ось ординат) . Численные значения приведе-
ны в табл. 14.4
ветствует пику кривой на рис. 14.3, б и составляет при Д = 0,005 менее чем
0,005 %. Она возрастает до 0,07 и 0,5 % при Д = 0,045 и Д = 0,125 соответ-
ственно.
Рассмотрим теперь свойства основной моды. Выражения в табл. 14.3, на-
пример для нормировки, получены подстановкой Fo в выражение в табл. 13.2
с использованием интегралов (37.92) и (37.93).
Часть мощности, переносимая модой по сердцевине. Ее определяет т?, вы-
ражение для которой приведено в табл. 14.3, а на рис. 14.3, а показана зави-
симость т?(Е), иллюстрирующая, что только при Ё<< 1 часть мощности в
сердцевине пренебрежимо мала.
Распределение мощности моды по поперечному сечению. Поток мощности
моды вдоль волоконного световода через единицу площади поперечного се-
чения, или интенсивность, определяется усредненным по времени вектором
Пойнтинга S (см. табл. 14.3, где а — амплитуда моды). Чтобы определить
зависимость распределения мощности моды от И, будем считать полную
мощность моды Р неизменной и пронормируем к ней интенсивность S -
271
= S/P = S /|а|2^. Используя характеристическое уравнение из табл. 14.3, по-
лучим искомое выражение
А_1Г У Jq(UR) р
Л(С7) J
1;
На рис. 14.3, в показана зависимость относительной величины S/S„ от ради-
альной координаты при разных V. Под понимается величина S при R = 0 и
V = оо. Для основной моды из табл. 14.5 имеем
= 1/[тгр2Т?(С7оо)]; «2,405, (14.17)
где иж является первым корнем функции Бесселя /0- Таким образом, толь-
ко при К = оо вся мощность моды сосредоточена в сердцевине. С уменьшени-
ем V поток мощности занимает все большую и большую площадь, включаю-
щую и часть оболочки, а максимальное значение5 на оси волоконного свето-
вода падает.
Глубина проникновения поля в оболочку. Как видно из рис. 14.3, в, ин-
тенсивность основной моды в оболочке может быть значительной. На доста-
точно большом расстоянии от оси волоконного световода с ростом R интен-
сивность спадает экспоненциально, как это видно из табл. 14.3 и разложений
(37.88). Количественно определим rpd как расстояние от оси световода до
точки, в которой S спадает в g < 1 раз по сравнению со своим значением на
границе сердцевины с оболочкой. Таким образом,
А?(Мр)=^0(Ю. ‘ (14.18)
Нормированное расстояние от границы сердцевины с оболочкой (rpd/p) — 1
определяет эффективную глубину проникновения поля сердцевины в обо-
лочку и показано на рис. 14.3, а в зависимости от К, при этом для нижней
кривой g = е"1, а для верхней — g = 0,1. Полученные зависимости позволяют,
например, утверждать, что при V = 2,5 около 84 % мощности основной моды
распространяется по сердцевине, а интенсивность, или плотность мощности
моды, спадает в е"1 раз на расстоянии от границы сердцевины с оболочкой
приблизительно р/2.
Распространение и уширение импульса. Если параметр волоконного свето-
вода К меньше 2,405, т. е. меньше значения, соответствующего отсечке вто-
рой моды (рис. 14.4), то световод является одномодовым и в нем могут рас-
пространяться только четная и нечетная основные моды. Обе моды имеют
одинаковую постоянную распространения 3 , поэтому их групповая ско-
рость tTg и время распространения (11.36) не зависят от поляризации волн.
В табл. 14.3 приведено выражение для полученное из соотношения (13.17)
в приближении слабонаправляющего волновода, а на рис. 14.3, д показана
зависимость безразмерной величины («сои^ - с)/сД от V.
Как отмечалось в разд. 11.12, уширение импульса в одномодовых воло-
конных световодах зависит от волноводной дисперсии и дисперсии матери-
ала. В отсутствие дисперсии материала уширение импульса пропорциональ-
но безразмерному параметру искажения, введенному в разд. 11.20. Исполь-
зуя определение D для слабонаправляющих световодов, приведенное в
табл. 13.2, получаем выражение в табл. 14.3. В таблице 14.4 даны численные
272
Рис. 14.4. Численное решение
характеристического уравне-
ния из табл. 14.6 с обозначе-
ниями мод и соответствую-
щими индексами I и тп. Зна-
чения параметра U, лежащие
на штриховой прямой, соот-
ветствуют частоте отсечки
каждой моды Vc
значения S9 а на рис. 14.3, д — график, из которого следует, что нулевая дис-
персия волновода, соответствующая минимальной групповой скорости, до-
стигается при V « 3.
Таблица 14.5. Приближенные выражения для основной моды
Г-0 оо
Параметры мод и ~ Г М23ехр(-А) и ~ 2.405 ехр(-р) W- V
N 10 W \к2/ np'nJso'V11 V1 ЙЧ-1 2 \Яо/ V2 W
dU dr 5.04 / 4 \ 1 т ехР —1 И4 V2 ) V V1
fl И2+ 2 ( 4 \ 1261 — «р( у,) i-d V3
с ( Г 4.492 /- 2\Т| d +т+^“рЫЛ с ( U2 ( 2 \)
Примечание. Эти выражения получены из соотношений, приведенных в табл. 14.3.
Подобные выражения можно получить и для НЕ1т-мод низших порядков» Пара-
метры определены в табл. I.
273
Приближенные выражения при больших и малых значениях V. В табли-
це 14.5 приведены приближенные выражения, описывающие свойства основ-
ной моды при больших и малых значениях параметра И Эти выражения по-
лучены предельным переходом Д 0 из соответствующих выражений в
табл. 12.4 с использованием приближений для функций Бесселя/ (37.82)
при малом значении аргумента. Остальные выражения в табл. 14.5 получены
из табл. 14.3 разложениями в ряд функций /<0 и К\, которые при малых зна-
чениях аргумента определяются выражениями (37.86) и (37^8). В этих пре-
дельных случаях можно считать, что V % V для малых V и W V для боль-
ших V. Точность каждого приближения может быть оценена, исходя из срав-
нения с точными значениями величин в табл. 14.4 при V = 1,05 или V = 4. Для
средних значений V прекрасную аппроксимацию дает линейная зависимость
И'(Е), а именно [5]
W = 1Д428Г - 0,996, 1,5 < 2,5, (14.19)
точность которой в этом интервале не хуже 0,2 %. Следует, однако, иметь в
виду, что производные от этого приближенного выражения не дают необхо-
димой точности как для групповой скорости, так и для параметра искажения.
14.7. Моды высших порядков (/ > 1)
Структура мод высших порядков была описана в разд. 14.3. В табл. 14.6
представлены решения F\ уравнения (14.4) и функции G^, выраженные че-
рез функции Бесселя и модифицированные функции Бесселя порядка I. Пол-
ные выражения для полей мод могут быть получены подстановкой этих вы-
ражений в табл. 14.1. Параметры мод определены в табл. 1.
Характеристические уравнения. К характеристическому уравнению для U
или W приводит условие непрерывности /^и dFyidR на границе сердцевины с
оболочкой, т. е. при R = 1. Оно в совокупности с рекуррентными соотноше-
ниями (37.72) и (37.73) дает уравнение в табл. 14.6. Из табл. 14.1 очевидно,
что решения характеристического уравнения при V > 0 и I > 0 дают значения
каждое из которых определяет свойства всех четырех четных и нечетных
HEl+1>m- и EHt_ l m-мод; последние типы мод в случае / = 1 обозначают
ТМОт и ТЕ0т. Увеличение U соответствует возрастанию индекса моды т.
На рис. 14.4 показано численное решение характеристического уравнения для
ряда низших мод, включаяНЕ^-моды, рассмотренные в предыдущем разделе.
Частота отсечки моды. Кроме основной НЕц-моды, каждая мода имеет
частоту отсечки, т. е., как сказано в разд. 11.18, такое минимальное значе-
ние К при котором мода распространяться не может. Значение U на частоте
отсечки Кс является решением характеристического уравнения в случае
W 0. Используя разложения (37.86), получаем J\_ AU) = 0 для всех мод,
в том числе для мод НЕ^ (т > 1), для которых ^(Е) = 0. Эти уравнения
приводят к значениям частот отсечки на рис. 14.4. Ясно, что для V < 2,405
волоконный световод является одномодовым, а £7 = V = 2,405 — частота от-
сечки моды с индексом I =т = 1. В случае W V -><»из характеристическо-
го уравнения и разложения (37.88) следует, что J\(U) = 0. Видно, что все
эти уравнения являются пределами выражений в табл. 12.4 при Д 0.
Поляризационная поправка. Поправка 8^ к скалярной постоянной рас-
пространения приведена в табл. 14.1 и выражена через интегралы Ц и /2-
274
Таблица 14.6. Свойства мод слабо направляющего волоконного световода со ступенчатым профилем показателя преломления
_ JAUR) _ K.WR)
1 Л(О) ’ 0^ R 1; ' F* ’ 1 R < с 00 G* = +и-Ш-2— J,(U) 0 R 1; 1 - K,(l₽j ’ 1 к < С 00
Характерней ическое уравнение (?+»>2 = f2 J,(0) К.ОП Производная параметра моды dl) _ и { K,3(5F) ) dF“ F?
Постоянная распространения /’ = р(2А)-{1"2Ди4 ; Полезный интеграл Jo 'd 2l)2 Kfl#)
I Поляризационные поправки / >0 ,.е,. ад _ _ 1 аи,. 6и,. wj. 2р F3 К.-ЛИ')! V1 K'-tiW) Нормировка = яр^ЛоХ-2 F»K„,QF)K,4,0F) 2 UJ U2 K,2(5F)
1>2 ...... .... ля ля K,QF) ] 5FU K,QF) др 2 = дРд. Z — дС/2 = дУл = Д = «— 2р F3K,tl0F)[ V1 K1+1(IF) Интенсивность
/= 1 (2А)3'2 ITU2 К, (Й>) Lr, К р Г3 Ki{W) j 1 V2 K2(W) Часть мощности в сердцевине . _ I/2 f>F2 K,(>T) I f>~ F2 [I?2 +KI.1(5F)KI+1(»#')J
1=1 . <504 = 0 j 6U4 = 0 Г рупповая скорость , _ c ( U2f 2K,2(»F) \) Ю‘ ”«l И K,.,OF)K,+I(^)/J
Отсечка U = F, W = 0 л-1«л = о Вдали от отсечки W Ъ и-* 00 J,(l/) = 0
Примечание. Векторные поля мод находятся подстановкой в табл. 14.1. Мощность моды равна \а 127V, где а — амплитуда моды. Пара-
метры определены в табл. I.
Рис. 14.5. Характеристики моды с индексом I = 1 волоконного световода со ступенча-
тым профилем показателя преломления:
а — нормированная векторная поправка б£7/Д(7 для ТМ01-моды; б — нормированное
распределение интенсивности; в — разность векторных поправок для двух пар мод с
индексом I ~ 1; г — качественное представление направления вектора электрического
поля, обозначенного стрелками
Производная df/dR в числителе каждого выражения равна дельта-функции
Дирака 6 (R — 1) (см. разд. 14.6), а интеграл в знаменателе определен в
табл. 14.6. В этой же таблице приведены выражения для и 6Ц. Поскольку
поля ТЕап-мод являются решением скалярного волнового уравнения, то по-
ляризационной поправки к скалярной постоянной распространения этих мод
не требуется.
Для ТМ-моды на рис. 14.5, а показана зависимость dUI&tJ (F), достигаю-
щая максимума 0,22 при К « 5. Сравнение скорректированного параметра
моды U + 8Uс точным U, определяемым характеристическим уравнением в
табл. 12.4, показывает, что относительная ошибка составляет менее 0,005 %
для Д = 0,005 и возрастает до 0,05 и 0,42 % для Д = 0,045 и Д = 0,125 соот-
ветственно.
Интерференция мод. Ненулевая поправка к постоянной распростране-
ния, рассмотренная выше, приводит к интерференции между парами мод с
одинаковой скалярной постоянной распространения. Например, предполо-
жим, что нечетные НЕ2г и ТЕогмоды возбуждаются одинаково, а мощность
всех остальных мод равна нулю. Если ошибочно пренебречь всеми поляриза-
276
ционными эффектами, то 5/3з = $04 = 0 и полное поперечное поле в волокон-
ном световоде можно на основании табл. 14.1 представить в виде
Et = tfet3exp(i|3z) + aet4exp(i/3z) = laF^in ^exp(i/3z)x, (14.20)
где a — амплитуда моды. Таким образом, в любом поперечном сечении
волоконного световода Et линейно поляризовано параллельно оси х (см.
рис. 14.5, г). Если в приближении слабонаправляющего волновода полное
поперечное магнитное поле записать в виде Ht = пс0 (eo/go)1/2z х Et, то рас-
пределение интенсивности (11.20) выражается как
S = |Et I2 = 2lal2«co (-^)1/2Л2 sin (14.21)
Z MO Mo L
Теперь рассмотрим те же поля с учетом поправки 5/33, приняв во внимание,
что поправка для ТЕ-мод равна нулю. Выражение, аналогичное (14.20), мож-
но записать в виде
Et = 2tfFt[xsin(pcos(5|33z/2) + /уcos <^sin(503<z/2)]exp [i(/T + 803l2)z],
(14.22)
Подстановка последнего выражения в (14.21) дает
5= |а|2исо(-^-)1/2К2 [sin2 (^+5/33z/2) + sin2 (^ ~ Sj33z/2) ]. (14.23)
Это выражение может быть просто физически интерпретировано. Оно пред-
ставляет собой суперпозицию двух распределений интенсивности (14.21) на
расстоянии z от входного торца волоконного световода, причем если первое
повернуто по часовой стрелке на угол 803z/2 относительно оси световода, то
второе — на такой же угол против часовой стрелки. Поэтому если, например,
803z = л, то электрическое поле волны линейно поляризовано вдоль оси у
(см. рис. 14.5, г), а ее амплитуда зависит от разности амплитуд полей ТЕОг
и НЕ2гмод. Распределение интенсивности описывается выражением (14.21),
а направление электрического поля повернуто на угол тг/2. И, наконец, на
расстоянии zb = 4тг/5/33, называемом длиной биений, поле (14.22) полно-
стью совпадает с полем (14.20).
Очевидно, что причиной интерференционных эффектов является разница
между поправками к скалярным постоянным распространения, и чем она
больше, тем быстрей изменяются направление поля и картина интенсивности.
Чтобы охарактеризовать количественно эти изменения с помощью выраже-
ний в табл. 14.6, для мод с индексами / = 1, т = 1 были оценены зависимо-
сти нормированных величин р(5/32 — 5/3 ^/Д372 и p(80t — Х/З3)/Д3/2 . Резуль-
таты представлены на рис. 14.5,в. Из полученных кривых следует, что при
V & 3,8 поправки 80! и 802 равны между собой, и поэтому любая линейная
комбинация полей etl и et2 из табл. 14.1 дает моду для этого частного значе-
ния V. Точные зависимости U для ТМ01- и НЕ21-мод, показанные на рис. 12.4,
в волоконном световоде с Д = 0,32, пересекаются при V ~ 3,4.
Мощность, переносимая модой по сердцевине. Величина if, рассчитанная
на основании выражения в табл. 14.6 с использованием выражения для U
из табл. 14.4, графически представлена на рис. 14.6 для первых двенадцати
мод. Эти кривые получаются из кривых на рис. 12.5 предельным переходом
277
Рис. 14.6. Часть мощности
мод, распространяющаяся по
сердцевине волоконного све-
товода со ступенчатым про-
филем показателя преломле-
ния. Значения rj на частоте
отсечки приведены в табл.
14.7
Таблица 14.7. Приближения для мод с индексом I > 1
Вблизи или на частоте отсечки Ис и « V, W 0 Вдали от частоты отсечки W « К, и
и 1{Г+(/-1)Гс} М-Т
к,-ДУНЛОП - 21n(0.89FT) (/=1) 1+р
ГЛ </>2)
dU dV 1 1 и» V2
N ~ 1 2 1 ~ •£ । О 1 оо 1 i 1 -17 -f :т * ! V 1 1 к 1 пР1п«, Y;* V 2 \к>/ Ul
/-1 / й2 i - V3
с (. .2-0 —-Н+Д—f "со 1 f J С fl — 11“ДТГ( "со 1 V j
Примечание. Выражения получены из соотношений, приведенных в табл. 14.6,
где Uсоответствует значению Uпри V = 00.
278
при Д -> 0. Следует подчеркнуть, что не для всех мод при отсечке тТ равна ну-
лю, и эти ненулевые величины т? приведены в табл. 14.7.
Распределение мощности моды. В предыдущем разделе была определена
нормированная интенсивность S для мод с индексом I ~ 0. По аналогии с вы-
ражениями (14.16) соответствующие соотношения для мод с индексом Z > 1
могут быть записаны в виде
V = -1 (X V Л(^)_
и Pv)
s=i ( и 2 _
я pv lyyw^ywy
0<А<1;
(14.24а)
(14.246)
1 < R < сю,
при выводе которых использовались характеристическое уравнение из
табл. 14.6 и рекуррентные соотношения^ (37.32) и (37.37). На рис. 14.5,6
приведена нормированная зависимость S/Sx цдя мод с индексом 1-1, где
- значение, которое достигает S при V = °°, т. е.
= J2(£?ooA1)/[7rp2J22(^oo)]. (14.25)
Из табл. 14.6 следует, что 3,83 (первый нуль функции Бесселя Ji), а
максимума функции Л достигает при U^R^ « 1,8. С ростом V мощность
моды все больше концентрируется в сердцевине.
Приближенные выражения для мод низших порядков. В табл. 14.7 приве-
дены приближенные выражения, описывающие свойства мод вблизи и вдали
от отсечки. Выражение для V вблизи отсечки получено в [7], а для случая
V -> °° выведено с помощью метода дифференциальных уравнений, описан-
ного в разд. 12.3 [8], согласно которому V выражается через ее предельное
значение при V = Остальные выражения являются следствиями соот-
ветствующих соотношений из табл. 14.6, полученных при использовании
асимптотических представлений функций Бесселя (37.86) и (37.88) соот-
ветственно для малых и больших значений аргумента.
Приближенные выражения для мод высших порядков. Поскольку моды
высших порядков могут распространяться только в волоконных световодах
с параметрами V >> 1,и поэтому V >> 1 или/>> 1. Приближенные вы-
ражения для мод высших порядков (см. табл. 14.8) могут быть получены
непосредственной подстановкой асимптотических выражений функции Бес-
селя (37.88) и модифицированной функции Бесселя (37.90) в соответству-
ющие соотношения в табл. 14.6. Характеристическое уравнение может быть
получено также непосредственно из скалярного волнового уравнения с
помощью метода ВКБ или теории локальных плоских волн, описанной в
разд. 36.7.
ВОЛОКОННЫЕ СВЕТОВОДЫ С ОБОЛОЧКОЙ И ГРАДИЕНТНЫМ ПРОФИЛЕМ
ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
В разд. 14.4 и 14.5 были рассмотрены световоды с неограниченным градиент-
ным профилем показателя преломления. Теперь рассмотрим свойства сла-
бонаправляющих световодов.
279
Таблица 14.8. Асимптотические выражения для мод высших порядков
Характеристическое уравнение ( Ш2 | /2 ) 1 /2 1аПх=|^р| . />1
Большое значение U и> 1, и Большое значение 1 1
U2 sin2x — I2 W2 cos2/ 1 + (^2+/2)1/2
сП/ d? /U\U2 —I2 — V2 cos2 х и
\И/ 17 2 sin2 х— J2 И(Л,2 + /2)1'2
N z-—X я lb с. Г? Q 5 W О м х х яр2”сс ( £р у/2 2 \Яо/ Г2 f 11 хи21 (ir2+/2),/2J
п U2 U2—I2 —V2 cos2 х 1 °2
И2 172 sin2 х-/2 ^'2(tf'2 + l2)^,2
с f U2 — ) 1+ДТ7 х "со 1 У V2 sin2/-2>F2cos2x — I2 1 с Ji л1)2 ^11-дйх Ji 2 11
U 2 sin2 х -12 J Т dF2+/2)1/2 JJ
х = (I/2-Z2)1'2—/cos'‘(//1/) —п/4
Примечание. Выражения получены из соотношений, приведенных в табл. 14.6.
Параметры определены в табл. I.
14.8. Пример. Аналитические решения
Существует всего лишь несколько типов профилей показателя преломления световодов
с оболочкой, для которых решение скалярного волнового уравнения можно предста-
вить в аналитической форме. Среди них - профили (м) и (о) на рис. 12.8, аналитичес-
кие выражения которых даны в табл. 12.9. Поля мод и характеристические уравнения
приведены там же для ТЕ-мод и, таким образом, являются решениями скалярного вол-
нового уравнения (14.4) при I = 1. Поэтому естественно обобщить эти решения На про-
извольные значения I. Для профиля (м) с постоянным показателем преломления серд-
280
цевины и градиентной оболочкой решение уравнения (14.4) можно записать следую-
щим образом [9]:
F^ = J^(UR), Q <R <1; F{ = K[v (WR)/K[v (W) t 1 (14.26a)
где v — (V2 - I2)1/2, а характеристическое уравнение имеет вид
UJ’{U) IJ^U) = мфио IK-W (i?), (14.266)
где штрих означает дифференцирование по аргументу, - функция Бесселя первого
рода, K-w - модифицированная функция Бесселя второго рода мнимого порядка. Соот-
ветствующие выражения для профиля (о) имеют вид [10]
F1=Mk M(^2)mK (Г), <1;
(14.27а)
Ft= K\(WR} , 1<Я<~,
где к = U2 /4 И, ц = 1/2 и
2ИГ и(Ю//Мк ц(Ю - 1 = WK'W/KAW), (14.276)
где Мк ц - функция Уиттекера первого рода. Ниже будет показано, как решить скаляр-
ное волновое уравнение с помощью разложения решения в ряд в случае параболическо-
го профиля световода с оболочкой.
14.9. Пример. Степенной профиль показателя преломления волоконного све-
товода с оболочкой
Этот класс профилей показателя преломления определяется следующим образом:
и2 (Я) = «ссЛ1 - 2ЛУ?Ч)> О<я<1; R=r/p, (14.28а)
= «’]= «cod “ 2Д), 1<Я< 0 <<?<“, (14.286)
где q - постоянная величина. На рис. 14.7, а приведены кривые, соответствующие раз-
личным q, включая параболический (q = 2) и ступенчатый (q = °°) законы изменения
показателя преломления. В приближении слабонаправляющего волновода «со »
или Д < < 1. Скалярное волновое уравнение для параболического профиля имеет ана-
литическое решение вида (14.27а), которое может быть обобщено на случай любого ра-
ционального q методом разложения решения в ряд.
Разложение решения в ряд. Во всех практических случаях показатель q является ра-
циональным числом и может быть представлен в виде q — p/s, где pus - целые числа.
Рис. 14.7. Изменение показателя преломления в волоконных световодах с усеченными
степенными профилями (а) и в предположении равного объема профилей (б)
281
Проводя замену переменных R -- Xs в уравнении (14.4), для поля в сердцевине имеем
[—- Ч- -1 + ~ (&x2s - r’x2s+ р - е2) 17’, = 0. (14.29)
dx2 -v ах V t
Решение, ограниченное при R = х — 0, можно представить в виде ряда [12]
г У v D^+n/s)
Л,- L ах = X a R 7, (14.30)
Ь п =- о п п = о п
где ап - константы, а() - произвольная величина. Подставляя (14.30) в уравнение
(14.29) и приравнивая члены с одинаковыми степенями х, получим следующие рекур-
рентные соотношения:
= ------------а т - 1, 2, .
'2ms 4m(m+Z) 2ms-2s
при n < 2s + p и
s2 ~
<2 —----------(V2a — U2a )
n n(n + 2ls) 1 n —2s —p n —2s7
(14.31a)
(14.316)
при n > 2s + p. Все остальные константы an равны нулю. Решение уравнения (14.4) для
оболочки с постоянным показателем преломления пропорционально модифицирован-
ной функции Бесселя второго рода/С^(И7?). Если решение нормировать таким образом,
что F^ = 1 при R — 1, то
L
S a„(Un/S)
п = О п
п — 0 п
0<Я <1;
(14.32)
K^WR)/K^W), 1 < °°,
a U, W определены в табл. I.
Характеристическое уравнение. Непрерывность dF^jdR в точке R = 1 и рекуррент-
ное соотношение (37.73) приводят к характеристическому уравнению
^t+1(IV)/K’V(lP) = - wZo«cn/(snSo«n); U2+W2 = V2. (14.33)
На рис. 14.8, а представлена зависимость решения U(И) основной моды (Z = 0, т = 1)
для различных значений q. Отметим, что лишь в случае ступенчатого профиля показате-
ля преломления параметр моды U стремится с увеличением V к^воему конечному зна-
чению, для всех остальных профилей показателя преломления U неограниченно возра-
стает при V -> °°. Сравнение величины U (14.9) для неограниченного степенного профи-
ля показателя преломления при V — 8 с учетом функции G(q) на рис. 14.2, в показы-
вает, что для данных q ошибка составляет менее 3,5 %. Это означает, что большая часть
мощности основной моды сосредоточена в сердцевине, при этом профиль показателя
преломления оболочки одинаков как для профиля с оболочкой, так и для неограни-
ченного степенного профиля, а область вне радиуса R = 1 оказывает незначительное
влияние.
Частота отсечки. Для мод высших порядков VQ является решением уравнения (14.33)
при U=V^VcnW=Q. Используя асимптотические выражения для функций
(37.86) при W -> о, находим, что Vc удовлетворяет условию
L (n + 2ls)a = 0. (14.34)
п— о
282
Рис. 14.8. Кривые параметра U основной моды в волоконных световодах с усеченными
степенными профилями показателя преломления (д), верхнего предела ^определяю-
щего диапазон одномодового режима (сплошная кривая), и его значений согласно вы-
ражению (14.45) (штриховая кривая) и параметра Кс, соответствующего кривой рав-
ного объема профилей на рис. 14.7, б
На рис. 14.8, б сплошной линией показана зависимость Vc(q) для мод с минимальной
частотой отсечки, Т. е. для ТЕ01-, ТМ01- и НЕ21-мод.
Распределение интенсивности. Выражение для интенсивности, или плотности, мощно-
сти S дано в табл. 13.2. Чтобы сравнивать распределение интенсивностей основных мод
в волоконных световодах с различными профилями показателя преломления, удобно
нормировать S таким образом, чтобы полная мощность моды равнялась единице, т. е.
Р = 1. Используя Р в табл. 13.2, получим выражение для нормированной интенсивности
S = F2l(2irp2 ^F2RdR). (14.35)
О
Подставляя выражение для Fo (14.32) в подынтегральное выражение в знаменателе
Рис. 14.9. Нормированные распределения интенсивности основной моды волоконных
световодов со степенными профилями при V = 2,405 и Ptot = 1 (д) и в случае равных
объемов профилей, соответствующих рис. 14.7, б (К = Vc — 2,405) (б)
6)
283
(14.35) и учитывая (37.93), получаем
^RdR = |
О 2
^(И/)
-1]+ 2
т=о
оо 7 /7 О. оо
2 2 )2
« = 0 2s + m + n и = 0 11
(14.36)
На рис. 14.9, а представлена нормированная зависимость яр2£ от радиальной координа-
ты R для различных параметров q при V = 2,405. Для ступенчатого профиля показате-
ля преломления (q = °°) S аналитически определяется (14.16).
Параметр искажения. В отсутствие дисперсии материала уширение импульса в
круглых одномодовых волоконных световодах пропорционально параметру искажения
D (13.18). Чтобы рассчитать его для имеющих различные степенные профили показате-
ля преломления волоконных световодов с оболочкой, представим выражение (13.18)
в следующем виде:
dv V v3 ’ V dV '
(14.37)
где величина к определена в табл. 13.2 через интегралы по поперечному сечению от Fo
(14.32). Дифференцирование последнего соотношения по V дает
<f-v-)F0^-RdR/'iF}RdR, (14.38)
ау о °у о
а дифференцирование выражений (14.32) и (14.31) по V приводит к [13]
°° п/с • 00 ^аг\
7F-^»(S <143”
где Ьо = 0, а остальные Ьп удовлетворяют рекуррентным соотношениям
Z? =-----Ц(£ЛЬ „ + 2Uxa ), (14.40а)
2ms 4т2 v 2ms —2s 2ms-2s
если n < 2s + p, и
. +2ГЯ „ -U*b „ -2ГКЯ ), (14.406)
n n2 1 n — 2s-p n—2s—p n —2s n —2s
если n > 2s + p. Величина an определена выражением (14.31). На основании проведен-
Рис. 14.10. Параметр искажения основных мод волоконных световодов со степенными
профилями показателя преломления (а) и значения нормированной частоты, на которой
волноводная дисперсия равна нулю (прямая q — °° соответствует ступенчатому профи-
лю) (б)
284
ного анализа получены кривые на рис. 14.10, а [13, 14]. На рис. 14.10, б показана зави-
симость ^(^), где под понимается значение параметра световода V, при котором
В = 0. Поскольку при D = 0 волноводная дисперсия отсутствует, то на основании
рис. 14.10, б можно сделать вывод, что это условие выполняется только для профилей
показателя преломления, параметр которых лежит в диапазоне 2 < q < Следует, од-
нако, подчеркнуть, что в одномодовых волоконных световодах волноводная дисперсия
никогда не равна нулю (см. рис. 14.8, б).
14.10. Профили показателя преломления равного объема
Выражение (14.1) описывает в общем виде профиль показателя преломле-
ния круглого волоконного световода. Если рассматривать волоконные све-
товоды с постоянным показателем преломления оболочки «с1, то с учетом
определения Д в табл. I, выражение (14.1) можно представить в виде
«2(А) =лг2с1[1 + Т^2Д-(1-Л]; 0СДС1, (14.41а)
= п2{, 1<А<оо. (14.416)
функция (1 —/) определяет форму профиля S (г), (4.13) и пропорциональ-
на превышению, или ’’высоте” п2 (А), над показателем преломления оболоч-
ки пср Рассмотрим теперь все профили показателя преломления волоконных
световодов с оболочкой, имеющие одинаковое значение Д, а поэтому и оди-
наковое значение псо, и определим эффективный объем профиля £2 как
интеграл по поперечному сечению от функции (1 —/), т. е.
S2=J (1 —f)dA = 2тгр27(1 — f)RdR,
О
(14.42)
где р — радиус сердцевины или характерный размер профиля. Профили рав-
ного объема имеют одинаковые £2, но в общем случае разные р.
Целью данного подхода является нормировка профилей показателя пре-
ломления с одинаковыми «с1 и Д с тем, чтобы таким образом разделить эф-
фекты, зависящие от формы профиля, от эффектов, которые практически не
зависят от закона изменения показателя преломления. В качестве иллюстра-
ции этой идеи рассмотрим некоторые профили показателя преломления, об-
суждавшиеся в предыдущем разделе.
Степенные профили показателя преломления волоконного световода с
оболочкой. В качестве эталонного профиля показателя преломления выбе-
рем ступенчатый (у = °°), который и определит величину £2 в (14.42). Далее
определим ре как рарцус сердцевины степенного профиля, имеющего тот же
объем £2. Если в выражении (14.28) R заменить на RQ = r/pQ и подставить в
(14.42), то получим
Ре = [(<7 + 2)/<?]1/2р. (14.43)
На рисунке 14.7, б показаны профили показателя преломления равного
объема.
Частота отсечки. На рис. 14.8, б дана зависимость частоты отсечки Vc от
параметра q. В случае профилей показателя преломления равного объема для
285
каждой формы профиля она определяется величиной К , которая теперь про-
порциональна ре. Если определить Vc, как частоту отсечки, выраженную че-
рез радиус ре, то из соотношения (14.43) имеем
Кс = (р/ре) Ис = [q/ (q + 2) ]1/2 кс. (14.44)
На рис. 14.8, б частота отсечки Vc практически не зависит от параметра q
(разница между значениями Кс при q = 1 и q = 00 составляет всего 5,1 %).
Другими словами, V фактически не зависит от формы профиля при измене-
нии q от 1 до 00 и с достаточной точностью может быть взят равной 2,405, что
соответствует ступенчатому профилю показателя преломления. Поэтому,
преобразуя выражение (14.44), имеем
Ис =» 2,405 [ (<7 + 2)/q] 1/2, (14.45)
которому соответствует штриховая кривая на рис. 14.8, б.
Распределение интенсивности. Распределение интенсивности основной мо-
ды в нормированной форме показано на рис. 14.9, а в предположении, что
для каждого профиля показателя преломления V = 2,405. Если сравнивать
профили равного объема и распределение интенсивности для каждого профи-
ля рассматривать на соответствующей частоте отсечки, определяемой соотно-
шением (14.45), то нормированная интенсивность irp2S при q > 1 практичес-
ки не зависит от формы профиля показателя преломления (см. рис. 14.9,6) .
Параметр искажения. В предыдущем разделе было показано, что параметр
искажения В может быть равен нулю при значениях К, достижимых на прак-
тике только в том случае, если q > 2. Следовательно, волноводная диспер-
сия в основном зависит от формы профиля показателя преломления.
Произвольная форма профиля показателя преломления. Выше было пока-
зано, что для степенных профилей показателя преломления равного объема
распределение интенсивности основной моды и частота отсечки Гс характе-
ризуются слабой чувствительностью к форме профиля. Проведенное рассмот-
рение можно обобщить на одномодовые волоконные световоды с произволь-
ной формой профиля показателя преломления, при этом распределение мощ-
ности описывается выражением (14.16) для ступенчатого профиля показате-
ля преломления, в котором
V = К(П/я)1/2 = Г[гГ(1 -f)RdR]V2,
О
(14.46)
а объемы профилей (14.42) предполагаются равными [15]. Аналогичным
образом можно обобщить и выражения для частоты отсечки (14.45)
Кс = 2,405 (П/тг)1/2 = 2,405 [2 Г (1 -f)RdR]1/2.
о
(14.47)
Выражения (14.46) и (14.47) справедливы лишь в случае одинаковых зна-
чений ис1 и Д у эталонного ступенчатого и рассматриваемого волоконных
световодов.
286
14.11. Свойства основной моды при малых значениях V
В одномодовых слабонаправляющих волоконных световодах с произволь-
ным профилем показателя преломления часть мощности, переносимая основ-
ной модой по сердцевине, становится ничтожной при V 0. Для волокон-
ного световода со ступенчатым профилем это видно из кривой для т? на
рис. 14.3, а. Одновременно с этим амплитуда поля в сердцевине становится
почти постоянной, о чем можно судить по кривой распределения интенсив-
ности на рис. 14.3, б\ и, следовательно, малочувствительной к форме про-
филя. Это позволяет утверждать, что поле в первую очередь зависит от объе-
ма профиля £2, определяемого соотношением (14.42), что, в свою очередь,
дает возможность связать поля в световоде с произвольным профилем пока-
зателя преломления и параметром V с известными полями в световоде со
ступенчатым профилем и параметром ^соотношением (14.46). Таким об-
разом, формально можно заменить V на‘К в выражениях в табл. 14.5, описы-
вающих свойства основной моды при малых значениях нормированной часто-
ты Г. Этот же вывод может быть получен формальным путем из скалярного
волнового уравнения, как будет показано ниже.
Вывод из скалярного волнового уравнения. Очевидно, что при-фиксиро-
ванной величине Д с уменьшением параметра V световода с произвольным
профилем показателя преломления, длина волны X возрастает. Когда V на-
столько мало, что X>> р, где р — радиус сердцевины, то электрическое поле
в сердцевине можно описать в рамках квазистатической аппроксимации вы-
ражением (11.52). Поскольку волоконный световод является слабонаправ-
ляющим, то членом Vt In и2 можно пренебречь и электрическое поле будет
описываться уравнением Лапласа для потенциала
у2ф=0; et =^Ф, (14.48)
где операторы V-2 и Vt определены в табл. 30.1. Решения этого уравнения
A cos и A sin конечные при R = 0, соответствуют четной и нечетной НЕП-
модам. В соответствии с рис. 14.1 для четной моды Ф = х и, следовательно,
et = х или Fq = 1, где х - единичный вектор, параллельный осих. Таким об-
разом, в сердцевине амплитуда поля и его направление постоянны, о чем го-
ворилось выше.
Размер оболочки всегда больше длины волны за исключением случая X =
= 00. Поскольку нормированная частота V мала, но конечна, для описания по-
ля в оболочке можно воспользоваться скалярным волновым уравнением.
Используя интегральную форму этого уравнения для V2 9 приведенную в
табл. 13.2, и полагая для оболочки / = 0, V2 = V2 - W 2,/ = 1, а для сердцеви-
ны Fo « 1 и dF0 /dR & 0, получаем
1 о© dF п
И2 J (1 -P)RdR - J RdR
W2 ---------------------1—E2----------. (14.49)
J- + jFlRdR
1 1
Поскольку первый интеграл в числителе пропорционален объему профиля £2
(14.42), а в оболочке Fo -Ко (WR)/Kq (W), то, используя интеграл (37.93),
получаем
W2/V2 = (14.50)
287
Подстановка сюда приближенного выражения для модифицированных функ-
ций Бесселя (37.86) и учет соотношения (14.16) дают простое выражение
W ъ 1,123ехр(—2тг/Ш/2) = 1,123ехр(—2/К2).
(14.51)
Для ступенчатого профиля показателя преломления f = 0, а £2 = я, и выраже-
ние (14.51) совпадает с асимптотическим выражением в табл. 14.5.
ГЛАВА 15. ГАУССОВО ПРИБЛИЖЕНИЕ ДЛЯ КРУГЛЫХ
ВОЛОКОННЫХ СВЕТОВОДОВ
Приближение слабонаправляющего волновода, рассмотренное в гл. 13, зна-
чительно упрощает определение полей мод оптических волноводов, посколь-
ку в его основе лежит решение скалярного, а не векторного волнового урав-
нения или уравнений Максвелла. В случае круглых волоконных световодов
с произвольной формой профиля показателя преломления скалярное волно-
вое уравнение может быть решено, как правило, только численными метода-
ми. В гл. 14 было рассмотрено несколько форм профиля показателя прелом-
ления, включая и представляющие практический интерес ступенчатый и сте-
пенной, которые допускают точное аналитическое решение через специальные
функции и ряды. Поэтому для количественной оценки физических свойств
мод необходимо либо использовать таблицы, либо проводить численные
оценки.
Исключением служит неограниченный параболический профиль показа-
теля преломления, рассмотренный в разд. 14.4, поле основной моды которо-
го (см. табл. 14.2) подчиняется гауссовой зависимости ехр(—йК2А2), а вы-
ражения для остальных характеристик моды имеют столь простой вид, что не
составляет труда их предсказать при изменении параметров волоконного
световода. Если к этому добавить, что распределение интенсивности основ-
ной моды, а следовательно и распределение поля, для световодов со ступен-
чатым и степенным профилями показателя преломления и оболочкой явля-
ется почти гауссовой функцией (см. рис. 14.9,я), то становится очевидной
целесообразность попытки описания ее в световоде с произвольным профи-
лем показателя преломления некоторой гауссовой функцией [1 — 3], что в
совокупности с простым вариационным методом является основой рассмат-
риваемого в этой главе гауссова приближения. Таким образом, основная
цель данной главы заключается в нахождении гауссовых полей в волоконных
световодах с заданным профилем показателя преломления. Постоянная рас-
пространения и другие характеристики мод одномодового волоконного све-
товода с достаточной точностью могут быть также выражены через простые
аналитические функции [5].
В разд. 14.10 было введено понятие объема профиля показателя прелом-
ления и показано, что в случае степенных профилей равного объема светово-
дов с оболочкой ряд таких характеристик, как диапазон одномодового ре-
жима работы и распределение интенсивности основной моды, малочувстви-
288
тельны к форме профиля, в то время как другие характеристики и в первую
очередь волноводная дисперсия сильно зависят от нее. Нечувствительность
распределения интенсивности моды по поперечному сечению от формы про-
филя получит прямое подтверждение в рамках гауссова приближения.
В этой главе гауссово приближение также обобщается на ряд мод низших
порядков, кратко описывается приближение эквивалентного ступенчатого
световода [4] и дается его сравнение с гауссовым приближением.
ОСНОВНЫЕ МОДЫ
Сначала вкратце напомним суть приближения слабонаправляющего волново-
да для основных мод круглого волоконного световода. В разд. 13.2 и 13.4
было показано, что две основные моды являются фактически ТЕМ-волнами,
поперечные поля которых поляризованы в ортогональных направлениях. По-
перечные компоненты полей НЕц-мод, поляризованные вдоль осей х и у на
рис. 14.1, определяются соотношениями (13.9). Пространственное распреде-
ление поля Fq (г) основной моды является решением скалярного волнового
уравнения, представленного в табл. 13.1 для случая / = 0, т. е.
[^Г +Т 1R +к2п"^ -P2]Fo=°, (15.1)
где п (г) — профиль показателя преломления, к = 2тг/Х и X — длина волны в ва-
кууме. Поскольку в данной главе будут рассматриваться только скалярные
величины, то знак ~, обозначающий ранее скалярную величину, опускается.
15.1. Гауссово приближение
Основная цель данного раздела состоит в нахождении достаточно точных
приближенных выражений радиальной зависимости поля Fo (г) и постоянной
распространения 0, входящих в уравнение (15.1). Выше было показано, что
функция Fq максимальна в точке г = 0 и монотонно спадает до нуля с ростом
г. Кроме того, в случае профилей показателя преломления, показанных на
рис. 14.9, a, Fq является почти функцией Гаусса. Следовательно, можно пред-
положить, что Fq можно аппроксимировать выражением
МО =ехр[-| (т;)2],
(15.2)
где г0 ~ размер пятна моды. Для определения г0 используем простой вариа-
ционный метод [4, 5]. Если зависимость (15.2) является хорошим прибли-
жением решения уравнения (15.1), то она может быть использована в каче-
стве пробной функции в стационарном выражении для 0, при этом значение
г о соответствует наибольшему значению 0 [6]. Напомним также, что по
определению основная мода имеет наибольшую постоянную распространения
0 или наименьший параметр моды U.
Для получения стационарного выражения для 0 умножим уравнение (15.1)
на tFq и, используя тождество
Д’ d2p0 dF0 d , п dF0 х ,dF0 4 2
<15J>
10 Зак 37
289
проинтегрируем уравнение от г = 0 до г ~ «>, учитывая, что Fo и dFQ/dr - экс-
поненциально спадающие функции, равные нулю при г = °°. В результате по-
лучим [5]
1[к2п2 (r)Fo - (dFQldr)2}rdr
02 =: 2--------------------------
IrF^dr
о
(15.4)
где к = 2тг/Х, а X — длина волны в вакууме. Полученное выражение в точности
совпадает с выражением в табл. 13.2 при 7 = 0. Таким образом, использование
стационарного значения для 02 приводит к тому, что ошибка первого поряд-
ка между гауссовым приближением для Fo и точным решением уравнения
(15.1) дает ошибку второго порядка в выражении для 02 . Другими словами,
приближенное выражение для (З2, получаемое подстановкой поля (15.2) в
соотношение (15.4), является более точным, чем исходное приближенное
выражение для Fo.
Для определения размера пятна подставим (15.2) в (15.4) и решим урав-
нение
д(32/дг0 = 0.
(15.5)
Постоянная распространения моды находится подстановкой решения урав-
нения (15.5) обратно в соотношение (15.4). Зная г0 и Д, можно полностью
описать поля мод одномодового волоконного световода, выражения для ко-
торых приведены в табл. 15.1.
Нахождение значений г0 и (3 облегчается, если использовать параметры Vи
U, поскольку это — безразмерные величины, a U, кроме того, не зависит и от
параметра высоты профиля Д. Подставляя зависимости (15.2) и выражение
для формы профиля показателя преломления из табл. 15.1 в соотношение
(15.4), интегрируя выражение в знаменателе непосредственно, а в числите-
ле _ по частям, получаем выражение для V2. Если под Ro понимать норми-
рованный размер пятна моды rQ/p, то уравнение (15.5) эквивалентно урав-
нению dU2/dR0 = 0, а подстановка полученного выражения для U2 приводит
к соотношению в табл. 15.1.
Приближенные выражения для характеристик основной моды. Подстав-
ляя гауссово приближение поля (15.2) в выражения в табл. 13.2, получим
приведенные в табл. 15.2 выражения для характеристик основной моды в
волоконном световоде с произвольным профилем показателя преломления.
Поскольку многие профили показателя преломления не имеют четкой гра-
ницы между сердцевиной и оболочкой, то имеет смысл обобщить функцию
?7, представляющую собой часть мощности, переносимую модой по сердцеви-
не, и определить т?(А) как часть мощности, переносимую модой внутри сече-
ния с нормированным радиусом R = г/р. Выражения для и D получаются
непосредственно из соотношений (13.17) и (13.18). Если для данного профи
ля показателя преломления уравнение для размера пятна моды может быт
290
Таблица 15.1. Гауссово приближение для полей основных мод слабонаправля-
ющих круглых волоконных световодов
Четная НЕц-мода (поляризованная вдоль оси х) Нечетная НЕц-мода (поляризованная вдоль оси у)
( 1 г2] Ех = ехр < - - -у f exp (iflz) [ 1 г2 ) Еу = ехр< --^->exp(/0z) 1 2 го )
/f \,/2 w, = (f) "“£x \A*O/ ЛоУ'2 \А*о/
n2(R) = П^{1 - 2A/(R)}; V = kpnjWir-. R=-p, Ro = ^
Вариационное уравнение для постоянной распространения fl
V2 1 U2 = 2K-^2=Rl+y ( Jo 1 ) )
Уравнение для размера пятна моды г 0
1 _ f"d/WR2 dS Г Я21 eXP)-^2fdR: r0 = PR0 1 Ко J
Примечание. Параметры определены в табл. I, а оси координат показаны на
рис. 14.1.
решено аналитически, то любая характеристика моды в табл. 15.2 может
быть выражена в явном виде через параметры волоконного световода.
Диапазон одномодового режима. Единственным параметром, который не-
возможно определить в рамках гауссова приближения, является максималь-
ное значение нормированной частоты Ис в одномодовом режиме волоконно-
го световода. В разд. 14.10 было показано, что она в первую очередь зависит
от объема профиля показателя преломления £2 (14.42) и малочувствительна
к его форме. Для профилей волоконных световодов с оболочкой при равных
максимальных значениях показателей преломления в сердцевине nCQ и обо-
лочки ис1 значение Vc оценивается по (14.47) исходя из предположения, что
профили показателя преломления одинакового объема имеют одну и ту же ча-
стоту отсечки, выраженную через объем ступенчатого профиля £2 из табл.15.2.
Гауссово приближение особенно полезно в тех случаях, когда рассматри-
ваются профили показателя преломления, для которых не существует анали-
тического решения скалярного волнового уравнения. В качестве первого
10* 291
примера рассмотрим один из таких профилей и продемонстрируем точность
гауссова приближения сравнением с численными решениями.
15.2. Пример. Гауссов профиль показателя преломления
На рис. 15.1, с показан гауссов профиль показателя преломления
п2 (R) = п2со {1 - 2Д [1-ехр(-Я2) ]}; О <R < ~, (15.6)
Таблица 15.2. Выражения для основной моды в гауссовом приближении
n2(K) = <{l-2AftR)}; R=r--, Ro = ^
Профиль Произвольный Гауссов
/(«) - 1 -exp(-R2)
«0 - 1
(И-1),/2
и - (2И-1)1/2
6U 6V 1
(2K-1),/2
S НИ—) nwexp{-(K2/*o)} 2 \Мо/ tCzO "соечЧ-^-ПК2} z \мо/
N я/>Ч>Л<>У/г„2 ~ 1 / Ло 2 \До/ яр^/соУ'2 1 2 W И-1
nW 1-ехр{-(К2/«о)} 1 - exp {- (V- 1)Л2}
v. Ct зк I К) ою| с ( д] n~|1+К2]
D 1 d f 1 ] VdV\VRl] 1 р
к f f® }l/2 2.405|2| (l-/)RdR| 2.405
292
1 (и2 )1/2 V = крИсо(2Д)*'2; 0 = -|2д "U2J
Профиль Ступенчатый Сглаженный
fW 0; 0 R < 1 1; 1 < R < оо 1 tme dt Г(м + 1) J (m+jm’
«0 1 1
{21пГ},/2 {(m+l)[K2/("+2) —1]}*/2
и {1+2In Г}*'2 {(m + 2)K2/<", + 2’ —(m+1)}1/2
dU dV 1 pr-m/(m + 2)
Г{1+21пГ}1/2 {(m + 2)K2/<" + 2) - (m+ I)}1'2
S ) n«,exp(- 2R2ln Г) 2 \До/ kl!M/2n x 2 Vpo/ exp [ —(m+1){И2/""+2) — 1}R2]
N «РЧо/вру* 1 4 In V яр2»со (eo Y/2 1 2(т+1)\Яо/ Г2'*-+2,-1
ч(«) 1—exp( —2R2 In И 1 - exp (-(m+ 1){Г2/<" + 2»- 1}R2)
vt C f A « } —J1+—(1-21пП^ n 1 V i “co I r J —|1+4[т+1-тГ2'<" + 2’]| "co I J
D 2 m+1[. ( m У/2/(,+ 2)1 P 1 U + 2/ J
К 2.405 2.405
Примечание. Характеристики даны в табл. 13.2. Приближенная частота отсечки вы-
числяется по формуле (14.47) . Параметры определены в табл. I.
где R = г/р, a f (R) — 1 - exp (-R2). Таким образом, n (R) с ростом R от 0 до °° умень-
шается плавно от исо до «ср Поскольку четкой границы между сердцевиной и оболоч-
кой нет, то форму профиля определяет характерный размер р. При р-> О профиль прини-
мает форму острия в области R = 0 и становится почти плоским при р-* «>. Такая фор-
ма профиля показателя преломления представляет практический интерес, поскольку яв-
ляется хорошим приближением реального случая, когда в процессе изготовления воло-
293
Рис. 15.1. Гауссов профиль показателя преломления (15.6) (а), параметр моды (/из
табл. 15.2 как функция нормированной частоты (6), распределение нормированной
интенсивности irp2S (15.8) при V = Vc ± 1, где Ис = 2,592 - частота отсечки второй мо-
ды (в), параметр искажения D из табл. 15.2 (г). На рйс. (б) - (г) штриховые кривые
получены при решении скалярного волнового уравнения [7]
конных световодов происходит взаимная диффузия материала сердцевины и оболочки.
Кроме того, в случае гауссова профиля выражения для характеристик основной моды
принимают особенно простой вид.
Подставляя выражение (15.6) в уравнение для размера пятна в табл. 15.1, получа-
ем [5]
г0 = Р/(И - 1) 1/2. (15.7)
Очевидно, что это выражение имеет физический смысл только при V > 1, однако это не
уменьшает его практической ценности, поскольку, во-первых, при V < 1 вблизи от оси
световода распространяется лишь малая доля мощности основной моды, а во-вторых, в
этом случае могут быть использованы методы, описанные в разд. 14.11.
Подставляя соотношение (15.7) в табл. 15.1, получим выражения для постоянной
распространения и параметра моды в табл. 15.2, которые позволяют получить все ос-
тальные характеристики моды.
Диапазон одномодового режима. Поскольку гауссов (15.6) и ступенчатый (14.12)
профили показателя преломления имеют одинаковый объем И, то частота отсечки для
обеих форм профиля должна быть одинаковой, т. е. Ис = 2,405. Численный метод [7]
дает значение Кс = 2,592, так что ошибка приближения составляет 7,2 %.
Постоянная распространения. На рис. 15.1, б представлена зависимость постоянной
распространения, выраженной через параметр моды U, от нормированной частоты, где
сплошная кривая построена на основании выражения из табл. 15.2, а штриховая - на
основании точного решения. При V — 1 ошибка составляет 1,4% и увеличивается до
294
1,8 % при V — 1,25, а затем монотонно уменьшается с ростом V. При V — VQ — 2,592
ошибка составляет 0,6 % [7].
Распределение интенсивностей. Определим величину S как распределение интенсив-
ности основной моды единичной мощности, т. е. hPTV - 1, где я - амплитуда поля мо-
ды, a N - коэффициент нормировки. Нормируя S на единицу поперечного сечения ради-
усом р, из табл. 15.2 имеем
<rp2S= (V - 1)ехр[-Л2 (V- 1)]. (15.8)
На рис. 15.1, в сплошными кривыми показаны нормированные распределения интенсив-
ности при И = VQ + 1 и V = Ис - 1, а штриховыми - точные расчетные зависимости. От-
метим, что с уменьшением V мощность концентрируется на большей площади попереч-
ного сечения. Этот эффект легко может быть объяснен с помощью зависимости т?(Я)
из табл. 15-2. При неизменной величине т? основной моды значение радиуса быстро рас-
тет при V -► 1, так как г р/ (V - 1)1/2.
Профиль, обеспечивающий максимальную концентрацию света. Найдем гауссов про-
филь, который обеспечивает максимальную концентрацию мощности основной моды
вблизи оси световода. Другими словами, необходимо определить такое -значение р, при
котором размер пятна rQ становится минимальным. Учитывая, что нормированная часто-
та световода V пропорциональна р, из соотношения (15.7) следует, что требуемое усло-
вие выполняется при г0 = р и V = 2, а тогда на основании табл. I р = X/ [я (и20 - и2р1/2 ].
Это совпадает с результатом разд. 10.2, полученным из физических соображений. Доба-
вим, что при таком значении г0 распределение интенсивности в точности повторяет фор-
му профиля показателя преломления.
Групповая скорость и уширение импульса. Если 0 < V < 2,592, то волоконный све-
товод с гауссовым профилем показателя преломления является одномодовым, время
распространения импульса обратно пропорционально групповой скорости (11.36), а
уширение импульса, обусловленное волноводной дисперсией, пропорционально ГДР =
- Д/И2, где D ~ скалярный параметр искажения, выражение для которого приведено в
табл. 15.2, а (на рис. 15.1, г сплошной кривой показана зависимость/) (К)). Сравнение с
численным расчетом (штриховая кривая на рис. 15.1, г) показывает, что максимальная
относительная ошибка составляет 9,6 % при V — 2,9 и 9,4 % при V — Кс. Отметим, что
нуля волноводной дисперсии не существует.
15.3. Пример. Ступенчатый профиль показателя преломления
В предыдущей главе свойства основной моды слабонаправляющих световодов со сту-
пенчатым профилем показателя преломления были рассмотрены на основании аналити-
ческого решения скалярного волнового уравнения, однако для получения количествен-
ных оценок необходимо было численно решить трансцендентное характеристическое
уравнение. В рамках же гауссова приближения выражение для постоянной распростра-
нения можно получить в явном виде, а основные характеристики моды с достаточной
точностью описываются простыми соотношениями [4, 5].
Выражения, приведенные в табл. 15.2, получены на основании соотношения табл. 15.1
и с учетом того, что для ступенчатого профиля df/dR есть 6-функция Дирака 6 (R - 1).
Точность приближения можно определить сравнением с соответствующими точными зна-
чениями в табл. 14.4. Дифференцируя выражение для размера пятна, находим, что мак-
симальная концентрация излучения вблизи оси световода достигается при V = е1/2 =
= 1, 65 и rQ = р или р « 0,83х/ [я (и*о - и^)1/2 ], что на 17 % меньше соответствующего
значения для гауссова профиля. Таким образом, плотность мощности в ступенчатом во-
локонном световоде выше.
295
15.4. Пример. Сглаженные профили показателя преломления
В качестве последнего примера рассмотрим профили (рис. 15.2, д), один из которых -
ступенчатый, а другой - гауссов. Форма такого типа профилей описывается следующим
выражением [5]:
n'(R) = и20[1-2Д/(Я)];
(15.9)
/(Я) = 1--- 1 j гтехр(_г)Л,
Г (т + 1) + 1)/?2
где Г - гамма-функция, т > -1 - постоянная величина, R — г/р. Если т - натуральное
число или нуль, то интегрирование по частям дает
f (R) = 1 - exp[-(m + I)/?2] Е /?2п (15.10а)
п “ О п-
= ехр [--(т + 1)Я2] S ,0я+ 1) д2п (15.106)
п = т+1 п'-
Гауссову профилю соответствуют т = 0, а ступенчатому - т = В случае R < < 1
разложение экспоненциальной функции в ряд в выражении (15.10) дает/(Я) « (т +
+ l)m7?2m + 2/w!, а (15.9) становится аналогичным (14.28а) для степенных профилей.
Свойства мод. Подставив (15.9) в соотношения табл. 15.1, получим выражения, опи-
сывающие основные свойства мод (см. табл. 15.2). Пределы т ->0и w соответ-
ствуют гауссову и ступенчатому профилям. При т -► 1 можно положить И2/(т + 2) —
— ехр [2 In VI (т + 2) ] и описать основные свойства мод выражениями для малых воз-
мущений световода со ступенчатым профилем, например,
р’/Н «= 2 In И + - In И (In V- 1); IP » 1 + 2 In V + - (In Г)2. (15.11)
Этот анализ свойств основной моды дает очень маленькую ошибку при определении
волноводного параметра U и частоты отсечки Vc, о чем свидетельствует табл. 15.3 [7].
На рис. 15.2, б” сплошными кривыми показаны зависимости параметра искажения от
нормированной частоты для т = 2 и т = <*>, построенные на основании выражения из
Рис. 15.2. Изменение показателя преломления в сглаженных профилях, форма кото-
рых описывается выражением (15.9) (т = 0) для гауссова профиля, т = «> - для сту-
пенчатого (а) и гауссово приближение для параметра D из табл. 15.2 (сплошная кривая)
и его значения, полученные численным решением скалярного волнового уравнения [7]
(штриховая кривая)
296
табл. 15.2. Штриховые кривые соответствуют точным зависимостям [7]. Если - нор-
мированная частота, на которой волноводная дисперсия равна нулю, т. е. D = 0, то
(15.12)
Видно, что только в случае гауссова профиля (т = 0) не существует нуля волновод-
ной дисперсии.
Профили равного объема. В разд. 14.10 было показано, что распределение интенсив-
ности основной моды и диапазон одномодового режима работы волоконного световода
главным образом зависят от объема профиля и малочувствительны к его форме, в то
время как волноводная дисперсия определяется в значительной мере формой профиля.
Гауссово приближение для сглаженных профилей дает возможность достаточно лег-
ко проверить эти выводы, поскольку все профили такого вида имеют одинаковый
объем, в чем можно удостовериться, если выражение для профиля (15.9) подставить
в выражение (14.42), изменить порядок интегрирования и учесть определение гамма-
функции (37.104).
Распределение интенсивности и параметр искажения. Распределение интенсивности
в поперечном сечении волоконного световода S (табл. 15.2) изменяется экспоненциаль-
но в зависимости от R2 /R2, где Ro - нормированный размер пятна. Поскольку для га-
уссова профиля 1/R2q = V - 1 (т 0), а для ступенчатого 1/R^ = 2 In V (т = то
размер пятна на частоте отсечки (2,592 и 2,405 соответственно) изменяется всего на
9 %, т. е. S слабо зависит от формы профиля. С другой стороны, данные табл. 15.2 или
соотношение (15.12) свидетельствуют о том, что параметр искажения зависит от формы
профиля, т. е. от т.
Диапазон одномодового режима. Если предположить, что размер пятна не зависит от
формы профиля при V — Кс, то, используя гауссово приближение, можно проверить,
как следствие этого предположения согласуется с точным значением Кс. Нормированная
интенсивность не зависит от формы профиля только в том случае, если размер пятна мо-
ды г0 является одинаковым для всех форм профиля. Поэтому для S/\а 12N из табл. 15.2
можно положить V = Ис и использовать в качестве эталонного ступенчатый профиль с
Ис — 2,405, значение г0 которого известно. В результате имеем
m + 2
rc=(l + irf) 2 ~2,405ехр(°^), m
(15.13)
Таблица 15.3. Параметры основной моды и относительная ошибка для различ-
ных сглаженных профилей
m Ц точное значение и, < гауссово приближение 1 Относительна! ошибка, % 1 ИС, точное значение VC, равные параметры пятна моды Относительная ошибка, %
0 2.034 2.045 -0.6 2.592 2.755 -6.3
2 1.818 1.826 —0.4 2.508 2.512 -0.2
4 1.758 1.766 —0.4 2.477 2.466 0.4
8 1.713 1.721 -0.5 2.451 2.437 0.6
16 1.683 1.694 -0.6 2.432 2.421 0.4
32 1.666 1.678 -0.7 2.420 2.413 0.3
оо 1.646 1.660 -0.8 2.405 2.405 0
Примечание. В таблице сравниваются приближенные и точные значения парамет-
ров основной моды U (при V = Vc) и Vc (приближенное значение Г, вычислено
согласно выражению (15.13))
297
В табл. 15.3 полученные по этой формуле значения частоты отсечки сравниваются с точ-
ными. Видно, что разница между приближенными и точными значениями пренебрежимо
мала за исключением гауссова профиля (т = 0), так как размер пятна действительно не
зависит от формы профиля при V — Ис, что позволяет считать частоту отсечки равной
2,405 для всех профилей равного объема, приведенных в табл. 15.2.
15.5. Поле вдали от оси волоконного световода
Во всех трех примерах, рассмотренных выше, показатель преломления обо-
лочки вдали от оси волоконного световода имел постоянное значение ис1.
В этой области решение скалярного волнового уравнения для основной мо-
ды пропорционально модифицированной функции Бесселя второго рода
KQ (WR), где R = г/р, а параметр W определен в табл. I. При больших значе-
ниях аргумента (ИТ? >> 1) функция Ко изменяется согласно выражению
(37.88) как R~1/2 ехр(-И7?), и поэтому гауссово приближение, при котором
поле меняется пропорционально ехр(—R2/2Rq) , в этой области дает боль-
шую погрешность. В большинстве случаев это дальнее (или слабое) поле иг-
рает второстепенную роль, однако оно становится существенным в случае
перекрестной связи двух волоконных световодов (см. гл. 28 и 29), посколь-
ку этот эффект обусловлен взаимодействием дальних полей, а поэтому их
поведение в этой области необходимо описать с достаточной точностью.
Для получения более точного выражения для дальнего поля используем
результаты гауссова приближения [5, 8]. Подставляя выражение для профи-
ля показателя преломления из табл. 15.1 в уравнение (15.1), перегруппиро-
вывая члены и переходя к безразмерным величинам, получаем
-’‘“l'7"=-(1514)
где параметр V определен в табл. I, а / = 1 при п =nCQ. Поскольку разность
(1 —/) значительна только вблизи оси световода, т. е. в области, где справед-
ливо гауссово приближение табл. 15.1, то в правой части уравнения (15.14)
можно положить Fo = exp(-R2/2Rq) . Полученное уравнение может быть ре-
шено методом функций Грина, описанным в разд. 34.9, а само решение -
первый интеграл в выражении (34.42) , т. е.
оо D
F0(R) « V2Ko(WR) J Л'[1 -/(^')]/o(^')exp(--^-)d/?', (15.15)
0 2Rq
где Iq — модифицированная функция Бесселя первого рода.
Гауссов профиль. Подставляя/, W = (V2 - t/2)1/2 иА0 =^о/риз табл. 15.2
для гауссова профиля, с помощью соотношения (37.101) получаем
Fo (R) ~ Г2Л-0 (ИК) Д?70 (WR')exp(—^F-R'2)dR', (15.16а)
о 2
[(Г— 1)Я]ехр[|-11^Н. (15.166)
При V = 2,5 и R > 1,5 это приближение отличается от точного результата ме-
нее чем на 4 % [7].
298
МОДЫ ВЫСШИХ ПОРЯДКОВ
Точное решение скалярного волнового уравнения для основной моды воло-
конного световода с неограниченным параболическим профилем показателя
преломления дает гауссову пространственную зависимость поля. Таким обра-
зом, суть гауссова приближения заключается в аппроксимации поля основ-
ной моды волоконного световода с произвольным профилем полем основ-
ной моды волоконного световода с некоторым параболическим профилем,
а конкретная форма профиля определяется из стационарного выражения для
постоянной распространения в табл. 15.1. Очевидно, что этот подход может
быть обобщен и на случай мод высших порядков подбором соответствующе-
го решения для волоконного световода с бесконечным параболическим про-
филем [9].
15.6. Приближения для полей
Пространственная зависимость поля любой моды аппроксимируется моди-
фицированными выражениями из табл. 14.2. Таким образом, имеем
FL = (/?/7?o)lZ^ .(Л2/^)ехр(-/?2/2Л20), (15.17)
m - 1
где _ j — обобщенный полином Лагерра, а обозначения определены в
табл. 15.1. Для определения Ro воспользуемся вариационным выражением
для U2 в табл. 13.2. Подставляя выражение (15.17) в знаменатель и исполь-
зуя соотношение (37.128), получаем
и’- <1518)
а величина RQ находится решением уравнения dU2/dR0 = 0 при минимальном
значении U2. Чтобы показать точность полученного приближения, рассмот-
рим ряд мод низших порядков в волоконном световоде с гауссовым про-
филем.
15.7. Пример. Гауссов профиль
В разд. 15.2 рассматривалось гауссово приближение для основной моды этого профиля.
Для всех мод с m = 1 выражение (15.17) имеет вид
F^~ (Я/Яо) ехр(-Яг/2Я2). (15.19)
Подставляя (15.19) в уравнение (15.18), полагая / = 1 - ехр(-7?2) и используя соот-
ношение (37.126), получаем
а также уравнение для Ro из табл. 15.1
(l + /? = )l+2= (15.21)
Кроме случая I — 0, соответствующего основным модам, это уравнение имеет аналити-
ческое решение при I = 1 и I — 2, являясь соответственно кубическим и полиномиаль-
ным уравнением четвертой степени. Решения для Ro и U2 представлены в табл. 15.4
[9], в которой также приведены точные значения частот отсечки [7]. Сравнение прибли-
женных и точных значений U показывает, что ошибка составляет менее 1,2 % для мод с
индексами I = m = 1 при V > 3 и менее 0,9 % для мод с индексами I = 2,т = 1 и И >
299
Таблица 15.4. Моды низших порядков волоконного световода с гауссовым профилем показателя преломления
n2(R) = 1 - 2Д(1 - ехр( - Я2))}; Я = ^; У=крпт{2(^2
I т F, К R R°-p V2 U2=--p2fi2 2Д
0 1 f IR2] ЧЙ - (r-D- (F>1) 2V- 1
1 1 R ( 1 R2 ] ^eXPU2Rl/ 2.592 l'T_1 + T(F2~6),'2sin(?_^}12 (J j \ J 0 / J a V27(27-4r2) “ (2И4- 18Г2 + 27) !*O - Ift; 1 4-
2 1 R2 f 1R2 ] я|еХРГ 2R2} 4.339 V2 ( K\ — + ЗИ-3 + (Г2-4Г)1/2( 2--i
Примечание. Размер пятна моды r0 = pR0 и постоянная распространения /3 получены на основании вариационного решения (15.18)
> 4,5. В обоих случаях ошибка растет по мере приближения V к частоте отсечки, по-
скольку распределение поля является неудовлетворительным приближением расплы-
вающихся вблизи отсечки полей волоконного световода с гауссовым профилем показа-
теля преломления.
ПРИБЛИЖЕНИЕ ЭКВИВАЛЕНТНОГО ВОЛОКОННОГО СВЕТОВОДА СО СТУПЕН-
ЧАТЫМ ПРОФИЛЕМ
Основная идея этой главы заключается в том, что поля мод волоконного све-
товода с произвольным профилем показателя преломления могут быть до-
статочно точно аппроксимированы соответствующими полями мод другого
волоконного световода с некоторой, заранее определенной, формой профиля
при условии соответствующего выбора параметров мод и параметров свето-
вода. Так, например, в основе гауссова приближения лежит бесконечный па-
раболический профиль, а размер пятна й постоянная распространения опреде-
ляются уравнениями из табл. 15.1. Альтернативным этому служит так называ-
емое приближение эквивалентного волоконного световода со ступенчатым
профилем [4], в основе которого лежит поле основной моды волоконного
световода со ступенчатым профилем показателя преломления. Оно является
справедливым в более широком диапазоне нормированных частот и для
большего числа параметров, чем гауссово приближение, но конечные выраже-
ния являются не столь простыми.
15.8. Основные моды
Предположим, что поля основной моды волоконного световода с произволь-
ным профилем показателя преломления можно аппроксимировать полями
основной моды некоторого ступенчатого волоконного световода. Зависи-
мость этих полей от радиуса запишем в виде (табл. 14.3)
Л>(*)
/о (UR)
Л) (СО ’
1;
Fo(R)
Ко (WR)
K0(W) ’
1 < R<°°,
(15.22)
где R = г/р, а параметры U и W определяются характеристическим уравнени-
ем и нормированной частотой
Таким образом, для заданных Кир функция Fo определена однозначно.
Следуя подходу, изложенному в разд. 15.1, подставляем функции (15.22)
в вариационное выражение для U2 из табл. 13.2 при I = 0. С помощью (37.92)
и (37.93), характеристического уравнения из табл. 14.6 и рекуррентных со-
отношений (37.72) и (37.73) получаем [4]
=2[W7^“]2 [Г2 + -Й-у], (15.24)
VKX(W) о Р 2
где J? =-г/р, а V, f(R) для произвольного профиля даны в табл. I. Чтобы най-
ти р и К, полностью определяющие ступенчатый волоконный световод, необ-
301
(15.25)
отноше-
решены
ходимо, чтобы параметр V2 одновременно являлся решением двух уравнений
<=0; ^=0.
др ’ dV
Иными словами, искомое решение должно минимизировать U2 по
нию к вариациям р и V. В общем случае эти уравнения могут быть
только численно. Более детальный анализ рассмотрен в работе [4].
Гауссов профиль. Использование приближения эквивалентного волокон-
ного световода со ступенчатым профилем при определении величин С/для ос-
новной моды световода с гауссовым профилем не требует ограничения на
диапазон нормированных частот V, как это было в случае гауссова прибли-
жения (табл. 15.2). Более того, разница между приближенными и точными
значениями U столь мала, что кривые на рис. 15.1, б, соответствующие этим
расчетам, неотличимы друг от друга. Кривая распределения интенсивности
вдали от оси световода, построенная на основании указанного приближения
фактически совпадает с точным решением особенно при малых V, в то время
как гауссово приближение приводит к значительным ошибкам (см. 15.1, в
кривую для V = 1,592). Последнее справедливо для дальнего поля, спадаю-
щего с ростом R очень быстро (см. разд. 15.5), тогда как выбор поля в вы-
ражении (15.22) обеспечивает необходимое поведение дальнего поля и для
R» 1.
Хотя приближение эквивалентного волоконного световода со ступенча-
тым профилем в этих двух случаях более пригодно, решения уравнений
(15.24) и (15.25) могут быть получены только численно. Соответствующие
выражения для гауссова приближения получены на основании уравнений в
табл. 15.1 и имеют простой вид (см. табл. 15.2) даже в случае скорректиро-
ванного выражения для дальнего поля.
15.9. Диапазон одномодового режима
Приближение для мод высших порядков, рассмотренное в разд. 15.6, не дает
необходимой точности при определении диапазона одномодового режима во-
локонного световода с оболочкой и произвольным профилем. На частоте от-
сечки при I = т = 1 поля мод волоконных световодов являются решениями
уравнения (11.54), в котором я (А) исо, и, таким образом, в цилиндри-
ческих координатах имеют радиальную зависимость R~1. Соответствующая
зависимость (15.17) всегда является экспоненциальной, что делает прибли-
жение неудовлетворительным. Поэтому для оценки Vc в табл. 15.2 использо-
вался метод профилей равного объема, однако значительно более высокую
точность дает приближение эквивалентного волоконного световода со сту-
пенчатым профилем.
Частота отсечки второй моды. Выше было показано, что на частоте отсеч-
ки поля мод волоконного световода с произвольным профилем показателя
преломления аппроксимируются полями мод эквивалентного ступенчатого
световода с индексами I = т = 1, т. е. U = V_= VQ = 2,405 и W= 0. Из табл. 14.6
и соотношения (37.86) следует, что если 0, то радиальную зависимость
этих полей можно представить в виде
302
^(Я)
Л (^)
Л (Vc)
1;
^<*>4
1 <оо.
(15.26)
Если в вариационном выражении для U2 из табл. 13.2 положить U = V = Vc,
1=1, перегруппировать члены, а некоторые интегралы вычислить с помощью
выражений (15.26), (37.91), (37.92) и табл. 14.6, то получим [4]
Ис = 2,892^4J [1 — f(R)] RdR + J [1 ~/(*)] . (15.27)
P to Ji(rc) 0 K J
Значение Kc находится решением уравнения dV^/др = 0 относительно р и
последующей подстановкой в выражение (15.27). В случае волоконного све-
товода с произвольным профилем показателя преломления эта процедура
может быть проделана только численно.
Гауссов профиль. Если для определения диапазона одномодового режима
волоконного световода с гауссовым профилем (15.6) использовать выраже-
ние (15.27), то получаемое значение Кс % 2,62 всего на 12% отличается от
точного из табл. 15.2 [4, 7].
ГЛАВА 16. ВОЛНОВОДЫ С НЕКРУГЛЫМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
В разделе 13.5 и 13.8 в общих чертах была рассмотрена структура мод слабо-
направляющих волноводов с некруглым поперечным сечением, интерес к ко-
торым обусловлен их анизотропными свойствами. В этой главе рассматрива-
ются волноводы, закон радиального изменения показателя преломления ко-
торых позволяет получить точное аналитическое решение скалярного волно-
вого уравнения, а в гл. 17 и 18 — приближенные решения. Основное внима-
ние уделяется эллиптическим волоконным световодам с неограниченным
параболическим профилем, поскольку, во-первых, в этом случае основные
характеристики моды, включая постоянную распространения, описываются
простыми выражениями, во-вторых, на примере таких световодов легко по-
казать, что даже небольшая асимметричность поперечного сечения приводит
к сохранению однородной поляризации всех мод световода и, в-третьих,
указанный профиль лежит в основе гауссова приближения для некруглых
световодов, которое рассматривается в гл. 17.
16.1. Планарные волноводы
Простейшим примером некруглого волновода может служить планарный
волновод, рассмотренный в гл. 12, моды которого являются либо ТЕ-, ли-
бо ТМ-модами (см. разд. 11.16). Электрическое поле каждой ТЕ-моды ле-
жит в плоскости поперечного сечения волновода и является однородно по-
ляризованным. Следовательно, решение в приближении слабонаправляюще-
го волновода полностью идентично точному решению, на основании которо-
го определяется поле еу и постоянная распространения. Оба эти решения
303
удовлетворяют скалярному волновому уравнению (12.16), а в аналитичес-
ком виде они приведены в табл. 12.7. В приближении слабонаправляющего
волновода поперечное электрическое поле ех каждой ТМ-моды также являет-
ся решением уравнения (12.16) , однако постоянная распространения опреде-
ляется не только ее скалярным значением, но и поправкой 60, обусловлен-
ной величиной двойного лучепреломления (13.11).
ЭЛЛИПТИЧЕСКИЕ ВОЛОКОННЫЕ СВЕТОВОДЫ С НЕОГРАНИЧЕННЫМ ПАРАБОЛИ-
ЧЕСКИМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
Круглые волоконные световоды с неограниченным параболическим профи-
лем детально рассмотрены в разд. 14.4. Если поперечное сечение световода
имеет эллиптическую форму, то профили показателя преломления можно
записать в виде
п2 (х, у) = п2о [1 - 2Д(^- +^)]; -°°<х,у<°°, (16.1)
Рх Ру
где рх и ру — характерные размеры поперечного сечения световода в х- и
^-направлениях. На рис. 16. 1 показаны кривые постоянного показателя пре-
ломления, представляющие собой семейство концентрических эллипсов, т. е.
эллипсов с одинаковым эксцентриситетом е, где
е= (1-Ру/Рх)1/2; Рх>Ру- (16-2)
Например, если п = п^? то согласно определению Д в табл. I получаем (х/рх)2 +
+ (у/Ру)2 = 1. Поскольку поперечное сечение волоконного световода зави-
сит от двух параметров рх и ру, то такой световод можно охарактеризовать
двумя нормированными частотами Vx и Vy и двумя параметрами моды Ux и
Uy, которые являются обобщением соответствующих параметров круглого
световода и даны в табл. 16.1. Профиль показателя преломления (16.1) фи-
зически нереализуем, но в силу соображений, изложенных в разд. 14.4,
приближение слабонаправляющего волновода будет справедливым при опи-
сании распространения волн, если мощность мод сконцентрирована вблизи
оси световода. Как будет показано ниже, это приводит к ограничению на воз-
можные значения параметров Vx или Vy.
Рис. 16.1. Кривые постоянного уровня
показателя преломления в поперечном
сечении эллиптических световодов с не-
ограниченным параболическим профи-
лем, форма которого определяется вы-
ражением (16.1)
304
Таблица 16.1. Основные моды эллиптического волоконного световода с не-
ограниченным параболическим профилем показателя преломления
[ /V2 \ ) ( Л2 ) 1/2 = 1-2Д ; е= 1-4 (. \Рх Ру / J 1 Рх J
к'х = крхпсо(2Л)112; Уу = крупа>(2А)':2; -^ = 4 к = Г г Рх Л
(к2 - 11/2 . (и2 - 11,2 и О их^\ — -р2хв2} ; С> --р2Л2\ ; = - ж (2Д РхР J ’ ' (2Д РуР \ Vx рх
Четная НЕп-мода (поляризованная вдоль оси х) Нечетная НЕц-мода (поляризованная вдоль оси >’)
Поперечные поля Ех = y)exp{i(0 + <5/3x)z} \Ро / Е, = T(x,y)exp{i(^ + <5^)z} /Р \1/2 ^=-(^) "«А \Ро/
Решение скалярного волнового уравнения ( ^^хК\1/2Гх2 /1) Т(х, у) = ехр< -1 — + — У 1 2 \ РхРу / _ Рх Ру _ J
Решение характери- стического уравнения 1414 = vx+vy; -СП"
Поляризационные поправки (2Д)3'2 Д ^х=--—6UX = ^ Рх 2pxVx х Ux (2Д)’/2 Д
px='p + wx
Скорректированные параметры мод UX = UX + 6UX Uy = Uy + 6Uy
Нормировка _япсо/е0у'2 рхру 2 \POJ (УхУу)112
Двойное лучепреломление е2 (2Д)’/2 ^-Р,-^-^^е22РжУ,
Примечание. Параметры приведены в табл. I.
305
16.2. Основные моды
Вывод выражений для поперечных полей двух основных мод слабонаправля-
ющего некруглого волоконного световода приведен в разд. 13.5. В табл. 16.1
эти поля выражены через решение Ф (х, у) скалярного волнового уравнения,
которое в декартовых координатах имеет вид
д2 ~
+ту +к2п2(х’У>= (16.3)
где Р - скалярная постоянная распространения, а остальные параметры опре-
делены в табл. I. Если в уравнение (16.3) подставить профиль (16.1), то лег-
ко показать, что решение для основной моды и характеристическое уравне-
ние определяются следующими выражениями:
f , V V v2 v2 •)
ф = ехр 4(р2Н)1/2(Тг + >) ; ^У=Гх+КУ’
/ Z Рхг'у Рх Ру I J J
(16.4)
из которых получаем формулу для постоянной распространения
___2Д
(У„Уу)“г
Ру Рх
(16.5)
которая имеет наибольшее значение для любой из основных мод. Детальный
вывод этих выражений приведен в разд. 16.3.
Поскольку волоконный световод является циркулярно несимметричным,
то, как было показано в разд. 13.5, поляризационные поправки 8рх и 8ру для
х- и ^-поляризованных мод различны. Чтобы определить их величину в урав-
нении (13.11), положим f (х, у) = (х/рх)2 + (у/Ру)2 и, подставив et = Фх
или et = Фу из уравнения (16.4), получим выражение в табл. 16.1. Продоль-
ные компоненты поля малы, и они могут быть оценены с помощью соотно-
шений (13.13).
Распределение мощности моды. Выражение для коэффициента нормиров-
ки в табл. 16.1, полученное на основании уравнения (16.4) и табл. 13.2,
позволяет получить следующую формулу для нормированного распределе-
ния интенсивности:
с 1 (К Г)1/2 VV у2
s = = ..ехр [- 1/2 ф + тт) ] • (16.6)
\a\N 11 Рхиу Рхиу Рх
Таким образом, кривые равной интенсивности представляют собой семей-
ство эллипсов, эксцентриситет которых меньше, чем у кривых с равным по-
казателем преломления.
Распространение импульса. Предположим, что импульсом света возбужда-
ются две собственные моды волоконного световода. Уширение импульса бу-
дет определяться волноводной дисперсией, однако в каждой моде оно будет
разное, поскольку световод является эллиптическим. Кроме того, небольшое
различие между постоянными распространения 8/Зх - 5 (Зу приводит к разным
306
групповым скоростям мод с ортогональными состояниями поляризации, а
следовательно, к межмодовой дисперсии , которую в этом случае часто назы-
вают двулучепреломлением.
Подставляя (16.4) в соответствующие выражения из табл. 13.2, получим,
что в скалярном приближении групповые скорости мод близки к скорости
света в среде с показателем преломления nCQ. Чтобы учесть поляризационные
эффекты, в (13.17) заменим £7 V и на (7Х, Vx и 6Ux/& соответственно,
и с точностью порядка А2 для моды, поляризованной вдоль оси х, получим
f л о )
Vgx=7r- 1-тЬ 4+ (р +1)2 • (16.7)
псо 2ИХ L JJ
Аналогичное выражение для моды, поляризованной вдоль оси у, получается
простой заменой индексов х на у и наоборот в выражении (16.7). Выражение
для волноводной дисперсии можно получить, если обобщить понятие пара-
метра искажения D, введенного в рассмотрение в разд. 11.20, на случай эл-
липтического волоконного световода, т. е. определить ^Х(К А) с помощью
выражений (11.58) и (11.59) при замене V на С точностью порядка Д
из (16.7) и (13.18) для моды, поляризованной вдоль осих, имеем
2)х (V, А) «= - [1 + { (^- - 1) ф + 3) ]. (16.8)
Аналогичное выражение для Dy(V, Д ) получается из (16.8) взаимной заме-
ной индексов х и у.
Межмодовая дисперсия может быть представлена как разность времен
распространения tx и ty двух мод надлине световодам. Подставляя (16.2) и
(16.7) в соотношение (11.36), для случая малого эксцентриситета эллипса
поперечного сечения имеем
t _t ______L)= 2£iAL£!co . (169)
У ‘x с l ТЛ2 y2 > V2 c
у v X v у
Таким образом, мода, поляризованная вдоль оси у, имеет большую группо-
вую скорость, и при фиксированной Vy дисперсия увеличивается с ростом
эксцентриситета.
Двойное лучепреломление — характеристика поляризационных свойств
волоконного световода. Проведенное рассмотрение свойств основных мод в
эллиптическом волоконном световоде дает основание провести аналогию с
распространением плоских волн в анизотропной среде, обсуждающееся в
разд. 11.23 [1]. Так, в частности, полное электрическое поле двух мод све-
товода Et эллиптически поляризовано, и характеристики эллипса поляриза-
ции меняются вдоль световода. С другой стороны, интерференция между по-
лями двух мод отсутствует и, следовательно, картина интенсивности полного
поля не меняется вдоль световода, что свидетельствует о линейной и одно-
родной поляризации мод.
Условия, при которых волоконный световод является слабонаправляю-
щим. В разд. 14.4 было показано, что приближение слабонаправляющего вол-
новода справедливо, если относительная разность показателей преломления
Д« 1 и значительная доля мощности основной моды сосредоточена в бли-
307
зи оси, т. е. (3 ъ кпс0. Из соотношения (16.5) следует, что для эллиптических
волоконных световодов последнее условие выполняется при
Гх» 2Д(1+рх/ру).
(16.10)
Для волоконных световодов с большим эксцентриситетом поперечного се-
чения рх » ру и приближение ограничивается достаточно большими значе-
ниями V*.
Поляризационная поправка к полям мод. Поправки первого порядка для
поперечного электрического поля могут быть получены из уравнения для
в табл. 32.1 при f = (х2 /рх) + (у2/р2). Для основной моды, поляризо-
ванной вдоль оси х, положим ej. = Фх, = 6t/x/A (см. табл. 16.1) и заме-
ним р, U и V на рх, Ux и Ух соответственно. Легко показать, что решением
этого уравнения будет функция
(П _ / х - 4V У х А ,т,
etx (РхХ Vx+V руУ)рхАФ’
А У J
(16.11)
а соответствующее выражение для ety получается из (16.11) взаимной заме-
ной х и у, включая индексы. Отметим, что эти выражения получены в предпо-
ложении << е+х и ety) << ety и, следовательно, являются справедливы-
ми прих« рх/Д172 иу« Ру!^'2 соответственно.
16.3. Моды высших порядков
Структура мод высших порядков некруглых волоконных световодов рас-
сматривалась в разд. 13.8. Поперечное поле каждой моды совпадает по на-
правлению и по форме с полями основных мод из табл. 16.1 за исключением
того, что Ф является соответствующим решением высшего порядка скаляр-
ного волнового уравнения (16.3). В случае поперечного сечения световода,
близкого по форме к круглому, такое представление полей мод становится
некорректным (см. разд. 13.9) и рассмотрено в следующем разделе.
Для определения функции Ф подставим выражение для профиля (16.1) в
скалярное волновое уравнение (16.3), проведем замену переменных и, вы-
разив решение в виде
+ Wv
* = F(wx)G (wy) exp (---’
(16.12)
получим два обыкновенных дифференциальных уравнения
d2F dF U2 к
‘(Х <1613а>
-2w-~ + l)G = 0, (16.136)
dw2 у dwy У27у Vx J v 7
где к — постоянная разделения, а параметры определены в табл. 16.1.
Решения, ограниченные при |х|, |.у| -> °°, являются полиномами Эрмита
Яп [2]. Коэффициенты при функциях F и G в уравнениях (16.13) должны
308
быть равны положительным целым числам или нулю. Исключение постоян-
ной разделения к приводит к характеристическому уравнению, из которого
получаем
, (^«Р [-1(^4 '’ (£ *^) 1.
(16.14а)
(16.146)
?7xC7y = (2т - 1) Vy + (2л - 1) Кх,
где т, п - 1, 2, . . . , а постоянная распространения определена в табл. 16.1.
Решению уравнения (16.4) для основной моды соответствует т = п = 1, а яв-
ный вид полиномов Эрмита для ряда мод низших порядков дается соотноше-
нием (37.107). Поляризационные поправки 60х и 6/Зу для каждой пары мод,
соответствующих решению Фтп, определяются выражением (13.11).
16.4. Почти круглые волоконные световоды
Опираясь на полученные выражения для мод эллиптического волоконного
световода, рассмотрим, каким образом однородно поляризованные моды
циркулярно несимметричного волоконного световода преобразуются в моды
круглого световода, выражения для которых приведены в табл. 13.1. Каче-
ственно этот вопрос был рассмотрен в разд. 13.9, здесь же дадим количе-
ственную оценку, для чего рассмотрим ближайшие к основной моды низших
порядков, поля которых описываются соответствующими решениями Ф21 и
Ф12 скалярного волнового уравнения. Из соотношений (16.14) и (37.107) с
точностью до постоянной величины имеем
V у v2 у2
РЛ = ЗГ,Ч. (16.15а)
У 1 У V у2 у2
(16.156)
В предельном случае круглого поперечного сечения р р р9 Vx^Vy-*V,
и поскольку у/р = R sin х/р = R cos (см. рис. 14.1), функции Ф2! и Ф12
переходят в соответствующие индексу I = 1 решения (14.3)
Фе = R ехр(— -у P7?2)cos Фо =R ехр(—у KR2)sin (16.16)
подученные в табл. 14.2 для круглого волоконного световода. Если /Зе и Ро —
скалярные постоянные распространения, соответствующие решениям Ф21 и
Ф12, то из (16.15) и (16.2) для малого эксцентриситета эллипса поперечного
сечения получаем
так как Ре, « кпсо и Vx/Vy = рх/ру, Ux/Vy = рх/ру.
Свойства мод почти круглого волоконного световода можно охарактери-
зовать параметром Л. Он был введен в разд. 13.9, а выражение для него полу-
309
чено методом возмущений в разд. 32.9. Используя определение Л, данное в
табл. 13.1, получаем выражение
Л~-е2К/4А~-Г(1 - ру/рх)/2Д.
(16.18)
При его выводе использовались данные табл. 14.2 для Z = 1 и соотношение
(16.17).
При |Л| << 1 поля мод подобны полям круглого волоконного светово-
да, т. е. являются линейной комбинацией выражений в табл. 14.1, а при
|Л| >> 1 моды являются однородно поляризованными модами эллипти-
ческого световода. Поскольку в реальных волоконных световодах относи-
тельная разность показателей преломления мала (А << 1), то становится
очевидным, что даже небольшая асимметрия поперечного сечения приводит
к однородной поляризации мод и, таким образом, круглый световод являет-
ся идеалом, который требует для своей реализации высокую точность.
АКСИАЛЬНО-НЕСИММЕТРИЧНЫЕ ПРОФИЛИ, ДЛЯ КОТОРЫХ СУЩЕСТВУЮТ
АНАЛИТИЧЕСКИЕ РЕШЕНИЯ СКАЛЯРНОГО ВОЛНОВОГО УРАВНЕНИЯ
В этой части главы рассматриваются некоторые примеры некруглых волно-
водов, профиль показателя преломления которых позволяет получить ана-
литические решения скалярного волнового уравнения и явные выражения
для основных характеристик моды.
16.5. Профили показателя преломления, описываемые однородной функцией
Форма таких профилей, введенных в рассмотрение в разд. 2.13, имеет вид
д?2 (х, у) = и20 [1 - 2Д/(х, у) ], <х, у < <», (16.19а)
где f (х, у) — однородная функция степени д, обладающая свойством
f(ax, ay) =aC[f(x, у). (16.196)
Используя это свойство, можно получить аналитические выражения для по-
стоянных распространения всех мод. Для этого подставим выражение для
профиля (16.19а) в скалярное волновое уравнение (16.3) и умножим его на
р2, где р — характерный размер поперечного сечения волоконного световода.
Затем, используя очевидную модификацию масштабного преобразования из
разд. 33.6 и формулу (33.26), получаем
t7=GK(2/q + 2)> (16.20)
где U и V определены в табл. I. Постоянная G зависит от q и от параметров,
описывающих асимметрию поперечного сечения, и не зависит от V. Напри-
мер, для эллиптического профиля (16.1) для q = 2, р = рх и решений (16.4)
имеем G = [2т — 1 + (2п — 1) (1 — е2)1/2 ]1/2, где е — эксцентриситет эллип-
са поперечного сечения (16.2).
Групповая скорость и волноводная дисперсия. Зависимость (J6.20) с точ-
ностью до неизвестной в общем случае функции G совпадает с зависимостью
U(V) для круглого волоконного световода с неограниченным степенным
профилем показателя преломления. Поскольку профиль (14.8) удовлетво-
310
ряет условиям однородности (16.196), то, следовательно, выражения для
групповой скорости и параметра искажения для асимметричных профилей
можно получить непосредственно из соответствующих соотношений (14.10)
и (14.11). Исключая из формул G, получаем
~ + п (2~q) и2
«СО (1 Д 2 + q Г2 ’ q (2 + Q)2 И3 ’
(16.21)
Из этих выражений видно, что в однородном профиле волноводная диспер-
сия отсутствует, если q = 2.
16.6. Профили показателя преломления с разделяющимися переменными
Этот класс профилей был введен в рассмотрение в разд. 2.14 и описывается
выражением вида
п2(х, у) =п2с0 {1 -2Д[/(х) +gO)]}; (16.22)
где f (х) и g (у) зависят соответственно только от х и у. Подставляя зависи-
мости для профиля (.16.22) в скалярное волновое уравнение (16.3) и пола-
гая Ф(х, у) = F(x)G(y), получим два обыкновенных дифференциальных
уравнения
d2F 'V2
р2 -ТТ + + K1F = °’ (16.23а)
ах £
d2 С ГЬ
Р2 + [ V - ^^у) - к] G = 0, (16.236)
dy2 2
где к — постоянная разделения, ар — характерный размер поперечного сече-
ния волновода. Требование ограниченности функций F и G на поперечном
сечении приводит к соотношению связывающему Un к, а исключение из не-
го к дает характеристическое уравнение. Параболический профиль (16.1)
является одним из примеров разделяемых профилей, для которого скаляр-
ное волновое уравнение в разд. 16.3 было решено описанным здесь методом.
Приведем теперь второй пример такого профиля.
16.7. Пример. Неограниченный линейный профиль показателя преломления
Показатель преломления в таком профиле изменяется линейно с изменением как х, так
и у и может быть записан в виде
Пг (х, у) = п’0[1 - 2Д(|х/рх| + Ij'/Pyl)]; -“ < х, (16.24)
где рх и Ру - характерные размеры поперечного сечения. Кривые постоянного показате-
ля преломления представляют собой ромбы и изображены на рис. 16.2, а. Граница меж-
ду сердцевиной и оболочкой представляет собой также ромб, описываемый уравнением
1*/рх1 + ly/Pyl = 1. Поскольку профиль является разделяемым, то решение скалярного
волнового уравнения можно получить (16.23), если f(x) = | х/рх |, a g О) = \у/ру |.
Проводя замену переменных
311
Рис. 16.2. Кривые постоянного уровня показателя преломления в волоконном световоде:
а — с неограниченным линейным профилем (16.24); б — с двойным параболическим
профилем (16.30) (d — расстояние между осями световодов)
8)
(16.25)
(16.26)
w = _ £L_k4-);
X к*3 Рх х 2 ps
= 1 М/’ Uy + <
г;'3 ( Py vy ~г ’
где параметры определены в табл. 16.1, получаем уравнения
dzF d'G
- w F = 0; г - w G = О,
dw? dw„ у
Л У
и решение Ф = FG. Таким.образом, обе функции F и G являются решениями уравнения
Эйри, а поэтому ограниченное решение определяется выражением
Ф = ±Лг(и>)Лг(™ ), (16.27)
у Л
где Ai - функция Эйри первого рода [2]. Знак функции Ф меняется при переходе из од-
ного квадранта на рис. 16.2, а в другой и определяется симметрией относительно осей х
и у. Условие непрерывности функций Ф, дФ/дх и д'У/ду вдоль осей приводит к характе-
ристическому уравнению. Например, решение для основной моды имеет знак + в каж-
дом квадранте и дает следующее характеристическое уравнение:
dAi (w ) dAi(w}
——5- = 0, X = 0; —-------у— = 0, у = 0.
dw dwv
А у
Значение постоянной распространения определяется первым нулем производной функ-
ции Эйри, а именно wx —1,018 при х = 0 и wy —1,018 при у — 0 [2]. Подставляя эти
значения в выражения (16.25) и исключая к, получим
(16.28)
Й.Ц, = 1,018 [(—)1/3 + (-^-)1/3 ] (Г К )2/3.
х У ру Рх х у
(16.29)
Поскольку линейный профиль также описывается однородной функцией, удовлетворя-
ющей условию (16.196) при q = 1, то соотношения (16.29) и (16.20) тождественны
между собой при q — 1 и рхр = р2 и, таким образом, можно определить параметри-
ческую зависимость функции (Тот рх и ру.
312
16.8. Пример. Двойной параболический профиль показателя преломления
В качестве заключительного примера в этой главе рассмотрим профиль, распределение
показателя преломления в котором описывается двумя смещенными относительно друг
друга неограниченными параболами [3]. Он имеет форму, изображенную на рис. 16.2, б,
и описывается функцией
п2 (х,у) = п2с0 {1 - 2Д[ (|х/р| - dj2p)2 + (у/р)2 ] •; - оо < х, у < (16.30)
где d — расстояние между вершинами парабол, ар- характерный размер поперечного
сечения. Поскольку профиль является разделяемым, то решение скалярного волнового
уравнения можно получить, если положить/(х) = (\х/р\ - d!2p)2 в уравнении (16.23а)
и g Су) = (у/р)2 в уравнении (16.236). Решение уравнения (16.30) находится по анало-
гии с решением уравнения (16.136), т. е.
1 У2 U2 к
С = ^п-1О/Р^Я)ехр(-|^-Г).; 2н-1 = ~-р (16.31)
где п — 1, 2, ... и Нп _ j - полином Эрмита порядка п - 1 [2], а параметры определены
в табл. I. Подставив выражение для к в уравнение (16.23а) и проводя замену перемен-
ных
w+ = (2K)‘;2-2X2~rf . X > 0; w_= х < 0, (16.32)
получим следующее уравнение:
d2F 1 w2
—+(р + _ __)F = 0> (16.33)
где w обозначает w+ или w_. Ограниченное решение этого уравнения выражается через
функции параболического цилиндра [2] и имеет вид
F = Dv (w+), х > 0, F= ±Dv(-wJ, x< 0, (16.34)
где знаки (+) и (—) относятся соответственно к симметричной и антисимметричной мо-
дам. Решение Ф скалярного волнового уравнения равно произведению функций F и G,
определяемых соотношениями (16.31) и (16.34). Характеристические уравнения могут
быть получены из условий непрерывности дЧ'/дх при х = 0 для симметричной и Ф при
х — 0 для антисимметричной мод и имеют вид
dDv I
—— = 0; D (w0) = 0,
dw I wo v
(16.35)
гдеи^0 = -(2V) 1/2 d/2р.
ГЛАВА 17. ГАУССОВО ПРИБЛИЖЕНИЕ ДЛЯ ВОЛОКОННЫХ СВЕТО-
ВОДОВ С ПОПЕРЕЧНЫМ СЕЧЕНИЕМ ПРОИЗВОЛЬНОЙ
ФОРМЫ
Гауссово приближение, рассмотренное в гл. 15, дает возможность получить
простые, но достаточно точные аналитические выражения для наиболее важ-
ных характеристик основных мод круглых волоконных световодов с произ-
вольным профилем показателя преломления. В этой главе дается обобщение
313
этого полезного приближения на случай волоконных световодов с произволь-
ной формой поперечного сечения.
Идея гауссова приближения для круглых волоконных световодов заклю-
чается в том, что, поскольку распределение поля основной моды световода
с произвольным профилем показателя преломления является приблизитель-
но гауссовой функцией, а распределение поля основной моды световода с
неограниченными параболическим профилем является точно гауссовой
функцией, поле волоконного световода с произвольным профилем аппрок-
симируется полем световода с неограниченным параболическим профилем, а
оптимальная аппроксимация находится вариационным методом, описанным
в разд. 15.1. В гл. 16 было показано, что распределение поля основной моды
в эллиптических световодах с неограниченным параболическим профилем
является также гауссовой функцией от обеих пространственных координат
поперечного сечения. Это дает основание аппроксимировать поле основной
моды некруглого световода с произвольным профилем показателя прелом-
ления полями такого световода (17.1, 17.2).
ОСНОВНЫЕ МОДЫ
Две основные моды слабонаправляющего световода с поперечным сечением
произвольной формы поляризованы линейно и однородно, а векторы элек-
трического поля параллельны оптическим осям световода (см. разд. 13.5).
Выражения (13.10) для поперечных электрических полей даны повторно в
табл. 17.1, где они представлены через фундаментальное решение Ф(х, у)
скалярного волнового уравнения для основной моды и скалярную постоян-
ную распространения <3. Волноводная структура обусловливает разные по-
стоянные распространения основных мод волоконного световода и выража-
ется в поляризационных поправках 60хи 6j3y. Поэтому основной целью гаус-
сова приближения в данном случае является получение простых аналитичес-
ких выражений для Ф, <3, 6j3x и 6j3y.
17.1. Гауссово приближение
По аналогии с решением скалярного волнового уравнения для основной мо-
ды эллиптического световода (см. табл. 16.1) предположим, что решение
уравнения (16.3) Ф(х, у) можно аппроксимировать следующей функцией
—
2 у2
Ф(х,у) =ехр[-у (~+ ~)],
~ ах ау
(17.1)
где ах и ау - размеры пятна моды, которые необходимо определить. Исполь-
зуя это выражение как пробную функцию в стационарном выражении для
постоянной распространения из табл. 13.2 и учитывая, что ах и ау соответ-
ствуют максимальному значению /3 [3], в декартовой системе координат
получим
314
Таблица 17.1. Гауссово приближение для основных мод волоконных светово-
дов с поперечным сечением произвольной формы
п2(х,у) = ^{1-2Д/(Х,У)}; Х = -\ У = А е = (1-4р2 Рх р, 1 р; J
Четная НЕ ц-мода (поляризованная вдоль оси х) Нечетная HEи-мода (поляризованная вдоль оси у)
£x = 'F(x,y)exp{i(^ + <5/?x)z} /г \1/2 Vt; "»£‘ \ио/ = *(*> у)ехр{|(Д + <5^)z} /р X1/2 Wx=~(f) "~£* \Мо/
ч f 1/№ у2\1 . вд . а, Ч'(х,у) = ехр^--(-у + -1 В; Ах~--, А,~-+ 1 х\Лх / J Рх Ру
.й - (2Д)3/2 2pxVlAi АЛ _ (2А)3/2 р” 2Р,ил:
Кх = крхПсо(2Д)‘«; Г, = кРЛо(2Д)*'2; £ = А к = у
Вариационное уравнение для постоянной распространения
1/ I/ Г® Гх ( X2 Y2 } 1 ( п п 1 V,U, ГГ f(X,Y)cxp\-^--AdXdY+-\ J- gQ gp У A.X Ay J 2 Py^y J
(V2 - )1/2 - (V2 - V/2 и о ^ = {^-P^2} ; = g
Уравнения для размера пятна моды
я 4х[“р а/ J х1 Y4 Й"л].ю]./а*ехр1 Al ^fdxdy А=Я" Г r^expf-^-^dXdy V2y Л J-оо J-« Pl *yf
Примечание. Параметры определены в табл. I, оси координат изображены на
рис. 16.1.
315
оо оо
J J [Л2и2 (х, ^)Ф2 - (d'i'/dx)2 - (d^/dyy]dxdy
~2 _ -со -оо
Р ------------------ОО--55-----------------------------
J / Ф2 dxdy
(П.2)
где к = 2я/Х, X — длина волны в вакууме. Размеры пятна мод могут быть
определены, если (17.1) подставить в уравнение (17.2) и найти решение,
удовлетворяющее одновременно двум уравнениям
-^7 =0; -^7 =0. (17.3)
<4 дау
Подстановка полученного решения обратно в уравнение (17.2) дает значение
постоянной распространения, а следовательно, и полностью определяются по-
ля в табл. 17.1. Выражения для поправок 6/3 х и 6/Зу получаются подстанов-
кой этих выражений в (13.11).
Вывод выражений для ах, ау и /3 из табл. 17.1 упрощается, если перейти
к нормированным относительно характерных размеров поперечного сечения
рх и р координатам X и У, нормированным частотам Vx и Vy, параметрам
моды их и Uy9 размерам пятна модЛх и Ау. Вариационное уравнение и урав-
нение для размера пятна моды непосредственно следуют из уравнений (17.2)
и (17.3) при использовании интегрирования по частям и коррекции постоян-
ных распространения уравнения (13.11).
В качестве иллюстрации данного метода рассмотрим конкретный пример.
17.2. Пример. Неограниченные степенные профили показателя преломления
Профили такого типа в декартовых координатах описываются следующим соотно-
шением:
пг(х,у) =л^[1 -2Д(|^|Ч + 1-Н4)], (17.4)
Рх Гу
где q - положительная постоянная. Параболический (q — 2) и линейный (q = 1) профи-
ли, рассмотренные в предыдущей главе, являются частными случаями неограниченного
степенного профиля показателя преломления. В рамках гауссова приближения в уравне-
нии для пятна моды из табл. 17.1 положим f = |X|q + | Y|q и с помощью интеграла
(37.107) получим
А = г _____________________ii/(q + 2). . — г____________________ii/(q + 2)
х 1<?Г(<?/2 + И)Г= J ’ У 1<7Г(<7/2 + И)Г^
(17.5)
где Г (х) - гамма-функция, а остальные параметры определены в табл. 17.1. Подстанов-
ка выражений (17.5) обратно в уравнение для постоянной распространения приводит к
уравнению
ss[Л)ТО.О ,
zq я Ру рх J
(17.6)
Степенные профили удовлетворяют условию (16.196) и, следовательно, являются одно-
родными функциями. Поэтому уравнение (17.6) должно являться частным случаем бо-
лее общего уравнения (16.20). Для неограниченного линейного профиля (q = 1) урав-
нение (17.6) сводится к точному характеристическому уравнению (16.29), если не учи-
тывать постоянные, множители 1,018 в правой части уравнения (16.29) и 3/(2тг1/3) =
= 1,024 в (17.6), что дает относительную ошибку 0,6 %. Отличное совпадение результа-
316
тов не зависит от рх и ру и показывает, что гауссово приближение справедливо при лю-
бом эксцентриситете поперечного сечения волоконного световода.
Величина двойного лучепреломления определяется разностью между скорректиро-
ванными постоянными распространения двух основных мод 60х — б/Зу. Из табл. 17.1
и выражений (17.5) получаем
(6/3 _5/3 )= ^-3ql 1/(ч + 2)[ф.)4Ч/(Ч + 2) _lb
( Х V 2рх V Я- J х J (17.7)
Для параболического профиля (q = 2) это выражение в точности совпадает с соответ-
ствующим выражением в табл. 16.1.
Отметим, что при произвольном q двойное лучепреломление растет с ростом эксцен-
триситета поперечного сечения.
ВОЛОКОННЫЕ СВЕТОВОДЫ С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
Рассмотрим теперь некоторые свойства волоконных световодов с эллипти-
ческим поперечным сечением, ограничившись случаем произвольного профи-
ля показателя преломления, при этом кривые постоянного показателя пре-
ломления представляют собой эллипсы с неизменным эксцентриситетом
(концентрический профиль). Одним из примеров такого профиля может слу-
жить параболический профиль, изображенный на рис. 16.1. В общем случае
закон изменения показателя преломления в концентрическом профиле мож-
но представить в виде
2 У
п2(х,у) = и£0[1 -j-)]; - оо < х, у < оо, (17.8)
Рх Ру
где f — произвольная функция одной переменной (х/рх)2 + (у/ру)2. Такая
форма профиля приводит к существенному упрощению уравнения для раз-
мера пятна моды и, как будет показано ниже, к тому, что эллиптический све-
товод имеет такую же постоянную распространения, что и круглый, при усло-
вии, что эксцентриситет эллипса невелик, а объемы профилей равны.
Уравнения для размера пятна основной моды. Эллиптическое поперечное
сечение трансформируется в круглое переходом к соответствующей системе
координат
X = х/рх = R sin <р, Y = у/ру =R cos<p. (17.9)
В этой системе координат функция профиля (17.8) является функцией
f(R2), соответствующей круглому световоду, а уравнения для размера пят-
на моды в табл. 17.1 принимают вид
2я A v оо лс 2л
—у = —ехр(-яЯ2) J (1 - cos 2^)exp(Z?^2cos 'l^dydR, (17.10а)
Их лу0 dR о
А.. °° ЛТ 2л
— р-f R2 ^-ехр(-ч?Л2) j* (1 + cos 2$) exp (bR2 cos l^dtpdR, (17.106)
Vy Ax о о
где a nb — постоянные величины, определяемые соотношениями
4- Д 2 _ А
а=—*_____Я- X____* .
2А2А2 ’
А у А у
(17.П)
317
Интегрирование по <р приводит к модифицированным функциям Бесселя пер-
вого рода. Поэтому, складывая и вычитая уравнения (17.10), получаем
-тЪ-+ R2 ^xp(-^R2)I0(bR2)dR, (17.12а)
лхгх Ау*у О аК
-V. - = ..2fS> (17.126)
^ХИХ Лу у 0
Для поперечного сечения с произвольным эксцентриситетом эти уравнения
могут быть решены только численными методами. Однако если эксцентри-
ситет мал, то можно получить аналитическое выражение.
17.3. Малая эллиптичность
Чтобы получить выражение, связывающее параметры эллиптического свето-
вода с параметрами круглого, предположим, что профиль показателя пре-
ломления (17.8) является ограниченным и имеет тот же объем £2, что и про-
филь круглого световода. Тогда, подставляя (17.8) в выражение (14.42),
интегрируя по сердцевине, ограниченной эллипсом (х/рх)2 + (//ру)2 = 1, и
учитывая преобразование (17.9), получаем выражение
рхРу=Р2, (17.13)
не зависящее от формы профиля, где р — радиус сердцевины круглого све-
товода. При небольшой эллиптичности поперечного сечения разложение вы-
ражения из табл. 17.1 в ряд и взятие членов порядка е2 дает
рх =р(1+е2/4); р = р(1—е2/4);
(17-14)
Кх = К(1 +<?2/4); Ку = К(1 - е2/4),
где V — нормированная частота круглого световода.
Если сравнить выражения (17.1) и (15.2), то при рх = ру = р для основной
моды получим Ах = Ау = Ro при е = 0. Здесь Яо нормированный размер мо-
ды в табл. 15.1. Поэтому в случае малой эллиптичности можно положить
Лх =Я0(1 + е2Рх); -4у =7?0 (1 + е2ру) (17.15)
и тем самым аппроксимировать выражения (17.11) следующим образом:
(П..6)
^0
а =
Д2О
Используя разложение (37.85) для функций IQ(x) и Ц(х) при малом значе-
нии аргумента, имеем
/о(6Я2) 1 +62Я4/4; Л (РА2) ~РА2/2. (17.17)
Подставим теперь выражения (17.14) - (17.17) в уравнение (17.12а) и при-
равняем коэффициенты при одинаковых степенях эксцентриситета е2. Коэф-
фициенты при нулевой степени дают уравнение для размера пятна моды круг-
лого световода в табл. 15.1, а коэффициенты при второй степени — соот-
ношения
px+py = 0; a = l/Rl
(17.18)
318
Если в табл. 17.1 положить ^х&у - £^2, то видно, что уравнение для постоян-
ной распространения совпадает с соответствующим уравнением в табл. 15.1
(с учетом интегрирования по частям). Таким образом, в рамках гауссова
приближения постоянная распространения эллиптического световода равна
постоянной распространения основной моды круглого световода при усло-
вии, что объемы профилей показателя преломления равны, а эксцентриси-
тет невелик.
Подставляя выражения (17.14) — (17.18) в уравнение (17.12а) и прирав-
нивая коэффициенты при нулевой степени е, получаем
1 V2 °° л df R2
''лЧ!1’ эдГ ^ехр(^)',кг' (1719)
Таким образом, если известен размер пятна основной моды круглого свето-
вода, то подстановкой (17.19) в соотношение (17.15) можно получить яв-
ное выражение для размера пятна основной моды эллиптического световода.
17.4. Пример. Ступенчатый профиль показателя преломления
В эллиптических световодах со ступенчатым профилем граница м.ежду сердцевиной с по-
казателем преломления исо и оболочкой с показателем преломления представляет
собой эллипс (л7рх) 2 + 07Ру) 2 = 1, где оси координат х и у изображены на рис. 16.1.
Уравнение для размера пятна моды (17.12) можно записать через функцию профиля
круглого ступенчатого световода. Поскольку df/dR = 8(R - 1), где 5 - 6-функция Ди-
рака, то, складывая и вычитая уравнения (17.12), получаем
Лу = ЛХГ’ [/0 -Л]е-а; Ax = AyVy(I0+I,)e\ (17.20)
где Io = IQ(b), = У, (b), а остальные параметры определены в табл. J7.1. Проводя не-
сложные алгебраические преобразования и используя определение (17.11), приходим к
соотношению
(2 - е2 - p2J 1
а = ~ьУГ7^ 57-77-=ln(W4ln(/’“/?)’ (17-21)
которое справедливо при любом эксцентриситете.
Предельный случай. Планарный волновод. Если зафиксировать Ру и устремить рх к
бесконечности, то эллиптический световод трансформируется в симметричный планар-
ный волновод, изображенный на рис. 17.1. При этом размер пятна моды а* а нор-
мированный размер пятна Лх = ^х/рх -> 0 (17.56). Поэтому а и Ъ в (17.11) становятся
неопределенными величинами. Чтобы избежать этого, подставим асимптотические выра-
жения (37.88) для модифицированных функций Бесселя во второе уравнение (17.20)
и, опустив члены высоких порядков, получим
Л’1п(2ЛуК’/х/7) = 1. (17.22)
С помощью таблицы 15.1 легко показать, что в рамках гауссова приближения это выра-
жение есть уравнение для размера пятна основной моды ступенчатого планарного волно-
вода с полушириной сердцевины ру
Малая эллиптичность. Решение уравнения (17.21) при малой эллиптичности, т. е. в
случае, когда в разложении параметров в ряд членами, порядок которых выше е2, мож-
но пренебречь, получается из соотношений (17.15) и (17.19), где согласно табл. 15.2
нужно положить df/dR = 8 (R ~ 1), а/?0 — (2 In V) ~1/2. Таким образом,
А*= (2 In Г)1/2 ~ Т (1 + In К) ’ АУ= (2 In И)1/2 +Т 1 +1п Г 1’ (17’23)
319
а двойное лучепреломление на основании табл. 17.1 определяется выражением
е2 (2Д)3,2 4 (In И)3
(17.24)
где р и V - радиус сердцевины и волоконный параметр круглого световода с объемом
профиля, равным объему профиля эллиптического световода.
17.5. Пример. Гауссов профиль показателя преломления
В эллиптическом световоде гауссов профиль определяется выражением
( у2 у"1 )
п2 (х,у) = п2со <1 - 24 [1 - ехр(- —-—)]>; -°° < х> У < °°- (17.25)
I рх ру J
Если в выражении (17.12) для круглого световода положить f — 1 - ехр(-А2), то, ис-
пользуя интеграл (32.102) , найдем, что нормированный размер пятна моды является ре-
шением системы связанных уравнений
V3 А3 у3 А3
А = (-У)1/2___У-_• А = (-^-)1/2__
* 1+а2’Ау (< 1+л’ ’
(17.26)
Исключение Л у приводит к уравнению четвертой степени для Л2, которое имеет явное
решение при произвольном эксцентриситете [2]. Выражения в приближении планарно-
го волновода могут быть получены способом, аналогичным изложенному в предыду-
щем разделе.
В случае малой эллиптичности в табл. 15.1 положим Ro = (V - 1)"1/2 и из соотноше-
ния (17.19) с учетом (17.15) получим
ЛХ (Г-1)1/2^ 4 (2Г-1)]’ АУ (Г-1)1/2^+4 (2Г—1)^’ (17'27)
где р и V - параметры круглого световода с гауссовым профилем равного объема. Из
табл. 17.1 получаем выражение для двойного лучепреломления
е2 (24)3/2
6'3х-5'?у=-------—
(К-1)3
(2И- 1)К3 ’
(17.28)
имеющее физический смысл только при V > 1.
ГЛАВА 18. МОДЫ ВОЗМУЩЕННЫХ ВОЛОКОННЫХ СВЕТОВОДОВ
До сих пор в ч. II рассматривались световоды, форма поперечного сечения и
профиль показателя преломления которых позволили получить точные или
приближенные выражения для полей мод. В гл. 12, 14 и 16 было показано,
что только для нескольких типов световодов существуют точные решения
скалярного волнового уравнения (как в случае произвольного, так и в слу-
чае слабонаправляющего световода). Однако в гл. 15 и 17 было рассмотрено
гауссово приближение для полей мод и показано, что даже при отсутствии
точного решения скалярного волнового уравнения они могут быть описаны
аналитически.
Эта глава посвящена рассмотрению свойств мод произвольных и слабона-
правляющих световодов с формой поперечного сечения и (или) профилем
показателя преломления, незначительно отличающимися от соответствующих
параметров световода, аналитические выражения для полей мод которого
320
известны. Поскольку под термином ’’незначительно отличающиеся” понима-
ются отклонения, влияния которых на свойства мод могут быть описаны в
рамках теории возмущений, например слабая анизотропия, слабое поглоще-
ние или небольшая эллиптичность, для краткости такие световоды в дальней-
шем будем называть возмущенными. Отметим также, что к этому типу от-
носится и сложный оптический волновод, содержащий две или более доста-
точно далеко расположенные сердцевины. В этой главе будет показано, как,
используя методы теории возмущений, получить выражения для полей мод
возмущенного световода, если соответствующие решения для невозмущен-
ного световода известны.
Возмущения с цилиндрической симметрией. Все возмущения, рассматри-
ваемые в данной главе, не зависят от продольной координаты z, поэтому воз-
мущенный световод обладает цилиндрической симметрией, или трансляци-
онно инвариантен, и его модам присущи все свойства, описанные в гл. 11.
Возмущенный световод характеризуется профилем показателя преломления
п (х, у) и неизвестными электрическими и магнитными полями мод, которые
для любой моды можно записать в виде (11.6)
E(x,y,z) = е(х, y)exp(i^); Н(х, у, z) = h(x, y)exp(ij8z), (18.1)
где /3 — постоянная распространения. Соответствующая мода невозмущенно-
го световода характеризуется профилем показателя преломления п(х, у) и
известными полями с постоянной распространения 0
Ё(х, у, z) = е(х, y)exp(ij3z) ; Н(х, у, z) = h (х, у) exp(i^z) . (18.2)
Таким образом, задача заключается в нахождении связи между выраже-
ниями (18.1) и (18.2), для чего следует рассмотреть отдельно слабонаправ-
ляющие и произвольные волоконные световоды. Поскольку в дальнейшем
рассматриваются главным образом определенные моды, в выражениях ин-
декс моды опускается.
МОДЫ СЛАБОНАПРАВЛЯЮЩИХ ВОЗМУЩЕННЫХ ВОЛОКОННЫХ СВЕТОВОДОВ
Если возмущенный и невозмущенный световоды являются слабонаправляю-
щими, то изменение показателя преломления п и п в сечении обоих светово-
дов мало и поля мод могут быть получены из решений скалярного волново-
го уравнения (см. гл. 13). Если Ф и /3 обозначают неизвестные решения и по-
стоянную распространения возмущенного световода, то они являются реше-
ниями уравнения
[V* + к2п2 (х, у) - 02]Ф = О, (18.3а)
а известные решения и постоянная распространения невозмущенного свето-
вода удовлетворяют уравнению
[^2 + к2^(х,у) -|Р]Ф=О, (18.36)
где V2 — поперечный оператор Лапласа, к = 2тг/Х и А — длина волны в ваку-
уме . Знак обозначающий в гл. 13 скалярные величины, для ясности
опущен.
Чтобы выразить Ф и /3 через Ф и 0, используем соотношение взаимности
этих двух решений. Как показано в разд. 33.5, оно следует непосредственно
из уравнений (18.3) и выражается уравнением (33.20)
1 1 Зак 37
321
J (г/2 - Г? )ФФ<±4
p2 _ 02 = k2 А»--------------, (18.4)
f ФФбМ
где Аж ~ бесконечное поперечное сечение, аФиФ для удобства предполага-
ются действительными функциями. Рассмотрим вначале возмущения в оди-
ночном световоде; а затем в сложной системе, состоящей из двух параллель-
ных световодов.
18.1. Решение для возмущенных изолированных волоконных световодов
Если профиль показателя преломления и (или) форма поперечного’ сечения
одного световода незначительно отличаются от соответствующих параметров
другого, то в большинстве случаев можно считать, что поперечные по л я_ мод
этих световодов идентичны, т. е. е ~ е\ h ~ h и, следовательно, Ф ~ Ф. Ис-
ключениями служат лишь поляризационные поправки к скалярной постоян-
ной распространения, для вычисления которых требуются поправки более
высоких порядков к Ф, получаемые либо разложением собственных функ-
ций волновода в ряд, как в разд. 33.9 и 33.10, либо, как в гл. 34, использова-
нием функций Грина.
Хотя поля мод возмущенного и невозмущенного световодов можно счи-
тать одинаковыми, предположить, что постоянные распространения этих мод
равны, нельзя, так как зависимость поля возмущенного световода (18.1)
от продольной координа1ы пропорциональна множителю j3z. Поэтому даже
небольшая ошибка при определении /3 приведет к большой ошибке при опре-
делении полного поля, поскольку величина z может быть достаточно боль-
шой. При этом поправка к постоянной распространения /3 может быть полу-
чена из уравнения (18.4), если положить Ф = Ф. В_случае слабонаправляюще-
го световода можно считать ff2 - /З2 2кпсо ((3 - 3) и и2 - п2 2«со (п - п) ,
предполагая, что псо — максимальный показатель преломления в возмущен-
ном иневозмущенномсветоводах.Такимобразом, из уравнения (18.4) имеем
0 = 0 + £[) (n-ri)^2dA]l J Ф2сМ,
А оо А оо
(18.5)
где интеграл в числителе не равен нулю в области, в которой параметры воз-
мущенного и невозмущенного световодов различны.
Для того чтобы описание полей мод возмущенного световода было пол-
ным, необходимо определить поляризацию поперечных компонент поля.
18.2. Поляризация возмущенных полей
Если невозмущенный световод имеет поперечное сечение произвольной фор-
мы, то поперечное электрическое поле каждой моды поляризовано вдоль од-
ной из оптических осей х0 или у0 (см. разд. 13.5 и 13.8). Направления опти-
ческих осей возмущенного световода определяют азимут поляризации воз-
мущенных полей мод и могут быть найдены либо из соображений симмет-
рии, либо формальными методами, изложенными в разд. 32.5.
322
Возмущения, нарушающие циркулярную симметрию. Во многих приме-
рах, приведенных ниже, невозмущенные световоды обладают циркулярно-
симметричными профилями и формой поперечного сечения. Если характер
возмущения таков, что циркулярная симметрия не нарушается, то поляриза-
ция каждой моды остается неизменной и подчиняется правилам, изложенным
в разд. 13.4 и 13.7. В противном случае моды поляризованы вдоль осейх0 и
у о возмущенного световода. В любом случае основные и НЕ 1т -моды остают-
ся линейно поляризованными в световодах как с круглыми, так и с произ-
вольными поперечными сечениями. Поляризация остальных мод при неболь-
шом отличии формы поперечного сечения от круглого определяется метода-
ми, рассмотренными в разд. 13.9.
Поляризационные поправки к постоянной распространения. В общем слу-
чае поправки и к скалярной постоянной распространения (3 мод воз-
мущенного световода с поперечным сечением произвольной формы разные,
что обусловлено анизотропией, или двойным лучепреломлением световода.
С этой точки зрения интерес представляют главным образом основные моды,
для вычисления поправок к постоянным распространения которых соглас-
но табл. 13.1 требуется определение поправки первого порядка к приближен-
ному решению скалярного волнового уравнения. В разд. 18.10 все эти поправ-
ки будут получены для волоконного световода с небольшой эллиптичностью.
Чтобы показать широкий диапазон применимости полученных результа-
тов, в данной главе используются результаты этого и предыдущих разделов
к решению различных проблем возмущенных световодов.
18.3. Однородные изменения профиля показателя преломления
Это довольно распространенный случай, что будет подтверждено ниже семью
примерами, при котором возмущение параметров световода эквивалентно
изменению показателя преломления на постоянную величину в некоторой
области поперечного сечения. В этой области профиль показателя преломле-
ния возмущенного световода имеет вид
п (х, у) = п (х, у) + би, (18.6)
где би - постоянная величина. Подставляя (18.6) в уравнение (18.5) и учи-
тывая определение плотности мощности из табл. 13.2, получаем
3 = 3 + ^рби, (18.7а)
где т?р — часть полной мощности невозмущенной моды, протекающей через
поперечное сечение А р области возмущения, т. е.
пр = J Ф2 dA/ J $2dA. (18.76)
А Аж
Р
Из (18.7) с очевидностью следует, что чем больше часть мощности моды в
во шущенной области, тем больше различие между (3 и(3. Чтобы получить ко-
1Р
323
личественную оценку, необходимо в (18.7) подставить выражения для Ф.
В гл. 14 и 16 для ряда форм поперечного сечения и профиля показателя пре-
ломления получены точные выражения Ф, а в гл. 15 и 17 дано гауссово при-
ближение в случае световодов с произвольным профилем показателя пре-
ломления.
18.4. Пример. Однородные изменения показателей преломления сердцевины
и оболочки
Предположим, что в волоконном световоде с градиентным профилем показатель пре-
ломления сердцевины повсюду отличается от показателя преломления невозмущенного
световода на 5«со- Тогда в (18.7) можно положить пр — п, би — б«со, гДе доля мощ-
ности моды, распространяющейся по сердцевине (см. табл. 13.2). Доля мощности в обо-
лочке равна 1 - г?, так что если показатель преломления оболочки отличается на 5«с| от
соответствующего параметра невозмущенного световода, то постоянная распростране-
ния в возмущенном световоде определяется соотношением
в = р+k[vsnco+ (1 -п)бис1], (18.8)
где к = 2тг/Х и X - длина волны в вакууме. Отметим, что в этом случае постоянная рас-
пространения не зависит ни от формы поперечного сечения, ни от профиля показателя
преломления. Поляризацию возмущенного поля моды можно определить на основании
соображений, изложенных в разд. 18.2. Точные и приближенные выражения для rj в слу-
чае круглого поперечного сечения приведены в гл. 14 и 15.
18.5. Пример. Трехслойный волоконный световод
Пусть невозмущенный круглый световод имеет сердцевину с радиусом р, профиль по-
казателя преломления п(г) и оболочку с однородным показателем преломления иср
Предположим теперь, что имеется третья область с показателем преломления п0
расположенная вне радиуса р0 > р, как это показано на рис. 18.1, а. При условии мало-
сти &п = п0 - «С1 возмущение является слабым и постоянная распространения моды
согласно (18.7) определяется выражением
(3 = 0+kfip(no - «cP’ (18.9)
где т?р - часть мощности модьГ, распространяющейся в области г > р0.
В качестве иллюстрации этого результата рассмотрим основные моды световода со
ступенчатым' профилем показателя преломления. Подставляя вместо Ф выражение для
Fq из табл. 14.3 и предполагая, что р0 достаточно велико, так что KQ (WR) можно заме-
нить асимптотическим выражением (37.88), с помощью интеграла из табл. 14.6 получим
Рис. 18.1. Поперечное сечение световода возмущенного третьим слоем (а); тонкой про-
межуточной оболочкой (б); изолированной неоднородностью (в)
324
{n^n , (18.10)
Р Р v 0 сР 2 WV 7 К} (ИО
где параметры определены в табл. I.
Случай тонкой промежуточной оболочки. Другой пример трехслойного световода
дан на рис. 18.1, б. Промежуточная оболочка представляет собой тонкое концентричес-
кое кольцо толщиной бри с показателем преломления п0. Поскольку дп = п0 - иср
то из (18.7) имеем
(3 = (3 +др (п0 - п^кр*2 (p)I°$ &rdr, (18.11)
О
где Ф(р) - поле невозмущенного световода на границе сердцевины с оболочкой.
Для основных мод ступенчатого световода Ф — Fo и, используя выражение для инте-
грала в табл. 14.6, получим
0 = ? + 2("о - I’ (18.12а)
где А*! - модифицированная функция Бесселя второго рода. Дальнейшее упрощение
формулы возможно, если использовать гауссово приближение (15.2) дляА0. Посколь-
ку размер пятна моды определяется выражением в табл. 15.2, то при условии, что V > 1,
имеем
др In И2
0 = 0 + 2(яо (18.126)
18.6. Пример. Изменение радиуса сердцевины
Рассмотрим ступенчатый волоконный световод с показателями преломления сердцеви-
ны и оболочки «со и и предположим, что радиус сердцевины увеличился и стал равен
р + др. Такое возмущение будет эквивалентно изображенному на рис. 18.1, б, если поло-
жить^ = п . Таким образом, из выражения (18.12) получаем
(18.13а)
' 0! v (io
в случае точного выражения для поля основных мод и
, Sp In V2
0«0+(2Д)1/2-з-----—; К>1, (18.136)
Р V
если использовать гауссову аппроксимацию. При выводе предполагалось, что «со
и поэтому в выражениях для V и Д можно положить я2 - «2i ~ 2яег. (ппе. - .
vv U1 VW LU UI
18.7. Пример. Изолированная неоднородность
Рассмотрим круглый волоконный световод с произвольным профилем показателя пре-
ломления п (г), в котором имеется небольшая неоднородность, остающаяся неизменной
вдоль всего световода (см. рис. 18.1, в). Пусть неоднородность имеет площадь попереч-
ного сечения <5 Л, средний показатель преломления nQ и расположена на расстоянии р0
от оси световода. Выражение для возмущенной постоянной распространения следует из
соотношения (18.7):
0 = p+k6A [n0 - «(p0)]^ (p0)/2TrJ^^, (18.14)
О
так как Ф зависит только от г. На первый взгляд приведенный пример является триви-
альным, однако поскольку неоднородность нарушает азимутальную симметрию, то по-
является необходимость в определении поляризации мод возмущенного световода. Со-
ображения, изложенные в разд. 18.2, и симметрия возмущенного световода позволяют
325
угверждать, что векторы поперечного электрического поля основных мод направлены
вдоль осей х и у (рис. 18.1, в). Ниже этот вопрос рассматривается при обсуждении
свойств световодов произвольной формы.
18.8. Пример. Волоконные световоды с поглощением
Некоторые свойства волноводов с поглощением рассматривались в гл. 11. Здесь рас-
сматривается световод, у которого коэффициент поглощения мал и который можно рас-
сматривать как возмущенный по отношению к световоду без поглощения.
Предположим, что имеется волоконный световод с произвольной формой поперечно-
го сечения. Поглощение в нем описывается мнимыми добавками i6«co и i5n соответ-
ственно к профилю показателя преломления сердцевины и к показателю преломления
оболочки. Поскольку в данном случае би в выражении (18-7) является мнимой величи-
ной, то и поправка к 0 будет мнимой. Если ее обозначить 01. то по аналогии с уравнени-
ем (18.8) имеем
? = Цп5Исо+ (1 -П)5и'с1], (18.15)
где г? - доля мощности моды, распространяющейся в сердцевине. Определив коэффици-
енты поглощения мощности в сердцевине и оболочке соответственно как асо = 2кбп1С0
и ас| ~ 2к8п*^ с помощью табл. 13.2 получим следующее выражение для коэффициента
затухания [1J:
7 == т?аСо + П ~ п) ас1’ (18.16)
т. е. мощность моды на длине z уменьшается в exp(~7z) раз.
Физическая интерпретация. Из выражения в табл. 13.2 следует, что при распростране-
нии моды по световоду с поглощением форма распределения интенсивности по попереч-
ному сечению 5 остается неизменной, а амплитуда распределения на расстоянии z от на-
чала световода уменьшается в exp(-7z) раз по сравнению с первоначальной. Если коэф-
фициент поглощения мощности а одинаковый по всему поперечному сечению, то у - а
и мощность, потерянная вследствие затухания, в любой точке поперечного сечения в
точности равна поглощенной. Этому частному случаю в уравнении (18.16) соответству-
ет асо = ас| - а, и поэтому у = а. Однако если величина а зависит от координаты по-
перечного сечения, то условие равенства потерь мощности вследствие затухания и по-
глощенной мощности для любой точки поперечного сечения нарушается и, следователь-
но, внутри поперечного сечения будет существовать поток мощности. В этом общем слу-
чае в уравнении (18.16) асо #= аср а поток мощности через границу сердцевины с обо-
лочкой поддерживает неизменной форму распределения интенсивности моды. Направле-
ние этого потока зависит от соотношения между асо и аср Так, например, в случае ас| =
= 0 наблюдается приток мощности в сердцевину.
18.9. Пример. Анизотропная сердцевина
Анизотропия и анизотропные волноводы рассматривались в конце гл. 11. В гл. 12 были
приведены примеры таких волноводов, а в разд. 13.12 обсуждались свойства слабона-
правляющих анизотропных волноводов. В этом примере волновод со слабой анизотро-
пией рассматривается как возмущенный по отношению к изотропному, при этом внима-
ние концентрируется на волоконном световоде с оболочкой, анизотропия которого
определяется сердцевиной. Это характерно для фоторецепторов зрения [2-4] и свето-
водов с кристаллической сердцевиной [5].
Неограниченная однородно-анизотропная среда. Для начала рассмотрим плоскую
волну, распространяющуюся в направлении z в неограниченной среде со слабой анизо-
тропией, характеризуемой показателем преломления п = п + 6«Х для электрического
поля, поляризованного вдоль оси х, и п = п + бПу — для электрического поля, поляризо-
ванного вдоль оси у, где п - показатель преломления изотропной среды, а 6«х и 6иу -
326
постоянные величины. Если в изотропной среде плоская волна может быть поляризова-
на в любом направлении, то в анизотропной среде возможны только два состояния по-
ляризации, характеризуемые двумя различными постоянными распространения. Волна,
поляризованная вдоль оси х, имеет постоянную распространения 0Х = кп + к8пх, а вол-
на, поляризованная вдоль оси у, - /Зу ~ кп + кЬпу. Если к тому же среда дихроичная, то
и коэффициент поглощения а зависит от состояния поляризации волны. Для удобства
предположим, что главные оси действительной и мнимой частей матрицы показателя
преломления, описывающей анизотропию, совпадают. В таком случае коэффициенты
поглощения мощности для двух поляризаций определяются выражениями
ах=2*6пх; ау = 2к6п . (18.17)
где i6пх и - малые мнимые компоненты, связанные с Ъпх и 5«у.
Анизотропный световод. Очевидно, что в круглом волоконном световоде с анизо-
тропной сердцевиной одна из основных мод поляризована вдоль оси х и имеет постоян-
ную распространения &х, а другая поляризована вдоль оси у и имеет постоянную распро-
странения 0у. Если п (х, у) — профиль показателя преломления изотропного световода,
то для моды, поляризованной вдоль оси х, п - п + а для моды, поляризованной
вдоль оси у, п = п + 6Пу. Если анизотропия мала и постоянна по поперечному сечению,
то Ьпх и <5Ну - константы. Тогда в уравнении (18.8) можно положить - 0 и заме-
нить 5исо на 6«х или на 6ny. В результате имеем [2, 3]
0Х = 0 + Лд6нх; 0у = /3 + кт]8пу,
(18.18)
где д - часть мощности основной моды, распространяющейся в сердцевине невозмушен-
ного (изотропного) световода, а /3 - постоянная распространения этой моды. Повторяя
рассуждения, приведенные в разд. 18.8, из выражений (18.16) и (18.17) получаем
^Х^^Х’ ^у-^У
(18.19)
Таким образом, световод одинаково влияет как на анизотропию, так и на поглощение.
18.10. Пример. Эллиптическая деформация
Рассмотрим круглый волоконный световод со ступенчатым профилем и показателями
преломления сердцевины и оболочки «со и соответственно. Предположим, что он
деформирован до небольшой эллиптичности (рис. 18.2, а), но площадь сердцевины оста-
лась неизменной, т. е.
рхру = р5; р = (1 - ру/рх) 1/3 < < 1, (18.20)
где р - радиус сердцевины круглого световода, рх, ру и е большая и малая полуоси и
эксцентриситет эллипса поперечного сечения возмущенного световода. Область возму-
щения состоит из четырех заштрихованных частей (рис. 18.2, я). Поскольку эллиптич-
ность поперечного сечения мала, то области возмущения очень тонкие и поля в них мож-
но аппроксимировать полем круглого световода на границе серди,евины с оболочкой,
т. е. положить Ф(г, = Ф(р, 99), где г и - цилиндрические координаты на рис. 18.2, а.
Радиальная ширина области возмущения 6р определяется эллиптичностью границы
между сердцевиной и оболочкой. Поскольку уравнение границы (х/р )2 + О/ру)2 — 1,
то, переходя к полярным координатам и разлагая уравнения (18-20) в ряд, с учетом
членов порядка е2 получим 6р = е2р/4 cos 2<р. Подставляя это выражение в формулу
для возмущенной постоянной распространения (18.7а), имеем
/3 = /3 +к (псо - нср (т?х + Пу), (18.21а)
327
Рис. 18.2. Поперечное сечение эллиптически деформированного световода со ступенча-
тым профилем показателя преломления и с площадью сердцевины, равной площади
сердцевины круглого световода (д), и зависимость нормированной величины двойного
лучепреломления В (18.25) и гауссово приближение этой величины^ (17.24) от нор-
мированной частотьт световода (б)
где (3 - постоянная распространения круглого световода, а дх и i?y определены выраже-
ниями
7Г/4 л оо2тг
nx = e2p2 J Ф2 (р, <р) cos 2<^J<^/ J J Ф2 {r, y)rdrdy, (18.216)
О 0 0
тг/2 оо2ТГ_
п - е2р2 J Ф2 (р, <р) cos 2<pd<p/J / Ф (г, <p)rdrd<p (18.21в)
у тг/4 0 0
и соответствуют заштрихованным областям, пересекающим соответственно оси х и у.
Основные моды. Поле основных мод круглого световода не зависит от <р. Следова-
тельно, в уравнениях (18.21) дх = -т?у и 0 = 0. Другими словами, если площади сердце-
вин круглого и эллиптического световодов с малым эксцентриситетом равны, то равны
и их постоянные распространения основных мод [б]. Условие равенства площадей экви-
валентно требованию равенства объемов профилей, как это следует из (17.13). Таким
образом, полученный результат является частным случаем более общего, полученного
в разд. 17.3. Согласно ему в рамках гауссова приближения при равенстве объемов про-
филя постоянные распространения основной моды круглого и эллиптического светово-
дов с произвольным профилем показателя преломления равны.
Поля мод эллиптического световода. Приближение Ф = Ф становится недействитель-
ным при определении векторных поправок к скалярной постоянной распространения
эллиптического световода. В разд. 34.8 методом функций Грина получены выражения
для полей мод эллиптического световода с учетом членов порядка е2
--------+ е ----- ------ --------- ---------
J0(U) 8 Л (to KQ(W) J,(U)
Ко (WR) + ^2 JQ(U) J2(U) «2 (W?)
/С0(Ю 8 Л (CO A W
(18.22а)
(18.226)
1 <2? < 00,
где — функции Бесселя первого рода, модифицированные функции Бесселя вто-
рого рода, R = r/p, a U, W определены в табл. I. Первый член в правой часта выражений
(18.22) описывает поля мод круглого световода, которые в табл. 14.3 выражаются
функцией Fo. Аналогичный результат может быть получен также методом разложения
собственных функций световода в ряд [7 ] (см. разд. 33.9 и 33.10).
328
Двойное лучепреломление. Из свойств симметрии поперечного сечения эллиптическо-
го световода следует, что поля основных мод на рис. 18.2, а поляризованы вдоль осей
х и у. В случае ступенчатого профиля показателя преломления поляризационные поправ-
ки к скалярной постоянной распространения 8/Зх и 6/Зу могут быть получены из выраже-
ния (33.26) подстановкой et = Фх и et = Фу соответственно, где хи у - единичные век-
торы, параллельные осям координат. С учетом членов порядка е2 двойное лучепрелом-
ление определяется следующим выражением:
6/?х - 6/3 = ( ---р J* (^x-- п ) Ф ds/ J* (18.23)
х У 4тгИ s дх У ду о
где $ - эллиптическая граница между сердцевиной и оболочкой, ds ~р[1 + %e2cos 2<p]d<p,
пх и Пу - декартовы компоненты единичной внешней нормали к s, определяемые со-
отношениями
пх = (1 - е2 sin2<p) cos <р; пу~ (1 + е2cos2^) sin <^. (18.24)
Переходя в уравнении (18.23) к полярным координатам и подставляя в него выраже-
ние (18.22) при R = 1 и выражение (18.24), с помощью рекуррентных соотношений
(37.72), (37.73), (37.47) и характеристического уравнения из табл. 14.3 получаем
6/зх_^у=^ф-^-[^
МУ
J3, (U)
+ (U2 - IV3)
П (U)
(Ю
+ и2].
(18.25)
На рис. 18.2, б представлена зависимость нормированного двойного лучепреломления
Rp — (6/?х - 6/3у)р/е2 Д3/2 от нормированной частоты круглого световода V. Зависи-
мость построена с учетом значений U и W в табл. 14.4. Кривая имеет максимум при
V — 2,48, т. е. в точке, где обе основные моды имеют одинаковую групповую скорость.
Для сравнения на этом же рисунке (кривая В) приведена та же зависимость, получен-
ная в рамках гауссова приближения (17.24). Она лежит немного ниже точной зависимо-
сти (относительная ошибка равна 19 % при V - 2,48), и максимум смещен к V — 2,33.
В остальном эти кривые подобны друг другу.
Моды с индексом 1=1. Рассмотрим теперь моды эллиптического световода, кото-
рым соответствуют моды круглого световода с индексом / = 1. В этом случае решения
скалярного волнового уравнения для круглого световода можно записать в виде
Фе = Fx (R) cos <р; Фо = (R) sin <р, (18.26)
где выражение для F г приведено в табл. 14.6, а постоянные распространения четной и
нечетной мод одинаковы и равны fi. В отличие от случая основных мод, постоянная рас-
пространения мод с Z — 1 зависит от распределения поля в заштрихованных областях на
рис. 18.2, а. С помощью интеграла из табл. 14.6 находим
е2 U2 К2 (ИО
ru + = ±— , (18.27)
'х у 4 j/г (W)K2 (IV)
где знаки (+) и (-) относятся соответственно к четным и нечетным решениям, мо-
дифицированная функция Бесселя второго рода, а остальные параметры определены в
табл. I. Выражения для постоянных распространения /Зе и /30 эллиптического световода
могут быть найдены из выражения (18.21а). Например, в приближении слабонаправля-
ющего волновода
« _ Я = £1 (2Д)1/2 U2 Ъ (И7)
Рр Рг> л ------------ ----
4 Р v К„ (W)K2 (Г)
(18.28)
Почти круглый волоконный световод. На рис. 18.3, а схематически изображена транс-
формация поляризации поперечного электрического поля мод с индексом / — 1 при из-
329
Рис. 18.3. Трансформация поляризации поперечного электрического поля мод с индек-
сом / = 1 при изменении формы поперечного сечения световода от круглой к эллипти-
ческой (стрелки обозначают направление вектора электрического поля, сами поля мод
определены выражениями (32.42) и изображены на рис. 32.1) (д) и нормированный
параметр 2Д|л±|/еа (18.29) как функция нормированной частоты световода (частота
отсечки мод равна V = 2,4, а вертикальная штриховая линия соответствует V = 3,8(6))
менении формы поперечного сечения световода от круглой до эллиптической. Рассмот-
рим случай, когда форма поперечного сечения занимает промежуточное положение меж-
ду круглой и эллиптической с большим эксцентриситетом. Некоторые свойства мод та-
ких почти круглых световодов были рассмотрены ранее в разд. 13.9, где было показано,
что количественно свойства мод можно описать параметром Л, который дан в табл. 13.1.
С учетом выражений из табл. 14.6 и (18.28) получим
I. I -<? И ко W
(18.29)
330
где значки (+) и (-) в знаменателе Л обозначают 6^ - 6(32 и8(33 - 6(34 соответственно,
а выражения для полей мод взяты из табл. 13.1. На рис. 18.3, б изображена зависимость
нормированного параметра 2Д |л± |/е3 от V. Минимальные значения |л+| и |л_| равны
приблизительно е2/Д, поэтому в случае слабонаправляющих световодов дяже неболь-
шой эксцентриситет поперечного сечения световода приводит к трансформации эллипти-
чески поляризованных мод круглого световода в линейно поляризованные, так как
Д < < 1 для слабонаправляющих световодов. При V = 3,8 поляризационные поправки
и 8(32 равны и |Л+1 — °°. В этом частном случае линейно поляризованные моды яв-
ляются модами как эллиптического, так и круглого световодов (см. разд. 14.7).
18.11. Неоднородные изменения профиля показателя преломления
Если возмущение является неоднородным, то отличие между возмущенны-
ми и невозмущенными профилями показателя преломления зависит от коор-
динат, т. е. _
п (Л У) = п (х У) + (X У) • (18.30)
Это существенно усложняет оценку интеграла в выражении (18.5), и простая
интерпретация формулы (18.7) становится недействительной. Однако при ис-
пользовании гауссова приближения (гл. 15 и 17) можно несколько упрос-
тить выражения.
Рассмотрим, например, круглый световод, в котором возмущение показа-
теля преломления подчиняется гауссову закону
5п(г) =6и(0)ехр[-(-^-)2]; |6и(г) | « п(г)у (18.31)
где а — характерный размер. Если Ф2 аппроксимировать гауссовой функ-
цией для основных мод ехр(—г2/го), где г0 — размер пятна основной моды
(см. табл. 15.1), то из уравнения (18.5) получаем
/3=|3 + fc5n(O) , (18.32)
где Ьп(г) = п - п. Для нахождения величины 0 остается только подставить
выражение для размера пятна моды. Примеры приведены в табл. 15.2.
МОДЫ ДВУХ ПАРАЛЛЕЛЬНЫХ ВОЛОКОННЫХ СВЕТОВОДОВ
До сих пор в этой главе исследовались возмущения параметров изолирован-
ных световодов. Теперь перейдем к рассмотрению возмущений, обусловлен-
ных взаимным влиянием двух параллельно расположенных волоконных све-
товодов. Сечение сложного оптического волновода изображено на рис. 18.4.
Анализ таких структур представляет практический интерес с’точки зре-
ния оптических перекрестных помех, которые подробно будут рассмотрены
ниже в гл. 29. В этой главе основное внимание уделяется волноводу, состоя-
щему из двух одинаковых или почти одинаковых световодов. В отличие от
рассмотренных выше возмущений одиночного световода, поле сложного вол-
новода нельзя достаточно точно аппроксимировать полем одиночного свето-
вода. Однако если световоды хорошо оптически разделены, т. е. амплитуда
поля одного из световодов на оси другого мала, и, кроме того, оба являются
слабонаправляющими, то поле сложного волновода достаточно хорошо ап-
проксимируется суперпозицией полей каждого из составляющих его светово-
дов в отдельности, при этом взаимным их влиянием можно пренебречь.
331
Рис. 18.4. Поперечное сечение сложного волновода с профилем показателя преломления
п (х, у), состоящего из двух волоконных световодов с радиусами сердцевин рх и р2.
Точка Р имеет полярные координаты и г2,<р2 относительно осей световодов, рас-
стояние между которыми равной
Ограничение на то, что световоды являются слабонаправляющими, весьма
существенно, поскольку, как показано ниже в разд. 18.21, простого извест-
ного метода возмущений в случае произвольных световодов не существует.
Поляризация и число мод. В оптическом волноводе, состоящем из одного
световода, существуют две ортогонально-поляризованные основные моды,
поля которых определяются фундаментальным решением скалярного волно-
вого уравнения (см. гл. 13). В случае же волновода, состоящего из двух све-
товодов, свойства симметрии структуры приводят к удвоению числа распро-
страняющихся мод. Таким образом, существуют два фундаментальных реше-
ния скалярного волнового уравнения и соответственно две пары основных
мод, т. е. четыре моды. Аналогично этому каждый набор из четырех мод выс-
ших порядков одиночного световода трансформируется в набор из восьми
мод сложного волновода. Поляризация полей мод такого волновода опреде-
ляется методами, изложенными в гл. 13, т. е. либо исходя из соображений
симметрии, либо методами теории возмущений.
Постоянная распространения. Вследствие асимметрии сложного волновода
постоянные распространения основных мод, определяемые фундаменталь-
ными решениями скалярного волнового уравнения, в общем случае разные.
Поэтому можно ожидать, что такой волновод будет обладать свойствами,
присущими анизотропным световодам, рассмотренным в разд. 18.9. В част-
ности, перекрестные помехи могут быть целиком объяснены в рамках скаляр-
ной теории, поскольку характерное расстояние, на котором проявляется этот
эффект, значительно меньше длин, на которых проявляются поляризацион-
ные поправки к скалярным постоянным распространения.
Обозначение параметров сложного оптического волновода. Профиль по-
казателя преломления сложного волновода обозначим п (х, у), где х и у —
оси координат, изображенные на рис. 18.4. Поля мод такого волновода опре-
деляются выражениями (18.1), в которых под е(х, у) и h(x, у) следует по-
нимать решения Ф(х, у) скалярного волнового уравнения (18.3), приведен-
ные в табл. 13.1. Изолированный невозмущенный световод 1 (см. рис. 18.4)
332
имеет профиль nCQ (х, у), а его поля мод определяет решение скалярного
волнового уравнения Ф j (х,_у). Соответствующие величины возмущающего
световода равны «с1 (х, у) и Ф2 (*, у) • Отметим, что в общем случае п Ф nQQ +
+ "cl-
18.12. Основные моды оптического волновода, состоящего из двух одинако-
вых волоконных световодов
Если оптический волновод состоит из двух одинаковых световодов, то фун-
даментальные решения Ф+ и Ф_ скалярного волнового уравнения определя-
ются симметрией поперечного сечения волновода и могут быть приближен-
но записаны в виде [9]
Ф+=Ф1+Ф2; ф_=ф1_ф2> (18.33)
где Ф1 и Ф2 - фундаментальные решения отдельного световода в системе
координат, изображенной на рис. 18.4. Эта же комбинация мод в разд. 18.18
получена методом теории возмущений.
Постоянные распространения. Постоянные распространения, соответству-
ющие решениям Ф+ и Ф_, обозначим соответственно (3+ и 0__, а под /3 будем
понимать общую постоянную распространения для решений Ф! и Ф2. В слу-
чае изолированных световодов /3+= /3_ = 0 .При достаточно большом расстоя-
нии между каналами в уравнении (18.4) можно положить (3 = (3±, Ф = Ф±,
п = исо, Ф = Ф!. Тогда с учетом приближения слабонаправляющёго волново-
да имеем
0+=0 + fc[J (п-п)^^+dA]/ J (18.34)
Ах с0 Ах
где п — профиль показателя преломления сложного волновода, А ж — беско-
нечное поперечное сечение, к = 2я/Х, X — длина волны в вакууме. Это выраже-
ние можно упростить, если в него подставить соотношение (18.33) и принять
во внимание ряд физических соображений, касающихся слабой электромаг-
нитной связи между световодами. Во-первых, вследствие экспоненциально
малой величины_Ф^ в сердцевине невозмущенного световода, в знаменателе
интегралом от Ф1Ф2 можно пренебречь по сравнению с интегралом Ф1.-Во-
вторых, основной вклад в интеграл в числителе вносит член Ф1Ф2, так как
разность п - nCQ отлична от нуля лишь вне сердцевины световода 1 (см.
рис. 18.4). Аналогичные аргументы применимы к профилям показателя пре-
ломления произвольной формы. Таким образом, имеем
0±=0±С; C = k[f (n-nC0)^^2dA]/f VjdA,
Aqo Аж
(18.35)
причем с увеличением расстояния между световодами С -> 0 по экспоненци-
альному закону.
Поляризационные поправки. Четыре основные моды двух одинаковых
световодов сложного волновода составляют пару симметричных и пару ан-
тисимметричных мод, соответствующих решениям (18.33) Ф+ и Ф_, где
Ф+ — симметричное, а Ф_ — антисимметричное решения. Поляризация полей
333
Симметричные (ч-) моЗы
Антисимметричные (-) моды
Рис. 18.5. Ориентация вектора электрического поля для четырех основных мод сложно-
го волновода, состоящего из двух одинаковых волоконных световодов
основных мод линейная, а ее азимут определяется симметрией поперечного
сечения и изображен на рис. 18.5. Если индексами х и у обозначить поляриза-
цию, а (+) и (-) - симметрию, то
ех+=еу+=Ф+; (18.36)
Поляризационные поправки 6j3x + , 5<Зу+ и 60х_, §Зу_ к скалярным постоян-
ным распространения (3+ и /3_ соответственно могут быть найдены из (13.11)
подстановкой соответствующих выражений для полей мод.
18.13. Перекрестная связь между двумя одинаковыми волоконными
световодами
Рассмотрим сложный волновод, состоящий из двух достаточно далеко рас-
положенных одинаковых световодов, каждый из которых является одномо-
довым. В предыдущем разделе обсуждались свойства фундаментальных ре-
шений Ф± и скалярных постоянных распространения /3± такого волновода.
Здесь же рассмотрим явление оптической перекрестной связи, суть которого
заключается в том, что в результате интерференции между полями мод, со-
ответствующих скалярным решениям Ф+ и Ф_, излучение, первоначально
распространяющееся в одном световоде, перекачивается в другой. Более под-
робно эта проблема рассматривается в гл. 29.
Предположим для простоты, что полное электрическое поле определяется
только модами, поляризованными вдоль оси х, т. е.
Е = /?+Ф+ехр(1)3+г) + />_Ф_ехр(10_з), (18.37)
где Ь+ и Ь_ — амплитуды мод. Поскольку световоды достаточно далеко раз-
несены, то можно приближенно считать, что если на входе сложного волново-
да (при z - 0) моды первого световода возбуждены с единичной мощностью,
то в окрестности второго световода поле равно нулю. Поэтому из (18.33)
следует, что вблизи второго световода Ф+ -Ф Ф2. Условие (18.37) при
z = 0 дает Ь+ Ь_. Выражение для поля Е2 в поперечном сечении второго све-
3 34
товода на расстоянии z от входного торца получаем из соотношений (18.37)
и (18.35):
Е2 = 2i#+^2exp(i0z)sin (Cz) . (18.38а)
Подобная зависимость для первого световода определяется выражением
Ех = 2Z>+^iexp(ij3z)cos (Си) . (18.386)
Перенос мощности и длина биений. Поток мощности Рг (и) или Р2 (z) в
каждом световоде определяется интегралом от интенсивности (мсо/2) х
х (Со/Мо)1/2 l^i I2 или (исо/2) (бо/До)1 1^212 по бесконечному поперечно-
му сечению. Предполагая, что на входе Pt (0) = 1 и Р2 (0) = 0, из (18.38)
получаем
Pi (и) = cos2 Cz; Р2 (и) = sin2 Cz. (18.39)
Таким образом, полная мощность, переносимая вдоль сложного волновода,
остается неизменной. Более того, она осциллирует из одного световода в
другой. Поведение такого волновода аналогично поведению дцух связанных
одинаковых маятников. Если zb - длина биении, т. е. расстояние вдоль оси
волновода, на котором мощность перекачивается из одного световода в дру-
гой и обратно, то из (18.35) и (18.39) получаем
_ Я 2я
Zb с е+- 0_'
(18.40)
При увеличении расстояния между световодами /3+ и длина биений воз-
растает по экспоненциальному закону. Физической причиной перекачки мощ-
ности является интерференция, или биения, полей основных мод,определяю-
щих полное поле (18.37); zb зависит только от разности скалярных постоян-
ных распространения. Поэтому при исследовании перекрестной связи в слож-
ном волноводе нет необходимости использовать поляризационные поправки
к постоянным распространения.
18.14. Пример. Волновод, состоящий из двух одинаковых волоконных све-
товодов со ступенчатыми профилями показателя преломления
Рассмотрим сложный волновод, состоящий из двух одинаковых ступенчатых одномодо-
вых световодов с радиусами сердцевины р — рх = р2 и расстоянием между осями свето-
водов d (см. рис. 18.4). В соответствии с принятыми ранее обозначениями в каждой
сердцевине п — псо, а в окружающей среде л — «ср nCQ = «со в сердцевине первого све-
товода и псо — «С1 в любой другой точке поперечного сечения волновода.
Длина биений. Прежде чем переходить к расчету Спо формуле (18.35) заметим, что
разность п - nCQ отлична от нуля только в сердцевине второго световода, а интеграл в
знаменателе пропорционален параметру нормировки N из табл. 13.2. Подставляя выра-
жение для , Ф2 и N из табл. 14.3 и переходя к цилиндрическим координатам, изобра-
женным на рис. 18.4, получаем
1 л 77* К р г
335
где параметры определены в табл. I и предполагается, что Д « 1 - пс\/псо- Чтобы вычис-
лить двойной интеграл, выразим Ко (Wrt /р) в системе координат г2, <р2 с помощью соот-
ношения (37.81) и учтем, что интегрирование по <р2 сводит разложение к одному чле-
ну, содержащему модифицированную функцию Бесселя первого рода/0 (Wr2/p), а инте-
грал по г2 является табличным и определен выражением (37.99). Принимая во внима-
ние, что WJQ (6/)^ (И7) + UJX (t/)70 (И7) с помощью характеристического уравнения из
табл. 14.3 и выражения (37.79) сводится к отношению Jo (t7) /Л*о (И7), получаем
(2Д)1Д Ц* К„ (Wd/p) ~ 1;2 ц* vyt-Wd/p)
Р V3 K(Wdp’ V3 K2t(W)
(18.42)
Приближенное выражение следует из (37.88) и является не менее точным, чем строгое
решение, поскольку для слабой связи между световодами Wd/p > > 1. Подстановка по-
лученного выражения в (18.40) приводит к экспоненциальной зависимости длины бие-
ний от расстояния между световодами, как и предполагалось в предыдущем разделе.
Более детально этот и другие вопросы рассматриваются в гл. 29.
Поляризационные поправки к постоянным распространения. Скалярные постоянные
распространения основных мод сложного волновода согласно равенству (18.35) опреде-
ляются постоянной распространения основной моды любого из световодов и параметром
С. Поскольку при одинаковых скалярных постоянных распространения каждая из ос-
новных мод существует в двух состояниях поляризации, то, как отмечалось в разд. 13.5,
для определения точных постоянных распространения мод необходимо вычислить по-
правки, обусловленные поляризационными свойствами волновода. Чтобы определить
каждую поправку, подставим приближенные выражения для поперечного электрическо-
го поля (18.36) в (13.12), где интегрирование теперь ведется вдоль границы между
сердцевиной и оболочкой обоих световодов. Из выражений (18.36) и (18.33) в соот-
ветствии с принятыми в разд. 18.12 обозначениями имеем
et = хех± = хФ± = х(^ ± Ф2), (18.43)
где х - единичный вектор, параллельный оси х на рис. 18.4. Соотношение (13.12) мож-
но существенно упростить, если принять во внимание соображения, которые привели к
переходу от (18.34) к (18.35). Поэтому в подынтегральном выражении в числителе
(13.12) членом ± 24\ Ф2 можно пренебречь по сравнению с членом 4^ + Ф2, который про-
порционален удвоенному параметру нормировки N из табл. 14.3. Таким образом, в си-
стеме координат, изображенной на рис. 18.4, имеем
(2А)М {/2 Kjw 27г- д% д _ _ п
5/3х± = k <18.44)
где в соответствии с табл. 14.3 и рис. 18.4
Ко /р) . _ _ K0(Wr2/p)
K0(W) ’ 2 Ко (И7)
д sin <р2 д д
—---_ _-----------—-------- -|- CQS —----
дх Р д<р2 дг2
(18.45а)
(18.456)
Здесь д/дг2 определяется при г0 — р, а параметры определены в табл. I. Выражая KQ(WrJp)
через г2 и <р2 с помощью (37.81) и проводя интегрирование, получаем
^х-+ = - * (£-- 1 ф - <w/p)b
х± 2р V3 ко
(18.46)
336
где Д - 7^(ИЭ и К. = Л*, (PV). Выражение для 60 + совпадает с (18.46), если изменить
Г.,,,,,, IT fUtsJiLx /______£>_ 1 Л __У_________________________________________ С
знак перед К2 (Wd/p). Видно (см. табл. 14.3), что множитель перед квадратными скоб-
ками описывает поляризационную поправку в случае изолированного световода, а взаи-
модействие полей световодов обусловило появление членов, зависящих от расстояния
между световодами d, Если световоды расположены достаточно далеко, то равенство
(18.46) можно несколько упростить, использовав асимптотические выражения (37.88).
Поляризационные поправки вызывают интерференционные эффекты между парами
основных мод с одинаковыми постоянными распространения. Например, если в волно-
воде возбудить только симметричные моды со скалярной постоянной распространения
/3+, то при распространении излучения по волноводу вследствие разницы между Ь&х+
и 60у+ вектор полного электрического поля будет вращаться [9]. Подобная ситуация
рассматривалась ранее в разд. 14.7 и может характеризоваться поляризационной длиной
биений 4тг/(6(Зх+ - 60 +). Сравнение с аналогичной величиной, обусловленной перекрест-
ной связью, показывает, что в слабонаправляющих волноводах даже при большом рас-
стоянии между световодами перекрестная связь является доминирующим эффектом в
пределах длины биений. С помощью (18.40), (18.42) и (37.88) имеем
60 . — 60v, I r ..
—S-t.-. .У+. «2ДИ/[Д (W)Kt (Ю -Л ЖДО]-
— р_ I
(18.47)
18.15. Пример. Волновод с двойным параболическим профилем показателя
преломления
Рассмотрим теперь основные моды волновода с двойным параболическим профилем по-
казателя преломления, форма которого описывается уравнением (16.30) и показана на
рис. 16.2, б. Несмотря на то что, как отмечалось в разд. 14.4, волноводы с таким про-
филем физически нереализуемы, метод возмущений, используемый в данном примере,
применим для любого волновода, состоящего из двух световодов. Предположим, что
профиль невозмущенного волновода можно представить в виде
= ”со - 2Д [ (х/р + dl2p>2 + O'/р)2 ]}’
(18.48)
где р - характерный размер поперечного сечения волновода. Профиль показателя пре-
ломления второго световода определяется выражением (18.48) с измененным переде?
знаком. Решение скалярного волнового уравнения для основных мод каждого светово-
да получается соответствующей модификацией решения из табл. 14.2:
где знаки (+) и (—) относятся соответственно к световодам 1 и 2, а параметр V опреде-
лен в табл. I. Для вычисления С подставим (16.30), (18.48) и (18.49) в уравнения
(18.35) и учтем, что величина п - п « (п2 - /2«со отлична от нуля только при
х> 0. После прямого интегрирования по х и у и нормировки на параметр N из табл. 14.2
при условии достаточно большого расстояния между световодами имеем
(18.50)
В отличие от экспоненциальной зависимости С в выражении (18.42) для ступенчатых
световодов в данном случае наблюдается гауссова зависимость, что является следстви-
ем параболического закона изменения показателя преломления. Скалярные постоянные
распространения и поляризационные поправки к ним могут быть получены из соотноше-
ний (18.35), (13.11) и табл. 14.2 аналогично тому, как это проделано в предыдущем
разделе.
Сравнение с точным решением. Точное решение скалярного волнового уравнения
для волновода с двойным параболическим профилем показателя преломления было по-
337
лучено в разд. 16.8. Постоянные распространения основных мод в неявном виде содер-
жатся в характеристических уравнениях (16.35) . Если нормированное расстояние между
световодами достаточно велико, так что dip >> 2/Е1/2, то легко показать, что асимп-
тотические выражения для параболических цилиндрических функций приводят к полу-
ченным ранее возмущенным решениям для (3+ и 0_. Подобным образом доказывается
и точность приближенного выражения (18.33). Более детально этот вопрос рассмотрен
в [10].
18.16. Моды высших порядков в оптическом волноводе, состоящем из двух
одинаковых волоконных световодов
В разделе 14.3 было показано, что в круглом световоде с каждым решением
скалярного волнового уравнения при I > 0 связано четыре моды. Если реше-
ния скалярного волнового уравнения для одной из этих четырех мод обозна-
чить Ф! и Ф2 соответственно для световодов 1 и 2 на рис. 18.4, то из сообра-
жений симметрии легко получить, что соответствующие возмущенные реше-
ния Ф+ и Ф_ определяются выражениями (18.33). Таким образом, четырем
модам круглого световода соответствуют восемь мод сложного волновода.
Поляризация поперечного электрического поля этих мод определяется сим-
метрией поперечного сечения и в соответствии с разд. 13.2 является однород-
ной и линейной, параллельной осям х и у на рис. 18.4. Поляризации мод
сложного волновода и круглого световода совпадают только при бесконеч-
ном удалении световодов друг от друга, как это показано на рис. 18.6, а
Рис. 18.6. Трансформация поперечного электрического поля моды с индексом I — 1,
содержащего две четные моды НЕ21 оптического волновода, образованного из двух све-
товодов при увеличении расстояния между ними (стрелки обозначают направление век-
тора электрического поля) (а); нормированный параметр 2Д|л| (18.53) как функция
нормированной частоты световода при различных значениях d/p (частота отсечки моды
равна V = 2,4, вертикальная штриховая прямая соответствует V — 3,8) (б)
338
для НЕ21-мод. По мере увеличения расстояния между световодами однород-
ность и линейность поляризации нарушается и при бесконечном удалении она
соответствует поляризации мод круглого волновода. На рис. 18.6, а такая
трансформация показана на примере двух четных НЕ2гМОД. Качественно этот
процесс рассматривался в разд. 13.9, а теперь количественную оценку влияния
расстояния между световодами на поляризацию дадим с помощью примера.
18.17. Пример. Сложный волновод, состоящий из двух волоконных светово-
дов со ступенчатыми профилями показателя преломления
Изменение поляризации мод от однородной для сложного волновода до соответствую-
щей модам с индексом 7=1 для одиночного световода может быть количественно оце-
нено параметром Л из табл. 13.1. Предположим, что /3Q и {3Q - постоянные распростране-
ния, соответствующие четному и нечетному скалярным решениям
Ф+е = ф1е + ф2е = F1 cos^i +Fi /р) cos </>2, (18.51а)
ф+о = *1о + ф2о = F1 <ri М)sin +F1 (г2/Р) s*n ^2 > (18.516)
где обозначения ясны из рис. 18.4, р = рх — р2 и функция определена в табл. 14.6.
Чтобы определить 0е, можно использовать уравнение (18.35), в котором Ч' = ,
Ф2 = Ф2е- Подобным образом можно определить и 0 . По аналогии с выводом, данным в
разд. 18.14, находим
= (2Д)1/2 U2 К2 (Wd/p}
е 0 РЕ3 Ко (W)K2 (ИТ) ’
(18.52)
Используя табл. 14.6 и 13.1, окончательно получаем [9]
j_K2(Wd/p) I ИТ/ГО(ИТ) 1-1
2Д К? (И7) I 2 к; (ИТ) I • (18,53)
На рис. 18.6, б изображена зависимость нормированного параметра 2Д|л| любого из
световодов от V при различном расстоянии между составляющими сложный волновод
световодами d/p, Соответствующие значения W находятся из характеристического урав-
нения с индексом 7 = 1 из табл. 14.6. Очевидно, что моды сложного волновода подобны
модам изолированных световодов при Л-> О, что имеет место либо при большом рассто-
янии между световодами, либо при V > > 1. В последнем случае мощность моды сосре-
доточена в основном в сердцевине, а спадающие поля в оболочке малы. При V — 3,8 и
любом расстоянии между световодами моды сложного волновода однородно поляризо-
ваны. Объяснение этого эффекта уже было дано в разд. 14.7 и 18.10.
18.18. Основные моды сложного оптического волновода, состоящего из двух
,различных волоконных световодов
Анализ удобно проводить отдельно — для волоконных световодов с суще-
ственно различными параметрами и с почти одинаковыми параметрами.
Световоды с существенно различными параметрами. Рассмотрим сложный
волновод, состоящий из двух параллельно расположенных волоконных све-
товодов, параметры которых значительно отличаются друг от друга, напри-
мер радиусы сердцевины (см. рис. 18.4). Фундаментальное решение (18.33)
для сложного волновода в данном случае не годится, поскольку волновод не
является симметричным. Однако поскольку световоды расположены доста-
точно далеко друг от друга, интуитивно ясно, что поля основных мод слож-
ного волновода подобны полям каждого отдельного световода. Таким обра-
339
зом, если они достаточно хорошо изолированы друг от друга, то в обозначе-
ниях разд. 18.12 имеем
Ф+=Ф15 Ф_=Ф2, 0_=02, (18.54)
где р!, 02 ~ постоянные распространения основных мод каждого световода.
Световоды с почти одинаковыми параметрами. Очевидно, что при вырав-
нивании параметров световодов должно существовать решение для основ-
ных мод, промежуточное между решениями (18.54) и (18.33) . Если парамет-
ры световодов почти одинаковые, оно может быть выражено по аналогии с
соотношениями (18.33) в более общем виде
Ф!+л+Ф2 _ Ф1+л_Ф2
(1+л2)1/2 ’’ ~~ (1+л2_)1/2
(18.55)
где используются обозначения,принятые в разд. 18.12, и а+, а_ — постоянные
величины. Для того чтобы определить эти постоянные и соответствующие по-
стоянные распространения 0+ и j3_, положим в (18.55) Ф = Фх, 0 - 0lf п =
= йсо, Ф = Ф± и представим в (18.4). Поскольку по предположению свето-
воды расположены друг от друга достаточно далеко, то, принимая во внима-
ние соображения, учтенные при переходе от выражения (18.34) к (18.35), с
помощью приближений, предшествующих (18.5), получаем
0± =0! + а±С12, (18.56а)
где 0± обозначает 0+ или 0_; под а± понимается а+ или а_; С12 - С (С опре-
деляется соотношением (18.35)) . Второе уравнение выводится аналогичным
образом при подстановке Ф = Ф2,0 = 02 и п=пс1 в (18.4) при Ф = Ф±. В ре-
зультате имеем
= аД2 + С21, (18.566)
где С21 - С (С определяется соотношением (18.35), в котором индексы пере-
ставлены местами). Исключение я+ из двух уравнений дает условие согласо-
вания нетривиальных решений. С точностью, которую дает выражение (18.56),
можно положить С12 = С21 = С, поскольку параметры световодов почти оди-
наковые. Отсюда получаем выражение для постоянной распространения
(18.57)
гдеСХ/7^ 1. Подстановка выражений (18.57) в (18.56) дает
(18.58)
Если световоды одинаковые, то 0г = 02, откуда F = 1, а± = ± 1, и соотно-
шение (18.55) с точностью до амплитудного множителя совпадает с соотно-
>10
шением (18.33). Если параметры световода существенно различные, то
1^1 — 021 >> 2С, откуда F -> 0, а+ -> 0, а_ -> <», и соотношение (18.55) сво-
дится к (18.54). Напомним, что в соответствии с выражением (18.35) срос-
том расстояния между световодами С спадает экспоненциально. Следователь-
но, если световоды расположены достаточно далеко друг от друга, даже не-
большое различие их параметров приводит к тому, что моды одного из них
не влияют на свойства и характеристики мод другого.
18.19. Пример. Сложный волновод, состоящий из двух волоконных свето-
водов со ступенчатыми профилями и почти одинаковыми радиусами серд-
цевины
Рассмотрим сложный волновод, состоящий из двух ступенчатых световодов с радиуса-
ми сердцевин р и р + 6р и одинаковыми показателями преломления сердцевин nCQ. По-
казатель преломления оболочек обозначим псу Согласно обозначениям предыдущего
раздела разность постоянных распространения основных мод Рх - /32 равна /3 - риз со-
отношения (18.13а), а параметр С определяется выражением (18.42), поскольку свето-
воды расположены достаточно далеко друг от друга. В результате имеем
= ^-( (lV)exp(^/p), (18.59)
где параметры определены в табл. I. При расстоянии между световодами d = 4р и часто-
те отсечки V = 2,4, используя данные табл. 14.4, находим, что правая часть (18.59)
приближенно равна 2806р/р. Таким образом, отличие радиусов сердцевин на 1 % дает
F ~0,3.
18.20. Перекрестная связь между двумя различными волоконными свето-
водами
Результаты, полученные при рассмотрении перекрестной связи в разд. 18.13,
справедливы и для сложного волновода, состоящего из двух различных све-
товодов. Необходимо только в выражение (18.37) вместо (18.33) подста-
вить (18.55). Вновь предполагаем, что световоды расположены достаточ-
но далеко друг от друга и первый возбуждается единичной мощностью.
Поле в окрестности второго световода равно нулю в точке z = 0, а поэтому
a+b+ (1 + cz^)"1/2 = a_b_ (1 + a2_Yi/2. Следовательно, поля, соответствующие
выражениям (18.38) , могут быть представлены в виде
b _ _ _ г С
Ei =+ 32)2-/2] [(а_ - a+)cos(— z)+ i(a_ + <z+)sin(—z)].
U _ Г г
(18.60a)
Ei =2ia+Z>+'?2exp[i(^1 + j32)z/2] sin (|?-z). (18.606)
Из выражений (18.57) и (18.58) по аналогии с (18.39) находим
(18.61)
Pi (z) = 1 - F2 sin2 (уz); Р2 (z) = F2 sin2 (£z).
341
Таким образом, часть полной мощности, перекачиваемая из световода в све-
товод, равна F2, а длина биений zb = 2nF/C. Из результатов предыдущего
раздела следует, что если радиусы сердцевин световодов различаются на 1 %,
то максимальная перекачиваемая мощность составляет 10 % от полной. Этот
вопрос рассматривается и в гл. 29.
МОДЫ ВОЗМУЩЕННЫХ ВОЛОКОННЫХ СВЕТОВОДОВ С ПРОИЗВОЛЬНЫМИ
ПРОФИЛЯМИ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
До сих пор при возмущении параметров волноводов предполагалось, что:
1) световоды являются слабонаправляющими, т. е. изменение показателя
преломления в поперечном сечении мало; 2) показатели преломления в воз-
мущенной области и той же области невозмущенного световода равны.
В этой части главы будет показано, что для нахождения полей мод и постоян-
ных распространения возмущенных световодов с произвольными профиля-
ми показателя преломления стандартные методы теории возмущений в об-
щем случае использовать нельзя. Это связано с поляризационными свойства-
ми возмущенных областей, В некоторых частных случаях могут быть исполь-
зованы альтернативные методы, что показано в приведенных ниже примерах.
Связь между модами возмущенного и невозмущенного световодов. Рас-
смотрим снова возмущения, характер которых не меняется вдоль светово-
да. Предположим, что неизвестные поля мод и постоянные распространения
возмущенного световода с профилем показателя преломления п (х, у) мож-
но представить в виде (18.1), а известные поля мод и постоянные распро-
странения невозмущенного световода с произвольным профилем показателя
преломления п(х, у) — в виде (18.2). Как показано в разд. 31.7, эти поля
мод можно точно связать уравнениями Максвелла, а постоянные распростра-
нения выражением (31.39), аналогичным (18.4). Опуская в (31.99) индек-
сы, имеем _
J («2 - д?)е • е*<14
’ <18'62)
-4 ОО
где Аж — площадь бесконечного поперечного сечения, z — единичный вектор,
параллельный оси световода, знак (*) обозначает комплексное сопряжение,
а остальные параметры определены в табл. I. Если оба световода (возмущен-
ный и невозмущенный) являются слабонаправляющими, это выражение сво-
дится к (18.4), что можно легко проверить с помощью табл. 13.1.
18.21. Решение, полученное методом возмущений
Рассмотрим возмущения, при которых /3 и 0 в выражении (18.62) близки.
Для удобства ограничимся случаем одиночного световода. Поскольку раз-
ность п2 - п2 может принимать произвольно большое значение, область воз-
мущения должна быть либо мала, либо сосредоточена вдали от оси светово-
да, где амплитуда полей мод мала. Для достаточно малых областей возмуще-
ния магнитные поля должны быть почти одинаковыми в любой точке попе-
речного сечения, т. е. h ~ h, поскольку из уравнений Максвелла вытекает
требование непрерывности h на границе возмущенной области. Однако это
утверждение для электрического поля в общем случае несправедливо. Усло-
342
Рис. 18.7. Показатели преломления сердцевины
исо и оболочки невозмущенного световода
со ступенчатым профилем показателя преломле-
ния и произвольным значением радиуса сердце-
вины р. Здесь же — область возмущения шири-
ной 6р < < рис произвольным показателем
преломления nQ расположена в оболочке
вие е ~ е имеет силу везде, за исключением области возмущения и, возмож-
но, вблизи нее. Эта оговорка возникает из-за того, что поле е является реше-
нием уравнений Максвелла и поэтому в точке разрыва профиля показателя
преломления необходимо выполнение" условия непрерывности нормальной
компоненты вектора лг2е. Это утверждение значительно проще пояснить
простым примером.
Ступенчатый разрыв профиля показателя преломления. Рассмотрим не-
возмущенный световод со ступенчатым профилем показателя преломления,
изображенным на рис. 18.7. Возмущенный профиль включает в себя узкое
кольцо с показателем преломления nQ. В полярной системе координат (см.
рис. 14.1) тангенциальные, т. е. азимутальные и продольные, компоненты
возмущенного электрического поля е^ и ez должны быть непрерывны на
границе (в точках г = гх и г = г2) • Отсюда ez % ez и е^ % е^ в любой точке,
включая область возмущения. Однако поскольку показатель преломления
на границе изменяется скачком от лс1 до и0, то нормальная, или радиальная,
компонента должна претерпевать разрыв, чтобы обеспечить непрерывность
функции и2ег . Следовательно, внутри области возмущения ет отличается от
ет , и эта разница увеличивается с ростом nQ - пс[. Более того, даже при
п0 ис1 нельзя считать, что внутри области возмущения ет « ег, как будет
показано ниже в первом примере. Подобные рассуждения справедливы и в
случае непрерывных профилей с резкоизменяющимися возмущениями.
Из приведенных выше рассуждений следует, что в общем случае в выраже-
нии^ (18.62) можно упростить только знаменатель, если положить е ~ е, h «
h, так как область возмущения дает пренебрежимо малый вклад в инте-
грал. В результате получаем
/ (п2 - п2) е • е*бМ
в = В + - (---) 1/2 Ар :------
2 мо /exh** idA
А оо
(18.63)
где Ар — площадь поперечного сечения области возмущения. Таким образом,
выражения, аналогичного (18.5), для световодов с произвольным профилем
показателя преломления не существует. Это существенно усложняет анализ,
поскольку необходимо находить приближенное выражение для возмущенно-
го поля е в области возмущения, а единого универсального метода определе-
ния поля е нет, и каждый случай необходимо рассматривать отдельно. При-
ведем теперь несколько примеров.
343
18.22. Пример. Бесконечно малая неоднородность
Рассмотрим изолированную неоднородность, о которой речь шла в разд. 18.7. Профиль
в сердцевине и показатель преломления неоднородности п0 (см. рис. 18.1, в) теперь бу-
дем полагать произвольными. Также считаем, что 6Л достаточно мало, так что наиболь-
ший линейный размер удовлетворяет условию d0 < < X, где X - длина волны в вакууме.
При этих условиях пространственные вариации поперечной компоненты электрического
поля внутри области возмущения пренебрежимо малы. Следовательно, продольная ком-
понента возмущенного поля, которая непрерывна на границе области возмущения, вну-
три области возмущения удовлетворяет условию ~ еъ (р0), где х — pQ, у ~ 0 - коор-
динаты неоднородности. С другой стороны, поперечное электрическое поле, которое
испытывает на границе разрыв, может быть найдено с помощью квазистатического приб-
лижения, т. е. временная зависимость ехр(-1аЯ) сохраняется, но зависимость от ради-
альной координаты et (д0) внутри области возмущения определяется из уравнения Ла-
пласа, а не из уравнений Максвелла. Этот же вывод может быть получен формально ум-
ножением векторного волнового уравнения (11.40а) Ha<7J, заменой п наи0 и пренебре-
жением членами, содержащими степени отношения <70/Х. Таким образом, для решения
поставленной задачи необходимо решить электростатическую задачу для бесконечно
длинного диэлектрического цилиндра с показателем преломления п0, который помещен
в среду с показателем преломления й(р0) и подвергается воздействию постоянного по-
перечного поля et(p0). Решения можно получить для световодов с эллиптическим и
круглым поперечными сечениями [11, 12].
В случае круглого поперечного сечения
et (Ро) =
2« (Ро) - , ,
w (Ро ) +«0
(18.64)
Поэтому если и0 и «(д0) достаточно сильно отличаются, то возмущенное и невозмущен-
ное поля внутри области возмущения могут существенно отличаться друг от друга. Да-
же если п0 п(р0), выражение (18.64) упростить нельзя, так как это приведет к невоз-
можности корректного описания поляризационных эффектов, обусловленных неодно-
родностью, например, разностью постоянных распространения основных мод.
Основные моды возмущенного световода со ступенчатым профилем показателя пре-
ломления. На рис. 12.6 схематически изображено направление вектора электрического
поля основной моды в сердцевине световода с произвольным ступенчатым профилем
показателя преломления. Если в сердцевине присутствует неоднородность, как это по-
казано на рис. 18.1, в, то симметрия световода с круглым поперечным сечением наруша-
ется. Однако если неоднородность является бесконечно малой, то ясно, что вектор элек-
трического поля основных мод ориентирован так, как изображено на рис. 18.8. Обо-
значим постоянные распространения мод, электрические поля которых показаны на
Рис. 18.8. Ориентация по-
перечного электрического
поля основных мод све-
товода со ступенчатым
профилем и небольшой
изолированной неоднород-
ностью:
а — с поляризацией вдоль
оси X ; б — с поляризацией
вдоль оси у
344
рис. 18.8, а и 18.8, б, через 0х и соответственно. Если теперь выражение (18.64) под-
ставить в (18.63) и учесть определение нормировки из табл. 11.1, то получим
(18.65)
где nCQ - показатель преломления невозмущенной сердцевины, а знак - для невозму-
щенных величин опущен. Выражение для (3 аналогично (18.65) - необходимо только
ех заменить на еу. Компоненты вектора е можно определить с помощью табл. 12.3, если
положить v — 1 и R = р0/р. Выражения полей четной и нечетной НЕ-мод с постоянными
распространения (Зх и (3 при = 0 соответственно имеют вид
a,J0(C/0) +d2/2(C/0) iu Jt (Ц>)
ev = ----------------------; e7 — ——-----•---, (18.66a)
x z P0 (IT)
a.JQ (t/0) - a2J2 (t/rf)
ey=~ ; = °’ (18666)
где Uo = UpQfp и ах, a2 определены в табл. 12.3. Теперь из соотношения (18.65) можно
получить количественную характеристику асимметрии, или двойного лучепреломления,
вносимую неоднородностью, а именно
о _ о - П° ПСО ( е° \ 1/2 Ir^l^o J J U2 2 fJ i
<x J}(U) 4 (M0) +п2С0 °(и)Л(и) pV 71 18’6
Она справедлива для любых п0 и nCQ. В приближении слабонаправляющего волновода
и о ~,7СО’ и с помощью табл. 12.3, 12.6 и 14.3 это выражение сводится к
(Зх-(Зу= 2Д1/2
”о ~”со
псо
6А U*
тгр3 V3
j2 (iv)
И (t/0) - 2^о (>? jo (У)Л (W ],
Ki (If)
(18.68)
где U = UpQlp, а параметры определены в табл. I. Из табл. 12.6 с очевидностью следует,
что полученный результат будет корректным, если компонента еъ известна с точностью
до Д1/2, a et - с точностью до А. Если в (18.63) вместо соотношения (18.64) использо-
вать приближенное равенство et « et, то выражение (18.68) никогда не будет получено,
даже в случае п0 ^nCQ.
18.23. Пример. Изменение радиуса сердцевины
Эффект, к которому приводит небольшое изменение радиуса сердцевины в слабона-
правляющем световоде со ступенчатым профилем показателя преломления, обсуждался
в разд. 18.6. Здесь рассматривается случай, когда разность между показателями прелом-
ления сердцевины и оболочки (исо - «ср может принимать произвольное значение. За-
метим, что эта задача не является оригинальной, поскольку известное решение для не-
возмущенного световода справедливо для любого радиуса сердцевины, но она позволя-
ет наглядно продемонстрировать очень простую основную идею. В отличие от предыду-
щего примера, ширина области возмущения может значительно превышать длину волны
X, необходимо лишь выполнение условия < < р. На рис. 18.9, а схематически изобра-
жено поперечное сечение такого световода.
Поле е в возмущенной области можно выразить через поле невозмущенного свето-
вода ё, использовав граничные условия уравнений Максвелла. Отсюда продольные и ази-
мутальные компоненты невозмущенного и возмущенного полей должны быть непре-
рывны соответственно при г — риг = р + 8р. Поэтому внутри области возмущения мож-
но положить е7 « ez (р), е ^ё^ (р). Радиальная компонента невозмущенного поля долж-
на быть такой, чтобы функция /Рёг была непрерывна при г = р. На основании рис. 18.9, б
имеем
345
Рис. 18.9. ( ечение световода со ступенчатым профилем, увеличение радиуса сердцевины
KOToporc'jia Ьр привело к возмущению полей (я); радиальные составляющие невозму-
шенною Cj. и возмущенного ег электрических полей в области возмущения (б)
"co^r =^ёт(р+), (18.69)
где индексы (-) и (+) относятся к внутренней и наружной сторонам границы. Посколь-
ку мало, то возмущенная компонента ет непрерывна при г = ри удовлетворяет усло-
вию сг(р_) «« ёт(р_). Подставляя последнее равенство в (18.69), получаем выражение
для радиальной компоненты поля внутри области возмущения
ег(Л («ci/«co)2®r~ ("сЙ’со^Ю- (18.70)
Другими словами, поле е фактически является аналитическим продолжением поля ё
в сердцевине в область возмущения. Поскольку п и п отличаются друг от друга только
внутри этой области, то ошибка, возникающая при предположении, что в (18.63) е ~е;
может быть произвольно большой. Однако если «со « иер то приближение е ~ ё вполне
приемлемо, так как возмущение не нарушает круговую симметрию поперечного сече-
ния световода, как это было в предыдущем случае. Можно легко показать, что при «со «
имеем ранее полученное выражение (18.13а).
18.24. Пример. Эллиптическая деформация
Рассмотрим вновь слабую эллиптическую деформацию поперечного сечения световода,
изображенного на рис. 18.2,6?. Если показатели преломления сердцевины и оболочки в
случае ступенчатого профиля могут принимать произвольные значения, то поля в четы-
рех областях возмущения могут значительно отличаться от полей круглого световода.
Если принять во внимание соображения, изложенные в предыдущем разделе, то возму-
щенное поле е в заштрихованной области, пересекающей ось х, определяется аналити-
ческим продолжением поля е в сердцевине круглого световода. Аналогично поле е в
заштрихованной области, пересекающей ось у, определяется аналитическим продолже-
нием поля в оболочке круглого световода. Учитывая это, из соотношения (18.63) полу-
чаем выражение для постоянной распространения возмущенной моды при условии, что
эксцентриситет эллипса мал. Если в (18.63) подставить выражения для полей четной и
нечетной основных мод из табл. 12.3, то с помощью разд. 18.10 и табл. 12.6 прямыми
вычислениями придем к соотношению (18.25), описывающему разницу между постоян-
ными распространения при исо ~^с] [8] •
18.25. Пример. Волоконные световоды с поглощением
В слабопоглощающих световодах с произвольным профилем показателя преломления
для расчета небольшой мнимой поправки’ к постоянной распространения достаточно
346
предположить, что е е. Положив в (18.63) /3 = /3 + /З1, п = пт + in1 и использовав опреде-
ления из табл. I и табл. 11.2, получим
7= 2^ 2* А) 1/2
MG
f 'nWlel2dA
J е X h* • idA
А ос
(18.71)
где у - коэффициент затухания мощности, поперечные компоненты поля невозмущен-
ного световода предполагаются действительными, индексы г и i обозначают действитель-
ную и мнимую части и и1 < < нг. Поскольку et и hf - действительные функции, то полу-
ченное выражение идентично выражению (11.63), выведенному с помощью теоремы
Пойнтинга.
ГЛАВА 19. ВОЛНОВОДЫ С ПЛАВНО ИЗМЕНЯЮЩИМИСЯ
ПАРАМЕТРАМИ
В предыдущей главе были рассмотрены возмущения, обусловленные неодно-
родностями, которые не зависели от длины световода. Однако в световодах
могут существовать и неоднородности, зависящие от продольной координа-
ты, например, изменения радиуса сердцевины круглого световода или скрут-
ка световода с эллиптическим поперечным сечением. Эта глава посвящена
методам, позволяющим описать свойства световодов с произвольными про-
филями показателя преломления и произвольными неоднородностями при
условии, что эти неоднородности изменяются достаточно плавно вдоль све-
товода. Формально этот метод является волновым аналогом лучевого анали-
за нерегулярных многомодовых световодов с плавно изменяющимися пара-
метрами, изложенного в гл. 5. Однако здесь основное внимание уделяется
одномодовьпм световодам.
ЛОКАЛЬНЫЕ МОДЫ
Световоды с изменяющимися по длине параметрами трансляционно неинва-
риантны, и поэтому моды, рассмотренные в гл. 11, распространяться в них не
могут. Более того, в общем случае для таких структур не существует точных
решений уравнений Максвелла. Однако, если параметры световода меняются
плавно, интуитивно ясно, что моды некоторого невозмущенного световода
TQ4HO аппроксимируются решением уравнений Максвелла внутри локальных
областей. По аналогии с локальными плоскими волнами, рассмотренными в
гл. 35, такие приближенные моды называются локальными. Свойства локаль-
ных мод наилучшим образом могут быть понятны при выводе выражений
их полей.
19.1. Поля локальных мод
Световод с плавно изменяющимися параметрами (рис. 19.1, а) имеет про-
филь показателя преломления п (х, у, z), зависящий от продольной коорди-
наты z. Чтобы сформировать поля локальных мод, аппроксимируем свето-
347
Рис. 19.1. Нерегулярный волоконный световод с профилем показателя преломления
п (х, у, z) и параметрами, изменяющимися вдоль его длины (а), и аппроксимация тако-
го световода последовательностью цилиндров, где — координата центра, a 8z - высо-
та данного цилиндра (б)
вод последовательностью цилиндров, как показано на рис. 19.1, б [1]. Вну-
три каждого цилиндра профиль показателя преломления не зависит от z и
определяется своим значением в точке zc, соответствующей центру цилиндра,
и совпадает с профилем невозмущенного световода, т. е. п -п(х, у, zc). Дру-
гими словами, поле внутри конечного цилиндра аппроксимируется полем
бесконечно длинного световода с профилем п(х, у, zc). Очевидно, что это
приближение будет достаточно точным при условии, что высота цилиндра
bz много больше характерной длины, на которой происходит заметное изме-
нение амплитуды поля. По аналогии с выражением (11.3) поле /-й локальной
моды внутри каждого цилиндра можно представить в виде
Е; = к У, Pj (zc) ] exp [ift (z )z];
(19.1)
Hj = hj [x, y, Pj (zc) ] exp [iPj (zc)z ],
где x и у — оси координат поперечного сечения световода. Векторы ej и hj
являются решениями векторного волнового уравнения (11.40), в котором
п = п(х, у, zc), а постоянная распространения /3- (zc), входящая неявно в ej
и h:, определяется из характеристического уравнения.
Мощность и фаза. Хотя амплитуда полей (19.1) изменяется с изменением
профиля от цилиндра к цилиндру, мощность локальной моды должна оста-
ваться неизменной вдоль неоднородного световода. Это требование выполня-
ется автоматически, если в каждом цилиндре использовать ортонормальные
моды (11.15), т. е. в выражении (19.1) заменить ej и hj на и hj соответ-
ственно.
При распространении локальной моды по световоду ее фаза в каждом ци-
линдре возрастает на величину, равную произведению постоянной распро-
странения j3j (zc) на высоту цилиндра <5z. Поэтому фаза в произвольном сече-
нии неоднородного световода равна сумме таких произведений. Однако плав-
ные изменения параметров световода означают и плавные изменения постоян-
ной распространения, таким образом, с достаточной точностью суммарную
Z
фазу можно аппроксимировать интегралом J P-(z)dz, а в выражениях для
о J
348
ej и hj заменить (zc) на /3- (z) • На основании этих соображений поле локаль-
ной моды в точке z имеет вид
Ej = [х, у, 3j (z) ] ехр [if (z) dz];
°z (19.2)
Hj = hj [x, y, £j (z) ] exp [if (z)dz].
j--------------------------------
Отсюда следует, что ej и hj неявно зависят от z через постоянную распро-
странения /3j (z). Этот же результат может быть получен формально из урав-
нений Максвелла, как показано в гл. 28.'
Приведенный вывод выражений для полей локальных мод иногда называ-
ют адиабатическим приближением, поскольку в его основе лежит предполо-
жение о том, что все изменения профиля происходят на длинах, значительно
больших характерных размеров поля, и поэтому изменением мощности ло-
кальной моды можно пренебречь [2]. Поэтому, хотя локальные моды — это
отличная аппроксимация мод световода с плавно изменяющимися парамет-
рами, они не являются точными решениями уравнений Максвелла. Неболь-
шая поправка к полям локальных мод может быть получена методом свя-
занных локальных мод (см. гл. 28) или методом наведенных токов (см.
разд. 22.10).
19.2. Критерий плавного изменения параметров
В нерегулярных световодах большинство важных для практики проблем
можно легко решить с помощью метода локальных мод, что демонстрируют
приведенные ниже примеры. Однако поля локальных мод будут хорошей ап-
проксимацией точных полей только в том случае, если неоднородности из-
меняются вдоль световода достаточно плавно. Поскольку поля локальных
мод формируются из полей мод локально эквивалентных световодов с ци-
линдрической симметрией, то соответствующее условие плавности определя-
ется наибольшим расстоянием, на котором полное поле такого световода силь-
но изменяется из-за фазового рассогласования между различными модами.
Длина биений. Напомним, что в соответствии с выражениями (11.2) и
(11.3), полное поле световода с цилиндрической симметрией может быть
представлено суммой полей мод. Поэтому ясно, что полное поле может под-
вергаться значительным изменениям на длине, равной длине биений между
парами мод zb. Определим наибольшую длину биений как
2я
гЬ ’ (19-3)
где /31 и j32 — две наиболее близкие по значению постоянные распростране-
ния. Тогда для обеспечения достаточной точности аппроксимации локальны-
ми модами необходимо, чтобы параметры световода изменялись на длине
> zb. Отметим, что zb много больше расстояния 2тг/(3^ необходимого для
значительного изменения фазы отдельной моды.
349
Одномодовые световоды. В круглых неоднородных световодах, в кото-
рых распространяется только основная мода с постоянной распространения
31, постоянная распространения /32 в выражении (19.3) относится к модам
излучения. Эти моды, свойства которых рассматриваются в гл. 25, формиру-
ют поле излучения. Если — показатель преломления оболочки, то постоян-
ная распространения мод излучения принимает любое значение внутри интер-
вала 0 < р2 аналогично плоской волне в неограниченной среде с пока-
зателем преломления лс1. Таким образом, наибольшее расстояние zb, на кото-
ром поле основной моды может изменяться, определяется выражением (19.3)
при З2 = ^ср Это эквивалентно приближению плоской волны, распространя-
ющейся в направлении оси z, и поэтому оно в большинстве практических
случаев является предельным. Если предположить, что световод слабонаправ-
ляющий, то эту верхнюю границу zb можно выразить через его параметры из
табл. I следующим образом:
2я 4ттр V
Zb~ - кпс1 ~ (2Д)1/2 Ж ’ (19’4)
поскольку 3 ~ Ь?со Дд2с1, где псо — максимальный показатель преломле-
ния сердцевины.
Многомодовые световоды. В многомодовых световодах разность между
ближайшими постоянными распространения уменьшается с ростом парамет-
ра V и отсюда критерий плавности (19.3) даетзь при Однако для
ряда задач, касающихся многомодовых световодов и рассмотренных в гл. 1
и 9, это требование не является необходимым. Дело в том, что критерий плав-
ности (19.3) возникает как следствие разности фаз между соседними парами
мод, а в результате диффузного освещения световода возбуждаются все мо-
ды, или лучи, распространяющиеся под всеми углами к оси световода, и поэ-
тому необходимость в согласовании фаз мод отпадает. В этом случае крите-
рием плавности служит так называемый модовый полупериод, т. е. расстоя-
ние вдоль оси световода, определяемое потоком мощности внутри моды и
неявно содержащееся в характеристическом уравнении. Для мод, распростра-
няющихся только в многомодовых световодах, модовый полупериод в точ-
ности равен лучевому полупериоду z , рассмотренному в разд 5.5. В свето-
водах с небольшим числом мод модовый полупериод обычно больше лучево-
го, что можно предвидеть, если принять во внимание продольный сдвиг, рас-
смотренный в разд. 10.6. Для планарных волноводов со ступенчатым профи-
лем показателя преломления модовый полупериод равен сумме zp и zs, что
иллюстрирует рис. 10.4, а.
Выводы. Используя выражения, полученные выше, можно теперь дать ка-
чественный критерий корректности метода локальных мод. В неоднородном
световоде с профилем показателя преломления п (х, у, z) на длине zb измене-
ние показателя преломления равно (dnI 2/dz)zb, и, таким образом, из выраже-
ний (19.3) и (19.4) для слабонаправляющих световодов, в которых распро-
страняются соответственно две (или более) и одна мода, получаем следую-
щие критерии плавности:
I___2тг____1 дп2 I « 1. 4яР — I—I « L fl9>5)
*01-02 ”2 dz ’ (2Д) 1/2 W2 П2 ' dz I
350
Значения величин 0 19 /32, И и W оцениваются в точке z. Несмотря на то, что
эти критерии являются только качественными, они дают возможность оце-
нить необходимую плавность изменений вдоль световода при распростране-
нии без существенной потери мощности. Ниже в гл. 28 на основании уравне-
ний Максвелла выводятся точные выражения критерия плавности.
19.3. Пример. Неоднородный радиус сердцевины
Рассмотрим световод, у которого радиус сердцевины p(z) изменяется так. как показа-
но на рис. 19.1, а. Для простоты предположим, что световод слабонаправляющий, а про-
филь показателя преломления ступенчатый. При распространении определенной локаль-
ной моды доля мощности этой моды в сердцевине 17(2) падает по мере уменьшения р (z).
Это с очевидностью следует из рис. 14.3, в, поскольку локальный параметр световода
V пропорционален р (z).
Сердцевина с поглощением. Если материал сердцевины слегка поглощающий с коэф-
фициентом поглощения мощности асо, то из уравнения (18.16) следует, что в точке z
коэффициент затухания мощности ?(z) = n(z}aQQ. Мощность моды P(z) находится за-
меной 7 на 7 (z) в уравнении (11.62) и интегрированием. В результате имеем
z
P(z) = Р(0) схр [—асо fv(z)dz] =P(0)exp(-acoTiavz), (19.6)
О
где nav - среднее значение r?(z) на длине световода z. Полученный результат также при-
меним к световодам, вдоль которых медленно меняются как радиус сердцевины, таки
профиль показателя преломления.
Критерий плавности. Полученный выше результат является корректным при условии,
что радиус сердцевины световода изменяется незначительно на расстоянии, равном соот-
ветствующей длине биений (19.5), т. е. \5p/p(z) | < < 1, гдебд — z^dp(z) /dz. Если кро-
ме основной распространяются моды высших порядков, z^ определяется выражением
(19.3), в результате чего имеем
|£2(z) | < < |0( — |p(z)/2ir, (19.7)
где 12 (z) « tg 12 (z) = dp(z)ldz ~ локальный угол конуса относительно оси z. Требова-
ние постоянства отношений в правой и левой частях неравенства (19.7) обеспечивает та-
кую форму конуса, что локальная мода в любом сечении конуса является точным ре-
шением уравнений Максвелла. В случае одномодового световода, используя выражение
для zb (19.4), имеем
|si(z)| << (2Д)Ш Й^/ДтгГ, (19.8)
где параметры определены в табл. 1, а значения величины W для каждой нормированной
частоты V приведены в табл. 14.4. Если это условие выполнено, то локальные основные
моды могут распространяться с пренебрежимо малыми потерями на излучение. Однако
при фиксированном угле конуса можно ожидать, что по мере уменьшения относитель-
ной разности показателей преломления Д световод становится более восприимчивым к
потерям на излучение.
19.4. Пример. Скрученные эллиптические световоды
Рассмотрим скрученный одномодовый эллиптический световод, в котором профиль по-
казателя преломления в зависимости от длины световода вращается относительно его
оси, как показано на рис. 19.2. Из разд. 13.5 следует, что в рамках приближения слабо-
направляющего волновода одно из основных мод эллиптического с цилиндрической
симметрией световода с постоянной распространения 0Х поляризована линейно, и век-
тор электрического поля параллелен оси х на рис. 19.2, а. Вектор электрического поля
второй моды с постоянной распространения /?у параллелен оси jv. Ясно, что векторы по-
перечных электрических полей двух локальных основных мод, распространяющихся
351
Рис. 19.2. Поперечное сечение эллиптического световода, закрученного вдоль своей оси.
Оси х и у связаны с большой и малой осями эллипса, а оси х0 и yQ зафиксированы в
пространстве
вдоль скрученного световода, направлены вдоль поворачивающихся осей х и у (см.
рис. 19.2, б), а моды имеют неизменные постоянные распространения 0Х и j3y соответ-
ственно. Таким образом, единственное различие между локальными модами и соответ-
ствующими модами трансляционно-инвариантного световода заключается во вращении
векторов электрического поля, в результате чего их направление в любом поперечном
сечении совпадает с полуосями эллипса. Качественно такая же картина наблюдается и в
скрученных анизотропных световодах.
Критерий плавности. Согласно ему скрутка должна быть мала на расстоянии, равном
длине биений между двумя основными модами. В этом случае приведенная выше каче-
ственная картина будет отвечать действительности. Положив в выражении (19.5) =
= isx и /32 = получим
R(Z) I << |?х- 0у|/2я, (19.9)
где t(z) = (1/и2)е)и2 /dz — локальный период скрутки.
В случае ступенчатого световода с небольшим эксцентриситетом е и средним радиу-
сом сердцевины р из соотношения (18.26) следует, что порядки разности 0Х - Зу и отно-
шения е2 (2Д)3/2 /Юр равны. Если zc - длина световода, на которой спираль скрутки со-
вершает полный оборот, то из неравенства (19.9) имеем
2тг
ZC = |т(2) | >> 4°я2р/[е2 (2Д)3'2]. (19.10)
Для типичного одномодового световода е2 » 0,5, 2Д = 0,02-и р ~ 3 мкм. Таким обра-
зом, для выполнения условия (19.10) zQ должна быть порядка нескольких метров.
ЛОКАЛЬНЫЕ МОДЫ ДВУХ НЕРЕГУЛЯРНЫХ СВЕТОВОДОВ
Метод локальных мод применим и к сложным волноводам с плавно изменя-
ющимися параметрами, состоящими как из двух одинаковых (рис. 19.3,а),
так и из пары разных световодов (рис. 19.4), и поэтому является мощным
средством исследований свойств неоднородных соединителей.
19.5. Поля локальных мод
Конструкция полей локальных мод сложного волновода является очевидной.
По аналогии с разд. 19.1 вначале оба световода аппроксимируются последо-
вательностью цилиндров (см. рис. 19.3, б) и, таким образом, каждый ци-
линдр рассматривается как часть сложного волновода, состоящего из двух
параллельных, трансляционно-инвариантных световодов, профили показате-
ля преломления которых соответствуют профилю в центральном сечении
352
Рис. 19.3. Сложный оптический волновод, состоящий из двух одинаковых неоднород-
ных световодов (а), и приближенная модель, в которой световоды представляются по-
следовательностью цилиндров, где zc обозначает координату центра, a 6z - высоту
цилиндра
цилиндра. Затем, предполагая, что световоды являются слабонаправляющи-
ми и расположены далеко друг от друга, из выражения (18.33) можно полу-
чить решение скалярного волнового уравнения для основной моды, а соот-
Рис. 19.4. Два конусообразных световода с равными радиусами сердцевины р в точке
z — zc (радиус сердцевины первого световода в точке zt равен радиусу сердцевины
второго в точке z2 и наоборот) (а); качественная картина поведения постоянных рас-
пространения локальных мод вдоль световодов (1) и (2) (б); ответвитель, состоящий
из двух световодов, радиусы изгибов которых постоянны (в); схематическое представ-
ление произвольного конусообразного ответвителя, состоящего из двух световодов
(1) и (2) с увеличивающимся и уменьшающимся радиусами сердцевины соответственно
(г)
12 Зак 37
353
ношение (18.34) дает возможность определить значение ее постоянной рас-
пространения. Поскольку, как было показано в разд. 19.1, локальные фунда-
ментальные решения Ф} [х, у, /3 (z) ], Ф2 [х У, P(z) ] и постоянная распростра-
нения (3(z) скалярного волнового уравнения для каждого световода в от-
дельности зависят от z, то и возмущенные решения Ф+, /3+ и Ф_, (3_ цля.
сложного волновода также будут зависеть от z. Следовательно, полная про-
странственная зависимость поперечного электрического поля для локальных
основных мод, поляризованных вдоль осей х и у, следует из выражений
(18.36) и (19.2) и может быть записана в виде
Z
Е± = Ф± (х, у, z)exp [i J Р± (z)dz]. (19.11)
о
Подобное выражение справедливо и в случае волновода, состоящего из двух
разных световодов, при усдовии,что выражения (18.33) и (18.34) заменены
на (18.55) и (18.57) соответственно, а а± в соотношении (18.58) теперь за-
висит от z. Критерий плавности для этого случая рассматривается ниже.
19.6. Пример. Перекрестная связь между одинаковыми световодами
Прямым следствием применения метода локальных мод к паре одиисковых световодов
с плавно изменяющимися параметрами является простое описание передачи мощности
за счет перекрестной связи между световодами. Если световод 1 на рис. 19.3, а первона-
чально возбужден единичной мощностью, а световод 2 не возбужден, то распределение
мощности вдоль сложного волновода может быть получено простой модификацией со-
ответствующей задачи для световодов с цилиндрической симметрией (см. разд. 18.13).
Z Z
Заменяя £z и Cz интегралом f (?(z)dz и J C(z)dz, где С (z) определяется выражением
о о
(18.35) через зависящие от z параметры, из соотношения (18.39) имеем
Z Z
Л (z) = cos2 [J C(z)Jz]; р2 (z) = sin2 [J C(z)Jz]'.
О О
(19.12)
Таким образом, две локальные основные моды интерферируют, и вся мощность переда-
ется от одной моды к другой и обратно на расстоянии, равном локальной длине биений
zb = 7JZ)”g_(z) -тк- (1913)
Такое описание перекрестной связи является корректным при условии, что изменением
параметров световодов надлине биений можно пренебречь.
КОНИЧЕСКИЕ ОТВЕТВИТЕЛИ
Рассмотрим теперь ответвители, состоящие из двух разных одномодовых све-
товодов. На рис. 19.4 приведены примеры таких ответвителей, представляю-
щие большой практический интерес [3]. Их свойства могут быть легко ис-
следованы методом локальных мод при условии, что световоды в ответвите-
лях расположены достаточно далеко, а параметры изменяются плавно.
19.7. Распространение локальных мод
В этом разделе рассматривается распространение локальных основных мод
вдоль сложного волновода или ответвителя, изображенного на рис. 19.4, а и
354
состоящего для простоты из двух параллельно расположенных световодов с
равными и противоположно направляемыми конусными углами. Результаты
разд. 18.18. показывают, что в каждой точке z вдоль ответвителя (за исклю-
чением малой области около z = zc, в которой радиусы световодов факти-
чески одинаковые), его локальные моды, по существу, являются локальны-
ми модами каждого световода в отдельности. Предположим, например, что
локальное фундаментальное решение Ф+ в выражении^ (19.11) удовлетворя-
ет в точке z =Zj на рис. 19.4, а условию Ф+ ~ Ф1, где Ф! — локальное фунда-
ментальное решение для изолированного световода 1. Отсюда локальная мо-
да ответвителя в точке z = zx определяется световодом с меныиим радиусом.
Та же локальная мода в точке z = z2, где меньшим радиусом обладает свето-
вод 2, по определению характеризуется локальным фундаментальным реше-
нием для этого световода, т. е. Ф+ ~ Ф2. Другими словами, поле Ф+ локаль-
ной моды, будучи сосредоточенным в точке z =Zj в световоде 1, при распро-
странении моды вдоль ответвителя перераспределяется в пространстве и в
точке z = z2 будет сосредоточено в световоде 2. Аналогично этому поле ло-
кальной моды Ф_ перейдет из световода 2 в световод 1 при распространении
моды из точки Zj в точку z2.
Необходимо отметить, что совсем не обязательно, чтобы ответвитель обла-
дал свойствами симметрии, как показано на рис. 19.4, а и 19.4, в. Описание
свойств таких ответвителей через поля Ф+ и Ф_ требует только плавного
уменьшения радиуса поперечного сечения сердцевины вдоль одного светово-
да по оси z, измеренного в плоскости, перпендикулярной оси z, при этом ра-
диус сердцевины другого световода должен плавно увеличиваться, как это
схематически показано на рис. 19.4, г. Критерий плавности изменения радиу-
са вдоль оси z будет рассмотрен ниже.
Математическое описание. К выводам, полученным выше на основании
физических соображений, можно прийти и аналитическим путем. Следуя рас-
суждениям разд. 19.5, выражения для поля Ф+ в точке z можно получить, ис-
пользуя соотношения (18.55), (18.57) и (18.58), т.е.
Ф+
(z) - (z) J [МО -М*)]%
[1 +аДг)р'2 ’ +,} 2C(z) Г 4^(г) J ’
(19.14)
где j3i (z), 02 (z) — постоянные распространения локальных мод каждого све-
товода, a C(z) - обобщенный параметр С из (18.35). В точке z = Zj на
рис. 19.4, ^радиусы сердцевины световодов сильно различаются, а поэтому
0i (zi) - 02 (zi) >> C(z^) (C(zj) > 0 по предположению) , и, следовательно,
из уравнения (19.14) следует: ~ 0 и Ф+ ~ Ф]. Из соображений симмет-
рии ясно, что постоянные распространения, схематически показанные на
рис. 19.4, б, в точке z2 примут значения, противоположные значению в точке
zi, а коэффициент связи С останется неизменным. Поэтому
0!(z2) -02(z2) =-[01(z1) -02(Z!)J| « C(z2) =C(zO, (19.15)
и из (19.14) получаем, что и Ф+ ~ Ф2.
12*
355
Переход полей локальных мод из световода 1 в световод 2 и наоборот
происходит в окрестности точки z = zc, в которой радиусы сердцевин свето-
водов фактически равны. Этот вывод следует из выражения (18.55), по-
скольку Ф+ и Ф_ в этой точке зависят как от Ф!, так и от Ф2.
19.8. Перекрестная связь
Метод локальных мод особенно просто позволяет проанализировать пере-
крестную связь в ответвителях. Если в точке z < — I (см. рис. 19.4) возбуж-
ден только световод 1, то из анализа, проведенного в предыдущем разделе,
ясно, что в (19.11) мода Ф+ является возбужденной, а Ф_ — невозбужден-
ной. Следовательно, характеристики распространения полностью определяют-
ся модой Ф+ и, таким образом, вся мощность этой моды переносится свето-
водом 2 при z I. Другими словами, в конусообразном ответвителе проис-
ходит фактически 100 %о-я передача мощности из одного световода в другой
при условии, что рассмотренный ниже критерий плавности выполняется.
19.9. Критерий плавного изменения параметров
Следуя рассуждениям, приведенным в разд. 19.2, можно утверждать, что при
описании свойств конических ответвителей метод локальных мод будет кор-
ректным, если критическая длина 21 (см. рис. 19.4), необходимая для пол-
ной передачи мощности из одного световода в другой, значительно больше
локальной длины биений zb в точке z = zc (см. рис. 19.4, а), в которой све-
товоды Ихмеют одинаковый радиус сердцевины р', а расстояние между их ося-
ми равно d. В разд. 18.13 было показано, что с ростом d длина биений для
двух одинаковых световодов увеличивается по экспоненциальному закону.
Поскольку в выражениях для Ф+ и Ф_ (18.33) расстояние между световода-
ми предполагается достаточно большим, то точность метода локальных мод
определяется им.
Если предположить, что в окрестности точки z = z^ угол конуса £2 светово-
дов одинаковый и противоположный по знаку, то критической длине 21 со-
ответствует изменение радиуса сердцевины обоих световодов 26р. Поэтому
из выражения (19.13) получаем критерий плавности
n = -/3- (^с)] =2^C(zc). (19-16)
В световодах со ступенчатым профилем различие радиусов сердцевины на
1 % достаточно для уменьшения передачи полной мощности на 10 % (см.
разд. 18.20). Следовательно, отношение бр/р должно составлять несколько
процентов, чтобы световоды были эффективно изолированы, а поскольку
C(zc), подчиняясь экспоненциальному закону, является малой величиной, то
угол £2 должен составлять несколько минут. Из условия 21» zb следует,
что критическая длина, необходимая для передачи полной мощности между
конусными световодами, должна значительно превосходить длину биений
полной мощности в сложном волноводе, состоящем из двух одинаковых ре-
гулярных световодов с радиусами сердцевины р. Более подробный анализ
точности метода локальных мод применительно к ответвителям дан в гл. 28.
356
ЛОКАЛЬНЫЕ МОДЫ ИЗОГНУТЫХ СВЕТОВОДОВ
До сих пор направление распространения локальных мод выбиралось прямо-
линейным, параллельным оси z световода или сложного волновода. Однако
в случае изогнутого световода, изображенного на рис. 19.5, а, в качестве на-
правления распространения локальных мод удобнее выбрать его изогнутую
ось. Тогда по аналогии с разд. 19.1 поля локальных мод формируются ап-
проксимацией изогнутого световода последовательностью цилиндров, изо-
браженных на рис. 19.5, б. Если профиль показателя преломления и форма
Рис. 19.5. Волоконный световод с радиу-
сом изгиба R (р - угловое смещение
вдоль изгиба) (а) и эквивалентная по-
следовательность цилиндров (б)
поперечного сечения световода не изменяются при изгибе, то поля локаль-
ных мод в окрестности световода в точности равны полям мод прямого све-
товода (11.3) при замене j3z на где R — радиус изгиба, а — угловое сме-
щение вдоль изгиба. Очевидно, что локальные моды, полученные таким об-
разом, будут хорошим приближением точных полей вблизи оси при условии,
что R достаточно велик.
Изгиб одномодовых световодов. Критерий плавности для локальных ос-
новных мод в изогнутом одномодовом световоде может быть получен на
основании соображений, изложенных в разд. 19.2, и подразумевает прене-
брежимо малое изменение угла на длине биений (19.4), т. е. zb/R << 1.
В приближении слабонаправляющего волновода это эквивалентно условию
Rip» 4я И/[ (2Д) 1/2 if 2 ], (19.17)
где р — радиус сердцевины, а остальные параметры определены в табл. I.
При выполнении этого условия можно ожидать достаточно хорошей аппрок-
симации полей световода вблизи оси полями локальных мод.
МНОГОМОДОВЫЕ СВЕТОВОДЫ И ЛУЧИ ,
В любой точке z вдоль нерегулярного многомодового световода локальные
моды высших порядков эквивалентны одиночному набору лучей, как это
следует из разд. 36.2. Каждый луч распространяется по пути, длина которо-
го медленно меняется на локальном полупериоде zp (z) (5.12). Видно, что
это аналогично свойствам многомодовых световодов, рассмотренных в
разд. 19.2. Более того, эквивалентность времен распространений мод и лу-
чей, рассмотренная в разд. 36.9; легко обобщается на световоды с плавно из-
меняющимися параметрами, для которых время распространения лучей опре-
деляется выражением (5.11).
Постоянная распространения мод /3 (z) является решением характеристи-
ческого уравнения для каждого значения z. Для мод высших порядков это
уравнение имеет вид, аналогичный уравнению для плоской волны (36.12) и
(36.13) в случае ступенчатого и градиентного профилей показателя прелом-
357
ления. Использование соотношения между параметрами мод и лучей из
табл. 36.1 показывает, что локальное характеристическое уравнение для выс-
ших мод имеет вид адиабатического инварианта (5.41).
Световоды со ступенчатым профилем показателя преломления. Рассмот-
рим параметр U моды нерегулярного ступенчатого световода с показателем
преломления сердцевины n(z) и радиусом сердцевины p(z). Из табл. 12.4
следует, что при V параметр U остается неизменным независимо от из-
менений параметров световода, если, конечно, эти изменения плавные. Соот-
ношение между U, /3 и 0z из табл. 36.1 для параметров, зависящих otz, име-
ет вид
U= kp(z)n(z) sin 6z(z) (19.18)
и является постоянным. Здесь 6Z (z) - угол между локальным направлением
луча и осью световода. Таким образом, U/k соответствует инварианту (5.20),
полученному ранее из лучевого уравнения, или соотношению (5.44), полу-
ченному из адиабатического инварианта.
ГЛАВА 20. ВОЗБУЖДЕНИЕ ВОЛОКОННЫХ СВЕТОВОДОВ
В предыдущих главах были определены свойства направляемых мод и рас-
смотрена структура их полей. Эта глава посвящена вопросам возбуждения
этих мод, когда входной торец световода освещается внешним источником,
например пучком света. При этом не вся падающая на входной торец мощ-
ность волны трансформируется в мощность, переносимую направляемыми
модами, — часть ее отражается от входного торца, а часть переходит в моды
излучения. Основное внимание в данной главе уделяется пространственно-
установившемуся режиму, рассмотренному во введении к части II. Это со-
стояние возникает достаточно далеко от входного торца и характеризуется
тем, что поле световода составляют только поля направляемых мод. В гл. 8
был изложен простой лучевой метод описания возбуждения многомодовых
световодов. В этой главе основное место занимают одномодовые и маломо-
довые световоды.
ВОЗБУЖДЕНИЕ МОД
Рассмотрим световод с произвольными профилем показателя преломления и
формой поперечного сечения (рис. 20.1,а), входной торец которою, т. е.
неограниченное поперечное сечение в точке z = 0 возбуждается произволь-
ным источником света. Амплитуды направляемых мод, возбужденных на
входном торце, легко могут быть найдены, если определено распределение
либо полного поперечного электрического поля Et в точке z = 0, либо соот-
ветствующего магнитного поля Ht. Разложив поле световода по полям его
мод, из соотношений ортогональности можно найти амплитуды мод. Однако
поля Et и Ht являются суммой поля возбуждения, которое задано, и поля,
отраженного от входного торца, интенсивность и распределение которого не-
известны, и определить его чрезвычайно трудно. К счастью, для слабонаправ-
ляющих световодов существует простое и точное приближение, которое бу-
358
Рис. 20.1. Входной торен (Z = 0) волоконного световода с произвольными профилем
показателя преломления и формой поперечного сечения (а) и преломление пучка ко-
нечной ширины на входном торне слабонаправляющего волоконного световода (б)
дет продемонстрировано на примерах после изложения общей теории [20.1 —
20.4].
20.1. Амплитуды мод и мощность
Полное поперечное поле на входном торце световода может быть представле-
но как поперечная составляющая разложения по собственным функциям вы-
ражений (11.2). Очевидно, что рассмотрению подлежат только вперед-рас-
пространяющиеся моды. Если поля направляемых мод представить в виде
(11.6), а поперечную составляющую поля излучения в точке z = 0 обозначить
Еп и Н^, то непрерывность поперечных полей на входном торце приводит к
соотношениям
Et (х, у) = S (х, у) + Efr (х, у), (20.1а)
/
Ht(x, = S ajhtJ(x,.>') + Ни(х, 7) (20.16)
для всех значений х и у, где постоянные а} являются амплитудами мод, а
7 = 1, . . . , М. Будем также предполагать, что источник излучения монохрома-
тический с той же неявной временной зависимостью exp(-icor), что и для по-
лей мод. В случае произвольного источника излучения, правая часть соотно-
шений (20.1) должна включать еще и суммирование по частотам.
В разд. 11.4 было показано, что поле каждой моды является ортогональ-
ным полю излучения и полю каждой другой направляемой моды. Имея это в
виду и предполагая, что световод является непоглощающим, умножим выра-
жение (20.1а) на h^, а (20.16) на и проинтегрируем по бесконечному по-
перечному сечению А м . С помощью соотношения (11.13) получим
“1 = Е' * 'idA' W7 х н' ’iJA- <2О2)
J -Ai оо J ОО
где z — единичный вектор, параллельный оси световода, а знак * обозначает
комплексное сопряжение. Если использовать условие (11.8) и выбрать в ка-
честве поперечных полей действительные функции, то коэффициент норми-
359
ровки TVj (11.12) будет также действительной величиной. Мощность Р-, пе-
реносимая каждой модой, определяется выражением (11.22), а следователь-
но, часть направляемой мощности полного поля равна
Р= SP; = S \а- |2М, (20.3)
/ J / J J
где суммирование проводится по всем направляемым модам.
ВОЗБУЖДЕНИЕ СЛАБОНАПРАВЛЯЮЩИХ СВЕТОВОДОВ
Для того чтобы определить амплитуды полей в выражении (20.2), необходи-
мо знать либо Et, либо Ht на входном торце световода. В общем случае ана-
литические выражения для этих полей получить невозможно. Однако, как
будет сейчас показано, проблема существенно упрощается, если световод яв-
ляется слабонаправляющим [20.2].
20.2. Поля мод на входном торце световода
Малое изменение показателя преломления в поперечном сечении слабона-
правляющего световода означает, что поля Et и Ht на входном торце прибли-
зительно соответствую! полям на границе между двумя полубесконечными
средами с показателями преломления п-х и п (х, у) « псо % ис1, что иллюстри-
рует рис. 20.1, б. Здесь п-х — показатель преломления области с z < 0, содер-
жащей источник излучения, псо, пс1 - соответственно максимальный показа-
тель преломления сердцевины и оболочки световода. Если световод возбуж-
дается пучком света диаметром 2ps >> X, то дифракционной расходимостью
пучка можно пренебречь. Таким образом, векторы Et и Ht могут быть опре-
делены из выражений, подобных полученным в случае отражения плоской
волны от границы раздела двух диэлектриков. В этом приближении прене-
брегают малыми эффектами рассеяния, обусловленными неоднородностью
профиля показателя преломления световода по поперечному сечению и пред-
полагают, что при z > 0 среда имеет неизменный показатель преломления ясо.
Преломление. Следуя изложенным выше соображениям, поле на входном
торце световода определяется полем возбуждения и представляется в виде
поля, изображенного на рис. 20.1, б. Если пучок света составляет с осью све-
товода угол 0р то в точке z = 0 он преломится и образует угол 0Z. Эти углы
связаны законом Снелля
пх sin = nCQ sin 0Z. (20.4)
На практике обычно пх < nCQ, так что 0Z < 0р и пучок преломится к оси све-
товода. Соотношения между Et, Ht и полями падающего пучка Ej, Hj опреде-
ляются коэффициентами отражения Френеля для случая отражения плоской
волны от границы двух диэлектриков и рассматриваются в разд. 35.6. В об-
щем случае эти коэффициенты зависят от поляризации пучка, но если угол
0j мал, то поляризация играет малую роль и коэффициенты определяются
выражением (35.18), в котором исо и ис1 необходимо заменить на п-х и nCQ
соответственно. Таким образом, из выражений (35.16), (35.15) и (35.17)
имеем
360
Et (0Z) *--------E; (0j) ; Ht (0J * Hj (0j) ,
1 Z «i+«CO * ’ ’ «i+«CO *
(20.5)
где E, и Hj являются почти поперечными составляющими поля, если вх<< 1,
т. е. когда в выражении (35.18) можно положить ~ ~ тт/2.
Переносимая мощность. Часть мощности пучка, переносимая через грани-
цу диэлектриков, зависит от произведения Et и Ht и определяется коэффи-
циентом передачи мощности Френеля Т (35.21), в котором а?со и «с| замене-
ны соответственно на пj и псо. Отсюда при < < 1.
7’ = 4ni«co/(ni+«co)2.
(20.6)
Другими словами, только часть мощности Т падающего пучка пересекает
плоскость, совпадающую с входным торцом световода.
Из выражения (20.5) видно, что амплитуду моды^ можно найти из уравне-
ния (20.2), если, во-первых, предположить, что исо = пх и = 0z (рис. 20.1,6),
а, во-вторых, в конечном выражении заменить tfj(0j) на Tl/2a^nfix/nCQ). На
практике фактически вся мощность пучка проходит через входной торец,
поскольку для типичного случая границы между воздухом и световодом
(flj = 1 и псо = 1,5) Т » 0,96. Везде в дальнейшем в этой главе предполагает-
ся, что исо = 77j и ez = 0j. Таким образом, поперечное поле на входном торце
является полем падающего пучка, т. е. Et = Ej и Ht = Hj. При исо Ф п-х полу-
ченные результаты могут быть скорректированы с помощью метода, описан-
ного ниже.
20.3. Поля возбуждающего пучка
Рассмотрим теперь возбуждение световода пучком света, параллельным или
направленным под небольшим углом 0j к его оси. Поле пучка при этом имеет
вид локальной плоской волны с волновым вектором, параллельным направ-
лению пучка. Если электрическое поле Ei однородно поляризовано вдоль
оси х (рис. 20.2, а) и пучок параллелен плоскости х, z, а функция распреде-
ления амплитуд f (г) является четной функцией г, то
Et = Ехх xf(r) exp [iknx (х0-х + z) ] = xf (r) exp [ikn{ (0/ cos + z) ]; (20.7a)
Hi = (eo/Mo)1/2 ИjZ x Ej я= Hyy, (20.76)
где x; у и z - единичные векторы, параллельные осям координат на рис. 20.2, а,
а остальные параметры определены в табл. I. Полная мощность пучка Р},
распространяющегося вдоль направления z, определяется уравнением (11.25)
Л = ЯП, (ео/мо)1/2 J rf (г) dr,
О
(20.8)
361
Рис. 20.2. Оси координат для описания полей падающего на входной торен пучка (а);
эффективность возбуждения гауссовым пучком мод световода с неограниченным пара-
болическим профилем как функция угла наклона (б); ориентация гауссова пучка
для: в - соосного; г — наклонного; д — смещенного возбуждений
которое справедливо как для ограниченного, так и для неограниченного
пучков,
20.4. Гауссов и однородный пучки
Ниже в этой главе рассматривается возбуждение гауссовым и однородным
пучками. Гауссов пучок имеет неограниченную ширину, а радиальное распре-
деление и полная мощность определяются выражениями
2
f (О = ехр (-1 -4-) ; Pj (ео/мо)1/2 п{р},
2 Ps 2
(20.9)
где ps - размер пятна. Радиальное распределение для ступенчатой функции
соответствует однородному пучку. В случае равенства радиуса однородного
пучка и размера пятна гауссова пучка переносится одинаковая мощность. Та-
ким образом, для однородного пучка имеем следующее выражение для
мощности:
fl, 0<г<ps _
/(0 = 1 ; Pj = 5 (eo/Mo)1/2njP2-
(О, ps<r<°°
(20.10)
Оно может быть получено из выражения (20.8).
362
20.5. Амплитуда мод и мощность
Поперечные поля etj и любой моды слабонаправляющего световода связа-
ны соотношением (13.1). Если предположить, что на рис. 20.1, б псо = п-, то
поля на торце световода определяются выражениями (20.7). При лсо пх
они несколько модифицируются, что отмечалось в разд. 20.2. Таким обра-
зом, из уравнений (13.1) и первого выражения (20.2) следует
(20.11)
где значение Ех оценивается в точке z = 0, a eXj - х-составляющая вектора
etj. Если использовать второе выражение (20.2), то результирующее соотно-
шение для а- согласуется с (20.11) только при малых углах падения пучка.
Это ограничение является следствием предположения о том, что на входном
торце световода Et = Ej и Ht = Hj, в то время как точные выражения для Et
и Ht зависят от структуры световода [2]. Однако это предположение вполне
соответствует интуитивному утверждению в конце разд. 20.2. Таким обра-
зом, соотношение (20.11) справедливо для слабонаправляющих световодов,
возбуждаемых пучком под небольшим углом к его оси. Если одно из этих
двух условий нарушено, то достаточно просто определить значение а} нельзя.
Соотношение (20.11) может быть получено и непосредственно из скаляр-
ного волнового уравнения, поскольку в приближении слабонаправляющего
волновода поля в выражении (20.1а) являются решениями этого уравне-
ния. Следовательно, (20.11) вытекает непосредственно из условия ортого-
нальности (33.56).
Ограничение 0j << 1 в слабонаправляющих световодах почти всегда вы-
полняется. В этом легко убедиться, если учесть, что в геометрической оптике
каждая направляемая мода распространяется относительно оси световода
под углом 0Z, который не превышает критического угла 0С » (1 - «с1/лсо^ 12 •
Поскольку по предположению исо ~ лс1, то 0с << 1.
Мощность мод. Выражение для мощности, переносимой каждой модой,
следует из соотношения (20.11) и табл. 13.2. Для световодов с произвольной
формой поперечного сечения имеем
Р= ^(е0/Мо)1/21 I E e^A\2l S |eJ2<M.
J 2 д л М л У
^ОО Z1 оо
(20.12)
В случае световодов с круглым поперечным -сечением это выражение с уче-
том табл. 14.1 преобразуется к виду
7
Р П оо 27Г оо
Р, =—^(воМо)1/2 IJ- J E^JZdRdrf/ f F2(R)RdR.
1 2тт о о 1 о 1
(20.13)
где р — радиус или характерный размер сердцевины, ^обозначает F^(R) cos
или F^(R) sin a F^(R) является решением скалярного волнового уравнения
363
(14.4). Азимутальная симметрия поперечного сечения круглого световода
приводит к независимости мощности, переносимой каждой модой, от поля-
ризации поля возбуждающего пучка, и поэтому полученный результат не за-
висит от того, какая компонента электрического поля используется в выра-
жении (20.7а).
Рассмотрим теперь некоторые конкретные примеры.
ВОЛОКОННЫЙ СВЕТОВОД С НЕОГРАНИЧЕННЫМ ПАРАБОЛИЧЕСКИМ
ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
На примере волоконных световодов с неограниченным параболическим про-
филем определим физическую природу возбуждения световода гауссовым
пучком [5 — 7]. Профили такого вида определяются выражением
и2(Д) =и20(1-2ДЯ2); 0<Я<~
(20.14)
где R = г/р и Д < < 1. Хотя такой профиль при R °° физически не реализу-
ем, приближение слабонаправляющего волновода вполне корректно при опи-
сании свойств основной моды (см. разд. 14.4), если V» 4А.
20.6. Пример. Соосный гауссов пучок
Если гауссов пучок падает перпендикулярно торцу световода (0j = 0 на рис. 20.2, в),
из соотношений (20.7а) и (20.9) следует, что электрическое поле при этом имеет вид
£х = ехр (-г2/2р2), где ps - размер пятна пучка. Таким образом, Ех не зависит от
что исходя из выражения 20.13 означает возбуждение только мод с индексом 1=0 или
НЕ1т-мод. Для основной моды, поляризованной вдоль оси х, из табл. 14.2 имеем Фо =
= Fo = ехр (-г2 /2г2), где r0 = p/V1'2 - размер пятна моды. Подставив полученные вы-
ражения в (20.13), разделив результат на соотношение (20.9) и предположив, чтог?| =
= «со, получим выражение для части мощности пучка, распространяющейся в основной
моде:
P„/Pj = [2ps''o/(Ps+z'o)r- (20.15)
Таким образом, только при совпадении пятен пучка и основной моды (r0 = ps) вся
мощность пучка распространяется в основной моде. Чем больше различие между ps и
г0, тем меньшая часть мощности распространяется в основной моде и тем большую
мощность переносят НЕ1т-моды высших порядков.
20.7. Пример. Наклонный гауссов пучок
Этот случай аналогичен предыдущему за исключением того, что теперь пучок направля-
ется под небольшим углом 0j к оси световода, как показано на рис. 20-2, г. Наиболее
существенным свойством внеосевого возбуждения световода является возбуждение
мод с Z > 0, а не только мод с индексом 1=0. Чтобы рассмотреть этот случай, с помо-
щью соотношения (37.80а) разложим выражение (20.3а) в ряд по функциям Бесселя
первого рода
°° -I
exp(ifcw:0f cos <р) =J0(kR) + 2 £ Zj (K/?)cos Z<z>, (20.16)
l- о 1
где к = kpn-fty Тогда из соотношений (20.7а), (20.13) и (20.9), полагая = nCQ, полу-
чаем следующее выражение для части мощности пучка:
364
р 2 I JFl(/?)Jl(K^)exp(-/?2p2/2p2s)^|2
1 = 2— 0________________________________
Pi ps jRF7(R)dR
0 L
(20.17)
Отметим, что в данном случае возбуждаются только моды четного порядка, т. е. =
= Fy(R) cos 1<р. Если для каждого значения I рассмотреть только моды низших поряд-
ков, то из табл. 14.2 следует, что 7^(7?) = (r/r0)'fexp (-г2/2гJ), гдег0 = р/К1/2 - размер
пятна моды. Подставляя это выражение в (20.17) и учитывая соотношения (37.1006)
и (37.125), получаем
Л л (4nco0i)21, ' '•oPs ,21+2 ,
~Г —л----------(} ехр 1~ “ТТ?------------
(20.18)
Это отношение определяет эффективность возбуждения мод гауссовым пучком как
функцию угла наклона 0j. Для каждого значения I максимальная эффективность дости-
гается при угле 0р определяемом дифференцированием выражения (20.18) по0р Та-
ким образом,
e-i = I'12 (fo + рр1/2 / (*р5”Л) •
(20.19)
В качестве иллюстрации к полученным результатам на рис. 20.2, б показаны зависимо-
сти от ^ps«j0| в предположении, что r0 = ps. Из них видно, что с ростом 0j часть
мощности в основной моде падает, а мощность, переносимая мрдами высших порядков,
растет, достигая максимума при угле 0-
20.8. Пример. Смещенный гауссов пучок
В этом случае гауссов пучок падает перпендикулярно торцу световода, но центр его сме-
щен на величину относительно оси (см. рис. 20.2, д). При таком асимметричном воз-
буждении основная мода будет переносить меньшую мощность, чем в случае, рассмот-
ренном в разд. 20.6. Кроме тогр, будут возбуждены моды высших порядков. В данном
случае из (20.7а) и (20.9) и с учетом координат, изображенных на рис. 20.2,а, полена
торце определяется выражением
£'x=exp{-[(x+rd)s+^]/2p^}. (20.20)
Если выразить Fo (7?) из табл. 14.2 в декартовых координатах и подставить полученное
соотношение в (20.13), то с помощью (30.127) и (20.9) определим часть мощности
пучка, переносимой основной модой (rq = п ):
Ро/Л = {2рЛ/(р1 ’expl-'Wo +рр]' (20.21)
Таким образом, эффективность возбуждения основной моды падает по экспоненциаль-
ному закону по мере смещения пучка от оси световода.
20.9. Пример. Соосный однородный пучок
Если в примере, рассмотренном в разд. 20.6, гауссов пучок заменить однородным с ра-
диусом ps, то, повторив вывод соотношения (20.15), получим эффективность возбуж-
дения основной моды
365
PJP^ (2r0/ps)5 [1 - exp(-p’/2r’)p,
(20.22)
Где r0 = p/V1/t2. Следовательно, в отличие от случая возбуждения гауссовым пучком эф-
фективность возбуждения основной моды никогда не достигает единицы, и всегда одно-
временно должны возбуждаться моды высших порядков HEJm- Максимальная эффек-
тивность возбуждения моды НЕП составляет 81 % при ps « 1.6г0.
Выражения, описывающие эффективность возбуждения основной моды Ро/Р[ Для
случаев, рассмотренных в этих трех примерах, приведены в табл. 20.1.
20.10. Пример. Наклонная плоская волна
Возбуждение торца световода неограниченной плоской волной эквивалентно возбужде-
нию однородным пучком с радиусом ps Повторив вычисления, проделанные в
разд. 20.7 для пучка, падающего под углом к оси световода, получим аналогично
(20.18) выражение
\ 1 -Цг2—ехр {кг°п^21 ’
(20.23)
Таблица 20.1. Эффективность возбуждения основной моды
Гауссов пучок
Соосный Рр _ 1 Гор1 Р, Ор+Р?)2
Наклонный под углом 0. к оси световода Ро _ л rjpl ( _ (кп^гор,)2 1 Pi (rp+P2)2CXP 1 Го+Р? J
Смещенный относительно оси световода на г d — = 4 ехр! Pi (r^+Ps2)2 Pl rp+PsJ
Однородный
Соосный Pp 'о/. / lp2\)2
Соосный с линзой P, “P(
Примечание. Приведенные выражения являются точными для световода с неогра-
ниченным параболическим профилем при r0 = p/V1/2 (в пределах гауссова прибли-
жения г0 равен размеру пятна, см. соотношение (20.24)). Здесь ps — размер пятна
пучка, Рг — полная мощность пучка и Ро — мощность основной моды.
366
при выводе которого предполагалось, что в (20.7а) /(г) = 1. Если 0j-*O, мощность ос-
новной моды равна 2тгг^И| (е0 /м0)1/2. Этот результат находится в полном соответствии
с результатами (20.22) и (22.10) при ps -> °°. Отметим, что мощность плоской волны
бесконечна, так как ее плотность равна п^/2 (е0 /д0)1/2.
ВОЗБУЖДЕНИЕ ОДНОМОДОВЫХ СВЕТОВОДОВ
Эффективность возбуждения основной моды круглого световода, поле ко-
торой описывается выражением (13.9), представляет особый интерес в слу-
чае, если он является одномодовым. Ранее в гл. 15 было рассмотрено гауссо-
во приближение, позволяющее описать свойства слабонаправляющих свето-
водов с произвольным профилем, если получить решение скалярного волно-
вого уравнения Fo (г) для основной моды невозможно. При этом радиальное
распределение поперечного поля основной моды аппроксимируется выраже-
нием (15.2):
F0(r) = ехр(—г2/2го), (20.24)
в котором размер пятна моды г0 зависит от конкретной формы профиля.
В этой же главе были рассмотрены примеры использования такого прибли-
жения для ряда профилей, включая ступенчатый и гауссов (см. табл. 15.2).
Таким образом, если поле основной моды аппроксимировать выражением
(20.24), то все результаты, полученные ранее для неограниченного параболи-
ческого профиля справедливы и для произвольной формы профиля показа-
теля преломления при условии, что в выражения в табл. 20.1 подставлено со-
ответствующее выражение для размера пятна моды rQ из табл. 15.2.
20.11. Соединение световодов
Гауссово приближение позволяет легко и просто получить достаточно точные
выражения, описывающие потери мощности при стыковке одномодовых све-
товодов. На практике эти потери обусловлены в большинстве случаев тремя
причинами: а) несоответствием геометрических размеров световодов; б) уг-
ловым рассогласованием (наклоном одного световода относительно оси дру-
гого) ; в) осевым рассогласованием (несовпадением осей). Все три случая
схематически показаны на рис. 20.3. Если поле основной моды излучающего
световода (z < 0) описывается гауссовой функцией с соответствующим раз-
мером пятна моды ps, т. е. FQ (г) = ехр(—г2/2р2), то каждое рассогласование
можно рассматривать как соответствующим образом ориентированный гаус-
а) z — 0
5) z = 0
Рис. 20.3. Соединение двух световодов:
а — различие в геометрических размерах; б — угловое рассогласование осей; в — несов-
падение осей
367
сов пучок, падающий на принимающий световод (z > 0). Если поле и этого
световода можно аппроксимировать гауссовой функцией, то часть мощности,
потерянная при соединении, равна 1 - Ро/Р? где эффективность PQ/PX для
разного вида рассогласований дана в табл. 20.1.
ВОЛОКОННЫЕ СВЕТОВОДЫ СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ
ПРЕЛОМЛЕНИЯ
В качестве дополнения к примерам, иллюстрирующим эффективность воз-
буждения мод световода с неограниченным параболическим профилем пока-
зателя преломления, получим теперь аналогичные выражения для слабона-
правляющего световода со ступенчатым профилем показателя преломления
при возбуждении его однородным пучком
20.12. Пример. Наклонный однородный пучок
Если однородный пучок, рассмотренный в разд. 20.1, падает на торец световода под уг-
лом 0j к его оси, то в соответствии с разд. 20.7 имеем
Ру р2 * * * * S
-=2-^1 J F,(R)J (xR)RdR\2 IS F(R)RdR, (20.25)
Л Ps 0 1 0 b
где к = kpnfi^ (см. рис. 20.2, а), а функция F^(R) определена в табл. 14.4. Используя
интегралы от произведения функций Бесселя (37.94) и (37.98) и интеграл в табл. 14.6,
получаем [2]
Л. = 4 и—___ -^s)A+i<KPPl f20 26a)
Pj V7 В * * * K{_ J (^)\+ J W (. (t/2 -k2)/^^) j
Если же ps > p, to
PA = f2pt/v
pi Psr
1 W JL(K) - K/t(tOA+I (X) p
(C/2 -k’)A(U) j’
(20.266)
[^(0/s)/L+! (ks) - JWl+ j ]ps - i (к) - ^L+ j W^Ck) ]p
(W2 +k2)aK‘iW
(20.26b)
где = Ups/p, = Wpjp, ks = *Ps/p и для ясности знак - при параметрах U и W опу-
щен. Напомним, что при выводе этих выражений предполагалось, что п-{ — ^со Если
же значительно отличается от показателей преломления световода, то в полученные
формулы необходимо ввести поправки, рассмотренные в разд. 20.2.
В качестве иллюстрации рассмотрим световод с параметром V = 5, который возбуж-
дается пучком, радиус которого равен радиусу сердцевины, т. е. ps = р. Если поле (20.7а)
пучка линейно поляризовано вдоль оси х, то из свойств симметрии пучка и рис. 14.4 сле-
дует, что возбуждаться будут только мода ТЕ01 и четные HEjr, НЕ12-, НЕ21-, НЕ31- и
ЕНп-моды. На рис. 20.4, а изображены зависимости отношений Р/Р^ vj\qP- полная мощ-
ность моды при данном значении U, и Р^т/Р^ гдеРьт - полная мощность всех мод, за-
висящая от нормированного угла 0|/0с- Здесь 0^ — критический угол, определяемый со-
отношением 0С « (2Д)1/2 ~ (1 - пс[/псо^12' Как видно из представленных зависимо-
стей, с увеличением 0j мощность основной моды падает, и возбуждаются моды высших
порядков, при этом полная мощность направляемых мод быстро уменьшается, посколь-
ку все большая мощность пучка излучается из световода.
368
Рис. 20.4. Зависимость эффективности возбуждения однородным пучком мод светово-
да со ступенчатым профилем от угла наклона 0^, где Рвключает мощность всех мод с
одинаковой величиной U (на рис. 14.4), а — суммарная мощность всех направляе-
мых мод [2] (а); зависимость эффективности возбуждения мод от нормированной
частоты отсечки световода V в случае осевого возбуждения (сплошная кривая соот-
ветствует точному решению (20.27в), а штриховая — гауссову приближению (20.28а))
(б); зависимость отношения полной мощности направляемых мод к мощности пучка
от нормированного угла наклона ручка для различных значений К (в). То же, что в
(б), для основной моды при различных отношениях радиусов пучка и сердцевины (кри-
вые соответствуют выражениям (20.27в) и (20.286)) (г)
Оптимальный угол наклона пучка. Очевидно, что при заданном значении параметра
V существует оптимальный угол наклона пучка 0р при котором зависимость эффектив-
ности возбуждения определенной моды имеет максимум (см. рис. 20.4,а). Ясно, что
максимальная эффективность возбуждения будет достигаться при угле 0р равном ха-
рактеристическому углу 0Z, который локальный волновой вектор поля моды (см.
разд. 36.2) образует с осью световода. Поскольку в слабонаправляющих световодах углы
0С и 0Z малы, из соотношений между волновыми и лучевыми параметрами (табл. 36.1)
следует, что 0^/0г « (0^/ес) V/U. Если значение 0j/0c соответствует максимуму эффек-
тивности возбуждения на рис. 20.4, я, a V/U при этом определяется рис. 14.4, то 0 j/0z «1.
Более строгий анализ показывает, что максимумы кривых на рис. 20.4, а для всех мод,
кроме основной, пропорциональны j (U) при условии, что V > > U [2]. Для моды
НЕП максимальная эффективность 85 % достигается в световоде с параметром V = 3,8
при угле 0j ~ 0.
20.13. Пример. Соосный однородный пучок
Если в предыдущем примере предположить, что пучок направлен вдоль оси, т. е. 0j =
= к = 0, то из свойств симметрии следует, что возбуждены будут только НЕп-и НЕ12-
моды. Таким образом, выражение (20.26) значительно упрощается [2]:
369
Ру г 2 W J,(C/S)
Pj ’ 1Р'7Г,(1П /0(С/) J
При равенстве радиусов сердцевины и пучка
2 И/
Ps = p-
(20.27а)
(20.276)
(20.27в)
Если радиус пучка значительно превосходит радиус сердцевины, то с помощью (37.88)
получаем
Py/Pi « ^-pV/'p^UWY1- Ps>> Р- (20.27г)
В последнем случае эффективность возбуждения каждой НЕ1т-моды зависит от от-
ношения радиусов сердцевины и пучка.
Численные результаты. На рис. 20.4, б для первых трех НЕ 1т-мод изображены зави-
симости отношения Ро/Р- (20.27в) от параметра И. Частота отсечки для моды НЕ 12 рав-
на 3,832, а для моды НЕ13 - 7,016. Максимум эффективности возбуждения основной
моды 0,85 достигается при V — 3,8. При этом гауссово приближение с учетом табл. 20.1
дает выражение
PQ/P{ = (2/1п Г) (И-1)2/И2, (20.28а)
при выводе которого предполагалось, что ps = р и г0 — р/ (21п V) 1/2. Эта приближенная
зависимость, изображенная на рис. 20.4, б штриховой линией, дает хорошую точность
при V < 2,4.
На рис. 20.4, г приведена зависимость (20.276), показывающая влияние радиуса
пучка на эффективность возбуждения основной моды. Видно, что при больших значени-
ях параметра V с ростом ps она падает. Штриховой линией на этом же рисунке показано
гауссово приближение (см. табл. 20.1) при r0 = pf (21п Г) 1/2, которое имеет вид
Ру /Pi = Р1рг /р^п Ю {1 - exp [-p’ln v/p1 ]} 2 (20.286)
и дает хорошую точность при V > 2,4.
Ранее было показано, что вблизи соответствующей частоты отсечки значительная
часть мощности мод НЕ12 или НЕ13 распространяется по оболочке (см. рис. 14.6). Поэ-
тому пучок, радиус которого значительно превышает радиус сердцевины световода, мо-
жет достаточно эффективно возбудить моды, находящиеся вблизи частоты отсечки, не-
смотря на то, что значительная часть мощности мод распространяется по оболочке. В слу-
чае же равенства радиусов эффективность возбуждения мод вблизи их частоты отсечки
пренебрежимо мала, что иллюстрируется на рис. 20.4, б для НЕ12- и НЕ13-мод.
20.14. Сравнение с геометрической оптикой
Полученные результаты весьма полезно сравнить с результатами анализа воз-
буждения однородным пучком многомодовых световодов со ступенчатым
профилем показателя преломления, которые были даны в разд. 4.9 с точки
зрения геометрической оптики.
Если предположить, что радиусы пучка и сердцевины световода равны, а
эффекты, обусловленные неидеальностью его торца, не учитывать, то в слу-
чае, когда угол наклона пучка к оси световода 0^ удовлетворяет условию 0 <
< < 0С, где вс — критический угол скольжения, вся мощность пучка транс-
формируется в мощность направляемых лучей и РЬт/Р^ ~ 1, где РЬг - полная
мощность направляемых лучей. Если же > 0 , то направляемых лучей не
370
возникает и Р^т/Р\ = 0- Графически это показано на рис. 20.4, в с помощью
кривой для V = °°.
Проводя соответствующие вычисления с использованием волновой тео-
рии, можно определить часть мощности пучка, которая .трансформировалась
во все направляемые моды, существующие при заданном значении парамет-
ра V. Таким образом, величина РЬг/Р| определяется суммой выражений
(20.26) при ps = р по всем направляемым модам. С ростом V возбуждается
все большее число направляемых мод, но только при V = °° результаты вол-
нового и лучевого анализов совпадают в точности [8]. Это объясняется тем,
что, как показано в гл. 10, при конечном значении V существенную роль иг-
рает дифракция на торце световода, приводящая к расширению поля пучка, а
этот эффект при лучевом анализе не учитывается.
ВОЗБУЖДЕНИЕ С ПОМОЩЬЮ ЛИНЗ
Линза, помещенная перед входным торцом световода, может значительно по-
высить эффективность возбуждения направляемых мод. Рассмотрим ситуа-
цию, изображенную на рис. 20.5. Параллельный соосный пучок радиусом рх
Рис. 20.5. Возбуждение свето-
вода с помощью линзы, ради-
ус которой равен радиусу пуч-
ка. Фокус линзы находится
в плоскости входного торна
световода
падает на собирающую линзу, расположенную таким образом, что ее фокус
совпадает с центром торца световода. Действие линзы на пучок света заклю-
чается в формировании дифракционной картины дальнего поля в фокальной
плоскости линзы, возникающей вследствие ограничения радиуса пучка апер-
турой линзы радиусом рг Предположим, что апертурный угол линзы 2в± мал,
тогда влиянием линзы на поляризационные свойства поля пучка можно пре-
небречь и считать, что потери мощности в линзе отсутствуют. Записав полное
поле падающего пучка в виде выражения (20.10), с помощью соотношения
(37.91) и табл. 13.2 определим нормированное дифракционное распределе-
ние дальнего поля линзы на торце световода [9]
’ к = кРпA’ R = Г/Р> (20.29)
г' J\
где Ji — функция Бесселя первого рода, пх — показатель преломления среды,
в которой распространяется пучок, 0* « pjf — апертурный угол линзы и
р — радиус или характерный размер сердцевины. Смысл радиальной коорди-
наты п ясен из рис. 20.2. Рассмотрим некоторые примеры.
20.15. Пример. Неограниченный параболический профиль
В данном случае в круглом волоконном световоде возбуждаются только НЕ1т-моды и
мощность каждой моды можно определить, если подставить соотношение (20.29) в
371
(20.13), учитывая, что выражение для F^(R) приведено в табл. 14.2. Для основной мо-
ды интеграл в числителе (20.13) определяется выражением (37.100а), так что эффек-
тивность возбуждения основной моды [10]
I PQ/Pt= (2/П)2 [1 — ехр (—П2/2) ]2; И = krQn^
I___________________________________________________
(20.30)
где r0 = plVxn - размер пятна моды. Функционально это выражение аналогично (20.22),
и поэтому при П = 1,6 максимальная эффективность возбуждения равна 81 %, что поз-
воляет сделать весьма интересный вывод о том, что максимальная эффективность воз-
буждения основной моды световода с неограниченным параболическим профилем пока-
зателя преломления не зависит от наличия линзы. Однако если плотность мощности
пучков в обоих случаях одинакова, фактическая мощность основной моды при исполь-
зовании линзы может быть значительно больше, нежели при ее отсутствии, поскольку в
первом случае можно одновременно увеличивать радиус пучка, радиус и фокусное рас-
стояние линзы, оставляя 0j неизменным и равным его оптимальному значению.
20.16. Пример. Гауссово приближение
Выражение для эффективности возбуждения основной моды световода с неограничен-
ным параболическим профилем (20.30) может быть также использовано и для оценки
эффективности возбуждения основной моды световода с произвольным профилем по-
казателя преломления.
В рамках гауссова приближения для поля основной моды (20.24) в выражение
(20.30) необходимо лишь подставить соответствующее выражение для размера пятна
моды. Например, для ступенчатого профиля из габл. 15.2 имеем г0 = р/(2 In К) 1/2, что
при V — 2,4 дает ошибку между точным результатом и полученным из (20.30), мень-
шую 1 % [10].
ДИФФУЗНОЕ ВОЗБУЖДЕНИЕ
До сих пор в этой главе рассматривалось возбуждение мод одним пучком,
направленным под определенным углом к оси световода. Теперь рассмотрим
случай, когда торец световода возбуждается несколькими пучками, направ-
ленными под разными углами к оси световода, т. е. диффузным источником
Рис. 20.6. Диффузный источник с радиусом р§ расположен на входном торце световода:
а — каждая точка источника излучает внутри конуса с углом 20т; б — модель, соглас-
но которой источник заменяется суперпозицией пучков с различными углами наклона 0
к оси световода
372
возбуждения, который схематично изображен на рис. 20.6, а. Такие источни-
ки иногда называют также (частично) пространственно-некогерентными ис-
точниками, в то время как однородный и гауссовы пучки, рассмотренные
выше в этой главе, являются почти пространственно-когерентными. Это
означает, что излучение во всех точках поперечного сечения пучка, падающе-
го под небольшим углом к оси световода, фактически имеет одинаковую
фазу, т. е. пучок рассматривается как плоская волна.
Частично диффузный источник, изображенный на рис. 20.6,я, можно рас-
сматривать как суперпозицию (когерентных) пучков, один из которых по-
казан на рис. 20.6, б. Поскольку фазы соседних пучков являются случайны-
ми, то полная мощность такого источника Ps равна сумме мощностей всех
пучков. Если предположить, что источник обладает осевой симметрией, то
0т
Р =2я JP(0)'sin0d0, (20.31)
s о
где Р(0) — полная мощность пучка, распространяющегося под углом в к оси
световода, приведенная к единичному углу. Пусть Pj — мощность, возбужден-
ная в /-Й моде. Поскольку она обусловлена всеми пучками, то имеем
0т
Р; = 27Г J* Л (0) sin 0d6, (20.32)
J о
где Pj (0) — часть мощности, возбуждаемой в моде пучком, распространяю-
щимся под углом 0 к оси световода. Тогда эффективность возбуждения /-й
моды определяется выражением
£l = _!______
Л 1 - cos 0m
emP:(0) 2 % Л(0)
Г sin0d0^~ ( 0d0.
о P 02mJo P
(20.33)
При выводе этого выражения предполагалось, что мощность источника не
зависит от угла, т. е. Р(0) = Р. Приближенное равенство справедливо при
0m << 1. Отношение Pj(0)/P, входящее в подынтегральное выражение
(20.33) в случае круглого световода, определяется соотношениями (20.13)
и (20.9), что подтверждает интуитивное представление о том, что мощность,
возбужденная в моде диффузным источником, равна мощности моды, усред-
ненной по всем пучкам, составляющим диффузный источник. Поэтому, если
известна эффективность возбуждения моды пучком с произвольным углом
0, то полная мощность определяется суперпозицией.
20.17. Пример. Одномодовые световоды
Предположим, что частично диффузный источник возбуждает одномодовый световод
(см. рис. 20.6, а). Поскольку в разд. 20.7 и 20.12 было показано, что основная мода на-
иболее эффективно возбуждается пучками, параллельными его оси, то ясно, что чем
ближе источник к диффузному, т. е. чем больше угол 0т, тем меньше эффективность
возбуждения основной моды. Чтобы подтвердить этот вывод количественно, рассмот-
рим источник, распределение интенсивности в поперечном сечении которого подчиняет-
ся гауссову закону, т. е. источник, представляющий собой некогерентную суперпозицию
гауссовых пучков. Выражение для эффективности возбуждения можно получить, если,
373
&
70
60
50
40
30
20
10
0 2 4 6 8 10 12 14 16 18 V
S)
Рис. 20.7. Эффективность возбуждения основной моды (20.34) как функция угла 0
диффузного источника для световодов со ступенчатым (у), гауссовым (g) и неограни-
ченным параболическим (р) профилями (а) и погрешность лучевого анализа при расче-
те (в процентах) эффективности возбуждения мод многомодового световода полно-
стью некогеренгным пучком как функция параметра V (сплошная кривая соответству-
ет точному расчету (20.39), а штриховая - приближению (20.41) [11]) (£)
использовав гауссово приближение, в подынтегральное выражение (20.33) вместо
Pj (0) /Р подставить соотношение P0/Pj из табл. 20.1 для случая наклонного гауссова пуч-
ка, заменив 0- на 0. Прямое интегрирование дает выражение
_Л = JL вс Рг г. , ет 'I
р г/2 п2 г2 . 2 U еХР ( ^2 г2 . '
Л v ro * P °c ro + P
(20.34)
где V - параметр световода, 0C » (1 - «с1/лсо^12 “ критический угол скольжения. Пред-
полагается, что радиусы пучка и сердцевины световода равны, т. е. ps = р, а отражение
от входного торца пренебрежимо мало, т. е. = исо< На рис. 20.7, а показана зависи-
мость отношения P0/Ps от нормированного угла 0т/0с для ряда профилей показателя
преломления на частоте отсечки второй моды. Согласно данным табл. 15.2 ступенчато-
му профилю (у) соответствует г0 — р/(2 In И)1/2 и V = 2,41, гауссову профилю (g) -
r0 = р/V - 1 и V ъ 2,59 и неограниченному параболическому профилю (р) - г0 =
— pfvv2 и V = 3, причем для последнего профиля выражение (20.34) является точным.
20.18. Пример. Многомодовые световоды
Рассмотрим слабонаправляющий многомодовый световод, который возбуждается диф-
фузным источником. Чтобы получить выражение для полной мощности направляемых
мод не°бходимо взять сумму выражений (20.32) для всех мод. Если предполо-
жить, что источник пространственно полностью некогерентный, т. е. 0т = я/2, то фаза
излучения каждой точки его поперечного сечения не зависит от фаз всех других точек и
полную мощность любой моды можно определить, зная эффективность возбуждения
данной моды от каждой точки поперечного сечения источника. Таким образом, Pj опре-
деляется выражением (20.12), в котором квадрат модуля интеграла заменен на инте-
грал от квадрата модуля подынтегральной функции. Однако это выражение не учиты-
вает, что каждая точка источника излучает свет, поляризованный вдоль осей х иу (см.
рис. 20.2, а) с равной вероятностью, а электрическое поле источника имеет одинаковые
х- и у-составляющие. Поэтому выражение (20.12) следует умножить на коэффициент
%, т. е.
374
Pj = 2T-O1'2 ' J le (20.35)
J О r*0 J J A j
<* QQ Z1 QQ
Если источник однородный и имеет площадь поперечного сечения, равную площади
сердцевины Ас, то с помощью табл. 13.2 выражение (20.35) можно преобразовать к
виду [11]
Pj = Cj|exj|’A4/J |etj|!<i4
/4 с А ос
(20.36)
где С = (лсо|£х|2/8) (е0/м0)1/2 и r?j - часть мощности моды, распространяющаяся в
сердцевине. Полученный результат был очевиден с самого начала: некогерентный источ-
ник возбуждает каждую моду с максимально возможной эффективностью т^. Полная
мощность направляемых мод определяется выражением
М М
/,ьт = /?/) = сД1^ <20-37)
где Л/ - число направляемых мод.
В многомодовых световодах параметр V настолько велик, что д- % 1 и, таким обра-
зом, Ррт в выражении (20.37) определяется числом мод. В разд. 36.13 показано, что
для ступенчатого световодаМ « Е2/2 и, учитывая определение V из табл. I,P^m пропор-
ционально 02, где 0С - критический угол скольжения. С точностью до коэффициента
нормировки, определяемого полной мощностью источника, выражение (20.37) совпада-
ет с (4.16), которое описывает полную мощность направляемых лучей при возбуждении
световода ламбертовым источником (4.2). Поскольку в рамках приближения слабона-
правляющего волновода Д < < 1, то распределение интенсивности ламбертова источни-
ка почти не зависит от угла и является лучевым эквивалентом диффузного источника.
20.19. Погрешность лучевого анализа
В предыдущем примере была установлена эквивалентность геометрического
и волнового анализов при рассмотрении эффективности возбуждения на-
правляемых мод слабонаправляющего ступенчатого световода с параметром
©о. Чтобы оценить погрешность лучевого анализа в случае, когда пара-
метр V конечен, рассмотрим выражение для полной мощности направляе-
мых мод Рс, полученное в рамках волнового анализа. Из соотношений (11.24)
и (20.37) имеем
м
Рсо=СЪ^, (20.38)
где С - постоянная величина и М « V2 /2. Пусть е — погрешность выражения
для мощности направляемых лучей, полученной с помощью геометрической
ОПТИКИ. ПОСКОЛЬКУ ПрЙ V “> оо 7?j -> 1, то
Р. — Р V2
&=.Ь г со =Л_( (20.39)
г со 7 — 1 J
Плотность решений характеристического уравнения приближается к конти-
нууму при V -> ©о, поэтому при конечном V можно сумму аппроксимировать
интегралом, a 7?j заменить асимптотическим выражением при больших V из
табл. 14.7. Хотя асимптотические выражения немного превышают истинные
375
для мод высших порядков, в результате тем не менее получается простое вы-
ражение для &. Таким образом,
Sn*~72[l-^W (20.40)
/ = 1 J О v
где непрерывная переменная £ имеет тот же смысл, что и / под знаком сум-
мы. При данном V параметр U удовлетворяет неравенству 0 < < К и £/2
% 2£. Подставляя это приближенное равенство в уравнение (20.40), раскла-
дывая его в ряд по степеням 1/V, получаем [11]
& = 1/V.
(20.41)
На рис. 20.7, б показана зависимость погрешности & от параметра V (штри-
ховая кривая соответствует (20.41), сплошная — (20.39)).
ГЛАВА 21. ИСТОЧНИКИ ИЗЛУЧЕНИЯ ВНУТРИ ВОЛОКОННЫХ
СВЕТОВОДОВ
В предыдущей главе рассматривалось возбуждение направляемых мод све-
товодов при освещении его торца (источники излучения как пространствен-
но-когерентные, так и пространственно-некогерентные, находились вне све-
товода) . Данная глава посвящена изучению мощности направляемых мод и
поля излучения источников тока, распределенных внутри световода и изобра-
женных на рис. 21.1. Интерес к исследованию этой специфической на первый
Z = Z2
Рис. 21.1. Расположение источников токов (тем-
ные пятна) с плотностью и направлением векто-
ра J, занимающих объем V между плоскостями
z — zx иг — z2
взгляд проблемы обусловлен тем, что неоднородности световодов, исследо-
ванию которых посвящена следующая глава, могут рассматриваться как ис-
точники, излучающие внутри однородных световодов. Ниже будет показано,
что изолированная неоднородность излучает подобно диполю, а неоднородно-
сти, возникающие на границе сердцевины и оболочки, эквивалентны трубча-
тому источнику тока.
ВОЗБУЖДЕНИЕ НАПРАВЛЯЕМЫХ МОД
Рассмотрим световод или волновод с произвольным профилем показателя
преломления и формой поперечного сечения, схематически изображенный
376
на рис. 21.1. Свойства полей мод такого волновода рассматривались в гл. 11.
Вне области источников тока полные поля Е и Н являются суммой полей
всех направляемых мод и поля излучения и определяются выражением
(11.2). Очевидно, что в области z > z2 (рис. 21.1) поле должно распростра-
няться в положительном направлении оси z и являться суммой полей вперед-
распространяющихся направляемых мод и вперед-распространяющихся со-
ставляющих Е^ц и Hjad . Аналогично приz < поле определяет только поля
назад-распространяющихся направляемых мод и назад-распространяющиеся
составляющие Efad и H^d поля излучения. Комбинация выражения (11.2) и
(11.4) позволяет представить полное поле в виде
Е(х, у, z) = Za^(x,y)exp(iPiz) + E^d(x, у, z); z>z2, (21.1a)
/
= Sa_je_j(x,y)exp(-i|3jZ) + E~&d(x,y, z); z<zt, (21.16)
H(x,y,z) = S«jhj(x, >’)exp(i/3Jz) + H^d(x, y, z); z>z2, (21.1b)
= Sa_jh_j(x,_p)exp (-if^z) + H~d(x,y,z); z <zn (21.lr)
где j = 1, . . . , M и a±j — амплитуды мод. В области zx <z <z2 зависимость
6z±j otz определяется соотношениями (31.35) и (31.36).
21.1. Амплитуда и мощность мод
Амплитуду направляемых мод определяют источники тока, изображенные на
рис. 21.1. Выражения для амплитуд могут быть получены из уравнений Макс-
велла (см. гл. 31). Из выражений (31.35), (31.36) и с учетом (11.7) полу-
чаем [1]
а1 = -1дГ J (etj + ezj£)* *Jexp(—i0jz)<r^; z>z2,
а-Г~мГ J (еЧ ~ ezj£)* ,Jexp(i0jZ)dr; z <zlt
(21.2а)
(21.26)
где У — объем, занимаемый источниками тока (см. рис. 21.1), в; =efi + eviz,
индексы t и z обозначают соответственно поперечную и продольные состав-
ляющие, z — единичный вектор, параллельный оси световода, а выражение
для коэффициента нормировки N-} приведено в табл. 11.1. Напомним также,
что если световод является непоглощающим, то сопряженные поля мод мож-
но выразить через несопряженные поля с помощью выражения (11.9) .
Мощность каждой моды определяется выражением (11.22)
Р. = ItfjPTVj P_j= (21.3)
где Pj — мощность вперед-распространяющейся моды (положительное на-
правление оси z на рис. 21.1), a P_j — мощность назад-распространяющейся
моды (отрицательное направление оси z). Полная мощность, возбужденная
во всех направляемых модах, равна
Л>т = *(Р1+Рч)=^(|а1|2 + М2)^Г (21-4)
Эффективность возбуждения каждой моды можно определить, если Р±] раз-
делить на полную мощность, излучаемую источником Ptot.
377
21.2. Слабонаправляющие волоконные световоды
Если световод является слабонаправляющим, го для упрощения выражения
(21.2) можно использовать приближения, рассмотренные в гл. 13. Предпола-
гая для удобства, что световод круглый, а источники тока излучают вдоль
оси х поперечного сечения световода, с помощью выражений из табл. 13.2
и табл. 14.1 и (21.3) получим мощность в каждой моде
Р+1 = ---е?-)1/21 J^xlexp(Ti^)6?n21/7 RFAR)dR,
1б7Тр 'I qq е0 г 0 L
(21.5)
где ех1 = Ftcos или exJ ~ F^sin Z^, (3^ - скалярные постоянные распростране-
ния, F^ - решения скалярного волнового уравнения (14.4), а остальные па-
раметры определены в табл. I. Это же выражение можно вывести непосред-
ственно из скалярного волнового уравнения с помощью метода, изложенно-
го в конце гл. 33. Если источник излучает вдоль оси световода, то соответ-
ствующее выражение имеет вид
р-л- Гб^7“ ФI’
(21.6)
где ezi определяется соответствующим выражением для ezi из табл. 14.1. В ка-
честве иллюстрации полученных результатов рассмотрим несколько простых
примеров.
21.3. Пример. Диполь в произвольном волоконном световоде
Выражение для вектора плотности тока J единичного диполя, длина которого d меньше
длины волны, и расположенного в точке с координатами rd, ^d, (см. рис. 12.3),
имеет вид
6 (г - rd)
J(r, <p,z) = —--5 ~ ¥>d)6 (z - zd)dl, (21.7)
”d
где 5 обозначает 6-функцию Дирака, I - вектор тока диполя, неявно включающий в се-
бя временную зависимость exp(-icjf) и определяющий направление вектора J. Подста-
новка (21.7) в (21.3) дает выражение для амплитуд мод, а мощность мод, возбужден-
ных диполем, может быть затем найдена из соотношения (21.2). Расчеты будут точны-
ми, если выражения для полей мод также являются точными (например, для световода
со ступенчатым профилем из табл. 12.3). Однако существует всего лишь несколько
форм профилей показателя преломления, которым соответствуют аналитические выра-
жения для полей. В дальнейшем будем рассматривать основные моды слабонаправляю-
щих световодов, поскольку при этом для мод световодов с произвольной формой про-
филя можно использовать гауссово приближение.
21.4. Пример. Поперечный диполь внутри слабонаправляющего волоконного
световода
Рассмотрим слабо направляющий световод с диполем, ориентированным вдоль оси х его
поперечного сечения (рис. 21.2, а). Очевидно, что основная мода, поляризованная вдоль
378
Рис. 21.2. Расположение дипо-
ля тока внутри световода в
точке с координатами
направление тока в кото-
ром параллельно оси х (д)
и оси z (б), и линии напря-
женности электрического по-
ля для этих двух случаев
(в), (г) при = 0 (влияние
световода на электрическое
поле не учитывается)
оси у, возбуждаться не будет, и полная мощность будет определяться мощностью Ро
одинаково возбужденных вперед- и назад-распространяющихся мод, поляризованных
вдоль оси х. Подстановка соотношения (21.7) в (21.5) дает
Ро = , (—) т(—)/ ГUWR, (21.8)
16яр3Исо е0 р о
где Fo - решение скалярного волнового уравнения для основной моды. В случае свето-
вода со ступенчатым профилем точное выражение для Fo приведено в табл. 14.3, а для
световодов с произвольным профилем используем гауссово приближение (15.2). В ре-
зультате имеем
8w>co
(^-)
ео
1/2 ехр
(21.9)
где г0 - размер пятна моды световода с данным профилем показателя преломления.
Это выражение, являющееся точным для световода с неограниченным параболическим
профилем, рассмотренным в разд. 14.4 (r0 = pIV1/2)> показывает, что мощность основ-
ной моды наибольшая для диполя, расположенного на оси световода, и уменьшается экс-
поненциально с ростом квадрата расстояния от оси.
21.5. Пример. Продольный диполь внутри слабонаправляющего волоконного
световода
В данном случае диполь ориентирован вдоль оси световода, как показано на рис. 21.2, б.
Подставляя соотношение. (21.7) в (21.6) и иёпользуя выражения из табл. 14.1, находим,
что возбуждаются обе основные моды, поляризованные вдоль осей х и у, мощности ко-
торых во вперед- и назад-распространяющихся модах Рох иРОу связаны соотношением
Р Р
Ох __ Оу
cos\d sin\^d
A|/d|2
8тгК?иС0
^0 ) 1/2
€0
RF2 (R)dR,
(21.10)
а параметры определены в табл. I. Используя гауссово приближение для поля моды
(15.2), выражение (21.10) можно записать в виде
379
fox = foy = ^I^Pl2 f^Aexp(_ A.
cos’^ sins^d 4’r^’r?"co e° r° ro
(21.11)
где r0 - размер пятна моды (см. табл. 15.2). Для световодов со ступенчатым и неогра-
ниченным параболическим профилями выражения (21.10) и (21.11) являются точны-
ми, если в (21.10) подставить выражение для Fo из табл. 14.3, а в (21.11) положить
г0 = • Из последнего выражения следует, что диполь, расположенный на оси свето-
вода, не возбуждает основных мод, а максимальная эффективность возбуждения дости-
гается при ~ го • Обратим внимание на тот факт, что мощность, возбужденная дипо-
лем, ориентированным вдоль оси световода, примерно в Д'1 раз меньше, чем в случае
диполя, ориентированного вдоль оси х. Такое различие становится очевидным, если рас-
смотреть распределение поля диполя на рис. 21.2, в и 21.2, г. Вблизи оси световода, где
поле основной моды имеет максимум и является фактически поперечным, поле диполя,
ориентированного вдоль оси z, параллельно оси световода, в то время как поперечный
диполь имеет и поперечное поле.
21.6. Пример. Трубчатый источник тока
Рассмотрим теперь случай, когда внутри световода находится трубчатый источник тока.
С помощью таких источников, как будет показано в следующей главе, можно модели-
ровать некоторые виды неоднородностей в световодах. На рис. 21.3 изображен трубча-
тый источник, представляющий собой цилиндрическую поверхность или тонкую трубку
радиусом г0, распределение плотности тока на которой Подчиняется закону [2]
J = fig(z) cosZC^-¥>0); -L<z<L, (21.12)
2w„
где - фиксированный угол, I - положительное целое число или нуль, 6 - дельта-
функция Дирака, п - единичный вектор, определяющий направление, ag (z) - распреде-
ление тока вдоль световода. Очевидно, что если такой источник рассматривать как су-
перпозицию диполей, то результаты, полученные в двух предыдущих разделах, будут
частными случаями данного.
Наибольший интерес представляет синусоидальный закон изменения плотности тока
на трубке произвольной длины, когда вектор тока параллелен заданному направле-
нию, т. е.
g (z) - ехр (iCz) sin £lz\ L(21.13)
и n — x или n — z, где С, П — постоянные величины, a x, z - единичные векторы, парал-
лельные осям координат на рис. 21.3. Если подставить выражения (21.12) и (21.13) в
Рис. 21.3. Трубчатый
источник тока длиной
2£, с радиусом г0 и
плотностью тока на по-
верхности J (21.12)
380
(21.5) или (21.6), то получим, что мощность, возбужденная во вперед- или назад-рас-
пространяюпщхся модах пропорциональна |/J2 или |/_|2 соответственно, где
L . . [sin(C + 0i - Г2)£ sin(C + 0i + Г2)£ )
4 = J exp{i(C + 0i)z} sinnzdz = i< ——!—-—-------------------?• (21Л4)
~L l с +01 C +0j4- I
Знак ~ опущен для ясности. Из полученного результата видно, что функции 1+ являются
резонансными. Другими словами, источники с пространственной частотой Г2 |С - 0j|
возбуждают главным образом вперед-распространяющиеся моды, а источники с про-
странственной частотой П « |С + 0j| — назад-распространяющиеся моды. Таким образом,
|/±Р n«|C±(3j| (21.15)
при условии, что трубка достаточно длинная.
ВОЗБУЖДЕНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
До сих пор в этой главе рассматривалась мощность возбуждения направляе-
мых мод. Она направляется световодом, а остальная часть полной мощности
источника излучается из него. Для определения поля излучения существуют
два общих метода, одним из которых является модовый подход, изложен
ный в гл. 25, согласно которому поле излучения представляется суперпози-
цией полей мод излучения. В этой главе дается подход, в котором использу-
ется функция Грина. Он основывается на определении вначале поля излуче-
ния от единичного диполя, а затем поля от произвольного источника в виде
линейной суперпозиции полей единичных диполей. Поскольку волноводы
предполагаются слабонаправляющими, то большая часть мощности источни-
ка излучается и лишь малая часть трансформируется в мощность направляе-
мых мод. Поэтому в первом приближении для оценки излучаемой мощности
можно считать, что источник находится в неограниченной среде с показате-
лем преломления, равным показателю преломления оболочки. Такое пред-
положение дает возможность использовать хорошо известные методы теории
антенн, которые идеально подходят к этой задаче. Влияние структуры свето-
вода в приближении свободного пространства можно учесть введением не-
больших поправок.
21.7. Слабонаправляющие волоконные световоды
Если источник тока локализован внутри световода с произвольным профи-
лем показателя преломления, определить поле излучения чрезвычайно слож-
но. Задача существенно упрощается в случае слабонаправляющего световода
[2]. Очевидно, при малых изменениях показателя преломления источник
возбуждает такое же поле излучения, какое он возбудил бы, находясь в од-
нородной бесконечной среде с показателем преломления, равным показате-
лю преломления оболочки ис1, что аналогично излучению антенны в свобод-
ном пространстве. Поэтому можно воспользоваться обычной теорией антенн
и выразить мощность, излучаемую из слабонаправляющего световода через
векторный потенциал А [3 — 5].
Представление полей через векторный потенциал. В разд. 34.3 показано,
каким образом классическое представление поля излучения в вакууме через
векторный потенциал А модифицируется в случае наличия световода. Элек-
трическая и магнитная составляющие поля излучения Е и Н связаны с век-
торным потенциалом соотношениями (34.13) , а именно
381
ik С 1 1 1
E= ta^lA+ft^V(V’A)r H=^VxA- <21,6)
где ис1 — показатель преломления оболочки, e0 и д0 — Диэлектрическая по-
стоянная и магнитная проницаемость вакуума. Волновое число в вакууме к
связано с угловой частотой со соотношением в табл. I. Временная зависимость
векторов Е, Н, А и J описывается множителем ехр(—icor), который для про-
стоты опущен. В приближении слабонаправляющего волновода векторный
потенциал А = А(х, у, z) является решением уравнения (34.14), т. е.
{V2 + к2п2} A = -m0J, (21.17)
где п = п (х, у) - профиль показателя преломления световода, J = J (х, у, z) -
заданное распределение тока и V2 - скалярный оператор Лапласа (37.36).
При выводе уравнения (21.17) предполагалось, что скалярные компоненты
вектора А относятся к фиксированной системе декартовых координат, а
пространственная зависимость поля может быть выражена в произвольной
системе координат. Основное различие между данной формулировкой и
обычным представлением поля в вакууме заключается в зависимости урав-
нения (21.17) от профиля показателя преломления и введении множителя
1/и21 в уравнение (21.16) .
Достаточно далеко в оболочке поля всех источников являются локально
плоскими. Как показано в разд. 34.4, выражения для полей в дальней зоне
имеют вид [3 — 5]
Е = - % 1/2 г х (г х А) ; Н = — г х А = п , (-^)l/2 f х Е.
(Мобо)1/2 Mo C1W
(21.18)
Из них находим вектор Пойнтинга S и полную мощность излучения Prad
S=^£L prad=£^4i ф1/2Лг-хАр^
5*00
(21.19)
Рис. 21.4. Возмущение вектора поля в точке Ристочником с плотностью тока J, располо-
женным в точке Q (л), и сферические полярные координаты точек Р и Q относительно
оси световода (б)
382
где с — скорость света в вакууме, — сферическая поверхность с радиу-
сом г = °° и £2 — пространственный угол. Единичный вектор г параллелен ра-
диальному вектору г на рис. 21.4 и 5 = | г| - радиус сферы.
Таким образом, подводя итог изложенному в этом разделе, можно ска-
зать, что задача определения поля излучения от источника поля с заданным
распределением плотности тока сводится к решению уравнения (21.17) для
векторного потенциала, в результате чего получаются выражения (21.18) и
(21.19).
21.8. Приближение свободного пространства
В данном случае под приближением свободного пространства понимается за-
мена слабонаправляющего световода неограниченной однородной средой с
показателем преломления [2, 6]. При этом небольшие изменения показа-
теля преломления не учитываются, о чем упоминалось в разд. 21.12. Интуи-
тивно ясно, что в случае слабонаправляющих световодов лишь излучение
вблизи его оси может сильно отличаться от излучения в свободном простран-
стве. Этим вызвана трудность возбуждения направляемых мод световода,
если источник излучает энергию не вдоль его оси. Этот вывод будет еще бо-
лее очевиден, если рассмотреть распространение лучей под углом 0Z к оси
световода, который меньше критического угла скольжения 0С. Они являют-
ся направляемыми и не излучают в свободное пространство. Поскольку
0С — (1 - ^cl/^co) 1/2 и исо ис1, то 0С « 1, и только параксиальные лучи
являются направляемыми. Следовательно, если говорить ,о полной излучен-
ной мощности, то ясно, что только источники с очень узкой, параксиальной
диаграммой направленности будут давать решения, существенно отличаю-
щиеся от решения в приближении свободного пространства. В большинстве
случаев, представляющих практический интерес, излученная мощность до-
статочно точно описывается в рамках приближения свободного пространства,
точность которого оценивается в разд. 21.13.
Поле излучения и излученная мощность. Выражения для векторного по-
тенциала в дальнем поле в рамках приближения свободного пространства
выведены в разд. 34.3 и 34.4 и могут быть представлены в виде
А = Мехр (iksnci); М - f J (г') ехр (-iks'n^cos х) d тГ'
(21.20)
Здесь интегрирование ведется по всему объему занятому токами, г' -
координатный вектор распределения плотности тока J(r') на рис. 21.4, а,
s - | г | и s' = |r | — радиусы, а х - угол между г и г'. Если (я, 0, ф) — сфери-
ческая система координат, изображенная на рис. 21.4,6' и ориентированная
так, что если азимутальный угол у равен нулю, радиус-вектор расположен в
плоскости z, то из уравнений (21.19) и (21.20) имеем
383
(21.21а)
(21.216)
где М0 и — 0 и (^-составляющие вектора М в точке Р. Используем теперь
полученные выражения для расчета поля излучения в примерах, рассмотрен-
ных в разд. 21.4 и 21.6.
21.9. Пример. Поле излучения диполя
В рамках приближения свободного пространства полная мощность, излученная дипо-
лем, рассмотренным в разд. 21.4 и 21.5, не зависит от его местоположения и ориентации.
Поэтому для простоты предположим, что диполь параллелен оси z (см. рис. 21.4). Под-
ставив выражения (21.7) (21.20), получим, что векторный потенциал,имеет только
z-составляющую, т. е.
Az = (M0Zfi?/47Ts)exp(iZ;swcl); MQ = -Id sin e, M = 0. (21.22)
Ненулевые составляющие дальнего поля можно получить из соотношений (21.18)
\к
Еа =-------------H7sin0; Н =---------Q-A sin 0, (21.23а)
в (M0e„)1/2 z ’ * М0 z
а уравнение (21.21) приводит к выражениям для потока мощности и полной излучен-
ной мощности
\ld\2k2n_1 * Л \ld\2k2n 1
S = ~32я\а (Мо /е°} " Sin 0Г; Prad = --------(^о /е0) ,Я
(21.236)
где параметры определены в табл. I.
Эффективность возбуждения. Определим теперь эффективность возбуждения дипо-
лем основных мод световодов с различными профилями показателя преломления. Если
диполь расположен в сердцевине световода со ступенчатым профилем на расстоянии
rd от его оси, то из выражений (21.8), (21.10), (21.236) и с учетом табл. 14.3 получим
для диполей, ориентированных вдоль осей х и у, соответственно
Ро „Л W1
Prad v (О) ’
г Л &dlp') (21’24)
= 6Д* —v~6 J} (U)
При выводе этих соотношений использовались характеристическое уравнение и прибли-
жение исо ~ ^ci- В последнем случае Ро - мощность, возбужденная в модах, поляризо-
ванных вдоль осей х и у. На рис. 21.5, а изображены зависимости отношений Р91^РХ^ и
P0/A2Prad от нормированного радиуса r^/р для диполей, ориентированных вдоль осей х и
z соответственно, в световоде с параметром V = 2,4. Численные значения были получе-
ны с помощью данных табл. 14.4. Из представленных зависимостей видно, что с ростом
rd/p эффективность возбуждения диполя, ориентированного вдоль оси х, падает и растет
для диполя, ориентированного вдоль оси z. В этом нет ничего удивительного, поскольку
384
а)
Рис. 21.5. Зависимости нормированных эффективностей возбуждения основных мод
Л}/Д^гас1 и ^oM2^rad от г&1? диполями, ориентированными соответственно вдоль осей
х и z (а), и нормированной мощности излучения Р от угла излучения в0 для осесиммет-
ричного трубчатого источника с продольной (In) (21.31) и поперечной (tr) (21.32)
ориентацией векторов тока (б)
в первом случае уменьшается амплитуда поперечного поля на оси световода, а во вто-
ром - увеличивается амплитуда продольного поля.
В рамках гауссова приближения выражения (21.24) можно получить с помощью со-
отношений (21.9), (21.11) и (21.236)
_^=2^ехр(_±);
Prad И го ''о
4 2 СЛР ' 2 * ’
И* / Г2 Г1
¥ ' О 10 ' О
(21.25)
где г0 - размер пятна моды, выражения которого для ряда форм профилей приведены
в табл.15.2.
21.10. Пример. Излучение трубчатого источника
Трубчатый источник тока был рассмотрен в разд. 21.6, где было показано, что эффек-
тивность возбуждения направляемых мод таким источником мала, если не выполнены
условия резонанса (21.15). Подобный вывод справедлив и для полей излучения. Если
длина трубки 2L значительно превосходит пространственный период 2л/Г2, где П - про-
странственная частота в выражении (21.13), то ясно, что мощность будете основном
излучаться под определенным углом к оси световода. Это также является следствием
теоремы Флоке [7]. Следует, однако, отметить, что теперь поле излучения зависит от
ориентации источника.
Продольно-ориентированный источник. Если ток в трубчатом источнике паралле-
лен оси световода (см. рис. 21.3), в рамках приближения свободного пространства
(разд. 21.8) вектор М имеет только продольную составляющую Mz. Чтобы получить
выражение для используем соотношение r»r' =cos х (см. рис. 21.4, б), где г и г' -
единичные векторы вдоль направлений ОР и OQ соответственно. В результате имеем
s cos х = sin 6 cos(<p - </) + z cos 0, (21.26)
где r0 = s' sin е' и z = s' cos в' на трубке. Подставляя это выражение в (21.20) и исполь-
зуя для J(r') соотношения (21.12) и (21.13), получаем
13 Зак 37 385
1 L 2л
Mz =— J sinQzexp[z (C-bzclcos0)z]c?z JcosZ(<p?-<p0) exp[ ikrji , sin0 cos(<p - </)]d<p'.
2я —L 0
(21.17)
Для интегрирования по используем выражение (37.62) :
1—1 rsin(x-S2)£ sin(x + n)Z1
Mz = (,-i) Vi (kron , sin 0) cos I(<p - >p0) [-----------------------], (21.28)
v X - Si x + Si
где x = C - kncy cos 0. При L -> «> первый и второй члены внутри квадратных скобок
имеют острые резонансы при х — & и х — соответственно. Как будет показано в
следующей главе, необходимо, чтобы выполнялось условие С + П > &иср а поэтому ва-
жен только первый член. Если 0О - угол 0 при резонансе, то
0n — ,arccos(~--------------------------------------------------------------------------------------------------------------------------------);
О<0
(21.29)
Положив в (21.21a) Mq — -Mz sin 0, = 0, из пространственной зависимости вектора
Пойнтинга получим, что мощность, излучаемая трубчатым источником, преимуществен-
но распространяется под углом 0О к оси световода.
Излученная мощность. При расчете полной мощности вторым членом в квадратных
скобках выражения (21.28) пренебрегают. Поскольку sin(x - П)£ является быстро-
осциллирующей функцией при 0 #= 0О, точность можно повысить, если для остальных
членов взять 0 = 0О. Таким образом, положив в уравнении (21-216) MQ = -Mz sin 0,
= 0, получим
Prad = 7 cos2Z (21.30)
32л ео и х_ х q
где х = (С - knci cos в - Г2)£ и х± = (С ± кпу- П)£ • Поскольку при L -> °° значения
х+ и х_ сильно расходятся, то можно считать, что х+ -> х_ -> -*>. Тогда с помощью
соотношения (37.111) находим
Лад = к~~ 1Л <! + 51,о) sin26Л(кГ<>"clsin ’
(21.31)
где символ Кронекера 6^ 0 равен единице при I = 0 и нулю во всех остальных случаях.
Таким образом, излученная мощность растет линейно с длиной, в то время как мощ-
ность направляемых мод увеличивается пропорционально квадрату длины трубки со-
гласно (21.15).
Поперечно-ориентированный источник. Пусть теперь в трубчатом источнике, имею-
щем пространственное распределение плотности тока такое же, как и в предыдущем
случае, токи параллельны оси х (рис. 21.4, б) . Вектор М (21.20) имеет только составля-
ющую Мх, которая идентична по величине составляющей Mz (21.28), а следовательно,
источник вновь излучает под углом е0 (21.29) к оси световода. Полная излученная
мощность находится подстановкой MQ - Мх cos в0 cos <р, = -Мх sin в уравнение
(21.216), что аналогично выводу выражения (21.31). В результате, полагая <р0 = 0, по-
лучаем [2]
(21.32а)
386
Множитель Dy определяется как
Do = 1 + cos50o; Z), = ~4~(1 + 3cos20o); £>t= у(1 + cos20o), Z > 2. (21.326)
На рис. 21.5,5 изображена нормированная мощностьизлученияР= 32Pracj (с0 /м0) '^(kL)
как функция угла 0О в случае осесимметричного источника .(/ = 0) и г0 •= р, V = 2,4,
Д = 0,005 и, следовательно, крпсу « 24. Осциллирующий характер кривых обусловлен
резонансами в поперечном сечении источника.
21.11. Поправка, обусловленная профилем показателя преломления воло-
конного световода
В предыдущих двух примерах при определении мощности, излученной ис-
точником, находящимся внутри световода, последний рассматривался как
неограниченная среда с постоянным показателем преломления лс1, а измене-
ние показателя преломления в его поперечном сечении не учитывалось. Те-
перь определим поправку к такому же результату, полученному в приближе-
нии свободного пространства и обусловленную профилем показателя пре-
ломления световода. Если предположить, что световод слабонаправляющий,
то ясно, что эта поправка будет существенна лишь для направлений, близких
к оси световода, т. е. при 0Q 0. Таким образом, можно ожидать, что в об-
щем случае приближение свободного пространства дает довольно точные ре-
зультаты.
Для того чтобы определить поле излучения в слабонаправляющем светово-
де, необходимо решить уравнение (21.17) для векторного потенциала. Од-
нако если решение данной задача в приближении свободного пространства
известно, то необходимо найти лишь поправку, обусловленную профилем по-
казателя преломления световода. Это решение является решением уравнения
(21.17), в котором в любой точке п (х, у) = лс1. Решение уравнения (21.17) в
случае, когда п (х, у) является переменной величиной, может быть найдено,
как линейная суперпозиция точных решений для трубчатого источника
(рис. 21.3), распределение тока в котором подчиняется уравнениям (21.12)
и (21.13). Таким образом, для решения поставленной задачи необходимо
лишь найти решение уравнения (21.17) для одного трубчатого источника.
Ограничим наше рассмотрение для простоты круглым поперечным сечением
источника.
21.12. Корректирующий множитель
Пусть Efs(s, 0, <р) — электрическое поле трубчатого источника (рис. 21.3) в
свободном пространстве, где S, в, у — сферические координаты на рис. 21.4, б.
Если E(S, 0, <р) — поле того же источника в световоде, то,в рамках прибли-
жения слабонаправляющего волновода поляризационные свойства этих двух
полей одинаковые. Для осесимметричного профиля показателя преломления
ясно, что небольшие изменения в направлении излучения зависят только от
6. Если этот вывод не кажется очевидным, то можно воспользоваться луче-
вым представлением, которое хотя и не очень точно при малых значениях па-
раметра V, однако дает качественно правильную физическую картину. В рам-
ках приближения свободного пространства лучи распространяются вдоль
крямых линий, а изменение показателя преломления сердцевины вызывает
387
преломление и поэтому изменение направления распространения лучей в
оболочке. Следовательно, можно положить [2]
E(s,0,<p) =Ct(0)Efs(5,0,^),
(21.33)
где — корректирующий множитель, обусловленный профилем пока-
зателя преломления. Формальный вывод этого соотношения приведен в
разд. 34.6. Здесь же отметим, что он получен из однородного скалярного
волнового уравнения и не зависит от поляризации поля. Таким образом, из
уравнения (34.26) имеем
q(0) = (21.34а)
где решение уравнения (34.25)
\ф + к2п2(г) -02]Ф cosZf.p-io), (21.346)
I и Г О
fs
а - решение этого же уравнения при п (г) - лс1. Оператор Лапласа опреде-
лен в табл. 30.1, л (г) — осесимметричный профиль, 0 = cos 0, г0 - радиус
трубки, 5 — дельта-функция Дирака. Отметим, что данное уравнение справед-
ливо, если распределение плотности тока подчиняется соотношениям (21.12)
и (21.13), когда все токи параллельны определенному направлению. Метод
решения уравнения (21.34) дан в разд. 34.7, здесь же рассмотрим простой
пример.
21.13. Пример. Световод со ступенчатым профилем показателя преломления
Предположим, что трубчатый источник радиусом г0 (см. рис. 21.3) расположен внутри
сердцевины или на границе сердцевины с оболочкой световода со ступенчатым профи-
лем радиусом р. Решение уравнения (21.34), полученное в разд. 34.7, можно записать
в виде [2]
I J^QrJp) W^U.Q) ’
(21.35)
где/^- функция Бесселя первого рода и
WAU, Q) = UJ,.. (U)H<p(Q) -QJAU)H^ (0; W AQ, Q) = 21/тг, (21.36)
I uf 1 L Ь 1+ 1 L
поскольку функция W^Q, Q) пропорциональна Вронскиану (37-77). ' - функция
Ганкеля первого рода, и остальные параметры связаны с 6 соотношениями
= (t/’-r2)1'2; у - kpn со (2Д) 1/2, (21.37)
где V - нормированная частота (параметр световода), к = 2тг/А и X - длина волны в
вакууме.
Физическая интерпретация. Корректирующему множителю можно придать простой
физический смысл, если представить его в виде произведения:
C;(0) = CC(J); ^(6)=-^°^ ; Сх(е) = Wy(Q, Q) IW^U, Q). (21.38)
о /Р)
Если соотношения (21.33) и (21.38) подставить в выражения (21.20), то вектор Пойн-
388
Рис. 21.6. Зависимости величины |СГ(0)|2 (21.38) от угла излучения 0О в случае осе-
симметричного источника, расположенного внутри световода со ступенчатым профилем
(а), и нормированной мощности Р от угла излучения 0О в случае осесимметричного
трубчатого источника, совпадающего с границей между сердцевиной и оболочкой свето-
вода со ступенчатым профилем (сплошная кривая соответствует выражению (21.416),
штриховая - выражению (21.32) (б)
тинга S, определяющий распределение излучения в дальнейшей зоне, можно представить
в виде
S= |C1(0)|2Sfs= |Cd(0) |2 |Cr(0) |2Sfc, (21.39)
где 5fs - амплитуда соответствующего вектора Пойнтинга в свободном пространстве.
Множитель Cd (0) описывает изменение направления потока излучаемой мощности.
Для стороннего наблюдателя это означает сдвиг кажущегося источника излучения. В гео-
метрической оптике это эквивалентно преломлению на границе сердцевины с оболочкой
согласно закону Снелля (35.4), т. е. изменению аргумента функции Бесселя U на Q.
Множитель Сг (0) описывает резонансы в поперечном сечении световода, возникновение
которых связано с вытекающими модами. Этот вопрос более подробно рассмотрен в
разд. 24.21. Если радиусы трубки источника и сердцевины разные, то резонансные пики
для источника тока и световода соответствуют различным значениям 0. При одинако-
вых радиусах трубки и сердцевины пики фактически совпадают, что иллюстрируют
рис. 21.5, б и 21.6,а, на которых зависимость |СГ (0) |2 от угла 0 дана для осесимме-
тричного трубчатого источника (Z = 0) и световода с параметром V — 2,4 [2]. Максиму-
мы кривых при Д = 5 ° 10‘3 и Д-5 ° 10"5 соответствуют 0 = 0С «5,7 и 0 - 0С « 0,57
соответственно, где 0с = (2Д) 1/2 - критический угол скольжения. Только если 0 < 0С,
IСг | действительно значительно отличается от единицы, а при возбуждении источником
направляемых мод С -* 0 (0 -> 0). Таким образом, в случае диффузного источника пол-
ная излученная мощность фактически равна полученной в приближении свободного
пространства, поскольку S «£fc почти для всех направлений.
Излучение диполя. Количественную поправку к мощности, излученной в свободном
пространстве, можно получить и для диполя, расположенного на оси световода и ориен-
тированного вдоль оси х. Интегрируя произведение |С(0) в выражениях (21.38) и
(21.236) по всем направлениям и учитывая, что I = rQ = 0, получим, что скорректиро-
ванное выражение для полной излученной мощности отличается от результата в прибли-
жении свободного пространства (21.236) менее чем на 0,1 % при V = 2,4 и Д < 0,01.
Градиентные профили показателя преломления. Подобная общая интерпретация кор-
ректирующего множителя для световодов со ступенчатым профилем показателя пре-
ломления справедлива и для слабонаправляющих световодов с градиентным профилем
и оболочкой. Профили, дающие точные аналитические решения уравнения (21.35), рас-
сматривались в гл. 14, а метод Вентцеля - Крамера - Бриллюэна (ВКБ), применимый
389
при решении однородного скалярного волнового уравнения (35.44), почти всегда мож-
но использовать для определения корректирующих множителей других форм профиля.
21.14. Пример. Скорректированное выражение для излучения трубчатого
источника
В разд. 21.10 было показано, что излучение трубчатого источника, распределение плот-
ности тока которого подчиняется выражению (21.13), направлено под углом 0О к оси
световода (21.19). Следовательно, полная мощность Р, излученная трубчатым источни-
ком длиной 2L и радиусом г0 < р, расположенным внутри ступенчатого световода, рав-
на [2]
Р= |Cl«?0)|’/’rad> (21.40)
где Prad - мощность, излученная в свободном пространстве. Таким образом, из выраже-
ний (21.35), (21.31) и (21.32) имеем
Р = 7^(Г)1/2 (1 + 6io)si"20
10 ео
I ^(e0,e0)
1
|2^(С/о^о/р)
(21.41а)
в случае, когда токи параллельны оси волновода и
(21.416)
в случае, когда точки параллельны оси х поперечного сечения световода. Величина
определена соотношением (21.326), - (21.36), в которых Uи Q заменены на Uo и
Qo (Со и 0q связаны соотношением (21.37) при 0 = fl0).
На рис. 21.6, б сплошной кривой показана зависимость нормированной мощности
р - 32P(e0/p0)yi /kL от угла 0О, построенная на основании выражения (21.416) дляис-
точника с радиусом г0 — ри I = 0. расположенного в световоде с параметрами V = 2,4 и
Д = 0,005. Штриховая кривая соответствует решению (21.32) в приближении свободно-
го пространства. Как отмечалось в предыдущем разделе, множитель С^(0О) (21.38)
описывает изменение направления излучения, которое может трактоваться как сдвиг
пиков при уменьшении 0О, в то время как множитель Сг (0О) связан с резонансами в по-
перечном сечении световода, которые влияют на амплитуду этих пиков.
ГЛАВА 22. НЕРЕГУЛЯРНЫЕ ВОЛОКОННЫЕ СВЕТОВОДЫ
Когда свет, распространяясь вдоль световода, падает на неоднородность, обус-
ловленную несовершенством структуры световода, часть световой мощности
рассеивается, что схематически изображено на рис. 22.1, а. Часть рассеиваю-
щейся мощности перераспределяется между вперед- и назад-распространяю-
щимися модами, а остальная часть излучается. Этот процесс наиболее удобно
описывать лучевыми методами, изложенными в гл. 5. Здесь основное внима-
ние уделяется световодам, в которых могут распространяться одна или не-
сколько мод. Неоднородности возмущенных (нерегулярных) световодов
будут трактоваться как источники вынужденных токов, находящиеся внутри
390
Рис. 22.1. Возмущенный световод с показателем преломления п (х, у, z) (темные пятна
обозначают неоднородности, на которых падающее излучение рассеивается в направля-
емые моды и поле излучения) (л) и невозмущенный световоде профилем п(х, >>) (тем-
ные пятна обозначают соответствующие вынужденные токи с плотностью J (х, у, z) (б)
невозмущенного световода, при этом результаты, полученные в предыдущей
главе, могут быть использованы для описания возбуждения направляемых
мод и поля излучения [1 — 3].
ПРЕДСТАВЛЕНИЕ НЕОДНОРОДНОСТЕЙ ВЫНУЖДЕННЫМИ ИСТОЧНИКАМИ ТОКА
В этой части главы будет показано, как неоднородности внутри световода
можно представить вынужденным электрическим полем источниками тока.
Неоднородности возмущенного световода, изображенного на рис. 22.1, а,
приводят к зависимости показателя преломления от продольной координа-
ты, т. е. п = п(х, v, z). Полные электрическое и магнитное поля Е(х, у, z) и
Н (х, у, z) в любой точке внутри возмущенного световода связаны между со-
бой уравнениями Максвелла для среды без источников. В частности, из урав-
нения (30.1а) имеем
Vx H = ~i(eo/Mo)1/2^2E, (22.1)
где параметры определены в табл. I. Если профиль показателя преломления
того же световода без неоднородностей обозначить п(х, у), то проведя пере-
группировку в правой части (22.1), можно записать
V X Н = i(eo/Mo) 1/2&(и2 - и2)Е - i(e0/M0) 1/2^и2Е. (22.2)
Если теперь сравнить это уравнение с уравнением (30.1а) для случая присут-
ствия токов, то первый член в правой части (22.2) можно трактовать как
фиктивный ток, направление и плотность которого подчиняются уравнению
J = i(eo/Mo) 1/2к (п2 - л2)Е.
(22.3)
Таким образом, J - это вынужденная плотность тока, обусловленная неодно-
родностями. Другими словами, поля возмущенного световода (см. рис. 22.1, а)
идентичны полям невозмущенного (см. рис. 22.1, 0, в котором имеются ис-
точники тока, распределение которых подчиняется соотношению (22,33).
391
22.1. Произвольные неоднородности
Источник вынужденного тока (22.3) существует только внутри области не-
однородности и целиком определен, если известно полное электрическое по-
ле Е. Однако поле Е является суммой известного падающего поля и неизвест-
ного рассеивающего поля, зависящего от поляризационных свойств неодно-
родности. Для неоднородности произвольного вида общего выражения для
рассеивающегося поля не существует, и поэтому совместно решать уравне-
ния (22.3) и (30.1) обычно не легче, чем уравнение Максвелла для возму-
щенного световода без источников. Исключением является бесконечно малая
неоднородность, представляющая собой сферу с постоянным показателем
преломления п и радиусом, малым по сравнению с длиной волны света; поле
внутри такой неоднородности может быть определено методом квазистати-
ческого приближения, рассмотренным в разд. 18.22. Из теории [4] имеем
Е^Зп2Ё/(и2 + 2п2), (22.4)
где п и Е — показатель преломления и электрическое поле в невозмущенном
световоде в месте нахождения сферы. Метод вынужденных токов может
быть также использован при расчете потерь локальных мод световодов с
плавно изменяющимися произвольными неоднородностями. Этот вопрос бо-
лее подробно рассмотрен в разд. 22.10.
22.2. Малые неоднородности
Под малыми понимаются неоднородности, практически не изменяющие про-
филь показателя преломления возмущенного световода, т. е. в уравнении
(22.3) можно положить п « п. Такое предположение приводит к значитель-
ным упрощениям при определении полей и дает минимальные потери в точ-
ности [1 - 3, 5 - 7]. Для удобства рассмотрим отдельно произвольные и сла-
бонаправляющие световоды. _
Произвольные световоды. В таких световодах изменения как п, так и п
являются произвольными, а в окрестности неоднородности п « п. В первом
приближении в соотношении (22.3) можно считать Е Е, т. е.
J = i(eo/Mo) 1/2к(п2 -п2)Е.
(22.5)
Таким образом, вынужденная плотность тока определяется известным полем
невозмущенного световода. Хотя это приближение не учитывает небольшие
поляризационные эффекты, обусловленные несферичностью центров рассея-
ния, оно является точным для сферических неоднородностей, поскольку из
формулы (22.4) имеем Е ~ Е. С помощью приближения (22.3) можно пока-
зать, например, как в результате рассеяния четная основная мода преобразу-
ется в нечетную. Электрические поля этих двух мод неортогональны друг к
другу и, как показано в разд. 22.8, связь между ними вызвана неоднородно-
стями. Однако если обе моды возбуждены одинаково, или если неоднородно-
сти расположены случайным образом, то в результате рассеяния происходит
усреднение мощности в модах и заметного ее перераспределения не про-
исходит.
392
Слабонаправляющие световоды. Если световод является слабонаправляю-
щим и п и, то, как показано в гл. 13, поля мод являются приблизительно
поперечными и в первом приближении можно считать, что Е ~Ё,где индекс
t означает поперечную компоненту. Таким образом, из (22.3) имеем
J = i(eo/Mo) 1/2^О2 -H2)Et. (22.6)
В этом выражении не учтены все поляризационные эффекты, обусловленные
неоднородностями, поскольку в рамках приближения слабонаправляющего
световода поперечные поля всех мод'ортогональны друг другу. В частности,
нечетная, или поляризованная вдоль оси у, основная мода не может быть воз-
буждена четной, или поляризованной вдоль осих, основной модой в отличие
от случая произвольного световода, рассмотренного выше. Подставляя выра-
жение (13.9а) в формулу (22.6), получим следующее выражение для плотно-
сти вынужденного тока, если на неоднородность в круглом световоде падает
основная мода, поляризованная вдоль оси х
J = ifli(eoMo) 1/2£(и2 - h2)F0 exp(i0z)x, (22.7)
где ах — амплитуда моды, F0(F) - фундаментальное решение скалярного
волнового уравнения (14.4), х — единичный вектор, параллельный оси х на
рис. 14.1, и /3 — скалярная постоянная распространения.
ПОТЕРИ ОСНОВНОЙ МОДЫ НА ИЗЛУЧЕНИЕ
В качестве иллюстрации больших возможностей метода вынужденных токов
приведем примеры, в которых определим мощность, излученную основной
модой круглого слабонаправляющего световода на небольших неоднородно-
стях различных типов.
22.3. Пример. Изолированная неоднородность
Рассмотрим небольшую неоднородность объемом б/ с постоянным показателем пре-
ломления л, расположенную на расстоянии от оси световода. Падающая основная мо-
да, поляризованная вдоль оси х, вызывает появление индуцированных токов с плотно-
стью, определяемой формулой (22.7) , в которой R = R j = r^/p ип = п(г&), где р - ради-
ус сердцевины. В рамках приближения ’’свободного пространства” (см. разд. 21.8) пол-
ная излученная мощность Pracj не зависит от поляризации моды и может быть получена
подстановкой /д = ах (е0/д0) тк (п2 - /?2)ГО6У в уравнение (21.236). Тогда выражение
для относительной излученной мощности получаем с помощью табл. 13.2:
<22-8>
где Pj - падающая мощность, V - параметр световода и по предположению п « nQQ №«cj.
Если неоднородность сосредоточена внутри сердцевины световода со ступенчатым про-
филем показателя преломления, то вычисляя непосредственно интеграл в выражении
(22.8) с помощью характеристического уравнения из табл. 14.6 для случая 7=0, имеем
393
Лас! _ _LLrJ2L "co ~ ”cl —.I2
Pj 24п2 д «’j p2
(22.9)
где параметры определены в табл. I. Это отношение можно выразить только через пара-
метр V, если для Fo(7?) в (22.8) использовать гауссово приближение (15.2) и табл. 15.2.
22.4. Пример. Случайное распределение неоднородностей
Рассмотрим световод, в котором небольшие неоднородности расположены случайным
образом. Плотность их распределения в единице объема равнаМ. Полная мощность, из-
лученная на длине световода dz, в точности равна сумме мощностей Ргад, излученных на
каждой отдельной неоднородности. Если P(z) - мощность моды в световоде длиной z, а
М - достаточно велико, то
dP(z) = -[ Г MPT^dA]dz, (22.10)
оо
где Аж - площадь бесконечного поперечного сечения, aPfaj связана с падающей мощно-
стью соотношением (22.8), в котором Pj заменена на Рг Обозначая первую часть (22.8)
через С(Р^), подставляя в (22.10) и интегрируя, получаем
P(z) =P(0)exp(-7z); 7 = fMCdA (22.11)
в предположении, что М и С не зависят от г. Здесь под Р(0) и у понимаются соответ-
ственно начальная мощность моды и коэффициент затухания мощности моды.
Равномерное распределение неоднородностей в сердцевине. Рассмотрим световод со
ступенчатым профилем и предположим, что в сердцевине с показателем преломления
исо с равномерной плотностью Мсо распределены неоднородности одинакового объема
5 i с0 с показателем преломления nQQ. Поскольку множитель С определяется правой
частью соотношения (22.8),то с помощью выражений (22.11), табл. 13.2, интеграла и ха-
рактеристического уравнения из табл. 14.6 при I — 0 получаем для коэффициента зату-
хания основной моды следующее выражение:
1 М о* Ка Гиа - и2 16 У '
7=2,Vf(Vft=^ [Пд^)сорЧ( (22.12)
где д - часть мощности основной моды, распространяющаяся в сердцевине. Если пара-
метры световода выразить через длину волны X, то коэффициент у будет пропорциона-
лен Х“4, что соответствует частотной зависимости рэлеевского рассеяния [8].
Равномерное распределение неоднородностей в сердцевине и оболочке. Обобщим те-
перь предыдущий случай и будем считать, что в оболочке также распределены неодно-
родности с плотностью Мср объемом 6 У^ и показателем преломления йср Непосред-
ственный расчет показывает, что в этом случае соотношение (22.12) принимает вид
7= 7?асо+ С1 -^сР (22.13)
где ас0 и aci -- объемные потери в материалах сердцевины и оболочки [8]. Выражение
для коэффициента асо может быть получено приравниванием правой части (22.12) и
первого члена в правой части (22.13) , а выражение для ас1 - заменой в полученном вы-
ражении для асо индекса со на cl.
394
22.5. Пример. Синусоидально возмущенная граница
Рассмотрим световод со ступенчатым профилем показателя преломления, в котором
граница между сердцевиной и оболочкой на длине 2 L деформирована по синусоидаль-
ному закону (рис. 22.2, с). Если p(z) - радиус сердцевины в точке z, то
p(z) = р + 6р sin Ш, (22.14)
где р - радиус невозмущенного световода, П - пространственная частота и 6р < < р
(т. е. по предположению возмущения малы). Эффект влияния деформированной грани-
цы на основную моду, поляризованную вдоль оси х, можно описать методом вынужден-
ных токов. Из рис. 22.2, а видно, что разность квадратов показателей преломления не-
возмущенного и возмущенного световодов п2 - п2 изменяется как ± (и^ - n2CG) в обла-
сти возмущения (знаки ± очевидны из рис. 22.2, а) и равна нулю во всех остальных об-
ластях. Поскольку 8р мало, то можно предположить, что токи сосредоточены в области
границы сердцевины с оболочкой. Поэтому из выражения (22.7) имеем
Jx = -ia(e0/p0)mk(n2CQ - п*с[) Ьр sin (Hz) exp (i0z)6 (г - р), (22.15)
где 6 - дольта-функция Дирака, знак ~ опущен для скалярных величин, и на границе
Fo (1) — 1 Таким образом, в соответствии с рис. 21.3 световод с деформированной гра-
ницей заменяется невозмущенным световодом, который возбуждается трубчатым источ-
ником, радиус которого равен радиусу сердцевины световода, ток направлен параллель-
но оси х (см. рис. 22.2, б), а амплитуда его определяется с помощью выражений (21.12)
и (21.13) при г0 - р, I = о и С = /3. Следовательно, можно непосредственно использо-
вать результаты, полученные в разд. 21.10 и 21.14.
Если длина деформированного участка достаточно велика, то излучение направлено
преимущественно под углом 0О к оси световода (21.30). Излученная мощность будет
пренебрежимо малой, если 0О не лежит в диапазоне 0 < 0О < я. Положив С = 0, получим
условие, эквивалентное следующему условию для пространственных частот:
0 - < И < 0 + Ъ?с|. (22.16)
Таким образом, имеем весьма полезное выражение, позволяющее оценить характерную
длину неровностей границы, вызывающих потери на излучение. Поскольку в слабона-
правляюших световодах р(0 - £ис1) « W2 (Д/2)1/3/V (см. табл. I), то из соотношения
(22.16) получим, что в случае неровностей с пространственным периодом 2тг/П более
0,5 мм малыми потерями на излучение в световоде с параметрами V = 2,4, р = 5 мкм и
Д = 0,005 можно пренебречь.
Излученная мощность. Полная мощность, излученная на деформированном участке
световода со ступенчатым профилем, пропорциональна величине, определяемой выраже-
ние. 22.2. Световод со ступенчатым профилем и показателями преломления сердцевины
и со и оболочки /?cj, граница между которыми деформирована по синусоидальному за-
кону между сечениями z = - L и z - L fa), и эквивалентное распределение токов в
направлении оси х на границе невозмушенного световода (б)
395
нием (21.416) с I = 0 и r0 = р. Из сравнения выражений (22.15) и (21.12) находим ко-
эффициент пропорциональности для источника тока и, возведя в квадрат модуль этого
коэффициента, получаем
где V — параметр световода и
wo (Uo> !2о) = ЦЛ (Ц>) #о(1) (So) - 6<Л (Ц>)Я,(1) (е0) ; (б0, е0) = 2i/TT, (22.176)
Qo =kpnclsm90 = (Ul - Г2),/2; cos 0O = (0 - П) fkncV (22.17b)
Здесь Ди функции Бесселя и Ганкеля первого рода.
Затухание мод. Мощность основной моды P(z) на длине z световода с синусоидаль-
но деформированной границей затухает вследствие потерь на излучение. Если деформи-
рованный участок разделить на отрезки длиной dz, малые по сравнению с длиной z, но
достаточно большие, чтобы приведенное выше описание было справедливым, то имеем
следующее выражение для изменения мощности моды на длине dz:
dP(z) = ~(Prad/2A)dz = -(Pad/2A£|ai|2)P(z)d2> (22.18)
в котором использованы соотношение P(z} = (^рДГи (11.22), где аг - амплитуда мо-
ды и N - параметр нормировки. Интегрируя (22.18), получаем
P(z) =Р(-1)ехр[-7(г + £)]; 7 = •Prad/2A7,|a1l2, (22.19)
где у - коэффициент затухания мощности и синусоидальные деформации начинаются в
точке z = —L. Подстановка выражения для N и использование характеристического
уравнения из табл. 14.3 и соотношений (22.17) дают
<“> “ «'•> ’ (22-20>
где параметры мод Un W определены в табл. I. На рис. 21.6, б сплошная кривая соответ-
ствует фактически зависимости у от П (без учета нормирующего множителя), посколь-
ку П и 0 связаны соотношением (22.17в). Видно, что за исключением области малых
углов, корректирующим множителем можно пренебречь.
ПЕРЕРАСПРЕДЕЛЕНИЕ МОЩНОСТИ МЕЖДУ НАПРАВЛЯЕМЫМИ МОДАМИ
Рассеиваемая на неоднородностях мощность преобразуется не только в излу-
ченную мощность, но и перераспределяется между как вперед- так и назад-
распространяющимися направляемыми модами, включая и падающую моду.
В этой части главы рассматривается применение метода вынужденных токов
для расчета мощности в каждой моде.
22.6. Одномодовые волоконные световоды с произвольным профилем пока-
зателя преломления
В круглом световоде, в котором распространяются только основные моды,
рассеиваемая (неизлученная) мощность может трансформироваться только
во вперед- и назад-распространяющиеся четные и нечетные основные моды.
396
Если вперед-распространяющаяся четная НЕп-мода падает на неоднородность
(см. рис. 22.1,а), то направляемая часть полного электрического поля в не-
возмущенном и возмущенном световодах соответственно равна
Ё = a1e1exp(i|3z); (22.21а)
Ё = [(flj +6Zj)ei + а2е2]exp(i(3z) + + я_2е_2 ] exp(-i|3z). (22.216)
Здесь /3 — постоянная распространения, одинаковая для обоих световодов,
индексы 1 и 2 обозначают вперед-распространяющиеся четные и нечетные мо-
ды, а отрицательные индексы — соответствующие назад-распространяющиеся
моды. Амплитуда а падающей моды постоянна повсюду, тогда как остальные
амплитуды постоянны лишь вне областей неоднородностей (см. рис. 22.1).
Из соотношения (11.27) следует, что полная мощность вперед-распространя-
ющихся мод Р+ в области z > z2 определяется выражением
Р+ = (|Д1 +<*112 + |а2 |2)№= Рг + IKefaafyN, (22.22а)
где Pi — мощность падающей моды, N — общий параметр нормировки, Re —
означает действительную часть, а знак * — комплексное сопряжение. В этом
приближении не учитываются члены более высоких порядков 6^ и а2, кото-
рые в случае малых неоднородностей значительно меньше ах. По аналогии
полная мощность Р_ назад-распространяющейся моды в области z <zx, опре-
деляется выражением
Л_ = (|а-1 I2 + l«_2 I2)N, (22.226)
где j и а_2 малы по сравнению с ах.
Представление вынужденных токов. Согласно этому методу неоднородно-
сти в световоде рассматриваются как источники вынужденных токов (см.
рис. 22.1, б). Подставляя выражение (22.21а) в (22.5), получим следующее
выражение для распределения плотности тока:
J =i<7i (е0/д0) 1/2£(и2 - «2)е exp (i0z), (22.23)
где пип— профили показателей преломления соответственно невозмущенно-
го и возмущенного световодов. Напомним, что, как отмечалось в разд. 22.2,
это приближение не учитывает поляризационные свойства неоднородностей,
обусловленные их несферичностью. Неизвестные амплитуды в выражении
(22.21) могут быть найдены подстановкой соотношения (22.23) в уравне-
ние (21.2), а именно
ai = ~д (£о/Мо)1/2 J (п2 -И2)в1 • (etj +ezjZ)=W~; z >z2,
<z , = T -^(eo/Mo)1/2 ( («2-и2)е! • (e^ - eZJz)*exp(2i/3z)dr'; z <Z1,
J 4 /V t
(22.24)
397
iде j = 1 или 2, индексы t из обозначают поперечную или продольную состав-
ляющие, z — единичный вектор, параллельный оси световода и / - объем
световода между плоскостями z =zv nz =z2 на рис. 22.1.
Многомодовые световоды. Приведенный выше анализ можно легко обоб-
щить на перераспределение мощности за счет неоднородностей в многомодо-
вых световодах, рассматривая все вперед- и назад-распространяющиеся на-
правляемые моды, поля которых описываются выражениями (22.21). Одна-
ко если источник падающего поля является диффузным, то более приемлем
лучевой метод, рассмотренный в гл. 5.
22.7. Слабонаправляющие одно модовые световоды
В разделе 22.2 утверждалось, что если неоднородности в слабонаправляющих
световодах малы, то пренебрежимо мала и связь между ортогонально-поля-
ризованными основными модами. Таким образом, в первом приближении
можно считать, что падающая четная (поляризованная вдоль оси х) мода воз-
буждает только вперед- и назад-распространяющиеся моды с такой же поля-
ризацией. Тогда выражение (22.21) можно записать в виде
Ё = 5’1Foexp(i^z)x; Е= [(?! + а^ехр^Зг) + exp(-i^z) ]Fox, (22.25)
где Fo = Fq (R) — фундаментальное решение скалярного волнового уравне-
ния (14.4), (3 — соответствующая скалярная постоянная распространения и
х — единичный вектор, параллельный оси х поперечного сечения световода.
Положив в формуле (22.6) Et = Е и использовав выражения (33.64в) и
(33.65а), получим
«1 =- / (п2 -n2)Fody-; z >z2,
4 уу До >
fl-i = 4 J ~ z72)FoexP(2i^)jy ; z <Zi,
Ч- уу МО у
(22.26а)
(22.266)
где N - скалярный параметр нормировки из табл. 13.2, Fo - действительная
функция для непоглощающего световода, и в данном случае можно считать
Р « кпсо, Фо =F0.
22.8. Пример. Изолированная неоднородность
Рассмотрим теперь рассеяние мощности в направляемые моды в случае, когда поля-
ризованная вдоль оси х мода НЕП падает на изолированную неоднородность, располо-
женную внутри одномодового световода со ступенчатым профилем показателя прелом-
ления. В рамках приближения слабонаправляющего волновода из выражений (22.26) и
табл. 14.3 получаем
= -a_lexp(-2ipzd) = -2-
”со - Ы Д,
р3 (2Д)1Я
7о (Frd/p)
V
(22.27)
в предположении, что неоднородность имеет объем bF, показатель преломления п и со-
средоточена в точке с г = rd и z - Остальные параметры определены в табл. I. Под-
398
ставляя это выражение в соотношение (22.22) и учитывая, что ах /ах является чисто мни-
мой величиной, находим, что во вперед- и назад-распространяющиеся моды рассеивает-
ся одинаковая мощность. Однако часть падающей мощности, рассеивающаяся в эти мо-
ды, весьма мала, поскольку пропорциональна квадрату объема неоднородностей и
разности квадратов показателей преломления.
Поляризационная связь. Приведенные выше результаты получены в рамках прибли-
жения слабонаправляющего световода, и поэтому в них не учтена небольшая поляриза-
ционная связь мод, обусловленная неоднородностями. Это можно сделать в случае цен-
тров рассеяния сферической формы, как это отмечалось в разд. 22.2. Если затем подста-
вить поляризационные поправки для полей HEjj-мод (ем. разд. 12.11) в уравнение
(22.24), то с учетом поправок второго порядка для etj и первого порядка для ezj полу-
чим выражения для я+2 порядка А. Таким образом, если на неоднородность падает мо-
да, поляризованная вдоль оси х, то мощность, рассеиваемая в нечетную (поляризован-
ную вдоль оси у) моду, в А"2 раз меньше мощности, рассеиваемой в четную (поляри-
зованную вдоль оси х) моду.
22.9. Пример. Синусоидально возмущенная граница
В разд. 22.5 методом вынужденных токов было исследовано излучение мощности ос-
новной моды на синусоидально возмущенной 'границе сердцевины с оболочкой слабо-
направляющего световода со ступенчатым профилем и показано, что мощность падаю-
щей моды, поляризованной вдоль оси х, рассеивается во вперед- и назад-распространяю-
щиеся основные моды с теми же состояниями поляризации. Следуя рассуждениям
разд. 22.5, в выражении (22.26) положим
п2 - и2 = - (п2С0 - n2cfi др sin(Qz) 6 (г - р) (22.28)
и предположим, что объем между плоскостями z = z1 = -L и z = z2 = L на рис. 22.2, б
равен Подставляя выражение (22.28) в (22.26), находим, что ах = 0, т. е. в рамках
данного приближения мощность во вперед-распространяющуюся моду не рассеивается.
По аналогии с выражением (21.15) можно заключить, что значительная часть мощности
рассеивается в назад-распространяюшуюся-моду только в случае выполнения условия
резонанса П 20, и
a «а — — (2Д)1/2 (22.29)
р р v J}(U)
Это обобщение получено с использованием нормированных выражений из табл. 14.3. Из
последнего выражения следует, что часть рассеиваемой мощности увеличивается пропор-
ционально квадрату длины неоднородности. Однако здесь следует иметь в виду, что ме-
тод вынужденных токов, основой которого в данном случае является уравнение (22.7),
при бесконечно больших L становится некорректным, поскольку он базируется на пред-
положении о фактической идентичйости полей возмущенного и невозмущенного свето-
водов. В таких случаях более удобным является метод связанных мод, изложенный в
гл. 27. Отметим, что из условия резонанса следует, что пространственный период синусо-
иды 2tt/Q должен быть сравним с длиной волны света.
ПЛАВНО ИЗМЕНЯЮЩИЕСЯ ПРОИЗВОЛЬНЫЕ НЕОДНОРОДНОСТИ
До сих пор в этой главе рассматривалось перераспределение мощности меж-
ду модами на малых неоднородностях трансляционно-инвариантных светово-
дов. Теперь покажем, как применить метод вынужденных токов при опре-
делении перераспределения мощности, рассеиваемой в направляемые моды и
моды излучения световодов с плавно изменяющимися вдоль их длины не-
однородностями.
399
22.10. Представление локальных мод вынужденными токами
Понятие локальных мод было введено в гл. 19 при описании свойств свето-
водов с произвольными неоднородностями. В разделах 19.1 и 19.2 отмеча-
лось, что поля локальных мод являются точными приближениями полей мод
световодов только в случае плавно изменяющихся по длине параметров. Не-
смотря на то, что поля локальных мод не являются точными решениями
уравнений Максвелла, получающуюся небольшую ошибку можно оценить с
помощью метода вынужденных токов.
Напомним, что структура /-й локальной моды формируется при разбиении
световода на последовательность маленьких аппроксимирующих цилиндров
(см. рис. 19.1). Профиль показателя преломления каждого цилиндра равен
п (х, у) = п (х, у, zc), где п (х, у, z) — профиль возмущенного световода, а
zc — координата центра аппроксимирующего цилиндра. Подобно этому точ-
ное электрическое поле Е^ аппроксимируется полем Et = е^(х, у) exp (i/3jz) бес-
конечно длинного^ цилиндра с профилем показателя преломления п. Посколь-
ку El Etи п « и, то, используя разложение Тейлора п вблизи п до линейных
членов с помощью уравнения (22.3), получаем
J = —i(eo/Mo)1/2 fcejexpCPjZ) (z - zc)dn2/dz|z ,
(22.30)
где значение производной соответствует центру цилиндра, — ортонормаль-
ное поле.
Метод определения потерь мощности аналогичен методу формирования
полей локальных мод, изложенному в разд. 19.1: вначале определяются поте-
ри в каждом аппроксимирующем цилиндре, которые выражаются через плот-
ность возмущенного тока J, и затем суммируются по всем цилиндрам в пред-
положении, что количество этих цилиндров стремится к бесконечности.
22.11. Перераспределение направляемой мощности
Рассмотрим теперь возбуждение всех остальных локальных мод /-й локаль-
ной модой. Начнем с определения вклада da} в амплитуду /-й вперед-распро-
страняющейся локальной моды. Он обусловлен вынужденным током с плот-
ностью внутри каждого аппроксимирующего цилиндра (22.30). Если перепи-
сать выражение (21.2а) относительно ортонормальных мод (см. разд. 11.5),
то для z > zc + 5z
da= — f e*J • exp(-i0.z)dAdz, (22.31)
4 zc-bz Лоо J
где 25z — высота цилиндра. Подставляя выражение для J в (22.31) , находим,
что dflj можно представить как произведение двух интегралов
1г zc + 5z 2
^=^(ео/До)1/2 S (z-z^expli^-^zjdz f • ^^n__\zdA.
(22.32)
Второй интеграл зависит от полей двух взаимодействующих мод, и поэтому
его удобно обозначить постоянной Сд
400
i ^-dA-, ]Ф1,
I dz
(22.33)
которая оценивается в точке z = zc- Ингегрируя по z и перегруппировывая
члены, находим, что выражение (22.32) можно представить в виде суммы
двух членов
da} = - 26zCjtexp [i(Pt - 3j)^c] cos [(PL- Pj)6z] + db}\ (22.34a)
iC,
= + -expti^-^-Sz)]]. (22.346)
Первая и вторая экспоненты в выражении для db} вычисляются соответствен-
но на левом и правом концах аппроксимирующего цилиндра. Рассмотрим те-
перь соответствующие члены для соседнего, расположенного справа, аппрок-
симирующего цилиндра (см. рис. 19.1, б) с центром в точке z'c и высотой
2dz'. Поскольку вариации параметров световода малы, то разницей между
Pt и можно пренебречь, а поэтому член exp [i(3i — Pj)(zc + 6z) ] в выраже-
нии для dbj должен сократиться с членом -exp [i(pt - Pj)(z^ - 3z') ] в выра-
жении для dbj, поскольку z^ = zc + dz + dz’. Таким образом, в результате сум-
мирования выражения (22.34а) по всем аппроксимирующим цилиндрам
вклад dbj в конечное выражение будет равен нулю. Аналогично тому, как это
сделано в разд. 19.1, заменим zc, (3^ Р- соответственно на z, P^(z) , Pj (z) и, по-
ложив dz = 2dz, для амплитуды /-й локальной моды в точке z в пределе по-
лучим
(22.35)
где C-X(z) — функция от z (22.33), для которой /3^ = Pj(z), Р( = P^(z), =
= [х, у, Pj (z) ], ej = et [x, у, Pt(z)], w =n (x, y, z) . С помощью этого результа-
та в гл. 28 оценивается точность метода локальных мод.
Моды излучения. Возбуждение локальных мод излучения, рассмотренное
в гл. 28, можно описать уравнением (22.35), если везде заменить/-ю локаль-
ную моду /-й локальной модой излучения.
ГЛАВА 23. ИЗГИБЫ
Эта глава посвящена в основном излучению мощности, обусловленному из-
гибами одномодовых волоконных световодов. Вначале будут рассмотрены
потери на изгибах с постоянным радиусом, а затем на случайных изгибах с
малым радиусом кривизны, которые известны больше как микроизгибы.
Потери на изгибах в многомодовых световодах рассмотрены в гл. 9 лучевым
методом.
401
ИЗГИБЫ С ПОСТОЯННЫМ РАДИУСОМ КРИВИЗНЫ
Прежде чем переходить к описанию модели для расчета потерь на излучение,
представляется целесообразным рассмотреть соответствующие физические
процессы.
23.1. Физические механизмы потерь на излучение
В прямом световоде с произвольным профилем показателя преломления по-
ле моды в каждой точке поперечного сечения распространяется параллельно
оси световода с одинаковой фазовой скоростью, так что плоскость постоян-
ной фазы ортогональна ей. Однако если световод изогнут в плоскую дугу с
постоянным радиусом, как это изображено на рис. 23.1, а, то ясно, что поля
Рис. 23.1. Изогнутый све-
товод с радиусом изгиба
Rc, профиль показателя
преломления которого в
сердцевине - нс0, в обо-
лочке — «ci (д), и эквива-
лентное возмущение, ап-
проксимированное наве-
денным током с плотно-
стью J (стрелки), занима-
ющим область сердцевины
световода (б)
и фазовые фронты вращаются вокруг центра кривизны изгиба с постоянной
угловой скоростью. Таким образом, фазовая скорость, параллельная оси
световода, должна линейно возрастать при увеличении расстояния от центра
кривизны С. Поскольку оболочка световода имеет постоянный показатель
преломления, то фазовая скорость может превышать скорости света в дан-
ной среде. Поэтому должен существовать некоторый радиус 7?rad в плоскости
изгиба, при превышении которого поле уже не может направляться светово-
дом и должно становиться излучающим, как это изображено схематически на
рис. 23.1, а. Вблизи и внутри сердцевины поля достаточно точно описывают-
ся с помощью метода локальных мод, рассмотренного в гл. 19, при условии,
что радиус изгиба достаточно велик.
23.2. Модель излучения
Чтобы рассчитать мощность, излученную на изгибе, достаточно использовать
приближенную модель световода, согласно которой изогнутый световод пред-
ставляется токовой антенной бесконечно малой толщины, излучающей в не-
ограниченную среду с показателем преломления, равным показателю пре-
ломления оболочки ис1 (приближение ’’свободного пространства”, рассмо-
тренное в разд. 21.8). Поэтому формулы теории антенн для дальнего поля,
например (21.21), могут использоваться при расчете поля излучения: необхо-
димо конкретизировать закон изменения плотности тока в антенне.
402
Выражение для тока в антенне получается в два приема [1,2]. Вначале си-
стема ’’световод - поля мод” заменяется соответствующим распределением
плотности тока J в однородной среде с показателем преломления «с1, что схе-
матически изображено на рис. 23.1, б. Правомерность такой замены следует
из рассуждений, аналогичных приведенным в начале гл. 22 и представлении
уравнений Максвелла в виде уравнений (22.1) - (22.3), в которых п заме-
нен на п р В результате получаем следующий закон распределения плотности
тока:
J = 1(е0/д0) 1/2^(«с1 “ "2)E>
(23.1)
где п — профиль показателя преломления, а Е - точное поле световода. Оче-
видно, что величина J отлична от нуля только внутри объема, соответствую-
щего сердцевине световода. Поле Е можно аппроксимировать полем локаль-
ной моды, т. е. полем световода, однородного в локальной области, если ра-
диус изгиба достаточно велик и подчиняется условию (19.17) .
Зтаем используются условия большого отношения радиусов изгиба и серд-
цевины (19.17) и тот факт, что для случаев, рассматриваемых в этой главе,
направление вектора J не меняется по поперечному сечению световода. Если
затем предположить, что распределение тока по поперечному сечению серд-
цевины сконцентрировано вблизи оси световода, то линейный ток определя-
ется выражением
I = и J JdA,
А
^со
(23.2)
где J — модуль вектора J в уравнении (23.1) , Лсо — площадь поперечного се-
чения сердцевины и и — единичный вектор, параллельный какому-либо фик-
сированному направлению в поперечном сечении световода.
С помощью этого результата в разд. 23.4 рассчитывается излученная мощ-
ность на изогнутом участке световода, представляемого в виде бесконечно
тонкой проволоки, ориентированной по его оси, вдоль которой течет ток
(23.2). Это позволяет выделить основные механизмы потерь на излучение.
Точность аппроксимации световода тонкой проволокой рассматривается в
разд. 23.7. Там же обсуждается влияние конечного поперечного сечения све-
товода.
23.3. Слабонаправляющие световоды
Основное внимание уделим излучению основной моды в изогнутых одномо-
довых волоконных световодах. В рамках приближения слабонаправляющего
волновода излученная мощность не зависит от состояния поляризации волны
при условии, что R >> р. Поэтому для удобства предположим, что вектор
поперечного электрического поля параллелен оси z на рис. 23.2, я, т. е. орто-
гонален плоскости изгиба. Вблизи и внутри сердцевины изогнутого участка
световода электрическое поле в рамках приближения локальных мод равно
а! F0(A)exp(ij3z), где ах — амплитуда моды, Fo — фундаментальное решение
403
Рис. 23.2. Ориентация декартовых осей координат OXYZ и сферических координат
(s, О, (s', 0 \ относительно тонкой круглой проволочной антенны с радиусом изги-
ба /?с, расположенной в неограниченной однородной среде с показателем преломления
лср Стрелки обозначают направление векторов тока с плотностью J, ориентированных
вдоль оси z (я), и эквивалентная антенна, представленная изогнутым световодом, по-
перечное сечение сердцевины которого описывается координатами (г, ф,
скалярного волнового уравнения из табл. 14.3 и /3 — скалярная постоянная
распространения. Для ясности знак ~ скалярных величин опущен. Координа-
та z представляет собой расстояние вдоль оси изогнутого световода, как это
изображено на рис. 23.2, а, и г — обычный радиус на рис. 23.2, б. Подстанов-
ка этих величин в уравнение (23.1) и использование параметров световода
и профиля показателя преломления из табл. I позволяет записать распределе-
ние эквивалентно! о тока в виде
J = I exp (i/3z)z;
и -Г(Л)]^0(Л), (23.3)
МО
где / = — i|J|, z — единичный вектор, параллельный оси z на рис. 23.2, а. От-
сюда ток антенны в выражении (23.2) равен
4=/сехр0^)х;
1С = -2та1Псор7(-^^)1/2 J [1 -f(R)]F0 (R)RdR,
° о
где /с = —i I Ia I, R = г/р, р - радиус сердцевины.
23.4. Излучение изогнутой антенны
Слабонаправляющий изогнутый световод, по которому распространяется ос-
новная мода, может быть заменен антенной или тонкой проволокой, распре-
деление тока в которой подчиняется выражению (23.4). Поскольку вектор
тока ортогонален продольной оси антенны, то весьма удобно рассматривать
систему как непрерывное распределение диполей, ориентированных вдоль
404
оси 2. При- расчете излученной мощности предположим для простоты, что
антенна , является замкнутой петлей с радиусом Rc, как это показано на
рис. 23.2, а. Если (s'; О'; </) - сферические координаты, ориентирующие
петлю относительно оси z, то выражение (23.4) определяет полное простран-
ственное распределение токов
Zc [6 (/ - Rc) /Rc] 6 (О' - тг/2) exp (i£/?c/) z, (23.5)
где 6 — дельта-функция Дирака, а координата z заменена на Rcp - расстоя-
ние вдоль антенны от оси х. Расчет излученной мощности будем вести в рам-
ках приближения ’’свободного пространства”, изложенного в разд. 21.7, ис-
пользуя понятие векторного потенциала. Если точка Р в дальнем поле имеет
координаты (s, 0, <р) (рис. 23.2,а), то подстановкой выражения (23.5) в
(21.20) при s ' = Rc находим, что вектор М имеет только z-составляющую
2я
Мъ = ICRC J exp {i/?c [(ty - Ъгс1 sin 0 cos(</? -</?)]} dp , (23.6)
где соотношение cos х = sin 0 cos(tp — </) очевидно из геометрических сообра-
жений. Положив ftp = —(3(р — </) + Рр и сравнивая полученный результат с
(37.61), находим хорошее приближение
IMz | = 27Г^с |/с11 Jv (kRcncX sin 0) |; v = (3RC (23.7)
при условии, что v >> 1. Если v — целое число, то выражение (23.7) являет-
ся точным. Полная излученная мощность находится подстановкой MQ =
= —sin О, = 0 в выражение (21.216). Переписывая это выражение и
учитывая, что nCQ « исР получаем
Лад = J (^С«С1 0)sin3fW0- (23-8)
Интеграл в этой формуле может быть оценен с помощью асимптотических
формул для функций Бесселя, так как v и kRc велики. Поскольку порядок
функции Бесселя больше ее аргумента, то, используя формулу (37.90), по-
лучаем следующее приближение для интеграла:
1 Ч2__________sin3#_______ J _2 г ft2 _ dn2fll 3/21 rlf) г да сп
I (|32-fc2«^sin20)1/2 ехр ( 3 sin3 б? [к2п2с1 1 j ( }
Главный вклад в интеграл дают значения 0, близкие к тг/2. Поэтому можно
воспользоваться методом Лапласа да я определения асимптотического значе-
ния интеграла. Подставляя выражение (37.131) в (23.8) и нормируя на на-
чальную мощность моды Р(0) = I#! |2jV, где N — коэффициент нормировки,
получаем
Лад _ я1/2 112 / ^с \ 1/2 / / \ 1/2 V2 71 со z 4 \ АЛ
Р(0) 32 Л1 1 ( Р ) °' ц/3/2 7УД р( 3 Р V‘
(23.10)
где параметры определены в табл. I, а /с задается выражением (23.4).
405
Коэффициент затухания мощности. Отношение PT2LJP(O) является частью
мощности, излученной из петли на рис. 23.2, я, и не учитывает затухания ло-
кальной моды вдоль антенны. Часть мощности, теряемой на единице длины,
или коэффициент затухания мощности у, находится делением выражения
(23.10) на длину петли 2тгАс. Поскольку у не зависит от z, то вывод выраже-
ния для P(z) аналогичен изложенному в разд. 22.4. В результате имеем
P(z) =P(0)exp(-yz); у =Prad/[2^(0) ].
(23.11)
Подставляя выражения (23.4), (23.10) и выражение для нормировки из
табл. 13.2 в (23.11), получаем коэффициент затухания мощности основной
моды в произвольном слабонаправляющем световоде
7= (Гб7^т)1/2еХр(“Т^4^") Ч ° 2l SJlRdR,
(23.12)
где f — функция профиля FQ — фундаментальное решение скалярного волно-
вого уравнения. Доминирующей в этом выражении является экспоненциаль-
ная зависимость от отношения радиусов изгиба и сердцевины, поскольку при
Rc » р коэффициент затухания очень мал и относительно ’’нечувствителен”
к остальным множителям, входящим в выражение (23.12) .
23.5. Пример. Ступенчатый профиль показателя преломления
Приближение, рассмотренное в предыдущем разделе, позволяет получить выражение
для коэффициента затухания мощности основной моды изогнутого слабонаправляюще-
го световода со ступенчатым профилем показателя преломления. Если в (23.12) поло-
жить в сердцевине / = 0, а вне ее/ = 1, то используя характеристическое уравнение, ин-
теграл из табл. 14.6 для индекса I = 0 и интеграл (37.91), получаем
где значения величин UvlW могут быть найдены из табл. 14.4.
23.6. Пример. Градиентный профиль показателя преломления
Для решения задачи, аналогичной рассмотренной в предыдущем разделе, для светово-
дов с градиентным профилем удобно использовать гауссово приближение, согласно ко-
торому Fo определяется выражением (15.2), a W - (V2 - £7*) 1/2 выражается через раз-
мер пятна моды с помощью соотношений из табл. 15.2. Так, например, в случае светово-
да с гауссовым профилем при V > 1 имеем
Подобное выражение может быть получено и через параметры световода со ступенчатым
профилем.
406
23.7. Излучение изогнутых волоконных световодов
В основе аппроксимации изогнутого световода тонкой проволокой, рассмот-
ренного в разд. 23.2, лежит представление поля такого световода суперпози-
цией диполей, расположенных на его оси. Поэтому результаты, полученные в
разд. 23.4, не учитывают эффекты, обусловленные конечными размерами по-
перечного сечения сердцевины. В этом разделе выводится выражение для ко-
эффициента затухания мощности основной моды с учетом распределения
плотности тока в некотором объеме, что позволяет определить поправки к
полученным выше результатам [1—3] .Как будет показано ниже,обусловлен-
ные конечными размерами сердцевины они в большинстве случаев весьма
малы и могут не учитываться, поскольку коэффициент затухания является
экспоненциально малым.
Для описания поперечного сечения световода введем полярные координа-
ты г и i//, изображенные на рис. 23.2, так что (г, ф,<р') представляет собой ор-
тогональную систему координат с метрическими коэффициентами (1, г, Rc +
+ г cos ф) соответственно. Проводя вычисления, аналогичные проделанным в
разд. 23.4, подставляя выражение (23.3) в (21.21) и предполагая, что свето-
вод свернут в замкнутое кольцо, получаем соотношение, аналогичное (23.6)
оо 2л 2л
Mz = J Irdr j (Rc + r COS ф)с!ф j exp[i(j3z - ks ncl cosx)]*fy', (23.15)
оо о
где из геометрических соотношений z = (Rc + r cos ф)<р', a x удовлетворяет
следующему равенству:
s' cos x = (Rc + r cos ф) sin 9 cos(</? - ip') +r cos 9 sin ф. (23.16)
По аналогии с выражением (23.7) интегрирование по приводит к
оо 2л
М - 2ttR J* Irdr J 4 [Ьгс1 (Rc + г cos ф sin 0] exp (~ikrnci sin ф cos 9)dф,
c о о
(23.17)
поскольку Ac >> r cos ф и v = j3(^c +r cos ф} & pRc >> i. Аргумент функ-
ции Бесселя всегда меньше ее порядка и, следовательно, можно использовать
приближение Дебая (37.90)
ехр[(р2 -z2)1/2 -parch(p/z)]
u(Z) ~ (27г) 1/2 (р2 -z2)1/4 ;
z = bzcl sin 9 (Rc + г cos ф). (23.18)
В этом выражении доминирующей является экспоненциальная зависимость,
и поэтому разложение (23.18) весьма ’’чувствительно” к небольшим измене-
ниям ее аргумента. Разложим его вблизи точки z0 = kRyi^ sin 9 по малому
параметру (krnc\ sin 9 cos ф), учитывая линейные члены. Подставляя это раз-
ложение в (23.18) и считая Rc » г cos ф, получим
J»(z) ^du(kRcndsinO)exp[r cos ф(Р2 - ^z^sin2#)]1/2. (23.19)
В свою очередь, подстановка этого выражения в (23.17) дает
Mz 2ttRcJv (kRcnci sin 9) J Irdr J* exp[Wft cos(\!/ + (23.20)
о о
407
где R = г/р, параметр W определен в табл. I и 6 = arsh [крпс^ cos 0IW]. Если
воспользоваться соотношением (37.65), то интеграл по ф равен 2тг/0(И^),
где /0 — модифицированная функция Бесселя первого рода. Таким образом,
функциональная зависимость Mz от 0 такая же, что и (23.7), а поэтому отно-
шение полной излученной мощности к начальной равно произведению правой
части выражения, (23.10) на масштабный множитель, равный квадрату отно-
шения соотношения (23.20) к (23.7) . Если этот масштабный множитель обо-
значить черезЛ,тоиз выражений (23.3) и (23.4) имеем
А =Л[1-/(7?)]F0(A)/0(^)^/f [1 — f (R)}FQ(R)RdR>2. (23.21)
(о о J
Таким с Зразом, коэффициент затухания равен произведению А и соотноше-
ния (23.12).
Зависимость от разности показателей преломления. Очевидно, что потери
на изгибах в слабонаправляющих световодах должны быть больше, чем в све-
товодах с большой разностью показателей преломления, поскольку в послед-
них мощность моды более эффективно направляется вокруг изгиба. Коли-
чественная зависимость потерь от относительной разности показателей пре-
ломления одинакова для световода и тонкой антенны и определяется экспо-
ненциальной зависимостью от Д в выражении (23.12). Поэтому, хотя слабона-
правляющие световоды и более ’’чувствительны” к изгибам, часть излучен-
Рис. 23.3. Зависимость нормированного коэффициента затухания ур от Д при различных
значениях нормированного радиуса изгиба RJp для световода со ступенчатым профи-
лем показателя преломления (23.23) (а) и с гауссовым профилем (23.25) (6)
ной на изгибе мощности пренебрежимо мала, если только отношение ра-
диусов изгиба и сердцевины не очень мало (см. рис. 23.3). Рассмотрим два
примера.
23.8. Пример. Ступенчатый профиль показателя преломления
Гели в выражении (23.21) в сердцевине положить / = 0, в оболочке/ = 1, адляГ0 ис-
пользовать соотношение из табл. 14.3, то с помощью интегралов (37.92), (37.99), ха-
408
рактеристического уравнения в табл. 14.3 и Вронскиана (37.79) получим следующее вы-
ражение для масштабного множителя:
А = [U2![WV2Ki w]]< (23.22)
Для световода с V — 2,4 из табл. 14.4 находим, что Л « 1,9. Тогда произведение Л и со-
отношения (23.13) дает следующее выражение для коэффициента затухания мощности
основной моды в изогнутом световоде со ступенчатым профилем показателя преломле-
ния [1 - 3]:
Я1Д , Р. „3 и2 1 ( 4 ]
2р (RC’ y2w3'2 /С?(ИОеХР1 3 Р V2 J '
(23.23)
На рис. 23.3, а изображены зависимости нормированного коэффициента ур от Д для раз-
личных значений RJpb световоде с V = 2,4. За исключением очень малых Д или практи-
чески недостижимо малых отношений RJp при определении коэффициента затухания
масштабным множителем можно пренебречь, поскольку коэффициент затухания экспо-
ненциально мал.
23.9. Пример. Градиентные профили показателя преломления
Для оценки масштабного множителя в световодах с градиентным профилем воспользу-
емся гауссовым приближением. Заменяя Fo выражением (15.2), a W соотношением
(Г2 - С/2)1/2 из табл. 15.2, с помощью (37.101) в случае гауссова профиля получаем
следующее выражение:
А = ехр[(Г- 1)2/(Г + 1)]; Г>1. (23.24)
На частоте отсечки второй моды V « 2,6 имеем Л ~ 2. Произведение А и соотношения
(23.14) дает выражение для коэффициента затухания мощности основной моды
-— ( Р )1/2-------------------ехр Г -------
2р ~R^ (Г+1)2 (Г - 1)1/2 1 Г+1
4 *с (Г-1)3
3 Р V2
(23.25)
На рис. 23.3, б изображены зависимости нормированного коэффициента затухания ур от
Д для различных Rc/p в световоде с V = 2,6. Здесь р - характерный размер профиля в
формуле (15.6). Как и в случае ступенчатого профиля, при определении порядка коэф-
фициента затухания, который мал, масштабный множитель можно не учитывать.
ПЕРЕХОДНЫЕ ПОТЕРИ
Кроме потерь на излучение, связанных с изгибом световодов, существуют
также переходные потери, обусловленные резким изменением радиуса кри-
визны изгиба, как это, например, показано, на рис. 23.4 в сечении АА'. При-
чиной потерь здесь является рассогласование полей, и поэтому падающее по-
ле возбуждают не только локальные моды, но и моды излучения, которые и
определяют переходные потери [4 — 6].
409
Рис. 23.4. Качественное представление сдвигов поля основной моды, обусловленных
одиночным изгибом (а); двумя изгибами с противоположными знаками кривизны (б)
и различными радиусами изгиба (в)
23.10. Изгибы с переменным радиусом
Для того чтобы рассчитать излучение, обусловленное резким изменением
кривизны, амплитуды полей мод изогнутого световода необходимо знать с
большей точностью, чем та, которую дает приближение локальных мод, рас-
смотренное в гл. 19. Суть этого приближения заключается в предположении,
что поля в любом поперечном сечении изогнутого световода идентичны по-
лям прямого световода и такое согласование полей наблюдается при любом
радиусе изгиба. В разделе 36.15 показано, что основное влияние изгиба на по-
ле основной моды проявляется в сдвиге распределения поля в плоскости
изгиба в радиальном направлении от центра кривизны на расстояние rd от
оси световода, что схематически показано на рие. 23.4, а. В случае светово-
дов с произвольным профилем в рамках гауссова приближения согласно
формуле (36.56) имеем
__ И р2 R » п
2Д Rc (р ’ с Р’
(23.26)
где г о - размер пятна моды (15.2), Rc - радиус изгиба, а остальные парамет-
ры определены в табл. I.
Прямые и изогнутые участки световодов. Переходные потери для случаев,
изображенных на рис. 23.4, а, обусловлены рассогласованием в плоскости
АА' между полями прямого участка световода и смещенными в радиальном
направлении полями изогнутого участка световода. Для описания радиально-
го распределения поля основной моды на этих участках воспользуемся гаус-
совым приближением (15.2). В результате для прямого и изогнутого участ-
ков соответственно имеем
Fo =ехр(-гг/2го); =exp[-(r-rd)2/2ro], (23.27)
I де rd — радиальный сдвиг (23.26). Таким образом, это полностью эквива-
410
лентно возбуждению световода смещенным гауссовым пучком, рассмотрен-
ному в разд. 20.8. Если предположить, что световод одномодовый, то часть
мощности падающей моды, которая преобразуется в направляемую, опреде-
ляется соотношением (20.21), где ps = г0 + Тогда часть излученной мощ-
ности, или переходные потери, при rd << г0 равны
(23.28)
Этот результат справедлив при падении волны на плоскость АА' с любой сто-
роны.
Два изогнутых участка. Рассмотрим два изогнутых участка световода с
радиусами R^ и А2, которые схематично изображены на рис. 23.4, б и в. Ве-
личина сдвига поля основной моды гг и г2 для каждого отрезка определяет-
ся выражением (23.26), в которой Rc необходимо заменить на R} или R2 со-
ответственно. В плоскости А А' относительный сдвиг rd также зависит от угла
X между плоскостями, в которых лежат изгибы, т. е.
rd = (Н + г2 -- 2гхг2 cos х) 1/2 • (23.29)
Когда изгибы лежат в одной плоскости, то rd =гг + г2 (х = 7Г)> если центры кри-
визны изгибов расположены по разные стороны от световода (см. рис. 23.4, б)
и rd = lri ~ r21 (х = 0), если центры кривизны лежат по одну сторону оси све-
товода (см. рис. 23.4, в). Отсюда относительный сдвиг и часть излученной
мощности для этих двух случаев определяются выражениями (23.26) и (23.28)
|7?i ± 7?2 |р2 К2 г0. 4 Ро Rx ± R2 .2 р2 У4 6
R.R22A W ’ Л'"1 ^1^2 } 8Д2
(23.30)
независимо от направления падения волн на плоскость А А
23.11. Микроизгибы
Если световод имеет большое число случайных изгибов с произвольным ра-
диусом кривизны и длиной други, то излучение на этих изгибах является не-
коррелированным, так что полные потери от изгибов и переходных участков
могут быть найдены простым суммированием. Поэтому полные потери на
микроизгибах вдоль световода равны суммарной мощности, излученной на
всех изгибах и переходных участках. Если отношение радиусов изгиба и серд-
цевины велико, что, как правило, реализуется на практике, то для определе-
ния потерь на микроизгибах могут быть использованы соотношения, полу-
ченные в этой главе. Так, если радиус изгиба велик, то переходные потери до-
минируют над потерями от чистого изгиба, поскольку последние имеют экс-
поненциальную зависимость от радиуса кривизны изгиба (23.12). Более под-
робный анализ потерь на микроизгибах приведен в [7, 8].
411
В случае, когда амплитуда микроизгибов достаточно мала, их можно рас-
сматривать как одну из форм возмущения границы и для оценки потерь ис-
пользовать методы, изложенные в разд. 22.5. Если это проделать, то окажет-
ся, что потери на излучение имеют значительную величину только тогда, ког-
да пространственная частота £2 микроизгибов (предполагается, что микроиз-
гибы вносят синусоидальное возмущение границы) лежит в диапазоне, опре-
деляемом соотношением (22.16).
23.12. Наклоны и смещения осей состыкованных световодов
В разделе 20.11 было показано, что в рамках гауссова приближения часть
мощности основной моды, переданная из одного световода в другой, в слу-
чае, когда эти световоды состыкованы вплотную, но имеется несогласование
профиля, а также несовпадение осей, определяется одним из выражений для
Ро/Л из табл. 20.1. Переходные потери, или часть излученной мощности, рав-
ны 1 - Ро/Л ПРИ условии, что световоды одномодовые.
Отраженная мощность. Переходные потери, рассмотренные в разд. 23.10,
не учитывают мощности, отраженной в назад-распространяющиеся моды в
местах соединений или при изменении радиуса изгиба. В разделе 20.2 было
показано, что от торца слабонаправляющего световода отражается пренебре-
жимо малая часть мощности, и поэтому потери на отражение можно не учи-
тывать.
ГЛАВА 24. ВЫТЕКАЮЩИЕ МОДЫ
В гл. 21 — 23 основное внимание уделялось полной мощности, излучаемой
источниками и на неоднородностях световодов, а распределение излученной
мощности по всему световоду не рассматривалось. Это распределение описы-
вает пространственный переход от источника возбуждения полей излучения
к пространственно-установившемуся режиму, возникающему затем в свето-
воде и характеризующемуся наличием в основном направляемых мод. Про-
странственный переход и пространственно-установившийся режим уже об-
суждались в разд. 8.1. Для источника, расположенного на входном торце
световода, получающаяся при этом картина схематически изображена на
рис. 8.1. В области пространственного перехода для описания распростране-
ния света вдоль волновода необходимы и направляемые моды, и поля излу-
чения. Длина пространственного перехода зависит от способности световода
направлять поля излучения от источника до полного их вытекания из сердце-
вины. Цель данной главы заключается во введении нового класса мод, назы-
ваемых вытекающими, описывающих ту часть поля излучения, которая мо-
жет распространяться на сравнительно большие расстояния вдоль световода
и сосредоточена главным образом вблизи его оси.
Основное внимание уделяется световодам, в которых могут распростра-
няться одна или несколько мод, поскольку пространственный переход в
многомодовых световодах рассматривался в гл. 8 с помощью вытекающих
лучей, свойства которых обсуждались в гл. 7. Напомним, что из формулы
412
(8.1) следует, что с ростом параметра V длина пространственного перехода
вдоль световода увеличивается по экспоненциальному закону. Например,
в световоде со ступенчатым профилем, для которого V = 50 и 0с « V 2Д =
= 0,1, длина пространственного перехода составляет примерно 10ир, где р -
радиус сердцевины, в то время как в световоде с той же величиной Д, но с
V = 2,4 длина пространственного перехода равна всего 17р. Хотя при малых
V формула (8.1) и не дает достаточной точности, однако она показывает,
что роль пространственного перехода при описании распространения света в
световодах с малыми V в которых распространяется небольшое количество
мод, невелика. Справедливости ради отметим, что свойства этого перехода
важны, в том числе, если длина световода мала, например при описании
свойств фоторецепторов зрения [1, 2]. Тем не менее представляется целесо-
образным рассмотреть свойства вытекающих мод, поскольку они позволяют
с хорошей точностью описать пространственный переход в световодах с ма-
лыми V, а физические свойства отдельных вытекающих мод дают достаточно
простую картину потерь на вытекание в световоде.
24.1. Излучение вблизи оси световода
Основная цель этой главы — описать свойства той части поля излучения, ко-
торая, концентрируясь вблизи или внутри сердцевины световода, может рас-
пространяться на сравнительно большие расстояния от источника возбужде-
ния. Таким образом, на конечном расстоянии световод эффективно направ-
ляет часть мощности поля излучения. Ясно, что внутри и вблизи сердцевины
поля, описывающие это излучение, должны иметь почти такой же вид, что и
поля, описывающие направляемую мощность. Единственное различие между
ними заключается в том, что поле излучения затухает при распространении
вдоль оси световода за счет потерь в оболочке. Таким образом, можно пред-
положить, что направляемая часть поля излучения может быть приближенно
описана вытекающими модами, т. е. модами, подобными направляемым
вблизи и внутри сердцевины, но имеющими комплексную постоянную рас-
пространения, обусловленную затуханием мощности моды в направлении ее
распространения.
Описание поля вытекающими модами может иметь несколько логических
подходов. Начнем с эвристического, а затем дадим детальный математичес-
кий анализ, справедливый для волноводов с произвольными формой попе-
речного сечения и профилем показателя преломления. Для простоты при об-
суждении свойств отдельных вытекающих мод опустим индекс моды.
24.2. Эвристический подход
В главе 11 было показано, что постоянная распространения /3 направляемой
моды определяется из характеристического уравнения при условии, что нор-
мированная частота световода V больше частоты отсечки Vc данной моды. Ес-
ли теперь исследовать эти решения для значений V, меньших частоты отсеч-
ки Кс, то обнаружится, что постоянная распространения (3 становится комп-
лексной величиной, а поля мод обладают свойствами вытекающих мод, опи-
санных выше.
Это можно также предвидеть, если исследовать свойства мод какого-либо
конкретного волновода. Например, сравним часть мощности направляемой
413
моды т] в сердцевине планарного волновода со ступенчатым профилем пока-
зателя преломления с такой же характеристикой волоконного световода со
ступенчатым профилем. Из табл. 12.2 с очевидностью следует, что для любой
моды планарного волновода т? -> О при V Кс, т. е. U= V = Vc, W = 0. С дру-
гой стороны, как следует из рис. 12.5, т? > 0 на частоте отсечки любой моды
волоконного световода за исключением ТЕ^-, ТМ^-, НЕ1т- и НЕ-мод.
Таким образом, между модами этих двух волноводов вблизи частоты отсеч-
ки мод существует различие. Если в планарном волноводе при приближении
к частоте отсечки моды вся ее мощность сосредоточена в оболочке, то в све-
товодах на частоте отсечки значительная часть мощности мод распространяет-
ся по сердцевине, за исключением мод, отмеченных выше.
Распространение на частотах, ниже отсечки. Рассмотрим источник, распо-
ложенный на торце световода с Д = 0,32 и возбуждающий моду НЕ31 на ее
частоте отсечки Кс = 4,399. Эта мода распространяется по световоду без за-
тухания, и в соответствии с рис. 12.5 примерно 60 % мощности моды перено-
сится по сердцевине. Если теперь чуть-чуть увеличить длину волны источника
X так, что параметр V будет ниже частоты отсечки моды VQ, то, несмотря на
то, что характеристики распространения световода изменятся мало, точный
волновой анализ показывает, что вся мощность моды является в основном
излучаемой. Вблизи или внутри сердцевины поле излучения может быть ап-
проксимировано полями направляемой моды НЕ31. Однако характеристи-
ческое уравнение показывает, что постоянная распространения моды /3 имеет
малую мнимую часть, что приводит к небольшому коэффициенту затухания.
Коэффициент затухания обусловлен постепенным рассредоточением мощно-
сти моды по всему поперечному сечению световода при распространении вы-
текающей моды и, как будет показано в разд. 24.14, мнимая часть /3 опреде-
ляет скорость излучения направляемой мощности вытекающей моды.
Приведенный пример подтверждает наше интуитивное представление о
том, что часть поля излучения, распространяющуюся вдоль и вблизи оси све-
товода, можно аппроксимировать направляемыми модами на частотах ниже
частоты отсечки. По-видимому, наиболее убедительными доказательствами
служат экспериментальные наблюдения картин распределения интенсивно-
стей полей мод в световодах [3, 4], волноводный параметр которых К ниже
частоты отсечки этих мод. Хотя свойства вытекающих мод планарных вол-
новодов исследованы давно [5 - 9], для волоконных световодов они были
описаны лишь недавно на примере моды HE3i [10 - 19].
24.3. Представление поля излучения полями вытекающих мод и простран-
ственной волны
Как отмечается в гл. 25 и 34, поле излучения оптического волновода может
быть определено либо методом мод, либо методом функции Грина. В гл. 26
показано, что в любом случае полные поля излучения Erad и Hrad могут быть
точно представлены суммой полей вытекающих мод и поля пространствен-
ной волны ЕСТ1, и Н . Таким образом,
SW bW х
414
4n Mlm
Erad = Д (ajEj +«_jE_j) +E,V; Hrad = (Д.Н. + %Н_р 4
(24.1)
где (7j и (?_j — амплитуды вперед- и назад-распространяющихся мод соответ-
ственно, — число вперед- и назад-распространяющихся вытекающих мод
(см. разд. 24.10). Поля мод Ej, Н.,Е_., Н ; являются полями направляемых
мод и определены выражениями (11.3) на частоте ниже частоты отсечки К
каждой моды. Поле пространственной волны представляет собой оставшую-
ся часть поля излучения. Мощность, связанная с полем пространственной
волны, быстро излучается из волновода.
При больших расстояниях от оси волновода поле пространственной волны
представляет собой поле излучения в чистом виде, в то время как в другом
предельном случае (на достаточно большом расстоянии от источника и вбли-
зи или внутри сердцевины) поле излучения можно приближенно описать по-
лями вытекающих мод. Исключением служит весьма редкая ситуация, когда
узкоколлимированный луч от источника возбуждения направлен под крити-
ческим углом 0С к оси световода. В этом случае поле пространственной волны
распространяется вдоль границы сердцевины с оболочкой на сравнительно
большие расстояния. Его вклад в поле излучения рассмотрен в гл. 26. Он уч-
тен в выражении (24.1).
ХАРАКТЕРИСТИКИ ВЫТЕКАЮЩИХ ВОЛН
В этой части главы исследуются свойства вытекающих мод непоглощающих
волоконных световодов с произвольными формой поперечного .сечения и
профилем показателя преломления. Ниже в разд. 24.20 кратко рассматрива-
ются свойства вытекающих мод планарных волноводов.
24.4. Параметры мод
Поскольку вытекающие моды являются направляемыми, распространяющи-
мися ниже частоты отсечки, то поля этих мод функционально идентичны по-
лям направляемых мод. Если индексами г и i обозначить действительную и
мнимую части комплексной величины, то
0=0Г +1У; U=Uc + ilJi-, W=WI + iW1, (24.2)
где U и И7 связаны с /3 и волноводным параметром Г соотношениями в
табл. I. Интервал значений постоянных распространения направляемых мод
определен выражением (11.46). Следовательно, для постоянной распростра-
нения вытекающей моды справедливы условия
0 < (Зт < Ь/с1 или t/ > К. (24.3)
В разделе 24.10 показано, что количество вытекающих мод конечно. По-
скольку чуть ниже отсечки W — почти чисто мнимая величина, то удобно вве-
сти новый параметр моды Q, определяемый соотношением
415
Q = p(k2n2cl-02)1/2=iW = (U2 - Г2)1/2. (24.4)
Таким образом, ниже частоты отсечки Q является почти действительной ве-
личиной. Для вперед-распространяющихся мод знаки перед действительны-
ми и мнимыми частями комплексных параметров следующие:
(Зг, U1, QT - положительный;
Л j i i (24.5)
и , w , W, Q — отрицательный.
24.5. Поля мод
Если выражение (24.2) подставить в (11.3), то получим следующую функ-
циональную зависимость полей вытекающих мод:
Е (х, у, z) = е (х, у) exp (i/3Tz) exp (~/3Tz) , (24.6a)
H (x, j, z) = h (x, y) exp (i/3Tz) exp (-tfz), (24.66)
где e и h зависят от комплексных параметров мод. Пространственная зависи-
мость векторов е и h в однородной оболочке произвольного световода иден-
тична зависимости в световоде со ступенчатым профилем (см. табл. 12.3)
за исключением постоянного множителя перед каждой компонентой. Ради-
альная зависимость амплитуды полей включает в себя модифицированные
функции Бесселя второго ряда Kv (И7?). Поскольку на частоте VQ W яв-
ляется почти чисто мнимой величиной, то используя выражения (24.4) и-
(37.71), заменим Кр функцией Ганкеля первого рода, аргумент которой
почти действительный. Таким образом, пространственная зависимость, на-
пример продольной компоненты поля четной моды, пропорциональна
(QR) cos (у<р) exp (ipz). (24.7)
На больших расстояниях от световода, таких что QR » v, функцию Ганке-
ля можно заменить ее асимптотической формой (37.87). Если учесть неяв-
ную зависимость от времени, то выражение (24.7) преобразуется к виду
(l/7?1/2)cos(z<v)exp {i [QA + pz - (2p + 1)тт/4 - cor]} . (24.8)
Выражение внутри фигурных скобок описывает волну, распространяющуюся
от световода. Направление распространения определяет направление излуче-
ния мощности вытекающей модой. В оболочке оно составляет угол 0Z с осью
световода, т. е. из выражений (24.8) и (24.4) имеем
cos 0Z = рт/кп^ tg 0Z = QT/PpT , (24.9)
где nс1 - показатель преломления оболочки.
24.6. Каустика излучения
Поля вытекающих мод характеризуются существенным изменением в их по-
ведении при достаточном удалении от оси световода. Определим радиус rrad
в оболочке как радиус, на котором порядок функции Ганкеля (24.7) и ее
416
аргумент равны, предполагая, что рассматриваются моды высших порядков,
т. е. v >> 1. Отсюда
'rad=PP/6r’> <24Л°)
где р — радиус сердцевины. Поведение полей в областях р <г<гт^ иrrad <
< г < «j описывается выражениями, полученными подстановкой асимптоти-
ческих форм функций Ганкеля (37.90) и (37.87) в соотношение (24.7).
Между границей сердцевины с оболочкой и поверхностью г = rrad поля явля-
ются спадающими, и амплитуда их уменьшается с ростом радиуса, в то вре-
мя как вне радиуса rrad поля имеют колебательный характер, и мощность
волны распространяется в направлении, определяемом (24.9). Таким обра-
зом, цилиндрическую поверхность с г = rrad можно считать источником излу-
чения, и поэтому назовем эту поверхность каустикой излучения. Описанная
картина схематически изображена на рис. 24.1, а. Внутри сердцевины и в об-
ласти р < г < rrad вытекающие моды ведут себя подобно направляемым, а
при г > rrad мощность излучается. Подчеркнем, что цилиндрическая поверх-
ность с радиусом rrad четко определена как фактический источник излучения
только для мод высших порядков.
5 Туннелирующие вытекающие моды Р< ггаи<о°
0 Преломленные вытекающие моды rrad ~ Р
г Направляемые моды rrad=o°
Рис. 24.1. Обусловленные каустикой с радиусом rrad и направленное под углом 0Z к
оси световода излучение мощности (затемненные области обозначают сердцевину, за-
штрихованные - спадающие поля в оболочке) туннелирующей вытекающей моды (а, б),
преломленной вытекающей моды (в) и направляемой моды (г) и таблица классифи-
кации мод в соответствии с величиной rrad
1 I Зак 37
417
24.7. Классификация вытекающих мод
Когда каустика излучения расположена на конечном расстоянии от границы
сердцевины с оболочкой, поля мод в области р < г<гхзА являются спадающи-
ми, и направление потока мощности, определяемое вектором Пойнтинга, па-
раллельно оси световода. Поскольку мощность излучается при г ~ riad, а поле
в любой точке внутри интервала 0 < г Orad затухает с одной и той же скоро-
стью, то часть излучаемой мощности должна передаваться из сердцевины. Фи-
зический механизм переноса мощности из сердцевины через спадающую об-
.ласть известен как туннелирование, или нарушение полного внутреннего от-
ражения (обсуждался в рамках геометрической оптики в гл. 7). По этой
причине вытекающие моды, для которых выполняется условие р <rrad <°°,
называются туннелирующими вытекающими модами. Ясно, что чем больше
rrad’ тем меньше затухание мощности моды, поскольку при rrad = 00 спадаю-
щее поле простирается в оболочку до бесконечности, и вытекающая мода
становится направляемой.
Если каустика излучения совпадает с границей сердцевины и оболочки,
т. е. rrad = р, то область спадания поля в оболочке отсутствует, и в соответ-
ствии с обозначениями лучей в гл. 7 моды называются преломленными выте-
кающими модами. Интервал изменения rrad для направляемых и вытекаю-
щих мод, а также глубина спадания поля даны на рис. 24.1.
24.8. Разложение на плоские волны
В разделе 36.2 показано, что в световоде со ступенчатым профилем показате-
ля преломления поля направляемых мод высших порядков можно разло-
жить по плоским волнам или лучам, причем каждый луч распространяется в
сердцевине световода под теми же характерными углами в7 и 0 . Такое раз-
ложение применимо и к полям вытекающих мод в сердцевине и подтвержда-
ет тот факт, что туннелирующие вытекающие моды состоят из туннелирую-
щих вытекающих лучей, а преломленные вытекающие моды - из преломлен-
ных вытекающих лучей [11]. Соотношения между параметрами мод v и /Зг
и лучевыми инвариантами I и /3 приведены в табл. 36.1, в которой /3 нужно
заменить на /Зт.
24.9. Слабонаправляющие волноводы
В главе 13 на основании решений скалярного волнового уравнения была
рассмотрена структура полей направляемых мод слабонаправляющих свето-
водов. Поперечные электрические поля et вытекающих мод имеют ту же
функциональную зависимость, что и поля et направляемых мод из табл. 13.1
при условии, что постоянная распространения /3 и параметры мод Un W заме-
нены их комплексными аналогами в соответствии с выражением (24.2). Вве-
дем также параметр моды Q, который определяется по аналогии с выражени-
ем (24.4). Для вперед-распространяющихся мод знаки перед действительны-
ми и мнимыми частями этих параметров подчиняются тем же правилам (24.5),
что и знаки перед точными параметрами.
Соответствующее поперечное магнитное поле h уже не связано с et соотно-
шением из табл. 13.1, поскольку /Зт лежит в том же диапазоне значений, что
и (Зт в выражении (24.3), и, таким образом, может значительно отличаться
418
от кпCQ. Поэтому используем упрощенную форму выражения (30.56) для
произвольных величин (3. В дальнейшем будет показано, что решение харак-
теристического уравнения для вытекающих мод можно приближенно запи-
сать в виде |0| кпсо, что является следствием того, что 0. быстро увеличи-
вается при уменьшении V ниже частоты отсечки Vc и компенсирует умень-
шение Рт. Следовательно, продольные поля (30.5в) и (30.5г) в (р0)-1 или
Д"1/2 V раз меньше, чем поперечные поля, и ими можно пренебречь. Отсю-
да уравнение (30.56) можно приближенно записать в виде
ht = (eo//A))1/2(0/fc)z х et,
(24.11)
где z - единичный вектор, параллельный оси световода.
24.10. Число вытекающих мод
В разд. 36.13 получено выражение для числа вытекающих модТИ^, которые
могут распространяться в произвольном многомодовом световоде с V>> 1.
Из (36.45) и (36.42) следует, число туннелирующих вытекающих мод Mtm
и преломляющих вытекающих мод Мт в световоде со ступенчатым профи-
лем равно соответственно
V2 (2Л)1/2
+ Д« 1. (24.12а)
= «-у [2Д- 1( д)1/2]’ (24.126)
где подразумевается, что число мод равно наименьшему целому числу, пре-
вышающему правую часть, а величина Д определена в табл. I. Эти выражения
включают все четные и нечетные НЕ-, ЕН-, ТЕ- и ТМ-моды. Число направляе-
мых мод7ИЬт определяется формулой (36.41), так что число всех мод
Л/fot = Л/Ьт +^tm +4m =^Ьт +Л4п = (24.13)
Число направляемых и туннелирующих мод приблизительно равно, если
Д<< 1.
МОЩНОСТЬ И ЗАТУХАНИЕ
Вытекающие моды являются полезным понятием, если их можно применить
для решения задач так же легко, как направляемые моды. Это обеспечивает-
ся разработкой обоснованного физического описания переносимой мощно-
сти и коэффициента затухания вытекающих мод [11, 13]. Поскольку четко-
го определения мощности, переносимой вытекающей модой, нет, то здесь
дадим качественное описание.
24.11. Качественное физическое описание
Принимая во внимание характерные свойства вытекающих мод, рассмотрен-
ные выше, исследуем структуру каждой моды [13]. Рассмотрим туннелиру-
ющую вытекающую моду в световоде длиной L (рис. 24.2, а). Пусть мода
14”
419
Рис. 24.2. Качественное описание потока мощности в световоде со ступенчатым профи-
лем для случая, когда вытекающая мода возбуждена в сечении z = 0 (л), и иллюстра-
ция потерь на излучение мощности вытекающей моды dPT с помощью бесконечно мало-
го цилиндра высотой dz (б)
возбуждена в сечении z = 0 и при распространении вдоль световода излучает
свою мощность с поверхности каустики излучения, рассмотренной в разд. 24.6.
По предположению направляемая часть мощности вытекающей моды сосре-
доточена в области 0 < г < rrad. Источником излучения для каждой точки в
поперечном сечении z = L является соответствующая точка на поверхности
каустики с радиусом г = rrad. Так, например, источником излученной мощно-
сти в сечении z = L с радиусом rQ является каустика в сечении z = 0, а с радиу-
сом Г1 - каустика в сечении z =2ьчто схематически изображено на рис. 24.2, а.
Поскольку при распространении вдоль световода мощность вытекающей мо-
ды падает, то, очевидно, что поле излучения в сечении z -L с радиусом г0 бу-
дет больше, чем в сечении с радиусом , так как в точке z = 0 излучается
бо'льшая мощность, чем в точке z = zx. Таким образом, можно ожидать, что
поле вытекающей моды вне радиуса г - rrad растет с увеличением радиуса,
достигая максимума при г = rQ. Вне г0 поле исчезает. Внутри радиуса г = гт^
полю вытекающей моды присущи свойства поля направляемой моды, за ис-
ключением того, что вследствие затухания мощности постоянная распростра-
нения вытекающей моды является комплексной величиной. Полезным будет
качественное сравнение этого затухания с затуханием, обусловленным име-
ющимся поглощением в среде в области г > гт^-
Увеличение амплитуды поля излучения в области г > гт^ следует и из
асимптотического выражения для поля (24.8). При постоянном z и увеличи-
вающемся г в соответствии с формулой (24.5) амплитуда поля растет про-
порционально (1/Rх/2)ехр(|2j| ’А).
24.12. Направляемая и излучаемая мощности
Поток мощности, изображенный на рис. 24.2, а, состоит из двух различных
частей: направляемой, сосредоточенной в сердцевине и области экспоненци-
ального спадания поля внутри радиуса rrad, и излучаемой, распространяющей-
ся под углом 0Z (24.9) и сосредоточенной в области г > rrad. Если полную
4 20
направляемую мощность в сечении z обозначить (z), то из выражений
(11.21а) и (24.6) имеем
I rt I 2
Р (z) = -4v~exp(-2/3z) Re ( J e x h* • zdA),
S 2 J j
rad
(24.14)
где а — амплитуда моды, Re означает действительную часть, * — знак комп-
лексного сопряжения, Xrad — площадь поперечного сечения с радиусом rrad,
z - единичный вектор, параллельный оси световода. Подобным образом
определим полную излученную мощность в сечении z
P (?) = exp (~2^z) Re ( J e x h* • idA),
A (z)
(24.15)
где A (z) - площадь кольца с внутренним радиусом rrad и внешним радиусом
ro =rrad-rtS0z-
Из этих определений следует, что Pr(z) есть вся направляемая мощность,
потерянная при излучении моды в световоде длиной z. Если первоначально
направляемая мощность не преобразуется в излученную, то при z -> ©© вся
направляемая мощность трансформируется в излученную. Таким образом,
можно записать
Р = Р(И) + Pr(z) = Р(0) =Рг(оо), (24.16)
поскольку полная мощность вытекающей моды вдоль световода не меняет-
ся. Входная направляемая мощность определяется эффективностью источни-
ка возбуждения (см. разд. 24.17)'.
Экстраполяция мощности направляемой моды. Излучаемая и направляе-
мая части мощности вытекающей моды рассматриваются здесь как интуитив-
ные понятия, поскольку граничная поверхность с радиусом rfad имеет смысл
только для мод высших порядков, а при определении угла 0z предполага-
лось, что затухание мощности моды мало. Тем не менее поскольку при
rrad -> ©о затухание становится очень слабым, можно ожидать что Pg (z) будет
иметь ту же функциональную зависимость, что и мощность направляемых
мод, если заменить W на -\Q и учесть множитель ехр(—2j3z). Другими слова-
ми, на частотах ниже отсечки выражение для направляемой части мощности
вытекающей моды является экстраполяцией выражения для мощности на-
правляемой моды. Этот вывод подтверждает соотношение (24.14), которое
при р1 -> 0 совпадает с соответствующим выражением для мощности направ-
ляемой моды (11.21а).
Световод со ступенчатым профилем показателя преломления. В случае
слабонаправляющего световода со ступенчатым профилем мощность направ-
ляемой моды равна Р = | а 12N, где выражение для коэффициента нормировки
приведено в табл. 14.6. Полагая И7 = -\Q и используя преобразование (37.71),
имеем
421
Pg(z) =^la|2P2«co(eo/Mo)1/2-^- Hx ]21 (g) ехР(~2^‘г) (24.17)
где знак ~ опущен, а Н^— функция Ганкеля первого рода. Поскольку
является действительной функцией, правая часть (24.17) вычисляется при
2 2Г -> 0, когда в первом приближении функция Ганкеля чисто мнимая и
U* U1,
24.13. Часть направляемой мощности в сердцевине
В разделе 11.8 величина т? была определена как часть мощности моды, рас-
пространяющаяся в сердцевине волновода. Хотя формального определения
такой же величины для вытекающих мод нет, на основании физических со-
ображений и, используя сведения из предыдущего раздела, определим т? для
вытекающей моды следующим образом
мощность, распространяющаяся / J е х h* • idA)
по сердцевине _ лсо
77 мощность, распространяющаяся' Re( f exh**zdA) ’
внутри каустики излучения 4rad
где обозначения определены в разд. 24.12.
Световод со ступенчатым профилем. В слабонаправляющем световоде со
ступенчатым профилем выражение для т? на частотах V < Кс может быть по-
лучено по аналогии с соотношением (24.17) из выражения, приведенного в
табл. 14.6,
[#1(1)(2)]2
Q2
- U2 J 1Д1 (2)Г Q2
71 “ I j (2)Я<*\ (2) “ U2
(24.19)
где знак ~ для скалярных величин опущен.
24.14. Коэффициент затухания мощности
При качественном описании свойств вытекающих мод в разд. 24.12 предпо-
лагалось, что при распространении моды ее полная мощность остается неиз-
менной. Это предположение имеет своей целью подчеркнуть то обстоятель-
ство, что коэффициент затухания мощности у представляет собой преобразо-
вания направляемой части поля в излучаемую часть того же поля, т. е.
Pg (z) = Р (0) ехр (-72 ); у = 2/31.
(24.20)
При распространении моды мощность, первоначально целиком сосредоточен-
ная в ее направляемой части, распределяется по все большему поперечному
сечению и в сечении z = L занимает область rrad <г < г0 (см. рис. 24.2, а) . Это
позволяет получить выражение для коэффициента затухания мощности [13].
Световод со ступенчатым профилем показателя преломления. Для удоб-
ства и простоты в качестве примера рассмотрим световод со ступенчатым
профилем. Возьмем бесконечно малый отрезок световода длиной dz, схема-
тически изображенный на рис. 24.2, б. Поскольку длина отрезка световода
422
достаточно мала, то из каустики излучения на излучение теряется лишь малая
часть мощности моды (z). Тогда коэффициент затухания мощности удов-
летворяет уравнению
dPx(z) ^P^z)dz, (24.21)
где Рг иА определены формулами (24.15) и (24.14) . Величину dPT(z) мож-
но оценить, если заметить, что мощность, излучаемая с поверхности радиусом
г " rrad ’ сосредоточена между двумя коническими поверхностями, составля-
ющие угол 0z с осью световода. Если г — средний радиус этих поверхностей
в сечении z, то из (11.20а) и (24.16) имеем
dP^z) =я|д|24г
р
[Re(e х h* • z)^
r,]exp(-20z)dz,
(24.22)
где a — амплитуда вытекающей моды, а скалярное произведение вычисляется
при г = г'. Из табл. 14.6, выражений (24.11) и (37.71) получаем
Re(«xb* |^|>. (24.23)
где - функция Ганкеля первого рода. Поскольку dP (z) не должна зави-
сеть от г, то весьма разумно положить г и дляЯ^цУ/р) использовать
асимптотическую форму (37.87). Подставляя выражения (24.17), (24.22) и
(24.23) в (24.21), окончательно имеем [13]
= 4 (2Д)1/2 (£Л)2________________1___________
7 Я Р К3 ]Н^ (2Г) | ’
(24.24)
где предполагается U V2 и Q « Q2. В разделе 24.18 будет подтверждено,
что этот результат, полученный на основе качественного физического описа-
ния, совпадает с формальным решением для малых значений у, полученным
на основе волновой теории.
Сравнение с вытекающими лучами. В разд. 7.1 рассматривалось затухание
вытекающих лучей в многомодовых световодах. Очевидно, что для мод выс-
ших порядков должно существовать хорошее соответствие между коэффи-
циентами ослабления для вытекающих мод и соответствующих вытекающих
лучей. Качественно и количественно этот вопрос рассматривается в разд. 36.11
применительно к планарным волноводам и волоконным световодам со сту-
пенчатым профилем показателя преломления.
ОРТОГОНАЛЬНОСТЬ И НОРМИРОВКА
Полное поле оптического волновода можно представить суммой полей дис-
кретных направляемых и вытекающих мод и поля пространственных волн.
Такое представление формально идентично разложению (11.2). Если ограни-
читься рассмотрением только вперед-распространяющихся мод, то
^bm
Е= , ajej exp(i/3 z) + S Ae exp(itf z)exp(-0‘ z) +E ; (24.25a)
J — 1 J- J J К — 1 K K K K sw
423
^bm ^lm
H= / = 1 ^еХр(^ + ^/kekexp(i^kz)exp("^kz) +Hsw’ (24.256)
где Afbm иЛГ1т — количество направляемых и вытекающих мод, а Е^, —
поля пространственных волн. Чтобы определить амплитуды поля Z>k вытека-
ющих мод, зависящие от эффективности возбуждения на входном торце све-
товода, потребуем выполнения соотношений ортогональности между вытека-
ющими модами, направляемыми модами и пространственными волнами и
используем выражение для коэффициента нормировки для каждой вытека-
ющей моды.
24.15. Соотношения ортогональности
Соотношения ортогональности для направляемых мод, полученные в разд. 11.4,
для вытекающих мод несправедливы. Это очевидно из выражения (24.8),
которое показывает, что поле растет как ехр(|£/|г/р) при Такие поля
не подчиняются условию ортогональности (11.10), в которое входит инте-
грирование по бесконечному поперечному сечению волновода, поскольку это
условие требу ?т нулевого значения поля при г ->°°.
Однако условия ортогональности можно сформулировать, если интегриро-
вать в плоскости комплексных г [20 — 22]. Предположим, что г имеет доста-
точно большую мнимую часть, способную скомпенсировать экспоненциаль-
ный рост амплитуды вытекающей моды при больших значениях Q\ Контур
комплексной плоскости г может быть выбран таким образом, что направля-
емые и вытекающие моды ортогональны как друг другу, так и полям про-
странственных волн. Следовательно, условие ортогональности для двух вы-
текающих мод функционально идентично условию (11.14), в котором бес-
конечное поперечное сечение Аж заменено на уЦ, где ЛД — действительное
поперечное сечение для конечных г и мнимое при г Таким образом,
(24.26)
Поля вытекающих мод имеют ту же функциональную зависимость, что и по-
ля направляемых мод, но параметры мод и постоянные распространения яв-
ляются комплексными величинами.
Необходимо подчеркнуть, что вытекающие моды не подчиняются соотно-
шению ортогональности мощностей (11.13), поскольку произведение х h*
не является аналитической функцией и, таким образом, не может быть рас-
пространено на комплексную область, что было необходимо для вышепри-
веденного обобщения.
24.16. Коэффициент нормировки
Из предыдущего раздела следует, что коэффициент нормировки определяет-
ся выражением
424
N= - j* e X h • zdA,
2Л'
(24.27)
где Ai - комплексное поперечное сечение, определенное выше, z - единич-
ный вектор, параллельный оси волновода. Подчеркнем, что для выполнения
условий ортогональности и для определения N необходимо детально знать
ЛД, и важно, чтобы ЯД обеспечивало нулевую амплитуду поля всех вытека-
ющих мод на бесконечном расстоянии от оси волновода. Поскольку, как по-
казано в разд. 11.3, для направляемых мод непоглощающих структур h* =
= h , то функциональная зависимость коэффициента нормировки N одинако-
ва для вытекающих и направляемых мод, что следует из интегрирования по-
лей вытекающих мод по бесконечному поперечному сечению ЛД. При вычис-
лении N необходимо соблюдать осторожность, поскольку аргументы е и h
являются комплексными величинами.
Световод со ступенчатым профилем показателя преломления. В качестве
иллюстрации рассмотрим слабонаправляющий световод со ступенчатым про-
филем, поля вытекающих мод в котором определяются выражениями
(24.6) и выражениями из табл. 14.1 и 14.6. Например, в сердцевине в направ-
лении z плотность мощности равна
= <24'28)
(При выводе этого соотношения использовалось выражение (24.11)). Для
слабовытекающих мод (3 « кпсо, так что (24.28) имеет такую же функцио-
нальную зависимость, что и для направляемых мод. Поэтому N также имеет
идентичную со случаем направляемых мод зависимость в табл. 14.6, в кото-
рой W заменяется на (—iQ). Тогда с помощью (37.71) имеем
*рЧо ге0)1/2 К2 ^(1)^077(0 (6)
2 Мо [я(»(е)]2 ’
(24.29)
где - функция Ганкеля первого рода, а знак ~ опущен.
Мощности направляемых и вытекающих мод. Несмотря на то, что коэф-
фициент нормировки N (24.27) формально справедлив для вытекающих
мод с произвольным вытеканием, прямой связи между мощностью, перено-
симой вытекающей модой, и коэффициент нормировки нет, хотя для направ-
ляемых мод такое соотношение существует — (11.22). Это объясняется тем,
что мощность вытекающей модыР (24.16) является интуитивным понятием,
введенным для понимания свойств вытекающих мод. Выразить мощность че-
рез коэффициент нормировки (11.22) можно только в случае слабовытекаю-
щих мод. Однако если рассматривать лишь мощность, сосредоточенную в
сердцевине, то выражение (11.28) справедливо как для направляемых, так
и для вытекающих мод.
24.17. Проблемы возбуждения и возмущения
Полученные соотношения ортогональности и выражение для коэффициента
нормировки позволяют обобщить некоторые результаты, полученные в пре-
425
дыдущих разделах для направляемых мод, на вытекающие моды. Так, в част-
ности, легко обобщаются выражения для. возмущенных световодов из гл. 18,
соотношения для эффективности возбуждения внешними источниками из
гл. 20, проблемы возбуждения и рассеяния излучения от внутренних источ-
ников тока, рассмотренные в гл. 21 — 23. В разделе 24.23 рассматривается
пример возбуждения вытекающей моды внутренним источником.
РЕШЕНИЕ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ
Выше рассмотрены все свойства, необходимые для понимания физического
поведения вытекающих мод и условий их возбуждения. Однако при этом
требуется знать комплексную постоянную распространения каждой вытека-
ющей моды. Решение характеристического уравнения для значений V, лежа-
щих ниже частоты отсечки, в общем случае может быть получено численными
методами. Аналитическое решение известно только для слабовытекающих
мод при К, близких к частоте отсечки [13]. Рассмотрим ряд примеров.
24.18. Пример. Аналитическое решение для волоконного световода со сту-
пенчатым профилем показателя преломления
Характеристическое уравнение для направляемых мод слабонаправляющего световода
со ступенчатым профилем приведено в табл. 14.6. Заменяя параметр W на -iQ, исполь-
зуя преобразование (37.71) и опуская знак получаем
1 (О .
Q* = и* - V\
(24.30)
где и функция Бесселя и Ганкеля первого рода, U, Q - комплексные величины
для каждой моды при V < 7С, за исключением основной моды, не имеющей отсечки. По-
лучим теперь* аналитические приближения для параметров мод при V < 7С> когда U и
Q - почти действительные величины с малой мнимой частью. Эти приближения дают также
точные начальные значения для численного решения, приведенного в следующем разделе.
Действительные части U и Q. Действительная часть U на частотах (7 < 7С) для всех
мод с индексом I > 1 приближенно определяется экстраполяцией выражения из табл. 14.7
в область V <. Vc, а действительная часть Q получается из соотношения (24.30), посколь-
ку Q1 « [((7Г)2 - 7а]1/3. Такая экстраполяция менее пригодна для НЕ 1т-мод высших
порядков (Z = 0, т > 1), так как на частоте отсечки каждой моды, как будет показано
в следующем разделе, существует разрыв функции U от V.
Мнимые части U и Q. Составляющие U1 и Q1 параметров мод могут быть найдены из
решения характеристического уравнения методом теории возмущения. Для этого опре-
делим функцию G следующим образом:
A+iW я1+\(е)
G (Ц) = . (24.31)
где U = if + it?. При V <VC U1 мало по сравнению с if, поэтому, разлагая G в ряд Тей-
лора вблизи UT, можно ограничиться лишь членом первого порядка малости. Учитывая,
что U является решением уравнения (24.30), дифференцируя (24.31) по U, с помощью
рекуррентных соотношений (37.72) имеем
(24.32)
426
Использование уравнения (24.30) позволяет выразить функции Бесселя через функции
Ганкеля
dG I = К2
du 'и=их и1 [я^се1)]3
Q1 = [((/)2 - Г2]1'2.
(24.33)
Вблизи частоты отсечки величина Q1 мала, и в функции Ганкеля преобладающей являет-
ся ее мнимая компонента. Следовательно, производная является фактически действи-
тельной величиной и, поскольку t/1 - действительная величина по определению, потре-
буем, чтобы компонента Im [G (£7Г) ] в выражении (24.31) была чисто мнимой. Послед-
нее выражение включает в себя только функции Ганкеля и, положив
(У^ ~ функция Бесселя второго рода), с помощью Вронскиана (37.766) находим
Im [G (£/)] = — --—1—— . (24.34)
я (^«(С1) |)2
Подставляя последнее соотношение и модуль выражения (24.33) в выражение (24.32)
с точностью, достаточной для возмущенного решения, получаем [13]
• Д 2 и1 ____________J___________ Л_ГД СД
’ (ег)| ; Q Q1 ’
где Q1 определяется из характеристического уравнения (24.30).
Коэффициент затухания мощности. Чтобы получить выражение для коэффициента
затухания мощности, приравняем мнимые части в выражении, определяющем параметр
U, т. е. игит = -р2^г. Для слабонаправляющих световодов вблизи частоты отсечки (Зг
^^псо= (24)1/3, и поэтому из соотношений (23.20) и (24.35) имеем
i 4 (24)1/2 (U1)3 1
7 ~ я pV3 |Я|(1) j (бг)Я1(р1 G2r) I ’ (24’36)
что идентично выражению (24.24), которое получено на основании интуитивных сообра-
жений о сохранении мощности. На частотах вблизи отсечки асимптотические выражения
для функции Ганкеля с малым аргументом (37.83) и (37.84) позволяют получить упро-
щенные выражения
(? = F), 1= 0; 1?=-я(Кс-К)/|1п2К(Кс-Г)|, /= 1, (24.37а)
Kc<Fc-О]1, 1>2; т*-2(2Д),/31?/(рП, (24.376)
при выводе которых предполагалось, что Ul « U « V * Кс, и использовались выражения
из табл. 14.7.
24.19. Пример. Численное решение для волоконного световода со ступенча-
тым профилем показателя преломления
Точное численное решение уравнения (24.30) для действительных и мнимых частей Uи
Q облегчается использованием табл. 14.7 и выражения (24.37) в качестве начальных
оценок для U при V < Кс. Решение уравнения для меньших V может быть найдено с по-
мощью метода итераций Ньютона - Рафсона, согласно которому выражение (24.31) для
G разлагается в ряд Тейлора вблизи известного нуля, при этом учитываются два члена
[21]. Полученные этим методом зависимости £7г(Г) и -С/1 (Г) изображена на рис. 24.3, а
для HEl+ j и ЕН^ t j-мод при I - 1, 2,.. ., 6. Основная мода HEn (Z = 0), не имею-
щая отсечки, приведена для сравнения. Решения для направляемых мод соответствуют
сплошным кривым для V > Vc. Штриховые кривые, берущие начало на частоте отсечки
V = Ус каждой моды - это решения U1 и U1 для туннелирующих вытекающих мод (ког-
да каустика излучения расположена на конечном расстоянии от границы сердцевины с
427
Рис. 24.3. Зависимости U1 и -U1 от параметра V в слабонаправляющем световоде со сту-
пенчатым профилем [21] для:
а ~ НЕ1+ 1,1“ и ЕН1— 1 1-мод (/ = 1, ...» 6) ; б — НЕ|т-мод (т = 2, 3, 4). Наклонная
прямая соответствует условию отсечки СЛ = V
оболочкой). Сплошные линии, продолжающие каждую кривую, соответствуют прелом-
ленным вытекающим модам (когда каустика излучения совпадает с границей сердце-
вины и оболочки). Необходимо помнить, что такое разграничение для мод низших по-
рядков является до некоторой степени искуственным, поскольку положение каустики
излучения в этом случае четко не определено.
На рис. 24.3, б даны зависимости Ur (Г) и -£/*(?) для НЕ1т-мод (Z = 0) при т =
= 2, 3, 4, включая основную моду (т = 1), приведенную для сравнения. Ниже частоты
отсечки каждая мода становится преломленной вытекающей модой, а области туннели-
рующих вытекающих мод не существует. Эти кривые отражают свойства, присущие ис-
ключительно НЕ1т-модам: ниже частоты отсечки не существует решения характеристи-
ческого уравнения, соответствующего вытекающим модам [19], что выражается в раз-
рыве кривых UT. Этот разрыв связан с нарушением непрерывности в rra(j для этих мод.
Его величина меняется скачком от г = °° для направляемых мод (на частотах чуть
выше частоты отсечки) до ггад = р для преломленных вытекающих мод (на частотах
чуть ниже частоты отсечки).
Коэффициент затухания. Характеристическое уравнение для вытекающих мод
(24.30) и его решения (7Г, U1 не зависят от параметра Д, но соответствующий коэффици-
ент затухания очень чувствителен к нему. Если приравнять действительную и мнимую
части U2, использовав определения в табл. I, исключить /Зг и подставить решение полу-
ченного квадратного уравнения относительно (01)3 в выражения (24.20), то получим
/ 2 С т/- 2 * • • | 1 / 2
7 = ~~ “ <С/Х)2 + а)а + 4 ((/(/)’]1/1 - Р’/2Д+ (£/)’ - (t/Уу
(24.38)
Легко показать, что у -> 0 при Д ->0. Кривые нормированного коэффициента затухания
ур, соответствующие величинам U1 на рис. 24.3, изображены на рис. 24.4 для световода
с Д = 0,005. Из рисунка видно, что вблизи частоты отсечки любая вытекающая мода
имеет произвольно малый коэффициент затухания. Такие вытекающие моды могут рас-
пространяться на значительные расстояния, существенно увеличивая продольную об-
ласть пространственного перехода к установившемуся режиму. В случае преломленных
вытекающих мод, которым соответствуют сплошные кривые на рис. 24.4, даже значение
наименьшего коэффициента затухания велико, так что эти моды быстро вытекают из
428
Рис. 24.4. Нормированный коэффициент затухания мощности ир как функция парамет-
ра V для мод, соответствующих рис. 24.3. Кривые рассчитаны по формуле (24.38) при
Д = 0,005 [21]
б)
световода. При фиксированном V затухание растет с ростом I. Это согласуется с соот-
ветствующими результатами для составляющих моду вытекающих лучей в гл. 7. Этот
вопрос более подробно обсуждается в разд. 26.11.
Часть мощности в сердцевине. Часть мощности вытекающей моды, распространяю-
щаяся по сердцевине, определяется формулой (24.19). Используя это выражение и беря
действительную часть отношения функций Ганкеля, можно получить зависимость 17 от
параметра V, изображенную на рис. 24.5 для мод рис. 24.3, а. Сплошные кривые отно-
сятся к направляемым модам, штриховые - к туннелирующим вытекающим модам.
Все преломленные вытекающие моды имеют т? = 1, так как гга(| = р и Лгас| = Лсо.
Точность приближения слабонаправляющего волновода. Точность решений для выте-
кающих мод, рассмотренных выше для случая слабонаправляющего световода, может
быть оценена сравнением с соответствующими решениями при Г < К точного характе-
ристического уравнения световода со ступенчатым профилем и произвольными показа-
телями преломления сердцевины и оболочки из табл. 12.4 [21]. Это сравнение показы-
вает, что величины UT и U1 незначительно отличаются от их точных значений при измене-
нии Д от 0 до 0,01 при условии, что мода находится ниже отсечки, но не слишком далеко.
Рис. 24.5. Зависимость части мощности в серд-
цевине от параметра V jjjwl мод, соответствую-
щих рис. 24.3, а [21]
429
24.20. Пример. Планарный волновод со ступенчатым профилем показателя
преломления
Характеристические уравнения для вытекающих ТЕ- и ТМ-мод планарного волновода в
приближении слабонаправляющего волновода можно получить, если в характеристи-
ческих уравнениях для ТЕ-мод в табл. 12.2 заменить W на -iQ. В результате имеем
Q = \U tg U (четные моды),
Q — -iU ctg U (нечетные моды),
(24.39)
где параметры определены в табл. I. Решение этих уравнений может быть найдено числен-
ными методами, подобными тем, которые использовались в предыдущем разделе. На
рис. 24.6, а изображены зависимости U1 (V) и -U1 (И) для первых пяти мод, включая ос-
новную или первую четную моду. На этих графиках сплошные кривые на частотах выше
Рис. 24.6. Зависимости (Л, -U1 (а) и 70 (А - 0,005) (б) от параметра V для четных и не-
четных ТЕ- и ТМ-мод слабонаправляющего планарного волновода со ступенчатым про-
филем. Наклонная прямая соответствует условию отсечки t/1 = V
частоты отсечки соответствуют направляемым модам. В области между V = Ис и V, при
которых наблюдается излом, или нарушение непрерывности наклона, решений для
вытекающих мод не существует. В этой области W - чисто мнимая и отрицательная
величина, и поэтому, как видно из табл. 12.1, с ростом расстояния от оси световода
поля мод в оболочке возрастают по экспоненциальному закону. Эти решения не явля-
ются решениями ни для вытекающих, ни для направляемых мод и не играют никакой
роли в описании полного поля (24.1). Для первой нечетной моды эта область простира-
ется от V = Vc до V - 0. При дальнейшем уменьшении V остальные моды становятся
преломленными вытекающими.
На рис. 24.6, б изображены зависимости нормированного коэффициента затухания
7Р (24.38) от параметра V для мод рис. 24.6, а в волноводе с Д = 0,005. Из рисунка вид-
но, что при соответствующем выборе V затухание может быть произвольно малым, что
приводит к большим длинам области установления стационарного режима.
ПРИМЕНЕНИЯ ВЫТЕКАЮЩИХ МОД
В оставшейся части этой главы приводится ряд примеров, иллюстрирующих
использование вытекающих мод для качественного и количественного описа-
ния свойств поля излучения световодов.
430
24.21. Пример. Поперечное распределение интенсивности излучения в даль-
нем поле
В разделах 21.8 и 21.11 было показано, что информация о профиле показателя прелом-
ления световода содержится в поперечном распределении интенсивности излучения в
дальнем поле, обусловленном находящимися внутри слабонаправляющего световода ис-
точниками, и это распределение может быть найдено из распределения излучения в при-
ближении свободного пространства с помощью корректирующего множителя. В свою
очередь, корректирующий множитель представим в виде произведения двух сомножите-
лей и Сг (0), что было показано в разд. 21.13 для световода со ступенчатым про-
филем. Сравнивая выражения (21.38) и (21.366) с выражением (24.31), легко заме-
тить, что если параметры U и Q выразить через 0 с помощью выражения (21.37), то
функция Сг (0) обратно пропорциональна функции G (U). Следовательно, при измене-
нии 0 пиковые значения |СГ(0) | совпадают с минимальными значениями |С ((/)|. Функ-
ция G (U) обращается в нуль только в случаях, если решение характеристического урав-
нения соответствует вытекающей моде, поскольку при этом (/не является действитель-
ной величиной. Из требования действительности параметра U (21.37) следует, что |G (U) |
имеет малое, но конечное минимальное значение, если (/приблизительно равно действи-
тельной части решения уравнения для вытекающей моды. Таким образом, пики функ-
ции |Cr(G) I соответствуют конечным минимумам функции |(7 ((/) \,а значит возбужде-
нию вытекающих мод, т. е. резонансам в поперечном сечении, что иллюстрируется на
рис. 21.6, а.
Излучение диполя. В качестве простого примера рассмотрим ориентированный вдоль
оси z диполь, расположенный на оси световода со ступенчатым профилем. Напомним,
что такой диполь уже рассматривался в разд. 21.9. Угловое распределение интенсивно-
сти излучения в приближении свободного пространства (26.246) пропорционально
sin2 0, где в - угол между радиусом-вектором точки поля и осью световода. В данном
случае г0 = 0, и поэтому в выражении (21.39) (в) — 1. Тогда распределение интен-
сивности излучения в случае присутствия световода изменяется по закону.
|Сг(е) |2sin20. (24.40)
На рис. 24.7 штриховой линией показана картина излучения в свободном пространстве,
а сплошной линией - описываемая выражением (24.40). Если предположить, что свето-
вод является одномодовым, то при увеличении 0 пики соответствуют возбуждению
вытекающих мод НЕ12, НЕ13, .... Симметрия задачи обусловливает возбуждение толь-
ко НЕ1т-мод. Кроме того, как явствует из выражений (21.37) и определения Q в
табл. I, угол 0, который каждый пик составляет с осью световода, совпадает с углом
0Z для вытекающих мод в выражении (24.9) , определяющем направление потока мощ-
ности в оболочке. Поэтому, зная постоянные распространения вытекающих мод, можно
легко определить направление пиков излучения в дальнем поле. Однако эти пики необ-
ходимо отличать от пиков, возникающих в свободном пространстве в более сложных
случаях.
Рис. 24.7. Диаграмма излучения диполя, располо-
женного на оси световода со ступенчатым профи-
лем показателя преломления. Пики соответству-
ют резонансам вытекающей моды (кривая -
картине излучения пространственной волны)
431
Как следует из выражения (24.1), поля излучения вблизи и внутри сердцевины со-
стоят из полей вытекающих мод и пространственных волн. Поэтому, если источник воз-
буждает в основном вытекающие моды, поле излучения приближенно описывается по-
лями вытекающих мод. Таким случаям соответствуют пики на рис. 24.7. Рассмотрим
пример, когда источник эффективно возбуждает отдельные вытекающие моды.
24.22. Пример. Синусоидальный линейный источник
Рассмотрим слабонаправляющий световод со ступенчатым профилем, на оси которого
расположен синусоидальный линейный источник длиной 2L, ориентированный вдоль
оси х поперечного сечения световода. Предположим, что распределение плотности тока
Jx соответствует трубчатому источнику и определяется выражениями (21.13) и (21.14)
при / = 0 и г -* 0. Тогда
Jx = [б (г - r0)/27ir0]exp(iCz)sin Ш;
(24.41)
где все обозначения определены в разд. 21.6. Из свойств симметрии следует, что возбуж-
даются только четные, или поляризованные вдоль оси х моды НЕ1т. Амплитуда каж-
дой вытекающей моды определяется соотношениями (31.35) и (31.36), в которых
бесконечное поперечное сечение Аж заменяется на комплексное поперечное сечение
(см. разд. 24.15), а коэффициент нормировки вычисляется способом, описанным
в разд. 24.16. Тогда амплитуда вперед-распространяющейся моды в области -L <£
равна
= / e*/xexp(-i^z)exp(^z)d4dz, (24.42)
1 «A'j -£ X, XJ Х J J
где ex и /3 = + i/3j - скалярные величины, определяемые из характеристического урав-
нения (24.30). Если подставить выражение для Jx (24.41) и предположить, что £ доста-
точно велико, то по аналогии с (21.16) получим, что эффективное возбуждение вперед-
распространяющейся вытекающей моды происходит в том случае, если постоянная рас-
J
(24.43)
(24.44)
(24.45)
пространения моды удовлетворяет условиям
Тогда по аналогии с (21.15) имеем
= е*.(0) exp(fl!z) - ехр(-(?Д)
°;(г) = 4 ~--------------—=-----------— ; <Z < £,
J 8 TVj
где значение exj (0) вычисляется на оси световода. Выражения для соответствующих по-
лей вытекающих мод следуют из формул (24.6) и (24.11)
i exi (°) 1 “ ехР Е*3!(z + L) 1 г
£«, = s ------------------,+-------
^у! = (6о/До) W %
Если L -* «>, то амплитуды полей |£х1 и |ЯХ1 фактически не зависят от z при z >> l/pj.
Это возможно когда поток мощности в вытекающую моду от источника возбуждения в
точности равен потоку мощности из вытекающей моды в поле излучения. Однако ам-
плитуда моды в установившемся состоянии зависит от мощности источника. Кроме то-
го, необходимо помнить, что (см. разд. 24.16) выражения, связывающего мощность вы-
текающей моды и амплитуды поля и моды и аналогичного выражению (11.22) для на-
правляемых мод, не существует.
24.23. Пример. Осевая синусоидальная неоднородность
В разделе 22.5 было определено затухание основной моды слабонаправляющего свето-
вода со ступенчатым профилем показателя преломления, обусловленное излучением на
432
синусоидальной неоднородности границы сердцевины с оболочкой. Коэффициент зату-
хания был вычислен с помощью методов теории антенн в приближении свободного про-
странства и введением корректирующих множителей. Рассмотрим ситуацию, когда по-
ле излучения достаточно точно аппроксимируется полем одиночной вытекающей моды,
это возможно в случае синусоидальной неоднородности вида (22.14). Азимутальная
симметрия неоднородности обеспечивает возбуждение вытекающих мод только типа
НЕ1П1- Направление излучения мощности из световода должно совпадать с направлени-
ем излучения вытекающей моды [23]. Если неоднородность световода и поля падающей
основной моды представить, используя метод наведенных токов, как это проделано в
разд. 22.5, то направление излучения можно определить с помощью выражения (24.43),
в котором С = /Зг, т. е.
я = ||8Г-I; 0|>> Ф
(24.46)
где индекс 1 обозначает основную моду. Как и в выражении (22.15), направление вы-
нужденного тока совпадает с осью х, а его плотность равна
/ 2 д ч жу <5 (Т____у '>
•/х . = - 16р(е0/м0)1/2—---- T777V ------г—— exp(i0,z)sin42z, (24.47)
НСО Л)(Ц) 'О
так как /?о(0) = 1М0(Ц). Для удобства предполагается, что начальная амплитуда моды
равна единице и подразумевается, что г0 -* 0. Амплитуда вытекающей моды получается
из выражения (24.44) нормировкой его на отношение правых частей в выражении
(24.41), а именно
exp(0?z) - ехр(-^Л)
п = с J
(24.48)
11 % Ъ
где TVj - коэффициент нормировки вытекающей моды (см. разд. 24.16), exj (0) опреде-
ляется выражением из табл. 14.3 и -L < z .
Затухание мощности основной моды. Непосредственно определить мощность, излу-
ченную основной модой, используя формулу (24.48), нельзя, поскольку общего выра-
жения мощности вытекающей моды через амплитуду моды а-^ (z) не существует. Извест-
ную амплитуду вытекающей моды можно использовать для расчета изменения амплиту-
ды основной моды аг (z) от ее начального значения ах (0) = 1 и, таким образом, опреде-
лить коэффициент затухания. Будем рассматривать поле вытекающей моды совместно с
неоднородностью световода как вынужденный ток с плотностью J в регулярном све-
товоде. По аналогии с выражением (24.47) получим
Jxi = -i6p(-^),/2 Е2?---—~ — ---- Г-^-а (z)exp(i^z - /з’г) sin(Gz). (24.49)
М Мо «со Л>(Ц) г« J J J
Теперь продифференцируем выражение (24.42) по z, поменяем местами индексы 1
и J и подставим в него (24.49). Учитывая, что выражения для ех1 и , соответствую-
щие основной моде, приведены в табл. 14.6, получим
(z) г _
--!- = -2iC. a. (z) exp [i(0. - 0, )z] sin(nz). (24.50)
dz---------------------------------------------------------Ji J J
где множитель Сц определен формулой (24.48). Из соотношений (11.22) и (24.49) на-
ходим, что мощность основной моды Рх (z) удовлетворяет уравнению
433
= Iй! (2Х(г)] * 4(V, sin(S3z)Jm [С. л. (z)exp [1(0. - 0, )z]], (24.51)
dz dz Ji J J
поскольку ax (z) 1. Подстановка выражения (24.48) и перегруппировка дает
dP, (z) 1 - exp[(~z+/,)0>]
= 2^.----------т--------LRe IC.C t [exp [itfj — Я - 0, ) z] —
dz
'’j
- exp [i(/3j + £2 - /3, ) z ] ]} ,
где символ Rc означает действительную часть. Если предположить, что неоднородность
достаточно длинная, то экспоненциальной зависимостью от L можно пренебречь, т. е.
2А > > 1/0?- Условие резонанса (24.46) показывает, что первый член внутри фигурных
скобок равен единице, а второй представляет собой осциллирующую функцию с пе-
риодом, вдвое меньшим пространственного периода неоднородности. Учитывая, что
L >> 7т/Г2, усредним правую часть (24.51) по периоду и получим выражение для коэф-
фициента ослабления основной моды
(24.52)
(z) 2
(24.53)
Эквивалентность с методами теории антенн и корректирующего множителя. Если /-я
вытекающая мода наводится сразу же за частотой отсечки (И < И ), выражение для ко-
эффициента затухания (24.53) совпадает с соответствующим выражением, полученным
в рамках приближения свободного пространства с учетом корректирующего множителя
для профиля показателя преломления световода. В случае осевого источника из выра-
жений (22.15) и (21.38) при подстановке г0 = 0 видно, что коэффициент затухания по
аналогии с (22.20) может быть выражен через параметры основной и вытекающей мод
8Р Р ' И/о (£Zj. L?)
Подставляя выражения для И'о (ф|, (?2) (22.176), из соотношения (24.9) получаем
cos0z = 1, поскольку вблизи частоты отсечки /3j ~кпсу Из формул (22.176) и (24.31)
с очевидностью следует, что Wo (f/j, (/) пропорциональна функции G (£/J), которая мо-
жет быть вычислена с помощью выражений (24.32) и (24.34). Отсюда
(<2j) I
\н Р
(24.54)
___1&р)2 <2дГ,г f w, Uj
7 Яр р 1 C/j 7(Ц)Л(^)
Первый множитель 1 /£Л выражается с помощью (24.35), а остальные — с помощью со-
отношений tTjfTj = = -pVfi\l (2Д)1/2. Если в характеристическом урав-
нении (24.30) Uи Q аппроксимировать величинами U* и Cj соответственно, т. е. в фор-
муле (24.31) G (tTj) « 0, то выражение (24.55) принимает вид
= д
Л- p v J, ({/,)J, (t/f)
J
При выводегв формулу (24.53) подставлено выражение (24.48) для и Cjp в кото-
ром U? « СЛ. Коэффициент нормировки определяется формулой (24.49), а - из
табл. 14.3. Условие С(С^) = 0 позволило выразить функции Ганкеля через функции
Бесселя. Следует напомнить, что такой подход справедлив только для излучения выте-
кающей моды, направленной под углом, определяемым соотношением (24.9).
И3
(24.55)
(24.56)
434
ГЛАВА 25. МОДЫ ИЗЛУЧЕНИЯ
Полные электромагнитные поля оптических волноводов могут быть пред-
ставлены в виде суммы двух составляющих. Первая составляющая, которая
может быть записана в виде суммы полей направляемых мод, описывает
пространственно-установившееся состояние, при этом мощность передается
непоглощающим волноводом на неограниченное расстояние. Вторая состав-
ляющая - поле излучения, описывающее пространственно-неустановившее-
ся состояние. В гл. 24 мы рассмотрели свойства полей вытекающих мод, ко-
торые являются частью полного поля излучения и играют значительную роль
при описании поля излучения вблизи или внутри сердцевины световода, если
источник излучения находится достаточно далеко. В таких случаях, представ-
ляющих наибольший практический интерес, для описания поля излучения
часто бывает достаточным знать лишь поля вытекающих мод. Оставшаяся
часть поля излучения, как это следует из формулы (24.1), включается в по-
ле пространственной волны, и, если источник излучения находится достаточ-
но далеко, долю этого поля удобно определять методами, описанными в сле-
дующей главе. В общем случае, однако, проще вычислять сразу полное поле
излучения, особенно если мощность вытекающих мод составляет малую
часть полной мощности поля излучения в сердцевине световода.
Решить уравнения Максвелла для полного поля излучения в общем случае
можно двумя методами. Метод функций Грина, рассматриваемый в гл. 34,
применялся в гл. 21 и 23 для нахождения амплитуды дальнего поля и расчета
мощности излучения. Второй метод описывает поле излучения с помощью
мод излучения подобно тому, как направляемая часть поля описывается на-
правляемыми модами. Каждый метод имеет свои достоинства и недостатки
и его выбор диктуется конкретной задачей. Так, метод мод удобно использо-
вать для определения амплитуды поля излучения в любой точке волновода,
а метод функций Грина для задач, в которых необходимо определить ампли-
туду излучения в дальнем поле.
Эта глава посвящена описанию полного поля излучения волновода с помо-
щью мод излучения. Вначале установим общие свойства мод излучения про-
извольных волноводов, а затем аналогично тому, как это было проделано в
гл. 13, рассмотрим моды излучения слабонаправляющих волноводов. В кон-
це главы будет приведен ряд примеров использования мод излучения в каче-
стве дополнения к решениям, полученным методом функций Грина в преды-
дущих разделах.
ОБЩИЕ СВОЙСТВА
Моды излучения подобно направляемым модам обладают почти всеми общи-
ми свойствами мод, рассмотренными в гл. 4. Как будет показано ниже, ос-
новное различие между направляемыми модами и модами излучения заклю-
чается в том, что для последних характеристического уравнения не существу-
ет вследствие смягчейия граничных условий, требующих исчезновения поля
при г Более того, на больших расстояниях от оси волновода поля мод
излучения имеют осциллирующий характер и не затухают, как поля направ-
ляемых мод [1,2].
4 35
25.1. Представление полей мод
Векторы электрического поля Ej и магнитного поля Hj отдельной моды излу-
чения являются решениями уравнений Максвелла для среды без источников.
Вследствие цилиндрической симметрии, или трансляционной инвариантно-
сти волновода, поля мод излучения можно записать в том же виде (11.6) , что
и поля направляемых мод, однако постоянная распространения (3 уже не яв-
ляется величиной, принимающей дискретные значения. Таким образом,
Ej(x,^, z) =ej(x,y)exp(iPz) = [e^x,/) + ezj(x, j^)z]exp(i/3z); (25.1a)
Hj(x,^, z) = hj(x,^)exp(i/3z) = [hjt(x,j) + hzj (x, j^)z] exp(i(3z), (25.16)
где j = 1, 2, . . . , °°, индексы t и z обозначают поперечную и продольную со-
ставляющие, z - единичный вектор, параллельный оси волновода. Если учесть
неявную временную зависимость ехр(—icor), то выражения (25.1) описыва-
ют вперед-распространяющиеся моды, поскольку по предположению 0 > 0.
Соответствующие выражения для полей назад-распространяющихся мод E_j
и H_j могут быть получены с помощью соотношения (11.7) . Отметим также,
что в непоглошающих волноводах для мод излучения справедливо правило
из разд. 11.3. Однако если выбрать поперечные составляющие поля и htj
как вещественные функции, то это приведет к неоправданному усложнению
описания свойств полей мод. Поэтому для удобства будем считать и
комплексными величинами.
25.2. Постоянная распространения
В разд. 11.17 мы установили, что постоянные распространения j3j направляе-
мых мод можно найти из характеристического уравнения, и для волноводов
с оболочкой они образуют набор дискретных величин, значения которых ле-
жат в интервале, определяемом выражением (11.46). Постоянные распро-
странения (3 мод излучения могут принимать непрерывные значения внутри
некоторого интервала. Если постоянная распространения моды — веществен-
ная и удовлетворяющая условию 0 < /3 < величина, то такая мода назы-
вается распространяющейся модой излучения, а если вещественная и мнимая
части постоянной распространения 3 удовлетворяют соответственно услови-
ям (Зт = 0 и 0 < З1 < °°, то такая мода называется затухающей. Распространя-
ющиеся моды переносят мощность, а затухающие описывают накопленную
энергию вблизи источника возбуждения. В табл. 25.1 приведены области зна-
чений постоянных распространения и параметры различных типов мод.
25.3. Разложение поля излучения
Дискретность набора постоянных распространения направляемых мод озна-
чает, что поля волновода в пространственно-установившемся состоянии мож-
но представить в виде конечной суммы (11.2), где суммирование проводит-
ся по всем направляемым модам. В противоположность этому каждая мода
излучения и каждая затухающая мода могут принимать любое значение из
диапазона значений постоянных распространения, приведенных в табл. 25.1,
и поэтому для описания поля необходимо проводить интегрирование по всем
значениям 3- Однако, как и в случае направляемых мод, при вычислении пол-
ного поля излучения в выражении (25.1) необходимо провести суммирова-
436
Таблица 25.1. Области значений постоянной распространения /3 и параметров
мод Uи Q для волоконных световодов
р и Q
Направляемые моды кПс1 < Pj «= кПт O^Uj< V Q’j = 0; е; > о
Моды излучения 0<:р< кпс1 V<U^kpnm -X V/ V о
Затухающие моды Р’ = 0; Р' > 0 крпт <U < ос kpnd <Q<x
Примечание. Индексы г и i обозначают вещественную и мнимую части величины,
а индекс / соответствует дискретным направляемым модам.
ние по всем индексам /, т. е. по всем поперечным полям отдельных мод. По-
этому вместо того чтобы использовать в качестве непрерывной переменной
постоянную распространения /3, которая является вещественной величиной
для мод излучения и мнимой для затухающих мод, воспользуемся парамет-
ром моды Q, определенным ниже, что значительно упрощает запись. Тогда
р является положительным корнем обратного соотношения
Q = p(k2n2d -02)1/2; /3 = 0(2) = (k2n2d-Q2/p2y/2.
(25.2)
Таким образом, Q всегда является вещественной и положительной величиной
как для мод излучения, так и затухающих мод.
Полное поле излучения можно теперь записать в виде
Erad (х, у, z) = S Г a. (Q) е (х, у, Q) exp [i /3 (2) z ] dQ;
i о J J
Hrad (x> Л z) = S Г«. (2)h (x, y, Q)exp [i0 (Q)z ]dQ,
7 о J J
(25.3а)
(25.36)
т. е. представить выражениями для вперед-распространяющихся мод излуче-
ния и соответствующих затухающих мод и аналогичными выражениями для
назад-распространяющихся мод излучения и соответствующих затухающих
мод, в которых j и Р заменены на -/ и ~р. В формулах (25.3) (Q) — ампли-
туда моды; для мод излучения интегрирование проводится по области 0 <
< Q < крп& а для затухающих мод - по области крпсХ < 2 < °°.
25.4. Ортогональность и нормировка
В разд. 11.4 было показано, что каждая направляемая мода ортогональна лю-
бой другой направляемой моде и всем модам излучения. Свойства ортого-
нальности мод излучения рассмотрены в разд. 31.3, из которого следует, что
в непоглощающем волноводе /-я и к-я вперед-распространяющиеся моды из-
лучения описываются соотношениями
437
J e (2) x h* ((?')• zd4 = J e*(g') x h.(2) ’ idA = 0,
A J к Д K J
oo oo
(25.4)
справедливыми для всех Q при j =£ к и Q^Q' при j = к, где А ж — бесконечно
большая площадь поперечного сечения, z — единичный вектор, параллельный
оси волновода, а звездочка означает комплексное сопряжение. Подчеркнем,
что условие ортогональности выполняется в случае j = к, если величины Q и
разные. Другими словами, мода излучения ортогональна сама по себе при
разных постоянных распространения.
Коэффициент нормировки TVj (2) /-й вперед-распространяющейся моды из-
лучения волновода без поглощения равен
1 f е-(2) х h*(2') • idA =N.(Q)b(Q- Q'),
2 л J J J
Л oo
(25.5)
где 6 — дельта-функция Дирака. Поскольку при Q-Q' интеграл нормировки
принимает бесконечное значение, то для определения TVj интеграл факторизу-
ется с помощью определения 5-функции, например выражением (37.108).
В следующем разделе показана физическая нереализуемость такого коэффи-
циента нормировки.
Ортонормированные моды излучения. Поля е^ и hj ортонормиро^ванных
мод излучения можно выразить через коэффициент нормировки Aj (£) так
же, как и поля направляемых мод (11.15). Любые две моды,/-я и к-я, удов-
летворяют условию ортонормировки
1 J е.(2) xh*(2) -zaL4 = l J ё*(2') xh:(2) ’^ = 3(2-2')^,
k 2 л», k J
(25.6)
где 5jk — символ Кронекера, т. e. 5jk = 1, если j = к, и 5jk = 0 в остальных слу-
чаях.
Назад-распространяющиеся моды излучения. Как и в случае направляемых
мод (см. разд. 11.4), назад-распространяющиеся моды излучения подчиняют-
ся соотношениям ортогональности, нормировки и ортонормировки, получае-
мым подстановкой выражения (25.4) в (25.6) с учетом формулы (11.7).
25.5. Мощность поля излучения
Полный, усредненный по времени поток мощности поля излучения Prad, пе-
реносимый параллельно оси волновода, может быть получен из выражения
(11.25):
Prad = I Re(J Erad X Н* d • idA), (25.7)
Л. Q0
где Re означает вещественную часть величины. Подставляя сюда выраже-
ния для полей (25.3) и меняя порядок суммирования и интегрирования,
получаем
438
P. =4ReH dQ? dQ'x(Q, Q') J e (g) x h*(2') ’ zdA; (25.8a)
rdd 2 о о 1 k
X (Q, Q') = exp i [0 (Q) - /3 (0') ] z s S a (0) a* (Q'). (25.86)
/ к J K
Соотношения ортогональности (25.4) и нормировки (25.5) приводят к
выражению
Р J \aAQWNAQ)dQ
d j о J J
(25.9)
для мощности мод, распространяющихся в положительном направлении оси
z волновода без поглощения. Сюда не входит мощность затухающих мод, ко-
торые по определению не распространяются.
Правая часть выражения (25.9) не зависит от z, и поэтому значение Prad
постоянно вдоль волновода. Такой же вывод справедлив и для полной
мощности направляемых модРы, определяемой формулой (11.27). Следо-
вательно, мощность мод излучения может быть определена по аналогии с
мощностью направляемых мод. Отдельная мода излучения, подобно направ-
ляемой моде, переносит энергию параллельно оси волновода, а полная мощ-
ность поля излучения равна сумме мощностей всех мод излучения, как это
и утверждается выражением (25.9) . Однако вследствие интерференции полей
различных мод излучения, включая одну и ту же моду с разными значениями
постоянной распространения, непрерывный спектр мод, выражаемый инте-
гралом (25.9), приводит к ожидаемому поведению полного поля излучения,
т. е. к излучению мощности из световода. Очевидно, что отдельная мода из-
лучения не имеет физического смысла и является всего лишь удобным поня-
тием при математическом описании процессов излучения.
25.6. Возбуждение мод излучения
Амплитуды мод излучения (2), возбужденных данным источником излуче-
ния, который расположен либо вблизи входного торца волновода, либо вну-
три волновода, находят аналогично амплитудам направляемых мод .
Возбуждение внешним источником. Пусть на входной торец волновода па-
дает электромагнитная волна, так что при z = 0 векторы поперечных полей
равны Et (х, у) и Ht (х, у). Часть этих полей трансформируется в поля излуче-
ния (20.1), которые можно выразить через поля мод излучения и затухаю-
щих мод (25.3) в сечении z = 0. Таким образом,
Etr(x, у) =S M(6)etj(e)Je;
(25.10)
Htt(x,jO -2 fa (Q)h (Q)dQ.
/ о J y
Выполняя векторное умножение первого уравнения на h*. (Q ), а второго на
etj (Q ) и используя условие ортогональности (25.4), получаем соотношения,
аналогичные (20.2) :
439
“И® =
(25.11a)
(25.116)
в которые входит коэффициент нормировки (25.5) .
Источники внутри волновода. Если источники тока с плотностью J нахо-
дятся внутри волновода, то поле излучения определяется второй суммой в
формуле (31.12), поскольку внутри области, где расположены источники то-
ка, амплитуды мод излучения и затухающих мод зависят от координаты z.
Вне этой области амплитуды мод - величины постоянные. Поэтому из фор-
мулы (31.37)
a±j(2) = * 4^W М0) + ezj(G) z]*Jexp [+ (25.12)
где Y — объем волновода между плоскостями z -zx hz = z2. Верхний и ниж-
ний знаки относятся к вперед- и назад-распространяющимся модам при z >
>z2 nz <zx соответственно, во всех остальных случаяха±] (2) = 0.
МОДЫ ИЗЛУЧЕНИЯ В ПРИБЛИЖЕНИИ СВОБОДНОГО ПРОСТРАНСТВА
Чтобы применять моды излучения для описания явлений в оптических вол-
новодах, необходимо показать, как находить их поля и коэффициент норми-
ровки из уравнении Максвелла для определенного волновода. Задача облег-
чается, если вначале рассмотреть моды свободного пространства, т. е. моды
излучения однородной неограниченной среды с показателем преломления
пej [ 1 ] - Моды в приближении свободного пространства имеют более простую
структуру, чем моды излучения волновода, и в то же время обладают всеми
общими свойствами, рассмотренными выше. Они полностью описывают из-
лучение источника в ’’свободном пространстве” и представляют собой аль-
тернативный способ описания по отношению к методам теории антенн, рас-
смотренным в гл. 21. К тому же моды излучения волновода переходят в мо-
ды ’’свободного пространства”, если показатель преломления не изменяется
в поперечном сечении волновода.
Структура мод. Чтобы обеспечить цилиндрическую симметрию мод ’’сво-
бодного пространства”, будем рассматривать среду как волновод с однород-
ной сердцевиной с поперечным сечением бесконечных размеров и показате-
лем преломления ис1. Самыми элементарными модами такой структуры яв-
ляются ТЕ- и ТМ-моды, продольные поля которых удовлетворяют соответ-
ственно условиям = 0 и /Л = 0, где индекс f обозначает ’’свободное про-
странство”. Для того чтобы сформировать остальные составляющие поля,
необходимо вспомнить (как было показано в разд. 11.15), что неисчезающие
продольные составляющие поля являются решениями уравнения (11.45)
в любой точке однородной среды. Поэтому
+e2)ftf. =0; (p2V’ + e2)4j=0 (25.13)
соответственно для ТЕ- и ТМ-мод, где параметр Q определен в табл. I. Чтобы
44 0
получить выражения для поперечных составляющих поля, необходимо под-
ставить ограниченные решения этого уравнения в формулы (30.6).
25.7. Пример. Решение в цилиндрических координатах
Чтобы связать моды ’’свободного пространства” с модами излучения круглых светово-
дов, которые будут рассмотрены ниже, получим выражения для составляющих полей
мод ’’свободного пространства” в цилиндрических координатах (г; <р; и). Ось? ориен-
Таблица 25.2. Моды ’’свободного пространства” в цилиндрической системе ко-
ординат
ТЕ-моды ТМ-моды
e'J 2v
4 гглеюм?) 2v - — J^QR)g^)
J,+1 (QR)f.+ xM + J.-x 1 (V) J,+ i(QR)f,+1(QR)-J.-1(QR)f.-lM
ef Cyj - J,+1 (QR)g,+1 ($»)+J, -1 (QR)g, -1 (y>)
0 2i^-J,(QR)f,(<p) pp
-2 - ^J'AQRKAp) \Mo/ * /p \ 1 /2 2fe) \До/ KVP
/ £0 \1/2 vB / p \ 1 /2 Lm2 -2(-) ^Л(6«)А(Р) \Мо/ P
^-JAQR)gA<P) \До/ kp 0
"j . .М'Ч (! >>0 2wU Iexh • -» к u .-о
r fcos(v</>) f —sin(v^); четные моды /,(¥>) = 1 • / J , v. (sin (v</>) ( cos (нечетные моды
Примечание. Штрих обозначает дифференцирование по аргументу. Параметры
определены в табл. I.
тируем вдоль направления распространения. Оператор определен в табл. 30.1, откуда
следует, что ограниченные решения уравнения (25.13) пропорциональны либо JV(QR) X
X cos(p<p), либо JV(QR) sin(p<p), где Jv - функция Бесселя первого рода, v - положи-
тельное целое число или нуль, R — г/р и р - характерный размер поперечного сечения,
например радиус сердцевины световода со ступенчатым профилем показателя преломле-
ния. Поперечные составляющие поля могут быть найдены из формул (30.9). выражения
441
итя полных полей ТЕ- и ТМ-поляризаций приведены в табл. 25.2, а формула (25.1) опре-
деляет полную пространственную зависимость этих полей. В данном случае удобно, что-
бы е*и ^удовлетворяли условию (11.8), т. е. чтобы, поперечные составляющие были ве-
щественными, а продольные ~ мнимыми величинами.
Коэффициент нормировки. Вывод выражения для коэффициента нормировки, при-
веденного в табл. 25.2, лучше всего проделать на примере. Рассмотрим нечетную ТЕ-мо-
ду с v = 1. Из формулы (37.75) находим, что левую часть (25.5) можно представить в
виде
2яр= А(Л»_) *'2 Г J, (ДО) J, (Q’R)RdR.
К Н-0 о
(25.14)
Нас интересует только случай Q = Q’. Из асимптотических выражений (37.87) для функ-
ций Бесселя с большим аргументом следует сингулярное поведение интеграла. Подста-
новка этих выражений в (25.14) дает
п !ехР П(бЯ ~ Зтт/4) ] + ехр [~i((ZK - Зтг/4) ]} [ ехр [i((27? - Зтт/4) ] +
+ ехр [-i(Q'R - Зтг/4) ] ] dR.
(25.15)
Сингулярность определяют только экспоненциальные члены, в которые входит разность
Q - Q'. Поэтому, пренебрегая остальными членами из формулы (25.5), имеем следую-
щее соотношение:
J exp[i(e-C')7?]d« =М(<2)6(£-Q'),
0 _оо
(25.16)
которое приводит к выражению для коэффициента нормировки в табл. 25.2. Заметим,
что при выводе этого соотношения использовалось одно из эквивалентных представле-
ний 6-функции Дирака (37.108).
СТРУКТУРА МОД ИЗЛУЧЕНИЯ
Если показатель преломления в поперечном сечении волновода не изменяет-
ся, т. е. если п = ис1 в любой точке или V = 0, то моды излучения волновода
должны становиться модами ’’свободного пространства”. Поэтому один из
подходов к формированию мод излучения заключается в модификации мод
’’свободного пространства” и представлении полей мод излучения в виде
суммы полей ’’свободного пространства” и полей рассеяния, обусловленных
профилем показателя преломления волновода [1]
е = ef+ es; h. = hf+ hs,
J J J J J J
(25.17a)
где индексы f и s обозначают соответственно поле ’’свободного пространства”
и поле рассеяния. Такое разложение является точным и дает возможность
сформировать моды излучения интуитивно. Кроме того, такая структура
мод обеспечивает те же условия ортогональности и нормировки, что и для
мод ’’свободного пространства” [1]. Таким образом,
442
1 J e.(0 x h*((2') • idA =1 J ef(G) x hf(£)* • idA =N. (2)5 (Q - 2') •
2 j J J 2 д J J J
oo ^oo
(25.176)
В следующем разделе этот вывод будет подтвержден на примере световода
со ступенчатым профилем показателя преломления. Доказательство в общем
виде для произвольной структуры приведено в [3]. Моды излучения, соот-
ветствующие ТЕ-модам ’’свободного пространства” (е?. = 0), называются
ITE-модами, а моды, соответствующие ТМ-модам ’’свободного пространства”
(/Л = 0), - ITM-модами* [1].
Аналитические решения. Выражения для полей мод излучения являются
решениями тех же уравнений, которым удовлетворяют и поля направляемых
мод, поэтому всякий раз, когда существуют точные решения для направ-
ляемых мод, существуют и соответствующие решения для мод излучения.
В гл. 12 было показано, что для волноводов с произвольной формой профи-
ля показателя преломления точное аналитическое решение уравнений Макс-
велла может быть получено лишь для нескольких известных форм профиля.
И даже в этих случаях выражения для полей мод излучения обычно имеют
значительно более сложный вид, чем для полей направляемых мод. В каче-
стве примера в следующем разделе мы рассмотрим волоконный световод со
ступенчатым профилем показателя преломления. Поля мод излучения для
планарного волновода со ступенчатым профилем могут быть получены ана-
логичным образом.
Разложение на плоские волны. Полная пространственная зависимость по-
ля каждой моды излучения определяется выражением (25.1), а значения по-
стоянных распространения лежат в интервале 0 < j3 < кп&. Для данного зна-
чения (3 поля мод могут рассматриваться как разложение в ряд Фурье полей
семейства плоских волн, распространяющихся под углом 0z к оси волново-
да. В случае оболочки с постоянным показателем преломления угол в7 свя-
зан с 0 соотношением
0 = £лс1 cos (25.18)
и, следовательно, 6Z удовлетворяет условию 0 < 0Z < тг/2.
25.8. Пример. Волоконный световод со ступенчатым профилем показателя
преломления
Поля мод излучения свсн >да со ступенчатым профилем показателя преломления фор-
мируются так же, как и поди направляемых мод в разд. 12.8. Вне границы между серд-
цевиной и оболочкой продольные составляющие поля являются решениями уравнений
(p2V2 + ^)ezj = 0; (p2V2 + [/’)/!zj = 0; 0<Я<1, (25.19а)
(p2V2 + e2)ezj = 0; (p2V2 + e2)/»ZJ = 0; 1 < R < (25.196)
где p — радиус сердцевины, U и Q определены в табл. I, а оператор V* - в табл. 30.1. Ре-
шения ezj и /zzj должны удовлетворять разложению (25.17). Этому условию удовлетво-
* Хотя в отечественной литературе обозначения ITE и ITM не приняты, мы сохранили
эти обозначения, введенные и определенные авторами. — Прим. ред.
443
ряют выражения в табл. 25.3, где b , csv и d„ являются постоянными величинами, ко-
торые необходимо определить: ud„ - константы ’’свободного пространства”, указан-
ные в табл. 25.3. Функция Ганкеля первого рода при R -> °° обеспечивает соответ-
ствие поля рассеяния удаляющейся от волновода волне.
Поперечные составляющие поля связаны с продольными соотношениями (30.9), а
условие непрерывности величин ezj, 7zzj, и h на границе сердцевины с оболочкой
позволяет определить постоянные. Приведенные в табл. 25.3 выражения для ITE- и
ITM-мод получены с помощью Вронскиана (37-77). По причинам, изложенным выше,
условия ортогональности и коэффициент нормировки каждой моды излучения идентич-
ны соответствующим выражениям в табл. 25.2 для мод ’’свободного пространства”.
Отметим, что коэффициент нормировки для TVj (Q) можно получить и непосредственно
из выражений для полей мод излучения методом, изложенным в разд. 25.7.
Качественный вид полей. Моды излучения с (3 < < кп^, т. е. при 0Z « я/2, можно пред-
ставить в виде плоских волн, падающих почти перпендикулярно к границе сердцевины с
оболочкой, так что сердцевина световода оказывает на эти волны слабое влияние. Поэ-
тому моды излучения с (3 < < кп i приближенно можно рассматривать как моды сво-
бодного пространства с ej ~ е и hj h., причем неявные условия, рассмотренные в
разд. 25.11, помогают облеппт/ь выполнение этого предельного перехода. В другом слу-
чае, когда /3 « кпсу, т. е. 0z « 0, на плоские волны, формирующие моды излучения, суще-
ственное влияние оказывает сердцевина световода.
СЛАБОНАПРАВЛЯЮЩИЕ ВОЛНОВОДЫ
В гл. 13 мы показали, как из решения скалярного волнового уравнения по-
лучить выражения для полей направляемых мод слабонаправляющих волно-
водов. Почти такой же способ применим и к полям мод излучения [4]. Од-
нако следует иметь в виду, что если направляемые моды являются почти
ТЕМ-волнами, поскольку Р ъ knCQ кпф то моды излучения таковыми не
являются, так как Р может принимать любое значение внутри интервала 0 <
< 0 < Лис1.
25.9. Пространственная зависимость полей
Рассмотрение свойств направляемых мод, проведенное в разд. 13.3, полно-
стью применимо и к модам излучения слабонаправляющих волноводов. Не-
обходимо только учитывать, что поля мод уже больше не являются преиму-
щественно перпендикулярными оси волновода. Однако декартовы составля-
ющие поперечного электрического поля (13.7) все-таки являются решения-
ми скалярного волнового уравнения. Таким образом, если под понимать
или evi, то
уз
(25.20)
[V^ + к2п2(х,у) -р2 (0]Ф = О,
где р (Q) в данном случае является непрерывной постоянной распростране-
ния мод излучения. Решение для может быть получено параллельно с ре-
шением для мод излучения произвольных волноводов. По аналогии с выра-
жением (25.17а) представим в виде суммы поля ’’свободного простран-
ства” и поля рассеяния
ф. = Ч^+Ф5, (25.21)
444
Таблица 25.3. Моды излучения волоконного световода со ступенчатым профи-
лем показателя преломления
Сердцевина Оболочка
ezj
h4
r (cos(v0) v f — sin(vq>); четные моды /.(*>) = i • , ,; . (Sin(v<^) ( COS(v^), нечетные моды
ITE-моды ITM-моды
av _4 P v Г2 1 _4 J F> nn^fipQJAU)H">(Q)M,
n kn^ kp U2Q3
Ь. _ i (* Y12 1 G> nci f €o Y/2 v И2 1
n\pj Qkp n nt UJ kp U2Q3
cfv 0 fiP
cs. _ 1JL v v2 1 _2.o_ J,(Q) A,
nkn^kpU2Q3 {H^(Q)}2M,
d\ \Яо/ Pk 0
d* 2i(Eo\lliQ MQ) B, \pj pk н?Ч0 м. 4 n2 /£0 V/2 v V2 1 pkV2Q3{H^(Q)}2My
NJ 1 1 X T? II V о о 2np2 /s0 V12 knd J 1; v>0 Q \Po) P X(2; v = 0
_ J'Jl/) _n2d H">(Q) ” UJ,(U) QH"4Qy ' UJ,(U) nlQH">(Q)
л - U Лс1 Fy . D _ Vf _ Bi 6* ' ’ n nL Q2JAQ)W"(Q)' M' n Q2JAQ)H<"(Q)
/ vB W V \* M. = hr4 7777 -F.G, \fc«co/ \UQJ
Примечание. Поперечные составляющие поля могут быть вычислены по форму-
лам (30.9) . Штрих обозначает дифференцирование по аргументу. Параметры опре-
делены в табл. I.
445
где — решение уравнения (25.20) при п = ис1, причем оно выражено через
параметр Q (25.2):
(p2V* + 22)Ф*'=0.
(25.22)
f f*
Таким образом, 4^ сводится к Ф^ при Д = 0 или V = 0. Выражения для Ф- и
Фj получены в разд. 25.11 для световода со ступенчатым профилем показа-
теля преломления.
25.10. Векторные свойства полей мод излучения
В гл. 13 для определения направления вектора etj и поправки 6j3j к постоян-
ной распространения скалярного приближения мы приняли во внимание по-
ляризационные свойства волновода. Однако поскольку постоянная распро-
странения 0 мод излучения может принимать любое значение в интервале
0 < Р < &ис1, такая непрерывная переменная величина не зависит от поляриза-
ционных свойств волновода и для полного описания последних необходимы
поправки к eXj и eyj более высоких порядков. Напомним, что поляризацион-
ные свойства направляемых мод начинают проявляться лишь на больших рас-
стояниях вдоль оси световода. Поэтому в случае мод излучения вследствие
того, что мощность этих мод вблизи оси волновода быстро уменьшается с
увеличением его длины, поляризационные эффекты малы. По этим причинам
в дальнейшем любым влиянием поляризационных свойств волновода на мо-
ды излучения будем пренебрегать. Соответствующая комбинация exj и eyj,
формирующая поле моды должна удовлетворять только условиям орто-
гональности полей мод излучения.
Соотношения ортогональности и нормировки. В рамках приближения сла-
бонаправляющего волновода остальные составляющие полей мод излучения
е} и /2j можно выразить через вектор etj, если в соотношении (30.5) опустить
все члены, включающие Vt In п2:
ezj р * etj’ ^zj p Vt htj, (25.23a)
где z - единичный вектор, параллельный оси волновода; векторные операто-
ры определены в табл. 30.1, а остальные параметры — в табл. I. Таким обра-
зом, в отличие от соответствующего поля направляемых мод поперечное маг-
нитное поле мод излучения не является решением скалярного волнового
уравнения. С использованием выражения (25.23) в разд. 32.11 показано, что
соотношения ортогональности (25.4) и нормировки (25.5) могут быть све-
дены соответственно к следующим:
446
J е (2) ’ е* (Q') dA =0; Q Ф Q', если j - к;
А„ J к
1 ф j ((?) . е* (Q’}dA = N ((?) § (е _ с/)
2 МО /С a J J J
оо
(25.24а)
(25.246)
Отметим, что в эти выражения входит полное электрическое поле, в то вре-
мя как в соответствующие выражения для направляемых мод (33.56) и
(33.6) входит только его поперечная составляющая.
Соотношения ортогональности и нормировки для мод ’’свободного про-
странства”. Комбинация е^ и е •, удовлетворяющая соотношению (25.24а),
не является однозначной. Однако если структура удовлетворяет разложе-
нию (25.21), то соотношения ортогональности и нормировки для мод ’’сво-
бодного пространства” автоматически обеспечивают соответствующие соот-
ношения для мод излучения [4]. Это подтверждается приведенным ниже
примером. Поэтому проще и значительно удобней сформировать etj таким
образом, чтобы поле в ’’свободном пространстве” было поляризовано и вы-
полнялось либо равенство ф = 0, либо равенство Zzzj = 0, т. е. чтобы это поле
можно было представить через поля либо ITE-, либо ITM-мод. Поскольку
каждая декартова составляющая полей точно удовлетворяет скалярному
волновому уравнению в ’’свободном пространстве”, то поля в табл. 25.2,
сформированные из продольных составляющих, могут быть получены с по-
мощью уравнения (25.22) и из поперечных составляющих электрического
поля. Другими словами, переходя в табл. 25.2 от радиальных и азимуталь-
ных составляющих вектора к декартовым, мы непосредственно определя-
ем комбинацию exj и eyj' Этот метод продемонстрирован ниже.
25.11. Пример. Волоконный световод со ступенчатым профилем показателя
преломления
Чтобы получить выражения для мод излучения слабонаправляющего волновода со сту-
пенчатым профилем и показателями преломления сердцевины и оболочки ”со и иср
начнем с решения уравнения (25.22) для свободного пространства. Если с помощью
табл. 30.1 оператор VJ выразить в полярных координатах, то только четное и нечетное
решения
ф[е = J{(QR) cos(Z^) ; Ф*° ~ J^QR) sin(Z^) (25.25)
являются повсюду ограниченными. Здесь - функция Бесселя первого рода, R = г/р,
р - радиус сердцевины, I - положительное целое число или нуль. Следующим шагом ре-
шения задачи является рассмотрение в соответствии с разложением (25.12) поля рассея-
ния Чд- Поскольку при г -> <» функция Чд должна представлять удаляющуюся от светово-
да волну, а функция Чд = Ф. + Ф^ должна быть ограничена при г = 0, то из уравнения
(25.20) находим, что этим требованиям удовлетворяют следующие функции:
Ф® = P^(UR) cos^); 0 <R < 1; (25.26а)
Ф® = [/((£•«) + q^^(QR) ] cos(Zi/>); 1 <R < (25.266)
а также подобные им выражения для Ф°, в которых cos(Z^) заменен на sin(Z^). В этих
формулах - функция Ганкеля первого рода, а параметр Uопределен в табл. I. Так
как Чд является решением скалярного волнового уравнения, то Ф®и б)Ф^/<)/? непрерыв-
447
ны при R — 1. Отсюда можно определить постоянные
учетом вронскиана (37.77) приведены в табл. 25.4.
и q^, выражения для которых с
Таблица 25.4. Моды излучения слабонаправляющего волновода со ступенча-
тым профилем показателя преломления
Tf = PiJi(UR) cos = {Л(ел)+^нрчел)}со8(М; Т?= Tftan (/</>) - 8 V/ V ОС ftJ V/ V/ о -1
л
1ТЕ-моды 1ТМ-моды
et/ = (Tf+, + , )х + (Т?+,, )у (четные) е,( = (44+, + 44-, )х - (Tf+, - 44-, )у (нечетные) е., = (4>f +, - 44., )х + (44+, + 44., )у (четные) е,, = (44-+, - 44-1 - (4»f+, + 44-, )у (нечетные)
ь _ (^®Y’Z2-2x •[«. -V /и -е, Д \До/ К 1 Р )
^2/ = д =
II to X 77^? II V о о 2’tpYe°Y/2kn'1 J1; />0 ' Q U/ Д (2; / = 0
Примечание. Параметры определены в табл. I, векторные операторы — в табл. 30.1.
Если ех| и являются декартовыми составляющими вектора etj, то, как было
объяснено в предыдущем разделе, линейная комбинация и , которая определяет
вид exi или еу|, получена сравнением с х- и ^-составляющими поля etj ’’свободного про-
странства” из табл. 25.2. Используя соотношение (37.49) для функций Бесселя, получа-
ем комбинации для четных и нечетных ITE- и ITM-мод, приведенные в табл. 25.4. Этот
метод формирования полей мод обеспечивает такую же нормировку, как и в случае мод
’’свободного пространства” и точных мод излучения из табл. 25.3.
Иногда полезно знать нормировку скалярных мод излучения, которая обсуждается
в разд. 33.7. Подставляя выражения из табл. 25.4 в формулу (33.31) и учитывая сообра-
жения, изложенные при выводе выражения для коэффициента нормировки в табл. 25.2,
получаем следующую формулу для искомой величины:
448
FAQ) = I 1<РЛ4 = J |ф°р<£4 . (25.26b)
I J I A L Q
Z1OO -^oo
Подчеркнем, что /^(S) и коэффициент нормировки Л^в табл. 25.4 для мод излучения
слабо направляющих световодов являются разными величинами. В этой главе рассматри-
вается последняя величина.
Неявные условия. Поля в табл. 25.4 являются предельным случаем точных подей в
приближении слабонаправляющего волновода из табл. 25.2. В этом пределе световод-
ный параметр V фиксируется, а —ис1. Однако чтобы корректно сформировать поля
слабонаправляющего световода, должны быть выполнены некоторые неявные условия
[5], а именно одно из следующих условий: либо
0 = кпс^} 0р — °о при А — О, (25.27а)
a Un Q - величины произвольные, либо
U-+°o при Д-0. (25.276)
Во втором случае налагать ограничения на 0 не нужно, так как 0 > 0. При уменьшении
Д и постоянном V второе условие справедливо для большего диапазона значений 0, а
при Д = 0 это условие выполняется для всех значений 0 за исключением 0 == кпсу
ИЗЛУЧЕНИЕ ИСТОЧНИКА В ’’СВОБОДНОМ ПРОСТРАНСТВЕ”
В этой первой серии примеров мы рассмотрим излучение источника в ’’сво-
бодном пространстве”, использовав моды излучения ’’свободного простран-
ства”, и сравним результаты рассмотрения с результатами, полученными ме-
тодами теории антенн в гл. 21.
25.12. Пример. Излучение диполя
Предположим, что диполь длиной d с силой тока I ориентирован вдоль оси х бесконеч-
ной однородной среды с показателем преломления лс| и расположен в начале осей коор-
динат, как изображено на рис. 25.1, а. При — 0 плотность тока диполя можно записать
в виде
= Idb (г - rM) (25.28)
л а а
где 6 — дельта-функция Дирака. Диполь возбуждает моды ’’свободного пространства”,
амплитуду которых можно определить, если выражение (25.28) подставить в формулу
(25.12):
Id 2я
= r’i®’'"' <25Л”
где верхний и нижний знаки относятся к вперед- и назад-распространяющимся модам
в областях z > 0 и z < 0 соответственно, aexj определяется в точке г = 0. Из табл. 25.2
следует, что возбуждаются только ТЕ- и ТМ-моды с индексом р = 1. Полагая для этих
мод / = 1 и / = 2 и учитывая, что при г = 0 ех1 - 1 и ех2 = -1, из выражения (25.29)
получаем
а±1 = ^Id^N, (0 ; а±2 = ± Zd/47V2 (Q) (25.30)
для четырех возбужденных мод.
Поля диполя. Если формулы (25.30) и выражения для полей из табл. 25.2 подста-
вить в формулу (25.3), то точные выражения для полей диполя могут быть получены
интегрированием по двум модам при z > 0 и z < 0. Асимптотическая оценка этих инте-
гралов при г — «j и переход от цилиндрической системы координат к сферической.при-
водят к выражениям (21.23) и (21.24а) для дальних полей диполя.
Мощность излучения. Полная мощность излучения диполя может быть найдена, если
выражение (25.30) и коэффициент нормировки из табл. 25.2 подставить в формулу
15 Зак 37
449
Рис. 25.1. Диполь дли-
ной d с силой тока I,
расположенный в нача-
ле координат и парал-
лельный оси х (а) ; по-
перечное сечение труб-
чатого источника (на-
правление тока парал-
лельно оси х) (б)
(25.9). Принимая во внимание вперед- и назад-распространяющиеся моды, имеем
р _ |/£/|г *Р”С1Г к
rad = 1^7(J + К,
(25.31)
Если положить Q — крп^ sin 0Z, /3 = кпс^ cos 0Z, то это выражение сведется к формуле
(21.246), полученной методами теории антенн.
25.13. Пример. Трубчатый источник излучения
Рассмотрим трубчатый источник, описанный в разд. 21.6, длиной 2L и радиусом г0, по
которому в направлении оси х течет ток с плотностью
Jx = 5 (г - r0)cos(/<p) sin (£2z) exp (iCz/2nr0) ,
(25.32)
где / - положительное целое число или нуль, а трубчатый источник ориентирован так,
как показано на рис. 25.1, б, и поэтому в формуле (21.13) <р0 = 0. Предположим, что
такой источник расположен в однородной среде с показателем преломления и, та-
ким образом, его поле излучения может быть описано полями мод ’’свободного про-
странства” в соответствии с геометрией на рис. 21.3. Подстановка выражения (25.32)
в формулу (25.12) позволяет найти амплитуды мод
। 2тг L
a±i (0 = + J exj(0c°s(M^ J sin (S2z) exp [i [С + 0 (0 ]z pz. (25.33)
J oroVj W) 0 J _£
где exj определяется в точке г = г0. Из табл. 25.2 следует, что при I > 1 возбуждаются
только четные ТЕ- и ТМ-моды с индексами р = 1+1ир = Z - 1, а при I — 0 - только чет-
ные моды с v — 1. В разд. 21.6 было показано, что результат интегрирования по z в ос-
новном определяется членами с П « |С - 0(0 I- Предположим, что 0(0 ~С - П, т. е.
включим в рассмотрение только вперед-распространяющиеся моды, что эквивалентно
учету только верхних знаков в формуле (25.33) и первого члена в фигурных скобках
формулы (21.15). Из табл. 25.2 следует, что
Кпе] 0(0)
соответственно для ТЕ- и ТМ-мод при / > 2, где
= ig ,Mov,3 sin [С-0(0 -n]Z
16W’hc1 4 C —0(0—fi
(25.34a)
(23.346)
Мощность излучения четырех мод находим подстановкой выражения (25.34) в (25.9):
:_'d'
О 1 [С-0(0-п]2 1£ис1 0(0
P =------------(—)1/3
rad 64яр2ис1 eo
(2'5.35)
450
Чтобы оценить интеграл, положим Q — крпс\ sin 0Z и (3 = cos 0Z и, приняв во внима-
ние соображения, изложенные в разд. 21.10, согласно которым основная часть мощно-
сти излучается под углом 0Z « 0О (21.30), получим
х .
kf LL ’ Я1Г1 Y
Prad ,П(1 + cos’®o)^(^o"ci sin е0) J —j-dx, (21.36)
где x = [С - 0 (Q) - ; x+ = (C - и x_ = (С - - SI)L. Используя резуль-
тат интегрирования по х выражения (21.31), приходим к выводу, что при I > 2 форму-
ла (25.36) сводится к выражению для дальнего поля антенны (21.33а). Аналогичным
образом можно получить выражения и для случаев I — 0 и I = 1.
ИЗЛУЧЕНИЕ ИСТОЧНИКОВ, НАХОДЯЩИХСЯ ВНУТРИ СВЕТОВОДОВ
Рассмотрим теперь, как поля излучения элементарного диполя и трубчатого
источника модифицируются в присутствии световода. Чтобы можно было
сравнить результаты этого рассмотрения с результатами, полученными с
учетом корректирующего множителя из разд. 21.12, будем предполагать све-
товод слабонаправляющим.
25.14. Пример. Диполь внутри световода со ступенчатым профилем показате-
ля преломления
Определим поправку к полю излучения диполя, рассмотренного в разд. 25.12, в случае,
когда он расположен на оси слабонаправляющего световода со ступенчатым профилем
показателя преломления. Если ось z на рис. 25.1, а совпадает с осью световода, то, пов-
торив весь анализ, проведенный в разд. 25.12, с учетом того, что моды ’’свободного про-
странства” необходимо заменить модами излучения слабонаправляющего световода, по-
лучим, что амплитуды полей на оси ех1 и ех2, а следовательно, и амплитуды мод, опре-
деляемые выражением (25.30), умножаются на величину р0, определенную в табл. 25.4.
Тогда формула для полной мощности излучения (25.31) должна содержать в подынте-
гральном выражении множитель |р0 I2. В результате с учетом того, что Q — крп^ sin 0,
/3 = lncy cos 0, получаем
р d = ^г~ Ис1(т£-),Я j sin 0Z(1 + cosJ0z)|po |’J0Z. (25.37)
гао 32я ео о
Из табл. 25.4 и формул (21.366) и (21.38) следует, что
Ро = И/о (Q, Q)/Wo (U, Q) = Ст (0) . (25.38)
Таким образом, выражение (25.37) идентично интегралу по переменной у от произведе-
ния мощности дальнего поля в ’’свободном пространстве”, определенной выражением
(21.236), на корректирующий множитель Со (0) (21.35) для источника, расположенно-
го на оси световода и рассмотренного в разд. 21.13.
25.15. Пример. Трубчатый источник внутри световода со ступенчатым профи-
лем показателя преломления
Рассмотрим трубчатый источник радиусом г0, симметрично расположенный внутри серд-
цевины слабонаправляющего световода со ступенчатым профилем показателя преломле-
ния, т. е. такой, что 0 < г0 < р, где р - радиус сердцевины. Повторим анализ из разд. 25.13,
приняв во внимание форму профиля показателя преломления световода и заменив мо-
ды ’’свободного пространства” из табл. 25.2 модами излучения слабонаправляющего
световода из табл. 25.4. В результате выражения для амплитуд мод (25.34а) принима-
ют вид
15
451
•W'ofc) kncl = _ G Jl<UrolP) &(Q)
*1-1 "*1+1 ~p\hI J^QrJp) P(Q) ’ *l~ 1 eUl -Pl U^QrJp) kncX
(25.39)
для ТЕ- и ТМ-мод соответственно, где I > 2, а функция определена выражением
(25.346). Конечное выражение для мощности излучения идентично выражению (21.416),
в котором представлено через члены, определенные формулой (21.366).
25.16. Влияние оболочки конечной толщины
Повсюду в этой главе мы определяли поля излучения в предположении, что
толщина оболочки не ограничена. На практике, однако, световоды имеют обо-
лочку конечной толщины, что схематически отражает рис. 1.1 во введении к
ч. I. Если толщина оболочки велика, то ее влияние на поля направляемых
мод мало, поскольку эти поля в оболочке затухают экспоненциально. Что ка-
сается мощности излучения, то часть ее будет отражаться от границы между
оболочкой и защитным покрытием, и в этом смысле оболочку одномодовых
световодов можно рассматривать как сердцевину многомодового световода,
оболочкой которого служит защитное покрытие. Таким образом, для таких
задач применимы, лучевые методы, описанные в ч. I, а коэффициенты переда-
чи мощности, рассмотренные в гл. 7 и 8, позволяют определить долю мощно-
сти, попадающую в защитное покрытие. Отраженная мощность затухает в
защитном покрытии при последующих отражениях и может быть проанализи-
рована лучевыми методами, предложенными в ч. I.
ГЛАВА 26. РАЗЛОЖЕНИЕ ПОЛЯ ИЗЛУЧЕНИЯ
Последние пять глав были посвящены рассмотрению с разных точек зрения
поля излучения оптического волновода. В гл. 24 мы ввели понятие вытекаю-
щих мод для описания поля излучения вблизи оси волновода на достаточно
больших расстояниях от источника излучения. Остальная часть поля излуче-
ния, как это следует из формулы (24.1), описывается полем пространствен-
ной волны. Поле излучения может быть представлено либо разложением по
полям мод излучения, как это сделано в гл. 25, либо суперпозицией полей
элементарных диполей с использованием метода функций Грина для волно-
вода, что продемонстрировано в гл. 21 и 34. В этой главе будет изложен ме-
тод нахождения составляющей волны поля излучения, основанный на фор-
мальном разложении поля в любом представлении на вытекающие моды и
пространственную волну.
Описания поля излучения с помощью мод излучения или полей элементар-
ных диполей формально идентичны. Применительно к световодам первый
метод включает в себя интегрирование по параметру Q, как это видно из
формулы (25.3), а во втором методе необходимо проводить эквивалентное
интегрирование по углу 0 (см. рис. 21.4). Затухающие моды имеют чисто
мнимую постоянную распространения 0, а параметр Q таких мод — величина
вещественная. Таким образом, хотя 0 может иметь мнимую часть, Q всегда
вещественная величина. В этой главе мы покажем, что, перейдя от интегриро-
вания вдоль вещественной оси QT к интегрированию в комплексной б-плос-
452
кости, поле излучения можно разложить на 1) конечную сумму полей выте-
кающих мод, соответствующих вкладу от дискретных комплексных полю-
сов и 2) поле пространственной волны, соответствующее значению интеграла
по комплексной плоскости. Для асимптотической оценки поля простран-
ственной волны на достаточно большом расстоянии от источника возбужде-
ния при интегрировании в комплексной 2-плоскости будет использован ме-
тод наискорейшего спуска [1].
ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ И РАЗЛОЖЕНИЕ
В дальнейшем рассмотрении поле излучения будем представлять в виде сумт
мы полей мод излучения (25.3). Поскольку этот анализ применим в равной
степени и для магнитного и для электрического полей, достаточно рассмот-
реть только последнее. Далее для простоты ограничим рассмотрение прибли-
жением слабонаправляющего волновода, а в примерах будем рассматривать
световоды со ступенчатым профилем показателя преломления. Таким об-
разом, °°
Erad (х, y,z}=?Sa (0 е. (х, у, Q) exp [i/3 (Q)z ] dQ, (26.1)
/ О J J
где flj (2) — амплитуды мод, а постоянная распространения моды 0 связана
с параметром Q соотношением, приведенным в табл. I. Интегрирование в об-
ласти 0 < Q < крпс\ соответствует вперед-распространяющимся модам'излу-
чения, а в области крпсХ <Q <°° — затухающим модам излучения, амплиту-
да которых экспоненциально уменьшается с ростом z.
Амплитуды мод a-(Q) могут быть выражены в явном виде с помощью
формул (25.12) и (25.11) , если конкретизирован источник возбуждения и,
таким образом, известны либо распределение плотности тока внутри свето-
вода J, либо поля возбуждения Et и Ht на торце световода. В любом случае
выражение для (2) следует подставить в формулу (26.1) и, используя сим-
метрию подынтегрального выражения, расширить область интегрирования до
2 = —00 • Для световода со ступенчатым профилем показателя преломления,
каждая декартова, или скалярная, составляющая поля пропорциональна ин-
тегралу /, который, как следует из (25.14) и (25.15), можно представить в
виде °° f (х v
I(x,y,z)=Z J w(un\ ^№<Q}z]dQ. (26.2)
Интегрирование ведется вдоль вещественной оси 2Г, Д — заданная, аналити-
ческая во всей комплексной 2-плоскости функция, которая при г °° про-
порциональна exp(i - Qr/p)\ функция ^(С/, 2) определена выражением
(21.366).
Поскольку цель данной главы — дать формальный метод разложения поля
излучения, детали вывода формулы (26.2) из выражения (26.1) опущены и
могут быть найдены в [1—3]. Вывод выражения (26.2) методом функций
Грина рассмотрен в [3,4].
26.1. Сингулярности подынтегрального выражения
Исследуем теперь сингулярности подынтегрального выражения в формуле
(26.2) в комплексной 2-плоскости с целью изменения пути интегрирования.
Интегралы такого вида рассматриваются в специальных монографиях [1,3].
453
Рис. 26.1. Комплексные плоскости:
а — (2-плоскость, иллюстрирующая ветвление функции в точках ±Ь, где b = крп^. Штри-
ховая линия соответствует границе разреза плоскости. Полюса направляемых и вытека-
ющих мод обозначены соответственно крестиками и точками, б — Ф-плоскость, где
прямоугольные области Т1 — Т4иВ1 — В4 соответствуют верхним и нижним квадран-
там римановых листов (2-плоскости, представленной на рис. 26.1, а. Штриховая линия
р соответствует границе разреза, sd ~ траектория наискорейшего спуска
Полюса интеграла являются нулями характеристического уравнения (24.30) .
Направляемые моды соответствуют чисто мнимому и положительному пара-
метру Q, что с очевидностью следует из формулы (24.4), и на рис. 26.1 пока-
заны крестиками на мнимой оси Q*. Вытекающие моды соответствуют комп-
лексным нулям функции И7! (U, Q), причем, как следует из формулы (24.5),
QT > 0, a Qi < 0, где индексы г и i обозначают вещественную и мнимую части.
Таким образом, полюса вытекающих мод расположены в четвертом квадран-
те на рис. 26.1, а.
Ограничение ветвлений. Из соотношения между постоянной распростране-
ния моды /3 и параметром Q
p2^(Q) = (kpndy -Q2 (26.3)
следует, что равенству /3 = 0 или Q = ± крпс^ соответствуют точки ветвления.
Появление этих точек обусловлено тем фактом, что для удовлетворения
условий, налагаемых на поля мод излучения при необходимо опреде-
лить знаки перед (3 и Q. Ограничения ветвлений могут быть введены произ-
вольным образом, но лишь в том случае, если они не пересекают путь инте-
грирования, проходящий вдоль вещественной оси (?г. На рис. 26.1, а ограни-
чения введены таким образом, что в верхней части рисунка 0* >0, а в нижней
части (3* < 0. Таким образом, вперед-распространяющиеся направляемые мо-
ды и вытекающие моды расположены в верхней части рисунка. Полюса су-
ществуют и в нижней части рисунка, однако они соответствуют модам, ам-
плитуда которых растет в направлении распространения. В случае световодов
без поглощения ограничения ветвлений могут быть введены вдоль веще-
ственной и мнимой осей 2-плоскости. Вследствие того, что полюса направля-
емых мод расположены вдоль мнимой оси 2\ удобно ввести небольшое по-
глощение в оболочку для более четкого различия между положениями полю-
сов и линий ветвления. Последние затем определяются из условий
454
Q'Q' = ^4141’ "cl = "cl + ’"cl (26-4)
и равенства мнимых составляющих выражения (26.3) .
Научившись описывать сингулярности в подынтегральном выражении
формулы (26.2) в комплексной (2-плоскости, мы теперь можем изменить
путь интегрирования в этой формуле, проходящий вдоль вещественной оси
(2Г. Однако, как можно видеть из рис. 26.1, а, для этой цели необходимо оце-
нить значения интегралов вблизи точек ветвления. Чтобы этого избежать,
введем преобразование, которое устраняет ограничения ветвлений.
26.2. Замена переменных интегрирования
Простая замена переменных позволяет устранить точки ветвления на рис. 261,а
и сделать подынтегральное выражение в формуле (26.2) однозначным, а
именно
Q = Ар/?с1 sin Ф; 0 = knci cos Ф; Ф=£+1т?. (26.5)
Отсюда верхняя и нижняя части комплексной Q-плоскости преобразуются в
комплексную Ф-плоскость, изображенную на рис. 26.1,6, а полюса преобра-
зуются в соответствующие области. Вещественная ось Q-плоскости становит-
ся контуром р, включающим в себя часть оси f (от f = —я/2 до f = я/2) вместе
с прямыми f = —я/2, т? > 0 и f = 7г/2, т? < 0. Таким образом, формула (26.2)
принимает вид
„ Ч-t V. г /L[x,b 6(ф)]
I(x,y, z) -kpnd (ф)]
exp (ifcz/?cl cos Ф) cos Фс/Ф. (26.6)
Интеграл вычисляется вдоль контурар, U(Ф) = [К2 + Q2 (Ф) ]1/2. Теперь,
когда точки ветвления исключены, становится ясным, что при соответствую-
щем выборе контура интегрирования р в интегралах (26.6) можно выделить
полюса, соответствующие вытекающим модам.
Если эту процедуру проделать, то окажется, что аналитические выражения
для направляемых и вытекающих мод одинаковые. Следовательно, поля вы-
текающих мод, рассмотренные в гл. 24, идентичны полям, полученным в
этом разделе. Более того, выражения для амплитуды мод a- (Q) в точности
равны выражениям, полученным в разд. 24.17 [2]. Однако интеграл вдоль
деформированной части контура остается’ Он дает вклад в пространственную
волну.
26.3. Метод наискорейшего спуска
С целью асимптотической оценки вклада поля пространственной волны в по-
ле излучения на большом расстоянии от источника изменим путь интегриро-
вания р на рис. 26.1, б таким образом, чтобы он проходил по траектории наи-
скорейшего спуска [1] и обозначим его sd. Тогда формулу (26.6) можно за-
писать в виде
Их, у, z) = S Я (х, у) exp(i(3:z) + S (х, у, z,
j J 1 I sd ь
(26.7)
455
где <Rjexp(ij3j) — вычет в полюсе, соответствующем каждой вытекающей мо-
де, заключенный в измененном контуре интегрирования, a обозначает
подынтегральное выражение в формуле (26.6). Чтобы определить вклад ин-
теграла вдоль траектории наискорейшего спуска, вспомним, что при г -> °°
функция gi ведет себя как ехр [i(Qr/p + 0z) ]. Если ввести безразмерные по-
лярные координаты (т; В), которые описывают радиальное и продольное
смещения, т. е.
г = рт sin z = рт cos 0; т = (г2 + z2) 1/2/р, (26.8)
•то с учетом определения переменной Ф [см. формулу (26.5)] функция
при г -> о© содержит множитель ехр [ikpnc]r cos(4< — В) ]. Таким образом, сед-
ловую точку при Ф = 0 и траекторию наискорейшего спуска находим из тре-
бования неизменности фазы, или вещественной части величины т cos (Ф — В).
Тогда [2]
cos (f - 0) ch т? = 1 (26.9)
соответствует пути, показанному на рис. 26.1, б. Отсюда получим, что вклад
в первую сумму в формуле (26.7) вносят только полюса вытекающих мод,
лежащие между контурами р и ,sd. Если координаты полюса q-й вытекающей
моды обозначить через (fq, r?q), то для того, чтобы этот полюс давал вклад
в первую сумму (26.7) ? необходимо выполнение следующих условий:
cos(fq - 0)ch7?q < 1; cos fq sh < 0. (26.10)
Рассмотрим теперь более подробно составляющие поля, соответствующие
вытекающим модам и пространственной волне.
ВКЛАД ПОЛЯ ВЫТЕКАЮЩИХ МОД В ПОЛЕ ИЗЛУЧЕНИЯ
Рассмотренное выше разложение дополняет наше качественное описание по-
лей вытекающих мод, данное в гл. 24, и формально показывает, что поля вы-
текающих мод имеют такое же аналитическое выражение, как и поля направ-
ляемых мод. Каждая вытекающая мода обусловлена резонансом в попереч-
ном сечении световода и определяется характеристическим уравнением
WyfU, Q) = 0. Поля вытекающих мод вносят вклад в поле излучения только
внутри сектора в плоскости (г; z), изображенного на рис. 26.2. Рассмотрим
полюс q-Й вытекающей моды с координатами (fq; r?q), который лежит меж-
ду траекторией наискорейшего спуска sd и контуром р на рис. 26.1, б. В этом
случае fq и r?q удовлетворяют неравенствам (26.10). Поскольку г и z явля-
ются переменными, то угол 0, определяемый из (26.10), будет также пере-
менным, а поэтому траектория наискорейшего спуска, определяемая выра-
жением (26.9), будет непрерывно изменяться. Ясно, что существует макси-
Рис. 26.2. Поле <?-й вытекающей моды вносит вклад в
поле излучения только в пределах заштрихованной
области. Вне этой области поле моды становится частью
поля пространственной волны
456
мальный угол 0q, для которого неравенства (26.10) еще выполняются. Это-
му углу соответствуют полюса вытекающих мод, лежащие на траектории
наискорейшего спуска. В этом случае cos(fq - 0q) ch ??q = 1, и, приравнивая
вещественные части в формуле (26.5) при w = fq + ii?q и исключая ??q, нахо-
дим, что для слабовытекающих мод
0q~arctg(e>3rq), (26.11)
где Qq и 0q — значения вещественных частей Q и (3 в полюсе, а мнимыми ча-
стями этих величин мы пренебрегаем. Другими словами, поле q-й вытекаю-
щей моды вносит вклад в поле излучения только в интервале углов 0 < 0 <
< 0q, изображенном на рис. 26.2. При 0 > 0q поле вытекающей моды стано-
вится частью пространственной волны. Этот результат находится в согласии с
интуитивным описанием полей вытекающих мод, приведенным в разд. 24.11,
где было показано, что поля вытекающих мод занимают область, ограничен-
ную углом 0Z, определяемым формулой (24.9) и идентичным углу 0q, рас-
смотренному выше.
Поля вытекающих мод не играют роли в описании полей излучения на
больших расстояниях от оси световода (т. е. при г -+<*>) и при конечном z.
Кроме того, поскольку мощность вытекающих мод экспоненциально умень-
шается вдоль световода, то вклад полей вытекающих мод в поле излучения
становится пренебрежимо малым при z -> Следует, однако, иметь в виду,
что эти расстояния могут быть действительно значительными, вследствие
того, что вытекающие моды многомодовых световодов могут иметь очень
малые коэффициенты затухания, как показано в гл. 8. Ниже покажем, что за
редким исключением поля вытекающих мод представляют собой хорошее
приближение поля излучения внутри и вблизи сердцевины световода, если
источник излучения находится достаточно далеко, а амплитуда поля излуче-
ния достаточно велика.
ВКЛАД ПОЛЯ ПРОСТРАНСТВЕННОЙ ВОЛНЫ В ПОЛЕ ИЗЛУЧЕНИЯ
Аналитического выражения для пространственной волны в произвольной
точке плоскости (г; z) не существует. Однако на достаточно большом рас-
стоянии от источника возбуждения такое поле может быть представлено ин-
тегралом вдоль траектории наискорейшего спуска, а этот интеграл затем
можно оценить методом наискорейшего спуска [1, 3, 5]. Таким образом,
на большом расстоянии от световода, когда г -> «>, а длина световода z фик-
сирована, вследствие вклада седловой точки в величину интеграла вдоль
траектории наискорейшего спуска амплитуда поля пространственной волны
изменяется пропорционально г~1/2 [1, 3, 4]. Такая зависимость хорошо из-
вестна для излучения в дальнем поле линейных источников.
Вклад поля пространственной волны в поле излучения вблизи или внутри
сердцевины световода на достаточно большом расстоянии от источника воз-
буждения, т. е. при z -> о© и г ~ р, может быть найден подстановкой 0 = 0 в
формулу (26.9), так что траектория наискорейшего спуска определяется
уравнением cos f ch т? = 1, или подстановкой /Зт = kncl в формулу (26.5).
В этом случае седловая точка не вносит вклад в величину интервала, и следу-
ющий член в интеграле вдоль траектории наискорейшего спуска определяет
зависимость амплитуды поля пространственной волны от z как z"3/2 [6, 7].
457
Рис. 26.3. Схематическое представление приповерхностных (боковых) волн:
а — на плоской границе между по л у бе с конечными средами с показателями преломления
лсо к ttcl < Л/СО’ о-в световоде со ступенчатым профилем показателя преломления
Такая зависимость характерна для дифракционных эффектов, связанных с
утечкой энергии вдоль границы двух диэлектрических сред. В случае полу-
бесконечных сред такие волны называются боковыми волнами [3]. Поэтому
в случае световода пространственную волну можно назвать поверхностной
волной, которая схематично изображена на рис. 26.3. Хорошо известно, что
поверхностные волны эффективно возбуждаются только в случае, когда
источник S обладает узкой диаграммой направленности и излучает под кри-
тическим углом вс. Поэтому за некоторыми исключениями на достаточно
большом расстоянии от источника излучения вытекающие моды достаточно
точно описывают поле излучения вблизи и внутри сердцевины световода при
условии, что амплитуда поля излучения достаточно велика.
Резюме. В заключение подчеркнем, что на достаточно большом расстоянии
от источника излучения, находящегося внутри волновода, вклад в дальнее
поле излучения вносит только поле пространственной волны, амплитуда ко-
торой при г -> оо пропорциональна г"1/2. На достаточно большом расстоянии
от источника, но вблизи или внутри сердцевины волновода наличие волново-
да изменяет эту зависимость, и основной вклад в излучение вносит поле,
распространяющееся вдоль границы между сердцевиной и оболочкой в фор-
ме приповерхностной волны, амплитуда которой приг->°° пропорциональна
z~3/2. Однако для того чтобы приповерхностная волна переносила значитель-
ную мощность, источник должен быть узконаправленным. В противном слу-
чае вытекающие моды описывают поле, энергия которого распределена вну-
три и вблизи сердцевины волновода и адекватно описывает поле излучения
достаточно большой мощности. Вблизи источника поля вытекающих мод и
пространственной волны велики и должны учитываться для корректного
описания полей излучения.
ГЛАВА 27. СВЯЗЬ МОД
Определить поля мод возмущенного волоконного световода можно несколь-
кими методами, а выбор конкретного метода зависит от характера возмуще-
ний. Если они невелики и не меняются вдоль световода, то для определения
полей мод целесообразно использовать методы теории возмущений, изложен-
ные в гл. 18. В то же время, если на величину возмущенцй не налагается ни-
каких ограничений, но вдоль волновода они меняются медленно, то наиболее
458
подходящим является метод локальных мод, описанный в гл. 19. В этой гла-
ве мы уделим основное внимание одиночным световодам со слабыми возму-
щениями, характер которых меняется произвольным образом вдоль про-
дольной оси световода.
При анализе таких световодов используется теория связанных мод, или те-
ория возмущений, зависящих от продольной координаты. Теория связанных
мод особенно полезна в случае, когда небольшие возмущения параметров
дают значительный эффект, например, когда условия резонанса приводят к
почти полному обмену мощностями между модами невозмущенного свето-
вода. За исключением таких экстремальных случаев небольшие возмущения
приводят к небольшому обмену мощностями и могут быть адекватно описа-
ны методом наведенных токов, изложенным в гл.22. В этой главе мы в ос-
новном будем рассматривать резонансную связь в волоконных световодах, в
которых распространяется одна или несколько мод. Такие же возмущения
в случае многомодовых световодов значительно проще описывать методами
геометрической оптики, что было продемонстрировано в гл. 5.
ТЕОРИЯ СВЯЗАННЫХ МОД
Если неоднородности меняются вдоль световода, то такая структура уже
больше не является цилиндрически симметричной и поэтому не может на-
правлять отдельные моды невозмущенного световода. Тем не менее поля
возмущенного световода в сечении z можно представить как суперпозицию
полей полной системы направляемых мод и мод излучения невозмущенного
световода. Любая отдельная мода из этой системы не является решением
уравнений Максвелла для возмущенного световода, и поэтому поля возму-
щенных мод в общем случае могут быть разложены по всем модам полной
системы мод невозмущенного световода. Характер этого разложения меняет-
ся вдоль световода и описывается системой уравнений связанных мод, кото-
рые определяют амплитуду каждой моды [1 — 3].
27.1. Уравнения связанных мод
Система уравнений связанных мод получается подстановкой разложения по-
ля мод возмущенного световода в уравнения Максвелла. В результате полу-
чаем бесконечную систему связанных дифференциальных уравнений первого
порядка для амплитуды каждой моды, зависящей от продольной координа-
ты z. Поскольку эта система получается непосредственно из уравнений Мак-
свелла, она точно описывает поля мод возмущенного световода. Однако в
общем случае такой метод не имеет никаких преимуществ перед уравнения-
ми Максвелла, так как общего аналитического решения системы не суще-
ствует. Задача значительно упрощается при наличии лишь двух мод, так как
это дает возможность использовать простые методы теории возмущений. Ин-
туитивно ясно, «что в этом случае поля мод невозмущенного световода долж-
ны быть хорошей аппроксимацией полей мод возмущенного световода, вклю-
чая и область возмущения. Это возможно только в случае, когда профили
показателей преломления возмущенного и невозмущенного световодов
лишь слегка различаются в любой точке световода (см. разд. 18.21). По-
скольку существует несколько задач, в которых рассматриваются световоды
459
с произвольным профилем показателя преломления и которые могут быть
решены в рамках этого условия, то ограничим наше рассмотрение слабона-
правляющими световодами, а всеми поляризационными эффектами, обуслов-
ленными их структурой, пренебрежем. Влияние поляризационных эффектов
мало, а их учет неоправданно усложнит рассмотрение, как это было видно на
примере из разд. 18.21.
27.2. Слабонаправляющие волоконные световоды
Рассмотрим невозмущенный световод с профилем показателя преломления
п (х, у) и возмущенный световод с профилем, зависящим и от аксиальной
координаты z, т. е. п (х, у, z). Поскольку предполагается, что световоды сла-
бонаправляющие и п & п & пс1, то по причинам, изложенным в предыдущем
разделе, поляризационные эффекты не учитываются и все операции прово-
дятся со скалярным волновым уравнением. Для удобства также предполо-
жим, что электрическое поле поляризовано вдоль оси х. Тогда
М
Ех (х, y,z)= [fej (z) + b_j (z) ] (x, y), (27.1)
где величины (z) и b_^ (z) содержат информацию об амплитуде и фазе впе-
ред- и назад-распространяющихся мод соответственно, М — число направляе-
мых мод и 'PjtX У) — решение скалярного волнового уравнения (13.8).
В принятых обозначениях это уравнение можно записать в виде
[V? + к2п2 (х, у) - ] *i = 0. (27.2)
t j j
Постоянная распространения скалярного приближения 3j определяется из
характеристического уравнения. В разложении (27.1) непрерывный спектр
мод излучения не учитывается, так как в дальнейшем в рассмотрение будет
приниматься только связь между направляемыми модами.
Система уравнений связанных мод, решениями которых являются амплиту-
ды мод, находится либо непосредственно из скалярного волнового уравне-
ния, как это показано в разд. 33.11, либо может рассматриваться как предел
соответствующих уравнений в приближении слабонаправляющего волновода,
выведенных в разд. 31.11 для световодов с произвольным профилем показа-
теля преломления. Последний подход приводит к следующей системе:
(27.3а)
для /-Й вперед
-распространяющейся моды и
db . м
(27.36)
для назад-распространяющейся моды, где — коэффициенты связи, завися-
щие от z и представляющие собой предел выражения (31.50) при исо -► лс1.
460
Тогда, учитывая, что продольные составляющие поля в рассмотрение не при-
нимаются, заменим • etl на и, приняв во внимание разницу в норми-
ровках между (31.45а) и (27.1), получим
1с —
£jl(z) -n2y*-*xdA/ J*2dA,
ZfZCO Лоо Лоо J
(27.4)
где Лоо — бесконечно большая площадь поперечного сечения.
Поскольку предполагается, что световод непоглощающий, то Ф| - веще-
ственные функции. В следующих разделах мы рассмотрим некоторые част-
ные случаи, в которых можно найти аналитическое решение уравнений свя-
занных мод.
Мощности возмущенных полей. Полную мощность направляемых мод в лю-
бом поперечном сечении вдоль световода можно найти, если просуммировать
мощности всех направляемых мод, использовав выражения из табл. 13.2 в
которых а заменено на b±] (z). Тогда мощность, переносимая в положитель-
ном направлении z,
М
Ры& = .fi^j(z)|27V,
(27.5)
где TVj — коэффициент нормировки. Выражение для мощности, переносимой
в отрицательном направлении z, аналогично (27.5) , только Щ (z) необходимо
заменить на b_^ (z).
27.3. Пример. Слабая связь мод
Если лишь малая часть полной мощности передается между модами возмущенного све-
товода, то уравнения связанных мод могут быть решены методом итераций. Решение
после первой итерации идентично решению, полученному в гл. 22 методом наведенных
токов. Чтобы продемонстрировать это, предположим, что в сечении z = 0 возмущенно-
го световода возбуждена только /-я вперед-распространяющаяся мода невозмущенного
световода. В первом приближении можно не учитывать взаимодействие со всеми осталь-
ными модами, и поэтому решение системы (27.3а) можно записать в виде
Z?l(z)=Z?l(°)exP(i^); &j(z) = O, / = Z, (27.6)
где Z>^(0) определяет полную начальную мощность. Итерация первого порядка получает-
ся подстановкой выражения (27.6) для £±^в правую часть системы (27.3). В результате
имеем
+ j =1 (°) ехР 0 ) > / *1-
Решение, удовлетворяющее начальному условию Z>±j (0) = 0, / #= I, имеет вид
z ~ ~
Z>±i = ± iZ\(0)exp(± ib.z) /Z) exp {i (0 + 0 )z }dz, j * I.
J * J о ь J
(27.7)
(27.8)
461
Если теперь ту же задачу решать, рассматривая /-ю моду возмущенного световода как
источник наведенного тока внутри невозмущенного световода, то в формуле (22.6)
нужно положить Et = Z^(0) Ф^ехр (ij3|Z). Тогда плотность тока, текущего вдоль оси х,
Jx= 1(е0/д0)1/2£(и2 - w2)Z?l(0)4'texp(i^lz). (27.9)
Далее соотношение для Z/ц (27.4) подставляем в формулу (27.8) и выражаем подын-
тегральную функцию через Jx. Если затем положить b + -^(z) ~ £+j(z)exp(± i^jZ), а под
объемом Упонимать объем между плоскостями z ~ 0 и z, то получим
а+; = expC+iftz)^/ J ЧМА. (27.10)
-J 2nco г J А J 'а„ j
Используя соотношения в табл. 13.2, легко заметить, что это выражение является пре-
делом выражения (21.2) в приближении слабонаправляющего волновода и, следова-
тельно, первая итерация уравнений связанных мод идентична решению, полученному ме-
тодом наведенных токов.
СИЛЬНАЯ СВЯЗЬ МОД
При определенных резонансных условиях небольшие возмущения парамет-
ров световода могут привести к передаче значительной мощности между дву-
мя модами полной системы мод невозмущенного световода. Примером мо-
жет служить резонансная связь в синусоидально деформированном светово-
де, которая будет рассмотрена ниже. Уравнения связанных мод описывают
передачу мощности между модами точно, тогда как метод наведенных то-
ков, рассмотренный в гл. 22, дает удовлетворительные результаты только в
случае слабой связи мод, т. е. если между модами перераспределяется малая
часть полной мощности. Если не рассматривать слабую передачу мощности
между всеми модами, а ограничиться рассмотрением резонансной связи
между двумя из них, то еистема уравнений связанных мод сведется всего
лишь к двум уравнениям для резонансных мод. Предполагая световод сла-
бонаправляющим и используя результаты разд. 27.2, рассмотрим связь мод
в этих двух случаях.
Две вперед-распространяющиеся моды. Когда связь между двумя вперед-
распространяющимися модами» с постоянными распространения (3lf /32 и
амплитудами b^z), b2(z) носит резонансный характер, то систему уравнений
(27.3) можно записать в виде
dz ~i(0i + ^ii)^i - iDi2b2 ; — Ц02 + D22)b2 -iZ>2i^i5 (27.11a) (27.116)
где коэффициенты связи определены формулой (27.4) . Для коэффициентов
перекрестной связи Dl2 и D21 справедливо равенство N2D2i = N\D12, где М,
N2 — коэффициенты нормировки мод, выражение для которых приведено в
табл. 13.2.
Одна вперед- и одна назад-распространяющиеся моды. Связь между впе-
ред- и назад-распространяющимися модами описывается системой уравнений
462
(27.11) в которой b2 заменяется на 6_2, а знак перед производной этой ве-
личины изменен. В частном случае, когда постоянная распространения назад-
распространяющейся моды равна —(^, система уравнений связанных мод
имеет вид
./х
~^~-i(0i =10^^,
db_,
+ i(3i +Z)11)Z?_l------------♦
(27.12a)
(27.126)
В более общих случаях сильной связи между несколькими парами мод урав-
нения (27.11) и (27.12) должны быть записаны для каждой такой пары. В ка-
честве иллюстрации полученных результатов рассмотрим резонансную связь
между парами мод синусоидально деформированного световода.
СИНУСОИДАЛЬНЫЕ ВОЗМУЩЕНИЯ
Рассмотрим слабонаправляющий волоконный световод с профилем показа-
теля преломления п(х, у) и предположим, что неоднородности по длине при-
водят к синусоидальной модуляции профиля с небольшой амплитудой, так
что его форму для возмущенного световода можно представить в виде
п2 (х, у, z) -п2 (х, у, z) + 8п2 (х, у) sin(S2z), (27.13)
где |6и21 << п2 и £2 — пространственная частота. Очевидно, что если посто-
янные распространения двух направляемых мод удовлетворяют условию ре-
зонанса или синхронизма, то между этими модами будет наблюдаться силь-
ная связь. Если для скалярных величин опустить знак то условие синхро-
низма примет вид
101 — 021 =Я. (27.14)
Для двух вперед-распространяющихся мод волоконного световода с оболоч-
кой эта разность не может превышать величины к(пх ~ п2). Следовательно,
£2 < (V/р) (Д/2)1/2, т. е. резонансная пространственная частота в световоде с
V = 2,4; Д = 0,005 и р = 10 мкм не больше 1,2 • 104 м-1. Рассмотрим теперь
резонансную связь в двух различных случаях.
27.4. Пример. Две вперед-распространяющиеся моды
В данном случае связь мод описывает система уравнений (27.11) . Если формулу (27.13)
подставить в (27.4), то каждый коэффициент связи может быть приведен к виду
D}l(z) = £)д8т(Ш); Яц =
— J* 6и2Ф.Ф/М/ J* Ф?<Х4,
2^со Л.» J Лоо J
(27.15)
Где £)ц - постоянный, не зависящий от z коэффициент. Чтобы получить приближенное
решение, вначале приведем уравнения связанных мод к безразмерным величинам. Для
этого выразим амплитуды мод через новые функции Хи Y:
X(z) = b^zyN^expi-i^z); Y(z) = b2 (z)7V"2exp (-i02z), (27.16a)
463
где 7VX и N2 - коэффициенты нормировки мод, а новой переменной является 0, связан-
ная с z соотношением
е = kz/2; к = <Z>12Z>21) (27.166)
Тогда с помощью безразмерных параметров
а= 1(Я-0,+02); r = ^G3j — ^2); s, =3,/*; s2 = Ь22/к (27.16в)
К к
и подстановки формул (27.15) и (27.16) в (27.11) уравнения связанных мод можно
записать в виде
— {exp(ia0) — exp [—i(а + 2т)0]} К + {exp [i(а+т)0] -
- exp [-i(a+ т)0] } X; (27.17а)
— (exp [i(a+2т)0] - exp (-ia0) } X + s2 {exp [i(а+т) 0] -
- exp [-i(a + т)0] } Y. (27.176)
Хотя эта система и не имеет простого аналитического решения, для больших простран-
ственных частот можно получить асимптотическое решение. В случае низких частот,
когда неоднородности медленно меняются вдоль световода, задачу можно решить ме-
тодом локальных мод, рассмотренным в гл. 19 и 28.
Асимптотическое решение. Поскольку амплитуда синусоиды мала, то из формул
(27.15) и (27.16) с очевидностью следует, что характерная длина 1/Д2> на которой про-
исходит значительное перераспределение мощности между модами, значительно превос-
ходит длину биений 2тт/|/Зх — /32 | ~ 2тг/£2, и, таким образом, из выражения (27.16) сле-
дует, что |т| >>1 и |т| >> |а|. Поэтому экспоненциальный член в формуле (27.17),
включаюшдй а + т и а + 2т, осциллирует значительно быстрее, чем соответствующие
члены, включающие только о. Отсюда можно заключить, что решение будет представ-
лять суперпозицию медленно меняющейся, не зависящей от т функции 0 с быстро ос-
циллирующей функцией 0, амплитуда которой порядка 1/т, в чем можно легко убедить-
ся, если проинтегрировать любое уравнение по частям и выделить в полученном выраже-
нии зависимость от 0. Если индексом 0 обозначить медленно меняющуюся составляю-
щую решения, то имеем [4]
—— = Уоехр (ia0); -°- = -Хо exp (-ig0). (27.18)
de de
Если первая мода на входе (z = 0) возбуждена с единичной мощностью, а вторая не воз-
буждена, то решения уравнений (27.18) с начальными условиями XQ = 1, Ко = 0 при
0—0 можно представить в форме
Хо = [cos (~) - oF sin (4-) ]exp(ia0/2); (27.19а)
г 2 г
=-F sin (—) exp (-iafl/2) ; F = 1/(1 + —) ,/2. (27.196)
F 4
Выражения для соответствующих полей легко могут быть получены с помощью формул
(27.1) и (27.16).
Распределение мощности вдоль световода. Выражение для мощности каждой моды
следует из формул (27.5) и (27.16) :
Л (z) = 1 - F2sin2 (0/F); Р2 (z) = F2sin2 (0/F), (27.20)
464
Рис. 27.1. Мощность Р2 (z), возбуждаемая во второй моде и обусловленная резонансной
связью с первой модой, первоначально возбужденной с единичной мощностью в светово-
де с небольшими синусоидальными неоднородностями:
а — медленно меняющаяся составляющая решение (27.20) выражена через угол 0,
определенный выражением (27.166) ; б' — быстро осциллирующая составляющая реше-
ния соответствует формуле (27.25)
откуда вытекает, что суммарная мощность остается неизменной вдоль световода. Из
этих формул видно, что коэффициент максимальной передачи мощности F2 (27.196)
чрезвычайно чувствителен к значению о, которая, в свою очередь, как это следует из
(27.16в), обратно пропорциональна разности между £2 и - 02. На рис. 27.1, а изобра-
жены зависимости Р2 (z) от 0 для различных значений о. При выполнении условий ре-
зонанса имеем а = О, F — 1, при этом происходит полная передача мощности от одной
моды к другой, в то время как при а = 2 и и = 5 передается соответственно 50 и 14 %
начальной мощности. Из формулы (27.20) также следует, что расстояние, на котором
происходит максимальная передача мощности, уменьшается с уменьшением F. И, нако-
нец, когда максимальная передаваемая мощность невелика, решение задачи можно по-
лучить, если принять в рассмотрение и остальные моды, использовав решение, получен-
ное в разд. 27.3 для случая слабой связи мод.
Поправки высших порядков. Поправки к медленно меняющимся составляющим
решения уравнений связанных мод, обусловленные членами с быстро осциллирующей
зависимостью от т, можно получить методом итераций из уравнений (27.17). Для опре-
деления первой поправки положим
Х=Х0+Х1; У=У0 + У1, (27.21)
где |Xj | < < |Х0 |, |У\ | < < |У0 |, и подставим эти выражения в уравнения (27.17).
Уравнения для медленно меняющейся составляющей исключаются из уравнений (27.18).
Положив в правой части Х= Хо, У = Уо, получим
бХ. Г 1
--- = - Уоехр [i(CT+ 2т) 0J + 2ist XQ sin (а + т)0; (27.22а)
dYi
—— — JVoexp [i (а + 2т) 0 J + 2is2 Уо8ш(а + т)0. (27.226)
U0
Поскольку медленно меняющаяся составляющая решения при интегрировании остается
постоянной, то решение, удовлетворяющее начальным условиям Хх — Ух = 0 при z = 0,
имеет вид [4]
Xs = --ib_ exp [-10 +2т) б] + ДД[1 — cos(a + т)в]; (27.23а)
У, . {1 — ехр [i(a +2т)в1 } - ~Д cos(a + r)0, (27.236)
о + 2т J О’ т
465
где функции Хо и Уо определены формулами (27.19). В рамках этой аппроксимации
получаем мощность каждой моды
РДз) = |Х0|’+2Re(X0JT*); Р2 (z) = | Уо |5 + 2Re(Уо У*), (27.24)
где символ Re обозначает вещественную часть функции, а знак * - комплексное сопря-
жение. Если выражения (27.19) и (27.23) подставить в формулы (27.24), то получим,
что члены с коэффициентами и D22, обозначенными теперь Sj, s2 (где sit s2 - веще-
ственные параметры), не вносят вклад в мощность мод. Тогда в предположении, что
|т| >> | а |, мощность во второй моде [4]
1 7 cts (О IF7)
Р2 (z) = F1 sin2 (0 /Р) <1 - - sin (т + а/2) в [а sin (т + За/2) 9 + —2— cos (т + 3ст/2) 0 ]
I т F
(27.25)
На рис. 27.1, б изображена зависимость Р2 (z) с учетом быстро осциллирующей составля-
ющей решения. Из приведенной зависимости видно, что разница между точным решени-
ем уравнений (27.17) и решением, в котором учитывается только медленно меняющая-
ся составляющая, невелика.
27.5. Пример. Одна вперед- и одна назад-распространяющаяся моды
В этом частном случае резонансная связь между вперед-распространяющейся и соответ-
ствующей назад-распространяющейся модами описывается системой (27.12). Подстав-
ляя факторизованный коэффициент связи (27.15) и проводя преобразование, анало-
гичное (27.16),
X(z) = Z>1(z)7V11/2exp(-i01z); Y (z) = b (z)7V]/2exp (i0tz) ; (27.26a)
A, 2 40,
в = ——z; о = ——(fi — 20.); r = ——, (27.266)
2 Dn Dn
получаем следующую систему уравнений связанных мод, выраженную через безразмер-
ные величины:
{exp(ia0) - exp [-i(a+2т)0]} У+ {exp [i (а + т) 0] -
- exp [—i(a+ т)0] } X; (27.27a)
d Y
--- = { exp(-ia0) - exp [i(a + 2т)е]} X - {exp [i(a + r)0] -
- exp [—i(a + r)0]} Y. (27.276)
Как и в задаче, рассмотренной в предыдущем разделе, |т | >> 1 и |т| >> |а|, откуда
получаем уравнения для медленно меняющейся составляющей
= Уо exp (i<70); = Х„exp (-iafl). (27.28)
de de
Решение для близкой к резонансной связи (а = 0) включает в себя функции, которые
растут или уменьшаются экспоненциально с ростом е. Следовательно, единственное при
е -► °° решение, удовлетворяющее начальному условию Хо = 1 при е — 0, имеет вид
Хо = exp (ia0) exp (-К0) ;
(ia—2к) <27’29)
У о = ---------exp(-ia0/2) exp (-К0),
466
где к ~ (1 - а2/4) 1/2 и |а| < 2. Далее из формул (27.5) и (27.26) получаем, что обе мо-
ды переносят одинаковую мощность
?! (z) = P_t (z) = exp (~kDx ), 0 < z < °°,
(27.30)
причем распространяются в противоположных направлениях. Этот результат находится
в полном соответствии с физической картиной, возникающей в данном случае. Ампли-
туда в пер ед распространяющейся моды уменьшается с ростом z, поскольку мощность
этой моды непрерывно перекачивается в назад-распространяющуюся моду, амплитуда
которой растет с уменьшением z. Скорость передачи мощности между этими модами за-
висит от ст И'достигает максимального значения Z)nexp (-5nz) при резонансе (а = 0).
С увеличением |а| эта скорость быстро падает и на первый взгляд может показаться,
что при | о | = 2 передача мощности прекращается, поскольку к = 0. Однако для опреде-
ления фактически переданной мощности необходимо учитывать быстро осциллирую-
щую составляющую решения. Поэтому при |а| > 2 решения для XQ и Ко могут быть по-
лучены из формул (27.19), в которых нужно положить? — (а2/4 - 1)1/2.
Слабая связь мод. В разд. 22.9 мы определили мощность, перекачиваемую в назад-
распространяющуюся основную моду, в случае, когда вперед-распространяющаяся ос-
новная мода падает на синусоидально возмущенную границу между сердцевиной и обо-
лочкой слабонаправляющего световода длиной 2L со ступенчатым профилем показате-
ля преломления. Решение (22.29) справедливо лишь для случая, когда потери мощно-
сти вперед-распространяющейся моды малы. Решение (27.29) также непригодно, по-
скольку при его выводе предполагалось, что световод имеет бесконечную длину. Если
же задачу из разд. 22.9 сформулировать в терминах этого разделай потребовать, чтобы
решения уравнений (27.28) удовлетворяли граничным условиям Хо = 1 при z = 0 = 0
и Уо = 0 при z = 2L или 0 = 0^ = , то в случае резонанса решение можно записать
в виде
Хо = ch 0 - sh-0 th 0L, Уо = sh 0 - ch 0 th 0(27.31)
Это решение сводится к (27.29) при L В случае слабой связи 0£ < < 1, и амплиту-
да назад-распространяющейся моды при z — 0 = 0 пропорциональна -0£. Если выраже-
ние для 8п2 из формул (22.28) и (27.13) подставить в выражение для (27.15) и
учесть, что = 1 при г = р, а интеграл в знаменателе (27.15) взять из табл. 14.6, то из
вычислений следует, что отношение а к ах в формуле (22.29) в точности равно -6^-
ГЛАВА 28. СВЯЗЬ ЛОКАЛЬНЫХ МОД
В предыдущей главе мы изложили теорию связанных мод применительно к
описанию распространения излучения в волноводах с небольшими возмуще-
ниями параметров, причем характер этих возмущений мог меняться произ-
вольным образом вдоль волновода. В этой главе будут рассмотрены волно-
воды с неоднородностями произвольной величины, но меняющимися очень
медленно вдоль волновода. При рассмотрении свойств таких волноводов в
гл. 19 было введено понятие локальных мод, которые являются прекрасным
приближением мод возмущенного волновода при условии, что любые иска-
жения цилиндрической симметрии последнего изменяются достаточно мед-
ленно. Однако поскольку локальная мода не является точным решением
уравнений Максвелла, при распространении моды вдоль волновода неболь-
467
шая часть ее мощности теряется вследствие связи с полем излучения или с
другими локальными модами. Поэтому главной целью данной главы явля-
ется изложение метода определения этих потерь.
Прежде чем начать описание метода, необходимо подчеркнуть, что теория
связанных локальных мод оказывается особенно полезной в случае сильной
связи между локальными модами, так как в случае слабой связи более удо-
бен метод наведенных токов, применение которого для подобных задач про-
демонстрировано в разд. 22.10 и 22.11.
ТЕОРИЯ СВЯЗАННЫХ ЛОКАЛЬНЫХ МОД
Точные выражения для полей мод волновода с произвольными возмущения-
ми параметров могут быть представлены в виде суперпозиции полей локаль-
ных мод и поля излучения. Если параметры волновода меняются медленно,
то при распространении локальной моды вдоль волновода ее мощность оста-
ется фактически неизменной. Тем не менее вследствие того, что локальные
моды не являются точными решениями уравнений Максвелла, между различ-
ными модами и полем излучения будет существовать связь, хотя и слабая.
Эту связь описывает система уравнений связанных локальных мод, которая
позволяет определить амплитуды каждой локальной моды и моды излу-
чения.
28.1. Уравнения связанных локальных мод
Разложение точных полей мод волновода можно записать в виде
Et (х,y,z)=Z [Ь.(z) + b_.(z) ]ё^. [х, у, 0 (z) ]; (28.1а)
Ht (х, у,г) = Ъ [Ь. (z) - 6_. (2) ] htj [х, у, 0. (z) ], (28.16)
где индекс t обозначает поперечную составляющую, знак л — ортонормаль-
ность, a Z?j (z) содержит информацию об амплитуде и фазе. Постоянная рас-
пространения локальной моды, а следовательно, и поле локальной моды из-
меняются вдоль световода, о чем уже упоминалось в разд. 19.1. Отрицатель-
ные индексы обозначают назад-распространяющиеся моды, а суммирование
неявно включает и моды излучения.
Получить уравнения для b- (z) можно двумя существенно различными спо-
собами. Менее формальный подход заключается в разбиении световода на по-
следовательность бесконечно малых отрезков, один из которых изображен
на рис. 31.2; затем в каждом таком отрезке определяется изменение ампли-
туды моды [1]. Детали такого способа изложены в разд. 31.16. Другой воз-
можный способ заключается в подстановке разложения (28.1) в уравнения
Максвелла, а использование соотношения ортогональности для локальных
мод позволяет получить систему уравнений связанных локальных мод [2, 3].
Такой способ, изложенный в разд. 31.14, приводит к системе уравнений
(31.65)
468,
db:
----ifi.b. = 2(C.b, + C. b ,);
dz j J i v Л I j - I -r
db •
—+i0.Z> . =-L(C .Д + С . fi .)
dz -j i -jl I -j -1 -I7
(28.2a)
(28.26)
для /-x вперед- и назад-распространяющихся мод соответственно. Коэффици-
енты связи (Гц определяются из соотношения
. л de, dhi ч
C.=-l f (h x-r^ “ ei х —-^-) ezcL4, j^l, C-=0,
А 4 J v J dz J dz 7
Л oo
(28.3)
где Лоо — бесконечно большая площадь поперечного сечения, z — единичный
вектор, параллельный оси волновода. При замене I -> -I или / -> -/ выраже-
ние для коэффициентов связи может быть получено с учетом свойств сим-
метрии поля [см. формулу (11.7)]. Необходимо помнить также, что j3, ер
hj и Сд зависят от z. Коэффициенты связи могут быть выражены и в ином ви-
де (см. 31.15 [4]), а именно
сг‘Ф“^ с. = ».
(28.4)
где знак * обозначает комплексное сопряжение.
В разд. 27.1 отмечалось, что применение уравнений связанных мод ограни-
чено рамками приближения слабонаправляющих волноводов. Такого ограни-
чения не существует для уравнений связанных локальных мод. Общее реше-
ние уравнений связанных локальных мод будет получено в следующем раз-
деле для случая слабой связи, а далее будут рассмотрены моды излучения.
Полная мощность направляемых мод. Поля локальных мод являются ор-
тонормированными и, следовательно, выражение для полной мощности на-
правляемых мод, распространяющихся в положительном направлении оси,
может быть получено из формул (11.16), (11.27) и (28.1) :
м
(28.5)
где М - число вперед-распространяющихся локальных направляемых мод в
сечении z. Замена Щ на Ъ_-} дает выражение для мощности направляемых
мод, распространяющихся в отрицательном направлении оси z.
Слабонаправляющие волноводы. В частном случае слабонаправляющих
волноводов, когда изменение профиля показателя преломления в попереч-
ном сечении мало, можно не учитывать все поляризационные свойства волно-
469
вода и выразить поля локальных мод и коэффициенты связи через решения
скалярного волнового уравнения. Этот подход эквивалентен тому, что мы
пренебрегаем продольными составляющими полей и выражаем ht- через
etj с помощью формулы (13.1). Уравнения связанных локальных мод и оба
выражения (28.3) и (28.4) для коэффициентов связи могут быть получены
и непосредственно из скалярного волнового уравнения, как это сделано в
разд. 33.12 и 33.13.
28.2. Слабая связь мод
Уравнения связанных локальных мод могут быть решены приближенно, ко-
гда только малая часть полной мощности возмущенного волновода перерас-
пределяется между его модами. Ранее было показано, что приближенное ре-
шение первого порядка идентично решению, полученному методом наведен-
ных токов в гл. 22. Для удобства предположим, что на входном торце свето-
вода (z = 0) возбуждена только l-я вперед-распространяющаяся локальная
мода, и в первом приближении связь с остальными модами учитывать не бу-
дем. Тогда решение системы (28.2) можно записать в виде
Z>t(z) = dl(0)exp[i(6l(z)dz]; b =(z) =0, j! *1. (28.6)
О
Уравнение для решения первого порядка получается подстановкой (28.6) в
правую часть системы (28.2), откуда для / / имеем
JZ? .(z) z
± i0jZ>±j (Z) = ± 6l(0)C±jl(z)exp [ij 0l(z)dz]. (28.7)
Решение, удовлетворяющее начальному условию b±] (0) = 0, имеет вид
< Z ) Z __
b±Az) =±Z^(0) < ехр[±Ц0;(г)б?7]? JC±il(z)exp(i5j3z)Jz, (28.8а)
( о Jo
где 5|3 — среднее отклонение постоянной распространения от ее среднего зна-
чения вдоль волновода, т. е.
__ л z
W) =4Ж(*) + & (*)]<&. (28.86)
о
Если теперь подставим выражение для коэффициента связи (28.4) в форму-
лу (28.8а) и предположим, что Z^(0) =1, то найдем, что конечное выражение
для Z>±j в точности совпадает с формулой (22.35), которая получена методом
наведенных токов и описывает слабое различие полей локальных мод и точ-
ных полей волновода. Таким образом, первая итерация уравнения связан-
ных локальных мод эквивалентна решению, полученному методом наведен-
ных токов.
28.3. Критерий медленного изменения параметров
Важным приложением решения уравнения связанных локальных мод в слу-
чае слабой связи мод является определение максимально допустимой скоро-
сти изменения параметров волновода вдоль его оси, при которой отдельные
локальные моды еще распространяются с пренебрежимо малыми изменения-
ми их мощности. Если предположить, что в волноводе первоначально воз-
470
J
(28.10)
буждена только Z-я локальная мода с единичной мощностью, т. е. Z?t(0) ~ 1, то
мощность, возбужденную в /-й вперед-распространяющейся моде, можно
определить из формул (28.5) и (28.8а) :
Z ___ Z __
Л(2) = [JC (z)exp(i8(3z)dz] [JC (z)exp(-i5/?z)dz], j ^l, (28.9)
J о’- 0 J
где Cj^ - согласно формуле (11.8) вещественная величина. Поскольку пара-
метры волновода меняются медленно, то из выражений (28.4) и (28.86)
следует, что С ц И <50 также меняются медленно, однако экспоненциальный
член в формуле (28.9) представляет собой быстро осциллирующую функ-
цию. Тогда, интегрируя выражение (28.9) по частям и опуская член, содер-
жащий (dC}lldz)lbp [4], для случая j получаем
(z) + F2 (0) - 2F(z)F(O)cos(50z);
F(z)=Cjt(z)M
где параметр F пропорционален отношению длины перекрестной связи 1/Сц
к средней длине биений 2тг/6/3. Таким образом, локальная мода распростра-
няется с малыми потерями, если на любом участке волновода |F(z) | << 1,
т. е. при условии, что длина связи значительно превышает локальную длину
биений. В формуле (28.4) наиболее чувствителен к вариациям профиля
вдоль z параметр откуда можно сделать вывод о том, что требование
|F(z) | « 1 эквивалентно интуитивному критерию, введенному в разд. 19.2,
согласно которому неоднородности должны заметно менять параметры вол-
новода на расстоянии, значительно превышающем локальную длину биений.
Мощность назад-распространяющейся моды определяется из выражения
(28.10) при условии, что в формуле (28.10) заменена на j3_j, а в формуле
(28.4) ej на e_j. В слабонаправляющих волноводах продольные поля малы,
и ими можно пренебречь, и поэтому мощность назад-распространяющихся
мод будет значительно меньше мощности вперед-распространяющихся мод.
Подобный вывод можно сделать и в отношении мод излучения, которые бу-
дут рассмотрены далее в этой главе.
В общем случае точные значения постоянных распространения локальных
мод могут быть получены из их характеристического уравнения численными
методами. Однако в ряде случаев можно получить аналитические выражения
для коэффициентов связи, что подтверждает следующий пример.
28.4. Пример. Волоконный световод переменного радиуса со ступенчатым
профилем показателя преломления
Ступенчатый профиль показателя преломления (г, z) световода с переменным радиу-
сом сердцевины можно представить в виде
=Цо {1-2ДЯ[г-р(г)]}, (28.11)
где ступенчатая функция Хевисайда удовлетворяет равенству Н(х} — 1 при х > 0 и
Я(х) — 0 в остальных случаях. Поэтому коэффициент связи, определяемый выраже-
нием (28.4), отличен от нуля только на границе сердцевины с оболочкой. Рассмотрим
два случая.
Слабонаправляющий световод. В этом случае продольными составляющими поля
можно пренебречь, а поперечные составляющие непрерывны на границе сердцевины с
471
оболочкой. Производную от функции профиля в подынтегральном выражении форму-
лы (28.4) представим через 6-функцию Дирака, а именно
— = ^ОД—6Ir-p(z)]- (28.12)
dz dz
Тогда выражение для коэффициента связи имеет вид [4]
с = - (-^-)1/3 Т (etj ’ etl) , dy. (28.13)
СЛ 4 4 (Sj-Л dz Wr = p(z)v
Выражения для ё^ и ёцприведеныв табл. 14.1 и 14.6, в которых р нужно заменить на p(z).
Интеграл по углу в формуле (28.13) содержит произведение тригонометрических функ-
ций, а это означает, что взаимодействуют только моды одинакового порядка. Если те-
перь полученное выражение подставить в формулу (28.10) и потребовать, чтобы выпол-
нялось условие |F| < < 1, то непосредственное вычисление показывает, что критерий
(19.7) применимости метода локальных мод несколько видоизменяется - в этом выра-
жении появляется множитель, описывающий изменение профиля показателя преломле-
ния вдоль световода.
Световоды с произвольной высотой1 профиля. Если Д может принимать любое значе-
ние, то определение величины Сд представляет значительные трудности, поскольку ра-
диальные составляющие поля ё| и ё^ претерпевают разрыв на границе сердцевины с обо-
лочкой. Эту трудность можно обойти, если учесть, что п2ё^ и и2ё^ непрерывны на гра-
нице сердцевины с оболочкой, а тогда подынтегральное выражение в формуле (28.4)
принимает вид
ё? • ё,-^— = (ё*. ё + ё*ё ,)-^- - (и2ё*.) (и2ё J -^-(^-), (28.14а)
J I dz <PJ .zj zl dz rj rl dz
где производная, no z во втором члене правой части может быть представлена аналогич-
но формуле (28.12):
да14б)
Таким образом, Сц определяется выражением (28.13), в котором подынтегральная
функция равна
[ё*.ё . +е*.ё .+ ё*) (-^-е ,)] _ , ч• (28.15)
1 <р] ipl zj zl rj rl r—p(z)
Выражения для ej и приведены в табл. 12.3 и 12.5, в которых необходимо заменить р
на p(z). Поскольку интеграл по углу содержит произведение тригонометрических функ-
ций, то и в этом случае взаимодействуют только моды одинакового порядка v.
28.5. Пример. Скрученный эллиптический волоконный световод
Рассмотрим слабонаправляющий световод с эллиптическим поперечным сечением, за-
крученный вокруг своей оси, как изображено на рис. 19.2. Описание свойств двух ос-
новных мод было дано в разд. 19.4 в рамках теории локальных мод. Предположим, что
в точке z — 0 моды, поляризованные вдоль осей х и у, имеют мощности 1 и 0 соответ-
ственно. поперечные электрические поля etl и ё^ параллельны соответственно большой
и малой осям, и общая постоянная распространения скалярного приближения равна (3.
Слабая связь мод. Если период скрутки достаточно мал, то мевду х- и у-поляризо-
ванными модами наблюдается слабая связь, которую можно рассчитать, используя ме-
тод анализа, изложенного в разд. 28.2. Вначале с помощью формулы (28.3) оценим ко-
эффициент связи С12.
Отличные от нуля составляющие полей двух мод вдоль единичных векторов х и у,
параллельных вращающимся осям х и у, имеют вид
472
ёН=^; et2=^ry; htl=(^),4o^6tf (28.16)
где Ф - фундаментальное решение скалярного волнового уравнения, N — коэффициент
нормировки, выражение для которого приведено в табл. 13.2, z - единичный вектор, па-
раллельный оси волновода; остальные параметры определены в табл. I. На следующем
шаге необходимо связать вращающуюся систему координат с неподвижной. Если х0 и
у0 - единичные векторы, параллельные осям х0 и у0 на рис. 19.2, то
х = х0 cos 0 (z) + у0 sin 0 (z) ; у = у0 cos 0 (z) - х0 sin 0 (z), (28.17)
где угол скрутки 0 (z) связан с периодом скрутки т (z) соотношением
Z
6(z) = jr(z)dz. (28.18)
О
Если теперь формулы (28.16) подставим в (28.3), продифференцируем выражение
(28.17) и вспомним определение нормировки, то получим
C12(z) = --^-(^),/2 J ё = -^(-^)1/22_ / &dA =т(г). (28.19)
2 Мо д u dz 2 Mo N д
QQ /1 QQ
Чтобы вычислить отношение F, определенное формулой (28.10), необходимо знать раз-
ницу между постоянными распространения 0Х = 0 + 60х и 0у = 0 + 60у двух мод, которая
обусловлена поляризационными свойствами эллиптического световода. Следовательно,
локальные, или основные, моды скрученного световода будут распространяться с пре-
небрежимо малой связью при условии, что |F| < < 1. Поскольку постоянные распро-
странения не зависят от z, это условие эквивалентно требованию, чтобы период скрутки
значительно превышал длину биений или чтобы выполнялось неравенство
|т(П|<< |й -0|. (28.20)
Л У
Это соотношение с точностью до множителя 2я идентично интуитивному критерию
(19.9). Напомним, что для световода со ступенчатым профилем показателя преломле-
ния и малым эксцентриситетом эллипса поперечного сечения, разность 0х - /?у определя-
ется формулой (18.25).
Сильная связь Мод. Если период скрутки мал, то между х- и у-поляризованными ло-
кальными модами и полем излучения одномодового световода будет существовать зна-
чительная связь. Для решения задачи теперь необходима полная система уравнений свя-
занных локальных мод, включая моды излучения, и в общем случае получить решение
невозможно. Однако задача становится разрешимой при резонансной связи между двумя
локальными модами. Характерной длиной, на которой происходит передача значитель-
ной доли мощности от одной моды к другой, является половина длины биений тг/ |/Зх -
- 0 |, что соответствует закручиванию световода на угол я/2 на участке световода
7г/2т. Тогда условие резонанса имеет вид
|2т| = |/Jx-Py|. (28.21)
Если это условие выполняется, то можно пренебречь связью между локальными модами
и полем излучения, что позволяет с помощью коэффициента связи, определенного фор-
мулой (28.19), привести уравнения связанных локальных мод (28.2а) к виду
db. db2
-j----= тЬ1’ "л----------i'V2 = ~Tbl ’ (28.22)
dz x dz у
где т, (Зх и /Зу не зависят от z. Исключив из этой системы bt или Ь2, легко получить ре-
шения,' удовлетворяющие начальным условиям Ьг — 1, Ъ2 = 0 (z = 0),
4 73
т ^х т т ^х + ^у
= [cos(— z) + i —z---F sin(—-z)]exp(i ——iz);
г Lt г 2
4-^3
b 2 (z) = -F sin (~ z) exp (i —-z) ;
b 2
p=1/[1+
(28.23а)
(28.236)
(28.23в)
Выражения для мощности каждой моды следуют из формулы (28.5):
Pj (z) - 1 - F2 sin2 (tz/F) ; P2 (z) = F2 sin2 (rz/F) . (28.24)
Таким образом, моды обмениваются мощностью, пропорциональной F2, и длина биений
составляет IixFIt. При выполнении условий резонанса (28.23) F2 = 1/2 и происходит
50 %-я передача мощности. Необходимо подчеркнуть, что решение (28.23) справедливо
только для случая, когда условия резонанса либо выполнены точно, либо расстройка
невелика. При этом перекачка мощности в моды излучения и в назад-распространяющи-
еся моды минимальна.
ЛОКАЛЬНЫЕ МОДЫ ИЗЛУЧЕНИЯ
Уравнения связанных локальных мод, рассмотренные в разд. 28.1, неявно
описывают связь с полем излучения. Оставаясь в рамках концепции локаль-
ных мод, которые описывают поток мощности, направляемой вдоль волно-
водов с медленно меняющимися параметрами, введем в рассмотрение си-
стему локальных мод излучения, которая описывает поле излучения, а сле-
довательно, и мощность, излученную из волновода. Структура полей каждой
локальной моды излучения идентична структуре полей локальных мод, толь-
ко теперь постоянная распространения (3 (Q) непрерывна и не зависит от z.
Таким образом,
Ej(x,^, z) =ё=(х, у, z)exp[i0(£>)z];
(28.25)
Hj (х, У, z) = hj (х, у, z) exp [i (3 (Q) z ],
где ej и hj — ортонормированные поля, определение которых было дано в
разд. 25.4, а их зависимость otz, как это отмечалось в разд. 19.1, обусловле-
на структурой полей в каждом сечении волновода.
Уравнения связанных локальных мод. Введение локальных мод излучения
в разложение (28.1) проводится, как и в случае уравнений связанных мод,
полученных в разд. 31.11. Например, амплитудная и фазовая зависимости
Z>j (zQ) /-й вперед-распространяющейся локальной моды излучения удовлет-
воряют уравнению связанных локальных мод
db
-ii3(e)dj= (28.26)
где в правой части подразумевается интегрирование по параметру £/ осталь-
ных мод излучения, как это сделано в формуле (31.51а). Коэффициент свя-
474
зи Сц(2), зависящий otz, определяется выражением (28.3) либо (28.4), где
0j нужно заменить на /3 (Q).
Полная мощность излучения. Полная мощность излучения вперед-распро-
страняющейся моды определяется выражением, аналогичным формулам
(28.5) и (25.9),
kpnd
?d = 2 J (28.27)
rad j 0 J
Для назад-распространяющейся моды в этом выражении необходимо заме-
нить на Ъ_у
Слабая связь мод. По аналогии с выражением (28.8) решение уравнения
(28.26) в случае слабой связи можно записать в виде
z
b}(Q) =Z>l(O)exp[i/3(e)z] J C.^QjexpfiSihjdz, (28.28)
где 60 определяется формулой (28.86), в которой 0j заменена на 0(0 и
предполагается, что первоначально возбуждена только 7-я локальная мода.
В качестве иллюстрации полученного результата ниже будет рассмотрен
простой пример, а пока отметим следующее. Из рассуждений, приведенных
после формулы (28.86), следует, что этот же результат может быть получен
методом наведенных токов, рассмотренным в разд. 22.10, при условии, что
/-я локальная мода заменяется/-й локальной модой излучения из разд. 22.11.
28.6. Пример. Конусообразный участок световода со ступенчатым профилем
показателя преломления
Рассмотрим конусообразный участок световода (рис. 28.1) со ступенчатым профилем
показателя преломления и предположим, что радиус сердцевины от одного конца кону-
сообразного участка, где он равен фиксированному значению р0, до другого конца
(р^) плавно уменьшается произвольным образом. В первую очередь нас будут интересо-
вать потери на излучение основных локальных мод такого конусообразного участка, од-
нако полученные результаты легко можно обобщить на случай локальных мод высших
порядков. Кроме того, этот пример позволяет оценить точность метода локальных мод.
Рис. 28.1. Нерегулярный участок световода со ступенчатым профилем показателя пре-
ломления с началом в сечении z = 0, где радиус сердцевины равен р0, и концом в сече-
нии z = L, где радиус сердцевины равен pL:
а — угол конусности резко изменяется на его концах; б — нерегулярный участок свето-
вода плавно переходит в световод постоянными параметрами
475
(28.30а)
(28.306)
(28.30в)
Слабая связь мод. Если основную моду и локальную моду излучения обозначить ин-
дексами I и / соответственно и предположить, что первоначально основная мода была
возбуждена с единичной мощностью, то из выражений (28.27) и (28.28) получаем, что
полная мощность, возбужденная в /-й моде,
крпс\ L
Р:= J |G(C)PdC; G(0 = jC(z)exp(i6Fz)dz, (28.29)
J о о
где C(z) обозначает зависящий от z коэффициент (Q). Интеграл G (Q) может быть
оценен асимптотически. Для того чтобы полученные результаты были применимы к обо-
им случаям, изображенным на рис. 28.1, проинтегрируем G(Q) дважды по частям и по-
ложим 6/3 = 5/? (z) = pt (z) - р (Q). В результате получим
G(Q~) = i<?0 + G1 -/exp(iSiSz)
Р az 60 az 60
C(0) C(Z)exp(i50Z)
° “ 60(0) 60 (Z) ;
G = exp(i50Z) d С I _ 1 d С I
1 60(Z) dz (60}|l 60(0) dz(60)lo’
где значение 6/3 в функциях Go и Gx оценивается в точке z = L. Поскольку при медлен-
ном изменении параметров конусообразного участка характерный линейный размер
С/Бр имеет порядок L, то предположив, что ЬБр > > 1, т. е. что длина конусообразного
участка много больше средней длины биений 2я/6/Г, получим, что Gx по порядку величи-
ны в ЬБр раз меньше Go, а интегралом в выражении (28.30а) можно пренебречь, так как
его порядок в (L Бр) 2 раз меньше, чем порядок Go. Из выражения для коэффициента
связи (28.13) следует, что С(0) и С(Ь) отличны от нуля, если конусообразный участок
имеет форму, изображенную на рис. 28.1, а, и поэтому G (Q) достаточно точно аппрокси-
мируется функцией Go. Если же он имеет форму, изображенную на рис. 28.1,6, то
С(0) = С(L) = 0 и Go = 0, а поэтому G (Q) аппроксимируется функцией Gr.
Мощность излучения. Если для простоты предположить, что радиус сердцевины кону-
сообразного участка меняется настолько сильно, что |6/3(Z) I < < |б/3(О) |, то в выраже-
нии (28.306) первым членом можно пренебречь. Подставляя (28.306) в формулу
(28.27), имеем
Т У гг «S-3D
соответственно для конусообразных отрезков, изображенных на рис. 28.1, а и б. Други-
ми словами, излучение в основном происходило вблизи узкого конца конусообразного
участка. Если теперь выражения для коэффициента связи (28.13) подставить в получен-
ные формулы, то окажется, что мощность излучения из конусообразного участка, изо-
браженного на рис. 28..1, а, пропорциональна квадрату угла раствора Конуса в точке z =
= L. Таким образом, если угол раствора конуса постоянен, то мощность излучения
пропорциональна Ь~2, где L - длина конуса. Аналогично этому мощность излучения из
конусообразного участка, представленного на рис. 28.2, 6, зависит от радиуса кривизны
образующей конуса в точке z — L, но в этом случае мощность излучения на порядок
меньше, чем в предыдущем. В обоих случаях интегрирование по Q осложняется зависи-
мостью поля излучения от коэффициента связи, т. е. зависимостью ё; (Q), и количествен-
ная оценка Pj может быть получена только численными методами. 1ем не менее крите-
рий медленного изменения параметров L |/3((?) - pt | < < 1 совпадает с интуитивным
критерием (19.7).
476
СЛОЖНЫЕ ОПТИЧЕСКИЕ ВОЛНОВОДЫ
Связь локальных мод в сложных оптических волноводах, состоящих, напри-
мер, из двух параллельных световодов с медленно меняющимися параметра-
ми, может быть описана в рамках ранее полученных результатов при условии,
что известны локальные поля мод такой сложной системы. В разд. 19.7 был
изложен метод описания этих полей суперпозицией полей локальных мод
каждого световода в отдельности, т. е. при расстоянии между световодами,
стремящемся к бесконечности. Здесь же мы, определив коэффициент связи
между основными локальными модами, исследуем точность такого описания
полей сложного волновода.
28.7. Пример. Конусообразные ответвители
Распространение излучения в конусообразных ответвителях с медленно меняющимися
параметрами (рис. 28.2) может быть описано, как это отмечалось в разд. 19.2, методом
локальных мод. В приближении слабо направляющего волновода фундаментальное ре-
шение Ф+ скалярного волнового уравнения дается формулой (19.14), а второе фунда-
ментальное решение Ф_ определяется аналогично. Тогда
Ф. + Д+Ф2 V Y2 Д1 “ @2
ф± = ; = х=-^- ’ (28‘32)
где и Ф2, 02 - зависящие от z решение и постоянная распространения, соответ-
ствующие локальным модам каждого световода в отдельности, а С - обобщение коэф-
фициента связи, определенного формулой (18.35), на случай его зависимости от про-
дольной координаты z. Если предположить, что профиль показателя преломления кону-
сообразного ответвителя ступенчатый, то разность и - пх отлична от нуля только в серд-
цевине второго конусообразного световода, где п - пх = «со - псу Поскольку п2С0 -
- "с! * 2"со ("со - "ср ’ то имеем
ъ- Ап* е
C(Z) = 4 (_JL) J- 4- *2dA, (28.33)
2 Ло2
a) 5)
Рис. 28.2. Примеры связи:
a — двух световодов с показателем преломления сердцевины и радиусами сердце-
вин (z) и р2 (z) ; показатель преломления оболочки равен ; б— двух» одинаковых
световодов
477
где Лсо2 ~ площадь поперечного сечения сердцевины второго конусообразного светово-
да, N - коэффициент нормировки, выражение для которого приведено в табл. 13.2.
Предположим, что на входе ответвителя, т. е. при z = 0, возбуждена только Ф+-мода с
амплитудой Z>+(0). Амплитуда b_(z) ф_-моды в случае слабой связи определяется
формулой (28.8), в которой индексы / и I необходимо заменить на индексы + и _ со-
ответственно. Тогда выражение для коэффициента связи следует из формулы (28.4),
которую для удобства запишем в виде
с е я /(z)
-+ 4 /?-/?. Mo Nl'2N^2 ’
~ (28.34)
/(z) = _ -L-- f Ф Ф dA,
д«со + “ dz
0+, 7V+ и 0_, N_ - постоянная распространения и коэффициент нормировки для Ф+-
и Ф_-мод соответственно. По аналогии с выражениями (28.12) и (28.13) имеем
tZp? dpi Ът
+1Г I (ф+фЛ2=рЛ” (2835)
где Pj, р2 - радиусы сердцевины в сечении z, азимутальные углы определяются относи-
тельно осей световодов, изображенных на рис. 28.2, а, и г2 - текущие радиусы. Из
формул (28.32) следует соотношение
Ф+ф_ = (Ф? - ^)/(4 + х2) 1/2, (28.36)
из которого видно, что в формуле (28.35) первую подынтегральную функцию можно
аппроксимировать функцией ф^, а вторую - функцией (-Ф^), поскольку х< < 1- Учи-
тывая, что в соответствии с табл. 14.3 = 1 при rv = рг и Ф2 — 1 при г2 = р2, получаем
(4 + х3)*'7(г) = 2я£-(р? -р2) = 2~(АсоХ -Мсо2), (28.37)
где Лсо j обозначает площадь поперечного сечения сердцевины f-го световода. Поскольку
из формулы (18.35) следует, что - (3_ = 2С, то, положив N+ + N2 для слу-
чая достаточно большого расстояния между световодами и подставив формулы (28.33)
и (28.37) в выражение (28.34), имеем
лАЛ я. г ,
С_+= ^=--^-(р’ - р?) / [(4 + хг)1/2 J Ф.МЛ]. (28.38)
м +1У2 dz Лсо2
Мощность Р_(и) в Ф_-моде определяется формулой (28.10), в которой F = С_+/8(3,
где 50 = 2С и С - среднее по всей длине конусообразного участка значение C(z). По-
скольку интегралы в выражениях для С_+ и С уменьшаются экспоненциально с увеличе-
нием расстояния между сердцевинами световодов, то становится ясным, что мощность
Р_ (z) мала только в случае, когда угол раствора конуса мал. Другими словами, при
данном угле раствора конуса поля мод чрезвычайно чувствительны к расстоянию между
световодами, что можно предсказать и на основании результатов разд. 19-9.
28.8. Пример. Одинаковые волоконные световоды
Анализ, проведенный в предыдущем разделе, можно использовать в частном случае та-
ких двух одинаковых световодов, какие изображены на рис. 28.2, б. В каждом сечении
вдоль сложного волновода рх = р2 и 0j = 02. Тогда из формул (28.32) и (28.37) получа-
ем, что х — I(z) • Другими словами, в пределах той точности, которую дает проведенный
анализ, связь с -модой отсутствует. Впрочем этот результат следует из свойств сим-
метрии волновода. Следовательно, связь существует только с локальными модами выс-
ших порядков и модами излучения, свойства симметрии которых подобны свойствам
Ф+-моды.
478
ГЛАВА 29, ПЕРЕКРЕСТНЫЕ ПОМЕХИ
В этой главе мы изучим явление оптических перекрестных помех между дву-
мя или множеством волоконных световодов с цилиндрической симметрией
или с медленным изменением параметров. Перекрестные помехи возникают
вследствие того, что поля мол световода простираются неограниченно далеко
в оболочку и взаимодействуют с полями мод других световодов, которые, в
свою очередь, воздействуют на поля мод исходного. В результате закого вза-
имодействия по мере распространения излучения происходит перекачка мощ-
ности из одною световода в другой и обратно. Доля перекачанной мощности,
или перекрестные помехи, зависит от перекрытия полей двух световодов.
В лучевом представлении перекрестные помехи обусловлены нарушением
полного внутреннего отражения или, что эквивалентно, оптическим туннели-
рованием.
Исследование перекрестных помех представляет интерес с точки зрения
создания оптических ответвителей или переключателей [1]. Кроме того, в
биологических приложениях перекрестные помехи могут также ограничи-
вать максимальную чувствительность фоторецепторов в сетчатке глаза жи-
вотных [2,3].
29.1. Два способа описания перекрестных помех
Описать перекрестные помехи можно двумя способами. В первом случае
определяются непосредственно моды сложного волновода,,а взаимодействие,
например, между модами двух идентичных световодов, приводящее к воз-
никновению перекрестных помех, проявляется в интерференции или биении
полей этих мод. Второй способ заключается в определении мод каждого из
световодов в отдельности, а перекрестные помехи характеризуются коэффи-
циентом связи между этими модами. Поскольку первый способ достаточно
подробно рассматривался в гл. 18 и 19, в этой главе мы уделим основное
внимание второму способу.
Несмотря на то, что анализ перекрестных помех с помощью коэффициента
связи мод отдельных световодов является формально точным*, по причинам,
изложенным в разд. 18.21, мы ограничим рассмотрение анализом слабона-
правляющих световодов, расположенных на достаточно большом расстоянии
друг от друга. Первое ограничение позволяет пренебречь всеми поляриза-
ционными эффектами, обусловленными сложной волноводной структурой,
а второе обеспечивает достаточную точность при простой суперпозиции ре-
шений.
ДВА ПАРАЛЛЕЛЬНЫХ ВОЛОКОННЫХ СВЕТОВОДА
Рассмотрение начнем с исследования случая, когда излучение распространяет-
ся вдоль двух параллельных цилиндрически симметричных волоконных све-
товодов (рис. 29.1), между которыми существует взаимодействие, приводя-
щее к перекрестным помехам, т. е. к перекачке мощности из одного светово-
* Это неверное утверждение. Теория связи мод отдельных световодов принципиаль-
но приближенна. - Прим. ред.
479
Рис. 29.1. Два параллельных световода:
а — световоды с показателями преломления сердцевин пх и и2 и радиусами рг и р2 со-
ответственно, окруженные однородной оболочкой с показателем преломления «с|. Оси
световодов расположены на расстоянии d; б — цилиндрические координаты и
г2, <р2, связанные с осями световодов
да в другой и обратно. Покажем, что перекрестные помехи определяются из
решения двух уравнений связанных мод. Будем предполагать, что сердцеви-
ны световодов окружены оболочкой неограниченной толщины с постоянным
показателем преломления, что достаточно легко достигается на практике
помещением такого сложного волновода в иммерсионную жидкость с пока-
зателем преломления, равным показателю преломления оболочки.
29.2. Вывод уравнений связанных мод
Рассмотрим два волоконных световода, схематически изображенных на
рис. 29.1, с профилями показателя преломления соответственно пх (х, у) и
«2 (х’ У) относительно общей системы координат. Показатель преломления
оболочки равен п^. Для удобства предположим, что каждый из световодов
является одномодовым, а поскольку исследование проводится в приближе-
нии слабонаправляющего волновода, будем рассматривать только основные
моды, поляризованные вдоль оси х. Если и N2 — коэффициенты норми-
ровки из табл. 13.2, то можно записать
Exi (х,у, z) (z)$j (x,y)exp(i^iZ)/N\/2 = bi (z)$i (x, y) /N\12; (29.1a)
Ex2(x, y,z) = a2 (z)<P2 (x,y)exp(i^2z)/M/2 = b2 (z) Ф2 (x, y)/Nl2/2, (29.16)
где вследствие связи между модами их амплитуды зависят от продольной
координаты z. Фундаментальное решение скалярного волнового уравнения
и постоянная распространения 01 и Ф2, З2 для каждого световода в от-
дельности, а также параметры bx(z), b2(z) полностью определяют зависи-
мость поля моды каждого световода от продольной координаты z (знак ~
скалярных величин для ясности опущен).
Предположим теперь, что профиль показателя преломления сложного
волновода определяется функцией п (х, у), т. е. п =пг в сердцевине первого
световода, п = п2 в сердцевине второго световода и п = нс1 в остальных точ-
ках поперечного сечения волновода, и пусть Ф обозначает соответствующее
решение скалярного волнового уравнения. Если второй световод рассматри-
480
вать как элемент, оказывающий возмущающее воздействие на поля мод пер-
вого световода, то уравнение для bx(z) можно получить из формулы (31.49)
подстановкой к = 1 и заменой Еиё* наФи Ф^Л^2 соответственно в пре-
дельном случае слабонаправляющего непоглощающего волновода. Здесь 7Vb
как и ранее, обозначает коэффициент нормировки. Таким образом,
4г -ЧгФ’'1 J (29.2)
1 -/I оо
где Ах ~ бесконечно большая площадь поперечного сечения сложного вол-
новода.
Решение с использованием уравнений связанных мод. Чгобы решить урав-
нение (29.2), необходимо знать функцию Ф, выражение для которой может
быть получено ее разложением по полной системе соответствующих решений
Фj для направляемых мод и мод излучения первого световода. Очевидно,
что такое разложение должно привести к бесконечной системе уравнений
связанных мод, выведенной в разд. 33.11. Недостаток такого подхода заклю-
чается в том, что в отдельности поле каждой моды первого световода являет-
ся плохим приближением поля во втором световоде, и поэтому для удовлет-
ворительной точности необходимо рассматривать большое число мод, что
приводит к практически неразрешимой системе уравнений.
Решение методом суперпозиции. Очевидно, что поля сложного волновода
можно с достаточной точностью аппроксимировать линейной комбинацией
полей основных мод каждого световода в отдельности при условии, что эти
два световода расположены достаточно далеко друг от друга, а параметры их
различаются не слишком сильно. Поэтому решение скалярного волнового
уравнения для сложного волновода можно записать в виде
ф(х,у, z) =bi(z)^1(xfy)/N\/2 + b2(z)$2(x,y)/N\'2. (29.3)
Подставляя это выражение в формулу (29.2), получаем первое уравнение
связанных мод. Второе уравнение можно получить, если рассматривать пер-
вый световод как элемент, возмущающий параметры второго световода.
В результате приходим к следующей системе уравнений [4] :
— i(0i + C11)Z>1 -iCi2b2’,
az
db2 - - _
~^z ~ i (Pz + C22) b2 = iС2фi,
(29.4а)
(29.46)
где Су - коэффициент связи, определяемый выражением
С..=------(—)1Z2 / (и2 -л2)Ф.Ф.<М; /,/=1,2 (29.5)
U 4 (N.N.)12 Лоо г 1 j v 7
й являющийся постоянной, не зависящей от z величиной. Поскольку по пред-
положению световоды расположены достаточно далеко друг от друга, ампли-
16 Зак 37 л Q1
туда Ф* экспоненциально мала в сердцевине световодаа поэтому С12 и С21
значительно меньше и 02. Более того, разность л2 -- л2 является исчезаю-
ще малой величиной в сердцевине световода /, и поэтому коэффициенты пе-
рекрестной связи С12 и С21 значительно больше коэффициентов Сц и С22,
которыми обычно пренебрегают. Отметим, что в принципе коэффициенты
Сц и С22 легко можно учесть, если в системе (29.4) переобозначить 0t и 02,
включив в них соответственно Сп и С22.
29.3. Идентичные и почти идентичные волоконные световоды
Несмотря на то, что коэффициенты связи могут быть очень малы, при выпол-
нении условий резонанса значительная доля полной мощности сложного вол-
новода может перекачиваться между двумя световодами. Если же условия
резонанса не выполняются, то разложение (29.3) становится недействитель-
ным, поскольку в таком случае необходимо учитывать и связь с назад-рас-
пространяющимися основными модами, и связь с полями излучения обоих
световодов. Резонанс наблюдается, когда параметры световодов идентичны
или почти идентичны. Тогда из формулы (29.5) имеем
J (н2 -н2)Ф1Ф2^.
Vo А~
(29.6)
Подставляя это выражение в (19.4) и опуская коэффициенты Си и С22 по
причинам, изложенным выше, исключим из полученной системы или Ь2.
В результате приходим к дифференциальному уравнению второго порядка с
постоянными коэффициентами. Решение, удовлетворяющее граничным усло-
виям bx (z) = Z?i (0) и b2 (z) = b2 (0) при z = 0, можно записать в виде
bi(z) = {й i(0) cos +
+ iF[bi(0) + ~-2d-24>.(0)]sin(y-z)} exp(i0az); (29.7a)
bit?) = { 62(0) cos (-^z) +
+ (0) - — ^-2- b2 (0) ] sin (-^-z)} exp(i)3az), (29.76)
где 0a и F определены выражениями
|За=(^+^)/2; F = l/[l + (0i -j32)W]1/2. (29.8)
Таким образом, амплитуда каждой моды изменяется вдоль световода по си-
нусоидальному закону.
482
Передача мощности между модами. Мощности в каждой моде в соответ-
ствии с формулами (11.22) и (29.1) равны
Pi (z) = |Z>j (z) |2 ; Р2 (z) = |Z>2(z)|2. (29.9)
Подставляя сюда выражения из (29.7), получаем
Рх (z) = Р. (0) + F2 {Р2 (0) - Р, (0) + [Л (0)Р2 (0) ]1/2} sin2 (-^z) ;
(29.10а)
Pi (z) = Pi (0) + F2{Pl (0) - P2 (0) - ~1^-- [Pi (0)P2 (0) ]1/2} sin2 (y-z),
(29.106)
где /\(0) — начальная мощность в i-й моде. Для простоты предполагаем, что
при z = 0 обе моды находятся в фазе и поэтому Ьх (0) и Ь2 (0) являются ве-
щественными величинами. Если на входе с единичной мощностью возбужде-
на только первая мода, т. е. Р{ (0) = 1, Р2 (0) = 0, то [5]
РДг) = 1-F2sin2 (~-z); Р2 (z) = F2 sin2 (-^z).
(29.11)
Таким образом, часть F2 полной мощности перекачивается из одного свето-
вода в другой и обратно на длине биений z^ = lirF/C. Полная перекачка до-
стигается только_в случае двух идентичных световодов и поскольку С значи-
тельно меньше 31 или j32, то для того, чтобы параметр F достигал больших
значений, параметры световодов должны быть фактически одинаковыми.
Если параметры световодов достаточно сильно различаются, то по причинам,
изложенным выше, точность получаемых результатов невелика.
Результаты, полученные в этом разделе, совпадают с результатами разд. 18.13
и 18.20, что подтверждается формулой (18.39) для F = 1 и формулой (18.61)
для случая F < 1, которые были получены из выражений для полей мод
сложного волновода. Кроме того, выражения (29.8) и (29.6), определяющие
соответственно параметры F и С в точности совпадают с формулами (18.57)
и (18.35), если в них положить п2 - п2 2л со (и - п j). Для численной оцен-
ки перекрестных помех рассмотрим ряд примеров.
29.4. Пример. Идентичные волоконные световоды со ступенчатым профилем
показателя преломления
Решение (29.11) зависит только от коэффициента связи, поскольку в идентичных све-
товодах F = 1. В разд. 18.14 было получено выражение для С в случае световодов со
ступенчатыми профилями показателя преломления, и на рис. 29.2, а изображена зависи-
мость нормированного коэффициента связи рС/ (2Д)1/2 от нормированного расстояния
между световодами d/p для различных значений световодного параметра V. Из этих гра-
фиков, например, следует, что длина биений z^ = Т/л/С равна приблизительно 2,8 • 104д,
если V — 2,4, Д = 0,005 и d/p = 4. Отметим, что при данном значении параметра V коэф-
фициент связи растет с уменьшением расстояния между световодами, поскольку увели-
чивается перекрытие полей. При фиксированном расстоянии между световодами коэф-
16*
483
Рис. 29.2. Для волоконных световодов со ступенчатым профилем показателя прелом-
ления:
а — нормированный коэффициент связи (18.42) как функция нормированного пара-
метра d/p в случае двух одинаковых световодов; б — часть мощности, передаваемая
из одного световода в другой в случае, когда радиусы сердцевин световодов различа-
ются на величину 5р
фициент С растет при уменьшении параметра V вследствие все большего проникновения
полей мод в оболочку, окружающую оба световода.
29.5. Пример. Идентичные волоконные световоды с гауссовым профилем по-
казателя преломления
Если каждый световод в отдельности имеет гауссов профиль показателя преломления,
то коэффициент связи можно определить в рамках гауссова приближения для основных
мод, рассмотренного в гл. 15. Для этой цели запишем выражение для профиля показа-
теля преломления сложного волновода в полярной системе координат, изображенной на
рис. 29.1, б, т. е.
"2 ="со{1 -2д[1 - ехр (-^-)-ехр (-—)]}, (29.12)
где р = = р2 - характерный размер поперечного сечения каждого световода. Профиль
п* определяется таким же выражением, но для г2 = °°. Вид подынтегральной функции в
выражении (29.6) наводит на мысль о том, что основной вклад в коэффициент связи
вносит область вблизи оси второго световода, а тогда
(2Д)1/2 ^Рпт €о 00 2п
С=--~--------т^-(—),/2/ / (29.13)
4 /Vi Мо 0 0
где R2 = г2 /р, а V - нормированная частота, одинаковая для обоих световодов. Если
использовать гауссово приближение для полей мод, то выражение для поля Ф2 вблизи
оси г2 следует из формулы (15.2) и из табл. 15.2, а приближенное выражение для поля
вдали от оси первого световода следует из формулы (15.16). В результате имеем
=^-Гехр [-у—-~К0[(К-1)Л]; %=ехр(-------UrD. (29.14)
где R2 — гх /р. Полученные выражения вместе с формулой для коэффициента нормиров-
ки из табл. 15.2 подставим в формулу (29.1’3) и с помощью (37.81) выразим аргумент
функции Ко в системе координат (R2, <р2). Поскольку после интегрирования по <р2 из
всей суммы в (37.81) останется только член с р = 0, то
С= (2Д)1ДГ3^-^хр[ ^-1^ ]К-„[(К-1) ±]G. (29.15а)
V + 1 2 (г + 1) Р
484
Для интеграла G можно получить аналитическое выражение, если использовать соотно-
шение (37.101) :
ОО V+1 1 (V — 1)2
G = p0 [(К - 1)Я2]ехр(-——--/?2)Я2</Я2 = -^хр [А ?--]. (29.156)
0 Z у т 1 Z (J т
И, наконец, заменим Ко асимптотической формой (37.88), поскольку (V - l)d/p » 1,
если световоды достаточно далеко разнесены, и получим окончательное выражение
С = ехр {(К- 1) - -]} (29.16)
dp (К + 1)2 г V +1 Р 1
При V = 2,6; Д = 0,005 и d/p = 4 длина биений составляет 1,7 ° 104д, что примерно в
6 раз больше, чем в случае световодов со ступенчатым профилем показателя преломле-
ния. Такое различие объясняется тем, что несмотря на то, что все параметры световодов
в обоих случаях одинаковые и взаимодействие основных мод рассматривается на часто-
те отсечки второй моды, разность п2 - п2 для гауссова профиля значительно меньше
разности я20 - л2| для ступенчатого профиля показателя преломления.
29.6. Пример. Волоконные световоды со слегка различающимися параметра-
ми и ступенчатыми профилями показателя преломления
Когда показатели преломления и радиусы сердцевин двух световодов, рассмотренных в
разд. 29.4, слегка различаются на величины 8псо и 6р соответственно (см. рис. 29.2, б),
постоянные распространения основных мод уже не будут равными, а будут различаться
на небольшую величину 60 = 0, - 02. Несмотря на то, что такое изменение параметров
световодов вызывает предельно малые изменения конфигурации полей (а это, в свою
очередь, почти не меняет коэффициент связи), даже небольшое отличие 60 от нуля при-
водит к значительному снижению доли перекачиваемой мощности, как это видно из
формул (29.8) и (29.11).
Без потери общности предположим, что показатель преломления и радиус сердцеви-
ны первого световода равны соответственно «со + 6исо и р + 6р. Тогда величина 60
определяется формулами (18.8) при Ьп cj = Ои (18.13а). Если теперь подставить выра-
жение для п из табл. 14.3 и выразить £ через параметр световода V, то после несложных
преобразований получим [5]
1 G2 1 f г IV2 ! (HQ . 8»ср + 2Д К1 (ИО i
Р V (24)1/2 I 1CZ2 К\ (ИО "со К? W Р J
где знак скалярных величин ~ опущен. Из этой^ формулы видно, как, например, ском-
пенсировать увеличение «со уменьшением радиуса, чтобы выровнить йостоянные рас-
пространения мод световодов и тем самым добиться максимальной передачи мощности.
Так, для V = 2,4 с помощью табл. 14.4 находим
6р/р«-(1,4/Д) (бисо/«со). (29.18)
Поскольку в слабонаправляющих световодах Д < < 1, малые изменения показателя
преломления приводят к значительно большему перераспределению мощности, чем та-
кие же в процентном отношении изменения радиуса сердцевины.
В случае изменения только радиуса сердцевины из формул (29-8) и (18.42) получа-
ем, что часть полной мощности, которой обмениваются световоды,
F2 = l/П (jf) lexp(2W-) (-^)2]. (29.19)
1 2я Р Р Р
485
На рис. 29.2, б эта зависимость изображена как функция от 8р/р при различных значени-
ях V й d/p.
29.7, Пример. Волоконные световоды с небольшим поглощением
Рассмотрим теперь случай, когда световоды, составляющие сложный волновод, облада-
ют небольшим поглощением. В этом случае профиль показателя преломления является
комплексной функцией (см. табл. 11.2), а постоянную распространения основной моды
каждого световода в отдельности можно представить в виде
Д. = £ + itfi - 71 = 2(з}. & = 02 + &, 72 = 2(3*, (29.20)
где индексы г и i обозначают вещественную и мнимую части величины, а , 72 - соот-
ветствующие коэффициенты затухания мощности. Связь между световодами с поглоще-
нием описывается системой (29.4), в которой коэффициенты связи (29.5), а также 0аи
F, определяемые решением (29.7) этой системы, являются комплексными величинами.
Если поглощение является доминирующим процессом, то отношение С/F в аргумен-
тах тригонометрических функций в (29.7) -- почти чисто мнимая величина, и поэтому
мощность, прежде чем перейти из одного световода в другой, успеет почти полностью
поглотиться в материале световодов. В другом предельном случае, когда поглощение
настолько мало, что С и F - приблизительно вещественные величины, решение (29.7)
отличается от решения для случая непоглощающих световодов лишь дополнительным
множителем exp [- + &)z/2]. Тогда мощности в каждом световоде при начальных
условиях (0) = 1 иР2 (0) - 0 равны [б]
Л (z) = [1 -Л'2 sin2 (~z) ] ехр (-7 z);
F а
(29.21)
P2(z) = F2sin2 (^-z)exp(-7 z),
г a
где 7a = (7i + 72) /2 - средний для двух световодов коэффициент затухания.
29.8. Пример. Многомодовые световоды
До сих пор в этой главе мы рассматривали взаимодействие основных мод одномодовых
световодов. Однако решение, полученное в разд. 29.3, имеет более общий характер, по-
скольку сильная или резонансная связь может наблюдаться между любой парой соответ-
ствующих мод двух многомодовых световодов с одинаковыми параметрами. Более то-
го, сильная связь возможна, даже если световоды и различные, так как постоянная рас-
пространения, скажем, ТЕ0т-моды одного световода может быть равна или почти рав-
на постоянной распространения НЕ1т-моды другого световода.
Рассмотрим два параллельных слабо направляющих световода с одинаковыми ступен-
чатыми профилями показателя преломления и равными радиусами сердцевин. Пусть
расстояние между осями световодов равно d. Предположим, что один из световодов
возбуждается однородным линейно поляризованным пучком лучей, который фокуси-
руется в центре его сердцевины, так что возбуждаются только НЕ1т-моды. Тогда во
втором световоде за счет связи будут возбуждаться такие же моды. Количественный
анализ показывает, что мощность Р2, возбуждаемая во втором световоде, определяется
выражением [7]
?г(г) = 1 (1 - 2HLL ); L = 2m (_8р_ ,;г Z (_ - 2р (29.22)
/>,(0) 2 L ecndvJp р
где Pj (0) - полная мощность на входе первого световода, V и 0С - световодный пара-
метр и критический угол, определенные в табл. I, 0т - апертурный угол линзы такой,
что 0т < 0С < < 1. Если световоды достаточно длинные, то в них достигается установив-
шееся распределение, при котором в световодах распространяется одинаковая мощ-
4 86
ность. Однако эта длина может оказаться очень большой, если только световоды не рас-
положены очень близко друг к другу. Например, если &с = 0,2, р = 7,5 мкм и V = 150,
то длина переходной области составляет около 1 м в случае соприкасающихся светово-
дов (J — 2р) и превышает 100 м, когда d — 2,04р. Кроме того, если радиусы сердцевин
световодов различаются всего лишь на 0,1 %, то перекачивается лишь пренебрежимо ма-
лая доля мощности.
ДВА ВОЛОКОННЫХ СВЕТОВОДА С МЕДЛЕННО МЕНЯЮЩИМИСЯ ПАРАМЕТРАМИ
Чтобы анализ перекрестных помех между двумя цилиндрически симметрич-
ными световодами был полным, рассмотрим пару световодов, параметры ко-
торых медленно меняются вдоль их длины, например, так, как это изображе-
но на рис. 19.3, а для случая одинаковых световодов и на рис. 19.4, а для слу-
чая конусообразного ответвителя. Распространение излучения в такой систе-
ме рассматривалось в гл. 19 с помощью локальных мод сложного волновода.
Целью данной части главы является описание перекрестных помех, возника-
ющих вследствие связи локальных мод каждого световода. Причем в этом
случае поля локальных мод определяются для каждого световода отдельно.
29.9. Уравнения связанных мод
Если параметры световодов меняются достаточно медленно, то поля мод
каждого из световодов в отдельности можно аппроксимировать полями ло-
кальных мод, рассмотренными в разд. 9.1, а перекрестные помехи определя-
ются коэффициентом связи между этими локальными модами. Для удобства,
как и ранее, будем предполагать, что световоды слабонаправляющие, одно-
модовые и расположены достаточно далеко друг от друга. По аналогии с
формулой (29.1) имеем
_ __ Z _
£'х1 = д1(г)Ф1 [х, у, (z)]exp[ij|31 {z)dz]INx(zY12 = Z>i GO'I'i/M СО1/2;
° (29.23a)
_ _ z „
£x2 = a2 (z) % [x, y, & (z) ] exp[i / Pi (0*1 /М (z)1/2 = b2 (O % l^i(01/2,
° (29.236)
где Pt и j32 медленно меняются вдоль осей световодов.
Уравнения связанных локальных мод из разд. 31.14 описывают взаимо-
действие между локальными модами одного и того же световода и поэтому
неприменимы для описания взаимодействия между модами двух разных све-
товодов по причинам, изложенным в разд. 29.2. Для решения поставленной
задачи обобщим вывод уравнений связанных мод (29.4) на случай светово-
дов с медленно меняющимися параметрами. В результате получим [8]
dh.
— - ipi(z)bi = iC(z)b2;
-iP2(z)b2 =iC(z)di,
(29.24а)
(29.246)
487
где bi и b2 определены формулой (29.23), a C(z) является обобщением фор-
мулы (29.6) на случай, когда Nifn, п, 4^ и Ф2 зависят от z. Отметим также,
что по причинам, изложенным в конце разд. 29.2, параметры связи Сц и С22
опущены.
29.10. Решение уравнений связанных мод
Прежде чем приступить к решению системы (29.24), заметим, что из физи-
ческих соображений следует, что распространение волны в сложной структу-
ре должно происходить со средней локальной фазовой скоростью. Поэтому
решение будем искать в виде
: Z „ _
Z»j(z) =£j(z)exp[^ J (0t + (J2)dz], (29.25)
J j z 0
где j = 1 или 2. Подставляя это решение в систему (29.24), получаем
dgl . 02~01 dg2 .02-0!
IT + 1~T~gl = iCg2; ~dT =lCgi- (29-26)
Исключая из этой системы функцию g2, приходим к следующему дифферен-
циальному уравнению:
dz2 dz dz *• 2 c dz^ C 4
(29.27)
Поскольку параметры световодов меняются медленно, производные от по-
стоянных распространения 31, З2 и от параметра С малы по сравнению с
остальными членами и их можно опустить. Тогда gi является решением гар-
монического уравнения
^-+^-^,=0; F=i/[1UI^A)2 (29.28)
где F и, следовательно, С/F являются медленно меняющимися функциями z.
Решение этого уравнения, полученное методом ВКБ, можно записать в виде
gl =P+(Z)I + p_(z)d_-
(29.29)
I+ =exp(± ij -£dz),
где p+ ир_ — произвольные, медленно меняющиеся функции z. Соответству-
ющие выражения для Ьх и Ь2 следуют из формул (29.25) и (29.24). Опуская
производные от р+ и р_, получаем
bi = (p+I+ + р_1_)1а; Ь2 = (а+Р+1+ + а_р_1_)1„ (29.30)
где медленно меняющиеся функции а+, а__ и интеграл определяются соотно-
шениями
Мг) = ~±4; Л = ехр4/(02 +0i)dz), (29.31)
ZC/ d о
которые справедливы для любого поперечного сечения сложного волновода.
488
Сохранение мощности. Решение (29.30) должно удовлетворять требова-
нию сохранения неизменной полной мощности локальных мод Рх (z) + Л(2)
вдоль световода. Подставляя формулу (29.30) в (29.9), получаем функцио-
нальные зависимости для р+ и р_:
p+(Z)=5+/[l+<(z)]1/2; p_(z)=5_/[l+a2_(Z)]1/2, (29.32)
где В+ и В_ — постоянные величины, не зависящие от z. Отсюда получаем
окончательно
&1(Z) ’ [ (1+а2)1'2 Л + (1 + <?)1/2 7-Ка;
я ,В, а_В_ , т
b2(Z) = [ (1+а2)1/2 Ц + (1+а2_)1/2 С] а’
(29.33а)
(29.336)
где 1± и Za определены формулами (29.29) и (29.31). Выражение для мощно-
сти в каждом световоде следует из формулы (29.9), а именно
В2 В2 2В В z С
Pi~ 1 +а2 + 1 + а2__ + (1 + а2)1/2(1 + a2_)i/2 C°S(2 ’ (2934а)
а2 В2. а2 В2 2В.В 2 С
+Т^- cos(2J^). (29.346)
При выводе этих выражений учитывалось, что в соответствии с соотношения-
ми (29.28) и (29.21) а+а_ = —1. Кроме того, для удобства предполагалось,
что при z = 0 моды имели одинаковые фазы, так что В+ и В_ являются ве-
щественными величинами.
29.11. Пример. Идентичные волоконные световоды
Если два световода с медленно меняющимися параметрами идентичны, как, например,
изображено на рис. 19.3, а, то = j32,a из формул (29.28) и (29.31) следует, что F = 1 и
а± = ± 1. Из решения (29.33), удовлетворяющего граничным условиям £х(0) = 1 и
Ь2 (0) = 0, вытекает, что В+ = В_ = 1 / %/ 2, а тогда из выражения (29.34) имеем [8]
z Z
P,(z) = cos2 [$C(z)dz] ; P2(z) = sin2 [ JC(z)dz].
о 0
(29.35)
Эти выражения в точности совпадают с результатами, полученными в разд. 19.6 мето-
дом локальных мод.
29.12. Пример. Конусообразные ответвители
Рассмотрим такой конусообразный ответвитель, какой изображен на рис. 19.4, а, и пред-
положим, что вначале возбуждена только мода первого световода, т. е. bl(0) = 1 и
^з(О) = 0. Решение (29.34) можно упростить, если предположить, что световоды доста-
489
точно хорошо оптически изолированы, т. е. >> |С|, |& | >> С. Кроме того, будем
предполагать, что параметры световодов достаточно сильно различаются, так что » Д2
при z = 0. Тогда из формул (29.28) и (29.31) получаем, что F * 0,я+ » 0и |я_| >> 1,
а это позволяет записать начальные условия в виде
^(0) р2(0)
(29.36)
Распределение мощности между двумя световодами по длине ответвителя следует из
формулы (29.34) :
1 а+
Л(2)= Pdz}= --— = 1-^(2).
1 + а\ 1 + а2.
(29.37)
В центральной части ответвителя, где параметры световодов практически одинаковые,
F *а+ « 1 и в каждом световоде распространяется половина полной мощности. В кон-
це ответвителя при z — L параметры второго световода соответствуют параметрам пер-
вого световода при z = 0 и наоборот, поэтому 02 » . В этом случае F » 0 и >> 1,
так что формула (29.37) сводится к выражениям РХ(Л) 0, Р2(£) « 1. Другими слова-
ми, вся мощность, первоначально распространявшаяся по первому световоду, перешла
во второй. Этот же результат был получен в разд. 19.7 при анализе таких ответвителей
методом локальных мод.
ПУЧКИ СВЕТОВОДОВ
Если произвольное число параллельных одномодовых световодов образует
пучок, то для описания перекрестных помех требуется система связанных
уравнений. Число уравнений равно числу элементов, поскольку для каждого
световода требуется одно уравнение, описывающее связь поля основной мо-
ды этого световода с полями основных мод других. Даже если предполагать,
что обмен мощностями происходит главным образом между основными мо-
дами, то в общем случае систему уравнений связанных мод решить чрезвы-
чайно сложно. Однако в ряде частных случаев, представляющих практичес-
кий интерес, симметрия пучка световодов в совокупности с симметрией
входного излучения позволяет описать перекрестные помехи двумя связан-
ными уравнениями, которые аналогичны уравнениям, исследованным в
разд. 29.2 и 29.9. Поэтому решение уравнений связанных мод для случая
двух параллельных световодов с цилиндрической симметрией или с медлен-
ным изменением параметров является основой для исследования более слож-
ных случаев. Для иллюстрации этой идеи рассмотрим несколько примеров.
29.13. Пример. Периодическое возбуждение пучка, состоящего из неограни-
ченного числа световодов
Рассмотрим пучок, состоящий из неограниченного числа одномодовых световодов с
одинаковыми параметрами, которые расположены в пространстве регулярным образом.
Предположим, что световоды являются слабонаправляющими, а в остальном на форму
профиля показателя преломления не накладывается никаких ограничений. Предполо-
жим также, что на входе пучка (z = 0) разные световоды возбуждены с мощностями
490
Рис. 29.3. Пучки, состоящие из неограниченного числа световодов, периодически воз-
буждаемых мощностями: Рх (0) и Р2 (0) (”+”и ”-”):
а — одномерные; б — из чередующихся столбцов; в — гексагональные; г — имеющие
шахматную структуру
РДО) или Р2(0) < Pj(O) как иллюстрирует рис. 29.3, где знаки + и - относятся соот-
ветственно к Рг и Р2. Под периодическим возбуждением понимается такое, когда ам-
плитуды bx(z} и b2(z) полей основных мод в выражении (29.1) равны у всех световодов,
возбужденных мощностями РДО) и Р2(0) соответственно, т. е. bx(z} относится к каж-
дому световоду, помеченному знаком b2(z) - к каждому световоду, помеченному
знаком
Если теперь предположить, что световоды расположены достаточно далеко друг от
друга, так что необходимо учитывать связь только между близлежащими элементами,
то определить амплитуды мод очень просто. Связь между близлежащими световодами
означает, что взаимодействуют лишь элементы с разными начальными мощностями воз-
буждения, поскольку у элементов с одинаковыми начальными мощностями моды не
взаимодействуют. Следовательно, решение для bx(z) и b2(z) определяется формулой
(29.7), в которой = /32 = 0, т. е. F = 1, 0а = 0, а коэффициент С теперь заменяется
взвешенным коэффициентом связи, учитывающим все близлежащие световоды, кото-
рые взаимодействуют с данным (например, на рис. 29.3 следует учитывать число плю-
сов, соседствующих с каждым минусом). Если под C(d} понимать коэффициент связи
между двумя световодами, оси которых расположены на расстоянии d друг от друга,
то соответствующий взвешенный коэффициент связи D для каждого случая, изображен-
ного на рис. 29.3, равен
a) 2C(d); б) 2C(d) + 4С( y/bd); в) 4С(<7); г) 4C(d). (29.38)
491
Теперь становится понятно, что связь между одним световодом и всеми остальными све-
товодами пучка может быть описана одной парой уравнений связанных мод, включаю-
щей взвешенный коэффициент связи и являющейся обобщением системы (29.38). От-
метим, что приближение взаимодействия близлежащих световодов является весьма
точным и может быть использовано в целом ряде задач.
Мощность, переносимая каждым световодом. Мощность в световоде, помеченном
знаком ”+” или определяется формулой (29.10), в которой =' {32, F = 1 и С =
= D, т. е.
Р, (Z) = Р, (0) cos2 (Dz) + Р2 (б) sin2 (Dz) ;
Р2 (z) = Р, (0) sin2 (Dz) + Р2 (0) cos2 (Dz).
(29.39а)
(29.396)
Значения коэффициента D, приведенные в формуле (29.38), показывают, что в пучке
световодов перекрестные помехи больше, нежели в случае двух световодов при одном
и том же расстоянии между ними. Кроме того, поскольку длина биений обратно пропор-
циональна D, максимальная передача мощности в пучках происходит на более коротких
расстояниях, чем в случае двух световодов.
29.14. Пример. Поглощение в пучке, состоящем из неограниченного числа
световодов
В добавление к перекрестным помехам рассмотрим эффекты, к которым приводит по-
глощение в световодах, составляющих пучок. Эта проблема интересна с точки зрения ис-
следования механизмов зрения животных, поскольку у многих из них фоторецепторы
представляют собой световоды, в большинстве случаев одномодовые и слабонаправля-
ющие [2, 3]. Информация о зашифрованном на фоторецепторах изображении содержит
распределение поглощенного света по поперечному сечению пучка. В этом разделе мы
рассмотрим, каким образом перекрестные помехи ухудшают качество изображения, ес-
ли фоторецепторы возбуждаются так, как показано на рис. 29.3.
Предположим, что коэффициент поглощения а одинаков для всех световодов в пуч-
ке и не зависит от продольной координаты. В этом случае, как показано в разд. 18.8, в
каждом световоде у = а, где у - коэффициент затухания мощности. Тогда по аналогии
с формулой (29.21) мощность в каждом световоде равна произведениюРу (z) или P2(z),
заданных формулой (29-39), на ехр (-az). Определим Р+ (z) и Р_ (z) как мощности, по-
глощенные на отрезке световодов длиной z, которые первоначально были возбуждены
мощностями Pi (0) (знак ”+”) и Р2(0) (знак ”—”) соответственно. Если перекрестные
помехи отсутствуют, то Р+ (z) — (0) и Р_ (z) — Р2 (0) при z — «>, т. е. каждый световод
пучка будет поглощать всю начальную мощность. Ситуация меняется, когда имеются пе-
рекрестные помехи. Если определить нормированную разность поглощенных мощно-
стей как
6N(z) = [Р+ (z) - Р_ (z) ] / [Р, (0) - Р2 (0) ], (29.40)
то при отсутствии перекрестных помех 67V (z) -► 1 при z ->«». Чтобы определить, как из-
меняется 8N при наличии связи между световодами, рассмотрим изменение мощности
на малой длине пучка dz. В соответствии с формулами (11.62) из табл. 11.2 и 13.2 по-
лучаем
с?Р+ (z) - dP_ (z) = а [Р, (z) - Р2 (z) ] ехр (-az)dz, (29.41)
поскольку по предположению иг «nCQ. Тогда на длине пучка L
SN(L) = Р?(0) -Р2(0) [ [P,(Z) -^Vl^-^z.
(29.42)
492
Подставляя сюда выражение (29.39) и учитывая (37.114), находим
6N(L) = {1 - [cos(2DZ) - ^sin (2D£) ] exp (-а£)} , (29.43)
где параметр D определен формулой (29.38), а отношение ID/а пропорционально от-
ношению длины участка 1/а, на котором происходит поглощение, к длине биений TnlD.
Из выражения (29.43) получаем, что при произвольном отношении 2D/a 8N(L) -*1/(1 +
+ 4D2 /а2) при L -* °°. В то же время если длинам конечна и длина участка, на котором
происходит поглощение, значительно превышает длину биений, т. е. если 2D/'a >> 1, то
ухудшение качества изображения, обусловленное перекрестными помехами, может
быть значительным.
29.15. Пример. Возбуждение одного световода в пучке, состоящем из неогра-
ниченного числа одномодовых световодов
Рассмотрим плоский пучок, состоящий из неограниченного числа одинаковых одномо-
довых слабонаправляющих световодов. Пронумеруем световоды индексами п = —°°,...
. . . , -1, 0, 1, . . . , как показано на рис. 29.4, а. Предположим, что световод, располо-
женный в центре (п = 0), возбуждается на входе (z = 0) единичной мощностью. По-
скольку световод одномодовый, его основная мода будет взаимодействовать с основ-
ными модами соседних световодов с индексами п = ± 1. Моды этих двух световодов
взаимодействуют с модами соседних, т. е. имеющих индексы п = ±2ии = 0и так далее.
В результате мощность, первоначально возбужденная в центральном световоде, распре-
деляется по все возрастающему числу световодов.
Чтобы промоделировать такой процесс, предположим, что взаимодействуют только
близлежащие световоды, а потери на излучение учитывать не будем. Такую ситуацию
описывают уравнения связанных мод для каждого световода, в которые входят ампли-
туда основной моды и-го световода и соответствующие амплитуды Z?n _ j (z) и + j (z)
Рис. 29.4. Одномерный пучок с бесконечным числом световодов, обозначенных индек-
сом и, с расстоянием d между осями (а). Примерами многомодовых пучков с конеч-
ным числом световодов являются пучки, в которых сердцевины световодов образуют
правильный треугольник (б) или правильный шестиугольник (в). Центральный свето-
вод может отличаться от окружающих световодов; расстояние между осями централь-
ного и окружающих световодов равно d
493
световодов с номерами п - 1 и п + 1 соответственно, где Z?n(z) определяется по аналогии
с формулой (29.1). Если коэффициент связи между модами соседних световодов обо-
значить С, то в соответствии с выражением (29.6) имеем [9]
-i^n = iC(*n_1+&n+1), -оо<„<оо,
(29.44)
где <3 - постоянная распространения основной моды, коэффициенты Сп и С12 опущены
и из соображений симметрии Z?_n = £п- Отметим, что это уравнение является обобщени-
ем уравнения (29.4а) на случай взаимодействия мод соседних световодов. Если уравне-
ния (29.44) записать в несколько ином виде
2 d^Cz\ [rI1ftn exP(-^z)] = [i-(n~ iexP(—i^z)] ~ [i“(n+1)Z> exp(-i/3z)]
(29.45)
и сравнить с рекуррентным соотношением (37-72), то легко увидеть, что решение, удов-
летворяющее начальным условиям до(0) = 1 и Z>n(0) = 0, п Ф 0, имеет вид
6n (z) = in4 (2Cz) exp (i0z), (29.46)
где /п - функция Бесселя первого рода. Мощность Pn (z) в каждом световоде следует
из формулы (29.9), т. е.
PnU) =7n(2Cz).
(29.47)
При больших z мощность в каждом световоде обратно пропорциональна его длине, что
следует из асимптотического разложения функций Бесселя (37.87).
29.16. Пример. Многоугольный пучок, состоящий из конечного числа
световодов
Рассмотрим теперь распространение излучения в пучках, состоящих из конечного числа
слабонаправляющих одномодовых световодов. Предположим, что световоды располо-
жены таким образом, что составляют правильный многоугольник, причем световоды,
расположенные в вершинах многоугольника, одинаковые, а центральный световод мо-
жет быть произвольным. В качестве примера на рис. 29.4, ^изображен пример треуголь-
ного расположения световодов, а на рис. 29.4, в - шестиугольного. В случае произволь-
ного возбуждения световодов описать взаимодействие всех пар очень сложно. Однако
если поля световодов, окружающих центральный, рассматривать как единое целое, то
распространение излучения в таком пучке можно описать двумя уравнениями связан-
ных мод, подобными системе (29.4) [4,5].
При рассмотрении будем учитывать только связь между близлежащими световода-
ми, а потерями на излучение пренебрежем. Центральный световод обозначим индексом
О, а окружающие его - индексами 1, 2, . . . , п. Расстояние между осями центрального
и соседних с ним световодов равно d. По аналогии с формулой (29.1) амплитуду поля
и-го световода обозначим bn(z). Обобщая уравнение (29.4а) на случай взаимодействия
мод центрального и соседних световодов, получаем
, — by
dz j.= i J
(29.48)
494
где р0 - постоянная распространения основной моды центрального световода, а С01 —
коэффициент связи между центральным световодом и любым из окружающих его, опре-
деляемый по формуле (29.6). Для каждого из окружающих световодов необходимо
учитывать связь с соседними световодами и с центральным:
—L = + iC01&0 (29.49)
uZ J J J 1
для / = 1, 2, . . . , и, где C12 - коэффициент связи между соседними окружающими све-
товодами, — постоянная распространения основной моды. Заметим, что + 1
при j = п и Z?j _ । -> Z?n при /=1. Следующим шагом решения является суммирование
выражения (29.49) по всем /. В результате получаем
d п п
eH-i/3,) S ft: = 2iC12 S ft+i«C01ft0- (29.50)
dz /=1J j=l J
Это выражение справедливо при п > 3. При п = 2 центральный и окружающие его све-
товоды являются коллинеарными, и поэтому связь между внешними световодами пре-
небрежимо мала. Далее, проводя замену переменных
1 п
а0 ~ = /2<?01 j $2 = @1 + ,
П j = 1 J 11
(29.51)
приходим к уравнениям
-i0ofto =iCa0; -i02a2 = iCbQ, (29.52)
az az
решение которых дают формулы (29.7) в соответствующих обозначениях.
Симметричное возбуждение. В частном случае, когда поля всех окружающих свето-
водов возбуждены с одинаковой амплитудой, то Ъг = Ь2 = ... = Ьп и мощность в цент-
ральном световодеР0(2), и полная мощность ?! (z) в окружающих световодах определя-
ются формулой (29.10), где
F= 1/[1+ (0О -0, -2С,2)г/4С2]‘п.
(29.53)
Следовательно, для обмена значительной частью мощности между центральным и окру-
жающими световодами необходимо, чтобы их параметры различались так, чтобы р0 =
= Pi + 2С12. Поскольку С12 является весьма малой величиной, даже небольшое различие
между параметрами световодов приводит к значительному перераспределению мощности.
ЧАСТЬ III. ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ
ВВЕДЕНИЕ
В ч. I и II сделана попытка (там, где это оказалось возможным) провести фи-
зический анализ так, чтобы обеспечить понимание основных явлений. Этому
способствовало также большое число простых рабочих примеров. В ч. III мы
дополним этот подход более строгим математическим обоснованием. Эта
часть включает, кроме того, важный сопутствующий материал, необходимый
для развития идей, изложенных в предыдущих главах.
ГЛАВА 30. УРАВНЕНИЯ МАКСВЕЛЛА
В этой главе приводятся основные уравнения электромагнитного поля для
анализа оптических волноводов. Из этих уравнений выводятся элементарные
свойства полей. Представленный материал используется на всем протяжении
ч. II и III, хотя в основном он применяется в гл. 11, где обсуждались свойства
направляемых мод.
Пространственная зависимость векторов электрического Е(х, у, z) и маг-
нитного Н(х, у, z) полей световода определяется уравнениями Максвелла.
Мы подразумеваем, что у векторов поля, плотности тока J и заряда о суще-
ствует временная зависимость ехр(—iatf). Диэлектрическая проницаемость
е(х, у, z) связана с показателем преломления п(х, у, z) соотношением е =
= п2 е0, где е0 — диэлектрическая проницаемость в свободном пространстве.
Для немагнитных материалов, из которых обычно изготавливаются светово-
ды, магнитная проницаемость р практически равна своему значению д0 в
свободном пространстве. Таким образом, на протяжении всей книги мы по-
лагаем р - р0, если нет специальных оговорок. При этом уравнения Максвел-
ла в единицах рационализованной системы MKS принимают вид [ 1 ]
V х Е = Цдо/^о) 1/2&Н; VxH= J - i(eQ/pQ')1/2 kn2 Е; (30.1а)
V • (и2 Е) = а/е0; V • Н = 0, (30.16)
где к = 2я/Х — волновое число и X — длина волны света в свободном про-
странстве. Соотношения между п, к, е0, Ро и другими электромагнитными
величинами даны в табл. I.
В областях, свободных от сторонних зарядов и токов, на границах разде-
ла сред с разными показателями преломления поля' удовлетворяют следую-
щим граничным условиям: 1) непрерывность магнитного поля и тангенци-
альных к поверхности раздела составляющих электрического поля; 2) не-
прерывность нормальной к поверхности раздела составляющей вектора элек-
трической индукции еои2Е.
496
30.1. П()ля трансляционно-инвариантных волноводов
Если профиль показателя преломления волновода не меняется с расстоянием
z вдоль волновода, т. е. и = п (х, у), то волновод является трансляционно-ин-
вариантным. Электрическое и магнитное поля в таком волноводе описыва-
ются суперпозицией полей с разделяющимися переменными [2] вида
Е (х, X z) = е (х, у) ехр (i/3z) ; Н (х, у, z) = 11 (х, у) ехр (ij3z), (30.2)
где (3 — постоянная распространения, а оси ориентированы, как показано на
рис. 11.1, а. Соответствующие выражения в цилиндрических координатах, по-
казанных на рис. 12.3, имеют вид
Е (г, <р, z) = е (г, ехр (i(3z) ; Н (rf <р, z) =h (г, <р) ехр (ifiz). (30.3)
Разложим эти поля на продольные и поперечные составляющие, соответ-
ственно параллельные и ортогональные к оси волновода, которые обозначим
индексами z и t:
Е = (et + ezz)ехр(i)3z) ; Н = (ht + hz£) exp(i|3z), (30.4)
где z — единичный вектор, параллельный оси волновода.
30.2. Соотношения между составляющими полей
Если мы подставим выражения (30.4) в уравнения Максвелла для полей без
источников, г. е. в уравнения (30.1) при J = 0, о = 0, и сравним продольные и
поперечные составляющие, то в результате получим
е =-(Мо/ео)1/2уХ zx {j3h + iV Л } ; 1 кгг 1 1 z (30.5a)
ht = (ео/Мо)1/2 z х {0et + iV^} ; (30.56)
ez =i(Mo/eo),/2-^r z • V x ht = i {vt ’ et + (et • Vt)lnn2 } ; КП L p (30.5b)
hz = —i(e0/g0)1/2 z- Vtxet =-|vt • hv (3O.5r)
где п = и(х, у) и к = 2тт/\. Векторные операторы определены в табл. 30.1, а
векторные тождества приводятся в разд. 37.2.
497
Таблица ЗОЛ. Векторные и скалярные операторы
¥ = ф(х, y)exp(iflz) А = а(х, y)exp(i0z)
V-A = Vt-At + iJ?4I
-5* Vt¥ = X—+ У-- дх dv = г—+^- — dr г or V -А + ‘ 1 Зх Зу 15 1 8А^
V2T = 7(2Т_^24< Vx А = Vtx At 4- ipi х А1 - i х Vt Лх
, а2^ з2у¥ V2T = -г-г + ч-т * Зх2 ду2 1 з ( а'Р) 1 а2* г дг ( dr j г2 д¥2 ЛЗА, ЗАЖ] VtxA, = i-^--^ ( дх ду J л f 1 д 1 дАг 1 = z<- —(гЛф) — — > (г дг г д^ )
Примечание. Даны разложения векторных и скалярных операторов на попереч-
ную и продольную составляющие, где Ф и А — некоторые произвольные скалярная
и векторная функции. Единичные векторы х, у, z, г и параллельны координатным
направлениям, приведенным на рис. 12.3.
30.3. Представление поперечных полей через продольные поля
Исключив et или ht из уравнений (30.5а) и (30.56), мы можем выразить по-
перечные поля через продольные [2]
е‘ = “ (Мо/ео) ткг х ;
^/v Г1 -- р J { J
ht = ~(PV-p2) + (ео/до)1/2кп2 i х Vtez|,
(30.6а)
(30.66)
где п = п (х, у) п к = 2я/Х. Эти выражения были особенно полезны при получе-
нии полей мод волновода со ступенчатым профилем показателя преломления
в гл. 12 и 25, когда волновое число связано с параметрами мод соотноше-
ниями
г к2п2С0 - Р2 = ЦЪ/р2 (сердцевина), (30.7а)
п2к2 — р2 = <
к2п2! — р2 = — W2!p2 (отражающая оболочка), (30.76)
где исо и ис1 — показатели преломления сердцевины и оболочки соответ-
ственно.
Планарные волноводы. Декартовы составляющие соотношений (30.6) для
планарных волноводов с профилем показателя преломления п (х) равны
е = -1 + (Цо_\ 1/2 е =— - f-^-0-)1/2 A? t
ех р1(^дГ+(е0) к ду J’ еу Р W Kdxi’
(30.8а)
498
h =1 (- c^-)1/2 h = Д + c^-)1/2 ^244>
X p (p dx v Mo dy J У P Ip dy Mo 7 dx J
(30.86)
где p = k2n2 — (32 и n = n (x).
Круглые волоконные световоды. Радиальная и азимутальная составля-
ющие уравнения (30.6) для круглых волоконных световодов с профилем
показателя преломления п (г) имеют вид
= .i,Мо_)1/2 к I
г Р 1 i^dT 1 ео > Г д<р ) 'О
h r^i/2— — I; h
Zr P Г dr ('Po) r d<p j ч>
_ i J P de7 _ »q , 1/2 dhz 1
“ p ( r ' e0 ' dr у
(30.9a)
= 1 p + (^L)
P (r dtp vMo dr J
(30.96)
где p = k2n2 -132 и n = n (r).
30.4. Поля непоглощающих волноводов
Поля волновода могут быть произвольно нормированы, при этом, вообще
говоря, е и h комплексные. Однако для волновода без потерь показатель
преломления веществен, и уравнениям (30.5) не противоречит возможность
выбора е и h так, чтобы либо их поперечные составляющие были веществен-
ными, а продольные — мнимыми, либо поперечные составляющие — мнимы-
ми, а продольные — вещественными. В этой книге мы примем первую из ука-
занных возможностей, так что
et, ht — вещественные, ez, 7zz — мнимые величины (30.10)
Поля же Е и Н уравнения (30.4) не подчиняются этому соглашению.
30.5. Вперед- и назад-распространяющиеся поля
Когда постоянная распространения (3 положительна, волны в волноводе рас-
пространяются в положительном направлении z, указанном на рис. 11.1, я.
Вперед- и назад-распространяющиеся волны просто преобразуются друг в
друга при замене /3 —/3. Если мы обозначим прямое и обратное направления
индексами ”+” и ” соответственно, то из уравнения (30.5) можно заклю-
чить, что имеются две возможности:
e~=-e^+^zi; h~=h^—^Zz; (30.11а)
или
е =e*-e^z; h = -h * + h \ i.
(30.116)
Будем использовать везде последнее соотношение. Для волноводов без по-
терь справедливы оба соотношения (30.10) и (30.116), так что комбинируя
их, мы получаем
е~ = (е+)*, h~ = (-h+)*, (30.12)
где символ * обозначает комплексное сопряжение.
499
ВЕКТОРНЫЕ ВОЛНОВЫЕ УРАВНЕНИЯ
Исключив электрическое или магнитное поле из уравнений Максвелла (30.1а),
мы получим неоднородные векторные волновые уравнения
{V2 + Л1 }Е = -V(Et -Vtlnn2) -i(-g-)1/2{*J+^V(^!)| ; (30.13а)
{V2 + п2к2} Н = (V х Н) х Vt In п2 - V х J - J х Vt In п2, (30.136)
где п = п(х, у), к = 2тг/Х и оператор V2 определен в уравнении (37.30). Под-
черкнем, что здесь V2 - векторный оператор, и его не надо путать со скаляр-
ным оператором V2. Если скалярные составляющие векторов Е и Н соотне-
сены с направлениями, определяемыми некоторой системой координат, то
V2 связывает составляющие так, как, например, в приведенных ниже соот-
ношениях (30.15) в случае цилиндрических полярных координат.
Когда источники отсутствуют, т. е. J = 0, поля с разделяющимися перемен-
ными вида (30.4) удовлетворяют однородным векторным уравнениям
{у2 + п2к2 - р2} е = ~(Vt + ij3z)et • Vt In n2; (30.14a)
{V2 + n2k2 - /32 }h = {(Vt + i0z)x h} x Vt In n2, (30.146)
где n = n(x, у), к = 27г/Х, а векторный оператор определяется соотношени-
ем (37.70).
Круглые волоконные световоды. Радиальные, азимутальные и продольные
составляющие уравнений (30.14), определенные цилиндрическими полярны-
ми координатами г, р, z на рис. 12.3, так что е = (ет, е , ez), h = (7?г, h , hz)9
в случае симметричного профиля показателя преломления и = и(г) имеют вид
Vfc - 2 def д_{ г2 др dr е г J Inn2 ) dr J -Ц- + fn2k2 - /32| r I ) er = 0; (30.15a)
1 [ J In П2 2 ) der e<£> f n
+ Г \ dr Г у Г J dp । n2k2 - p2 j e „ = 0; (30.156)
™ .. d In и ,2 ( —er + ^n zk2 - 32 j ez =0; (30.15b)
- -1- t г у2 д^р -4 + r2 J \n2k2 -02 = 0; (30.15г)
ж-;- dhn2 д , , ч dr dr 1 Minn r( dr 2 2I - +— r-v-1 £- + r J dip r2 [n2k2 - |32} = 0;
(30.15д)
Jin n2 dh7 + — - dr dr ,n d In n2 -hT + ^n2k2 - 02J h2 , =0, (30.15e)
где п = п (г), а поперечный оператор Лапласа определен в табл. 30.1.
30.6. Декартовы составляющие полей
Как подчеркивалось выше, векторный оператор V2, вообще говоря, связыва-
ет составляющие полей в произвольной системе координат. Однако, если
векторы поля имеют составляющие, отнесенные к фиксированным направле-
500
ниям декартовых координат, такой связи не существует, и векторный опера-
тор V2 заменяется скалярным лапласианом V2. Так, если положить
Е = £хх + £уу + £z i; Н = Ях + Яуу + 1, (30.16)
в уравнениях (30.13), где х, у и z — единичные векторы, параллельные осям
на рис. 11.1, а, то получим
{V2 + n2k2} Е = -V{Et -Vtlnn2} ; (30.17а)
{v2 + n2k2} H=(VxH)xVtlnn2-VxJ-JxVtlnn2, (30.176)
где V2 определяется соотношением (37.37) нп = п(х, у). Подчеркнем, что
хотя составляющие поля соотнесены с фиксированными направлениями де-
картовых координат, их пространственное изменение может быть выражено
в любой цилиндрической системе координат, как, например, приведенные ни-
же уравнения (30.23) в случае цилиндрических полярных координат.
30.7. Однородные векторные волновые уравнения
Если мы имеем дело с декартовыми составляющими (30.16) полей с разде-
ляющимися переменными вида (30.4), то в областях, свободных от источни-
ков, уравнения (30.17) приводятся к однородным векторным волновым
уравнениям, поперечная и продольная составляющие которых имеют вид
{V2+K2*2 -f32}et=-Vt(et -Vtlnn2);
{ Vf + n2k2 - /32} ez = — i(3et • Vt In n2 ;
{V2 + n2k2 - 02} ht = (Vt x ht) x Vt In n2 ;
+ n2k2 -02} h2 = (Vt/zz - i0ht) • Vt In n2,
(30.18a)
(30.186)
(30.18b)
(30.18г)
где n =n(x, y) ,k = 2я/Х, поперечные поля определены соотношениями
et = ехх + еуу, ht = йхх + йуу, (30.19)
а операторы V^, Vt определены в табл. 30.1.
Планарные волноводы. В планарном волноводе с профилем показателя
преломления п (х) поля с разделяющимися переменными имеют следующую
пространственную зависимость:
Е (х, z) = е (х) exp (i j3z) ; Н (х, z) = h (х) exp (i(3z). (30.20)
При этом уравнения для составляющих полей получаются из (30.18) и имеют
вид
+~(ex d-^n ) + (n2k2 - (Р)ех = 0; (30.21а)
dx2 dx v х dx v ' x >
d2e
+'(n2k2 - (32)ey =0; (30.216)
+ ex+ {n2k2 -02}ez =0, (30.21b)
501
- X dx2 + 1[П2к2 - 02}\ = O; (30.21r)
d2hy dx2 din n2 dx dh^r f ) + -j n2k2 - 02 7 h = 0; dx l j у (30.21д)
d2h7 d In n2 (30.2 l.e)
dx2 dx 5 ifih —f + \n2k2 - j32f h = 0, <. x dx J 1 J z
гдеп = п(х) ик = 2тг/Х.
Круглые волоконные световоды. В круглом волоконном световоде с осе-
симметричным профилем показателя преломления п (г) поля с разделяющи-
мися переменными имеют вид (30.3), где
е(г, <р) = ех(г, <р)х + еу(г, ф)у + ez(r, <р) 1; (30.22а)
h (г, </>) = hx (г, </?) х + hy (г, <р)у + hz {г, </>) z. (30.226)
Тогда из (30.18) получаем уравнения для составляющих
{v2 + п2к2 — 02} е + J[е cos ip + ev sin - 0; (30.23а)
et J х ох (1 х у dr '
{v^ + п2к2 - 02} еу + |[ех cos + еу sin ] = 0; (30.236)
{ V2 + п2к2 — fi2} ez + W-[ex cos у + ey sin = 0; (30.23b)
{v?+n42 -02] + sin =0; (30.23r)
{^ + n2k2 -02} --^4 cos . =0; (30.23д)
{V2 + n2k2 -02\ hz + {[10Л - 4^- ] cos p + [i/Зй -sin = 0,
(30.23e)
где n = n(r), к = 2тт/Х, а оператор определен в табл. 30.1. Декартовы со-
ставляющие оператора связаны с полярными соотношениями (37.47) :
д д sin'ir д д . д cos <р д
dx or г dip dy dr г dip
(30.24)
а декартовы и полярные координаты так, как показано на рис. 12.3. Решение
уравнений (30.23) для е и h идентично решению уравнений (30.15), так как
поля не зависят от выбора координат.
30.8. Уравнения для продольных составляющих
Продольные составляющие eL и/г2в уравнениях (30.186) и (30.18г) зависят
от поперечных полей et и ht. Если использовать соотношения (30.6), чтобы
выразить et и ht через ег и /zz, то получаем систему связанных уравнений
{v2 + p]ez - vtez • Vt In п2 = -(Мо/е0)1/2 ' (^hz х Vt In и2 );
(30.25a)
502
+ p}ftz - Vtftz • vt In n2 = (eo/Po)1/2 2 • (Vtez x Vt In n2),
(30.256)
где p = k2n2 -&2,n=n(x,y) ик- 2я/Х.
ПОГЛОЩАЮЩАЯ СРЕДА
Уравнения Максвелла непосредственно применимы к поглощающей среде с
комплексным показателем преломления, как пояснено в гл. И. Здесь мы
покажем, как определить поглощаемую мощность электромагнитного излу-
чения.
30.9. Поглощаемая мощность
Теорема Пойнтинга может быть выведена из уравнений Максвелла как след-
ствие закона сохранения энергии. Согласно ей средняя по времени мощность,
выделяемая распределением токов с плотностью J в объеме <,
2 у
(30.26)
где для J и Е подразумевается временная зависимость exp(-iotf).
Можно использовать представление наведенных токов из гл. 22 для опре-
деления мощности, поглощенной в материале. Используя обозначения гл. 22,
будем считать п показателем преломления поглощающей среды, а показатель
преломления соответствующей непоглощающей среды обозначим через п.
Влияние поглощения тогда может быть описано с помощью наведенного тока
с плотностью J согласно соотношению (22.3), т. е.
J = i (е0 /До.)1/2 к(п 2 - п2 ) Е,
(30.27)
где Е — вектор электрического поля поглощающей среды. Если веществен-
ная и мнимая части показателя преломления поглощающей среды равны пт
и п1 соответственно, то полагая в (30.27) п = п1 + in1, п = п1 и подставляя по-
лученное выражение для J в (30.26), находим потери мощности электромаг-
нитного поля в виде*
Р = -А:(-^-)1/2 JnWlElMVC
МО у
(30.28)
Это выражение является точным при условии, что точно известно электри-
ческое поле в непоглощающей среде.
АНИЗОТРОПНАЯ СРЕДА
Обобщим уравнения Максвелла в соответствующие волновые уравнения на
случай распространения полей в анизотропных материалах [3]. Это обобще-
* Заметим, что для вычисления реально поглощаемой мощности надо фактически
брать вещественную часть выражения (30.26), что и было сделано при выводе (30.28). -
Прим, перев.
503
ние следует из того, что в общем случае вектор электрической индукции D
не параллелен вектору электрического поля Е. При этом
D = eon2 • Е, (30.29)
где п2 — тензор с девятью составляющими, т. е. составляющие вектора D
определяются соотношением = еоп^Ек, где i, к = 1, 2 или 3, и подразуме-
вается суммирование по к. Эти составляющие зависят от выбранной систе-
мы координат.
Для простоты будем считать, что оси декартовых координат ориентиро-
ваны параллельно главным осям анизотропной среды, как рассматрива-
лось в разд. 11.23.- В этом случае отличны от нуля только диагональные со-
ставляющие тензора: п\ъ и22 и и23. Для удобства обозначим эти составляю-
щие через и2, Пу и и2 соответственно.
30.10. Векторные волновые уравнения
Уравнения Максвелла в анизотропной среде без источников имеют вид
V х Е = i(/i0/e0)1/2АгН; V х Н =-Це0/м0) 1/2*п2 • Е; (30.30а)
V • (п2 • Е) = 0; V • Н = 0, (30.306)
где параметры определены в табл. I. Взяв ротор от уравнений (30.30а), ис-
ключив затем либо Н, либо Е и использовав векторные тождества (37.30) и
(37.31), получим следующие векторные волновые уравнения для декарто-
вых составляющих полей:
V2E + fc2n2 • Е = V(V • Е); V х { п~2 • (V х Н)} =£2Н, (30.31)
где п-2 — диагональный тензор с составляющими п~2 , пу2 и п”2 . Эти уравне-
ния аналогичны уравнениям (30.17) для изотропной среды без источников
(J = 0). Так как вектор п2 • Е не параллелен Е, то член V(V • Е) из первого
уравнения (30.31) в общем случае невозможно представить аналогично чле-
ну ~V(Et * Vt In и2) из уравнения (30.17а). Однако в особых случаях, как
мы сейчас покажем, возможны упрощения векторных волновых уравнений.
30.11. Планарные волноводы
Если волновод имеет планарную структуру, т. е. однороден в направлениях
осей у и z (см. рис. 12.1), а главные оси анизотропных материалов, из кото-
рых он сделан, параллельны осям декартовых координат, то такая структура
поддерживает ТЕ- и ТМ-моды. Аналогично ТЕ- и ТМ-модам изотропных вол-
новодов, которые обсуждались в разд. 12.14 и 12.15 соответственно, электри-
ческое поле каждой ТЕ-моды и магнитное поле каждой ТМ-моды имеют толь-
ко составляющие по оси Подставляя выражение для поля (30.20) в первое
уравнение (30.31), получаем
{ d2 1
) + k2n2v - 02 ? ev = 0, (30.32а)
( dxz У J У
где иу = иу(х), так что электрическое поле ТЕ-моды удовлетворяет скалярно-
му волновому уравнению. Аналогично из второго уравнения (30.31) находим
С J2 din и2 j „ о 1
ITT - —3-— -7Г + k nz ~ = ° (30.326)
(dx2 dx dx z J У v
504
для ТМ-мод, где nz = nz (х). Если показатель преломления nz постоянен в
поперечном сечении волновода, то /гу удовлетворяет скалярному волново-
му уравнению. Остальные составляющие находим из уравнений Максвелла
(30.31а), и по аналогии с (12.17) и (12.23) имеем
ТЕ-моды ТМ-моды
N ;з- о> 11 * X | II П 1 и *5:1 m /-s ° ° -Г- 1 О 1 о и 5 ° ф / 05 N о> II * _ II II N w -СО ) ° 1? ф II го ь- р 4? И 1
(30.33)
Параметры определены в табл. I.
30.12. Одноосные волноводы
Главные показатели преломления одноосного анизотропного волновода удов-
летворяют соотношению пх = пу =£ nz, и если ось z параллельна оси волново-
да, то векторные волновые уравнения можно упростить. Легко показать, что
продольные составляющие уравнений (30.31) имеют вид
+ k2n2z - р2 (nz/nt)2} ez = —ij3(et • Vt ln^); (30.34a)
{V* + k2n2 - p2} hz = (Vt/?z - ij3ht) • V{ In n\, (30.346)
где nx = nx = ny. Эти уравнения сводятся к уравнениям (30.186) и (30.18г)
соответственно для изотропного волновода, когда п = пх = nz.
Нетрудно убедиться, что поперечные составляющие могут быть выражены
через ez и hz, если заменить в уравнении (30.6) п напх. Так, например, ради-
альная и азимутальная составляющие поля в круглом волоконном световоде
с nt =nt (г) задаются соотношениями (30.9) с р = к2п2 — Р2.
30.13. Поле, поляризованное параллельно главным осям
При определенных условиях, обсуждавшихся в конце гл. 13, возможно рас-
пространение моды, у которой вектор электрического поля фактически па-
раллелен либо оси х, либо оси у, если считать эти оси главными. В этих слу-
чаях вектор электрической индукции параллелен вектору электрического
поля, так что используя представление поля в виде (30.4), находим, что в де-
картовых координатах поперечная составляющая et удовлетворяет попереч-
ной составляющей векторного волнового уравнения (30.31)
+ к2п} - 02 ) et = -Vt (et • Vt In n2), (30.35)
где nx = их, et = exx для мод, поляризованных мод вдоль оси х, и = пу,
et = еуу для мод, поляризованных вдоль оси у. Единичные векторы х и у
параллельны осям координат. Не считая того, что значения различаются
для двух направлений поляризации, уравнение (30.35) идентично уравнению
(30.18а) для изотропного волновода.
505
ГЛАВА 31. МЕТОДЫ МОД ДЛЯ УРАВНЕНИЙ МАКСВЕЛЛА
Имеются два общих метода решения уравнений Максвелла или, что эквива-
лентно, неоднородных векторных волновых уравнений. В одном методе ис-
пользуются функции Грина (см. гл. 34), в другом, называемом методом мод,
используются собственные функции*. Основная цель этой главы заключается
в обосновании второго подхода: выводятся основные свойства мод и пока-
зывается, как с их помощью можно представить поля в световодах. Поэтому
содержание главы в основном заключается в математическом дополнении
к описанию свойств мод в гл. 11, 25 и 28.
Рассматриваемые здесь моды являются точными решениями уравнений
Максвелла. В гл. 33 мы сравним результаты, полученные в этой главе, со
свойствами мод слабонаправляющих волноводов, получаемых из решений
скалярного волнового уравнения.
Начнем с вывода важного интегрального соотношения для двух решений
уравнений Максвелла — теоремы взаимности, В своей двумерной форме эта
теорема идеальна для вывода свойств мод трансляционно-инвариантных све-
товодов. Она имеет разнообразные применения — от доказательства ортого-
нальности мод и вычисления амплитуд мод, возбувденных источником тока,
до вывода уравнений связанных мод, а также стационарных выражений для
постоянной распространения и групповой скорости.
Существуют две формы теоремы взаимности — сопряженная и несопря-
женная, зависящие от того, какие используются поля — комплексно-сопря-
женные или без комплексной сопряженности. На протяжении ч. II мы посто-
янно использовали сопряженную форму теоремы взаимности, которая до-
пускает простую физическую интерпретацию в терминах потоков мощности.
Результаты, полученные при использовании сопряженной формы, обычно
предполагают, что световод непоглощающий, однако эффекты поглощения в
материале используемых на практике световодов обычно так малы, что мо-
гут рассматриваться как слабое возмущение непоглощающего волновода.
ТЕОРЕМА ВЗАИМНОСТИ
Вывод сопряженной и несопряженной формы теоремы взаимности требует
рассмотрения двух различных электромагнитных ситуаций: одна характери-
зуется показателем преломления среды п, плотностью тока J, а также векто-
рами электрического Е и магнитного Н полей, другая — соответственно вели-
чинами и, J, Ей Н. Все векторные величины содержат не указанный явно вре-
менной множитель ехр(—loot), где со - угловая частота. Показатели прелом-
ления п и п могут зависеть от всех трех пространственных переменных, маг-
нитная же проницаемость равна значению в свободном пространстве, если
не оговорено противное.
31.1. Сопряженная форма
Определим векторную функцию Fc соотношением
Fc = Е х Н* + Е* х Н, (31.1)
* Этот метод называется также методом спектрального разложения поля по собствен-
ным волнам или модам. - Прим. ред.
506
где знак * обозначает комплексное сопряжение. Поля, не отмеченные чертой
сверху, удовлетворяют уравнениям Максвелла (30.1), а поля с чертой удов-
летворяют сопряженной форме этих уравнений.
V х Ё* =-i(—)1/2 &Н*; Vx H* = J* + i(-5“-)1/2A?(n*)2E*, (31.2)
ео До
где До, е0 и к — вещественны. Используя векторное тождество (37.28), по-
лучаем
V •Fc = -i(^-)1/2fc !(й*)2 - и2} Е • Ё* - (Ё* • J + Е • J*). (31.3)
Двумерная форма теоремы о дивергенции (37.56) для Fc имеет вид
J V . Fcd4 =~ J F • idA + fF • nd/, (31.4)
А с dz J с ic
где А — площадь поперечного сечения волновода, az — единичный вектор, па-
раллельный оси z. Криволинейный интеграл берется по периметру площади
А; п — единичный вектор внешней нормали к контуру Z, лежащий в плоско-
сти сечения А. Этот результат справедлив как для непрерывных, так и для
ступенчатых профилей. Вблизи разрывов профиля показателя преломления
скалярное произведение Fc • п определяется только составляющими полей,
ортогональными к нормали п, как это следует из соотношения (31.1). Из
граничных условий уравнений Максвелла, приведенных в начале гл. 30, вид-
но, что произведение Fc • п непрерывно на разрывах среды. Следовательно,
разрывы не вносят дополнительный вклад в криволинейный интеграл.
Для оптических волноводов возьмем бесконечно большое поперечное се-
чение А ж. Тогда криволинейный интеграл по окружности г -> <», где г — ради-
ус цилиндра, становится пренебрежимо малым, если одно из полей или оба по-
ля — с чертой и без черты сверху — представляют собой направляемые моды,
так как при этом Fc обращается в нуль при г -+ °° из-за экспоненциального за-
тухания полей направляемых мод. В результате из (31.4) получаем сопря-
женную форму теоремы взаимности
~ JF • idA = J V*Fd4,
dz л L л v
Zl oo Л oo
(31.5)
где Fc определяется соотношением (31.1), a V • Fc задается формулой (31.3).
Этот результат справедлив для произвольных профилей показателя прелом-
ления, включая случай поглощающего материала, когда п — комплексная
величина.
Вытекающие моды и моды излучения. В случае вытекающих мод, как мы
показали в разд. 24.15, их поля для комплексных г затухают быстрее, чем
г"1/2 при | г | [1]. Если Fc состоит из полей мод излучения, обсуждавших-
ся в гл. 25, то криволинейный интеграл в уравнении (31.4) быстро осцилли-
рует при г -► оо, поскольку поля в любой цилиндрической структуре изменя-
ются как ехр {IQr/p } /у/r при больших значениях г (см. разд. 25.8). Таким
507
образом, значение криволинейного интеграла трудно определить в общем
случае, так же как затруднительно его вычислить точно для конкретной за-
данной структуры. Однако, положив этот интеграл равным нулю, мы полу-
чим правильные свойства мод излучения. В гл. 25 мы показали, что один из
методов построения мод излучения состоит в использовании направляемых
мод волновода с металлической оболочкой в предельном случае бесконечно-
го поперечного сечения. На границе с металлом тангенциальная составляю-
щая электрического поля равна нулю, так что исчезает член Fc • п, а следова-
тельно, и криволинейный интеграл равен нулю.
Другой подход состоит в том, что можно исходить из факта нефизичности
индивидуальных мод излучения: хотя они и хорошо определены математи-
чески, каждая из них переносит бесконечно большую мощность. Только су-
перпозиция континуума мод излучения может правильно воспроизвести фи-
зические поля. Таким образом, хотя криволинейный интеграл не может быть
разумно определен, когда Fc составлена из полей отдельных мод излучения,
ясно, что этот интеграл исчезнет при суперпозиции большого числа быстро
осциллирующих функций, формирующих континуум в дальнем поле при
г оо [2]. При строгом математическом выводе используются некоторые
свойства поперечного векторного волнового уравнения в предельной точке
на бесконечности [3]. Таким образом, мы можем отбросить криволинейный
интеграл как для вытекающих мод, так и для мод излучения, и такие моды
подчиняются сопряженной форме теоремы взаимности (31.5).
Формулировка теоремы взаимности с помощью криволинейного интегра-
ла. Мы можем переписать равенство (31.5), заменив поверхностный интеграл
в правой части криволинейным. Для этого определим А как некоторую пло-
щадь в поперечном сечении, где либо отличны от нуля токи, либо и* =£ п. Ес-
ли положить А = А ж - Л , то левая часть уравнения (31.4)' обращается в
нуль, как это ясно из выражения (31.3). Криволинейный интеграл в правой
части (31.4) вычисляется по контуру I = + Z , где Zp — периметр площади
Ар. Интеграл по контуру обращается в нуль, как отмечено выше, и мы по-
лучаем равенство
/ F • zdd =—£ F • &#, (31.6)
dz А _ а I
которое формально идентично уравнению (31.5)
31.2. Несопряженная форма
Вторая форма теоремы взаимности связывает поля с чертой и без черты свер-
ху через векторную функцию F, которая определена соотношением
F=ExH —ЁхН. (31.7)
Из соотношений (30.1) и (37.28) находим
V • F = i(-g-)1/2/c(n2 - и2)Е • Ё + Ё • J — Е • J. (31.8)
Далее, поступая, как в предыдущем разделе, и заменяя в равенстве (31.4)
Fc на F, приходим к несопряженной форме теоремы взаимности
508
-f- f F 'idA = S V • FdA, (31.9)
dz A. A,,
где F определена соотношением (31.7), a V • F — соотношением (31.8).
31.3. Ортогональность мод
В качестве первого применения сопряженной формы теоремы взаимности
продемонстрируем вывод ортогональности направляемых мод, мод излуче-
ния и вытекающих мод в непоглощающих волноводах. Рассмотрим две впе-
ред-распространяющиеся моды с постоянными распространения j3j и (Зк. Ин-
дексы / и к могут относиться к двум различным направляемым модам, а в
случае мод излучения — к модам с различными значениями постоянной рас-
пространения 0. Положим
Е = е. exp(ij3.z) ; Н = h. exp(i|3.z) ;
J J _ J j (31.10)
E = ekexp(i|3kz) ; H = hkexp(i0kz)
и J = J - 0. Обе моды принадлежат одному и тому же непоглощающему вол-
новоду, так что п* = п. Подстановка выражений (31.1) и (31.10) в равенство
(31.5) дает
(j3j - 0k) / {е. х h*+е*х h.} ’ЫЛ=0, j*k, (31.11)
Л ОО
где Аж — неограниченно большая площадь поперечного сечения, az — единич-
ный вектор, параллельный оси волновода. Теперь рассмотрим вторую пару
мод, состоящую из той же вперед-распространяющейся /-й моды и назад-рас-
пространяющейся к-й моды с полями
E = e_kexp(-i0kz), Н = h_kexp(-i/?kz). (31.12)
Связав эти поля с полями вперед-распространяющейся моды с помощью со-
отношения (11.7), из равенств (31.1) и (31.5) получим
(0, + 0 ) J {е х h* — е* х h } • idA = 0, (31.13)
J к л J к к J
Л оо
так как рассматриваются только поперечные составляющие поля. Складывая
и вычитая (31.11) и (31.13), получаем соотношения ортогональности в виде
J е. х h* • zdA = / е* х h. • zdA =0, / =# к,
л J k Л k J
rloo SI oo
(31.14)
которые выполняются для всех вперед-распространяющихся направляемых
мод и мод излучения в непоглощающем волноводе. В частности, каждая на-
правляемая мода ортогональна всем модам излучения и поэтому ортогональ-
на полным полям излучения Ега(^ и Hrad волновода. Таким образом,
(31.15)
509
Для вытекающих мод (см. гл. 24) ортогональность выражается также со-
отношениями (31.14), если Аж заменить на комплексное поперечное сечение
А^, как было указано в разд. 24.15.
Несопряженная форма соотношения ортогональности. Мы можем повто-
рить приведенный выше вывод, используя несопряженную форму теоремы
взаимности, выражающуюся равенством (31.9). Выражение, соответствую-
щее соотношению (31.14), очевидно, имеет вид
J* ej х hk • zdA = J ek x hj • zdA = 0, / Ф k, (31.16)
A oo -^1 OO
что верно как для поглощающего, так и для непоглощающего волноводов.
Для волноводов без потерь соотношения (31.14) и (31.16) идентичны, так
как поперечные составляющие поля вещественны по условию (11.8).
Ортогональность мод излучения. Из полученных выше результатов также
следует, что сопряженная и несопряженная формы соотношений ортогональ-
ности выполняются и для мод излучения волновода без потерь, если только
различаются их постоянные распространения, т. е. если Q Ф Q' в обозначени-
ях (25.2) и (25.4). К этому же можно прийти, рассматривая каждую моду
излучения как предельный случай направляемой моды волновода с металли-
ческой внешней оболочкой, когда поперечное сечение неограниченно увели-
чивается. Для металлического волновода направляемые моды удовлетворя-
ют обеим формам соотношений ортогональности, так что это свойство пере-
носится и на моды излучения.
Если металлический волновод ничем не заполнен, то процедура предельно-
го перехода приводит к ортогональности мод излучения в свободном про-
странстве. Если же внутри металлического волновода находится диэлектри-
ческий волновод, то та же процедура приводит к ортогональности мод излу-
чения диэлектрического волновода.
31.4. Интегральные соотношения для постоянной распространения
Другое применение теоремы взаимности приводит к точным выражениям
для постоянной распространения направляемых мод. Аналогично выводу,
данному в разд. 31.1, заменяя там Fc на Gc, где
Gc = Е х Н*, (31.17)
и считая, что a?=h,J=J = O, с помощью уравнений (30.1) и (37.28) получаем
V-G =1^(^-)1/2Н*Н*- (-^-)1-/2(н2)*Е"Ё*к (31.18)
t е0 МО J
Заменяя Fc на Gc в равенстве (31.5), приходим к соотношению
4~ J Ех Н* • idA = ifc J { (-^-) 1/2Н • Н*- (-2-)1/2 (и2)*Е • Ё*)л4.
dz а а I е0 До
Л оо оо 4 J
(31.19)
Поля с чертой и без черты — это вперед- и назад-распространяющиеся мо-
ды с постоянной распространения (3j. Таким образом, мы полагаем
Е = ej exp (i|3jZ) ; Н = hj exp (i/3jZ); (31.20a)
Ё = e_ j exp (-i/3jZ); H = h_j exp (-i(3}z). (31.206)
510
Подстановка этих выражений в (31.19) с использованием равенств (11.7)
дает
(31.21)
Это выражение справедливо для волноводов без потерь. Тождество [4]
к f п2е. х h*-idA f J(ifo.)|h.|2 + (-^)1/2n21e. |4 dA (31.22)
J J 2 Хе ( eo J Mo J J
приводит ко второму выражению для непоглощающего волновода
& =к(^-)У2 J п2е. х h*’ zdA/ J п2 |е= |2d4,
J 4 J J л J
(31.23)
где | ej 12 = ej • е? и было использовано равенство запасенных электрической
и магнитной энергий, т. е; соотношение (11.18).
31.5. Запасенные электрическая и магнитная энергии
Усредненные по времени электрическая и магнитная энергии и опре-
делены соотношениями (11.17). В световоде без потерь при_отсутствии дис-
персии обе энергии равны. Это доказывается путем замены Е на Е и Н на Н в
равенстве (31.19). Интеграл в левой части не зависит от z, поэтому получаем
f n2leA2dA f lhA2dA,
J 4 A J
(31.24)
где использованы выражения для полей (31.20).
31.6. Фазовая и групповая скорости
Фазовая и групповая скорости моды, распространяющейся вдоль волново-
да, определяются соответственно соотношениями
_ со _ 2яс _ doo _ 2ттс dX
ирГ Pj ~ vgj " “ 15“ dPj ’
(31.25)
где связь угловой частоты со с длиной волны X дана в табл. I. Мы можем вы-
разить vpj через поля мод, используя выражения для из разд. 31.4. Здесь
мы выведем аналогичное выражение для с учетом дисперсии материала,
если п и ц изменяются с длиной волны, т. е. п = п (X) и ц = ц (X), в дополнение
к пространственной зависимости и.
Обобщенная теорема взаимности. Для вычисления групповой скорости не-
обходимо вывести обобщенную теорему взаимности, в которой учитывают-
ся изменения частоты со во временной зависимости полей. Пусть Е и Н — по-
511
ля /-й моды для длины волны X. Эти поля удовлетворяют уравнениям Мак-
свелла для полей без источников, которые, если учесть и изменение прони-
цаемости д, имеют вид
Vx E = 27tw-£h, V х Н =-27псе0Ц—Е, (31.26)
A X
где с — ^корость света в свободном пространстве. Если Е и Н — поля волны с
длиной X, то они удовлетворяют уравнениям, аналогичным (31.26) , где Е, Н,
X, д и п заменены на Е, Н, Х, д - д ( X) и п = п ( X) соответственно.
Тогда из уравнения (31.1) с помощью соотношения (37.28) находим для
непоглощающего волновода
V-F =2тс\(~- А—)е0Е*Ё* + (£-#)Н‘Н*к (31.27)
с I X * X J
Переменные в выражениях для полей разделяются, поэтому
Е = е- exp(i0z); Н = h exp(10 z);
_ _ _ _ _ _ (31.28)
Е = е. exp(iffjZ); Н = h exp (10,z).
Подставляя выражения (31.1), (31.27) и (31.28) в соотношение (31.5) по-
лучаем
(0; — 0;) _ _ ( и2 п2 —
—1-----A / {е( х h* + е* х к } • zdA = J) ------— )еое • е* +
2тгс J J J J а~ I X х J J
+ (А- - |) h. • h* J dA. (31.29)
Разделив обе части уравнения (31.29) на X — X, перейдя к пределу X -> X
и положив X — X ->dX, Pj — Pj из (31.25) для непоглощающего светово-
да найдем
J е. х h* • zcL4
2Л„ J J
\2
A- J {е01 е 12 (d/dX) (п2 /X) + | h, |2 (d/dX) (д/Х)} dA
4 Д J J
Z1 QQ
(31.30)
Если к тому же среда волновода не имеет дисперсии, то, комбинируя соотно-
шения (31.30) и (31.23) и полагая д = д0, можно получить
c0i
и . =—L Г exh*’ idA/ f п2е. х h*’ z<£4.
gJ к л J J л J J
Л1 OO ^oo
(31.31)
Здесь было использовано также соотношение (31.24) . Обобщение равенства
(31.31) на световоды, изготовленные из анизотропных материалов, рассма-
триваемые в конце гл. 11 и 30, получаем заменой «2ej х Н?ип2 • ej х h* где
п2 — тензор показателя преломления.
512
ВОЗБУЖДЕНИЕ МОД ИСТОЧНИКАМИ ТОКА
Здесь мы определим амплитуды направляемых мод и мод излучения, воз-
буждаемых заданным распределением токов J в объеме У' между перпенди-
кулярными к волноводу плоскостями z = Zj и z = z2 (рис. 31.1). Поля в вол-
новоде разложим по полной системе вперед- и назад-распространяющихся мод
Е = Z !«j(z)ejexp(il3jz) + а_ =(z)e_=ехр(-ifyz)} + SJ {adz, 2)ej(2)exp{i|3(2)z] +
/ j о
+ «_j(X Q')e_j(Q)exp[-iP(Q)z]} dQ-, (31.32a)
Н = 2{Л;(г)11:ехр(1/12) + а_;(и)Ь_:ехр(-1(3:г)} +Z J {a (z,Q)h(Q) x
/ j о J J
x exp[i|3(2)z] +a_j(z, 2)h_j(2)exp[-i/3(2)z]} dQ, (31.326)
где амплитуды мод зависят от z только в объеме и постоянны (или равны
нулю) вне этого объема. В соотношении (31.1) поля без черты сверху опре-
деляются выражениями (31.32), а поля, отмеченные чертой, эквивалентны
полям /-й вперед-распространяющейся направляемой моды волновода без
источников, т. е. при J = 0, п = п
Е = ej exp(ifLz); Н = h. exp (i/3jZ) . (31.33)
Подставляя Fc в выражение (31.5) и используя соотношения ортогонально-
сти (31.14), находим
da- (2) 1
4^ К ‘ (31.34)
J -^OO
где TVj — коэффициент нормировки (11.12). Интегрируя no z и предполагая,
что при z <Zj не существует вперед-распространяющихся мод, получаем
0j(z)=O, z<Zj;
1 z t t
а;(г)=-——/ J e* • J exp(-i/3.z )dAdz , z1=Cz<z2;
J 4/Vj Zj Aqo J J
“i(z)=
J exp(—z>zj.
(31.35a)
(31.356)
(31.35b)
Рис. 31.1. Заданное распределение токов с плотно-
стью J в объеме тГ между плоскостями поперечного
сечения z = zx и z = z2 волновода. Вне объема^
токов нет
17 Зак 37
513
Соответствующие выражения для а_} получаются с помощью аналогичной
процедуры, но с использованием полей /-й назад-распространяющейся моды
вместо полей, определяемых по формуле (31.33) :
«_j(z) = 1N Iе*; ’J exp(i/3z)Ji< z<zi; J ty! V j у J J (31.36a)
1 ^2 / J e*. * J exp(i(3.z)cL4dz, z1^z<z2; J 4/Vj z Аж J (31.366)
a . (z) = 0, z > z2. (31.36b)
Используя подходящие поля мод излучения вместо полей, определяемых по
(31.33), легко вывести следующие выражения:
aj(^Q) =-^e)-Je*(e) z>22; (31.37а)
a_j(z,Q) / e*.(e)-Jexp[i/3(2)z]J>; (31.376)
для вперед- и назад-распространяющихся мод излучения, где коэффициенты
нормировки Nj(Q) определяются соотношением (25.5). Выражения для ам-
плитуд в области, содержащей источники (см. рис. 31.1), выводятся по ана-
логии с (31.35) и (31.36). Можно также выразить амплитуды мод через по-
верхностные интегралы, используя соотношение (31.6) вместо (31.5).
МЕТОДЫ МОД ДЛЯ РЕГУЛЯРНЫХ волноводов
Если поля и постоянные распространения мод известны для одного волново-
да, то можно, используя теорему взаимности, определить поля и постоянные
распространения мод для некоторого другого волновода. Пусть второй вол-
новод регулярен в том смысле, что он трансляционно-инвариантен, т. е. его
параметры не зависят от z. Выводимые ниже соотношения являются точными
и составляют основу для анализа методом теории возмущений, проводимого
в разд. 31.10, если волноводы не слишком отличаются друг от друга.
31.7. Постоянные распространения
Пусть Ё, Н и - известные поля и постоянная_распространения к-й моды
волновода с профилем показателя преломления и, а Е, Н и 0j - неизвестные
поля и постоянная распространения /-й моды волновода с профилем показа-
теля преломления п. Считая, что моды обоих волноводов имеют различные
значения (Зк или 0j , положим
Е = ej exp(ij3jZ) ; Н = hj exp(i0jZ) ; (31.38а)
Ё = ekexp(i^kz) ; Н = hkexp(i0kz). (31.386)
Подставляя (31.1) и (31.38) в выражение (31.5) и учитывая соотношение
(31.3) для поля без источников, получаем
514
f (n2 -n2)t. • e*dA
0. = 0 + *(-£».) «'*---. (-31.39)
J k Mo f {e. x h * + e* X h.} • idA
л ) k k J
oo
Мы считаем, что оба волновода имеют магнитную проницаемость ц0 , равную
магнитной проницаемости свободного пространства, и первый из них являет-
ся непоглощающим, т. е. показатель преломления п — вещественный. Это вы-
ражение стационарно относительно вариаций величин, отмеченных сверху
чертой [5,6].
Представление постоянных распространения с помощью криволинейного
интеграла. Использование соотношения (31.6) вместо (31.5) приводит к вы-
ражению, альтеративному (31.39),
£{е. х h* +ё* х h.} • ndl
I 1 J k- k j
0. - /3. = —i---E---------=----—------:------ , (31.40)
J k f {e. x h* + e* x h.} • zd/1
A -A J k k j
где Zp — контур, ограничивающий площадь поперечного сечения Лр, на кото-
рой п Ф п\ п - единичный вектор внешней нормали к контуру /р, лежащий в
плоскости А .
31.8. Поля мод
Поперечные составляющие поля /-й моды во втором волноводе могут быть
формально найдены с помощью разложения их собственных функций по пол-
ной системе вперед- и назад-распространяющихся-мод первого волновода.
Положим
etj =S{«k+«_k}etk + S П\(2) +«_k(2)}etk(e)J2; (31.41а)
hti = S -<Lk> htk + S Г { ak(2) ^_k(2)} htk (Q}dQ, (31.416)
где и flk(2) — амплитуды вперед-распространяющихся направляемых мод
и мод излучения соответственно, а я_к и я_к(2) — амплитуды соответствую-
щих назад-распространяющихся мод. Назад- и вперед-распространяющиеся
поля связаны соотношением (11.7). Продольная составляющая поля ezj на-
ходится_подстановкой выражения (31.416) в уравнение (30.5в) с учетом то-
го, что ezk и htk также связаны соотношением (30.5в). Аналогично выраже-
ние для &ZJ следует из (31.41а) и (30.5г). Таким образом, считая, что магнит-
ная проницаемость световода такая же, как в свободном пространстве, т. е.
До, получаем
п 2 f — оо _ ]
К - + I I ; (31.42а)
°! К * “.s.Kk * ‘ I [«k(e)+»_k<e)i\k(e)«- (31-426)
Важно отметить, что при получении выражений для ezj и 7zZj мы поменяли
порядок действия оператора интегрирования по модам излучения и операто-
pa Vt. Это возможно, если первые производные от и etk по поперечным
координатам непрерывны [7]. Поля мод волноводов с непрерывным профи-
лем показателя преломления удовлетворяют -этому условию. Для ступенча-
тых профилей выражения (31.42) неприменимы. Однако их можно интерпре-
тировать в определенном смысле как предельные, как указано в рэзд. 31.10.
Составляющие е- и могут быть также найдены из вторых равенств в соот-
ношениях (30.5в) и (30.5г), если известны и h^.
31.9. Амплитуды мод
Амплитуды мод в выражениях (31.41) определяются подстановкой послед-
них в знаменатель уравнения (31.39) с учетом соотношений ортогональности
(31.14) для полей, отмеченных чертой сверху. Тогда для вперед- и назад-рас-
пространяющихся направляемых мод имеем
(3L43a)
• е*.dA,
— к
(31.436)
где коэффициент нормировки Доопределяется соотношением (11.12) и вы-
ражен через поля ек и hk, а поле е*к. связано с ек соотношением (11.9). Из
соотношений ортогональности (25.4) (для полей, отмеченных сверху чер-
той) получаем для амплитуд мод измерения
a (Q) =----------*---------
k 4tfk(C) [0j-13(2)]
(-J41/2 J(«2-«2)e. '^AQ)dA\ (31.43b)
Мо л J K
oo
a AQ)=-~------z---
~k 4Nk(Q) [&}+№)]
(-—)1/2 («2 ~n2)ej
° A ” (31.43r)
где коэффициент нормировки 7Vk(2) определяется соотношением (25.5) и
выражен через поля ек (Q) и hk (Q), а поле el к (Q) связано с ек (2) соотно-
шением (11.7). Отметим, что равенствами (11.9) нельзя пользоваться, так
как наш выбор полей мод излучения не удовлетворяет условию (11.8), как
было показано в разд. 25.1.
Вывод соотношений (31.43) основывается на использовании выражения
(31.39) в предположении, что выполнено некоторое дополнительное условие
для определения постоянной распространения /3j и амплитуд мод. Последние
определяются с точностью до произвольной постоянной. Это условие следует,
например, из задачи на собственные значения для второго волновода, выра-
женной в интегральной форме соотнощением (31.23). Подстановка разложе-
ний (31.41) и (31.42) в уравнения (31.23) и (31.43) приводит к системе с
бесконечным числом нелинейных уравнений для амплитуд связанных мод.
Решение этой системы уравнений в общем виде не существует, однако ее ре-
шение возможно, когда второй волновод лишь слегка отличается от первого.
516
31.10. Слабовозмущенные волноводы
Решение (31.43) для амплитуд мод можно получить в аналитическом виде,
если волноводы мало-отличаются, т. е. если один из волноводов получается в
результате слабого возмущения другого и это возмущение не меняется
вдоль его длины. По причинам, объясненным в разд. 18.21, профили показа-
телей преломления в обоих волноводах должны быть близки друг другу во
всей области действия возмущения. Это фундаментальное ограничение мето-
дов теории возмущения эквивалентно требованию
е.~е • h~h (31.44)
tj tj tj tj
которое должно выполняться везде, включая область возмущения. С этой
оговоркой из уравнений (31.39) и (31.41а) с очевидностью следует, что «
~ 0j и flj « 1. Амплитуды остальных мод находятся методом итераций, начи-
ная с замены & наfi и ej на в выражениях (31.43) при условии, что кФ j
в уравнении (31.43а). Таким образом, поправки первого порядка к соотно-
шениям (31.44) относятся ко всем модам излучения и всем направляемым
модам, кроме /-й.
Разрывные профили. Как отмечено в разд. 31.8, интегральные выражения
для мод излучения в формулах (31.42) для ezj и имеют смысл только в
случае непрерывных профилей показателя преломления; там же указано, что
eZj и /zzj могут быть найдены и непосредственно из вторых равенств в соотно-
шениях (30.5в) и (30.5г), если только известны поля и h^. В случае раз-
рывного профиля тоже можно получить правильные результаты для ezj и hz-,
если поля в (31.42) рассматривать как предельные, т. е. для профиля, полу-
ченного из сглаженного непрерывного профиля. Однако при этом решающее
значение имеет то обстоятельство, что область сглаживания должна быть мно-
го меньше, чем область возмущения.
МЕТОДЫ МОД ДЛЯ НЕРЕГУЛЯРНЫХ ВОЛНОВОДОВ
Здесь мы рассмотрим распространение волн вдоль волноводов с неоднород-
ностями, изменяющимися с расстоянием z, т. е. вдоль нерегулярных волно-
водов, уже не обладающих трансляционной инвариантностью по z. При рас-
смотрении используется полная система направляемых мод и мод излучения
регулярного, т. е. невозмущенного трансляционно-инвариантного волновода,
что приводит к уравнениям связанных мод для амплитуд мод, зависящих otz.
31.11. Уравнения связанных мод
Пусть оба волновода имеют магнитную проницаемость р0, п(х, у) — профиль
показателя преломления регулярного волновода, а п (х, у, z) — профиль воз-
мущенного волновода. Для удобства мы используем выражения для орто-
нормированных мод, взятые из разд. 11.5 и 25.4, и положим
Е = S fo (z) + Z>_j (z) ] ё + 2 J [Z> (z, Q) + b (z, Q) ]e. (Q)dQ; (31.45a)
1 j J J J j о J J J
H = s [ij (z) - b (z) ] h + s Г [*= (z, G) - b (z, Q) ] h, (Q)dQ, (31.456)
/ J J J / 0 J J J
где Et и Ht — полные поперечные составляющие поля возмущенного волно-
517
вода. Функции (z) и Щ (z, Q) вперед-распространяющихся направляемых
мод и мод излучения включают зависимость от z и фазы, и амплитуды, а
^_j (z) и Z?_j (z, 0) соответствуют назад-распространяющимся модам. Мы ис-
пользовали здесь соотношения (11.7) для связи полей вперед- и назад-рас-
пространяющихся мод. Мощность каждой направляемой моды определяется
величиной | Z?j (z) |2. По аналогии с выводом уравнения (31.42) получим для
продольных составляющих полей возмущенного волновода следующие выра-
жения, имеющие смысл, если функция п(х, у, z) везде непрерывна (см.
разд. 31.10):
2 ( 00 )
Ez=~\^[b(z}-b (z)]e +S J [b(z,Q)-b (z, Q)]e.(Q)dQ ;
(31.46a)
Я = S[Z> (z) + b (z)]hzj + S Г [b-(z, Q) + b . (zf Q)]hz:(Q)dQ.
j ] ~J J j о “J J
(31.466)
При выводе мы полагали, что поля в уравнениях (31.1) и (31.3), отмечен-
ные чертой сверху, равны полям вперед-распространяющейся к-й направляе-
мой моды, т. е. _ __
E = ekexp(i0kz); Н = hkexp(i0kz). (31.47)
Считая волновод непоглощающим, находим из уравнения (31.5), что
*{Et Х *4 + Х ’ 2 exP(-i0kz)dA = i(-g-) k J (и2 -
- й2)Е • e* exp(-ij3kz)cL4. (31.48)
Подставляя здесь в левую часть разложение (31.45), используя соотношения
ортогональности (11.16) и (25.6) и связь вперед-и назад-распространяющих-
ся полей, задаваемую соотношением (11.9), находим
— i/З Ъ =4 (— У'2к J (и2 - й2)Е -e*dA.
dz k k 4 'до 7 J v ' k
OO
Подстановка вместо E разложений (31.45a) и (31.46a) приводит к уравне-
нию для к-й вперед-распространяющейся направляемой моды [9]
(31.49)
+ГKkl(2)W) +
I l о
+ck 1(2)b 1(2)]de|,
(31.50а)
где коэффициенты связи определяются соотношениями
("’ -"М -ё«+<31'50б>
У J ’МО (3I.5OB)
«4 оо J
518
Уравнения для амплитуд Ь_к получаются из (31.50а) после замены Ьк на
Ь_к, 0к на —0к, к на -fc,a ё*к на — ё*к. Уравнения для связанных мод излуче-
ния получаются аналогичным образом, если поля в выражениях (31.47) за-
менить полями fc-й вперед-распространяющейся моды излучения невозмущен-
ного волновода. Таким образом, [9]
- i0 (2)Ьк (2) = i S 1[Ск| (2) ъх + ск _! (2) м +
+Г ки(2, е')^(2') + ск _ 1(2, е')меш}>
(31.51а)
где коэффициенты связи задаются соотношениями
г<-2-5’){ёгк(е) • + ^к(0«г,}^; (31.516)
caio. е"> - -J I - "> {«1 (0 • еисе’>, <е)ёа(е’>]м
00 (31.51в)
Для назад-распространяющихся мод излучения уравнения получаются из
(31.51а) после замены b^(Q) на £_к(2), 0(2) на —0(2), к на —к, ёк на
ё-к-
Система уравнений связанных мод (31.50) и (31.51) представляет собой
точный эквивалент уравнений Максвелла для волноводов с непрерывными
профилями показателя преломления. Последнее ограничение является след-
ствием того, что мы использовали разложения (31.46). Однако уравнения
связанных мод можно сделать применимыми и в случае разрывных профи-
лей, если провести процедуру сглаживания, указанную в разд. 31.10. Уравне-
ния^ связанных мод могут быть решены методом теории возмущений при п «
« п по причинам, указанным в разд. 31.10.
31.12. Физическое рассмотрение
Уравнения связанных мод, полученные в предыдущем разделе, могут быть
выведены также с помощью интуитивного подхода, что позволяет глубже по-
нять физический смысл связи мод. Рассмотрим бесконечно малый участок
возмущенного волновода длиной dz, как показано на рис. 31.2, и определим
Рис. 31.2. Бесконечно малый участок нерегулярного
волновода между плоскостями поперечного сечения
z и z + dz
519
его влияние на вперед-распространяющуюся направляемую моду. Зависи-
мость от z коэффициентов Z>k(z) в разложениях (31.45) можно представить
в виде
Mz) = «k(z)exp(i/3kz), (31.52)
где ак (z) и (3kz — амплитуда и фаза моды соответственно. Изменение Z?k (z)
на рассматриваемом бесконечно малом участке волновода описывается
очевидно, соотношением
dbk(z) = i(3kbk(z)dz + dak(z)exp(i/3kz), (31.53)
где первый член в правой части учитывает изменение фазы. Изменение ампли-
туды dak(z) возникает из-за наличия нерегулярности, при этом все моды
вносят в него вклад. Для определения этого вклада заменим неоднородно-
сти на участке волоконного световода, показанном на рис. 31.2, наведенным
током с плотностью J, обсуждавшимся в гл. 22. Из соотношения (22.3)
следует
J=i(^-)1/2fc(n2 -и2)Е, (31.54)
где п и п — пгюфили показателей преломления возмущенного и нёвозмущен-
ного волноводов, а Е — полное электрическое поле возмущенного волново-
да. Интерпретируем тогда J как источник в невозмущенном волноводе. Его
вклад в dak (z) следует из выражения (31.34)
/7т
<&k(z) =—^".Jek ’ J exP(-i^kz)Jyl> (31.55)
так как Nk = 1 для ортонормированных полей. Если мы подставим этот ре-
зультат в формулу (31.53), представим J в виде разложений (31.45а) и
(31.46а) с помощью (31.54) и учтем выражения для коэффициентов связи
(31.506) и (31.50в), то придем к уравнению связанных мод (31.50а).
ЛОКАЛЬНЫЕ МОДЫ
В гл. 19 мы ввели понятие локальных мод, чтобы описывать поля в волново-
дах с большими, но медленно изменяющимися по длине неоднородностями.
Поскольку отдельная локальная мода является лишь аппроксимацией точно-
го поля, то в процессе распространения ее мощность оказывается связанной
с мощностью других локальных мод. Наша цель здесь — вывести систему
уравнений связанных мод, определяющих амплитуды каждой моды [10].
Сначала, однако, необходимо получить соотношения, которым удовлетворя-
ют поля в таких волноводах.
31.13. Поля в нерегулярных волноводах
В волноводе, не обладающем трансляционной инвариантностью, профиль по-
казателя преломления изменяется с координатой z, отсчитываемой вдоль оси
волновода, т. е. п = п (х, у, z). Следовательно, мы не можем больше записы-
вать точные поля Е и Н в форме с разделяющимися переменными (30.4). Од-
нако мы можем разделить поля на поперечную и продольную составляющие
E = Et +ЯД H = Ht +tfzi, (31.56)
520
где каждая составляющая зависит от z. Векторный оператор V определяется
соотношением
V = Vt+ zd/dz, (31.57)
где Vt определен в табл. 30.1. Подставляя выражения (31.56) в уравнения
Максвелла для полей без источников (30.1) и приравнивая соответствующие
составляющие, получаем
е.=-Ь ф 2 * Ps1 - v>"4 4 Ф “1 (v>х н->
( яг 1 (31.58а)
Н« = - 1/2 2 х hr - г = - i Ф1,2 2 • (vtх Е») •
(31.586)
Исключение продольных составляющих и использование соотношений
(37.27) приводит к следующим уравнениям для поперечных составляющих
полей:
Е>=Г Ьф “2 * 4^ 4 v>х х е 4 <з1-59а>
ГЬМ- (31-S96)
где параметры определены в табл. I.
31.14. Уравнения связанных локальных мод
Для удобства мы рассматриваем здесь только направляемые моды: моды из-
лучения легко включаются в уравнения по аналогии с тем, как это было сде-
лано в уравнениях связанных мод в разд. 31.11. Представим поперечные со-
ставляющие поля возмущенного волновода в виде разложения по полной си-
стеме вперед- и назад-распространяющихся локальных мод
Et = S {b.(z) + b_-(z) } ё^(х.л 0j(z)); (31.60а)
Н = S {b. (?) - Ь_} (?)} hjj (х, у, 3, (?) ), (31.606)
где знаком * отмечается ортонормировка, a Ъ-} (z) описывает как амплитуд-
ную, так и фазовую зависимости моды, т. е.
6±j(z) =e+j(z)exp(±i/3j(z)<fe>. (31.61)
I о J 1
Постоянная распространения j3j (z) и поле каждой локальной моды удов-
летворяют уравнениям (31.59) при каждом фиксированном значении zвдоль
волоконного световода, т. е. неявная зависимость ё^- и htj от z игнорируется
при дифференцировании. Таким образом,
ё«" -ф {ф1'1^2 *h» 4 v<х <v>х ; <з1-б2а)
4{Ф''!,’/гх 4V>х <444 (31-626)
521
Поперечные же составляющие полного поля волновода удовлетворяют
уравнениям (31.59) точно, поэтому, подставляя в них разложения (31.60),
с учетом соотношений (31.62) получаем
( - db\ db-\ - 1
2 - *_j) z x - i0. (b. + Z>_p z x h4 + ----^i-) z x hjj} = 0;
(31.63a)
f ^ti dbi db_\ ч 1
2 {(*j +M z x -J- - i0j(br b_}) z x + (-^L +-^) i x j =0.
(31.636)
Локальные моды локально ортонормированы и, таким образом, удовлет-
воряют соотношениям (11.16). Умножим скалярное уравнение (31.63а) на
etk, а уравнение (31.636) на htk и проинтегрируем в плоскости поперечного
сечения. Считая волновод непоглощающим, т. е. что efV = ё* , h+v = h* , по-
LK IK LX tK
лучаем
db- db i 1 dh,,
л лоо
(31.64a)
db, db 1 .
IT
(31.646)
где опущен нижний индекс t, поскольку только поперечные составляющие
входят в подынтегральные выражения. Складывая и вычитая (31.64а) и
(31.646), получаем
где — коэффициенты связи, определенные соотношениями
(31.65а)
(31.656)
Cik = - J I h- х - ё. х 4^-1 ’ ZdA, j Ф к, С. = 0.
4 A J dz J dz J JJ
ЛОО k '
(31.65b)
Коэффициент Cji равен нулю вследствие дифференцирования единичной нор-
мы. При замене к к, j / получаем коэффициенты Cjk с отрицательными
индексами, используя свойство симметрии полей, определяемое соотноше-
ниями (11.7).
31.15. Альтернативная форма коэффициентов связи
Мы покажем здесь, что коэффициенты связи (31.65в) могут быть выражены
в более компактной форме. Комбинируя составляющие поля в уравнениях
522
(31.58) и подставляя поля для /-й вперед-распространяющейся локальной
моды из уравнений (19.2), получаем
-1 (—)1/2 кп2 ё. = Vt х h; + i&z х L; (31.66а)
Mo j t J j j
x ej +ij3jZx6j; (31.666)
мы игнорируем неявную зависимость векторов ej и hj от z. Умножая уравне-
ние, сопряженное к уравнению (31.66а), на ё^, а уравнение, сопряженное к
уравнению (31.666), на h^, где штрих означает частную производную otz,
и почленно вычитая полученные уравнения, находим
[к 1/2*** ’ + 1,2пЧ\ ’ёк}= % ’ vt х и;-й; • vt х е* +
+ i(3. {ё* х ht -h*x ё' } "z. (31.67)
j j к J к 7
Второе уравнение получается из (31.66) заменой индекса / на А: и диффе-
ренцированием обоих уравнений по z. Далее умножим первое уравнение на
ё*, а второе — на h*, вычтем их друг из друга и в результате получим
+(-^-)1/2«2ё*-ё:) -ёк =
ре0' j Тс J kJ ’ dz J k
= • Vt x h' -M" Vtx e' - {(z x ёк) • h»- (f x hk) • ё*} -
-^к{ё*х^-ь*х ё^} * z. (31.68)
Если сложить уравнения (31.67) и (31.68) и результат проинтегрировать в
плоскости поперечного сечения, то условия ортогональности локальных мод
(11.16) приводят к тому, что член, содержащий множитель d^/dz, исчезает.
С помощью соотношений (37.28) четыре члена с оператором Vt можно выра-
зить в виде
J V • { h*x ё' -ё* х &}dA. (31.69)
A J * J *
оо
Из двумерной формы теоремы о дивергенции (37.55) следует, что поверх-
ностный интеграл идентичен криволинейному интегралу на бесконечности и
он обращается в ноль, так как функция полей и их производные экспонен-
циально уменьшаются до нуля на бесконечности. Поскольку мы считаем вол-
новод непоглощающим, то ёт и ht можно выбрать вещественными, откуда
вытекает, что [12]
\ = (—)1/2 ---Ц-Т J ё* • ё ^-dA.
jk 4(^-0к)Лте1 k<)z
(31.70)
Здесь Cjk — тот же коэффициент связи, что в выражении (31.65в).
523
31.16. Вывод уравнений связанных мод на физическом уровне
Система уравнений связанных локальных мод может быть выведена интуи-
тивно путем рассмотрения участка нерегулярного волоконного световода
[12], заключенного между двумя сечениями, отстоящими друг от друга на
бесконечно малую величину dz. Здесь мы приведем краткое описание этого
метода. Участок световода длиной dz показан на рис. 31.2. Вперед-распро-
страняющаяся /-я локальная мода с амплитудой (z) падает на рассматрива-
емый участок световода в точке z. Изменение величины bXz) вдоль рас-
сматриваемого участка световода согласно соотношению (31.61) имеет вид
( z 'j
db. = ifi.b.dz + da. exp <i f /3,(z )dz' >. (31.71)
J J J J l о J
Здесь первый член в правой части учитывает изменение фазы, а второй — из-
менение амплитуды. Для того чтобы определить изменение da-^ исследуем
отраженные и прошедшие поля, когда к-я вперед-распространяющаяся ло-
кальная мода падает на рассматриваемый участок волоконного световода.
Поперечная электрическая составляющая полного поля непрерывна на
рассматриваемом участке, т. е. Et = Ер где Et включает в себя поле к-й впе-
ред-распространяющейся и всех назад-распространяющихся локальных мод в
точке z, a Ej — поле всех вперед-распространяющихся локальных мод в точке
z + dz. Следовательно,
akEtk + Sa_jEti=S<E^ (31.72)
I I
где Е — обозначение ортонормированной локальной моды, включающее ее
фазовую зависимость; отрицательные индексы здесь обозначают назад-рас-
пространяющиеся локальные моды, для которых Et _ * = Eti.
Умножая векторно обе части (31.72) на (Hj) */2 и интегрируя в плоскости
поперечного сечения с учетом условий ортонормировки (11.16), получаем
для непоглощающего волновода
а. = -^- J Ё. хй;* * idA + J Ё= х Н> • zdA. (31.73)
J 2 А К J i 1 д J
Л оо » ХЧ оо
В первом порядке по dz магнитное поле в точке z + dz связано с полем в
точке z соотношением
И! =Hj + -^-dz, (31.74)
подстановка которого в выражение (31.73) с использованием условий
(11.16) приводит к выражениям
a. = akDkjdz + a-i + ? J * (31.75а)
д! = а. (1 + D..dz) + а_- + S а_р_-dz, j = к, (31.756)
где
, - <1Н*
IE (31.75b)
1J 2 Лоо 1
524
Вторая пара уравнений получается аналогичным образом с использовани-
ем условия непрерывности поперечной составляющей магнитного поля, т. е.
Ht = . Соотношение, соответствующее (31.72), имеет вид
(31.76)
так как Ht _ * = — Hti. Используя условие ортонормировки и выражение для
Ej , аналогичное (31.74), находим
а. = -aiAjdz~ a-i - ? а- iF- Hdz’ J'*k’ (31 -77a)
aj = a. (1 _ Fjjdz) - a_j - S a_ {F_ {jdz, j = k, (31.776)
где
, . <ЭЁ*
'Wy/i x^'taA’ <з1-77в)
Дифференцируя соотношение (11.16) no z, получаем и, склады-
вая соответствующие уравнения (31.75) и (31.77), находим
2a! = йк (Dkj- Djk)dz + 2 a-i(я-ij -Dj j*k> <3L78a>
2a! =2flj + Sa_i(Z>_ij-Z>j_i)dz, / = Л. (31.785)
С помощью уравнений (31.61), (31.65в), (31.75в) и (31.77в) легко убедить-
ся, что уравнение (31.78) эквивалентно
(а -а)ехр{1 /0 (z)dzl = С Ъ + S С- _ J dz. (31.79)
1 J I о J J V. j )
Если мы суммируем по к вклады в aj кавдой вперед-распространяющейся
моды, положим aj - 4?j = dbj-в соотношении (31.71), и разделим результат
на dz, то получим систему уравнений связанных мод (31.65).
ГЛАВА 32. ПРИБЛИЖЕНИЕ СЛАБОНАПРАВЛЯЮЩЕГО ВОЛНОВОДА
В гл. 13 мы показали, как построить поля для направляемых мод в слабона-
правляющих волноводах, используя простую физическую аргументацию, и
затем в гл. 25 распространили этот метод на моды излучения. Чтобы допол-
нить физическое рассмотрение, мы здесь даем формальный математический
подход, используя теорию возмущений для векторного волнового уравнения.
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ
Электрическое и магнитное поля моды произвольного волновода предста-
вимы в виде функций с разделяющимися переменными (11.3) и (11.6):
Е(х, у, z) = е(х, y)exp(i(3z) = {et + ezz} exp(ij3z) ; (32.1a)
H(x,j, z) = h(x,/)exp(ij3z)= {ht + ftzz} exp(i/3z), (32.16)
где 3 — постоянная распространения, z - единичный вектор, параллельный
оси волновода, а индексы t и z обозначают соответственно поперечную и про-
525
дольную составляющие. Мы опускаем индекс моды, так как в этой главе рас-
сматриваются только отдельные моды, и считаем, что et и ht имеют декарто-
вы составляющие, т. е.
et = + еуУ’ ht = М + М’ (32.2)
где х и у — единичные векторы, параллельные осям х и у (см. рис. 11.1, а).
При этом е удовлетворяет векторному волновому уравнению (11.40а), а его
поперечная составляющая — уравнению (30.18а)
{V^+^л2 -02} et =-Vt{et • Vtln«2} , (32.3)
где п = п (х, у) — профиль показателя преломления, к = 2тт/Х и X — длина вол-
ны в свободном пространстве. Операторы определены в табл. 30.1. Все дру-
гие составляющие е и h получаются из et с помощью соотношений (30.5).
Параметрическая зависимость полей. Мы обсуждали в гл. 11 параметри-
ческую зависимость полей мод и показали, что электрическое поле всегда за-
висит от волноводного параметра V и относительной высоты профиля Д, ко-
торые безразмерны. Следовательно,
е = е(К Д), (32.4)
где V и Д определены в табл. I. Подчеркнем, что оба эти параметра независи-
мы друг от друга.
32.1. Разложение полей направляемых мод
Если волновод является слабонаправляющим, то его профиль мало изменя-
ется и Д « 1. Предположим также, что поперечная составляющая электри-
ческого поля et может быть разложена в ряд по степеням Д с учетом того,
что V и Д — независимые параметры [1 - 3]. Таким образом,
et(,K Д) =et + Де{(1) + Д2е2 + ..., (32.5)
где верхний индекс обозначает степень Д, а коэффициенты при кавдой сте-
пени Д зависят только от V; знаком ~ обозначается решение при Д = 0.
Удобно векторное волновое уравнение выразить в безразмерной форме.
Для профиля вида
«2 (X, Я = {1 - 2Д/(х, у); , (32.6)
где исо — максимальное значение показателя преломления, f > 0, параметр
сердцевины U и волноводный параметр V определены в табл. I. Пусть р — ха-
рактерный размер поперечного сечения волновода, тогда уравнение (32.3)
можно переписать в виде
{р2 V2 + V2 - v2f\ et = -pVt {et • pVt In n2} .
(32.7)
Разложение для U имеет вид
U(V, Д) = U + MJW +... ; U=p(k2n2m -32)1/2, (32.8)
где U — значение U при Д = 0, 0 — соответствующая постоянная распростра-
нения. Если мы подставим это разложение в соотношение, связывающее U
и точную постоянную распространения 0, приведенную в табл. I, выразим
кп^ через V и Д и применим биномиальное разложение, то получим
526
L_
P (2Д)1/2 Г V2) ’
. = К 1 _ £1 f A V/2 _ V4+4UV2U(l) ( Д V/2
p P (24)1/2 pV 1 27 PV3 2 7
(32.9a)
(32.96)
Выразив 3 через U с помощью соотношения (32.8), находим, что (3 и(3 связа-
ны равенством
^=^_4_^21(Д)3/2 (3210)
с точностью до членов порядка Л3/2 включительно. В гл. 13 первые поправки
к (5 и Uобозначены через 6/3 и bU соответственно. Таким образом, из уравне-
ний (32.8) и (32.10) получаем
0^+60; 50 = — -^(24)1/2 =- (32.11а)
р V pV 2
U^U+dU- 8U = UW Д = — { р И/t/(2Д)1/2} 50. (32.116)
Чтобы разложить член Vt In п2 в уравнении (32.7), подставим в него выраже-
ние (32.6)
VtW =Vtln(l — 2Д/) = —2AVt/—2Д2 Vtf2 — . .. (32.12)
Для ступенчатого профиля, когда п = nCQ в сердцевине и « = «с1 в оболочке,
из определения Д, приведенного в табл. I, получаем
f=H, Vt In и2 = —2Д6§ + ..., (32.13)
где Н — единичная ступенчатая функция, т. е. Н = 0 в сердцевине и Н = 1 в
оболочке, 6 — дельта-функция Дирака, которая отлична от нуля только на
границе раздела, s — единичный вектор внешней нормали к границе раздела.
Остальные составляющие поля. При заданной поперечной составляющей
электрического поля et остальные составляющие можно выразить через et с
помощью соотношений (30.5). Если мы используем определение волновод-
ного параметра, приведенное в табл. I, и выразим к через V и Д, то получим
ez=70 {pVt’et + (et -pVt)ln«2} ; (32.14а)
\ = "со (-S')1/2 -^^2 х {р0е + ipVtez} ; (32.146)
Ф“ фГ- 17 z »jV' • h.1' (3214в)
где р — характерный размер поперечного сечения волновода. Члены разло-
жения этих составляющих получены в следующем разделе.
32.2. Вывод разложений поля
Дадим систематический вывод уравнений, которым удовлетворяют члены
разложения et, и покажем, как получить соответствующие члены разложений
остальных составляющих поля. Подставим разложения (32.5), (32.8) и
(32.12) в уравнение (32.7) и приравняем члены при одинаковых степенях Д.
527
Нулевой порядок. В низшем (нулевом) порядке по Д находим, что et
удовлетворяет уравнению (32.7) при Д = 0, т. е.
р2 v2 + т _ v2f > et = 0.
(32.15)
Это скалярное волновое уравнение обладает свойствами, рассмотренными в
разд. 33.1, а именно et и его первая производная везде непрерывны. Член низ-
шего порядка в разложении поперечной составляющей магнитного поля ht
обозначим как Ht. Если подставить разложения (32.5) и (32.9) в уравнение
(32.14, б) и учесть, что член низшего порядка в разложении для ez пропорци-
онален Д1/2, как будет показано ниже, то получим
Rt =«co(-^-)1/22xgf
(32.16)
(32.17)
Следовательно, ht тоже удовлетворяет скалярному волновому уравнению.
Соответствующие члены низшего порядка в разложении продольных состав-
ляющих ez и hz получаются подстановкой (32.5), (32.9) и. (32.12) в уравне-
ния (32.14а) и (32.14в) и поэтому имеют порядок Д1/2. Если верхним ин-
дексом (Обозначать степень Д, то
z Э1/2
е<‘и -е,),
В отличие от поперечных составляющих et и Ht продольные составляющие
не являются решениями скалярного волнового уравнения.
Первый порядок. Поправка первого порядка е^1) удовлетворяет неодно-
родному уравнению, приведенному в табл. 32.1, которое получается прирав-
ниванием членов порядка Д в уравнении (32.7). Так же поправки Ц1), Z/2 и
h2^2 находят приравниванием членов порядка Д в уравнении (32.146) и по-
рядка Д^2 в уравнениях (32.14а) и (32.14в).
Резюме. Если объединить полученные выше результаты, то поля направ-
ляемых мод слабонаправляющих волноводов можно представить в виде
разложений
е = е + Д1/2е*/2 z + Де^ + Д^2 е^3^ z + .. .,
I z t z
h = ht + Д1/2/Л1/2) z + Ahj1) + Д372/?72 z + ...,
(32.18a)
(32.186)
где et и e^1) удовлетворяют уравнениям, Приведенным в табл. 32.1, а осталь-
ные члены выражены через et и ер\ Пример этого разложения дан в табл. 12.6
528
Таблица 32.1. Уравнения для членов разложения нулевого и первого порядков
по степеням Д поперечной составляющей электрического поля для слабонаправля-
ющего волновода
{p2V2+1/2 - К2/}е, = О
{p2v,2+ О1 - Г2/}®!1» = 2pVt{et-pV,/}—2йи,1'е,
/£„\‘/2 21/2
К = "«(—) ^,,2, = i—pV,-6,
\Мо/ *
21/2 п /р \1/2
Ла/2> = 1__р?,А= -'2,/2f(^ 2-pV.xi,
/£л\1/2 ( и2 2 1
h!‘* = "со^—j 2х !<*’ —рЛ ~у2 P^l (PVt -*t) j
«<x3'2, = '-p|₽Vt-e;*’ + p2pVt-«t-2el-pVt/j
и /г'Х1/2 I?1/2 С г'/2 ~ 1
Л<з/г>= _(2i/2^( J» ) i.pVixe!» = ^ pVl-hl") + —jpV.-h,
V \ До / V I V J
Примечание. Остальные составляющие поля выражены с точностью до членов по-
рядка Д3/2 включительно через решения указанных уравнений.
для основной моды волоконного световода со ступенчатым профилем пока-
зателя преломления.
В разд. 32.4 рассматривается постоянная распространения, а в последую-
щих разделах показывается, как строить поля мод с-помощью решения ска-
лярного волнового уравнения.
32.3. Физическая интерпретация предельного приближения при Д О
Первые члены е t и Ht в разложениях (32.18) представляют собой точные ре-
шения при Д = 0 или, что эквивалентно, при «со = «с1. Хотя V и Д рассматри-
ваются в разложениях как независимые параметры, в определении V, приве-
денном в табл. I, фигурирует величина Д. Следовательно, если Д = 0, мы
должны положить также X = 0, чтобы в пределе при Д О, X 0 волноводный
параметр остался конечным и, вообще говоря, произвольным. Если Д = О,
то из выражения (32.9) следует, что 0 = °°, а это означает, что поля мод вол-
новода с «со = ис1 теряют физический смысл. Однако если Д и X малы, но не
равны нулю, а /3 велико, но конечно, то поля мод и постоянные распростра-
нения волновода с «со = ис1 являются хорошей аппроксимацией для опреде-
ления полей мод и постоянных распространения слабонаправляющего волно-
вода, как было показано в гл. 13.
Хотя et является очень хорошей аппроксимацией поперечной составляю-
щей точного поля, некоторые читатели могут быть неудовлетворены тем, что
эта аппроксимация основывается на не имеющей физического смысла моде-
ли волновода, для которого nCQ = ис1 [2]. Однако она аналогична общеприня-
529
той аппроксимации в виде единичных диполей для реальных физических ди-
полей. Вспомним, что электростатический потенциал диполя может быть вы-
ражен через два независимых параметра: дипольный момент р -Qd и рассто-
яние d между двумя одинаковыми по величине и противоположными по зна-
ку зарядами ± Q. Если d достаточно мало, то потенциал в некоторой точке
поля равен <р(р, d) & ip(p, 0), где 0) — потенциал элементарного диполя
при d = 0. Элементарный диполь не имеет физического смысла, так как Q
должен быть равен °° для того, чтобы значение р осталось произвольным и
конечным. Тем не менее поле реального диполя с d Ф 0 хорошо аппроксими-
руется полем элементарного диполя с d = 0. Параметрыр, dnQ диполя игра-
ют здесь роль соответственно параметров V, Д и X”1 оптического волновода.
На первый взгляд скалярное волновое уравнение (13.8), выраженное че-
рез (3, не определено при Д -► 0, j3 -> °°. Однако оно идентично уравнению
(32.15) , в которое входит параметр ZZ Поскольку значение j3 должно лежать
в интервале, указанном в табл. I, то значение Uдолжно лежать в интервале
0 < U< V. Следовательно, при Д 0 и фиксированном V значение Uостается
конечным даже при Д = 0. Таким образом, оба уравнения — (13.8) и (32.15) —
вполне определены в указанном пределе.
32.4. Постоянные распространения
В разд. 32.2 мы получили разложение для полей направляемых мод слабона-
правляющих волноводов. Члены этого разложения зависят, в свою очередь,
от разложения модового параметра U (32.8). Здесь мы покажем, как найти
эти члены.
Постоянная распространения скалярного приближения. Член низше-
го порядка для U появляется в скалярном волновом уравнении (32.15).
В разд. 33.1 будет показано, что решение скалярного волнового уравнения и
его первые производные должны удовлетворять условию непрерывности.
Это приводит к задаче на собственные значения для допустимых значений
U. В общем случае это уравнение трансцендентно и должно решаться числен-
ными методами, как ясно из примеров, приведенных в гл. 14. Для данного
U значение постоянной распространения скалярного приближения j3 получа-
ется из соотношения, приведенного в табл. I.
В выражениях (32.1) поля мод зависят от произведения где 0 - точ-
ная постоянная распространения. Так как значение z может быть произволь-
но большим, то необходимо знать поправки высших порядков к постоянной
распространения скалярного приближения 3, чтобы наши приближенные вы-
ражения для полей были достаточно точными на конечных расстояниях вдоль
волновода. Эти поправки учитывают поляризационные эффекты, обуслов-
ленные направляющими свойствами волновода.
Соотношение меаду точным значением постоянной распространения и ее
значением для скалярного приближения. Для того чтобы подправить скаляр-
ное приближение для постоянной распространения, мы сначала выведем со-
отношение между полем et и постоянной распространения полученными из
скалярного волнового уравнения, и точным значением поля et и постоянной
распространения /3, полученными из векторного волнового уравнения. Та-
ким образом, из уравнений (32.15) и (32.3) имеем
; + k2n2 -Д*} et =0; (32.19a)
{V^ + k2n2 -fi2} et =-Vt.{et • Vtlnn2} , (32.196)
где n = n(x, у). Умножая скалярное уравнение (32.19a) на et, уравнение
(32.196) — на et, вычитая полученные соотношения одно из другого и инте-
грируя по неограниченной площади поперечного сечения А ж , получаем [2]
02 -pi = J ? • V {е • У1пи2}сМ/ | £ -е dA, (32.20)
Аж 1 1 Аж 1 г
где члены с исчезли. Чтобы показать это, преобразуем поверхностный ин-
теграл от этих членов в криволинейный с помощью тождества (37.57) :
;{ё -V’e -е .VJe}^=HeVt.e -eV -ё} . ndl, (32.21)
A I II I II 1 I 1 I I 1 t
оо Zqq
где Zoo — периметр сечения А ж , а и — единичный вектор внешней нормали к
1Ж , лежащий в плоскости сечения А ж . Так как поля направляемых мод и их
производные экспоненциально уменьшаются до нуля на бесконечно больших
расстояниях от волновода, то криволинейный интеграл обращается в нуль.
Подынтегральное выражение в числителе правой части (32.20) имеет вид
et • УгФ, где Ф - скалярная функция. Его можно заменить, используя век-
торное тождество (37.26), на Vt • (Фёг) - ФУг • et. Поверхностный инте-
грал от УДФ^) преобразуется в криволинейный с помощью тождества
(37.55), который обращается в нуль по тем же причинам, по которым обра-
тилась в нуль правая часть в (32.21). Если мы вспомним определения UnU,
приведенные в табл. I, то окончательно получим альтернативное выражение
(32.22)
которое является точным и справедливо для любого профиля показателя
преломления, ступенчатого или градиентного.
Постоянные распространения ТЕ-мод. Из гл. И и 12 мы знаем, что моды
с е7 = 0 являются ТЕ-модами. Из табл. 31.2 следует, что член Vt • et в уравне-
нии (32.22) пропорционален еО/2) для слабонаправляющего волновода. Сле-
довательно, Vt • et = 0, и постоянная распространения скалярного приближе-
ния совпадает с точной постоянной распространения. Это согласуется с ре-
зультатами гл. 12, где мы показали, что точные поля ТЕ-мод можно вывести
из скалярного волнового уравнения.
Поправки теории возмущений к постоянной распространения скалярного
приближения. Мы определим здесь первую поправку к Она обозначена
как 8(3 в гл. 13. В этой главе показано [см. (32.11а) ], что поправка имеет по-
рядок Д372. Преобразуя левую часть (32.22) и подставляя в нее выражения
(32.9) и (32.11а), получаем в низшем порядке по Д
Р -J32 = -(0-0) (0 + 0) = -(И/р)(2/Д)1/250. (32.23)
531
Подобным образом мы подставим разложения (32.12) и (32.18,а) в правую
часть уравнения (32.22) и сохраним только члены низшего порядка. Сравни-
вая результат с (32.23), получаем
(32.24)
Соответствующее выражение для 6(/следует из соотношения (32.116) :
8U = -^ / (pVt -ё )ё -p\fdA/f &dA, (32.25)
где U — решение задачи на собственные значения для скалярного волнового
уравнения.
Поправки теории возмущений для ступенчатого профиля. В случае волно-
вода со ступенчатым профилем показателя преломления член Vt In п2 в
(32.22) задается 6-функцией с весовым множителем из (32.13), и выраже-
ния (32.24) и (32.25) приводятся к виду
50 = - (2^LbbU= ^^(pVt -et)g • ndl/ f^dA, (32.26)
l Лоо
где криволинейный интеграл берется по периметру I поперечного сечения
волновода, ап — единичный вектор внешней нормали к I.
НАПРАВЛЕНИЯ ВЕКТОРОВ ПОЛЯ НАПРАВЛЯЕМЫХ МОД
Мы показали в гл. 13 с помощью физической аргументации и выше с помо-
щью метода теории возмущений, что пространственная зависимость попереч-
ного электрического поля et слабонаправляющего волновода приближенно
описывается решениями скалярного волнового уравнения. Так как далее мы
будем иметь дело только с решениями скалярного волнового уравнения, то
опустим знак ~, использованный в первых разделах этой главы. Вообще го-
воря, et представляет собой линейную комбинацию решений скалярного
волнового уравнения, причем каждое решение имеет одно из двух ортого-
нальных состояний поляризации [2]. Направление вектора было найдено в
гл. 13 с помощью простых физических соображений; здесь мы покажем, как
это направление может быть определено с использованием теории возмуще-
ний соответственно для каждого случая, рассмотренного в гл. 13.
32.5. Волноводы с некруглым поперечным сечением
Если поперечное сечение волновода некруглое, то скалярное волновое урав-
нение (13.8) имеет только одно рещение Ф для каждого дискретного значе-
ния постоянной распространения скалярного приближения 0*. Вектор et, как
показано в (13.7), тогда принимает вид
* Правильнее было бы здесь сказать, что снимается вырождение, связанное с круго-
вой симметрией сечения волновода, так как, вообще говоря, возможно вырождение
мод по другим причинам. - Прим. ред.
532
et = (ах + 6у)Ф, (32.27)
где а и b — постоянные. Имеется всего два Возможных значения отношения
а/b, соответствующих двум ортогонально-поляризованным модам. Мы опре-
делим эти значения, используя соотношение теории возмущений для слабона-
правляющих волноводов, подобное (34.24). Это соотношение выводится за-
меной в (32.22) et на st, где st обозначает либо Фх, либо Фу, а Ф удовлетво-
ряет уравнению (13.8). Таким образом,
/2ДЧ 3/2
60 = J (pVt • st)et • pVtfdA/ J s • e dA. (32.28)
Аж Аж
Это выражение связывает поправку 60 к постоянной распространения ска-
лярного приближения с правильной линейной комбинацией (32.27). Чтобы
определить 30 и отношение а/b, составим два уравнения, подставляя et из вы-
ражения (32.27) и полагая: 1) st = Фхи 2) st = Фу. Это дает соответственно
a{D -5(3} +bD =0, aD + b {D -6/3} =0, (32.29)
где величины/) определяются выражениями
Dna J <pVt • • P^dA/ J <32-30>
pq 2pr Ax ' A~
a p, q обозначают либо x, либо у. Таким образом, система уравнений (32.29)
приводит к квадратному уравнению для а/b с решениями [2]
6/3= {Dyy+D^l [(Dyy-D^y + 4Z>xy]1/2 }/2; (32.31а)
a/b= {D^- Dyy± [(Dyy-D^Y +4Z»2xy]1/2} /2Пху, (32.316)
где мы положили £>ху = /)ух-
Доказательство тождества = /)ух. Равенство Dxy -D^ следует из ска-
лярного волнового уравнения. Заменим et на Ф в уравнении (32.15) и опре-
делим оператор У в виде
^Ф = {pV2 + £2 - К2/} Ф = 0. (32.32)
Дифференцируя по х и у, получаем соответственно
= И2Ф-^ • (32.33)
дх дх ду ду
Если умножить первое равенство на дФ/ду, вторбе — на д^/дх и подставить в
(32.30), то найдем
D - D = (2Д)3/ г С дФ ^2 дФ дФ у2 б)Ф ) , г ф2
^ху ^ух 2Кз I дх t ду ду t дх J
(32.34)
По аналогии с (32.21) правая часть может быть преобразована в криволиней-
ный интеграл, который стремится к нулю, так как Ф и ее первые производ-
ные экспоненциально уменьшаются до нуля на бесконечно больших расстоя-
ниях от оси волновода, и мы получаем требуемый результат.
Если подставить поочередно два значения а/b из (32.316) в выражение
(32.27) и перемножить скалярно полученные для et выражения, то получим
нуль; следовательно, поля мод ортогональны.
533
Определение оптических осей. В разд. 13.5 мы использовали физические
соображения, чтобы показать, что поперечное электрическое поле мод долж-
но быть поляризовано в направлении оптических осей слабонаправляющего
волновода. Если х0 и у0 — единичные векторы, параллельные оптическим
осям, то обе составляющие выражаются в виде
et=^x0, е^Фуо, (32.35)
где Ф - решение скалярного волнового уравнения (13.8). Сравнивая эти со-
отношения с (32.27), находим, что направления оптических осей задаются
выражениями
- _ * + а+У . х+а_у
Х° " (1+а2)1/2 ; У° = (1+а2_)1/2 ’
(32.36)
где а+ и а_ обозначают значения отношения а/b, соответствующие знакам
”+” и в правой части равенства (32.316). Обычно эти направления оче-
видны из симметрии волновода.
Результаты этого раздела применимы ко всем как основным, так и выс-
шим модам слабонаправляющих волноводов с произвольным поперечным
сечением и соответствуют результатам разд. 13.5 и 13.8, полученным с помо-
щью физических соображений. Кроме того, они применимы и к основным
модам световодов с круглыми поперечными сечениями, обсуждаемым в сле-
дующем разделе.
32.6. Круглые ролоконные световоды
В решениях скалярного волнового уравнения для круглого световода с про-
филем показателя преломления п (г) переменные разделяются:
Ф = F^R) cos (Ар), Ф = F{(R) sin (Up), (32.37)
где Л = r/p, a F^) удовлетворяет обыкновенному дифференциальному
уравнению
С (F 1 d ~ )
W+«5stt,!-^--pMFi=0’ <32J8)
как было показано в начале гл. 14. Выражение для профиля и другие пара-
метры определяются в табл. I.
Основная мода и НЕ1т-моды. Это те моды круглого световода, для кото-
рых имеется лишь одно решение скалярного волнового уравнения для дан-
ного значения ft или, что эквивалентно, U, соответствующее I = 0 в (32.37).
Следовательно, направление et описывается с помощью анализа методов, при-
меняемых в предыдущем разделе. Положив Ф = FQ (R) в формуле (32.30),
непосредственно получим, что Dxx = Dyy и Dxy = 0. Значения отношения а/Ь
в этом случае не определены, так что направление et может быть выбрано па-
раллельным любой паре ортогональных направлений, как и было показано
в разд. 13.4.
Моды высших порядков. Круглый световод уникален, так как для него
скалярное волновое уравнение при каждом значении j? имеет два решения
534
для мод высших порядков, соответствующих (32.37) с I > 1. Таким обра-
зом, направление вектора et, как это следует из формулы (13.7), определя-
ется соотношением
е = {[a cos (Zy?) + b sin (Z<p) ] x + [c cos (kp) + d sin (kp) ] у}, (32.39)
где a, b, с и d — постоянные. Имеются четыре набора значений этих постоян-
ных, соответствующих двум парам ортогонально-поляризованных мод. Вы-
ведем уравнения для этих постоянных способом, аналогичным приведенно-
му в разд. 32.5. Подставляя (32.39) в (32.28), получим четыре уравнения со-
ответственно:
1) st =FlC0S(Mx; 2) st =Flsin(/(p)x;
3) st = cos (Л/>) у; 4) st = sin (/</>) y.
Если поверхностные интегралы выражены в полярных цилиндрических ко-
ординатах (г, , то dA = p^RdRd^p, где R = г/р, а интегрирование проводится
по области 0 < R < °°, 0 < ip < 2я. Интегрирование по у проводится легко, и
четыре уравнения соответственно принимают вид
ад0 = аЦ + dl2; bb(3 = ЬЦ - cl2; (32.40a)
cbp = ch - bl2; db(3 = dh + al2 (32.406)
для I > 1, а при Z = 1
W = {3a + d)A + {a + 3J)/2 J 2bb(3 = (b + c) (h ~h} \ (32.40b)
2cbfi = {b +с)(Л -Z2); 2J5j3 = (a + 3J)A + (3a +J)/2. (32.40r)
Множители h и h определяются соотношениями
(2A)3/2 I(df/dR)dR i(2S)V2 f F2 (df/dR) dR
4pV lRF^R 2 4pV JRF^R
(32.40д)
Четыре независимых решения этих уравнений и соответствующие попереч-
ные поля (см. табл. 13.1) имеют вид
etl а = -d = 1, b =с = 0; е : a =d = 1, b = с = 0; (32.41а)
е • b = с — 1,а = б? = 0; е : b = -с = 1, a = d = 0. (32.416)
t3 t4 v 7
Поправки 50 j к постоянной распространения скалярного приближения выра-
жаются через параметры Ц и 12, приведенные в табл. 14.1. Ясно, что etl и et3,
et2 и et4 — пары ортогонально-поляризованных мод.
32.7 . Свойства симметрии мод высших порядков в круглых волоконных
световодах
Комбинации решений скалярного волнового уравнения для поперечных по-
лей слабонаправляющих круглых световодов даны в табл. 13.1. Как было
показано в предыдущих разделах, эти комбинации могут быть выведены с
помощью теории возмущений. В этом разделе мы покажем, как эти комби-
нации могут быть выведены только из соображений симметрии [2]. Начнем
с четырех векторных решений, построенных из решений скалярного волно-
535
Четные НЕ21~моды TMQ1 Нечетные НЕ21-моды ТЕ01
5)
/
Рис. 32.1. Поперечные электрические поля в сердцевине круглого световода:
а — качественное представление полей, определенных формулами (32.42) для мод с
I = 1; заштрихованные области соответствуют более высокой интенсивности поля;
б — результаты комбинации полей, представленных на рис. 32.1, й\ стрелки показывают
направление поперечного электрического поля
вого уравнения с произвольной постоянной распространения Д, и обозначим
их следующим образом:
е = F\ cos ехо = Fi sin (32.42а)
ли I XU L
еуе = C0S У’ еуо = F](R) sin (М У> (32.426)
где I > 1 и F(R) — решение уравнения (32.38).
Круглый световод инвариантен относительно вращения вокруг его оси.
Следовательно, если мода световода вращается аналогичным образом, то она
должна сохранить ту же постоянную распространения, хотя и не обязательно
остаться той же самой модой. Например, если поле ехе для I = 1 повернуто на
произвольный угол, оно будет представлено линейной комбинацией всех че-
тырех полей, приведенных на рис. 32.1, а. Однако если ехе — поле моды све-
товода, то все четыре поля в формулах (32.42) должны иметь одинаковые
поправки к постоянной распространения 3- Поскольку же четыре поправки
при I > 1 в табл. 14.1 неодинаковы, то получается, что ни одно из полей
(32.42) не представляет моду световода.
Чтобы вывести правильную линейную комбинацию, отберем моды, обла-
дающие одинаковыми свойствами при повороте на 90° и при зеркальном от-
ражении относительно осей х и у. Для облегчения вывода рассмотрим здесь
любой конкретный пример, скажем моду с I = 1, показанную на рис. 32.1, б.
Так, ехе комбинируется с еуо, поскольку они переходят друг в друга при
вращении, а ехо комбинируется с еуе, так как при вращении они переходят
друг в друга с точностью до обратного знака. Учет симметричной и антисим-
метричной комбинаций приводит к выражениям для поперечных полей четы-
рех мод слабонаправляющего волоконного световода, представленных в
536
табл. 13.1. Можно показать, что эти комбинации соответствуют свойствам
симметрии световода. Распределения полей et2 и et4 на рис. 32.1, б не изменя-
ются при зеркальном отражении относительно осей световода и при поворо-
те на произвольный угол; это говорит о том, что они являются полями мод
световода. Однако при поворотах на произвольный угол и зеркальных отра-
жениях etl переходит в поле, которое является линейной комбинацией etl
и . Симметрия требует, чтобы эта новая комбинация также была модой,
что, в свою очередь, требует равенство постоянных распространения полей
eti и et3* Это очевида° из табл. 14.1, так как 301 =
32.8 . Альтернативное представление для мод круглых волоконных
световодов
При рассмотрении слабонаправляющих круглых световодов как в этой гла-
ве, так и в гл. 13 и 14, подразумевалось, что комбинации, приведенные в
табл. 13.1, образуют наилучшую основную систему мод для описания при-
ближенных решений векторного волнового уравнения. Однако мы могли бы
рассмотреть, например, набор четырех право- и лево-циркулярно поляризо-
ванных полей, имеющих комплексную форму вида
eu = (х + i >0^(7?) ехр (iZ^); etb = (х - iу)F{(R) ехр(iZ<?), (32.43а)
etc = e*; etd=e*, (32.436)
где значком * отмечается комплексное сопряжение, aF\(R) — вещественное
решение уравнения (32.38). Исследуем теперь вопрос о том, может ли эта,
даже более простая система полей быть системой мод векторного волнового
уравнения в приближении слабонаправляющего волновода. Начнем с замеча-
ния о том, что поля мод в табл. 13.1 связаны с полями, определенными фор-
мулой (32.43), соотношениями
et!=Re<eta>; et2=Re<etb); (3244)
et3=Im<eta); et4=Im(etb),
где Re и Im обозначают вещественную и мнимую части. Если каждое из по-
лей (32.43) есть приближенное решение векторного волнового уравнения
(32.3) с уточненной постоянной распространения Д + ОД, то при приравнива-
нии вещественной и мнимой частей каждого поля становится ясно, что обе
они также являются решениями с той же самой постоянной распространения
(3. Поэтому, в частности, Re(eu) и Im(eta) имеют одинаковые постоянные
распространения для всех I > 0, соответствующих 8/31 = 8/3 3 в табл. 14.1.
Однако это, вообще говоря, не так для Re(etb) и Im(etb), поскольку при
1=1 поправки 8/32 и ОД для ТЕ0т-мод и ТМ0т-мод различаются. Следова-
тельно, представление полей (32.43) применимо ко всем модам круглого
световода за исключением ТЕОт- и ТМ0т-мод. В случае неограниченного
параболического профиля, как показано в табл. 14.2, 8(32 = 8(3ц для мод с
1=1, если только не учтены поправки высших порядков.
32.9 . Световоды с почти круглым поперечным сечением
Мы рассмотрели в разд. 13.9 моды высших порядков световодов с почти
круглыми поперечными сечениями и показали, что поперечное электрическое
537
поле должно иметь такой вид, как в нижней части таблицы 13.1. Здесь поля
выражены через решения скалярного волнового уравнения вида (32.37) и
неизвестные постоянные и а_. Для круглого поперечного сечения оба ре-
шения имеют одну и ту же постоянную распространения. Однако, если попе-
речное сечение лишь приближенно круглое, решения скалярного волнового
уравнения имеют близкие, но различающиеся постоянные распространения
и $о, как показано в разд. 13.8.
Значения а* и а_ и поправки 80е и 80о соответственно к постоянным рас-
пространения скалярного приближения 0е v 0О непосредственно связаны
между собой. Соответствующие соотношения находим с помощью процеду-
ры, подобной той, которая была приведена в разд. 32.5. Положим в формуле
(32.28) et - etl или е( = et2, где еп и et2 взяты из табл. 13.1, и составим четы-
ре выражения, считая, что: 1) 80 = 80е, st = F cos(/^)x и 2) 80 = 800, st =
= Fj sin (Up) у. В рамках сделанных выше приближений при вычислении Vt/
достаточно взять f таким, как для профиля круглого световода. Тогда по
аналогии и с формулами (32.40) получим
30е=Л+л/2; л6(30= h +аЦ, l> 1; (32.45а)
280е = (3+д)Л + (1 +Зл)/2; 2л80о = (3 + a)I2 + (1 + За)Л, /= 1,(32.456)
где а обозначает или а_, а параметры Ц и /2 определяются уравнениями
(32.40д). С учетом соотношений табл. 14.1 решение этих уравнений можно
выразить через поправки 80! и 302 для круглого световода [2] в виде
д±=Л± (1+Л2)1/2; А=(0е-0о)/(50! -602); ' 1>\. (32.46)
Поправки для круглого световода находим подстановкой а± в выражения
(32.45). Если повторить вычисления с et = et3 или et = et4, то получим иден-
тичное выражение для а± с той лишь разницей, что 8|3i — 802 изменяется на
803 - 804 в формулах (32.46).
32.10 . Поправки высшего порядка к полям мод
Фактически для всех применений слабонаправляющих волноводов, рассмот-
ренных в ч. II, достаточно знать поля мод низшего порядка^ и ht. Эти поля
с опущенным знаком ~ рассматривались на протяжении предыдущих пяти
разделов. В разд. 32.2 мы показали, что первыми поправками являются про-
дольные поля еи 9 которые точно выражаются через et и ht (см.
табл. 32.1). Однако, как отмечено в разд. 13.11, для задач, в которых важ-
ны поля е(V2) и ^(1/2) , 0бь1ЧН0 также требуется знать поправки и hO).
В табл. 32.1 приведены поправки М1), е @/2) и /Л3/2), которые полностью опре-
делены, если известно решение уравнения для еW . Поправка U W , входящая
в это уравнение, вычисляется с помощью решений низшего порядка с исполь-
зованием выражений (32.116) и (32.25). Известны два общих метода реше-
ния*: с помощью разложения по собственным функциям или с помощью
функций Грина.
* Здесь имеется в виду решение волнового уравнения с правой частью для
Прим, ред.
538
Решение методом собственных функции. В методе собственных функций
уравнения, являющиеся х- и ^-составляющими уравнения для ер), решают-
ся по отдельности с помощью разложения декартовых составляющих е (0 и
по полной системе собственных функций Ф| и 'J'j(C), принадлежащих
соответственно дискретной и непрерывной частям спектра собственных зна-
чений скалярного волнового уравнения, где удовлетворяют уравнению
(13.8), Ф^ (0) - уравнению (25.20), а переменная Q определена в табл. I
[4]. Например, пусть
е® = 2ЖФ. + S Г a.(Q)^ (Q)dQ, (32.47)
х / J J j о J J
где а. и a. (£?) — амплитудные коэффициенты. Это разложение подставляется
в ураЬненЬе для х-составляющих
{p2V\ + U2 _ V2f}e® =2p2^{et * V/} - 2UUme*, (32.48)
где ex - х-составляющая поля et. Амплитудные коэффициенты находят за-
тем с помощью соотношений ортогональности собственных функций, рас-
смотренных в разд. 33.2.
Решение методом функций Грина. Решение для е^ получается с помощью
функции Грина G (г, г') скалярного волнового уравнения, где гиг'- радиус-
векторы точек в поперечном сечении волновода [5], и
{p2V2 + £2 - Г2/}С = р26(х-х')6(>-У), (32.49)
где 6 — это дельта-функция Дирака. Следовательно,
е® = / G(r,r')g(r')^', (32.50)
1 Аж
где Аж — неограниченно большая площадь поперечного сечения, г = (х, у),
г = (х, у) , a g обозначает правую часть уравнения для ер), приведенное в
табл. 32.1.
Для конкретных профилей имеются более прямые методы определения
ер). В табл. 14.2 решение для ер) найдено с использованием метода разделе-
ния переменных и решения обыкновенных дифференциальных уравнений.
Для усеченных степенных профилей, рассмотренных в разд. 14.8, было пока-
зано, что решения скалярного волнового уравнения выражаются через сте-
пенные ряды. Декартовы составляющие поля ер) могут быть определены за-
тем в виде степенных рядов [6].
Как было показано в гл. 13, все моды волноводов с некруглыми попе-
речными сечениями и основные моды круглых световодов однородно по-
ляризованы, т. е. силовые линии поля образуют ортогональную сетку пря-
мых линий по всему поперечному сечению. Поправки высших порядков к
полю рассматриваются как небольшое искривление линий поля, при этом
электрическое и магнитное поля в общем случае уже не будут строго орто-
гональны.
ВЕКТОРНОЕ ВОЛНОВОЕ УРАВНЕНИЕ ДЛЯ ВОЛНОВОДОВ С ИСТОЧНИКАМИ
Если в волноводе присутствуют источники тока, полные поля связаны с то-
ками через уравнения Максвелла или, что эквивалентно, через неоднородные
539
векторные волновые уравнения. Декартовы составляющие Ех, Еу и £z пол-
ного электрического поля Е удовлетворяют уравнению (ЗО.17а)
{V2 + к2п2} Е= -V[Et ’ Vtln«2} (-^-)1/2 ^2J +v( Vn2J )j- ,(32.51)
где J = J(x, y, z) — объемная плотность тока источников, п = п (х, у), V2 —
по существу скалярный лапласиан (37.36), а остальные величины определе-
ны в табл. I. Напомним (см. разд. 11.16), что члены, содержащие Vt In п2,
описывают поляризационные свойства волновода. Если волновод слабона-
правляющий, то изменения профиля показателя преломления малы, и интуи-
тивно ясно, что поляризационные эффекты также малы. Приближенную фор-
му уравнения (32.51) в этом случае получаем, пренебрегая всеми членами,
содержащими производные от профиля, и заменяя п на «с0 в правой части.
Следовательно [7],
{v2 +к2п2} Е = -i(-^)1/2 ffcj + V(V-- JH . (32.52)
e° t *«co J
В этом уравнении не учитываются поляризационные свойства волновода, и
за исключением пространственной зависимости коэффициента преломления
в левой части оно идентично обычному уравнению для поля источников в
свободном пространстве [8]. Таким образом, в общем случае необходимо
сохранить оба члена в правой части (32.51). Мы обсудим решения этого
уравнения в следующих двух главах.
МОДЫ ИЗЛУЧЕНИЯ
В разд. 25.9 и 25.10 мы показали, как определять моды излучения слабона-
правляющих волноводов, используя поперечное электрическое поле et, ко-
торое формируется из решений скалярного волнового уравнения. Однако в
отличие от случая направляемых мод соответствующее магнитное поле ht,
полученное из соотношения (25.236), не удовлетворяет скалярному волно-
вому уравнению. Это означает, что соотношения ортогональности и коэффи-
циент нормировки мод излучения отличаются по форме от соответствующих
соотношений для направляемых мод, приведенных в табл. 13.2, как будет
показано ниже.
32.11 . Ортогональность и нормировка
Рассмотрим две различные моды излучения с электрическими полями ej =
= ej(2) и ek = ek((/) и образуем смешанное произведение ej х hk • z, где
знаком * обозначается комплексное сопряжение, az — единичный вектор,
параллельный оси волновода. В это произведение входят только попереч-
ные составляющие полей, так что подставив для выражение из (25.236)
и проведя преобразования с помощью соотношений (37.24) и (25.23а),
получим
е. X h. Z, Ф» - V,el} . (32.53)
540
Проинтегрируем обе части этого уравнения по всей площади поперечно-
го сечения и, используя тождество (37.26), преобразуем второй член в фи-
гурных скобках. В результате получим
— Je.xh* • z = A(-^Q-)1/2 j fe о е* + i* у . е ± у . (е е*
2Лоо J к 2 мо7 к Лоо| tj tk р zk t tj p t v tj zk'J
(32.54)
Из двумерной формы теоремы о дивергенции (37.55) следует, что интеграл
от третьего члена в фигурных скобках эквивалентен криволинейному инте-
гралу по периметру сечения Аж . Этим интегралом пренебрегаем по причинам,
изложенным в разд. 31.1, и в результате, используя соотношение (25.23а),
чтобы выразить Vt - через ezj, находим
1 J ex h*/ е.(С) .е*(С')^. (32.55)
^оо х4оо
Таким образом, соотношения ортогональности (25.4) сводятся к соотноше-
ниям (25.24а) для слабонаправляющего волновода, а выражение для коэф-
фициента нормировки (25.5) заменяется выражением (25.246).
ГЛАВА 33. МЕТОДЫ МОД ДЛЯ РЕШЕНИЯ СКАЛЯРНОГО
ВОЛНОВОГО УРАВНЕНИЯ
В гл. 11 были рассмотрены основные свойства мод оптических волноводов.
В гл. 30 и 31 эти свойства были выведены из уравнений Максвелла. Для сла-
бонаправляющих волноводов, рассмотренных в гл. 13, мы получили упро-
щенные выражения для мод в гл. 32, которые суммированы в табл. 13.2.
Соответствующие упрощения выражений для мод излучения были даны в
гл. 25. Существуют два пути, которыми эти упрощенные выражения могут
быть получены. Один путь — перейти к пределу Д 0 в точных выражениях
при фиксированном значении К Другой путь — вывести свойства мод из ре-
шений скалярного волнового уравнения, с самого начала считая, что попе-
речное электрическое поле et моды слабонаправляющего волновода удов-
летворяет этому уравнению. В этой главе мы следуем второму, более непо-
средственному подходу. Подчеркнем, что при этом поляризационные эффек-
ты, которые обусловлены структурой волновода и обсуждались в гл. 13,
здесь не учитываются.
33 Л. Скалярное волновое уравнение
В разд. 13.3 было показано, что декартовы составляющие вектора попереч-
ного электрического поля являются решениями скалярного волнового урав-
нения. Если Ф обозначает любую составляющую вектора (13.7), а $ — посто-
янная распространения скалярного приближения, то
{V* + k2n2 (х,у) -Р2} Ф = 0, (33.1)
где п (х, у) — профиль показателя преломления, к = 2я/Х, X — длина волны в
свободном пространстве, а оператор V2 определен в табл. 30.1. Как мы по-
541
кажем ниже, решение Ф скалярного волнового уравнения и его первые про-
изводные везде непрерывны и тем самым связаны граничными условиями.
Это приводит к задаче на собственные значения для ft.
Свойства непрерывности. Свойства непрерывности решений уравнения
(33.1) доказываются от противного. Предположим, что функция Ф — не не-
прерывна, так что где-нибудь она имеет ступеньку, или скачок значений. Пер-
вые производные тогда будут содержать сингулярность, описываемую 6-функ-
цией Дирака, а вторые производные — производную от 6-функции. Так как
профиль п(х, у) может иметь ступенчатые разрывы, то ясно, что уравнение
(33.1) не может быть удовлетворено. Следовательно, Ф должна быть непре-
рывна. Аналогично доказывается непрерывность первых производных. При
этом отнюдь не обязательно, чтобы вторые производные были непрерывны.
Например, если п(х, у) — ступенчатый профиль, то, по крайней мере, одна из
вторых производных от Ф должна быть разрывна. Наконец, так как поле
et строится из решений скалярного волнового уравнения, то оно должно
иметь те же свойства непрерывности, что и Ф.
НАПРАВЛЯЕМЫЕ МОДЫ КАК РЕШЕНИЕ СКАЛЯРНОГО ВОЛНОВОГО
УРАВНЕНИЯ
Здесь выводятся свойства мод слабонаправляющих волноводов исходя из
решений скалярного волнового уравнения.
33.2. Ортогональность и нормировка
Обозначим через Фj и Ф^ два различных решения уравнения (33.1) с посто-
янными распространения^ и .
Считая волновод непоглощающим и придерживаясь введенного в разд. 11.3
соглашения, можно считать функции Ф^ и Фк вещественными. Таким образом,
!V? + к2п2 - $2; ф. = 0; {V2 + к2п2 - & } Ф1 = 0, (33.2)
t J J t k k v 7
где n = n(x, у). Умножение первого уравнения на Фк, второго — на Фр вычи-
тание одного уравнения из другого и интегрирование полученного соотноше-
ния по неограниченной площади поперечного сечения А м , дают
(0? ~№) f = J {Ф, 72Ф. -Ф.У?Ф, } dA.
'•Ч к7 ? Г к ? к t j j к к*
оо оо
С помощью двумерной формы теоремы Грина (37.58) правая часть этого со-
отношения преобразуется к криволинейному интегралу
$ [Ф. ¥+Ф. - Ф.УхФ, } • hdl,
1 k t J J t
‘co
где Zoo — периметр площади поперечного Аж , а п — единичный вектор внеш-
ней нормали к /оо, лежащий в плоскости Аж . Этот интеграл равен нулю, так
как решения для направляемых мод и их первые производные экспоненци-
ально стремятся к нулю при удалении на бесконечность. Поэтому из соот-
ношения (33.3) следует, что все направляемые моды слабонаправляющих
волноводов удовлетворяют условию
(33.3)
(33.4)
/ Ф.Ф.Л4 = 0, j*k.
(33.5а)
542
Это выражение включает и назад-распространяющиеся моды с постоянными
распространения $_ = -j3j и $_к - Рк в соответствии с соглашением (11.4).
Если etj и etk обозначают решения скалярного волнового уравнения, состав-
ленные из (13.7), с постоянными распространения j3j и |Зк соответственно,
то можно повторить приведенное выше доказательство и получить
(33.56)
Напомним (см. табл. 11.1), что ортогональность точных полей мод описыва-
cj tk ’ z*
Выражение для ht, приведенное в табл. 13.1, показывает, что это произве-
дение пропорционально etj • etk для слабонаправляющего волновода. Так как
et вещественно для непоглощающего волновода, то из (33.5) следует, что
для направляемых мод в приближении слабонаправляющего волновода ска-
лярная и векторная форма соотношений ортогональности эквивалентны.
Нормировка. Удобно нормировать решения скалярного волнового уравне-
ния с помощью коэффициента нормировки 7V, приведенного в табл. 11.1.
Повторяя приведенные выше рассуждения, находим
N =4 I I exh*’ zdA I = -^2-(-^2-)1/2 J e?dA. (33.6)
2 I л I 2 Mo д t
Подставляя сюда выражения из табл. 13.1, получаем следующие соотношения
для волноводов с некруглым поперечным сечением и для круглых световодов:
N J N = ™со Отт-)1/2 S^^dr
2 Ах О
(33.7)
соответственно для основных мод и всех мод высших порядков.
33.3. Интегральные выражения для постоянной распространения
В разд. 11.13 мы показали, что точную постоянную распространения можно
строго выразить через интегралы от векторных полей мод. Здесь мы выведем
аналогичную формулу, в которой постоянная распространения скалярного
приближения будет выражена через решения скалярного волнового уравне-
ния. Начнем с уравнения (33.1). Умножив его на Ф и проинтегрировав обе
части по неограниченной площади поперечного сечения А ж, найдем
З2 J Ф2<£4 = к2 J и2Ф2б£4 + J ФУ2ФбД4. (33.8)
А А А *
оо оо 21 оо
Второй интеграл в правой части преобразуется с помощью двумерной формы
теоремы о дивергенции (37.55) и тождества (37.26). Таким образом,
J Ф?2ф<£4 = ^Ф(^Ф) - nJ/- J (\Ф)2^Л, (33.9)
А оо 4эО A QO
где /оо — периметр площади поперечного сечения А ж , а п — единичный вектор
внешней нормали к в плоскости Аж . Криволинейный интеграл обращает-
543
ся в нуль, так как Ф и ее первые производные экспоненциально уменьшают-
ся до нуля на бесконечности. Комбинируя (33.8) и (33.9), получаем
02 = J- (£2и2Ф2 - (V^)2} dA/ J ^dA,
/4 оо Л оо
(33.10).
где п = и (х, у). Это уравнение представляет собой интегральную форму зада-
чи на собственные значения для скалярного волнового уравнения, обсуждав-
шегося в разд. 33.1. Это также стационарное выражение относительно вариа-
ций Ф [1,2]. Далее, рассматривая соответствующее выражение для точной
постоянной распространения (31.21) , убеждаемся, что в приближении слабо-
направляющего волновода соотношение (33.10) не может быть непосред-
ственно получено при аппроксимации полей е и h выражениями для et и ht
из табл. 13.1. Иными словами, в разложении (32.18) необходимо оставлять
члены высших порядков.
33.4. Фазовая и групповая скорости
Фазовая и групповая скорости для направляемых мод скалярного волново-
го уравнения определяются соотношениями
~ со 2яс
vn =— =—
Р 3 ХЗ
Jco
2ъс dX
X2 d(3
(33.11)
соответственно, где угловая • скорость со и длина волны в свободном про-
странстве X связаны, как указано в табл. I. Мы можем выразить ир через ре-
шение Ф уравнения (33.1) с помощью соотношения (33.10). Ниже мы полу-
чим аналогичные выражения для vg. Иначе скорость ug может быть найдена
дифференцированием скалярного волнового уравнения задачи на собствен-
ные значения. В дополнение к пространственным изменениям профиля пока-
зателя преломления учтем также дисперсию материала, если «ид изменяют-
ся с длиной волны, т. е. п = п(Х) ид = д(Х), как это пояснялось ранее в
разд. 31.6.
Обозначим решение задачи (33.1) для длины волны X через Ф(Х) и соот-
ветственно Р (X). Так как к = 2тг/Х, то
{V2 +4тг2и2 (Х)/Х2} Ф(Х) = £2 (Х)Ф(Х). (33.12)
То же решение для длины волны X удовлетворяет уравнению
[V2 +4тг2п2 (Х)/Х2} Ф(Х) = 02 (Х)Ф(Х). (33.13)
Умножая уравнение (33.12) на Ф(Х), уравнение (33.13) — на Ф(X), вычитая
одно из другого и интегрируя по неограниченной площади поперечного сече-
ния, получаем
{02(Х)-02(Х)} / Ф(Х)Ф(Х)<?Л=4тг2 _^!1А)|ф(Х)ф(Х)Л4+4
Л” Х (33.14)
где / — интеграл вида
J {Ф(Х)72Ф(Х) -Ф(Х)72Ф(Х)} dA. (33.15)
Л t t
544
Этот интеграл преобразуется в криволинейный на бесконечности с помощью
двумерной формы теоремы Грина и обращается в нуль, так как Ф(Х), Ф(Х)
и их первые производные экспоненциально стремятся к нулю на бесконечно-
сти. Разделив обе части уравнения (33.14) на X — X и перейдя к пределу
X ~>Х, найдем
оо Л оо
(33.16)
Для волноводов без дисперсии материала это выражение сводится к виду
ve=Cy- J Ф2<М/ J «2Ф2<7Л.
g кАх А„
(33.17)
Из табл. 13.1 ясно, что выражение для групповой скорости (31.31) в случае
точных полей в приближении слабонаправляющего волновода сводится к
(33.17).
Производная модового параметра. Весьма полезно выразить производную
dU/dV через решение скалярного волнового уравнения. Это может быть сде-
лано аналогично приведенному выше выводу выражения для групповой ско-
рости, но с той лишь разницей, что начинать надо с уравнения (32.15) вместо
(33.12) и считать среду необдадающей дисперсией. При этом если U и К но
не f изменяются с длиной волны, то результат, аналогичный (33.17), непо-
средственно получается с помощью выражения из табл. 13.2. Подробности
этого вывода могут быть найдены в [3].
33.5. Соотношения взаимности
Исходя из скалярного волнового уравнения, мы можем получить соотноше-
ния взаимности для мод различных волноводов. Пусть Ф и /3 — поле и посто-
янная распространения моды одного слабонаправляющего волновода с про-
филем показателя преломления п = п (х, у), а Ф и (3 — поле и постоянная рас-
пространения моды другого^ слабо направляющего волновода с профилем по-
казателя преломления п = п(х, у). Для простоты мы опускаем знак ~ у по-
стоянных распространения. Обе моды удовлетворяют скалярному волново-
му уравнению, так что согласно (33.1) имеем
{V2 + к2п2 -/З2; Ф = 0; !v* + к2п2 -02} Ф =0. (33.18)
Умножив первое из этих уравнений на Ф, второе — на Ф, вычитая их друг из
друга и проводя интегрирование по неограниченной площади поперечного
сечения, получаем
(02-02) { ФФбМ=&2 J (и2 - п 2)ФФбМ + J |Ф72Ф —ФУ2Ф}dA.
А°° (33.19)
С помощью тождества (37.58) второй интеграл в правой части преобразует-
ся в криволинейный интеграл на бесконечности, который обращается в нуль,
18 Зак 37 545
так как Ф, Ф и их первые производные экспоненциально уменьшаются до
нуля для направляемых мод. В результате получаем
/З2 -|32 = к2 J (п2 - «2)ФФ<7Л/ J-
^4 ОО оо
(33.20)
Это выражение получается из (31.39) в приближении^лабонаправляющего
волновода. В этом нетрудно убедиться, полагая 02 — /3 2 ъ 2кнсо(/3 — (3) и
подставляя выражения для полей из табл. 13.1. Выражение (33.20) также
стационарно относительно вариаций величин, обозначенных чертой сверху
[1,2].
Выражение соотношения взаимности через криволинейные интегралы.
Можно также получить соотношение между модами различных волноводов,
выраженное через криволинейные интегралы. Для этого заменим в соот-
ношении (33.19) на Аж - Др> где Ар — площадь области поперечного сече-
ния, в которой п(х, у) Фп(х, у). Тогда первый интеграл справа в (33.19) ра-
вен нулю, а второй интеграл так же, как и выше, преобразуется к криволи-
нейному интегралу по контуру + Z , где Z — периметр области Л . Инте-
грал по равен нулю, и поэтому остается соотношение
(З2 - 0 2 = $ - Ф^Ф) • hdl/ J ФФбМ. (33.21)
Аоо р
Здесь использовано тоадество (37.58), где п — единичный вектор внешней
нормали к Z , лежащий в плоскости Аж . Легко убедиться, что это соотноше-
ние получается из (31.40) в приближении слабонаправляющего волновода.
33.6. Аналитические выражения для постоянных распространения
Имеется всего несколько профилей показателя преломления, для которых
получаются замкнутые решения скалярного волнового уравнения, как уже
указывалось в разд. 14.8, и еще меньше профилей, для которых к тому же
имеются аналитические выражения для постоянных распространения. Одна-
ко в случае неограниченных степенных профилей в круглых световодах для
постоянных распространения можно получить замкнутые выражения, хотя
этого и нельзя сделать для самих решений скалярного волнового уравнения,
исключая случай неограниченного параболического профиля (см. табл. 14.2).
Эти профили имеют вид
n2(R) = w2o(l -2ДЯ4), R>0, q>0, (33.22)
где R = r/p, а другие величины приведены в табл. I. Для круглого световода
решения уравнения (33.1) можно выразить через функции /^(Я) [см. фор-
мулу (32.37) ]. Подстановка (33.22) в (32.38) приводит к уравнению
(33-23)
При масштабном преобразовании A -+aR этого уравнения получаем [4]
( (j2 1 j /2 ~ )
W+r ™ ~ +а2 иг ~ v2a 4+2*q h=°- (33-24)
546
Для заданных I и q параметр U зависит только от волноводного параметра
V, т. е. U = U(V). Так как значение параметра U должно быть одинаково для
обоих уравнений, то приходим к выводу о том, что параметр О удовлетво-
ряет функциональному уравнению
aU(V) = + 2)/2). (33.25)
Это уравнение имеет решение
Й = бТ2/(2 + 7), (33.26)
где G — постоянная, зависящая от I и q, но не зависящая от V. Можно опре-
делить G при I = 0, учитывая, что соотношение (33.26) должно выполняться
и для V -+ °°. В этом пределе выражения для tj получены в разд. 36.8 с помо-
щью метода ВКБ. Сравнивая (33.26) и (36.19), определяем G, откуда следу-
ет [4]
Г(1/, + И)(1, + 2)(2т-1)я"К«
1 2Г(1/?) 1 '
где индекс т = 1, 2,... обозначает номер моды, как в табл. 14.1. Выражая V
через аэ и U через & с помощью соотношений, приведенных в табл. I, непо-
средственно из (33.11) находим выражение для групповой скорости
где /Т выражается через G с учетом (33.27).
МОДЫ ИЗЛУЧЕНИЯ КАК РЕШЕНИЕ СКАЛЯРНОГО ВОЛНОВОГО УРАВНЕНИЯ
Решениями скалярного волнового уравнения являются как скалярные на-
правляемые моды, так и скалярные моды излучения. Направляемые моды
аналогичны элементам .ряда Фурье, а моды излучения могут рассматриваться
как элементы интеграла Фурье. Вместе они образуют полную систему мод
для представления произвольного поля. Моды излучения характеризуют-
ся скалярным полем Ф (0 и постоянной распространения /3 (Q), которые
удовлетворяют скалярному волновому уравнению
{V2 + к2 п2 (х, у) -02(0} Ф(0 =0. (33.29)
Таким образом, дискретные значения (3 для направляемых мод в уравнении
(33.1) заменяются континуумом значений /3(0). В гл. 25 мы объяснили, по-
чему более удобно работать с параметром мод излучения Q, определенным в
табл. I. Напомним также, что как электрическое et, так и магнитное ht по-
перечные поля векторных направляемых мод слабонаправляющих волново-
дов являются решениями скалярного волнового уравнения. Однако, как по,-
казано в гл. 25, только поле et (0 векторных мод излучения удовлетворяют
скалярному волновому уравнению.
33.7. Ортогональность и нормировка
Континуум скалярных мод излучения, удовлетворяющих уравнению (33.29),
трактуется аналогично векторным модам излучения волновода. Для опреде-
18*
547
ления соотношений ортогональности повторяем процедуру из разд. 33.2, за-
менив Skj на Фк на M/j (б) и Фк (б). Затем подобно тому, как было сделано
в разд. 31.1, для получения правильных свойств ортогональности потребуем
обращения в нуль криволинейного интеграла в формуле (33.4). Таким обра-
зом получим
5 Ф.(б)Ф*(б')<М =0, Q*Q'. (33.30)
A J к
оо
Заметим, что это соотношение ортогональности относится и к модам излуче-
ния с различными значениями 2 и с j = к. Определим F-} (Q) как коэффици-
ент нормировки каждой скалярной моды излучения
F- (б) S (Q - Q') = J Ф. (б) <7 (б') dA, (33.31)
J д J J
Z1 оо
где 6 — дельта-функция Дирака. Подчеркнем, что Fj (б) не надо путать с ко-
эффициентом нормировки N: (б) для векторных мод излучения, определен-
ным соотношением (25.5). Между этими двумя выражениями, вообще го-
воря, нет простой связи.
33.8. Вытекающие моды
Поле излучения в скалярном волновом уравнении может быть представлено
континуумом скалярных мод излучения, обсуждавшихся выше, или дискрет-
ной суммой скалярных вытекающих мод и пространственной волной. Это яс-
но по аналогии с обсуждением в гл. 25 и 26 векторных мод излучения и выте-
кающих мод слабонаправляющих волноводов. Скалярные вытекающие мо-
ды соответствуют решениям Ф уравнения (33.1) ниже значений отсечки,
когда параметр fi становится комплексным. Многими свойствами направляе-
мых мод, установленными в этой главе, обладают также вытекающие моды.
Например, соотношение ортогональности (33.5а) применимо к вытекающим
модам, если только поперечное сечение А ж заменено комплексным попереч-
ным сечением Х>, введенным в разд. 24.15, чтобы обеспечить обращение в
нуль криволинейного интеграла (33.4).
МЕТОДЫ МОД ДЛЯ АНАЛИЗА РЕГУЛЯРНЫХ ВОЛНОВОДОВ
Если для одного волновода известна полная система решений скалярного
волнового уравнения, то она может быть использована для представления
скалярной моды другого волновода. Второй волновод можно рассматри-
вать как трансляционно-инвариантный, слабо отличающийся от первого.
33.9. Поля мод и постоянные распространения
Пусть Ф]- и -- неизвестные поля и постоянная распространения /-й моды
второго волновода, имеющего профиль показателя преломления п (х, у).
Представим Фj в виде разложения по полной системе решений Фк для на-
правляемых мод и Фк (б) для мод излучения первого волновода с профи-
лем п (х, у) . Таким образом, имеем
Ф .(х, у) = Ъа Ф (х,у) +S fa у, Q)dQ, (33.32)
J к к к к о к к
где и (Q) — амплитуды мод, которые должны быть определены, а Фк
548
и Фк(2) удовлетворяют соответственно уравнениям (33.1) и (33.29) ели
(3, замененными на и и (3 .
Для простоты мы опустили знак ~. Подставим разложение (33.32) в
(33.20), положив Ф = Фр Ф = Фк, (3 = (3- и (3 = (Зк. Используя соотношения
ортогональности (33.5а) и (33.30), находим
к2 1 — —
а, = ! (я1 - (33.33а)
1,2 1 -
(3333б)
где Fk и Fk (Q) — скалярные коэффициенты нормировки, определенные со-
отношениями
F = J Ф2/Л; F (2)5(2-2') = J Ф.(2)Фк(2')^, (ЗЗ.ЗЗв)
К л к к к к
оо оо
а 5 - дельта-функция Дирака. Для окончательного определения амплитуд
мод необходимо еще составить уравнение для (З^. Как в разд. 31.9, можно
получить из (33.10) нелинейную систему связанных уравнений. Хотя эта
система уравнений и не имеет общего решения, в случае слабо отличающих-
ся волноводов методом теории возмущений можно найти ее приближенное
решение.
33.10. Слабовозмущенные волноводы
Процедура, описанная в предыдущем разделе, формально является точной,
но она не приводит к определенным выражениям для Фj и /3^. Однако если
второй волновод представляет собой лишь слабовозмущенныи аналог перво-
го, можно получить решение уравнений (33.33) методом итераций.
В низшем порядке имеем
Ф. Ф., 0. (3. (33.34)
и, следовательно, « 1 в разложении (33.32). Поправки следующего поряд-
ка_находятся подстановкой & = (L и Фj = Ф| в (33.33) и (3 = , (3 = (3j, Ф =
= ф = ф. в соотношение (33.20). В результате получаем
к2
а. -------
k
в2 = в 2 +
Ч Р j F
- 4- J («2 -л2)Ф.Ф.<М;
Fk А„ J k
f(n2-n2)^2dA
^к Аж J
(33.35)
и аналогичное выражение для ак (Q). Этот метод использовался для опреде-
ления мод слабо эллиптичного волоконного световода через моды круглого
световода. Подробности приведены в [5].
МЕТОДЫ МОД ДЛЯ НЕРЕГУЛЯРНЫХ ВОЛНОВОДОВ
Если волновод неоднороден по длине, то распространение волн вдоль него
может быть описано системой уравнений связанных мод, основывающейся
на полном наборе мод скалярного волнового уравнения. При таком описа-
549
нии игнорируются все поляризационные свойства волновода. Последнее эк-
вивалентно тому, что полное поперечное электрическое поле остается парал-
лельным фиксированному направлению. Здесь мы покажем, как вывести
эту систему уравнений, исходя из скалярного волнового уравнения.
33.11. Уравнения связанных мод
Пусть п (х, у) и п (х, у, z) — профили показателя преломления регулярного
и нерегулярного волноводов соответственно. В рамках приближения слабо-
направляющих волноводов поле в нерегулярном волноводе удовлетворяет
трехмерному скалярному волновому уравнению, которое можно записать
в виде .
V2 + к2п2 (х, у, z) + Ф = О, (33.36)
где оператор V2 определен в табл. 30.1, к = 2я/Х, X — длина волны в свобод-
ном пространстве. Выразим функцию Ф в виде суперпозиции полной системы
скалярных направляемых мод и мод излучения
Ф = S a (z) Ф (х, у) + S Г Q) U Л Q)dQ, (33.37)
/ 1 I /о 1 1
где и ax(z, Q) содержат полную зависимость от z вперед- и назад-рас-
пространяющихся мод, а функции Ф| и Ф[(б) удовлетворяют уравнениям
(33.1) и (33.29)
{Ч2+к2п2(х, у) -0?; =0; \Ф+кгп2(х,у) - H2(Q) ] Ф AQ) =0.
I L L I и t
(33.38)
Для простоты здесь опущен знак ~. Подставляем разложение (33.37) в урав-
нение (33.36) и используем уравнения (33.38) для исключения членов V^L.
Умножая полученное уравнение на Фк и интегрируя его по неограниченной
площади поперечного сечения, получаем с помощью ортогональности (33.5а)
уравнение
d2a. f оо )
= <33'39а)
и аналогичные выражения для як((2). Здесь J9kl и Z>kl(2) - коэффициенты
связи; _
О = ifc2 J (п2 - п 2уъЪЛА/ J Ф2dA, (33.396)
д к ь д к
а выражение для £>kl«?) получается из (33.396) при замене Ф1 на Ф[(2)-
Таким образом, эти коэффициенты являются функциями z. После того как
решения для становятся известны, амплитуды Jk и d^ вперед- и назад-
распространяющихся мод можно найти из соотношения
ak =4exPO0kZ) +й?_кехР<-'0к2)- (33.40)
Иногда может оказаться полезной процедура, аналогичная приведенной ниже
после соотношения (33.63), где определяются амплитуды мод, возбужден-
ных источниками тока.
Сопоставление с уравнениями связанных мод для произвольных волново-
дов. В разд. 31.11 была получена система уравнений связанных мод для опи-
550
сания распространения волн по произвольным нерегулярным волноводам,
полученная на основе точных мод регулярного волновода. Если мы приме-
ним к этим уравнениям приближение слабо направляюще го волновода, то
окажется, что, например, уравнение (31.50а) останется таким же, но вид ко-
эффициентов связи (31.506) и (31.50в) изменится. Пренебрегая в выраже-
нии для ezk членами, порядок которых выше, чем у членов в выражении для
etk и учитывая соотношение ортонормировки, приведенное в табл. 11.1 и в
соотношениях (33.7), получаем
CkifeZ)kl/(2toco); Ск1Ш) ^£>к1(С)/(2^лсо) (33.41)
Далее необходимо продифференцировать уравнение (31.50а) по z и в резуль-
тирующем соотношении выразить db^/dz через Z?k. Опуская для простоты
связь с модами излучения, имеем
4^ . <33-«*)
)-^»С (33.426)
I I 1 — ь dz кь dz dz J
где учтено, что в приближении слабонаправляющего световода Ск = Ckv
Подобным же образом исходя из уравнения, аналогичного (31.50а), получа-
ется и второе уравнение для b - к, В результате находим
-4^ + № к= А2 +ь ? -х’ <33-43)
где учтено, что С_к1 = Ск _ = Ск1. В пределе слабонаправляющего волновода
j3k Следовательно, если дополнительно в правых частях уравнений
(33.42а) и (33.43) заменить |Зк на Ь?со, положить як = Z?k + ^-к и использо-
вать соотношение (33.41), то получим систему уравнений
ci
<3344>
идентичную систему уравнений (33.39а).
ЛОКАЛЬНЫЕ МОДЫ
Локальные моды были введены в гл. 28 для упрощения описания распростра-
нения волн по волноводам с большими, но медленно меняющимися нерегу-
лярностями. Мы получили уравнения связанных локальных мод для произ-
вольных волноводов в разд. 31.14. Здесь мы получим уравнения для локаль-
ных связанных мод из скалярного волнового уравнения. Так же, как и в
разд. 33.11, будем игнорировать все поляризационные свойства волновода.
33.12. Уравнения связанных локальных мод
В слабонаправляющем нерегулярном волноводе полное скалярное поле
Ф(х, у, z) удовлетворяет трехмерному скалярному волновому уравнению
(33.36). Представим Ф в виде суперпозиции ортонормированных локаль-
ных мод
551
^Vk = 2Mz)V’M(z))/! J ^kU^i3k(z))^}, (33.45)
Аг к L-/4 qq
где предполагаются включенными также моды излучения. Функция (z)
описывает зависимость от z как вперед-, так и назад-распространяющихся
мод. По аналогии с рассмотрением, проведенным в разд. 19.1, здесь скаляр-
ное поле локальной моды Фк удовлетворяет двухмерному волновому урав-
нению в каждой фиксированной точке z вдоль волновода
{^+k2n2(x,yfz')*k=0, (33.46)
где п (х, у, z) — профиль показателя преломления нерегулярного волновода;
знак ~ опущен. Подставим разложение (33.45) в уравнение (33.36) и исполь-
зуем уравнение (33.46) для исключения члена \7^Фк. Результирующее выра-
жение имеет вид
f d2av о л da*
Умножим это уравнение на Фр проинтегрируем результат по неограниченной
площади поперечного сечения и применим соотношение ортогональности
(33.5а), выполняющееся при каждом значении z. В результате получаем
(Ра- Г da. )
—zl + 02а. =2 +Е..а.\,
dz2 J J к t dz Jk kJ
где Z)jk и — коэффициенты связи, определенные соотношениями
D = - -
Jk x
б)Фк d2 Фк
dz “к dz2
(33.47)
(33.48а)
J ф.
A J
Zl оо
----dA\
dz
(33.486)
02Фк
---,dA,
I dz2
[ J Ф2</л11/2,
А к (
являются функциями z. Как и при решении уравнений связанных мод (33.39а),
после получения решений уравнений (33.48а) амплитуды вперед-и назад-
распространяющихся локальных мод можно определить из соотношения
{Z t J ( z f f
i f 0.(z')dz' > +d . exp <-i (z')dz'
о J J ~J l о J
Fjk X
X =| J
Л» J
Ф2<7Л
J
(33.48в)
(33.49)
при анализе зависимости от z.
Сопоставление с уравнениями связанных локальных мод для произволь-
ных волноводов. В разд. 31.14 была получена система уравнений связанных
локальных мод для произвольных волноводов. В приближении слабонаправ-
ляющего волновода поля мод в выражениях для коэффициентов связи
(31.65в) имеют только поперечные составляющие. Используя связь этих со-
ставляющих с соответствующими нормированными решениями скалярного
волнового уравнения (33.45), (см. табл. 13.1), находим с помощью выраже-
ний (33.486):
с. =-С . ,^D.J2, С. = Г ~0. (33.50)
jk -j - k, jk j - к _jk v 7
552
По аналогии с уравнениями (33.42) и (33.43) систему уравнений связанных
локальных мод для слабонаправляющего волновода представим в виде
d2b-
—Л + р2Ь = 10 S С b + х+; (33.51а)
az J J J £ JK к
d2b =
—fl + 02b = -ip SC b + X , (33.516)
dz J -J J £ J* -к -
где
f rfCik db , ) dp-
X+ = S ) b + С-,- > ± ib . -f- . (33.51b)
1 k I ±k dz jk dz J ±j dz v 7
В приближении слабонаправляющего волновода j3j « кпсо = К/p (2Д)1/2 и,
таким образом, 00 при Д -> 0. Кроме того, из (31.61) получаем, что в
низшем порядке ab±k/dz » ± i(3kb±k. Следовательно, в правых частях уравне-
ний (33.51а) и (33.516) доминирует член с j3j, а в определении параметра
Х± — член с db±k/dz. Соответственно если пренебречь остальными членами,
сложить уравнения (33.51а) и (33.516) и положить^ = b} + Z?_j,то получим
d2a-
(33-S2)
Из соотношений (33.49) и (31.61) находим, что dak/dz ^ij3k(Z>k — Z?_k) при
Д -> 0. Так как 0к & кпс0 для всех мод, то приходим к выводу, что уравне-
ния (33.52) и (33.48а) эквивалентны.
33.13. Альтернативная, форма коэффициентов связи
Здесь мы, проводя параллель с разд. 31.15, получим альтернативную форму
коэффициентов связи (33.48). Дифференцируя уравнение (33.46) для Фк
по z, находим
{^+к2п2-р-[}^ + 4^---^Ц*к=0- (33-53)
t к’ dz [ dz dz J к
Умножая это уравнение на Фр уравнение — (33.46) на d'kjdz и вычитая один
результат из другого, получаем
С дФ. дФ. ) f дФ. дФ. 'j
)^-^2Ф. - Ф; V2 + (£2И2 ~02) Ф. -г-1 - Ф. ) =
( dz t к J t dz J v к7 ( к dz J dz j
f dn2 d& 'I
= U2-f--------Цф.ф (33.54a)
( dz dz J J k
Второе уравнение получается аналогично при замене Ф- на Ф. ;
J к
(дФ, дФ- ) ( <)Ф^ 1
J к «гф _ ф V2_________11 + (к2п2 _ р-2\ 2ф____к _ ф ---11 -
t dz Vt J kvt dz J (* " PP( J dz к dz f
,2 dn2 1 у
&2— --------з-l- > ФФ,-
dz dz J J к
(33.546)
553
Сложим эти уравнения и проинтегрируем по неограниченной площади попе-
речного сечения Аж. Члены, содержащие V*, преобразуются с помощью тож-
дества Грина (37.58) в криволинейный интеграл по периметру площади А ж .
Этот интеграл обращается в нуль, так как функции SPj, Фк и их первые про-
изводные экспоненциально уменьшаются до нуля на больших расстояниях
от волновода. Соотношение ортогональности (33.5а) приводит к исчезнове-
нию членов с dfi2jdz и dftydz при i ^к. Перегруппировав оставшиеся члены,
с учетом (33.50) находим
к2
?jk = 02 - 02
J к
J -^-Ф. ф] dA =------5-----— J- -^-Ф. Ф, dA (33.55)
Л, J к 2псо (0. - 0к) dz J к
1
где использовано соотношение & + Зк ~ 2&исо ПРИ А << 1- Это выражение
идентично выражению для коэффициентов связи, полученному из (31.70)
в приближении слабонаправляющего волновода, с учетом соотношений ор-
тонормировки (см. табл. 11.1) и нормировки (33.7).
ВОЗБУЖДЕНИЕ МОД ИСТОЧНИКАМИ ТОКА
В гл. 32 было получено уравнение, связывающее полное электрическое поле
Е в слабонаправляющем волноводе с плотностью тока J источников тока.
Использовав определение волноводного параметра, приведенное в табл. I,
уравнение (32.52) можно выразить в виде
{V2 + к2п2(х,у)} E = -i*(^-)1/2|j+^-pV(pVx J)j , (33.56)
где V2 определяется соотношением (37.36), к = 2л/Х, X — длина волны в сво-
бодном пространстве, а поле Е выражено через декартовы составляющие.
Рассматривая возбуждение направляемых мод, пренебрежем вторым членом
в фигурных скобках справа, что можно сделать независимо от скорости из-
менения J при достаточно малом значении Д. Поперечные поля можно найти,
как только станет известно решение уравнения (33.56) для Ег В это реше-
ние входит только поперечная составляющая плотности тока Jt. Продольная
составляющая плотности тока Jz связана с Et только через поле Ez, которое
дает поправки высших порядков здесь не рассматриваемые. Соответственно
уравнение (33.56) сводится к виду
{V2 + к2п2(х,у)} Et=-ifc(Mo/eo)1/2Jf (33.57)
Так как все поляризационные эффекты в волноводе игнорируются, можно
разложить поле Et на декартовы составляющие и решать оба неоднородных
волновых уравнения для этих составляющих по отдельности.
Определение скалярных полей. Пусть Ф(х, у, z) nJ(x, у, z) обозначают ли-
бо Ех и Jx, либо Еу и Jy в уравнениях для составляющих (33.57). Тогда ана-
логично уравнению (33.36) уравнение для Ф может быть переписано в виде
+ к2п2 (х, у) + Ф = 1/2Jv (33.58)
Разложим Ф по полной системе скалярных мод
ф = s {ak(z)exp(i0 z) + a_k (z)exp(—i/3 z)} Ф = ЕЛ (г)Ф , (33.59)
к к
554
где як (z) и а_к (z) ~ зависящие от z амплитуды к-х вперед- и назад-распро-
страняющихся мод соответственно, а Ак (z) отражает полную зависимость от
z, связанную с Фк. Здесь опущены для простоты скалярные моды излучения.
Каждая скалярная функция Фк удовлетворяет уравнению
+ к2п2 (х, у) - j32k; Фк = о. (33.60)
Подставляя разложение (33.59) в уравнение (33.58) и используя уравнение
(33.60) для исключения членов с 572Фк, приходим к соотношению
Г d2А 1
+^K=-i*C),'v (зз-б1)
Умножим обе части этого соотношения на Фр проинтегрируем по неограни-
ченной площади поперечного сечения и, использовав соотношение ортого-
нальности (33.5а), получим уравнение
d2 А
+Ц2А. =g. ; g. = -ik №-)1/2 J V.JdA/ J Ф2Л4, (33.62)
J J J J 6° Лоо J Лоо J
где gj — функции z. Это неоднородное обыкновенное дифференциальное
уравнение второго порядка может быть решено такими стандартными мето-
дами, как, например, вариация произвольных постоянных. Решение имеет
вид
i ( z Z2 )
Aj = - Г gi ^ехр (Z ~ dt+ S g- О)ехр {ip. (г - z)} dt\,(33-63)
где zt и z2 - постоянные. Считаем, что токи распределены в объеме между
плоскостями z = Zj и z = z2 поперечных сечений волновода, как показано на
рис. 31.1. Таким образом, сравнивая (33.63) и (33.59), получаем следующие
выражения для амплитудных коэффициентов:
я. = 0, (33.64а)
а. =-~ Sg.(t)exp(-ipt)dt, zt<z<z2-, (33.646)
J 7 J J
а. = 1 i 22 J'gi(Oexp( I0.t)dt, ZPj J J z > z2, (33.64b)
для вперед-распространяющихся мод и i а - = -~— J ^(Oexp(iP t)dt, j 2 p j 2 J z < z i; (33.65a)
a . -j i = -57- J g-(t)exp(iP t)dt, Zpj 2 J J Zj <z <z2; (33.656)
a . -J = 0, z>z2 (33.65b)
для назад-распространяющихся мод, где^ определяется выражением (33.62).
Соответствующие выражения для мод произвольных волноводов даны в
формулах (31.35) и (31.36). В пределе Д -> 0 с учетом соотношения норми-
ровки (33.7) эти выражения сводятся к приведенным выше, так как
& ^псо9 а ФУНК1*ИЯ считается вещественной.
555
ГЛАВА 34. МЕТОДЫ ФУНКЦИЙ ГРИНА
В трех предыдущих главах мы описали решение уравнений.Максвелла для
полного электромагнитного поля произвольных и слабонаправляющих во-
локонных световодов в терминах направляемых мод и мод излучения. Не-
обходимость использовать суперпозицию всех этих мод не всегда делает
этот путь простейшим, особенно в случае одномодовых волоконных свето-
водов, когда представляет интерес только основная мода. Здесь мы приво-
дим основные сведения об альтернативном подходе — методе функций Гри-
на [1—3] — в качестве приложения к его применению в задачах о малых
возмущениях в гл. 18 и в задачах об излучении поля источниками тока в
гл. 21. В последнем случае этот метод эквивалентен методу вычисления по-
ля, возбужденного элементарным диполем, и последующего построения по-
лей распределенных токов методом суперпозиции. Однако для случая произ-
вольного распределения токов этот метод может оказаться не проще, чем ис-
пользование разложения по собственным функциям. Иными словами, пре-
имущества использования метода функций Грина или метода разложения по
собственным функциям зависят от особенностей рассматриваемой конкрет-
ной задачи.
ПОЛЕ ПРОИЗВОЛЬНО РАСПРЕДЕЛЕННЫХ ТОКОВ
В гл. 31 мы использовали теорему взаимности для уравнений Максвелла,
чтобы выразить амплитуды мод произвольного волоконного световода через
заданное распределение тока. Здесь мы используем эту теорему, чтобы пока-
зать, как полные поля, обусловленные этим распределением, могут быть по-
лучены с помощью линейной суперпозиции полей единичных диполей.
34.1. Вывод из теоремы взаимности
Рассмотрим два случая возбуждения полей. В первом произвольное распре-
деление токов с плотностью J создает в волоконном световоде электричес-
кое Е и магнитное Н поля, а во втором — элементарный диполь с плотностью
тока J порождает поля Е и Н. Все шесть электромагнитных величин содер-
жат временную зависимость ехр(—icof). Местоположение и ориентация ди-
поля учитываются выражением
J =5(r-r'){7x + 7yy + 7zz}, (34.1)
где 7Х, 7у, 7Z - произвольные величины, х и г - радиусы-векторы точек
наблюдения и положения диполя соответственно, х, у, z — единичные векто-
ры, параллельные декартовым осям координат; при этом ось z направлена
вдоль оси волоконного световода, а 6 — известная дельта-функция Дирака.
Свяжем оба указанных случая с помощью трехмерной формы сопряженной
теоремы независимости. Считая световод непоглощающим, так что его коэф-
фициент преломления п веществен, и подставляя выражение (34.1) в уравне-
ние (31.3), получаем
V • Fc = -(Ё* • J + E • J*), (34.2)
где знаком * обозначается комплексное сопряжение, п = п, а вектор Fc опре-
делен соотношением (31.1). Если проинтегрировать обе части этого выраже-
ния во всем пространстве по координате г' и применить теорему о диверген-
556
ции (37.55), то его левая часть преобразуется в поверхностный интеграл на
бесконечности, обращающейся в нуль, так как поля в выражении для Fc до-
статочно быстро убывают при |r'| Таким образом, остается соотношение
V* + EJ* + EJ* = -S Ё* (г, г') • J (/)dr (34.3)
где левая часть вычислена при г ' = г, а Г" —объем, в котором распределены
источники тока. Составляющую Ех можно найти, если положить Jx = 1, Jy =
= 7Z =0, так что Е при этом представляет собой поле в точке г, обусловлен-
ное ориентированным по оси х элементарным диполем, расположенным в
точке г'. Аналогичным образом определяются составляющие Еу и Ez. Пола-
гая Е = Ехх + Еуу + Ez z, окончательно получаем
E(r) =- J E*(r,r') : J'(r')d^',
(34.4)
где Е называется диадной функцией Грина, а знаком обозначено опреде-
ленное ниже диадное произведение. Очевидно, что Е имеет девять составля-
ющих для того, чтобы учитывать вклады в каждую составляющую поля Е от
диполей, ориентированных вдоль осей х, у, z, с составляющими тока Jx, Jy и
Jz в точке г'. Если Ехх, Еху и Exz — составляющие поля Е, дающие полный
вклад в Ех от составляющих тока Jx, Jy и Jz источника соответственно, то
; чу,+ А’Л+а* <34-5>
аналогичные выражения имеются для Еу и Ez.
Вычисление полей диполей. Если поле элементарного диполя в волокон-
ном световоде известно, то электрическое поле, обусловленное заданным
распределением тока, определяется из формулы (34.4), а соответствующее
магнитное поле — из формулы (30.1а). Для нахождения поля диполя можно
использовать такие разложения по модам, как (31.32), и вычислить амплиту-
ды мод из выражений (31.35) и (31.37). Это было сделано в разд. 25.14 для
диполя, расположенного на оси световода. Однако в этом случае было бы
проще непосредственно определить поля, создаваемые распределением тока,
с помощью аналогичного разложения по модам. Можно было бы также ре-
шить неоднородное векторное волновое уравнение (30.13а), плотность тока
J в котором задается выражением (34.1), однако в общем случае решение
этого уравнения затруднительно из-за наличия связи между составляющими
электрического поля, обусловленной членом Vtln п2 . Задача становится раз-
решимой для световода со ступенчатым профилем показателя преломления,
так как в этом случае член Vt In п2 обращается в нуль везде, кроме границы
раздела между сердцевиной и оболочкой, и уравнение (30.13) может быть ре-
шено с помощью продольных составляющих поля, как указано в разд. 11.15.
Но даже в этом особом случае вычисление полей диполя и полных полей ока-
зывается слишком громоздким [4].
Приведенные выше соображения относятся к произвольным волоконным
световодам. Если же ограничиться только слабо направляющими волоконны-
ми световодами, то метод функций Грина может быть значительно упрощен.
557
Чтобы понять это упрощение, выведем сначала выражение для векторного
потенциала поля в световоде с произвольным профилем показателя прелом-
ления, а затем получим из него выражение для частного случая слабонаправ-
ляющего световода.
34.2. Представление векторного потенциала для произвольных волоконных
световодов
Решение уравнений Максвелла для полного поля в световоде с произволь-
ным профилем показателя преломления можно выразить через известный
векторный потенциал А, взятый в лоренцевой калибровке. Стандартный вы-
вод этого представления предполагает среду однородной [5, 6], но его лег-
ко модифицировать, как это сделано ниже, чтобы учесть неоднородность
среды световода.
Независимо от изменения среды уравнение для дивергенции магнитного
поля (30.16) удовлетворяется, если положить
H=(l/Mo)Vx А, (34.6)
где до — магнитная проницаемость свободного пространства. Подстановка
этого выражения в (30.1а) дает
Vx Е= {i*/(Moeo)1/2} Vx А. (34.7)
Это уравнение имеет общее решение вида
Е = i&A/(poeo)1/2 + VX) (34.8)
где х — произвольная функция координат, а для Е, Н, А и х подразумевает-
ся временная зависимость ехр(—icof). Связь угловой частоты со с другими
параметрами приведена в табл. I. Подставляя выражения (34.6) и (34.8) во
второе из уравнений Максвелла (30.1а) и используя векторное тождество
(37.30), получаем
{V2 + £2и2} A = V(V- A) -MoJ + ib*2 (juoeo)1/2Vx, (34.9)
где п = п (х, у) — профиль показателя преломления волоконного световода.
Составляющие вектора А,направлены вдоль декартовых осей, так что мож-
но заменить векторный лапласиан V2 скалярным, как это разъяснено в
разд. 30.6. Если мы теперь выберем функцию х в виде
X = i(V • А)/{&л2 (доео)1/2 } , (34.10)
то уравнение (34.9) запишется следующим образом:
{V2 + к2п2} А = -д0J + (V • A) Vt In и2.
(34.11)
При этом электрическое поле
(34.12)
558
что следует непосредственно из соотношений (34.8) и (34.10). Если показа-
тель преломления везде постоянен, то уравнение (34.11) ивыражение (34.12)
сводятся к хорошо известным результатам для однородной среды [5, 6].
34.3. Представление векторного потенциала для слабонаправляющих воло-
конных световодов
Представление полей через векторный потенциал в слабонаправляющем све-
товоде существенно упрощается, так как мы можем пренебречь всеми чле-
нами, содержащими Vt In и2, по причинам, изложенным выше, после уравне-
ния (32.51). Таким образом, выражения (34.6) и (34.12) заменяются следу-
ющими:
1
H = t-Vx А;
(Моео)1/2
V (V • А)
(34.13)
а из уравнения (34.11) вытекает, что декартовы составляющие вектора А
удовлетворяют уравнению
{V2 + к2п2} А = -До-*-
(34.14)
В (34.13) мы положили п ъ ис1, чтобы согласовать результат с приближени-
ем свободного пространства, рассмотренным в следующем разделе. Выведен-
ные уравнения отличаются от стандартных уравнений для однородной среды
[5, 6] учетом зависимости А от профиля показателя преломления световода
только в левой части уравнения (34.14).
Решение для векторного потенциала. Каждая декартова составляющая
векторного потенциала удовлетворяет скалярному волновому уравнению.
Следовательно, решение уравнения (34.14) для каждой составляющей вы-
ражается через одну и ту же функцию Грина, и суперпозиция дает
А(г) =мо JG(r,r')J(r')rfH
(34.15)
где — объем, в котором распределены источники тока, а г и г' - радиусы-
векторы точки наблюдения поля и точки расположения источника соответ-
ственно. Функция Грина определяется уравнением
{V2 +к2п2} G(r, г') = -6(г — г')
(34.16)
с подходящими граничными условиями, где 5 — дельта-функция Дирака.
Нас интересуют, главным образом, только поле излучения или дальнее по-
ле. Как пояснено в разд. 21.8, излучение источников в слабонаправляющих
559
световодах близко к излучению в свободном пространстве, т. е. в ненаправ-
ляющей среде с однородным показателем преломления ис1. Соответственно
решим сначала уравнение (34.16) для среды, в которой везде п = мс1, а за-
тем введем поправки, отражающие присутствие световода.
34.4. Функция Грина свободного пространства
В среде с однородным показателем преломления ис1 решение уравнения
(34.16) хорошо известно. Оно имеет вид [1-3]
С(Г.И= (34 |7)
4я|г - г'|
где |г — г'| - расстояние между точкой наблюдения и местоположением ис-
точника. Если ограничиться рассмотрением дальнего поля, когда |г| >> |г'|,
то, используя тождество
|г - г'| = {s2 + s'2 - 2ss' cos X i 1/2 , (34.18)
чтобы получить разложение выражения (34.17) (где s = |r|, s' = |г'|, а х —
угол между векторами г и г', как показано на рис. 21.4, б), найдем главный
член [7]
f exp {ib«cl} f
G(r, г ) =----—--------exp {—iks ис1 cos x} •
(34.19)
Подстановка (34.19) в (34.15) приводит к выражению для А в дальнем поле
(21.20). Кроме того, для области, достаточно удаленной от всех источников,
где s » s', из (34.19) выводим, что V i£zzclr, где г - единичный вектор,
параллельный вектору г, представленному на рис. 21.4, а. В соответствии с
тем, как выражения (21.18) и (21.19) были найдены из (21.16), находим
вектор Пойнтинга S = 56 Re (Е х Н*), где Re обозначает вещественную часть, а
знак * - комплексное сопряжение.
34.5. Трубчатые источники в слабонаправляющих волоконных световодах
Установив способ вычисления поля излучения источников тока в свободном
пространстве, обратимся теперь к влиянию световода на это поле. Можно
продолжать решать уравнение (34.16) для заданного профиля показателя
преломления, что приведет к выражениям для полей, полученным с помощью
формул (34.15) и (34.13). Однако вместо того, чтобы суммировать даль-
ние поля от единичных источников, предпочтительнее определить функцию
Грина для трубчатого источника, введенного в разд. 21.6 и изображенного
на рис. 21.3 [7] • Преимущество такого трубчатого источника состоит в том,
что его геометрия обладает той же симметрией, что и круглый световод.
К тому же произвольный источник тока может быть описан с помощью не
только распределения диполей, но и полной системы трубчатых источников.
Мы рассмотрим здесь этот последний подход.
560
Произвольное распределение токов источника. Распределение токов труб-
чатого источника, определенного выражением (21.12) в обозначениях, приве-
денных на рис. 21.3, имеет вид
(34.20)
где 2L — длина отрезка световода с областью токов, &1 — положительное це-
лое число или нуль. Для удобства мы считаем единичный вектор и параллель-
ным некоторому фиксированному направлению. Мы можем выразить произ-
вольное распределение токов в виде суперпозиции токов трубчатых источни-
ков, интегрируя (34.20) по r0, <Po и суммируя по /. Для учета зависимости
от продольной координаты, выраженной функцией g (z), проведем преобра-
зование Фурье распределения токов, векторного потенциала и полей по 0.
Если индексом I отмечать определенную трубку тока, то, например, для нее
получим
= 7^exp(-i0z)Jz; E^z) = 7 Elexp(i0z)c?|3. (34.21)
2л
Чертой сверху обозначаются образы Фурье электромагнитных величин, свя-
занные друг с другом соотношениями (34.13) и полученные путем преобра-
зования величин Е, Н, А в Е^, Ц и соответственно, и представления опера-
тора V в виде V = Vt + ij3z, где Vt — оператор поперечного градиента (см.
табл. 30.1), az — единичный вектор, параллельный оси световода. Аналогич-
но, подставляя выражение (34.20) в уравнение (34.14) после его преобра-
зования по Фурье, получаем
{v^ + к2п2 - £J2} ^ = - Mog—2^,- —cos I (<? - <Po)n,
(34.22)
где g — образ Фурье функции g, V* — поперечный оператор Лапласа из
табл. 30.1, а п = п (г) — профиль показателя преломления световода. Таким
образом, учет влияния световода на поле излучения в свободном простран-
стве сводится к решению этого простого уравнения. Напомним, что при та-
ком описании игнорируются все поляризационные эффекты в слабонаправ-
ляющем световоде, так как член, содержащий Vt In п2, в уравнении опущен.
34.6. Корректирующий множитель
Поле излучения трубчатого источника определяется решениями уравнения
(34.22) для декартовых составляющих вектора At. Тем не менее мы можем
сделать определенные заключения об этом поле независимо от профиля по-
казателя преломления световода [7]. Прежде всего рассмотрим решение для
случая свободного пространства, когда везде п = ис1. Пространственная зави-
симость А^ при значениях г, соответствующих точкам вне трубки, пропорци-
ональна в цилиндрических полярных координатах функции
561
(Qr/p) cos /(</>- <p0), Q = P {к2п2{ - (?} 1/2, (34.23)
где//^ ~ функция Ганкеля первого рода, которая вместе с неявной времен-
ндй зависимостью ехр(—iatf) описывает уходящую волну при г -+°°. Если до*
пустить теперь наличие световода, то, хотя показатель преломления в сердце-
вине п (г), входящий в уравнение (34.22), изменяется^ но везде в оболочке
п = "cl- Следовательно, пространственная зависимость At в дальнем поле сно-
ва пропорциональна выражению (34.23), но при ином коэффициенте пропор-
циональности. Если*, обо значить решение уравнения (34.22) для свободного
пространства как , то решение при наличии световода выражается в виде
= СХ^}А[\ (34.24)
где коэффициент Q аналогичен корректирующему множителю в (21.34),
который был выведен в разд. 21.11, исходя из интуитивных физических со-
ображений. Если для удобства считать, что_вектор п в (34.22) параллелен оси
х поперечного сечения световода, тогда А^ имеет только х-составляющую,
которую мы обозначим через Ф^. Таким образом, Ф| удовлетворяет неодно-
родному скалярному волновому уравнению, имеющему в цилиндрических
полярных координатах вид
IA- + -уу + к2п2 - /32| Ф = Ь^-—--cos /(^> - ^о), (34.25)
[or r or г д<р J 1 г°
где b = —p.Qgl'1'п. Если Ф^ обозначает решение для свободного пространства
при п = ис1, то корректирующий множитель для трубчатого источника в вы-
ражении (34.24) задается для поля в оболочке отношением
Г>р.
(34.26)
Произвольное распределение токов источника. Мы можем теперь постро-
ить поле, возбужденное произвольным источником внутри волоконного све-
товода. Для отдельного трубчатого источника электрическое и магнитное по-
ля линейно связаны с векторным потенциалом. Поэтому соотношения, со-
ответствующие (34.24), имеют вид
VciE[s> <34-27)
После обратного преобразования Фурье в соответствии с формулами (34.21)
находим и, учитывая вклады в полное электрическое поле от всех трубча-
тых источников, получаем
E(r, <p,z) = 77- S J exp(ij3z)dp7cro^o J Ё^о, (34.28)
2Я l = о о 1 0 1
где Q зависит в общем случае не только от 0, но и от rQ и .
34.7. Пример. Ступенчатый профиль показателя преломления
Здесь мы выведем выражение для корректирующего множителя в случае трубчатого
источника, расположенного в сердцевине слабонаправляющего волоконного световода
со ступенчатым профилем показателя преломления. Решение уравнения (34.25) выра-
жается в виде
562
JX(UR)
'Vl~P"j~(U) C0s/^~^o); 0<r<ro; (34.29a)
( J, (UR) /Л0 (UR))
'J', = ) 9 f rfA +S—tjt-lcos/(<p ~^0), r0<r<p; (34.296)
1 I hV>(U) J
Ф=Г—--------- cos/(v?-<p0), p<r<°°, (34.29b)
1 Яр* (Q)
где p, q, s, I - постоянные, которые надо определить, J уи l/)l> - функции Бесселя и Ган-
келя первого рода соответственно, U и Q связаны с (3, как указано в табл. I, R - г/р, а
г0,р-радиусы трубчатого источника и сердцевины соответственно. На граничной поверх-
ности г — р обе функции Ф^ и дъ^/дг непрерывны, а на трубчатом источнике при г ~ rQ
непрерывна только Фр Четвертое граничное условие связывает скачок дЧ^/дг при г = г0
с правой частью уравнения (34.25). Умножая это уравнение наг, интегрируя по малому
интервалу г0 - 6г < г <г0 + 6г и вспоминая, что Ф^ непрерывна, получаем
./“о [>]^l=^cos/(.-.o). (34.30)
Примененные к выражениям (34.29) эти четыре условия вместе с вронскианом (37.77)
приводят к следующему решению:
ф -b^L^fL.H^(QR)cosl(>p-^(,), Г>р- (34.31а)
1 WX(U, Q) I
W}(U, Q) = QJV(U)H^' (Q) _ UH\(Q)J{(U), (34.316)
где штрихом отмечено дифференцирование по аргументу. Соответствующее решение
для свободного пространства Ф^ дается тем же выражением, в котором везде Uзаменен
на Q. Отсюда корректирующий множитель (34.26) принимает вид
Л(^о/Р) &
Cl ^(Qro/p) H\(U, Q) ’
(34.32)
где W](Q, Q) - вронскиан (37.77). Похожее выражение может быть получено, когда
трубчатый источник расположен в оболочке, т. е. при г0 > р.
ПРИМЕНЕНИЕ ТЕОРИИ ВОЗМУЩЕНИЙ
Функции Грина также могут быть использованы для решения неоднородных
скалярных дифференциальных уравнений, которые получаются при приме-
нении метода возмущений для анализа слабонаправляющих волоконных све-
товодов. Пусть нужно найти решение Ф = Ф(г) уравнения
{У* +к2п2 _р2} ф = х, (34.33)
где х = х(г) — заданная функция векторной координаты г в поперечном сече-
нии световода, п = л (г) - профиль показателя преломления, а оператор V*
определен в табл. 30.1. Если G = (7(г, г') обозначает функцию Грина этого
уравнения, то, подчиненная соответствующим граничным условиям, она
удовлетворяет уравнению
{V2 + к2 п2 _ ^2 | G = 5 (г _ г') , (34.34)
563
где 6 — дельта-функция Дирака, аг' - фиксированная точка пространства.
Решение уравнения (34.33) тогда дается выражением
Ф(г) = J G(r,r')x(r')d>S' (34.35)
где У"' — обозначает объем, в котором х отлична от нуля. Для иллюстрации
этой методики рассмотрим примеры.
34.8. Пример. Эллиптические волоконные световоды с малым
эксцентриситетом
Используем методы теории возмущений из разд. 18.10 для определения свойств мод эл-
липтического ступенчатого волоконного световода с малым эксцентриситетом. Этот
подход требует знания решения Ф скалярного волнового уравнения (18.3а). для возму-
щенного волоконного световода. В низшем порядке Ф = Ф, где Ф- известное решение
скалярного волнового уравнения (18.36). Поправки первого порядка получаются при
преобразовании уравнения (18.3а) к виду [8]
{V2 + к2п? - 02} Ф = к2 {п2 - п2} Ф, (34.36)
где п — показатель преломления круглого световода, а р - постоянная распространения
эллиптического световода. Правая часть равна нулю везде, кроме четырех заштрихован-
ных областей, показанных на рис. 18.2, а. В этих узких областях мы можем положить
Ф » Фи аппроксимировать правую часть 6-функцией на поверхности г — р с весовым
множителем к2 (п2 - п2)8г, где 6г - ширина области, выражение для которой приведе-
но после формулы (18.20) . Следовательно, (34.36) заменяется уравнением
{V* + к2 п2 - р2} Ф = - е-У - 6 (г - p)cos 2</?,
1 4р
(34.37)
(34.38)
так как Ф= 1 при г = р (см. табл. 14.3), а п = пс\, п = псо в заштрихованных областях,
пересекающих ось х на рис. 18.2, а. По аналогии с решением уравнения (34.25) (см.
разд. 34.7) получаем
JAUR} „ K2(WR}
ф = cos2<^ ^1; Ф = cos2^’ 1
где R = г/р. Постоянные р и q определяются из условия непрерывности Ф при г = р и
условия, аналогичного (34.30) с / — 2, г0 = рнЬ — -е2 V2 /4. С помощью решения зада-
чи на собственные значения из табл. 14.3 и рекуррентных соотношений (37.72) и (37.73)
находим, что решение, правильное с точностью до величин порядка е2, дается выраже-
нием (18.22).
34.9. Пример. Поправки к дальнему полю
В разд. 15.5 было показано, как получить дальнее поле слабонаправляющего волокон-
ного световода, зная гауссово приближение для основной моды. Как разъяснено после
формулы (15.14), для этого требуется получить решение уравнения
f d2 1 d I f R2 1
(iF • 'Г' -1"11 -"’’ЫГ <34”>
где R — r/р, Ro = r0/p, а параметр W определен в табл. I. Размер пятна поля, считающий-
ся заданным, равен r0 a f - вариация профиля (14.1). Используя такие стандартные ме-
тоды [1 - 3] как вариация произвольных постоянных, легко получить решение урав-
нения
) d2 1 d I ,
= (34-40)
564
для функции Грина G (R, R ), выраженной в виде [8]
G(R, R) = -Ко (WR)Io(WR')R', (34.41а)
G(R, R) = -Io(WR)Ko(WR')R', R ^R' < (34.416)
где Io и KQ — модифицированные функции Бесселя первого и второго рода соответ-
ственно. Далее решение уравнения (34.39) может быть записано по аналогии с решения-
ми уравнений (34.34)-и (34.35):
F„ (R) = -К„ (WR) f Ia(WR')x (R')R'dR' - I0(WR) J K<,(WR')x (R')R'dR’, (34.42)
0 R
где функция x (R ) из (34.33) заменена правой частью уравнения (34.39) сR вместо/?.
В оболочке световода R 1, в выражении для Fo доминирует первый интеграл,
и в пределе R -* °° мы получаем выражение (15.15).
ГЛАВА 35. ЛУЧИ И ЛОКАЛЬНЫЕ ПЛОСКИЕ ВОЛНЫ
Поведение электромагнитных волн в многомодовом волноводе, волновод-
ный параметр которого удовлетворяет условию V» 1, может быть описа-
но в лучевом приближении, изложенном в ч. I. Такое распространение волн
вдоль волновода описывалось с помощью непрерывной суперпозиции лучей,
поток мощности которых вдоль траекторий определяется классическими за-
конами геометрической оптики. В этой главе мы рассмотрим поведение от-
дельных лучей и связанных с ними потоков мощности, исходя из представле-
ния о локальных плоских волнах для электромагнитных полей в однородной
и неоднородной средах.
В следующей главе мы рассмотрим полные электромагнитные поля, сум-
мируя поля многих мод многомодового волновода. Это менее прямой путь,
чем лучевой подход, так как при этом требуется знание свойств отдельных
мод и таких величин, как постоянная распространения, определяемая из ха-
рактеристического уравнения. Это приводит к алгебраическим и концепту-
альным усложнениям задач, которые могут быть решены проще с помощью
лучевого анализа. Кроме того, модовая природа полных полей многомодо-
вых волноводов редко наблюдается [1], а потому несколько абстрактна.
ЛОКАЛЬНЫЕ ПЛОСКИЕ ВОЛНЫ
Если показатель преломления п везде постоянен, то среда ненаправляющая
и электромагнитные поля могут быть представлены в виде отдельных плос-
ких волн. Если предположить теперь, что п почти постоянен и мало меняет-
ся на расстояниях порядка длины волны света, то интуитивно ясно, что в
каждой точке поля похожи на локальные плоские волны, исключая ситуации,
когда существенны эффекты дифракции, либо эффекты, обусловленные за-
висимостью от длины волны, либо эффекты в каустиках или в фокусах. Ис-
пользуя это простое представление, мы получим в разд. 35.3 основные свой-
ства локальных плоских волн. Можно использовать также формальный под-
ход. Предположим, что каждая составляющая поля имеет пространственную
зависимость вида ехр {1Ф (х, у, z)} , которая подставляется в уравнения
Максвелла. Условие медленного изменения среды, выражающееся* в виде
565
X|Vln n21 << 1, где X — длина волны излучения в свободном пространстве,
приводит к уравнениям, определяющим распространение локальных плоских
волн, включая уравнение лучевых траекторий, или эйконала, (1.18). Такой
подход достаточно полно описан в [2 — 4] и не нуждается в повторении. Так
как наш интуитивный подход основан на распространении волн в однород-
ной среде, мы сначала суммируем все относящиеся к этому основополагаю-
щие результаты, включая законы Снелля.
35.1. Однородная среда
Пусть электрическое Е и магнитное Н поля в неограниченной среде с одно-
родным показателем преломления п имеют вид [5]:
Е(г) =Еоехр(шк • г); Н(г) = Ноехр(шк • г), (35.1а)
где Ео и Но — постоянные векторы, г — радиус-вектор, и подразумевается
временная зависимость вида ехр(—iatf). Волновой вектор к = Х'к, где к —
единичный вектор, параллельный направлению распространения волны, к =
- 2тг!\, X - длина волны в свободном пространстве. Векторы Ео и Но ортого-
нальны друг другу и вектору к и связаны соотношением
Но =и(ео/мо)1/2кх Ео, (35.16)
где параметры определены в табл. I.
Поток мощности. Интенсивность или плотность потока мощности S име-
ет величину и направление, определяемые усредненным по времени векто-
ром Пойнтинга. Таким образом, из (35.16) мы находим, что
8 = Ш[Е(г) хН*(г)] =-5 (-—)1/21 Ео 12 к, (35.2)
где Re обозначает вещественную часть, а знаком * отмечено комплексное со-
пряжение. Следовательно, поток мощности течет в направлении распростра-
нения волны. Кроме того, энергия света переносится вдоль лучей, направле-
ние которых задается волновым вектором, а мощность сосредоточена в лу-
чевой трубке, т. е. трубке параллельных лучей с поперечным сечением dAr
изображенной на рис. З5‘.2,я. При этом |S|t£4 не изменяется вдоль трубки.
Вдоль каждого луча или лучевой трубки происходит набег фазы
ик • г = «а • r = ^-L = ^-Lo, (35.3)
X р X °
где Zp и Lq - геометрическая и оптическая длины траектории луча соответ-
ственно.
35.2. Закон Снелля
Отражение и прохождение плоских волн или лучей, падающих на плоскую
границу раздела между двумя полубесконечными однородными средами,
определяются законами Снелля [2]. На рис. 35.1 представлены показатели
преломления нижней среды п и верхней среды с ис1 < исо, а также крити-
ческий угол ас = sin"1 (ис1/лсоУ Обозначим углы падения, отражения и пре-
ломления, отсчитанные от нормали QN, через с^, аг и at соответственно.
566
Рйс. 35.1. Отражение от плоской поверхности раздела двух сред с показателями пре-
ломления и лс1 < Лсо:
а — полное внутреннее отражение; б — частичное отражение и преломление
Падающий, отраженный и преломленный лучи и нормаль лежат в одной
плоскости.
Если Qj > ас, то падающий луч испытывает полное внутреннее отражение
(см. рис. 35.1, а), при этом аг = но если < ас, то имеется как частич-
ное отражение, так и частичное или преломление (или прохождение) (см.
рис. 35.1, б), а углы удовлетворяют соотношениям
а. =а ,п sin a. = n}sina . (35.4)
1 т ьо ] Cl t
Для планарных волноводов, описанных в гл. 1, удобно выразить законы
Снелля через углы скольжения, дополнительные к углам падения, отражения
и преломления, т. е. 0z = тг/2 — = л/2 — аг и 0t = л/2 — аг
Критический угол скольжения 0С = л/2 — &с используется во всей книге.
35.3. Медленно изменяющаяся среда
Выражения, приведенные в разд. 35.1 для однородной среды, могут быть ин-
туитивно обобщены при условии, что показатель преломления п (г) мало из-
меняется на расстояниях порядка длины волны света. Так, набег фазы (35.3)
становится интегральной величиной
2л
/лк • dr - -т— J nds, (35.5)
Р Л Р
где 5 — расстояние, отсчитанное вдоль траектории луча р, которая теперь ис-
кривлена из-за градиентности профиля показателя преломления среды. Со-
Bic. 35.2. Лучевые трубки:
а — с постоянным поперечным сечением dA в однородной среде; б — с изменяющимся
поперечным сечением dA (г) в среде с градиентным профилем
567
ответственно ноля вдоль траектории даются выражениями, аналогичными
(35.1а), где к • г заменяется на (35.5), а векторы Ео, Но теперь являются
медленно изменяющимися функциями координат. Следовательно, поля пред-
ставляются локальными плоскими волнами
Е(г) = Ео (г) ехр Ji pk • dr j,; H (г) = Но (r)cxpf i pk • dr I . (35.6a)
I P J ’ P J
Касательная к 1раектории p задает направление локального волнового век-
тора к и потока мощности и определяем ирощ ранет венное изменение единич-
ного вектора k(r). Поэтому подходящее обобщение соотношения (35.16)
имеет вид
Но (г) =п(г)(ео/мо)1/2 к (г) х Е0(г). (35.66)
Для данного профиля траектория р определяется из уравнения лучевых тра-
екторий (уравнения эйконала), как было показано в гл. 1 и 2.
Поток мощности. Если построить из искривленных лучевых траекторий
лучевую трубку, как показано на рис. 35.2, о, то по определению поток мощ-
ности в трубке сохраняется, т. е. величина S(r) • к(г)<±4(г) постоянна вдоль
трубки; здесь dA (г) — элементарная площадь в поперечном сечении, а вектор
S(r) дается выражением (35.2) с п, Ео и к, замененными на и (г), Е0(г) и
к (г) соответственно. Следовательно, и величина п (г) | Е0(г) |2 dA (г) постоянна
вдоль трубки, а если через г0 обозначить какую-либо точку сечения трубки,
то пространственная зависимость электрического поля локальной плоской
волны, распространяющейся в среде с градиентным профилем показателя
преломления, как это следует из (35.6а), имеет вид
=Е0(г0) -ехрJ „к (35.7)
где г — произвольная точка траектории. Для магнитного поля получается ана-
логичное соотношение, если заменить Ео (г0) на Но (г0) и выразить Но (г0) че-
рез Ео (г0) с помощью (35.66).
Поляризация. Мы определяем единичный вектор Е0(г) = Е0(г)/|Е01 (г) |
в направлении электрического поля, как поляризационный вектор. Это на-
правление фиксировано в однородной среде, но изменяется при распростра-
нении локальной плоской волны в медленно изменяющейся среде в соот-
ветствии с уравнением [2, 4]
z/P 1 Л
= - у k(r){Ёо • V In п2 (г)} . (35.8)
Напомним, что член с Vt In п2 появляется в векторном волновом уравне-
нии (11.40) и имеет геометрическую интерпретацию, рассмотренную в
разд. 11.16. Однако в слабонаправляюших многомодовых световодах обыч-
но пренебрегают как фазовыми, так и поляризационными эффектами и
трактуют распространение излучения в скалярном приближении, так как эти
эффекты обычно маскируются многократными отражениями большого чис-
ла лучей, распространяющихся по световоду. Но в слабонаправляющих све-
товодах, по которым распространяются одна или несколько мод, поляриза-
568
ционные эффекты часто оказываются важными при распространении на боль-
шие расстояния, как это отмечалось в гл. 13.
Резюме. Если показатель преломления среды изменяется медленно, то по-
ля в среде ведут себя как локальные, т. е. как пучки лучей, причем каждый
луч переносит энергию по лучевой траектории. Таким образом, такие наибо-
лее интересные явления в многомодовых волноводах, как распространение
импульсов, уширение импульсов и облучение, могут быть описаны с помо-
щью лучевых методов классической геометрической оптики, представляю-
щих основу для рассмотрения в гл. 1 — 5. Вследствие пренебрежения малыми
дифракционными эффектами эти явления при описании лучевыми методами
не зависят от длины волны. Однако по причинам, обсуждавшимся в разд. 10.3,
для этого необходимо, чтобы волновод был многомодовым с К» 1; при
этом описание лучевыми методами будет правильным.
35.4. Уравнения составляющих для траекторий лучей
При построении лучевых траекторий в сердцевине волноводов со ступенчаты-
ми профилями показателей преломления в гл. 1 и 2 используются прямоли-
нейные траектории, являющиеся решениями лучевого уравнения (1.18) вод-
нородной среде. Если сердцевина имеет градиентный профиль показателя пре-
ломления, то декартовы составляющие лучевого уравнения получаются не-
посредственно, как в (1.19) и (2.49). Здесь мы выведем соответствующие
уравнения для составляющих в цилиндрических полярных координатах г,
у, z (см. рис. 2.1) для световодов с градиентными профилями п (г), рассмат-
риваемых в гл. 2, и с помощью простого обобщения — для медленно изменя-
ющихся нерегулярных волоконных световодов с профилями и (г, z), рас-
сматриваемых в гл. 5.
Представим радиус-вектор в уравнении (1.18) в виде
r = rf+zz, (35.9а)
где гиг — единичные векторы в радиальном и продольном направлениях со-
ответственно. Используя выражения для пространственных производных
единичных векторов (37.54), получаем выражение для производной вдоль
луча:
dr . dr dr . .dz .dr - dp dz
— = r— + r— + z— = r— + rp— + z —, (35.96)
ds ds ds ds ds ds ds
p — единичный вектор в азимутальном направлении. Повторяя эту проце-
дуру, находим
-^ -/и(г) -—-I = гА |и(г)-уЦ; (35.10а)
ds ( v 'ds J r ds ( v 7 ds J v 7
A d f , 4 z x,dp г d ( , .dp\ , dr dp
AT =— \n(r)—> - rn(r)(—) , Ai=~—lrn(r)~~> + n(r)—— .
r ds ( v 7 ds j 4 7V ds7 ’ ds 1 ' ds J v 7 ds ds
(35.106)
Приравнивая подобные члены в уравнении (1.18) сл(г) = и(г) в правой
части, получаем для составляющих уравнения (2.13). Аналогично, заменив
п (г) на п (г, z) в обеих частях уравнения (1.18), получаем уравнения для со-
ставляющих (5.3).
569
ОПИСАНИЕ ПОТЕРЬ С ПОМОЩЬЮ ЛОКАЛЬНЫХ ПЛОСКИХ ВОЛН
Приведенное выше описание распространения волн с помощью локальных
плоских волн или лучей дает возможность прямо определить потери на по-
глощение вдоль каждого луча, как было показано в гл. 6. Однако этот под-
ход не позволяет непосредственно увидеть, каким образом теряется мощ-
ность лучей из-за наличия полей локальных плоских волн за пределами лу-
чевой траектории, что происходит в случае поглощающей оболочки или на
изгибе волновода. Эти потери обычно пренебрежимо малы на малых длинах
волновода, так как поля за пределами луча бесконечно малы, а их амплиту-
ды экспоненциально спадают при удалении от луча. Тем не менее эти потери
накапливаются с расстоянием вдоль волновода и в конечном счете могут
стать существенными.
В последующих разделах мы выведем выражения для коэффициентов
прохождения для учета указанных механизмов потерь. Эти коэффициенты
передачи совместно с траекториями классической геометрической оптики
полностью описывают распространение волн по многомодовым волноводам,
как показано в гл. 6 — 9. Все волноводы с градиентным профилем показате-
ля преломления, рассмотренные в ч. I, имели профили показателя преломле-
ния, почти однородные на расстояниях порядка длины волн света. Аналогич-
но, все криволинейные поверхности раздела и каустики были почти плоски-
ми на тех же расстояниях. Следовательно, электромагнитные поля имеют ха-
рактеристики плоских волн в локальных областях, исключая непосредствен-
ную окрестность каустик, где происходит быстрый переход от осциллирую-
щих полей локальных плоских волн к экспоненциально спадающим полям
за пределами лучевой траектории. В соответствии с этим аппроксимируем по-
ля волновода локальными плоскими волнами, обсуждавшимися в разд. 35.3,
и будем рассматривать лучи как локальные плоские волны.
Ключевые задачи. Как показано ниже, нам необходимо решить только две
электромагнитные задачи, играющие роль ключевых для определения коэф-
фициентов прохождения мощности любого многомодового волновода. Вот
эти задачи:
1) падение плоской волны на плоскую границу раздела двух сред- На ре-
шении этой классической задачи основано определение коэффициента про-
хождения мощности для всех волноводов со ступенчатыми профилями пока-
зателей преломления;
2) падение локальной плоской волны на плоскую каустику. На решении
этой задачи основано определение коэффициентов прохождения мощности
для всех градиентных волноводов. Этот подход применяется ниже как к вы-
текающим лучам, так и к направляемым лучам волноводов с поглощающей
оболочкой.
Приближение слабонаправляющего волновода. Для упрощения выкладок
и в соответствии с результатами гл. 6 — 9 ограничимся определением коэф-
фициентов прохождения мощности только для слабонаправляющих волново-
дов. Это означает, что получаемые нами выражения не зависят от поляриза-
ции падающей волны.
570
35.5. Прохождение мощности и коэффициенты затухания
Мы показали в разд. 35.3, что электромагнитная мощность в сердцевине вол-
новода распространяется по лучевым трубкам. Полная энергия в трубке мо-
жет изменяться только при отражении от поверхности раздела, когда направ-
ление трубки резко меняется, как показано на рис. 35.3,а, либо в окрестно-
сти точки поворота, или каустики, где площадь поперечного сечения трубки
dA = 0, как показано на рис. 35.4, а. Чтобы описать потери мощности, связан-
ные со слабым проникновением полей локальной плоской волны в оболочку
за пределы траектории луча, сохраним в сердцевине геометрическую траек-
торию луча и введем коэффициент прохождения мощности, или потерь, Т
определенный соотношением
(35.11)
1
Рис. 35.3. Частичное отражение и преломление на плоской границе раздела (а); заштри-
хованы области распространения потока мощности по лучевым трубкам. Штриховкой
отмечена область поглощения мощности, если луч отражается от плоской границы с
поглощающей средой (б)
Рис. 35.4. Явления на границе раздела двух сред:
а - туннелирующий луч в среде с градиентным профилем частично отражается от кау-
стики точек поворота и частично распространяется дальше от каустики излучения; за-
штрихованы области распространения потока мощности по лучевым трубкам, а штри-
ховкой обозначена область спадающего поля; б — частичное отражение и прохождение
на поверхности раздела между средой с градиентным профилем и однородной средой
571
где Pj — мощность падающего луча, Рт — мощность отраженного луча. Этот
коэффициент определяет относительную потерю мощности в области отраже-
ния или поворота. Коэффициент затухания мощности у на единице длины
волновода, вычисляемый усреднением Т по расстоянию между последова-
тельными точками отражений или поворота, задается выражением
y = 77zp=7Vr, (35.12)
где Zp — полупериод луча, a N — число точек отражения или поворота на еди-
нице длины волновода, как показано на рис. 1.5 и 1.9.
Лучевая мощность. Обозначим через P(z) мощность в лучевой трубке в
точке с координатой z, отсчитанной вдоль волновода. Изменение P(z) на бес-
конечно малой длине dz согласно определению (35.12) имеет вид
dP(z) = -yP(z)dz = —NTP(z)dz. (35.13)
Отсюда получаем, что экспоненциальное затухание начальной мощности
Р(0) описывается выражением
P(z) = P(0)exp(-yz),
или
( z )
P(z) =P(O)e^l-jt(z)dz\ (35.14)
I 0 j
в зависимости от того, обладает волновод трансляционной инвариантностью
или нет. Мы показали в гл. 1, 2 и 5, как определять zp и 7V; теперь наша
цель — в оставшейся части этой главы использовать теорию локальных плос-
ких волн для определения Т и, следовательно, у.
35.6. Плоские границы раздела
Рассмотрим падение плоской волны на плоскую границу раздела, чтобы впо-
следствии определить коэффициент прохождения для плоских волноводов
со ступенчатыми профилями показателя преломления. Эта классическая за-
дача рассматривается в большинстве учебников по электромагнитной теории,
тем не менее мы повторяем здесь ее решение, так как оно понадобится нам
для обобщения задачи на среду с градиентным профилем показателя прелом-
ления, а также потому, что анализ имеет специфические особенности в случае
слабонаправляющих волноводов.
Рассмотрим две полубесконечные среды с показателями преломления псо
и яс1 < псо, разделенные плоскостью х = 0, как показано на рис. 35.3, а. Луч,
или плоская волна, падает из более плотной среды на поверхность раздела
под углом скольжения 07 к направлению оси z. Отражение плоской волны в
этом случае хорошо изучено, и коэффициент прохождения (35.11) иденти-
чен классическому коэффициенту прохождения Френеля [2].
Скалярное приближение. Представляет интерес специальный случай, ког-
да исо ~ /7ср В этом предельном случае известные классические выражения
не зависят от явлений поляризации, т. е. коэффициенты прохождения не за-
висят от направления вектора электрического поля волны. Таким образом,
если пренебречь всеми поляризационными эффектами, то поля являются ре-
шениями скалярного волнового уравнения, а не уравнений Максвелла. Это
важно, так как решения скалярного волнового уравнения имеют более про-
572
стые свойства, уже обсуждавшиеся в разд. 33.1. Для удобства примем, что
электрическое поле волны направлено в направлении оси .у, параллельном по-
верхности раздела сред. Следовательно,
Еу = Ф(х)ехр(10г) ; 0 = Ьгсо cos 0Z, (35.15)
где 0 — z-составляющая волнового вектора падающей волны, подразумева-
ется временная зависимость поля ехр(—iccr), а функция Ф(х) удовлетворя-
ет скалярному волновому уравнению
* = 0. (35.16)
Здесь п (х) = псо для х < 0, п (х) = для х > 0,к = 2я/Х, X - длина волны в
свободном пространстве. Обозначая решения для полей падающей и отражен-
ной волн при х < 0 верхними индексами /иг соответственно, получаем с по-
мощью (35.15)
Ф* -A exp(iA?2c0 х sin 0z); Фг = В ехр(—iknCQ х sin 0z), (37.17а)
где А и В — постоянные. Напомним законы Снелля из разд. 35.2, согласно ко-
торым мощность проходит через поверхность раздела только в случае, если
02 > 0С, где 0С — критический угол скольжения, определенный в табл. I. При
выполнении этого условия происходит частичное отражение от границы раз-
дела (см. рис. 35.3, а), и решение уравнения (35.16) при х > 0, отмеченное
верхним индексом t, имеет вид
Ф1 = Cexp(ifcncl х sin 0t) ; ncl cos 0t = nco cos 0Z, (35.176)
где С — постоянная, a 0t — угол между преломленным лучом и направлением
оси z, связанный с углом 0z законом Снелля. Для определения постоянных
В и С вспомним (см. разд. 33.1), что любое решение скалярного волнового
уравнения и его первая производная должны быть непрерывны. Следователь-
но, Ф* + Фг и Ф1, а также их производные по х непрерывны при х = 0, что
приводит к соотношениям
В = «со sin вг - "cl sin et С _ 2nco Sin ez >
A nCQ sin 0z + ??с1 sin 0t ’ A nCQ sin 0z + ncl sin 0t
справедливым при 0c < 0Z < я/2. При падении, близком к нормальному, по-
лучаем
~2«со/(«со+«с1); ^^тг/2, (35.19)
что представляет собой коэффициент прохождения, использованный в
разд. 20.2.
Коэффициент прохождения мощности, или коэффициент Френеля. Лучевые
трубки, образованные падающими и отраженными лучами (см. рис. 35.3, а),
имеют одинаковые в направлении оси z сечения, и поскольку функция Ф
комплексна, плотность потока мощности в каждом луче изменяется как
|Ф|2, что ясно из табл. 13.2. Из (35.11) и (35.18) получаем, что коэффици-
ент прохождения определяется выражением 1 - |В/Л|2 для 0С < 0Z < я/2,
которое приводится с помощью (35.176) к коэффициенту Френеля
4rtco,7cl sin sin _ 4sin (sin2 ^z “ sin2 *c) 1/2
(исо sin Oz + ncl sin 0t) 2 (sin Oz + {sin2 Oz — sin2 Oc} 1/2)2
где sin 0C = {1 — n2c]/n2ro} 1/2• Обобщение для цилиндрической поверхности
раздела требует лишь изменения углов, определяющих Т, как это указано в
разд. 35.12. Предельное выражение для падения луча в направлении, близ-
ком к нормальному, получается при ~ ~ тг/2, а при падении под углом,
близким к критическому, 0z & 0с> В обоих этих случаях соответственно
получаем из (35.20)
Т*-------C1 . 0Z л/2; 7^4/1 (35.21)
(«co+ncl) >
поскольку 0с « 1 при Исо % Ис1.
Спадающие поля. Если падающий луч испытывает полное внутреннее отра-
жение, то мощность не переходит через границу раздела. Поэтому поля при
х > 0 быстро спадают до нуля, и выражение (35.176) заменяется на
= Сехр(-£2Ь?сох); £2 = (sin2 0С - sin2 0Z)1/2, (35.22а)
а выражения, соответствующие (35.18), имеют вид
В sin0z — Ш С 2sin07
~Т= sin0z + iS2 ’ Т ~ sin вг + in (35.226)
Кроме того, на границе раздела при отражении происходит изменение фазы Ф,
т. е. В = А ехр(1Ф) прих = 0, откуда получаем
((sin2 0 - sin2 07) 1/2
Ф = -2 arctg 1 ----------ъ-—
sin 0Z
так как 0 < 0Z < 0С « 1.
С 02 1
-2 arctg - 1? 1/2
I ^z '
(35.23)
35.7. Плоские границы раздела между поглощающими средами
Если среды, изображенные на рис. 35.3, а, являются поглощающими, то пока-
затели преломления становятся комплексными:
Л со “ п со + i^co’ пcl ” пcl + *"с1 ’
где верхние индексы i иг обозначают вещественную и мнимую части. Соот-
ветствующие решения скалярного волнового уравнения даются выражения-
ми (35.17а) с комплексным значением исо и (35.22а), где sin2 0С заменен
комплексной величиной 1 - л^/^со* Затем, проводя анализ, подобный пред-
ставленному в предыдущем разделе, находим, что для всех значений 0Z коэф-
фициент прохождения мощности, вообще говоря, отличен от нуля и выража-
ется в виде
т _ 4 sin 6>z Re (и2, /п2С0 - cos2 flz)1/2
I sin 0Z + {n2j /n2o - cos2 ez}1/2 |2 ’
(35.24)
574
где Re обозначает вещественную часть. Таким образом, лучи, которые полно-
стью отражались бы в случае непоглощающей среды, теперь испытывают по-
тери мощности при отражении. Если поглощение слабое, т. е. п[с0 «лгсо,
wcl « п cl ’ 0 0с Д'™ значений вг, не слишком близких к 0С, то выра-
жение (35.24) хорошо аппроксимируется формулой
4
(я2с-^)1/2 d«rcrd‘
(35.25)
Заметим, что Т < 0 в особом случае, когда = 0. /?со > 0, так как мощ-
ность передается из непоглощающей среды в поглощающую. Хотя в этом слу-
чае луч как бы приобретает дополнительную мощность при отражении, одна-
ко эта мощность теряется впоследствии на поглощение при дальнейшем рас-
пространении луча по траектории. Соответствующий коэффициент затухания
у в волноводе представляет собой сумму коэффициента затухания в сердце-
вине ус0 и коэффициента ус1, учитывающего обмен мощностью между серд-
цевиной и оболочкой, как это выражено формулой (6.30).
Альтернативный подход. Возможно альтернативное решение задачи для
поглощающей оболочки, которое легко обобщается на случай среды с гради-
ентным профилем показателя преломления. Пусть среда сердцевины непо-
глощающая, т. е. пгсо = 0, а среда оболочки — слабо поглощающая, т. е.
игС1 »и*1. Лучевая трубка, сформированная падающими и отраженными лу-
чами (см. рис. 35.3, б), испытывающими полное отражение при п1^ = 0, теперь
(т. е. при п'с0 Ф 0) проникает на некоторое расстояние в область х > 0, обра-
зуя трубку, которая заштрихована на рис. 35.3. Интуитивно ясно, что полная
поглощенная мощность спадающего поля в заштрихованной области равна
мощности, теряемой падающим лучом, и, следовательно, коэффициент про-
хождения определяется отношением поглощенной мощности [6] к падающей.
Если ширина трубки падающих лучей (см. рис. 35.3, б) равна 6/, то шири-
на заштрихованной области приближенно равна 6//^7 при 0z < « 1. Так
как среда слаббпоглощающая, то полная поглощенная мощность Pabs хорошо
аппроксимируется выражением, получающимся при интегрировании \dP\ из
табл. 13.2 по всей заштрихованной области при замене функции IЕj I на функ-
цию Ф1, приведенную в (35.22) для непоглощающей среды. Таким образом,
при псо « игс1 находим
I б?1 Я/
(>)-, (35.26)
где учтено, что £2 (в/ _ 02)1/2. Мощность в трубке падающих лучей
с помощью табл. 13.2 и выражения (35.17а) запишем в виде (51/2) \А\2п “х
х («о/Ро)1/2 • Подставляя в отношение Pabs/P-mc выражение (35.226) для С/А,
получаем для коэффициента прохождения формулу, идентичную (35.25) с
«со = °-
575
35.8. Решения скалярного волнового уравнения методом ВКБ
В последующих двух разделах мы распространим представления, получен-
ные в предыдущих разделах, на среды с градиентным профилем. Прежде
чем это сделать, полезно запастись некоторыми предварительными резуль-
татами. Напомним рассмотрение, проведенное в разд. 35.3, где было показа-
но, что решения уравнений Максвелла могут быть аппроксимированы ло-
кальными плоскими волнами, если профиль показателя преломления мед-
ленно меняется на расстояниях порядка длины волны света. Такие решения,
известные .как асимптотические, могут быть получены либо интуитивно с
помощью физических соображений, либо математическими методами. Если
ограничить рассмотрение слабонаправляющими волноводами, то распростра-
нение электромагнитного поля в этой ситуации также описывается локаль-
ными плоскими волнами, но поля представляют собой решения скалярного
волнового уравнения, а не уравнений Максвелла, т. е. описывают явления, не
зависящие от направления векторов поля. Таким образом, решение скаляр-
ного волнового уравнения для локальных плоских волн может быть полу-
чено с помощью тех же интуитивных соображений, которые приведены в
разд. 35.3.
Решение с помощью локальных плоских волн. Касательная к лучевой тра-
ектории в областях х < и х > xrad среды с профилем показателя прелом-
ления п (х) (рис. 35.4, а) образует угол 0z (х) с направлением оси z. Постоян-
ная распространения (3 является z-составляющей локального волнового век-
тора к(х). Если х-составляющую обозначить кх (х), то
к (х) = [&х (х), 0] = [кп (х) sin 6Z (х), кп (х) cos 0z (х) ]. (35.27)
Лучевая трубка на рис. 35.4, а ограничена идентичными лучами, сдвинутыми
относительно друг друга на расстояние 6z параллельно оси z, и поэтому име-
ет ширину 6/(х) = .6z sin 0z (х). Если заменить п (r)dA (г) на п (х)6/ (х) в вы-
ражении (35.7) и положить dr = \dx, dz\, то из (35.27) найдем следующее ре-
шение скалярного волнового уравнения для локальных плоских волн:
, , \ - I z V 1/2 ехР j ±i J (*) sin вг (*)dx I еХР ’ <35 -28)
{п (х) sin0z(x) J 1/2 ( J
где знаками ”+” и ” обозначены соответственно положительное и отрица-
тельное направления распространения лучей относительно осих. Опустим за-
висимость от z и заменим 0z(x) на (3 с помощью соотношения (35.27). Та-
ким образом, решение уравнения (35.16) примет вид
ф(х) =~Д2»2(х) -132}1/4 ехр 'k2fl2(x) -02} 1/2
(35.29)
где множитель перед экспонентой и аргумент экспоненты учитывают соответ-
ственно постоянство мощности и набег фазы. Этот осциллирующий тип реше-
ния справедлив в областях, где кп (х) — (3 » 1, и часто называется асимпто-
тическим ВКБ-решением скалярного волнового уравнения [7].
Если выполняется условие (3 — kn (х) » 1, то решение скалярного волно-
вого уравнения, полученное методом ВКБ описывает спадающие поля [7] :
576
Ф(%) =Ъ2"'^ 'м)1/4 eXP {" W2 ~ k2n2 W ) 1/2M •
i P ~ К П \X) ] t J
(35.30)
Заметим здесь, что в последующих приложениях (З2 — к2п2 (х) заменяется
на |&2и2 (х) - 021.
Лучевые каустики. Расположение лучевых каустик на рис. 35.4, а дается
выражением (1.26) через лучевой инвариант 0. Если заменить 0 на постоянную
распространения (3 с помощью соотношений из табл. 36.1, то найдем, чтох1р
и xrad удовлетворяют уравнениям
A;n(xtp)=(3; kn(xIad)=p (35.31)
соответственно. В непосредственной окрестности этих каустик имеется рез-
кий переход от осциллирующего поля (35.29) к спадающему (35.30), и ни
одно из решений, полученных методом ВКБ, здесь не имеет силы. Однако не-
обязательно знать детали поведения решения скалярного волнового уравне-
ния в этой области, чтобы связать эти два типа решения. Имеются формулы,
которые соотносят эти решения друг с другом [7]; они используются ниже.
35.9. Плоские каустики и туннелирование лучей
В этом разделе мы обобщим решение задачи о падении плоской волны на
плоскую границу раздела сред и рассмотрим падение локальной плоской
волны на каустику в медленно изменяющейся среде с градиентным профи-
лем показателя преломления. Наша цель — определить коэффициент прохож-
дения мощности через границу для туннелирующих лучей.
Рассмотрим среду с непрерывным профилем показателя преломления
п (х), мало меняющимся на расстояниях порядка длины волны света. Луче-
вая траектория в области х < р на рис. 35.4, а касается прих =х^ каустики
точек поворота. Если в области выше каустики траектории отсутствуют, то
луч полностью отражается от каустики и мощность не теряется, т. е. Г = 0.
Однако если прошедший луч снова возникает на каустике излучения х =
= xrad, то имеет место оптическое туннелирование, как указано в гл. 7, й
мощность переходит от траектории при х = х^ к траектории при х = xrad.
Если поля локальных плоских волн имеют постоянную распространения 0,
то значения х^ и xrad определяются уравнениями (35.31) .
Решения методом ВКБ. С помощью х-составляющей локального волново-
го вектора (35.27) и решений (35.29), полученных методом ВКБ, решения
скалярного волнового уравнения для падающей, отраженной и преломлен-
ной локальных плоских волн записываются соответственно в виде
i Л ( *tp ) В ( 1
(35.32а)
в области х <Хф и
=/Г (-fv 1/2 eXp{i * (35.326)
I xrad J
19 Зак 37
577
в области х > xT2Ld> r&e А £ и С — постоянные величины, связанные с ампли-
тудами соответствующих полей. Поля в области <х < xrad экспоненци-
ально спадают при увеличении х. Если Фе обозначает решение скалярного
волнового уравнения, то из (35.30) следует, что
Фе = .. Д|1/2 ехр(- J (x)|cfrl, (35.32в)
kx(*)l (. J
где kx (x) — мнимая, a F — постоянная величины.
Формула для сшивания решений. Связь между лучевыми трубками на кау-
стиках осуществляется через заштрихованную область шириной 6z (см.
рис. 35.4,а). Мощность, потерянная падающим лучом на каустике прих^,
туннелирует через эту область и передается прошедшему лучу при xrad. На
каустиках и вблизи них теория локальных плоских волн неприменима, но
если каустики расположены не слишком близко друг к другу, то нет необхо-
димости знать поля в этих областях, чтобы определить коэффициент прохож-
дения. Мы можем связать решения (35.32) с помощью формулы для сшива-
ния решений, полученных методом теории ВКБ, которая приводится в учеб-
никах [7]. Следовательно,
В =А ехр(—1я/2) ; F =А\ C = Fexp^-J I(х) |dx >. (35.33)
Первое выражение описывает хорошо известное явление уменьшения фазы
на тг/2 при касании лучом каустики; это явление уже выходит за пределы
представлений о плоских волнах.
Коэффициент прохождения для туннелирующих лучей. Для заданной Ф1
мощность Р^с в трубке падающих лучей может быть вычислена с помощью
табл. 13.2 и выражения (35.22а) как произведение ширины трубки и интен-
сивности излучения, что приводит к формуле
Лпс = 7^)1/25/(х)п(х)|ф112 = (7Г)1/215а~ ’ (35-34)
2 МО МО Z/v
так как 6/(х) = 5z sin 0Z (х) и кх (х) = кп (х) sin 0z (х) . Аналогично мощность
Ptr в трубке прошедших лучей дается таким же выражением с заменой по-
стоянной А на С. Коэффициент прохождения мощности (35.11) в этом слу-
чае дается отношением Ptr/Лпс- Выражая кх (х) через лучевой инвариант Р с
помощью соотношения (35.27) и табл. 36.1, получаем [8]
Г rad - / 1
Т = ехр ] -2к / [ 0 - П (х) ]12 dx к
t *tp
(35.35)
Если длина волны X -> 0, то к -> «> и Т -> 0. Это подтверждает, что туннелирова-
ние представляет собой явление, существенно зависящее от длины волны.
Нарушение полного внутреннего отражения. Потери на туннелирование
лучей, распространяющихся по планарным волноводам, выражаются в фор-
муле (35.35) через координаты плоских каустик в сердцевине и оболочке.
578
В планарной геометрии туннелирование обусловлено нарушением полного
внутреннего отражения [2]. Поскольку значения профиля на каустиках оди-
наковы по определению-, т. е. п(х^} - «(xrad) = j3, в планарных волноводах
туннелирование может происходить только, если имеется минимум профиля
между каустиками. Хотя такие профили не рассматривались в ч. I, мы приве-
ли формулу (35.35) для того, чтобы показать, как получить коэффициент
прохождения для простейшей возможности геометрии. Кроме того, обобще-
ние выражения (35.35) на случай цилиндрической геометрии проводится не-
посредственно, как это показывается ниже в разд. 35.12.
Преломленные лучи. Планарные волноводы с оболочкой и непрерывными
градиентными профилями в сердцевине имеют резкий скачок наклона произ-
водной профиля на границе раздела между сердцевиной и оболочкой — см.,
например, усеченный параболический профиль на рис. 1.10. Как отмечалось
в разд. 7.2, скачок производной профиля приводит к отражению лучевой
мощности от границы раздела. Эту ситуацию иллюстрирует рис. 35.4, б, где
среда х > р имеет однородный показатель преломления ис1, а среда х < р име-
ет такой градиентный профиль п (х), что п (0) = пс1. Падающий и отраженный
лучи описываются выражениями (35.32а) с xto = р, а прошедший луч — пер-
вым выражением в (35.176). Параметры В и С выражаются через А с помо-
щью условий непрерывности функций Ф1 + Фг и Ф* и соответствующих пер-
вых производных при х = р. Производная от кх (х) получается при дифферен-
цировании соотношения (35.27), содержащего п (х) и (3, и с учетом того, что
кх (р) = кпс\ sin 0t. Образуя комбинацию 1 — |2?/Л|2, получаем следующее
выражение для коэффициента прохождения [9] :
т= i/Ь + (—_2£_—)
I 8кп^ sin3 et
1 - (—^—)2—
_ 8кп3} sin6 3t
dn2(x) I C1 1
гдек=___|р_.
(35.36a)
(35.366)
приближенная формула справедлива, когда второй член мал по сравнению с
единицей. Производная берется на границе раздела со стороны сердцевины.
Когда длина волны Х~>0, то&-х»иГ->1. Другими словами, в приближении
классической геометрической оптики вся мощность падающих лучей прохо-
дит через поверхность раздела, как и предполагалось в гл. 1 и 2.
35.10. Плоские каустики и поглощающая среда
В этом разделе мы обобщим процедуру, рассмотренную во второй части
разд. 35.7, чтобы применить ее к среде с градиентным профилем показателя
преломления и, таким образом, исследуем ситуацию, представленную на
рис. 35.5,а, которая возможна для планарных волноводов с непоглощающей
сердцевиной и поглощающей оболочкой. Среда при х > р однородна, слабо
поглощает и имеет показатель преломления «с1 = «с! + *>41 ’ где Пс1 « Лс1 ’
а среда при х < р непоглощающая, имеет градиентный профиль показателя
преломления п (х), удовлетворяющий условию п (р) = п2^ . Луч, который дол-
Рис. 35.5. Явления на границе раздела однородной с лабопоглощающей среды и непогло-
щающей среды с градиентным профилем:
а — луч отражается от каустики точек поворота, но часть потока мощности проходит
(заштрихованная область) и поглощается в заштрихованной области; б — градиентные
профили; непрерывной линией показан произвольно меняющийся профиль, а штрихо-
вой — профиль с линейным изменением л2 (х)
жен был бы полностью отразиться при = 0, касается каустики при х = х^.
По аналогии с рис. 35.3 распространим лучевую трубку на область выше кау-
стики, как показано на рис. 35.5, а. Спадающие поля описываются выраже-
нием (35.32в) для Ф1 с F = А. При х > р функция |£х(х) I = Iкх (р) |
\/32 — &2(игс1 )2} 1/2 постоянна, и мы получаем
W)l4 <35-37)
iMrti I «tp >
Мощность спадающего поля, поглощаемая в заштрихованной на рис. 35.5,а
области, дается первым выражением в (35.26). Подставляя в него выраже-
ние для Ф1, получаем
Ф'"“Р{~2 Ь*i <3538)
Отношение мощностей Pabs к где взята из (3534), дает коэффици-
ент прохождения. Выражая j3 через лучевой инвариант (3 с помощью соотно-
шения, взятого из табл. 36.1, и , выраженного через коэффициент погло-
щения мощности ас1, находим
ОС 1 п ( р )
т = ---Тфф” exp ]-2к / [02 - п2 (х) ] i/2dx >.
2к 02-(игс1)2 ( хф >
(35.39а)
Это выражение применимо ко всем направляемым лучам, исключая неболь-
шое число лучей с каустиками точек поворота, почти совпадающими с по-
верхностью раздела. Если среда сердцевины (при х < р) также поглощаю-
щая, то нужно сложить коэффициенты затухания мощности для полей в серд-
цевине и оболочке, как это выражено формулой (6.30).
Линейное приближение. Существенные потери мощности испытывают
лишь лучи, каустики точек поворота которых расположены не слишком да-
580
леко от поверхности раздела, т. е. при & р на рис. 35.5, а. Пи аналогии с
выражением (6.23) мы можем тогда разложить в ряд Тейлора подынтеграль-
ную функцию в (35.39а) при х = xtp. Следуя выводу выражения (6.24), на-
ходим, что на границе раздела волновода, т. е. при х = р
2
Т-Ъ expj-^Pl-O^L.l (1 - >)»}• (33.396)
где производная берется на границе раздела со стороны сердцевины.
35.11. Непрерывные и разрывные профили
В предыдущих разделах при получении выражений для коэффициентов про-
хождения мы рассматривали градиентные и ступенчатые профили раздельно.
Это разделение было необходимо потому, что решение для локальных плос-
ких волн или решение методом ВКБ скалярного волнового уравнения в слу-
чае непрерывного градиентного профиля не подходит для ступенчатого про-
филя, у которого изменение коэффициента преломления сконцентрировано
на границе раздела. Рассмотрим, например, степенной профиль, усеченный
при х = р (см. рис. 1.10). При увеличении q профиль становится круче и нару-
шается требование медленного его изменения на длинах порядка длины вол-
ны света. Именно поэтому коэффициент передачи (35.35) для градиентного
профиля не сводится к соответствующему выражению (35.20) для ступенча-
того профиля для случая, когда каустика точек поворота приближается к по-
верхности раздела, т. е. при х^ -+р на рис. 35.4, а.
Однако если бы мы знали точное решение скалярного волнового уравне-
ния для градиентного профиля, то должны были бы увидеть, что результаты
для ступенчатого профиля являются соответствующим пределом результа-
тов для градиентного профиля. Ступенчатый профиль эквивалентен любому
градиентному профилю (см. рис. 35.5, б, сплошная кривая), меняющемуся
от постоянного показателя преломления исо до постоянного показателя пре-
ломления ис1 на расстоянии 6х, меньшем длины волны света. Соответственно
мы можем смоделировать ступенчатый профиль любым градиентным профи-
лем такого типа и, взяв предел при 6х 0 от выражения для коэффициента
прохождения в случае градиентного профиля, получить коэффициент Френе-
ля (35.20). Это было проверено для случая, когда вариация профиля была
линейной, как показано штриховой линией на рис. 35.5, б. Решения скалярного
волнового уравнения в этом случае выражались через функции Эйри [10].
Градиентные профили со ступенчатым скачком. В выражении для коэф-
фициента прохождения в случае туннелирующих лучей (35.35) предполага-
ется непрерывность профиля. Если ввести скачкообразный разрыв на грани-
це раздела х = р (см. рис. 35.4, а) и считать, что поля по обеим сторонам раз-
рыва остаются спадающими, то можно показать, что влияние разрыва сводит-
ся к умножению коэффициента прохождения на дополнительный множитель
|Гг1,такчто [11]
581
f Arad _ )
T= |Tflexp l-2k J {j32-n2(x)} 1/2dxL (35.40a)
<• *tP J
f {(HT-0)1/2 + (n2_-i32)1/2;2 ’ J
где n+ и n_ обозначают значения n(x) по разные стороны ступеньки (n+ >
> n_)9 a Tf является аналитическим продолжением для коэффициента Фре-
неля (35.20), поскольку квадратные корни в нем становятся мнимыми.
35.12. Цилиндрические поверхности раздела и каустики
Проведенные выше вычисления коэффициентов прохождения применимы не-
посредственно для планарных многомодовых волноводов. С небольшими из-
менениями их можно применить также к многомодовым волоконным све-
товодам с круглым поперечным сечением, где лучи падают на цилиндричес-
кие поверхности раздела и каустики. Для этого требуется, чтобы цилиндри-
ческие поверхности можно было рассматривать как плоские на расстояниях,
сравнимых с длиной волны света. Зависимость коэффициентов прохождения
(35.35) и (35.39а) от профиля всегда выражается через величины -
- п2 (х)}1/2. В областях, где лучи распространяются, поперечная составляю-
щая локального волнового вектора записывается в виде &х(х) ,как в (35.27),
а в области, где поля спадают, используется величина | kx (х) |. Интуитивно
ясно, что на цилиндрическую геометрию волоконного световода можно рас-
пространить результаты, полученные для планарной геометрии, просто заме-
няя кх (х) на кт (г), где кт (г) — радиальная составляющая локального волно-
вого вектора в области, где лучи являются распространяющимися, определя-
емая выражением
t ( ,.2 ) ( Л2 Л
кт(г) = kn (г) cos а (г) = j&2«2(r) - /З2-~ >1/2 = £)И2(г) - j32 -/2-^-?1/2,
(35.41)
где п(г) — профиль показателя преломления световода, а (г) — угол между
волновым вектором и радиальным направлением, а и —_по рядок азимуталь-
ной зависимости поля. Соотношения между а (г), /3 и I даются формула-
ми (2.14), (2.16) и (2.17), а соотношения между (3, и, 13 и 7 приведены
в табл. 36.1.
Решение скалярного волнового уравнения. Изложенная выше процедура,
конечно, должна давать те же результаты, что и при асимптотическом реше-
нии скалярного волнового уравнения, аналогичном проведенному в разд. 35.8.
Соответственно этому решим волновое уравнение аналитически, используя
ВКБ-приближение, а затем покажем, что полученные решения идентичны ре-
шениям в виде локальных плоских волн, рассмотренных в разд. 35.3. Наибо-
лее общую ситуацию для волоконного световода радиуса р с градиентным
профилем п(г) в сердцевине и однородным показателем преломления обо-
лочки ис1 = п (р) иллюстрирует рис. 35.6. Туннелирующий луч падает на кау-
стику точек поворота радиуса rtp, а прошедший луч появляется в оболочке
582
на каустике излучения радиуса rrad. Вследствие азимутальной и осевой сим-
метрии ищем решение скалярного волнового уравнения в виде
X (г, z) = Ф (г) exp (i exp (i j3z), (35.42)
т. е. в цилиндрических полярных координатах, отнесенных к оси световода,
где 0 — постоянная распространения, ар- порядок азимутальной зависимо-
сти поля. Функция Ф (г) удовлетворяет уравнению
С /7 2 1 /У )
h^+г +*2"2(г) ~НФ=О- (35-43а)
Для его решения введем новую независимую переменную w = In г. В резуль-
тате получим уравнение
f d2 )
< + к2 (w) exp (2w) > Ф (w) = 0, (35.436)
(dw2 г )
в котором фигурирует только радиальная составляющая волнового вектора,
определенного выражением (35.41). Поскольку п(г) и, следовательно, кт (г)
изменяются медленно, то решения в виде локальных плоских волн вне кау-
стик идентичны решениям уравнения (35.16) для случая планарной геоме-
трии с лг, замененным на w, а к2п2 (х) — j32 на к2 (w)exp(2w). Например, ре-
шение для падающих лучей в области г < rtp следует из выражения (35.32а)
и имеет вид
A С Г ¥г\ Л
i С tp j
Ф = {гкх(г)} 1/2 еХр [7 dr Г (35,44)
Положения каустик и rrad даются решениями уравнения кх (г) = 0.
Эквивалентность описания с помощью локальных плоских волн. Множи-
тель перед экспонентой в выражении (35.44) учитывает постоянство мощ-
ности вдоль луча. Это ясно из физических соображений и из рис. 35.6, где
траектории лучей, образующих трубку, идентичны, не считая смещения вдоль
волоконного световода и поворота вокруг его оси. Таким образом, проек-
ция поперечного сечения трубки 8А (г) на радиальное направление должна
возрастать линейно с г, т. е. величина SA (г) /г cos а (г) должна быть инвариант-
на вдоль трубки; здесь а (г) — угол между касательной к траектории и ради-
альным направлением. Плотность потока мощности в трубки изменяется как
Рис. 35.6. Туннелирующий луч
касается каустики точек по-
ворота при rtr, а прошед-
ший луч вновь появляется на
каустике излучения rrad. Об-
ласти, заштрихованные силь-
нее, отмечают распростране-
ние потока мощности по лу-
чевым трубкам с площадью
поперечного сечения дА (г),
а в области, заштрихованной
слабее, поле спадает
583
п (г) | Ф112 в соответствии с табл. 13.2, и по определению к (г) = кп (г) cos а (г).
Следовательно, полная мощность трубки 8А (г)п (г) |Ф* г сохраняется вдоль
траектории.
Коэффициент прохождения для туннелирующих лучей в волоконных све-
товодах с градиентным профилем показателя преломления. Если заменить в
формулах из разд. 35.9 х на г, Ы(х) на 8А (г) и кх (х) на кт (г), то вычисление
коэффициента прохождения при туннелировании для круглого световода
проводится так же, как для планарного волновода. Соответственно мы полу-
чаем из формул (35.35) и (35.41) [6]
f гга<2 — — л2
Т=ехр\-2к $ [j32 + I2 n2(r)]1/2dr
( 'tp r
(35.45)
при условии, что значения rtp и rrad не слишком близки друг к другу.
Коэффициент прохождения для туннелирующих лучей в волоконных свето-
водах со ступенчатым профилем.Соответствующий результат для волоконно-
го световода со ступенчатым профилем показателя преломления может быть
также получен из формул в разд. 35.9 с теми же заменами обозначений, кото-
рые указаны перед выражением (35.45), и с использованием дополнительных
требований х^ = р в формулах (35.32) и (35.33) и п(х) = «со в (35.32а).
Применим формулы для сшивания поля (35.33), чтобы выразить С через F,
и затем выразим F через А, потребовав непрерывность функций Ф* + Фг и
Фе и их первых производных при х = р. Это приведет к выражению [12, 13]
f rad __ _ п2
Г= |Tflexp <-2Л J- [02+r А-
to Г
где Tf — аналитическое продолжение коэффициента Френеля;
‘ _ 4(«2С0_-72 -02)1/2(и2с1 -Г -Д2)1/2
f {(«со" I2 -02)1/2 + (и2с1 -I2 -02)1/2}2 ’
(35.46а)
(35.466)
Для туннелирующего луча первый радикал в числителе вещественный, а вто-
рой — чисто мнимый. Следовательно,
4 _
|7>‘ («2со - I2 -в2У'2(Р+И2 -л2с1)1/2- (35.46в)
1 со с!
Этот результат представляет собой частный случай формулы (35.40) для ци-
линдрической границы раздела, когда, с одной стороны, граница раздела по-
ля описывается локальными‘Плоскими волнами, а, с другой стороны, имеет-
ся спадающее поле.
Линейное приближение. Если каустики находятся не слишком далеко от
поверхности раздела между сердцевиной и оболочкой, то интегралы в фор-
мулах (35.45) и (35.46а) могут быть вычислены приближенно. Например,
вклад от сердцевины в диапазоне < г < р получается линеаризацией выра-
жения в квадратных скобках подынтегральной функции с номощью’разложе-
584
ния в ряд Тейлора при г = р и сохранения только первых двух членов. Следо-
вательно, получаем
{2г + (3S.47)
Подстановка нижнего предела не дает вклада в результат интегрирования,
так как левая часть последнего уравнения равна нулю при г = Таким
образом, получаем интеграл
р _ _ л2 , ? (j32 +72 - л2])3/2
; [02 '+ 12 - п2 (г) ] i/2dr я» -|р
'tp Г 3
1 dn2 (г) I
~dr 1'-= р_’
крп\ - 212
(35.48а)
выраженный через производную профиля сердцевины на поверхности разде-
ла. Аналогично, вклад в интеграл от оболочки имеет вид
}ad[j32 + Z2 ^--n2cl]1/2Jr«4^-(|32 +Т2 -л2с1)1/2, (35.486)
л Г 3 1
а выражение для коэффициента прохождения следует из формулы (35.45):
f 2» (02+/2-^)3/2
Т ехр < - — кр---;----=т~ --------------
I 3 и крп2сХ-212 п2х-р2
(35.49а)
где к — определяется в (35.48а), а /2 п2х р2, так как rrad » р. Подобное же
приближение возможно для световода со ступенчатым профилем показателя
преломления, при этом из (35.46) и (35.486) получаем
(35.496)
где |7f| дается выражением (35.46в), а I п2с$2 в этом приближении. От-
сюда вытекает, что Т -+ 0 при /3 лс1, т. е. получаем предельное значение для
направляемых лучей.
Преломленные лучи. В сердцевине волоконного световода со ступенча-
тым профилем показателя преломления нами был использован коэффици-
ент Френеля для описания части мощности, теряемой лучами, испытывающи-
ми преломление на поверхности раздела. На рис. 35.1, б падающий и прошед-
ший лучи образуют с нормалью или радиальным направлением углы сь и at
соответственно. Если пренебречь поляризацией, то формула (35.20) заменя-
ется на 4п п . cos a- cos at
гтр _ VU Vi________1_______L
z \ *2
(и_п cos a- + n cl cos a J
v VvJ 1 VI т
ncn sin a. = n sin a .
co 1 cl t
(35.50)
Соответствующее выражение для градиентных профилей рассмотрено в
разд. 7.3.
35.13. Цилиндрические поверхности раздела, каустики и поглощающая среда
Коэффициент прохождения для туннелирующих лучей в световоде с градиент-
ным профилем показателя преломления дается выражением (35.45), кото-
рое является простым обобщением соответствующего выражения (35.35)
для планарного волновода. Из рассмотрения, приведенного в предыдущем
разделе, и из решения, полученного в разд. 35.9, должно быть очевидно, что
для номинально направляемых лучей, распространяющихся в световоде с
градиентным профилем показателя преломления, непоглощающей сердцеви-
ной и слабопоглощающей оболочкой, выражение для коэффициента прохож-
дения является соответствующим обобщением формулы (35.39). Следова-
тельно,
а , и ( р п2 1
r = 2F
(35.51)
где ис] = нгс1 + i«ci ~ показатель преломления оболочки. Соответствующее
выражение, справедливое в рамках линейного приближения, выводится в
разд. 6.7 (формула (6.24)).
Волоконные световоды со ступенчатым профилем показателя преломле-
ния. Выражение для коэффициента прохождения в случае, когда номинально
направляемые моды распространяются по световоду со ступенчатым профи-
лем и слабо поглощающими сердцевиной и оболочкой, получается из (35.25)
при отсчете направления луча от радиального направления, т. е. при замене
угла 0Z на я/2 — . Отсюда
4_ ff/2~ai J ”cl ”со I
вс ^с- (тг/2 — ttj)2} 1/2 I игс1 игс0 J
(35.52)
при условии, ЧТО угол я/2 - не слишком близок К 0С.
35.14. Поверхности раздела и каустики, определяемые двумя радиусами
кривизны
В общем случае концепция коэффициента прохождения мощности для выте-
кающих лучей, распространяющихся по волноводам с произвольными профи-
лем показателя преломления и поперечным сечением, имеет смысл только
тогда, когда коэффициент прохождения определяется локальной геометрией.
Так, в разд. 7.13 мы ввели концепцию локальных коэффициентов прохожде-
ния для описания потерь лучевой мощности в волноводах, где кривизна по-
верхности раздела или каустики изменяется вдоль траектории, например в
круглых или скрученных волоконных световодах. Использование коэффици-
ента прохождения локально обосновано при условии, что точка поворота или
граница раздела находятся не слишком далеко от каустики излучения. В
противном случае передаваемая мощность зависит от формы волновода в це-
лом и локальное описание оказывается несправедливым.
586
Отражение на границе раздела. Ступенчатый профиль. Рассмотрим сначала
границу раздела между средами с однородными показателями преломления
псо и Пс1 (Рис- 35.7, а). На поверхности в точке Р направления осей у и z ле-
жат в главных плоскостях кривизны (т. е. эти оси, находясь в касательной к
поверхности плоскости, принадлежат также главным нормальным сечениям),
и соответствующие главные радиусы кривизны равны ру и pz. Луч, отражаю-
щийся в точке Р, образует углы 0у и 0Z с направлениями нормали и осей у
и z соответственно. Коэффициент прохождения для туннелирующих лучей
может быть выведен на основе коэффициента прохождения для цилиндри-
ческой поверхности раздела, выражение для которого получено в разд. 35.12.
Туннелирующие лучи, каустики излучения которых находятся не слиш-
ком далеко от поверхности раздела круглого световода, имеют коэффици-
ент прохождения, определяемый (35.496). Заменяя лучевые инварианты в
экспоненте их выражением (2.7) через углы, показанные на рис. 2.3, получаем
sin2 а
sin2 а
Г ? „ (sin2 а - sin2.а )3/2 ] -
|7\|ехр< - 4£ри--------------—-------------У; р = р . 2~ 2 ,
f [ 3 с0 sin2 a j sin 0Z cos 6^
(35.53)
где ас = arcsin (д2с1/л2со) - критический угол. Из выражений (2.7) и (35.46в)
также следует, что | Tf I зависит только от а - С помощью теоремы Эйлера
[14] (см. разд. 37.5) можно показать, что р — это радиус кривизны линии
пересечения границы раздела и плоскости, проходящей через падающий луч
и нормаль (т. е. плоскости падения). Таким образом, для данной длины вол-
ны коэффициент прохождения полностью определяется направлением луча
относительно нормали и параметром р. Это верно также и в более общем
случае, представленном на рис. 35.7,а. Другими словами, коэффициент про-
хождения дается формулой (35.53), а радиус кривизны в плоскости паде-
ния - выражением (37.133) [12]
Рйс. 35.7. Поверхность раздела произвольной кривизны:
а - луч отражается от границы раздела между средами с показателями преломления п
и лсГ» “ в среде с градиентным профилем траектория луча касается поверхности про-
извольной кривизны h = п (^р) » описывающей каустику точек поворота
587
p p sin2 а
Р=-------> (35.54)
р cos2 0 + р cos2 0
У L. L у
которое сводится к выражению для цилиндрической поверхности раздела,
когда pz -> оо. Это утверждение может быть доказано прямым анализом [12,
15], для которого также следует, что формула (35.53) справедлива только
при условии kpnCQ » 1/cos3 а.
Отражение от каустик. Среда с градиентным профилем показателя пре-
ломления. Подобный результат применим и к среде с градиентным профилем.
Соответствующую ситуацию иллюстрирует рис. 35.7, б с использованием обо-
значений из рис. 35.7, а. Луч касается каустики в точке Р, а касательная к
траектории, лежащая в плоскости каустики, образует углы 0Z и я/2 — 0Z с на-
правлениями осей z и у соответственно. Поверхность постоянного показате-
ля преломления п (г) =п (Гф) имеет главные радиусы кривизны ру и pz.
В рамках линейного приближения туннелирующие лучи в круглом свето-
воде с градиентным профилем и с каустиками точек поворота и излучения,
расположенными не слишком далеко от поверхности раздела, имеют коэф-
фициент прохождения, определяемый выражением (35.49а). Если лучевыми
инвариантами являются 0и Z, то из формул (2.17), (2.19) и из рис. 35.7, б
ясно, что Р2 +12 п2 (д-ф) и Т ъ п (r^), так как Гф « р, следовательно,
Т = ехр (- 4кРпа-^—Г [- ~ 1]3/21 Р = . 2О '» (35.55)
[ 3 с1 кр - 2 п2! J sin2 0г
так как п (Гф) » nCQ «с1. В разд. (37.5) на основании теоремы Эйлера показа-
но, что р - радиус кривизны поверхности раздела в плоскости, определяемой
касательной к лучу в точке поворота и радиальным направлением, т. е. в
плоскости падения. Мы утверждаем теперь, что формула (35.55) справедли-
ва и для ситуации, представленной на рис. 35.7, б, когда радиус кривизны в
плоскости падения дается выражением (37.134) :
— PyPz
р =-------Г -у . "2 п . (35.56)
ру cos2 0Z + pz sin2 0Z v 7
Общий результат (35.55) может быть выведен формально [16] и справедлив
при условии kpnсо » 1.
35.15. Поля в окрестности каустик
Поля волновода в окрестности каустик излучения или точек поворота нельзя
представить плоскими или затухающими волнами, полученными методом
ВКБ в разд. 35.7. Вот почему выражения для коэффициента прохождения,
выведенные ранее в этой главе, несправедливы в случае, когда эти каустики
приближаются друг к другу. В большинстве практически интересных случаев
такая предельная ситуация не реализуется, так как большая часть лучевой
мощности теряется при каждом отражении и луч затухает очень быстро вдоль
волновода. Однако при таких вычислениях, как расчет скрученного светово-
да в гл. 9, удобно иметь выражения, одинаково справедливые для любых
588
значений коэффициента прохождения независимо от того, является ли выте-
кающий луч туннелирующим или преломленным.
Решение скалярного волнового уравнения. Если пренебречь поляризацией,
то свойства полей волн в световоде описываются решениями скалярного
волнового уравнения такого вида, как (35.43а). В окрестности, например,
каустики точек поворота преобразуем второй член в фигурных скобках
преобразованного уравнения (35.436) к виду
к] (w)exp(2w) « (w - wtp) [ ^\к2 (w)exp(2w)} | ] (35.57)
Здесь учтено, что ^(w^) = 0 по определению, a = In Подставляя
(35.57) в уравнение (35.436) и изменяя независимую переменную, для Ф по-
лучаем уравнение Эйри [17]
{ у2 /УС ) I
f = -(» - »„) [£" W«p(2»)] Ц" (35.S8)
с общим решением
Ф(Г) =CAi(f) +PBi(O, (35.59)
где Ai и Bi — функции Эйри первого и второго рода, а С и D — постоянные.
Аналогичное выражение имеется для окрестности каустики излучения. По-
стоянные определяются сшиванием асимптотических решений в области до-
статочно далекой от каустик, т. е. при £ -> ± ©°, с полями локальных плоских
волн при условии непрерывности Ф и ее первой производной на поверхности
раздела [4, 9]. Коэффициент прохождения для лучей, у которых каустики
излучения и точек поворота близки друг к другу, строится с помощью выра-
жения (35.59) и, как можно показать, сводится к выражению для туннелиру-
ющих лучей (35.49а) в одном предельном случае и к выражению для прелом-
ленных лучей (35.35) в другом предельном случае [9].
Единое приближение. В соответствии с приведенным выше рассмотрением
имеются три формы для коэффициента прохождения, применимых соответ-
ственно к туннелирующим, преломленным лучам и к промежуточному слу-
чаю. Это неудобно при численных расчетах, когда оказываются существенны-
ми много лучевых направлений. Этого можно избежать, применяя единооб-
разный метод аппроксимации для решения скалярного волнового уравнения
[17]. При этом три различные формы заменяются одним выражением, оди-
наково применимым для всех вытекающих лучей [18].
ГЛАВА 36. ЛУЧИ И АСИМПТОТИЧЕСКОЕ ОПИСАНИЕ МОД
В предыдущей главе были рассмотрены интуитивные представления, касаю-
щиеся распространения лучей или локальных плоских волн, с целью допол-
нить лучевое описание распространения излучения по многомодовым свето-
водам, представленное в ч. L Альтернативное описание проведено методами
мод в ч. II. Для описания полей в многомодовом волноводе в общем случае
требуется суммирование полей большого числа мод. В результате роль от-
589
дельных мод становится мало заметной. Это делает возможным переход к
непрерывной суперпозиции лучей. Подчеркнем, что асимптотический анализ
методами мод включает излишний промежуточный шаг — решение задачи
на собственные значения (получение характеристического уравнения). Эта
задача вносит концептуальные усложнения и в общем случае может быть ре-
шена только численными методами.
Основная цель данной главы — продемонстрировать эквивалентность лу-
чевого описания и асимптотического описания методами мод многомодовых
волноводов. Мы начнем с рассмотрения асимптотического соответствия меж-
ду модой волновода и эквивалентным семейством лучей или локальных,
плоских волн, а затем перейдем к обратной ситуации и найдем, как может
быть построена мода с помощью локальных плоских волн путем использо-
вания простых соотношений соответствия.
ЛУЧЕВОЕ ПРЕДСТАВЛЕНИЕ МОДЫ
Поле моды в произвольном волноводе в области, где возможно распростра-
нение лучей, выражается в общем случае в виде суперпозиции полей локаль-
ных плоских волн, соответствующих лучам всевозможных направлений. За-
мечательным исключением является планарный волновод со ступенчатым
профилем показателя преломления, рассматриваемый ниже, для которого в
разложение моды включаются лучи только двух направлений. Как будет по-
казано ниже, каждая из мод, распространяющихся в многомодовых волново-
дах, асимптотически эквивалентна одному семейству лучей, где каждый луч
имеет одни и те же характеристики распространения, например, в круглом
световоде — это одинаковые значения лучевых инвариантов /3 и I.
36.1. Планарный волновод со ступенчатым профилем показателя
преломления
Тригонометрическая функциональная зависимость полей в сердцевине
для мод планарного волновода со ступенчатым профилем, приведенных
в табл. 12.1, может быть разложена на две составляющие. Например, электри-
ческое поле четных ТЕ-мод выражается в виде
- {ехр(П7х) + ехр(-П7х)} /2 cos U =е+ + е~, (36.1)
где знаки ”+” и ” соответствуют экспонентам с положительной и отрица-
тельной фазами. Определим волновые векторы относительно декартовых
осей, изображенных на рис. 12.1, их составляющими
k4 = (± U/p,O,0) = knc0(± sin 0Z, 0, cos 0Z) = k(± {п2С0-р2}'12 ,0,0),
(36.2)
где 0Z — угол между направлением распространения и осью волновода, а
остальные параметры определены в табл. I. С помощью характеристическо-
го уравнения* из табл. 12.2 и величин из табл. 12.1 получаем соотношения
h±=<S’)1/2Tk±x,±; e±'h± = 0- <36-3)
Каждая тройка векторов (е+, h+, k+), (е~, h~, k~) состоит из взаимно орто-
гональных векторов. Таким образом^ поля в произвольной точке?в сердце-
590
вине световода представляются суперпозицией полей двух плоских волн, рас-
пространяющихся под углом 0Z по направлению к оси и от оси, как показано
на рис. 36.1, а. Нетрудно показать, что аналогичная интерпретация применима
ко всем оставшимся модам, приведенным в табл. 12.1.
36.2. Волоконный световод со ступенчатым профилем показателя
преломления
В отличие от полей планарного волновода поля в сердцевине круглого све-
товода, выражающиеся через функции Бесселя (см. табл. 12.3), нельзя
представить единым семейством лучей [1]. Однако поля мод высших поряд-
ков, имеющие U » 1, асимптотически эквивалентны одному семейству.
Для того чтобы это продемонстрировать, используем сначала рекуррентные
соотношения (37.72) для Jv ± р взятые из табл. 12.3 и позволяющие выра-
зить их через J
и U - и » и1'3
и ее первую производную. Затем при условии, что U » 1
, можно использовать дебаевскую аппроксимацию (37.89).
Азимутальная зависимость от sin(p^) или cos(p<p) разлагается подобно выра-
жению (36.1). Если знаки ”+” и обозначают поля, изменяющиеся как
ехр(± соответственно, то
eT =f{l±i^~r} exp(±ix); (36.4а)
hx i*); (36.46)
+ i7?2 } exp^ ix-* ’ (36.4b)
h* ± 4 exp(± ix); (36-4r)
е±ъ = iX)’ (36.4д)
hi (-77-) -----— exp(+ ix), (36.4e)
K “° PS*
Рис. 36.1. Разложение полей мод на плоские волны:
а — ъ сердцевине плоского волновода со ступенчатым профилем; б — в поперечном се-
чении сердцевины волоконного световода со ступенчатым профилем
591
где Fj и F2 определены в табл. 12.3 и связаны между собой так, как показа-
но в табл. 12.4. Функции f ng даются выражениями
f = igl{(2irynURJv(U)}, g = (U2R2 - р2У/4. (36.4ж)
Учитывая зависимость otz в формуле (12.10), получаем следующее выраже-
ние для набега фазы
Х + pz = (U2R2 - р2) 1/2 - v arccos(p/C7F) - тг/4 + + 0z. (36.4з)
Определим теперь волновой вектор плоской волны к* его составляющими
относительно радиального, азимутального и продольного направлений (см.
рис. 12.3) следующим образом:
к±=|± (U2R2 — р2) 1/2/Яр, vfRp.P } = (36.5а)
= knCQ {± cos а (г), sin cos 0^ (z), cos 0Z| = (36.56)
= fc{± (n2Q - P2 -I2 IR2Y12 J/R, 0}, (36.5b)
где 0Z и a(r) — углы между направлением распространения и продольными
поперечным направлениями в точке Р на рис. 36.1, б, г — расстояние от оси,
а 0 (г) - угол между азимутальным направлением и проекцией волновых
вейоров на поперечное сечение световода. Эти соотношения следуют из
обобщений формул (2.7) и соотношений из табл. 36.1 между 0, р и лучевыми
инвариантами. Легко проверить, что поля (36.4) удовлетворяют соотноше-
ниям (36.3). Поля мод в точке Р асимптотически эквивалентны суперпози-
ции полей двух плоских волн, распространяющихся по направлению к по-
верхности раздела и от нее под углом а (г) к радиальному направлению.
Как следует из выражений (36.5) при а (г) = тг/2, все лучи касаются цилин-
дрической поверхности радиуса ric = pvfU, показанной на рис. 36.1, б. Это и
Таблица 36.1. Сопоставление лучевых параметров и параметров мод для воло-
конных световодов и планарных волноводов со ступенчатым профилем показателя
преломления
^=y?=/c? = /cncoCOS0I
V cos 02
р Sin0c
v = ~ pT— kpT = krn^ sin 0Z cos 0^,
— U - cos 0„
P v
= крпюзт02 = fcp«-j82)1/2
|zsin02 V ( g2]1/2
sin0c sin0c(
/cpnco (sin2 0c-sin2 0Z)12 = kp(ft2 - n2,)1/2
[ sin20cJ
V f?2 I1'2
tan 0C ( n2, J
Q' = крпю (sin2 0t - sin2 0C)112 = V -1
(sin и _
V f Б2)1/2
= М^-Д2),/2=~ i-M
tan0c (
Примечание. Параметры определены в табл. I.
592
есть внутренняя каустика, введенная в разд. 2.2. Далее получаем, что только
ТЕОт- и ТМ0т-моды (р = 0) состоят из меридиональных лучей, так как ric =
= 0, а все HEvm- и £’Ярт-моды образуются из косых лучей. Напомним, что в
приближении слабонаправляющего волновода все моды образуются из па-
раксиальных лучей.
36.3. Лучевое представление для свободного пространства
В случае свободного пространства, т. е. ненаправляющей однородной среды с
показателем преломления п, любое решение уравнений Максвелла может
быть выражено в виде суперпозиции плоских волн или лучей, распространя-
ющихся во всевозможных направлениях. Так, например, если вектор элек-
трического поля в плоскости z = 0 везде параллелен направлению оси х и
имеет пространственное распределение Е (х, у), то [2]
Е(х, у) = -д- / f S(kx,ky)cxp{i(kxx + kyy)} dkxdky, (36.6)
где кх = кп cos 0Z, ку = кп-cos 0у соответственно — х- и.у-составляющие вол-
нового вектора плоской волны пк, имеющего величину пк = л?(к( = 2тт/\ и
образующего углы 0Х и 0у с направлениями осей х и у. Длина волны в сво-
бодном пространстве равна X. Обратное соотношение имеет вид
S(kx,ky) = J J* Е(х, y)exp$-i(kxx + £уХ)} dxdy, (36.7)
-------------ОО -оо
где S(kx, ку) — угловой спектр плоских волн.
Цилиндрические долны. Можно преобразовать выражения (36.6) и (36.7)
к цилиндрической геометрии; заменяя (х, у) на цилиндрические полярные
координаты (г, <р) с помощью соотношений (37.46) й определяя и как ради-
альную составляющую вектора пк. Если волновой вектор образует угол 0Z с
направлением оси z, то из формул (37.49) получаем
к*х + к= nkr sin 0Z = иг. (36.8)
В случае, когда рассматриваемое поле обладает круговой симметрией, т. е.
Е=Е(г), из формулы (36.6) иопределения (37.62) находим [3]
Е (г) = J S (и) JQ (иг) rdr, (36.9)
о
где Jo — функция Бесселя нулевого порядка. Формула (36.7) дает для рас-
сматриваемого случая симметричный угловой спектр
S(и) = 2я J Е(г) Jo (иг)rdr. (36.10)
Спектральную функцию удобно пронормировать для сравнения с результата-
ми разд. 10.1. Соответственно определяем
А («) =4^ = ? J° ^rdrEE(r)rdr, (36.11)
о о
так что Л (0) = 1.
593
АСИМПТОТИЧЕСКОЕ ОПИСАНИЕ РАСПРОСТРАНЕНИЯ МОД
В этой части главы мы приведем асимптотическое описание распространения
излучения по слабонаправляющим волноводам с помощью мод и продемон-
стрируем эквивалентное ему описание с помощью лучей или локальных
плоских волн, как в ч. I. Ограничение рассмотрения слабонаправляющими
волноводами введено для упрощения, а отнюдь не по принципиальным при-
чинам.
36.4. Поля мод
Поля мод слабонаправляющих волноводов строятся из решений скалярного
волнового уравнения, как объяснено в гл. 13. Однако, если волноводный па-
раметр велик, т. е. V » 1, решения скалярного волнового уравнения для
мод в многомодовых волноводах хорошо аппроксимируются решениями,
полученными методом ВКБ [4]. В разд. 35.8 и 35.12 было показано, что эти
решения идентичны решениям в виде локальных плоских волн. Соответствен-
но поля мод высших порядков асимптотически идентичны полям локальных
плоских волн, что строго эквивалентно разложению мод, рассмотренному в
примерах разд. 36.1, 36.2, в которых учитываются как пространственная за-
висимость, так и направление векторов полей мод. Более того, суммарный
эффект асимптотических полей большого числа мод приближенно описывает-
ся при V -> °° интегралом по континууму мод. Этот интеграл идентичен инте-
гралу по континууму полей локальных плоских волн или лучей. Мы проде-
монстрировали это предельное представление для частного примера, рассмот-
ренного в разд. 20.19’.
36.5. Постоянные распространения
Постоянные распространения мод определяются характеристическим урав-
нением, которое получено при решении скалярного волнового уравнения,
как объяснено в разд. 33.1. Однако для мод высших порядков характеристи-
ческое уравнение может быть получено асимптотически без использования
решений скалярного волнового уравнения. Напомним, что в многомодовом
волноводе поля мод существенны только в области сердцевины, где они име-
ют осциллирующий характер. Поскольку поля практически равны нулю вне
этой области, то ясно, что осцилляции полей должны существовать только в
этой области. Ниже мы приведем примеры, показывающие как этот простой
критерий приводит к характеристическому уравнению.
Такая же асимптотическая форма характеристического уравнения может
быть выведена также с помощью локальных плоских волн. Этот подход на-
лагает условие на набег фазы вдоль траектории лучей, т. е. на число полупе-
риодов волн, что демонстрируется в последующих примерах.
36.6. Планарный волновод со ступенчатым профилем показателя
преломления
Рассмотрим планарный волновод со ступенчатым профилем и показателями
преломления nQQ и ис1 в сердцевине и оболочке соответственно. Постоянная
распространения 0 является z-составляющей волнового вектора локальной
плоской волны, величина которого равна knCQ. Соответственно поперечная
594
составляющая дается выражением (^«^ “ 02)1/2 = U/p через модовый пара-
метр. Поля осциллируют между границами разделах = ± р (см. рис. 12.1).
Если мы учтем еще изменение фазы Ф на самих границах, где Ф дается выра-
жением (35.23), то условие того, что поле в поперечном сечении имеет целое
число осцилляций, имеет вид
р U
/ Л + Ф=Мг,А = 0, ± 1, . . . . (36.12)
-Р р
Выражая Ф через модовый и волноводный параметры волновода, используя
соотношения, приведенные в табл. I, и проводя преобразования, получаем ха-
рактеристические уравнения для четных и нечетных ТЕ-мод, приведенные в
табл. 12.2, при четном или нечетном N соответственно. Таким образом, в
этом частном случае условие, выраженное соотношением (36.12), является
точным для всех мод.
Вывод с помощью локальных плоских волн. В разд. 10.7 мы продемон-
стрировали, как простые условия постоянства фазы, основанные на трансля-
ционной инвариантности планарного волновода, приводят к преимуществен-
ным направлениям лучей или локальных плоских волн. Выражая в уравне-
нии (10.16) углы через модовый и волноводный параметры и используя со-
отношения, приведенные в табл. I, легко убедиться, что уравнение (10.16)
идентично характеристическому уравнению для ТЕ-мод, представленному в
табл. 12.2. Таким образом, преимущественные направления лучей соответ-
ствуют дискретным значениям постоянной распространения моды.
36.7. Волоконный световод с неограниченным параболическим профилем
показателя преломления
Здесь мы приведем два вывода характеристического уравнения для волокон-
ного световода с неограниченным параболическим профилем показателя пре-
ломления (14.5), аналогичных представленным в предыдущем разделе. На-
помним (см. гл. 2), что траектория луча или локальной плоской волны ле-
жит между внутренней каустикой и каустикой точек поворота с радиусами
ric и rtp соответственно. Поэтому поля мод осциллируют между этими двумя
каустиками. Аналогичное (36.12) условие существования целого числа ос-
цилляций между двумя каустиками имеет вид
rtp
f к (r)dr - — = Ш7г, т = 0, ± 1, . . . , (36.13а)
'ic Г 2
где кТ (г) — радиальная составляющая волнового вектора локальной плоской
волны в точке с радиусом г, а член —тг/2 учитывает изменение фазы на кау-
стике. Подставляя для кТ(г) среднюю часть выражения (35.41), заменяя и
/3 соответственно волноводным параметром световода V и модовым парамет-
ром Uи полагая и = Z, получаем
( /2 )1/2 .
J W dR = (т + 1)я, (36.136)
V' *
где R = г/р. Заметим, что пределы интегрирования являются корнями подын-
тегрального выражения. Полагая R2 = А + В sin в, где А = LP/IV2 и В =
595
= (U*I4V4 — l2/V2)1/2, вычисляем интеграл с помощью формулы (37.113).
После преобразования имеем
U2 = 2Г(2т + I — 1)1/2, Z = 0,l,...; т = 1,2,.... (36.14)
Это соотношение является характеристическим уравнением, приведенным в
табл. 14.2. Указанный выше диапазон значений параметров 1пт обеспечива-
ет вещественность параметра U. Таким образом, наше асимптотическое ха-
рактеристическое уравнение справедливо для всех мод световода с неограни-
ченным параболическим профилем показателя преломления.
Вывод с помощью локальных плоских волн. Траектория луча в световоде с
параболическим профилем рассматривалась в разд. 2.10. На расстоянии вдоль
световода, равном полупериоду zp, траектория, показанная на рис. 36.2, я,
начинается в точке Р на каустике точек поворота, касается внутренней кау-
стики в точке Т и снова встречается с каустикой точек поворота в точке Q.
Относительно оси световода траектория между точками Р и Q закручивается
на угол я радиан в поперечном сечении световода, как показано на рис. 36.2, б.
Следуя концепции разд. 10.7, характеристическое уравнение получается
наложением условия согласования на набег фазы на отрезке траектории меж-
ду точками Р и Q, возникающего в результате трансляционной и вращатель-
ной симметрий световода [5]. Набег фазы состоит из двух составляющих.
Первая представляет собой интеграл от волнового вектора локальной плос-
кой волны вдоль траектории. Так как к (г) = кп (г), этот интеграл пропорцио-
нален оптической длине траектории LQ согласно формуле (2.26). Вторая со-
ставляющая представляет собой уменьшение фазы при касании траекторией
каустик и образуется из потери фазы я/2 на внутренней каустике и потери
фазы я/2 на каустике точек поворота, поскольку траектория начинается и за-
канчивается на последней. Таким образом, набег фазы равен kL0 — я.
Траектория на рис. 36.2, а инвариантна при перемещении на zp параллель-
но оси световода и вращении на угол я относительно этой же оси. Поэтому
соответствующее изменение фазы имеет вид
zp^(rtp)n(/'tp)cos0z(''tp) +m'tpfc(/'tp)"(rtp)sin0z(rtp)’ (36.15)
где к(г*р)п (Гф)соз 0z (г^) представляет собой составляющую волнового
вектора локальной плоской волны в точке Q, параллельную оси световода,
а к(Гф)п (Гф)зт 0z (г^) является составляющей в азимутальном направле-
нии. Траектория луча образует угол 0z (г^) с направлением оси z в точке Q.
Вспомнив определение лучевых инвариантов /3 и I из табл. 2.1 и положив
Рис. 36.2. Траектория луча в
волоконном световоде с не-
ограниченным параболичес-
ким профилем:
а — винтовая траектория
между последовательными
точками поворота; б — проек-
ция траектории на поперечное
сечение волоконного свето-
вода
596
r ~ Сф и ^z_(rtp) = убедимся, что изменение фазы (36.15) эквивалентно
k(zpp + Ttpl). Условие соответствия требует, чтобы это выражение отлича-
лось от набега фазы вдоль траектории на четное кратное числа я. Следова-
тельно,
kLQ — я = k(zp(3 + яр/) + 2тя, т = 0, ± 1,. .. . (36.16)
Подставляем для Lq и zp выражения из табл. 2.1 для параболического про-
филя и выражаем р и I через параметры (3 и р, используя соотношения из
табл. 36.1. Непосредственное преобразование с использованием модовых и
волноводных параметров приводит к условию (36.14). Аналогичное рас-
смотрение траекторий лучей в сердцевине волокна со ступенчатым профи-
лем показателя преломления приводит к асимптотической форме характе-
ристического уравнения, представленной в табл. 14.8 [5].
36.8. Неограниченные степенные профили
Если световод имеет какой-либо профиль из семейства неограниченных сте-
пенных профилей, определенных выражением (14.8), то можно вывести
асимптотическое характеристическое уравнение для всех осесимметричных
мод с / = 0. Таким образом, подставляя (14.8) в уравнение (36.13а) и пола-
гая I = 0, г = 0, приходим к уравнению, аналогичному (36.14) :
гм
J (U2 - V2R^yl2dR = (т - -)я, т=0, + 1,... . (36.17)
О 2
Сделав затем подстановку R = (xU2/V2) получим
-----— J (1-*)1/2* 1 q^ qdx = (m - ~—)я. (36.18)
qV 14 q 2
Интеграл выражается через 0-функцию (37.104) , связанную с у-функцией со-
отношением (37.105). После преобразования имеем
и- г О-1М^(<7 + 2)Г(1/^^)Г^ qKq + 2)
1 2Г(1/?) J • 1 ’
Это соотношение выполняется для всех мод с I = 0 для световодов с неогра-
ниченными степенными профилями показателя преломления, в частности
для световода с параболическим профилем (q = 2), когда уравнение (36.19)
сводится к (36.14).
36. 9. Время прохождения
Время прохождения модой расстояния z в световоде выражается через груп-
повую скорость vg с помощью (11.36), где для удобства опущен индекс мод.
Здесь мы покажем, что если использовать асимптотическую форму характе-
ристического уравнения (36.13а) для вычисления групповой скорости, то вре-
мя прохождения моды равно времени прохождения луча [4]. Это равенство
выполняется и тогда, когда материал световода обладает дисперсией [6].
Подставим среднюю ча<>ть из выражения (35.41) для кТ(г) в уравнение
(36:13а), заменим п (г) на Д (г, X), чтобы учесть дисперсию материала, и поло-
жим к - Itt/X. Результирующее уравнение продифференцируем по X. Хотя
597
пределы интегрирования зависят от X, они не дают вклад в производную от
интеграла, так как подынтегральное выражение равно нулю на обеих каусти-
ках. Преобразовав оставшиеся члены, получим
к2 nn.dr rtp dr
9 W77’ <36-2O)
1C Г 1C J
где nty — групповой показатель (3.33a). Выразим кт(г) через лучевые инва-
рианты с помощью соотношения (35.4) и табл. 36.1 и положим /3 = к(3. Инте-
грал в знаменателе (36.20) пропорционален полупериоду луча (2.28), а ин-
теграл в числителе пропорционален оптической длине траектории (2.336).
Следовательно, время прохождения расстояния z, получающееся из выра-
жений (11.31) и (11.36),
_ г zX2 бф _ z £т_
vg 2яс dX с zp ’
совпадает с выражением (2.336) для времени прохождения луча.
36.10. Поглощающие волноводы
В этом разделе мы сравним затухание мощности моды, обусловленное сла-
бо поглощающей средой, с соответствующим затуханием лучевой мощности.
Для простоты рассмотрим планарный волновод со ступенчатым профилем
показателя преломления и сердцевиной шириной 2р. Отметим верхними ин-
дексами г и i вещественную и мнимую части показателей преломления серд-
цевины и оболочки л?со = игсо + in*CQ и «с1 = игс1 + in^ соответственно, где
псо « п со’ wcl « wcl' Постоянная распространения моды комплексна, (3 =
= /Зт + 1/3\ и является решением характеристических уравнений из табл. 12.2.
При этих условиях имеются два метода определения поглощения. В одном
методе используются результаты теории возмущений (18.16), справедливые
для слабопоглощающих волноводов, где параметр т? берется из табл. 12.2
для ТЕ-мод. В другом методе решается характеристическое уравнение из
табл. 12.2 с помощью разложения по теории возмущений. Так как оба мето-
да приводят к одинаковым результатам, мы рассмотрим здесь только вто-
рой. Для четных ТЕ-мод имеем
K’=C7tgt/; W=Wr + iW‘; £/={/ +it?. (36.22)
Приравнивая члены низшего порядка, получаем
W1 = и1 tg и1. (36.23)
Малые мнимые части параметров U и V находим, приравнивая мнимые части
уравнения (36.22). Используя соотношения (37.3), (37.5) и (37.6) для раз-
ложения tg(t7r + iW) и полагая tg(it?) iU\ находим с точностью до перво-
го порядка малости
UTw‘= [#(И'Г+ 1)+ (t/r)2} и1. (36.24)
Модовые параметры свяжем с постоянными распространения, приравняв ве-
щественные и мнимые части в определениях, представленных в табл. I и оста-
вив в каждом случае только члены низших порядков. В терминах коэффици-
ентов поглощения мощности в сердцевине и оболочке асо и ас1, определен-
598
ных соотношениями (6.10) и (6.19) соответственно, и коэффициента зату-
хания мощности у из табл. 11.2 получаем
и1 = р{(£игсо)2 - (0Г)Ч'/2 ; 2^ = р2(^гсоасо-/Згу); (36.25а)
иА = р{(|Зг)2 - (К1)2}1'2 ; 2И/^ = р2(|31т-^1с1ас1). (36.256)
Волноводный параметр и критический угол скольжения в этой ситуации опре-
деляются через вещественные части показателя преломления.
V = кр {(пгс0)2 - (лс1)2}12 > Cos0c =лс1/'7со- (36.26)
Подставляя (36.25) и (36.26) в уравнение (36.24), после преобразования на-
ходим, что коэффициент затухания мощности дается выражением
W (cos вс)«с| + ««(Г1 t
7 ------------^(ГГЙЛ)----------------- <36-27)
справедливым, если поглощение достаточно слабое.
Затухание лучевой мощности. Для того чтобы связать коэффициент зату-
хания мощности моды с коэффициентом затухания лучевой мощности, вы-
разим правую часть равенства (36.27) через характеристики луча. Веществен-
ная часть постоянной распространения связана с углом 0Z, образуемым тра-
екторией луча с осью волновода (рис. 36.3), с помощью замены пс0 на игсо в
соотношении, приведенном в табл. 36.1. Аналогично волноводный параметр
связывается с 0С с помощью соотношения (36.26). Так как волновод счита-
ется слабонаправляющим, то оба угла, 0Z и 0С, малы, и для простоты исполь-
зуем аппроксимацию
^кп^- V^kpnJcoec. (36.28а)
Соответствующая аппроксимация соотношений (36.25) имеет вид
I? * kpnrco0z; И/г * крптсо - 02)1/2 (36.286)
Подставляя (36.28) в выражение (36.27) и преобразуя, находим
7 = «C0 + T/(zp+s), (36.29)
где z_ — полупериод траектории луча (1.10), Т — коэффициент прохождения
(35.25), as — боковой сдвиг (10.8). В рамках сделанных приближений выра-
жения для этих величин, как легко убедиться, имеют вид
7 ~ 2р. 2р в_г_ “с! - “со _ 2р бс 1
Р V V 0С (02 - 02)1/2 ’ V 0Z (02 - 02)1/2 ’ 1 '
Многомодовые волноводы. Для мод, распространяющихся в планарном
волноводе, если он многомодовый и К>> 1, член с s в выражении (36.29)
может быть опущен при условии, что 0Z Ф 0С. Кроме того, вклад в 7 от со-
ставляющей Т, включающей в себя асо, пренебрежимо мал по сравнению с
первым членом в правой части (36.29), поскольку К» 1 и, поэтому может
быть также опущен. В результате имеем
7 = aCo + 77Zp=yCo+7cl- (36-31)
В соответствии с траекторией луча, приведенной на рис. 36.3, а, первый член
в правой части представляет собой коэффициент затухания мощности 7С0 в
однородно поглощающей сердцевине, как это выражено формулой (6.10)
599
Рис. 36.3. Траектория луча в сердцевине толщиной 2р поглощающего плоского волново-
да со ступенчатым профилем показателя преломления (а) ; эффективная сердцевина
шириной 2ре, учитывающая продольный сдвиг s
при 07 « 1. Аналогично T/z^ является коэффициентом затухания мощности
ус1 в однородно поглощающей оболочке, как это выражено формулой (6.17)
при 0Z, 0С « 1. Суммарное выражение показывает, что коэффициенты зату-
хания для моды и луча одинаковы.
Волноводы с малым V. Если параметр V мал, то распространяться могут
только моды низших порядков. Член с s в выражении (36.29) должен быть
удержан для учета дифракционных эффектов, как указывалось в разд. 10.4,
для Т также требуется теперь полное выражение. Однако простая физическая
интерпретация все еще возможна. Напомним (см. разд. 10.6) , что явление бо-
кового сдвига представляет собой увеличение полупериода траектории луча
от zp до zp + 5 в соответствии с добавкой ST к траектории (см. рис. 36.3, б) .
Если ввести эффективную полуширину сердцевины как показано на ри-
сунке, и заменить траекторию луча PSTR на зигзагообразную траекторию
PQR, то выражение (36.29) описывает затухание вдоль новой траектории [1].
Это утверждение подтверждается тем, что поглощение в сердцевине не зави-
сит от траектории, так как угол 0Z мал и поэтому не изменяется при указан-
ной замене траектории. Кроме того, знаменатель второго члена в правой ча-
сти (36.29) zp + 5 является точно полупериодом новой траектории луча, т. е.
аксиальной проекции отрезка PQ. Наконец, составляющая коэффициента
прохождения, зависящая от асо, учитывает слабое прохождение мощности из
оболочки в сердцевину. Этот обмен возникает из-за различия коэффициентов
поглощения в сердцевине и оболочке.
36.11. Вытекающие моды и вытекающие лучи
В разд. 24.18 мы ввели выражение для коэффициента затухания мощности
для туннелирующих вытекающих мод в слабонаправляющем световоде со
ступенчатым профилем показателя преломления. Теперь мы покажем, что
для мод высших порядков выражение (24.36) эквивалентно коэффициенту
затухания мощности для соответствующих косых туннелирующих лучей.
Аргумент функций Ганкеля в выражении (24.36) меньше их порядка. Кро-
ме того, считаем, что параметр I достаточно велик, так что порядок обеих
функций Ганкеля можно считать приближенно равным I. При этих условиях
можно использовать приближенные выражения (37.90) и для простоты ап-
600
про к си ми ров ать параметр х средней частью выражения (37.906). Следова-
тельно,
Если заменить р, U и Q на /, U* и QT соответственно в соотношениях с луче-
выми инвариантами в табл. 36.1, то
2 K2CO-F (Д2 + I2 - И2])1'2 Г (Т2^2-^)3'2 )
7 « - —- -----------п--------ехР 1 - т ;----Г •
Р «со - «с1 I 3 (З2 - И2С1 J
(36.33)
Выражение для соответствующего коэффициента затухания лучевой мощно-
сти следует из (7.2) и (7.19), так что
Т IT’fl Г 2
7 = — = ~----ехР)-7
zp zp 13
{I2 + /З2 - л2])3/2
кр---------------------
02 - пл
(36.34)
Подставляя для | | выражение (7.196), а для zp выражение из табл. 2.1 и
замечая, что в приближении слабонаправляющего волновода j3 « исо, нетруд-
но убедиться, что и коэффициенты затухания для моды и луча одинаковы
[7]. Аналогично аналитическое сравнение может быть проведено для прелом-
ленных вытекающих мод и лучей в планарном волноводе со ступенчатым
профилем показателя преломления [8].
Численное сравнение. Выражение для коэффициента затухания мощности
моды, полученное выше, выведено методами теории возмущений из характе-
ристического уравнения для световода со ступенчатым профилем показателя
преломления. Мы* можем проверить соответствие между коэффициентами за-
тухания мощности моды и луча, решая характеристическое уравнение числен-
но для комплексных значений постоянной распространения. Это решение рас-
сматривалось в разд. 24.19. Хорошее соответствие имеется для мод с наи-
меньшими коэффициентами затухания, в то время как для мод с большими
коэффициентами затухания лишь включение бокового сдвига для вытекаю-
щих лучей и использование уточненной модели при вычислении коэффициен-
та затухания мощности луча приводят к хорошему согласию результатов. Де-
тали приведены в [9, 10].
ЧИСЛО МОД В МНОГОМОДОВЫХ ВОЛНОВОДАХ
Можно вывести простое асимптотическое выражение для числа направляе-
мых и вытекающих мод, которые могут распространяться в многомодовых
волноводах. Поскольку для них V» 1, большинство мод распространяется
достаточно далеко от отсечки Кс, и их поля резко спадают в оболочке, убы-
вая достаточно быстро за границей раздела, так что можно рассматривать
только поля в сердцевине. Обратимся к модификации часто используемого
в квантовой электродинамике метода определения плотности мод в двумер-
ном ящике [11] • Полное число мод 4ftot как направляемых, так и вытекаю-
щих находится интегрированием по площади поперечного сечения сердцеви-
ны Лсо и по соответствующей области в двумерном пространстве волно-
вых векторов. Таким образом [12], получаем выражение
601
dk dk i
Mm-2 Jdxdy j (3635)
лсо лк
в котором учитываются две возможные поляризации каждой моды, напри-
мер ТЕ- или ТМ-моды в планарном волноводе. Примеры приводятся ниже.
Мы считаем, что в (36.35) и последующих выражениях число мод равно наи-
меньшему целому числу, превосходящему правую часть. Число направляе-
мых или вытекающих мод находится с помощью подходящего ограничения
диапазона значений кх и ку, как показано ниже [13].
36.12. Планарный волновод со ступенчатым профилем показателя
преломления
Полное число мод, которые могут распространяться в планарном волноводе,
дается одномерным аналогом выражения (36.35). Если полуширина сердце-
вины равна р, а ее показатель преломления равен nCQi то для любой точки в
поперечном сечении значение кх лежит в пределах от — кп со до knQQ. Следо-
вательно,
р кпсо dk 4 у
(36'36)
где использован волноводный параметр V. Число направляемых модМЬт да-
ется выражением, подобным выражению для Mtot, но пределы интегрирова-
ния по кх уменьшены до ± кп CQ sin 0С, где 0С - критический угол скольже-
ния. Таким образом,
j р кпсо ™ вс
^bm ~ dx J
-p ~knco sin 6C
dk=^ V.
х 7Г
(36.37)
Из рис. 12.2 для значений отсечки параметра V ясно, что этот результат верен
для всех значений V. Туннелирующие вытекающие моды не распространяют-
ся в планарных волноводах, и число преломленных вытекающих мод да-
ется разностью между полным числом мод и числом направляемых мод:
4 Г 1 }
Мг^ = —V\---------77Г- -17.
Лгт tot bm 7Г ( (2Д)1/2 J
(36.38)
Поскольку Д« 1, то очевидно, что число направляемых мод слабонаправ-
ляющего волновода является лишь малой частью полного числа мод.
36.13. Волоконный световод со ступенчатым профилем показателя
преломления
Если 0Z и 0^ - углы в сферической системе координат относительно оси све-
товода с осесимметричным профилем показателя преломления п (г), где г —
радиус, то декартовы составляющие волнового вектора в поперечном сече-
нии световода равны
кх = кп (г) sin 0Z cos 0^, ку= кп (г) sin 0Z sin 0^. (36.39)
С помощью якобиана (37.129) выражение для полного числа мод (36.35)
преобразуется к виду
602
к2 Р о я/2 27Г
Mtoi = п (f)rdr J Мг J sin 02 COS • (36.40)
0 0 0
Подставляя сюда n(r) = nCQ, получаем Mtot для световода co ступенчатым
профилем. Число направляемых мод дается выражением (36.40), в ко-
тором верхний предел интегрирования по 0Z заменяется на вс. Следователь-
но, с помощью параметров световода, определенных в табл. I, получаем сле-
дующие выражения:
Л/tot =^2/4Д; Mbm = И/2. (36.41)
Тогда число туннелирующих и преломленных вытекающих мод
К2 Г 1 )
“^tot ~ ^bm J” t 2Д ~ j ’ (36.42)
Граница между углами, соответствующими туннелирующим и преломлен-
ным модам, следует из (2.6), т. е. из условий а = ас, 0 = тг/2 - 0С на поверхно-
сти раздела между сердцевиной и оболочкой. Таким образом, выражение
(2.3) приводится к виду
sin 0 = sin 0Z sin 0^. (36.43)
Если обозначить через число туннелирующих вытекающих мод, то из
(36.40) и (2.6) получаем
V ”/2
= Та" J* / sin °z cos ez sin2 °* dOv ’ (36.44)
7TA0c
где 0^ = arcsin {sin 0c/sin 0Z } , а множитель sin2 0^ появляется из-за круглой
формы сечения [13]. Интегрируя по 0^ и проводя преобразование W =
= sin 0z/sin 0С, находим с помощью соотношения (37.1136), что
, ~ ZiJ1 + (2Д)1/21
tm 2 [ Зтг J
(36.45)
при Д « 1. Число преломленных вытекающих мод равно .
Усеченные степенные профили. Число направляемых мод, которые могут
распространяться в многомодовом волоконном световоде с усеченным сте-
пенным профилем показателя преломления, получается из выражения (36.40)
и подстановкой для п(г) соответствующей функции из табл. 2.1 и заменой
верхнего предела интегрирования по 0Z на критический угол скольжения
0С (г) (2.29). Таким образом,
р V2 а
МЬт = 2k2 Jп2 (г) rdr J- sin 0Z Cos 0ZJ0Z = --. (36.46)
0 0 2 q + 2
Так, например, в световоде с усеченным параболическим профилем показате-
ля преломления имеется только половина от числа направляемых мод в све-
товоде со ступенчатым профилем.
СДВИГ ПОЛЯ В ИЗОГНУТОМ ВОЛОКОННОМ СВЕТОВОДЕ
В разд. 23.10 мы обсуждали сдвиг полей мод, обусловленный изгибом све-
товода. Если радиус изгиба много больше радиуса сердцевины, то для описа-
603
ния этого сдвига можно воспользоваться методами теории возмущений. По-
кажем, что влияние изгиба может быть описано с помощью прямого светово-
да с эффективным профилем показателя преломления. Цоля изогнутого
световода могут тогда быть найдены решением скалярного волнового урав-
нения для прямого световода с эффективным профилем.
36.14. Вывод эффективного профиля
Ситуацию иллюстрирует рис. 36.4. Пусть прямой участок слабонаправляюще-
го волоконного световода переходит в изгиб с постоянным радиусом Rc,
основная мода световода имеет постоянную распространения j3 и электри-
ческое поле поляризовано по оси х, которая параллельна плоскости изгиба.
Таким образом, в прямом световоде
E=F0(r)exp(ij3z)x, (36.47)
где х — единичный вектор, параллельный оси х, z — расстояние вдоль свето-
вода, г — радиальная координата, a Fo (г) — фундаментальное решение ска-
лярного волнового уравнения (14.4). Очевидно, что на изгибе то же самое
поле должно иметь угловую зависимость вида ехр(1к0), где к — постоянная,
а 0 — угловая координата по изгибу, отсчитываемая от оси х (рис. 36.4) . Ес-
ли теперь z обозначает расстояние вдоль изогнутого световода, т. е. вдоль
кривой с радиусом кривизны, постоянным относительно оси изгиба, прохо-
дящей через точку С, то можно определить локальную постоянную распро-
странения (3 соотношением
exp(iK0) = exp(i/3z). (36.48)
Считая z = О при 0=0. Если г и - полярные координаты в поперечном
сечении изогнутого световода, как показано на рис. 36.4, то из геометричес-
кого рассмотрения получаем
z = (Rc +г cos <р)0. (36.49)
На оси световода в начале изгиба должно быть /3 = /3. Подставляя (36.49) в
(36.48), находим, что к = (3RC, и, следовательно,
( г 1
Р=~Б~7---------—H-cos<4, (36.50)
Яс + ГСО8(£ Rc J v 7
где считается, что Rc » г. Напомним, что поле основной моды существенно
только в области вблизи оси световода.
Локальную постоянную распространения можно рассматривать как моди-
фицированную постоянную распространения, учитывающую изгиб. Другими
Рис. 36.4. Волоконный световод с профилем
показателя преломления п (г), изогнутый в
виде дуги с постоянным радиусом RQ. По-
лярные координаты (г, <р) даны в попереч-
ном сечении световода в положении точки
О, где ось СО параллельна плоскости изгиба
604
словами, можно приближенно определить поле изогнутого световода, решая
скалярное волновое уравнение для прямого световода, но с заменой парамет-
ра /3 на /3. В цилиндрических полярных координатах (г, <р, z) эта подстановка
из (36.50) в (14.4) после преобразования приводит к уравнению
(-TV + ТТТ + Со =о, (36.51)
dr2 г дг г2 д<р2 е J
где имеем (3 & knCQ в приближении слабонаправляющего волоконного свето-
вода. Эффективный профиль показателя преломления nQ связан с профилем
п(г) прямого световода соотношением [14]
«е ~п2 (r) + 2псо (r/^c)C0S
(36.52)
при Rc » г. Таким образом, для учета изгибав эффективный профиль вклю-
чается линейная добавка. Сдвиг поля из-за изгиба находим, сравнивая реше-
ние Go уравнения (36.51) с соответствующим решением/^ для прямого све-
товода.
36.15. Пример. Гауссово приближение
Уравнение (36.51) можно решить для произвольного профиля п (г), если использовать
для поля основной моды гауссову аппроксимацию из гл. 15. Решение скалярного волно-
вого уравнения для прямолинейного световода выражается через размер пятна г0, зави-
сящий от конкретного профиля [см. (15.2) ]. Чтобы решить уравнение (36.51), положим
Go = {1 +А (r/Rc) cos^ Fo; Fo = exp (-r2 /2r2), (36.53)
где A - постоянная, и опустим члены порядка (r/Rc)2 • Поскольку Fo аппроксимирует
решение уравнения (14.4) при I = 0, то получаем, сравнивая члены порядка r/RQ в урав-
нении (36.51), что Л=(Лт0исо)2. Это выражение можно переписать, используя параметры
световода, определенные в табл. I, в видеЛ = rj V2/2Др2. Следовательно, электрическое
поле изогнутого световода ориентировано в радиальном направлении и приближенно
равно
ехр (- ) ехР О0ЛС0) ’ (36.54)
где R - единичный радиальный вектор в плоскости изгиба.
Сдвиг максимального значения поля. Максимальное значение электрического поля
сдвигается во внешнюю сторону изгиба относительно своего положения на оси в пря-
мом световоде. Вычислим этот сдвиг в плоскости изгиба <р = 0. Второй член в фигурных
скобках выражения (36.54) мал по сравнению с единицей, и, следовательно, оба члена
хорошо аппроксимируются выражением ехр {(г* К2/2Др2) (r/RJ cos <р J. Подставляя его
в (36.47), получаем с точностью для величин порядка r/RQ в экспоненте
Е = R ехр|- j^-(r - ZL zj. ехр , (36,55)
где V - волноводный параметр, определенный в табл. I. Если через обозначить сдвиг
максимального значения поля, то
Е = К ] 1 +-------— cos ip
I 2Др2 F
605
= r°
fd 2Д R^p2
(36.56)
Этот сдвиг является основным эффектом влияния изгиба на поле. В направлении, пер-
пендикулярном плоскости изгиба (<р = тт/2), сдвига нет, так что все искажение поля
сводится к сдвигу в сторону от центра изгиба.
ГЛАВА 37. МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ
В этой заключительной главе для удобства ссылок сведены вместе математические фор-
мулы, которые используются на протяжении всей книги. Этот список мы отнюдь не счи-
таем исчерпывающим, но он позволяет избежать необходимости обращаться к другим,
особенно к менее знакомым, источникам. Все приведенные ниже результаты содержат-
ся в книгах [1 - 4], либо могут быть выведены с их помощью.
37.1. Тригонометрические, гиперболические и связанные с ними функции
Тригонометрические соотношения
sin 6 = {е10 - e-i0}/2i; cos е = {ei0 + e~i0} /2; (37.1)
sin2 6 + cos2 0=1; 1 + tg2 0 = 1/cos2 0; (37.2)
1 + ctg2 0 = 1/sin2 0; tg 0 = 1/ctg 0 = sin 0/cos 0; (37.3)
cos 20 = 2 cos2 0 — 1 = 1 - 2 sin2 0; sin 20 = 2 sin 0 cos 0; (37.4)
sin(0t ± 02) = sin 0t cos 02 ± sin 02 cos ; (37.5)
cos(0^ ± 02) = cos 0j cos 02 + sin 0j sin 02; (37.6)
arcsin 0 = тт/2 - arccos 0; tg (arcsin 0) = 0/(1 - 02) V2. (37.7)
Правило синусов
Если длины сторон треугольника равны а, b и с, а углы, расположенные против этих сто-
рон, обозначены А, В и С, то
я/sin А = b/sin В = e/sin С. (37.8)
Разложения для малых значений аргумента
sin 0 « 0 - 03 /6 + . . . ; cos '0 » 1 - 02/2 + . . . ; (37.9)
tg 0 « 0 + 0 3/3 + . . . ; ctg 0 « 1/0 - 0/3. (37.10)
Гиперболические функции
sh z = (ez—е—z)/2; ch z = (cz + e~z) /2; (37.11)
ch2z-sh2z=l; 1 - th2z = 1/ch2z; (37.12)
cth2 z - 1 = l/sh2 z; .th z = 1/cth z = sh z/ch z; (37.13)
ch 2z = 2ch2z — 1 — 1 + 2sh2z; shz=2shzchz; (37.14)
sh^ ± z2) = sh zx ch z2 ± sh z2 ch zx; (37.15)
ch(zt ± z2) = chzt ch z2 ± sh zv sh z2; (37.16)
arshz= In |z + (z2 + 1) 1/2 j ; arch z = In4 z + (z2 - 1) 1/2(37.17)
606
Разложения вблизи z = 1
arch z « (z2 - 1) и - (z2 - l)12/6 + ... ; z >1; (37.18)
arch(l/z) « (I - z2) v2 + (I - z2) V2/3 + . . . ; z£l. (37.19)
Логарифмическая функция
lim (In z) /za = o, a > 0; lim alz l/a - 1| = 0. (37.20)
Разложение в ряды
ln(l +z) -z2/2 +z3/3 - . . . ; ln(l -z) ~-z -z2/2 -z3/3 - . . . . (37.21)
37.2. Векторы, векторные операторы и интегральные теоремы
Векторные операции
Лх А • А = А2; Лу Л2 А • А* = |А|=; (37.22)
А • (В X С) = *х By Bz ; а • (В X С) = В • (С X А) = С .(А X В), (37.23)
Су cz — -А • (С X В).
А X (В X С) = -А X (С X В) = (А • С) В - (А • В) С. (37.24)
Векторные операторы
Индекс t отмечает поперечный оператор, как определено в табл. 30.1
V Ф2) = % Уф2 + Ф2 ;
V • (ФА) = ФУ • А + А • Уф;
V X (ФА) = ФУ X А + УФ X А;
V • (А X В) = В • (V X А) - А • (У X В);
У2Ф = У • (УФ);
V2 А = У (У - А) - V X (УХА);
У^Ф^) =Ф1У(Ф2 +Ф2У1Ф1; (37.25)
У^ФАр - ФУ* • At + At • УГФ; (37.26)
Vt X (ФА^ = ФУ1 X At +У{ФХ At; (37.27)
Vt • (А X В) = В • (Vf X А) - А • (Vt X В); (37.28)
У2Ф- Vt • (^Ф); (37.29)
V2A = Vt(Vt • А) - Vt X (Vt X А). (37.30)
Следующие соотношения выполняются только в том случае, если А имеет декартовы
составляющие
У2А=У2А, У2А=У2А, А= (Лх,Лу,Л2). (37.31)
Декартовы составляющие
Скалярная функция Ф и векторная функция А зависят от декартовкоординат (х, у, z).
Если х, у и z - единичные векторы, параллельные осям х, у и z соответственно, а А име-
ет декартовы составляющие Ах, Ау и /4Z, то
А= (ЛХ,Л У’Л z) =Лхх+Луу+Л (37.32)
УФ - дФ . , дФ А , дф. х + у + z; (37.33)
дх ду dz
дА„ дАу дД7 <)Л7
А= ^ + - + —= V . At ч Z , (37.34)
дх ду dz 1 1 dz
607
X У Z
V X А = д дх д ду д dz дА ’ VtXAt=(^- ду (37.35)
^х ЛУ ^z
П2 т д2Ф д2Ф д2Ф 2 д2Ф
V2 Ф =--- +----- + ---= у2ф + ----;
дх ду2 dz2 * dz2
V2A= V2 А = (VMx)x+ (VMy)y + (VMz)z;
d2 A
V+2A=V2A; V2A=V!A+——— .
1 1 1 dz2
(37.36)
(37.37)
(37.38)
Цилиндрические полярные координаты
Скалярная функция Ф и векторная функция А зависят от цилиндрических полярных ко-
ординат (г, ^р, z). Если г, <р и z - единичные векторы, параллельные радиальному, ази-
мутальному и продольному направлениям соответственно, а А имеет цилиндрические
полярные составляющие Аг , А^ и Л7, то
А — (A j-, А A g) A j.f + Афкр + Azz,
(37.39)
V • A =
Т7т дФ., 1 дФЛ . дФЛ _ т дф.
УФ = — г + — —ф + —z = Vt Ф - ----------z;
dr r dip dz * dz
дА.„ дА7 дА7
___i*L +___£ — v • А + ______—•
dip dz t t dz ’
F fw+F
f
z
(37.40)
(37.41)
VX A= —
d
dr
d
dip
d
dz
1 f d dAr )
Z;
(37.42)
A
72Ф =
d21
~dr
1 4-Х + д2Ф ^72ф+ХХ-
Г дг г2 dip2 dz2 t dt2
(37.43)
V2A —
2 dAy
r2 dip
, 7 dAr
v 2лср+4-—1
r2 dip
z; (37.44)
Vt2A = V2A
d2A
dz2
(37.45)
Соотношения между декартовыми и цилиндрическими полярными
координатами
Ориентация систем координат показана на рис. 14.1. С учетом определенных выше обо-
значений имеем
х — г cos у — г sin ip; г = (х2 +у2)1/2; <р = arctg (у/х);
дФ б)Ф sin дФ дФ дФ , cos ср дФ
- = cos <р -------------------- = sin <р —- +-------------------------;
дх dr г dip ду dr г dip
(37.46)
(37.47)
608
~dr~ = cos^ + sin^±L; 1 ±t = -sin^ +cos^; dx * dy r dtp dx dy (37.48)
AT = Ax cos <p + Ay sin <p; Ay = -Лх sin <p + Ay cos <p; (37.49)
Ax = AT cos <p - Ay sin <p; Ay = AT sin <p +Ay cos (37.50)
Соотношения между единичными векторами
r = x cos <p + у sin ip; £ = - x sin <p + у cos <p; (37.51)
x = r cos ip — ip sin ip; у = f sin <p + £ cos <p; (37.52)
fx£ = z; z X f = (37.53)
=o, = |*=o, d± = -i. dr d<p dr dtp (37.54)
Интегральные теоремы
Следующие теоремы применяются к плоской поверхности S с периметром I, единичный
вектор внешней нормали к которой равен n, a z - единичный вектор, ортогональный к
поверхности S и параллельный положительному направлению оси z. Исключение состав-
ляет второе из соотношений (37.55), которое применяется к объему У, ограниченно-
му поверхностью S, единичный вектор внешней нормали к которой есть п.
fVt ‘ $А • nJZ; JV • Adr = $А • hdS\ (37.55)
S I S
/ V • MS = £fA • zdS + f A • hdl ; (37.56)
J {At • V*Bt - Bt • V’At}<75 = f (At (Vt • Bt) - Bf (Vt • At)} • hdl, (37.57)
J {W’tx - х^ф}dS = f {'I'VjX - xVt*} • hdl. (37.58)
S I
37.3. Функции Бесселя
Дифференциальные уравнения
Функции Бесселя первого и второго рода Jp(z) и (z), а также функции Ганкеля пер-
вого и второго рода Н^(г) и (z) удовлетворяют одному и тому же дифференци-
альному уравнению. Если F» (z) обозначает одну из этих функций, то
J2F, dF
z2-----+z —v- + (z2 - p2)F = 0. (37.59)
dz2 dz v
Если Gv (z) обозначает модифицированную функцию Бесселя первого или второго рода
Iv (z) или Kv (z), то
d2G dG
z2-----v- +z—v- - (z2 +p2)G = 0. (37.60)
dz2 dz v
Интегральные представления и разложения в ряд
В дальнейшем v берется вещественной и неотрицательной, a.m - неотрицательной целой
величиной.
J (z) = — J cos(z sin 0 - »0}d0 - f exp(-z sh Г - vt)dt‘, (37.61)
nn Я 0 77 0
20 Зак 37
609
т / \ _ J- f iH 1
'm- ' “ « m J exp(iz cos 0) cos (m0)d0 = — f exp (-iz cos 0) cos (m0)de; (37.62)
2я1 о 2я о.
4(Z) = (f)P s -^z2/4)J ; (37.63)
2 /=о /!П/ + ^ + 1)
1 2,r
7m(z) — у COS ^0^exP (z cos ’ (37.64)
0
1 2Я
Iq = 2тГ J* exp cos(<9 “ ix^ 1 d0 ’ (37.65)
0
Kv (z) = J exp(-z ch r)ch (vt)dt, (37.66)
0
z
Kw(z) ~ j* exP(“z ch t)cos{vt)dt, (37.67)
0
гдеK‘ - модифицированная функция Бесселя второго рода мнимого порядка.
Соотношения между функциями Бесселя, Ганкеля и модифицированными
функциями Бесселя
Я<°(2) = Jp(z) +irp(z); Я<2>(г) = 4(z) -irp(z); (37.68)
•/m(iz)= im/m(z); J0(iz) = Z0(z); J1(iz)= iZ,(z), (37.69)
-2_m(z) = (-DmJm(z); (37.70)
/Cm(-iz) = (я/2) im + 'f$ (z); K_m(z) =K-m(z). (37.71)
Рекуррентные соотношения
Приведенным ниже рекуррентным соотношениям для также удовлетворяют функ-
ции Г.„, Я(1) и Я<2>.
m m m
Z f ) ^m(Z) 1 ( >
| Ли - 1 (z) + dm + i (z) j ’ у ~ у Y?n — i (z) ~ Ли + 1 J ’ (37.72a)
j (z} _ ™ j dJrvSz>> . j (7. _ m j J7m(z) .
Jm+rz> ~~Y~ m<z)----------, 4?-i(z) - T m(Z) --------------------’ (37.726)
z ( 1 ^^(z) i f
^*m(z^ ~ + 1 (z^ ~ - i (z) j ’ ~fz ~ ~ - 1^ + + l(z^ j ’
(37.73a)
+ A-m_1(z) = -—X-m(z)-------------(37.736)
An(z) = A~m \jm ~ ~ Ifn + ’ Jz = - f(z^ +/и? + i(z) j » (37.74a)
Im + ; Im _ 1(Z) = Zm(z) + ylT; (37.746).
6J0
вронскианы
k/2)’ ym<2)} = - rm(2)-“- = tz = (37’76a)
= Yxn(z^m + 1 ~ dm^Ym + Л2) = (37.766)
~ dm(z^Ym — l(z> ~~ Ym^z^m — i^z) (37.76b)
И'рт^’ (*)} = =^= (37 77a)
= (zVm + i(^) - Jm(zyH<V+1(Z) = (37.776)
= У^Нт- 1<У - >‘У - 1 <2>; (37.77b)
r 1 ^m(z) ^m(Z) 1
^K(2Um(2>}=^m(z>->--7m(2)^!-------= F (37.78)
k/Co^Wz)} = K^zyi^z) + /„(2)^(2) = ! (37.79)
Ряды функций Бесселя и модифицированных функций Бесселя
exp(iz cos 6) = J0(z) + 2 S iniJm(z)cos(w0); (37.80а)
т = 1
cos(z cos 0) ~J0(z) + 2 (-l)mJ2w(z)cos(2w0); (37.806)
m = 1
sin(zcos0) = 2 S (-l)mJ2OT +1(2)cos(2ot + 1)0 . (37.80b)
m — о
Для биполярных координат, приведенных на рис. 18.4, имеется дополнительная формула
fcos(w<p.) SS « fcos(p<p,);
, \ =± L (“DVKm + MI (агг) (37.81)
m Lsin^J р = _оо т+р р |_sin(pv?2).
Предельные выражения для малых значений аргумента (z -► 0)
<37-82>
11 l;l" * 0); 1(f^ '’-(j-)”1 (37.83)
r„(z) =* (2/n) In 2; Hp (2) «(2iAr) In z; (37.84)
w^(|)m; Л(г)яг<+тГ (37'85)
(m - 1)! 0 m
«m(2)“ ---S-----(7} ('”*0); /C0(z) ~-In z + (in 2 - 7), (37.86)
где 7 » 0,577 - постоянная Эйлера.
20* 611
Асимптотические разложения при больших значениях аргумента (z ->0)
7p(Z)" <^-)V2cos{z-"f ^1)(z)«(~),/2exp{i(z-^ - J)|; (37.87)
<37-8s>
Асимптотические разложения Дебая
Если аргумент больше, чем порядок, и выполняется условие z - v >> vy3, то
C0SX /7(1\z> ~ r2V2 —• f37 8oa1
J"(Z) (n> (z2 - i/2)1'4 ’ Hv (Z)~(7) (Z2_^)W> (37'89a)
<7/,,(z) 7 /72 .,2x1/4 (z) 0 (72 ,,2-j 1/4
—£— « - (-) ----— Sin x; --v « i (-) 1,2 ( ~ j —exp (ix); (37.896)
dz tt z dz к z
X = (z2 - г2)1/2 - v cos -1 (y/z) - — . (37.89b)
4
Если аргумент меньше, чем порядок, и выполняются условия v >> 1. v - z >> р1/3, то
X = nch(n/z) - (Н -z2)1'2^-1—(и2 -z2)3'2«|(^_- I) 3'2, (37.906)
3z 3 z
где приближенно^ выражение для х справедливо, если z близко к v.
37.4. Интегралы от функций Бесселя
Неопределенные интегралы
$zJ0(az)dz = Lj, (az); ^-1^-dz = - ±-{j2(az) + /?(az)} , (37.91)
JzJ^zWz = ^-{j'm(az) -Jm_ 1(azym+l(az)} ; (37.92a)
f zJ2(az)rfz = l2-pj(flz) + J] (az) | ; (37.926)
JzX^(az)dz = ^^m(az) - Km _ l(az)Kfn+ /az)} ; (37.93a)
p/C2(az)dz = («) - K2, (az) | ; (37.936)
Jz7m(«Vm(Z>z)dz = - Z_b-^ { bJm(az)Jm _ '(bzy-aJ^bz)^ _ ^az)} ; (37.94)
f zKm(az)Km(bz.)dz = - z_ b2 jbKm(az)Km + ^bz) - aKm(bz)Km + j(az) j. ; (37-95)
z2
f zV0 (az)Ji (az)dz = (az); (37.96)
f z2^(az)^(az)dz = - — K\ (az); (37.97)
2a
612
jzJm(az)Km(bz)dz - — ? { aKm(bz)Jm _ ^az) - bJm(az)Km + j^z)} ; (37-98)
fzJ^azyi^bzydz = ~-~ bj j bJ0(az)Ii (bz) + aJt (az)IQ(bz)j .
(37.99)
Определенные интегралы
Г r 7 •> <> 7 1 - exp(-b2 /4а2) (37.100а)
0 b
°c ^m+\r zl ч / 2 2x_r Z>mexp(-Z>2 /4а2) J z V (*z)exp(-a3z2)dz = 52—2 0 (la2)™ 1 Г r ZL ч z 2 exp(Z)2/4а2) J zIQ(bz)Qxp(-a2z2)dz = — 0 2<Z2 (37.1006) (37.101а)
°° 1 (37.1016)
J 70(^)cxp( a±)a± - _b^y2 ,
f zK (bz) exp (—az)dz — - . (37.102а)
j oV. /caj. v _ ^2)3/2 , 00 h
(37.1026)
J z/t (bz) exp (-az)dz - 3/2 ;
где я > b > 0 в формулах (37.1016) и (37.102).
37.5. Прочие функции и интегралы
Специальные функции
Полные эллиптические интегралы первого и второго рода соответственно имеют вид
. я/2 de я/2 (37.103)
/ (l-psin’0)- ’ Ev~ I (1^Sin e) ze'
a 7 и /3-функции соответственно определяются следующим образом:
00 7 1 t ^7 1 W 1 Г (z) = J t е dt, B(z, w) = J t (1-0 dt. 0 0 (37.104)
Приведем некоторые специальные соотношения и их частные значения:
00 — t Г {m + 1) = т\ = J Гте dt\ B(z, w) = г (z) г (w)/r (z + w). 0 r(z+ 1) =zr(z); Г(-) «3,625; Г (A) «2,679; 4 3 (37.105) (37.106а)
Г (у) = я1/2 « 1,772; Г (|) « 1,354; Г (у) 1,225, (37.1066)
где т = 0, 1, • • . . Полиномы Эрмита низших порядков имеют вид
Но = 1; H.=2Z‘, H2=4z2-2; Н3 = Sz3 - 12z. (37.107)
613
Некоторые эквивалентные определения 6-функции Дирака имеют вид
1 +оо
6(z —z0)— J ехр(± i(z - z0)r)(7r; (37.108а)
2тг „оо
6(z-z0)=-~- S cos m(z - z0) = exp| im(z - z0) I. (37-1086)
2я m — _oo 2я rn = —o° '
Если г и r0 - радиусы-векторы точек пространства, то в декартовых и цилиндрических
полярных координатах имеем соответственно
6 (г — г0) = 6(х - х0)«(у - y0)6(z - z0); 6 (г — г0) =2^—— 6 (р - ip0)6(z - z0).
ro
(37.109)
Неопределенные и определенные интегралы
я J cos(m0)sin(z cos 0)d0 = 0, (m ~ четное); 0 я Jcos(w0)cos(z cos O)d0 = 0, (m — нечетное); 0 2я + *> - 2 / ~х J sin(ди0)exp(± iz cos 0)c?0 = 0; J sl-n- ~ dz = an (a > 0); 0 "OO Z "p d = n . (37.110a) (37.1106) (37.111) (37.112a)
-я/2 1sin20 (a2 + 1)1/2 ’
г = 1 . Г, a . v2. o I . (37.1126)
a + b cos’ в (a + £>)} 'n dL^l^a + b^ f de sin e , 1 |n L..f + e Д .
(37.113a)
cos2 0 2 cos2 0 2 t 4 2 J
J z arcsin(y)6?z - arcsin(i) + (z2 - 1) "1/2; (37.1136)
J- {a2 sin2 (Z?z) +ab sin(2Z?z) + 2b2} cxp(-flz) (37.114a)
sin (ftz)exp( flZ)dx. a(a2 +4ft2)
] {a2 cos2 (Z?z) - ab s\n(2bz) + 2bA cxp(-tfz) (37.1146)
cos2(*z)exp(-az)dz- - fl(^+4Z>2) f dz 1 In [ g + eZ ~ (g2 ~ 1)1,2 I (a> 1);
(37.115)
я + ch z (a2 - 1)1/2 u [ a + ez + (a2 - 1)1/2 J
oo 1 +z2 ’ I fl2 + z2 a a — OO Q (37.116)
О A N A 1 N 1 <3 + n | a c 1! £ '—> (37-117)
f К _ Л1'2 dz . a in a + I - - b^ = Z,b2 ) lb b i (37.118a)
= a ch- (аБ) - - Й1) m ~ -1- (a- - (37.1186)
где а > b > 0, а приближенное выражение справедливо при Ъ <а.
614
J-?-----dz = (?2-а2)'л- jh)'•%= (Z2 - o2)1/2--a cos“‘(-|); (37.119)
{1 - (a/z)2j 1/2 I z2 j z
f____________dz______= j_ , f 2z2 - a1 |
-o {z2 -a2 - (b/z)2 j.1'2 2 ( (4Z,2 +a4)1/2 J ’ 1 '
где z0 - наименьший корень знаменателя подынтегрального выражения
z zdz - - Icos- -[ (g2 ~z2) ~ (z' -&2) I
J (a2 - z2)1/2 (z2 - b2)1 1/2 2| a2 -b2 } ’
где a>b >0na>z > b.
z3dz S {a2 -z2)1/2(z2 - _b.)m ~4^2+b^ (*>*>0); (37.122)
J- }^7= J z 1 [(z2-a2)t/2(z2 - b2)V2- (a2 +b2)X+abY]; (37.123a)
x=in {-<? 2 -fl2)1/2 + (z2 -b2)172 1 (a2 -b2)v2 ) ’ (37.1236)
f {a - b)2 + Г (z2 -a2) 1/2 + (z'2 - b2)172!2 )
Y = In <- — jb-— J— > , z > a, z > b; (37.123b)
| (a + b)2 + [(z2 — a2)1/2+ (z2 -Z>2)V2]2 j
z j z exp (~a2z7 0 ">dz = ~7~ fl - exp(<z2z2)l ; 2a2 I J (37.124a)
Jz3 exp(-fl2z2)t/z = 0 = _^г{1 - (1 +o2z2)exp(-<z2z2)| ; (37.1246)
Г F 7m / /щ = J Z eXP (~C ?z2>dz-, Li r{(w+1)/2l; (37.125a)
0 2fl
r y/n 1 x/^7 1
° ~ ~ia ’ Ц 2fl2 ’ 2 4fl3 ’ 3 2fl4 ’ (37.1256)
4 oo
J z exp{-a2z2)dz = - г {(m + 1)/2|, m = 0, 2, 4, (37.126a)
arrc 1 f
+f°° m / J z exp(- -a2z2)dz =0, rn = 1, 3, . . . ; (37.1266)
+ oo о , f л )i/2 f {b +q)2 )
J exp (-az2 - Z?z) exp (- pz2 - qzjdz _< У exp У r , I fl + p J l4(fl+p)J (37.127)
где a > 0, p > 0. Если ^z) - обобщенные полиномы Лагерра, то
V dz = ! , 1 > 0, m > 1. J (m - 1) ! (37.128)
Якобиан преобразования
Якобиан двумерного преобразования (и, v) -> (р, q) имеет вид
у_ д(и,и) _ ди dv ди dv
д (р, q) др dq dq др ’
615
Метод Лапласа
Если х - большая положительная величина, а функция h(z) достигает своего максималь-
ного значения на нижнем пределе интегрирования z = а в интервале
b
G(x)= Jg(z)exp{x/z(z)| Jz, (37.130)
а
то значение G (х) хорошо аппроксимируется выражением [3]
G(x) =5(<г)ехр|хЛ(а)И —---------Г* , (37.131)
k } I 2xh (a) J
где h” (а) - обозначение производнойd2h(z)!dz2 при z = а.
Теорема Эйлера
Если декартовы оси координат ориентированы в точке Р на поверхности произвольной
кривизны так, что ось х нормальна к поверхности, а плоскости х ~ у и х - z содержат
главные радиусы кривизны ру и pz соответственно, то в произвольной плоскости, со-
держащей ось х и образующей угол £2 с осью z, радиус кривизны р дается выражением
[4]
1 cos2 П Sin2 П - Py^z
— —---------+--------, ИЛИ р = -----------------.
- р, р о cos2 П + р sin2 £2
Р z у у Z
(37.132)
Для ситуации, изображенной на рис. 35.7, а, очевидно, что угол П между плоскостью па-
дения и осью z связан с углами а и 0Z соотношениями cos £2 = cos 0z/sin а и sin П =
= cos 0y/sin а. Следовательно,
Р -
PyPz sin2 а
Ру cos2 ez + Pz cos2 0y
(37.133)
На рис. 35.7, в плоскость падения в точке Р образует угол 0Z с осью z. Таким образом,
П = 0Z и
pypz
О А •
р cos2 0+P sin2 0,_
у z Z *
(37.134)
СПИСОК ЛИТЕРАТУРЫ
К введению ч. I
1. Keck, D. В. (1981) ‘Fiber design for cables.’ Third International Conference on
Integrated Optics and Optical Fiber Communications, San Francisco, April, 1981.
2. Miller, S. E. and Chynoweth, A. G. (eds.) (1979) Optical Fiber Communications,
Academic Press, New York.
* 3. Midwinter, J. E. (1979) Optical Fibers for Transmission, Wiley, New York
К главе 1
* 1. Born, M., and Wolf, E. (1970) Principles oj Optics, Pergamon Press, Oxford.
* 2. Marcuse, D. (1972) Light Transmission Optics, Van Nostrand, New York.
* 3. Jackson, J. D. (1967) Classical Electrodynamics? Wiley, New York.
4. Krueger, D. A. (1980) Spatial varying index of refraction: an open ended under-
graduate topic. Am. J. Phys., 48, 183-8.
5. Ankiewicz, A. and Pask, C. (1977) Geometric optics approach to light acceptance and
propagation in graded index fibres. Opt. Quant. Elect., 9, 87-109.
6. Fletcher, A., Murphy, T. and Young, A. (1954) Solutions of two optical problems.
Proc. Roy. Soc., A223, 216-25.
7. Gloge, D. and Marcatili, E. A. J. (1973) Multimode theory of graded-core fibres. Bell
Syst. Tech. J., 52, 1563-78.
К главе 2
1. Snyder, A. W. (1974) Leaky-ray theory of optical waveguides of circular cross-
section. Appl. Phys., 4, 273-98.
2. Rawson, E. G., Herriott, D. R. and McKenna, J. (1970) Analysis of refractive index
distributions in cylindrical, graded-index glass rods (GRIN) used as irtiage relays.
Appl. Opt., 9, 753-9.
3. Ankiewicz, A. and Pask, C. (1977) Geometric optics approach to light acceptance and
propagation in graded-index fibres. Opt. Quant. Elect., 9, 87-109.
4. Lipson, S, G. and Lipson, H. (1969) Optical Physics, Cambridge University Press, p.
80.
5. Barrell, K. F. and Pask, C. (1979) Geometric optics analysis of non-circular graded-
index fibres. Opt. Quant. Elect., 11, 237-51.
6. Ankiewicz, A. (1979) Ray theory of graded non-circular optical fibres. Opt. Quant.
Elect., 11, 197-203.
К главе 3
1. Gloge, D. and Marcatili, E. A. J. (1973) Multimode theory of graded-core fibres, Bell
Syst. Tech. J., 52, 1563-78.
2. Fletcher, A., Murphy, T. and Young, A. (1954) Solutions of two optical problems.
Proc. Roy. Soc., A223, 216-25.
3. Olshansky, R. and Keck, D. B. (1976) Pulse broadening in graded-index optical
617
fibres. Appl. Opt., 15, 483-91.
4. Ankiewicz, A. and Pask, C. (1977) Geometric optics approach to light acceptance and
propagation in graded index fibres. Opt. Quant. Elect., 9, 87-109.
5. Barrell, K. F. and Pask, C. (1979) Geometric optics analysis of non-circular graded-
index fibres. Opt. Quant. Elect., 11, 237—51.
* 6. Jackson, J. D. (1967) Classical Electrodynamics, Wiley, New York, pp. 208-15.
7. Adams, M. J., Payne, D. N., Sladen, F. M. E. and Hartog, A. H. (1978) Wavelength-
dispersive properties of glasses for optical fibres: the germania enigma. Electron.
Lett., 14, 703-5.
8. Hammond. C. R. (1978) Silica-based binary glass system: wavelength dispersive
properties and composition in optical fibres. Opt. Quant. Elect., 10, 163-70.
9. Marcatili, E. A. J. (1977) Modal dispersion in optical fibres with arbitrary numerical
aperture and profile dispersion. Bell Syst. Tech. J., 56, 49-63.
10. Pask, C. (1978) On the derivations and interpretation of the Marcatili profile
condition for optical fibres. Electron. Lett., 14, 13-15.
11. Olshansky, R. (1978) Optical waveguides with low pulse dispersion over an
extended spectral range. Electron. Lett., 14, 330-1.
К главе 4
* 1. Jackson, J. D. (1967) Classical Electrodynamics, Wiley, New York.
* 2. Born, M. and Wolf, E. (1970) Principles of Optics, Pergamon Press, Oxford.
3. Snyder, A. W. (1974) Leaky-ray theory of optical waveguides of circular cross-
section. Appl. Phys., 4, 273-98.
4. Pask, C. and Snyder, A. W., (1974) Illumination of multimode optical fibres-leaky
ray analysis. Opto-electronics, 6, 297-304.
5. Albertin, F., Di Vita, P. and Vannuci, R. (1974) Geometrical theory of energy
launching and pulse distortion in dielectric optical waveguides. Opto-electronics, 6,
369-89.
6. Ankiewicz, A. and Pask, C. (1977) Geometric optics approach to light acceptance and
propagation in graded index fibres. Opt. Quant. Elect., 9, 87-109.
7. Barrell, K. F. and Pask, C. (1979) Ray launching and observation in graded-index
optical fibres. J. Opt. Soc. Am., 69, 294-300.
8. Barrell, K. F and Pask, C. (1980) Pulse dispersion in optical fibres of arbitrary
refractive-index profile. Appl. Opt., 19, 1298-1305.
К главе 5
1. Personick, S. D. (1971) Time dispersion in dielectric waveguides. Bell Syst. Tech. J.,
50, 843-59.
2. Marcuse, D. (1972) Higher-order processes and the loss penalty of multimode
operations. Bell Syst. Tech. J., 51, 1819-36.
3. Pask, C. (1980) Pulse propagation in optical fibres with index profile slowly varying
along their length. Opt. Quant. Elect., 12, 281-90.
4. Ankiewicz, A., Love, J. D., Pask, C. and Snyder A. W. (1982) Slowly varying optical
fibres. J. Opt. Soc. Am., 72, 198-203.
5. Marcuse, D. (1979) Multimode fiber with z-dependent а-value. Appl. Opt. 18,
618
2229-31.
* 6. Landau, L. D., and Lifshitz, E. M. (1960) Classical Mechanics, Pergamon Press,
Oxford, p. 154.
* 7. Marcuse, D. (1972) Light Transmission Optics, Van Nostrand, New York, p. 98.
8. Arnaud, J. A. (1976) Beam and Fibre Optics, Academic Press, New York.
9. Allan, W. B. (1973) Fibre Optics Theory and Practice, Plenum, New York, p. 21.
10. Winston, R. (1970) Light collection within the framework of geometric optics. J.
Opt. Soc. Am., 60, 245-7.
11. Snyder, A. W., Mitchell, D. J. and Pask C. (1975) Pulse propagation in multimode
optical fibres. Electron. Lett., 11, 275-6.
12. Jackson, J. D. (1962) Classical Electrodynamics, Wiley, New York, p. 489.
13. Gloge, D. (1972) Optical power flow in multimode fibers. Bell Syst. Tech. J., 51,
1767-83.
14. Marcuse, D. (1974) Theory of Dielectric Optical Waveguides, Academic Press, New
York, p. 237.
15. Snyder, A: W. (1976) Pulse distortion in the ultimate multimode optical fibre. Appl.
Opt., 15, 1290-4.
16. Jones, D. S. (1964) The Theory of Electromagnetism, Pergamon Press, Oxford, p.
510.
К главе 6
1. Snyder, A. W. (1974) Leaky-ray theory of optical waveguides of circular cross section.
Appl. Phys., 4, 273-98.
2. Snyder, A. W. and Love, J. D. (1976) Attenuatior. coefficient for rays in graded fibres
with absorbing cladding. Electron. Lett., 12, 255-7.
3. Ankiewicz, A. and Pask, C. (1977) Geometric optics approach to light acceptance and
propagation in graded index fibres. Opt. Quant. Elect., 9, 87-109.
4. Gloge, D. (1975) Propagation effects in optical fibres. I.E.E.E. Trans. Microwave
Theory Tech., 23, 106-20.
* 5. Born, M. and Wolf, E. (1970) Principles of Optics, Pergamon Press, Oxford, p. 40.
6. Barrell, K. F. and Pask C. (1978) The effect of cladding loss is graded-index fibres.
Opt. Quant. Elect., 10, 223-31.
К главе 7
1. Snyder, A. W. (1974) Leaky-ray theory of optical waveguides of circular cross-
section. Appl. Phys., 4, 273-98.
2. Snyder, A. W. and Love, J. D. (1974) Tunnelling leaky rays on optical waveguides.
Opt. Commun., 12, 326-8.
3. Love, J. D., Pask, C. and Winkler, C. (1979) Rays and modes on step-index
multimode elliptical waveguides. Micro waves, Opt. Acoust., 3, 231-8.
4. Snyder, A. W. and Love, J. D. (1975) Reflection at a curved dielectric interface-
electromagnetic tunnelling. I.E.E.E. Trans. Microwave Theory Tech. 23, 134—41.
5. Snyder, A. W. and Love, J. D. (1976) Attenuation coefficient for tunnelling leaky
rays in graded fibers. Electron. Lett., 12, 324-6.
* 6. Born, M. and Wolf, E (1970) Principles of Optics, Pergamon Press, Oxford, p. 40.
7. Snyder, A. W. and Mitchell, D. J. (1974) Generalized Fresnel’s laws for determining
619
radiation loss from optical waveguides and curved dielectric structures. Optik, 40,
438-59.
8. Love, J. D. and Winkler, C. (1978) Refracting leaky rays in graded-index fibers.
Appl. Opt., 17, 2205-8.
9. Love, J. D. and Snyder, A. W. (1975) Fresnel’s and Snell’s laws for the multimode
optical waveguide of circular cross-section. J. Opt. Soc. Am., 65, 1241-7.
10. Pask, C. (1975) On the neglect of refracting rays in optical power calculations. Opt.
Quant. Elect., 7, 428-9.
11. Kapany, N. S. and Burke, J. J. (1972) Optical Waveguides, Academic Press, New
York.
12. Stewart, W. J. (1975) Leaky modes in graded fibers. Electron. Lett., 11, 321-2.
13. Adams, M. J., Payne, D. N. and Sladen, F. M. E. (1975) Leaky rays on optical fibers
of arbitrary (circularly symmetric) index profiles. Electron. Lett., 11, 238-40.
14. Love, J. D. and Winkler, C. (1977) Attenuation and tunnelling coefficients for leaky
rays in multilayered optical waveguide. J. Opt. Soc. Am., 67, 1627-33.
15. Love, J. D.and Winkler, C. (1978) The step index limit of power law refractive index
profiles for optical waveguides. J. Opt. Soc. Am., 68, 1188-91.
16. Love, J. D. and Winkler, C. (1978) A universal tunnelling coefficient for step- and
graded-index multimode fibers. Opt. Quant. Elect., 10. 341-51.
*17. Abramowitz, M. and Stegun, I. A. (1972) Handbook of Mathematical Functions,
Dover, New York, p. 448.
18. Ramskov Hansen, J. J., Ankiewicz, A. and Adams, M. J. (1980) Attenuation of leaky
modes in graded noncircular multimode fibers. Electron Lett., 16, 94-6.
19. Love, J. D. and Winkler, C. (1980) Generalized Fresnel power transmission
coefficients for curved graded-index media. I.E.E.E. Trans, Microwave Theory
Tech., 28, 689-94.
20. Jones, D. S. (1978) Electromagnetic tunnelling. Quart. J. Meeh. Appl. Math., 31,
409-34.
21. Love, J. D. and Winkler, C. (1978) The effects of material absorption on ray power
attenuation in multi-layered optical waveguides. Opt, Quant. Elect., 10, 383-92.
22. Love, J. D. and Snyder, A. W. (1975) Generalized Fresnel’s laws for a curved
absorbing interface. J. Opt. Sdc. Am., 65, 1072-4.
К главе 8
1. Snyder, A. W. (1974) Leaky-ray theory of optical waveguides of circular cross
section. Appl. Phys., 4, 273-98.
2. Snyder, A. W. and Pask, C. (1975) Optical fibre: spatial transient and steady state.
Opt. Commun., 15, 314-16.
3. Snyder, A. W., Mitchell, D. J. and Pask, C. (1974) Failure of geometric optics for
analysis of circular optical fibres. J. Opt. Soc. Am., 64, 608-14.
4. Ankiewicz, A. and Pask, C. (1977) Geometric optics approach to light acceptance
and propagation in graded-index fibres. Opt. Quant. Elect., 9, 87-109.
5. Ankiewicz, A. and Pask, C. (1978) Tunnelling rays in graded-index fibres. Opt.
Quant. Elect., 10, 83-93.
6. Love, J. D. and Pask, C. (1976) Universal curves for power attenuation in ideal
multimode fibres. Electron. Lett., 12, 252-3.
7. Pask, C. (1978) Generalized parameters for tunnelling ray attenuation in optical
620
fibres. J. Opt. Soc. Am., 68, 110-16.
8. Pask, C. (1975) On the neglect of refracting rays in optical power calculations. Opt.
Quant. Elect., 428-9.
9. Pask, C. and Snyder, A. W. (1974) Illumination of multimode optical fibres - leaky
ray analysis. Opt. Quant. Elect., 6, 297-304.
10. Barrell, K. F. and Pask, C. (1978) The effect of cladding loss in graded-index fibres.
Opt. Quant. Elect., 10, 223-31.
11. Barrell, K. F. and Pask, C. (1979) Ray launching and observation in graded-index
optical fibres. J. Opt. Soc. Am., 69, 294-300.
12. Ramskov Hansen, J. J., Ankiewicz, A. and Adams, M. J. (1980) Attenuation of leaky
modes in graded noncircular multimode fibres. Electron. Lett., 16, 94-6.
13. Barrell, K. F. and Pask, C. (1980) Leaky ray correction factors for elliptical
multimode fibres. Electron. Lett., 16, 580-1.
14. Potter, R. J. (1961) Transmission properties of optical fibres. J. Opt. Soc. Am., 51,
1079-89.
* 15. Kapany, N. S. (1967) Fiber Optics, Academic Press, New York.
16. Pask, C. and Snyder, A. W. (1976) Multimode optical fibres: interplay of absorption
and radiation losses. Appl. Opt., 15, 1295-8.
К главе 9
1. Snyder, A. W. and Mitchell, D. J. (1974) Bending losses of multimoded optical fibres.
Electron. Lett., 10, 11-12.
2. Winkler, C., Love, J. D. and Ghatak, A. K. (1979) Loss calculations in bent
multimode optical waveguides. Opt. Quant. Elect. 11, 173-83.
3. Love, J. D. and Winkler, C. (1978) Power attenuation in bent multimode step-index
slab and fibre waveguides. Electron. Lett., 14, 32-4.
4. Winkler, C., Love, J. D. and Ghatak, A. K. (1978) Power attenuation in bent
parabolic-index slab and fiber waveguides. Electron. Lett., 14, 570-1.
5. Snyder, A. W. and Mitchell, D. J. (1974) Generalized Fresnel’s laws for determining
radiation loss from optical waveguides and curved dielectric structures. Optik, 40,
438-59.
6. Snyder, A. W. and Mitchell, D. J. (1974) Whispering-gallery rays within dielectric
circles and spheres. Electron. Lett., 10, 16-17.
К главе 10
* 1. Sommerfeld, A. (1953) Optics, Academic Press, New York, chap. V.
* 2. Goodman, J (1968) Fourier Optics, McGraw-Hill, New York, p. 48 and chap. 4.
3. Johnson, С. C. (1965) Field and Wave Electrodynamics, McGraw-Hill, New York,
p. 331.
4. Bracewell, R. N. (1978) The Fourier Transform and Its Applications, 2nd Edn, New
York, pp. 244-50.
.5 . Lotsch, H. К. V. (1970) ‘Beam displacement at total reflection: the Goos-
Hanchen shift. Optik, 32, 116-37, 189-204; 1971 32, 299-319, 553-69.
6. Renard, R. H. (1964) Total reflection: a new evaluation of the Goos-Hanchen
shift. J. Opt. Soc. Am., 54, 1190-8.
7. Horowitz, B. R. and Tamir, T. (1971) Lateral displacement of light beam at a
621
dielectric interface. J. Opt. Soc. Am., 61, 586 95.
8. Kapany, N. S. and Burke, J. J. (1972) Optical Waveguides, Academic Press, New
York.
9. Kogelmk, H. and Weber, H. P. (1974) Rays, stored energy, and power flow in
dielectric waveguides. J. Opt. Soc. Am., 64, 174-85.
10. Snyder, A. W. and Love, J. D. (1976) Goos-Hanchen shift. Appl. Opt., 15, 236-8.
11. White, I. A. and Pask, C. (1977) Effect of Goos-Hanchen shifts on pulse widths
in optical waveguides. Appl. Opts., 16, 2353-5.
12. Love, J. D. and Snyder, A. W. (1976) Optical fiber eigenvalue equation: plane
wave derivation. Appl. Opts., 15, 2121-5.
13. Tien, P. K. (1971) Light waves in thin films and integrated optics. Appl. Opt.,
10, 2395-413.
К введению ч. II
1. Collin, R. E. (1965) Field Theory of Guided Waves, McGraw-Hill, New York.
2. Johnson, С. C. (1965) Field and Wave Electrodynamics, McGraw-Hill, New York.
3. Felsen, L. B. and Marcuvitz, N. (1973) Radiation and Scattering of Waves, Prentice-
Hall, Englewood Cliffs, N.J.
* 4. Miller, S. E., Marcatili, E. A. J. and Li, T. (1973) Research toward optical fiber
transmission systems. Proc. I.E.E.E. 61, 1703-51.
5. Gambling, W. A.,' Matsumura, H. and Ragdale, С. M. (1978) Loss mechanisms in
practical single-mode fibers. Proceedings ,of the Fourth European Conference on
Optical Communication, Genoa, Italy.
6. Gambling, W. A., Matsumura, H. and Ragdale, С. M. (1979) Mode dispersion,
material dispersion and profile dispersion in graded-index, single-mode fibers.
Microwaves, Opt. Acoust. 3, 239-46.
7. Snyder, A. W. and Menzel, R. (eds.) (1975) Photoreceptor Optics, Springer-Verlag,
Berlin.
8. Snyder, A. W. (1979) in Handbook of Sensory Physiology, Vol. VII/6A (ed. H.
Autram), Springer-Verlag, Berlin, pp. 279-81.
9. Hondros, A. and Debye, P. (1910) Electromagnetic waves in dielectric waveguides.
Ann. Phys., 32, 465-76.
К главе 11
1. Adler, R. B. (1952) Waves on inhomogeneous cylindrical structures. Proc. I.R.E.,
40, 339-48.
* 2. Landau, L. D. and Lifshitz, E. M. (1960) Electrodynamics of Continuous Media.
Pergamon Press, Oxford.
3. Snyder, A. W. and Pask, C. (1973) Incoherent illumination of an optical fiber. J.
Opt. Soc. Am., 63,. 806-12.
4. Miller, S. E. and Chynoweth, A. G. (eds.) (1979) Optical Fiber Communications,
Academic Press, New York.
5. Dyott, R. B. and Stern, J. R. (1971) Group delay in fiber waveguides. Electron Lett.,
7, 82-4.
6. Gambling, W. A., Matsumura, H. and Ragdale, С. M. (1979) Mode dispersion,
material dispersion and profile dispersion in graded-index, single-mode fibers.
622
Microwaves, Opt. Acoust., 3, 239—46.
7. Johnson, С. C. (1965) Fields and Wave Electrodynamics, McGraw-Hill, New York.
8. Snitzer, E. (1961) Cylindrical dielectric waveguide modes. J. Opt. Soc. Am., 51,
491-8.
* 9. Born, M. and Wolf, E. (1970) Principles of Optics, Pergamon Press, London, chap.
XIV.
10. Stokes, A. R. (1963) The Theory of Optical Properties of Inhomogeneous Materials,
E. & F. N. Spon, London, chap. 4.
К главе 12
1. Snyder, A. W. and de la Rue, R. (1970) Asymptotic solution of eigenvalue equations
for surface waveguide structures. /.fe.E.E. Trans. Microwave Theory Tech., 18,
650-1.
2. Marcuse, D. (1974) Theory q} Dielectric Optical Vaveguides, Academic Press, New
York, chap. 1.
3. Snyder, A. W. (1971) Approximate eigenvalues for a circular rod of arbitrary
dielectric constant. Electron. Lett., 7, 105-6.
* 4. Marcuse, D. (1972) Light Transmission Optics, Van Nostrand, New York, p. 331.
5. Snyder, A. W. (1969) Asymptotic expressions for eigenfunctions and eigenvalues of
a dielectric or optical waveguide. I.E.E.E. Trans. Microwave Theory Tech., 17,
1130-8.
6. Kawakami, S. and Nishida, S. (1974) Characteristics of a doubly clad optical fiber
with a low-index inner cladding. I.E.E.E. Trans. J. Quantum Electron., 10, 879-87.
7. Yeh, C. (1962) Elliptical dielectric waveguides. J. Appl. Phys., 33, 3235-42.
8. Kogelnik, H. (1975) in Integrated Optics (ed. T. Tamir), Springer-Verlag, Berlin,
pp. 53-61.
* 9. Landau, L. and Lifshitz, E. (1958) Quantum Mechanics, Pergamon Press, Oxford,
p. 70.
10. Gordon, J. (1966) Optics of general guiding media. Bell Syst. Tech. J., 46, 321-32.
11. Ankiewicz, A. (1978) Comparison of wave and ray techniques for solution of
graded index optical waveguide problems. Opt. Acta, 25, 361-73.
12 Love, J. D. and Ghatak, A. K. (1979) Exact solutions for TM modes in graded index
slab waveguides. I.E.E.E. Trans. J. Quantum Electron., 15, 14—16.
* 13. Abramowitz, M. and Stegun, I. A. (1965) Handbook of Mathematical Functions.
Dover, New York.
14. Burman, R. (1968) Some electromagnetic wave functions for propagation along
cylindrically stratified columns. I.E.E.E. Trans. Microwaves Theory Tech., 16,127-9.
15. Love, J. D. (1984) Exact, analytical solutions for modes on a graded-profile fiber.
Opt. Quant. Elect, (submitted).
16. Yamamoto, S., Koyamada, Y. and Makimoto, T. (1972) Normal-mode analysis of
an anisotropic and gyrotropic thin-film waveguide for integrated optics. J. Appl.
Phys., 43, 5090-7.
17. Ramaswamy, V. (1974) Ray model of energy and power flow in anisotropic film
waveguides. J. Opt. Soc. Am., 64, 1313-20.
18. Kapany, N. S. and Burke, J. J. (1972} Optical Waveguides, Academic Press, New
York, p. 141.
623
К главе 13
1. Snyder, A. W. and Young, W. R. (1978) Modes of optical waveguides. J. Opt. Soc.
Am., 68, 297-309.
2. Snyder, A. W. (1969) Asymptotic expressions for eigenfunctions and eigenvalues of
dielectric or optical waveguides. I.E.E.E. Trans. Microwave Theory Tech. 17,
1130-8.
3. Gloge, D. (1971) Weakly guiding fibers. Appl. Opt., 10, 2252-8.
4. Arnaud, J. A. (1976) Beam and Fiber Optics, Academic Press, New York.
5. Kaminow, I. P. (1981) Polarization in optical fibers. I.E.E.E. Trans. J. Quantum
Electron., 17, 15-22.
6. Snyder, A. W. (1974) Light absorption in visual photoreceptors. J. Opt. Soc. Am.,
64, 216-30.
7. Snyder, A. W. (1979), in Hana^ook o] Sensory Physiology, Vol. VII/6A (ed. H.
Autrum), Springer-Verlag, Berlin, pp. 279-81.
8. A. W. Snyder and F. Riihl (1983) Novel polarization phenomena on anisotropic
multimoded fibres. Electron. Lett., 19, 401-2.
9. A. W. Snyder and F. Riihl (1983) New single-mode single-polarization optical fiber.
Electron. Lett., 19, 185-6.
10. A. W. Snyder and F. Riihl (1983) Single-mode, single-polarization fibers made of
birefringement material. J. Opt. Soc. Am., 73, 1165-74.
11. M. P. Varnham, D. N. Payne, R. D. Birch and E. J. Tarbox (1983) Single
polarisation operation of highly birefringent bow-tie optical fibers. Electron. Lett.,
19, 246-7.
К главе 14
1. Snyder, A. W. and Young, W. R. (1978) Modes of optical waveguides. J. Opt. Soc.
Am., 68, 297-309.
2. Snyder, A. W. (1969) Asymptotic expressions for eigenfunctions and eigenvalues of
a dielectric or optical waveguide. I.E.E.E. Trans. Microwave Theory Tech. 17,
1130-8.
3. Kurtz, C. N. and Streiffer, W. (1969) Guided waves in inhomogeneous focussing
media, Part I: Formulation, solution for quadratic inhomogeneity. I.E.E.E. Trans.
Microwave Theory Tech., 17, 11-15.
4. Pask, C. (1979) Exact expressions for scalar modal eigenvalues and group delays in
power-law optical fibres. J. Opt. Soc. Am., 69, 1599-1603.
5. Rudolph, H. D. and Neumann, E. G. (1976) Approximations for the eigenvalues of
the fundamental mode of a step index glass fiber waveguide. Nachrichtentech. Z.,
29, 328-9.
6. Sammut, R. A. (1979) Analysis of approximations for the mode dispersion in
monomode fibres. Electron. Lett., 15, 590-1.
* 7. Marcuse, D. (1972) Theory of Dielectric Optical Waveguides, Academic Press, New
York.
8. Snyder, A. W. and de la Rue, R. (1970) Asymptotic solution of eigenvalue equations
for surface waveguide structures. I.E.E.E. Trans. Microwave Theory Tech., 9,650-1.
9. Love, J. D. (1984) Exact, analytical solutions for modes on a graded-profile fibre.
Opt. Quant. Elect, (submitted).
10. Yamada, R. and Inabe, K. (1974) Guided waves in an optical square-law medium. J.
624
Opt. Soc. Am., 64, 964-8.
11. Gambling, W. A., Payne, D. N. and Matsumura, H. (1977) Cut-off frequency in
radially inhomogeneous single-mode fibre. Electron. Lett., 13, 139-40.
12. Love, J. D. (1979) Power series solutions of the scalar wave equation for cladded,
power-law profiles of arbitrary exponent. Opt. Quant. Elect., 11, 464-6.
13. Love, J. D., Hussey, C. D., Snyder, A. W. and Sammut, R. A, (1982) Polarization
corrections to mode propagation on weakly guiding fibres. J. Opt. Soc. Am., 72,
1583-91.
14. Snyder, A. W. and Sammut, R. A. (1978) Dispersion in graded, single-mode fibres.
Electron. Lett., 15, 269-71.
* 15. Snyder, A. W. (1981) Understanding monomode optical fibres. Proc. I.E.E.E., 69,
6-13.
К главе 15
1. Gambling, W. A. and Matsumura, H. (1977) Simple characterization factor for
practical single-mode fibres. Electron. Lett., 13, 691-3.
2. Snyder, A. W. (1977) Acuity of compound eyes: physical limitation and design. J.
Comp. Physiol., 116, 161-82.
3. Marcuse, D. (1978) Gaussian approximation of the fundamental modes of graded
fibres. J. Opt. Soc. Am., 68, 103-9.
4. Snyder, A. W. and Sammut, R. A. (1979) Fundamental (НЕц) modes of graded
optical fibers. J. Opt. Soc. Am., 69, 1663-71.
* 5. Snyder, A. W. (1981) Understanding monomode optical fibres. Proc. I.E.E.E., 69,
6-13.
* 6. Mathews, J. and Walker, R. L. (1965) Mathematical Methods of Physics, Benjamin,
New York.
7. Anderssen, R. S., de Hoog, F. and Love, J. D. (1981) Modes of Gaussian profile
optical fibres. Opt. Quant. Elect., 13$ 217-24.
8. Snyder, A. W., Love, J. D. and Sammut, R. A. (1982) Green’s function methods for
perturbed optical fibres. J. Opt. Soc. Am., 72, 113-35.
9. Love, J. D. and Hussey, C. D. (1984) Variational approximations for modes of
weakly guiding fibres, Opt. Quant. Elect. 16.
К главе 16
* 1. Born, M. and Wolf, E. (1970) Principles of Optics, Pergamon Press, Oxford.
* 2. Abramowitz, M. and Stegun, I. A. (1965) Handbook of Mathematical Functions,
Dover, New York.
3. Sharma, A., Khular, E., Thyagarajan, K. and Ghatak, A. K. (1979) Coupling of two
parallel multimode parabolic index waveguides: an exact analysis in the weakly
guiding approximation. Opt. Commun., 30, 166-9.
К главе 17
* 1. Snyder, A. W. (1981) Understanding monomode optical fibers. Proc. I.E.E.E., 69,
6-13.
2. Love, J. D. and Hussey, C. D. (1984) Variational approximations for modes of
21 Зак 37 6 25
noncircular waveguides. Opt. Quant. Elect, (submitted).
* 3. Mathews, J. and Walker, R. L. (1965) Mathematical Methods oj Physics, Benjamin,
New York.
К главе 18
* 1. Snyder, A, W. (1972) Power loss on optical fibers. Proc. I.E.E.E, 60, 757-8.
2. Snyder, A. W. and Menzel, R. (1975) Photoreceptor Optics, Springer-Verlag, New
York.
3. Kirschfeld, K. and Snyaer, A. W. (1976) Measurement of a photoreceptor’s
characteristic waveguide parameter. Vision Res., 16, 775-8.
4. Snyder, A. W. (1979), in Handbook of Sensory Physiology, VII/6A (ed. H. Autrum),
Springer-Verlag, Berlin, pp. 279-81.
5. Kaminow, I. P. (1980) Polarization in optical fibers. I.E.E.E. Trans. J. Quantum
Electron., 17, 15-22.
6. Tsuchiya, H. and Sakai, J. I. (1975) Characteristics of single-mode optical fiber
with elliptical core. Technical group of the IECE Japan, OQE74-86.
7. Sammut, R. A., Hussey, C. D., Love, J. D. and Snyder, A. W. (1981) Modal analysis
of polarization effects in weakly-guiding fibers. I.E.E. Proc., Pt. H, 128, 173-87.
8. Love, J. D., Sammut, R. A. and Snyder, A. W. (1979) Birefringence in elliptically
deformed optical fibers. Electron. Lett., 15, 615-16.
9. Snyder, A. W. and Young, W. R. (1978) Modes of optical waveguides. J. Opt. Soc.
Am., 68, 297-309.
10. Thyagarajan, K., Kumar, A. and Ghatak, A. K. (1981) Perturbation analysis of the
coupling between two cylindrical parabolic index waveguides. Opt. Commun., 39,
26-30.
11. Stratton, J. A. (1941) Electromagnetic Theory, McGraw-Hill, New York.
12. Smyth, W. R. (1941) Static and Dvnamic Electricity, McGraw-Hill, New York.
К главе 19
1. Snyder, A. W. (1965) Surface mode coupling along a tapered dielectric rod. I.E.E.E.
Trans. Antennas Propag., 13, 821-2.
2. Jackson, J. D. (1964) Electrodynamics, Wiley, New York, p. 419.
3. Wilson, M. G. F. and Teh, G. A. (1975) Tapered optical couplers. I.E.E.E. Trans.
Microwave Theory Tech., 23, 85-92.
К главе 20
1. Snyder, A. W. (1966) Surface waveguide modes along a semi-infinite dielectric fiber
excited by a plane wave. J. Opt. Soc. Am., 56, 601-10.
2. Snyder, A. W. (1969) Excitation and scattering of modes on a dielectric or optical
fiber. I.E.E.E., Trans. Microwave Theory Tech., 17, 1138-44.
3. Cardama, A. and Kornhauser, E. T. (1975) Modal analysis of coupling problems in
optical fibers. I.E.E.E. Trans. Microwave Theory Tech. 23, 162-70.
4. Kapany,N. S. and Burke, J. J. (1972) Optical Waveguides, Academic Press, chap. 5.
5. Stern, J. R., Peace, M. and Dyott, R. B. (1970) Launching into optical-fiber
waveguides. Electron Lett., 6, 160-2.
626
6. Marcuse, D. (1970) Excitation of the dominant mode of a round fiber by a Gaussian
beam. Bell Syst. Tech. J., 49, 1695-1703.
7. Mostafavi, M., Itoh, T. and Mittra, R. (1975) Excitation of an optical fiber by a
Guassian beam. Appl. Opt., 14, 2190-3.
8. Snyder, A. W., Pask, C. and Mitchell, D. J. (1973) Light acceptance property of an
optical fiber. J. Opt. Soc. Am., 63, 59-64.
* 9. Born, M. and Wolf, E. (1970) Principles of Optics, Pergamon Press, London.
10. Barrell, K. F. and Pask, C. (1979) Optical fiber excitation by lenses. Opt. Acta, 26,
91-108.
11. Snyder, A. W. and Pask, C. (1973) Incoherent illumination of an optical fiber. J.
Opt. Soc. Am., 63, 806.
К главе 21
1. Adler, R. B. (1952) Waves on inhomogeneous cylindrical structures. Proc. I.R.E., 40,
339-48.
2. Snyder, A. W. (1980) Weakly guiding fibers. J. Opt. Soc. Am., 70, 405-11.
3. Ramo, S., Whinnery, J. R. and Van Duzer, T. (1965) Fields and Waves in
Communication Electronics, Wiley, New York, sect. 12.04.
4. Jones, D. S. (1964) Theory of Electromagnetism, Pergamon Press, Oxford.
5. Papas, С. H. (1965) Theory of Electromagnetic Wave Propagation, McGraw-Hill,
New York, sect. 2.2.
6. Snyder, A. W. (1970) Radiation losses due to variations of radius on dielectric or
optical fibers. I.E.E.E. Trans. Microwave Theory Tech. 18, 608-15.
7. Brouillon, L. (1946) Wave Propagation in Periodic Structures, electric fitters and
lattice structures, McGraw Hill, New York.
8. Hussey, C. D. (1983) Radiation from graded-index single-mode fibers. I.E.E. Pt H.
130, 225-9.
К главе 22
1. Snyder, A. W. (1969) Scattering due to irregularities on dielectric or optical fibers.
I.E.E. Electron. Lett., 5, 2,71-72.
2. Snyder, A. W. (1969) Excitation and scattering of modes on a dielectric or optical
fibre. I.E.E.E. Trans. Microwaves Theory Tech. 17, 1138-44.
3. Snyder, A. W. (1970) Radiation losses due to variations of radius on dielectric or
optical fibers. I.E.E.E. Trans. Microwaves Theory Tech. 18, 608-15.
4. Stratton, J. A. (1941) Electromagnetic Theory, McGraw-Hill, New York.
5. White, I. A. and Snyder, A. W. (1977) Radiation from dielectric optical waveguides.
Appl. Opt., 16, 1470-2.
6. Marcuse, D. (1975) Radiation losses of the HEj j mode ot a fiber with sinusoidally
perturbed core boundary. Appl. Opt., 14, 3021-25.
7. Rawson, E. G. (1974) Analysis of scattering from fiber waveguides with irregular
core surfaces. Appl. Opt., 13, 2370-7.
8. Jones, D. S. (1964) Theory of Electromagnetism, Pergamon Press, Oxford.
К главе 23
1. Snyder, A. W., White, I. A. and Mitchell, D. J. (1975) Radiation from bent optical
2P 627
waveguides. Electron. Lett., 11, 332-3.
2. White, I. A. (1979) Radiation from bends in optical waveguides: the volume-current
method. Microwaves, Opt. Acoust., 3, 186-8.
3. White, I. A. (1977) Radiation losses in dielectric optical waveguides. Ph.D. Thesis,
The Australian National University.
4. Gambling, W. A., Matsumura, H. and Ragdale, С. M. (1978) Field deformation in a
curved single-mode fibre. Electron. Lett., 14, 130-2.
5. Gambling, W. A., Payne, D. N. and Matsumura, H. (1976) Radiation from curved
single-mode fibres. Electron. Lett., 12, 567-9.
6. Marcuse, D. (1976) Field deformation and loss caused by curvature of optical fibres.
J. Opt. Soc. Am., 66, 311-20.
7. Gambling, W. A., Matsumura, H. and Ragdale, С. M. (1979) Curvature and
microbending losses in single-mode optical fibres. Opt. Quant. Elect., 11, 43-59.
8. Sakai, J. I. (1980) Microbending loss evaluation in arbitrary-index single-mode
optical fibers. I.E.E.E. J. Quant. Elec., 16, 36-49.
К главе 24
1. Snyder A. W. and Menzel R. (eds) (1975) Photoreceptor Optics, Springer-Verlag,
Berlin.
2. Snyder, A. W. (1978) Handbook of Sensory Physiology, Vol. VII/6A (ed. H.
Aiitrum), Springer-Verlag, Berlin, pp. 279-81.
3, Snitzer, E. (1961) in Advances in Quantum Electronics, Columbia University Press,
New York, p. 360.
4. Stewart, W. J. (1975) Proceedings of the First European Conference on Optical
Communication, London.
5. Collin, R. E. (1960) Field Theory of Guided Waves, McGraw-Hill, New York,
chap. 11.
6. Collin, R. E. and Zucher, F. J. (eds) (1969) Antenna Theory, Part II, McGraw-Hill,
New York.
7. Kapany, N. S. and Burke, J. J. (1972) Optical Waveguides, Academic Press, New
York.
* 8. Felsen, L. B. and Marcuvitz, N. (1973) Radiation and Scattering ofWaves, McGr’aw-
Hill, New York.
9. Tamir, T. (1973) Inhomogeneous wave types at planar structures. III. Leaky waves.
Optik, 38, 269‘97.
10. Snyder, A. W. and Mitchell, D. J. (1973) Leaky rays cause failure of geometric optics
on optical fibres. Electron. Lett., 9, 437-8.
11. Snyder, A. W. and Mitchell, D. J. (1974) Leaky rays on circular optical fibers J. Opt.
Soc. Am., 69, 599-607.
12. Snyder, A. W., Mitchell, D. J. and Pask, C. (1974) Failure of geometric optics for
analysis of circular optical fibers. J. Opt. Soc. Am., 64, 608-14.
13. Snyder, A. W. and Mitchell, D. J. (1974) Leaky mode analysis of circular optical
waveguides. Opto-electronics, 6, 287-96.
14. Snyder, A. W. (1974) Leaky-ray theory of optical waveguides of circular cross
section. Appl. Phys. 4, 273-98.
15. Snyder, A. W. and Love, J. D. (1974) Tunnelling leaky modes on optical
waveguides. Opt. Commun., 12, 326-8.
628
16. Snyder, A. W. and Pask, C. (1975) Optical fibre: spatial transient and spatial steady
state. Opt. Commun., 15, 314-16.
17. Adams, M. J., Payne, D. N. and Sladen, F. M. E. (1975) Leaky rays on optical fibres
of arbitrary (circularly symmetric) index profiles. Electron. Lett., 11, 328-40.
18. Stewart, W. J. (1975) Leaky modes on graded fibres. Electron. Lett., 11, 321-2.
19. Sammut, R. and Snyder A. W. (1976) Leaky modes on a dielectric waveguide-
orthogonality and excitation. Appl. Opt., 15, 1040-4.
* 20. Shevchenko, V. V. (1974) The expansion of the fields in open waveguides in proper
and improper modes. Radio Phys. Quantum Electron., 14, 972-7.
21. Sammut, R. and Snyder, A. W. (1975) Leaky modes on circular optical waveguides.
Appl. Opt., 15, 477-82.
22. Marcuse, D. (1974) Theory of Dielectric Optical Waveguides, Academic Press, New
York.
23. Sammut, R. A. and Snyder, A. W. (1979) Radiation from optical waveguides:
leaky mode interpretation. Electron. Lett., 15, 58-9.
К главе 25
1. Snyder, A. W. (1971) Continuous mode spectrum of a circular dielectric rod. I.E.E.E.
Trans. МТГ, 19, 720-7.
2. Marcuse, D. (1974) Theory of Dielectric Optical Waveguides, Academic Press, New
York. The radiation modes derived here are not orthogonal, and lead to errors.
3. Sammut, R. A. (1982) Orthogonality and normalization of radiation modes in
dielectric waveguides. J. Opt. Soc. Am., 72, 1335-37.
4. Snyder, A. W. and Sammut, R. A. (1979) Radiation modes of optical waveguides.
Electron. Lett., 15, 4-5.
5. Snyder, A. W. (1980) Weakly guiding optical fibres. J. Opt. Soc. Am., 70, 405-11.
К главе 26
1. Carrier, G. F., Krook, M. and Pearson, С. E. (1966) Functions of a Complex Variable,
McGraw-Hill, New York.
2. Sammut, R. A. (1975) The theory of unbound modes on circular dielectric
waveguides. Ph.D. Thesis, The Australian National University.
* 3. Felsen, L. B. and Marcuvitz, N. (1973) Radiation and Scattering of Waves, Prentice-
Hall, Englewood Cliffs, N.J.
4. Collin, R. E. (1960) Field Theory of Guided Waves, McGraw-Hill, New York,
pp. 485-506.
* 5. Morse, P. M. and Feshbach, H. (1953) Methods of Theoretical Physics, McGraw-
Hill, New York.
6. Tamir, T. and Oliner, A. A. (1963) Guided complex waves. Proc. I.E.E., 110,310-34.
7. Tamir, T. and Felsen, L. B. (1965) On lateral waves in slab configurations and their
relation to other wave types. I.E.E.E. Trans. Antennas Propag., 13, 410-22.
К главе 27
1. Snyder, A. W. (1972) Coupled-mode theory for optical fibers. J. Opt. Soc. Am., 62,
1267-77.
629
2. Marcuse, D. (1973) Coupled mode theory for round optical fibers. Bell Syst. Tech.
J., 52, 817-18.
3. Marcuse, D. (1974) Theory of Dielectric Optical Waveguides, Academic Press, New
York, p. 101.
* 4. Snyder, A. W. and Davies, O. J. (1970) Asymptotic solution of coupled mode
equations for sinusoidal coupling. Proc. I.E.E.E., 58, 168-9.
К главе 28
1. Snyder, A. W., (1965) Surface mode coupling along a tapered dielectric rod. I.E.E.E.
Trans. Antennas Propag., 13, 821-2.
2. Snyder, A. W. (1970) Coupling of modes on a tapered dielectric cylinder. I.E.E.E.
Microwaves Theory Tech., 18, 383--92.
3. Marcuse, D. (1974) Theory of Dielectric Optical Waveguides, Academic Press, New
York, p. 106.
4. Snyder, A. W. (1971) Mode propagation in a nonuniform cylindrical medium.
I.E.E.E. Trans. Microwaves Theory Tech. 19, 402-3.
5. McIntyre, P. and Snyder, A. W., (1978) Light propagation in twisted anisotropic
media: application to photoreceptors. J. Opt. Soc. Am., 68, 149-57.
К главе 29
1. Kapany, N. S. and Burke, J. J. (1972) Optical Waveguides, Academic Press, New
York, chap. 7.
2. Snyder, A. W. and Menzel, R. (eds) (1975) Photoreceptor Optics, Springer-Verlag,
Berlin, p. 50.
3. Snyder, A. W. (1979) Handbook of Sensory Physiology, Vol. V1I/6A (ed. K. Autrum),
Springer-Verlag, Berlin, pp. 279—81.
4. Snyder, A. W. (1972) Coupled-mode theory for optical fibers. J. Opt. Soc. Am., 62,
1267-77.
5. McIntyre, P. and Snyder, A. W. (1973) Power transfer between optical fibers. J. Opt.
Soc. Am., 63, 1518-27.
6. McIntyre, P. (1975) Crosstalk in absorbing optical fibers. J. Opt. Soc. Am., 65,
810-13.
7. Snyder, A. W. and McIntyre, P. (1976) Crosstalk between light pipes. J. Opt. Soc.
Am., 66, 877-82.
8. McIntyre, P. and Snyder, A. W. (1974) Power transfer between nonparallel and
tapered optical fibers. J. Opt Soc. Am., 64, 285-8.
9. Jones, A. L. (1965) Coupling of optical fibers and scattering in fibers. J. Opt. Soc. Am.,
55, 261-9.
К главе 30
* 1. Stratton, J. A. (1941) Electromagnetic Theory, McGraw-Hill, New York.
2. Adler, R. B. (1952) Waves on inhomogeneous cylindrical structures. Proc. I.R.E., 40,
339-48.
* 3. Born, M. and Wolf, E. (1970) Principles of Optics, Pergamon Press Oxford, chap.
XIV.
630
К главе 31
1. Sammut, R. and Snyder, A. W. (1976) Leaky modes on a dielectric waveguide:
orthogonality and excitation. Appl. Opt., 15, 1040-4.
* 2. Marcuse, D. (1973) Light Transmission Optics, Van Nostrand, New York, p. 323.
3. Friedman, B. (1956) Principles and Techniques of Applied Mathematics, Wiley, New
York, pp. 230-50.
4. Brown, J. M. (1966) Electromagnetic momentum associated with waveguide
modes. Proc. I.E.E., 113, 27-34.
* 5. Mathews, J. and Walker, R. L. (1965) Mathematical Methods of Physics, Benjamin,
New’ York.
6. Rumsey, V. H. (1954) Reaction concept in electromagnetic theory. Phys. Rev., 94,
1483-91.
* 7. Whittaker, E. T. and Watson, G. N. (1969) A Course of Modern Analysis;
Cambridge, London, p. 67.
8. Snyder, A. W. (1970) Mode propagation in optical waveguides. Electron. Lett., 6,
561-2.
9. Snyder, A. W. (1972) Coupled-mode theory for optical fibers. J. Opt. Soc. Am., 62,
1267-77.
10. Snyder, A. W. (1969) Coupling of modes on a tapered dielectric cylinder. I.E.E.E.
Trans. Microwave Theory Tech., 18, 650-1.
11. Snyder, A. W. (1965) Surface mode coupling along a tapered dielectric rod. I.E.E.E.
Trans. Antennas and Propagation, 13, 821-2.
12. Snyder, A. W. (1971) Mode propagation in a non-uniform cyclindrical medium.
I.E.E.E. Trans. Microwave Theory Tech., 19, 402-3.
К главе 32
1. Snyder, A. W. (1969) Asymptotic expressions for eigenfunctions and eigenvalues of
dielectric or optical waveguides. I.E.E.E. Trans. Microwaves Theory Tech. 17,
1130-8.
2. Snyder, A. W. and Young, W. R. (1978) Modes of optical waveguides. J. Opt. Soc.
Am., 68, 297-309.
3. Tjaden, D. L. A. (1978) First-order correction to ‘weak-guidance’ approximation in
fibre optics theory. Philips J. Res., 33, 103-12.
4. Sammut, R. A., Hussey, C. D., Love, J. D. and Snyder, A. W. (1981) Modal analysis of
polarization effects in weakly-guiding fibres. I.E.E. Proc., 128, 173-87.
5. Snyder, A. W. and Love, J. D. (1982) Green’s function methods for analyzing optical
fibre perturbations. J. Opt. Soc. Am. 72, 1131-35.
6. Love, J. D., Hussey, C. D., Snyder, A. W. and Sammut, R. A. (1982) Polarization
con ections to mode propagation on weakly guiding fibres. J. Opt. Soc. Am., 72,
1583-91.
7. Snyder, A. W. (1980) Weakly guiding optical fibres. J..Opt. Soc. Am., 70, 405-11.
8. Ramo, S., Whinnery, J. R. and Van Duzer, T. (1965) Fields and Waves in
Communications Electronics, Wiley, New York.
К главе 33
* 1. Mathews, J. and Walker, R. L. (1965) Mathematical Methods of Physics, Benjamin,
631
New York, pp. 315-23.
* 2. Morse, P. M. and Feshbacn, H. (1953) Methods of Theoretical Physics, McGraw-
Hill, New York, p. 1112.
3. Love, J. D., Hussey, C. D., Snyder, A. W. and Sammut, R. A. (1982) Polarization
corrections to mode propagation on weakly guiding fibres. J. Opt. Soc. Am., 72,
1583-91.
4. Pask, C. (1979) Exact expressions for scalar modal eigenvalue and group delays in
power-law optical fibres. J. Opt. Soc. Am., 69, 1599-1603.
5. Sammut, R. A., Hussey, C. D., Love, J. D. and Snyder, A. W. (1981) Modal analysis of
polarization effects in weakly-guiding fibres. I.E.E. Proc., 128, 173-87.
К главе 34
* 1. Morse, P. and Feshbach, H. (1953) Methods of Mathematical Physics, McGraw-Hill,
New York, chap. 7.
2. Friedman, B. (1956) Principles and Techniques of Applied Mathematics, Wiley, New
York, chaps. 3 and 4.
* 3. Mathews, J. and Walker, R. L. (1964) Mathematical Methods of Physics, Benjamin,
New Yoik, chap. 9.
4. Yip, G. L. (1970) Launching efficiency of the HEj j surface wave mode on a dielectric
rod. I.E.E.E. Trans. Microwave Theory Tech., 18, 1033-41.
5. Papas, С. H. (1965) Theory of Electromagnetic Wave Propagation, McGraw-Hill,
New York, chap. 2.2.
6. Ramo, S. Whinnery, J. R. and Van Duzer, T. (1965) Fields and Waves in
Communications Electronics, Wiley, New York, sect. 12.04.
7. Snyder, A. W. (1980) Weakly guiding optical fibers. J. Opt. Soc. Am., 70, 405-11.
8. Snyder, A. W., Love, J. D. and Sammut, R. A. (1982) Green’s function methods for
analyzing optical fiber perturbations. J. Opt. Soc. Am., 72, 1131-35.
К главе 35
1. Stewart, W. J. (1975) Proceedings of the First European Conference on Optical
Communication, London.
* 2. Born, M. and Wolf, E. (1975) Principles of Optics, Pergamon Press, Oxford.
3. Jones, D. S. (1964) The Tbeory of Electromagnetism, Pergamon Press, New York.
* 4. Felsen, L. B. and Marcuvitz, N. (1973) Radiation and Scattering of Waves, Prentice-
Hall, Englewood Cliffs, N.J.
5. Johnson, С. C. (1965) Field and Wave Electrodynamics, McGraw-Hill, New York.
6. Snyder, A. W. and Love, J. D. (1976) Attenuation coefficient for rays in graded
fibers with absorbing cladding. Electron. Lett., 12, 255-7.
* 7. Mathews, J. and Walker, R. L. (1965) Mathematical Methods of Physics, Benjamin,
New York.
8. Snyder, A. W. and Love, J. D. (1976) Attenuation coefficient for tunnelling leaky
rays in graded fibers. Electron. Lett., 12, 324-6.
9. Love, J. D. and Winkler, C. (1978) Refracting leaky rays in graded-index fibers.
Appl. Opt., 17, 2205-8.
10. Love, J. D. and Winkler, C. (1978) The step index limit of po.wer law refractive index
profiles for optical waveguides. J. Opt. Soc. Am., 68, 1188-91.
11. Love, J. D. and Winkler, C. (1977) Attenuation and tunneling coefficients for leaky
rays in multilayered optical waveguides. J. Opt. Soc. Am., 67, 1627-33.
632
12. Snyder, A. W. and Love, J. D. (1975) Reflection at a curved interface -
electromagnetic tunneling. I.E.E.E. Trans. Microwave Theory Tech., 23, 134—41.
13. Love, J. D. and Winkler, C. (1978) The effects of material absorption on ray power
attenuation in multi-layered optical waveguides. Opt. Quant. Elect., 1G, 383-92.
* 14. Korn, G. A. and Korn, T. M. (1968) Mathematical Handbook for Scientists and
Engineers, McGraw-Hill, New York.
15. Jones, D. S. (1978) Electromagnetic tunnelling. Quart. J. Meeh. Appl. Math., 31,
409-34.
16. Love, J. D. and Winkler, C. (1980) Generalized Fresnel power transmission
coefficients for curved graded-index media. I.E.E.E. Trans. Microwave Theory
Tech., 28, 689-94.
*17. Abramowitz, M. and Stegun, I. (1964) Handbook of Mathematical Functions,
Dover, New York.
18. Love, J. D. and Winkler, C. (1978) A universal tunnelling coefficient for step- and
graded-index multimode fibers. Opt. Quant. Elect., 10, 341-51.
К главе 36
1. Kapany, N. S. and Burke, J. J. (1972) Optical Waveguides, Academic Press, New
York, p. 74.
2. Johnson, С. C. (1965) Field and Wave Electrodynamics, McGraw-Hill, New York.
3. Goodman, J. (1968) Fourier Optics, McGraw-Hill, New York.
4. Gloge, D. and Marcatili, E. A. J. (1973) Multimode theory of graded-core fibers.
Bell. Syst. Tech. J., 52, 1563-78.
5. Love, J. D. and Snyder, A. W. (1976) Optical fiber eigenvalue equation: plane wave
derivation. Appl. Opt., 15, 2121-5.
6. Ankiewicz, A. (1978) Comparison of wave and ray techniques for solution of
graded index optical waveguide problems. Opt. Acta., 25, 361-73.
7. Snyder, A. W. and Mitchell, D. J. (1974) Leaky rays on circular optical fibres. J. Opt.
Soc. Am., 69, 599-607.
8. Marcuse, D. (1974) Theory of Dielectric Optical Waveguides. Academic Press, New
York, p. 33.
9. Love, J. D. and Winkler, C. (1978) Goos-Hanchen shift tor leaky rays on step-index
waveguides. Electron. Lett., 14, 379-81.
10. Love, J. D., Winkler, C., Sammut, R. and Barrell, K. (1978) Leaky modes and rays
on multimode step-index waveguides-a comparison. Electron. Lett., 14, 489-90.
* 11. Feynman, R. P., Leighton, R. B. and Sands, M. (1965) The Feynman Lectures on
Physics, Addison-Wesley, New York.
12. Snyder, A. W. and Pask, C. (1973) Incoherent illumination of an optical fibre. J.
Opt. Soc. Am., 63, 806-12.
13. Pask, C., Snyder, A. W. and Mitchell, D. J. (1975) Number of modes on optical
waveguides. J. Opt. Soc. Am., 65, 356- 7.
14. Gambling, W. A., Matsumura, H. and Ragdale, С. M. (1979) Curvature and
microbending losses in single-mode optical fibres. Opt. Quant. Elect., 11, 43-59.
К главе 37
* 1. Abramowitz, M. and Stegun, I. A. (eds) (1965) Handbook of Mathematical Functions,
Dover, New York.
* 2. Gradshteyn, I. S. and Ryzhik, I. M. (1965) Tables of Integrals, Series and Products,
Academic Press, New York.
* 3. Erdelyi, A. (1956) Asymptotic Expansions, Dover, New York, p. 36.
# 4. Korn, G. A. and Korn, T. M. (1961) Mathematical Handbook for Scientists and
Engineers, McGraw-Hill, New York, sect. 17-3-5.
СПИСОК РАБОТ, ПЕРЕВЕДЕННЫХ НА РУССКИЙ ЯЗЫК, И РАБОТ
СОВЕТСКИХ АВТОРОВ
Борн М., Вольф Э. Основы оптики: Пер. с англ. - М.: Наука, 1970. - 855 с.
Градштейн М. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений: Пер. с
англ. - М.; Л.: Наука, 1971.
Гудмен Дж. Введение в Фурье - оптику: Пер. с англ. - М.: Мир, 1970. - 364 с.
Джексон Дж. Классическая электродинамика: Пер. с англ. - М.: Мир, 1965- - 702 с.
Зоммерфельд А. Оптика. - М.: ИЛ, 1953. - 486 с.
Капани Н. С. Волоконная оптика: Пер. с англ. - М.: Мир, 1969. - 464 с.
Корн Г., Корн Т. Справочник по математике: Пер. с англ. - М.: Наука, 1977. - 831 с.
Ландау Л. Д., Лифшиц Е. М. Механика. - М.: Наука, 1973. - 208 с.
Ландау Л. Д., Лифшиц Е. М. Квантовая механика. М.: Наука, 1974. - 752 с.
Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред. М.: Наука, 1982. - 620 с.
Маркузе Д. Оптические волноводы: Пер. с англ. - М.: Мир, 1974. - 576 с.
Мидвинтер Дж. Волоконные световоды для передачи информации: Пер. с англ. - М.: Ра-
дио и связь, 1983. - 336 с.
Миллер С., Маркатили Е., Ли Т. Исследование световодных систем связи//ТИИЭР. -
1973. -Т. 61, №12.-С.46.
Морс Ф. М., Фешбах Г. Методы теоретической физики: Пер. с англ. - М.: ИЛ, 1958. -
Т. 1 - 2.
Мэтьюз Дж., Уокер Р. Математические методы физики: Пер. с англ. - М.: Атомиздат,
1972. - 398 с.
Снайдер А., Девис О. Асимптотическое решение уравнения связанных мод для случая
симметричной связи//Труды ИРЭ. - 1958. - № 2. С. 117.
Снайдер А. Потери энергии в оптических волокнах//ТИИЭР. - 1972. - Т. 60, № 6. -
С. 132 - 133.
Снайдер А. Теория одномодовых волоконных световодов. - ТИИЭР. - 1981. Т. 69,
№7. - С. 7 - 15.
Справочник по специальным функциям с формулами, графиками и математическими
таблицами: Пер. с англ./Под ред. М. Абрамовица,И.Стиган:-М.:Наука, 1979.-832 с.
Стреттон Дж. А. Теория электромагнетизма: Пер. с англ. - М.: Гос. изд-во технико-те-
орет. лит-ры, 1984.- 540 с.
Уиттекер Э. Т., Ватсон Дж. Н. Курс современного анализа: Пер. с англ. - М.: Физматгиз,
1963. -Ч. 1 -Ч. 2.
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике: Пер. с англ. - М.:
Мир, 1967.
Фельсен Л., Маркувиц Н. Излучение и рассеяние волн: Пер. с англ. - М.: Мир, 1978. -
Т.1 - 2.
Шевченко В. В. Потери на излучение в изогнутых волноводах поверхностных волн//Изв.
вузов, Радиофизика. - 1971. - Т. 14, № 5. - С. 768 - 777.
Шевченко В. В. О разложении полей открытых волноводов по собственным и несоб-
ственным волнам//Изв. вузов, Радиофизика. - 1971. - Т. 14, № 8. - С. 1242 - 1249.
Эрдейи А. Асимптотические разложения: Пер. с англ. - М.: Физматгиз, 1962. - 127 с.
ДОПОЛНИТЕЛЬНЫЙ СПИСОК ЛИТЕРАТУРЫ
Д1. Miller S. Е. Coupled wave theory and waveguide applications//Bell Syst. Techn. J. -
1954. - Vol. 33, No. 3.- P. 661 - 719.
Д2. Schelkunoff S. A. Conversion of Mazwell's equations into generalized telegraphist's
equations//Bell Syst. Techn. J. - 1955. - Vol. 34, No. 5 - P. 991 - 1043.
634
ДЗ. Каценеленбаум Б. 3. Теория нерегулярных волноводов. - М.: Изд. АН СССР,
1961. - 216 с.
Д4. Шевченко В. В. Плавные переходы в открытых волноводах. - М.: Наука, 1969- -
192 с.
Д5. Marcuse D. Theory of dielectric optical waveguides. - New York: Academic Press, 1974.-
257 c.
Д6. Никольский В. В. Вариационные методы для внутренних задач электродинамики. -
М.: Наука, 1967. - 460 с.
Д7. Шевченко В. В. Методы формул сдвига в теории диэлектрических волноводов и
волоконных световодов//Радиотехника и электроника. - 1986. - Т. 31, № 5. -
С. 849 - 864.
Д8. Маркузе Д. Оптические волноводы: Пер. с англ. - М.: Мир, 1974. - 576 с.
Д9. Унгер Х.-Г. Планарные и волоконные оптические волноводы: Пер. с англ. - М.:
Мир, 1980. - 656 с.
ДЮ. Семенов Н. А. Оптические кабели связи. - М.: Радио и связь, 1981. - 152 с.
Д11. Передача оптических сигналов по световодам/ А. С. Беланов, В. В. Григорьянц,
В. Т. Потапов, А. Д. Шатров//Итоги науки и техники. Сер. Радиотехника. - 1984. -
Т. 30. - С. 60 - 88.
Д12. Grudinin А. В., Sulimov V. В. Degree and state of polarization in an anisotropic single-
mode optical fibre//Optics Communications. - 1984. - Vol. 49, No. 5. - P. 321- 323.
Д13. Грудинин А. Б., Сулимов В. Б. Когерентные и поляризационные свойства излуче-
ния в одномодовых волоконных световодах//Труды ИОФАН. -1987. - Т.5. - С.18 - 35
Д14. Дедловский М. М., Коршунов И. П., Шевченко П. П. Исследование когерентности
поля излучения многомодового оптического волокна//Радиотехника и электрони-
ка. - 1980. - Т. 25, № 3. - С. 481 - 486.
Д15. Исследование межмодовой дисперсии в оптических волокнах методом корреляци-
онного анализа поля излучения/М. М. Дедловский, И. П. Коршунов, Р. Ф. Матвеев,
В. Н. Тутубалин //Радиотехника и электроника. - 1982. - Т. 27, № 2. - С. 220 - 232.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Адиабатический инвариант 90, 349
Анизотропия материала 254
структурная 254
Антенные методы 381, 556
Апертура числовая 29
локальная 29, 63
Асимптотические методы мод 589
Бесселя функции 609
Боковая волна 458
Вариационные методы 288, 313
Векторные операции 607
Векторный потенциал 558
Взаимности соотношения 545
- теорема 506
----обобщенная 511
----форма несопряженная 508
----сопряженная 506
---формулировка с помощью криволи-
нейного интеграла 508
ВКБ-решения 488, 576, 577
круглые волоконные световоды 582
планарные волноводы 577
формулы сшивания 578
Возбуждение 58, 358
волоконного световода многомодо-
вого 58
-----одномодового 367
диффузное 62, 372
лучей 58
мод 358
- вытекающих 426
- излучения 439
- направляемых 376
неоднородное 65
поля излучения 381
635
пучком 65, 361
- гауссовым 362, 364
- коллимированным 65
- наклонным 364
- однородным 362, 365
- осевым 364
- смещенным 365
слабонаправляющих волноводов 360
Возмущения 320
однородные 323
радиуса сердцевины 325, 345
синусоидальные 395
слабоанизотропные 326
Волновод
анизотропный 199, 233, 504
- двуосный 200
- одноосный 200
- планарный 236
- слабонаправляющий 201, 238, 253
- сохраняющий поляризацию 257
многослойный 209, 223
нерегулярный 79, 347
- затухание мощности луча, моды 598
- коэффициент прохождения мощ-
ности 574, 579, 584
- слабонаправляющий 249
- форма импульса 114
планарный 11, 203
- градиентный 18, 226
- коэффициент прохождения мощнос-
ти 572, 574
- лучевые параметры 21
траектории 18
- многомодовый 12
- направляемые лучи 11
с металлической оболочкой 508
- поглощением 105,197, 346, 503,598
- несимметричный 27, 209
слабонаправляющий 240, 525
— вытекающие моды 418
- круглые волоконные световоды 243,
258, 534
- методы мод 541
- моды излучения 446, 540
- некруглый 244, 303
- общие свойства 247
- параксиальное приближение 23
- поляризационные поправки для по-
лей мод 525, 538
-------постоянной распространения
530
сложный оптический 331
ступенчатый волоконный 210, 267
- планарный 203
Волноводный параметр 12, 29, 192
Волноводный переход параболический 96
Волновое уравнение 187, 189
векторное 187, 500, 525
- в координатах декартовых 501
---цилиндрических 500
---пределе малых значений V 194
— для анизотропной среды 503
---волноводов одноосных 505
---слабонаправляющих 5 25
---ступенчатых 202
скалярное 189, 243, 306, 541
- для анизотропной среды 504
---волновода со степенным профи-
лем 189
- свойства непрерывности 542
Волоконный параметр 29
Волоконный световод
идеальный 174
круглый 28, 258
— основные моды 243
- слабонаправляющий 258
медленно изменяющийся 83, 347, 487
---изогнутый 357
некруглый 44, 303
- анизотропный 256
— вытекающие лучи 129
- лучевая дисперсия 53
- слабонаправляющий 240
- эллиптический 304
нерегулярный многомодовый 79
- одно модовый 347
одномодовый 9, 193
одноосный 200, 238, 505
почти круглый 248, 309
с градиентным профилем 35, 226
---многомодовый 35
---одномодовый 288
---точное решение 226
с регулярным возмущением 320
слабоэллиптический 309
сохраняющий поляризацию 257
трехслойный 324
эллиптический 223, 304, 327, 346
- скрученный 351
Временная зависимость поля 178
Время прохождения
луча 17, 22,27,41,51,597
моды 185, 209
Ганкеля функции 610
Геометрическая оптика 9, 565
применимость 165
636
Гиперболические функции 606
Глубина проникновения 272
Гсоса-Генхена сдвиг 168
Граничная поверхность сердцевина — обо-
лочка 11, 28, 176
Грина функции 556
Г рупповая
задержка 185
скорость 184, 511
- время прохождения луча, моды 597
- гауссово приближение 292
- поправки высшего порядка 252
— слабонаправляющих волноводов
250
Групповой показатель 17, 23, 42, 187
Двойное лучепреломление 199, 254, 329
геометрическое 307
материала 199, 254
структурное 253
Диполь 378, 384
излучение 384
Дисперсия 186
внутримодовая 186
волноводная 186, 195
- нулевая 297
линейная 55
лучевая 49
материала 17, 23, 42, 49, 52, 54, 79,
186, 199
межмодовая 49
нелинейная 5 7
профиля 54
Дифракция 161
Диффузионное уравнение 102
Диффузное возбуждение 62, 372
источник 59, 69
Диэлектрическая проницаемость 496
Длина
биений 335, 337, 342, 349
пути 15, 21, 34, 41
- оптического 15, 21, 34, 41
Затухание 197
поглощение 105, 197
туннелирующие лучи 126, 141
Защитное покрытие 9
Изгиб 153,401
волоконного световода многомодово-
го 159
--одномодового 401
каустика излучения 156
классификация лучей 154
переходные потери 409
планарного волновода 154
сдвиг поля 603
Излучение 135, 381, 435
волоконного световода 93, 116
диполя 384, 449
источника диффузного 135
- трубчатого 385, 450
Импульс 49, 58
уширение 49, 88, 146, 186
- пространственное 50
форма 58, 75, 114
Импульсный отклик 58, 75
средняя квадратическая ширина 76
Инвариант адиабатический 90
- лучевой 14, 20, 31, 40, 45, 75, 195
Инвариантность трансляционная 11, 497
Интегральные теоремы 609
Интенсивность 182, 250
- распределение 59, 68, 149
Искажения параметр 195, 250, 292
Источник
дипольный 378
диффузный 59, 69, 135, 372
Ламбертов 59
мощность 62, 382
трубчатый 380, 385, 451
частично диффузный 60, 69, 71
эффективность 63
Каустика 19, 582, 586
внутренняя 30, 37, 73
излучения 39, 416
произвольной кривизны 130
точек поворота 19, 37, 73
Количество отражений 17, 22, 34
Концентрация света 67, 95
Компоненты поля в декартовых коорди-
натах 242, 526
Косые лучи 34, 37, 54, 191
Коэффициент затухания 106, 111, 118,
156, 197
- поглощения 326
- прохождения универсальный 129
- связи 460, 469, 522
Крамерса-Кронига соотношение 182
Критический угол 13, 22, 30, 41, 567
скольжения 13, 208, 567
- локальный 22, 41
Лазер 60
Ламбертов источник 59
Лапласа уравнение 194, 287
Лиссажу фигуры 48
637
Лучевой траектории построение 13, 18,
29, 35
Лучи
вытекающие 31, 45, 116, 149, 600
- возбуждение 135
- классификация 123, 125
- рефрагирующие 31, 116
- туннелирующие 31, 116, 600
классификация 31, 37, 47, 123, 125,
159
меридиональные 30, 36, 54, 122, 190,
593
направляемые И, 28
параксиальные 23
полупериод траектории 15,21
предпочтительное направление 171
рефрагирующие 14, 20, 31, 37, 136
точка поворота 19
траектория 15, 21, 29
туннелирующие 31, 38, 116, 122
- затухание 126
— коэффициент прохождения мощнос-
ти 578
- полное внутреннее отражение нару-
шенное 578
- рефрагирующие 45, 48, 116, 129
уравнение 18
- траектории 18, 35, 45, 81
’’шепчущей галереи” 157
Лучевые параметры 15, 21, 34, 40
- трубки 58, 566
- углы 30, 35
Магнитная проницаемость 188, 496
МаксвелЛа уравнения 187, 496
Методы мод
для уравнений Максвелла 506
- скалярного волнового уравнения
541
Микроизгибы 411
Моды
вытекающие 412, 452, 456, 600
— возбуждение 425
- затухание 419
- классификация 416
— мощность 419
- нормировка 423
- ортогональность 423, 547
- разложение поля излучения 452
- рефрагирующие 417
- туннелирующие 417
- уравнение собственных значений 426
гибридные 190
- лучевое разложение 593
- природа поля 190
- физический смысл 191
излучения 435
— возбуждение 439
- локальные 474
- мощность 438
- нормировка 437, 446
- ортогональность 437, 446
— постоянная распространения 436
- разложение по плоским волнам 443
- скалярные 446, 547
— слабонаправляемые 445
- ТЕ и ТМ 443, 447
локальные 347, 467
— волоконного световода многомодо-
вого 350, 357
----неоднородного 352, 354, 477
- длина биений 349, 354
- излучение 350, 474
- изогнутого волоконного световода
357
- коэффициенты связи 469, 522, 551,
554
- мощность 348
- связь 467
--перекрестная 354, 356
- скалярные 552
направляемые 176
- векторное волновое уравнение 187
- возбуждение 358, 376
- волноводов без поглощения 179
--с поглощением 197
- нормирование полей 180
- ортогональность 180
- переносимая мощность 182, 197
— слабонаправляющих волоконных
световодов 240
ортонормированные излучения 438
- направляемые 181
основные 174, 194
- в пределе малых значений К 194,
287
- двух параллельных волоконных
световодов 333, 339
- однополяризационных волоконных
световодов 257
- постоянная распространения 243
- приближение 274, 287
-- гауссово 289, 314
--эквивалентного ступенчатого про-
филя 301
--LP-мод 244, 246
638
- слабонаправляющих волоконных
световодов 243
НЕ 190
- лучевое представление 590
LP 244
ТЕ 189, 190,504, 531, 593
ТЕМ 242
ТМ 190,504,593
Мощность направляемых лучей 63, 70
коэффициент затухания 106, 111,113,
118, 571
- поглощения 106, 197, 326
- прохождения 62, 109, 118, 571
плотность 182, 250
поток 182
распределение по направляемым лу-
чам 71
распространяющаяся в сердцевине 183
Направляющие углы 30, 35
Нерегулярности 79
излучение 93, 393, 395
изменение радиуса сердцевины 395
изолированные 393, 398
малой амплитуды 83, 87
малые 87, 92, 392
медленно изменяющиеся 83, 347, 399
наклоны 367
поверхностные шероховатости 395,
399
распределенные 394
резкие 100
связь мод 395, 401
сдвиг оси 367
случайные 82
стыки 367
Оболочка 9, 12, 28, 177
ограниченная 452
поглощение 108, 113
распространение 165
Одно модового режима область 291
Однородная диэлектрическая среда 198,
240, 326
Ответвитель направленный переменного
сечения 354, 477, 489
Отражение плоских волн
от границы раздела 131
- каустики 131
Ось главная 199, 254
оптическая 244, 254, 534
Параметры мод 193
Переход волноводный 95
линейный 97
Плоские волны локальные 565
в однородной среде 566
потери 570
слабонаправляющих волноводов 570
Снелля закон 566
туннелирующие 574
Френеля коэффициенты 573, 586
Плоскость падения 130, 587
Поглощение в материале 326
Пойнтинга вектор 182, 503
Поле излучения 413
вклад вытекающих мод 456
- пространственной волны 457
интегральное представление 453
полная мощность 438
Полное внутреннее отражение 166, 241,
566
нарушенное 418, 578
от поверхности изогнутой 122
--плоской 117
Полупериод модовый 350
Постоянная распространения 178, 188,
192
волноводов с потерями 197
- слабонаправляющих 242
волоконного световода возмущенно-
го 342, 514
--слабоэллиптического 318
волоконных световодов параллель-
ных 333
Гауссово приближение 292
интегральное приближение 188, 250,
510
мод вытекающих 413
- излучения 437
Потерь механизмы
изгиб 153, 402
излучение 93, 393
микроизгибы 411
неоднородности 79, 93, 393
поглощение 105, 197, 326
рассеяние 103, 394
рефракция 116
сдвиг поперечный 367, 411
соединение 367
туннелирование 116
Приближение
адиабатическое 90, 349
асимптотическое 83, 349, 565
вариационных методов 289, 314
ВКБ 676
гауссово 289, 314
квазистатическое 344
639
локально плоских волн 565
метода возмущений 320
параксиальное 23, 208
свободного пространства 383
скалярное 240, 525
слабонаправляющее 240, 525
ступенчатого профиля 301
---эквивалентного 301
Приповерхностная волна 458
Пространственная волна 414, 457
- когерентность 373
Профиль показателя преломления 242,
258
гауссов 292, 320
гиперболический секансный 16, 25
- тангенсный 227
градиентный 10
двойной параболический 313
дисперсия 54
неограниченный линейный 311
- степенной 265, 597
обратно квадратичный 227
объем 63
одинакового объема 63, 64, 297
описываемый однородной функцией
46,310
оптимальный 51, 56, 148
параметр высоты 24, 193, 259
с разделяющимися переменными 47,
311
сглаженный 296
степенной некруглый 44
ступенчатый 25, 55, 64, 66, 202, 210,
267
тангенсный 227
усеченный 177
- обратно квадратичный 230
---линейный 230
— параболический 25, 64, 65, 227, 230
- степенной 43, 55, 64, 75
- экспоненциальный 227
форма 297
эллиптический гауссов 320
- концентрический 304
- ступенчатый 319, 329
эффективный 604
Пучок волоконных световодов 490
Пучок гауссов 162
коллимированный 60, 65
однородный 162
освещающий 361
Разложение
по модам 177
---вытекающим 423
---излучения 436
---направляемым 176
---скалярным 539
- плоским волнам 208, 223, 418, 443
- собственным функциям 205, 515,
539
полей мод 222, 526
поля излучения 452
Размер пятна моды волоконного свето-
вода
круглого 289
некруглого 315
Рассеиватели 100
Решение в виде степенного разложения
281
Рэлеевское рассеяние 103
Светодиод 59
Связь мод 390, 458
в волоконных световодах неоднород-
ных 467
локальных 467
перекрестная 331, 352, 479
пучка волоконных световодов 490
Сдвиг оси 365
- продольный 167
Сердцевина 9, 12, 28, 106, 113, 177
Синусоидальные деформации 432, 463
Система единиц MKS рационализованная
496
Скорость света локальная 17, 23, 192
Снелля закон 13, 18, 29, 61, 566
Соединение 367
Статистические неоднородности 82, 398
Стационарные выражения 250, 289, 515
Среда с поглощением 105, 1 97, 503
Тензор показателя преломления 504
Уравнение
диффузионное 102
Лапласа 194, 284
Максвелла 187, 496
связанных мод 459, 480, 519
характеристическое 178, 185, 188
Условия
граничные для скалярного волнового
уравнения 542
---уравнений Максвелла 497
резонансные 177, 381, 462, 473
слабой направленности 265
Фазовая скорость 178, 511, 544
Формулы сшивания 5 78
Цилиндрическая симметрия 12, 178, 321
Цилиндрические полярные координаты
608
Частота отсечки 194, 285
Число мод
вытекающих 419
направляемых 178, 194
Эйконала уравнение 18, 566
Эйлера теорема 616
Эксцентриситет 304, 318
Электромагнитное поле 496
ОГЛАВЛЕНИЕ
Предисловие авторов к русскому изданию................................ 5
Предисловие редакторов перевода....................................... 6
Предисловие........................................................... 7
ЧАСТЬ I. ЛУЧЕВОЙ АНАЛИЗ МНОГОМОДОВЫХ ОПТИЧЕСКИХ
ВОЛНОВОДОВ ............................................................ 9
Введение ............................................................ 9
Глава 1. Направляемые лучи в планарных волноводах..................... 11
1.1. Планарные волноводы.......................................... 11
Планарные волноводы со ступенчатым профилем................ 12
1.2. Построение лучевых траекторий................................ 13
1.3. Лучевой инвариант............................................ 14
1.4. Лучевые параметры............................................ 15
1.5. Время прохождения луча...................................... 17
Планарные волноводы с градиентным профилем.................. 18
1.6. Построение лучевых траекторий................................ 18
1.7. Лучевой инвариант............................................ 20
1.8. Лучевые параметры........................................... 21
1.9. Время прохождения луча...................................... 22
Слабонаправляюшие волноводы................................. 23
1.10. Параксиальное приближение.................................. 23
Градиентные профили, допускающие аналитические решения...... 24
1.11. Пример. Параболический профиль............................. 24
1-12. Пример. Гиперболический секансный профиль.................. 25
1.13. Пример. Усеченный степенной профиль........................ 26
Несимметричные волноводы.................................... 27
Глава 2. Направляемые лучи в волоконных световодах.................. 28
2.1. Волоконные световоды с круглым сечением.................... 28
Волоконные световоды со ступенчатым профилем................ 29
2.2. Построение лучевых траекторий............................... 29
2.3. Лучевые инварианты.......................................... 31
2.4. Лучевые параметры........................................... 34
2.5. Время прохождения луча...................................... 34
Волоконные световоды с градиентным профилем................. 35
2.6. Построение лучевых траекторий и лучевые инварианты.......... 35
2.7. Классификация лучей......................................... 37
2.8. Лучевые параметры............................................40
2.9. Время прохождения луча.......................................41
Градиентные профили, допускающие аналитические решения.......42
2.10. Пример. Параболический профиль..............................42
2.11. Пример. Усеченный степенной профиль.........................43
Волоконные световоды с некруглым сечением....................44
641
2.12. Лучевые уравнения...........................................
2.13. Пример. Профиль, описываемый однородной функцией............ 46
2.14. Пример. Профиль, описываемый функцией с разделяющимися пере-
менными .......................................................... 47
2.15. Пример. Параболический эллиптический профиль ............... 48
Глава 3. Уширение импульсов........................................ 48
Лучевая дисперсия в планарных волноводах................... 50
3.1. Ступенчатый профиль......................................... 50
3.2. Усеченный степенной профиль................................. 51
Лучевая дисперсия в волоконных световодах.................... 52
3,3. Некруглые волоконные световоды............................ 53
Дисперсия материала и дисперсия профиля...................... 54
3.4. Дисперсия материала......................................... 54
3.5. Дисперсия профиля........................................... 54
3.6. Линейная дисперсия.......................................... 55
3.7. Пример. Волоконный световод со ступенчатым профилем......... 55
3.8. Пример. Волоконные световоды с усеченным степенным профилем. . . 55
3.9. Нелинейная дисперсия........................................ 57
Глава 4. Возбуждение волоконных световодов и форма импульса........ 58
Источники излучения.......................................... 58
4.1. Диффузный, или ламбертов источник............................ 59
4.2. Коллимированный пучок........................................ 60
Прохождение излучения через торец волоконного световода...... 60
4.3. Отражение и преломление...................................... 60
4.4. Прохождение мощности......................................... 61
Диффузное возбуждение........................................ 62
4.5. Полная мощность источника.................................... 62
4.6. Полная мощность направляемых лучей........................... 63
4.7. Пример. Ступенчатый и усеченный степенной профили............ 64
4.8. Неоднородное возбуждение..................................... 65
Возбуждение коллимированным пучком........................... 65
4.9. Пример. Ступенчатый профиль.................................. 66
4.10. Пример. Градиентные профили.................................66
Возбуждение с помощью линзы..................................67
4.11. Коллимированный пучок.......................................67
4.12. Пример. Распределение интенсивности.........................68
4.13. Пример. Косое падение пучка.................................68
4.14. Диффузный источник..........................................69
4.15. Пример. Распределение интенсивности.........................70
4.16. Частично диффузный источник.................................71
Распределение мощности по направляемым лучам.................71
4.17. Вывод функции распределения.................................72
4.18. Функция распределения, зависящая только от 0................73
4.19. Пример. Ступенчатый и усеченный степенной профили...........74
Импульсный отклик............................................75
4.20. Время прохождения луча, зависящее только от 0...............75
4.21. Пример. Ступенчатый профиль.................................76
4.22. Пример. Усеченные степенные профили.........................77
4.23. Время прохождения луча, зависящее от обоих инвариантов......78
4.24. Дисперсия материала.........................................79
642
Глава 5. Нерегулярные волоконные световоды........................ 79
Непрерывно изменяющиеся нерегулярности....................... 80
5-1. Время прохождения луча...................................... 80
5-2. Уравнения лучевой траектории.............................. . 81
5.3. Пример. Волоконный световод со ступенчатым профилем и продольно
изменяющимся показателем преломления сердцевины................... 82
Случайные нерегулярности..................................... 82
5.4. Уменьшение уширения импульса................................ 82
Медленно изменяющиеся волоконные световоды................... 83
5.5. Время прохождения луча...................................... 84
5.6. Пример. Усеченный степенной профиль......................... 86
5.7. Малые нерегулярности........................................ 87
5.8. Пример. Малые изменения радиуса сердцевины.................. 88
5-9. Пример. Малые изменения показателя степени.................. 89
5.10. Адиабатический инвариант.................................... 90
511. Пример. Ступенчатый профиль................................. 91
5.12. Пример. Усеченные степенные профили......................... 92
5.13. Потери на излучение......................................... 93
514. Пример. Ступенчатый волоконный световод с изменяющимся радиу-
сом сердцевины.................................................... 94
5.15. Пример. Световод с усеченным степенным профилем и изменяющим-
ся радиусом сердцевины............................................ 95
Конусные переходы и фокусировка света........................ 95
5.16. Возбуждение коллимированным пучком.......................... 96
5.17. Пример. Параболический переход.............................. 96
5-18. Пример. Линейный переход.................................... 97
519. Возбуждение диффузным источником............................ 98
5.20. Точность приближения для перехода с медленным изменением ра-
диуса............................................................. 99
Резкие нерегулярности и рассеиватели......................... 100
5.21. Распределение мощности направляемых лучей................... 100
5.22. Пример. Диффузионное уравнение............................. 102
5-23. Пример. Рэлеевское рассеяние................................ ЮЗ
Глава 6. Поглощение в материале.......................................105
6.1. Поглощающая среда и затухание...............................105
Поглощение в сердцевине......................................106
6.2. Пример. Сердцевина с однородным поглощением.................107
6.3. Пример. Сердцевина с неоднородным поглощением...............108
Поглощение в оболочке........................................108
6.4. Спадающие поля..............................................108
6.5. Коэффициент прохождения мощности............................109
6.6. Пример. Ступенчатый профиль.................................110
6.7. Градиентные профили.........................................111
6-8- Пример. Усеченный параболический профиль....................112
6.9. Пример. Волоконные световоды с усеченными степенными профи-
лями.........................................................11J
Суммарное поглощение в сердцевине и оболочке.................113
Влияние поглощения на форму импульса.........................114
6.10. Пример. Ступенчатый профиль.................................114
6Л1. Пример. Усеченный параболический профиль....................116
643
Глава 7. Вытекающие лучи...........................................116
Рефрагирующие лучи...........................................117
7-1. Планарный волновод со ступенчатым профилем...................117
7.2. Планарные волноводы с градиентным профилем...................119
7.3. Волоконный световод со ступенчатым профилем..................120
7.4. Волоконные световоды с градиентным профилем..................121
Туннелирующие лучи...........................................122
7-5. Волоконные световоды с градиентным профилем................ 122
7.6. Волоконный световод со ступенчатым профилем..................124
7.7. Затухание туннелирующих лучей................................126
7.8. Пример. Градиентные профили. . ,.............................126
7.9. Пример. Усеченный параболический профиль.....................127
7.10. Пример. Ступенчатый профиль..................................127
7.11. Переход от туннелирующих к рефрагирующим лучам...............128
7.12. Универсальные коэффициенты прохождения.......................129
Некруглые и нерегулярные волоконные световоды................129
7.13. Локальные коэффициенты прохождения мощности..................130
7.14. Границы сердцевины и каустики произвольной кривизны..........130
Поглощающие волоконные световоды.............................132
Глава 8. Пространственно-неустановившийся режим....................133
8-1. Пространственно-неустановившийся и пространственно-установивший-
ся режимы ........................................................133
Излучение из волоконных световодов, возбуждаемых диффузным
источником...................................................135
8.2. Возбуждение вытекающих лучей в волоконных световодах со ступен-
чатым профилем....................................................135
8.3. Пространственно-неустановившийся режим для волоконных свето-
водов со ступенчатым профилем.....................................137
8.4. Возбуждение вытекающих лучей в волоконных световодах с градиент-
ным профилем......................................................139
8.5. Пространственно-неустановившийся режим для волоконных светово-
дов с усеченным параболическим профилем...........................140
Обобщенные параметры.........................................141
8.6. Обобщенный параметр для волоконных световодов со ступенчатым
профилем..........................................................142
8.7. Обобщенный параметр для волоконных световодов с градиентным
профилем........................................................ 143
8.8. Пример. Диффузное возбуждение волоконных световодов со ступен-
чатым профилем................................................... 144
8.9. Пример. Диффузное возбуждение волоконных световодов с усечен-
ным параболическим профилем...................................... 145
Уширение импульса........................................... 146
8.10. Пример. Лучевая дисперсия в волоконных световодах со ступенча-
тым профилем....................................;.................147
8.11. Пример. Лучевая дисперсия в волоконных световодах с усеченным па-
раболическим профилем............................................ 148
Некруглые волоконные световоды.............................. 149
Распределение интенсивности на конце волоконного световода...149
8.12. Пример. Волоконный световод со ступенчатым профилем......... 150
8.13. Пример. Волоконные световоды с усеченным степенным профилем. . . 151
Потери на излучение и поглощение................................. 152
644
8.14. Пример. Волоконный световод со ступенчатым профилем.........152
815. Пример. Волоконный световод с усеченным параболическим про-
филем ............................................................153
Глава 9. Изгибы........................................................153
Изогнутые планарные волноводы................................154
91. Классификация лучей на изгибе................................154
9-2. Затухание световой мощности................................ 156
9-3. Пример. Ступенчатый профиль..................................157
9-4. Пример. Усеченный параболический профиль.....................158
Изогнутые волоконные световоды...............................159
9-5. Пример. Ступенчатый и усеченный параболический профили.......160
Глава 10. Дифракционные явления....................................161
Дифракция пучка света........................................162
10.1. Однородные и гауссовы пучки.................................162
10.2. Удержание света волоконным световодом.......................164
10.3. Применимость геометрической оптики.....•....................165
Влияние дифракции на полное внутреннее отражение.............166
10.4. Продольный сдвиг............................................167
10.5. Время прохождения продольного сдвига.......................168
10.6. Продольный сдвиг в планарных волноводах.....................169
10.7. Предпочтительные лучевые направления........................171
Дифракционные эффекты в произвольных волноводах.............172
ЧАСТЬ II. ВОЛНОВОЙ АНАЛИЗ ОПТИЧЕСКИХ ВОЛНОВОДОВ.............174
Введение...............................................................174
Глава 11. Основные свойства мод........................................176
Волновой анализ распространения света.......................176
11.1. Постоянная распространения и фазовая скорость...............178
11.2. Свойства симметрии составляющих поля........................179
11.3. Поля непоглощающих волноводов...............................179
11.4. Соотношения ортогональности и нормировка....................180
11.5. Ортонормальные моды.........................................181
Энергия и мощность..........................................181
11.6. Запасенные электрическая и магнитная энергии................181
11.7. Поток мощности..............................................182
11.8. Часть мощности моды в сердцевине............................183
11.9. Полная переносимая мощность.................................183
11.10. Часть полной мощности в сердцевине.........................184
Групповая скорость..........................................184
11.11. Групповая задержка................................,........185
Уширение импульса...........................................186
11.12. Уширение импульса в одномодовых волоконных световодах......186
Свойства полей мод..........................................187
11.13. Характеристическое уравнение...............................188
11.14. Решение, выраженное через продольные составляющие поля.....189
11.15. Взаимодействие составляющих поля...........................189
11.16. Гибридная природа полей мод................................190
11.17. Постоянная распространения.................................192
Волноводные параметры и параметры мод.......................192
645
11.18. Частота отсечки моды........................................194
11.19. Число направляемых мод......................................194
11.20. Параметр искажения..........................................195
11.21. Связь с лучевым инвариантом.................................195
Волноводы с поглощением.......................................197
11.22. Затухание мощности..........................................197
Анизотропные волноводы........................................199
11.23. Однородная анизотропная среда............................. 199
11.24. Анизотропные волноводы......................................200
Глава 12. Волноводы, для которых уравнения Максвелла имеют точные ре-
шения ..................................................................201
12.1. Волноводы со ступенчатым профилем показателя преломления....202
Планарные волноводы со ступенчатым профилем показателя прелом-
ления ........................................................203
12.2. Поля мод.....................................................203
12.3. Постоянные распространения...................................206
12.4. Свойства мод.................................................207
12.5. Слабонаправляющие волноводы..................................208
12.6. Разложение полей мод по плоским волнам.......................208
12.7. Асимметричные и многослойные волноводы.......................209
Волоконные световоды со ступенчатым профилем показателя пре-
ломления......................................................210
12.8. Поля мод.....................................................210
12.9. Постоянные распространения...................................211
12.10. Свойства мод................................................218
12.11. Слабонаправляющие волоконные световоды......................222
12.12. Разложение полей мод по плоским волнам......................223
12.13. Многослойные и эллиптические волоконные световоды...........223
Волноводы с градиентным профилем показателя преломления......226
12.14. Пример. ТЕ-моды планарного волновода с градиентным профилем
показателя преломления.............................................226
12.15. Пример. ТМ-моды планарных волноводов с градиентным профилем
показателя преломления.............................................228
12.16. Пример. ТЕ-моды волоконных световодов с градиентным профилем
показателя преломления >......................................... 228
12.17. Пример. ТМ-моды волоконных световодов с градиентным профилем
показателя преломления.............................................230
12.18. Пример. Гибридные моды волоконного световода с градиентным про-
филем показателя преломления.......................................232
Анизотропные волноводы............*...........................233
12.19. Планарный волновод со ступенчатым профилем показателя прелом-
ления .............................................................236
12.20. Одноосный волоконный световод со ступенчатым профилем показа-
теля преломления...................................................238
Глава 13. Слабонаправляющие волноводы...............................240
13.1. Поляризационные явления, обусловленные волноводной структурой . 240
Моды слабонаправляющих волноводов.............................241
13.2. Аппроксимация мод ТЕМ-волнами................................242
13.3. Пространственная зависимость полей мод.............".........242
Векторные свойства полей мод..................................243
646
13.4. Основные и НЕ1т-моды круглых волоконных световодов..........243
13.5. Основные моды волноводов с поперечным сечением произвольной
формы.............................................................244
13.6. Поляризационные поправки к скалярной постоянной распространения 245
13.7. Моды высших порядков круглых волоконных световодов..........246
13.8. Моды высших порядков волноводов с поперечным сечением произ-
водной формы......................................................248
13.9. Моды высших порядков почти круглых волоконных световодов .... 248
Свойства мод слабонаправляющих волноводов....................... 249
13.10. Зависимость поглощения от поляризации......................249
13.11. Поляризационные поправки высших порядков...................252
Анизотропные слабонаправляющие волноводы....................253
13.12. Моды анизотропных волноводов...............................255
13.13. Одномодовые однополяризационные волоконные световоды.......257
Излучение через вытекающие моды в анизотропных световодах...257
13.14. Одномодовые однополяризационные световоды на вытекающих
модах.............................................................257
Глава 14. Волоконные световоды круглого поперечного сечения...........258
Направляемые моды круглых волоконных световодов.............258
14.1. Структура полей мод.........................................259
14.2. Основные и НЕ 1т (/= 0)-моды................................262
14.3. Моды высших порядков (/> 1).................................262
14.4. Пример. Неограниченный параболический профиль показателя пре-
ломления..........................................................263
14.5. Пример. Неограниченный степенной профиль показателя преломления 265
Волоконные световоды со ступенчатым профилем показателя пре-
ломления..........................................................267
14.6. Основные и НЕlm (Z = -моды................................ 267
14.7. Моды высших порядков (/>1) .................................274
Волоконные световоды с оболочкой и градиентным профилем пока-
зателя преломления..........................%...............279
14.8. Пример. Аналитические решения...............................280
14.9. Пример. Степенной профиль показателя преломления волоконного
световода с оболочкой.............................................281
14.10. Профили показателя преломления равного объема..............285
14.11. Свойства основной моды при малых значениях V...............287
Глава 15. Гауссово приближение для круглых волоконных световодов......288
Основные моды...............................................289
15.1. Гауссово приближение........................................289
15.2. Пример. Гауссов профиль показателя преломления..............292
15.3. Пример. Ступенчатый профиль показателя преломления..........295
15.4. Пример. Сглаженные профили показателя преломления...........296
15.5. Поле вдали от оси волоконного световода.....................298
Моды высших порядков........................................299
15.6. Приближение для полей.......................................299
15.7. Пример. Гауссов профиль.....................................299
Приближение эквивалентного волоконного световода со ступенча-
тым профилем ...............................................301
15.8. Основные моды...............................................301
15.9. Диапазон одно модового режима...............................302
647
Глава 16. Волноводы с некруглым поперечным сечением....................303
16.1. Планарные волноводы..........................................303
Эллиптические волоконные световоды с неограниченным параболи-
ческим профилем показателя преломления.......................304
16.2. Основные моды................................................306
16.3. Моды высших порядков......................•..................308
16.4. Почти круглые волоконные световоды...........................309
Аксиально-несимметричные профили, для которых существуют ана-
литические решения скалярного волнового уравнения. ..........310
16.5. Профили показателя преломления, описываемые однородной
функцией...........................................................310
16.6. Профили показателя преломления с разделяющимися переменными . . 311
16.7. Пример. Неограниченный линейный профиль показателя преломления. 311
16.8. Пример. Двойной параболический профиль показателя преломления. . 313
Глава 17. Гауссово приближение для волоконных световодов с поперечным
сечением произвольной формы............................................313
Основные моды................«...............................314
17.1. Гауссово приближение.........................................314
17.2. Пример. Неограниченные степенные профили показателя преломления 316
Волоконные световоды с эллиптическим поперечным сечением.....317
17.3. Малая эллиптичность..........................................318
17.4. Пример. Ступенчатый профиль показателя преломления...........319
17.5. Пример. Гауссов профиль показателя преломления...............320
Глава 18. Моды возмущенных волоконных световодов.......................320
Моды слабонаправляющих возмущенных волоконных световодов . . . 321
18.1. Решение для возмущенных изолированных волоконных световодов . . 322
18.2. Поляризация возмущенных полей................................322
18.3. Однородные изменения профиля показателя преломления..........323
18.4. Пример. Однородные изменения показателей преломления сердцеви-
ны и оболочки......................................................324
18.5. Пример. Трехслойный волоконный световод.....................324
18.6. Пример. Изменение радиуса сердцевины........................325
18.7. Пример. Изолированная неоднородность........................325
18.8. Пример. Волоконные световоды с поглощением..................326
18.9. Пример. Анизотропная сердцевина.............................326
18.10. Пример. Эллиптическая деформация............................327
18.11. Неоднородные изменения профиля показателя преломления.......331
Моды двух параллельных волоконных световодов.................331
18.12. Основные моды оптического волновода, состоящего из двух одина-
ковых волоконных световодов........................................333
18.13. Перекрестная связь между двумя одинаковыми волоконными све-
товодами ..........................................................334
18.14. Пример. Волновод, состоящий из двух одинаковых волоконных све-
товодов со ступенчатыми профилями показателя преломления...........335
18.15. Пример. Волновод с двойным параболическим профилем показателя
преломления........................................................337
18.16. Моды высших порядков в оптическом волноводе, состоящем из
двух одинаковых волоконных световодов..............................338
18.17. Пример. Сложный волновод, состоящий из двух волоконных свето-
водов со ступенчатыми профилями показателя преломления.............339
648
18.18. Основные моды сложного оптического волновода, состоящего из
двух различных волоконных световодов.............................339
18.19. Пример. Сложный волновод, состоящий из двух волоконных свето-
водов со ступенчатыми профилями и почти одинаковыми радиусами
сердцевины.......................................................341
18-20. Перекрестная связь между двумя различными волоконными свето-
водами ..........................................................341
Моды возмущенных волоконных световодов с произвольными про-
филями показателя преломления.............................342
18.21. Решение, полученное методом возмущений.....................342
18.22. Пример. Бесконечно малая неоднородность....................344
18.23. Призер. Изменение радиуса сердцевины.......................345
18.24. Пример. Эллиптическая деформация...........................346
18.25. Пример. Волоконные световоды с поглощением.................346
Глава 19. Волноводы с плавно изменяющимися параметрами................347
Локальные моды..............................................347
19.1. Поля локальных мод..........................................347
19-2. Критерий плавного изменения параметров......................349
19.3. Пример. Неоднородный радиус сердцевины......................351
19.4. Пример. Скрученные эллиптические световоды..................351
Локальные моды двух нерегулярных световодов.................352
19.5. Поля локальных мод . j......................................352
19.6. Пример. Перекрестная связь между одинаковыми световодами....354
Конические ответвители......................................354
19-7. Распространение локальных мод..............................'354
19-8. Перекрестная связь..........................................356
19.9. Критерий плавного изменения параметров......................356
Локальные моды изогнутых световодов.........................357
Многомодовые световоды и лучи...............................357
Глава 20. Возбуждение волоконных световодов...........................358
Возбуждение мод.............................................358
20.1. Амплитуды мод и мощность....................................359
Возбуждение слабонаправляющих световодов....................360
20.2. Поля мод на входном торце световода.........................360
20.3. Поля возбуждающего пучка....................................361
20.4. Гауссов и однородный пучки .....’...........................362
20.5. Амплитуда мод и мощность....................................363
Волоконный световод с неограниченным параболическим профи-
лем показателя преломления..................................364
20.6. Пример. Соосный гауссов пучок...............................364
20.7. Пример. Наклонный гауссов пучок.............................364
20.8* Пример. Смещенный гауссов пучок.............................365
20-9. Пример. Соосный однородный пучок............................365
20.10. Пример. Наклонная плоская волна............................366
Возбуждение одномодовых световодов..........................367
20.11. Соединение световодов......................................367
Волоконные световоды со ступенчатым профилем показателя пре-
ломления....................................................368
20.12. Пример. Наклонный однородный пучок.........................368
20.13. Пример. Соосный однородный пучок...........................369
649
20.14. Сравнение с геометрической оптикой..........................370
Возбуждение с помощью линз...................................371
20.15. Пример. Неограниченный параболический профиль...............371
20.16. Пример. Гауссово приближение................................372
Диффузное возбуждение........................................372
20 I7- Пример Одномодовыс световоды.............................373
2018. Пример. Многомодовые световоды...............................374
20.19. Погрешность лучевого анализа................................375
Глава 21- Источники излучения внутри волоконных световодов.............376
Возбуждение направляемых мод............................... 376
21.1. Амплитуда и мощность мод.....................................377
21.2 Слабонаправляющие волоконные световоды.......................378
21.3 Пример. Диполь в произвольном волоконном световоде...........378
21.4. Пример. Поперечный диполь внутри слабонаправляющего волокон-
ного световода.....................................................378
21.5 Пример. Продольный диполь внутри слабонаправляющего волокон-
ного световода.....................................................379
21.6. Пример. Трубчатый источник тока..............................380
Возбуждение поля излучения................................. 381
21-7. Слабонаправляющие волоконные световоды.......................381
21.8. Приближение свободного пространства..........................383
21.9. Пример. Поле излучения диполя................................. . 384
21.10. Пример. Излучение трубчатого источника......................385
21.11. Поправка, обусловленная профилем показателя преломления воло-
конного световода..................................................387
21.12. Корректирующий множитель....................................387
21.13. Пример. Световод со ступенчатым профилем показателя преломления 388
21.14. Пример. Скорректированное выражение для излучения трубчатого
источника..........................................................39U
Глава 22. Нерегулярные волоконные световоды............................390
Представление неоднородностей вынужденными источниками тока . . 391
22.1. Произвольные неоднородности..................................392
22.2. Малые неоднородности.........................................392
Потери основной моды на излучение............................393
22.3. Пример. Изолированная неоднородность.........................393
22.4. Пример. Случайное распределение неоднородностей..............394
22.5. Пример. Синусоидально возмущенная граница....................395
Перераспределение мощности между направляемыми модами.......396
22.6. Одномодовые волоконные световоды с произвольным профилем по-
казателя преломления............................................. 396
22.7. Слабонаправляющие одномодовые световоды.................... 398
22.8. Пример. Изолированная неоднородность.........................398
22.9. Пример. Синусоидально возмущенная граница....................399
Плавно изменяющиеся произвольные неоднородности..............399
22Л0. Представление локальных мод вынужденными токами.............400
22.11. Перераспределение направляемой мощности.....................400
Глава 23. Изгибы.......................................................401
Изгибы с постоянным радиусом кривизны........................402
23.1. Физические механизмы потерь на излучение.....................402
650
23.2. Модель излучения.............................................402
23.3. Слабонаправляющие световоды..................................403
23.4. Излучение изогнутой антенны..................................404
23.5. Пример. Ступенчатый профиль показателя преломления...........406
23.6. Пример. Градиентный профиль показателя преломления...........406
23.7. Излучение изогнутых волоконных световодов....................407
23.8. Пример. Ступенчатый профиль показателя преломления...........408
23.9. Пример. Градиентные профили показателя преломления...........409
Переходные потери............................................409
23.10. Изгибы с переменным радиусом................................410
23.11. Микроизгибы.................................................411
23.12. Наклоны и смещения осей состыкованных световодов............412
Глава 24. Вытекающие моды..............................................412
24.1. Излучение вблизи оси световода...............................413
24.2. Эвристический подход.........................................413
24.3. Представление поля излучения полями вытекающих мод и про-
странственной волны 414
Характеристики вытекающих мод................................415
24.4. Параметры мод................................................415
24.5. Поля мод.....................................................416
24.6. Каустика излучения ,.........................................416
24.7. Классификация вытекающих мод.................................418
24.8. Разложение на плоские волны..................................418
24.9. Слабонаправляющие волноводы..................................418
24.10. Число вытекающих мод...................................... 419
Мощность и затухание.........................................419
24.11. Качественное физическое описание............................419
24.12. Направляемая и излучаемая мощности..........................420
24.13. Часть направляемой мощности в сердцевине....................422
24.14. Коэффициент затухания мощности..............................422
Ортогональность и нормировка.................................423
24.15. Соотношения ортогональности.................................424
24.16. Коэффициент нормировки......................................424
24.17. Проблемы возбуждения и возмущения...........................425
Решение характеристического уравнения........................426
24.18. Пример. Аналитическое решение для волоконного световода со сту-
пенчатым профилем показателя преломления...........................426
24.19. Пример. Численное решение для волоконного световода со ступен-
чатым профилем показателя преломления..............................427
24.20. Пример. Планарный волновод со ступенчатым профилем показате-
ля преломления.....................................................430
Применения вытекающих мод....................................430
24.21. Пример. Поперечное распределение интенсивности излучения в даль-
нем поле...........................................................431
24.22. Пример Синусоидальный линейный источник.....................432
24.23. Пример. Осевая синусоидальная неоднородность................432
Глава 25. Моды излучения...............................................435
Общие свойства...............................................435
25.1. Представление полей мод......................................436
25.2. Постоянная распространения...................................436
651
25.3. Разложение поля излучения.....................................436
25.4. Ортогональность и нормировка..................................437
25.5. Мощность поля излучения.......................................438
25.6. Возбуждение мод излучения.....................................439
Моды излучения в приближении свободного пространства..........440
25.7. Пример. Решение в цилиндрических координатах..................441
Структура мод излучения.......................................442
25.8. Пример. Волоконный световод со ступенчатым профилем показате-
ля преломления.....................................................443
Слабонаправляющие волноводы...................................445
25-9. Пространственная зависимость полей............................445
25.10. Векторные свойства полей мод излучения.......................446
25.11. Пример. Волоконный световод со ступенчатым профилем показате-
ля преломления.....................................................447
Излучение источника в ’’свободном пространстве”...............449
25.12. Пример. Излучение диполя.....................................449
25.13. Пример. Трубчатый источник излучения.........................450
Излучение источников, находящихся внутри световодов...........451
25.14. Пример. Диполь внутри световода со ступенчатым профилем пока-
зателя преломления.................................................451
25.15. Пример. Трубчатый источник внутри световода со ступенчатым про-
филем показателя преломления.......................................451
25.16. Влияние оболочки конечной толщины............................452
Глава 26. Разложение поля излучения.....................................452
Интегральное представление и разложение.......................453
26.1. Сингулярности подынтегрального выражения......................453
26.2. Замена переменных интегрирования..............................455
26.3. Метод наискорейшего спуска....................................455
Вклад поля вытекающих мод в поле излучения....................456
Вклад поля пространственной волны в поле излучения............457
Глава 27. Связь мод.....................................................458
Теория связанных мод..............................•...........459
27.1. Уравнения связанных мод.......................................459
27.2. Слабонаправляющие волоконные световоды........................460
27.3. Пример. Слабая связь мод......................................461
Сильная связь мод.............................................462
Синусоидальные возмущения.....................................463
27.4. Пример. Две вперед-распространяющиеся моды....................463
27.5. Пример. Одна вперед- и одна назад-распространяющаяся моды.....466
Глава 28. Связь локальных мод...........................................467
Теория связанных локальных мод................................468
28.1. Уравнения связанных локальных мод.............................468
28.2. Слабая связь мод..............................................470
28.3. Критерий медленного изменения параметров......................470
28.4. Пример. Волоконный световод переменного радиуса со ступенча-
тым профилем показателя преломления................................471
28.5. Пример. Скрученный эллиптический волоконный световод..........472
Локальные моды излучения......................................474
652
28.6. Пример. Конусообразный участок световода со ступенчатым про-
филем показателя преломления.....................................475
Сложные оптические волноводы...............................477
28.7. Пример. Конусообразные ответвители.........................477
28-8. Пример. Одинаковые волоконные световоды....................478
Глава 29. Перекрестные помехи........................................479
29-1. Два способа описания перекрестных помех....................479
Два параллельных волоконных световода......................479
29.2. Вывод уравнений связанных мод..........................•. . . 480
29.3. Идентичные и почти идентичные волоконные световоды.........482
29.4. Пример. Идентичные волоконные световоды со ступенчатым про-
филем показателя преломления.....................................483
29.5. Пример. Идентичные волоконные световоды с гауссовым профи-
лем показателя преломления.......................................484
29.6. Пример. Волоконные световоды со слегка различающимися пара-
метрами и ступенчатыми профилями показателя преломления..........485
29.7. Пример. Волоконные световоды с небольшим поглощением.......486
29-8. Пример. Многомодовые световоды.............................486
Два волоконных световода с медленно меняющимися параметрами . . 487
29.9. Уравнения связанных мод.................................. 487
29.10. Решение уравнений связанных мод...........................488
29.11. Пример. Идентичные волоконные световоды...................489
29.12. Пример. Конусообразные ответвители........................489
Пучки световодов...........................................490
29.13. Пример. Периодическое возбуждение пучка, состоящего из неограни-
ченного числа световодов.........................................490
29.14. Пример. Поглощение в пучке, состоящем из неограниченного числа
световодов..................................................... 492
29.15. Пример. Возбуждение одного световода в пучке, состоящем из нео-
граниченного числа одномодовых световодов........................493
29.16. Пример. Многоугольный пучок, состоящий из конечного числа све-
товодов..........................................................494
ЧАСТЬ III. ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ...............................496
Введение.............................................................496
Глава 30. Уравнения Максвелла........................................496
3 0.1. Поля трансляционно-инвариантных волноводов............497
30.2. Соотношения между составляющими полей......................497
30.3. Представление поперечных полей через продольные поля.......498
30.4. Поля непоглощающих волноводов..............................499
30.5. Вперед-и назад-распространяющиеся поля.....................499
Векторные волновые уравнения...............................500
30.6. Декартовы составляющие полей...............................500
30.7. Однородные векторные волновые уравнения....................501
30-8- Уравнения для продольных составляющих......................502
Поглощающая среда..........................................503
30.9. Поглощаемая мощность.......................................503
Анизотропная среда.........................................503
30.10. Векторные волновые уравнения..............................504
653
30.11. Планарные волноводы.........................................504
30.12. Одноосные волноводы..........................................505
30.13. Поле, поляризованное параллельно главным осям................505
Глава 31. Методы мод для уравнений Максвелла............................506
Теорема взаимности............................................506
31.1. Сопряженная форма.............................................506
31.2. Несопряженная форма...........................................508
31.3. Ортогональность мод...........................................509
31.4. Интегральные соотношения для постоянной распространения.......510
31.5. Запасенные электрическая и магнитная энергии..................511
31.6. Фазовая и групповая скорости..................................511
Возбуждение мод источниками тока..............................513
Методы мод для регулярных волноводов..........................514
31.7. Постоянные распространения....................................514
31.8. Поля мод......................................................515
31.9. Амплитуды мод............................................... 516
31.10. Слабовозмущенные волноводы...................................517
Методы мод для нерегулярных волноводов........................517
31.11. Уравнения связанных мод......................................517
31.12. Физическое рассмотрение......................................519
Локальные моды................................................520
31.13. Поля в нерегулярных волноводах...............................520
31.14. Уравнения связанных локальных мод............................521
31.15. Альтернативная форма коэффициентов связи.....................522
31.16. Вывод уравнений связанных мод на физическом уровне...........524
Глава 32. Приближение слабонаправляющего волновода......................525
Векторное волновое уравнение................................ 525
32.1. Разложение полей направляемых мод.............................526
32.2. Вывод разложений поля.........................................527
32-3. Физическая интерпретация предельного приближения при А -> 0...529
32.4. Постоянные распространения....................................530
Направления векторов поля направляемых мод....................532
32.5. Волноводы с некругцым поперечным сечением.....................532
32.6. Круглые волоконные световоды..................................534
32.7. Свойства симметрии мод высших порядков в круглых волоконных
световодах.........................................................535
32.8. Альтернативное представление для мод круглых волоконных све-
товодов............................................................537
32.9. Световоды с почти круглым поперечным сечением.................537
32.10. Поправки высшего порядка к полям мод.........................538
Векторное волновое уравнение для волноводов с источниками....539
Моды излучения................................................540
32.11. Ортогональность и нормировка.................................540
Глава 33. Методы мод для решения скалярного волнового уравнения........541
33.1. Скалярное волновое уравнение..................................541
Направляемые моды как решение скалярного волнового уравнения . . 542
33.2. Ортогональность и нормировка..................................542
33.3. Интегральные выражения для постоянной распространения.........543
33.4. Фазовая и групповая скорости..................................544
33.5. Соотношения взаимности........................................545
33.6. Аналитические выражения для постоянных распространения........546
Моды излучения как решение скалярного волнового уравнения....547
33.7. Ортогональность и нормировка..................................547
33.8. Вытекающие моды...............................................548
Методы мод для анализа регулярных волноводов..................548
33.9. Поля мод и постоянные распространения.........................548
654
33.10. Слабовозмущенные волноводы..................................549
Методы мод для нерегулярных волноводов.......................549
33.11. Уравнения связанных мод.....................................550
Локальные моды...............................................551
33.12. Уравнения связанных локальных мод.......................... 551
33.13. Альтернативная форма коэффициентов связи....................553
Возбуждение мод источниками тока.............................554
Глава 34. Методы функции Грина.........................................556
Поле произвольно распределенных токов........................556
34.1. Вывод из теоремы взаимности..................................556
34.2. Представление векторного потенциала для произвольных волокон-
ных световодов . . ............................................. 558
34.3. Представление векторного потенциала для слабонаправляющихся
волоконных световодов.............................................559
34.4. Функция Грина свободного пространства........................560
34.5. Трубчатые источники в слабонаправляющих волоконных световодах . 560
34.6. Корректирующий множитель....................................561
34.7. Пример. Ступенчатый профиль показателя преломления...........562
Применение теории возмущений.................................563
34.8. Пример. Эллиптические волоконные световоды с малым эксцен-
триситетом........................................................564
34.9. Пример. Поправки к дальнему полю.............................564
Глава 35. Лучи и локальные плоские волны...............................565
Локальные плоские волны......................................565
35.1. Однородная среда.............................................566
35.2. Закон Снелля.................................................566
35.3. Медленно изменяющаяся среда..................................567
35 4. Уравнений составляющих для траекторий лучей. .............569
Описание потерь с помощью локальных плоских волн.............570
35.5. Прохождение мощности и коэффициенты затухания................571
35.6. Плоские границы раздела......................................572
35.7. Плоские границы раздела ме>ВДУ поглощающими средами..........574
35.8. Решения скалярного волнового уравнения методом ВКБ...........576
35.9. Плоские каустики и туннелирование лучей.................... 577
35.10. Плоские каустики и поглощающая среда........................579
35.11. Непрерывные и разрывные профили........................... 581
35.12. Цилиндрические поверхности раздела и каустики...............582
35.13. Цилиндрические поверхности раздела, каустики и поглощающая среда 586
35.14. Поверхности раздела и каустики, определяемые двумя радиусами
кривизны........................................................ 586
35.15. Поля в окрестности каустик............................. • • 588
Глава 36. Лучи и асимптотическое описание мод......................589
Лучевое представление моды...................................590
36.1. Планарный волновод со ступенчатым профилем показателя прелом-
ления 590
36.2. Волоконный световод со ступенчатым профилем показателя прелом-
ления ............................................................591
36.3. Лучевое представление для свободного пространства............593
Асимптотическое описание распространения мод.................594
36.4. Поля мод.....................................................594
36.5. Постоянные распространения...................................594
36.6. Планарный волновод со ступенчатым профилем показателя прелом-
ления 594
36.7. Волоконный световод с неограниченным параболическим профи-
лем показателя преломления........................................595
655
36.8. Неограниченные степенные профили............................597
36.9. Время прохождения...........................................597
36.10. Поглощающие волноводы......................................598
36.11. Вытекающие моды и вытекающие лучи..........................600
Число мод в многомодовых волноводах.........................601
36.12. Планарный волновод со ступенчатым профилем показателя прелом-
ления ............................................................602
36.13. Волоконный световод со ступенчатым профилем показателя прелом-
ления ............................................................602
Сдвиг поля в изогнутом волоконном световоде.................603
36.14. Вывод эффективного профиля.................................604
36.15. Пример. Гауссово приближение...............................605
Глава 37. Математические формулы......................................606
37.1. Тригонометрические, гиперболические и связанные с ними функции. . 606
37.2. Векторы, векторные операторы и интегральные теоремы.........607
37.3. Функции Бесселя.............................................609
37.4. Интегралы от функций Бесселя................................612
37.5. Прочие функции и интегралы................................ 613
Список литературы.....................................................617
Список работ, переведенных на русский язык, и работ советских авторов.634
Дополнительный список литературы . ...................................634
Предметный указатель................................................. 635
Монография
АЛАН СНАЙДЕР, ДЖОН ЛАВ
ТЕОРИЯ ОПТИЧЕСКИХ волноводов
Заведующая редакцией О. В. Толкачева
Редакторы: С. Н. Удалова, С. Т, Симонова
Художественный редактор Т. В. Бусарова
Переплет художника А. А. Соломатина
Технический редактор Л. А. Горшкова
Корректор Л. С. Глаголева
ИБ № 1320
Подписано в печать 31.07.87 Формат 60x90/16 Бумага офс. № 1 Гарнитура
’’Пресс-роман” Печать офсетная Усл. печ. л. 41,0 Усл. кр.-отт. 41.50 Уч.-изд. л. 44,58
Тираж 5000 экз. Изд. № 21479 Зак № 37 Цена 5 р. 60 к.
Издательство ’’Радио и связь”. 101000, Москва, Почтамт, а/я 693
Московская типография № 4 Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли.
129041, Москва, Б. Переяславская ул., д. 46
Таблица I
Некоторые параметры поля и среды
€ = €0И2 Диэлектрическая проницаемость
£0 Диэлектрическая проницаемость свободного пространства
До Магнитная восприимчивость свободного пространства
1 0) С~(«оДо)’/2 * Скорость света в свободном пространстве
со — кс Угловая частота
ехр( - icot) Временная зависимость
Параметры мод
Точные выражения (лсо , пс1 — произвольные) В приближении слабонаправляющего волновода {пео ъ пс1)
Постоянная распространения гч гч ’—‘Io. II 1 ( 17 2 ~ )1/2 р = -{ — -и2> р р ( 2Д J
Параметр моды в сердцевине 1/ = р(к2п^ ~Р2)'12 U = р(к2п£, -р2)1'2
Параметр моды в оболочке (направляемые моды) W = р(Р2 -к2^)*'2 W = Р(р2 -fc2^)1/2
Параметр моды в оболочке (моды излучения) Q = р(к2п& — Д2)112 = iW Q = р(к2^ ~р2)'12 - iW
Соотношения между волноводным параметром и параметрами мод V2 = l/2+IF2 = U2 — Q2 v2 = u2+iy2 = U2-Q2
Условие отсечки и = К= К; ^ = 0 V = V= К; (Г = 0
Диапазон существования направляемых мод кп^ < Р кп^ к^ < р < кп^
Диапазон существования мод излучения 0 р < ktici 0 Р <кп^
Таблица I
Лучевые параметры
Числовая апертура
{«2(И-"с1}1/2 ? Локальная числовая апертура >
С п2 Р/2 0c(r) = sin‘4 1--—-> 1 п W J - 1 f Лс1 1 = cos 1 < —— > 1 "(0 J Локальный критический угол скольжения
Угол между траекторией луча и осью
0Дг) Угол между проекцией траектории на поперечное сечение световода и азимутальной осью
<х(г) Угол между траекторией и радиальным направлением
J = n(r) cos вх(г) Осевой инвариант
Т= - n(r) sin 0z(r) cos 0Лг) Р Азимутальный инвариант
ГК Радиус внутренней каустики
г>р Радиус каустики точек поворота
рТ ГаЛ (п2.-72),/2 Радиус каустики излучения
г₽=й Полупериод траектории луча, отсчитываемый вдоль оси световода
N = - zp Число отражений, или точек поворота на единице длины световода
Lp Геометрическая длина пути луча на полупериоде траектории
io Оптическая длина пути луча на полупериоде траектории
Локальная скорость света
t Время прохождения луча
Таблица I
Параметры волновода или световода
n(x,y) or n(r) Профиль показателя преломления
л2(х,у) = п^,{1 -2Д/(х,у)} "2(г) = "»{1 -2ДДг)} Представление профиля
<3п п‘=п~лГа Групповой показатель
Л2О-И2 sin20c Л* - 2 Параметр высоты профиля
0С= sin-41 -^-1 ' = cos' 4 —) I \"со/ Критический угол скольжения
(/'0) Максимальное значение показателя преломления в сердцевине
ис1 =Псо(1-2Д)1/2 (/=1) Однородный показатель преломления оболочки
S = 1-/ Форма профиля
п= (1-лал= хал J л, J л* Объем профиля
Неограниченное поперечное сечение
Поперечное сечение сердцевины
p Радиус сердцевины (для градиентных световодов - полуширина)
Длина волны в свободном пространстве
_ In _ V ~ a ~ ри^гд)1'2 Волновое число в свободном пространстве
V = M"t-"ci)I/2 = крМ2Д)1/2 == kpnco sin 0C Волноводный, или волоконный параметр
"co = "cl or Д < 1 A ~ "co-"cl Д = "co / и2 V/2 I n \ 0CS (2Д)1'2 1-~ ) scos"‘I — I \ nco / \ПСО/ Приближение слабонаправляющего волновода, или параксиальное приближение
Таблица I
Некоторые параметры поля и среды
€ = €0И2 Диэлектрическая проницаемость
£0 Диэлектрическая проницаемость свободного пространства
До Магнитная восприимчивость свободного пространства
1 со С ~ (СоЯо)111 к Скорость света в свободном пространстве
со — кс Угловая частота
ехр(-шя) Временная зависимость
Параметры мод
Точные выражения (псо ' пс1 ~ произвольные) В приближении слабонаправляющего волновода (псо ъ ncJ)
Постоянная распространения 1 (V2 )1/2 Р 1 2Д J . 1 (г2 - )1/2 Р = _< — -и2У Р 1 2Д J
Параметр моды в сердцевине V = p(k2r£ -р1)112 V = р(к2п^-P2)ti2
Параметр моды в оболочке (направляемые моды) И,= р(Р2-к2г$)212 W = р(Р2 -к2^)'12
Параметр моды в оболочке (моды излучения) Q = р(к2п^ — Р2)112 ~ iW Q = р(к2^ -р2)'12 = iW
Соотношения между волноводным параметром и параметрами мод V2 = U2+W2 = U2-Q2 V2 = 1/2+Й'2 = и2-С2
Условие отсечки [/= Г= Гс; W = 0 и = Г = К; fT = O
Диапазон существования направляемых мод кц-t < р кп^ bid < Р < кп^
Диапазон существования мод излучения 0 < Р < /сця 0 Р < кп^