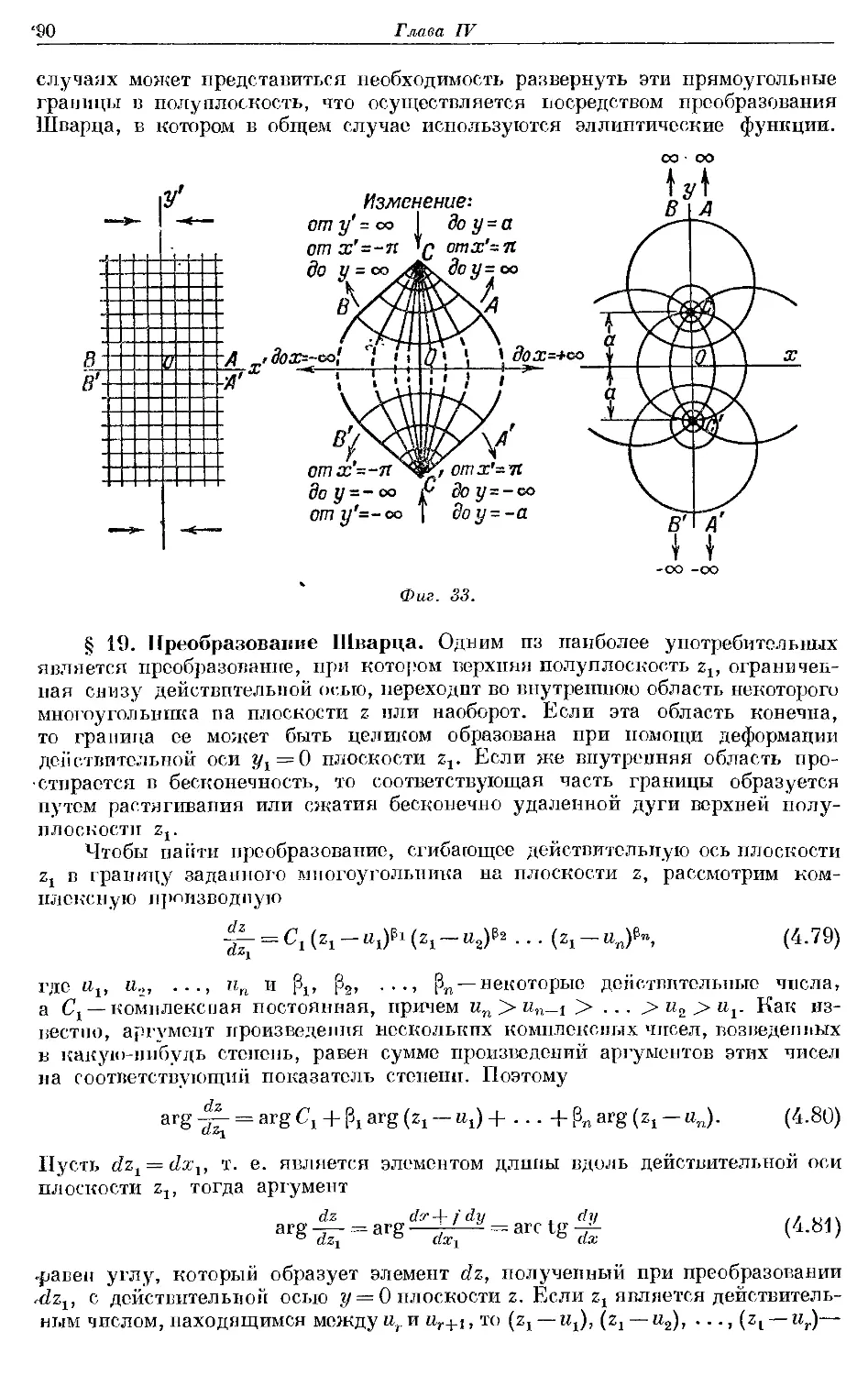
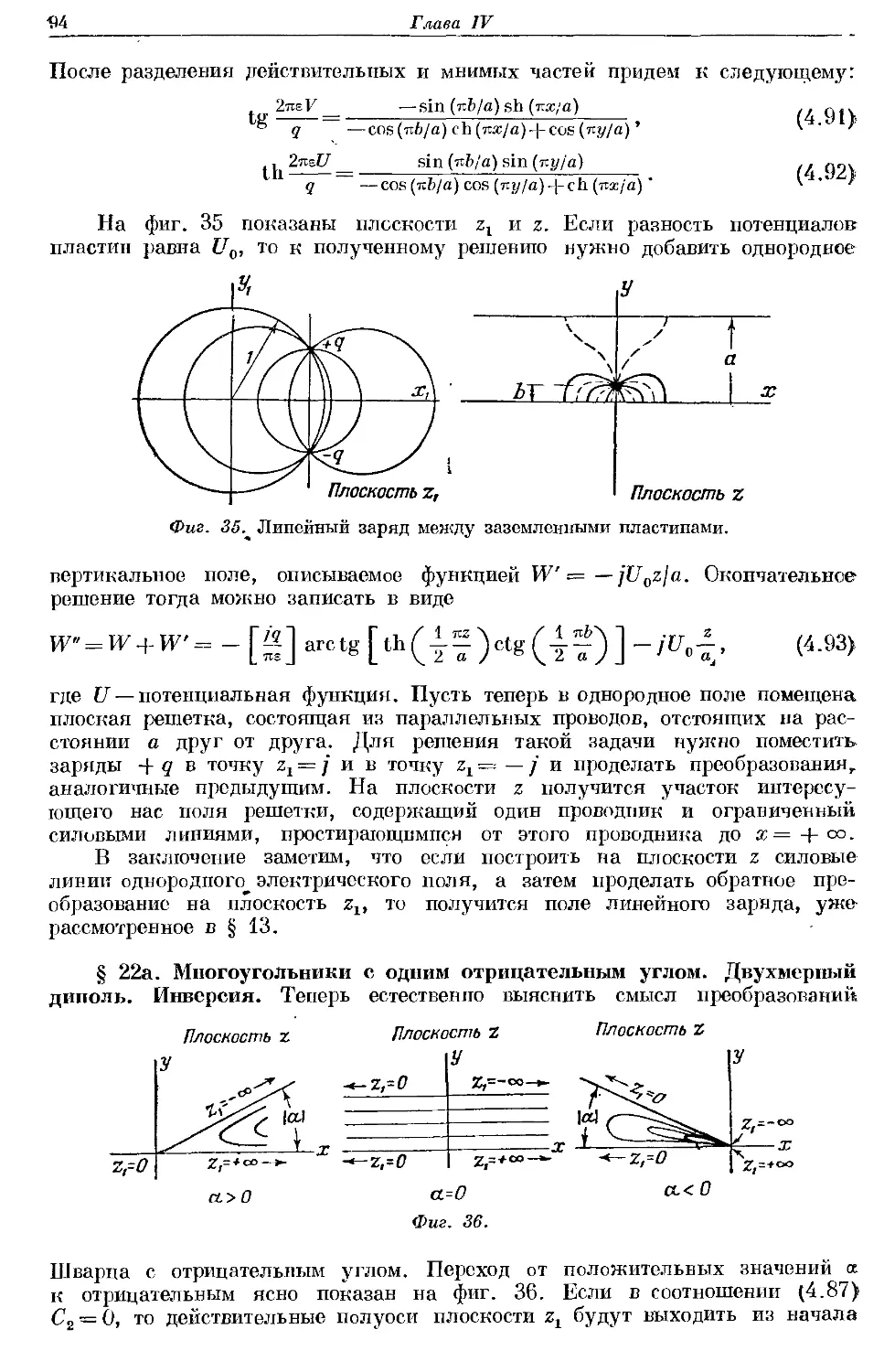
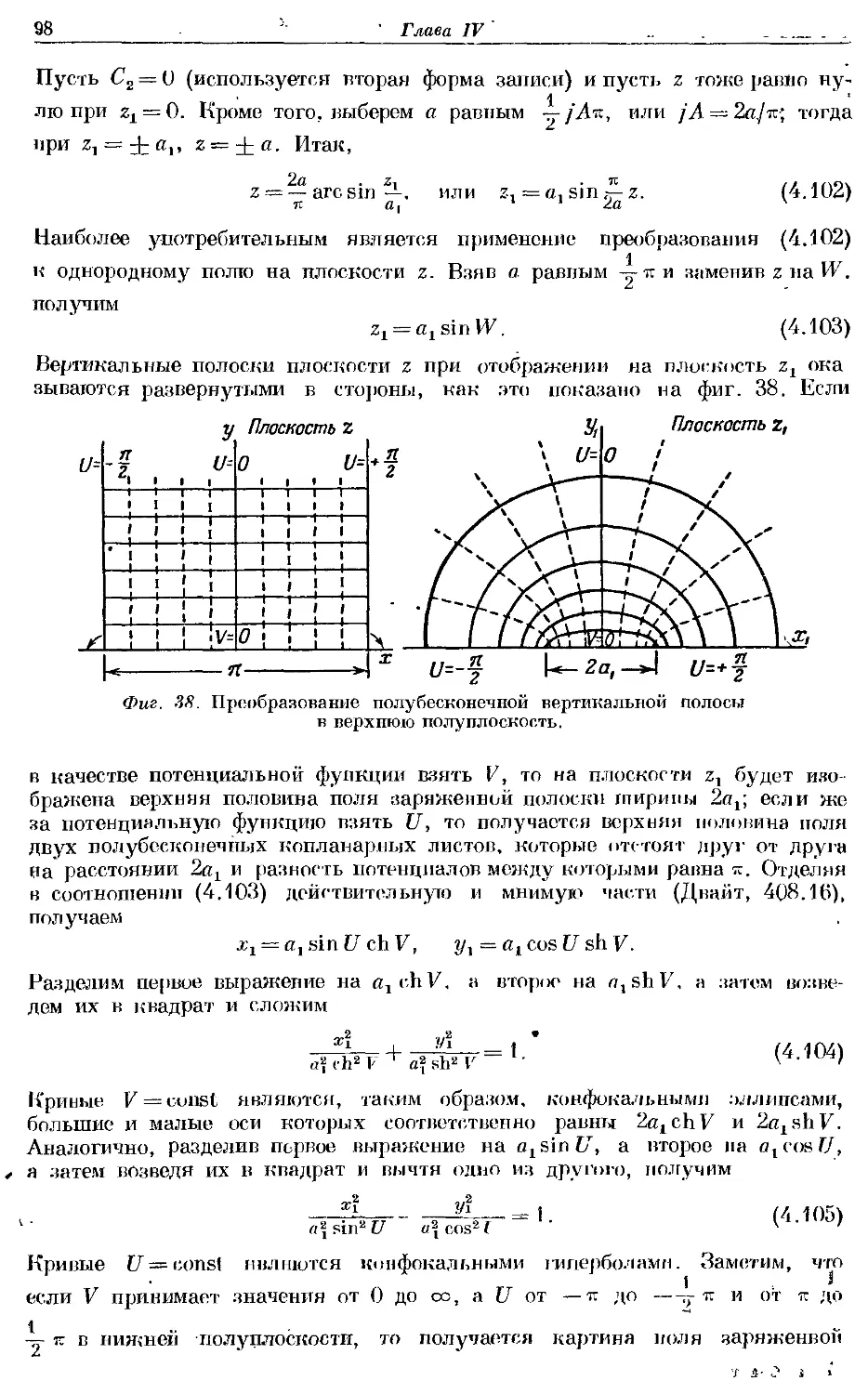
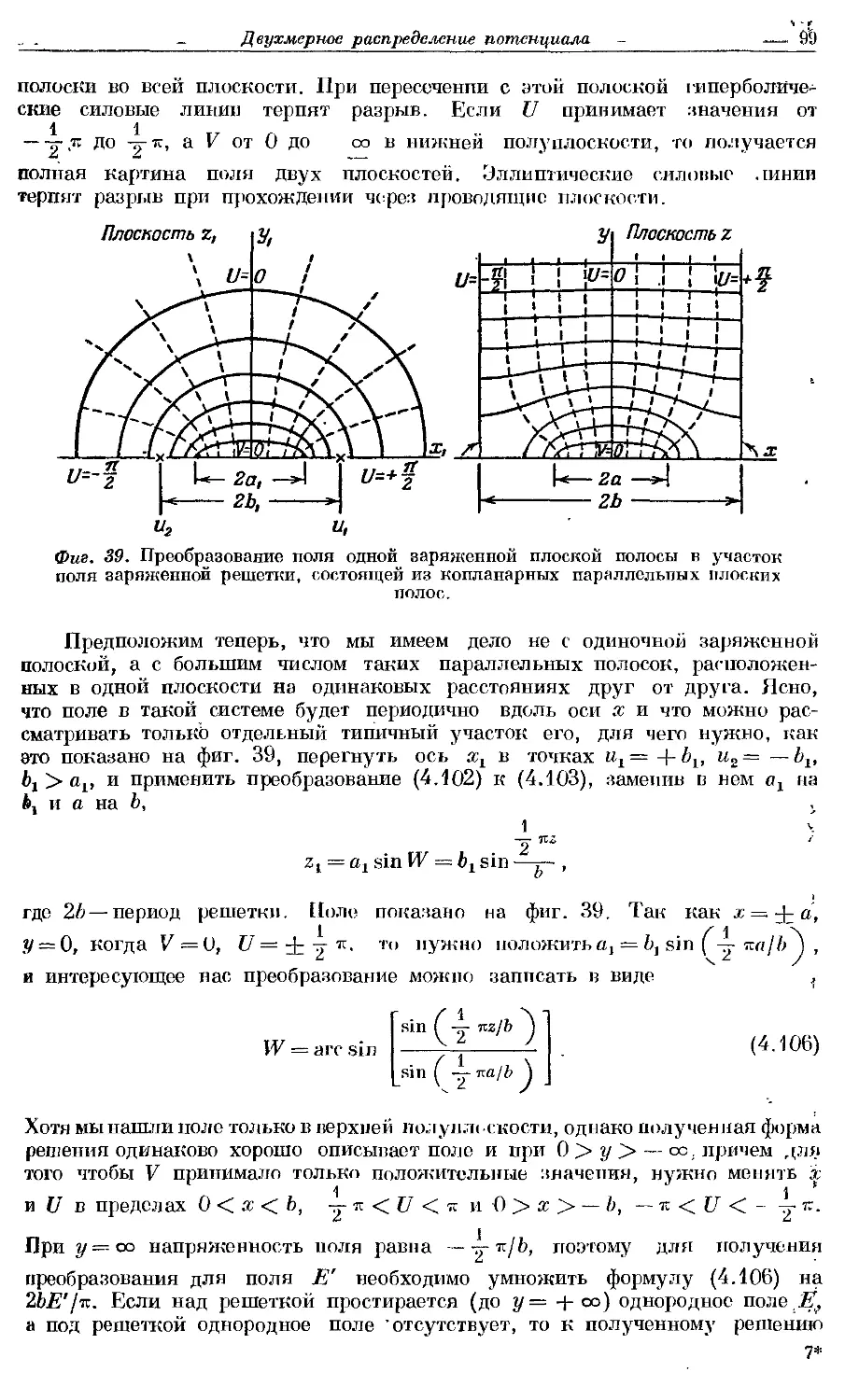
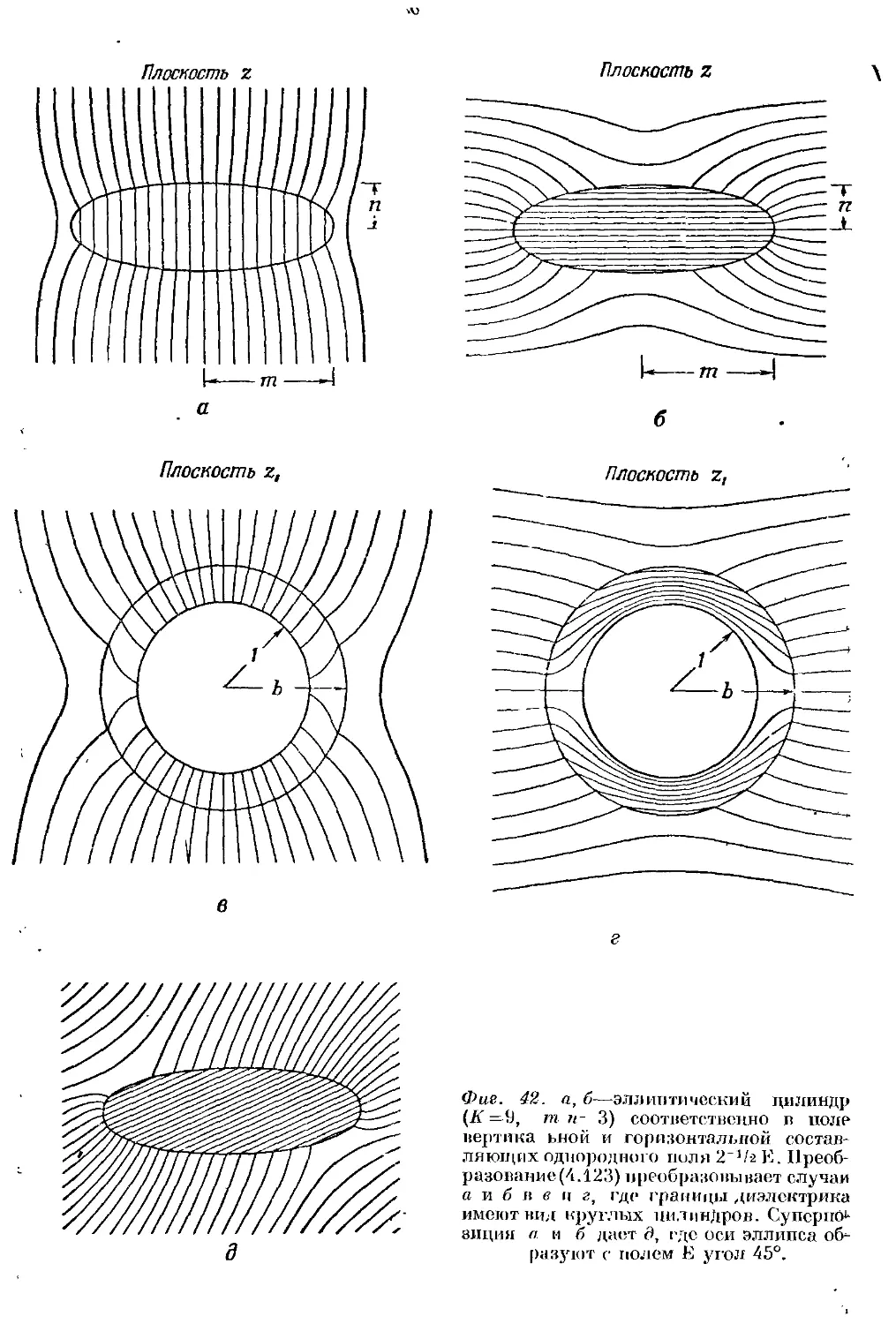
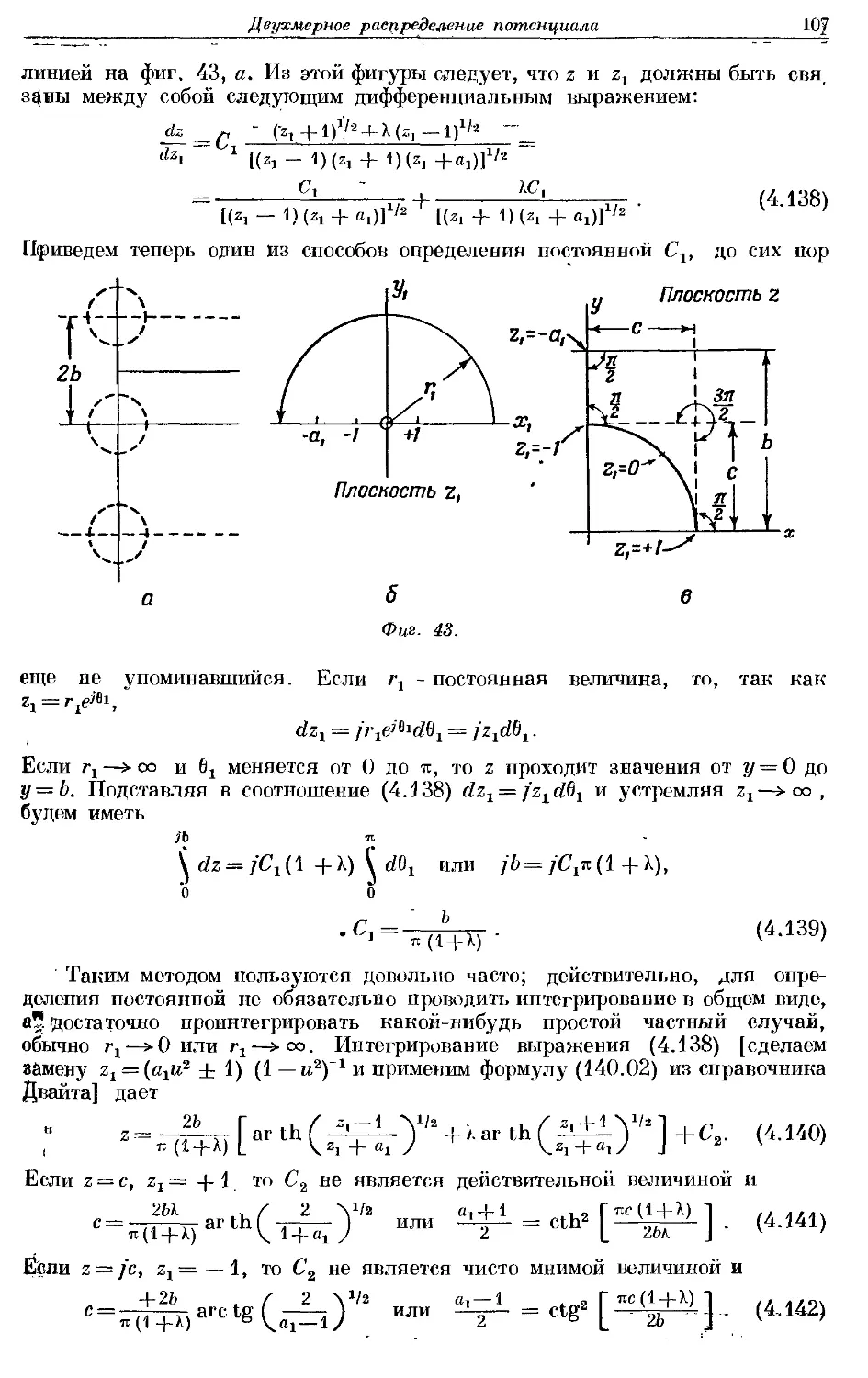
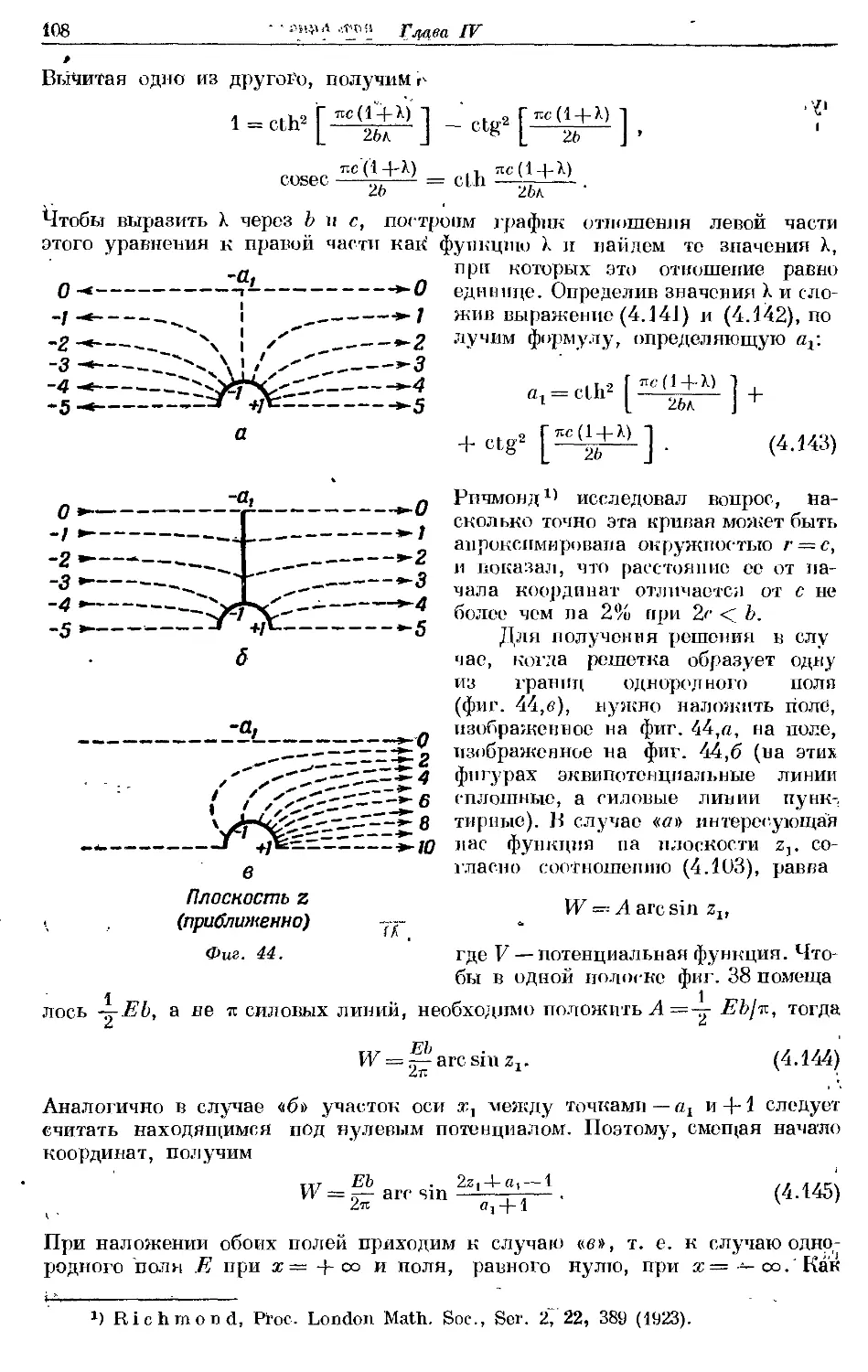
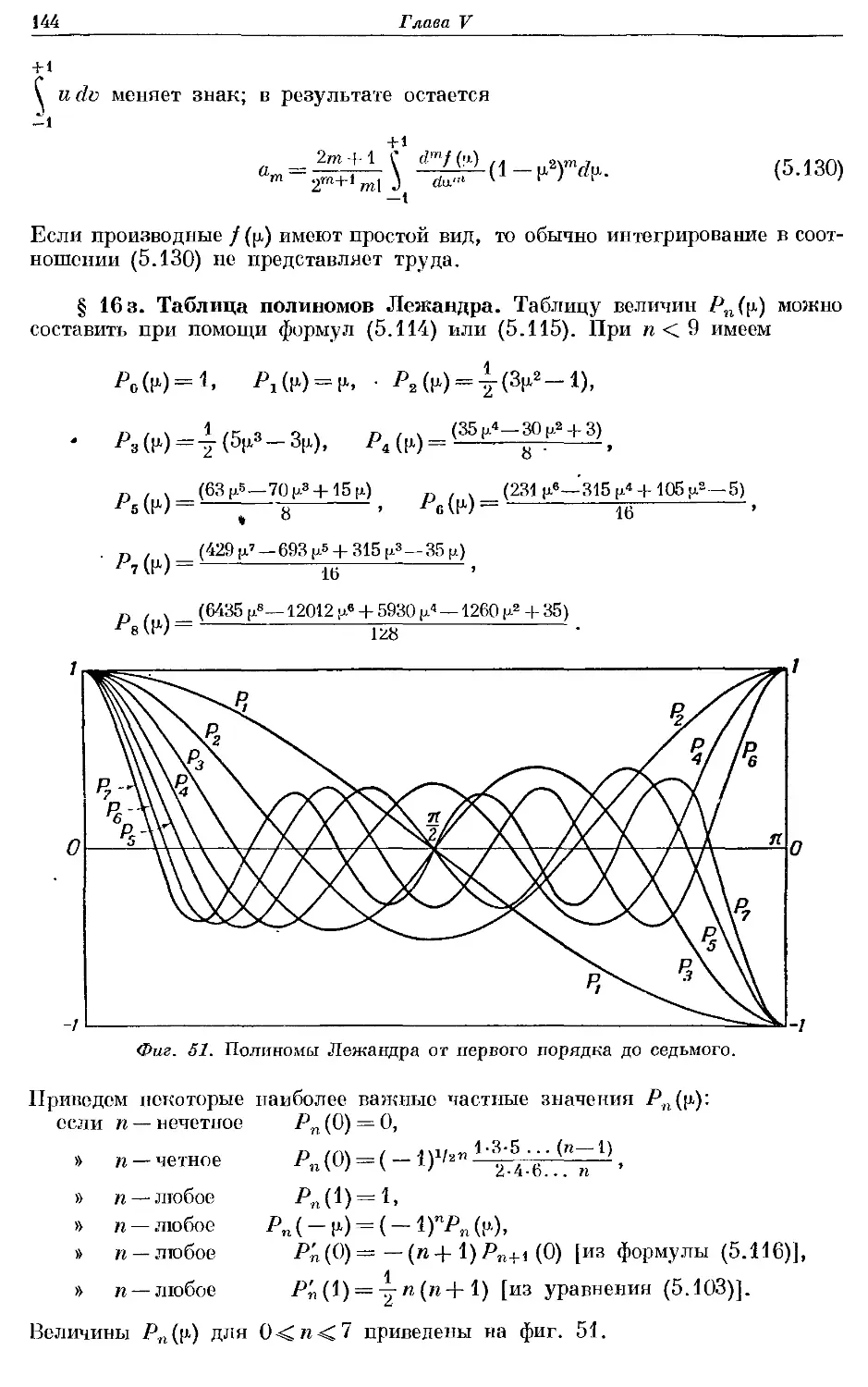
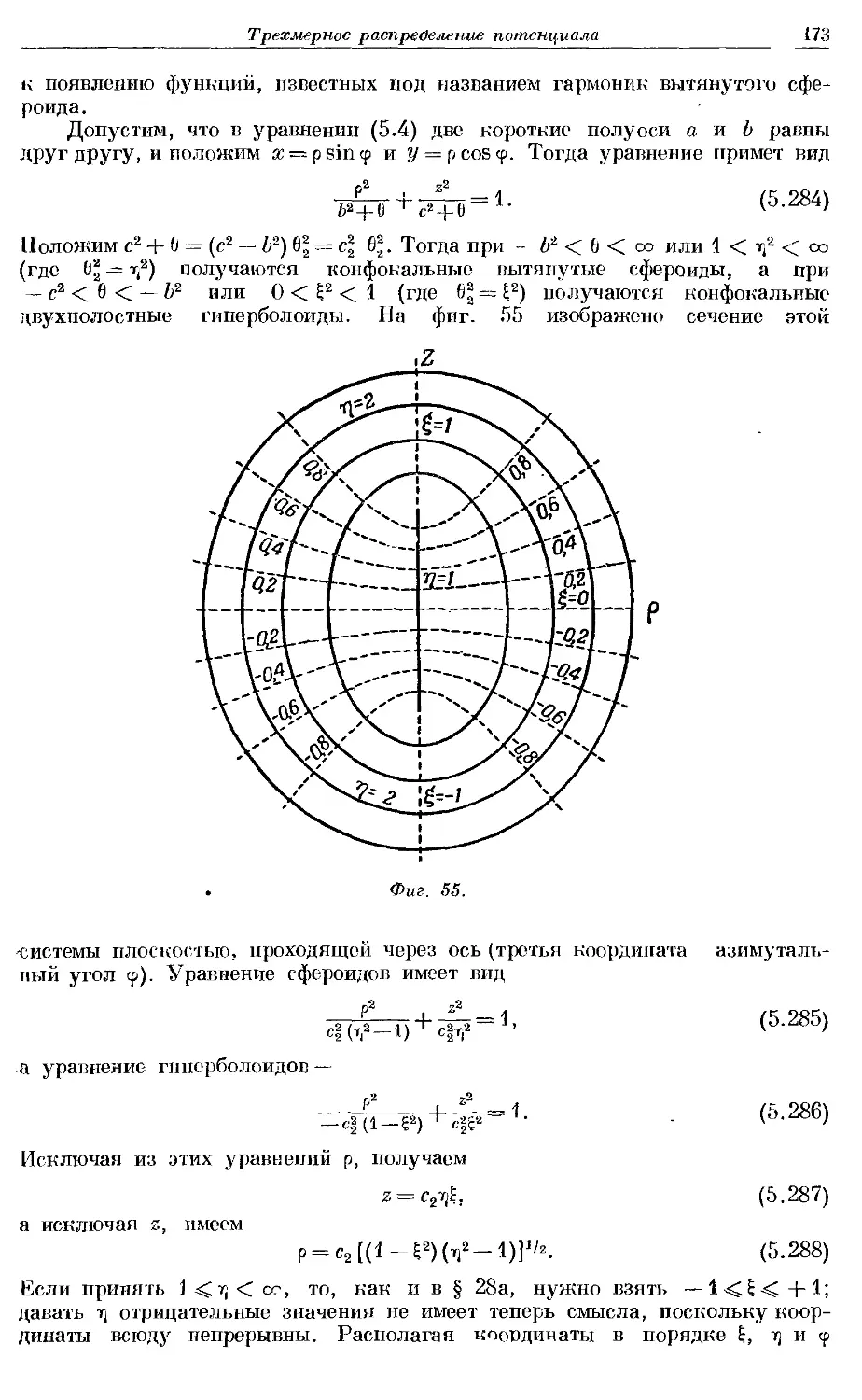
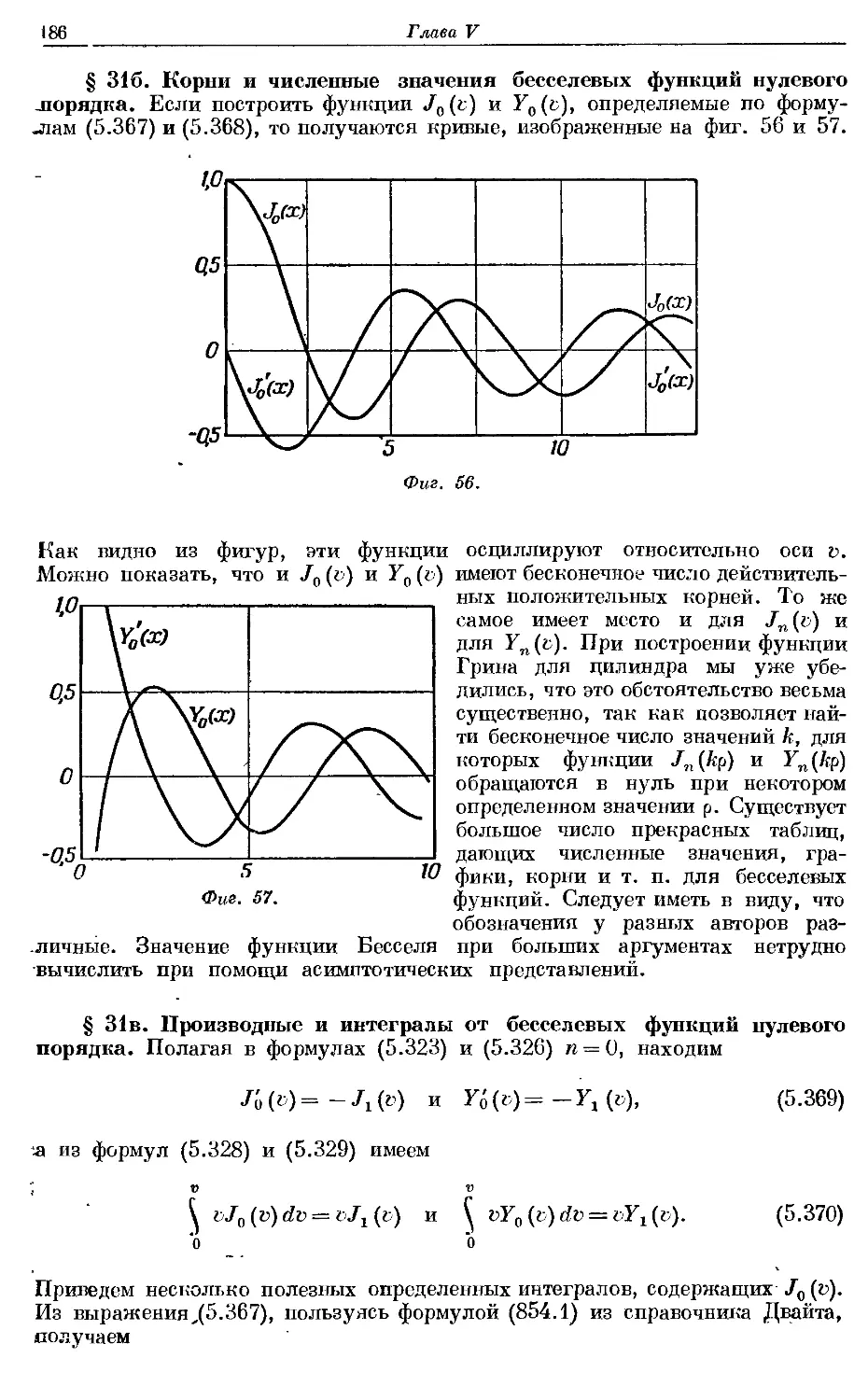
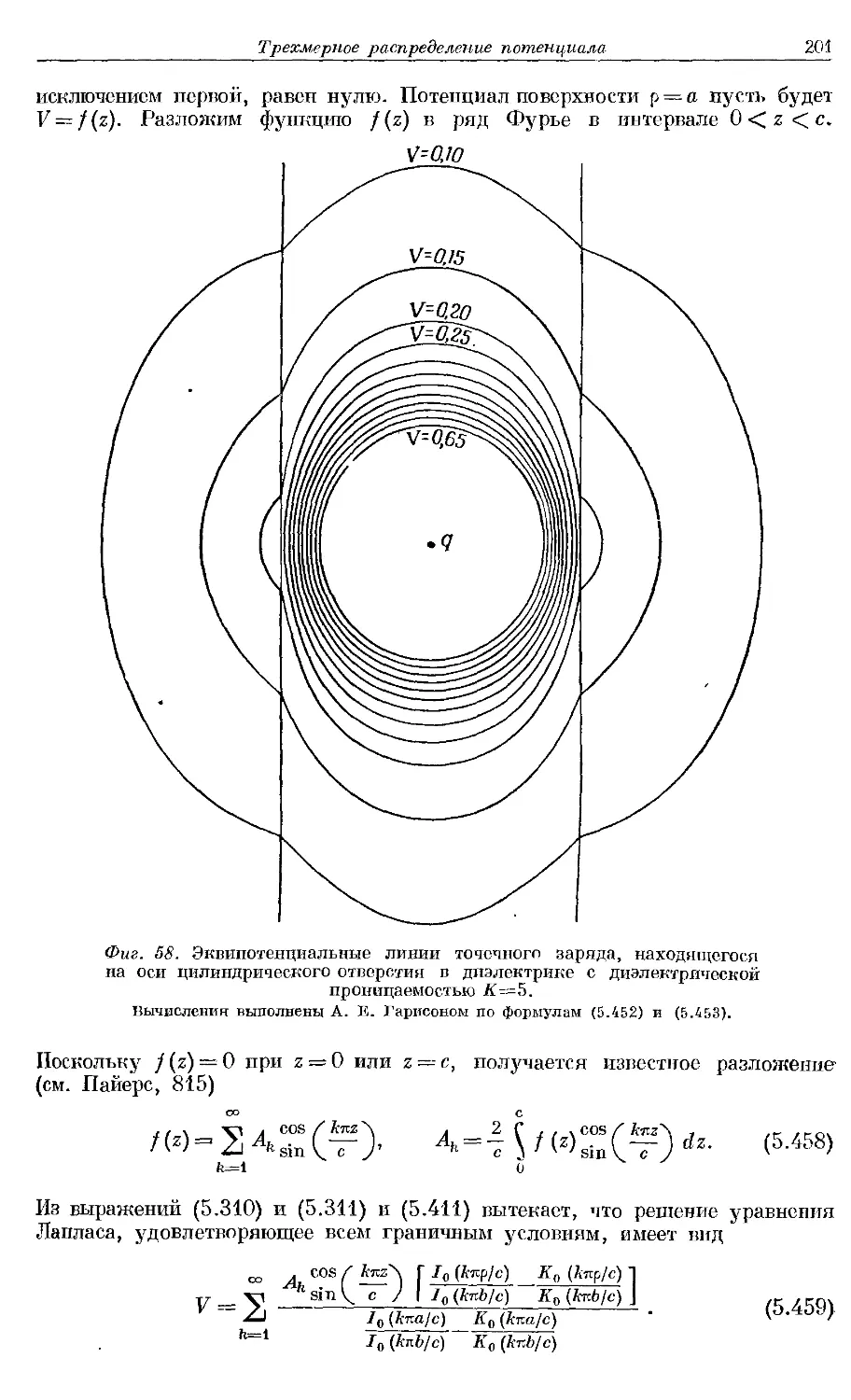
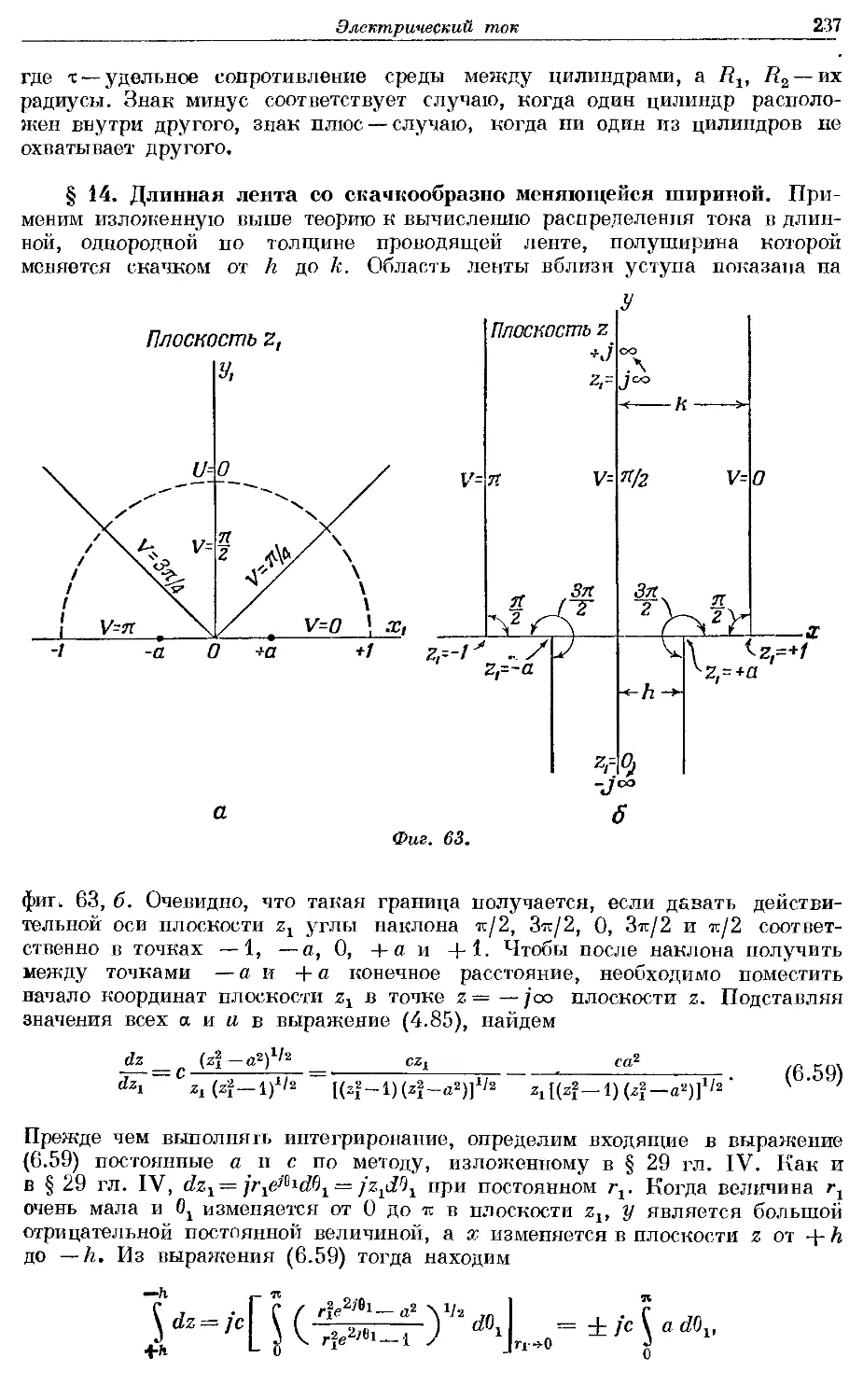
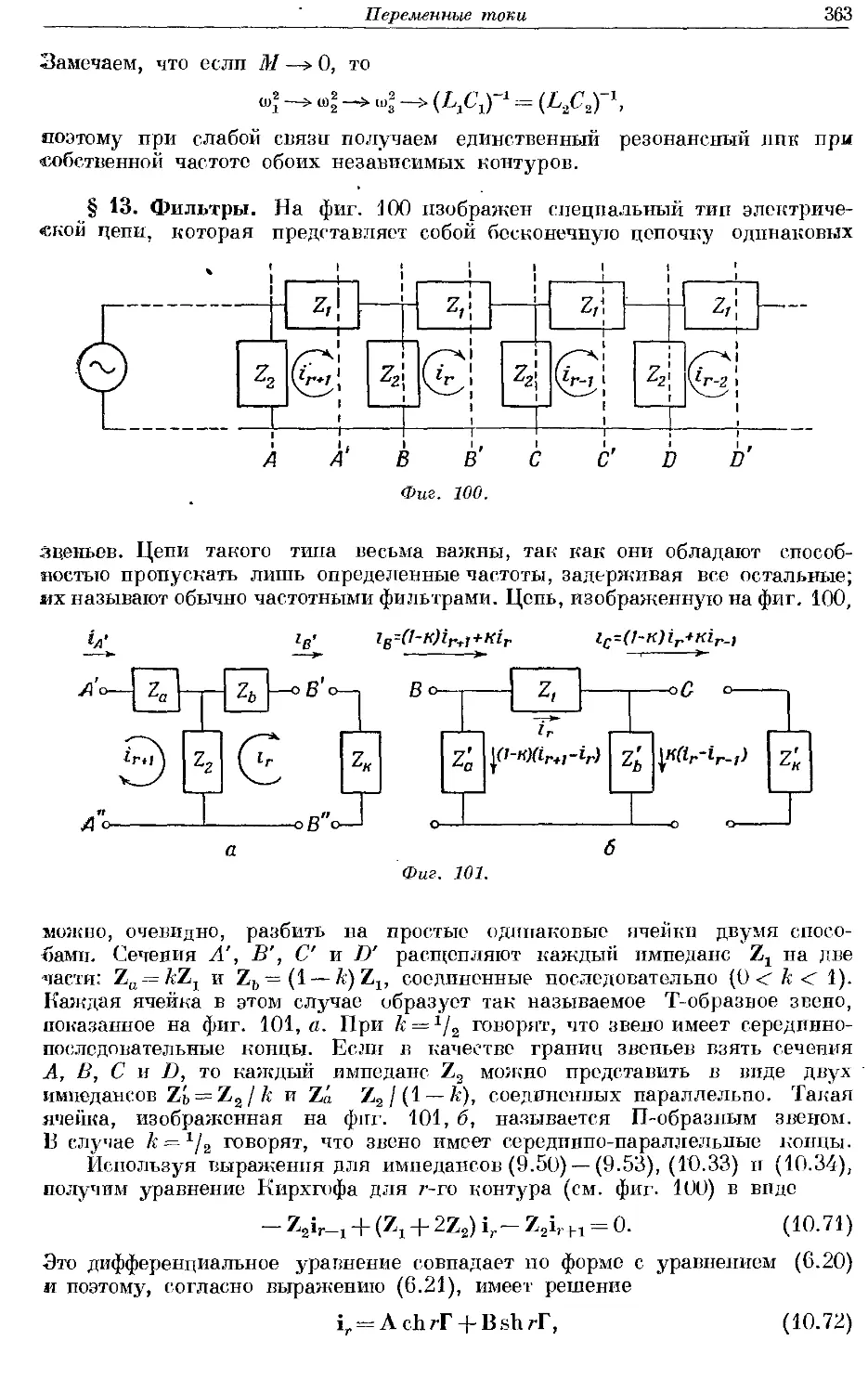
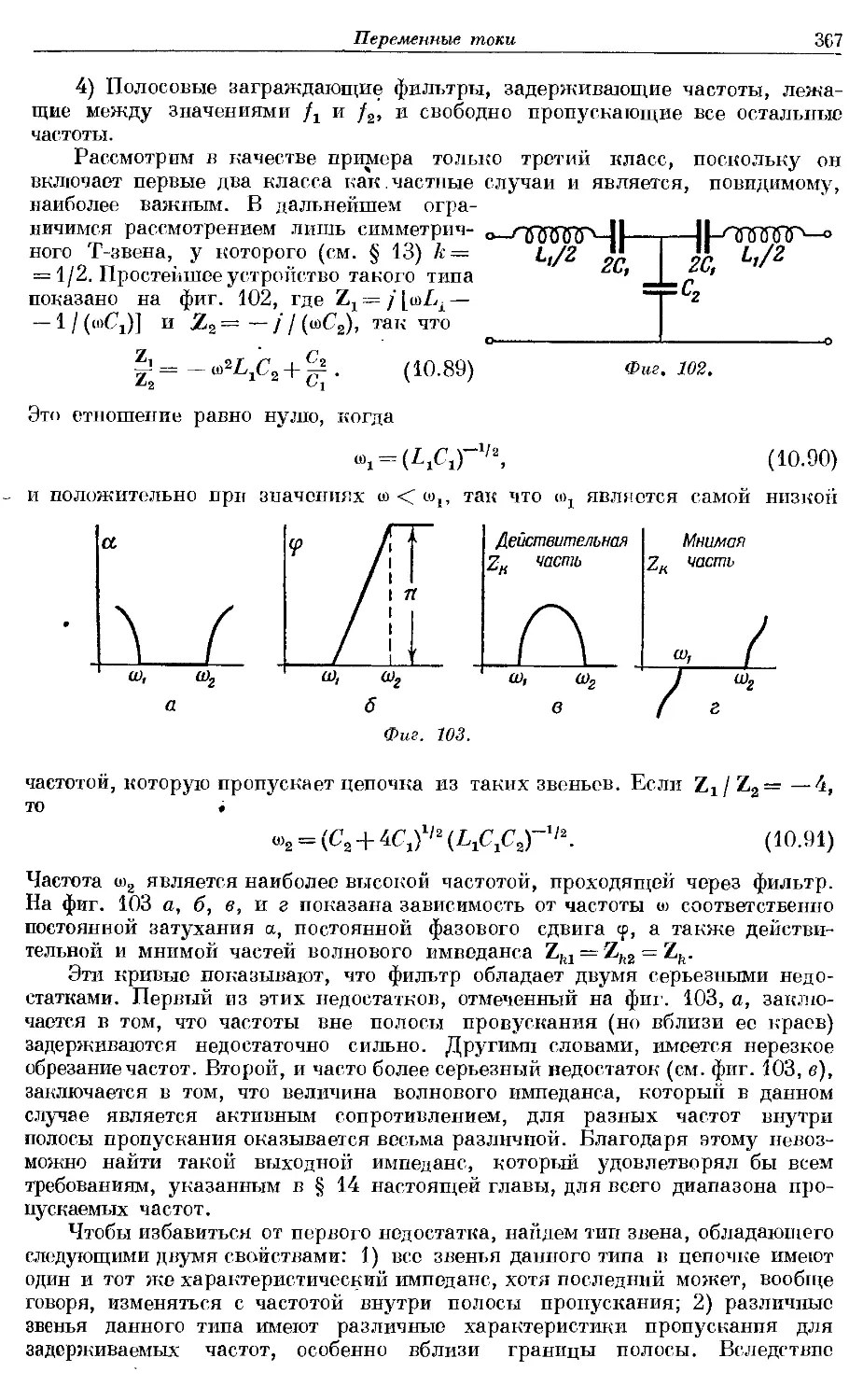
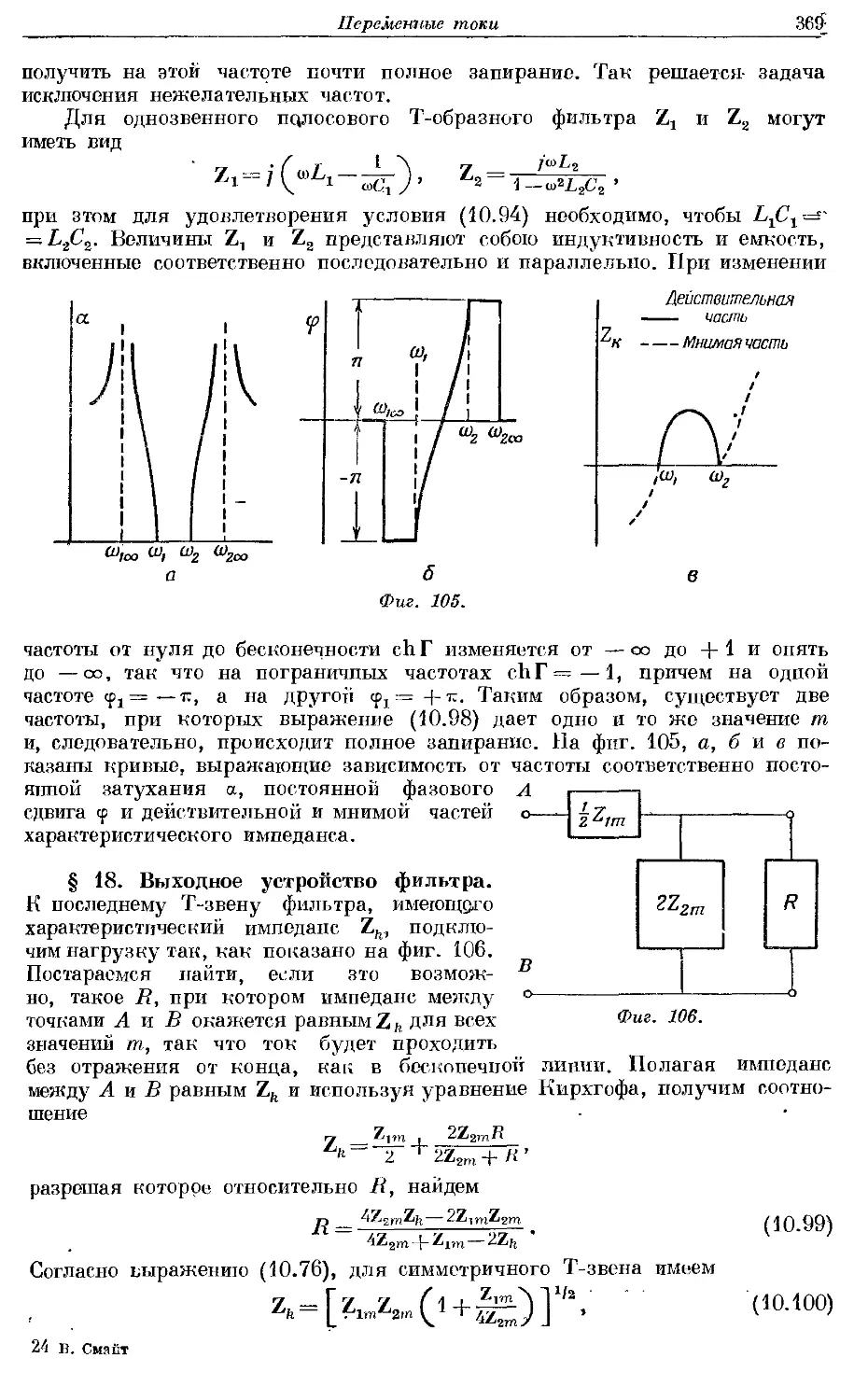
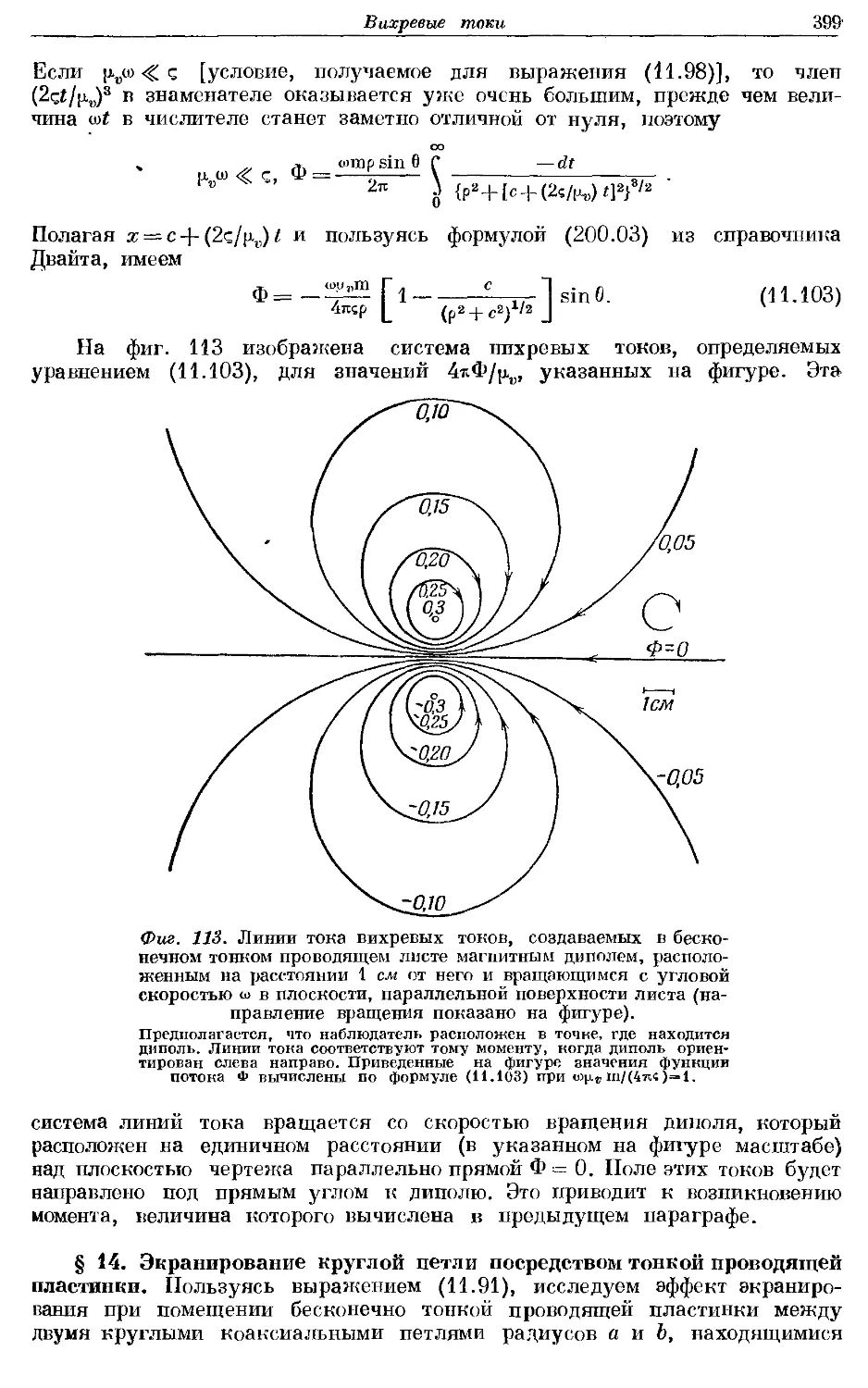
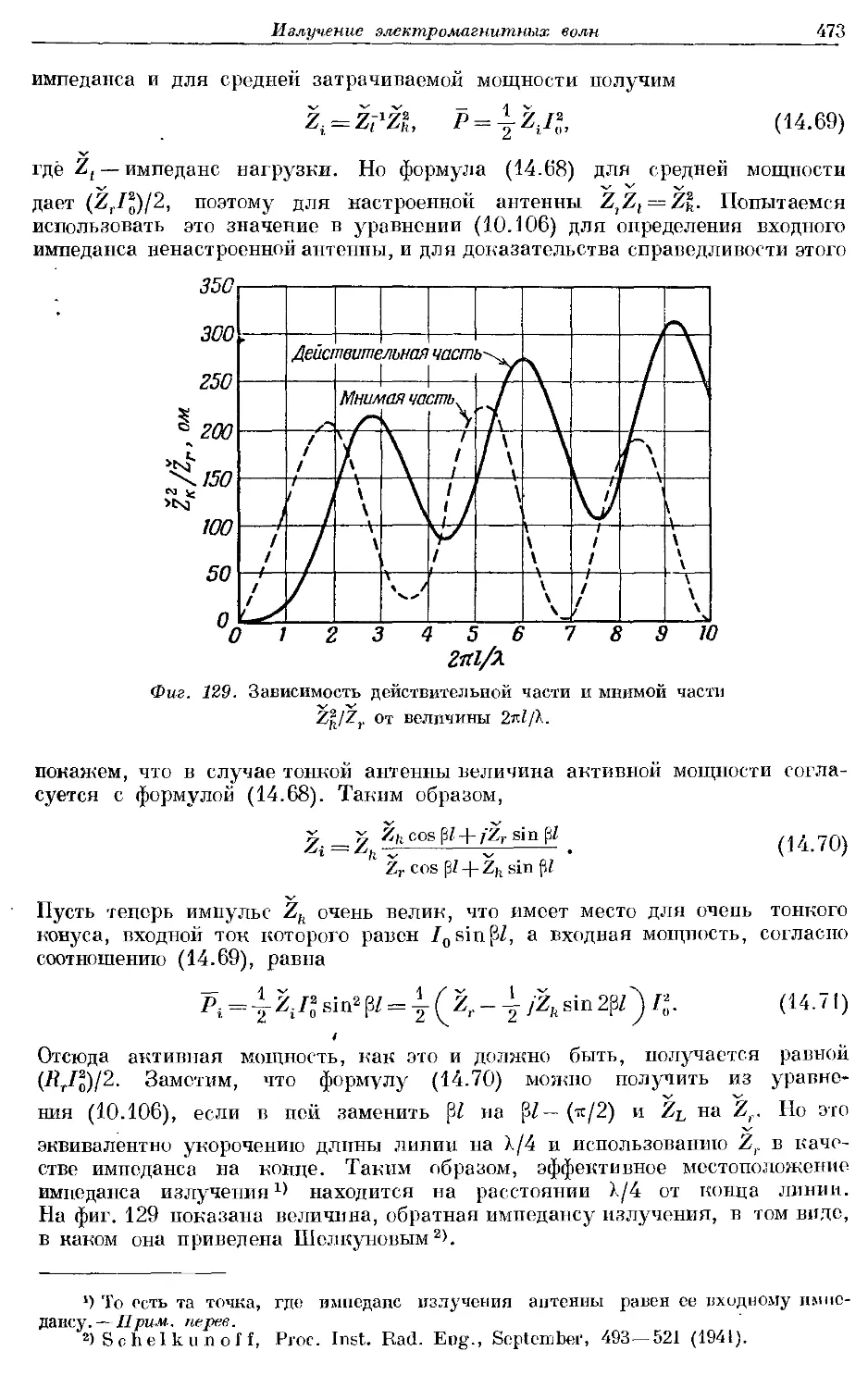
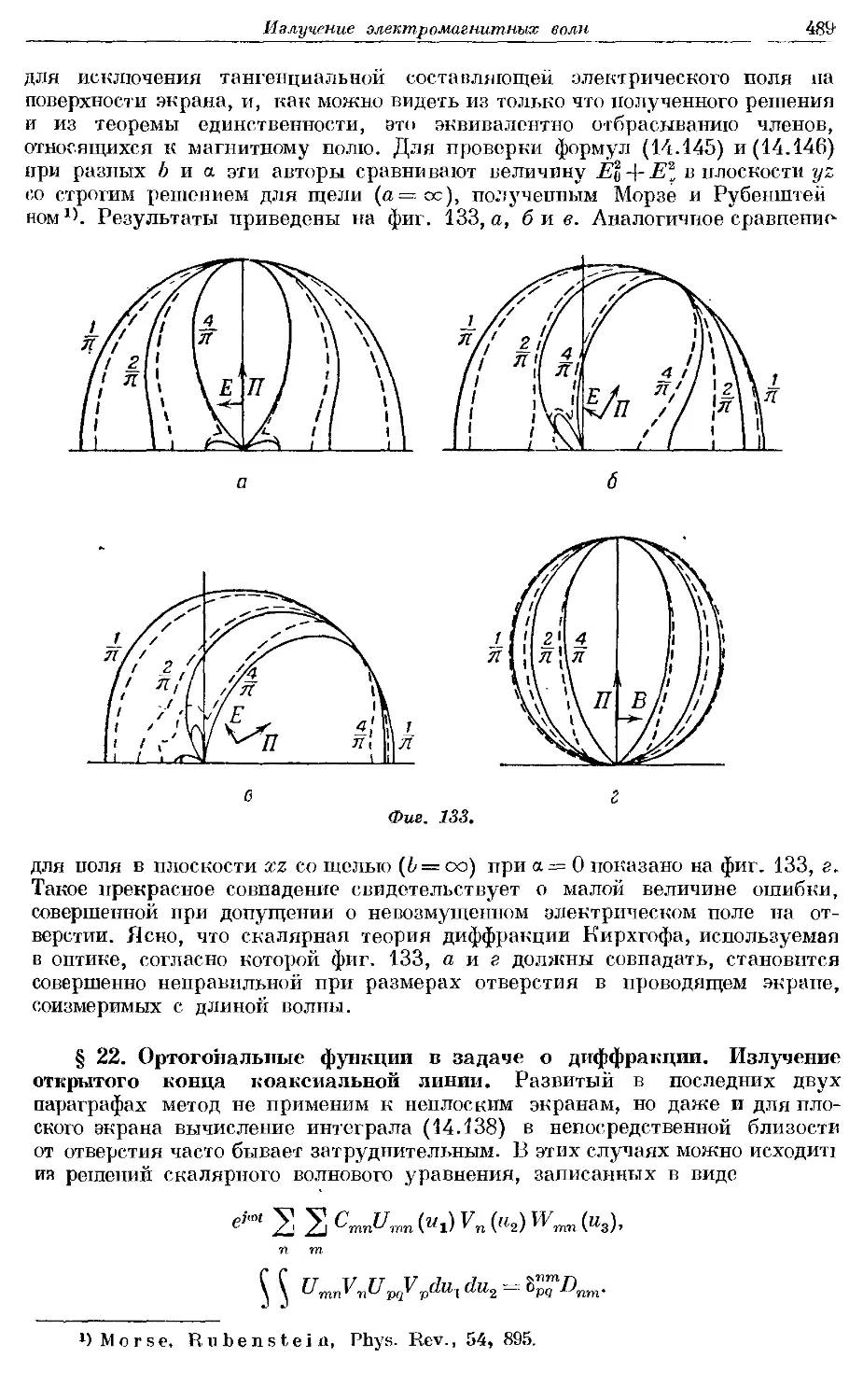
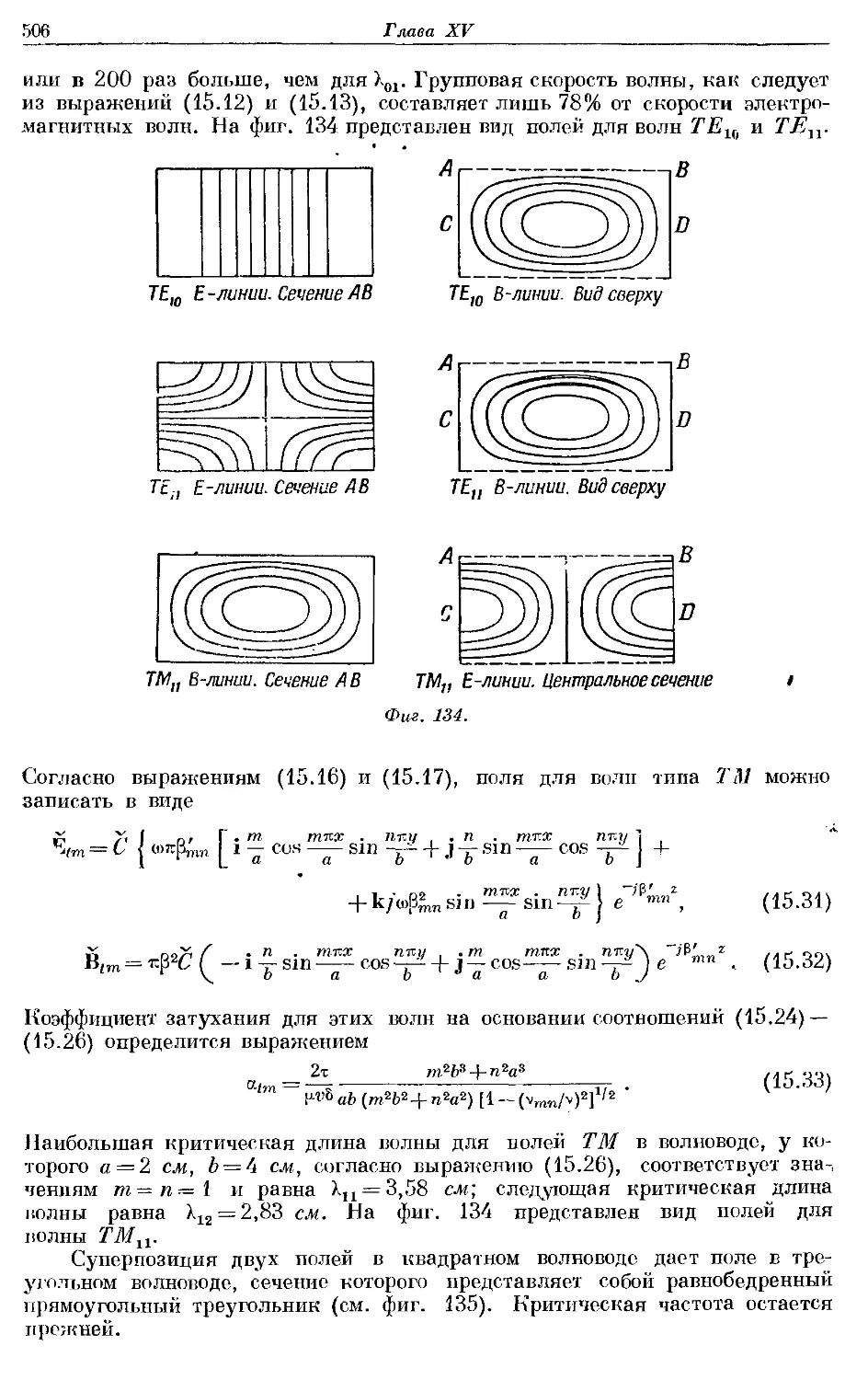
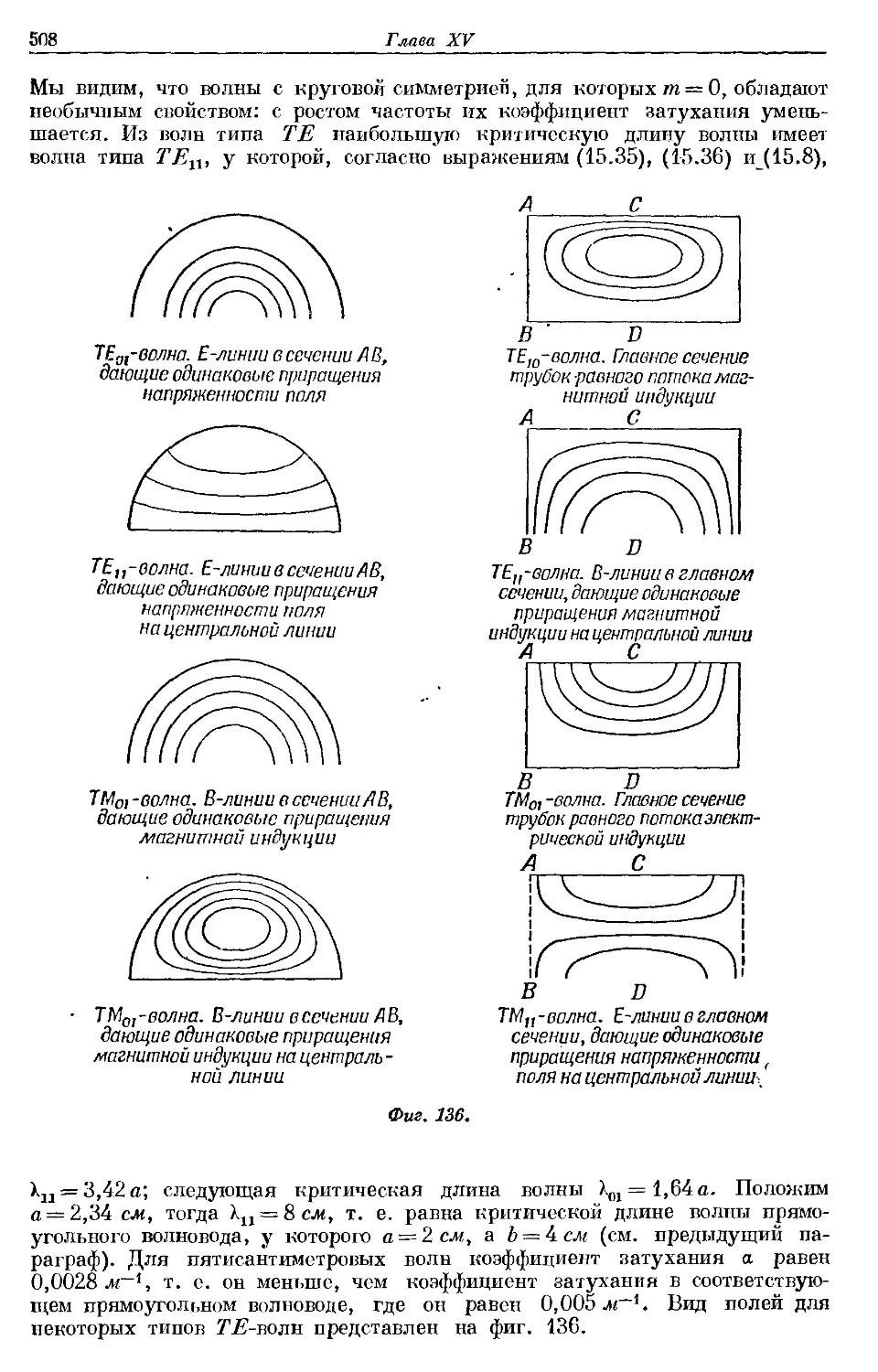
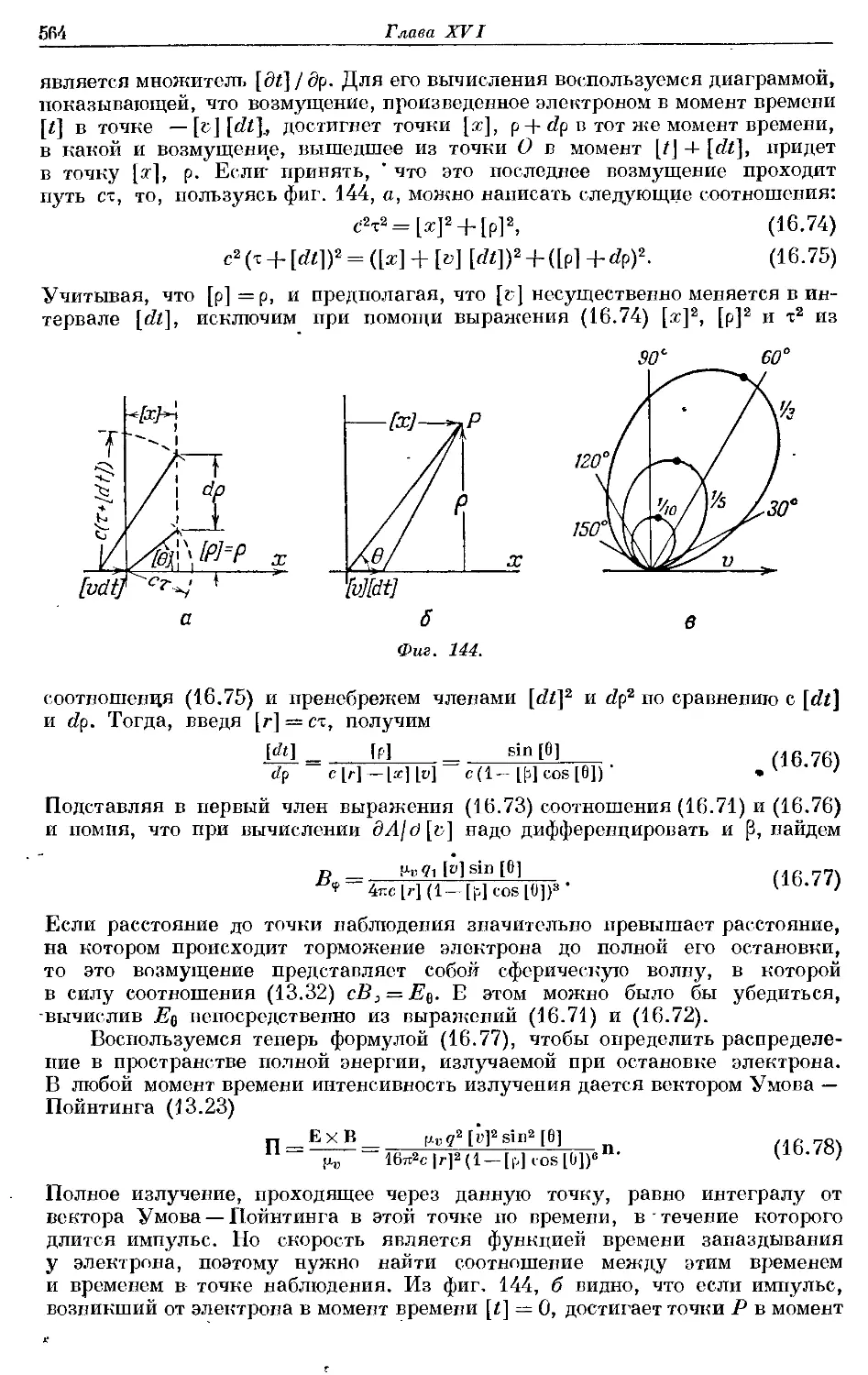
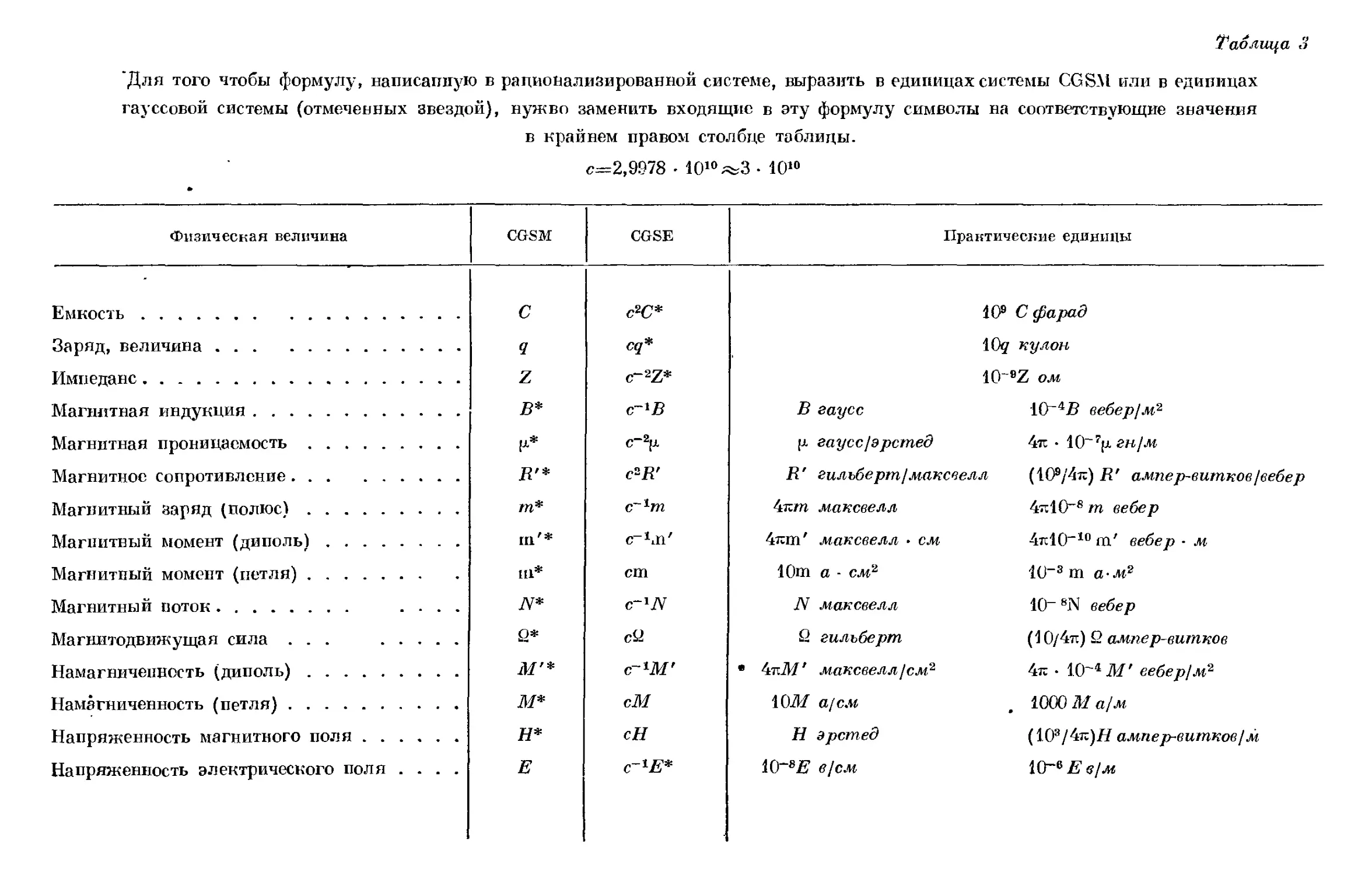
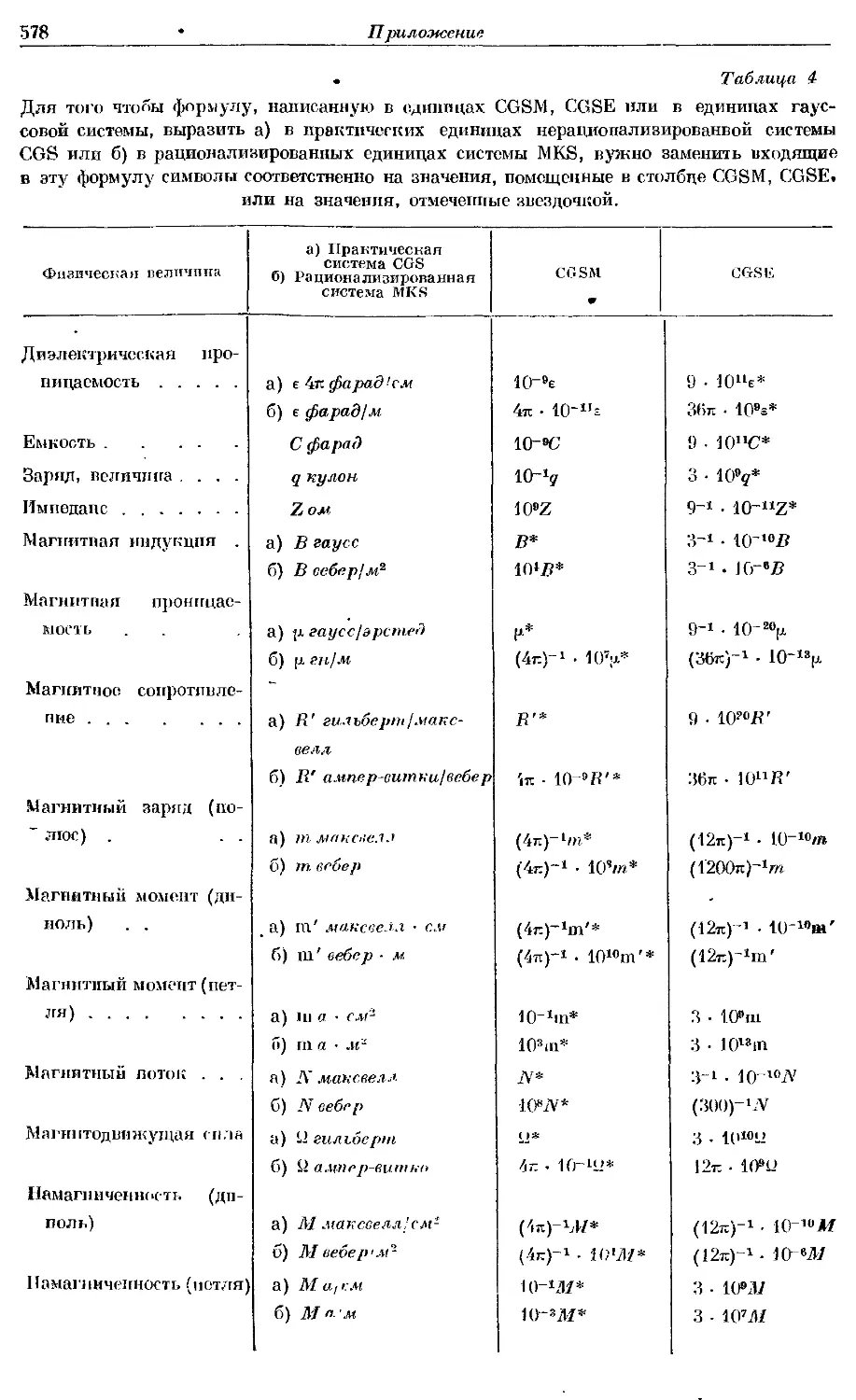
Text
В. СМАИТ
ЭЛЕКТРОСТАТИКА
и
ЭЛЕКТРОДИНАМИКА
Перевод со второго американского издания
А. В. ГАПОНОВА и М. А. МИЛЛЕРА
и * л
ИЗДАТЕЛЬСТВО
ИДСЩТРАННОИ ЛИТЕРАТУРЫ
Москва, 1954
Библиотеке
профессора Саеочкнна Ю,В.
STATIC AND DYNAMIC
ELECTRICITY
by
WILLIAM R. SMYTHE
SECOND EDITION
NEW YORK TORONTO LONDON
1 9 50
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКОВ
Предлагаемая вниманию советского читателя книга Смайта «Элек-
«Электростатика и электродинамика» содержит изложение основ классической
макроскопической теории электромагнитного поля. В отличие от большин-
большинства подобных курсов в книге наряду с последовательным освещением обще-
общетеоретических вопросов значительное место отводится изложению основных
методов решения электродинамических задач, а также приводятся вспомо-
вспомогательные математические сведения, необходимые для овладения этими
методами. С этой точки зрения книга Смайта занимает промежуточное по-
положение между учебником, где задачи, как правило, приводятся лишь для
иллюстрации отдельных теоретических положений, и сборником задач,
в котором если и сообщаются некоторые результаты теории, то только в весьма
конспективной форме. Систематическое изложение теоретического материала
и, что особенно существенно, большое количество задач, рассмотренных
непосредственно в тексте, а также задач, помещенных вместе с ответами
в конце каждой из глав, составляют несомненное достоинство книги и де-
делают ее не только ценным пособием для студентов и аспирантов, изучающих
теорию электромагнитного поля, но и полезным справочником для специа-
специалистов, работающих в смежных областях.
Перевод этой книги на русский язык был осуществлен благодаря ини-
инициативе покойного академика А. А. Андронова, считавшего издание такого
пособия по теории электромагнитного поля весьма целесообразным. Вместе стем
А. А. Андронов отметил и некоторые присущие книге Смайта существенные
недостатки, в частности: отсутствие теории электромеханических систем,
имеющих большое значение в приложениях (электромашины), теории рас-
распространения радиоволн, а также до некоторой степени утилитарное изло-
изложение основ специальной теории относительности.
Не менее важным недостатком книги является также игнорирование
автором достижений советских ученых, что приводит, естественно, к неко-
некоторому снижению общего уровня книги и особенно глав, относящихся
к применению теории быстропеременных полей в современной радиотехнике.
В этой области нашим физикам и инженерам принадлежит ряд фундамен-
фундаментальных результатов, позволяющих подойти к рассматриваемым вопросам
с несколько иных и в научном и в педагогическом отношении позиций.
Подробное комментирование соответствующих мест настолько бы отвлекло
от оригинального текста, что мы сочли целесообразным оставить их вообще
Предисловие переводчиков
без примечаний, отсылая читателя к оригинальной литературе, список
которой помещен в конце книги. Сделанные нами примечания относятся
лишь к некоторым допущенным автором фактическим ошибкам и неточно-
неточностям. Ряд явных опечаток, замеченных при переводе, был исправлен без
оговорок.
Всюду, где математические преобразования не носят принципиального
характера, в книге практикуются ссылки на соответствующие формулы
из математических справочников Двайта (Dwight, Tables of Integrals and
Other Mathematical Data, Macmillan, 1934) и Пайерса (Р e i г с е, A Short
Table of Integrals, Ginn, 1929), первый из которых имеется на русском
языке (Г. Б. Д в а й т, Таблицы интегралов и другие математические фор-
формулы). При переводе ссылки на справочник Пайерса сохранены только в тех
немногих местах, где ссылки на справочник Двайта отсутствуют.
А. В. Гапонов.
М. А. Миллер.
ПРЕДИСЛОВИЕ АВТОРА
КО ВТОРОМУ ИЗДАНИЮ
Широкое распространение практической рационализированной системы
единиц, а также возросшее значение высокочастотных колебаний заставило
в корне пересмотреть первое издание книги. Во втором издании прежде
всего всюду изменена система единиц.
К главам, посвященным электростатическим полям, добавлено еще 40 за-,
дач по трудности выше средней. Они охватывают главным образом при-
примеры на такие граничные условия, которые не рассматривались в первом
издании. Более подробное изложение вопросов, связанных с электромаг-
электромагнитными волнами, заставило переписать заново некоторые части пятой
главы, касающиеся функций Бесселя, и привело к введению векторных по-
поверхностных гармоник, что сильно упрощает ряд вычислений. Пере-
Переписана также большая часть гл. XI о вихревых токах. Электромагнитным
волнам посвящены три главы, из которых две совершенно вовые. И в самом
тексте и в 150 задачах к этим главам содержатся некоторые впервые публи-
публикуемые результаты и методы. Для приобретения навыка в решении задач
на волновые поля по этой книге обучались две группы аспирантов. Мвогие
задачи оказались чересчур трудными для аспирантов первого года обучения,
но любая задача была решена, по крайней мере, хотя бы одним аспирантом
старшего курса. Путь решения той или иной задачи либо непосредственно
вытекает из содержания книги, либо требует некоторого почти очевидного
его обобщения. Поскольку в задачах приводится ряд весьма полезных све-
сведений, о них упоминается и в'лпредметном указателе—это должно облег-
облегчить пользование книгой в качестве справок при решении задач. Во втором
издании опущена гл. XV первого издания, так как приведение ее содер-
содержания в соответствие с современными воззрениями потребовало бы слишком
много места.
Ни одна из новых тем второго издания ие требует от читателя допол-
дополнительной математической подготовки по сравнению с предполагавшейся
в первом издании. Опыт работы автора с первым изданием книги показал,
что успешное решение электрических задач определяется в большей сте-
степени физической интуицией, чем математической. Поэтому студенты, спе-
специализировавшиеся при окончании в области математики, сильно уступают
в этом отношении тем, кто кончал по физике или электротехнике.
375 студентов Калифорнийского технологического института внима-
внимательно изучили первое издание книги. Можно надеяться поэтому, что оста-
осталось незамеченным лишь незначительное число ошибок, неясностей или
сомнительных утверждений.
Вильям Р. Смайт.
ИЮЛЬ 1950
Предисловие автора к первому изданию
ПРЕДИСЛОВИЕ АВТОРА
К ПЕРВОМУ ИЗДАНИЮ
Средний специалист, окончивший высшее учебное заведение, даже если
он достаточно близко знаком с современной теорией электромагнетизма,
в большинстве случаев не в состоянии решать встречающиеся ему задачи,
требующие некоторых отступлений от стандарта и некоторой разработки
основных известных ему положений. Настоящая книга появилась в ре-
результате двенадцатилетней работы автора по обучению аспирантов первого
курса—физиков, электротехников, геофизиков и математиков, которые
должны были обладать в области приложений основных принципов электри-
электричества и магнетизма знаниями в объеме требований, необходимых для полу-
получения кандидатского звания. Книга может служить для справок о методах
решения достаточно обширного класса задач, не решаемых путем простого
применения формул из справочников. Предполагается, что читатель обла-
обладает математическими познаниями в размере обычвых требований по курсу
математической физики, читаемому в высших учебных заведениях, а именно,
что он знаком с векторным анализом, дифференциальным и интегральным
исчислениями и с элементарными дифференциальными уравнениями. Все
математические вычисления, выходящие за пределы указанного курса,
проводились таким образом, чтобы читатель, имеющий требуемую подго-
подготовку, мог проследить за ними. Несмотря на некоторые трудности, автору
удалось избежать применения контурных интегралов на комплексной пло-
плоскости, однако он уверен, что при более глубоком изучении предмета нужно
овладеть этим могучим математическим инструментом.
Как уже было упомянуто, эта книга написана скорее для физиков-экспе-
физиков-экспериментаторов и инженеров, чем для теоретиков". Поэтому в нее включены
лишь те разделы теории, которые имеют непосредственное применение,
а изложение их сделано кратким и доступным читателю с указанной выше
подготовкой.
В книге нет ни одной темы, представляющей лишь чисто исто-
исторический интерес. В самом тексте разобрано много задач—больше, чем это
принято обычно. При их отборе принималась во внимание степень важности
результата задачи в приложениях или то, насколько задача поясняет теорию,
доказывает полезность тех или иных положений теории. Помимо этого,
обширное собрание задач имеется в конце каждой главы. Ohpi охватывают
почти все положения теории, приведенные в тексте. Многие из этих задач
взяты из Кэмбриджских экзаменационных вопросов и опубликованы в книге
Джинса [Jeans J. H., The Mathematical Theory of Electricity and Mag-
Magnetism, Cambridge, 1925]. Наиболее способные аспиранты решили все за-
задачи, однако средний аспирант это сделать был не в состоянии. Читатель,
занимающийся самостоятельно, может, очевидно, проверить себя на этих
задачах. Многие важпые результаты помещены, за недостатком места,
не в тексте, а в задачах, поэтому они также перечислены в предметном
указателе.
Порядок расположения материала и само изложение несколько отли-
отличаются от общепринятых. Прежде всего все рассуждения основываются
непосредственно на макроскопических экспериментальных фактах, а не на
представлениях о микроскопической структуре проводников и диэлектриков.
Это вызвано двумя причинами: во-первых, хотя микроскопическая теория
и выдержала основпую проверку, а именно, дала (в пределах точности
экспериментов) наблюдаемые макроскопические законы,—это еще не говорит
за то, что она является единственной теорией, или за то, что верны и все
другие выводы и.ч нее; во-вторых, изложение наиболее удовлетворительной
теории, опирающейся на'квантовую механику, требует такой математической
Предисловие автора.к первому изданию
техники, наличие котором не предполагается у читателя в начале изучения
книги, но которой он должен обладать по прохождении двух третей ее мате-
материала. Поэтому изложение этой теории, краткое в силу необходимости,
приводится лишь в последней главе. Второе отступление от общепринятого
состоит в рассмотрении теории магнетизма на основе взаимодействия элек-
электрических токов и движущихся зарядов и в отказе пользоваться понятием
одиночного магнитпого полюса. Это логически неизбежно приводит к при-
применению не скалярного магнитного потенциала, как обычно, а магнитного
вектор-потенциала, широко (хотя и не исключительно) используемого во
всей теории магнетизма и электромагнетизма. Для многих читателей может
показаться удивительным, что это иногда значительно упрощает выкладки,
особенно при вычислении коэффициентов самоиндукции и взаимной индук-
индукции, а также при изложении теории вихревых токов и электромагнитного
излучения.
Другие незначительные отклонения от обычпых курсов заключаются
в более широком использовании функций Бесселя, конформных пре-
преобразований, а также методов специальной теории относительности при
нахождении, например, силы взаимодействия двух движущихся зарядов.
Последнее позволяет, опираясь на надежное экспериментальное подтвер-
подтверждение, освободиться от необходимости делать те или иные гипотезы о форме
и размерах электрических зарядов и отчетливо понимать пределы примени-
применимости обычных формул без привлечения этих гипотез./
Некоторые разделы, обычно включаемые в книги по электричеству
и магнетизму, просто опущены. Так, совершенно не затрагиваются пи элек-
электролитическая проводимость, ни фотоэлектрические и термоэлектрические
эффекты и т. д., хотя в общем и предполагаются у читателя элементарные
познания в этих вопросах. Трактовка же их на том уровне, на котором на-
написана остальная часть книги, потребовала бы знаний основ физиче-
физической химии, термодинамики и квантовой теории. Также опущена теория
электрических машин и приборов, включая и вакуумные лампы, так как
представляется наиболее целесообразным излагать эти разделы в непос-
непосредственной связи с лабораторными курсами. За недостатком места мы не
касались операторного метода Хевисайда и динамического метода анализа
контуров.
Перед тем, как приступить к чтению книги, читатель должен ознако-
ознакомиться со всеми употребляемыми системами электрических единиц и отдать
предпочтение той или иной системе. Совершенно несущественно, какая
система используется в действительности, если только об этом ясно указано.
В каждом разделе курса автор выбирал ту систему единиц, с которой легче
всего было работать. Так, в гл. I—V употреблялась электростатическая
система CGSE, в гл. VII—XII—электромагнитная система CGSM,
а в гл. XIII—XV—гауссова система. Во избежание недоразумений внизу каж-
каждой страницы указана употребляемая па ней система единиц. Кроме того, в
приложении даны достаточно полные таблицы перевода величин из одной си-
системы в другую, позволяющие результаты любых вычислений представлять
в любых единицах. Чтобы увидеть, насколько употребление рационализи-
рационализированных единиц упрощает вычисления, были тщательно исследованы
все занумерованные формулы предварительного литографического изда-
издания. При этом обнаружилось, что сложность 169 формул уменьшилась,
123—возросла, а 1 196 формул по сложности остались неизменными. Таким
образом, существует очень мало данных в пользу рационализированных или
нерационализированных единиц. Ответы задач с этой точки зрения не
исследовались. .
При взятии интегралов или производстве математических преобразо-
преобразований всюду практиковались ссылки (при помощи номера) на соответствующие
Предисловие автора к первому ивданию
формулы у Пайерса [Р е i г с е, A Short Table of Integrals, Ginn, 1929]
или у Двайта [D w i g h t, Table of Integrals and Other Mathematical
Data, Macmillan, 1934 (см. перевод: Д в а й т, Таблица интегралов и другие
математические формулы, М.—Л., 1948)]. Поэтому желательно, чтобы чита-
читатель запасся хотя бы одной из этих книг. Библиография, помещенная в конце
каждой главы, ни в коей мере не является полной, но включает в себя
почти все те книги, которые, по мнению автора, содержат полезный дополни-
дополнительный материал или поучительное изложение вопроса.
Автор принял все меры, какие только знал, чтобы исключить ошибки,
однако он совершенно уверен, что они еще остались, поэтому он будет
благодарен всякому, указавшему их.
Вильям Р. Смайт.
АВГУСТ 1939
ОБОЗНАЧЕНИЯ
Символы, напечатанные жирным шрифтом, применяются для обозначе-
обозначения векторов (v, и, <р, ...) всюду, за исключением гл. X, где жирным
шрифтом обозначены комплексные амплитуды (I, 8, ...) или сопряженные-
им величины (I*, fe*, ...). В последующих главах знаком ~ отмечаются
Ч> V V v v
комплексные амплитуды (/, Щ, ...) и комплексные векторы (Е, В, П, ...),
а знаком <~ — комплексно-сопряженные амплитуды (/, Щч ...) и комплексно-
сопряженные векторы (Е, В, П, ...). Величины векторов и скаля-
скаляры как зависящие, так и не зависящие от времени не отмечаются
никак.
А, Ач, Ах и т. д.—вектор-потенциал.
А0 -нормированный вектор-потенциал.
alf ах и т. д.—квазивектор-потенциал.
В, By, Вх и т. д.—магнитная индукция.
В—реактивная проводимость.
В0—нормированная или относительная реактивная
проводимость, BZh.
С—емкость. Постоянная величина.
С0—нормированная или относительная емкость.
с—скорость света. Длина.
спп—собственная емкость. В § 8 гл. IX—оператор.
стп—взаимная емкость. В § 8 гл. IX—оператор.
D, ?)9, Dx и т. д.—электрическая индукция.
ds—дифференциальный элемент длины вдоль s.
dr—дифференциальное изменение г.
Е, Е, Е, Е и т. д.—напряженность электрического поля.
Е {к)—полный эллиптический интеграл.
е—заряд электрона; основание натурального лога-^
рифма 2,71828.
8, Ш, 8, Ш и т. д.—электродвижущая сила.
Ше—эффективное значение электродвижущей силы.
F, Fx—сила.
G—активная проводимость, Y — G-\- JB.
g—ускорение силы тяжести.
Н, Н, Н, Н и т. д.—напряженность магнитного поля.
{р), Н{п\Н™(v)—функции Ханкеля.
h—постоянная Планка.
hlt h2, h3—применяются в ортогональных криволинейных,
координатах. Элементы длины при этом равньь
hsdua, hadu3.
10 Обозначения
n\ hn\v), An2), h'n\v)—сферические функции Ханкеля.
1,1, 1,1 и т. д.—электрический ток.
1е—эффективное значение силы тока.
ie—эффективное значение плотности тока.
i, i, i, ix и т. д.—плотность тока. Ток.
i, j, k—единичные векторы по осям х, у, z.
Jn, Jn(v)—функции Бесселя.
/=(-1I/2.
in' jn(v)—сферические функции Бесселя.
К—относительная диэлектрическая проницаемость,
К (к)—полный эллиптический интеграл.
Кт-—относительная магнитная цроницаемость [л/[л„.
Кп, Кп (р)—модифицированные функции Бесселя.
кп, кп («)—модифицированные сферические функции Бесселя.
к—постоянная Больтцмана.
L, Lnn, Ln-—самоиндукция.
Lmn—взаимная индукция.
LP—нормированная или относительная самоиндук-
самоиндукция.
I, т, п—направляющие косинусы (с осями х, у, z).
М, М—намагниченность.
М—взаимоиндукция.
шх, ш, ю, т, т и т. д.—момент диполя или петли.
т', т'—классический магнитный дипольный момент
(гл. XII).
т—масса. Число (обычно целое).
N—поток электрической или магнитной индукции.
п—единичный вектор в направлении нормали.
п—показатель преломления. Число.
пп, nn{v)~~сферическая функция Бесселя.
2!! = 2-4.6...2п.
) = 1-3-5 ...Bп+1).
Р—поляризация.
Р, Р—м ощност ь.
Р—средняя мощность.
Рп, Р™ ([>•)—присоединенная функция Лежандра.
р, р—импульс. Количество движения.
р-—число. шр,-у. ш.
Q—электрический заряд. Добротность полого резо-
резонатора.
Q—квадрупольный момент.
Q™, Qn {&)—присоединенная функция Лежандра.
q—точечный или переменный заряд.
Я, Rr, Rnn, Rmn—активное сопротивление.
R, R (г)—функция только г.
Rn, Rn(v)—решение уравнения Бесселя.
¦ i?? Rn, («)—решение модифицированного уравнения Бесселя.
R, i?—расстояние между двумя точками.
г, г—расстояние от начала координат.
S—площадь поверхности.
< Sc, So—поперечное сечение полости.
S, Sn, S™— поверхностная Гармоника.
Обозначения 11
S, Sn, Smn, Snn—потенциальный коэффициент.
snn—собственный потенциальный коэффициент.
smn—взаимный потенциальный коэффициент.
s—расстояние вдоль кривой. Число.
Т, Т—механический момент.
Т—абсолютная температура. Период.
t—время.
ТЕ—поперечно-электрическое ноле.
ТМ—поперечно-магнитное поле.
te — индекс для величин, относящихся к полям ТЕ.
tm—индекс для величин, относящихся к полям ТМ.
U—фувкция потока, или потенциальная функция.
[U]—ф dU по кривой постоянного значения V.
и, и—скорость.
и =¦ cos Ь.
м1? м2, м3—ортогональпые криволинейные координаты.
V—потенциальная фувкция, или функция потоки.
[V]—ф dV по кривой постоянного значения U.
v—объем.
v, v—скорость.
W, W, W, W—решения скалярного волнового уравнения.
W— энергия. U + j'V ¦
Wte-—решения, описывающие волны ТЕ.
Wtm—решения, описывающие волны ТМ.
X—реактивное сопротивление.
х, у, z—прямоугольвые координаты.
Yn, Yn(i)—функции Бесселя.
Y, Y—полная проводимость, G-\-j'B.
Y°—нормированная или относительная полная про-
проводимость, YZk.
Z, Z—вектор Герца.
Z, Z, Z, Znn, Zn—полное сопротивление.
Zh—характеристическое или волновое полное сопро-
сопротивление.
Z0—нормированное или относительное полное сопро-
тивление, Z/Zh.
Z, Z(z)—функция только z.
z—комплексная переменная, х -f- /у.
а' с ^' ' ff—часто используются для обозначения углов.
Р—отношение у/с. Отношение (ц — ^в)/(^ + ^„).
Р—волновое число для плоской волны, w(pisI/2.
pm«— волновое число в волноводе, (р2 — РтпI/2.
Ртп—критическое волновое число.
Pmnp—собственное волновое число полого резонатора.
Г, Г—комплексная постоянная распространения.
Y—электрическая проводимость.
А, Дгч—детерминант. Малая часть чего-либо.
8—толщина скин-слоя. Разность фаз.
8—малая величина. Малая часть чего-либо.
12 Обозначения
8™—символ Кронекера, равный нулю при тФп,
и единице при т = п.
е—диэлектрическая проницаемость. Малая величнна.
ev~диэлектрическая проницаемость вакуума.
е, еп—фазовый угол.
0, 0F)—функция только б.
6—полярный угол.
6—единичный вектор в направлении б.
6, 6', б"—углы падения, отражения и преломления.
%—магнитная восприимчивость, A — р2)/2.
X—длина волны.
Хпп—критическая длина волны.
\—длина волны в волноводе.
Xmnp—резонансная длина волны в полом резонаторе.
[J.—магнитная проницаемость, cos б.
;1„—магнитная проницаемость вакуума, 4тг-10~7.
v—частота в периодах в секунду.
vmn—критическая частота.
vm«p—резонансная частота полости.
Е, S (I)—функция только 5.
?, С, ср—сплюснутые сфероидальные координаты.
5, Ъ 9—вытянутые сфероидальные координаты.
П, П, П—вектор Умова—Пойнтинга.
П—эффективное значение вектораУмова—Пойнтинга.
р—расстояние от осей z или б. Плотность заряда.
Рх—единичный вектор в направлении р.
о—поверхностная плотность электрического заряда.
?—площадь или удельное поверхностное сопротив-
сопротивление.
1—удельное объемное сопротивление. Плотность.
Время.
Ф(9)—функция только ср.
9—единичный вектор в направлении ср.
ср—азимутальный угол. Фазовый угол.
Ф—скалярный потенциал.
Q—магнитодвижущая сила. Телесный угол,
ы—частота в радианах в секунду.
V—векторный оператор, \д/дх-{- jd/dy + kdjdz.
^2—двухмерный векторный оператор.
а-Ь—скалярное произведение а и Ь.
а X Ь—векторное произведение а и Ь.
V8—оператор Лапласа.
[v]—запаздывающее значение v.
Глава I
ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОСТАТИКИ
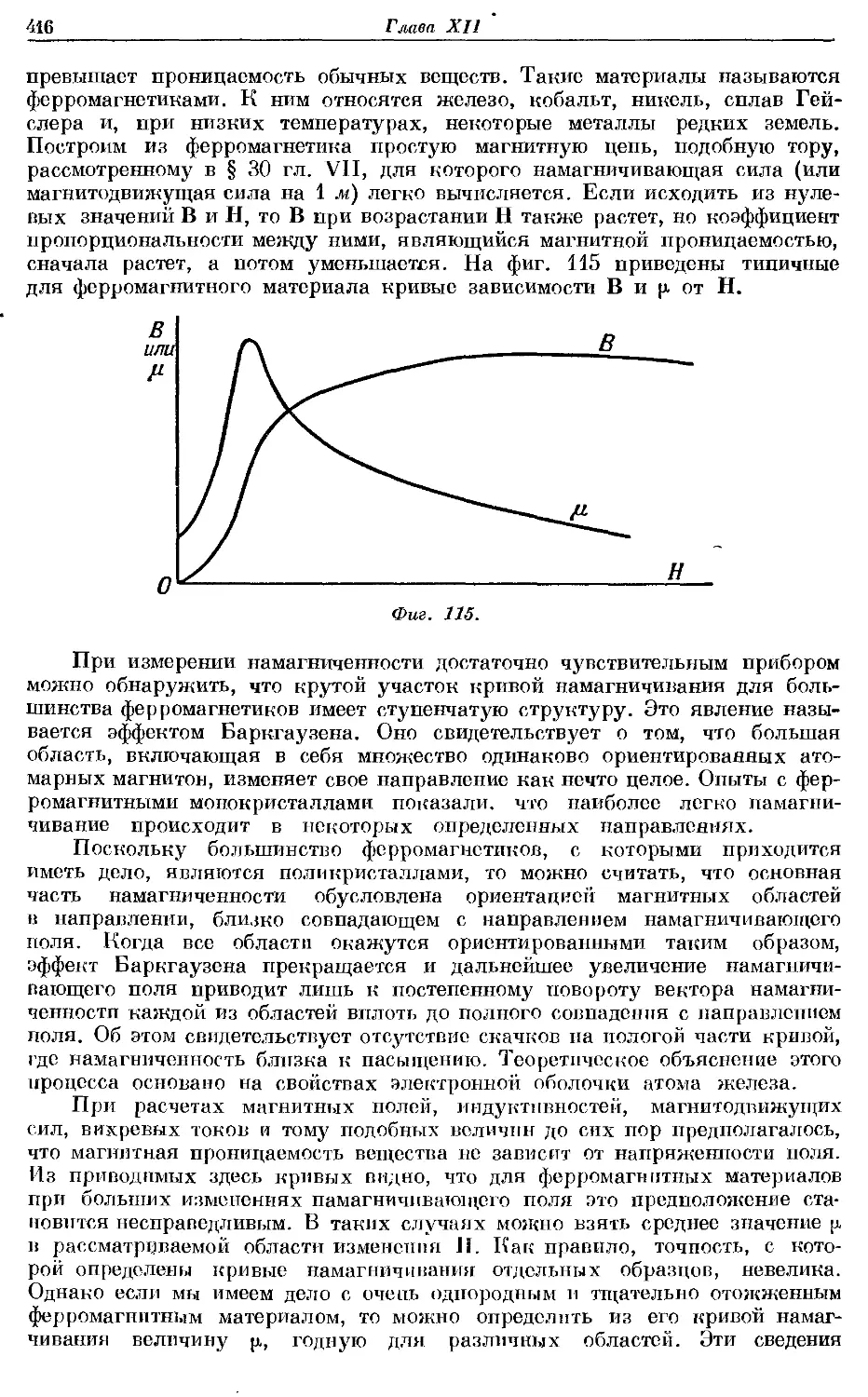
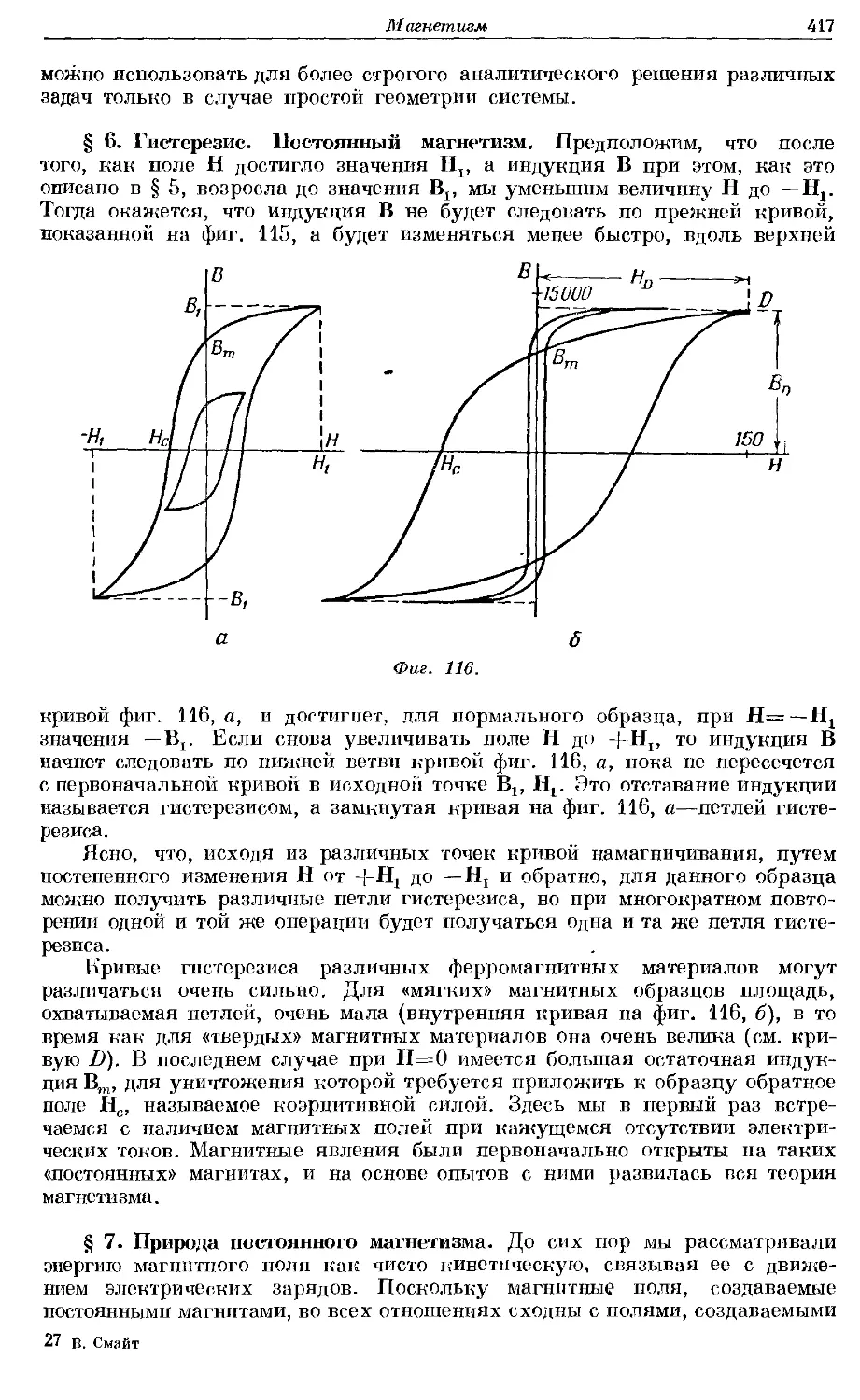
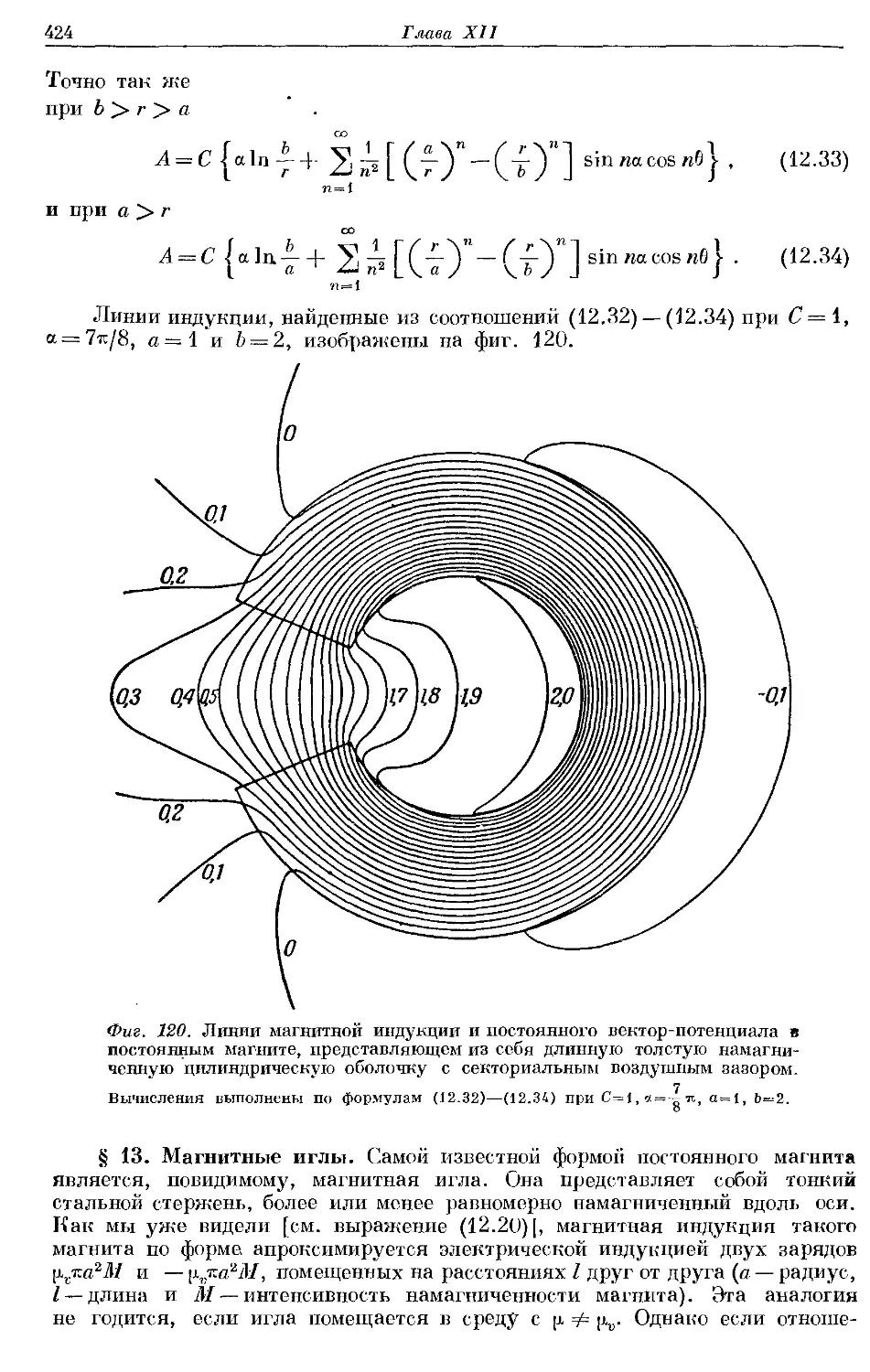
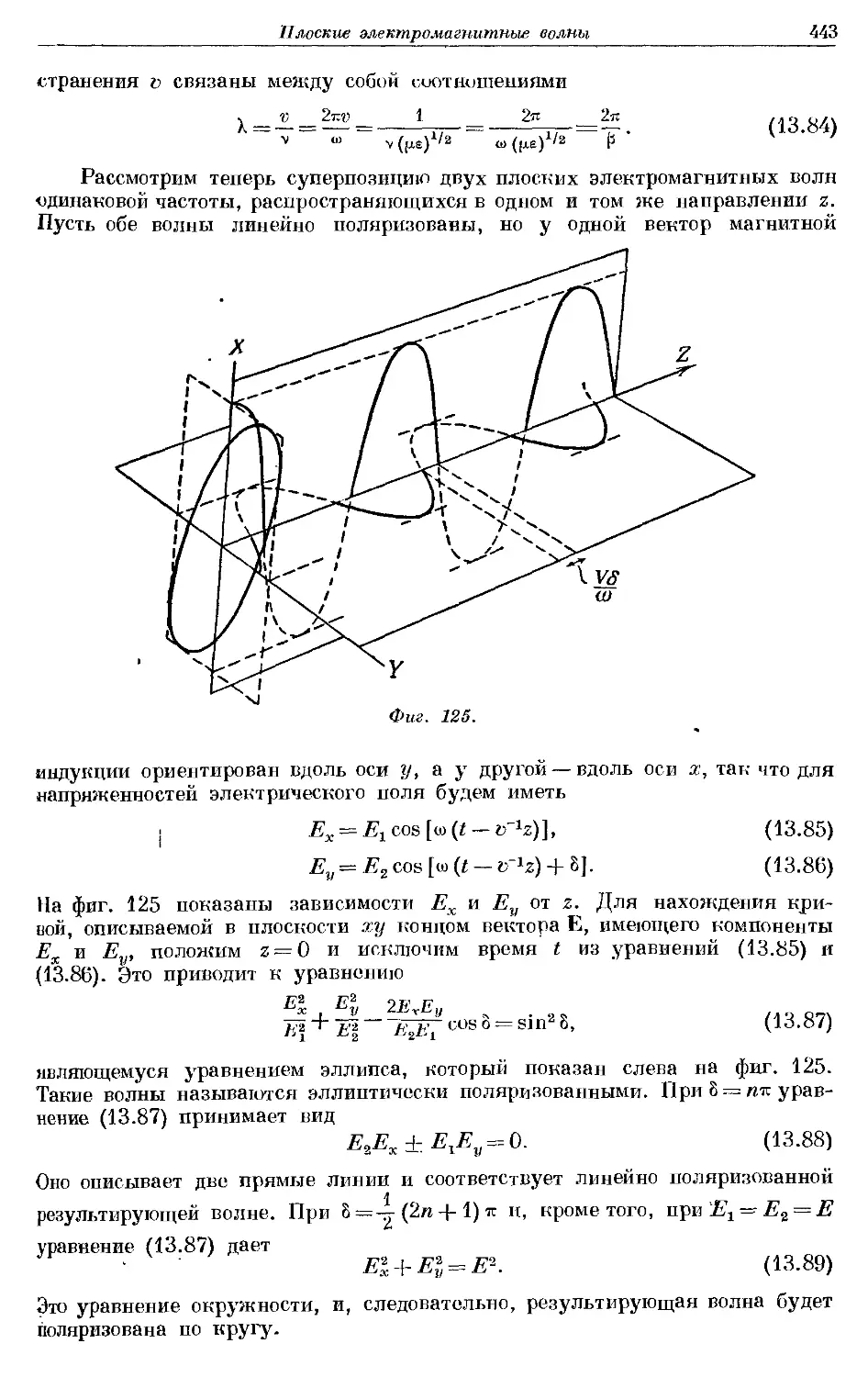
§ 1. Электризация. Проводники и изоляторы. Слово «электричество»
происходит от греческого слова, означающего янтарь. Около 600-х годов
до нашей эры Фалес Милетский, невидимому;* первый открыл, что янтарь,
если его потереть, притягивает к себе легкие тела. В настоящее время изве-
известно, что этим свойством в той или иной степени обладает большинство веществ.
Если потереть куском шелка стеклянную палочку или металлическую па-
палочку со стеклянной ручкой, то обнаружится, что они притягивают к себе
маленькие кусочки бумаги. Поэтому их называют наэлектризованными.
В случае металлической палочки состояние электризации может быть уничто-
уничтожено прикосновением пальца. Далее, держа в руках куски различных ве-
веществ и дотрагиваясь ими до наэлектризованной металлической палочки,
можно обнаружить, что металлы и влажные предметы уничтожают электри-
электризацию, а такие вещества, как стекло и шелк,—не уничтожают. Вещества,
снимающие электризацию, называются проводниками, а вещества, не сни-
снимающие ее,—изоляторами. Существуют, однако, и такие вещества,
которые снимают электризацию очень медленно и поэтому с одинаковым
правом могут быть названы плохими проводниками или плохими изолято-
изоляторами. Таким образом, нет определенной границы между этими двумя груп-
группами веществ. *
§ 2. Положительное и отрицательное электричество. Потрем стеклянную
палочку шелком и коснемся этой палочкой или этим шелком какого-нибудь лег-
легкого проводящего тела, например позолоченного шарика, подвешенного на
шелковой нитке,—он окажется наэлектризованным. Два шарика притяги-
притягиваются, если один из них наэлектризован стеклом, а другой шелком, и оттал-
отталкиваются, если оба наэлектризованы стеклом или шелком. Отсюда следует,
что существуют два рода электричества и что тела, одинаково наэлектризо-
наэлектризованные, отталкиваются, а противоположно наэлектризованные—притяги-
наэлектризованные—притягиваются. Проводя опыты со многими веществами, мы приходим к выводу, что
существуют только два рода электричества. Электричество на стеклянной
палочке принято называть положительным, а на шелке—отрицательным.
§ За. Закон Кулона, единица заряда, диэлектрики. Далее оказывается,
что сила, действующая между шариками, быстро уменьшается при удалении
их друг от друга. Кулон при помощи крутильных весов исследовал эти силы
и нашел, что сила взаимодействия двух наэлектризованных тел пропорцио-
пропорциональна произведению их зарядов, обратно пропорциональна квадрату
расстояния между ними и направлена вдоль линии, соединяющей эти
тела. Этот закон известен под названием закона Кулона. Его форму-
формулировка содержит в себе определение количества электричества или
электрического заряда: электростатической единицей заряда является та-
такое количество электричества, которое отталкивает равное ему количество
14 Глава I
электричества, находящееся в вакууме на расстоянии одного сантиметра,
с силой в одну дину. Практической единицей электричества является кулон,
равный 0,3 • 1010 электростатических единиц.
Этот закон обратных квадратов остается справедливым и в однородных
изотропных непроводящих средах, но там сила, действующая между оди-
одинаковыми зарядами, меньше по величине, и ее в единицах MKS можно
записать в виде
где F—сила, действующая на заряд q' кулонов со стороны заряда д, г—
вектор, направленный от q к q', г—его величина (в метрах), rt—единичный
вектор вдоль г, е—диэлектрическая проницаемость, являющаяся постоян-
постоянной характеристикой среды. Для вакуума эта величина (обозначим ее е„)
численно равна 8,85 ¦ 10~12 фарад 1м. Относительная диэлектрическая проницае-
проницаемость К, равная отношению е/ев, является величиной безразмерной и не
зависящей от выбора системы единиц.
§ 36. Пределы применимости закона Кулона. Точность измерений Кулона
значительно превзойдена современными методами, и, как недавно было под-
подтверждено, величина показателя у г в формуле A.1) равна 2 с точностью до
10~9. Однако нужно помнить, что закон Кулона можно применять с уверен-
уверенностью лишь в пределах тех размеров, при которых он подтверждается.
Закон строго применим только к заряженным телам, размеры которых
значительно меньше расстояния между ними. Форма же и состав этих тел
несущественны. На протяжении всей книги мы постараемся избежать построе-
построения какой бы то ни было макроскопической теории, основанной на предполо-
предположении применимости закона Кулона для атомных расстояний.
§ 4. Электростатическая индукция. Электрические заряды в проводни-
проводниках могут свободно перемещаться. Поэтому при поднесении электрического
заряда к незаряженному проводнику заряды противоположного знака пере-
переместятся в нем ближе к поднесенному заряду, а одинакового знака—дальше
от него, хотя в целом проводник останется, конечно, незаряженным. Так как
по закону Кулона сила взаимодействия тем больше, чем меньше расстояние
между зарядами, то в результате незаряженный проводник будет притяги-
притягиваться к заряду. Появляющиеся при этом на проводнике заряды называются
индуцированными. Если заряд, индуцированный на удаленных частях про-
проводника, не снят (например, прикосновением руки), то при удалении инду-
индуцирующего заряда проводник возвращается в нейтральное состояние.
Если же, оставляя индуцирующий заряд на месте, отделить друг от друга
ближние и дальние части проводника, следя за тем, чтобы они оставались
изолированными, то обнаружится, как и следовало ожидать, что обе части
несут на себе заряды противоположного знака.
Приншга действия многих «электростатических машин» заключается
в автоматическом повторении этой операции и накапливании разделенных
зарядов.
Используя значительно более чувствительные методы, можно обнаружить,
что заряд обладает небольшой притягивающей силой также и по отношению
к незаряженным изоляторам1). Это показывает, что даже в изоляторах при-
г) Нетрудно видеть, что для обваружения силы взаимодействия между электриче-
электрическим зарядом и везаряженным изолятором нет необходимости в более чувствительных
методах. При относительной диэлектрической проницаемости К, не слишком близкой к
единице, эта сила того же порядка, что и сила взаимодействия заряда с металлом.
См., в частности, задачу, приведенную в § 5 гл. IV. —Прим. перев.
Основные положения электростатики 15
сутствуют электрические заряды и что они не являются абсолютно неподвиж-
неподвижными, а могут испытывать некоторые смещения. Мы не будем здесь обсуждать
гипотез, относящихся к действительному поведению зарядов в проводниках
и изоляторах. Теории этих явлений еще несовершенны, хотя и значительно
продвинуты по сравнению с 1930 г.
§ 5. Элементарные электрические заряды. Как было обнаружено, элек-
электрический заряд не может быть бесконечно делимым. Наименьшим извест-
известным нам отрицательным зарядом обладают отрицательный электрон и
мезон. Впервые этот заряд с большой точностью был определен Миллике-
ном. Принятое в настоящее время его значение равно 1,60-10~19 кулонам.
Наименьшим известным нам положительным зарядом обладают позитрон
(или положительный электрон) мезон и протон. С очень высокой степенью
точности все элементарные заряды равны по величине. Масса электрона,
а также, повидимому, и позитрона равняется 9,1 • 10~31 кг. Масса протона при-
приблизительно в 1850 раз больше массы электрона.
При рассмотрении электрических задач мы будем считать электриче-
электрические заряды бесконечно делимыми и пользоваться понятием плотности за-
заряда. Ясно, что это справедливо лишь в том случае, если приходится иметь
дело с величинами зарядов, значительно превышающими 1,60-10~19 кулон.
В пределах же атомных размеров, например, подобное рассмотрение, ко-
конечно, становится бесполезным. Как мы уже видели, электрические заряды
могут свободно перемещаться в проводнике, и, поскольку они обладают
инерцией, естественно ожидать, что при ускорении тела заряды будут отста-
отставать от него, создавая тем самым электрический ток, который можно обна-
обнаружить по магнитному полю. Этот эффект, оказавшийся очень незна-
незначительным, был предсказан еще Максвеллом, но обнаружен и измерен лишь
вскоре после его смерти Толменом, Барнетом и другими. Результаты опытов
показали, что подвижное электричество в проводнике—отрицательное и что
отношение электрического заряда к его массе совпадает, в пределах погреш-
погрешности эксперимента, с соответствующим отношением у электрона.
Почти все явления, с которыми нам придется иметь дело в этой книге,
связаны с распределением или движением электронов, а положительные
заряды проявляются лишь как недостаток электронов, хотя с математиче-
математической точки зрения совершенно безразлично, осуществляется ли перенос
электричества отрицательными зарядами или положительными или зарядами
обоих знаков одновременно.
§ 6. Напряженность электрического поля. Если на бесконечно малый
электрический заряд, помещенный в некоторую область пространства,
действует сила, то говорят, что в этой области существует электрическое поле.
Напряженность электрического поля в некоторой точке определяется век-
вектором, равным силе, отнесенной к единице заряда и действующей на поло-
положительный заряд, расположенный в данной точке. Этот заряд должен быть
достаточно мал, чтобы его присутствие не вызывало перераспределения дру-
других зарядов. Последнее ограничение необходимо из-за явления электроста-
электростатической индукции.
Подобно тому, как действие на тело нескольких механических сил
может быть сведено к действию одной результирующей силы, являющейся
их векторной суммой, результирующая напряженность электрического поля,
созданного некоторым распределением зарядов, может быть получена как
векторная сумма напряженности полей, созданных отдельными элементами
этого распределения. Таким образом, напряженность электрического поля
в точке Р, созданного п зарядами, находящимися в бесконечной однородной
16
Глава I
среде с диэлектрической проницаемостью е, равна
A.2)
где Ер — напряженность электрического поля (в вольтах ва метр), rt —
вектор, равный по модулю rt и направленный из точки Р к заряду qt.
§ 7. Электростатический потенциал. При перемещении заряда в элек-
электрическом поле совершается работа. Потенциалом (в вольтах) точки Р электро-
электростатического поля называется работа (в джоулях на кулон) по перемещению
заряда из точки нулевого потенциала в точку Р. Выбор точки нулевого
потенциала — дело удобства. Очень часто, хотя и не всегда, она выбирается
на бесконечности. Величина заряда долж-
должна быть достаточно малой, чтобы не выз-
вызвать перераспределения электричества. Во
избежание явлений неэлектростатического
характера перемещать заряд нужно очень
медленно.
Вычислим потенциал поля точечного
заряда q. Работа dV, необходимая для пе-
перемещения единичного заряда на расстояние ds в поле Е, равна — Е ¦ ds
или — Eds cos 6, где б —угол между Е и ds. В случае поля точечного заряда
она равна
где г — вектор, направленный от заряда q к элементу пути ds, и б — угол
между г и ds, как показано на фиг. 1. Очевидно, что dr = ds cos 6, поэтому
для потенциала (в вольтах) имеем
?
О г0
Если выбрать г0 бесконечным, то
(L4)
Электростатический потенциал является скалярной функцией точки и не
зависит от пути, по которому заряд приносится в эту точку. Потенциал в
любой точке электростатического поля может быть получен путем сложения
потенциалов отдельных зарядов, создающих поле; таким образом,
п
Fp = J_2-fr-, A.5)
где jv — расстояние между Р и qt (в метрах).
Поскольку скалярная сумма значительно проще вокторной, то ясно,
почему при вычислениях предпочитают иметь дело с выражением A.5), а не
с A.2). Напряженность поля в точке Р можно найти из выражения A.5)
Е= -gradF= -W. A.6)
В прямоугольных координатах компопенты напряженности поля равны
Е = —— Е = , Е = • A-^)
х дх ' v ду z dz
Основные положения электростатики 17
Компоненты градиента в любой другой фиксированной координатной системе
можно получить, если выразить V, х, у и z через координаты этой системы.
Методы перехода от одной системы координат к другой приведены в
§ 4 и 5 гл. Ш.
Если расстояние между элементарными зарядами мало по сравнению со
всеми остальными рассматриваемыми размерами (что обычно и имеет место
на практике), то распределение зарядов можно считать непрерывным и можно
говорить об их объемной плотности р (заряд на единицу объема) и о поверх-
поверхностной плотности а (заряд па единицу поверхности). Сумма A.5) переходит
в этом случае в пптеграл
i С*!* C?, A.8)
1 4гаг J r ^ 4та
v S
где dv — элемент объема, dS — элемент поверхности. Необходимо заметить,
что эти формулы применимы только тогда, когда все окружающее простран-
пространство, а также находящиеся в нем материальные тела имеют диэлектрическую
проницаемость е. В противном случае нужно применять методы, развитые
в гл. IV и V.
§ 8а. Электрические диполи и мультиполи. Сложим потенциалы поля,
создаваемого зарядом — q, находящимся в точке х0, у0, z0, и поля, создава-
создаваемого зарядом -\-q, ваходящимся в точке xo + dxo, у0, z0. Тогда в некоторой
точке Р с координатами х, у, z результирующий потенциал будет равен V
или
4тау = -1-+ * f-S-W-—= - qdx° дðР-gdXa{x-Xa) - gdx° дг°р
op " ¦ op " op op ° op op
Если устремить dx0 —> 0, a q —> oo так, чтобы их произведевие q dx0 оста-
оставалось конечным, то получится система, известная под названием электри-
электрического диполя. Мощность или момент этого диполя определяется векторной
величиной m = q dx0, направленной от отрицательного заряда к положи-
положительному. В полярных координатах потенциал, в точке г, б, созданный ди-
диполем, помещенным в начале координат, раве.н
у_ nifos6 ^ m-r A g.
Очевидно, это выражение может быть обобщено, так что, если потенциал
Vp в точке Р, созданный системой п зарядов, дается выражением A.5), где
/v — радиус-вектор из q- в Р, то потенциал V'p, созданный системой п ди-
диполей, таких же по знаку и по величине и расположенных в тех же точках
пространства с осями, параллельными оси х, будет равен
Путем дифференцирования выражения для потенциала единичного элек-
электрического диполя, представленвого в прямоугольвых" координатах, можно
получить потенциал единичного квадруполя, размерность которого QL2.
Таким образом, выражения
дхду
И Т. Д.
представляют потовциалы линейного квадруполя (фиг. 2, а) и поверхност
ного квадруполя (фиг. 2,6). Дальнейшее дифференцирование приведет к по
2 в. Смайт
Библиотека
профессора Саночкина Ю.В.
18 Глава I
тонциа'ам более сложных мультгшольных систем, суммарный заряд которых
всегда равен нулю. Другие случаи будут рассмотрены в § 13.
Сила, действующая на диполь m в поле Е, равна векторной сумме
сил, действующих па каждый из зарядов, образующих диполь. Так как
заряды равны и противоположны, она сводится а векторной разности напряжеп-
ностой полей (ds • V)E на двух концах диполя, умноженной на q', таким
образом,
F = #(ds ¦ V)E = (m- V) Е. A.11)
В однородном поле эта сила равна нулю.
У
ах dx
Фиг. 2.
В однородном поле заряды находятся под действием сил -f- gE и — gE,
приложенных на расстоянии efcsinO F —угол между ds и Е). Поэтому на
диполь действует механический момент
) = юхЕ, A.12)
где t — единичный вектор, нормальный к m и Е,
§ 86. Взаимодействие диполей. Потенциальная энергия диполя в про-
произвольном поле с потенциалом V равна суммарной работе, совершаемой при
внесении в это поле каждого из зарядов в отдельности. Если потенциал
поля в точке Pv где расположен заряд +<7> равен F1? а в точке Р2, где
расположен заряд — у, равен F2, то ¦
• &V dV
' S7 " m л7 ' (^ • ^)
ндесь m — дшгольный момент, a s отсчитыкаетея в направлении оси диполя.
В задкторных обозначениях это можно записать в виде
W = (m-V)F. A.14)
Пусть mt и т2 — моменты двух диполей А и В, а г—вектор, направленный
из Л в В. Тогда потенциал в точке В, созданный диполем А, согласно
A.9), равен
i^ ^ (i) A.15)
Подстановка этого выражения для V в A.14) дает
A-ksW = + m2 • V (тх • ry~s) = m2 ¦ (rVm1 • г + хщ
= m2 • (m^" — nij ¦ r3ir) = m1 ¦ m2r~3 — ?m1 ¦ rm2 • rr'&.
Если mt и m2 образуют с г углы б и б', а ср —угол между ними, то
— 3 cos 6 cos 0'). (l.W)
Обозначим через ф угол между плоскостями, содержащими nij и m2 и uepe
секающимися вдоль г; тогда, беря г в направлении -х, a mt — лежащим в
Основные положении электростатики 19
плоскости ху, для направляющих косинусов получим Z1=cosft, /2 = cos&',
ml = sin 6, m2 = sin 6' cos ф, тгх = 0. Таким образом,
cos cp = Zj/2 -f- TOj/Wg -f и^ = cos б cos 6' -f sin 6 sin 0' cos ф,
ose'). A.17)
Сила, действующая между двумя диполями, получается путем дифферен-
дифференцирования
^ |^. A.18)
Она имеет максимум при ф = 0, 6 = 6' = О. Аналогично определяется момент,
стремящийся повернуть диполь в направлении а,
Т=-^-. A.19)
да v '
§ 9. Силовые линии. Одним из наиболее полезных способов наглядно-
наглядного представления электрического поля является изображение его при по-
помощи «силовых линий» или «эквипотенциальных поверхностей». Силовая
ливия электрического поля —это такая ваправленная кривая, касательная
к которой в любой точке совпадает по направлению с напряженностью
электрического поля в этой точке. Отсюда следует, что если ds—элемент
дуги этой кривой, го
ds = XE, A.20)
где X — скалярный множитель. Выразив векторы через их компоненты
в прямоугольной системе координат и исключив X, мы получим дифферен-
дифференциальное уравнение силовых линий
их dy dz .. «..
Аналогичные уравнения можно ваписать е в других координатных систе-
системах, если воспользоваться результатами § 3 и 5 гл. III. Существуют более
простые методы получения уравневий силовых линий, не требующие интег-
интегрирования этих уравнений. Однако один пример на их непосредственное
интегрирование мы все же приведем здесь. Рассмотрим поле, созданное
двумя зарядами: + q в точке х = а и ± g в точке ж=—а. Поскольку
в силу симметрии поле одинаково в любом сечении, содержащем ось х, то,
в частности, за это сечение можно принять плоскость ху. Сумма ж-со-
ставляющих напряженности электрических нолей, созданных двумя этими
зарядами в любой точке пространства, равна Ех, где
Или, произведя замену
и » = ^. A-22)
получим
qv . qu
\2 у2/1_|_м2|°/2
Аналогично
20
Глава I
Уравнение A.21) примет вид
d-L — ^" =
dx ~~ Ex ~
\
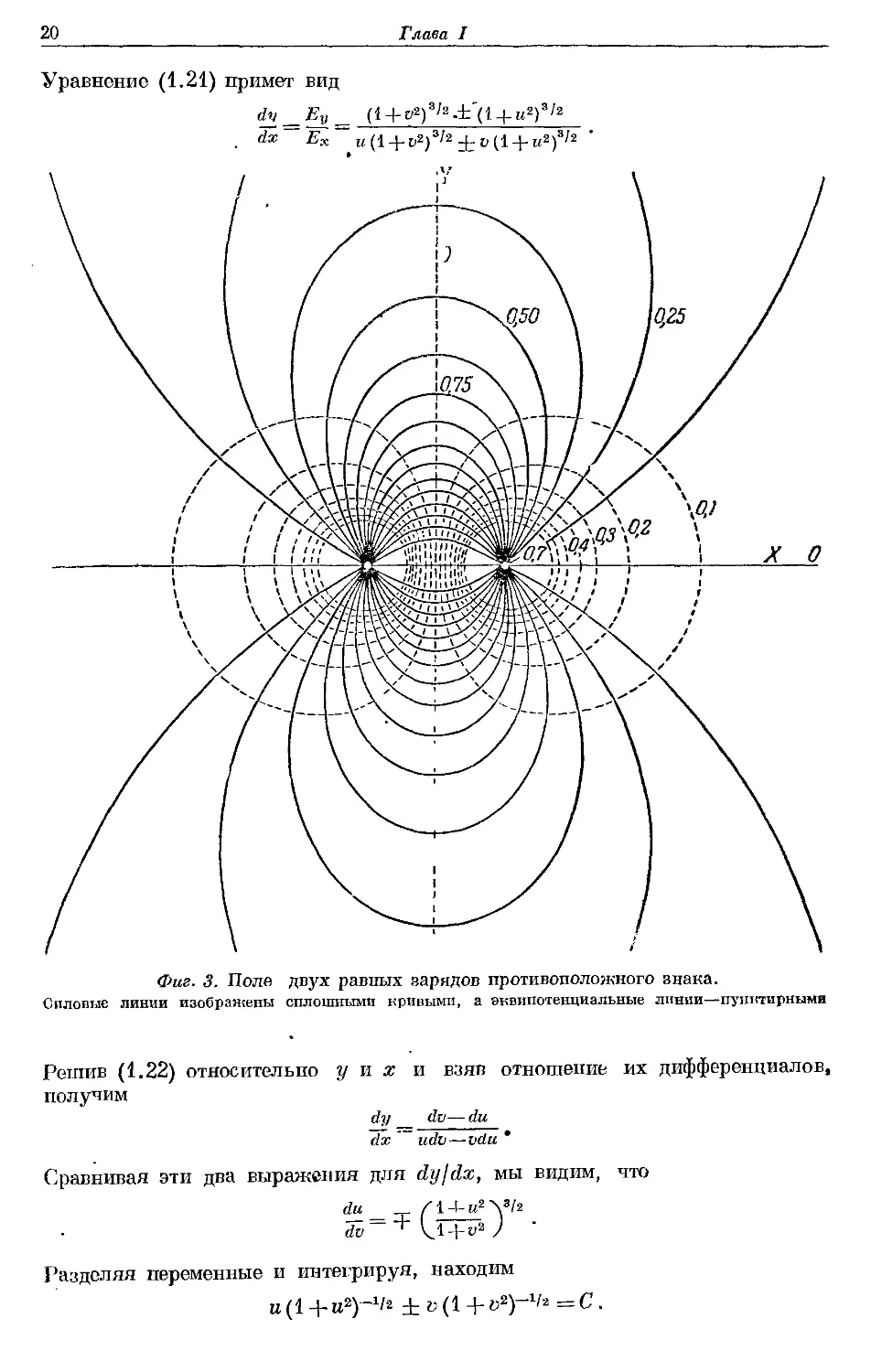
Фиг. 3. Поле двух равных зарядов противоположного знака.
Силовые линии изображены сплошными кривыми, а эквипотенциальные линии—пунктирными
Решив A.22) относительно у и х и взяв отношение их дифференциалов,
получим
dy dv— du
dx ' udv—vdu '
Сравнивая эти два выражения для dyjdx, мы видим, что
du _ /1 -1-м2 у/2
Разделяя переменные и интегрируя, находим
в A + »2)-1/f ± »A + v2)'1'2 = С •
Основные положения электростатики
21
Или, возвращаясь к х и у,
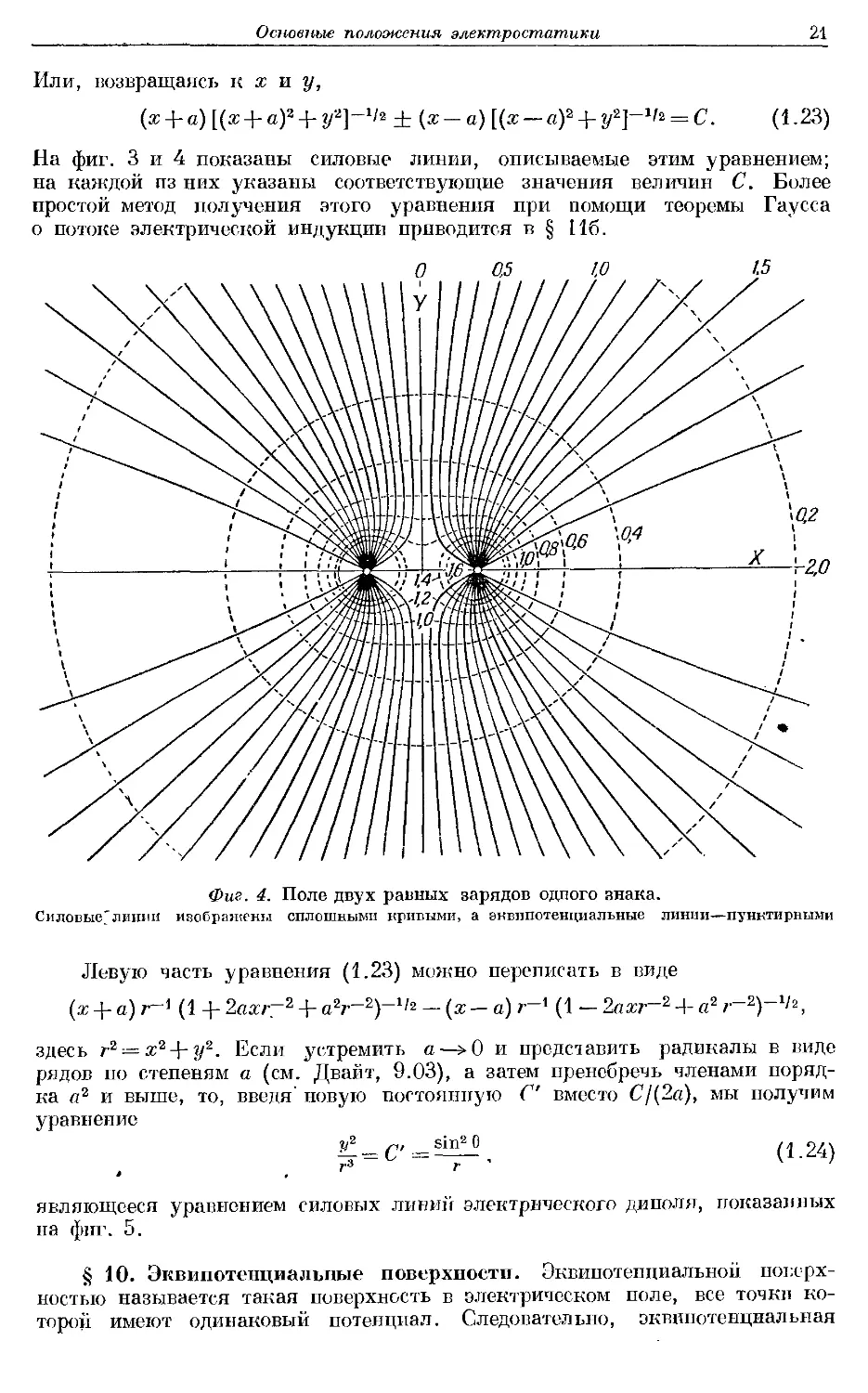
-Ч* = С. A.23)
На фиг. 3 и 4 показаны силовые линии, описываемые этим уравнением;
на каждой из них указаны соответствующие значения величин С. Более
простой метод получения этого уравнения при помощи теоремы Гаусса
о потоке электрической индукции приводится в § 116.
Фиг. 4. Поле двух равных зарядов одного знака.
Силовые'линии изображены сплошными кривыми, а эквипотенциальные линии—пунктирными
Левую часть уравнения A.23) можно переписать в виде
(ж + а) г-* A + 2ахгг2 + о8/--2)-1/* - (ж- о) г A - 2ахг~2 4- а2 л-2)-1'*,
здесь г2 = ж24-?/2. Если устремить о—>0 и представить радикалы в виде
рядов но степеням а (см. Двайт, 9.03), а затем пренебречь членами поряд-
порядка я2 и выше, то, введя новую постоянную С вместо С/Bа), мы получим
уравнение
^С'^:^-0 A.24)
< , г3 г ' '
являющееся уравнением силовых линий электрического диполя, показанных
на фиг. 5.
§ 10. Эквипотенциальные поверхности. Эквипотенциальной поверх-
поверхностью называется такая поверхность в электрическом поле, все точки ко-
которой имеют одинаковый потенциал. Следовательно, эквипотенциальная
22
Глава I
поверхность описывается уравнением
A.25)
где С — постоянная. В последующих главах будут приведены картины раз-
различных электрических полей с нанесенными на них эквипотенциальными
п силовыми линиями. Заметим, что поскольку при движении заряда вдоль
эквипотенциальной поверхности не затрачивается никакой работы, силовые
линии должны быть к ним ортогональны. В качестве примера использова-
использования уравнения A.25) возьмем только что рассмотренный случай. Точки,
потенциал которых равен С, определяются уравнением
Это уравнение эквипотенциальных поверхностей, сечение которых показано
Фиг. 5. Силовые линии электрического диполя.
на фиг. 3 и 4 при помощи пунктирных линий. Значения С даны для
величины заряда q = 4тс.
В электростатическом поле часто можно отыскать такие точки или
линии, где эквипотенциальные поверхности имеют по крайней мере двойное
пересечение и где, следовательно, VF становится равным нулю. Их назы-
называют нейтральными, равновесными или сингулярными (особыми) точками
или линиями. Такой точкой является, например, начало координат на
фиг. 4. В § 24е гл. V будут рассмотрены некоторые свойства этих точек.
§ 11а. Теорема Гаусса о потоке электрической индукции1). Мы
будем доказывать эту теорему, исходя из закона обратных квадратов и
предполагая, что все' пространство заполнено однородным диэлектриком.
Последнее предположение будет в дальнейшем снято.
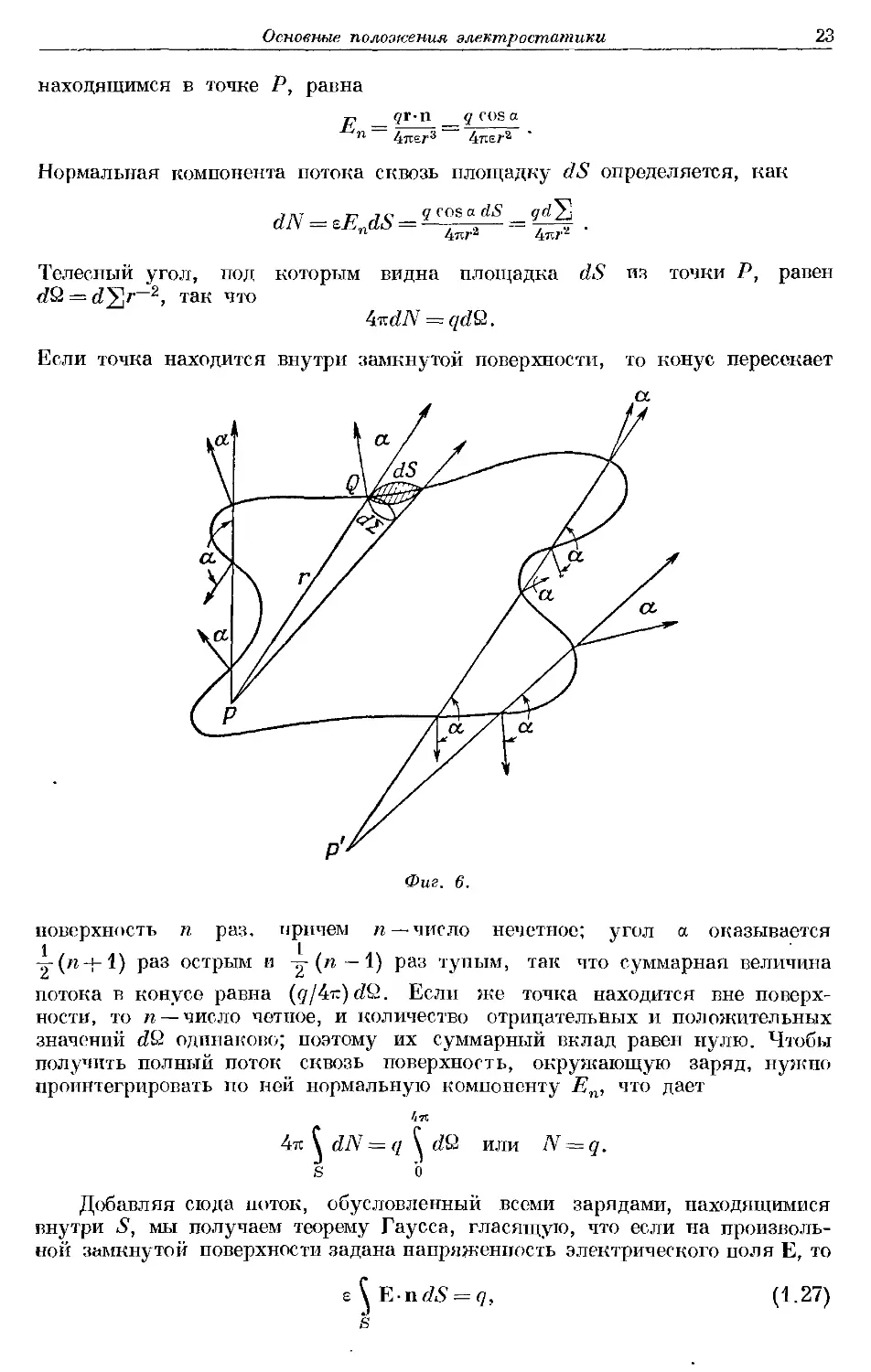
Рассмотрим малый элемент dS замкнутой поверхности (фиг. 6), внешняя
нормаль к которой образует угол а с радиус-вектором из точки Р, в кото-
которой расположен точечный заряд д. Каждую точку границы элемента dS
соединим прямой линией с точкой Р, так чтобы образовался малый конус.
Этот конус имеет сечение d^ со сферической поверхностью, проходящей
через точку Q и имеющей центр в точке Р; поэтому d^]=dS cos а. Нормаль-
Нормальная составляющая напряженности поля, созданного в точке Q зарядом q,
*) Определение вектора электрической индукции будет дано с § 14. В оригинале
а"втор пользуется понятием электрического потока (electric flux).—Прим. перец.
Основные положения электростатики
23
находящимся в точке Р, равна
Р qr-n q COS a
п = 4nir3 = 4тсег2 "
Нормальная компонента потока сквозь площадку dS определяется, как
Телесный угол, под которым В1чдна площадка dS та точки Р, равен
Q ^]2, так что
Если точка находится внутри замкнутой поверхности, то конус пересекает
а.
Фиг. 6.
поверхность п раз, причем и —число нечетное; угол а оказывается
1 I
у(п~|-1) раз острым и у (и — 1) раз тупым, так что суммарная величина
потока в конусе равна (q/ir.)dQ. Если же точка находится вне поверх-
поверхности, то и —число четное, и количество отрицательных и положительных
значений dQ одинаково; поэтому их суммарный вклад равен нулю. Чтобы
получить полный поток сквозь поверхность, окружающую заряд, нужно
проинтегрировать по ней нормальную компоненту Еп, что дает
i я
4тг \ dN = q \ dQ или N = q.
S О
Добавляя сюда поток, обусловленный всеми зарядами, находящимися
внутри S, мы получаем теорему Гаусса, гласящую, что если на произволь-
произвольной замкнутой поверхности задана напряженность электрического поля Е, то
е \ F,-ndS = <
S
A.27)
24
Глава I
где n — единичный вектор внешней нормали к поверхности, а интегрирова-
интегрирование производится ио всей поверхности, охватывающей заряд q.
Если пространство вне рассматриваемой 1юверхности является неодно-
неоднородным и содержит различные диэлектрические и проводящие тела, то
необходимо ввести определенные предположения относительно электрических
свойств веществ в электростатических полях. Поэтому при рассмотрении
таких полей мы будем считать, что природа всех тел чисто электрическая
и что они состоят из положительных и отрицательных зарядов, ноля кото-
которых подчиняются закону обратных кяадратов. Ята гипотеза позволяет
объяснить электростатические явления в любом материальном теле путем
сложения полей всех составляющих его зарядов. Следовательно, уравнение
A.27) остается в силе независимо от природы диэлектрических или прово-
проводящих веществ, находящихся вне рассматриваемой поверхности, так как оно
учитывает поля, созданные внешними зарядами. Принятая нами гипотеза
содержится в явном или неявном виде в большинстве курсов по электро-
электростатике.
§ 116. Силовые линии системы коллинеарных зарядов. Для иллю-
иллюстрации применения этой теоремы воспользуемся ею при нахождении урав
нения силовых линий систе-
мы коллинеарных электриче-
электрических зарядов <7ц <7г> Яз' ¦ ¦ •>
расположенных в точках хх,
х2, х3, ... оси х. Из симмет-
симметрии системы ясно, что ни од-
одна силовая линии не может
пересечь поверхность, образо-
образованную вращением вокруг оси
х силовой линии, лежащей
в плоскости ху. Применяя
теорему Гаусса к объему, ог-
ограниченному этой поверх-
поверхностью вращения и плоско-
плоскостями ж = 4 и ж - В (фиг. 7),
мы получим, что полный ноток N, входящий через сечение А, равен полному
потоку N, выходящему через сечение В, так как поток сквозь боковые стенки
равен пулю. Для получения уравнения поверхности необходимо, таким образом,
приравнять N постоянной величине. Как следует из A.2), N равняется
сумме потоков от каждого из зарядов в отдельности, поэтому, по только
что доказанной теореме Гаусса, получаем
Фиг. 7.
здесь Q1% 62, 63, ...—телесные углы, иод которыми видно сечение из
ху, х„, xs, . . . Переходя к углам аг, сс2, а3, . . . (см. фиг. 7), получим
> = С"—-^ У о. COS a..
Объединив постоянные в левой части уравнения и выразив косинусы чере;$
координаты х, у плоскости ху, мы приходим к уравнению силовых лилий
п
C^^q.ix-x^Kx-x^ + y^lK A.28)
Уравнение A.23) является его частным случаем.
Основные положения электростатики 2S
§ Ив. Силовые линии на бесконечности. Введем г = [(ж — жJ + у2]1!*
и будем пренебрегать значениями [(ж— ж;)/г]п при ж — ж; <С J" и тг>>2, тогда
можно написать
п п п
vi /— \ ^ — ж" VI , л пгч
2 ^ (*¦-*<)=-=--2 ?» (-1-29)
i=l i=j
где ж — координата «центра тяжести» зарядов. Таким образом, поле на
бесконечности совпадает с полем заряда, помещенного в центре тяжести
зарядов и равного их алгебраической сумме. Это положение можно распро-
распространить и нк неколлинеарные заряды. Действительно, разбивая произволь-
произвольную систему зарядов на пары п применяя в каждой паре формулу A.29),
а затем группируя попарно центры тяжести предыдущих пар и т. д., мы
придем в конце концов к центру тяжести всей системы.
§ 12. Максимумы и минимумы потенциала. Теорема Ирншоу. Рас-
Рассмотрим маленькую сферическую поверхность, охватывающую точку Р
электрического поля. Среднее значение потенциала на этой поверхности
равно
]
я о о
Беря производную и применяя теорему Гаусса, получим
dV I С c'dV . Л ,n , 1 Г dV ,c q
-т- = г- \ \ т-sin " db d® = -.—s \ -г- dS — — —г— ,
dr in J J dr ~ Anr2 ) dr 4uer2
S
0 0
где q -заряд внутри сферы. После интегрирования приходим к результату
В случае q = 0 среднее значение потенциала на малой сфере, охватывающей
точку Р, такое же, как и в точке Р. Отсюда вытекает теорема о том, что-
потенциал не может иметь ни максимума, ни минимума в тех точках про-
пространства, где отсутствуют электрические заряды. IIз определения потен-
потенциала следует, что для устойчивого равновесия положительный заряд должен
находиться в точке минимума потенциала, а отрицательный—в точке, где
потенциал максимален; при атом потенциал самого заряда, очевидно, исклю-
исключается из рассмотрения. Поскольку по доказанному выше в электростати-
электростатическом иоле нет ни максимумов, ни минимумов потенциала, то отсюда
следует также теорема Ирншоу, утверждающая, что заряд в электрическом
поле не может удерживаться в равновесии одними электрическими сплами.
Следовательно, если мы считаем природу вещества чисто электрической,
т. е. все тела состоящими из положительных и отрицательных зарядов,
между которыми действуют электрические силы, то эти силы взаимодействия
должны быть отличны от электростатических.
§ 13. Потенциал двойпого электрического слоя. В § 8а мы видели, что
потенциал диполя можно получить из потенциала одиночного заряда путем
дифференцирования в ваправлеиии оси диполя. Подобным же образом мы
получаем, что если потенциал точки Р, созданный элементом поверхности.
dS с плотностью заряда с, равен
dV^-г^- dS,
26 Глава I
где ;—расстояние от dS до Р, то
-.— dS -рг- ( —
4пг дп\г
является потенциалом точки Р, созданным диполем с моментом adS, направ-
направленным вдоль п. Итак, потенциал двойного электрического слоя с моментом
Ф (на единицу плошали) равен
4л.е ) дп
S
Но n-rr3dS = dQ, где dQ — телесный угол, под которым виден элемент
поверхности dS из точки Р (см. § 11а). Поэтому
F = —V'ErfQ. A.31)
4ле J v '
В случае двойного слоя с постоянным моментом W это дает
4ие v '
где Q — полный телесный угол, под которым виден двойной слой из Р.
§ 14. Вектор электрической индукции и силовые трубки. Очень
часто приходится иметь дело с произведением диэлектрической проницаемости
на напряженность электрического поля. В слу-
случае изотропных диэлектриков это произведе-
D2 ние называют вектором электрической индук-
индукции D или вектором электрического смещения;
таким образом,
D==eE. A.33)
В системе единиц MKS индукция D измеряется
в кулонах на квадратный метр, а напряжение
электрического поля Е —в вольтах на метр.
Линии электрической индукцки аналогичны
Фиг. 8. линиям напряженности электрического поля;
в изотропных диэлектриках они совпадают по
направлению, но в силу того, что е больше е„, линии электрической индукции
расположены плотнее. Взяв малый элемент площади, нормальный к линии
индукции, и яроведя линии индукции через псе точки его границы, мы
выделим в пространстве некоторую область, называемую силовой трубкой
(см. фиг. 8). Применим теорему Гаусса о потоке вектора еЕ, т. е. о потоке
электрической индукции, к свободному от зарядов пространству, ограни-
ограниченному двумя нормальными сечениями такой силовой трубки. Поскольку
интеграл по боковой поверхности равен нулю, поток, входящий в один
конец трубки, равен потоку, выходящему из другого конца, так что если
¦«Sj и S2 — площади поперечных сечений, то поток в трубке равен
В последующих главах будет приведено много фигур, на которых показаны
силовые трубки. Единичной силовой трубкой называется трубка, ноток
сквозь любое сечение которой равен единице. Сфера единичного радиуса.,
окружающая заряд q, имеет площадь 4xjk2, поэтому на ней D = qj^kr..
Следовательно, из заряда q выходит q единичных силовых трубок. Таким
•образом, заряд на конце единичной мшовой трубки равен одному кулону.
Основные положения электростатики
27
§ 15. Натяжения в электрическом поле1). Понятие о силовых линиях
и силовых трубках было введено нами лишь для более наглядного пред-
представления электрического поля. Возможно, однако, следуя Фарадсяо, пойти
значительно дальше в развитии этих идей, а именно — рассматривать трубки
как средство передачи электрических сил. Поскольку при решении ряда
задач такая точка зрения может быть
чрезвычайно полезной, посмотрим, какую
систему натяжений надо постулировать
для получения наблюдаемых электриче-
электрических сил. Выясним, как должно зависеть
иатяшение вдоль силовой трубки от на-
напряженности электрического ноля для
того, чтобы сила взаимодействия между
двумя равными зарядами противополож-
ного знака, расположенными на расстоя-
расстоянии 2о друг от друга, выражалась бы законом Кулона. Обозначим эту
зависимость через Ф(Е). Из формулы A.2) напряженность поля в плоскости
«симметрии (см. фиг. 9) равна
р, 2nq _ q COS3 6
(Tins* О
кольцевой элемент площади
cos8 В
m
Выписав силу Кулона в левой части, а натяжения в плоскости yz в пра-
правой части уравнения и разделив обе части на 2-ка2, получим
т. 12
32кЧа* ~ 2ла2
A.34)
Положим x = qlBnsa2) и представим Ф п виде степенного ряда по Е; тогда
со -Г./2
1Г = ^5 2 cnEnds=^cn^ \ cos3(-Desinerfo.
n=0 ii=0 0
Это равенство должно иметь место для любых значений qua и, следова-
следовательно, для любых значений х. Поэтому все Сп = 0, за Х1склгочентгем и = 2.
Сокращая на ж2, получаем
Итак,
A.35)
¦Это и есть то натяжоние"вдоль силовой линии, которое требуется для со-
создания в соответствии с законом Кулона гилы притяжения двух зарядов
противоположного знака.
х) В английской литературе различаются два термина: stress—напряжение и ten-
tension—натяжение. Во избежание путаницы с напряжением электрического поля оба
«лова всюду переведены как натяжение. — Прим. перев.
28 Глава I
Очевидно, что если бы в исследованном нами случае имели место
только силы натяжения, действующие вдоль силовых трубок, то эти трубки
стремились бы, по возможности, укоротиться и расположились бы в конце
концов вдоль линии, соединяющей заряды. Однако мы знаем, что ири
равновесии силовые линии заполпяют все пространство вокруг зарядов,
следовательно, между ними должны существовать пекоторые силы отталки-
отталкивания, препятствующие их стягиванию. Для определения этого давления
Чг (Е) рассмотрим силу, действующую между двумя зарядами одного знака.
Этот случай отличен от только что рассмотренного, потому что теперь
силовые линии оканчиваются на бесконечности. Натяжение, приходящееся
на единичную площадку сферы большого радиуса, убывает с расстоянием
обратно пропорционально четвертой степени радиуса, как это ясно из выра-
выражения A.35) и из закона обратных квадратов. Площадь поверхности сферы
возрастает пропорционально квадрату радиуса, так что по этому направле-
направлению не передастся никаких сил. Поэтому полную силу можно рассматри-
рассматривать как результат отталкивания силовых линий в плоскости симметрии.
Из выражения A.2) для напряженности поля в этой плоскости имеем
2qy ~=?c°s2flfn0. A.36)
Выполняя действия, аналогичные предыдущим, вместо выражения A.34)
получим
L J
2зш2
На том же основании, что и раньше, _" (Е) можно представить в виде
С2Е2 и тот же самый путь вычисления С2 приводит к
эт/2
Таким образом,
-~. A.38)
Эта величина представляет собой силу отталкивания (на единицу площади)
между двумя соседними силовыми линиями, необходимую для получения
закона Кулона в случае двух зарядов одинакового знака. Эти результаты
можни записать в следующих эквивалентных друг другу формах:
еЕ* ED Л» . чч
Так как Ф и W являются функциями только е и Е, то они имеют одина
ковый вид для любых полей независимо от их источников.
§ 16. Теорема Гаусса о потоке электрической индукции для неод-
неоднородных сред1). Теперь мы уже подготовлены для обобщения теоремы
Гаусса о потоке электрической индукции па случай изотропной среды с мс-
«
г) Оставаясь п рамках макроскопической электродинамики, невозможно доказать
тсорому Гаусса о потоке электрической индукции для неоднородной среды, исходя
только из закола Кулона. В частности, нрмлодешшй здесь вывод непоследователен,
так как при применении теоремы Гаусса к енлешом трубке с переменной диэлектри-
диэлектрической проницаемостью е автор уже предполагает, что для незаряженного диэлектрика
V-D = O. Вывод теоремы Гаусса о потоке электрической индукции можно найти в книге-
И. Е. Та мм а, Основы теории электричества, 1940. — Прим. перев.
Основные положения электростатики
29
няющейся от точки к точке диэлектрической проницаемостью. Предположим,
что в такой среде, внутри замкнутой поверхности S, в точке Р расположен
точечный заряд q. Окружим точку Р столь малой сферой S', чтобы внутри
¦ее величину е' можно было бы считать постоянной. Затем на поверхности
S выделим элемент dS тоже настолько малый, чтобы величина е на нем
оставалась постоянной, и рассмотрим силовую трубку, имеющую своими
сечениями элементы dS на S и dS' на S' и оканчивающуюся на заряде q.
Применил! теорему Гаусса к свободному от
зарядов диэлектрику внутри трубки между
dS и dS'. Так как нормальная составляю-
составляющая D на стенках равна нулю, то единст-
единственный вклад в поверхностный интеграл
дадут dS и dS', поятому
S
Интегрируя по двум поверхностям, мы имеем
»' dS' — \ еЕ • n dS,
8 Фиг. 10.
так как е' одинакова для всех элементов
¦dS'. Но в § 11а было доказано, что интеграл, стоящий и левой части,
равен q, так что
^eE-ndS=q, A.40)
s
где и е и Е являются функциями координат. Это выражение, как и раньше,
нетрудно обобщить на тот случай, когда q включает в себя все заряды
янутри S.
Сложные поля могут быть суммой полей простых источников. Приме-
Применение выражения A.40) в таких случаях упрощается, если сначала вычис-
вычислить потоки от отдельных источников, а затем просуммировать их:
E2-ndS+...
Иногда этого бывает достаточно для решения задачи.
A.41)
§ 17. Граничные условия и натяжения на поверхности проводников.
Если заряд находится на проводнике в статическом равновесии, то ни внутри
проводника, ни вдоль его поверхности не существует никаких полей: в про-
противном случае, поскольку по определению заряды в проводнике могут
свободно перемещаться, возникло бы движение зарядов, что противоречило бы
постулированному состоянию равновесия. Отсюда следует, что проводник
целиком находится под одним потенциалом и что силовые линии подходят
нормально к его поверхности и оканчиваются на ней.
Пусть а — плотность поверхностного заряда (в кулонах на квадратный
метр). На' каждую единицу заряда приходится одна единичная силовая
трубка, выходящая при положительном значении а из поверхности. Поэтому
D = eE=--a. A.42)
Поскольку силовые линии выходят из проводящей поверхности нормально
к ней, то они могут взатшно пересекаться только на бесконечно острых
краях или остриях. Мы видели, что это происходит в математических точках
30
Глава I
или ребрах. Ясно, что имеет место и обратное утверждение. На дне V-об-
разного желобка или конической впадины- Duo равны нулю.
Из § 45 следует, что вдоль силовых линий существует натяжение,,
равное по величине
F =?.= ?-. A.43)
Очевидно, это есть сила, действующая на квадратный метр заряженной
'проводящей поверхности. Она направлена всегда в сторону внешней норма-
нормали, независимо от знака поверхностного заряда.
Следует заметить, что мы не рассматривали гидростатических сил,.
могущих присутствовать в диэлектрике благодаря его способности расши-
расширяться или сжиматься в электрических полях. Выражение учитывающее-
такие силы, будет получено позже в § 10 гл. П.
§ 18. Граничные условия и натяжения на поверхности диэлектрика.
Применим теорему Гаусса о потоке электрической индукции к малому
дискообразному объел.у, плоские поверхности
которого имеют площадь dS и расположены
с двух противоположных сторон границы раз-
раздела двух диэлектриков е' и е" (фиг. 11).
Этот диск настолько сплюснут, что площадь
его боковой поверхности исчезающе мала по
сравнению с площадью оснований. Если на
поверхности границы раздела двух сред сво-
свободные заряды отсутствуют, то, обозначив
нормальные компоненты электрической индукции через D'n и D"n, из § 16
найдем
D'ndS = D'n dS или D'n = D'n ¦ A.44)
Натяжение на границе, созданное нормальными компонентами индукции*
должно равняться разности натяжения по обе стороны от границы; поэтому,
пользуясь выражением A.39), получаем
_ D'n2 D^_ _ _ Р'„*(г' — г") _ _ Щ? К'—К" .
«~ ~2Р ~ ~5Р ~~ W^' 2еи К'К" ¦ {
Рассмотрим работу, совершаемую при перемещении единичного заряда
вдоль пути, показанного на фиг. 12; участки этого пути, перпендикуляр-
перпендикулярные к границе, г радиол агаются исчезают»-
малыми. Поскольку энергия сохраняется,
то работа, совершаемая при перемещении
единичного заряда вдоль этого пути, рав-
равна нулю, и, следовательно, E[ds = E'[d&
или
Фиг. 12. Е\ = Е\. A.46)
Давление па границу равно разности да-
давлений по обе стороны от нее; поэтому из выражения A.38) имеем
Фиг. 11.
Рп =~*'Е?-У"Е? = ~Е?
A.47)
Таким образом, можно сформулировать следующее положение: на неза-
незаряженной границе раздела двух диэлектриков нормальная составляющая
вектора электрической индукции и тангенциальная составляющая напря^
Основные поломсения электростатики
31
женности, электрического поля непрерывны. Эти граничные условия можно-
записать при помощи потенциалов
дп
=- В
dV"
дп
Т7, SV TS., 0V"
ИЛИ Л —— = К -х— ,
дп дп
V =V",
A.48)
A.49)
где V и V" — потенциалы в средах в' и в".
нуль потенциала в обеих сгедах выбран
так, чтобы в некоторой точке границы со-
соблюдалось равенство V — V". Далее, пу-
путем интегрирования соотношения A.46) убеж-
убеждаемся в справедливости условия A.49) для
всех точек границы раздела.
Пользуясь соотношениями A.45) и A.47),
можно выразить нормальные натяжения, воз-
возникающие на границе раздела двух диэлек-
диэлектриков и направленные из в' в в", в виде
Условие A.49) означает, что
Фиг. 13.
F =Т —Р = —
n -*n l п
v
I)'2
к.
Л'2
21
2е'
При выводе этой формулы не было принято во внимание, что некото-
некоторые диэлектрики обладают способностью сжгшаться или расширяться в при-
присутствии электрического поля. В таких средах на границу раздела будут
действовать дополнительные силы гидростатического происхождения. Выра-
Выражение, учитывающее эти силы, будет получено в § 10 гл. II.
На границе раздела двух изотропных диэлектриков силовые линии
и линии электрической индукции преломляются одинаковым образом. В сре-
среде с ех обозначим угол между Ех (или DJ и нормалью к границе через а1г
а соответствующий угол в среде е2 — через <х2 (фиг. 13). Тогда из соотно-
соотношений A.44) и A.46) получим
D1 cos ax = s1i?1 cos ах = D2 cos а2 == ?2E2 cos <x2,
D^e~J sin a, = Ex sin ax = D2e^1 sin a2 = E2 sin a2.
Разделил первое уравнение на второе, найдем
ejClga^tjdg^. A-51)
Это и есть закон преломления векторон D и Е на границе раздела двух
изотропных сред с различными диэлектрическими проницаемостями.
§ 19. Электрическая индукция и напряженность поля в твердых
диэлектриках. Диэлектрическая проницаемость была впервые введена нами
при формулировке закона Кулопа A.1) в качестве множителя, характери-
характеризующего среду, в которой, измеряются электрические силы. На первый
взгляд трудно представить себе, каким образом могут быть выполнены эти
гипотетические измерения в твердых диэлектриках. Однако, используя
только что полученные граничные условия, можно предложить метод опре-
определения электрической индукции п напряженности поля, а следовательно,
и диэлектрической проницаемости в таких средах.
Для определения электрической индукции и напряженности поля
в твердом диэлектрике сделаем в нем маленькую безвоздушную дискооб-
дискообразную полость, толщина которой несоизмеримо мала по сравнению с ради-
радиусом. Напряженность поля внутри полости вдали от ее краев полностью
Глава I
определяется граничными условиями на плоской границе раздела, как по-
показано на фиг. 14, а.
Для определения индукции ориентируем полость так, чтобы напря-
напряженность полн внутри нее была нормальна к плоскости основания
<(c\i. фиг. 14, а). Из § 18 известно, что электрическая индукция в диэлек-
диэлектрике и в полости в этом случае одинаковы; поэтому, измеряя напряжен-
напряженность поля в полости и умножая ее на sv, можно найти электрическую
индукцию в диэлектрике.
Для определения напряженности поля в твердом диэлектрике надо
•ориентировать длинную тонкую цилиндрическую полость так, чтобы вектор
напряженности поля внутри нее был параллелен оси (см. фиг. 14, б).
Но из равенства A.46) следует, что напряженность поля внутри полости
такая же, как и в твердом диэлектрике. Отношение индукции к напряжен-
Фиг. 14.
ности. поля дает диэлектрическую проницаемость; ири этом необходимо,
•чтобы размеры полости были значительно меньше размеров окружающего
диэлектрика и чтобы внешнее поле оставалось постоянным. .
Найденные таким путем величины электрической индукции и напря-
напряженности поля, конечно, не представляют собой истинных молекулярных
полей внутри диэлектрика, а являются результатом их усреднения. Всякие
другие значения средних величин будут находиться в противоречии с резуль-
результатами макроскопических наблюдений.
§ 20. Кристаллические диэлектрики. Применим теперь эксперимен-
экспериментальный метод § 19 к нахождению отношения электрической индукции D
и напряженности поля Е в однородном кристаллическом диэлектрике.
От граней большого диэлектрического куба, плоскости которого перпенди-
перпендикулярны к осям х, у и z, отрежем три плоскопараллельные пластинки
толщиной d. На поверхности этих пластинок нанесем проводящий слой
"и приложим к каждой из пластинок разность потенциалов V. Рассмотрим
участки пластинок, достаточно далекие от краев. Граничные условия
для потенциалов на всех таких участках для всех пластинок одинаковы,
следовательно, одинаково и распределение потенциалов на центральных
участках всех пластинок. Таким образом, эквипотенциальные поверхности
вблизи центра пластинок параллельны проводящим плоскостям, и напряжен-
напряженность электрического поля Е, согласно формуле A.6), равна V/d. Проводя
далее опыты с дискообразной полостью, размеры которой несоизмеримо
малы по сравнению с d (во избежание нарушения распределения зарядов
на проводящих поверхностях), находим, что D пропорционально Е, но направ-
направления их различны. Поэтому для х, у и z пластинок соответственно имеем
(Dx)x - впЕх, (Dy)x = haEf, (Dz)x = в13Ех,
= ЧзЕу,- A.52)
(Dx)z = b31Ez, (Dy)z = B3iEz, (Dz)z = b33Ez.
Даже если напряженность Е одинакова во всех пластинках, нормальная
¦составляющая D, вообще говоря, может быть различной. Однако, как пока-
Основные положения электростатики 33
зывает эксперимент, в любом случае имеет место
(Dx)yEx = (Dy)xEy, (DX)ZEX = (DXEZ, (Dy),Ey = (Dz)yEz. A.53)
Из выражения A.52) следует
Ac = hiEx + 4iEv + b31Ez,
Dv = в12Ех + в22Еу + ЧгЕг, A.54)
Dz = 4sEx + 4zEv + bssEz.
Сравнивая соотношения A.53) и A.52), мы видим, что
S12=e2U el3=E31> е23 = Е32- A.55)
Таким образом, если в изотропной среде величины D и Е связаны простым
множителем е, то в кристаллах вместо него появляется величина, известная
под названием симметричного тензора, имеющего девять компонент, шесть
из которых различны между собой.
Посмотрим, нельзя ли так ориентировать оси, чтобы по возможности
упростить вид соотношений A.54). Произведение E-D, будучи величиной
скалярной, не должно зависеть от выбора осей координат. Представляя
его через значения компонент Е и используя соотношения A.54) и A.55),
имеем
Е D = впЕ% + в22Е1 + в33Е% + 2в12ЕхЕу + 2е13ВД + &23ЕуЕг. A.56)
Это уравнение поверхности второго порядка относительно Ех, Еу и Ez.
Поворотом осей координат можно менять величины Ех, Еу, Еъ, сохраняя
постоянным Е% + Еу -\- El. В частности, будем ориентировать оси так, чтобы
исчезли все смешанные произведения ЕхЕу, EXEZ и EyEz. Уравнение
квадратичной формы относительно новых осей можно записать в виде
Ъ-Ъ^^ЕЬ + г^ + ъЕХ, A.57)
а компоненты электрической индукции относительно этих осей будут соот-
соответственно равны
Г>х = вгЕх, Dy = e2Ey, DZ = 4EZ. A.58)
Направления координатных осей в соотношениях A.58) совпадают с направ-
направлениями электрических осей кристалла. Если величины въ в2 и е3 одинаковы,
то среда изотропная. В случае равенства только двух величин кристалл
называется одноосным. Если же все три величины различны, мы имеем
дело с двухосным кристаллом.
ЗАДАЧИ 1)
1. Два топких параллельных коаксиальных проводящих кольца одинакового
радиуса а находятся па расстоянии Ъ друг от друга. Работа, которую необходимо
затратить при внесении точечного заряда q в центр каждого из колец, равна соответ-
соответственно FKj и W2- Показать, что величины зарядов на кольцах равны
2. Четыре одинакопых параллельных линейных наряда расположены вдоль ребер
квадратной призмы, причем заряды, лежащие па копцах одной диагонали, положи-
х) Здесь и в дальнейшем задачи, отмеченные авездочкой (*), заимствованы, как
указывает автор, из экзаменационных вопросов Кэмбриджского увисерситета в том
виде, о каком они были приведены в книге Джинса (J. H. Jeans, The Mathemati-
Mathematical Theory of Electricity and Magnetism, Cambridge, 1925). При переводе этих задач мы
пользовались современной терминологией и практической системой единиц (JVIKS).—
Прим. перео.
в. Смайт
34 Глава I
тельные, а на концах другой—отрицательные. Найти чагть полного потока индукции,
входящую внутрь призмы.
3. Заряд q находится в точке ж = а, j/ = 0, z = 0. Найти величину заряда, который
нужно поместить в точку т.= —a, i/ = 0, 2 = 0 для того, чтобы поток индукции, прохо-
проходящий в положительном направлении сквозь круг х = 0, у2 + z2 = a2, был равен N.
4. Два тонких концентрических кольпа лежат в одной плоскости. Радиусы колец
равны 1 и 2, а заряды соответственно ¦—Q и +B7I'2Q. Покпзать, что единственные
нейтральные точки (точки равновесия) в поле находятся в sc = O и =(Г2"'2.
5. Показать, что уравнение силовых линий двух параллельных линейных заря-
зарядов q и —q (па единицу длины), расположенных в a- = e n sc= —а, можно записать
через поток индукции (на единицу длины) N между силовой линией к осью х в виде
6*. Заряды -\-iq, —q находятся в точках А та. В, точка же С является точкой
равновесия. Доказать, что гиловая линия, проходящая через точку С, пересекает линию
АВ в точке А под углом 60°, а в точке С под прямым углом. Найти угол в точке А
между линией АВ и той силовой линией, которая выходит из точки В под прямым
углом к АВ.
(Выписать выражение для потенциала в полярных координатах с цептром в С для
малой окрестности точки С.)
7*. Два положительных заряда q1 и д2 расположены соответственно в точках А
и В. Показать, что касательная на бесконечности к той силовой линии, которая выхо-
выходит из 9, под углом а к ВА, образует с линией ВА угол
2 arc sin ( q\'2 (gi + q2) -1'2 sin ^
и пересекает ее в точке С такой, что
AC:CB = q2: ди
8*. В точках А к В находятся точечные заряды -\-q, —q. Силовая линия, выхо-
выходящая из А под углом а к АВ, пересекает плоскость, проходящую через середину
отрезка АВ, перпендикулярно к нему, под прямым углом в точке Р. Показать, что
sin4=21/2sin4-^ PAB.
9*. Показать, что на произвольной замкнутой поверхности S, не содержащей
внутри себя заряженных тел, существует замкнутая линия, в каждой точке которой S
пересекается под прямым утлом с эквипотенциальной поверхностью, проходящей череа
эту точку.
10*. Заряды о?, —q, —q расположены соответственно в точках А, В и С, причем
В находится в середине АС. Нарисовать примерную картину силовых линий. Пока-
Показать, что сплоная линия, выходящая из точки А под углом а к АВ, большим, чем
arc cos (— 1/з), не может достигнуть ни точки В, ни точки С. Показать, что асимптота
силовой линии, соответствую цей углу а = arc cos (— 2/3), перпендикулярна к АС.
11*. [1а прямой линии имеются три заряженные точки А, В, С причем AC=f,
BC = a2lj\ заряды в этих точках равны соответственно q, —qa/f, insVa. Показать,
что в поле этих зарядов всегда существует сферическая эквипотенциальная поверхность.
Найти положение точки равновесия на линии ABC в случае 4яе1/ = <7 (f + a)/(f — аK
и н случае 4-neF = q (/ — а)/(/ faJ.
12*. Сферические проводники А и С несут па себе заряды, равные соответственно
(? + ?') и —Ч- Показать, что ¦ зависимости от относительных размеров и расположе-
расположения сфер, а также от отношения q'/q (уществует либо точка, либо линия равновесия.
Нари ¦опять для каждого случая картину силовых линий и сечений эквипотенциальных
поверхностей пло. костью, проходящей через центры сферы.
J3*. Заряженное тело расположено вблизи проводпика, поверхность которого
имеет непрерывную кривизну. Показать, что на любой силовой линии, проходящей
от тела к проводнику, и точке, где сила минимальна, главные радиусы кривизны соот-
ветстпующей эквипотенциальной поверхности равны по величине и противоположны
по знаку.
14*. Если две заряженные концентрические проводящие сферы соединить проводом,
то внутревпяя сфера полностью разрядит!я. Доказать, что если бы сила взаимодей-
взаимодействия зарядов была пропорциональна r~'¦i"P'>t т0 На внутреннем проводнике остался
бы варяд В такой, что приближенно
Основные положения электростатики 35
где А—заряд на внешнем проводнике, а / и g— соответственно сумма и разность
радиусов сфер.
15*. Три бесконечных параллельных провода, несущих заряды (па единицу длины)
1, 2> ~ч' 1 пересекают перпендикулярную к ним плоскость в точках А, В. С, явля-
являющихся вершинами равностороннего треугольника. Доказать, что крайняя силовая
линия, идущая из А в С, образует с линией АС углы
если только q' }> 2q.
16*. Отрицательный точечный заряд —52 лежит на линии, соединяющей два
положительных точечных заряда §i и <7з> на расстоянии а и fl от каждого из этих
зарядов соответственно. Показать, что если величины зарядов удовлетворяют соотно-
соотношению
причем
то в поле существует такая окружность, в каждой точке которой сила равна нулю.
Найти (в общем виде) эквипотенциальную поверхность, на которой находится эта
окружность.
17*. Электрические заряды qv —qz, 53 (?з > ?i) расположены на одной прямой;
отрицательный заряд—на середине отрезка между положительными. Показать, что
если
то число единичных силовых трубок, приходящих из J] в q2, равно
(
18*. Точка .Р находится на расстоянии 1 см от бесконечной плоскости, поверх-
поверхностная плотность заряда которой равна с Показать, что половина полной напряжен-
напряженности поля 2тоз в точке Р обусловлена зарядами, расположенными в пределах 2 см
от точки Р, а половина—всеми остальными.
19*. Эбонитовый (непроводящий) диск радиусом 10 см заряжеп при помощи тре-
трения равномерно распределенным поверхностным зарядом. Найти напряженность элек-
электрического поля на оси диска на расстояниях 2, 6, 10, 14 см от его поверхности.
20. Два параллельных коаксиальных кольца радиусами о и Ъ несут на себе рав-
равномерно распределенные заряды Q, и Q2. Расстояние между плоскостями колец равно с.
Показать, что между кольцами действует сила
«и* (ей)8'» Ч-*" >> ' " 1~с^ + (в
и ?—полный эллиптический интеграл модуля к.
21. Показать, что на больших расстояниях поле кольцевого заряда —Q радиуса Ь
в концентрического, конланарного с ним другого кольпевого заряда Q радиуса с сов-
совпадает с полем линейного квадруполя, у которого крайние йаряды —Q отстоят от
центрального 2Q на расстоянии а; при этом б2 — с2 = 4а2.
ЛИТЕРАТУР IA
Abraham M., Becker R., Klassische Electrizitat und Magnetismus, Berlin, 1932,
(См. перевод: Абрагам М., Беккер Р., Теория электричества, 2-е изд.,
М.—Л., 1939.)
Geiger-Scheel, Handbuch der Physik, Bd. XII, Berlin, 1927.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925,
Mason M., Weaver W., The Electromagnetic Field, University of Chicago Press,
192&.
Maxwell J. C, Electricity and Magnetism, v. I, Oxford, 1881.
Poor V. C, Electricity and Magnetism, Wiley, 1931.
Ramsey A. S., Electricity and Magnetism, Cambridge, 1937.
Stratton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: С т р э т-
тон Дж. А., Теория электромагнетизма, М.—Л., 1948.)
Thomson J. J., Mathematical Theory of Electricity and Magnetism, Cambridge, 1921.
Thomson W., Papers on Electrostatics and Magnetism, Macmillan, 1884.
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
Wien-H arms, Handbuch der Experimentalphysik, Bd. X, Leipzig, 1930.
3»
Глава II
КОНДЕНСАТОРЫ, ДИЭЛЕКТРИКИ,
СИСТЕМЫ ПРОВОДНИКОВ
§ 1. Теорема единственности. Прежде чем решать задачу о нахож-
нахождении потенциалов в системе проводников с заданными зарядами или обрат-
обратную задачу о нахождении зарядов по заданным потенциалам, полезно убе-
убедиться в том, что обе они имеют единственное правильное решение.
Предположим сначала, что двум различным распределениям поверх-
поверхностной плотности заряда на проводниках о и а' соответствуют одинаковые
потенциалы. Тогда потенциал точки Р на поверхности одного из провод-
проводников, обусловленный разностной плотностью поверхностных зарядов а — а'.
окажется, согласно формуле A.8), равным
т. С с—с' ,„ 1 Г а ,о i f о' JO
VP = \ —. dS = — \ - dS — -г- \ — dS,
S S S
где г —расстояние от Р до элемента поверхности dS и интегрирование
производится по поверхности всех проводников. Ток как стоящие в правой
части интегралы по условию равны между собой, то Fp=0, т. е. все про-
проводники имеют нулевой потенциал. Но это означает, что в такой системе
вообще не существует электрического поля и а — а' — 0. Следовательно,
а = а' и распределение одинаковое. Заданное распределение является, таким
образом, единственным.
Предположим теперь, что одной и той же величине полного заряда Q
на проводниках могут соответствовать различные плотности распределения
ana'. В этом случае при разностной плотности а — а' полный заряд любого
проводника будет равен нулю, а поэтому плотность заряда а —а' может
или равняться нулю всюду, или же на одной части поверхности провод-
проводника быть положительной, а на другой отрицательной. Последнее, однако,
невозможно, потому что при этом силовые трубки, оканчивающиеся на отри-
отрицательно заряженных участках, должны были бы исходить из точек с более
высоким потенциалом, а оканчивающиеся на положительно заряженных
участках — из точек с более низким потенциалом. Это рассуждение приме-
применимо к любому находящемуся в поле проводнику. Поэтому ни один из про-
проводников с поверхностной плотностью заряда а —о' не может быть рас-
расположен в точке максимума или минимума потепциала. Следовательно,
их потенциалы просто равны, что опять приводит к исчезновению поля
и к равенству а = а'. Итак, если па каждом проводнике задан полный заряд,
то соответствующее ему распределение плотности поверхностного заряда
единственно.
§ 2. Емкость. Вследствие того, что электрические натяжения в среде
зависят (§ 15 гл. I) от напряженности поля всюду одинаковым образом,
равновесие системы не нарушается при изменении напряженности поля
всюду в одно и то же число раз. Так, при удвоении поверхностной плот-
Конденсаторы, диэлектрики, системы проводников
37
ности заряда в каждой точке системы заряженных проводников конфигу-
конфигурация поля остается неизменной, а напряженность увеличивается вдвое,
и, следовательно, возрастает в два раза работа, совершаемая при переме-
перемещении малого заряда от одного проводника к другому. Это постоянное
отношение заряда изолированного проводника к его потенциалу называется
емкостным коэффициентом или емкостью, а обратное ему отношение назы-
называется потенциальным коэффициентом. Если в поле находятся другие про-
проводники, то эти термины становятся неточными, за исключением того случая,
когда все эти другие проводники заземлены и незаряшены. Пусть С — емкость
(в фарадах), «S1 — потенциальный коэффициент (в фарадах), V— потенциал
(в вольтах), a Q — заряд (в кулонах), тогда, по определению,
= CV, V^SQ.
B.1)
Два близко расположенных изолированных проводника образуют про-
простейший конденсатор. Пусть они несут на себе равные по величине и про-
противоположные по знаку заряды, тогда емкость конденсатора есть отношение
заряда на одном из проводников к разности потенциалов между ними.
(Отношение берется всегда таким, чтобы емкость была положительной.)
Таким образом, для конденсатора имеем
= C(V1-V2),
B.2)
§ 3. Последовательное и параллельное соединение конденсаторов.
Возьмем п простых незаряженных конденсаторов; одну из пластин каж-
каждого из них подсоединим к клемме А, а другие соединим с клеммой В, как
А
А° !
-<?4
a
Фиг. 16.
это показано на фиг. 15. Приложим теперь между А и В разность
потенциалов V, тогда
где Cv Ct, ..., Cn — емкости конденсаторов, a Qlt Q2, -••, Qn—заряды
на них. Полный заряд, очевидно, равен
Таким образом, эти конденсаторы (их принято называть соединенными
параллельно) ведут себя подобно одиночному конденсатору, имеющему
емкость
С = С1 + С2+...+Сп. B.3)
Рассмотрим теперь п простых незаряженных конденсаторов, соединен-
соединенных так, как показано на фиг. 16; одна пластина конденсатора 1 подклю-
подключена к А, а другая соединена с первой пластиной конденсатора 2, вторая
пластина конденсатора 2 соединена с первой пластиной конденсатора 3
и т. д. и наконец, вторая пластина n-го конденсатора подключена к В.
Такое соединение конденсаторов называется последовательным. Прикладывая
38 Глава II
разность потенциалов между А и В, имеем
Здесь F,- — разность потенциалов между пластинами г'-го коиденсатора.
Поскольку любая пара соединенных проводпиков остается изолированной,
ее суммарный заряд равен нулю. По если все силовые трубки, выходящие
из одной пластины конденсатора, оканчиваются на другой пластине того же
конденсатора, то
<?i = <?2= ...=Qn = Q
и величину Q, являющуюся общим множителем, можно вынести за скобки
в правой части равенства. Таким образом, конденсаторы, соединенные
последовательно, ведут себя подобно одному конденсатору, имеющему
емкость С и потенциальный коэффициент S, соответственно равные
i-k + ?+-+h S = S1 + S2+...+Sn. B.4)
Полученная формула является приближенной, так как в общем случае
нельзя ограничиться рассмотрением только полей подобного рода. Однако
©ели пластины конденсатора расположены близко друг к другу и если
диэлектрическая проницаемость между пластинами значительно превышает
проницаемость окружающего пространства, то дополнительной «распреде-
«распределенной» емкостью, обусловленной полями рассеявия, можно пренебречь.
Формула B.4), в частности, теряет смысл в случае воздушного конденсатора
с далеко разведенными пластинами.
§ 4. Сферический конденсатор. Рассмотрим две концентрические про-
водящио сферы: внутреннюю -радиуса а, несущую на себе заряд +Q,
и внешнюю — радиуса Ъ, несущую заряд — Q. Пространство между ними
будем считать заполненным однородным изотроивым диэлектриком с про-
проницаемостью е. В силу симметрии вектор электрической индукции должен
быть направлен по радиусу, а его величина может зависеть только от г.
Следовательно, применяя теорему Гаусса о потоке электрической индукции
к концентрической сферической поверхности радиуса г (Ь > г > а), получим
eE-n dS=4™-zeE=
s
откуда
9V Q
Поэтому разность потенциалов между сферами окажется равной
у _v = _о_\& = JL(' 1 1>)^ь~а п
а ^ 4тг? j г2 4тге \ fl Ь J Aizzab '
¦что приводит к следующему значению для емкости сферического конден-
конденсатора
С = р^. B.5)
Устремляя Ь—>оо, можно получить из формулы B.5) емкость одиночной
сферы радиуса а, помещенной в среду с диэлектрической проницаемостью е:
B.6)
Конденсаторы, диэлектрики, системы проводников 39
Следует заметить, что при выводе формулы B.5) предполагалось, что
пне радиуса Ь нет никаких зарядов. Это было необходимо для того, чтобы
сфера с г =Ь была под нулевым потенциалом. В противном случае необхо-
необходимо учитывать дополнительную емкость между внешней поверхностью
сферы радиуса Ъ и бесконечностью, вычисленную по формуле B.6)а).
§ 5. Цилиндрический конденсатор. Рассмотрим теперь ива круглых
концентрических проводящих цилиндра бесконечной длины: внешний —
радиуса Ъ с зарядом — Q (на единицу длины) и внутренний — радиуса а
с зарядом -\-Q (на единицу длины). Обозначим через е диэлектрическую
проницаемость однородной изотропвой среды между цилиндрами. В силу
симметрии вектор электрической индукции должен быть направлен по радиусу
(в направлении внешней нормали) и лежать в плоскости, перпендикулярной
к оси, причем величина его должна зависеть только-от г. Применяя теорему
Гаусса к объему, ограниченному концевтрическим круглым цилиндром радиуса г,
b > г > а, и двумя перпендикулярными к оси плоскостями, расположенными
на расстоянии одного метра друг от друга, и учитывая, что последние
не дадут никакого вклада в поверхностный интеграл, получим
eE • n dS =
откуда
E= — — ¦
а разность потенциалов между цилиндрами равна
?=_j2_ln.?. B.8)
ь
Таким образом, для емкости (на единицу длипы) длинного цилиндрического
конденсатора имеем
С = . 2Z , ¦ B.9)
In (Ь/а) v '
Если теперь устремить Ь —ь со, то С —* 0. Следовательно, конечный заряд
(на единицу • дливы) на круговом цилиндре конечного радиуса и бесконеч-
бесконечной длины создает бесконечную разность потенциала между поверхностью
этого цилиндра и бесконечностью. Так как в действительности мы имеем дело
только с цилиндрами конечной длины, то эта трудность и не возникает;
однако это свидетельствует о том, что результаты настоящего параграфа
применимы лишь в тех случаях, когда расстояние до поверхности цилиндра
мало по сравнению с расстоянием до его оснований.
§ 6. Плоский конденсатор. Пусть две бесконечные параллельные про-
проводящие плоскости, несущие на себе заряды + Q и — Q, расположены па
расстоянии а друг от друга, а пространство между ними заполнено одно-
однородным изотропным диэлектриком. Тогда из соображений симметрии поле
внутри должно быть однородным и нормальным к проводящим плоскостям.
х) С общем определении емкости B.2) предполагается, что два проводника, из ко-
которых состоит конденсатор, имеют равные по величине и противоположные по знаку
заряды. В противном случае введение емкости, вообще говоря, ве имеет смысла, и сле-
следует пользоваться емкостными или потенциальными коэффициентами (см. § 16—18).
Однако если один из проводников полностью охватывает другой, как это имеет место
в случае сферического конденсатора, то емкость, определенная как отношение заряда
иа внутреннем проводнике к разности потенциалов между проводниками, не зависит,
очевидно, от наличия зарядов во внешнем пространстве.—Прим. перев.
40
Глава II
Обозначим через а заряд, приходящийся на 1 м2. Тогда, как следует из
§ 14 гл. I, с каждого квадратного метра проводящей поверхности должно
выходить а единичных силовых трубок. Таким образом, для электрической
индукции и напряженности поля между плоскостями мы получаем
а для разности потенциалов между плоскостями
B.10)
Поэтому емкость (на единицу площади) равна г/а, а емкость, соответствующая
площади А,
На практике поле может быть однородно только вдали от краев конден-
конденсатора. Поэтому формула B.11) представляет лишь приближение к дей-
действительности и том лучшее, чем меньше а по сравнению со всеми разме-
размерами плоской поверхности и чем больше проницаемость диэлектрика между
плоскостями по сравнению с проницаемостью внешнего пространства.
§ 7. Защитные кольца. При получении формулы B.9) для емкости
на единицу длины цилиндрического конденсатора, а также формулы B.11)
для емкости плоского конден-
конденсатора размеры проводников
предполагались бесконечными.
Чтобы эти формулы можно бы-
было бы применить к реальным
конденсаторам, используется
WJ
'Фиг. 17.
Фиг. 18.
приспособление, известное под названием защитного кольпа. В цилиндриче-
цилиндрических конденсаторах, как показано на фиг. 17, крайние участки одной ив
пластин отделены от центральной части узким зазором, но поддерживают-
поддерживаются под одним и том же потенциалом. Искаженное поле вблизи краев, та-
таким образом, не оказывает влияния на поле в центральной части, за исклю-
исключением очень незначительного искажения вблизи зазора, поэтому отноше-
отношение заряда центральной части конденсатора к разности потенциалов будет
определяться формулой B.8).
Аналогичное устройство применяется и в случае плоского конденсатора:
в поверхности одной из пластин прорезается узкая щель, отделяющая, как
показано на фиг. 18, центральную часть пластины от ее краев, причем по
обе стороны от щели поддерживается один и тот же потенциал. Поле между
центральными участками является однородным, если не учитывать незна-
Конденсаторы, диэлектрики, системы проводников 41
чительного влияния узкой щели, поэтому отношение заряда ва централь-
центральном участке к разности потенциалов можно определять по формуле B.10).
§ 8. Энергия заряженного конденсатора. Взаимную энергию любой
системы зарядов можно вычислить непосредственно из определения потен-
потенциала. Работа (в джоулях), требуемая для помещения /-го заряда на его
место, согласно формуле A.5), равна
Полная работа, необходимая для того, чтобы все заряды разместились по
их местам, будет
Введение множителя х/2 обусловлено тем, что при суммировании учить -
вается ве только работа, совершаемая при помещении z'-ro заряда на его
место в поле /-го заряда, но и работа, совершаемая при помещении /-го
заряда на его место в поле z'-ro заряда, что, очевидво, есть одно и то же.
Если через Vi обозначить потенциал в точке, где расположен z'-й заряд,,
то, согласно формуле A.5), выражение B.12) можно записать в виде
Когда все заряды расположены на одном и том же проводнике а, они
находятся под одним потенциалом. Поэтому, обозначив их сумму через Qa,
получим
W« = T 2 <^=1Г 2 4i =4<?Х,- B-14)
no a no a
Введя емкость проводника С и пользуясь соотношениями B.1), мы придем
к следующим эквивалентным друг другу выражениям для энергии заря-
заряженного проводника
ii-? = icv*. B.15)
В конденсаторе, пластины которого несут на себе заряды Q и — Q и имеют
потенциалы Vx и V2 соответственно, эта энеггия равна
\j^-V2). B.16)
что можно, учитывая формулы B.2), записать и в форме, аналогичной B.15).
§ 9а. Энергия электрического поля. Выше было показано, что законы
электростатики согласуются с наглядными представлениями о передаче
электрических сил посредством натяжений, имеющихся всюду, где есть поле.
Но где существуют натяжения, там должна быть запасена потенциальная
энергия, плотность которой мы сейчас и вычислим. Для этого рассмотрим
бесконечно малый дискообразный элемент объема с основаниями, совпадаю-
совпадающими с эквипотенциальными поверхностями. В силу достаточней малости
объема эти основания можно считать плоскими и параллельными друг другу,
а поле между ними — однородным полем бесковечно малого плоского кон-
конденсатора. Пусть ds — толщина диска, п — единичный вектор нормали к era
42 Глава II
поверхности (Е = Еп). Тогда разность потенциалов между основаниями
будет равна (dV/ds)ds = —Eds, а зэряд на основании, имеющем площадь
dS, равен
Учитывая, что объем конденсатора dv = dsdS, из формулы B.15) для энер-
энергии получим
И для плотности энергии электрического поля окончательно имеем
dv 2 N '
В изотропном диэлектрике D-E = 1)Е и
dW еЕ2 DE D2 ,о „ о\
В кристаллическом диэлектрике, согласно соотношению A.56),
~ = \ {вУ1Е\ + в22Е22 + в33Е23 + 2*12ЕгЕ2 + Тв^Е, + 2e23E2Es), B.19)
или, если оси координат совпадают с направлением электрических осей
кристалла [см. выражение A.57)],
^ = i &E* + г,Е1 + ЧЕ1). B.20)
§ 96. Плоский конденсатор с кристаллическим диэлектриком. Вьс-
"числим емкость плоского конденсатора, приходящуюся на 1 ж2 площади
пластин; в качестве диэлектрика в конденсаторе служит кристаллическая
пластинка толщиной d. Диэлектрические проницаемости в направлении осей
кристалла х, у и z обозначим соответственно через в1г е2 и е3, а направля-
направляющие косинусы углов, образуемых нормалью к пластинам конденсатора и
этими осями,—через I, m и п. Так как с электрической точки зрения один
участок конденсатора ничем не отличается от пругого, то эквипотенциаль-
эквипотенциальные поверхности должны быть параллельны плоскостям конденсатора и
располагаться' на одинаковом расстоянии друг от друга, а напряженность
электрического поля должна быть направлена вдоль нормали. Таким образом,
где V — разность потенциалов, приложенная к конденсатору. Отсюда
х—— у—— 7-nV aiw
Подставив эти выражения в формулу B.20), умножив на d объем конден-
конденсатора, приходящийся на 1 м2 поверхности пластины, и воспользовавшись
соотношениями B.15), находим
Откуда емкость, приходящаяся на 1 м2 равна
2?2 + п2в3 ,9 9„.
2 \&&ь)
§ 10. Натяжения в случае зависимости диэлектрической проницае-
-мости от плотности среды. До сих пор при рассмотрении натяжений
Конденсаторы, диэлектрики, системы проводников 43
в диэлектрике (§ 17 и 18 гл. I) мы не учитывали того, что диэлектриче-
диэлектрическая проницаемость может в действительности меняться при изменении
плотности вещества т, т. е. что в среде могут существовать еще и натяже-
натяжения гидростатического происхождения, стремящиеся сжать или растянуть
диэлектрик. Оперируя с элементом объема точно такой формы и ориен-
ориентации, что и в § 9а, мы можем упростить наши исследования, сведя их
к изучению маленького плоского конденсатора с зазором 8 и площадью пла-
пластин AS. Комбинируя формулы B.15) и B.11) и предполагая, что диэлек-
диэлектрик изотропный (проницаемость равна е), для энергии конденсатора будем
иметь
AW — 5 /72 _ т п2 _ тГ>2 д е
где через т обозначена масса диэлектрика, приходящаяся на единицу пло-
площади между пластинами конденсатора, так что т = т8. Если предположить,
что масса т постоянна, а проницаемость е является функцией плотности т,
то сила, действующая на площадь пластины конденсатора AS, определится
следующим образом:
дЬ "" di дЬ ~~ ~2& ~Ы~ *
Итак, натяжение или сила, действующая на единицу площади и стремя-
стремящаяся растянуть поверхность диэлектрика, равна
AF D2 д (st) (9 ?оч
Произведя дифференцирование и сравнив с выражением A.43), мы опре-
определим дополнительное гидростатическое натяжение
D2 дг Е2 де в^Е2 дК ,о о/\
На границе между двумя диэлектриками наряду с теми натяжениями,
которые уже были рассмотрены нами, необходимо учитывать разность
гидростатических давлений, что вместо соотношения A.50) даст нам
«следующее выражение для полного натяжения, направленного от К' к К":
р _ 1 К--К» (D't2 , Р'п2\ Д'V дК' , Р"Ч" дК" 1 ,„«..
Гп-~2Г„\ к1 \1ГЛ"к7') Т* аТ"+ "Т7^ д%" J • {¦*°>
На границе диэлектрика с пустотой, положив К" = 1 и dK"fdx" — 0,
получим
_ 1 rJT'-l/ДУ . п-2\ Р'Ч 8К'1
n^2eBL К' УК' + Un ) К'2 дъ' \ —
^f^^^'-^-x'l^l-iHp!^'-!J, B.26)
где
Знак дК'/дх' может быть либо положительным, либо отрицательным;
поэтому в тех случаях, когда этот член является преобладающим в выра-
выражении B.26), диэлектрик под действием поля может сжиматься или растя-
растягиваться. Это явление известно под названием электрострикции, его наблю-
наблюдал Квинке и другие.
§ 11. Электрострикция в жидких диэлектриках. Существует соот-
соотношение, известное под названием формулы Клазиуса —Мозотти, свя-
связывающее плотность жидкости с ее относительной диэлектрической
44 Глава II
проницаемостью
Ы=с*> B-27)
где С — некоторая постоянная, характеризующая жидкость.
Хотя теоретический вывод этой формулы основан на некоторых неточ-
неточных утверждениях, тем не менее во многих случаях ова очень хороню под-
подтверждается экспериментально 1). Дифференцируя ее, получим
дК _(К + 2)*_ (g + 2)(JT-l)
5т 3 Зт
Подставляя в соотношение B.24), мы находим гидростатическое давление,
стремящееся сжать жидкость
р =
(Заметим, что мы всюду жидкость считали почти несжимаемой, т. е. т — по-
почти постоянной.) Таким образом, при погружении, например, заряженной
сферы в большой но объему жидкий диэлектрик давление, определяемое
по формуле B.28), будет меняться обратно пропорционально четвертой сте-
степени расстояния от центра сферы. В частности, если диэлектрик слегка
сжимаем, то он будет иметь наибольшую плотность около поверхности
сферы (конечно, без учета других явлений, таких, например, как грави-
гравитация).
§ 12. Силы, действующие на проводник в диэлектрике. При нахо-
нахождении силы, действующей на заряженную границу раздела диэлектрика и
проводника, предполагалось, что заряд расположен на диэлектрической сто-
стороне границы, поэтому все поле находилось внутри ииэлектрика и сила
(па единицу площади), без учета электростршщии, согласно формуле A.43),
равнялась D2/{2e). Рассмотрение энергии заряженного конденсатора под-
подтверждает правильность этого результата. Исследуем теперь силу при пред-
предположении, что заряд расположен на проводящей стороне границы. Если
диэлектрическую проницаемость проводника обозначить через е', то эта сила
будет равна ZJ/Be'). Но поверхность диэлектрика должна считаться теперь
находящейся в электрическом поло, поэтому на ней существует натяжение,
определяемое формулой B.25), которое стремится сжать проводвик. Пре-
Пренебрегая электрострикцией и помня, что поле всюду направлено нормальт
к поверхности, мы получаем суммарную силу "натяжения в виде
Р .— К —К' j~,2 е е' „2
2 ~~ 2evKK' ~ 2ге' U '
Тогда полная сила, действующая на проводник, будет равна
Итак, различные предположения относительно места нахождения заряда
приводят к одним и тем же результатам.
Если относительная диэлектрическая проницаемость не претерпевает
скачка, а непрерывно, хотя и быстро, меняется в некотором пограничном
участке, то натяжения должны быть определены путем интегрирования.
Полное результирующее натяжение получится таким же, как и раньше,
однако распределение патяжения вблизи границы может быть, вообще го-
говоря, различным.
Geiger-Scheel, Handbuch der Physik, Bd. XII, 1927, S. 518.
Конденсаторы, диэлектрики, системы проводников 45
§ 13. Теорема взаимности Грина. Докажем, что если проводники при
зарядах на них QL, Qs, ... , Qn имеют потенциалы Vlt V2, ... , Vn, а при
зарядах Q[, Q'2, ... , (^ — потенциалы V[, V'2, ... , Vn, то справедливо сле-
следующее соотношение:
п п
'ZQiV'i = 'ZQ'iVi. B.30)
i = l i=l
Рассмотрим систему точечных зарядов и напишем для нее матрицу, со-
состоящую из п2 членов, каждый из которых представляет собой произведе-
произведение величины одного точечного заряда на потенциал другого точечного
заряда. Воспользовавшись формулой A.5), запишем сумму каждого столбца
в нижнем ряду, а сумму каждой горизонтальной строки—в крайнем правом
столбце. Тогда
Г)
^7+ 4таг
0 ^
4лег2
gign . g2gn , qsqn . + о =<
QlVl qkV* q'3Vs ¦¦¦ q'nVn '
Так как порядок суммирования произволен, то, складывая все члены
в нижнем ряду или складывая все члены в крайнем правом столбце, мы
должны получить одинаковые результаты
Следует заметить, что величина Vs является потенциалом, создаваемым
в точке расположения заряда gs всеми нештрихованными зарядами, за
исключением самого gs. Все заряды, расположенные иа одном проводнике,
должны быть умножены на один га тот же потенциал, что позволяет про-
просуммировать эти заряды
откуда и следует формула B.30). Рассмотрим один важный частный слу-
случай этой теоремы. Если в формуле B.30) положить Q[, Q's, ... , (>n = 0,
ф2, Q3, ... , Qn = Q, a Q1—Q'%, то V[ = Vt. При помещении заряда <^ на про-
проводник В потенциал незаряженного проводника А меняется точно на
такую же величину, на какую изменился бы потенциал незаряженного про-
проводника В при помещении заряда Q на проводник А. Как будет доказано
в § 8 гл. III, эта теорема остается в силе и при наличии границ раздела
двух или нескольких диэлектриков с различными проницаемостями.
§™14ДСуперпозиция полей. Прибавим к обеим частям формулы B.30)
Y.QiVi ИЛИ ^Q'iV'i и сравним результаты с первоначальным соотношением
B.30). Мы видим, что если заряды Qlt Q2, ... , Qn создают потенциалы
VltV2, ... , Vn и т. д., то заряды Q1 + Q'^ Q2 + Q'2, ¦¦¦ , Qn+Q'n создают
потенциалы Vx + V[, V2 + V'2, ... , Vn + V'n- Путем такого сложения уже
46 Глава II
известных решений можно решить большое количество новых задач. Рас-
Рассмотрим в качестве примера п концентрических проводящих сфер радиусов
/-,, г2, . .. , гп с зарядами Qlt Q2, ... , Qn. Пусть требуется найти потен-
потенциал какой-нибудь, скажем, s-й сферы. Для этого можно сложить потен-
потенциалы, создаваемые на s-й сфере каждой из сфер в отдельности,
4таГя = (<?х f <?2 + •'• ¦ + Q,)гГ1 + <?s+i гТ+i + • - ¦ + Qnrn', B.32)
где учтено, что внутри заряженной проводящей сферы радиуса а потен-
потенциал равен Q (iizea)-1, а снаружи он не зависит от а и равен Q Dиег)-1
(г — расстояние до центра).
§ 15. Индуцированные заряды на заземленных проводниках. При
помещении точечного заряда q в некоторую точку Р, находящуюся вблизи
системы заземленных проводников, на последних появляются индуциро-
индуцированные заряды. Величину заряда Q, индуцированного на одном из провод-
проводников, можно определить из формулы B.30), если известен потенциал V'p
точки Р в том случае, когда заряд в ней отсутствует, а потенциал этого
проводника равен V. Действительно, из формулы B.30) имеем
... = Q'-O + 0-VP + ^-0+ q'2-0 + ... ,
откуда
Q=-^4- B.33)
Например, пусть единственным проводником в поле является проводящая
сфера, а точка Р находится на расстоянии г от ее центра. Тогда из фор-
формулы B.6) находим V = qx Dnea)—1 и Vp = g1(ii^er)~1, и величина заряда,
индуцированного на сфере точечным зарядом q, расположенным в точке Р,
будет равна
<?=-^. B.34)
Если теперь точка Р находится между двумя проводниками, один из
которых расположен внутри другого, и известен ее потенциал V'p в том
случае, когда потенциалы проводников равны V[ и V'2, то при заземлении
этих провод ников заряды Q1 и Q2, индуцированные на них точечным заря-
зарядом q, помещенным в точку Р, можно найти по формуле B.30)
Q1V1 + Q2V2 + qVP = 0.
Но так как все силовые трубки, исходящие из q, должны кончаться на
проводниках, между зарядами имеет место соотношение G, + Qz = — q. Раз-
Разрешая относительно Ql и Q2, получим
Q*=w=nq и Q*-n=nq- B-35)
Так, папример, если точка Р находится между двумя заземленными
сферами (см. § 4), заряды, индуцированные на внутреннем и внешнем про-
проводниках, соответственно равны
Vl г{г2—Г1L V2 r(r2— гг) ч к '
Здесь г — расстояние ст точки Р до центра (гх< г < г2).
Если же точка Р находится между двумя заземленными цилиндрами
(см. § 5), то заряды, индуцированные на внутреннем и внешнем провод-
проводниках, соответственно равны
„ In jr2/r) n In (г,/г)
Конденсаторы, диэлектрики, системы проводников
47
И, наконец, если точка Р находится между двумя заземленными плоско-
плоскостями (см. § 6) на расстоянии а от одной и на расстоянии Ъ от другой, то
а + Ь
И &=--
B.38)
§ 16. Потенциальные коэффициенты. Рассмотрим п заряженных про-
проводников, форма и расположение которых неизменны. Мы знаем, что заряд,
помещенный на один из проводников, определенным образом изменяет
потенциалы всех других проводников и что это изменение зависит только
от геометрической конфигурации системы и от ее диэлектрической прони-
проницаемости. Отношение изменения потенциала Vr г-го проводника к заряду Qs,
помещенному на s-й проводник и вызвавшему это изменение, называется
потенциальным коэффициентом sJr. Из теоремы взаимности Грина (§ 13)
следует, что ssr = srs. Суперпозиция решений для зарядов Qr, Qs, Qt и т. д.,
расположенных на проводниках г, s, t, дает
V2 =
B.39)
Vn = SinQt
snnQn-
Таким образом, ssr является потенциалом, приобретаемым г-м проводником
при помещении единичного заряда на s-й проводник, если заряды на всех
других проводниках при этом равны нулю. Помещение положительного
заряда на проводник всегда повышает потенциал соседних изолированных
проводников, поэтому коэффициент srs всегда положителен. Коэффициент srT
называется собственным потенциальным коэффициентом.
§ 17. Собственная и взаимная емкости. Решив систему уравнений B.39),
мы получим выражение для зарядов на проводниках через их потенциалы.
Эти решения будут иметь вид
где
Qn = CinV1 + C2nV2 + H
S22S32 • • '
¦ ¦ ¦ Sn
S21S3
'2SS33
21 .41
B.40)
• • «пЗ
Д =
B.41)
гак что cri является минором srs в А, деленным на Д.
Величина сгг называется собственным емкостным коэффициентом, или
собственной емкостью, и определяется как отношение заряда к потенциалу
на г-м проводнике при условии, что все другие проводники заземлены.
Знаки потенциалов и зарядов всегда совпадают, поэтому коэффициент crt
веегда положителен.
48 Глава II
Величина счг называется емкостным коэффициентом, коэффициентом
индукции, или взаимной емкостью, и определяется как отношение индуци-
индуцированного заряда на г-м проводнике к потенциалу s-го проводника при
условии, что все проводники, кроме .9-го, заземлены. Знаки индуцирующего
и индуцированного зарядов всегда противоположны, поэтому коэффициент crs
либо отрицателен, либо равен нулю. ,
§ 18. Электростатическая экранировка. Предположим, что проводник 1
окружен, как это показано на фиг. 1У, проводником .2. Все силовые трубки,
исходящие из проводника 1, оканчиваются на проводнике 2, поэтому если
потенциал V2 = 0, то заряд на проводнике 1 зависит только от его собствен-
собственного потенциала. Это означает, что в уравнениях B.40)
с31 = с41=...=Сщ=0. B.42)
Таким образом, между проводником 1 и любым проводником вне 2 не суще-
существует никакого взаимодействия. Эти проводники, как говорят в таком
случае, экранированы, т. е. защищены от
проводника 1. Заметим также, что по-
поскольку Qz= — <?j и все проводники,
кроме проводника 1, заземлены, то
Ввиду полной однотипности уравне-
уравнений B.39) и B.40) потенциальные коэф-
коэффициенты можно выразить через емко-
емкостные простой заменой s на с в форму-
19. лах B.41). В интересующем нас случае
экранирования проводника 1 проводником
.2, учитывая соотношение B.42), получим
sir = «2r, Кг. B.43)*
Заменяя в первом уравнении B.39) Sir на $2Г и вычитая из него второе,
находим
Vi-Vt = (sJ1sVi)Q1.
Если Vx > V2, то силовые трубки идут от Vt к V 2 и заряд Q1 положителен,
но тогда su— s12 > 0. Из соотношения B.43) следует s12=s22, поэтому
*u">*ia и *ц>*22- B.44)
§ 19. Потенциальные и емкостные коэффициенты в случае двух
¦отдаленных проводников. Пусть одиночный проводник 1 имеет емкость СЛ,
а другой одиночный проводник 2 — емкость С2. Считая проводник 1 незаря-
женпым, поднесем к нему проводник 2, несущий на себе заряд Q2, на неко-
некоторое расстояние г, значительно провосходящез линейные размеры (порядка а)
каждого из проводников. При этом потенциал проводника 1 увеличится
па величину <?2Dттзг)~1 [если пренебречь незначительным (порядка а/Акег2)
изменением потенциала па участке, занимаемым самим проводником 1].
Сопоставив это с первым уравнением B.39), получим s21 = (Aizer)—1. На ближ-
ближней части проводника 1 будет индуцироваться заряд, противоположный
по знаку заряду Q2 и равный по порядку величины Q2a Dтгег)~1. Такой же
заряд, но только того же знака, что и Qo, будет находиться на отдаленной
части проводника 1. На больших расстояниях г поле этих двух одинаковых
по величине и противоположных по знаку зарядов, отстоящих друг от друга
не дальше, чем на а(а< г), по существу является полем диполя, потенциал
которого на проводнике 2 [см. формулу A.9)] по крайней мере имеет
порядок величины Q2a2 Dтсг3)~'. Следовательно, с точностью до членов
Конденсаторы, дия^ьектрики, системы проводников 49
этого порядка присутствие незаряженного проводника 1 не оказывает влияния
на величину потенциала проводника 2, так что из второго уравнения B.39)
мы имеем s22 = V2Q^1 = C^~l и аналогично su = C^1. Таким образом, и первом
приближении
Решив детерминант B.41) и опустив члены порядка )—3, дль собственных
и взаимных емкостей будем иметь
1_
2—C,C2 '
§ 20. Энергия системы зарядов. Если известны напряженность поля
и электрическая индукция во всех точках вокруг заряженных проводников,
то энергию всей системы можно получить путем интегрирования выраже-
выражения B.17), а именно:
^ B.47)
где интегрирование распространяется на всю область вне проводников.
Часто, однако, известными являются не поля во всех точках, а заряды
и потенциалы проводников, а также их собственные и взаимные емкости.
Для нахождения энергии в этом случае предположим, что заряды Qxa,
Q2a, ..., Qna доставляются на проводники бесконечно малыми порциями
Qtda, Q2da, ..., Qnda, начиная от того состояния, когда проводники
не заряжены, т. е. <х = 0, и кончая значением а = 1. При зарядах (?j<x,
Q2a, . .., Qna потенциалы проводников равны FjGc, F2a, . . ., Vna, поэтому
работа, совершаемая при внесении очередной порции заряда, равна
dW = F^jGc da + V2Qsa da -f . .. + VnQna da.
А энергия системы в конечном состоянии будет
п 1 п
W = 2 VrQ, \ a da = 1 V V.Q.. B.48)
i=i о i=i
Или, заменяя Qt в соответствии с соотношением B.40), имеем
Wv = \ (cuVl + 2cl2VLV2 + c22V\ +-..). B.49)
Аналогично, заменяя Vi в соответствии с соотношением B,39), получим
| s22Ql +...). B.50)
§ 21. Силы и моменты сил, действующие на заряженные проводники.
Если известны напряженность поля и электрическая индукция в каждой
точке поверхности проводника, то суммарную результирующую силу, дей-
действующую на проводник в направлении единичного вектора р, можно
получить путем интегрирования выражения B.29) по всей поверхности про-
проводника, что дает
\^v.ndS, B.51)
где п— единичный вектор нормали к элементу поверхности dS.
Если известны заряды и потенциальные коэффициенты системы провод-
проводников, то ее потенциальная энергия определяется по формуле B.50), где su,
s12 и т. д. зависят от конфигурации системы. Точно так же, как и в меха-
в. Смайт
50 Глава II
нике, мы определим силу или момент, стремящиеся произвести изменения
какого-либо параметра, характеризующего эту конфигурацию как производ-
производную потенциальной энергии по этому параметру, взятую со знаком минус:
т-=—тг( 4йQ\ + 2-4^ОлО? +•••]• B.52)
В зависимости от того, является ли т\ длиной или углом, это выражение
определяет соответствующую компоненту силы или момента, стремящихся
увеличить значения •»). В рассматриваемом случае заряды остаются неизмен-
неизменными и изменение электрической энергии равно совершаемой механической
работе. Если же пользоваться выражением B.49), поддерживая при помощи
батареи или каким-нибудь другим путем потенциалы постоянными, то энер-
энергия системы увеличится. Сила же в обоих случаях должна быть одинаковой,
так как она зависит только от начального состояния системы, которое
можно описать и при помощи зарядов, и при помощи потенциалов.
Чтобы выразить силу череа потевциалы, объединим формулы B.48) —
B.50) в следующее равенство:
W^Wq + Wv-J] V& = 0, B.53)
дифференцируя которое получим
rf4T = у. тгр- dO. 4- у. -— (IV- + У гт- dt), = 0. B.54)
Но из соотношений B.53), B.50) и B.39)
и из соотношений B.53), B.49) и B.40)
^_^1_л -уе V
Подстановка в соотношение B.54) дает
Поскольку сумма равна нулю для совершенно произвольных значений d\,
то каждый из членов этой суммы в отдельности должен равняться нулю.
Поэтому, заменив W через соответствующее выражение B.53), получим
f^ ^ ^ a <255>
Но нам известно, что — 5FFq/5tjs есть сила (или момент), стремящаяся уве-
увеличить tjs, так что она выразится через потенциалы следующим образом:
Итак, при постоянных зарядах работа, совершаемая при малых перемеще-
перемещениях, дается выражением B.52), а при постоянных потенциалах — выраже-
выражением B.56). Разность этих выражений составляет работу, совершаемую тем
прибором, который поддерживает потенциал постоянным:
0Wv dwn \ dWv
^^)^ч = 2-—-diis. B.57)
^____^ Задачи ^^ 51
ЗАДАЧИ
1. Центры трех одинаковых сфер радиуса а расположены па одной прямой на рас-
расстояниях Г] и г2 друг от друга. Сначала только центральная сфера 2 имела заряд Q.
Затем ее соединили со сферой 1, а потом, отсоединив от сферы 1, подсоединили к сфере 3.
Показать, что если расстояния между сферами значительно больше а, то заряд на
сфере 3 ранен
0з=-т- [ ¦ —— И 1 •
2. Четыре одинаковые незаряженные проводящие сферы расположены по углам
кнадрата. Заряд Q сообщается проноднику 1, затем при помощи тонкой пронолочки
проводник 1 соединяется на мгновение по очереди с проводниками 2, 3 и 4 (нумерация
проводников циклическая). Показать, что в результате
„ Q SU—S24 п Q SU—
8 Sj] slt 8 sxl — S]4
3. Пусть сферы 1 a 2 (см. предыдущую задачу) сначала несут на себе ааряды,
соответственно ранные +Q и — Q, и пусть, как и раньше, сфера 1 подключается па
мгновение по очереди к сферам 3 и 4. Показать, что если сторона кнадрата г значи-
значительно больше радиуса сфер а, то сфера 4 окажется заряженной зарядом Q4, прибли-
приближенно равным
2~S/2Q Г21'2/4 B*'г 3) а\
Найти также заряды Q3 и Qt.
4. Три одинаковые сферы расположены по углам равностороннего треугольника
на очень большом расстоянии друг от друга. Сначала каждая сфера имела наряд Q.
Затем по очереди сферы на мгнонение заземлялись. Показать, что после этого заряд
на сфере 3 стал равен
' ¦?)
[[ найти также заряды на сферах 1 -а 2.
5. Четыре одинаконых проводника расположены по углам правильного тетраэдра,
причем каждый из пронодников совершенно симметричен по отношению к трем другим.
Первоначально нее они не были заряжены. Затем один из проводников приобрел зарнд Q
от батареи с напряжением V, которую от него тотчас же отключили. После этого его
на мгнонение по очереди подключали к каждому из трех пронодников, а потом зазем-
заземлили. На проводнике остался заряд —Oi- Показать, что все нзаимные емкости равны
2i-7Q)I,
кроме того, найти потенциальные коэффициенты.
6. Два проводника, янляющиеся зеркальными изображениями друг друга, перво-
первоначально незаряжены. Сфера с зарядом Q сначала соединяется с некоторой точкой на
одном из проводвикон, а затем с ее зеркальным отображением на другом. В каждом
из этих случаев заряд поровну распределяется между сферой и проводником. Показать,
что после большого числа таких попеременных подключений заряд равномерно рас-
распределяется между тремя проводниками.
7. Три одинаковых изолированных проводника расположены так, что любой из них
совершенно симметричен относительно двух других. Проволочкой, подключенной к ба-
батарее, напряжение которой неизвество, по очереди касаются каждого проводника. Заряды
на вервых двух оказываются после этого равными Qt и Q2. Найти заряд на третьем.
8. Из трех концентрических проводящих сферических оболочек радиусоп а, Ъ и с
внутренняя и внешвяя заземлены, а средняя разрезана на дне половины и заряжена.
Найти, сколь велик должен быть радиус а (а < b < с), чтобы воспрепятствовать отде-
отделению друг от друга этих половин.
9. Три проводника соединены тонкой проволокой и заряжены. Определить, как
распределяются между ними заряды, если известно, что
SJ1 =523 Ф S22> S12 ~ S2i Ф S13i 5
10. Два концентрических сферических проводника, радиусы которых равны в ¦ Ъ,
соединены проволокой. От внутреннего проводника отделяется точечный заряд q и дви-
движется радиально во направлению к внешнему с постоянной скоростью V. Показать,
что скорость перемещения индуцированного заряда с внутреиней сферы на внешнюю
равна
^-= — gab (b—a)-1 v (с-И0~2-
4*
52 Глава II .
11. Кольцо радиуса а, несущее ва себе полвый заряд Q, расположено ннутри
заземлевной сферы радиуса Ь, так что ось кольца совпадает с диаметром сферы, а его
плоскость отстоит от цевтра сферы иа расстоявии с. Найти потенциал в центре.
12. Точечвый заряд д, ломещенвый ва оси тонкого зазсмлеввого проводящего
кольца радиуса а на расстоявии Ъ от его певтра, индуцирует па кольце заряд — Q.
Показать, что емкость кольца равва AneQg-1 (a2-^- fc2I'2.
13. Проводящая сфера радиуса а находится внутри концентрического с ней ди-
диэлектрического шара радиуса Ъ, относительная диэлектрическая проницаемость которого
равна К. Показать, что емкость проводящей сферы равна
b — a)-1.
14. Пусть (см. предыдущую задачу) проводящая сфера заземлена, а на расстоянии г
от ее центра (г > Ъ > а) находится точечный заряд д. Показать, что на сфере будет
индуцирован заряд
КаЬд
~7
15. Сферический ковденсатор, радиус ввутреннего проводника которого а, а ввега-
иего Ъ, заполпен двумя концентрическими сферическими слоями диэлектрика с нрови-
цаемостямп ег и в2. Радиус г их границы раздела равен -п- (а + Ь). Найти отношение
ej/-2> если изнестно, что точечный заряд, расположенный на этой границе, ивдуцирует
одинаковые заряды на внутренней и пиешвей проводящих сферах, когда они обе за-
зсмлевы.
16. Незаряжевная проводящая сфера массы М плавает в диэлектрической жид-
жидкости с проницаемостью е, погрузившись в нее па одну четверть своего объема. До
какого потевциала нужно зарядить сферу, чтобы она плавала ногруженвой наполовиву?
17*. Показать, что если алгебраическая сумма зарядов системы проводников
положительва, то поверхностная плотность заряда, но крайней мере на одном из них,
пеюду положительна.
18*. Пусть имеется несколько изолированных проводвиков, положение которых
задано и неизмевво. Собственные емкости двух каких-вибудь проводников в этой
системе равны Сх и С2, а взаимная емкость равна В. Доказать, что если эти лроипдвшш
соединить тонкой проволокой, то емкость объединенного проводника будет равна
19*. В системе изолировавных проводников заряжеивых произвольным образом,
заряды переносятся с одного проводника иа другой до тех пор, пока все проводники
не окажутся под одним и тем же потенциалом V. Показать, что F = Z?/(s1 + 2s2), где st u
?2—алгебраические суммы соответственно собствевных и взаимвых емкостей (коэффп-
лпеитон нвдукции), а Е—сумма всех зарядов.
20*. Доказать, что в результате операции, опксашюй в предыдущей задаче,
электростатическая энергия системы уменьшается иа величину, равную уменьшению
энергии при понюкевии потевциала каждого проводника на V.
21*. Два одинаковых сферических ковдевсатора, радиусы внутревних и внешних
проводников которых равны а и Ь, изолированы и находятся иа большом расстоянии г
друг от друга. Внутренним сферам сообщаются заряды е и е', а затем ввешвие сферы
соединяются проволокой. Показать, что убыль эвергии при этом приближенно будет
равна •
A6 7is)-'(e—e'Y(b-i — г-1).
22*. Конденсатор образован двумя товкими концевтрическими оболочкзми радиу-
радиусов а и Ь. Во ввсшней оболочке имеется веболыпое отверстие, сквозь которое проходит
нзолироваввый провод, соединяющий ввутреннюю сферу с третьим проводником, распо-
расположенным на большом "расстоянии г от конденсатора и имеющим емкость с. Внешняя
оболочка конденсатора подключева к земле, а суммарный заряд соединенных провод-
проводников равен Е. Доказать, что сила, действующая иа третий проводник, нриближевно
равва
r3)-1 [ineab (й —uj-^c].
23*. Замквутая эквипотенциальная поперхвость потенциала Vx содержит ннутрп
себя другую замкнутую поверхность потенциала Fo. Потевциал некоторой точки Р,
лежащей между этими поверхвостямп, равен Vp. Если в точку Р поместить заряд Е,
а обе эквипотенциальные поверхности заменить проводящими сферами, соединенными
с землей, то заряды Ег и EQ, нвдуцированные на них, будут удовлетворять соот-
соотношению
Задачи 53
24*. Проводник заряжается от электрофора путем повторяющихся подсоединений
к пластинке, которая после каждого подсоединения снова заряжается от электрофора
до заряда Е. Пусть е-—заряд на проноднике после первой операции. Доказать, что
конечный зарнд равен
Ее(Е-е)-1.
25*. Четыре одинаковых незаряженных заземленных пронодника расположены
симметрично по углам правильного тетраэдра. При помощи подвижного заряженного
сферического проводника касаются по очереди каждого из них, дотрагиваясь лишь до
наиболее близко расположенных к центру тетраэдра точек. Показать, что получаемые при
этом проводниками величины зарядовelt е2, е3, е4 образуют геометрическую прогрессии».
26*. Заменив в задаче 25* тетраэдр на квадрат, доказать, что
(ei—ег) (е1ез—e|) = ei(e2e3 — «A)-
27*. Два неподвижных изолированных проводника несут на себе заряды Е1 и Е2
и имеют некоторые заданные значения потенциалов. Их потенциальные коэффициенты
равны su, S]2, s22- Еслп эти проводники окружить сферическим пронодником, имего-
щим очень большой радиус R и центр вблизи них и находящимся под нулевым по-
потенциалом, то для сохранения на проводниках тех же значений потенциалов их пужно
зарядить зарядами Е[ п Е2. Доказать, пренебрегая величиной Вт2, что
(Е[ — Е1){Е'2 — Е2)-1 =(s22 — Si2)(?ii — s^)-1.
28*. Показать, что геометрическое место точек, из которых единичный заряд
индуцирует ва некотором заземленном проводнике постоянный заряд, совнчдает с экви-
эквипотенциальной поверхностью поля этого проводника в отсутствие точечного заряда.
29*. Показать 1) что если изолированный проводник, находящийся п свободном
пространстве и имеющий единичный потенциал, создает в какой-нибудь точке Р потен-
потенциал (Р), то единичный заряд, помещенный в точку Р, будет индуцировать на этом
проводнике (теперь заземленном) заряд —(Р); 2) что если (PQ) — потенциал, созданный
л точке Q индуцированным зарядом, то (PQ) является симметричной функцией поло-
положения Р и <?.
30*. Две маленькие заземленпые сферы расположены рядом друг о другом между
двумя большими параллельными пластинами, одна из которых заряжена, а другая
соединена с землей. Представить графически характер возмущений, вносимых сферами
в однородное поле в случае, когда линия их центров 1) перпендикулярна к пластинам,
2) параллельна пластинам.
31*. Полый проводник А находится под нулевым потенциалом и содержит внутри
себя еще два других изолированных проводника В и С — один внутри другого. Про-
Проводник В положительно заряжен, а проводник С не заряжен. Проанализировать раз-
различные типы силовых линий, которые могут существовать внутри полости, классифи-
классифицируя их согласно тому, на каком проводнике они начиваются и па каком оканчи-
оканчиваются. Доказать невозможность существования тех типов линий, которые хотя гео-
геометрически и допустимы, но почему-либо отвергаются. Доказать, что потенциалы про-
проводников В п С положительны и что потенциал С меньше В.
32*. От проводника, емкость которого равна С, отделена некоторая часть Р. 11а
большом расстоявпи от всех других ироводников емкость этой отделевной части равна с.
Сам проводпик остается изолированным, а часть его Р на большом расстоянии от него
заряжается зарядом е, и ей предоставляется возможность свободно двигаться под
действием сил взаимного притяжевия вплоть до достижения проводника. Описать и
объяснить изменения, которые произойдут в электрической энергии системы.
33*. Проводник, несущий на себе заряд Qt, окружен проводящей оболочки!
с зарядом Q2. Внутренний проводник при помощи проволоки соединяется с очень
далеким незаряженным проводником. Затем проволока отсоединяется от внутреннего
проводника и присоединяется к впешней оболочке. Показать, что заряды Q[ n Q^ ста-
станут равными
q, ^ mQt—nQz _ (m + п) Q2-f mnQ[
41 m-t-n+mn' V2 m + n
где С, С A + m)-—собственные емкостные коэффициенты близких проводников, а Сп —
удаленного проводника.
34*. Показать, что еслп из общего числа и + 1 проводников один проводник содер-
содержит внутри себя п других, то существует п соотношений между потенциальными
или емкостными коэффициентами. Показать также, что если потенциал самого
большого проводника равен Vo, a потенциалы остальных равны F,, V2, ..., Vn, то
наиболее общее выражение для энергии будет равняться сумме -^-CVjj и некоторой
54 Глава II
кнадратичной функции F,— Fo, F2—Fo, ..., Vn—Vo, где С—постоянная, не занисящая
от положения внутренних проводников.
35*. Вяутренвяя обкладка сферического конденсатора (радиусы а, Ь) несет на себе
постоянный заряд Е, а ннешняя ваходится под нулевым потенциалом. Под дейстнием
ннутренвих сил ннешний проводник сжимается от радиуса b до радиуса Ь1. Доказать,
что сонершаемая электрическими силами работа раина
— Ьх)/(8квфЬх).
36*. Пусть (см. предыдущую задачу) потевциал V нвутреннего пронодника под-
деряшнается постоянным, а заряд может меняться. Показать, что совершаемая работа
раина
2jisF2a2F — Ь1)/[(Ь1 — а) (Ь — а)].
Найти неличиву энергии, затраченной батареей.
37*. Пользуясь обычными обозначениями, доказать, что
SuSiS > S12Sl3.
38*. Показать, что если после ввссения в систему проводников нового проводника
нотенциальвые коэффициенты sTr, srs, sss становятся ранными s'rr, s'rs, s'ss, то
(srrSss — SrrSssX (Srs — SrsJ.
39*. Система состоит из p-\-g-\-2 пронодников Ax, Аг, ..., Ap, Bx, B2, ¦¦¦, Bq,
C, D. Доказать, что при известных зарядах на нсех пронодниках А и С н при изнест-
ных потенциалах на всех проводниках В и С не может существовать более одного
ранновесиого распределения зарядов, если только проводник С не экранирован электри-
электрически от пронодника D.
40*. Имеются четыре проводника А, В, С и D, причем пронодпик В окружает
проводник А, а пронодник D окружает пронодник С. Найти собственные и взаимные
емкостные коэффициенты 1) для А и В, если С и D удалены; 2) для С и D, если
А и В удалены; 3) для В и D, если А и С удалены, и, наконец, определить эти
коэффициенты для полной системы из четырех проводникон.
41*. Два одинаковых проводвика А и В одинаково заряжены и расположены сим-
симметрично по отношению друг к другу; третий, подвижный пронодник С последовательно
занимает дна положения: одно паходится практически целиком ннутри пронодвика А,
другое—в пределах пронодника В. Оба положения симметричвы относительно друг
друга, и н любом из них потевциальные коэффициенты для С, расположенные в по-
порядке возрастания, ранны р, д, г. В каждом из этих положений С по очереди соеди-
соединяется сначала с окружающим его пронодвпком, потом заземляется и, ваконец, изо-
изолируется. Определить заряды на пронодниках н результате произвольного числа таких
операций и показать, что конечные неличины зарядон будут ваходиться н отношении
1 : — fi:fJ2—1, где р — положительный корень уравнения гх2—дх-\-р — г = 0.
42*. Собствевная емкость одного нронодника раина СЛ, а другого С2. Они нахо-
находятся на большом расстоянии друг от друга и имеют потенциалы Ft и F2. Доказать,
что сила отталкинания между ними определится выражением
С точностью до какой степени г спранедлино это выражение?
43*. Дна одинаковых изолированных пронодвика расположены симметрично отно-
относительно друг друга, причем один из вих не заряжен. При помощи третьего изолиро-
нанного проводника симметричным образом попеременно касаются каждого из этих двух
пронодникон, начиная с заряженного. Пусть е, и е2—заряды на нроподвиках после
перного касания каждого из них. Показать, что после того, как произойдет г касаний,
эти заряды будут ранны
J
(Для задач 43* и 44* см. разностные ураннения § 96 гл. V.)
44*. Имеются три проводника AL, A2 и .43, причем пронодник Аь практически
находится внутри проноднпка А2. Пронодник Ах при помощи тонкой пронолоки попере-
попеременно соединяется с проводниками А2 и А3, начиная с As. Первоначально проводник
Лх имел заряд Е, а А2 и А3 были ве заряжены. Показать, что заряд на проноднике Аг
после п соединений с А3 будет ранен
где через а, р, f обозначены соотнетстненво su—s12, s22—s12, sss—s12.
Задачи 55
45*. Пространство между обкладками сферического конденсатора радиусон а и Ь
наполнено воздухом. На внутревнюю сферу наносится слой краски постоянной тол-
щипы t и диэлектрической проницаемости К. Найти происшедшее при этом изменение
емкости конденсатора.
46*. Заряд проводника равен е, a F, и F2—потенциалы двух полностью окру-
окружающих его эквипотенциальных иоверхвостей (F, > FjT' Пространство между этими
двумя поверхностями заполняется диэлектриком с относительной проницаемостью К.
Показать, что изменение энергии системы равно
(FF)(tf
47*. Воздушный конденсатор образован двумя концентрическими сферами. Поло-
Половина пространства между сферами заполнена твердым диэлектриком с относительной
диэлектрической проницаемостью К. Граница раздела между ним и воздухом есть
плоскость, проходящая через центр сфер. Показать, что емкость такого конденсатора
будет равна емкости конденсатора, псе пространство между сферами которого запол-
иено диэлектриком, имеющим относительную проницаемость — A+.ЙГ).
48*. Радиусы внутренних и внешних оболочек двух одинаковых сферических
конденсаторов, удаленных один от другого и помещенных в бесконечную диэлектри-
диэлектрическую среду проницаемости К, равны соответственно а и Ь, а относительная прони-
проницаемость диэлектрика внутри конденсаторов рапна Кх и К2. Обе поверхности первого
конденсатора изолированы и зарнжены, а второго—не заряжены. Внутренняя поперх-
иость второго конденсатора заземляется, а внешняя при помощи проволоки с превебре-
жимо малой емкостью соединяется с пнешней поверхностью первого конденсатора.
Показать, что убыль энергии будет рапна
Q2[2(b — a)
где Q—количество электричества, протекшего по проводу.
49*. Внешняя обкладка длинного цилиндрического конденсатора представляет
собой тонкую оболочку радиуса а; диэлектрик между цилиндрами по одну сторону
от плоскости, проходнщей через ось, имеет проницаемость К, а по другую — прони-
проницаемость К'. Показать, что если внутренний цилиндр заземлен, а внешний имеет
на единицу длины заряд д, результирующая сила, действующая на внешний цилиидр,
равна
д2(К — К') ,
J (Ha
50*. Неоднородная диэлектрическая среда состоит из п концентрических сфери-
сферических слоен с относительными диэлектрическими проницаемостями Кл, К2, ..., Кп.
Первый слой имеет форму шара, а внешний, п-й, простирается до бесконечности.
Радиусы границ раздела диэлектриков равны соответственно а,, а2, ..., an_j. Доказать,
что потенциал, создаваемый зарядом Q, расположенным л центре, будет на расстоянии
г от него (в среде с провнцаемостыо Ks) рапен
51*. Конденсатор образован двумя прямоугольными параллельными проводящими
пластинами, ширипа которых Ь, а площадь А п которые расположены на расстоянии d
друг от друга. Между пластинами параллельно им помещена плитка из диэлектрика
толщиной t, площадь которой равна площади пластины. Эта нлитка выдвигается
ив конденсатора, так что между пластинами остается только часть ее, имеющая длину,
равную х. Доказать, что сила, стремящаяся возвратить плитку в первоиачальное
положение, определяется по формуле
d— t')
где t'=t (К — i)/K, К — относительная диэлектрическая проницаемость плитки, Е—
заряд конденсатора. При решении пренебречь влиянием краев.
52*. Три замкнутые поверхности 1, 2, 3 являются эквипотенциальными поверх-
поверхностями электрического поля. Пространство между поверхностями 1 и 2 заполнено
диэлектриком с проницаемостью е, а между поверхностями 2 и 3—диэлектриком
с проницаемостью г'. Показать, что емкость конденсатора, образованиого поверхностями
1 и 3, раина величине С, определяемой выражением
UC=sv/{sA)+sv/(s'B),
56 Глава II
где А и В—емкости воздушных конденсаторов, образованных соотпетственпо поверх-
поверхностями 1, 2 и 2, 3.
53*. Граница раздела двух диэлектриков (Кг, К2) имеет плотность заряда а
(на единицу площади). Напряженности электрического поля по разные стороны
от границы равны Flt F2 и образуют с общей нормалью к границе углы с,, с2. Указать,
как определить величину F2, и доказать, что
54*. Пространство между двумя концентрическими сферами радиусов а и Ь,
потенциалы которых поддерживаются равными А и В, заполнено неоднородным дп-
электриком. Его диэлектрическая проницаемость меняется, как п-я степень расстояния
от общего центра сфер. Показать, что потенциал в любой точке между поверхностями
равен
АаР*1 — Bbnhl /ab-\n г А—В
on+i__ftnn \~7) orm__fcnn •
55*. Конденсатор образован двумя параллельными пластинами, находящимися
на расстоянии h друг от друга. Одна из пластин имеет нулевой потенциал. Простран-
Пространство между пластинами заполпепо диэлектриком, проницаемость которого линейно
возрастает от одной пластины к другой. Показать, что емкость на единицу площади
равна
где A"i и К2—значения диэлектрических пронидае.мостеы на поверхности пластин.
Искажения в распределении поля на краях пластин не учитываются.
56*. Сферический проводник радиуса а окружен концентрической с пнм сфери-
сферической проводящей оболочкой, внутренний радиус, которой 6. Пространство между
ними заполнено диэлектриком с проницаемостью, меняющейся но закону (с + г)/г, где
г—расстояние от центра. Доказать, что если внутренняя сфера изолирована и имеет
заряд Е, а внешняя заземлена, то потенциал в диэлектрике на расстоянии г от центра
будет равеи
47tsc V г с-\-Ъ J
57*. Сферический проподпик радиуса а окружен концентрической с пнм сфери-
сферической оболочкой радиуса Ь. Пространство между ними заполнено диэлектриком, про-
2
ницаемость которого на расстоянии г от центра равна \>.e~v р~3, где р — га-1. Доказать,
что емкость такого конденсатора будет
1а -е).
58*. Показать, что емкость конденсатора, состоящего из двух проводящих сфер
г = а и г = Ь, между которыми находится неоднородный диэлектрик с проницаемостью
К = /@, <j>). равна
znab (Ь — a)-1 \\ f @, 9) sin С d() dy.
53*. Пусть в некоторой воображаемой кристаллической среде молекулы имеют
форму дисков, расположенных параллельно плоскости ху. Показать, что компоненты
напряженности поля и электрической индушши связаны между собой уравнениям™
вида
1У, ir.g =sJ2
60*. Плитка из диэлектрика проницаемости К и толщины .-с помещена внутрь
плоского конденсатора, параллельно его пластинам. Показать, что натяжение на поверх-
поверхности диэлектрика равно
61*. Для газа /С = 1-{-6р, где р—плотность, а 0 — малая величина. В газ помещен
проводник. Пренебрегая членами порядка О2, показать, что механическая сила, дей
ствующая на единицу поверхности пронодинка, равпа — as/ev. Дать физическую интер-
интерпретацию этого результата.
62*. При вращении кривой
1 9а ( - а-\-х а — х \ 1_
(ж2 + ^2I/2"6<\[(а. + оJ + 2/2]3/2 + [(а._оJ + 2/2]3/2^ а
Литература 57
вокруг осп х образуется замкнутая поверхность, которую принимают за границу
проводника. Показать, что его емкость равна ineva, а поверхностная плотность заряда
на конце оси равна е/Cтш2), где е—полный заряд.
63. Отношения потенциалов Prs системы п проводников можно определить выра-
выражениями
F2+ ... + PinVn,
Vn = PniV, + Pn2V2
Показать, что Р^ выражаются через потенциальные п емкостные коэффициенты следую-
следующим образом:
~ • • • 4~^rs^sr4~ • • • 'r srnCnr'
ЛИТЕРАТУРА
Abraham M., Becker R., Klassische Electrizitat und Magnetismus, Berlin, 1932.
(См. перевод: А б р а г а м М., Б е к к е р Р., Теория электричества, 2-е изд.,
M.—Л., 1939.)
Geiger-Scheel, Handbuch der Pbysik, Bd. XII, Berlin, 1927.
Gray A., Absolute Measurements in Electricity and Magnetism, Macmillan, 1888.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
Mason M., Weaver W., The Electromagnetic Field, University of Chicago Press,
1929.
Maxwell J. C, Electricity and Magnetism, v. I, Oxford, 1881.
Planck M. К. Е. L., Theorie der Electrizitat und Magnetismus, Berlin, 1932.
Ramsey A. S., Electricity and Magnetism, Cambridge, 1937.
Russell A., Alternating Currents, Cambridge, 1914.
Thomson J.J., Mathematical Theory of Electricity and Magnetism, Cambridge, 1921.
Thomson W., Papers on Electrostatics and Magnetism, Macmillan, 1884.
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
Wien-Harms, Handbuch der Experimentalpliysik, Bd. X, Leipzig, 1УЗО.
Глава III
ОБЩИЕ ТЕОРЕМЫ
§ 1. Теорема Остроградского —Гаусса. Приступим теперь к нахожде-
нахождению связи между интегралом от нормальной компоненты некоторого непре-
непрерывного в пространстве вектора А, взятым по замкнутой поверхности S и
по (т—1) замкнутым поверхностям, лежащим внутри S, и интегралом от
дивергенции вектора А, взятым по объему v между этими поверхностями.
Пусть компоненты вектора А в прямоугольных координатах равны Ах,
^ ¦ -.,_ ^ч Ау, Аг, тогда дивергенцию
-х» А, которую мы будем обоз-
обозначать V - А, можно пред-
представить в виде
V . \—
^Лх | dAJL I дАг
дх *~ ду dz
Фиг. 20.
C.1)
Предположим, что объем v
разделен на тонкие призмы
с прямоугольным попереч-
поперечным сечением dydz. Одна из них (см. фиг. 20) вырезает из поверх-
поверхности Sj элементы dS'h dS", координаты которых равны соответственно х$
и х'/, а единичные векторы нормали п] и п" направлены наружу. В по-
поверхностном интеграле элементам dS'j и dS'/ будут соответствовать значения
подинтегральной функции, равные
По из фиг. 20 следует, что i • п'} dS'f = — i • ri/ dS'/ = dy dz, поэтому общий
вклад всех сечений призмы, составляющей часть объема v и пересекающей
(Я — Р) поверхностей, равен
Q q ж)'
2 dy dz (AX', — Ах>/) =2 dy dz\ -4^- dx.
х.
Теперь просуммируем но всем призмам, на которые разделен объем v.
Составляя подобные выражения для',4,, и Аг и складывая их, после под-
подстановки V • А из соотношения C.1)лмы получим окончательно
/= i s.
= J
C.2)
Общие теоремы 59
где dv = dzdydz. Эта формула известна под названием теоремы Остроград-
Остроградского — Гаусса
§ 2. Теорема Стокса. Непосредственно из теоремы Остроградского —
Гаусса можно получить другую важную теорему. Применим формулу C.2)
к бесконечно малому прямому цилиндру, имеющему высоту h, площадь
основания S, периметр основания s и площадь боковой поверхности S'.
Обозначим через кип, единичные векторы нормали к основанию и к боко-
боковой поверхности, а через F некоторую векторную функцию и заменим А на
п X F. Поскольку п — постоянный вектор, то в выражении
VnxF = FVxn-nVxF
F ¦ V X п — 0, но на плоских поверхностях и [п X F] • п = 0, поэтому поверх-
поверхностный интеграл от этого выражения по S исчезает и формула C.2) при-
принимает вид
^ п X F • п, dS' = С F • пх X ndS' = — \ п ¦ V X ?dv.
S' S' v
В силу того, что dv = h dS и dS' = h ds, поверхностный и объемный инте-
интегралы превращаются соответственно в линейный и поверхностный
&F nt X nds= - { п ¦ V X FdS.
Далее, nxn,= — ^хп является единичным вектором, направленным вдоль
границы, поэтому, выбрав его положительным для положительного направ-
направления s, мы получим nt X nrfs= —ds и после суммирования по всем бес-
бесконечно малым цилиндрам, охватываемым поверхностью, будем иметь
5
s
При суммировании линейных интегралов обход всех внутренних контуров
совершается дважды в противоположных направлениях, и, следовательно,
интегралы по ним взаимно уничтожаются. Остается только интеграл по
наружному контуру всей области. Сумма поверхностных интегралов равна,
естественно, интегралу по всей поверхности, так что
F ds=^n- V xFdS. C.3)
Это и"*Ъсть теорема Стокса. Она может быть сформулирована следующим
образом: линейный интеграл от вектора F по некоторому замкнутому кон-
контуру равен поверхностному интегралу от ротора вектора F по поверхности,
опирающейся на этот контур.
§ 3. Уравнения Пуассона и Лапласа. Пусть в теореме Остроградского —
Гаусса вектор А будет вектором электрической индукции D = eE. Если к
поверхностному интегралу применить теорему Гаусса о потоке индукции
A.40), то
где р — плотность электрического заряда. Таким образом, для исчезающе
малого объема dv будем иметь
=V-D=4g=P. C.4)
вО Глава III
Обозначим D = eE= — sgradF = — b\V, тогда
div(egradF) = V-FVF)=-P. C.5)
Мы получили уравнение Пуассона для неоднородного диэлектрика. В случае
однородного диэлектрика е — постоянная величина и ее можно вынести нз-
под знака дифференцирования, что дает
divgradF = V • VF = ^2F= -±. C.6)
При р = 0 это уравнение называется уравнением Лапласа. Для неоднород-
неоднородного, но изотропного диэлектрика уравнение Лапласа можно записать в
прямоугольных координатах следующим образом:
т-( е^г- ) + т-( е -=г- )+v-( s —- ) = 0. C.0
дх\ дх J ' ду\ ду J ' dz\ dz J v '
Если диэлектрик однородный, но не изотропный, и если координатные оси
направлены вдоль главных осей кристалла [см. соотношение A.58)], то
а^^ & 0- (о.8)
Если ?ке диэлектрик и изотропный и однородный, уравнение принимает вид
§ 4. Ортогональные криволинейные координаты. В большинстве элек-
электростатических задач заданными величинами являются: заряды или потен-
потенциалы всех проводников системы, величины остальных зарядов и их рас-
расположение, а также диэлектрическая проницаемость среды как функция
точки. Задача считается решенной, если определен потенциал во всех точ-
точках. Для этого необходимо найти решение уравнения Пуассона, удовлетво-
удовлетворяющее заданным граничным условиям. Обычно существует такая система
координат, в которой эти условия можно выразить наиболее просто и кото-
которой естественно поэтому пользоваться при решении уравнения. Наиболее
употребительными являются криволинейные ортогональные системы координат.
Рассмотрим три семейства взаимно ортогональных поверхностей таких,
что через каждую точку данной области проходит одна из поверхностей
каждого семейства. Любая из поверхностей первого семейства характеризует-
характеризуется определенным численвым значением величины их, а второго и третьего
семейств — численными значениями величин и2 и и3. Бесконечно малый
прямоугольный параллелепипед образуется шестью поверхностями ult ut +
+ dult u2, щ + du2, u3, u3 + du3. Поскольку лишь в немногих случаях величины
uv u2, и3 непосредственно выражают расстояния, для получения истинных
длин ребер параллелепипеда необходимо, вообще говоря, умножить duJ, dtu
и du3 соответственно на множители hl7 h2, h3lK
Последние могут меняться от точки к точке, т. е. являться функциями
их, и2 и щ. Таким образом, длины ребер параллелепипедов (см. фиг. 21)
равны
ds1 = h1du1, ds2 = h2du2, ds3 = h3du3. C.10)
J) Эти обозначения совпадают с обозначениями, приводимыми в книгах: II о u s-
ton, Principles of Mathematical Physics, Abraham M., Becker R., Klassischc
Electrizitat und Magnetismus, Berlin, 1932. (См. перевод: А брагам М., Беккер Р.,
Теория электричества, 2-е изд., М. — Л., 1939.) В справочниках Peirce и Smithsonian
Tables, а также в книге Jeans J. H., The Mathematical Theory of Electricity and
Magnetism, Cambridge, 1925, через Л,, Л2, hs, обозначены обратные величины.
Общие теоремы
61
Если V есть некоторая скалярная функция, то, по определению, ком-
компонентами ее градиента будут
дУ
дУ
ht ди1 '
дУ
ds2
дУ
h2 ди2
дУ
ds3
дУ
h3 ди3 '
C 11)
Для вычисления дивергенции в этих координатах нужно применить
теорему Остроградского — Гаусса C.2) к бесконечно малому объему, пока-
показанному на фиг. 21. Нормальная составляющая потока
вектора А, выходящего через грани OCGB и ADFE,
равна
(А ds d) d (/г/4) ddd \
—
(А1 ds2 ds3) dst =
4) duxdu%dus =
Добавляя соответствующие два слагаемые для четырех
других граней и сравнивая полученное выражение с
формулой C.2), находим
divA=V • А = ^- [^
hxh2h3
C-12)
Далее, замевяя A = eVF и подставляя в уравнение Пуассона C.5), имеем
д ( hJl**~ dV Л д МАЕ дУЛ д / h,h2z дУ\1 __ __
du\ hx дих)^~ди2\ h2 дщ) +~дп~3 \ h3 ~дп3) J "~ ~"Р>
V-(eVF)=-p. C.13)
При p = U соотношение C.13) дает уравнение Лапласа для неоднородного
изотропного диэлектрика. Если диэлектрик однородный и изотропный, то
в —постоянная величина и ее можно вынести из-под знака дифференциро-
дифференцирования.
§ 5. Представление ротора в ортогональных криволинейных коор-
координатах. Применим теорему Стокса к грани О ABC элементарного криволи-
криволинейного куба, изображенного на фиг. 21. Пусть Fv F% и F3 являются ком-
компонентами вектора F вдоль и1г и2 и и3. Тогда из соотношения C.11) линей-
линейный интеграл вдоль ОА и DC окажется равным
\h1 (&j, u%) Ft (w1
а вдоль AD и СО
[h2(u1 + du1, u2)
) — hx (иг, и2 + du2) Ft (и1г u2 + du2)] dux =
"' ~ P, (ЫЛ-\ CtlZam
Su2 J z
ux, u2)]du2 =
u1, u2) — h2
Суммирование этих выражений дает линейный интеграл вдоль OADCO, кото-
который по теореме Стокса равен интегралу от нормальной компоненты ротора
F по площади h1h2du1du2 этой грани. Сокращая на duxdu2, получим
(V X F)8 *
C.14)
62
Глава 111
Аналогично и для других граней
§ 6. Представление оператора V • (eV) в различных системах коор-
координат. В сферических координатах, где г = иг — расстояние до начала коор-
координат, 6 = и2 — полярный угол и <р = м3 — азимутальный угол (см. фиг. 22,а),
мы имеем
ds1 = h1 dut = dr, hx= 1,
Согласно соотношению C.13), уравнение Лапласа принимает следующий
вид:
1 д
В цилиндрических координатах, где р = ггг— расстояние от оси 2,
Ф=ы2 —азимутальный угол, z = u3 — расстояние до плоскости я?/ (см. фиг. 22, б),
имеем
dsx = hx dUj =dp, кг = 1,
ds3 = h3 du3 = dz, h3=i.
Уравнение Лапласа, согласно формуле C.13), в этих координатах можно
записать в виде
Позже, в связи со специальными задачами, мы встретимся с некоторыми
другими системами координат, например с эллипсоидальной.
§ 7. Теорема Грина. Положим в выражении C.2) А = (еgrad Ф) Ф =
= ?еуФ, где W и Ф — скалярные функции, конечные и непрерывные в об-
области интегрирования и дважды дифференцируемые, а е — дифференцируемая
скалярная неличина, которая может иметь разрывы на некоторых границах
внутри области. Исключим эти границы, окружив их узкими областями,
Общие теоремы 63
тесно примыкающими к ним с двух сторон. Пусть п'р и пр' — единичные
векторы нормали с двух сторон р-ш границы, a AJ, и Ар' — значения А по
обе стороны от нее. Если имеются q таких областей, включающих q разрывов
непрерывности, то интеграл по ним равен
я
p=i S
где dSp — элемент поверхности разрыва. Прибавив эти члены к формуле C.2)
и подставив А = *Ре^Ф, получим
т Ч
2 S?
^ C.19)
V V
Напишем теперь подобное же выражение, поменяв местами W и Ф, и вычтем
одно нэ другого. Тогда
Если е—жостоянна и непрерывна, то выражение C.19) принимает вид
j = ^ (V4r-^Ф + ЧТ2Ф) dv. C.21)
v
И яэ выражения C.20) имеем
)$ C-22)
j=l S,-
Стрэттоном был предложен следующий полезный векторный аналог
этих формул. Заменим в выражении C.2) А на 4*X(VX<J>), где Ч* и
Ф — конечные, непрерывные в области интегрирования и дважды дифферен-
дифференцируемые векторы. Тогда
^ ^ V-[4*X(VX<I>)]dv,
^ . C.23)
S,- v
Вычитая из выражения C.23) аналогичное выражение с переставленными
Ч* и Ф, нолучим
C.24)
64 Глава III
§ 8. Теорема взаимности Грина для диэлектрических сред. Пусть
имеется два распределения электрических зарядов. Обозначим в выраже-
выражении C.20) через VP = F потенциал одного из них, через Ф = V — потенциал
другого, а через е — диэлектрическую проницаемость среды. Если поверхность
раздела двух сред с разными е незаряжена, то на ней, согласно ¦ усло-
условию A.48),
, дФ' _ ,, дФ" _ „ дФ"
опр опр дпр
а из условия A.49)
Подобное же соотношение можно написать и для W, так что интегралы
по поверхностям разрыва исчезают. При отсутствии объемпых зарядов,
т. е. при V-(eV4P"][=0 и V-(eV<I)) = 0, исчезает и объемный интеграл,
поэтому
ИЛИ
или
m m
Таким образом, теорема взаимности Грина B.30) остается в силе п в при-
присутствии диэлектриков.
§ 9. Функция Грина. Пусть ЧГ— потенциал, создаваемый единичным
зарядом, находящимся в точке Р, а Ф — потенциал, создаваемый индуци-
индуцированным поверхностным зарядом плотности р, расположенным на некоторой
замкнутой заземленной поверхности S, окружающей точку Р. Единичный
заряд в точке Р можно рассматривать как заряд, объемная плотность кото-
которого всюду равна нулю, за исключением бесконечно малого объема dv
«близи Р, в котором Ф можно считать величиной постоянной и равной Фр.
Учитывая, что W = Dиег), где г — расстояние от Р, и что У2Ф = 0 всюду
внутри v, a V24?"= —р/е внутри dv, а вне dv равно нулю, и принимая во
внимание, что Ч?'= —Ф на поверхности S, из выражения C.22) получим
где, как и в § 1 и 7, за положительное направление п принято направле-
направление из объема v. Обозначим Ф + Dтгет-)'1 через G. Тогда
-^-[-dS. C.26)
Мы будем называть функцию G функцией Грина, хотя многие авторы
именуют функцией Грина функцию Ф. Очевидно, что G является решением
уравнения Лапласа, равным нулю на границе S и имеющим простой полюс
в точке Р. С электрической точки зрения это решение представляет потен-
потенциал, создаваемый единичным зарядом, находящимся в некоторой точке Р
Общие теоремы 65
внутри заземленной проводящей поверхности S. Как правило, по формуле
C.26), совпадающей с формулой A.8), нельзя определить G, так как очень
редко плотность заряда па проводнике о оказывается известной. В после-
последующих главах будет приведено много методов определения фупкции G для
систем с различными формами границ.
Силу Flt действующую вдоль направления гг1 на заряд д, находящийся
в точке с координатами и[, гг'2, и'3 (см. § 4), можно выразить через функцию
G(ult и2, и3) по формуле
J l
о ,. ( Г dGfu-,, и'о, и',)~] .
l-lim { v ,'_ -—— +
/ II П fill \ t
Первое выражение имеет место в силу того, что при малых о создаваемые
индуцированными зарядами поля в точках и[ + 8 и и\ — 8 одинаковы, в то
время как поля, создаваемые самим зарядом, равны по величине и проти-
противоположны по направлению и, таким образом, уничтожаются. Второе выра-
выражение следует из формулы B.13), так как изменение и[ не вызывает изме-
изменения энергии самого заряда, а влияет только на энергию индуцированных
зарядов.
§ 10. Решение уравнения Пуассона. Потенциал точки Р, созданный
в вакууме зарядом плотности р, находящимся в объеме dv, согласно фор-
формуле A.4), равен </F = pDit?7-)~1c?v, где г — расстояние от объема dv до
точки Р. Таким образом, потенциал в точке Р, созданный всеми зарядами,
будет равен
C.28)
Но из формулы C.6) следует, что этот потенциал удовлетворяет уравнению
Пуассона
Г2у=_-1. C.29)
Таким образом, выражение C.28) является решением уравнения C.29).
Однако уравнение C.29) можно решить непосредственно при помощи
теоремы Гаусса. Применим ее к области v, заключенной между двумя
концептричпыми сферами с центрами в точке Р, одна из которых мала
и имеет поверхность о, а другая, большая, имеет поверхность 2 и радиус/?.
Пусть функция lF в соотпошешш C.22) равна г'1, а Ф = У, тогда
у I
дп дп
= \ [ т ^w - FV2 (т) ]
Рассмотрим первый из этих интегралов. На малой сфере д/дп^=—д/дг
и телесный угол, под которым виден элемент dS из точки Р, равен
dQ = r~2dS. Поэтому в силу конечности oVjdr
_ г \ ~ dQ - \ VdQ -> - Ы'р. C.31)
Если весь заряд Q, создающий потенциал V, расположен в коночном
области, то при R—>¦ оо V—>Q Dт:е/?)'1 и на поверхности 2 °^а члена
в подинтегральном выражении стремятся к Q (^eR3)^1, n то время как
площадь поверхности равна 4т:/?2. Слсдоватольво, второй интеграл стре-
5 в. Смайт
66 Глава III
мится к нулю как Q (&R) '. Поскольку г г является решением уравпспия
Лапласа (^2т-~1 = 0), то, учитывая уравнение C.29), выражение C.30) можно
переписать в виде
$^i$f dv, C.32)
откуда опять следует решение C.28) уравнения C.29).
§ 11. Теорема единственности при наличии диэлектрических сред.
Если уравнение Лапласа имело бы несколько решений, удовлетворяющих
одипаковым граничным условиям, то нужное решение пришлось бы выби-
выбирать путем эксперимента и от всей теории потенциала было бы очень мало
пользы. Пусть в некоторой области заданы величины и положения всех
фиксированных зарядов и известен также потенциал по всей границе обла-
области, за исключением, может быть, некоторых замкнутых проводящих по-
поверхностей, на которых заданы полные заряды. Докажем, что в этом слу-
случае потенциал V определен однозначно. Предположим, что существуют два
значения V и V', удовлетворяющие граничным условиям и уравнепиго Лап-
Лапласа. Тогда и разность их также должна удовлетворить уравнению Лапла-
Лапласа, т. е., согласно формуле C.5),
что справедливо, так как фиксированные заряды выпадают. Положим в со-
соотношении C.19) Ф = 47 = V — V. Согласно § 8, интегралы но границе раз-
раздела двух диэлектриков исчезают, если на границах нет поверхностных за-
зарядов. Подстановка дает
2
C.33)
Те поверхностные интегралы в левой части, которые соответствуют 'грани-
'границам с заданным потенциалом, исчезают в силу того, что F = F' в каждой
точке. Поверхности же с заданным зарядом являются, по условию, прово-
проводящими, т. е. па них V и V постоянны я могут быть вынесены за знак
интегрирования. Поэтому для s-й поверхности имеем
ik{V*- v's} dS° =(F* ~ v's) ®' ~
По предположению, полный заряд на этой поверхности фиксирован, так
что Qs — Q's — O и вся левая часть выражения C.33) обращается в нуль.
Поскольку подинтегралыюе выражение справа всегда положительно, 'то
величина V(V —F') всюду должна быть равпа нулю. Таким образом, раз-
разность V — V должна быть постоянной, но на границе она равна нулю,
значит она равна нулю во всей области. Теорема доказана.
§ 12. Внесение нового проводника. Докажем, что если при внесении
незаряженного или заземленного проводника в электрическое поле, создан-
созданное некоторой системой заряженных проводников, величины зарядов всех
проводников остаются неизменными, то энергия системы умсч1ьшается. Обо-
Обозначим энергию поля в начальном состоянии через W, напряженность поля
через Е, а объем через v. Те же величины после внесений проводника
Общие теоремы 67
обозначим через гг" , Е', V. Тогда имеем
W - W = \ ^ Е2 dx - у ^ Е'* dv
J \ [(E-E'J-2E'-(E'-E)]dv. C.34)
Подставляя теперь в соотношение C.21) W = V' и Ф = Г — V и помня,
что во всем объеме У2Ф = 0, получим
5
m m.
так как Q'j — Qj- Таким образом, второй член в последнем интеграле C.34)
равен нулю и, следовательно, W—W' является величиной положительной.
Поскольку при заземлении никакой работы не совершается, то любое возни-
возникающее при этом перераспределение зарядов должно происходить за счет
электрического поля и вызывать уменьшение его энергии.
§ 13. Эквивалентный слой Грина. Обозначим через Vp потенциал
в точке Р. находящейся вне замкнутой поверхности S, созданный зарядом,
распределенным с плотностью р (х, у, z) в объеме v, ограниченном этой по-
шзрхпостьк S. Положим в соотношении C.22) W = r г иФ = Р, так что,
согласно формуле C.6), V2iI'=—р/е. Используя формулу A.8), получаем
\±.dSvidS= = _Wp, C.35)
S S v
где г — расстояние от точки Р до объема d\. Отсюда видно, что нотен-
циал Vp в точке Р можно выразить либо в впде объемного интеграла от
плотности заряда в объеме v, либо в виде двух интегралов по поверхности
S, ограничивающей объем v. Сравнение соотношения C.35) с A.6) и A.30)
показывает, что Vp не изменится, если убрать объемный заряд р и заме-
заменить его поверхностным слоем, совпадающим с S и несущим заряд
— e(dVjcin) (на единицу поверхности) и, кроме того, некоторое распределение
диполей с моментом eV (на единицу площади), ориентированных вдоль
внешней нормали к S.
Пусть -5" совпадает с, эквипотенциальной поверхностью. Тогда в соот-
соответствии с формулой C.2), вынося V за знак интеграла, второму интегра-
интегралу можно придать вид
G) ^^) C.36)
S v
Так как !.//• является потенциалом точечного заряда 4тс, находящегося
в точке Р, то интеграл C.36) равен нулю, и, следовательно, внутри v
V2(l//-) = 0. В этом случае двойного (дипольного) слоя не требуется. Следо-
Следовательно, любой участок эквипотенциальной поверхности в электрическом
поле можно заменить очень тонким незаряженным проводящим листом, так
как последний можно рассматривать как две бесконечно близкие эквипотен-
эквипотенциальные поверхности. Чтобы потепцпал Vp остался неизменным, эти
5*'
68 Глава III
поверхности, как видно из соотношения C.35), должны иметь па внешних
своих сторонах равные по величине и противоположные по знаку плотности
зарядов.
§ 14. Энергия диэлектрического тела в электрическом поле. Из пре-
предыдущего параграфа следует, что силы, действующие на неподвижные
внешние заряды со стороны заданного объемного распределения или экви-
эквивалентного ему поверхностного слоя, одинаковы. По закону Ньютона спра-
справедливо и обратное утверждение. Это упрощает вычисление работы, совер-
совершаемой при перемещении незаряженного диэлектрического тела в поле,
созданном неподвижными источниками в среде с проницаемостью е0. Если
слой вносится в уже полностью сформированное поле, то энергия элемен-
элемента поверхности dS л этом поле определяется выражением A.14) с учетом
результатов § 7 гл. I, а именно:
dW=[oV + {m-V)V]dS, C:37)
где о — плотность заряда, m — плотность дипольного момента, а V — потен-
потенциал, создапный внешними неподвижными зарядами. Поляризация диэлек-
диэлектрика, а следовательно, и величины о и m эквивалентного слоя пропор-
пропорциональны в этом случае напряженности внешнего поля; они создаются
этим полем и равны нулю при его отсутствии. Поэтому полная работа со-
составляет половину той, которая дается выражением C.37). Подставляя зна-
значения о и т, приведенные в § 13, и интегрируя по поверхности слоя, по-
получим
^ W)dS. C.38)
где Vo — результирующий потенциал на внешней стороне эквивалентного
слоя или поверхности диэлектрика. Согласно условиям A.48) и A.49), по-
потенциал на внутренней стороне слоя связан с Fo соотношениями
V^V, и B^-VV^en-VV,, C.39)
где е — диэлектрическая проницаемость тела. Подставляя соотношения C.39)
в C.38) и применяя теорему Остроградского — Гаусса C.2), получим
ибо Ч2У = Ч2Уг~0. Пусть напряженность электрического поля, создаваемого
некоторым фиксированным распределением зарядов в объеме v однородной
изотропной среды с проницаемостью е0, равна Е, а Е;—напряженность поля
в этом же объеме, заполненном однородным изотропным диэлектриком е.
Тогда разность энергий равна
W = 4" 5 (ео - Е)Е • Ei rfv- C.^1)
V
Момент или сила, действующие на тело в направлении 0, равны
§ 15. Изменение электрической энергии системы при увеличении
диэлектрической проницаемости. Если заряды на проводниках, создаю-
создающие электрическое поле, сохраняются постоянными, то при увеличении
Общие теоремы 69
диэлектрической проницаемости п какой-либо точке среды энергия всей
системы уменьшается. Чтобы доказать это, введем следующие обозначения;
W — энергия системы, Qj — заряд па /-м проводнике, р — объемная плотность
заряда, V — потенциал произвольной точки не — диэлектрическая проницае-
проницаемость. Предположим, что при изменении в Q. и р остаются постоянными,
а V и W меняются. Тогда
W = у ^ s?2 rfv = у ^ е (Wf d\,
V
Заменим n соотношении C.19) W на bV и Ф на F, подставим V- (EV^0= —P
и предположим, что границы раздела различных диэлектриков незаряшены
(соответствующие им поверхностные интегралы обращаются в нуль)
=2 \ bVBW-dSi+ \
J1S П}
J=1S,-
потому что
j=l V
Подставляя результат в соотношение C.43) и перенося 28ТУ о левую часть,
находим
bW = —^Д 8е (\'VJdv. C.44)
V
Таким образом, bW — отрицательно при положительном os.
§ 16. Потенциал аксиально-симметричного поля. Путем непосред-
непосредственной подстановки в уравнение C.18) и проведения соответствующего
интегрирования по частям можно убедиться, что если е — постоянная вели
чипа и потенциал V не зависит от угла ф, уравнение Лапласа имеет сле-
следующее решение:
)dO, C.45)
где Ф (z) — действительная функция z. Разложение этой функции в ряд
Тейлора (см. Двайт, 39) имеет вид
Ф (г, р) = Ф (г) + Ф' (z) /p sin 6 + B!)-1 Ф" (z) (/psin G)s + ... C.46)
Подставляя ряд C.46) в выражение C.45) и интегрируя от 0 до 2т, полу-
чпм
n=0
70 Глава III
Отсюда видно, что V (z, 0) совпадает с Ф (z). При отсутствии зарядов на оси
решение C.47) лает значение V, однозначное во всех точках, не отделенных
от оси заряженной поверхностью.
ЗАДАЧИ
!. Показать, что компопспты ротора в цилиндрической системе координат равны
i дАг дАу
rot. А = — ~х ¦ -^— ,
Р р O'-f OZ
.дАР дАг
lA
2. Показать, что компоненты ротора в сферической системе координат равпы
> (sin вач) эа6
dti да
3. Показать, что для эллипсоидальной системы координат (см. § 2 гл. V) коэф-
коэффициенты hu h2, h3 в выражении C.10) можно записать в виде
'i/if = (u1 — и2) (щ — Из)^'!. 4й| = (н2 — и3) (н2—h1)B2i ^з = (мз — ui) (мз — м2) В3,
где
Di, 2, 3 = [(ffi2 + Ml, 2, 3) (Ь2 + «,, 2, 3) (с2 + м1, 2, 3)ГХ-
причем О Ь> а, —Ъ2 < и2 <—а2, — а2 < г*, < оо. О частных случаях сплюснутого
и вытянутого сфероидов см. § 28 и 29 гл. V.
4. Пусть три семейства ортогональных поверхностей заданы концентрическими сфе-
сферами u\ = x2-\-yz-\-z2 и двумя семействами конусов: х2и~\-\-у2 (м| — Ь2)~1 + г2(м| — с2)~1 = 0
и х2щ2-\-у* (ui — fc^-i+z2^2 — c2)-1 = 0. Показать, что
5. Три семейства ортогональных поверхностей выражаются уравнениями: х2 с~2и~2-\-
у2с~2(и2 —1)-1 = 1, х2с~2щ2 — j/2c-2(l_м|)-!=1 и z = m3. Показать, что
и Л3 = 1.
6. Показать, что если ортогональные поверхности заданы уравнениями у2 ='icul x -
2и2, у2=—• 4си2 х + 4с2к| и z = m3, то
7. Показать, что если семейство ортогопальпых поверхностей задало уравнениями
( ) 2\2 i22 и 3/ = a;tgM3> то
8. Доказать, что в случае, когда ортогональные поверхности заданы уравнениями
-2/2I'2 = csh ul (ch uv — cos u2)~l, j/ = a;tgM3 и z = c sin м2 (ch Mt — cos u2)~1, коэффп-
Литература 71
циенты равны
Эта система координат известна под названием Тороидальной. Ортогональные поверх-
поверхности представляют собой тороиды, сферы и плоскости.
9. Доказать, что для ортогональных поверхностей, заданных уравнениями
(a:2-f-?/2I/2 = esin и2 (ch Mt — cos мг)~г, y^xigua, г = сяЬм1(сЬм1 — cos иг)~\ коэффи-
коэффициенты равны
h1 = c(cbu1 — cos мг)~г, /:2^=hl и ks = esinu2 {chul — cos u2)~1.
Это—биполярные координаты, так как если rj и гг—векторы, направленные из точки Р
в точки z=+e и z=—с, то M]=ln(r2rj1) и cos м2 = (Г1-1"г) ГГ1 Г21-
10*. Пусть относительная диэлектрическая проницаемость среды меняется по за-
закону е~г'а, где г—расстояние от некоторой фиксированной точки. Требуется убедиться
в том, что решением дифференциального уравнения для потенциала будет функция
а2г-2 [е~г1а__ , _ ra_i _ гг Ba2)-l] cos 6 .
Найти потенциал впутри диэлектрического тара, помещенного в однородное ноле при
условии, что диэлектрическая проницаемость шара является вышеуказанной функцией
расстояния от центра.
И*. Пусть в электрическом поле, созданном системой проводников с заданными
потенциалами, диэлектрическая проницаемость среды е произвольным образом измени-
изменилась! но так, что в любой точке среды величина е по крайней мере не уменьшилась,
и ее изменения были всюду малы. Доказать, что энергия поля при этом возросла.
12. Найти условие, при котором из семейства двухмерных эквипотенциальных
линий F2 = / (z, у) можно путем вращения вокруг оси z образовать семейство экви-
эквипотенциальных поверхностей. Показать, что если это возможно, выражение для потен-
потенциала будет иметь вид
'y(\vt)* ду-
ЛИТЕРАТУРА
Abraham M., Becker R., Klassische Elcktrizitat and Magnelismus, Berlin,
1932. (См. перевод: А б р а г а м М., Б е к к е р Р., Теория электричества,
2-е изд., М.—Л., 1939.)
Gciger-Scheel, Handbuch der Physik, Bd. Ill and XIJ, Berlin, 1927, 1928.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
Mason M., Weaver W., The Electromagnetic Field, University of Chicago Press,
1929.
Maxwell J. C, Electricity and Magnetism, v. I, Oxford, 1881.
Peirce В. О., Newtonian "Potential Function, Ginn, 1902.
Planck M. K. E. L., Theorie der Electrizitat und Magnetismus, Berlin, 1932.
Ramsey A. S., Electricity and Magnetism, Cambridge, 1937.
Stratton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: С т р э т-
тон Дж. А., Теория электромагнетизма, М.—Л., 1948.)
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
Wien-Harms, Handbuch der Experimentalphysik, Bd. X, Leipzig, 1930.
Глава IV
ДВУХМЕРНОЕРАСПРЕДЕЛ EUL1E П0ТЕ11Ц НАЛА
§ 1. Двухмерные поля и потепциалы. Задача о нахождении потенциала
называется двухмерной тогда, когда все эквипотенциальные поверхности
в поле цилиндрические, т. е. все они могут быть образованы пугем пере-
перемещения бесконечной прямой линии параллельно некоторой фиксированной
линии. Под единичным зарядом в этом случае мы будем понимать линей-
линейный заряд, равномерно распределенный вдоль некоторой оси и равный по
величине одному кулону на метр. Как уже было показано [см. формулу
B.7)], напряженность поля, созданного линейным зарядом на расстоянии г
от него, в однородном изотропном диэлектрике имеет лишь радиальную со-
составляющую, равную
Отсюда, интегрируя, получаем выражение для потенциала
Ясно, что теперь ужо нельзя положить потенциал равным нулю на беско-
бесконечности, так как это приведет к бесконечному значению постоянной С.
Как правило, мы будем выбирать значения С так, чтобы по возможности
упростить вычисления.
Строго говоря, задача о двухмерных электростатических полях не мо-
может возникнуть в действительности, так как все проводники имеют конеч-
конечные размеры. Однако существует очень много важных задач о нахождении
поля в системе параллельных цилиндрических проводников, длина которых
значительно превышает расстояния между ними, так что вдали от краев,
где краевые эффекты сказываются несущественно, такую задачу можно
трактовать как двухмерную.
§ 2. Круговые гармоники. Термин «гармоника» в наиболее общем
смысле этого слова употребляется по отношению к любому решению урав-
уравнения Лапласа. Обычно, однако, его применяют к более узкому классу
решений, именно к таким решениям, которые можно в определенных коор-
координатных системах записать в виде произведения трех функций, каждая
из которых зависит только от одной координаты. Решение задачи, удовле-
удовлетворяющее заданным граничным условиям, образуется путем суммирования
некоторого числа таких гармоник, взятых с надлежащими коэффициентами.
В обычных цилиндрических координатах, описанных в § 6 гл. III, ци-
цилиндрические гармоники записываются в виде
. D.3)
В частном случае, когда функция Z (z) — постоянная величина, задача сво-
сводится к двухмерной и гармоники называются круговыми. В дальнейшем
Двухмерное распределение потенциала 73
мы будем вместо р употреблять г, а вместо <р употреблять 6. В этих обозначе-
обозначениях уравнение Лапласа C.18) для однородной изотропной диэлеЕ^трической
среды, если его умножить на г2, примет вид
Будем искать его решения в виде
У = Д(г)вF). D.5)
Подставляя решение D.5) в уравнение D.4), получим
—-о
Очевидно, что этому уравнению удовлетворяют решения следующих урав-
уравнений:
^=-иЭД, D.6)
5? + 1^ = п«4. D.7>
dr2 ' г dr r2 v '
Уравнение D.6) является уравнением гармонического осциллятора; его ре-
решением будет
Q = Acosne + BsmnG. D.8)
Легко убедиться, что решением уравнения D.7) при п Ф 0 является функ-
функция
R = Crn + Dr-n, D.9)
а при п= О
D.10)
D.11)
Число /г называется показателем гармоники. Круговые гармоника бывают
с показателем, равным нулю,
V = (AO+B)(Clnr + D), D.12)
и с показателем, отличным от нуля,
+ Drn). D.13)
Сумма таких гармоник, взятых с различными множителями для каждого п,
иди интеграл но п тоже, очевидпо, являются решением уравнения D.4)
У = 2впЯи или V = \f{n)HnRndn. D.14)
и
Следует замешть, что мы не накладывали никаких ограничений па значе-
значение п.
Если для любых значений 0 при п— целых числах, имеет место равенстло
^(АпсоБпв + Вт^тпВ)=,у_ (CncosnO + Dnsin nO), D.15)
то из него вытекает, что
Ап = Сп и Bn = Dn D.16)
74 Глава IV
Чтобы доказать это утверждение, необходимо помножить правую и левую
части равенства D.15) на cosmG, а затем проинтегрировать в пределах от 0
.до 2т., что даст
2-к 2-к
2 ( Ап \ cos пВ cos rnO dO + Bn\, sin яб cos mOdQ) =
о • б
2-к 2т.
cos nO cos mO dd + Dn
6 о
Бее члены, для которых т ф п, равны нулю (см. Двайт, стр. 445 и 465).
При т = п (см. Двайт, 450.11 и 858.4) мы имеем
1 1
При помощи аналогичной процедуры, используя только sinmG, легко дока-
доказать, что Bn = Dn.
§ 3. Представлрние потенциала поля липейного заряда в виде ряда
«о гармоникам. При использовании круговых гармоник часто бывает
необходимо иметь разложение потенциала поля
линейного заряда, координаты которого мы
" обозначим через г0, б0. Пусть Я— расстояние
/1 между линейным зарядом q и точкой Р (фиг. 23).
1° Тогда, полагая в выражении D.2) постоянную С
равной нулю, для потенциала V в точке Р
Фиг. 23. имеем
'= ~2qlnR = -gln[r2 + ^-2/Tocos@-0o)] =
= -2qlnr-qln [ 1 --? е»(в-вв) ] [ 1 --^ e~i<е-во)] .
При г0 < г (Двайт, 601) получаем
2qlnr-\-q I — Г0 (в—6o)-j_g—У (в—во)] -[_ _ ( 1л. ) ("е?2 (б—6o)_i_g—j2 (9—60)j i _ I __
Перепишем это в виде суммы, разложив cos/г (б — 0о) (см. Двайт, 401.04),
тогда
D.17)
Это справедливо для г > г0. Соответствующее выражение для ?• <* г0 можно
получить из D.17), если в нем поменять местами г и г0, а именно:
1пг0] . D.18)
и есть искомые нами разложения.
§ 4. Проводящий или диэлектрический цилиндр в однородном поле.
J3 качестве примера, в котором используются граничные условия на поверх-
поверхности металла и на границе раздела двух диэлектриков, рассмотрим задачу
•о бесконечном проводящем цилиндре радиуса а, покрытом слоем диэлектрика
Двухмерное распределение потенциала 75
а •< г < Ъ с относительной проницаемостью К и помещенном в однородное
электрическое поле Е, перпендикулярное к оси цилиндра. Потенциал этого
первоначального поля вне цилиндра можно представить в виде
Потенциал, обусловленный индуцированными зарядами в цилиндре, должен
исчезать на бесконечности, поэтому выражение для него не может содержать
членов типа гп. Кроме того, поскольку этот потенциал должен быть сим-
симметричным относительно оси х, в выражении отсутствуют члены, содержа-
содержащие sin/гб. Таким образом, окончательное выражение для потенциала вне
цилиндра должно иметь вид
со
yo = ?rcose+ 2 Anr'nccsn0. D.19)
Потенциал поля внутри диэлектрического слоя также не может содержать
членов вида sin nb, но члены гп и г'п могут в него входить, так как зна-
значения г — 0 и г = оо находятся вне пределов этого слоя
со
Vo = S {Bnrn + Crrn) cos nO. D.20;
• л=1
Если начало координат выбрано на оси цилиндра, то потенциал проводпика
V = 0. Таким образом, мы нашли решения уравнения Лапласа, удовлетво-
удовлетворяющие условиям на бесконечности и обладающие симметрией относительно
оси х. Теперь необходимо удовлетворить граничным условиям на поверх-
поверхности металла и на границе раздела двух диэлектриков, что позволит опре-
определить коэффициенты Ап, Вп и Сп. Граничными условиями при г= Ъ, согласно
соотношениям A.48) и A.49), будут
е„-^- = е~1Г- или ~1Г^ = К ~- и Vn=V-. D.21)
" dr dr dr dr « i v /
Подстановка выражений D.19) и D.20) в уравнение D.21) дает
Е cos б — 2 nAJr"-1 cos nO = К 2 п{ВпЬп'г — CJf1^1) cos «6,
ЕЬ cos 0 + 2 AJfn cos nO = ^ (ВпЪп + CJfn) cos пв.
Для п Ф 1 из соотношений D.16) мы имеем
_ Аф-^1 = KBJf'x - KCJfn'\ D.22)
Anb^ = Bnbn + Cnb-n. D.23)
На поверхности проводника r = a, V{ = 0, поэтому
0 = В„ап + Сп<Гп. D.24)
Умножая уравнение D.22) на b и складывая с D.23), получаем
(К+1)Вп = (К-1)СпЬ-^. D.25)
Системе уравнений D.24) и D.25) можно удовлетворить, либо полагая
Вп = Сп 0, либо (К + 1)/'(К— 1)= —(а/ЬJП. Последнее, однако, невозможно
в силу независимости величин К и а. Поэтому, учитывая первое соотно-
соотношение и подставляя его в уравнение D.23), имеем
Ап = Вп = Сп = 0. D.26)
76
Глава IV
Для я=1 вместо уравнений D.22) — D.24) получаем
Е - АХЪ~* = ЯБ, - КСХЪ-*,
Решая эти уравнения относительно Av В1 и Сг, имеем
— 1)Ь2
Следоштельно, потенциалы D.19) и D.20) соответственно равны
На фиг. 24,я показаны линии электрической индукции.
а
Фиг. 24.
D.27)
D.28)
Полагая в соотношениях D.27) К=\, мы получим решение для метал-
металлического цилиндра радиуса а
D.29)
Поле для этого случая показано на фиг. 24,6.
Решение для диэлектрического цилиндра радиуса b получим, если
положим в соотношениях D.27) а = 0
а
1 —
АГ+1 г
IE
K+l
г cosS.
D.30)
Заметим, что внутри диэлектрического цилиндра поле однородно. Линии
индукции изображены на фиг. 25 для К = 5.
§ 5. Диэлектрический цилиндр. Метод изображений. Рассмотрим
теперь, как влияет диэлектрический цилиндр радиуса а на поле линейного
Двухмерное распределение потенциала
77
заряда q, расположенного в точке r = b, 6=0 (см. фиг. 26). Потенциал,
обусловленный самим линейным зарядом, определяется по формуле D.18),
в которой нужно положить ro — b, б,, = 0. К нему необходимо добавить
потенциал, обусловленный поляризацией диэлектрика. Этот потенциал должен
исчезать на бесконечности и быть симметричным относительно осп х. Таким
Фиг. 25. Фиг. 26.
образом, полный потенциал в области а < г < b ранен
и=1
Так как потенциал внутри цилиндра остается конечным при г = 0 и сим-
симметричным относительно оси х, его можно представить в виде
D.32)
Полагая Vo = V{ при г = а. получим
и c^-
D.33)
Кроме того, ev (dVJdr) = е (dVJdr) при г = а или (dVoldr) = K(dVJdr), что
дает
^-^4 = л-4- D.34)
Решим уравнения D.33) и D.34) относительно Ап и ^,г:
2
ш. Вп =
Итак, для потенциала вне цилиндра имеем
пЪп'
п=1
и внутри цилиндра —
,} , D.35,
Если теперь положить
78 Глава IV _^___
то выражение D.35) в точности совпадает с формулами разложения потен-
потенциала D.17) и D.18), создаваемого тремя линейными зарядами, расположен-
расположенными на оси х: зарядом q' в точке х = а2/Ь, зарядом — д' в точке х = 0
и зарядом q в точке х = Ъ. Точно так же потенциал D.36) совпадает с потен-
потенциалом линейного заряда q", расположенного в точке х = Ъ, причем
Таким образом, незаряженный диэлектрический цилиндр радиуса а,
помещенный на расстоянии Ъ от параллельного его оси линейного заряда q,
по своему действию на поле вне цилиндра эквивалентен двум параллельным
оси линейным зарядам, один из которых (— q') распределен вдоль оси
цилиндра, а другой (q') находится между линейным зарядом q и осью
цилиндра па расстоянии а2/Ь от последней. Этот заряд q' можно рассма-
рассматривать как «изображение» заряда q в цилиндре радиуса а. Потенциал
внутри цилиндра с точностью до постоянной совпадает с потенциалом поли
в отсутствие цилиндра при замене линейного заряда q на q". Некоторые
авторы в числителе выражения для q" вместо 2 ставят 2К. Тогда потен-
потенциал внутри цилиндра нужно вычислять как потенциал линейного заряда q"
в однородном пространстве, заполненном диэлектриком с проницаемостью А".
Отсюда следует, что при внесении диэлектрического цилиндра в любое
электрическое поле, созданное любым двухмерным распределением линей-
линейных зарядов, параллельных оси цилиндра, структура этого поля внутри
цилпндра не меняется, а напряженность поля умепыиается в 2/GT-j- 1) раз.
§ 6. Изображение в проводящем цилиндре. Из соотношения A.51)
следует, что при К —^ со силовые линии подходят нормально к понерх-
ности диэлектрика, что является граничным
условием на поверхности проводника. По-
Поэтому закон изображения в проводящем пена
ряженном цилиндре можно получить, поло-
положив в формуле D.37) К—->ос; это дает
д' = —q. Таким образом, если линейный за-
заряд q расположен параллельно оси неза-
ряженного проводящего цилиндра радиуса
а па расстоянии Ь от нее, то дополнитель-
дополнительный потенциал вне цилиндра, обусловлен-
обусловленный присутствием цилиндра, совпадает с потенциалом поля, создаваемого
двумя параллельными линейными зарядами, один из которых равен q и
распределен вдоль оси, а другой равен — q и находится между линейным
зарядом q и осью на расстоянии a-jb от последней.
Как это показано на фиг. 27, для определения положения изображе-
изображения необходимо из точки q провести касательную к диэлектрическому или
проводящему цилиндру. Тогда перпендикуляр, опущенный из точки каса-
касания на линию — qq', пересечет последвюю в искомой точке q'.
§ 7. Изображение в плоской поверхности проводника или диэлек-
диэлектрика. Пересекающиеся проводящие плоскости. Устремим радиус цилпн-
цилпндра к бесконечности, сохраняя постоянным расстояние d=b— а между
линейным зарядом и поверхностью цилиндра. Тогда расстояние между изо-
изображением q' и этой поверхностью будет
a-a2b-l = ab~l (b-a)-^d.
Таким образом, полученный пами закон изображения можно распро-
распространить и на случай линейного заряда, расположенного параллельно
Двухмерное распределение потенциала
79-
плоской поверхности полубесконечной диэлектрической среды или проводя-
проводящей пластинки. Изображенный заряд располагается на таком же расстоя-
расстоянии от поверхности, что и действительный, но только по другую сторону
от нее. Для проводника q' = — q, для диэлек-
диэлектрика q' и q" определяются из выражения D.37).
Из фиг. 28 очевидно, что две плоскости,
пересекающиеся в начале координат под углом
¦к/т, где то — целое число, будут являться экви-
эквипотенциальными плоскостями в поле линейных
зарядов, параллельных линии пересечения пло-
плоскостей и расположенных на поверхности цилин-
цилиндра г — г„ под углами б0, 2vnrx -f б(), 4тгто~1 ¦+-
+ 60, ..., 2(то— ^г.тг1-^ б0 (заряды + q) и
2-ютг1 — б0, 4-п:то~1 — б0, ..., 2т. — б0 (заряды — q).
§ 8. Задача о диэлектрическом клине. Уравнение D.4) имеет еще-
одво решение, соответствующее значениям я ф 0. Для получения его необхо-
необходимо в соотношениях D.6) —D.9) постоянную п замолить па /я. Тогда
О, D.38)
n lnr = C cos (л In r) + Dsin (n In r). D.39)
Это решение периодично не по б, а по In г, поэтому в интеграле и в ряде
D.14) взаимно ортогональными будут теперь функции Rn, а не в„. Эти
гармоники можно использовать при реше-
аии задачи о диэлектрическом клине, огра-
ограниченном двумя плоскостями 6 = — а и
О —а, имеющем диэлектрическую прони-
проницаемость е2 и находящемся в поле линей-
линейного заряда q, распределенного вдоль
линии б --- -у, г = а в среде с диэлектриче-
диэлектрической проницаемостью е1 (см. фиг. 29). По-
Поскольку в такой системе отсутствуют ци-
цилиндрические границы, на которых долж-
должны исчезать члены, содержащие синусы
или косинусы в решепии D.39), нельзя
ограничиваться дискретными значениями
я, а следует считать я меняющимся непрерывно,
искать по форме интеграла D.14). Обозпачнм
через Р и запишем потенциалы в виде
V,
Фиг. 29.
п поэтому решение задачи
величину (sj — e24'/(ei ~\~ ег)
V1 = A + р) ^ [А (к) в*» + В (A) r-h«] cos [ * In (? ) ] dk + CD, D.4U)
о
У2 = \ [С (к) еы + D {k) e-"G] cos [ ft In (¦?-) ] dk + Co, D.41)
о
CO
Vs = ^ [E (ft) e^ + F (k) e-**] cos [ ft In ( ~ ) ] dh-\ Co, D.42)
о
где Vt относятся к области — а < 0 < a, V2 — к области а<б<Г^ н V3 —
к области -с < 6 < 2г. - а. Постоянную С„ можно выбрать так, чтобы потен-
потенциал V равнялся нулю в любой заданной точке. Если в качестве такой
?0 Глава IV
точки оыбрать точку г — а, б = 0, то постоянная Со будет равна величине
Окружность /• = а проходит через точку q и является силовой линией,
потому что всюду вдоль нее dV/dr = O. Отсюда следует, что половина пол-
полного потока индукции приходится на долю силовых линий, уходящих в бес-
бесконечность, другая же половина связана с силовыми линиями, оканчиваю-
щимися в точке г = 0, где, таким образом, находится заряд — -^q. По тео-
теореме об интегралах Фурье, если два из интегралов вида D.40) —D.42)
равны между собой при любых значениях In (г/а), то равны между собой
и их подиптегральные функции. Используя граничные условия A.48) и A.49)
при 0 = а, после некоторых преобразований подинтегральных выражений
для Vx и F2 получим
С = А + $е~2'<°В, D = [ie2haA + B. D.43)
Аналогичная процедура для Vx при 6= —а и для V3 при 6 = 2- — а дает
Е = (А + $Ве2ы) е-2'™. F = фАе-2ка + В) e2f™. D.44)
Теперь остается удовлетворить еще одному условию при 6 = f. Для этого
напишем выражение для плотности потока индукции сквозь плоскость 0 — f
оо
о
о
Умножим обе части на cos [tin (г/а)] dr и проинтегрируем в пределах от г=0
до г=оо. Тогда выражение, стоящее слева, по теореме Гаусса равно q,
так как интегральная функция отлична от нуля только вблизи г = а;
правая же часть находится по теореме о разложении в интеграл Фурье.
В результате получим
Кроме того, Vz равно V® при 6 = f, поэтому
(С- Е) #1 =—(D-F) e-^.
Исключив D и F или С и Е из этих уравнений, получим
Из выражении D.43) — D.45) для А и В имеем
sh к
А Я - q [eT* (T*} yh 7;K-e±k '"^ sh к (д
' 2n?tA:[sh2fti:— [з2 sh2 А (тг—2а)]
где иерхиие злаки относятся к ^4, а пижние — кВ. В частном случае, когда
система симметрична относительно плоскости ~{ = т., потенциал внутри ди-
диэлектрического клпна равен
2a)]
Двухмерное распределение потенциала 81
Подинтегральное выражение остается конечным при к = 0 и экспоненциально
убывает с ростом к. Построив график этой функции в зависимости от к,
можно вычислить интеграл D.47) при помощи планиметра. Если существует
только один заряд в точке r = a, S = -j-, то члены, обусловленные заря-
зарядом— у q, расположенным в начале координат, и входящие в решение
D.40) — D.42), можно исключить из него путем добавления к Vt, V2 и V3 члена
¦igln-lla^-g-^]-'. D.48)
Если на некотором цилиндре r—h потенциал поддерживается равным нулю,
то решение находится в виде суммы двух решений: одного для линейного
заряда q, расположенного в точке г —a, 6 = f, а другого —для линейного
заряда —q, расположенного в точке г=Ь2/а, 6 = ^. Если же нулевой потен-
потенциал имеют два цилиндра г = b и г — с, то необходимо применять дискрет-
дискретный набор величин п в соотношении D.39) и искать решение для потен-
потенциальной функции не в виде интеграла, а в виде ряда.
§ 9. Комплексные величины. Прежде чем переходить к сопряженным
функциям и конформным преобразованиям, напомним вкратце некоторые
наиболее важные свойства комплексных величин.
Если z = x-\-jy, то очевидно, что каждой точке
плоскости ху, называемой в связи с этим z-roio-
скостыо, соответствует одно значение z. В поляр-
полярных координатах (см. фиг. 30) величина z записы-
записывается в виде (Двайт, 408.04)
z = x + /у = r cos S + jr sin 6 = reJ'e. D.49) Фиг. 30.
Длина вектора г называется модулем z и обозначается через |z|. Угол б
называют аргументом, амплитудой1), фазой или углом z. При возведении
комплексного числа z в степень h получается
zn=.rnel-nB> D.50)
т. е. модуль величины z" равен п-й степени модуля z, а аргумент zn равен
аргументу z, помноженному на п. Аналогично и для произведения двух
комплексных чисел
D.51)
т. е. модуль произведения двух комплексных чисел равен произведению
их модулей, а аргумент произведения равен сумме их аргументов. Заменив
теперь в формуле D.51) zx на Zj1, получаем, что модуль частного от деле-
деления двух комплексных чисел равен частному от деления их модулей,
а аргумент равен разности их аргументов.
Пусть z1 = z1 + jy1 = f(z) = f(x + jy), тогда величина z* = хг — ]УХ =
= /(х — /у) называется комплексно-сопряженной z. Последнее соотношение,
имеющее место для аналитических функций, могкно доказать путем разло-
разложения функции / (х ± /у) в степенной ряд с действительными коэффициен-
коэффициентами: всюду, где ;Ь/ возводится в четную степень, соответствующий член
г) Этот термин широко употребляется математиками для обозначения угла (L
Однако амплитудой называют также максимальное отклонение некоторой переменной
неличины, например н теории переменных токов. В этом случае при использовании
комплексных обозначений амплитуда практически совпадает с модулем соответствующей
комплексной величины.
6 в. Смяйт
82 Глава IV
ряда будет действительным и одинаковым при любом знаке перед ], там же,
где ± / возводится в нечетную степень, соответствующий член ряда будет
чисто мнимым, а знак перед / остается прежним. Для | zx |2 имеем
I ч I2=А + у\ = чА = / (*+fy) f & - fy) ¦
Таким образом, для получения модуля функции комплексной переменной
необходимо помножить эту функцию на комплексно-сопряженную ей
и извлечь квадратный корень.
§ 10. Сопряженные функции. Напишем двухмерное уравнение Лапласа
в прямоугольных координатах
-&г-+^г = °- D-52)
Это уравнение второго порядка в частных производных. Его общее решение
должно содержать две произвольные функции и, как легко убедиться путем
дифференцирования, может быть записано в виде
U = Ф (х + jy) + «" {х- jy).
Заметим, что для того, чтобы Ф и W были решениями уравнения D.52),
они должны иметь конечные производные в той области, где справедливо
это уравнение, и, следовательно, должны являться аналитическими функ-
функциями, т. е. функциями, разлагаемыми в степенной ряд1). Величина U,
являющаяся электростатическим потенциалом, должна быть действительной,
что возможно только, если мнимая часть Ф равна по величине и противо-
противоположна по знаку мнимой части W, т. е. если Ф (x + jy) = u-\- ft,
а ЧГ (ж — fy) = w—jv, где и, v, w — действительные величины. Аналити-
Аналитические функции Ф и I разлагаются в степенной ряд
во оо со
Ф(х+ jy) = Ф (ге*) = 2 AnrneW = 2 Лпгп cos габ + / 2 A/1 sin nO,
п=0 , п=0 тг=О
со оэ со
W (х - fy) = W (ге-Я) = 2 Впгпе-™» = 2 A/1 cos габ - / 2 Bj» sin nb.
п=0 тг=О я=0
В силу того, что мнимые части Ф н 47 равны по величине и противоположны
по знаку при любых б, мы получаем, что Ап — Вп [см. соотношение D.16)],
и, следовательно, реальные части этих функций в точности равны между
собой, т. е. u — w. Поэтому U = 2u.
Пусть V — другая действительная величина, такая, что V = 2v, тогда
U + fV = 2 (и + jv) = 2Ф (х + jy) = / (х + fy). D.53)
Функция V также удовлетворяет уравнению Лапласа, что можно показать,
либо воспользовавшись написанным выше разложением, являющимся разложе-
разложением в ряд по круговым гармоникам, либо путем умножения выражения D.53)
па —/:
V - fU = - jf {x + fy) = F(x + jy).
Отсюда ясно, что V равна реальной части функции F\x-\-jy), точно так же
как Ь является реальной частью функции f(x-hjy)- В дальнейшем мы
будем U + jV обозначать через W, а х 4- jy через z, т. е.
W = f(z). D.54)
Функции U (х, у) и V (х, у) называются сопряженными.
х) Whit la k с г, Watson, Modern Analysis, Ch. V. (См. перевод Уиттекер,
В а тс он, Курс современного анализа, 1933, ч. I, гл. V.)
Двухмерное распределение потенциала 8?
§ 11. Функции потока. Продифференцируем выражение D.54) по х и у:
dW _ви_. ¦ 9V _ ,, . dz _ .,
dx ~~ dx + ' dx ~ I W дх ~'
™L ?Е+ j dV f (z) ± j/
L + j f (z) ± j/ (z)
Умножим второе соотношение на / и прибавим к ному первое, тогда из
равенства нулю реальной и мнимой частей суммы получим
dV dU dV _ dU . ,.r
и ~ду~-~д~- V4-'^
дх~~1)у
Но это есть условие взаимной ортогональности семейств кривых U (х, у) —
= const и V (х, у) = const. Как мы уже видели, любое из этих семейств
можно выбрать в качестве эквипотенциальных линий; тогда функция, описы-
описывающая это семейство, называется потенциальной. Другое же семейство
кривых, ортогонально пересекающееся с первым, будет представлять в этом
случае силовые линии. Функция, соответствующая этому семейству, назы-
называется функцией потока.
§ 12. Напряженность электрического поля. Поток электрической
индукции. Рассмотрим производную
dW _ dU + jdV _(dU/dx) dx+(dUjdy) dy + /'[(dV/dx)dx-\-(dV/dy) dy]
dz dx + / dy dx -j- / dy
В соответствии с соотношениями D.55) заменим bUjdx и dUjdy, тогда
dW _ (dVldy) (dx + j dy) + / (dV/дх) (dx + /dy)_ dV . dV _ dU . dU /Л rfix
dz dx+jdy ~ dy +1 dx ~~ dx 1 dy ' \q:-i)K>)
Таким образом, если в качестве потенциальной функции выбрана V, то
мнимая часть выражения dW/dz равна ^-составляющей напряженности
электрического поля, а реальная часть dW /dz равна его ^-составляющей.
Независимо от того, выбрана ли в качестве потенциальной функции U или Vг
амплитуда вектора Е в данной точке определяется модулем функции dW/dz
в этой точке. Обозначим через dn элемент длины в направлении макси-
максимального увеличения потенциала, а через ds — элемент длины в направлении,
полученном при повороте dn на угол и/2 против часовой стрелки, тогда
из соотношений D.56) получим
dW
dz
dU _ dV
dn ds
ИЛИ
dW
dz
dV__ dU
dn ds
D.57)
в зависимости от того, являются ли потенциальными функциями U или V.
Пусть, например, V — потенциальная функция. Найдем поток индукции
сквозь произвольный участок эквипотенциальной поверхности, ограничен-
ограниченный кривыми Uу и f/2. Для этого воспользуемся формулой A.27):
1/2 U2
Поток = - е J ¦§? ds = е С Щ-ds = е (Г/2- U,). D.58)
i/i i/i
Таким образом, подобно тому как разность потенциалов между любыми
двумя точками определяется разностью значений потенциальных функций
в этих двух точках, так и полный поток индукции, проходящий сквозь
линию, соединяющую две произвольные точки в поле, равен произведению
диэлектрической проницаемости е на разность значений функции потока
в этих двух точках.
С*
У4 Глава IV
Если поверхности V1 и F2 являются замкнутыми и если при этом псе
заряды расположены на одной стороне одной из поверхностей и на про-
противоположной стороне другой поверхности, то в области между V1 и V'г
исо силовые линии проходят от одной поверхности к другой и, следова-
следовательно, дакая система, как это следует из § 2 гл. II, образует конден-
конденсатор. Заряд Q на любой из поверхностей равен полному потоку сквозь нее
(на единицу длины). Из выражении D.58) этот поток определяется как
произведение е на приращение U за один оборот вдоль кривой V (обозна-
(обозначим это приращение через [U]). Поскольку разность потенциалов равна
\V2~ Fj|, то емкость в случае вакуума будет
§ 13. Функции U и V для поля линейного заряда. Прежде чем при-
приступать к описанию общих методов нахождения функции /{х-\- fy), рас-
рассмотрим один из наиболее простых примеров,
когда вид этой функции почти очевиден. В поляр-
полярных, координатах (Двайт, 408.04) для величины z
мы имеем
z = х + fy = r cos 6 + jr sin S = гё*. D.60)
По формуле D.2) потенциал линейного заряда,
расположенного в начале координат, равен Z7 =
Фиг. 31. i
= — у <7 (та) х In г. Ясно, что это выражение яв-
является реальной частью — — <7(та)-11п Zj поэтому искомую нами функцию
можно записать в виде
W — U+ jV — 9lnZ — gin r fqb _
__ _ gln(x + /y) _ q In(x24-y2I/2 jg arctg (yjx\ //сл\
¦Для проверки будем менять угол 6 от 0 до —2тг (см. фиг. 31). Тогда
функция eV будет пробегать значения от 0 до q и, следовательно, полный
поток индукции, создаваемый линейным зарядом д, равен д, как это и тре-
требуется в § 12 настоящей главы.
Нетрудно теперь написать выражение для /(z) в случае линейного
заряда, расположенного в произвольной точке г0, 60 или z0. Потенциал
такого заряда равен
U = - 4 <7 W11п^ = -т ^ (таГ ln I''2 + г20 - 2rr0 cos F - 0о)]
4
4"9 ACS^1 ln ^г CCS ° "" Г" C0S 6оJ + (r Sin б — ro sin °nJ] =
Но из формулы D.61), заменив в ной х на А а. у на В, мы видим, что
1п(А2-\- В2I'2 является реальной частью 1п(А + /.В), поэтому искомая функ-
¦цин имеет вид
W= -j?ln(A+/fi)= --^ln (|-^-гоеЛо)= -^ln(z -z0). D.62)
Двухмерное распределение потенциала 85
В случае п линейных зарядов, расположенных в точках zlf z2, .. ., zrt,
функция W будет равна
D-63)
s=i
§ 14. Емкость между двумя круглыми цилиндрами. В § 6 мы видели,
что эквипотенциальные поверхности в поле двух одинаковых по величине,
но противоположных по знаку линейных зарядов представляют собой круг-
круглые цилиндры. Рассмотрим поле, создаваемое двумя линейными зарядами: заря-
зарядом 2та, расположенным в точке у = а, и зарядом —2та, расположенным
в точке у— —а. Такой выбор величины q упрощает коэффициенты. Выра-
Выражение D.63) для W можно несколько видоизменить, а именно (Двайт, 601.2
и 505.1):
W = ln^±Zj = 2/ arctg iL = 2/arcctg -J-. D.64)
Решая это уравнение относительно z (Двайт, 408.19), имеем
— U + /V _ -asin(U//) + asmV
z-actg 2/ - t-os(t///)-fosF •
Выделим теперь отдельно действительные и мнимые части:
я sin V a sh U ,. „ri
Исключив из этих уравнений V, получим
x2+y2 — 2aycihU+a2 = 0, D.66)
что можно записать следующим образом:
= a2 cosech2 U. D.67)
Как и следовало ожидать, эквипотенциальные линии образуют семейство
окружностей с центрами на оси у. При у > 0 значения потенциала поло-
положительны, а при у < 0 значения потенциала отрицательны. Если из урагаю
ний D.65) исключить U, то получим уравнение
х2 — 2ах ctg V + у2 — а2 = 0,
которое можно переписать в виде
(х — a ctg VJ ±у2 = а2 cosec2 F. D.158;
Итак, силовые линии тоже образуют семейство окружностей, проходящих
через точки оси У(У— +а и у= —а).
Для определения емкости (на единицу длины) между двумя цилиндрами
U —¦U1 и U=U2 необходимо, как это следует из формулы D.59), разделить
заряд 2тс на разность потенциалов U2 — Ux. Пусть нам заданы радиусы этих
двух цилиндров Дх и R2 н расстояние I) между их осями. Сначала нужно
выразить через них величины а, иг и U2. Из уравнения D.67) имеем //j =
= а | cosech Ut\, R2 = а | cosech Uz\ и D — a (| cth U1 \ ± (cth f/21), причем ниж-
нижний знак относится к случаю положительных значений и Ux и Uz, т. с. когда
один цилиндр находится внутри другого, а верхний знак со(^вотствуот случаю
отрицательного значения f/1; т. е. когда ни один тгз цилиндров не охватывает
другого. Руководствуясь далее этим правилом выбора знака, можно написать
(Двайт, 651.02)
c-h (Ut — Ux) = ch U2 ch Ux ± | sh U2 sh Ux | = (| cth f/a cth Ut | ± 1) | sh f/2 sh
86
Глава IV
1 1
Подставляя вместо ~Ь 1 равное ей выражение 4:у ±у (Дсайт> 650.08),
нолучим
ch (U2 ~ иг) = [ | clh l\ cth ГУ21 ± у (clh2 U2 - cosoch2 U2) ±
± у (cth2 f/, - cosoch2 C/x) ] | sh Lrx sh t/?. | =
+ (cth C/2 + cth Uxf -q= гoscch2 t/, T coscrh2 t/2
4 \
If^l 1
Фиг. 32.
Подставим сюда значения D, Яг и Л2, что даст
Таким образом, емкость (на единицу длины) между двумя цилиндрами равна
С = 2тге arch(±—^~ 1 ~ 2 j | , D.69)
где ишкний знак относится к случаю, когда одтга цилиндр находится внутри
другого, а верхний знак — к случаю, когда ни один из цилиндров не охваты-
ваит другого. Оба эти случая показаны па фиг. 32, а и б.
§ 15. Емкость монаду цилиндром и плоскостью. Емкость между двумя
одинаковыми цилиндрами. Устремим величину R1~ D-\-h, показанную
на фиг. 32, а, к бесконечности, тогда окружность внешнего цилиндра совпа-
совпадает, по крайней море, в некоторой конечной области с осью х. Пренебрегая
RI ио сравнению с R\ и IJ и h по сравнению с 2Rlt получим R1 + D =
= 2R1 — h ^ 2R±. Поэтому
-D* . (Д,-Д)(Д,+Д) ^ h
Двухмерное распределение потенциала 87
Таким образом, емкость (на единицу длины) между проводящим цилиндром
радиуса 11 и бесконечной проводящей плоскостью, расположенной парал-
параллельно оси цилиндра на расстоянии h от нее, равна
C = 2«e arch-jj-) . D.70)
Два одинаковых цилиндра, расстояние между центрами которых I) = 2h,
имеют емкость (на единицу длины) в два раза меньшую, чем емкость, опре-
определяемая по формуле D.70), так как их можно рассматривать как два таких
конденсатора, соединенных последовательно. Окончательное выражение для
емкости двух одинаковых цилиндров можно получить п непосредственно
из формулы D.69), полагая Д1 = Я.2 и D = 2h:
Х . D.71)
§ 16. Конформные преобразования. Очевидно, что метод сопряженных
функций является могучим средством решения двухмерных задач о распре-
распределении потенциала. Но для того чтобы им пользоваться, надо уметь на-
находить нужные функции. Прежде чем излагать общие методы пх отыскания,
мы сейчас изучим некоторые специфические свойства функций комплексных
переменных. Нанесем на одну из плоскостей значения z = x-\-jy, а на дру-
другую— значения z, = ж, +/г/, н предположим, что z является аналитической
функцией zx, так что каждой толке на плоскости z1 соответствует по крайней
море одна точка на плоскости z. Если функция z =/(гх)—непрерывная,
то при перемещении точки по плоскости zx вдоль некоторой кривой соот-
соответствующая ей точка па плоскости z тоже опишет некоторую кривую.
Если же функция /(z,) не является непрерывной функцией, то точка на
плоскости z будет перескакивать при этом с одного места в другое. Пусть,
когда точка на плоскости z,, описав замкнутую кривую, возвращается
в первоначальное положение, соответствующая точка на плоскости z также
возвращается в первоначальное положение; тогда в той области плоскости z,
где это имеет место, функцию /(z,) называют однозначной. По правилу
деления двух комплексных чисел (см. § 9) имеем
dz
dz.
IdzI ds
| dz,
D.72)
где ds —длина элемента dz дуги кривой в плоскости z, a ds,—длина соот-
соответствующего элемента dz1 соответствующей дуги кривой в плоскости zt.
Таким образом, модуль dz / dzy служит мерин изменения элемента длины
вблизи некоторой точки плоскости z при преобразовании этой точки в соот-
соответствующую точку плоскости г,.
Построим теперь боскопочио малый треугольник, образованный пере-
пересечением трех кривых па плоскости z,, и обозначим длины сторон этого тре-
треугольника через dsl7 ds[, dk\. Тогда длины сторон треугольника, трансфор-
трансформированного на плоскость z, будут ds=hdslt ds' = hds'1, ds" = hds, откуда
ds1:ds[:dsl = ds:ds':ds", т. е. эти треугольники оказываются подобными.
Отсюда ясно, что углы, образованные при пересечении соответствующих
кривых, при таких преобразованиях не меняются. Эти преобразования назы-
называются конформными.
При делении двух комплексных чисел их аргументы вычитаются, по-
поэтому аргумент отношения dz / dzx равен углу, па который поворачивается
при преобразовании элемент кривой.
§ 17. Уравнение границы в параметрической форме. Пусть f (х, у) = 0
является уравнением одной из интересующих пас эквипотенциальных поверх-
88 Глава IV
ностой, причем х и у могут быть представлены в виде действительных аи а
литических функций некоторого действительного параметра t, который ме-
меняется в таких пределах, что х и у описывают всю поверхность проводника.
Тогда существует очень простой метод получения решения уравнения Лаиласа,
удовлетворяющего граничному условию V — 0 на зтой поверхности. Действи-
Действительно, если
* = /i@. У = М), D.73)
то искомым решением будет
На поверхности проводника V = 0, потому что при подстановке этого зна-
значения в соотношение D.74) получаем параметрическое уравнение поверхности,
в котором только вместо параметра t используется bU.
К сожалению, число задач, при решении которых можно применять
этот метод, чрезвычайно ограниченно. Среди них следует упомянуть задачи
о нахождении поля в системе конфокальных конусов или в системе провод-
проводников с различными циклоидальными поверхностями. В качестве примера
определим, насколько исказится однородное электрическое поле при внесении
и него волнистой металлической поверхности, образующая которой описывает-
описывается уравнением циклоиды
ж = аF —sin6), ?/ = аA — cos<2). D 75)
Отсюда z = a(bW — smhW) + aj{l—w^bW) = a{bW + j — ]'е-'ш), что дает
x = a{bV— ehY smbU), y — a(bV + 1 — ebVcos hU). При больших отрицатель-
отрицательных значениях потенциала x = abU, y~- + abV, так что мы действительно по-
получаем однородное поле, направленное вдоль у, его напряженность равна Е —
= + dV j ду = аГ1 Ь'1. Отсюда находится постоянная Ь, и выражение для z
принимает вид
Для определения поля в любой точке продифференцируем это выражение
в результате получим
Е dz Е dz
dW
~~dz
= E A - 2ev/«E cos
~
На поверхности проводника F = 0 и y = a[i—cos(UfaE)], поэтому для
плотности заряда на ней имеем
= е
dW
dz
v=o V 2У
— [ n~ ) SE.
Этот результат отпогится к полю с той стороны поверхности, на которой
имеются острые края. С другой стороны поверхности поле отсутствует, так
чго на поверхности происходит разрыл непрерывности.
§ 18. Нахождение сопряженных функций. В большинстве случаев по-
поиски функции W, удовлетворяющей заданным граничным условиям в пло-
плоскости z, начинаются с поисков такого преобразования, которое упростило
бы формы границ. Если и новые граничные условия окажутся незнакомыми,
нужно искать второе преобразование, еще более упрощающее граничные
условия. В конце концов можно прийти к такой системе, в которой решение
написать сравнительно просто. После этого необходимо проделать обратный
Двухмерное распределение потенциала
путь — к решению исходной задачи. Часто, однако, возможно, опуская
промежуточные этапы, написать сразу функцию f(W, z) = 0 путем исключе-
исключения промежуточных комплексных переменных. Но даже если это и невоз-
невозможно, промежуточные переменные служат в качестве параметров, связываю-
связывающих между собой W и z.
При совершении таких преобразований часто очень полезно представлять
себе рассматриваемую область плоскости zx в виде упругой мембраны, обла-
обладающей свойством сохранять углы между любыми нанесенными на ней ли-
линиями при любых деформациях ее границ. При этом мембрана не может
отрываться от границ, но может скользить вдоль них, а также бесконечно
растягиваться и сжиматься.
Предположим, например, что в интересующей нас задаче границы про-
проводника представляют собой две неконцентричные и непересекающиеся
окружности, или две пересекающиеся окружности, или же, наконец, две
окружности одного типа и одну или две другого типа, пересекающиеся
ортогонально. При помощи соотношения D.64) любую из этих областей
можно преобразовать п прямоугольную:
±^ D.7E)
i ^
1 z—/a
Мы употребляем здесь z1 = х1 + fy1 вместо W = U + /V, чтобы подчеркнуть
чисто геометрический характер этого преобразования. Из уравнений D.67)
и D.68) следует, что когда х и у принимают значения - со < х < оо,
— оэ < у < со, хг и у1 меняются в пределах —0 < yt < 2тг и — со < хх < оо.
Таким образом, функция D.76) преобразует горизонтальную полоску шири-
шириной 2тг плоскости zx во всю плоскость z. Вертикальные линии внутри этой
полоски превращаются, согласно уравнению D.67), в окружвости, описы-
описываемые уравнением
х2 + {у — а cth хгJ = a2 cosech2 хг, D.77)
а горизонтальные линии превращаются в окружности, проходящие через
точки у=±а, х = 0 и описываемые уравнением D.68)
(х - a ctg г/jJ + у2 = a2 cosec2 yt. D.78)
Это преобразовагие можно представить себе, вообразив бесконечную горизон-
горизонтальную полоску упругой мембраны ширияой 2тг, вращаемую в направлении
против часовой стрелки вплоть до достижения ею вертикального положения
в плоскости г'. При этом точки х1 — 0, уг = 0 и ,гх = 0, уг = 2тг превращаются
соответственно в линии А А' и ВВ'. Сожмем теперь эту полоску около
точек у' — — со (С) и у' = + с° (О и начнем сближать точки С и С", пере-
перемещая их вдоль оси у, при этом центральная часть полоски будет растяги-
растягиваться в горизонтальном направлении. Линии СА, СВ и С А', С'В' подобно
вееру развертываются соответственно около точек С и С до тех пор, пока
СА не совпадет с СВ, а С А' с С В'. В результате мембрана оказывается
растянутой на всю плоскость z, а ее бесконечно малые дуги АА' и ВВ'
становятся бесконечно удаленными дугами, разделяемыми осью х на две
равные части.
Все эти преобразовании, за исключением первого поворота, показаны
на фиг. 33. Если вдоль линий соединения СА с СВ и С А' с" СВ' нет
никаких нарушений непрерывности, то потенциал в горизонтальных полосках
на плоскости z1 должен быть периодичным по уг с периодом 2тс.
Задачи, в которых рассматриваются линейные заряды и прямоугольные
границы с проводником или отдельные участки таких границ, находящиеся
под разными потенциалами, можно решить методом изображепий. В других
'90
Глава TV
случаях может представиться необходимость развернуть эти прямоугольные
границы 13 полуплоскость, что осуществляется посредством преобразования
ЗЦварца, в котором в общем случае используются эллиптические функции.
оэ • оо
•
Rf
О
¦>
-*
У'
7
-¦А'Х
Изменение:
от у'= I
от
*
Изменение:
у'= со I доу=а
х'=-п *? отх'=п
от со'--п ^W, cmx'=it
у = -°° Р
у'=-оо |
оту
у
до у--а
-оо -оо
Фиг. S3.
§ 19. Преобразование Шварца. Одним из наиболее употребительных
является преобразование, при котором верхняя полуплоскость zx, ограничен-
ограниченная снизу действительной осью, переходит во внутреннюю область некоторого
многоугольника па плоскости z или наоборот. Если эта область конечна,
то граница ее может быть целиком образована при помощи деформации
действительной оси ^! = 0 плоскости zx. Если же внутренняя область про-
простирается в бесконечность, то соответствующая часть границы образуется
путем растягивания или сжатия бесконечно удаленной дуги верхней полу-
полуплоскости Zy.
Чтобы nail™ преобразование, сгибающее действительную ось плоскости
Zj в границу заданного многоугольника на плоскости z, рассмотрим ком-
комплексную производную
/J^T 1 V 1 1/ V 1 2/ \ 1 71/ f y^tm у
где и,у, и.,, ..., ип и р\, Р2, ..., j3n — некоторые донствптельные числа,
а Су — комнлексмая постоянная, причем ип > м„_1 > ... > п„ > их. Как из-
иестио, аргумент произведения нескольких комплексных чисел, возведенных
в какую-нибудь степень, равен сумме произведений аргументов этих чисел
на соответствующий показатель степени. Поэтому
= ar
p\ arg (Z
... +18narg(z1 — un).
D.80)
Пусть dz1^=dxl, т. е. является элементом длины вдоль действительной оси
плоскости Zj, тогда аргумент
dz dr-\-idy . rf?/ .. ....
arg = arg ——- = arc tg —— D.81)
.равен углу, который образует элемент dz, полученный при преобразовании
¦dzy, с действительной осью у = 0 плоскости z. Если zx является действитель-
действительным числом, находящимся между иг и ur+i, то (zt — иу), (zy — и2), ..., (zt — иг)—
Двухмерное распределение потенциала
91
дейстайтельные положительные числа, аргумент которых равен 0, a {z1 — wr+i),
(z1— ur+2), • ¦ ¦, (z1 — Mn) —действительные, но отрицательные числа, аргумент
которых равен тт.
Поэтому на основании соотношений D.80) и D.81) найдем
бг = arc tg -g = arg С,
D.82)
Итак, все элементы оси хг, лежащие между точками иг и urtl (фиг. 34),
после преобразования сохраияют свое направление и остаются прямолиней-
прямолинейными; их наклон к оси х определяется формулой D.82). Аналогично, те
Плоскость z,
dx,
Ur+2
Фиг. 34.
элементы, которые лежат между иг+1 и wr+2, также остаются прямолиней-
выми, но имеют другой наклон
бг+1 = arc tg -g- = arg С, + (Pr+2 + pm + ... + pn) те.
Угол между этими линиями равен
D.83)
Мы построили две стороны многоугольника. Подобным же образом, подби-
подбирая значения C и и, можно построить и весь многоугольник, имеющий нуж-
нужные длины сторон и нужные углы при вершинах.
Предположим, что требуется найти поле пад ломаной линией в пло-
плоскости z, показанной на фиг. 34. Любой угол, например <хг+1, измеренный
между двумя прилегающими сторонами многоугольника в области, где
ищется поле, называется внутренним углом многоугольника. Так как
т. — аг+1= —1Г?,+]7 то Для определения этого угла мы имеем
Подставим соотношение D.84) в D.79)
~ =C1(Z1-B1)"~iBl
D.84)
D.85)
,. D.86)
Подбирая для Сл тот или иной аргумент, можно, как это видно из
соотношения D.82), произвольным образом ориентировать многоугольник
Интегрируя это выражение, приходим к искомому преобразованию
92 Глава IV
на плоскости z. Размеры многоугольника определяются модулем постоянной С1.
Помимо этого, многоугольник можно без всякого вращения, меняя лишь
постоянную С2, располагать в любом требуемом направлении.
Чтобы убедиться в правильности выбора стороны границы при отсчете а,.,
положим zx = W, тогда действительная ось у1 = V = О совпадет с экви-
эквипотенциальной линией. При аг < тг напряженность поля dW/dz = dz1/dz
должна в вершинах обращаться в нуль, а при аг > тг — становиться там
бесконечной. Полагая в соотношении D.85) x1=U— ur, легко убедиться
в правильности наших результатов.
§ 20. Многоугольники с одним положительным углом. Если действи
тельная ось в ходе преобразования претерпевает излом только в одной
точке, то без ограничения общности эту точку можно принять за начало
координат; тогда, положив в выражении D.86) ul — 0 и считая а > 0,
получим
C^ C D.87)
Пусть С2 = 0, а Сг равна некоторой действительной постоянной. Тогда
вершина полученного многоугольника будет совпадать с началом координат,
а его стороны с лучами 6 = 0, 6 = а. Третья сторона многоугольника бес-
бесконечно удалена. Модуль zn равен п-м степени модуля z (см. § 9), по-
поэтому круг радиуса г1 = аг на плоскости zl переходит в круг радиуса г = а
на плоскости z. В частности, задачи, рассматривающие область, ограни-
ограниченную дугой окружности и двумя ее радиусами, можно при помощи пре-
преобразования D.87) свести к задачам, рассматривающим область в виде
полукруга.
При а = 2тг верхняя полуплоскость % преобразуется во всю плоскость г.
Разделение действительных и мвимых частей дает у — 2С1х1у1 и х — Сх {х\ — у\).
Исключив по очереди ух и xlt мы получим уравнения двух взаимно орто-
ортогональных семейств конфокальных парабол г/2 = — ^Схх\ (х — Схх1) и ?/2 =
— 1кС{у\ (х +0^1). Таким образом, однородное поле И/ = г1 на плоскости z5
преобразуется на плоскости z в поле полубескопечной заряженной прово-
проводящей плоскости. Поле линейного заряда па плоскости z1? расположенного
над заземленной горизонтальной проводящей плоскостью, проходящей
через начало координат, преобразуется на плоскости z в поле линейного
заряда вблизи полубескопечной проводящей плоскости, край которой
параллелен линейному заряду.
При <х = Зтг/2, положив W = zlt мы получим в плоскости z поле заря-
заряженного проводящего прямоугольного клина, образующие которого совпа:
дают с положительной частью оси х и отрицательной частью оси у. Таким
же путем, как и для а = 2тг, можно найти поле линейного заряда, распо-
расположенного вблизи прямоугольного клпна.
При а = тг плоскость zt не претерпевает, очевидно, никаких изменений,
не считая изменений в масштабе за счет множителя Сх.
4
При а=у7Г7 положив W = %, получаем на плоскости z поле внутри
проводящего прямоугольного уголка, образованного положительными полу-
полуосями х и у. В этом случае СЦУ — х2—у2 и C\V=2xy, т. о. эквипотен-
эквипотенциальные и силовые линии образуют два взаимно ортогональпых семейства
равнобочных гипербол. Поле линейного заряда, параллельного краю такого
уголка, находится так же, как и в случае а~2тг.
§ 21. Многоугольник с углом, равным нулю. В этом очень важном
случае ось хг складывается до тех пор, пока обе стороны угла а не ста-
станут параллельными друг другу и, следовательно, верхняя часть полупло-
Двухмерное распределение потенциала 93
скости не окажется сжатой между ними. Две параллельные, но пересека-
пересекающиеся линии, могут находиться на конечном расстоянии друг от друга,
если их точка пересечения бесконечно удалена. Тогда вместо преобразо-
преобразования D.87) имеем
z-C^lnz^C.,. D.88)
Как и раньше, будем считать Сх действительной величиной, а Гг = 0.
Начало координат zx = 0 преобразуется в z= — оо, а новое начало коор-
координат соответствует точке zx ¦¦= 1. Запишем zx в виде zx = rxe>ul и положим 01 = 0,
тогда z = C1lnr1, что соответствует действительной оси плоскости z. Если
же положить дх = те, то х = Сг In r1 и у -- Сх те, что соответствует линии,
расположенной над действительной осью на расстоянии Схк от нее. Таким
образом, верхняя полуплоскость zx преобразуется на плоскости z в гори-
горизонтальную полоску. При этом радиальные линии бх = const становятся
горизонтальными линиями у = const, а полуокружности rx = const переходят
в вертикальные линии, имеющие длину Схк. Часто приходится встречаться
с задачами, в которых конфигурация системы периодична; это означает,
что и поле в системе можно разбить па одинаковые полоски. Оказывается,
что при решении таких задач большую пользу может оказать преобразова-
преобразование D.88). Для примера найдем поле в системе, состоящей из заряженной
нити, находящейся между двумя параллельными проводящими заземленными
плоскостями. Возвращаясь к плоскости zx, мы получаем задачу о поле
нити над параллельной проводящей, заземленной плоскостью. При помощи
метода изображений, рассматриваемого в § 7. и формулы D.63) легко
папиеать требуемую функцию
Пусть при zx= + 1 W — 0, т. е. С= — In ( — е>ь°), тогда
W = - 4~ Ь -'~СС° . D.89)
Преобразуем это поле на плоскость z, положив С2 — 0, Схъ—--а и СгЬь = Ь
и подставив в выражение D.89) zx из формулы D.88), в результате получим
wz/a_е;яЬ/о т. (г-}ЪI2а_е— я (z—jb)/2o
Т/Т/ __- J . 1 v» ". ?_ 1J-. "
2ле ln(z+;b)/a 2tcs
. _ J
2ле l_en(z+;b)/a 2tcs ,.-¦п (г+/Ь)/2о_(?п (z+,'b)/2o '
Используя (Двайт, 654.1, 655.1 и 702), мы получим
1 —/th (J^ м/a ^ ctg (^ 1
= _ IJL arc tg [ th A ^/e ) clg ( -1*m) ] . D.90)
Глава IV
После разделения действительных и мнимых частей придем к следующем}':
fiT2msF_ — sin (nb/a)sh (та/а) D 91>
D.92)
sin (r.b/a) sin (ny/a)
-cos (тсЬ/а) cos
сЬ (та/а)"
На фиг. 35 показаны плоскости zx и z. Если разность потенциалов
пластин равна Uo, то к полученному решению нужно добавить однородное
Плоскость z
Фиг. 35.^ Линейный заряд между заземленными пластинами.
пертикальное поле, описываемое функцией W = —jUozja. Окончательное
решение тогда можно записать в виде
)D?)]/^, D.93)
где U — потенциальная функция. Пусть теперь в однородное поле помещена
плоская решетка, состоящая из параллельных проводов, отстоящих на рас-
расстоянии а друг от друга. Для решения такой задачи нужно поместить
заряды -f q в точку z1 = / и в точку z1== —/и проделать преобразования Т
аналогичные предыдущим. На плоскости z получится участок интересу-
интересующего нас поля решетки, содержащий один проводник и ограниченный
силовыми линиями, простирающимися от этого проводника до ж= + оо.
В заключение заметим, что если построить на плоскости z силовые
линии однородного^ электрического поля, а затем проделать обратное пре-
преобразование на плоскость zlf то получится поле линейного заряда, уже-
рассмотренное в § 13.
§ 22а. Многоугольники с одним отрицательным углом. Двухмерный
диполь. Инверсия. Теперь естественно выяснить смысл преобразований
Плоскость z
Плоскость Z
Плоскость Z
+ Z.-0
-*—z =0
У
CL>0
a=0
Фиг. 36.
CL<0
Шварца с отрицательным углом. Переход от положительных значений а
к отрицательным ясно показан на фиг. 36. Если в соотношении D.87)
С2 — 0, то действительные полуоси плоскости гг будут выходить из начала
Двухмерное распределение потенциала 95-
координат на плоскости z, образуя между собой угол а. На этой же фигуре
показан примерный вид кривых у1 = const на плоскости z.
Наиболее интересным случаем, относящимся к этой категории, является
случай а= —it. Будем исходить из однородного поля W = г1г считая функ-
функцию U потенциальной. Это однородное поле можно представить себе со-
созданным бесконечно большим положительным зарядом, расположенным
в точке ж1=+оо, и бесконечно большим отрицательным зарядом, распо-
расположенным в точке х1 = — оо. Из рассмотрения фиг. 36 следует, что при
интересующем нас преобразовании эти два заряда бесконечно близко под-
подходят друг к другу, оставаясь все же по разные стороны осп .у плоскости z.
По определению, двухмерным диполем называется система, состоящая
из двух бесконечно больших, одинаковых по величине и противоположных
по знаку линейных зарядов, расположенных бесконечно близко друг
к другу, так что произведение величины зарядов (на единицу длины)
на расстояние между ними остается конечным. Оно называется дипольным
моментом (па единицу длины) и обозначается через т. Упомянутое преобра-
преобразование можно получить непосредственно из соотношения D.64), заменив
)а на а и устремив а—» О (Двайт, 601.2),
а
W——^-ln — >-^L = -HL_> D.94V
кг.г а а->0 mz 2tcez v '
' z
Отсюда
jj m cos 6 _. m sin 0
~ 2mr ' 2тс-г '
а также
:0. D.95)'
Эквипотенциальные линии представляют собой окружности, касающиеся
оси у в начале координат; силовые линии, тоже являющиеся окружностями,,
касаются в начале координат оси х.
Другим важным примером, относящимся к случаю а = — it, является
преобразование, получаемое из соотношения D.87) при С1 = аг,
В полярных координатах, разделяя действительные и мнимые части,
имеем
ггг = а2 и G=— Oj.
Каждой точке вне круга радиуса f1 = a на плоскости z1 поставлена в соот-
соответствие определенная точка внутри круга радиуса /- = а на плоскости z.
Если W = / (Zj) есть решение уравнения Лапласа, то W = f (zjj1), где z* — вели-
величина, комплексно-сопряженная с Zj, —тоже будет решением, причем опи-
описываемое им поле является зеркальным изображением первого, т.е. гг = г*
и б1=—б*. Сравнивая плоскость z с плоскостью z*, мы видим, что
rr; = a* и 6 = в;. D.97)-
Точки, удовлетворяющие этому соотрошенгао, называются инвертироши-
ными, а величина а называется радиусом ипверсии. Если суммарный
заряд на плоскости z отличен от пуля, то это значит, что на бесконеч-
бесконечности должен находиться заряд, равный ему по величине и противоположный
по знаку, на котором бы оканчивались простирающиеся в бесконечность.
•96 Глава IV
«иловые линии. Иа плоскостях zt или z* эти линии окажутся вблизи начала
координат. Таким образом, мы приходим к следующему правилу инверсии
is цнух измерениях.
Если в поле зарядов д' и д" и т. д., находящихся в точках z\ z"
11 т. д., поверхность S является эквипотенциальной, то инвертированная
поверхность будет эквипотенциальной в поле зарядов д', д" и т. д., нахо-
находящихся в точках z'*, z'l* и т. д., и заряда — 2<7> расположенного в на-
начале координат. Этот метод позволяет, исходя из известного решения
задачи, рассматривающей плоские пересекающиеся границы, получать реше-
решения задач, в которых рассматриваются границы в виде пересекающихся
цилиндров. В полярных координатах уравнение окружности на плоскости z
можно записать в виде
г2 — 2urcos(G~a) = R2-и2, D.98)
где R — радиус окружности, а и и а — координаты ее центра. Умножим
уравнение D.98) на г*2 и подставим, согласно соотношениям D.97), 6*
вместо в и а* вместо а; тогда
(/г,"J - 2rrlur{ cos F* - а*) = (R2 - гг2) г*Л2.
Учтя, что ?т* = а'г, получим
или
.г*2 - 2ivJ cos F* - а*) = R\ - и\, D.99)
где
и - °2м и р _ °2-» // 100^
Таким образом, при инверсии окружность преобразуется в окружность.
Если же первоначальная окружность проходит через начало координат,
то |w|=7? и \иг\—>R1 = co, т. е. после инверсии получается окружность
бесконечного радиуса с центром на бесконечности, или, другими словами,
прямая линия. Кратчайшее расстояние от этой линии до начала координат
равно
а уравнение перпендикулярного к ней радиуса-вектора будет в* = а*.
Справедливо и обратное, а именно — прямая линия в результате инверсии
преобразуется в окружность, проходящую через начало координат.
§ 226. Изображения при двухмерной инверсии. Оставим на некоторое
иремя в стороне обсуждение преобразований Шварца и приведем пример
на применение метода инверсии к двухмерным системам. Используя только
что сформулированное правило, найдем выражение для поля бесконечно
большого линейного заряда + q (на единицу длины), расположенного
параллельно бесконечному цилиндрическому проводнику, внешняя поверх-
поверхность которого образована в результате ортогонального пересечения двух
круговых цилиндров и заряжена зарядом —д (на единицу длины). Пло-
Плоскость z показана на фиг. 37, я, линейный заряд находится в точке Р,
а контур поверхности проводника обведен сплошной линией. Из пре-
предыдущего параграфа известно, что если произвести инверсию относительно
точки О, то обе проходящие через нее окружности превратятся в прямые
лилии, пересекающиеся в силу конформности отображения ортогонально.
Двухмерное распределение потенциала
97
Для простоты в качестве круга инверсии выберем круг, ограниченный
показанной на фиг. 37 пунктирной окружностью, которая является каса-
касательной окружностью к цилиндру с наибольшим диаметром. На фиг. 37, б
приведена система, получаемая в результате инверсии, на плоскости z*.
Задача о нахождении поля линейного заряда, параллельного линии пере-
пересечения двух ортогональных проводящих плоскостей, уже рассматривалась
в § 7, где было показано-, что поле внутри такого прямоугольного уголка
совпадает с полем в этой области, когда все проводники удалены и когда,.
Плоскость z
Фиг. 37. Двухмерная инверсия.
кроме заряла, в точке Р' имеются еще линейные заряды — q, -f q и — q
в точках Р[, Р'2 и Р'3 соответственно.
Из п ранил а инверсии следует, что поверхность цилиндрического про-
проводника на плоскости z, соответствующая диум проводящим плоскостям
на плоскости z*, совпадает с эквипотенциальной поверхностью в поле
зарядов + <7> —<7> +? и —Ч< расположенных соответственно в точках
Р, Рх, Р2 и Ps, являющихся инвертированными но отношению к Р', Р[,
Р'2 и P's. Пусть СР = гс и ВР — гь, тогда точка Р1 на линии ВР будет
находиться на расстоянии b2jrh от В, точка Ря на линии СР — на расстоя-
расстоянии c2jrc от С н, наконец, Р2 — н точке пересечения BPsuCPx. Поскольку
точки Р', Р[, Р'2 и P's на плоскости z* лежат на окружности, пересекаю-
пересекающейся под прямым углом с лилиями Q'Q\ и Q'Q'z, то и точки Р, Рг, Р2
и Р3 на плоскости z будут находиться на окружности, пересекающейся
под прямым углом с окружностями, образующими поверхность проводвиков.
§ 23. Многоугольник с двумя углами. Среди большого числа различ-
различных примеров, относящихся к этому случаю, выберем лишь одив, а именно,
преобразование действительной оси в прямоугольник шириной 2а. Поло-
Положим в соотношении D.85) а1 — а2 — -^-, щ= + а1( и2 = — аг; тогда
dz
IT,
А
D.1U1)
Интегрирование этого выражения (Двайт, 260.01 или 320.01) дает
z = A ar ch ( J- ^ + Сх = /A arc sin f -J-) + C2.
7 В. Смайт
98
Глава IV
Пусть С2 = О (используется вторая форма записи) и пусть z тоже равно ну-
нулю при z1 = 0. Кроме того, выберем а равным — /Arc, или /Л==2й/тг; тогда
нри z, = ± flj, z = ± а. Итак,
2а . г,
z — — arc sin —,
тс а.
или z,=a,sinK-z.
1 ' 2а
D.102)
Наиболее употребительным является применение преобразования D.102)
к однородному полто на плоскости z. Взяв а равным -у те и заменив z на W.
получим
z1 = «1sinVy. D.103)
Вертикальные полоски плоскости z при отображении на плоскость zx ока
зываготся развернутыми в стороны, как .что показано на фиг. 38. Если
у Плоскость Z
Плоскость г,
п
U-
-1—I-
U=
i i i i
i i
0 !
I I
i i
¦91-
и-Ц
U-2a,-*\
Фиг. SS. Преобразование полубесконечной вертикальной полосы
н верхнюю полуплоскость.
в качестве потенциальной функции взять V, то на плоскости zl будет изо
бражена верхняя половина поля заряженной полоски ширины 2аг; если же
за потенциальную функцию взять U, то получается верхняя половина поля
двух полубесконечных копланарных листов, которые отстоят друг от друга
на расстоянии 2а1 и разность потенциалов между которыми равна те. Отделяя
в соотношении D.103) действительную и мнимую части (Двайт, 408.16),
получаем
x1 = «1sinf/chF, yl=al cos U sh V.
Разделим первое выражение на «jc
дем их в квадрат и сложим
+
второе на nlshV, а затом возве-
возвеy\
а? eh2 V + а\ sh2 V
D.104)
К'риные V = coiist являются, таким образом, конфокальными :иитпсами,
большие и малью оси которых соответственно равны 2«1chF и 2«1shF.
Аналогично, разделив первое выражение на a1sii\U, а второе на OjCosT/,
а затем возведя их в квадрат и вычтя одно из другого, получим
У\
U a\ cos2f
1.
D.105)
Кривые J7 = cons1 нвлнются конфокальными гиперболами. Заметим, что
если V принимает значения от 0 до то, а U от —те до —,у те и от тс до
•у тс в нижней полуплоскости, то получается картина коля заряженвон
Двухмерное распределение потенциала
полоски во всей плоскости. При пересечении с этой полоской гиперболиче-
гиперболические силовые линии терпят разрыв. Если U принимает .чначения от
~-n-,it До jx, а К от 0 до га в нижней полуплоскости, то получается
полная картина поля двух плоскостей. Эллиптические силопыо линии
терпят разрыв при прохождении через проводящие плоскости.
Плоскость z,
Плоскость z
Фиг. 39. Преобразование поля одной заряженной плоской полосы в участок
поля заряженной решетки, состоящей из копланарных параллельных плоских
полос.
Предположим теперь, что мы имеем дело не с одиночной заряженной
полоской, а с большим числом таких параллельных полосок, расположен-
расположенных в одной плоскости на одинаковых расстояниях друг от друга. Ясно,
что поле в такой системе будет периодично вдоль оси х и что можно рас-
рассматривать только отдельный типичный участок его, для чего нужно, как
это показано на фиг. 39, перегнуть ось х1 в точках ul= +^i, uz= —blt
fcj > av и применить преобразование D.102) к D.103), заменив в нем Oj па
6, и о на b, ;
= ai
= o, sin
где 2b—период решетки. Поло показано на фиг. 39. Так как х = -]-а,
г/ = 0, когда V = U, U= i -х к. то нужно положить at — bt sin ( -^ najb J,
я интересующее нас преобразование можно записать в виде ,t
W = arc sin
sin ( -zr nz/b J
sin ( — Tzajb )
D.106)
Хотя мы нашли поле только в верхней полуплоскости, однако полученная форма
решения одинаково хорошо описывает поле и при 0 > у >¦ — со. причем дл»
того чтобы V принимало только положительные значения, нужно менять х
1 1 *
и U в пределах 0<ж<Ь, у!г<?/<тг и О > ж > — Ь, — к < J7 < - у г..
При у—-со напряженность ноля равна — у к/b, поэтому для получения
преобразования для поля Е' необходимо умножить формулу D.106) на
2ЬЕ'/п. Если над решеткой простирается (до у— + оо) однородное попе,Е?
а под решеткой однородное поле 'отсутствует, то к полученному решению
7*
100
Глава IV
нужно прибавить Е' = -т> Е, что даёт
W = ~ { z + — arc sin
sin ( у nz/b J
sin ( -у тга/b \
При этом величина напряженности поля в любой точке равна
dW
Е
1±
cos ( -7т- nz/b
Г сор2 ( у тсг/г- ^ — cos2fу ла/Ь
D.107)
D.108)
§ 24. Щель, прорезанная в бесконечной плоскости. Для получения
поля вблизи плоского проводящего экрана, в котором прорезана щель
У
G\ гС^Х
Фиг. 40. Плоскость со щелью, имеющая одну границу с однородным полем.
шириной 2я, можно отогнуть участок действительной оси, лежащий между
точками ж = +я и х= —я, и растянуть его так, чтобы он охватил всю
нижнюю полуплоскость z, поверхность которой на плоскости zx протяги-
протягивается сквозь разрыв в начале координат. Из фиг. 40 видно, что а, = 2тг,
а2 =—it, а3 = 2it, ю1=+,в1, и2 = 0, us= — ях, поэтому из соотношения
D.85) получаем
dz „ л? —«Г
13 результате интегрирования имеем
Необходимо, чтобы при zl=-^a1 z=-^a. Это выполняется при Са = 0 и
2а1С1 = а, так что окончательно имеем
D.109)
I \ax z,
Если исходить из однородного вертикального ноля W = — Ezl на
плоскости z1 и положить 2ях — а, то такое преобразование оставляет па
плоскости z без изменений поле на бесконечности и искажает его вблизи
экрана со щелью; при этом часть поля проникает еккозь щель. Из соотно-
соотношения D.109), взяв в качестве потенциальной функции V, находим
W = - Ez1=-4r
D.110)
Если мнимую часть корня всегда брать положительной, то, чгобы л верх-
верхней полуплоскости поля складывались, а i: нижней— вычитались, нужно
в выражении D.110) выбрать знак плюс.
Двухмерное распределение потенциала
101
Плотность погерхностного заряда на экраье дается выражением
dW
dz
¦)•
y=0 Z V -(^-a2I/* J ' D.111)
& знак выбирается так, чтобы в верхней полуплоскости оба члена скла
дывались, а в нижней — вычитались.
Пользуясь преобразованием D.109). легко получить на плоскости г
поле заряженной нити, расположенной вблизи заземленной металлической
плоскости с прорезанной в ней щелью, исходя из поля заряженной нити
над заземленной плоскостью на плоскости zl.
Запишем правую часть соотношения D.109) в полярных координатах
и решим полученные уравнения относительно х и у:
-^-^=-^—стЬ1г D.112)
J.1 „2
г1 — а1
-sin I
Возведем оба ураш ения в квадрат и сложим
D.113)
D.114)
Таким образом, если г1 > аг, то полуокружности рачиуса rt и радиуса
а\/г1 преобразуются на плоскости z соответственно в верхвгою и пижпюю
половины элллиса. описываемого уравнением D.114). Полуок]>ужности
радиуса rl=a1 распрямляется, превращаясь в отрезок действительной оси
— а<ж< -\-а.
§ 25. Рямановы поверхности. Для более отчетливого представлений
всех возможностей, заключающихся в том или ином преобразовании, часто
Фиг. 41. Риманова поверхность.
бывает полезно пользоваться понятием римановой поверхности, что можно
показать на примере предыдущего параграфа. Хотя все точки плоскости г
уже были использованы нами для представления положительных значений
Ух, соотношение D.109) дает также значения z и при отрицательных уу,
для которых — тг < fej < 0. Из уравнения D.113) следует, что область'
0<т>1<я1и — Tt<6j<0 соответствует верхней полуплоскости z, а область
аг < /•( < со и —-п < 6j < 0 — нижней полуплоскости. Таким образом, каж
дои точке на плоскости z соответствуют две точки на плоскости zt. Однако
эту двухзначность можно исключить, сделав плоскость z из двух листов.-
Соединяя эти листы между собой, нужно проявлять крайнюю осторожность,
следи за тем, чтобы - при прохождении некоторой точкой непрерывного
102 Глава IV
контура на одной из плоскостей соответствующая ей точка на другой плоско-
плоскости описывала также непрерывный контур. На фиг. 41, справа, изображен цен-
центральный участок такой поверхности, .называемой римановой поверхностью.
Линии, относящиеся к нижнему листу, сделаны пунктирными; кроме того,
для большей наглядности оба листа показаны разнесенными. Из А в В и
из С в В можно перейти только через участок х2 < я2, а из Л в С и из
В a D через участки х2 > я2. Окружность радиуса гх — гх при st—>0
становится на плоскости z бесконечно удаленной окружностью, лежащей
на поверхности АС. Римановы поверхности можно построить для большого
числа различных преобразований.
§ 26. Задача о круглом цилиндре, расположенном внутри эллипти-
эллиптического. Из двух последних параграфов следует, что область плоскости z,,
внешняя по отношению к кругу rl = ai, при помощи преобразования
D.115)
может быть превращена во внешнюю (по отношению к участку действитель-
действительной оси — я<ж<я) область поверхности BD плоскости z. Поскольку на
плоскости z1 мы ограничились областью вне круга радиуса гх~-=ах, то,
Следовательно, нельзя пересекать ось хх на отрезке —я1<з;1<+я1.
Поэтому и на плоскости z нельзя пересекать ось х на отрезке —я < х < + я.
Линия, соединяющая точки + я и - а, называется линией разреза плос-
плоскости z.
С точки зрения электростатики зто позволяет преобразовывать любое
поле на плоскости z,, имеющее в качестве эквипотенциальной или силовой
линии окружность радиуса г1 = ах, в поле на плоскости z, имеющее в ка-
качестве эквипотенциальной или силовой линии линию соединения точек
ж=+я и х== — а. В более общем случае можно получить решение задачи,
рассматривающей конфокальные эллиптические границы, исходя из решения
задачи с границами в виде концентричных круговых цилиндров, так как
преобразование D.114) превращает любую окружность радиуса rl = b1, где
6j > ах, в эллипс на плоскости z. Если же эти окружности на плоскости zi
взять эксцентричными по отношению к окружности радиуса гх = ах, то после
преобразования получится профиль самолетного крыла. Поэтому это преоб-
преобразование используется в аэродинамике и называется «преобразованием
крыла».
§ 27а. Условия на границе раздела двух диэлектриков. При помощи
соотношенийA.48), A.49)иD.55) определим j раничные условия, которым удо
влетворяют потенциальные функции и функции потока. Пусть функции
Wt = Ux + /Vx — fl (z) и W2 — U2 + /V2 = /2 (z) описывают электростатиче-
электростатические поля по разные стороны от границы раздела двух диэлектриков с про-
ницаемостями ех и е2. Обозначим через д/дп и d/ds соответственно производ-
производные вдоль нормали и вдоль касательной к границе. Тогда из соотношений
A.48) и D.55), приняв U за потенциальную функцию, находим
ас/, ас/2 svx ev2 ,, ..„.
s1-iri = s2 з-5 или s. —-1 = е, -~^ . D.116)
Если принять, что в некоторой точке границы соединяются между собой
линии нулевого потока, описываемые функциями Wx и W2, то соотношения
D.116) можно проинтегрировать в пределах от этой точки до точки Vx или
цо V2 и, следовательно, получить
или KXVX = K2V2, D.117)
Двухмерное распределение потенциала 103
где ЛГ,, А^ —относительные диэлектрические проницаемости. Из условия
A.49) имеем
Пх = иг. D.118)
Таковы граничные условия для V и U в случае, если последняя выбрана
в качестве потенциальной функции. Если же за потенциальную функцию
взять V, то граничными условиями будут
Vx = Va и ?1C/i = s2t/2 или KlU1 = KtUt. D.119)
§ 276. Эллиптический диэлектрический цилиндр. Конформные пре
образования могут применяться не только для решения задач, рассматрива
ющих границы, совпадающие с эквипотенциальными или силовыми линиями
поля, но и при решении многих других задач,, в которых нужно удонлетво
рить условиям на границе раздела диэлектрических сред. Так как при
таких преобразованиях углы сохраняются, то закон преломления силовых
линий A.51) бу-дет удовлетворен. Предположим, например, что нужно
решить задачу о нахождении сопряженных функций, описынающпх поле,
в случае эллиптического цилиндра, помещенного в однородное поле, направ-
направление которого составляет угол а <; большой осью эллипса. Уравнение
диэлектрической границы запишем и виде
Преобразование, описанное в § 26, позволяет получить эту эллиптическую
границу на плоскости z, исходя пз окружности радиуса r1 = b на плоско-
плоскости Zj. Для простоты положим в § 24 и 26 aj = l, так что вся плоскость z
будет соответствовать той области плоскости zl, которая расположена вне
единичного круга. Запишем уравнение D.114) в форме D.120) и прирав-
приравняем соответствующие коэффициенты, в результате получим
и Ь* = '"-^-. D.121)
т — п ч '
В системах с эллиптическими границами удобнее пользоваться не прямо-
прямоугольными координатами х и у, а эллгттическими (конфокальными) коор-
координатами и и v, показанными на фиг. 38 и 39. Соотношения между пря-
прямоугольными и эллиптическими координатами можно получить из выраже-
выражения D.103):
z—asinw, x = a sin и chw, у = а cos u she. D.122)
Тогда преобразование D.115) запишется и виде
или
Zy = /е ->™ = ]<г->и+* = ~ [z -г- (z2 — a2I^] =a[z~(z'z- a2I'*]-*. D.123)
Отсюда видно, что на больших расстояниях от начала координат (л,—^оо)
1 1
z= Y"flzi- T- °- однородное поле W^ — aEzy преобразуется в однородное
иоле W = Ez. Мнтересутоп(ее нас поле может быть, очевидно, представле-
представлено в виде суммы двухполен: вертикального Esina и горизонтального Ecosa.
Эти составляющие поля показавы на фиг. 42, а и б. Ось, проходящая
,через фокусы, совпадает в случае «ав с эквипотенциальной линией, а в
случае «бв— с силовой линией. Поэтому на плоскости zx картины силовых
линий будут такими, какими они изображены на фиг. 42, в и г.
Плоскость z
Плоскость z
Плоскость z,
Плоскость z,
Фае. 42. а, б—эллиптический цилиндр
(К =9, т п- 3) соответственно л поле
иертика ьной и горизонтальной состав-
составляющих однородного ноля 2~Va К. Преоб-
Преобразование^!.123) преобразовывает случаи
а и б в в и г, где границы диэлектрика
имеют вид круглых цилиндров. Супсрпо1-
8иция а и б дает д, где оси эллипса o6t
разуют с полем Е угон 45°.
Двухмерное распределение потенциала 105
Но поле, изображенное на фив. 42, в, уже было вычислено нами п
§ 4. Примем V за потенциальную функцию и положим U[ = О на единич-
единичной окружности, тогда
E'(-zi + A'z'i'i)' D.124)
W'i-= --^faB'EsmaiZi+z-*), D.125)
где с учетом D.121.) обозначено
а, =
(/С—1) + (АГ+1N2 (те — п)(Кт + п)
jn±n
(.ЙГ— 1) + (К + 1)Ь*~~ Кт + п '
Для случая, изображенного на фиг. 42, е, можно использовать те же гармо-
гармоники. При z1 = e;'fl Vi=O, поэтому решение должно иметь вид
+A"z-i), D.128)
W'i = ±-аВ'Е cos a (Zl+z-4). D.129)
Согласно § 27а, при г =6 и^ — Щ и УЦ = .КУ?, поэтому
62 + Л" = В"(^2 + 1) и б2-Л" = /?•?"(б2-1).
Решая относительно А" и В", получим
А„_ ЪЦ(К + 1)-(К-1)Ъ2] (m-; i»)(m-gn) .,
Ь2(/Т + 1) — (/С— 1) (m — n)(m + ATn)' К
— = т + п D.131)
1) — (АГ — 1) т+Кп " ^ '
Беря суперпозицию этих полей н применяя преобразование D.123), для
области вне цилиндра находим
Wo = i- «jE1 [е-/« zx + (Л'' cos a + /А' sin а) zf1 ] =
2
= -j afE [e-> <a+№> - {A" cos a + /A' sin a) e>w] =
= Y E {e~i" [z + (z2 - a2I'*] + (A" cos a -f /A' sin a) [z - (z2 — я2I/*]}.
D.132)
Аналогично и для области внутри цилиндра
1 . —1
Wi = -п- я-Ё" (/?" cos a — /о sin a)(z1-{- zi ) =
n / i \ /" COS a . sin a \ .. ,о„,
— ? (m + и) ( :— / -p—i— ) z. D.133)
V ' ' \m -\- Kn ' Km + n J v
Заметим, что внутри цилиндра ноле остается однородным. На фиг. 42, О
показаны линии электрической индукции для того случая, когда внешнее
поле наклонено на угол 45° по отношению к осям эллипса.
" § 27в. Момент, действующий на диэлектрический цилиндр. Момент Т,
действующий на единицу длины бесконечного диэлектрического цилиндра,
находящегося в однородном электрическом поле, ориентированном перпенди-
106 , . Глава IV
кулярно к оси цилиндра и под углом а к главной оси эллипса, можно
найти, исходя из результатов предыдущего параграфа и из формул C.41)
и C.42). Таким образом, •• я?
т^ — 4-'\ 4-ЕЛ1—к
где <? — угол между внешним полем Е и однородным полем внутри цилин-
цилиндра _?";. Величины Е, Е. и cos<p постоянны внутри v, поэтому их можнр
вынести из-под интеграла, после чего интеграл будет равен \ dv = nmn (на
единицу длины). Относительные иаправлепия и величины векторов Е и Ei
даются выражением D.133), в котором при определении Е надо положить
ЛГ1
Oz
t=\E\
D.135)
Подстанлян прсизнеденио этих величин в D.134), получим
| Е || Е, | cos (в - в.) = Re ЕЕ\ = | .Е(г)#?г) | +1 E(i) E? \ , D.136)
,., 1 ZP9 / ts л\ I i \ d / COS2 a sill2 a "\
I — тг,Е (К — i) vmn (m -\- n) тг( ^— + ^—;— ) =
2< v ' v ' ' da.\m-\- Kn ' Km -\-n J
w== пг„Е2 (К — IJ mn (n^—nfi) sin 2a ., ..„,
Этот момент стремится повернуть главную ш;ь эллипса вдоль поля.
§ 28. Многоугольник с закругленным углом. Существует несколько
методов, позволяющих заменить острые углы в преобразовании Шварца на
.округленные. Один из них состоит в замене множителя Zj ^~ в выражении
. на [Zj + >• (zi - lyi'Y'M-i, где | ип | > | и?,_, | > ... | «я | > 1 и /. < 1.
Другой метод заключается в замене множителя zia/1t)~' на
{z1 + l)(a^)-' + >• (z, - 1 )W«)-i.
И обоих случаях аргумент нового множителя равен нулю при z1 > 1 и равен
a — ix при Zj<< - 1, так что стороны многоугольника, соответствующие обла-
области вне — 1 < Zj < +1, образуют между собой те же углы, как и в случае
применения множителя z'/^ . Между точками zx = + 1 и z1 — — 1 полу-
получается теперь некоторая кривая, форму которой можно менять при помощи
множителя д.
§ 29. Плоская решетка из цилиндрических проводов большого
диаметра. В § 21 мы пришли к выводу, что задача о нахождении поля
около плоской решетки, образованной из цилиндрических проводов малого
радиуса, может быть сведена к задаче, в которой вместо цилиндрических
поверхностей проводов рассматриваются эквипотенциальные поверхности ре-
решетки, состоящей из линейных зарядов. Если же диаметры проводов, обра-
образующих решетку, соизмеримы с расстояниями между ними, то использован-
использованное приближение совершенно несправедливо. Однако в этом случае можно
воспользоваться методом, изложенным в предыдущем параграфе. Возьмем в
качестве типичного участка поля решетки область, отмеченную сплошной
Двухмерное распределение потенциала
Щ
линией на фиг, 43, я. Из этой фигуры следует, что z и z, должны быть свя,
з^ны между собой следующим дифференциальным выражением:
1С,
D.138)
Приведем теперь один из способов определения постоянной Сг, до сих пор
У> „ Плоскость г
2Ь
I —._». __
еще не упоминавшийся. Если л, - постоянная величина, то, так как
dzx = /r1el6ldb1 = fz1d61.
Если т-j—> со и 6Х меняется от 0 до тг, то z проходит значения от у = 0 до
j/=6. Подставляя в соотношение D.138) dz1 = fz1d61 и устремляя z1—> со ,
будем иметь
Wz = /С1! A + X) { dO1 или /6 == /CjTt A + X),
о о
.С|=_Ь__ D.139)
Таким методом пользуются довольно часто; действительно, для опре-
определения постоянной не обязательно проводить интегрирование в общем виде,
а" достаточно проинтегрировать какой-нибудь простой частный случай,
обычно /•1—^-0 или г1—»оо. Интегрирование выражения D.138) [сделаем
замену z1 = («1u2 ± 1) A — и2) и применим формулу A40.02) из справочника
Двайта] дает
,. D.140)
Если z = с, Zj = + 1 то С2 не является действительной величиной и
с =
Если z — fc, zt= —1, то С2 не является чисто мнимой величиной и
к A+1)
или
, —1
V
. 2
108
[у
Вычитая одно из другого, получим г
I
cosec
= cth -Ч
26л
Чтобы выразить X через & и с, построим график отношения левой части
этого уравнения к правой части как функцию X и найдем то значения X,
при которых это отношение равно
единице. Определив значения X и ело-
жшз выражение D.141) и D.142), по
ф
О -*
-/-* __
-2-* ^
-3 -* -1"""^
*~0
•*-1
__ 9-2
11
() ()
лУчим формулу, определяющую ах:
D.143)
0»-—
-a,
-3 —
-4*-~
-5»»-
6
+0
—3
—5
-a,
—*-0
i''Vs?Sz?^\
i <''>--
??—"ZZZZZ^.jo
Плоскость z
(приближенно)
Фие. 44.
Ричмонд1' исследовал вопрос, на-
насколько точно эта кривая может быть
анпоксимнрована окружностью г = с,
и показал, что расстояние оо от па-
чала координат отличается от с не
более чем на 2% при 2с < Ъ.
Для получения решения в слу
чае, когла решетка образует одну
из границ однородного поля
(фиг. 44,в), нужно наложить поле,
изображенное на фиг. 44,а, на ноле,
изображенное на фиг. 44,6 (на этих
фигурах эквипотенциальные линии
сплошные, а силовые линии пунк-
пунктирные). Н случае «с» интересующая
нас функция па плоскости Zj. со-
согласно соотношению D.ЮЗ), равва
W — A arc sin zlf
лось
где V — потенциальная функция. Что-
Чтобы в одной полоске фиг. 38 помеща
-гг-ЕЬ, а не тг силовых линий, необходимо положить А =— ЕЬ/п, тогда
Z &
W = garcsmz,. D.144)
Аналогично в случае «б» участок оси x,j между точками — аг и +1 следует
считать находящимся под нулевым потенциалом. Поэтому, смещая начало
координат, получим
W^^-arcsin^-^-. D.145)
При наложении обоих полей приходим к случаю «в», т. е. к случаю одно-
однородного поли Е при х— + оо и поля, равного нулю, при х= — оо. Как
Richmond, Proc. London Math. Soc, Ser. 2, 22, 389 A923).
Задачи 109
и в соотношении D.103), за потенциальную функцию выбрана V. В упомя-
упомянутой выше работе можно найти аккуратно выполненные графики полей в
таких системах.
§ 30. Случай углов, нецелократных л/2. Задачи, н которых углы
многоугольника не составляют целого кратного тс/2 или в которых имеется
несимметричный многоугольник с более чем двумя прямыми углами, или в
которых два или более проводника прямоугольного сеченля находятся под
различными потенциалами на конечном расстоянии друг от друга и т. д.,
также могут быть решены при помощи преобразования Шварца, но интегри-
интегрирование в этих случаях приводит к эллиптическим функциям Якоби.
С этими функциями можно манипулировать таким же образом как, напри-
например, с тригонометрическими или гипорболичоскими функциями, но все опе-
операции значительно осложняются. Мы не приводим здесь примеров, требую-
требующих применения эллиптических функций.
ЗАДАЧИ
i. Пусть полоска у = 0, О-^аг^а имеет потенциал VB, а остальная часть полу-
полуплоскости xz а < х < ее, а также вся плоскость yz находятся под нулевым потенциа-
потенциалом. Показать, что потенциал в любой точке х > 0, у > 0 определяется) выражением
arc tg —^ 2arc tg — + arc tg
ь х — а ь x ^ b
2arc tg + arc tg
а ь x ^ bx-\-a
2. Полуплоскости x = 0, у^О и у = 0, ж^-0 представляют собой проводящие
экраны, поверхности которых заземлены всюду, кроме участка, расположенного вблизи
линии пересечения полуплоскостей и ограниченного линиями х=а и у - -Ь. Этот участок
изолирован и находится - под потенциалом F. Найти плотность поверхностного заряда
на экранах.
3. Используя метод иннерсии, установить закон отображения линейного заряда
и расположенном параллельно ему круглом проводящем цилиндре.
4. Поверхность проводника имеет форму лнешней поверхности тела, нолученвого
при ортогональном пересечении двух одинаковых круглых цилиндров радиуса а. Пока-
Показать, что плотность поверхностного заряда на таком нроноднике равна
qBr2 — a2) (iitar2)-1,
где q—-заряд на единицу длины, а т—расстояние от оси.
5. Показать, что отпошопие максимальной плотности поверхностного заряда
к минимальной в случае заряженного проводящего эллиптического цилиндра равно
отношению большей оси эллппса и меньшей.
6. Провод, несущий на себе заряд q (на единицу длины), протянут вертикально
внутри вертикальной цилиндрической полости радиуса а, находящейся в среде с относи-
относительной диэлектрической проницаемостью К. Показать, что если провод расположен
на расстоянии с от центра полости, то на него действует сила, стремящаяся переме-
переместить провод еще ближе к стенке полости и равная (на единицу длины)
[2эте„(а2— с2) |
7. Две тонкие фибровые нити натянуты вертикально внутри заземленного про-
проводящего круглого цилиндра радиуса а. Показать, что если расстояние между нитями
равно 2E1'2—>2I'2 а и если они заряжены до равных по величине п противоположных
но знаку потенциалов, то действующая на нити сила будет равна нулю.
8. Бесконечная проиодящяя цилиндрическая оболочка радиуса а разрезана вдоль
на четыре одинаковых части. Одна из них имеет потенциал -\-V\, другая, диаметрально
противоположная,—потенциал —F,, а две остальных—заземлены. Показать, что потен-
потенциал внутри оболочки }>авен
il Vx Г 2ау 2ах
9. Рассмотрим область пространства, ограниченную с. одной сторопы плоскостью
xz, а с другой—поверхностью 'цилипдря в-2-{-у2 — Ъ2. Поверхность цилиндра и часть
110 _. Глава IV
плоскости, проходящая через папосу а < ] х | < Ъ, ваходятся под потенциалом, равным
нулю. Часть плоскости, лежащая в полосе ¦—а < a; <-f-a, имеет потенциал Fo. По'Кй-
зать. что уравнение силовых линий при а-^г^Ь имеет вид "гг.
it "^о V а
где суммирование происходит по нечетным п.
10*. Три д;шнных тонких одинаково заряжевных параллельных провода располо-
расположены на одинаковом расстоянии 31'2с друг от друга. Показать, что уравнение экви-
эквипотенциальных поверхностей такой системы в полярных координатах запишется в виде
с6 — 2r3c3 cos 36 = const,
где за начало координат взята точка, равноудаленная от всех трех нронодов, и в каче-
качестве нулевой поверхности взята поверхность, проходящая через один из проводов.
11*. Полый цилиндрический проводник большой длины разделен на две части
плоскостью, проходящей через его ось; эти части отдалепы друг от друга на небольшое
расстояние и поддерживаются под потенциалами V, и V2. Потенциал в любой точке
внутри цилиндра радиуса а равен
1 .гг , ., . , V, — F2 2arcos6
где /—расстояние от оси, а 0—угол между плоскостью, проходящей через ось перпен-
перпендикулярно к плоскости разделения, и плоскостью, проходящей через точку, где ищется
поле, и ось.
12*. Заряженная линия, имеющая им единицу ^лииы заряд е, расположена парал
лельно диэлектрическому цилиндру с относительиой проницаемостью К н радиусом о.
Показать, что если с—расстояние между линией и осью цилиндра, то сила, дейст-
действующая на единицу длины прогюда, равна
К—1 а2е2
13*. Бесконечно длинный цилиндрический проводник, поперечное сечение которого
представляет собой внешнюю границу трех одинаковых ортогонально пересекающихся
окружностей радиуса а, имеет на единицу длины заряд е. Доказать, что плотность
заряда на расстоянии г от оси рапна
е (Зга + а2) C/-2--а2—01/2 аг) (Зг2--а2 + 61/2 аг)
бяа г2 (9г4 — За2 г2 + «")
14. Край горизонтальной плоскости, имеющей нулевой потенциал, расположен на
расстоянии с от параллельной ему вертикальной плоскости, нотепциал которой равен
— п. Показать, что плотность заряда на вертикальной плоскости равна г (?/2 + с2)~ '3,
а на горизонтальной она равна —е (ж2 — с2)—1'2, где хну отсчитываются от той линии
в вертикальной плоскости, которая расположена ближе всего к краю горизонтальной
плоскости.
15. Показать, что емкость на единицу длины между плоской полоской шириной
2с и эллиптическим цилиндром, фокусы которого совпадают г краями полоски, равна
( аг сп — ) ,
где а,—большая полуось эллипса.
16. Показать, что сила притяжения (на единицу длины) между двумя одинако-
одинаковыми параллельными проводами радиуса а. несущими на себе заряды, равные соответ-
соответственно -\-q и —q (па единицу длины), равна
где с—расстояние между центрами проводов. ¦
17. Плоская решетка состоит из плоских конланарных параллельных полосок
шириной 2а, расстояние между центрами которых равно 2Ъ. Считая решетку заряжен-
заряженной, показать, что эквипотевциальвая поверхность, расположенная в среднем на рас-
расстоянии 6 от решетки, отличается от плоской поверхности приблизительпо на величину
0,028Ъ cos2
i-«./*).
Задачи Ш
"' 18. Найти приближенное выражение для поля решетки, составленной из парал-
цельных проводов радиуса а, отстоящих друг от друга на расстоянии 2л, считая, что
эта решетка имеет потенциал Uo и находится на расстоянии Ь (расстояние измеряется
от центров проводов) от параллельной ей заземленной плоскости и что а < b и а < 2л,
т. е. получить
— Е/о e^-^cosy + c*
С/, " с2е2х — 2сех tos у + 1 '
где
¦fo - _ e2b —2ceb cos a
'~~ cV*
и
с = ch b cos a -; (ch2 b cos2 a —
Здесь мы приняли, что 2а— максимальная толщина слоя, содержащего замкнутые экви-
эквипотенциальные линии вокруг линейных зарядов, а Ъ—расстояние между этим слоем
и заземленной плоскостью.
19. Используя результаты § А и § 26, найти преобразование, дающее поле около
проводящей заземленной полоски шириной 2с, ввесенной в однородное поле, параллель-
параллельное плоскости полоски. Если за потенциальную функцию принять U, то
W = ±li(z2—с2I'2.
20. Добавляя однородное иоле к решению, полученному в задаче 19, найти пре-
преобразование, дающее поле плоской проводящей полосы шириной 2с, помещенной
в однородное электрическое поло, ориентированное перпендикулярно к оси полосы
и под углом а к ее плоскости. Найти также вращающий момент (на единицу длины),
действующий нн полосу
W —Е[± (г2 — «2I/2со.ча — /г sin а], Г = ~ uec2 E2 sin 2o.
21. При помощи обратного преобразования Шварца найти поле, создаваемое двумя
полубесконечными копланарными плоскостями, потенциалы которых равны +^о и —Uo,
а параллельные края отстоят на расстоянии 2с друг от друга. Показать, что если U-
потенциальная функция, то
г = с sin —j-j— .
22. Повервув преобразование, используемое и задаче 21, на 90е и применив
преобразование Шварца, найти ноле свободно заряженной горизонтальной ренгетки,
образованной из одинаковых параллельных вертикальных полос шириной 2а, располо-
расположенных на расстоянии 2Ъ одна от другой. Пусть V—потенциальная функция, а еС/„—за
ряд отдельной полосы (на единицу длины), тогда
23. Сместив начало координат в задаче 21 и применив логарифмическое преобра-
преобразование, найти преобразование, дающее поле в том случае, когда решетка, описанная
в задаче 22, образует одну из границ -однородного поля. Пусть V—потенциальная функ-
функция, а е?/0—заряд' полосы, тогда
Ч = —- arc si n
1
2я sh (rra/fc)
24. Положив в задаче 21 с = 1 н взяп V я качестве потенциальной функции, при-
применим логарифмическое преобразование и получим ноле в системе, состоящей из набо-
набора полубесконечных пронодящих параллельных плоскостей, расстояние между которыми
равно Ь. Края этих плоскостей расположены на оси у. а потенциалы их попеременно
равны -f Uо и ~и„.
"'*• з. - — In sin Т-Г7- .
25. Показать, что можно так видоизменить форму краев пластин во многонластин-
чатом конденсаторе, состоящем из параллельных пластин, что попе вдоль вгей его по-
Глава IV
верхности, включая и края, будет постоянным. Показать, что такой поверхностью
является в задаче 24 поверхность U=U0/2, уравнение которой будет /
Ь .
х——— In
2
о 2т/Л
2 cos-— )
b J
верх
/
26. Воздушный конденсатор переменной емкости состоит из тонких плоских пла-
пластин, перемещающихся между неподвижными пластинами. Используя решение за-
задачи 24, показать, что дополнительная емкость, обусловленная изгибом силовых линий
на краях пластин, экгшлалентна добавлению к краям пластин полосок шириной (fc/тс) 1п2,
где Ь — расстояние между соседними неподвижными пластинами.
27. Найти поле линейного заряда +— Q, расположенного и начале координат,
в центре кривизны цилиндрического желоба единичного радиуса, если секториальный
угол желоба ранен 2а, а заряд на единиицу длины равен—Q.
W = т^- arc sin
/me
/ (r-1) cos (-1 0 )-(г+1) singl
2,1'2 si
sin
При решении следует использовать преобразование, приводимое в § 23, положив в нем
Ь-=п, повернув его на WP н применил к нему логарифмическое преобразование.
28. Добавляя к полю, полученному в последней задаче, поле линейного заряда
— — <5, находящегося в начале координат, получить выражение для потепциала сво-
свободно заряженного цилиндрического желоба единичного рмдиуса, центр кривизны ко-
которого совпадает с началом координат, а образующий угол равен 2а:
4ШЗ
2 arc sin
/(r-l)eos (l-
/ , -
i- / In r-
20. Показать, что в предыдущей задаче отношение заряда на выпуклой стороне
поверхности желоба к заряду на вогнутой стороне равно
(t+a)/(n — а).
30. Показать, что плотность поверхностного заряда в задаче 29 равна
1-де плюс, относится к выпуклой стороне.
31. Края двух полубесконечных тонких проводящих плоских экранов представ-
представляют собой прямые, параллельные между собой. Эти экраны находятся под пулевым
потенциалом и образуют одну из границ электростатического поля, располагаясь всег-
всегда так, что один из них является отображением другого в плоскости у. Найти преоб-
преобразования для следующих случаев:
а) экраны параллельны: поле снаружи:
г= —Y ^Л (/W2a-2_2/ In И- —п —/ + 2/ In a),
б) угол между экранами 90°; поле снаружи;
п) угол между экранами 9U"; поле внутри:
2 = A + /) ~ V
a2) — /60.
32. Найти преобразование, дающее поле бесконечной нити, несущей заряд д (на
единицу длины) и расположенной над центром щели, прорезанной в плоском зазем-
заземленном проводящем экране, если ширина щели раина 2fc, а расстояние от ее центра
до нити d:
(«*¦ -fc«I/g-/ Id j
Задачи ИЗ
33. Электроскоп Вольфа состоит ив двух одинаково заряженных фибровых нитей
радиуса с, расположенных на расстоянии 2d одна от другой. Эти нити протянуты
внутри заземленного цилиндра радиуса Ъ симметрично относительно его оси и парал-
параллельно ей. Показать, что емкость на единицу длины между этими двумя нитями и за-
заземленным цилиндром находится в пределах
Г
Здесь пренебрегли величинами с* и d4 no сравнению с Ь4.
34. Два одинаковых параллельных проводящих цилиндра, несущих полный за-
заряд g (на единицу длины), касаются между собой. Показать, что емкость (на едини-
единицу длины) между этими цилиндрами и третьим большим цилиндром, ось которого
совпадает с линией касания двух малых, приближенно равна
1пBЬ/таг) '
где Ъ> а.
35. Пластина (толщиной 2А) переменного воздушного конденсатора перемещается
вдоль середины зазора (шириной 2В) между двумя другими пластинами. Показать,
что преобразование для поля вблизи края подвижной пластины дается выражением
^th(^) (Д-Л) ah D-
z = A — arch тг + / — -arch
1*
тг + / — -arch —Tl—<- .
[ABB—A)I** * ABB—A)fl2
Показать также, что кажущееся увеличение ширины пластины, обусловленное краевым
эффектом, приближенно равно
2 Г 2В—А .. [АBВ—А)I'2 1
36. В тонкой бесконечной пластинке, находящейся под потенциалом V—1, проре-
прорезана бесконечно длинная щель шириной 2К. На расстоянии h от этой пластинки рас-
положена другая, параллельная ей, потенциал которой равен нулю. Показать, что
поле в произвольной точке х, у определяете.и из выражений
Г 2g2 shrcE/ "I
~ L«(i — a2) chnU + cosnV + J '
_ Г 2а2
~ L
где U — функция потока, а величина а определяется уравнением
37. Требуется найти поле вблизи плоской заряженной пластины толщиной 2Л,
имеющей закругленный край радиуса h. Показать, что подходящим преобразованием
для этого случая будет
2tc-4V (W2—1I/2 +2/тх-1агс sin W),
где F = 0 на поверхности, описываемой при 0 < х < Л уравнением
2й fV а- у/а /\ х~\Чг . / ж у/г
и при х > h урашшнием
y=±h.
Показать, что эта кривая отклоняется от окружности радиуса h меньше чем на 0,14ft.
38. Поперечное сечение проводящего цилиндра представляет собой гипоциклоиду
с п точками возврата. Цилиндр имеет потенциал V—0 и несет на себе заряд Q (на
сдивицу длины). Показать, что потенциал поля снаружи нилиндра дается преобразо-
преобразованием
z= ?.
где а-— расстояние от оси до точки возврата.
8 В. Смаит
114 Глава IV
39. Показать, что правильная призма, каждая из п сторон которой имеет ширину
может быть вписана в эквипотенциальную поверхность
2тсеп
ноля, полученного в предыдущей задаче, таким образом, что каждая сторона будет
касаться поверхности вдоль двух линий, расположенных одна от другой на расстоянии
1/п
Показать, что с увеличением п поверхность призмы приближается к эквипотенциальной
поверхности и, в частности, уже при п = 5 разница в максимальных расстояниях от
оси не превышает 6%, а в минимапьных расстояниях она менее 1%.
40*. Поперечное сечение цилиндра, потенциал которого поддерживается равным
нулю, представляет собой одну из ветвей равнобочной гиперболы. С вогнутой стороны
гиперболы параллельно ее оси расположен линейный заряд. Доказать, что изображение
зтого заряда в гиперболе будет состоять из трех таких зарядов. Найти распределение
индуцированных зарядов на цилиндре.
41*. Даны некоторая цилиндрическая область, ограниченная двумя коаксиальными,
конфокальными параболическими цилиндрами, фокальные параметры которых равны 2а
и 2Ь, и равномерно заряженная линия, параллельная образующим цилиндра. Эта ли-
линия пересекает оси парабол на расстоянии с от их фокусов (а > с > Ъ). Показать, что
потенциал поля внутри такой цилиндрической области равен
сп _2
Ala а1/г —Ь
cos —¦ ч ^ ' г с
1 п 1Л> Л
-^-6 —с /2 \
¦кг '* cos -~- В тс
ch ТТ. Т7- + cos -
где г, в—полярные координаты в поперечном сечении, начало которых выбрано в фо-
фокусе. Выразить А через заряд на единицу длины линии.
42*. Бесконечно длинный эллиптический диэлектрический цилиндр с проницае-
проницаемостью К, поверхность которого описывается уравнением 5=а, гдеж + /у=с chE + /v)),
помещен в однородное поле Р, параллельное большой оси эллипса. Показать, что по-
потенциал внутри цилиндра равен
—Рх A + cth a)/(K-{- cth a).
43*. Два изолированных незаряженных круглых цилиндра, расположенных один
вне другого, поверхности которых описываются уравнениями rj=a и rj=—р, где
x-\-jy=c tg — (? + /rj), помещены в однородное поле с потенциалом Fx. Показать, что
потенциал, обусловленный распределением зарядов на цилиндрах, равен
,. V/ л e1 sh np + e shna
sh n (a
44*. Поверхности двух заземленных круглых цилиндров, расположенных один
1
вне другого, описываются уравнениями rj=a и rj= — C, где ж+/^=с tg— (? + />]).
Цилиндры помещены в поле лпнейного заряда д (линия х=0, у = 0). Показать, что по-
потенциал, обусловленный индуцированными зарядами, снаружи цилиндров равен
д v I e~™ sh n (tj + P) +e~^ sh n (a-rj)
~-^2jTT sh«(a+fi)
Суммирование производится по всем нечетным положительным целым значениям п.
Задами 115
45*. Поперечные сечения двух бесконечно длинных металлических цилиндрор пред-
представляют собой кривые
где Ь> а > с. Доказать, что если потенциалы цилиндров поддерживаются соответствен-
соответственно равными Ул и F2, а пространство между ними заполнено воздухом, то плотности
поверхностных зарядов (на единицу длины) на двух противолежащих сторонах поверх-
поверхности соответственно равны
a2In(Ъ/а) Ь2In{b/a)
46*. Какие задачи можно решить при помощи преобразования
где а > 1?
47*. Какую электростатическую задачу можно решить при помощи преобразо-
преобразования
где W взята в качестве потенциальной функции, а Ф — в качестве функции, сопряжен-
сопряженной ей?
48. Однородное поле Ео ограничено верхней поверхностью (у = 0) бесконечной
проводящей пластинки толщиной 6. Часть этой пластинки, расположенная между
х=а и х-~=—а, удаляется, и в пластинке образуется бесконечная щель. Показать, что
если за потенциальную функцию принять U, то преобразование, дающее поле, можно
записать в одпом из следующих видов:
IE f arc sin— , m j+C^^,,
)F [arc si
c sin
-2E [
arc sin Q^y12 , A- -m2I'2] +faE0,
где F(p, q) и E (p, g) — эллиптические интегралы первого и второго рода модуля </.
Постоянпые Clt C2 и т удовлетворяют уравнениям
ЪЕ0=— (
где Е и К—полные эллиптические интегралы модуля т.
49. Бесконечный проводящий лист, находящийся под нулевым потенциалом, сов-
совпадает с плоскостью ж = 0 всюду, за исключением выступа или выема, сечение кото-
которого представляет собой окружность радиуса Ъ с центром в точке х = с. Эта поверх-
поверхность образует одну из границ поля Е, простирающегося до х=со и являющегося
неоднородным только вблизи выема или ныступа. Показать, что потенциал является
мнимой частью следующей функции:
(Ь2 — с2I'2^ [z-j-f (Ь2 — с2I/2]"/" + [S — / (Ь2 —с2I/2]д/"
"" a [z + /(b2—c2I^]^ —[z—/(Ь2 —с2I'2]"/"'
где cos а = с/6 для выступа 0 < а < тс и для выема тс < а < 2те.
116 Глава IV
50. Показать, что решение двухмерного уравнения Лапласа в прямоугольных гар-
гармонических функциях будет
V = (A sin тх-\-В cos тх) (Сshmy + D chmy), если тфО
и
V = (A + Bx)(C + Dy) при т = 0.
51. Грани бесконечно длинной проводящей прямоугольной призмы задаются урав-
уравнениями х = 0, х = а и 2/= 0, у = Ъ Линейный заряд д (на единицу длины) расположен
в точке а; = с, y = d, где 0 < с < а и 0 < d < Ь. Показать, что потенциал внутри приз-
призмы равен:
для 0 < у < d
1 , m-nb , ттс ,
m=l
V =— У. — cosech sh—(Ъ -rf)sh—-sin sin ,
us +—* m a a a a (i
для d < у < b
\т« 2о vn I nmb mr.d ттс , тле ткх
У =— >, — cosech sh sh — (о — у) sin sin .
¦us ZJ m a a a v J! a a
m=--l
Показать также, пользуясь формулой C.27), что спла, действующая на едппнцу
длины заряда, равна
о2 vi Г i , тка ткBс — а) . „innd j mr.b , mr.Bd — b) . „ mnc "I
— >, -г- cosech —— sh —. '- sm! — ^— cosech sh i ^-sin2 .
e ^J |_ fc b b b a a a a J
m=l
Заметим, что всюду, за исключением малых с и d, эти ряды сходятся очень быстро.
52. Показать, что поле системы, состоящей из трех линейных зарядов: д в г10,
q в zYo и —9 n начале координат плоскости Zj (см. § 276), преобразуется в невозму-
q Yo д рд t ( § ), рру
щенное поле одиночного линейного заряда д в z0 на плоскости z, где Zg =^
53. Используя вакон изображения, сформулированный в § 5 для случая круглого
диэлектрического цилиндра, и закон изображения, установленный в предыдущей задаче
для единичной окружности, найти сопряженные функции, дающие поле линейного за-
заряда д, расположенного параллельно оси эллиптического диэлектрического цилиндра
с проницаемостью К. Заряд находится на линии и0, v0 вне цилиндра, поверхность кото-
которого определяется уравнением » = »1 (используются эллиптические координаты § 276).
Получить следующие результаты:
в области внутри цилиндра
со
2 (f^)n
n=0
в области вне цилиндра для поля, обусловленного только поляризацией диэлектрика,
где верхний знак для п четных, а нижний —для п нечетных.
'"¦ 54. Линейный заряд д расположен параллельно образующим диэлектрического па-
параболического цилиндра. В параболических координатах у = 2$-(\, ос = Ч2—т,2, где
-^о5'<'5 < +оо и 0 < ~t\ < оо, координаты заряда равны Чо н т\0, а поверхность ци-
цилиндра определяется уравнением тг] == тг]1. Показать, что внутри диэлектрика преобразо-
ваппс, дающее поле, будет иметь вид
In
v я + i у
п=0
Задачи 117
а снаружи для поля, обусловленного только поляризацией диэлектрика, получим
(АГ+1J
2 (fri У
ln
где верхний знак для и четных, а нижний для п нечетных.
55. Цилиндр (х/аJп + C//6J" = 1 несет на себе заряд —Q (на единицу длины).
Применив теорему Гаусса для поверхности Т/ = 0, показать, что
Применяя затем теорему Гаусса к цилиндру г = сс, показать, что заряд, содержащийся
инутри, равен nQ (на единицу длины). Следовательно, окружающее цилиндр простран-
пространство может быть свободным от зарядов только при п=1.
56. Проводник, границы которого заданы уравнениями 0 = а, 6=—а и г=\, несет
на себе заряд тсе (на единицу длины). Показать, что потенциальная функция V опре-
определяется из преобразования
, „ { . тс sin W тс —а (тс — а) sin И' \
In s = — 2/ ) arc sin =7- -| arc i.g ' т-г- > .
\ [аBтс — а)]1^ ^ - [аBт= — а)-тс2 sin2 W]1'2 j
57. Бес.конечиая проводящая призма квадратного сечения со стороной шириной а
имеет на единицу длины заряд Q. Показать, что плотность поверхностного заряда на
призме определяется следующими уравнениями н параметрической форме:
4
D
где а: — расстояние от центра призмы до точки на поверхности, a F и ?—эллиптиче-
?—эллиптические интегралы первого и второго рода.
58.. Две проводящие ленты лежат в плоскости i/ = 0 и занимают области а < х < Ъ
и —а > х > — 6. Показать, что емкость (на единицу длины) между ними раина
гК{т)
К(п) '
где К (к) — полный эллиптический интеграл модуля к, т = (Ь2 — а2I'2^, а п=а/Ъ.
59. Показать, что емкость на единицу длины между двумя проводящими поло-
полосками, лежащими соответственно в плоскостях ж = Ь и х= ¦— Ъ и ограниченными пло-
плоскостями у = а и у=—а, равна
еК(к')/К(к),
где К{к') и К(к) — полные эллиптические интегралы, модули которых к' и fc = (l — A-'2I'2
удовлетворяют уравнению
а _ К (к1) Е {aiccos[E (к')/К (к1)], А'} — ?'(*') F {are cos [У? (*')/# (к1)], к'}
Ъ~ Е{к')К(к) — (к/к')*Е{к)К{к')
Значение А, близкое к действительному, можно найти из грубой оценки емкости С.
60. Поверхность Т/ = тс состоит из двух координатных полуплоскостей х = 0, у < О
к j/=0, х < 0, а поверхность Т/=0 определяется уравнениями x = h при у < к и у = к
ври х < h. Показать, что преобразование, определяющее поле и такой системе, будет
иметь нвд
у пг = Л arc tg [A(ew + II/2 (h*e№'— A2)~1/2] — A ar th [A (e^ + lI'2 (Л2еН/ —A2)" 1/2].
Показать, что дополнительная емкорть (на единицу длины) по сравнению с той, кото-
которая была бы, если в области х < 0 и у < 0 между F = 0 и F = tc существовало только
однородное поле, равна
2г Г, Л2 + А АЛ Л А ~|
4ЛА h g A A h \ '
118 Глава IV
ЛИТЕРАТУРА
13 а 1 о m a n П., Partial Differential Equations. Cambridge, 1932.
G e i g e r-S с h e e 1, Handbuch der Physik, Bd. XII, Berlin, 1927.
Jeans J. H., Tho Mathematical Theory of Electricity and Magnetism. Cambridge
1925.
Maxwell J. C, Electricity and Magnetism, v. I, Oxford, 1881.
Moullin E. В., Principles of Electroinagnetism, Oxford, 1932.
Rot he R., OllendorffF., Pohlhausen K., Theory of Functions, Technology
Press, 1933.
Russell A., Alternating Currents, Cambridge, 1914.
Sokolnikoff I. S., So к о 1 n i к о f f E. S., Higher Mathematics for Engineers
and Physicists, McGraw-Hill, 1934.
Thomson i. J., Recent Researches in Electricity and Magnetism, Oxford,
1893.
Walker M., Conjugate Functions for Engineers, Oxford, 1933.
Webster A. G., Electricity and Magnetism, Macniillan, 1897.
Wion-Harms, Handbuch 5er Experimentalphysik, Fd. X, Leipzig, 1930.
Глава V
ТРЕХМЕРНОЕ РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА
§ 1. При каких условиях поверхности некоторого семейства могут
быть эквипотенциальными? На первый взгляд кажется, что трехмерное
распределение потенциала, обладающее аксиальной симметрией, можно по-
получить путем такого вращения поперечного сечения двухмерного распреде-
распределения потенциала, при котором границы трехмерной области образуются
из границ поперечного сечения соответствующей двухмерной области.
В общем случае, однако, это оказывается несправедливым. Найдем условие,
которому должно удовлетворять семейство непересекающихся поверхностей,
чтобы оно могло быть семейством поверхностей равного потенциала. Пусть
уравнение поверхностей имеет вид
F{x,y,z) = C. E.1)
Поскольку каждому значению С соответствует одна из поверхностей семей-
семейства, то, если эта поверхность эквипотенциальная, каждому значению С
должен соответствовать определенный потенциал
удовлетворяющий уравнению Лапласа. Дифференцирование дает
т. д.
Подставляя в уравнение Лапласа, получим
w=?+w + S=r {C) (VCJ+r
откуда
(VCJ Г
Таким образом, поверхность F (х, у, z) — C может быть эквипотенциальной
только в том случае, если отношение V2C/(VCJ является функцией только С.
Путем интегрирования уравнения E.2) можно найти действительное
значение потенциала. Поскольку /" (С)//' (С) = d [In /' (C)]fdC, мы имеем
J Ф {С) dC = -In [/' (С)] + А',
или
Повторное интегрирование дает
^$*<C)dC E.3)
120 Глава V
Постоянные А и В можно определить, если задано значение потенциала на
двух поверхностях, принадлежащих семейству E.1).
§ 2. Потенциал поверхностей второго порядка, определяемых уравне-
уравнением ж2/(а2 + 6) + у2\{Ь% + G) + «2/(с2 + в) = 1. В качестве примера примене-
применения полученной выше формулы покажем, что любое из трех семейств не-
непересекающихся поверхностей второго порядка, определяемых уравнением
где с>й>а и —с2 < © < со , можно рассматривать, как семейство экви-
эквипотенциальных поверхностей. Чтобы представить себе эти поверхности, будем
менять б в указанных пределах. В интервале — а2 < б < оо каждый член
уравнения E.4) положителен, так что соответствующие поверхности суть
эллипсоиды. При 6 = оо мы имеем сферу с бесконечным радиусом, а при
6 = — а2 эллипсоид сплющивается в эллиптический диск, лежащий в пло-
плоскости yz.
Изменению 6 в пределах от — а2 + 8 до — а2 — 3 соответствует переход
на плоскости yz из области, лежащей внутри диска, во внешнюю область.
Последняя представляет собой предельный случай однополоетиого гипер-
гиперболоида, описываемого уравнением E.4) при — Ъ2 < 6 < — а2. Когда б = — Ь2,
однополостный гиперболоид сплющивается в участок плоскости xz, вклю-
включающий ось х и лежащий между гиперболами, пересекающими ось z в
точках
z=±(cs —
Изменения) © в пределах от — W + о до — Ь2 — В соответствует переход на
плоскости xz в область, лежащую по другую сторону этих гипербол. Эта
область есть предельный случай двухполостного гиперболоида, описывае-
описываемого уравнением E.4) при —с2 < 6<—Ъ2, сплющенного в плоскость xz.
При в — — с2 получается другой предельный случай: два «листа» этого
гиперболоида сливаются друг с другом в плоскости ху. Таким образом,
через каждую точку пространства проходит одна поверхность каждого
семейства. Нетрудно показать, что ати три семейства являются взаимно
ортогональными, и, следовательно, к ним можво применить теорию, изло-
изложенную в § 5 гл. III, приводящую к эллипсоидальным гармоникам.
Ввиду сложности последних мы не будем здесь рассматривать их в общем
виде и ограничимся, несколько позднее, исследованием лишь частного
случая сфероидальных гармоник.
Возвращаясь к нашей задаче, положим
Л/ —_^ L У. L.
(са+0)п
В этих обозначениях уравнение E.4) сведется к Мг=1, и после дифферен-
дифференцирования будем иметь
2х Л/Г дЬ п ав 2х
+?-м*^=0' или Ш = м{а*
так что
Трехмерное распределение потенциала 121
Повторное дифференцирование дает
дЧ 22х86 2х J Г 2х
[
дх* ~Af2(o2 + 0) Af2(a2 + BJ9a: a2 + (j Af| [ (a2 + BJ 3
4а;2
*
Прибавляя аналогичные выражения для у и z, получим
Т72й _ 27V 8Мз 8Д?2М3 _ 27V
Л/2 М| + Ml ~ М2 -
Подставляя полученные выражения в уравнение E.2), находим
У20 _ 27V Ж2 _ N
(VB? ~ Щ ~4~ ~ ~2
и, следовательно,
+ ^в). E-6)
Таким образом, поверхности рассматриваемого семейства могут быть эквипо-
эквипотенциальными, а их потенциал определяется по формуле E.3):
G
V = A i\j.[(a2 + b)(b2 + O)(c2 + B))-1^dd + B. E.7)
Эллиптический интеграл вида E.7) можно найти в книге Пайерса [формулы
E42) —E49) при х= —6]. Постоянные А и В могут быть выбраны действи-
действительными пли мнимыми, лишь бы потенциал V был действительным.
§ 3. Заряженный проводящий эллипсоид. Если выбрать V = 0 при
б=оо, то формула E.7) примет вид
V= - А ^ [(a2 + 6)F2 + e)(c2+6)]-1/2d0. E.8)
Полагая Tr=F0 при 0 = 0 и подставляя в формулу E.8), получим
со
- А = Vo J ^ [(а2 + 6) {V + 6) (с2 + 6)]-V. dO у1 . E.9)
п
Если полный заряд эллипсоида равен Q, то поле, созданное им на беско-
бесконечности, должно быть равно Qj^-кгг2). Согласно уравнению E.4), при
б—*оо х2 + у- + z2 = г2—>0, и, следовательно, 96/9/-—>2г. Поэтому
SV _ &V дЬ _-±2 = —
дг г^> дЬ dr~~"rs г2 '
так что
8tzbA=-Q. E.10)
Согласно формуле E.9), емкость эллипсоида равна
[(а2 + G) (^ + 6) (С2 + e)]-i/2
а поверхностная плотность заряда определяется выражением
Из формулы E.8) следует, что (дУ1дВ)ъ=о = A (abc)'1, а из уравнения E.5),—
что | V6| = 2A/71/a> откуда
Q
122 Глава V
§ 4. Эллиптический и круглый диски. Емкость эллиптического диска,
получаемая из формулы E.11) при а = 0, выражается при помощи эллип-
эллиптического интеграла. Чтобы найти плотность поверхностного заряда, запишем
формулу E.12) в виде
- ¦ ' aV ^
9 ТГ 1.Л ~Т~
Пусть теперь а—>0 и членами, содержащими у и г, можно пренебречь.
Поскольку и х и а равны нулю, первое слагаемое необходимо преобразо-
преобразовать при помощи уравнения E.4), положив в нем 6 = 0. Для плотности
заряда будем иметь
Полагая в формуле E.11) а = 0 и 6 = с, получим выражение для емкости
круглого диска (см. Двайт, 186.11):
СО
С = 8tts ^ 6-V2 (Ь2 + б)'1 dep = 8таг (-|- | arc tg 6-^ "V1 = 8efc. E.14)
о
#
Если положить ^2 + z2 = p2 и с=Ь, то из из формулы E.13) следует, что
ллотность заряда на каждой из сторон круглого диска равна
а= Я. E.15)
4тсЬF2 — р2I'2 ч '
Потенциал, созданный таким диском, дается формулой E.8), если положить
в ней о = 0 и Ь=с:
,т 2Vr.r тс е1/2^ 2F0 Ь
У = —°( -s— arc tg -г- ) = —- arc tg -rr .
71 V2 Ъ Ь J ТС Ь g!/2
Подставляя сюда значение 6, полученное из соотношения E.4) при а —О,
Ъ=с и ж2 + ^2 + 22 = г2, находим
от/
F = ^-° arc tg B1/2 6 {г2 - b2 + [(r2 - b2J +4i2x2]1/-' }~^). E.16)
Эту задачу можно также решить при помощи гармоник сплюснутого сфероида
(см. § 28а настоящей главы).
§ 5. Метод изображений. Проводящие плоскости. Применение кри-
критерия, выведенного в § 1, показывает, что для систем, содержащих более
одного точечного заряда, потенциал нельзя получить при помощи двухмерной
аналогии. Тем не менее два метода, используемые для решения двухмерных
задач, можно использовать в трехмерном случае. Одним из них является
метод изображений. В любом случае, когда уравнение замкнутой проводя-
проводящей поверхности, находящейся в поле точечного заряда q, записывается
в виде
п
(где г—расстояние от q до точки Р на поверхности, rs — расстояние от неко-
некоторой точки s, находящейся по другую сторону поверхности, до Р), задачу
можно решить методом изображений. Мы рассмотрим только простейшие
поверхности — сферу и плоскость. Из симметрии очевидно, что для решения
задачи о точечном заряде, расположенном в плоскости ху вблизи бесконечг-
Трехмерное распределение потенциала 123
ной проводящей плоскости или вблизи двух таких плоскостей, пересека-
пересекающихся вдоль оси z под углом -к/т, следует поместить его изображения
в плоскости ху в тех же точках, что и в двухмерном случае (фиг. 28).
Сложение потенциалов точечного заряда q и его изображений дает в области,
заключенной между пересекающимися плоскостями, точно такой же потен-
потенциал V, какой создается зарядом q и равным ему по величине индуциро-
индуцированным зарядом противоположного знака, распределенным по плоскостям.
Поверхностную плотность этого индуцированного заряда о можно найти,
вычислив —sdV/dn на поверхности металла. В случае точечного заряда q,
помещенного на расстоянии а от заземлевной проводящей плоскости,
плотность индуцированного заряда в точке Р, согласно § 15 гл. I и фор-
формуле A.42), равна
где г—расстояние от q до Р. Из § 18 гл. II известно, что никакое рас-
распределение истинных зарядов в пространстве, отделенном от q заземленной
проводящей плоскостью, не может повлиять на величину плотности зарядов а,
индуцированную на стороне, обретенной к q.
§ 6. Плоская граница двух диэлектриков. Однородный линейный
заряд, расположенный параллельно плоской границе раздела двух диэлект-
диэлектриков, можно рассматривать состоящим из равномерно распределенных
вдоль линии одинаковых точечных зарядов, для которых изображения
строятся так же, как для линейного заряда. Естественно поэтому пред-
предположить, что для точечных зарядов справедлив тот же закон изображений,
что и для линейных.
Пусть относительные диэлектрические проницаемости областей, соот-
соответствующих положитатьным и отрицательным значениям z, равны соот-
соответственно Кг и К2. Рассмотрим систему зарядов, расположенных в ди-
диэлектрике Кг; пусть потенциал системы я отсутствие диэлектрика равен
Fvac = / (Ж, У, г),
так что в том случае, когда все пространство заполнено однородным ди-
диэлектриком Кг, потенциал, в соответствии с формулой A.5), имеет вид
Потенциал изображения в плоскости г = 0 будет
Закон изображений, изложенный в § 5 гл. IV, говорит, что в присутствии
диэлектрика К2 поля в областях Кх и К2 записываются в виде
**i=jt / (:';- У'z) + CJ &' у' -z) E-18)
V2 = C2f(x,y,z). E.19)
При z = 0 V1 = V2 и [см. условия A.48)] K1(dV1jdz) = K2(dV2ldz); поэтому
1+К1С1 = КгС2 и 1 - К1С1 = К2С2.
Разрешая эти уравнения и подставляя результат в выражение E.18) и E.19),
получим
i[i ] E-20)
124 Глава V
Пусть заряд q расположен в диэлектрике Кх в точке Рх; принимая во вни-
внимание формулу A.5), мы видим, что поле в области Кх такое, как будто
все пространство заполнено диэлектриком Klt а в отраженной точке Р2
находится добавочный заряд q'. Поле в области К2 совпадает с полем
заряда q", находящегося в точке Рг; оно вычислено в предположении,
что все пространство заполнено диэлектриком Кп. При этом
if %- E-22)
Для «ычисления поля выбор пеличииы Кп несущественен, но обычно ее при-
принимают равной Кг, 1 или К2. Здесь принято Kn = Kv
§ 7. Изображение в сферическом проводнике. В § 6 гл. IV было
показано, что цилиндр радиуса р = а является эквипотенциальной поверх-
поверхностью в поле двух лилейных зарядов — заряда q
при р = ?> и заряда — q при р= -\-a2jb. Покажем
теперь, что сфера радиуса г = а имеет нулевой по-
потенциал в ноле двух точечных зарядов: q в точке
г = b и </' в точке r = a2jb, причем последний, как
будет показано ниже, уже не равен — q. Потенциал
V, созданный зарядом q' на сфере радиуса г = а,
Фиг. 4о. как это видн0 цз фиг 45, равен
4tteF' = q' (а*Ь-2 + а2 — 2ФЬ^ cos 6)-V-2 =
= ha-^q (а2 +№ — 2ab cos 6)-x/2 = ha^R^q'.
Потенциал, созданный на этой сфере зарядом q, равен qj^t-KER). Для того
чтобы результирующий потенциал был равен нулю, эти потенциалы должны
быть равны по величине и противоположны по знаку, т. е.
<7'=-Т?. E-23)
Следовательно, потенциал в произвольной точке определится выражением
V = (ii:e)-lq [(г2 + Ъ2 — 2Ьг cos 6)-х/2 _ а (b2r2 +а*- 2аЧг cos Ь)~^\, E.24)
а плотвость поверхностного заряда на сфере будет равна
(<W\ ¦ 9 Г а~ bcosb Ъ(Ъ — о cos 6) a2 — b2 /t- о-\
а = — е ( ,— ) =/- — -^ — ' = -—— q. E.2o)
Потенциал сферы можно, очевидно, сделать равным любой заданной вели-
величине V, если прибавить к полученному решению потенциал точечного
заряда
q = fomV, E.26)
помещенного в центр сферы. Если требуется найти поле, созданное точеч-
точечным зарядом q и проводящей сферой, несущей заряд Q. достаточно при-
прибавить к формуле E.24) потенциал заряда Q + aq/b, находящегося в центре.
Можно показать, что, в противоположность аналогичному двухмерному
случаю, простым изображением нельзя построить решение для диэлектри-
Трехмерное распределение потенциала
125
ческого шара в поле точечного заряда. Для решения этой задачи требуется
применение сферических гармоник.
§ 8. Пример применения метода изображений для нахождения поля
точечного заряда. В качестве примера, иллюстрирующего содержание
последних трех параграфов, построим
изображения в случае заземленного ме-
металлического листа, лежащего в пло-
плоскости yz и имеющего сферическую вы-
выпуклость радиуса а с центром в начале
координат; пространство, лежащее ниже
плоскости xz, заполнено диэлектриком
с относительной диэлектрической про-
проницаемостью К. Точечный заряд q на-
находится в точке хс, у0, z0 и х\ -\- у\ -\-
-f-Zp = i2. Чтобы найти требуемые изо-
изображения, дополним границы пунктир-
пунктирными 'пиниями, как это показано на
фиг. 46. Потенциал над плоскостью
xz можно найти как сумму потенциа-
потенциалов самого заряда q и его семи изо-
изображений, расположенных следующим
образом: ф
Фиг. 46.
q в точке х0, ?/0, г0,
q в точке
— ?;с,
- q в точке ~х0, у0, z0, - </' а точке — хь, - у0, z0,
ag (a\2 ( а у ( а \" ад' ( а \2 I а \2 ( а \2
-тв точке [Т)х0, [Т)уь, [T)z0, -т в точке [т)х0, -(т)уь, (т)г0,
ад (а\2 (а\2 (а\* ад' (а\- { а\2 (а'\1
тп точке -{T)X(l,{T)y0,{T)z,, -^ 1. точке (-)з-0, ~(т)у0. (T)z0,
где, согласно соотношению E.22),
1—А'
Потенциал в диэлектрике, ниже плоскости xz, можно получить, используя
только изображения выше плоскости xz п подставляя, н соответствии
с выражением E.18), вместо q заряд
Сечение проводника плоскостью ху и проекция изображении на эту пло-
плоскость показаны на фиг. 40.
§ 9а. Бесконечная система изображений. Задача о двух сферах.
Часто оказывается-, что при помощи конечного числа точечных зарядок
нельзя получить эквипотенциальные поверхности нужной формы. В неко-
некоторых случаях, однако, можно сначала сделать эквипотенциальной одну
поверхность, располагая внутри нее точечные заряды, а затем при помощи
подходящей системы изображений сделать эквипотенциальными и другие
поверхности. При этом, однако, первая поверхность искажается. Тогда при
помощи третьей системы изображений ей можно придать опять первона-
первоначальную форму, но за счет искажения других поверхностей, и т- д. Если
126
Глава V
эффект каждой последующей группы изображений стремится к нулю
либо в силу уменьшения величины зарядов, либо из-за их удаления,,
либо за счет тенденции к взаимной компенсации, то при достаточном числе
изображений получается сколь угодно близкая апроксимация точного
решения1).
Воспользуемся этим методом для вычисления собственных и взаимных
емкостей двух сфер. Пусть радиусы сфер 1 и 2 суть а и Ъ, а расстояние
между их центрами равно с. В соответствии с § 17 гл. II коэффициент си
есть заряд на сфере 1, а с12 —на сфере 2, когда сфера 2 заземлена,
а сфера 1 имеет потенциал, равный единице. Коэффициент е22 можно полу-
получить, поменяв местами а и Ъ в с11. На фиг. 47,а и б приведены соот-
соответственно случаи с<(Ь — а) и с>(Ь-\-а) при значениях а/с = т, bjc = n-
Фиг. 47.
Создадим сначала на сфере 1 потенциал, равный единице, поместив-
в ее центр О' заряд q = iTzea. Затем, поместив изображение д' = —4-ктЬ/с =
= — ккта на расстоянии Ь2/с=пЬ влево от точки О [см. формулу E.23)],
добьемся равенства нулю потенциала сферы 2. Потенциал сферы 1 можно
опять сделать равным единице при помощи изображения
q" —
i
(c—nb) A — п2)
расположенного на расстоянии а2/(с— nb)^=maj{l — /г2) вправо от точки О'
и опять привести потенциал сферы 2 к нулю, поместив изображение
1 ~ c—ma/(i — n2) ~~ 1 —/и2—п2
на соответствующем расстоянии от точки О и т. д. Величина каждого после-
последующего изображения уменьшается, а соответствующее решение прибли-
приближается к точному. Складывая заряды на сфере 1, получим
т2п2
где верхний знак относится к случаю «б». Складывая заряды на сфере 2,
для случая «б» будем иметь
-па- t_n2^ffl2- • • • J ¦ (-28)
!) \втор выражается неточно: недостаточно, чтобы вклад каждой послед^щей
группы изображений стремился к нулю, —необходима сходимость соответствующего
ряда.—Прим. перев.
Трехмерное распределение потенциала 127
Б случае «о», согласно § 18 гл. II, с12 = — сп. В силу симметрии для
случая «б» можно написать
mzn2 , ~) гг- оп,
+ ] E.29)
В случае «о» емкость с22 не представляет интереса.
Сила притяжения между двумя сферами при F2=0, согласно соотно-
соотношению B.56), равна
p_Vl дси_ WFf Г mn m»wM2(t-w»)-m»] ,
^-""а^- Г~ i A=^M + [A2J2]2 +••
Чтобы получить потенциал в некоторой точке Р, следует сложить потен-
потенциалы, созданные в этой точке всеми изображениями. Если потенциалы
сфер равны Vx и V2, причем V2 фО, то в случае «б» появится вторая си-
система изображений, для получения которой нужно начинать с зарядок
qt= 4-KmV-L и q2-= tiTzzbVо, расположенных соответственно в центре сфер
1 и 2. Величины зарядов этой системы и их расположение получаются при
перестановке О ш О' ш а и b в соответствующих выражениях для первой
системы изображений.
§ 96. Уравнения в конечных разностях. Задача о двух сферах.
Для точных расчетов формулы последнего параграфа не очень удобны,
если только m и вне малы. Установив общее соотношение между после-
последовательными изображениями и решая полученное разностное уравнение,
можно найти более компактные выражения, содержащие гиперболические
функции. Обозначим п-е изображение в сфере 1 через qn, так что перво-
первоначальный заряд в ее центре равен д1 = 47гео; изображение qn в сфере 2
обозначим через рп. Расстояние от точки О' до qn равно sn, а от точки О
до рп равно гп (фиг. 47). Тогда
P = t Г = E31)
где нижний знак относится к случаю «о», а верхний — к случаю «б».
Исключая с ^f sn из соотношений E.32) и E.33), получим
n+1 в
так что
Исключив sn из соотношений E.32) и E.34), приведем результат к виду
J L *-''-*!. E.35)
gn-i
Это есть, очевидно, уравнение в конечных разностях иторого порядка
с постоянными коэффициентами. Согласно общему методу решения таких
уравнений, следует подставить в уравнение E.35) 1/д„ = и", разделить результат
128 Глава V
на ип~1 и решить полученное квадратное уравнение для и алгебраически.
Если два его решения суть и1 и м2, то решение разностного уравнения
имеет вид
— = Au?i-Bu2, E.36)
где А а В определяются начальными условиями. Рассматриваемый случай
особенно прост, поскольку коэффициенты при l/gn+j и l/^n_i одинаковы.
Пользуясь формулами F51.03) и F51.04) из справочника Двайта, согласно
которым
sh (и + 1) 6 + sh (и — 1) 6 = 2 eh 6 sh иб,
ch (п + 1) в + eh (п ¦*-1) 6 = 2 ch О oh nO,
получаем, что решение уравнения E.35) можно записать к виде
— = Achm + Bshna, E.37)
Чп
•если выбрать
Чтобы вычислить А и /?, напишем для первых двух изображений
А= JL=:^clia-f-^sha,
— = ± ^-^-2^-1- = f 2cha ±-|Л г^- = J ch2a -f B»h2a.
q2 йЬ 4лга \_ о J -mui
Умножая первое из этих ураввений на 2cha и записывая его члены через
ch2a и sh2<x, найдем величины А и В.
4 = тАг, В = Ь.±а,с1а. E.39)
4jtso wzab sh a ч '
Если подставить значепия Л и i? в решение E.37), то, используя (Двант, 651.1I),
получим
— = s "а — a,s . — E.40)
Складывая заряды на сфере 1, находим
со
cu = 4~sabsha 3 [bshna ± ash(?t —1) я] ], E.41)
п 1
где нижний знак относится к случаю «а» (фиг. 47, а), а верхний —к слу-
случаю «б» (фиг. 47, б). В случае «а», согласно § 18 гл. II, ci2= — cu.
Чтобы найти с12 в случае «б», следует определить /?„. Взяв верхний знак
и исключив из соотношений E.31) и E.32) c—sn, получим
1 __ а 1 Ъ 1
Подставим значения l/r/n+i и 1/^„ из ссотношения E.40) п воспользуемся
формулами E.38) и (Двайт, 651.06); тогда
А-кгаЪ ph a '
Трехмерное распределение потенциала 129
гак что сложение зарядов на сфере 2 дает
»
оо
с12= J>j cosech/га. .E.43)
гг=1
Емкость с22 в случае «б» в силу симметрии и соотношения E.41) равна
^ [ ( — l)a]^. E.44)
§ 9в. Сфера над плоскостью и две одинаковые сферы. Представляет
интерес частный случай рассмотренной задачи—задача о сфере над про-
проводящей плоскостью. Этот случай можно получить, положив d-\-c=b—>со
в случае «о» или с — d=b—> со в случае «б», если d— расстояние от центра
сферы 1 до плоскости. При этом /г —¦* 1, т—^0, т/\ 1 — п| = a/d, так что
» то
сп = 4тао ( 1 + т^ + / °_ а + • • • ) = 4тео sh a ^ cosech na, E.45)
n=l
где d = flcha и а—^бесконечво малая величина по сравневию с Ъ. В обоих
случаях («о» и <<б») Л12= —Cjj. Сила, действующая между сферой и пло-
плоскостью, будет равна
/,__F|9?ll 2 2 2 fj_ _8ad_ I
CO
= 2ireFj J [cosech/га (cth a — n oth /га)]. E.46)
я = 1
Для двух одинаковых сфер радиуса а, расположенных на расстоянии с
Друг от друга, формулы § 96 несколько упрощаются, если ввести пара-
параметр р = 1/2а; тогда при а — Ъ имеем (см. Двайт, 652.6)
2=J. E.47)
В этих обозначениях, полагая в соотношении E.41) a-=bf имеем
оо
cu = c22 = 4ireashp Y cosechBn-l)P E.48)
n=l
и из соотношения E.43) получаем
оо
с1О = — 4тао sh p 5j cosech 2/гр. E.49)
1! = 1
§ 10. Инверсия в пространстве трех измерений. Геометрические
свойства. Если на плоскости проведена окружность радиуса К с центром
в начале координат и пересекающая ее радиальная прямая, то две точки
на этой прямой, расположенные на расстояниях г и г' от центра, называются,
согласно § 22а гл. IV, инвертированными точками в том случае, когда
rr' = IP. E.50)
8 § 22а гл. IV окружность представляла собой сечение цилиндра, но ее
с равным основанием можно рассматривать как главное сечение сферы.
Таким образом, каждой точке некоторой поверхности соответствует в про-
9 В. Смайт
130
Глава V
странстве инвертированная точка; поверхность, образованная инвертирован-
инвертированными точками, носит название инвертированной поверхности. Если уравнение
исходной поверхности в сферических координатах было /(г, 0, ср) =0,
то уравнение инвертированной поверхности имеет вид f(Ks/r, 6, ср)=О.
В § 22а гл. IV было показано, что прямые линии инвертируются (преобрази -
готся) в окружности, лежащие в той же плоскости и проходящие через
центр инверсии, и наоборот, тогда как окружности, не проходящие чере;'.
центр, инвертируются также в окружности. Следовательно, в трехмерном
случае пЛоскостп инвертируются в сферы, проходящие через цептр ппверсмгг,
а сферы, не проходящие через центр, инвертируются в сферы. Поскольку
в § 22а гл. IV законы инверсии были получены при помощи конформных
преобразований, углы при инверсии не изменяются. Отсюда, очевидно, сле-
следует, что если малый конус с телесным углом dQ n вершиной в начале
коордипат вырезает на поверхности S н инвертированной ей поверхности Л"
элементы площади dS и dS', а угол 6 между осью конуса и элементами
площади один и тот же, то
dS _ г2 dQ cos 6 _ г2 E 51}
dS7 ~~ r'2'dU cos 6 " У2 ' V • )
§ 11а. Инверсия потенциала и зарядов-изображений. Покажем, что
законы инверсии можно сформулировать для электрических величин таким
образом, что из решения одной задачи
можно получить решение другой, в кото-
которой границы раздела являются поверх-
поверхностями, инвертированными по отношению
к соответствующим поверхностям первой
задачи. Рассмотрим фиг. 48, на которой
точки/', R' и Q' — инвертированные по
отношению к точкам Р, R и Q, а О — центр
инверсии. Заряд q в точке Р создает потен-
потенциал V = ql(tfne.PQ) в точке Q, а заряд q'
в точке Р' создает потенциал V = q' j{At.&P'Q') в точке Q'. Треугольники OQ'P'
и OPQ подобны, поскольку К2 = ОРОР' = OQOQ' и угол а —общий.
Искомое соотношение между потенциалом V в точке Q до инверсии и потен-
потенциалом V в точке Q' после инверсии имеет, следовательно, вид
у _g'PQ _ д' ОР
V ~~ q P'Q' ~~ qOQ' '
Чтобы использовать это соотношение, следует установить подходящий закон
инверсии зарядов. В § 7 было показано, что сфера радиуса К имеет нуле-
нулевой потенциал в поле заряда q, расположенного в точке г=Ъ, и заряда
|<?'|— +-^|*?|/^> расположенного в инвертированной точке г'=К21Ъ. Если
потенциал сферы после инверсии относительно самой себя (т. е. меняющей
местами заряды) остается равным нулю, то закон инверсии зарядов должен быть
К
ь
к
' ОР
ОР'
'' к
E.52)
Отношению приписан положительным знак, поскольку мы потребовали,
чтобы инверсия сохраняла знаки зарядов неизменными. Подставляя эти
величины в уравнение для инверсии потенциала, получим соотношение
V _ К ОР __ К _OQ
V ~ OP CQ' ~~ OQ' ~~ К
E.53)
Формула E.53) показывает, что если при конечном расстоянии OQ потенциал
V = 0, то V' — 0. Это означает, что если некоторая поверхность имеет пулевой
Трехмерное распределение потенциала
потенциал в поло точечных зарядов ql7 q2, . .., qn, находящихся в точках
Pv Р2, ...,Рп, расположенных па коночных, отличных от нуля расстоя-
расстояниях от центра инворспи, то инвертированная поверхность будет иметь
нулевой потенциал в иоле инвертированных зарядов q[, q\, ....q'n, находя-
находящихся в точках Р[, Р'2, ..., Р'п. Уиомян}"юо выше ограничение необходимо,,
поскольку соотношение E.52) не имеет места, когда ОР равно нулю пли
бесконечности. Из сказанного выше следует также, что и тех случаях, когда
некоторая задача решается при помощи изображений, «шшертироватшан»
задача также решается при помощи, изображений.
•
§ 116. Пример инверсии изображении. Вычислим (.илу, делелнующую
на точечный заряд q, находящийся в плоскости симметрии двух соприкасаю-
соприкасающихся заземленных сфер радиуса а; заряд расположен в точке Р на рас*
стоянии b от точки соприкосновения сфер. Очевидно, что две сферы можно
-я'
-я'
*ч'
Инвертированная система
а
Фиг. 49.
получить инверсией системы плоскостей, изображенной на фиг. 49, а. Вычис-
Вычисления упрощаются, если в качестве сферы инверсии выбрать сферу, касаю-
касающуюся обеих плоскостей (изображенную на фиг. 49, а пунктиром). Потенциал
в точке Р', созданной изображениями до инверсии, равен
¦1н2.
2tis
Точка Р' является точкой равновесия (нейтральной точкой) поля изобра-
изображений, так что величина потенциала V внутри сферы радиуса 3' с центром
в точке Р' (V'p) постоянна, если пренебречь членами порядка 8 при п > 1.
Закон инверсии E.53) дает для потенциалов, созданных изображениями
в точке Р и на расстоянии 8 над точкой Р (изображения лежат на окруж-
окружности, проходящей через Р и точку касания), следующие выражения:
лт 2а лт, т/ 2а тг, тг 2аЬ тг,
Vb — -7-Vp, Кь+8«
Согласно соотношению E.52), заряд q' при инверсии преобразуется в заряд
2aq/b, так что сила, действующая на q, оказывается равной
§ llrs. Инверсия заряженной проводящей поверхности. Рассмотрим^
проводящую поверхность S, заряженную до потенциала 1/К и несущую
у*
132
Глава V
поверхностный заряд плотности о; пусть Q — некоторая точка на этой по-
поверхности. Согласно закону E.53), потенциал в соответствующей точке Q'
на инвертированной поверхности S' равен V'q = 1 jOQ'. Поскольку потенциал
в точке Q', созданный отрицательпым зарядом 4те, находящимся в точке О,
равен —ijOQ', то очевидно, что при наложении потенциала такого заряда
потенциал инвертированной поверхности обращается в нуль. Обращение
этой операции дает важное правило, согласно которому, зная решение
задачи для проводника с нулевым потенциалом в поле положительного
заряда 4тс, можно при помощи инверсии с центром в той точке, где
находится этот заряд, получить решение задачи для инвертированной про-
проводящей поверхности, заряженной до потенциала — К'1. Для инверсии
поверхностной плотности заряда в точке Р будем, согласно соотношениям
.E.50) -E.52), иметь
? _ ML Ё? _ JL (°рJ _ (°р? _ 1{3 т «\
о dS' д
ОР (ОР'J К3 (ОР'K " v ;
§ 11г. Преобразование емкости при инверсии. В качестве примера
применения метода, изложенного в § Ив, найдем емкость проводника,
у
Инвертированная система
а а
Фиг. 50.
образованного двумя сферами радиусов а и Ь, пересекающимися под прямым
углом. Очевидно, что инвертированная система имеет вид, изображенный
на фиг. 50,а: две заземленные плоскости, пересекающиеся под прямым
углом, находятся в поле точечного заряда q' = 4та. Это поло совпадает
с полем, созданным зарядами-изображениями, показанными на фигуре. Про-
Проводник требуемой формы, полученный прп помощи инверсии, будет иметь
потенциал F=— \\К =—1/2о. Согласно формуле A.27), заряд па этой
поверхности равен сумме зарядов-изображений qv q2 и qs, т. е., в соот-
соответствии с соотношением E.52),
_ . Г —а аЪ ^ 1
^-<7l + <72 + <73— "е1~2а~ 2а(а* + Ъ2I12 2а]'
а емкость равна
E.56)
Потенциал в пространстве, окружающем проводпик, можно найти непосред-
непосредственно по зарядам-изображениям qu q2 и q3 или при помощи инверсии
Трехмерное распределение потенциала 133
потенциала, создаваемого зарядами-изображениями внутри угла, образо-
ванпого плоскостями.
§ 12а. Пространственные гармоники. В § 1 было показано, что враще-
вращением семейства ортогональных кривых, представляющего поперечное сечение
двухмерного поля, нельзя, вообще говоря, получить семейство трехмерных
эквипотенциальных поверхностей. Однако таким образом можно получить
семейство поверхностей, которые вместе с плоскостями, пересекающимися
вдоль оси вращения и характеризуемыми азимутальным углом, образуют
систему ортогопальных криволинейных координат; последнюю можно изучить
при помощи метода, изложенного в § 4 гл. III. Если меридианалыюе сече-
сечение поставленной трехмерной краевой задачи образует двухмерную границу,
для которой решение можно получить при помощи конформного преобразо-
преобразования, то существует метод, позволяющий построить такую систему коор-
координат, в которой первоначальные краевые условия имеют весьма простой
лид. Задача, таким образом, заключается в нахождении общего решения
уравнения Лапласа в такой системе координат.
Пусть иг = fx (х, у) и и2 = /2 (х, у) — сопряженные функции в плоскости z,
определяемые соотношением
z = х + /у = / К + }и2) = /(и). E.57)
Тогда, согласно выражению D.56),
— =/'(м), или dx+jdy = f'{u) (du-L + fdiiz).
Умножая это равенство на комплексно-сопряженное, получим
dsl = dx2 + dy2 = | ^ \\dul 4- du\).
Если эта система вращается относительно оси у, то для элемента длины
будем иметь
ds2 =
(du\ + dul) + x2 №J- E-58)
Сравнение с соотношением C.10), где dy = du3, дает
h —h — —
1 2 du
И Л3 = Ж.
так что уравнение Лапласа, согласно соотношению C.13), имеет вид
dz |-2 г э г av ~\ a f sv\~\ 'aw „ ,к cn.
-г т—(ж^г- )+т—(Жт— L--т-? = 0. E.59)
х
Последний член здесь без труда отделяется, если, как было указано в § 2
гл. IV, искать решение в виде
V = U(ult к2)Ф(ф). E.60)
Разделив уравнение E.59) на V и полагая последний член равным —т2,
получим, как и в решении D.8), функцию Ф в виде
Ф = А^™* + ВЛ e~3mv = A cos mw + В sin my. E.61)
Для U(к., и2) получается уравнепие в частных производных
1 a f аи
( ж
ж
аи \ , 1 a f аи л тг
ди
= 0.
Трудности, связанные с интегрированием этого уравнения, определяются видом
функции х(щ,и2) и \dz/du\. Во многих важнейших системах координат,
\'М Глава V
в частности во всех системах, рассмотренных в настоящем главе, х имеет вид
^^ЮйгЫ. E.63)
откуда, используя соотношение D.56), имеем
dz 2 дос . дх 2 / дх\% f дх. Л2 л •> •> ,2 /г „..
— = 7 =( ) +( ) = s 1 й + Я Я'9 • » E.64)
йи диу ди2 \ди1 / \ди2 J 0102 0102 \
Положим
и подставим выражения E.63) —E.65) в уравнение E.62). Разделив резуль-
результат на U1 (ггх) U2(u2), получим, что каждый член уравнения содержит только
одну переменную. Приравнивая члены с щ постоянной +(s + m2c), а члены
с и2 постоянной —(s-)-m2c), будем иметь дифференциальные уравнения
в полных производных
-n* ГГISV-Л + s = 0. E.67)
Весь остальной материал настоящей главы посвящен решению этих урав-
уравнений и примепению их решений [а также решения E.61)] к задачам о на-
нахождении потенциала.
Из соотношения D.61) заменой х на у л наоборот получаются сфери-
сферические координаты, так что
g1 = e=7- и g2 = sin гг2 = sin 6. E.68)
Если положить с= — 1 и s — и(и+ 1) в уравнениях E.66) и E.67) и восполь-
воспользоваться переменными г и 6, то эти уравнения переходят в уравнения
E.836) и E.102).
Из преобразования D. 03) получаются гармоники сплюснутого сферо-
сфероида, если положить
^. E.69)
IIpii (;=-{-! Ti .s- = —п (п -(- 1) уравнения E.66) и E.67) совпадают в пере-
переменных I и С с уравнениями E.244).
Гармоники вытянутого сфероида получаются из преобразования D. ЮЗ)
заменой х на у и наоборот при
^ = 0,008^ = ^A-^2 и g2 = shK2 = G12-lI-'2. E.70)
Если в уравнениях E.66) и E.67) положить с= +1 н s= —и (и +1),
го и переменных 5 и t] получится уравнение Лапласа в обычной для
«иытянутых» сфероидальных координат форме, рассмотренное в § 29а.
Цилиндрические координаты получаются вращением преобразования
z = a, так что для них g1 = u1 = p = k~lv и g2 = l. Полагая п уравнении
E.66) с = 0, s= —к2, т=п и разделив уравнение на к2, получим уравне-
уравнение Бесселя E.302). Аналогичная подстановка в уравнение E.67) дает
уравнение E.301).
§ 126. Задача о клипе, ортогонально пересекающемся с поверх-
поверхностью вращения. В частном случае, когда т f= 0 и соотношение E.63)
удовлетворено, решение уравнений E.66) и E.67) можно получить в весьма
простой форме. Пусть w1 = f1(x, у) и w2=-f2(x, у) — сопряженные функции,
которые должны быть подвергнуты вращению. Выберем новые ортогональные
Трехмерное распределение потенциала 135
координаты и1 и и2 так, что
gl (и,) = (A, e»i + В, e-«i) = F1 К), E.71)
g2 (и2) = (-4, cos гг2 + Z?2 sin м2) = /^ (ш2). E.72)
Обозначая через р радиуг вращения некоторой точки, будем, согласно
соотношению E.63), иметь
Р = gi Ю 82 Ю = Fi (Щ) Fz (Щ)- E-73)
Если положить тс=1 и s = 0 u уравнениях E.66) и E.67), "то, как
нетрудно убедиться посредством подстановки, решениями этих уравнений
будут
Ux = C,gT E-74)
Ua = Cagf. E.75)
Соответствующие дифференциальные уравнения — уравнения второго порядка,
поэтому каждое из них должно иметь еще одно решение. Поскольку метод
нахождения второго решения по одному известному решению может ока-
оказаться полезным не только в рассматриваемом случае, выведем его здесь
в общем виде. Предположим, что y = v есть частное решение уравнения
g + M% + Ny = 0, E.76)
где М и N — функции х. Подставляй y — cz в это уравнение, обозначая
z' = dzjdx и исключая v при помощи уравнения E.76), получаем
" dx ' V dx
Умножая на dxjvz' и интегрируя, будем иметь
In %' + In ъ~ + [ М dx = С,
или
Z'^ dx ^ BV~2 e ' Х-
Интегрирование дает
так что
у = с(А + в\ к-2 е~$ м dxdA . E.77)
Б рассматриваемом случае, выполнив дифференцирование и умножив на l/i,2,
можно привести уравнения E.66) и E.67) к виду E.76), тогда Mi,2 будет
равно
М ==S'i'2 _z=dll>Sl,2
1>2 ~^1,2 ~ d"l,2
Принимая v равным выраженшо E.74) или E.75), получаем при помощи
формулы E.77) при Л = 0 вторые решения
136 Глава V
Следовательно, решение уравнения Лапласа можно записать в виде
V = 8Т[С, + D, J ^)g™ {С, + ?2 Jф^ cos{тщ + Р). E.80)
Решение в такой форме удобно, в частности, когда поверхность заряжен-
заряженного проводника образована поверхностью вращения и клином, ребро кото-
которого лежит на оси вращения.
Применение полученного решения можно проиллюстрировать простым
примером. Пусть бесконечный проводящий заряженный клин, внешний угол
которого равен а, имеет сферическую выпуклость радиуса о, пересекающую
обе его стороны под прямым углом. Тогда, взяв цептр сферы за начало коор-
, 1 г
динат и расположив стороны клина под углами <p = i~ai будем иметь
p = rsinO, gl = eui = r, g2 = sinu2 — sin0. Бое граничные условия выпол-
выполняются, если выбрать
Таким образом, получаем
[(^I+B7C/tt)]os^. E.81)
Эта формула дает V = 0 на поверхности клпна и сферы, а вдали от начала
координат совпадет с решением § 2U гл. IV.
§ 13. Сферические гармоники. Когда граничные условия электростати-
электростатической задачи имеют простой вид в сферической системе координат, целесо-
целесообразно воспользоваться общим решением уравнения Лапласа в этой системе.
Это решение можно получить точно таким же путем, что и в § 2 гл. IV.
Пусть г —расстояние от начала координат, 6 —полярный угол, отсчиты-
отсчитываемый от оси z, ср — азимутальный угол, отсчитываемый вокруг оси z от
плоскости zx\ в этих переменных уравнение Лапласа имеет, согласно
C.17), вид
д( oOV\ , ir>/. ndV\ 1 ff'-V ,e сип
7Г( r -я- I + ^—fi 5« ( sm^^77 ) + -^V7iT-?- = f'- E.82)
dr\ dr J ' sin 0 d% \ di) J ' sm! 0 dy2 v '
Будем искать решение в виде
-RS, E.83а)
где Д — функция только г, в — функция только 0, а A> — функция только <р
Функция S = Ф© называется поверхностной сферической гармоникой, а функ-
функция в (при Ф = const) —зональной гармоникой. Подставив V — RS в урав-
уравнение E.82) и разделив на RS, будем иметь
) +
) + Л1 sinО вО ^БШ дЬ J
Н dr \! dr ) + Л1 sin.О вО ^БШ дЬ J + S sin2 (J ду* — J-
Первый член этого уравнения зависит только от г, другие содержат только
угловые координаты. Уравнение удовлетворяется, следовательно, в любой
точке только в том случае, если
К dr
Трехмерное распределение потенциала 137
Нетрудно видеть, что решением последнего уравнения является
\ E.84)
где п(п +1) = К. Подставляя это значение К в первое уравнение и умножая
на S, получим
ST^V+"(" + 1)lS = 0- E-85)
Решение E.83а) приобретает, таким образом, вид
n~l )Sn. E.86)
Очевидно, что V будет решением уравнепия Лапласа только в том случае,
если величины п в обоих членах одинаковы и равны индексу функции Sn.
Сумма (или интеграл) по п, состоящая из членов типа E.86), также будет
решением.
В частном случае при п = О уравнение E.85) принимает вид
^=u- E-87)
В § 21 гл. VI будет показано, что или U, пли V удовлетворяют этому
уравнению, если
^ '\ E-88)
Таким образом, каждая сопряженная функция предыдущей главы даст два
решения уравнения Лапласа в трехмерном пространстве после замены х
* 1 1
на coscptg-g-^, У на smcptg-^-S и умножения на (А + Br-1). Особенно важ-
важные решения, получающиеся при W = z±m и W = In z, имеют вид
V = {А +Вг-1) (С ctgm4"e +#tgmie) cos(mT + 8J, E.89)
V = (А+Вг-')(СIn tg~Ь + D^ . E.90)
§ 14a. Общие свойства поверхностных гармоник. Прежде чем решать
уравнение E.85), выведем при помощи теоремы Грина важное свойство функ-
функций Sn. Вывишом еще раз формулу C.22)
С (ПЛ/2Ф - ФЧ*ЧГ) dv = \ ( W д~ - Ф^Л dS. E.91)
V S
Положим W—rmSm и Ф = гп5„, так что V2tD = V24? = 0 и объемный интеграл
равен нулю. В качестве поверхности интегрирования выберем сферу единич-
единичного радиуса; обозначив через dQ элемент телесного угла, будем иметь
и, аналогично, дФ/дп = nSn. Подстановка в формулу E.91) дает
(nSnSn - mSnSm) dQ = (п - т) J SnSm dQ = 0,
т. е. при п i= m
JnSmdQ = O. E.92)
138 Глава Г
§ 146. Потенциал гармонического распределения заряда. Пусть
на поверхности сферы задана конечная непрорывная плотность электри-
электрического заряда ап, такая, что в любом месте поверхности можно выбрать
настолько малую площадку AS, что па ной можно пренебречь величииой
(ап — оп) по сравпению со средним значением ап плотности заряда ап на пло-
площадке AS. Этот заряд создает потенциал Fo вне сферы и потенциал V.
внутри нее. Применяя теорему Гаусса о потоке электрической индукции A.27)
к маленькому объему, охватывающему элемент оболочки AS, будем иметь
E.93)
Рассмотрим плотность ап такую, что
Тогда, поскольку F0=F; при г —а, должно иметь место равенство
Подстановка выражений E.94) и E.95) в уравнение E.93) дает
°» = Sn. E.96)
Впоследствии будет показано, что если 0 входит в функции Sv через Р™ (cosO),
то эти функции удовлетворяют условиям, наложенным на on d начале
настоящего параграфа. Используя найденные выше формулы, а также
формулу A.8), можно получить два весьма полезных интеграла:
s
Углы, сходящие в функцпго Sn, суть координаты концов Rt или Ro. В силу
принципа суперпозиции потенциал, обусловленный некоторым поверхност-
поверхностным распределением заряда, которое можно представить в виде
o = S0 + S1 + S2+..., E.98)
дается формулами
ЧПЧI*] -<¦¦
при г>а-
§ 15. Дифференциальные уравнения поверхностных гармоник. Пере-
Переменные 0 и ср в дифференциальном уравнении понерхностных гармоник
tS" = («)Ф E.85) можно разделить обычным методом. Подставив fcMfc вместо 5
в уравнение E.85) и разделив уравнепно на e<i>/sin2G, получаем
sinfl d
-e-do
Dio уравнение удовлетворяется для любых значений б и ср только гз том
случае, если
1 ?/2Ф ^
Грехмррнор распределение потенциала 139
Если положить Кг = тп2, то решение второго уравнения имеет, очевидно, вид
U> = Ccosm's> + Dsinmy, E.100)
за исключением случая m =0, когда
Ф^Му+N. E.101)
Полагая К1 = тп2 в первом уравнении и умножая его на 6/sin2 6, будем иметь
е = °> <5-102>
т. с. дифференциальное уравнение для функции в.
§ 16а. Зональные гармоники. Уравнение Лежандра. Прежде чем
исследовать общее решение уравнения E.102), рассмотрим наиболее важный
частный случай, когда V не зависит от ер, Ф — постоянная и, согласно
решению E.100), тп = 0. Если обозначить cos Ь через [х, то уравнение E.102)
примет вид
[^]в(» + 1)в- = 0- E.103)
Это уравнение называется уравнением Лежапдра, а его решения — зональ-
зональными гармониками.
§ 166. Решение уравнения Лежандра при помощи рядов. Чтобы
получить решение уравнения E.103) в виде ряда, положим
вге = 2>у. E.104)
Подстановка выражения E.104) в уравнение E.103) дает
S (> (г - 1) о^-2 + I и (и + 1) - г (г + 1)] aAS} = 0.
Чтобы это равенство удовлетворялось при любых значениях [х, коэффи-
коэффициенты при различных степенях [х должны порознь равняться нулю, т. е.
Г) «г .-а = (п_г)(л + ,. + 1) Ог+2. E-105)
Отметим, что если ог = 0, то ог_2 = аг— 4 = ... = 0 и, согласно соотноше-
соотношению E.105), o_i и о_2 равны нулю при коночных а0 и ох; таким образом,
иго отрицательные степени [х в решении отсутствуют. Следовательно, если
выбрать о0 = 1 и сохранить четные степени jj., решение можно записать в виде
рп = 1 __ Л^1 ц + _ ^ _ _ _ (
Кгли 1!ыбрать Oj^^-1 и сохранить нечетные степени ;х, то решение будет
Общее решение уравнения E.103) в интервале — 1 < |а < + 1 имеет вид
независимо от того, является ли п целым числом или дробью, действитоль-
пым или комплексным; необходимо лишь, чтобы ряды были сходящимися.
140 Глава V
Рекуррентные формулы для рп и qn можно получить вычитанием p-n+i из /?n_i:
т, п - Г(» + 1)(» + 2)и(п-1) g
Pn-i ~ Рп+1 — [ 2! ¦ Iх
(n-I)(n + 2) 4 "I _
3! I* +•¦¦ J ~
E.108)
Аналогично получаем
{п + IJ <7n+i - n*qn-i = Bл + 1) [хрп. E.109)
Дифференцируя ряд E.107) и прибавляя п dqTI-i[dp и (n+
будем иметь
' ¦ / ¦ л\ ' Го л (п — 2-\-п-\-'д) п (n + i) „
"9«-i + (и + 1) ?«+i = [2и + 1 —v ^
(n-4 + n+5)nfn — 2)fn + l
+ ^
и, аналогично,
(и + 1)/?;_! + пК+1 = - п (п+ 1) Bп + 1) 9п. E.111)
§ 16в. Полиномы Лежандра. Формула Родрига. Если п — четное
положительное целое число, то ряд E.1U6) имеет, очевидно, конечное
число членов, равное -у (п + 2), и может быть записан в виде
n (и + 2г)!
Zj v ~ I П
r=0 2n^2(n2
В этом случае полиномы Рп (р.) определяются как
P(F)= ~} ^n- E-112)
Если /г — положительное нечетное целое число, то ряд E.107) имеет конеч-
конечное число членов, равное -^-(я+ 1), и его можно записать в виде-
В этом случае полиномы Рп(\>-) определяются следующим образом:
Трехмерное распределение потенциала 141
При целом положительном п полиномы Лежандра .Р„([х), представленные
в виде E.112) и E.113) по возрастающим степеням [х, можно записать
1 1
в обратном порядке, если подставить s = —и —г в E.112) и s = —(и—1)—г
в E.113); подстановка в обоих случаях дает
EЛ14)
s=0
1 1 . ..
где т равно -^ п или -^(п—1) в зависимости от того, которое из этих
чисел целое.
Из выражения E.114) для .Рп([х) можно получить формулу, известную
под названием формулы Родрига:
т
= _1_ _^1 V ^ _ 1 V4 "! .. 2п-28
s=0
Последняя сумма есть разложение бинома ((J-2—-1)", так что
Формулы E.114) и E.115) дают решение уравнения Лежандра* E.103)
независимо от величины переменной [х. Для гармоник вытянутого сферо-
сфероида 0 < р. < оо. При очень больших значениях р. член с высшей степенью [х
много больше остальных, поэтому
§ 16г. Коэффициенты Лежандра. Обратное расстояние. Полиномы,
рассмотренные в § 16в, известны также под названием коэффициентов
Лежандра; чем обусловлено это название, будет ясно из дальнейшего. Если
две точки расположены на расстояниях а и b от начала координат F > а),
а угол между а и Ъ равен G([x = cosO), то величину, обратную расстоянию
между этими точками, можно записать в виде
-L = (а- -Ь 6»- 2аЬ^Ь =
а 3|а2— 1/nV , V — За ( а
Нетрудно видеть, что коэффициент при (а/fc)" совпадает с выражением E.114)
для /^((х), так что можно записать
В последующем это разложение будет неоднократно использовано при реше-
решении задач.
142 Глава V
§ 16д. Рекуррентные формулы для полиномов Лежандра. Если п —
нечетное целое число, то, подставив в формулу E.10b) pn—t, Pn^i " Цп
из формул E.112) и E.113) и разделив полученное равенство на
оудем иметь
Точно такое же выражение получается для четных п из формулы E.109).
Аргумент полиномов в тех случаях, когда это не может привести к недо-
недоразумению, не выписывается.
Если «—четное целое число, то, подставив в форму ту E.110) рп, G«-ь
q'n-ui из формул E.112) и E.113) и разделив па
2пBи + 1
получаем
р;+1-р;_, = Bи+1)р„. E.П9)
Такое же выражение можно получить при нечетном п из формулы E.111).
Интегрированием формулы E.119) можно получить выражение для
интеграла от Рп(\>-)'-
Производную полинома Рп(\>-) можно получить путем сложения последова-
последовательности уравнений типа E.119)
/>;(|*) = Bп-1)Л1_, + Bп-5)Д1_3+... E.121)
Если продифференцировать выражение E.118) и исключить из результата
P'n—i при помощи выражения E.119), то получится другая важная формула
для производной
P'n+i=V-P'n+(n + i)Pn или Кг =[*/>;_!+ «Лг-1. E.122)
Исключая отсюда P'n-i и P'n+i при помощи выражения E.119) и исполь-
используя выражения E.118), E.119) или E.120), будем иметь следующие
эквивалентные друг другу формулы:
р, С + 1) №nPn+i) _ (!У,
71 ~ 1 —(X2 1—[
-п(га
§ 16е. Интеграл от произведения полиномов Лежандра. В приложе-
приложениях полиномов Лежандра весьма важен интеграл от их произведения,
вычисленный в пределах от 6 = 0 до б = к или от [х=—1 до [х=+1.
Согласно формуле E.92),
[ />n(l*)/>m(l*)rf|i = 0 при тФп. E.124)
—1
Трехмерное распределение потенциала 143
При т.— п можно подставить значение одного из 1>п по формуле E.115)
+1 -И
\
—i
Проинтегрируем правую чаек, раненстла по частям п ра:;, выбирая каждый
раз (горный член за и, а второй за сГс. Поскольку сГ (;х2—l)n/d\).r содержит
всегда множитель (;х2 — \IМ', v всегда обращается в нуль пргг подстановке
пределов, так что произведение иг выпадает; окончательно получаем
—1
Согласно формуле E.114),
так что
)_ Bп)\п\ _ Bи)!
2 п\ п\ 2 п\
л \ •
и интегрирование (см. Двайт, 854.1) дает
—-1
§ 16ж. Разложение функций по полиномам Лежандра. Функцию,
которую можно разложить в ряд Фурье в интервале —1 < jj. <-(-!, можно
аналогичвым методом разложить в ряд и по полиномам Лежандра в этом же
интервале. Запишем этот ряд в виде
/W = ^oW + «AW+-.+^nW+-- E-128)
Умножим это равенство на /^„(р.) и проинтегрируем от[х=— 1 до ji= +1;
в результате, согласно формуле E.92), все члены, кроме т-го, исчезают.
При помощи формулы E.127) получаем
+1
E.129)
Отметим, что при /(р-) = 0 в интервале—1<[х<: +1, am = 0. Это означает,
что если ряд по полиномам Лежандра равен нулю, то должны равняться
нулю коэффициенты при каждом из его членов. Как и в случае рядов Фурье,
в точках разрыва сумма ряда равна полусумме звачений /(р.) по обе сто-
стороны точки разрыва. Посредством подстановки формулы Родрига E.115)
в формулу E.129) можно получить другое, часто более удобное, чем E.129),
выражение для ат. Подстановка дает
$
Иптегрируя это соотношение несколько раз по частям, принимая каждый
раз первый член за и, а второй за dv, находим, что | uv |*j равно пулю и
144
Глава V
+ 1
\ и do меняет знак; в результате остается
2m
Y
E.130)
Если производные / (р.) имеют простой вид, то обычно интегрирование в соот-
соотношении E.130) не представляет труда.
§ 16з. Таблица полиномов Лежандра. Таблицу величин /'„(р.) можно
составить при помощи формул E.114) или E.115). При п < 9 имеем
C5 [л4—
B31 [х6
_ D29 tx7—693 [л* + 315 |л3—35 p.)
_F435[л8—12012 ^ + 5930 [л4 —1260 [Л2 +35)
ITS
^г—5)
Фиг. 51. Полиномы Лежандра от первого порядка до седьмого.
Принедом некоторые наиболее важные частные значения Рп{^)'-
если п — нечетное Рп @) = 0,
» «-четное
» п — лгобое
» «-любое
» и —любое
» и —любое
Величины
для
@) [из формулы E.116)],
уравне
7 приведены на фиг. 51.
^п@)= — (и+
Р'п (I) = — п (п + 1) [из уравнения E.103)].
Трехмерное распределение потенциала
145
§ 16и. Полиномы Лежандра мнимого аргумента. При изучении гар-
гармоник сплюснутого сфероида приходится иметь дело с Рп{]Х), где / = (—II'2
и 0<С< оо. Подставляя /С вместо р, в формулу E.114), получаем
Рп (/Г) = ( -
Bn-2s)\
V '
1 1
где m = Yn или иг = у(и —1) в зависимости оттого, которое из этих чисел
целое. Аналогичная подстановка в формулу E.116) дает
BвI
2" (n!J
E.132)
§ 17. Потенциал заряженного кольца. Допустим, что потенциал V
симметричен относительно оси х и его величина в каждой точке этой оси
известна и может быть представлена в виде
конечного или бесконечного (но сходящегося)
ряда, содержащего только целые степени х.
Тогда потенциал it любой точке пространства
можно получить умножением п-го члена на
/>n(cos6) и заменой х на г. Полученное выра-
выражение справедливо, пока г меняется в тех
же пределах, что и ж в исходном разло-
разложении.
Воспользуемся этим методом для вычисле-
вычисления потенциала кольца,- полный заряд которого
равен Q (фпг. 52). В этом случае
4таУд = О (с2 -f х2 — 2сх cos а)—1!*.
Разлагая Va в ряд, согласно формуле E.117), получаем
при ж>с
-;&2 (fT*.<—>.
при х
V А —
Потенциал в любой точке Р с координатами г, б оказывается равным
при г > с или 0 Фа, г = с
при /• < с или 6 ^= а, /• = с
у=
E.133)
гг=О
С тУ р« (
cos а)
Другие примеры приме1:ения изложенного метода будут даны в конпе
настоящей и в последующих главах.
№ В. Смайт
146 Глава V
§ 18. Заряженное кольцо в проводящей сфере. Если в некоторой
области известен потенциал, обусловленный заданным фиксированным рас-
распределением заряда, то можно найти и потенциал, обусловленный этим
распределением в присутствии проводящей сферической оболочки. Разложим
первоначальный потенциал по сферическим гармоникам и прибавим к нему
второй потенциал, обусловленный индуцированным зарядом и разложенный
по тем же гармоникам. Последвий должен быть таким, чтобы сумма потен-
потенциалов обращалась в нуль на сфере; он стремится к нулю на бесконеч-
бесконечности, если первоначальный заряд находится вне сферы, и конечен в центре
сферы, если заряд расположен внутри.
В качестве примера найдем потенциал в произвольной точке, находя-
находящейся внутри сферической ионизационной камеры радиуса Ь, если коллектор
представляет собой тонкое круглое концентрическое кольцо радиуса о.
В рассмотренной в предыдущем параграфе задаче полоишм а = -гт-7г и г > а,
подставим значение Рп @) из § 16 з и заменим п на 2п, поскольку в реше-
решении сохраняются только четные степени; для потенциала, обусловленного
только кольцом, находим
Потенциал индуцированного заряда должен быть конечным в начале коор-
координат, поэтому он имеет вид
со
Но Vi + Vr = 0 при г = Ъ, поэтому, согласно формуле E.129), можно порознь
приравнять нулю коэффициенты при каждом .Pn(cos6), так что
А2п— К Ч 2-4-6... 'in Ъг
и, если a<r<cb или г = а, б Ф — it, потенциал ранен
Если г < а или г = а, б Ф-zr к, то
При применении этого метода к полям, созданным некоторым распределе-
распределением заряда на проводниках, следует соблюдать осторожность. В действи-
действительности поле индуцированных зарядов влияет, вообще говоря, на инду-
индуцирующие заряды и вызывает их перераспределение; по этой причине
результат может оказаться ошибочным.
§ 19. Сферическая диэлектрическая оболочка в однородном поле.
Вычислим поле внутри диэлектрической оболочки, внутренний и внешний
радиусы которой равны о и b и которая помещена в однородное электро-
Трехмерное распределение потенциала 147
статическое поле напряженности Е. Как и в последней задаче потенциал
снаружи можно рассматривать как потенциал первоначального поля
i?rcos6 плюс потенциал, обусловленный поляризацией диэлектрика. Послед-
Последний должен стремиться к нулю на бесконечности и, следовательно, содер-
содержать только обратные степени г. Кроме того, граничные условия на бес-
бесконечности содержат только одну поверхностную гармоническую функцию
Рг (|а) = cos 6, так что потенциал снаружи должен иметь вид
В диэлектрике с относительной диэлектрической проницаемостью К ввиду
того, что г не обращается ни в нуль, ни в бесконечность, сохраняются оба
члена
V» = (Вг + ~Л cos6.
В полости потенциал должен быть конечным, так что единственно возможное
решение есть
Vs = Dr cos 6.
Четыре граничных условия, необходимые для определения А, В, С и D,
имеют вид
r=b, IV-=F2, или Eb+^ = Bb + -?r, E.136)
-t± = K~ , или Е—-гт==КВ jv-, E.137)
of or о о
r-—a, V^ — Vz, или Ba-\—j = JPa, E.138)
K-~=-~ , или KB ^- = D. E.139)
or or a
Решая эти уравнения, получаем
D== 9?? .
Из выражения для Vs видно, что формула E.140) представляет собой на-
напряженность электрического поля внутри оболочки.
§ 20. Сферический конденсатор с малым расстоянием между цен-
центрами внутренней и внешней обкладок. В качестве примера граничных
условий, содержащих поверхностные гармонические функции, вычислим
приближенно распределение заряда на внутренней обкладке сферического
конденсатора, предполагая, что расстояние между центрами внутренней
и внешней обкладок невелико. (Если внутренний радиус а почти равен
внешнему Ь, то для получения удовлетворительной точности приходится
учитывать очень много членов в формулах, найденных в § 9а методом
изображений.) Выберем начало координат в центре внутренней сферы; тогда
приближенное уравнение внешней поверхности будет
r=b + cP1(v.)t E.141)
где с —расстояние между центрами и [x = cos6. Это соотношение вытекает
из формулы E.117), так как, если пренебречь членами порядка еп при
п>1, формула E.117) даст
Ъ = г [1 + сг-^ ([х)Г = г - сРг О»).
10*
148 ¦ Глава V
Поскольку граничные условия содержат и Ро (р.) и Рг (р.) и поскольку точки
/• = 0 и г = оо находятся вне поля, потенциал должен иметь вид
1(p). E.142)
где С и D — малые поправки порядка с. Граничные условия записываются
<'ледующим образом:
при г = а
1фЦ Г = Ь + С/5! ([Д.)
(произведениями Сс и /)с пренебрегаем). Коэффициенты при Ро(\>.) и Р1(\>.)
следует, согласно формуле E.129), порознь приравнять нулю, откуда
находим
—Vz = O, -
Решая уравнения, получим
д в* (Г,-Г,) г_
6 — a ' F — a)(bs — a3) ' (b — a) (b3 — a3) '
Можно вычислить также плотность поверхностного заряда
/ dV\ sab(Vi — V2)/l Зс ,.\
О = — Ё ( -5— = 4г — —5 — Г5 5 cos о
(членами порядка с" пренебрегаем). Отметим, что при интегрировании о
но поверхности сферы поправочный член выпадает, так что с точностью
до члепов порядка с емкость конденсатора получается такой же, как
и в случае концентричных сфер.
§ 21. Задачи с простой конической границей. В§ 146 было показано,
что потенциал заряда, распределенного по поверхности сферы, можно вы-
выразить через сферические гармонические функции. Можно также показать,
что если потенциал V на поверхности круглого конуса, описываемой урав-
уравнением 6 = а, можно представить в виде
где п — целое число, то потенциал в любой точке простравства будет
рп (сов 0)
V = V (АпГп+ВпГ-"-1) рп (сов 0)
: ¦ ^-1 Рп (сова) ' \ • /
Нетрудно проверить, что это решение удовлетворяет уравнению Лапласа
¦и граничным условиям. « ч
,г § 22а. Зональные гармоники второго рода. Второе решение уравнения
Лежандра, определяемое бесконечными рядами E.106) или E.107), назы-
называется зональной гармоникой второго рода и обозначается Qn(\>-). Эти гар-
гармоники определяются п©..формулам, аналогичным формулам E.112) и E.113):
Трехмерное распределение потенциала
если п — нечетное число,
Qn Ы = (- 1I/2(Г1+1) — ^ Рп. E-144)
если п — четное число,
Определение пригодно при — 1 < р, < -|- 1.
Хотя в рассмотренных выше решениях уравнения Лежандра [x = cos6.
впоследствии при использовании сфероидальных гармоник потребуются
рошопия, в которых будет р.'2 > 1. Поэтому необходимо распространить
ряд E.104) на отрицательные степени г. Формулу E.105) можно записать
в виде
Мы видим, что если аг+2 = 0, то ari.i — al.^6= ... =0, а если а.г+1= 0, то
a_r+3 = a_r+s-=° . .. =0. lio an+2 равно пулю, если ап конечно, и а_п+1 равно
нулю, если aJn_1 конечно. Если выбрать а,1 = 2п!/[2н(и!J], то мы получим
формулу E.114) для полинома Рп (р.); но если принять а_„_1 = 2п (n\JjBn+ 1)!,
то, полагая в формуле E.146) /•=—п — 3, г=—п — 5 и т. д., получим
коэффициенты ряда
Vn VP-^ — B» + 1>I L [л'1 "г 2 Bn-f3) (л"*3 ' ' ' J
2»("'J VI (»+г)!(и+2/-)! Bга+ 1)! n-2r-i
Заменив, согласно обозначениям формулы E.114), г на s, будем иметь
оо
П /„\ _ 2п У (» + *)'(гс + 2s)! п_28.г /5
Ряд, очевидно, сходится при [х2 > 1 и определяет в этой области Qn(v)-t
При очень больших р. член с наименьшим отрицательным показателем
степени в формуле E.147) превышает все остальные, так что
§ 226. Рекуррентные формулы для функций Лежандра второго рода.
Посредством подстановки в формулы E.108) и E.109) величин рп и qn,
определенных из формул E.144) и E.145), можно получить точно таким же
образом, как и формулы E.118) — E.128), следующие соотношения, связи
ваюшие Qn{y.) различных порядков:
(и
1 + B«-5)<?„^+ ... +[хA-[х2I, E.152)
л' _ (rc + l)(^Qn—Qn-,) E
150 • Глава V _ ^
§ 22в. Выражение функций Лежандра второго рода через полиномы
Лежандра. Полезное выражение для Qn(\>.) можно получить из уравнения
Лежандра, если известно, что Рп(\>-) является его решением. Из уравнений
E.76) и E.77) следует, что если v является одним из решений дифферен-
дифференциального уравнения
-g + M-g+M/ = 0, E.154)
где М и ^V —функции х, то второе его решение будет
У = v С А + В С гГ2е~! Шх dsA . E.155)
Для уравнения Лежандра E.103) v = Pn(\>.) и Ж= — 2[хA —р.2), так что
\ Md\). = In (I — р.2), или е J ^ = A — р.2), и формула E.155) принимает вид
Чтобы определить постоянные А и В, положим п = 0 и п=1. Интегрируя
при помощи формул A40) и A52.1) справочника Двайта и используя при-
приведенное там же разложение F01.2), получим
Из формул E.144) и E.145) следует, что #0 (р.) = qb и Qx (р.) = — р{, исполь-
используя для величин q0 и рг выражения E.106) и E.107), будем иметь
Л = 0 и ?=1.
Таким образом, общая формула для @п([х) имеет вид
в частности
0О (,,,)=.*. 1„ 1±? E.157)
и
• (?i (Iх)= ~2 V- ^п 1—~ — ^- E.158)
Используя формулу E.149), получим
E.159)
Повторное применение формулы E.149) дает
Это выражение справедливо при р,2 < 1. Общее решение уравнения Лежандра
будет
Трехмерное распределение потенциала 151
Если положить А'—А—п- В1п( —1) и подставить в решение E.160), то
nnF-JVi М- • ¦ • ] ¦
Следовательно, при [х2 > 1 в качестве формулы, определяющей (?„([х), можно
принять
Полагая и = 0 и п = 1 и используя разложение (Двайт, 601.3), получаем,
что определенные таким образом выражения для величин Qb ([х) и Q1 ([х) сов-
совпадают с E.147).
§ 22г. Некоторые значения функций Лежандра второго рода. При
немощи формул E.160) и E.161) нетрудно найти численные значения
функций (?п([х); для удобства приведем некоторые важные частные значения
этих функций при действительном аргументе:
если п — четное число,
?„@) = 0, E.162)
если и —нечетное число,
если п — любое число,
^(-riH-r^W, E 164)
<?n(l) = co, Qn{co) = 0. E.165)
§ 22д. Функции Лежандра второго рода мнимого аргумента. При-
Применение гармоник сплюснутого сфероида связано с использованием функций
(?n(/Qi где /--( — II'2 и 0<С< оо. При С> 1 выражение для Qn (/?) полу-
получается просто подстановкой /X вместо [х в формулу E.147):
s=0
Аналогичная подстановка в формулу E.161) не приводит к однозначному
результату, поскольку логарифмический член в формуле E.161) много-
многозначен. Применяя формулы F01.2) и E06.2) из справочника Двайта, не-
нетрудно получить
Dii )=-2/
Если представить коэффициенты в формуле E.161) в виде E.131) и ис-
использовать приведенный выше ряд для логарифма, то получится выраже-
выражение, совпадающее с выражением E.166). Таким образом, имеет место сле-
следующее соотношение:
<?п(/9= -/^саЕ^РА/ч-^Рп-ЛГч-^Е^РпАГч----, E-167)
где arcctg меняется в пределах от 0 до и. Это выражение можно исполь-
использовать для определения Qn{J4 Б0 всем интервале —оо < С < со, по-
поскольку оно не имеет особенности при С=1. Отметим, что при конечных С
функция Qn(fQ конечна и что,
если п — четное число,
f ^le"??^ ' <5-168)
152 Глава V
если и —нечетное число,
E-169)
При больших С член с наименьшим отрицательным показателем степени
в формуле E.166) много больше всех остальных, так что
Ц(- >)пп ^ • EЛ70)
Весьма полезную формулу можно получить, если продифференцировать
выражение E.156), а интегралы, содержащиеся в найденном соотношении,
исключить при помощи выражения E.156). Подстанлян /1 вместо [х, будем
иметь
К (/С) Qn (/С) - Р'п (/С) Qn (/С) = A + С2)- E.171)
§ 22е. Применение функций Лежандра второго рода в теории по-
потенциала. Наиболее важные применения зональных гармовик второго рода
связаны с использованием сфероидальных гармоник. Поскольку функции Qn (jj.)
обращаются в бесконечность при ц = 1, ови используются в качестве сфериче-
сферических гармоник главным образом в тех задачах, в которых коническая гра-
граница исключает ось (jx=l) из области, где ищется электростатическое поле.
Рассмотрим, например, случай двух коаксиальных конусов. Пусть
потенциал равен нулю па конусе 6 = р и равен Va = V (Лпгп + Впг~п~а) на
конусе б = а. Тогда в пространстве между конусами потенциал будет
v _ -у wlTl. -r^w'^lQr, (cos 6) Pn(v) — Pn(ros$)Qr,
где [j, = cos б. Проверка показывает, что это решение удовлетворяет гра-
граничным условиям.
Интересен тот частный случай, когда один конус имеет потепциал,
равный нулю, а другой — потевциал, равный Vx. Поскольку Р0([х) = 1, то
в этом случае
V __ A Qo(fOSp) —QoffOS-») _ .
v- ло<?0(,-ов М-Qo (cos a)-Не-
a)-Несогласно формуле D06.2) из справочника Дваата,
Qv (cos б) =А In [A + cos 6) / A - cos 0)] = - In tg @/2)
и выражение для потенциала между конусами имеет вид
V = Vl ln-f- / In-f- . E.173)
§ 23. Зональные гармоники нецелого порядка. Во многих случаях,
когда область, н которой ищется потепциал, имеет конические границы,
применение гармоник только с целыми значениями п оказывается недоста-
недостаточным. В этих случаях необходимо обобщить выражения для гармоник
па значения п, определяемые таким образом, чтобы Рп(\у) или Qn(\>.) об-
обращались в нуль на соответствующих конусах. Многие из приведенных
выше соотношевий [например, рекуррентные формулы для Рп([>-) и (?п(р.)]
справедливы и при нецелых значениях п; однако основные определения
нуждаются в соответствующей модификации. Так, выражением для Рп(\>.),
Трехмерное распределение потенциала 153
пригодным для любых значений п, будет ряд
у (nA-\)(nA-2)...(n-\-r)(-n)(\ — n)...(r — \-n)
()
Этот ряд сходится при любых [j. = cos 6, за исключением б = ir. Пример гар-
гармоник такого рода можно найти в § 27а — 27в настоящей главы, если при
нять, что заряд расположен на оси полости и, следовательно, ж = 0.
Если v не является целым числом, то Ру (jj.) и /\ (— jj.) будут незави-
независимыми решениями уравнения Лежандра и будут связаны с <Qy (jj.) cootho
шением
Если п — цслоо число, то функция (?„([а), определенная п § 22а, яиляетс.я
пределом Qv (u.) при v —> п.
§ 24а. Присоединенные функции Лежапдра. В § 13 и 15 настоящей
главы было показано, что решением урашюпия Лапласа в сферических
координатах является произведение ДЙФ, где
R^A^+Br-"-1, E.176)
Ф = С cos mtp + D sin mtp, E.177)
«I
а в является решением уравнения E.102), которое, если ввести [х вместо
cos G, принимает нпд
При накождеттпи решения этого уравнения мы исходили из уравнении Ле-
гкаидра, соответствующего /п = 0. Выполняя дифференцирование произведе-
пия в первом члене уравнения Лежандра, можно привести последнее к виду
Решениями этого уравнения являются у = Рч(^) и l/ = Qn([>-)- Диффореици-
руя уравнение Лежапдра т раз и обозначая dmy/d[>.m через V, получаем
A-р*)$-2р{т+1)^+(п-т)(п4-т + 1)» = 0. E.179)
Вводя ш = A — [х2I/27Пу, или v=-'-{i—^Y^mw, получим уравнение E.179)
в виде
^^[ ^] = U. E.I80)
Это уравнение совпадает с уравнением E.178), в чем нетрудно убедиться,
выполнив дифференцирование в первом члене E.178); следовательно, ре-
решения уравнения E.178) имеют вид
Поскольку у является решением уравнения Лежапдра, то общее решение-
уравнения E.178) записывается следующим образом:
154 Глава V
где Р™([>) и (?™([х) при — 1 < [х< +1 определяются по формулам
К (I*) = A - №>*m~jP- , E-182)
^- E-183)
Для — 1 < [х < +1 Гобсон вводит в правые части множитель (— I). В тех
случаях, когда [х, будучи действительной или мнимой величиной, по мо-
модулю больше единицы, функции Р™{[>.) и Q™(jx) определяются следующим
образом^:
E.184)
E.185)
Эти функции известны как присоединенные функции Лежандра первого и
второго рода. Их можно получить при помощи формул E.182) и E.183)
из уже известных выражений для Рп(\>.) и Qn([>-).
Для действительных значений [х, меньших единицы, формулы E.182)
и E.183) дают
Р\ (V) = A - ^2I/2. Р% Ы
РЪ(р) = 3 A - Ц«) V. [X, Р\ ([Х) = А A _
- 1), Р\ М = Ю5 A - [х2K/2 [х,
[хгJ. E.186)
Для больших значений т и /г используются рекуррентные формулы § 24г.
При действительных значениях [х, больших единицы, формулы для
функций Р™ ([х) и $?([а)> определяемых согласно выражениям E.184) и
E.185), можно получить заменой в приведенных выше выражениях E.186)
•множителя A —[х2I^ на ([х2— lI^ и, кроме того, заменой 1 — [х на [х-1
в логарифмическом члене функции Q™ (jx). Для больших значений тип
используются рекуррентные формулы § 24г.
Трехмерное распределение потенциала 155
Для мнимых значений аргумента, согласно § 16з, § 22д и формулам
E.184) и E.185), будем иметь
= С arc ctgC-1,
E-187)
В формулах для (C(/Q-arcctg изменяется от 0 до тс при значении С, изме-
изменяющемся от + °° Д° — °° •
Если [х—»оо, то, подставляя формулы E.116) и E.148) в E.184) и
E.185), получаем
ЯМ^шЩ^*"' EЛ88>
• E-189)
В случае т = п при подстановке формулы E.114) в E.182) сохраняется
только член, соответствующий s = 0; в результате получается решение,
найденное в § 126 [формула E.81)]:
P?(cose) = Bm-l)!!sinm6. E.190)
Для Р^(х) можно дать интегральное представление; пригодное при любых п
и ж>1:
riff (*) = (» + !) (и+ 2) .-
Т.
...(п + т){ [x + (x2 — lI^cos<f]ncosm(fd(f. E.191)
Подстановка в уравнение E.178) и двукратное интегрирование по частям
показывает, что выражение E.191) удовлетворяет уравнению Лежандра.
Постоянный множитель нетрудно проверить, если устремить ж—» оо (инте-
(интеграл при этом вычисляется) и сравнить результат с формулой E.188).
§ 246. Интегралы от произведений присоединенных функции. Урав-
Уравнение E.92) показывает, что при п -/= п'
+ 1 2-я
[ \ [рп М Рп- ((J-) (A cos my -Ь В sin mep) (A' cos iw'<p -f-
Bdd . E.192)
Благодаря наличию произведения тригонометрических функций этот инте-
интеграл равен нулю и в том случае, если т — целое число и т фт' незави-
независимо от значений п и п' (см. Двайт, 435, 445 и 465).
Чтобы определить значение интеграла E.192) при /г = /г' и т = т',
необходимо вычислить интеграл от квадрата Р™^) по поверхности сферы
единичного радиуса.
156 Глава V
Используя для Р™{[>.) выражения E.182) и E.115), получим при помо-
помощи интегрирования по частям
2[х= \ udv =
—i —1
*>2tt / \\9~ \ I Vr* / ^7 n+m \Г* *) I " I j r>4.?n— 1 \Г* 1J I ^^
-1
+ 1
Повторим интегрирование ш> чистим, полагая кайчдый раа
Произведение г<« обращается в пуль на граштцах интервала, поскольку и
содержит множитель (J.2 — l при m^s, а г — при m <' s. Поэтому поело
(т + и)-кратного интегрирования по частим получим
= \ -gj^jjl- {^ [(^ 1Г|-_^(^_1)«] j f/[x. E.193)
1
— i . ¦—1
Так как степень [х при дифференцировании понижается, второй множитель
в подинтегральном выражении оказывается, очевидно, постоянным. Поэтому,
сохраняя лишь наивысшую степень \х и заменив ;х2—1 па ;х2, получим,
что этот множитель равей
[2nBn-l)Bn-2).. (n- ^Ч*0'
Весь интеграл с учетом формул E.126) и E.127) оказыпается равнг^м
-1 —1
+1 2
) l n\rn i 2
При w ф= п' из формулы E.192) следует
+1
(п — т)\ ) l n\rn i 2п + 1 (п — т)! ч '
\ Р?ЫР1?МФ = 0. E.195)
—1
В случае m =/= т' весьма полезным является следующее интегральное соот-
соотношение:
t1 F М Рт' (и.)
^ 1Ц^ AЛ) ф = 0. E.196)
-1
Для доказательства этой формулы запишем уравнение E.178), обозначив
сначала в = г/ и т = т, а потом в=г/' и т = т'; умножим первое уравне-
уравнение на у', второе—на у, вычтем и проинтегрируем от —1 до +1. Для
интегрирования в случае т = т' перенесем средний член уравнения E.205)
Трехмерное распределение потенциала 157
в правую часть, возведем в квадрат, заменим исюду п на п — 1, умножим
на п + т и исключим из результата Ф^/в™"/ при помощи уравнения E.208),
возведенного в квадрат и умноженного на п — т. При интегрировании от
— 1 до -t-1 все члены, не содержащие 1—;х2, интегрируются согласно
формуле E.194) и взаимно уничтожаются; в результате остается
J —[л.2 п — т J 1 — (J.2 Bт)! (п — т)! ^ 1—[а2 "
Подставляя Н^ по формуле E.190) и интегрируя (см. Двайт, 854.1), на-
находим
(^ !^Mi i^ E.197)
m (n — m)\
-1 0
При применении вектор-иоте.пциала нам придется пользоваться свойствами
ортогональности поверхностных векторных функций cos6, определяемых
соотношением
Р™М= I A-^I/2РГ Ы ± I тA-».*)-*» Kb). E.198)
Интегрирование скалярного произведения двух таких функций дает
-1
+1
Г г,л 2\ pW / N Dm' / \ i 2 (Л 2\-1 Рт / N Рт I
— 1
Заменяя второй член при помоши уравнения E.178) и группируя члены,
находим
+1 - +1
ЙЙ d\x =
{ [A - V-2) Рп'] Pf +1 [A - !-2) Рп'} K
+ i
п'Рр]1\ + п(п + 1) J ЙЙф = я(п
—1 —1
—1
Согласно формулам E.192) и E.194), результат равен нулю при п Ф р
и равен
+1
С 2
(n-m)! (
при n = p.
§ 24в. Присоединенные функции от мнимого аргумента. Применение
гармоншг сплюснутого сфероида приводит к появлению функций Р™ (/С)
и ^5Г(/С) <>т мнимого аргумента, где С изменяется от 0 до оо. Представление
этих функций в виде рядов можно получить, применяя формулы E.184)
и E.185) к E.131) и E.166). Следует отметить, что окончательные ряды
для Р™ (/С) содержат только пулевые или положительные степени ",, так
158 Глава V
что Pn(f-O) конечны, а Р™ (j ¦ ее) бесконечны. Ряды для (С (/С) содер-
содержат только отрицательные степени С, так что Q™ (j ¦ оо) обращается в нуль.
Получим теперь для этих функций важное соотношение, аналогичное
соотношению E.171). Согласно выражению E.155),
Продифференцируем это равенство и исключим при помощи полученной
формулы интеграл из правой части; в результате (после замены [х на /С)
будем иметь
? • E-200>
Полагая С —» оо и учитывая формулы E.188) и E.189), находим
B = (-l)m&±!!&. E.201)
§ 24г. Рекуррентные формулы для присоединенных функций Лежандра.
Как было показано в § 16д и 226, рекуррентные формулы для функций
Рп ([х) и Qn ([>.) одинаковы. Знак в соответствующих формулах для функций
в™ = АР™ ([>.) + BQ™ ([х) зависит от того, изменяется ли [х в интервале
— 1 < [х < +1 или [х > 1 или же [х является величиной мнимой. Ниже
будут получены эти формулы, причем верхний знак будет относиться к слу-
случаю [x = cos6. Продифференцируем выражение E.122) т раз, умвожим на
sinm+1 6 или на ([х2—l)V2(w+i)j B результате, согласно формулам E.182)
и E.183) или E.184) и E.185), будем иметь
в^+11 = (т + п + 1)[±A-^)]1^е^ + [хеГ+1. E.202)
Теперь продифференцируем выражение E.119) т раз и умножим на
[± A— [i,2)ji/2(m+i)- принимая во внимание формулы E.182) и E.183) или
E.184) и E.185), получим
е^,1 - ей1=Bп+1) [± A - (х2)]1^ е™. E.203)
Вычтем выражение E.203) из E.202), в результате найдем
E.204>
Заменим в формуле E.202) и на и—1 и исключим @™-f и в|Г_ь исполь-
используя для этого соотношение E.204) и соотношение, получающееся из E.204)
заменой т на т — 1. Если разделим результат на — A — jx2), то получим
формулу
A-[х2)Г1/2 @т±(т + п)(п-т+ 1)вГ"' =0, E.205)
являющуюся рекуррентной относительно т.
Если умножим формулу E.202) на т— п и формулу E.204) на т + п+ 1,
вычтем одну из другой и заменим в результате т + 1 на т, то получим
рекуррентную формулу относительно п:
(т - л - 1) е?+1 + Bи + 1) [хв™ - (т + п) K-i = 0. E.206)
Трехмерное распределение потенциала 159'
Дифференцируя выражения E.182) и E.183) или E.184) и E.185) и поль-
пользуясь приведенными выше формулами, нетрудно получить
= rp I (m + и) (и - ттг + 1) в™ + J-<C+1 =
= Т Щ. [± A - (х2)]-1'2 в™ Т (т + п)(п- т +1) eJT1 • E.207)
Иногда желательно выразить [± A — jj.2)]'2 в™ через функции Лежапдра.
Для этого заменим в формуле E.202) /и на т — 1, разделим на [±A — у-2)]1'2,
подставим [а[± A — [А2)]~1/2в™ из формулы E.205) и заменим в окончатель-
окончательном выражении п на п—1; в результате будем иметь
2т[±A-[х2)Г1/2е^ = ±еЙ1-1-(п+т-1)(т + и)е^Г11. E.208)
Замена т на т — 1 в формуле E.203) и подстановка в последнее из выра-
выражений E.207) дает
A-[х2)е^'= ± т[хв^=Р (m + и) (и-т + 1)Bи+1Г1 (©-+!-©«-О-
Преобразуя, согласно формуле E.206), последний, первый и средний члены
этого равенства, получим соответственно
= ± Bи+ I) [{т-п- 1) в™+1 +(п + l)(m + n)
= Т и[а©™ ± (/и + п) Qt-i • E.209)
§ 24д. Некоторые значения присоединенных функций Лежандра.
При помощи рекуррентных формул предыдущего параграфа, а именно E.205)
и E.207), совместно с результатами § 16з и §22г, получаются следующие
соотношения:
если п + т — четное число,
Рт (Q\ = ,' _ 1W2 (п-т) 1-3-5...(n + m — 1)
n ^ ; V ; 2-4.'о... (и —mj '
если п-\-т — нечетное число,
если п + т — нечетное число,
2-4-6
1.3-5...(n—m)
если п + тп — четное число,
160 Глава V
§ 24е. Равновесные (нейтральные) точки и линии. Чтобы исследовать
характер точки равновесия, выберем начало координат в этой точке и вос-
воспользуемся разложением потенциала но сферическим гармоникам. Внутри
сферы достаточно малого радиуса (настолько малого, что внутри нее не
содержится зарядов) потенциал должен быть конечным и, следовательно,
иметь вид
со п
V = 2 2 AnnrnP™(cos 0) cos (икр + 8m). E.210)
В точке равновесия VF равен нулю, так что oVjdr—^O при /• —^0 и коэф-
коэффициенты Ат1 равны нулю. В основу классификации точек равновесия
можно положить соответствующее данной точке наибольшее значение р,
такое, что псе Атп (п < р) обращаются в нуль при г—»0. Таким образом,
для точки равновесия р-ro порядка р есть наибольшее целое число, для
которого при любых значениях 6 и »
дУ 3^F dPV
В достаточно малой окрестности точки (или линии) равновесия р-то порядка
V = Ло + /-р+1 2 А». р+1 ^р+1 (cos 6) cos (пщ + Bm). E.212)
Потенциал в точке равновесия равен Аы,. Уравнение эквипотенциальных
поверхностей, пересекающихся в этой точке, получается для малых г путем
приравнивания нулю суммы, в выражении E.212). Для аксиально-симме-
аксиально-симметричного поля m равно нулю, и эквипотенциальные поверхности имеют вид
конусов, угол раствора которых 2а определяется уравнением Pp+i (cos a) = 0.
Согласно § 16з, для точек первого порядка угол а равен 54°44' и 125°36';
для течек второго порядка угол а равен 39°!4', 90° и 140°46' и т. д.
Простейшая линия равновесия соответствует тому случаю, когда все члены,
кроме тп = р -{-1, равны нулю. На этой линии равновесия пересекаются
р + 1 эквипотенциальных поверхностей, являющихся плоскостями, образую-
образующими менту собой угол и/(/? + 1).
§ 25. Биаксиальные гармоники. Б некоторых случаях может потребо-
потребоваться представить зональную поверхностную гармонику Рп (cos б') через
поверхностные гармоники Sn F, ср), отнесенные к другой оси. Пусть две оси
пересекаются в начале координат и координаты оси 6' в системе б, ср равны
0 = 0 и ср = 0. Требуется найти коэффициенты разложения
т~п
¦ Рп (cos б') = У| АтР™ (cos 6) cos /иср. E.213)
тп=0
Умножим правую и левую части этого равенства на Р"п (cos 6) cos (scp) и про-
проинтегрируем по поверхности единичной сферы. В правой части все члены,
согласно" § 246, обращаются в нуль, за исключением одного, содержа-
содержащего Sn; с учетом выражения E.194) он равен
Am ) [PZ Ы В)}* cos* rn^dS-^V^^ An. E.214)
s
Интеграл, стоящий в левой стороне, имеет «ид
Трехмерное распределение потенциала 161
Точно такой же интеграл появляется в качестве коэффициента при Ъп в вы-
выражении для потенциала Vp, создаваемого в точке 6' = 0, r==b зарядом,
распределенным но поверхности единичной сферы с плотностью ?„F, ср).
;)та задача была решена в § 146, и, следовательно, искомый интеграл можно
приравнять коэффициенту при Ьп в соответствующем решении, пригодном
при любых Ь ¦< 1. Таким образом,
Используя разложевпе E.117) и принимая во внимание, что интегралы от
произведений типа Pr(casb')SnF, <р) обращаются, согласно формуле E.92),
в нуль, получаем ь правой части один член:
faeVp = Ьп \ Pn (COS 6') Sn F, cp) dS.
s
Но потенциал Vp был вычислен п § 146 [формула E.97)]:
i\ нашем случае координаты точки Р относительно оси О равны 6 = 0
и ср = О, так что Sn (G, ср) = Р™ (cos в), и равенство коэффициентов при Ьп
в двух различных выражениях для Vp означает
\ Рп (cos в') Рп (cos G) cos гщ dS = 5^-т К (cos в). E.215)
s
Приравнивая интегралы E.214) и E.215), определяем Ат
Если нг = О, то интегралы E.214) и E.215) вычисляются при помощи фор-
формул E.127) и E.97):
s s
Подстановка в соотношение E.213) дает
т=0
где 8$п=1 ири т — 0 я 8^=0 при т ф 0. Этот символ носит название
символа Кронекера и в более общем виде записывается 8™, причем 8™ = 1
при ю=и и 3™ = 0 при т ф п.
§ 26. Конические границы. Потенциал, созданный внутри конуса за-
зарядом, распределенным произвольным образом по его поверхности, можно
найти, если постоянные разделения в уравнении E.82-) выбраны так, что
функции R и Ф оказываются ортогональными. Так, если п равно jp — 1/2>
го К равно - /?2 + 1/4i H К> согласно выражению E.84), имеет вид
Rv = А'г'р-1'* + В'г-™-1!* = г-J/2 A cos (p In /• + 8Р). E.218)
Произведение RvRV'dr оказывается равным cos(/?^ + 8p)cos(/>'^ + V)^
(где ф = 1пг), что приводит к ряду или интегралу Фурье по In г.
В. Смайт
162
Глава V
В множителе в появляются функции Лежандра порядка jp - г/2. Эти функ-
функции носят название конических функций; они были рассмотрены Гобсоном,,
Гейне и др. Гобсон приводит для них такой ряд:
Решение, соответствующее верхнему знаку и обращающееся в бесконечность
при [а=1, следует использовать для области, лежащей вне конуса; нижний
знак соответствует решению для внутренней области. Эта функция не
является периодической. Формула E.182) была получена без специальных
предположений относительно п, поэтому
dmPi±lX) E-220)
§ 27а. Присоединенные функции Лежандра нецелого порядка. Как
уже было указано в предыдущем параграфе, при наличии конических
границ приходится пользоваться функциями -Р™([*) или (?™(;л,), у которых
ипдекс п не является целым числом. В частности, приходится пользоваться
разложением в ряд по функциям Лежандра, порядок которых п таков,
что 8™ (fj,0) = 0. Для этого необходимо иметь формулы, аналогичные фор-
формулам E.92) и E.194). Пусть 6™([х) = г/ и в™ (\х) = у' — решения уравнения;
E.178), такие, что
е?Ы = вяЫ = 0. E.221)
Тогда
Умножая первое уравнение на у', второе — на у и вычитая одно из дру-
другого, находим
Интегрируя от {а0 до 1, будем иметь
1
}>¦(,
(п—п')(п+п'-\-\)
Откуда при п ф п', согласно соотношению E.221), следует
1
E.222)
E.223)
Для п=п' поступим следующим образом. Пусть п—п'~&п'. Подставив.
у = у' -\-(ду'}дп')Ьп' в выражение E.222), найдем
di/ , dy , ду' , дч' ду' . , , ду' , д2у' . ,
* rf(j " ф " dfx ' др дп " ду. J
( ф f р дп " ду. J д\>.дп'
Поскольку при [а = {х0 у' = 0, то при п^-п' получим
Трехмерное распределение потенциала
Для вычисления значений йв™/5п можно воспользоваться представлением
функции 6™ в виде ряда [например, ряда E.104)] или в виде определев
ного интеграла (последнее можно найти в работах, список которых при-
приведен в конце настоящей главы).
§ 276. Функция Грина для конуса. Рассмотрим задачу о точечном
заряде q, расположенном внутри заземленного конуса б = а в точке г = а,
б = р, <р = <р0. Под точечным зарядом мы будем понимать такой заряд, раз-
размеры которого достаточно малы, но все-таки отличны от нуля, так что
напряженность поля и потенциал в математическом смысле являются функ-
функциями ограниченнымиг). Граничные условия (F = 0 на конусе) автомати-
автоматически удовлетворяются, если пользоваться разложением по функциям Лежанд-
ра, порядок которых п подобран таким образом, что Р™ (\i0) = 0, где [а0 = cos a.
Из формул E.176), E.177) и E.182) следует~что при таком выборе п ре-
решение уравнения Лапласа, конечное при г = 0 и г= оо, непрерывное при
г = а и имеющее должную симметрию относительно ср0, имеет вид
при г < а
^i=2 2 А^(~У Рп Ы cos m (cp-To), E.225)
при г > а
^ СО
^0 = 2 2 A™(y)n+1^Mcosm(cp-To). E.226)
п т=0
Чтобы определить коэффициенты Атп, введем новую переменную tp' = <р — tp0,
составим, как в § 8 гл. IV, разность dVJdr — dVojdr, умножим правую и
левую части на Р^ (fj,)cos/?cp' d\xdy' п проинтегрируем от ср' = 0 до ср' = 2-п
и от [а = {а0 до jj.= 1. Тогда (см. Двайт, 445) все члены в правой части
обращаются в нуль, кроме членов т=р; последние, согласно формуле
E.223), также обращаются в нуль, за исключением членов n = s. После
умножения на а2 получаем
27С+1
+ 1 2г.
[Р* (р)]Ыр \ cosVcp'rfcp'. E.227)
b
Интегралы в правой части вычисляются при помощи формулы E.224)
и формулы (Двайт, 440.20), кроме случая, когда р — 0. Для вычисления
левой части заметим, что a2 dp efcp' = — a2 sin 6 d6 dy' = — dS. Поле непре-
непрерывно на сфере радиуса г = а, за исключением бесконечно малого участка
поверхности AS около точки б = р, ср = ср0 (или ср' = 0), где сосредоточен
заряд. Поэтому dVijdr = dVoldr и подиитегралъное выражение обращается
в]нуль везде, кроме площадки AS, которая выбирается настолько малой,
что под интегралом Р^ ([i) можно заменить на Ps([>-i) (tAi = cosP)i а cos/ко' —
на 1. Поскольку на внутренней стороне AS dVJdr= —dV/dn, а на внеш-
внешней стороне AS dVoldr = dV/dn, левая часть уравнения E.227), согласно
Ч Здесь и в дальнейшем (§ 28е, ЗОи и т. д.) автор фактически рассматривает точеч-
точечный заряд, плотность которого описывается В-фупкцией Дирака. Вопрос о сходимости
соответствующих рядов ие затрагивается.—Прим. перев.:
И*
1E4 Гдава V
теореме Гаусса о потоке электрической индукпии A.27), оказывается равной
n e s vrl/ v '
Разрешая уравнение ^5.227) относительно Aps и изменяя р на то и s на w
п соответствии с обозначениями в формулах E.225) и E.226), получаем
где 8т = 1 при т — 0 и 8т = 0 при т ф О.
§ 27в. Функция Грина для конической полости. Предположим, что
заряд д находится между заземлеивыми сферами r = d иг = си внутри
заземленного конуса 0 = а, так что с < а < d и 0 < р < а. В этом случае
к функции Грина для конуса надо прибавить потенпиал, обращающийся
в нуль на самом конусе и дающий при /¦ = d и /¦ = с суммарный потенциал,
равный нулю. Поскольку точки г=0 и г—со исключены из области, в
которой ищется поле, этот потенциал должен иметь вид E.225) или E.226),
где (г/а)п или (a//-)n+I заменены на Су* + Dvr~n~l. Если прибавить полу-
полученное выражевие к выражению E.225) и положить г = с, то суммарный
потенциал должен обратиться в нуль, откуда
?1=0- E-23°)
Приравнивая к нулю суммарный потенциал при r = d, получаем
^=0. E.231)
Определив Сп и 1)п из соотношения E.230) и E.231) и прибавив новый
потенциал к потенциалу E.225), найдем для г < а
i cos то (<f — <р0) • E.232)
п m=0
Аналогично, для /• ^> а, согласно формуле E.226), находим
<р0). E.233)
Если, кроме того, плоскости ф = + ~( и ср = 0 (-(¦ > срп > 0) имеют нулевой
потенциал и если -(= iz/s (s — целое число), то решение можно получить
при помощи метода изображений в виде суммы потенциалов типа E.232)
м E.233). Если -(-f=- тс/s, следует использовать гармоники нецелочисленных
порядков вида sin (ттсср/-^). Благодаря этому в коэффициенте Атп появляет-
появляется множитель 2г./-(, а в выражениях E.232) и E.233) cosm(<p — cpn) заменяет-
заменяется на sin (m-n:cpo/-c)sm(mir.f/Y).
§ 28а. «Сплюснутые» сфероидальные координаты. Обычными геомет-
геометрическими объектами, встречающимися в электрической аппаратуре, являются
тонкий круглый диск и тонкий лист с круглым отверстием. Ни одна из
изученных до сих пор координатных систем не образует таких естествен-
естественных границ, за исключением конфокальной системы, описанной в § 2 и 3.
В этой системе, фиксируя значение одной из координат и не ограничивая
Трехмерное распределение потенциала 16Й
пределов изменения остальных, можно получить поверхность требуемой
формы. Наличие аксиальной симметрии, когда трехосные эллипсоиды
превращаются в сплюснутые сфероиды, сильно упрощает задачу. Ниже
рассматривается решение уравнения Лапласа в такой системе координат;
оно содержит функции, известные под названием гармоник сплюснутого
сфероида.
Положим в уравнении E.4) большие полуоси Ь и с равными друг
другу и обозначим у = р cos <р и z = p sin <p. Тогда уравнение можно записать
в виде
х2 , Р2 „4 /
Положим в этом уравнении а2 + 0 = (Ь2 — а2) ®\ = с\ Ь\. Тогда при — а* < 0 < со
или 0 < ?2 < со (где 6^ = I?) мы получаем конфокальные сплюснутые сфе-
сфероиды, а при — Ъ2 < 6 < — а2 или 0 < I2 < 1 (где — ti\ = ?2) — конфокальные
однополостные гиперболоиды. Третьей координатой является, очевидно,
азимутальный угол <р. Уравнение сфероидов имеет вид
а уравнение гиперболоидов —
_?L^+ р!__=1. E.236)
fiZ^Z 1 учи /Л t I *
Исключив р из этих уравнений, получим
а исключив х —
E.238)
Координата р всегда положительна, а х принимает значения от — со до
+ со. Поэтому если выбрать 0 < С < со, то следует принять — 1 < \ < + \
(см. фиг. 54), а если выбрать —со<С< + со, то следует принять
O<L<1 (см. фиг. 53).
Чтобы написать уравнение Лапласа в такой системе координат, необ-
необходимо вычислить коэффициенты hl7 h2 и h3 в уравнении C.13). Согласно
выражениям C.10),
1 as . ао, \ э'с дь,
кг дп ' дп h2 дп дп
При помощи формулы E.5) получаем
ае, 1 ае \\U\ i
an 2c|(J, ci
Записывая координаты в порядке Е, 'С, ч. \\ подставляя вместо х и р их
значения E.237) и E-238), находим
E-241)
166 Глава V
Уравнение Лапласа C.13) можно записать и виде
§ 286. Гармоники сплюснутого сфероида. Решение уравнения E.242),
имеющее вид F=EZ<I>(rfle В, Z и Ф — соответственно функции только
f Д и <р), называется гармоникой сплюснутого сфероида. Умножая урав-
уравнение E.242) на A + С2) A — S2) [аЯФ($2 + С2)], получаем, что последний
член зависит только от ср. Чтобы найти решение уравнения, как и в § 13,
приравняем этот член —т2, а остальные члены -4-и?2, тогда
Последнее уравнение удовлетворяется, если
E.244)
Полагая С = /С, приводим второе из этих уравнений к виду
0. E.245)
Решение уравнения E.243), согласно выражению E.177), будет
Фт = С cosm?+ D sin тр. E.246)
Уравнения E.244) и E.245) совпадают с, E.178), поэтому их решение
имеет вид E.181)
E.247)
E.248)
it, следовательно, общее решевие будет
2тпФт. E.249)
Поскольку сфера есть частный случай сфероида, естественно ожидать, что
сферические гармоники — частный случай сфероидальных. Проследим, как
решение, определяемое выражениями E.246) —E.249), переходит в решение
E.177), E.181) и E.176) при стремлении эксцентриситета эллипсоида
к нулю. При сх —*¦ 0 ¦ диск, соответствующий С = 0, стягивается в точку
= 0. Из выражения E.237) вытекает, что С—»оо при сх—а-0 (так как
?0), ив выражении E.238) можно пренебречь 1 по сравнению с С2
P1()(
ci->0 c
¦ Из этого выражения находим 5:
S-»a;(a;2 + P2)-1/2==coso = (x. E.250)
ci->-0
Таким образом, решение E.247) переходит в решение E.181).
Трехмерное распределение потенциала
167
Из выражения E.237) получаем, чтп
„ х
г
Используя формулы E.188) и E.189), находим
A2rn и
E.251)
E.252)
Откуда следует, что решение E.248) переходит в решение E.176).
Формулы E.250) и E.252) во многих случаях позволяют сразу найти
гармоники сплюснутого сфероида, требуемые для решения данной задачи,
«ели известен вид решения соответствующей задачи в сферических гармо-
гармониках.
§ 28в. Проводящий лист с круглым отверстием. Рассмотрим беско-
бесконечный тонкий плоский металлический лист с круглым отверстием, кото-
который либо сам заряжен, либо является границей внешвего однородного
поля.
Фиг. 53.
Чтобы координаты были непрерывными во всем пространстве, где
существует электрическое поле, выберем 0<?<!l и —оо< С< + °о; при
этом С имеет тот же знак, что и х. Как показано на фиг. 53, уравнение
листа имеет вид ? = 0. Рассмотрим случай, когда такой лист, имеющий
потенциал, равный нулю, является границей однородного внешнего поля.
При ж=со поле должно совпадать с невозмущенным однородным полем,
а при х= — со оно должно быть равно нулю. Поскольку при С2—>оо
можно пренебречь 1 по сравнению с С, выражения E.237) и E.238) дают
т. е. С—>±г/с1 и ? = х/(с^)—>| ж|/г = | cos б |. Уравнение однородного поля
при ж=оо имеет вид V = Er cosO, т. е. S входит в него только через cos б;
иными словами, решение содержит только Рг(Ч) и, следовательно, соот-
соответствует т — 0, п—\. Поэтому с учетом E.249), E.247) и E.248)
168 ' Глава V
потенциал равен
V = P, (?) [А'Р1 (/С) + B'Q, (/С)]. E.253)
Подставив сюда значения Р1 и Q1 ич формул E.187), получаем
F=c[M'C + fi'(CarcctgC-l)]. E.254)
Чтобы вычислить А' и i?', рассмотрим C=rfc °°- При С= + со коэффи-
коэффициент при В' обращается п нуль и
^, откуда Ес1 = /А'. E.255)
При ? = —оо постоянным членом можно пренебречь, поэтому
0=cosg(^ + ^). откуда «В'= /А', E.256)
пли
В'=-^ E.257)
Ксли край отверстия соответствует р — а, то, поскольку С и ? равны при
этом нулю, из выражения E.238) следует, что (^ = 0. Для потенциала,
таким образом, получаем
F = a_7E [;-i-(Carcctg;- 1I . E.258)
Плотность заряда на поверхности листа дается формулой
0= ~ eS~>=Fsr ¦ E.259)
Из выражения E.238) вытекает, что аС=±(р2 - а2I/з при Ё = 0; поэтов
и, согласно формулам E.258) и E.259),
го cos—Ь —гг~ > , (^ 9(Ч)\
где знак плюс соответствует верхней стороне поверхности, а минус —
нижней.
§ 28г. Момент, действующий на диск в однородном ноле. Если незаря:
женный проводящий диск радиуса а расположен такпм образом, что нормаль
к нему образует угол а с электрическим полем Е (однородным до внесения
диска), то внешнее поле Е можно рассматривать как суперпозицию двух одно-
однородных полей: поля Z?cosa, перпендикулярного к плоскости диска, и поля
Е' = Е sin a, параллельного плоскости диска. Для решения задачи во втором
случае можно воспользоваться гармониками сплюснутого сфероида. Непре-
Непрерывность координат достигается тогда при 0<С<°° и — l<l<-fl:
такая система координат изображена на фиг. 54. Как и в предыдущем
параграфе, при г=оо С—> г fa и Z—^-^cosB, причем знак ? совпадает
со знаком х. В бесконечности, где сохраняется невозмущенвое поле,
~Vco = b р costp = b, а [A ^ ?2) A + lj)] '2 costs. E.261)
Поскольку tp «ходит в решение только в виде cos^, в решениях E.246)
E.249) т должно быть равно единице. Но н>т, поэтому наименьшее воз-
Трехмерное распределение потенциала
16!»
можное значение п есть п = 1. Далее, при г = оо .зависимость F^ от ? и С
E.261) соответствует множителю A — [л,2I^™ в формулах E.182) и E.183).
Следовательно, значение п > 1 невозможно, так как г. этом случае» при
Фиг. 54,
дифференцировании в формулах E.182) и E.183) ? и С появились бы в кн
честве множителей. Согласно формулам E.187),
а из формул E.186) следует
Ввиду конечности потенциала при k = i 1 множителя (^ (I) быть не может
и потенциал должен иметь вид
V = Р1 (?) И/3! (/С) + В# (/С)] cos 9
cos «р. E.262)
При С = 0 потенциал V = 0, поэтому /Л = —^ ir/?. Если же С = оо, то послед
ние два члена в выражении E.262) малы по сравнению с первым; поэтому .
приравнивая выражения E.262) и E.261), находим
„, 1 р ,> 2Е'а
Еа= -тгъВ, пли «= .
Z тс
После этого для потенциала получаем окончательное иыражриие
V = 2И ?'а 1A - 52) A 4-С2)]1^ Qirc tgc + ^i^) cos<p. E.263)
Подставляя значения р из формулы E.238), запишем это выражение в виде
V = 2^! ^'Р (^ arc tg С + j-^ cos ср. ' E.264>
170 Глава V
Внесение незаряженного диска не возмущает компоненту поля i?cosa,
перпендикулярную к плоскости диска; поэтому состветствующии потенциал
имеет вид V" — Ex cos a, а решение в общем случае V=V +F" можно за-
записать п виде
[^( ^^) ] E.265)
где С связана с р и х соотношениями E.237) и E.238).
Пользуясь формулой E.265), нетрудно вычислить момент, действующий
на диск: определив плотность поверхностного заряда о, мы найдем силу,
действующую на единицу поверхности, равную -^ °2 / е. Чтобы упростить
расчет, заметим, что действие поля Е sin а на поверхностный заряд, индуци-
индуцированный полем Ecosa, не создает момевта, так как плечо соответствующей
силы равно нулю. Следовательно, весь момент обусловлен действием поля
.Ecosa на поверхностный заряде', индуцированный полем Esma. Согласно
выражению E.264),
dV> 1 _ 2sE'p
J ~
sE'p f Г
Но из выражения E.237) С = ж/(а?), так что дС j дат = (йЁ) . При С = 0
а2?2 = й2—р2 [см. формулу E.236)], поэтому
Q,= _4^iDa pCoS9
m (а2 — р2) /2
Для силы, действующей на элемент площади рс?рс?ср, плечо равно pcostp,
откуда выражение для полного момента, учитывая действие поля Ecosa на
заряд на обеих сторонах диска, имеет вид
„, 8eZ?2 Sill a COS ol f р3 COS
m J j (а2 — p1
Принимая во внимание, что 2 sin a cos a = sin 2а, и интегрируя по формуле
(Дкайт, 858.3), находим
Инте]рируя еще раз (Двайт, 323.01), получаем для момента
Т = - 4е?? sin 2a [4" («2 - Р2)8/2 - «2 («2 - Р2I/2 ] ° = - 8ea'/?'sin2g . E.267)
§ 28д. Потенциал заряда, распределенного по поверхности сфероида.
Допустим, что на поверхности сплюснутого сфероида С = Со задана плотность
'поверхностного заряда ап) удовлетворяющая условиям, сформулированным
в § 146 гл. V. Этот заряд создает потенциал Vo вне сфероида и Vi внутри
него. Применение теоремы Гаусса о потоке электрической индукции A.27)
к маленькому объему, охватывающему элемент поверхности сфероида, дает
е ~\ f)n дп /S" L^A К ЭК
.Пусть ап такова, что
g^| E.269)
cos m(T-TJ. E.270)
Трехмерное распределение потенциала 171
Благодаря такому выбору потенциал Fo конечен при С=°°. Чтобы i
был бы конечным при С = 0, Е = 0 и чтобы Vi = Vo при С == Со, F, должен
иметь вид
gg />™ (/X) .С. E.271)
Подставляя выражения E.269) и E.271) в уравнение E.268) и используя
выражение E.200), получаем
Полагая
^^A+ф, E-273)
можно при помощи выражений E.269), E.271), E.272) и A.8) получить
два весьма важных интеграла:
2_ л,с _ л рт (,г \ пт
S = Атп Q™ (/Со) К 0D Sn. E.274)
Рассмотрим теперь плотность поверхностного заряда, являющуюся суммой
плотностей вида csr, так что потенциалы будут суммой потенциалов вида
E.274). Таким образом,
\1 \! j —1 riS \l \1 j — 1 /-f 7^S / f.\ / \
°=ZjZj^2 <Jr = 2jZj«2 Csrt>r{k)COSS((f — cp,).
Для определения коэффициентов Стп умножим с на
fC (i) cos m (cp — cpm) hxhs dk dtp
и проинтегрируем по поверхности сфероида. При этом все члены обратятся
в нуль, кроме тех, для которых m = s и п = г. Для них, используя фор-
формулу E.214) при т Ф 0, получаем
+ 1 2-к
*°— 1 О
Потенциал, создаваемый зарядом, распределенным по полерхности с плот-
плотностью с, будет равен
при С < Со
со п
V. = 2 2 Af™,Р™(/С)/*"(?) сов т(<р-фт), E.276)
при С> Со
m=0
Qn (/Q ^ (?) cos m (cp - cpm), E.277)
где, согласно формулам E.275) и E.271),
X \ \ оРп (?) cos wi (ю - срт) Л^ЛдОс аср, (О.Z/o)
-1 ^
172 '__ ^ Глава V
здесь &m — I при т = 0 и &m = 0 при т Ф 0. Из формулы E.271) вытекает
' E-279>
Множитель 2 - 8'™ появляется потому, что в случае нг = О интегрирование
по ср при выводе формулы E.275) дает множитель 2т: вместо ъ.
§ 28е. Представление потенциала точечного заряда через гармоники
силюснутого сфероида. Результатом предыдущего параграфа можно восполь-
воспользоваться для вычисления потенциала, создаваемого точечным зарядом, рас
положенным в точке ?0, Со, ср0. Под точечным зарядом подразумевается заряд,
размеры которого слишком малы, чтобы их можно было измерить физически,
но математически они отличны от пуля, благодаря чему напряженность
поля н потепциал являются всюду ограниченными функциями. Допустим,
что плотность заряда с равна нулю везде, за исключением площадки S,
находящейся в точке ср = <р0, ? = ?0. Площадка 5 предполагается настолько
малой, что на ней функция Р™ (?) постоянна и равна Р™ (?0) и cos т (ср — <рт) =
= cosm(cp — сро) = 1. При этом интеграл в формуле E.278) вычисляется
следующим образом:
Р™ (У \ [ оА A dh d<p = К (|0) \adS = qP™ F0)
и коэффициенты, определяемые по формуле E.278), оказываются равным»
Д/тп = /B С)д(-1Г^ [{^]2<2№о)^п (?0). E.280)
Из формулы E.279) находим
^±1 [^3]2(У- E-281)
Потенциал точечного заряда q имеет вид
при С < Со
V, = S 3 А^™, ^« (/О Кг F) cos m (ср ?0). E.282)
при С > Сп
СО ?7
П= S 2^„п<?п(/С)^E)сс6т(ср-ср0). E.283)
При помощи этих формул можно (используя те же методы, что и в случае
сферических гармоник) построить функцию Грина для областей, границы
которых образованы координатными поверхностями сплюснутой сфероидаль-
сфероидальной системы координат.
§ 29а. Гармоники вытянутого сфероида. Закругленные концы двух
коаксиальных стержней (электродов), образующих искровой промежуток,
обычно хорошо апроксимируются поверхностями двухполостного гиперболой
да вращения. В некоторых устройствах встречаются также удлиненные про-
проводники, похожие по форме на вытянутые сфероиды. Поверхности ил
яиляются естественными границами в «вытянутой» сфероидальной системе
координат, так как определенному значению одной координаты соответствует
одна, и только одна, из поверхностей для всего ивтервала изменения осталь-
остальных координат. Решение уравнения Лапласа в этих координатах приводит
Трехмерное распределение потенциала
173
к появлению функций, известных под названием гармоник вытянутого сфе-
сфероида.
Допустим, что в уравнении E.4) две короткие полуоси а и Ъ равны
ДРУГ другу, и положим a; = psincp и ?/ = pcoscp. Тогда уравнение примет вид
E.284)
Положим с2 + 0 = (с2 - Ь~) Ь\ = с\ 6*. Тогда при - Ь1 < 6 < оо или 1 < tj2 < оо
(где Ъ\ -= tj2) получаются конфокальные вытянутые сфероиды, а при
— с2 < б < — Ь2 или 0 < S2 < 1 (где 6| — ?2) получаются конфокальные
двухполостные гиперболоиды. На фиг. 55 изображено сечение этой
Фиг. 55.
-системы плоскостью, проходящей через ось (третья координата азимуталь-
азимутальный угол ср). Уравнение сфероидов имеет вид
72 =1, E.285)
а уравнение гиперболоидов —
+ —=1
Исключая из этих уравнений р, получаем
а исключая s, имеем
Если принять J < г; < ее, то, как и в § 28а, нужно взять
E.286)
E.287)
E.288)
давать -ц отрицательные значения не имеет теперь смысла, поскольку коор-
координаты всюду непрерывны. Располагая кооюдинаты в порядке Ё, г\ и ср
174 Глава V
и вычисляя так же, как и в § 28а, коэффициенты кг, hs и h3, находим
=Ру"', E.290)
E.291)
Уравнение Лапласа в этом случае имеет вид E.242), если в последнем
заменить 1+^2 на tf — 1 и ?2 + ?,2 на yf — ?2. Полагая, что решение равно
ЕНФ, и повторяя рассуждения § 286, получаем для S и Н то же самое
уравнение E.244). Уравнение для Ф имеет, как и прежде, вид E.246). Та-
Таким образом,
™ $ E.292)
Hmn = A'P^(ii) + B'Q^(ii), E.293)
Фт = С cos m® + D sin my, E.294)
а общее решение имеет вид
y = 2 2SmB#,A- E.295)
т п
§ 296. Вытянутый сфероид в однородном поле. В качестве примера
применения результатов предыдущего параграфа вычислим поле заземлен-
заземленной плоскости, имеющей проводящую сфероидальную выпуклость высо-
высотой с и основанием радиуса Ъ, при наличии внешнего однородного поля.
Такая ситуация имеет, например, место d том случае, когда наэлектри-
наэлектризованная плоская грозовая туча оказывается над находящимся на земле
мокрым стогом сена или над елью. Пусть при z = со потенциал равен
Er cos б. Как и раньше, при
тп —> со т —> — и 5 —> — = cos о.
с2 г
Принимая во внимание формулу E.188), мы видим, что ? мошет входить
в решение только через Рхф). Поэтому потенциал, согласно выражению
E.161), имеет вид
При z=co tj = co, -q—1 = 0 и arcthnj = O, так что
E
или
Сфероид с полуосями cub можно получить, если в уравнении E.284)
положить 6 = 0, или с?2г^ = с2. Следовательно,
О = с2Е -f В ( аг cth tj0 \ или # =— c2i? ( ar cth 7j0 — — J
Окончательное выражение для потенциала имеет вид
/ ar clh ij \
V = Ezll 1 , E.296)
\ ar cth т0- '
¦<1о
Трехмерное распределение потенциала 175-
E.297)
и т], ?, z связаны соотношениями E.287) и E.288).
§ 30а. Уравнение Лапласа в цилиндрических координатах. Б тех
случаях, когда граничные условия выражаются наиболее просто в ци-
цилиндрической системе координат, для нахождения потенциала следует
пользоваться решением уравнения Лапласа в цилиндрических координатах.
В этой системе координат уравнение Лапласа имеет вид
~^г + 7 W + ~f Щ*+~Ы?=0' E.298)
г;ге ? = pcoscp и г/ = р sin ср. Частный случай, когда потенциал V не зави-
зависит от z, был уже рассмитрен в § 2 гл. IV; в связи с этой задачей были
сведены круговые гармоники. Будем искать теперь решение в виде V = БФ2,
где Б, Ф и Z — суть соответственно функции только р, ср и z. Это решение
мы будем называть цилиндрической гармоникой. Подставив значение V
в уравнение E.298) и разделив на ЯФЕр~2, получим
=0. E.29»)
§ 306. Уравнение Бесселя и функции Бесселя. Положим в уравне-
уравнении E.299)
*^=-пя E.300)
и
— d2Z — к2 (
Тогда функция R должна удовлетворять уравнению
Если положить кр — с, то это уравнение примет вид
^ + С1^д = 0. E.302)
dv ' V. v%J ч '
Общие решения уравнений E.300) и E.301) будут
Ф = Ае1пч + Бе-* = A' cos nw + В' sin щ, E.303)
Z = Cefez + De-h* = С ch kz + D' sh kz. E.304)
Решение уравнении E.302) —уравнения Бесселя — носит название функции
Бесселя и-го порядка. Цилиндрическая гармоника, таким образом, запи-
записывается в впде
, E.305)
за исключением случая А==0, когда, согласно уравнению D.7) и выраже-
выражению D.39),
Fo = (Mpn + Nfn) {Cz + D) (A cos wp + В sin щ), E.306)
V0=[M cos (и In p) + N sin {n In p)] (Cz + D) (Л ch мер + Б sh ncp). E.307)
Если и к и и равны нулю, то
Vm = (М In р + N) (Cz + D) (Лср + Б). E.308)
17C Глава V
§ ЗОв. Модифицированное уравнение Бесселя и модифицированные
функции Бесселя. Несколько иной результат получается при замене к
ira /к в уравнении E.301). Вместо уравнения E.302) тогда получаем
уравнение
которое носит название модифицированного уравнения Бесселя, а его ре-
решения—модифицированных бесселевых функций. Вместо решения E.304)
будем иметь
Z = Ce>hi* + De~№ = С ros kxz + D' sin kxz. E.310)
Цилиндрические гармоники теперь можно записать в виде
V = Л ° (&lP) с*'"* e±*iz. E.311)
Решения такого типа будут рассмотрены в § 33—37.
§ 30г. Решение уравнения Еесселя. Положим в уравнении E.302)
«n= Ъ«**>™\ тогда
оп2 [в Bга + s) asis-2 + аьия] = 0 E.312)
п, следовательно,
as=-\s{2n + s)]-*a_a. E.313)
Кслн коэффициент а0 конечен, то коэффициенты а_2, о_4 и т. д. равны
нулю. Пусть о0= [2'Т (n+1)], что сводится к B"и!)~1 при целых п.
Тогда, применяя последовательно формулу E.313) и заменив Rn(v) на
Jn {b), получим
Г ( \— vn Г1 г?2гг»п
г=0
Функция /п («) носит название функции Бесселя первого рода n-го по-
порядка. Очевидно, что при пфО /п@) = 0 и, как будет показано в § 31г,
/„{оо)=--0.
Поскольку дифференциальное уравнение E.302) второго% порядка, оно
должно иметь еще второе решение. В случае, когда п — не целое число,
jthm решением будет J_n(i), но когда и —целое число, решения ./„(у) и
J_n(t) не являются независимыми. Чтобы показать это, заменим п на —га
в выражении E.314); тогда, так как [Г (-—и)]'1 = 0, ряды для J_n(v) и
(— 1)" /„(г>) совпадают. Когда п — не целое число, второе решение дается
формулой
¦7v(,)Cosv.-7_vW_
V V ' Sill V7t N '
Ксли v — целое число, то формула C.315) дает 0/0. Для раскрытия неопреде-
юнности заменим в выражении E.314) п на —v, разобьем сумму по г от
О до со на две суммы - от п до со и от 0 до /г—1, заменим в первой г
на n + s м во второй {Г [1 — (v — г)]} на тГ1 Г (v — г) sin vn (Двайт, 850.3).
Трехмерное распределение потенциала 177
Если подставить полученное выражение в формулу E.315) вместо /_v(t>)
и заменить cos^v на (— 1)", то будем иметь
2r— v
Согласно выражению E.314), скобка обращается в нуль при v = n, так
что первый член опять дает 0/0. Чтобы раскрыть неопределенность, про-
продифференцируем каждый множитель по v и подставим п вместо v. Вос-
Воспользовавшись справочником Янке и Эмде (стр. 108), находим
_r ' \
dz L Г (z) J Г (z) dz Г (z)
7M=1
где С = 0,5772157 —постоянная Эйлера. При помощи этой формулы, а
также формулы E63.3) из справочника Двайта неопределенность 0/0 рас-
раскрывается; если обозначить С — In 2 через In а, то
. / i \ 2r—n
r=0
\n+2r
A \n . -.
Zj nrl I
r=0
Общее решение уравнения Бесселя, когда п — целое число, имеет, таким
образом, вид
Bn(v):=A>Jn(v) + B'Yn(v). E.317)
Отметим, что функция Yn @) обращается в бесконечность; в § 31г будет
показано, что функция Уп(оз) обращается в нуль. Для функции, определяемой
формулой E.316), существует много обозначений. В книге ВатСона и British
Association Tables используется Yn(v), Янке и Эмде, Щелкунов и Стрэт-
тон пользуются Nn(v), Грэй, Метьгоз и Макроберт —К„(и).
Подстановка М = 1/е и N == 1 -- (njvJ в уравнение E.76) приводит к урав-
уравнению E.302), так что, если Jn (v) — известное решение, формула E.77) дает
E.318)
Дифференцируя это равенство- и опуская аргумент, получаем
Согласно рекуррентным формулам,"-величина В не зависит ни от п, ни от
v и, следовательно, может быть вычислена для простейшего случая и=0
и малых у. В зтом случае в выражении E.316) существенен только лога-
логарифмический член; этим членом и его производной можно заменить Yn(v)
и Y'n (v) в уравнении E.319). При подстановке логарифмический член
сокращается, и величина В оказывается равной 2/тс, так что уравнение E.319)
принимает вид
'n(e) Jn{v)-Jn(v)Xn(с) =~ ¦ E.320)
12 в. Смайт
178 Глава V
Для цилиндрических электромагнитных волн пользуются функциями
Ханкеля
H^{v) = Jn(V) + jYn(v), Ei2)(v) = Jn(v)-jYn(v), E.321)
которые в комбинации с е'ф1 лают бегущие волны.
§ ЗОд. Рекуррентные формулы для функций Бесселя. Если умножим
выражение E.314) на vn и продифференцируем, то найдем
[v)\ _ v2™-1 Г - г'2 v*
dv ' = 2»-*Г(гс) I ~'lM~l
Выделив в правой части множитель ьп и сравнив с выражением E.314),
получим
Выполнив дифференцирование в левой части, разделив на vn и обозначив
дифференцирование по v штрихами, наймем
Jn = J^~Jn. E.322)
Повторяя ту же операцию с умножением на гГп вместо ип, будем иметь
J'n= —Jn+i + —Jn= -^(Jn-i—Jn+i)- E.323)
Подстановка выражения E.322) в E.323) дает
^/п = /п_1 + /и+1. E.324)
Замена в выражениях E.322) — E.324) Jn (v) на (— 1)" /_п(у) приводит
к рекуррентным формулам для /_m(t). Дифференцируя формулу E.315) и
подставляя /v{^) из выражения E.322) и Jl_v (v) из аналогичного выраже-
выражения, получаем, что при v—»/г [когда cos yr —» — cos (v—l)-к и sinw—>
—»• — sin(v—1) тс]
J'_^ 7v_j cos(v — 1)те—/_v+i v GV cos w—7_v)
sin vie v-ж sin (v—1) те vsinwt
Аналогичную операцию можно применить и к выражению E.323), так что
F' у , п у /к чос;\
„ — in-i—— * п> ^o.ozo;
После вычитания одной из этих формул из другой получим
^п у У _1_ V /t; 497V
~~-in— in—lT-'n+l" V°" °^'/
Полезные интегральные формулы получаются путем интегрирования равен-
равенства, послужившего для вывода выражения E.322), и аналогичного ему
равенства, связанного с формулой E.325),
юп/„_1 (о) do = »"/„(»), E.328)
vnYn_x (v) dv = tn Fn (e). E.329)
Трехмерное распределение потенциала 179
Такое же интегрирование выражений E.323) и E.326) дает
« Jn+t (v) dv=- v-nJn (с), E.330)'
nYn+l {v)dv = -v-nYn(v). E.331 >
§ ЗОе. Значения функций Бесселя на бесконечности. Для решения
задач, в которых возможны значения р= со, необходимо знать, как ведут себя
при этом функции /п(Лр) и Yn(kp). Чтобы найти предельные значения функ-
функций, мы воспользуемся приемом, который часто употреблялся Зоммерфельдом.
В качестве первого приближения при v —*• со пренебрежем в уравневии E.302)
членами, содержащими гГ1 и гГ2. Получим приближенное дифференциаль-
дифференциальное уравнение
решение которого имеет вид
R = R'e±>v. E.333)
Подставим теперь это «пробное» решение в уравнение Бесселя E.302)
и предположим, что R' меняется с изменением V, но настолько медленно,
что членами d2R'/dv2, v^dR'/dv и v'2R' можно пренебречь по сравнению»
с членами dR'/dv и гг1/?'. Тогда
2-^1 + — = 0, или Я' = С«-1/2.
Асимптотическое решение, таким образом, будет
R = Cv-^e^. E.334)
Отсюда видно, что наибольший из членов, которым мы пренебрегли, оказы-
оказывается порядка v~*l2. Функции Jn(v) и Yn(v) должны быть действительг
ными линейными комбинациями двух решений, соответствующих знаку
плюс или минус в выражении E.334), т. е. должны иметь вид
cos (у + а), E.335)
^ Bv-1'* cos (у + р). E.336)
Чтобы найти зависимость А и а от п, подставим выражение E.335) в фор-
формулы E.322) и E.323), которые при v—*• со дают соответственно J'n = Jn—i
и /п=—Jn+x- Подстановка приводит к уравнению аэт± i = ап Ц1 -^-, кото-
рое удовлетворяется при ап= —^"/гтс + Т и показывает, что А не зависит
от п. Поскольку п не обязательно целое число, положим в выражении E.335)
n=-i? и сравним результат с формулой E.394). Сравнение показывает,
1
что ^= —тп' и ¦иает
где членом v~ml2 следует пренебречь, если т>3 и п — действительное чиело.
Чтобы получить Yn(v), подставим выражение E.337) в E.315), заме-
заменив предварительно п ва v и на — v. При целом v получаем в резуль-
результате 0/0, однако, заменив и числитель и знаменатель их производными
12*
Ш Глава V
no v, находим для v = п
V I \ f 2V/2 • f t 1 \ /г ППО\
У« (у) * ( — ) sin c-tbi:-tt: . E.338)
Таким образом, обе бесселевы функции обращаются в нуль на бесконеч-
бесконечности. На основании выражения E.337), E.338) и E.321) для функций
Хапкеля будем иметь
_2у'2 >{v-2nT—v
7V0 /
. E.339)
§ 30:к. Интегралы от бесселевых функций. 15 § 276 настоящей главы
был получен ряд по сферическим гармовикам, удовлетворяющий на конусе
6 = а условию V — 0. Для этого порядок п гармоник в™ (cos б) был подобран
таким образом, чтобы в™ (cos a) = 0. Для определении коэффициентов раз-
разложения необходимо было (см. § 27а) вычислить интеграл по б в пределах
от 0 до а от произведения двух гармоник. Точно так же для получения
ряда по бесселевым функциям, удовлетворяющего условию V = 0 и Е = 0
на цилиндре р = а, необходимо вычислить интеграл от произведения Rn(kpp)
и Rn(kQp), где кр и kQ подобраны так, чтобы удовлетворить граничным
условиям.
Пусть u = Rn(kpp) и v == Rn(kqp) — два решения уравнения Бесселя.
Тогда, согласно § 306, 1
Умножая первое уравнение на pv, второе — иа ри, вычитая одно из другого
и интегрируя, находим
оо
При интегрировании по частям интегралы сокращаются и остается
-\' ¦¦
/.12 121 С t f du dv \o
1 - (к„ — kn) \ put dp^= — pw-з- — PM-^— ) =
4 *^ j V яр яр у о
= - a L V4 (V) я» (M - ЛА (V) R'n (Ml •
ch'O «ыражение обращается в пуль, если
Rn(kpa) = Rn(kqa) = Q, E.340)
или если
R'n(kpa)=R'n(kQa) = 0, E.341)
или если , 0. -
Поэтому при кр Ф kq имеем
а
[ PRn (kpP)Rn (kQp) dp = 0. E.343)
Трехмерное распределение потенциала
18!
Когда Rn{kpa) = Rn
поскольку
= O, имеет место
E.344)
Ь а
f{x)dx=^ С f{x)dx— С f{x)dx.
Для вычисления интеграла в случае кр = кд умножим уравнение Бесселя
E.302) на v2{dRJdv)dv; это даст
dv \ dv J
dv
dv + v
dv
dv
Проинтегрируем это выражение от 0 до а и применим интегрирование
по частям в первом и третьем членах. В результате получим следующее
выражение, которое равно нулю:
о J
о
2 o"
Второй и третий члены в нем сокращаются; разрешая это уравнение отно-
относительно пятого члена, имеем
E.345)
Подстановка производных из выражения E.323) дает
v [Rn (г;)]2 dv = 1 a* {[Rn (a)]2 + [Rn+i (о)]»} - паДп (а) /?эт+1 (а) =
4 «(°I2 + lfl«-i (a)]2} ~ ™Rn (а) Д„-1 (а). E.346)
При применении вектор-потенциала нам представится случай воспользо-
воспользоваться ортогональными свойствами векторных функций
Интеграл от нуля до а от скалярного произведения этих функций равен
?- E-348)
182 * Глава V ^
При помощи формул E.322) — E.327) это выражение можно записать в виде
суммы двух интегралов типа E.343)
а
i (кдР) р dp + 1 $ Я„_, {крР) Rn^ (kgp) p dp. E.349)
Вычислим каждый из интегралов по приведенной выше формуле для
\ puv dp, сложим результаты и затем исключим производные посредством
формул E.322) и E.323). В полученном выражении члены, не содержащие
функций л-го порядка, исчезают; группируя в оставшихся членах функции
(п—1)-го и (и+1)-го порядков, применим к ним те же формулы E.322)
и E.323). В результате описанной выше операции, считая v — kva и v>'_ = kqa,
будем иметь
Rn (ftpP) ¦ Rn {kQp) p dP = (ft* - ft*)-* [vRn (»') R'n (») - v'Rn (v) R'n (v')]. E.350)
При kv Ф kq интеграл обращается в нуль, если выполнено одно из усло-
условий E.340) — E.342). В случае kp — kq сумма интегралов, входящих в выра-
выражение E.349) и вычисленных при помощи формулы E.346), равна
И °2 - ( i У ] [Rn <V)]2+т
Таким образом, поверхностную векторную функцию р и ер, одна из компо-
компонент которой обращается в нуль при р = а, можно представить в виде суммы
членов вида
§ ЗОз. Разложение в ряд по функциям Бесселя. Рассмотрим функ-
функцию f{v), удовлетворяющую в интервале от гз = О до v = a условиям, необ-
необходимым для разложения в ряд Фурье, и одному из следующих гранич-
граничных условий:
а) /(о) = 0. Этот случай имеет место, если f(v) является потенциаль-
потенциальной функцией, а потенциал границы равен нулю.
б) /'(о) = 0. Этот случай имеет место, если границей области является
поверхность, касательная всюду силовым линиям.
в) af (а) 4 Bf (а) = 0. Этот случай сводится к случаю «а» при В — оо
и к случаю «б» при В = 0. Пример такого условия приводится в § 9 гл. XI.
Функцию f(v) можно разложить в ряд
/(г>)=1МЛ(М. E-352)
прячем величины [аг выбираются таким образом, чтобы в случае «а»
Jn (|iro) = 0, в случае «б» J'n (p-ra) = 0 и в случае «в» praJ'n (р-га) 4- BJn (|х?.а) = 0.
Для определения Аг умножим выражение E.352) на к/„(р.,г;) и проинте-
проинтегрируем от v = 0 до v = а. Все члены в правой части, согласно формуле
E.343), исчезают, за исключением Д. \ v[Jn{[i.sv)]2dv, так что
а
I Vf (V) Jn (l^s*) dv
. . A. = ±- ¦ • ; E.353)
Трехмерное распределение потенциала 183
Интеграл в знаменателе этой функции можно вычислить при помощи соот-
соотношения E.346)
V-sO.
$°bUiv>)]2<fo = |i72 $ x[Jn{x)]*dx =
О О
{ М]2}-^4(^аL±1 foe). E-354)
случае «а» подстановка выражения E.354) в формулу E.353) дает
В случае «б» подстановка выражения E.354) в формулу E.353) дает
а
А = -—5 j—„. ,, .—775- \ vf(v)Jn(u,«v)dv. E.356)
0
Б случае «в» подстановка выражения E.354) в формулу E.353) дает
§ ЗОи. Функция Грина для цилиндра. Обратное расстояние. На основе
материала, изложенного в последних параграфах, можно решить задачу
¦о потенциале точечного заряла q, расположенного в точке z = 0, р = Ь,
<р = ср0 внутри заземленного проводящего цилиндра. Под точечным зарядом
мы будем подразумевать такой заряд, размеры которого хотя и слишком
малы, чтобы их можно было бы измерить физически, однако отличны от
.нуля, благодаря чему напряженность поля и потенциал — функции всюду
ограниченные. Из выражения E.305) вытекает, что решение, обращающееся
в нуль при z = оо, симметричное относительно плоскости ср = ср0, дающее
У — О при р = а и справедливое для положительных значений z, имеет вид
= 2 2 Arse~^Js (W) cos s (cp - cpc), E.358)
r i s0
2
где значения p.r выбраны так, что /s(|xra) = 0. Функции Ys (p.rp) отсутствуют,
поскольку они бесконечны на оси.
В силу симметрии вся плоскость z = 0 состоит из силовых линий,
за исключением той точки, где находится точечный заряд. Чтобы сфор-
сформулировать граничные условия на этой плоскости, примем, что (dV/dzH
равно нулю всюду, кроме маленькой площадки AS в точке ср = ср0, р = Ь.
Дифференцируя выражение E.358) и подставляя z = 0, получим
,\ vrrs,(w)coss(? -
r=ls=0
Коэффициенты Ars этого разложения определяются, как и в § ЗОж и ЗОз
настоящей главы, посредством умножения на р/р (р-чр) cos р (ср — срп) и инте-
интегрирования от р = 0 flti р—а и от ср = О до cp = 2tc. Согласно формуле E.343)
и (858.2) из справочника Двайта, все члены в правой части выражевия, за
исключением p = s и q=r, исчезают. В последнем случае, как видно из
формулы (858.4) справочника Двайта, интегрирование по ср дает множи-
184 Глава V
тель ж при s > 0 и 2тс при « = О, поэтому, согласно формуле E.355),
S S
где &s = 1 при s =¦- О и 8° = 0 при s ф 0. Область Л61 в плоскости z = 0, в
которой (&V /dzH Ф 0, выбирается настолько малой, что в ней /s (jJ-rp) имеет
постоянное значение Js (jj,rb) и cos s (<р — (р 0) = 1. Используя теорему Гаусса
о потоке электрической индукции A.27) и учитывая, что рассматриваемый
интеграл дает половину полного потока, находим
Подставляя л формулу E.359), получаем.
Для потенциала, таким образом, будем иметь
|-?„). E.361)
Это есть функция Грина (см. § 9 гл. III) для круглого цилиндра. Если
координаты заряда q суть р= b, z = z0 и <р = <р0, то в выражении E.361)
следует заменить | z| на \z — zo\. Если заряд расположен на оси, то все
члены суммы по s, кроме первого, исчезают, а /с ([лгЬ) = 1.
При а—> оо выражение E.361) дает потенциал точечного заряда q n
свободном пространстве. При [ira —> оо функция /n([i.ra) меняется, согласно
выражению E.337), синусоидально, так что ее нули отличаются друг от
A \ —1/г
•у ^ra J .когда /„ ([i.ra) = 0.
Вырангение для потенциала E.361) принимает вид
V = о_.„а ^1 B — 8") cos s (<p — <p0) V е~гЛ^ I z~zo I Js (Mfxb) X
Если M[i. = ft, то при Д[л,—^-0 и г—*¦ оо это выражение записывается ь инте-
интегральной форме:
оо оо
У = "dhr = h S B - 8") cos s (? ~ %) J e~*' -« ' Js (kb) /. (AP) dft, E.362)
8 = 0 0
где fl2=(z —zoJ + p2 +62~2pbcos(<p —<pc). При 6 = zo = 0 получаем
ft. E.363)
Положим z, z0, <p0 равными нулю и заменим в выражении E.363) р на R;
тогда после сравнения выражений E.362) и E.363) найдем _
Л, [(Р2 + б2 - 2рЬ cos T)V2] = 2 B - 8») /s (p) /s F) cos («p). E.364)
8=0
Трехмерное распределение потенциала 185.
§ ЗОк. Функция Грина для цилиндрической полости. Используя супер-
суперпозицию решений вида E.361), можно при^ помощи метода изображений
(§ 8 и § 116) получить потенциал, обращающийся в нуль не только на по-
поверхности цилиндра р — а, но и на плоскостях z = 0 и z = L. Если коорди-
координаты положительного заряда q суть z = c, p=b и <р = <р0, то положитель-
положительные изображения следует поместить в точках z = 2nL + с, а отрицатель-
отрицательные—в точках z — 2nL — с, где п — целое число, принимающее значения
от —оо до +°°- В результирующем потенциале множитель, зависящий
от z, при z < с оказывается равным
V е~^г BrlL+c-z> _J_ V e~V-r B«L-c+z) _ VI g-nr BnL~c-z) __ VI e~V-r BnL+c+z) _
2
n=0 n=i ^
¦= 2 [(e-^c - e+11r«=) 2 e-2"^1" + e^0 ] sh M.
Суммируя ряды (Двайт, 9.04), умножая числитель и знаменатель суммы на
е^г и приводя к общему знаменателю, получаем
2 sh fxr (? — г) gh u,.z
Подстановка этой величины в выражение E.361) дает при z<c выражение
для потенциала
( _ } E365);
r=l s=0
В случае z > с в этом выражении следует заменить z на L — 2 и с на
L — с. Если заряд находится на оси цилиндрической полости, то сумма по
s исчезает и остается лишь член, соответствующий s = 0.
Если потенциал должен обращаться в нуль не только на перечислен-
перечисленных выше поверхностях, но и на плоскостях <р = 0 и ср = <рх (где 0 < <р0 < fj)
и если <р1 = тс/тг (где п — целое число), то функцию Грина, согласно методу
изображений (см. § 8), можно построить, как суперпозицию 2/г решений
типа E.365).
§ 31а. Функции Бесселя нулевого порядка. В важном случае полей,
симметричных относительно оси z, потенциал не зависит от <р и уравнение
Бесселя E.302) принимает вид
dИ , 1 dR , п г\ /с оппх
-j-5-Ч—-T-+R — 0. E.366)
dv2 v dv v '
Его решение E.314) можно записать в виде
Этот ряд сходится, очевидно, для любых г;. Так же как и Jn(v), У0(оо)==0;
однако /с@) = 1. Формула E.316) при п — 0 дает
1
^)щ^ 2C!) -...]. E-368)
где In и равен —0,11593.
186
Глава V
§ 316. Корни и численные значения бесселевых функций нулевого
лорядка. Если построить функции /0(г;) и Y0(v), определяемые по форму-
формулам E.367) и E.368), то получаются кривые, изображенные на фиг. 56 и 57.
W
Q5
-Q5
Л
/
Л
\
У
J0(X)
Л
J0(X)
5 Ю
Фиг. 56.
Как видно из фигур, эти функции осциллируют относительно оси v.
Можно показать, что и /0 (v) и Yo (v) имеют бесконечное число действитель-
действительных положительных корней. То же
самое имеет место и для /„(&) и
для Yn{b). При построении функции
Грина для цилиндра мы уже убе-
убедились, что это обстоятельство весьма
существенно, так как позволяет най-
найти бесконечное число значений к, для
которых функции Jn{kp) и Yn{kp)
обращаются в нуль при некотором
определенном значении р. Существует
большое число прекрасных таблиц,
дающих численные значения, гра-
графики, корни и т. п. для бесселевых
функций. Следует иметь в виду, что
обозначения у разных авторов раз-
.личные. Значение функции Бесселя при больших аргументах нетрудно
•вычислить при помощи асимптотических представлений.
§ 31в. Производные и интегралы от бесселевых функций нулевого
порядка. Полагая в формулах E.323) и E.326) п = 0, находим
Д \Y0(x)
1 \У
Q5 V=*
О
-°-5о
5
Фиг. 57.
10
/о (е) = - Л (v) и У5 (») = - У, (»),
.а из формул E.328) и E.329) имеем
E.369)
и
E.370)
Приведем несколько полезных определенных интегралов, содержащих /0 (v).
Из выражения„E.367), пользуясь формулой (854.1) из справочника Двайта,
получаем
Трехмерное распределение потенциала 187
( —1)«2«;2п п 1 . 3 ... Bп —1)
: ^-1 Bn)! 2 г- It ...In
n=0
Изменив порядок суммирования и интегрирования и воспользовавшись фор-
формулой (Двайт, 415.02), будем иметь
oW-vS 2 (-^"^щГ^^Т^ cos (e cos 0 Л,
0 n=-0 - 0
откуда
ic т:
Jo (ftp) == — \ cos (ft p cos t) dt=z — \ cos (ftp sin t) dt. E.371)
о о
Применяя известные тригонометрические формулы для суммы и разности
двух углов и интегрируя по частям, нетрудно показать, что выражения,
удовлетворяющие рекуррентным формулам E.322) — E.324), имеют вид
1С
/n (V) = — \ cos (nt — v sin t) dt. E.372)
о
При п = 0 выражение E.372) сводится, очевидно, к выражению E.371).
Непосредственная подстановка в уравнение E.302) и интегрирование по
частям показывает, что выражение
Ce . E.373)
удовлетворяет уравнению Бесселя при и > — у - Постоянная определяется
путем сравнения значений ( -гг v j /n (у) при г; —> 0, определяемых соот-
соответственно по формулам E.373) и E.314).
Нетрудно показать, что соотношение E.363) сохраняется при замене z
на /z; таким образом,
^ е-**/0 (ftp) dft - (р2 - z*)-1/..
о
Откуда, разделяя действительную и мнимую части, находим, что при р2 > z2
cos ftz /0 (ftp) dft = (р2 - z2)-V2, E.374)
sinftz/o(ftp)rfft = 0. E.375)
() !
188 Глава V
При р2 < z2 будем иметь
С
\ cos kz Jn (Ар) dk =-- 0, E.376)
sin kz Jo (kp) dk = (z2 - P2)-x/2. E.377)
§ 31г. Поле точечного заряда, расположенного над диэлектрической
пластинкой. Применим результаты двух последних параграфов к вычисле-
вычислению потенциала, создаваемого по одну сторону от бесконечной диэлектри-
диэлектрической пластинки толщиной с и относительной диэлектрической проница-
проницаемостью К точечным зарядом q, расположенным с противоположной сторовы.
Примем, что точечный заряд находится в начале координат, а ось z перпов-
дикулярва к пластинке. Уравнения поверхностей, ограничивающих пластинку,
будут z = a и z = Ь, причем Ь — а = с. Согласно соотношению E.363), по-
потенциал, обусловлевный одним лишь точечным зарядом, равен
V = -r^ = 72-Xj0(kp)e-*Wdk. E.378)
Поскольку это выражение представляет собой решение уравнения Лапласа,
зависящее только от z и р, очевидно, что в результате внесения под знак
интеграла произвольной функции к мы также получим решение. Обозначим
через Vl потенциал в области — оо < z < а и запишем
V1 = Dга,,)-1? [ J /0 (кр) е-* И dk + J Ф (к) /n (k9) e+k* dk I . E.379)
оо -"
Последний член представляет собой потенциал в области ниже пластинки,
обусловленный ее поляризацией и, следовательно, конечный в указанвой
области. Потенциал внутри пластинки можно представить в виде
^ W (к) Jo (кр) г** dk+^в (к) Jo (kp) e+te dk ] . E.380)
о о
Это выражение остается, разумеется, конечвым при а < z <Cb. Потенциал
над пластинкой, т. е. в области 6<z< +oo, должен обращаться в нуль
при z = оо и, следовательно, имеет вид
оо
^з = ^%ГЧ \ 2 {Щ /о (кр) е-** dk. E.381)
о
Определим теперь Ф(к), Ч?(/с), в (к) и Q(k) так, чтобы граничные условия
удовлетворялись для любых значевий р от 0 до оо. Для этого необходимо,
чтобы тем же условиям удовлетворяли соответствующие подинтегралыше
выражения. Последнее утверждение можно доказать, если воспользоваться
интегралом Фурье — Бесселя
/ («) = \ tJn (tX) [ \ Uf (U) Jn (Ш) du ] dt
0 0
(некоторые ограничения, налагаемые на п, и нид функции f(x) предпола-
Трехмерное распределение потенциала 189
гаются выполненными). Таким образом, из равенства
"о о
после умножеппя обепх частей па р/0 (тр) dp, интегрирования от О до со и
последующего умножения па т получаем
Л ("О = Mm).
Применительно к рассматриваемой задаче это означает, что условие V1=Vi
при z = а после исключения /0 (кр) дает
e-fta + ф (?) ека_ ЦТ (?) e-fta __ Q (&) gfea = 0) E.382)
а условие dVJdz = AT dVJdz после исключения /с (&р) сводится к
— (r~ha + Ф (к) eha+KW (к) е~Ьа - А'Н (ft) efea = 0. E.383)
Точно так же при z = Ь условие V2 — V3 дает
47 (к) е~кЬ + в (к) еы - Q (к) е~ feb = 0, E.384)
а из условия KdV2/dz = dVs/dz находим
- KW (к) e~hb + Кв (к) <*ь + Q (к) ег™ = 0. E.385)
Разрешая соотношения E.382)— E.385) относительно Q(k), получаем
• Q(k)= — ... . м . E.386)
Положим, для простоты, Ь — а —с и (К — l)/(it + 1) = р, так что 1— Р2 =
4^(АГ1J; тогда
Подстановка в выражение E.381) приводит к следующей формуле для F8:
у flj-Wf/.W^a. E.387)
Для представления полученной формулы в виде ряда разложим к ряд ее
знаменатель (см. Двайт, 9.04):
СО
5 ^*г^ + Р2 ^ Jo №) е~к (z+2c) d*
о о
Подставляя значения интегралов из соотношения E.363), будем иметь
3 4ТОЦ, 1(z2+p2)l/2 ^[(Z+2cJ+[2]1/2 [(Z + 4CJ + P2]1/2
или
V = g С*'?2)
у ! .
E.388)
Этот же результат можно получить более длинным путем при помощи
метода изображений. Потенциал в других областях можно найти, разрешив
190 Глава V __
соотношения E.382) —E.385) относительно Ф(/с), W (к) и в (ft) и подста-
подставив полученные выражения в формулы E.379) и E.380). Этот метод
Применим и в случае любого числа диэлектрических пластинок.
§ 31д. Потенциал внутри полого цилиндрического кольца. В качестве
другого примера вычислим потенциал в каждой точке области, ограни-
ограниченной двумя цилиндрами р = а и р = Ь, потенциал которых равен нулю,
и двумя плоскостями — плоскостью z = 0 с нулевым потенциалом и z = с
с потенциалом F = /(p). Поскольку значения р = 0 и р=оо исключены
из рассматриваемой области, в решении будут и /0 (ftp) и Yo (ftp). Очевидно,
что, в соответствии с формулами E.304) и E.317), решение уравнения
Лапласа, удовлетворяющее граничным условиям при z = 0 и р= Ь, имеет вид
Vh = Л sh (М [ /о (М - f^f Yo (M ] • E.389>
Условию Fft = 0 при р = а можно удовлетворить, если выбрать значения
так, чтобы
Следовательно, всем граничным условиям, кроме условия при z = c, удо-
удовлетворяет и сумма таких решений
со
F= S Vk. E.390)
Последнее граничное условие V = / (р) при z = с удовлетворяется, если
]выбрать Ар так, чтобы
оо
/ (р) = 2 A sh (^kC) [ /0
Так как выражение в скобках удовлетворяет уравнению Бесселя, обозна-
обозначим его через Ro (^ftp). Далее умножим правую и левую части равенства
на р-йо(|*«Р) [где ^0([i.8a) = i?0(|Asb) = 0] и проинтегрируем от а до Ъ. Бла-
Благодаря тому, что Ro ([i.ftc) = Ro ((xftb) = 0, все члены в правой части, согласно
формуле E.344), обращаются в нуль, за исключением одного, для кото-
которого k = s. Для этого члена, в силу выражения E.345), мы имеем
ь
2 ( dR0 Л2 2 f dB0 "Л2 1 АЬ Sh |lfcC
f
а
Дифференцируя i?0([j,ftp) по формуле E.369), находим
К (М = - {Л (М - ^у ^1 (М } •
Для Ah, таким образом, получаем
ь
2 I р/ (р) Ro (w)
Подстановка выражения E.391) в E.389) и затем E.389) в E.390) дает иско-
искомое решение.
Чтобы получить потенциал внутри заземленного цилиндра р = а в по-
потенциалом У = 0 при z = 0 и V — / (р) при z = c, следует опустить член
Трехмерное распределение потенциала 1JH"
с Yo в формуле E.389); тогда выражение E.391) примет вид
Ah = 2°, г i 412 ь—• E.392)'
§ 32. Функция Бесселя нецелого порядка. Сферические функции
Бесселя. Если п — нецелое число, то общее решение уравнения Бесселя
имеет вид
Hn(v) = AJn(v) + BJ_n(v). E.393)
Функция Yn{v) в этом случае не нужна, поскольку она является линей-
линейной комбинацией Jn(v) и /_„(&). Формулы § ЗОд справедливы и для функ-
функций Бессепя нецелого порядка. Особенно простой вид имеют функщиг
/ . _1\(г>), где и —целое число; так, например, если подставить в выра-
выражение E.314) п — 1/^ и п = — х/2 и сравнить полученный результат с ря-
рядами для синуса и косинуса (см. Двайт, 415.01 и 415.02), то получим
E.394)-
Подстановка и = 1/г и n~ —V2 B Ф°РмУлУ E.324) дает
А*(°) = (JiI'2 (lTsinv~~cosy) ' E.395)
¦J-»/2(«)= (^)I/2(~ siny— ^C0S^}- E.396)
В случае п — 8/2 и n = — 3/2 получаем
04] E-397>
E.398>
Таким же путем можно получить, очевидно, выражение
I^-i (— I)8 (п
Ь Bs)l(n —2
8=0
8=0
E 399)
где верхним пределом каждой из сумм является целое число, наиболее
бливкое к указанному в формуле. Заметим, что, согласно формуле E.315),
Y , (в) = ( —!)»+«/ , (у), E.400)
поскольку cos ( n -f- у J -я равен нулю. Заменяя п на (и+у)в формуле-
E.314), получаем, что при v —» 0
192 Глава V
Сферические бесселевы функции /„ («) и пп (v) определяются следующими
выражениями:
. , -. ( 71 \ ХЫ -г , . 1 4 , .
„+f-
где/п(гз) и iVn (г) —функции, используемые Шелкуновым. Последние появ-
появляются при изучении сферических электромагнитных волн и недавно были
затабулированы. Из выражений E.402), E.320), E.322) и E.323) следует, что
п'п (о) /п (о) - *„ (о) /{, (о) = «-2, E.403)
Bя +1)у-1 /п = /„_! + /„, 1, /; = ± /„J:i ^ ^и + у ± -f )°"! /п- E-404)
Аналогичные формулы имеют место и для nn(v). Дифференцирование
формул E.404) и исключение /„_! (о) дает дифференциальное уравнение
для функции fn(v) или nn(^):
] [i ]n{v) = 0. E.405)
§ 33а. Модифицированные бесселевы функции. Решение модифици-
модифицированного уравнения Бесселя E.309)
f^W E.406)
dv2 v dv
можно получить подстановкой /v вместо v в формулу E.314). При этом
выражение в скобках оказывается действительным, но появляется общий
коэффициент ]'п. Искомое действительное решение дается, таким образом,
выражением
со I l \v+2r
/v («) = /-/v (/«) = S ri ?(* + , + !) • ¦ Г5-407)
r=0
Если v —нецелое число, то вторым решением уравнения будет
- E.408)
Если v является целым числом, то ^(v + r-j-l) можно заменить на (
и убедиться, что функция In(v) совпадает с /_„(?;). Поэтому второе реше-
решение можно определить следующим образом:
Кп (v) = 4 «/¦"+' [/„ (/о) + /У„ (/о)] - E.409)
При помощи выражений E.314), E.316) и E.407) это решение можно
привести к виду
П~1 (-Iff jr Ч (n-i—1I
2^^+
г=0
Г
У [у V E.410)
\m=l
Трехмерное распределение потенциала 193
где 1па=—0,11593. Общее решение уравнения E.406), когда п — целое
число, имеет вид
B°n(v) = AIn(») + BKn(v). E.411)
Согласно выражениям E.407), E.409) и E.320), имеет место равенство
=»-». E.412)
Из выражений E.409), E.321) и E.407) следует, что
?) Кп (в) = ДИ //?> (/„) = (- /)«+i Н<? (- /Ъ), (
Таблицы этих функций приведены в книге Янке и Эмде.
§ 336. Рекуррентные формулы для модифицированных бесселевых
функций. Выражение E.322) можно записать в виде
Подставив в него ]п1п{ь) вместо Jn(jc) и разделив на ]п~1, получим
/; = /„_!-?/„. E.414)
Аналогично из выражения E.323) будем иметь
/; = /„+!+ ¦?/„. E.415)
Вычтя выражение E.414) из E.415), получим
^/п = /„_! -/„+1. E.416)
Преобразуя решение E.409) при помощи рекуррентных формул § ЗОд, по-
получаем
-K'n = Kn_i+^Kn, E.417)
-#; = #„+!--?#„, E.418)
-2~Кп = Кп„1 Kn+i. E.419)
Здесь использованы обозначения, принятые у Ватсона и у Грэя, Метыоза
и Макроберта. Некоторые авторы опускают множитель ( — 1)" в формуле
E.410), благодари чему рекуррентные формулы для /п и Кп оказываются
одинаковыми. Путем интегрирования выражений E.4i4) и E.417) можно
получить (как это было сделано в § ЗОд) две полезные интегральные формулы:
J »"/„_! (e)de = »"/„(»), E.420)
J ьпКп^ (г-) dv = - ьпКп (е). E.421)
Аналогичное интегрирование выраяюыий E.415) и E.418) дает:
¦¦^/„+1 (е) Аз = в-*/„(»), E.422)
" Kn+i (е) Аз = - »-"/?„ (»). E.423)
13 в. Смайт
194 Глава V
§ ЗЗв. Значение модифицированных бесселевых функций на бесконеч-
бесконечности. Значения 1п{ь) и Kn(i.) при ь-^-со можно получить из соответству-
соответствующих значений функций /п(г) (см. § ЗОе) путем замены ь на /Ъ. Точность
полученных выражений та же: они пригодны, если величиной с~~3/2 можно
пренебречь по сравнению с v~~112. Заменим в выражении E.337) ь на jt>,
запишем /—'/г в виде e~~ll4i7Z и представим тригонометрические функции через
экспоненциальные (см. Двайт, 408.02); тогда, пренебрегая членом e'v, по-
получим
Если и—целое число, то, вычислив последний множитель (см. Двайт, 409.04
и 409.05), будем иметь
i1
Из соотношений E.413) и E.339) получим
Хотя приведенные выше формулы были получены в предположении, что
и —целое число, подставляя их в уравнение E.406), убеждаемся, что они
справедливы при любых п1).
§ 33г. Интеграл от произведения модифицированных бесселевых
функций комплексного аргумента. В гл. XI для определения мощности,
рассеиваемой в проводнике при протекании в нем вихревых токов,- по-
потребуется вычислить интеграл от произведения модифицированных бесселевых
функций Вп [(/рI/2 х] и соответствующих комплексно-сопряженных функций
ПпК-jpI'**], где (/I/2 = 2-1/2A+/) и (_/у/2==2-1/2A_/). в задачах
с цилиндрической симметрией число п обычно целое, а в задачах со сфери-
сферической симметрией п равно половине нечетного числа. Используя формулы
§ ЗОж, можно вычислить этот интеграл для любых значений п. Обозначим
К = - / UpI" = (- fp)lh и кд = / (- jpfi* =
и = Д„ [ - / UpI'* А = (- /Г Д» К/»1/2«]
е = Rn[f (- /р)Ч*х] = /"RI [( - /»»/2х],
Подставив эти величины в уравнения § ЗОж, предшествующие условию
E.340), и изменив р на х, получим
xR°n [(jpL* х]Я°п[{- /рI" x]dx=^ xR°n (kqx) R°n (kpx) dx =
¦ 0
= 1 at1 P-1'* [I1* m (kpa) Д»' (kqa) - ( - /)VS ^ (kqa) /?»' (ftpfl)] =
[ Vя" (^Pfl) Д«-1 (А9а) + Vя" (V) Д"-« (V)l =
[A;pa^n-2 (Лра) Лп-i (V) + Л5«Д«-2 (V) Л"-1 (V) -
- 4 (п - 1) Д»_! (Арв) Д»_, (ftga)]. E.426)
Точнее, не для любых п, а только для п <?v. — Прим. перев.
Трехмерное распределение потенциала 195
§ ЗЗд. Функция Грина для кольцевой цилиндрической полости.
В качестве примера использования модифицированных бесселевых функций
вычислим потенциал, обусловленный маленьким зарядом q, расположенным
в точке г = с, р = b и <р = »0, внутри цилиндрической кольцевой полости
с проводящими стенками, уравнения которых суть z = О, z — L, р = d и р = с
(a>d). Частвый случай, d = 0 соответствует цилиндрической полости, для
которой в § ЗОк было получено решение, содержащее бесселевы функции.
Поскольку ни /т(г), ни Кт{с) не имеют действительных корней, для
получения функции, обращающейся в нуль при заданном значении р, по-
потребуется, очевидно, их комбинация. Ясно, что искомая функция имеет вид
R°m (k, s, t) = Km (ks) Im (to) - Im (ks) Km {kt). E.427)
Так как эта функция обращается в нуль, вообще говоря, лишь при одном
значении t(t = s), то в областях вблизи внутренней и вблизи ввешвей гра
ниц необходимо пользоваться различными функциями, которые должны,
конечно, совпадать при р = Ь. Нетрудно написать две такие функции, обра-
обращающиеся к нуль на поверхности проводников и совпадающие друг с другом
при р = Ъ. Они имеют вид
при с?< р < b или р = Ь, со Ф ср0
E.428)
при b < p <; а или p = b, cp Ф cp0
n=l m=0
E.429)
Эти решения имеют должную симметрию относительно ср = ср0. Для определе-
определения коэффициентов Стп можно воспользоваться теоремой Гаусса о потоке
электрической индукции, применив ее к области, окружающей заряд.
Доиустим, что заряд q сосредоточен в маленькой области на поверхности
цилиндра р = 6 в окрестности точки z = c, у = у0. Эта область принимается
настолько малой, что физически ее невозможно измерить, однако математи-
математически она не является точкой, благодаря чему потенциал и напряженность
поля всюду конечны. Согласно формуле A.27), интеграл по дпум сторонам
поверхности цилиндра S2 равен
s2 s
Из выражений E.428) и E.429) следует
со со
OV dV" VI V\ л ПТ
dp dp Z_l ZJ '
71=1 771=0
-j- , d, b ) I sin -j— cos m (cp — cp(!).
При помощи решения E.409) это выражение можно записать следующим
образом:
со со
dV SV^__ y у„ ±r>of]}]i_ d Л- s^_ I _ ч /5 431 \
П = 1 771=0
13*'
?96 Глава V
Положим теперь ср — ф0 = сР'> умножим правую и левую части иа
sin (pr.z I L) cos qy' b dy' dz
я проинтегрируем по поверхности цилиндра p = b. Все члены в правой части,
за исключением тех, для которых р = п и q = m, обращаются в нуль (см.
Двайт, 858.1 и 858.2). Оставшиеся интегралы, кроме q=m = O, вычисляются
по формуле (Двайт, 858.4). Для вычисления интеграла в левой части заметим,
что если размеры заряда достаточно малы, то cos дар' и sin {nr.z I L) имеют
постоянные значения, равные соответственно единице и sin (пт.с / L), и могут
быть вынесены из-под знака интеграла. Поэтому, учитывая, что dS = b <icp' dz,
я левой части получаем интеграл E.430). При то Ф 0 имеем
| sin ^ = - i Cmn LkRI ( i?L, d, e) . E.432)
При то = 0 коэффициент х/2 в правой части отсутствует, поскольку \ tZcp = 2ти.
о
Определяя Стп из соотношения E.432) и подставляя в выражения E.428)
м E.429), находим
» - B-С) 24 (~ , a, b) tf^J.
X sm-j-sm-^-cosTO(cp —cp0), E.433)
ZJ ZJ „ / пъ \
n=l m=0 i»ml —j-,a, a)
TITZC . tlTlZ , % /г/од
X sin — sin -=r- cos m (cp - cp0), E.434)
где oj, = U при т Ф1) и 8^ = 1 прп m = 0.
Для цилиндрической полости (случай, рассмотренный в § ЗОк с при-
применением бесселевых функций) следует положить d = 0, так что приведен-
пые выше выражения для потенциала примут вид
у
у. ^А- /—kAsin^Sin^
E.435)
(C)
F'=^f2 S , ГппаЛ ^
E.436)
Как видно из выражения для потенциала V, последний удовлетворяет всем
граничным условиям, конечен, но не обращается в нуль на оси. Когда
заряд расположен на оси, следует пользоваться формулой E.436), опустив
суммирование по то и положив то = 0.
Трехмерное распределение потенциала
§ 34а. Модифицированные бесселевы функции нулевого порядка.
При п=0 формула E.407) дает
Д(»)=1+|- + ~ + ~^+... E.437)
Таким образом, функция /0 (v) действительная (но не имеет действительные
корней) и
/0@).= 1 и /0(оо)=оо. E.438)
Формула E.410) при и = 0 принимает вид
V2 ЗУ --- E.439)
Производные от /0(г) и K0(v) определяются выражениями E.415) и E.418)
и равны
Гй = 1х и К'^-К,. E.440)
Из формул E.420) и E.421) получаем
/0(e)dc =»/,(»), E.441)
5
о
v
^ vK,t (e) dv=- vK1 (»). E.442)
о
§ 346. Интегральное представление модифицированных бесселевых
функций второго рода. Значение на бесконечности. Подстановка
со
= \ е~" ch 'f d<? в левую часть уравнения E.406) дает при и = 0
о
7?°
о
[ ch2 сре~" ch'* cZcp — — { ch ере-" ch "> dep — \ e~s ch " d<?.
0 0 0
Объединяя первый и третий члены (Двайт, 650.01) и интегрируя по ча-
частям, будем иметь
ОО ОО ОЭ
(sh ср) [е-*сЬ5? d (ch ср)] = С м dfc = 1 ^-^ е""с11 ? + \ \ ch cpe-"ch ? rfo,
0 0
Полученное выражение совпадает со вторым членом, и, следовательно,
рассматриваемый интеграл удовлетворяет уравнению E.406). Поскольку
любое решение уравнения E.4U6) должно иметь вид R° = Alo(v) + BKo(v)
и поскольку интеграл обращается в нуль при гз=^оо, /0(в) не входит в ре-
решение и № = ВК0{ь). В § 36а будет показано, что в соответствии с выра-
выражением E.439) следует принять В=1, так что
К, (с) = \ е-" ch f da = 4 /«#}>} (/») = - 4 /™^о ' (- /»)• E.443)
о
Выражение
ОО
«m dnK°fjj) = (_ 1)" ^ tm chn сре~" ch ip dep
о
?lS8 Глава V
также обращается в нуль при в=оо, поскольку v входит в иодинтеграль-
ное выражение в виде vme~av, где а > 1. Из рекуррентных формул E.418)
и E.419) следует, что
К1=—К'о, откуда Я,(оо) = 0.
Из формулы E.419) тогда получим
где р = 1 при и нечетном и р = 0 при п четном. Формула E.417) показы-
показывает, что Кп(сс) = 0 и т. д.
Другое интегральное представление для Ku(v) имеет вид
со
K0(v) = [ cos(?;shtp)rftp. E.444)
о
Еейтман выводит это соотношение следующим образом.
Рассмотрим функцию
со
W = \ е~х ch v cos (у sh cp) dq,
где x = r cos д и у = r sin б. Дифференцирование ее даст
ой оу ^ ох
оо
= — V е~х cU *р [х sh cp sin (?/ sh cp) — у ch cp cos (у sh cp)] do =
о
= ^ ^- [е-ж ch f sin
о
e-50 ch
* sin (y sh cp)
= 0.
Таким образом W не зависит от в. Полагая 0 = 0, получаем х = ?-,
г/ = 0, так что, согласно формуле E.443), W =^К0(г). Подстановка Ь—-^~
дает х = 0, y = r; W совпадает в этом случае с интегралом E.444), что и
доказывает (.праведлнвость формулы E.444).
Для вывода интегральной формулы, применяемой при исследовании
диффракции на щели, подставим формулу E.443) в формулу E.442), заме-
иим интеграл от 0 до оо половиной интеграла от — оо до оо и изменим
порядок интегрирования. В результате получим (см. Двайт, 567.1)
со
2vK1(v) = kvH?)( — /Ъ)= \ e-™hlP(l + fcchcp)sech2cpd'f. E.445)
—ОО
§ 35. Интегральное представление бесселевых функций нулевого
порядка. Подстановка v/j вместо ь в формулу E.443) дает
Ко CV\ — [ e>v ch ¦" d<? = ^ cos (c ch cp) dtp + / ^ sin (г; ch cp) dcp.
0 0 0
Сделав аналогичную замену в выражешги E.409) и приравняв действитель-
действительные it мнимые части, получим (в обозначениях, принятых Ватсоиом;
Трехмерное распределение потенциала i99
см. § ЗОг) для функций J0(v) и Y0(ij) следующие формулы:
E.446)
со
уо (г;) = _ 1 ^ cos (v ch cp) dcp. E.447)
о
§ 36a. Представление обратного расстояния через модифицирован-
модифицированные бесселевы функции. Найдем выражение для обратного расстояния ме-
между двумя точками с координатами р0, ср0, z0 и р, cp, z в цилиндрической
системе координат. Для этого можно воспользоваться методом, изложен-
вым в § 31д; однако проще исходить из выражения для потенциала точеч-
точечного заряда, находящегося посередине между двумя плоскостями, распо-
расположенными па расстоянии L друг от друга. Потенциал такого заряда можно
получить из выражения E.435), если положить а=оо и сдвинуть начало
координат на L/2. Поскольку при этом сохраняются только нечетные зна-
значения п, для р < р0 будем иметь
со со
где N=Bn+ l)n/L. Полагая 2mz[L —-un и 2n/L = Au, получим
i „
m=0
Допустим теперь, что L—» со и, следовательно, Ди—*0. При этом сумми-
суммирование по п в пределах 0 <! п < со переходит, по определению, в интегри-
интегрирование по и в пределах 0^и< оо. Следовательно,
+ ^p] cos [(«,+?)*] Да.
= „ 2 2 B — §т) \ Кт (ир0) /т (up) cos uz du cos m (cp — cp0). E.449)
m-0 0
При p > р„ в выражении E.449) следует поменять местами р и р0. Если
оо = 0, то суммирование исчезает и
со
cos kz Ke (kp) dk. E.450)
В случае z — О и ср0 = 0 заменим в выражении E.450) р на Д и сравним
с выражением E.449). Из сравнения следует, что при р < р0
Ко [(Р2 + Рае - 2РРо cos tfi* ] = 2 B - 8°m) KM Im (P) cos m<p. E.451)
Для проверки выбора произвольной постоянной в выражении E.443) под-
подставим определяемое этой формулой значение Ке(кр) в выражение E.450).
Интегрируя сначала по к (см. Двайт, 577.2), а затем по ср (см. Двайт,
120.01), убеждаемся, что равенство E.450) удовлетворяется.
200 Глава V
§ 366. Цилиндрические границы раздела двух диэлектрических сред.
Полученное выше выражение для обратного расстояния можно попользовать
для решения задач при наличии в системе цилиндрических границ, допу-
скающих распространение электрического поля до бесконечности. В таких
Задачах разложение в ряд по функциям Бесссля невозможно, поскольку,
как нетрудно видеть из асимптотических представлений § ЗОе, интегралы
п § ЗОз обращаются в бесконечность при а=оо. Решение в этих случаях
получается обычно в виде определенного интеграла, численную величину
которого можно найти графически.
В качестве примера найдем поле точечного заряда q, расположенного
на оси бесконечной цилиндрической полости радиуса а, прорезанной в бес-
бесконечной диэлектрической среде с относительной диэлектрической прони-
проницаемостью К. Пусть потенциал внутри полости будет F, а вне полости
Vk- Воспользуемся методом, аналогичным изложенному в § 31д.
Будем рассматривать У как сумму потенциалов, первый из которых обу-
обусловлен одним лишь точечным зарядом и имеет вид E.450), а второй обу-
обусловлен поляризацией диэлектрика и должен быть конечным на оси поло-
полости. Таким образом, потенциал V имеет вид
v=ikv\ №»№>) + w(*O*(ftp)lcoskzdk- E-452)
Потенциал в диэлектрике должеп быть конечным на больших расстояниях
и, следонательно, должен иметь вид
со
ук = у4- \ Ф (*) Ко (*Р) cos kz dk. E.453)
Согласно грапичному условию V = V& при р = а, необходимо, чтобы
Ко(ка) + W (к) /„ (ко) = Ф (к) Ко (ка). E.454)
Граничное условие dV/dp = КдУк/др при р = а дает
К'о (ка) + W (к) Го (ка) = К® (к) К'о (ка). E.-455)
Исключай W (к) из соотношений E.454) и E.455) и упрощая полученное
выражение при помощи соотношения E.412), получим
Ф М =
l-ka(K-l)Jo{ka)K-(ka) '
Подставляя выражение E.456) н соотношение E.454), находим
ка(К-\)Кй(ка)К'й(ка)
\-ka(K-\)lu{ka)K'v(ka) ' (
На фиг. 58 изображено поле, вычисленное но формулам E.452) и E.453)
с использованием E.456) и E.457); интегрирование было выполнено для
случая /*Г = 5 при помощи планиметра.
§ 37. Потенциал внутри кольцевой цилиндрической полости. Из
электродинамических задач, для решения которых применяются модифици-
модифицированные функции Бесселя, наиболее важными являются задачи о пере-
переменных токах в цилиндрических проводниках. Однако и при решении не-
некоторых электростатических задач также применяются модифицированные
бесселевы функции. Рассмотрим, например, потенциал в области, ограни-
ограниченной поверхностями р = а, р = 6, z = 0 и z = c, потенциал которых, за
Трехмерное распределение потенциала
201
исключением первой, равен нулю. Потенциал поверхности р = а пусть будет
V = f(z). Разложим функцию f(z) в ряд Фурье в интервале 0 < z < с.
v=aio
Фиг. 58. Эквипотенциальные линии точечного заряда, находящегося
на оси цилиндрического отверстия в диэлектрике с диэлектрической
проницаемостью ЛГ=5.
Вычисления выполнены А. Е. Гарисоном по формулам E.452) и E.453).
Поскольку / (z) = 0 при z = 0 или z —- с, полз'чается известное разложение
(см. Пайерс, 815)
cos
cos
Из выражений E.310) и E.311) и E.411) вытекает, что решение уравнения
Лапласа, удовлетворяющее всем граничным условиям, имеет вид
ю А совАЬгаЛ Г/о
_ V sin у с / I /0
(fatp/c)
(кпЪ/с) ^0 (ЫЬ/с)
/0 (kna/c)
То (knb/c)
Ko (kna/c)
Ko (knb/c)
E.459)
202 Глава V
Для потенциала в области, лежащей внутри цилиндра p = ft, на поверхно-
поверхности которого задан потенциал F = /(z), и ограниченной двумя заземлен-
заземленными плоскостями z=0 и z=c, выражение E.459) дает
V = y,Ah sin ^ 7; (,У°\ . E.460)
Для потенциала в области, лежащей вне цилиндра р = а, на поверхности
которого задан потенциал V — f (z), и ограниченной заземленными плоско-
плоскостями z = 0 и z = c, будем иметь
E.461)
§ 38. Модифицированные бесселевы функции нецелого порядка. Об-
Общее решение модифицированного уравнения Бесселя в том случае, когда п
не является целым числом, молено получить в результате замены в выра-
выражении E.393) j-nJn(jv) на In(v)
R°(о) = Aln (») + 2?/_n («). E.462)
Функция Kn{v) является линейной комбинацией /„(у) и /_и(и). Для этих
функций справедливы полученные выше рекуррентные формулы. Формулы
E.394)-E.398) дают
E.463)
' E.464)
E.465)
= (|I/S (sh»--i-ch«) , E.466)
E.467)
E.468)
Общая формула принимает наиболее простой вид, если воспользоваться
экспоненциальными функциями
8=0
где в обеих частях нужпо выбрать либо верхний, либо нижний знак.
Как / 1 (г;) так и / i (v) обращаются в бесконечность при у=со.
Решением, обращающимся в нуль при v—>оо, является функция К
П+2
определяемая соотношением E.409), в котором следует заменить п на п -f--j .
Исключим из этого соотношения функцию У i (/Ъ) при помощи формулы
{5.400), введем, согласно выражению E.407), функции / / i\(v) и иред-
Трехмерное распределение потенциала
203
ставим их в виде E.4G9). В результате экспоненциальные функции с поло-
положительными показателями степени сокращаются и мы получаем
S\(n-S)\Bvf ¦
0
(ОЛЮ)
В простейших случаях
С1 +4
, . . / 2 Л г/2 r, . 1 xn (n4-s)le-v
К (V) = ( — ) К 1 iP) = — > 1/ ч|/ч >s •
n ч ' ^тгоу n+4 ю •<--' s! (n — •?)! (Ivf
При » = 0 основную роль в сумме E.470) играет член n — s, так что
К i{v) у Г ny-HBn-i)\\ E.472)
Сферические бесселевы функции Лп(«) можно определить следующим
¦образом:
п
E.473)
E.474)
Отсюда, принимая во впиманпе соотношение E.403), получим
kn (jv) jn (v) — /7^ (jv) /„ (v) = — /-"+' v'2. E.475)
Рассматриваемые функции связаны с функциями Kn(v) Шелкунова и
"ri) (v) Стрэттона следующим образом:
— — / Un\]v') +]nn\!v)]- (о.47b)
с § 336 и выражением E.473),
При помощи выражений E.409) и E.400) находим
Рекуррентные
имеют вид
фо^
мулы,
— Bга-
в
-f'
соответствии
- ft
n+,,
± (n+4 ± I
E77)
§ 39. Приближенные решения. Электростатические линзы. Для пе-
лого ряда практических задач, точные решения которых получить невоз-
невозможно или затруднительно, можно найти прибли-
приближенные решения, достаточно (с точки зрения экспе-
эксперимента) близкие к точным. Один, часто весьма эф-
эффективный, приближенный метод заключается в том,
что при решении задачи добиваются выполнения гра-
граничных условий не всюду, а лишь в конечном числе
точек. Рамо и Виннери рассматривают в качестве
примера аксиально симметричную электростатиче-
электростатическую электронную линзу (фиг. 59). Линза состоит
из плоской проводящей пластинки толщиной 2Ъ с
отверстием радиуса а; пластинка имеет потенциал Уо
и'^помещается посередине между параллельными
заземленными плоскостями, расположенными на рас-
расстоянии 2с друг от друга. Фокусирующие свойства
такой лиизы выражаются обычно через поле на оси симметрии.
искомой величиной является в данном случае поле на оси.
•<—
/¦
/
/' Уу
У ¦'¦•'//////,
'у '/
—2с-
>-
\о
V
s
у
/
Фиг. 59.
Поэтому
у В соответствии с
выражением E.311) и § 34а решение, обладающее соответствующей симметрией
204 Глава V
и обращающееся в нуль на заземленных плоскостях, имеет вид
sin p±i>^] . E.478)
и=0
Если пренебречь в этом выражения всеми членами, для которых п > 4, то
можно добиться, чтобы потенциал E.478) был равен Т7„ в четырех точках
границы. Пусть эти точки имеют координаты z = 0 u z=b при р = ои
р= 1,5ft и p = 3ft при z=b. Тогда в случае а = Ь = 0,3с постоянные Ап ока-
оказываются равными
Л1 = 1,15, Л= -0,172, Л8 = 0,02И, Л4 = 0,00098. E.479)
Эти значения дают, очевидно, удовлетворительную точность для точек на
оси, где /0@) = 1.
§ 40. Функции клина. Функции, введенные в § 306 и ЗОв, оказыва-
оказываются неадэкватными в тех случаях, когда искомый потенциал обращается
в нуль на поверхности цилиндров р = р1; р = р2 и на плоскостях z = zv
z = z2n имеет некоторое произвольное значение на плоскостях ср = ср1; ср — ср2.
Для решения этой задачи требуются функции, ортогональные по риги
получающиеся заменой п на /v и к на jk в уравнениях E.300) — E.302).
Таким образом,
ф (vcp) = С ch vcp + D sh v<p = C'e^ + D'e~^, E.480)
Z (kz) = E sin kz+F cos kz, E.481)
R^(kP) = AFw(kP)+BGy{kp), E.482)
где функция Rv (v) удовлетворяет дифференциальному уравнению
1 dR
Функция F^ (v) —> со при v —s- со и определяется формулой
Fv (v) = cose ch vit { ev cos в ch v6 JO — ^ e~v ch (sin vi dt. E.484)
о о
Функция Gv (v)—»0 при v—> со и определяется следующим образом:
СО
Gy (v) = \ е-* сЪ * cos vtdt^K^iv). E.485)
о
Если v меньше некоторого определенного значения, увеличивающегося
с ростом ч, то обе эти функции — периодические и при v, стремящемся к нулю,
осциллируют как sin v In ( -тг v j \ и cos v In f -^ v j \. Интеграл по v от
произведения этих функций, умноженного на V, обращается в нуль, за
исключением того случая, когда индексы v одинаковы у обоих сомножите-
сомножителей. Поэтому любую функцию, допускающую разложение в ряд Фурье,
можно разложить и по функциям JRv(kp). Задача о трехмерном диэлектри-
диэлектрическом клине решается точно таким же методом, как и аналогичная двух-
двухмерная задача в § 8 гл. TV.
Задачи 205
ЗАДАЧИ
1. Два одинаковых точечных заряда помещены па расстоянии 26 друг от друга.
Показать, что помещенная посередине между ними заземленная проводящая сфера
уничтожает их взаимное отталкивание, если радиус сферы равен приблизительсо Ь/8.
2. Пусть с—радиус-вектор, проведенный из центра проводящей сферы радиуса а
в точку, где находится точечный заряд д. Показать, что если заряд с&еры Q равен
то сила, действующая па заряд д в однородном поле Е, совпадающем по направлению
с радиус-вектором с, обращается в нуль.
3. Бесконечная проводящая плоскость является границей однородного поля, на-
напряженность которого X неизвестна. На заданный заряд д, помещенный на расстоянии г
от плоскости, действует некоторая (неизвестная) сила F. Если прямо под зарядом по-
поместить на плоскости проводящую полусферу радиуса а, то оказывается, что сила,
действующая па заряд, не изменяется. Показать, что
р_ д2 Г
4яе L
J
4. Сферическая проводящая полость радиуса а наполнена до половины диэлек-
диэлектриком. Сила, обусловленная изображениями, не действует на заряд, помещенный
па оси симметрии на расстоянии а/3 от плоской поверхности диэлектрика. Показать,
что проницаемость диэлектрика равна 1,541 е„.
5*. Заряд расположен в точке О над бесконечной проводящей плоскостью, потен-
потенциал которой равен нулю. Показать, что заряд любого участка плоскости пропорцио-
пропорционален углу, над которым виден этот участок из точки О.
6*. Две бесконечные заземленные проводящие плоскости пересекаются под углом 60°.
Заряд е расположен на одинаковом расстоянии от обеих плоскостей н на расстоянии г
от линии их пересечения. Найти плотность поверхностного заряда на плоскостях.
Показать, что и точке, находящейся на расстоянии г 3 '2 от вершины угла в плоско-
плоскости, проходящей через точечный заряд и перпендикулярной к линии пересечения,
плотность поверхностного заряда равна
_
73/2
7*. Точечный заряд е находится вне проводящей изолированной сферы на рас-
¦стоянии г от ее центра. Какой минимальный положительный заряд следует поместить
на сферу, чтобы поверхностная плотность заряда была яа ней всюду положительна?
8*. Заземленная проводящая сфера находится в поле точечного заряда, располо-
расположенного в точке Р вне сферы. Найти отношение индуцированного заряда, приходящегося
на ту часть поверхности сферы, которая видна из точки Р, к индуцированному заряду
остальной ее части.
9*. Точечный заряд е подносится к проводнику, имеющему форму шара радиуса а.
Заряд проводника равен Е^>е. Показать, что точечный заряд будет отталкиваться от
сферы, если расстояние от него до ближайшей точки поверхности сферы не превосхо-
превосходит (приближенно) ^ а
10*. Полость в проводнике представляет собой четверть сферической полости,
•ограниченную двумя взаимно перпендикулярными диаметральными плоскостями. По-
Построить изображения-точечного заряда, расположенного внутри полости.
11*. Проводящая поверхность образована дпумя бесконечными плоскостями, пере-
пересекающимися под прямым углом, и заключенной между ними четвертью сферической
поверхности радиуса а. Потенциал поверхности равен нулю. Точечный заряд е распо-
расположен симметрично относительно плоскостей и сферической поверхности на большом
расстоянии / от центра последней. Показать, что заряд, индуцированный на сфериче-
сферическом участке описанной поверхности, равен приблизительно —5ев3/(л/3).
12*. Тонкая плоская проводящая пластинка произвольной формы и размера нахо-
находится в поле заряда, распределенного с заданной плотностью по одну сторону от нее.
Пусть Oj—плотность индуцированного поверхностного заряда в точке Р на той стороне
пластинки, которая обращена к заданному заряду, а о2— плотность поверхностного
заряда в соответствующей точке противоположной стороны. Доказать, что
а. — а9 =
где ао—плотность поверхностного заряда, индуцированного заданным зарядом в точке Р
бесконечной проводящей плоскости, совпадающей с пластинкой.
206 Глава V
13*. Проводящая плоскость имеет выпуклость в виде полусферы радиуса а. На ее
оси, на расстоянии / от центра, находится точечный заряд е. Показать, что если по-
потенциал плоскости и выпуклости равен нулю, то заряд, индуцированный па последней г
равен
14*. Заземленная проводящая сфера радиуса а находится в поле заряда, равно-
равномерно распределенного с плотвостью а по внешней поверхности непроводящего сегмента
радиуса с, концентричного со сферой. Показать, что плотность заряда на поверхности
сферы, обращенной к сегменту, в точке пересечения А оси сегмента со сферой равна
где В — точка пересечения оси с поверхностью сегмента и D—точка на его краю.
15*. Два проводящих диска радиусов а и а' расположены перпендикулярно к пря-
прямой, соединяющей их центры. Расстояние между ними г велико по сравнению с а.
Первый диск имеет потенциал V, а второй заземлен. Показать, что заряд первого
диска равен
8пЧаг2У
(я2г2—Ааа') '
16*. Тонкое проволочное кольцо радиуса с, несущее заряд Q, расположено в пло-
скости, касательной к заземленной проводящей сфере диаметра а, таким образом, что
центр кольца лежит в точке касания плоскости* и сферы. Доказать, что плотность
поверхностного заряда, индуцировапвого на сфере в точке, направление на которую
из центра кольца образует угол ф с нормалью к его плоскости, равна
c2Q sec3
\ (а2 + с2 sec2 ф — 2ас tg ф cos 6)/2 d6.
17. В колбе радиуса а с проводящими стенками, из которой выкачан воздух,
на расстоянии с от ее центра образовался неподвижный ион с зарядом д и массой те.
Показать, что иоя достигнет стенки через промежуток времени, равный
г = 5-1^Dят?а3I/2(/Г— Е), где к2 = (а2 — с2) а~2,
К и Е—полные эллиптические интегралы модуля к.
18. Центр заземленной проводящей сферы радиуса а находится ва оси заряжен-
заряженного кольца. Радиус-вектор с, проведенный из центра сферы к кольцу, образует угол о.
с его осью. Показать, что сила, втягивающая сферу в кольцо, равна
_Q'2E_(c2 — а2) к3 cos a 4rz2c2sin2a
16я2ес2«2 gins о A —ft2) ' д а* + с* — 2а2с2 cos 2a '
Е—полный эллиптический интеграл модуля ft.
19*. Частица с зарядом е находится в средней точке лияви, соединяющей центры
двух одинаковых проводящих сфер, потенциал которых равен нулю. Пренебрегая выс-
высшими степенями т—отношения радиуса сфер к расстоянию между их центрами, пока-
показать, что заряд, индуцированный на каждой из них, равен
— 2ет A — т -f m2—3m3 +4m4).
20*. Две изолированные проводящие сферы радиусон а и Ь, несущие заряды Q,
и Q2, расположены таким образом, что расстояние между их центрами с велико но
сравпепшо с а и Ь. Показать, что потенциальная энергия системы равна приближенном
(8га)-i [(е-* —Ус-4) QI + 2c-^Q1Q2 + {h-^asc-^) Q|].
21*. Две изолированные проводящие сферы радиуса а находятся в однородном
электрическом поле напряженности Е, перпендикулярном к прямой, соединяющей
центры сфер. Показать, что сила взаимодействия между сферами равна
A — 2esc-8 —
где с—расстояние между их центрами.
Задачи 207
22*. Две незаряженные изолированные сферы радиусов а и Ъ вносятся в однород-
однородное электрическое поле, иараллельвое прямой, соединяющей их центры. Расстояние
между центрами сфер с много больше их радиусов а и Ъ. Показать, что плотность
поверхностного заряда в точке пересечевия сферы а с прямой, соодмвяющей центры
сфер, приближенно равна
23*. Две одинаковые проводящие сферы радиуса а касаются друг друга. Показать,
что емкость полученного таким образом проводника рапна 8-кга in 2.
24*. Радиусы двух касающихся проводящих сфер равны соответственно а п Ъ.
причем a J> Ь. Показать, что если потенциал сфор равен V, то их заряды будут
V b (a -r Ъ)г J 3 (a + 6J
25*. Проводящая сфера радиуса о касается бесконечной проводящей плоскости.
На продолжении диаметра, проходящего через точку касания, ва расстоянии с от этой
точки находится единичный точечный заряд. Показать, что заряды, индуцированные
на плоскости и на сфере, равны соответственно
тш / па \ тш ^гаЛ
-Tct*u; и t^UJ-1-
26*. Расстояние между понтрами двух одинаковых заземлевных проводящих сфер
радиуса о равно 2с. Показать, что единичный заряд, находящийся посередине межд^
сферами, ивдуцирует на каждой ив них заряд
со
У (— 1)" sech па,
1
где с = о ch a.
27. Расстояние между центрами двух одинаковых сфер радиуса о равно с. Сферы
соединены тонкой проволочкой. Показать, что емкость такой системы равна
со
8raa sh fi ^ (— l)n+1 cosech n|3,
где ch P = -^- с/а.
28. Две одинаковые сферы радиуса а, центры которых находятся на расстонии с
друг от друга, заряжены до одинакового нотепциала V. Показать, что сила отталкива-
отталкивания между ними равна
со
2-nsV2 ^ (—IO (cth P—n cth пЩ cosech n\,
тг=1
где ch|3 = -— с/а.
29*. Изолированная проводящая сфера радиуса а помещена посередине между
двумя бесконечными параллельными заземленными плоскостями, находящимися иа
большом расстоявии 2с друг от друга. Пренебрегая величинами порядка (а/сJ, пока-
показать, что емкость такой сферы равва приблизительно
I In 2].
30*. Две сферы радиусов га и г2 касаются друг друга. В таком положении пх
емкости равны соответственно сх и г2. Показать, что
222
1 1 1
где / = '11(г1 + '12)-
31*. Между двумя параллельными бесковочпымп заземленными плоскостями нахо-
находится точечный заряд е. Расстояния от заряда до плоскостей равны соответственно а
и Ь. Показать, что потенциал в точке Р па прямой, перпендикулярной к плоскостям
и проходящей через заряд, равен
a+b) L
где z—расстояние от заряда до точки Р, W (z) = JT' (z)/r B),
208 Глава V ^___
32. Электрон с зарядом е и массой те, летящий первоначально в горизонтальном
направлении со скоростью v, должен пролететь (в вакууме) над плоской незаряженной
горизонтальной поверхностью пластинки из диэлектрика длиной d. Пусть в тот
момент, когда электрон проходит над краем пластинки, расстояние между ними равно а.
Пренебрегая краевым эффектом, показать, что под действием сил, обусловленных
изображением, электрон будет втянут в диэлектрик, прежде чем достигнет противо-
противоположного его края, если
{К
334 Точечный заряд расположен над плоской бесконечной поверхностью диэлектри-
диэлектрика. Угол между силовой линией электрического ноля в диэлектрике и нормалью к его
поверхности равен а; угол между этими же липиями вблизи точечного заряда равен ^.
Показать, что аир связаны соотношением
34*. Заряды е, и е2 расположены на прямой, перпендикулярной к плоской границе
раздела двух диэлектрических сред с относительными диэлектрическими проницае-
мостями Кг и К2, на равных расстояниях а от границы. Найти силы, действующие
на заряды, и объяснить, почему эти силы не равны.
35*1). Два проводника, емкости которых в воздухе равны сх и е2, помещены
на прямой, иерпендикулярной к плоской границе раздела двух диэлектриков с. относи-
относительными диэлектрическими проницаемостями ft, и кг. Расстояния от проводников
до границы раздела, равные соответственно а и Ъ, велики по сравнению с размерами
самих проводников. Проводники соединены между собой тонкой проволочкой и заряжены.
Доказать, что заряд распределяется по проводникам (приближенно) в отношении
Г Ы к,-к2 2к2 И .
L vc2 26 (ftx +*2) (к, + А-2) (а + Ь) \ ¦
4Я
с +
36*. В воздухе, над плоской поверхностью бесконечного диэлектрика, находится
проводящая сфера радиуса а. Расстояние между центром сферы и поверхностью диэлек-
диэлектрика равно с. Показать, что ее емкость равна
/ v. VI Г (К— I)"!"-1 ^
47teuasna- V I }-= -^ cosecn па,
^ L(-ff+i) J
где ch a = c/o.
37. Заземленный проводник' состоит из двух одинаковых проводящих сфер радиуса а,
пересекающихся ортогонально. В плоскости пересечения на расстпявии За2~~1'2 от оси
симметрии находится точечный заряд д. Показать, что заряд, индуцированный на про-
/ 1 2 Л
воднике, равен ( -^—~Щ2)Ч-
38. Плоский заземленный проводящий лист имеет круглое отверстие радиуса а.
В плоскости листа на расстоянии Ъ от центра отверстия находится точечный заряд д.
Показать, что плотность поверхностного заряда, индуцированного на листе на расстоя-
расстоянии с от центра отверстия и на расстоянии г от заряда д, равна
— д (а2 —Ь2I/2/[2я2г2 (с2 — а2I1*].
39. Показать, что если в предыдущей задаче заряд распределен но кольцу радиуса Ъ,
лежащему в плоскости листа концентрично с отверстием, то плотность индуцирован-
индуцированного поверхностного заряда в точке Р равва
40. Пользуясь решением предыдущей задачи и теоремой взаимности Грппа,
показать (при помощи метода инверсии), что потенциал в точно Р поверхности сферы,
часть которой покрыта тонкой металлической оболочкой, имеющей форму чаши
х) Ввиду ошибки у автора эта задача приведена непосредственно из книги Джннса
с соответствующим переводом в практическую систему единиц. —Прим. перес.
Задачи 209
и заряженной до потенциала Fo, равен
2Vn . cos a
—- arc sin j. .
¦к cos О
Здесь 0—угол между осью симметрии системы и примой, соединяющей точку пере-
пересечения этой оси и поверхности листа с точкой Р, о—угол между осью и прямой,
соединяющей ту же точку с краем «чаши».
41. Используя решепие предыдущей задачи, найти первый член разложения потен-
потенциала заряженной сферической «чаши» по сферическим гармоникам. Все точки поверх-
поверхности «чаши» находятся на одинаковом расстоянии а от начала координат, а угол
между ее осью и прямой, соединяющей начало координат с краем «чаши», равен -^- р.
Пользуясь полученным выражением, показать, что емкость такой системы равна
42. Используя решение задачи 39 и применяя метод инверсии, найти плотность
поверхностного заряда, индуцированного на заземленной сферической проводящей «чаше»
зарядом, распределенным равномерно (с плотностью — о,) по поверхности, дополняющей
«чашу» до сферы. Путем наложения заряда, равномерно распределенного по всей поверх-
поверхности сферы с плотностью о1? показать, что плотности поверхностного заряда на внут-
внутренней и внешней сторонах «чаши», заряженной до потенциала Fo, равны соответственно
eFn Г sin a . sin а Т eFn
°i = —- п arc sin ——г , о0 = —-4-е;.
™ L(sin2e — sin2<xI/2 smflj a ^
Обозначения те же, что и в задаче 40.
43*. Поверхность проводника образована внешними поверхностями двух одинаковых
сфер, пересекающихся таким образом, что угол между их радиусами в точке пересече-
пересечения равен 2п/3. Показать, что емкость такого проводника равна
2лаеE — 3~1/2-4),
где а — радиус сфер.
44*. Изолированный незаряженный проводник, образованный двумя одинаковыми
сферами радиуса а, пересекающимися под прямым углом, вносится в однородное элек-
электрическое иоле напряженности Е таким образом, что прямая, соединяющая центры
сфер параллельна силовым линиям. Показать, что заряды, ипдуцированпые на сферах,
равны ± Ипга^Е/2.
45*. Поверхность проводпика состоит из больших (внешних) частей поверхностей
двух одиваковых сфер радиуса а, пересекающихся под углом тс/3, и третьей сферы
радиуса с, пересекающейся с каждой из одинаковых сфер под прямым углом. Показать,
что емкость такого проводника раина
-|—~ З1'О —ас Г 2 (а2
46*. Сферическая оболочка радиуса а с маленьким отверстием, площадь которого
равна S, заряжена до потенциала V. Доказать, что заряд на внутренней стороне
j
оболочки меньше — e.VSja.
47*. В тонкой проводящей сферической оболочке вырезано отверстие. Оболочка
заряжена. Доказать, что в любой точке разность плотностей поверхностного заряда
на внутренней и внешней сторонах оболочки постояппа.
48*. Показать, что емкость эллиптической пластинки с малым эксцентриситетом е
и площадью А равна приближенно
49*. Объем эллипсоидального проводника, мало отличающегося от шара, равен
объему шаря радиуса г. Оси эллипсоида равны 2r(l + <x), 2r(l + fJ), 2r({-{-f)- Прене-
Пренебрегая кубами величин a, fi, -у. показать, что его емкость равна
50. Заряд сплюснутого сфероидального проводника с полуосями о и Ъ (а < Ь)
равен Q. Показать, что две половины, на которые сфероид рассекается диаметральной
14 в. Смайт
210 | Глава Г
плоскостью, отталкиваются друг от друга с силой
Q2[16jisF2—а2I-Чп—.
51*. Заряд вытянутого сфероидального проводника с полуосями аи Ь (а > Ъ)
равен Q. Показать, что две половины, на которые сфероид рассекается диаметральной
плоскостью, отталкиваются друг от друга с силой
Q2 [\6т (а2 - b2)]-1 In ~.
Найти величину этой силы в случае сферы.
52*. Топкий круглый диск радиуса а окружен сфероидальным проводником, поверх-
поверхность которого получается вращением эллипса с фокусами S, лежащими на краю диска.
Заряд диска равен Q, заряд с-феропда Qx. Показать, что энергия такой системы равна
[Q2/l BSC + iQ + Q^Z. SBC]/(8Ksa),
где В — точка пересечения оси вращеппя с поверхностью сфероида, С—центр диска
(сфероида).
53*. Конденсатор состоит из двух концентричных и коаксиальных сплюснутых
сфероидов с малыми эксцентриситетами S и 8'. Оси сфероидов, совпадающие по направ-
направлению с осью симметрии, равны 2е и 2с'. Пренебрегая квадратами эксцентриситетов,
показать, что емкость такого конденсатора равна
4леес' (с' — с) Г с' — с + -| Eс' — 8'е) 1 .
Найти с той же степенью точности распределение заряда на каждой из обкладок кон-
конденсатора.
54*. Относительная диэлектрическая проницаемость среды, которая заполняет
конденсатор, состоящий из двух ковфокальных вытянутых сфероидов, является функ-
функцией точки и равна Kl/ш, где 5> — расстояние от данной точки до оси вращения.
Показать, что емкость такого конденсатора равна
°i + W \ '
где a, b и Oj, Ъг—полуоси эллипсов, вращением которых получаются поверхности
сфероидов.
55*. Тонкая сферическая «чаша» образована частью поверхности сферы ж2+y2-\-z2 = cz>
лежащей внутри конуса [х/'а)г + (y/bJ = (zjcJ. «Чаша» соединена с землей при помощи
тонкой проволоки. Виедем обозначения: О — начало координат, С—точка, диаметрально
противоположная О («вершина чаши»), Q—произвольная точка на краю «чапш»,
р—точка дуги большого круга CQ. Доказать, что заряд Е, помещенный в точку О,
индуцирует на сфере поверхностный заряд, плотность которого в точке Р равна
Ее CQ Г <й>
¦ — где т— ч
J (a2 sin2l
4nablopz(OP2 — OQ2I'*' ' 3 (а2 sin2 6 + Ь2 cos2 6I'2 '
56. Заряд д находится на расстоянии с от центра сферической полости радиуса а,
нырстзанной п бесконечном диэлектрике с относительной диэлектрической проницае-
проницаемостью К- Показать, что сила, действующая на заряд, равна
(ff-l)g2 y n{n + l) / с уп+1
4гсе„с2 ^ n+K{n + i)\ a J
п=0
57. Проводящая заземленная сфера радиуса а расположено таким образом, что
ее центр находится на оси заряженного кольца, а радиус-вектор с, проведенный из
центра сферы к кольцу, образует с осью последнего угол а. Показать, что сила,
втягивающая сферу в кольцо, равна
Задачи 211
58. Сферические координаты круглого кольца равны а, а. Шар радиуса Ъ из
диэлектрика с относительной диэлектрической проницаемостью К расположен так, что
его центр находится в начале координат. Принимая плотность линейного заряда кольца
равной т, показать, что выражение для потенциала между кольцом и сферой имеет вид
59. Участок поверхности сферы радиуса а, лежащий между углами 8 = а и 6 = тг—и,
несет поверхностный заряд, распределенный с постоянной плотностью о. Доказать,
что выражение для потенциала вне сферы имеет нид
со
аа f a ^> I fa N
— j_cosa+J>j ^q^-IPsn+ifcosa) —P2rl_!(cosa)] ( — )
60. В заземленной фотоэлектрической камере, представляющей собой сферу ради-
радиуса Ъ, в качестве коллектора используется круглое кольцо радиуса а. Кольцо помещено
в центре; заряд его равен Q. Показать, что напряженность ноля на поверхности сферы
ранна
' 2-4... 2и Ь*
61. Точечный заряд q находится на расстоянии Ь от центра днух концентрических
проводящих заземленных сфер, радиусы которых равны соответственно а а с (причем
а < Ь < с). Показать, что в области а < г < Ь выражепие для потенциала имеет пид
Р„(со8б).
62. На бесконечной проводящей плоскости помещена половина диэлектрического
шара радиуса а, прилегающая к плоскости всей площадью большого круга. Прямо над
ней, на расстоянии Ь от плоскости, находится точечный заряд q. Показать, что вне
диэлектрика Плотность поверхностного заряда, индуцированного на плоскости, равна
Ч_ Г Ь ъ (l-jr)Bn + l)Bn + 2)l-3...Bn + l) ain>3 I
'*n LOP + r2)*1* ^ l + (Zn+l)(JT-fl) 2-4 ... Bn + 2) b*n**rin*3 J
0
63. Круглый диск радиуса с заряжен до потенциала Vx. Показать, что потенциал,
создаваемый таким диском в окружающем пространстве, при г > с равен
Найти значение потенциала в области г < с.
64. Два одинаковых кольпа радиуса а расположены друг против друга в парал-
параллельных плоскостях таким образом, что радиус одного из них виден из центра другого
под углом а. Считая заряды колец равными Q и Q', доказать, что сила отталкивания
¦между цими равна
QQ'
У, (— 1)п т, (sin аJп*3Р',ги.1 (COS a).
4J Z-4'o...Zn ' '( '
47teo2
n=0
65. Проводящие стенки сферической полостп радиуса а покрыты изиутри слоем
однородного диэлектрика; внутренний радиус такой изоляции равен Ь. Показать, что
на точечный заряд q, находящийся н полости на расстоянии с от центра, действует
сила
2"-1 !(К—\) (га + 1) аг"^+ [(K + l) n + 1] Ь2-1}
14*
212 Глава V
• 66. Точечный заряд q находится на расстоянии с от центра заземленной проводя-
проводящей сферы радиуса а, покрытой слоем диэлектрика, внешний радиус которого равен Ъ,
а относительная диэлектрическая проницаемость равна К. Показать, что выражение
для потенциала в диэлектрике имеет вид
п=0
67*. В однородное электрическое поле напряженности F вносится изолированная
проводящая сфера радиуса а, полный заряд которой равен нулю. Показать, что если рассечь
сферу на две половины плоскостью, перпендикулярной к направлению ноля, то полу-
чевные полусферы будут стремиться раздвинуться и гюгребуется сила, равная —г
чтобы удержать их вместе.
68*. В изолированном незаряженном сферическом проводнике имеется сферическая
полость радиуса Ь. В полости находится проводящий шар радиуса а, заряд которого
равен Q. Расстояние с между центрами шара и полости очень мало. Пренебрегая чле-
членами порядка с2 найти потенциал внутри полости и показать, что плотность заряда
н точке Р поверхности шара равна
Q_f J Зс cos 6 N
где 6 — угол между радиусом, проходящим через точку Р, и прямой, соединяющей
центры полости и шара.
69*. Уравнение поверхности проводника имеет вид г = а A-\-ЬРп), причем величина о
очень мала. Проводник вносится в однородное электрическое поле напряженности F,
параллельное оси гармоник Рп. Показать, что плотность индуцированного заряда
в любой точке поверхности такого проводника больше плотности заряда, который воз-
возник бы, если бы поверхность проводника была сферической, на величину
[5+т] Кп
70*. Уравнение поверхности проводника, заряженного до потенциала У, имеет
Вид г = аA +ЬРп). Проводник окружев слоем диэлектрика (К), причем поверхность
раздела диэлектрика с окружающей средой (воздухом) задана уравнением r — b (l4-fjPn)-
Пренебрегая квадратами и более высокими степенями величин й и yj, .показать, что
потенциал в окружающей среде на расстоянии г от начала координат равен
KabV
71*. Поверхность заземленного проводника задала уравнением
где величина yj очень мала. Показать, что точечный заряд, находящийся на расстоя-
расстоянии / от начала координат в точке с угловыми координатами 6 и <р, индуцирует на
проводнике заряд, равный приближенно
72*. Заземленпвя проводящая сфера радиуса с окружена концентричным ей круг-
круглым проволочным кольцом радиуса а. Заряд, приходящийся па единицу длины кольца,
равен е. Показать, что плотность поверхностного заряда на сфере равна
73*. Диэлектрический шар окружен тонким круглым проволочным кольцом, несу-
несущим заряд Q. Радиус кольца о значительно больше радиуса шара. Показать, что потен-
потенциал внутри шара имеет вид
°° 1-3-5... Bп—1)
A + JT) 2-4-6... 2п
Задачи 213
74*. Проводящая сфера радиуса а окружена конпентричной диэлектрической
(с относительной проницаемостью К) оболочкой, внешний радиус которой равен 2а.
Показать, что. когда такая система вносится в однородное электрическое поле напря-
напряженности F, на проводнике появляются заряды, противоположные по знаку и равные
по величине
75*. Проводящий шар радиуса а окружен оболочкой из однородного диэлектрика К.
Внешний радиус оболочки равен Ь, а центр ее находится на малом расстоянии f от
центра шара. Предполагая, что потенциал шара равен V, а других проводников в окру-
окружающем пространстве пе имеется, показать, что плотность заряда ва поверхности шара
равна приближенно
BvKVb г ^ | 6 (А'—1) -уя2 cos 0 ]
а [(АГ— 1)о + 6]
где 6 — угол между радиусом, проведенным в ту точку, где ищется плотность заряда,
и прямой, соединяющей центры шара и оболочки.
76*. Внутри стеклянной оболочки, ограниченной концентрическими сферами ради-
радиусов а и Ь (а < Ь), находится заряд q, расположенный в точке Q на малом расстоянии с
от центра сфер О. Показать, что потенциал в точке Р вне оболочки на расстоянии г
от точки Q равен приближенно
2с (Ь3—а3) (К— IJ cos6
J'
где К—относительная диэлектрическая проницаемость стекла, а 0—угол между QP
и 0Q.
77. Показать, что диэлектрический шар радиуса а (относительная проницаемость
шара равна К) и точечный заряд q, расположенный на расстоянии с от его центра,
притягиваются с силой
n(n
п\с J
п=\
78. Проводящая сфера радиуса а насажена на проводящий конус, поверхность
которого пересекается с поверхностью сферы под прямым углом, а угол раствора
равен 2(п—а). Показать, что в том случае, когда такая система заряжена, выражение для
потенциала имеет вид
A f-a^^r"-1) Pn (cos 6),
1
где 0< n < 1 и Рп (cosа) = 0 при а>— тт.
79. Два коаксиальных проводящих конуса, углы раствора- которых, измеренные
от положительного направления оси, равны соответственно 2а и 2р, пересекаются орто-
ортогонально с проводящей сферой радиуса а. Показать, что если такая система заряжена,
то потенциал вне сферы в пространстве между копусами равен
А (Г«—a2«+1r-n~i) [Qn (cos p) Pn (cos ft) — Pn (cos p) Qn (cos ft)],
где п — наимепьшее число, для которого
Qn (cos Р) Рп (cos а) — Рп (cos P) Qn (cos а) = 0.
80. Сплюснутый диэлектрический сфероид с поверхностью ^0 вносится в однород-
вое электрическое попе Е, параллельное оси ?= 1. Показать, что поле внутри сфероида
однородно и его напряженность равна
Е
(К—1) Со 1A + Cg) arc ctg Со—Со] — ^ "
81. Сфероид, описанный в предыдущей задаче, вносится в однородное поле Е,
перпендикулярное к оси ? = 1. Показать, что поле внутри сфероида однородно и его
напряженность равна
IE
82. Вытянутый диэлектрический сфероид с поверхностью т10 вносится в однородное
электрическое поле Е, параллельное оси ? = 1. Показать, что поле внутри сфероида
214 Глава V
однородно и его напряженность равва
Е
(if — 1) rI0 1A —ч|) аг ctbijo + ijo]— ЛГ
8Н. Сфероид, описанный в предыдущей задаче, вносится в однородное поле Е, пер-
перпендикулярное к оси Е = 1. Показать, что поле внутри сфероида однородно и его напря-
напряженность равна
2Е_ *
2 + (К— l)ij0 1A — ^arcthijo + ijoJ '
84. Сфероид, относительная диэлектрическая проницаемость которого равна К,
вносится в однородное электрическое поле Е таким образом, что его ось вращения обра-
образует угол « с полем. Показать, что па сфероид действует момент, равный
— tibv (К —1) тР-пЕ (El — E2) sin 2a,
о
где п — полуось в направлении оси вращения и т— полуось, перпендикулярная к ней.
Дли сплюснутого сфероида Е1 и Е,— поля, полученные соответственно в результате
решения задач 80 "и 81, причем ?0 = п {т*— п2)'2. Для вытянутого сфероида Е1 и Е2 —
поля, полученные соответственно в результате решения задач 82 и 83, где iH =
= n(n2—те2р1/2.
85. Заземленный проводящий диск радиуса а, ураввепие которого имеет вид ? = 0,
находится в поле точечного заряда q, расположенного в точке 1, Со, 0. Показать, что
потенциал, обусловленный индуциропаппьш па диске зарядом, равен
2 ». (/С) Р2„ F).
п=0
86. Пользуясь теоремой взаимности Грипа и результатами, полученными в § 28е
гл. V, показать, что потенциал, созданный заряженным кольцом, уравнения которого
имеют вид С = ?о> ? = ?о> равен
S п 1Ы Р« («о) Qn (/С) Рп F),
п=0
где О Со и Q—заряд кольца. Найти выражение для потенциала, справедливое при С < 10.
87. Заземленный лроводящий диск радиуса а находится в поле заряженного кольпа,
уравнения гсоторого имеют вид ?=?0- ? = ?0- &аряд кольца равен Q. Показать, что потев-
циал, создаваемый индуцированным зарядом, равен
88. Верхняя и нижняя половины сплюевутого сфероида С = ?о изолированы друг
от друга и заряжены соответственно до потенциалов -\-V0 и —-Vo. Показать, что выра-
выражение для потенциала во внешнем пространстве имеет вид
Найти выражение для потенпиала внутри сфероида.
89. По поверхности вытянутого сфероида i) = i)o распределен с плотностью а (€, tp)
поверхностный заряд. Пользуясь методом, изложенным в § 28д гл. V, показать, что
ныражение для потенциала внутри сфероида имеет виц
Задачи 215
где коэффициенты Мтп равны
-1 О
Величины ht, h3 определяются формулами E.289) и E.290). Найти аналогичное выра-
выражение для потенциала во внешнем пространстве.
90. Используя решение предыдущей задачи, показать, что потенциал точечного
заряда q, расположенного в точке ?0, г10, ^о при rt > т]0, равен
n=0 m=0
X Pn F) Qn (Ч) С Ы К (So) cos m (9-9o).
Получить соответствующее выражение при •/) < rl0.
91. Внутри цилиндрической полости радиуса а, ограниченной заземленными прово-
проводящими стенками, расположено (коаксиальио полости) заряженное кольцо радиуса Ь.
Пользуясь выражением для потенциала внутри полости, обусловленного точечным заря-
зарядом q, находящимся на оси полости, и теоремой взаимности Грина, найти потенциал,
поддаваемый кольцом на оси. Показать, что при z < с этот потенциал равен
со
;sh[xft(L —с) Jofa
причем координаты оснований полости и плоскости кольца равны соответственно z = 0,
z= L и z = с, а значения [% выбраны так, что /0 (№й) — 0. Показать', что, согласво фор-
формуле C.27), на кольцо действует сила
/i=l
направленная к основапию полости.
92. Цилиндрическая полость ограничена проводящими стенками z = ^c и р = я.
Полость рассечена плоскостью z = 0; верхняя и нижняя части изолированы друг от друга
и заряжены соответственно до потенциалов +V0 и —Vo. Показать, что потенциал
инутри полости лается выражением
— У sh^k(c — \z\)]Jp(№) \
где /„ ((j-feo) ^ 0, а знак совпадает со знаком z. Другое выражение для потенциала
имеет вид
Ti=l
93. Цилиндрическая полость ограничена проводящими стенками z = ^c, р = я.
•Стен1си полости заземлены, за исключением площадок на основаниях, имеющих вид
дисков радиуса Ь и заряженных соответственно до потенциалов -\-Ve м —Fo. Показать,
что потенциал внутри полости при р > 6 равен
bV0 yr\
«2 ZJ
з Jo ([%я) = 0, или
со
2bV0 чг\ , »\пКа (птаг/'с) 70 (пър/с) — /0 (итш/с) Кй (ппр/с)
п=1
? У ] » ' I I -и —я I л\ 1 \ я J
216 Глава V
а потенциал в области р < Ь равен
/ »в кй (ппа/с) 1г (пъЫс)-\-10(ппа/с) КЛ (nnb/c) J / ппр "\^n(n
п=1
94. Полубесконечная цилиндрическая труба радиуса а имеет проводящие стенки
и ограничена с одного конца плоской проводящей пластинкой, перпендикулярной к ее
оси и имеющей тот же потенциал, что и труба. На оси трубы на расстоянии b от пла-
пластинки находится точечный заряд д. Показать, что на заряд действует сила
где
fe=l
95. Область, лежащая ниже плоскости z = 0 внутри цилиндра с проводящими стой-
стойлами радиуса а, заполнена диэлектриком с относительной диэлектрической проницае-
проницаемостью К. На оси цилиндра в точке z=6 находится заряд q. Показать, что потенциал
в области z > О определяется ныражснмем
fe=l
где /0 ((^fte) = 0. Найти выражение для потенциала в диэлектрике.
96. Поверхность проводника образована вращением окружности радиуса а вокруг
одной из ее касательных. Показать, что емкость такого проводника равна
Jt=i О
где /0 (v-ha) = 0.
97. Проводник, описанный в предыдущей задаче, вносится, будучи незаряженным,
в однородное электрическое поле Е, параллельное оси вращения проводника. Показать,
что потенциал результирующего поля, выраженный в полярных координатах, равен
оо
2Еа2 v-\ —у-ha2r~l cos В /„ (иъа2г~х «in в)
/Iе —^т^ г;? i
Ь=1
98. Проводник, рассмотренный в предыдущей задаче, повернут так, что внешнее поле Е
стало перпендикулярным к оси вращения. Показать, что при /o((*ke) = O потенциал равен
оо
4Еа2 уф —v.lla2r~i cos 6 /, ([ifja2r-'1 sin 6)
Еа2 уф
99. Показать, что выражение для потенциала, созданного заряженным кольцом
радиуса а, имеет вид
при р < а
со
-„ 2 \ Ко (ka) Io (kp) cos kz dk
О
или при р > а
оо
Q
\ /0 (ка) Ко (kp) cos kz dk,
Ъ-Ч
О
где Q—заряд кольца.
100. Кольцо радиуса а, несущее заряд Q, расположено так, что его ось совиадаег
с осью бесконечного диэлектрического цилиндра радиуса Ь. Показать, что потенциал
в диэлектрике равен
со
^ ^ W (к) /0 (Ар) Ко (ka) cos Az dk,
0
где 4f (k) — [l-\-kb(K— 1) /о(АЬ) Ко
. Задачи
217
101. Посередине между плоскостями z = c и z =—с, потенциалы которых равны
соответственно Ее и —Ее, расположено заземленное тороидальное кольцо, поверхность
которого получается путем вращения окружности радиуса а с центром в точке р = Ь
относительно оси, лежащей в плоскости окружности. Показать, что иотенциал «коль-
«кольцевых мультиполей», расположенных на окружности р = 6, z = 0, обращающийся в нуль
при z = 0 и соответствующий полю, перпендикулярному к плоскостям, равен d2iTVl/dzzr,
где Fj — потенциал «кольцевого диполя» с моментом М, равный
при р < Ь
со
., .. У пК0 ) /0 .—*- ) sin
п=1
и при р > Ь
со
-7Г~Г У nlo ) Ко ( —!- ) sin ¦— .
n=l
Показать далее, что потенциал, обращающийся в нуль не на всей поверхности кольца,
а на 2т окружностях p = ps, г=^?,8, где 0 < s^m и (ps — 6J + -г^ = «2, равен
= Ez+
n=l
sin
Последнее выражение справедливо при р < 6; для случая р > 6 р и 6 надо поменять
местами. Коэффициенты Аг равны
.s. Vn
12 . . . Vr-\, 2 Z2 fr-n,
tl,m
T/ T/
^ 21 • • • 'mi
V22 ¦ • • ^Я2
V V
Если ps < b, то
П=1
В области ps > Ь надо поменять местами р?и 6. Если воспользоваться только коэффи
циентом Лц то условие F = 0 будет удовлетворяться на окружностях р = Ь, z =-)-«,
что дает прекрасный результат в случае в <С с и а <^Ь. Данная задача является типич-
типичным примером нахождения приближенного решения.
102. Пользуясь формулами E.15), E.375) и E.377), показать, что потенциал, создан-
.ный в окружающем пространстве диском радиуса а, несущим заряд Q, равен
103. Потенциал, обусловленный плоским бесконечным проводящим листом, несущим
на обеих сторонах равномерно распределенный (с плотностью с0) поверхностный заряд,
равен Vq. Используя результаты § 28в и 31в гл. V, показать, что потенциал, создан-
созданный таким листом при наличии в нем отверстия радиуса а, равен
dk.
104. Цилиндр радиуса р = « опирается на заземленную плоскость z = 0. Вдоль
цилиндра поддерживается равномерное падение потенциала, причем потенциал цилиндра
в том месте, где он пересекается со второй заземленной плоскостью z=c, равен Vo.
(Цилиндр и вторая плоскость изолиронлны друг от друга.) Показать, что выражение
для потенциала вне цилиндра между плоскостями имеет вид
п=1
К01птш1с)
218 Глава V
105. Потенциалы стенок кольцевой цилиндрической полости р = «, р = Ь, z = 0,
z = c равны соответственно fx (z), /2 (z), /3 (p), /4(р). Показать, что потенциал внутри
полости является суперпозицией четырех функций: двух функций, типа рассмотренных
в з 31д гл. V, и двух, тина рассмотренных в § 37 гл. V.
106. Точечный заряд q находится в точке z—z0, p = 6, <( = $. Плоскости <р=0 и
9 = а, а также цилиндр радиуса р=в имеют потенциал, равный нулю, причем 0< р < а
и 0 < Ъ < а. Показать, что пыражение для потенциала имеет вид
V- 2п У У /CT/,(^fe)sin(s^/g) u_zo
sK/a.()
107. Полу бес конечный заряженный проводящий лист имеет выпуклость в виде
сплюснутого сфероида, ось которого совпадает с краем листа. Уравнение поверхности
сфероида ? = ?0. Показать, что выражение для потенциала имеет впд
108. В диэлектрическом шаре радиуса а вырезан сектор: плотадью среза шар
прилегает к бесконечному проводящему клину с углом раствора а, причем поверхности
шара и клина пересекаются ортогонально. Показать, что если клин заряжен, то потен-
потенциалы внутри и вне шара равны соответственно
Fi==C • ° + 2* (г sin 0)«'« cos S ,
109. Заряженный проводящтгй клин со сторонами ср= +а и 9==—а пересекается
под прямым углом с заряженной проводящей плоскостью z = 0.. Показать, что в облас-
области --а<ср<-}-а и 0<z потенциал равен
Cz[Jm COS те;р,
где in — наименьшее число, для которого
110. Даны три заряженные ортогональные проводящие поверхности: клиц со сто-
сторонами <f>=+« и 9 = —а, плоскость z = 0 и цилиндр р — а. Показать, что в области
— а<9<+<*> z>0 и р>а потенциал равен
Cz (pm — а2т р~т) cosmf,
где те — наименьшее число, длн которого cosm.a = 0.
HI. Дапы три заряженные ортогональные проводящие поверхности: клин со сто-
1
ронами 9=+а и <f>=—а> плоскость 6=-^-7t и сфера г = а. Показать, что в области
— a < 9 < +a> z > 0 и г > а потенциал равен
С (гтн_а2га*з r-m-2) cos g sjnm g cos те 9>
едемте — наименьшее число, для которого cos те a = 0.
f: 112. Заряженный проводник имеет глубокое прямоугольное углубление, стенки
которого определяются уравнениями х = 0, х = а, у = 0, у = Ь и z = 0. Показать, что
потенциал внутри углубления, вдали от открытого его конца, равен
F=Csin — sin -r- i
а о
113. Стенки бесконечной заземленной проводящей трубы прямоугольного сечения
определяются уравнениями а;=0, х = а и у=0, у^=Ь. В точке х-=х0, у = у0, z — z0
внутри трубы находится точечный заряд. Показать, что потенциал в такой системе ра-
равен
оэ со
X sin е sin sin
«e
Задачи 219
114. В заземленном проводнике вырезана полость, стенки которой определяются
уравнениями йг = О, ж = «, ?/ = 0, у = Ъ, z —0, z = e. В точке ж0, у0, z0 находится точеч-
точечный заряд q. Показать, что потенциал внутри полости будет равен
со со
4ф >г> 'ст sh Amn (с — z0) sh Amn z . ппж0 . nv.x . mm/0 . т-ку
ваЬ *—I 4-} -Amn sh Amn с a a b b
n=l m—\
гдеЛтп = я (те2в2 + п2Ь2) '2/яЬ. Эта формула справедлива в области z < z0; в области z > z0
надо поменять местами а и z0. Показать, что z-компонснта действующей на заряд
силы равна
со со
п=1 m=l
Чтобы получить компоненту Fa-, следует в формулах для Fz и Атп заменить а на с,
с ня а, хк на z0 и z0 на ж0. Соответственно для Fy следует в выражении для Fz и ^4тц
заменить 6 на с, с на Ъ, z0 на ?/0 и у0 на z0.
115. Показать, что выражение для потенциала диполя т, параллельного оси 6 и
расположенного в точке Ь, а, 0, имеет вид
m Х< Х' '" *"" ..i"—-#¦/' ^ ~m (COSa)P™(cos6)c.OSTO9.
Формула спраисдлина при г < b. В случае г > Ь следует заменить (r/b)n на (Ъ/г)п*1.
116. Центр шара, изготовленного из диэлектрика с относительной проницаемостью
К и имеющего радиус а, совпадает с началом координат. В точке г находится диполь
ш, причем угол между m и г ранен а. Показать, что на диполь действует момент,
равный
to п
(К — l)m2 v, XI B — Ь^)п(т—п — 1)(п — те) ! ,
sina/J ^-J (пАГ + n + l) (n + те)!
1 т=0
X [I
(аргумепт cos a у функций Лежандра опущен). Показать, что на диполь действует сила
(К— l)m2c.osa -у ^ B — Ь°„) п (п + l) (п + 2) (те—п — 1) (п— те) I
' 2j 2j ~ (пА: + 'г + 1)(п + те)! Х
117. Путем вращения вокруг оси ж преобразования, рассмотренного в § 14 гл. IV,
получить (полагая щ = и и u2=V) уравнение E.62) для этого случая. Подставить в
уравнение E.62) вместо U выражение (ch и1 — cosu2)J'2 Vx (щ) V2 () и показать, что
дифференциальные уравнения для U2 и Ul имеют вид
i
Последнее совпадает с уравнепием E.178), если п заменить па п—^- и ,и на сЪи1.
118. Тор, полученный вращением окружности радиуса Ь. заданной уравнением
м1 = м0 (гм. предыдущую яадачу), заряжен до потенциала Fo- Показать, что выражение
для потенциала во внешнем пространстве имеет вид
ч1/2 v () (+ ) Цл,я ( ,) Pw_1/8 (chut)
2F0 (chit,—cos и, '! >. ,, ., , . ' cosnit2,
0 ^ B + l)!!(shI/2^i/(chtto)
где сЬм0 равен с/Ь (с—расстояние от центра окружности и0 до прямой %=0).
220 Глава V
119. Найтп полный заряд тора, описанного в предыдущей задаче, путем сравне-
сравнения потенциала при мг = 0 и и2 = 0 с потенциалом q/Aner. Показать, что емкость тора
равна
8.S2V* Ь (sh и^Л (-
8Пв2 ЪEЪи0) ^ (
120. Тор, описанный в задаче 118, вносится в однородное ноле Е, параллельное
его оси вращения. Показать, что потенциал результирующего поля равен
F = Ex-\- (ch ux — cos м2) "V An Pn x (ch щ) sin nu2,
n=l
где
4 Bn +1) (—2)" n«B0 РЦ1/2 (cth м0)
Значения а определяются из уравнения D.67) и U=u0.
121. Тор, описанный в задаче 118, вносится в однородное поле Е, перпендикуляр-
перпендикулярное к его оси вращения. Показать, что потенциал во внешнем пространстве равен
со
Е cos <f> p4-(chMx—cosmjI'2 2 Ап Р„—1/2 (ch щ) cos m2 ,
где
^ _ Bn-l) Bn+1) (-2Г+1 6 (sh Mo)x/2 РГ/а (cth и,)
122. Путем вращения вокруг оси у преобразования, рассмотренного в § 14 гл. IV,
получить (полагая u1 = U и m2 = F) уравнение E.62) для этого случая. Подставить в
уравнение E.62) вместо V выражение (ch их — cosм2I;'2 их(щ) Пг (м2) и показать, что
дифференциальные уравнения для Ux и U2 имеют вид
d2Z7, Г IV d2U2 dU2 , Г , , , те2 тт
1 = ( n-i ) ил, 5^4-ctgM2-i—-+I п(п4-1) .—5— Z72 = 0.
йи\ \ 2 у «м| ° вм2 L sm'1M2J
Последнее совпадает с уравнением E.102), если 0 заменить на и-,.
123. Две сферы м,=м0 и щ = —и0, полученные в предыдущей задаче, вносятся
в однородное поле, имеющее потевциал Ez, таким образом, что прямая, соединяющая их
центры, параллельна полю, а потенциалы сфер оказываются равными соответственно
у0 и — Fo. Показать, что выражение для потенциала во внешнем пространстве имеет
вид
n=0
где
3
f n + Y ) Mi Pn
«
В лоследнем выражении chM0=c/6, b—радиус сфер, с —расстояние между их центрами.
124. Предполагая в предыдущей задаче, что сферы незаряжены, получить следу-
следующее выражение для потенциала:
V0 = Eb sh щ
^,_
125. Показать, что между сферами, рассмотренными в предыдущей задаче, дей-
действует сила, определяемая выражением
п—2 (n-f-1) ^In+il ^4n>
лат»
n=0
Литература 221
где коэффициенты Ап получаются подстановкой Fo из задачи 124 в выражение для Ап
задачи 123.
126. Потенциал внешних источников имеет на поверхности сферы радиуса а зна-
значение /F), где 6—полярный угол. Используя разложение § 1Вж гл. V и суммируя
ряды под знаком интеграла (см. § 17 гл. V), показать, что в области г < а
я/'2 д С С r1/2/(a) sin a da I
дг )
—я 0 '
ЛИТЕРАТУРА
а) Электричество
G e i g e r-S с h e e I, Handbuch der Physik, Bd. XII, Berlin, 1927.
Gray A., Absolute Measurements in Electricity and Magnetism, v. I, Macmillan, 1888.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
Mason M.,' Weaver W., The Electromagnetic Field, Universitv of Chicago Press,
1929.
Maxwell J. C, Electricity and Magnetism, v. I, Oxford, 1881.
Peirce В. О., Newtonian "Potential Function, Ginn, 1902.
Planck M. K. E. L., Theorie der Elektrizitat und Magnetismus, Berlin, 1932.
Ramsey A. S., Electricity and Magnetism, Cambridge, 1937.
Schelkunoff S. A., Electromagnetic Waves, Van Nostrand, 1943.
Stratton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: С т р э т-
тон Дж. А., Теория электромагнетизма, М.—Л., 1948.)
Thomson W., Tait P. G., Treatise on Natural Philosophy, Cambridge, 1912.
Thomson W., Papers on Electrostatics and Magnetism, Macmillan, 1884.
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
Wi en-Harms, Handbuch der Experimentalphysik, Bd. X, Leipzig, 1930.
б) \Ыатематика
Bat e'm a n H., Electrical and Optical Wave Motion, Cambridge, 1915.
Batemau !H., Partial Differential Equations, Dover, 1944.
British Association, Bessel Inunctions, Part 1, Cambridge, 1937.
Byerly W. E., Fourier's Series and Spherical Harmonics, Ginn, 1893. \
С a r s 1 a w H. S., Mathematical Theory of the Conduction of Heat in Solids, Macmillan,
1921. (См. перевод: Карслоу, Теория теплопроводности, М. — Л., 1947.)
Copson E. Т., Theory of Functions, Oxford, 1935.
Fletcher A., Miller J. С P., R о s e n h e a d L., An Index of Mathematical
Tables, Scientific Computing Service, London, 1946.
G e i g e r-S с h e e 1, Handbuch der Physik, Bd. HI, Berlin, 1928.
Grav A., Mathews G. В., Ma "с Robert Т. М., Bessel Functions, Macmil-
Macmillan, 1922.
Harvard Universitv Computation Laboratory, Tables of Bessel Functions of the First Kind
of Orders 0 to 78, Harvard University Press, 1946—1950.
Heine E., Anwendungen der Kngelfunctionen, Berlin, 1881.
Hobson E. W., Spherical and Ellipsoidal Harmonics, Cambridge, 1931. (См. перевод:
Гобсон Е. В., Теория сферических и эллиисоидальных функций, М Л., 19о2.)
J a h n k e, Emde, Tables of Functions, Dover, 1943. (См. перевод: Янке Е. и
Э м д е Ф., Таблицы функций, М.—Л., 1948.)
М а с R о b e r t Т. М., Spherical Harmonics, Dutton, 1927.
Magnus W., Oberhettinger F., P'ormulas and Theorems for the Special
Inunctions of Mathematical Physics, Chelsea, 1949.
McLachlan N. W., Bessel Functions for Engineers, Oxford, 1934.
Morgan S. P., Tables of Bessel Functions of Imaginary Order and Imaginary Argument,
California Institute of Technology, Pasadena, 1947.
Prasad G., Spherical Harmonics..Г, 2 v., Benares, 1930, 1932.
Riemann, Weber, Differentialgleichungen der Physik, Braunschweig, 1925.
W a t s о n G. N., Theory of Bessel Functions, Cambridge, 1922. (См. перевод: Ватсон Г.,
Теория бессолевых фумкпий, М.—Л., 1949.)
Webster A. G., Partial Differential Equations, Leipzig, 1927.
Whit taker E. Т., W a t s о n G. N., Modern Analysis, Cambridge, 1935. (См
перевод: Уиттекер Е. и Ватсон Г., Kvpc современного анализа,
М.—Л., 1937.)
Глава VI
ЭЛЕКТРИЧЕСКИЙ ТОК
§ 1. Плотность электрического тока. Уравнение непрерывности.
Если два проводника А и В, заряженные соответственно до потенциалов
Vа и Vb, привести в соприкосновение с двумя точками третьего провод-
проводника, то, как мы видели в § 1 гл. I, заряд переходит от одного провод-
проводника к другому до тех пор, пока потенциалы проводников А а В не срав-
сравняются. Можно наблюдать два явления, связанных с переходом заряда:
нагревание проводника и появление магнитного поля вблизи проводника,
по которому перемещаются электрические заряды. Второе из этих явлений
будет рассмотрено в следующей главе. Скорость перехода заряда от про-
проводника А к В называется силой электрического тока. Сила тока в любой
системе единиц определяется, следовательно, выражением
'=§• (•¦•)
где / получается в амперах, еслп Q выражено в кулонах и ? — в секундах.
Если при помощи какого-нибудь электромеханического приспособления,
например движущейся изолированной ленты, непрерывно переносить заряд
от точки соприкосновения проводника В с соединительным проводником
к соответствующей точке проводпика А с такой скоростью, что разность
потенциалов Va — У в будет оставаться постоянной, п в то же самое время
охлаждать соединительный проводник так, чтобы его температура не меня-
менялась, то окажется, что ток п магнитное поле также останутся неизмен-
неизменными. Последнее поэтому можно не рассматривать в теории постоянных
токов. Очевидно, что электрический ток в любой точке характеризуется
величиной и направлением. Если в точке Р проводящей среды взять эле-
элемент поверхности dS, нормальный к направлению тока в этой точке, и если
ток, текущий через dS, равен dl, то плотность тока в этой точке опреде-
определяется выражением
i=5... F.2)
R случае постоянного тока количество электричества, втекающего в любой
элемент объема, должпо равняться количеству электричества, вытекающему
из него. Следовательно, интеграл от нормальной составляющей плотности
тока, взятый по поверхности, ограничивающей этот объем, должен быть
равен нулю. Отсюда, по теореме Остроградского—Гаусса C.2), следует
i-n dS =
S v
Так как это равенство выполняется для всех элементов объема, то
= 0. F.3)
Электрический ток 223
Уравнение F.3) называется уравнением непрерывности, а вектор, удовле-
удовлетворяющий этому уравнению, называется соленоидальным.-
§ 2. Электродвижущая сила. В рассмотренном выше опыте движу-
движущаяся лента действует на переносимые ей электрические заряды с силой
как раз достаточной для преодоления электростатических сил в простран-
пространстве между проводниками А и В ж обусловливает тем самым электродви-
электродвижущую силу (э. д. с). Величина э. д. с. Ь измеряется работой в джоу-
джоулях, совершаемой лентой при перемещении от В до А заряда в 1 кулон,
за вычетом потерь на трение в движущем механизме. Если сила, движу-
движущая ленту, увеличивается, то лента будет двигаться ускоренно до тех
пор, пока добавочные заряды пе увеличат разность Va — У в настолько,
что электростатические силы опять уравновесят механическую силу, при-
приложенную к лепте. При разрыве проводника между А и В лента остана-
останавливается (так как механизм не может преодолеть возросшие электроста-
электростатические силы) и работа против сил трения прекращается. Следовательно,
в этом случае э. д. с. S в точности равна V7^ — Vb-
При обычных температурах, чтобы поддерживать силу тока в цепи
постоянной, необходимо иметь некоторый источник э. д. с. В разобранном
выше примере вопрос о локализации э. д. с. не вызывает затруднений:
э. д. с. распределена между А и В вдоль ленты. В химических истопниках
э. д. с, например гальванических элементах и аккумуляторах, э. д. с.
локализована на поверхностях электродов. В термоэлементах она локали-
локализована на поверхности соприкосновения двух проводников. В случае метал-
металлического контура, помещенного в переменное магнитное поле, возникает
э. д. с. индукции (рассматривается в гл. VIII), которая может быть рас-
распределена по всем элементам цепи. В динамомашине, замкнутой на внеш-
внешнюю цепь, э. д. с. распределена по обмотке машины. Во всех этих слу-
случаях, если контур разомкнут и разность потенциалов в месте разрыва
измеряется прибором, не потребляющим тока (например, электростатическим
вольтметром или потенциометром, заэкранированным от внешних воздейст-
воздействий), результат измерения дает сумму э. д. с. в контуре.
Электродвижущая! сила вдоль заданного пути обычно определяется иным
способом. Напряженность электростатического поля в какой-либо точке
была определена как сила, действующая на помещенный в эту точку еди-
единичный положительный заряд. О характере этой силы не было сделано
никаких высказываний, за исключением того, что она пропорциональна
величине заряда. Как будет показано ниже, электрическое сопротивление
среды пе оказывает влияния па измерение напряженности поля, поскольку
сопротивление, подобно вязкому трению, действует только на. движущиеся
тела. Следовательно, полная сила, действующая на находящийся на ленте
заряд, равна нулю, так как электростатическая и механическая силы урав-
уравновешиваются. В той части контура, где течет ток, действуют только
электростатические силы. Поэтому линейный интеграл от Е по замкнутому
контуру равен разности потенциалов между проводниками А и В, которая,
как было показано, равна с- Таким образом,
g=(?)Eds. F.4)
Эта формула определяет э. д. с. по замкнутой^ пути интегрирования.
Напряженность электрического поля Е полезно иногда рассматривать как
сумму двух компонент: электростатической компоненты Е', которая опи-
описывается скалярным потенциалом п для которой интеграл по любому
замкнутому пути равен нулю, и компоненты Е" (по природе соленоидальной),
224 Глава VI
которая обусловлена э. д. с. и для которой интеграл по замкнутому
пути отличен, вообще говоря, от нуля. Компонента Е" полезна при рас-
рассмотрении распределенных э. д. с; но для э. д. с, локализованных
в поверхностном слое, введение Е" излишне, так как в этом случае Е"
обращается в бесконечность в самом слое и равна нулю во всем остальном
пространстве. Значение интеграла от Е" зависит от выбора пути интегри-
интегрирования. В частности, в примере с лентой интеграл от Е" равен нулю
по любому замкнутому пути, лежащему целиком на ленте или целиком
вне ее.
Во многих случаях можно выбрать границы, пересечение которых при
интегрировании запрещено, таким образом источники э. д. с, например
лента в рассмотренном выше примере, оказываются исключенными. Тогда
интеграл от Е по всем разрешенным замкнутым путям оказывается равным
нулю и в рассматриваемой области можно пользоваться скалярным потен-
потенциалом. Даже при распределенной э. д. с. могут существовать такие гра-
границы, что для всех разрешенных путей интегрирования интеграл F.4)
обращается в нуль. В этом случае невозможно провести различие между
Е' и Е" и термины э. д. с. и потенциал равнозначны. Именно в этом
смысле используется Ш в следующем параграфе; для напряженности поля
в этом случае можно написать
E=-V^ = V?- F.5)
§ 3. Закон Ома. Удельное сопротивление. Если в эксперименте,
описанном в § 1, все физические условия, такие, как температура и коэф-
коэффициент полезного действия, остаются неизменными, а э. д. с. увеличи-
увеличивается, то после достижения стационарного состояния окажется, что ток
увеличился пропорционально э. д. с. Это закон Ома. Для устройства,
в котором отсутствуют механические потери, отношение э. д. с. между
точками А и В к протекающему току называется электрическим сопротив-
сопротивлением RA& между этими точками, так что
1АВ
Построим в точке Р проводящей среды элементарный цилиндр, основания
которого dS перпендикулярны к току в точке Р, а боковые стенки, длина
которых равна ds, параллельны току. Э. д. с. между основаниями цилиндра
будет равна (dSjds)ds=^ ^ Ш-As, и через цилиндр будет протекать ток idS.
Применяя закон Ома к этому цилиндру, запишем соотношение F.6) в виде
il±J- idS tdS
где а —угол между ~^Щ и ds. Сопротивление Rt> цилиндра, у которого ds
численно равно dS, обозначается через т и называется удельным сопротив-
сопротивлением среды в точке Р. Таким образом,
т = -!-^—Lcosa. F.7)
Если т не зависит от направления тока, то угол а должен равняться нулю,
так что направления градиента потенциала и тока совпадают. В этом слу-
случае проводящая среда называется изотропной. Величина, обратная удельному
сопротивлению т, называется проводимостью. Обозначая проводимость
через т> можно записать формулу F.7) в виде
F.8)
Электрический ток 225
На основании формул F.8) и F.4) для замкнутого пути в проводящей
среде будет иметь место равенство
•ds — ~\S. F-9)
§ 4. Тепловое действие электрического тока. В § 1 было отмечено,
что проводник нагревается проходящим по нему током. Температуру про-
проводника можно поддерживать постоянной, удаляя выделяющееся тепло.
Но если в проводнике по происходит никаких изменений, то очевидно, что
выделившаяся в нем энергия каким-то способом была внесена в систему
извне. В случае с движущейся лентой, перенося заряды от проводника
В к А, мы, очевидно, совершаем работу против электростатических сил.
Из определения потенциала следует, что эта работа W равна Q (VA — Vb)-
так что подводимая мощность будет выражаться формулой
2 \ —(Va—VtA 1 ,т> ((\ Ю\
. I I У А У М) '-ЛИ* IU.JLUI
Отсюда при помощи соотношения F.6) получим
F.11)
Если /, V и R выражены в электростатической или абсолютной электро-
электромагнитной системах единиц, то Р получается в эргах в секунду. Если /
выразить в амперах, V — в вольтах и R —в омах, т. е. воспользоваться
практической системой единиц, то Р получится в ваттах. Полная таблица
ОДИВ1Щ приведена в приложении. Тепло выделившееся при прохождении
тока, называется джоулевым теплом.
§ 5. Линейные проводники. Законы Кирхгофа. Последовательные
и параллельные соединения проводников. Рассмотрим задачу о распреде-
распределении тока в системе проводников, поперечные сечеьшя которых достаточно
малы по сравнению с их длиной, так что изменение потенциала в узлах
(так мы будем называть места соединения двух или большего числа про-
проводников) мало по сравнению с изменением потенциала между соседними
узлами. Будем называть такую систему цепью, составленной из линейных
проводников. При расчете таких цепей удобнее оперировать не с. плот-
плотностью тока, а с полным током, проходящим через сечениь проводника.
Из § 1 и 2 вытекают два очень важных правила, известных под названием
законов Кирхгофа. Если применить уравнение непрерывности к любому
узлу цепи, считая токи, направленные к узлу, положительными, а направ-
направленные от узла отрицательными, то получается первый закон:
1. Алгебраическая сумма токов, сходящихся в любом узле, равна нулю.
Из определения э. д. с, данного в § 2, и закона Ома следует, что,
обходя один за другим проводники, образующие замкнутый контур в элек-
электрической цоплг, и считая при этом токи, текущие в направлении обхода,
и э. д. с, стремящиеся создать ток в этом направлении, положительными,
а токи, текущие в обратном направлении и- соответствующие э. д. с,—
отрицательными, мы получим второй закон:
2. В любом замкнутом контуре алгебраическая сумма произведений IR
равна алгебраической сумме э. д. с.
Если п проводников так подключены друг к другу, что ток последо-
последовательно проходит один за другим все проводники, то такое соединение
называется последовательным. По закону Ома разность потенциалов между
концами такой цепи будет равна
IR1 + IRz±... + IRn.
15 в. Смайт
22В
Глава VI
Если всю цепь**рассматривать как один проводник с сопротивлением Н,
то разность потенциалов будет равна IR. Приравнивая эти выражения,
получаем
Я = Я1+Я2+...+Я)|. F.12)
Таким образом, когда новый проводник образован при помощи последо-
последовательного соединения проводников, его сопротивление равно сумме сопро-
сопротивлений отдельных проводников.
Соединение проводников называется параллельным, если несколько
проводников соединены так, что ток, поступающий в систему, разделяется
на отдельные токи, каждый из которых проходит не более, чем по одному
проводнику. Разность потенциалов между концами проводников будет в этом
случае одна и та же, т. е.
ЛЯ, = /2Да =...=/„«„.
Пусть / — полный ток и R— эквивалентное сопротивление цепи. Тогда
JiR1 = I2R2— . .. = InRn = IR. Ток /s в проводнике с сопротивлением^
будет равен
F.13)
* а ГГ 1 •
Составляя из выражений вида F.13) сумму всех токов, ранную общему
току /, и разделив ее на IR, получим
r2
-1
F.14)
Таким образом, когда новый проводник образуется при помощи параллель-
параллельного соединения нескольких проводников, величина, обратная его сопротив-
сопротивлению, равна сумме величии, обратных сопротивлениям отдельных провод-
проводников.
§ 6. Расчет электрических цепей. Контурные токи. Мост Уитстона.
Задачу, с которой обычно приходится иметь дело при расчете цепей, можно
сформулировать так: даны сопро-
сопротивления всех ветвей, величины
и направления всех э. д. с, тре-
требуется найти токи во всех вет-
ветвях. Иногда оказывается возмож-
возможным разбить цепь на группы по-
последовательно и параллельно сое-
соединенных проводников и найти
решепие но формулам предыду-
предыдущего параграфа. Общее реше-
решение поставленной задачи можно
получить, вводя специальное обо-
обозначение для тока в каждой вет-
Фиг. 60.
ви и написав 1-й закон Кирх-
Кирхгофа для q узлов (что дает q уравнений) и 2-й закон Кирхгофа для п
независимых контуров (что дает еще п уравнений). Всего получается (и-f- q)
уравнений, определяющих (п-{-q) токов. Объем работы можно сильно сокра-
сократить, введя так называемые контурные токи, автоматически удовлетворя-
удовлетворяющие 1-му закону Кирхгофа, после чего остается решить систему только
из п уравнений. Ток в каждой ветви можно записать как сумму зтих
контурных токов. В качестве примера рассмотрим схему, называемую
мостом Уитстона (фиг. 60). Она часто применяется для сравнения неизвест-
неизвестного сопротивления с известным. Во' «внешвий» контур включена э. д. с. Ш;
Электрический ток 227
сопротивление этой ветви равно г. Контурные токи можно выбрать
по-разному. Выбор контурных токов должен допускать различные токи
в каждой из ветвей. Выбрав контурные токи так, как это показано
на фиг. 60, и написав 2-й закон Кирхгофа для контуров DBA, BCD
и АВСЩ, получим
*гД0---;а(Д1 + Д,) + /Я8 = 0; ' (C.15)
h (Д„ + я2 + Д4) + h (R2 + R*) - 1R, = 0; F.16)
ixR2+ i2{R1 + R2) + Ir = %. F.17)
Если задача заключается в том, чтобы выразить один ток через другой,
например ток ii через /, то можно обойтись только двумя из этих урав-
уравнений. Из уравнений F.15) и F.16) находим
Если же заданы только э. д. с. дг сопротивления, то приходится решать
систему из трех уравнений F.15) — F.17). Это нетрудно сделать, пользуясь
теорией определителей. Для i1 будем иметь
(R, R, - Д9 Д8) Ш • [ До (Яг + Д2) (Д8 +R 4) + RBr (R, +
Н- R2 + Rs -f- Rt) + r (R, + Д8) (Да + Д4) + Rx R2 R3 + R2 R3 R, +
-ЬД8Д4Д1 + Д4Д1ДаГ1- F-19)
Ток в любой ветви равен алгебраической сумме протекающих по ней
контурных токов. Например, в ветви ВС ток равен /'j + i2. На практике
одно из сопротивлений Rlt R2, Rs и Л4 моста Уитстона неизвестно,
а остальные, из которых, по крайней мере, одно переменное, заданы. Регу-
Регулировкой переменного сопротивления добиваются отсутствия тока г\ в галь-
гальванометре, который включают вместо Rg. При этом условии, как легко
видеть, соблюдается равенство RlRi = R2R3, откуда л определяется неи,ч-
вестное сопротивление.
§ 7. Цепи из одинаковых звеньев. В некоторых случаях приходится
иметь дело с цепями, которые можно разделить на большое число одина-
одинаковых звеньев, причем связь каждого звена с соседними одинакова.
Тогда вместо решения системы, состоящей из большого числа уравнений,
можно сформулировать соотношение между токами в соседних контурах
в виде разностного уравнения, при решении которого следует учиты-
учитывать условия на концах цепи. В качестве примера применения этого
метода рассмотрим цепь, состоящую из генератора и нагрузочного сопро-
сопротивления R, причем ток от генератора к нагрузке подводится по одному
проводу, а обратным проводом служит земля. Провод подвешен на п оди-
одинаковых изоляторах, расположенных на одинаковом расстоянии друг от
друга. Сопротивления участков провода между генератором и 1-м изоля-
изолятором, между каждой парой изоляторов и между последним изолятором
и нагрузкой одинаковы и равны р, а сопротивление земли ничтожно мало.
В сухую погоду, когда никакой утечки через изоляторы нет, ток генера-
генератора равен /j, но при влажной погоде для получения того же тока в нагрузке
от генератора приходится брать ток 12. Определим величину сопротивления
каждого изолятора г, считая, что утечка во всех изоляторах одинаковая.
Для решения этой задачи начертим схему цепи (фиг. 61), перенумеруем
изоляторы от 1 до и и введем контурные т^ки. Закон Кирхгофа для кон-
контура s имеет вид
h-ir - h Br + р) + is+1 r = 0,
15*
228
Глава VI
ИЛИ
s IT s + 1 ^ r у s
Решение уравнения F.20) (см. Двайт, 651.03) имеет вид
причем
или
(chfi —1)
F.20)
F.21)
F.22)
Фиг. 61.
Чтобы найти А к В, заметим, что в первом контуре
а в (п 4- 1 )-м контуре /, = A ch (п + 1) б + В sh (п + 1) б. Из этих урав-
уравнений определяем А и В:
(n + lN — /, shO
sh nfi
sh nfi
Подстановка значений А ш В ь решение F.21) дает
. _ /g sh (n — s +1) 04- A sh (s— 1) 6
sh nb
F.23)
Для последнего контура получим
Подставляя г из выражения F.22) и гп из выражения F.23), после упро-
упрощений найдем
2ILRsh.n6sh^6 + pIlCh [у B/г + 1) б] — p/2ch-|-6 = 0. F.24)
Уравнение F.24) можно решить графически, цостроив его левую часть как
функцию б и найдя пересечение этой кривой с осью б. Подстановка най-
найденного значения 6 в формулу F.22) дает величину г. Если сопротивление
провода мало ио сравнению с сопротивлением изолятора, то 4 sh2 у 6 —> б2,
так что гсб—^.«(р/гI'2. Если эти величины малы, то можно считать
(см. Двайт, 657.2), что сЬж=1 + ^^2> shx=x, и тогда решение для ба
будет иметь вид
^ 8р (/,-/,)
Электрический ток 229
Ввиду того, что /j — /2 мало по сравнению с llt этой величиной в знаме-
знаменателе можно пренебречь, и, поскольку, согласно'формуле F.22), г = р8~2,
получим
где /?j — сопротивление всего провода без учета утечки.
§ 8. Линия с непрерывно распределенной утечкой. От случая отдель-
отдельных изоляторов легко перейти к случаю линии с непрерывно распределен-
распределенной изоляцией. Расстояние между изоляторами теперь нужно считать бес-
бесконечно малым, так что, если сопротивления провода и утечки на единицу
длины соответственно равны Т и S, то p = Tdx и S=rdx. Следовательно,
имеет место уравнение
Разностное уравнение F.20) переходит теперь в дифференциальное:
?-(?)'• <•¦*>
Интегрирование этого уравнения дает
x.
Предполагая, что граничные условия, как и прежде, имеют вид i = /2 при
х = 0 и i = 1Х при х = L, получим
Это выражение соответствует выражению F.23) и позволяет найти ток
в любой точке линии. Напряжение на изоляции в любой точке линии по
закону Ома равно —S(di/dx), так как ток, протекающий через изоляцию
между точками х и х -f- dx, равен — (di/dx) d.v, а сопротивление утечки этого
участка равно S/ dx.
Примем, как и раньше, что изоляция идеальна при сухом кабеле и. что
при влажном кабеле приходится брать от генератора ток /2, чтобы полу-
получить в нагрузке ток /х. Пусть по этим данным требуется вычислить S.
Если R — сопротивление нагрузки, то напряжение на конце линии будет
/,/?=— S(di/dx)x=L- Подставляя сюда значение dijdx из выражения F.27),
найдем
[(jy/][(jy/]2 = 0. F.28)
Это уравнение соответствует уравнению F.24) и точно так же может быть
решено относительно S графически. Если S много больше Т, то можно
ограничиться тем же приближением, что и при получении выражения F.25).
В результате получим
<-, BR+LT)LI1
Л= 2G,-7.)
230 Глава VI
Выражение F.29) соответствует выражению F.25). Оно показывает, что
сопротивление равномерно распределенной утечки эквивалентно сосредото-
сосредоточенному сопротивлению утечки SjL, включенному посередине линии.
§ 9. Общая теория цепей. В § 6 было отмечено, что выбор контурных
токов можно сделать по-разному, лишь бы они были независимыми и допу-
допускали бы существование различных токов в каждой отдельной ветви цепи.
Если число узлов цепи q и число ветвей р, то полное число независимых
контурных токов п определяется формулой
n = p-q+l. F.30)
В мосте Уитстона (см. § 0) р = 6, гу = 4 и w = 3. Обозначим сопротивление
ветви, по которой протекает только один контурный ток ip, через Rp,
а сопротивленце ветви, по которой протекают два или большее число токов, —
через Rpq (ip и iq— два тока из тех, которые протекают по данной ветви).
Сумму сопротивлений всех ветвей, по которым протекает ток гр, обозначим
Rpv, так что если ни в одной ветви не протекает больше двух токов, то
. F.31)
Если ток is нигде не протекает по ветви, общей с током ip, то в фор-
формуле F.31) отсутствует индекс .<?.
Выбрав независимые контурные токи и используя введенные выше обо-
обозначения, можно написать законы Кирхгофа для п независимых контуров цепи
в следующей форме:
± Д2] i, + R22 i2 ±R23i3±...± R2n in = ± i2, F.32)
4-R i 4- R i 4- R ; 4- A- R I = -I- %
В этих уравнениях Дрр всегда положительно; в уравнениях, где встречается
Rpp, Rpq следует брать со знаком плюс, когда токи ip и iq проходят по
общей ветви в одном и том же направлении, и со знаком минус, когда
они текут навстречу друг другу. Электродвижущая сила Ш%> берется со
знаком плюс, если она помогает току ip, и со знаком минус, если она ему
противодействует. Если токи г;- и ik нигде не проходят по одной и той же
ветвп, то в уравнениях F.32) член Rjh отсутствует. Заметим, что, по опре-
определению,
Если две ветви не имеют общего узла, то контурные токи всегда можно
выбрать таким образом, что в каждой из них будет протекать только один
ток, хотя для этого приходится, вообще говоря, вводить ари (или большее
число) тока в некоторых других ветвях. Выбрав таким образом токи, обо-
аначим через Др5 алгебраическое дополнение элемента Rpq в определителе
И 4- R 4- Я
А = ±Rpl ... ±Rpq ... ±Rpn F.34)
Заметив, что вследствие равенства F.33)
% Ар9 = Дда- F-35)
Найдем из системы уравнений F.32) ток iq дли случая, когда единствен-
единственная з. Д. с. Ш-п, действующая в цепи, включена в ветвь, по которой проте-
Электрический ток 231
каст только один ток ip, и, наоборот, найдем ток ip, когда единственная
э. д. с. Eq включена п ветвь, несущую ток iq. Мы получим
jg = -I^??- и ip==-h*?L. F.36)
Иа формул F.35) и F.36) следует важное соотношение взаимности: если
gp=gg7 то'ip~iq- Иными словами, если э. д. с, включенная в одну из
двух ветвей, вызывает некоторый ток и другой ветви, то та же самая э. д. с,
будучи включенной во вторую ветвь, вызывает в первой такой же ток.
Если э. д. с. J? включена в г-го ветвь, то вместо формул F.36) мы будем
иметь
(Л д С? А
• В Г "ТО • Вг игр
Ы ~~ Д V — Д
Откуда, поделив одно равенство на другое, находим
j- = |a- F.37)
Формула F.37) позволяет выразить отношение любых двух токов через
-сопротивления элементов цепи.
Докажем теперь теорему Тевсннна, которая иказываотся иногда полез-
полезной при расчете цепей. Эта теорема утверждает, что, если напряжение
разомкнутой цепи между двумя ее [концами A и В равно Ftl, а ток, тону-
тонущий между А и В, при замыкании их пакоротко, равен /, то сопротивле-
сопротивление всей цени, измеренное между точками А и В при условии, что из цепи
удалены все источники э. д. с, а все сопротивления остались неизменными,
будет равно R = VJI. Из теоремы следует, что подключение точек А и В
к любой другой цепи равносильно подключению к ней батареи с э. д. с. Fy
и внутренним сопротивлением R. Чтобы доказать теорему, предположим,
что к точкам А и В подклычено очень большое сопротивление Яр. Тогда
в детерминанте F.34) все члены, не содержащие Rp, будут пренебрежимо
малы по сравнению с членами, содержащими Лр, так что, принимая во вни-
внимание выражение F.31), Д—>/?р Дрр при Rp—+oo. Разность потенциалов
между А и В, создаваемая всеми э. д. с, включенными в цепь, как видно
ш формулы F.36), будет равна
Если точки А и В замкнуты накоротко, то, сопоставляя это выражение
с формулой F.36), получаем
Сравнивая полученную формулу с выражением для сопротивления цепи
между точками А и В, которое можно получить из формулы F.36), будем
иметь
/? = l? = A==ij2, F.38)
гр Дрр I ¦ v I
что и доказывает теорему.
Существует класс цепей, имеющих большое практическое значение,
для которых контурные токи можно выбрать так, что будут удовлетворены
следующие условия: имеется по крайней мере одна ветвь, через которую
проходит только один ток; в ветвях, где текут два тока, они направлены
навстречу друг другу; через любую ветвь протекает не более двух токов.
В этом случае в детерминанте F.34) и в левых частях уравнений F.32) все
232
Глава VI
члены вида Rpp положительны и члены вида Rpq отрицательны. Токи мы
имеем право перенумеровать как нам угодно, поэтому при решении уравне-
уравнений относительно ix можно допустить, что в ветви, где включена э. д. с. t,
протекают токи i2 и i3. В правых частях уравнений F.32) мы заменим ?»
на —^23' ^а на +^2з и положим §р = 0 при рф2 или 3. Вместо фор-
формулы F.35) получаем
1^2 ~Г 1 6 3
д ~
1
1
1
1
«12
«32
«42
— «П2
— «13 • ¦ •
+ «зз ¦ ¦ ¦
— «43 ¦ • ¦
— «ПЗ • • ¦
- «Ш
— «Зп
-«4п
+ «пп
+
-«12-
+ «22 —
2
_и. _
«13
«23
«43
«in
... — R2n
... Rin
... 4-й
|
J
Два определителя в скобках отличаются только своими вторыми строками.
Их сумма равна, следовательно, определителю, вторая строка которого
получается сложением соответствующих элементов вторых строк этих опре-
определителей и имеет вид
~ «32 + «22» + «33 «I
23 >
¦«34 «21»
«Зп~«2
а остальные строки такие же, как у каждого из складываемых определи
телей. Величина определителя не меняется, еслп к каждому элементу
какой-нибудь строки прибавить соответствующие элементы любой другой
строки. Заменим поэтому вторую строку суммой всех строк, так что окон-
окончательное выражение с учетом соотношений F.31) и F.33) примет вид
— «12 —«13 —«
+ «2
— «42
+ «3 +«4
«43 + «J
14
«in
- ¦ «4
+ Rn
В2
F.89)
Если обозначить этот определитель мере.) А123, то для рассматриваемой цеп»
получаются формулы, аналогичные формулам F.36),
и i23 =
F.40)
Формулы F.40) обычно оказываются более удобными, чем формулы F.3(i),
так как знаки уже приняты во внимание при выборе контурных токов.
§ 10. Сопряженные проводники. Двойной мост Кельвина. Дда про-
проводника в электрической цепи называются сопряженными, если источник
э. д. с, будучи включенным в одиь из них, не создает тока в другом
и наоборот. Если Rp и Rq — Два сопряженных проводника, то условие их
сопряженности, как следует из формул F.36), имеет вид
Дрв = 0. F.41)
Если контурные токи выбраны так, что справедлива формула F.39), то
условие сопряженности проводников Rx и R23 принимает вид
Д123=0. F.42)
Условие баланса для моста Уитстона, описанного в § 6, можно получить,
исходя из соотношения F.42), если обозначить иа фиг. 60 через i\ ток /,
Электрический ток
233
а через i2 и i3 соответственно токи в треугольниках ABD и BCD. Мост
Уитстона не пригоден для измерения очень малых сопротиплсний, так как
сопротивления контактов делаются сравнимыми с измеряемым сопротивле-
сопротивлением. Этот недостаток устраняется в измерительной схеме, показанной на
фиг. 62, где измеряемое сопротивление заключено между точками А и В,
а ток к нему подводится через контакты С и D. Сопротивление контактов
АиВ много меньше сопротивлений i?12+ В13 и B2i + B3i. Требуется найти,
при каких условиях ток через гальванометр равен нулю, пли, что то нес
самое, найти условие сопряженности сопротивлений В1 и В23. Ввиду того,
что токи it и i4 не имеют общей ветви, Вы следует положить равным нулю.
Условие баланса моста, согласно со-
соотношениям F.42) и F.39), имеет вид
С А кг В D
-т г—VWVWV*—| •-
— /?12 —
+в2
+ вя +в4
- BiS + В,
= 0. F.43)
Фиг. 62.
Уже отсюда видно, что искомое усло-
условие баланса моста не зависит от Вг
и, значит, от сопротивления контак-
контакта С; но нужно, чтобы оно также
не зависело от сопротивления контак-
контакта D, т. е. от 7?4. Таким образом,
в определителе F.43) коэффициент при Bi и коэффициент при членах, не
содержащих 7?4, должны порознь равняться нулю. Последние, согласно
соотношению F.31), все входят в 7?44; следовательно, минор элемента 7?44
в определителе F.43) должен обращаться в нуль, т. е. — В12В3 + В13В2 — 0.
Кроме того, должен быть равен нулю минор элемента 7?4, т. с. —B12Bi3-\-
В4д = 0. Из этих двух выражений следует
в*
В,
F.44)
Итак, если ток в ветви В23 отсутствует, В2 можно выразить через В3 при
условии, что отношения В12/В18 и В2А/ВЫ известны и равны друг лругу.
§11. Постоянные токи в проводящих средах. 13 § 1 [формула F.3)]
было показано, что если в установившемся состоянии в проводящей среде
нигде не происходит накопления зарядов, то дивергенция плотности тока i
всюду равна нулю. Согласно закону Ома [формула F.8)], плотность тока i
it изотропной среде пропорциональна градиенту потенциала и обратно про-
пропорциональна удельному сопротивлению. Из этих формул следует, что
= 0. F.45)
Если среда однородная, то ~z постоянная величина и уравнение F.45)
принимает вид
Г^=0. F.46)
Сравнивая уравнения F.45) и F.46) с уравнениями C.5) и C.6), мы видим,
что эти уравнения совпадают с уравнением Лапласа, а величина, обратная
удельному сопротивлению -с, т. е. проводимость среды, играет ту же роль,
что и диэлектрическая проницаемость среды в электростатике. Отсюда выте-
вытекает возможность использования в теории постоянных токов математического
аппарата электростатики. Трубки тока находятся в таком же отношении
к эквипотенциальным поверхностям, как и силовые трубки в электро-
234 Глава VI
статике. На границе двух проводящих сред потенциал и нормальная компо-
компонента плотности тока должны оставаться непрерывными, так что в соот-
соответствии с условиями A.48) и A.49) условия на границе имеют вид
1 av _ 1 av ,6 47)
V' = V". F.48)
Эти соотношения полностью определяют связь значений градиента потен-
потенциала сю обе стороны границы. Поэтому, если относительные диэлектри-
диэлектрические проницаемости обоих сред также различны и не пропорциональны
соответствующим проволимостям, то для удовлетворения добавочному гра-
граничному условию необходимо ввести еще одну переменную. Считая, что
на границе распределен поверхностпый заряд с плотностью а, на основании
уравнения F.45) получаем
^-=„г^1__2^ = -(*Л-ВД V F-49)
Рассматривая магнитные силы, действующие между проводниками, несущими
токи (см. следующую главу), можно, казалось бы, придти к заключению,
что распределение токов, вычисленное путем решения уравнений F.45) и
F.46), неправильно, вследствие смещения элементов тока, обусловленного
магнитным взаимодействием. В действительности в изотропных ноферромаг-
питных проводниках при наличии магнитного поля всегда имеет место
увеличение сопротивления, называемое иногда «продольным эффектом
Холла» г). Вследствие этого в тех областях проводника, где напряженность
магнитного поля больше, сопротивление возрастает относительно сильнее,
чем в областях с меньшей напряженностью магнитного поля, и относи-
относительная плотность тока там уменьшается. Например, в случае постоянного
тока в цилиндрическом проводнике плотность тока вблизи оси несколько
больше, чем на периферии. Если этот проводник помещен во внешнее одно-
однородное поперечное магнитное иоле, которое складывается с собственным
магнитным полем тока на одной стороне цплиндра п вычитается из него
на другой, то появляется боковое смешение тока в направлении, совпа-
совпадающем с направлением силы, действующей на проводник. При этом поло-
положение эквипотенциальных поверхностей не изменяется и не возникает
никаких дополнительных поперечных сил, действующих на проводник, по
которому течет ток. Хотя изменение сопротивления проводника можно из-
измерить, однако соответствующее смещение тока при обычных температурах
слишком мало, чтобы его можно было заметить. Обычный поперечный
эффект Холла вызывает изменение положения эквипотенциальных поверх-
поверхностей, зависящее от свойств проводника, но распределение тока в этом
случае остается неизменным. Однако можно поставить опыт таким образом,
что распределение тока в контуре изменится; это изменение наблюдается
при помощи чувствительных приборов лишь в очень сильных полях. Итак,
изменение распределения тока в проводниках, обусловленное магнитными
взаимодействиями, пренебрежимо мало, и результаты, полученные путем
решения уравнений F.45) и F.46) при заданных граничных условиях,
можно рассматривать, поскольку речь идет о влиянии этого взаимодействия,
как точные.
Так как удельное сопротивление зависит от температуры, а проте-
протекающий по проводнику ток выделяет тепло, то при сильных токах найден-
найденные решения окажутся неточными; наибольшие отклонения будут наблю-
*) Классическую теорию эффекта Холла можно найти в книге Р. Беккера.
Электронная теория, М.—Л., 1936. — Прим. перев.
Электрический ток 235
даться там, где большая плотность тока вызывает сильное нагревание
среды. Поэтому наши результаты будут точны только в юм случае, если
температурный коэффициент сопротивления среды и плотность тока малы
или если токи кратковремениы.
§ 12. Общие теоремы. Общие теоремы, выведенные в гл. III из тео-
теоремы Грина, можно запасать в форме, удобной для решения рассматривае-
рассматриваемых в настоящей главе задач.
1. Если всюду на границах проводника задано значение потенциала V,
а также заданы величина и местонахождение всех источников или стоков
тока внутри него, то потенциал V однозначно определен во всех точках
проводника.
2. Если всюду па поверхности проводника задано значение нормальной
компоненты плотности тока, а также заданы величина и местонахождение
всех источников или стоков тока внутри него, то тем самым определено
значение разности потенциалов между любыми двумя точками проводника.
3. Если удельное сопротивление части проводника возрастает, то сопро-
сопротивление всего проводника возрастает или остается неизменным.
4. Если удельное сопротивление части проводвика уменьшается, то
сопротивление всего проводника уменьшается или остается неизменным.
К этим теореь.ам можно добавить еще одну, доказательство которой
¦будет дано ниже.
5. В проводнике всегда устанавливается такое распределение тока,
при котором выделяется минимальное количество тепла.
Чтобы доказать ату теорему, предположим, что имеется отступление
от распределения, задаваемого законом Ома F.8), и что добавочная плот-
плотность тока равна j. Так как не должно быть накопления зарядов, эта
добавочная плотность тока j должна удовлетворять уравнению непрерыв-
непрерывности V-j = O. Тепло, выделяющееся в элементе трубки тока в проводнике,
согласно выражениям F.8) и F.11), равно
Здесь dS— поперечное сечение элементарной трубки и ds — ee длина. Ин-
Интегрирование дает
Р = ^ [i(VFJ + 2j-VF + xf ]rfv. F.50)
V
Применив теорему Грина C.21) ко второму интегралу, полагая j=VcI» и
V = V, будем иметь
\ j \V dv= -Л W-jdv + ^ VnjdS.
Первый член в правой части равен пулю, так как V"j = O- Второй член
также равен нулю, поскольку величина полного тока через электрод
задана. Следовательно, в правой части выражения F.50) отличны от нуля
только первый и третий интегралы. Первый дает количество тепла, выде-
выделяющееся в проводнике, в том случае, когда выполняется закон Ома. Тре-
Третий интеграл всегда положителен, поэтому при всяком отклонении от закона
Ома количество выделенного тепла увеличивается.
§ 13. Двухмерный ток. Как было отмечено в § 1 гл. IV, в электро-
электростатике, строго говоря, не существует двухмерных задач ввиду того, что
любой цилиндрический проводник имеет конечную длину, а получить
236 Глава VI
резкую границу электрического поля на концах цилиндра ненозможно, так
как в природе нет сред с нулевой диэлектрической проницаемостью. На-
Напротив, многие задачи о токах в проводниках являются строго двухмер-
двухмерными, так как ток можно сосредоточить в конечной области, ограничивая
эту область изолирующей поверхностью. К этому типу задач принадлежат
ссе задачи о токах в тонких плоских проводящих пленках. Для решения
этих задач применимы все методы, описанные в гл. IV. Наиболее эффек-
эффективным из них является метод сопряженных функций.
В § 10 гл. IV было показано, что решение уравнения F.48) в случае
потенциала, зависящего только от х и у, имеет вид
U{x, у) или V(x, у), F.51)
где
W = U + /V=:f(z) = f(x + /y). F.52)
Если V — потенциальная функция, то плотность тока i в любой точке, со-
согласно формулам D.57) и F.7), будет равна
__
X
3W
IT
1 dV __ I dU
т дп т ds
F.53)
Если выбрать в качестве потенциальной функции U, то
i=i|»=±*u+i*:. F.54)
В формулах F.53) и F.54) принято то же самое правило знаков, что
и в формуле D.57).
Таким образом, если проводник ограничен эквипотенциальными лини-
линиями Ux и V2 и силовыми линиями V1 и V2, то ток через него будет равен
V2 V2 Vz
, Г . , 1 Г dU , 1 С dV , V2 — V,
I = \ ids = — \ 7j— ds = — \ ^-- ds = — .
Vi Vi V)
Сопротивление проводника по закону Ома равно
Если в формуле F.55) эквипотенциальные линии U1 и ~U2 являются зам-
замкнутыми крлвыми, то электростатическая емх^псть между электродам»,
находящимися в вакууме, будет равна (см. § 12 гл. IV)
т—и\7 {ь.щ
I и2 — t^i |
где через [V] обозначен интеграл от V, взятый по замкнутому контуру едоль
V\ или U2- Таким образом, зная С, можно найти сопротивление между И\
и U2, если проводящая среда заполняет то же самое пространство, что и
электростатическое поле. При помощи формул F.55) и F.56) находим
R = ^. F.57)
Так, из формулы D.69) следует, что сопротивление на единицу длины
между двумя параллельными цилиндрическими электродами, оси которых
находятся на расстоянии D друг от друга, равно
Электрический ток
237
где х —удельное сопротивление среды между цилиндрами, a Rx, R2 — их
радиусы. Знак минус соответствует случаю, когда один цилиндр располо-
расположен внутри другого, знак плюс — случаю, когда ни один из цилиндров не
охватывает другого.
§ 14. Длинная лента со скачкообразно меняющейся шириной. При-
Применим изложенную выше теорию к вычислению распределения тока в длин-
длинной, однородной по толщине проводящей ленте, полуширина которой
меняется скачком от h до А. Область ленты вблизи уступа показаиа на
У
Плоскость z,
У,
-I
-а
О
Плоскость z
п
V--
-/
Зп
"Г
Л
Kz,=+a
О
-J
Фиг. 63.
фиг, 63, б. Очевидно, что такая граница получается, если давать действи-
действительной оси плоскости z1 углы наклона тс/2, Зтг/2, 0, Зи/2 и я/2 соответ-
соответственно в точках —1, —а, 0, +а и +1. Чтобы после наклона получить
между точками — а и + а конечное расстояние, необходимо поместить
начало координат плоскости z1 в точке z = — /оо плоскости z. Подставляя
значения всех а и и в выражение D.85), найдем
dz
dz1
F.59)
Прежде чем выполнять интегриронание, определим входящие в выражение
F.59) постоянные а и с по методу, изложенному в § 29 гл. IV. Как и
в § 29 гл. IV, dzi — jr1e^dd1 = fzldrI при постоянном гг. Когда величина гг
очень мала и^ 01 изменяется от 0 до it в плоскости zlt у является большой
отрицательной постоянной величиной, а х изменяется в плоскости z от +h
до —h. Из выражения F.59) тогда находим
23& Глава VI
I
откуда h = '^- -Tj- /ежа. Аналогично, у — большая положительная постоянная
величина при rt—» оо, так что
Откуда к =^-~- ]съ. Решая относительно с и а, будем иметь
—I— "/Л ... !• 1\\
а = ~к и с= + ~- (Ь.ЬО)
Подставим эти значения в выражение F.59), заменим z2 в первом члене
и a2/z2 —во втором на («2-f-я2)/A + к2) н проинтегрируем (см. Двайт, 120).
В результате получим
2 [, t r(z?— a2)l'/2 , г (i__zfI/2
Постоянная интегрирования отсутствует, так как из этой формулы следует,
что, когда yt = 0 и хх = ± я, z = ± /г, а когда ух = 0 и ^ = ± 1, z = ± ft.
Физически очевидно, что вдоль разных границ проводника проходят
различные линии тока. Если положить И* = 1пг1, или z1 — ew, где U —
потенциальная функция, то (см. фиг. 63, а) линия тока F=0 будет про-
проходить от хг— + со до ж1 = 0 и линия тока F = tc—от хг= —оо дож1=0.
Следовательно (см. фиг. 63, б), эти линии тока будут проходить соответ-
соответственно по правой и левой границам ленты, сверху вниз, а полный ток
в ленте будет равен / = тг/<;. Подставляя z1 = ew, получим
.. и„ -
F.61)
причем действительная часть z положительна, если положительна действи-
действительная часть z1.
Если ; — сопротивление между противоположными-сторонами квадрата
с площадью 1 м2, вырезанного из того же самого листового проводника,
что и лента, то сопротивление широкого участка ленты (длиной ук) будет
Rk = с,|yk|/2ft, а узкого (длиной yh) Rh- c,\yh\/2h. Когда два таких уча-
участка ленты, широкий и узкий, соединены между собой так, как это пока-
показано на фиг. 63,6, сопротивление всей ленты будет ие Rk -f Rh, a Rh + Rh+ ДЙ,
где Д7? — добавочное сопротивление, обусловленное деформацией линий
тока вблизи места соединения. Если ?/fe > к и ?/,, > h, то эквипотенциаль-
эквипотенциальные линии на фиг. 63, б параллельны оси. Вычислим для этого случая Д/?.
На оси у F = yTC, так что e2w = —e2U и выражение F.61), если заменить
arc tg /и на / ar th и и положить х = 0, даст
у = — I ft ar th ( ¦ 2гГ ) — Л ar th g f —^ ) . F.62)
Пусть U=U1—>+со, тогда е2и очень велико и (см. Двайт, 4 и 5.3)
уъ= — ( ftar th ^ „., /гаг tha " „,, ).
Электрический ток 239
Пользуясь формулой G02) из справочника Двайта и пренебрегая 1, а и а2
по сравнению с е^и, получим
Если U—U^—>~<x>, то е2и очень мало ir, как п раньше,
2 Г, . 2а2 + е2G2 , - а2 B + е2G2)
г/. = — к ar th —577 Л ar th —' ¦>,-, =
'' m L аB + е2G2) 2а2 + е2G2 J
i Г , , 1 + a , , 4а2 Т
2hU2 , 1 /. , Л + Л. , , 4Л2 \ 2AE/
= ? + — ( к In y^i- _ /< In T-—^ ) =
те те \_ /с — h к* — IP J тс
Вычитая из первого выражения второе, найдем U1 — V2
ТТ ТТ —^УЪ nVh (А _ В
Ui~U2-H~ ~th~ Я V2A 2T
и, с силу формулы F.55),
Подставляя значения ^1 и 5, для Д7? после упрощений получим следу-
следующее выражение:
. „ « Г/г2 + Л2, k + h 91 Л2 —Л2 1 . .„„,,
А7? = — —X— 1п5—- + 21п ... F.63)
2те [_ hk к—h Ahk \ v '
Другие примеры применения этого метода можно найти в задачах, поме-
помещенных в конце главы.
§ 15. Трехмерное распределение тока. Если пространство можд\
двумя электродами целиком заполнено однородной изотропной проводящей
средой, то распределение тока и сопротивление между электродами можно
получить, решая электростатическую задачу о емкости между теми же
самыми электродами, при замене проводящей среды диэлектриком. В обоих
случаях нужно найти решение уравнения
V2F-0. F.64)
В электростатической задаче, если электроды находятся в вакууме, гра-
граничные условия, согласно формуле A.40), имеют вид
s^LdSn. F.65)
on
8
В задаче о токе соответствующие условия, согласно формуле F,5), можно
записать в виде
V = Va, Ia^-\\^dSa. F.66)
s
Так как граничные условия одинаковы, эквипотенциальные поверхности
в обоих случаях в точности совпадают. Сопротивление, по закону Ома,
будет равно
„_ Wb-Va\ . \Vb-Va\ тг„ ,аа~
ТТЛ
I Va I
240 Глава VI
где С—емкость между электродами, находящимися в вакууме. Если можно
найти такую электростатическую задачу, в которой боковые стенки сило-
силовой трубки имеют ту же форму, что и граница между проводником (с удель-
удельным сопротивлением -с) и изолирующей средой и, кроме того, эквипотен-
эквипотенциальные поверхности концов силовой трубки совпадают по форме с иде-
идеально проводящими контактами на концах проводника, то сопротивление
проводника можно выразить, согласпо формуле F.67), через «емкость»
силовой трубки. Под емкостью в этом случае подразумевается отношение
заряда на конце трубки к разности потенциалов между ее концами.
§ 16. Системы электродов. Две сферы. Удаленные электроды. Если
в однородную изотропную проводящую среду с удельным сопротивлением т
помещены п идеально проводящих электродов, то все соотношения между
потенциалами электродов и вытекающими из них (или втекающими в них)
токами можно найти при помощи методов, изложенных в § 14 — 19 гл. III.
Для этого нужно только заменить заряд ^s в электростатической задаче
на ток /s s-ro электрода и умножить емкостные коэффициенты на (те.,)^1,
а потенциальные — на хе^.
Например, для двух сфер с радиусами а и Ь, одна из которых нахо-
находится внутри или снаружи другой и расстояние между центрами которых
равно С, из уравнений B.39), учитывая, что /1== —/2, получим
так что сопротивление между ними равно
= «r(sll-2s12 + sa2). F.68)
В § 9а гл." V методом изображений были вычислены значения си, с12 и с2,
для этого случая. Используя эти величины, для сопротивления В в соот-
соответствии с определителем B.41) получаем
+С2А- F.69)
' 22
Формула F.69) мало пригодна, если одна сфера находится внутри другой.
В этом случае можно использовать метод, изложенный в § 20 гл. V.
Если два электрода находятся в бесконечной проводящей среде на
большом расстоянии друг от друга, то из формул F.68) и F.69) следует, что
где г—расстояние между электродами, а Са и Сь — электростатические
емкости каждого из них в отдельности.
§ 17. Задача о проводящем шаре. Для иллюстрации применения
метода сфзричоских гармоник к решению задач, в которых рассматриваются
границы между проводником и изолятором, вычислим потенциал во всех
точках проводящего шара с удельным сопротивлением г, в том случае,
когда ток / входит в один его полюс 8 = 0 и вытекает из противоположного
6 = it. В силу симметрии потенциал экваториальной плоскости можно при-
принять равным нулю, так что в соответствии с § 16 и гл. V в разложении
потенциала будут присутствовать только нечетные гармоники. Для потен-
потенциала, который должен быть конечным в начале координат, получаем
V = S i42n+ira»+ti>2n4.i (cos 6). F.71)
п=0
Электрический ток 241
Чтобы определить А2п+\, продифференцируем выражение F.71) по г, поло-
положим г = а, умножим на P2m+i ((*) dp и проинтегрируем от (а = 0 до (а= 1. Из
соотношения E.92) следует, что в правой части останется только член,
для которого т— п, так что, заменив т на п,- получим
1 1
P()d Bn + i)A^ [ [iW()]2^. F.72)
о
Применим формулу E.127) к интегралу в правой части. При г = а произ-
производная dV/dr равна нулю всюду, за исключением площадки AS поверхности
электрода, т. е. окрестности (л = >1; эта площадка так мала, что на ней
/*2гг+1 ((*) можно заменить на /^m-i A) = 1- Согласно формуле F.8),
dV)dr = \ V?? | = «V; поскольку dS = — 2-ка2йр, для А2п\\ находим
.. ,е il 4/г + З 1
и, следовательно, выражение F.71) принимает вид
со
ТГ т1 утл 471 + 3 /г\2п+1
Этот ряд можно разбить на четыре более простых ряда и заменить в них
2и +1 на т. Таким образом, получим,
Обозначая расстояния до полюсов через i?e и i?^, можно, согласно выраже-
выражению E.17), произвести суммирование этих рядов:
Пусть Ro и i?m образуют с осью шара углы а0 и аЛ) так что i?0cosa0 =
= a — r cos б и /?те cos a-n, = a + г cos б. Появляющиеся при интегрировании
(см. Пайерс, 182) в выражении F.74) логарифмические члены In r сокраща-
сокращаются, и для потенциала V получаем
Очевидно, что
так что исходное разложение F.73) остается верным вблизи полюсов.
В рассматриваемом случае в силу симметрии границы трубок тока
являются поверхностями вращения. Уравнение поверхности трубки, по кото-
которой протекает ток Ilt можно получить, интегрируя нормальную компоненту
плотности тока — A/т) (dVjdr) по сегменту, вырезанному трубкой на сфере,
и приравнивая результат интегрирования току + Ii- Для этой цели выра-
выражение F.74) более удобно, чем F.75). Интеграл от членов, содержащих
величины, обратные расстояниям, был вычислен в § 116 гл. I; поскольку
элемент поверхности равен 2irr2 sin 6 db, для тока II будем иметь
в в
l_rosa0 . 1—cosa^x , r/ / f sin6d6 С sin в db~\
16 В. Смайт
•242 Глава VI
Полагая х — cos б и интегрируя (см. Двайт, 191.01), получим
Если р~ тупой угол между Ro и Rn, то
Яп — 2а cos ап = Ro cos р, До — 2а cos а0 = R^. cos fi
и уравнение трубок тока приводится к виду
) F.76)
Эта формула подтверждает выполнение граничных условий, так как на поверх-
поверхности шара второй член в скобках равен нулю и 1г = /.
§ 18. Задача о сплошном проводящем цилиндре. Для иллюстрации
применения бесселевых функций к задаче о проводнике, ограниченном
цилиндрической изолирующей поверхностью, вычислим распределение потен-
потенциала в сплошном проводящем круглом цилиндре, длина которого равна 2с,
радиус а, удельное сопротивление т, в том случае, когда ток / подводится
к нему при помощи электродов, имеющих вид узких кольцевых поясков, при-
прижатых к цилиндру на расстоянии Ь по обе стороны от его экватора. Ширину
пояска будем считать настолько малой, что физически измерить ее невоз-
невозможно, но в то же время отличной от нуля в математическом смысле, так
что плотность тока и потенциал всюду будут конечны. Принимая эква-
экваториальную плоскость за плоскость нулевого потенциала, получаем, что
решение уравнения непрерывности, остающееся конечным на оси, в соответ-
соответствии с § 33а гл. V и формулой E.311), имеет вид
V = 2 АЛ (К?) sin knz. F.77)
На границе z = c должно быть dV/dz = 0. Это граничное условие удовле-
удовлетворяется, если, имея в виду, что cos [Bлг + 1)тг/2] = 0, положить
К = (Щ^- F.78)
Чтобы определить Ап, продифференцируем выражение F.77) по р [используя
соотношения E.440)], положим р = а, умножим результат на sinknz и про-
проинтегрируем от 0 до с. В правой части останется только тот член, для
которого кр = кп (см. Двайт, 435), Поэтому, заменив р на п, получаем
с fenc
С* гЬЛ1 С
\ j- sin knz dz = Ап1г (кпа) \ sin2 knz d (knz).
о о
Применим к интегралу в правой части выражение D30.20) из справочника
Двайта. На границе р = а, OV/dp равно нулю всюду, за исключением поверх-
поверхности AS, покрытой электродом и лежащей в окрестности z = b. Эта
поверхность настолько мала, что на ней sin knz можно принять равным sin knb.
Из формулы F.8), полагая 2\adz = dS, получим для интеграла в левой части
J Lr.a
Постоянные Ап будут равны
Формулы F.77) —F.79) дают искомое решение.
sin hnb ,n
ftna) " V '
Электрический ток 24S
В рассмотренной задаче границы трубок тока являются поверхностями
вращения. Уравнение поверхности трубки, несущей ток /', можно получить,
интегрируя плотность тока —A/т) (dV/dz) по поверхности диска, вырезан-
вырезанного трубкой, и приравнивая результат интегрирования току — /':
^ I0{knp)pdp.
п=0 О
Интегрируя это выражение при помощи формулы E.441) и подставляя
значение Ап из формулы F.79), получим
со
Т> _ 4/Р V sin ЬпЪ cos hnzl^ (knp) .„ „„.
1 -~^ 2l B/г + 1)/1(М) ' ( Щ
2l
71 = 0
где значения кп вычисляются по формуле F.78).
§ 19. Сопротивление земли. В геофизике существует метод исследова-
исследования структуры земной коры, основанный на измерении распределения
потенциала на земной поверхности при прохождении тока между двумя
или большим числом поверхпостных электродов. Рассмотрим простейший
случай, когда до глубины а удельное сопротивление земли равно тх, а на
большей глубине оно равно т2. Применим метод, изложенный в § 31г гл. V,
для нахождения распределения потенциала около точечного электрода.
Решение в случае двух или большего числа электродов можно найти при
помощи -суперпозиции. Потенциал, созданный уединенным электродом,
можно получить из выражения E.378), заменяя, согласно § 15, заряд q
на 2те/. Следует иметь в виду, что в этом случае 2/ соответствует току,
рассмотренному в § 15, так как весь ток протекает в нижнем полупро-
полупространстве. Таким образом, для потенциала одного электрода имеем
оо
V ^lk^-i\J^h)e-^dk. F.81)
Как и в § 31г гл. V, для получения решения в области т, мы должны
учесть добавочный потенциал, обусловленный разрывом непрерывности при
z — a; этот потенциал может содержать как члены e~kz, так и члены ehz
ввиду того, что z в данной области является конечной величиной. Таким
образом,
^ W (к) Jo (кр) е+ь* dk+^J0 (йр) е-"* dk ] . F.82>
о о
На поверхности земли z = 0 и линии тока должны быть горизонтальны;
так как последний член формулы F.82) уже удовлетворяет этому условию,
то этому же условию должны удовлетворять и остальные члены формулы
F.82). Следовательно, условие дУг/дг = 0 при z = 0 дает
-Ф(к) + У(к) = 0. F.83>
Потенциал в области т2 должен обращаться в нуль на бесконечности и,
следовательно, может иметь только такой вид:
• ¦ (€.84>
¦. ;¦¦
16*
244 Глава VI
Граничные условия при z = a, согласно соотношениям F.47) и F.48), запи-
записываются следующим образом:
12 т, 5z т2 dz
После подстановки соответствующих выражений из формул F.82) — F.84)
и исключения Jo (Jcp) получаем
e-ha + ф (?) (gfta + e-ha) _ Q (&) g-fta = 0> F.85)
- x2e-fea + т2Ф (к) {еы - е~ка) + ^в (к) е~ы = 0. F.86)
Исключив в (к) из этих уравнений, обозначив (тх — Тг)/(Т1 + тг) через f)
и подставив в формулу F.82), находим распределение потенциала на поверх-
поверхности земли (где z = 0)
^[1^S F.87)
* °
Разлагая знаменатель выражения F.87) в ряд (см. Двайт, 9.04) и меняя
порядок суммирования и интегрирования, получим
F* = 2^ [ [ J» (kp) dk+2Hi (- 1ТРП [ e~2nha Jo (kP) dk] •
п=1
Подстановка интеграла из выражения E.372) дает
Если принять теперь поверхность земли за плоскость осу, то при токе /
между электродами, находящимися в точках ж=+6иа;= —Ь, для потен-
потенциала на поверхности (поскольку р+=[(ж—ЬJ + у2]1/2 и р_=[(ж-Ь&J + У2]1/2)
можно написать
} F.89)
Случай любого числа слоев был рассмотрен Стефанеско и Шлюмбергером *>.
§ 20. Токи в тонких изогнутых пленках. Если тонкую однородную
по толщине изогнутую пленку можно развернуть на плоскость, то, выполнив
ату операцию, мы сведем задачу к двухмерной и сможем применить для ее
решения методы § 13. Если же развертывание на плоскость невозможно,
то приходится применять другие методы. Из уравнений C.13) и F.46)
следует, что уравнение непрерывности в ортогональных криволинейных
координатах имеет вид
^A^^XVf^V F 90)
дщ \ /ij дщ J ди2 V Л2 ди2 J ди3 \ hs ди
и8
Пусть пх и и2 — ортогональные криволинейные координаты на рассматри-
рассматриваемой поверхности, а и3 — расстояние, отсчитанное в направлении, нормаль-
нормальном к поверхности. Пленка настолько тонкая, что распределение тока
на обеих ее сторонах одинаково и, следовательно, dV/du3 = 0. Толщина
— ¦ ¦ — '#
*) Stef anesco, Schlumberger, Journ. d. Phys., I, 132 A930).
Электрический ток
245
цленки всюду одинаковая, так что h3 не зависит от
условиях уравнение F.90) принимает вид
Sm V Й duj дщ \h du/
При этих
9
Это уравнение и следует решить, чтобы найти распределение тока.
§ 21. Распределение тока в сферической пленке. Считая, что для
сферической пленки V не зависит от г, можно на основании уравнения C.17)
представить уравнение F.91) в виде
smb~
F.92,
п
где б — полярный, а <р — азимутальный угол.
Хотя сферическую пленку нельзя развер-
развернуть на плоскость, однако каждую точку
сферической поверхности можно спроектиро-
спроектировать на бесконечную плоскость таким обра-
образом, что величины углов не изменятся. Эта
операция называется стереографической про-
проекцией и весьма похожа на инверсию. На
одном из концов диаметра строят плоскость,
касательную к сфере. Линия, проходящая Фиг. 64.
через другой конец диаметра О и точку Р
(фиг. 64), пересекает плоскость в точке Р',
которая называется проекцией точки Р. Пусть ^' — решение уравнения
непрерывности для плоскости, где это уравнение, согласно D.4), имеет вид
' N ¦ " F.93)
дг
\ дг J dtp2
При проектировании на сферу системы кривых, изображающих W, азиму-
азимутальный угол не меняется. Из фиг. 64 видно, что г и 6 связаны соотношением
Уравнение спроектированных кривых можно получить, если в уравнение F.93)
подставить 6 и <р вместо г и <р:
д
дВ д
д дВ д . „ д
-5- = г "а" Чп = Sln ° яп !
дг or m 90
тогда уравнение F.93) примет вид
sne
Это уравнение совпадает с уравнением F.92). Таким образом, стереографи-
стереографическая проекция решения уравнения непрерывности для плоскости дает
решение этого уравнения для тонкой однородной сферической пленки.
В § 10 гл. IV было показано, что U и V являются решениями урав-
уравнения V2F = 0, где
f(z + /у) = / (г cos cp -I- jr sin cp),
Ч Ортогональные криволинейные координаты иу и и2 всегда можно выбрать таким
образом, чтобы внутренняя и внешняя поверхности пленки совпадали с координатными
поверхностями M3=const. Если пленка тонкая и однородная по толщине, то, очевидно,
при этом коэффициент ha, по крайней мере внутри пленки, не зависит от щ и м2.—
прим. перее.
246 Глава VI
если / (z) — аналитическая функция. Из сказанного выше вытекает, что если
F.94)
то и U и V будут решениями уравнения непрерывности на поверхности
сферы радиуса а, причем, если [/ — потенциальная функция, то V — функция
потока, и наоборот. Из законов инверсии следует, что прямые на плоскости
при проектировании на сферу дают окружности, проходящие через точку О,
а окружности на плоскости переходят в окружности на сфере.
В качестве примера найдем распределение потенциала в сферической
пленке радиуса а, имеющей поверхностное удельное сопротивление с, когда
ток / втекает в нее в точке б = а, ср = -g- ir и вытекает в точке б = а,
<р = —2~тс. Заменяя, согласно § 15, величину заряда 2теи в соотноше-
соотношении D.66) на е„с/, мы получим для распределения потенциала U в плоской
пленке следующее выражение:
th
s/ " 2by 2br sin 9
Но, как видно из фиг. 64, r = 2atg-y-B, так что
1 1
., 2tiU tg2 6 + tg2 " 1 — cos a cos 6 ,» ot-4
Cth —=-= ¦: -. =- : -jr--. -. (D.9O)
si оi 1 n i 1 • sin a sm 6 sin 9 ч '
2 tg -у и tg — a sin 9
Таким же путем из соотношения D.68) можно получить уравнение линии тока:
. 2kV г2—б2 cos a —cos 6 /с пс\
ctg —г- = ,-п ¦ — . —й . (о.96)
° s/ 26r cos 9 sin а sin 6 cos 9
§ 22. Поверхность вращения. В качестве другого примера найдем
решение уравнения F.91) для поверхности, образованной вращением кривой
?/ = /(z) вокруг оси z[f(z) — однозначная функция z]. Очевидно, что на такой
поверхности положение любой точки Р можно определить ортогональными
координатами z и <р, где ср — азимутальный угол, отсчитываемый вокруг оси г.
Положим в § 20 координату пх численно равной z, а м2 = ср. В силу сим-
симметрии ht и h2 не зависят от ср. Тогда уравнение F.91) принимает вид
-r^w [ —^-^г- ) + -^г-о = 0. (о.97)
hi oz \^ h\ oz J ^9
Чтобы найти решение этого уравнения, введем новую переменную и, равную
нулю при z = z0 и удовлетворяющую соотношению
* и• ho о \ hi 7 ta c\o>\
•^-=-ri-^r или и = \ -г*- dz. @.У0)
oil hi oz J
Тогда уравнение F.97) принимает вид
Как было показано в § 10 гл. IV, решениями этого уравнения являются
функции U (и, ср) или V (и, ср), причем
F(u + j<p). F.100)
Электрический ток
247
Чтобы выразить и через заданные величины, нужно вычислить hx и h2.
Уравнение поверхности имеет вид
p = /(z), F.101)
так что
откуда
dp = /' (z) dz
ds2 = ф2 + dz2 + p2 tfT2 = {[/' (z)]2 + 1} dz2 + [/(z)]2 dy\
Подставляя эти значения в соотношение F.98), получим
F.102)
F.103)
Фиг. 65.
Поскольку при увеличении <р на 2пъ мы возвращаемся к той же линии на
поверхности, для однозначности полученного решения необходимо, чтобы
F(u + jtp) была периодической функ-
функцией <р с периодом 2гс. По форме ре-
решение совпадает с решением для ци-
цилиндрической поверхности, которую
можно развернуть в плоскую ленту.
Если, как показано на фиг. 65, по-
поверхность вращения замкнута на од-
одном конце, то /(z) = 0 в точке пере-
пересечения поверхности с осью z и, со-
согласно выражению F.103), эквива-
эквивалентный цилиндр будет простираться
до и=—оо. Если один из концов
поверхности ве замкнут (фиг. 65), то
эквивалентный цилиндр также будет
оканчиваться при некотором* поло-
положительном значении и и граничные
условия на краю цилиндра будут
выражаться той же функцией угла <р, что и граничные условия на краю
поверхности вращения, изображенной на фигуре.
§ 23. Предельные значения сопротивления. Общие теоремы, изложен-
изложенные в § 12, часто дают возможность найти предельные значения, между
которыми заключено сопротивление проводника, даже в том случае, когда
нельзя вычислить точное значение. Для нахождения нижнего предела со-
сопротивления разместим внутри проводника тонкие идеально проводящие
слои таким образом, чтобы они, с одной стороны, совпадали по возмож-
возможности точвее с действительными эквипотенциальными поверхностями, а с дру-
другой стороны, давали возможность вычислить сопротивление полученного
проводника. Как следует из § 12, это сопротивление будет равно сопроти-
сопротивлению исходного проводника или будет меньше его. Чтобы найти верхний
предел, введем внутрь проводника как можно ближе к действительным
линиям тока тонкие слои изолятора с таким расчетом, чтобы оказалось
возможным вычислить сопротивление измененного проводника. Как известно
из § 12, это сопротивление будет равно сопротивлению исходного провод-
проводника или будет больше его.
248
Глава VI
Например, сопротивление между двумя электродами данной формы
имеет промежуточное значение между сопротивлениями, соответствующими
электродам, поверхности которых описаны вокруг данных электродов
и вписаны в них. В качестве характерного примера рассмотрим сопро-
сопротивление между идеально проводящими электродами, прижатыми к концам
А и В подковообразного проводника с треугольным поперечным сечением
(фиг. 66). Для получения верхнего предела сопротивления введем в про-
проводник бесконечно тонкие слои изолятора и расположим их на очень ма-
малом расстоянии друг от друга
таким образом, чтобы ток в
проводнике протекал только
по прямым линиям и полу-
полуокружностям. Длина такого
слоя, как видно из фиг. 66,
равна 2c+iz{b-\-x). Площадь
соответствующего поперечного
течения равна xdx, и, следо-
следовательно, сопротивление
dR _
и
Фиг. 66.
xdx
Все слои параллельны, гак
что, согласно формуле F.14),
верхний предел сопротивления (см. Двайт, 91.1) будет равен
xdx
2c -\- тсЬ -\- тех
2с + гс (a-f 6)-1-1
J
9 Г m , гл! 2с + те (я-f 6) 1
F.104)
Чтобы найти нижний предел сопротивления, введем в сечения М и ЛГ
проводника идеально проводящие слои. В прямолинейных частях провод-
проводника AM и NB ток распределится равномерно, и сопротивление их будет
равво AcTJa2. В закругленной части MN проводник имеет форму треуголь-
треугольной силовой трубки в двухмерном электростатическом поле, описываемом
функцией W = In z. Отсюда следует, что функция потока и потенциальная
функция имеют вид
U = lnr и F = 6. F.105)
Сопротивление полоски, лежащей на расстоянии у (см. фиг. 66), в силу
формулы F.55), равно
Полоски соединены параллельно, следовательно, (см. Двайт, 620),
1/8»
1 ) Ш
Так как изогнутая часть проводника и обе прямолинейные части соеди-
соединены последовательно, то нижнее предельное значение сопротивления будет
равно
Электрический ток 249
§ 24. Токи в анизотропных средах. Слои в земной коре. Взяв ди-
дивергенцию выражения F.8), мы получим
V-(tV*0=—V-» = 0. F.107)
Если среда не изотропна, то ее проводимость в различных направлениях
различна, и f нельзя выносить из-под знака V. Однако если среда одно-
однородна, то проводимость ее по любому направлению одинакова. В этом
случае можно, как это было сделано в соотношениях A.58) и C.8), выбрать
систему прямоугольных координат таким образом, что уравнение F.107)
примет вид
+ ^ = О. F.108)
Вследствие особенностей образования земной коры часто оказывается, что
ее проводимость в горизонтальном направлении больше, чем в вертикальном.
Если направить ось z по вертикали, то уравнение F.108) можно записать
следующим образом:
Если ввести новую переменную, определяемую соотношением
u^(^yhz=az, F.110)
то уравнение F.109) примет вид
Для решения уравнения F.HI) применимы все методы, изложенные в гл. V,
однако необходимо либо выразить граничные условия в координатах х, у, и
и потребовать, чтобы решение уравнения F.111) им удовлетворяло, либо,
наоборот, перейти в решении уравнения F.111) к переменным х, у, ъ.
Предположим, что сферический электрод радиуса R до половины погружен
в землю. Граничное условие имеет в этом случае вид V = Vo при х2 + У2 ^~
+ z2 = х2 -{-у2 -+- (и/аJ = R2. Следовательно, в системе х, у, и это условие
должно выполняться для сфероида
Из выражений E.8) и E.9), полагая a2 = b2 — R2 и c2 — a.2R2, получаем
решение
==v гГ ^ 1. г Г
Полагая x = a2-\-Q и принимая во внимание, что а > 1, будем иметь
(см. Двайт, 192.11)
0 arthl(c2 —a2)/c2]1/2
Но из уравнений E.284) и E.285) следует, что
с2+е = (с2 — a2) yf,
и выражение для потенциала принимает вид
arth- =
y(i) F.112).
250 Глава VI
Согласно соотношениям E.287) и E.288),
U = az = i?(a2-
жя+уа = Дя(о2
Исключая ?, получим
Наименьшее значение т] будет на электроде, где 7j = a/(a2—II'2. Поэтому
знаменатель первого члена всегда больше, чем знаменатель второго, так
что эквипотенциальные поверхности имеют форму неконфокальных сплюс-
сплюснутых сфероидов. На поверхности земли z = 0 и эквипотенциальные линии
определяются уравнением
V = V0 ГагсЬГ ^ГагвЬД [ ^ J'". F.114)
Для точечного'электрода, когда величина R очень мала, в выражении F.114)
можно заменить arsh через угол. Учитывая, что остальная часть выраже-
выражения F.114) пропорциональна току /, получим
+ y*)-lh. F.115)
Кривые, определяемые этим уравнением, имеют тот же вид, что и в случае
изотропной среды.
§ 25. Ток, обусловленный движением пространственного заряда.
Уравнение Чайльда. До сих пор мы рассматривали токи в проводниках,
•суммарный заряд которых был равен нулю. Рассмотрим теперь токи в про-
проводниках, несущих заряды только одного знака, так что суммарный заряд
•отличен от нуля. Движение зарядов следует считать настолько медленным,
что формулы электростатики остаются справедливыми. В этом случае должно
удовлетворяться уравнение Пуассона C.6), согласно которому
V2F== Pf F.116)
¦где V — потенциал и р — плотность заряда. Допустим, что все заряды оди-
одинаковы, что каждый из них связан с массой т и что всю свою энергию
¦они получают от наложенного поля. Тогда энергия частицы, скорость кото-
которой равна v, а заряд qt в точке с потенциалом V будет
, mv* = 2q(V0-V), F.117)
.где Vo —потенциал в начальной точке. Плотность тока в произвольной
точке будет равна
i = pv. F.118)
В простейшем случае заряды в неограниченном количестве эмиттируются
плоскостью х = 0 и ускоряются по направлению к плоскости х=Ь под дей-
действием приложенного напряжения Vo. На плоскости х = 0 эмиссия зарядов
продолжается до тех пор, пока не исчезнет увлекающее их электрическое
иоле. Поэтому граничное условие имеет вид
(Т) =0- F-119)
Скорости всех зарядов направлены по оси х, так что, исключая р и v из-
уравнения F.116) при помощи формул F.117) и F.118), получим
dW _ i [ m "]
~W i; [2g(V0-V)\
Электрический ток 251
Умножая это выражение на dVjdx и интегрируя от V = Vn и dV/dx — О
до V и dV[dx, будем иметь
Извлекая из обеих частей квадратный корень и интегрируя от V = V0,
л; = 0 до V = 0 и х=Ь, найдем плотность тока
FЛ21)
д т b v '
Это выражение известно под названием закона Чайльда. Оно показывает,
что при неограниченной эмиссии зарядов из одной пластины ток между
пластинами пропорционален потенциалу в степени 3/2. Такой ток называется
«током, ограниченным пространственным зарядом». Как видно из формулы
F.121), ограничение пространственным зарядом значительно сильнее ска-
сказывается на заряженных атомах, чем на электронах, вследствие их большей
массы.
На практике эмиттер часто имеет вид тонкого, круглого цгглиндра,
а эмиттированные заряды перемещаются по направлению к большому цилинд-
цилиндру, концентричному с эмиттером. В этом случае удобно воспользоваться
цилиндрическими координатами, и если / — полный ток на единицу длины
цилиндров, то уравнение F.118) принимает вид
F.122)
Записав уравнение F.116) в цилиндрических координатах при помощи урав-
уравнения C.18), исключив, согласно формулам F.117) и F.122), р и v и за-
заменив Vo — V на V, получим
г™ + ™='( ^Y'2. F.123)
Непосредственное решение этого уравнения затруднительно, если даже вообще
возможно. Можно, однако, получить его решение в виде ряда следующим
•способом: предположим, что q, m и V входят в искомое решение в такой же
¦форме, как и в выражение F.121), и будем искать решение F.123) в виде
9 ут
1=4" ?ГУ- F-^)
Нужно определить pi2 так, чтобы удовлетворялось уравнение F.123). Под-
Подстановка выражения F.124) в уравнение F.123) дает
?Ч1)!о' FЛ25)
где
7 = 1п(?). F.126)
Решение этого уравнения можно найти обычным методом в виде ряда
!^-- FЛ27)
В формуле F.126) через а обозначен радиус внутреннего цилиндра. Таблица
значений В как функции rja опубликована Ленгмюром.
252 Глава VI
ЗАДАЧИ
1. Некоторый прибор должен работать от 6-вольтовой аккумуляторной батареи.
Батарея, хотя и имеет весьма малое сопротивление, но не может давать нужный ток
достаточно долгое время. Чтобы преодолеть это затруднение, генератор постоянного
тока, э. д. с. которого может колебаться от 100 до 120 в, соединяют последовательно
с сопротивлевдем, подобранным так, что когда генератор с последовательно подклю-
подключенным сопротивлением присоединяется параллельно к батарее, последняя ве дает
тока при наибольшем значении э. д. с. генератора. Какую часть тока будет давать бата-
батарея, когда э. д. с. генератора имеет наименьшее значение?
2. Требуется, чтобы температура печи не выходила за известные пределы, не-
несмотря на то, что напряжение в линии колеблется от 100 до 120 в. При наивысшей
температуре печь потребляет 1,5 а при 60 в и при низшей температуре 1а при 30в.
В распоряжении имеется «балластная лампа», через которую проходит ток, равный
точно 2 а при любом напряжении от 30 до 50 в. Показать, что при использовании двух
реостатов существует, по крайней мере, два способа решения поставленной задачи и что
требуемые пределы сопротивлений реостатов в одном случае будут 70—140 ом и 6,67—
40 ом и в другом 5—20 ом и 30—120 ом.
3. Через некоторый прибор независимо от величины приложенного напряжения
проходит ток ?,. Напряжение на прибор подается с потенциометра, имеющего сопро-
сопротивление В. и подключенного к батарее с э. д. с. % и внутренним сопротивлением г.
Параллельно прибору включен вольтметр, сопротивление которого R1# Найти ток, те-
текущий через батарею, как функцию показаний вольтметра.
4. Батарея с э. д. с. %Л включена между точками А и В цепи. Ветви AD, АС,
CD, ВС, СЕ и BE имеют сопротивления, соответственно раввые г, 2г, г, R, 2R, Я.
Когда к точкам D и Е подключается вторая батарея, то оказывается, что ток через
первую батарею равен нулю. Показать, что э. д. с. второй батареи равна
DB 3)lg/Br( + R)]
( I(( )]
5. Напряжение на стрелку электрометра подается от неподвижного в подвижного
контактов А ж В присоединенного к батарее потенциометра АС, имеющего большое
сопротивление. При помощи вольтметра с большим, но неизвестным сопротивлением
измеряются напряжения V, УЛ и V2 соответственно между точками АС, ВС и АВ.
Показать, что после того как вольтметр будет отключен, истинное напряжение,
поданное на стрелку электрометра, будет равно V2VJ(V1 + V2)-
6. К батарее, имеющей внутреннее сопротивление г и э. д. с. %, подключены
параллельно друг другу две проволоки, каждая из которых имеет длину D и сопро-
сопротивление р (на единицу длины). На каждой из проволок имеется подвижной контакт,
расположенный на одной проволоке на расстоянии х от конца, а на другой—ш> рас-
расстоянии у от того же конца. Между контактами включено сопротивление R. Показать,
что ток через R равен
' 2Рр(у-х)Щ
7. Углы квадрата А, В, С, D соединены между собой и с центром квадрата про-
проволокой, сопротивление которой на единицу длины равно г. В сторону АВ включен
гальванометр, а в диагональ АС, между точкой С и центром, включена батарея. Пока-
Показать, что если проволоку между точкой В и центром в диагонали BD заменить
сопротивлением rB-\-2 '23)-1, то ток через гальванометр будет равен нулю.
8*. Однородная проволока длиною 4 а согнута в квадрат, противоположные
вершины которого соединены прямолинейными кусками такой же проволоки. К точке
пересечения диагоналей подведен ток заданной неличины, выходящий через одну и»
вершин квадрата. Найти силу тока в различных ветвях цепи и показать, что полное
сопротивление цепи равно сопротивлению куска проволоки, имеющего длину
9*. Из однородной проволоки изготовлен каркас в виде прямоугольника со сто-
сторонами 2а и За, разделенный проволоками, параллельными его сторонам на квадраты
со сторонами а. Сопротивление контактов во всех точках пересечения проволок счи-
считается ничтожно малым. Показать, что для тока, входящего в один угол каркаса
и выходящего из противоположного угла, полное сопротивление цепи равно сопротив-
сопротивлению куска проволоки длиною 121 «/69.
10*. На телеграфной линии возникает повреждение, вследствие которого в неко-
некотором месте между линией и землей появляется сопротивление определен-
определенной величины. Показать, что при неизменной батарее на передающем конце линии
ток на приемном ее конце будет наименьшим, если повреженио находится посередине
линии.
11*. Сопротивление трех проволок ВС, СА, АВ одинакового сечения и материала
равны соответственно а, Ъ, с. Четвертая проволока, имеющая постоянное сопротивле-
Задачи 253
ние d, соединяет точку А со скользящим контактом на стороне ВС. Показать, что
для тока, входящего в точку А и выходящего из скользящего контакта, наибольшее
¦сопротивление равно (а ц-6 + с) dfta + Ь-\-с-\-Ы), и найти наименьшее сопротивление.
12*. Гальванический элемент имеет э. д. с. 0,85 в и внутреннее сопротивление
10 ом. Показать, что наибольший ток, который можно получить в проволоке, имею-
имеющей сопротивление 22,5 ом, от батареи, составленной некоторым способом из 5 таких
элементов, равен в точности 0,06 а.
13*. Шесть точек А, А', В, В', С, С соедивены медными проволоками, длины
которых равны (в метрах): АА'= Щ ВС=В'С = 1; ВС' = В'С'=2; АВ=А'В' = 6;
АС' = А'С' = 8. ToqKH В а В' также соединены проволоками (каждая длиной в 1 м)
с зажимами батареи, внутреннее сопротивление которой рявно сопротивлению г метров
проволоки. Все проволоки имеют одинаковое сечение. Показать, что ток в проволоке
АА' равен току в простом контуре, состоящем из той же батареи, замкнутой проноло-
кой длиною C1г -|-104) метров.
14*. Две станции А и В соединены телеграфной линией, один конец которой в А
соединен с одним из зажимов батареи, а другой конец в В—с одним из зажимов
приемного аппарата. Вторые зажимы приемвого аппарата и батареи заземлены. В резуль-
результате повреждения линии в точке С между линией и землей появляется сопротивление г.
Сопротивлениями батареи, приемного аппарата и земли можно пренебречь, а сопротив-
сопротивление участков АС и СВ линии равны соответственно р ш q. Показать, что при воз-
пикновении утечки ток в приемном аппарате уменьшается в отношении г (р+д): +
15*. Два гальванических элемента, э. д. с. которых равны соответственно ел и е2,
а внутренние сопротивления равны тл и г2, присоединены параллельно друг другу
к проволоке с сопротивлением R. Показать, что ток в проволоке равен
{e1r2-^-e2r1)/(r1R-\-r!iR-\- глг2) и найти отношение токов, протекающих через элементы.
16*. Цепь имеет форму тетраэдра PQRS; в ветвь PQ включена батарея с э. д. с. Е,
-сопротивление этой ветви вместе с внутренним сопротивлением батареи равно jR. Co-
противлевие каждой из ветвей QR и RP равно г, каждой из ветвей PS и RS равно
1 2
-5-г, и сопротивление ветви QS равно —г. Найти ток в каждой ветви,
о о
17*. Пусть А, В, С, D—четыре вершины моста Уитстона; сопротивления плечей
моста АВ, BD, AC, CD равны соответственно с, р, Ъ, -\. Ток в диагонали ВС, куда
включен гальванометр, равен нулю. В эту диагональ включают батарею с э.д.с. Е,
причем полное сопротивление в цепи гальванометра после включения батареи равно а.
Найти ток через гальванометр.
18*. Нужно найти место повреждения в кабеле АВ длиной 50 км. При включении
иа конце А батареи с э.д.с, равной 200 в, найдено, что если изолировать конец В,
«го потенциал будет равен 40 в. Если, наоборот, изолировать конец А, то для полу-
получения на нем потенциала в 40 в нужно подключить к концу В батарею с э. д. с, рав-
равной 300 в. Показать, что расстояние от места повреждения до конца А равно 19,05 км.
19*. В контур с заданной величиной э. д. с. и заданным сопротивлением вклю-
включается добавочное сопротивление. Найти величину этого сопротивления, при которой
в нем будет выделяться наибольшее количество тепла.
20*. Сопротивления противолежащих плечей моста Уитстона равны соответственно
¦а, а' и Ь, Ь'. Показать, что если поменять местами диагонали, содержащие гальвано-
гальванометр и батарею, то будет соблюдаться равенство
A 1 Л
С С J
(а-д') (Ь-Ь'НС-Д)
(аа' — ЬЬ1)
где С и С—токи через гальванометр в обоих случаях, G и R—сопротивления ветвей,
¦содержащих гальванометр и батарею, н Е — э.д.с. батареи.
21*. Несколько ламп накаливания (N), каждая из которых имеет сопротивление г,
питаются от генератора с постоянной э.д.с. и сопротивлением, равным R (включая
я сопротивление проводов). Считая, что световой поток, излучаемый каждой лампой,
пропорционален квадрату выделяемого тепла, показать, что для получения максималь-
максимальной светоной отдачи при заданвом количестве горючего для двигателя следует соеди-
пять лампы в параллельные группы, каждая из которых содержит п ламп, где п —
целое число, ближайшее к числу BNRjrI^2.
22*. К батарее, имеющей э. д. с. Е и внутреннее сопротивление В, подключены
дне параллельные ветви. Первая ветвь с полным сопротивлением R содержит вольт-
вольтметр, в котором имеется скачок потенциала такой величины, что протекающий через
пего единичный ток сонершает в единицу времени работу, равную р единицам работы.
Сопротивление второй ветви равно г. Показать, что если Е > р(В-\-г)/г, то тек через
батарею равен [E(R +г) — pr]/[Rr + В (R + г)].
23*. Тридцать проводников одинакового сопротивления соединены между собой
•так же, как ребра додекаэдра. Показать, что сопротивление всей цепи току, подведеа-
254 Глава ГI
ному к днум противолежащим нершинам, равно 7/в сопротивления отдельного про-
проводника.
24*. Цепь состоит из проводникон РА, РВ, PC, PD, АВ, ВС, CD, DA с сопро-
сопротивлениями, равными соответственно а, C, -у, Ь, т + 8> Ь + а, а + Р, р+-|- В ветвь Л/>
включена батарея с э. д. с. Е. Показать, что ток в ветви ВС равен
Р(сф + 76)?/[2Р2<2 + ([ИВ-аТJ], где Р = а+р+т + Ь, <2 = рт + 7<х + ар + а6 + РЬ + ?6.
25*. Из проволоки изготовлен каркас в ниде правильного шестиугольника, верши-
вершины которого соединены с центром проволоками, каждая из которых имеет сопротивле-
пие, равное 1/п сопротивления стороны шестиугольника. Показать, что сопротивление
каркаса току, подведенному к двум его противоположным вершинам, равно сопротивле-
сопротивлению стороны шестиугольника, умноженному на 2(п + 3)/[(м +- 1)(м + 4)].
26*. Концы В и В' днух длинных одинаконых параллельных пронолок АВ и А'В'
соединены проволокой пренебрежимо малого сопротивления, а концы А и А' подклю-
подключены к зажимам элемента, внутреннее сопротивление которого ранно сопротивлению
куска проволоки длиною г. Длина каждой проволоки равна I. Точно такой же элемент
подключается к перемычке между проволоками на расстоянии х от концов А и А'.
Показать, что после подключения второго элемента ток в проволоке ВВ' увеличится
в отношении
27*. На одной и той же телеграфной линии расположены три станции А, В, С.
Оператор, находящийся на станции А, знает, что между А и В возникло поврежде-
повреждение, и обнаруживает, что от одной и той же батареи ток на станции А равен i, если
линия в В изолирована, а в С заземлена, равен i', если линия заземлена в В, и равен
г", если В а С изолированы. Показать, что понрежденио возникло на расстоянии
ка- k'b+(b—аI1* {ка-к'ЬI'*
к—к'
от станции А, где АВ = а, ВС — Ь—a, k=i"/(i — i"), k' — i"l{i'— i").
28*. Шесть проводников соединяют попарно четыре точки А, В, С, D. Сопротивле-
Сопротивления этих проводников равны а, а, Ъ, C, с, -у, где а, а означают соответственно сопро-
сопротивления пронодников ВС, AD и т. д. Показать, что сопротивление такой цепи между
точками А и В лежит в пределах от [с~1 + (а + 6)~1 + (а + Р)~1]~1 до
29*. Каждая из двух одинаковых прямых проволок А^А^ и В0Вп разделена на п
равных участков точками А17 ..., А,^, Ви ..., В„_г. Сопротивление каждого участка, а
также замыкающей проволоки АпВп равно R. Соответственные точки проволок от 1-й
до п-й соединены поперечными проволоками, и к концам ^%Ве подключена батарея.
Показать, что если через все поперечные проволоки протекает одинаковый ток, то со-
сопротивление пронолоки ASBS должно быть равно [(п — sJ-{-(n—s)-\-l]R.
30*. Каждая из п точек соединена со всеми остальными проволоками, имеющими
одинаковые сопротивления г. К двум из этих точек подключена батарея с э. д. с. Е и
внутренним сопротивлением R. Показать, что тон в проволоке, соединяющей те две
точки, к которым подключена батарея, равен 2Е/Bг~\-пВ),
31*. Шесть точек А, В, С, D, P, Q соединены девятью проводниками АВ, АР,
ВС, BQ, PQ, QC, PD, DC, AD. В проводник AD включена э. д. с, а в проводник
PQ—гальванометр. Обозначив сопротивление проводника XY через rXY> показать, что
ток через гальванометр равен нулю, если
Q + rCQ) (rAB TDP~rAP rDc) + rBC (rBQ rDP~rAPrCQ) = 0-
32*. Цепь образована путем соединения каждой из пяти точек 1, 2, 3, 4, 5 со
всеми остальными. Показать, что условие сопряженности проводников 2—3 и 1—4
имеет вид
№б+ #25 +#35 + Ktf) (К12Кз4 К13КМ) =
= #52 (#54#13 #34#15)+#ВЗ (#24#S1 #54#1г)»
где через Кт обозначена проводимость между точками р и д.
33*. Каждая из двух замкнутых проволок разделена на тпп равных частей,
соединенных проводниками. Сопротивление каждой из тпп частей равно R. В каждый
соединяющий m-ik проводник включена одинаковая батарея; полные сопротивления этих
проводников равны между собой. Сопротивление каждого из остальных (тп—п) соеди-
соединяющих проводников равно h. Доказать, что ток через соединяющий г-й проводник
; Задачи 255
(считая от ближайшей батарея) равен
tgo — tgma
где С—ток через каждую батарею и sin 2о=Л/(й + )
34*. Длинная телеграфная линия ААгА2.. .АпАп^1 подвешена на га равноотстоящих
изоляторах в точках Аи А2, ..., Ап. К концу А подключен один из полюсов батареи
с э. д. с. Е и внутренним сопротивлением В; другой полюс батареи, так же как и
конец линии Ап+1, заземлен. Сопротивления отрезков линии AAlt AtA2, ..., AnAn+l
одинаковы и равны R. При влажной погоде возникает утечка через изоляторы на землю;
сопротивление каждого изолятора равно г. Показать, что сила тока на участке линии
Ар Apt j равна
?chBra —2p-j-i)a
В ch Bn + 1) a + (i?rI/2 sh Bга+ 2) a '
где 2sha=(R/rI/2.
35*. Из га кусков однородной проволоки, каждый из которых имеет сопротивление
о, изготовлен каркас в виде правильного многоугольника АХА2 ... А^,, Вершины много-
многоугольника соединены с его центром О прямолинейными кусками той же проволоки.
Показать, что, если точка О имеет постоянный потенциал, равный нулю, а точка А1 —
потенциал V, то ток в проводнике АгАг*г будет равен
2Fshash(n —
с ch па
где а определяется уравнением ch 2a = 1-}-sin (я/га).
36*. Из однородной проволоки изготовлен каркас, имеющий форму приемы с 2п гра-
гранями. Основания призмы имеют вид правильных многоугольников с 2п сторонами,,
каждая из которых имеет сопротивление г. Сопротивление каждого из ребер призмы
равно R. Показать, что сопротивление между двумя противоположными вершинами-
ранно
пт R th 6
Т+ 2thraO '
1 »•
где sh2O = — -^.
37*. Цепь обраяована проводниками, соединяющими каждую из га точек со всеми
остальными. Сопротивления всех проводников одинаковы, и в проводник, соединяющий
точки Aj и А2, включена э. д. с. Показать, что токи протекают только в проводниках,
проходящих через точки А, и А2, и найти эти токи.
38*. Каждая предыдущая точка из последовательности га точек А},А?,...,Ап
соединена с последующей пронодником сопротивлением р; то же имеет место для после-
последовательности точек В\, В2, ..., Вп. Между каждой парой соответствующих точек обеих
последовательностей, например между Аг и Вг, включено сопротивление R. К точкам
Л] и Вп подведен постоянный ток i. Показать, что в точке Ах ток распределяется
между ветвями АХА2 и АХВЛ в отношении
shraa—sh(ra — 2) о—2sha
(ra —2)a —2sh(ra —l)o '
где сЬа (+р)/
39*. Подземный кабель длиной а имеет плохую изоляцию, так что по всей его*
длине имеется равномерно распределенная утечка. Проводимость утечки равна 1/р' на
единицу длины кабеля, а сопротивление единицы длины кабеля равно р. К одному из
концов кабеля подключен полюс батареи, другой полюс которой заземлен. Доказать,
что ток на протиноположном конце кабеля имеет такую же величину, как в случае
кабеля без утечки, имеющего полное сопротивление
40. Две прямые проволоки сопротивлением г на единицу длины соединены на
одном конце. Точки Аи А2, -.., Ат одной проволоки соединены через сопротивления
R, 2Е, ..., mR с точками Вх, В2, .... Вт другой пронолоки. Расстояния точек Ап и Вп
от соединенных концов проволок равны соответственно п2х и п2у. Разность потенциа-
25fi Глава VI
лов между Ат и Вт равна <§. Показать, что между точками Ап и Вп течет ток
где (x = l + r( )
41. Проволока, рассмотренная в предыдущей задаче, перерезана между точками
/4S_X и As к 2?s_! и 2?s. Показать, что если s < п < т, то ток между Л„ и 2?„ будет
равен
*n (m т 1) Л 1(Рт-Лп+1) <?„
где аргумент функций Лежандра равен 1 + г (x~\-y)IR.
42. Цилиндрический стержень длиной I и радиуса а, изготовленный из вещества
с удельным сопротивлением т, установлен перпендикулярно к плоским параллельным
поверхностям двух полубесконечных масс того же вещества. Показать, что сопротив-
сопротивление R между связанными таким образом массами заключено в пределах
+ R<
¦ка2^2а 2[я« — ПпA + па/1)\ '
При ?=0 оба предела дают одно и то же точное значение.
43*. Цилиндрический кабель состоит из медного провода, покрытого тонким изо-
изолирующим слоем из материала с заданным удельным сопротивлением. Показать, что
при заданных значениях сечений провода и оболочки сопротивление утечки кабеля
будет наибольшим в том случае, когда поверхности провода и оболочки представляют
собой прямые круглые коаксиальные цилиндры.
44*. К однородному круглому диску подводится ток при помощи двух идеально
проводящих проволок круглого сечения. Радиус проволок равен а, и расстояние между
их центрами равно d. Проволоки расположены перпендикулярно к краю диска.
Показать, что сопротивление между проволоками равно 2 (?/-п) ar ch (d/2a), где ?—удель-
?—удельное сопротивление.
45. Два электрода малого радиуса 8 расположены на средней линии бесконечной
ленты, окруженной изолятором. Расстояние между электродами равно 2а. Ширина
ленты -к, ее удельное сопротивление s. Показать, что сопротивление между электрода-
электродами приближенно равно
е , sh2«
— In—=— .
Ь
46. В отличие от предыдущей задачи электроды расположены симметрично на
линии, перпендикулярной к краям ленты. Показать, что в этом случае сопротивление
между ними приближенно равно
47. Электроды расположены так же, как и в задаче 45, но края ленты ограни-
ограничены идеальным проводником. Показать, что сопротивление между электродами при-
приближенно равно
48*. Круглый медный диск с удельным сопротивлением sx (на единицу поверх-
поверхности) помещен на очень большой лист оловянной фольги с удельным сопротивле-
сопротивлением «о- К такому сложному проводнику при помощи электродов подводится ток.
Показать, что функция тока в листе фольги, соответствующая электроду, через кото-
который к фольге подводится ток е, является мнимой частью функции
где а — радиус медного листа, z—комплексная переменная (начало координат в центре
листа, действительная ось проходит через электрод), с—расстояние от электрода до
начала координат.
49*. Однородная проводящая пленка имеет вид поверхности, полученной враще-
вращением цепной линии ?/2-|-22 = с2 еЬ2 W<?)- Доказать, что при протекании тока С через
электрод, находящийся в точке х0, у0, z0, потенциал в точке х, у, z будет равен
4rc 1 с [
Задачи 257
50. В круглый цилиндр радиуса R и длины L, изготовленный ив проводящего
материала с удельным сопротивлением г, вставлены два электрода в виде тонких пла-
стивок, края которых параллельны оги цилиндра. Оба электрода и ось цилиндра
лежаг в одной плоскости, причем расстояние между краем каждого ив электродов и
осью цилиндра с мало по сравнению с К. Показать, что сопротивление между элек-
электродами приближенно равно
7TT/2L *
51. К точке Р бесконечной плоской проводящей плешей подводится ток, который
выходит из нее в бесконечности. В пленке выревано круглое отверстие, не затрагива-
затрагивающее точки Р. Показать, что разность потенциалов между двумя любыми точками на
краю отверстия вдвое больше разности потенциалов, которая существовала между этими
точками до того, как отверстие было прорезаио.
52. Изолятор имеет форму усеченного конуса с высотою h, радиусом нижнего
основавия а, и радиусом верхнего основания а2. Нижнее основание конуса находится
на металлической пластине, а на его верхнем основании установлен круглый металли-
металлический стержепь, ось которого является продолжением оси конуса. Радиус стержня
равен а3. Показать, что поверхностное сопротивление изолятора между пластиной и
стержнем равно
где s — удельное сопротивление поверхности изолятора.
53. К точке 6 = a, tf=O сферической пронодящей пленки подводится ток, вытека-
вытекающий из пее в точке 6 = о, ср = я (здесь 6 — полярный, а ср— азимутальный угол).
Показать, что распределение потенциала в пленке дается выражением
. /" I —rosooos Ч-т-sin о sin 6 roscp Л „
\L — cos a cos U -\- sin a siu о cos cp J
54. В шар радиуса а, изготовленный из изолятора, вставлены концы двух метал-
металлических стержней радиуса Ъ. Удельное сопротивление изолятора очень велико, а по-
поверхностное сопротивление равно «. Продолжения осей обоих стержней пересекаются
в центре сферы под углом а. Показать, что поверхностное сопротивление между стерж-
стержнями равно
— ar ch
¦к
Ъ 2 J
55. Ток протекает по тонкой пленке, уравнение которой имеет вид (z/aJ + (p/bJ=l,
где р2 — х2-\-у2 и а > Ь. Показать, что потенциал V на пленке равен либо Ul, либо ?/2,
где. г71 + /г72 = /(« + /9), tgcp = y/:c и
bz \ , () .
l + !^arc sin
Л
J
Фувкция /(a + /V) — периодическая функция ср с периодом 2п и, кроме того, dV/da = Q
при z=^f а или а = -{1о':, если в этих ючках нет источников или стоков тока; в про-
противном случае dV/dy = 0.
56. Вместо иытянутой сфероидальной пленки, о которой шла речь в предыдущей
8адаче, рассмотреть пленку в виде сплюснутого сфероида, для которого а < Ь. Показать,
что результат будет таким же, как в предыдущей задаче, за исключением того, что а
будет иметь новое значение
.,/ bz \ (б2 —а2I'2 , rz(fc2_a2\1/2 -1
o = arth ¦ rrl— ;—-—ar sn —^ ~— .
\[a4+(b2_a2)z2]l/2y b I a2 J
57. Будем считать поверхность земли плоской, а ее удельное сопротивление рав-
равным т0 всюду, за исключением области ннутри полубесконечного вертикальвого конуса
с вершиной на поверхности. Удельное сопротивление земли внутри KOHyi а обозначим
череэ г,. Ток / полводится к поверхности земли в точке ср — 0 на расстоянии г=я от
вершины конуса. Показать, что потенциал в произвольной точке г < а вне конуса
17 в. Смайт
258 Глава VI
выражается формулой
со
^ [Ат (р) pJV^ (ц) + Вт (р) Р™_1/2 (-ц)] cos {рЫ r)dP.
m=0 0
3[Pp_i/2()]/()
•j ™ ¦ > <-> —
(- COS a)\ld (COS a) P™ _1/2 ( - cos a)
58. Источник тока /, имеющий форму круглой тонкой петли, находится внутри
сплошного цилиндра, изготовленного из проводящего материала. Петля расположена
коаксиально цилиндру; длина цилиндра равна L, радиус равен а. Основания цилиндра
имеют бесконечно большую проводимость и заземлены. Показать, что распределение
потенциала в цилиндре при z < с выражается формулой
СО
г1 y sh [xfez sh [Xfe (L - c) /q (n b) Je
2
sh (J-hZ, [xh [Jo
где [^й выбраны гак, что /( (^а) = 0, а координаты петли р = 6, z = c.
59. Два кольца, сделанные из тонкой проволоки радиуса й, расположены коакси-
коаксиально с бесконечно длинным цилиндром радиуса а, изготовленным из проводящего
материала. Кольца погружены в поверхность цилиндра на глубину d. Показать, что
если [i-k ныбрано так, что J1{\>fla) — 0, то сопротивление между кольцами приблизи-
приблизительно равно
где с—расстояние между центрами колец.
60. В круглом проводящем цилиндре, внутренний и внешний радиусы которого
равны соответственно а и Ъ, прорезана во всю длину узкая продольная щель. Края
1 1
щели поддерживаются при потенциалах — Vo и —- Vo, так что ток обтекает вокруг
цилиндра. Показать, что электростатическое поле при г < а н г > Ъ определится
соответственно преобразованиями
и W^
61. Ток i подведен к полюсам тонкой проводящей сферической пленки радиуса а,
имеющей поверхностное удельное сопротивление s. Показать, что электростатический
потенциал в любой точке внутри пленки дается формулой
«=о
62. Ось цилиндрической проволоки радиуса а, изготовленной из проводящего
материала с удельным сопротивлением -с,, совпадает с осью 2. Среда вне проволоки
между 2= -с и 2=с имеет удельное сопротивление т2. Все остальное пространство
заполнено изолятором. Показать, что отношение сопротивления участка, заключенного
между г=си2= -с, в случае идеально изолированной пронолоки к сопротивлению
того же участка при наличии конечного сопротивления среды та > хх равно приолижевно
Л
Литература 259
63. Углы широкой ленты (фиг. 63, 6) срезаны под углом 45° так, что полуширина
леиты линейно возрастает от h до к. Показать, что при наличии такого перехода сопро-
сопротивление вблизи середины длинной ленгы превышает сумму сопротивлевий обеих ее
частей (с песрезанвыми углами) на не.чичину
ЛИТЕРАТУРА
Abraham M., Becker К., Klassische Elektrizatel und Magnetismus, Berlin, 1932.
(См. перенод: А б р а г а м М., Б е к к е р Р., Теория электричества, М.—Л.,
1939.)
G e i g e r—S с h e e I, Haudbuch der Physik, Bd. XIII, Berlin, 1928.
Gray A., Absolute Measurements in Electricity and Magnetism, v. I, Macmillan, 1888.
Jeans J.H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
Mason M., Weaver W., The Electromagnetic Field, University of Chicago Pres?,,
1929.
Maxwell J.C., Electricity and Magnetism, v. I, Oxford, 1881.
К a m s e у A. S., Electricity and Magnetism, Cambridge, 1937.
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
W i e n - H arms, Handbuch der Expenmentalphysik, Bd. X, Leipzig, 1930.
Глава VII
МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ТОКОВ
§ 1. Определение единицы силы тока (ампера) через величину магнит-
магнитного момента. Как уже было упомянуто в предыдущей главе, между про-
проводниками с током возникают силы взаимодействия, известные под назва-
названием магнитных сил. Это магнитное взаимодействие было тщательно иссле-
исследовано Ампером. В одном из своих экспериментов он обнаружил, что если
два проводника, по которым циркулируют противоположно направленные
токи равной величины, расположить достаточно близко друг к другу, то
они перестают взаимодействовать с остальными контурами. Возьмем не-
несколько небольших плоских проволочных петель, ток к которым подво-
подводится через два плотно сплетенных изолированных провода, так что
наблюдаемые магнитные силы будут обусловлены только петлями. Рас-
Располагая петли на расстояниях, больших по сравнению с их размерами,
и пропуская через них постоянный ток, можно заметить, что они действуют
друг на друга с такими же силами и моментами, как электрические диполи,
расположенные на месте петель и ориентированные вдоль нормали к их
плоскостям. Рассмотрим три небольшие петли, несущие постоянные токи.
Для каждой выбранной из них пары можно измерить силу взаимодействия
и, зная расстояния между петлями, определить при помощи выражения
A.18) произведения т1т? = А, т1т3 — В и т2т3 = С и отсюда найти
nij = АВ/С, т\ = АС /В и т% = ВС/А. Считая окружающую среду вакуумом
и заменив 1/е на jj.e = 4it-10~7, мы получим, что величина «магнитного мо-
момента» m отдельной петли равна произведению площади петли (в квадрат-
квадратных метрах) на ток в ней (в амперах). Отсюда ампер можно определить
как такой ток, который, протекая по небольшой плоской проволочной петле,
создает магнитный момент, равный по величине площади петли. В среде,
отличающейся от вакуума, силы и моменты будут другими. При этом всюду
вместо \>.v появляется множитель |х, называемый магнитной проницаемостью
среды.
§ 2. Магнитная индукция и магнитная проницаемость. Если на про-
проводник с током, помещенный в некоторую область, действует магнитная
сила, то говорят, что в этой области существует магнитное поло. Будем
измерять распределение магнитного поля при помощи небольшой петли-
пробника точно так же, как можно было бы измерять распределение элек-
электрического поля посредством небольшого электрического диполя. Если
петля может свободно поворачиваться, то под действием поля она примет
определенную ориентацию. Положительным направлением магнитного поля
условимся считать такое нормальное к плоскости петли направление,
в котором перемещался бы винт с правой резьбой при его вращении в напра-
направлении протекания тока по петле. Как и в электростатике, напряженность
магнитного поля можно найти, измерив величину момента, действующего
на петлю. Таким образом, мы определим магнитную индукцию В или
Магнитное взаимодействие токов 261
плотность магнитного потока как такой направленный вдоль магнитного поля
вектор, величина которого (в веберах на квадратный метр) равна вращаю-
вращающему моменту (в ныотон-метрах), действующему на петлю с единичным
магнитным моментом, ориентированным перпендикулярно к полю. Этот
вращающий момент, а следовательно, и В зависят от среды,- в которой про-
производится измерение. Относительную магнитную проницаемость веще-
вещества Кт мы определим как отношение магнитной индукции в некоторой
точке пространства, полностью заполненного данным веществом, к зна-
значению магнитной индукции в той же точке в вакууме при сохранении кон-
конфигурации проводников и величин протекающих в них токов. Магнитная
проницаемость \х равна произведению \ivKm.
Осуществление экспериментов, на которых основываются определе-
определения (л и В, в случаях жидких и газообразных сред не вызывают принци
пиальных затруднений. Но внутри твердого тела производить измерения
при помощи проволочной петли, очевидно, уже невозможно. Если все про-
пространство вне небольшой области, в которой находится петля, заполнено
одной жидкостью, а эта область заполнена другой жидкостью, то измеряе-
измеряемое значение В не будет зависеть от формы и размеров выделенной области
только в том случае, когда обе жидкости имеют одинаковые магнитные
проницаемости. Таким образом, для определения В и |х в некоторой точке Р
однородного изотропного твердого тела следует вырезать л нем маленькую
полость, содержащую точку Р, и заполнить ее такой жидкостью, чтобы
измерение в точке Р не зависело от формы и размера полости. Полученные
значения В и |х в точке Р будут такими же, как и до создания полости.
В § 25 настоящей главы, используя граничные условия, выведенные в § 22,
мы опишем экспериментальный метод определения В и |х, пригодный
и в случае магнитно-анизотропных кристаллов.
Пусть в нашем распоряжении имеется большое число маленьких петель,
в каждой из которых циркулирует ток /. Не изменяя площади петель,
составим из них сетку таким образом, чтобы векторы магнитной индукции,
обусловленные двумя близлежащими петлями, всюду оставались парал-
параллельными друг другу. Из опыта Ампера следует, что магнитный эффект
всех внутренних петель при этом исчезает л результирующее магнитное
поле будет таким же, как если бы ток / протекал лишь по границе, обра-
образованной крайними петлями независимо от формы самой поверхности сетки.
Но, как известно, магнитная индукция, обусловленная каждой элементар-
элементарной петлей с площадью dS, совпадает с электрическим полем, порождае-
порождаемым электрическим диполем с моментом \>.г1 dS. Следовательно, магнит-
магнитная индукция, обусловленная контуром, несущим ток /, будет такой же,
как напряженность электрического поля однородного электрического
двойного слоя мощностью |хе7, опирающегося на этот контур (см. § 13
гл. I). Этот магнитный эквивалент двойного слоя называют обычно маг-
магнитным листом. Однако если мы в поисках этого листа будем следо-
следовать вдоль маиштной силовой линии, создаваемой некоторым электри-
электрическим контуром, то окажется, что наше движение будет происходить
по замкнутому путн, нигде не пересекающему магнитной неоднородности,
соответствующей электрическому двойному слою. Таким образом, маг-
магнитный лист в действительности не существует и является лишь удобным
понятием, используемым при вычислении магнитных полей. Более того,
отсюда следует, что не существует магнитных источников или стоков, соот-
соответствующих зарядам в электростатике, так что
divB=V-B=0. G.1)
Из формулы A.32) следует, что работа, затрачиваемая при перемеще-
перемещении единичного электрического заряда с одной стороны однородного
262 Глава VII
электрического двойного слоя мощностью |хе/ на другую сторону по пути,
огибающему край слоя, равна |х/, поскольку разность между телесными
углами, под которыми виден двойной слой из начальной и конечной точек
пути,. составляет 4тг. Таким образом, если напряженность электрического
поля равна Е, то
где ds —элемент пути. Но, как мы видели, магнитная индукция, обуслов-
обусловленная током /, будет всюду такая же, как напряженность электрического
ноля, создаваемая однородным электрическим двойным слоем мощностью
;j.e/, опирающимся на контур, по которому протекает ток I, поэтому в ва-
вакууме ф B-ds — \xvl, а в однородной среде с магнитной проницаемостью р.
G.2)
Но, согласно формуле F.2), /= \ i-ndS, где i — плотность тока, a S
площадь, ограниченная кривой s; таким образом, (V)B-ds = |j, \ i-ndS. Пре-
Преобразовав левую часть этого равенства при помощи теоремы Стокса C.3),
получим
\ VxB-nd5 = p, ^ i-ndS. G.3)
s s
Легко заметить, что ранснство G.3) выполняется для любого замкнутого пу-
пути, даже если этот путь включает только часть полного тока, ибо в по-
последнем случае любая часть поверхности, пронизываемая токами, кото-
которые этим путем не охватываются, будут пересекаться с ними дважды:
один раз в положительном направлении и один раз в отрицательном, или
не будет пересекаться совсем, что в любом случае не даст никакого вкла-
вклада в интеграл. Таким образом, соотношение G.3) должно иметь место и
для подынтегральных выражений; для области с однородной магнитной
проницаемостью из G.3) вытекает
VxB = jj,i. G.4)
§ 3. Магнитный вектор-потенциал. Однородное поле. Как известно,
дивергенция вектора, являющегося ротором другого вектора, тождественно
равна нулю, и, следовательно, этот вектор удовлетворяет уравнен-шо G.1).
Таким образом, можно ввести новый вектор А, называемый магнитостати-
ческим вектор-потенциалом, такой, что его дивергенция равна нулю, а ро-
ротор равен В, т. с.
VXA = B, V-A = O. G.5)
Обычная формула для rot rot А дает
VX[VXA] = V(V-A) (V-V)A=-V2A.
Подставляя в соотношение G.4) для области с однородной магнитной про-
проницаемостью, находим
-?*А = |и, G.6)
или, выписывая компоненты векторов,
. G.7)
Магнитное взаимодействие токов 263
Таким образом, компоненты Ах, Ау, Аг удовлетворяют уравнению Пуас-
Пуассона C.6). Решение этого уравнения было найдено в § 10 гл. III C.28):
Складывая компоненты, получим
В области вне проводника i обращается в пуль, а внутри тонкого провода,
поперечное сечение которого равно dS, ixdv = idSdx — Idx. Поэтому, скла-
складывая компоненты векторов, получим
Физически такое представление является более удовлетворительным, чем
оперирование с магнитным листом, так как величина А зависит только oi
конфигурации контура, силы тока и места нахождения точки наблюдения
»i так как при этом не вводится никаких искусственных неоднородностей.
¦ ho выражение приводит к правильному значению линейного интеграла
от В по любому пути. Очевидно, вектор А можно рассматривать как сум-
сумму векторов, каждый из которых обусловлен некоторым элементом тока
замкнутого копту[а и параллелен этому элементу.
В декартовых координатах вектор-потенциал, описывающий однород-
однородное магнитное иоле В, направленное вдоль оси х, имеет только две компо-
компоненты:
Ау= — azB, Az = {i—a)yB, G.11)
где а — произвольное число. Очевидно, отличной от нуля будет лишь
.х-компонента ротора этого выражения, равная В. В сферических координа-
координатах вектор-потенциал однородного поля, параллельного оси 6 = 0, равен
Ач = ^-ВгятЪ. G.12)
В цилиндрических координатах для вектор-потенциала однородного поля,
параллельного оси z, будем иметь
Ач = ^Вр. G.13)
В сплюснутых сфероидальных координатах вектор-потенциал однородного
поля, параллельного оси 5=1, равен
A<f = <~7-P\(i)P\(]rJ, G-14)
а п вытянутых сфероидальных координатах
А СУ** Р1 lt\ Р1/-уЛ 11 Л Е\\
<р — —V— 1 \^/ 1 \^/* \ /
Разумеется, все эти формулы не представляют собой наиболее общую фор-
форму записи вектор-потенциала А, описывающего данное поле В, ибо это
лоле не изменяется, если к А добавить градиент любой скалярной вели-
величины.
§ 4. Теоремы единственности в магнитостатике. В § 11 гл. III
были найдены необходимые условия внутри и на границе области для
однозначного определения электростатического потенциала внутри нее. ¦
264 Глава VII
Это доказательство без всяких изменений применимо и в магнитостатике —
к системам, содержащим магнитодвижущую силу (см. § 29 настоящей гла-
главы), при условии, что в рассматриваемой области отсутствуют электриче-
электрические токи, которые могут привести к неоднозначности в определении маг-
магнитодвижущей силы. Но при использовании вектор-потенциала требуется
иное доказательство единственности. Покажем, что если заданы положение
и величина всех токов внутри замкнутой поверхности, а также значение
тангенциальной составляющей вектор-потенциала или магнитной индук-
индукции на самой поверхности, то значение магнитной индукции внутри
рассматриваемой области определяется единственным образом. Та часть по-
поля, которая обусловлена внутренними источниками, определяется формула-
формулами G.5) и G.10) однозначно. Допустим теперь, что одним и тем же внеш-
внешним источникам и одинаковым значениям указанных выше величин на гра-
границе области соответствуют два различвых поля В и В' внутри нее. Если
V-A=V-A' = 0, то V2(A —А') обращается в нуль но всем рассматривае-
рассматриваемом объеме и, следовательно, при подстановке функции
в выражение C.23) мы получим
\ A V).[(B-K')xn]dSr G.16)
Если на поверхности S пхА=пхА' шш Вх п = В' х п, го ииверхностпый
интеграл обращается в нуль, так что в любом случае В = В' в каждой
точке внутри обт>ема v, поскольку величина (В — В'J является положительной.
Но если разность В — В' равна нулю внутри всего объема, то А и А'
могут отличаться друг от друга внутри лишь на градиент скаляра. Однако»
как было показано в § 11 гл. IIT, при обращении градиента скаляра
в нуль на поверхности S он оказывается равным нулю во всем объеме vr
поэтому при обращении разности А —А' в нуль на поверхности S она
равна нулю всюду ввутри v; тем самым А однозначно определяется чере:*
свое значение на поверхности S.
§ 5. Разложение вектор-потенциала но ортогональным функциям.
В электростатике после нахождения потенциала, обусловленного заданным
распределением зарядов, для того, чтобы удовлетворить условиям на
границах с диэлектриком или проводником, к этому потенциалу добав-
добавляют подходящий возмущенный потенциал. Пользуясь этим методом в слу-
случае вектор-потенциалов, нужно, найдя по формуле G.9) ту часть вектор-
потенциала, которая обусловлена заданным распределением токов, добавить
к ней такой вектор-потенциал возмущенного поля, чтобы их суперпозиция
удовлетворяла магнитным граничным условиям.
Метод непосредственного решения уравнения Лапласа для сектор-потен-
сектор-потенциала весьма сложен, так как оператор Лапласа, применяемый к вектору,
действует не только па величины составляющих вектора, по и на единич-
единичные векторы, как это видно из выражений A1.46) и A1.47). За исключе-
исключением случая декартовых координат, это проводит к системе трех диффе-
дифференциальных уравнений в частных производных, решение которых может
оказаться очень сложным. Следует поэтому попытаться отыскать более-
простой способ решения. '
Как мы уже видели [см. формулу C.4)], и свободном пространстве,
где нет - электрических зарядов, дивергенция электрического поля равна
нулю, и поскольку это поле можно представить как градиент скаляра [см.
Магнитное взаимодействие токов 265
выражение A.6)], его ротор также обращается тождественно в нуль. Анало-
Аналогично, пользуясь выражениями G.1) и G.4), находим, что в свободном
пространстве, где нет электрических токов, дивергенция и ротор магнит-
магнитной индукции равны нулю. Следует ожидать, что в таких областях для
этих двух полей можно написать разложение по ортогональным функ-
функциям в одинаковой форме. Подобное разложение уже было получено в гл. V
при решении уравнения Лапласа, являющегося уравнением второго поряд-
порядка в частных производных. Это уравпение разбивалось на три дифференци-
дифференциальных уравнения в полных производных, каждое из которых содержала
единственную координату и было связано с другими при помощи днух
индексов (постоянных разделения). Таким образом, каждый член в разло-
разложении содержал два индекса и шесть постоянных интеграции. Как только
что указывалось, исходя из математического подобия электрического и маг-
магнитного нолей, можно ожидать, что в разложении вектор-потенциала, опре-
определяющего вектор магнитной индукции, будет содержаться то же самое
число индексов и постоянных.
Этот потенциал должен определяться тремя скалярными потенциаль-
потенциальными функциями, потому что в декартовых координатах каждая компонен
та вектор-потенциала удовлетворяет уравнению Лапласа. Однако эти ком
поненты не являются независимыми, а связаны соотношением V-A = Of
поэтому можно использовать самое большее две незавпспмые скалярные функ-
функции. Более того, ниже будет показано, что при соответствующем их выборе
магнитостатическое поле может определяться только одной из этих функции.
Общее выражение для вектор-потенциала, приводящее к равной нулю дивер-
дивергенции, имеет вид
A = VxW, G.17)
где W является вектором, определяемым двумя скалярными потенциаль-
потенциальными функциями. В дальнейшем для удовлетворения граничным условиям
в задачах о вихревых токах и о электромагнитном излучении будет удобно
разложить W на две взаимно ортогональные компоненты, каждая из кото
рых определяется своей скалярной потенциальной функцией, т. е.
W^ul^-Lux V^a. GЛ8)
где и—произвольный вектор, выбираемый так, чтобы
*(vxW) = vx(v*W) = o,
^o и v*w2=o. { ¦ }
Легко проверить путем представления в декартовых координатах, что если
u = I, j, k или г, то
и V2 (u X ^W2) = u X V {v4v%)r- Г''-Щ
так что выбор и в соответствии с условием G.1 У) возможен. Из аналогии
между В к Е вытекает, что В подобно Е можно представить через одну скаляр-
скалярную потопциалъную функцию. Это предположение подтверждается исследо-
исследованием той части А, которая соответствует функции IF2. Действительно,
u = i, j, k, Vx(uxV^2) = u(VW2)-V(u-V^2), G-21)
u = r, V X (u X VW2) = u (VW2) - V (u-
Поскольку VW2 = 0, то часть вектор-потенциала А, определяемая функ-
функцией W2, оказывается градиентом скаляра, и поэтому в магнитостатическом
случае она не влияет на значение величины В.
266 Глава VII
Пусть uv и2, us — ортогональные криволинейные координаты, а век-
вектор и, оиределенвый выше, ориентирован в направлении и,; тогда, выражая 1Уг
в виде U (uJF (и2, и3), будем иметь В-А = 0. (Доказательство см. у Ласса,
стр. 48 и 57.)
В последующих параграфах развитая здесь теория будет применена
для нахождения решения уравнения
0 G.23)
в форме
А = uJJ^U^U^ + U2U21U22UM
где uj, uj>, из —единичные векторы в направлении координат ult щ, и3,
a Urs — функция только us. Решение должно быть записано в таком виде,
чтобы вектор-потенциал можяо было вычислить в любой точке внутри объе-
объема, не содержащего источников и ограниченного семейством поверхностей,
на каждой из которых одна координата сохраняется постоянной и танген-
тангенциальные компоненты вектор-потенциала заданы.
§ 6. Вектор-потенциал в цилиндрических координатах. В гл. V бы-
было найдено, что общее решение уравнения Лапласа в цилиндрических коор-
координатах выражается в виде суммы членов, содержащих, за исключением
Некоторых частных случаев, функции Бесселя. Найдем теперь аналогичное
решение для вектор-потенциала, который на поверхности прямого круглого
цилиндра можно разложить по ортогональным функциям. Выражая танген-
тангенциальную компоненту вектор-потенциала на поверхности в виде суммы таких
решений, можно тем самым определить его значение в любой внутренней
точке цилиндра. Пользуясь решением уравнения V2W1 = 0, выраженном
в функциях Бесселя (см. § 306 гл. V), и полагая u = k для функ-
функции W, входящей в соотношение G.17), получим
W = k/г1 (Аеы + Веы) [CJn (кр) f DYn (кр)] sin (щ + Ьп). G.24)
Тогда из соотношения G.17) для вектор-иотенпиала имеем
At=-(Аеы + Be**) [CJn(кр) + DYn(кр)] п(кр)^cos(щ + 8П),
Ач = (Aehz + Be'hz) [CJ'n (кр) + DY'n (кр)] sin (л? + 8„), G.25)
что совпадает с ортогональной поверхностной векторной функцией, опреде-
определенной ранее выражением E.347). Если для данного значения z какая-либо
из компонент вектора к X А при р = а обращается в нуль, то при этом зна-
значении z вектор к X А можно представить в виде суммы таких функций.
Редко употребляемая форма записи, содержащая <р, получается, если 8П
положить равным нулю, п—>0, а произведения пА и пБ сохранить конеч-
конечными.
Чтобы получить решение, соответствующее тангенциальной компоненте
лектора А, заданной на боковой поверхности, воспользуемся функциями
E.311), ортогональными по z и ср. Тогда вместо выражения G.24) получим
А = ~ [С1п (кр) + DKn (кр)] п (кр)'1 cos {kz + Tft) cos (щ + 8n),
Д, = [СГп (кр) + DK'n (AP)] cos (kz + Th) sin (щ + Ъп).
Компонента z удовлетворяет скалярному уравнению Лапласа; ее можво
записать в виде
At = [C'In (кр) + D'Kn (кр)] cos (kz + Th) cos (щ + 8;). G.27)
Магнитное вааимодейст&ие токов 267
Решения, полученные выше, непригодны при значениях А: = 0 и п Ф 0. В этом
случае решения, соответствующие выражениям G.26) и G.27), будут
А9 = (яр"-1 + БР-"-') (Cz Н- D) sin (гор + 8„),
Л9 = (- Арп~1 + БР-"-») (Cz + D) cos (rep + 8„), G.28)
Д. = (А'Рп -+ Я'р"*1) (Cz + D') cos (»p + К)-
При А = О не существует решений, одновременно ортоговальных по р и ср
и приводящих к заданному значению А на торцах цилиндров. Если же
равны вулю А; и и, то из соотношения E.308) можно вайти некоторые пред-
представляющие интерес формы решений, если положить
G.29)
А9 = Ap~l z In р + Бр~1 In р + Ep~l z + F,
А3= -Ap-lz^ — Bp~l^ — Cp-lz-Dp-1, G.30)
Другие крайне редко требующиеся решения можно найти путем использо-
использования в выражении для функции W векторов i, j или г.
§ 7. Вектор-потенциал в сферических координатах. В гл. V общее
решение уравпелия Лапласа в сферических координатах было представлено
ь виде суммы членов, содержащих сферические гармоники. Теперь требуется
получить аналогичное решение для вектор-потенциала, которое обладает
свойством ортогональности на поверхности сферы, так что можно выразить
тапгенциальвые компоненты вектор-нотенциала на поверхности в виде суммы
таких решений и тем самым определить его величину в любой внутренней
точке. Пользуясь решением уравневия \Ч?г — 0 в виде сферических гармоник
(см. § 24 гл. V) и полагая u = r, получим для W и А (см. § 5) следующие
выражения:
W = г (Агп + Яг-»-») [СР™ (cos б) +¦ DQn (cos G)] sin (пир + 8J, G.31)
A6 = (Arn + Br-"-1) [CP™ (cos 6) + DQ™ (cos 6)] m cosec 6 cos (mep + 8J,
п' (cos6) + DQ' (cosb)]sm6sm(m^ + bm) (
Здесь А — ортогональная поверхностная векторная функция, упоминаемая
в § 246 гл. V. При т = 0 и 8т = тг/2 эю соотношение принимает вид
wa1>)\- G.33)
Часто бывает полезно выражать В через W. При u = r получим
B = Vx(VXrH/)= -Vx(rxVW) = r -^(VW) +
пли, выписывая компоненты этого выражения, будем иметь
я я 7
§ 8. Выражение для вектор-потенциала через значение магнитной
индукции на оси. Применяемые для фокусирования электронных пучков
магнитвые линзы обычно конструируются из коаксиальных катушек с током
или эквивалентных им магнитов, так что вектор-иотенциал имеет только
•^-компоненту. Для расчета фокусирующих характеристик таких линз удобно
иметь выражение для вектор-потенциала через значение магнитной индук-
индукции и се производных на оси системы. Пусть W = kPF, где W — решение
268 " Глава VII
уравнения Лапласа [см. C.45)], тогда из выражения G.17) имеем
_ ' 2л
A°:=^jf = 4^[ <I>(z + /psin6)sin6eZe, G.35)
о
где Ф (z) —¦ действительная функция, разложение п ряд Тейлора которой
имеет вид (Двайт, 39)
*(^P) = *W+^/psinfl + ^-^(/psmflL... G.30)
Подстановка выражения G.36) в G.35) и интегрирование от 0 до 2тс дают
л*> -2) И1(п+1I &»'^ V.Ty • (/-<5/)
п=0
Магнитная индукция Vx^j на оси, где р = 0, равна
rjL^n =_»w G-38)
ov ' L p ^p Jp=o 3z v '
Теперь, подставляя это в выражение G.37), можно выразить А-(р, z) через
индукцию B()(z) и ее ироизводные
n=f)
Элементы тока, возбуждающего поля подобного рода, представляют собой
коаксиальные круговые петли, поэтому значения р и z, в пределах которых
справедливо выражение G.39), будут такими же, как и в случае круглых
петель. Для нахождения этих пределов подгтавпм Бп (z) из формулы G.55)
в выражение G.39) и сравним результаты с решением задачи 27, справед-
справедливым при любых значениях риг. Для этого следует, воспользовавшись
выражением E.314), разложить функцию ^(Лр) в ряд, изменить порядок
суммирования и интегрирования и подставить вместо интегралов производ-
производные выражения E.357). Совпадение результатов показывает, чю выраже-
выражение G.39) однозначно определяет вектор-потенциал для всех значений риг.
которые можно достигнуть, не пересекая поверхностьй с током. Последнее
ограничение необходимо потому, что внешние поля любых токов, цир-
циркулирующих внутри замкнутой поверхности, не изменяются, если эти
токи заменить соответствующим образом подобранными токами, текущими
по поверхности.
§ 9. Уравнение аксиально симметричных трубок магнитной индукции.
Магнитное поле можно представить наиболее наглядно путем нанесения
линий потока или линий магвцтной индукции. При аксиальной симметрии
картина поля в любой плоскости, проходящей через ось, бучет одинаковой,
а токи — ортогональными к этим плоскостям; и этом случае уравнение линии
магнитной индукции легко можно получить цз выражения для вектор-по-
вектор-потенциала, имеющего лишь Л^-составляющую. Путем вращения вокруг осп
симметрии каждой линии потока образуется поверхность трубки магнитной
индукции. Каждую трубку можно охарактеризовать величиной магнитного
потока N внутри нее. Эту величину можно получпть путем интегрирования
нормальной составляющей индукции по любому сечению S трубки. Таким
образом, уравнение поверхности такой трубки будет
=Д B.ndS = /(p,z). G.40)
Магнитное взаимодействие токов
269
Пользуясь теоремой Стокса C.3), преобразуем это выражение к виду
G.41)
Для сечения, расположенного в плоскости, перпендикулярной к оси z, путь
интегрирования s является окружностью длиной 2тср, на которой величина А9
постоянна, поэтому уравнение поверхности силовой трубки будет
N = 2крА9(р, z).
G.42)
В системе ортогональных криволинейных коордиват м1, и2 и ф, обладающей
аксиальной симметрией, расстояние р является функцией uL и м2, поэтому
уравневие силовой трубки имеет вид
N =
в1? и2)
1; u2).
G.43)
х
§ 10. Вектор-потенциал и поле
двухпроводной линии. Применим
сначала формулу G.10) для нахожде-
нахождения магнитного поля токов, один из
которых течет в длинном прямом про-
ноде в одном направлении, а дру-
другой — в параллельном проводе, нахо-
находящемся от первого на расстоянии а,
в обратном направлении. Поскольку
все элементы проводов напраълены
вдоль оси х (фиг. 67), вектор А имеет лишь компоненту Ах- Согласно фор-
формуле G.10),
G.44)
Фиг. 67.
=i \ (тг~^)^=-^5[К
Г2 -у-
Отсюда видно, что поверхности постоянного вектор-потенциала являются
поверхвостями круглых цилиндров, совпадающими с эквипотенциальными
поверхностями в электростатике, когда заряды двух проводов равны + jj,e/
и -[ле7, а V— — <7Bке)'11п(«2/«1). При \xl = 2тг уралнением этих цилиндров
будет уравневие D.67), если заменить в нем U па Ау и х на z. Магнитное
поле f хА направлено под прямым углом к соответствующему электри-
электрическому полю TF, а их численные значения одиваковы. Из соотношений
C.14) — C.16) следует, что компоненты магнитной индукции в вакууме
соответственно равны (так как h1 = k2 = k3 --= 1)
в дЛг
Ввиду того, что «г =
имеем
dz
= 0,
G.45)
*
1-Л
а\ ) '
G.46)
G.47)
270
Глава VII
§ 11. Вектор-потенциал и поле круглой петли. Вычислим вектор-
потенциал в точке Р (см. фиг. 68), пользуясь сферическими координатами.
Вследствие симметрии величина А, очевидно, не зависит от <р- Поэтому для
простоты выберем точку Р в плоскости xz, где <р = 0. Объединяя попарно
равноотстоящие от Р элементы длиною ds, имеющие координаты -f-<p и — <р,
мы видим, что результирующий вектор А направлен нормально к плоско-
плоскости pz. Следовательно, вектор А имеет
только одну компоненту As. Пусть
dSy — составляющая элемента ds в этом
направлении, тогда формулу G.10)
можно записать в видо
7S
!>.! С
~~ 2л J (а
a cos <p dtp
Фиг. 68.
2 —2ар cos ?I
Для очень маленькой петли г0 = (р2
+ z2I'a>a, и поэтому
орсоР9
чп 6
Введя магнитный момент петли m (см. § 1), равный it«2/ и направленный
вверх, находим
А = |х (т X г) Dит-3) 1.
G.49)
Если это приближение не годится, то, полагая ср = и-}-2©, так что с/<р = 2<f6
и cos <р = 2 sin2 б—1, будем иметь
4 _
VaI
B sin2 0 —
2 —4apsin20]1/2'
Введем величину
G.50)
и после некоторых преобразований получим
A—Л2 sin2
_ JL С (l_k%sin2 b)*l2dQ] =
G.51)
где К п Ь — полные эллиптические интегралы первого и второго рода.
Для определения магнитной индукции следует написать, пользуясь
выражениями C.14)—C.16), компоненты ротора в цилиндрических коорди-
координатах. Как известно (см. § 6 гл. III), в этом случае h1 = l, Л2 = р, hz = i,
Магнитное взаимодействие токов 271
поэтому
G 52)
Производные от К и Е соответственно равны (см. Двайт, 789.1 и 789.2)
дК _ Е К дЕ _ Е К
дк ~ АA — к2) к ' дк ~ к ~к "
А из соотношения G.50) имеем
дк zk3 дк к А3 к3
dz Аар ' dp 2p 4р 4а
Выполняя дифференцирование, группируя члены и заменяя к, согласно
выражению G.50), получим
1
Численные значения Bf и i?z для любых риг находятся путем опреде-
определения к из выражения G.50) с последующим отысканием в таблицах
(см. Двайт, стр. 208—210) соответствующих значений К и Е. На оси
симметрии, где р = 0, имеем
#* = ¦?-» 0 и Bz = — 57-. G.55)
§ 12. Поле токов, текущих по сферической пленке. Введем функцию
потока ф и определим ее значение в некоторой точке Р на тонкой сфе-
сферической пленке радиуса а как полный ток, протекающий по пленке через
любую кривую, проведенную на пленке между точкой Р и точкой, где зна-
значение ф равно нулю. Компоненты плотности тока оказываются, таким
образом, связанными с функцией <Ji уравнением
ц г G.0b)
а до
Найдем вектор-потенпиал и магнитное поле, обусловленное этими токами.
Поскольку любую возможную функцию ф можно выразить в виде суммы
поверхностных гармоник, то достаточно вычислить поле распределения
1С- "^i?("» f)> а затем посредством суперпозиции найти поле, соответ-
соответствующее произвольной функции ф. Обозначим магнитную индукцию вне
пленки через Во, а внутри—через В(. Применяя соотношение G.2)
к небольшому контуру длиной йв, окружающему элемент пленки и лежа-
лежащему в плоскости ер — const, получим
ле.
Воспользуемся соотношениями G.56) и введем скалярную функцию W
из выражения G.34), тогда
аф _ о2 (rw0) g2 (rWj)
Р дЬ~ дгди дгдЬ '
272 Глача VII
Аналогично, взяв контур в направлении <р, получим
dty1 д*{1У„)
'f ' si
j_ _
sin й <9<у sin в drd'f ' sin ti <9r dy
Умножим первое уравнение на db, а второе —на sin 6 d<p и затем вычтем
одно из другого. В результате обе части оказываются полными дифферен-
дифференциалами, поэтому после интегрирования, помня, что при г = а Ц;а=Ш^,
будем иметь
{) G.57)
Рассматривая ф в виде ?™F, у), мы обязаны, исходя из соотношения G.31),
взять решение в форме
так как при этом выполняются требуемые условия, а именно: Wo = \?г
при r = a, Wv конечная функция на бесконечности, a Wi — конечная
функция в дачайе координат. Следовательно, согласно выражению G.17),
вектор-потенциал и.^еет вид
(at+;;„„„
В каждой из этих составляющих множитель, содержащий 6, можно выра-
выразить посредством соотношений E.207) и E.2С8) в виде суммы двух при-
присоединенных функций Лежандра.
§ 13. Зональные токи в сферической пленке. Практически наиболее
важвым является тот случай, когда токи текут в сферической пленке
по линиям постоянной широты. Вследствие аксиальной симметрии все
величины в этом случае не зависят от ер. Функцию потока можно записать
следующим образом:
Ф= 5 CnPn (cos 6). G.60)
Плотность тока имеет только ер-составляющую
со оо со
__ 1 5ф >-, Сп дРг, (ц) -у C,,sin6 дРп(и) __ v C« pi ,,л п М\
l'~7i-2j т 5в. - ~ 2.—а лг~- ~ Z т *^ }> ^ 1;
Г!=1 П = 1 Г!=1
где и = cos G. Если магнитная проницаемость во всем пространстве равна jx,
то в соответствии с выражениями G.58) функция W примет вид
71=1 И=1
Вектор-потенциал, согласно соотношениям G.59), равен
Магнитное взаимодействие токов 273
для г < а
для г > а
Г!=1
Заметим здесь, что поскольку (<р)х-=—sin ep, (^j^coscp, то величины
Ах и Ау удовлетворяют уравнению G.7) для свободного пространства
(i = 0). Легко видеть, что выражение для А имеет ту же форму, что и G.33).
Компоненты магнитной индукции получаются из соотношений G.62) или
G.63) и G.64). Таким образом, пользуясь выражениями G.34),- имеем
для г < а
T7=t
для г> а
^^(f) G-66)
А из выражений G.63) и G.64) получаем
для г < а
для г > а
•Di(«). G-68)
Эти выражения но только позволяют определить магнитную индукцшо
тока, текущего по проводу, намотанному на зферу с произвольной плот-
плотностью, но и показывают также, каким образом следует намотать этот
провод на сферу, чтобы получить заданное поле. Так, например, в случае
однородного поля внутри сферы Br = Bcos6 и В$——BsinO, поэтому,
согласно выражениям G.65) и G.67), все С„ = 0, за исключением Су.
Таким образом, из соотношения G.61) следует, что плотность намотки
провода пропорциональна величине d[Pn(cos6)]/d6= — sin6. Если вос-
воспользоваться выражениями G.63) и G.64), то, согласно формуле G.42), урав-
уравнения поверхности силовых трубок, можно записать в виде
iV = 2irrsmOA,. " G.69)
§ 14. Представление поля круглой петли через сферические, гар-
гармоники. Предположим, что плотность тока на поверхности сферы всюду
равна нулю, за исключением полосы 6 = а, ширина которой настолько
мала, что физически ее трудно измерить, но все же она отлична от нуля,
так что плотность тока и векторгйотенциал—функции всюду ограничен-
ограниченные. Пользуясь выражениями G.61) и G.62), можно написать
18 В. Смяйт
274 Глава VII
Будем вычислять величины Сп, так же как и в гл. V, путем умножения
обеих частей равенства на Р\п{и) и интегрирования от и= — 1 до и=1.
Согласно соотношению -E.92), все члены справа исчезают, кроме тех, для
которых п = т, и в соответствии с выражением E.194) имеем
1
п (п — 1)! 2ге4-1 v
с { )
Плотность тока г отлична от нуля лишь в полосе б = а шириной As;
эта полоса настолько узка, что функцию P*(cos6) на ней можно считать
постоянной, имеющей значение P*(cosa). Тогда интеграл оказывается
равным
Pi (cos a) \ ia sin б effl = Pi (cos a) sin a \ ids = I sin aP* (cos a).
J в
Таким образом,
/-г B?г4-1) / sin a nl . . /n nrw
Cn——v ., , ; , ..— PKcosa). G.70)
Пользуясь выражением G.63), находим вектор-потенциал в области г < а
а из выражений G.65) и G.67) получаем компоненты магнитной индукции
со
Вг = "Чг- 2 (тТ Р.1 <«»«)/>„(соав), G.72)
n=l
G.73)
где cos 6 = и. Для области г > а аналогичные выражения получаются, как
и прежде, при помощи соотношений G.66) и G.68). Пусть начало коор-
координат находится в центре петли, тогда a = it/2, cosa = 0 и Р,'@) =
= —(я+ 1) /)п+1@), так что четные значения п исключаются; пользуясь
результатами § 16з гл. V, для г < а получим
(п—нечетное)
(я—нечетное)
Если г больше а, то в выражении G.74) следует заменить (г/а)"-1 на
(а/г)п+2, а в выражении G.75) (гja)"-1 на — n (a/r)n+2/(n + 1)-
Согласно уравнению G.42) и соотношению G.71), уравнения поверх-
поверхности силовых трубок будут иметь вид
Ач. G.76)
Магнитное взаимодействие токов
275
§ 15. Закон Био и Савара. Поле прямолинейного провода. Применим,
операцию ротора к обеим частям выражения G.10)
где
~
(l)xds.
Поскольку координаты точки, дтя которой вычисляется В, не входят в ds.
ибо последний зависит только от конфигурации контура, то по отношению
к оператору V величина ds является постоянной и
первый член в правой части последнего выражения
равен нулю. Но V A/г) = — г/г3, так что
в="^-
ds х г
G.77)
Если~[6 есть угол, измеряемый от ds к г, то можно
написать
причем В направлено перпендикулярно к плоскости, Фиг. 69.
содержащей ds и г1). Если 6 отсчитывается по часо-
часовой стрелке, то В направлено от наблюдателя. Био и Савар установили этот
закон только для прямолинейных токов.
В этом случае, обозначая через а расстояние от точки Р до провода
(фиг. 69), имеем
= а2 + s2, sin 6 = — ,
так что выражение
(см: Двайт, 200.03)
В = 7,—
для магнитной индукции G.78) принимает вид
оо
ads [л/
о
о
G.79)
§ 16. Поле солевоида с произвольным шагом намотки. В качестве од-
одного из элементов электрической цепи очень часто применяется соленоид.
Он состоит из провода, намотанного в виде спирали, изображенной на
фиг. 70. Пусть уравнение этой спирали имеет вид
x — acosip, y = asinip, z = flcptga, G.80)
где а —шаг намотки, т. е. z возрастает на 2imtga при увеличении ср на 2тт.
Напишем z-компоненту вектора В [см. выражение G.77)]
rydsx — rxdsy
Компоненты г и ds для точки наблюдения, расположенной на оси соленои-
соленоида, будут равны
гх =-- — a cos ер, dsx = — a sin ep dtp,
гу=—a sin ер, dsy = a cos ер йер,
rz = — а ер tg a 4- С, dsz = a tg a dtp.
*) ПосколЕку г и ds в выражении G.77) стоят под знаком интеграла, утверждение
автора об их перпендикулярности вектору В лишено смысла (только в случае прямо-
линейных токов вектор В перпендикулярен г и ds). ¦— Прим. перев.
18*
276
Глава VII
Найдем поле на оси соленоида, имеющего N витков; поле подводящих
проводников не будем принимать во внимание, считая, что его можно вы-
вычислить отдельно. Расположим начало координат в точке, где требуется
вычислить Вг, и подставим в выражение G.81) значение г = (ж2 + уг + z2I'2 =
= а A Ч- tp2 tg2 аI'2. Выбирая пределы интегрирования
N +
<Pl = — N-K-]
И
ф, = Nk +
о tg а Т2 ' о tg а '
находим после интегрирования (см. Двайт, 200.03), что компонента Вг на
расстоянии Ь от цептра соленоида равна
tg
«\[a2
tg a + Ъ
Nna tg а —
^ V
а-ЬJ]1'* /
a2 + (JVnatga + bJ]lli [o2+ (aNn tg <
Обозначая через fit и Р2 углы между осью соленоида и векторами, прове-
проведенными из точки b к концам провода, образую-
образующего соленоид, полученное выражение можно за-
записать в виде
В. = -
G.82)
Следует заметить, что если точка b находится
внутри соленоида, то один из углов фг или C2)
должен быть больше тс/2, поэтому один из коси-
косинусов всегда отрицателен. Пусть расстояние меж-
между крайними концами провода соленоида равно
L, тогда
L --= 2izNa tg a
и при наличии п витков на единицу длины Л^ =
= Ln, так что
i?z = ljj,n/(cosp2 —cosp,). G.83)
Формулы G.82) и G.83) для аксиальной компо-
компоненты поля на оси являются совершенно строги-
строгими. Однако если а Ф- О, то кроме этой компоненты
существуют также и другие. Вычисления, аналогичные только что про-
проделанным, дают
Фиг. 70.
— ryds,
о2 tg a (— <f cos tp + sin t
Это выражение, вообще говоря, отлично от нуля.
У 4я
dsz—rz dsx
4л J
— о2 tg a (cos tf> + ф sin
G.84)
G.85)
Этот интеграл в обшем .случае также не равен нулю. Таким образом, сило-
силовые линии не являются прямыми, а имеют вид спиралей.
В важном случае бесконечно длинного соленоида выражения G.82) и
G.83) принимают вид
" :- • ¦' ' - ¦ ¦ Bz= , **[ = щу.1. G.86)
Магнитное взаимодействие токов
277
При этом ж-компонента обращается в нуль, так как выражение G.84)
будет представлять собой интеграл от нечетной функции, а вместо выра-
выражения G.85) получаем
Bv=~
cos 9 + 9 sin 9
dtp.
Проинтегрируем «торой член, стоящий под знаком интеграла, но частям,
полагая и — sin ер, do = <р [BтгтсаJ-|-<р2]~3'2 d<p, после чего получим
cos 9 dtp
cos 9 rftp
Если положить ер = 2/гтвд sh ф, то второй интеграл оказывается, согласно
формуле E.444), равным Ко Bтга): эта величина является модифицирован-
модифицированной функцией Бесселя второго рода, рассматривавшейся в § 346 гл. V.
Очевидно, значение первого интеграла можно получить посредством диф-
дифференцирования второго интеграла но аргументу 2итга и деления резуль-
результата на —2п-ка, так что в соответствии с формулой E.444) имеем
Ву = - npl [2mzaK0 Bшга) + Кг {2пъа)\. G.87)
Если а = 0 или /г=оо, то Ву=0 и поле является аксиальным. При
а = тс/2 или п = 0 соленоид превращается в прямолинейный провод, парал-
параллельный оси z и расположенный от нее на расстоянии а. В этом случае
Bz=0 и, как следует из результатов § 34а гл. V, Ко—> — 1пBитш) v
Кг—> 1/ B/гтш), откуда
п->0
2toj
что вполне согласуется с выражением G.79).
§ 17. Поле в цилиндрической полости внутри проводящего круглого»
стержня. Вычисление магнитного поля, обусловленного задапным распре-
распределением плотности тока, часто силь-
сильно упрощается, если пользоваться
суперпозицией известных решений.
В качестве примера применения это-
этого метода рассмотрим проводящую
среду (с единичной относительной
магнитной проницаемостью), запол-
заполняющую все пространство между
двумя бесконечными цилиндрически-
цилиндрическими поверхностями. Найдем магнит-
магнитную индукцию внутри малого ци-
цилиндра радиуса а, лежащего внутри
большого цилиндра радиуса Ь, счи-
считая расстояние между их осями рав-
равным с (см. фиг. 71). Пусть плотность
тока всюду в поперечном сечении
одинакова и имеет лишь z-состав- Фиг. 71.
лнющуго (iz). В отсутствие полости
значение В$ на окружности радиуса г, проведенной через точку Р, было
бы постоянным и, согласно формуле G.2), раьнялось бы
В' =
X г.
278
Глава VII
Добавление такого же выражения для тока с плотностью — i, протекаю-
протекающего только по внутреннему цилиндру, приводит к тему, что суммарная
плотность тска вс внутрсппом цилиндре оказывается равней нулю, а маг-
магнитная индукция равной
— ' С — ">— — " — —u'fk ' \— " — и '
в
G.88)
где it, j и k — единичные векторы в направлении осей х, у и z. Полный
ток / равен (nb2 — тта2) /, и однородное поле в полости определяется
выражением
\>.с1
п(Ь2—а2)"
G.89)
§ 18. Поле токов, текущих вдоль цилиндрической проводящей
?нки. Предположим, что в бесконечней круглей цилиндрической пленке
пленки
теки текут параллельно оси z и что плотность
тока i можно выразить через круговые поверх-
поверхностные гармоники, т. е.
G.90)
n=0
Как следует пз § 10, вектор-потенциал в точке
/', находящейся на расстоянии R от бесконечного
провода, несущего ток /, параллелен ему и
равен
In R. Таким образом, согласно
Фив. 72.
выражениям G.8), вектср-пстенцпал, обусловлен-
обусловленный всей цилиндрической пленкой (см. фиг. 72),
определяется выражением
1 С
Az— -tj-jj-tc-1 V ia In R da.
G.91)
По на выражения D.18) следует
1л R = In а— 2~ Г-^-Т*(cos mO cos mx + sin mO sin лиа). G.92)
т = 1
Подставляя выражения G.90) и G.92) в G.91), получим интегралы в пре-
пределах от 0 до 2тг от произведений cos mx cos nx, sin mx sin nx и sin mx cos nx.
Бее эти интегралы (см. Двайт, 858.1 и 852.2) при т -ф п обращаются
а пуль. При т — п интеграл от sin 2ma= 2 sin mx cos ma тоже равен нулю,
а от sin2ma и cos2ma равен г(см. Двайт, 858.4); отсюда выражение
G.91) принимает вид
-j)" (Cncos nO
i nO). G.93)
§ 19. Сила, действующая на электрический контур в магнитном
иоле. Из эксперимента, списанного в § 1, найдено, что силы, действующие
и магнитном поле на небольшую проволочную петлю с током, являются
точно такими же, как и силы, действующие в электрическом поле на
электрический диполь. Мы видели также, что любой электрический контур
можно рассматривать как границу сетки, каждая ячейка котором представ-
Магнитное взаимодействие токов 279
ляст собой одну из таких петель. Используя формулу A.11), можно, таким
образом, написать выражение для силы, действующей на элемент сетки
dS с током /, Подставляя nf dS вместо m и В вместо Е, получим
dF = J(n-V)BdS. G.94)
Воспользуемся далее хорошо известным соотношением
(Vxn) + (n-V)B + nx(VxB). G.95)
Поскольку оператор V не действует на п, первые два члена справа обра-
обращаются в нуль. Согласно соотношению G.4), V xB = ;j.i, а так как внутри
петли тока нет, то VxB = O. Подставляя VxA вместо В [см. формулу
G.5)], получим следующее выражение для полной силы, действующей на
контур:
Применим теорему Стокса C.3) и носпользуемся опять соотношением
G.95), где заменим п на ds, а В на А. Замечая, что оператор V не дей-
действует на ds, имеем
F=/V $ A ds = / ^ ftds-V)A + dsx(V х А)]. G.96)
Однако
^s • V) А = ^ (Шх + jdAy -f ЫАХ) = О,
потому что dAx, dAy и ЙА —полные дифференциалы, а Ах, Ау и А^~
однозначные функции. Помня, что Vx А = В, из выражения G.96)
находим
или l?BsinOds = &dF, G.97)
где б < тг — угол, отсчитываемый от ds к В. Если линия наблюдения пер-
перпендикулярна к ds и В. а 6 отсчитывается по часовой стрелке, то сила
направлена в сторону от наблюдателя.
Эксперименты Ампера не приводят к однозначному закону для сил,
действующих между элементами контуров. В самом деле, из выражений
G.97) ц G.77) следует, что сила взаимодействия между двумя контурами
равна
Линейный интеграл цо контуру s л первом члене последнего выражения
обращается в пуль, потому что г/г3 является градиентом скаляра 1/г.
Отсюда получаем два выражения для силы взаимодействия между элемен-
элементами контуров
п dsx(ds'xr) /-,r(ds-ds') „ ,,,„
С Lj L или - С \я > . (/.99)
Сопоставляя выражения G.77) и G.97), нетрудно видеть, что в случае
двух почти совпадающих контуров, по которым циркулируют ранные и про-
противоположно направленные токи, когда, согласно опытам Ампера, магнитное
иоле обращается почти в нуль, основной вклад в выражение для силы
дают лишь близко расположенные элементы, для которых г мало. При этом
сила 'оказывается направленной в сторону положительных значений г.
280
Глава VII
Следовательно, контуры отталкиваются, в результате чего появляется маг-
магнитное поле. Этот случай составляет полную противоположность случаю
электрического поля, где сила взаимодействия между равными по величи-
величине и противоположными по знаку зарядами стремится их сблизить и тем
самым уничтожить имеющееся электрическое поле. Таким образом, в при-
природе энергии электрического и магнитного полей имеется коренное разли-
различие. Более подробно этот вопрос будет рассмотрен в следующей главе,
в связи с законом индукции- Фарадся. Все эти формулы для сил, дей-
действующих на контуры в магнитном поле, хорошо подтверждаются экспе-
экспериментально.
§ 20. Примеры на вычисление сил взаимодействия между электри-
электрическими контурами. Для двух бесконечных параллельных проводов, нахо
дящихся на расстоянии а друг от друга и несущих токи / и /', согласно
выражениям G.79) и G.97), поскольку
sin 6 = 1, мы имеем
ds' х [s, xal.
Отсюда, очевидно, сила отталкивания на
единицу длины равна
G.100)
Фиг. 73.
1 -1- 2таг "
Положительный знак берется при нротиво-
полошном направлении токов / и /', а от-
отрицательный — при одинаковом направлении
их.
Вычислим теперь силу взаимодействия двух коаксиальных проволочных
петель радиусов а и Ъ, по которым протекают токи / и /', как показано
на фиг. 73. Вследствие симметрии очевидно, что сила взаимодействия являет-
является силой притяжения, поэтому, согласно выражению G.97), единственной
эффективной компонентой магнитной индукции оказывается Bf; величина
этой компоненты одинакова для всех элементов каждого из контуров.
Поскольку координаты контура с током /' равны р = Ъ, z = с, то сила
определяется выражением
= l'B9(a, Ъ,
{а, Ь, с).
Подставляя сюда значение В9 из соотношения G.53), получим
г} ixll'с Г т-г (я2 -4- ^2 Л~ с2) Е ~\
~^|_-^+ (fl_fcJ + c2 J.
где, согласно выражению G.50), модуль к равен
, 2 4аЬ
Сила будет иметь обратное направление, если один из токов направить
в противоположную сторону.
Это выражение для силы нетрудно представить в виде ряда. Действитель-
Действительно, объединяя выражения G.97) и G.72), при с2-(-^2>й2 будем иметь
F= -г
sin а
п=1
)Рп@),
G.102)
Магнитное взаимодействие токов 28 Л
потому что в выражении G.72) cos6 = m = 0 и г = а, а в выражении G.97)
ds = 2-rai.
Другой более быстро сходящийся ряд можно получить следующим
способом.
Если две петли имеют разные радиусы, то можно выбрать начало-
координат в вершине кругового конуса, проходящего через эти петли
и имеющего угол раствора, равный 2[3. Пусть /• — радиус-вектор малой
петли, s — радиус-вектор большой петли; тогда сила взаимодействия между
петлями равна
F = 2W sin р (Br sin р + Въ cos Р),
где Вг и В6 определены выражениями G.72) и G.73). Таким образом,.
СО
F = щх1Г sin3р 2 (тУ IT P* (cos Р) InjP» (cos'6) ~ cos PP" (cos Р)Ь
п=2
Суммирование начинается с п = 2, потому что член, соответствующий /г =» 1 г
равен нулю. Последнее выражение можно упростить, используя результаты
§ 2 гл. IV и соотношение E.119). Заменим п па п-\-1, где 1</г< со, и
учитывая, что rjs = ajb при b > а, получим
^15?)- G03>
§ 21. Вектор-потенциал и вектор намагниченности. Определение
вектор-потенциала, данное выражением G.9), оказалось достаточным во-
всех рассмотренных выше случаях, когда вся область предполагалась
заполненной средой с постоянной магнитной проницаемостью. Если же (х
изменяется непрерывно или имеет разрывы непрерывности, то для одно-
однозначного определения вектор-потенциала необходимо рассмотреть природу
намагничивания. В § 7 гл. XII будет приведено экспериментальное под-
подтверждение того, что намагниченность обусловливается круговыми токами
или вращением электрических зарядов внутри тела. Введем вектор М —
магнитный момент (на единицу объема), обусловленный этими токами (или
спинами), и назовем его вектором намагниченности. При помощи выраже-
выражения G.49), полагая |х = |хг и измеряя г от точки наблюдения, для вектор-
потенциала, описывающего поле, создаваемое намагниченностью М, пблучим
v. G.104)
V V
Преобразуем это уравнение, пользуясь векторными тождествами
q G.105)
V xMdv= JnxMiS, G.106)
S
где п—единичный вектор, направленный вдоль внешней нормали к поверх-
поверхности S, ограничивающей объем v. Соотношение G.106) доказывается при
помощи теоремы Остроградского—Гаусса C.2), если подставить в нее-
А = Мха, где а— постоянный вектор, так что V-(Mxa) = a-VxM и
' = a-\nxM dS.
'282 Глава VII
Поскольку эти справедливо для произвольного вектора а, то отсюда выте-
вытекает справедливость соотношения G.106). Применение соотношений G.105)
и G.106) к выражению G.104) дает
|L Ам= ) ^dv- \ V X (^) dv= \ ^Mrfv+ \ ~ dS. G.107)
v v v S
При однородной намагниченности внутри рассматриваемой ограниченной
области выражение G.107) более удобно, чем G.104), ибо в этом случае
интеграл по объему в выражении G.107) обращается в нуль. Пусть i —
плотность истинного тока, тогда полный вектор-потенциал равен
4л: J
v S
^,fMxn^ G108)
Еслгг заданы только распределения тока и величины магнитной про-
проницаемости, как это и имеет место в большинстве случаев, то для примене-
иия этой формулы нужно выразить М через |х и В. Для этого заметим,
что на больших расстояниях от замкнутых контуров конечных размеров
магнитная индукция и, следовательно, намагниченность обратно пропор-
пропорциональны квадрату (или более высоким степеням) г, поэтому интеграл
по поверхности в выражении G.107) исчезает. Если магнитная проницаемость
|х в этой области постоянна и магнитный момент М обусловлен лишь током i,
то вектор-потенциал должен также определяться выражением G.9), откуда,
сравнивая его с соотношением G.108), имеем
M). G-109)
Мы определяем |х в изотропной, но не однородной среде таким образом,
чтобы это уравнение оставалось в силе. При помощи его исключим |xi из
соотношения G.4) и, принимая во внимание, что при постоянном значении |х
окончательное уравнешге должно сводиться к соотношению G.4), а также
учитывая, что в соответствии с экспериментальными данными вектор М про-
пропорционален В и имеет одинаковое с нпм направление, получим
i = VX?-' GЛ10)
Аналогично тому, как соотношение G.2) получается из G.4), нетрудно
вывести из G.110) следующее соотношение:
В—=/. G.112)
§ 22. Граничные условия для магнитных полей и для вектор-потен-
вектор-потенциалов. В предыдущем параграфе мы определили вектор-потепциал А для
тех областей, где намагниченность не является однородной, а также на
поверхностях, где она терпит разрыв. Найдем граничные условия, которым
должен удовлетворять лектор-потенциал А. Каждая из трех компонент А
определяется скалярным выражением, аналитически совпадающим с выра-
выражением A.8) и имеющим в случае вакуума вид
Ото выражение определяет электростатический потенциал в свободном про-
пространстве, обусловленный распределением электрических зарядов с объемной
Магнитное взаимодействие токов 283
плотностью рис поверхностной плотностью а. Из электростатики известно,
что значение потенциала F,- на внутренней стороне поверхности S, опре-
определяемое этими интегралами, равно значению потенциала FA на внешней
стороне поверхности S. Далее, применяя теорему Гаусса о потоке электри-
электрической, индукции к небольшому дискообразному элементу объема, примыка-
примыкающему к элементу dS поверхности и настолько тонкому, что dv можно
¦считать пренебрежимо малым но сравнению с (dSf^, после сокращения на dS
получим соотношение
дп дп ev
Таким образом, мы знаем граничные условия, которым удовлетворяют
интегралы вида A.8), а следовательно, н каждая компонента выражения
iG.108). 'Складывая все компоненты и заменяя 1/s,, на |х0, получим
А0 = А;. G.113)
и, как следует из выражения G.111),
^Ai)Xn]. G.114)
Если с одной стороны от границы имеется намагниченность М', а с другой
стороны М", то для получения граничных условий достаточно представить
себе, что граница является тонким слоем с некоторой магнитной прони-
проницаемостью, для границ которого можно написать условия G.113) и G.114),
относя их к одной и той же нормали. Исключая затем А,, и дА0 / дп,
найдем
А'=А" G.115)
и
^^ -M-)xn]. G.116)
Чтобы выразить второе граничное условие через величину магнитной про-
проницаемости, вместо дI дп напишем n-V и воспользуемся соотношением
n-V(A'-A") = V[n-(A'-A")]-nx[Vx(A'-A")]-
-(A'-A")-Vn-(A'-A")X(Vxn).
вследствие условия G.113) последние два члена пропадают. Заменяя
Vx(A'-A") на В'— В" и используя выражение G.5), после некоторых
преобразовании получпм
V[n- (А' - А")] = п X (В' - [хсМ' - В" + ^М").
Подставляя значение М из соотношения G.111), найдем
Согласно условию G.115), А'п — А'п равно нулю на всей границе, поэтому
градиент этого выражения вдоль границы также обращается в нуль. Таким
образом, V (А'п — А'п) является вектором, нормальным к границе. Но правая
часть вышенаписанного соотношения представляет собой вектор, направлен-
направленный вдоль поверхности границы, поэтому
Теперь можно написать граничные услошгя, накладываемые на ком-
компоненты вектора А, в системе ортогональных криволинейных коордилат
284 Глава VII
ur, us и ut, рассмотренных в § 4, 5 и 6 гл. III. Пусть на границе коор-
координата иг является постоянной, тогда, согласно условию G.115), имеем
а'г=а;., а; = а; и а\ = а\. G.И8)
Введем в- левую часть выражения G.117) V X А вместо В, после чего,
используя соотношения C.14) — C.16), получим
1 Г d(KsA'r,s) a(*t,r4',rI 1 Г d(hr,s^,s)
(л' L дЩ,г d"r,s J ,"•" L dut,r
Соотношения G.118) и G.119) являются искомыми граничными условиями.
Чтобы получить граничные условия, накладываемые на В, заметим,
прежде всего, что, согласно условию G.115), разность вектор-потенциалов
в двух точках на границе раздела двух сред сохраняется при переходе через
границу. Следовательно, производные от вектор-потенциала по обе сто-
стороны от границы, взятые в одинаковом направлении, параллельном границе,
должны быть также равны между собой. Вектор п X А лежит в касательной
плоскости к границе, поэтому V-nxA содержит только подобные произ-
производные. Напишем известное векторное тождество для дивергенции вектор-
векторного произведения
V-nx A= -n-VxA + A-Vxn. G.120)
При подстановке сюда А' — А" вместо А последний член, согласно усло-
условию G.115), исчезает, и мы получаем
nVxA' = nVxA".' G.121)
Подставляя В вместо V X А, находим
п-В'= п. В". G.122)
Таким образом, нормальные компоненты магнитной индукции на границе
раздела двух сред меняются непрерывно. Исходя из выражения G.117),
для тангенциальных компонент магнитной индукции находим следующее
соотношение:
¦jJ-(nxB') = l(nxB'). G.123)
- Часто. оказывается возможным ввести два вектора а' и а", отличаю-
отличающихся от А' и А" и являющихся более простыми. Роторы этих векторов
всюду дают то же значение магнитной индукции, что и роторы А' и А";
однако эти векторы, как будет показано в § 5 гл. VIII, удовлетворяют
вместо условия G.115) следующим граничным условиям:
в?Ф&; и aj,, = »?,,. G.124)
На примере, разбираемом в следующем параграфе, будет ясно видно, что
эти векторы являются более удобными при вычислении, чем А' и А". Они
не определяются однозначно (как А' и А") при помощи интегралов типа
G.1U8). Мы будем называть их квазивектор-потепциалами.
§ 23. Пример использования векторов а и А. В качестве примера
использования граничных условий, выведенных в предыдущем параграфе,
рассмотрим бесконечный провод с током /. простирающийся в z-направлении.
Пусть окружающая провод среда в области положительных значений z
обладает магнитной проницаемостью |х', а в области отрицательных зна-
значений z — магнитной проницаемостью |х". Из выражения G.10) видно, что
простейшими векторами а' и а", которые удовлетворяют условию G.119)
Магнитное взаимодействие токов 285
и не удовлетворяют условию G.115) и роторы которых дают правильное
значение В' и В", являются
а' = —kQ-n-^u'lnp) и a"=-k^«-1/|i,"lnp). G.125)
Вектор, определяемый выражением G.108), должен удовлетворять на гра-
границе раздела двух сред условию А' = А". Часть объемного интеграла
о выражении G.108), содержащая /, дается выражением G.10). К этому
решению необходимо добавить другой потенциал для того, чтобы удовле-
удовлетворить новому граничному условию. Рассмотрение решений G.30), записан-
записанных в цилиндрической системе координат, показывает, что наиболее под-
подходящей формой является форма cz/p. Подставляь это и вводя произволь-
произвольные постоянные С1 и С2, мы получим
А' = 1 *-!/ { - k^ (In р + Q + р Ц[х' - ц„) zp-i + C2]}, G.126)
± }. G.127)
Вторые члены соответствуют значениям вектор-потенциала, даваемым инте-
интегралом G.104). Векторы магнитной индукции В' и В", получаемые из со-
соотношений G.126) и G.127), совпадают с теми, которые получаются
из соотношений G.125).
§ 24. Метод изображений для токов в случае плоской границы.
Сходство граничных условий для В, полученных в § 22 настоящей главы,
с условиями для D, полученными в § 18 гл. I, приводит к мысли о том,
что метод изображений, развитый в § 6 гл. V, можно применить и при
вычислении магнитного поля, создаваемого электрическим контуром, рас-
расположенным вблизи плоской границы полупространства, заполненного
средой с магнитной проницаемостью |х. Пусть граница раздела совпадает
с плоскостью z = 0, контур расположен в области положительных значений z,
а среда с проницаемостью |х — в области отрицательных значений z. Обо-
Обозначим через А вектор-потенциал магнитного поля, создаваемого одним этим
контуром. По методу изображений (§ 6 гл. V) квазивектор-потенциал над
границей можно представить в виде А + а', а под границей — в виде а", где
А=1/,(ж, у, z) + jfa(x, у, z) + kfs(x, у, z), G.128)
л' = \С'хи(х,у, -z) + iC'J2(x,y, -z) + kC'J3{x,y, -z), G.129)
a" = iC'1'f1(x, у, z) + jC'2'f2(x, у, z) + kC'3'fs(x, у, z). G.130)
Исходя из условий G.124) при z = 0, получаем
az + a'z 1= а" и аж, „ + a'Xt у = a'x\ v
или
G.Ш)
Граничные условия при z = 0 для производных, определяемые соотноше-
соотношением G.119), будут удовлетворены, если положить
= h,c;\ G.Ш)
Поскольку а" и А имеют одинаковую форму, получим
lM^ ^ Gлзз)
286 Глава VII
Таким образом, магнитная индукция вне среды с проницаемостью и об-
обусловливается как бы двумя контурами: первоначальным контуром с током /
и контур-изображением с током /' = [(и — [х„)/([л -f- и^)] I. Направление тока Г
таково, что проекции / и /' на границу раздела сред совпадают друг
с другом и по положению и по направлению. В среде с проницаемостью |i.
магнитную индукцию можно представить себе как обусловленную одним
лишь первоначальным контуром, по которому вместо тока / циркулирует
ток /" = 2//( )
§ 25. Магнитная индукция и магнитная проницаемость в кристаллах.
Сходство граничных условий для В, выведенных в § 22 настоящей главы,
и условий для D, полученных в § 18 гл. I, подсказывает, что метод
измерения D и Е, описанный в § 19 гл. I, можно применить для Вии.
Вырежем в исследуемом теле небольшую дискообразную полость, толщина
которой пусть будет очень малой по сравнению с ее радиусом, так что
магнитная индукция в полости, вдали от ее краев, будет определяться
лишь граничными условиями на плоских поверхностях. Если полость
ориентировать таким образом, чтобы магнитная индукция внутри оказалась
направленной нормально к плоским границам полости, то, согласно соот-
соотношению G.122), значение В в полости будет равно значению В в среде.
Вырежем теперь полость в виде длинного тонкого цилиндра. Магнитная
индукция внутри нее вдали от концов будет полностью определяться
граничными условиями на боковых стенках цилиндра. Если полость ориен-
ориентировать таким образом, чтобы магнитная индукция оказалась направлен-
направленной вдоль оси цилиндра, то, пользуясь выражением G.123), нетрудно
убедиться, что отношение В'/[лц внутри полости равно отношению В/и в среде.
Эти два измерения позволяют определить В и и. Если произвести этот опыт
в магнитноанизотропной среде! то обнаружится, что, вообще говоря, напра-
направления В и В' будут различными. Однако в кристалле существуют по крайней
мере три такие ориентации поля, вдоль которых В и В' совпадают
по направлению. Эти направления являются магнитными осями кристалла;:
вдоль каждой из них величина и может принимать разные значения.
В некоторых кристаллах В и В' имеют одинаковое направление для всех
ориентации поля в некоторой плоскости и для поля, перпендикулярного
к этой плоскости. К этому вопросу мы еще возвратимся в § 3 и 4 гл. XII.
§ 26. Двухмерные магнитные поля. В прямоугольных координатах
граничные условия для тангенциальной составляющей магнитостатического
вектор-потенциала совпадают с условиями для электростатического скаляр-
скалярного потенциала, если величину е заменить на 1/и. В двухмерном случае,
когда имеются только магнитные поля, параллельные плоскости ху, токи
должны протекать лишь в z-направлении и, следовательно, вектор-потенциал
может иметь только одну компоненту Аг, которая с необходимостью оказы-
оказывается тангенциальной ко всем поверхностям. Если отношение u/u0 очень
велико, то, согласно условию G.119), все поверхности, на которых А,—
постоянная величина, т. е. поверхности равного вектор-цотеициала (эгсви-
векторпотенциальныё поверхности), будут ортогональными к границе. Таким
образом, величина А, ведет себя как электростатическая функция потока
на электрической эквипотенциальной поверхности. Величина В вычисляется
из Az точно так же, как электрическое поле вычисляется из функции потока.
Действительно, в прямоугольных координатах, где /г1 = /г2 = /г3 = 1, поль-
пользуясь выражением C.15) и C.16), имеем
что совпадает с соотношением D.56).
Магнитное взаимодействие токов
287
При отсутствии тока уравнение G.7) принимает вид
G.135)
для решения его применимы все методы, рассмотренные в гл. IV.
§ 27. Магнитное экранирование двухпроводной линии. Для иллюстра-
иллюстрации применения результатов предыдущего параграфа вычислим величину
магнитной индукции снаружи цилин-
цилиндрического экрана с внутренними и
внешними радиусами а и Ь, имеющего
проницаемость |х и окружающего два
параллельных прямолинейных прово-
провода, расположенных симметрично отно-
относительно оси цилиндра и несущих
противоположно направленные токи
(см. фиг. 74). Очевидно, при решении
этой задачи следует использовать кру-
круговые гармоники, с которыми мы име-
имели дело в § 2 гл. IV. В § 10 гл. VII
было показано, что вектор-потенциал
двух противоположно направленных то-
токов определяется выражением
2=%г1пг- GЛ36)
Фиг. 74.
Из соотношения D.17), полагая там 60=0 и 60 = тг, а также ро = с, Для:
р > с получим следующие ряды:
оо
71=1
Составим их разность, тогда четные члены сократятся; заменяя затем п
на 2тг + 1, получим
71 = 0
G.137)
Для нахождения потенциала в области, окружаемой экраном, нужно
добавить к полученному выражению потенциал, обусловленный присутствием
экрана и конечный в начале координат; тогда
п=0
0. G.138)
В области 2, обладающей магнитной проницаемостью |х, р не принимает
ни нулевое, ни бесконечное значение, поэтому следует написать
G.139).
п=0
288 Глава VII
Снаружи экрана потенциал должен исчезать на бесконечности
• 2J ^2n+l p-^7—1 COS
n=0
Граничные условия G.118) и G.119) должны удовлетворяться при всех
-значениях 6, поэтому каждый член рядов G.138)—G.140) должен удовлетво-
удовлетворять этим условиям; в результате этого после умножения на a2n+i или
/,2n+i ПрИ р_ а получаются следующие соотношения:
= B2n+i a^+2 + C2n+i G.141)
*n+2-ftA..+ i- G.142)
При р = b получаем
B2n+i 64и+2 + C2n+i = ?>2п+1
Разрешая относительно Z^n+i, находим
аЛ4и+2т-1 1
г) J 2^ТТ
и=0
G.
G.
.143)
.144)
cosBn+lN.
G.
.145)
Поле снаружи экрана определяется выражениями C.15) и C.16), где,
согласно § 6 гл. Ill, hx = \ и h2 — p
§ 28. Метод изображений для токов в двухмерных системах. Выра-
Выражения для векторного потенциала поля прямолипойного тока / и для
скалярного потенциала поля линейного заряда q имеют одинаковую форму.
Более того, как было показано, двухмерные магнитный векторный потен-
потенциал и электростатический скалярный потенциал удовлетворяют одинаковым
по форме уравнениям Лапласа и граничным условиям (если К заменить
на l/.ffm). Отсюда следует, что результаты § 5 гл. IV применимы к прямо-
прямолинейному току /, параллельному оси круглого цилиндра с проницаемостью |х
и радиусом а и находящемуся от этой оси на расстоянии Ь. Таким образом,
вектор-потенциал в области вне цилиндра, обусловленный наличием послед-
последнего, является таким же, как если бы вместо цилиндра был помещен
ток — изображение /', расположенный между током / и осью цилиндра
(параллельно оси и на расстоянии a2jb от нее), и ток — /', протекающий
вдоль оси. Вектор-потенциал внутри цилиндра оказывается таким же, как
при замене тока / на ток /". Токи /' и /" определяются выражением D.37),
если К заменить на i-IKm, т. е.
1' = тЧ}\1 и l"=w^hl- GЛ47)
лт1-1 лт-)-1
При Кт—> оо /'—>•/, поэтому законы изображений для токов на гра-
границах сред с большой относительной магнитной проницаемостью совпадают
с законами изображений для электрических линейных зарядов в провод-
проводниках,' с тем лишь важным отличием, что изображения тока имеют тот же
Магнитное взаимодействие токов 289
:шак, а изображения заряда — противоположный знак. Таким образом,
системы изображений, рассмотренные в § 5, 6 и 7 гл. IV, можно исполь-
использовать и для токов. При этом нужно только помнить о знаках и замене К
на ЦКт.
§ 29. Магнитодвижущая сила и напряженность магнитного поля.
При изучении магнитного поля сразу же поражает наличие многих общих
свойств у вектора магнитной индумцгти и у электрического тока. Прежде
всего имеем [соотношения F.3) и G.1)]
V-i = 0 и V-B = O. GJ48)
Далее, для простого замкнутого пути имеем [соотношения F.9) и G.112)]
^ = Ш и §~ = 1- G.149)
Магнитный вектор-потенциал вычисляется на основании соотношения G.108).
Совершенно ясно, что можно с таким же успехом, как это было проделано
в гл. VI, провести аналогичное рассуждение п определить новую скалярную
величину, подобную f, которую будем называть магнитодвижущей
силой Q (м. д. с). Таким образом, для замкнутого пути вокруг тока /
магнитодвижущая сила равна
Q = I, G.150)
где / измеряется в амперах, a Q — в ампервитках. Ввиду того, что магнито-
магнитодвижущая и электродвижущая силы являются функциями многозначными,
их величины зависят от выбранного пути интегрирования. Используя
метод, примененный в § 2 гл.VI к if, часто можно ввести соответствую-
соответствующие перегородки так, чтобы вдоль любого разрешенного замкнутого пути
интеграл G.149) обращался в пуль. В этом случае Q приобретает харак-
характер скалярного потенциала. В простейших случаях такая перегородка из-
известна под названием магнитного листа. Легко видеть, что в выражении
G.149) магнитная проницаемость |х играет роль проводимости а (см. гл. VI),
поэтому для магнитных контуров можно установить соотношение, анало-
аналогичное закону Ома F.8), т. е.
В=—[iVQ. G.151)
Для градиента магнитодвижущей силы удобно ввести особое обозна-
обозначение. Введенную таким образом величину, взятую с обратным знаком
(—Н), мы будем называть напряженностью магнитного поля:
H=-VQ = —. G.152)
В системе MKS Н измеряется в ампервитках на метр. Выражая интеграл
G.149) через Н, получим
~Hds = /. G.153)
Это соотношение не зависит от магнитной проницаемости среды. Из
выражений G.148) и G.151) нетрудно получить соотношение, аналогичное
соотношению F.46), а именно:
V2Q=0. G.154)
Исходя из соотношений F.3), F.9) и F.46), были получены условия,
которым должна удовлетворять электродвижущая сила на границе двух
сред с различными проводимостями. Подобным же образом можно было бы,
19 В. Смайт
290 Глава VII
исходя из соотношений G.148), G.149) и G.154), вывести условия, кото-
которым должна удовлетворять магнитодвижущая сила Q на границе двух
сред с различными магнитными проницаемостями. Проще, однако, обра-
обратиться к соотношениям G.122) и G.123) и использовать G.152). Тогда
из соотношения G,122) найдем
[x'H'-n^-ix''H''-п, G.155)
а из соотношения G.123) получим
Н'хп = Н"хп G.156)
или, вводя магнитодвижущую силу, имеем
G' = G". G.158)
Следует отметить, что магнитодвижущая сила удовлетворяет точно таким
же соотношениям [см. G.154), G.157), G.158)], как и электростатический
потенциал [см. C.6), A.48) и A.49)]. Однако она отличается от послед-
последнего тем, что является неоднозначной функцией, если в поле не создавать
перегородок, препятствующих обходу по замкнутому пути вокруг любого
тока; при наличии перегородок магнитодвижущая сила Q является одно-
однозначной функцией в области вне этих перегородок, и ее можно исследо-
исследовать методами электростатики. При таком ограничении величина Q назы-
называется скалярным магнитным потенциалом; им мы будем пользоваться
для получения решения магнитостатических задач по аналогии с соответ-
соответствующими электростатическими решениями.
Например, для нахождения экранирующего действия сферической обо-
оболочки, внешний и внутренний радиусы которой равны Ъ и а, а магнитная
проницаемость равна |х, и которая помещена в однородное магнитное поле
с индукцией В, можно воспользоваться выражением E.140). Мы видим,
что поле внутри оболочки остается однородным, а величина магнитной
индукции внутри оказывается равной
г>
*~9Ят
Ввиду того, что соотношения G.157) и G.158) совпадают по форме
с соотношениями A.48) и A.49), закон преломления магнитных силовых
линий на границе двух изотропных магнитных сред, получаемый из пер-
первых соотношений, будет совпадать с законом преломления электрических
силовых линий, который выводится из вторых соотношений и выражается
формулой A.51). Таким образом, на границе двух сред магнитные сило-
силовые линии резко изменяют свое направление, согласно закону
fx'ctga' = fx"ctga", G.160)
где а' — угол, образуемый силовой линией и нормалью к границе в среде
с магнитной проницаемостью |х', а а" — соответствующий угол в среде
с,магнитной проницаемостью jx".
§ 30. Магнитный контур. Тор. В предыдущем параграфе была ука-
указана близкая математическая аналогия между магнитной индукцией и плот-
плотностью электрического тока. Чтобы яри решении магнитостатических задач
можно было пользоваться методами, развитыми в гл. VI для решения дина-
динамических задач, удобно ввести несколько новых магнитных величил.
Магнитное взаимодействие токов
291
Магнитный поток N через поверхность S соответствует электрическому
току /, что видно из их определений:
indS. G.161)
s s
Единицей потока в системе MKS является вебер. Магнитное сопротивление R'
между двумя точками в контуре соответствует электрическому сопротив-
сопротивлению; они определяются аналогичными
соотношениями:
*АВ
1АВ
"АВ
G.162)
Фиг. 76.
Для иллюстрации расчета таких конту-
контуров найдем поток в торе, который имеет
магнитную проницаемость [J. и на который
намотано п витков провода, несущего
ток /. Пусть радиус сечения тора равен
Ь, а расстояние от центра этого сечения
до оси тора равно а. Из определения G.150) следует, что магнитодвижу-
магнитодвижущая сила для замкнутого пути вдоль тора (от 0 до 2тс) равна nl. Поскольку,
вследствие симметрии, величина Н не зависит от 6, то магнитодвижущая
сила на отрезке пути, заключенном между 0 и 6, будет пропорциональ-
пропорциональна 6, т. е.
Й = ^. G.163)
Согласно выражению G.152), имеем
дО.
"гдЬ
In
2кг
Таким образом, при заданном значении г величина Н$ является постоян-
постоянной и тор можно разбить на ряд цилиндрических слоев, как это пока-
показано на фиг. 75, не изменяя его магнитного сопротивления. Магнит-
Магнитное сопротивление одного такого слоя будет равно
dR' =
Длина 2лг
Но dS = 2 [b2 — (a —
параллельно, имеем
Площадь"
и ввиду того, что эти
слои соединяются
J
R'
а-Ъ
Интегрируя (см. Пайерс, 187) и подставляя пределы, получаем
Пользуясь выражением G.162), найдем поток внутри тора
N = ^r=pnl[a~ (a2 — Ь2I'*]. G.164)
§ 31. Магнитный контур с воздушным зазором. Очевидно, что в случае
непрерывного магнитопровода с высокой магнитной проницаемостью и до-
достаточно большой всюду площадью поперечного сечения магнитный поток
в контуре будет почти полностью сконцентрирован внутри магнитопровода.
19*
292 _ Глава VII
Однако если в этом магнитопроводе имеется разрыв, то поток, про-
проходя через зазор, распределится таким образом, что магнитодвижущая сила
будет удовлетворять всюду уравнению G.154), а на границе зазора —
условиям G.157) и G.158). Если магнитная проницаемость среды fi" очень
велика по сравнению с магнитной проницаемостью зазора [j.', to, как сле-
следует из соотношения G.160), а'~>0 и силовые линии в зазоре подходят
перпендикулярно к границе среды. В случае, когда произведение jj,' на
часть длины пути магнитного контура, лежащую в среде с высокой маг-
магнитной проницаемостью, мало по сравнению с произведением у." на длину
воздушного зазора, можно практически считать полное магнитное сопро-
сопротивление сосредоточенным в зазоре при условии, что поперечное сечение
магнитной среды нигде не является слишком малым. Это имеет место,
например, для многих электрических машин. Если поверхности, ограни-
ограничивающие зазор, параллельны и их площадь А велика по сравнению
с расстоянием d между ними, то поле в зазоре можно считать однородным
и краевым эффектом пренебречь; тогда магнитное сопротивление зазора
равно dfA.
Для получения строгого решения в других случаях следует пользо-
пользоваться вектор-потенциалом или непосредственно вектором магнитной индук-
индукции, используя закон Био и Савара, а также граничные условия, рассмотрен-
рассмотренные в § 22. Этот путь, однако, часто бывает сопряжен с длительными
математическими вычислениями, что не оправдывается требуемой на прак-
практике точностью. В таких случаях достаточно точный результат можно
получить и при помощи скалярного магнитного потенциала, применяя
методы, развитые в гл. IV и V. Как уже упоминалось в § 29, при этом
возникает необходимость создавать искусственные перегородки обычно где-
нибудь в той части магнитного контура, которая обладает большой маг-
магнитной проницаемостью. При большой магнитной проницаемости мы при-
приписываем потенциалу в этой части среды одно значение с одной стороны
от перегородки и другое значение—с другой стороны. Когда конфигурация
системы позволяет расположить перегородку вдали от зазора, вносимая
при этом ошибка ничтожно мала.
§ 32. Поле в трансформаторе броневого типа. В качестве примера
нахождения приближенного решения путем введения предположения о бес-
копечной магнитной проницаемости вычислим поле тока, протекающего
в проводе, намотанном в виде тонкого симметрично расположенного
цилиндрического слоя на цилиндрическом сердечнике броневого трансфор-
трансформатора. Напишем уравнение стенок, образующих «окно» трансформатора,
в цилиндрических координатах в виде z = —h, z — -\-h, p = a и p=b.
Равномерная плотная обмотка, намотанная на каркасе р = с в пределах
от z= —к до z= -t к, имеет п витков на единицу длины, по которым
течет ток /. Эту обмотку можно рассматривать как одиночную однородную
оболочку с полным током /0 -- 2nlk, обтекающим сердечник параллельно
плоскости z, как показано на фиг. 76. Найдем магнитную индукцию
в «окне». В силу симметрии вектор-потенциал будет иметь лишь одну
компоненту А?. Из § 6 следует, что в цилиндрических координатах реше-
решение содержит либо обычные, либо модифицированные функции Бесселя.
В нервом случае применимы методы, изложенные в § ЗОз и ЗОи гл. V
(окончательные результаты приведены в задачах 31 и 32 в конце этой
главы).
Пользуясь методом, рассмотренным в § 37 гл. V, найдем решение,
содержащее модифицированные функции Бесселя. Если А имеет лишь
ср-компоненту, величина которой не зависит от ср, то решение получается
из выражения G.26), где следует положить и = 0 и 6 = т:/2. Поскольку
Магнитное взаимодействие токов
293
р = 0 и р = со находятся вне рассматриваемой области, то нельзя исключить
ни /х(Ар), ни К1(кр), т. е. решение запишется в виде
= 2
m=l
где учтено, что Вр= — dA.Jdz обращается е нуль при 2 = ±/г, а также
принята во внимание симметрия относительно плоскости z = 0. В дальнейшем
/
L
V/////////
fn
—1.
////У/
г\
1±
Фиг. 76.
удобно пользоваться следующими обозначениями Гсм. формулы E.441^
E.442)]: i * f j v „
B)(=>()(^) G.166)
^ <?>(?)(?>(?). G.167)
Легко видеть, что
Лп ("».*,*) = 0. G.168)
Обозначим вектор-потенциал при а < р < с через А'ч и при с < р < Ъ
через i4J. Тогда три из четырех остающихся граничных условий запишутся
в виде
А'у —А'у, если р = с,
еСЛИ P =
1 З(рЛф) л
= 7~~^-= ' еслн p = fe-
G.169)
G.170)
Из выражений G.167) и G.168) очевидно, что все эти условия будут удо-
удовлетворены, если положить
, b, c)R1(m, a,
-4;= 2 CmRi(m, a, ciR^m, b, p) cos
G.171)
G.172)
Определим Сто из граничного условия на поверхности катушки. Для полу-
получения этого граничного условия заметим, что линейный интеграл вдоль
пути, окружающего витки и расположенного между z = 0 и z = z, не зави-
зависит от величины индуцированной намагниченности и что для путир = с, плотно
294 Глава VII
примыкающего к стенке цилиндра, этот интеграл, согласно формуле
G.2), равен
(f В • ds = \ (B'z - В"г\„с dz = ^nlz.
Дифференцируя полученный результат по z, находим
(Я?-ДОг-.с = л,и/, если ~k<z<+k, G.173)
(B'z-B-z)r_c = 0, если k<\z\<h. G.174)
Из выражений G.169) —G.172) получаем
B'z — В" = ^j —г- Cm [Ro (m, a, c) R1 (m, b, c) — R1 (m, a, c) Ro (m, b, c)] cos —r— ,
что при помощи соотношения E.412) сводится к следующему:
со
т=\
Для определения Ст умножим обе части этого выражения на cos (qnz/h) dz
и проинтегрируем в пределах от— h до + h. Все члены спраяа (см. Двайт,
858.2) пропадают, за исключением того, для которого m = q. Из соотноше-
соотношений G.173) и G.174) видно, что интеграл слева равен нулю для всех зна-
значений z, кроме — к < z < + к, отсюда
Т С nvnz , 2txvnlh . mnk „ h „ . ,.
ix,,wi \ cos -j— dz— — sin —r— = Lm — RJm, a, b).
rv j h rrm h m c v\ > /
Разрешая это относительно Cm и подставляя в выражения G.171) и G.172),
получаем
для й < р < с
2^ ^ J_ Bl (m Ь, С) Дг (m, a, P) g}п Ы cQg m*z ?
* it /J m Ло (пг, а, 6) /г /г ' v
«г=1
ДЛЯ С < р <
2^n/? ^, 1 Д1(»»а,С)Д1(т,Ь,Р)
* тс ZJ m Bo(m,a,b) h
Согласно выражению G.43) уравнение силовой трубки имеет вид
N = 27cpAf. G.177)
В случае соприкосновения катушки с внутренним сердечником а — с и век-
вектор-потенциал внутри «окна» трансформатора равен А^. При соприкосно-
соприкосновении катушки с внешней стенкой с=Ь и вектор-потенцпал внутри «окна»
трансформатора будет равен А'Р. В обоих случаях выражения G.175) и
G.176) значительно упрощаются, поскольку в силу соотношений E.412) и
и E.440)
R1(m,s,s) = -^-. G.178)
Выражения G.175) и G.176) показывают, что если обмотка занимает всю
высоту окна (h = k), ноток рассеяния будет отсутствовать, так как магнит-
магнитная проницаемость железа предполагается бесконечной. На фиг. 77,а, б и в
а б в
Фиг. 77. Линии индукции потока рассеяния в плоскости сечения окна трансформатора броневого типа, изобра-
изображенного на фиг. 76.
а—обмотка расположена при р=1, б—обмотка расположена при р=1,5, в—обмотка расположена при р=2. Кривые вычислены
по формулам G.175)—G.177) при а=1, Ь~2, h=—n, h=jg-n, ц=со, vvnI=-l0.
296
Глава VII
изображен поток рассеяния при расположении катушки во внутреннем
сердечнике, в середине «окна» и у внешней стенки. В каждом случае
число ампервитков предполагается одним и тем же, а обмотка—располо-
обмотка—расположенной в пределах от z= —/г/4 до z= -\-hji..
§ 33. Полюс с расщепленным наконечником. Эффективный воздуш-
воздушный зазор. Предположим, что в одной из плоских границ воздушного
зазора, ширина которого равна В, проделаны два параллельных паза
шириной 2А, расстояние между серединами которых равно 2С Если С—А
велико но сравнению с В, то на иоле вблизи одного из пазов наличие
другого паза не оказывает практически никакого влияния, поэтому пиле
вблизи каждого паза можно вычислять совершенно независимо. Пусть
глубина паза велика по сравнению с его шириной, тогда влиянием на
поло со стороны дна паза можпо пренебречь и считать паз бесконечно
У,
У
Плоскость z
Плоскость z,
AVK\\M\\\\\N
R S
6
Фиг. 78.
глубоким. Таким образом, участок RS на фиг. /8, а можно рассматривать
как участок RS на фиг. 78, б, где впешние границы простираются до
бесконечности. Пусть магнитная проницаемость материала настолько велика,
что м. д. с. полностью падает в воздушном зазоре, как это упоминалось
в § 31. Отверстие паза имеет форму многоугольника с нулевыми внутрен-
внутренними углами при ж= ^оо и углами Зтс/2 при х— ±-А, у = В. Таким
образом, обратное преобразование Шварца переведет эту границу в дей-
действительную ось на плоскости zx. Пусть вершины углов, равных Зтс/2,
переходят в точки ^=±1, тогда углы, равные нулю, перейдут в точки
^1=±я. где а2<1. Согласно выражению D.85), точки на плоскостях
z и Zj связаиы между собой соотношением
dz __ r,
dz
G.17У)
Магнитная цепь в плоскости zlt сечение которой показано на фиг. 78, е,
представляет собой двухпроводную линию, рассмотренную в § 10. Поскольку
магнитное сопротивление той части цепи, которая находится под осью ;г1?
равно нулю, вектор-потенциал над осью х1 равен удвоенному выражению
G.44), т. е.
^(^) G-180)
что, согласно выражению D.62), является действительной частью функции
¦a a — Zy v '
Прежде чем определить W в плоскости z, следует проинтегрировать соот-
соотношение G.179). В результате получим
z= С
(*!-!)
Магнитное взаимодействие токов 297
В первом интеграле выпишем в явном виде / и воспользуемся формулой
C20.01) из справочника Двайта, а во втором интеграло положим z1 =
=¦ аи (и2 — 1)—х/г и применим формулу B00.01) из справочника Двайта.
Заменив С на /С, можно написать эти интегралы в нескольких эквива-
эквивалентных формах, причем правильность знака в каждой из этих форм
должна быть проверена путем дифференцирования и сравнения с выраже-
выражением G.179). Эти формулы следующие:
(-1—а2I'2 , Г 1 —а2 ]/2 .„ ,оо v
KJarsh(j G.182а)
r . . -^A— И2I'2 . I Г1-О2 И 1/2 1 ,, .„..„
z = С arc sin zx + /С —arcsmsz! -g ^ f> G.1826)
, G.182b)
z — С arc sin z, -\- it —-—-— \-C '-—ar ch < -,—>-, 4,> . G.182r)
/o a U —(a/2!J) N '
j
Если zt > 1, то a; = + yl = -n-^''IC из соотношения G.182в), откуда С = 2Ajtz,
а если 1 > z1 > а, то у — В = — A — о2I^ из соотношения G.182г), откуда
а = Л (Л2+ Б2)~1/2. Согласно выражению G.181) (см. Двайт, 702), имеем
?, или Zl = athCT- 17.183)
а
Тогда (см. Двайт, 650.08)
l — a2I''2
После подстановки этого выражения в соотношение G.182в) получим
2 ( . .г A tU t\v "I ,
z = — I A arc sin ту- In -—T -\-
u | [ (A* + B*) l2 4h>* J
- ^_—-sh^-11. G.184).
(A2 + Б2I'2 *Ы J / V '
В нашем распоряжении имеются эквивалентные формы записи функции
преобразования G.1826), G.182в) и G.)82г). Для учета влияния паза на
величину магнитного сопротивления воздушного зазора следует вычислить'
поток на участке между R и S при наличии паза и в его отсутствие.
Из выражения G.183) следует, что точкам действительной осп соответствуют
действительные значения W. Для бол» ших значений U = Аъ на оси х, что-
имеет место, когда величина С— А значительно больше В, мы имеем
я, поскольку arc sin [A/{A* + B2fh] = arc tg (А/В) = (и/2) -
выражение G.184) можно написать в виде
ж = л -\- — ^ —.
или
—А) .А . В
298 Глава VII
и, в случае (х— .4) > В,
А В
arctg
G.185)
Так как в начале координат <Az = 0 [см. выражение G.181)], то его значе-
значение в любой точке х, согласно соотношениям G.134), равно
о 'о
Этот интеграл представляет собой магнитный поток, выходящий из нижней
¦плоскости на участке от х = 0 до х = С. Для создания на этом же участке
такого же магнитного потока в отсутствие паза (т. е. когда ^4'=0), но
при прежнем значении магнитодвижущей силы, ширина воздушного зазора
В' должна быть выбрана равной
в, i^/ (А + С)
Таким образом, зазор шириной В' при отсутствии пазов обладает таким же
магнитным сопротивлением, как и зазор шириной В при наличии пазов,
•если ширина последних равна 2А, а расстояние между ними равно 1С.
ЗАДАЧИ
1. Показать, что магнитная пндукция в центре проволочной петли, по которой
•протекает ток и которая имеет форму правильного плоского многоугольника с 2п сто-
сторонами и расстоянием 2а между параллельными сторонами, равна
anl . тс
-— sin — ,
па Zn
где I—ток в петле.
2. Провод протянут по окружности радиуса а всюду, за исключением дуги с уг-
углом 2ф, где он следует вдоль хорды. Образованная таким образом проволочная петля
подвешивается в точке, противопопожпой центру хорды, так, что плоскость петли при
¦этом оказывается перпендикулярной к другому прямолинейному проводу, проходящему
через ее центр. Показать, что если токи в петле и в проводе равны i и V, то момент,
действующий на петлю, ранен
txii'a , .
¦ (sm<p—9 cosy).
3. Провод образует плоскую спираль, уравнение которой н полярных координатах
имеет вид r = i?6/BniV), где iV — число всех витков, a R —радиус-вектор, пронеденный
из центра к наружному концу спирали. Показать строго, что при протекании по спи-
спирали тока / аксиальная составляющая магнитной индукции вдоль оси на расстоянии z
от плоскости спирали равна
4. Плоскость круглой проволочной петлп радиуса Ъ, по которой протекает ток i,
образует с однородным магнитным полем В угол E. Показать, что если внутрь петли
поместить концептрично шар радиуса а, обладающий магнитной проницаемостью (л,
то действующий момент возрастет на неличину
*^т~\ 2izBia3b-1 cos В.
5. Две пронодящие полосы шириной А располагаются параллельно на расстоянии В
друг от друга, образуя противоположные стороны прямоугольной призмы. По этим
¦яолосам протекает один и тот же ток I в противоположных направлениях. Показать,
Задачи 299
что при равномерном распределении тока сила отталкивания между полосами равна
^яа единицу длины)
6. Электродинамометр состоит из двух квадратных проволочных петель, длина
сторовы каждой из которых равна о; Однч из петель может вращаться вокруг оси, про-
проходящей через середину противоположных сторон обеих петель. Считая петли пересе-
пересекающимися на этой оси, показать, что момент, действующий на подвижную петлю
*! том положении, когда она образует с неподвижной петлей угол л/2, равен
]+4arcctgF1b.2)-2arccos-i} ,
¦где /—ток, протекающий по обеим петлям.
7. Два круглых цилиндра, по каждому из которых в г-направлении протекает
1 т
равномерно распределенный ток — /, расположены так, что их оси имеют координаты
ж=+с и х=—с. Эти цилиндры находятся внутри круглой цилиндрической оболочки
с осью, проходящей через точку ж = 0; по оболочке протекает в противоположном на-
«равлении равномерно распределенный ток /. Показать, что сила, направленная
j; центру и действующая на один из внутренних цилиндров, равна (л72/A6ле).
8*. Показать, что в любой точке ндоль силовой линии вектор-потенпиал, описы-
описывающий поле тока, протекающего по окружности, обратно пропорционален расстоянию
между центром окружности и основанием перпендикуляра, опущенного из данной
точки на плоскость, в которой расположена окружность. Пользуясь этим свойством,
начертить линии постоянного лектор-потенциала.
9*. Ток i течет в контуре, имеющем форму эллипса, длина которого I, а пло-
площадь А. Показать, что магнитная индз'кция в центре равна -у-^И/А.
10*. Ток i протекает по окружности радиуса а, а ток i'—в очень длинном пря-
прямом линейном проводе, лежащем л той же плоскости. Показать, что сила взаимного
притяжения между ними равна
[jut' (sec а—1),
где 2а—угол, под которым видна окружно.-.ть из ближайшей к окружности точки пря-
прямолинейного провода.
11*. Две проволочные петли с радиусами а и Ъ, имеющие общий центр, могут
свободно вращаться вокруг изолированной оси, являющейся общим диаметром обеих
петель. Показать, что при протекании по петлям токов i и i' для удержания плоско-
плоскостей петель под прямым углом требуется приложить момент
J Ь2 f,9 Ъ2Л ..,
7Ш. ( 1 — —- III.
При этом отношение Ь/а предполагается настолько малым, что величиной (Ь/аL можно
пренебречь.
12*. Токи i и С протекают по квадратным петлям, длина стороны каждой из кото-
которых равна а; стороны взаимно параллельны, а плоскости петель расположены под
прямым углом к прямой длиной с, соединяющей центры петель. Показать, что петли
притягиваются с силой
2[j.W Г с Bа2 4-c2)V2 o2 + 2c2 )
" I «2 + С2 Н с(а2+с2I/2 J '
13*. Ток i протекает в прямоугольной петле со сторонами длипой 2а и 26; петля
может свободно вращаться вокруг оси, проходящей через ее центр и параллельной
сторонам длииой 2а. Другой ток Г течет в длинном прямолинейпом проводе, парал-
параллельном оси и расположенном от нее на расстоянии rf. Доказать, что для удержания
петли в положении, при котором плоскогть петли образует угол <р с плескостью, про-
проходящей через центр петли и прямолипейный провод, требуется приложить к петле
момент
— 262d2 cos 2<?) "
300 Глава VII
14*, Круглая прояолочная петля радиуса а конпентрична сферической оболочке
из мягкого железа (внутренний радиус оболочки Ъ, внешний радиус с). Показать, что
при протекании по петле постоянного тока / наличие железной оболочки приводит
к возрастанию числа линий магнитной индукции, пронизывающих петлю, приблизи-
приблизительно на величину
(с3- Ь3)
2ЬЩКт + 2) BJCm+l) с3- г (Кт-1J Ь3] '
15*. В железе, заполняющем лее пространство и имеющем магнитную проницаем
мость [л, вырезана круглая цилиндрическая полость. Внутри полости параллельно ее
оси проходит провод, по которому течет постоянный ток /. Доказать, что провод при-
притягивается к ближайшей стенке полости с силой (на единицу длины)
где d—расстояние между проводом и его электростатическим изображением в полости.
16*. Показать, что при наличии в среде с магнитной проницаемостью [л однород-
однородного магнитного поля можно удалить любую шаровую область и поместить в образо-
образовавшуюся полость (концентрично) шар с магнитной проницаемостью [л, и сферичсскук>
оболочку с магнитной проницаемостью [л2, не исказив внешнего поля, при условии,
что [л, ё [л 5 № и чт0 выбрано соответствующее отношение объемов шара и оболочки.
Доказать также, что поле, внутри шара однородно, а его напряженность больше или
меньше напряженности внешнего поля в зависимости оттого, больше или мевыне (л
по сравнению с [л,.
17*. Шар радиуса о. изготовленный из мягкого железа, помещен п однородное
магнитное поле, параллельное оси z. Показать, что г ил оные линии вне шара распола-
располагаются на поверхностях вращения, уравнения которых имеют вид
где г—расстояние от центра шара.
18*. Шер из мягкого железа с магнитной проницаемостью [л помещается в магнитное-
поле, скалярный потенциал которого является однородным полиномом степени п
относительно х, у, г. Показать, что скалярный потенциал внутри шара равен перво-
первоначальному значению, умноженному на Bп-\-\I(пКт + п-\-\).
19*. Показать, что если вма-то шара, описанного в предыдущей задаче, поместить
оболочку с радиусами а, Ъ, то поле внутри полости изменится в отношении
(a -\2п+1
~ъ)
20*. Бесконечно длинный полый железный цилиндр с магнитной проницаемостью [л,
внутренний и внешний радиусы которого равны а и Ъ, помещается в однородное
магнитное поле, направление которого перпендикулярно к образующим цилиндра.
Показать, что число линий ршдукции, пронизывающих область, занимаемую цилиндром,
изменяется при помещении цилиндра в поле в отношении
21. В сплюснутой сфероидальной пленке ? = Ео ток имеет зональное распределение^
так что между ? = 1 и ? = ?0 функция распределения тока ф Eо)= 2 СпРп E0)- Исполь-
Используя полученный н § 11 интеграл, вычисляемый по формулам § 28д гл. V, показать,
что при С<С0 вектор-потенциал поля этого тока равеп
со
1/S 2 nn Q(Д) р(Д)рE)
71 = 1
22. Пользуясь предыдущей задачей, показать, что для области ? < Со вектор-потен-
вектор-потенциал, описывающий поле тока /, циркулирующего в проволочной петле Ко, ?0, выра-
выражается формулой
Получить результат для области t >
.. Задачи^ 301
23. Показать, что если сфероид, описанный в задаче 21, является пе сплюснутым,
вытянутым, то в области г] < rj0
n = i
24. Вытянутые сфероидальные координаты проволочной петли, но которой цирку-
циркулирует ток /, раины |0, yj0. Показать, что вектор-потенциал поля этой петли равен
25. Пусть в систему, описанную в предыдущей задаче, вносится вытянутый сфе-
сфероид, обладающий магвитной проницаемостью р.. Показать, что если поверхность этого
сфероида задана в виде yj = ttj1 , то изменение вектор-потевциала в области yj > rju
обусловленное внесением сфероида, равно
26. Показать, что вектор-потенциал, обусловленный током /, протекающим в пло-
плоской проволочной петле радиуса а, расположенной в плоскости z = 0, определяется
и области р > а формулой
А = \mIk~1 \ /j (Аа) Кг (Ар) cos kz dk.
Для р < а следует в этой формуле поменять местами р и а.
27. Показать, что ветор-потенциал, обусловленный током /, циркулирующим
в плоской проволочной петле радиуса а, равен
со
i ' f Ji (Ао) Jj (Ар) (
28. Ток / циркулирует по проволочвой петле радиуса а, расположенной коакси-
ально с бесконечным цилиндром радиуса 6. Проницаемость цилиндра равна и. Пока-
Показать, что часть ьектора-потенциала, обусловленная наличием цилиндра, определяется
вне циливдра формулой
„а/я-1 ^ Ф (A) i?"i (Аа) Кл (Ар) cos Az dk,
где
( > (Кт
Написать формулу, определяющую вектор-потенппал во внутренней области.
29. На участке длиной 2с поверхности круглого цилиндра радиуса а циркулирует
вокруг оси цилиндра равномерно распределенный ток /. Показать, что в области р > а
вектор-потенциал определяется формулой
^ — t^L С i. i1 (ка) Кг (А-р) cos kz sin Ac dk.
О
30. Iln плоской круглой проволочной петле радиуса а, расположенной парал-
параллельно бесконечной пластине толщиной I на расстоянии 6 от поверхности воследпей, про-
протекает ток 1. Показать, что если материал, из которого изготовлена пластина, обладает
магнитной проницаемостью р., то вектор-потенциал перед пластиной (где находится
302 Глава VII
петля), внутри пластины и за пластиной определяется соответственно формулами
со
О
СО
А3 = 2^Кта1 \ Jx (А-р) Jx (ka) Се'** dk,
О
где р отсчитывается от оси петли, z—от плоскости петли и
31. Бесконечный сплошвой круглый цилиндр радиуса аг и магнитвой проницае-
проницаемости [л=оо расположен коаксиальио с бесконечной цилиндрической трубой, выполнен-
выполненной из того же материала и имеющей инутренний радиуг а2. В пространстве между
ииыи помещено коаксиальное проводящее кольцо, ограниченное поверхностями: p = 6i
и р = #2, z = c1 и z = c2. По кольцу циркулирует ток /, точное значение плотности-
которого [см. выражения F.105)] задано строго в виде t»=/[p(c2—Ci) In F2/Ь,)]~*.
Показать, что вектор-потенциал в области z> с2 > сх при % < р < о3 определяется-
формулой
где Дт (Апр) = Уо (knui) Jm (А^р)—Jo (Anoi) Fm (Anp), a kn выбрано так, что Ro (A^ o2) = 0 и
32. Предположим, что железо в трангформаторе броневого типа обладает бесконеч-
бесконечной магнитной проницаемостью, а стенки «окна» заданы уравнениями р = о,, р = о2, z = 0,
z = L. Используя результаты предыдущей задачи и результаты, полученные в § 30 и-
гл. V, показать, что поле тока, циркулирующего в проводящем кольце, ограничен-
ограниченном поверхностями р = &t, р = Ь2, z = clt z = c2, описывается снаружи проводника вектор-
потенциалом следующего вида:
в области z < в! < с2
со
а в области сх < с2 < z
со
где постоянные определяются так же, как и в предыдущей задаче. В области сг < z < сг
имеем
33. Стенки бесконечно длинной трубы, обладающие бесконечной магнитной про-
проницаемостью, заданы уравнениями
Параллельно стенкам вдоль линии sr = e, y = d(Q<c<a и 0<d< b) протянут провод,
по которому течет ток /. Показать, что вектор-потенциал внутри трубы равен
в области 0 < у < d
со
2ixl хл 1 ттЬ , тгт ., ... mm/ rime ткх
Л' = -!— >. — cosech • ch ¦ F — d) ch —•- cos —— cos — ,
г n ZJ m a a v 'a a a
Задачи 303".
в области d < у < b
... 2u/ vi 1 . тъЪ , rrmd , пи тгс ттта;
Л''=—г— >. —cosech ch ¦ en -F—у) cos cos ..
i -к t-l m а а оч/ а а
34. Показать, что компоненты силы (на единицу длины) в предыдущей задаче равны
оо
и р!2 ЧЛ l mnb пи ттсс
F,,=i-— >, cosech sh Bd— 6) cos2 -—-,
Fx = ?-— >. cosech sh -T-Bc - о) cos2—г—.
о *—i b b b
m=l
Заметим, что всюду, за исключением очень малых с и d, ряды сходятся очень быстро.
35. Бесконечно длинный провод, по которому течет ток /, расположен вдоль,
линии х = а, у=Ъ между двумя бесконечными пластинами (v = 0 и у = с), обладающими.
бесконечно большой магнитной проницаемостью. Показать, что вектор-потенциал между
пластинами определяется выражением
тт (^ 1 \С Т-Ь , т: (х—а) куЛ2 , ,, ^ (я-—а) . „ку!
U=—Ц— In cos ch — -'cos— ) +sh2—5 -'sin2— .
ад LV c с с J с с _\
Это выражение представляет собой действительную часть функции
W=— V- In cos ch—^ i .
2л |_ с c J
Заметим, что поле является однородным и имеет противоположное направление при
ж>а и а; ¦Со.
36. Бесконечный провод, по которому течет ток /, расположен в плоскости z — z0,
справа от бесконечного полупространства, заполненного веществом с бесконечной
магнвтпой проницаемостью. Граница этого полупространства представляет собой пло-
плоскость ж = 0, имеющую круглый цилиндрический бугорок или круглую цилиндри-
цилиндрическую выемку радиуса 6 с центром в точке я = е. Используя результат задачи 49>
гл. IV, показать, что вектор-потенциал является действительной частью функции
где
a {[Z + /C'2 —с2I/2ГУо — [г—/(Ь2— с2I'2]^"}
и cos a—c/b. Для бугорка 0 < а < тс, а для выемки тс < 2а < 2тс.
37. Используя соотношение —In (z—о)=\ k'1 \e~h ^z~a^ — е~ь] й/с, где действи-
действительная часть (z—о) положительпа, показать, что поле провода, по которому течет
ток 1 и который расположен в плоскости х=а между двумя плоскими границами (ж = О
и х = Ь, где 0 < а < Ь) двух полубесконечных сред с магнитной проницаемостью [л*
находится посредством следующих преобразований:
в области 0 < х < b
ehb ^g-kb 1—|
0
в области b < x
и области x < 0
Wa = —, „¦v , ,. \ —p- e^1 ¦¦; E dk,
n(Km-\-i) J ft |_ \ k2g~2hb 1 fi J
¦304 Глава VII
где U—вектор-потенциал, prW—скалярный потенциал, W = U-j-/V и & = (Km-^i)x
x(JTm+ !)-•.
38. Показать, что поле пронода, по которому течет ток 1 и который расположен в пло-
плоскости х = d между двумя шюс кими границами (ж = — сих= ~\-с, где — с < d -j-c) двух
полз'бесконечных гред с магнитной проницаемостью ц, находится посредством гледу-
ющих преобразований:
и области ¦—с < х < с
( + У fl
и области с < a;
в области х < — с
тдс p = (^m—i)(Km-\-i)-*, U— вектор-потенциал, \х~Чт — скалярный потенциал в W =
= U-\-/V. Этот результат можно получить непосредственно путем применения метода
изображений или путем разложения знаменателя в функции преобразования, рассмо-
рассмотренной в предыдущей задаче, г последующим интегрированием и заменой z на z~\-c,
Ь на 2с и а — с на d. Чтобы неличина U вблизи начала координат была конечной, сле-
следует добавить к ней бескопечпо большую постоянную неличину
39. Сраннить первый интеграл в § 11, определяющий А , с выражевием E.191)
т показать, что вектор-потенциал поля, обусловленного током /, циркулирующим
я круглой проволочной петле радиуса а, ранен
А = 2-х/2[х/ (ch к, — cos м2I/2 Pi1/2 (ch щ),
¦rpfi в соответствии с § 14 гл. IV 2ар cthul = r2-j-a2 и 2ozctgM2 = ''2—°2-
40. Используя задачу 117 гл. V, результаты § 14 гл. IV, ныражения G.32) и
E.206), добавить к выражению для А , данвому в предыдущей задаче, такие члены,
чтобы магнитное поле оказалось тангенциальным к тору (ihu, = c/b), полученному
лутем вращения окружвости радиуо 6 вокруг прямой, лежащей в плоскости этой
окружности не расстоянии с от ее центра. Показать, что полученная сумма равна
- cos nu2.
ЛИТЕРАТУРА
Abraham M., Becker R., Klassische Elektrizalet und Magnetismus, Berlin, 1932.
(См. перенод: А б р а г а м М., Б е к к е р Р., Теория электричества, М.—«П.,
1939.)
Attwood S. S., Electric and Magnetic Fields, Wiley, 1932.
Curtis H. L., Electrical Measurements, McGnw-Hill, 1937.
¦Geiger-Scheel, Handbuch der Physik, B. XV, Berlin, 1927.
Cray A., Absolute Measurements in Electricity and Magnetism, v. II, Macmillan, 1888.
Hague В., Electromagnetic Problems in Electrical Engineering, Oxford, 1929.
(См. перевод: Хэг Б., Электромагнитные расчеты, М.—Л., 1934.)
Литература 305
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
Lass, Harry, Vector and Tensor Analysis, McGraw-Hill, 1950.
Mason M., Weaver W., The Electromagnetic Field, University of Chicago Press,
1929.
Maxwell J. C, Electricity and Magnetism, v. II, Oxford, 1881.
Moullin E. В., Principles of Electromagnetism, Oxford, 1932.
P e i г с е В. О., Newtonian Potential Function, Ginn» 1902.
Planck M. K. E. L., Theorie der Electrizitat und Magnetismus, Berlin, 1932.
Poor V.C., Electricity and Magnetism, Wiley, 1931.
Ramsey A. S., Electricity and Magnetism, Cambridge, 1937.
Russell A., Alternating Currents, Cambridge, 1914.
Stratton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: Страт-
тои Дж. А., Теория электромагнетизма, М.—Л., 1948.)
Walker M., Conjugate Funktions for Engineers, Oxford, 1933.
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
Wien-H arras, Handbuch der Experimentalphysik, B. XI, Leipzig, 1932.
Глава VIII
S
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
§ 1. Закон индукции Фарадея. Сто лет тому назад Фарадей и, неза-
независимо от него, Генри обнаружили, что если магнитный поток N [см. выра-
выражение G.161)], пронизывающий замкнутый проводящий г.онтур, изменяется,
то в контуре возникает ток. Направление этого индуцированного тока таково,
что его собственный магнитный поток препятствует изменению первоначаль-
первоначального магнитного потока. Таким образом, если поток через контур в неко-
некотором направлении увеличивается, то поток, обусловленный индуцирован-
индуцированным током, направлен в сторону, противоположную этому направлению;
если же первоначальный поток уменьшается, то поток/ обусловленный
индуцированным током, направлен в ту же сторону, что и первоначальный
поток. Индуцированные токи всегда стремятся сохранить статускво магнит-
магнитного поля. Электродвижущая сила индукции (в вольтах) равна взятой с обрат-
обратным знаком скорости изменения потока (в веберах в 1 сек.)
Здесь возможны некоторые ограничения, о которых будет сказано позднее.
Совершенно несущественно, благодаря чему изменяется поток: можно
перемещать относительно контура источник, создающий этот поток, можно
изменять величину потока, перемещать контур или изменять его форму.
Фарадей доказал справедливость соотношения (8.1) для замкнутого метал-
металлического контура, но поскольку мы знаем, что тангенциальная состав-
составляющая V2? = Е одинакова по обе стороны поверхности проводника, соот-
соотношение (8.1) должно быть справедливо и для электродвижущей силы
вдоль пути, проходящего вне проводника. Можно, следовательно, утвер-
утверждать, что соотношение (8.1) справедливо для любого замкнутого пути,
и написать, пользуясь выражением G.161), для двухсторонней поверхно-
поверхности S
^-ds = -~^ В-в AS. (8.2)
s
Преобразуя левую часть соотношения (8.2) на основании теоремы Стокса
C.3), получим
S S
Поскольку это должно выполняться для произвольной поверхности, мы
имеем
• VxE=-f- (8.3)
в вебер 1(м • сек)г. Если Е возникло исключительно вследствие электро-
электромагнитной индукции (специальный случай Е", рассмотренный в § 2 гл. IV)
Электромагнитная индукция 3(}Т
й не имеет ни источников, ни стоков, то дивергенция Е равна нулю:
Если вектор А получен из формулы G.10), то его дивергенция также
равна нулю. Заменим теперь в соотношении (8.3) В на V X А и переменим
местами djdt и rot; тогда нетрудно видеть, что роторы векторов Е и
— dA/dt раввы между собой. Если два вектора обладают всюду одинаковыми
роторами и дивергенциями, то они равны друг другу; отсюда получаем
соотношение
которое связывает напряженность электрического поля или э. д. с. на 1 м
с вектор-потенциалом, изменение которого порождает это поле.
Соотношение (8.1) применимо во всех случаях, когда происходит измене-
изменение потока сквозь недеформируемые контуры, а также в тех случаях, когда
поток изменяется вследствие деформации контура, при условии, что все
элементы контура, соединенные вначале, не разъединяются в течение всего
процесса. Можно придумать такие эксперименты с использованием сколь-
скользящих контактов, когда возможность применения соотношения (8.1) является
сомнительной или просто неясной. Эти случаи можно было бы рассмотреть,
концентрируя внимание не на области, охватываемой цепью, а на элементах
самой цепи, и затем уже прилагая соотношение (8.4).
Другая формулировка закона индукции дается в гл. XVI, где пока-
показывается, исходя из специальной теории относительности, что если наблю-
наблюдатель перемещается относительно неподвижного контура, создающего
магнитную индукцию В, то он обнаружит, вообще говоря, наличие
некоторой электродвижущей силы. Пусть v — скорость движения, Е — напря-
напряженность электрического поля, возникающего благодаря движению; тогда
из соотношения A6.93) получим
E = [vxB], (8.5)
где Е измеряется в в/м, v—в м\сек и В—в еебер/м2-
§ 2. Взаимная энергия двух контуров. Рассмотрим теперь работу,
необходимую для сближения двух контуров, в которых циркулируют по-
постоянные токи / и /'. Каждый контур содержит э. д. с, являющуюся
источником или поглотителем энергии и обеспечивающую постоянство токов
в течение всего времени. Для контура 1, пользуясь законом Ома F.6) и
(8.1), имеем
а4
где Ш — вышеупомянутая э. д. с. Энергия, потребляемая в контуре 1 при
его перемещении из бесконечности за время t, равна, согласно соотноше-
соотношению F.11).
t t N t
PR^dt^I ^gdt±I J dN^I^gdt± N1,
0 0 0 0
где N — поток через первый контур, создаваемый вторым контурож при их
окончательном взаимном расположении. Очевидно, последний член выражает
работу, совершенную в первом контуре благодаря наличию магнитного поля
второго контура. В то же время для поддержания во втором контуре тока
постоянным в нем затрачивается работа ± NT. Таким образом, общая
энергия, затраченная источниками э. д. с. в двух контурах для поддержа--
ния постоянства токов при сближении этих контуров, равна
± {IN + FN').
20»
308 Глава VIII
Подставляя вектор-потенциал в соотношение G.161) и пользуясь теоремой
Стокса и формулой G.10), получим
N= { В' -ndS= ^VxA' -ndS= <J3 A' - ds = ^-
s s
и аналогично
<8-6>
так что затраченная энергия представляется в виде
^-. (8.7)
Закон Фарадея показывает, что если два контура притягиваются друг к
другу, то индуцированная э. д. с. приводит к возникновению такого поля,
которое стремится изменить направление тока в каждом контуре, поэтому
источники э. д. с. должны доставлять энергию для поддержания постоянства
токов / и /'. В случае, когда контуры отталкиваются друг от друга, про-
происходит обратное явление.
Рассмотрим механическую работу, совершаемую против магнитных сил
при движении двух контуров. Согласно соотношению G.98), сила, дей-
действующая на контур 1, равна (в ньютонах)
При интегрировании по контуру 1 первый член пропадает, поскольку под-
интегральное выражение г/г3 можно представить как градиент скаляра 1/г.
Тогда механическая работа, затраченная только на перемещение от г=оо
до г— г, равна
Сравнивая соотношения (8.7) и (8.8), мы видим, что половина энергии,
Затрачиваемой батареей в цепи, идет на совершение механической работы.
Но поскольку единственная разница между начальным и конечным состо-
состояниями заключается в изменении магнитного поля, окружающего контуры,
то и разница в значениях энергии должна быть равна изменению энергии
магнитного поля. Таким образом, при относительном перемещении двух
контуров, несущих постоянные токи, механическая работа, совершаемая
контуром, возрастает или уменьшается в той же мере, как и энергия
магнитного поля. Это объясняет кажущийся парадокс, упоминаемый в
§ 19 гл. VII. Отсюда также следует, что если известна энергия Wb маг-
магнитных полей двух контуров, то можно вычислить механическую силу или
момент, стремягцихся увеличить координату 0, беря производную этой
энергии по 6, т. е.
р 8WB ¦ ,г> сп
F=+-ar- (8-9>
§ .3. Энергия магнитного поля. Найдем энергию, требуемую для соз-
создания магнитного поля одиночного контура. Воспользуемся результатами,
полученными в последнем- параграфе, и будем считать, что все простран-
пространство заполнено однородной изотропной средой с проницаемостью [а. Построим
поле, составляя контур из бесконечно тонких нитей тока. Пусть резуль-
результирующая плотность тока всюду конечна. Знаменатель в соотношении (8.8)
Электромагнитная индукция 308
не может обратиться в нуль, так как конечные нити тока расположены
друг от друга на конечном расстоянии. Чтобы получить правильное зна-
значение энергии, в соотношение (8.8) для одиночного контура необходимо
добавить множитель 1/2, поскольку интегрирование учитывает не только
работу при приближении нити а к Ь, но также работу при приближении
нити Ъ к а. Введем, кроме того, в соотношение (8.8) плотность токов в
соответствии с формулой F.2); тогда оно примет вид
V V'
где г— расстояние между элементарными объемами dv и dv', i и i'— плот-
плотности тока в этих объемах; интегрирование по пространству производится
дважды, причем, как и в § 2, мы полагаем, что в области интегрирования
[а постоянно. Заменяя i согласно выражению G.4), а \ (i'/r) dv' соглас-
v
но выражению G.8), имеем
WB-^- WxB • Adv. (8.11)
V
Пользуясь формулой для дивергенции векторного произведения
A- VxB = B- [VxA]-V • [AxB] = ?2_v . [АхВ],
получим
WB=±-[ B2d\ — ^-[ V -[AxB](fv,
V V
где интегрирование распространяется на все пространство. По теореме
Остроградского — Гаусса C.2) второй интеграл можно преобразовать в по-
поверхностный интеграл по бесконечной сфере. Этот интеграл исчезает, по-
поскольку из выражения G.8) следует, что А стремится к нулю как 1/т\
B = VxA как 1/г2, а площадь поверхности возрастает только как г2,
так что
\ V • [AxB]dv= \ [АхВ] -ndS~*0.
v S
Таким образом, окончательное выражение для энергии получаем в виде
(8.12)
Энергию можно считать локализованной в пространстве, где находится
магнитное поле, окружающее ток; плотность энергии равна -^В21р,. Сравни-
Сравнивая это с выражением B.18), определяющим энергию электростатического
поля, мы видим, что магнитное поле так же, как и электростатическое,
можно, для наглядности, трактовать при помощи системы натяжений.
§ 4. Коэффициент взаимной индукции. Коэффициент взаимной индук-
индукции Ж]2 двух контуров определяется как поток 7V12 через контур 1, об-
обусловленный единичным током в контуре 2. В системе единиц MKS едини-
единицей взаимной индукции является генри. Математическая запись определе-
определения М12 имеет вид
ilf[2= ^B2-ndSu . (8.13)
Si
310 Глава VIII
или
М12 = (? А, • ds1? (8.14)
где А2 — вектор-потенциал поля, созданного единичным током в контуре 2.
Пользуясь выражением (8.6), можно написать
^L = Mai. (8.15)
Поток через контур 1, обусловленный током /2 в контуре 2, будет равен,
как ато вытекает из формулы (8.13),
NM = M12IV (8.16)
Из формулы (8.1) получаем, что э. д. с. в контуре 1, наводимая при изме-
изменении тока в контуре 2, равна
Шг^-М^. .(8.17)
Из соотношения (8.8) видно, что взаимную энергию двух контуров можно
представить следующим выражением:
Wlt = MtsI1Ia. (8.18)
Согласно выражению (8.12), общая энергия двух контуров равна
Wt =± \ (В1 + В2) • (B1 + B2)dv= 1( [ B\dv + 2 $ В, • B2dv + \ B\dv) .
V V V V
Первый член определяет энергию, требуемую для установления тока 11F
а последний — тока /2; средний член выражает энергию их взаимодействия.
Следовательно, из выражения (8.18) имеем
¦^i2V2=-^^B1.B2dv. (8.19)
V
Согласно формуле (8.9) сила или момент, стремящиеся увеличить неко-
некоторую координату 6, определяющую положение одного контура относи-
относительно другого, выражается соотношением
§ 5. Граничные условия для а. В § 22 гл. VII были использованы усло-
вия для производных квазивектор-потенциала а на границе раздела двух
сред с различной проницаемостью. В предыдущем параграфе мы впервые
лстретились с соотношением (8.14), содержащим шттеграл от а, поэтому
теперь нужно рассмотреть те граничные условия, которые необходимо нало-
наложить на вектор а, для того чтобы это соотношение было пригодно и
is местах нарушения непрерывности. Возьмем небольшой прямоугольный
контур, длинные стороны которого находятся близко друг к другу, но
расположены по обе стороны от границы раздела двух сред с различной
проницаемостью. По мере сближения этих сторон площадь прямоугольника
стремится к нулю, так что поток через этот контур, обусловленный током /„,
текущим во втором контуре, должен исчезать. Но, согласно соотношениям
{8.14) и (8.16), этот поток равен N = /„ т a2ds. Поскольку короткие сто-
стороны прямоугольника исчезагоще малы, основной вклад в интеграл дадут
большие стороны длиной L, которые, однако, настолько коротки, что век-
вектор а вдоль них можно считать постоянным.
Электромагнитная индукция
311
Но, согласно выражениям G.122) л G.123), тангенциальная компо-
компонента вектора а имеет одинаковое направление но обе стороны поверхности
раздела, поэтому, ориентируя прямоугольник вдоль us и ut, мы получим
для соответствующих тангенциальных компонент вектора а
ф
s,< = L (a'Stt — a's[t) = 0
Таким образом,
<* = <«. (8.21)
§ 6. Коэффициент взаимной индукции простейших коитуров. В каче-
качестве простого примера вычисления коэффициента взаимной индукции рас-
рассмотрим две плотно намотанные катуш-
катушки А и В, изображенные на фиг. 79.
Катушка В содержит п витков и намо-
намотана на кольце с проницаемостью р.. Ка-
Катушка А имеет т витков. Поскольку
весь поток проходит через кольцо, из
соотношений G.164) и (8.16) получим
M12 = [ircm[a-(a2 — б2I'*]. (8.22)
Если а > Ь, то а можно вынести из-
под корня и остаток разложить в ряд
{Двайт, 5.3), оставляя лишь квадратич-
квадратичные члены. Тогда
., \i.nmb2
2а
(8.23)
Фиг. 79.
Если А = кЬ2, щ = n/Biw.) — число вит-
витков на единицу длпны, то коэффициент
взаимной индукции между бесконечным
соленоидом, намотанным на цилиндр площади А и проницаемости \х,
и окружающей цилиндр катушкой, содержащей т витков, равен
М12 = \т1тА. (8.24)
Этот результат можно было бы сразу получить, воспользовавшись непо-
непосредственно выражением G.86).
§ 7. Коэффициент взаимной индукции двух колец. Используя соот-
соотношение (8.14), можно написать выражение для коэффициента взаимной
индукции двух коаксиальных проволочных колец. Вектор - потенциал
кольца А (см. фиг. 80) имеет лишь ср-составляющую и одинаков для всех
элементов кольца В, поэтому из соотношения (8.14) получим
Me
L = ф Аа ¦ dsB = 2-кЬ
Таким образом, согласно выражению G.51), имеем
М12 = 2,!*-1 (ahI'* [ С 1 - 4 й2) К - Е ] ,
где, как видно из выражения G.50),
(8.25)
+ c2]-1. (8.26)
Численное значение К и Е можно найти в справочнике Двайта A040 и
1041). Точно таким же образом, исходя из соотношения G.71), получается
312
Глава VIII
другое выражение для М12. Считая а= -^-
§ 16з гл. V, при Ь2 -\- с2 < я2 находим
T1=I
(и—нечетное)
б = р и используя результаты
). (8-27)
В случае Ь2 + с2>а2 следует написать вместо [(Ь2 + с2)/а2]1/2П выражение
[2/(fcs 2)](+1)/2
[/( )]
Исходя из выражений (8.14), G.72) и E.217), можно вычислить вза-
взаимную индукцию двух произвольно ориентированных колец, если их оси
Фиг. 80.
пересекаются. Так, в случае, изображенном на фиг. 80, б, при Ъ > а, взяв
за начало координат точку пересечения осей и отсчитывая угол 6 между
ними от оси кольца а, получим
[Br]bevaBdQdtf.
(8.28)
о о
Если 6' — угол, отсчитываемый от оси кольца Ь, то, заменяя в соотноше-
соотношении G.72) величину ,Pn(cos6') в соответствии с выражением E.217), где
f = в, а = г и 1=1, будем иметь
г]ь = ^ ? (т)"р- <cos Р) S B -8») ё
п=1
т=0
e)
После подстановки этого выражения в соотношение (8.28) и интегрирова-
интегрирования по <р остаются лишь члены, содержащие т~0. Согласно соотношению
E.118), интегрирование по б дает
cos «
=_ Sin а П (COS a)
и для коэффициента взаимной индукции получаем выражение
со
' = ^а sin a sin р ^
§ 8. Переменная взаимная индукция. На фиг. 81 изображено устрой-
устройство, часто употребляемое для получения переменной взаимной индукции
(вариометр). Каждая катушка содержит один слой провода, намотанного
на каркас со сферической поверхностью. Одна катушка вращается относи-
Электромагнитная индукция
313
тельно другой, находясь с ней на общей оси. Обозначим через f угол
между плоскостями катушек, через а и Ь радиусы двух сферических поверх-
поверхностей и через 2А и 1В угловую ширину обмоток катушек. Допустим, что-
катушки состоят из плоских проволочных колец, равномерно распределен-
распределенных с плотностью п колец на единицу длины. Число витков п' на еди-
единицу угла для каждой катушки будет тогда п'а = паa sin а и n{,= nbbsin р
соответственно. Взаимная индукция между элементами двух катушек,
согласно выражению (8.29), равна
dMab =
ab
sin® a sin*
?Р" W P'n Ы Pn (cos T) da
Общая взаимная индукция получится после интегрирования по обеим ка-
катушкам, т. е.
я=-п+А
- S г
dM,
аЪ'
—В
Обозначая cos a или cosp через и, при-
ходим при помощи соотношения E.123)
к интегралам вида
Интегрируя [см. соотношение E.120)] и
производя упрощения, согласно выраже-
выражению E.118), получаем
(8.31)
Если и — четное число, то оба предельных значения равны и, следо-
следовательно, исчезают, так что остаются значения лишь для случая, когда
п — нечетное число.
Для п = 1 необходимо специальное исследование. В этом случае иа
выражения (8.30) имеем
f)]iA |-sin^). (8.32Y
(8.33)
Аналогичные выражения получаем для В. В результате находим
со
Т1=1
(и—нечетное)
Коэффициенты, зависящие от заданных размеров катушки, можно вычи-
вычислить, после чего формула принимает вид
Маъ= ^ ^A
(и—нечетное)
где 7 — угол между плоскостями катушек.
(8.34)
Глава VIII
§ 9. Самоиндукция. Как следует из выражения (8.12), магнитная
энергия одиночного контура, по которому течет ток 11г пропорциональна
В2; но, поскольку индукция В пропорциональна 11г имеем
Коэффициент пропорциональности Llu являгопщйся величиной постоянной,
называется коэффициентом самоиндукции или самоиндукцией контура. Другая
полезная формула для вычисления самоиндукции получается путем подста-
подстановки выражения G.4) в выражение (8.11), а именно:
-Adv = YL"/B' (8-36)
где интегрирование производится но области, в которой имеется ток.
Б системе MKS единицей индуктивности является гепри.
Самоиндукция контура, состоящего из бесконечно тонкой проволоки,
ло которой течет конечный ток, оказывается бесконечной, так как
величина В вблизи провода обратно пропорциональна расстоянию до него.
Следовательно, при конечной длине провода интеграл в выражении (8.35)
логарифмически расходится (dv можно представить в виде rdrdG). Это
означает, что при вычислении самоиндукции мы обязаны учитывать
геометрические размеры провода и нигде не принимать плотность тока i
бесконечной. Будем рассматривать провод как пучок нитей тока, каждая
из которых обладает бесконечно малым поперечным сечением dS и несет
ток idS. При установлении тока в таком проводе магнитный поток
каждой нити тока пересекает соседние нити и по закону Фарадея (8.1)
возбуждает в них э. д. с. индукции, направленную противоположно току
и равную Щ ——dN/dt, где dNjdt—изменение потока, пронизывающего
контур, в 1 сек. Для поддержания тока 1г источник энергии должен
кроме работы, затрачиваемой на преодоление сопротивления, совершать
еще работу, равную (в 1 сек.)
Ш1г = 1^. (8.37)
Энергия, запасаемая магнитным нолем в 1 сек., равна dW/dt, поэтому из
выражений (8.35) и (8.37) имеем
т dN1 _ г т dl-t
Il~dT ~^iyi"dT-
Сокращая /t и интегрируя от момента времени, когда ток отсутствовал
до момента окончательного установления тока, получим
JVu = JVi- (8.38)
Таким образом, можно определить самоиндукцию контура как приращение
потока, пронизывающего контур, при изменении тока иа единицу. Электро-
Электродвижущая сила, наведенная в контуре при изменении тока, равна
§ 10. Вычисление самоиндукции. Тонкий провод. Из всего вышеска-
вышесказанного естественно следует, что при вычислении самоиндукции нужно
отдельно рассматривать две области: область вне провода и область внутри
провода. Вклад последней бывает часто пренебрежимо малым, однако если
даже он существенен, но радиус провода мал по сравнению с остальными
размерами контура, то можно допустить, что иоле снаружи равно иолю
Электромагнитная индукция 315
тока, сконцентрированного на оси провода, а поле внутри идентично с по-
полем длинного прямого провода данного поперечного сечения, по которому
течет тот же самый ток. Силовые линии вблизи поверхности являются при-
приблизительно окружностями, концентричными оси провода, так что весь
поток снаружи провода связывает осевую нить с любой линией, проведен-
проведенной параллельно ей на поверхности провода. Чтобы получить эту часть
самоиндукции, нужно, следовательно, найти коэффициент взаимной индук-
индукции между двумя параллельными криволинейными контурами, располо-
расположенными друг от друга на расстоянии, равном радиусу провода.
Внутри провода м. д. с. вдоль окружности радиуса г (с центром на оси)
зависит, согласно определению G.150), только от тока, протекающего вну-
внутри этой окружности. Так как вследствие симметрии В зависит только
ют г, из § 15 гл. VII следует, что
h L (8.40)
где /—полный ток, а —радиус провода. Энергия внутри провода, как
видно из выражения (8.35), равна
где через L обозначена длина провода. Отсюда внутренняя самоиндукция
на единицу длины равна
где [i/ — магнитная проницаемость провода.
§ 11. Самоиндукция круглой петли. Пользуясь методом, развитым
в предыдущем параграфе, и результатом рассмотренного примера, вычис-
вычислим самоиндукцию проволочной петли радиуса Ъ, проницаемости fi/ (радиус
привода а). Длина проьода составляет 2тг5, поэтому внутренняя самоин-
самоиндукция, согласно выражению (8.41), равна
I*=iv'b. (8-42)
Как было показано в § 10, мы можем получить остальную часть самоин-
самоиндукции, применив соотношение (8.25) к двум замкнутым контурам, один
из которых совпадает с осью провода, а другой — с его внутренним краем.
В этом случае, согласно соотношению (8.26), полагая с = 0 и а <С Ь, получим
. /2 . 4Ь(Ь-а) а2
1 к — L
При А; як 1 значение Е, согласно соотношению (8.25), равно
7С/2 75/2
Е= С A— sin2eI/2rf8= (Cos6d6=l.
о о
Для получения К положим <р = -^-тг—0 и разобьем нптервал интегрирова-
интегрирования на две части."
Tt/2 ?>0
_ (iA;sine) A —/f2cos2<pI/2 J A—A:2 cos2 <pI/2 '
0 0 'f0
316
Глава VIII
где A — A;2) <g tp0 < 1. Поэтому положим в обоих интегралах к=1, а в пер-
первом интеграле, кроме того, заменим sintp на tp, тогда
к= С
> (&'2
^/2
С rfy
J Sin <у "
sm<f>
и * * ©
Далее производим интегрирование (Двайт, 200.01 и 432.10), полагаем
) = tgtp0 и, пренебрегая к'2 по сравнению с ср2,, находим
— —1 Л —1 **
^ ~ п "fc7 ~~ п о
Подставляя значение К в соотношение (8.25) и прибавляя найденное вы-
выражение для внутренней индуктивности (8.42), получаем окончательно
(8.43)
где [х' — проницаемость внутри провода, [i — снаружи.
§ 12. Самоиндукция соленоида. Рассмотрим соленоид в виде цилин-
цилиндра, в бесконечно тонком поверхностном слое которого течет ток в напра-
. 21 = L *-\ влении, перпендикулярном к оси
цилиндра (см. фиг. 82). Для стро-
строгого вычисления самоиндукции та-
такого цилиндра следует воспользо-
воспользоваться соотношением (8.25), позво-
позволяющим найти взаимную индукцию
отдельных элементов оболочки, а
затем проинтегрировать найденное
выражение по всей оболочке. Однако
результат получается довольно слож-
сложным. Но если длина соленоида ве-
велика по сравнению с его диаметром, то поле внутри него в любом
сечении, перпендикулярном к оси, можно приближенно считать одно-
однородным. Для вычисления самоиндукции при помощи соотношения (8.38)
нам нужно знать поток, пронизывающий любой элемент оболочки, после
чего проинтегрировать по поверхности. Согласно выражению G.83), поток
(отнесенный к единице тока) через ndx витков в интервале dx равен
Фиг. 82.
1-х
;jdx.
Проводя интегрирование (Двайт, 201.01) от —/до +1, имеем
Ln = тг[ш2гс2 [DZ2 + а2I'2 -а] = ^а2п2 [(IJ + а2I'2 - а].
(8.44)
§ 13. Самоиндукция двухпроводной линии. Используя соотношение
(8.36), вычислим строго самоиндукцию на единицу длины двухпроводной
линии. Будем полагать (см. фиг. 83), что ток одного направления равно-
равномерно распределен в проводе радиуса а, а обратного направления—в про-
проводе радиуса с; оси проводов параллельны и расположены одна от другой
на расстоянии Ъ. Магнитную проницаемость окружающей среды и проводов
примем равной единице. Вектор-потенциал и плотность тока имеют, оче-
очевидно, лишь z-комионенту. Если / — полный ток, то плотности токов будут
равны
Электромагнитная индукция 317
Для нахождения вектор-потенциала А' ноля внутри провода, обусловлен-
обусловленного током, текущим по этому проводу, напишем уравнение G.6) в цилин-
цилиндрических координатах [см. уравнение C.18)] и получим, помня, что А'
является функцией лишь р,
д Г дА'\ . jxl и./ „ .
—тг( Р~а~ )— — F— —-*-«¦ или +^~т ¦ (8.46)
р dp V др У та2 тсс2 v '
Интегрируя дважды от 0 до р, имеем
4^#4 ^4 (8.47)
Вне провода, полагая i = 0 в соотношении (8.46), интегрируя дважды
от внешней границы провода до ру и замечая, что нижний предел при
каждом интегрировании получается подстановкой рг — а в выражение
(8.47), имеем
Аналогично
A't' = C +^-+^- \п&¦ (8 49) Фиг- 83'
Для того чтобы соотношения (8.48) и (8.49) согласовались с соотношением
G.44), мы должны положить
Сх= -С2. (8.50)
Согласно соотношению (8.36), имеем
lxxp = ^ ix {a\ + a;') dsx + ^ г2 (^ + a;') dS2. (8.51)
Si S2
Сперва вычислим лишь первый интеграл, а затем, используя симметрию,
сразу напишем значение второго интеграла. Пользуясь формулой (868.4)
из справочника Двайта и опуская С1г находим
о о
а
0 0 0
Аналогично для второго провода имеем
Складывая соотношения (8.52) и (8.53), получаем
^нК1+21п50- (8-54)
Если провода одинаковы, т. е. а = с, то
4) . .... (8-55)
318 Глава Г III
§ 14. Энергия п контуров. Пусть имеется п контуров, по которым
текут токи Iv /2, ..., 1п, и магнитная индукция, обусловленная этими
токами, равна В1; Bg, -.., Ви соответственно. Посколыгу результирующая
индукция является их векторной суммой, общая энергия поля, согласно
формуле (8.12), будет равна
. (8.56)
V 4=1 i=ly=
В двойную сумму произведения В4-В; и Ву-В; входят так, что, пользуясь
соотношениями (8.35) и (8.19), выражение (8.56) можно представить в виде
Как мы видели в § 2, сила или момент, стремящиеся увеличить коор-
координату б ?-го контура, равны производной от энергии поля по этой коор-
координате; таким образом,
4<§ ^). (8.58>
§ 15. Натяжения в магнитном поле. Мы видели в соотношениях (8.12)
и B.18), что плотности энергии dW/dv магнитного и электрического нолей
даются выражениями
™Л * Г™-) =?-. (8.59)
Из соотношения G.1) известно, что всюду V-B = 0, а из соотношения C.4)
следует, что в отсутствие электрических зарядов V • D = 0. Поэтому состоя-
состоянию равновесия в магнитном ноле соответствует та же система натяжений,
что и в электрическом поле, если в последнем заменить D на В и е на р.
Таким образом, на основании результатов § 15 гл. I магнитные силы можно
представить в "виде натяжения Т, направленного вдоль силовых линий,
и давления Р, направленного перпендикулярно к ним, причем
т=и=|:- (8-60>
В случае, когда магнитная проницаемость является функцией шютпо-
сти г, можно привести те же рассуждения, как и в § Ю гл. II, учитывая
только, что вместо конденсатора, заполненного диэлектриком, мы имеем
дело с магнитной цепью, содержащей магнетик. В результате мы придем
к выводу, аналогичному B.24), что в магнетике, наряду с вышеуказан-
вышеуказанными натяжениями, должно существовать гидростатическое давление
Для нахождения силы, действующей в магнитном поле на плоскую-
границу между двумя средами с различными проницаемостями ]>.' и ]>.",
сложим нормальные компоненты натяжений, определяемых выражениями
(8.60) и (8.61); таким же путем, каким были получены соотношения A.50)
Задачи319'
й B.25), придем к формуле
"
1 Г ц'-ц» Г В? В'п2
~ 2 | ' ^ ' + "
2 |_ ц' ^ jj.' + jj." ^ ,/2 Их' + (л <Эх
уГ -1
х" J •
Эга сила действует но нормали к поверхности и направлена от [>,' к jj,".
Нормальная и касательная составляющие индукций В' и В" в двух средах
имеют соответственно индексы п и t. Для границы среды с проницаемостью jj.
и вакуума, вводя ^" = щ., у.' = щ. Кт и полагая др"/дг" = 0, получаем
/"=• ^- (/С, — 1) — г—~ \-\ ^—— i (8.63)
где
. (8.64)
Формулы, выведенные в этом параграфе, вполне пригодны для обыч-
обычных сред, но непригодны для ферромагнитных материалов, которые будут
рассмотрены в гл. XII. В ферромагнетиках наблюдается много сложных
явлений (например, изменение формы без изменения объема), которые
нельзя учесть никакой простой формулой.
§ 16. Энергия магнетика в статическом магнитном поле. В преды-
предыдущем параграфе было показано, что сила, действующая на тело с прони-
проницаемостью ji, помещенное в среду с проницаемостью [j..e, при наличии
магнитостатического поля В, создаваемого постоянными токами, численно
равна силе, которая вычислялась в § 14 гл. III [см. выражение C.42)]
для диэлектрика ем = [j.r, помещенного в электрическое поле с индукцией
Ю = В, обусловленное неподвижными электрическими зарядами. Из фор-
формулы (8.9) явствует, что в случае магнитного поля сила или момент, дей-
действующие в направлении 6, равны производной по 6 от энергии магнит-
магнитного поля, т. е.
Сравнение с выражением C.41) показывает, что если в области с магнит-
магнитной проницаемостью ^ создать при помощи системы постоянных токов
магнитную индукцию В внутри некоторого объема v и потом заполнить
этот объем средой с проницаемостью \>. (после чего установится индукция В7),
то энергия, затрачиваемая на намагничивание этой среды, равна следующему
интегралу но объему:
v
Здесь среда предполагается изотропной, а проницаемость р, —не зависящей
от напряженности поля; при этом в систему не вносится дополнительных
источников магнетизма. При помощи вектора намагниченности G.111) это
выражение можно написать в виде
(8.67).
ЗАДАЧИ
1. Показать, что коэффициент взаимной индукции между длинным прямым просо-
дом и копланарным с ним проволочным равносторонним треугольником равен
320 Глава VIII
где а—высота треугольника, Ъ—расстояние от провода до ближайшей параллельной
ему стороны треугольника.
2. Круглая проволочная петля радиуса а расположена параллельно плоской гра-
границе полубесконечной среды с относительной магнитной проницаемостью Кт и нахо-
находится от нее на расстоянии d. Показать, что увеличение самоиндукции петли из-за
наличия среды равно
где введено обозначение с=а(а2 + й2) х'2.
3. Шар радиуса Ъ, обладающий очень большой магнитной проницаемостью, поме-
помещается концентрично с проволочной петлей радиуса а. Показать, что добавочная само-
самоиндукция, обусловленная присутствием шара, равна
^ 1-3-5 ...(
4. Показать, что коэффициент взаимной индукции между двумя концентрическими
прополочными окружностями радиусов а и Ъ, лежащими в одной плоскости, равен
n=0
1-3-5...( )|
2.4-6... Bn + 2)J
51). Внутри тонкой проводящей цилиндрической оболочки радиуса а находится
коаксиальный с ней провод радиуса Ь. Показать, чго самоиндукция такой линии на
единицу длины равна
т?['+"¦(*)] ¦
6. Плоский контур произвольной формы лежит на плоской поверхности нолубеско-
яечной среды с проницаемостью (J-. Пренебрегая полем внутри провода, показать, что
присутствие среды увеличивает самоиндукцию контура в 2fj./(fx-)-[).„) раз.
7*. Длинная прямолинейная нить тока пересекает под прямым углом диаметр
(или его продолжение) тонкой круглой петли, по которой течет ток, и образует
с ее плоскостью острый угол а. Показать, что коэффициент взаимной индукции равен
[л» [с sec а — (с2 sec2 а — а2I'2]
или
1
и зависимости от того, проходит ли прямолинейный ток вне или внутри кругового то-
тока; здесь а—радиус окружности, с—расстояние прямолинейного тока от центра петли.
8. Цилиндрический провод с проницаемостью [л., окруженный копцентрично толстым
слоем изоляции с проницаемостью цц помещен в жидкость с проницаемостью \х3 пер-
перпендикулярно к полю с индукцией В. Показать, что поперечная сила на единицу
длины, действующая на поверхность изоляции, равна
IB,
а поперечная сила, действующая на поверхность проводника, равна
причем результирующая сила равна IB.
9. В некоторой точке вблизи контура, по которому течет единичный ток, создается
магнитная индукция В. Показать, что если поместить небольшую сферу радиуса а
и проницаемости [л. так, чтобы центр сферы был в этой точке, то самоиндукция контура
увеличивается приблизительно на величину
+ 2)
Ввиду ошибки у автора задача приведена в измеяейном виде.—Прим. персе.
Задачи 321
10. Цилиндрический слой проницаемости р. с внутренним и внешним радиусами
и и 6 окружает два параллельных провода, но которым текут токи в противоположных
направлениях. Эти провода расположены параллельно оси (в одной плоскости с нею)
и находятся от пие на одинаковом расстоянии с. Показать, что наличие слоя увеличи-
увеличивает самоиндукцию на единицу длины двухпроводной пинии на величипу
где [хи i/m
11*. Круглая петля радиуса а кшщеитрнчна со сферическим слоем проницаемости р.,
имеющим внутренний и внешний радиусы соответствии но Ъ м с. Показать, что наличие
слоя увеличивает самоиндукцию петли приблизительно на величину
где н-1) - \i-IKm, а радиус а очень мал но сравнению с Ь и с.
12. Координаты проволочного кольца радиуса а в вытянутой сфероидальной
системе координат равны 6 = {, и k]=iji. В кольцо помещается вытявутьш сфероид
щюницаемоми \>., поверхность которого определяется уравнением т) = тH. Показать, что
вследствие этого самоиндукция кольца возрастает на величину
Z
91 = 1
где \h) = V-IKm-
13. Координаты двух проволочных колец радиусов а1 и аг в вытянутой сферо-
сфероидальной системе координат равны %, 5j и if]2, 52- В кольца помещается вытянутый
сфероид проницаемости р., поверхность которого определяется уравнением •*] = %>•
Показать, что наличие сфероида приводит к увеличению взаимной индукции колец на
величину
(Кт—\) V 2n + l p} i^)Q}, (tj,) PJ, (g2
где щ,=[/
14. Центры двух параллельных коаксиальных проволочных петель радиусов я и с
находятся на расстоянии s друг от друга. Показать, что взаимная ивдукцня между
петлями при внесении коаксиально им бесконечного цилиндра радиуса 6 и проницае-
проницаемости jj. возрастает на величиву
со
2,хфс \ Ф (к) Кг (ка) Кг (kc) cos ks dk,
где рл> = р.1Кт, а выражение для Ф (к) дано в задаче 28 гл. VII.
15. Показать, что самоиндукция проволочной петли радиуса а при внесении
коаксиально ей бесконечного цилиндра радиуса 6 и проницаемости р. увеличивается
на величину
оо
^{к){К1(ка)}гйк,
где |л„=[л./.йГт, а выражение для Ф (к) дано в задаче 28 гл. VII.
16. Имеется два контура, один из которых образован участком поверхности
пилиндра f = et, заключенным между z= -\-с, и 2=^-с,, а другой—участком поверх-
поверхности цилиндра ? = а2 (а2 , а,), заключенным между г=+с2 и г=—с2. Показать,
что если токи в контурах (кольцах) распределяются равномерно, то взаимная индукция
между ними равна
со
k~2Ij (ftax) JiTj (Aa2) sin ксг sin kc% dk.
17. Используя результат задачи 30 гл. VII. показать, что если плоскость круглой
проволочной петли радиуса а параллельна бесконечвой пластине толщиной t и
21 В. Смайт
322 Глава VIII
проницаемости р. и находится от нее на расстоянии Ъ, то самоиндукция петли
возрастает на величину
со
где
а ЛГП и Еп—полные эллиптические ритегральг горного и второго рода модуля кп.
18. Бесконечная пластина толщиной t и проницаемостью р. помещается парал-
параллельно между петлями, изображенными иа фиг. 80, а. Показать, что взаимная индук-
индукция между петлями теперь становится равной
где
г, С-—С-в ,о 4аЬ
а Ж'п и ?п—полные эллиптические интегралы модуля кп.
19. Показать, что самоиндукция соленоида с малым шагом намотки, имеющего /V
витков, длину с и диаметр d, равна
4-
о
где rf'c = tga, а! я Z?—полные эллиптические интегралы модуля sin a.
20. Проволочное кольцо радиуга а коакгиально с соленоидом радиуса 6, имеющим п
витков на единицу длины. Пусть наибольшее расстояние от точки на кольце до ближ-
нрго конца соленоида равно с, а до дальнего конца равно d. Показать, пользуясь
формулой G.51) (без дальнейшего интегрирования), что сила взаимодействия между
кольцом и соленоидом, когда но ним текут токи / и /', определяется выражевием
где модули полвых эллиптических интегралов равны fc, =2(abI'2/c и /f2 = 2 (оЬI'2^.
21. Два коаксиальных соленоида с малым шагом намотки, имеющие соответственно
пит виткоп на единицу длины и диаметр d, раслоложевы так. что расстояние между
ближними концами равно 6, а между дальними концами равно с. Длина одного из
соленоидов равна а. Показать, что их взаимная индукция выражается формулой
4
i- ^iimd? 2 (-1)" sec ап [A - tg2 ап) Е (kn) + tg2 апгК (*п)Ь
п=1
где tgai = c/d, tga2 = (c — a)/d, tga3 = 6/rf, tg a4 = (a + b)/d, A-n = COSan.
22. Показать, что если по соленоидам, рассмотренным в задаче 21, текут токи
/ и 1', то сила взаимодействия между соленоидами равна
4
-i ^nmir 2 ( — l)nsinansec2an[?(An) — К {kn)\.
п=1
23. Оси двух колец радиусов а и 6 параллельны и расположены на расстоянии
с друг от друга. Расстояние между плоскостями колец рнвио d. Показать при помощи
соотношения E.451), чю взаимная индукция между кольцами определяется выра-
выражением
Vab Г
\ ! 1 ika) fi (kb) Ko C?c) cos Ad dk,
0
если с > а + Ъ.
323
24. Показать, что в случае 6 > а-\-с взаимная индукция, определяемая в преды-
предыдущей задаче, равна
^\ Кх (ка) 1Х (кЪ) Io (kc) cos kd dk.
25. Пользуясь выражением E.364), показать, что результаты задач 23 и 24 можно
записать в виде
у \тЪ { J, (ка) J, (кЪ) Jo (кс) е~м dk.
26. Два соленоида, радиусы которых равны а и Ь, а длины А и В, имеют соот-
соответственно тип витков на единицу длины. Оси соленоидов параллельны и находятся
на расстоянии с друг от друга; расстоявие между плоскостями центральных витков
равно d. Показать (см. задачу 23), что при с > а-\-Ъ взаимная индукция соленоидов
равна
с
УаЪтп [ а-2/, {ка) Jj (kb) Ko (kc) sin кА sin kB cos kd dk.
J
27. Пусть соленоид радиуса а (см. задачу 26) расположен внутри соленоида
радиуса Ъ. Исходя из решения задачи 24, показать, что
= ^аЪтп Г
О
28. Исходя из решения задачи 26, написать выражения для взаимной индукции
в вадачах 26 и 27 в виде
со
2[хв& ^ 1гЧх (ha) Jx (kb) Jo (kc) sh kA sh kB e~hd dk.
О
29. Взаимное положение колец, радиусы которых равны а и Ь, определено, если
8аданы величины: с—кратчайшее расстояние между осями колец, А и В — расстояния
центров колец от линии с и fl—угол между осями. Показать, что взаимная индукция
определяется в виде
со со
И
о о
(costp сойф' cos p + sin о sin<p') dtp dtp'
' + sin^ sin9'cos |з) —
где D=(c2-f-yl2 + B2—2у1В cos PI'2 — расстояние между центрами колец и
/(ф> 9') = в (с cos f 4-В sin ^ sin fl) + 6 (c cos 9'+ ^4 sin f' sin $),
30. Двухнроподггая линия помещается симметрично между двумя параллельными
листами 6ei конечной проницаемости, находящимися один от другого на расстоянии а,
так что плоскость, проведенная через два провода, перпендикулярна к плоскостям
листов. Расстояпие между проводами равно с Показать, что присутствие листов уве-
увеличивает самоиндукцию (на единицу длины) двухпроводной линии на величину
21»
324 Глава VI11
ЛИТЕРАТУРА
Abraham M., Becker R., Klassische Elektrizitat und Magnetismus, Berlin,
1932. (См. перевод: Абрагам М., Б е к к е р Р., Теория электричества,
2-е изд., М.—Л., 1939.)
Curtis H. L., Electrical Measurements, McGraw-Hill, 1937.
Geiger-Scheel, Handbuch der Physik, Bd. XV, Berlin, 1927.
Gray A., Absolute Measurements in Electricity and Magnetism, v. II, Macmillan, 1888.
Heaviside 0., Electrical Papers, Boston, 1925.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge,
1925.
Maxwell J.C., Electricity and Magnetism, v. II, Oxford, 1881.
M о u 11 i n E. В., Principles of Electromagnetism, Oxford, 1932.
Planck M. К. Е. L., Theorie der Elektrizitit und Magnetismus, Berlin, 1932.
Russell A., Alternating Currents, Cambridge, 1914.
Stratton J.A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: С т р э т-
т он Дж. А., Теория электромагнетизма, М.—Л., 1948.)
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
Wien-Harms, Handbuch der Experimentalphysik, Bd. XI, Leipzig, 1932.
Глава IX
ПЕРЕХОДНЫЕ ЯВЛЕНИЯ
В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
§ 1. Неустановившиеся электрические процессы. Термин «неустано-
«неустановившийся» (переходный) процесс употребляется для обозначения явлений,
наступающих после внезапного изменения в электрическом контуре, по кото-
которому течет ток. Строго говоря, эти явления оказываются переходными
лишь в том случае, когда в контуре содержится сопротивление, рассеива-
рассеивающее энергию. Практически сопротивление всегда имеется, поэтому пере-
переходные явления редко продолжаются более нескольких секунд, даже в самом
крайнем случае. В качестве примеров возникновения переходных явлений
отметим разряд или зарядку конденсатора, внезапное изменение магнитного
потока, охватывающего контур, или внезапное выключение или включение
источника э. д. с. В этой главе мы рассмотрим неустановившиеся процессы
в контурах, содержащих индуктивность и сопротивление, емкость и сопро-
сопротивление или все три элемента сразу, считая источник э. д. с, если он,
конечно, имеется, постоянным.
В общем случае, когда электрическая цепь предоставлена самой себе,
т. е. она не получает и не отдает энергию, все процессы в ней можно
описать при помощи линейного однородного дифференциального уравнения
с постоянными коэффициентами, в котором в качестве независимой пере-
переменной взято время, а зависимыми переменными являются заряды и токи.
Решение этого уравнения, содержащее произвольные постоянные, число
которых равно порядку уравнения, называется дополнительной функцией.
Значение произвольных постоянных находится из начальных условий. При
наличии источника постоянной э. д. с. дифференциальное уравнение будет
содержать постоянный член. В этом случае по прошествии достаточно дли-
длительного времени останутся постоянные токи или заряды на конденсаторах,
так как все члены дополнительной функции обратятся практически в нуль.
Эти токи или заряды, не включающиеся в дополнительную функцию, соот-
соответствуют стационарному состоянию системы. Они выражаются частным
интегралом дифференциального уравнения. Сумма дополнительной функции
и частного интеграла или, пользуясь терминологией, принятой в электро-
электротехнике, сумма нестационарного и стационарного решений является полным
решением задачи.
§ 2. Энергетические соотнешевия в электрической цени. В электри-
электрическом контуре, содержащем емкость, сопротивление и индуктивность,
энергия может накапливаться в электростатическом поле, создаваемом
постоянными зарядами на конденсаторах, а также в ипде кипотической
энергии магнитного поля, возбуждаемого движущимися зарядами в индук-
тивностнх; кроме того, в сопротивлениях происходит рассеивание энергии
в виде тепла. Без внешних воздействий электрическая энергия, в конечном
счете, излучится или превратится в тепловую энергию. Потери вследствие
излучения будут нами рассмотрены ниже в связи с электромагнитными
326
Глава IX
волнами. Там мы увпдим, что эти потери сильно зависят от скорости изме-
изменения тока в контуре. Однако для колебаний с частотой до 100 кгц и даже
несколько выше этими потерями по сравнению с потерями в сопротивлении
обычно можно пренебречь, что и будет принято в этой главе. Потенциаль-
пая энергия контура [см. формулу B.15)] равна Wc — — ^ qljcs джоулей,
где заряд qs выражен в кулонах, емкость cs — в фарадах. Кинетическая
энергия контура [см. формулу (8.35)] равна WL = —- ^ Lri% джоулей, где
самоиндукция Lr выражена в генри, ток ir — в ампс-
r р р r
pax. Мощность рассеяния [см. формулу F.11)] равна
Р = у 2 гв^« ватт, где сопротивление Rq выражено в омах,
n амперах. Таким образом, общий запас энергии
о
8 ток i
о магнитного и электрического полой равен
<9Л>
8=1 Г=1
Скорость уменьшения этой энергии должна быть равна
скорости теплового рассеяния, т. е.
р п . т р
S*vs=—тег- или 2-^+2ма+2ОД=°. (9-2)
q=1 s=l г=1 0=1
где точкой обозначено дифференцирование по времени.
§ 3. Контур, состоящий из емкости, индуктивности и сопротивления.
В контуре, показанном на фиг. 84, L, С и R включены последовательно,
• • • •
так что q — i, q = i. В этом случае, после деления на общий множитель i,
уравнение (9.2) принимает вид
= 0.
(9.3)
Согласно выражению (8.39), Li = Lq представляет собой падение напряже-
напряжения в катушке самоиндукции. Из закона Ома F.6) следует, что Ri — Rq
является падением напряжения на сопротивлении. Точно так же, согласно
формуле B.1), величина qjc является падением напряжения на конденса-
конденсаторе, так что уравнение (9.3) выражает просто закон Кирхгофа (см. § 5,
гл. VI), а именно: сумма падений напряжения вдоль замкнутого контура
равна нулю.
Общим решением уравнения (9.3) будет
q = CieW + C2ek*, (9.4)
где Clt С2 — постоянные интегрирования, определяемые начальными значе-
значениями величин q и i, а через кх и &2 обозначены величины
O. LY/2
L2 LC
2L
Если (Rj2L)>{LC)-ll2, то кг и к2 — величины действительные, и изме-
изменение тока имеет апериодический характер. Введем в решение (9.4) величину
/2
)
Переходные явления в электрических цепях 327
Тогда
q = e-wm i (dc»' + C2e-<°() ¦-=¦ e-W2w г (^ ch ы + 5 sh coi) =
= e-№/2i.)«/)ch(u)i + <J;)> (9.6)
где Л^^ + С,, В = С1 — С2, D = (A2 — B2I'* и th<|> = .B/4.
В случае (R/2L) < (LC)~1/2 At и &2 — величины комплексные, и измене-
изменение тока носит колебательный характер. Заменяя в решении (9.6) со на /со,
получим решение в виде
q = е- №/2*0« (Су""* + С2е-"°') = e-W2*-)' (A cos со г + Б' sin о>г) =
= e-№/24«.D'cos(urf + <p), (9.7)
где
Л 67 + ^ В'ЦСС) D' (A* + B'*yh и
Период колебаний Т равен 2т/со, а собственная частота контура равна
<о/2тг. Логарифмический декремент затухания а, определяемый как логарифм
отношения амплитуд двух последовательных колебаний, равен
а = In [е-(л/2Ь)«е+[ВД+Т)/2Ц] = jg. = ?*_ . (9.8)
Если со = 0, то говорят, что контур имеет критическое затухание. Разлоншм
в решении (9.7) cos и sin в ряд (Двайт, 415.01, 415.02), отбросим все
члены, кроме первого, и пводя В" вместо со/?', получим решение (9.7)
в виде
). (9.9)
§ 4. Зарядка и разряд конденсатора. Если контур (см. фиг. 84) зам-
замкнуть при помощи ключа S в момент времени t = 0, когда на конденсаторе
имеется заряд ^0, то, полагая в решениях (9.6). (9.7) или (9.9) q = q0
и t = 0, получим
А=дп. (9.10)
Падение напряжения в катушке самоиндукции L (di/dt) = L (d2q/dt2) должно
быть конечным все время, включая и начальный момент. Таким образом,
при t = Oi=q = O. Дифференцируя выражения (9.6), (9.7) или (9.9) по
времени и подставляя в них эти значения, получим
Д = Я'=—= ^Л. (9.11)
Тогда в любой момент времени t заряд на конденсаторе равен
при JL > (LC)~lh q = qoe-R4*L (%h <at + ~ sh a>*) , (9.12)
при -?=(LCr1/s ? = ?ое-и/2ьA + -5г0' (9ЛЗ)
при
-^- < AС)~Чл q = q0e~™l2L Г cos coi + ^ sin w*) . (9.14)
Ток г в каждом случае равен q. На фиг. 86, а показаны кривые зави-
зависимости q от t, где буквами А, В, С обозначены соответственно случаи
<9.12)-(9.14).
328
Глава IX
Цепь для зарядки конденсатора показана на фиг. 85. Уравнение Кирх-
Кирхгофа для этого контура имеет точно такой же вид, как и уравнение (9.3),
только в правую часть теперь будет входить Ш — э.д.с. батареи. Мы
можем решить это уравнение двумя способами: 1) ввести новую пере-
переменную У = д — С?, сведя тем самым новое ураштение к форме (9.3);
2) добавить к общему решению (9.6), (9.7)
и (9.9) однородного уравнения частное ре
шение, соответствующее стационарному со-
С~— стоянию, которое, как нетрудно убедиться,
равно q=C?. При любом способе, полагая
7 = 0 при t = 0, получим
;i нтъщтр
I
R
-ЛЛЛЛАЛЛЛЛ/V
Фиг. 85.
(9.15)
Дифференцирование дает для i прежнее выражение, поэтому, полагая
г = 0 при t = 0, имеем, как и раньше,
" "' В" R '.. (9.16)
(9.17)
(9.19)
Значение тока в каждом случае равно i = д. Кривые зависимости q от
времени / показаны на фиг. fc6, б, где буквами А, В, С обозначены
Полное решение для случаев (9.12) — (9.14) имеет соответственно вид
rll ы + JL
Фиг. 8G. а—разряд конденсатора, включенного последовательно с актилныы
сопротивлением и индуктивностью, б—зарядка этого же кондепсатора; А—в слу-
случае большого затухания в контуре, В—в случае критического затухания,
С—в случае малого затухания.
соответственно случаи (9.17) —(9.19). Б случае /t = 0 выражение (9.14) для
разряда конденсатора принимает вид
q=qoza&[t(LC)-l% (9.20)
а выражение (9.19) для зарядки конденсатора будет
q = C% {I -cos [t(LC)~lh]}, (9.21)
Переходные явления в электрических цепях 320-
т. е. в обоих случаях имеем незатухающие колебания, продолжающиеся
бесконечно долго, с, частотой [2л (LC) /2].
В случае L = 0 ш—>оо, так что 2shu)?^e( и 2chu)f^e"". Разлагая
выражение (9.5) в ряд (Дваит, 5.3) и отбрасывая члены, содержащие L
в числителе, получаем
<0=""ЙЛ ~НЮ J ^2L~~BCJ
так что выражения (9.12) и (9.17) принимают соответственно кид
(9.22)
(9.23)
Таким образом, конденсатор разряжается через сопротивление по экспо-
экспоненциальному закону.
§ 5а. Нарастание и спадание тока в катушке индуктивности. Если
в контурах, изображенных на фиг. 84 и 85, конденсатор отсутствует,
то уравнения, выражающие закон Кпрхгофа, будут иметь вид
+' <
Введем в уравнение (9.25) новую переменную х== i — (§//?), тогда оба
уравнения (9.24) и (9.25) можно записать в форме
dx R „ dx R
+ з; 0 или
тз; = 0, или
dt ' L
После интегрирования имеем
1пж= -~t+Cv или x = Ae-Wt. (9.26)
J-j
Таким образом, если в момент времени г = О i = i0, то в последующие
моменты времени ток будет уменьшаться по закону
i = ior№. (9.27)
Если же контур, содержащий последовательно включенные сопротивление,
индуктивность и батарею, замкнуть в момент времени 1 = 0 (i—О), тогда,
согласно уравнению (9.25) и решению (9.26), получим нарастание тока по
закону
i = -J(l-e-№L)O. (9.28)
Постоянная времени контура равна, по определению,
Х = 7р (9-29)
Для спадающего тока это есть время, к течение которого величина тока
уменьшается относительно своего первоначального значения в е раз.
§ 56. Индуктивно связанные контуры. Как было ноказано в § 4 гл. VIII
[см. выражение (8.17)], если магнитное поло одного контура охватываоч
второй контур, го изменение тока в одном из контуров наводит и
другом контуре э. д. с. индукции. Таким образом, написав уравнение?
330
Глава IX
Кирхгофа для цепи, изображенной на фиг. 87, мы должны включить
в него член (8.17), после чего получим
dt
dt
dt
(9.30)
(9.31)
Если магнитные потоки, созлаваемые токами г\ и г2, складываются, то
перед М принято писать знак плюс; если же потоки направлены проти-
противоположно, то пишут знак минус. Исклю-
Исключим из уравнения (9.30) величину г'2.
Разрешив уравнение (9.30) относительно
di2\dt, подставим полученный результат
в уравнение (9.31), разрешив которое от-
2 носительно R2i2 и умножив затем на М,
найдем
Ч- MR2i2 = (ЬгЬ2 - Л/2) -§- +
§
Фиг. 87. (9.32)
Для получения di2/dt продифференцируем
это выражение и подставим в уравнение (9.30), которое после умно-
умножения на R2 примет вид
{LXL2 -
(9.33)
Точно так же, как и в § 4, мы можем сделать правую часть этого уравне-
уравнения равной нулю, введя новую переменную i'1 = i1—(^/^i)> или можем
прибалить частное решение, соответствующее стационарному режиму,
i1 = ^//?1, к общему решению однородного уравнения, получающегося из
уравнения (9.33), если правую часть положить равной нулю. Полное
решение имеет вид, аналогичный решению (9.4),
= е"" (А c
Здесь А;,, и ^ — действительные величины, равные — а
(9.34)
(9.35)
(9.36)
Когда t = 0, i, = 0, отсюда Л=— %\RX.
Очевидно, общее решение уравпеннй (9.30) и (9.31) будет одинако-
одинаковым, но стационарное значение для i2 равно нулю, так что решением
для i2 будет
i2 = e-at (Cchfit + Dsh$t). (9.37)
В начальный момент времени (t — 0) i2 — 0, отсюда С — 0.
Подстаиляя решения (9.34) и (9.37) в уравнение (9.31) и учитывая,
что A = igjR1 и G = 0, после сокращения на e~at получим
-где
и
(R2 -
(9.38)
(9.39)
Переходные явления в электрических цепях 33f
Поскольку уравнение (9.31) удовлетворяется для всех значений t,
величины Р и Q должны быть приравнены нулю по отдельности. Разрешая
полученные уравнения относительно В и D и подставляя затем выраже-
выражения для А, В, С и Л и решения (9.34) и (9.37), получаем
(9.40)
(9.41)
Из выражения (9.40) видно, что ток i1 асимптотически приближается
« своему конечному значению Щ\КХ. Полагая di^dt=O и разрешая полу-
полученное уравнение относительно t, находим, что i2 достигает максимума
при
t^i-arthi- (9.42)
и затем асимптотически стремится к нулю.
В момент, когда i2 = 0 и г\ = ?/Rv разомкнем цепь (см. фиг. 87) посред-
посредством выключателя и исследуем полученный эффект. Если бы мы разомк-
разомкнули цепь мгновенно, прекратпв ток it в нулевой промежуток времени, то
производная di^jdt в этот момент оказалась бы бесконечной, и, согласно
формуле (8.39), на выключателе возникло бы бесконечно большое напря-
напряжение. Поскольку ни одна физическая система не выдержит такого напря-
напряжения, то это значение никогда не может быть достигнуто. В действитель-
действительности, в момент разрыва цепи небольшая емкость, всегда существующая
между контактами и проводами цепи, заряжается до тех пор, пока потен-
потенциал не упадет. По этой причине очень трудно пайти точные начальные
условия для ij.
В обычных условиях мгновенное прекращение тока it должно инду-
индуцировать в индуктивности второго контора бесконечную э. д. с, поро-
порождающую искрение, если распределенная емкость контура по будет доста-
достаточно большой. Впрочем, существует важный практический случай, где
это утверждение неверно. Предположим, что вся самоиндукция L, второго
контура равна взаимной индукции М и что можно найти такое отношение
токов i[ и i'2, что при протекании тока i[ или i'2 каждый виток самоиндук-
самоиндукции L2 будет охватывать одинаковый поток. Тогда во втором контуре можно
мгновенно установить такой ток ь2, что поток L2i2 через этот контур будет
одинаков с потоком M"&/Rlt существовавшим до того, как прекратился
ток ij. В этом случае э. д. с. во втором контуре конечна, а начальное зна-
значение тока i2, получаемое приравниванием потоков, равно
Этот случай можно приближенно осуществить на практике, если Lt и L2
представляют собой однослойные соленоиды одинаковой длины, плотно
намотанные на одном каркасе.
Закон Кирхгофа для тока г2 выразится уравнением
^ 2 = 0. (9.44)
Решением этого уравнения, дающим правильное начальное значение i2,
будет, как легко проверить, следующее выражение:
(9.45)
332 Глава IX
§ 6. Кинетическая энергия и электрокинетический импульс. Из фор-
формулы (8.39) следует, что мгновенное изменение потока L11il должно было
бы привести к возникновению бесконечной э. д. с. в катушке индуктив-
индуктивности. Как было показано в предыдущем параграфе, это физически невоз-
невозможно, поэтому Lilil должно иметь одинаковое значение до и после вне-
внезапного изменения в электрической вепи. Величина L11i1 называется
электрокинстическим импульсом, потому что она находится в такой
же связи с кинетической энергией Lnij/2, в каком находится меха-
нический импульс mv с механической кинетической энергией -у тпъ2. Только
что установленный принцип неизменности потока известен так же, как
принцип сохранения электрокинетического импульса. Поскольку для рас-
рассеяния в сопротивлении конечного количества энергии требуется при нали-
наличии конечного тока конечное время (как и для зарядки конденсатора на
конечную величину), то кинетическая энергия — Llti\ в контуре должна
также оставаться постоянной при мгновен-
мгновенном изменении в цепи. Эти законы сохра-
сохранения часто дают возможность сразу на-
написать начальные значения переходных
токов. В цепях, где нот рассеяния энер-
энергии, обо величины — полный электроки-
нетический импульс и полная энергия —
Фиг. SS. остаются постоянными. Пользуясь этим,
можно ответить на многие вопросы без
решения дифференциальных уравнений. Рассмотрим, например, систему,
изображенную на фиг. 88. Пусть вначале конденсатор имеет заряд Qo и вы-
выключатель замыкает цепь; требуется найти максимальные значения токов
fj и i2. Электрокинетический импульс остается равным нулю, поэтому
?iii + ?2i2 = 0. (9.46)
Общая энергия остается равной QHBC), поэтому, когда конденсатор разря-
разрядится, кинетическая энергия будет равна
С Г С
Решив эти уравнения для максимальных значений i1 и i2, получим
2 ¦ (9-48)
§ 7. Общий вид уравнений переходных процессов в цепях. Восполь-
Воспользуемся методом, аналогичным методу, примененному в § 9 и 10 гл. VI при
рассмотрении электрических цепей, состоящих из активных сопротивлений.
Введем п независимых токов, как и в § 9 гл. VI, так, чтобы в каждой
ветви цепи могли протекать различные токи. В этой связи следует заме-
заметить, что взаимная индукция между двумя контурами рассматривается
как самоиндукция некоторого проводника, общего для обоих контуров.
При этом условии, если цепь содержит q узлов и р ветвей, величина п
определяется" формулой
п = р-д+\. (9.49)
Активные сопротивления будут обозначены так же, как и в § 9 гл.
VI, т. с. Rrx — общее сопротивление для контуров, по которым текут токи
ir и is; Rr — сопротивление, по которому течет один ток ir; Rrr — полное
сопротивление контура, по которому течет ток ir. Обозначение индукций
Переходные явления в электрических цепях- 333
осложняется из-за наличия взаимных ипдукций. Если L'rs — общая самоин-
самоиндукция контуров, по которым текут токи ir и is, a M1S — взаимная индук-
индукция между ними, то, по определению, самоиндукция Lrs будет равна
Ln = L'rs±Mn. (9.50)
Знак минус соответствует случаю, когда взаимная индукция Мп и само-
самоиндукция L'rs направлены в противоположные стороны. Обозначим через L'r
самоиндукцию катушки, в которой протекает один ток ir, и через Lrf пол-
полную самоиндукцию контура, сто которому протекает ток ir, так что если
ни по одному из контуров не проходит более чем два тока, то
Lrr=L'r + L'lr + L'2r + ... +L'nr = Lr-i-Llr + L2r+ ...+Lnr. (9.51)
Заметим, что, согласно этому определению, Lr включает в себя и взаимную
индукцию.
В контурах, которые мы будем рассматривать, каждый конденсатор
может заряжаться и разряжаться одним или более чем одним током, при-
причем будем считать, что данному току соответствуют только конденсаторы,
соединенные последовательно, а не параллельно. Как известно [см. фор-
формулу B.4)J, при последовательном соединении нескольких конденсаторов
обратная величина результирующей емкости равна сумме обратных величин
составляющих емкостей. С целью упрощения обозначений, введем новую
величину, обратную емкости, так называемый потенциальный коэффициент S.
Обозначим через Srs общий потенциальный коэффициент контуров, по ко-
которым протекают токи ir и is, через Sf потенциальный коэффициент, свя-
связанный с единственным током ir, и через Srr сумму потенциальных коэф-
коэффициентов в контуре, по которому течет ток ir, так что
StT=Sr + Slr + S9r + ••• + -V (9.52)
Если ни в одном из контуров не протекает более двух токов, то
Д„ = Д„, Ln = Lsr и Sn = Sa. (9.53)
Эти величины называются взаимными параметрами цепи, a Rrr, Lrr и STr
называются параметрами контура.
Согласно формуле (9.1), сумма падений напряжений в контуре г, за-
зависящая от тока ir, равна
( Lrr S + Rrr Tt + Srr ) Vr = arrqr, (9.54)
T
где dqjdt = ir, arr— дифференциальный оператор, действующий на q
только в том случае, если он написан впереди qr. Электродвижущая сила,
наведенная в r-ом контуре током ?н, протекающим в общей с ним ветви, равна
± (Lrs *, + Rrs ± + Srs) gs = arsqR. (9.55)
Перед скобкой следует взять знак плюс, если токи ir и is имеют в общей
ветви одинаковое направление, или минус, если их направление проти-
противоположно.
В случае, когда э.д.с. в цепи отсутствует, уравнение Кирхгофа можно
записать, пользуясь операторным обозначением, в следующей форме:
•• +-a2nqn = 0, (9.56)
-•• +annqn=0.
334 . Глава IX
§ 8. Решение для цепей общего вида. Мы видели [см. решения (9.4)
и (9.6)], что для одной ячейки с оператором ап решение имеет вид
где рг и р2 — два значения р, получаемые после подстановки Qev в диффе-
дифференциальное уравнение (9.3) и решения соответствующего алгебраического»
уравнения. Амплитуды Q\} и Q\^ — это постоянные интеграции, опреде-
определяемые заданными начальными условиями, а именно: во-первых, начальной
энергией магнитного поля, создаваемого токами в катушках индуктивности,
и, во-вторых, энергией электрического поля, создаваемого зарядами на
конденсаторах. Вполне естественно попытаться сделать подобную же под-
подстановку в систему дифференциальных уравнений (9.56). Решение будет
найдено, если в результате этой подстановки мы сумеем определить вели-
величины р так, чтобы удовлетворить системе дифференциальных уравнений и,,
кроме того, получить число произвольных постоянных, равное максималь-
максимальному числу начальных условий, которые мы можем задать. Число началь-
начальных условий, очевидно, равно числу независимых электрических и маг-
магнитных полей, определяющих энергию системы. Бе следует задавать лишь
ток, протекающий по сопротивлению, поскольку он не определяет энергию-
и мгновенно прекращается, как только выключается э. д. с. Если имеется л
независимых контурных токов, то может существовать самое большее 2ге
постоянных интеграции.. Таким образом, искомая подстановка имеет вид
; qr = Qrept. (9.57)
Введем для удобства полую алгебраическую величину crs, определяемую
соотношением
arsgs = ± (LrsP* + RrsP + Srs) Q^ = crsQsept. (9.58)
Тогда, после сокращения на ept, система уравнений (9.56) примет вид
' " c11<I+clS(J+ ... +cln<?n=0,
C21V1 ~^~ C22V2 "T~ • • • + c2nQn — "? /g '
¦ cnnQn = 0.
Как и в § 9 гл. VI, выпишем определитель
С11С12
(9.60)
д= СочС'
21С22 • • • С2п
Поскольку начальные условия, определяющие величины Q, не были исполь-
использованы в уравнениях (9.59), то эти уравнения нельзя разрешить относи-
относительно (?j, Q2, ..., Qn. Вследствие того, что все правые части —нули, мы
получим, употребляя обычный метод детерминантов, следующий результат:
& = ! • (9-61)
Тривиальное решение Qr — 0, очевидно, удовлетворяет системе уравнений
(9.59), но не удовлетворяет начальным условиям. Ясно, что начальные
условия могут быть удовлетворены совместно с соотношениями (9.61) только
в том случае, если •«•>... ....
Д=0. (9.62)
Переходные явления в электрических цепях 335-
Этот детерминант называется характеристическим. Раскрывая его, получим
для р алгебраическое уравнение степени не выше 2п, так как р входит
в выражение для сг, не более, чем во второй степени. Решение этого урав-
уравнения дает возможные значения р, выраженные через параметры электри-
электрической цепи. Каждое значение р, полученное таким способом, определяет
собственную частоту и затухание некоторого процесса в системе. Подставляя
его в выражение (9.57), получим для v-й частоты
9г=<2(Л^. (9.63)
Для этой частоты система уравнений (9.59) принимает вид
(9>64)
Эти уравнения совпадают по форме (за исключением того, что их правые
части равны нулю) с уравнениями F.32), поэтому соотношения, аналогичные
соотношениям F.37), не зависящим от правой части, выполняются и для
этих уравнений. Таким образом, если AfeS—алгебраическое дополнение Chs
в определителе (9.60), то
Очевидно, этому уравнению удовлетворяют величины
Q^ = A(h%^ и Q^^&tfG™, (9.65)
где G(v) — постоянная, соответствующая частоте v. Можно положить к равным
любому числу от 1 до п.
Полное выражение для qr представляет собой самое большее сумму 2п
членов вида (9.63), т. е.
qr = QM&ii + QWeP2t -f . . . + Q^e^n' . (9.66)
Подставляя выражения (9.65) в (9.66), получим не более п уравнений,
содержащих q^, q2, ..., qn. Дифференцируя, получим еще п уравнений^
содержащих ilt i2, • • •, in- Таким образом, будем иметь
Полагая в этих уравнениях ( = 0 и используя начальные значения для
9и 9г. • ¦ ¦, Яп, «1» h> ¦ ¦> г™. можпо ыапти GA), GB), . .., GBn),
¦33fi Глава IX
выраженные через Д$, А$, . .. , Ь.^1, Д^, Д^г, • • •, Н« и т. д. Последние
определяются через с^); в выражение для которых, согласно соотноше-
соотношению (9.58), входят величины р.., полученные из уравнения (9.62) и опре-
определяемые, в конечном счете, параметрами цепи. Таким образом, задача
полностью решена.
§ 9. Типы собственных колебаний. В случае простого контура, рас-
рассмотренного в § 4, мы нашли, что в зависпмости от параметров контура
возможны три. типа собственных колебаний. Первый тип, называемый
колебательным, получается при комплексных /?v, когда активное сопротивле-
сопротивление цепи мало по сравнению с емкостным и индуктивным и^и вовсе отсутст-
отсутствует. Поскольку заряд qr, входящий в выражение (9.66), должен быть
действительной величиной, хотя Qr и комплекспы, необходимо, чт'»бы вели-
величины р были комплексно-сопряженными, т.е. величины Q? ev-x -\- Qr ePfe( —
действительные. Подобные два члена можно объединить и записать в форме
Аеы cos at -\- Веы sin at = Cebt cos (at -f- <p).
Другой тип собственного колебания соответствует критическому затуханию
(см. § 4); в этом случае несколько корней уравнения (9.62) одинаковы.
Если, например,
Ps = Ps+1 ~ • • ' — Р2П-1 = Pir,.
то члены в уравнениях (9.67), содержащие ps, . . . , р2п, должны быть за-
заменены следующим выражением:
где г пробегает все значения от 1 до и. Соответствующие изменения должны
быть сделаны и к выражениях для ir.
Третий тип собственных колебаний можно получить, если р — дейст-
действительные величины. Это соответствует случаю очень большого затухания
(см. § 4 ). В этом случае колебания отсутствуют и ток, или заряд, умень-
уменьшается, не меняя знак. Это — единственный тип, который имеет место,
когда контур состоит только из индуктивности и сопротивления или из
емкости и сопротивления.
§ 10. Цепь, содержащая постоянную э.д.с. Если электрическая
цепь, которую мы рассматривали, содержит источники постоянной э. д. с,
то в правых частях некоторых из уравнений (9.56) будут стоять не нули,
я. постоянные Шр, Шп и т. д. Полное решение этих уравнений представляет
собой сумму общего решения однородного уравнения (неустановившийся
режим) и частного решения (стационарный режим). Общее решение дается
выражениями (9.67). Для получения частного решения заметим, что в ста-
стационарном состоянии все конденсаторы становятся разрывом цепи, а все
индуктивности — коротким замыканием. Таким образом, если вновь изо-
изобразить цепь, опустив все ветви, содержащие ышденсаторы, и заменив индук-
индуктивности идеальными проводниками, то полученную эквивалентную схему
можно исследовать методом, описанным в § 9 и 10 гл. VI, дающим ста-
стационарное значение токов. Зная значения тока и сопротивления в каждой
ветви, можно найти напряжение, а отсюда и заряд на конденсаторах в ста
ционарном режиме. Добавляя теперь к общему решению (9.67) стационар-
стационарное значение соответствующего тока или заряда, мы получим полное
решение задачи. Постоянные G(i\ ?B), . . . , ?(п) определяются попрежнему
из уравнения, которое получается из общего решения, если положить
4, — (J, а токи и заряды считать равными своим начальным значениям.
Переходные явления в электрических цепях
337
§ 11. Собственные частоты двух индуктивно связанных контуров.
Применим полученные результаты к системе, показанной на фиг. 89. Два
контура, по которым текут токи г\ и г2, на- Р
зываются индуктивно связанными.
Здесь
Л7
о
о
Or
о 2
о
Фс,
Из соотношения (9.58) имеем
Фиг.
^-. (9.68)
Характеристическое уравнение (9.60) будет иметь вид
Подставляя в него значения с11; с22 и с12 из соотношений (9.68), получим
O, (У.69)
(9.70)
. ¦Rl^'2-b^2^'l
/^ __
Т> __
L.U—M*
Собственные частоты системы являются корнями уравнения (9.69); этц
корни мы обозначим через рг, р2, р3, р^. (Подробности решения уравне-
уравнения четвертой степени см. в книгах по теории уравнений и в учебниках
по алгебре.) Значения корней равны
Риг= - ¦
где
Знак квадратного корня следует брать таким, чтобы
и
(Pi + Ps) РзЛ + (ЛЗ + />*) PlP2 =—С
Если обозначить
Л7— i/BD \ АВС °2
(9.71)
(9.72)
(9.73)
(9.74)
(У.75)
(9.76)
8 108у '
то значения г1; t2 и г3, которые используются в соотношении (9.72), даются
следующими выражениями:
22 в. Смайт ~
338
Глава IX
Если К>0, iV{^.}0, N2>K3, то, полагая chcp = {±} NK~3^, имеем
t1-={±}2(KIl2ch±<?, tz,3= -Yfi± f@K)lhsh^V- (9-77)
Если К < 0, то, считая shcp = iV( — K)~z^, получим
5h4?- (9.78)
(9.79)
Если # > 0, N2 < ЙГ3, то, полагая coscp =NK~sl2, имеем
cos -i cp, tz,s =—jh± (ЗЛГI/а sin -1 ?.
Тип собственных колебаний можно определить без непосредственного вы-
вычисления корней р1г р2, р3 и р4. При K3>N2, 48 (ifI'2 > (8В — ЗА2) и
Фиг. 90.
8В > ЗЛ2 корни образуют две комплексно-сопряженные пары, которые
можно записать в форме
И
— а2 ±
Так как в этом случае в каждом кошуре имеются два затухающих гармо-
гармонических колебания, то возникают биения, подобные наблюдаемым на воде
— t
Фиг. 91.
или в звуковых волнах. Если эти колебания окажутся в фазе, то ампли-
амплитуда результирующего колебания будет максимальной. Частота биений
равна ^-(№2 — (fli)/Tt- Энергия переходит с этой частотой от одного контура
к другому и обратно до тех пор, пока полностью не рассеется в сопротив-
сопротивлениях. На фиг. 90 изображен ток во втором контуре системы, показан-
показанной на фиг. 89, когда после замыкания выключателем цени первого кон-
контура конденсатор С1 разряжается.
При K3~>N2, а 8В< ЗА2 и 48 (iTI^ < 8В — ЗА2 все корни действи-
действительны и отрицательны и токи уменьшаются, но совершая никаких коле-
колебаний.
Переходные явления в электрических цепях
339
При К < 0 имеются два действительных корня и пара комплексно-со-
комплексно-сопряженных [см. соотношения (9.78)]. В этом случае в системе совершается
одно затухающее колебание, не сопровождаемое явлением биений. Такой
тип колебаний изображен на фиг. 91. Когда K = N, то два или несколько
корней одинаковы.
§ 12. Амплитуды колебаний в двух связанных контурах. Мы опре-
определили частоты колебаний и коэффициенты затухания. Остается теперь из
начальных условий найти амплитуды колебаний. Из определителя (9.60)
имеем
= С
22.
Д12 = - с 12 =
Таким образом, при к=\ полное решение для рассматриваемой системы,
записанное в форме (9.67), будет
(9.80)
= -M
Ё2 = - Л/
Пусть при t = 0 ql = Q, q2 = 0, гх = 0 и г'2 = 0. Подставляя эти значения
в уравнения (9.80) и сокращая на — М, нетрудно разрешить их относи-
относительно GA) и получить
Pz Pz Pi
p\
Pi
p\
cB)
L22
Pl
cC)
L22
pi
pAV pAV
В числителе умножим верхнюю и нижнюю строки детерминанта соответ-
соответственно на R2 и на L2 и вычтем их из средней строки, тогда все члены ее
станут равными 1/С2. После вычитания третьего столбца из первого и вто-
второго столбцов первые два члена средней строки обращаются в нуль, по-
понижая тем самым порядок детерминанта, так что его теперь можно пред-
представить в виде произведения сомножителей. Таким образом, числитель при-
принимает вид
- Pi) \P3 ~ Pt) (Рз ¦
(9.81)
В знаменателе умножим вторую строку детерминанта на L2 и вычтем из
первой, потом умножим вторую и четвертую строки соответственно на R2
и L2 и вычтем из третьей, после чего из этой строки можно будет вынести
общий множитель 1/С2. Умножим теперь третью строку на R2 и вычтем
из первой, тогда все члены этой строки станут равными 1/С2; эту вели-
величину можно также вынести в качестве общего множителя. После вычита-
вычитания четвертого столбца из первого, второго и третьего столбцов первые
три члена первой строки обращаются в нуль, понижая тем самым порядок
детерминанта. Теперь за знак детерминанта можно вынести множитель
(Pi~Pz)(Pz — Pi) (Рз — Pi)' после чего во второй строке останутся только
единицы. Вычитая в полученном детерминанте третий столбец из первого
и второго, опять понижаем порядок детерминанта и выносим затем множи-
множитель (Рх— Рз)(р2 — Рз)- Оставшийся детерминант второго порядка сводится
22*
Зад . Глава IX .
к р2— plt так что знаменатель принимает вид
(Р\ — Pi) (Рг — Р*)(Рз — Pa) (Pi — Pa* (Р2 — Ря) (Р2—Р,) /g g2)
Таким образом, для GO получаем следующий результат:
P2PiP<fi2Q (9 83)
(Р2 — Pi) (Рз—Pi) (Pi — Pi)'
Для получения G^2) нужно лишь заменить индекс 2 на 1 в выражении
(9.81) и изменить знак в выражении (9.82), тогда
/у
(Рз — Р2> (Рй — P2){Pi — Рг)
Аналогично
P4P1P2C2Q
(Pi— Рз) (Л— Рз) (Р2— Рз) '
(Pi — Pi) (P2— Pi) (Рз — Pi)
При начальных условиях, заданных в наиболее общей форме, т. е.
когда величины qlt q2, ix и i2 в начальный момент ( = 0 не равны нулю,
мы получим для каждого G выражения, очень похожие по форме на выше-
написанные. Способ их получения тот же самый.
§ 13. Колебательный режим. В этом случае корни уравнения (9.69)
т вид
= а' + jb', 2p3cC>GC) = а" + jb". (9.88)
имеют вид
Положим
Тогда, поскольку p-^d^G^ и р3с<$&3^ являются комплексно-сопряженными
pzc$&2) и Pi^2^^ соответственно, мы можем представить ток it (см.
Двайт, 408.01 и 408.02) в форме, определяемой соотношением (9.80),
ix = e~ait (a' cos ш^ — b' sin ш^) -|- e~t (a" cos u>2t — b" sin ш21) =
= flle-oi« sin («v + ?i) + fl2fi~O2( sin (ш2г + ^), / (9.89)
где
a1=(a'a+6'aI/*. а2 = (а"а+й"8I/» (9.90)
В N
cPi = y + arctg^>> cp2 = -^ + arctg^. (9.91)
Аналогично, полагая
-2Mps1Gil) = c'+fd' и -2MplGC) = c" + jd", (9.92)
имеем
г2 = e~0lt (с' cos Wjif — d' sin uijf) + e~( (c" cos ш2^ — d"' sin ш2?) =
= Cje-^' sin (ш/ + Ф1) + c2e-°2( sin (ш2г -|- ф2), (9.93)
где
1/2, cg=-(c + dI/2 (9.94)
Переходные явления в электрических цепях 341
И
(9.95)
Подставляя d соотношение (9.83) вместо рг, р2, р3, pt соответствующие
им выражения (9.87), получим
( + /)( + |)GQ (9 96)
ш1 + ш2)] '
— 2/a>j [a2 — «! + / (<oj — <о2)] [а2 — а1
Последние множители в знаменателе можно написать в виде
К - а2J + W — ш!) + 2/<"i (a2 — ai)-
Согласно выражению (9.68), имеем
4V = [^ (<*? - «>?) - ДЛ + CI1] + /Ч (Дя - 2ttlL2). (9.97)
Так как
cC
мы получаем
1,2
Г [Ь2С2(п|2д)||2)Д2С2а1 ;24 1] + <,2С1(Д2-2сч,2Ь2J 1 i/2
Xl [(a2-».)B + K—.)8][(«2-ai)e+K + -i)s] I ^' ( }
где индексы перед запятой относятся к а1г а индексы после запятой —
к а2.
Согласно соотношению D.51), выражение для arctg(b'/a'), являющего-
являющегося аргументом а' -\- jb', можно получить, если из суммы аргументов с|У
и числителя pxG ' вычесть аргументы множителей знаменателя G . Вычис-
Вычисляя эту разность и пользуясь формулой (9.91), находим
_г Ш12^2(^2 — 2а 12-^2) r
<pi ,2 = arc tg 1_а^
— arc tg ——— Т arc tg "' 2 . (9.99)
Ct2 д-л &2, ^1
Подобным же образом получаем
ci ,2 = - (с'- + d'^Yь = _ ЧМ (р\,3PuSG(l'3)G(i •3)')V* =
„л-,„. „\-/п„ ._и,.,„ лп (9.100)
Согласно соотношению D.51), выражение для аргумента c'-\-]d' можно
получить, если из суммы аргументов р\ и числителя pxG ' вычесть аргу-
аргументы множителей знаменателя G( . В результате после использования
формулы (9.55) имеем
•1.1,2= -2arctg^i-arctg^=^ =F arctg-^±^. (9.101)
tt| 2 a2 al a2 al
§ 14. Индуктивно связанные контуры, обладающие малым актив-
активным сопротивлением. Если активное сопротивление мало, т. е. токи
являются в обоих контурах сильно осциллирующими, то собственные
342 Глава IX
частоты определяются выражениями j»i,2= — а2 ± }'и>1у Рз.ь— — а2 ± /оJ.
Подставим эти значения в уравнение
(Р - Pi) (P - ft) (P - Рз) (Р ~ Pi) = О,
перемножим скобки и сравним полученные коэффициенты с коэффициента-
коэффициентами уравнения (9.69). В результате будем иметь соотношения
(9.102)
2, (9.103)
С = 2ai(af 4-0,2) +2^2 + 0J), (9.104)
JD = (a124-u,2)(a2 + uJ), (9Л05)
Сравнивая выражения (9.102) и (9.104) с выражениями (9.70), мы видим,
что ах и а2 —такого же порядка малости, как R1 и R2, ш-этому величи-
величинами a2, af и аха2 можно пренебречь по сравнению с о>2 и ш|. Таким обра-
образом, имеем
A = 2ax + 2a2, (9.106)
jS^cuf-fo,!, (9.107)
G^2^0J 4-2^0J, (9.108)
D ъ оJо)|. (9.109)
Из соотношений (9.107) и (9.109) получим
4 [J5±(J52
Пользуясь выражениями (9.70) и пренебрегая величиной /?х/?2, эту форму-
формулу можно привести к виду
Из соотношений (9.106) и (9.108) получим выражения для gcj и а2 и, заме-
заменив С и А их значениями (9.70). будем иметь
,) ' (9.111)
где первый индекс относится к аи а второй — к а9.
Пренебрегая в выражении (9.98) величинами a2, R2 и а/?, находим
1>2 Ш1 2 I Ш1 — Ш1 I <i)j 2 [(L-fix — L2C2J-\-4C1C2M2]112
Если затухание мало и а2 — а1<Сш1 — ш2, то последние члены в выраже-
выражении (9.99) очень велики, поэтому сумма углов близка к тс, а разность —
к нулю. Чтобы устранить неопределенность, воспользуемся формулой
-=- т: — arc tg A = arc tg (A'1).
Поскольку все арктангенсы малы, заменим arc tg А на А и пренебрежем
величиной As, в результате чего получим
ТС A4-1) Ш1 2^2 (^2 %al %L2) 21DJ 2(а2 Oj)
A—<»fii!
Переходные явления в электрических цепях 343
Из выражения (9.100) находим
МС2Лш12(ш1и,2)^">i2MC2iQ
Учитывая, что все углы в выражении (9.101) велики, воспользуемся опять
соотношением
— тг — arc tg A = arc tg (A)
и напишем всюду А вместо arc tg А. Можно несколько упростить резуль-
результат, добавив 2тг, и получить
+
_
-1,2 И" -S)
(L,C, -L2C2) (П,С, -В2С2)
cd1j2[(L,C1—
Подставляя эти значения в (9.89) и (9 93), получим окончательное выра-
выражение для токов г\ и i2.
§ 15. Настроенные индуктивно связанные контуры, обладающие
малым активным сопротивлением. Пусть дга контура, рассмотренные
к предыдущем параграфе, настроены, каждый в отдельности, на одну и ту
же частоту. Тогда, если пренебречь членами с R2, Ьг Сх = L2 C2 и выра-
выражение (9.110) можно записать в ьиде
«12= Г, " Г, • (9.116)
В этом случае выражение (9.111) также можно упростить
Ci -f- R2 Су ,ц ip,
U(CCI"[(W4M]"
После подстановки в выражения (9.112) —(9.115) получим
«12 = Г, Q i, тт. (9.118)
п A ± 1) (С,В,-С, Д,)
VJ'2 2 "^ гмс
i 2= (CiC2I|'Q jt-, (9.120)
(9.121)
§ 16. Цепи из одинаковых звеньев. Иногда приходится иметь дело
с цепями, которые состоят из одинаковых повторяющихся звеньев (см.
фиг. 92). Все индуктивности равны L, и все емкости, за исключением пер-
первой, равны С. Для /--го звена уравнение (9.59) имеет вид
Cr, r-i Qr-i + cr, rQr + cr<rhl Qr^ = 0, (9.122)
где
1 га2
cr>r_i = cr,r+i = —¦?-, cr> r = Ьрг -[- — .
344 Глава IX
Это уравнение можно написать в форме
Qr-i + Qr+1 = B - LC^) Qr = 2 cos 2cp Qr, (9.123)
^ = /(U = /(LC)-1/2 2sm<?. ¦ (9.124)
Так как краевые условия наиболее просто выражаются через напря-
напряжения в узловых точках (первого и последнего контуров), представим урав-
уравнение (9.123) также через напряжение. Заменим в уравнении (9.123) г
на r+'l и полученное выражение вычтем из [уравнения (9.123), тогда,
поскольку
CV QQ
мы получим
Fr-i+Vr+i = 2cosi2?yr. (9.125)
Уравнения (9.123) и (9.125) аналогичны уравнению F.20) и имеют своим
C /Г^ [? /TS [? /Г-*- \С JC /
II
Фиг. 92.
решением (см. Двайт, 401.05 и 401.06) следующее выражение:
(9.126)
Поскольку конец линии заземлен, то
0 = Acos,2n<? + Bsm2n't. (9.127)
В первом контуре
Исключая г"х и заменяя р2 выражением (9.124). a Fo и Fx выражением
(9.126), получим
^^V cp. (9.128)
Заменим cos2cp и sin 2cp выражениями D03.02) и D03.22), взятыми их
справочника Дваита> тогда получим
Приравнивая найденное выражение к значению В/А, получаемому из соот-
соотношения (9.127), приходим к следующему уравнению:
Cctg2n<? = BC0 — Qtgcp. (9.129)
Подстановка корней этого трансцендентного уравнения в выражение (9.124)
дает собственные частоты рассматриваемой системы. Корни урапне-
пия (9.129) наиболее легко найти путем графического построения функции,
получаемой после перенесения всех членов пз нравом части в левую. Тогда
Переходные явления в электрических цепях
34S
пересечение построенной кривой с осью ср и даст искомые значения ср.
Вычисление амплитуд, удовлетворяющих заданным начальным условиям,,
до некоторой степени упрощается вследствие большого числа нулей в урав-
непиях (9.67).
§ 17. Интегральный эффект переходного процесса. В некоторых изме-
измерительных электрических схемах, где употребляются баллистические гальвано-
гальванометры, измеряется интегральный эффект переходного процесса. В таких
случаях для получения нужного результата
можно проинтегрировать соответствующее
дифференциальное уравнение. Рассмотрим в
качестве примера электрическую цепь, изо-
изображенную на фиг. 93. Это устройство иногда
применяется для сравнения величин взаим-
взаимной индукции и емкости. Цепь считается
сбалансированной, если замыкание или раз-
размыкание ключа не вызывает отклонения
стрелки баллистического гальванометра. Пе-
Перед тем как ключ замыкается в первый раз,
г1=г = г3 = ^ = <72 = 9з ~ 0. После того как
установится стационарный режим, г2 = is = О, q2 = г\ R± С и, если цепь сба-
сбалансирована, q2 — qs — 0, откуда q3 — г\ RjC. Пусть LG и Rq — самоиндукция
и сопротивление гальванометра, тогда уравнение Кирхгофа для контура,
по которому проходит ток г3, будет иметь вид
Фиг. 93.
dt
(9.130)
Предположим, что в момент Бремени t = 0 ключ замыкает цепь, а к мо-
моменту t = T достигается стационарное состояние. Умпожая уравнение (9.130)
на dt, интегрируя но t между этими пределами и пользуясь упомяпутымт
начальными и конечными значениями для токов и зарядов, получим
Сокращая на iv приходим к результату
M=-R1R2C. (9.131)
Это— искомое условие баланса схемы. Если значения S и М не подобраны
специальным образом, то ток через гальванометр не будет равен нулю
в продолжение переходного процесса, а будет протекать спачала в одном
направлении, а затем в противоположном.
§ 18. Переходные явления при импульсах конечной продолжитель
ноети. До сих пор в этой главе рассматривались переходные явления,
наступающие после мгновенных изменений в цепи. Обратимся теперь к слу-
случаю, когда прилагаемая э. д. с. требует для достижения своего стационар-
стационарного значения конечного времени Тй. Пусть в интервале О < t < То ее зна-
значение равно f{t). Подставляя эту функцию вместо ?-, решаем полученные
уравнения, как и прежде, и находим общее решение однородной системы
и частное решение неоднородной системы. Определяем далее произвольные
постоянные из начальных условий (при t = 0). Полученное решение будет
справедливо для интервала 0 < t < Jo. Затем будем искать решение урав-
уравнений, имеющих место после мгновенного изменения в цепи в момент вре-
времени t — Jo. При отсутствии дополнительных изменений общее решение1
будет прежним, а частное решение—другим. Мы определим постоянные
интеграции, полагая t = T0 в этом втором решении и подставляя в него
346 Глава IX
значения qv q2, ..., qn и t\, i%. .....
при t = T0. Второе решение имеет место в интервале То < / < со.
В случае, когда f(t) — сложная функция, нахождение частного интег-
интеграла для первого решения может оказаться очень трудным или даже не-
невозможным, особенно для сложных цепей. Если, одвако, импульс э. д. с.
имеет прямоугольную форму, то в интервале 0 < t < То
<—г э. д. с. постоянна и частный интеграл для первого
с решения * можно найти методом, рассмотренным в
Р § 10. Если в интервале Го < t < со э. д. с. равна
—I 1 нулю, то для этого интервала сохранится лишь об-
общее решение однородного уравнения.
Для контура, изображенного на фиг. 84, со-
Фиг. 94. стоящего из индуктивности, емкости и сопротивле-
сопротивления, включенных последовательно, в интервале
0 вместо уравнения (9.3) будем иметь
'о
Если ввести
то общее решение в случае, когда i?2/DZ/2) Ф it'(LC), принимает вид
q = Сх еш + С2 е^ + J?L-) \f{l)e-^dt- T^) { / (t) e~™ Л. (9.134)
Если i?a/DL2)=l/(/^), то Х = Х1 = Хг= -B/BL)=-1ЦЩ1'» и
^ f(t)e~» dl-^tf(t)er-»dt] . (9.135)
о о
Пусть в начальный момент (f=0) </=</„ и i=iv, тогда, подставляя
t=0 в решение (9.134) и в его производную, получим
Gо — Сг + С2, i0 = 'klC1 -f- X2C2, ?*i= ^ ^_^ ° , С2 = ^ °_j-- ° • (9,136)
^_^ 2 ^
В случае критического затухания, согласно соотношению (9.135), имеем
С; = 20 и C'a = io-\qo. (9.137)
В качестве специального примера рассмотрим импульс, показанный на
фиг. 94 и описываемый функцией
/@ = 12*, (9.138)
причем <7о=го — 0 при t = Q. Пусть этот импульс посылается в контур
•с критическим сопротивлением. Для такого контура справедливы соотноше-
соотношения (9.135) и (9.137), так что С[ =С!2 = 0. Тогда из соотношения (9.135)
получаем
' 1- '
п Ля pxtft \ tf-м tjt С t2 p~u <lt Л (9 1391
0
Задачи 347
После интегрирования (см. Двайт, 567.1 и 567.2) получим ¦. *я
<9Л4<>
выражения определяют г и q в интервале 0 <r t < Тп. Решение в интер-
интервале То <с t < оо, определяемое выражением (9.9), имеет вид
q = e-ia/2L(A + Щ, i =
Подставляя сюда значения г = гх, # = </х при ? = Г0) находим
(9.142)
(9.143)
Значения гг и ^х в формулах (9.142) и (9,143) определяются из выраже-
выражений (9.140) и (9.141), в которых нужно положить t = T0. Тогда формулы
¦(9.142) и (9.143) определяют заряд и ток в интервале Ти < t < со.
ЗАДАЧИ
1. Звено, состоящее из параллельно включенных конденсатора С,2 и индуктив-
индуктивности L2, соединено последовательно с конденсатором Сл, ивдуктивностью Lx и выклю-
выключателем. Вначале Сг имеет заряд Q- Показать, что в любой момент времени после замы-
замыкания цепи выключателем величина заряда на конденсаторе Сх определяется формулой
Q {р\—Р2Г1 [(^Г1^!1—Ръ) cos Р\г—(^Г1^!1 — Pi) cos Рг1]<
где
л_
2. В обмотке электромагнита, индуктивность которого равна 1 гк, циркулирует
постоянный ток 10 а. Пренебрегая сопротивлением, найти величину емкости конденса-
конденсатора, который следует подключить к концам обмотки электромагнита для того, чтобы
при внезапном разрыве цепи не произошел пробой изоляции, выдерживающей напря-
напряжение в 10 000 е. Используя этот конденсатор, показать, что при сопротивлении обмотки
электромагнита в 1 ом действующая э. Д. с. в ней будет приблизительно равна 9 992 е.
3. Катушка самоиндукции L, конденсатор С и батарея, обладающая э. д. с. % и
шутренним сопротивлением R, соединены параллельно. Показать, что через ( сек. после
присоединения батареи ток через нее равен
«|_ [1 _ (шКС)-1 е-нС sin юг],
.а ток через катушку самоиндукции раной
%- {1 — е~иШС [BСОЙС)-1 sin cot + cos cot]},
где
1/
Написать решение для случая, когда величина ш мнимая или когда она равна нулю.
4. Посие того как в контуре, рассмотренном в предыдущей задаче, установилось
стационарное состояние, батарея отключается. Показать, что через / сек. после отсо-
отсоединения батареи заряд на конденсаторе, равен
348 Глава IX
5. Коэффициент взаимной индукции двух связанных контуров равен М. Первый
контур состоит из <§, R, I] и выключателя, соединенных последовательно, а второй
контур содержит L2 и С, также соединенные последовательно. Показать, что дифферен-
дифференциальное уравнение для тока в первом ковтуре будет
С (ЬЛЬ2 — М2) i + CL^Ri + L^ + Ri=%,
а для тока во втором контуре — такое же, только с правой частью, рчвной вулю. При
каких значениях параметров контура в системе возможны колебания?
6. Показать, что если после установления стаппонарвого состояния в системе,
рассмотренной в предыдущей задачр, цепь первого контура внезапно разрывается, то
через t сек. после разрыва ток во втором контуре будет равен
7. Основной контур состоит из двух одинаковых индуктивностей L и L и кон-
конденсатора С, соединенных последовательно. Параллельно конденсатору подключается
батарея % с внутренним сопротивлением R. Каждая из индуктивпостей L связана с
контуром, состоящим из последовательно соединенных ипдуктивности L и кондевсатора
С, причем коэффициент взаимной индукции равен М. После достижения стационарного
состояния цепь батареи разрывается. Показать, что ток в освовном ковтуре равен
у % Вгх [(cos prt + cos p2t) + (i2 + 8M2)^1/2b(cosp1i — cos p2t)].
в то же время ток в каждом из связанных контуров равен
% MR-1 {L2 + 8M*)-112 (cos Plt — cos p2t),
где
' A,2 =[3i T (L2 + 8M2I/2] [4" (.L2 — M2)]-1.
8. Сопротивление R и конденсатор С,, соединенные параллельно, пключаются по-
последовательно с батареей <§, конденсатором С2 и выключателем. Вначале конденсаторы
зарядов не имеют. Показать, что через t сек. после замыкания цепи заряд па конден-
конденсаторе С2 равен (внутренним сопротивлением бятареи можно пренебречь)
С2й11-С2(G]+С2)-1е-^],
где m = [R(CJ-\-Ci)]~1. Найти также заряд на копденсаторе Ct.
9. В обмотке большого электромагпита, индуктивность которого L, циркулирует
постоявный ток /. Цепь разрывается при помощи ключа, устроенного так, что разом-
разомкнутые концы расходятся с постоянной скоростью и через 1/]0 сек. образуют зазор в
1 см. Пробивное напряжение ла ключе равно 1 500 в/мм. Показать, что для предотвра-
предотвращения искрения в ключе его следует блокировать кондепсатором, емкость которого равна
I2L
A5000J' ^ 150 000 '
в зависимости от того, которая из величин больше.
10. Три ветви соединяются в двух узлах. Первая ветвь содержит Lr и Rlt вторая
содержит L2 и Д2, а третья содержит %, Ли выключатель. Показать, что через t сек.
после вамыканип цепи ток через батарею равен
где
11. Три ветви соединяются в двух узлах: первая ветвь содержит конденсатор Сх в
выключатель, вторая — конденсатор G2 и выпрямитель К, третья — индуктивность L.
Вначале конденсатор Сл имеет заряд Qo, а полярность выпрямителя такова, что сразу
после замыкания цени (при г = 0) конденсатор 6\ не может раврядиться через вторую
ветвь. Показать, что ток через индуктивность L в указанные ниже промежутки временя
равен при 0 < t<\ тт 1!
Задачи = 34&
при -i л (LCO1'2 <t<-|-« {(iCiI/2 + [L (Сг + С,)]1'*}
при г > -^«{(ZC^I/» + [L (Сх + С2)]1/2}
12*. Коэффициент взаимной индукции двух связанных контуров с параметрами L,
R, и N (индуктивность), R2 равен М. В один из контуров включается э. д. г.. %.
Показать, что полное количество электричества, протекающее через второй контур,
равно %MI1\R2.
13*. Коэффициент взаимной индукции двух евпзапных контуров с параметрами С,
R, L и N, S (сопротивление) равен М. В начальный момент на конденсаторе находился
заряд Q. Показать, что если LN = M2, то начальные токи равны
NQ MQ
C(RJN+SL) Я C(RJN+SL)'
Найти токи в любой последующий момент времени.
14*. Два изолировавных провода А и Б с одинаковыми активными сопротивлениями
я с самоипдукциями L имеют коэффициент взаимной индукции, мало отличающийся от L.
К концам провода В присоединяется проволока малого активного сопротивления, а к
концам провода А — батарея с малым внутренним сопротивлением. Через t сек. uoi ле
присоединения в проводе А наблюдается ток i. Доказать, что для не очень малых t
ток приблизительно равен
1=4" ('"о+'").
где 10 — постоянный ток в А, V ¦—ток, который протекал бы через t сек. в А н В при
их последовательном соединении с батареей.
15*. Два заряженных проводника, емкостные коэффициенты которых равны ^lt 4B1
Г, соединяются посредством катушки, имеющей большую самой вдукцию L и сопротив-
сопротивление R. Показать, что частота собственных колебаний системы равна
-Г2 1 i?^ у/2
1 L 4V •
16*. Две параллельно соединенные катушки (#, S — сопротивления, L, М, N —
«оэффициевты индукции} расположены так, что постоянвый ток, разветвляющийся
жежду ними, создает такие магнитные поля, что результирующая сила, отклоняющая
«трелку гальванометра, равна нулю. Доказать, что при внезапном возникновении тока
в цепи, содержащей катушки, начальная сила, действующая на стрелку, не будет,
вообще говоря, равна нулю и что в результате получится такое отклонение стрелки
¦гальванометра, которое возникает при постоянном (установившемся) токе, проходящем
в одной первой катушке в течение времеви
М—L M—N
R S
17*. Конденсатор С разряжается через две пени: первая состоит из сопротивления
R и самоиндукции L, другая —из сопротивления R' и конденсатора С. Показать, что
яаряд Q на конденсаторе в любой момент времени удовлетворяет дифференциальному
Дфавневию
"• 4Н?+*+"О §+(?+?+?) %+&-*¦
18*. Мост Уитстона используют для сравнения коэффициента взаимной индукпии
М двух катушек с коэффициентом самоиндукции L третьей катушки. Одна из парных
катушек помещается в диагональ АС, содержащую батарею, другая катушка присо-
присоединяется к концам диагонали BD в качестве шунта к гальванометру (баллистическому)
и третья катушка помещается в плечо AD. Мост вначале балансируется на постоянном
токе (сопротивления плеч АВ, ВС, CD, DA равпы Rlt R2, R3, Ri)', сопротивление
шувта изменяется до тех пор, пока при размыкании и замыкав ии цепи батареи стрелка
гальванометра перестает отклонятся. Пусть в сбалапсированиом мосте сопротивление
шунта равно R. Доказать, что
350 Глава IX
19. Два конденсатора С, и С2 пключеиы последовательно с индуктивностью L..
В начальный момент заряд па С, равен Q, а на С2—нулю. Показать, что через t сек-
после замыкания цепи ток через катушку индуктивности равен
/%in [Gife)
Показать, что если Cj > C2, то заряд на первом конденсаторе никогда не изменит
свой знак.
20. Три ветви соединяются в двух узлах. Каждая из двух ветвей содержит конден-
конденсатор С и индуктивность L, а третья ветвь — только конденсатор С. Показать, что кру-
круговые частоты собственных колебаний системы равны (_LC)—1'2 и З1'2 {LC)~ '2.
21. Между двумя пластинами желательно создать поле, которое за яремя То ли-
линейно возрастает до значения Fo, а потом за такое же время линейно уменьшается до-
нули. Емкость такого конденсатора равна С, и при наличии поля Fo заряд на нем
равен Qo. В пепи конденсатора находится сопротивление R. Найти форму импульса,
который должен быть приложен для создания вышеописанного поля.
22. Электрическая цепь представляет собой равносторонний треугольник, каждая
сторона которого содержит емкость С, а вершины соединены с общей центральной точ-
точкой гшдуктивностями L. Показать, что в системе возможны колебания с периодом
Т = Чъ CLCI'2.
23. Два одинаковых конденсатора С соединены последовательно с соленоидом
индуктивности L. Показать, что соединение средней точки соленоида с точкой между
конденсаторами приводит к появлению новой круговой частоты со2, определяемой
выражением
где coj — первоначальная круговая частота, а М — взаимная индукция между двумя
половинами соленоида.
ЛИТЕРАТУРА
Berg E. J., Heaviside's Operational Calculus, McGraw-Hill, 1929.
Bush V., Operational Circuit Analysis, Wiley, 1929.
Carson J. R., Electric Circuit Theory and the Operational Calculus, McGraw-Hillr
1920.
Cohen L., Heaviside's Electrical Circuit Theory, McGraw-Hill, 1928.
Gardner M. P., Barnes J. L., Transients in Linear Systems, Wiley, 1942.
(См. перевод: Г a p д я e p M. Ф., Б з р н с Дж. Л., "Переходные процессы
в линейных системах, М., 1949.)
Geiger-Scheel, Handbuch der Physik, Bd. XV, Berlin, 1927.
G u i 1 1 e ma n E. A., Communication Networks, Wiley, 1931, 1935.
Heavisi'de O., Electrical Papers, Boston, 1925.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
Kurtz E. В., С о г с о г a n G. F., Introduction to Electrical Transients, Wiley, 1935.
Maxwell J. C, Electricity and Magnetism, v. II, Oxford, 1881.
M с I 1 w a i n K., Brainard J. G., High Frequency Oscillating Circuits, Wiley, -
1931.
Ollendorf F., Die Grundlagen der Hochfrequenztechnik, Berlin, 1926.
Pierce G. W., Electric Oscillations and Electric Waves,"McGraw-Hill, 1920.
Poor V. C, Electricity and Magnetism, Wiley, 1931.
Russell A., Alternating Currents, Cambridge, 1914. n
Shea Т. Е., Transmission Networks and Wave Filters, Van Nostrand, 1929.
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
\\ ien-Harms, Handbuch der Experimentalphysik, Bd. XI, Leipzig, 1932.
Глава X
ПЕРЕМЕННЫЕ ТОКИ
§ 1. Гармонические электродвижущие силы. Частное решение. Если-
в системе все э. д. с. являются периодическими функциями времени, то они:
создают ток, называемый переменным. Наиболее распространенной и важной
из этих функций является гармоническая или синусоидальная функция.
Электродвижущая сила такого типа индуцируется в плоской проволочной
петле, имеющей форму окружности радиуса а, яри ее вращении с постоянной
угловой скоростью (и вокруг диаметра, который расположен под прямым
углом к однородному магнитному полю В. Когда плоскость петли обра-
образует с направлением поля угол я = Ы, поток через нее равен N = •ка2В sin Ы.
Согласно формуле (8.1), индуцированная э. д. с. будет равна
Ш= — — = -'Ka2Biocoswt^=e(lcoswt. A0.1)
В случае неоднородного магнитного поля или неравномерной угловой ско-
скорости Ш нельзя, вообще говоря, выразить в такой простой форме; но если
эти отклонения периодические, то э. д. с. можно представить в виде супер-
суперпозиции подобных простых колебаний с разными частотами. Такие случаи
будут рассмотрены в конце настоящей главы.
Дифференциальное уравнение, в котором t является независимой пере-
переменной, будет содержать теперь в правой части вместо постоянного члена
выражение вида
g1 = g0 cos (wt -f cp) = A cos Ш -f В sin Ы =
= Re{g0e>'(l0'+?>} = Re{>e>'""}, A0.2)
где A~E0coS(f, B-— —^„sincp. Полное решение такого уравнения состоит
из общего решения однородного уравнения, получаемого путем приравни-
приравнивания правой части нулю, плюс частное решение неоднородного уравнения,
или стационарное решение. Первое решение неустановившегося режима
подробно исследовалось в предыдущей главе, где было установлено, что
при наличии в схеме сопротивления каждый член решения содержит мно-
множитель, в который время входит в снригателышй показатель экспонент
цналыюй функции. С течением времени эта часть общего решения стре-
стремится к нулю и остается только частное решение, которое и будет рас-
рассматриваться в настоящей главе.
§ 2. Контур, содержащий сопротивление, емкость и индуктивность.
На фиг. 84 был показан наиболее общий вил электрической цепи, которая не
содержит взаимной индуктивности и в которой Я, L и С включены последова-
последовательно. Для простоты выберем t = 0 в тот момент времени, когда синусоидаль-
синусоидальная э. д. с. достигла мяксимума. Тогда в выражении A0.2) <р = 0. Уравнение-
352 Глава X
Кирхгофа для рассматриваемой цепи имеет вид
Lq + Rq + ?=I{e{eoe^}. A0.3)
После того как переходные процессы, о которых шла речь в § 3 гл. IX,
прекратятся, естественно ожидать, что ток в контуре будет иметь ту же
периодичность, что и э. д. с. Попытаемся отыскать частное решевие в форме
i = Re {ie*°<} = Re {le^1} = Re {Уо ё («"+*)}. A0.4)
Вектор I является, вообще говоря, комплексной величиной и называется
комплексной амплитудой, содержащей как амплитуду /0, так и фазу ф иско-
искомого тока. НапишемI = /' + //", где /' и /" — действительные величины, тогда
Имея в виду, что i = g, подставим в уравнен ie A0.3) вместо q его значение
м, опустив общий множитель е'ю1, получим
[i? + /(«»L-JL)]l = g0> A0.5)
или
Это выражение по форме полностью совпадает с выражением F.6), однако
вместо сопротивления здесь стоит величина Z, известная иод названием
комплексного импеданса контура, комплексная амплитудаJ) тока I вместо
тока / и амплитуда SS0 синусоидальной э. д. с. вместо ?. При использова-
использовании этих символов всю теорию электрических цепей, развитую в гл. VI
на базе законов Ома и Кирхгофа, можно полностью применить к цепям
переменного тока в стационарном режиме. Амплитуду тока можно всегда
найти, взяв квадратный корень из произведения I и сопряженной ей вели-
величины I*, так как II* =Г2 + 1. В гл. IV мы уже рассматривали подобные
операции с комплексными величинами. Б нашем случае, в частности, имеем
Вектор Z называется полным сопротивлением контура (импедансом), а
X = шЬ — 1 / (шС) — реактивным сопротивлением, причем первый член wL
(индуктивное реактивное сопротивление) и второй член 1 /(юС) (емкостное
реактивное сопротивление) измеряются в тех же единицах, что и сопротивле-
сопротивление. Умножим числитель и знаменатель выражения A0.6) на Z*; тогда
знаменатель будет действительной величиной, а /" / /' будет равно отноше-
отношению мнимой части Z* к действительной. Следовательно,
-Согласно выражению A0.4), ток равен:
; = 4^os((d? + <L). A0.9)
См. примечание к § 9 гл. IV.
Переменные токи 353
Если конденсатор отсутствует, то
i = ^—тг cos (tot - arc tg ^ V A0.10)
(R2 + <fl2L2I/2 V ь R J y >
В этом случае говорят, что ток по фазе отстает от э. д. с. Если контур
состоит только из конденсатора и сопротивления, то, полагая L = 0, получим
+ arctg *Л. A0.11)
В этом случае ток опережает э. д. с. При наличии одной лишь самоиндукции,
полагая в выражении A0.10) R = 0, находим ( поскольку yir = arctgoo J
A0.12)
В этом случае ток отстает на 90°. При наличии одной лишь емкости,
полагая в выражении A0.И) R = 0, имеем
(+ уя\ A0.13)
т. е. ток опережает э. д. с. на 90°.
§ 3. Мощность, эффективные значения, резонанс. Мощность, затрачи-
затрачиваемая в контуре в каждый момент времени, определяется выражением,
аналогичным выражению F.10),
Р = 1% = Щ. cos tot cos (tot + <]>) =
— -у- (cos2 tot cos ф — cos tot sin tot sin <]>) =
= -?¦ (cos ф + cos 2tot cos ф — sin 2tot sin ф), A0.14)
где i и g —мгновенные значения тока и э. д. с, входящие в выражение
A0.3); A0.4) и определяемые соотношением A0.6). Изменение мощности
на протяжении одного периода показано на фиг. 95. Большую часть времени
мощность поступает в контур, но в течение некоторого промежутка времени
она передается из контура обратно в генератор. Если мы усредним мощность,
определяемую выражением A0.14), по целому числу периодов, то члены
с cos 2tot и sin 2tot выпадут и останется только постоянный член, так что
il
Z*
=!Re{8i*}, A0.15)
2
где 8* и Z* — комплексно-сопряженные величины 8 и Z соответственно.
Введем величину хе, получаемую после извлечения квадратного корня
из квадрата переменной величины х, усредненного но периоду. Как известно
(см. Двайт, 858.4), среднее значение квадрата синуса или косинуса равно
1/2. Следовательно, квадратный корень из среднеквадратичного значения
тока и э. д. с. равен соответственно
и ge = B)-V*g0. A0.16)
Соотношение (Ю.7) можно записать теперь в виде
23 в. Смайт
354 Глава X
Целесообразность введения этих величин станет очевидной, если, используя
формулы A0.16) и A0.17), записать в такой же форме выражение A0.15):
Р = ie Ше cos ф = i* Z cos ф = ~ cos ф = Ц R = Re [8e i?}. A0.18)
Мы видим, что и случае ф = 0 эти формулы совпадают с соответствующими
формулами для постоянного тока § 4 гл. VI. Поэтому величина ie назы-
называется эффективным током, a <fe — эффективной электродвижущей силой.
Величина cos ty, называемая коэффициентом мощности, выражается через
параметры контура; используя формулу D00.12) из справочника Двайта
и выражение A0.8), имеем
COS Л = — J5- . A0.1У)
Величина iesin<jj называется реактивной или безваттной составляющей тока,
поскольку опа ничего не вносит в среднее значение мощности.
Из соотношения (Ю.7) следует, что при i»2 = (LC)~1 Z достигает мини-
минимума, а ток принимает максимальное значение. Частота, при которой ток
максимален, называется резонансной. Согласно формуле (9.5), при малом
сопротивлении в цепи контура резонансная частота близка к частото соб-
собственных колебаний контура. Резонанс, конечно, возможен и в том случае,
когда сопротивление настолько велико, что контур не может находиться
в колебательном режиме. Если контур настроен в резонанс, то, как вытекает
из соотношений A0.15) и A0.19), коэффициент мощности равен единице
и цепь потребляет максимальную мощность. В случае контура с очень
малым сопротивлением и емкостью, но с большой индуктивностью ток
в нем будет, согласно выражению A0.12), очень малым и в то же время
1
<}).—> —— тс, т. е. cos ф —>0. Такая цепь, не потребляя мощности, препятствует
прохождению переменного тока и в то же время пропускает постоянный;
это устройство называется дросселем. С другой стороны, при включении
очень большой емкости постоянный ток будет проходить плохо, но зато
переменный ток, согласно выражению A0.13), пройдет без всякой потери
1
мощности, потому что и в этом случае ф = -^тс.
§ 4. Графическое представление. Векторная диаграмма *К Как было
показано в § 9 гл. IV, значение комплексного числа z = x-\-jy можно
представить точкой на комплексной плоскости. В полярной системе коор-
координат это можно записать в виде ге^, где 6 — угол между осью абсцисс
и радиус-вектором г, проведенным в эту точку. Выражения для э. д. с.
и установившегося тока A0.3) и A0.4) имеют ту же форму, поэтому их
также можно представить в полярной системе координат. Эти два вектора
длиной /0 и (So, отложенные из начала координат и составляющие между
собой постоянный угол ф, вращаются с постоянной угловой скоростью ш
вокруг начала координат. Мгновенные значения i и Щ в момент времени t
равны проекциям радиус-векторов на действительную ось Ох. Вектор Ш
представляет собой результирующую э. д. с. в контуре, являясь суммой
трех компонент: 1) э. д. с. jwLIQ в катушке индуктивности, опережающей
ток, согласно выражению A0.12), на 90°, 2) компоненты I0R, находящейся
в фазе с током, и 3) э. д. с. —/70/ (шС) на конденсаторе, отстающей от тока,
согласно выражению A0.13), на 90°. Векторная диаграмма э. д. с. н ее
Ц Автор не делает различия между векторной и круговой диаграммами. При пе-
переводе принят термин «векторная диаграмма». — Прим. перев.
Переменные токи
355
компонент изображены на фиг. 95, слева. В центре фиг. 95 показаны
осциллограммы тока, э. д. с. и мощности. Справа изображена векторная
диаграмма компонент мощности.
Фиг. 9Si
§ 5. Последовательное и параллельное соединение импедансов. Как
уже упомивалось выше (см. § 2), комплексные обозначения позволяют
написать для переменных токов закон, аналогичный закону Ома для по-
постоянных токов. Это обстоятельство, совместно с законами Кирхгофа, дает
возможность установить для импедансов, соединенных последовательно п
Фиг. 96.
параллельно, теже самые правила, которые были получепы в §5 гл. VI для
сопротивлений. Так, общий импеданс Z цепи, состоящей из нескольких
импедансов Z1; Z2, ..., Zn, соединенных последовательно, выражается
следующим образом:
+... + Zn. A0.20)
Поскольку мы имеем дело с векторами, следует брать векторную сумму
23-
356 Глава X
вместо алгебраической. Для параллельного соединения импедансов имеем
Так как обратная величина-комплексного числа ге>н равна в~'ь / г, то при
параллельном соединении импедансов нужно откладывать на диаграмме
векторы, длины которых —обратные величины длин Zv Z2, ..., Zn, а аргу-
аргументы имеют противоположный знак. Для получения результирующего
вектора Z следует взять обратную величину модуля суммы этих величин
и сменить знак аргумента суммы па обратный. На фиг. 90 показаны век-
векторные диаграммы: слева — для случая последовательного соединения трех
импедансов Z1; Z2 и Z3 и справа — для случая параллельного соединения
тех же импедансов, когда складываются обратные величины импедансов.
Обратная величина импеданса часто называется полной проводимостью.
Масштаб длин векторов на фиг. 95 задается окружностями единичного
радиуса. Следует заметить, что при параллельпом соединении сумма обрат-
обратных величин конечных импедансов Ъ^1 может оказаться равной нулю. В этом
случае результирующий импеданс Zp равен бесконечности, т. е. ток такой
частоты через цепь проходить пе может.
§ 6. Передача мощности. Предположим, что источник, имеющий
импеданс Zs, генерирует э. д. с. Шье^1, а импеданс нагрузки равен ZL.
Тогда, согласно выражениям A0.7) и A0.20), ток в цепи равен
и, в соответствии с выражением A0.19),
^ц-. A0.23)
Пользуясь выражением A0.19), находим среднюю мощность, потребляемую
нагрузкой,
^- (Ю.24)
Для определения значения Zl, при котором в нагрузке поглощается макси-
максимальная мощность, приравниваем частные производные дР / dRL и дР/ dXL
нулю, в результате чего найдем
Rl=KI + (Xs + XLY A0.25)
и
XS=-XL. A0.26)
После подстановки выражения A0.26) в A0.25) получаем
RL = RS. A0.27)
Таким образом, максимальная мощность передается в том случае, когда Zt
и Zs являются комплексно-сопряженными величинами. При выполнении
этого условия
§ 7. Мостик импедансов. Точно также как мост Уитстона (см. фиг. 60)
служит для сравнения сопротивлений, мост, изображенный па фиг. 97,
Переменные токи
357
употребляется для сравнения импедансов. Пусть /Ocoso>? — ток, питающий
мост, тогда ток через индикатор Zg является [в выражении F.18) следует
заменить R на Z] действительной частью выражения
,• Z,Z4—ZaZ3Т )fOt
Aс •
Если ток равен нулю, то должно выполняться соотношение
Z7 11 1А1Л ЧП\
14— 2 3* ^lU.OU^
Отсюда получаются два условия баланса вместо одного, ибо это соотношение
должно выполняться независимо как
для действительной, так и для мнимой
части.
Наиболее распространенными мо-
мостами такого типа являются: емкостный
мост
у !_ 1 _ / 1 _ r
в котором
условие
а также
ности,
и Z4 = JR4,
при балансе выполняется
С1Л2 = С8ДЛ, A0.31)
мост, содержащий индуктив-
индуктивФиг. 97.
И Z4 =
в котором при балансе
it-lift =^ Jticylin If l^-til/, = iVo/Xo. tlU.OZl
§ 8. Цепь переменного тока в общем случае. Задачу о нахождении
токов в произвольной цепи можно решить точно так же, как и в § 9 и 10
гл. VI, если удастся ввести величины Zpq, связь которых с комплексными
э. д. с. и контурными токами будет аналогична связи jRpQ с постоянными
токами и э. д. с. Выражения (9.50) — (9.53) определяют взаимные пара-
параметры Lrs, Rrs и Srs, а также собственные параметры Lrr, Rrr и Srr таким
образом, что в стационарном состоянии, когда все токи и э. д. с. изменяются
с одной и той же частотой, уравнение (9.54) можно записать в виде
(
/o,Lrr + Rn - 'in j i, = Zrr ir = 8,,.,
в виде
s + JR,s-^)is= ± Zrsi,, =
A0.33)
а уравнение (9.55)
± (/o,Lrs + JR,s-^)is= ± Zrsi,, = 8,.,. A0.34)
Импеданс Zr определяется соотношением
Ъ„ = Zr + Zlr + Z2r + ... + Znr A0.35)
и, таким образом, содержит коэффициенты взаимной индукции, включенные
в Lrs. Сумма э. д. с. 8^ 82, ..., 8П в контурах, несущих токи ilf i2, ..., in,
имеет вид
t'liii ± Z12i2 ± .. - ± Zlnin= S^
± • • • ±
A0.36;
±
±
358
Глава X
Эти уравнения по форме совпадают с уравнениями F.32); знаки опреде-
определяются в соответствии с выбранным направлением токов. Решение будет
иметь также прежнюю форму, поэтому, согласно выражениям F.36), мы
приходим к выводу, что если единственный источник э. д. с. r?v находится
в ветви, где протекает единственный ток ip, то амплитуда а фаза тока ig
в д-й ветви выражаются соотношением
^2, A0.37)
4 =
где ApQ — алгебраическое дополнение элемента Zpg в детерминанте
Zn ... ± Ъш
A0.38)
± Znl ... Znn
Отсюда также следует, что стационарный ток в некоторой ветви, появля-
появляющийся при помещении переменной э.д.с. во вторую ветвь той же цепи,
равен, по амплитуде и фазе, току, который появится во второй цепи, если
тот же самый источник э. д. с» поместить в первую ветвь. Если источник
э. д. с. находится в г'-й ветви, то, согласно выражению F.37), отношение
любых двух стационарных токов в электрической цепи равно
Теорема Тевенина для переменных тг-ков утверждает, что если при
разомкнутом контуре потенциал на концах А и В в рассматриваемой
цени равен 80 и если (на той же частоте) при замене всех источников
э. д. с. их внутренними имнедансами цепь между концами А и В имеет
импеданс Z, то при соединении А и В проводом с нулевым импедансом
ток через него будет равен
A0.39)
Равенство A0.39) получается из A0.37) так же, как выражение F.38)
из F.36). Это позволяет включать данную цепь с концами А и В в другие
цепи как источник э. д. с. 80, имеющий внутренний импеданс Z.
Как мы увидим, в большинстве случаев возможно ввести контурные
токи таким образом, что будут выполняться следующие условия: 1) по
меньшей мере в одной ветви протекает только один ток ijj 2) в ветвях,
где протекают лишь два тока, эти токи направлены противоположно;
3) в любой ветви протекает не более двух токов. Тем самым определяются
все знаки и можно использовать выражение F.39), причем теперь в детер-
мипапте Д все собственные импедансы Zpp берутся со знаком плюс, а вза-
взаимные импедансы Zpr, — со знаком минус. Пусть в ветви, в которой поме-
помещена э. д. с, протекают два тока i2 и i3, тогда
A -i- Аз + А • • • + А
Z42 — Z4
44
-z
'in
Ai4
Ami
A0.40)
Если имеется несколько э. д. с, то их следует рассматривать по отдель-
отдельности и полученные результаты сложить, принимая во внимание фазу
каждой из э. д. с.
Переменные токи
359
Для получения полного решения с учетом переходных явлений следует
стационарные решения добавить к общему решению (9.67), после чего
определить постоянные интегрирования из начальных условий.
§ 9. Сопряженные ветви в электрической цепи. Мостик Андерсопа.
Две ветви в цепи называются сопряженными, если источник э. д. с, поме-
помещенный в одну из ветвей, не вызывает тока в другой ветви. Пусть в каж-
каждой из рассматриваемых ветвей протекает по одному току ip и ig; тогда
условие сопряжения, согласно соотношению
A0.37), имеет вид
Ди = 0. A0.41)
Если токи введены так, что применимо со-
соотношение A0.40), то, обозначая детерми-
детерминант в этом уравнении через Д123, будем
иметь следующее условие сопряжения:
Д1а=0. A0.42)
Найдем при помощи этой формулы усло-
условие баланса в мостике Андерсона (фиг. 98),
применяемом для сравнения величин ем-
емкости и самоиндукции. Импедансы, стоя-
стоящие в соотношении A0.40), в данном
случае равны: Z12 = jR3, Z13 = 0, Z14 = jR4,
-J-jR4 — fl(wC). Написав соотношение A0.42)
~ — Z12Z3Z44 -f- Z14Z2Z43 — Z14Z3Z42 = 0,
являющееся условием балапса мостика, и приравняв нулю действительную
часть, находим
1.A0.43)
Фиг. 98.
Z48=-//(«O и
= 0, или L =
Приравняв нулю мнимую часть, получаем
: -~ = О, ИЛИ
Ri = R:iR2. A0.44)
Выполнения условия баланса A0.44) можно добиться, используя постоян-
постоянный ток, как в обычном мостике Уитстона; затем, включая источник пе-
переменной э. д. с. и регулируя величину сопротивления R, можно удо-
удовлетворить условию A0.43).
§ 10. Вынужденные колебания в индуктивно связанных контурах.
Найдем токи ii и U в контурах, изображенных па фпг. 99. В этом слу-
случае, согласно соотношениям A0.33) и ПО.34), а также (9.50) —(9.53),
имеем
= R2 + /X2.
Пользуясь соотношением A0.37), получим выражения для токов
Z22t> (^2"Ь/-<^2) «о . : 2|2<Э
где
^12
D
D '
:2-х1ха +
19= — :
42
D
/{R.X,-f
A0.45)
A0.46)
A0.47)
360
Глава X
Взяв действительную часть произведения ije3tD(, как это делалось в выра-
выражении A0.4), находим
—¦ COs(<i)?-|-<p),
где
| D |
A0.48)
A0.49)
г2 — ||)| '
Далее
где
Исходя из выражения A0.46) или A0.50) и A0.52), получаем
A0.50)
A0.51)
A0.52)
A0.53)
Представляет особый интерес найти те значения ш, при которых
величины ix и i2 максимальны или минимальны. Прежде чем излагать
обычные приближенные методы, наметим
строгий путь вычисления этих значений.
Приведем выражение | D | к форме, бо-
более удобной для дифференцирования; срав-
сравнив соотношение A0.45) с (9.68) и заме-
заменив р на /ш, получим
/<i)Zjj = Cj,, /u>Z12 = С12, /o>Z22 = С22.
Таким образом, при помощи уравнения
(9.69) находим
rj rj у2 С11С22 f12 Г)
^11^22 4*12 „л
| ЛДЛЛ/WV—|
Фиг. 99.
— /Аш3 — Вт2 + /Сш + D)
L,L2 —
Умножая эту величину на комплексно-сопряженную и извлекая из полу-
полученного результата квадратный корень, будем иметь
| D | = L'Li~M2 К + (А2 - 2В) (»fi +
+ (J32— 2АС + 21)) (о4 + (С2 — 2BD) ш2
A0.54)
Определить максимальное и минимальное значения амплитуды ц без
построения кривой трудно, но для г2 вычисления упрощаются; дифферен-
дифференцируя выражение амплитуды mMEJ | D | тока i2 по ш и приравнртвая ре-
результат нулю, получаем в дополнение к ш2 = 0 следующее соотношение:
_ (?2 _ 2АС + 2D) 0L-2 (С2 - 2В?>) ш2 - 3D2 = 0.
A0.55)
Это — уравнение четвертой степени относительно ш2, корни его находятся
при помощи формул § 11 гл. IX. Каждому положительному дейст-
действительному корню соответствует максимум или минимум тока /2. Для.
выяснения вопроса о том, какому корню соответствует максимум, следует
Переменные токи . 361
подставить этот корень в уравнение A0.54). Тем самым определится также
величина амплитуды.
Обычно частоту переменного тока в электрической цепи определяют,
связывая эту цепь с контуром, имеющим откалиброванное реактивное
сопротивление; изменяя реактивное сопротивление, можно получить ма-
максимальную амплитуду тока в контуре. Такой контур называется волноме-
волномером. Пусть параметры электрической цепи Rv Lx, C1 и частота <о зафикси-
зафиксированы, тогда максимум тока i2 возникнет, согласно выражению A0.51),
при условии
Получаемое после дифференцирования соотношение разрешим относительно
Xf\ тогда
'л = щ+х* ¦ A0-56>
Отсюда, соглагио выражениям A0.51) и A0.49), находим для тока г
2
При очень слабой связи М —»0, ХBМ) = 0 и в соответствии с соотношением
A0.56) получаем
w = (L2Q-1/2. A0.58)
Эта частота совпадает с собственной частотой волномера, если Rz мали.
Сохраняя частоту постоянной, настроим теперь оба контура, тогда к соот-
соотношению A0.56) добавляется условие
Ш Aа5э>
Для удовлетворения соотношений A0.56) и A0.59) необходимо, чтобы
X1 = Xs = 0 A0.60)
или
где Х1 и Х2 имеют одттаковый знак. По, поскольку Xt и Х2 — действи-
действительные величины, соотношение A0.61) не может иметь места, если
М2ш2 < RtR2\ поэтому при слабой связи (М мало) справедливо соотноше-
соотношение A0.60) и максимум оказывается при
Формула A0.57) принимает вид
При сильной связи М2«J > Rfl2 имеет место соотношение A0.61) и
1<2М) = у f о (Я^Г1" «»s (Ы + ф), A0.64)
где
\L/2
362 Глава X
Выражение A0.64) показывает, что при достаточно сильной связи макси-
максимальный ток не зависит от М и ю. Следует помнить, что при больших
значениях L и С выражения для Хх и Х2 A0.61) являются положитель-
положительными, а при малых значениях — отрицательными.
§ 11. Индуктивно связанные контуры, обладающие малым активным
сопротивлением. Тот факт, что Вг и 112 малы, ие ведет к значительному
упрощению полученных выше выражений для тока, потому что членами,
содержащими /?а, можно с уверенностью пренебречь лишь при частотах,
довольно далеких от резонансных, когда другие члены не так малы. Однако
вычисление резонансных частот упрощается, ибо, обращаясь it выражениям
(9.70), легко видеть, что теперь в уравнении A0.55) членами АС и С2 можно
пренебречь и разложить его левую часть на два множителя
0. A0.65)
Первый множитель дает два положительных корня:
Максимальные значения тока i2 в этом случае получаются точно при нор-
нормальных частотах собственных колебаний связанных контуров [см. выра-
выражение (9.110)]. Второй множитель имеет один положительный корень ш2,
2 2
р
лежащий между ю2 п ю2.
2=2С,С2(Ь,Ь2
этой частоте получается минимум тока. Заметим, что если М—>0, то
т. с. частоты, при которых г2 максимален, стремятся к парциальным ча-
частотам (к резонансным частотам двух отдельных контуров).
Уравнение, соответствующее A0.55), но относящееся к максимуму
и минимуму тока 1г, можно теперь также разложить на множители
т-^)ш2-^]=0. A0.68)
Первый множитель совпадает с множителем в выражении A0.65), поэтому
г1 имеет максимумы при тех же частотах шг и юо, как и г. Второй множи-
множитель представляет относительно ю2 кубическое уравнение, которое решается
стандартным методом и п,ает один положительный корень, лежащий между
ш, и (в2, по отличный от (в3. Этому корню соответствует мгашмум тока.
§ 12. Настроенные индуктивно связанные контуры, обладающие
малым активным сопротивлением. Если два только что рассмотренные
контура настроены независимо на одну н ту же частоту, то hxCx = Ь2С2,
и результаты предыдущего параграфа несколько упрощаются. Максималь-
Максимальный ток в обоих контурах имеет теперь место при частотах и>1 и ю2,
которые [см. соотношение A0.66)] определяются выражением
<« = гг* "—Ч^ • A0.69)
Минимум тока i2 получается [см. соотношение A0.67)] при частоте
(В2 = г-; — ¦ . A0.70)
(СгС2) '2{L1L2—M2\ ^ '
Переменные
363
Замечаем, что если М —*• 0, то
поэтому при слабой связи получаем единственный резонансный пик при
собственной частоте обоих независимых контуров.
§ 13. Фильтры. На фиг. j 00 изображен специальный тип электриче-
электрической цепи, которая представляет собой бесконечную цепочку одинаковых
А
Z'\
к
<?!
Z,
в в
Фиг. 100.
С' D
—г~
Ь'
звеньев. Цепи такого типа весьма важны, так как они обладают способ-
способностью пропускать лишь определенные частоты, задерживая все остальные;
их называют обычно частотными фильтрами. Цепь, изображенную на фиг. 100,
ic=(!-K)ir+Kir_,
В
-о В'
¦J
Во
о
Z'a
z
7"
0
1Я
—о
Фиг. 101.
можно, очевидно, разбить на простые одинаковые ячейки двумя спосо-
способами. Сечения А', В', С и D' расщепляют каждый импеданс Zt на две
части: Ъа=кЪх и Zb=(l — к) Zv соединенные последовательно (О < к < 1).
Каждая ячейка в этом случае образует так называемое Т-образное звепо,
показанное на фиг. 101, а. При /с = 1/2 говорят, что звено имеет середиино-
поелсдовательные концы. Если в качестве грании звеньев взять сечения
А, В, С и D, то каждый импеданс Z2 можно представить в виде двух
импедансов Z'b = Z2j к и Ъ'а Z2/(l — к), соединенных параллельно. Такая
ячейка, изображенная на фиг. 101, б, называется П-образным звеном.
Б случае к = 1/2 говорят, что звено имеет серединпо-параллельные концы.
Используя выражения для имиедансов (9.50) —(9.53), A0.33) и A0.34),
получим уравнение Кирхгофа для г-го контура (см. фиг. 100) в виде
iJ.-Zair1.1 = 0. A0.71)
Это дифференциальное уравнение совпадает по форме с уравнением F.20)
и поэтому, согласно выражению F.21), имеет решение
i^Ach/T + Bsh/T, A0.72)
364 Глава X
где
^ A0.73)
Комплексная величина Г называется коэффициентом пропускания или
постоянной передачи звена. На фиг. 100 отсчет числа звеньев производится
от конца, где расположен приемник. Пусть этот конец находится беско-
бесконечно далеко, тогда г стремится к бесконечности, и. поскольку при х—> оо
2chx—>2sha;—>еж, в соответствии с фиг. 101, а имеем
iB. \г ~ AchiT+Bsh/T
Аналогично в соответствии с фиг. 101, б
или
Г = 1пЫ. AU.74)
Следовательно, постоянную передачи звена в бесконечной цепи И образной
или Т-образной структуры можно определить как натуральный логарифм
векторного отношения стационарного тока в звене к соответствующему
току в соседнем звене, более удаленном от источника э. д. с. При таком
определении действительная часть Г оказывается положительной и назы-
называется постоянной затухания а, а мнимая часть ср называется фазовой постоян-
постоянной или постоянной фазового сдвига.
Поскольку, согласно выражению A0.74), в бесконечной цепочке отно-
отношение ip+i/ip не зависит от р, постоянная передачи звена, составленного
из п простых одинаковых звеньев, равна
= In D2-Y=nT, A0.75)
Vlp17 '
0 (
-l lp-2 lp-П J V.lp-1
где Г — постоянная передачи одного простого звена. Представляет интерес
определить, какой импеданс следует присоединить к концу линии для
того, чтобы получить такой же эффект, как при бесконечном продолжении
линии. Такой импеданс называется итеративным, характеристическим или
волновым импедансом и обозначается Zfe для Т-звсна или Zfe< для П-звена.
Очевидно, если добавить или убрать одно звено из такой бесконечной
цепочки, то ее импеданс не изменится, например (см. фиг. 101, о) импеданс
между А'А" с импедансом Zh, присоединенным к В'В", будет таким же,
как между концами одного Zh. Отсюда получается соотношение
разрешая которое относительно Zftl и помня, что Za-|-Zb = Z1, будем иметь
Zhl = j(Za-Zb)+[ziZ2(l+-i|)]1/2. A0.76)
Из соотношения A0.74) следует
IDJ^Z^hF. A0.77)
Переменные токи
365
Изменив направление токов в линии на обратное (что сведется к тому,
что ZH и Zb поменяются местами), получим другой волновой импеданс
2 • ¦ A0-78)
Аналогично для П-звена (фиг. 101, б) имеем
I. I « I I
* T-
- , ! Zl
T4
§ 14. Условия на ковцах в частотных фильтрах. Постоянные А и В
в выражении A0.72) определяются из условий в первом и последнем звеньях
цепи. Рассмотрим цепь Т-образных звеньев. Если мы присоединим
к правому концу линии (фиг. 101, а) импеданс ZR, то, составляя уравне-
уравнение Кирхгофа для получившегося контура, пользуясь выражениями A0.72),
A0.73), A0.76) и A0.77) и считая г=0, получим
A0.81)
Пусть ZB=Zbl. В этом случае А = В и выражение A0.72) принимает вид
ir = Aerr. A0.82)
Если Zj--импеданс генератора и 8 —его э. д. с, то для первого звена
цепи имеем
Ток в последнем звене цепи, согласно выражению A0.82), равен
а ток в генераторе —
A0-85)
Поскольку, как мы покажем позднее, можно сконструировать цепь так,
что Г будет чисто мнимой величиной для какой-либо заданной частоты, то
для этой частоты ток в последнем звене будет иметь такую же амплитуду, как
и в генераторе. Это свойство является наиболее желательным, поэтому
всегда стремятся конструировать фильтры так, чтобы Zr (выходной импе-
импеданс) был равен волновому импедансу фильтра (измеренному в направле-
направлении к выходу). Из выражений A0.26) и A0.27) следует, что для того, чтобы
в пинию поступала наибольшая мощность, Z, должно равняться Zti- Как
будет показано в следующем параграфе, для пропускаемых частот Z Z^
366 Глава X _____
Следовательно, необходимо, чтобы импеданс генератора, питающего линию,,
или входной импеданс Z, был бы рдвен волновому сопротивлению филь-
фильтра (измеренному в направлении к входу). Точно к такому же выводу
можно было бы прийти в результате анализа цепи из П-звеньев, поэтому
ответ на вопрос, какой тип звеньев использовать, зависит от того, какие
из волновых импедансов Zhl п Zft2 или Zft^ и Zfc'2 можно наиболее простым
способом сделать равными заданным входному и выходному импеданса»
при исследуемых частотах.
§ 15. Частотные характеристики фильтров. Условие, при котором
ток данной частоты проходит через фильтр без потерь, нетрудно получить
из выражения A0.72). Действительно, если амплитуда тока ir одинакова
при всех значениях г, то члены, содержащие г, должны быть тригонометри-
тригонометрическими функциями; но, поскольку ch/6 = cos6 и sh/6~/sin6, это приво-
приводит к тому, что постоянная передачи звена Г должна быть чпсто мнимой
величиной. Следовательно, правая часть выражения A0.73) должна быть
действительным числом, заключенным между +1 и —1, т. е. Zx и Za.
должны быть чисто реактивными сопротивлениями. Эти идеальные условия
приближенно осуществляются на практике. Таким образом, условие идеаль-
идеальной передачи выражается неравенствами
Cl, или — 4<?!<0. A0.86)
__,2 ?2
Поскольку Zl и Z2 — чисто мнимые величины, из выражений A0.86),
A0.76), A0.78) —A0.80) следует, что для пропускаемой частоты Zhi=Zfc2:
и Zh-i = Zb'2- Поэтому при симметричных звеньях Zk и Zw для пропу-
пропускаемых частот являются активными сопротивлениями.
Рассмотрим теперь передачу тока через бесконечный фильтр при часто-
частотах, но удовлетворяющих неравенству A0.86). Выражая ток i's в s-м звене
через ток ?„, поступающий в линию, согласно выражению A0.74), имеем
ц = _;_-»г. (Ю.87>
Если отношение Zx / Z2 положительно, то спГ — действительное число,
большее единицы, откуда Г — действительное число, также [согласно
выражению A0.74)] положительное. Если
то спГ< — 1 и (см. Двайт, 655.2) Г=|Г|±/те. Поэтому вместо A0.87)
будем иметь
_;=-_;_-1П. A0.88)
Таким образом, амплитуда тока при частотах, но удовлетворяющих нера-
неравенствам A0.86), при прохождении тока от генератора вдоль линии зату-
затухает экспоненциально.
§ 16. Полосовой фильтр. Фильтры обычно разделяются на четыре
класса, а именно: 4
1) Низкочастотные фильтры, пропускающие все частоты, лежащие
ниже определенной частоты /2, и задерживающие все остальные.
2) Высокочастотные фильтры, пропускающие все частоты, лежащие
выше некоторой частоты /х, и задерживающие все остальные.
3) Полосовые фильтры, пропускающие частоты, заключенные между
значениями f1 и /2, и задерживающие все остальные частоты.
Переменные токи
367
4) Полосовые заграждающие фильтры, задерживающие частоты, лежа-
лежащие между значениями fl и /2, и свободно пропускающие все остальные
частоты.
Рассмотрим в качестве примера только третий класс, поскольку он
включает первые два класса как.частные случаи и является, повидимому,
наиболее важным. В дальнейшем огра-
ограничимся рассмотрением лишь симметрич-
симметричного Т-звена, у которого (см. § 13) к —
= 1/2. Простейшее устройство такого типа
показано на фиг. 102, где Zj = / [ш/^ —
— 1 / (iflC^)] и Ъг = — / / (юС2), так что
L,/2
гс,
A0.89)
Фмг.
Это отношение равно нулю, когда
(Ю.90)
- и положительно при значениях ю < <»,, так что шг является самой низкой
а
w, юг
а
Ч>
Действительная
часть
А
Мнимая
ZK часть
си,
1
и/? со, (ог
б в
Фиг. 103.
си,
частотой, которую пропускает цепочка из таких звеньев. Если Z1/Z2= —4,
то .
о>2 = (О2 -\- 4Cj) K'-'v^i^z) • (HJ.ai)
Частота ш2 является наиболее высокой частотой, проходящей через фильтр.
На фиг. 103 а, б, в, и г показана зависимость от частоты ш соответственно
постоянной затухания а, постоянной фазового сдвига ср, а также действи-
действительной и мнимой частей волнового имведанса ZM = Zh2 = Zb.
Эти кривые показывают, что фильтр обладает двумя серьезными недо-
недостатками. Первый из этих недостатков, отмеченный на фиг. 103, а, заклю-
заключается в том, что частоты вне полосы провускания (но вблизи ее краев)
задерживаются недостаточно сильно. Другими словами, имеется нерезкое
обрезание частот. Второй, и часто более серьезный недостаток (см. фиг. 103, в),
заключается в том, что величина волнового импеданса, который в данном
случае является активным сопротивлением, для разных частот внутри
полосы пропускания оказывается весьма различной. Благодаря этому невоз-
невозможно найти такой выходной импеданс, который удовлетворял бы всем
требованиям, указанным в § 14 настоящей главы, для всего диапазона про-
пропускаемых частот.
Чтобы избавиться от первого недостатка, найдем тип звена, обладающего
следующими двумя свойствами: 1) все звенья данного типа в цепочке имеют
один и тот же характеристический импеданс, хотя последний может, вообще
говоря, изменяться с частотой внутри полосы пропускания; 2) различные
звенья данного типа имеют различные характеристики пропускания для
задерживаемых частот, особенно вблизи границы полосы. Вследствие
:_8_ Глава X
первого свойства цепочка из таких последовательно соединенных звеньев
образует для пропускаемых • частот фильтр, приближающийся по своим
свойствам к бесконечному однородному фильтру. Пользуясь вторым свой-
свойством, можно скомбинировать различные звенья так, что одни будут сильно
задерживать то частоты, .которые другие звенья задерживают слабо, и гем
самым можно добиться наиболее полного задерживания всех частот вне
полосы пропускания. Оказывается, что такой фильтр можно выполнить
из звеньев Т-образного и 11-образного типа; это будет показано в сле-
следующем параграфе.
Хотя второй недостаток — изменение величины волнового импеданса
внутри полосы пропускания — нельзя ликвидировать полностью, однако,
как будет показано в § 18, он в значительной степени исправляется под-
подбором соответствующего конечного звена фильтра.
§ 17. Производные звенья типа 31. Под таким названием известны
наиболее важные звенья, применяемые в фильтрах. Рассмотрим лишь сим-
симметричное Т-образное звено, изображенное
J-7
±7
на фиг. 104. Соотношения между Zl
в звене такого типа будут
A0.92)
A0.93)
Z1Z2 = k2. A0.94)
ф ^ Постоянная величина к называется номи-
номинальным характеристическим импедансом
звена и не зависит от частоты. Согласно
выражению A0.76), где теперь Z0 = Zb, характеристический импеданс вы-
выражается соотношением
(Л |_ ^лт \ I '2 Гу 7 /4 L ^1 ) I 14С\ QK\
*т" /у— J — ^1^2 V ~Т~7~7~ / " ^Хи.УО;
Этот импеданс не зависит от выбора т. Согласно выражению A0.73),
постоянная передачи Г равна
оЬГ = 1+|р-. A0.96)
Из выражений A0.92) и A0.93) следует, что
—. A0.97)
Это отношение обращается в нуль, когда Zj/Z2 равно нулю, и равно —4,
когда Zj/Zg равно —4, поэтому на основании условия A0.86) можно за-
заключить, что пограничные частоты полосы определяются отношением Zj7Z2
и также не зависят от величины т. Знаменатель выразкения A0.97) обра-
обращается в нуль, если
Отсюда, выбрав полосу пропускания и зная величину отношения 2JZt
для пограничных частот, можно найти его величину на любой частоте вне
полосы и затем, пользуясь выражением A0.98), подобрать т так, чтебы
Переменные токи
369'
получить на этой частоте почти полное запирание. Так решается- задача
исключения нежелательных частот.
Для однозвенного по.лосового Т-образного фильтра Zj и Z2 могут
иметь вид
J—
при зтом для удовлетворения условия A0.94) необходимо, чтобы L1C1=?"
=. L.2C2. Величины Z, и Z2 представляют собою индуктивность и емкость,
включенные соответственно последовательно и параллельно. При изменении
а>1со со, сог со2со
а
Действительная
— часть
jk Мнимая часть
,си,
со,
6
Фиг. 105.
частоты от нуля до бесконечности ch Г изменяется от — со до +1 и опять
до — оо, так что на пограничных частотах спГ=—1, причем на одной
частоте срх =—те, а на другой <р1== -\-ъ. Таким образом, существует две
частоты, при которых выражение A0.98) дает одно и то же значение т
и, следовательно, происходит полное запирание. На фиг. 105, а, б и в по-
показаны кривые, выражающие зависимость от частоты соответственно посто-
постоянной затухания а, постоянной фазового
сдвига ср и действительной и мнимой частей
характеристического импеданса.
§ 18. Выходное устройство фильтра.
К последнему Т-звену фильтра, имеющего
характеристический импеданс Zh, подклю-
подключим нагрузку так, как показано на фиг. 106.
Постараемся найти, если зто возмож-
возможно, такое R, при котором импеданс между
точками А и В окажется равным Z ^ для всех
значений т, так что ток будет проходить
без отражения от конца, кап в бесконечной линии. Полагая импеданс
между А и В равным Zk и используя уравнение Кирхгофа, получим соотно-
соотношение
В
о
1Z
R
<
Фиг. 106.
разрешая которое относительно R, найдем
Согласно иыражению A0.76), для симметричного Т-звена имеем
A0.99)
"A0.100)
24 В. Смэит
370
Глава X
а для симметричного П-звена [см. выражение A0.79)] имеем
Исходя из выражений A0.100) и A0.101), получаем
fe> = ZlmZ
2m
A0.101)
A0.102)
A0.103)
A0.104)
Те же самые соображения применимы и ко входу цепи; поэтому в отно-
отношении характеристического импеданса цепь подобна П-образному звену
и имеет постоянную передачи, равную
постоянной передачи симметричного про-
производного Т-звена типа т. Согласно
выражениям A0.102), A0.92) и A0.93),
„ 4ZZ24-(l-m2):
Подставляя эти выражения в знаменатель A0.99), имеем
«ft
A0.105)
Фиг. 107.
Если принять /?? равным Z^g-номиналь-
ному характеристическому импедансу
системы, то в полосе пропускания отно-
отношение Z0/Zh> для различных т будет
зависеть от -rZ./Z, так. как это показа-
но на фиг. 107. Согласно изображенным
здесь кривым, выбор т = 0,6 для ко-
конечного звена обеспечивает характери-
характеристический импеданс, постоянный почти
во всей полосе пропускания; тем самым
ликвидируется второй недостаток просто-
простого фильтра. В линиях связи употребляются и другие, более сложные фильтры,
но основные принципы, па которых они построены, аналогичны рас-
рассмотренным выше. Влияние рассеивания энергии в сопротивлениях, кото-
которым мы всюду пренебрегли, сказывается в том, что все углы и острые
пики на кривых фиг. 103, а, б, в и г и фиг. 105, а, б и в сглаживаются.
§ 19. Линии передачи. В гл. VI мы легко перешли от линии с пе-
периодически повторяющимися последовательно включенными активными со
противлепиями и сопротивлениями утечки к линии с распределенными
параметрами. Подобно тому, как было проделано в § 2 для перехода о»
линии передачи на постоянном токе к линии передачи на переменном токе,
заменим в F.4) последовательно включенное сопротивление Т последо-
последовательным импедансом Zl на единицу длргны, а сопротивление утечки
S — параллельным импедансом Zc (также на единицу длины). Таким образом,
комплексная амплитуда тока i в линии удовлетворяет дифференциальному
уравнению
~ = ^ i = zLYci = F'2i, A0.106)
интеграл которого можно записать в виде суммы экспоненциальных функций
A0.107)
• Переменные топи 371
Действительная часть комплексной постоянной передачи Г' называется по-
постоянной затухания а', а мнимая часть /|3' определяет фазовый сдвиг Р'.
На отрезке dx ток между двумя элементами линии равен — (di/dx) dx
и протекает по импедансу ZJdx, поэтому, согласно закону Ома, на этом
участке создается падение напряжения
При малых значениях а' вдали от генератора, где х велико, i = 0, так что
в выражении A0.107) В = 0. В этом случае характеристический импеданс равен
Zft= ~ B=0 = Zcr = (ZcZLLi = (^J • (Ю.109)
Если В не равно нулю, то отношение Ь к i при х — 0, получаемое из вы-
выражений A0.107) — A0.109) и называемое обычно входным импедансом, равно
Пусть линия длиною / имеет при х — 1 нагрузку ZL, тогда из выраже-
выражений A0.107) и A0.108) следует, что
zL= Х- x=l=zh Ае-,'Г vi ¦ (юли)
Исключая из соотношений A0.110) и A0.111) величины А и В, получим
для входного импеданса следующее выражение:
7Р7 ¦ A0.112)
Если линия на концах разомкнута или, наоборот, закорочена, то входные
импедансы будут равны соответственьо Z^clhP'/ и Zfethr'Z. Заметим, что
ZpZs = Zfe. Ток в линии, поступающий от генератора с внутренним импе-
импедансом Zt и э. д. с. 8, равен
Выражение A0.27) показывает, что для передачи в линиях максимальной
мощности нужно, чтобы Z, = Z|. Таким образом, наилучшие условия пере-
передачи получаются в том случае, когда импедансы нагрузки и генератора
являются величинами, комплексно-сопряженными характеристическому им-
импедансу линии. В § 9 в 13 гл. XIII этот вопрос будет рассмотрен еще
с другой точки зрения, исходя из уравнений Максвелла.
§ 20. Электродвижущие силы несинусоидальной формы. Метод рядов
Фурье. Существует несколько методов исследования периодических э. д. с.
частоты ш1; имеющих форму колебаний, отличную от синусоидальной.
В одном из этих методов э. д. с. рассматривается как суперпозиция не-
нескольких э. д. с. с частотами и>17 2o>j, 3u>1 и т. д., называемых гармониками.
Пользуясь разложением функции / (t) в ряд Фурье, нетрудно определить
амплитуды и фазы составляющих э. д. с, которые в сумме образуют задан-
заданную функцию j (t). Таким образом, имеем
= Ао + ^ (An <=°s mwj + Вт sin m<V) =
m
= AQ + 2 [ {A2m -b B2mI12 cos (»,« - arc tg|?) ] =
m
= Л+2 Re {CmeMu>l(}. (
m
24*
372
Глава X
где
Am — — \ / (я) cos пио^а da,
В ~~ \ f(a)s\niwo,ada
A0.115)
A0.116)
Cn=-- An- jBm, A0.117)
Последнее выражение A0.114) имеет как раз такую форму, которая
употреблялась в этой главе с самого начала. Таким образом, если дей-
действующая э. д. с. задана в виде функции f(t),
¦ х мы решаем задачу отдельно для э. д. с. вида
i
Шх = Re {Cxe^i'j, g2 = Re
g, = Re{CBe*e«'} и т. д.
A0.118)
Складывая действительные части полученных
фиг jgg решений, получаем искомое решение нашей
задачи,
В качестве типичного примера рассмот-
рассмотрим э. д. с. пилообразной формы (фиг. 108), приложенную к контуру, им-
импеданс которого при частоте ти>г равен Zm. Согласно выражению A0.115),
А —0, а из выражения A0.116) получим (см. Двайт, 430.11)
V
5 \
о «3
da —
">1 60
1«0 1
sin тш,о —
cos
Таким образом, приложенная э. д. с. представляет собой суперпозицию
9. д. с. вида
g = Re { LlL^Ll2!l° gfimit I A0.119)
Если в рассматриваемом контуре сопротивление, емкость и индуктивность
соединены последовательно, то для тока, согласно соотношениям A0.7) —
A0.9), будем иметь выражение
i = -
sin (m<fl,?-f ф)
L (towjC) J J
a j 1/2 '
где
A0.120)
A0.121)
Наличие / в выражении A0.119) приводит к тому, что в соотношении A0.9)
косинус заменяется на синус.
§ 21. Электродвижущие силы несинусоидальной формы. Метод повто-
повторяющегося переходного режима. Другой метод исследования стационарного
режима, когда в. %, с. повторяется с периодом У и ее можно представить
на интервалах @, J,), (?„ f2), ..., (Vi. Л функциями f1(t), J2(t), . .., fn(t),
основан на использовании общих решений дифференциальных уравнений
р праЫыми частями f1(t), /2(t), ...,, fn(t) (см. § 18 гл, IX). Постоянные
.интегрирования для стационарного процесса определяются (при наличии
Переменные токи 373
в контуре самоиндукции и емкости) из условия непрерывности то,ка и за-
заряда на границах временнйх интервалов, а также из условия равенства
значений тока и заряда в моменты ; = 0 и г = Г.
В качестве примера решим этим методом задачу, рассмотренную в пре-
предыдущем параграфе. В зависимости от величины постоянной затухания
в контуре (большое, малое или критическое затухание) возможны три форму
решения. Рассмотрим случай, ¦ когда в контуре возможны колебания,
т. е. угловая частота ш= (LCy1—r-i?2L~2 2 — действительная величина.
Уравнения контура записываются в виде
d*q R dq д _ %0 . (лг) л oov
йЧ Я di , i %0
Вместо того чтобы использовать общий, но громоздкий метод (9.134), ре-
решим уравнение A0.123) при помощи подстановки х = i — Щ„ (С/Т). Уравне-
Уравнение для х имеет вид (9.3), поэтому [см. выражение (9.7)] имеем следующее
решение, описывающее колебательный процесс:
i==M + e-w2L(Acosu>* + JBsinu>*). A0.124)
Первое граничное условие /(=_т = г'(=т дает
^ ^ ~ A0.125)
Согласно второму граничному условию gt=—r = Qt=T, получим
+т
\idt = O. > A0.126)
—т
Интегрируя (см. Двайт, 577.1 и 577.2) и подставляя пределы, находим
Т = А (Й sh S cos wT + ш ch S"sin w2'
Объединяя это с соотношением A0.125), получим
^l = Ach~sino,T + Bsh^coswT. A0.127)
Разрешая теперь соотношения A0.125) и A0.127) относительно А и В,
будем иметь
Ч 0 ch С 4- RT/L Л sin »г
Л = A0Л28)
sh2 ( yrt'l ) + sin2«r
2?=— -Y r^ т. (Ю.129)
Выражения A0.124), A0.128) и A0.129) определяют стационарный тон
в интервале —T<_t<.T. Эти значения тока периодически повторяются.
Полученное выражение можно рассматривать как сумму ряда A0.120).
374
Глава X
§ 22. Контур с отрицательным активным сопротивлением. Переход-
Переходный характер явлений, рассмотренных в гл. IX, обусловлен тем, что в кон-
контуре содержится активное сопротивление, рассеивающее энергию. При обыч-
обычных температурах невозможно сделать контур без сопротивления. Однако
можно поместить в контур устройство, которое содержит источник энергии
и в определенных пределах изменения тока будет проявлять себя как отри-
отрицательное активное сопротивление —R. Если его поместить последова-
последовательно с активным сопротивлением контура Я, то результирующее сопро-
сопротивление будет
r = R-R, A0.130)
а при параллельном соединении получим
RE
A0.131)
В первом случае /- = 0, если R = R, а во втором случае —если R = 0, так
что любые заданные колебания будут продолжаться бесконечно долго
с постоянной амплитудой. Если, в первом
[I случае, R < R или, во втором случае, R < R,
¦ то г отрицательно и показатель степени у
е экспоненты (см. гл. IX) становится положитель-
положительным. В этом случае колебания, однажды воз-
возникнув, будут возрастать (по амплитуде) экс-
экспоненциально до тех пор, пока ток не
превысит тех пределов, в которых это устрой-
устройство действует как отрицательное сопротивле-
сопротивление. При помощи такого устройства обычно
осуществляется генерация переменного тока
при частотах, слишком высоких для враща-
вращающихся электрических машин.
Мы приведем только один пример такого контура. Возьмем простой
случай, рассмотренный в задаче 3 гл. XIII, когда L, С, R соединены па-
параллельно (см. фиг. 109). Если 4/?2С > L, то в контуре возможны колебания
с частотой ш, равной
A0.132)
Фиг. 109.
и амплитудой, затухающей со временем экспоненциально. Поместим теперь
Параллельно с R электронную лампу, которая в ограниченных пределах
ведет себя как отрицательное сопротивление. В цепи, изображенной на
фиг. 109, будем рассматривать только переменные токи. Выходной ток i
источника управляется пренебрежимо малой энергией, поступающей из ко-
колебательного контура по специальному элементу связи. Например, в случае
электронной лампы контур в цепи сетки можно индуктивно связать с L.
Тогда анодный ток i будет некоторой функцией напряжения на сопроти-
сопротивлении R, которую для малых значений V можно считать линейной.
Таким образом,
A0.133)
A0.134)
A0.135)
Согласно обозначениям, указанным на фигуре, имеем
±
Переменные токи 375
Дифференцируя соотношение A0.135) и подставляя значения производных
тока из A0.133) и A0.134), после преобразований получим
dW \ d V
^- + ^^[У — Щ{У)]+~ = 0. A0.136)
Допустим, что величина ф (V) достаточно велика и, следовательно, второй
член при малых V отрицательный. Будем искать периодическое стационар-
стационарное решение в виде
оо
F = 5Jencos(««o* + <Pn)- A0.137)
Для нахождения связи между основной частотой и амплитудами гармоник
умножим уравнение A0.136) на V и проинтегрируем по всему периоду.
Второй член обращается в нуль, и ,
после интегрирования по частям пер- * 1
вого члена получаем
1t~W *
Подставляя значение V из выраже- ч л \ 1—
ния A0.137) и разрешая получен-
полученное соотношение относительно ш, бу-
будем иметь
оо оо
Г 53 ««• (Ю.138)
Рассмотрим случай, когда система
только что перешла за порог само-
самовозбуждения. В этом случае второй член в уравнении A0.136) оказы-
оказывается с малой отрицательной величиной и в первом приближении им можно
пренебречь; в результате получаем частоту to = (L?)~/a, совпадающую
с собственной частотой контура в отсутствие активного сопротивления.
Исследуя выражение A0.138), мы видим, что амплитуды гармоник в этом
случае также пренебрежимо малы.
Чтобы определить амплитуду основного колебания в стационарном
состоянии, необходимо принять определенное выражение для функции <}» (V)
в формуле A0.133). Разумно определить i следующим аналитическим
выражением:
A0.139)
согласно которому при малых V второй член в уравнении A0.136) отрица-
отрицательный, если ар > 1. На фиг. 110, представляющей функцию ^ = arctg 10 х,
видно, что полученная кривая сильно напоминает сеточную характеристику
триода, когда рабочая точка находится в середине характеристики (в точке
перегиба). При помощи выражения A0.139) можно определить постоянные
аир через параметры характеристики лампы и величину обратной связи.
После этого уравнение A0.136) принимает вид
??+ ** (F_BarctgaF) + j?=O. A0.140)
Умножим зто уравнение на \ V dt и проинтегрируем по t каждый член
по частям (см. Двайт, 79), принимая в каждом случае м= \ Vdt, так что
du = Vdl. После выбора пределов интегрирования t=—тг/ш и г = тг/ш
376 Глава X „____________
.первый и третий члены исчезают, а произведение uv от второго члена дает
С (у2 — $V arc tg aV) dt = 0. A0.141)
-Подставляя сюда вместо V его выражение A0.137), полагая я„=0 дпя
всех в^1и выбирая, начальный момент времени, когда tpt = 0, можно
проинтегрировать по частям второй член, принимая M = arctg<xF и dv—Vdt.
Произведение uv при подстановке пределов исчезает и, пользуясь форму-
формулой (858.3) из справочника Двайта, находим
sin2 юг ,. _
1 _ JL С "а
ИЛИ
таг2 2тф рA+а2а2) Г
о а<о а<о J
1 + а2а2 COS2 u>t
Выполняя интегрирование (см. Двайт, 460.1, где следует вместо Ь2 взять 1,
а вместо а2 взять 1+<х2а2) и умножая на.аш/т;, получим ¦ j i
Избавляясь от дробн9го показателя степени, будем иметь
Из этого выражения следует, что возможна нулевая амплитуда. Это озна-
означает, что для • получения колебаний с. амплитудой, отличной от нуля,
необходим начальный толчок, например-разряд конденсатора. Из выражения
в_квадратных скобках получаем амплитуду стационарных колебаний г;.г я
а
Заметим, что в стационарном состоянии, когда второй член в уравне-
уравнении A0.136) мал, частота зависит только от L и С, в то время как ампли-
амплитуда определяется -только величиной R и свойствами генератора. Болей
сложные системы рассматриваются у Ван дер Поля и в других работах,
список которых указан в конце главы. ;
ЗАДАЧИ
1*. Катушка вращается с постоянной угловой скоростью со (вокруг оси, лежащей
в плоскости катушки) в однородном магнитном поле, силовые линии которого перпен-
перпендикулярны к оси вращения. Найти ток в катушке и показать, что его величина будет
наибольшей, когда плоскость катушки образует с направлением магнитных силовых
линий угол, равный
arc tg
(.Ю-
2*. Катушка обладает сопротивлением R и самоиндукцией L; ее концы А и В при
помощи провода, сопротивлением которого можно пренебречь, присоединяются к кон-
конденсатору емкостью С. В цепи, соединяющей точки А и В, наблюдается ток / cos ptr
причем заряд конденсатора изменяется в фазе с током. Показать, что заряд равен
Ы
-?- • COS pt
И что
Найти ток в катушке. -
Задачи 377
3*. Концы В и D провода, обладающего сопротивлением R и самоиндукцией L*
присоединены к пластинам конденсатора С. Провод вращается вокруг вертикальной
прямой BD с угловой скоростью и> и расположен так, что в плоскости, в которой ле-
лежит провод и прямая BD, между ним и BD заключается площадь величиною А.
Пусть М~-горизонтальная составляющая магнитного поля земли. Показать, что для-
поддержания вращения требуется затрачивать в среднем мощность, равную
4*. Замкнутый соленоид образован из большого числа N катушек, у каждой из-
которых провод равномерно намотан на круглый цилиндр радиуса а и высотой 2ft.
В центре цилиндра помещается маленькая катушка, ось которой совпадает с осью ци-
цилиндра, а магнитный момент изменяется по закону М sin pi. Показать, что сила тока,
протекающего через соленоид, равна
¦где R, L—сопротивление и самоиндукция соленоида и tg a = R/pL.
5*. Круглая катушка радиуса а, имеющая N витков и сопротивление R, вра-
вращается с угловой скоростью ш вокруг вертикального диаметра в горизонтальном маг-
магнитном поле земли Н. Показать, что при атом катушка испытывает противодействие'
величиной
1
R2 -f *>2L2
6*. Ток / sin pt, протекающий в катушке А, индуцирует ток в катушке В.
Показать, что средняя сила, ¦ стремящаяся увеличить любую координату катушки 6,
равна
где L, М, N—коэффициенты индукции катушек, a R—сопротивление катушки В.
7*. Плоский контур площадью S вращается с постоянной скоростью ч> вокруг
оси 2, лежащей в его плоскости на расстоянии h от центра тяжести площади- На оси .г,
н.а большом расстоянии а от начала координат, укреплена проволочная петля с маг-
магнитным моментом ш, направленным вдоль оси Ох. Доказать, что в момент времени I
ток приближенно равен
S . ,
-—соч (.ог — е)-|
L2^)l>-i 4т
где kj, e—постоянные.
8. Генератор с заданной э. д. с. и импедансом Zf соединен с нагрузкой Z^ пере-
передающей линией с характеристическим импедансом Z^. Показать, что при максимальном.
токе в нагрузке Z2.=Z[ZZ.
9*. Две точки А ш В соединены проводом с активным сопротивлением R (без
самоиндукции); точка В соединяется с третьей точкой С двумя проводами, каждый из
которых имеет сопротивление R, а один, кроме того, обладает самоивдукциеи L. Пусть
между концами А, С поддерживается напряжение Е cos pt. Показать, что напряжение-
между точками В ж С будет
где
V'2 _ pLR
10*. Кондевсатор С присоединен параллельно катушке с сопротивлением R и-
самоиндукцией L при помощи проводников, обладающих сопротивлением г. Получен-
Полученный таким образом контур включается в цепь с э. д. с, имеющей период 2-п/р. Пока-
Показать, что этот контур эквивалентен проводу без самоиндукции, если
378 Глава К
и что сопротивление этого провода должно быть равным
11*. Точки А и В соединены двумя ветвями с сопротивлениями соответственно
В и S, самоиндукциями L и N и коэффициентом взаимной индукции М. Доказать,
что для внешней цепи, которая подключена к точкам А и В и по которой течет ток
частоты р, эти две ветви эквивалентны одной ветви с самоиндукцией
NB2 + LS2 + 2MBS + p2(LN—М2) (L + N—ZM)
и сопротивлением
(L т Л — 2iW
12. Три точки а, 6 и с соединены следующим образом: между а и с находятся две
ветви—одна содержит сопротивление В, а другая—генератор переменного тока и ин-
индуктивность; между Ъ и с находятся также две ветви—одна содержит гальванометр
переменного тока, а вторая — сопротивление Р и индуктивность L; между а и Ъ поме-
помещаются емкость С и сопротивление S. Между двумя индуктивностями имеется связь
(коэффициент взаимной индукции равен М). Показать, что для того, чтобы стрелка
гальванометра не отклонялась, должно выполняться условие
13. Генератор с э. д. с. jf0coso>t, выключатель, индуктивность Lu сопротивление В
• соединены последовательно. Показать, что после замыкания цепи в ней не будет на-
наблюдаться переходных явлений, если в момент замыкания цепи значение э. д. с. было
равно
л
14. Общая индуктивность и сопротивление цепи (включая и вторую обмотку транс-
трансформатора) равны соответственно L и В. В первичной обмотке течет ток 70сови>1.
В каждом полупериоде существует момент времени, когда разрыв вторичной цепи
может произойти без искры. Показать, что в этот момент ток в первичной цепи равен
15. В контур, состоящий из емкости С и индуктивности L, включена последова-
последовательно периодическая э. д. с. прямоугольной формы, такая, что V= Vo, если2ля/ш < t <
< Bn + l) it/*0, и F=0, если Bга + 1)-п;/<о < t < {2п -\-2) -п/ш, где и—целое положительное
число. Показать, что после установления стационарного состояния токи it или /2 опре-
определяются выражениями
при 2птъ/<х> < t B 1
li~~T-\ Т) sec ТТ sln ' {Щ \ *—~—Z \ I •
при Bп -\-1) п/со < t < Bга+ 2) п/<о
Исследовать случаи, когда u> = (LC)~1'2 и <о = а/а ()
16. Решить предыдущую задачу методом рядов Фурье и показать, что ток опре-
определяется выражением
СО
^ — 1Г1 cos [Bm+ 1)^1.
17. Электродвижущая сила, описанная в задаче 15, но с пределами-)-—Fo
1
и —— Vo, вместо Vo и 0 прикладывается к катушке Llt связанной с контуром,
имеющим индуктивность L2 и емкость С, соединенные последовательно (коэффициент
лззаимной индукции равен М). Показать, что в стационарном режиме заряды Qt и Q2
Задачи 379
«а конденсаторе в интервалах, времени, указанных в задаче 15, равны
п _ MVnCzccm"' tin l (в Т ""Л sin 1 6
где
18. Решая предыдущую задачу методом рядов Фурье, показать, что заряд на
кондевсаторе равен
2МУВС ^ sin Bm + 1) о.t
п
19. Э. д. с. включается в первичную обмотку трансформатора, имеющую индуктив-
индуктивность L] и сопротивление Rt. Вторичная обмотка трансформатора, имеющая сопроти-
сопротивление /?2 и индуктивность L2, нагружена импедансом Z?. Коэффициент взаимной ин-
индукции между обмотками трансформатора равен М. Показать, что если u>L2 много
больше чем R2-{-RL—//(wCL), то отношение токов в первичной и вторичной обмотках
мошет не зависеть от частоты.
20. Показать, что в предыдущей задаче отношение э. д. с. в первичной и во вто-
вторичной обмотках трансформатора не зависит от частоты в случае, если wI^Z^ много
больше чем (М2—L,L2)ib2 и R,(R2 + Zl) и « (L2Rl + L1R2).
21. Пусть круговая частота синусоидальвой э. д. с, используемой в контуре, опи-
описанном в § 2 настоящей главы, равва и>1. Показать, что отвошение у среднего квадрата
тока при LC = a>12 к среднему квадрату тока при любой величине L и С равно
J-
22. Пусть L, С и R в предыдущей задаче заменены на Lz, C2 и R2> a M достаточ-
достаточно мало. Показать, что результат предыдущей задачи годится и для тока в контуре 2,
изображенном на фиг. 99 (<ох—круговая частота э. д. с, включенной в контур 1).
23. Доказать, что электрическую цепь, составленную из импедаисов Z,, Z2, ...
... , Zn, соединяющих точки Рл, Pz, ... , Рп с одной общей точкой, можво заменить
цепью из импедансов Z12, ZC, Z23» ¦ - - . соедивяющих попарно точки Р (индексы ука-
указывают вомера соединяемых точек), где
* п
Zrs=Z,-Zs 2^j Zp . ,
24. Можно доказать, что импеданс любого двухполюсника, содержащего только
чисто реактивные сопротивления, записывается в форме
глК-о.*)И-о.11) ¦¦¦ (of».,,-0,2)
/Ы(ы| —(О2) ... (ы|„—ы2)
где А—положительная постоявная и 0 ^ш, ^ш2 ... <^<i>2n+i -<^°°- Пользуясь этим,
показать, что Z можно образовать последовательными контурами и последовательной
комбинацией параллельных настроенных контуров с антирезовансвыми круговыми часто-
частотами <о2, Ш4> • • •. Ш2п или при помощи параллельной комбинации настроенных контуров
с резонансными круговыми частотами ш,, ш3, ..., и>2п-ц-
25. Показать, что если два реактивных импеданса имеют одинаковую резонансную
и одинаковую антирезонансную частоту, то их отвошение постоянно для всех частот.
26. Показать, что реактивность импеданса, пе содержащего активного сопротив-
сопротивления, на участке между резонансной и антирезонансной частотами всегда возрастает
с увеличением частоты.
27. Один контур состоит из сопротивления Elt емкости Сх и индуктивности Lx.
Второй ковтур содержит сопротивление В2, емкость С2 и индуктивность L2. Часть
ивдуктиввости является общей обоим контурам. Показать, что если М определево как
поток, пронизывающий одни контур, когда но втором контуре протекает единичный ток,
то уравнения для i, и г2 будут (овпадать с уравнениями § 10настоящей главы при усло-
условии, что элемент, общий обоим контурам, обладает нулевым активным сопротивлением.
Такая связь между контурами называется прямой или автотрансформаторной.
28. Пять контуров соединены цепочкой так, что все взаимные импедансы равны
«улю, за исключением тех, которые соединяют смежные контуры. В центральный
380 Глава X
(т. е. третий) контур помещается синусоидальная э. д. с. Показать, что комплексные
амплитуды токов определяются выражениями
; ry у y2 /у у yg \—l у у2 /у у y2 \—ji—i Cjg
I3 L^33 ^11 23 \ 11 22 ^12) ^55^34 \ 44^55 ^n5) i {5 »
'4 ~ ^55^34^(^44^*55 ^45) *3» *5 =: ^'45^'6514t
29. Два контура состоят соответственно из ипдуктивностсй L, и L2, емкостей Ct
и С2 и сопротивлений Tiv и i?2. Часть г сопротивлений Rv и /?2 является общей обоим
контурам. В первый контур включена периодическая э. д. с, изменяющаяся с круго-
круговой частотой «о,. Показать, что ток по втором контуре будет максимальным при усло-
условии, что реактивность каждого контура в отдельности для этой частоты равна нулю
и что максимальный ток равен r% (RjR2—г2). Такая связь между контурами назы-
называется связью через активпое сопротивление.
30. Три контура соединяются цепочкой так, что Z13 = 0, a Z12 и Z23 являются
мнимыми величинами. В первый контур включается э. д. с. частоты о>1ш Сопротивле-1
ни я контуров равны соответственно Rv, R2 и Я3- Показать, что если RVR2RS^ \ R3Zl2 —
— /?iZ|3 |, то в третьем контуре ток будет максимальным при частоте ч>г, когда реакч
тивность каждого контура в отдельности обращается в нуль. Это максимальное значен
ние равно
«о | Z12Z23 | (R.^g-Z^Rs-ZfjRJ-1.
31. Показать, что если в предыдущей задаче RjR2Rs^.R3Zi2 — R\Z\Z, то макси-
максимальный ток в третьем контуре может быть получен при Х1Л =0, -3T22Xi3l= —Z|3 | Z^2 |,
и что амплитуда тока будет равна
\_
2
-ЗГц> -Угг и -Узз — реактивные сопротивления.
32. Показать, что если в той же задаче i?[/?2-R3 -"С -RjZfg — -R3Z22, то максимальный
ток в третьем контуре может быть получен при JSTS3 = O, -2T22Xj^ = —Z22|ZJi|, и что
амплитуда тока будеэ> ранна
т
41 Z2s I Ч«
33. Два импеданса называются взаимно инпертировашшми, если Z,Z2 = k2, где к—
действительное число, не зависящее от частоты. Показать, что если импеданс Z, эквива-
эквивалентен hx и С], соединенным последовательно, то Z2 должен быть эквивалентен L?
и С2, соединенным параллельно, т. в. LXC\^ — L«C\1 = k2.
34. Два импеданса, удоилетворяющие условию A0.94), называются взаимно, инвер-
инвертированными. Пусть Z1Zi = Z2Z2^=/f2. Показать, что импеданс, полученный параллельным
соединением Zi и Z2, и импеданс, полученный последовательным соединением Z\ и Z2,
будут взаимно инвертированными и нелпчина А:2 останется прежней.
35. Линия передачи (или фильтр)' имеет нагрузку, совпадающую с выходным
импедансом Z^x. К началу линии подключен генератор с импедансом, совпадающим
с входным импедансом Z^2 линист. Показать, что при любой заданной частоте ничего-
не изменяется, если заменить линию (или фильтр) одним Т-звеном, подобным ийобра-
женному на фиг. 101, а, при условии, что
2ZR1 = (Zo + ZbI/2 Ba + Zb + 4Z,I'2 + Zo- Zb
и
2Zh2 = (Zo + ZbI'2 (Zo + Zb+4Z2I/2 _ Za + Zb.
36. Показать, что Т-звено (см. фиг. 101, а) и П-звеио (см/ фиг. 101, б) ведут себя
одинаково при всех частотах при условии, что для любой частоты
37. Пусть Zol и Zsl — входные импедансы фильтра при разомкнутом и соответ-
соответственно закороченном выходе, а Zo2 и Zs2 — соответствующие импедансы, если вход
и выход помепять местами. Показать, что
Литература 381
= (ZOI+Z02)[ZOI(Z02-Z.42)r1/2.
38. Пусть №m—резонансная частота контура с импедансом Ъх, рассматривавшимся
в § 17 настоящей главы, и пусть Lr — его эффективная индуктивность. При помощи
результатов задачи 32 показать, что выражение A0.95) примет вид
39. Используя предыдущую задачу и рассматривая фильтр, о котором шла речь
и конце § 17 настоящей главы, где обе границы обрезаемых частот получались при
сЬГ=—1, показать, что величину Z& можно выразить через граничную частоту ш2
в виде
40. Пользуясь предыдущим результатом, показать, что если ш1 к ш2—граничные
частоты полосы пропускания, а шт—резонансная частота контура с импедансом Zlt то
»т = ш1<1>2-
41. Сравнивая выражение A0.95) и выражение для Z^, полученное в задаче 39,
показать, что для заданных зпачений т, ш2 и и>т частоту ш^, при которой происходит
полное запирание, можно найти из уравнения
J?2L_^L=r J^_^n\ A_
шт шоо V шт ш2 У
42. Передающая линия, характеристический импеданс которой равен R^, нагру-
нагружена импедансом R^-^-fX^. Показать, что линия и нагрузка могут быть согласованы,
если последовательно с narpj3Kofi поместить четверть-волновую линию, имеющую
характеристический импеданс (RkRL)^2, а в месте соединения нагрузки с главной
линией подключить короткозамкиутый отрезок линии длиной I с характеристическим
импедансом R^, при этом tg $1 = HL/XL. —
43. Показать, что линия и нагрузка в предыдущей задаче могут быть также
согласованы посредством четверть-волновой линии, имеющей характеристический импе-
данс [(Rl-\-Xl) Rk/RL]112, путем подключения в месте их соединения с нагрузкой
короткозамкнутого отрезка линии длиной I с характеристическим импедансом /?^, при
этом
V2
ЛИТЕРАТУРА
В а г 11 e 11 А. С, The Theory of Electric Artifical Lines and Filters , Wiley, 1930.
(B a t e m a n H., Electrical and Optical Wave Motion, Cambridge, 1915.
Bode H. W., Network Analysis and Feedback Amplifier Design, Van Nostrand, 1945.
Carson J. R., Electric Circuit Theory Operational Calculus, McGraw-Hill, 1920.
Geiger-Scheel, Handbuch der Physik, Bd. 15, Berlin, 1927.
Guilleman E. A., Communication Networks, Wiley, 1931, 1935.
Heaviside O., Electrical Papers, Boston, 1925.
Johnson K. S., Transmission Circuits for Telephonic Communication, Van Nostrand,
1925.
К e n n e 11 у А. Е., Electric Lines and Nets, McGraw-Hill, 1928.
Ollendorf E., Die Grundlagen der Hochfrequenztechnik, Berlin, 1926,
Pierce G. W., Electric Oscillations and Electric Waves, McGraw-Hill, 1920.
Russell A., Alternating Currents, Cambridge, 1914.
Shea Т. Е., Transmission Networks and Wave Filters, Van Nostrand, 1929.
Staff M. I. T., Electric Circuits, Wiley, 1940.
Starr А. Т., Electric Circuits and Wave Filters, Pitman, 1934.
Van der Pol В., Non-linear Theory of Electric Oscillations, Proc. Inst. Rad.
Eng., 20, 1051 A934).
Ware L. A., Reed H. R., Communication Circuits, Wiley, 1942.
Webster A. G., Electricity and Magnetism, Macmillan, 1897.
Wien-Harms,, Handbuch der Experimentalphysik, Bd. XI, Leipzig, 1932.
Глава XI
ВИХРЕВЫЕ ТОКИ
§ 1. Индуцированные токи в объемных проводниках. Две последние
главы были посвящены применению законов магнитного взаимодействия
токов, а также закона Фарадея к системам, состоящим из линейных про-
проводников. В настоящей главе мы получим, опираясь на эти законы,
результаты, относящиеся к системам с объемными проводниками. Прежде
всего следует заметить, что приводимое здесь рассмотрение, как и все,
предшествующее ему, является приближенным, а именно — всюду пред-
предполагается мгновенность распространения электрических и магнитных полей,
или, другими словами, предполагается, что можно пренебречь максвеллов-
ским «током смещения». Совершаемая при этом ошибка совершенно
ничтожна, если частота процесса такова, что длина волны колебаний в
системе значительно превышает размеры самой системы. В противном слу-
случае, т. е. если это условие оказывается невыполненным, необходимо решить
полную систему уравнений Максвелла, о которой будет идти речь в гл. XIII.
Закон индукции Фарадея устанавливает, что при изменении магнитной
индукции В в проводнике появляется электрическое поле Е, величина
и направление которого определяются соотношением
или, пользуясь магнитным вектор-потенциалом А (8.4), это можно записать
в виде
Е=-?. A1.2)
Как только в проводнике появляется электрическое поле, в нем по закону
Ома возникает электрический ток. Пусть т —удельное сопротивление,
a i — плотность тока; тогда при помощи соотношения F.8) уравнения A1.1)
и A1.2) можно переписать в виде
x(Txi)=-f, A1.3)
Эти токи, протекая по проводнику, имеющему магнитную проницаемость (а,
создадут в нем магнитное поле, определяемое уравнениями
TxB = (xi, A1.5)
V2A=-Ixi. A1.6)
Из уравнений A1.3) —A1.6) легко получить уравнения, которым должны
удовлетворять меняющиеся во времени величины i, В и А внутри провод-
проводника. Исключая при помощи уравнения A1.3) величину В, дифференцируя
Вихревые токи 383
уравнение A1.5) по времени, а также учитывая соотношение F.3), получим
Исключив i из уравнений A1.4) и A1.6), имеем
х at
A1.8)
Аналогично можно исключить i из уравнений A1.3) и A1.5), после чего,
пользуясь выражением G.1), находим
Ji^= -[^x(VxB)] = V2B-V(?.B) = V2B. A1.9)
Уравнения A1.7)— A1.9) имеют форму хорошо известного уравнения тепло-
теплопроводности, с той лишь разницей, что зависимая переменная величина
является вектором, а не скаляром. В прямоугольных координатах каждая
компонента, рассматриваемая как скаляр, удовлетворяет тому же самому
уравнению. Однако это не имеет места для компонент в любой системе коор-
координат,, за исключением некоторых специальных случаев.
Задачи о вихревых токах, как и задачи о токах в линейных провод-
проводниках, естественно, распадаются на два класса: к первому относятся задачи
о неустановившихся, а ко второму —об установившихся процессах. Послед-
Последние проще всего рассматривать, исходя из понятия комплексной амплитуды,
как это делалось в предыдущей главе. Начиная с этой главы, нам придется
иметь дело с комплексными векторами. Поэтому условимся в дальнейшем
комплексные и комплексно-сопряженные амплитуды обозначать знаком «V»
и «Л» соответственно, поставленными сверху над символом. Те величины,
у которых указанные знаки сверху отсутствуют, подразумеваются действи-
действительными, хотя в общем случае и зависящими от времени.
Внутри достаточно малого элемента объема ток пропорционален при-
приложенной э. д. с. и импеданс этого объема равен просто его активному
сопротивлению T.dx/(dydz). В стационарном состоянии ток в элементе
равен idydz. Таким образом, в соответствии с соотношением A0.15) средняя
мощность, рассеиваемая внутри такого элемента, определится по формуле
dF=\$idv=*±-nidv. A1.10)
§ 2. Решение уравнения для вектор-потенциала вихревых токов.
Решение уравнения A1.8), где т ф со, можно получить точно таким же
путем, как для случая т~ оо в § 5 гл. VII. Представим А в'виде [см. выра-
выражения G.17) и G.18)]
, A1.11).
где u=i, j,-k или г. Согласно соотношениям G.19) и G.20), имеем
V2A = V X [и\?Щ\ + uxV (V2W2)].
Подставив эти два выражения в уравнение A1.8), получим
Если Wt и VF2 являются решениями уравнения теплопроводности
¦z at
384 Глава XI
то при помощи соотношения A1.11) можно выразить через них решение
уравнения для вектор-потенциала вихревых токов.
. Пользуясь соотношениями G.21) и G.22), найдем, каким образом
лыражается поле В через функции Wx и W2'
, " A1.13)
A1.14)
где u = i, j, k или г. Поскольку В и А удовлетворяют одинаковым урав-
уравнениям A1.8) и A1.9), то можно было ожидать, что и решения A1.11)
и A1.14) будут иметь сходный между собою вид. Мы видим, что теперь
значецио В определяется обеими функциям: Wx и W2. Принимая во внима-
внимание соотношение G.22), можно произвести дальнейшее упрощение написан-
написанных выше выражений
f A1.15)
u==r, B=-75('XWl + rlF1) + r.V(W1) + 2V^. A1,16)
Если направить и вдоль иг и искать решение уравнения A1.12) в виде
U(u^)F{u2, u3, t), то, как и в § 5 гл. VII, полученное в результате поле В
будет перпендикулярно к А. -
§ 3. Скин-эффект в стационарном случае. Уравнение A1.7) имеет
простое решение в том случае, когда среда, обладающая проницаемостью [J.
и удельным сопротивлением т, заполняет полупространство z > 0. Пусть
плотность тока, частота изменения которого равна ш, имеет в плоскости
z — 0 только компоненту ix, не зависящую ни от х, ни от у. Тогда уравне-
уравнение A1.7) дает
дЧ<г d2ix /л л лп\
^ <11Л7>
так как ix является функцией только z. Решением этого уравнения будет
4 = Се-<^ ¦>'I/2z + DeU«>v- iI/2z. A1.18)
Если плотность тока ix конечна при z = оо, то I) = 0. Заменяя B/) /2 на 1 + /
и добавляя временной множитель, получим
ixeM = ^e-Wa^-YI'2* ejt»'-A/2>B^fI'2z]j A1.19)
где i0 —значение ix на поверхности z = 0. Взяв теперь действительную
часть, будем иметь
W [^У'] A1.20)
Таким образом, амплитуда плотности тока ix экспоненциально уменьшается,
а фаза изменяется линейно.
Применяя формулу разложения косинуса и используя формулы (863.1)
и (863.2) из справочника Двайта, для полного тока Icos(wt + ф), текущего
в полосе шириной 1 м, найдем
dz = i0 Bo)[iT)~1/2 (cosu>t + siniot) = i0 (шр.т)~1/2 cos(^wt — ^ тг^. A1.21)
Заметим, что существуют такие значепия z, при которых ток меняет свое
направление на. обратное, и поэтому удаление части проводящей среды,
лежащей ниже некоторой определенной глубины, приведет к увеличению
Вихревые токи 385
полного тока1'. Мощность, поглощаемую в виде тепла и приходящуюся
на 1 м2 поверхности, можно вычислить по формуле A1.10) с учетом фор-
формул D40.20) и E65.1) из справочника Двайта:
со
¦ 2яЛ Л ixataz- 2 \^e dz-
о
= -Г тг'о (\ ^лУЦ% = т/1 Г4- '"Н'Т Y/2 = Я (т8) = 4" шр.8/1, A1.22)
где/е = 2~ / — эффективное значение тока /. Таким образом, активное
сопротивление равно такому сопротивлению, которым при постоянном токе
обладает поверхностный слой (скин-слой) толщиной
8=Г4
Рассмотренные здесь вихревые токи могли бы появиться в проводнике
Лишь при наличии вблизи его поверхности однородного магнитного поля
B0coswt, направленного вдоль оси у. Поведение i и В в проводнике
описывается одним! п теми же дифференциальными уравнениями [см. A1.7)
и A1.8)], поэтому обе эти величины затухают экспоненциально по мере
удаления в глубь проводника. Чтобы вычислить рассеиваемую энергию,
возьмем контурный интеграл от В вдоль сторон прямоугольника, располо-
расположенного перпендикулярно к оси х и вытянутого вдоль оси z настолько,
что одна из его сторон длиной 1 м лежит вне поверхности проводника
(но в непосредственной близости от него), где индукция равна Во, а другая
сторопа — далеко в глубине проводника, где индукция практически уже
равна нулю. В интеграл войдет лишь значение Во, поэтому, согласно
соотношению G.2) (пли из первого уравнения Максвелла), получим
Bo = lxl = 21l*lxle. A1.23)
Из выражения A1.22) следует, что рассеиваемая вихревыми токами мощ-
мощность, приходящаяся па поверхность с площадью S и определяемая через
амплитуду Во магнитной индукции вне поверхности проводника (в непосред-
непосредственной близости от него), равна
Р== [ Т\ dS = {2^-fi)-1 \ BldS. A1.24)
S s
Самоиндукция Ц, приходящаяся на 1 ж2 поверхности и обусловленная
наличием магнитного поля впутрп проводника, находится из соотноше-
соотношений A1.20), (И.22), (8.36) и A1.3):
»\ \ i-Adtdz = -^[ { i%dtdz=~ = ^. A1.25)
0 0 0 0
J J J J
0 0 0 0
Сопоставление выражения A1.25) с выражением для сопротивления Н'
Aга 1 м2 поверхности) приводит к соотношению
Д=-.=4- = -\ A1.26)
соо шО-( со ч '
1) Аргументация автора неубедительна, поскольку в бегущей волне A1.20) нот,
очевидно, неподышшых в пространстве узлопых поверхностей, на которых вектор плот-
плотности тока меняет свое направление на обратное.—Прим. перее.
?5 в. Смайт
386 - Глава XI
Отсюда следует, что величиной L[ при высоких частотах можно полностью
пренебречь.
§ 4. Скин-эффект в случае полого цилиндрического проводника.
Если частота настолько велика, что глубина проникновения мала по
сравнению с радиусом кривизны поверхности проводника, то результаты
предыдущего параграфа вполне можно применить к обычному цилиндриче-
цилиндрическому проводу или к круглой цчлиндричейкой трубе. Если же это условие
не выполняется, то следует решать задачу заново, пользуясь цилиндрически
ми координатами. В этом случае в силу полной симметрии относительно оси
цилиндра ток iz является функцией лишь р, и уравнение A1.7) принимает вид
/ши. У . У .У 32г, , 1 di7 ... „m
'— it = ]^ix = ipiz = -^+ ~^- A1.27)
Введя обозначение v — (jpI^p, получим
Это уравнение является модифицированным уравнением Бесселя E.309)
нулевого порядка. Его решение имеет вид [см. E.411)]
Г2 = CI0 (v) + Шо (в) = С/о [(/рI!* р] + 1)К0 К/»1/* р]. A1.29)
Из выражения G.89) следует, что вследствие симметрии магнитное поле
во внутренней полости трубки существовать не может. Если через а и Ъ
обозначить соответственно внешний и внутренний радиусы трубки, то
граничным условием при р = Ъ будет В = О, что в соответствии с уравне-
уравнением A1.3) дает
(Vxi)P=b = 0 или (-§-)р_„ = 0. A1.30)
При р = а имеем следующее граничное условие:
?)р=а = *„. (И.31)
Используя соотношение E.440), из выражений A1.29) и A1.30) получим
0 = CIX [(jp)lb b] - DKX [dpI'*]*
а из выражений A1.29) и A1.31) будем иметь
i0 = С/о [(/рI'* а] + DK0 [{jpL* a].
Отсюда
?^ К, \{fPfh Ь] го
/о К/»1/2 «J ^ [UPL* Ь\ + A [(/ji,I'* Ь] Кв [(/рI'* а]
Г7
§ 5. Скин-эффект в сплошном цилиндрическом проводнике. В слу-
случае сплошного металлического стержня нужно в уравнении A1.3) поло-
положить D—0, потому что, согласно § 34а гл. V, при х = 0 функция К0(х)
обращается в бесконечность. Тогда вместо выражений A1.29), A1.32)
и A1.33) для iz будем иметь следующее:
Вихревые токи 38Т
Для получения численных значений необходимо величины /0 [(/I/2 х]
и Ко [О'I'2 ж] разбить на действительную и мнимую части. Это произво-
производится при помощи функций her, bei, her и kei, введенных Кельвином; для
этих функций существуют таблицы (см., например, Двайт, 1050). Таким
образом, имеем
h К/У'2 Ж1 = bero х + / beio x> A1.35)
о ж. A1.36)
Подставляя A1.35) и A1.36) в E.437) и E.440), можно найти разложение этих
функций в ряд. Используя функции Ъег и bei в выражении A1.34),
умноженном на eJ<fl(, и взяв от него действительную часть, получим выра-
выражение для плотности тока в цилиндрическом проводнике радиуса а в виде
e] -it te
a - arc tg6e?0 f(p)/ a] Ш° HpI'2 Pl^6c> Kp)I/2 Pl 6f'° f(/>-/2 a| A138)
be[(I^alber{(pI^P]tbei[(pI^P]bei\{I^a] '
Полный ток в проводе в любой момент времени мошно выразить через
величину магнитного поля на поверхности проводника, поскольку они
связаны между собой соотношением # = |а//Bтся). Из соотношений A1.34)
и E.440) после сокращения на е;№' имеем
«Wo
или
о_/,_*!/,.г. „.-_w«e] A1.39)
Средняя рассеиваемая мощность, приходящаяся на единицу длины в кольце
радиуса р и толщины dp, согласно выражению A1.10), равна
dPav = Т т ! к !2 2тр t?p = T:Ti2i2p dp,
где i2 — величина комплексно-сопряженная iz. Отметим здесь же, что вели
чине (-}- /I/а = 2~1/2 A 4- /), часто встречающейся в рассматриваемых уравнени-
уравнениях, соответствует комплексно-сопряженная величина_( —/) /2 = 2~ /2A — /) =
= -/(/I/2- Поэтому
= /о К - /»1/2 Р] = Го [ ~ / (/»1/2 Pi-
Полная мощность, рассеиваемая в проводе (на единицу его длины), равна
S '.1-
Этот интеграл является частным случаем интеграла E.426) и получается
из последнего при п — 0, вследствие чего результат, записанный череа
функции berox и beiox, будет иметь вид
р ^ тка_ Ьег0 [(рI'* a] bei'0\(P)lh a]-berB [{pI^ a] beiB [(рI'2 а] (
"" 1' «1/ gl'«
25*
B
388 - Глава XI
В соответствии с выражением A1.39) квадрат эффективного значения /с
равен
/2 ^ 2я*х*ра'
6 22
1J р Mi 41)
]}2 °"
Если Л = т/(тся2) — сопротивление на единицу длины при постоянном токе,
то высокочастотное сопротивление R' равно
R, = Т^ва» R = a (рI^ to- [(pI^ а] tei' [(рI^ a]-ter' [(рI'* aj ftrf f(pI/» a] R
¦с/1 2 {be'KJ^JP + ^'KI'"^]}2
A1.42)
где, как и во многих таблицах, индекс «нуль» опущен и, согласно выра-
выражению A1.27),
р = т'^ш = -ур.ш A1.43)
и а — радиус цилиндра.
Энергию магнитного поля внутри провода можно определить, восполь-
воспользовавшись соотношением A1.39):
Тогда для средней энергии внутри провода, согласно выражению (8.12),
получим
где введены сокращенные обозначения /0 вместо I0[{jp)ll2p] и 1'0 вместо
д10(х)/дх. Поскольку, в силу соотношения E.440), Г0(х) = 1г(х), этот инте-
интеграл совпадает с интегралом E.426), если в последней положить и=1,
поэтому его значение через функции Ьегг х и bei^ x равнп
ар-1!* [Ьегг (рх1*а) bei[ (рх^а) — bei\ (р^д) beix (p1'^)].
При помощи формул (828.1), (828.2), (829.3) и (829.4) из справочника
Двайта эти функции сводятся к функциям нулевого порядка. Учитывая,
что средняя энергия равна — Ьг11 и что 1% определяется выражением A1.41),
для L{ — внутренней самоиндукции па единицу длины — получим
j __ ?(РI/2 ber[(pfh a]ber' \{рУ:2 a] + bei\{pf^ a] bet' [(рI^ а] Щ Щ
Л ^яшв {be/-'[(pI/2aj}2+|fcei'l(pI/2aD2
§ 6. Решение в сферических координатах при аксиальной симметрии.
Предположим, что магнитное иоле, вызывающее вихревые токи, не зави-
зависит от <р и не имеет ф-составляющей. Тогда вектор-потенциал имеет только
(р-составляющую, т. е.
А = чА9(г, 6, t), A1.45)
где (f — единичный вектор в направлении ер, равный
4= — isincp-f jcostp. A1.46)
Применим оператор Лапласа C.17) к выражениям Ах — — ^?sincp и
А = А9 cos <p по отдельности. После некоторой перегруппировки членов
Вихревые токи
389
уравнение A1.8) примет вид
Выписывая V2 в сферических координатах C.17) и опуская q>, получим
х dt г2 дг X дг ) Tr2sinflaer 36 1 г2 sin2 О
, (Н 48)
дг
ди*
где введено обозначение и = cos G.
Рассмотрим теперь стациоцарные вихревые токи, предполагая, что
магнитное поле осциллирует с круговой частотой ш. Как и в § 13 гл. V,
будем искать решение в виде произведения двух функций, одна из кото-
которых зависит только от 6, а другая — только от г, т. е.
-l? = Re{9?-1/2Re'M(}. A1.49)
Подставим это в выражение A1.48), умножим все на г2 и разделим на
Re3U>(, тогда получим
где
/j = x'1[xi« = 7!Jj())- A1.51)
Как и при решении уравнения E.82), приравняем члены, зависящие от б,
величине —и(и+1), а члены, зависящие от г, приравняем п(п-\- 1); тем
самым уравнение A1.50) будет тождествепно удовлетворено. После диф-
дифференцирования уравнения A1.50) получаем
dt2
1 „ J-,
Д„=0.
A1.53)
Первое из ураБненин совпадает с дифференциальным уравнением E.180)
для присоединенных функции Лежандра, соответствующим значению т = 1,
а второе является модифицированным уравнением Бесселя E.406), в кото-
котором х =UpYl%r- Таким образом, в соответствии с соотношением E.181)
и § 33 гл. V. А9 является действительной частью выражения
/-^[Л^И + ЗДИ] {СпК+1,2 [(jpyi*r]+bnKn+ih [{jPyhr]}e^. A1.54)
Если п — целое число, а это так и должно быть для Р\ (и) и Q\ (и) при
Отсутствии коцических границ, то можно для второго решения вместо
Kn+iy2 использовать /_(n+i/2), как в § 38 гл. V.
В области, где проводимость равна нулю, левая часть выражения A1.48)
обращается в нуль, и если положить Аче'">1 =R'QeP'ot, то мы получим, как
и раньше, уравнение A1.52), но вместо уравнения A1.53) будем иметь
A1.55)
390 , Глава XI
Решение этого уравнения [см. E.84)] имеет вид
R'^A^ + Br^'1. A1.56)
В непроводящих областях члены в соотношении A1.54), зависящие от г,
следует заменить этим выражением.
§ 7. Проводящий шар в переменном поле. Пусть шар, имеющий
удельное сопротивление т, магнитную проницаемость р. и радиус а, поме-
помещен в однородное переменное магнитное поле Be1Uit, направленное вдоль
«си z. Опуская множитель е-', получим следующее выражение для ком-
комплексного вектор-потенциала:
А = <р-| fir sin 6 = <p-Ifi/-i>l (cos 6). A1.57)
Это выражение можно легко проверить, применяя к нему оператор ротора
ет учитывая соотношения C.15) и C.16). Таким образом, в выраже-
выражениях A1.54) и A1.56) нужно положить и = 1,и, поскольку вектор-потенциал
вихревых токов должен в бесконечности обращаться в нуль, снаружи
шара будем иметь
a<r<oo, Ао = <р у fi (r+ /V-2) sin 6. A1.58)
л
При /• = 0 величина А; конечна, поэтому, согласно выражениям E.465).
я E.466), внутри шара остается только /з/2 [(//>I/2 г]. Таким образом, пола-
полагая в выражении A1.54) п—1, находим
0 < г < а, А; = <р±ВСг-11*1»ы [(/рI/» г] sin в. A1.59)
из соотношений G.118) и G.119) следует, что при г = а должны выпол-
выполняться следующие граничные условия:
Л = Л и ^(rzinBAJ-v.-^irsintij. A1.60)
Полагая в выражениях A1.58) и A1.59) г —а, используя соотношения
E.414) —E.416) и обозначая для краткости In[(fp)ll2a] через /п и (fp)ll2a
через v, получим
а* + Z>= h [/2 h],
Bа?-D) |х = jyf/i [1 /3/2 + vllh] С = №*!* [(v-+ V'1) /1/2 - /_1/2] С.
Разрешив эти уравпения относительно С и D, будем иметь
^СИ 61)
выражения можно представить также при помощи гиперболических функ-
функций [см. § 38 гл. Уили Двайт, 808.1 и 808.3]. Согласно уравнению A1.4),
.плотность тока всюду внутри шара определяется следующим образом:
i = -/oryAi- - jpv.-1 A,., A1.63)
Вихревые токи 391
где Aj дается выражением A1.59). В соответствии с соотношениями A1.58),
C.15) и C.16) магнитное поле снаружи сферы равно
e, (И.64)
(И.65)
Подобным же образом из соотношения A1.59) находятся В.в и Bir. Сра-
Сравнение выражений A1.64) или A1.65) с G.49) показывает, что поле вихре
вых токов подобно полю магнитного диполя, т. с. полю кольца радиуса а,
несущего ток /е;ш', где \xoa2J = 2BD. Если магнитное поле не является
переменным, то ш = 0 и в выражении A1.51) р—> 0. Поэтому [см. § 38
гл. V и Двайт, 657.1 или 657.2] имеем
и /-i"<*>J^W
Выражения A1.61) и A1.62) упрошаются, так что соотношения A1.58)
и A1.59) принимают вид
AL67)
Это точные выражения для статических полей. Из соотношения A1.63)
в качестве первого приближения для медленно меняющихся полей имеем
К такому же результату мы придем и в том случае, когда удельное
сопротивление становится бесконечно большим.
При очень высоких частотах
А4->0, Ао -»<р-1В (г-a3/-2)sin 6, A1.69)
потому что, согласно результатам § 38 гл. V,
/l/2 (Ж) -^ ^8/2 (Ж) -^ /_1/2 (Ж) -* . . . ->( — \ т,
т. е. внутри шара магнитное поле отсутствует, а вихревые токи, как
и следовало ожидать, становятся поверхностными.
Чтобы иметь представление о порядке встречающихся здесь величин,
вычислим, пользуясь выражением A1.51), значение р для переменного
поля, изменяющегося с частотой 60 гц (т. е. ш = 120тг). Пусть т и |i даны
в единицах MKS, тогда для меди т ^ 1,7-10~8 ом-м, \х «к pv — 4ii-l0-7 ен/м
и /7^28 000. Для типичных железных образцов т=10~7, \х ^ 480тг-10~7
(в магнитном поле напряженностью 1,5-105/Dтг) ампервитков на метр)
и /? = 57ОООО. Для графита т:^8-10-6, [х % 4тг- Ю и /? = 600. Таким
образом, при этой частоте при расстояниях порядка нескольких санти-
сантиметров выражение A1.69) могло бы быть пригодным для железа или меди,
но не для графита. Предположение о том, что Aj. =0, а Во тангенциальна
к поверхности, сильно упрощает вычисление.
Так как мы оперировали в этом параграфе с комплексными ампли-
амплитудами, то полученные результаты позволяют найти и амплитуду и фазу
392 Глава XI
искомых величии. Аналогичные граничные условия и такого же вида
электродвижущие силы встречаются при решении задачи об экранирующем
действии произвольного числа концентрических толстостенных сферических
оболочек, но результаты в этом случае записываются в более сложной
форме. В частности, оказывается, что если некоторое заданное количество
материала распределить между несколькими отдельными концентрическими
оболочками, то экранирующее действие усиливается. Более того, суще-
существуют онтимальные значения толщин оболочек и расстояний между ними
§ 8. Мощность, поглощаемая шаром в переменном магнитном поле.
Вычислим теперь мощность, поглощаемую шаром в случае, рассмотренном
в предыдущем параграфе. Как следует из выражения (И. 10), внутри эле-
элементарного объема dv поглощается мощность
dP = — т i i dv = тгтг i г2 sin б dr d6.
Подставляя значения гиг из соотношений A1.63) и A1.59) и интегрируя
по б в пределах от 6 = 0 до 6 = тг, получим
о
Р ^ ? ] / К/»1'2 г] /3/2 [(- /»1/2 г] г dr. A1.70)
Применим последнюю формулу E.426) и учтем, что в соответствии
г. § 38 гл. V
1l(±/»1/3«]=|i-^(r
В результате вычисления интеграла (см. Двайт, 651.06—651.09) находим
(тг/г'/га)-1 {-^Bра?)Ч* fsh B/M2I/2+sin BpaiIl^]~ch ftpa2I'* + cos {2pa2f^ \
Исключив произведение С С из соотношения A1.70) при помощи гшра
жений A1.71), A1.61) и A1.51), получим
«)-
v.o) раЫ (S—
где u = BpI/2a, С = сЬм, с = cos и, S = shu, s — sinit.
§ 9. Переходные явления в проводящем шаре. 15 двух последних
параграфах рассматривалась задача о шаре с удельным сопротивлением т
и проницаемостью [-i, находящемся в однородном переменном установившемся
магнитном поле. Решим теперь задачу в случае переходного режима, когда
та же самая сфера помещена в однородное магнитное поле В, которое
в момент времени 2=0 внезапно становится равным пулю. Совершенно
ясно, что в этом, как и в предыдущем, случае А также будет иметь
только ср-состаиляющую. В момент временп t = 0 поверхностные вихревые
токи воспрепятствуют мгновенному изменению внутреннего поля, и поскольк}
вектор-потенциал при переходе через границу должен быть непрерывным.,
то из выражения A1.67) в момент времени t. = 0 мы будем иметь
Вихревые токи 39S
Ввиду того, что вне сферы т=оо, последующее поведение вектор-потен-
вектор-потенциала А будет определяться решением уравнений
=0. A1.73)
Решение первого уравнения, экспоненциально зависящее от времени, было
найдено нами в § 6. Попытаемся теперь удовлетворить граничным усло-
условиям, взяв сумму таких решении. Ясно, что в рассматриваемом случае
колебания отсутствуют и, следовательно, нужно /W .заменить на —qst.
Введем величину
A1.74)
Тогда в формулах § 6 следует /р везде заменить на — h\. В частности,
в выражении A1.54) вместо (/jdI'2 теперь появляется fks, и'мы приходим
к обычным функциям Бесселя. Поскольку вектор-потенциал А4 должен
быть конечным при /• = О и зависеть от 0 так же, как и в выражении
A1.72), то из выражения A1.54), подставляя sin 6 вместо Р\(и), получим
следующее соотношение:
Ai = ? 2 А 8/-1/2/з/2 (Л./-) sin 0 erbst. A1.75)
s
Вектор-потенциал Ао конечен в бесконечности и равен А{ при г = а лля
всех значений t. Отсюда, согласно выражению A1.56), имеем
Ao = ?2^s^2sinee-9*'. A1.76)
Кроме условия A1.72),' при t=U нужно удовлетворить также условию
A1.60), имеющему при г = а (после сокращения на sinO) вид
Ао- vi> h, dr — Iх дг ¦
Отсюда при г = а для всех значений t должно выполняться уравнение
Продифференцируем второе уравнение, а затем умножпм первое уравнение
на [л и сложим его со вторым, после чего, сокращая на As, получим
!\« #а F^/2 (й.я)| + ( V- + ~ft,) J'l, (К°) = U- (H.78)
( ~)
Таким образом, для того чтобы удовлетворить гранпчным условиям, нужно
найти корни ks этого j-равнения; знание этих корней позволит
определить при помощи выражения A1.74) величины qs, входящие в спит
ношения A1.75) и A1.76). Значения Ая можно найти при помощи выра
жения E.395) и таблицы тригот метрических фупкций.
Умножая A1.72), A1.75) и A1.76) на r1^ w полагая j! = 0, получим
Это выражение совпадает с последним выражением E.352), где n = s/s,
и из соотношения A1.78) величина В равна ([*¦/[*¦„)+у • Из выражения
E.328) имеем
-394 Глава XI
В соответствии с соотношениями A1.78) и E.323) получаем
/5/2 (ква) = -7,/2(ква) + ~-аЛ/, (М = -^-^ Л,2 (ksa).
Используя выражение E.337), находим
а ШтВа /2
Подставив это выражение в A1.75) и A1.76), определим Аг и Ао. Плот-
Плотность тока внутри шара в соответствии с уравнением A1.4) дается выра-
выражением
§ 10. Вихревые токи в плоских пластинках. Пусть в плоскости z = U
расположена очень тонкая пластинка, обладающая удельным сопротивле-
сопротивлением с (на единицу поверхности). Вычислим вектор-потенциал А(х, у, z, t)
поля вихревых токов, которые индуцируются в такой пластинке под дей-
действием переменного магнитного поля, описываемого вектор-потенциалом
А' (х, у, z, t). Будем обозначать плотность этих токов через i. Появление
электрического поля —d(A'z4-Az)/dt внутри пластинки приводит к появле-
появлению поверхностных электрических зарядов, электростатическое поле которых
в точности компенсирует первоначальное. Токи, сопровождающие это пере-
перераспределение зарядов, настолько незначительны, что ими можно вполне
пренебречь и рассматривать лишь тангенциальные составляющие As и А^.
Таким образом, используя уравнение A1.4), можно написать
Пусть вихревые токи находятся в некоторой конечной области пластинки,
последняя может быть как конечной, так и бесконечной. Введем функцию
потока Ф (х, у), определенную в каждой точке Р пластинки, как ток,
протекающий через любое поперечное сечение, проведенное от точки Р
до края пластинки. Пользуясь соотношением G.2), для замкнутого пути,
взятого по контуру этого сечения и не включающего поверхность, .и
учитывая, что В симметрично относительно пластинки, будем иметь
оо
xdx = 2{\j Bvdy, A1.83)
V
где путь интегрирования при положительных z проходит в направлении
положительных значений х или у. Дифференцируя выражение A1.83),
получим
. _дФ_ 2ВУ _ 2 дАх . _дФ _2Вж_ 2 дАу
или в векторной форме
i=_2^. A1.84)
Подставим это выражение в уравнение A1.82), тогда для области внутри
пластинки получим
at (л„ dz
Вихревые токи 395
Вне пластинки вектор-потенциал А состоит из двух частей: магнитной
части, порождаемой вихревыми токами, и электрической части, являющейся
градиентом скаляра и порождаемой электрическим двойным слоем, возник-
возникшим под действием A'z и Az. Так как тангенциальная компонента А^
вектор-потенциала возбуждающего поля известна и так как As меняется
непрерывно при переходе через каждую границу двойного слоя, то соотноше-
соотношение A1.85) является для As граничным условием на внешней стороне поверх-
поверхности пластинки. Это условие вместе с уравнением F2A = 0 определяет А
всюду вне пластинки. Если пластинка обладает конечными размерами, то гра-
граничным условием на ее крае (в плоскости пластишш) будет i = 0 или
j)As/dz = 0. Правая часть уравнения A1.85) конечна в любой момент
времени; это означает, что если bt, —*• 0, то о (А^ 4- As) —> 0. Поэтому скачко-
скачкообразное изменение А' мгновенно индуцирует такие вихревые токи, кото-
которые сохраняют А 4-А' и В + В' неизменными внутри пластинки. Таким
образом, при заданном изменении А' начальное значение А известно, и
если дальше никаких изменений не происходит, то последующие значения А
в процессе уменьшения вихревых токов можно найти, полагая в уравне-
уравнении A1.85) дA's/dt = 0 и решая полученное уравнение. Второе внезапное
изменение А' приведет к возникновению второй серии вихревых токов
и т. д. В любой заданный момент времени поле вихревых токов будет
являться суперпозицией найденных полей. Если скачки внешнего поля
становятся меньше и - интервалы между ними короче, то в пределе мы
приходим к непрерывному изменению магнитного поля во времени.
§ 11. Решение задачи о вихревых токах в плоской бесконечной
пластинке методом изображений. Представим себе, что тонкая бесконеч-
бесконечная плоская проводящая пластинка (z = 0) находится в магнитном поле,
источники которого расположены в области z > 0. Пусть в момент времени
t—О поле изменяется так, что если при t < 0 его вектор-потенциал был
равен А[ = f1 (х, у, z), то при t > 0 А'2 = f2 (х, у, z). Из результатов преды-
предыдущего параграфа следует, что вихревые токи, появляющиеся в момент
времени t — 0, сохраняют прежней величину вектор-потенциала на поверх-
поверхности пластинки, поэтому вначале поле в отрицательной области z остается
неизменным. Таким образом, на отрицательной стороне пластинки началь
ный вектор-потенциал, обусловленный только вихревыми токами, равен
(А),_о = А;-А4 = /!(*, у, z)-/2(x, у, z). A1.86)
Это поле могло быть создано старым источником совместно с н вым источ-
источником, если у последнего изменить знак на обратный. Эти воображаемые
источники, которые могут заменить действительно действующие вихревые
токи, являются изображениями, подобными изображениям в электростатике.
Поскольку AJj не зависит от t, то уравнение A1.85) сводится к урав-
уравнению
общим решением которого, удовлетворяющим при /=0 условию A1.86),
является следующее:
A = U(x, у, _|z[-2q^)-/a(*, у, -И-2^1*)- (И.88)
Знак z выбран таким, чтобы сделать А одинаковым при ± z, как того
требует симметрия задачи, и чтобы величина А затухала со временем.
Таким образом, уравнение показывает, что к полю А^, которое существовало бы
в отсутствие пластинки, добавляется по обе стороны от пластинки
396 Глава XI
затухающее поле, порождаемое вихревыми токами, которое можно представить
как иоле источников, находящихся сверху и снизу пластинки и удаля
гощихся от нее с постоянной скоростью 2с/[л„.
Максвелл предложил формулу для этого закона изображений, которук.
можно использовать при любом характере изменения ноля. Пусть вектор-
потенциал возбуждающего поля равен
A' = f(t,x,;j,z). A1.89)
За бесконечно малый интервал времени di это иоле изменится на вели
чину
ЭХ' д ,. . ,
~0f-dz = —tf(t, x, у, z)dz.
Первоначальное поле вихревых токов, появляющееся в тот же интервал
времени, должно быть равно этому изменению по величине и противопо-
противоположно по направлению. Как мы видели, это поле уменьшается со време-
временем так, как поле воображаемых источников, находящихся по обе стороны
пластинки и удаляющихся от нее с постоянной скоростью 2с/[л„. Таким
образом, вектор-потенциал вихревых токов в момент времени t, описывающий
поле источников-изображений, возникших до момента времени t, в течение
интервала (х, x-(-dx) будет определяться выражением
И\— —~ i С t— - г 11 — 1И 2?
ал — Qt I \J- — '¦¦> х> У' — I z | — 7Г
В момент времени t полный вектор-потенциал вихревых токов равен
-т, х, у, -|z|-gx)dx. A1.90)
При z < 0 величину — | z \ надо заменить на z, и, поскольку (см. Пайерс,
863) df/dx=—dfldt-\-Bc/i>.v)dfldz, подстановка этого выражения вместо
df/dt в соотношение A1.90) и интегрирование, при условии, что / = 0прп
х=оо и /= V при х = 0. дают полное результирующее поле
(^). A1.91)
Вычислить этот интеграл часто проще, чем A1.90).
§ 12. Момент, действующий на вращающуюся петлю с током или
магнитный диполь. При вращении магнитной системы вокруг оси, распо-
расположенной перпендикулярно к плоскости проводящей пластинки, поле
индуцированных вихревых токов создаст, вообще говоря, тормозящий
момент, пропорциональный, как мы увидим далее, угловой скорости вра-
вращения системы, если эта скорость не слишком велика. Измеряя этот момент,
можно найти угловую скорость (на этом принципе работают некоторые
типы автомобильных спидометров). Простейшей магнитной системой
является диполь или небольшая петля с током, которая может вра-
вращаться вокруг центра, сохраняя направление магнитного момента парал-
параллельным пластинке. Для уяснения построения изображений мы, не
пользуясь формулой A1.90), поступим следующим образом: представим
себе, что через равные промежутки времени х диполь мгновенно поворачи-
поворачивается на угол «их. Рассмотрев этот случай, мы сумеем затем, устремив
длину интервалов к нулю, получить результат и для непрерывного
Вихревые токи
397
движения. На фиг. 111 показаны изображения (как они выглядят сверху),
образованные при последних четырех скачках, в то мгновение, когда диполь
с моментом m занимает указанное на фигуре положение. Вращающий
момент, действующий на т, будет являться суммой моментов от всех
изображений. Поскольку все диполи-изображения направлены перпенди-
¦1
кулярно к оси вращения, в выражении A.16) G1 = 0'2 = —-тг и, согласно
выражению'A.19) и § 1 гл. VII, момент, обусловленный одним изображе-
изображением, составляющим с m угол ф, равен
A1.92)
Тогда, если р = ш^/с,, момент от всех изображе-
изображений равен
„,
{л«ш2
sin пых—sin
l^/>3m2
32л
со
/ I
n=0
DO
л sin n mi — sin n шт cos <ox — cos лшт sin шт
и)Т
и=0
(рс -\-гш
A1.93)
При переходе к непрерывному движению х —> dt,
т. —¦>/ и sinшт —¦> шт—>wdt, так что сумма в вы-
выражении A1.93) превращается в интеграл
Т' —
[xvu>psm2 С — cos
т
^ \о
гот
гаг
H.V
A1.94)
Фиг. 111.
Введем x — pc-j-wt, так что cos wt — cos (ж — рс) и, следовательно,
со со
/ Г rosa; , , . Г sin x , Л
¦ ( cos рс \ —^- dx -j- sin рс \ —?- аж j,
32я
или (см. Двайт, 441.13 и 431.13)
cos ar
-sm pc
f si
\ —
sin а;
A1.95)
рс
Эти интегралы можно выразить в виде рядов (см. Двайт, 431.11 и 441.11)
или записать в форме известных функций интегрального косинуса Ci
и интегрального синуса Si, определяемых следующим образом:
(И.96)
рс
рс
Таблицы и графики интегралов Ci и Si даны в справочнике Янке и Эмде и
других книгах по математике.
Если величина рс значительно больше единицы, то, проинтегрировав
трижды соотношение A1.94) по частям, мы получим для Т такое выра-
выражение:
sin u>t
3 ros vit 12 sin
(pc-\-u>t,L '
398
Глава XI
Если пренебречь величиной 20ш/(/?сJ по сравнению с единицей, то найдем
joc»l, ^ = §7^- A1.97)
Если же пренебречь величиной и>(рсJ по сравненшо с единицей, то полу-
получим
vc <? 1 Т — ^"^т /11 о,Я"\
рс «. 1, i _ 64лс2 . A1.у»)
Для медной пластинки толщиною 0,1 мм с = 0,00017, так что при частотах
100, 10 000 и 10 000 000 гц величина р будет соответственно равна 4,67,
467 и 467 000. Таким образом, при этих частотах при с «к 0,01 м нужно
было бы пользоваться соответственно соотношениями A1.98), A1.95) и A1.97)
§ 13. Вихревые токи, возбуждаемые вращающимся диполем. Весьма
поучительно вывести непосредственно выражение для вихревых токов, кото-
которые будут индуцироваться вращающимся
диполем, описанным в предыдущем пара-
параграфе. На фиг. 112 воспроизведено одно
из изображений, показанных на фиг. 111.
Обозначим на фиг. 112 буквой Р точку на
пластинке, имеющую координаты р, 0, и
найдем в этой точке значение функции по
тока Ф. Согласно выражению A1.83),
A1.99)
где путь интегрирования выбран в ра-
радиальном направлении и принято во внима-
внимание, что интегралы вдоль нижнего и верх-
верхнего пути равны между собой. На фиг. 112
показано п-е положительное изображение.
Очевидно, для Вр важна только р-компо-
нента этого изображения. Используя при
вычислении В9 соотношения G.52) и G.49),
прибавляя затем величину, получаемую от
n-го отрицательного изображения, и сум-
сумб й
Фиг. 112.
р
мируя результат по всем изображениям, найдем
. A1.100)
Подставляя теперь это выражение в A1.99), интегрируя и разлагая второй
косинус (см. Двайт, 401.03), имеем
cos (лит + 6) —cos (тот 4-6) cos «от +sin
sin шх
5?
2л
П--Й
.A1.101)
Переходя к интегралу точно так же, как это было сделано в предыдущем
параграфа, получаем
Ф
штр Г —sin(cot-|-6) dt
A1.102)
Вихревые токи
399'
Если |хюш < с [условие, получаемое для выражения A1.98)], то член
Bсг/[х„K R знаменателе оказывается уже очень большим, прежде чем вели-
величина о>? в числителе станет заметно отличной от нуля, поэтому
— dt
(У» «С, Ф=_
Полагая х — с + Bс/р„) t и пользуясь формулой B00.03) из справочника
Двайта, имеем
rj-lsinO. A1.103)
На фиг. 113 изображена система нпхревых токов, определяемых
уравнением A1.103), для значений АъФ/у^, указанных на фигуре. Эта
Фиг. 113. Линии тока вихревых токов, создаваемых в беско-
бесконечном тонком проводящем листе магнитным диполем, располо-
расположенным на расстоянии 1 см от него и вращающимся с угловой
скоростью о) в плоскости, параллельной поверхности листа (на-
(направление вращения показано на фигуре).
Предполагается, что наблюдатель расположен в точке, где находится
диполь. Линии тока соответствуют тому моменту, когда диполь ориен-
ориентирован слева направо. Приведенные на фигуре значения функции
потока Ф вычислены по формуле A1.103) при ч>у.ъ т/D7Ч)=1.
система линий тока вращается со скоростью вращения диполя, который
расположен на единичном расстоянии (в указанном на фигуре масштабе)
над плоскостью чертежа параллельно прямой Ф = 0. Поле этих токов будет
направлено под прямым углом к диполю. Это приводит к возникновению
момента, величина которого вычислена в предыдущем параграфе.
§ 14. Экранирование круглой петли посредством тонкой проводящей
пластинки. Пользуясь выражением A1.91), исследуем эффект экраниро-
экранирования при помещении бесконечно тоикой проводящей пластинки между
двумя круглыми коаксиальными петлями радиусов а и Ъ, находящимися
400 Глава XI
одна от другой на рассточнии с. При отсутствии пластинки вектор-потен-
вектор-потенциал первой петли в месте расположения второй петли, в соответствии
с § 11 гл. VII, был бы равен
где м2 = а24-б2 —2a6coscp. В соответствии с выражением A1.91), в случае
наличия экрана нужно взять действительную часть следующего выражения:
. , ,, sal д С f F e^V-V dz
А + А\COSCP( \
( \ г , ,•, ^./o , i i2iV2 Jd<?- A1Л05)
С целью упрощения вычислений рассмотрим лишь случай, когда 2<;/(шр,€) < 1.
Проинтегрируем по х несколько раз по частям и после и-го интегрирования
получим
Комплексная амплитуда вектор-потенциала в месте нахождения второй
петли равна •
Щ^УЦ^,. A1.106)
Н соответствии с § 7 гл. VIII, отношение нового потока сцепления к ста-
старому равно
Если величина 2<;/(u>ixv) кала, то в рядах можно ограничиться одним пер-
первым членом, и тогда
*4^^, A1Л08)
где В{1 и Лф определяются соответственно выражениями G.53) и G.50)
и вычисляются при р = Ъ, z = с. Если, кроме того, а или Ъ малы по срав-
сравнению с с, то из выражения G.48) получаем
д 6;сA1.109)
Как мы видели в § 13, для медной пластинки толщиной 0,1 мм при ча-
частоте 1 мггц отношение и>[\,/<; равно 46 70U, что вполне удовлетворяет ггред-
положениго, сделанному при выводе соотношения A1.108). Отсюда при
а = 1 см, 6 = 10 см и с = 10 см, согласно соотношению A1.109), Во^ 0,0006,
т. е. экранирующее действие пластшши весьма значительно.
§ 15. Зопальные вихревые токи в сферической пленке. Рассмотрим
вихревые токи в тонкой сферической проводящей пленке. При наличии
аксиальной симметрии все вихревые токи текут по коаксиальным окруж-
окружностям. Пусть полный вектор-потенциал равен А' + А, где А — вектор-по-
вектор-потенциал вихревых токов. Э. д. с. Ш, вызывающая появление токов в кольце
шириною а A6, соответствующем углу 0, индуцируется, как известно, в ре-
результате изменения величины полного потока сквозь это кольцо. Пользуясь
Вихревые токи 401
соотношениями (8.1) и результатами § 8 гл. VII, можно выразить Щ через
А' + А и затем —при помощи закона Ома F.6) — через ток
fdN d ro . а/л/ , л \i Ъаач sin 6 .
= ~-JT= -5г[2та8ш0D + Л)]V
Откуда, если вектор-потенциалы равны нулю при 6 = 0, имеем
-±Щ + А„) = щ, A1.110)
где i9 — плотность тока, ; —удельное поверхностное сопротивление. Пусть
выражение для вихревых токов в пленке представлено в виде ряда по
зональным гармоникам, где in — тг-я гармоника тока. Из выражений G.61)
и G.64) можно найти простое соотношение между in и и-м членом разло-
разложения вектор-потенциала этих токов, а имонно:
in. A1.111)
Если А\ также разложить в ряд по сферическим гармоникам, то, подста-
подставляя выражение A1.111) в A1.110), мы видим, что разложения A't и Л9
связаны между собой на поверхности пленки (/¦ = а) уравнением
-2|(л;+^)=22-^-Чс. (И.И2)
Если при t > 0 возбуждающее поле А? постоянно, а в момент времени
? = 0 поле вихревых токов известно и равно
Др=2с„л. (и-из)
Г!
то, очевидно, решение уравнения A1.112), определяющее закон убывания
вихревых токов, имеет вид
Л = 2С'пЛ1е-[Bг!+1)/11г]?'- A1.114)
п
Предположим, что значение вектор-потенциала возбуждающего поля
на поверхности сферы можно записать в форме
Изменение этого ноля, происшедшее за i сек. до момента времени / за
бесконечно малый интервал времени d~, равно
Возникающие за тот же интервал времени dx вихревые токи создают поле,
полностью нейтрализующее это изменение в момент его возникновения;
но с течением времени поле вихревых токов убывает по закону A1.114),
и к моменту времени t мы имеем
п
Полный вектор-потенциал вихревых токои на поверхности сферы в момент
времени t равен .
t ^ ^ g A1.116)
71 0
26 в. Смайт
¦402 Глава XI
Заменим df/dt на —df/ck и проинтегрируем по частям; тогда, пользуясь
соотношением A1.115), получим следующее выражение при г = а для вектор-
потенциала от всех источников:
В случае стационарного переменного поля величина А'^, которая может
являться результирующим потенциалом поля как внешних, так и внутренних
источников, определяется при г~а выражением A1.115), где
Ans = Pl(cosb), f (t) = cos Ы. A1.118)
Обозначая величину Bn -f-1) ?/(ivO через N и интегрируя выражение A1.116)
(см. Двайт, 863.1 и 863.2), для вектор-потенциала поля только вихревых
токов при г = а получим следующее соотношение:
со
* ' Лв == 2 CnAns со (со2 + jV2) (N Sin w* - со COS u*) =
0
4
= ~ S CnA« «»<!>„ cos («ot + iJO, A1.119)
где tg^n = ^V/o). Таким образом, отставание по фазе еп равно —фэт. Вели-
Величина Ас, которая обращается в нуль при т-=ос и определяется выраже-
выражением A1.119) при г = а, будет являться вектор-потенциалом поля' вне
.сферы, обусловленного только вихревыми токами. Следовательно,
A0 = ^2j-('b(-) Pn (cos 6) cos en cos (wt — ej, A1.120)
«=0
B» + 1)б_ A л j
Внутри пленки вектор-потенциал поля вихревых токов Ai должен быть
всюду конечным, поэтому (a/r)n+1 следует заменить на (/"/а)". Для внешних
источников г входит в выражение для А' в виде (/"/a)n. Согласно соотно-
соотношениям A1.115), A1.118) 1и A1.119), результирующее внутреннее поле
равно (см. Двайт, 401.03)
Это выражение можно было бы получить непосредственно из соотношений
.A1.115), A1.117) и A1.119). Отношение тг-го члена в разложении по гар-
гармоникам новой амплитуды к соответствующему члену в разложении по гар-
гармоникам старой амплитуды равно
ЯОп= M,"Jf' =si"V A1.123)
Из выражения A1.120) следует, что если ? очень велико, то отношение
A1.123) близко к единице и поле остается неизменным., но если пленка
является хорошим проводником, т. е. если с, мало по сравнению с jjyu,
I то /?оп становится очень малым и происходит почти • полное экраниро-
экранирование.
Вихревые токи " 403
Плотность вихревых токов в пленке, определяемая выражениями
A1.111) и A1.119), равна
^^ Bn). A1.124)
Согласно формуле F.11), мгновенное значение мощности, рассеиваемой на
' элементарной площадке dS пленки, равно г2? dS, а для всей пленки, учиты-
учитывая, что и = cos б, получим
/! ТС +1
i2 sin 6 db = - 2<;тга2 \ t2 da.
-1
Если возвести в квадрат выражение A1.123) и проинтегрировать от и— — 1
до к =4-1, то все члены, содержащие смешанные произведения, согласно
соотношению E.92), исчезнут и останется сумма интегралов от квадратов
величин. Таким образом, каждая гармоническая составляющая incos(wt — еп)
тока i ведет себя как независимый ток, так что средняя мощность рас-
рассеяния в соответствии с выражением A0.18) равна
+i +i
-^ i*is = Cirea \ [ ^ inVdu = vi:a* ^ \ ^а-
S 1 1
[
-1 -1
Интегрируя при помощи соотношения E.194), найдем окончательно мощ-
мощность, рассеиваемую в сферической пленке:
со
Р = 2тгф2 n(n+l)Bn + l)Clcos2en. A1.125)
§ 16. Вихревые токи в тонкой цилиндрической пленке. Когда все
вихревые токи в тонкой бесконечной приводящей цилиндрической пленке
радиуса а текут параллельно ее оси, вектор-потенциал поля, индуцирую-
индуцирующего эти токи, должен также быть направлен параллельно оси, и магнит-
магнитное поле в этом случае является двухмерным. При этом, как мы видели
в § 26 гл. VII, вектор-потенциал обладает свойством электростатической
функции потока: его значение в каждой точке представляет поток между
этой точкой и некоторой другой фиксированной точкой. Пусть Az—вектор-
потенциал поля вихревых токов, a A'z + Az — полный вектор-потенциал; тогда
для э. д. с. на единицу длины, индуцируемой в полосе а, В шириною ad&
при изменении полного потока N, приходящегося на единицу длины этой
полосы, получим, используя закон Ома F.6), следующее соотношение:
S A1Л26>
где iz — плотность тока, а с,—удельное сопротивление пленки. Если разло-
разложить ток i в ряд по круговым гармоникам, то, согласно выражениям G.90)
и G.93), будет существовать простое соотношение между п-м членом этого
разложения и п-м членом разложения в ряд вектор-потенциала Az поля
этого тока. На поверхности пленки это соотношение имеет вид
(Ап)^а = \^ап-Чп. A1.127)
Пусть А'г и Ах разложены по круговым гармоникам; тогда, подставляя выра-
выражение A1.127) в A1.126), мы видим, что эти разложения удовлетворяют
2С*
404 Глава XI
следующему уравнению:
4 2-?К. (И.128)
С точностью до постоянного множителя это уравнение совпадает с урав-
уравнением A1.112), так что, задав возбуждающее поле при р = а в виде A1.115),
со
A'zs= -%СпАт/пA), A1.129)
Г1=1
можно определить вектор-потенциал вихревых токов [см. выражение A1.116)]
следующим образом:
со
A1.130)
ri=l 0
Заменяя dfjdt на —(df/дх) и интегрируя по частям, получим
$ A1.131)
Для синусоидального возбуждающего поля [см. выражение A1.118)]
имеем
Ans = cos{n6 + bn), f(t) = coswt. A1.132)
¦ Аналогично выражениям A1.120) и A1.121), вектор-потенциал ноля вихре-
вихревых токов при р > а определяется следующим образом:
os(otf— sn), A1.133)
: n = l
tgsn = 2«? ((Ofj^a). A1.134)
1 Для р < а нужно заменить (а/р)п на (р/а)п и, если источники поля нахо-
\ дятся вне цилиндра, то, так же как и в § 15, имеем
со
Отношение п-х гармоник поля при наличии пленки и соответствующих
(_ гармоник поля при отсутствии пленки равно
= sinen. A1.136)
t" Те замечания, которые были- сделаны относительно выражения A1.123),
, полностью относятся и к этому. При расположении источников внутри
цилиндра отношение новой амплитуды к старой в области вне пленки
определяется попрежнему соотношением A1.136). Согласно выражениям
/ A1.127) и A1.133), плотность вихревых токов в иленке равна
— kZ (ivz) 2 пСпc°s (пв4-8„) cosencos{Ы - вп). A1.137)
Вихревые токи 405
Согласно соотношению A0.18), средняя рассеиваемая мощность на еди
ницу длины цилиндра равна
¦'\"
Если выражение A1.137) возвести в квадрат и проинтегрировать от 0 до
2тс, то все члены, содержащие смешанные произведения, исчезнут и оста-
останется только сумма интегралов от функции cos2(ra6 + 8n), каждый из кото-
которых (см. Двайт, 854.1) равен тт. Таким образом, каждому члену разложения
можно сопоставить независимый контур, поэтому средняя рассеиваемая
энергия в единицу времени равна
оо
7> = 2т:а(^ау1 2 nWl cos2 вп. A1.138)
n = i
§ 17. Переходные явления при экранировании с помощью толстой
цилиндрической оболочки. В § 3 были рассмотрены продольные синусо-
синусоидально меняющиеся вихревые токи внутри толстостенной цилиндри-
цилиндрической оболочки, a d | 15 — произвольно изменяющиеся во времени про-
продольные вихревые токи в тонкой оболочке. В качестве сравнительно просто-
простого примера, содержащего как продольные, так и поперечные компоненты то-
токов, рассмотрим бесконечный цилиндр, имеющий магнитную проницае-
проницаемость [л, проводимость -(. внутренний радиус а, внешний радиус Ъ\ ось
цилиндра составляет угол а с однородным магнитным полем В. Найдем
поле внутри цилиндра по прошествии времени t после исчезновения или
появления внешнего поля. Из выражения G.28) следует, что решения для
статического вектор-потенциала при р > Ь, 6>р>а ио>р должны соответ-
соответственно иметь вид
] A1.139)
, A1.140)
A1.141)
Эти выражения определяют заданное поле при р = оо и остаются конечными
при р—-О. Значение постоянных определяется из условия непрерывности Aj и.
{Вхр)/(А при р = а и р = Ь; заменив ([л — [а„)/([а + [xj на (J, b2j(Ь2 — $2а2}.
на G, получим
=i, A1.142)
^)G. A1.143)
После момента времени ? = 0 имеют место те же решения уравнения A1.8),
где ~{=0, за исключением того, что в Ах пропадают р-члены, так как при
р = оо В = 0. В решении для а < р < b величина Аг должна иметь множи-
множитель sin ср, а Др —не зависит от <р. Как и в § 9, попытаемся искать это
решение в виде суммы экспоненциально затухающих функций, т. е.
2 n9e-«st]- A1.144)
S
Для А2 уравнение A1.8) является скалярным; из него множитель
sincpe""9*' выпадает и оно после подстановки v2 = [J^sP2 переходит
в уравнение E.302) с и— 1. Для А? уравнение A1.8) принимает вид A1.47).
406 Глава XI
Подставляя в последнее —9Р 2 вместо V2y, отбрасывая e~Pst и обозначая
PIPsP2 чеРез v2, мы опять получаем уравнение типа E.302) при Л —1.
Таким образом, для ?>0 выражения A1.139) — A1.141) заменяются сле-
следующими:
2 ], A1.145)
S
А, = В ^ {? sin «ВД [(^ТАI/2Р] е-м + k cos aZ)^
A1.146)
[<? sin a^pe-P*'+ к cos а/'зр sin (ре-в«( ], A1.147)
где i^x и Pj являются функциями Бесселя. Приравнивая Ах и А2 при р = Ь
обозначая ([AfftI'2 через ks и (fJ.'f'ZsI'2 через ls и опуская sin 9 в Az,
будем иметь
9CS + kC's = «рбДЛ, (AS6) + kbD'sP, (/,6). A1.148)
Приравнивая при р=6 тангенциальные составляющие ji~1B = }i~1V X А,
пуская sin 9 в <р-компоненте и умножая все на б2, получим
[ksbR[ (A.*) + ^х (*«&)] - wJsb2D'sP[ (lsb). A1.149)
"¦ Так как k-член равен нулю, то, согласно § 30 г гл. V, Л()(Л66) = 0, и
в соответствии с соотношением E.320) имеем
4 ). A1.150)
Аналогичным образом из граничных условий при р = а, выписывая выра-
выражение для РхDа), получаем
9/> + kF'sa = 9A#! (A8a) + кД [jB*^ (/sa) + У, (/во)], A1.151)
A1.152)
Исключение /"s, Z)s, F's и Z>s из четырех уравнений дает
; ksaR0 (ksa) - 2 ((x"V) Дх (Aeo) = ksaR[ (ksa) + A - 2^» Д, (А„а) = О, A1.153)
O = vJtaPi(l,a)~vI>l(lsa). A1.154)
Можно использовать только значения ps = kll([>.^), удовлетворяющие соотно-
соотношению A1.153). Подставляя Yu(ksb) из соотношения A1.153) в R^(ksa) и
применяя соотношение E.320), получим
R1 (ksa) = 2[х,/0 (ksb) тг-i [KksaJ6 (ksa) - 2{,J, {ksa)]-\ A1.155)
Исходя из соотношений E.323) и E.324), выразим Р[ и Рг через Ро и Ра
и'обозначим ([л — [^/([л + !^и) через р; тогда выражение A1.154) можно пре-
преобразовать к следующему виду:
Здесь можно использовать только значения 9s = ^l/(^f). удовлетворяющие
второму равенству. Подставляя выражение для E's в Pt(lsa) и РгAаЬ) и
используя рекуррентные формулы § 30 г гл. V и соотношение E.320),
получим
Ъ A п\ 2A — р) р j , -2A —р)
f»AW ~ w [р/ (^) + J2 (V)]' ^1 V»°> - *1ф [Jo (isb) + v±
Задачи 407
Остается определить Д, и D's так, чтобы при / = 0 выражение A1.146)
совпадало с A1.140), когда а < р < Ь. Опуская общие для каждой компоненты
множители, имеем
9 (Z)oP - i?oP-i) + к (Цр - E'oP-i) = ^ l?Ai?i (ASP) + кДРх &р)]. A1.158)
Умножим обо части скалярно на p[yR1(krip)-b-kP1(lnp)]dp и проинтегри-
проинтегрируем в пределах от а до Ь, представив этот интеграл в виде разности двух
интегралов: от 0 до а и от 0 до Ь. В силу соотношений A1.146), A1.153),
A1.154) и E.342) в правой части остается только п-й член, а значение Ач
дается выражением E.357), где В= 1 — 2[х~1;х. Интегрируя левую часть при
помощи соотношений E.328) и E.329) и разрешая полученное равенство
относительно Dn, для Рп из выражения A1.151) найдем
Выражение E.357) при i? = [x^V определяет правую часть соответствую-
соответствующего выражения для Аг. Интегрируя левую часть при помощи соотноше-
соотношений E.328) и E.329) и разрешая полученное равенство относительно D'n,
для F'n из выражения A1.143) получим
Полное поле внутри оболочки в любой момент времени определяется фор-
формулами A1.147), A1.159), A1.160), A1.155) и A1.157), где кп и 1п вычи-
вычисляются из соотношений A1.153) и A1.156). Если при ?<0 поля не 6bmOj
а в момент времени t = 0 возникло иоле В, то из выражений A1.141) и
A1.147) следует, что вектор-потенциал А^ внутри оболочки окажется
равным
Р<а, А; = (А3)о-А3. A1.161)
Эти решения были также получены другим методом х). При произволь-
произвольном изменении В во времени на основании полученных результатов поле
можно найти методами, аналогичными развитым в предыдущем параграфе.
ЗАДАЧИ
1. Бесконечная железная пластина ограничена параллельными плоскостями ж = Л,
я=—А; на пластину равномерно намотан провод в направлении, параллельном оси у.
При прохождении по проводу пероиепного тока снаружи пластины возбуждается магнит-
магнитное поло Но cos pt, параллельное оси z. Доказать, что напряженность магнитного поля
внутри пластины на расстоянии, х от ееродшш определяется выражениями
ch 2тх -J- cos 2mx \ */г
ch 'Imh -f- cos 2mh J
—shm(r«4-a-)sin m(h — x) — shm (h—x) sin m (h-\-x)
"' ch in (h -t- x) cos m (h—.r)f chm(/i—x) cos m{h-\-x) '
где m2=-7-jj.j5/T Исследовать частные случаи, когда rah лгало и когда mh велико.
2. Все точки круглой проволочной петли, несущей ток 1 cos ы, находятся на
расстоянии с от центра шара радиуса а, проницаемости jj. и удельного сопротивления -с;
радиус-вектор, проведенный из центра шара в любую точку петли, образует с прямой,
О См. Phil. Mag., 29, 18 A940). -
408 Глава XI
проходящей через пентры шара и петли, угол а. Показать, что вектор-потенциал
внутри шара равен действительной части следующего выражения:
71=1
где
И />=A0l/t.
3. Шар радиуса а с проницаемостью ц и удельным сопротивлением т помещается
в область, где в момент времени г = 0 появляется поле, которое при отсутствии шара
было бы однородным полем с индукцией В. Пользуясь обозначениями § 9, показать, что
при t ^s- 0 потенциалы определяются выражениями
4. Бесконечно длинный круглый цилиндр радиуса а, обладающий магнитной про-
проницаемостью A и удельвым сопротивлевием г, обмотан проводом, по которому проходит
переменный ток. Показать, что если на поверхности цилиндра поле Иг однородно и его
величина равна Но cos шг, то магнитное поле внутри цилиндра определится выраже-
выражениями A1.37) и A1.38), где вместо i: и гй нужно подставить иеличипы В2 и Во. Поль-
Пользуясь соотношением A1.5), найти плотвость и направление вихревых токов.
5. Круглая прополочная петля имеет координаты г = а, 6 = а, а сферическая про-
проводящая пленка с новерхностпым удельным сопротивлением ? совпадает с поверх-
поверхностью г = 6. В петле создается ток, меняющийся по закону i=/(l — e~~RtlL). Показать,
что если за прем я, в точение которого вихревые токи затухают, перемещением сферы
и петли можно пренебречь, то сообщаемый петле импульс определится выражением
ъ Vn+t Bп+1)?Е,-4-2|х„ЬД „i . . „i .
— ) ,-, Л г i ,р Pn(cosa)Pn+l (cosa).
«/ (^п+1)?Ь + |х^6й v
2? Л (n + l)Bn + l)
Г1=1
6. Над бесконечной тонкой пластиной, обладающей удельным поверхностным сопро-
сопротивлением ?, помещается небольшая проволочная петля с магнитным моментом
М coscoj, направленным порпепдикулярпо к плоскости пластины. Показать, что если
1 ^ шхо> 11й 3> ihft т0 магнитная индукция на противоположной стороне пластины равна
4?
J
6
7. Показать, что в предыдущей задаче плотность тока г'9 на расстоянии р от оси.
а также средняя рассеиваемая энергия в единицу времени приближенно равны
8. Магнитный момент небольшой петли с током уменьшается линейно от значе-
значения М при г —0 до нуля при г = Г. Петля помещается на расстоянии с над бесконеч-
бесконечной тонкой пластиной, обладающей удельным поверхностным сопротивлением с. Маг-
Магнитный момент петли перпендикулярен к плоскости пластины. Показать, что поле В на
оси в точке, находящейся на расстоянии z от пластины, благодаря присутствию пла-
пластины возрастает на величину
+ z) +it]
и на величину .
4
B^[l,(c + z) + 2i(tT)V\i^(c + z) + 2itY Р
Задачи 409
9. Магнитный диполь с моментом М расположен параллельно бесконечной тонкой
пластине, обладающей удельным поверхностным сопротивлением ?, и находится от нее
на расстоянии с. Пусть диполь перемещается с постоянной скоростью v параллельно
пластине в направлении, перпендикулярном оси диполя. Показать, что в стационарном
режиме со стороны вихревых токов на диполь будет действовать тормозящая сила,
равная
^-¦я-^МЧс Bс)-4 [D?2 + plv*I1* + 2c]-2.
10. Магнитный диполь с. моментом М движется с постоянной скоростью v по пря-
прямой линии на расстоянии с от бесконечной пластины, обладающей удельным поверх-
поверхностным сопротивлением с. Показать, что если М и v образуют угол <р, то тормозящая
сила, действующая на дииоль, равна
где FB — значение тормозящей силы, полученное в предыдущей задаче.
11*. Через небольшую кольцевую катушку, обладающую при прохождении еди-
единичного тока магнитным моментом М, пропускают медленно изменяющийся ток
I caswt. Катупша окружена тонкой сферической оболочкой с радиусом о и удельным
сопротивлением ?; центр оболочки лежит на оси катушки, на расстоянии / от центра
катушки. Показать, что индуцируемые в оболочке токи текут по окружностям, лежа-
лежащим в плоскостях, перпендикулярных оси катушки, и что плотность тока на окруж-
окружности, радиус которой виден из центра под углом а, определяется выражением
Ml (А-кРа)'1 2 Bп +1) U~lo)n Pn (cos a) cos ?„ cos (сог —en),
где
Bп+1)с
12. Тонкая сферическая пленка радиуса а, обладающая удельным поверхностным
сопротивлением ?, вращается с постоянной угловой скоростью о вокруг оси, перпенди-
перпендикулярной однородному магнитному полю В. Показать, что при этом возникает тормо-
тормозящий момент, равный
13. Показать, что если в предыдущей задаче сферу поместить в поле В cos u>t, то
средняя рассеиваемая мощность в ней будет равна
14. Показать, что поле внутри пленки в предыдущей задаче определяется выра-
выражением
— ЗВ? (Ос2 + (х2а2ш2)-1/2 sin (ш« — е),
где tg е = -1— .
15. Тонкостенный цилиндр радиуса о, обладающий удельным поверхностным со-
сопротивлением ?, помещается в поле Bcoswi, нормальное оси цилиндра. Показать, что
поле внутри цилиндра определяется выражением
( + ^)-1/2 sin (ш« —е),
где tge = 2?/(nwoa).
16. Показать, что если в предыдущей задаче цилиндр вращать вокруг оси с угло-
угловой скоростью ш в однородном магнитном поле В, перпендикулярном к оси вращения,
то при этом возникнет тормозящий момент, равный (на единицу длины)
17. Два параллельных провода, по которым текут противоположно направленные
токи, изменяющиеся по закону /coswt, имеют в цилиндрической системе координаты:
Ь, 0 и Ъ, тс (ось z направлена вдоль проводов). Показать, что вектор-потенциал
в точке г, 6 вне тонкой трубы радиуса р = о, обладающей удельным поверхностным
сопротивлением », определяется выражением
оо
2 t4 Bи +1J ?2+ !xB»*aarVl! (р ЬJп+1 со? Bп +1N sin (о>г — е„),
«=0
410 Глава XI
где
2 , а>Ъ.
18. Толщина тонкой сплюснутой сфероидальной пленки ? = С0 изменяется так,,
что удельное поверхностное сопротивление можво считать равным ? = Л2«0. В момент
времени 1 = 0 мгновенно устанавливается однородное магнитное поле В, параллельное
оси сфероида. Показать, что плотность возникающих при этом вихревых токов равна
_ A—
где JV2[(l + qs^Qi(t]
)Qi@)]
19. Длинный сплошной цилиндр радиуса а = (а-2 + ?/2I/2, обладающий магнитной
проницаемостью ц и удельным сопротивлением т, помещается в переменное магнитное
поле Re {BeJwt}, направленное пдоль оси or. Показать, что вектор-потенциалы Ai и Ао,
направленные вдоль оси z, внутри и снаружи цилиндра равны соответственно
Аг= Re {ChKipI'*?] е>^ sin <(}, A=Re {В (p + JDp) e3 sin 9} ,
где /0 [(/» '2 а] обозначено через /0 и /2 [(/pI'2 a] —через /2,
20. Показать, что средпяя рассеиваемая мощность в случае, рассмотренном в пре-
предыдущей задаче, определяется выражением
[Ьегй (рЧ*а) bei2 (р1/2а) — bei0 (р1/аа) Ье
_
— Ы
где (ber2x-^jbei2x) написаны вместо /2 (/" '2ж), а аргументы функций в знаменателе
такие же, как в числителе. Показать, что при малых р это выражение переходит
в следующее:
Р = у V
21. Длинный сплошной цилиндр радиуса а, обладающий магнитной проницае-
проницаемостью (х и проводимостью f. вращается вокруг своей оси с постоянной угловой ско-
скоростью со в магнитном поле В, перпендикулярном к оси цилиндра. Показать, что
вследствие вихревых токов появляется тормозящий момент (на единицу длины)
^...,—^ „ '¦ \bern (pl^a) bei2 \рх'^а) — beiu (p '2a) Ъегг
где /> = 7|j-<j), а аргументы функций в знамепателе и числителе одинаковы.
22. Петля радиуса а коакспальна с цилиндрической полостью радиуса Ъ и вы-
высоты с и паходится от ео дна на расстоянии d. Показать, дао если скин-эффект вастолько
велик, что вектор В почти тангенциален к стенкам полости, то самоиндукция петли
уменьшается на величину
.- \ 2
*>
где модуль А! = а[а2 + (пс —rfJ]'2 и модуль ? = a (a2 + n2c2)"'2.
23. Пусть глубина скин-слоя в случае, рассмотренном в задаче 21, равна В, про-
проводимость цилиндра f и ток /. Пользуясь выражением A1.24), показать, что если кт
выбрано так, что Jx (ftm6)=0, то рассеиваемая мощность равна
I be
(»?a/c) sin(»7td/c)
&) sh (Amc)J2
Задачи 411
24. Тонкий диск радиуса а, обладающий удельным поверхностным сопротивле-
сопротивлением s, находится в области, где до помещения диска существовало однородное поле
B0cos<o?, перпендикулярное плоскости диска. Найти вторичные токи исходя из вы-
выражения для вектор-потенциала поля первичных вихревых токов, наведенных полем
B0coso>i. После этого показать, что суммарная плотность вихревых токов равна
где модуль функций К и Е равен 2 (яр) /г(а + р)~1, а члены, содержащие (<о[хя/?J, от-
отброшены. Показать, что на частоте 60 гц это выражение применимо для пластинки
толщиною 0,1 мм.
25. Пусть в предыдущей задаче частота колебаний настолько велика, что тол-
толщина скин-слоя 8 много меньше толщины диска и вектор В можно считать танген-
тангенциальным к поверхности диска. Показать, что плотность вихревых токов, включая обе
поверхности, на расстоянии р от центра диска равна
¦кВр2
* [ля (в2— р2I/2 *
ЭтО'йыражение для L является совершенно строгим при идеальной проводимости
диска.
26. Плотность вихревых токов в бесконечно длинной цилиндрической пленке
радиуса в, обладающей удельным поверхностным сопротивлением ? и толщиной, много
меньшей, чем толщина скив-слоя, равна (^H при t = 0 и i при t = i. Показать, что
если ток (?„H можно записать в виде интеграла Фурье, то
со со
(» H = \ Ч/ (к) cos kz dk, i = V W (к) cos kze~
0 0
27. Пусть в предыдущей задаче вектор-потенциал возбуждающего поля на поверх-
поверхности пленки равен
со
3? (к, я, t) cos kz dk.
Пользуясь решением задачи 26 и результатами § 15, показать, что вектор-потенциал
поля вихревых токов равен
"г cos fa; dkdi.
28. Петля радиуса Ъ, но которой циркулирует ток icosoi, коаксиальна с очень
длинной цилиндрической пленкой р = а, обладающей удельным поверхностным сопро-
сопротивлением « и толщиной, много меньшей толщины скин-слоя. Показать, что наличие
пленки приводит к возрастанию сопротивления и индуктивности петли на величину
sin2 6 [Я, (А*)]2 Кх {ka) [Ix (ka)]'1 dk,
о
sin 6 cos 0 № (№)]2 ?j (ka) [/x (te)]-i dft,
о
где /?!(№) = /!(№), если b < a, R1(kb) = Kl(kb), если 6 > я, и
tg В = S о^я/^/ся) #! (/от).
29. Исходя из задачи 40 гл. VII и используя результаты § 5 гл. VII, показать,
что внешняя самоиндукция тора, образованного вращением окружности радиуса Ь
вокруг прямой, лежащей в одной плоскости с окружностью на расстоянии с метров от
412 Глава XI
ее центра, при высоких частотах, когда проявляется сильный скин-эффект, равна
где Ща = Ъ/с, а модуль к функций К н Е определяется выражением
к2 = cos a seca-rp .
30. Проволочная петля радиуса а коаксиальна с бесконечно длинным проводящим
цилиндром радиуса Ъ и находится вне этого цилиндра. По петле циркулирует пере-
переменный ток 1 такой высокой частоты, что возникающие в цилиндре вихревые токи
можно считать пши;рхногтными. Пользуясь результатом задач 2б и 28 гл. VII, пока-
показать, что плотность вихревых токов определяется выражением
° , (ка) , „
cos kz dk.
K^kb)
i)
31. Пользуясь выражением (8.25), показать, что наличие цилиндра н предыдущей
задаче уменьшает самоиндукцию петли на величину
оо
_1_
Z
где К и Е являются полными эллиптическими интегралами модуля к = 2 (аЬI'2 (а-
Показать, что потери на вихревые токи приводят к возрастанию сопротивления петли
на неличину-
со
где ^—проводимость, а 8 — толщива скин-слоя для цилиндра.
ЛИТЕРАТУРА
В a t е ш а и П., Electrical and Optical Wave Motion, Cambridge, 1905,
Frenkel J., Lehrbuch der Elektrodynamik, Bd. II, Berlin, 1928. (Френкель Я. И.,
Электродинамика, т. II, М.—Л., 1935.)
Geiger-Scheel, Handbuch der Physik, Bd. XV, Berlin, 1927.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge,
1925.
MacDonald H. M., Electromagnetism, Bell, 1934.
Maxwell J. C, Electricity and Magnetism, Oxford, 1881.
M о ц 11 i n E. В., Principles of Electromagnetism, Oxford, 1932.
Ollendorf P., Die Grundlagen der Hochfrequenztechnik, Berlin, 1926.-
Russell A., Alternating Currents, Cambridge, 1914.
Schelkunoff S. A., Electromagnetic Waves, Van Nostrand, 1943.
S t r a 11 о n J. A., Electromagnetic Theory , McGraw-Hill, 1941. (См. перевод: С т р э т-
тон Дж. А., Теория электромагнетизма, М.—Л., 1947.)
Глава XII
МАГНЕТИЗМ
§ 1. Парамагнетизм и диамагнетизм. Для большинства веществ,
не считая некоторых особых исключений, рассмотренных в § 5, магнитная
проницаемость очень незначительно зависит от напряженности поля, и ее
с достаточной степенью точности можно считать постоянной, как это и при-
принималось до сих пор. В отличие от диэлектрической проницаемости отно-
относительная магнитная проницаемость может быть как больше, так и меньше
единицы.
Вещества с магнитной проницаемостью больше единицы называются
парамагнитными, а с магнитной проницаемостью меньше единицы — диама-
диамагнитными. Рассмотрим силы, действующие на такие тела при помеще-
помещении их в поле, создаваемое некоторым неподвижным контуром, по которому
течет постоянный ток. Из соотношений (8.9) и (8.16) или (8.38) ясно, что
если при бесконечно малом смещении или вращении контура происходит
возрастание потока индукции через него, то, следовательно, существует
сила или момент, стремящиеся вызвать это движение. Пусть в поле этого
контура находятся какие-нибудь тела, смещение или вращение которых
увеличивает поток индукции сквозь контур. Тогда, по третьему закону
Ньютона, должны существовать соответствующие силы или моменты, дей-
действующие на эти тела.
Из § 30 гл. VII следует, что магнитная индукция (или плотность
потока индукции) и проницаемость в магнитных цепях находятся между
собой точно в такой же зависимости, как плотность тока и проводимость
в электрических цепях. Поэтому теоремы 3 и 4 § 12 гл. VI можно сформу-
сформулировать применительно и к магнитным цепям. Если проницаемость какого-
нибудь элемента в магнитном поле тока возрастает (или уменьшается),
то магнитное сопротивление цепи тоже возрастает (или уменьшается).
Но, как мы видели, существуют силы, способствующие возрастанию потока
и, следовательно, уменьшению магнитного сопротивления. Так, в неодно-
неоднородном поле тела, более парамагнитные или менее диамагнитные, чем
окружающая их среда, имеют тепденндпо перемещаться в направлении
к участкам с большей напряженностью поля. При помещении пара- или
диамагнитного тела удлиненной формы в однородное поле возникает момент,
стремящийся повернуть ось тела но цолто. Это можно видеть в случае
сфероида, рассмотренного в задаче 84 к гл. V, заменив там е на [>., ео
на \\ и Е на Н пли на Bjy.. Формула для вращающего момента содержит
разность И1~Н2, куда входит множитель (^. — ^J, и знак его оказывается
одним и тем же как при \х > \>.v, так и при \х < \\,.
В квантовой механике дается теоретическое обоснование установлен-
. ного на опыте факта независимости магнитной проницаемости диамагнитных
веществ от температуры. Для слабо парамагнитных веществ проницаемость
, в большинстве случаев также не зависит от температуры. У сильных пара-
1 Магнетиков, но не ферромагнетиков, изменение проницаемости с темпера-
414 Глава XII
турой обычно происходит по закону
где С и 0 — постоянные, а Т — абсолютная температура. Это эмпирическое
соотношение носит название закона Кюри. Его обоснование приводится
в квантовой механике. Для газов величина 6 обычно равна нулю.
§ 2. Магнитная восприимчивость. Часто бывает удобно пользоваться
еще одной величиной, а именно магнитной восприимчивостью, определяемой
для изотропной среды (через уже рассмотренные в § 21 и 29 гл. V1T
величины) по формуле
Л A2.2)
Восприимчивость и проницаемость связаны между собой соотношением
* = 1*7* A*-Ю = *«,-!• -A2.3)
Парамагнитное тело при помещении в магнитное поле уменьшает эпергию
последнего, а диамагнитное — увеличивает. Согласно соотношениям (8.12)
и (8.11), это изменение энергии определяется в виде
ЛИ/ "'>" ¦" _ \Yv— У-1 " V-v „ГГ2 /4 9 /,\
A^_ — -^-^- - _ -xU . (UA)
Заметим, что для парамагнитных тел величина у. положительна, а для
диамагнитных —отрицательна. Для магнитной восприимчивости закон
Кюри можно записать в более простой форме:
*=щгь- A2>5)
§ 3. Магнитные свойства кристаллов. Многие вещества, особенно
кристаллы, обладают неодинаковыми магнитными свойствами в различных
направлениях. Используя некоторые материалы, такие, например, как
графит, можно даже изготовить вещество, являющееся в одном направлении
диамагнетиком, а в другом — парамагнетиком. Обнаружено, однако, что
в таких случаях для любой заданной ориентации магнитная индукция В
пропорциональна напряженности поля Н и составляет с ней постоянный
угол а. Подобное же соотношение существует в кристалле и между век-
векторами D и Е. Поэтому для векторов магнитного поля, как и в § 20 гл. I,
можно написать систему уравнений вида A-52) и A.53), а именно считать,
что компоненты В и Н связаны между собой следующим образом:
Bz = \).13НХ
где
1*12 = 1*21» 1*13 = 1*31. 1*23 = 1*32- A2-7)
Итак, компоненты В и Н связаны между собой тремя уравнениями, содер-
содержащими девять коэффициентов, шесть из которых различны. Проницаемость
теперь является уже не числом, а симметричным тензором. При соответ-
соответствующей ориентации осей уравнения A2.6) можно записать в форме,
аналогичной A.58),
A2.8)
Магнетизм
415
Если имеют место соотношения A2.8), то считают, что координатные оси
направлены вдоль магнитных осей кристалла.
Используя формулу A2.2), можно написать соответствующие уравнения,
.связывающие М и Н,
МХ=.ЧНХ, Му = чНу, АГг = хаН„ A2.9)
где (^л = (j,j — (j,t, и т. д. При вращении координатных осей получается ана-
аналогичная A2.6) система уравнений для М и Н, содержащая тензор магнчт-
ной восприимчивости.
§ 4. Кристаллический шар в однородном магнитном поле. В каче-
качестве примера использования формул последнего параграфа найдем момент,
действующий на кристаллический, шар,
помещенный в однородное магнитное
поле с индукцией В. Пусть угол между
В и осью х равен а и (х2 —(х3. Граничные
условия, очевидно, будут удовлетворены
суперпозицией двух полей: поля с ин-
индукцией Bcosa, направленного но оси х
и действующего на изотропный шар с
проницаемостью \хг, и поля с индукцией
/isina, направленного по оси у и дей-
действующего на изотропный шар с проницае-
проницаемостью Uo.
Если взять поле В в сечении ху
(см. фиг. 114), то из § 7 гл. XI и из
соотношения G.49) видно, что вне шара поле в точности равно суперпози-
суперпозиции первоначального поля, поля магнитного диполя с моментом тж, на-
направленным по оси х, и поля диполя с моментом ту, направленным по
оси у, где
Фиг. 114,
т.. =
V-v
cos a
И П1 =
У
\>.% — ц^ irza3B sin a
Суммарное поле этих диполей эквивалентно полю одного диполя, момент
которого m образует угол Р с -осью х, т. е.
- p.v)* (ца + 2^K A -sin a) + (f*a
? sin aI'2
Угол между моментом га и полем можно найти из выражения (см.
Двайт, 405.02)
Тогда из § 19 гл. VII для момента имеем
A2.13)
была
— a).
Этот момент стремится повернуть сферу так, чтобы ось (Xj при
направлена по полю, а при (^1<(х2—перпендикулярно к немуъ
1 ' § 5. Ферромагнетизм. Существует очень важная группа материалов,
у которых магнитная проницаемость изменяется при изменении намагни-
намагничивающего поля, зависит от предыдущих состояний образца и намного
416
Глава XII
превышает проницаемость обычных веществ. Такие материалы называются
ферромагнетиками. К ним относятся железо, кобальт, никель, сплав Гей-
слера и, при низких температурах, некоторые металлы редких земель.
Построим из ферромагнетика простую магнитную цепь, подобную тору,
рассмотренному в § 30 гл. VII, для которого намагничивающая сила (или
магнитодвижущая сила на 1 м) легко вычисляется. Если исходить из нуле-
нулевых значений В и Н, то В при возрастании Н также растет, но коэффициент
пропорциональности мегкду ними, являющийся магнитной проницаемостью,
сначала растет, а потом уменьшается. На фиг. 115 приведены типичные
для ферромагнитного материала кривые зависимости В и (i от Н.
Б
или
О
И
Фиг. 115.
При измерении намагниченности достаточно чувствительным прибором
можно обнаружить, что крутой участок кривой намагничивания для боль-
большинства ферромагнетиков имеет ступенчатую структуру. Это явление назы-
называется эффектом Баркгаузена. Оно свидетельствует о том, что большая
область, включающая в себя множество одинаково ориентированных ато-
атомарных магнитон, изменяет свое направление как нечто целое. Опыты с фер-
ферромагнитными монокристаллами показали, что наиболее легко намагни-
намагничивание происходит в некоторых определенных направлениях.
Поскольку большинство ферромагнетиков, с которыми приходится
иметь дело, являются поликристаллами, то можно считать, что основная
часть намагниченности обусловлена ориентацией магнитных областей
в направлении, бли.жо совпадающем с направлением намагничивающего
ноля. Когда все области окажутся ориентированными таким образом,
эффект Баркгаузена прекращается и дальнейшее увеличение намагничи-
намагничивающего поля приводит лишь к постепенному повороту вектора намагни-
намагниченности каждой из областей вплоть до полного совпадения с направленном
поля. Об этом свидетельствует отсутствие скачков на пологой части кривой,
где намагниченность близка к пасыщению. Теоретическое объяснение этого
процесса основано на свойствах электронной оболочки атома железа.
При расчетах магнитных полей, индуктпвностей, магнитодвижущих
сил, вихревых токов и тому подобных величин до сих пор предполагалось,
что магнитная проницаемость вещества не зависит от напряженности поля.
Из приводимых здесь кривых видно, что для ферромагнитных материалов
при больших изменениях памагничпвагощего поля это предположение ста-
становится несправедливым. В таких случаях можно взять среднее значение \х
в рассматриваемой области изменения I!. Как правило, точность, с кото-
которой определены кривые намагничивания отдельных образцов, невелика.
Однако если мы имеем дело с очень однородным и тщательно отожженным
ферромагнитным материалом, то можно определить из его кривой намаг-
чивания величину \х, годную для различных областей. Эти сведения
Магнетизм
417
можно использовать для более строгого аналитического решения различных
задач только в случае простой геометрии системы.
§ 6. Гистерезис. Постоянный магнетизм. Предположим, что после
того, как поле Н достигло значения Hj, а индукция В при этом, как это
описано в § 5, возросла до значения В17 мы уменьшим величину Н до — Нх.
Тогда окажется, что индукция В не будет следовать по прежней кривой,
показанной на фиг. 115, а будет изменяться менее быстро, вдоль верхней
Н
Фиг. 116.
кривой фиг. 116, а, н достигнет, для нормального образца, при Н=— Нх
значения — Bj. Если снова увеличивать поле II до -fHI; то индукция В
начнет следовать по нижней ветви кривой фиг. 116, а, пока не пересечется
с первоначальной кривой в исходной точке Вх, Нх. Это отставание индукции
называется гистерезисом, а замкнутая кривая на фиг. 116, а—петлей гисте-
гистерезиса.
Ясно, что, исходя из различных точек кривой намагничивания, путем
постепенного изменения Н от +НХ до — Нх и обратно, для данного образца
можно получить различные петли гистерезиса, но при многократном повто-
повторении одной и той же операции будет получаться Одна и та же петля гисте-
гистерезиса.
Кривые гистерезиса различных ферромагнитных материалов могут
различаться очень сильно. Для «мягких» магнитных образцов площадь,
охватываемая петлей, очень мала (внутренняя кривая на фиг. 116, б), в то
время как для «твердых» магнитных материалов она очень велика (см. кри-
кривую D). В последнем случае при Н=0 имеется большая остаточная индук-
индукция Вт, для уничтожения которой требуется приложить к образцу обратное
поле Нс, называемое коэрцитивной силой. Здесь мы в первый раз встре-
встречаемся с наличием магнитных полей при кажущемся отсутствии электри-
электрических токов. Магнитные явления были первоначально открыты на таких
«постоянных» магнитах, и на основе опытов с ними развилась вся теория
магнетизма.
§ 7. Природа постоянного магнетизма. До сих пор мы рассматривали
энергию магнитного поля как чисто кинетическую, связывая ее с движе-
движением электрических зарядов. Поскольку магнитные поля, создаваемые
постоянными магнитами, во всех отношениях сходны с полями, создаваемыми
27 в. Смайт
418 Глава XII
токами, естественно предположить, что они имеют то же происхождение. При-
Природу постоянного" магнетизма можно раскрыть из анализа ряда явлений,
известных под названием гиромагнитных эффектов. Поскольку элек-
электрические заряды не поступают извне внутрь постоянного магнита и не
выходят из него наружу, движение электричества внутри магнита должно
быть циркулярным, и это вращение должно происходить около осей, ориен-
ориентированных в среднем около одного определенного направления, создавая
определенное внешнее поле. Если, как это упоминалось в § 5 гл. I, носи-
носители электричества обладают механической инерцией, то при вращении
по замкнутым траекториям они обладают вращательным моментом и, сле-
следовательно, подвержены действию гироскопических сил. Эти силы были
предсказаны еще Максвеллом, но техника того времени была слишком
несовершенна для их обнаружения. В связи с этим можно ожидать двух
эффектов. Первый—намагничивание при вращении. В механике хорошо
известен факт, что если подвес гироскопа вращать таким образом, что его
ось а может поворачиваться только в плоскости, проходящей через эту
ось и ось вращения системы Ь, то й стремится расположиться параллельно Ъ.
Таким образом, если ненамагничениос тело обладает вращающимися
электрическими ззрядами с произвольно ориентированными осями, то
вращение этого тела вызовет ориентировку этих осей по оси вращения
и тело намагнитится. Эти явления в ферромагнитных материалах были
обнаружены и измерены Барнетом. Второй эффект заключается в появле-
появлении вращения при намагничивании. Из закона сохранения момента нра-
щсиия следует, что если первоначально произвольно ориентированные осп
располагаются затем вдоль магнитного поля, то, чтобы результирующий
момент был равен нулю, тело в целом должно повернуться в противопо-
противоположном направлении. Этот эффект был впервые измерен Эйнштейном
и Дс-Гаазом, а потом уже, с большей точностью, другими эксперимента-
экспериментаторами. Оба эффекта показывают, что в ферромагнитных телах происходит
вращение отрицательных электрических зарядов, причем средний магнитный
момент оказывается несколько большим по величине, чем чисто спиновой
магнитный момент. Считают, что этот избыток обязан «орбитальному» ира
щению электрона. Таким образом, магнитные поля постоянных магнитов
ire отличаются от уже изученных нами нолей.
§ 8. Равномерное намагничивание. Эквивалентный поверхностный ток.
В постоянных магнитах намагниченность М, по определению, не зависит
от приложенного поля. Ее можно определить (см. § 21 гл. VII) как маг-
магнитный момент круговых постоянных токов (или спинов), отнесенный к еди-
единице объема. Согласно соотношениям G.104) и G.107), вектор-потенциал
поля, создаваемого заданной намагниченностью М, выражается в виде
^^dS, A2.14)
где объемные интегралы берутся но всему объему магнита, а поверхност-
поверхностные—по его поверхности.
Мы будем называть область равномерно намагниченной, если всюду
внутри нее намагниченность М постоянна по величине и направлению.
Для такой области второй объемный интеграл в выражении A2.4) равен
нулю. Рассмотрим остающийся интеграл по поверхности. Предположим,
что М направлено по оси х, т. е. M — iM. Пусть б — угол между i п п,
a ds и dst — ортогопальные векторы, лежащие на поверхности магнита
(ds нормально к i и п). Тогда
М X n dS = М sin^O dsY ds = М dx ds,
Магнетизм
419
так что
A =
М dx
ds.
A2.15)
По форме это выражение совпадает с выражением G.10), поэтому
магнит в целом можно заменить пленкой, которая совпадает с поверхностью
магнита и токи по которой текут в плоскостях, нормальных направлению
намагничивания х. Плотность тока не зависит от х и равна интенсивности
намагниченности М. При рассмотрении систем, содержащих постоянные
магниты, очень удобно вводить такую пленку, называемую эквивалентной
пленкой тока.
§ 9. Намагниченный шар и цилиндр. Магнитные полюсы. Для
однородно намагниченного шара ток, текущий по эквивалентной цленке
между б и 6 — dO (см. фиг. 117), равен
i dG = M dx = Ma sin 6 dQ,
где г—угловая плотность тока. Тогда функ-
функция потока выражается в виде
A2.16)
= Л1а[Р1(и)-Р0(и)]7
Фиг. 117.
где и = cos 6. По форме это выражение сов-
совпадает с выражением G.60). Поэтому, пола-
полагая в соотношениях G.64) и G.62) п — 0 и и==1, мы найдем вектор-потен-
вектор-потенциал во внешнем пространстве:
^ = ^siDfj. A2.17)
Из сравнения с выражением G.48) видно, что это поле совпадает с полем
маленькой петли с током, магнитный момент которой равен
A2.18)
П1 =
3
В § 1 гл. VII было показано, что магнитное поле на некотором расстоянии
от такой петли совпадает с электрическим полем электрического диполя,
имеющего тот же самый момент.
Для правильного круглого цилиндра, намагниченного вдоль оси, экви-
эквивалентная пленка тока представляет собой соленоид с нулевым шагом
намотки, у которого ток на единицу длины равен М. Магнитная индукция
в любой точке Р иа оси такого соленоида, согласно § 16 гл. VII, пыра-
жается формулой
Вх = у IV""* (cos Р2- cos P0, A2.1У)
где Pt и Р2 — углы, образованные с осью линиями, соединяющими Р с кон-
концами цилиндра. Если радиус цилиндра а мал по сравнению с его длнпой I,
то в точках, удаленных от концов,
Разделив числитель и знаменатель на х-^-~1 и разложив в ряд
(Двайт, 9.03), пренебрежем членами а4, а6 и более высоких порядков. Тогда
• ¦ 27*
420 ¦ Глава XII
после подстановки в формулу A2.19) получим выражение
A2.20)
аналогичное выражению для вектора -электрической индукции на оси х,
1 1
если в точке ж = —/ имеется заряд qY = \^а2М и в точке х= —-г^/—заряд
92= — \xv-na2M. Так, естественно, в опытах с магнитной иглой возникла
гипотеза о магнитных зарядах или полюсах. Область, из которой выходят
магнитные силовые линии, называется северным полюсом, а область, в кото-
которую они входят,—южным полюсом. Как мы уже видели, в действитель-
действительности магнитные заряды существовать не могут, так как дивергенция
магнитной индукции всюду равна нулю.
§ 10. Условия на границе с постоянным магнитом. Как видно
из названия, предполагается, что поля, в которые помещается «постоянный»
магнит, не влияют на интенсивность его намагничивания1). Это означает,
что если заменить магнит эквивалентной ему пленкой тока, то область
внутри нее будет иметь магнитную проницаемость jj^. При помещении
магнита в область с магнитной проницаемостью [>., где существует внешнее
магнитное поле, последнее искажаемся на поверхности магнита так, чтобы
удовлетворить граничным условиям на границе двух сред с различными
магнитными проницаемостями |лг и [>.. Эти граничные условия были полу-
получены в § 22, 23, 29 гл. VII.
§ 11. Сферический постоянный магнит в однородном поле. Вычислим,
для примера, вращающий момент, действующий на равномерно намагни-
намагниченный шар, помещенный в среду с магнитной проницаемостью (л, магнитная
индукция в которой до внесения шара была всюду однородна. Пусть а —угол
между М и В. Очевидно, что момент, действующий на пленку тока в поле,
создаваемом этим током, равен нулю, и поэтому достаточно вычислить
индукцию, обусловленную наличием внешнего поля. Вектор-потенциал,
описывающий поле В, в сферических координатах равен
А? = ~ Br sin 0. A2.21)
Выражение G.48) для вектор-потенциала содержит подобную зависимость
от 6, но стремится к нулю на бесконечности. Поэтому логично выбрать
добавочный член, обязанный присутствию шара с проницаемостью \xv именно
в такой форме. Итак, вне шара имеем
)ne. A2.22)
*) Определение постоянного магнита, данное автором, не совпадает с общеприня-
общепринятым. Обычно (см., например, книгу II. Е. Тамма «Основы теории электричества)))
к постоянным магнитам относят более широкий класс сред, намагниченность которых
складывается из постоянной, сторонней (не зависящей от внешнего поля) намагничен-
намагниченности Мо и индуцированной намагниченности, линейно зависящей от напряженности
внешнего поля Л/п=-——Н. При замене постоянной намагниченности Мо эквивалент-
ной пленкой тока среду внутри нее следует считать отличной от вакуума. Если же
ввести пленку тока, эквивалентную суммарной намагниченности, то шла и распределе-
распределение тока g пленке окажутся зависящими от внешнего поля. Предлагаемый автором
метод соответствует, следовательно, случаю, когда индуцированной памагниченностыо
можно пренебречь по сравнению с постоянной. — Прим. иерее.
Магнетизм
421
Поскольку Ai должно быть конечным в начале координат и иметь ту же
самую зависимость от 6, -то
Ai9 = Drsm0. A2.23)
Чтобы определить Си/), используем граничные условия G.118) и G.119)
при г = а. Это дает уравнения
Решая относительно С и подставляя в выражение A2.22), получим
пв- A2-25>
При г = а это выражение по форме совпадает с выражением A2.21), и,
согласно A2.23), оно представляет однородное поле в направлении В.
Момент, действующий на кольцевой элемент тока, лежащий между Ьх
и 61-\-dfI (где В1 — полярный угол, отсчитываемый от оси намагничивания),
равен произведению силы тока в кольце, площади кольца, магнитной индук-
индукции и sin а:
dT =--- iza2 sin2 вг В Г 1 - 2 .f"^ I i ddt sin а.
Подставляя из § 9 выражение для idfij и интегрируя (Двайт, 854), найдем
т==
sin а
A2.26)
Можно было бы вычислить силу и момент, действующие на шар при
помещении его в неоднородное поле. В этом случае выра?кение для силы
состояло бы из двух членов: один относился бы к силе, действующей на
шар с проницаемостью jxu, а другой — к силе, действующей на поверхностный
ток, проходящий по сфере. Эти силы можно вычислить, используя резуль-
результаты § 19 гл. VII и соотношение A1.69).
§ 12а. Подъемная сила подковообразного магнита. Для подъема фер-
ферромагнитных предметов часто применяют постоянный магнит в форме под-
подковы. При рассмотрении его для простоты предполо-
предположим, что «ноги» удалены и осталось только полу-
полукольцо, показанное на фиг. 118. При паличии «йог»
можно было бы использовать приближенный ме-
метоп, как и в § 23 гл. VI. Предположим, что это
полукольцо было намагничено путем соприкоснове-
соприкосновения с другим таким же полукольцом, дополняю-
дополняющим его до полного кольца; последнее было обмотано
проволокой, по которой пропускался электриче-
электрический ток. В первом приближении намагниченность
М будет зависеть от г — расстояния до центра коль-
кольца,—так же, как зависела магнитодвижущая сила
[см. выражение G.163)]
М = -. A2.27)
Фиг. 118.
Чтобы найти эквивалентный поверхностный ток, возьмем тонкий слой тол-
толщиной dr и радиусом г, в котором намагничевиость М можно считать постоян-
постоянной. Тогда если г —угловая плотность тока, то для тока, текущего между
422 • Глава XII
О ж 6 — с№ (как и в §«9), найдем
C^ A2.28)
При сложении поверхностных токов смежные слои уничтожаются и полу-
получается постоянная угловая плотность тока С по любому сечению кольца.
Теперь предположим, что наш магнит приложен к бруску с бесконечно
большой проницаемостью, причем контакт между ними идеальный. Внутри
поверхности эквивалентной пленки тока линии магнитной индукции будут
полуокружностями, так как, согласно соотношению G.114), они нормально
входят в брусок и нормально выходят из него. Магнитодвижущая сила
ь цепи, в соответствии с соотношением G.150), равна
%C. A2.29)
Магнитное сопротивление слоя dr, как и в § 30 гл. VII, будет опреде-
определяться по формуле
,п _ Длина _ та-
^„Xl (лошадь
потому что проницаемость внутри эквивалентной пленки тока равна \xv.
Поток индукции в этом слое равен
А для натяжения в поперечном сечении слоя, согласно выражению (8.60),
получим
Сила притяжения бруска каждым контактом равна
с
„, \М,аС2 Г dr tj.vaC2(c — b)
1=-^—)^= W
Верхним предел для С можно грубо оценить по кривой намагничен-
намагниченности стали. Если общее число витков в катушке при первоначальном
намагничивании было равно п, а ток в ней imi то магнитодвижущая сила
на 1 ж была равна, следовательно, nim/(it7-) ампервитков на метр (см. 7.150).
Предположим, что исследуемому образцу соответствует широкая петля
на фиг. 116,6 и что Нг,--=тт1(ъЪ). Тогда для всех величин г, больших Ъ,
намагничивающая сила окажется меньше, чем HD, и петли гистерезиса
будут лежать внутри указанной кривой. Пусть отношение Вт к Вр (обо-
(обозначим его через Р) одинаково для всех этих петель и отношение Вц к Нц
(обозначим его через ;х') также постоянно. Тогда из выражения A2.27)
имеем
д г С_ Вт ni-mp/P
~~ r ~ 14 ~ \>v*r '
так что
^^. A2.31)
Эти является верхней границей для С, если не принимать в расчет меха-
механические толчки, влияние тепловой обработки, «мягкость» стали, снижа-
Магнетизм
423
у
ющие С, особенно после разделения кольца на два магнита. Ошибка, совер-
совершаемая при предположении, что ;х = оо, не является серьезной, так как
для большинства мягких образцов [х/[хщ > 500.
§ 126. Поле цилиндрического магнита. Для создания сильных магнит-
магнитных полей на маленьких участках постоянные магниты часто выполняют
в виде колец с малым зазором. Эти кольца намагничиваются, как описано
в предыдущем параграфе, путем равномерной обмотки их проводом и про-
пропусканием по нему тока. Чтобы упростить расчет поля в этом случае,
предположим, что кольцо является столь
широким вдоль оси, чго его можно счи-
считать длинным цилиндром с внешним и
внутренним радиусами а и Ъ (см. фиг. 119).
До создания зазора цилиндр намагничи-
намагничивается током, текущим параллельно оси
цилиндра по обмотке, равномерно намо-
тапной вдоль его стенок. Как было пояс-
пояснено в предыдущем параграфе, результи-
результирующая намагниченность М оказывается
обратно пропорциональной расстоянию г.
После намагничивания вырезается зазор
<¦- радиальными стенками, не нарушающий
намагниченность М, а именно — удаляется
чагть металла и остается только уча-
участок, лежащий между 6=-j-a и 6= —а.
Если Ъ достаточно мало по сравнению с длиной цилиндра, задача вдали
от краев становится двухмерной. В этом случае линии магнитной индукции
совпадают, как доказано в § 26 гл. VII, с линиями постоянного вектор-
потенциала, и их можно очень просто найти при помощи метода круговых
гармоник, рассмотренного в § 2, 3, 4 гл. IV и§ 18 гл. VII.
Как показано в предыдущем параграфе, эквивалентный поверхностный
слой состоит из той части первоначальной намагничивающей обмотки, кото-
которая охватывает неудаленные части кольца и ток в которой между 6 и
6 + dB равен I db. Поскольку все элементы обмотки параллельны оси и отда-
отдаленные торцы цилиндра не влияют на величину вектор-потенциала А,
то последний также всюду параллелен оси и элементы тока можно счи-
считать бесконечно длинными. Считая вклад внешних элементов положитель-
положительным, а внутренних — отрицательным, находим, что вектор-потенциал dA
поля в точке Р (г, 6), созданного элементами тока, расположенными между -+- 0г
и — 0х, выражается, согласно соотношению G.44), следующим образом:
Фиг. 119.
dA =
х - In Д, - In R3 + In Д4)
Подставляя вместо логарифмов их значения из выражения D.17) и
получаем
dA=с 2 4" (°
cos n6icos пв dei-
Интегрируя от Ох — 0 до 0г = а, имеем
при /¦ > Ъ
и=1
i Гап — Ъп\ .
sinncccos/гО.
A2.32)
424
Глава XII
Точно так же
при Ъ > г > а
сю
= cUln-j+ Е^[(т")П-(т)"] sin no cos лб} , A2.33)
и при а > г
. A2.34)
Линии индукции, найденные из соотношений A2.32) — A2.34) при С=\,
a=7it/8, a=l и fc = 2, изображены на фиг. 120.
Фиг. 120. Линии магнитной индукции и постоянного вектор-потенциала в
постоянным магните, представляющем из себя длинную толстую намагни-
намагниченную цилиндрическую оболочку с секториальным воздушным зазором.
7
Вычисления выполнены по формулам A2.32)—A2.34) при С=1,«=— л, а=1, Ь=2.
о
§ 13. Магнитные иглы. Самой известной формой постоянного магнита
является, повидимому, магнитная игла. Она представляет собой тонкий
стальной стержень, более или менее равномерно намагниченный вдоль оси.
Как мы уже видели [см. выражение A2.20) [, магнитная индукция такого
магнита по форме, апроксимируется электрической индукцией двух зарядов
\).ътм2М и —\хгг~а2Л1, помещенных на расстояниях I друг от друга (а — радиус,
/ — длина и М — интенсивность намагниченности магнита). Эта аналогия
не годится, если игла помещается в среду с ;х Ф \xv. Однако если отноше-
Магнетизм 425
ние длины иглы к ее диаметру очень велико, то можно воспользоваться
другим приближением. В случае иглы с магнитной проницаемостью \xv,
помещаемой в среду ;х, поверхность эквивалентной пленки тока (как следует
из § 25 гл. VII и § 19 гл. I) представляет собой поверхность длинной
узкой полости. Аксиальный поток через нее от внешнего источника выра-
выражается произведением \xvH или [х(,?/[х на таг2 cos 6, где 6 —угол между В
и осью полости. Как следует из § 8, ток в элементе dl эквивалентной
плепки тока, охватывающий этот поток, равен М dl, где М — намагничен-
намагниченность. Согласно соотношениям (8.18) и "G.152), энергия эквивалентного
поверхностного тока равна
W = ikMtm2 {Hcosddl = jx^/ад2(S2 — Qx). A2.35)
По форме это выражение сходно с выражением A.13), так что тонкая,
равномерно намагниченная игла ведет себя аналогично двум равным по вели-
величине, но противоположным по знаку, зарядам \хгМгм2, помещенным в элек-
электрическое поле с потенциалом V = Q, где Q — магнитодвижущая сила, или
скалярный магнитный потенциал,
В отсутствие источников внешнего магнитного поля поток, пронизы-
пронизывающий эту узкую полость, практически не зависит от магнитной прони-
проницаемости окружающей среды, так как магнитное сопротивление цепи почти
полностью сосредоточено внутри полости, куда не проникает внешняя среда
и где проницаемость равна [х„. Таким образом, поток магнитной индукции
от достаточно тонкой магнитной иглы, как и поток электрической индукции
от электрического диполя, не зависит от окружающей среды. Поэтому ска-
скалярный магнитный потенциал, или магнитодвижущая «ила, такой иглы
обратно пропорционален магнитной проницаемости окружающей среды.
Эти величины можно вычислить по формулам § 76 гл. I, считая, что магниты
обладают взаимной потенциальной энергией. Пусть г—радиус-вектор, про-
проведенный от магнитного диполя с моментом т,' к магнитному диполю
с моментом т'2 и составляющий с ними утлы Ь% и 02, а — угол между
m't и т'2, a <j> — угол между пересекающимися по г плоскостями, содержа-
содержащими т[ и т^. Тогда из соотношений A2.35), A.16) и A.17) потенциальная
энергия выражается в виде
W = jg^ (cos a - 3 cos 6j cos G2), A2.36)
W = ^^ (sin G,, sin G2 cos A - 2 cos G,, ,-.os 02). A2.37)
Силы или моменты, действующие со стороны одного диполя на другой,
можно найти из этих формул путем дифференцирования по соответствующей
координате. В частности, сила отталкивания равна
2cos^cos62)- A2-38)
Потенциальная энергия иглы с моментом т' в поле с индукцией В выра-
выражается следующей формулой [см. G.14)]:
W-^m'R^m'By.-1, A2.39)
откуда силы определяются путем дифференцирования. В сферических коор-
координатах вектор-потенциал поля магнитной иглы на расстоянии г от нее опре-
определяется по формулам § 11 гл. VII, которые при г > Z дают
А, =???. A2.40)
426 Глава XII
Вектор-потенциал, как и полный поток, не зависит от проницаемости среды.
Следует отметить, что классический магнитный момент т', используемый
в этом параграфе, отличается по размерности от магнитного момента рамки,
определенного в § 1 гл. VII и в соотношении G.49). Выведенные в этом
параграфе формулы точны только для случая бесконечно тонких магнитов.
Силы или энергию постоянных магнитов с,.большим поперечным сечением,
помещенных в среду (х Ф \xv, нельзя найти путем интегрирования этих
формул.
ЗАДАЧИ *)
1. Под землей л направлении с востока на запад протянута железная труба. Для
обнаружения се местонахождения производятся измерения магнитного склонения через
каждые о футов A,525 м) в северном направлении, начиная с некоторой фиксирован-
фиксированной точки. При этом оказывается, что отклонения от нормального склонения 60° в за-
зависимости от х равны
х 185 190 195 200 205 210 215 220 225 230 235
¦А? -4,5° -5,0° -5,5° -7,5° -6,0° +0,0° +14,5° +0,0° -1,5° -1,2° -1,0°
Найти координату х, соответствующую центру трубы, и расстояние от поверхности
земли до трубы.
2. Стальпая гиря маятника радиуса а равномерно намагничепа в вертикальном
направлении с интенсивностью /. Пусть в данной точке земного шара вертикальная
компонента напряженности поля земли равна V, а ускорение силы тяжести равно g. Найти
отношение периода колебаний этого маятника к периоду колебаний ненамагниченного
маятника, если масса его равна га, расстояние от центра тяжести до точки подвеса
раино I, а колебания происходят в плоскости восток—запад.
3. Сфера с пропицаемостыо 1000 и радиусом 10 см помещена на 1 м северо-восточ-
северо-восточнее (относительно магнитного меридиана) магнитной иглы компаса. Показать, что, если
пренебречь силами изображения, отклонение иглы от магнитного меридиана будет
равно 5', с точпос.тыо до 1%.
4. Найти магнитное ноле внутри и,снаружи полости, образованной толстой сфе-
сферической оболочкой, равномерно намагниченной в направлении х с интенсивностью М.
5*. Два маленьких магнита плывут горизонтально но поверхности воды, один
вдоль линии, соединяющей их центры, а другой — перпендикулярно к ней. Доказать,
что взаимодействие магнитов сводится к единственной силе, действующей под прямым
углом к прямой, соединяющей их центры и приложенной на расстоянии одной трети
се длины от магппта, перемещающегося вдоль линии, соединяющей центры магнитов.
6*. Маленький магнит АСЕ может свободно вращаться около своего центра С.
Он взаимодейстлует с маленьким закрепленным магнитом PQ. Доказать, что в положе-
1
шш равновесия огь АС В лежит в плоскости PQC и что tg 6: -—— tg в', где 6 и 6' —
углы, которые оба магпита составляют с соединяющей их линией.
7*. Три маленьких магнита, расположенвые в вершинах равностороннего треуголь-
треугольника 1ВС, могут свободно вращаться около своих центров. При равновесии магнит А
параллелен ВС, а магниты В и С перпендикулярны соответственно сторонам АВ и АС.
Доказать, что магнитные моменты относятся как З1'2 : 4 : 4.
8*. Ось маленького магнита составляет с нормалью к некоторой плоскости угол <р.
Доказать, что линия, соединяющая магнит с точкой на плоскости, в которой плотность
пересекающих се силовых линий максимальна, составляет с осью магппта угол 6, такой,
что
2lge = 3lg2(<p-6).
9*. Два маленьких магнита лежат в одной плоскости и составляют углы 0 и 6'
с лшшей, соединяющей их центры. Показать, что прямая, направленная вдоль равно-
равнодействующей сил взаимодействия между ними, делит линию центров в отношении
10*. Центры двух маленьких магнитов удалены на расстояние г друг от друга.
Оси их составляют углы 0 .и 6' с линией, соединяющей их центры и угол е между
собой. Показать, что продольная составляющая силы, действующей па первый маг-
*) Во всех задачах речь идет о классическом магнитном моменте.
Задачи 427
пит, равна
Зтщ' DтС(лт-'1)-1 E cos2 6 cos 6' —cos 6' —2 cos e cos 6).
Показать также, что момент пары сил, приложенных к плечу ;¦ и действующих со
стороны одного магнита на другой, равен
mm' (^jxr4) d sin e,
*
где d — кратчайшее расстояние между их ося.ми.
11*. Две магнитные иглы с моментами m я т' спаяны таким образом, что их оси
составляют угол ч. Показать, что если их подносить в однородном горизонтальном
магнитном ноле таким образом, чтобы они свободно качались, то их оси составят
углы 6 и 6' с силовыми линиями, причем
sin 6 sin 6' , о , ,, , „ , , г/о .
= = fm2 + m 2 + 2mm cos a) >- sin а.
m' m
12*. Доказать, что если центры двух молекул, имеющих магнитные моменты mum',
неподвижно закреплены в точках А и В(АВ = г) и одна из молекул может спободпо
вращаться вокруг своего центра под действием некоторого заданного момента сил,
обусловленного полем второй молекулы, так что в состоянии равновесия ось этой моле-
молекулы наклоняется относительно АВ па угол 6, то в отсутствие внепшего поля момент
сил равен
3mm' sin 26
871^C cos2 6+ 1I/2 "
13*. Центры двух одинаковых маленьких магнитов фиксированы, а сами магниты
могут вращаться вокруг них. Эта система ваходится в однородном магнитном ноле Н,
направленном перпендикулярно к отрезку длиной г, соединяющему центры магнитов.
Показать, что положение, в котором оба магнита ориентированы по силовым линиям
однородного поля, является устойчивым только при
Н > Зт Dт:(лг3)-1.
14*. Центры двух частиц с одинаковыми магнитными моментами фиксированы в точках
-\-а, 0 и —а, 0. М'оменты этих частиц параллельны оси z и направлены в одну сторону.
Показать, чтп если некоторая другая молекула (обладающая магнитным моментом) мо-
может свободно вращаться вокруг своего центра, находящегося в точке @, у, z), то ось ео
будет лежать в плоскости ж = 0 и будет наклонена относительно оси z на угол
Зуг
arc tg тт-5 s г .
° Zz2—а2—yz
Исследовать, какое из двух положений равновесия будет устойчивым.
15*. Доказать, что существует четыре положения, при помещении в которые дан-
данный магнитный стержень полностью нарушает возможность контроля магнитного поля
земли посредством стрелки компаса, т. е. стрелка становится безразличной по отноше-
отношению к любому направлению (не испытывает действия никаких сил). Ликазать. что если
размеры стержпя малы по сравнению с расстоянием до стрелки, то одна пара этих
положений отстоит от стрелки в 1,25 раза дальше, чем два других положении.
16*. Три маленьких магнита, магнитный момент каждого из которых равен ш,
закреплены в вершинах равностороннего треугольника ABC, так что их северные полюсы
ориентированы соответственно в направлениях 1С, АВ и ВС. Другой маленький магнит
с моментом т' находится в центре треугольника, вокруг которого он может свободно
поворачиваться. Доказать, что при малых колебаниях период колебаний центрального
магнита равен периоду колебаний маятника длиной
C51I/2mm' '
где b—длина стороны треугольника, а Г — момент инерции подвижного магпнта отно-
относительно центра.
17*. Три частицы с одинаковыми магнитными моментами, расположенные в вершинах
равностороннего треугольника, могут вращаться вокруг своих центров, оставаясь все
время ориентированными в направлении, лежащем в плоскости треугольника. Доказать,
что существует четыре, и только четыре, таких положения равновесия, в которых углы,
отсчитываемые в одном направлении, между осями магнитов и биссектрисами соответст-
соответствующих углов треугольника, равны. Доказать также, что два симметричных положе-
положения равновесия являются неустойчивыми.
428 Глава XII
18*. Четыре маленьких одинаковых магнита расположены по углам квадрата
и совершают колебания под действием сил взаимодействия. Доказать, что периоды
осиовпых колебаний равны
Г АщхткЧ fh I АтцыпкЧ J/* Г
где m — магнитпый момент магнита, ткг—момент инерции магнита, a d — длина сторо-
стороны квадрата.
19*. Система магнитов расположена в одвой плоскости. При перемещении оси малень-
маленькой стрелки по замкнутому контуру, лежащему в плоскости и не содержащему магнит-
магнитных полюсов, стрелка совершает полный оборот. Доказать, что этот контур включает
по крайней мере одпо положение равновесия.
20*. Доказать, что скалярный потенциал поля, создаваемого телом, равномерно
намагниченным с интевсивностью /. в любой внешней точке совпадает с потенциалом
поля, создаваемого двойным слоем, совпадающим с поверхностью тела, если магнитный
момент этого слоя равен 1х, где х—координата, измеряемая параллельно направлению
намагничивания.
21*. Шар из твердой стали равномерно намагничен в определенном направлении.
В некоторой внешней по отношению к шару точке находится магнитная частица, ось
которой параллельна оси намагничивания шара. Найти моменты пар сил, действующих
на шар и на частицу.
22*. Сферическая магнитная оболочка радиуса а радиально намагвичена так, что
магнитный момент некоторой произвольной точки ее поверхности равен Sit где iSj—
поверхностная сферическая гармоника положительного порядка i. Показать, что
скалярный потенциал на расстоянии г от центра оболочки равен
при г < а
при г > а
23*. Показать, что если земной шар был бы равномерно намагничен, то тангенс
угла склоневия оказался бы равным удвоенному тангенсу угла магнитной широты.
24*. Доказать, что по известной на всей поверхности земли горизонтальной со-
составляющей (в меридианном направлении) магнитного поля земли можно теоретически
вычислить все другие компоненты этого поля.
25*. Исходя из того, что интеграл по замкнутому коптуру от напряженности
магнитного поля в отсутствие токов равен нулю, показать, что горизонтальную со-
составляющую магнитного поля в некоторой произвольной точке можно приближенно
выразить через известные поля в трех других точках, расположенных вокруг первой.
Показать, что эти шесть извествых величин также не являются независимыми, а свя-
связаны между собой одним условием.
26*. Доказать, что если бы земля была шаром и ее магнетизм был обусловлев
двумя маленькими прямыми стержневыми магнитами, расположенными в полюсах и
имеющими магнитные моменты, равные по величине и одинаково ориентированные вдоль
земной оси, то магнитное склонение В выражалось бы через угол магнитной широты I.
следующим образом:
( 1 ) i 1 1X.
8 ctg ( 6 +-1 x) = ctg i X-6 tg 1 X-3tg3 1
27*. Предположим, что земля является шаром радиуса а, а ее поле описывается
скалярным потенциалом
Показать, что величину й можно полностью определить по значениям горизонталь-
горизонтальной напряженности поля, наклонению и склонению, измеренным в четырех точках,
и по значениям склонения, измеренным дополнительно еще в четырех точках.
28*. Считая, что в разложении магнитного потенциала поля земли можно пре-
пренебречь пятой и высшими,.гармониками, показать, что из наблюдений результирующего
магнитного поля в восьми точках на поверхности земли можно найти значение, потен-
потенциала всюду.
29*. Предполагая, что земной магнетизм полностью обусловлен наличием внут-
внутренних источников и что северная компонента горизонтального поля выражается через
Литература 429
широту А как A cos А -| В cos3 X, доказать, что вертикальная компонента на данной ши-
широте, направленная вниз, зависит от широты следующим образом:
2 ( А-\-—г ) sin A — -^- sin3 X.
30*. Магнитная частица, имеющая момент ш, находится на расстоянии а над
плоской границей бесконечного бруска, сделанного из мягкого железа. Ось частицы
перпендикулярна к этой границе. Найти силу, действующую на частицу, и показать,
что потенциальная энергия системы равна
31*. Маленький магнит с моментом m находится вблизи большого неподвижного
куска мягкого железа с проницаемостью р., имеющего очень большую плоскую поверх-
поверхность. Расстояние от этой поверхности до магнита равно а, а угол, который состаиляет
ось магнита с кратчайшим расстоянием до поверхности куска, равен 6. Показать, что
для того, чтобы удержать магнит в этом положении, необходимо приложить некоторую
силу и момент, ранный
(р. — (л.„) m2 sin 6 cos 6
ЛИТЕРАТУРА
Abraham M., Becker R., Klassische Elektrizitiit und Magnetismus, Berlin,
1932. (См. переиод: А брагам М., Беккср Р., Теория электричества,
2-е изд., М.—Л., 1939.)
A 11 w о о d S. S., Electric and Magnetic Fields, Wiley, 1941.
Bitter F. Т., Introduction to Ferromagnetism, McGraw-Hill, 1937.
Ewing J. A., Magnetic Induction in Iron and Other Substances, Van Nostrand, 1900.
Geiger-Scheel, Handbuch der Physik, Bd. XII, 1927.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge,
1925.
M а в о n M., Weaver W., The Electromagnetic Field, University of Chicago Press.
1929.
Moullin E. В., Principles of Electromagnetism, Oxford, 1932.
Planck M. К. Е. L., Theory of Electricity and Magnetism, Macmillan, 1932.
Ramsey A. S., Electricity and Magnetism, Cambridge, 1937.
S p о о n e г Т., Properties and Testing of Magnetic Materials, McGraw-Hill, 1931.
Wien-Harms, Handbuch der Experimentalphysik, Bd. XI, Leipzig, 1932.
Williams S. R., Magnetic Phenomena, McGraw-Hill, 1931. ,
Глава XIII
ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
§ 1. Уравнения Максвелла. Мы будем считать, что в тех областях
пространства, где |л и е являются непрерывными функциями координат и
где можпо ввести понятия плотности электрических зарядов и плотности
токов проводимости (или конвекционных токов), электрические и магнит-
магнитные величины связаны между собой следующими уравнениями:
A3.1)
VxE=~f>
V-D = Pf A3.3)
VB = 0. A3.4)
Уравнение A3.2) выражает собой закон индукции Фарадея (8.3), а два
последних уравнения, A3.3) и A3.4), совпадают, очевидно, с уравнениями
C.4) и G.1). Новым является лишь уравнение A3.1), которое без послед-
последнего члена представляет собой просто закон Ампера G.4). Этот последний
член, введенный Максвеллом, делает при отсутствии зарядов и токов всю
систему уравнений более симметричной, а уравнение A3.1) сходным по
структуре с уравнением A3.2).
Если запои индукции Фарадой утверждает, чти изменение потока
магнитной индукции сквозь некоторую замкнутую кривую вызывает появ-
появление электродвижущей силы на этой кривой, то уравнение A3.1) устанав-
устанавливает появление магнитодвижущей силы при изменении потока электри-
электрической индукции. Сам Максвелл, повидимому, считал появление магнит-
магнитного поля следствием действительного перемещения электрических зарядов,
однако для подтверждения справедливости уравнения A3.1) в таком пред-
представлении нет необходимости. Справедливость всей системы уравнении
Максвелла подтверждается правильностью многочисленных следствий и вы-
выводов, вытекающих из них. Может быть, в действительности уравнения
Максвелла являются лишь приближенными, но в пределах современном
точности измерений их можно считать точными. Поскольку электрический
заряд сохраняется, то имеет место уравнение непрерывности F.3)
V-i+| = 0. A3.5)
В изотропных средах i и Е связаны между собой законом Ома F.8)
E = xi, или i = ?E. A3.C)
Для анизотропных сред при соответствующем выборе осип из выражения
F.108) имеем
i
Плоские электромагнитные волны 431
В изотропных средах D и Е связаны между собой соотношением A.33)
D = sE. A3.8)
В анизотропных средах из соитношения A.58) при соответствующем выборе
осей получаем
Di j A3.9)
Предположив, что \>. и все величины, входящие в уравнения A3.6) —
A3.9), не зависят от напряженностей полей, мы несколько ограничим пре-
пределы применимости уравнений Максвелла, в частности, при некоторых
частотах это ие позволит применить их к ферромагнитным веществам.
§ 2. Волновое уравнение. Электромагнитные потенциалы. Вектор
Герца. Считая магнитную проницаемость ja постоянной, применим опера-
операцию ротора к уравнению A3.1)
Подставим сюда значение V В из уравнения A3.4), a V-E. из уравнения
A3.2), тогда получим
™ = wjr+v-*W- <13J0>
Аналогично, взяв ротор от обеих частей уравнения A3.2) и заменив V-E,
согласно уравнению A3.3) (считая р = 0), а V X В, согласно уравнению
A3.1), получим
V2E = ,xTf + V*~- A3.11)
Мы пришли к волновым уравнениям для вектора магнитной индукции п
вектора напряженности электрического поля. Как будет видно из дальней-
дальнейшего, первый член и правой части этих уравнений обусловливает тепловое
рассеивание энергии поля в среде. В непроводящих средах G = 0) этот член
отсутствует.
До сих пор мы широко пользовались скалярным электростатическим
потенциалом, градиент которого со знаком минус давал напряженность
электрического поля, а также магнитостатическим вектор-потенциалом,
дивергенция которого была равна нулю, а ротор был равен вектору маг-
магнитной индукции. Желательно теперь обобщить определения потенциалов
на случай быстропеременпых полей. Для этого выберем обобщенный маг-
магнитный вектор-потенциал А так, чтобы ротор его всегда был равен векто-
вектору магнитной индукции В и, следовательно, для постояппых полей вектор-
потенциал А совпадал бы с магнитостатмческим. Таким образом,
;B = VxA. - A3.12)
Исключая В из уравнения A3.2) и меняя порядок дифференцирования,
получаем
В результате интегрирования этого уравнения набавляемся от ротора, по
при этом появляется постоянная интегрирования, которую можно предста-
представить как градиент некоторого скаляра ф, так как ротор градиента тожде-
тождественно равен нулю
^ A3.13)
432 Глава XIII
Введенная, таким образом, скалярная величина ф называется электричес-
электрическим потенциалом и совпадает для статических полей с электростатическим по-
потенциалом, рассмотренным в § 7 гл. I. Представляется удобным, хотя, как
будет показано в § 2 гл. XIV, в этом нет необходимости, выбрать вели-
величины А и ф так, чтобы они удовлетворяли тем же уравнениям, что и век-
векторы Е и В, а именно:
f^ A3.14)
f g A3.15)
Это накладывает на А и ф определенное, ограничение. Действительно,
взяв дивергенцию от обеих частей уравнения A3.13) и положив р = 0, т. е.
V-E = O [см. уравнение A3.3)], получаем А
Сравнение этого уравнения с уравнением A3.15) показывает, что послед-
последнее может иметь место только при условии
^-А^-[хТф-,хв§. A3.16)
Это условие совместимо также й с уравнением A3.14). Чтобы доказать
последнее, необходимо взять градиент от обеих частей уравнения A3.16)
и преобразовать левую часть, снова пользуясь векторным тождеством, при-
приведенным в начале настоящего параграфа. Произведя замену V X В в соот-
соответствии с уравнением A3.1) с учетом выражений A3.6) и A3.8), а Уф,
согласно уравнению A3.13), после соответствующих сокращений мы придем
к уравнению A3.14).
Покажем теперь, что полное электромагнитное поле можно описать
при помощи одного вектора Z, называемого вектором Герца, через который
потенциалы А и ф выражаются следующим образом:
V = [*TZ + [^, if=-\.Z. A3.17)
Для удовлетворения уравнения A3.16), а также и A3.13) необходимо
взять
Vx(VxZ), A3.18)
Выразим вектор магнитной индукции, используя выражения A3.12) и
A3.17), через вектор Герца Z
Уравнение A3.19) описывает все свойства электромагнитных волн. Для
непроводящих сред, исключив ф из уравнений A3.13) и A3.16), получим
-^' B = VXA'. A3.21)
Как следует из уравнения A3.3), при р = 0 дивергенция ноного вектор-
потенциала А' равна нулю.
Плоские электромагнитные волны 433
§ 3. Вектор Умова—Пойнтинга. Умножим уравнение A3.1) на —Е, а
уравнение A3.2)—-на В/[л и сложим результаты
-i-E-D-^-^. A3.22)
dt fj. at v/
Проинтегрируем левую часть уравнения A3.22) по некоторому произвольному
объему v и применим теорему Остроградского—Гаусса C.2), тогда получим
Объемный интеграл в правой части оставим без изменения, в результате
будем иметь %
^(^^K^g)]^ A3.23)
Первый член, стоящий в правой чаетг^ соотношения A3.23), представляет
собой, как это следует из закона Ома и из выражения F.11), мощность,
выделяемую в объеме v в виде тепла. Второй же и третий члены, соглас-
согласно выражениям B.18) и (8.12), представляют собой скорости изменения
электрической и магнитной энергий в этом объеме. В силу закона сохра-
сохранения энергии, если все эти члены больше нуля, энергия, поглощае-
поглощаемая в объеме, должна поступать в него извне. Поток энергии, проходящей
сквозь поверхность, окружающую объем v, должен определяться левой
частью соотношений A3.23). Тэешм образом, взятая в направлении внеш-
внешней нормали и проинтегрированная по замкнутой поверхности компонента
вектора
П = ^5. A3.24)
, представляет собой поток энергии, выходящей в единицу времени из объ-
объема, ограниченного этой поверхностью. Вектор П называется ввЕггором
Умова—Пойнтинга. Следует подчеркнуть, что нами был вскрыт физический
смысл только интеграла от этого вектора по замкнутой поверхности и не
было показано, что вектор П представляет собой поток энергии сквозь
отдельный элемент поверхности1).
§ 4. Плоские волны в однородном незаряженном диэлектрике.
Электромагнитное возмущение называется плоской волной в том случае,
если фазы мгновенных значений величин В, Е, ф, А и Z постоянны вдоль
любой из взаимно параллельных плоскостей. Эти плоскости называются
фронтом волны, а нормаль к ним, задаваемая единичным вектором п,—
волновой нормалью. Б диэлектрических средах величина f равна нулю, и
поэтому первый член в правой части уравнения A3.19) исчезает. ЭДожно
проверить дифференцированием, что общее решение будет тогда иметь вид
= U [(n-r+rt')-B(t+O] + h [(n-r-ot') + v (t + f)], A3.25)
где у = ([ле)~х/2. Таким образом, значение функции f1 в точке n-r-htt' в
момент времени t + t' совпадает с ее значением в точке пг в момент I,
т. е. /х описывает волну, движущуюся со скоростью v в направлении п.
Ч О локальном значении вектора Умова—Пойнтинга см. книгу И. Е. Таима,
Основы теории электричества, М., 1946. — Прим. перее.
28 в. Смайт
434 Глава XIII
Аналогично, функция /2 описывает волну, движущуюся с такой же ско-
скоростью в противоположном направлении —п. Скорость распространения
электромагнитной волны в пустоте с = ([лге1)—1/а равна 3• 108 м/сек. Отноше-
Отношение скорости с в пустоте к скорости v в среде называется показателем
преломления зтой среды п
Поскольку уравнения A3.10), A3.11), A3.14), A3.15) и A3.19) одинаковы,
то решение для плоской волны, распространяющейся в направлении п.
можно записать в виде
D = D0/(n-v -vt), A3.27)
E = E0/(n-r-«i), A3.28)
В = В0 ^(n-r — vl), A3.29)
где Do, Ео и Во —векторные амплитуды ^величин D, Е и В, a f (n-r — ct) —
скалярная функция. При плотности заряда р, равной нулю, выражение
A3.27) вместе с уравнением A3.3) дает
Отсюда либо функция /' равна нулю, что приводит к случаю статического
ноля, не представляющему здесь интереса, либо
' n-D0 = 0. A3.30)
При помощи аналогичной подстановки решения (J3.29) в уравнение A3.4)
получаем такой же результат:
п-В0 = 0. A3.31)
Это означает, что D и В лежат в плоскости фронта волны. Далее из ре-
решений A3.28), A3.29) и уравнения A3.2) имеем
Это справедливо для любого момента времени, поэтому величина /х должна
быть пропорциональна /, и можно принять
пхЕ0 = уВ0, или пхЕ = уВ. A3.32)
Точно так же, если величина i равна нулю, то подстановка решений A3.27)
и A3.29) в уравнение A3.1) дает
п X Во = — jJ.yD0, или пхВ=— JJ.&D. A3.33)
Умножая скалярно соотношение A3.32) на A3.33) и учитывая, что
п. Ве = 0, получим
(п х Ео) • (п X Во) = - цоЧ),,• Во = (п- II) (Ео• Во) - (п• Во) (п¦ Ео) - Ео• Во.
В силу соотношения A3.33), правая часть этого уравнения равна нулю,
поэтому
Е0-В0 = 0 и D0-B0 = 0. A3.34)
Итак, векторы Ео и Do перпендикулярны к вектору Во. Из выражения
A3.24) для вектора Умова — Пойнтинга получаем
A3.35)
Плоские электромагнитные волны
435
тогда как волновая нормаль совпадает по направлению с Do х Во, что
очевидно из выражений A3.30) и A3.31). Следовательно, направление
распространения энергии П образует с волновой нормалью n угол* равный
углу между векторами Е и Ю. Если вектор В остается всюду параллель-
параллельным некоторому .фиксированному направлению, то и вектор Е вследствие
соотношения A3.34) тоже будет обладать этим свойством. Такая волна
называется линейно или плоско поляризованной. В оптике под плоскостью
поляризации подразумевают плоскость, в которой лежат векторы П и В.
В радиотехнической литературе плоскостью поляризации обычно считают
плоскость векторов П и Е.
§ 5. Скорость распространения волны в анизотропных средах.
Рассмотрим распространение электромагнитных волн в однородной анизотроп-
анизотропной непроводящей среде с магнитной проницае-
проницаемостью [л„. Совместим направления осей координат
с электрическими осями среды. Тогда из соот-
соотношения A.58) имеем
Dx = BrEx, Dv = b2Ev, Dz = s3Ez. A3.36)
Согласно § 9а гл. II, объемная плотность элек-
электрической энергии равна
dW
A3.37)
Фиг. 121.
При получении последнего соотношения исполь-
использованы выражения A3.9) для вектора D и A3.32)
для п X Е и изменен порядок следования вектор-
векторного и скалярного произведений. Это соотношение свидетельствует о равен-
равенстве плотностей электрической и магнитной энергий. Плотность полной
электромагнитной энергии равна удвоенному выражению A3.37). Обозначим
направление распространения энергии (направление луча) через и'.
На фиг. 121 показана ориентация векторов В, D, E, n и п'. Очевидно,
что D, E, n и п' лежат в одной плоскости, поскольку они ортогональны
к В. Заметим также, что
п-Е n''D /.о on.
sma = —= — . (I0.08)
Для нахождения скорости v перемещения фронта волны вдоль п преобра-
преобразуем сначала соотношения A3.32) и A3.33) к виду
Затем введем три характеризующие кристалл постоянные vt, &2 и гK
Исключив теперь Е из выражения A3.39) при помощи соотношений A3.36)
и A3.40), получим
[х„{ю\- У3) Dx = I (n • Е), ^ (vl - г;2) Du = m(a- E),
|xo(i5*-i52)?)z = /i(n-E), A3.41)
где I, т, п — составляющие вектора п, т. е. его направляющие косинусы.
Согласно соотношению A3.30), п • D = Шх + mDy -f nDz = 0. Если сюда под-
подставить Dx, Dy и Dz из выражения A3.41), то получим
Т?П^2" + v2 — v% ^~ r?-—v\ = ' " v1^-1-)'1
436 Глава XIII
Это уравнение называется уравнением Френеля; оно выражает скорость
распространения фронта волны через значения направляющих косинусов
волновой*, нормали. В общем случае для любого определенного направления
нормали существует два различных значения скорости распространения.
Путем непосредственной подстановки в соотношение A3.42)_ легко убедиться,
что если vt > t>2 > v:i, то только для двух направлений величина с имеет
одно-единственное значение
«0 = 0, no=±{p\-W*[p\-i%-4* A3.43)
и что это значение равно v2. Направления, определяемые косинусами /0, ти„
и п0, называются оптическими осями двухосного кристалла. Если
ijj-sr. e2 y= es, то скорость распространения v однозначна только в направ-
направлении z, для которого по=1, а т0 = 10 = 0. Если же vt f^i2 — i3, то v
однозначна только в направлении х, для которого Zo= I, mo= nu = 0. J3 обоих
случаях существует только одна оптическая ось, т. е. кристалл является
одноосным.
§ 6. Поверхность, образованная, лучом, и поляризация в анизотроп-
анизотропных средах. Для нахождения скорости распространения энергии ь' в про-
произвольном направлении в кристалле необходимо поделить выражение A3.24)
па E2lpv и умножить на п-Е, используя соотношение A3.32). Тогда
п-Е П ЕЕхВ—п(п-Е^ (пЕJЕ МЗ 44}
Решив уравнение A3.39) относительно п(п-Е), перепишем его в проекциях
на оси х, у и z и при помощи соотношений A3.41) исключим Dx, Dy и Dz,
а результат подставим в правую часть уравнения A3.44):
. „ п Е „ Г . »* (п-Е)*
Как ясно из соотношений A3.38), а также из фиг. 121, величины v и с'
связаны между собой соотношением
= Cos2a = l-sin2a = l-(-^2. A3.46)
Поскольку Пж, v, z = ПдИос, у, z, выражение A3.45) можно переписать в виде
n'x.y.z Е2 j-,
( о V ( « V
V «1,2, 3 / V С'У
Пусть V, ш', п' — составляющ,ие вектора п', т. е. его направляющие коси-
косинусы, тогда
п' - Е = 1Е'Х + т'Еу -+ п'Ег.
Поэтому, умножая написанные выше уравнения на V, т' и га', а затем
складывая полученные результаты, мы приходим к уравнению, опреде-
определяющему лучевую скорость г/ в направлениях Г, т' и га' как функцию
постоянных кристалла сг, v2, vs:
Для каждого отдельного направления существуют, вообще говоря, две раз-
личныб лучевые скорости. Если в некоторой момент времени в начале
Плоские электромагнитные волны
437
координат появилось электромагнитное возмущение, то за \ сек. оно пере-
переместится на расстояние r=v'. На фиг. 122 изображена форма волны в'пер-
вом октанте для случая v1 > v2 > cs. В направлении OP, а также вдоль
его зеркального изображения в плоскости YZ лучи имеют одинаковые ско-
скорости. Из уравнения A3.47) вытекает, что эти направления луча связаны
с направлениями оптических осей кри-
сталла соотношениями
I
~
_
A3.48)
Оптической осью на фиг. 122 является
прямая 00'. Один из листов двухсвяз-
двухсвязной поверхности, изображенной на
фиг. 122, пересекается с координат-.
ными плоскостями по окружностям ра-
радиусов vlt v2 или*"гз3. Если из трех ве-
величин vlt v2 и v3 две равны между
собой, то один лист волновой поверх-
поверхности образует вытянутый или сплю-
сплюснутый сфероид, а другой—сферу,
причем ось сфероида равна диаметру
сферы. Луч, образующий сферическую поверхность, называется обыкновен-
обыкновенным лучом, а образующий сфероидальную поверхность — необыкновенным.
Будем обозначать два решения уравнения A3.42) через va и vb, а соот-
соответствующие им значения компонент электрической индукции—через D^,v, г
и D^v,z- Помножим каждое из уравнений A3.41), написанное для t> — va,
на аналогичное уравнение, написанное для v — г;ь, и сгруппируем резуль-
результаты; тогда
Фиг. 122.
x, у, z x, у, z
2
Их, у, г
(«1.2,3 —
A3.49)
Разбивая правую часть на элементарные дроби и складывая теперь эти три
уравнения, получим
2 2
(п-Е)»
Е{ак следует из A3.42), каждый член суммы, стоящей в правой части,
равен нулю; поэтому
D<°>.D(b) = 0. A3.50)
Это означает, что лучи са и vb плоско поляризованы. Их плоскости поля-
поляризации расположены под прямым углом.
§ 7. Энергия, давление и импульс плоской волны. Представим себе
плоскую волну в изотропной среде, падающую нормально на бесконечный
плоский лист из поглощающего материала, и рассмотрим прямоугольную
призму единичного поперечного сечения, основания которой параллельны
поглощающему листу и расположены по разные стороны от него. Для опреде-
определения потока энергии, входящей внутрь призмы, необходимо проинтегрировать
вектор Умова—Пойнтинга П по поверхности призмы. Но на боковых поверх-
поверхностях [см. соотношения A3.30), A3.31)] оВп = Ен=0, т.е. Пп = 0. Также
равен нулю поток энергии сквозь основание, расположенное за поглощающим
¦438 Глеев XIII
листом. Поэтому единственным интегралом, отличным от нуля, будет ин-
интеграл по поверхности основания, расположенного со стороны падающей
полны. Следовательно, согласно выражениям A3.35), A3.32), мгновенное
значение скорости поглощения энергии в листе (в ваттах на квадратный
метр) равно
П -ЕхВ _nfc'2 — (n-E)E
~ ~ п> ¦
В изотропных средах n-E = 0 и В = (\>.еI1*Е [см. выражение A3.32)]; поэтому
П, = п "-ГГ- = п гт- = п -—г-
Для плотности энергии электромагнитного поля [см. соотношения B.6)
и (8.12)] мы получили выражение
8W гЕ2 В2
~W = ~г~ + |Г • A3.52)
Скорость распространения волны равна (це)'*; поэтому за 1 сек. сквозь
площадку, равную 1 м2, проходит количество энергии, заключающееся
в цилиндре, имеющем единичную площадь основания A м2) и высоту,
равную (|л.е)—1/2 м.
Как было показано выше [см. соотношения A.39) и (8.60)], в электри-
электрических и магнитных полях существует давление, равное соответственно
1 1
17-е.Е'2 и -7гВ2/[). и направленное перпендикулярно к силовым линиям1).
Если плоская волна падает на поглощающий лист, то, поскольку поле
отлично от нуля только с одной стороны от листа, последний должен испы-
испытывать давление, равное (в ньютонах на 1 м2)
р^^еЕ^ + ^^В2. A3.53)
Сравнивая выражение A3.53) с A3.52), мы видим, что электромагнитное
давление равно плотности энергии вблизи поверхности листа.
Предположим теперь, что поглощающий лист может свободно переме-
перемещаться; скорость перемещения листа иод действием давления Р будем
считать очень незначительной, т. е. его массу будем считать большой2).
Тогда между давлением Р и импульсом р справедливо соотношение
Применим к этому случаю механический закон сохранения импульса. Тогда
импульс, получаемый поглощающим листом, должен отдаваться волной.
Сравнивая между собой соотношения A3.54) A3.53) и A3.51), мы приходим
к выводу, что электромагнитная волна обладает имнульсом, равным (на еди-
единицу объема) в направлении распространения п
§ 8. Отражение и преломление плоских волн. Рассмотрим падение
плоской волны на бесконечную плоскую границу раздела двух сред, маг-
магнитные и диэлектрические проницаемости которых соответственно равны (i, e
1) Давление электромагнитных волн (спотоиое давление) вперпые было обнаружено
и измерено П. Н. Лебедевым в 1901 г.—Прим. перев.
2) При большой массе будет мало ускорение листа. Для обеспечения малой скорости
листа необходимо, чтобы интервал времени, в течение которого действует давление Р,
был бы не слишком велик. — Прим. перев.
Плоские электромагнитные волны
439
и [л", в". Благодаря наличию границы раздела в этом случае могут воз-
возникнуть еще две волны: отраженная волна, возвращающаяся обратно в пер-
первую среду, и преломленная волна, входящая во вторую среду. Обозначим
единичные векторы в направлении распространения падающей, отраженной
и преломленной волн соответственно через и, а' и а". Пусть углы, обра-
образованные единичными векторами а, а" и а' с нормалью к плоской поверх-
поверхности раздела равны 6, б" и 6' соответственно;
при этом условимся для случая падающей и
преломленной волн нормаль направлять во
вторую среду, а для отраженной волны — в пер-
первую (см. фиг. 123). Будем подразумевать под
плоскостью падения плоскость, перпендикуляр-
перпендикулярную к границе раздела и содержащую вектор а.
Пусть М и N—две произвольные точки в
пространстве, а р — вектор, направленный из
М в N. Будем, как и раньше, под п пони-
понимать единичный вектор, ориентированный нор-
нормально к фронту волны. Тогда волна, имею-
имеющая скорость с, пройдет через точку N лишь
спустя п-р/г: сек. после того, как она пройдет
через точку М. В рассматриваемом нами слу-
случае один и тот же фронт волны дважды прой-
пройдет через некоторую заданную точку Р в пер-
первой среде: один раз до отражения, а другой
раз после отражения. Если фронт волны в мо-
момент времени t = 0 проходит через точку О на
границе раздела, то он должен был пройти •
через точку Р до отражения в момент вре-
времени < = ст-r/гэ и после отражения в момент времени t -=а'-г/с, где г —
радиус-вектор, направленный из точки О в точку Р. Считая закон от-
отражения одинаковым для всех точек границы раздела, мы получаем, что
промежуток времени между этими двумя прохождениями будет таким же
, и для любой другой точки Q, расположенной на одинаковом с точкой Р
расстоянии от границы раздела. Вектор, направленный из точки О в точ-
точку Q, равен r + s (s лежит в плоскости раздела). Поэтому, приравнивая эти
интервалы времени и умножая результаты на v, получим
Фиг. 123.
о • г — <т' • г = a¦ (r -j- s) — <j' • (г + s), пли
= a -s.
A3.56)
Следовательно, а и а' образуют одинаковые углы с любым вектором, лежа-
лежащим в плоскости раздела двух сред, это возможно только в том случае,
если <т является зеркальным отображением <т' в плоскости раздела. Таким
образом, волновые нормали к падающей и отраженной волнам лежат в пло-
плоскости падения с двух противоположных сторон от нормали к границе
раздела и образуют с этой нормалью равные (острые) углы.
Найдем теперь направление преломленного луча. Для прохождения
фронта волны из точки Р, находящейся в первой среде, в ее изображе-
изображение Р", находящееся во второй среде, требуется определенное время. Пусть
г —радиус-вектор, направленный из точки О в точку Р, а г"—радиус-
вектор, направленный из точки О в точку Р". Если две другие точки
(Q и ее изображение Q") расположены на таком же расстоянии от границы
раздела, что и точки Р и Р", то время прохождения фронта волны из Q
в Q" будет одинаково со временем прохождения из Р в Р". Радиус-векторы
точек Q и Q" равны r + s и r" + s (s лежит в плоскости раздела). При-
Приравнивая интервалы времени аналогично тому, как это было проделано
440 Глава ХШ
для отраженной волны, мы получим
(r»e")V* (е- • г») - (^)V. (в. г) = ((."г"I/* fсг" ¦ (г" + в)] - (цвI'2 [а • (г + в)],
(()."е"I/2 (о* ¦ s) = (,,.?)г/2 („. 8). A3.57)
Если s направить перпендикулярно к а, т. е. перпендикулярно к плоско-
плоскости падения, то правая часть соотношения A3.57) будет равна нулю, и,
следовательно, вектор а" тоже будет перпендикулярен к s, Это означает,
что волновые нормали отраженной и преломленной волн лежат в плоскости
падения. Выбрав теперь s лежащим в плоскости падения и обозначив
через v и t>" скорости распространения волн в первой и во второй средах,
мы получим закон преломления Снеллиуса:
у-"*-" У/г = v _ cos os ^ sin U _ п A3 58}
(хе / «" cos="s sin й" ' \ ¦ t
Величина п, равная отношению sin б к sin б", называется показателем пре-
преломления. Проделанный нами вывод одинаково справедлив и для случая
анизотропных сред, с той лишь разницей, что там v и v" различны для
разных углов падения, и поэтому п зависит от б. ^
§ 9. Интенсивности отраженной и преломленной волн. Закон сохра-
сохранения энергии требует, чтобы поток энергии, проходящий через 1 м2-
поверхности раздела, был равен разно-
разности потоков энергии падающей и отражен-
отраженной волн. Поэтому, как это очевидно и»
фиг. 124 и формулы A3.35),
(П - Д') cos е = П" совв". A3.59)
В дальнейшем мы будем рассматривать
отдельно волны, у которых в плоскости
падения лежит вектор В, и волны, у ко-
Фиг 124 торых в плоскости папения лежит вектор
Е. В связи с этим все векторы, относя-
относящиеся к первому случаю, будем отмечать
индексом 1, а ко второму — индексом 2.
Если вектор В! лежит в плоскости падения, то пектор Ех параллелен
границе раздела. Поэтому, исходя из соотношения A.45), имеем
?,+?;=?;'¦ A3.60)
В этом случае, воспользовавшись формулой A3.51) и положив в ней
[). = [>." = [>.„, выражение A3.59) можно представить в виде
Ei/2 (El - Е[2) cos 6 = г"^Е"\ cos 6".
Разделив теперь это выражение на выражение A3.60) и учтя соотношение
A3.58), найдем
8?"всове>;. A3.61)
?
sin
Решим систему линейных алгебраических уравнений A3.60) и A3.61) отно-
относительно Е[ и E"x; в результате получим
р, Sin F—6") F мо fi9v
asme-cose 3.63)
1 sin(U-ttr) 1 v '
Плоские электромагнитные волны 44!
Из соотношений A3.32) и A3.58) следует
Используя выражение A3.51), можно определить интенсивность отраженной
волны в виде
тт, sin2F—6") „ ..„ „„.
ni=sin4J + u-}ni- A3-66)
Подставив выражение A3.66) в A3.59), для интенсивности преломленной
волны получим
, ¦„„ 2 sin 6" cos 6 sin 2в „ ,,„ „,.
1 П Д A3Ь7>
Рассмотрим теперь тот случай, когда вектор Е2 лежит в плоскости паде-
падения, а В2, следовательно, параллелен границе раздела. Полагая jxv= jx" = jxt,,
вместо выражения A3.60) будем дметь
52+б; = б;'. A3.68)
Соотношение A3.59), согласно выражению A3.51), можно представить
в виде
s
i/2 ф1 - В?) .-.и 6 = Я^е"-1'* cos 6".
Разделив его на выражение A3.68) и воспользовавшись соотношением A3.58),
получим
Решим уравнения A3.68) и A3.С9) относительно B't и В; в результате
найдем
t.g(B-6") ,„ _п
sin 26
Из соотношений A3.32) и A3.58) имеем
2 sin 6" cos 6 F мя 7ov
Интенсивность отраженной волны будет равна
п, tg«@-O*) п
Подставляя это в соотношение A3.59), получим интенсивность преломлен-
преломленной волны в виде
„„ 2 sin 6" cosfi sin 26 тг пч 7п
sin*
При нормальном падении cos б и cos 0" в соотношении A3.59) равны еди
нице, поэтому вместо выражения A3.61) получим
442 Глава ХШ
Учитывая выражение A3.60), найдем
ЕГ=-^=?Е. A3.76)
^Е- <13-77)
Из соотношения A3.51) определяем интенсивность отраженной волны
и интенсивность проходящей волны
Необходимо отметить, что интенсивности, даваемые выражениями A3.66),
A3.67), A3.74), A3,75), A3.78) и A3.79), представляют собой энергию,
проходящую в 1 сек. сквозь 1 м2 площадки, параллельной фронту волны.
Чтобы получить плотность электромагнитной энергии в волне, необходимо
разделить П на v — скорость распространения волны в среде.
Как очевидно из выражения A3.70), при fl + t/' = ir/2 B'2 = 0. Это озна-
означает, что если вектор Е лежит в плоскости падения волны, то существует
такой угол, при котором отраженная волна отсутствует. Его называют
углом поляризации, так как падающая под этим углом неполяризованная
волна отражается от границы раздела, линейно поляризованной, а именно,
вектор В в ней лежит в плоскости падения. Угол поляризации, называе-
называемый также «углом Брюстера», можно определить из соотношения A3.58)
в виде
sin6" ¦ с =^=п. A3.80)
§ 10. Частота. Длина волны. Эллиптическая поляризация. До сих
пор при исследовании законов отражения и преломления ноли мы пользо-
пользовались для описания плоской волны решением волнового уравнения в об-
общем виде /(nr — tt). Теперь же при обсуждении вопросов, связанных
с круговой и эллиптической поляризацией, удобнее иметь дело с регуляр-
регулярными периодическими функциями, которые можно всегда представить
в виде ряда Фурье, состоящего из синусоидальных членов. Поэтому поло-
положим
f{nr-vt) = D cos [ш (t — v^n • г) + <р], A3.81)
где п — единичный вектор в направлении распространения. Все вычисли-
вычислительные операции значительно упрощаются, если воспользоваться [см. вы-
выражение A0.2)J тем. что
Dcoslutf-v^nr) -i-<p] = Re Dei;fe v . A3.82)
Как и в § 2 гл. X, величину De"f обычно принято записывать в виде ком
гшексной амплитуды D. Круговая частота ш связана с циклической v соот-
соотношением
№ = 2™. A3.83)
Длиной волны X называется кратчайшее расстояние, которое измеряется
п направлении распространения волны и через которое все ее электри-
электрические свойства повторяются. Частота, длина волны и скорость распро-
Плоские электромагнитные волны
443
странения v связаны между собой соотношениями
X = = — = Т-, = —,
Рассмотрим теперь суперпозицию двух плоских электромагнитных волн
¦одинаковой частоты, распространяющихся в одном и том же направлении z.
Пусть обе волны линейно поляризованы, но у одной вектор магнитной
индукции ориентирован вдоль оси у, а у другой — вдоль оси х, так что для
напряженностей электрического поля будем иметь
: Ex = E1cos[io{t — o-1z)], A3.85)
Ey=Ezcos[u(t — y-!z) + 8]. A3.86)
На фиг. 125 показаны зависимости Ех и Еу от z. Для нахождения кри-
кривой, описываемой в плоскости ху концом вектора Е, имеющего компоненты
Ех и Еу, положим z — 0 и исключим время t из уравнений A3.85) и
A3.86). Это приводит к уравнению
F2 F2 пи г
8, A3.87)
щ
cos 8 =
являющемуся уравнением эллипса, который показан слева на фиг. 125.
Такие волны называются эллиптически поляризованными. При 8 = итг урав-
уравнение A3.87) принимает вид
Ео_Ех±-Е^Еу=--0. A3.88)
Оно описывает две прямые линии и соответствует линейно поляризованной
результирующей волне. При 8=у Bи+1) тг и, кроме того, при Е1 — Ег = Е
уравнение A3.87) дает
Е1Л-Е1^Е*. A3.89)
Это уравнение окружности, и, следовательно, результирующая волна будет
поляризована по кругу.
444 . Глава ХЩ
§ 11. Полное отражение. Первый пример эллиптически поляризован-
поляризованного излучения мы приведем в связи с явлением, называемым полным
отражением. Пусть в формуле .A3.58) е" < е, тогда 6" > б. В частности,
6" может равняться тг/2 при 6 < -к/2. Значение б, при котором 6" = тг/2,
называется критическим' углом 6с. Явление полного отражения подтверж-
подтверждается экспериментально. Ниже будет показано, как можно его исполь-
использовать. Предположим, что б > бс и перепишем соотношение A3.58) для
случая (х = (х", тогда получим
Затем выражение A3.61) запишем в виде
^ К A3.90)
Объединяя выражение A3.90) с A3.60), будем иметь
Е>х = "-!=/ Ц*»1»Ь(.-_/.)]* Е =
1 cos6+/[sin2e —(е"/е)]/2
Соответственно из выражения A3.69) получим
Ft fr- / ((«/О [('/О sin» 6-I]}1'» т>
Объединяя последнее выражение с A3.68), найдем
COs6 —/{(e/e")[(e/E)sin6 l]}^
ц i . ,—гттт—„ч • 2fi—пш В., = е>^В„, A3.93)
COS в + / {(?/?) [(е/е) S1I12 6—1]}V2 2 2> V /
_ 2 cos 6 {(г/г") [(г/г") sill2 6-
Поскольку, как это очевидно из соотношений A3.91) и A3.93), 1^1 = 1^^
|Z?2| = |i?2|, то падающие и отраженные лучи имеют одинаковые интен-
интенсивности. Поэтому из закона сохранения энергии следует, что преломлен
ный луч не переносит никакой энергии. Это подтверждается также непо-
непосредственным вычислением Е\ ш В"^ и затем П". Сравнивая соотношений
A3.91) и A3.93) с соотношением A3.82), мы видим, что при отражении
волны, в которой вектор В лежит в плоскости падения, фазовый угол
меняется на величину фх, а при отражении волны, в которой вектор В
перпендикулярен к плоскости падения, — на величину ф2. Таким образом,
в случае падения линейно поляризованной волны, имеющей компонентами
напряженности электрического поля Ех и Е2, отраженная волна будет по-
поляризована по эллипсу. Разность фаз 8 можно определить, поделив выра-
выражение A3.91) на A3.93) и учитывая, согласно соотношению A3.32), что
В; A/^ В№ЧЕ
= е' «*-*¦> =
sin2 6 — / cos 6 [sin2 6 -(г"/е)]1/2 "
Отношение мнимой части этого выражения к действительной дает tgS.
Пользуясь формулой D06.02) из справочника Двайта, для tg8/2 можно
получить
S _ C0s6 [Sin2 6-(г"/г)I/2
Плоские электромагнитные волны 445
§ 12. Электромагнитные волны в однородных проводниках. Для
сред с отличной от нуля проводимостью необходимо учитывать все члены
в волновых уравнениях A3.10) и A3.11). При выводе уравнения A3.11)
предполагалось, что р = 0. Чтобы показать справедливость этого предполо-
предположения для проводящих сред, возьмем дивергенцию от уравнения A3.1),
т. е.
Вместо eV-E, согласно уравнению A3.3), можно написать р и проинте-
проинтегрировать в пределах от 0 до t' и от р^ до р'; в результате получим
p'=p'oe-W. A3.96)
Таким образом, всякое распределение плотности электрического заряда
р'о постепенно убывает до нуля совершенно независимо от электромагнитных
возмущений. Если р'о первоначально было равно нулю-, то р' будет все время
равно нулю. Поэтому мы вообще можем положить р = 0. Время релаксации
Т определяется по формуле
Г = те = ^1е. A3.97)
Рассмотрим простой периодический процесс, для которого векторы В и Е
можно представить в виде
В = Re Be'"* = Re B(le>" <••>'+?).
Производная по времени djdt сводится к умножению на /ш; поэтому вместо
уравнения A3.10) и A3.11) получим
A3.98)
A3.99)
По своей форме эти уравнения совпадают с уравнениями A3.10) и A3.11),
написанными для периодических процессов в диэлектриках, только вместо
е для проводящих сред нужно писать е — д/ш. Действительная и мнимая
части часто встречающейся комплексной величины (fieI'2 соответственно
равны (Двайт, 58.2)
A3.100)
§ 13. Плоские волны в однородных изотропных проводниках. Неко-
Некоторые свойства плоских волн в проводящих средах можно получить не-
непосредственно при помощи описанной выше подстановки, исходя из свойств
плоских волн в диэлектриках, рассмотренных в § 4. Действительно, в слу-
случае изотропных сред соотношения A3.30) —A3.32) не зависят от характера
величины е, поэтому и в однородных проводниках векторы В и Е парал-
параллельны фронту волны. Из соотношения A3.33) имеем
Во = (и -+ jk) Ео = (и2 + ft2I/* Еое>Л1С *« <*/">, A3.102)
т. е. векторы напряженности электрического поля и магнитной индукции
сдвинуты по фазе относительно друг друга на угол arctg(&/n). Перепи-
Переписывая Е в форме A3.82) и подставляя в соотношение A3.102), получим
>, A3.103)
я) (и2 + А2I/2 А^-'еЯ^ «-™-r)+arc tg №/«)i? A3.104)
446 Глава XIII
где е — единичный вектор вдоль Ё, а а—единичный пектор, нормальный
к фронту полны. Мы видим, что по мере проникновения волны в сред\
Е и В экспоненциально убывают. Ято свидетельствует о наличии поглоще-
поглощения в среде. Поглощение растет с увеличением к. Величина п называется
показателем преломления, як — коэффициентом затухания.
Иногда бывает полезно 'з«ать порядки этих величин, например, для
неферромагнптпых сред с магнитной проницаемостью, близкой к [!„. Точное
значение диэлектрической проницаемости проводников неизвестно, но,
повидпмому, по порядку величин она совпадает с проницаемостью диэлек-
диэлектриков. В качестве типичного примера возьмем медь, проводимость кото-
которой приблизительно равна 5,8-107 1/ом-м. Обозначив длину волны в
вакууме через Х„ и используя выражение A3.84), получим для меди
(# = е/<0
iA -3,38- 10е.
К
we 2ясе К
Эта величина значительно больше единицы всегда, за исключением очень
коротких волн, поэтому п is. к в выражении A3.101) с большой точностью
равны
п ъ - к *, (± [хХоТI/2 (т,с)-У2. A3.105)
При помощи соотношения A3.104) подсчитаем расстояние, на котором
величины Е и В уменьшаются в е27С = 5-102 раз. Это расстояние равно
При Хо равном 1 см, 1 м, 100 м, 10 км величина d для меди принимает
соответственно значения 0,0025 мм, 0,024 мм, 0,24 мм, 2,4 мм. Пред-
Представляет также интерес сравнить средние значения электрической и маг-
магнитной энергий в волне. Из соотношений A3.104) и A3.52) имеем
WP Е2 р.г
Предположим, что е = 2е1;, тогда для только что рассмотренных длин волн
это отиошевие соответственно равно We/Wm = 5,7А0~8, 5,7-Ю0, 5,7-Ю2,
5,7-10~14, т. е. полная энергия почти целиком магнитная.
§ 14. Отражение от проводящей поверхности. В § 12 было показано/
что в проводящей среде величину (^"е"I/2 нужно заменить на
[fi" (е" — /<й~1т)]1'2 = п + ]к-
Таким образом, из соотношения A3.58) при помощи выражения A3.100)
для sin 6" и cos 6" получаем
Из предыдущего параграфа следует, что для длин волн порядка 1 см и
более
— къп> 1,4-104.
Поэтому угол 6", определяемый формулой A3.108). оказывается комплексной
величиной, очень малой по модулю. Если вектор магнитной индукции
лежит в плоскости падения, то, согласно выражению A3.66), имеем
^SSJCTJnW1'.- . A3.109)
Плоские алектромагнитные волны 447'
Если же в плоскости падения лежит вектор напряженности электрического
поля и, кроме того, угол падения 6 не слишком близок к тг/2, то из выра-
выражения A3.74) получаем
Ч-ТЙ^П11*™**- A3-110)
Итак, сравнительно длинные электромагнитные волны полностью отра-
отражаются от проводящей поверхности независимо от поляризации и угла
падения. При меньших значениях проводимости те же результаты справед-
справедливы для более длинных волн. Та незначительная часть поля, которая
проникает внутрь проводника, очень быстро затухает в нем по мере уда-
удаления от его поверхности, так что даже очень тонкий металлический лист
почти совершенно непрозрачен по отношению к коротким волнам. Для опре-
определения поляризации отраженного луча разделим выражение A3.62) на
выражение A3.72), в результате чего получим
Е'ъ созСО + В»)^ (coS6"-sm6"tg0)iy2 /14 1111
Е{~ cos F — Ь")Ь\ (cos 0" + sin b" tg 0) Ех " ( " '
И рассмотренном нами диапазоне длин волн
п-\- jk «; иA — /).
Если |[1е/(и + jkJ1 <С 1, то cosG"=l, и из формулы A3.108) имеем
Е2 __ ["-(У*I'2 sin 0 tg 6-/»] Е2 _ Цп-ЬхгI'* sin 6 tg 0]^ + п*)*'* ^Е2 .^ {
E' 1 — /n]E1 \[n-r((xe)l/2sinetge]2 + n4 - Ei' ' '
Поскольку n—величина большая при любых углах падения 6, за исключе-
исключением близких к те/2, то
ЩЕ
При tg6—> оо появляются изменения не только величин Е'2 и i?j, но и
сдвига по фазе 8. Таким образом, для длин волн порядка 1 см и более
эллиптически поляризованное излучение получается только при скользящем
падении линейно поляризованной волны.
§ 15. Плоские волны вдоль идеально проводящих цилиндрических
проводников. Плоские волны могут распространяться не только в свобод-
свободном пространстве пли в бесконечно протяженной диэлектрической среде
с плоскими границами, но и вдоль системы идеально проводящих цилиндри-
цилиндрических проводников, т. е. в некотором направлении г, вдоль которого
поперечные сечения проводников не меняются. Согласно § 3 гл. XI, электро-
электромагнитное поле не проникает внутрь идеального проводника, а-токи текут
лишь в бесконечно тонком слое по его поверхности, поэтому с идеальным
проводником не связано никаких потерь энергии. Интересующую нас задачу
можно решить несколькими способами. При получении результатов § 26
гл. VII считалось, что вектор-потенциал, а следовательно, согласно § 2,
и вектор Герца ориентированы вдоль направления z, т. е. параллельно
токам. Решение волнового уравнения для вектора Герца дает и скалярный
потенциал и вектор-потенциал. Если, воспользовавшись уравнением A3.16),
исключить скалярный потенциал, то полученный вектор-потенциал будет
лежать в плоскости, нормальной z. Тот же результат можно получить
448- Глава XIII
непосредственно, решая скалярное волновое уравнение
dy2 J
d"-w л „ ..„ ....
— Pe = 0. A3.114)
Решение получается, если каждую из скобок по отдельности приравнять
нулю1'. Это решение имеет вид
W = V, (х, у) jx [z - (це)-1/21] + F2 (х, у) U [^ + (И'2 «J. A3.115)
где Vt и F2—решения двухмерного уравнения Лапласа. Пусть Wt и W2 —
комплексные потенциальные функции, рассмотренные в гл. IV, тогда
W^U. + jV^F^x + jy), W2=U2 + jV2 = F2(x + jy). A3.116)
Если V2F определен как i (dV/dx) + j (dV/ду), то из § 11 гл. IV мы имеем
-kxV2F=V2C/, kxV2C/=V2F, Vx[V2Uf(z)]=kx.VaUf'(z). A3.117)
Из соотношения A1.11) вектор-потенциал поперечного электрического поля
равен
i*t]. A3.118)
Очевидно, что первый член соответствует волне, распространяющейся в поло-
положительном направлении оси z, а второй—в отрицательном направлении
оси z. Поля определяются по формулам
A3.119)
^ A3.120)
Верхний знак относится к волне, распространяющейся в положительном
направлении. Из уравнений A3.117), A3.119) и A3.120) имеем
A3.121)
Будем различать две группы проводников, предполагая, что токи втекают
в проводники одной группы и возвращаются по проводникам другой группы.
Тогда из уравнения A3.120) с очевидностью следует, что если при некото-
некотором значении z потенциалы проводников, относящихся к одной и той же
группе, одинаковы, то они останутся одинаковыми и при любых других
значениях z. Для нахождения соотношения между полным током и сум-
суммарным зарядом в любой из групп, состоящей из и проводников, нужно
воспользоваться формулой A3.121), уравнением G.2), а также привлечь
теорему Гаусса A.40). В результате получим
Я, еЦ = (ре)^ I. A3.122)
Обозначим через L самоиндукцию на единицу длины, через С —емкость
на единицу длины, а через S—площадь поперечного сечения z = const, не
занимаемую проводниками. Тогда из соотношений B.15), B.47) и (8.35)
имеем
J) Полагая в уравнении A3.114) постоянную разделения равной нулю, автор огра-
ограничивается рассмотрением только главных волн, не оговаривая этого.—Прим. перее.
Плоские электромагнитные волны 449
Таким образом, L и С оказываются связанными между собой соотношением
LC = (хе = гГ2. A3.124)
Произведение LC равно величине, обратной квадрату скорости распростра-
распространения электромагнитной волны в окружающей проводники среде.
Если в некоторой плоскости z = О задана зависимость векторов Е и В
от времени, то, пользуясь уравнением A3.118), легко получить выражение
для А, пригодное при любых z,
z]}. A3.125)
Пусть U и V даются формулой A3.116), тогда выражение A3.125) при-
приводит к следующим значениям полей в сечении z = 0: /
о = - (FI/2 ^2 V (х, у) g' (t). A3.126)
Столь же просто, пользуясь уравнением A3.118), написать выражение для
А, если в момент t = 0 векторы Е и В заданы в виде функции от z:
А = Л- V2 U (х, у) {/ [(це)'/. z+t]-f [(реI/, г - t] -
-*]}. A3.127)
Пусть U и F определены но формуле A3.116), тогда из выражения A3.127)
для А получим следующие значения полей в момент времени t = 0:
Ео= -VtU(X,y)f[Mll»z\, Bo= -WVaV(x,y)g'l(VeIi*z]. A3.128)
§ 16. Характеристический импеданс среды '). Если вместо идеального
диэлектрика, с которым мы имели дело в предыдущем параграфе, рас-
рассматривать среду с проводимостью 7> то уравнение A3.114) необходимо
переписать в виде
Если теперь вторая скобка равна нулю, то решение уже нельзя! записать
через произвольные функции. Поэтому мы используем метод разделения
переменных, описанный в гл. V, согласно которому уравнение в частных
производных разбивается на два уравнепия, содержащих полные производ-
производные. Решение последних можно представить в виде экспоненциальных
функций, причем в зависимости от того, будет ли постоянная разделения
действительной или мнимой величиной, решение будет гармоническим в
пространстве (переходный процесс) или гармоническим во времени (устано-
(установившийся процесс). Сейчас мы будем рассматривать только установившиеся
решения, предполагая зависимость от времени заданной в виде фактора
е1'"* (см. § 10 настоящей главы). Функцию W, удовлетворяющую уравне-
уравнению A3.129), можно представить в виде произведения двух множителей;
второй множитель удовлетворяет дифференциальному уравнению A0.106),
поэтому функции / [z ± ([ae)~^2 t], входившие в ряд формул предыдущего
*) Термин «характеристический импеданс» здесь и далее сохранен ва отношением
Е/Н, термин «волновое сопротивление» — за отношением V/T п бегущей волне.—
Прим. переч.
29 в. СмаПт
450 . Глава XIII
параграфа, необходимо теперь заменить на e±Tz+'wt, где
Г2 = /Ш[1 (Т + /we) = (а + /РJ, A3.130)
40*6' + ^1/2 ~ we] |1/2' Р = { ( Т ш0 Kw2e2 + Т2I'2 + we1 j1/2 •
A3.131)
Здесь Г — постоянная распространения, а — коэффициент затухания волны,
а р — волновое число (или фазовая п< стояиная). Теперь вместо уравнений
A3.119) и A3.120) для волн, распространяющихся в положительном или
отрицательном направлениях оси z, будем иметь
В = Re [ т rV2 V (ж, у) еч=**+*«] =
= q: V2 V (ж, у) <?*" [a cos (utf T Pz) - р sin (<of q: pZ)], A3.132)
E = Re [ - /« V2*7(ж, ?/) e 1*2+>"'] = «V2 ^7 (ж, г/) е*« sin (ш* =F Pz), A3.133)
f'E=q:/<fl(kxB), или fkxE = ± /<oB. A3.134)
Согласно формуле F.57), произведение сопротивления R между провод-
проводниками на емкость С равно те или e/f (и сопротивление и емкость отне-
отнесены к единице длины). Поэтому шунтирующая полная проводимость Y
и последовательный импеданс Zl, фигурирующие в § 19 гл. X, равны
Тогда из соотношения A0.109) для волнового сопротивления линии получим
. A
В . ГС Ч
Рассмотрим теперь частный случай линии, состоящей из двух беско-
бесконечных параллельных проводящих плоскостей, расположенных на рассто-
расстоянии 1 м друг от друга. Емкость на единицу длины участка линии, име-
имеющего площадь поперечного сечения в z-направлении 1 м2, равна е, поэтому
волновое сопротивление будет равно
)ll J A3.136)
причем V = Е, B=pi (i —плотность тока). Мы видим, что ^зависит толь-
только от свойств среды. Конфигурация поля в такой линии совпадает с кон-
конфигурацией поля в плоско поляризованной волне. Поэтому разумно, следуя
Шелкунову, назвать Zh. характеристическим импедансом среды. Сравнение
формул A3.136) и A3.58) показывает, что для оптически прозрачных сред,
когда т = 0, а [i — [ir, характеристический импеданс пропорционален пока-
показателю преломления. Пользуясь выражениями A3.131) и A3.136), можно
определить характеристическую постоянную распространения среды и виде
К = а+ /Р = [hv- (Т + /«к)]1'* = W Zh1 ¦ A3.137)
§ 17. Отражения от иеодпородностей. Согласующие секции. Предпо-
Предположим, что описанная в последнем параграфе плоская волна, бегущая
в направлении z, встречает на своем пути плоскую гр. ницу раздела
(z = const) двух сред, причем среда, простирающаяся за этой границей,
имеет диэлектрическую проницаемость е„, магнитную fi2 и проводимость ia.
Соотношения между значениями напряжения и тока, соответствующими
Пдоские электромагнитные волны 451
падающей, отраженной и проходящей волнам, согласно выражению A3.135),
имеют вид
\\=Zji, Vi=-ZX V2 = ZJz- A3.138)
На самой границе потенциалы и токи должны быть непрерывны, что дает
V1 + V'1=V2 и i1 + i'1=i2. A3.139)
В результате совместного решения написанных выше уравнений для
V Х' V V
^i> Ve> h и h получим
2 — Z, V2
110.
Если обе среды непроводящие, то, как легко видеть из выражений A3.131),
A3.135) и A3.58), отношение Zi/Zl можно заменить на отношение г:2/с1г т. е,
на отношение скоростей распространения волн в двух средах. Следовательно,
закон отражения потенциалов при нормальном падении такой же, как и для
напряженностей электрического поля [см. выражения A3.76) и A3.77)]. Опе-
Оперируя с отдельными компонентами, можно использовать формулы линий
передачи при получении законов отражения для произвольных углов падения.
Путем введения согласующей секции можно избежать отражений при
переходе электромагнитной волны из одной непроводящей диэлектрической
среды (i^Sj) в другую (^Зез)- При идеальной передаче входной импеданс
согласующего слоя или секции должен быть равен характеристическому
импедансу первой среды. Согласно соотношению A3.135), нужно положить
в выражении A0.112)
Для согласования необходимо удовлетворить следующему уравнению:
1/ 2I/2sin Bтг//Х2)
3
inB7rZA2) " ;
Зто уравнение будет иметь место, если положить *)
1 A3.142)
Таким образом, длина согласующей секции равна нечетному числу Х2/4,
а ее характеристический импеданс — среднему геометрическому импедансов
первой и второй сред; пользуясь оптической терминологией, можно сказать,
что показатель преломления согласующего слоя должен быть равен среднему
геометрическому показателей преломления сред, расположенных справа и
слева от согласующего слоя. Четверть-волновые слои широко применяются
для уменьшения отражений от поверхностей линз.
§ 18. Комплексный вектор Умова—Пойнтинга. Выражение для век-
вектора Умова — Пойнтинга в комплексном виде полезно в тех случаях, когда
г) Формула A3.142) испрашльная. Ошибка при выгоде заключается в том, что
самоппдукция L магнетика равна [л, т. е. равная в различных средах. Следовательно,
вместо A3.142) должно иметь место следующее условие согласования:
Wj1 = (рI* е- V2) ([Л>/2 eri/S). ! = iu B„ + !) Х2.
В оптике обычно [л = [л1), поэтому формула A3.142) дает правильное соотношение между
диэлектрическими проницаемостями.—Прим. перев.
2fl*
452 Глава XI11
поля меняются со временем синусоидально и, следовательно, оператор d/dt
нельзя заменить на множитель /ю. Перепишем уравнение A3.2) и уравне-
уравнение, комплексно сопряженное с A3.1). Последняя операция является вполне
законной, так как она не изменяет реальной части ура'внения
VxE= -/«В, VxB = [i(i- /юе)Ё. A3.143)
Умножив первое уравнение на В, а второе на —Е и сложив результаты,
получим
В -(VxE) — E-(VxB) = — ОТЁ • Ё —/(«(jj.eE • Ё —В - В)].
Как и в § 3, левую часть зтого выражения, равную V • (ЕхВ), проинте-
проинтегрируем по объему v и применим теорему Гаусса. По закону Ома F.8)
вместо Е можно написать i/f, или xi, где i — плотность тока; в результате
долучим
— jr-1 [ п ¦ (ЁхВ) dS= С тг2 dv — /to \ (еЁ • Ё —^В • B)dv. A3.144)
S v v
Из выражения A1.10) следует, что реальная часть члена, стоящего в левой
части, равна удвоенной величине средней энергии, поглощаемой в течение
1 сек. внутри объема интегрирования. Таким образом, проинтегрировав
нормальную компоненту вектора
ffi1E ^iE E A3.145)
(нормаль направлена внутрь объема) по замкнутой поверхности, окружаю-
окружающей зтот объем, мы получим скорость поглощения электромагнитной энергии
внутри него. Эту формулу можно использовать, например, для определения
потока энергии, проходящего сквозь плоскость z = Zo линии передачи, опи-
* ч/ •
санной в § 1В. Исключив при помощи выражения A3.134) Е из выражения
A3.145) и используя соотношения A3.123) и A3.135) для волны, бегущей
в положительном напрайлении оси z, получим
^l k^. A3.146)
2
i ( I I * 2Г 2
Как и в выражении A3.122), потенциал предполагается положительным
на тех проводниках, по которым ток течет в положительном направлении z.
Если изменить знак напряжения или тока (какую-либо одну величину,
а не обе сразу), то направление потока энергии сменится па обратное.
§ 19. Квазиплоские волны вдоль неидеальных проводников. Двух-
Двухпроводная линия Лехера. Если линия передачи, рассмотренная в § 15
и 16, образопана проводниками, имеющими конечную проводимость, то из-за
наличия вихревых токов часть энергии будет выделяться в виде тепла на
поверхности зтих проводников. Напряженность электрического поля будет
иметь z-компоненту, что приводит к появлению составляющей вектора
Умова — Пойнтинга, направленной внутрь проводника. Очевидно, что теперь
волна уже не будет чисто плоской. В большинстве практически важных слу-
случаев потери Мощности на единицу длины малы по сравнению с мощностью,
передаваемой вдоль линии, поэтому направление вектора П незначительно
отклоняется от оси z. Поскольку потери энергии пропорциональны квадрату
напряженности поля, то поле экспоненциально убывает вдоль z, что при-
водит к появлению в последовательном импедансе Z^ активной составляв
Плоские электромагнитные волны 45й
ющей R-. Кроме того, благодаря проникновению магнитного поля внутрь
проводника к Z^ добавляется еще и внутреннее индуктивное сопротивле-
сопротивление /wLj. Учитывая все зто, для волнового сопротивления, определяемого
по формуле A3.135), получаем
Z --= ( ZlY/2 = fL[Ri + /">(L +-U)\ V/2 A3.147)
V у J V ' (ЛG + /<ОЕ) J
Для большинства линий передачи R- < wL, Lt < L и -у <С <ое, поэтому для
линии в вакууме волновое сопротивление и постоянная распространения
соответственно равны
:„)-1/2 = 3 . 108L = C • ЮеС)~1, A3.148)
.)]. A3.149)
В качестве примера найдем Zh и Г для системы Лехера, состоящей
из двух параллельных проводов диаметра d, расстояние между осями
которых равно Ъ. Пользуясь формулами D.71) и A3.124), можно определить
внешнюю индуктивность в виде
Z, = ^ = ilarch-^-. A3.150)
Заметим, что L зависит только от конфигурации и не зависит от отдель-
отдельных размеров. Будем теперь считать частоту и проводимость настолько
большими, чтобы глубина проникновения 8 была значительно меньше d.
Тогда для сопротивления R[ (на единицу площади) и для индуктивности
Ц. (на единицу площади) можно использовать формулу A1.26), в резуль-
результате имеем
A3.151)
где is—ток, текущий в цилиндрическом поверхностном слое, приходящийся
на дугу единичной длины, а множитель 2 обусловлен наличием двух про-
проводников. Согласно соотношению A3.119), на цилиндре, имеющем потенциал
U = иг, тангенциальная составляющая В равна dV Ids. Применяя к злемепту
поверхности формулу G.4), получим \>.is = B. Таким образом,
Из соотношений G.44), D.57) и D.64) имеем
dW\ dV V.I . тс ([/, + /!') . 74A7, —/F) y.l f ,2^7г i^V\
— = — ='— sin ' - sm —— ¦ = — i ch2 -~ — cos2 —r },
F_-=/ich^i A3.152)
0
^ ^U2. A3.153)
ch^,
d \xl
Последнее следует из соотношения D.66). Подставляя выражения A3.152)
и A3.153) в A3.151) и разделив все на I2, получим
п _ 2Rjb _ 2t'b A3 154)
1 Ted ^ - d^ ТЫ (Ь* - d2I/2 ' I
Li = 2L'ib , = 2z'b „ . A3.155)
¦nd (b2 — d2)l/2 d(b2 d2I'2
454
Глава XIII
Рассмотрим теперь частный случай, когда отношение d/b = 1,5 и линия
находится в пустоте или в воздухе, так что fi=jAi; = 4it • 10~7. Тогда само-
самоиндукция L, определенная по формз'ле A3.150), равна 3,85 • 10~7 гп. Для
подсчета B.i и Lt необходимо, помимо d/b, знать еще частоту, удельное сопро-
сопротивление, магнитную проницаемость и один из размеров проводников. Для
одного из наиболее важных проводников—меди y'=1/t'=5,8- Ю*, а ji, = jj,,,.
Остановимся на частотах 3 мггц, 300 мггц и 30 000 мггц, которым соот-
соответствуют длипы волн 100 м, 1 м и 1 см. Индуктивное сопротивление u>L
для этих частот соответственно равно 72,5 ом, 72.5 ом и 7250 ом, а толщина
скин-слоя 3,82 ¦ Ю-5 м, 3,82 • 10 м, 3,82 • 10 м. Поэтому в соответ-
соответствии с формулами A3.152), A3.153) и A3.149) можно составить следую-
следующую таблицу.
Л, М
0,01
0,01
1,00
1,00
100
100
d, м
0,001
0,01
0,001
0,01
0,001
0,01
Я„, ом
38,5
3,85
3,85
0,385
0,385
0,0385
L., ги
1,225-М-1»
1,225-1С-11
1,225-10-»
1,225-10-ю
1,225-10-8
1,225-10"9
я
5,1 -Ю-2
5,1-Ю-3
5,1-Ю-3
5,1-Ю-4
5,1-10-"
5,1-Ю-5
Р
19
19
1,9
1,9
0.19
0,19
Очевидно, что во всех случаях /?; и wL{ малы по сравнению с coL; поэтому
волновое сопротивление, определенное по формуле A3.148), будет равно
115,5 ом.
§ 20. Групповая скорость. Амплитуду любого из векторов поля в плос-
плоской волне, распространяющейся в линии передачи, можно записать в виде
— f (alt к2) cos (ю* —
A3.156)
j и м2 — ортогональные координаты в плоскости, перпендикулярной к
оси z, а Р — волновое число или фазовая постоянная. Если фазовая скорость
волны зависит от частоты, как это имеет место, например, в волноводах
или диспергирующих средах, то сигнал, образованный группой волн раз-
различных частот (волновым пакетом), будет менять свою форму (искажаться)
по мере продвижения вдоль %. Пусть такой пакет образован волнами,
волновые числа которых расположены в интервале Ро — Ь и[В04-?>, а ампли-
амплитуда волны в интервале бф равна А ф). Тогда амплитуда сигнала опре-
определится из выражения
Этот интеграл можно представить в виде произведения двух множителей
S = Се> ("о'-Рог), где С = \ А (Р) е> Кш—)<»<- (Р
Р8
один из них представляет несущую волну, фазовая скорость которой
равна с0 — соо/р„, т. е. равна средней фазовой скорости. Другой множитель
(модулирующий фактор) является огибающей пакета, перемещающейся со
Задачи 455
скоростью (о> — WO)/(P — Ро)- Средняя амплитуда волнового пакета равна ]/2 С/8.
Таким образом, на несущую частоту ш0 накладывается еще модулирующая
частота w — w0. Пусть теперь мы хотим определить скорость перемещения
плоскости, в которой амплитуда модуляции С, образующая сигнал, постоянна.
По теореме о среднем значении интеграла
С = 28Л (Р ) е' t(<»i—<»о)'— (Pi—Po) z]j
где Ро — 8 < Рх<Р0 4-8. Если диапазон частот, входящих в колновой пакет,
настолько мал, что Pj - Ро и (%— <о0 бесконечно малы, то скорость сигнала
будет равна
^=J!iZ^L__ ^ . A3.157)
ЗАДАЧИ
1. Два самолета летят па высоте // над плоской поверхностью воды на расстоянии d
друг от друга. С одного самолета на другой послан радиосигнал. Приемная и пере-
передающие антенны на самолетах представляют собой короткие металлические проволочки
длиной I, ориентированные вертикально. Полагая h > /, d > I и А ^> / и считая диэлек-
диэлектрическую проницаемость воды равпой в, показать, что отношение мощности сигнала,
принятого после отражения от воды, к мощности прямого сигнала равно
2. Плоская электромагнитная ваппа, поляризованная под углом 45е по отношению
к плоскости падения, испытывает полное отражение внутри призмы, в которую она
входит и из которой она вы-ходит под прямым углом к ее граням. Показать, что
мощность волны, выходящей из призмы, равяа Itin2 (l+n)->/0, где п — показатель пре-
преломления. Показать также, что выходящая волна будет эллиптически поляризованной
с разностью фаз у, определяемой соотношением
tg — <? = cos 6 (sin б) (sin2 6— и-2) '\1
где 6 —угол падения на заднюю грань призмы. При решении задачи пренебречь много-
многократными отражениями.
3. Плоская электромагнитная волна с длиной вотны X падает на бесконечную
диэлектрическую плоско-параллельную пластинку толщиной а. Показать, что интен-
интенсивность отраженной волны, поляризованной нормально или параллельно плоскости
падения, дается выражением
462sin2 Г-1 о
где Ь— отношение интспсивногтп волны, отраженной только от перепней грани пла-
пластинки, к интенсивности падающей волны, Ь—Ыпа\~'> соэф — угол преломления, п — по-
показатель преломления. При решении необходимо учитывать фэзоиые соотношения и
многокрптпые отражения; пластинку считать нспоглощлющей.
4. Показать, что для вектора Умова - Пойитикга па границе раздела с анизотропной
средой в общем случае нельзя пользоваться законом преломления, приведенным
в § 7 гл. XIII.
5. Показать, что плоскость, проходящая через точку пересечения оптической оси
с лучевой поверхностью перпендикулярно к оптической оги, япляртся плоскостью,
касательвой к окружности, проведенной вокруг оси .луча (см. фиг. 122).
6. Плоская волн.ч палае? иод углом 0 на плоскую поверхность одноосного кри-
кристалла, нормаль к которой образует угол а. с оптической осью. Пусть <? — угол между
плоскостью падения и плоскостью, содержащей нормаль п оптическую ось, пусть также
'—' -*• =з- Показать, что направления иолноьых нормалей 0о и 0е двух преломленных
456 Глава XIII
волн определяются из выражении
. „„ sinfl . ,.,,
Sln6o = ~^ • sm 6e =
— COS2a-\ — , P = sina ?0sa COS
N= F* M* .»,
cos2 а Е
M
cos2 а Е«(гз—e
1 . 1
При углах <y<—7i необходимо брать знак минус, а при -^ т. < <у < и—знак плюс.
7. Показать путем непогродственной проверки, что волны, вектор В в которых
перпендикулярен к оси г, описываются вектор-потенциалами вида
= С, {i/p' cos [(pi- р'2I'2х] -к (р2 - р'»I/я sin [(PI -p»«/'2 я]} <J («tf-ГО,
р| = <я2[л2Е2 и рг > Pi- В гвязи с этим решить задачу о распространении
плоской поверхпогтной волны над бесконечной плоской идеально проводящей поверх-
поверхностью, покрытой слоем диэлектрика толщиной а. Магнитная и диэлектрическая про-
проницаемости диэлектрика равны ссответствонво \i2 и е2> а окружающего пространства—
p.j и Sj. Показать, что скорость распространения волны определяется из уравнения
E2lP Pi) —=-1 (P2 H ) l6 l\H2 i5 ) a\- I
Если р,а = 1,ОО, [i2=[i, и 52=46!, то приблизительно Pj : р': р2 = 1 :1,636 :2, так что
амплитуда уменьшается в 10 раз относительно своего максимального значения на рас-
расстоянии я- = 1,78а.
8. Показать путем непосредственной проверки, что волна, вектор Е в которой
перпендикулярен к оси г, описывается вектор-потенциалами вида
-р'2>, А2 - jC2 sin [(PI- p'») x]
где
и
В связи с этим решить задачу о распространении плоской поверхностной волны над
бесконечной идеально проводящей поверхностью, покрытой слоем диэлектрика толщи-
толщиной а. Магнитная и диэлектрическая проницаемости диэлектрика равны соответственно
[i2 и е2, а окружающей среды — \хг и 2j. Показать, что скорость распространения волны
определяется из уравнения
Если р,я=1,00, ,u8 = fii и e2 = 4s]F то приблизительно р, : S': Р2 = 1 :1,03 : 2, так что
амплитуда уменьшается в 10 раз относительно своего максимального значения на рас-
расстоянии х- 9,4а.
9. Пусть два одинаковых цилиндрических проводника, ограниченных плоскостями
z = 0 и z = l, имеющими диэлектрическую и магнитную проницаемости, равные нулю,
несут на себе равные по величине и противоположные по знаку заряды, так что раз-
разность потенциалов между ними равна Fo. В момент г = 0 поверхности плоскостей ста-
становятся проводящими (R—i опротивление между цилиндрическими проводниками).
Показать, что потенциал между проводниками можно записать в виде
у
R + Zk t^Q
где
0<z<l и S{l,.eIl4< t<
10. Однородная линия передачи, имеющая длину I и волновое сопротивление Zfc.
подключена одним концом к цепи, состоящей из последовательно соединенных батареи
с э. д. с. %, сопротивления R и выключателя. Пренебрегая искажениями поля па коп-
цах, показать, что если в момент г = 0 цепь замыкается, то через сопротивление R
потечет ток
*2
Литература 457
11. Однородная линия передачи, имеющая длину I и волновое сопротивление Z^,
в сечении z — l закорочена, а в сечении z=0 подключена к цепи, состоящей из после-
последовательно соединенных батареи с э. д. с. %, сопротивления R и выключателя. Прене-
Пренебрегая искажениями поля на конце линии, показать, что если в момент t = 0 цепь
замыкается, то ток, текущий через батарею, будет равен
2п
12. Если вектор Герца имеет только z-состанлпющую, то он удовлетворяет скаляр-
скалярному волновому уравнению A3.114). Показать, что в случае плоской линии передачи
потенциалы имеют вид
Показать также, что в результате исключения скалярного потенциала при помощи
формулы A3.21) мы придем к выражению для результирующего вектор-потенциала А',
совпадающему с выражением A3.118).
13. Линия передачи состоит из двух не охватывающих друг друга цилиндров ра-
радиусов а и Ъ, расстояние между осями которых равно с. Показать, что волновое сопро-
сопротивление такой линии определяется по формулам A3.147) и A3.148), а постоянная рас-
распространения в ней — по формуле A3.149), где
2ab ' l l 2каЬЪ[(Ь2 — а2J — 2с2 (Ь2+а2) + с4]1'2 '
14. Линия передачи состоит из двух конфокальных эллиптических цилиндров,
главные оси которых равны 2а и 2Ъ (а < Ъ). Обозначив через 2с расстояние между фо-
фокусами, а через К—полный эллиптический интеграл, показать, что Zj, определяется
по формулам A3.147) и A3.148), а Г—но формуле A3.149), где
Т_Р. Ь+^-с2I'2 „ _..г ,'
15. Линия передачи состоит из двух параллельных плиских полосок шириной Ъ,
имеющих удельное сопротивление т'. Плоскости этих полосок отстоит одна от другой
на расстоянии а (а <^Ъ). Показать, что постоянная распространения и волновое сопро-
сопротивление приближенно равны
Г2
]
16. Линия передачи состоит из днух параллельных цилиндров рядиусов а и Ъ,
расстояние между осями которых равно с; причем один цилиндр находится внутри
другого. Показать, что волновое сопротивление определяется по формулам A3.147) и
A3.148), а постоянная распространения—по формуле A3.149), где
Х--11 arch
2л
— а2J— 2с2 (а2+
17. В среде с магнитной проницаемостью (х и диэлектрической проницаемостью е
плоская юлна падает нормалыш на плоское идеально отражающее зеркало. Показать,
что можно избежать отражений; поместив на расстоянии четверти волны от зеркала
тонкую пластинку (толщиной d) из вещества с диэлектрической проницаемостью е' и
с проводимостью -у\ если -у'^5^ (Е/^) '2 и 7'-^>а>г#
ЛИТ Е РАТУРА
Abraham M., Becker R., Klassische Elektrizitat und Magnetismus, Berlin,
1932. (См. перевод: А бр a r a м Ы., Б е к к е р Р., Теория электричества,
2-е изд., М.—Л., 1939.)
В a t e m a n H., Electrical and Optical Wave Motion, Cambridge, 1915.
Biggs H. F., The Electromagnetic Field, Oxford, 1934.
Born M., Optik, Berlin, 1933. (См. перевод: Борн М., Оптика, М.—Л., 1935.).
458 Глава XFFI
Drude P., Theory of Optics, Longmans, 1920. (См. перевод: Д р уде П., Оптика,
М.—Л., 1935.)
Forsterling К., Lehrbuch der Optik, Leipzig, 1928. *
Frenkel J., Lehrbuch der Elektrodynamik, Bi. 2, Berlin, 1926, 1928. (Френкель
Я. 11., Электродинамика, М.—Л., 1935.)
Geiger-Schell, Handbuch der Physik, Bd. XII, XV, XX, Berlin, 1927, 1927, 1928.
Heaviside O., Electrical Papers, Boston, 1925.
Hertz H. R., Electric Waves, Macmillan, 1893.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
King R. W. P., Mimno H. R., Wing A. H., Transmission Lines, Antennas
and Wave Guides, McGraw-Hill, 1945. (См. перевод: Кинг Р., Мимно Г.,
У и н г А., Передяющие линии, антенны и волноводы, М.—Л., 1948.)
Livens G. H., Theory of Electricity, Cambridge, 1926.
MacDonald H. M., Electromagnetism, Bell, 1934.
Mason M., Weaver W., The Electromagnetic Field University of Chicago Press,
1929.
Maxwell J. G., Electricity and Magnetism, Oxford, 1881.
Plank M. К. Е. L., Theory of Electricity and Magnetism, Macmillan, 1932.
R a m о S., W h i n n e г у J. R., Fields and vVaves in Modern Radio, Wiley, 1944.
(См. перевод: Р а м о С, В и н н е р и Д., Поля и волны в современной
радиотехнике, 2 изд., т-е М.—Л., 1948.)
ScbelkunoTf S. A., Electromagnetic Waves, Van Nostrand, 1943.
Stratton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: С т р э т-
т о н Д. А., Теория электромагнетизма, М.—Л., 1943.)
Webster A. G., Electricity and Magnetism, Macniillan, 18U7.
Wien-Harms, Handbuch der Experimentalphysik, Bd. XI, 1932.
Глава XTV
ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
§ 1. Постановка задачи. Любая неэкранированная полностью система,
генерирующая электромагнитные колебания, теряет часть энергии за счет
волн, расходящихся в окружающее пространство. Если система не пред-
предназначена специально для излучения, то эти потери в ней рассматриваются
как утечки, и тогда обычно требуется знать только мощность излучения.
Если же излучение составляет основное назначение системы, как, например,
в случае антенн или рупоров, то, помимо этого, нужно иметь сведения о
Поляризации излучаемых волн, о распределении излучаемой энергии в про-
пространстве, о потерях, не обусловленных излучением, о распределении заря-
зарядов и токов в системе и, наконец, о ее входном импедансе. Эти характе-
характеристики зависят от приложенных электродвижущих сил, частоты, разме-
размеров системы и ее конфигурации, а также от материала, из которого сделаны
эти системы, и от свойств окружающей ее среды. Например, для антенны,
находящейся в свободном пространстве, полное решение задачи должно
заключаться в нахождении полек, удовлетворяющих уравнениям Максвелла *
снаружи антенны и внутри нее, а также удовлетворяющих соответствующим
граничным условиям на поверхности антенны. В частности, полученные
при этом напряженность электрического поля и распределение тока должны
быть согласованы на поверхности соединения антенны с линией передачи
с полями и токами в этой линии. Такое полное решение задачи для
существующих систем, повидимому, невозможно.
Существуют, однако, методы, позволяющие с необходимой точностью
вычислять одну или несколько из перечисленных выше характеристик
антенн. При помощи запаздывающих потенциалов по заданному распреде-
распределению зарядов и токов всегда можно найти электромагнитное поле. Часто
оказывается, что вдали от антенны это поле чувствительно только по отно-
отношению к существенным изменениям в распределении токов или зарядов в
антенне, и поэтому последнее можно задавать приближенно. Приближенное
распределение позволяет с достаточной точностью определить и джоулевы
потери, если они малы. Посредством теоремы Умова — Пойнтинга можно
найти действительную (но не мнимую) часть входного импеданса антенны.
Формулы скин-эффекта позволяют определить омические потери, если
известно магнитное поле непосредственно вблизи поверхности металла.
Распределение тонов в а"нтеннах, выполненных из идеально проводящего
проводника простой геометрической формы (сфера, сфероид), можно найти
из строгого решения задачи, основанного на применении системы ортого-
ортогональных функций, подобных тем, которые встречаются в электростатике,
но только более сложных. Но, за исключением случая конической антенны,
такое строгое решение дает мало сведений относительно входного реак-
реактивного сопротивления. Излучение из отверстий часто сначала вычисля-
вычисляют в предположении, чго поля на отверстии известны, а затем эти поля
«стараются подобрать так, чтобы удовлетворить граничным условиям.
460 Глава XIV
В нижеследующих параграфах будут приведены примеры на применение
большинства из этих методов.
§ 2. Два типа вектор-потенциалов. По заданному распределению
токов источника можно при помощи" уравнения непрерывности найти и
распределение его зарядов. В § 4 будет показано, что запаздывающие
скалярные и векторные потенциалы можно представить в виде интегралов
соответственно от зарядов и токов, подобно тому, как это имеет место в
электростатике и в магнитостатике. Запаздывающий вектор Ге"рца, описы-
описывающий все поля, выражается через токи при помощи одного интегриро-
интегрирования, так как уравнение непрерывности в источнике предполагается при
этом удовлетворенным.
В общем случае в указанных выше методах имеют дело с вектор-
потенциалами, дивергенция которых не равна нулю и которые имеют
отличные от нуля тангенциальные составляющие на поверхностях антенн.
Однако в том случае, когда заряды располагаются tra идеально проводящих
поверхностях, ограничивающих область, где ищется поле, часто бырает
проще пользоваться вектор-потенциалом другого типа, обладающим равной
нулю дивергенцией, и тем самым полностью избавиться от скалярного
потенциала, как это было указано выше [см. соотношение A3.21)]. Такой
вектор-потенциал всегда перпендикулярен к поверхности антенны. Если же
существуют заряды вне проводников, то целесообразно разбить вектор-
потенциал А на две части: соленоидалытую А" и потенциальную А'.
В частности, производная по времени от А' равна градиенту скаляра ЧГ'-
Взяв дивергенцию от обеих частей уравнения A3.13) и воспользовавшись
A3.3), получим
V • Е= -V • ^-'— V ¦ VW= — V2 (ЦГ' + ЦГ) = -?-.
Обозначая W-\-W через новую скалярную функцию Ф, имеем
72Ф=— |-. A4.1)
Таким образом, единственное осложнение, вносимое зарядами, заключается
в необходимости решить уравнение Пуассона, что можно сделать методами
электростатики. Заметим, что Ф всегда находится в фазе с р. Это свиде-
свидетельствует о том, что с полем, описываемым потенциалом Ф, не связано
никакого распространения энергии.
§ 3. Сферические электромагнитные волны. Диполь. Как следует
из результатов § 2 гл. XIII, все векторы электромагнитного поля удовлетво-
удовлетворяют одному и тому же волновому уравнению; поэтому если в изотропной
непроводящей среде каждая компонента uXtVtZ является функцией только г.
то она должна удовлетворять следующему уравнению в полярпых коорди-
координатах:
~дГ2 ь '' u*.v.z--pr0
где г.'2 = ([л,е). Пусть w = ruXtViZ, тогда
В § 4 гл. XIII было показано, что решением этого уравнения будет
w = rux, v,t = fl[t- (V-Ф'2 г] + /я [t + (И1/2 г]. A4.4)
Как и в решении A3.25), первый член означает расходящуюся волну,
а второй — сходящуюся волну. Дифференцируя уравнение A4.2) последова-
Излучение электромагнитных волн 461
тельно по х, у и z и меняя порядок дифференцирования, мы придем к выводу,
что производные и по х, у и z также являются решениями уравнения A4.3);
поэтому решение уравнения A4.2) можно представить в виде
, у. г
{ Т /l V ~ (И1/2 Г] + | U Г* + Ы1/» Г] } . A4.5)
Это решение позволяет написать выражение для поля, создаваемого любым
электрическим мультииолем с изменяющимся во времени моментом. При
¦г—>0 вблизи начала координат электрический потенциал должен совпадать
с электростатическим потенциалом, приведенным в § 8а гл. I. Таким образом,
скалярный потенциал вблизи начала координат и соответствующий вектор
Герца для мультиполей единичного момента, описанных в § 8а гл. I,
в частном случае, диполя и линейного квадруполя, ориентированных в на-
направлении z, будут, согласно соотношениям A4.5) и A3.7), равны
], («.в)
Поле излучения поверхностного квадруполя не определяется однозначно
электростатическим потенциалом: оно зависит от направления токов, текущих
между зарядами. В случае совершенно симметричного квадруполя получаем
Z= -i
Нетрудно заметить, что из девяти вторых производных независимыми
между собой являются только шесть, так как порядок дифференцирования
можно менять. Каждый из этих секторов после умножения на произвольную
постоянную можно рассматривать как компоненту некоторого квадруполя
общего вида, момент которого является симметричным тензором второго
ранга, каким, например, являлась диэлектрическая проницаемость среды,
рассмотренная в § 20 гл. I. Аналогично и моменты мультиполей более
высоких порядков являются тензорами более высоких рангов. Более полное
изложение этих вопросов содержится в книге Стрэттона. Заменяя В на Е
и [аеЕ на В, можно из поля электрического мультиполя получить поле ана-
аналогичного магнитного мультиполя (см. § 11 гл. VII).
Наиболее важным видом мультипольного излучателя является электри-
электрический диполь, момент которого мы обозначим через mcosiui. Из соотноше-
соотношений A4.6), A3.17) и A3.18) получим
Z = ^Гг(г1 cos 6 -6 sin В) cos(urf-pr), A4.10)
-Pr)J, A4.11)
А = (ле^= _-^ (ri Cos 6 - 6 sin 6) sin (ш; - \ir), A4,12)
,-, дАг 3W m ros 0 r ,. йч D •/. ь ., ,л/ло\
E= f==^os^t^ ^^HN (!413)
cos (ш/ ~ '3r) -
A4.15)
A4.16)
462 Глава XTV
Вторая часть вектор-потенгиала, определяемая как А' = — \ Е dt, также
дает магнитную индукцию A4.15). Как уже было указано в § 2, при исполь-
использовании потенциала А', дивергенция которого равна нулю, нет нужды
в скалярном потенциале. Эта форма представления полей получается при
применении соотношения A1.11) к скаляру аи / dz, определяемому выраже-
выражением A4.4).
Если представить себе диполь в виде двух проводников, соединенных
между собой тонким проводом длиной /, так что зарядом на проводе можно-
было бы пренебречь по сравнению с зарядом на концевых проводниках,
то диполышй момент окажется равным m = Ql, где Q — максимальная вели-
величина заряда на одном из проводников. Максимальная величина тока в про-
проводе / равна Ц9, а В- при малых г находится в фазе с током /. Поэтому
для получения поля диполя, ток в котором меняется по закону /cosutf,
необходимо в выписанных выше формулах mm заменить на 11, аи/- на
Ы — (тс / 2). На больших расстояниях от излучателя выражения A4.13) —
A4.15) принимают вид
= -^^-вап(ш«-рг). A4.17)
Мгновенное значение потока излучаемой энергии, согласно выражению A3.23)^
равно
У—: 2vR2 sine dO = |^- sin2 (mt — ^г). A4.18)
S 0 ^
Средняя мощность излучения равна половине амплитуды мгновенной мощ-
мощности, т. е., как следует из соотношения A3.32), для вакуума
— _ f;g /212 _ (.i2/2ff _ я/Ч2 _395/2/2 ... .q
где I и X измеряются в любых, но одних и тех же единицах, Р— в ваттах,
а /—амплитуда тока в диполе—в амперах. Для реальных антенн эта
формула не является точной, даже если не принимать во внимание влияние
зрмли и других близлежащих объектов, потому что ток вдоль антенны
распределен неравномерно; однако ею можно пользоваться при / < X, введя
среднюю неличину амплитуды /. Потери мощности на излучение, кап
и омические потери, пропорциональны квадрату тока, поэтому обычно вводят
понятие сопротивления излучения, определяя его как козффигиент про-
пропорциональности между мощностью излучения и квадратом эффективного
значения тока
ом. A4.20).
§ 4. Запаздывающие потенциалы. Для нахождения решений уравнений
Максвелла (см. § 1 гл. ХШ) часто пользуются методом запаздывающих
потенциалов. Согласно уравнениям A3.14) и A3.15), векторные и скалярные
потенциалы распространяются в однородной диэлектрической среде со ско-
скоростью ([хе)-1/2. Попытаемся написать решения этих уравнений, аналогичные
решениям G.10) и C.28). Дли этого будем считать, что распределение
плотности тока i и плотности заряда р фиксировано в пространстве и меняется
только во времени, отложив рассмотрение движущихся изолированных заря-
зарядов до последней главы. Нам нужно вычислить значение потенциалов А
и W в точке Р в некоторый момент времени t. Сигнал, посылаемый в точку Р
элементом c?v, находящимся в точке ж,, уг, zx на расстоянии г от Р, пройдет
Излучение электромагнитных волн 463
это расстояние со скоростью (|j.s)—xh и, слеповательно, выйдя из dv в момент
времени t — (i^sI'2 r, будет определяться условиями, характеризовавшими
элемент d\ в этот момент времени. Суммируя сигналы от всех элементов,
для потенциалов в точке Р в момент времени t, согласно решениям G.10)
и C.28), будем .иметь следующие выражения:
А<*. у, г, *) = ?
W (х, 2/, z, 0 = ^ ^ ^ Pt'.-y,.»..;-^-] dXl dyi dZi. A4.22)
Поля определяются по этим запаздывающим потенциалам так же, как
и в § 2 гл. XIII. Нетрудно убедиться в том, что выражения A4.21) и A4.22)
действительно удовлетворяют волновым уравнениям, так как подинтеграль-
ные выражения у Ах, Ау, Аг и 47 в точности совпадают с общим видом
решения / [t — ((isI^/•]//•, полученным в § 3 [см. A4.4)].
В свободном пространстве, как следует из соотношений A3.17), А = (is —- ;
поэтому для запаздывающего вектора Герца непосредственно из решения
A4.21) имеем
Z = -G
Но нужно еще убедиться в том, что это выражение не противоречит реше-
решению A4.22), учитывая, что i и р связаны между собой уравнением непре-
непрерывности A3.5). Для получения ЧГ и Z возьмем дивергенцию от Z по коор-
координатам точки наблюдения, так что оператор V будет действовать в выра-
выражении A4.23) только на г. Поскольку г2 = (х — ххJ + (у — угJ + (z — zxJ,
то любая производная от г по координатам точки наблюдения х, у, z равна
взятой со знаком минус соответствующей производной Vx по координатам
точки xv ух, zx элемента источника dv. Вид функции i в выражении
A4.23) показывает, что
где оператор VJ действует только на .хх, у1 и zt и не действует на t или г.
Заменив теперь —^гг на Vr и применяя уравнение непрерывности к элементу
источника в момент времени t — (^sI'2 r, после подстановки в выражение
A4.23) получим
Первый интеграл по объему исчезает, потому что его можно (по теореме
Остроградского—Гаусса) преобразовать в поьерхностный интеграл и выбрать
поверхность вне источника, где i равно нулю. Второй член после интегри-
интегрирования по t принимает вид A4.22), т. е. мы показали, что из выражений
A4.23) и A3.5) можно получить A4.21) и A4.22).
Возможность использования выражений A4.21) — A4.23) зависит от той
точности, с которой можно задать распределение зарядов и токов в источ-
источнике. Если последний представляет собой очень тонкий, идеально проводящий
провод, протянутый вдоль кривой s, то необходимо потребовать, во-первых,
чтобы вдоль провода равнялась нулю ^-составляющая напряженности
электрического поля, определяемая формулой A3.13), и, во-вторых, чтобы
¦464 Глава XIV
•было удовлетворено уравнение непрерывности A3.5), т. с.
" ?s=_^_4^ = u, ^ + |L=U. A4.24)
s ds dl ds ' dt v '
Но поскольку провод бесконечно тонкий, можно приблизиться к нему на
бесконечно малое (по сравнению с радиусом кривизны кривой s) расстоя-
расстояние г, на котором А и Ф определяются по формулам, выведенным для
¦бесконечно длинного прямого провода,
^ A4.25)
Подставляя эти значения в уравнения A4.24) и дифференцируя по времени t
и по длине s, после исключения As и Ф будем иметь
дч ач а-2р д*Р ... „„.
-м^^-дё- d^^ae- A4-26)
Для гармонических во времени процессов решение уравнения A4.26) за-
записывается в виде
/ (S) = Iie> Ы-№ + /ge,- M+pS) A4.27)
Таким образом, ток вдоль провода распределен синусоидально.
§ 5. Излучение линейной антенны. Запаздывающие потенциалы можно
применить при вычислении поля, создаваемого линейной антенной. Введем
цилиндрическую систему координат р, у и z; обозначим через z' координату
некоторой точки антенны, расположенной вдоль оси z между zj[ и zj. Пусть
¦отношение диаметра антенны к ее длине настолько мало, что ток в ней
распределен в виде синусоидальной стоячей волны. Начало координат по-
поместим в той точке антенны (или ее продолжения), где имеется (или должен
бы иметься) узел тока. Таким образом,
/ = /0sinPz'cosurf. A4.28)
Для определения поля можно воспользоваться либо потенциалами, либо
вектором Герца. Однако при употреблении потенциалов более ясно виден
физический смысл условий на концах антенны, в зависимости от которых
ток на конце может равняться или не равняться пулю. Плотность линей-
линейного заряда, согласно выражению A3.5), равна
• о = — ([isI/* /0 cos pz' sin mt. A4.29)
Заметим, что плотность о всюду конечна, поэтому решение применимо
только в тех случаях, когда сосредоточенные на концах заряды не излучают.
Однако, если это необходимо, к полученному решению нетрудно добавить
поле, обусловленное этими источниками. Из выражений A4.21) и A4.23)
для запаздывающих потенциалов получим
1
4та
cos P*' sin (")f - И dz', A4.31)
r
__ Излучение электромагнитных волн 465
где r2 = (z' — zJ + p2. Для определения величины Ег из уравнения A3.13)
положим
sin (чл — р#Л Зи Йи „ , dv D ¦ п ,
dz dz'
Таким образом, из уравнения A3.13) для Ez имеем
22 cou/0 Г cos ft z[ sin (<ot — ВгЛ cos ft Zo sin(<uz — Sr2) 1 /. , nn.
иг" i~~Z~'— I • A4.oz)
Величины 2?р и Н9 можно найти, не интегрируя выражения A4.30) и
A4.31), а подставив в них u — r-^-z'—z и v = r—z' -\-z, откуда rdu = udz'
и rdv = — с dz'. Тогда эти интегралы (Двайт, 401.01) запишутся в виде
Г sin (cot — Rz — fiu) , _,_ Г sm(u)t + Sz — fiv) , A4.33)
— \ —-—rr ¦—аи ^F \ 5——! —dv, '
где верхний знак относится к выражению A4.30), а нижний—к выраже-
выражению A4.31). Заметим, что р входит только в пределы интегрирования и что
\Л —. LA— Р /¦-!/, ч/л
поэтому дифференцирование этих интегралов по р дает
рГ sin(ot — $r+fa') sin (cot — |4r + fo
Приводя к общему знаменателю, подставляя r'2 — (z'—zJ вместо р2, а также
используя формулы для синуса суммы и разности аргументов Ы — fir и
Pz', получаем
Е* = —5 = - ^ [ cos (wf - ^) «in К - cos И - Pz-i) ^n 8 z; -f
+ ^^ sin ((of - \ir2) cos Pz; - ?i-—? sin (tof - prx) cos $z[ 1 , 'A4.36)
#. = 5 _ ~ [sin (tof — pr2) cos pz2 — sin (u>f — firj cos pzj +
+ ^=^cos(o)f —P/^sinPz; —^^cos(o)f-Pr1)sinpz;]. A4.37)
Выражения A4.3i!), A4.36) и A4.37) применимы и к антеннам с отлич-
отличными от нуля нагрузками на концах, но при условии, что излучение от
этих нагрузок отсутствует. Последнее можно осуществить при помощи
заземленных экранов, как, например, в случае антенны, оканчивающейся
коаксиальной линией, изображенной на фиг. 126, а.
На фиг. 126, б и в показаны два типа нагрузок на конце; их действие
учитывается путем добавления к скалярному потенциалу A4.31) запазды-
запаздывающего потенциала, обусловленного зарядом на конце. Если нагрузку
заменить участком антенны, продолженным до ближайшего узла тока,
то заряд на этом участке будет равен заряду нагрузки, так как в них
текут одинаковые заряжающие токи. Проинтегрировав выражение A4.29)
для плотности заряда а от ближайшего узла до z\ и от точки z\ до
30 в. Смайт
Глава XIV
ближайшего к ней узла, мы получим выражения для зарядов Qx в точке z[
и (?2 в точке z'2:
Q\ = — ы~х10 sin fizj sin Ы, Q2 = m~1I0 sin ftz'2 sin int.
Если нагрузки сосредоточены на малом участки антенны, то их можно
рассматривать как точечные заряды. В этом случае к скалярному потен-
потенциалу A4.31) нужно добавить соответствующий запаздывающий скалярный
потенциал вида
Д 47 = 7° [ shl ft 4 sin (юг — pr2) _ sin p 21 sin (mt — prt) "I A4 38}
4iXU)? L r2 rl J
Соответствующие добавки к полям Ez и Ef окажутся равными
A4.39)
-rin К
Магнитное поле, определяемое выражением A4.37). не претерпевает изме-
изменений. Интересно отметить, что при-
приводимые Стрэттоном вычисления Бех-
мана для поля линейного осциллятора
(в них используется вектор Герца) при-
приводят к наличию нагрузки такого типа
на обоих концах антенны.
Если концы антенны совпадают с уз-
узлами тока, то, как следует из выраже-
выражения A4.28), [iz[ и [iz!2 должны быть
равны тхк и m2ic, где т1 и т2 — поло-
положительные или отрицательные целые
числа; соответствующие же косинусы
будут равны (—l)mi и (-—1)тз. В этом
случае поля, определяемые выражениями
A4.32), A4.36) и A4.37), можно запи-
записать в более простом виде, а именно:
в
(-ir^siiKW-
j —z)sin(cot —
( —l)
mi
14
A4.42)
-^a)]; A4.43)
здесь m2 — m1 = n — число пучностей тока, укладывающихся вдоль антенны.
Пусть антенна имеет длину 21, один ее конец (а) находится в точке
z' =—/, а другой (Ь) — в точке z' = /; возбуждение происходит в центре;
частота колебаний произвольная, и хотя на концах всегда имеются нули
тока, на самой антенне может ие существовать ни одной пучности тока.
По формулам A4.32), A4.36),* A4.37) найдем поля, создаваемые каждой
из половин антенны в отдельности, а затем сложим результаты. При
этом при вычислении величин, относящихся к концам а и Ь, положим
Z1 — О, Z2 — L,
— Га
[Z — 2. =1\ COS I
z — z'2 = r2 cos S;
¦ z., = r9 cos (
Излучение электромагнитных волн 4(>7
Углы б, Ва и бь отсчитываются от положительного направления оси z.
Подставляя эти значения в формулы A4.32), A4.36) и A4.37) и учитывая,
что й) = ф, получим
„ _с(л/0 Г sin (cot — Brra) sin(coi —Br^ 2 cos p* sin (mi — 6r)
Ea = Г ° [2 cos б cos p/ sin (iat — fir) — cos 6a bin (wt — fira) —
— cos бь sin (id* — $rb)], A4.45)
В„ = у-9- [2 cos pZsin (ш^ — fir)— sin (Ы — fira)— sin (mt — fir,)]. A4.46)
Заметим, что амплитуда тока может достигать максимального значения /0
в любой точке в пределах антенны за исключением ее концов.
§ 6. Поля на больших расстояниях от линейной антенны. Получим
теперь диаграмму направленности излучения на больших расстояниях от
линейной антенны длиной 21, возбуждаемой в центре генератором произ-
произвольной частоты. Ток на концах антенны будем считать равным нулю.
/\
/' \
\ /
/' V
ч/
Фиг. 127.
Выражение A4.46), положив в нем ra = r-\-l cos б, rb = r — l cos 0 и p = rsm9,
можно записать в виде *
П („г.\Ч2 /Г M-Zq [cos 67 — cos (rfil cos 6)] sin (<oi— pr) ... ,?,
но из соотношения A3.145) следует, что средний по времени поток энергии,
излучаемой в /--направлении, равен
П = ^ IЕ* 11н* I = j г'*12 ?"/21в* I2- A4-48>
Если антенна является резонансной ^ и имеет в центре пучность токат
т. е. 2р/=да:, то совершенно ясно, что, изобразив П в виде радиус-вектора
в полярной системе координат, мы получим, что число максимумов и мини-
минимумов в результирующей кривой соответствует числу узлов и пучностей
в стоячей волне тока. Пунктирная кривая изображенная на фиг. 127,
относится к случаю п = 3. Полная излучаемая мощность равна интегралу
от П ио сфере большого радиуса с центром в начале координат. Вычислим
этот интеграл только для случая резонанса. Подставив п-к/2 вместо р/ и
выразив квадрат знаменателя в выражении A4.47) по формулам двойного
]) Резонансной антенной называют иногда антонну, реакттшое сопротивление кото-
которой равно нулю. В этом случае длина резонансной антенны оказывается, вообще говоря,
слегка отличной от rik/2. См. далее стр. 472. — Прим. перев.
30*
458 Глава XIV
угла (Двайт, 404.22), получим
8л ) 1 — cos2fi v '
0
Обозначив теперь cos 6 через й и разбив при помощи разложения на эле-
элементарные дроби этот интеграл на два, мы убеждаемся, что полученные
интегралы равны между собой (для этого в одном из них переменную ин-
интегрирования и надо заменить на —и):
+1 +1 +1
f 1 + cos пни , Г 1 ^ cos пни , С 1 -j- cos пни ,
\ ~iT7i r~ au+\ ~t —— du = \ ^ du.
j 2A —«) л 2A + и) J 1+и
-i -i -i 9
Положим v = итг A -f и), тогда выражение A4.49) можно записать в виде
^^ ^ c)], A4.50)
где Ci Bити) — интегральный косинус, таблицы которого имеются у Янке
и Эмде, а С = 0,5772. Подставляя численные значения, для сопротивления
излучения получим .
4 72430130аF28 A4.51)
При п=\ оно равно 73,13 ом. В § 10 будут получены формулы для со-
сопротивления излучения антенны, у которой распределение тока не имеет
пучности в точке возбуждения.
Предположение о бесконечной тонкости антенны составляет только один
из недостатков приведенного выше рассмотрения задачи. Для поддержания
постулированного режима стоячей волны в антенне необходимо в каждый
ее элемент поставлять энергию, компенсируя расходы на джоулевы потери
и на излучение. Причем если первые максимальны в центре антенны,
где максимален ток, то, как нетрудно видеть из выражений A4.41) и A4.43),
последние достигают наибольшей величины вблизи кондов антенны. Таким
образом, очевидно, что, во-первых, невозможно при помощи возбуждения
п одной точке поддерживать данное распределение тока вдоль всей антенны
и, во-вторых, что для восполнения потерь энергии в антенне должна при-
присутствовать затухающая бегущая волна, в которой нет узлов и которая
излучает совершенно по-другому, чем стоячая волна тока. Грубую качествен-
качественную оценку влияния уменьшения амплитуды тока вблизи концов антенны
можно получить, например, взяв суперпозицию полей, созданных двумя ан-
антеннами, в одной из которых возбуждаются колебания первого типа (/г=1),
а в другой — колебания третьего типа (и = 3). Если частоты и амплитуды
этих колебаний совпадают, то в результате получится поле, создаваемое
линейной антенной длиной ЗХ/2, в которой амплитуда тока в центральной
полуволне в два раза превосходит амплитуду тока в крайних полуволнах.
Используя выражение A4.47) и считая р/ = итг/2, после некоторых- упро-
упрощений (Двайт, 403.23) получим
В, = fo6)V» Е, = Ji^o cos (I^cose) cos (.cos») s.n ( _ g (М 52
vr ' sir sin 0 \ i / \ /
Диаграмма направленности, вычисляемая нутом подстановки выражения
A4.52) в A4.48), пзобрагкена на фиг. 127 сплошной кривой. Мы видим,
что, хотя амплитуды крайних полуволн такие же, как и раньше, однако
величина крайних лепестков сильно уменьшилась, а центрального лепестка
увеличилась в 4 раза.
Малу\шние электромагнитных волн 469
§ 7. Излучение бегущей волны. Рассмотрим волну тока о постоянной
амплитудой /Ocos(u>? — Cz'), бегущую вдоль провода от точки z'=—/'2
к точке z' = -\-1/2, где она полностью без отражений поглощается. По фор-
формуле A4.21) -поле, создаваемое в точке х, у, z на больших расстояниях
r=(p2 + z2I'2 от антенны, равно
где r'= [(z —z'J +p2Y^^r— z' cos6 и p = rsin 6. При г' >/ членами порядка
r~2 можно пренебречь, и тогда (Двайт, 401.11)
в _y.I0 sin6sin(<Bf —fo-) sin [|pZ(l-cos 0)]
2-кг 1 — cos 6
53)
Среднюю излучаемую мощность можно получить путем интегрирования
выражения A4.48), а именно:
Заменив [3/A—cos 6) на и и используя формулу D03.2) из справочника
Двайта, получим
2pl - 2pi
С 1 —Cos'm , If/,,
du-W \ d-
о о
Первый интеграл выражается через Gi 2pZ (см. Янке и Эмде, стр. 98),
так что подстановка численных величин и замена [3 на 2т:/Х окончательно
приводит к следующему выражению:
Р = 30Р0 [2,108 +In l + Ci^ + ^^J - A4.55)
§ 8. Коническая линия передачи. Формулы A4.44) —A4.46) дают
поле излучения, создаваемое линейной антенной, возбуждаемой в центре,
а формула A4.51) определяет сопротивление излучения такой антенны для
случая, когда пучность тока совпадает с точкой возбуждения. Но из рас-
рассмотрения бесконечно тонкого провода нельзя получить никаких сведений
о реактивном сопротивлении антенны, так кап самоиндукция провода на
единицу длины равна бесконечности. Если же для избежания этой труд-
трудности радиус провода принять отличным от нуля, то вычисление реактив-
реактивного сопротивления все же окажется затруднительным вследствие появле-
появления бесконечной емкости в бесконечно узком зазоре на входе антенны.
Шелкунов сумел преодолеть обе трудности путем рассмотрения бикониче-
ской антенны, состоящей из двух конусов, вершины которых находятся
в точке возбуждения. Для простоты изложения про дискутируем сначала
вопросы, связанные с конической линией передачи.
Волновое уравнение в сферической системе координат, описывающее
волну с круговой частотой ш, согласно § 2 гл. XIT1 и соотношениям C.17),
A3.131), имеет вид
(> ) ^ 0 A4.56)
Чтобы разбить это уравнение на два, приравняем первую и вторую пары
членов по отдельности нулю и получим уравнения E.87) и A4.2), где
470
Глава XIV
Г2 = у2/иJ. Но из решений E.88) и A4.4) для расходящейся полны имеем
W = r-lV(B, <p)e-«-Cos(otf — \ir), A4.57)
где х — коэффициент затухания, а р — волновое число
U (О, 9) + }Т(В, ?) = /-( (e^lg-*-O). A4.58)
Лектор-нотеициал для волны поперечно-электромагнитного ноля ТЕМ равен
Л = V X vW = — г1 х V2Fe-°r cos (mt — Qr) = V2C^e~cir cos (Ы — $r), A4,59)
где V2 имеет только 6- и ср-составляющие. По форме это выражение совпа-
совпадает с выражением A3.118); это свидетельствует о том, что при прило-
приложении переменного потенциала к вершинам двух юга нескольких идеально
f
ZR,
В
ER,
Фиг. 128.
проиодящих конусов,' поверхности которых образованы путем вращения
радиус-вектора, вдоль этих конусов будет распространяться сферическая
волна, эквивалентная плоской волне, распространяющейся вдоль цилиндри-
цилиндрической линии передачи, задаваемой уравнением
a; = cos®tg-^-0, у = sines tg -^ 6, z = r. A4.60)
Рассмотрим теперь частный случай двух круговых конусов с углами при
вершинах, равными Ъул и 2у2, оси которых пересекаются, как это пока-
•аано на фиг. 128, под углом 2ф. Стереографическая проекция линий пере-
пересечения этих конусов со сферой радиуса г на тангенциальную к ней пло-
плоскость (см. § 21 гл. VI) приводит к эквивалентной линии передачи, со-
состоящей из двух цилиндров радиусов R1 и R2 с расстоянием между
осями D; поперечное сечение линии показано на фиг. 32, б. Из фиг. 128 следует
Беря отношение этих равенств, применяя формулу (Пайерс, 602) и затем
разрешив относительно Z)/B/?li2), найдем
D Ешф A46])
2 К
1,2
] ,2
Емкость (на единицу длины) эквивалентной цилиндрической линии, согла-
согласно соотношениям D.71) или D.69), равна (при x = Xi —Хг или Xi ^ Хг)
С
е 1
или -?г = 7Г
С In
— sin27i—б1
~ ^
2 sm Xi sinxs
/л/ со\
A4.62)
Излучение электромагнитных волн 471
Знак минус соответствует двум вложенным друг в друга конусам, в про-
противном случае надо употреблять знак плюс. Согласно выражению A3.135),
волновое сопротивление равно
z *f^iY/2 = ^L^, A4.63)
с
где |х — магнитная проницаемость, г — диэлектрическая проницаемость, а
1 — проводимость окружающей конус среды.
При <1>=х/2, беря, для простоты, направление 6 = 0 за ось одного
ил конусов, мы получаем, что U не зависит от координаты ср, и, положив
в выражении A4.58) F(и) равным Clnu, из соотношения E.157) найдем
гттг In tg @/2) _ Qo (cos 6) ,, „,
где разность потенциалов между конусами и емкость на единицу длины
соответственно равны
= т.г (hi ctgyx) • A4.65)
§ 9. Бпконическая антенна. Если оба конуса в бикопической линии
передачи имеют конечные размеры, то они образуют биконическую антенну.
Независимо от того, замкнуты ли концы конусов сферической оболочкой,
или открыты, целесообразно решать задачу, о вычислении ноля как крае-
краевую задачу в сферической системе координат (см. § 13). Этот метод осо-
особенно хорошо использовать для конусов с углами при вершинах, близкими
к U или к 180°. В случае малых углов численные результаты можно найти
и другими методами.
Возьмем два идеально проводящих коаксиальных конуса одинаковой
длины, у которых угол при вершине 2у настолько мал, что распределение
тока, согласно соотношенпям A4.24) и A4.27), можно записать в виде
i = /0 cos wit sin (PZ — Pr). A4.66)
Тогда поля определяются по формулам A4.44) — A4.46), а излучаемая мощ-
мощность находится путем интегрирования вектора Умова — Пойнтинга по поверх-
поверхностям конуса. Пусть уа, у, у^ь — углы, под которыми виден из точек
z=~l, z = Q и z~l соответственно радиус конуса р, оканчивающийся
на поверхности конуса на расстоянии /• от его вершины. Пользуясь выра-
выражением для вектора Умова — Пойитинга A3.23), а также теоремой о цир-
циркуляции Н G.2), для мгновенной мощности, излучаемой обоими конусами,
получим
I I
: (Ez cos у + Ef sin у) dr. A4.67).
Подстановка выражений A4.44) для Ег, A4.45) для Е9 и A4.66) для i
дает
" I'OS ffl
где Sa — sin (wt — $ra) и Sb = sin(wt — $rh). Члены, содержащие cosp/, исче-
исчезают, потому что p=rsin^. Поскольку угол у_ выбран малым, ю га и гь
можно заменить на 1-\-г и / — г, a cosya, cos/ и i-us)rb считать равными
единице. Если ^"а я Sb разбить на множители, то при помощи формул
472 Глава XIV
D01.05) —D01.07) из справочника Двайта для 2кР (ф/-2)-1 будем иметь
(-6
sin 2ш . , , - . , , . , . „, . , ^ . . , . ., г,, i ,
I — г ¦ г , > — R) \ аг —
(—8
COS2 4>t
где Л = 2рг, a L=2p/. Величины 8 и 8' нужно положить равными нулю
всюду, где это не приводит к появлению бесконечных членов. В книге
Янке и Эмде можно найти формулы для интегральных синусов и косинусов
а а
С sin Ах , _. . С 1— cosAk , ,, , , . . . ,i. , Л .
\ —-— ах = Si (Аа), V dx = С + In (Aa) — Ci (Aa),
о о
где С = 0,5772. При помощи этих формул легко проинтегрировать выраже-
выражение для мощности, и поскольку In 8 и In 8' выпадают, то все члены оста-
остаются конечными. Таким образом,
р =
+ ln (PZ)] cos BpZ) + [Si DpZ) - 2 Si {2Щ sin BpZ)}. A4.68)
Сравнение с выражением A0.14), где Щ'1 заменяется на I^Z2, показы-
показывает, что коэффициент при Ilsin2wt равен 2Zrsinty или 2ХГ, где Хг —
реактивное сопротивление излучения, а коэффициент при I\ cos2 u>2 равен
Zrcos^ или Rr, где Rr — сопротивление излучения. Если в точке возбужде-
возбуждения находится пучность тока BpZ = mr, где и —нечетное число), то вели-
величина Rr имеет то же значение, что и в выражении A4.51). Если же
в точке возбуждения находится узел тока и п — число четное, то резуль-
результат получится другой, потому что при получении выражений A4.66)
и A4.67) направление тока в обеих половинах антенны предполагалось
одинаковым, в то время как при выводе соотношения A4.50) токи счита-
считались текущими в противоположных направлениях.
Несмотря на то, что мощность потерь в антеннах уже определена,
еще ничего не известно о том, где нужно подключить антенну к линии,
чтобы получить правильное значение входного импеданса1). Из распреде-
распределения A4.66) следует, что Ну, а следовательно, и мощность потерь обра-
обращаются в нуль в узлах тока; поэтому нельзя подсоединять линию к кон-
концам антенны. Чтобы найти наиболее простым способом место подключения,
нужно рассмотреть случай, когда идеально проводящая антенна настроена
так, что поступающая в нее мощность расходуется только на излучение.
Тогда в точке возбуждения находится пучность тока $1 =-^ {2п-\-\) к ,
а амплитуда входного тока равна /0. Подставляя ее значение в уравне-
уравнение A0.106) и полагая коэффициент затухания равным нулю, для входного
г) Непраьидьиая постановка задачи. Вопрос о распределении мощности потерь
на излучение ьдоль антенны, строго говоря, не имеет смысла. При правильной поста-
постановке задача заключается в определении входного импеданса антенны и в согласовании
последней с соответствующей Ливией передачи.—Прим. перее.
Излучение электромагнитных волн
473
импеданса и для средней затрачиваемой мощности получим
Z. = Z~A P = ^ZJl, A4.69)
где Zt — импеданс нагрузки. Но формула A4.68) для средней мощности
дает (ZrP0)/2, поэтому для настроенной антенны ZrZt = Zk- Попытаемся
использовать это значение в уравнении A0.106) для определения входного
импеданса ненастроенной антенны, и для доказательства справедливости этого
0
о
8
4 5 6
гт/х
Фиг. 129. Зависимость действительной части и мнимой части
Z?/Zr от величины 2к1/\.
покая^ем, что в случае тонкой антенны величина активной мощности согла-
согласуется с формулой A4.68). Таким образом,
cos CZ + /Z,. smp/
Zrcos
A4.70)
Пусть теперь импульс Zh очень велик, что имеет место для очень тонкого
конуса, входной ток которого равен /osin[3Z, а входная мощность, согласно
соотношению A4.69), равна
^(l):. A4.71)
Отсюда активная мощность, как это и должно быть, получается равной
(RTIl)/2. Заметим, что формулу A4.70) можно получить из уравне-
ния A0.106), если в пей заменить $1 на pZ—(тс/2) и ZL на Zr. Но это
эквивалентно укорочению длины линии на Х/4 и использованию Zr в каче-
качестве импеданса на конце. Таким образом, эффективное местоположение
импеданса излучения1) находится на расстоянии Х/4 от конца линии.
На фиг. 129 показана величина, обратная импедансу излучения, в том виде,
в каком она приведена Шслкуновым2).
1) То есть та точка, где импеданс излучения антенны ранен ее входному импе-
импедансу.— Прим.. перев.
2) Sohelkunof i, Proc. Inst. Rad. Eng., September, 493—521 A941).
47i Глава XIV
Из формулы A4.70) ясно, что резонансная длина волны, при которой Z^
является чисто действительной величиной, зависит от реактивного сопро-
¦v
тивления излучения, но при \Zh\ > Хт она находится вблизи 28/ = тт.
§ 10.- Сложные антенны. Линейная антенна имеет симметричную диа-
диаграмму направленности относителыю оси. Для концентрации излучения
к одном направлении требуется «направленная система», диаграмма кото-
которой формируется при помощи нескольких, обычно одинаковых излучателей
длиной 21, расположенных параллельно друг друг}'. Амплитуды и фазы
токов в антеннах могут быть различными. Пусть излучатели расположены
параллельно оси z в положительном октанте прямоугольной системы коор-
днггат в виде решетки, расстояния между двумя близлежащими элементами
которой в направлениях осей х, у и z соответственно равны а, Ъ и с. Рас-
Расстояние от начала координат до излучателя, характеризуемого целыми чис-
числами и, v, w, определяется выражением
ruvw = *и« + №*> -f кшс. A4.72)
Обозначим радиус-вектор, проведенный из начала координат О в очень
удаленную точку наблюдения Р, через гг^, тогда ра.шость путей прохожде-
прохождения сигналов из точки О в точку Р и от излучателя uvw в точку Р будет
Г1"гшж- Предположим, что размеры системы малы по сравнению с г и что
при вычислении амплитуды поля в точке Р все излучатели можно рас-
рассматривать расположенными на одинаковом расстоянии от точки Р. Если
колебания в антенне uvw отстают по фазе от колебаний в антенне 000
на фазовый угол ф1ГОЮ, а ток в ней равен 1№Ш„ то, согласно соотноше-
соотношению A4.47), вклад этой антенны в поле Bv, создаваемое в точке Р, будет
определяться реальной частью следующего выражения:
—cos
2кг sin 6
нг)го_р(г_Г1 -ггшш)]
Обозначая первый мпожитсль через Fmw, для всей системы в целом,
получим
В, = (И1'2 !„ = е~*г 2^2 V'P'rW W . A4.73)
uvw
В случае одинаковых излучателей множитель F постоянен, и эта формула
упрощается. Пусть в направлениях х, у и z каждый последующий излу-
излучатель имеет по сравнению с предшествующим постоянный сдвиг фазы,
равпый соответственно ?, т] или С. Тогда тройная сумма в выражении A4.73)
распадается на произведение трех сумм:
uvw
= F 2 ey"(Pri-ia-;) 2 e^V^) 2 e^Vkc-'> . A4.74)
uvw
Каждый ряд представляет собой геометрическую прогрессию, и его можно
просуммировать (см. Двайт, 26):
¦ !_ 1
'i-lL e-iWbr-w t A4.75)
Излучение электромагнитных волн
475
где тх — номер осциллятора в направлении х. Из выражения A3,146) для
среднего
поэтому
значения вектора Умова — Пойнтинга имеем у
a — 6I sin2
, ¦ jb—Q] siu»
b—v))] sin2 [V2
g
Кап уже было сказано, система предназначается для концентрации излу-
излучения в определенном направлении. Коэффициент направленного действия
или выигрыш системы G определяется как отношение максимальной интен-
интенсивности излучения Фдг к интенсивности Фо, усредненной по сферической
поверхности большого радиуса, концентричной с излучающей системой.
Выигрыш, выраженный в децибеллах, мы будем обозначать через Gd.
Итак,
*" A4.77)
'АГ
Функция выигрыша GF, <p) для любого направления является отношением
Ф (б, ср) к Ф,,. Например, для иолуволиовой антенны, как следует из соот-
соотношений A4.48) и A4.50), отношение максимальной интенсивности к
Фиг. 130.
средней равно 4 [In Bjt) -\-C — Ci Bж)\~1, что дает для экваториальной плоско-
плоскости ?=1,64 или Cd = 2,15 дб. Нормированная диаграмма направленности
есть поверхность
G@, ф) Ф(й, ф) ., . „о.
г = —-=т-- =—ж—*-- • A4.78)
м м
Рассмотрим теперь частный случай системы, состоящей из т одипа-
ковых п-полуволновых антенн, колеблющихся в фазе и находящихся па рас-
расстоянии Х/2 одна от другой. Положим my = mz—l, E=0, ра = рХ/2 = тг
и р/=птг/2, так что в выражении A4.76) Si-j-ia = jt cos <p sin 6, и поэтому
" cos A/2ил cos 6) 2 Г sin A/2тл cos 9 sin 0) 2
sin 0
cos Ф si
A4.79)
Такая система называется антенной тина бродсайд (broadside array), так
как при ср = тг/2 второй множитель в выражении A4.79) максимален, и, сле-
следовательно, максимум диаграммы направленности антенны лежит в плоскости,
перпендикулярной оси системы. На фиг. 130 показаны относительные зна-
значения 11 в плоскости 6=0 (дополнительные максимумы отгущены). Около
максимума синусы, входящие во второй множитель, малы, поэтому этот мно-
множитель равен т2. Однако отсюда нельзя сделать вывод, что при равенстве
полных мощностей излучение системы в этом направлении в т раз больше,
чем излучение одиночного осциллятора, потому что излучатели взаимодей-
взаимодействуют между собой. Для определения действительного выигрыша нужно
подсчитать Фо. Заметим, что из соотношения A4.75) следует, что послед-
последний множитель в выражении A4.79) можно, введя а — п cos <p sin 6, запи-
записать в виде
m—1 т—1
sin Vz"
2«
p=0
= т-\-2 ^ (m-p)cospa.
476 Глава XIV
Преобразуя косинус по формуле D15.02) из справочника Двайта, интегрируя
по ср (Двайт, 854.1), а затем объединяя члены, не зависящие от б, получим
иг—1 2те
2ямг + 2 (т~ Р) \ cos (Рп cos 9 sin Щ d<p =
т—1 со
- 2тг Г т2 + У V (m-rt(/>s'"eJs I
Для определения излучаемой мощности это выражение надо умножить
на оставшийся множитель в выражении A4.79) и на r2sm6d6, а затем
проинтегрировать в пределах от 0 = 0 до б = тг. Первый член уже был про-
проинтегрирован в § 6. Другие же интегралы имеют вид
^^^ ^ [I ~t-cos(n*cos0)]
о о
В результате интегрирования получим (см. Двайт, 854.1)
2y-i/8
B,-1)! + "SF
Суммироваьше по ^ в первом члене приводит (Двайт, 442.11) к результату,
выражаемому через интегральный косинус (Янке и Эмде, стр. 98). Таким
образом,
со ртс
о VI ( — i)s(pKJs о С 1 —C0S3?
2Z ^Й = ~2 J —
= ~2 J
О
s=l 0
Объединяя все члены, для полной излучаемой мощности получим
Р = ^|? J т*С + т2 In Bnir) — m2 Ci Bmr) -f
m—1 со
+ 4 2 (»*-/>) \&(рк)-С-1п
[
V=i s=l
Из соотношений A4.77) и A4.78) выигрыш в децибеллах получается равным
10lg[l/г\).cI2m2j(nP)\. Для п=1, т = 2 отношение Фм/Ф0 равно 3,81, что
более чем в два раза превышает Фм/Ф0 у полуволновой антенны. Выигрыш
равен 5,81 дб.
§ 11. Влияние земли. Диэлектрические или проводящие тела, нахо-
находящиеся вблизи антенны, оказывают влияние на нее и искажают ее поле.
Чаще" всего таким телом является поверхность земли. Для волн, близких
к сферическим, можно применить законы отражения и преломления на
границе раздела с проводящей средой, полученные в § 14 гл. XIII. Если
же антенна расположена вблизи поверхности, то определить угол падения
очень сложно, и пользоваться этими законами затруднительно. Часто,
однако, поверхность можно считать плоской и идеально проводящей. Тогда
поле над ней останется неизменным, если эту идеально проводящую плос-
плоскость заменить второй, антенной, представляющей собой отражение первой
и расположенной и ориентированной таким образом, чтобы результирующее
электрическое поле было нормально к поверхности земли. Если все первона-
первоначальные антенны располагались перпендикулярно или параллельно земной
поверхности, то результирующее поле, очевидно, можно вычислить по фор-
формулам предыдущего параграфа.
Излучение электромагнитных волн . АП
»
§ 12. Единственность решения. Прежде чем находить решения волно-
волнового уравнения, соответствующие данной краевой задаче, следует опреде-
определить, какие величины надо задать, чтобы решение было единственным.
Рассмотрим область, не содержащую источников и ограниченную изнутри
поверхностями «S^, ..., Sn, а снаружи поверхностью So. Пусть е, [j. и f
являются функциями координат, по не зависят от напряжешгостей попей.
Предположим, что два решения уравнений Максвелла Е, В и Е', В' совпа-
совпадают между собой в любой точке области при t = 0. Теорема Умова — Пойн-
тинга (§ 3 гл. XIII) и закон Ома для разностных полей ДЕ = Е—Е',
ДВ = В — В' и т. д. дают следующее соотношение:
Чтобы поверхностный интеграл равнялся нулю, должно выполняться равен-
равенство
ДЕхАВ-п = ДВхп-ДЕ = пХ ДЕ-ДВ=0.
Таким образом, если п X ДВ или п х ДЕ равны нулю при t > 0, то поверх-
поверхностные интегралы исчезают. Член в квадратных скобках либо равен
нулю, либо положителен, но при t — 0 он был равен пулю, поэтому если
он вообще меняется, то он должен становиться положительным. Но пер-
первый член в левой части тоже либо равен нулю, либо больше нуля. Сле-
Следовательно, подинтегральное выражение равно нулю, т. е. ЬЕ = ДБ = 0.
Таким образом, решения Е, В и Е', В' одинаковы и полностью опреде-
определяются начальными значениями полей внутри области и тангенциальными
компонентами Е или В на поверхности, ограничивающей эту область, задан-
заданными для любого момента времени t > 0. Практически обычно имеют дело
со стационарными решениями задачи; в этом случае значения величин
в какой-нибудь момент времени полностью определяют значения этих величин
во все предшествующие моменты времени.
§ 13. Решения волнового уравнения в сферических координатах.
В изотропной непроводящей среде на расстояниях, значительно превыша-
превышающих размеры источника, все волны являются сферическими. Поэтому
в задачах об излучении наиболее полезной формой решения волнового
уравнения является решение в сферических координатах, имеющее вид
суммы произведений ортогональных функций, взятых с коэффициентами,
определяемыми заданными граничными условиями. Как мы видели
в § 2 гл. XIII, полное поле излучения в этом случае описывается вектор-
потенциалом, дивергенция которого равна нулю и который можно выра-
выразить,"как было указано в § 2 гл. XI, через два решения Wte и Wlm
скалярного волнового уравнения, т. е. если, согласно уравнению A1.12),
tm, A4.81)
то решение первого уравнения определяется через решения остальных
по формуле
VW VWJ. A4.82)
Заметим, что решение, соответствующее Wte, приводит к всктор-нотен-
циалу, а следовательно, и к электрическому полю, направленному перпен-
перпендикулярно к г. Эти ноля называются поперечно-электрическими волнами
и отмечаются индексом te. По формуле A1.14) вектор магнитвой индукции
будет равен
В = _ V X (|шо*г1-Г,т+ г X VIFfc). (I i.83)
478 Глава XIV
Отсюда видно, что магпитное поле, определяемое из W(m, ориентировано
нормально к г, поэтому эти волны называются поперечно-магнитными.
Уравнение A4.81) решается так же, как и в § 6 гл. XI, по только для
большей общности мы добавим множитель Ф(г-р):
# = г-1/2/Т(г)вF)Ф(9). A4.84)
Подставив выражение A4.84) в A4.81), получим для R дифференциальное
уравнение A1.53), для в — уравнение E.102), а для Ф — уравнение й2Ф/й<р2 =
— — т2Ф. Таким образом, если полошить и = cos б, р = оз((леI/2> то решение
для W запишется в виде
W = [ЛРЪ (и) + BQ™ (и)] [Cjn (рг) + Ъ\ (/{Jr)] cos (т9 + 8 J. A4.85)
Сферические функции Бесссля обозначепы здесь так же, как и в § 32
и 38 гл. V, а именно:
/„ (Рг) = *Ч* Bpr)~V2 Jn+1/2 (pr); кп (/рг) = (| /«Pr)~1/S Kn+lh (/рг)- A4.86)
Первая функция в комбинации с множителем е'иЯ представляет стоячую
волну, а вторая, в зависимости от того, является ли п положительным
или отрицательным числом, представляет соответственно расходящуюся
или сходящуюся волну.
§ 14. Разложение плоской волны по полиномам Лежандра. Для
удовлетворения граничным условиям на сферических поверхностях часто
бывает необходимо иметь разложение плоской волны по функциям A4.85).
Хотя для простоты мы будем рассматривать волну, распространяющуюся
вдоль оси 6 = 0, однако полученные ниже результаты можно отнести
и к волнам, распространяющимся вдоль любых других осей. Из выраже-
выражений A3.132) и A3.133) можно видеть, что координата z = rcosO, будучи
умноженной на Г, входит в формулы для плоских волн только через пока-
показатель экспоненциальной функции. Поэтому в качестве коэффициента перед
Р„ (cos 6) при разложении в ряд по полиномам Лежандра нужно взять
охр [Г г cos 0]. Из выражения E.130)
+1
Тг)" J е^и A - u2)" du. A4.87)
—i
Разложение в ряд экспоненциальной функции (Двайт, 550) дает
со v +1
При s-нечетных этот интеграл равен нулю; поэтому заменим s на 2т
IX, взяв пределы интегрирования от 0 до 1, поставим перед интегралом
множитель 2. В знаменателе этого выражения вместо Bт)! можно написать
22т/н! тг-^зГ {m-\-lj2) (Двайт, 850.7 и 855.1), тогда при помощи соотно-
соотношения E.407), заменив п\ на Г(п-|-1), получим
~ _ Bп + 1) я1/2 ^ (I>)i+am Г(то+1/2)Г(п+1)_
т=0
??г=0
Излучение электромагнитных волн 479
При отсутствии затухания Г можно заменить на /(8 и, учитывая соотно-
соотношение E.407), получить
а„ = Bп + 1) Г (-2^I/2 Jn+^ Фг) = Г Bп + 1) /п фг). A4.90)
Таким образом, искомое разложение будет иметь вид
со
0%г = eftr COS в = ^ /" Bп + 1) ]'п (Рг) />„ (COS б). A4.91)
п=0
Для волны e~i$z надо заменить р на — р, или, что то же самое, cos б на
cos (тс — б). Это эквивалентно [см. соотношение E.314) или § 13 гл. V]
введению в правую часть множителя (—1)"
со
е-т = «г-ypr cos е = Д (_ jf Bп + 1) /„ (рг) Рп (cos б). A4.92)
§ 15. Излучение кольцевого тока. Магнитный диполь. Разложение
решений по ортогональным функциям, даппое н § 13, обычно применяется
в краевых задачах, но оно может оказаться предпочтительным и для
источников с заданным распределением тока. Например, на больших рас-
расстояниях от круглой петли, ток вдоль которой распределен равномерно,
поле можно легко найти при помощи метода запаздывающих потенциалов
(см. § 4), но вблизи петли это сделать довольно трудно. Из соображений
симметрии ясно, что такой источник создает только поперечно-электриче-
поперечно-электрические волны, и, согласно выражениям A4.21) и A4.22), эти волны можно
описать, не привлекая скалярного потенциала, при помощи только ср-ком-
поненты вектор-потенциала. Поэтому из выражения A4.85) при г > а мы имеем
Wte = Д АпРп (cos 0) /п (ра)\ (/рг). A4.93)
При г <. а надо переставить местами г и а. Согласно выражению A4.82),
вектор-потенциалы равны
г > а А, = 2 АП (cos б) /„ (ра) \ (/рг), A4.94)
71=0
СО
г<а \= 2 \Pl (cos б) /п (Pr) kn (/ра). A4.95)
Ясно, что эти потенциалы равны между собой при г —а. Кроме того,
поскольку поле должно быть симметричным относительно плоскости 6 = тс/2,
в рядах могут существовать только члены, соответствующие нечетным п,
поэтому п следует заменить на Bт-|-1)- Из выражения A4.27) ясно, что
ток может быть однородным только в случае очень малых Ра, для которых
]пфг) sf (PrJm+1/Dm + 3)!! и кп(/фа) «в D?п+ 1)!! (/Ра)*" при г<а [см. соот-
пошения E.401) и E.472)]. За исключением временного множителя, выра-
выражение 'A4.95) является чисто действительным и совпадающим по форме
с выражением G.71), если а = тс/2, так что оно, будучи умноженным па
costn/, дает значения А$ при г*Са. Учитывая, что, согласно § 16 гл. V
и соотношению E.182), jP^m^j @) = ( —l)mBw +1)И и подставляя найден-
найденные из выражения A4.95) значения Ат в A4.94), получим
ее
г > а Аъ — -г- -7J- (л/ "S
480 ¦ Глава XIV
Для нахождения действительной части от A.fe7wt по формуле E.474) можно
заменить
Re [е^к2т+1 (/>•)] = ( - l)m [ntm?1 (Pr) cos со/ _ /2т+1 @Г) sin о>*].
При больших г, в силу малости [За, всеми членами, кроме т — 0, можно
пренебречь и пг и /х определять по формулам E.395), E.396), E.400)
и E.402). Тогда выражение для Ас принимает вид
А, = -^(л/а2/* sine [cos (mt — $r) — $r sin (ut — $r)]. A4.97)
Если тса2/ заменить на М, то напряженность электрического поля — OAjdt
оказывается равной магнитной индукции, создаваемой электрическим дипо-
диполем [см. выражение A4.15)], а компоненты вектора магнитной индукции Вг
и jBg — равными умноженным на — [ле соответствующим компонентам напря-
напряженности электрического поля, создаваемого электрическим диполем. На
больших расстояниях поле становится равным
cos ((Bi _ рг)> A4.98)
Е, = ((хе)^ Вь =
что совпадает с выражением D4.17), умноженным на чс^аЧ'1, так что излу-
излучаемая мощность" и сопротивление излучения определяются по форму-
формулам A4.19) и A4.20) с учетом квадрата того же множителя
Р = 153 900 а4/2/-; /?г = 307 800 а*Г*. A4.99)
Таким образом, мощность излучения, будучи выраженной через ток
в антенне, оказывается обратно пропорциональной четвертой степени длины
волны, тогда как в случае линейной антенны она обратно пропорциональна
всего лишь второй степени X.
§ 16. Свободные колебания проводящей сферы. Приводимые в § 13
решения волнового уравнения можно с успехом применить для изучения
электромагнитных колебаний сферических тел. Как следует из выраже-
выражения A4.82), возможны два типа колебаний: поперечно-электрические и по-
поперечно-магнитные. Исследование выражения A4.85) показывает, что при
Ъ = 0 снаружи сферы будет существовать стоячая волна [см. соотноше-
соотношение E.399)], а при С = 0— расходящаяся волна [см. соотношение E.473)].
Решение Q™ должно быть исключено, так как оно равно бесконечности
при 6 = 0, 0 = тс. В случае диэлектрического или не идеально прово-
проводящего шара поле будет существовать и внутри него. Мы восполь-
воспользуемся суммой решений типа A4.85), взятых пока с неопределенными, но
различными для внешней и внутренней областей коэффициентами. Найден-
Найденные при помощи выражения A4.85) по этим решениям значевия вектор-
потенпиала должны удовлетворять граничным условиям G.118) и G.119),
как это имело место в § 7 гл. XI.
В качестве простого и интересного примера рассмотрим случай идеально
проводящей сферы. Если начальное поле внутри сферы было рашю нулю,
то оно будет отсутствовать и во все последующие моменты времени, так
что потери энергии обусловливаются только излучением. Входящую в выра-
выражение A4.85) неизвестную, вообще говоря, частоту колебаний нужно опре-
определить из граничных условий. Сначала исследуем колебания поперечно-
магнитного типа, могущие возникнуть, например, при перемещении сферы
в статическом электрическом поле. Простейшее колебание соответствует
Излучение электромагнитных волн 481
.-течениям т = 0 и га=1 в выражении A4.85), для которого, учитывая
соотношение A4.82),
= 2 4 { -2-^. (/V) + ^1 И, </М1} ¦
^ »
Условие равенства нулю-тангенциальной компоненты —dA^/dt электриче-
электрического поля при г—а, согласно соотношению E.473), дает
Подставляя в выражение A4.85) найденные отсюда два значения р =
= шр([хеI/2, для Wtmelwt получим
—2}t( s)-xh _-2_____/_.
sinв Аг\ [ —--??— I * °'+3l/2)a + ^ А Г "У 1 e (;-3l/2)a •
A4.102)
При помощи соотношений E.471), E.473) и подстановки
± ^ ^ A4.103)
после объединения произвольных постоянных действительную часть Wtme>iOt
можно записать в виде
Cra sin 0 [31/2 (а — j-) sin (u>t — fir — ф) —
— {a + r)em((ut — fir — ty)e~'Jt+~2a r). A4.104)
Из формул A4.103) и A3.84) видно, что длина волны колебаний равна
7,26а и при прохождении волной расстояния, равного диаметру сферы,
ее амплитуда уменьшается в е раз. Таким образом, колебания очень быст-
быстро затухают, исчезая уже через несколько периодов. Аналогичным путем
можно рассмотреть и колебания поперечно-электрического типа.
Подобный, но только более сложный анализ применим и по отноше-
отношению к вытянутому, сфероиду. Если эксцентриситет сфероида велик, то он
прекрасно апроксимирует собой прямой провод конечной длины.
§ 17. • Вынужденные колебания диэлектрического или проводящего
шара. Формулы, полученные в § 13 и 14, позволяют строго решить задачу
об установившемся процессе дчффракции плоской электромагнитной волны
на однородном шаре. Мы ограничимся случаем, когда шар является иде-
идеально диэлектрическим или идеально проводящим. Пусть плоская волна
распространяется в направлении z и имеет только х-компоненту поля Е.
Тогда из соотношений A3.132), A3.133) и A3.21) для комплексной ампли-
амплитуды напряженности электрического поля, магнитной индукции и вектор-
потенциала, относящихся к этой волне, будем иметь
И Ех и Bv имеют /--составляющие, поэтому для описания полны в сфери-
сферических координатах потребуются и поля ТЕ и поля ТМ. Из выражений
31 В. Смайт
4«2 Глава XIV
A4.82) и A4.83) находим
Аг = Ах sin б cos ср = [V х (г X VW[m)]r,
Ъг = Ву sinflsins=[Vx (гх VW{e)]r.
В разложении A4.92) функция e~^z представлена в виде суммы членов
типа A4.85). Путем дифференцирования по 0 введем множитель sin 0, вхо
дящий в соотношение A4.106):
со
= -п2 (- /Г B« + 1) /„ фг) Pk (cos 6), A4.107)
СО
~i~ 2 (~ ')" Bп + *) /т. (>В/") Р« (cos 6)' A4.108)
СО
^?F2 (-7)BB»+l)/n(P/-)^(cos0). A4.109)
ri=l
Применив оператор A4.106) к /г-му члену в выражении A4.91) с учетом
соотношения E.85), получаем
Итак, тс части ^'т и W'te функщгй Wtm и VK,e, которые описывают падаю-
падающую плоскую волну, можно найти путем умножения п-то члена рядов
A4.108) и A4.109) на — г [п(п + I)]. Те же части, которые описывают
¦v
диффрагированньте волны, должны содержать функцию kn(j$r), так как
эти волны являются расходящимися. Таким образом, имеем
), A4.111)
ri=l
Vy(e = ^JL 2 ";+J1} [(-/)» /„ фг) + IiX (/?/•)] i>?(cos 6). A4.112)
Внутри шара поля должны оставаться конечными в начале координат; по-
поэтому
со
), A4.113)
к 1
A4.114)
Приравняв нормальные компоненты воктора электрической индукции,
согласно выражениям A4.110) и A4.106), найдем
еД„,/„ Ф'а) = е [jn фа) + ГАА (/№ A4.115)
Приравняв нормальные компоненты вектора магнитной индукции, согласно
выражениям A4.110) и A4.106), придем к следующему соотношению:
Излучение электромагнитных волн 483
Тангенциальная составляющая вектор-потенциала А в соответствии с вы-
выражениями A4.110) и A4.82) равна
Г 1 дП'1е 1 8*ir\V,m)-l m[6Wte
L0 дц, 7". dbdr J ? [ ао
[
[
Равенство тангенциальных компонент Е или А включает в себя только
производные Wlm по г, так как члены, относящиеся к Wip, уже равны в
силу соотношения A4.116). Условия, накладываемые на 6- или <р-состав-
лшощие, приводят к одному и тому же соотношению
Г д[а/п{?'а)] ^ д[а/„(?а)] -Y д[акп($а)] A4 1181
ni да da ' п да \ • >
Сравнение A4.82) с A4.83) показывает, что Wtm входит в выражение для
At таким же образом, как Wte—выражение для Вг Равенство 6- или <р-
составлягощих вектора [х^В при г = а включает в себя только г-производ-
ные от функции Wte, потому что члены, содержащие функцию \Vlm, уже
равны между собой, всилу соотношений A4.115), A4.117) и A4.83). Поэтому
1 Y» д [afn (Уа)] 1 Г d\ajntfa)] .пЪ д[а\(/?а)] ] MAi1Q\
- ^„i- Ya -j{ d~a h^« Та )' A4Л1У)
Приравнивая величины Ani в выражениях A4.115) и A4.118) и разрешая
полученное уравнение относительно Ап при помощи соотношений E.474),
E.403) и E.404), получим An=(l — jNy1, где N равно
) — г?'агпп ($а) ,п_х (p'a) — n(sl — e) /п (р'а) пп (ра) , „
{ '
Такие же формулы, но только с ;х{ и ;х вместо ei и е, получаются и для
Вп путем решения уравнений A4.116) и A4.119). В случае идеально
проводящей сферы для нахождения Ап и Вп нужно левые части соотноше-
соотношений A4.116) и A4.118) приравнять нулю, что дает
а ¦ Pa^n-i (Ра) — ппп (М 1 '! ft in {» /л/, мп
} bo,jn^№)-njn(M) ' n" /n(pa)-/ren(fia) ' V '
Энергия, рассеянная сферой в некотором направлении, равна, согласно выраже-
выражению A3.143), действительной части комплексного вектора Умова — Пойнтинга
у 1ГЧЗ X В = i- [x-i (!хеI/2Ё х (гх X Ё) = \- v^l^h (ЕйЕ„ + EJEJ. A4.122)
Но из соотношения E.473) на больших расстояниях, где при р > 1 можно
пренебречь членами г'р, имеем
? *^*n(/Pr)] = _1 у», A4Л23)
Подставляя это в выражения A4.111), A4.112) и A4.117) для тангенциаль-
тангенциальной компоненты напряженности электрического поля, рассеянного на шаре,
на больших расстояниях от него получим
n' (cosO) +
сов,-? [Л^^+^йпв^Ссобв)] sin,} . A4.124)
31*
Глава XIV
Для получения полной рассеянной энергии выражение A4.122) надо умно-
умножить на г2 sin Odd dy и проинтегрировать в пределах 0<<р <2и и 6<0<u.
Подстановка выражения A4.124) в A4.122) и проведение интегрирования
по <р, дающее множитель и, приводят, если опустить аргументы полиномов
Лежандра, к выражению
+ {AnK + BJm) (РпРш + P'nPln)]- A4.125)
"Умножая на г2 sin Odd и интегрируя от 0 до и, получаем, что первая груп-
группа полиномов Лежандра сводится к интегралу E.198), который равен ну-
нулю при тфп, и к E.199) при т = п. Интеграл от первого члена второй
группы сокращается с интегралом от второго члена. 15 результате полная
рассеянная мощность получается величиной действительной и равной
ln\ +|-о„|). A4.12Ь)
В книгах Макдоиальда и Стрэттона, названия которых приведены в конце
этой главы, дискутируются некоторые интересные случаи диффракции
на шаре.
§ 18. Решения волнового уравнения в цилиндрических координатах.
В § 15 гл. XIII был рассмотрен частный случай цилиндрической волны, распро-
распространяющейся в направлении z; при этом в волновом уравнении приравни-
приравнивались нулю по отдельности члены, содержащие z и t. Если теперь вместо
этого первую группу членов положить равной ± $тп> а вторую—равной
^F рт„ и зависимость от времени считать синусоидальной (Р2== ш2е[х), то
получим следующие уравнения:
w)Z = 0, W = UZ. A4.127)
Сравнение с уравнениями E.300), E.304) и E.317) показывает, что в си-
системе координат р, <р, z функция И^ имеет вид
W = (Ив*™* +Ве-*тп') [CJm фт1р) + DYn ф^р)] cos (пир + 8т), A4.128)
W = (Ае*тп* + BerK.n') [CIn (BmnP) + DKm фтпР)] cos (mT + 3m), A4.129)
где Jcmn = P2 — %m и k'?n = p2 + %,,„. Если С, D, kmn и к^п являются дей-
действительными, то обе функции описывают волны, распространяющиеся вдоль
«си z. При Щ„,п > р2 величина ктп становится мнимой, и выражение A4.128)
•описывает волны, экспоненциально убывающие в направлении z. Если С дей-
действительная, a D комплексная величина, то это значит, что выражение
•A4.128) определяет также и распространение в радиальном направлении.
Если же наконец, зависимость от z отсутствует, т. е. ктп и k'mv равны нулю,
то выражения A4.128) и A4.129) описывают волны с цилиндрическим
•фронтом. щ
Определим поперечно-электрические и поперечно-магнитные волны
как волны, электрические и, соответственно, магнитные поля в которых
юриентированы перпендикулярно к оси z. Тогда, полагая в соотноше-
Иалучение электромагнитных волн
ниях A1.11) и A1.15) u = k, получаем
§ 19. Разложение плоской волны по цилиндрическим гармоникам
Для плоской синусоидальной волны, распространяющейся в направлении и,
согласно § 16 гл. XIII, имеем
#°' = /(мх, и2) еЛ^'-Р"-^ = / (м1? м2) e^o'e->Pr-cos(o-?)> A4.132)
где направление п перпендикулярно к оси z и составляет с плоскостыо
» = 0 угол а, а к, и и2 — координаты в плоскости, нормальной к п. Пло-
Плоскую волну можно выразить через цилиндрические гармоники. Для этого
нужно последний экспоненциальный множитель в формуле A4.132) разло-
разложить в комплексный ряд Фурье. Однако, чтобы использовать уже полу-
полученные соотношения, проще разлагать в ряд отдельно действи'ельнук
и мнимую части. Разложим сначала в ряд Фурье функцию cos (жsirup):
2 — 6° Г
ап — " V cos (ж sin ф)соБ/гф^ф. A4.133)
—-к
Воспользовавшись формулой D01.06) из справочника Двайта и учитывая,
что в случае четной подинтегральной функции вместо интеграла от —к
до те достаточно взять интеграл от О до п и умножить его на 2, получим
2-6°
° г г г -,
" \ cos (иф — х sin ф) dty + \ cos (геф + ж sin ф) йф A4.134)
о о
Но, согласно соотношению E.372), эти интегралы равны Jn(x) и/„( — ж) =
= ( — \)nJn(x)\ поэтому все ап, соответствующие «-нечетным, равны нулю,
и если п обозначить через 2т, то
со со
cos(a;sin^)= 2 {2 — b°m)Jam(x)cos2mty= 2 Jn(x)cosnty A4.135)
m = 0 n=—со
Точно таким же путем разлагается в ряд и функция sin (x sin ф), для ко-
которой вместо суммы /п(х) и Jn{— х) получаем их разность
со со
sin(a:sin<]0= S 2/2m+, (ж) sin (^m + 1) ф = *2 /n(a;)sin иф. A4.136)
m=0 ri=—со
Помножив A4.135) на / и сложив с A4.134), мы придем к разложению
экспоненциальной функции, для которой, тз прежних обозначениях (ж = ррг
ф= —-{-'<р — а), ряд имеет следующий вид:
/n7n(pp)cos«(a-«p). A4.137)
§ 20. Излучение из отверстий в плоском проводящем экране. Стро-
Строгое решение задачи о нахождении поля, излучаемого сквозь отверстие.
486
Глава XIV
\
Экран
Экран
б
Фиг. 131.
чрезвычайно сложно. Поля должны удовлетворять не только волновым урав-
уравнениям вне отверстия и определенным условиям на его границах, но и непре-
непрерывно соединяться с полями, существующими на самом отверстии. Последние
обычно очень сильно меняются под действием отраженного излучения, воз-
возникающего вследствие наличия экрана. Поэтому строгое решение задачи воз-
возможно лишб в очень ограниченном числе случаев, когда математически можно
рассматривать все пространство, где существует поле, как единую область.
В § 12 было доказано, что задание начальных значений полей во всей
области, а также задание тангенциальных компонент электрического или маг-
магнитного полей на поверхности, ограничивающей эту область, однозначно опреде-
определяют поля в любые последующие моменты времени. Для установившихся
процессов имеет смысл только одно второе условие. В случае идеально про-
проводящего экрана целесообразно оперировать
с электрическим полем, потому что его тан-
тангенциальная составляющая на поверхности
экрана равна нулю, т. е. известна. В ка-
качестве первого приближения при нахожде-
нахождении неизвестного электрического поля на
отверстии лучше всего, повидимому, взять
значения поля, существующего в отсут-
отсутствие экрана. Приводимое ниже рассмотре-
рассмотрение относится только к случаю плоских
проводящих экранов; на форму и количе-
количество отверстий, равно как и на структуру
падающей волны, не будет накладываться
никаких ограничений.
Нам нужно найти источник, создающий
такое ноле Е, тангенциальная компонента ко-
которого исчезает на всей бесконечной плоскости,
кроме ее участка S, где она равна некоторой заданной величине. Рассмотрим
тонкий двойной лист с током. Пусть расстояние между слоями тока очень мало,
а плотности токов в них равны по величине а противоположны по направ-
направлению, как это показано на фиг. 131-, а. Если ток постоянен вдоль своего
направления, то он весь проходит через края, где его направление меняется
на обратное; если же плотность тока в центре больше, чем на краях, то,
как это показано на фиг. 131, б, часть тока возвращается назад еще до
достижения краев. Поскольку лист считается очень тонким, то внешнее
магнитное поле пренебрежимо мало по сравнению с полем между слоями.
Поэтому, применяя теорему о циркуляции Н к прямоугольному контуру abed,
ориентированному перпендикуляно i и своей большой стороной плотно при-
прилегающему к верхнему слою (фиг. 131, а), мы найдем, что Bi=\u. Далее,
под действием изменения потока магнитной индукции N = B^dl сквозь
площадку контура a'h'c'd' в последнем возникнет э.д.с. — (dN/dt), равная,
в силу симметрии, 2Edl при 3—->0, так что напряженность электрического
поля Е непосредственно над поверхностью листа будет равна ^- /iu[xoi.
Такой двойной слой тока можно, очевидно, выполнить при помощи беско-
бесконечно малых соленоидов длиной dc, имеющих поперечное сечение bdl
и магнитный момент n x ibdldc, равный, если его выразить через Е, величине
— 2 (juijx)"^ х EdS. Эти элементарные соленоиды нужно распределить таким
образом, чтобы они создавали требуемое изменение поля Е вдоль поверх-
поверхности. Из симметрии очевидно, что вне границ двойного слоя создаваемое
им поле Е будет нормальным к поверхности экрана. Согласно выражению
A4.97), вектор-потенциал, описывающий поле, создаваемое в некоторой
точке Р маленькой петлей тока, ориентирован перпендикулярно к оси
Излучение электромагнитных волн " 487
последней и прямо пропорционален синусу угла между этой осью и радиус-
вектором г, направленным от петли в точку Р. Подстановка только что
найденной величины момента вместо момента петли тса2/, входящего в вы-
выражение A4.97), дает
А = Ае** = ^е** \ l/-fr)(nxE)x>1 ^dS, A4.138)
где rx— единичный вектор вдоль направления г. На больших расстояниях
членом с / в подинтегральном выражении можно пренебречь по сравнению
с Рг. В общем случае амплитуда, направление и фаза Е могут меняться
вдоль поверхности отверстия.
Рассмотрим систему источников электромагнитного поля, находящихся
над плоскостью ху, а .также систему их изображений с противоположными
знаками, находящихся под этой плоскостью. Ясно, что на плоскости ху
тангенциальные составляющие электрического и нормальные составляющие
магнитного полей, создаваемых обеими системами, вычитаются и исчезают,
тогда как нормальные составляющие электрического и тангенциальные
составляющие магнитного полей складываются. Поэтому если любую часть
плоскости ху покрыть тонким листом идеально проводящего металла, то
это не приведет к искажениям поля. Если после этого изображенные
источники убрать совсем, то на отверстии нормальные составляющие элек-
электрического и тангенциальные составляющие магнитного полей, создаваемые
истинными источниками, останутся без изменений, так как вихревые токи,
текущие в проводящей плоскости, оказывают действие только на нормаль-
нормальные составляющие магнитного и тангенциальные составляющие электри-
¦ ческого полей. Таким образом, когда электромагнитная волна произвольного
вида падает на плоский и идеально проводящий лист произвольной формы,
нормальные составляющие электрического и тангенциальные составляющие
магнитного полей остаются невозмущенными на отверстиях, прорезанных
в этом листе. Поэтому из выражения A4.138) имеем
Это интегральное уравнение можно решить относительно п X Е на отверстии.
Подставив результат в выражение A4.138), мы получим совершенно строго
диффрагированное поле в случае бесконечно тонкого плоского проводящего
экрана произвольной формы.
Если магнитное поле в падающей волне ориентировано параллельно
экрану и длина волны значительно превосходит размеры отверстия, то часто
можно найти, исходя из теории потенциала, точную величину отношения нор-
нормальной и тангенциальной компонент вектора магнитной индукции на от-
отверстии и отсюда уже определить величину тангенциальной составляющей
напряженности электрического поля. Перемещение прямоугольника a'b'c'd'
вдоль Вг уменьшает величину 2Edl ровно настолько, насколько умень-
уменьшается величина dN/dt. Это уменьшение, в свою очередь, равно скорости
изменения потока магнитной индукции, выходящего через обе поверхности
двойного слоя на участке между двумя соседними положениями контура
d'b'c'd'. Таким образом, на отверстии, прорезанном в плоскости ху, если Е
имеет только ^-составляющую, имеем
Ц~ = 1шВг- A4.140)
Путем интегрирования этого уравнения находим тангенциальную состав-
составляющую Е, входящую в выражение A4.138). Решение статической задачи
488
Глава XIV
позволяет определить В, на отверстии через значение тангенциальной к пло-
плоскости экрана компоненты В вдали от отверстия. Эта величина относится
к стоячей волне, поэтому она в два раза превышает величину В в падающей
волне, появляющейся в отверстии. В конце главы помещены примеры,
в которые включены результаты Бете о диффрактщи на малых отверстиях.
§ 21. Диффракция на прямоугольном отверстии в проводящем пло-
плоском экране. Формулы, полученные в предыдущем параграфе, позволяют
найти диффрагированное поле в случае прямоугольного отверстия в идеально
проводящем экране, совпадающем с плоскостью ху. Пусть магнитное поле
направлено вдоль оси х, а вектор Умова — Пойнтинга наклонен относительно
оси z на угол а, как это показано на фиг. 132. Если через хг и уг
обозначить координаты элемента dS
чере.-! г — радиус-вектор, проведенный
из dS в точку Р, а через /? —радиус-
вектор из точки О в точку Р, то при
R > а и Я > b приближенно будем
иметь
г «= R — хг cos cp sin б — уi sin cp sin 6.
A4.141)
Тангенциальная компонента Et в
плоскости z — U имеет непостоянную
фазу, а именно:
Фиг. 132.
Ete^1 = Ecos(xey(«>(-PwsinO)_ A4.142)
Так как векторное произведение n x E параллельно оси х, то вектор
(nxE)xR лежит в плоскости yz и перпендикулярен к DP, а следовательно,
и R, и пропорционален по величине sin б'. Таким образом, имеем
Av= — cosO cosecO'A, Az = sin 0since cosecO'A, A4.143)
Aq ¦= -AtJsin<p cos 6 — Azsin 6, Ar_ — .A^coscp, -lr = 0. A4.144)
Если теперь выражение A4.138) подставить и выражение A4.143), то
cosec 0' сократится с sin 0'. Пренебрежем х\ и у\ по сравнению с R2, со-
хранив члены хг и ух в выражении для А только в показателе. Тогда,
переписав выражение A4.142) для Et и учитывая выражение A4.144),
получим
a Sln у
с-'РR
1 dyt —
2Е cos a sin <f sin ( —- [3<я cos cp sin 0 j sin | — f* (sin <f sin 0 — sin a)
aR cos 9 sin 0 (sin ф sin в — sin a)
COSO.
h, A4.145)
A4.146)
Единственное допущение, сделанное при выводе этих формул, заключается
в предположении о невозмущенном электрическом поле на отверстии. Стрэттон
и- Чу1) получили эти формулы путем суперпозиции или «отражения» двух
решений уравнений Максвелла., при этом электрическое и магнитное поля
на отверстии предполагались невозмущенными. Суперпозиция пеобходима
^Stratton, Chu, Phys. Rev., 56, 106.
Излучение электромагнитных волн
48»
для исключения тангенциальной составляющей электрического поля на
поверхности экрана, и, как можно видеть из только что полученного решения
и из теоремы единственности, это эквивалентно отбрасыванию членов,
относящихся к магнитному полю. Для проверки формул A4.145) и A4.146)
при разных Л и а эти авторы сравнивают величину Ец-\-Е1 в плоскости yz
со строгим решением для щели (а=ос), полученным Морзе и Рубенштей
ном1'. Результаты приведены на фиг. 133, а, бив. Аналогичное сравнение
((
_
..1 ..
r/
/
2/1
j\
/
I
4 ,
Л'\
ii
i/n
/
4
"/
I
]
/ 1
H
i....
\
i
i
n
1
1
7T/<
//
I-
1 I /
''4
1 УГ-Л
/ /^
fit
^\
n
1
Si
?
Фиг. 133.
для иоля в плоскости xz со щелью (Ь = оо) при а= 0 показано на фиг. 133, г.
Такое прекрасное совпадение свидетельствует о малой величине ошибки,
совершенной при допущении о невозмущенном электрическом поле на от-
отверстии. Ясно, что скалярная теория диффракции Кирхгофа, используемая
в оптике, согласно которой фиг. 133, а и г должны совпадать, становится
совершенно неправильной при размерах отверстия в проводящем экране,
соизмеримых с длиной волны.
§ 22. Ортогональные функции в задаче о диффракции. Излучение
открытого конца коаксиальной липни. Развитый в последних двух
параграфах метод не применим к неплоским экранам, но даже и для пло-
плоского экрана вычисление интеграла A4.138) в непосредственной близости
от отверстия часто бывает затруднительным. В этих случаях можно исходив
ия решений скалярного волнового уравнения, записанных в виде
еу"" 2 2 CmnUmn К) Vn (в2) Wmn (u3),
Morse, Rubenstein, Phys. Rev., 54, 895.
490 Глава XIV
Координата и3 отсчитывается в направлении, нормальном к экрану, а иг, и2
являются ортогональными криволинейными координатами на его поверх-
поверхности. Интеграл берется по поверхности экрана и отверстия; 8™ = 0 при
„любых п, тп, р, д, кроме р — п и д = тп. Такие решения у?ке встречались
нам [см. A4.85), A4.128) и A4.129)], мы будем иметь с ними дело также
и в ряде задач о волноводах. Для проводящего экрана величина Стп вычис-
вычисляется по значению тангенциальной составляющей напряженности электри
ческого поля н& отверстии.
Этим методом можно, например, найти излучение от открытого конца
коаксиальной линии. Поле на больших расстояниях проще вычислять по
формуле A4.138), но при нахождении поля вблизи отверстия используе-
используемый здесь метод предпочтительнее. Область существования электромагнит-
электромагнитного поля в линии ограничена изнутри и снаружи цилиндрами радиусов
р — а и р = Ь. Линия соединена с плоскостью z = 0, являющейся идеально
проводящей всюду, за исключением а < р < Ъ. При вычислении поля излу-
излучения в области z >0 мы будем предполагать, что & < X, и для отыскания
поля при г < Ъ будем пользоваться методами электростатики. Для любого
радиального распределения потенциала оно находится путем интегрирова-
интегрирования последнгго по плоскости z =0, потенциал которой считается равным
нулю всюду, кроме узкого кольца радиуса р и ширины dp, имеющего
потенциал V (р). Потенциал Vp, созданный этим кольцом в точке Р на оси,
можно найти при помощи теоремы взаимности Грина, исходя из значения
заряда dg, индуцированного зарядом д, находящимся в точке Р, на коль-
кольцевом элементе заземленной плоскости. Чтобы определить dg, надо в фор-
формуле E.25) положить b—a — z и а~>Ь—-> оо. При z>p разложение в ряд
(см. Двайт, 9.05) дает
^^ A4-147)
Для получения dV в точке г, 6 подставим г вместо z и умно?ким на
P2n+i(cosb). Потенциал в плоскости z=0 будет иметь значения
P>b, F(P) = 0, b>P>a,
а>р>0, V(p) = Vo. A4.148)
Если подставить jto в выражение A4.147) и проинтегрировать (Двайт,
-610.9), то
у.
In (bye) 2j ( l> (
Для нахождения поля излучения надо положить в A4.85) А = \ и
В — С = т — Ъ=0., в результате чего получится расходящаяся волна. Вели-
чипы Д, определяются путем приравнивания коэффициентов при Р2п+1 (cos о)
в выражении для Е6, полученном из Wim, соответствующим коэффициентам
в выражении для Е%, даваемом соотношением A4.149), при r—b.
Из выражений A4.85) и A4.82) получим
Поскольку fib мало, то вместо производных в этом выражении можно,
Задачи 491
согласно E.472) и E.473), написать: Bп+ 1)Dи + 1)!1 (ftb)-Bn+2) ¦
Чтобы найти Е6 при г = 6, в выражении A4.149) вместо P2n+1(cos6) на-
напишем — Ь~*д [Р2п+1 (cos 6)]/d6 = b^P^n+i (cos 6), а вместо г2П+2 подставим &2"+2
Приравнивая коэффициенты и разрешая относительно JJn, находим
Электрическое и магнитное поля при г, больших Ь, определяются из соот-
соотношений A4-82), A4.85), A4.110) и A4.83) в виде
?е= -^^ ^r~[rk2n+iUM]Pln+l(cosb), A4.151)
со
Ег = /о 2 V Bп +1) Bй + 2) к2п+1 (JM P2n+1 (cos 6), A4.152)
оо
В?= -Р2 ^ bAn+1(/Pr)P|n+1 (cos 6). A4.153)
n=0-
Эти выражения дают поля в области г > ft. Если ft < К- они удовлетво-
удовлетворяют совершенно строго граничным условиям A4.148). Пренебрегая высокими
степенями pb и (За и удерживая только первые члены в рядах, для поля
на больших расстояниях, где fc2n+i (j$r) можно заменить на (f^r)'1 e—^r,
получим
1/ ^^-Pr). A4.154)
Как ясно из сравнения с выражением A4.17), это поле эквивалентно полю
на больших расстояниях, создаваемому элементом тока—11 sin Ы, где
// = тсшеF2 —a2) F0/ln(fc/a), так что мощность, излучаемая в верхнее полу-
полупространство, равна половине мощности, определяемой выражением A4.19)
(Р-а*)* Fg _ 2rc2ce (b»-a«)i Fg
(fc/«)]2 ~ 311н (fc
Fg ЗЦп (Ь/а)]П«
Этот же метод применим и в случае неплоских экранов, таких, например,
как бесконечный проводяший коаксиальный конус с подключенной к нему
линией. Ход решения здесь тот же самый, однако отправным пунктом должен
быть § 276 гл. V. В приводимых ниже задачах содержатся другие примеры
на применения этого метода.
ЗАДАЧИ
1. Линейный квадруполь состоит из зарядов •—д, -j-2g> и —д, расположенных
соответственно в точках z=—а, 0, +а. Квадрупольный момент Q равен a2qsin<i>t.
Показать, что поля на расстоянии г > а будут равны
—3cos2fi)
4ite
Qo sin 26
4Я?
#.„==-
492 Глава XIV
2. Показать, что средний ио времшш поток энергии, излучаемой квадруполем
описанным о предыдущей задаче, равен 1Gk*cQ% A51Ч)-1.
3. Плоский квадруполь гостоит из зарядов —д, -\-д, — д и +д, расположенных
по углам квадрата, стороны которого длиной а параллельны соответственно линиям
V — 0, -тг л, я и — ж. Квадрупольный момент равен Q = a2g cosmf = Q0 cos cot. Показать,
что на расстояниях г ^> а ноля будут равны
„ 3Q0 sin2 0 sin 2<р Г / 3 82 Л . . . 33 . , .,]
г g0 sin 0 cos 2<р
%=—8^—-
Q0psin6ros29 Г 332 /-рт ЗИ
4. Показать, что средний по времени поток энергии, излучаемой описанным ь
предыдущей задаче квадруполем, равен 4n6cQg E1Ч)-1.
5. Электрический диполь, лежащий в плоскости ху в начале координат, вращается
вокруг оси z с угловой скоростью ш, причем в момент времени г = 0 диполь ориентиро-
ориентирован вдоль оси х. Показать, что составляющие вектора магнитной индукции будут равны
= —-—- [rfisin (cot — Э)— у)- cos (o)t—fir —<p)],
CD[xiIfCOS6r o , , .
¦P= 4т!г2 [^cos('"f -fir —<(>) +sin И — Рг —<(.)].
7 x). Две антенны одинаковой длины Bп-|-1)Х/2 расположены параллельно оси г
и имеют центры в точках ж=0 и х = а. Колебавия в антенне х = а запаздывают по
фазе относительно колебаний в аитенве х — 0 на 90°. Показать, что интенсивность излу-
излучения такой антенны будет
— [xc/gcos2 Г-ттBге+ ?)ftcos6 I cos2 Г-т-те (l—у sin 6 cos 9
llx= 2r.2r2 sin2 6 '
Изобразить приблизительно форму сердцевидной диаграммы направленности при а = Х/4
в плоскости 0 = 7i/2.
8. Показать, что при а = Х/4 выигрыш двойной антенны, описанной н предыдущей
задаче, в два раза превышает выигрыш одиночной антеивы. возбуждаемой на том же
типе колебаний.
9. Система состоит из р синфазных пар антенн, описанных в задаче 7 и располо-
расположенных вдоль оси у ва расстоянии А/2 друг от друга. Показать, что диаграмма на-
направленности для интенсивности излучения дается функцией
sin2 ( — рк sin 6 sin <f j
[ --я sin 0 siiiy J
1 sin2
где интенсивность llj равна интенсивности в задаче 7 при я = Х/4. Показать, что выиг-
выигрыш в два раза больше, чем у системы, состоящей из р одиночных антенн, располо-
расположенных вдоль оси у на расстоянии Х/2 друг от друга.
10. Система состоит.ив р полуволновых синфазных антенн, расположенных друг
за другом вдоль оси z. Показать, что интенсивность излучения на больших расстоя-
расстояниях равна
-лс1% cos2 ( -г- те cos 0 ) sin2 ( — р те cos 6 )
8тс2г2 sin2 6 sin2 ( -^- п cos 0 )
х) Вследствие неправильной постановки яадача 6 при переводе опущена.-
Прим перее.
Задачи 493
Заметим, что такая система совпадает с длинной линейной антенной, нагружен-
нагруженной через каждые Х/2 таким образом, чтобы ликвидировать наличие переменных фаз.
11. Распределение тока в круглой проволочной нетле радиуса а имеет вид
Io sin n <f0 cos wt. Используя запаздывающие потенциалы и привлекая формулы § 18, по-
показать, что при больших г в точке г, О, у потенциал А равен
-грцаг^/о/п ((Basin fi)sin ny sin <— nv~-{-t»t — '
12. Электромагнитные волны рассеиваются проводящим шаром, радиус которого
мал но сраввению с длиной волны. Показать, что на расстояниях от шара, значитель-
значительно превышающих его радиус, поле, излучаемое под углом г/3 по отношению к направ-
направлению падающего луча, будет линейно поляризованным.
13. Лииейво поляризованная электромагнитная волна надает на непроводящий
шар, имеющий диэлектрическую проницаемость et и магнитную [ij. Радиус этого шара
мал по сравнению с длиной волны. Показать, что рассеиваемое излучение равно излу-
излучению системы, состоящей из расположенных в начале координат электрического ди-
диполя, ориентированного вдоль вектора Е падающей волны, и перпендикулярного
к нему магнитного диполя. Показать, что моменты этих диполей равны
Е
—coso>f.
14. Плоская электромагнитная волпа, вектор Е которой ориентирован вдоль оси у
т равен Е cos {«it — fiar), падает на идеально проводящий цилиндр радиуса а с осью
вдоль z. Показать, что полное полв определяете и действительной частью следующих
выражений:
Jn (РР) ^ (Ра)]
^- — JSpS Ыра)-,ТЦр5) '
п=0
15. В среде [лв плоская электромагнитная волна, электрический вектор которой
равен Ecos(u>t — fk) и ориентирован вдоль оси у, падает на цилиндр [л'е' (радиус ци-
цилиндра а, а ось направлена вдоль z). Показать, что рассеиваемое поле определяется
действительной частью следующих выражений:
(- Пп.B-5°) [(tt'eI/«7n (За) J'n (P'a)-(^e'I/^ fn (|Ja) Jn
16. Плоская электромагнитная волна, электрический иектор которой ориептиро-
иан вдоль оси z и равен ?cos(<»<—?s.t), падает на идеально проводящий цилиндр ра-
радиуса а с осью вдоль z. Показать, что полное поле определяется действительной
частью следующих выражений:
Ez =
Е Z, (-,У B-Е&) [Jn (pa) Yn {\i9)-Jn
^ 2 Й
Е Z,
17. В среде [ле плоская электромагнитная нолва, электрический вектор которой
ориентирован вдоль оси z и равен Е cos (u>t—fa), падает на цилиндр [л'е' (радиус ци-
цилиндра а, а ось направлена вдоль z). Показать, что рассеиваемое ноле определяется
действительной частью следующих выражений:
494 Глава XIV
n=0
p'a) [Jn (pa) — jYn^a)} — (ixe') >2 Jn(p'a) [Jn (pa) — /Yn (pa)]
18. Часть идеально проводящего шара радиуса а, расположенная между В = -( в
В=эт — y- удалена, а между конусами поддерживается разность потенциалов Vcosu>i
при г = а. Принимая, что распределение потенциала ь зазоре при r = a определяется
по формуле A4.64), показать, что поле излучения равно действительной части сле-
следующих выражений:
со
Е6 — V0r~lelWt 2 ^" tBn+2) X2n+1 (/» —JH^2n+2 (/?'•)] Р2n+l(cOs °).
п О
со
71=0
со
$ ^^ Y /З2^^^' ^S^ О ^ f/3/Л /* (cos 6)
X — ши.Dл + 3)Р2п+1 (cosy)
[B71 + 2) /f2n+1 (;ра)-/> /с2п+2 (/[^)]
где Zft определяется по формулам A4.63) и A4.65)
19. Подсчитать входной импеданс системы, оппсаппой в предыдущей задаче, дока-
доказав ее эквивалентность конической линии передачи, нагруженной при г = о бесконечным
множеством параллельно соединенных импедансов Zlt Z2, ..., где
~CT— ~ ^n«2n+i \Jpa) J 2n+i (COS 7).
Zn
20. Среда [ле заполняет пространство между бесконечным диэлектрическим цилинд-
цилиндром ц'е' радиуса а и идеально проводящим цилиндром р = 6. Показать, что вдоль ци-
цилиндра могут распространяться поперечно-электрические волны при каждом значении «„,
удовлетворяющем уравнению
(vnb/a)—Y1 {vn)Jj (vnb/a)]= 1>-R, (vn)
У0(уи)/, (vnb/a)] vnBa (vn) '
а также при условии, что ш2я2[л'г' > ип и ш2я2це > Ъп ¦
Показать, что скорость п-й волны равна
и что поля в среде [л'е' определяются по формуле
n J{/); —/и>аВг = ипСпе nJ0{unp/a),
где ш2а2[л'е' — ип =ш2я2ае — Vn = kna2-
21. Позсазать, что если отражатель ври р = 6 в носледцей задаче отсутствует, то
при тех же частотах и значениях материальных коистаит плоская волна не может
существовать, но результаты предыдущей задачи остаются в силе, если Ro и R, заме-
заменить па функции Ханкеля Jo —jY0 и /, — jY^.
22. Бесконечная среда (ае окружает бесконечный диэлектрический цилиндр [х'е'
радиуса а. Показать, что плоская поперечно-электрическая волна может распростра-
распространяться вдоль такого цилиндра при каждом значении ип, удовлетворяющем уравнениям
а также при условии, что ш2я2[л'е' > ип и е' > е.
3ndnvu 495
Показать, что скорость волны равна ша (ш2л21а'е/ — мп)"'2 и что поля снаружи опре-
определяются по формулам
^^ ¦ If? 2
Кй
23. Удостовериться в том, что при У,(г;п6/а) = 0 условия задачи 20 приближенно
удовлетворяются при s = 1,99e' = 1,99з„, \± = ц' = |л„, шя = 1С9, и=1, » = 3,46, и пока-
вать, что фазовая скорость приблизительно равна 3,15-10s м/сек.
24. Удостовериться в том, что условия задачи 22 приближенно удовлетворяются
при
e' = l,72e = l,72s0, [л = [л ' = [4,, шя = 109, м=2,65, »=J,
и показать, что фазовая скорость в' z-папраялснип приблизительно равна 2,87-108 м/сек.
25. Среда [>л заполняет пространстно между бесконечным диэлектрическим цилинд-
цилиндром [х'е' радиуса а и идеально проводящим цилиндром р=6. Показать, что плоские
поперечно-магнитные волны могут распространяться вдоль цилиндра при любых зна-
значениях ип, удовлетворяющих уравнению
[Л (Уп) Уо (vnb/a)—Y0 (vn) Jo (Vnb/a)] = «ЭТ2?О (г'п)
а также при условии, что ш2а2и.'е' > ип и ш2я2|ле > Vn .
Показать, что скорость п-й волны равна ma^aVs'—ипу и что поля в среде
и-'е' определяются по формулам
v v v- —jh z v v- —j7tnz
/i1 = A'n (coja'e')/? _ /Се J1(unp/a), knaEz = unCne Jo (unp/a),
„ „ , , 2 „ , 2 ,2 o
где ш^яг|л е •—un —и>~а*\).Е—Vn =кпй--
26. Показать, что если отражатель при р = 6 в последней задаче отсутствует, то
при тех же частотах и значениях материальных констант плоская волна не может
существовать, однако результаты предыдущей задачи остаются в силе, если Щ и Л,
заменить на функции Ханкеля Jo — /Yo и /, — /У,.
27. Бесконечная среда ц.е окружает бесконечный диэлектрический цилиндр ц'е'
радиуса а. Показать, что плоская поперечно-магнитная волна может распространяться
вдоль цилиндра при каждом значении ип, удовлетворяющем уравнениям
Vn*'Ji (ип) K0[Vn) + unEj0 (ип) Кг (vn) = 0, ш2яVе' — и„ = <»га2! " ' ~? 1? '
а также при условии, что
Показать, что скорость n-й волны равна
cuo(<D2a
и что поля снаружи цилиндра определяются по формулам
/спяА2= /VfiCn^ -"-о (^тгя р)-
28. Удостовериться в том, что если Уо (vnb/a) = 0, условия задачи 25 приближенно
удовлетворяются при
е = 2г' = 2вг), lx. = y.' = lxv. ша = 1,2.109, ип=1, «п = 3,
и показать, что фазовая скорость в направлении z приблизительно равна 3,10-10е м/сек.
29. Удостовериться в том, что условия задачи 27 приближенно удовлетворяются при
e'=l,81e=l,8lEt), 1л = [х' = [х„, о)я = 0,99.109, и„ = 2,8 п »п=1,
к показать, что фазовая скорость приблизительно равна 2,88-108 м/сек.
4U6 Глава XIV
30. Бесконечная плоская идеально проводящая поверхность покрыта слоем ди-
диэлектрика [л2е2 толщиной а, над которым простирается бесконечная диэлектрическая
«реда [л,е,. Используя результаты § 18, показать, что расходящаяся поверхностная
волна ТМ, которая может существовать в такой системе, описывается вектор-по-
вектор-потенциалами, равными действительным частям следующих выражений:
" А^С, [р, ({."-Р!I
А,-С, {Pl (Pf-p'»I'11 sin [(pi -p'*I/s s]
-kp' cos [(Pi-P'»I'* z\ Я<2> (Р'р)} e*
где
Pf =«0^
Локазать, что скорость этой полны точно такая же, как у плоской волны, рассмотрен
ной в вадэче 7 гл. XIII.
31. Бесконечная плоская идеально проводящая поверхность покрыта слоем диэлек
грика [л2е2 толщиной а, над которым простирается бесконечная диэлектрическая среда [IjE, .
Используя результаты § 18, показать, что расходящаяся поверхностная волна ТЕ,
которая может существовать в такой системе, описывается при помощи вектор-потен-
вектор-потенциалов, равных действитрльвым частям следующих выражений:
^^^ (р'р) ^1, А2^?С2 sin
где
Локазать, что скорость этой волны рама скорости плоской волны, рассмотренной
п задаче 8 гл. XIII.
32. Бесконечный идеально проводящий цилиндр радиуса а покрыт слоем диэлек-
диэлектрика [л2?2> внешний радиус которого равен Ъ, и паходится в бесконечной диэлектриче-
диэлектрической среде [J^e,. Пользуясь результатами § 18, показать, что иозможными вектор-потен-
вектор-потенциалами, описыпающими поверхностную волну ТМ, являются действительные части
следующих выражений:
At = С, I -ЫР'К, (р,р) + кр1К0 (Ар)] в«"*-Р'*>,
А2 =
где
= -S"o (P2e) 7o (ftp) —^o (P2«) Ko (p2p),
= Ko {p2a) /, (p2p) + /0 (/¦»:«) A
Показать, что скорость можно найти из уравнения
— *2PiK0 (Pib) -Ri (p2b) = «
Пусть о = 1, 6 = 2, [л2 = [л,, е2=4а, и р4Ь = 1 000; показать, что ^ : р' : р2 = 1: 1,163 : 2
и что при р = 3,445 Ь компонента В0 равна Vio своего вначения цри р = 6.
33. Получить формулу A4.158), исходя непосредственно из выражения A4.138).
34 Плоскость поляризации падающей волны, показанной на фиг. 132, пращастся
так, что вектор Е остается параллельным оси х. Показать, что вектор-потенциал диф
фрагированной волны на больших расстояниях равен
а - costp Y VcosB ~Л,
* *й '—
8
COS a Sin if 4 ° COS а "
гДе Ау определяется по формуле A4.145).
35. Пусть отверстие, о котором шла речь в § 21, имеет форму не прямоугольника,
а кольца, внешний и внутренний радиусы которого соответственно равпы а и Ъ. Пока-
Показать, что вектор-потенциал диффрагированного поля на больших расстояниях имеет пил
А 18У ^ Е cos a S'D f 1„ ftR
Задачи 497
где
Q= (sin2 a + sin2 0 — 2 sin a sin 6 sin yI'2.
36 Пусть плоскость поляризации падающей волны, рассмотренной в последней
задаче, вращается, сохраняя вектор Е параллельным оси х. Показать, что вектор-потен-
вектор-потенциал диффраг.ированного поля на больших расстояниях имеет вид
37. Показать, что если в § 21 или в последних трех задачах имеется не одно, а
два одинаковых отверстия с центрами в точках у = е и !/ = —с, то цри R J> с потенциал
для одиночного отверстия надо умножить на фактор
2 cos [{".с (— sin a -j- у/Щ].
38. Пусть пентры отверстий, рассмотренных в последней задаче, расположены
в точках х = с и я = —с. Показать, что необходимым множителем в этом случае будет
2 cos {?сх/Щ.
39 Сферическая оболочка радиуса а является совершенно поглощающей изнутри
и идеально проводящей снаружи. Электрический диполь М cos tut находится в центре,
в начале координат, и ориентирован вдоль направления Ь = 0. Часть оболочки, распо-
расположенная между 0=а' и 0 = о", удалена Показать, что выражение для вектор-йотен-
циала диффрагироваиного поля определяется но формулам § 13, где
со
# ? АпРп(cosb)kn(/[ir),
l
(п — i)(n + 2)d[akn(fpa)\jda
=cosa'
40. Пусть в предыдущей зодаче в центре оболочки находится не электрический
диполь, а маленькая коаксиальная с осью симметрии системы проволочная петля
радиуса Ъ. по которой течет ток 1е*'°1. Показать, что выражение A4.82) определяет
значение вектор-потенциала диффрагироваиного поля снаружи, если
гг=1
П~~в L
41. Маленькая проволочная петля радиуса Ъ. не-ущая ток Icosmt, расположена
на расстоянии с от центра коаксиального с пей отверстия радиуса а, прорезанного в бес-
бесконечном плоском проводящем экране. Доказать, что если а <С X, 6<с и с < X, то
векчор-иотолцн&л диффрагироиа иного ноля .равен
A.eimt= — ^2/62 A6т-)-1 [2с —Bс2 + Я2)(с2 + а2)~1/2] sin 20 еЯ™«-РК) _
42. Плоская волна, вектор напряженности электрического поля которой равев
Eoemt~^tJ) и направлен вдоль оси г, падает нормально на бесконечный плоский иде-
идеально ироподягцми тонкий экран. В экране прорезана щель шириной 2а, такая, что ось z
делит ее по длине на две ранные части. Пренебрегая разно тью фаз на щели, пока-
вать при помощи результатов § 24 гл. IV и 5 20 нгитоящей главы, что на расстояниях
от щели R > а электрические поле, прошедшее через щель, будет равно
Z si и и
г 2к
где t' = t + 7i/Dra) и 6 —угол между R и нормалью. Заметим, что амплитуда В, соответ-
соответствующая стоячей волне (см. § 24 гл IV), в два раза превышает амплитуду бегущей волны.
43-. Вектор напряженности электрического поля в стоячей волне, равный в пучности
величине Е^е1', ориентирован нормально к бесконечной идеально проводящей плоско-
плоскости, в которой имеется щель шириной 2а. Пренебрегай разностью фаз на щели,
показать при помощи § 24 гл. IV и § 20 настоящей главы, что на расстояниях от щели
32 в. Смайт
498 Глава XIV
а прошедшее поле равно
где г' = г-{-те/D<») п 6 — угол между R и нормалью.
44. Оставляя в последней задаче значение Ео неопределенным, вычислить из А^
величину 'Bz. Взять выражение для Вг, в котором еще не проведено интегрирование
по х, и вычислить Bz при ж.= 0 и 'fa < 1, т. е. при малом аргументе функции Ханкелн.
Выразить Ео через B0e^ot и показать, что если плоская волна, у которой Вг = Вйе^Ф1~Ъх\
падает на тонкий плоений идеально проводящий экран с прорезанной в нем щелью
шириной 2я и осью, совпадающей с х = 0, то при я<Х диффрагироваштое поле
равно
4 In pa
где г' = «-{-те/Dсо) и 0 — угол между R и нормалью. При решевии воспользоваться
формулой E.445).
45. Плоская волем, вектор-магнитной индукции в которой Вве! (№'~~Р") ориентирован
вдоль оси z, надает нормально ва бесконечный плоский идеальво проводящий тонкий
экран, совпадающий с плоскостью у = 0. В экране имеется щель шириной 2а, такая,
что- ось- z делит ее по длине на две равные части. Пренебрегая разностью фаз на
щели, показать при помощи результатов § 23 гл. IV и § 20 настоящей главы, что на
расстояниях от щели R^> а проходящее поле равно
где I' =t + я:/Dо>), 6 — угол между R и нормалью, а неличива Bz вычисляется в центре
щели, где она приравнивается Во.
46. Линейно поляризовавная электромагнитная волпа, фронт которой накловеи
па угол а относительно плоскости yz, падает ва щель, описанную в задаче 42. Пусть
вектор магнитной индукции волны параллелен щели. Показать, что если ра мало
и развостью фаз на щели можво пренебречь, то интенсивность излучения диффраги-
рованного поля на больших расстояниях R от щели равпа
47. Пусть вектор вапряжеввостп электрического поля волны, рассмотренной в по-
последней задаче, параллелен щели. Показать, что если 'ра очень мало и можно пренебречь
разностью фаз на щели, то из задачи 42 интенсивность диффрагированиого излуче-
излучения равва
—_ др3а4 cos2 6 cos2 a --
ьн
48. Отверстие радиуса а прорезано в бесконечном плоском идеально проводящем
экране, представляющем собой границу однородного электрического ноля типа стоячей
волны Еое)ю1. Пренебрегая разностью фаз на отверстии и пользуясь выражениями
E.258) и A4.138), показать, что вектор-потенциал на больших расстояниях от центра
щели равен
¦г —/?¦„ [sin (Ря sin 6)— р« sin 6 cos (jSa sin 6)] —j$n
8 no>[iflsm2e e
49. Показать, пользуясь методами § 286 гл. X, что если в однородной стоячей волне
магнитная индукция равна B0e3lot и направлена вдоль оси ж параллельно бесконечному
тонкому идеально проводящему экрану, совпадающему с плоскостью z = 0, в котором
имеется небольшое отверстие радиуса я, то z-составлнющая В на отверстии равна
Задачи Ш\)
При помощи § 20, пренебрегая разностью фаз, показать, что на больших расстоя-
расстояниях от центра щели вектор-потенциал диффрагированного ноля равен i
~ 2/Д0 sin у [sin (Pg «n O)-Pa aii, 6 cos (jig sin 6)] ^ Х
8 ?cfi2fisin')e ' 8
где <f— азимутальный угол, отсчитываемый от оси i, ad- полярный угол, измеряемый
от оси щели.
50. Линейно поляризованная волна надает на тонкий плоский идеально проводящип
экран пед углом а к его нормали. В экране имеется малое отверстие радиуса а. Пусть
вектор Ео параллелен плоскости экрана. Показать, что если в залаче 49 jia мало, то
интенсивность диффрагированного излучения равна '
ff_ Щ*а* cos2 а A - -sin2 6 cos2 <f) T
1 Н
Заметим, что Во в стоячей волне задачи 49 в два раза больше, чем в бегущей.
51. Показать, что средняя излучаемая отверстием мощпость в последней задаче
равва
52. Пусть вектор Ео, рассмотренный в задаче 50, лежит в плоскости падения волны.
Показать, что если в задачах 48 и 49 ря очень мало, то интенсивность диффрагирован-
диффрагированного излучения равна
4В4а6 —
[4 sin2 у cos2 6 + B cos <p — sin 6 sin aJ] По.
Заметим, что амплитуда стоячей полны в задачах 48 ц 49 в два раза превышает амилш-
туду в По.
53. Показать, что средняя излучаемая отверстием мощность и последней задаче равна
-р 16^D + sin2 a) ^
54. Электродвижущая сила <S приложена в середине, очень узкой щмш, про-1
резанной в бесконечном плоском проводящем экране j/ = 0 и имеющей границы я = ^8(
z=±l. Предполагая, Что попе в щели в плоскости j/=0 равно E0 = i8-1(| sin [fi(J — z)],
показать при помощи выражения A4.138), что напряженность электрического ноля вне
щели при у > 0 равва
± 1/2A ТО
где R2 = х24-у2 + (z — ZjJ. Показать путем сравнения с ротором от A4.138), что
так что поле одинаково по виду с полем антенны, возбуждаемой в центре, если поменять
местами В и Е. Следовательно, из A4.45)
¦ Е= -~% (яр)-1 [2 cos ЦЛ sin(<»i — p/-) — sin (o.t — $ra) — sin (•»< —Ргь)],
где ra и гь—расстояния между концами щели и точкой наблюдепия.
55. Применить результаты предыдущей задачи к случаю резонансной щели l^1/^
и показать при помощи A4.50), чю сопротивление излучения щели при излучении в обо
стороны равно 363 ом. t
Замечание. Содержание нижеследующих задач базируется на теории диффракцйи.
Кирхгофа, которая не только полезна при решении оптических задач, ио с некоторой
Осторожностью может быть применена и в других случаях. !
56. Пусть функция ?/=ф(а;> У? %)е?1 является составляющей вектора Герца в не-
непроводящей среде, т. о. удовлетворяет уравнепию A3.19) при т=оо. Пусть также
г = г-1е/(«>*-И = 9(а;, у> z)ei"*
—аналогичная составляющая для сферической волны, возникающей в точке Р, как она
определена в A4.5). Подставив <\> и у в формулу Грина C.22) и выбрав объем интегри-
интегрирования между очень маленькой сферой, окружающей Р, и некоторой очень большой
поверхностью S, содержащей внутри себя сферу, показать, что
= \
S
32*
500 Глава XIV
где typ—значение ф в Р. Эта формула, лежащая в основе теории диффрагщии Кирхгофа,
выражает эффект в точке Р через интеграл по поверхности, окружающей точку Р.
57. Пусть поверхность S имеет отверстие, a U является сферической волной,
возникающей в точке Q, расположенной вне S. Предполагая, что функция U имеет на
отверстии те же значения, какие она имела бы при отсутствии S,' и считая U равной
нулю на остальной части S, показать, что
4л
S
где rj и г — радиус-векторы из Q и Р в пекоторую точку на отверстии; величины обоих
радиус-векторов значительно больше fr1; 6" —площадь отверстия.
58. Нугть в поверхности имеется отверстие 6''. Обозначим через В и R, средние
расстояния из центра отверстия О до точек Р v Q, я через .т' и г/' коордииоты некото-
некоторой точки отверстия, отсчитываемые от центра О. Разложить г и г1 в ряды по степе-
степеням х' и у' и показать, что
n-R П-R, Л
П-R, Л 2тц№+Д|)/Д
Б'
где р = 2пХ-1.
59. Рассмотрим плоскую волпу с интенсивностью 70, падающую нормально на круг-
круглое отверстие радиуса а, так что Л1=оо, и выберем R^>a, a P в точке ж = а:, у = 0;
тогда
F(x', у', В~1, Бг1)^ — za;'.R-» =
где а — угол, под которым видно ж из точки 0. При помощи E.370) и E.371) подсчитать
интеграл и показать, что интенсивность диффрагнроваиного излучения равна
1 Sin a)\*.
60. Взяв Q и Р на оси круглого отверстия радиуса а и считая, что В, и R много
больше а, показать, что если интенсивность падающей волны /0, то интенсивность в точ-
точке Р равна
4Я2/0 (Й! + В)-2 sin2 [па2 BX)-i (В + ЙГ1)]-
ЛИТЕРАТУРА
Biggs H. F., The Electromagnetic Field, Oxford, 1934.
Frenkel J., Lchrbuch der Elektrodynamik, 2 В.1., Berlin, 1926, 1928. (Френ-
(Френкель Я.. И., Электродинамика, М.—Л., 1935.)
Geiger-Scheel, Handbnch der Physik, Bd. XII, XV, XX, Berlin, 1927, 1927, 1928.
Hertz H. R., Electric Waves, Macmillan, 1893.
King R'. W. P., Mini no H. R.,-Wing A. H., Transmission Lines, Antennas,
and Wave Guides, McGraw-Hill, 1945. (См. перевод: Кинг Р., М и м н о Г.,
У и н г А., Передающие линии, антенны и волноводы, М., 1948.)
М а с D о ri a I d H. M., Electromagnetism, Bell, 1934.
Mason M., Weaver W., The Electromagnetic Field, University of Chicago
Press, 1929.
Maxwell J.G., Electricity and Magnetism, Oxford, 1881.
Page L.,. Adams N. I., Jr., Electrodynamics, Van Nostrand, 1940,
Schelkunoff S. A., Electromagnetic Waves, Van Nostrand, 1943.
Silver S., Microwave Antenna Theory and Design, McGraw-Hill, 1949. (См. перевод:
Сильв ер С, Антенны сантиметровых волн, ч. I и 11, VI., le.lO.)
Stratton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод:
Отрэттон Дж. А., Теория электромагнетизма, М.—Л., 1948.)
W.i е п.- Н а г m s, Handbuch dor Experimentalphysik, Bd. XI, 1932.
Глава XV
ВОЛНОВОДЫ И ПОЛЫЕ РЕЗОНАТОРЫ
§ 1. Волны в полых цилиндрических трубах. В § 15 — 19 гл. XIII
было показано, что вдоль двух или большего числа идеально проводящих ци-
цилиндров, расположенных один внутри другого, могут распространяться плос-
плоские электромагнитные волны. Если эти цилиндры окружить еще одним, внеш-
внешним, идеально проводящим цилиндром, то на очень высоких частотах внутри
такой системы появятся незатухающие волвы других типов; в частности,
внутри одиночного проводящего цилиндра простые плоские волны не могут
существовать1). Любую, как внутреннюю, так и внешнюю, границу цилин-
цилиндрического волновода можно получить путем перемещения образующей
параллельно оси z. Часто рассматривают волноводы, замкнутые в сечении
z = 0 и простирающиеся от z = 0 до z = oo. Как было доказано раньше
[см. выражение A3.21)], любую волну можно описать при помощи вектор-
потенциала А, который в соответствии с § 15 гл. XIII выражается через
решение W скалярного волнового уравнения двумя способами, один из
которых приводит к волне поперечно-электрического типа (ТЕ), а другой —к
волне поперечно-магнитного типа (ТМ). Соответствующие дифференциальные
уравнения имеют вид
^ ^. A5.1)
Нас будут интересовать установившиеся решения, соответствующие процес-
процессам, происходящим с круговой частотой со. В этом случае, как следует
из § 2 гл. XI, вектор-потенциал, удовлетворяющий первому уравнению,
а также ротор этого вектор-потенциала можно выразить через решения
скалярных уравнений следующим образом:
), A5.2)
где P2 = (u2e]j.. В формулах A4.130) и A4.131) эти выражения даны в цилин-
дрических координатах. Как и в § 18 предыдущей главы, W можно пред-
представить в виде произведения двух функций, одна из которых зависит
только от z, а другая — только от поперечных координат. Тогда скалярное
уравнение A5.1) распадается на два
W = UZ, V|ff± &„# = (), ^|+(P2T$nn)Z = 0. A5.3)
Здесь V зависит только от поперечных координат их и м2, а $тп опре-
определяется граничными условиями и симметрией системы. Обозначим через п
*) Классификация волн, которой придерживается здесь автор, не совпадает с обще-
общепринятой. В частности, волны в волноводе принято называть плоскими неоднород-
неоднородными.— Прим. перев.
502 Глава XV
единичный вектор, нормальный к поверхности границы, т. е. совпадающий
по направлению с А. Согласно соотношениям A5.2), граничные условия
можно записать в виде
I или ^f = 0, A5.4)
O = nx[Vx(kxV#(J] = nX[kVW(m-k.V(V№-J] =
, d2Wtml , d2W,m Q2 тЪ i
I * "l I __^ It- ' С К * I/I/ ^__ It-
I Д—о l ~^~" —Д—5" * I HwiK / Ytl
Здесь s— координата, измеряемая на цилиндрической поверхности вдоль
линии пересечения ее плоскостью, перпендикулярной к оси z, так что
s, = kxn. Таким образом, функция U на границе должна удовлетворять
условиям
Utrn = U или pmn = u и ^-" = 0. A5.5)
Второе и третье условия в соотношениях A5.5) совпадают с теми,
которые встречались нам при рассмотрении главных волн (см. § 15
и 19 гл. XIII), т. е. волн, скорость распространения которых не зависит
от частоты. Такие волны возможны только при наличии двух или более
проводящих цилиндров.
Поскольку дифференциальные уравнения A5.3) являются уравнениями
второго порядка, то каждое из них имеет два независимых решения, а их
q6uj,ee решение можно записать в виде
= [AU1 (и„ uJ + BUs(ult u2)](Ce-T«>nZ + De^z), A5.6)
" ll A5.7)
При р > Pmn постоянная распространения Гти является часто мнимой вели-
величиной (<х = 0), и экспоненциальные множители в выражении A5.6) свиде-
свидетельствуют о наличии двух незатухающих волн, распространяющихся соот-
соответственно в положительном и отрицательном направлениях оси z. Если же
j3 < pmn, то, поскольку поля должны оставаться конечными, необходимо
положить С = 0 при z > 0, а при z < 0 положить D = 0. Тогда в оставшемся
члене Гтп — величина чисто действительная (Рт«=0), что приводит к экспо-
экспоненциальному убыванию поля вдоль z. Критическая частота vmri и крити-
критическая длина волны типа тп соответственно равны
Лп« = ^ (И = ^Г - Кпп = ^ ¦ A5-8)
Чтобы распространить на волноводы понятие характеристического
импеданса, подставим в определение A3.136) значения Е и В из соотно-
соотношения A3.134). Это дает
\ у №le _^ ±/v^\VxkWte\ _±/Q>ji.WxkWte\_ j^ /V A5.9)
kB |kx[Vx(Vxkif,e)]| \d(VxkWie)/dz\ Tmn'
,% . _ , H-lkxEtml _ /|fcx[Vx(kxVHrtm)]| ^
\/-Jh\lm — ± v
|B,m| («
kW")/6>z| _ T /fmn ^ A5.10)
Волноводы и полые резонаторы 503
Выражая эту же величину через критическую частоту, получаем
/2l1 -(v/vJ]1'2. A5-11)
Как и в соотношении A3.134), знак выбирается в зависимости от направле-
направления распространения волны: верхний знак соответствует волне, распростра-
распространяющейся в положительном направлении оси z, а нижний — волне, рас-
распространяющейся в отрицательном направлении оси z. Заметим, что при
частотах выше критической характеристический импеданс для обеих волн
представляет действительную величину, что свидетельствует о передаче энер-
энергии вдоль волновода; при частотах ниже критической характеристиче-
характеристический импеданс является чисто мнимым. В этом имеется отличие от того
определения линии передачи, которое было дано в § 17 гл. XIII.
Из соотношений A5.6) и A5.7) получаем выражение для фазовой
скорости распространения волны при р > $тп
Vmn==^_ = ш2 = v ^ = v A5.12)
где v — скорость распространения света в среде, заполняющей волновод.
Групповая скорость на основании соотношений A3.157) и A5.12) равна
да) 1 <93 Вгл« 1 V2
Итак, vmn > v > («,),„„. При очень высоких частотах фазовая и групповая
скорости приближаются к скорости волн в свободном пространстве. Выразим
лекторы электрического и магнитного полей Е и В через U при помощи
соотношений A5.2) и A5.3):
Ё(е = - /<оА,е = /сок X Vf/(ee-;P™'z, A5.14)
В/е = V х А,е = (- ft'mnV2Ute + Щппи1е) e~№'™z, A5.15)
Е,т = - /<oAfm = (o»P^V2C/(m + b№lrnU,m) е~'*'тпг - A5.16)
B(m = V X A(m = B% x *и,пе-»™г. A5.17)
Здесь Ute и Utm удовлетворяют уравнению A5.3); как видно из соотноше-
соотношений A5.2), размерность их различна.
§ 2. Учет затухания в волноводах. Волноводы применяются для
передачи высокочастотной энергии из одной точки в другую. Поэтому очень
важно знать величину потерь в волноводах. В случае заполнения волновода
неидеальным диэлектриком в последнем будет поглощаться часть энергии,
ни в обычных волноводах с воздушным заполнением эти потери редко
имеют значение, и поэтому расчет их отнесен нами в задачи, помещенные
и конце главы. Помимо этих потерь, в стенках волновода неизбежно
дазникают потери, обусловленные наличием вихревых токов, которые, как
правило, следует учитывать. Во всех практических случаях проводимость
стенок столь велика, что при вычислении Р можно в качестве очень хо-
хорошего приближения использовать решение, полученное для случая идеаль-
идеальных проводников. Если уменьшение некоторой величины пропорционально
значению самой величины, то в таких случаях всегда имеет место экспонеп-
504 Глава XV
циальное затухание. Как видно из формулы A1.24), мощность потерь
в проводящей поверхности пропорциональна квадрату тангенциальной
составляющей магнитного поля на поверхности. Поэтому поля при распро-
распространении вдоль трубы затухают экспоненциально, и если коэффициент затуха-
затухания для поля равен а, то для вектора Умова—Пойнтиига он равен 2а. При
усреднении по времени мощности Р, передаваемой вдоль волнов- да, множи-
множители, периодически зависящие от времени, исчезают, и мы имеем Рё~ az.
Вычислив производную от Р но z при помощи выражения A1.24)
и поделив ее на Р, получим
где dP/dz — средняя мощность потерь на единицу длины, В—вектор маг-
магнитной индукции непосредственно вблизи стенок, т — удельное сопротивление
материала стенок, о —толщина скии-слоя. На стенке V2Z7(e = s1 oUtejos,
поэтому из выражений A5.15) и A5.17) имеем
+ FmnUte, Blm.Blm = ^Y2Utm-Y2Utm. A5.19)
Но, согласно соотношению A3.145), среднее значение энергии, проходящей
в z-направлении через единичную площадку в одну секунду, равно
Ref -|i-'ExB ), или, пользуясь выражениями A5.14) —A5.17), получаем
|П,в|,= -уЦ-'юР' № X VUte) X V2ffJe]2 = l,*-i<o (PS-PU1/8 V2fVV2C/(e,
A5.20)
. I П(т |2 = у H-^P'P* [Vafffm X. (k x VUtm)]z =
= y^-1^2(P2-PU1/2V2^m.V2C/(m. A5.21)
Для упрощения поверхностного интеграла представим скалярное произведе-
произведение, входящее в выражения A5.20) и A5.21), в развернутом виде и, кроме
того, воспользуемся соотношением A5.3), тогда получим
VV(CT\U)-UV\U]dS = p«in [ U*dS. A5.22)
s
Первый интеграл по поверхности, т. е. \ V2-(W2U)dS, равен нулю, в чем
s
можно убедиться, преобразовав его в линейный интеграл по контуру границы
и воспользовавшись соотношениями A5.4) или A5.5), согласно которым
на границе или U, или V2Z7 равно нулю. Из выражений A5.18) —A5.20)
находим коэффициент затухания поперечно-электрической волны
т
Pmn I*- Km/v)*! ф (dUteldS)* ds + (%n/v)« (^ Ute ds
Здесь 8 = f — (ujj.'y J 2 —глубина проникновения, jj.'—магнитная проницае-
проницаемость стенок, v— частота, vmn — критическая частота, v—скорость света в сре-
среде с магнитной проницаемостью jj. и диэлектрической проницаемостью е.
Волноводы и полые резонаторы 505
a Ptrm=2-^"vmn. Поскольку вектор VU ортогонален поверхностям стенок,
то на основании' выражений A5.18), A5.19) и A5.21) можно написать
(dUtm/dn)* ds
Эта формула показывает, что затухание поперечно-магнитных волн
с увеличением частоты возрастает одинаково при любой форме поперечного
сечения волновода. Затухание поперечно-электрических волн, как видно
из формулы A5.23), зависит от формы поперечного сечения трубы и увели-
увеличивается с ростом частоты только в том случае, когда иервый член
в числителе выражения A5.23) не равен нулю (первый член равен нулю
для некоторых типов круглых волноводов).
§ 3. Прямоугольный волновод. Рассмотрим трубу, ограниченную
плоскостями х~0, х = а, у 0, у = Ь. Легко видеть, что решениями урав-
уравнения A5.3), удовлетворяющими граничным условиям A5.4) и A5.5), будут
ТТ ^ m~x п~г/ тт /-, . тих . п*у ,.е пг-,
^(e = Cmncos —cos —. kr(m=^Cmnsin —sin—, A5.25)
если m и n — целые числа. Согласно выражениям A5.14) и A5.15), поля
ТЕ можно записать в виде
a-sm—-—j— sin —cos—'Je ;Pm" , A5.27)
В<„ = С I ]тф'тп [ i — sin— cos -f + iT cos -j- sin -^J +
^^. A5.28)
На основании соотношений A5.23), A5.25) и A5.26) затухание этих волн
равно
,a , =_^ ¦ -w\; , A5.29)
2т Цт*Ь+п*аI*-ЫпМЧ1я , (fl + b)K^/vJ 1 ,* г от
Наибольшая критическая длина волны для полей ТЕ в волноводе,
у которого a =-• 2 слг и & = 4 cjw, согласно выражению A5.26), соответствует
значениям т = 0 и и=1 и равна X0i=8 см. Величина XOj не зависит от «.
Следующая по длине волна соответствует т=\ и и — 0 и равна Х10^=4слг.
Величина Х10 не зависит от Ъ. Как мы увидим в дальнейшем, волновод
можно выполнить таким образом, чтобы в нем возбуждались только волны
вполне определенного типа. Для пятисантиметровой волны, распространяю-
распространяющейся в волноводе только в виде волны типа TEqi, толщина скин-слоя
8«=8,5-10-7 м (для меди). Поэтому коэффициент затухания ate, определяемый
го формуле A5.29), приблизительно равен 0,005, так что (см. Двайт, 550.2)
на 1 м длины волновода напряженность поля убывает на 1/2%, а энер-
энергия—на 1%. Из соотношенияA5.12) коэффициент затухания при X = Xj0 равен
aio = /PJo = 0,3* = 0,94,
506
Глава XV
или в 200 раз больше, чем для Хо1. Групповая скорость волны, как следует
из выражений A5.12) и A5.13), составляет лишь 78% от скорости электро-
электромагнитных волн. На фиг. 134 представлен вид полей для волн TEUl и ТЕ
ТЕ,0 Е-линии. Сечение А В
ТЕЮ В-линии. Вид сверху
ТЕп Е-линии. Сечение АВ
ТЕи В-линии. Вид сверху
В
В
ТМп В-линии. Сечение А В ТМ„ Е-линии. Центральное сечение
Фиг. 134.
Согласно выражениям A5.16) и A5.17), поля для воли типа ТМ можно
записать в виде
. m m« . n-ny . . п
1- COS — Sin -^ + Л_
4-
Вт = ъ$2С I — 1 у sin cos-t-^ + j —
mit-x y
cos sm-~)e
nity\
A5.31)
mn . A5.32)
Коэффициент затухания для этих волн на основании соотношений A5.24) —
A5.26) определится выражением
2т m2fc3-f-nzas /it моч
Наибольшая критическая длина волны для нолей ТМ в волноводе, у ко-
которого « = 2 см, & = 4 см, согласно выражению A5.26), соответствует зна-
значениям т=п—1 и равна Хп = 3,58 см; следующая критическая длина
полны равна Х12 = 2,83 см. На фиг. 134 представлен вид полей для
полны TMlV
Суперпозиция двух полей в квадратном волноводе дает поле в тре-
треугольном волноводе, сечение которого представляет собой равнобедренный
прямоугольный треугольник (см. фиг. 135). Критическая частота остается
прежней.
Волноводы и полые резонаторы
507
§ 4. Круглый волновод. Рассмотрим круглый волновод радиуса а.
Как следует из § 18 гл. XIV, решение уравнения A5.3), конечное на оси,
будет иметь вид
U(p, <р) = Jm (Pmn р) (Стн ы»пир -Ь Dmn sin irap), A5.34)
где, исходя из соотношений A5.4) и A5.5), Pmrt надо выбрать таким, чтобы
(е=0, |/m(Pmn«)|(m = 0. A5.35)
А
да
Е-лииии. Сечение А В В-линии. Вид справа
Б
В-линии. Сечение А В Е-линии. Вертикальное сечение
Фиг. 135.
Ниже приведены наиболее важные нулевые точки этих функций:
/; C,832) = /; G,016) = /; (i,84i)=/; E,зз1) = о, A5.36)
/0 B,405) = /0 E,520) = J1 C,832) = Jx G,016) = 0. A5.37)
Поля для волн ТЕ, согласно соотношениям A5.4) и A5.15), определяются
следующим образом:
[Е],„ = /со [pj mp-1 Jm $mn p) (Cmn sin mcp - Dmn cos m <p) +
m (Kn P) Фгпп ™ ТП? + L>mn Sin mf)] ^W, A5.38)
n [ - PlPmn /m (Pmn p) (^mn COS Щ + Dmn Sin ГЩ) +
/m (pmn p) (Cmn sin mcp - Dmn cos mcp)] + ^
m(pmnP)(Cmncosmcp-b4wsmmcp)} e"ip'm"z. A5.39)
Из соотношений A5.34), A5.35), A5.23) и E.337) находим выражение
для коэффициента затухания волн ТЕ
[B]le =
508
Глава XV
Мы видим, что волны с круговой симметрией, для которых т — 0, обладают
необычным свойством: с ростом частоты их коэффициент затухания умень-
уменьшается. Из волн типа ТЕ наибольшую критическую длину волны имеет
волна типа ТЕп, у которой, согласно выражениям A5.35), A5.36) и A5.8),
А С
ТЕа,-волна. Е-линии в сечении Л В,
дающие одинаковые приращения
напряженности поля
ТЕ „-волна. Е-линии в сечении АВ,
дающие одинаковые приращения
напряженности поля
на центральной линии
TMoi -волна. В-линии в сечении/IB,
дающие одинаковые приращения
магнитной индукции
ТМО1-волна. В-линии в сечении АВ,
дающие одинаковые приращения
магнитной индукции на централь -
ной линии
В ' D
ТЕю-волна. Главное сечение
трубок равного потока маг-
магнитной индукции
А С
В В
ТЕ „-волна. В-линии в главном
сечении, дающие одинаковые
приращения магнитной
индукции на центральной линии
А С
В В
ТМсу, -волна. Главное сечение
трубок равного потока элект-
электрической индукции
А С
В В
Ши-волна. Е-линии в главном
сечении, дающие одинаковые
приращения напряженности,
поля на центральной линии..
Фиг. 136.
Хй1 = 3,42а; следующая критическая длина волны Х01 = 1,64а. Положим
а = 2,34 см, тогда Хп = 8см, т. е. равна критической длине волны прямо-
прямоугольного волновода, у которого а = 2см, а Ь = Асм (см. предыдущий па-
параграф). Для пятисантиметровых волн коэффициент затухания а равен
0,0028 м~1, т. е. он меньше, чем коэффициент затухания в соответствую-
соответствующем прямоугольном волноводе, где он равен 0,005 м~1. Вид полей для
некоторых типов ТЕ-вопъ представлен на фиг. 136.
Волноводы и полые резонаторы 509
Поля для волн ТМ, согласно соотношениям A5.16) и A5.17), опреде-
определяются по формулам
Ё<т = {ш$'тп [рДпп J'rrm Cmn p) (Cmtl COS т<р + Ьтг1 sin mcp) —
- <рт р-1 /т (Pmn p) (Cmn sin т«р - ?>mn cos ту)] +
/wpJU Jm фтп р) (Стп cos mcp + Д™ sin mcp)} е~*'тп\ A5.41)
Pan4>-f^m QrpnP) Фтп sin mcp — Ътп cos mtp) +
Р) (Cmn COS Щ + L>mn Sin 1йф)] в~УР W. A5.42)
Коэффициент затухания волн ТМ на основании соотношений A5.34),
A5.35), A5.24) и E.337) равен
Наибольшими значениями Хтп являются ХС1 = 2,61 а, Хи= 1,64 а и Хоа = 1,14 а.
§ 5. Коаксиальный волновод. Линии передачи, образованные двумя
проводящими цилиндрами — внутренним (радиуса а) и внешним (радиуса Ь),
относятся к классу линий, по которым мо1'ут распространяться волны
любых частот (такие линии рассмотрены в § 15 гл. XIV). Сопротивление
линии на единицу длины равно [см. соотношение A3.151)]
b
Характеристический импеданс, определенный выражением A3.147), равен
Zu = \ ¦—-г- г—— } , A5.45)
где
= .Т- In — .
<?тс а
Формула для коэффициента самоиндукции на единицу длины была полу-
получена, исходя иа соотношения LC = |ie и щ выражения B.9). Если самоин-
самоиндукция L?., обусловленная скин-эффектом, и проводимость диэлектрика f
малы, то при d(HJL)jd{bja), равном нулю, коэффициент затухания имеет
тупоп• минимум. Значение минимального коэффициента затухания, получаю-
получающееся при 6 = 3,6а, всего лишь иа 5% меньше значения коэффициентов
затухания при Ь = 2,5 а и ири Ь~ 5,0а.
При достаточно коротких длинах волн в коаксиальной линии могут
существовать волны высших порядков, подобные описанным в предыдущем
параграфе. Эти волны появляются главным образом при удовлетворении
граничных условий на неоднородностях. Поскольку область вблизи оси в
этом случае исключена из поля, необходимо в решении писать обе функ-
функции Бесселя. Таким образом, в соответствии с выражением A4.128) имеем
U = (Стп cos лир + Ътп sin mcp) Rm фтп р), A5.46)
[Дт (Ртп Р)Ьв = Jra (Р™, I') Y'm фтп а) - Ym (?тп р) Гп C„т «), A5.47)
[Дт Фтп Р)]„„ = Jm Фтп р) Ym ®тп а) - Ym Qmn р) /т фтп а), A5.48)
где, согласно соотношениям A5.4) и A5.5), pmn нужно выбирать таким,
чтобы выполнялись условия
A5.49)
510 Глава XV
Из выражений A5.47) —A5.49) видно, что при р = а и р—Ь граничные
условия, определяемые соотношениями A5.4) и A5.5), удовлетворяются.
Выражения для полей, коэффициентов затухания и т. д. можно опреде-
определить так же, как и в предыдущем параграфе, но для коаксиального волно-
волновода они представляют меньший практический интерес. • ",
§ 6. Плоские неоднородности в коаксиальной линии. При решении
некоторых задач о распространении электромагнитных волн в ряде случаев
можно получить достаточно точные результаты, воспользовавшись метода-
методами электростатики. Действительно, введя в уравнение A5.1) длину волны Л,
мы видим, что
V2E = - ш VE = - 4те*>г8Е ->¦ 0. A5.50)
;.->-эо
Таким образом, если длина волны значительно превышает размеры обла-
области, то мгновенные значения полей в последней не отличаются от полей,
описываемых решениями уравнения Лапласа, удовлетворяющими тем же-
граничным условиям."
Рассмотрим две коаксиальные линии, коаксиально соединенные между
собой в плоскости z = 0, которая является идеально проводящей всюду,
за исключением отверстий, соединяющих области распространения волн
в линиях. Пусть длина волны настолько велика, что в коаксиальных
линиях может распространяться только главная волна. Ясно, что если она
имеет характер стоячей волны и узел электрического поля совпадает
с плоскостью z = 0, то неоднородность не будет оказывать никакого влия-
влияния, так как в этой плоскости отсутствует радиальная составляющая
электрического поля, а линии магнитной индукции всюду касательны к этой
плоскости. В любой линии передачи картина распределения стоячей волны
вдоль линии не нарушается только в том случае, если, в узел электри-
электрического поля помещают шунтирующий элемент. Поэтому действие рас-
рассматриваемой нами неоднородности эквивалентно действию шунтирующего
элемента в плоскости z = 0.
Рассмотрим теперь частный случай коаксиального кольцевого отвер
стия и предположим, что плоскость z = 0 находится точно посередине
между двумя соседними узлами стоячей волны электрического поля.
Очевидно, что радиальная составляющая поля главной волны не перпенди-
перпендикулярна к плоскости z -— 0, поэтому для удовлетворения граничных усло-
условий здесь необходимо присутствие местных полей высших порядков, вид
которых определяется соотношениями A5.47) или A5.48). Все они содер-
содержат фактор е~'р6иг' [см. соотношение A5.38)], т. е. поля существенно от-
отличны от нуля лишь вблизи сечения z = 0, в области, значительно
меньшей, чем длина волны. Таким образом, местные поля находятся в
фазе. Согласно выражению A5.50), мгновенное значение электрического
поля в сечении совпадает со статическим полем между внутренним и
внешним проводниками, а емкость линии в сечении z = 0 равна разности
между действительной емкостью этого сечения и суммой емкостей концен-
концентрических цилиндрических конденсаторов по обе стороны сечения.
В качестве простейшего примера может служить случай, когда отно-
отношение внешнего радиуса ко внутреннему близко к единице. Небольшой
участок цилиндрического конденсатора можно заменить узкой пластинкой
плоского конденсатора и решить задачу при помощи конформных преоб-
преобразований. Такое решение для случая плоского конденсатора с параллель-
параллельными пластинами, имеющими уступ с одной стороны, изображено на
фиг. 63,6 (линии V=0 и V = те/2) и рассмотрено в § 14 гл. VI. Полови-
Половина величины дополнительного сопротивления (на единицу длины) опреде-
определяется по формуле F.63), а соответстпующап добавочная емкость (на единицу
Волноводы и полые резонаторы 511
длины), согласно соотношению F.67), будет равна 2е/(тД.Д). Емкость
неоднородности определяется как произведение этой емкости на периметр
2тгг области, в которой распространяются волны. Таким образом, из соот-
соотношения F.63) имеем
о
A5.51)
Виннери и Джемисон1) эмпирически показали, что если имеется уступ
только в одной стенке, то нужно умножать добавочную емкость на пери-
периметр другой стенки. При отношении внутреннего радиуса к внешнему,
равном 5, этот способ дает ошибку только около 10%. Отражения от
таких препятствий вычислены в § 17 гл. XIII [см. выражение A3.140)],
где Zhl и Zh2 — волновые сопротивления линий по разные стороны от пре-
препятствия (ступеньки)
Z^Zhl, LrJ.C + ±-r^f+±.2. A5.52)
§ 7. Возбуждение волноводов. Строгое решение задачи о возбуждении
волновода посредством петли связи или штыря представляет исключитель-
исключительные трудности. Одиако в этом случае, как и для антенн (см. § 4 — 7
гл. XIII), можно получить приближенные решения, если принять определен-
определенное распределение тока вдоль провода и считать, что весь ток сконцен-
сконцентрирован вдоль оси провода. Тем самым задается магнитное поле вблизи
провода, которое затем можно представить в виде суперпозиции полей различ-
различных типов волн. Если принятое распределение тока является правильным,
то электрическое поле сторонних э. д. с. на поверхности провода будет
полностью скомпенсировано тангенциальной составляющей электрического
поля, создаваемого данным током. Поэтому импеданс излучения некоторо-
некоторого участка провода будет равен взятой со знаком минус сумме линейных
интегралов от электрических полей различных типов (интегралы берутся
вдоль провода в направлении тока), деленной на величину тока. Таким
образом, поле каждого типа действует как некоторый независимый
контур, подключенный к концам этого участка провода. Данный элемент
тока возбуждает такие типы волн, у которых имеется составляющая
электрического поля вдоль провода, что подразумевает также наличие
магнитного потока, сцепленного с проводом. Рассмотрим элемент тока,
лежащий в плоскости z = z0 бесконечного волновода, простирающегося от
z= — оо до z=co. Составляющую В, тангенциальную к этому сечению,
(В,), можно записать в виде бесконечной суммы, каждый член которой
относится к определенному типу волны и имеет вид ¦AmnUmn(u1)Vm{u2),
где Vmn (Mj) и Vm (u2) — ортогональные функции поперечных координат их и
и2. Умножим это равенство на Uvq (иг) Vv (м2) du>\ du2 и проинтегрируем по
всему сечению. Тогда с одной стороны равенства останется только член,
соответствующий pq. Величина Bt всюду равна нулю, за исключением
малой области (и[, и'2), в которой UVQ(u'1)Vv(u'i) можно заменить средним
значением ит(и'г) Vv(u2). Согласно закону о циркуляции магнитного поля
[см. выражение G.2)], интеграл от В, в направлении, перпендикулярном
к направлению элемента тока, равен -^ \xl. С этим методом мы уже встре-
встречались в магнитостатических задачах в § 12, 14 и 32 гл. VII. Обычпо
такой элемент возбуждает и волны ТЕ и волны ТМ. Если поместить
в точку z= — z0 второй элемент тока, равный первому по величине и про-
противоположный по знаку, то суммарное электрическое поле будет перпенди-
перпендикулярно к плоскости z = 0 и, следовательно, будет совпадать с полем,
Ч Whinne.ry, J am i so n, Proc. Inst. RacU Eng., 32, 98.
512 Глава XV
возбуждаемым в волноводе, замкнутом в сечении z = 0 идеально проводя-
проводящей плоскостью.
Элемент тока, ориентированный 'вдоль оси z, возбуждает только
волны ТМ. Метод, описанный в § 3 гл. XIV, оставляет неопределенными
и длину й фазу дипольного источника, полученного путем дифференциро-
дифференцирования поля точечного источника по координате z, совпадающей с направ-
направлением распространения. Поэтому лучше взять дипольный источник, распо-
расположенный в плоскости постоянной фазы, как это и было сделано в § 22
гл. XIV [см. выражение A4.147)], где плоскость z0 была всюду заземлена,
за исключением бесконечно малого отверстия, на котором поддерживался
потенциал V0e''ot. Электрический дипольный мгмент этого источника, как
и магнитный дипольный момент маленькой петли с током, пропорциона-
пропорционален его площади dS0. Таким образом, формула A4.154) для элемента тока
с моментом / dzu cos wt дает
7° dz° = /W/T)F
Выпишем выражение для тангенциаленои составляющей Etm в плоскости z0
в виде бесконечной суммы членов вида AmnUmn (мх) Vm (м2) и определим
коэффициент Ар1, умножив эту сумму на Um (мх) Vp (м2) dux du, и проинте-
проинтегрировав по сечению. Тогда в правой части останется только член, содер-
содержащий Ат, а в левой части мы возьмем dS0 в виде криволинейного
квадрата, ограниченного линиями и\, и[ -\-^и[, u'i, u\ -\-Аи[. На элементе dS0
и вне его Elm равно нулю, но интеграл от Elm при переходе через гра-
границы элемента dSn равен ± Vo. Если элемент тока несет на себе еще
и свободные заряды, как это должно быть в случае штыря, введенного
внутрь волновода, то, согласно выражению A4.1), скалярный потенциал будет
совпадать по фазе с зарядом, что удовлетворяет электростатическим условиям
и не оказывает влияния на распространяющиеся волны. Это местное поле
приводит к наличию емкостною реактивного сопротивления. В случае произ-
произвольной ориентации элемента тока его можно разложить на продольную и
поперечную составляющие и рассматривать каждую из них в отдельности.
При возбуждении волновода через отверстие метод, изложенный в § 22
гл. XIV, часто позволяет получить приближенное решение, если постули-
постулировать, что на отверстии сохраняется тангенциальная составляющая невоз-
невозмущенного поля.
§ 8. Возбуждение круглого волновода элементом тока. Применим
метод, описанный в предычущэм параграфе, для вычисления волнового
режима внутри круглого волновода, возбужденного радиальным или про-
продольным элементом тока. Для элемента тока, ориентированного нормально
к указанным двум направлениям, вычисления сходны с вычислениями
в случае радиального тока, и поэтому они помещены (вместе с аналогич-
аналогичными примерами для прямоугольных волноводов) в задачи, находящиеся
в конце главы.
Рассмотрим элемент тока pje1"*, длина которого в точке р0, 0 в пло-
плоскости z0 равна dp0. Если бы этот элемент находился не в точке ср = О,
а й точке ср=ср0, то в формулах § 4 достаточно было бы заменить ср на
ср — ср0. Полное поле типа ТЕ равно двойной сумме по m и п членов, опре-
определяемых соотношениями A5.38) и A5.39). Чтобы найти амплитуду члена рд,
положим в выражении A5.39) t 0, z = z0 и Стп = 0, а затем, учитывая,
что Ер — четная функция ср, умножим его скалярно на величину
p'1^ (Ppgp) cos /><p] pdp efy
Волноводы и полые резонаторы 513
и проинтегрируем в пределах от ц.-= — тг до ср = тг и от р = 0 до р = а.
В результате периого интегрирования в сумме по т исчезнут все члены,
кроме р-го, а интегралы от sin2pcp и cos2pcp будут равны ¦к. Обозначим
Рр„р через tj, а Рир—через i2, тогда оставшийся интеграл по р примет вид
1Л-1- A5-54)
Но, согласно соотношению E.350), этот интеграл равен нулю для любых п,
кроме n = q, когда он [см. соотношение E.351)] равен
В плоскости z0 поле В? всюду .равно нулю, а поле Bv отлично от нуля
только на элементе ctoo вблизи точки р0, 0. На основании соотношения G.2)
i * 1 ¦ v
ф В^р cfo = —— \xl при р = рс. Решая относительно Dm, имеем
\Ъ „],е = _fj^jPp-MIWcj e*™z.o. A5.55)
"9 гР/"(в*Л[/(Р0)]2
Для полей ТЛ/, возбуждаемых радиальным элементом тока, в выражении
A5.42) .положим t = 0, z = z0 и Дпп = Ои помножим его скалярно на величину
а затем проинтегрируем в пределах от <р = — тг до ср — тг и отр = Одор = а.
Полученные интегралы совпадают с рассмотренными выше, за исключе-
исключением множителя B- 8Р), а интеграл, входящий в выражение A5.54), равен
2~lPpsG^p(Pp<ja)]2' потому что /р(Рма)=О. Таким образом, получаем
op)_e,^
В случае продольного элемента тока, используя источник, характеризуемый
соотношением A5.53), положим в выражении A5.41) z = z0, Dmn = 0 и умно-
умножим скалярно обе части его на величину
[pipPp/p (РрЧР) cos № - 4PJp (Рр«Р)sin Л>] dP dT = Rpq dP d?>
а затем проинтегрируем в пределах О< р<а и 0<ср< 2тг. В результате
интегрирования по ср правой части, используя соотношения E,350) и E.351)
и помня, что Jv (РР4а) == 0, получаем
RpqdP Af = ^#i fma2 [Гр фрдй)Г e~^^ (l5.57)
J ¦) ±j On
о и
1 1
Площадка dS0 ограничена дугами c-fy^ и с —-г-& и радиальными линиями
1 1
— Л<р и ——&'?. Интеграл вдоль дуг, где подинтегральная функция не зависит
от <р, равен
.. xV0^— -Ри1Рис/р' (PPQc) -г-/Р(Рр,с)]У0ВДт. A5.58)
33 в Смайт
514 Глава XV
На радиальных сторонах В настолько мало, что можно положить р—с,
тогда получим
- Ърс 4V (Ppgc) [ sin (i рДср ) - sin ( - у />Д<р) ] Vo =
F0/p(PpBc). A5.59)
Сумма выражений A5.58) и A5.59) равна левой части выражения A5.57).
Заменив сбАср на йб",,, подставив VodSo из выражения A5.53) и комбинируя
функции Бесселя при помощи уравнения Бесселя E.314), для Cpq получим
Следует отметить, что в выражениях A5.56) и A5.60) функцию /р(Ррд«)
можно в силу соотношения E.134) заменить на—•^¦i(PPQ«), потому что
§ 9. Возбуждение круглого волновода петлей с током. Применим
формулы предыдущего параграфа к плоской квадратной петле, располо-
расположенной в плоскости <р = 0 круглого вол-
-d-*~[ повода радиуса о, замкнутого в сечении
z = 0 проводящей степкой, граничные ус-
LJ
0
LJ
in
i LJ лови я на которой удовлетворяются
" in
если
*; взять зеркальное изображение петли, как
ето показано на фиг. 137. Будем предпо-
лагатъ, что распределение тока в петле
фиг 137 однородно, хотя интегралы можно вычи-
вычислить для любого заданного распределе-
распределения. Волны ТЕ возбуждаются только ра-
радиальными участками петли. Суммируя прирост амплитуды Dmn за счет
элементов / dp0 в точке р0, d, — I dp0 в точке р0, Ь, 1 йр0 в точке р0, — Ь
и — Idp0 в точке р0, — d [см. соотношение A5.55)] и интегрируя в пре-
пределах от ро = с до ро — а, для области |z|>d получим
,Х , 2wu/[sin(p^nd) —sintp^^)] Г"л„(с), ,,,„..
|//mn|(e= ; ^- \ tt, ^ 10.01/
где Pmn определяется выражением A5.35), a f^?n = Р2 - ?тп- Интеграл в соотно-
соотношении A5.61) можно вычислить путем разложения Jm (t) вряд [см. E.314)],
в котором обычно бывает достаточно взять лишь несколько членов. Поля
волн ТЕ определяются выражениями A5.38) и A5.39), в которые необхо-
необходимо подставить выражение для Ьтп, а Стп положить равным нулю.
Из предыдущего параграфа следует, что волны ТМ возбуждаются всеми
участками петли. Действуя так же, как и при нахождении волн ТЕ, но
применяя соотношение A5.56) вместо соотношения A5.55), находим, что
боковые стороны петли для области z > d дают
г^/ ! ¦ __ /У-/о B — Ът) [sin (pmtirf) — Sin (;-mnb)| Jm (PWO C15 62^
Для продольного участка, как видно из фиг. 137, нужно просуммировать
действие элементов в z0 и — z0, а затем проинтегрировать^ пределах от
zu = b до ze — d, что приводит к следующему:
7 ХГ" Л —<2 —8m)Wo[sin(;d) Sin(°6)l J(PC)
/
Волноводы и полые резонаторы 515
Суммируя выражения A5.62) и A5.63) и учитывая, что на основании
соотношения A5.7) Р2.= Pmn + Pmn, для волн ТМ, возбуждаемых петлей,
окончательно получаем
гл I __ / B—Ь°т) pip [sin (^nrirf) — sin (&nnb)] Jm j$mnc) ,j^ g^.
Поля определяются путем подстановки этой величины в выражения A5.41)
и A5.42). Для распространяющихся волн р„„ — величина действительная,
так что входящие, в числитель тригонометрические члены можно записать
(см. Двайт, 401.09) в виде
sin ф'тпй) - sin ф'тпЬ) — 2 sin [u (d — b) \'~n] cos [n (d + 6)Х^]. A5.65)
Совершенно очевидно, что если длина петли d — b равна целому числу
длин волн в волноводе или если расстояние -^-(d-\-b) от центра петли
до замыкающей стенки равно нечетному числу полуволн, то соответству-
соответствующий тип волны не будет возбуждаться. Если же нижняя часть петли
лежит на оси волновода, то возбуждается только симметричная волна ТМ,
потому что Jm @) = 0 при т =j= 0.
§ 10. Возбуждение круглого волновода через отверстие. Б последнем
параграфе решалась задача о возбуждении волновода в случае заданного
распределения тока в антенне или в петле. Теперь решим ее для задан-
заданного значения тангенциальной составляющей электрического поля на от-
отверстии. Рассмотрим коаксиальную линию, состоящую из двух цилиндров
радиусов р — Ъ и р — с (с > Ь) и ограниченную с одного конва идеально
проводящей плоскостью z=0, в которой прорезано кольцевое отверстие.
Эта плоскость замыкает круглый полубесконечный волновод р = а, z—- 0,
z=oo. Из симметрии ясно, что в волноводе может возбуждаться только
не зависящая от ср волна ТМ, а из соотношений A5.49) и A5.41) мы
получаем
Jo (М = 0, Ёр = о, 2 СЛЛ (рпР) е~*"\ A5.66)
51=1
Как и в выражении A4.148), мы принимаем для плоскости z = 0 следу-
следующие граничные условия:
0 < р < Ъ, Et = 0;
1; С<Р<«- Д>=0- A5-67)
Подставляя эти значения для Ev в соотношение A5.66), умножая затем
обе части на р/х(Рпр)йр и интегрируя в пределах от р = 0 до р = а, для С„
получим
Для вычисления входного импеданса волновода, подсоединенного к коакси-
коаксиальной линии, проинтегрируем вектор Умова—Пойнтинга по площади отвер-
отверстия. На основании формулы A3.97), используя отношение Е9/В^, опреде-
определяемое выражениями A5.41) и A5.42), имеем
Л =1 J ?Д сИ - Р I E!2,,dP = Л. . A5.69).-
33*
Глава XV
Возведем выражение A5.66) в квадрат и произведем интегрирование при
помощи соотношения E.354):
Таким образом, волновод эквивалентен цепи, состоящей из параллельно
включенных импеданеов, каждый из которых соответствует определенному
типу волны. Для распространяющихся волн $'п — действительная величина
и импеданс получается чисто активным. Для других волн $'п — мнимая
величина, т. е. импеданс реактивен. Точное решение требует согласования
нолей на отверстии со стороны волновода и со стороны коаксиальной линии
с использованием соотношения A5.48).
л,
1 • § 11. Плоские неоднородности в прямоугольных волноводах. Плоская
неоднородность может быть образована путем соединения двух прямоуголь-
прямоугольных волноводов, расположенных с двух сторон от перпендикулярной к ним
идеально проводящей плоскости z = d, в которой прорезаны отверстия,
соединяющие внутренние области волновода. Пусть в обоих волноводах
распространяется только волна типа TEW. Тогда можно создать такую
сд'оячую волну, у которой узел электрического поля (см. § 6) будет совпа-
совпадать с плоскостью z d. Следовательно, но тем же причинам, что и в § 6,
такое сочленение должно действовать, как некоторый шунтирующий эле-
мент Zs, помещенный в линию в сечение z = d. Рассмотрим теперь частный
случай, считая длину волны Х]0 одинаковой для обоих волноводов и пред-
предположив, что стоячая волна TJE10 имеет узлы электрического поля в точках
z = 0 и z = 2d. Напряженность электрического поля для волны ТЕ10, в соот-
соответствии с соотношением A5.27), равна
JS^J^sin^sinp^zcosurf, A5.71)
Где 0 < z < d. Поскольку это поле дает отличную от нуля тангенциальную
слагающую па металлических поверхностях в сечении z = d, в волноводе
должны присутствовать также и волны высших типов, которые ее ком-
компенсируют. Как видно из соотношения A5.27), содержащего множитель
е— 11 jnn(z~d)l ^ ПрИ достаточно большой величине Х10 поля высших типов лока-
локализованы в очень небольшом интервале z. Следовательно, их колебания
совпадают по фазе, что позволяет, учитывая соотношение A5.50), опре-
определить конфигурацию этих полей статическим методом.
Отрезок волновода 0 < z < 2d эквивалентен Т-образному звену (изо-
(изображенному на фиг. 101), замкнутому накоротко в сечениях A'A" (z = 0)
¦v" v ¦v v
и В'В" (z = 2d), причем Za = Zb, Z2 — Z/, в этом звене происходят колебания
такого типа, при которых ir+i = —ir и — Za-\-Zs — 0. Обычно при рассмо-
рассмотрении неоднородностеи в волноводе пользуются понятием «нормированного»,
или отвосительного импеданса, который мы будем обозначать через Z0.
Нормированный на единицу импеданс равен действительному импедансу,
отнесенному к характеристическому импедансу волновода. Для волны
ТЕ10, распространяющейся без затухания, соотношение A0.112) дает
ДсИ1к1+/1вк.1 A5>72)
fol '
Волноводы и полые резонаторы 517
В случае коротко замкнутого Т-образного звена z? = 0 и l = d, поэтому
при резонансе
ZS = -| ZI- -1 /tgp;orf. A5.73)
. i
Остановимся теперь на специальном случае, когда геометрия волновода
в любом сечении, параллельном плоскости х = О, а следовательно, и
электрическому полю, одинакова. В сечении z = d это могут быть устут
пы в стенках, или диафрагмы, или комбинация и тех и других. Элек-
Электрическое поле ориентировано параллельно плоскости х — О, так что на
участке вблизи z'=d, где можво пренебречь изменениями фазы, вектор Е
при любых значениях х должен быть непрерывен по у и z и должен
выражаться через потенциал, удовлетворяющий двухмерному уравнению
Лапласа, записанному в координатах у и z. В любых узлах электрического
поля ток одинаков, поэтому полный заряд на верхней и нижней стенках
волновода между узлами Е также одинаков. Пусть в интервале 0 < z < 2d
заряд на единпцу ширины стенки (вдоль х) при х=х0 равен (?10 для
волны ТЕ10 и Qu для всех других типов волн. Обозначим статическую
емкость неоднородности (на единицу • ширины) через Сг. Разность потен
циалов между верхней и нижней стенкой волновода при х = ос0 и z = d
равна Vd=bEd. Тогда на основании выражения A5.71) имеем
4АЮ d
0 ^
о о
Подстановка этой величины в выражение A5.73) дает
Z\^ * =J74 .тли C° = ^.CV A5.75)
Таким образом, такая неоднородность имеет емкостный характер.
В качестве примера рассмотрим такую диафрагму в волноводе, кото-
которая образует в нем окно высотой с (высота сечения волновода равна b)r
как это изображено на фиг. 39, где все эквипотенциальные поверхности,
за исключением граничных поверхностей, на которых С/ = 0 и U-— ic,
показаны пунктирными линиями. Подставляя в выражение A4.106) а —с,
W = /V, z — jd, для V (при d—>оо) получим
., rtrf -, TZC ltd , ,
Заряд на единицу длины на расстоянии от 0 до d равен tV. Последний
член, умноженный на в, равен половине дополнительного заряда па слепке
волновода, обусловленного присутствием диафрагмы, при условии, если
разность потенциалов равна ти/2. Поэтому для получения С1 нужно второй
член умножить на 2 и на 2е/ти. Подстановка Сг в гыражение A5.75) и
замена (ij0 на 2iik~l дает для нормированной реактивной проводимости В"
следующее выражение:
Во = шСо=-J'lncosec^. • A5.77)
В случае симметричной диафрагмы, о)раниченной поверхностями
U= — тг/2 и СУ = тс/2 (см. фиг. 39), единственная разница будет заключаться!
втом, что разность потеншгалов равна не ти/2, а ти, и, следовательно, выра-1
жение A5.77) нужно разделить на 2. Поскольку ближайшая экспоненциально
спадающая волна ТЕп исключается теперь в силу симметрии, то результаты
518
Глава XV
рказываются несколько более точными. Из фиг. 39 ясно, что емкост-
емкостная полоска в центре ведет себя в точности так же, как и симметричная
диафрагма.
Другой интересный случай имеет место тогда, когда геометрия вол-
волновода в любом сечении, параллельном плоскости у = 0, а следовательно,
и магнитному полю, одинакова.
Согласно выражению A5.28), амплитуды составляющих В в плоскости
z = d равны
icos (PiVO s*n —ь zj mA I
m=2
ch | '?
sin
^ sin (p10d) cos - - 2j —
| cos
A5.78)
A5.79)
где Рт0 = тт:/а. Умножив выражение A5.78) на sin (ux/a) dx, a выражение
У О
Фиг. 138.
A5.79) на cos(rcx/a)dx, произведем интегрирование в пределах от х =
до ж = а и исключим Ах; это дает
[iioa f B2 cos (та/а) da:
О
a
Ti ^ Bx sin (nx/a) dx
A5.80)
Здесь требуется статическая апроксимация высших типов волн только
в плоскости z = d, а не во всей области их существования, поэтому это
выражение может привести к более точным результатам, чем выраже-
выражение A5.74).
На фиг. 138, а показан частный случай симметричной диафрагмы
с зазором, равным с. Очевидно, что магнитные силовые линии проходят
по обе стороны от центра окна в противоположных направлениях. Приве-
Приведенные на фиг. 138, а и б схемы связаны между собой так же, как схемы
на фиг. 39. Поле, изображенное на фиг. 138, б, получается от щели, шири-
ширина которой равна 2 и которая вырезана в бесконечной плоскости, имеющей
нулевую магнитную проницаемость. Эта плоскость является границей раз-
раздела двух равных но величине, но противоположно направленных однород-
однородных магнитных полей. На фиг. 40 показана верхняя часть поля при а = 1.
Суперпозиция двух полей в соответствии с соотношением DЛ10) приводит
к полю, изображенному на фиг. 138, б. Применив к последнему преобра-
преобразование D.107), указанное на фиг. 39, но несколько измененное (начало
координат ^помещается у основания диафрагмы), получаем поле, показанное
Волноводы и полые резонаторы 519
на фиг. 138, а. Таким образом,
W = C'(z'* — \yi*, z[ = Ьг sin v —-. A5.81)
Исключая z[ и требуя выполнения равенства z' = y(a —с) при z[=l, на-
находим
(^'^Y/2. A5.82)
В сечении волновода плоскостью z — d у' = О, что с учетом выражения
D.56) дает
= ± С§-х (cos^^-sin^I'2. A5.83)
Таким обра"зом, Вх является четной функцией относительно оси волновода,
равной нулю при*у(а — с) < х < -у (а-)- с), a В2 является нечетной функ-
1 1
цией, равной нулю при 0<х<-^-(х— с) и при — (а + с) < Х < а- Инте-
гралы в выражении A5.80) можно взять по частям, если в одном из них
положить dv--Bxdx и и = sin(irx/a), а в другом dv=-Bzdx и u = cos(tzx/o).
Произведение uv равно нулю, и если в одном интеграле sin(itx/a) заме-
заменить на t cos ( -у ¦KCJa J , а в другом cos (тгх/a) — на t sin ( -j ъс\а J, то они све-
сведутся к интегралу C50.01), приведенному в справочнике Двайта. Под-
Подстановка их значений в выражения A5.80) и A5.73) дает
& = /?tg8g=/u>LS. A5-84)
Рассматриваемая диафрагма является индуктивной, и соответствующая ей
нормированная шунтирующая реактивная проводимость равна
Б° = 4-= L=_^?.ctg2^. A5.85)
В конце главы имеются задачи на расчет других видов диафрагм.
§ 12. Полые резонаторы. Собственные колебания. При возникновении
электромагнитного возмущения внутри замкнутой полости с идеально про-
проводящими стенками волны будут бесконечное число раз отражаться от
¦стенок, так как в системе отсутствует рассеяние энергии. Поскольку на
стенках тангенциальная составляющая электрического поля обращается
в нуль, волна произвольной формы должна быть образована из элементар-
элементарных стоячих волн, соответствующих таким частотам, при которых на стен-
стенках создаются узлы электрического поля. Эти стоячие волны образуют
¦собственные (нормальные) колебания полости. Ясно, что если две непре-
непрерывные волны с одинаковой частотой, поляризацией и амплитудой распро-
распространяются в линии передачи или волноводе в противоположных направ-
направлениях, то через каждые полволны образуется узел поперечного электри-
электрического поля. Если в любых двух узлах электрического поля пересечь
волновод двумя идеально проводящими плоскостями, перпендикулярными
к его оси, и образовать таким образом полость, то часть «пойманной» между
ними волны будет описываться одной из собственных функций колебания этой
полости. Очевидно, при произвольном расстоянии между плоскостями собст-
собственные частоты будут характеризоваться тем, что для них на длине волновода
между плоскостями будет укладываться целое число полуволн. Это сооб-
520 Глава XV
ражеиие можно использовать при нахождении частот собственных (нор-
(нормальных или свободных) колебаний полости, образованной из отрезка
волновода описанным выше путем. Амплитуды двух волн, распростра-
распространяющихся в волноводе в противоположных направлениях, равны меж-
между собой, т. е. в выражении A5.6) С1 = ± Z). Если рассеяние энергии
в полости отсутствует, а ее торцевые степки совпадают с плоскостями
z = () и z=-d, то для р-то поперечно-электрического типа колебаний,
взяв действительную часть выражения A5.6), получим
Wte = [Аиг (ult ия) + BU2 (и,, u2)]te sin ^ cos (V + %)te, A5.86)
а для p-m поперечно-магнитного типа колебании имеем
u1,ut)]tmcosJ^-cos(iapt + ^p)lm, A5.87)
где Pmn выбрано равным piz/d, что обеспечивает исчезновение тангенциаль-
тангенциальной составляющей электрического поля на торцевых стенках полости. Гра-
Граничные условия A5.4), A5.5) и A5.7), из которых находится величина pmn.,
остаются при этом выполненными, заменив теперь л на Pmnp и Ь'т„ на
ръ/d и решив выражение A5.7) относительно собственных частот колебаний
типа тпр для эвакуированной полости, найдем
«W,p = М~г1* KnV = *fW = f (&» + Р^*I" = v [[&„ + рЫсП]1!*. A5.88)
Для прямоугольного волновода Bmn дается формулой A5.26), для круг-
круглого- формулой A5.35), а значения pwm, соответствующие волнам высших
типов в коаксиальном волноводе, определяются по формуле A5.49). В слу-
случае главной волны в коаксиальной линии, согласно выражению A5.5),
§ 13. Типы независимых собственных колебаний полости. Обычно
электромагнитное воамущение возбужлает в полости одновременно несколько
типов собственных колебаний. Мы докажем, что мгновенное значение пол-
полной энергии равно сумме мгновенных значении энергии- собственных коле-
колебаний каждого типа, составляющих заданное возмущение, т. е., что
п
= 2 \ Bfdv. A5.89)
v i=l v v i—1 v
Для этого подставим в формулу C.24), являющуюся векторным аналогом
теоремы Грина, Е; или В; вместо Ф и Ё, или В,- вместо Ф и заменим
оператор rot rot, согласно соотношениям A3.10) и A3.11) на шг\>.в. Тогда
lie (cof-co?) ^Е,,.Е^у= JJ [Е} X (\ X Е,)- Е. X (V х Е,)] ¦ ndS. A5.90)
v S
11 ' Ej и Е7- имеют на гратшпах лишь нормальные составляющие, поэтому
оба вектора, стоящие в прямых скобках, тангенциальны к поверхности
границы, и, следовательно, их скалярное произведение на единичный
вектор нормали п равно нулю. Таким образом, поверхностный интеграл
обращается в нуль и в силу соотношения Е= —/соА мы получаем
i-A;dv = 0. A5.91)
Итак, внутри произвольной полости с идеально проводящими стенками,
заполненной неиоглощающим диэлектриком, собственные колебания, име-
Волноводы и полые реаонаторы 521
ющие разные частоты, являются совершенно независимыми. Но если потери
в полости настолько велики, что резонансные кривые, соответствующие
колебаниям двух типов, перекрываются, то этот вывод оказывается
несправедливым, потому что первый множитель в левой части выра-
выражения A5.90) может тогда быть равен нулго в отдельные моменты
времени.
Используемый здесь вектор^потенциал всегда определяется как ротор
W, так что его дивергенция раина нулю. Как было показано в § 2 гл. XIV.
при отсутствии зарядов такой вектор-потенциал описывает все поля,
удовлетворяющие уравнениям Максвелла. Если же внутри полости нахо-
находится электрод, несущий изменяющийся во времени заряд, то в соответ-
соответствии с выражением A4.1)' к решению необходимо добавить еще скаляр-
скалярный потенгиал поля, колебания которого во всей полости совпадают но
фазе с колебаниями заряда. Этот скалярный потенциал удовлетворяет
уравнению Пуассона. Чтобы доказать независимость энергии поля — ^Ф
от энергии поля —/шА или —jei^xft, нужно воспользоваться форму-
формулой C.2):
^ \ ^ = 0. A5.92)
Поверхностный интеграл равен нулю, поскольку ТФ параллелен п.
§ 14. Емкость и индуктивность цилиндрической полости. В общем
случае распределение зарядов, токов и потенциалов вдоль стенок полости
таково, что невозможно дать строго последовательное определение этих
величин, исходя из представления о контуре с сосредоточенными постоян-
постоянными, эквивалентном рассматриваемой полости. Чтобы эти определения
были полезны, они должны приводить к значениям тока, самоиндукции,
емкости, энергии и резонансной частоты, имеющим такой же порядок
величины, что и в эквивалентном контуре с сосредоточенными постоянными.
Мы будем определять эквивалентный ток полости для какгго-гшбудь типа
колебаний как эфф ктивпое значение объемной плотности тока смещения,
умноженное на площадь среднего поперечного сечения полости Sc — 2~JI~SO
для волн ТМ или на площадь среднего продольного сечения Sc = ( — Sn J ~d
для волн ТЕ. Ясно, что такое определение совпадает с обычным опреде-
определением тока в линейном контуре LC с поперечно-магнитным полем,
если ноле в конденсаторе однородно, а площадь его пластин равна Sc.
Таким образом, из первого уравнения Максвелла A3.1) мгновенное зна-
значение тока в г-м типе колебаний, учитывая, что oJ[ieA = V xVx А, равн. >
2, A5.93)
где V—объем полости. Из соотношений (8.11), A3.1) и (8.12) получаем
мгновенное значение магнитной энергии
522 Глава XV
Из соотношения A5.93) и A.39) находим мгновенное значение электри-
электрической энергии
Если теперь вместо . \ /{ dt написать qit то выражения A5.94) и A5.95)
будут представлять энергию в тг-м независимом эквивалентном контуре
LC [см. соотношение (9.1)]; при этом величины L4 и Ci определятся сле-
следующим образом:
т _ r*v j^ __frfL /
с —-^i с — ^s с — —
A5.97)
Заметим, во-первых, что резонансное соотношение ш = IjC удовлетворяется
и, во-вторых, что для всех колебаний одного типа (например, типа ТЕ
или ТМ) величина емкости для данной полости одинакова.
§ 15. Затухание собственных колебаний. Активное сопротивление
полости. До сих пор при вычислении нормальных частот мы считали
стенки полости идеально проводящими. Большинство применяемых металлов
являются настолько хорошими проводниками, что затухание свободных
колебаний начинает сказываться только после значительного числа коле-
колебаний. Поэтому при определении мощности, поглощаемой стенками, можно
пользоваться уже полученными нами в § 3 гл. XI формулами скин-эффекта.
Таким образом, согласно выражению A1.26),
Р = B[x2T8)-i ^ В, - В( dS, A5.98)
где -у и 8 — соответственно проводимость стенки и толщина скин-слоя,
а В, — амплитуда тангенциальной составляющей вектора магнитной индук-
индукции на поверхности стенки. Поглощающие свойства полого резонатора
обычно принято выражать через его добротность Q, величина которой опре-
определяется из соотношения
Wt = Woer«*l<i, A5.99)
где W,~энергия в момент времени t. Разделив это выражение на его
производную по времени, получим
а1Г A5Л00)
Заметим, что, согласно выражениям A5.94) и A5.95), энергия периоди-
периодически изменяется* от чисто электрической до чисто магнитной, но сумма
магнитной и электрической энергий все время остается постоянной с точ-
точностью до множителя, определяющего затухание. Поэтому полную энергию
можно считать равной максимальной магнитной энергии, определяемой
выражением A5.94), так что
toV'n8 ^ A-Arfv cou/f&J B-Bdv 2(* J В2dv
$ BfBi
Волноводы и полые резонаторы 523
В выражении (9.7) показатель, характеризующий затухание, и для q и для
i был равен —-^-(.ff/^)^ т. е. —(RjL)t для W. Отсюда, пользуясь фор-
формулами A5.100) и A5.96), находим активное сопротивление полости, име-
имеющей объем v, при колебании i-то типа:
]- A5.102)
При наличии потерь в стенках резонансная частота будет меньше, чем
•ш0 = (LC)'1. Заменив в дифференциальном уравнении колебаний полости
djdt на /ш и предполагая Й настолько малым, что ш -\- ш0 *с 2ш0 и о>ш0 =ь ш^,
мы придем к следующему результату1):
— Lw* + /o,R + C-1 = 0 или До) = |ш0 — о)| ^ i-0,^-1. A5.103)
§ 16. Собственные колебания цилиндрической полости. Выражения
для собственных частот свободных колебаний цилиндрической полости были
получены нами в § 12 [см. выражение A5.99)], а для эквивалентной емкости и
•самоиндукции— в§15 [см. соотношенияA5.96) иA5.97)]. Теперь найдем выра-
выражения для эквивалентного тока, добротности Q и для напряженностей полей
через величины, характеризующие размеры полости. В целях упрощения
этих вычислений можно воспользоваться следующей формулой, справедли-
справедливость которой доказывается при помощи соотношения A5.22):
(V X kVF) • (V X kVF) dv=\ (V2WJ d\ =
v
Л
So 0 p So
A5.104)
Применяя эту формулу, а также учитывая соотношения A5.2) и A5.93),
для эквивалентного тока в полости получим
^{ ^]lh). A5.105)
Для колебаний типа ТМ выразим объемный интеграл не через А, а через В,
как это было сделано в соотношении A5.101). Тогда, воспользовавшись
выражениями A5.104) и A5.2), придем к следующему:
^) в-Bdv
V
j =
?= I ^tAtv \ (С^^Г'-сшН +¦ f). A5.106)
В соответствии с соотношениями A5.2), A5.86) и A5.87) поля в полом
резонаторе можно записать в виде
(«У
cos (V + «PP), A5.108)
x) Следует иметь в виду, что автлр при оценке изменения частоты не учитывает
влияние самоиндукции скин-эффекта, сказывающееся в том же порядке. — Прим. перев.
524 Глава XV
in(V + ?P), ¦ A5-109)
B,m = - P™P (к X VUtn) cos-^ cos (<y + ?p). A5.110)
Для определения (? нужно вычислить поверхностный интеграл, входящий
в выражение A5 101). Для одной торцевой поверхности из соотношений
A5.105), A5.108) и A5.22) находим
\ Ble.Bled5 = i? \(W7(e)^ = ^3™ \ Ui.dS = g??ll.. A5.111)
So So So ^Pd' ,
Подставим теперь в выражение A5.101) объемный интеграл из соотношения
A5.105); тогда получим J ;
Qte= ^dSf (l+ ,fc"Prf< С Bf.rfsV, A5.112)
Si
где iSj — боковая поверхность полости. В случае колебаний типа ТМ для
одвой торцевой поверхности из соотношений A5.110), A5.22) и A5.20)
имеем
U}mdS = ^\{2-fv) l\m. A5.113)
Подстановка объемной) интеграла из соотношения A5.93) в выражение
A5.101) дает
^ Г ^У ^ D2 ЛСП /¦'Iе;
(md J • A
В последующих параграфах подробно разбираются свойства прямоуголь-
прямоугольного, круглого и коаксиального цилиндрических резонаторов. Результаты,
относящиеся к резонаторам других форм, помещены в задачах г. конце
главы.
§ 17. Свойства прямоугольного резонатора. Собственные частоты
колебаний прямоугольной еолости, согласно выражениям A5.88) и A5.26),
равны
"'* " ' I2 . П2 , 1
В соответствии с соотношениями A5.25) и A5.107) —A5.110) поля в таком
резонаторе определяются по формулам
Еп Г . п шпх . ппу
fe = ™mnpC [-lyCOS —^- Sin -у- +
, . т . тих пт.у 1. pnz . , ... ,агалп*
+ ^"^Б1П~1ГСОБ~0~ J Sin-VSin(<D*-r'!')nmP. A5.116)
В, =тг26 -{ V 1 S1I1 COS —~ -f 1-T-COS SIB —г^ COS -?-т- +
le i d \_ а а Ь ' J b a t J rf
os —cos-^sin ^r] cos (id* ¦+ ф)тг7р, A5.117)
.,, о л, I в Г . га тих . пъу . п . тт.х. л.пи 1 • P^z
^tm = ^ 0>п,н,^ < -v i — f-os sm -—- + j-sin cos —f- sin-—
im mnp у d I a a b J b a 6J d
A5.118)
Волноводы и полые резонаторы 525
(,n— — ^Рт-п-юС I 1— Sin— COS
A5.119)
Если один из индексов т, п или р равен нулю, то вектор Е будет ориен-
ориентирован вдоль соответствующей оси, a v не будет зависеть от длины резо-
резонатора в этом направлении. В этом наиболее распространенном случае, если
принять /) = 0и заменить тг2 {т2оГ'2 i n2b~2) С на Со, поля можно записать
следующим образом:
Ez= -"wAjsiii —rsin -rsm (mi- ф)тп, A5.120)
В = *С0 (^1Т sin -^- cos — 1 — cos —sin -f- J cos(oii-f ф)^. A5.121)
Если же электрическое поле ориентировано вдоль другой оси, то поля
можно найти при помощи циклической перестановки х, у, z, а, Ь, с и
т, п, р. Для определения значений L-, С- и 1х, близких к значениям
в соответствующем эквивалентном контуре с сосредоточенными параметрами,
последний нужно рассматривать как систему с колебаниями типа ТМ.
На фиг. 133 представлена структура поля в полом резонаторе, совпадающая
€ соответствующей структурой поля в волноводе за исключением верхнего
рисунка: его надо рассматривать как вид в сечении CD, а не АВ. Кроме
того, вся картина уже не изменяется во времени, а является стационарной,
причем там, где Е обращается в нуль, В достигает максимума и наоборот.
Поперечные границы должны ставиться так, чтобы линии i? пересекали их
ортогонально. Если исключить для колебаний ТЕ случай m = 0 и п О,
то для эквивалентных токов прямоугольного резонатора на основании соот-
соотношений A5.105) и A5.106) будем иметь
^g^ ). A5.122)
Добротность Qle при отличных от нуля тп, п, р, согласно выражению A5.112),
равна
-i- ц^Ък (mW -, п2а*) (т?ЬЧ* + п*аЧ* + р2а2Ь2K'2
^(е= p*a->b-> \n*a (a + dj-t т?Ь (b + d)[ т d-> (а + Ь) (т*Ь* , п-а2J ' ^ '
Поскольку при т — 0 или п — 0, А1т = 0, то для Qtm из соотношения A5.114)
получим
цхчЬъ{т*Ь21П2а*){тЧЧ2 + п*аЪA2 ' pWb2I'2 . - . „,.
' К • I
Как видно из формулы A5.115), наименьшую возможную частоту колеба-
колебаний резонатор аможно получить, если индекс, соответствующий наименьшему
размеру рез натора, равен нулю, а два остальных равны единице. Пусть,
например, р = 0, a d — наименьший размер резонатора. Тогда
Для полости с квадратным сечением (а = Ъ) и для кубической полости
(о = Ъ = d) соответственно получим
526 Глава XV
где v — скорость распространения волны в свободном пространстве, магнит-
магнитная проницаемость которого равна jj,, 7 — проводимость стенок, а 8 — толщина
скин слоя. В задачах в конце главы приведены числовые примеры.
§ 18. Свойства резонатора, имеющего форму круглого цилиндра.
Собственные частоты колебаний такого полого резонатора, как следует
из § 12, выражаются через скорость v-и длину волны Xmnp электромагнит-
электромагнитных волн, распространяющихся в среде, заполняющей резонатор, еледуюшим
образом:
?&(^)-?-^- A5Л27>
Здесь волновое число p,mn выбрано таким образом, чтобы удовлетворялись
условия A5.35). Из выражений A5.34) а A5.110), положив
sin (wt + а) = s (t) и cos (ш? -|-а) = c(t),
получим следующие выражения для полей:
] in-^-s(t), A5.128)
c(t), A5.129)
= <omr,pC' {-^ [piPmn-^mC (?) - ? ~ JmS (?) ] Sill
tt), A5.130)
B,m= -P^pC' [Ply/mS(cp) + ?Pmn/«C(?)]cos^-c(/). A5.131)
Согласно соотношениям A5.105), A5.106) и E.350), эквивалентные токи
полого•резонатора равны
^e) cos («rf + a), A5.132)
'P^^p^ [2 B- 8°) B - ВД-V*/;, (pmnc) cos (o,f + a). A5.133)
Поскольку рфО для волн Ji?, то из выражений A5.112) и A5.114) имеем
Wfiads$mnp (fimna2- та2) М 5 134"»
ЦтЦA2а) 2&аЗ]+$аЧЗ) ' (
M5 135V
Числовые примеры приведены в § 26.
§ 19. Многосвязные цилиндрические полые резонаторы. В многосвяз
ной полости всегда можно провести такую замкнутую кривую, которую
нельзя сжать в точку без пересечения границ полости. Если полость огра-
ограничена снаружи двумя параллельными плоскостями и нормальной к ним
цилиндрической поверхностью, а изнутри одной или более цилиндрическими
поверхностями, также нормальными к этим плоскостям, то внутри полости
возможны такие типь! колебаний, частота которых определяется только
Волноводы и полые реаонатпоры 527
расстоянием между плоскостями. Эти типы колебаний называются основ-
основными (главными). Они удовлетворяют второй системе граничных условий,
определяемых выражениями A5.5), причем Pmn = 0, и представляют собой
стоячую волну типа тех волн, которые существуют в линиях передачи
(см. § 14—19 гл. XIII). Ба основании соотношения A5.88) резонансные
частоты, соответствующие главным типам колебаний, для такой многосвяз-
многосвязной полости равны
Поля можно записать при помощи выражений A3.119) и A3.120) в виде
Е = CpVJJ (х, у) sin-^ sin wpt, В = Ср'A*еIЛТв7 (х, у) cos ^ cos wpt, A5.137)
где U (х, у) и V (х, у) — сопряженные функции, рассмотренные в гл. IV,
причем U (х, у) на одном семействе цилиндрических поверхностей прини-
принимает значение [/г, а на другом — значение Uz *\ Согласно соотношению D.55),
интеграл от \U или VF по замкнутому контуру, на котором U = const,
равен приращению [F] величины V. Обычно эта величина равна 2тг, как,
например, для эллиптических цилиндров (см. фиг. 38, где вместо V нужно
подставить U). Пусть мгновенное значение заряда на метр для р-то глав-
главного типа колебаний в сечении z равно ар. Определим эквивалентный заряд
полого резонатора через среднее значение с? при помощи соотношения A.40)
следующим образом:
9p = (d \ 4«b)Ih-[rt5 (§ Epdsjdz]4t =
= 2-1/2Ef/[F]Cpsinu)/. A5.138)
Пусть мгновенное значение тока в р-м главном типе колебаний на поверх-
поверхностях с потенциалами U1 и U2 в сечении z равно 1р. Определим- экви-
эквивалентный ток полого резонатора через среднее значение /р при помощи
выражения G.2) следующим образом:
= -^. A5.139)
Тогда мгновенные значения электрической и магнитной энергий будут
равны
* = гЙг. ^^^[nd^^il, A5-140)
о
где Сг и Lj —емкость и самоиндукция на единицу длины. Если Lp и С —
эквивалентные самоиндукция и емкость полости, то на основании выра-
выражений A3.124) и A5.136) они связаны между собой следующим образом:
bp = Jgr. C = Cxd, LpC = -±-, Lfi^v*. A5.141)
1) Автор не учитывает, что главная волна (N—1)-кратно вырождена.—Прим
перев. ' '
528 Глава XV
Если Fo — максимальная разность потенциалов между стенками полости
в некоторый момент времени, то электрическая энергия в полости равна
й
4 \ CF 81П2^ d
где Vp = 2~ 1/2F0. Следовательно, при таком определении Vр все соотноше-
соотношения между L, С, i, q и F, имеющие место для контуров с сосредоточенными
параметрами, сохраняют силу и для главных типов колебаний. Дли определе-
определения потерь вычислим поверхностный интеграл в выражении A5.98). Ьа тор-
торцевых плоскостях на основании соотношений A5.137) и A5.140) имеем
2 \B.BdS = ^\B.Bdv = ^(Wm)p = 4-^il. A5.143)
So V
Так как величины VF, dV/ds и [ cW/dz1 | такие же, как для соотноше-
соотношения A5.137), то на двух семействах цилиндрических поверхностей, име-
имеющих потенциалы иг и U2, имеем
-A5.144)
1,2
Подстановка выражений A5.140), A5.143) и A5.144) в формулы A5.98) —
A5.100) дает
Для вычисления линейного интеграла необходимо выразить zt как функ-
функцию W, как это было сдельно в выражении D.103), откуда ясно, что
dzJoW — функция U и V. В первом интеграле U нужно положить рав-
равным L\, а во втором — равным ?/2, а область интегрирования в обоих слу-
случаях необходимо распространить на все значения V, покрьшающие поверх-
поверхность U = const.
§ 20. Отрезок коаксиального кабеля как резонатор. Простейшим
случаем многосвязного полого резонатора с криволинейными поверхностями
янляется полость, образованная двумя коаксиальными круговыми цилинд-
цилиндрами. Главный тип колебаний в ней определяется таким же образом, как
и в предыдущем параграфе. Из § 13 гл. IV имеем
A5.146)
Следовательно, поля, определяемые по формулам A5.136) и A5.137), будут
равны
^^ ^^. A5.147)
Приращение V, обозначаемое нами через [V], равно 2тг. По.тому, если Ъ —
внешний радиус, а а — внутренний, то
In±, §Щ~ХМ = е~^ ^ = 2«r*i«?. A5.148)
Волноводы и полые резонаторы 529
Аналогичным путем для другого линейного интеграла получим 2-KJb. Под-
Подставляя эти результаты в соотношение A5.145), получаем для р-ro главного
типа колебаний
Q¦, = ДГ1 + Да,+ »? Л~'. 05.149)
ХР 2р.'8 L //ablnF/a)J v '
Из соотношений A5.136), A5.139) и A5.141) имеем
(±)~1. A5.150)
Ток ip равен радиальному току смещения / [см. выражение A5.93)], если
средняя площадь поперечного сечения определяется выражением
Помимо колебаний главных типов в коаксиальном резонаторе существуют
также и колебания других типов, которые выражаются через функции Бес-
Бесселя первого и второго родов [см. соотношения A5.46) — A5.49)]. Если d
значительно больше b — а, то колебания этих типов имеют частоты, зна-
значительно превышающие частоту главного типа колебаний р = 1. Эти частоты
можно вычислить методами, рассмотренными в § 16.
§ 21. Собственные колебания сферической полости. Решение вол-
волнового уравнения, рассмотренного в § 13 гл. XIV, состоит из произведе-
произведений сферических гармоник на сферические функции Бесселя. В соотноше-
соотношении A4.85) в членах 0 и R необходимо сохранить только Pn(cos6) и/п(Рг),
потому что Оп (cos 6) обращается в бесконечность на оси, а кп (/Рг) пред-
представляет волну, бегущую в радиальном направлении, тогда как в случае
колебаний полости с идеально проводящими стенками могут существовать
только стоячие волны. Из соотношений A4.85), A4.83), A4.110) и A4.117),
полагая sm(m<? + tym) = s(<?), cos (mcp + фт) = с (ср) и }„фрпг) = /п, получим
следующие выражения для напряженности электрического ноля и магнит-
магнитной индукции:
Е,е = «уС [ 6 ^ Р™ (cos 6) s (9) - <р sin В Pf (cos б) с (<р) ] /„ sin (о* + т)> A5.152)
В,. = С [ г, ^±^1 р" (cos 6) с («р) /„ - 6 НН-° Pt (cos 0) с («р) I {rjn) -
^п (со8в)*(<р)|:(г/„)] совН-нт), A5.153)
Е(ж = о,С [ г, ii!t±ll Р- (cos 6) с (9) /„ - 6 s4-° РГ (c,,s 6) с (?) | (r/J -
-? ^/С (cos 6) s(cp) |-(,7п)] sinH + т), A5.154)
B,m = id» (xeC [ 6 JJg P™ (cos 6) s (cp.) - <p sin & P™" (cos 6) r (9) ] /n cos («t + T).
A5.155)
На границе полости (r = a) тангенциальная составляющая Е должна обра-
обращаться в нуль, так что |Зрп необходимо выбрать так, чтобы удовлетворялись
граничные условия
[/„(РР»«I|в = 0> ^[«/;(Ppila)]lm=O. A5.156)
34 в. Смайт
530 Глава XV
Эквивалентный ток полости можно представить в виде выражения,
аналогичного выражению A5.93), т. е. как эффективное значение объем-
объемного тока смещения при средней площади поперечного сечения, равной
— тш2. Это значение является точным для колебаний типа ТЕа1, при кото-
которых ток смещения течет вокруг оси, но оно приемлемо также и для коле-
колебания типа ТМ1(). Возводя выражение A5.152) в квадрат и проинтегри-
проинтегрировав по объему v, получим в результате интегрирования по ср 2тг/B —8„),
а в результате интегрирования по другим координатам, согласно соотно-
соотношениям E.198), E.402) и E.346), найдем
= ?о^^с/1(рпа)[22„B^1 ,J . A5.157)
Для определения эквивалентного тока, соответствующего колебаниям типа
ТМ, выразим Wm через А и В. Учитывая, что объемный интеграл от А2
равен объемному интегралу от В2, деленному на Рр„, и, пользуясь выраже-
выражением A5.155), мы придем к такому же интегралу, что и раньше, но только
входящая в него величина [Зрп должна удовлетворять второму условию
A5.156). Таким образом,
Ы УУ[г2{^ 2]\'2. A5.158)
2B-8Я,)Bп+1)(п-то)!
Из выражений A5.94) и A5.100) находим самоиндукцию и емкость:
Вычисление Q по формуле A5.101) упрощается благодаря тому обстоятель-
обстоятельству, что, согласно выражениям A5.152) и A5.153), интегрирование но 6
и <р приводит к появлению одинаковых множителей в объемном и поверх-
поверхностном интегралах, которые сокращаются; поэтому достаточно только про-
провести в объемном интеграле интегрирование по г. Используя в случае
волн ТЕ первое выражение A5.101), а в случае волн ТМ второе выра-
выражение A5.101) и выполняя интегрирование при помощи соотношений E.402)
и E.346), после упрощений, связанных с выполнением условия A5.156),
получаем
§ 22. Собственные колебания реальных полых резонаторов. До сих
пор мы рассматривали полости, образованные замкнутыми идеально про-
проводящими поверхностями. Если же в стенках имелись потери, то они
определялись по формуле A5.103). На практике для введения энергии
в полость в ее стенках проделываются отверстия или внутрь полости вво-
вводятся электроды. Обычно стремятся лишь незначительно исказить поля
в резонаторе, и поэтому отверстия и электроды делают по возможности
небольшими. Обозначим вектор-потенциал и резонансную частоту идеаль-
идеальной полости соответственно через А(| и ш0, а реальной полости — через А
и ш. Полагая в соотношении C.24) Ч* = А, Ф = Ао и учитывая, что умно-
умножение на ш2 (ае равносильно применению оператора rotrot, получим
цеК-ш^ A.Aodv=$[AX(VxAj-AoX(VxA)]-ndSr. A5.161)
v S
Пусть v—объем идеальной полости, a S — ee поверхность, к которой
Волноводы и полЫе резонаторы
вектор Ао ортогонален. Тогда второй член в поверхностном интеграл* равен
нулю. Если отверстие мало, то ш «%* ш0, ю -\- юц =к 2ш0 и А*А0 в большей
части объема v, так что
f EvR-.nrf.V / $E,xB0-nd?
~ I^Tw ' (lo.lbZ)
где Wm, Е( и Во—соответственно мгновенные значения магнитной энергии
в полости и тангенциальные компоненты действительного поля Е и поля Во
в случае отсутствия отверстия. Часть поля Е,, обусловленную полем Во,
можно найти путем решения магнитостатической задачи о бесконечной
плоскости (с нулевой магнитной проницаемостью), в которой проделано
отверстие заданной формы и которая является границей поля Во, однород-
однородного и параллельного плоскости всюду, за исключением области вблизи
отверстия, где имеются искажения. Из этой задачи определяется связь
между нормальной составляющей Вп на отверстии и полем Во. Влияние
отверстия можно полностью скомпенсировать, если закрыть его двойным
слоем тока (см. § 20 гл. XIV), излучение которого в точности равно погло-
поглощению энергии в нем. _
Поля Вп и Ej, создаваемые этим двойным слоем тока, равны по вели-
величине, но противоположны по энаку соответствующим полям отверстия,
а поле В, дополняет поле отверстия до поля стоячей волны Во. Если от-
отверстие прорезано в плоскости ху, а поле Во направлено вдоль х, то (Et)v
можно найти путем интегрирования выражения A4.140), зная величину Вп.
В задаче 49 гл. XIV дана величина Вп для круглого отверстия в тонкой
металлической стенке. Если в отсутствие отверстия электрическое поле,
перпендикулярное к поверхности, было равно Ео,. то для определения со-
составляющей Ё( на отверстии, обусловленной наличием поля Ео, необходимо
найти решение электростатической задачи о плоской поверхности с отвер-
отверстием, которая является границей поля Ео, однородного вдали от отвер-
отверстия. В § 28в гл. V рассматривается случай круглого отверстия в тонком
экране. При определении добротности Q нужно к потерям в стенках доба-
добавить еще потери на излучение сквозь отверстие.
-гъ-
§ 23. Полые резонаторы сложной формы. Одним из наиболее важных
видов полых резонаторов является сложный резонатор, состоящий из не-
нескольких простых соединенных меж-
между собой полостей, границы которых \*~
только частично совпадает с коорди-
координатными поверхностями. Как прави-
правило, в каждом таком отдельном слу-
случае требуется специальное решение
задачи. Рассмотрим в качестве при-
примера полость, представляющую со-
собой прямой круглый цилиндр радиу-
радиуса b и длины с, внутри которого с Фиг. 139.
одной стороны вставлеп другой, бо-
более короткий прямой круглый замкнутый цилиндр (радиуса а), коаксиаль-
коаксиальный с первым. Между основаниями цилиндров с другой стороны об-
образуется при этом зазор с высотой, равной d. Полость такой формы
(ее сечение показано на фиг. 139) нельзя отнести к категории уже рас-
рассмотренных нами полых резонаторов. Сначала мы укажем путь отыска-
отыскания точного решения задачи по методу Хана *>; затем приведем менее точ-
точное решение, справедливое в том важном для практики случае, когда d
м
+—2а
N
—~
t
d
М
\
С
1
У
-1) Hahn, Journ. Appl Phys. 12, 62.
34*
532 Глава XV
много меньше a, b или X. И, наконец, в заключение нами будет рассмот-
рассмотрена грубая апроксимация, использующая аналогию с линией передачи.
Будем интересоваться только пилями в полости и наименьшей собственной
частотой колебаний. Согласно § 16 и 18 гл. XV, компоненты векторов
поля ТМ в областях М, удовлетворяющие граничному условию Et = 0
при р = b, z --= 0 и z = c можно записать в виде
со
ti о ^^ ~— I ~~Б—о г Г"
/оз L Ро ¦**() \^оа)
= /0 (ft.6) ^o (PoP) - П (РьЧ Л, (РоР). A5.165)
= 'о (P» ^0 (Pmp) - Ko (Pm6) /0 (PmP),
-2, W = K-^, K = P = «V = ^- A5.166)
•В области N поля, остающиеся конечными при р = 0 и удовлетворяющие
условию Е = 0 при z = 0 и z = d, равны
а)
A5Л68)
v v
Приравнивая между собой В9 и В'^ при р = я и умножая обе части равен-
равенства на cos (pizz/d) dz, а затем интегрируя в пределах от z = — d до z — d,
мы получим выражение для коэффициента ,Лр через все коэффициенты Ст.
Аналогично, полагая Ez —E'z при 0 с |z| < б? и Ez — 0 при d < |z| < с,
а затем умножая обе части равенства на cos (qizz/c) dz и интегрируя в пре-
пределах от z = — с до z = с, мы найдем выражение для Cq через все коэффи-
коэффициенты Ап. Исключая из этих уравнений коэффициенты Ап и поделив на Со,
выразим величину CJCO через отношение Сгп/С0. Таких уравнений мож-
можно написать бесконечное число (по одному для каждого значения q), по-
поэтому для определения Ст/С0 нужно вычислить бесконечный детерминант.
Подстановка этих значений CJC0 в уравнение, соответствующее q ~ О, при-
приводит к следующему соотношению:
1 = Л) (Зо а) Г ^ До (Ро а) ! Ро с у Ст До (Зт а) ,;1д m^d 1 ^ /15 169)
Наименьшая величина [30, удсшлетвор>иощая этому уравнению, определяет
величину Ро, входящую в выран{енио E.166). Амплитуду колебаний всегда
можно выбрать таиой, чтобы Ао было равно единице.
Осуществление изложенного выше способа решения, очевидно, пред-
представляет собой основную трудность всей задачи. Таким образом, намечен-
намеченный путь только теоретически дает точное решение, практически же он
неприемлем, так как решение бесконечной системы уравнений требуют,
большой затраты времени. Однако для облегчения этой операции Хан
Волноводы и полые резонаторы 533
составил специальные таблицы. Если d много меньше, чем a, b и X, то можно
предложить другой метод, позволяющий найти X с большей точностью,
чем та, с которой обычно измеряются величины а, Ь и с. Кроме того, при
помощи этого метода можно подсчитать и Q. В случае достаточно малых d
тангенциальная составляющая электрического поля можду М и N при
р = а не зависит от а и Ь, а определяется только размерами d и с и раз-
разностью потенциалов в зазоре. Взяв а и Ъ бесконечно большими, мы придем
к двухмерной задаче, решенной в § 14 гл. VI (в этом решении вместо d
и с входят h и к). При с > d задача еще более упрощается (на фиг. 63, о
следует при этом убрать полосы при хг = ± !)• Из § 14 гл. VI имеем
[(zji^ft + acsmI A5.170)
дх
= im
dW
dz
= Im
A5.171)
где z и z1 — комплексные переменные, a 2V0—разность потенциалов на
зазоре. Для определения Ех на оси х, как функции х, найдем такие ком-
комплексные значения величины zlt которые соответствуют в выражении A5.170)
значению y = U. Подстановка этих значений в выражение A5.171) позво-
позволяет получить связь х и Ех. С точностью до 1/чооо выражение для Ех будет
иметь вид
Ех = Vo d'1 [ A + В cos (та d) + С (х <Г*J + ?> [ sec ( у тос d~i) ] °'355 } ,
A5.172)
где А = 0,34091, В=— 0,00656, С= -0,07785 и /) = 0,49910. В резуль-
результате интегрирования выражения A5.167) в пределах от z = 0 до z — d при
р -- а получим, что Vo — Ао. Подставив эту величину Vo в выражение A5.172)
и заменив х на z, приравняем между собой выражения A5.172) и A5.163)
при —d < z < d и потребуем равенства нулю выражения A5.163) при
d < | z | < с, а затем, умножив обе части равенства на cos (pizz/c) dz, про-
проинтегрируем в пределах от z= — с до z — c. Решим теперь последнее
уравнение относительно Ср и подставим найденные значения Ср в вырат
жение A5.169), которое после этого методом подбора можно решить отно-
относительно р. Морено1) приводит кривые для таких полостей. Очевидно,-
подстановка в выражения A5.164) и A5.168) значений Ап и Ст дает
вектор магнитной индукции, и, следовательно, Q можно подсчитать по
формуле A5.101).
Приближенное значение резонансной частоты можно найти, исходя
из аналогии с линией передачи. При d <С с область полого резонатора М
напоминает отрезок коаксиальной линии, коротко замкнутой в сечении
z — c, входной импеданс которого, согласно соотношениям A0.112) и A5.51),
равен -7J- /р (raw)-1 tg Be. Область N представляет собой конденсатор, шунти-
рующий линшо и имеющий импеданс (j^o)- При резонансе оба эти
импеданса должны быть равны по величине и противоположны по знаку,
поэтому приближенное значение Р находится из соотношения
<15Л73>
Мы можем только оценить Со. Рассматривая область N как плоский
конденсатор и пренебрегая краевым эффектом, мы определим нижвкяо
l) Moreno Т., Microwave Transmission Design Data, McGraw-Hill, 1948.
534 Глава XV
границу величины емкости Со ч= ека2/с1. В частном случае, когда d < а,
d С с и a «s 6, величину Со можно найти довольно точно, как это, напри-
например, сделано в задаче 65.
§ 24. Возбуждение полого резонатора петлей с током. В наиболее
общем случае колебания в полости представляют собой суперпозицию
рассмотренных выше колебании отдельных типов. При этом не только
колебания каждого типа совершаются независимо, как в отдельных линей-
линейных контурах, но и отношение возбуждающего тока к эквивалентному
току полости для колебаний какого-либо типа зависит только от геомет-
геометрической конфигурации системы, как это имеет место и в случае линейных
контуров с сосредоточенными параметрами. Кондон*) для упрощения вычис-
вычисления взаимной индукции предложил разбить вектор-потенциал, соответ-
соответствующий i-му типу колебаний, ла два множителя: Ci и А". Первый,
<:калярный, множитель определяет зависимость от времени и интенсив-
интенсивность; величина его подбирается таким образом, чтобы интеграл по объему
полости от квадрата второго, векторного, множителя был равен v. Векторы
А", зависящие только от геометрии системы, являются «нормированными»
безразмерными вектор-потенциалами. Из § 13 следует, что они обладают
свойством взаимной ортогональности, а из выражения A5.1), в котором
нужно положить ю-(?к, так что остается только член А", видно, что они
удовлетворяют следующему уравнению:
V2A? = - р?А?. A5.174)
Из соотношения A5.93) можно выразить Ci через эквивалентный ток
резонатора /\ и, следовательно, записать А как функцию А" и /4:
\ Al.Aidv=-^-2=^- = Cl \ A?.A?dv = vC?, A5.175)
V V '
OD OD
A(r, *¦)= 2 Ci(t)M(r)=?- 2 75A?. A5.176)
i=o ci=ollt
Задача заключается в определении входящих в это разложение коэффи-
коэффициентов через плотность возбуждающего тока i'(r, t). При отсутствии
зарядов дивергенция i' (r, t) равна нулю, и поэтому плотность тока можно
представить в виде ряда
Г (г, 9=2 А (9 А? (г). A5.177)
i=0
Коэффициенты -Dj (9 находятся путем умножения соотношения A5.177)
иа Ap(r)dv и интегрирования по объему v. Пусть полный возбуждающий
грк У течет по такому тонкому проводнику, что на его поперечном сече-
сечении вектор Ар можно считать постоянным. Тогда, обозначая через ds
элемент длины провода, мы сведем интеграл, стоящий в левой части,
к линейному интегралу вдоль s. В правой же части равенства все члены,
кроме р-го, будут равны нулю, т. е.
i' (r, t) ¦ Ар (r)|rfv = /' ф A» ds =
. , , A5-178)
!) Condon E. U., Rev. Mod. Phys., 14, No 4. [См. перевод: Усп. Физ. Наук,
27, 211 (Ы5).~Прим. перев.] ¦ ¦
Волноводы и полые резонаторы 535
Заметим, что взаимная индукция Мр между колебанием р-го типа и про-
проводом определяется совершенно так же, как в формуле (8.14),-где Ар//р—
вектор-потенциал, отнесенный к единичному току. Поскольку А и i' пред-
представлены в виде ряда по одно.й. и той же полной системе ортогональных
функций, то уравнения Максвелла A3.10), связывающие между собой
выражения A5.176) и A5.177), можно применить к каждому из членов
в отдельности. Таким образом, выражая В и D через А и учитывая, что
V • А — 0, получим
-$$?м= -*D*M- A5Л79)
Подстановка V2A" и Di из соотношений A5.174) и A5.178) и деление
«беих частей на А° приводят к следующему уравнению:
Э ^/'@- A5.180)
Приведенное уравнение получено при предположении, что стенки резона-
резонатора являются идеально проводящими, и, следовательно, Qi бесконечно
велико. Чтобы учесть небольшое поглощение, которое обычно и имеет
место на практике, необходимо добавить к левой части уравнения член
вида («Bj/^i) dljdt, заменить она на LiCl [значения Lfi^ определяются
по формулам A5.96) и A5.97)] и ввести сопротивление й,, опреде-
определяемое соотношением A5.102). Таким образом, уравнение A5.180)
примет вид
Mi дЧ'. (\
Поскольку /' является периодической функцией времени, меняющейся
€ круговой частотой ю, то колебание каждого типа будет подчиняться
уравнению вынужденных колебаний осциллятора A0.3). Для определения
амплитуды установившегося процесса нужно записать Ii в виде | /{| e'mt,
а /'—в виде | /' | е;т', разделить уравнение на е'ю' и решить его относи-
тельно |/,-|. Резонанс наступает приблизительно при (в = (в{, так что
, У . _ М,\У'\ .у. _ щМ; \I'\ _Mi\I'\Ql м
При резонансе эквивалентный ток полости | /4 |рез отстает от /' на фазо-
фазовый угол 90°. ' у
Суммарное магнитное ноле в резонаторе определяется из векторного
потенциала А, равного сумме векторных потенциалов, описывающих коле-
колебания отдельных типов. Из соотношения A5.178) следует, что полное
магнитное поле, пронизывающее петлю, равно 2^;^t> T- е- члены, дающие
отдельно самоиндукцию, здесь не выделены. Электродвижущая сила в петле,
имеющей сопротивление R, равна
оо
? = Д/Ч- 2 f*Mj: A5.183)
i=0
Подставляя сюда из соотношения A5.182) выражение для 74 через /', для
импеданса петли получим
мМ- - и ¦
i
536 Глава XV
Так как Q. обычно очень большая величина, то первые члены в знамена-
знаменателе велики по сравнению с последними,.за исключением значений w яв к>г.
Те колебания, для которых к>- > ш, дают индуктивную часть реактивного
сопротивления, а колебания, для которых ш{ < ш, — емкостную часть реак-
реактивного сопротивления. Эта формула позволяет качественно судить об изме-
изменениях реактивного сопротивления петли, возбуждающей резонатор. Если же
несколько видоизменить выражение для Mt, то можно получить и коли-
количественные данные. Основная трудность определения AI- заключается
в предположении о бесконечной тонкости провода, так как при этом вблизи
него поле В бесконечно велико, а следовательно, и L также обращается
в бесконечность. В действительности, если толщина провода значительно
меньше длины волны, то поля в резонаторе будут такими же, как если
бы возбуждающий ток был сконцентрирован на оси провода, а поверхность,
последнего совпадала бы с границей силовой трубки индукции. Пра-
Правильное значение потока сцепления можно, следовательно, найти путем
интегрирования А от одного конца петли до другого вдоль любой из кривых,
лежащих на поверхности провода. Соответственно необходимо видоизменить
и определение Мр, данное в соотношении A5.178). Заметим, что путь
интегрирования в выражении A5.178) можно замкнуть, возвратившись,
в начальную точку на границе полости, что никак не скажется на вели-
величине Мр, так как вектор А перпендикулярен к гюанице. Этот интеграл
будет равен, очевидно, поверхностному интегралу от В по .площади петли.
§ 25. Возбуждение круглого цилиндрического резонатора петлей
с током. Развитую теорию можно пояснить на примере полого резонатора,
имеющего форму круглого цилиндра. Пусть возбуждение происходит
на наинизшей собственной частоте, которая соответствует колебаниям
типа ТЕп (см. фиг. 135) и для которой риа=1,84. Согласно соотноше-
соотношению A5.127),
($1Т(У- A5Л85>
Из соотношения A5.129) находим, что амплитуда вектора магнитной индук-
индукции пропорциональна величине
] , A5.186)
где заменили ?5Ц на р. Для возбуждения этого типа колебаний необходимо
ввести сквозь стенку внутрь резонатора маленькую петлю. Из выраже-
выражения A5.186) с очевидностью следует, что поток индукции сквозь такую
петлю в поле ТЕХХ будет максимальным (а следовательно, будет макси-
максимальной и связь петли с резонатором), если петлю поместить вблизи
плоских стенок резонатора в центре (перпендикулярно к линиям Вр), или
на краю (перпендикулярно к линиям В.#), или же если поместить петлю
вблизи боковых цилиндрических поверхностей в центре (перпендикулярно
к линиям Bz), или около основания (перпендикулярно к линиям BJ).
Отношение потоков в направлении z при р яв а, ср = 0, z*-^diB направ-
направлении р при р=ъО, ср = 0, za: 0 равно
Mz I Bz Imax _ Prf-Л (И _ 0,682d (\*> \R1\
Таким образом, при 0,682 d > а максимальная связь петли, имеющей задан-
заданные размеры, с полостью осуществляется вблизи боковой поверхности
Волноводы и полые резонаторы 5о7
цилиндра на середине расстояния между его основаниями. Предположим,
что маленькая петля площади S расположена в плоскости z = у d (<р = 0)
настолько близко от стенки, что значение Вг на протяжении всей петли
можно считать равным значению Bz на поверхности стенки. Чтобы убе-
убедиться в этом, заметим, что при р= 0,95а, /г(Рр) = 0,997 J1(^a). Коэффи-
Коэффициент взаимной индукции равен пронизывающему петлю потоку индукции,
обусловленному единичным эквивалентным током полости, т. е., в спит
ветствии с выражениями A5.129) и A5.132),
м_ \Bz\S 2faV l,3-10-'.Srf
Из соотношений A5.134) и A5.184) для резонатора с медными стенками
(Y = 5,7-107) добротность Q и дополнительное сопротивление петли при
резонансе определяются следующим образом:
12SSS4}
- *l1 •
Максимальная разность потенциалов в полости имеет место вдоль линии
z = yrf и (р=-о"К. Поэтому из соотношения A5.128), полагая т — р = \
и используя формулу E.314), имеем
а со 1,84
г=0 0
= 1 ,60шС = 582а/х (d2 + 2,92а2)-1'2. A5.190>
Из соотношений A5.185), A5.188), A5.190) и A5.183) можно найти коэф-
коэффициент усиления по напряжению, а из соотношений A5.188), A5.189)
и A5.183) эквивалентный ток полого резонатора
V __0,812g2 ]В.'\Г\ 1,748 SQ . ,,
Входящая сюда величина й является той частью электродвижущей силы
в петле, которая совпадает по фазе с /'.
Представляет интерес привести некоторые числовые величины. Пусть
площадь петли S= 1 см2, радиус цилиндрической полости а = 10 см, а длина
d = 20 см. В качестве заполняющей полость среды возьмем вакуум. Тогда
со^7,25.109 радиан/сек., v^ 1,15-Ю9 гц, X я» 26,0 см,
гн, (?я
Коэффициенты самоиндукции и взаимной индукции полости, согласно-
соотношениям A5.96) и A5.97), равны
Lu = 2,15-10-8 гн, Си = 8,85-10'12 фарад.
Если пиковое значение электродвижущей силы, совпадающей по фазе с Г,
равно 1000 в, то go^1000e, 7^ = 0,583 a, Fmax = 81200e, /O = 367 a
и Р=292 вт. Расчеты некоторых других способов возбуждения отнесены
в задачи, помещенные в конце главы.
§ 26. Возбуждение полого резонатора при помощи электрода. Если
полый резонатор возбуждается неравномерно распределенным током, как
-538 - Глава XV
это имеет место в случае электрода, введенного в полость, то дивергенция
плотности тока i отлична от нуля, и, следовательно, в резонаторе при-
присутствует электрический заряд, плотность которого мы обозначим через о.
В таких случаях, как было показано в § 2 гл. XIV, поля можно описать
при помощи суммы Соле нон дальнего иектор-потепциала и скалярЕгого потен-
потенциала, удовлетворяющего уравнению Пуассона. Коэффициенты взаимной
индукции для каждого типа колебаний попрежнему определяются форму-
формулой A5.178), потому что, как было доказано при помощи соотношения
A5.92), наличие потенциальной части у i не вносит никаких изменений
ни в объемный интеграл, ни в значеЕте эквивалентного тока полости.
Поле, описываемое скалярным потенциалом, приводит к появлению допол-
дополнительной электрической энергии, меняющейся в фазе с зарядом на элек-
электроде, т. е. к появлению дополнительного реактивного сопротивления
чисто емкостного характера. Здесь возникает трудность, подобная той,
которая имеет место в антенных задачах, а именно — каким образом опре-
определить распределение зарядов и токов на электроде. Если электрод очень
тонкий, то емкость его ничтожна, а коэффициент самоиндукции почти
полностью определяется его радиусом1), так что, следуя результатам
§ 4 гл. XIV, мы получим синусоидальное распределение, описываемое
выражением A4.27). С увеличением радиуса реактивное сопротивление
полости начинает сказываться относительно сильнее и распределение тока
меняется. Почти точные результаты получаются в том случае, когда резо-
резонатор возбуждается при помощи тонкой проволоки, имеющей на конце
металлический электрод. Тогда можно считать, что ток в тонком проводе
распределен равномерно и что заряд полностью сосредоточен на электроде
и его можно определить методами электростатики. При этом формулы
A5.174) —A5.182) § 24 остаются без изменений, а к выражению A5.183)
нужно будет только добавить д'/С0, где I' = fu>g', а Со — емкость элек-
электрода:
Z = R L+ V /т"'У . A5.192)
При ш = ш4 из-за наличия Со импеданс Z уже не будет действительной
величиной, но если ш =& ш4, то существенное значение будет иметь только
¦ i-й член суммы, поэтому, приравнивая реактивное сопротивление нулю,
получаем
i = O. . A5.193)
Часто коэффициент при wf — w2 значительно больше коэффициента при
(ш1—is2J, поэтому, удерживая только два последних члена и считая
-(в + (в4 = 2(в;, получим
о,-—о>_ Li _ 1 ..
В качестве примера рассмотрим шар радиуса г, центр которого нахо-
.дится на расстоянии / от стенки. Шар поддерживается при помощи тонкой
проволоки. Пусть вся эта система преднаЗЕтчается для возбуждения
колебания типа ТЕи, рассмотренного в предыдущем параграфе. Как
видно из соотношения A5.92), максимальная связь резонатора с проводом
будет осуществляться при помещении последнего вдоль максимальной
составляющей вектор-потенциала. Наилучшим таким положением будет
¦ х) Коэффициент самоиндукции почти полностью определяется радиусом и длиной
-электрода,— Прим. перев.
Волноводы и полые резонаторы 539
1 1
z = -jd, ip = yi: [см. соотношение A5.128)]. Как и при вычислении выра-
выражения A5.188), для небольших расстояний от границы можно заменить
J^kp) на J1(ka). Таким образом, формулы A5.128), A5.132) и A5.178)
приводят к следующему соотношению:
М-\ V*- 2^P"ldP 3,84-10-^
a-l Kud I Y^tfiia2 — 1) I
Согласно выражению A5.184), дополнительное активное сопротивление
контура связи равно
R' = 109,2 aQ (d? + 2,92a2)-1/2 {ln [a (a - ly1]}2. A5.196)
Если шар очень мал и находится вблизи стенки, то входящая в выра-
выражение A5.192) емкость Со приблизительно равна емкости между шаром
и плоскостью, которую на основании соотношения E.45) можно предста-
представить в виде
r2)-1+...]. A5.197)
При любом разумном выборе соответствующих величин условия примени-
применимости уравнения A5.194) выполняются очень хорошо, так что w очень
близка к iflj. Из соотношений A5.192), A5.190) и A5.182) отношение
максимальной разности потенциалов в полости и разности потенциалов
вдоль провода, обусловленной наличием R' и Со, а также величина экви-
эквивалентного тока полости равны
n^. (.5.198)
При подсчете % не учтено реактивное сопротивление, соответствующее
колебаниям высших типов. Если же им пренебрегать нельзя, то его можно
найти по формуле A5.192). Рассмотрим колебания того же типа, что и в
предыдущем параграфе, предполагая значения о>, v, X, Q, L;. и Ci равными
приведенным там, а I и г положим равными соответственно 1 с* и 1 мм:
Со *» 1,17 • Ю-13 фарад, М ъ 3,08 • 10-ю гн,
R' ~ 16 560 ом, ^=^- = 0,99 ¦ Ю-6.
Ч!
При пиковом напряжении на штыре, равном 1000 в, пренебрегая влия-
влиянием высших типов колебаний, получаем
Fmax ~ 27 100 в, П * 0,0604 а,
1пъ 118,4 а, ?^30,2 вт.
-<>
1 § 27. Возбуждение полого резонатора через отверстие. Если полый
резонатор соединен через отверстие в его стенке с волноводом, то для по-
получения строгого решения необходимо согласовать значения вектор-потен-
вектор-потенциала на отверстии. Поскольку выражение для вектор-потенциала с обеих
сторон от отверстия имеет вид бесконечных рядов, то эта задача аналогична
задаче, решенной в § 23 при помощи метода Хана. Часто, однако, можно
получить хорошее приближение, задаваясь распределением поля на отвер-
отверстии, подобным приведенному в § 10. Среди приводимых ниже задач можно
найти примеры таких решений.
540 - Глава XV
ЗАДАЧИ
1. При данной частоте движение электромагнитного возмущения вдоль волновода
можно представить себе как перемещение серии одинаковых волновых ячеек со ско-
скоростью, равной фазовой скорости волны. Вследствие того, что П-Vxll =0, каждая ии
этих ячеек содержит замкнутые волновые поверхности, обладающие тем свойством, чт«
в любой точке Е и В направлены по касательной к ним. Для волн ТЕ можно ири
помощи таких поверхностей разбить каждую ячейку на трубки магнитной индукции
одинаковой величины. Показать, что для волн ТЕто, описанных в § 3. уравнение вол-
волновых поверхностей в ячейке с центром в z = 0 при t= 0 имеет вид
.1 . / птх \
= cos fi?no z sin ( 1,
V a. J
где С — часть полного потока магнитной индукции, приходящаяся на площадку, рас
положенную между силовой трубкой, проходящей через х, z, и стенкой ячейки. Пока-
Показать, что эти поверхности являются гиперболическими вблизи углов ячейки и эллип-
эллиптическими около центра ячейки.
2. Показать, что уравнение волновых поверхностей для волн ТЕ в прямоугольном
волноводе имеет вид
С = \Е— К cos2 (raroccr1) cos2 (nnyb-1)] cos pmn z,
где С—часть полного потока магнитной индукции в волновой ячейке, приходящаяся
на площадку, расположенную между волновой поверхностью, проходящей через точку
х, у, z, и границей ячейки, а Е и if—полные эллиптические интегралы модуля
[1 — cos2 (m-izxa-1) cos2 (ni^ir1)]1'2.
3. Показать, что уравнение волновой поверхности волны ТМ в прямоугольном
волноводе имеет вид
С = [Е — К sin2 (mnxar1) sin2 {nnyb~l)\ sin [WnZ,
где С—та часть полного потока вектора Е, которая находится впутри волновой поверх-
поверхности, проходящей через точку х, у, г, и Е и К — полные эллиптические интегралы
модуля
[1 — sin2 (типа»-1) sin2 (пгф-1)]1'2.
4. Волновые ячейки для аксиально-симметричных волн в круглом цилиндрическом
волноводе имеют, вообще говоря, форму колец. Для волн ТЕ первая r-я ячейка ограии-
j
чена поверхностями p = pr. P=pr+i и z=J--j-ln, где /-—целое число, 0<r<n; J1{^0nPr)=
= Jl (PonPr+i) = 0. Показать, что волновые поверхности в ячейке совпадают с вихревыми
кольцами магнитного поля
С = рУ1 (Роп р) [Рм J, (Son p^f)]-1 cos rfm z,
ГДС Л> (PonPjif) = 0, pr < Рм < P'+ i И С —часть потока магнитной индукции в r-и кольце,
проходящем между рТ и р, z. Сделать эскиз.
5. В цилиндрическом круглом волноводе аксиально-симметричные волны ТМ обра-
образуют кольцеобразные ячейки, включая и половинную ячейку, граничащую со стеиками
волновода, причем для r-й ячейки pr<p<Pr+i и 0 < z < -ц-Х, где г — целое число.
00 < п; Jx (Ponpr)=./i (Sonpr+i) = 0. Показать, что волновые поверхности, за исключе-
исключением ближайшей к стенке волновода, представляют собой вихревые кольца электриче-
электрического поля
C = pJj (Pon Р) [рм -Л (Роп Рм)! sin Pon z,
где Jo (РопРм) = 0, рг < Рм < pr+i> а ? — часть полного потока вектора Е в r-й ячейке,
приходящаяся на площадку между р и р,.. Для половинной ячейки, граничащей со стен-
стенками, рм = в.
6. Исходя из выражения A5.7) и из результатов § 16 гл. XIII, показать, что если
проводимость диэлектрической среды, заполняющей волновод, равна f, то волновое число
и коэффициент затуханий можно записать соответственно в виде
а' = 2-1'2 {[(Р2 - f&J + шу-f2]1''2- <f + fm}lh¦
Эти формулы одинаково справедливы для частот ниже и выше критической.
Задачи 541
7. Показать, что если в волноводе отношение проводимости к диэлектрической
проницаемости мало по сравнению с разностью между частотой сигнала v, распространя-
распространяющегося в виде волны те-го типа, и критической частотой vm, то коэффициент затухания
i' и фазовая скорость v'm приближенно раины
1
где v — скорость распространения волны в свободном пространстве, а «т-— фазовая ско-
скорость при равной нулю проводимости.
8. Между двумя параллельными идеально проводящими поверхностями расположен,
перпендикулярно к их поверхности, идеально проводящий цилиндр р = а, вдоль которого
течет равномерно распределенный по нему ток J cosa>t. Показать, что комплексная
амплитуда вектор-потенциала, описывающего электромагнитное поле между плоскостями
снаружи цилиндра, равна
где р2 = а>2[ле и, согласно выражению E.316), при (За, стремящемся к нулю, ?г (fia) —*
—>2/(тфа). Наметим, что, согласно таблицам Янке и Эмдс, при а < 0,0181 X
[J, (?а)] < 0,01 [У, (Вй)].
9. Показать, что в предыдущей задаче активная и реактивная части входного
импеданса цилиндрического провода соответственно равны
д !*1/2* Y .У*1 \Jq (Р«0 Jx (Р«0 + Уо (P«0 Y, (pa)]
где А/ = 1/! (Ра)]2+[1'] (Р<*)]2, а I — расстояние между плоскостями.
10. Пусть плоскости, рассмотренные в задаче 8, соединены между собой идеально
проводящим цилиндром р = Ь. Показать, что комплексная амплитуда нектор-потешшала
между плоскостями равна
Г __ V-I [Го (pb) Jo (Pp) -Jq (pb) Ур (ррI
г 2па$ [Jo $Ь) У, (|1в) - YB (В6) /х (pa)] '
Вычислить входное реактивное сопротивление.
11. Электромагнитная волна распространяется ь радиальном направлении между
двумя параллельными идеально проводящими плоскостями, перпендикулярными к ocuz.
Пользуясь выражениями A4.128), A4.130), A4.131), показать, что если электрическое
поле этой волны имеет только «-составляющую и по зависит от координаты у и если
p = Za при р = а, то при р= h это отношение равно
J) (?<*) Уо (i16)- Л (P*) У i (Pa)l
Htp h ^vZa[J1(iia)Y]Qb) — J1(^b)Y,('jia)}-\-i[Je{^a)Yj(fib) JL (S6) Уо (pa)]
1 12. В круглом волноводе радиуса 6 при v > v0, распространяется волна типа ТМ01
^см. фиг. 135). Чтобы электромагнитная волна могла пройти через участок волно-
волновода, имеющий кольцевой зазор (кольцевую щель) в бокоиой поверхности, необходимо,
чтобы в зазоре существовало отличное от нуля электрическое ноле. Исходя из ре-
результатов предыдущей задачи, показать, что па некоторой частоте vc > v0l можно до-
добиться полного отражения волны от щели, если прикрыть щель сверху цилиндри-
цилиндрической, коаксиальной с волноводом коробкой, плоские основания которой совпадают с
краями щели, а радиус определяется из соотношения
Уо [2л ((j.EI'2vcaJ = Je [2л ((j.e) '2vca]y, [2я((ле) '-vcb].
13. Предположим, что два участка ьвепшей оболочки коаксиального волновода
радиуса Ъ необходимо изолировать друг от друга по постоянному току. Исходя из за-
задачи 11, показать, что это можно осуществить без нарушения углопни распространения
волны с частотой vc, если между этими участками оставить небольшой зазор, к каждому
краю которого присоединить по коаксиальному с волноводом плоскому параллельному
флянцу, имеющему радиус; а, определяемый из соотношения
Jo [2п (у*I!» vcft] У, [2* (И1'* vco] =- J, [2-к (.агI''2 vca] Уо [2я [у*I'* vc6].
При решении считать, что на краях флянца имеется узел магнитного поли или тока.
542 Глава XV
*» 14. Пусть в предыдущей задаче /—ток в коаксиальной линии, г—ширина зазора,
a (fieI/a = ». Показать, что разность потенциалов на внешних краях флянца равна
— Jt {шЪ/v)
15. Секториальный рупор, образованный плоскостями z = 0, z — b и tp = O, 9 = °'г
возбуждается током klcosmt, равномерно распределенным вдоль тошного провода р = сг
tf = a. В бесконечности (р=оо) волна полностью поглощается. Найти, пользуясь соот-
соотношениями A4.128) и A4.130), подходящий для этого случая вид записи вектор-потен-
вектор-потенциалов: Ах при р < с и Аг при р > с. Показать, приравнивая Az и Az при р=с и инте-
интегрируя разность В —В'у по поверхности р=с, а затем примевяя закон о циркуляции
V V
вектора В [см. выражение G.173)], что A'z и Аг можно представить в виде следующих
рядов Фурье: t
при 0 < р < с
* со
m = l
при с < p < oo
16. Используя предыдущую формулу, проинтегрировать вектор Умова — Пойнтинга»
[см. выражение A3.146)] по сечению рупора при больших р и показать, что сопротив-
сопротивление излучения равво
17. Пусть угол раствора рупора, рассмотренного в задаче 15, а' = я/и, где п- -целое
число, а радиус провода равен а. Считая а <? и-с и а <С \{п1п)—°] с, показать, что гра-
граничные условия будут удовлетворены суперпозицией полей типа описанных в задаче И,
если воспользоваться методом изображения (см. фиг. 28). Показать также, что при
полном поглощении волны на бесконечности (р=оо) входной импеданс при а<^Х при-
приблизительно равен
я—1
п—1
8=0
где R—активное сопротивление провода. Обычно сумма членов, содержащих Уо^
ничтожно мала по сравнению с логарифмическим членом. „
18. Показать, что электромагнитная волва, имеющая в г-направлении п максиму-
максимумов электрического поля, может распространяться в радиальном направлении внутри
рупора, ограниченного идеальво проводящими плоскостями z = 0, z = 6, 9 = 0 и у=а
при условии
л
19. В круглой проволочной петле р = с, лежащей в плоскости z = d между двумя
бесконечными идеальво проводящими плоскостями 2 = 0 и z = a, течет равномерно рас-
распределенный по проводу ток ф/е;ю(. Показать (см. § 18 гл. XIV), что при X > 2а энер-
энергия между плоскостями не распространяется, а вектор-потенциал, описывающий поле
в области р > с, в этом случае имеет вид
nrtd . nnz 2л Г/геХ\2 , ~| гЫ
= 2nr^Y_1-j1
Задачи 543^
20. Если в предыдущей задаче а < X < 1а, то между плоскостями будет распро-
распространяться волна одного типа. Показать, что тогда в области р > с комплексная ампли-
амплитуда вектор-потенциала имеет вид
оо
- ^ { ъН^ (Plp) Л (Pjc) sin % sin-f + 2/ ^ *х (М /, <?»«) sin ^ sin ^ } ,
где #„ (PiP) — функция Ханкеля [см. соотношение E.321)],
21. Секториальиый рупор, ограниченный плоскостями z = 0, z = a и ср = О, у = а,
возбуждается при помощи товкой изогнутой проволоки р = е, z = d, вдоль которой
течет равномерно распределенный ток ip/cosu>;. Показать, что если а < X < 2а и радиус
провода г значительно меньше с, то из задачи 20 при условии полного поглощения
излучения в бесконечности (р=оо) следует
Написанные выше ряды сходятся очень быстро.
22. Показать, что если в предыдущей задаче Х = 1,5а, с—а, а=^18°, d=a/2, то
реактивное сопротивление будет равно нулю при радиусе провода 0,0114 а, а сопротив-
сопротивление излучения при этом будет равно 274,5 ом.
23. Прямоугольный волновод возбуждается при помощи петли, находящейся
в плоскости x = d. Показать, применяя метод изображений, что все компоненты век-
вектор-потенциала параллельны этой плоскости, и, следовательно, волны, возбуждаемые
петлей, можно найти, исходя из результатов § 1 гл. XV, т. е.
~ V, . ТО71Ж '
W = Cmnsm c
a
E= - o>Cmrl I jpmn cos -^-+k/-y- sin—-^- \ sin -j-
B=Cmn |i [p.-.--s- J sin— cos— -— |_л_
cos
где (PmnJ==P2 — Pmn- Заметим, что эти волны представляют собой комбинацию волн
типа ТЕ и ТМ.
24. Прямоугольный волновод возбуждается при помощи штыря, ток в котором
направлен вдоль оси у. Показать, пользужь методом изображений, что B-j = O и, сле-
следовательно, волны, возбуждаемые штырем, согласно § 1 гл. XV, должны описываться
следующими выражениями:
= -cmn sin ^ cos ^ е-*™* , а = V х (j X VW),
ппу . f „„ ?г2я2 \ . тпх ппу
+ k ^ra" sin ^ sin ^ ]
В = Р26'т„ у i/p^n sin ——hk -^- cos — J cos -^ e ;p»»«r
.544 Глава XV
25. Пользуясь методом, приведенным в § 8 гл. XV, показать, что вектор-потен-
вектор-потенциал, описывающий поле элемента тока kldz^1, расположенного в точке х0, yOr z0
а прямоугольном волноводе, при z > zB имеет вид
оо оо
21 dzn vi VI . rmtxr,' . птсуп f. tmt mrtx . nrty
n—j- Y ), sin "sin—^f! cos sm__»
ZJZJ a b \ a
a b \ a a b
a=l n=l
26. Исходя из задачи 24, показать, что всктор-иотенциал, описывающий поле
.элемента тока j/ dyue , находящегося в точке x0, y0, zB в прямоугольном волноводе,
при z > z0 имеет вид
/\i.J dy0 vi vs и . пижц гел.?/о Г • чт-nrt2 mrtx nrty
A=—,.„ ,' >, >, -— sin cos —V— I i •—7— cos sin —т
ab a b
m=ln=0
n2rt2 Л . mrtx mty nrt . тяж . гели 1 — j'b' (г—гп)
-—r?- sin • cos-^ k7fC,,-r sin sin-—- I e >Vmn l "' .
Ьг J a o, Tnn о a 6 J
27. Исходя из задач 25 и 26, показать, что при возбуждении прямоугольного
волновода маленькой проволочной петлей, по которой течет ток /е31 (площадь петли
dS, петля лежит в плоскости хв в точке у=у0, z = z0, eo магнитный момент направлен
вдоль оси х), вектор-потенциал, описывающий поле, при z > z0 имеет вид
г [ij dS
А=
ab ZJ ^J v
т=1п=О
^ 1
ft J
sin
28. Исходя из задачи 26, показать, что при возбуждении прямоугольного волновода
маленькой петлей, по которой течет ток /е3' (площадь петли dS, петля лежит в пло-
плоскости 20 в точке х = х0, у = ув, ее магнитный момент направлен вдоль оси г), вектор-
иотеициал, описывающий поле, при г > z0 имеет вид
pxl dS -^a vi 2 — Bm — ои
пиу0 Г.
Ь L
H± sin
a
29. Прямоугольный волновод, коротко замкнутый в сеченый г=-0, возбуждается
при помощи одной половины прямоугольной петли, два вертикальных провода кото-
которой перпендикулярны к оси у, а горизонтальный прояод длины с протянут вдоль
линии сс = сс0, z — z0. Предполагая, что в волноводе распространяются только волны
ТЕ10, показать, что сопротивление излучения равно
2ош.с2 . тсх0 . „о, ., 2п Г /- Л \2г/2
, 2п Г /- Л \2
30. Прямоугольный волновод, коротко замкнутый и сечении z = 0, возбуждается
полукруглой тонкой проволочной петлей радиуса о, ток вдоль которой распределен
равномерно. Петля лкжит в плоскости x = d, а ее центр и концы находятся в плоско-
плоскости z=0- Предполагая, что при заданной частоте в волноводе может распространяться
только волна ТЕ10, показать, пользуясь результатами задачи 26, что сопротивление
излучения равно
о,
-, где Ko =
31. Применяя метод изображений и пользуясь результатом задачи 20, а также
учитывая соотношение E.451), показать, что в задаче 30 реактивное сопротив-
Задачи 546
лепие излучения равно
Р=2
где 2Г0 — значение реактивного сопротивления, определенного н задаче 21, при а= и и
За исключением случая больших размеров легли, первый член много больше суммы
членов, обусловленных отражением.
32. Круглый бесконечный полиовод радиуса а возбуждается элементом тока
¦fIBfBdcfe3, находящимся в точке с0, 0, zB. Показать, что амплитуды волн ТЕ в фор-
формулах A5.38) и A5.39) равны
где Jm((Wa)=0, а амплитуды ноли ТЫ, входящие в формулы A5.41) и A5.42), равны
где Jrn(Primn) = 9-
33. Круглый бесконечный волновод радиуса а возбуждается маленькой петлей
с. током, имеющей магнитный момент kl dSe3' и лежащей и плоскости z — zB в точке
рв, 0. Показать, что при этом п волноводе возникают только волны ТЕ, амплитуды
которых, входящие в формулы A5.38) и A5.39), равны
,7, , / B — С) V-1 dS^mnJm (PmnPo) Jt'mn2* in i n
l^mnjte -—7 —§ ; r——— —- e Lb>mnlte = 0
l^mnjte7 § ; r> Lmnlte 0.
2njJmn (ртпаг — тг) [Jm (pmna)]2
34. Круглый бесконечный колиипод радиуса а возбуждается при помощи малень-
маленькой петли с, током, имеющей магнитьый момент ql dSe*1 и лежащей в плоскости
<j)=0 в точке z = zB, p = f0- Показать, что и области z > z0 амплитуды воли ТЕ, входящие
в формулы A5.3S) и A5.39), и волн ТМ, входящие в формулы A5.41) и A5.42), соот-
соответственно равны
ma/ dSJm
Г:
- m2) [Jm (р,ппа)]2
t/61 B —?m
\П 1, -
lmnltm'г7'
Artpmrfrmn [aJm (
35. Коаксиальная лииия, внутренний и внешний радиусы которой равны соот-
ветствеш.о г, и 7'2, юедпнена с, прямоугольным волноводом через кольцевую щель
в его широкой стенке. Центр щели находится в точке x~-d, y=0, z = c. Прямоуголь-
Прямоугольный волновод закорочен в сечении г = (). Показать, что если частота такова, что
в волноводе может распространяться только волна ТЕ10, то сопротивление излучения,
обусловленное этой волной, равно
y In2 (/-г/г,)
(тМ/а) sin2 р'с [Jo Bnr2/~k) — J0 Bго-,/Л)]2 '
[s 1 N2 -1 1/2
1 — \~2^-1а ) ¦ 1'Р1' расчете возбуждения волновода воспользо-
воспользой
ваться методом двойвого слоя тока, описанным в § 20 гл. XIV, считая, что кольцо
тока имеет прямоугольное сечение (г2 — г,) г, и устремляя затем к) к нулю при посто-
постоянном произведении ч] на плотно ть тока.
36. Прямоугольный волновод (< м. § 3), замкнутый в сечении 2 = 0 идеально про-
проводящей плоскостью, воабуждаетл я при помощи провода радиуса г, расположенного
параллельно оси у вдоль x=d, z = с и не ущего равпомерво распределенный ток
j/ (os wt. Считая ?• -С а, г -С X, ?• < с и г <g^ d, показать, пользуясь суперпозицией решений,
35 в Смайт
546 Глава XV
типа приведенных в задаче 8, что реактивное сопротивление равпо
+00
п=0 и=—со
37. Пусть в предыдущей задаче с имеет тот же порядок величины, что и г, но
провод все же не касается торцовой стенки. Показать, что пренебрегая членами
р4с4, р*с6 и т. д. и .комбинируя оставшиеся члены попарно, для реактивного сопротив
леция можно пилучить следующее выражение:
2М^
принимающее при d=—a пид
7J=1
38. Прямоугольный волновод (см. § 3), замкнутый в сечении z = 0 идеально про-
проводящей плоскостью, возбуждается при помощи провода ралнуса г, расположенного
вараллельно оси у вдоль x = d, z—c и песущсто ток j/coswf. Показать, что при
малом г поля в области z > с можно записать в виде
к = _±^п у j _^_ sin ^^ sh у^гС sin:
о, ?j р'т . а
т-1
-=— >. sin—sh/K,c i sin k —.— Ir.oS'
l
m=l
где Pm = (">VE—¦nPrnPar*I!2. Для получения полой в области z<c следует поменять
местами z и с.
39. Задаваясь в предыдущей задаче частотой v, удовлетворяющей неравенству
nv < 2av < (« + l)v, где »—скорость света в среде, заполняющей волновод, показать
путем интегрирования вектора Умова—Пойнтинга по сечению трубы при больших z,
что сопротивление излучения равпо
п
2о)[аЬ -л 1 . тта?
Дг = —р Утг sin2 Pi,c sin2 -—- .
• 7П=1 *
40. В прямоугольном волноводе (а = 10 см, 6=2 см), замкпутом в сечевии z = 0,
распрострлняется волна; соответствующая ей длина полны в свободном пространстве
равна 15 см. Волна возбуждается при помощи провода радиуса 0,5 мм, протянутого
поперек волновода вдоль линии z=^c, #=5 см. Показать, что для получения совро-
тивлсния излучения 100 ом нужно выбрать с равным 2,62 см или 14,0 см и т. д.
Показать, что фазовая и групповая скорости полны соответственно равны 1,52»; и 0,66 v.
а реактивное сопротивление, имеющее индуктивный характер, равно 261 ом.
41. Пусть волновод, опиганный в задачах 38 и 39, замкнут накоротко при помощи
идеально проводящего провода, протянутого вдоль линии z = d2, z = c2. Имподансы
^ ^.
Zj и Z2, определяемые для каждого из проводов, помещаемых по отдельности в волно-
волновод, можно найти из задач 38 и 39. Показать, что при помещении в волновод одно-
одновременно обоих проводов импеданс ZJ первого провода окажется равным
Задачи Ы7
где
ее
2y.b vi I . miuli . mnd2 . r. — jf>' с.
м = > —г- sin ¦ sin sin pmce m г .
" *-> Pm a a
Для распространяющихся волн $'т — действительная величина.
42. Пусть в системе, описанной в задаче 40, требуется уничтожить реактивное
сопротиплепие. Показать, пользуясь результатами задачи 41, что это можно осуще-
осуществить без изменения активного сопротивления путем замыкания волновода при помощи
тонкой проволоки, расположенной вдоль центральной линии па расстоянии с2 = 11,39 см
от конца. Величина М будет действительной, если радиус провода равен 3,45 мм
is если, конечно, предположить справедливость выведенных формул для цроводов такого
радиуса.
43. Прямоугольный волновод (а=1, & = 2), замкнутый в сечении 2 = 0, возбу-
возбуждается при помощи расположенной в плоскости х~1/2 прямоугольной петли, к концам
которой приложены равные но величине и противоположные по знаку потенциалы.
Вертикальные стороны иетли расположены вдоль линий у = 1/2 и г/ = 3/2; длина этих
сторон неизвестна. Петля возбуждается на частоте, соответствующей длине волны
в свободном пространстве, равной 0,5 см. Показать, что в волноводе будут раецро
страняться только полны следующих типов:
Поясвипъ, нечему исключены волны других типов.
44. Поперечное сечение волновода предстаньяет собой прямоугольный равнобедрен-
равнобедренный треугольник, длина каждой из одинаковых сторон которого равна а. Показать,
что критическая частота vc, соответствующая первой распространяющейся волпе ТЕ,
равна -г v/а и что
где v—скорость распростраиевия света в среде, заполняющей волновод.
45. Поперечное сечение волновода представляет собой прямоугольный равнобедрен-
равнобедренный треугольник, длина каждой из одинаковых сторон которого равна а. Показать,
что критическая частота vc, соответствующая перпой распространяющейся волне ТМ,
р
равна — б1^2 via и что
V. v J J
где v—скорость света в среде, заполняющей волновод. ~
46. В круглом цилиндрическом полноподе плоскость <р = 0 представляет собой
бесковечно тоякий ироподящ4ш лист. Показать, что наименьшая критическая частота,
соответствующая волнам ТЕ, определяется но формулам
(
р1/2 , или
47. Показать, что наименьшая критическая частота, соответствующая волнам ТМ
6 задаче 46 равна -^ via.
48. В одном из сечений прямоугольного волнопода (см. § 3) помещена тонкая про-
проводящая диаграмма, в которой от х=^0 до х-=а прорезана щель шириной d, с центром
в точке ?/ = с. Показать, что для вол вы ТЕ1В нормированная шувтирующая проводи
месть.[см. выражение A5.77)] равна
_. о>С 4b./. ъс . nd~
= соС0 = ^= —^—In Sin —-Sin —
yt \9 :V b 2b
49. Пусть половива диафрагмы [см. выражение A5.82)], симметричной отвоси-
тельно начала координат, удалена так, что зазор между оставшейся половиной и стен-
стенкой волновода стал равен d. Показать, что ноле в этом случае дается преобразованием
V2
548 Глава XV
яде начало отсчета находится на пересечении диафрагмы со стенкой волновода.
Доказать далее, что нормированная реактивная проводимость диафрагмы будет опре-
определяться не выражением A5.85), а выражением
50. Индуктивная диафрагма (см. § 11) представляет собой полоску шириной с,
расположенную в центре. Из соображений симметрии следует, что одинаковые участки
на верхней и нижней стенках волновода будут иметь одинаковые по величине,
но противоположные по знаку заряды, так что вокруг окна по будут циркулировать
токи, и, следовательно, функция потока будет принимать одинаковое значение (V=0)
м на полоске а на стенках. Показать, что в плоскости полоски
s ъх Е ~\ / пс та"\ х/г
Ч а & J Ч '2а a J
аде Е и К — полные эллиптические интегралы модуля к = cos ( -тр ш-/а }. Показать
также, что нормированная шунтирующая проводимость равна
*-4«
?}" — = -
?—(l—i
51. Волноводы, описанные в задачах 1 — 5, превращены в полые резонаторы путем
юведения в них проводящих плоскостей z- -О и z—d. Показать, что уравнения вол-
иовых поверхностей останутся прежними, если в них заменить для воли ТЕ
а для волн ТМ —
,,, . / imz \
cos p'z на sin ( — J ,
sin $'z на cos ( ^^ ) .
4 d J
52. Показать, что аксиально-симметричные волновые поверхности в сферической
полости сонпадают с вихревыми кольцами магиитвого поля и что они ппходятся в ячей-
ячейках, ограниченных сферами r = rs, r = rs+l и конусами b = 6p, O = Gp<]; s и р- целые
числа O^s < t, 0<!/> < п, /n(fWs)=0 и sin (Jp/','(cos Ом) = 0. Уравнение волпоиых
поверхностей имеет вид
с_ Пп ($оуг) sin OP* (cos 0)
~гм/п (Роп>ш) sin UMt i (cos <IM) '
где
d
rs < rM < rs+], -—lrMin($0nrM)] = V, Op < 6M < 6p+1 и Рп(cos bM) = 0.
arM
"Часть потока магнитной индукции сквозь нлощадку, ограниченную границей ячейки
и г, 0, равна С, а радиус полости г< равен а.
53. Показать, что волновые поверхности аксиально-симметричных полей ТМ
в сферической полости представляют собой вихревые кольца электрического поля,
уравнения которых совпадают с уравнениями, полученвыми в предыдущей задаче,
но только flj0 имеет в этом случае другое значение и вблизи стенок полости появляются
половинные ячейки.
54. Плоскости х = 0, у = 0, х4-у = а, 2 = 0 и z = d являются границами полого
резонатора. Показать, что собственная частота простейшею колебания ТЕ равна
и что
-где v — скорость света в среде, заполняющей резонатор.
[л'6[2а-»+A + 21/2)а
Задачи 549
55. Плоскости ж = 0, у = 0, я:-\-у = а, 2 = 0 и z = d являются границами полого
резонатора. Показать, что собственная частота простейшего колебания ТМ равна
и что
„ y.ad
где v — скорость света в среде, заполняющей полость.
56. Полость ограничена плоскостями г = 0 и # = я и поверхностью призмы у=юг
y—b, y = z, z — у —2b. Предполагается, что напряженность электрического поля имеет
только я-составляюшую и что единственное периодическое решение, дающее значение
Лх=0 при у=0 и х = у, имеет вид
АХ = С[sinp(z —у) sinq (г-} у) — sin? (z — у) sin p (z +y)],
где /> я b — нераввые между собой произвольные постоянные. Показать, что наибольшая
резонансная длина волны полости равна 2&/51'2 и определяется значопиями р=—тс/1>
и q — —i:lh.
57. Исследование в последней задаче узловых линий паинизшего колебания
типа ТМ показывает, что поле можно разбить на четыре ячейки, имеющие форму
равнобедренных треугольников. Исходя лз этого и пользуясь задачей 55, «оказать-
(путем суммирования потерь ва четырех сторонах, двух диагоналях и посьми стенках),
что
<? = [лВ (;л')-1 М [B + 21/2) d-\- 2b]-1.
Это превышает добротность Q простейшего колебания типа ТМ в квадратной и круглой
полости с плоскими освованмпми.
58. Полый резонатор образован из коротко замкнутой бинонической линии пере-
передачи и ограничен двумя конусами 6 = а и В = л — а и сферой r — d. Показать, что резо-
резонансная длина волны главного типа колебания равна
Ы
2p+i
и что
2fjt4 sin a In ctg— а
Q — Г
— a i
где С—постоянная Эйлера, равная 0,5772. •
59. Определим эквивалентный ток полого резонатора, рассмотренного в предыдущем?
задаче, как ток, текущий по внешней оболочке, и выберем Sc таким образом, чтобы
выполнялось соотношение A5.93). Показать, что для главного колебания коэффициент
самоиндукции и емкость полости соответственно раины
L=?lnctg-a,
'" ' -"inliictg-ia
60. Полый резонатор ограничен дпумя плоскостями z = 0, z = d и двумя кон-
конфокальными эллиптическими цилиндрами, ортогональными к этим плоскостям, г.рпчем
большие и малые оси эллипсов равны Мл, т, и Ж2, т2- Показать, воспользовавшись
результатами § 23 гл. IV и § 19 гл. XV, что для р-то главного колебания такого
полого резонатора
J^_
2u/6p
где M2 > Mlf a Xt и K2 — полные эллиптические интегралы, модули которых соответ-
соответственно равны (М\ — т\I1*1Мл и (M\ — m\fhjM2.
61. Полый резонатор ограничен двумя плоскостями z = 0 и z = d и дпумя круг-
круглыми цилиндрами, оси которых перпендикулярны к плоскостям и находятся на
Г>50 Глава XV
расстоянии с друг от друга, причем а > 6+с, где а и b — радиусы цилиндров. Показать,
используя результаты § 14 гл. IV и § 19 гл. XV, что для р-то гласного типа колебания
4аЬ[(а2—б2J—2(a2 + 62)c2 + c4]l/2arch[(a2 + 62 —c2)/Ba6)]
1-1
I
62. Прямоугольный резонатор (шириной а, высотой 6, длиной d > 2а) частично
перегорожен в цептре от у=а до у=Ъ при помощи тонкой проводящей диафрагмы.
В резонаторе возбуждается колебание типа TEi0. Рассматривая его как Т-образное зве-
звено волновода, шунтированное на копнах емкостью, подсчитанной в § 11, показать, что
длину волны н свободном пространстве, соответствующую наименьшей резонансной
частоте полости, можно найти из формулы
, 2а\л 86/. п<ЛЛ 2лА
А= !—г;—, I == =г— I In cosec — Н tp —— i
63. Пуств в предыдущей задаче о = 2, 6 = 1, с = 1/2 и d = 4. Показать, что \ = 4,692.
64. Пусть в задаче 62 плоскость z = 0 является стенкой резонатора. Показать,
используя результаты задачи 23 и формулу D.10В) и применяя интеграл Мелера — Ди-
Дирихле для функций Лежандра. что вектор-потенциал, описывающий поле в области
0 < z < d, имеет вид
со
\—Л „:„ пх Г : sin Ро2 i V с f t ~~- ППу I t- /n7Z -:» ПпУ~\ sh (I Pn | z) 1
a L sinporf' ^J "V Ь \pn\b Ъ J s\a{\$n\d) \
если длива волны в свободном пространстве, входящая в задачу 62, удовлетворяет
неравенству
а2Х2> 4я262 —Х2&2>0
и
я Dа2—Х2I/2
65. Используя результаты задачи 60 гл. IV, показать, что если в полом резона-
резонаторе, описапном в § 23, d <С a, d <С с и а «к 6. то емкость Со, входящая в формулу
A5.173), приблизительно равна
,,, d2 + F , 2a.k d , 2orf , A 2catf "I
+2aln -4й-+-5-агсtg т+^гагсtg т - T-J •
где k=b -h. При «= 0,1; 6 = 0,015; (/ = 0,001; c = 0,02; величина j5 = 42,7. Графики Мо-
Морено дают и этом случае [5=41,0. Точность увеличивается с уменьшением разности Ъ—а.
6G. Прямоугольный полый резонатор имеет в направлениях х, у, z размеры а, Ь, d.
В резонаторе при помощи тонкого провода, протянутого параллельно оси z вдоль ли-
линии я —а], у=Ь], возбуждается колебание ТМпо. Провод подключен к источнику та-
таким образом, что ток ндоль участка провода, находящегося внутри полости и имею-
имеющего сопротивление R, распределен равномерно. Считая, что размер d значительно
меньше, чем а или 6, показать, что входное сопротивление равно
ab(a2Jt-b2)-\-2d{as-\-b3) а Ъ
Показать также, чго усиление по папряжеиию в такой системе будет равно
таг, nftj
cosec—-cosec—-г- ¦
a b
67. Пользуясь методом изображений и результатами задачи 8, показать, что если
в предыдущей задаче провод имеет радиус с, то входное реактивное сопротивление
провода равно
-^lnc+^2 2 ((l-
—оо —оо
Литература 551
Ламетим, что прп малых с псриый член написанного выше выражения значительно
превосходит остальные, из которых наиболее существенными являются гп = п = 0.
68. Пусть стенки полого резонатора, рассмотренного в задаче 66, сделаны из меди
(-у = 5,8-107) и пусть полс-ть имеет размеры a—iO см, 6 = 20 см, d = 2 см. Показать,
что резонансная частота, соответствующая колебанию ТМио, равна 1,670-109 щ, а доб-
добротность Q приближенно равна 9100. Показать, что активное входное сопротивление
будет равняться 100 ом, сел» возбуждающий провод имеет координаты ж = 0,0512 см,
(/ = 10 см или ж = 5 см, у = 0,1024 см или если о и расположен гдо-либо на кривой
sin (raj,/10) sin (лб,/20) = 0,0160. Показать также, что при .мощности на входе 1 em
эффективное значение напряжения в цеитрс равно 625 в.
69 Прямоугольный резонатор возбуждается полукруглой петлей радиуса г, лежа-
лежащей в плоскости у = Ь1 и имеющей центр в точке z — dt, x = 0. Показать, что коэффи-
коэффициент взаимной индукции между петлей и полем типа ТЕтпр равен
м = 8
70. Прямоугольный резонатор возбуждается полукруглой петлей радиуса г, лежа-
лежащей в плоскости ,'/ = 6| и имеющей центр н точке z = d1, ж = 0. Показать, что коэффи-
коэффициент взаимной индукции между этой петлей и полем типа ТМтпр равен
„. 2т^тг[2B—Ьр)] Т ,„ х . nub,
71. Сферическая полость с медными стенками радиуса а возбуждается при помощи
маленькой плоской петли площади S, расположенной настолько близко к стенке по-
полости, что значение магнитной индукции В па протяжении ъгем петли можно считать
равным значению В на стенке полости. Показать, что при возбуждении этого полого ре-
зопатора на резонансной частоте, соответствующей колебанию ТМол, входное сопротив-
сопротивление будет равно
3
и что если pola = 2,744, а К—активное сопротивление петли, то коэффициент усиления
по напряжению будет равен
J/_^2_ [Si(M_ ] =
•6 KSL() I
72. Пусть полый резонатор, рассмотренный и предыдущей задаче, имеет радиус
10 см, а стенки его сделаны из меди. Показать, что для получения входного активно-
активного сопротивления в 100 ом площадь петли должна быть приближенно равна 0,225 см2
и что при этом получится усиление по напряжению в 436 раз.
ЛИТЕРАТУРА
King R. W. P., Mimno H. It., Wing A. H., Transmission Lines, Antennas and
Wave Guides, McGraw-Hill, 1945. (См. перевод: Кип г Р., Мимно Г.,
У и и г А., Передающие линии, антенны и иолпоноды, М., 1947.)
Marcuvitz N.. Waveguide Handbook, McGraw-Hill, 1950. (См. перевод: Спра-
Справочник по волноводам, М., 1952.)
Montgomery С. G., Dicke R. H., Pur с ell К. М., Principles of Microwave
Circuits, McGraw-Hill, 1948.
Moreno Т., Microwave Transmission Design Dam, McGraw-Hill, 1948.
Radio Research Laboratory Staff, Very High Frequency Techniques, McGraw-Hill, 1947.
R ag an G. L., Microwave Transmission Circuits, McGraw-Hill, 1948.
R a m о S., W b i n n e г у J. R., Fields and Waves in Modern Radio, Wiley, 1944. (См.
перевод: Р о м о С, В и и е р и Д ж., Поля и волны в современной радиотех-
радиотехнике, изд. 2, М.—Л., 1950.)
Sarbacber R. I., Edson W. A., Hyper and Ultrahigb Frequency Engineering,
Wiley, 1943. (См. перевод: Сарбахер Р., Эдсон В., Техника сверх-
сверхвысоких частот, М., 1947.)
Schelkunoff S. A., Electromagnetic Waves, Van Nostrand, 1943.
Slater J. С, Microwave Electronics, Van Nostrand, 1950.
Slater J. C, Microwave Transmission, McGraw-Hill, 1942. (См. перевод".
С л э т е р Дж. К., Передача ультракоротких радиоволи, М.—Л., 1946.)
s tra t ton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: Страт-
тон Дж. А., Теория электромагнетизма, М.—Л., 1948.)
Watson W. H., Wave Guide Transmission and Antenna System, Oxford, 1947.
Глава ХМ
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
И ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ
§ 1. Постулаты специальной теории относительности. 1? предыдущих
главах при рассмотрении электрического и магнитного взаимодействия
зарядов л токов предполагалось, что величины последних могут меняться
со временем, но их взаимное расположение, а также положение относительно
некоторого наблюдателя остается неизменным. При трактовке вопросов,
связанных со взаимодействием систем, прямолинейно перемещающихся и
пространстве относительно друг друга пли относительно наблюдателя,
специальная теория относительности опирается, повидимому, на наиболее
твердо установленную экспериментальную базу.
13 основу специальной теории относительности положены два постулата.
1. Все физические законы, или описывающие их уравнения, имеют
одинаковый лид в пустоте во всех декартовых системах координат, совер-
совершающих относительно друг друга равномерное поступательное движение.
2. Скорость света в пустоте одинакова для любого наблюдателя, нез.а-
висимо от относительной скорости источника спета и наблюдателя.
Исследование большого количества доступных наблюдению явлений
механического, оптического и электрического характера, существование
которых было предсказано на основе этих постулатов, показало, что во
всех случаях результаты опытов, проводимых на земле, подтверждают эти
постулаты.
§ 2. Преобразование Лоренца. Рассмотрим две системы координат
(см. фиг. 140), оси х и х' которых совпадают. Пусть система S' движется
, относительно системы S вдоль
q
Y
q
направления х с постоянной ско-
скоростью v. Для нахождения со-
соотношений, связывающих х, у, z
и г с ж', у', г' it t' и удовле-
тгоряющих двум постулатам спе
й
v <r циалыюй теории относительно-
*" сти, проделаем мысленно следую-
щий простой опыт. Предположим,
Фиг. 140. что к момент времени t =--1' = 0
оба начала координат О и О'
совпадали и что в этот момент из общего для обеих систем начала коорди-
координат был послан световой импульс. Согласно постулатам § 1, п каждой си-
системе S и iS" должна наблюдаться сферическая волна, расходящаяся из
начала координат со скоростью с. Поэтому в любой последующий момент
времени уравнение, описывающее фронт волны в системе S, будет иметь
вид
x2 + y2 + z2 = c2t2, A6.1)
Специальная теория относительности 55S
а в системе S'
x'2 + y'2 + z = c4'2. A6.2)
В силу симметрии фронта волны при наблюдении в системах S и S' можно
положить z = z' и У—у'. Тогда для удовлетворения уравнений A6.1) и
A6.2) должно выполняться следующее равенство:
х* — сг1? = х'* — с4'2. A6.3)
В системе S в момент времени t точка О' будет иметь координату ы, а
в системе S' в момент времени t' точка О имеет координату — Ы'. Наиболее
простыми соотношениями *>, приводящими к этому результату, будут
ж' = х(:г— vt), -х ¦=¦*.' (х' + ?¦*')• A6.4)
Исключение х' дает
Подставляя значения х' и i' из пыражеггпй AE.4) и A6.5) в A6.3) полу-*
чаем соотношение, содержащее переменные х2, at и г2, но поскольку оно
должна выполняться при любых положительных значениях t и любых
значениях х, то коэффициенты при ж2, х/ и г2 должны порознь равняться
нулю. Приравнивая их к нулю и решая относительно % и %', находим
Таким образом, из выражений A6.4) и A6.5) получаем искомые формулы
преобразования
•V.' __ „ / л, ^. *\ л, -.
ni1 О/ я-' <7 ?/ . iji1
U U, 4у -О 5 ;/ ¦ (J
V с2 У '
§ 3. Преобразование скорости и ускорения. Будем определять скорости
движения относительно системы координат S следующим образом:
dx dy dz ,.COl
U^df' uv<=W> u*=dF> <l6-8)
а относительно системы -S"
«Нг- <=W' *=W- A6-9>
Дифференцируя первые три уравнения первой группы A6.7) по ?, а второй
группы по г и исключая из правых частей соответственно dt\dt' и dt'jdt
путем дифференцирования четвертого уравнения противоположной группы,
получим
A6.10)
UxV
A6.11)
х) Простота не является, очевидно, достаточно убедительным аргументом. Автор не
вводит понятие интервала, хотя фактически постулирует инвариантность последнего.—
Прим. перее.
554
Глава XVI
Это — уравнения преобразования скорости. Интересно отметить, что если
даже системы движутся с относительной скоростью v = с и некоторая
точка в системе S' имеет скорость и'=с, то величина и, определяемая
формулой A6.10), равна с. Таким образом, скорость света можно рассма-
рассматривать как верхний предел возможной скорости.
При помощи аналогичных операций, дифференцируя выражения A6.9)
и A6.10), получим для ускорений следующие соотношения:
( Л
V
dP
uxV
-3du'x
Соответствующие уравнения для du'x/dt' и du'VtZ \dt' можно получить из
выражений A6.12) и A6.13) путем перестановки величин, отмеченных
штрихами, и величин, не отмеченных штрихами, и замены -\-v па —v.
Заметим, что постоянное ускорение в системе S' в общем случае не
обусловливает постоянного ускорения в системе S.
§ 4. Зависимость массы от скорости. По первому постулату закон
«охранения энергии и импульса должен выполняться для всех наблюдателей.
В
О.
У
V
s
и
~х
(
.а
)
X
Чтобы выяснить результат, к которому приводит это требование, рассмо-
рассмотрим простой эксперимент, предложенный Толманом и проиллюстрирован-
проиллюстрированный на фиг. 141. Пусть в тот момент, когда оба начала координат совпа-
совпадают, из точки В' в системе S' по направлению к точке О' начинает дви-
двигаться шар со скоростью и, а из точки А в системе S — другой шар,
перемещающийся параллельно у также со скоростью и.
Выберем отрезки ОА и ОБ такими, чтобы в момент соударения центры
шаров располагались вдоль направления Y. На фиг. 141 показано, как
это соударение будет паблгодаться из систем S и S'. Будем считать, что
в состоянии покоя но отношению к любому наблюдателю масса каждого
из шаров равна т0, и предположим, что масса является функцией вели-
величины скорости
т = /(м2) и /гао=/@). A6.14)
.'По формулам предыдущего параграфа начальные скорости равны
Для системы S Для системы >S"
пах = 0, Uay = U,
иах = —v,
A6.15)
Uby = — U ¦
Специальная теория относительности 555
Будем отличать скорости после удара при помощи черточек сверху. По
законам соударения двух гладких шаров их импульс по оси х должоп
сохраняться относительно любого наблюдателя. Таким образом, в системе
5 для составляющей в направлении х имеем тьО—Таф, или
Это приводит к требованию
Иь=—и и, следовательно, 7nb — mt>. (,16.16)
Знак минус выбран из предельного случая малых скоростей, когда «= 1
В системе S для составляющей п направлении у получим
Принимая во внимание соотношение A6.16) и учитывая известный резуль-
результат при v = 0, мы видим, что это уравнение удовлетворяется только, если
ио= —и. Разделив его на и, найдем
/fu*) = iraa = ^-. A6.17)
Если скорость и мала, то
mo. A6.18)
Итак, масса тела, движущегося со скоростью v относительно данного на-
наблюдателя, кажется последнему увеличившейся в х раз по сравнению с
массой покоя, где
Для дальнейшего удобно ввести величины к, и *.[, определяемые сле-
следующим образом:
1/2, A6.20)
,; = (l-""+f ¦'¦«?) 1/2, • A6.21)
где их, иу и мг — компоненты скорости частицы в системе^, d u'x, u'y, u'z —
компоненты скорости той же частицы в системе S'. Используя выражения
A6.10) и A6.11), можно получить такие соотношения:
(ib.ll)
A6.23)
§ 5. Преобразование сил. Характер уравнении, связывающих силы в
системах S и S', зависит от того, определяется ли сила как произведение
массы на ускорение или как производная импульса по времени. Мы будем
придерживаться последнего определения; поэтому, учитывая выражение
A6.18), запишем
556 " Глава XVI
Записывая это уравнение в компонентах, можно видеть, что при таком
определении в общем случае сила и ускорение не совпадают по неправда-
нито. Выполняя дифференцирование, получим
„ du , dm du , 3 и du
Пусть сила приложена в направлении и1г a u = u,w и
du u, du
dt ~~ dt '
тогда
§ = Щ$Г- A6.26)
Если dujdt — O, т. е. если скорость меняется только по направлению, а не
по величине, то из соотношения A6.25) следует, что сила снова будет
совпадать по направлению с ускорением, перпендикулярным к скорости и,
„ du du /лс г>г,.
?t = mo4-^=™fdT- A6-2/)
Величины т1 = тох? я т, = т^ принято называть соответственно продоль-
продольной и поперечной массой частицы.
Силы, наблюдаемые в системе S', должны записьшаться в той же
форме, что и в системе S,
F'-m rf
° dt'
Подставим в уравнение A6.24) для ж-компоненты силы вместо х,мя соот
ветствующие выражения из соотношений A6.10) и A6.22) и вместо dt'/dt
выражение, получаемое путем дифференцирования формулы A6.7); тогда
Ho
, ux uv -\-uz , 1
c*dt' + c'dt' *i2 dt'
так что, производя подстановку, получим
duz . , d
C2+UxV
Аналогичные операции для Fy и Fz дают
^ + /'z- (lb.Zb)
Это и есть уравнение преобразования сил.
Специальная теория относительности 557
§ 6. Сила, действующая на заряд, движущийся в магнитном ноле.
Первый постулат специальной теории относительности требует, чтобы законы
электростатики были одинаковыми для любого наблюдателя. Если пред-
предположить дополнительно к этому неизменность величины заряда, то отсюда
будет следовать, что в системе S силы взаимодействия движущихся в ней
зарядов отличаются от электростатических. Как будет ясно из дальнейшего
(см. § 14), инвариантность заряда является следствием инвариантности
уравнений Максвелла. Эти дополнительные силы можно было бы назвать
электрокинетическнми, но вскоре мы увидим, что они совпадают с силами,
которые мы назвали магнитными.
Предположим, что в системе S' имеется два точечных заряда q и qx,
расположенные на плоскости х'у' соответственно в точках х' = 0, у' = у[ и
х' = х', у' = 0. По закону Кулона, компоненты силы, действующей па заряд q
в системе «S", будут равны
F'x = =Wj?__, F'= q-^—,sT , F't = 0. A6.30)
В системе S эти заряды будут двигаться в положительном направлении
оси х со скоростью t, поэтому силы, наблюдаемые в системе 6', можно
получить путем подстановки соотношений A6.7) и A6.30) в вырая5ение
A6.28). Для обоих наблюдателей в системах S и S' сила не будет зависеть
от времени, и, следовательно, ее можно рассматривать в момент / = 0,
t'=—x'vc—2. Поскольку u'x=u'v = u'z = V, х' = кх и т. д., это дает
Fv = ^^п-, Fz = 0. A6.31)
4тсевх (х2ж2 + 7/f) /2
Теперь посмотрим, какие силы наблюдаются в системе S, если вместо
заряда qx имеется бесконечная линия зарядов, равномерно распределенных
вдоль х м движущихся со скоростью I. Заряд любого элемента оси, со-
согласно принятой гипотезе, одинаков для любого наблюдателя, так что
сила, обусловленная этим элементом, получается при помощи подстановки
в выражение A6.31) величины
q1 = adx = a'dx'. A6.32)
Заметим, кстати, что так как в силу соотношения A6.7) dx' = v.dx, то
из утверждения об одинаковости заряда q± для обоих наблюдателей с не-
необходимостью вытекает, что
о=хо', A6.33)
т. е. плотность заряда для систем S и S' оказывается разной. Подстав-
Подставляя соотношение A6.32) в формулу A6.31) и интегрируя в пределах от
а;=—оо до ж= -|-оо, мы получим для силы, с которой действует движу-
движущаяся заряженная лента на заряд q, следующие выражения (см. Двайт,
200.03 и 201.03):
^ = 0,^ = 0, F^lV-^" , A6.34)
где р = в/с. Полагая P = U, можпо определить наблюдаемую в системе S
электростатическую силу, равную qaJB-Keny), так что дополнительная сила,
обусловленная движением, будет
^^v, A6.35)
а измеренный в системе S ток i - ас. Как вытекает из формулы G.79),
в системе <Ь' с этим током связано магнитное поле, направленное по оси z
558 Глава XVI
и имеющее в точке х = 0, у — Уг значение Bz = jx,i/Bit?/j). Подставляя это
значение в формулу A6.35), мы видим, что обусловленная движением
дополнительная сила, действующая на д, равна
bFy=-Bzqv. A6.36)
Таким образом, на точечный заряд </, движущийся с постоянной ско-
скоростью V в однородном магнитном поле В, действует сила, направленная
перпендикулярно к v и В и равная
Fm=?[vxB]. A6.37)
В прямоугольных координатах это можно записать в виде
Fm = <?[i {^z-vA,) + i^A-^Bz) + k{VxBy-vvBx)}. A6.38)
В § 14 будет показано, что соотношение A0.37) также является след-
следствием инвариантности уравнения Максвелла. Если положить vq = Ji\s,
то получится в точности закон, определяющий силу, действующую на
помещенный в магнитное ноле В элемент ds, по которому течет ток 1.
Из опытов Ампера, описанных в § 19 гл. VII, этот закон можно было
вывести только как интегральный закон для замкнутых контуров.
Теперь мы распространим его и на случай изолированных движущихся
зарядов. Следует заметить, что формула A6.37) остается совершенно
точной и для полей В, меняющихся во времени и в пространстве, при
условии, что эти изменения настолько медленны, что индукцию В па про-
протяжении области, занимаемой зарядом, можно считать однородной и посто-
постоянной. Можно ожидать, что выражепие A6.37) окажется неверным для
каких-нибудь действительных заряженных частиц, если применять его для
субатомны^ расстояний и частот*
§ 7. Движение зарядов в однородном магнитном поле. Предположим,
что частица, имеющая заряд q и массу т, движется в магнитном поле В
со скоростью v. Пусть единичный вектор Sj, направленный вдоль v(v = csj),
составляет с полем В угол а. Тогда из соотношения A6.37) имеем
Или, записывая это уравнение в компонентах, получим
8,1^2 = 0, A6.40)
т. е d — постоянная величина и
^ В], A6.41)
т. е. вектор ds1 перпендикулярен к sx и В и, согласно выражению A6.27),
массу т нужно брать равной поперечной массе. Обозначим через dcp —
угол между векторами sx и s,+ dst, измеряемый в плоскости, перпенди-
перпендикулярной к В, а через р—радиус кривизны траектории на участке dy.
Тогда, раскрывая векторное произведение в выражении A6.41) и раз-
разделив обе части этого уравнения па ^sina, мы придем к следующему
соотношению:
mfds, _mtd<f _ reusing _ ^ A6.42)
s^sinadt dt p
Таким образом, траектория частицы представляет собой спираль с угловым
Специальная теория относительности 559
шагом, равным -^-п — а; эта спираль охватывает круглый цилиндр, радиус
которого равен
mnv sin a
(lb.43)
а ось параллельна В. В частном случае, если вектор v перпендикулярен
„1 _.
к В, то угол a = Ylt> и заряд движется по круговой орбите.
§ 8. Энергия движущейся заряженной частицы. Энергию, сообщаемую
частице под действием силы, мы определим как работу, совершаемую этой
силой. В течение бесконечно малого промежутка времени dt частица прой-
пройдет расстояние dr = udi. Тогда, согласно выражению A6.16). совершаемая
работа будет равна
Подставляя значение х, из.выражения A6.16) и интегрируя от 0 до иТ
получим
W = (mt - m0) с2 = (*! - 1) m0c2. A6.45)
Отсюда вытекает, что увеличение энергии связано с увеличением массы.
Этот закон представляет собой теперь один из наиболее точных и пол-
полностью подтвержденных законов физики. Он был подтвержден главным
образом большим количеством данных о ядерных распадах. Таким обра-
образом, мы имеем достаточные экспериментальные основания, чтобы утвер-
утверждать, что
\W = с2Дт. A6.46)
Согласно выражениям A6.44) и A6.37),- заряженная частица не получает
энергии от магнитостатической части статического электромагнитного поля.
Поэтому" она ие может попасть в область, электростатический потенциал
которой превышает сумму потенциала точки вылета частицы и потенциала,
необходимого для сообщения частице ее начальной скорости.
§ 9. Критическое магнитное поле в магнетроне. В качестве примера
расчета движения заряда при наличии электрического и магнитного полей
рассмотрим устройство, известное под казванием магнетрона. В простран-
пространстве между двумя концентрическими круговыми проводящими цилиндрами
создан вакуум. С поверхности внутреннего цилиндра вылетают заряженные
частицы, обычно электроны, причем начальная скорость их ничтожпо мала.
Между цилиндрами поддерживается разность потенциалов такого знака,
что заряженные частицы приобретают ускорение в направлении от внут-
внутреннего цилиндра радиуса а к внешнему цилиндру Ь. Магнитное поле
ориентировано вдоль оси цилиндров, а индукция В является функцией
только расстояние от оси р. Найдем, при каком значении В частицы пере-
перестают достигать внешнего цилиндра, если принять потенциал последнего
равным V. Если через <р обозначить азимутальный угол, то частицы еще
достигают анода, но уже перестают попадать иа него в том случае, когда
на аноде dpjdt = р = 0, так что
-56U Глава XVI
Приравнивая производную момента импульса частицы моменту действую-
действующих на нее сил, получим
^^ A6.47)
В начале пути <р = 0, а в конце p — b, py = v, и m = x1m0, поэтому в резуль-
результате интегрирования уравнения A6.47) вдоль пути получим
ь
s^Wpte = - q [ pB dp. A6.48)
а
Обозначим через N полный поток магнитной индукции между цилиндрами
ь
N = 2tl \ pBdp, тогда
а
x1mofe=-^-. A6.49)
Поскольку знергия заряда определяется только потенциалом V в точке,
где этот заряд находится, то, согласно выражению A6.45), имеем
F<? = (x1-I)muc2. A6.50)
Исключая при помощи соотношения A6.50) xt и v из формулы A6.49),
полу им
Если потенциал достаточно мал, то вторым членом в правой части можно
пренебречь. Решая выражение A6.51) относительно V, получаем
A6.52)
§ 10. Траектория космической частицы в однородном поле. В каче-
качестве примера вычисления траектории заряженпой частицы, на которую
действуют электрические и механические силы, рассмотрим частицу, дви-
движущуюся в плоскости, перпендикулярной к однородному полю В,, считая,
что сила торможения частицы в среде пропорциональна скорости. Экспе-
Эксперимент показывает, что заряженные частицы космического происхожде-
происхождения, обладающие большими скоростями, рассеивают свою энергию
почти равномерно вдоль всего пути, так что предположение о характере
тормозящих сил соответствует действительности. Пользуясь выражениями
A6.24) и A6.37), напишем уравнения движения в проекциях на оси х и ?/:
A6.53)
A6.54)
Проинтегрируем теперь эти два уравнения в пределах от некоторой точки
на траектории до начала координат, где х=г/-0иж = ?/ = 0, и возьмем
отношение полученных результатов:
У ау —QmjX-—пу /л о сс\
T=rf7 = qBy-Kx ¦ A6'55)
Полагая ?/ = rsin6 и х = г cos 6, имеем
Специальная теория относительности
561
Выбрав в —0 при г—1 и проинтегрировав от этой точки до некоторой
точки на траектории, получим
или
A6.57)
- 5
Таким образом, траектория представляет собой спираль с постоянным
шагом. Для космических электронов, движущихся с большими скоростями, К
примерно равно 3qP ¦lO~'i, где Р— давление воздуха в атмосфере.
§ II. Магнитное поле движущегося заряда. Вернемся снова к силе
взаимодействия двух движущихся зарядов, определяемой формулами A6.31).
В соответствии с выводами § 6 можно считать, что наблюдатель в системе S,
рассматривая силы, действующие на заряд, пересекающий ось у, со сто-
стороны другого заряда, движущегося вдоль оси х, приписывает их комбиниро-
комбинированному действию электрического и ма
гнитного полей второго заряда. Состав-
Составляющая силы по оси х, т. е. вдоль на-
направления движения заряда q, должна
быть чисто электростатического характе-
характера, тогда как составляющая силы по
оси у содержит и электрическую и маг-
магнитную части. Таким образом, имеем
Fv = Fesine-Fm, A6.58)
•Fv=-Fx~-Fy A6.59)
Здесь мы ввели угол б (фиг. 142), учи-
учитывая, что, как будет показано в § 17, аберрация сигнала, посланного
из qx в q, равна нулю. Подставляя значения сил из соотношения A6.31),
получим
»-, qq,y(t?—1) qq^Tufiil ,.п П1Л*
Fm~= jr-= '— ——-. A6.60)
В системе S эта сила не меняется со временем, и поскольку q предста-
представляет собой точечный заряд, то наблюдатель, находящийся в системе S,
может считать, что заряд движется в однородном магнитном поле, индук-
индукцию которого вполне законно вычислять по формулам A6.37) и A6.38).
Таким образом, магнитное поле, создаваемое зарядом qt, оказывается равным
lJ.vq.VI/-K
A6.61)
Радиальная составляющая напряженности электрического поля по опреде-
определению и в силу соотношения A6.58) равна
Fe
Ч
&х?
qx
izzv (ч?х* -f- y2f'2 '
Используя формулы § 2 гл. XIII, находим
A6.62)
36 В, Смайт
562 Глава XVI
Легко убедиться в том, что векторный и скалярный потенциалы, соответ-
соответствующие выражениям A6.61) и A6.62), определятся следующим образом:
Ах = -^ Yf! (lb.bo)
? = — тг ¦ A6.64)
Следует заметить, что формулы A6.61)—A6.64) применимы к случаю
точечного заряда, движущегося равномерно и прямолинейно. Входящие
в них пространственные величины определяют действительное положение
заряда в момент измерения.
§ 12. Запаздывающие поля и потенциалы движущегося заряда.
Поскольку электромагнитные поля распространяются с конечной скоростью с,
то сигнал, полученный в точке Q в момент времени t, когда пославший
его заряд ql находится уже в точке Р,
будет в действительности представлять
собой сигнал, посланный зарядом qx из
некоторой предшествующей точки [Р]
на траектории заряда. Если даже после
^г прохождения через точку [Р] заряд из-
[r]\ ^v менил свое движение, то поле в точке Q
^v в момент времени t останется все же
~1@\ г TtjV > прежним. Таким образом, в случае не-
^Шы.—^Г х равномернгго движения поле в момент
времени t целесообразнее описывать как
Q^P функцию движения заряда в момент
' t — ([r]lc)' гДе ([^]/с)—время запаздыва-
Фиг. 143. имя, а [г] — радиус-вектор, проведенный
из точки [Р\ в точку наблюдения Q. Но
так как поле в точке Q не зависит от пути заряда д1 после прохождения
им точки [Р], то мы будем предполагать, что движение заряда q1 после
прохождения точки [Р] остается неизменным, т. е. он движется прямолиг
н> йно с постоянной скоростью [г;] по направлению к некоторому фиктив-
фиктивному положеншо Р'. Тогда поле в точке Q можно вычислить методом, опи-
описанным в предыдущем параграфе. Бапйшем необходимые соотношения
между фиктивными и запаздывающими величинами (см. фиг. 143)
A6.65)
A6.66)
где через [[3] обозначено [f]/c. Член, входящий в знаменатель выражения
A6.60), можно теперь переписать в виде
х2х2 + ?/2=[х]2(г2— [p]2?/2)=[*]2[/-]2(l-[p]cos[6]J. A6.67)
Подставляя соотношения A6.66) и A6.67) в формулу A6.61), получаем
выражение для магнитной индукции движущегося заряда через запаздываю-
запаздывающие величины
Вг = ¦ 2 ^у" ' ¦ m %. A6.68)
Это выражение, очевидно, можно применять для медленно меняющихся
скоростей при условии, что значения [[3] и [v] берутся в точке [Р]. В век-
Специальная теория относительности 563
торных обозначениях соотношение A6.68) будет иметь вид
Электрическое поле, определенное в § 11, направлено вдоль г. Как
видно из фиг. 142,
где [гх] — единичный вектор, направленный вдоль [г]. Таким образом, вводя
в выражение A6.62) запаздывающие величины [р] и [v], для электрического
поля найдем
(ф)
Е = 4*е1,И1|A-[Н«>8[в])» • A6.70)
Подстановка соотношений A6.65) и A6.66) в выражения A6.63) и A6.64)
позволяет определить запаздывающие потенциалы поля, создаваемого дви-
движущимся точечным зарядом
A6.72)
['] (!-[?] cos [б])"
Для малых [р] эти выражения, очевидно, совпадают с выражениями A4.21)
и A4.22), если в последних считать размеры заряда малыми. При больших
[р] можно из выражений A4.21) и A4.22) получить соотношения A6.71)
и A6.72), если принять во внимание изменения времени запаздывания
-в пределах бесконечного .малого объема заряда. Этим изменением нельзя
пренебрегать, даже если заряд сжимается в точку. Более полная дискуссия
этих вопросов дана Мэзоном и Уивером.
§ 13. Излучение равномерно ускоренного, прямолинейно движущегося
электрона. Результаты предыдущего параграфа можно применить к случаю
ускоренного движения реального заряда, например электрона, при условии,
что ускорение достаточно мало и, следовательно, можно пренебречь измене-
изменением времени запаздывания на протяжении размеров электрона. В противном
случае для нахождения поля необходимо было бы знать конфигурацию
электрона, что при современном уровне знаний неосуществимо. Предполагая
ускорение достаточно малым, чтобы можно было воспользоваться формулами
A6.71) и A6.72), подсчитаем поле излучения прямолинейно движущегося
электрона на больших расстояниях от него, если электрон испытывает
постоянное торможение (постоянное отрицательное ускорение). Такая ситуа-
ситуация имеет место, например, внутри антикатода в рентгеновской трубке.
Для нахождения В проще оперировать с вектор-потенциалом А. Согласно
выражению A6.71), вектор-потенциал А имеет только ж-составл-яющую, а
следовательно, В имеет только ^-составляющую, где <р — азимутальный угол,
отсчитываемый вокруг оси движения. Мы знаем зависимость [ь] от [t]
и хотим найти зависимость А от р в некоторой удаленной точке. Так как В
равен ротору А, то
9 dp ~ d[V] I dt J dp d\x] dp d[P] dp
Поскольку cos [6] можно записать в виде [ж] ([r]2-f-[p]2)~1/2, то все члены,
кроме первого, имеют в знаменателе величину [т*]2, поэтому на больших
расстояниях можно сохранить только первый член, в котором неизвестным
36*
5fi4
Глава XVI
является множитель [dt]/ др. Для его вычисления воспользуемся диаграммой,
показывающей, что возмущение, произведенное электроном в момент времени
[t] в точке —[г;] [dt\, достигнет точки [х], р -+¦ dp в тот же момент времени,
в какой и возмущение, вышедшее из точки О в момент [/] 4- [dt], придет
в точку [ос], р. Если- принять, ' что это последнее возмущение проходят
путь ст, то, пользуясь фиг. 144, а, можно написать следующие соотношения:
A6.74)
A6.75)
Учитывая, что [р]=р, и предполагая, что [г;] несущественно меняется в ин-
интервале [dt], исключим при помощи выражения A6.74) [ж]2, [р]2 и т2 из
[vdtj
x
fvjfdt]
5
Фиг. 144.
соотношения A6.75) и пренебрежем членами [dt]2 и dp2 по сравнению с [dt]
и dp. Тогда, введя [г] — ст, получим
[dt\ = [f] sin [6] ... fi „
dp c[r]-[x][v] сA-[[»]со8[в])- 9У"-'Ч
Подставляя в первый член выражения AE.73) соотношения A6.71) и A6.76)
и помия, что при вычислении dA\d\v] надо дифференцировать и [i, найдем
d _
[6]
A6.77)
Если расстояние до точки наблюдения значительно превышает расстояние,
на котором происходит торможение электрона до полной его остановки,
то это возмущение представляет собой сферическую волну, в которой
в силу соотношения A3.32) сВ^ = Е^. Е этом можно было бы убедиться,
¦вычислив ?е непосредственно из выражений A6.71) и A6.72).
Воспользуемся теперь формулой A6.77), чтобы определить распределе-
распределение в пространстве полной энергии, излучаемой при остановке электрона.
В любой момент времени интенсивность излучения дается вектором Умова —
Пойнтинга A3.23)
л ЕхВ и,,о2 \v]2sin2 [61 уЛ«г,оч
Полное излучение, проходящее через данную точку, равно интегралу от
вектора Умова — Пойнтинга в этой точке по времени, в течение которого
длится импульс. Но скорость является функцией времени запаздывания
у электрона, поэтому нужно найти соотношение между этим временем
и временем в точке наблюдения. Из фиг. 144, б видно, что если импульс,
возникший от электрона в момент времени [t] — 0, достигает точки Р в момент
Специальная теория относительности 565
т, а импульс, возникший от электрона в момент [dt], попадает в Р в момент
т-f-efa, то справедливы следующие соотношения:
р2 4-[ж]2 = с2т2, A6.79)
Р2 + (И - [е] И]J = с2 (т - [dt] + dtf. A6.80)
Исключая при помощи соотношения A6.79) р2, [х]2 и т2 из выражения
A6.80), опуская члены с [dt]2 и dt2, малые по сравнению с [dt] и dt,
и введя cos [б] вместо [ж]/ст, получим
dt = (l —[$] cos [в]) [dt]. A6.81)
Таким образом, для полной энергии, излученной в направлении б, найдем
Тй = J П Л = J П A - [р] cos [В]) [dt].
Или учитывая, что [v] [dt] = — [dv], получаем (см. Двайт, 90)
г ^,дЦу] sin^jb] С d\v] tJ.vqh,sin^ Г. 1 1
6 16л2сИг J A —[Metis 1«]M ь4тА-2 tos О L A — f>cos6LJ •
О
Н последнем члене опущены обозначения запаздывания, так как, по
предположению, расстояние, па котором возникает возмущение, мало
по сравнению с расстоянием до точки наблюдения. Формула A6.82), полу-
полученная Зоммерфельдом, дает хорошее совпадение с измеренным распределе-
распределением интенсивности «белых» рентгеновских лучей, если принять во внима-
внимание поглощение излучения антикатодом. На фиг. 144, в изображены соот-
соответствующие кривые при разных р.
§ 14. Преобразование уравнений Максвелла. По первому постулату
специальной теории относительности уравнения Максвелла должны иметь
одинаковую форму в системах S и iS". Запишем их теперь в несколько
более общем виде, проведя обобщение на случай движущихся изолирован-
изолированных зарядов. Введем ри вместо i в соотношениях A3.1). Тогда для свобод-
свободного пространства будем иметь следующую систему уравнений:
т? В . дЕ «В' , , , Ж'
A6.83)
Из формулы A6.7) получаем следующие дифференциальные соотношения:
Поэтому
дх' dt' v дх' ot' i.n ai\
~я— — х; "я~ =—х"-5-> -^—=—ХГ-, ——= у.. A6.84)
дх дх с2 dt dt v '
d __ d дх' д df _ ( d а л ,КЙ.
о — "о 7 о —1 о / о — I ~о # ' t/ ^—г I. 1А0.О*-'/
dt dx dt dt dt \dt dx J v '
JL — JL JE. JL
Меняя теперь при помощи соотношений A6.85) независимые переменные
в первой группе уравнений A6.83), т. е. переходя от слгстемы S к S',
566 Глава XVI
и используя соотношение между скоростями, полученное в § 3, мы находим
искомые уравнения преобразования для Е, В и р, которые, как можно
убедиться, приводят ко второй группе уравнений A6.83),
Ех = Е'х, Ev,г = х (Е'у,г ± vB't,у), A6.86)
ВХ = В'Х, BViZ = *(B'ViZT<r^E'z,v), A6.87)
A6.88)
где нижний знанс соответствует второму индексу. Эти уравнения показывают,
что разделение электромагнитного поля на электрическую и магнитную
части зависит от характера движения наблюдателя. Чтобы получить выра-
выражения для Е', В' и р' через Е, В и р, необходимо только поменять местами
величины со штрихами и величины без штрихов и изменить знак перед ?$ и v.
Мы можем теперь показать, что предполагавшаяся в § 6 инвариантность
электрического заряда непосредственно следует из соотношения A6.88).
Исключая последний множитель в соотношении A6.88) при помощи выра-
выражения A6.22), получаем рк'^ — р'-к^ где хх и v.[ определяются по формулам
A6.20), A6.21). Таким образом, в системе Sc, неподвижной относительно
заряда, имеем
Но, согласно выражению A6.84), элементы объема в системах S и S'
сжимаются., так что
dsn = Г 1 — ( —
Объединяя выражения A6.89) и A6.90), мы видим, что в системах S и S'
величина заряда будет одинакова, поскольку
p'ds' = q. A6.91)
Можно показать также, что уравнения A6.86) и A6.87) приводят
к уже полученному нами выражению для силы, действующей на заряд,
движущийся в магнитном поле [см. выражение A6.37)]. Предположим,
что в системе S' заряд покоится и поле имеет электростатический характер.
Тогда
*",.v.i=q'E'x,v.z. A6.92)
Используя уравнения преобразования для сил A6.28) и полагая их = v,
иу = 0 и uz = 0, из соотношений A6.86) и A6.87) получим, учитывая, что
Fx=qEx, Fy,z=q(Ey,z^uxBz,v). A6.93)
Или в векторной форме
FE xB)], A6.94)
что совпадает с выражением A6.37).
§ 15. Определение скорости самолета относительно земли. Одной из
наиболее трудных экспериментальных проблем в авиации является опре-
определение скорости самолета относительно земли в условиях плохой види-
видимости. Поскольку при горизонтальном полете самолет пересекает верти-
вертикальную составляющую земного магнитного поля, то на его горизонталь-
горизонтальных проводниках должна возникать электродвижущая сила, величина
Еготорой пропорциональна скорости движения. Идея определения скорости
Специальная теория относительности 567
самолота относительно земли при помощи измерений величины этой э. ц. с.
была предложена и даже запатентована. Можно привести несколько спо-
способов осуществления этой идеи, из которых наиболее очевидным является
вращение вытянутого проводника в горизонтальной плоскости. Если само-
самолет неподвижен, то при равномерной скорости вращения индуцированные
заряды постоянны. При движении самолета э. д. с. индукции в северном
полушарии всегда направлена справа налево, что приводит к перемеще-
перемещению зарядов с одного конца проводника на другой, т. е. к появлению
переменного тока, частота которого равна частоте вращения проводника,
а амплитуда пропорциональна скорости самолета относительно земли.
Величина этого тока очень мала, но все же в хорошо экранированной
лаборатории его можно измерить достаточно чувствительными приборами.
Возникает вопрос, исчезнет ли этот эффект в случае применения на само-
самолете электрически экранированной аппаратуры. Известно, что магнитное
поле проникает сквозь немагнитные металлические проводники, но известно
также и то, что индуцированная в экране э. д. с. создает такие электри-
электрические поля, которые противодействуют полям, проникающим внутрь
экрана. До сих пор мы рассматривали эту задачу с точки зрения непо-
неподвижного наблюдателя в системе S, связанной с землей, и пришли к выводу,
что эта задача довольно сложная. Посмотрим теперь на нее с точки зре-
зрения наблюдатели в системе S', находящегося на самолете и производящего
измерения. Обозначим вертикальное направление через z, направление
движения через х, а компоненты магнитного поля земли через Вх, Ву и Bz.
Обычно существует также и вертикальное электрическое поле, напряжен-
напряженность которого мы будем считать равной Ez Это поле определим в системе S,
а затем при помощи соотношений A6.87) определим магнитное поле, наблю-
наблюдаемое в системе >S",
ВХ = ВХ, Bl,t = *(BVtZ±c-1№z.v)'*-Bv,z. A6.95)
Так как скорость самолета значительно- меньше скорости света, то [3 я» О
и ¦/ =ь 1 и, следовательно, магнитное поле в системе S' равно магнитному
полю в системе S. Что же касается электрического поля, то
Е? = 0, Е'у=— *vBz ^ - vBz, Е'г = x2?r4 *vBy *, Ez. A6.96)
Таким образом, наблюдатель в системе S' обнаружит, что самолет нахо-
находится в поперечном электрическом поле vBz, поэтому он не может приме-
применить металлическое экранирование своей аппаратуры. Кроме того, это
поле значительно меньше нормального атмосферного электрического поля Ez,
и при малейшем крене самолета результаты измерений окажутся совершенно
неверными.
§ 16. Движение заряженной частицы в перекрещивающихся электри-
электрическом и магнитном полях. В предыдущем параграфе был приведен при-
пример, показывающий, насколько упрощается задача, если при помощи
уравнений преобразования A6.86)—A6.88) ввести в рассмотрение новое
поле, появляющееся в движущейся системе координат. Теперь мы приме-
применим эти уравнения для исключения одной из компонент поля путем пере-
перехода к новой системе отсчета. Рассмотрим заряженную частицу, выле-
вылетающую из начала координат с компонентами начальной скорости vx, vy
и vz и находящуюся под действием однородного электрического по-
поля, паправлевного вдоль оси у, и однородного магнитного поля, направ-
направленного вдоль оси z. Для наблюдателя, движущегося вдоль оси х с
568 Глава XVI
постоянной скоростью v, эти поля, согласно соотношениям A6.86) и A6.87),
будут равны
- - - - A6.97)
A6.98)
Если Еу < сВ, и если выбрать скорость движения S' такой, что
Ey = vBz, A6.99)
то наблюдатель в системе iS" обнаружит только однородное магнитное поле,
направленное вдоль оси z и определяемое выражением A6.98). Пусть
заряд вылетел в тот момент, когда начала координат систем S ш S' совпа-
совпадали, тогда начальными условиями будут t = t' = x = х' = у = у' = z = z = 0.
В системе S' компоненты начальной скорости заряда равны t'x, t'v и v'z.
Как видно из соотношения A6.43), в системе S' заряд будет двигаться
с угловой скоростью о' по траектории, имеющей вид спирали с угловым
шагом Y> закручивающейся вокруг круглого цилиндра радиуса а, где
и tgT'= ,,P',v/a • A6.100)
(Vx -г Vy ) П
qBz
Воспользовавшись соотношениями A6.20), A6.21) и A6.23) для •/.[, можно
написать
('2
i-^
_р ^) =
Подставляя выражения A6.98) и A6.101) в формулу A6.100), получим
[с2 feJ?-? 4
Угловая скорость вращения вокруг оси цилиндра будет равна
^ , A
где, если смотреть в положительном направлении оси z, угловая скорость
вращения со' для положительного заряда д направлена против часовой стрелки.
В большинстве случаев Е > vxB, так что величина ь'х отрицательна.
Тогда линия, перпендикулярная к оси z и тангенциальная к поверхности
цилиндра, образует в начале координат с отрицательным направлением
оси х' острый угол ф0, тангенс которого на основании формул A6.10)
и A6.11) равен
Мы можем написать теперь координаты заряда в системе <S" в зависимости
от времени
х' = а [ — s'mu/t' совф0 + A — co.sw'f')sin^0] —a [sin ф0 —sin (u>'t' + Ф0)],
у' — a [sin o/z' sin фо+ A — cos o/z') cos фс] == a [cos ib0— cos (w'l' -\- Фо].
Введем величины ф и fc, определив их следующим образом:
фо, A6.105)
Специальная теория относительности
569>
Выразив х и у через х', у' и V [см. формулы A6.7)] и f через ф и Ьг
получим
х( L гпг ) = &ф—6ф0-f-a sin ф„ — автф, A6.107)
г/ = асо8ф0—асовф. A6.108)
Мы получили точные уравнешга траектории частицы в параметрическом
виде. Заметим, что при значении ф = 2mz J- ф0 частица находится в точке
Таким образом, траектории всех частиц, вылетающих из начала коорди-
координат и характеризуемых одним и тем же значением Ъ, будут периодически
в одних и тех же точках пересекать ось z. Из соотношения A6.1С6) видно
далее, что если начальные скорости значительно меньше скорости света,
а>Ь
X'
Фиг. 145.
ш расстояние между точками пересечения зависит только от напряжен-
ностей полей и от отношения заряда частицы к ее массе. Это обстоятель-
обстоятельство использовано в одном из типов масс-спектрографа.
Пусть, например, напряженность электрического поля равна 100000в/м,
а магнитная индукция составляет 0,1 вебер\м*, тогда входящая в выраже-
выражение A6.107) величина Е2/(сВJ будет равна 1/90000. В этом случае фор-
формулы A6.107) и A6.108) превращаются в параметрическое уравнение
трохоиды (циклоиды), описываемой точкой, лежащей на радиусе круга,,
катящегося без скольжения по прямой линии. Выберем начало координат
так, чтобы этот круг катился вдоль оси х' в плоскости у'х', тогда
У =
у' = т/ — а
Найденные нами траектории изображены на фиг. 145, где Ъ — радиус катя
тцегося круга, а а — расстояние вдоль радиуса от центра круга до точтиг Р,
описывающей искомую кривую. Циклоидальные траектория при а = h были
использованы Дж. Дж. Томсоном в 1899 г. для определения отношения
ejrn0 у фотоэлектронов.
§ 17. Аберрация п эффект Допплера. Как было показано в § 2 гл. ХПI,
все свойства электромагнитных волн можно описать при помощи вектора
Герца Z, удовлетворяющего в свободном пространстве волновому уравне-
уравнению A3.20),
4-S- A6.109)
ибщее решение этого уравнения для случая плоской волны дается выра-
выражением A3.25). Для монохромат(гческой волны с частотой v это решение,.
570 Глава XVI
учитывая выражение A3.84), а также то, что ?> = с, можно записать в виде
Z = Acos —(п-г-<й). A6.110)
Такая волна будет наблюдаться в системе iS". Но эта же волна из
системы S' будет наблюдаться распространяющейся вдоль направления п',
¦а частота ее будет равна v'
Z' = A'cos^p-'(n'-r'-c«'). A6.111)
По второму постулату § 1 скорости распространения в обеих системах ?
и S' должны быть одинаковыми. Уравнения преобразования A6.7) должны
преобразовывать формулу A6.111) в A6.110), а это, как можно видеть,
приводит к требованию равенства аргументов, стоящих под знаком коси-
косинусов в формулах A6.110) и A6.111), если выразить их через v, n, r и I.
Чтобы полученные соотношения были справедливы при всех значениях
величин х, у, z и t, коэффициенты при каждом из них должны быть
-соответственно равны для обоих аргументов. Мы можем написать
n-r— cl = lx + my + nz — ct. A6.112)
Используя преобразование A6.7) и производя группировку членов, получим
п' • г' — ct' = I'x' + m'y' -j- n'z' — ct' =
= x С V + -^Л х + m'y + n'z — x (с + I'v) t. A6.113)
Приравнивая коэффициенты, найдем
_= —= — =^?±ii> = JL. A6.114)
Эти соотношения позволяют обнаружить движение источника электро-
электромагнитного излучения относительно наблюдателя путем измерения излу-
излучения в точке наблюдения. Эффект изменения направления называется
аберрацией, а эффект изменения частоты —эффектом Допплера. Предполо-
Предположим, что источник неподвижен относительно системы S', а наблюдатель
неподвижен относительно системы ?. Тогда наблюдателю', находящемуся
в системе S, будет казаться, что свет распространяется в направлении
I, т, п, а для наблюдателя, находящегося в системе iS", направление
распространения света будет Г, т', п'; причем связь между I, m, n и V,
т', п' дается соотношением A6.114). Приравнивая в соотношении
A6.114) первый и четвертый члены и полагая I = cos6 и Г = cos в', будем
иметь
,, cosO' + P .,,
где [i — v/c. Это—строгая формула аберрации. Приравнивая в соотноше-
соотношении A6.114) два последних члена, получим
v==l + Pco6 6'v>j g
A —f>*)V2 V '
Это — строгое выражение для изменения наблюдаемой частоты электро-
электромагнитного излучения при движении источника относительно наблюдателя.
Если источник приближается к наблюдателю, то cos в' положителен, если
же источник удаляется, то cos в' отрицателен и, следовательно, в первом
-случае частота увеличивается, а во втором случае уменьшается. Согласно
•основным постулатам, аберрация и эффект Допплера появляются только
Задачи 571
при относительном движении наблюдателя и источника. Таким образом,
формулы A6.115) и A6.116) остаются справедливыми и в случае, когда
источник покоится, а наблюдатель перемещается. Можно было бы ожидать
отклонений от этих формул для астрономических расстояний, так как
¦специальная теория относительности полностью подтверждена только
на опытах, производившихся на земле, однако, повидимому, эти формулы
являются точными и в астрономии.
ЗАДАЧИ
1. Длинный прямой катод радиуса а, по которому течет ток /, испускает элек-
электроны с ничтожной начальной скоростью. Под действием потенциала V эти электроны
приобретают ускорение по направлению к длинному концентрическому цилиндрическо-
цилиндрическому аноду радиуса Ъ. Пренебрегая зависимо-тью массы от скорости, показать, что напря-
напряжение, при котором электроны перестают попадать на анод, равно
2. Решить предыдущую задачу строго для случая, когда Е > cB.f, путем перехо-
перехода к системе координат, движущейся параллельно оси цилиндра с такой скоростью,
что в этой системе магнитное ноле исчезает. Показать таким же образом, что вылетев-
вылетевший из катода электрон не может вернуться на него обратно.
3. Решить задачу 1 строго при Е < сВр путем перехода к системе координат,
движущейся параллельно оси цилиндра со скоростью, при которой электрическое поле
в этой системе исчезает. Показать, что электропы перестают попадать на анод при
условии
где Л = 1»|2-|-?>22, a Vi, v2 выражаются через начальные скорости ил и v2 в направле-
направлениях жир следующим образом:
где Vx — EJBу. Начальная скорость v^ пренебрежимо мала.
4. В накуумной лампе имеется цилиндрический катод радиуса г0, окруженный
коаксиальным с ним анодом радиуса ;-,. Лампа расположена таким образом, что ее
ось совпадает с осью вращения конфокальных гиперболических поверхностей полюсов
электромагнита. Показать, что если магпитное поле в плоскости симметрии равно
Вф (''2 + 62)~1'2, то для того, чтобы электроны могли в этой плоскости достичь анода,
необходимо приложить напряжение, точное значение которого равно
5. Параллельный пучок электронов, ускоряемый напряжением V, создает ток,
равный /. Сечение пучка представляет собой круг радиуса а. Показать, что величина
нормального к пучку ускорения, приобретенного электроном на поверхности пучка
под действием электрических и магнитных сил, выражается следующим образом:
6. Точечный заряд g двигается в поле другого неподвижного точечного заряда Q.
Применяя закон сохранения момента количества движения р и закон сохранения энер-
энергии и используя выражение A6.45) для кинетической энергии, показать, что уравне-
уравнение траекторий будет иметь вид
где
'' ~ \k
572 Глава XVI
7. В каждом из двух плоских листов, находящихся в вакууме па расстоянии а
ДРУГ от ДРУга> имеется отверстие диаметра Ъ. Отверстия расположены таким образом,
что линия, соединяющая их центры, перпендикулярна обеим плоскостям. Сквозь первое
отверстие испускается внутрь поток заряженных частиц, имеющих одинаковую энергию,
причем максимальный угол расхождения частиц в пучке, отсчитываемый от нормали,-
равен а. Пренебрегая величиной а по сравнению с единицей, найти зпачения магнит-
магнитного поля, приложенного нерпендикулярво листам, при которых пучок частиц пройдет
и через второе отверстие. Показать, что максимальный диаметр пучка между отвер-
отверстиями равен
1а .
Sin a + 6,
пп
где п — целое число.
8. Показать, что если пучок, рассмотренный в предыдущей задаче, имеет вид
конуса, т. с. псе частицы исходят из одной и той же точки оси, и если эта точка
также находится в магнитном поле, то минимальное зпачепие последнего, необходимое
для сведепия пучка частиц н фокус, расположенный за вторым отверстием в точке,
представляющей собой зеркальное изображение источника, равно
2nmva [q (aa-J-6)],
где a — угол, под которым виден радиус первого отверстия из точки, где находится
источник. Показать также, что это поле увеличивает число ионов, проходящих
первое отверстие, в число раз, равное
Г •
aa-f-b
9. Две одинаковые параллельные круглые цилиндрические проводящие оболочки
имеют заряд на единицу длины, равпый соответственно + Q и —Q. Вьутри каждой
из них протянут провод, расположенный так, что если ток I течет в проводах в проти-
противоположных направлениях, то поверхности оболочек совпадают с силовыми линиями
магнитного поля. Найти, в какой движущейся системе координат при cQ < / будет
существовать только магнитное поле.
10. Показать, что если заряженные частицы вылетают с поверхности одного из ци-
цилиндров (см. предыдущую задачу), где до этого они покоились, то составляющая их
скорости, параллельная цилиндру, в точке rlt r2, равна
r2rw та
где г10 и г20 — расстояния от точки вылета до каждого из проводов.
11. Вектор-потепдяал двухмерного магпитостатического поля имеет только z-co-
ставляющую. Пусть ион с зарядом q и массой покоя т0 ил!еет скорость v. В точке,.
где вектор-потенциал равеп Alt составляющая этой скорости по оси z равна vz. Пока-
Показать, что в точке, где вектор-потевциал равен Л2, составляющая скорости по оси z
определяется выражением
vz-g (moc)~i (c2-u2I/2 (А2—Ах).
12. Показать, что в случае любых двухмерных электрических и магпитиых полей,
пересекающихся ортогонально, всегда можпо перейти к такой движущейся системе
координат, п которой Е или сВ (в зависимости от того, которое из них меньше) будут
исключепы. ч
13. Положение заряда q задапо уравнением s — acosv>t. Показать, пользуясь выра-
выражениями A6.71) и A6.77), что при мае <С 1 и а < г периодическая составляющая
полей Е и В, создаваемых зарядом q, описывается соотношениями A4.13) — A4.15),
где г — расстояние от среднего положения заряда до точки наблюдения, 6 — угол между г
и s, a m = <7«.
14. Положения sx и s2 двух одинаковых зарядов q заданы уравнениями Si = —s2 =
f " \
= 2а cos I ~y co{ j . Следуя предыдущей задаче и считая а/ <^ ыас-1 <g I, Q0 = qa?r
показать, что тта больших расстояниях периодическая составляющая поля равпа
сВ. =ED=
'—-')•
Сравнить с полем линейного квадруполя, рассмотренного в задаче 1 гл. XIV.
Литература 573
15. Электрон движется в аксиально симметричном магнитостатическом поле, для
которого
Показать, что если угловая скорость вращения электрона вокруг оси в точке p = Pi,
г — Zj равна м„ а в точке р = р2, z = z2 равна w2i то
mpfcoj—тр|ш2 = е [fH^tpx, zx) — t>2Af (p2, Ъ)]-
16. Частица, летящая в направлении оси х со скоростью #0 и имеющая заряд д
и массу покоя ти0, в момент времени t=t0 входит в точке х = 0, у = —6, z = 0 внутрь
эвакуированного прямоугольвого волновода, вдоль которого распространяется волна ТЕ01.
Показать, что уравнение движения частицы в системе, движущейся со скоростью,
равной групповой скорости волны, имеет вид
где Ео—максимальное значение напряженности электрического поля в покоящейся
системе координат. Показать, что при vx <g с положение частицы в произвольный
момент времени t в этой системе будет описываться уравнением
\
x~qE0(isPma)-i[o> (I — @)cosco{0_sino)t + sinco{0] + tH(t—r0), j/= —b, z=0.
ЛИТЕРАТУРА
Biggs H. P., The Electromagnetic Field, Oxford, 1934.
G e i g e r-S с h e e 1, Handbuch der Physik, Bd. XII, Berlin, 1927.
Jeans J. H., The Mathematical Theory of Electricity and Magnetism, Cambridge, 1925.
Livens G. H., Theory of Electricity, Cambridge, 1926.
Lorentz H. A., Theory of Electrons, Leipzig, 1916. (См. перевод: Л о р е н т п,
Теория электронов, М. 1934.)
Mason M., Weaver W., The Electromagnetic Field, University of Chicago Press,
1929.
Stratton J. A., Electromagnetic Theory, McGraw-Hill, 1941. (См. перевод: С т р э т-
т о н Дж. А., Теория электромагнетизма, М.—Л., 1948.)
То! man R. С, Relativity. Thermodynamics and Cosmology, Oxford, 1934.
W i e n-H arms, Ilandbuch der Experimentalphysik, Bd. XI, 1932.
Zworykin V. K., Morton G. A., Ram berg E.G., Hillier J., Van-
Vance A. W., Electron Optics and tbe Electron Microscope, Wiley, 1945.
ПРИЛОЖЕНИЕ
СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ ЕДИНИЦ
Существует три способа классификации абсолютных систем электрических единиц,
В соответствии с употребляемыми механическими единицами системы электрических
едивиц могут принадлежать к системе сантиметр—грамм—секунда (COS) или к системе
метр—килограмм—секунда (MKS). В зависимости от принятых величин освовных
единиц измерений система называется классической или практической. И, наковец,
по способу введения множителя 4л различают рационализированные и иеранионализиро-
вавные системы единиц. Применяемая в этой книге система MKS принадлежит к группе
практических рациовализиронаввых систем MKS. Приведенные в приложении таблицы
содержат соотношения между этими единицами, практическими нерациовализирован-
ными CGS единицами и классическими верационализировавными CGS единицами.
Во всех рационализированных системах эквивалентные формулы имеют очень
сходный пид. Однако способ введения множителя 4л и определенно единиц в системе-
Джорджи MKS отличается от того способа, который принят в соответствующей клас-
классической системе, а именно, система строится таким образом, чтобы рационализация
не влияла да наиболее распространенные практические единицы кулон и вольт. Это
осуществляется путем введения множителя 4л в диэлектрическую и магнитную про-
проницаемость. Поскольку во всех таблицах, в которых приводятся числовые значения
электрических и магнитных свойств материалов, принято употреблять относительную^
диэлектрическую проницаемость K — tjtv и относительную магнитную проницаемость
ЛТт = [л/[л,„ то часто в практических системах единиц предпочитают применять величины
Ktv и Km\>-V, где е„ и ,и.о диэлектрическая и магнитная проницаемости для: вакуума.
Если формула дава в одной какой-либо системе единиц, то ее всегда можво напи-
написать и в любой другой системе, выражая входящие в нее величины и требуемых еди-
единицах и подставляя их и формулу. Чтобы пояснить это, для примера выразим закон
Кулона о силе взаимодействия друх зарядов в классической неранионализировавной
системе CGS электростатических единиц. Физические величины, выраженные в едини-
единицах CuSE, мы будем обозначать буквами без индексов, а аналогичным величинам,,
выраженным и единицах Джорджи MKS, будем приписывать индекс 1. В соответствии
с табл. 2
?1 = 3-1.10-"? и ?1 = C6i:)-1-10-1e. A)
Из табл. 1 для мехапическлх единиц мы пидим, что
F1==10-5F и /•1 = 10-2г. B).
Формуле A.1) для закона Кулона в системе MKS имеет вид
Подставляя сюда значения Fu glt el и rl из формул A) и B) и упрощая, получаем
Аналогичную процедуру, разумеется, можно произвести и при преобразовании формул,
содержащих магнитные величины. Подробное рассмотрение этого вопроса содержится
в сэатье Кевслли1). Заметим, что если в формулах C) и D) е положить равной еди-
единице, то формулы все же будут отличаться одна от другой. Такпм образом, даже
в тех случаях, когда результат относится к процессам и вакууме, формула, которую-
нужно выразить в системе CGSE или CGSM, должна быть написана для среды с отлич
лымм от единицы [л или е.
*) Kennelly, Amer. Phi]. Soc. Proc, 76, 343 A936).
Системы влектрических единиц
575
А. Чтобы формулу, написанную в систе-
системе единиц CGS, выразить в единицах
MKS, нужно заменить входящие в эту
формулу символы на соответствующие
значения в крайвем иравом столбце
таблицы.
Таблица 1
Б. Чтобы формулу, написанную в рационали-
рационализированной системе единиц MKS. выразить
в единицах CGS, нужно заменить входящие
в эту формулу символы на соответствующие
значения в крайнем иравом столбце таблицы.
Длина . .
Масса . . .
Мощность .
Сила . . .
Энергия . .
1 м
т кг
Р ет
F ньютонов
W джоулей
102
103
10'
105
10'
1 см
т г
Р эрг/'сек
F дин
W эрг
Длина. . .
Масса . . .
Мощность .
Сила . . .
Энергия . .
1 см
т г
Р эрг/сек
F дин
W эрг
ю-2
ю-3
ю-'
10-5
ю-'
1 м
т кг
Р ет
F ньютонов
W джоулей
Таблица 2
Для того чтобы формулу, написанную в рационализированной системе MKS, выра-
выразить в единицах системы CCSE или в единицах гаусговой системы, нужно заменить
входящие в эту формулу символы на соответгтвук щие значения в крайнем иравом
столбце таблицы. сяьЗ-1010 При очень точных вычислениях множитель 3 надо каждый
раз заменять на 2,9978.
Физическая величина
CGSE
CGSM
Практическая система
Диэлектрическая про-
проницаемость
Емкость
Заряд, величина . . .
Импеданс
Напряженность элек-
электрического поля . . .
Потенциал электриче-
электрический скалярный . . .
Потенциальный коэф-
коэффициент
Проводимость
Проводимость удельная
объемная
Проводимость удельная
поверхностная ....
Реактивное сопротив-
сопротивление
Самоиндукция
Сопротивление . . . .
Сопротивление удель-
удельное объемное ....
Сопротивлевие удель-
удельное поверхностное
Ток, объемная плот-
плотность
Ток, поверхностная
плотность
Ток
Электрическая индук-
индукция
Электродвижущая сила
?
С
я
Z
Е
V
S
G
1
7'
X
L
R
9-il0-"e47i фарад/см (Уок)'1 ¦ \(ГЧфарад/м
9-1. Ю-"С фарад
З-МО-»? кулон
9-10"Zojk
сЕ
сГ
c2S
300.Е в/см
30 OOOjB в/м
300Fe
9-4O-»G i/ом
c2L
c2R
сЧ
с-Ч
с'1!
D
З-МО-Ч' а/см З-МО!"' а/м
З-ЧО-о/ а
З-1- 10-9?>4т1 кулон/см2 A2т:)-110-5?> кулон/м*
Таблица
"Для того чтобы формулу, написаггную в рационализированной системе, выразить в единицах системы CGSM или в единицах
гауссовой системы (отмеченных звездой), нужво заменить входящие в эту формулу символы на соответствующие значения
в крайнем правом столбце таблицы.
с=2,9978-
Физическая величина
CGSJI
CGSE
Практические единицы
Емкость
Заряд, величина
Импеданс
Магнитная индукция
Магнитная проницаемость
Магнитное сопротивление
Магнитный заряд (полюс)
Магнитный момент (диполь)
Магнитный момент (петля)
Магнитный поток . . . .
Магнитодвижущая сила ...
Намагниченность (диполь)
Намагниченность (петля)
Напряженность магнитного поля
Напряженность электрического поля . . . .
с
q
z
в*
t,*
R'*
m*
m'*
m*
TV*
Q*
M'*
M*
H*
E
cW*
eg*
c~2Z*
cm
сЯ
cM
cH
В гаусс
(х еаусс/эрстед
R' гилъберт/максвелл
4ит максвелл
4тап' максвелл • см
Ют а - см2
N максвелл
Q гилъберт
4ттА/' максвелл /см2
ЮМ а/см
Н эрстед
1Сг8Е в/см
109 С фарад
10? кулон
10-"Z ом
10-4jB вебер/м2
471 • Щ-т^гн/м
(lO9/^) R' ампер-витков/вебер
4я10"8 т вебер
4тс10~10 т' вебер ¦ м
l(J-3m а-м2
10-SN вебер
A0/4тт) Q ампер-витков
Ы ¦ 10~4М' еебер/м2
1000 Ш а/м
A03/4л)// ампер-витков/м
10-" Е в/м
со
ы
Потенциал магнитный векторный ...
Потенциал электрический скалярный,. . .
Потенциальный коэффициент
Проводимость
Проводимость удельная объемная
Проводимость удельная поверхностная . .
Реактивное сопротивление
Самоиндукция . .
Сопротивление
Сопротивление удельное объемное . . . .
Сопротивление удельное поверхностное . .
Ток, объемная плотность
Ток, поверхностная плотность
Ток
Электродвижущая сила
А*
V
S
а
1
Г
х
L
R
х
s
i
i'
I
c~l A
с-Н'*
c~2S*
c2G*
ci*
а'*
ci*
.1 гауг
IO~6 A «eoepJM
W~K V e
10 9 Л' i/фа pad
109G 1/o.w
10е-,' 1/(ли • f.«) 1°П7 1/(°-и ' ¦«)
10~9Т О.И - CM
lOi а/см2
10»"' в/ел
io-!
10i
10-
' л ол<
101' ом ¦ м
'; о.и
lO5/ a/.mz
103t' й/л
a
8VS e
578
Приложение
- Таблица 4
Для того чтопы формулу, написанную в единицах CGSM, CGSE или в единипах гаус-
гауссовой системы, выразить а) в практических единицах нерациопализированвой системы
CGS или б) в рационализированных единицах системы MKS, нужно заменить входящие
в эту формулу символы соответстненно на значения, помещенные в столбце CGSM, CGSE.
или на значения, отмеченные зиездочкой.
Физическая величина
Диэлектрическая про-
пицаемость
Емкость
Заряд, величина ....
Импедапс . ...
Магнитная индукция .
Мпгиитпая проницае-
проницаемость
Магнитное сопротлнле-
пие
Магнитный заряд (по-
~ лгос) . . .
Магнитный момент (ди-
(диполь) . .
Магнитный момент (пет-
ля) ....
Магнитный поток . .
Магнитодвижущая шля
Намагниченность (дц-
поль)
Намагниченность (петля]
а) Практическая
система CGrS
б) Рационализированная
система MKS
а) е 4гс фарад!'см
б) е фарад/м
С фарад
q кулон
Zom
а) В гаусс
б) В себер/м?
a) jj. гаусс/эрстед
б) (х гн/м
-
a) R' гилъберт!макс-
гилъберт!максвелл
б) R' ампер-витки/вебер
а) т Mnnciie.i.'
б) т. вебер
_ а) га' максвелл • см
б) т' бебер ¦ м
а) ш а • см"
о) т а • м-
а) Л" максвелл
С) Л7 вебер
у) U гил ьберт
б) И ампрр-випит
а) М максвелл!см:
б) М вебер'м-
а) Ма/гм
б) Мп.-М
CGSM
W
10"9е
4tl • 10-"s
io-»c
109Z
в*
10*/?*
,,*
Dk)-1 • Ю'-х*
R'*
'in ¦ urnv*
Dit)-lm*
Dk)-1 ¦ Ю'/й*
Dr:)-1m'*
D7t)-» • 10wm'*
10-^n*
10sm*
N*
iCfiJV*
o*
'tr. • 1fr4.»*
CGSE
9 • 10"e*
Звп • 10"s*
9• JOnC*
3 • 10 V
9-1 . io-»z*
3-i . X0~">B
3 • ](•>-•?
9-1 • 10-2V
(ЗЬк)-1 • 10-13(x
9 • 10?0«'
36it • 10llR'
A2it)-» • iO-lom
A200л)-»/»
-
A2л)-1 • 10-lem'
A2n)-1m'
3 ¦ 10»ш
3 • 1018in
:)-i . lo-«>iV
C(H)~^V
3 • 1(>1OU
12it • 10»U
A2л)-1 ¦ lO-^Af
A2л)-1 - 10-»Л/
3 - 10»Л/
3 ¦ 107АГ
Системы электрических единиц
579
Физическая величина
Напряженность магнит-
магнитного поля
Напряженность элс:к-
трического поля . . .
Потенциал магпитпый
векторный
Потенциал электриче-
электрический скалярный . . .
Потенциальный коэффи-
коэффициент . .
Проводимость
Проводимость удельная
объемная
Проводимость удельная
поверхностная ....
Реактивное сопротивле-
сопротивление ... ...
Самоиндукция . . .
Сопротивление
Сопротивление удель-
удельное объемное ....
Сопротивление удель-
удельное поверхностпое . .
Ток . . -
Ток, объемная* плот-
плотность . ...
Ток, поверхностная
плотность
Электрическая индук-
индукция (смещение) . . .
Электродвижущая сила
а) Практическая
система CGS
б) Рационализированная
система MKS
а) Н эрстед
б) В ампер-витков/м
а) Е в/см,
С) Ее/м
а) А гаусс ¦ см
б) Лсебер/м
Vo
S 1/фарад
G \]ом
a) f \/(ом-см)
б) -у 1/(ом-м)
f 1/ом
X ом
L гп
В ом
а) г ом ¦ см
б) 1 ОМ ¦ М
? ОМ '
I а
a) i а/см2
б) i а/м~
а) г' а/см
б) V а/м
a) D 4те кулон/см2
б) D кулон/м2 '
%в
Таблица
CGSJI
Я*
4гс • 10-3Я*
108Я
WE
Л*
10е А*
108F
10-"G
10-4Y
10-у
\0°L
10° R
104
10"г
104
lO-i/
10~Ч
\о~ч -
10-V
¦хо-ч1
4и • iO-'D
4 (nродолжение)
CGSE
3 • 1010Я
12ти . Ю'Я
C00)-i#
З • Ю~"Е
з-i. ю-1ол
з-1 • ю-4л
(ЗОО)-1!'*
9-1 • Ю-11^'*
9 . 10»G*
9 ¦ 10п7*
9 • 10«7*
9 - 10"f'*
9-1 . 10-iiX*
Q-i . io-ii?*
9-1 . Ю-"Б*
9-1 - Ю-"г*
9-i - 10-«г*
9-i . Ю-*
3 ¦ 10е/*
в
3 • 1№*
3 . 105i*
3 • 10V*
3 • 10V*
3 • 10"D*
12те • 105jD*
(зоо)-1^* '•¦
37*
580
Приложение
Таблица 5
В этой таблице приведены физические размерности электрических единип: I—длп-
на, т—масса, { — время, д — заряд, е—диэлектрическая проницаемость, jx —магнитная
проницаемость. Для определевия размерности в любой системе единиц можно пользо-
пользоваться любым столбцом таблицы, но проще всего л системе CGSE пользоваться значе-
значениями, помещенными в первом столбце, положив е=1, в системе CGSM -зпачспиями
во втором столбце (|х=1) и, наконец, в системе MKS—значениями, помешенными
в третьем столбце.
Физическая величина
Сим-
Символ
CGSE
MKS
Диэлектрическая проницаемость
Емкость
Заряд, величина
Импеданс
Магнитная индукция
Магнитная пропицаемость . .
Магпитное сопротивление ....
Магнитный заряд
Магнитный момент (диполь) .
Магнитный момент (петля) .
Магнитный поток
Магнитодвижущая сила . . .
Намагниченность (диполь) . . .
Намагниченность (петля) ....
Напряженность магнитного поля
Напряженность электрического
поля
Потенциал магнитный векторный
Потенциал электрический ска-
скалярный
Потенциальный коэффициент . .
Проводимость
Проводимость удельная объемная
Проводимость удельная поверх-
поверхностная
Реактивное сопротивление . . .
Самоиндукция
Сопротивление
Сопротивление удельное объемное
Сопротивление удельное поверх-
поверхностное ".
Ток
Ток, объемная плотность . . .
Ток, поверхностная плотность
Электрическая индукция (сме-
(смещение)
Электродвижущая сила
С
,Q
Z
в
т
т'
m
N
у
М'
м
н
Е
А
V
S
G
1
Y
х
L
R
т
i
i'
D
е.'4-Ч
Vsm"/2 ?
pit-1
mll'°qx
тГЧ-tq-1
elf1
е-Ч
е-Ч-Ч
\xlt~1
ml3tq-
l-4-iq
Системы электрических единиц
581
Таблица 6
Числовые величины, характеризующие вакуум
и рационализированной системе MKS
Скорость света
Диэлектрическая проницаемость
Магнитная проницаемость . . .
Характеристический импеданс .
Характеристическая проводи-
проводимость
du-»/E»)
/2
Ом»Г1/а = 2,99776- W м/сек
8,85525-lO8^ C6г.-109)-1 фа рад/м
4я-10-' ъ 1,25664-10-° ен/м
376,707 о.и
2,65458-10 1/ом
Таблица 7
Значения атомных констант в рационализированной системе MKS *
Постоянная Фарадся (О16=16) F = 96 522 4:7 кулон/граммэквивалент.
Число Лвогадро(О16 = 16) N= F,0251 ± 0,0004). 1023 i/молъ
Постоянная Планка й = F,6234 + 0,0011). 10~34 джоуль-сек
Заряд электрона е=A,60199 ± 0,00016)-10"» кулон
Удельный заряд электрона . е!т = A,75936 ± 0,00018)- 10й кулон/кг
* DuMond J. W. M-, Cohen E. It., Rev. Mod. T'hys., 20, 82 A948). (В табл. 6 и 7 при-
приведенные данные относятся] к 10 48 г. Данные на денабрь 1950 г. см. Du Mond J. W. M.,
Cohen E. R., Phys. Rev., 8-2, 855 A951), а также Усп. Физ. Наук. 45, 458 A951). Специально
относительно скорости света см. Усп. Физ. Наук, 42, 485 A950) и 48, 599 A952).— Пргич. перев.)
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА')
а) По общим вопросам электродинамики
А б р а г а м М., Б е к к е р Р., Теория электричества, М.—Л., 1936.
Б е к к е р Р., Электронная теория, М.—Л., 1936.
В у л ь ф А. А., Сборник упражнений по теории электромагнитного поля, М., 1939.
Говорков В. А., Электрические и магнитные поля, М., 1951.
Гольдштейн Л. Д., Электромагнитные колебания и волны, Л., 1951.
Г о л ь д ш т е й н Л. Д., 3 е р н о u H. В., Электромагнитные колебания и волны,
ч. II, Л., 1953.
Гринберг Г. А., Избранные вопросы математической теории электрических и маг-
магнитных явлений, М.—Л., 1948.
Иваненко Д. Д. и С о к о л о в А. А., Классическая теория поля, М.—Л., 1951.
К а л а н т а р о в П. Л. и Нейман Л. Р., Теоретические основы электротехники,
ч. Ill, M.—Л., 1948.
Л а н л а у Л. и Лившиц Е., Теория поля, М.—Л., 1948.
Л о р е п т ц Г. А., Теория электромагнитного поля, М.—Л., 1933.
Максвелл Д. К., Избранные сочинения по теории электромагнитного поля, М., IQW.
Мандельштам Л. И., Полное собрание трудол. т. V, М., 1950.
М и т к е в и ч В. Ф., Магнитный поток и его преобразования, М.—Л., 1946.
П а п а л с к с и Н. Д. (иод редакцией), Курс физики, т. II, М.—Л., 1947.
С т р э т т о н Дж. А., Теория электромагнетизма, М.—Л., 1948.
Та мм И. Е., Основы теории электричества, М.—Л'., 1949.
Френкель Я. И., Электродинамика, т. I и II, М.—Л., 1934.
Э й х е н в а л ь д А. А., Теоретическая физика, ч. VI, М.—Л., -1931.
б) По теории быстропеременных полей и ее приложениям
Вайиштейн Л. А., Диффракция электромагнитных и звуковых волн на открытом
конце волновода, М., 1953. *
Введенский Б. А. и Аренберг А. Г., Радиоволноводы, ч. I, M.—Л., 1946.
Г у р е в и ч А. Г., Полые резонаторы и волноводы, М., 1952.
Де Бройль Луи, Электромагнитные волны в волноводах и полых резонаторах,
М., 1948.
К и с у и ь к о Г. В., Электродинамика полых систем, Л., 1949.
Купрадзе В., Основные задачи математической теории диффракции, М.—Л., 1953.
Л с о н т о в и ч М. А., О приближенных граничных условиях для электромагнитного
ноля на поверхности хорошо проводящих тел (статья в сборнике «Исследование но
распространению радиоволн», под ред. Введенского Б. А., М.—Л., 1948).
Леонтович М. и Левин М., О возбуждении вибраторов в антеннах, Изв.
АН СССР, серия физич., 8, 3, 156 A944).
М а л о в Н. Н., О расчете контуров, эквивалентных полому резонатору, ЖТФ, 18, 4,
421 A948.)
Нейман Н. С., Выпуклые эндовибраторы, ИЭСТ, 9, 1 A939).
II о т е х и н А. И., Некоторые задачи диффракции электромагнитных волн, М., 1948.
Пнстолькорс А. А., Антенны, М., 1947.
1' а м о Си В и и и е р и Дж., Поля и волны в современной радиотехнике, М.—Л.,
1948.
Рыто в С. М., К расчету поглощения электромагнитных волп в трубах, ЖТФ, 10,
17fi A940).
Самарский А. А. и Тихонов А. П., О возбуждении радиоволноводол, ЖТФ,
17, И, 1283, A947); 17, 12, 1431 A947); 18, 8, 971 A948).
С л а т е р Дж. К., Передача ультракоротких волн, М.—Л., 1У46.
Ф е л ь д Я. II., Основы теории щелевых аитепп, М., 1948.
Фок В. А., Диффракция радиоволн вокруг земной поверхности, М.—Л., 1940.
Антенны, Сов. радио, М., 1951.
Линии передачи сантиметровых волн, т. 1, Сов. радио, М., 1951.
Справочник по волноводам, Сов. радио, М., 1952.
Теория линий передачи сверхвысоких частот, т. I и П, Сов. радпо, М., 1951.
Техника сверхвысоких частот, т. I, Сов. радио, М., 1952.
Дополнительная литература составлена переводчиками.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
НОМЕРА ЗАДАЧ НАПЕЧАТАНЫ КУРСИВОМ И ЗАКЛЮЧЕНЫ В СКОБКИ ПОСЛЕ НОМЕРА
СТРАНИЦЫ, НА КОТОРОЙ ОНИ НАХОДЯТСЯ
Абберация электромагнитных воли 509. 570
Ампер, единица силы тока 222, 2'Ю
Ампера опыт 260, 279
Андерсона мостик 359
Анизотропная среда, диэлектрический jij u-
шщаемость 33, 436
— — магнитная проницаемость 28E, 414,
436
— — плотность энергии 42
— — уравнение Лапласа 60
— — электрические оси 33
—- — электромагнитные волны 435—437
А нтенна 464—476
— биконическая 471—473, 493 A8), 494 A9)
— в полом резонаторе 537—539
— влияние земли 476
— входной импеданс 473
— выигрыш -475
— кольцевая (петля) 479—480, 492 A1)
— коэффициент направленного действии
475
— линейная 464—469
— —¦ возбуждаемая в центре. 407
— — диаграмма направленности 41>7, 475,
492 G, 9, 10)
— — излучаемая мощность 468, 470
излучение бегущей волны i(>9
— — нагрузка на конце 466
— — плотность зарядов 465
поля вблизи 464, 46—
¦ ¦ — вдали 467, 468
потенциалы поля 464
потери на излучение 467
сопротивление излучении Wu
— системы 474—476, 492 G, 10)
¦— сопротивление излучения 4С>8, 472, 473,
480
—щелевая 500 E9, 60)
Аргумент комплексного числа 81
Б
Баркгаузена эффект 416
Барнетта опыт 15
— эффект 418
Ьег и bei функции 387—389, 410 C0, 21)
Бесселевы функции 175—192
— — бесконечного аргумента 17!) .
— -— векторные поверхностные 181, 20(>,
512, 513, 526
Бессслсвы функции второго рода 176—179
185, 186, 91—193
интегралы 178, 179—182, 187, 188
— — пулевого порядка 185—190
— — — — график 186
— — — — Корин и численные значения
186
— — — —¦ обратное расстояние 183
— — — — производные и интегралы 180
187
— — первого рода 176
— — — — нецелого порядка 191
— — — — отрицательного порядка 191
полуцелого порядка 191, 388—
394, 407 B), 408 C)
— — представление в виде опреде-
определенного интеграла 187, 198
применения 183—185, 187—190,
215 (91—93), 216 (94—98), 242, 258E5),
266, 302 B7, 30, 31, 32), 392—393, 405,
406, 408 C), 478—485, 492 A1), 493 A4—
17), 494 B0—22), 495 B3), 496 C5, 36),
Ш1D2—15), 500E9), 508—510, 512—515,
532, 535, 540 D, 5, 8, 9), 541 A0—16),
Г>42 A7, 20, 21), 544 C0—32), 545 (S3—37),
550 F7), 551 F9, 70).
— — разложение в рады 182
— — рекуррентные формулы 178
сферические 191, 192, 203, 478—484,
490, 493 A8, 19), 497 C9, 10), 530, 537
548 E2) 551 G1)
— — теорема сложения 184
Бссселя модифицированное уравнение 176,
192
решение 192
— дюдифнцированные функции 192, 203
— — — Ъсг и bei функции 386—388,
ilO B0, 21)
— — — бесконочного аргумента 194
— — — лторого рода 192—194
интегралы 193, 194—199
— — — комплексного аргумента 194
¦ интегралы 194, 386—388
— — — мнимого порядка 204
— — — нецелого порядка 202
нулевого порядка 197—202
• интегралы 197, 199
— — — представления в виде опре-
определенных интегралов 197, 199
¦— — — обратное расстояние 199
— — — полуцелого порядка 202, 203,
388—398, 477, 478 (см. также Бесселевы
функции сферические)
584
Предметный указатель
Бесселя модифицированные функции при-
применения 194—196, 199—202, 215 (92,
93), 210 (99, 100), 217 A01), 242, 243,
292—294, 301 BS, 29), 321 A4—16),
386—390, 407 B), 410 A9, 22, 23),
411 B6, 28, 30, 31), 478, 479, 485, 494 B2),
495 B7, 32), 542 A9—21), 544 C1)
— рекуррентные формулы 193
сферические 203, 477—480, 482,
490, 491, 493 A8, 1!>) (см. также Бсссе-
лслы функции сферические; Хапкеля, функ-
функции)
— — — теоремы сложения 199
— уравнение 175
— решение 176, 177
Био и Сапарра закон 275
Биполярные координаты 71 B), 220 A22—
124)
Брюстера угол 442
Веоер, единица магнитного потока 291
Векторные поверхностные гармоники 157
181
Бесееля 181. 266, 267, 513, 520
— — — Лсжандра 157, 267, 529
Векторный аналог теоремы Грина 63
Вектор-потенциал 262
Взаимная емкость 47—49, 126—129, 240
Взаимный потенциальный коэффициент
46—49, 240
Взаимоиндукция 309, 534, 535
Вмхрепые токи 382—412
и плоских пластинках 395—400
¦— — — •— — метод изображений ЗЙ5—
399
— — ¦— — — момент, действующий на
вращающийся диполь 3!N, 397
¦— полом цилиндрическом проиод-
ПИ1.-1' 380. 387, 405—407
— — — полубесконечном среде с плоской
границей 384, 385
•— сплошном цилиндре 386—388
таре 388—394
— — — толстой цилиндрическом ооо-
лочке 385, 386, 405—407
— — — тонкой сферической пленке 3',)9—
403
— — — — цилиндрической пленке 403—
405
¦— — ментор-потенциал ноля 382—384,
388—3!)(i, 400—407
— — мощность рассеиваемая 382, 385,
403, 405
— — распределение в проводнике 383
Вихрь 59, 61 (см. Ротор)
Воздушный зазор в магнитной цепп 291,
296—298
— — — кольпсиом магните 423, 124
Во. ша, определение 433
Волиопод 501—519
— возбуждение 511— 516, 543B-?), 547 ( /.?)
— — через отверстие '512, 515, 516
— лплповис поверхности 540 A, 2), 5-50
C—5)
•— полны, скорость сигнала 503
— фазовая 503
Волновод затухание 503—505, 507, 540 F, 7)
— коаксиальный 509, 510
— — излучение из открытого конца 489—
491
— внутрь круглого волновода 515,
516
прямоугольного полновода
545 (За)
— критическая длина волны 502
— круглый цилиндрический 507—509
— — — возбуждение диполем 512—51 5,
545 C2—34)
коаксиальной линией 514
затухание 503
с продольной перегородкой 547
D6, 47)
— нормированный (относительный) импе-
импеданс 516
— поля в общем виде 503
— — в частных случаях 505, 507—509
— поперечно-магнитные полны 478, 501
— поперечно-электрические полны 477,
501
— прямоугольный 505. 506
— — возбуждение диполем 543 B4, 26),
Г>'м B5)
— — — коаксиальной линией 545 (-35)
— маленькой петлей 543 B3, 27),
514 B8)
— — — поперечным цроводом 545 C6,
37, 3S)
¦— — затухание 503—505.
— — плоские неоднородности 510—519,
547 D8, 49, S0)
емкостные 517, 518, 547 D8)
¦ индуктлппые 518, 519, 549
(P.), S0)
— сиязь с волноводом 511—516, 543—551
B3—43)
— треугольного поперечного сечения 500,
Г>'|7 'A1, 43)
— характеристический импеданс 502
Полномер 361
Волны, форма псеппугопдалышн периоди-
периодическая 371—373
— — пилообразная, разложение • и рял
Фурье 372
— метод помторнющегосн переход-
переходного режима 372, 373
— — прямоугольная 378 A5—IS)
— — елмм/оилальшш 351—382
— электромагнитные (см.~ Электромагнит-
Электромагнитные волны)
Гальнанометр баллистический 345
Гармоники биаксиалыше 160, 161
— зональные 139 (см. также Поверхност-
Поверхностные гармоники)
— кругопые 72—80
— — для двухпроводной .'миши с маг-
магнитным пилипдрпческнм экраном 287,
288
— — — линейного заряда 74
— — ¦— то кон в цилиндрической пленке
278
¦— поверхностные 138, 152, 164
Предметный указатель
585
Гармоники пространственные 133—204
— сфероидальные 164—175
— цилиндрические 72, 133 (см. также.
Бесселсвы функции)
векторные поверхностные 182, 266,
267
Гаусса теорема о потоке электрической
индукции 22—24, 28, 83, 137, 184, 195
Гауссова система единиц 575, 579
Герца вектор 432, 461, 403
аббераштя 569, 570
— — волновое уравнение 431, 432
— — для сферической волны 460, 401
— — Допплер-эффект 569—571
¦— — запаздывающий 403
Гиромагнитные эффекты 417, 418
Гистерезис 417
Градиент п криволинейных координатах 01
Грина теорема 45, 02—05, 137
— — некторный аналог 03
— — взаимности 45, 04
— — — при наличии неоднородного ди-
диэлектрика 64
— функция 64, 05
для диска 214
— — — кольца nil л ого цилиндрического
195—190
конуса 161, 162
— — — полости конической 163
• прямоугольной 219 A14)
— ¦ цилиндрической 185, 195
— — — призмы прямоугольной 218 A13)
сферы 124
— —• — цилиндра 183—185
— экшталентпый слой 07, 68
д
Даллсппе гидростатическое п диэлектри-
диэлектрике 43
— плоской электромагнитной волны 438
Двойной лист тока 486
— слой магнитный 201, 289
— — электрический 25, 26, 67
Декремент логарифмический 327
Детерминант характеристический 335
Джорджи система единиц 574—580
Джоуля закон 225
Диамагнетизм 413
Диамагнитная восприимчивость 414
Дивергенция 58—61
—• в криволинейных координатах 61
Диполь магнитный (см. Магнитный диполь)
— — вектор-потенпиал ноля 270, 425, 426
взаимодействие диполей 425
вращающийся 396—399
— — колеблющийся, излучение 479
— — момент, определение 424, 425
— — — петли, определение 424, 425
— электрический 17—21, 460
— — взаимодействие диполей 18
колеблющийся, излучение 400
— — линейный 95, 96
— — момент, действующий на диполь, 18
потенциал поля 17
—- — силы, действующие на диполь, 18
Диск круглый в однородном поле 108, 169
емкость 122
Диск круглый и кольцевой заряд 214 (87)
— — —• точечный заряд 21 i (85)
— — поверхностная плотность заряда 122
— — потенциал 122
— — — в выражении через бсссслепы
функции 217 A02)
— эллиптический, емкость 122
— — поверхностная плотность заряда 122
Диэлектрик, граничные условия 29—31,
102, 103
Диэлектрическая проницаемость 14, 10,
23, 20, 32, 33, 68, 09
Добротность полого резонатора Ъ'2.2—529,
5150, 537, 548 E4, 55, 57, 58, G0, 61)
Дополнительная функиия 325, 336^
Дотьгор-эффек'г 509—571
Единицы взаимоиндукции 309
— гауссовы 575—579
— емкости 37
— заряда 14
-— магнитного сопротивления 289—291
— магнитной индукции 260
— — проницаемости 200
— магнитодвижущей силы 289—291
-— мощности 225
-— напряженности поля магнитного 28У
электрического 16
-— плотности магнитного потока 261
— потенциала 10
-— потока магнитного 291
— размерности 580
— самоиндукции 314
-— сопротивления 224
— CGSE 14
— таблицы перехода 575—-579
— тока 222, 261
— электродвижущей силы 223, 224
— электромагнитные 574—579
Единственности теорема для распределе-
распределения токов 235
— -— —- электромагнитных волн 477
— — магнитостатики 263
— — электростатики 36, 00, 67
Емкостные коэффициенты" 47—49
Емкостный мост 357
Емкость в электрических цепях '327
— взаимная 47—49, 120, 128, 129, 240
— выражение через сопряженные функ-
функции 84
— двух полосок конланарных Ц7 E9)
¦— диафрагмы и волноводе 510, 547
D8, 49)
— диска круглого и эллиптического 122
— кольца 207 B6), 220 A19)
— определение 36
— неременного воздушного конденсатора,
поправка на краевой эффект 112 B6),
ИЗ C5)
— плоского конденсатора с кристалличе-
кристаллическим диэлектриком 42
— •— прямоугольным изгибом 117
F0)
— полого резонатора 522
— полоски и конфокального цилиндра 110
A6)
586
Предметный указатель
Емкость последовательное и параллельное
соединения 36, 37
— при инверсии 132
— распределенная 37
— собственная 47—49, 126, 128, 129, 240
— сфер 37, 111 B3), 126—128, 131, 207
B7), 209 D3, 45)
— сферического конденсатора 37, 126, 127,
128, 147
¦— сферы и плоскости 127
и плоского диэлектрика 208 C9)
двух плоскостей 207 B9)
— схема для измерения 345, 356, 357, 359
— цилиндра и плоскости 86
— цилиндрического конденсатора 39,
84—88 -
— цилиндров 84—86, ИЗ C<?)
— эллипсоида 121
3
Заряд 13, 14
— в проводнике 15, 445
— движущийся в магнитном поле 555—560
— — — магнитном и цилиндрическом
электрическом полях 557, 558
— — в перекрестных электрическом и маг-
питном полях 567—569
— единица 13
— коллинеарный 24
•— конденсатора 36
— линейный вблизи диэлектрического кли-
клина 79—81
— — — плоскости со щелью 100
¦— — законы изображений 76, 79
— — между плоскостями 93, 94
— — потенциал 72, 74, 82
— на проводнике (индуцированный) 14,
4В, 65
— •— -—¦ плоском 40
— — — сферическом 46
— цилиндрическом 46
— потенциал поля 16
¦— пространственный 250—251
-— распределение, единственность 36, 66
— сохранение (инвариантность) при пре-
преобразовании Лорентца 557, 558, 566
—- точечный 16
— элементарный 15
Заряда плотность 17
— — в двойном слое 25, 67, 68
•— эквивалентиом слое 67, 68
— — единственность распределения 36
¦ задачи 110 A3, 14), 112 C0), 114 D5),
205 F, 12, 14), 206 A6), 208 C9), 209 D2,
47), 211 F2), 212 F5, 69, 72).
¦ инверсия 129
¦ на антенне 464
¦— •— — диске заряженном 122
— — — — в продольном поле 168
— ¦ конденсаторе плоском 39
сферическом эксцентрическом
147
— ¦— — плоскости в присутствии точечно-
точечного заряда 123
— проводнике 29
— сфере в присутствии точечного
заряда 124
Заряда плотпогть на экране с круглым
отверстием 167
— — -—¦ — с циклоидальной поверхно-
поверхностью 88
— — — — со щелью 100
— — — эллипсоиде 121
Затухание в электрическом контуре 327—
331
— вихревых токов 392—394, 405—407
— критическое 327, 337, 338
Затухания коэффициент (постоянная) 362—
370, 450
— — в полых трубах 503, 508
— — -—¦ производном М-звене 368, 369
— — ¦— простом фильтре 362, 366
•— — линии передачи 370
Защитные кольца 40
Земля, влияние на антенну 476
Зональные гармоники 136, 148
Излучепие электромагнитное 430
реактивное сопротивление 472
сопротивление 462, 468, 472, 480, 491
Изображения в волноводах 511, 514, 542
A7), 543 B3, 24), 544 C1), 545 C6, 37)
— ¦— диэлектрической пластинке 189
— — плоскостях пересекающихся 78, 96
сферах касающихся 131
— пересекающихся 132
— — — разделенных 125—128
— в сфере проводящей 122
¦— — цилиндре круглом проводящем 77, 78
диэлектрическом 76, 77
пересекающимся с другим ци-
цилиндром 96
— вихревых токов в плоском листе 395,
398
— зарядов линейных в проводниках 76—
78, 96, 97
— — ¦ диэлектриках 76—78
¦— — точечных в проводниках 121—128,
130, 131, 185
— диэлектриках 123, 124
— контурных токов 285, 288
— при инверсии 77, 131, 132
Изолятор 13
Импеданс 352—371
— взаимный 357
— волновой 363—370, 502, 503
— входной 365, 371, 450
— — антенны биконической 473, 494 A9)
— щелевой 499 E5)
¦— — волновода, присоединенного к коак-
коаксиальной линии 515
¦— — нормированный 516
— — радиальной линии 541 (9)
секториального рупора 542 A5, 16),
542 A7, 18, 21, 22)
электрода в прямоугольном волново-
волноводе 545 C0, 31), 545 C6, 37)
— выходной 365, 369, 371, 450
— мост импедансный 356, 357
-— последовательные и параллельные со-
соединения 355
— сложение импедансов как векторов 355
— характеристический среды 449, 450
Предметный указатель
587
Импульс плоской волны 437, 438
— электрокинетический 332
Инверсия 96—97, 129—132
— в пространстве двух измерений 96, 97, 98
— трех измерений 129—131
— плоскостей пересекающихся 132
— поверхностей проводящих заряженных
131, 132
— сфер пересекающихся 132
Индуктивная связь 329—331, 337—343,
359—363, 536, 537
Индуктивное реактивное сопротивление 352
Индуктивность 309—318
¦— взаимная в электрических цепях в об-
общем случае 332—336, 357
— — коаксиальных катушек 311, 312, 322
B1), 323 B6)
контуров 309—313, 329—331, 333—
344, 357, 359, 362
— — — намерение 345
— — круглых колец коаксиальных 311, 312
копланарных 320 D)
некоаксиальных 311, 312, 322
B3), 323 B5)
— — расположенных вокруг цилип-
дра из магнетика 321 A4)
— — определение и единицы 309, 310
— — переменная 312, 313
— — соленоида бесконечного и петли 311
— — тороидальной катушки и охватывак>-
>цего се кольца .411
-— — электрода и резонатора 535—539
— собственная (самоиндукция) 314
— — в цепих общего вида 332—334, 357
— — ныражение "(Срез вектор-потенциал
314, 317
— — диухпроводной линии 316, 317
— собственная двухпроводной линии экра-
нирпианной 321 A0)
— — контура переменного тока 353—375
— — контур г самоиндукцией 326—381
круглой петли 315, 316
— — — — вокруг цилиндра из магнети-
магнетика 321 A5)
— — на векторной диаграмме 354, 35Г>
— — определение и единицы 314
соленоида 316
— -— тонкого провода 314, 315
— — цилиндра сплошного на высоких
частотах 387
Индукция магнитная 261, 2E2
— Фарадея закон 306, 314, 351
— электрическая 15, 26, 27, 29, 31, 430
— электромагнитная в линейных цепях
ЗОв—324
— ¦— •— объемных проводниках 382—412
Индуцированный заряд 14
Интеграл частный 325, 328, 336, 351—372
Ирншоу теорема 25
К
Квадруполь электрический 17, 461, 491
A—3), 492 D)
Кельвина мост 232, 233
Кег и kei функции 387
-.— — — -— в теории диффракции 409
E6— 60)
Кирхгофа законы 225—227, 230, 320—333,
352, 355, 363, 365, 369
Клаузиуса—Мозотти формула 44
Клин диэлектрический 78, 79
-— ортогональный к поверхности вращения
134, 135
— проводящий 92
Комплексные амплитуды .'$52—.472
— числа 81, 82
Конденсатор, емкость 36
— зарядка 327—329
— защитные кольца 40
— определение 36
-— переменный воздушный, поправка на
краеной эффект 112 B6), ИЗ C5)
— плоский 39
— — с кристаллическим диэлектриком 42
— — —; прямоугольным изгибом 117 F0)
— — энергия 41
— последовательное и параллельное со-
соединения 37, 38
— разрядка 327—329
¦— сферический 38
¦ неконцентрический 125—129, 147, 148
— цилиндрический 39, 86, 87
— — некоаксиальный 86, 87
— энергия 41
Коническая полость, функция Грина 163,
164
Конические: границы 148, 161—1(И
— координаты 70 D)
Контур магнитный 280—292
— - - воздушный аазор 291, 2D2
— — магнитное сопротивление 291
— — магнитодвижущая сила 289
поток в магнитных контурах 291
— — тороидальный 290, 291
— электрический 329—331, 337—343
— — колебания 340, 341
— — нестационарный ток .425—350
— — — — энергетические соотношении
325, 326
переменного тока 351—36:>
— электрический переменного тока, коэф-
коэффициент полезного действия 354
— — — -— мощность передаваемая 356
— — — — мощность потребляемая 353,
ЗГ>4
¦— — — — несинусоидальная э.д.с. 371 —
373, 378 A5—18)
— — — — отрипательное сопротивление
374—376
— — — — установившийся режим 351 —
356
— — последовательный 326—-429
¦— — — зарядка конденсатора i>27, 328
затухание 427
— — — постоянная Бремени 329
-— — — разрядка конденсатора 327, 328
-— — — частота колебаний 327
— — постоянного тока
-— — — — изображение 285, 288
¦— — — — магнитное поле 260—305
— — — — сила взаимодействия магнит-
магнитная 278—281, 308, 310, 318
-— — — — —• действующая на контур
в магнитном поле 278—281
— — — — энергия взаимная двух кон-
контуров 308, 310, 318
588
Предметный укаватель
Конус, функция Грина 162—164
Конфокальные координаты 104, 164—174
(ог. также Эллиптические координаты)
— сфероиды сплюснутые 164—17.'!
— — вытянутые 172—174
— цилиндры гиперболические 98, 9!)
параболические 92
— — эллиптические 98, 99 л
— эллипсоиды 120, 121, 164—174
Конформные преобразования 87—1о9
гипербол конфокальных 98, 99
равнобочных 92
— — границы в параметрической форме 88
— -— двух цилиндров 85—87, 89, 90
— — крыла самолета 102
— — мпогоугольника с закругленным уг-
углом 10fi
— •— парабол конфокальных 92 .
— — плоскости в плоскость со щелью 100
— с круглым цилиндрическим высту-
выступом или выемкой 115 D9)
¦ полоски в биполярные ортогональ-
ортогональные окружности 89
— — применения, двухмерный диполь 94
инверсия 96, 97
— — — к клину 92
-— — ¦— — магнитным полям 296—298,
303, 304 C5—38)
токам 235—239, 246—247
— — электрическим полям 88, 92—
109
— — — — электромагнитным волнам 453,
518
на римановой поверхности 101
решетки 94, 99, 106—108, 111 B2)
— — сопряженных функций 88—90
— — циклоидальной волнистой поверх-
поверхности 88
— — цилиндра круглого в эллиптиче-
эллиптический—102
Шварца 90—109
— — — двухмерный диполь 94, 95
— — — лвух углов 97—99
— — — инверсия 94, 97
— — — клина 92
— — — крыла самолета 102
на римановой поверхности 10J
— — — полуплоскости л полоску 98—
00
— — — угла нецелократного л/2 109
— — — ¦— отрицательного 94, 95
— — — — положительного 92
— "— — — равного пулю 92
электрических токов 235—239, 246—
247
— — эллипсов конфокальных !)8, 99, 102
Коэрцитивная сила 416
Криволинейные координаты 60—62
Кристалл, электрические свойства .'И, .42
Круглые петли с током, вектор-потенцпал
ноля 270, 271, 273, 274
— — — —• взаимоиндукция 311, 312
— — коаксиальные, сила взаимо-
взаимодействия при постоянных токах 280, 281
— — — — магнитное ноле постоянных
токов 270, 271. 273, 274
— — — — переменный ток, излечение
479—481
¦— — -— — самоиндукция 315, 316
Круглые петли с тиком экранирование
при помощи плоского листа 399, 400
Круговые гармоники 72—78
Кулона закон 13, 27, 28
— ¦— ограничения 14
Кюри закои 414
Л
Лапласа оператор (лапласиан) 60—63
применительно к векторам 262, 265—
267, 382—384, 387, 388, 393, 431, 455,
501, 510
— уравнение 60—62, 69,- 82, 133, 137, 166
175, 176, 233, 510
— — в анизотропном диэлектрике 61
неоднородном диэлектрике 60—62
ортогональных криволинейных
координатах 61
— — — прямоугольных координатах 60
— -— — сферических координатах €2, 134,
136
— — ¦— сфероидальных координатах 134,
164, 172 «
— — — цилиндрических координатах 62,
175
при вращении сопряженных функ-
функций 133
— — применительно к токам 233
решения в двух намерениях 72—117
трех измерениях 133—221
Лежандра коэффициенты 141
— полиномы 140
— — график 144
интегралы 142, 143
¦ мнимого аргумента 145
— — ¦— — и бесконечного 145
применения 145—148, 210—213 E7—
79), 240, 241, 267, 273, 274, 280, 281,
312, 313
— — производные 140
— — разложение 141
— — рекуррентные формулы 142
Родрига формула 140
— — таблица 144
— уравнение 139
— — решение в виде рядов 139
рекуррентпые формулы 139, 140
— функции 148—174
— — второго рола 148—153
— — — — выражение, через полшшлш
150, 151
мнимого аргумента 151, 152
— — — — применение к теории потен-
потенциала 152
рекуррентпые формулы 149,
158, 159
ряды 149, 151
чиелсипые значения 151
— ¦— дробного порядка 153
— — комплексного порядка 162
— — первого рода 153
гипоргеометрические:ряды15й
— — присоединенные (см. Присоединен-
Присоединенные функции Лежандра)
Линзы электростатические 203, 204
Линия передачи переменных токов, двух-
двухпроводная 452—454
Предметный указатель
589
Линия передачи переменных токов, двух-
двухпроводная неидсальные проводники
452—454
диэлектрическая 494 B0, 21),
49Г> B6—29)
- коаксиальная 509, 510, 515
— — — — — излучение открытого кон-
конца 489, 490
— — — — — не отражающие уступы 541
A2, 13)
__ -, . плоская неоднородность
5 К), 511
— коническая 409—471
— — — — конфокальная эллиптическая
457 A4)
— — отражение от неоднородности
450, 451
— — — — переход от сосредоточенных
параметров к распределенным 370, 371
-— — — — полые трубы 501-—519
— — — — рупор секториальный 549 A5,
16), 542, 543 A7, 18, 21, 22)
с диэлектрическим покрытием
496 C0—32)
— — -— — цилиндрическая 447—450, 457
A3, 16)
Логарифмический декремент затухания 327
— потенциал 72—74, 84
Лорентца преобразование 552, 553
М
Магнетрон 559, 560
— критическая частота 559, 560
Магнит, игла 420, 424, 425
-— кольцевой с воздушным зазором 422,
424
— подковообразный 421—423
— постоянный 417—426
— — граничные услоинн 420
— сферический 420, 421
в среде из магнетика 421
— цилиндрический 419, 423, 424
— эквивалентная пленка тока 418, 419
Магнитная восприимчивость 414, 415
— игла 419, 420, 424, 425
— индукция 260—262
— — антенны 465 (см. также Антенна)
— — Био и Савара закон 274
— — в анизотропной среде 280, 435, 436
двухмерных нолях 286—288
полых резонаторах 519
— шаре 390—394
— — — электромагнитных волнах 434
¦— — вихревых токов в плоском листе 394
— — инутри цилиндрической поломи в
цилиндрическом стержне 277, 278
выражение через вектор Герца 432
вектор-потенциал 383, 384
¦— — две скалярные фупкцпи 1583,
;;84
граничные условия 283—284
— — движущегося заряда 5G1, 563, 564
двухпроводной линии 269
¦ экранированной 287, 288
-— — пивергенщш 262
-— — диполя колеблющегося магнитного
479
Магнитная индукция диполя колеблюще-
колеблющегося электрического 460, 461
— — единственность 263, 264
интеграл по замкнутому контуру
262, 279, 282
¦ контура линейного 275
— — определение 260, 261
— — остаточная 417
— — переменного тока при экранировании
399
в проводниках 386—394, 403—
407
петли круглой 270, 271, 273, 274
— — распространение 383, 431, 432
— — — в проводнике 382, 445, 446
¦ ротор 262, 382
сила, действующая на движущийся
заряд 557—559
— — соленоида с произвольным шаголт об-
обмотки 275—277
— ¦— токов в сферической пленке 271—¦
273
цилиндрической пленке 278
¦— — электрона, движущегося прямоли-
прямолинейно ускоренно 563—565
— проницаемость 261, 413, 414
— — анизотропной среды 286, 414
— — в цепи магнитной 289, 290
— — выражение через намагничение 281
¦— — граничные условия 281—284
зависимость от температуры 414
— — и энергия ноля 309, 319
— — относительная 261
— — переменная 282
— — ферромагнитных сред 415—418
Магнитное взаимодействие токов 260—304
— поле, вектор-потенциал 262
— — действие на контуры 310, 318, 378—
381
напряженность 289—291, 415—417
— — — граничные условия 290
единица, эрстед 289
натяжения 318, 319
— — плотность энергии 309
потенциал скалярный 289—291 (см.
также Магнитодвижущая сила)
— сопротивление 289—292, 296—298, 422
Магнитный гистерезис 417
— диполь 260, 261, 270, 424, 425, 426
и волноводе 544 B8), 545 C3, 34)
— "контур 289—292
— лис/ 261
— момент 2E0, 419, 425
— полюс 420
— потенциал векторный 262
скалярный 289, 290
— ноток трубки 268
Магнитодвижущая сила 289—291, 421, 422
граиичпые условия 290
Максвелла гиромагнитные аффекты 418
— метод изображений для вихревых токол
395—399
— ток смещения 382, 430
— уравнения 430
— — инвариантность up и преобразовании
Лорснтца 557, 565, 506
Масса, изменение со скоростью 554, 556
— продольная п поперечная 550
Мезоп 15
590
ITредметный указатель
Милликсна опыт 15
Модуль комплексного числа 81
Момент, действующий на диамагнитные те-
тела 319, 413
— — — диполь магнитный 424, 425
— ¦ вращающийся над прово-
проводящим листом 398—400
— — — — электрический 17
— — вблизи диэлектрического
шара 219 A16)
— диск в электрическом поле 168—
170
— — — диэлектрический сфероид 214 (84)
— — — •— эллиптический цилиндр 103—•
106
диэлектрическое тело 68
— — — заряженные проводники 49, 111
B0), 168, 169
— — — кристаллический шар магнитный
415
— — — магнитные иглы 425
парамагнитные тела 318, 319, 413
¦— — — петлю с током 260
— полоску в однородном электри-
электрическом поле 111 B0)
¦ сферический магнит (шар) в одно-
однородном магнитном поле 420, 421
— ¦ неоднородном магнит-
магнитном поле 420
¦ — сферическую оболочку, вращаю-
вращающуюся в магнитном поле 409 A2)
— •— — цилиндрическую пленку, вра-
вращающуюся в магнитном поле 409 A6)
Мощности коэффициент 354
Мощность 353
¦— векторная диаграмма 355
— излучаемая антенной 467—469
¦— минимальная 235
— проходящая через отверстие 491
— рассеиваемая в волноводе 503—505
полости 522—523
полупространстве с плоской гра-
границей 385
— сопротивлении 225, 235
— — — сплошном цилиндре 387
— тонкой сферической пленке 403
— ¦ — цилиндрической пленке 405
. шаре 392
вихревыми токами 383, 385, 387,
392, 403, 405, 503—505, 522, 523
¦— — при скин-эффекте 385, 387, 392
— эффективная 353, 354
Мультиполь 17, 461
— излучение 461, 479, 480, 491 A—3)
II
Намагниченность 281—283, 413, 414, 418,
419
— в кристалле 415
— иглы 419, 420, 424, 425
— интенсивность 281—283, 413, 418, 419
— кольцевого магнита 423, 424
— кривая намагничивания ферромагне-
ферромагнетика 416
— подковообразного магнита 421, 422
— при вращении 418
— равномерная 418, 419
Намагничивающее поле 415
в подковообразном магните 421, 422
Напряженность магнитного поля 289, 290
— граничные услоиия 290
единица 289
— электрического поля 16, 30, 83
в анизотропной среде 31—33 40,
435—437
диэлектрике 30
— — плоской волне 433—437
— — поле излучения 431—43й
— ¦ выражение через вектор Герца
432
вектор-потенциал 307, 382
— ¦— — — — электродинамические по-
потенциалы 431
граничные условия 29, 31 102,
103
1 — ротор 306, 382
Натяжения в диэлектрике жидком 43, 44
— • сжимаемом 43
магнитном поле 318, 319
электрическом поле 27, 28
— на границе диэлектрика 30, 43
— ¦ с проводником 29, 30, 42, 43,
— силовых трубок 27, 28
Непрерывности уравнепис 223, 225, 245,
249, 430, 464
— ¦¦— в анизотропной среде 249
— ¦ двух измерениях 235—239
¦ тонкой пленке 244
трех измерениях 223, 233, 249
Обратное расстояние 141
О
Однородная намагниченность 417, 418
Однородное иоле магцитостатическое, вск-
тор-потенциал 263
в цилиндрической полости 277
— — — впесение в поле тел различной
формы 290, 300 A7, 20), 415, 418, 419, 425
— — — движение заряда 558, 559, 5fi7—
509
— релятивистское преобразованно
565—569
экранирование оболочкой из маг-
магнетика 290
•— энергия 309
релятивистское преобразование 507—
509
-— — электрическое, внесение в поле тел
различной формы 76—78, 103, 405, 111
A8, 20), 125 A23, 124), 168—170, 172,
174, 175, 209 D4), 212—214 F9, 74, 80—
84), 216 (97), 220 A20, 121)
движение заряда 567—569
— — — ограниченное 88, 94, 99—101,
Ю6—108, 111 B2, 23), 115 D8, 49), 167,
168, 174, 175
Ома закон 224, 225, 352, 432
Операторы в общей теории цепей 333—335
Оптические оси кристалла 436
Ортогональность сопряженных функций 83
Ортогональные и эквипотенциальные по-
поверхности 120
Ортогональные координаты 60—02
градиент 61
Предметный указатель
591
Ортогональные ксордипаты дивергенция
61
Лапласа уратшеппс 61
— — при вращении сопряженных функций
133, 134
— — Пуассона уравпение 61
— — ротор 61
Остатонная магпитная индукция 416
Остроградского—Гаусса теорема 58, 59,
E4, 222, 281, 309
Относительности специальная теория 552—
571
— — — инвариантность заряда 557, 558,
566
— — — — уравнений Максвелла 557,
565, 566
Лорентца преобразование 552,
553
— масса зависимость от скорости
554, 555
— — поперечная и продольная 556
— постулаты 552
— — — применение 561—563
П
Параболические цилппдрцческие коорди-
координаты 70 (б)
Парамагнетизм 414
Переходило процессы в линейных цепях
325—350
вихревые токи 392—394, 400, 401,
405—407
Плоская решетка 94, 99, 106—108
Плоские волны 430—458
Плоско-параллельные проводящие пласти-
пластины 39, 40, 93, 94, 112 B6, 31), ИЗ, 207
C1, 35, 36)
— бесконечный набор 111 B4)
— для создания однородного поля
111 B5)
Плоскость диэлектрическая, изображение
линейного заряда 78
точечного заряда 122, 123
— проводящая 39, 40, 78, 79, 94, 97, 115 D9)
¦ изображения линейного заряда 78,
79
точечного заряда 122, 123
и сфера 129
цилиндр 85, 86
— — полубесконечная со щелью 100
— —¦ преобразование 93
с отверстием 167, 168
Поверхностная плотность заряда 17
Поверхностные гармоники 137, 138, 152
— — векторные, сферические 157, 267
цилиндрические 182, 266, 267
— — дифференциальное уравнение 136
— — зональные 139, 148 (см. также Ле-
шандра полиномы)
— — — второго рода 148—152
— •— — выражение через полиномы
Лежандра 150, 151, 152
— — — мнимого аргумента 151,152
•— — —г- рекуррентные формулы
149
¦ ряды 148, 140
— — — численные значения 151
Поверхностные гармоники зональные комп-
комплексного порядка 161
¦— нецелого порядка 152, 153
ортогональность 137
Позитрон 15
Пойнтинга—Умова вектор 433
— — в волноводе 504, 515
— — — кристалле 436
¦— проводнике 446
диффрагированного поля 408 D6,
47), 499 E0, 52)
— — для линейной антенны 467
комплексный 451
— — определение 433
— — отраженный и преломленный 44и—
442
¦— от проводника 446—447
— — угол с фронтом волны 434
— — энергии плотность 437, 438
Показатель преломления 439
Полый резонатор 519—539
-— — биконический 549 E8, 59)
— — возбуждение 534—539, 550, 551
F6—70)
— — волновые поверхности 548 E1—53)
— — длина волны резонансная 519
добротность Q 522—530, 537/ 548,
549 E4, 55, 57, 58, 60, 61)
— — емкость 521
поля 523—526, 529, 532
призматический 549 E6, 57)
прямоугольный 524
с диафрагмой 550 F2—64)
— — резонансная частота 520, 523, 524,
526, 527, 530—534, 536—538, 548, 549
E4—56, 60)
— — с отверстиями 530
— — влияние затухания 522
самоиндукция 521, 522, 527—529
— — сложной формы, метод Хана 531—
533
— — собственные колебания 519—531
— — сопротивление активное 523
сферический 529, 551 G1, 12)
ток эквивалентный 521, 523, 525—
530, 534—539
— — треугольный 548, 549 E4, 55)
цилиндрический 519—521, 523, 524
— — ¦—• многосвязный 526—528
— — — —• коаксиальный 528
— — — — конфокальный эллиптический
549 F0)
— — — ¦— некопцентричесгаш круглый
549 F1)
Поляризации угол 442
Поляризация электромагнитной волны 435
440—443, 447
— — — и анизотропной среде 436, 437
волноводе 501—519
поле антенны 465—469
диполя 462, 479
круговая 443
¦ при диффракции 481—484
отражении от проводника 446,
447
— — — ¦— — полном 444
— эллиптическая 442
Потенциал векторный аксиально-симме-
аксиально-симметричного поля 268
592
Предметный указатель
Потенциал векторный вихревых токов,
метод изображений 394—399
— — волновое уравнение в проводнике 383
— —¦ выражение для электрического поля
через потенциалы 307
-— через две скалярные функции
383, 384
— — граничные условия 282—284
— — единственность 264
— — неустановившийся режим в сфериче-
сферической пленке 402
¦— — — ¦— — толстой цилиндрической
оболочке 405—407
• шаре 392—394
— —• поля диполя 270
двухмерного 286—288, 296—
298
—- — — иглы магнитной 425
— линии двухпроводной 269
— — ¦ экранированной 287, 288
магнита кольцевого 423, 424
однородного 263
— переменного тока в проводниках
383—385, 388—390
—- — — — — — сферической пленке
400—403
• шаре 390—394
петли круглой 270, 271, 273
¦ выражения 300 B2), 301
B4, 26, 27)
— — — пленки сферической с током
271—274
— тока линейного 285
— — — перпендикулярного грани-
границе раздела 285
— токов в цилиндрической оболочке
(пленке) 278
трансформатора броневого типа
423, 424
— трехмерного 262—288, 292—295
— — экранирование тонким плоским ли-
листом 395, 398—400
— тонкой сферической пленкой 400,
401
— — цилиндрической пленкой
403—405
электродинамический 431, 432
— —-.— в резонансной полости 519—539
— — — волн в трубах 501—519
— плоских 440—466
— сферических 460—500
— волновое уравнение 431
— выражение через вектор Гер-
Герца 432
— дивергенция 432
— — —¦ единственность 477
— — — запаздывающий 462, 563
— — — — движущегося заряда 561, 5G2
— — —¦ — поля антенны 64
¦ конической линии передачи 4G9
— —¦ — нормированный в полости 534,
535
— — — перпендикулярный В 384
петли с током 479, 480
— — — решение в сферических коорди-
координатах 477
— — — — — цилиндрических координа-
координатах 484
— — — свойство ортогональности 534
Потенциал векторцый электродинамиче-
электродинамический, связь со скалярным потенциалом
432, 460
— квазивектор 284, 285, 310
граничные условия 284, 310
— —• линейного тока, перпендикулярного
границе раздела 285
— распределения тока 224
— — — в проводшцих средах 234—244
— — — — слоистой земле 243, 244
— — — — сплошном цилиндре 242, 243
сферической пленке 245, 246
— — тонкой пленке 244
— — — граничные условия 234
— — —¦ двухмерный 235—239
— — — на поверхности вращения 246,
— скалярный магнитостатический 289—291
— — электродинамический 431, 432, 462
— — — волновое уравнение 432
— — — выражение через вектор Герца
432, 457 A2)
— движущегося заряда 561—563
диполя 460, 461
— — — запаздывающий 462
— — — связь с векторным потенциалом
электростатический 16—221
— — — аксиально-симметричного поля 69
¦— — — в кольце полом цилиндрическом
190, 218 A06)
— — системе с коническими гра-
границами 148, 152, 160—162, 213 G8, 79)
сферической оболочке 146,
147
вблизи нейтральных (равновес-
(равновесных) точек 160
— гармоническое распределение за-
ряда 138, 171, 172, 214, (89)
— — — градиент 16, 61
— — — граничные условия 30—32, 102,
1иЗ
— двойного слоя 25, 26, 67
— — — двухмерного поля 72—118
диполя 17, 219 A15)
диска проводящего 122, 167—
17U, 211 F3), 214 (86—87), 217 A02)
— — — дифференциальное уравнение 61,
62 (см. также Лапласа уравнение)
— — — единственность 36, 66
—. — — заряда линейного 72, 74, 84 (см.
также Круговые гармоники)
— — — — — н диэлектрического кли-
клина 78—81
— —¦ объемного 17, 65, 66
— поверхностного 17, 64
— — — и функция потока 83, 84, 102
— — — квадруполп 17
клина с выпуклостью 134, 135
— — — кольцевого заряда 145, 214 (86),
210 (99), 217 A01)
¦— — — логарифмический 72, 74, 84
— — — максимумы и минимумы 25
— — — многоугольника 90 (см. также
Конформные преобразования)
— — — нуль 16
прп изображениях 78, 79, 122—
128, 130, 131
инверсии 96, 97, 130, 131
Предметный указатель
593
Потенциал скалярный электростатический
проводника в однородном поле 76—
78, 167—169, 174, 175, 220 A20, 121,
123)
суперпозиция 17, 45, 46, 78, 79,
06, 100, 103—105, 108, 123, 145, 146,
169, 185, 188, 200
тора заряженного 219 A18)
—• — — — незаряженного между плоско-
плоскостями 217 A01)
— ¦ точечного заряда 16, 172, 183,
199
— •— -— — — в цилиндрической поло-
полости внутри диэлектрика 200—202
— вблизи диэлектрической
пластины 188, 189
выражение 136, 138. 145—
148, 158, 163, 164, 166—172, 183, 199,
215 (90)
— — — трехмерного поля 119—132
¦ функция потенциальная 82—84
— эквипотенциальные линии 20, 21,
22, 90, 100, 104
— — — электростатической линзы 203
Потенциальная энергия диполей магнит-
магнитных 425
— — — электрических 18
конденсатора заряженного 41
Потенциальный коэффициент 47—49
взаимный 47—49, 240
—¦ — собственный 47—49, 240
Поток магнитной индукции в воздушпом
зазоре 291, 296—298
— торе 290, 291
¦ единица, вебер 291
переменный 306, 351
рассеяния в трансформаторе 292—
296
Потока плотность магнитного 261 (см.
также Магнитная индукция)
Постоянная времени контура 329
— распространения 363—371
Преломление магнитных силовых линий
290
— оптическое 438—442
— электрпческих силовых линий 31
Преобразование Лореитца 552, 553 (см.
также Относительности специальная те-
теория)
Присоединенные функции Лежавдра 153—
164, 167—174
—¦- бцаксиальные гармоники 1C1)
161
большого аргумента 155, 167,
174
— — — выражение через функции Лежан-
дра 153 .
действительного аргумента 153—
174
— — — дифференциальное уравнение
153
— — — интеграл Лапласа 155
— — от произведения 155, 157
— мнимого аргумента 155, 157,166—
173, 263, 300 B1, 22)
¦— нецелого порядка 161, 162, 219
A8), 220 A19—121), 257 E7)
¦— поверхностные векторные гар-
гармоники 157
38 в. Смайт
Присоединенные функции Лежандра, при-
применения 159, 163, 164, 168—175, 214
(89), 215 (90), 263, 267, 272—274, 300
B1—24), 301 B6), 312, 321 A2, 13),
389, 392, 402, 403, 408 B, б), 40&
A1, 18), 411 B9), 478, 479, 482—484,
491, 493 A8, 19), 497 C9, 40), 529
рекуррентные формулы 158, 159
специальные значения 159
таблицы 154, 155
Проводимость 224
Проводник, граничные условия для токов
234
— в электростатике 29, 30, 44
— емкость 36
— заряды внутри 15
— — на поверхности 29 (см. также Заряд;
Заряда плотность)
— линейный, токи 225—233
— момент, действующий на заряженный
проводник 49, 50
— натяжения на границе с диэлектриком
43
— поверхности проводника 29, 43
— объемный (массивный), распределение
токов 233
— определение 13
— сила, действующая на заряженный про-
проводник 30, 44, 49, 50
— электромагнитные волны в проводнике
445, 446
— энергия системы заряженных провод-
проводников 49
Пуассона уравнение 61, 65—67, 250, 251,
460
— — в ортогональных криволинейных
координатах 61
решение 65, 66
Равномерная намагниченность 418, 419
Разностные уравнения 127, 227, 228
Распространения постоянная 363—371
— ¦— в линии передачи 370, 371
свободном пространстве 450
— фильтре простом 363—370
— типа М 368—369
Реактивная проводимость 355
Реактивное сопротивление 352
Резонатор полый (см. Полый резонатор)
Релаксации время 445
Релятивистские преобразования для силы
555, 556
— •— •— скорости 553, 554
ускорения 554
Рентгеновское излучение ускоренного элек-
электрона 563—565
Решетка заряженная 94, 98, 99, 106—10$
Риманова поверхность 101
Родрига формула 140, 141
Ротор 61, 62
— в ортогональных координатах 61, 62
—¦ — сферических координатах 70 B)
цилиндрических координатах 70 A)
—,Грина векторная теорема 63
Рупор секториальный 542 A6, 16), 542.
A7, 18, 21, 22)
594
Предметный указатель
Самоиндукция 314—317, 32У—331 , 337—
344, 359—363
Связанные контуры 329—331, 337—344,
359—363
Сила, выражеппе через функцию Грина 65
— действующая на диамагнитные тела 319,
413
— диполь магнитный со стороны ви-
хрепых токов 398, 399
— — — — электрический 18
— — — диэлектрические тела 68
— — — заряды, движущиеся 557—559,
566
—• контуры электрические 278—281,
298 (о), 299 {6, 7, 10—13), 300 A5), 308,
310, 318, 323 (8)
— — — парамагнитные тела 413
— —¦—¦ постоянные магниты 421—425
¦— проводники заряженные 49, 127
сферы 127, 131, 220 {125)
— коэрцитивная 417
— между магнитными иглами 425
— — сферой и плоскостью 129
— преобразования сил 555, 556
Силовые линии магнитного поля 295, 433
(см. также Магнитная индукция)
электрического поля 20, 21, 22, 76,
77, 86, 94, 97, 98, 99, 100, 104, 108, 201
— —г — — диполя 19, 21
— — — — дифференциальное уравпсние
19, 20
¦ зарядов 19
— — -— — — коллинеарных 24
— — — — на бесконечности 25
— — — — — границе диэлектрика 30
— — — — -— •— проводника 29
— ¦— — — натяжения 27, 28
Синусоидальная э.д.с. 351—376
Скип-слой, толщина 384, 504, 521
Скин-эффект 384—388 -»
— в цилиндре полом круглом 386
— сплошном 386—388
шаре 390—394 (см. также Вихрение
токи)
-— па плоской поверхности 384
Смещение электрическое 22, 26, 29, 30
(см. также Электрическая индукция)
Собственная емкость 47—49, 126, 127, 240
Соленоид 275—277 (см. также Индуктив-
Индуктивность; Магнитная индукция)
Сопротивление биконической антенны 473
¦— в цепях переменного тока 352 (см. так-
также Импеданс)
— выражение через емкость 236, 239
— высокочастотное цилиндра 386, 387
— земной коры 243, 244
— излучения 462, 4E8, 473, 480, 491
—¦ коаксиальной линии, соединенной с
прямоугольным волноводом 516
— лепты переменной ширины 237-—239,
259 F3)
— линии передачи 370
— магнитное 291, 292, 296—298, 422, 424
¦ воздушного зазора 292, 296—298
тора 291, 292
-— между электродами удаленными 236, 240
Сопротивление на векторной диаграмме
354, 355
¦— определение 224
— отрицательное 374—376
— петли в полости 537
— полого резонатора 523
— предельные значения 247, 248
— при неустановившихся процессах 325—
350
— резонансной щели 499 F5)
— удельпое 224
анизотропной среды 249, 250
— штыря в полости 538
Сопряженные ветви в цепях переменного
тока 357—359
— — — — постоянного тока 232
— функции для двухмерного диполя У4
инверсии 94—96
— — — клина 92
— — — линейного заряда 84
— — — вблизи плоскостп'.со щелыо
100, 101
— — — — — между плоскостями 86
магнитного поля 296, 297
— -— — плоскости со щелью 100, 101
— — — полоски зарпжеппой 99
— — — проводников в линии передачи 452
— решетки из круглых цилиндров
106—108
плоских полосок 99
— — — тонких проводов 94
цилиндра 85, 86, 98, 102—106
на римановой поверхности 101, 102
— — нахождение 88, 89
— — ортогональность 83
¦ применение в з'адачах 110—117 A7—
60), 256—257 D3—50), 257 E5), 303 C5—
38), 457 A3, 14, 16), 547 D8—55)
— теории токов 236—239
— — — к полоске переменной ширины
237—239
Статические машины 14, 222, 223
Стационарный процесс в контуре перемен-
переменного тока 351—381
после переходного 328, 330, 331
Стереографическая проекция 245, 246
Стокса теорема 59, 308
Сферические гармоники 136—164 (см. так-
также Поверхностные гармоники)
¦ вихревых токов 388—391, 400—403,
iO7 B, б), 409 A1)
в линейных контурах 273, 274, 280,
312, 313
— — — теории электромагнитных волн
477—479, 480, 493, 500, 504 A8, 19),
506 C9, 40), 538
— электростатике 138, 145—147,
160, 162—164, 212 G0), 213 G9)
разложение вектор-потенциала 268
распределение токов 341
— координаты дивергенция 61
• оператор Лапласа 62
ротор 70 B)
Сфероидальные гармоники вытянутого сфе-
сфероида 172—174
— — выражение для взаимной ин-
индукции 321 A3)
— диэлектрический сфероид 214
(82, 83, 84)
Предметный указатель
595
Сфероидальные гармоники вытянутого
сфероида, обратное расстояние 215 (90)
-— — потенциал векторный поля пе-
петли с током 301 B4)
гармонического распреде-
распределения зарядов 214 (89)
-— — применения п электростатике
214 (82—84, 89), 215 (90)
— ¦ к линейным цепям 301
B4, 26), 321 A2, 13)
самоиндукция 321 A2)
¦— — — — сфероид в однородном поле
174
— -— сплюспутого сфероида 133, 134, 164—
172
-— — — — векторные поля петли с током
300 B2)
¦— ¦— диска потенциал 168—171
¦— — диэлектрический сфероид 213
(80, 81), 214 (84)
— — — •— обратное расстояние 172
¦— плоскости с круглым отвер-
отверстием 167
— — применения в линейных цепях
300 B2)
электростатике 167—
172, 213 (80, 81), 214 (84—88)
— координаты 164, 165, 172, 173
Т
Тевешша теорема 358
-— — для постоянного тока 231
Тензор диэлектрической проницаемости 33
Ток в земной коре 249, 250
— вихревой 382—412
— неустановившийся 325—331, 341—343,
345—347
в цепях общего вида 332—336
— переменный 351—381
— — безваттная составляющая 354
•— — и антенне 464—476
¦ ветвях цепи 356, 357
¦— — ¦— контурах, индуктивно связан-
связанных 359—363
— — — полом резопаторс 521
-— проводниках объемных (массив-
пых) 385—412
-— — графическое представление 354
— — комплексные обозначения 352
мощность 353—356, 383
¦— — па векторной диаграмме 354
¦ резонанс 353
— пленка, эквивалентная магниту 418, 419
-— постоянный 222—259
¦— — и анизотропных средах 249, 250
¦— — — ветвях цепи 231
-— — — пространстве двухмерном 235—
239, 286—288
трехмерном 233—235, 239—
244, 249, 250
¦— — вектор-потенциал 262, 263
-— — граничные условия 234, 239, 244
единица 222, 260
-— — изображения в цонерхиости магне-
магнетика 285, 288
Кирхгофа законы 225, 226, 227, 230,
326—333, 352, 360, 367
Ток постоянный, магнитное поле 260—305
(см. также Магнитная индукция)
-— — непрерывность 223, 225, 245
плотность 222, 225, 233—236
¦— — пространственного заряда 250, 251
•— — распределение в ленте переменной
ширины 237-—239
— — — — объемных проводниках 233—
247
— — — — поверхности вращения 246,
247
— слоистой земле 249, 250
— — — — сплошном цилиндре 242, 243
¦ • шаре 240—242
¦ сферической пленке 245—246
— — — общие теоремы 235
¦— —¦ тепловой эффект 225, 235
¦— смещении 430
Тока функция для вихревых токов 394,
398, 399
¦— — — установившихся процессов 236,
246
Тор в однородном поле 220 A20, 121)
— емкость 220 A19)
— незаряженный между плоскостями 217
A01)
— свободно заряженный 219 A18)
Тороидальные координаты 70 (8), 214 A17)
Трансформатор 359, 363
¦— броневого типа, утечка 292—296
Трубки магнитной индукции 268, 269
— тока 233, 234, 241'
У
Уитстона мостик 226'
Умова—Пойнтинга вектор (см. Пойнтшг-
га—Умова вектор)
Ф
Фаза переменного тока 352—354
Фазовая постоянная в линии передачи
370, 371
— •— — М-производном звене фильтра
368
фильтрах 363—368
— электромагнитных волнах 450,
451
Фарадея закон ипдукции 306, 314, 351
— в линейных цепях 306, 314, 351
-— — объемных проводниках 382,
430
— — — -— поверхностях 401, 403
— уравнениях Максвелла 430
Фильтры, импеданс 363—370
— полосовые 366—368
— постоянная затухания 363—368
— — распространения 363—368
— производное М-звено 368, 369
— простые Т- и П-звеньп 363—368
— серединно-параллельное звено 363
— серединно-последовательное звено 363
— сложные 368, 369
¦— — выходное устройство 369, 370
— условие на конце 365, 366, 369
— частотные характеристики 366—369
38*
596
Предметный указатель
Френеля уравнение 435, 436
Фуко токи (см. также Вихревые токп)
Фурье—Воссели интеграл 188
Фурье ряды 73, 74, 201, 371, 372
— — в теории волноводов 505, 506
— — для полей в полости 520, 523—527
— — переменная э.д.с. синусоидальная
371, 372
— — — — пилообразная 372
¦— — прямоугольная 378 A6, 18)
(см. также Бесселя модифицированные
функции)
X
Ханкслп функции, значения на бесконеч-
бесконечности 180
¦— — определение 178, 193
— — представления через определенные
интегралы 197
— — применения 494 B1), 495 B6, SO, SI),
541 (8), 542 A6, 17, 20) (см. также Бес-
селевы функции)
— •— сферические 203
Холла эффект 234
Ц
Цепь магнитная (см. также Контур магнит-
магнитный)
Цепь электрическая, нестационарный ток
325—350
— — — — в контуре 325—350
— — — — интегральный эффект 345
— — — — общая теория цепей, амплиту-
амплитуды 335
— — параметры 333
— — — — при постоянной э.д.с. 336
¦— — — — процессы колебательные 334—
336
— — — — решение 334—336
— — — типы собственных колебаний
33C
— — переменного тока 351—381
общая теория 357—359
параметры 357
— — — — соотношение взаимности 358
— — — — сопряженные ветви 359
— Тевенина теорема 358
— — установившейся режим 351—
381
— фильтры 363—370
: — эквивалентная 379 B3, 21)
— — постоянного тока, общая теории
2:50—232
— — — — параллельное соединение 226
— — — •— последовательное соединенно
226
— — — — сопрпжепные ветви 227—229,
232, 233
Тевегшна теорема 231
— ¦— — — Уитстона мостик 226, 227
— — энергия 235, 326
— — составленная из одинаковых
звеньев 343, 344
Цилиндрическая пленка, поле токол 278
— полость, Грппа функпип 184
Цилиндрические гармоники 72—77
— координаты, Лапласа уравнение 62,
¦ — решение 175, 176 (см. также
Бесселевы функции)
ротор 70 A)
Цилиндрическое кольцо, потенциал вну-
внутри 190, 200—202
Чайлда уравнение 250, 251
Частный интеграл 325, 328, 336, 351—372
Частота, Допплер-эффект 569—571
— переменного тока 351—381
— полосы пропускания в фильтрах 366—
369
— собственная контуров, индуктивно сли-
слизанных 360—363
— — индуктивно связанных контуров
359—363
— — полости 520 (см также Полый резо-
резонатор)
— — резонансная 353, 354
— —¦ сферы проводящей 480, 481
— — цепей общего вида 334—336
— — — составленных из одинаковых
звеньев 343, 344
— электромагнитных волн 442
Частотные характеристики волноводов
502—509 (см. также Волновод)
оконечного звена фильтра 369, 370
— — фильтров с производными звеньями
типа М 368, 369
— ¦— — — простыми звеньями 366
Э
Эйнштейна и де Гааза эффект 418
Эквивалентный слой Грина 67, 68
Эквипотенциальные поверхности 20—22,
98—100, 120, 201
Экранирование квазимагнитостатическос
вихревыми токами 396, 399, 400—403,
405
— магнитостатнческое 287, 288, 290
—¦ электрическое 48
Электрический диполь 17—21
— заряд 13, 14
-г- — в проводнике 445, 446
Электрическая ипдукцпя 22, 23, 28, 30,
31, 430
— — в кристаллах 31, 32, 435—437
— — ¦— плоской волне 434
граничные условия 29, 30
Электрический мулыиполъ 17
Электрическое поле аксиально-симметрич-
аксиально-симметричное 69
— — в волноводах 503—509, 517
— — — полом резопаторе 520, 532
— — двухмерное 72—119
заряда движущегося 561—563
— — нейтральные (равновесные) точки н
линии 160
однородное 18, 40, 75, 99, 100, 106,
107
— — плотность энергии 42
Предметный указатель
597
Электрическое поле при внесении диэлек-
диэлектрика 6в, 68
суперпозиция 46, 78, 94, 99,
103—105, 107—109, 125, 145, 146, 169,
185, 200
функция потока 83, 84, 102, 103
Электродвижущая сила перемепного тока
351—381
— —¦ взаимоиндукции 310
— —¦ гармоническая (синусоидальная)
351—371
— — градиент 306, 430
— —¦ комплексная 351—371
— — определение 223, 224
— — переходный процесс е контуре 345—
347
— — периодическая, несинусоидальнап
1571—373, 378 A5, 17, 18)
постоянного тока 223, 224
самоиндукции 314
Электромагнитная индукция 300—323,
382—412
Электромагнитные волны 430
— — аберрация 569, 570
— —-в анизотропной среде 435—437
— —¦ — волноводе 502—503
¦ — линиях передачи. 370, 371, 447—
454, 456 A0—16)
— — — в полых резонаторах 519—539
• проводнике 445, 44G
— — -—• трубах 501—519
— — волновое уравнение 431, 432
решение 477, 478, 484
— — — число 450
групповая скорость 454
— — давление 438
— — диффракцпп, Кирхгофа формулы
',99—500 F6—60)
на отверстии 485—489, 486—490
{SJ—36, 39—53), 500 E9, 60)
сфере 481—484, 493 A3)
цилиндре 493 A4—17)
— — длина волны 442
Допплер-эффект 569—571
— — излучаемые из конца коаксиальной
линии 489—491
— — импульс 437
— — интенсивность 433
между7 плоскостями 540 F—8), 541
A0, 11)
— — отражение 438—442, 441, 446, 447,
450, 451, 455 C)
Электромагнитные волны плоские 447—
450, 452, 453, 456 G, 8), 485, 494 B0—
25), 496 B9—32)
— — поляризация 435, 442, 443
постоянная распространения450, 451
— — преломление 438—442
скорость 454, 503
сферические 457 A2), 460, 461, 464—
477, 479, 480, 562
— — теорема единственности 477
фазовая постоянная 442, 450
характеристический импеданс 449,
450
— — частота 442
эллиптическая поляризация 442, 443
— — энергия, плотность 437, 438
—направление распространения 433,
434, 437
Электрон 15
— спин 418
Электростатическая линза 203, 204
Электрострикпип 43
Эллипсоид заряженный 121, 122
Эллипсоидальные координаты 120
Эллиптические координаты 99
— цилиндрические координаты 70 E)
Энергия в цепях тока 326
— взаимная двух контуров 307—311
— —¦ магнитных игл 425
¦ гс-контуров 318
— — электрических диполей 17
— диссипация 225, 235
— диэлектрического тела в поле 68
— заряда движущегося ?59
— - и диэлектрическая проницаемость 69
— излучаемая линейно ускоренным элек-
электроном 563—565
осциллятором 461
— кинетическая, в контуре 326, 332
— конденсатора заряженного 41, 326
— магнетика в поли 319
— плотность в магнитном поле 309, 310
— — — электрическом ноле 41, 42
— полого резонатора 520, 521
— потенциальная в контуре 41, 326, 332
— проводников заряжепных 41, 49
— распространение 363—371
— — в волноводах 501—519
линиях передачи 363—370
• фильтрах 363—370
— сохранение 332, 440, 554, 559
О Г Л А В Л В Л II Е
Предисловие переводчиков 3
Предисловие автора ко второму изданию ... 5
Предисловие автора к первому изданию 6
Обозначения . . . . . 9
Глава I, Основные положения электростатики 13
§ 1. Электризация. Проводники и изоляторы A3). § 2. Положительное
и отрицательное электричество A3). § За. Закон Кулона, единица заряда,
диэлектрики A3). § 36. Пределы применимости закона Кулопа A4).
§ 4. Электростатическая индукция A4). § 5. Элементарные электрические
заряды A5). § 6. Напряженность электрического поля A5). § 7. Электро-
Электростатический потенциал A6). § 8а. Электрические диполи и мультиволи
A7). § 86. Взаимодействие диполей A8). § 9. Силовые линии A9).
§ 10. Эклипотенциальные поверхности B1). § 11а. Теорема Гаусса о по-
потоке электрической индукции B2). § 116. Силовые линии системы кол-
линеарных зарядов B4). § Ив. Силовые линии на бесконечности B5).
§ 12. Максимумы и минимумы потенциала. Теорема Ирншоу B5).
§ 13. Потенциал двойного электрического слоя B5). § 14. Вектор электри-
электрической индукции и силовые трубки B6). § 15. Натяжения в электриче-
электрическом поле B7). § 16. Теорема Гаусса о потоке электрической индукции
для неоднородных сред B8). § 17. Граничтше условия и латяжеиия па по-
перхгюсти проводников B9). § 18. Граничвые условия и натпжепип на
поверхности диэлектрика C0). § 19. Электрическая индукция и папря-
жепность поля в твердых диэлектриках C1). § 20. Кристаллические ди-
диэлектрики C2).
Задачи 33
.Литература 35
Глава II. Конденсаторы, диэлектрики, системы проводников 36
§ 1. Теорема единственности C6). § 2. Емкость C6). § 3. Последователь-
Последовательное и параллельное соединение конденсаторов C7). § 4. Сферический кон-
конденсатор C8). § 5. Цилиндрический конденсатор C9). § 6. Плоский кон-
конденсатор C9). § 7. Защитные кольца D0). § 8. Энергия заряженного
конденсатора D1). § 9а. Энергия электрического поля D1). § 96. Пло-
Плоский конденсатор с кристаллическим диэлектриком D2). § 10. Натяжения
и случае зависимости диэлектрической проницаемости от плотности сре-
среды D2). § 11. Электрострикцип в жидких диэлектриках D3). § 12. Силы,
действующие на проводник в диэлектрике D4). § 13. Теорема взаимностп
Грина D5). § 14. Суперпозиция полей D5). § 15. Индуцировавные заря-
заряды на заземленных проводниках D6). § 16. Потенциальные коэффициен-
коэффициенты D7). § 17, Собственная и взаимная емкости D7). § 18. Электростати-
Электростатическая экранировка D8). § 19. Потенциальные и емкостные коэффициен-
коэффициенты в случае двух отдаленных проводников D8). § 20. Энергия системы
нарядов D9). § 21. Силы и моменты сил, действующие на заряженные
проводники D9).
Задачи * 51
Литература * : 57
Оглавление 599
Глава III. Общие теоремы 58
§ 1. Теорема Остроградского—Гаусса E5). § 2. Теорема Стокса E9).
§ 3. Уравнения Пуассоиа и Лапласа E9). § 4. Ортогональные криволи-
криволинейные координаты F0). § 5. Представление ротора в ортогональпых кри-
криволинейных координатах F1). § 6. Представление оператора V • (eV)
в различных системах координат F2). § 7. Теорема Грина F2). § 8. Тео-
Теорема взаимности Грина для диэлектрических сред F4). § 9. Функция
Грина F4). § 10. Решение уравнения Пуассона F5). § 11. Теорема един-
единственности при наличии диэлектрических сред F6). § 12. Впесение пово-
го проводника F6). § 13. Эквивалентный слой Грива F7). § 14. Энергия
диэлектрического тела в электрическом поле F8). § 15. Изменение элек-
электрической энергии систедш при увеличении диэлектрической проницаемо-
проницаемости @8). § !6. Потенциал аксиально-симметричного поля F9).
I Задачи 70
Литература 71
Глава IV. Двухмерное распределение потенциала 72
§ 1. Двухмерные поля и потенциалы G2). § 2. Круговые гармоники G2).
§ 3. Представление потепциала поля линейного заряда в виде ряда по гар-
гармоникам G4). § 4. Проводящий или диэлектрический цилиндр в однород-
однородном поле G4). § 5. Диэлектрический цилиндр. Метод изображений G6).
5 6. Изображение в проводящем цилиндре G8). § 7. Изображение в пло-
плоской поверхности проводника или диэлектрика. Пересекающиеся проводя-
проводящие плоскости G8). § 8. Задача о диэлектрическом клине G9). § 9. Ком-
Комплексные величины (81). § 10. Сопряженные функции (82). § 11. Функ-
Функции потока (83). § 12. Напряженность электрического поля. Поток элек-
электрической индукции (83). § 13. Функции U и V для поля линейного ва-
рпда (84). § 14. Емкость между двумя круглыми цилиндрами (85).
§ 15. Емкость между цилиндром п плоскостью. Емкость между двумя
одинаковыми цилиндрами (86). § 16. Конформные преобразования (87).
§ 17. Уравнение границы в параметрической форме (87). § 18. Нахожде-
Нахождение сопряженных функций (88). § 19. Преобразование Шварца (90).
j 20. Многоугольники с одним положительным углом (92). § 21. Много-
Многоугольник с углом, равным вулю (92). § 22а. Многоугольники с одним
отрицательным углом. Двухмерный диполь. Инверсия (94). § 226. Изобра-
Изображения при двухмерной инверсии (96). § 23. Многоугольник с двумя
углами (97). § 24. Щель, прорезанная в бесконечной плоскости A00).
$ 25. Рпмаиовы поверхности A01). § 26. Задача о круглом цилиндре, рас-
расположенном внутри эллиптического A02). § 27а. Условия на границе раз-
раздела двух диэлектриков A02). § 276. Эллиптический диэлектрический ци-
цилиндр A03). § 27в. Момент, действующий на диэлектрический цилиндр A05).
§ 2S. Многоугольник с закругленным углом A06). § 29. Плоская решетка
из цилиндрических проводов большого диаметра A06). § 30. Случай
углов, нецелократных it/2 A09).
Задачи .... 109
Литература . 118
I лава V. Трехмерное распределение потенциала 119
§ 1. При каких условиях поверхности некоторого семейства могут быть
эквипотенциальными? A19). § 2. Потенциал поверхностей второго порядка,
определяемых уравнением *2/(я2 + 6) + Л'(Ь2 + 0) + 22/(е2 + В) = 1 A20).
§ 3. Заряженный проводящий эллипсоид A21). § 4. Эллиптический и круг-
круглый диски A22) § 5. Метод изображений. Проводящие плоскости A22).
§ 6. Плоская граница двух диэлектриков A23). § 7. Изображение в сфери-
сферическом проводнике A24), § 8. Пример применения метода изображений
для нахождения поля точечного заряда A25). § 9а. Бесконечная система
изображений. Задача о двух сферах A25). § 96. Уравнения в конечных
разностях. Задача о двух сферах A27). § 9в. Сфера над плоскостью и две
¦одинаковые сферы A29). § 10. Инверсия в пространстве трех измерений.
Геометрические свойства A29). § Иа. Инверсия потенциала и зарядов-изо-
зарядов-изображений A30). § 116. Пример инверсии изображений A31). § Ив. Инвер-
Инверсия заряженной проводящей поверхности A31). § 11г. Преобразование
емкости при ипверсии A32). § 12а. Пространственные гармоники A33).
§ 126. Задача о клине, ортогонально пересекающемся с поверхностью вра-
вращения A34). § 13. Сферические гармоники A36). § 14а. Общие свойства
поверхностных гармоник A37). § 146. Потенциал гармонического распре- .
600 Оглавление
деления зарпда A38). § 15. Дифференциальные уравнения поверхностных
гармоник A38). § 16а. Зональные гармоники. Уравнение Лежандра A39).
§ 166. Решение уравнения Лежандра при помощи рядов A39). § 16в. По-
Полиномы Лежандра. Формула Родрига A40). § 16г. Коэффициенты Лежанд-
Лежандра. Обратное расстояние A41). § 16д. Рекуррентные формулы для полино-
полиномов Лежандра A42). § 16е. Интеграл от произведения полиномов Лежанд-
Лежандра A42). § 16ж. Разложение функций по полиномам Лежандра A43).
§ 16з. Таблица полиномов Лежандра A44). § 16и. Поливомы Лежйндра
мнимого аргумента A45) § 17. Потенциал заряженного кольца A45).
§ 18. Заряженное кольцо в проводящей сфере A46). § 19. Сферическая ди-
диэлектрическая оболочка в однородном поле A46). § 20. Сферический кон-
конденсатор с малым расстоянием между центрами внутренней и внешней
обкладок A47). § 21. Задачи с простой конической границей A48).
§ 22а. Зональные гармоники второго рода A48). § 226. Рекуррентпые фор-
формулы для функпий Лежандра второго рода A49). § 22в. Выражение функ-
функций Лежандра второго рода через полиномы Лежандра A50). § 22г. Неко-
Некоторые значения функций Лежандра второго рода A51). § 22д. Функции
Лежандра второго рода мнимого аргумента A51). § 22е. Применение функ-
функций Лежандра второго рода в' теории потенциала A52). § 23. Зональные
гармоники нецелого порядка A52). § 24а. Присоединенные функции Ле-
жапдра A53). § 246. Интегралы от произведений присоединенных функ-
функций A55). § 24в. Присоединенные функппи от мнимого аргумента A57).
§ 24г. Рекуррентные формулы для присоединенных функций Лежандра A58).
§ 24д. Некоторые значения присоединенных функций Лежандра A59).
§ 24е. Равновесные (нейтральные) точки и линии A60). § 25. Биаксиальные
гармоники A60). § 26. Конические границы A61). § 27а. Присоединенные
функции Лежандра нецелого порядка A62). § 276. Функция Грива для
конуса A63). § 27в. Функция Грина для конической полости A64).
§ 28а. «Сплюснутые» сфероидальные координаты A64). § 286. Гармоники
сплюснутого сфероида A66). § 28в. Проводящий лист с круглым отверсти-
отверстием A67). § 28г. Момент, действующий па диск в однородном поле A68).
§ 28д. Потепциал заряда, распределенного по поверхности сфероида A70).
§ 28е. Представление потенциала точечного заряда через гармоники сплюс-
сплюснутого сфероида A72). § 29а. Гармоники вытянутого сфероида A72).
§ 296. Вытянутый сфероид в однородном поле A74). § 30а. Уравнение
Лапласа в цилиндрических координатах A75). § 306. Уравнение Бесселя
и функции Бесселп A75). § ЗОв. Модифицированное уравнение Бесселп и
модифицированные функции Бесселя A76). § 30г. Решение уравнения Бес-
Бесселп A76). § ЗОд. Рекуррентные формулы для функций Бесселп A78).
§ ЗОе. Значения функций Бесселя на бесконечности A79). § ЗОж. Интегра-
Интегралы от бесселевых функций A80). § ЗОз. Разложение в рпд по функциям
Бесселп A82). § ЗОи. Функция Грипа для цилиндра. Обратное расстоя-
расстояние A83). § ЗОк. Функция Грина для цилиндрической полости A85).
§ 31а. Функции Бесссля нулевого порядка A85). § 316. Корни и числен-
численные значения бесселевых функций нулевого порядка A86). § 31в. Произ-
Производные и интегралы от бесселевых функций нулевого порядка A86).
§ 31г. Поле точечного заряда, расположенного над диэлектрической пла-
пластинкой A88). § 31д. Потенциал внутри полого цилиндрического коль-
кольца A00) § 32. Функция Бссселя нецелого порядка. Сферические функции
Бесселп A91). § 33а. Модифицированные бееселевы функции A92).
§ 336. Рекуррентные формулы для модифицированных бесселевых функ-
функции A93). § ЗЗв. Значении модифицированных бесселевых функций на бес-
бесконечности A94). § 33г. Интеграл от произведения модифицированных бес-
бесселевых функций комплексного аргумента A94). § ЗЗд. функция Грина
для кольцевой пилиндричсской полости A95). § 34а. Модифицированные
бееселевы функции нулевого порядка A97). § 346. Интегральное представ-
представление модифицированных бесселевых функций второго рода. Значение ва
бесконечности A97). § 35. Интегральное представление бесселевых функ-
функций нулевого порядка A98). § ЗСа. Представление обратного расстояния
через модифицированные бееселевы функции A99). § 366. Цилиндрические
границы раздела двух диэлектрических сред B00). § 37. Потенциал вну-
внутри кольцевой цилиндрической полости B00). § 38. Модифицированные
бееселевы функции нецелого порядка B02). § 39. Приближенные решения.
Электростатические лпвзы B03). § 40. Функции клипа B04).
Задачи . .
Литература
Оглавление 601
Глава VI. Электрический ток 222
§ 1. Плотность электрического тока. Уравнение непрерывности B22)
§ 2. Электродвижущая сила B23). § 3. Закон Ома. Удельное сопротивле-
сопротивление B24). § 4. Тепловое действие электрического тока B25).' § 5. Линей-
Линейные проводники. Законы Кирхгофа. Последовательные и параллельные
соединения проводников B25). § {5. Расчет электрических цепей. Контур-
Контурные токи. Мост Унтстоиа B28). § 7. Цени из одинаковых звеньев B27)
§ 8. Линия с непрерывно распределенной утечкой B29). § 9. Общая тео-
теория цепей B30). § 10. Сопряженные проводники. Двойной мост Кельви-
Кельвина B32). § 11. Постоянные токи в проводящих средах B33). § 12. Общие
теоремы B35). § 13. Двухмерный ток B35). § 14. Длинная лента со скач-
скачкообразно меняющейся шириной B37). § 15. Трехмерное распределение то-
тока" B39). § 1С. Системы электродов. Две сферы. Удаленные электроды B40).
§ 17. Задача о проводящем шаре B40). § 18. Задача о спловшом проводя-
проводящем цилиндре B42). § 19. Сопротивление земли B43). § 20. Токи в топ-
топких изогнутых пленках B44). § 21. Распределение тока f сферической
пленке B45). § 22. Поверхность вращения B46). § 23. Предельные значения
сопротивления B47). § 24. Токи в анизотропных средах. Слои в земной
коре B49). § 25. Ток, обусловленный движением пространствешюго заряда.
Уравнение Чайльда B50).
Задачи . . . 252
Литература . . . 259
Глаш VII- Магнитное взаимодействие токов W0
§ 1. Определение единицы силы тока (ампера) через величину магнитного
момента B60). § 2. Магнитная индукция и магнитная проницаемость B60).
§ 3. Магнитный вектор-потенциал. Однородное поле B62). § 4. Теоремы
единственности в магнитостатике B63). § 5. Разложение вектор-иотенциала
по ортогональным функциям B64). § 6. Вектор-потенциал в цилиндриче-
цилиндрических координатах B66). § 7. Вектор-потенциал в сферических координа-
координатах B67). § 8. Выражение для вектор-потенциала черев значение магнит-
магнитной индукции на оси B67). § 9. Уравнение аксиально симметричных тру-
трубок магнитной индукции B68). § 10. Вектор-потенциал и поле двухпро-
двухпроводной линии B69). § 11. Вектор-потенциал и поле круглой петли B70).
§ 12. Поле токов, текущих по сферической пленке B71). § 13. Зональные
токи в сферической пленке B72). § 14. Представление поля круглой пет-
петли через сферические гармоники B73). § 15. Закон Био и Савара. Поле
прямолинейного провода B75). § 16. Поле соленоида с произвольным ша-
шагом намотки B75). § 17. Поле в цилиндрической полости внутри проводя-
проводящего круглого стержня B77). § 18. Поле токов, текущих вдоль цилиндри-
цилиндрической проводящей пленки B78). § 19. Сила, действующая на электриче-
электрический контур в магнитном поле B78). § 20. Примеры на вычисление сил
взаимодействия между электрическими контурами B80). § 21. Вектор-по-
Вектор-потенциал и вектор намагвиченности B81). § 22. Граничные условия для
магнитных полей и для вектор-потенциалов B82). § 23. Пример использо-
использования векторов а и А B84). § 24. Метод изображений для токов в случае
плоской границы B85). § 25. Магнитная индукция и магнитная проницае-
проницаемость в кристаллах B86). § 26. Двухмерные магнитные ноля B86).
§ 27. Магнитное экранирование двухпроводной линии B87). § 28. Метод
изображепий для токов в двухмерных системах B88). § 29. Магнитодви-
Магнитодвижущая сила и напряженность магнитного поля B89). § 30. Магнитный
контур. Тор B90). § 31. Магнитный контур с воздушным зазором B91).
§ 32. Поле в трансформаторе броневого типа B92). § 33. Полюс с расщеп-
расщепленным накопечником. Эффективный воздушный зазор B96).
Задачи 298
Литература 304
Глава VIII. Электромагнитная индукции ' 306
§ 1. Закон индукции Фарадея C06). § 2. Взаимная энергия двух конту-
контуров C07). § 3. Энергия магнитного поля C08). § 4. Коэффициент изапшшй
индукции C09). § 5. Граничпые условия для а C10). § С. Коэффициент
взаимной индукции простейших контуров C11). § 7. Коэффициент взаи.м-
пой индукции двух колец C11). § 8. Переменная взаимная индукция C12).
§ 9. Самоиндукция CJ 4). § 10. Вычисление самоиндукции. Тонкий про-
провод C14). § 11. Самоиндукция круглив петли C15). § 12. Самоиндукция
соленоида(ЗШ. § 13. Самоиндукция двухпроводной линии C16). § Н. Энергия
602 Оглавление
п контуров C18). § 15. Натяжения в магнитном поле (П18). § 16. Энергия
магнетика в статическом магнитном поле C18).
Задачи 319>
Литература ... 324
Глава IX. Переходные явления в электрических цепях 325
§ 1. Неустановившиеся электрические процессы C25). § 2. Энергетические
соотношения в электрической цепи C25). § 3 Контур, состоящий из емко-
емкости, индуктивности и сопротивления C26). § 4. Зарядка и разряд копдппса-
тора C27). § 5а. Нарастание и спадание тока в катушке индуктивно-
индуктивности C29). § 56. Индуктивно связанные контуры C29). § 6. Кинетическая
энергия и электрокиветичоский импульс C32"). § 7. Общий вид уравнений
переходных процессов в цепях C32). § 8. Решепие для цепей общего ви-
вида C34). § 9. Типы собственных колебаний C36). § 10. Цепь, содержащая
постоянную э.д.с. C36). § 11. Собственные частоты двух индуктивно свя-
связанных ковтуров C37). § 12. Амплитуды колебаний в двух связанных кон-
контурах C39). § 13. Колебательный режим C40). § 14. Индуктивно связан-
связанные контуры, обладающие малым активным сопротипленисм C41). § 15. На-
Настроенные индуктивно связанные контуры, обладающие малым активным
сопротивлением C43). § 16. Цепи из одинаковых звеньев C43). § 17. Ипте-
тральный эффект переходного процесса C45). § 18. Переходные яллешш при
импульсах конечной продолжительности C45).
Задачи . . 347
Литература . . 350
I лача X. Переменные токи 351
§ 1. Гармонические электродвижущие силы. Частное решепие C51).
§ 2. Контур, содержащий сопротивление, емкость и индуктивность C51).
§ 3. Мощвость, эффективные значения, резонанс C53). § 4. Графическое
представление. Векторная диаграмма C54). § 5. Последовательное и парал-
параллельное соединение импедансов C55). § 6. Передача мощности C56).
§ 7. Мостик импедавсов C56). § 8. Цепь переменного тока в общем слу-
случае C57). § 9. Сопряженные ветви в электрической цепи. Мостик Андерсо-
Андерсона C59). § 10. Вынужденные колебания в индуктивно связанных конту-
контурах C59). § 11. Индуктивно связанные контуры, обладающие малым актив-
активным сопротивлением C62). § 12. Настроенные индуктивно связанные кон-
контуры, обладающие малым активным сопротивлением C62). § 13. Филь-
Фильтры C63). § 14. Условия на ковцах в частотных фильтрах C65). § 15. Ча-
Частотные характеристики фильтров C66). § 16. Полосовой фильтр C66).
§ 17. Производные звенья типа М C68). § 18. Выходное устройство фильтра C69).
§ 19. Линпи передачи C70). § 20. Электродвижущие силы яесииусоидаль-
ной формы. Метод рядов Фурье C71). § 21. Электродвижущие силы носи-
нусоидальной формы. Метод повторяющегося, переходного режима C72).
§ 22. Контур с отрицательным активвым сопротивлением C74).
Задачи . . 37Р
Литература . . . . 381
Глава XI. Вихревые токи . . ЗЯ2
§ 1. Ипдуцированные токи в объемных проводниках C82). § 2. Решение
уравнения для вектор-потенциала вихревых токов C83). § 3. Скин-эффект
в стационарном случае C84). § 4. Скин-эффект в случае полого цилиндри-
цилиндрического проводника C8С). § 5. Скин-эффект в сплошном цилиндрическом
проводнике C86). § 6. Решите в сферических координатах при аксиаль-
аксиальной симметрии C88). § 7. Проводящий шар в пере.менном поле C00).
§ 8. Мощность, поглощаемая шаром в перемевном магнитном ноле C92).
§ 9. Переходные явления н проводящем таре C92). § 10. Вихревые токи
и цлоскях пластинках C94). § 11. Решение задачи о вихревых токах в пло-
плоской бесконечной пластинке методом изображений C95). § 12. Момент,
действующий на вращающуюся петлю с током или магнитный диполь C96).
§ 13. Вихревые токи, возбуждаемые вращающимся диполем C98). §14. Экра-
Экранирование круглой петли носредством тонкой проводящей пластинки C99).
§ 15. Зопальвые вихревые токи в сферической пленке D00). § 16. Вих-
Вихревые токи в тонкой цилиндрической пленке D03). § 17. Переходные-
Оглавление 603
явления при экранировании с помощью толстой цилиндрической обо-
оболочки D05).
Задачи ¦ 407
Литература 412
Глава XII. Магнетизм ' 413
§ 1. Парамагнетизм и диамагнетизм D13). § 2. Магпитпа» восприимчи-
восприимчивость D14). § 3. Магнитные свойства кристаллов D14). § 4. Кристалличе-
Кристаллический шар в однородном магнитном поле D15). § 5. Ферромагнетизм D15).
§ 6. Гистерезис. Постоянный магнетизм D17). § 7. Природа постоянного
магнетизма D17). § 8. Равномерное намагничивание. Эквивалентный по-
поверхностный ток D18). § 9. Намагниченный шар и цилиндр. Магнитные
полюсы D19). § 10. Условия па границе с постоянным магнитом D20).
§ П. Сферический постоянный магнит в однородном поле D20). § 12а. Подъ-
Подъемная сила подковообразного магнита D21). § 126. Поле цилиндрического
магпита D23). § 13. Магнитные иглы D24).
Задачи . . 420
Литература .... 420
Глава XIII. Плоские электромагнитные волны 430
§ 1. Уравнения Максвелла D30). § 2. Волновое уравнение. Электромагнит-
Электромагнитные потенциалы. Вектор Герца D31). § 3. Вектор Умова—Пойнтиига D33).
§ 4. Плоские волны п однородном иезаряженвом диэлектрике D43). § 5. Ско-
Скорость распространения волны в анизотропных средах D35). § 6. Поверх-
Поверхность, образованная лучом, и поляризация в анизотропных средах D30).
§ 7. Энергия, давление и импульс плоской волны D37). § 8. Отражение
и преломление плоских волн D38). § 9. Интенсивности отраженной и
преломленной воли D40). § Ю. Частота. Длина волны. Эллиптическая поля-
поляризация D42). § 11, Полное отражение D44). § 12. Электромагнитные волны
п однородных проводниках D45). § 13. Плоские полны в однородных
изотропных проводниках D45). § 14. Отражение от проводящей поверх-
поверхности D46). § 15. Плоские волны вдоль идеально проводящих цилиндриче-
цилиндрических проводников D47). § 16. Характеристический импеданс среды D49).
§ 17. Отражения от неоднородностей. Согласующие секции D50). § 18. Ком-
Комплексный вектор Умова—Пойнтинга D51). § 19. Квазиплоскис волны вдоль
неидеальных проводвиков. Двухпроводная линия Лехера D52). § 20. Груп-
Групповая скорость D54)
Задачи .... . . .... .... ... . 455-
Литература 457
Глава XIV. Излучение электромагнитных волн 459
§ 1. Постановка задачи D59). § 2. Два типа вектор-потенциалов D00).
§ 3. Сферические электромагнитные волны. Диполь D00). § 4. Запазды-
Запаздывающие потепциалы DG2). § 5. Излучение линейной антеииы D04).
§ 6. Поля на больших расстояниях от линейпой антенны D07). § 7. Излу-
Излучение бегущей волны D09). § 8. Копическая линия передачи D69). § 9. Би-
коиическая антенна D71). § 10. Сложные антенны D74). § 11. Влияние
земли D70). § 12. Единственность решения D77). § 13. Решения волнового
уравнения в сферических координатах D77). § 14. Разложение плоской
волны по полиномам Лежандра D78). § 15. Излучение кольцевого тока.
Магнитный диполь D79). § 16. Свободные колебания проводящей сфе-
сферы D80). § 1.7. Выпужденные колебания диэлектрического или проводяще-
проводящего шара ^481). § 18. Решения волнового уравнения в пилиндрических коор-
координатах D84). § 19. Разложение плоской волны по цилиндрическим гар-
гармоникам D85). § 20. Излучение из отверстий в плоском проводящем экра-
экране D85). § 21. Диффракция на прямоугольном отверстии в проводящем
плоском экране D88). § 22. Ортогональные функции в задаче о диффрак-
ции. Излучение открытого конца коаксиальной линии D89).
Задачи 491
Литература . 500
Глава XV. Волнободы и полые резонаторы 501-
§ 1. Волны в полых цилиндрических трубах E01). § 2. Учет затухания
в волноводах E03). § 3. Прямоугольный волновод E05). § 4. Круглый вол-
604 Оглавление
повод E07). § 5. Коаксиальный волновод E09). § 6. Плоские неоднородно-
неоднородности в коаксиальной линии E10). •§ 7. Возбуждение волноводов E11)..
§ 8. Возбуждение круглого волновода элементом тока E12). § 9. Возбуж-
Возбуждение круглого волновода "петлей с током E14). § 10. Возбуждение круг-
круглого волновода через отверстие E15). § 11. Плоские неоднородности в пря-
прямоугольных волноводах E16). § 12. Полые резонаторы. Собственные коле-
колебания E19). § 13 Типы независимых собственных колебаний полости E20).
§ 14. Емкость и индуктивность цилиндрической полости E21). § 15. Зату-
Затухание собственных колебаний. Активное сопротивление полости E22).
§ 16. Собственные колебания цилиндрической полости E23). § 17. Свой-
стна прямоугольного резонатора E24). § 18. Свойства резонатора, имею-
имеющего форму круглого цилиндра E20). § 19. Многосвязные цилиндрические
полые, резонаторы E26). § 20. Отрезок коаксиального кабеля как резона-
резонатор E28). § 21. Собственные колебания в сферической полости E29).
§ 22. Собственные колебания реальных полых резонаторов E30). § 23. По-
Полые резонаторы сложной формы E31). § 24. Возбуждение полого резона-
резонатора петлей с током E34). § 25. Возбуждение круглого цилиндрического
резонатора петлей с током E36). § 26. Возбуждение полого резонатора при
помощи электрода E37). § 27. Возбуждение полого резонатора через от-
иерстие E39).
Задачи . .
Литература
Г дача XVI. Специальная теория относительности н движение заряженных
частиц 552
§ 1. Постулаты специальной теории относительности E52). § 2. Преобразо-
Преобразование Лоренца E52). § 3. Преобразование скорости и ускорения E53).
§ 4. Зависимость массы от скорости E54). § 5. Преобразование сил E55).
§ 6. Сила, действующая на заряд, движущийся в магнитном попе E57).
§ 7. Движение заряда в однородном магнитном поле E58). § 8. Энергия
движущейся заряженной частицы E59). § 9. Критическое магнитное поле
is магнетроне E59). § 10. Траектория космической частицы в однородном
поле E60). § 11 Магнитное поле движущегося заряда. E61). §12. Запазды-
Запаздывающие поля и потенциалы движущегося заряда E62). § 13. Излучение
равномерно ускоренного, прямолинейно движущегося электрона E63).
§ 14. Преобразование уравнений Максвелла E65). § 15. Определение ско-
скорости самолета относительно земли E66). § 16. Движение заряженной ча-
частицы в перекрещивающихся электрическом и магнитном полях E67).
§ 17. Аберрация и эффект Допплера E69).
Задачи ... 571
Литература . . . . . 573
Приложение. Системы электрических единиц . ... 574
Дополнительная литература . . 582
Предметный указатель . . . . 583
В. С м а й т, Электростатика и электродинамика
Редактор Е. И. МАЙКОВА. Художниц Н. А. Лгтин. Технический редактор Б. Ы. Ильин
Корректоры К. И. Иванова и А. II. Окорокова
Сдано в производство 2/IX 1053 г. Подписано к печати 28/XII 1953 г. Т-09087. Бумага
70xl08I/i6=lfl-0 бум. л. 52.1 печ. п. Уч.-адд. д. 55,1. Изд. № 2/1642. Цена 40 р. 55 к. Зак. 1216.
Издательство иностранное литератур ы. Москва, Ново-Алексеевская. 52.
16-я типография Союзполиграфпрома Главиздата Министерства культуры СССР.
Москва, Трехпрудный пер., 9 "
О П К Ч А Т К И
Стр.
Строка
Напечатано
Слеоует читать
391
445
483
49R
525
Формула A1.65)
Формула AЛ.102)
10 св.
1 си.
Формула A5.121)
1 д
"/•sin О <Э0
(sin О А)
, как Wfe — выражение
, как VK(e— в пыражепив
. те
В. Смайт
В СМАЙТ
ЭЛЕКТР ОС ТАТИКА
и
Э КТРОа НАМИК *