ББК 39.33-01я73 Г85
УДК 629.113(075.8)
Рецензенты: кафедра «Автомобили и двигатели» Завода-втуза при Московском автомобильном заводе имени И. А. Лихачева; д-р техн, наук проф. кафедры «Автомобили» .Московского автомобильно-дорожного института Я. Е. Фа-робин
ПЕРЕЙТИ К ОГЛАВЛЕНИЮ
Гришкевич А. И.
Г 85 Автомобили: Теория: Учебник для вузов.— Ми.: Выш. шк., 1986.— 208 с.: ил.
Изложены методы расчета параметров автомобиля, обеспечивающих заданные эксплуатационные свойства, и методика расчета оценочных характеристик. Описаны алгоритмы расчетов и программы.
Для студентов вузов, обучающихся по специальности «Автомобили и тракторы», может быть использован инженерами-автомобилест-роителями.
Г
3603030000—088
-------------о о—оо
М(304)05—86
ББК 39.33-01я73
(б) Издательство «Вышэйшая школа», 1986.
А.И. ГРИШКЕВИЧ
АВТОМОБИЛИ
Теория
Допущено
Министерством высшего и среднего
специального образования БССР в качестве учебника для студентов
специальности "Автомобили и тракторы" высшйх технических учебных заведений


Минск "Вышэйшая школа" 1986
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ.............................. 5
ВВЕДЕНИЕ ................................... 7
1.
ОСНОВЫ ТЕОРИИ КОЛЕСНОГО ДВИЖИТЕЛЯ
1.1.	Скорость движения автомобильного колеса............................. 10
1.2.	Момент сопротивления качению эластичного колеса в ведомом режиме ..................................15
1.3.	Уравнение движения колеса по не-деформнруемой поверхности . . .	16
1.4.	Сцепление колеса с дорогой ...	20
1.5.	Моделирование процесса движения автомобильного колеса на ЭВМ 25
3.
ТЯГОВЫЙ РАСЧЕТ АВТОМОБИЛЯ
3.1.	Техническое задание.................64
3.2.	Выбор характеристик двигателя	68
3.3.	Выбор параметров трансмиссии	71
3.4.	Особенности тягово-скоростных расчетов при наличии в трансмиссии гидромеханической передачи..................77
4.
ТОРМОЗНЫЕ СВОЙСТВА АВТОМОБИЛЯ
4.1.	Основные	определения...............86
4.2.	Замедление автомобиля при торможении ...................................88
4.3.	Оценка тормозных свойств автомобилей ...................................94
4.4.	Регулирование тормозных сил ...	98
2.
ТЯГОВО-СКОРОСТНЫЕ СВОЙСТВА И ТОПЛИВНАЯ ЭКОНОМИЧНОСТЬ АВТОМОБИЛЯ
2.1	Силы и моменты, действующие на автомобиль или автопоезд при прямолинейном движении....................27
2.2.	Окружная сила на ведущих колесах	28
2.3.	Силы сопротивления движению	35
2.4.	Нормальные реакции опорной поверхности .............................42
2.5.	Тяговый баланс автомобиля ...	43
2.6.	Оценка тягово-скоростных свойств автомобиля ..............................48
2.7.	Топливная экономичность автомобиля	54
2.8.	Влияние конструктивных и эксплуатационных факторов на тягово-скоростные свойства и топливную экономичность автомобиля.......................59
5. ПЛАВНОСТЬ ХОДА
5.1.	Основные характеристики подвески	103
5.2.	Характеристики дорожных неровностей ..................................108
5.3.	Критерии оценки плавности хода	113
5.4.	Расчетные схемы, применяемые при анализе плавности хода автомобилей	115
5.5.	Расчетные методы оценки плавности хода автомобилей.......................125
6.
УПРАВЛЯЕМОСТЬ И УСТОЙЧИВОСТЬ АВТОМОБИЛЯ
6.1.	Основные определения.............133
6.2.	Увод автомобильного колеса . . . 135
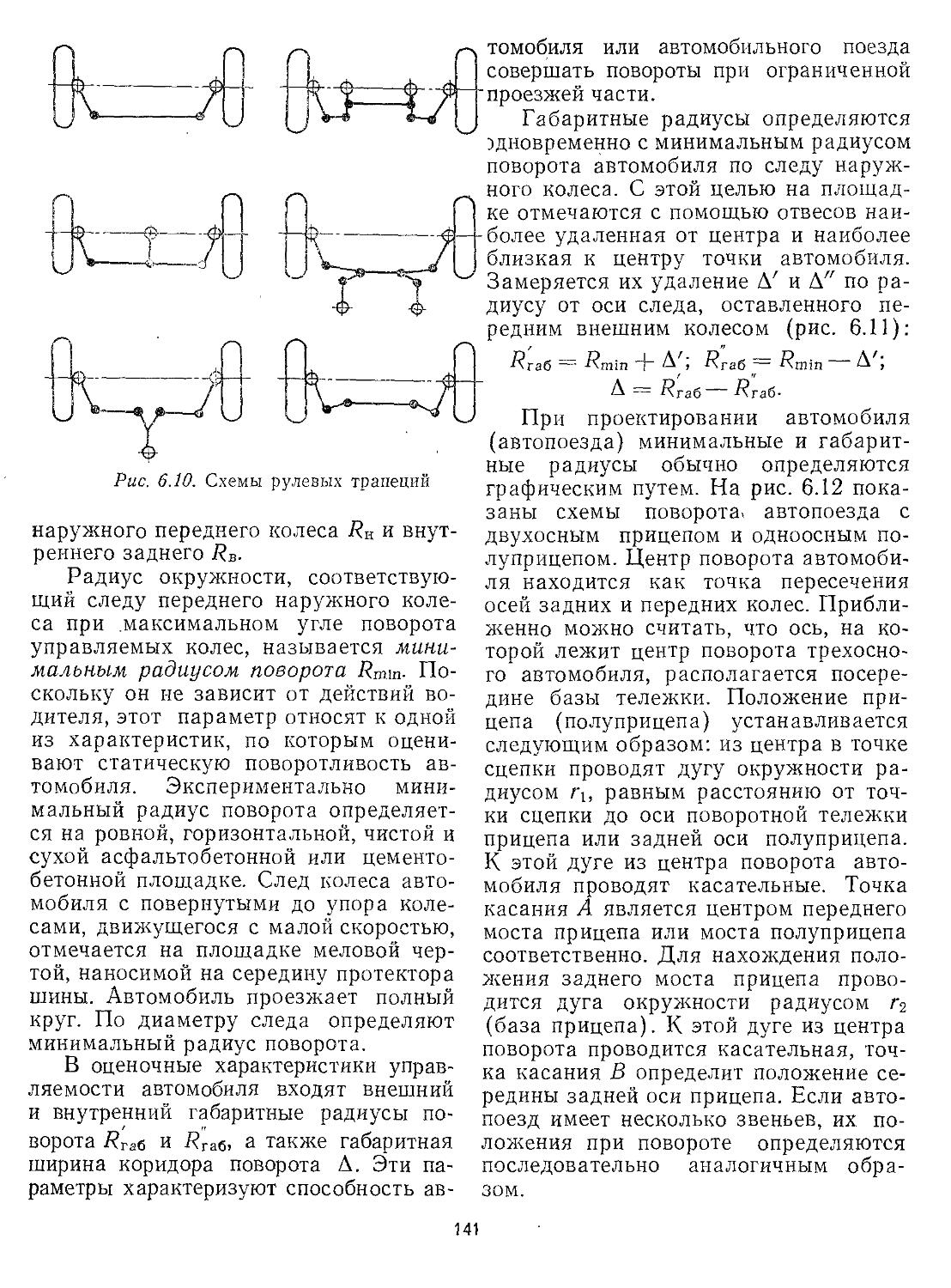
6.3.	Кинематика поворота автомобиля 139
6.4.	Силы, действующие на автомобиль при криволинейном движении . . . 144
3
6.5.	Траекторная н курсовая устойчивость автомобиля......................150
6.6.	Занос и опрокидывание автомобиля 163
7. ПРОХОДИМОСТЬ АВТОМОБИЛЯ
7.1.	Основные определения..............168
7.2.	Профильная проходимость .... 169
7.3.	Опорно-сцепная проходимость . . . 173
8.
МОДЕЛИРОВАНИЕ ПРОЦЕССА ДВИЖЕНИЯ АВТОМОБИЛЯ
8.1.	Общие принципы моделирования 185
8.2.	Основные характеристики автомобильных дорог....................187
8.3.	Методика построения модели автомобильной дороги...................194
8.4.	Моделирование динамики автомобиля и логики действий водителя . . . 200
Литература	205
Предметный указатель	206
ПРЕДИСЛОВИЕ
Важнейшей задачей народного хозяйства страны уже в первые годы Советской власти было создание автомобилестроения. Развитие его характеризуется несколькими этапами. В период становления автомобильной промышленности (1924...1931 гг.) были созданы первые советские автомобили АМО-Ф15 и Я-3, начала развиваться отечественная наука о проектировании автомобиля. При Высшем Совете народного хозяйства (ВСНХ) в 1918 г. была организована научная автомобильная лаборатория, на базе которой создан впоследствии головной научный центр автомобильной промышленности — Научно-автомоторный институт (НАМИ),— первые центры формирования научных кадров в области проектирования и исследования автомобильной техники. В этих центрах под руководством основателя советской автомобильной школы Е. А. Чудакова были начаты первые плановые работы по исследованию и испытанию автомобилей.
В период 1931...1945 гг. главное внимание уделялось созданию материальной базы для массового производства автомобилей. Были построены крупнейшие автомобильные заводы: Горьковский и Московский, значительно расширен Ярославский, а во время Великой Отечественной войны начал работать автомобильный завод на Урале. Уже в 1937 г. годовой выпуск автомобилей достиг 200 тысяч, что способствовало успешному выполнению пред
военных пятилеток и имело большое значение в победе советского народа в Великой Отечественной войне.
Послевоенный период характеризуется развитием автомобильной промышленности, строительством новых автомобильных и автоагрегатных заводов, увеличением выпуска автомобилей и повышением их качества.
В настоящее время автомобильная промышленность Советского Союза занимает одно из ведущих мест в мире.
Одним из основных факторов, определяющих качество создаваемого автомобиля, является уровень подготовки инженерных кадров, занятых его проектированием, изготовлением и испытанием. Инженеров-конструкторов и инженеров-испытателей для автомобильных заводов и научно-исследовательских организаций готовят автомобильные кафедры конструкторского профиля более двадцати высших учебных заведений страны. Кафедра «Автомобили» Белорусского ордена Трудового Красного Знамени политехни-Чс^иОго института подготовку специалистов указанного профиля ведет уже около 40 лет. Работа кафедры проходит в тесном сотрудничестве с конструкторскими отделами автомобильных заводов, и в первую очередь с заводами объединения БелАвтоМАЗ. В подготовке специалистов принимают участие сотрудники Минского автомобильного завода, работающие на заводской кафедре «Большегрузные автомобили».
5
Сотрудниками обеих кафедр подготовлен к изданию комплекс учебных пособий по дисциплинам: «Теория автомобиля», «Конструирование и расчет автомобиля», «Испытание автомобилей», «Специализированный подвижной состав», а также «Организация производства большегрузных автомобилей», читаемым в Белорусском политехническом институте. Предполагается, что комплекс под общим названием «Автомобили» будет состоять из восьми книг: «Теория», «Конструкция, конструирование и расчет. Трансмиссия», «Конструкция, конструирование и расчет. Системы управления и ходовая часть», «Основы проектирования», «Машины особо большой грузоподъемности», «Специализированный подвижной состав», «Испытания» и «Лабораторный практикум».
При создании комплекса учебных пособий авторы использовали отечественный и зарубежный опыт конструирования автомобилей, а также опыт подготовки инженеров в вузах страны и Белорусском ордена Трудового Красного Знамени политехническом институте.
В настоящем учебнике, являющемся первой книгой комплекса, рассмотрены основные свойства автомобиля, обеспечивающие его подвижность, описаны методы-расчетного и экспериментального определения измерителей и пока
зателей этих свойств, а также методы расчета параметров автомобиля с требуемыми показателями подвижности. В учебнике изложены все вопросы программы курса «Теория автомобиля» для специальности 0513 «Автомобили и тракторы» и вопросы, связанные с моделированием на ЭВМ. движения автомобиля. Применение моделирования движения для оценки эксплуатационных свойств автомобилей на стадии проектирования позволяет существенно уменьшить объем экспериментально-доводочных работ при создании новых конструкций или модернизации существующих.
При написании учебника использованы материалы научных работ, учебников и учебных пособий, опубликованных в отечественной и зарубежной печати. Основная использованная литература, а также литература, рекомендованная студентам для углубленного изучения отдельных разделов, приведена в конце книги.
Автор выражает благодарность рецензентам — кафедре «Автомобили и двигатели» Завода-втуза (при ЗИЛе) и профессору кафедры «Автомобили» Московского ордена Трудового Красного Знамени автомобильно-дорожного института Я- Е. Фаробину, сделавшим замечания, направленные на улучшение содержания комплекса учебных пособий.
Заслуженный деятель науки и техники БССР д-р техн, наук проф. А. И. Гришкевич
ВВЕДЕНИЕ
При проектировании автомобиля его конструкции придают определенные свойства, которые принято называть потенциальными. Степень реализации этих свойств, а соответственно и качество изделия, зависит от уровня конструкторской проработки, принятой технологии его изготовления, используемых материалов.
Для оценки свойств автомобиля применяют измерители и показатели. Измеритель характеризует свойство с качественной стороны, показатель — число, указывающее количественное значение измерителя. Показатель позволяет обычно оценить свойство автомобиля лишь при частном сочетании условий его работы. Поэтому для полной оценки рассматриваемого эксплуатационного свойства в достаточно широком диапазоне условий применяют несколько показателей.
Различают две группы основных свойств, имеющие принципиально разную природу. Первая группа — функциональные свойства, вторая — свойства надежности.
Функциональные свойства автомобиля обеспечивают изделию возможность выполнять свои функции, определяемые его назначением. Применительно к автомобилю эти свойства называют эксплуатационными. Автомобиль может выполнять свои функции, если он будет находиться в работоспособном состоянии, т. е. в том случае, когда значения всех параметров, характеризующих способ
ность выполнять заданные функции, соответствуют требованиям нормативно-технической или конструкторской документации.
Свойства надежности — группа свойств, которая характеризует способность автомобиля сохранять работоспособное состояние. Они определяются сочетанием свойств: безотказности, долговечности, ремонтопригодности, сохраняемости. Безотказность —• свойство автомобиля сохранять работоспособное состояние в течение некоторого времени (наработки). Долговечность характеризует способность автомобиля сохранять работоспособное состояние до наступления предельного при установленной системе технического обслуживания и ремонта. Ремонтопригодность оценивает приспособленность автомобиля к предупреждению и обнаружению причин возникновения отказов, повреждений и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонта. Сохраняемость — свойство автомобиля сохранять безотказность, долговечность и ремонтопригодность в течение хранения и позже.
Для суждения о возможности использования того или иного автомобиля в заданных условиях эксплуатации выработан ряд критериев, позволяющих объективно оценить соответствие существующей или перспективной конструкции автомобиля предъявляемым требованиям. В качестве основного критерия, характеризующего эффек
7
тивность эксплуатации автомобиля, используют относительные затраты на перевозку 1 т груза или одного пассажира. Эти показатели зависят не только от конструкции автомобиля, но и ряда других факторов: дорожных условий, уровня организации перевозок, технического обслуживания и ремонтов. Критерием, более тесно связанным с конструкцией автомобиля и достаточно полно характеризующим эффективность его использования, является производительность. Последняя определяется грузоподъемностью или пассажировместимостью автомобиля и средней технической скоростью.
Грузоподъемность — максимальная масса груза, перевозимого автомобилем; зависит от размеров и прочности основных несущих узлов и агрегатов шасси. При ограничении по дорожным условиям полной массы автомобиля грузоподъемность его определяется снаряженной массой. Поэтому оценку грузоподъемности автомобиля производят по массе перевозимого груза тт и коэффициенту использования грузоподъемности kT, представляющему отношение массы перевозимого груза к полной массе автомобиля. Чем выше этот коэффициент, тем более совершенна конструкция грузового автомобиля.
Возможность полного использования грузоподъемности автомобиля зависит от размеров кузова и плотности предполагаемого к перевозке груза. Удельная объемная грузоподъемность — отношение грузоподъемности к вместимости кузова. По ней можно судить о степени использования грузоподъемности автомобиля при перевозке грузов различной плотности.
Пассажировместимостью называется количество пассажиров, которые могут одновременно перевозиться в автобусе или легковом автомобиле. Она зависит от прочности деталей и узлов шасси, кузова и от размеров пассажирского помещения. При этом каждое пассажирское место должно
соответствовать установленным требованиям к габаритным размерам сидений и размерам свободного пространства перед и над ними. Измерителями пассажировместимости являются: количество пассажирских мест (номинальная пассажировместимость); площадь пола автобуса, приходящаяся на одно место для сидения; площадь пола городского автобуса для проезда пассажиров стоя. Вместимость (номинальная) легкового автомобиля определяется количеством пассажирских мест.
Средняя техническая скорость автомобиля характеризует его способность доставлять грузы или пассажиров с минимальными затратами времени. Она зависит от тягово-скоростных и тормозных свойств автомобиля, его управляемости и устойчивости, плавности хода, проходимости.
Следовательно, эксплуатационные свойства автомобиля' могут быть подразделены на две группы. Свойства первой группы связаны с компоновочными характеристиками автомобиля и особенностями его использования при эксплуатации, а свойства второй группы обеспечивают подвижность автомобиля.
В теории автомобиля изучаются функциональные свойства автомобиля, связанные с его подвижностью. Ее задачей является разработка методов расчета конструктивных параметров, при которых обеспечивается требуемая подвижность автомобиля в заданных условиях эксплуатации.
Основные положения теории автомобилей как науки были разработаны Е. А. Чудаковым и сформулированы в учебнике «Теория автомобиля», впервые вышедшем в 1935 г. В последующем отдельные разделы теории автомобиля получили дальнейшее развитие в трудах многих советских и зарубежных ученых.
Совершенствование методов расчета тягово-динамических и топливноэкономических свойств автомобиля на
8
шло отражение в трудах Зимеле-ва Г. В., Фалькевича Б. С., Яковлева Н. А. Вопросы управляемости и устойчивости автомобиля разрабатывались Литвиновым А. С., Певзнером Я- М., методы расчетов плавности хода и обоснование выбора параметров автомобиля как колебательной системы — Ротенбергом Р. В., Певзнером Я- М. и др. В работах Бухарина И. А., Фрумкина А. К- изложены методы расчета тормозной динамики автомобиля.
Использование ЭВМ для расчетов параметров проектируемого автомобиля позволило существенно повысить достоверность расчетов, результаты которых в этом отношении стали близки к результатам натурных испытаний. Для наиболее полного использования возможностей ЭВМ потребовалось разработать новые методики аналитических расчетов, основанные на теории вероятностей и теории случайных процессов. Созданию общей теории системы водитель — автомобиль — дорога предшествовало создание представительных математических моделей отдельных звеньев системы. Разработка этих моделей, их исследование и уточнение— результат многолетней работы
коллективов научно-исследовательских институтов, конструкторских бюро автомобильных заводов, кафедр высших учебных заведений.
Применение теории случайных процессов к исследованию характеристик автомобиля впервые в комплексном виде было изложено в работах Пархи-ловского И. Г. и коллектива научных работников под руководством Хачатурова А. А. Методы расчетов характеристик управляемости автомобиля получили дальнейшее развитие в работах Антонова Д. А., Иларионова В. А., Фаробина Я- Е. Разработке современных методов оценки проходимости автомобилей посвящены работы Агейкина Я- С., Безбородовой Г. Б. Большой вклад в развитие1 теории автомобиля сделали зарубежные ученые М. Мич-ке, Дж. Вонг и др.
Необходимо отметить, что «Теория автомобиля» является относительно молодой наукой и многие ее разделы нуждаются в дальнейшей разработке и уточнении. На современном этапе основным направлением в развитии теории автомобиля следует считать разработку методов оптимизации его параметров с помощью электронно-вычислительных машин.
(ОСНОВЫ ТЕОРИИ КОЛЕСНОГО ДВИЖИТЕЛЯ
1.1.	Скорость движения автомобильного колеса
Прежде чем приступить к изучению закономерностей движения автомобиля, необходимо рассмотреть основные зависимости, связанные с работой одного из его важнейших устройств •— колеса. Колесо с пневматической шиной является характерным движителем автомобиля. Под движителем понимается рабочий механизм, взаимодействующий с опорной поверхностью дороги и обеспечивающий передвижение мобильной машины. Известны различные типы движителей: колесный, гусеничный, шнековый, шагающий и др. Характерная особенность автомобиля заключается в том, что его движителем является система колес с эластичными пневматическими шинами.
На автомобильное колесо, взаимодействующее с опорной поверхностью, действуют силы, которые удерживают автомобиль на дороге, передвигают и останавливают его, заставляют изменить направление движения. В процессе взаимодействия колеса с опорной поверхностью деформируется в различных направлениях как колесо, так и опорная поверхность. В зависимости от соотношения деформации колеса и опорной поверхности возможны следующие условные виды движения колеса: 1) эластичного (деформируемого) колеса по недеформируемой поверхности; 2) жесткого (недеформируе-мого) колеса по деформируемой поверхности; 3) деформируемого колеса по деформируемой поверхности.
К первому виду движения можно
относить случаи, когда деформация опорной поверхности значительно меньше деформации шины, что наиболее характерно для автомобиля как транспортного средства, предназначенного для движения по дорогам с твердым покрытием.
Второй вид движения наиболее часто наблюдается при работе трактора на рыхлых или болотистых почвах, при движении автомобиля по снежной целине или сыпучему песчаному грунту.
В некоторых условиях деформации колеса и опорной поверхности соизмеримы, например при движении автомобиля с пониженным давлением воздуха в шинах по грунтам с малой несущей способностью (пашня, размокший грунт и др.).
Автомобильное колесо может катиться прямолинейно (при прямолинейном движении автомобиля) или криволинейно (при повороте автомобиля).
Ниже рассматривается прямолинейное движение автомобильного колеса по недеформируемой поверхности. При этом считается, что все силы и моменты, действующие на колесо, располагаются в вертикальной плоскости.
Особенности работы колеса в других условиях движения будут рассмотрены в соответствующих разделах.
Пневматическая шина представляет собой тонкостенную оболочку, наполненную сжатым воздухом. При качении колеса по дороге происходит деформация этой оболочки и проскаль
10
зывание элементов протектора относительно поверхности дороги.
Размер автомобильного колеса в свободном, ненагруженном состоянии характеризуется свободным радиусом гс. Свободный радиус колеса — половина наружного диаметра Da: гс = = 0,5 Он.
Под наружным диаметром колеса понимается диаметр наибольшего окружного сечения беговой дорожки колеса при отсутствии контакта с дорогой. Наружный диаметр колеса зависит от давления воздуха в шине и, как правило,возрастает с его увеличением, определяется непосредственно замером. Значение наружного диаметра колеса при номинальном давлении воздуха в шине указывается в ГОСТах или каталогах.
При действии на колесо вертикальной нагрузки происходит деформация части шины, соприкасающейся с опорной поверхностью., При этом расстояние от оси колеса до опорной поверхности становится меньше свободного радиуса. Это расстояние, замеренное у неподвижного колеса, называется статическим радиусом rCt. Статический радиус при номинальных нагрузках и давлении воздуха в шинах также указывается в их характеристиках. Обычно шины конструируют таким образом, чтобы при номинальных нагрузке и давлении прогиб шины составлял 13... 20 % от высоты профиля. Статический радиус при известных конструктивных параметрах шин можно находить из соотношения:
//'ст = 0,5 d-\-'kzH, где d — посадочный диаметр обода шины; /.z— коэффициент вертикальной деформации, зависящий от типа шин: для тороидных шин Xz = 0,85...0,87; для шин с регулируемым давлением и арочных /,2 = 0,8...0,85; Н — высота профиля.
При качении нагруженного колеса в силу ряда причин (динамическое действие нагрузки, передаваемый ко-
Рис. 1.1. К определению скорости колеса лесом крутящий момент, скорость вращения и др.) расстояние между осью колеса и опорной поверхностью меняется. Это расстояние называют динамическим радиусом гЛ. При качении колеса по твердой опорной поверхности с малой скоростью статический и динамический радиусы его практически одинаковы. Поэтому при приближенных расчетах динамический радиус часто принимают равным статическому.
Для вывода основных кинематических соотношений представим протектор колеса в виде плоской недеформи-руемой в тангенциальном направлении ленты, как это показано на рис. 1.1. При качении колеса его точки участвуют в двух видах движения: переносном вместе с осью и автомобилем, совершаемом со скоростью их, и относительном — относительно оси колеса. Абсолютная скорость любой точки, например точки А, может быть найдена сложением этих скоростей:
Va = vx+voA, где voA — скорость перемещения точки А относительно оси колеса.
Относительная скорость точки А, расположенной на периметре колеса,
VoA = СОкГ с, где (ок — угловая скорость вращения колеса.
В силу принятого допущения о не-деформируемости в тангенциальном направлении протектора колеса такую
11
Рис. 1.2. Тангенциальная деформация шины от вертикальной нагрузки:
4- — зона сжатия
Рис. 1.3. Зависимость радиуса качения колеса в ведомом режиме от его нагрузки
же скорость будут иметь все принадлежащие протектору точки (например, точка В, находящаяся в контакте с опорной поверхностью). Поскольку в зоне контакта векторы относительной и абсолютной скоростей располагаются по одной прямой, абсолютная скорость точек шины, находящихся в зоне контакта,
=	УоА'
Поступательную скорость оси колеса vx можно выразить через его угловую скорость:
Пх = СОцГ к,	(1.1)
где гк— радиус качения колеса.
Радиус качения колеса можно представить как радиус условного недефор-мируемого кольца, которое, катясь без скольжения, совершит число оборотов и пройдет путь, одинаковый с реальным колесом. Радиус качения колеса является условной величиной и непо
средственно не связан с его размерами. Он определяется как отношение поступательной скорости колеса к угловой скорости его вращения:
к= Пх/<ЙК-
При качении колеса на него могут действовать крутящий момент и толкающая сила. Если колесо катится под действием только толкающей силы, такое колесо называют ведомым. Радиус качения колеса в ведомом режиме гко не равен свободному его радиусу, поскольку при действии на шину вертикальной нагрузки происходит сжатие протектора в тангенциальном направлении по нижней полуокружности шины (рис. 1.2). Поэтому периметр колеса в нагруженном состоянии оказывается меньше периметра свободного колеса. Этому способствует и то, что точки протектора, находящиеся на различном расстоянии от центральной плоскости колеса, имеют неодинаковые относительные скорости. Поэтому в зоне контакта тангенциальные деформации шины также оказываются различными по ее ширине.
Радиус качения колеса в ведомом режиме можно определить по экспериментально установленной зависимости: г .. rePs+vlFz ' кО — ' с
'сРв + V2F2 ’
где рв — давление воздуха в шине, . МПа; Fz — нагрузка, приходящаяся на шину, кН; vi, V2 — константы, определяемые экспериментально (v2>vi).
Характер изменения радиуса колеса в ведомом режиме от нагрузки показан на рис. 1.3.
При номинальных давлении и нагрузке радиус качения колеса в ведомом режиме больше его статического радиуса и меньше радиуса колеса в свободном состоянии. При расчетах его можно принимать равным 0,95...0,97 свободного радиуса.
Реальное автомобильное колесо в тангенциальном направлении не явля-
12
ется абсолютно жестким. Под воздей- а ствием передаваемого крутящего момента протектор деформируется в тангенциальном направлении. Если направление передаваемого момента совпадает с направлением угловой скорости колеса, элементы шины, находящиеся в набегающей полуокружности, подвергаются сжатию, а с противоположной стороны — растяжению, как это показано на рис. 1.4. На этом же рисунке показана эпюра тангенциальных напряжений в протекторе шины.
Элементы шины, находящиеся в контакте с опорной поверхностью, нагружены в тангенциальном направлении неодинаково: элементы, входящие в контакт, сжимаются, а выходящие —• растягиваются. При возрастании передаваемого крутящего момента увеличивается площадь, в пределах которой происходит проскальзывание шины относительно дороги (рис. 1.5). При некотором значении момента начинается одновременное перемещение всех находящихся в зоне контакта точек колеса. Перемещение части точек колеса, находящихся в контакте с дорожным покрытием, относительно опорной поверхности, когда в зоне контакта есть точки, неподвижные относительно этой поверхности, называется упругим проскальзыванием колеса. Одновременное же перемещение всех находящихся в контакте точек колеса называется скольжением колеса.
Вследствие упругого проскальзывания или скольжения путь, проходимый колесом за один оборот, оказывается меньшим, чем путь, проходимый в ведомом режиме. При возрастании передаваемого крутящего момента увеличивается тангенциальная деформация шины, скольжение и уменьшается путь, проходимый колесом за один оборот. В соответствии с принятым выше определением, уменьшение пути перемещения центра колеса за определенное число его оборотов равносильно уменьшению радиуса качения. Если
Рис. 1.4. Деформация шины (а) и эпюра напряжений в протекторе (б) при приложении к колесу крутящего момента:
4--зона сжатия;---зона растяжения
Рис. 1.5. Зависимость площади скольжения колеса (заштрихованная зона) от передаваемого им момента Л4К:
а Л<к = 0; б — Мк = 0.46Мктах. в Мк= 0,ДМ[<тах. г ~	= ^ктах
направление передаваемого момента будет противоположным направлению угловой скорости вращения колеса (тормозящее колесо), при увеличении момента радиус качения будет возрастать.
Зависимость радиуса качения колеса от передаваемого ему крутящего момента показана на рис. 1.6. На участке 2—3 радиус качения линейно зависит от передаваемого момента, и его изменение определяется упругим про-
13
о
Рис. 17. Экспериментальная зависимость радиуса качения колеса от передаваемого момента для шины ОИ-25 14,00—20:
А —рв=0,36 МПа, Рг = 13 кН;Лт =0,00765 м/(кН  м); □ —рв = 0,36 МПа, f^=40 кН,хт =0,0039 м/(кН-м); О —рв=0,18 МПа, Гг=13 кН, ZT — 0,0065 м/(кН • м)
Рис. 1.6. Зависимость радиуса качения колеса от передаваемого им момента
скальзыванием колеса. Акад. Е. А. Чудаковым, впервые установившим эту зависимость, предложена следующая формула для нахождения радиуса качения по передаваемому колесу моменту:
т/ /'к = /'кО 7.тА1в,	(1-2)
где гк0 — радиус качения при нулевом крутящем моменте, который соответствует радиусу качения колеса в ведомом режиме; 7.т — коэффициент тангенциальной эластичности шины, зависящий от типа и конструкции шины.
На участках 1—2 и 3—4 изменение радиуса качения определяется как упругим проскальзыванием, так и скольжением колеса. Пунктирной линией на графике показано, как изменялся бы радиус качения при отсутствии скольжения. Очевидно, что на участках 1—2 и 3—4 он может находиться также по формуле (1.2). В последующем радиус качения, определенный при отсутствии скольжения, будем называть радиусом качения без скольжения и обозначать rQ.
На участках 0—1 и 4—5 происходит полное скольжение элементов шины относительно опорной поверхности. Точка 5 соответствует буксующему колесу при неподвижном автомобиле, а точка 0 — колесу, движущемуся юзом.
На рис. 1.7 показаны некоторые зависимости радиуса качения от переда
ваемого крутящего момента, полученные в лабораторных условиях. Если обозначить радиусы качения и передаваемые колесом моменты в начале и в конце линейного участка соответственно через Мч, гк? и М3, гк3, то коэффициент тангенциальной эластичности шины
л __ гк2 гкЗ
Т~|М2|-|М3|-
Экспериментально радиус качения находят путем определения числа оборотов колеса N на отрезке пути s при заданном режиме движения:
Гк = 5/(2лА).
Согласно рис. 1.1, скорость точки В (скорость us) можно рассматривать как скорость скольжения элементов шины относительно опорной поверхности. В соответствии с принятыми обозначениями
Vs = Иц (/'к — Го) •
Отсюда следует, что при гк = г0 колесо катится без скольжения. Если гк>г0, скорость скольжения положительна и ее направление совпадает с направлением поступательной скоро-
14
Рис. 1.8. Положения мгновенных центров вращения колеса
сти колеса (колесо движется юзом). При гк<Го скорость скольжения отрицательна и направлена в сторону, противоположную вектору поступательной скорости центра колеса (колесо движется с буксованием).
На рис. 1.8 показаны планы скоростей для рассмотренных трех случаев качения колеса. Из рисунка следует, что радиус качения является расстоянием от центра колеса до его мгновенного центра вращения Ot и в зависимости от режима движения может изменяться от нуля (буксующее колесо при неподвижном автомобиле) до бесконечности (заблокированное колесо при движущемся автомобиле).
1.2.	Момент сопротивления качению эластичного колеса в ведомом режиме
Шина деформируется под действием нормальной к опорной поверхности составляющей нагрузки на колесо (нормальной нагрузки). Площадь контакта ее с дорогой увеличивается до тех пор, пока не наступит равновесие между подъемной силой (нормальной реакцией дороги) и нагрузкой. У неподвижной шины контактная поверхность имеет форму, близкую к эллипсу, большая ось которого находится в плоскости симметрии шины. Распределение давления по площади контактной поверхности неравномерное, оно примерно пропорционально деформа
ции шины. Характерная эпюра давлений под неподвижной шиной показана на рис. 1.9, а.
При движении автомобильного колеса в работе участвуют все элементы шины. За один оборот колеса каждый элемент профиля шины, например элемент b — b (рис. 1.10, а), подвергается полному циклу нагружения и разгрузки.
С достаточной для практической цели точностью можно считать, что нагружение (деформирование) элементов шины происходит в зоне полуокружности 0—1—2. а восстановление формы — полуокружности 2—3—0. При этом наиболее интенсивное деформирование и восстановление происходят в зонах полудуг 1—2 и 2—3 соответственно.
По мере перемещения элемента шины от точки 1 к точке 2 увеличивается его деформация и, следовательно, воспринимаемая им нагрузка. Зависимость нагрузки AF, передающейся на элемент, от его деформации представлена на графике рис. 1.10, б (линия 1—2). При перемещении элемента от точки 2 к точке 3 происходит уменьшение деформации (уменьшение нагрузки, приходящейся на элемент). На графике линия, характеризующая зависимость AF=7(/i) вследствие неизбежных гистерезисных потерь пройдет ниже линии, показывающей ту же зависимость при увеличении деформации (линия 2—3). Площадь, заключенная между
15
Рис. 1.9. Эпюры давлений: а — неподвижной шины; б — катящейся
Рис. 1.10. Деформация элементов шины при качении
линиями нагружения и разгрузки, пропорциональна потерям энергии на деформацию элемента шины при одном обороте колеса.
Вследствие того что при одинаковых прогибах в зонах увеличения и уменьшения деформации на элементы шины приходится разная нагрузка, эпюра давлений для катящегося колеса оказывается несимметричной отно
сительно середины контактной поверхности: в передней части контактной поверхности нормальные давления будут большими, нежели в задней. Поэтому равнодействующая нормальных реакций смещена на расстояние а от середины контактной поверхности (см. рис. 1.9, б). За счет этого смещения создается момент относительно оси колеса
Mf^aRz,
где Rz — нормальная к опорной поверхности составляющая реакции дороги.
Этот момент препятствует качению колеса. Поэтому его можно считать моментом сопротивления качению колеса. Из приведенного видно, что на недеформируемой поверхности момент сопротивления качению обусловлен внутренними (гистерезисными) потерями энергии на деформацию шины.
1.3.	Уравнение движения колеса по недеформируемой поверхности
Схема сил и моментов, действующих на колесо, катящееся по недеформируемой поверхности, показана на рис. 1.11. На схеме обозначены: F? — нормальная нагрузка колеса, представляющая перпендикулярную к опорной поверхности составляющую всех сил, приложенных к колесу со стороны автомобиля, включая вес колеса; Fx — продольная сила колеса, т. е. составляющая равнодействующей сил, приложенных к колесу со стороны автомобиля, параллельная опорной поверхности (считается положительной, если ее направление совпадает с направлением поступательной скорости колеса); Rx — продольная составляющая реакции дороги; Rz — нормальная составляющая реакции дороги, смещенная относительно середины контактной поверхности на расстояние а; Мк — момент, действующий на колесо со стороны автомобиля (положителен, если его направление совпадает с направлением
16
Рис. 1.11. Силы и моменты, действующие на катящееся колесо
угловой скорости колеса); Мкз — момент сопротивления ускорению вращения колеса.
При составлении схемы сил учитывалось, что автомобильное колесо не может перемещаться в продольном направлении относительно кузова. Поступательное движение колеса можно рассматривать совместно с движением всего автомобиля, а продольную силу Fx считать передающейся от колеса к автомобилю, масса которого включает и массу колес.
Для нахождения характеристик движения колеса составим уравнение мощностей (при этом для общности будем считать, что мощность подводится к колесу через крутящий момент и продольную силу и затрачивается на преодоление сопротивления качению, сопротивления, обусловленного проскальзыванием элементов шины относительно опорной поверхности, и сопротивления разгону колеса):
Р« + Px = Pf + Ps + PKj,	(1.3)
где Рк — мощность, подводимая к колесу посредством момента Мк:
Рк = Мкак‘,	(1Д)
Рх — мощность, подводимая к колесу через толкающую силу Fx:
Px=Fxvx=FxrRaR-, (1.5)
Pf — мощность, затрачиваемая на преодоление сопротивления качению:
Р/ = Л>К;	(1.6)
PKj — мощность, затрачиваемая на разгон колеса:
Ркз=Мкзсок;	(1.7)
Ps — мощность, рассеиваемая в зоне контакта колеса с опорной поверхностью:
Ps= |PxVs| = |РхСОк (Гк-Го) |.	(1-8)
В последнем выражении мощность, рассеиваемая в зоне контакта колеса с опорной поверхностью, определяется произведением силы, действующей в этой зоне по направлению скорости скольжения, на скорость скольжения. Поскольку эта мощность рассеивается, произведение Rxvs как при буксовании, так и при юзе колеса всегда положительно.
Из схемы сил, приведенной на рис. 1.11, следует, что
RX=FX.	(1.9)
Тогда выражение (1.3) с учетом зависимости (1.9) можно преобразовать следующим образом:
— = —Рг-Рх + -^.	(1.10)
rQ г0	Г0
Введем обозначения:
— = FK; — = Л /рг = Ff, = FKj.
rQ	ro	ro
При принятых обозначениях выражение (1.10) запишется в	и
Fk+Px	' ^(1.1Г)
где FK — окружная сила колеса; Ff—-сила сопротивления качению колеса; Ркз- — сила сопротивления разгону колеса.
Закономерность, устанавливаемая уравнением (1.11), формулируется следующим образом: в общем случае движения сумма продольной и окружной сил колеса равна сумме сил сопротивления качению и разгону.
17
Рис. 1.12. Режимы качения колеса
vx
колесом и рамой автомобиля в продольном направлении. Участок 3—4 характеризуется действием положительной силы FK, а продольная сила передается от колеса на раму автомобиля (ведущий режим). Следует отметить, что при установившемся движении по горизонтальной поверхности нейтральный и свободный режимы качения могут быть только у колес мно-v гоприводных автомобилей.
Рассмотрим характерные режимы движения автомобильного колеса (рис. 1.13). Уравнение движения ведог мого колеса

Fx=Ff+FK5-,
Рис. 1.13. Силы и моменты, действующие на ведомое колесо
При равномерном движении сопротивления разгону колеса нет и
FK + Fx = F/.	(М2)
Графически зависимость (1.12) представлена на рис. 1.12. На участке 1—2 колесо катится под действием продольной силы Fx. Сила FK направлена в сторону, противоположную движению колеса. Такой режим качения называют тормозным. В точке 2 сила Гк равна нулю, колесо движется только под действием продольной силы — это соответствует ведомому режиму качения; на участке 2—3 на колесо действуют продольная и окружная силы (нейтральный режим движения), а в точке 3 — только окружная сила. Этот режим называют свободным: отсутствуют силы взаимодействия между
в развернутом виде
dt ’
О
где 7К — момент инерции колеса.
При равномерном движении Fx = = Ff. Поэтому можно дать следующее определение: сила сопротивления качению колеса численно равна силе, которую необходимо приложить в продольном направлении к оси колеса для того, чтобы обеспечить его равномерное качение.
Сила сопротивления качению вводится в расчет условно. Ранее было дано понятие момента сопротивления качению. Поэтому под силой сопротивления качению можно понимать силу, которую необходимо приложить к оси колеса в продольном направлении для преодоления момента сопротивления качению. Следовательно,
Mf = aRz = r0Pz = fr0Rz-го
Толкающая сила Fx и продольная составляющая реакции дороги Rx образуют пару сил, обеспечивающих качение колеса. Поскольку значение Rx ограничено трением между колесом и дорогой, соответственно будет ограничен и момент, при котором возможно качение колеса. В частности, для обес-
18
Рис. 1.14. Силы и моменты, действующие на ведущее колесо
печения качения колеса при установившемся режиме движения необходимо, чтобы соблюдалось условие Fxs^Rx max. Максимальное значение продольной составляющей реакции дороги
Rx тах = <pRz,
где ф — коэффициент, определяющий трение между шиной и опорной поверхностью дороги. Он называется коэффициентом сцепления.
Тогда условие качения колеса будет иметь вид
Fx=Ff^((>Rz или/^ф.	(1-13)
X Это значит, что ведомое колесо будет катиться, если коэффициент сопротивления качению не превышает коэффициент сцепления. Если это условие не соблюдается, колесо движется юзом (например, движение автомобиля по гладкому льду при пониженном давлении воздуха в шинах). Поскольку обычно коэффициент сопротивления качению значительно меньше коэффициента сцепления, качение ведомого колеса обеспечивается.
\ В едущее колесо катится под действием крутящего момента (рис. 1.14). При этом на раму автомобиля передается сила, совпадающая по направлению со скоростью автомобиля, а на колесо действует противоположно направленное усилие. Усилие, передающееся от колеса на раму автомобиля,
называется силой тяги колеса (FT). Так как FT = — Fx, уравнение движения ведущего колеса запишется в виде:
л Ек=FT + Ff-J-Fitj или FT = FK F/ — F^j., <-------- ------------------ (1.14)
Это значит, что сила тяги колеса равна окружной силе за вычетом силы сопротивления качению и силы, затрачиваемой на разгон колеса.
Максимальный момент, который может быть реализован ведущим колесом по условиям сцепления, находится из уравнения (1.14) с учетом равенства Rx =FT:
FK = Rx + F	г о;
Мк max — Rx max^oF F/ro + Alj;
44 K max = (ф f) Rz?0 4“ 4K •
При установившемся движении
44I; max = (ф+№г0.	(1.15)
Максимальный момент, который колесо может реализовать по сцеплению, будем обозначать М9. Если крутящий момент, подводимый к колесу, будет больше определяемого выражением (1.15), начнется ускоренное вращение колеса.
Ведущее колесо автомобиля является механизмом, преобразовывающим вращательное движение колеса в поступательное движение автомобиля. Поэтому к ведущему колесу, как любому механизму, передающему или преобразовывающему энергию, применимо понятие коэффициента полезного действия (КПД):
T]k = Fx/Fk,
где Рх — мощность, передаваемая от колеса к раме автомобиля; Рк — мощность, подводимая к колесу.
При движении автомобиля с постоянной скоростью
Ft<Vk FT Лк
Пк = —------= —-----•
F к Г0
Отношение FT/FKo можно рассматривать как силовое передаточное число,
19
Рас. 1.15. Силы и моменты, действующие на тормозящее колесо
а отношение гк/г0 — как кинематическое. Тогда КПД ведущего колеса будет равен произведению силового и кинематического передаточных чисел.
Учитывая соотношение (1.15) и считая /7к; = 0, для ведущего колеса можно записать:
где Ff/FK — относительные силовые потери; (г0 — гк)/г0 — относительные кинематические потери.
\ У тормозящего колеса движущей является толкающая сила, передающаяся от рамы автомобиля, а момент Мх, который будем называть тормозным, направлен в сторону, противоположную вращению колеса (рис. 1.15).
Учитывая, что Л1Т =—Мк, уравнение движения колеса в тормозном режиме будет:
'	+ Ff + Fк) — Fx-\- Ff + F^
где Fx — тормозная сила.
При торможении, как правило, колесо вращается с замедлением. Если обозначить скорость автомобиля при торможении их, а угловую скорость вра-dr	Ац
щения колеса <йт, то ---------------;
dt	dt
do>T	d(oK
	= -	. Угловое замедление ко-dt--------dt
леса при торможении
da>_ rn [ Мх	\
~Г{—-Fx + fRz > (1-16) 'к\ г0	/
причем FX = RX.
Учитывая, что в режиме торможения, так же как и при других режимах движения автомобиля, продольная реакция опорной поверхности ограничена сцеплением, максимальный тормозной момент, который реализуется колесом,
•Л^гтах — (ф f) PzT0 4“ 7к —.
Для практических расчетов иногда используют зависимость
Мх max — tyRzf О-
1.4.	Сцепление колеса с дорогой
Установленную в параграфе 1.1 зависимость радиуса качения колеса от передаваемого крутящего момента удобно представить не в абсолютных, а относительных показателях. С этой целью произведем преобразование общего уравнения движения автомобильного колеса. Разделив все члены уравнения (1.11) на Rz, получим
Ук — kx+f+yj,	(1.17)
где ук — удельная тангенциальная сила:
Yk = Fk/Rz=Mr/ (г oRz) ;
kx — коэффициент продольной силы колеса:
kx=Rx/Rz— FxfRz",
Уз — удельная инерционная сила колеса:
Rz r0Rz dt
Для случая установившегося движения kx = yK—f.
Если обозначить скорость поступательного движения центра колеса при отсутствии проскальзывания или скольжения через t>xo, то выражение (1.1) можно записать в виде
Ох0 = f о<йк, а реальную скорость поступательного
20
движения оси колеса наити по выражению
vx = vx0±vs, где знак минус принимается, если колесо является ведущим, а плюс — ведомым или тормозящим.
Скольжение колеса удобно характеризовать коэффициентом скольжения 5 — отношением скорости скольжения к скорости качения колеса без скольжения при ведущем режиме или реальной скорости при тормозном режиме.
В ведущем режиме:
VS	vxO~vx	г0~гк
86 = --= -------=---------»
vx0 vx0	r0
в тормозном:
vs	vx~vxO	rK-r0
s = — =---------=---------.
vx	vx
Коэффициент скольжения может изменяться от нуля до единицы. Так, при ведущем и тормозном режимах при отсутствии скольжения (гк=Го) V коэффициент скольжения равен нулю, \Ка при полном скольжении — единице. /При ведущем режиме полное скольже-। ние будет при буксующем колесе и неподвижном автомобиле (гк=0), а при 1 тормозном режиме — при движении колеса юзом (гк=оо).
Используя полученные соотношения, можно построить график зависимости коэффициента продольной силы от коэффициента скольжения (рис. 1.16.), аналогичный показанному на рис. 1.6. Правая часть графика соответствует ведущему режиму качения колеса, левая — тормозному, линейный участок — линейному участку зависимости (см. рис. 1.6). На этом участке по мере увеличения передаваемого момента пропорционально увеличивается тангенциальная деформация шины и возрастает число скользящих элементов. При определенном значении коэффициента скольжения (0,1... 0,15) продольная реакция дороги достигает максимального значения. Ра-
Рис. 1.16. Характерная зависимость коэффи-циента продольной силы колеса от коэффициента скольжения
бота колеса на этом участке является устойчивой: при увеличении передаваемого момента возрастает и продольная реакция дороги.
При дальнейшем увеличении крутящего момента начинают скользить все точки колеса в зоне контакта его с дорогой. Это сопровождается уменьшением продольной составляющей реакции дороги и коэффициента продольной силы колеса, поскольку определяющим становится трение скольжения, меньшее, чем трение покоя. В результате в ведущем режиме имеет место быстрый разгон колеса (буксование), а в тормозном — его остановка, т. е. работа колеса на рассматриваемом участке является неустойчивой.
Коэффициент продольной силы колеса при полном скольжении (коэффициент сцепления) характеризует тот крутящий момент, который может быть реализован колесом в данных дорожных условиях по условиям сцепления его с дорогой. Максимальное значение коэффициента продольной силы колеса определяет максимальный реализуемый колесом момент и называется
21
Рис. 1.17. Зона расположения значений коэффициентов <ртах и <р, замеренных для шии 6,40-и 6,00—15 с нагрузкой 3,7 кН при бетонном (а, в) и асфальтобетонном (б, г) покрытиях
максимальным коэффициентом сцепления (фтах)-
В справочной литературе, как правило, приводятся значения коэффициентов сцепления при полном скольжении. Это связано с тем, что наиболее распространен метод определения коэффициента сцепления путем измерения силы, необходимой для движения заблокированного тормозом колеса, или измерения крутящего момента буксующего колеса.
Значения ф и фтах зависят от многих факторов, основными из которых являются: тип и состояние покрытия, конструкция и состояние шины, ско
рость движения автомобиля, нагруз на колесо. Некоторые эксперимента; ные зависимости коэффициента п| дольной силы колеса и коэффициенч сцепления в продольном направлен приведены на рис. 1.17...1.21. Наибе, шие значения коэффициента сцеш ния характерны для дорог с сух твердым асфальтобетонным или i ментобетонным покрытием. В эт условиях коэффициент сцепления < ределяется в основном трением меж шиной и покрытием дороги. При ка1 нии колеса по дороге с твердым г крытием резина протектора дефорл руется гораздо больше, чем матери
22
Рис. 1.18. Зависимость коэффициента продольной силы колеса от коэффициента скольжения на различных дорожных покрытиях (шина Данлоп С41 5,90—15; Fz = 30 кН; рв = 0,16 МПа; va = 30 км/ч):
1 — сухой бетон; 2 — мокрый; 3 — уплотненный снег
Рис. 1.19. Зависимость коэффициента продольной силы от коэффициента скольжения при различной скорости движения по асфальтобетонному шоссе:
1 — иа = 10 км/ч; 2 — 25 км/ч; 3— 40 км/ч
покрытия. Твердые выступы покрытия внедряются при этом в контактирующую с ним поверхность шины. Поэтому для обеспечения хорошего сцепления дорожное покрытие должно иметь определенную шероховатость (оптимальная высота микронеровностей 2... 5 мм).
При наличии на покрытиях пленки грязи или влаги глубина вдавливания его неровностей в резину протектора значительно уменьшается и коэффици-
Рис. 1.20. Изменение коэффициента продольной силы колеса в зависимости от коэффициента скольжения шины 6,50—15:
1 — Fг=2 кН; 2 — 3 кН; 3 — 4 кН
Рис. 1.21. Зависимость коэффициента сцепления от скорости движения автомобиля при различной толщине (Л) водяной пленки на покрытии (шина 5,6—16; fz = 30 кН; рв =
= 0,15 МПа):
1 — ft = 0,2 мм; 2—1 мм; 3 — 2 мм
ент сцепления снижается. Он будет тем меньше, чем толще слой грязи н'а покрытии дороги. На мокрых дорогах коэффициент сцепления определяется гидромеханическими свойствами жидкой пленки, находящейся между шиной и опорной поверхностью, давлением в зоне их контакта и в значительно меньшей степени, чем на сухих дорогах, зависит от типа покрытия. Сцепные качества покрытия уменьшаются по мере его изнашивания. Наименьший коэффициент сцепления характерен для заснеженных и обледенелых дорожных покрытий.
23
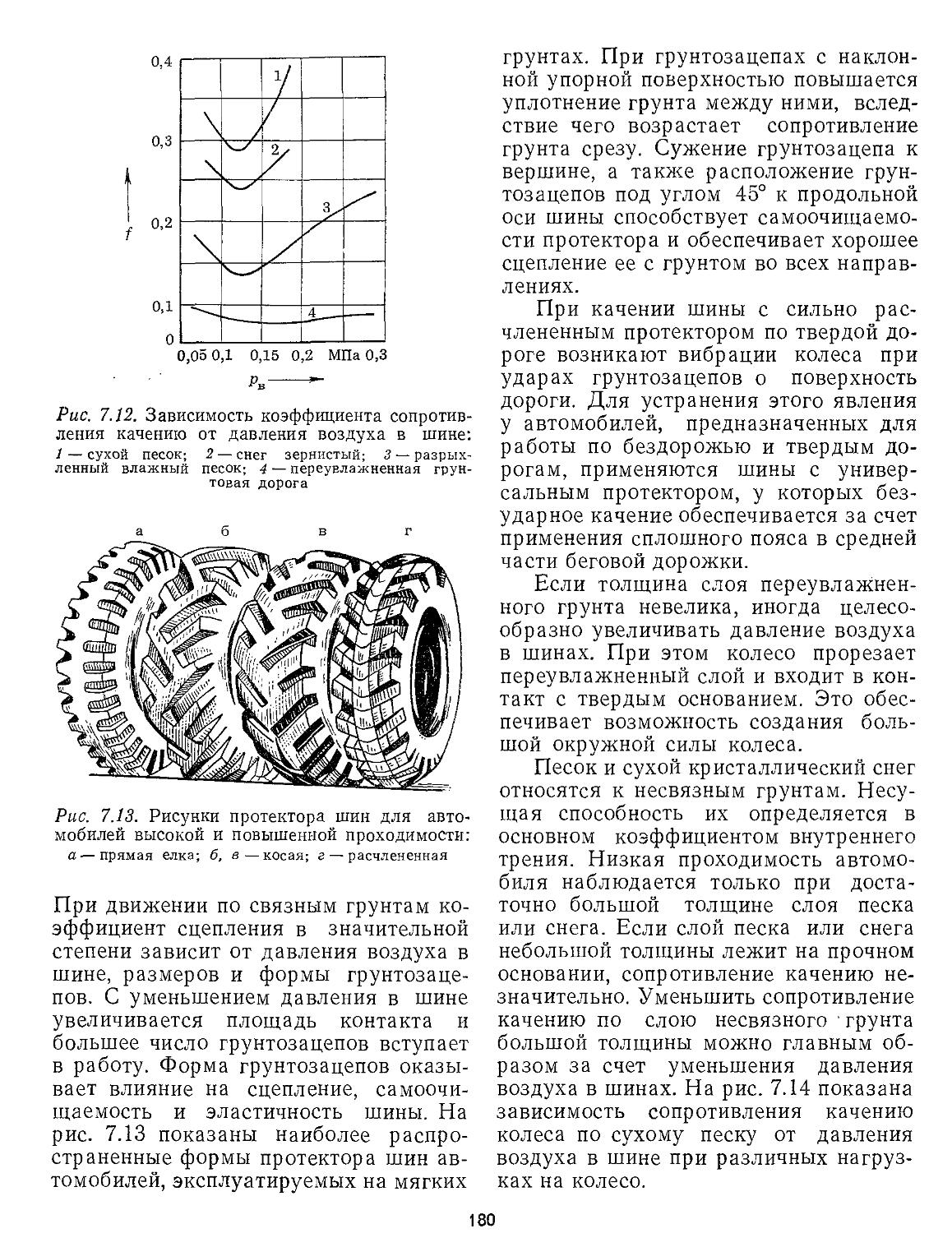
Рис. 1.22. Характерные рисунки протекторов дорожных шин
Коэффициент сцепления зависит также от конструкции шины, в основном от конструкции ее протектора. Шины с гладким протектором при всех режимах движения на асфальтовых мокрых, заснеженных и обледенелых дорогах имеют минимальное сцепление. Шины с шашечным рисунком протектора обеспечивают в этих условиях максимальный коэффициент сцепления, однако при движении по сухим твердым дорогам они интенсивно изнашиваются. Наиболее целесообразен с точки зрения обеспечения высоких средних коэффициентов сцепления и высокой износостойкости протектор с продольными ребрами, расчлененный надрезами различной формы под углом 45° (рис. 1.22). При таком рисунке протектора пленка жидкости на дорожном покрытии выдавливается в сторону (в прорези), что обеспечивает восстановление контакта резины протектора с опорной поверхностью.
Для повышения сцепления шины со скользким дорожным покрытием протектор выполняют из резины специальных составов или устанавливают в него специальные металлические шипы. Шипы противоскольжения позволяют повысить на обледенелых покрытиях коэффициент сцепления в 1,5... 2 раза.
Среди эксплуатационных факторов, влияющих на коэффициент сцепления, наиболее существенным являет
ся скорость движения автомобиля. С увеличением ее уменьшается коэффициент продольной силы колеса и, соответственно, коэффициент сцепления. Это обусловлено упруговязким характером деформаций резины протектора, протекающих во времени. При больших скоростях движения резина протектора не полностью зацепляется за неровности покрытия. На мокрых дорогах с увеличением скорости затрудняется выжимание влаги из зоны контакта шины и дороги, где образуется прослойка жидкости, и резко снижается коэффициент сцепления. Возрастает динамическая прочность жидкостной пленки, поэтому затрудняется ее разрыв и удаление с контактирующих поверхностей. При определенной толщине пленки жидкости и скорости движения под действием гидродинамических сил шина всплывает на поверхность пленки. В этом случае сцепление колес с дорогой очень мало и определяется трением в слое жидкости. Такое состояние шины на мокрой дороге называется аквапланированием, а скорость, при которой оно возникает,— критической по аквапланированию.
При динамических расчетах автомобиля в ряде случаев возникает необходимость учитывать изменение коэффициента продольной силы колеса в зависимости от скорости движения. Если нет более точных данных, то в
24
Табл. 1.1. Значение коэффициента сцепления
Дорожное покрытие	Состояние	Коэффициент сцепления
Асфальтобе-	Сухой	0,7...0,8 тон	Мокрый	0,45... 0,55 Булыжное	Сухое	0,4...0,55 Щебенчатое	Сухое	0,5..,0,7 Мокрое	0,3...0,5 Грунтовая	Сухая	0,4...0,6 дорога	Мокрая	0,2... 0,45 В период рас- 0,15...0,25 . путицы Песок	Сухой	0,2... 0,4 Мокрый	0,35... 0,5 Снег укатан-	0,15...0,25 ный Гладкий лед	0,08... 0,2		
первом приближении можно воспользоваться соотношением:
‘ А И ) ,
где kxv, kx0 — коэффициенты продольной силы колеса соответственно при скорости v и малой скорости, м/с; А — коэффициент, зависящий от типа шин и дорожных условий. Для асфальтобетонных покрытий можно принимать 4=0,015.. .0,03.
Аналогичное соотношение используется для коэффициента сцепления:
фхи = фхо(1 — Av).
• Коэффициент сцепления зависит от нагрузки на колесо и давления воздуха в шине. На дорогах с твердым покрытием увеличение нагрузки на колесо приводит к уменьшению коэффициента сцепления, причем на заснеженной дороге и'при гололедице относительное изменение коэффициента сцепления больше, чем на дорогах с асфальтовым покрытием.
Для каждой шины коэффициент сцепления имеет максимальное значение при определенном давлении воздуха в ней. При движении по мягким поверхностям коэффициент сцепления возрастает с уменьшением давления воздуха в шине благодаря увеличению
площади контакта и улучшению характеристик взаимодействия колеса с грунтом. В этих условиях шины с низким давлением воздуха имеют более высокий коэффициент сцепления, чем шины с высоким давлением.
В табл. 1.1 приведены рекомендуемые для расчетов значения коэффициентов сцепления автомобильных шин для некоторых типичных дорожных условий, соответствующие условиям полного скольжения и малой скорости движения. Меньшие значения относятся к шинам высокого, а большие — к шинам низкого давления.
1.5. Моделирование процесса движения автомобильного колеса на ЭВМ
В некоторых случаях при изучении тяговой или тормозной динамики автомобиля возникает необходимость определять характеристики движения автомобильного колеса на переходных режимах. Такие расчеты целесообразно выполнять на электронных цифровых или аналоговых вычислительных машинах. Ниже излагается методика расчета применительно к аналоговым вычислительным машинам, позволяющим обычно более четко проследить силовые и кинематические связи в
изучаемых механизмах.
При анализе динамики автомобильного колеса заданными параметрами являются: нормальная нагрузка колеса Fz-, крутящий момент, действующий на колесо, Мк; скорость vx и ускорение dvxldt оси колеса. Необходимо определить продольную силу колеса Fx, угловые скорость ®к и ускорение dta^dt вращения колеса.
Основным расчетным уравнением является (1.16), которое можно представить в виде, удобном для набора на АВМ:
т Мк
Л /к
^R<-^-fRz.
'к
(1.18)
25
Рис. 1.23. Блок-схемы моделирования на АВМ процесса движения тормозящего колеса
На рис. 1.23 показаны принципиальные блок-схемы моделирования режима работы тормозящего колеса.
Схемы рис. 1.23, а...г соответствуют формулам (1.18...1.21):
vx — °Vo
(1.19)
(1-20)
kxv=kxO-AkxOv; kx0=f(s); Rx —
Для моделирования режима разгона необходимо заменить формулу (1.19) и соответствующую ей блок-схему на формулу расчета коэффициента скольжения колеса при буксовании.
Диод на выходе интегратора (рис. 1.23, а) обеспечивает нулевое значение угловой скорости колеса (блокировку) в случае, когда тормозной мо--мент оказывается больше момента сцепления Му. При этом коэффициент скольжения принимается равным единице и операционный блок (ОПР, рис. 1.23, а) разрывает контакты k, что равносильно приравниванию нулю силы сопротивления качению колеса. В схемах предусмотрено, что vx, \lvXf> Rz — переменны; напряжения, пропорциональные им, подаются с системы моделирования движения автомобиля.
2 ТЯГОВО-СКОРОСТНЫЕ СВОЙСТВА И ТОПЛИВНАЯ ЭКОНОМИЧНОСТЬ АВТОМОБИЛЯ
2.1. Силы и моменты, действующие на автомобиль или автопоезд при прямолинейном движении
Схема сил, действующих на автомобиль-тягач, изображена на рис. 2.1. На рисунке показан наиболее общий случай, когда автомобиль-тягач ускоренно движется на подъем крутизной а.
При изображении сил приняты следующие основные допущения: дорожные условия под правыми и левыми колесами одноименных мостов автомобиля одинаковы, поэтому все силы, действующие на мост, могут быть приведены к его середине; автомобиль симметричен относительно продольной
оси; нормальные составляющие реакции дороги приложены в середине контактной поверхности, а их смещение учтено в моментах сопротивления качению колес мостов.
Все силовые факторы, действующие на автомобиль-тягач, можно разделить на три группы: движущие; сопротивления движению; нормальные.1 к направлению движения.	;
К первой группе относится окружная сила на ведущих колесах FK.
Вторую группу составляют:
М/2 — моменты сопротивления качению колес автомобиля; FB •— сила со- 1 противления воздуха; F, — продольная составляющая силы тяжести автомобиля; FjX—сила сопротивления по
Рис. 2.1. Силы и моменты, действующие на автомобиль-тягач при прямолинейном движении
27
ступательному ускорению масс автомобиля; Fnx — продольная составляющая силы сопротивления прицепа. У одиночного автомобиля сила сопротивления прицепа отсутствует.
К третьей группе относятся: Rzi, RZ2 — нормальные реакции дороги; Gacos а—нормальная составляющая веса автомобиля; Fnz — нормальная составляющая силы сопротивления прицепа (крюковая нагрузка). Силы, входящие в эту группу, направлены перпендикулярно к вектору скорости автомобиля. Поэтому их влияние на динамику движения автомобиля не непосредственное, а косвенное.
2.2. Окружная сила на ведущих колесах
Окружная сила на ведущих колесах возникает в результате того, что к ве-,чдущим колесам подводится через ^трансмиссию крутящий момент от двигателя, установленного на автомобиле.
В настоящее время на автомобилях в основном применяются двигатели внутреннего сгорания. Их мощностные свойства принято оценивать скоростными характеристиками, представляющими зависимость эффективной мощности или крутящего момента на коленчатом валу при установившемся режиме работы от частоты вращения двигателя^.’ Скоростная характеристика, полученная при полной подаче С топлива, называется внешней скоростной характеристикой, а полученные при неполной подаче топлива — частичными.. Скоростные характеристики определяют на специальных тормозных стендах. При этом обычно непосредственно находят зависимости эффективного момента двигателя от частоты его вращения, а мощность определяют расчетом.
Частичные скоростные характеристики получают при определенном положении органа, регулирующего подачу топлива. У карбюраторных двига
телей таким органом является дроссельная заслонка, а у дизельных двигателей — пружина регулятора. Поэтому частичные характеристики у карбюраторных двигателей соответствуют открытию дроссельной заслонки на определенный угол, а у дизельных — определенному натяжению пружины регулятора (определенному положению педали подачи топлива).
На рис. 2.2 показаны типовые внешние характеристики карбюраторного и дизельного двигателей.
Частичные характеристики карбюраторного и дизельного двигателей различаются значительно. При неизменном проходном сечении дросселя и изменении нагрузки на карбюраторный двигатель зависимость момента двигателя от частоты его вращения подобна зависимости, полученной при максимальном проходном сечении дросселя. У дизельных двигателей изменение натяжения пружины регулятора равносильно изменению максимальной частоты вращения двигателя. Поэтому линии, характеризующие связь между частотой вращения двигателя и крутящим моментом при постоянном положении педали подачи топлива, оказываются практически параллельными аналогичной зависимости при полной подаче топлива.
При очень малой подаче топлива для вращения двигателя необходимо, чтобы крутящий момент, подводимый извне, был равен моменту сопротивления вращению двигателя. В этом случае считается, что двигатель работает в тормозном (пассивном) режиме.
Таким образом, область возможных режимов работы двигателя (соотношений между частотой вращения двигателя и крутящим моментом на коленчатом валу) оказывается ограниченной: сверху — внешней скоростной характеристикой двигателя, снизу— внешней тормозной. Область режимов работы двигателя ограничена также справа и слева: справа — мак-
28
Рис. 2.2. Скоростные характеристики двигателей: а — карбюраторного; б — дизельного
симальной, а слева — минимально устойчивой частотой вращения.
Поскольку внешняя характеристика определяет предельные режимы работы двигателя, именно она является наиболее существенной при оценке скоростных свойств автомобиля.
V Важнейшими параметрами внешней скоростной характеристики двигателя являются: Ре тах — максимальная эффективная мощность (кВт); М>тах—максимальный крутящий момент (кН • м); Мр — крутящий момент при максимальной мощности (кН • м); «етаХ— максимальная частота вращения коленчатого вала двигателя (об/мин); пР — частота вращения коленчатого вала при максимальной мощности (об/мин); Пщ — часто- та вращения коленчатого вала при максимальном крутящем моменте (об/мин); kw—коэффициент приспособляемости по моменту:
= тах/Лфр;	(2.1)
f ka — коэффициент приспособляемости \ по частоте вращения:
ka = пР!пм.	(2.2)
У карбюраторных двигателей, име
ющих ограничитель частоты вращения, максимальная частота вращения коленчатого вала при движении автомобиля с максимальной скоростью может на 10...20 % превосходить частоту пР, соответствующую максимальной мощности двигателя. Ограничитель, устанавливаемый с целью повышения долговечности карбюраторных двигателей, включается в работу на той части внешней характеристики, где мощность практически не возрастает с увеличением частоты вращения коленчатого вала. Это соответствует пе0= (0,8...1)«р. Поэтому при расчетах внешней характеристики за максимальную мощность принимается та, которая была бы получена при отсутствии ограничителя. Мощность, соответствующая началу работы ограничителя, будем обозначать Ре0. Максимальная частота в этом случае будет иметь место при работе двигателя без нагрузки. Обычно она на 5...15 % выше пе0.
Внешняя характеристика дизельного двигателя в рабочем диапазоне час
29
тот вращения не достигает максимума, и максимальное значение мощности соответствует началу работы регулятора.
По известной зависимости мощности двигателя от частоты вращения коленчатого вала можно найти и крутящий момент двигателя
Ме= (60 Ре) / (2лЛе).
Если известны характеристики двигателя, принятого к установке на автомобиль, необходимо их использовать при выполнении тягово-динамических расчетов. Часто при проектировании автомобиля характеристики двигателя неизвестны, и тогда расчет ведут по приближенным скоростным характеристикам.
Основанием для построения приближенных скоростных характеристик является то, что внешние характеристики двигателей внутреннего сгорания могут быть представлены зависимостью:
где а, Ь, с — коэффициенты, значения которых зависят от типа и конструкции двигателя; Ре, сос — текущие значения мощности и угловой скорости вращения коленчатого вала двигателя.
В соответствии с методикой, разработанной в М.АДИ, система уравнений, необходимая для нахождения коэффициентов а, b и с, может быть получена из следующих соображений. Поскольку уравнение (2.3) имеет общий характер, оно должно удовлетворяться и в точке пе=пР. Это возможно при условии
а+ф + с=1.	(2.4)
Если из правой части уравнения (2.3) вынести за скобки сое/сор, после преобразования получим выражение для построения зависимости крутяще
го момента от угловой скорости вращения коленчатого вала:
Ме = МР
ае
<лр
(2.5)
а + b
Приняв ие = им и Ме=Метах, с учетом соотношений (2.1) и (2.2) имеем второе уравнение
км — п Ыка elk,.,.	(2.6)
Третье уравнение получается из условия наличия экстремума функции (2.5) при ие = (0м и соответственно равенства нулю производной
<4
Мр[~ +2— — =0
ИЛИ
9r
b + ~ = Q.	(2.7)
Решение системы уравнений (2.4), (2.6) и (2.7) дает
а =	*.
М2-М-1 ’
Ь =----^(^м-1)	(2g)
М2-М-1
= _ fe24feM-l)
с М2-М-1
Поскольку в характеристиках двигателей обычно приводятся значения Ре max, Пр, Л4е max и Им, по формулам (2.3), (2.8) можно построить внешнюю характеристику двигателя.
На рис. 2.3 изображена экспериментальная характеристика двигателя ЯМ.3-238. Точками показаны значения, рассчитанные с использованием формул (2.3), (2.5) и (2.8).
Ориентировочно значения коэффи-. циентов приспособляемости могут быть приняты для карбюраторных двигателей: kM — 1,05...1,45; ka = 1,5...2,5; для дизельных: !гм= 1,1...1,5; ka = 1,45...2. Коэффициент приспособляемости карбюраторного двигателя в сильной степени зависит от его литровой мощно-сти — отношения максимальной мощно-
30
Рис. 2.3. Внешняя скоростная характеристика двигателя ЯМЗ-238
к рабочему объему цилиндров
ста двигателя Ул (рис. 2.4).
В табл. 2.1 приведены некоторые параметры современных карбюраторных и дизельных двигателей.
Необходимо учитывать, что при стендовых испытаниях двигатель комплектуется дополнительным оборудованием (глушитель, вентилятор, радиатор, компрессор и др.) в соответствии с принятыми в каждой стране стандартами. Полученная при испытаниях мощность двигателя приводится к нормальным условиям: атмосферному давлению 760 мм рт. ст. и температуре 15 °C.
Для приведения к нормальным условиям используется формула международного бюро стандартов:
D _ d 760 530 + z
*е * вО р	»
°о	545
где Рео — мощность при температуре окружающего воздуха t (°C) и барометрическом давлении Во (мм рт. ст.).
Рис. 2.4. Зависимость коэффициентов приспособляемости карбюраторных двигателей от их литровой мощности
Условия работы двигателя, установленного на автомобиле, отличаются от стендовых; двигатель работает с другими впускными и выпускными системами; на нем устанавливаются дополнительные механизмы, на привод которых затрачивается определенная мощность; двигатель работает при другом температурном режиме. Поэтому мощность двигателя, установленного на автомобиле, несколько меньше полученной при стендовых испытаниях. При использовании для тягово-скоростных расчетов стендовых внешних характеристик значения мощности, соответствующие определенным частотам вращения коленчатого вала, уменьшают путем умножения на коэффициент kc, зависящий от типа двигателя и автотранспортного средства. В приближенных расчетах можно принимать /гс = 0,85...0,9. В последующем параметрам двигателя, полученным при стендовых испытаниях, будем присваивать индекс «с», параметрам, соответствующим работе установленного на автомобиль двигателя при полной подаче топлива,— «е», а при неполной — «д». Например: Рс — мощность двигателя, полученная при стендовых
31
Табл. 2.1. Параметры отечественных карбюраторных и дизельных двигателей
Марка	Гл. л	Тип	S и го Е «У Ом	7 К S S со” Ом е	и • и -хеш	7 К со” с	kM	^(0	Коэффициенты			Расход топлива, г/(кВт • ч	
									а	ъ	с		
												Sa	Sp
МеМЗ-968	1,197	К4Р	'29,4	4,3	74,5	2,8	1,14	1,54	0,65	1,5	1,15	327,3	405 ВАЗ-2105	1,295	К4Р	50,7	5,6	94,1	3,4	1,09	1,65	0,88	0,69	0,57	299,2	340 4087	1,36	К4Р	36,8	4,75	91,2	2,97	1,23	1,6	0,58	2,07	1,65	326,4	390 451М	2,445	К4Р	55,2	4	166,7	2,35	1,26	1,7	0,72	1,83	1,55	312,8	340 ГАЗ-52-04	3,48	К6Р	55,2	2,8	205,9	1,5	1,094	1,87	0,97	0,46	0,43	340	360 ЗМЗ-66	4,25	K8V	88,6	3,3	284,4	2,25	1,16	1,47	0,44	2,12	1,56	306	326 ГАЗ-14	5,53	K8V	161,8	4,2	451,1	2,75	1,23	1,53	0,41	2,5	1,91	272	292 ЗИЛ-130	6	K8V	110,3	3,2	402	1,9	1,22	1,68	0,75	1,59	1,34	321	355 ЗИЛ-375	7	K8V	132,4	3,2	465	1,9	1,18	1,68	0,80	1,3	1	321	355 КамАЗ-740	10,85	D8V	154	2,6	637	1,7	1,13	1,53	0,68	1,38	1,06	224	244 ЯМЗ-236	11,15	D6V	132,4	2,1	666,7	1,5	1,107	1,4	0,44	1,87	1,31	223	240 ЯМЗ-238	14,84	D8V	176,5	2,1	882,6	1,5	1,099	1,4	0,48	1,73	1,21	223	240 ЯМЗ-240	22,3 D12V 264,8 2,1 1274,8 1,5 1,061 1,4 0,68 1,07 0,75 223 240 Примечание: К4Р — карбюраторный, четырехцилиндровый, рядный; D6V — дизельный, шестицилиндровый, V-образный.													
Рис. 2.5. Изменение эффективного момента двигателя в зависимости от ускорения вращения коленчатого вала
испытаниях; Ре— мощность двигателя, установленного на автомобиле, при работе по внешней характеристике; Рк — мощность двигателя при работе по частичным характеристикам.
При работе на неустановившемся режиме мощность, отдаваемая двигателем, меньше мощности на установившемся режиме. Это обусловлено динамикой наполнения цилиндров воздухом и парами топлива и тепловой инерцией двигателя. Из экспериментального графика, приведенного на рис. 2.5, видно, что уменьшение момен
та двигателя при работе на неустано-вившихся режимах невелико (не более 3 %) и примерно линейно зависит от ускорения вращения коленчатого вала: dco.
ДМ =
где ус — коэффициент: уе = 0,001...0,002.
При разгоне автомобиля часть момента двигателя затрачивается на разгон маховика и связанных с ним деталей. Поэтому ведущим колесам автомобиля от трансмиссии передается крутящий момент
где 1М—момент инерции маховика и связанных с ним деталей; ит — передаточное число трансмиссии; т]т — коэффициент полезного действия трансмиссии.
Таким образом, сила, обеспечивающая движение автомобиля, — окружная сила на ведущих колесах при не-
32
установившемся режиме F'K может быть найдена по формуле:
Af_uTnT ,	ч и da
Fk =	-	“I- Al) ~ йт —
'о________	'о dt
/„ da„
(2-W)
n где n — число ведущих колес. При установившемся движении
F к — А1дНтТ]т/го.	(2.11)
Если двигатель работает по внешней характеристике, а движение автомобиля является установившимся, окружная сила на ведущих колесах оказывается наибольшей для данного режима движения. Такую окружную силу называют полной и обозначают Fk0. В соответствии с формулой (2.11) полная окружная сила определяется по выражению:
Fkq~ М.еи^х\^1г о-
В ряде случаев максимальное значение окружной силы на ведущих колесах определяется сцеплением колес с дорогой. В этих условиях максимальный реализуемый колесом крутящий момент находится по формуле (1.15). Если считать, что коэффициенты сцепления под колесами моста одинаковы, окружная сила ведущих колес моста, ограниченная сцеплением ГКф, может быть найдена по выражению:
Ек<₽ = М^/го = (<р 4- /) Т?г2, где Rz2 — нормальная реакция дороги, действующая на колеса ведущего моста автомобиля.
В практических расчетах сопротивлением качению колес пренебрегают, т. е. окружную силу ведущих колес моста принимают равной силе тяги
Ек<р = ф7?22.	(2.12)
л Коэффициент полезного действия ; трансмиссии характеризует потери ; мощности при передаче ее механизмами трансмиссии и равен произведению
2 А. И. Гришкевич	33
коэффициентов полезного действия ее механизмов. Наибольшие потери мощности имеют место в коробках передач, раздаточных коробках, главных передачах, колесных редукторах. Потери мощности в отдельных механизмах и трансмиссии в целом могут быть найдены экспериментально на специальных испытательных стендах или путем испытаний автомобилей. Исследованиями установлены некоторые общие закономерности изменения КПД трансмиссий в зависимости от типа агрегата и режима его работы. Это позволяет давать приближенную оценку КПД трансмиссии проектируемого автомобиля.
Экспериментальными исследованиями показано, что потери мощности в трансмиссии можно представить двумя составляющими: потерями, обусловленными наличием трения в узлах, передающих нагрузку (трение в зацеплении шестерен, в карданных сочленениях, в подшипниках), и потерями, вызванными разбрызгиванием масла в картерах (гидравлические потери), причем к этой же группе можно отнести потери мощности на трение в сальниках.
Первая группа потерь характерна тем, что при увеличении передаваемого через трансмиссию крутящего момента потери на трение возрастают медленнее, чем возрастает передаваемый трансмиссией момент. Вследствие этого увеличивается КПД механизмов. Гидравлические же потери практически не зависят от передаваемого момента, а определяются только скоростью вращения валов, вязкостью и объемом масла в картерах. При увеличении частоты вращения валов потери мощности на перемешивание и разбрызгивание масла в картерах возрастают более интенсивно, чем передаваемая мощность, и КПД редукторного механизма уменьшается. КПД редукторных механизмов возрастает при уменьшении вязкости масла, уменыпе-
Рас. 2.6. Экспериментальные зависимости КПД коробки передач от:
а — относительного крутящего момента на первичном валу; б — относительной частоты вращения первичного вала; А — высшая передача; В — промежуточные передачи; С — первая передача
Вязкость
Рис. 2.7. Зависимость момента трения от вязкости масла в коробке передач
нии объема (уровня) масла в картере и повышении температуры его до пределов, при которых масло не теряет своих смазочных качеств. Поэтому наибольшие КПД характерны для редукторов с сухим картером и принудительной подачей масла к рабочим поверхностям.
Экспериментальные графики, характеризующие потери мощности в редукторных механизмах в зависимости от режимов работы механизмов, показаны на рис. 2.6...2.8. Некоторые из них приведены в относительных величинах, определяемых отношением текущего значения величины к номинальному.
Для расчета потерь мощности на трение в узлах, которые передают на-
Рис. 2.8. Зависимость КПД коробки передач от относительного момента при смазывании под давлением (/) и разбрызгиванием (2)
грузку, можно использовать экспериментально установленные значения КПД шестеренчатых зацеплений. Считается, что пара цилиндрических шестерен передает мощность с КПД, равным 0,98, а конических — 0,97.
Поскольку гидравлические потери мощности практически не зависят от передаваемого крутящего момента, они могут быть найдены экспериментально путем измерения момента, необходимого для прокручивания незагруженного редуктора. Гидравлические
34
потери во всей трансмиссии автомобиля обычно определяют экспериментально совместно с потерями в подшипниках ведущих колес, прокручивая трансмиссию с заданной скоростью при вывешенных ведущих колесах. Если известен крутящий момент Л4х.х, потребный для прокручивания незагруженной трансмиссии, ее КПД можно найти по формуле:
Т]т = Т1ш(1	Л4х.х/Л4е),
где т)ш — КПД шестеренчатых зацеплений, через которые передается момент двигателя Ме, необходимый для обеспечения движения автомобиля в заданных условиях.
Следовательно, КПД редукторных механизмов зависит от режимов работы. В частности, на низших передачах КПД коробок передач вследствие передачи крутящего момента через две пары шестерен будет ниже, чем при работе на прямой передаче. В то же время при движении автомобиля на низших ступенях через главную передачу передается большой крутящий момент, а ее валы вращаются с малой скоростью. Поэтому ее КПД будет выше, чем при движении автомобиля с высокой скоростью. Это позволяет считать, что КПД механической трансмиссии автомобиля практически не зависит от режима ее работы.
Для проектных расчетов рекомендуются следующие значения КПД отдельных механизмов: коробки передач— т]к.п=0,96...0,98; раздаточной коробки— т]р.к = 0,93...0,97; колесной передачи — t'It.-.p = 0,96.. .0,98; карданного шарнира — т]к.ш = 0,995; главной передачи— т]о = О,93...О,97. При работе двигателя по внешней характеристике КПД механической трансмиссии можно считать равным рт = 0,8...0,92 (меньшие значения относятся к многоприводным грузовым автомобилям, большие — к легковым).
2.3. Силы сопротивления движению
Сила сопротивления качению (К/), как показано в гл. 1, вводится в расчет условно вместо момента сопротивления качению, что более удобно при изучении тягово-скоростных свойств автомобилей.
При движении по твердым дорогам сопротивление качению обусловлено гистерезисными потерями энергии в шине при ее радиальной, тангенциальной и боковой деформациях, скольжением в зоне контакта с опорной поверхностью и сопротивлением воздуха. При этом гистерезисные потери составляют 90...95 % общих потерь энергии.
Сопротивление качению зависит от многих конструктивных и эксплуатационных факторов: конструкции шины, давления в ней воздуха, температуры, нагрузки и передаваемого шиной момента, скорости движения автомобиля, состояния дорожной поверхности. Колеса автомобиля работают в различных условиях: разная нагрузка, передаваемый момент, состояние опорной поверхности. Так как невозможно учесть особенности работы каждого колеса, используют осредненные значения коэффициентов сопротивления качению, а общую силу сопротивления качению автомобиля определяют по выражению:
2
= Ffi = fG& cos a « fGa, (2.13) t=i
где f — осредненный коэффициент сопротивления качению, который обычно находится экспериментально для определенных дорожных условий и шин; z — число колес автомобиля.
В наибольшей степени сопротивление качению зависит от таких конструктивных параметров шин, как число слоев и расположение нитей корда, толщина и состояние протектора. Уменьшение числа слоев корда, толщины протектора, применение синтетиче-
2*
35
б
Рис. 2.9. Зависимость сопротивления качению от:
а — скорости движения (1 — шина диагональная; 2—радиальная; 3 — с протектором уменьшенной толщи* ны); б — крутящего момента: в — давления воздуха в шине; г — диаметра шины (/— при контакте с бетонным покрытием; 2 — грунтом средней плотности; 3 — песчаным); д — температуры шины
ских материалов с малыми гистерезис-ними потерями способствуют снижению сопротивления качению. С увеличением размера шины при прочих равных условиях сопротивление качению также снижается.
Влияние эксплуатационных и конструктивных факторов на сопротивление качению иллюстрируется экспери
ментальными графиками, приведенными на рис. 2.9. Так, с повышением давления воздуха в шине и ее температуры сопротивление качению уменьшается. Наименьшее сопротивление качению имеет место при нагрузке, близкой к номинальной. С увеличением степени изношенности шины оно уменьшается.
36
Табл. 2.2. Коэффициенты сопротивления каче-
нию
Дорожные условия	f	
Асфальтобетонная дс»ога	0,013..	.0,02
Гравийная	0,020..	.0,025
Булыжная	0,025..	.0,05
Грунтовая: сухая	0,025..	.0,035
после дождя	0,05..	.0,15
, Песчаная поверхность: сухая	0,1..	.0,3
влажная	0,06..	.0,15
Снежная укатанная	0,03..	.0,05
На дорогах с твердым покрытием сопротивление качению во многом зависит от размеров и характера неровностей дороги, обусловливающих повышенное деформирование шин и подвески и, следовательно, дополнительные затраты энергии. При движении по мягким или грязным опорным поверхностям затрачивается дополнительная работа на деформирование грунта или выдавливание грязи и влаги, находящихся в зоне контакта колеса с дорогой.
Рекомендуемые для расчетов значения коэффициентов сопротивления качению приведены в табл. 2.2.
Исследования показывают, что при ^движении автомобиля со скоростью до У 50__км/ч сопротивление качению можно ^считать постоянным. Интенсивное увеличение сопротивления качению наблюдается при скорости свыше 100 км/ч. Объясняется это увеличением -затрат энергии при ударах и колеба-. тельных процессах, происходящих в шине при высоких скоростях движения. Предложено несколько эмпирических зависимостей для определения коэффициента сопротивления качению fv- при высокой скорости движения. Приводим некоторые из них:
fv = a + b (0,01wa)2’5;
Ь = 0,01 (l + Wa/160);
fv = fo[l + (0,006Уа) 2],
Рис. 2.10. График для определения коэффициентов а и b
где а, b — коэффициенты, выбираемые по графику (рис. 2.10) в зависимости от давления воздуха в шине; ца — скорость автомобиля, км/ч; f0 — коэффициент сопротивления качению при малой скорости.
Сила сопротивления подъему автомобиля (F^)— составляющая силы тяжести автомобиля, направленная параллельно опорной поверхности и приложенная в центре масс автомобиля на высоте hg. Если углы подъемов считать положительными, а спусков — отрицательными, сила сопротивления подъему определяется выражением:
Fi = Gasin а.
Крутизну профиля характеризуют уклоном — тангенсом угла наклона плоскости дороги к горизонтальной плоскости. В дорожной документации уклон обычно выражают в тысячных (промилле, %о)  При расчетах движения автомобиля уклон обозначают буквой I и задают в тысячных, сотых (процентах) или непосредственно значением тангенса угла уклона. Например, уклон одной и той же крутизны может быть обозначен: z = 3O°/o0; i=3 %; i= = 0,03. Последнее обозначение является предпочтительным.
Поскольку обычно уклоны дороги невелики, принимают
sin а «г; Ft=i Ga. (2-14)
В ряде случаев при расчетах тяговоскоростных свойств автомобиля целесообразно рассматривать совместно сопротивление качению и сопротивле-
37
Рис. 2.11. Обтекание автомобиля воздухом ние подъему. Сумма этих сопротивлений называется сопротивлением дороги
F^ = Ff + Ft = (/ + t) Ga = фСа, (2.15) где ip — коэффициент сопротивления дороги. Обычно значение сопротивления дороги, при котором должны быть обеспечены требуемые тягово-скоростные свойства автомобилей, определяют в техническом задании на их проектирование.
Сила сопротивления воздуха (FB) существенно влияет на тягово-скоростные свойства автомобилей, особенно при высоких скоростях движения. Основной составляющей сопротивления воздуха является лобовое сопротивление, которое достигает 60 % общего. Лобовое сопротивление вызывается тем, что при движении автомобиля впереди его создается зона повышенного давления, а сзади — зона разряжения (рис. 2.11). За счет различия давлений воздуха впереди и сзади автомобиля и создается сила лобового сопротивления. При этом она будет тем больше, чем большая энергия необходима для перемещения воздуха, а последняя зависит от характера вихре-образования. Поэтому чем больше при движении автомобиля образуется вихрей воздуха, тем больше сила лобового сопротивления. Поскольку вихреобра-зование в воздухе зависит от формы движущегося в нем тела, лобовое сопротивление называют сопротивлением формы. Различают также сопротивление, вызываемое выступающими частями автомобиля (добавочное сопротивление) ; сопротивление, обуслов
ленное трением воздуха о наружные поверхности автомобиля; сопротивление, возникающее при прохождении воздуха через подкапотное пространство, и др.
Лобовое сопротивление в основном определяет затраты мощности двигателя при высоких скоростях движения, а следовательно, и расход топлива. Сила лобового сопротивления
Fax — CvP ~2~Лв,
где сх — коэффициент лобового сопротивления (коэффициент обтекаемости); р—плотность воздуха; v—скорость относительного движения воздуха и машины; Ав — лобовая площадь (площадь наибольшего поперечного сечения машины).
Обычно коэффициенты лобового сопротивления определяют путем продувки автомобиля или его модели в аэродинамических трубах.
Принципиальная схема аэродинамической трубы показана на рис. 2.12. Установленный в трубе вентилятор создает поток воздуха, обтекающий модель, помещенную в рабочую часть трубы. Специальным весовым устройством измеряется сила, действующая на испытываемую модель, равная силе лобового .сопротивления.
Сопротивление формы в основном обусловлено фронтальным давлением воздуха. На рис. 2.13 показана зависимость (в условных единицах) лобового сопротивления от конфигурации кузова простейшей формы. Из схемы видно, что при удлиненной передней части сопротивление воздуха уменьшается на 60 %, в то время как при удлиненной задней — только на 15 %. На сопротивление формы автомобиля значительное влияние оказывают конфигурации капота, крыльев, ветрового стекла, крыши, боковых стенок, багажника, основания.
Накопленные материалы исследований аэродинамики легковых автомоби-
38
Рис. 2.12. Схема определения сопротивления воздуха в аэродинамической трубе
Рис. 2.14. Рациональная аэродинамическая форма кузова легкового автомобиля
Рис. 2.13. Влияние формы тела на лобовое сопротивление
лей с жестким закрытым кузовом позволяют дать определенные рекомендации по наиболее рациональной и приемлемой с аэродинамической точки зрения форме кузова. У такого автомобиля передняя часть в плане имеет скругленные углы. Передняя часть средней высоты на виде сбоку имеет скругленную форму и понижается в направлении вперед. Ветровое стекло в плане скругленное. Крыша в плане несколько сужающаяся вперед и назад от средней стойки или имеет постоянную ширину. Должны быть обеспечены плавные переходы от крыши к задней панели и багажнику. Допускается грань в месте перехода крыши к заднему скату. Пол кузова цельный с выступающими механизмами. Примерная
схема такого кузова показана на рис. 2.14.
Добавочные сопротивления, возникающие при установке на автомобиль различных выступающих деталей, могут значительно увеличить общее сопротивление воздуха. Например, установка отдельных небольших фар может вызвать дополнительное сопротивление сх = 0,04, антенны — сж=0,02, наружного зеркала — сж = 0,01.
В последнее время в связи с увеличением средних скоростей движения грузовых автомобилей, а также повышением требований к их топливной экономичности особое значение придается аэродинамическим качествам грузовых автомобилей, в первую очередь — магистральных автомобилей и автопоездов. Коэффициенты лобового сопротивления у грузовых автомобилей обычно выше, чем у легковых. Обусловлено это худшей аэродинамической формой грузовых автомобилей, а также тем, что зазор между кабиной и платформой, выступающие части платформы и кузова создают дополнительные источники вихреобразования. На рис. 2.15, а показан характер обтекания воздухом автопоезда.
Наибольшие коэффициенты лобового сопротивления характерны для автомобилей, перевозящих контейнеры, автомобилей с открытой бортовой платформой. Установка тента на автомо-
39
Рис. 2.15. Характер обтекания воздухом седельного автопоезда (а); приспособления для уменьшения сопротивления воздуха (б):
1 — обтекатель; 2 — гибкая оболочка
биль способствует снижению коэффициента сопротивления на 12...15 %. Наименьший коэффициент сопротивления характерен для автомобилей, перевозящих цистерны.
Уменьшение сопротивления воздуха для грузовых автомобилей может достигаться за счет скругления углов в местах перехода от лобовой плоскости к верхней и боковым поверхностям, установки лобового стекла с наклоном, увеличения выпуклости передней панели, а также путем применения специальных аэродинамических приспособлений, улучшающих обтекание автомобиля или автопоезда воздухом. В идеальном виде дополнительное аэродинамическое приспособление для седельного тягача (рис. 2.15,6) можно представить в виде обтекателя 1, установленного на крыше тягача, и гибкой оболочки 2, закрывающей зазор между тягачом и полуприцепом. Поскольку основное воздушное сопротивление движению автопоезда создается за счет воздуха, обтекающего кабину и набегающего на переднюю стенку полуприцепа, установка отклонителя на крыше кабины, направляющего основной поток воздуха выше передней стены
Рис. 2.16. Приспособления для уменьшения аэродинамического сопротивления грузовых автомобилей
полуприцепа, может дать значительный эффект. На рис. 2.16 схематично показаны различные аэродинамические приспособления, применяемые на грузовых автомобилях, а также процентное уменьшение коэффициента сопротивления, полученное по результатам испытаний в аэродинамической трубе.
В расчетах тягово-скоростных свойств автомобилей обычно используют не коэффициент обтекаемости сх, который определяется в основном формой автомобиля, а коэффициент сопротивления воздуха /гв, которым учитываются и другие сопротивления, не зависящие непосредственно от формы автомобиля. При этом сила сопротивления воздуха рассчитывается по формуле:
' F* = k*ABv2.	(2.16)
Следовательно, приближенно можно считать, что /гв = 0,5рсхр (р— коэффициент, учитывающий дополнительные сопротивления).
Иногда для удобства сравнительной оценки аэродинамических качеств автомобиля вводят понятие «фактор обтекаемости», являющийся произведением
40
Табл. 2.3. К определению площади лобового сопротивления автомобилей
Тип автомобиля	Нг X вг, м2
Легковые: особо малый класс	1,4... 1,9 малый класс	1,6...2,1 средний класс	1,9...2,3 большой класс	2,2...2,6 Грузовые грузоподъемностью: 0,5...2,0 т	4,2...5,7 2,0...5,0 т	5,2...7,5 5,0...15,0 т	6,9...9,0 свыше 15 т	9,0... 15	
езда больше, чем для одиночного автомобиля, на 20...30 %, а у седельного автопоезда — примерно на 10 %.
Сопротивление воздуха принято рассматривать в виде сосредоточенной силы, приложенной в точке, называемой центром парусности автомобиля. Расстояние от опорной поверхности до центра парусности называется высотой центра парусности hB.
Сила сопротивления поступательному разгону автомобиля (Fjx) — это сила его инерции
Табл. 2.4. Коэффициенты сопротивления воздуха
Тип автомобиля	£в, Н-с^-м"-4
Гоночные	0,13...0,15
Легковые	0,15...0,35
Автобусы	0,25...0,4
Грузовые	0,5...0,7
Автопоезда	0,55...0,95
коэффициента сопротивления воздуха и лобовой площади (£ВЛВ).
Входящая в выражение (2.16) площадь лобового сопротивления может быть определена по технической документации, а при ее отсутствии — приближенно по выражению
Д в — схВг//г,
где а — коэффициент заполнения площади: для легковых автомобилей а = = 0,78...0,8; для грузовых а = 0,75...0,9 (большие значения принимаются для более тяжелых автомобилей); Вг и Нг— наибольшие ширина и высота автомобилей соответственно.
В табл. 2.3 приведены произведения ширины и высоты современных автомобилей различных типов, а в табл. 2.4— значения коэффициентов сопротивления воздуха. При наличии прицепа коэффициент сопротивления для по-
Сила сопротивления прицепа (Рпх) включает составляющие: силу сопротивления качению прицепа Fnf, силу сопротивления подъему прицепа Fnf, силу сопротивления воздуха движению прицепа Рв.п; силу сопротивления поступательному разгону прицепа Fnj- Эти силы, за исключением сил сопротивления воздуха и сопротивления качению, определяются по тем же формулам, что и соответствующие силы сопротивления движению автомобиля, в которых вместо силы тяжести автомобиля Ga подставляется сила тяжести прицепа Оп. Силу сопротивления воздуха приближенно можно считать равной одной трети силы сопротивления воздуха для автопоезда. При расчетах сил взаимодействия в сцепном устройстве тягача и прицепа эта сила обычно не учитывается.
Поскольку колеса прицепа являются ведомыми, силу, необходимую для обеспечения качения колес, можно найти суммированием сил сопротивления качению каждого колеса. Таким образом, для случая прямолинейного движения автомобильного поезда по ровной дороге продольное усилие в сцепке
Fnx = fGn + lGa +
dt rQ dt
При расчетах тягово-скоростных
41
свойств автопоезда обычно рассматривают силы, действующие на автопоезд в целом, которые определяются по формулам (2.13)...(2.16) путем подстановки, где это необходимо, вместо силы тяжести автомобиля силы тяжести автопоезда.
2.4. Нормальные реакции опорной поверхности
Нормальные составляющие реакции дороги (нормальные реакции), действующие на колеса автомобиля, непрерывно изменяются в процессе движения. Они определяют сопротивление качению колес автомобиля, а в предельных режимах движения — максимальные значения окружных сил и устойчивость автомобиля.
При движении автомобиля по ровным дорогам задача нахождения нормальных реакций сводится к определению внешних сил и моментов, действующих на автомобиль, и составлению уравнений моментов относительно центра площади контакта одного из мостов автомобиля с опорной поверхностью.
Например, для нахождения нормальной реакции в соответствии со схемой, изображенной на рис. 2.1, необходимо составить уравнение моментов относительно центра контакта передних колес с опорной поверхностью:
7?z2E = FB/iB4-FjXhg-{~Fihg~\~ Gacos о.' fl-p + F пх^кр 4-Fnz(T4- с) +Л1/1 + ЛД2;
Rz2 — [FB/lB 4“ T'/jTlg Fthg -[•- Ga X
X cos a • ci 4- FnAP -f- Fnz (L 4" c) 4~ 4- Мц 4- Mf2].
Если рассматривать движение автопоезда, состоящего из тягача и прицепа, можно принять
Fт = 0; Fnx — (f 4* i) Gn 4- ma
j	dv.
r0 dt
Mfl + M}2 = fr0Ga; sina = i, cosa=l.
В этом случае после преобразований получим следующее выражение для нахождения реакции Т?г2:
Т?г2 =	[(я + frо) Ga	(Ga/ig 4- Gn/tKp)t4-
4- (mah& 4~ бп/^пй-кр) -^- 4~ /Gn/iKp 4- FB/iB],
где <5„ = I 4-—
r0mn
Для одиночного автомобиля:
Т?г2 = —— [(fl 4“ fr0 4“ i^-g) Ga 4“	—— 4"
L	dt
4~ FB/iB].
Если автомобиль стоит неподвижно на горизонтальной площадке,
Rz2=G2= (a[L) Ga.
Аналогично для автопоезда:
T?2i = у[(& — fr0)Ga—(GJig 4- Gn/iKp) i —
(jnahg -J- 6п/7?п^кр) ~— —• j^Gn^-кр ^в^в]? at
для одиночного автомобиля: ,
Rzi =-£-[(& — fro — ihg) Ga —
— ma/ig^-FB/iB]; dt
для неподвижного автомобиля:
7?zi= Gt= (6/L)Ga.
Так как продольный профиль дороги включает и криволинейные участки, при движении автомобиля возникает центробежная сила, увеличивающая на вогнутых кривых или уменьшающая на выпуклых кривых нормальную к опорной поверхности составляющую силы тяжести автомобиля. Изменение при этом нормальных реакций дороги незначительно и в расчетах обычно не учитывается.
Нормальные реакции, действующие на колеса неподвижного автомобиля, равны осевым весам (Gi, G2). Отноше-
42
Табл. 2.5. Значения коэффициентов перераспределения реакций
Условия движения	kRl	kR2
Разгон с макси- мальным ускоре- нием	0,85...0,9 1,05...1,12 Преодоление предельных подъе- мов автомобилем: легковым	0,75...0,8	1,08... 1,12 грузовым	0,85...0,9	1,05... 1,1 повышенной про- ходимости	0,4...0,6	1,18...1,22 Торможение с максимальной ин- тенсивностью	1,4...1,2 0,65...0,75 - Торможение на спуске	1,4...1,6 0,45...0,55		
Fx2~ FB+Fi+Fjx~\-Fx\,	(2-18)
где Fx\ — сила, необходимая для обеспечения качения ведомых колес:
2 ZK1 л
Fxl =//?21 +(2.19) rQ dt
Окружная сила на ведущих колесах определяется выражением (2.10).
Подставив выражения (2.19) и (2.10) в уравнение (2.18), имеем:
МдМт ,Ъ( , г , Щ го
О 27к2 dw п___ ишк
го
dt
d<J\.:	dv
dt 2'к1 -----X
го
ние нормальных реакций дороги к осевому весу движущегося автомобиля называется коэффициентом перераспределения нормальных реакций:
kRi =-Rzi/Gi', kR2 = Rz^iGz.	(2.17)
Иногда эти коэффициенты используются при приближенных расчетах некоторых тягово-скоростных свойств автомобилей. Характерные значения коэффициентов перераспределения реакций приведены в табл. 2.5.
При определении нормальных реакций дороги в случае многоосных автомобилей общий подход остается таким же. Однако при этом необходимо составлять дополнительные уравнения, учитывающие кинематику и характеристики подвески.
2.5. Тяговый баланс автомобиля
Силой, движущей автомобиль, является окружная сила ведущих колес, определяемая по формуле (2.10). От ведущих колес к раме автомобиля передается продольная сила Fx2 = FT, которая необходима для преодоления сил сопротивления и качения ведомых колес:
Используя
а>, = со£/нт, после преобразований получим:
Л'кЩ	(
~ Пт = F;- — F, FB -j- tns 1 -|-
'0	\
соотношения
а>к = ц/го;
(Ve^e + dM) Ч2Т	~ к
--------- — Пт П---Д
ma ro m-Jo
Введем обозначения:
V I
щ М +1 ) и2	к
- , □_ п^+м) т	J (2 21)
Фа
dv
(2-20>
‘ 1	2	1|т -Г
"Vo
где k — число ведомых колес; число ведущих колес; z=n + k.
Тогда силу, затрачиваемую на гон поступательно движущихся и щающихся масс - автомобиля, можно представить в виде:
/	с du
Faj ~ О/72а ——. dt
Коэффициент 6 называется коэффициентом учета вращающихся масс. Если известны конструктивные параметры автомобиля, его можно подсчитать по выражению (2.21). Коэффи-
п —
раз-вра-
(2.22)
43
циент учета вращающихся масс иногда представляют в виде:
6 = 1 -J- 4~	(2.23)
где
?/к „ (VVt-M Oj = ----, 02 — ------
таг0	та'о
ик.п — передаточное число коробки передач.
Для одиночных автомобилей при номинальной нагрузке можно считать <Ji = O,03...0,05; 02 = 0,04...0,06. Меньшие значения относятся к более тяжелым автомобилям.
Если загрузка автомобиля отличается от номинальной, коэффициенты и о2 могут быть получены путем умножения их значений для автомобиля с номинальной нагрузкой на отношение та/та, где та, та— масса автомобиля при расчетной и номинальной нагрузках соответственно.
Аналогичным образом можно определить силу сопротивления разгону автомобильного поезда:
/7а.п/ = 6а.пта.п-^.	(2.24)
at
Коэффициент 6а.п может быть также определен по формуле (2.23), если значения Oi и о2 для одиночного автомобиля умножить соответственно на отношения (maZa.n)/(fna.nZa) и та/та.п, где та, тал1; za, za.n — соответственно полная масса одиночного автомобиля и автопоезда и число колес автомобиля и автопоезда.
Учитывая соотношения (2.10) и (2.22), уравнение (2.20) можно записать в следующем виде:
FK = Ft+Fi + FB + Faj.	(2.25)
Уравнение (2.25) называется уравнением тягового баланса автомобиля: сумма всех сил сопротивления движению автомобиля, включая силу сопротивления разгону, в любой момент времени равна окружной силе на ведущих
Рис. 2.17. Тяговая характеристика автомобиля
колесах, определенной для случая установившегося движения.
Графическое изображение уравнения тягового баланса в координатах полная окружная сила — скорость называется тяговрй_ характеристикой автомобиля. На рис. 2.17 кривые пока-зывагбт зависимость полной окружной силы от скорости движения автомобиля на соответствующих передачах (количество кривых тяговой характеристики автомобиля равно числу его передач). Для построения тяговой характеристики используются зависимости:
FK() = —— цт; va = 0,377-^ (1 — s), го	ит
(2.26) где s — коэффициент скольжения, определяемый по зависимостям, приведенным в гл. 1.
На рис. 2.18, а показана тяговая характеристика, построенная для случая движения легкового автомобиля на первой передаче по твердой сухой дороге. На рис. 2.18, б показан аналогичный график для случая движения автомобиля на высшей передаче по сухой
44
вания шин даже при небольших значениях окружной силы.
С помощью графика тягового баланса можно решать целый ряд задач, связанных с движением автомобиля. Однако использовать этот график для сравнительной оценки тягово-скоростных свойств автомобилей трудно, поскольку в автомобилях разной массы имеют место и разные окружные силы на ведущих колесах.
Окружная сила и сила сопротивления воздуха при заданной скорости движения целиком зависят от конст-
Рис. 2.18. Влияние буксования на тяговую характеристику легкового автомобиля:
а —тяговая характеристика на первой передаче (/ — без учета скольжения; 2 — с учетом скольжения); б — тяговая характеристика на прямой передаче (1 — без учета скольжения на сухой дороге; 2 — с учетом скольжения; 3 — с учетом скольжения на заснеженной дороге); в — зависимость окружной силы от коэффициента скольжения (/ — сухая дорога; 2 — заснеженная)
и заснеженной дорогам. Там же показана зависимость окружной силы на ведущих колесах от коэффициента скольжения для этих условий. Из графика видно, что только при больших значениях окружной силы (движение на низших передачах) учет скольжения дает заметный эффект. Поэтому в ряде случаев для автомобилей, предназначенных для движения по твердым дорогам, когда длительность использования низших передач незначительна, графики тягового баланса строят без учета скольжения колес. В случае же движения по дорогам с малым сцеплением определение скорости автомобиля необходимо вести с учетом проскальзы-
рукции и состояния автомобиля. Разность окружной силы и силы сопротивления воздуха — свободная сила тяги, которая может быть использована для преодоления сил сопротивления дороги и разгона автомобиля. Отношение свободной силы тяги к весу автомобиля (автопоезда) называется динамическим фактором D;
D=(FKQ-FB)/Ga. (2.27)
Динамический фактор — величина безразмерная.
Уравнение тягового баланса, следовательно, можно записать в виде:
D = f + i + -L^\	(2.28)
g
где g — ускорение свободного падения.
45
Рис. 2.19. Динамическая характеристика автомобиля
Графическое изображение зависимости динамического фактора от скорости движения автомобиля называется динамической характеристикой (рис. 2.19).
С помощью динамических характеристик можно сравнивать тягово-скоростные свойства автомобилей различной массы. В то же время необходимо отметить, что при изменении нагрузки автомобиля изменяется и динамическая характеристика. Пересчет динамического фактора при нагрузке, отличающейся от номинальной, может быть проведен по формуле:
D'=Dmoltna,
где D' — динамический фактор при заданной нагрузке; D — то же, при номинальной нагрузке.
Максимальные значения окружных сил обычно ограничены по условиям сцепления. Поэтому на тяговых и динамических характеристиках показывают линии, соответствующие максимальным по сцеплению окружным силам ГКф и динамическим факторам Dv. Окружную силу по сцеплению подсчитывают по выражению (2.12).
Поскольку максимальное сцепление имеет место при движении автомобиля
с малой скоростью, при подсчете динамического фактора, ограниченного сцеплением, в выражении (2.27) пренебрегают силой сопротивления воздуха:
Dtp = FK<P/Ga = <p (GJGa).
Отношение G2/Ga называют коэффициентом сцепного веса. Этот коэффициент показывает, какая доля веса автомобиля приходится на ведущие колеса. С увеличением коэффициента сцепного веса повышается проходимость автомобиля.
Особыми точками динамической характеристики, по которым целесообразно проводить сравнение тягово-скоростных свойств автомобилей, являются: максимальная скорость va max и динамический фактор при максимальной скорости Dv; максимальное значение динамического фактора на высшей передаче О® тах и соответствующая ему скорость vK (критическая); максимальный динамический фактор на низшей передаче £)тах и соответствующая ему скорость vD. Соответствующие параметры динамических характеристик некоторых отечественных автомобилей приведены в табл. 2.6.
На каждой передаче динамический фактор имеет максимальное значение при определенной скорости движения, являющейся критической для данной передачи. Движение автомобиля со скоростью, превышающей критическую, будет устойчивым. Действительно, если при коэффициенте сопротивления дороги ф1 ( рис. 2.20) автомобиль движется со скоростью oai, то при некотором повышении сопротивления, например до значения ф2, скорость автомобиля уменьшится, а динамический фактор увеличится до значения, равного ф2. При уменьшении ф до значения ф1 скорость автомобиля возрастет, а динамический фактор уменьшится. Таким образом, при движении автомобиля со скоростью, большей укр, автоматически поддерживается устойчивый режим движения. При движении со скоростью.
46
Табл. 2.6. Параметры динамических характеристик автомобилей
Автомобили	va max» км/ч	Ч’а	max	vK , км/ч	^max	V£). км/ч
Легковые: ЗАЗ-966	120	0,024	0,08	60	0,37	17 ВАЗ-2101	140	0,025	0,065	60	0,3	22 Москвич-412	140	0,037	0,07	60	0,35	23 Волга-М-24	145	0,025	0,10	65	0,4	20 Автобусы: РАФ-977Д (Латвия)	ПО	0,02	0,068	45	0,26	20 ПАЗ-625Б	80	0,018	0,045	40	0,32	7 ПАЗ-672	80	0,022	0,042	60	0,32	9 ЛАЗ-695Е	75	0,03	0,045	45	0,35	7 ЛАЗ-699А	100	0,02	0,036	40	0,31	7 Грузовые: УАЗ-451 Д	95	0,032	0,067	60	0,26	20 ГАЗ-53А	85	0,022	0,045	58	0,34	9 ЗИЛ-130	90	0,018	0,043	48	0,36	5 Урал-377*	75	0,017	0,038	45	0,33	6 КамАЗ-5320	85	0,015	0,037	50	0,35	6 КрАЗ-257	70	0,02	0,036	43	0,3	6 ЗИЛ-131*	80	0,013	0,018	40	0,57	5 Седельные автопоезда: КАЗ-608 «Колхида»	75	0,01	0,025	44	0,21	5 Урал-375С	75	0,013	0,022	35	0,23	5 КамАЗ-5410	85	0,01	0,017	40	0,18	6 ♦ Высшая ступень в раздаточной коробке.						
Рис. 2.20. График критической скорости по динамическому фактору
меньшей vK (например, цаз), увеличение Ф будет сопровождаться уменьшением скорости и динамического фактора, что в итоге должно привести к тому, что двигатель заглохнет, если своевременно не будет включена более низкая передача.
В некоторых случаях для оценки тягово-скоростных свойств и топливной экономичности автомобилей используют уравнение мощностного баланса,
Рис. 2.21. Мощностной баланс автомобиля с дизельным двигателем
иллюстрирующее распределение мощности двигателя по видам сопротивлений. Для получения последнего необхо
47
димо все члены уравнения (2.25) умножить на скорость автомобиля:
FKv = F^v+FBv+FajV;
P:-;=	PВ
где PK — мощность, подводимая к ведущим колесам; Рв — мощность, затрачиваемая на преодоление сопротивления воздуха; /V;— мощность, затрачиваемая на разгон автомобиля.
Так же, как и уравнение тягового баланса, уравнение мощностного баланса может быть представлено в графическом виде (рис. 2.21). На графике показана зависимость мощности, подводимой к ведущим колесам, а также суммарной мощности, затрачиваемой на преодоление сопротивления дороги и воздуха, от скорости движения на различных передачах. Разность этих двух мощностей дает мощность, которую можно реализовать для разгона автомобиля.
2.6.	Оценка тягово-скоростных свойств автомобиля
Основным показателем, по которому наиболее полно можно оценить тягово-скоростные свойства автомобиля, является средняя скорость движения vm — отношение пройденного автомобилем пути s ко времени чистого движения tR, vm = s/tR.
Средняя скорость движения вновь создаваемых автомобилей или автомобилей, проходящих контрольные испытания, определяется при пробеговых и эксплуатационных испытаниях, проводимых в различных дорожных и климатических условиях. Поскольку средняя скорость определяется не только конструкцией автомобилей, но и условиями движения, по этой характеристике не всегда представляется возможным дать объективную оценку тяговоскоростных свойств автомобилей.
В настоящее время для оценки скоростных свойств автомобилей используются различные критерии. При этом
Табл. 2.7. Коэффициенты парной корреляции
Критерии оценки скоростных свойств	Коэффициенты парной корреляции	
	при простой зави- симости	при логарифмической зависимости
Удельная мощность, кВт/т	0,51	0,13
Максимальная скорость, км/ч Динамический фактор при максимальной скоро-	0,43	0,48
сти	0,37	0,39
Динамический фактор при скорости 60 км/ч	0,57	0,41
Время разгона на высшей передаче с 15 до 60 км/ч, с	—0,26	—0,25
Время разгона с 15 до 60 км/ч с переключением передач, с	—0,73	—0,85
степень объективности оценки в сильной степени зависит от назначения автомобиля и условий его эксплуатации. Для примера в табл. 2.7 показаны коэффициенты парной корреляции между некоторыми критериями оценки скоростных свойств и средней скоростью движения грузовых автомобилей по твердым грунтовым дорогам.
Из таблицы видно, что в рассматриваемых условиях наиболее тесно корреляционно связаны со средней скоростью время разгона автомобиля с 15 до 60 км/ч с переключением передач и динамический фактор при скорости 60 км/ч. Это является достаточно очевидным, поскольку при движении по твердым грунтовым дорогам вследствие неровностей дороги приходится ограничивать скорость, при этом мощность двигателя, как правило, не используется полностью, а движение автомобиля характеризуется частыми циклами, состоящими из разгонов и торможений. Исследования показывают, что наибольшее количество разгонов осуществляется в диапазоне скоростей 15...40 км/ч. Поэтому в указанных
48
условиях характеристика разгона с переключением передач наиболее полно характеризует и среднюю скорость движения. Динамический фактор при скорости 60 км/ч определяет тот коэффициент сопротивления дороги, при котором в этих условиях автомобиль может двигаться без снижения скорости. Поэтому он также характеризует среднюю скорость движения.
При работе автомобиля, в других условиях, например на магистральных перевозках, средняя скорость может оказаться более тесно корреляционно связанной с другими критериями, такими, как максимальная скорость, удельная мощность.
В нормативных документах, определяющих методы оценки скоростных свойств автомобилей, приводится комплекс критериев, позволяющих провести сравнительную объективную оценку автомобилей с учетом возможных условий эксплуатации. Проверка скоростных свойств автомобилей выполняется по ГОСТ 22576—77, а комплекс измеряемых параметров определяется программами контрольных испытаний. Основными оценочными показателями тягово-скоростных свойств автомобилей и автопоездов являются: максимальная скорость и характеристики приемистости.
- Испытания по оценке тягово-скоростных свойств автомобилей и автопоездов проводятся при номинальной нагрузке на прямолинейном отрезке горизонтальной дороги с цементобетонным или асфальтобетонным покрытием. Уклоны ее не должны превышать 0,5 % и быть более 50 м. Испытания проводятся при скорости ветра не более 3 м/с и температуре воздуха —5...
; +25 °C.
Максимальная скорость автомобиля (автопоезда) —это максимальная скорость, развиваемая на горизонтальном ровном участке дороги. Определяется она путем измерения времени проезда автомобилем мерного
Рис. 2.22. Скоростная характеристика «разгон — выбег»:
а — по времени; б — по пути; 1, 3 — разгон; 2,4-выбег
участка дороги длиной 1 км. До въезда на мерный участок автомобиль на участке разгона должен достичь установившейся скорости.
Условная максимальная скорость — это средняя скорость прохождения автомобилем последних 400 м участка длиной 2000 м при интенсивном разгоне с места.
К характеристикам приемистости автомобиля, т. е. его способности быстро увеличивать скорость движения, относятся: скоростные характеристики «разгон — выбег» и «разгон на высшей и предшествующей передачах», время разгона на участках длиной 400 и 1000 м, время разгона до заданной скорости.
Разгон — выбег — скоростная характеристика, представляющая собой зависимость скорости уа от пути s и времени t разгона автомобиля с места и выбега до остановки (рис. 2.22). Разгон осуществляется с передачи, используемой при трогании с места. Подача топлива в процессе разгона мак-
49
Рис. 2.23. Скоростная характеристика «разгон на высшей передаче»:
1—по времени; 2—по пути
Рис. 2.24. Скоростная характеристика автомобиля при движении по дороге с переменным профилем
ных испытаний находят преодолеваемый автомобилем максимальный
симальная. Разгон автомобиля проводится на участке длиной 2000 м, после чего выключается передача в коробке передач и автомобиль по инерции движется до полной остановки. Характеристикой «выбег» оценивается сопротивление движению автомобиля. При контрольных испытаниях оценочным параметром является также путь выбега со скорости 50 км/ч.
Разгон на высшей и предшествующей передачах — скоростные характеристики, представляющие зависимость скорости иа от пути s и времени t разгона при движении автомобиля на высшей и предшествующей высшей передачах (рис. 2.23). Разгон начинается с минимально устойчивой для данной передачи скорости путем резкого нажатия до упора педали подачи топлива.
Время разгона на участках 400 м и 1000 м, а -также время разгона до заданной скорости устанавливают обычно по характеристике «разгон — выбег». Для грузовых автомобилей заданной скоростью является 60 км/ч, а для легковых — 100 км/ч.
Кроме перечисленных характеристик, определяют скоростную характеристику автомобиля или автопоезда при движении по дороге с переменным профилем, а по программе контроль-
подъем.
Скоростная характеристика при движении автомобиля по дороге с переменным профилем представляет собой зависимость средней скорости движения от максимальной допустимой (ограничение скорости) при проезде измерительного участка протяженностью 10...15 км. Участок должен иметь прямолинейный профиль, причем на нем должно быть не менее одного подъема и спуска длиной 600... 800 м и крутизной не менее 4 °/о • Для определения точки на графике производится пробег автомобиля по измерительному участку с наибольшей по техническим возможностям скоростью, но не превышающей допустимой скорости, задаваемой для каждого заезда. Ограничение скорости устанавливается в зависимости от номинальной таким образом, чтобы на графике скоростной характеристики автомобиля (рис. 2.24) было не менее четырех точек. Минимальная скорость ограничения — 30 км/ч, остальные устанавливаются кратными 10 км/ч.
Максимальный преодолеваемый автомобилем (автопоездом) подъем определяется на участках с ровным сухим покрытием или естественным сухим, задерно
50
ванным грунтом. Подъем преодолевается на низшей передаче в коробке передач и раздаточной коробке с включенным (при наличии) приводом передних ведущих колес и заблокированными дифференциалами. Автомобиль, движущийся на низшей передаче с минимальной устойчивой скоростью, подводится к началу подъема, после чего педаль подачи топлива нажимают до отказа.
Оценочные характеристики тяговоскоростных свойств автомобиля могут быть получены в результате решения уравнения тягового баланса автомобиля. Решается оно графическим способом с использованием тяговых и динамических характеристик или аналитически. В последнем случае внешняя характеристика двигателя задается в виде функции типа (2.3) или численно (таблица). Задача решается, как правило, на ЭВМ. Графические и аналитические решения выполняются, принципиально по одинаковой методике. Поэтому графический метод решения можно рассматривать как алгоритм программы для решения задачи на ЭВМ.
Максимальная скорость автомобиля, так же как и максимально возможная скорость при данном сопротивлении дороги, может быть найдена непосредственно по тяговой и динамической характеристикам. Для этой цели на тяговой характеристике строится зависимость суммарного сопротивления дороги и воздуха по формулам (2.15) . и (2.16) (см. рис. 2.17). Точка пересечения кривой сопротивлений с тяговой характеристикой соответствует максимально возможной для данных условий скорости движения. Кривая тяговой характеристики, которой принадлежит эта точка пересечения, указывает также номер возможной для движения передачи. Если линия суммарного сопротивления проходит между кривыми, соответствующими силе тяги на смежных передачах, движение возможно на передаче, для которой эта
кривая лежит выше линий сопротивлений, при скорости, соответствующей работе двигателя по частичной характеристике.
При определении максимальной скорости сопротивление дороги принимается равным сопротивлению качению автомобиля по дороге с ровным цементобетонным или асфальтобетонным покрытием.
Если для решения тех же задач используется динамическая характеристика, на графике наносится только линия зависимости коэффициента сопротивления дороги ф от скорости движения (см. рис. 2.19). Точки пересечения этой линии, так же как и на графике тяговой характеристики, указывают номер передачи и скорость движения. Если масса автомобиля отличается от номинальной, коэффициент сопротивления дороги нужно умножить на отношение расчетной и номинальной масс автомобиля (та/^о)-
Максимальная для заданных условий движения скорость автомобиля может быть найдена также по графику мощностного баланса. Для этого необходимо построить график зависимости суммарной мощности, потребной для преодоления сопротивления дороги и воздуха, от скорости автомобиля. Точка пересечения линии этой зависимости с линией зависимости мощности, подведенной к ведущим колесам, укажет максимальную для данных условий скорость автомобиля (см. рис. 2.21).
Для нахождения максимального преодолеваемого автомобилем подъема по графику тяговой характеристики определяется максимальное значение окружной СИЛЫ Fk max- ПОСКОЛЬКУ При преодолении максимального подъема ускорение автомобиля и сопротивление воздуха можно считать равными нулю,
Fk max'— (f + 1’max) Ga	(2.29)
ИЛИ
l'max = Eft max/Ga f 
51
Для решения той же задачи по динамической характеристике необходимо найти Дшах и определить imax:
imax = Дтах f 
По приведенной методике можно вычислить с достаточной точностью максимальные подъемы, при которых sina~tga. Это уклоны крутизной до 10°. Методы определения преодолеваемых автомобилем более крутых подъемов (внедорожных) описаны' в гл. 9.
Оценку приемистости автомобиля расчетным путем можно проводить по максимально возможным ускорениям, а также по характеристикам разгона.
Максимально возможные ускорения автомобиля при движении в заданных дорожных условиях наиболее удобно вычислять, используя динамическую характеристику. Из уравнения тягового баланса (2.28) имеем
=	(2.30)
dt о
С помощью этой формулы можно построить график зависимости ускорений автомобиля на передачах при заданных дорожных условиях. Используя график ускорений, можно определить оценочные критерии приемистости автомобиля.
Поскольку этап трогания автомобиля с места зависит от темпа включения сцепления и темпа подачи топлива, т. е. определяется индивидуальными особенностями водителя, то при расчете принимается, что разгон начинается с минимальной устойчивой скорости на передаче, с которой происходит трогание автомобиля. Минимальная устойчивая скорость определяется исходя из минимальной устойчивой частоты вращения двигателя. Разгон осуществляется при полной подаче топлива, т. е. двигатель работает по внешней характеристике. Время разгона автомобиля на определенной передаче от скорости ПпНп до скорости v находится исходя
Рис. 2.25. Выбор момента переключения передач из следующих соотношений:
V
dv	,, dv , f dv	.f.
ax = —; dt =——; t= —. (2.31) dt	ax	J dx
°min
Интегрирование этого выражения производят численным методом. Предполагается, что в небольшом интервале скоростей \Vi = Vi — Vi-i движение автомобиля является равноускоренным, причем ускорение равно полусумме ускорений в начале и в конце этого интервала. Время движения автомобиля \ti, при котором его скорость возрастает на Дщ, определяется по закону равноускоренного движения:
Ан,	2 Ан,
д/. =---L = ---------‘-----=
аср	ах(1—1) "b axi
=__________25 (^.-^._1)
+ ^-1) - (^ + ^--1)1 ’
Суммарное время разгона автомобиля на передаче k от скорости Ukmin до скорости Oftmax находится суммированием времени разгона в интервалах.
Для обеспечения наибольшей интенсивности разгона скорость переключения на высшую передачу va должна соответствовать максимальной частоте вращения коленчатого вала двигателя, если ускорение на низшей передаче при всех скоростях движения больше ускорения на высшей передаче (рис. 2.25, а), или скорости автомобиля, при которой кривые ускорений на низшей и высшей передачах пересекаются
52
б
Рис. 2.26. Разгон автомобиля на I и II передачах: а — по времени; б — по пути
(рис. 2.25, б). Во время переключения сопротивление движению можно принимать постоянным и равным принятому значению ф. Потеря скорости за время переключения
АЦп~^1ф^п/6п,
где ta — время переключения. В зависимости от способа переключения tn= = 0,8...1,5 с; 6П—коэффициент учета вращающихся масс при переключении передач: 6Л= 1,03...1,05.
Путь разгона автомобиля
t
s = ^vdt.	(2.32)
о
Этот интеграл также вычисляется численными методами. При равноускоренном движении в интервале скоростей ^Vi = Vi~ V'i-1 путь, проходимый автомобилем,
Asj = uCpA/j= 0,5 (и,~ 1 + Уг) А^-
Путь разгона автомобиля от скоро-
сти Vk min ДО скорости Vk max S =
(=1 {п—число интервалов). Путь, пройденный автомобилем за время переключения tn с k-й передачи на (&+1)-ю передачу,
’ А?п = (,Vk щах 0,5Дуп)^п.
Табл. 2.8. Время разгона легковых автомобилей до скорости 100 км/ч
Модель	Время, с	Модель	Время, с
ЗАЗ-968	38	Москвич-	
ВАЗ-2103	19	412 ИЭ	19
ВАЗ-2106	17,5	ГАЗ-24	22
ВАЗ-2121	25	ГАЗ-13	20
Москвич-2138	33	ГАЗ-14	15
Москвич-2137	24	ЗИЛ-117	13
Табл. 2.9. Расчетное время разгона автобусов и грузовых автомобилей до скорости 60 км/ч
Модель	Время, с	Модель	Время, с
ПАЗ-672	41	КамАЗ-5320	42
ЛАЗ-699А	32	Урал-375	55
УАЗ-4510М	18	Урал-377	62
ГАЗ-53	36	КрАЗ-257	55
ГАЗ-66	28	КАЗ-608А +	
ЗИЛ-130	38	+ ОдАЗ-885В	80
		КамАЗ-5410+	
		+ ОдАЗ-9370	90
На рис. 2.26 показан характерный график разгона автомобиля на I передаче и переход на II передачу.
Характеристики выбега автомобиля могут быть получены из уравнения тягового баланса при FK = 0. Время и путь, в течение которых скорость умень-
53
шается с до v%, определяются по формулам (2.31) и (2.32), азамедление а [ й А Д2 \
°'—#+^Н-
Характерные графики пути и времени разгона показаны на рис. 2.22, а в табл. 2.8, 2.9'—-время разгона до заданной скорости некоторых отечественных автомобилей. Расчетный анализ тягово-скоростных свойств автомобиля целесообразно проводить на ЭВМ.
2.7.	Топливная экономичность автомобиля
Себестоимость автомобильных перевозок в значительной степени зависит от топливной экономичности автомобилей — свойства, характеризующего расход топлива автомобилем или автопоездом при движении.
Топливная экономичность непосредственно зависит от конструкции автомобиля. Она определяется степенью совершенства рабочего процесса в двигателе, коэффициентом полезного дей-? ствия и передаточными числами трансмиссии, соотношением между снаряженной и полной массой автомобиля и автопоезда, сопротивлением движению.
Топливная экономичность оценивается по путевому расходу топлива — расходу топлива (в литрах или килограммах) на 100 км пути, проходимого автомобилем.
В США и Англии расход топлива принято выражать пройденным путем, соответствующим расходу топлива в одну объемную единицу. За единицу пути принимают милю, а единицу объема — галлон. Учитывая, что одна миля равна 1,609 км, 1 галлон США — 3,785 л, а 1 галлон английский — 4,546 л, перевод расхода, топлива шз одной системы в другую может осуществляться по соотношениям:
Qs = 235/mpg (t/S); Qs = 282[mpg (Imp), где Qs — путевой расход, л/100 км; mpg(US), mpg (Imp)—путь (в ми
лях), проходимый автомобилем при расходовании 1 галлона топлива соответственно США и английского.
Путевой расход топлива (иногда его называют средним расходом) определяют экспериментально при испытаниях или эксплуатации автомобилей в определенных дорожных условиях. Обычно испытания совмещаются с про-беговыми, при которых одновременно оценивают средние скорости движения и другие эксплуатационные свойства автомобилей.
Расход топлива автомобилем определяется и внешними факторами, не зависящими от конструкции автомобиля: рельефом местности, интенсивностью движения, состоянием дорожного покрытия, климатическими условиями и др. Существенное влияние на эксплуатационный расход топлива оказывает нагрузка. Поэтому более объективную сравнительную оценку топливной экономичности автомобилей дает не средний расход топлива, а удельный: отношение среднего расхода топлива к выполненной полезной работе по перевозке грузов или пассажиров. Такими показателями являются: (л/(т-км)) или <7п (л/(пасс.-км)):
7г= Qs/(1002T); 7n=Qs/(ЮОп), где zT, п — соответственно масса перевозимого груза (т) и число пассажиров. Для оценки топливной экономичности автомобилей используют следующие показатели: средний расход топлива в типовых дорожных условиях; топливную характеристику установившегося движения; контрольный расход топлива и топливную характеристику при движении по магистрально-холмистой дороге. Дополнительно для автомобилей, работающих с частыми остановками (городских и пригородных автобусов, специальных автомобилей), определяют топливную характеристику при циклическом движении.
' Средний расход топлива определяют путем измерения объема
54
Рис. 2.27. Типовая топливная характеристика установившегося движения грузового автомобиля по дороге с асфальтобетонным покрытием:
1 — с грузом; 2 — без груза
горючего, израсходованного автомобилем на определенном пути в заданных дорожных условиях (обычно—при движении автомобиля по равнинным, магистрально-холмистым, горно-холмистым и горным дорогам).
V- Топливная характеристика установившегося движения — график зависимости путевого расхода топлива от скорости установившегося движения в заданных дорожных условиях. Экспериментально ее определяют на горизонтальном ровном участке дороги с усовершенствованным покрытием при различной степени загрузки автомобиля: при полной нагрузке; без груза; с прицепом и др. Точки характеристики находят путем измерения объема израсходованного автомобилем топлива при проезде с заданной скоростью мерного километрового участка. Требования к этому участку такие же, как и при оценке скоростных качеств автомобиля. Обычно испытания скоростные и на топливную экономичность совмещают.
На рис. 2.27 показана топливная характеристика установившегося движения автомобиля при движении на высшей передаче, а на рис. 2.28 — при движении на различных передачах. С увеличением скорости путевой расход, как правило, сначала несколько уменьшается1 и достигает минимума при некоторой, зависящей от условий движения,
Рис. 2.28. Топливная характеристика легкового автомобиля «Шкода-100» при движении по дороге с асфальтобетонным покрытием
скорости. Затем по мере увеличения скорости расход топлива довольно быстро возрастает. При малой скорости и, соответственно, малой мощности, развиваемой двигателем, он возрастает и вследствие уменьшения механического КПД двигателя (увеличивается относительная доля механических потерь мощности) и ухудшения условий сгорания горючей смеси в цилиндрах. При большой развиваемой двигателем мощности расход топлива возрастает из-за переобогащения горючей смеси и соответственного уменьшения эффективного КПД двигателя. Зависимость расхода топлива от скорости движения более резко выражена у автомобилей с карбюраторными двигателями, поскольку удельный расход топлива у последних значительно больше зависит от степени использования мощности, чем у дизельных.
Минимальный расход горючего при движении автомобиля с номинальной нагрузкой по твердой горизонтальной дороге называется контрольным расходом (см. QK на рис. 2.27).
В связи с тем что зависимость расхода топлива от скорости в зоне минимальных расходов является пологой, контрольный расход обычно определя-
55
б
Рис. 2.29. Методика определения эксплуатационного расхода топлива:
а — для автомобиля с карбюраторным двигателем; б — с дизельным; Э.Р — эксплуатационный расход топлива
ют как расход топлива при определенной для данного автомобиля скорости, близкой к скорости, соответствующей минимальному его расходу.
Стандартами регламентируется скорость, при которой измеряют контрольный расход топлива. Контрольный расход измеряется при скорости 40... 100 км/ч. Отношение этой скорости к максимальной составляет 0,55...0,8.
По контрольному расходу топлива оценивают техническое состояние автомобиля, и поэтому он обычно указывается в технических характеристиках автомобиля.
Топливная характеристика установившегося движения дает лишь приближенную оценку топливной экономичности автомобилей. В то же время имеется определенная связь между этой характеристикой и эксплуатационным расходом горючего. Исследованиями, выполненными в ряде стран, установлено, что эксплуатационный путевой расход топлива примерно на 10 % больше расхода по топливной характеристике установившегося движения по твердым дорогам при скорости, составляющей две трети максимальной для автомобилей с дизельными двигателями и три четверти — с карбюраторными. Методика определения эксплуатационного путевого расхода показана на рис. 2.29.
Топливная характеристи
ка при движении автомобиля по магистрально-холмистой дороге представляет собой зависимость путевого расхода топлива от допустимой на маршруте скорости движения (Пдоп). В некоторых случаях строят зависимости расхода топлива от средней скорости движения. Эти характеристики позволяют судить о топливной экономичности автомобилей при переменных режимах движения в условиях, когда скорости ограничены.
у Топливная х ар а к те ристи-й'а циклического движения — зависимость путевого расхода топлива от средней скорости движения автомобиля циклами, состоящими и» этапов разгона, установившегося движения и остановки. Измерения проводятся на прямом горизонтальном уча-_ стке с усовершенствованным покрытием. Расстояния между остановками, -а также диапазоны скоростей установившегося движения определяются типом автомобиля.
Расчетные методы оценки топливной экономичности автомобилей основаны на следующих предпосылках! В каждый момент времени режимы; движения автомобиля и работы двига-. теля определяются номером ступени в коробке передач, скоростью и ускорением движения, сопротивлением дороги. В пределах достаточно малого участка пути Д$г указанные характеристи-
56
Рис. 2.30. Характеристика топливной экономичности двигателя ЯМЗ-238:
1—внешняя скоростная характеристика; 2— 8е= = 210,8 г/(кВт,-ч); 3 — ge=209,4; 4 — ge=212,2; 5 — ,ge = 213,5;	6 — ge = 217;	7 - gg=224,4;	8 - ge=
= 231,2 г/(кВт • ч)
ки можно считать постоянными. Расход топлива двигателем определяется по затрачиваемой им мощности и удельному расходу топлива. При этом допускается, что КПД двигателя при установившихся и неустановившихся одинаковых режимах одинаков.
Удельный расход топлива ge —отношение массы топлива, г, расходуемого двигателем за один час работы, к его эффективной мощности, кВт. Он зависит от режима работы двигателя, его мощности и частоты вращения. Получаемые при стендовых испытаниях зависимости представляют графически (рис. 2.30) или в числовой форме (таблица). Средняя мощность, которая должна подводиться к ведущим колесам автомобиля на участке пути Д$г-, Рк1 =	+ kBABv3 + bmaaxiVi. (2.33)
Расход топлива (в литрах) при проезде участка Д${ с учетом потерь мощности в трансмиссии и на привод агрегатов двигателем
AQz = 2,8 • Ю-^-, где р — плотность топлива. При расчетах можно принимать плотность бензина равной 730 кг/м3, а дизельного топлива — 860 кг/м3.
Расход топлива при проезде всего маршрута:
Q = 1 AQn 4—1
где п — число участков, на которые разделен весь маршрут.
Путевой расход топлива (в литрах на 100 км пути) на маршруте: Qs = = MQ/s.
Характеристики режимов движения автомобиля, входящие в уравнение (2.33), определяют путем моделирования на ЭВМ методами, описанными в гл. 8.
В тех случаях, когда топливно-экономические характеристики предполагаемого к установке двигателя неизвестны, для определения удельных расходов топлива используют приближенные методы.
Статистической обработкой топливно-экономических характеристик двигателей внутреннего сгорания установлено, что удельный расход топлива определяется удельным расходом его при максимальной мощности двигателя и степенью использования мощности и частоты вращения (под степенью использования мощности И понимается отношение мощности двигателя при рассматриваемом режиме работы Рк к его мощности по внешней характеристике при данной частоте вращения Ре—АА = РЛ/Ре, а под степенью использования частоты вращения Е — отношение текущего значения частоты вращения двигателя пе к частоте вращения при максимальной мощности пР — Е = пе/пР);
ge = gepknkE,	(2.34)
где gep — удельный расход топлива
57
Рис. 2.31. Мощностной баланс автомобиля с карбюраторным двигателем при движении на высшей передаче
двигателем при максимальной мощности; kn и кв — коэффициенты, зависящие от степени использования мощности и частоты вращения двигателя.
При сравнительных или приближенных расчетах можно принимать: для дизельных двигателей
kn = 1,2 + 0,14И—1,8И2+1,46И3; для карбюраторных двигателей
kn = 3,27 —8,22И + 9,13И2 —3,18И3; для всех типов двигателей
kE= 1,25 —0,99Е + 0,98Е2 —0.24Е3.
Удельный расход топлива двигателем при максимальной мощности обычно на 5...10 % больше минимального удельного расхода gprnln. Последний зависит от типа и конструктивных особенностей двигателя и составляет 300...340 г/(кВт-ч)— для карбюраторных двигателей и 220...260 г/(кВт-ч) — для дизельных.
При расчетах топливных характеристик установившегося движения для определения степени использования мощности и частоты вращения удобно применять график мощностного баланса автомобиля. Такой график для случая
движения автомобиля на одной из ступеней в коробке передач приведен на рис. 2.31. На графике показано изменение стендовой мощности двигателя Рс, на коленчатом валу Ре, мощности,, подведенной к ведущим колесам, РК и мощности, требуемой на преодоление сопротивления дороги, Рц в зависимости от скорости движения автомобиля..
Мощность, затрачиваемая на преодоление сопротивления воздуха, Рв вычитается из мощности, подведенной к ведущим колесам. Это позволяет, используя один график, рассчитывать параметры работы двигателя при различных сопротивлениях дороги. При установившемся режиме движения, например со скоростью vai по дороге с коэффициентом сопротивления фь двигатель затрачивает мощность, определяемую суммой потерь мощности, связанных с установкой двигателя на автомобиль (отрезок Л1), при передаче через трансмиссию (Л2), на преодоление сопротивления воздуха (Л3) и сопротивление дороги (Л4). Мощность, которую двигатель мог бы развивать при данной скорости движения автомобиля, определяется отрезком В. Следовательно, степень использования мощности двигателя
И = (Л1 + Л2+Лз+Л 4)/S, где В = P,Jkc.
Степень использования частоты вращения определяется отношением отрезков С и D:
Е = С/D — v^i/vp, где vP — скорость, соответствующая максимальной мощности двигателя.
Определение удельного расхода топлива по выражению (2.34) дает определенную погрешность, обусловленную особенностями конкретных двигателей. Учитывая невысокую точность данного метода расчета, часто степень использования мощности двигателя упрощенно принимают как отношение мощности, затрачиваемой на
58
движение автомобиля, к мощности, которая может быть подведена к ведущим колесам:--’
Г и = ?1),+ -в .	\
у	Т’е'Нт
Часовой расход топлива при движении автомобиля в заданных условиях: Q4 = 1(Г6£Л = 10~Wh£e Р^ + Рв .
11т
Путевой расход топлива:
ю Q4 = io~WhM^ + pb) РЧ>	Р^т
2.8.	Влияние конструктивных и эксплуатационных факторов на тягово-
/ скоростные свойства и топливную / экономичность автомобиля
/А Тягово-скоростные и топливно-экономические характеристики автомобиля зависят от многих факторов: параметров двигателя, трансмиссии; весовых и компоновочных параметров автомобиля; характеристик шин; условий эксплуатацией^
Движение автомобиля осуществляется за счет энергии сжигаемого в двигателе топлива. Уравнение топливного баланса, характеризующее расход выделяемой при сгорании топлива энергии, можно представить в виде:
Fq=Ft + №C,
где IFq — количество теплоты, выделяемой при сгорании топлива; W't — потери энергии при ее преобразовании в двигателе и при передаче к ведущим колесам (тепловые и механические потери в двигателе, затраты энергии на привод вспомогательных агрегатов, потери в трансмиссии); Wc— затраты энергии на преодоление сил сопротивления движению автомобиля (дороги, воздуха и разгону).
Анализ составляющих топливного баланса показывает, что основными потерями энергии являются термоди
намические и механические потери в двигателе (при установившемся режиме работы двигателя — 50...55 % общей энергии, выделяемой при сгорании топлива, на режимах разгона — до 70 %). Поэтому одним из резервов повышения экономических показателей работы автомобильного транспорта является уменьшение термодинамических и механических потерь энергии непосредственно в двигателе. Пути повышения эффективного КПД двигателя изучаются в курсах двигателей внутреннего сгорания.
Затраты энергии на привод вспомогательных агрегатов совместно с потерями во впускном и выпускном трубопроводах и подкапотном пространстве составляют 7...9 % энергии, выделяемой при сгорании топлива. В связи с этим следует обращать особое внимание на конструктивное оформление места установки двигателя. Целесообразно максимально уменьшать сопротивление всасывающих и выхлопных трактов, применять различные устройства, включающие вентилятор и другие вспомогательные механизмы только на тот период, когда это необходимо.
Тягово-скоростные и топливно-экономические характеристики автомобиля в значительной мере определяются типом и максимальной мощностью используемого двигателя. Сравнительная оценка автомобилей обычно производится по удельной мощности Руд — отношению максимальной эффективной (стендовой) мощности двигателя к массе автомобиля. Минимальное значение удельной мощности обычно регламентируется. Это способствует выравниванию скоростей транспортных потоков на дорогах.
Уменьшение удельной мощности до определенных пределов способствует, как правило, снижению расхода горючего и стоимости автомобильных перевозок. В то же время при слишком малой удельной мощности путевой расход горючего может увеличиться за
59
Рис. 2.32. Зависимость средней скорости и путевого расхода топлива от удельной мощности магистрального автопоезда
Рис. 2.33. Влияние формы внешней характеристики на запас мощности двигателя
счет более частого использования промежуточных ступеней в коробке передач. На графике (рис. 2.32) видно, что при принятых дорожных условиях минимальный путевой расход топлива имеет место при удельной мощности около 8,5 кВт/т. При дальнейшем увеличении удельной мощности средняя скорость движения автомобиля практически не изменяется, путевой же расход топлива возрастает значительно.
При одинаковой номинальной мощности двигателей характер изменения их внешних скоростных характеристик может быть различным. На рис. 2.33 показан график мощностного баланса
автомобиля с двумя двигателями одинаковой максимальной мощности, но» коэффициенты приспособляемости по< крутящему моменту которых различны. Из графика видно, что при установке двигателя с большим коэффициентом приспособляемости (характеристика 1) запас мощности, который может быть использован автомобилем для разгона при движении по дороге с определенным сопротивлением, будет большим, чем в случае установки другого двигателя (характеристика 2). Из-этого следует, что при установке двигателя с характеристикой 7 автомобиль будет обладать лучшей приемистостью и, соответственно, большей' средней скоростью, а расход горючего будет ниже за счет уменьшения времени использования промежуточных передач.
Указанные положения подтверждаются опытом эксплуатации и испытаний автомобилей. Например, в результате испытаний дизельного автопоезда, проведенных на скоростной трассе автополигона НАМИ, было установлено, что увеличение коэффициента приспособляемости kM с 1,07 до 1,13 привело к увеличению средней скорости на 10 % и уменьшению расхода топлива на 7...8 %. Время же разгона до скорости 60 км/ч сократилось на 10 %-Уменьшение расхода топлива достигается также в случае понижения номинальной частоты вращения коленчатого вала двигателя при одновременном соответствующем увеличении крутящего момента.
"-Проектируя автомобиль, конструк-тбр при выборе мощности двигателя должен учитывать различные факторы: назначение автомобиля, предполагаемые условия эксплуатации, тип и характер трансмиссии, форму внешней характеристики и др/ Рекомендации по методам выбора характеристик двигателя при проектировании автомобиля приведены в гл. 3.
В определенных дорожных услови-
60
26
б
Рис. 2.34. Зависимость путевого расхода топлива от массы автомобиля: а — грузового; б — легкового
ях силы сопротивления движению зависят от массы и размеров автомобиля.
Сопротивление дороги пропорционально массе автомобиля. Поэтому увеличение массы всегда приводит к увеличению расхода топлива. Это наглядно видно на графиках рис. 2.34, где показаны статистические зависимо-лсти путевых расходов топлива от пол-. ной массы грузовых и легковых автомобилей. Путевой расход топлива у грузовых автомобилей практически пропорционален их массе. У легковых автомобилей эта пропорциональность не наблюдается. Объясняется это тем, что основным сопротивлением движению грузовых автомобилей является сопротивление качению, пропорциональное их массе; у легковых автомобилей сопротивление воздуха оказывается соизмеримым, а при больших скоростях движения — и превосходящим сопротивление качению. В условиях, когда максимальные скорости ограничены и примерно одинаковы у всех легковых автомобилей, сопротивление воздуха практически не зависит от массы автомобиля, поскольку площадь лобового сопротивления не пропорциональна ей.
Пропорциональная зависимость между расходом топлива и массой перевозимого груза не наблюдается. Это
объясняется тем, что с увеличением полной массы автомобиля уменьшается коэффициент снаряженной массы, представляющий отношение снаряженной массы автомобиля т0 к номинальной массе груза. Поэтому с точки зрения экономии топлива всегда выгоднее осуществлять перевозку грузов большегрузными автомобилями и автопоездами.
Снижение расхода топлива при одновременном повышении тягово-скоро-,'стных свойств автомобиля может быть ^достигнуто за счет уменьшения сил сопротивления движению: сопротивления качению и сопротивления воздуха. Несмотря на то что работы в этом направлении ведутся, есть и неиспользованные резервы. Так, коэффициенты сопротивления качению современных шин при движении по дорогам с твердым покрытием в зависимости от конструкции и применяемых материалов составляют пока 0,009...0,018, коэффициенты обтекаемости однотипных автомобилей также различаются более чем в два раза. Снижение потерь энергии на сопротивление воздуха особенно важно для автомобилей, работающих на магистралях.
I "Йсследования показали, что при снижении коэффициента обтекаемости магистральных автомобилей на 12 %
61
путевой расход топлива уменьшается на 20...25 %ЛОсновные конструктивные мероприятий^, способствующие уменьшению дорожного сопротивления и сопротивления воздуха, были показаны в гл. 2.
Важным условием эффективной реализации мощности двигателя в различных условиях эксплуатации является рациональный выбор параметров трансмиссии: передаточного числа главной передачи, числа и диапазона передаточных чисел коробки передач, а также закономерности построения ряда передаточных чисел.
При проектировании трансмиссии нужно стремиться обеспечивать наиболее высокие средние скорости движения и наименьшие расходы топлива в тех условиях эксплуатации, для которых автомобиль предназначен. |
Автомобильный двигательв реальных условиях эксплуатации только незначительную часть времени работает на режимах максимальной мощности. Причем, чем больше удельная мощность автомобиля, тем реже используется режим максимальной мощности. Одна и та же мощность двигателя при его работе на частичных режимах может быть получена при различной частоте вращения. Например, как следует из рис. 2.30, мощность в 150 кВт реализуется при угловой скорости коленчатого вала 120...230 рад/с. Однако в зависимости от частоты вращения удельный расход топлива будет разным: минимальный — 209,4 г/(кВт-ч) и максимальный — 224,4 г/(кВт-ч). Очевидно, что наиболее выгодным будет режим, при котором удельный расход топлива будет наименьшим. На рис. 2.30 пунктиром показана линия, объединяющая точки, соответствующие режимам работы двигателя с максимальными при данных удельных расходах топлива мощностями.^Идеальная трансмиссия и система управления работой двигателя должна обеспечивать такое регулирование передаточных чи
сел трансмиссии, чтобы при любых дорожных сопротивлениях и скоростях движения двигатель работал бы по характеристике, соответствующей наименьшим удельным расходам топлива. С этой точки зрения применение бесступенчатых и ступенчатых трансмиссий с большим числом ступеней должно способствовать повышению топливной экономичности и средних скоростей движения автомобилей в любых условиях эксплуатации. (
Практически при слишком большом числе ступеней механической трансмиссии усложняется ее конструкция, повышается материалоемкость и стоимость. При такой трансмиссии водитель не всегда правильно ориентируется в выборе необходимой передачи. Это в конечном итоге приводит к тому, что потенциальные возможности многоступенчатых передач оказываются не реализованными.
В последнее время на некоторых автомобилях применяют механические многоступенчатые передачи с системами автоматического переключения и системами управления режимами работы двигателя, созданными на базе специализированных ЭВМ. Такое направление развития автомобильных трансмиссий является перспективным. Предварительные расчета показывают, что внедрение таких систем на магистральных автомобилях приведет к уменьшению расхода топлива на 10... 15 % при одновременном повышении их тягово-скоростных свойств. Еще больший эффект может дать применение таких систем на автомобилях, работающих с резко изменяющимися режимами движения.
уТЛередаточное число главной передачи определяет диапазоны дорожных сопротивлений и скоростей движения, в пределах которых автомобиль работает на высшей ступени в коробке передач. Поскольку движение на высшей ступени является наиболее экономичным, от правильности согласования ха
62
рактеристик двигателя, назначения автомобиля и передаточного числа главной передачи в значительной степени зависит себестоимость перевозок^ Рекомендации по выбору передаточных чисел трансмиссии приведены в гл. 3.
Средняя скорость и расход топлива в немалой степени зависят от дорожных условий. При работе автомобилей в высокогорных условиях вследствие снижения плотности воздуха и соответствующего уменьшения коэффициента наполнения цилиндров двигателя средняя скорость автомобилей снижается на 40...50 %, а расходы топлива увеличиваются на 10...15 %. В высокогорных условиях примерно в 5...6 раз возрастает путь, проходимый автомобилем на низших ступенях в коробке передач. В качестве мероприятий, позволяющих частично компенсировать потери мощности в этих условиях, принимают специальные регулировки карбюраторов или топливоподачи у дизельных двигателей, регулировку фаз газораспределения, повышение степени сжатия двигателей, турбонаддув. По имеющимся данным, использование турбонаддува может полностью компенсировать разреженность воздуха на высотах до 4000 м.
Средняя скорость и расход тщх при движении автомобиля, особенК-1 сложных условиях, в немалой степенк. зависят от квалификации водителя и стиля управления автомобилем.
Достижению низких расходов способствует плавное движение без резких разгонов и торможений. Вследствие того что экономичность двигателя всегда выше при работе с высоким крутящим моментом и малой частотой вращения, чем при работе с малым моментом и высокой частотой, целесообразно осуществлять переход на высшую передачу как можно раньше. Следует, где это целесообразно, использовать накат при выключенной передаче в коробке передач.
При движении автомобиля в городских условиях обычно наблюдается повышенный расход горючего. Это обусловлено необходимостью остановок на перекрестках, небходимостью частых разгонов и торможений. В зимние месяцы расход больше, чем летом. Существенное влияние на расход горючего оказывает техническое состояние автомобиля, главным образом состояние двигателя и ходовой части.
3 ТЯГОВЫЙ РАСЧЕТ АВТОМОБИЛЯ
3.1. Техническое задание
Общие положения. Задачей тягового расчета является определение характеристик двигателя н трансмиссии, обеспечивающих требуемые тягово-скоростные свойства и топливную экономичность автомобиля в заданных условиях эксплуатации.
Тяговые расчеты выполняются при проектировании нового автомобиля или модернизации существующего. Исходные данные для тягового расчета определяются в техническом задании, являющемся первичным документом, на основании которого выполняются эскизный н технический проекты.
Техническое задание устанавливает основное назначение, условия эксплуатации, технические характеристики, показатели качества, технико-экономическое обоснование необходимости разработки автомобиля новой конструкции или модернизация существующего, а также при необходимости и специальные требования к автомобилю.
В техническом задании для тягового расчета указываются: тип автомобиля, его назначение, условия эксплуатации, грузоподъемность пли пассажировместимость, максимальная скорость, максимальный преодолеваемый подъем, тип двигателя н трансмиссии, колесная формула. Иногда в техническом задании указывается двигатель, который должен использоваться на автомобиле. В этом случае максимальная скорость в задании не оговаривается.
На основании технического задания конструктор, анализируя технические характеристики существующих близких по назначению автомобилей и оценивая перспективы их развития, а также традиции и уровень технической оснащенности завода-изготовителя, качество предполагаемых к использованию материалов, выбирает ряд характеристик, необходимых для проведения тягового расчета. К таким характеристикам относятся: весовые и размерные параметры, размеры шины, коэффициент полезного действия трансмиссии, коэффициент сопротивления воздуха.
Масса автомобиля и автопоезда. В СССР приняты следующие определения. Масса сухого автомобиля (тс) — масса автомобиля без снаряжения, т. е. без инструмента, запасного колеса, дополнительного оборудования (например, радиоприемника, кондиционера и др.) и заправки (топлива, жидкого смазочного материала и воды). Сухая масса автомобиля включает массу жидкости в амортизаторах, смазочного материала в агрегатах и шарнирах, а также электролита в аккумуляторной батарее.
Масса снаряженного автомобиля т<у—масса автомобиля с заправкой и снаряжением, но без водителя и пассажиров.
Полная масса тл — суммарная масса снаряженного автомобиля, полезной нагрузки (тг), снаряжения, водителя и пассажиров.
Масса автомобильного поезда
64
Табл. 3.1. Характеристики легковых автомобилей
Класс автомобиля	Группа	Рабочий объем двигателя, л		Сухая масса, кг		Масса снаряжения, кг	
I — особо малый	1	До	0,849	До 649		30..	50
	2	0,85.	..1,099	650	. .799	50..	65
II — малый	1	1,1.	..1,299	800	..899	65..	90
	2	1,3.	..1,499	900	..1049		
	3	1,5.	..1,799	1050	..1149		
III — средний	1	1,8.	..2,499	1150	..1209	90..	НО
	2	2,5.	..3,499	1300	..1499		
IV — большой	1	3,5.	..4,949	1500	..1900	ПО..	120
	2	Свыше 5		Не регламентирована			
(та.п) —суммарная полная масса тягача и прицепа (полуприцепа).
Полную массу автомобиля можно найти по формулам:
для грузовых автомобилей:
ma = т0 + тг + тч{п+1) +«iq;
для автобуса городского типа: т&=т0 + гпч{п + к+1) + т§\ для автобуса междугородного типа: та=т0 + «ч(п + 2) +«6;
для легкового автомобиля: тЛ = т0 + тчп + т5, где тч — масса водителя или пассажира. При расчетах принимают тч= = 75 кг; п — число мест для сидения пассажиров; k — число мест для проезда стоя; «б — масса багажа.
Число мест для проезда пассажиров в автобусах городского типа стоя определяется исходя из площади, в пределах которой возможно их размещение. В нормальных условиях предполагается размещение на одном квадратном метре свободной от сидений площади до 5 человек, а в часы «пик» — до 8.
В число мест для сидения в легковых автомобилях включается место водителя. Массу багажа водителя и пассажира грузовых автомобилей и городских автобусов принимают равной 5 кг, автобусов междугородных перевозок— 15 кг и легковых автомобилей— 10 кг на одного человека.
Рис. 3.1. Зависимость удельной снаря-женной массы автобусов от их вместимости
Снаряженная масса легковых автомобилей зависит от класса и группы. В табл. 3.1 приведен рабочий объем двигателя (Ул) — основной параметр, определяющий принадлежность автомобиля к соответствующему классу и группе, а также масса автомобилей в соответствии с типажом.
Снаряженная масса автобуса зависит от его номинальной вместимости. Снаряженную массу можно определить по удельной снаряженной массе, т. е. массе автобуса, приходящейся на од-
3 А. И. Гришкевич
65
Рис. 3.2. Зависимость коэффициента грузоподъемности от полной массы бортовых автомобилей н автопоездов
Рис. 3.3. Зависимость коэффициента грузоподъемности от полной массы автомобилей-самосвалов
ного пассажира. На рис. 3.1 показана зависимость этой массы от номинальной вместимости городских и пригородных автобусов. При этом под номи-
нальной вместимостью понимается число пассажиров, перевозимых автобусом при нормальных условиях движения (не в часы «пик»). Огибающие кривые соответствуют наименьшим и наибольшим удельным массам.
Если задана грузоподъемность грузового автомобиля,его предполагаемую полную массу можно найти по статистическим данным исходя из коэффициента грузоподъемности /гг: kr=mrlm&. На рис. 3.2 показана зависимость этого коэффициента от полной массы бортовых неполноприводных и полноприводных автомобилей и седельных автопоездов. Огибающие кривые соответствуют наиболее высоким коэффициентам грузоподъемности рассмотренных бортовых автомобилей и седельных автопоездов. На рис. 3.3 показаны аналогичные зависимости для автомобилей-самосвалов.
Приведенные на рис. 3.1...3.3 зависимости характеризуют современный уровень автомобилестроения. Следует полагать, что с улучшением качества применяемых материалов и технологии изготовления автомобилей коэффициенты грузоподъемности последних будут повышаться.
Распределение веса грузовых автомобилей по мостам определяется целесообразностью полного использования грузоподъемности шин, а также необходимостью соблюдения норм, ограничивающих максимальную допустимую нагрузку на дорогу. В СССР по допускаемой на одиночный мост нагрузке автомобили делятся на две группы: А и Б. У автомобилей первой группы на одиночный мост допускается нагрузка до 100 кН, второй —- до 60 кН. Отдельную группу составляют внедорожные автомобили, нагрузки на мосты которых обычно не регламентируются. Движение таких автомобилей по дорогам общего пользования, как правило, запрещено. Допускаемая нагрузка на мост тележки зависит от расстояния между осями смежных мостов и состав-
66
ляет 70... 100 % от нагрузки, допускаемой на два одиночных моста при расстояниях между мостами 1 ...2,5 м.
При распределении веса грузовых автомобилей по мостам следует иметь в виду, что увеличение нагрузки на ведущий мост приводит к увеличению сцепного веса автомобиля и соответственно к повышению его проходимости. Грузоподъемность автомобиля при этом уменьшается. Например, грузоподъемность шин у автомобиля 4x2, имеющего на заднем мосте четыре шины, будет полностью использоваться в случае, когда на этот мост приходится 67 % нагрузки. При этом коэффициент сцепного веса
k<p = Gq/Ga, определяющий проходимость автомобиля по сцеплению, будет равен 0,67, а полная масса автомобиля группы А может составлять 15 т. Если для повышения проходимости такого автомобиля принять коэффициент сцепного веса 0,75, полная масса автомобиля будет 13,3 т, что, естественно, приведет к уменьшению его грузоподъемности. Применение на таком автомобиле мостов с широкопрофильными шинами позволит повысить массу автомобиля примерно до 20 т, а коэффициент сцепного веса станет равным 0,5.
Обычно вес, приходящийся на ведущий мост, колеса которого имеют сдвоенные шины, принимают у автомобилей группы А 0,67...0,7, а у автомобилей группы Б — 0,7...0,75 полного веса автомобиля.
Распределение веса легковых автомобилей по мостам зависит от схемы автомобиля. При переднем двигателе и заднем ведущем мосте на задний мост приходится 52...55 % полного веса, при переднем двигателе и переднем ведущем мосте — 43...47 %, а при заднем двигателе и заднем ведущем мосте — 56...60 %.
Распределение веса у городских, пригородных и междугородных автобу
сов принимается таким же, как и у автомобилей группы А, а у автобусов, предназначенных для местных перевозок,— как у автомобилей группы Б. У полноприводных автомобилей с одинарными колесами распределение веса выбирается таким, чтобы обеспечить примерно равномерную загрузку всех мостов. При этом нагрузку на передний мост принимают на 4...8 % меньше, чем на остальные.
Масса буксируемого прицепа зависит от назначения автопоезда, массы тягача, числа ведущих мостов тягача и других факторов. Отношение массы прицепа к массе тягача (коэффициент массы прицепа /гПр) у автопоездов, предназначенных для движения по твердым дорогам, равно 0,5...1,2. При этом большие значения относятся к автомобилям группы А. Для автомобильных поездов с полноприводными тягачами при движении по грунтовым дорогам &цр=0,3...0,6.
После определения массы и распределения веса автомобиля по мостам конструктор, используя ГОСТы с сортаментом шин, выбирает размеры шин и основной расчетный радиус колес Го-
Коэффициент сопротивления воздуха и площадь лобового сопротивления проектируемого автомобиля определяют по методике, изложенной в гл. 2.
Диапазон максимальных скоростей грузовых автомобилей определяется условиями безопасности движения, действующими нормативными документами, скоростными показателями автомобилей-аналогов и тенденциями развития автостроения. По ГОСТ 21398— 75 нижний предел максимальной скорости составляет 75 км/ч для полностью нагруженных одиночных автомобилей и автопоездов, движущихся по горизонтальной дороге с твердым покрытием, и 30 км/ч на подъеме с крутизной 3 %.
Максимальная скорость большинства современных грузовых автомобилей находится в пределах 80...100 км/ч.
з*
67
Предполагается, что в перспективе скорость тяжелых грузовых автомобилей магистрального типа не будет превышать 100 км/ч.
Максимальная скорость полноприводных грузовых автомобилей — также 80... 100 км/ч (только у автомобилей массой до 2 т достигает 120 км/ч), легковых автомобилей в зависимости от их класса— 100...220 км/ч. Максимальная скорость автомобилей особо малого класса обычно не превосходит 140 км/ч, малого класса— 170 км/ч, а среднего и большого — 220 км/ч.
Коэффициент полезного действия трансмиссии выбирают по методике, изложенной в гл. 2.
3.2. Выбор характеристик двигателя
Выбор характеристик двигателя является одним из наиболее ответственных этапов тягового расчета. При повышенной мощности двигателя улучшаются динамические качества автомобиля, возрастает средняя скорость движения. Однако при повышении мощности двигателя увеличиваются его размеры и масса, размерность трансмиссии, определяющие стоимость изготовления автомобиля, а также расход топлива и масла. При недостаточной мощности двигателя автомобиль, обладая низкими тягово-скоростными свойствами, будет создавать помехи для других более скоростных автомобилей, движущихся в общем транспортном потоке. При этом чем хуже тягово-скоростные свойства автомобиля, больше его размеры и масса, тем больше он создает помех в транспортном потоке. Это, естественно, уменьшает эффективность автомобильных перевозок.
Необходимую максимальную мощность двигателя находят из условия обеспечения максимальной скорости движения автомобиля при заданном дорожном сопротивлении ЧД и сравнивают с мощностью двигателей автомобилей-аналогов, и на этой базе делает
ся заключение о пригодности двигателя к установке на проектируемый автомобиль.
Поскольку при максимальной скорости ускорение автомобиля равно нулю, исходя из уравнения мощностного баланса, необходимая мощность двигателя (кВт) при движении автомобиля массой та (т) со скоро-СТЬЮ У а шах (км/ч) определяется по выражению:
71	/	1? А 71^	\
n	a max I _	.	, в в а max ]
+ 13000 )
(3.1)
Для расчетов по формуле (3.1) значения дорожного сопротивления принимают: для легковых автомобилей в зависимости от их класса фа = 0,025... 0,04, автобусов — 0,018...0,03, грузовых автомобилей — 0,015...0,025, автопоездов— 0,01...0,015, полноприводных автомобилей повышенной и высокой проходимости — 0,015...0,05.
Так как при максимальной скорости движения двигатель работает с максимальной частотой вращения, в случае установки на автомобиле дизеля Рег,= = Ре max. У карбюраторного двигателя максимальная частота вращения пе max и частота при максимальной мощности Пр, как правило, не совпадают. В этом случае максимальную мощность можно найти исходя из соотношения (2.3):
Ре max — Р ev
А пе max ।	тах\^
р	у Tip J
/ П	\ 3 1 —1
I ‘ о т о v \
Отношение петах/«р у современных карбюраторных двигателей легковых автомобилей составляет 0,9...1,15, а у грузовых — 0,9... 1.
Максимальная стендовая мощность двигателя Рс тах = Ре тах/^с. Значения kc принимаются согласно рекомендациям, приведенным в параграфе 2.2.
По найденной стендовой мощности выбирается двигатель из числа выпу-
68
Рис. 3.4. Зависимость максимальной скорости от удельной мощности легковых автомобилей
скаемых промышленностью, имеющий мощность, близкую к требуемой. При этом одновременно изучается возможность форсирования или при необходимости ограничения мощности двигателя. Выбранный двигатель должен удовлетворять и другим требованиям, оговоренным техническим заданием на проектирование автомобиля.
В случае, если двигатель с требуемыми параметрами не производится, принимается решение о целесообразности изготовления нового двигателя с требуемыми характеристиками. Для проведения тяговых расчетов по методике, изложенной в параграфе 2.2, строится внешняя характеристика с учетом потерь мощности при установке двигателя на автомобиле, а также внешняя стендовая характеристика для технического задания на проектирование двигателя.
Необходимую максимальную стендовую мощность двигателя сравнивают с мощностью двигателей на автомобилях-аналогах. При этом следует учитывать, что в характеристиках автомобилей приводится максимальная стендовая
Рис. 3.5. Время разгона легковых автомобилей до скорости 100 км/ч в зависимости от их удельной мощности
мощность двигателя, измеренная в соответствии с действующими государственными стандартами в разных странах. Различные автомобили сравниваются ПО удельной МОЩНОСТИ Руд.
Статистически установлены определенные закономерности, связывающие удельную мощность и тягово-скоростные свойства автомобиля.
На рис. 3.4 показана взаимосвязь удельной мощности, максимальной скорости и класса легковых автомобилей, а на рис. 3.5 — зависимость времени их разгона до скорости 100 км/ч от Руд. Из графиков видно, например, что автомобили особо малого класса характеризуются удельной мощностью до 40 кВт/т, максимальной скоростью до 140 км/ч и временем разгона до 100 км/ч — 19...23 с. Удельная мощность автомобилей среднего и большого класса достигает 90 кВт/т, максимальная скорость — 220 км/ч, при этом время разгона до скорости 100 км/ч составляет 8...10 с.
Удельная мощность грузовых автомобилей зависит от их назначения и массы (рис. 3.6). Для автобусов удельная мощность дизельных двигателей
69
a
Рис. 3.6. Зависимость удельной мощности от полной массы автомобилей:
а — неполноприводных; б — полноприводных
составляет 8...12 кВт/т, а карбюраторных — 9...13 кВт/т.
На рис. 3.7 показаны зависимости времени разгона грузовых автомобилей до скорости 60 км/ч от их удельной мощности.
С уменьшением удельной мощности (до определенных пределов) снижается расход горючего и стоимость автомобильных перевозок. В то же время автомобиль с малой удельной мощностью будет иметь плохие динамические свойства. Это в конечном итоге связано с уменьшением средних скоростей движения и увеличением народнохозяйственных затрат. Поэтому определение минимальной допустимой удельной мощности двигателя является важной проблемой.
Рис. 3.7. Время разгона грузовых автомобилей до скорости 60 км/ч в зависимости от их удельной мощности
Рис. 3.8. Изменение средней скорости движения и расхода топлива в зависимости от удельной мощности магистральных автопоездов
На рис. 3.8 показано изменение средней скорости движения и расхода горючего в зависимости от удельной мощности магистральных автопоездов. График получен по результатам эксплуатационных испытаний, проведенных в ФРГ и Франции. На рис. 3.9 изображена экспериментальная зависимость условной максимальной скорости некоторых автопоездов от их удельной мощности. Условная максимальная скорость характеризует скоростные качества автомобиля при переменных режимах движения. Из приведенных графиков следует, что в диапазоне 4,5...6,5 кВт/т увеличение удельной
70
Рис. 3.9. Зависимость условной максимальной скорости автопоездов от их удельной мощности
Рис. 3.10. Графическое определение максимальной скорости автомобиля
ХЩИЯ к для других более скоростных мащ пя-В связи с этим можно считать, что п^ч. проектировании автопоездов Руд должна быть в пределах 7,5...8 кВт/т.
Когда в техническом задании определен двигатель, который должен быть использован на автомобиле, при выполнении тягового расчета определяется возможная максимальная скорость исходя из мощностного баланса автомобиля. При этом мощность (кВт), подводимая к колесам автомобиля, определяется по формуле:
ко — Рс гпах^сЦт Ч
i tl \ 2
у ftp J
Отношение nemax/«p, как показано выше, зависит от типа используемого двигателя. Решение уравнения мощностного баланса и определение максимальной скорости может быть выполнено графически, как это показано на рис. 3.10, или аналитически путем решения уравнения:
Щ max Ц^а max ‘ Ь = 0,	(3.2)
где а= 1,27-l05fmB/(kBAB); Ь=4,7Х] X 104Рко/ (&в-Ав) •
Решение уравнения (3.2) по формуле Кардано дает
мощности приводит к повышению скоростных качеств автопоездов при незначительном возрастании расхода горючего. Исследования скоростных и экономических характеристик автопоездов показывают, что при дальнейшем увеличении Руд скорости движения практически не повышаются. В результате расчетов экономической эффективности междугородных перевозок установлено, что оптимальной для тяжелых автопоездов является Руд порядка 6... 7,5 кВт/т. Если же рассматривать движение транспортного потока в целом, автопоезда с удельной мощностью 6 кВт/т создают значительные помехи
3.3. Выбор параметров трансмиссии
К характеристикам трансмиссии, определяемым при тяговом расчете автомобиля, относятся: передаточное число главной передачи п0, диапазон передаточных чисел Дк, количество ступеней п в коробке передач и ряд передаточных чисел.
71
Рис. 3.11. Влияние коэффициента высшей передачи на мощностной баланс автомобиля
Гп ер е д а то ч но е число главной передачи выбирают исходя из максимальной кинематической скорости автомобиля Унтах. Кинематическая скорость — это скорость, соответствующая максимальной частоте вращения двигателя при высшей ступени в коробке передачу
Ок max = 0,377tle тах^о/^т.в, где ит.в — передаточное число трансмиссии при высшей ступени в коробке передач.
ГВ' общем случае кинематическая скорость может не совпадать с максимальной скоростью автомобиля Уатах, определяемой исходя из баланса мощностей. Степень их совпадения оценивается коэффициентом высшей передачи Су ~ Оа max/Ок max- Для Оценки ВЛИЯНИЯ этого коэффициента на тягово-скоростные и топливно-экономические показатели автомобиля с дизельным двигателем рассмотрим график его мощностного баланса при различных значениях cv (рис. 3.11).
На графике показана мощность, подводимая к ведущим колесам, при с®<1; с«=1 и СвЖ Сопротивление фи является для данного автомобиля расчетным.,'Как видно из графика, максимальная- скорость будет наибольшей при cv=l. Во всех других случаях она
меньше или из-за недостатка мощности двигателя (с^<1), или вследствие перехода двигателя на работу по регуляторной ветви (cr> 1). При движении автомобиля со скоростью запас мощности для разгона будет тем больше, чем больше значение cv- В то же время степень использования мощности двигателя при движении с этой скоростью будет тем выше, чем меньше cv. Поскольку степень использования мощности двигателя определяет топливную экономичность автомобиля, то при уменьшении cv последняя повышается.
При изменении дорожного сопротивления, например при уменьшении его до ф1, максимальная скорость автомобиля при cv—l изменится мало, а степень использования мощности двигателя значительно уменьшится. У автомобиля, имеющего с^<1, максимальная скорость возрастает. Если максимальную скорость принять за расчетную, возрастет степень использования мощности двигателя.
\ТЛри магистральных перевозках сопротивление движению часто ниже расчетного: движение по отдельным высококачественным магистралям, при попутном ветре, на затяжном спуске, при неполной загрузке автомобиля. В то же время при магистральных перевозках средняя скорость движения автомобиля практически не зависит от его приемистости. Поэтому для магистральных автомобилей в ряде случаев целесообразно принимать кинематическую скорость больше максимальной, особенно в том случае, когда имеется достаточное число ступеней в коробке передач и различие в передаточных числах высшей и предшествующей ступеней не очень большое.^
У легковых автомобилей cv=1. Условие сг>1 обеспечивают в тех случаях, когда требуются хорошие динамические качества автомобиля при ограниченной мощности двигателя и небольшом числе ступеней в коробке передач.
72
Передаточное число главной передачи находят по формуле:
«0 = 0,377 пе maxr0Cvl (fa шах^в), где «в — передаточное число высшей передачи в коробке передач.
Высшая передача в коробке передач заднеприводных автомобилей бывает прямой или повышающей. Повышающая передача наиболее часто применяется на автомобилях средней и большой грузоподъемности, предназначенных для работы с прицепами, а по производственным соображениям и с целью унификации коробок передач — и на грузовых автомобилях других типов. Передаточное число повышающей передачи принимается 0,65...0,8.
Передаточное число высшей передачи для переднеприводного автомобиля определяется конструкцией коробки передач и привода. В этом случае целесообразно находить суммарное передаточное число трансмиссии на высшей передаче «т.в, а разделение передаточных чисел между коробкой передач и главной передачей производить исходя из конструктивных соображений.
Главные передачи заднеприводных легковых автомобилей имеют передаточные числа 3,1...4,9, а переднеприводных— 3,7...5,1. У грузовых автомобилей главные передачи изготовляют с передаточными числами 4,5...9. При этом на автомобилях одного типа в зависимости от условий эксплуатации главные передачи могут быть с различными передаточными числами.
Диапазон передаточных чисел коробки п ер еда чДк равен частному от деления передаточных чисел крайних ступеней («1/«в). Диапазон передаточных чисел и число передач являются основными характеристиками коробок. Определяются типом и назначением автомобилей.
У легковых автомобилей применяют коробки передач с 3...5 ступенями. Наиболее распространенными в настоящее время являются четырехступенча
тые, хотя и наблюдается тенденция к увеличению количества моделей с пятиступенчатыми коробками передач. Трехступенчатые применяют только на автомобилях с большой удельной мощностью двигателя. Диапазон передаточных чисел трехступенчатых коробок передач составляет обычно 2,3...2,6, пятиступенчатых — 3,5...4,5, четырехступенчатых— 3,4...4, а отдельных из них — 3,1...3,2 и 4,5...4,7.
Диапазон передаточных чисел и число ступеней коробок передач грузовых автомобилей отличаются большим разнообразием. Применяют коробки передач с числом ступеней п = 5...22 при Дк = 5...25. Количество ступеней находится в прямой зависимости от диапазона передаточных чисел коробки. Это видно из данных, полученных статистической обработкой многих моделей автомобилей: диапазону передаточных чисел коробки передач 5,7...8,5; 7,9... 9,35; 8...10; 9,2...18,5; 13...19,4; 17...24,7 соответствует число ступеней 5; 6; 8; 10; 16; 20.
Общей тенденцией является увеличение числа ступеней и диапазона передаточных чисел коробки передач при возрастании общей массы автомобиля и автопоезда. У большегрузных автомобилей и автопоездов увеличение п и Дк позволяет более эффективно использовать двигатель при работе их с различной степенью загрузки и в различных дорожных условиях.
Передаточное число первой передачи должно быть таким, чтобы автомобиль (автопоезд) мог преодолеть максимальное Сопротивление ДОРОГИ фтах, заданное техническими условиями, и мог двигаться с минимальной устойчивой скоростью для обеспечения возможности маневрирования в стесненных условиях. Уравнение тягового баланса для этого случая с учетом формулы (2.29):
Me тахЦ)М1Т]т/го= бафmax*	(3.3)
73
Отсюда необходимое передаточное число первой передачи
= фтахОа/'о/(Л4е тах^оТ]?). (3-4)
При расчетах по формуле (3.4) фтах для одиночных автомобилей должно быть не менее 0,35, а для автопоездов— не менее 0,18. Обычно принимают для легковых автомобилей фтах = = 0,35...0,5 и грузовых — фтах = 0,35... 0,4.
Возможность реализации окружной силы на колесах автомобиля при передаточном числе Ui, подсчитанном по формуле (3.4), проверяется по условиям сцепления ведущих колес с дорогой:
тах^О^ЛЛт/^О — фбф.
Следовательно, передаточное число первой передачи, при котором окружная сила реализуется по сцеплению,
tJ __
(3-5)
тахио4т где бф— сцепной вес автомобиля.
Для полноприводных автомобилей Gq, = Ga, автомобилей с задним расположением ведущих мостов Сф = ki&Gz, с передним ведущим мостом — G,t = = kmGi. В этих выражениях Gj и G2 — доля веса автомобиля, приходящаяся соответственно на задний и передний мост; km и k$2 — коэффициенты перераспределения нагрузки. Можно принимать km = 0,8...0,9 и km = 1,1...1,3. Расчеты проводятся для условий движения по хорошему «сухому» шоссе (<р = 0,7...0,8).
Если Ui по формуле (3.4) будет больше, чем рассчитанное по формуле (3.5), необходимо принять меры к увеличению сцепного веса автомобиля, поскольку при данном сцепном весе автомобиль не сумеет преодолеть подъем, определенный техническим заданием. При невозможности увеличения сцепного веса следует принять значение Ui, найденное по формуле (3.5),
согласовав с заказчиком изменение технического задания.
Передаточное число первой передачи должно удовлетворять условию обеспечения минимально устойчивой скорости движения:
U\r = 0,377 Пе min^o/ (fZo^a min) , (3-6) где /Zemin—минимальная устойчивая частота вращения коленчатого вала двигателя, мин-1; па mm — минимально устойчивая скорость движения, принимаемая 4...5 км/ч.
Если передаточное число, определенное по формуле (3.6), больше найденного по формуле (3.4) или (3.5), оно принимается в качестве расчетного для первой передачи.
Если предварительно на основании статистических данных устанавливается диапазон передаточных чисел коробки передач, принимается и1 = ДкЦв. В этом случае также нужно провести проверку обеспечения возможности преодоления автомобилем заданного подъема и движения его с минимальной устойчивой скоростью.
Передаточные числа промежуточных передач выбирают из условия обеспечения максимальной интенсивности разгона автомобиля, а также возможности длительного движения при повышенном сопротивлении дороги.
Для того чтобы в процессе разгона двигатель работал с наибольшей средней мощностью, его частота вращения должна быть в диапазоне частот, близком к частоте максимальной мощности. Допустим, что этот диапазон определяется частотами вращения п\ и п2 (рис. 3.12). Если принять такое условие, после начала движения автомобиля при достижении частоты вращения двигателя п2 должен произойти переход на вторую ступень. При этом частота вращения двигателя в начале движения на второй ступени в коробке передач составит п\.
Если пренебречь уменьшением скорости за время переключения ступеней,
74
Рис. 3.12. Выбор передаточных чисел промежуточных передач
скорость в конце движения на первой ступени V[ должна быть равна начальной скорости движения на второй ступени v2:
= O,377n2ro/(uoUi);
v2 = О,377П1ГО/(«о«2);
V[ = v2; u2/ui = njn2.
Очевидно, что при переходе со второй на третью ступень это условие будет сохраняться:
v2 = о3; п2и2 = nfa; и3/и2 = п\1п2, и3 = «i {njn2y.
При переходе на m-ю ступень
—1 =	Чп!Чт—I = ^1/^2 = Qi
и,п = um-\q = щдт-х.
Следовательно, при постоянном диапазоне частот вращения двигателя передаточное число каждой последующей ступени получается из предыдущего умножением на постоянный множитель 7 = П1/«2. Такой ряд чисел называется геометрической прогрессией.
Если n-я передача имеет передаточное число ип, знаменатель геометрической прогрессии определяется из соотношения:
ип = un-iq = «17"-1; q = (ип/щ) Передаточное число m-й пер т—1	п—т т—1
ит = U\(Un/Ui)n~1 — «1 П-1 Ип "-1. (3.7)
Если в коробке передач имеется Прямая передача, передаточные числа промежуточных ступеней определяются по формуле п—т
ит = и^,	(3.8)
где п — номер прямой передачи.
Пользуясь формулами (3.7) и (3.8), можно найти передаточное число промежуточных ступеней для любой коробки передач. Например, для трехступенчатой
«2 = V , для четырехступенчатой „ _ „2/3„1/3. „ _ ,,1/3„2/3
Если ряд промежуточных передаточных чисел выбран по геометрической прогрессии, средняя мощность двигателя при разгоне автомобиля будет максимальной в случае одинакового использования ступеней по времени и мощности на каждой ступени. В действительности же время движения автомобиля на двух высших передачах составляет 80...90 % общего времени разгона. Примерно такую же долю составляет и путь, проходимый автомобилем на этих передачах. Поэтому ряд передаточных чисел целесообразно скорректировать таким образом, чтобы шаг q между высшими ступенями был меньше, чем между низшими. У большинства выпускаемых в настоящее время автомобильных коробок передач передаточные числа высших ступеней сближены на 5... 15 % по сравнению со значениями, получаемыми из геометрической прогрессии, а между низшими — соответственно на 5...15 % увеличены. При этом шаг между передачами не должен быть больше 1,7...1,8 у автомобилей с дизельными двигате-
75
Рис. 3.13. Отношения передаточных чисел коробок передач грузовых автомобилей:
а — четырехступенчатых: I — Ui/u4; 7/— «2/«4; ///— «з/«4; б — пятиступенчатых; I — uJus-, П — и^ие, III — Us/U5‘ /V — U4/U5; в — шестиступенчатых: 1 — uJuq- II — Uzfue, 111 — из/ие, ZV —w4/«e; V — us/u6
v
a max
6
Puc. 3.14. Отношения передаточных чисел коробок передач легковых автомобилей:
а — трехступенчатых: 1 — Wi/w3; ZZ — w2/w3; б— четырехступенчатых-. Z —	ZZ —а2/«4*. III — U3IU4
лями и 2 — с карбюраторными. В противном случае будет затруднено переключение на высшую ступень из-за того, что начальная частота вращения двигателя на высшей ступени может оказаться слишком низкой. У современных автомобилей с четырех-, шестиступенчатыми коробками передач в среднем шаг q составляет 1,5... 1,8, между высшими ступенями—1,4...1,6, а
между низшими—1,6...1,8. С увеличением числа ступеней различие в q на высших и низших передачах уменьшают, так как наличие большого числа ступеней позволяет практически на всех передачах работать на режимах, близких к максимальной мощности двигателя или наибольшей его экономичности. Средний шаг передаточных чисел у многоступенчатых составных коробок передач выбирают в пределах 1,2...1,4.
При проектировании коробок передач целесообразно сопоставить полученные передаточные числа с передаточными числами коробок передач существующих автомобилей. Графики, приведенные на рис. 3.13 и 3.14, построены по результатам анализа конструкций современных коробок передач. На них показаны отношения передаточных чисел промежуточных передач и высшей у легковых и грузовых автомобилей. Отношение передаточных чисел первой и высшей передач определяет диапазон передаточных чисел коробок передач. У легковых автомобилей он зависит от максимальной скорости— при увеличении максимальной скорости уменьшается; у грузовых автомобилей зависит от массы — возрастает с увеличением массы.
В раздаточных коробках полноприводных автомобилей имеются, как пра
76
вило, две передачи: высшая и низшая. Высшая является прямой или имеет передаточное число, близкое к единице. Передаточное число низшей передачи определяют так же, как и у коробок передач, т. е. из условий: преодоления автомобилем максимального подъема
Пн — Galpmaxfо/ (Л1е тахИоП1Т]т) полного использования его сцепного веса
Un = СафГо/ (Л1е тах^оИ1Т]т) обеспечения минимальной устойчивости скорости движения
«н = 0,377 Пе min/o/^iUot’a min.) 
При расчетах принимают фтах = = 0,7...0,9, ф = 0,7...0,9, Uamin=2...3 км/ч.
Отношение передаточных чисел низшей и высшей передач в современных раздаточных коробках полноприводных автомобилей составляет 1,65...2,1.
Оптимальность выбранных при тяговом расчете параметров (мощности двигателя, передаточных чисел главной передачи и коробки передач) целесообразно проверять путем моделирования движения проектируемого автомобиля в характерных условиях эксплуатации (гл. 8). Передаточные числа трансмиссии окончательно уточняются при определении параметров шестерен в процессе конструирования агрегатов трансмиссии.
3.4. Особенности тягово-скоростных расчетов при наличии в трансмиссии гидромеханической передачи
На автомобилях различных типов достаточно широкое применение получили трансмиссии с гидромеханическими передачами. Гидромеханическая передача (ГМП) состоит из гидродинамической передачи (гидромуфты или гидротрансформатора) и механического вального или планетарного редуктора.
Гидромуфта имеет два рабочих колеса, находящихся в общем картере, заполненном рабочей жидкостью.
Насосное колесо связано с двигателем, а турбинное — с ведущим валом механического редуктора непосредственно или через механическое сцепление. Насосное и турбинное колеса располагаются с малым зазором, так чтобы межлопастные каналы одного были продолжением каналов другого. Лопатки насосного колеса воздействуют на жидкость, которая, выйдя из межлопастных каналов насосного колеса, попадает в межлопастные каналы турбинного, заставляя его вращаться. Поскольку на гидромуфту внешние крутящие моменты не действуют, крутящий момент на насосном колесе Л4„ всегда будет равен моменту на турбинном Мт. В тяговом режиме угловая скорость турбинного колеса <вт ниже угловой скорости насосного <Вц. Отношение угловой скорости турбинного колеса и угловой скорости насосного колеса гидродинамической передачи называется кинематическим передаточным отношением 1т.н: 1‘т.н=<Вт/сон. Поскольку моменты на насосном и турбинном колесах гидромуфты одинаковы, КПД гидромуфты равен кинематическому передаточному отношению: Т]н.т = 1т.н. Гидротрансформатор имеет не менее трех лопастных колёс — насос, турбину и реактор, причем последний обязательно должен быть соединен с внешней опорой. Вследствие этого гидротрансформатор позволяет изменить не только кинематическое передаточное отношение, но и силовое.
Силовое передаточное отношение — отношение момента на турбинном колесе к моменту на насосном — называют коэффициентом трансформации k: k = MT/MH. КПД гидротрансформатора Т]н.т = МтСОт/ (Л4НСОН) = /jlTI1.
Гидротрансформаторы, у которых турбинные и насосные колеса вращаются в одном направлении, называются гидротрансформаторами прямого
77
Рис. 3.15. Кинематические схемы автомобильных гидротрансформаторов:
I — входной вал; II — выходной; Н — насосное коле-со; Т — турбинное; Р — реактор; М — муфта свободного хода; Ф — блокировочный фрикцион
хода. Если у гидротрансформатора отсоединить реактор от внешней опоры, момент на турбинном колесе станет равен моменту на насосном. В этом случае трансформатор будет работать как гидромуфта. Гидротрансформатор, у которого на некоторых режимах реактор может отсоединяться от внешней опоры, называется комплексным.
В трансмиссиях автомобилей применяют комплексные трансформаторы прямого хода. Наибольшее распространение получили комплексные трех- и четырехколесные трансформаторы, имеющие соответственно один и два реактора, установленные на муфтах свободного хода. Принципиальные схемы таких трансформаторов показаны на рис. 3.15. Муфта свободного хода блокирует реактор с внешей опорой на режимах преобразования крутящего момента. На этих режимах крутящий момент на реакторе противоположен направлению вращения насосного колеса. При перемене знака момента на реакторе последний разблокируется и начинает вращаться свободно. Гидротрансформатор, лишенный внешней опоры, переходит на режим гидромуфты. Применение двух реакторов позволяет расширить зону работы гидротрансформатора с высоким КПД. В комплексных трансформаторах автомобилей, работающих преимущественно на дорогах с твердым покрытием, для повышения их топливной экономичности иногда устанавливают фрик
цион, блокирующий насосное и турбинное колеса.
Применение на автомобилях гидродинамических передач способствует увеличению срока службы двигателя и трансмиссии, уменьшению числа передач в механическом редукторе и числа их переключений, повышению проходимости автомобиля и комфортабельности за счет более плавного трогания с места. Гидромеханические передачи по сравнению с механическими имеют более сложную конструкцию, повышенную материалоемкость и стоимость. В случае замены механической передачи гидромеханической наблюдается некоторое ухудшение характеристик разгона автомобиля при повышенном расходе топлива.
Проектирование гидродинамических передач производится на базе теории подобия. Установлено, что одинаковые по относительным размерам конструктивных элементов гидромеханические передачи имеют одинаковые относительные характеристики: коэффициент трансформации — k, КПД — цн.т, коэффициент насоса — Хн. Последний определяет нагружающие . свойства трансформатора и находится по формуле
Хн = Мн/(р^О5Д (3.9) где р — плотность рабочей жидкости, кг/м3; Пн — частота вращения вала насоса, об/мин; Da — активный диаметр (максимальный диаметр круга циркуляции, соответствует максимальному диаметру насосного колеса), м.
Свойства гидродинамических передач полностью отражаются безразмерными характеристиками. Безразмерная характеристика определяет зависимость коэффициента полезного действия, коэффициента трансформации и коэффициента насоса от передаточного отношения гидродинамической передачи и строится по результатам испытаний конкретных гидродинамических передач.
78
Рис. 3.16. Безразмерные характеристики: а— гидромуфты; б — однореакторного гидротрансформатора; в — двухреакторного
На рис. 3.16 приведены безразмерные характеристики гидромуфты одно-и двухреакторных комплексных гидротрансформаторов.
Основными режимами работы гидродинамических передач являются: 1 — режим «стоп» (iT.H = 0, Хн = Хн.о, k = = k0, т]н.т = 0); 2 — холостого хода или синхронного вращения (tT.H = 1; k = 0, т]н,т = 0); 3 — равенства моментов (Л1И = — Л4Т; k = 1, 1т.н = i'h.m, = ^н.м)> 4 наибольшего коэффициента насоса (Хн = = ^итах); 5 — режим максимального КПД (i't.h — i-r.ni Т|н.т = T]H.rmaxi ^-н — ^н)-
Из приведенных характеристик видно, что КПД гидромуфты линейно зависит от ее передаточного отношения, а КПД однореакторного трансформатора имеет максимум при определенном значении передаточного отношения. При коэффициенте трансформации, близком к единице, целесообразно осуществлять переход на режим гидромуфты (точка Л). Таким образом, участок АВ является участком работы гидротрансформатора в режиме гидромуфты. На кривой КПД четырехколесного трансформатора (двухреакторного) можно выделить три участка: ОС — оба реактора неподвижны; СА — первый вращается, а второй неподвижен; АВ — оба реактора вращаются. В точке В может происходить включе
ние фрикциона блокировки. При полностью сблокированном фрикционе гидротрансформатор выполняет функцию жесткого звена.
Рабочий диапазон трансформатора определяется минимальным допустимым КПД на основных режимах работы автомобиля. Принято обозначать: максимальный коэффициент трансформации в рабочем диапазоне — кр, минимальный КПД,— т]Р, соответствующее им передаточное отношение — iT.H.p. У автомобилей обычно принимают т]р в рабочем диапазоне равным 80 % и соответственно обозначают yiso, iso-
Максимальное значение передаточного отношения в рабочем диапазоне определяется режимом равенства моментов (&=1). Обычно Ip max = 0,84... 0,85, а рабочий диапазон передаточных отношений трансформатора составляет 0,4-0,85.
Прозрачность — свойство гидродинамической передачи, характеризующее ее способность нагружать двигатель в соответствии с изменением сопротивления движению автомобиля. Оценивается коэффициентом прозрачности П — отношением коэффициентов насоса при двух значениях передаточных ОТНОШеНИИ 1*т.н1 И 1*т.н2 (ii.nl< <^1т.н2): П=Хт.м1/^т.м2- Если П>1, передача считается прозрачной. При такой
79
передаче с изменением сопротивления движению изменяется нагрузка, передающаяся на двигатель. При П=1 передача непрозрачная, двигатель не реагирует на изменение сопротивления. При П<1 передача имеет обратную прозрачность — уменьшение сопротивления приводит к увеличению нагру-женности двигателя.
На различных режимах работы гидродинамическая передача может иметь разные показатели прозрачности. Например, на рис. 3.16, а гидромуфта на участке й.н=0, /т.н=Ш обладает обратной прозрачностью, а на участке гт.н= = 1н, Ьг.н= 1 — прозрачная.
Если специально не оговаривается, под коэффициентом прозрачности понимается отношение коэффициентов момента насоса на стоповом режиме (iT.H=0) и на режиме равенства моментов (&=1):
П = Лн.о//-Н.М.	(3.10)
В зависимости от числового значения коэффициента прозрачности, определяемого по формуле (3.10), все гидротрансформаторы условно делят на непрозрачные и прозрачные. К непрозрачным и малопрозрачным относят гидротрансформаторы, имеющие П = = 0,7...1,5. Гидротрансформаторы, имеющие большие значения коэффициента прозрачности, считаются прозрачными.
Наибольшие значения коэффициента трансформации в рабочем диапазоне имеют непрозрачные и малопрозрачные трансформаторы (Ар= 1,35...1,5).
При тягово-динамических расчетах автомобиля с гидродинамической передачей необходимо помимо передаточных чисел трансмиссии определить следующие характеристики гидродинамической передачи: активный диаметр или передаточное число согласующего редуктора; нагрузочную характеристику системы двигатель — гидродинамическая перадача; выходную характеристику системы двигатель — гидродинамическая передача. Для определения
этих характеристик следует выбрать принципиальную схему передачи и соответствующую ей безразмерную характеристику.
При известной конструкции трансформатора активный диаметр рассчитывают, используя правила подобия для лопастных машин:
Da = 5/мн/(рМн2) •	(3.11)
Плотность жидкости р должна соответствовать рабочей температуре 90...120 °C. В автомобильных ГМП рабочей жидкостью являются минеральные масла (индустриальное, турбинное, трансформаторное и др.). Для этих масел при указанной температуре р = = 850...870 кг/м3.
При непосредственном соединении двигателя внутреннего сгорания (ДВС) и ГМП в формулу (3.11) вместо Мн и Пн следует подставлять крутящий момент и частоту вращения двигателя, соответствующие определенной точке внешней характеристики. Если значение D известно, выбор характеристик совместной работы осуществляется подбором передаточного числа согласующего редуктора, устанавливаемого между двигателем и ГМП. В этом случае:
Мн = МеЦс.пГ]с.п; Ин = tte/^c.n, где uc.n, ric.n — соответственно передаточное число и КПД согласующей передачи:	__________________
^с.п “	P^H^e7)a/(M/r]c.n) •
Согласование характеристик двигателя и ГМП заключается в выборе активного диаметра гидропередачи или передаточного числа согласующего редуктора, обеспечивающих наилучшее использование возможностей двигателя и ГМП. Основной задачей является обеспечение при определенной передаче в механической! коробке ГМП наибольшего диапазона регулирования передаточных чисел трансмиссии при наименьшем расходе топлива. Процедура согласования заключается в по-
80
Рис. 3.17. Характеристики совместной работы двигателя с прозрачным (а) и непрозрачным (б) гидротрансформаторами
строении характеристик входа системы двигатель — гидропередача и выборе оптимальной из них. Характеристика входа получается в результате совместного решения уравнений крутящего момента двигателя, работающего по внешней характеристике Me=f(ne), и крутящего момента на насосном колесе Л1Гт=f (/гн). Решение может быть выполнено аналитически или графически. Точки пересечения графиков указанных уравнений определяют соответствующие режимы работы.
Для построения характеристики входа необходимо на график внешней характеристики двигателя нанести на
грузочные кривые (параболы) гидродинамической передачи для ряда значений передаточного отношения iT.H. Нагрузочные кривые рассчитываются исходя из выражения (3.9), в котором Хн определяется по выбранной безразмерной характеристике трансформатора.
На рис. 3.17, а показана характеристика входа или так называемый график совместной работы двигателя с прозрачным трансформатором.
Все параболы проходят через начало координат, их крутизна возрастает при увеличении Хн. Точки пересечения парабол с внешней скоростной характеристикой двигателя определяют крутящий момент двигателя, частоту его вращения и передаточные отношения гидротрансформатора при работе двигателя на установившемся режиме с полной подачей топлива. Для каждой частичной характеристики будут свои точки согласования. Таким образом, возможные режимы совместной работы двигателя и гидротрансформатора с прямой прозрачностью ограничиваются слева параболой нагружения, соответствующей стоповому режиму, а справа — параболой, соответствующей максимальному передаточному отношению гидротрансформатора, сверху — внешней характеристикой двигателя, снизу — тормозной.
У непрозрачных трансформаторов, (см. рис. 3.16, б) с постоянным Хн на графике совместной работы будет только одна парабола. Зона совместной работы в этом случае ограничивается точками пересечения этой параболы с внешней и тормозной характеристиками двигателя.
У некоторых трансформаторов Хн при увеличении передаточного отношения от 0 до 1 изменяется следующим образом: вначале возрастает от %н.о до. Хитах и затем уменьшается до Хн.м-Считают, что такие гидротрансформаторы обладают смешанной прозрачностью. Характеризуются они двумя
81
коэффициентами прозрачности на участках с прямой (П1 = Хнтах/Хн.м) и обратной (П2=Хн.о/Хнmax) прозрачностью. В этом случае на графике совместной работы сектор нагрузочных кривых участка с обратной прозрачностью располагается внутри сектора участка с прямой прозрачностью.
При установке между двигателем и ГМП согласующего редуктора для построения характеристики входа следует предварительно перестроить внешнюю скоростную характеристику двигателя путем приведения ее к валу насосного колеса, используя при этом зависимости:
пр — MeUc.nT]c.n', /1епр = Це/Цс.п.
Обычно согласование начинается с выбора основного режима, определяемого характеристиками трансформатора и двигателя, типом и предполагаемыми условиями эксплуатации автомобиля. При этом следует иметь в виду, что общий диапазон силового регулирования системы ДВС — ГМП при определенной ступени механического редуктора зависит от коэффициента трансформации k и коэффициента приспособляемости двигателя по моменту kM, а расход топлива-—от удельного его расхода двигателем на рассматриваемом режиме и коэффициента полезного действия гидротрансформатора.
Дизельные двигатели обладают малым коэффициентом приспособляемости по моменту. Поэтому общий диапазон силового регулирования системы ДВС — ГМП обеспечивается в основном за счет высокого коэффициента трансформации ГМП. В этом случае целесообразно применение непрозрачных или малопрозрачных гидротрансформаторов, обладающих более высокими, чем прозрачные, коэффициентами трансформации. При применении непрозрачных трансформаторов для обеспечения полного использования мощности двигателя и малого расхода топлива на всех эксплуатационных режимах
Da или цс.п выбирают таким образом, чтобы нагрузочная кривая гидротрансформатора, соответствующая его максимальному КПД, пересекала кривую внешней характеристики двигателя в точке максимальной мощности. Принято говорить, что в этом случае совмещены режимы максимальной мощности двигателя и максимального КПД гидротрансформатора.
Для малопрозрачных трансформаторов с целью максимального использования мощности на режимах трансформации согласование проводят так, чтобы соблюдалось условие пе0 = = (0,8...0,9)пр, где пе0 — частота вращения вала двигателя при полной подаче топлива на режиме «стоп». Наибольшая же топливная экономичность обеспечивается при пе0= (0,8...1)пед, где neg — частота вращения вала двигателя при минимальном удельном расходе топлива.
У грузовых автомобилей, самосвалов, городских автобусов наиболее часто трансформаторы согласовывают так, что Пео— (0,5...0,75)пР. Для повышения топливной экономичности таких автомобилей целесообразно применять блокировку трансформатора. •
Высокая приспособляемость карбюраторного двигателя может быть использована для достижения хороших динамических качеств автомобиля. Прозрачность гидротрансформатора должна быть такой, при которой бы двигатель во время трогания автомобиля с места развивал бы наибольший крутящий момент, а затем по мере его разгона переходил на режим максимальной мощности. Удовлетворительная топливная экономичность в этом случае может быть достигнута путем согласования режима наиболее часто используемой мощности с режимом максимального КПД.
На легковых автомобилях применяют прозрачные трансформаторы с относительно малым коэффициентом трансформации при стоповом режиме
82
Рис. 3.18. Характеристики выхода системы двигатель — гидротрансформатор
Рис. 3.19. Динамическая характеристика автомобиля ГАЗ-13 «Чайка»
(& = 2,0...2,5). Для снижения шума от работы двигателя при трогании автомобиля с места, а также уменьшения интенсивности его изнашивания и расхода топлива следует при стоповом режиме нагружать двигатель при частоте его вращения, меньшей соответствующей максимальному крутящему моменту, несмотря на то что это снижает окружную силу на колесах. С целью
снижения шума и для городских автобусов рекомендуются пе0 = (0,5...0,75)пР.
При проектировании трансмиссий с гидропередачами, обладающими большой прозрачностью, необходимо анализировать положение кривой нагружения с максимальным значением коэффициента насоса (Хн max ). С целью предотвращения перегрузки или остановки двигателя при трогании автомобиля точка пересечения этой параболы с внешней характеристикой двигателя должна быть правее минимальной устойчивой частоты вращения двигателя.
Основной характеристикой для расчета тягово-скоростных свойств автомобиля с ГМП является характеристика выхода системы двигатель — гидропередача, представляющая собой зависимость мощности Рт, крутящего момента Мц на валу турбинного колеса от частоты вращения вала турбины пт при полной подаче топлива в двигателе. Исходными данными для расчета являются точки, характеризующие совместную работу двигателя и гидропередачи, и соотношения: Мт=Мпк; Пт^п^.н;. Рт = 0,105Л1тПт.
Характеристика выхода системы двигатель •— гидротрансформатор показана на рис. 3.18.
Тяговая и динамическая характеристики автомобиля с ГМП строятся с использованием зависимостей, приведенных в гл. 2 для механических трансмиссий, в которых вместо значений Ме и пе подставляются соответственно значения Мт й пт с выходной характеристики системы двигатель — гидротрансформатор. Динамическая характеристика автомобиля с гидромеханической передачей показана на рис. 3.19.
Для нахождения ускорений автомобиля при разгоне можно использовать формулу (2.30). Коэффициент учета вращающихся масс б определяется исходя из следующих соображений.
Если трансмиссия включает гидродинамическую передачу, при разгоне
83
автомобиля необходимо затрачивать энергию на разгон маховика и связанных с ним деталей (в том числе и насосного колеса), а также турбинного колеса с соответствующими деталями. Энергия также затрачивается на разгон жидкости в межлопаточных пространствах турбины и насоса. Если /н— момент инерции насосного колеса с учетом связанных с ним деталей и находящейся между его лопатками жидкости, а /т — момент инерции турбинного колеса, уменьшение момента на выходном валу гидродинамической передачи АЛ1Т при неустановившемся режиме вследствие затрат энергии на разгон деталей, связанных с насосным и турбинным колесами, то
da„	d<j).
АМТ = /н—М + /т — dt	dt
dco„ . \ da
Х "я	~я
аш_ / а
Учитывая, ЧТО d(OH/</®T = rfrtH/d«T, имеем
Л*—5-
dn.r
da>, ~dt
Если учесть уменьшение крутящего момента двигателя при его работе на неустановившемся режиме, общее уменьшение момента на выходном валу гидротрансформатора
АЛ4Т/ = (УеМе 4“ Iн) k
dcoT dt (3.12)
dri
Уменьшение окружной силы на ведущих колесах автомобиля при этом режиме АЕ£ может быть получено из выражения (3.12) с использованием соотношений:
АРК =
АМт]ит.Ы . го
__ V
<0т — Ит.м> г0
где Мт.м; г]т.м — передаточное число и КПД механической части трансмиссии.
Коэффициент учета вращающихся масс автомобиля с гидродинамической
передачей по аналогии с формулой (2.21):
6 = 1 -f- {УеМе IH) k------1- /т X
dn„
ц?.м
"Vo
к 2
—о
г0та
При отсутствии необходимых данных можно принять: для легковых автомобилей /н=/т = 0,1 ...0,6 кг-м2; для грузовых автомобилей и автобусов /н=/т=0,6...3 кг-м2; для грузовых автомобилей особо большой грузоподъемности /н = 4...6 кг-м2; /т = 7...8 кг-м2. Большие значения относятся к ГМП, работающим с двигателями большой мощности.
Если гидродинамическая передача соединяется с двигателем через согласующий редуктор,
/н = /н0 + У, /г-Ц2,
где До — момент инерции насосного колеса; Ui — передаточное число механизма от насосного колеса до детали с моментом инерции Л.
По данным характеристики входа системы двигатель — гидропередача строится кинематическая характеристика — зависимость частоты вращения насоса от скорости вращения турбины (рис. 3.20) с использованием соотношения Пт = 1т.н«н. Графическим или аналитическим дифференцированием этой зависимости определяются значения производной dtiildtin при заданных частотах вращения вала турбины пт или скоростях движения автомобиля. У непрозрачного трансформатора при полной подаче топлива двигатель и насосное колесо вращаются с постоянной скоростью (б?пт/с?Цн=0). При блокировке трансформатора k=l и dn^ldn^—X.
На рис. 3.21 показаны графики разгона автомобиля с гидромеханической передачей.
Общий диапазон силового регулирования ГМП определяется как произведение соответствующего диапазона
84
Рис. 3.20. Графический метод определения diiu/dn-r
Рис. 3.21. Ускорение (а), время и путь разгона (б) автомобиля ГАЗ-13 «Чайка»
трансформатора при КПД не менее 80 % (&so) и диапазона передаточных чисел механической коробки передач Дк. Его обычно принимают близким к диапазону механических коробок передач. Передаточные числа главной передачи, высшей и первой передач механического редуктора рассчитывают исходя из тех же соображений, что и при аналогичных расчетах для механических трансмиссий. При этом ввиду возможности плавного изменения силы тяги при движении автомобиля в тяжелых условиях расчетный коэффициент сцепления принимают большим, чем для механических трансмиссий: Ф = 0,8...1.
При определении минимального количества ступеней механического ре
дуктора ГМП исходят из условия обеспечения на всех режимах движения, кроме режима трогания автомобиля с места, работы гидротрансформатора при КПД не менее минимального расчетного (80%). По безразмерной характеристике трансформатора определяют диапазон передаточных отношений iT.Hl И 1т.н2, При КОТОРЫХ КПД трансформатора не меньше расчетного. Используя характеристики входа и выхода системы двигатель — гидротрансформатор, находят соответствующие этим отношениям пц и цТ2, определяющие минимальную и максимальную частоту вращения вала турбины при работе трансформатора в расчетном режиме. Отношение nTi/nT2 = <7 является знаменателем геометрической прогрессии ряда передаточных чисел механического редуктора. В этом случае минимальное число ступеней п находится следующим образом:
Дк = Ц1/ив; ив = щ<7п-1; Дк = <7"(п“1); n^lg J\K/lg q — l.
В ГМП грузовых автомобилей применяют механические редукторы с тремя — пятью ступенями при диапазоне передаточных чисел 2,5...4,2. ГМП легковых автомобилей имеют от двух до четырех ступеней при диапазоне 1,6.4.
Главные передачи автомобилей с ГМП имеют такие же передаточные числа, как и у автомобилей с механическими трансмиссиями. В некоторых случаях с целью повышения топливной экономичности легковых автомобилей передаточное число главной передачи принимают на 15...20 % меньшим, чем в механических трансмиссиях. В этом случае при движении автомобиля в условиях повышенного дорожного сопротивления с включенной в механическом редукторе высшей передачей гидротрансформатор работает в режиме трансформации.
85
ТОРМОЗНЫЕ СВОЙСТВА АВТОМОБИЛЯ
4.1.	Основные определения
Скорость и безопасность движения автомобиля в значительной степени определяется его тормозными свойствами. Под тормозными свойствами понимают способность автомобиля быстро снижать скорость движения вплоть до полной остановки при минимальном тормозном пути, сохранять заданную скорость при движении под уклон, а также оставаться неподвижным при действии случайных сил.
Уменьшение скорости движения автомобиля при торможении происходит за счет искусственного создания момента сопротивления вращению колес. При этом кинетическая энергия автомобиля превращается в тепловую вследствие трения, возникающего в тормозных механизмах и при контакте шин с опорной поверхностью.
Автомобиль должен иметь несколько тормозных систем, выполняющих различные функции: рабочую, стояночную, вспомогательную, запасную.
Рабочая (основная) тормоз ная система служит для уменьше ния скорости автомобиля и полной его остановки. У современных автомобилей тормозными -механизмами рабочей тормозной системы являются колесные тормоза. В процессе торможения кинетическая энергия автомобиля переходит в работу трения между фрикционными накладками и тормозным барабаном или диском, а также между шинами и дорогой. Тормозной момент Мх, раз
виваемый тормозным механизмом, зависит от его конструкции и давления в тормозном приводе:
М-с = «рп,
где а — коэффициент пропорциональности, зависящий от конструкции тормозного механизма и привода, а также давления в приводе; рп — избыточное давление в тормозном приводе.
В общем случае эта зависимость нелинейная.
Управление рабочей тормозной системой осуществляется от ножной педали.
Стояночная тормозная система предназначена для удержания автомобиля на месте. Привод стояночной тормозной системы воздействует на колесные тормоза рабочей тормозной системы или на специальный дополнительный тормоз, связанный с трансмиссией автомобиля. Управление стояночной тормозной системой ручное.
Вспомогательная тормозная система используется при длительном торможении автомобиля (например, на длинных спусках). Она состоит из моторного или трансмиссионного тормозов-замедлителей. Управление ею автоматическое или ручное.
Запасная тормозная система служит для остановки автомобиля при отказе рабочей тормозной системы. У некоторых автомобилей функции запасной выполняет стояночная тормозная система.
86
Рис. 4.1. Диаграмма торможения автомобиля: а —изменение замедления во времени; б — то же, скорости во времени
Различают аварийное (экстренное) и служебное торможение.
Аварийное торможение производится с максимальной для данных условий интенсивностью. Обычно их количество не превосходит 5... 10 % общего числа торможений.
Служебное торможение применяют для плавного уменьшения скорости автомобиля или его остановки в заданном месте. Оно производится с небольшой интенсивностью, не вызывающей неприятных ощущений у водителя и пассажиров. Замедление при служебном торможении обычно не превосходит 1... 1,5 м/с2.
Служебное торможение может осуществляться: а) двигателем — водитель уменьшает или прекращает подачу топлива в цилиндры двигателя. При этом двигатель начинает работать в тормозном режиме. Тормозная сила создается за счет трения в двигателе и агрегатах трансмиссии. Такой способ торможения применяется при необходимости получения малых замедлений; б) двигателем и тормозами совместно — применяется в случае, когда необходимое замедление не обеспечи
вается только торможением двигателем. Это наиболее часто используемый способ служебного торможения. На дорогах с малым коэффициентом сцепления при таком способе торможения уменьшается возможность возникновения заноса; в) торможение при отсоединенном двигателе — применяется так же, как и торможение совместно двигателем и тормозами, в тех случаях, когда торможение двигателем не обеспечивает нужного замедления, а также при необходимости остановки автомобиля.
Если в момент времени t = 0 (рис.
4.1)	возникает ситуация, вынуждающая водителя тормозить, он оценивает обстановку и переносит ногу с педали подачи топлива на тормозную педаль. Этот процесс занимает время, называемое временем реакции водителя (te).
Время реакции водителя включает время психической реакции tp (оценка обстановки и принятие решения тормозить) и время физической реакции /р (перенос ноги с педали подачи топлива на тормозную педаль).
Проведенные экспериментальные исследования показывают, что время реакции зависит от индивидуальных особенностей водителя, его психического и физического состояния и составляет 0,2... 1,5 с. При расчетах обычно принимают £р = 0,8 с.
После нажатия на педаль в течение некоторого времени t3 происходит передача усилия от педали к тормозным механизмам. Это время, которое называют временем запаздывания тормозного привода, зависит от типа тормозного привода, его конструктивных особенностей, технического состояния и возрастает при увеличении длины трубопроводов и количества тормозных механизмов. При расчетах можно принимать для гидравлического привода t3=0,05...0,1 с, для пневматического — /3 = 0,2 с.
Тормозной момент и, соответствен
87
но, замедление автомобиля нарастают в течение промежутка времени, называемого временем нарастания замедления tH. Это время определяется интенсивностью нажатия водителем педали тормоза, а также временем, необходимым для наполнения емкостей и деформации механизмов привода и тормоза. Оно зависит от типа и конструкции привода и тормозных механизмов. При расчетах тормозной динамики автомобиля обычно считают, что водитель быстро (мгновенно) нажимает тормозную педаль. При этом нарастание замедления происходит по линейному закону, а максимальное замедление достигается за время /н = 0,4...0,5 с.
Суммарное время /3 + ^н называют временем срабатывания тормозного привода tn- Максимальное время срабатывания тормозного привода регламентировано стандартами и не должно быть больше 0,6 с. При этом t3 не должно превышать 0,2 с.
В течение некоторого времени tx автомобиль движется с заданным замедлением ах. При достижении автомобилем требуемой скорости водитель отпускает тормозную педаль. Происходит оттормаживание— уменьшение замедления автомобиля. Время оттормажива-ния (t0) при гидравлическом приводе составляет примерно 0,2 с, а при пневматическом— 0,5... 1,5 с. Если торможение производится до полной остановки, в момент остановки замедление уменьшается до нуля практически мгновенно.
Весь путь, проходимый автомобилем от момента, когда водитель заметил препятствие, до полной остановки называют остановочным путем (s0)-
Остановочный путь складывается из пути, проходимого автомобилем в течение времени реакции водителя и срабатывания тормозного привода, и пути торможения:
So = 5р.з -f- Sr,
где sp 3 — путь, проходимый автомоби
лем за время реакции водителя и время запаздывания тормозного привода; St — путь торможения — расстояние, проходимое автомобилем за время действия на него тормозных сил.
4.2.	Замедление автомобиля при торможении
Внешние силы, действующие на автомобиль при торможении, показаны на рис. 4.2. Основными силами, обеспечивающими замедление автомобиля, являются тормозные силы Fxi и Ft2, действующие в плоскости контакта колес с дорогой и направленные противоположно направлению движения автомобиля. При достаточном сцеплении силы Fti и Ft2 определяются тормозными моментами, развиваемыми тормозными механизмами мостов,
F Xi = МХ(1 Г Q.
Максимально возможные значения тормозных сил ограничены по сцеплению:
Ft; = qRzi-
Кроме тормозных сил, на автомобиль действуют силы сопротивления качению колес F/j и Ff2, сила сопротивления подъему Fi и аэродинамическое сопротивление FB.
Сумма проекций всех сил на плоскость, параллельную опорной поверхности, равна инерционной силе автомобиля:
6xmaax = FX1 + Ft2 + Ffi + Ff2 + F;+ F^ (4-1) гдебт— коэффициент учета вращающихся масс автомобиля при торможении: 6Т= 1,03... 1,05.
К вращающимся массам в процессе торможения обычно относят только массы колес. Связано это с тем, что при торможении с отсоединенным двигателем маховик не связан с колесами автомобиля, а моменты инерции других деталей трансмиссии малы. Пр»
88
Рис. 4.2. Силы, действующие на автомобиль при торможении
торможении же двигателем к ведущим колесам через трансмиссию передается тормозной момент, равный разности тормозного момента двигателя и инерционного момента маховика.
Обозначим:
Fx\ + Ft2 = FT; FT = yTg/na;
где Ут — удельная тормозная сила.
Подставив эти обозначения в (4.1) и выразив силы сопротивления качению и подъему через коэффициент сопротивления дороги, после преобразований получим
ах = 4-(^т + Ф)-' т
По аналогии с динамическим фактором Dx может быть назван тормозным фактором. Предельное значение его полностью определяется параметрами автомобиля.
Максимальное значение тангенциальной силы (см. гл. 1), в рассматриваемом случае тормозной, достигается при определенном проскальзывании в зоне контакта колеса с дорогой. Поэтому тормозные системы автомобилей
и автопоездов целесообразно конструировать таким образом, чтобы при торможении коэффициенты скольжения колес всех мостов были бы одинаковыми. Только в этом случае можно полностью использовать сцепной вес автомобиля при аварийных торможениях, а также исключить блокировку колес. Как было установлено ранее, при блокировке колес уменьшается значение удельной окружной силы.
Нецелесообразно колеса доводить до полного скольжения (юза) также и с точки зрения устойчивости и управляемости автомобиля, так как при полном юзе колесо не может воспринимать боковые силы. В случае полного скольжения даже небольшие силы или моменты, действующие на автомобиль, могут вызвать боковое скольжение колес моста.
Когда первыми блокируются колеса заднего моста, автомобиль теряет устойчивость. Это наглядно видно на схеме, приведенной на рис. 4.3. При блокировке задние колеса неспособны воспринимать поперечную силу. Поэтому незначительная боковая сила, воздействующая на автомобиль, вызванная, например, ветром, неровностями дороги, центробежной силой, или поворачивающий момент, обусловленный различием тормозных сил на правых и левых колесах, могут вызвать боковое скольжение колес заднего моста. Это приведет к тому, что продольная ось автомобиля повернется на некоторый угол (угол (3, см. рис. 4.3). Поскольку при торможении инерционная сила направлена по направлению движения, при отклонении оси автомобиля от прямолинейного направления движения она создает момент, стремящийся увеличить занос автомобиля.
При блокировке передних колес водитель не способен управлять автомобилем: автомобиль продолжает прямолинейное движение, но устойчивость его при этом не теряется.
При поперечном отклонении перед-
89
Рис. 4.3. Схема заноса автомобиля при блокировке колес заднего моста на дороге с малым сцеплением
Рис. 4.4. Силы, действующие на автомобиль при торможении на горизонтальной дороге
него моста инерционная сила создает момент, стремящийся возвратить автомобиль в положение, соответствующее прямолинейному движению. Потеря управляемости водителем воспринимается быстро, и управление может быть восстановлено за счет уменьшения тормозной силы.
При блокировке же задних колес после определенного углового отклонения автомобиля водитель уже не в состоянии даже путем полного растормаживания восстановить устойчивость автомобиля. Поэтому блокировка задних колес более опасна, чем передних. Особо опасна блокировка задних колес при малом коэффициенте сцепления их с дорогой. При торможении в этих условиях кинетическая энергия автомобиля рассеивается слабо и автомобиль, обладающий большой кинетической энергией при входе в занос, может длительно совершать вращательное движение с большой угловой скоростью.
Для того чтобы обеспечить одинаковое скольжение колес всех мостов, необходимо, чтобы удельные тормозные силы yxi на всех мостах были одина-Хковыми:
—	уxi = FxtlRzi,	(4.2)
где Fxt и Rzi — тормозная сила и нормальная составляющая реакции дороги, действующие на i-й мост.
Из формулы (4.2) видно, что для обеспечения наиболее эффективного торможения необходимо, чтобы тормозные силы (тормозные моменты) распределялись между мостами автомобиля пропорционально нормальным реакциям дороги.
При торможении происходит изменение (перераспределение) нормальных реакций. Чтобы выяснить основные его закономерности, рассмотрим торможение двухосного автомобиля на ровной горизонтальной дороге (рис. 4.4). При этом будем считать, что сопротивление воздуха не оказывает влияния на распределение реакций, а силы сопротивления качению малы по сравнению с тормозными. Реакции Rz\ и 7?z2 могут быть найдены из уравнений моментов относительно центров площадей контакта колес с дорогой противоположных мостов:
Яг1 = у- {gtnab + F//ig);
R24 = у- (gmaa — F/hg).
Отсюда видно, что при торможении
90
Рис. 4.5. Зависимость оптимального коэффициента распределения тормозных сил от коэффициента сцепления:
1 — грузового автомобиля с полной нагрузкой; 2 — то же, без груза; 3 — легкового автомобиля
автомобиля реакция под передним мостом увеличивается, под задним уменьшается. Степень их перераспределения зависит от интенсивности торможения — инерционной силы Fj.
При принятых допущениях инерционная сила равна тормозной, а значения нормальных реакций определяются выражениями:
Rzt = gma (b + Vxhg)/L;
Rz2 = gma(a — Vxhg), (4.3)
где Ут — удельная тормозная сила автомобиля:	= Fx/Ga.
Если торможение осуществляется с максимальной интенсивностью, а суммарная тормозная сила распределяется между мостами автомобиля так, что обоими мостами полностью используются сцепные свойства дороги,
Fx = фДг! + фДг2 = фСа-
Следовательно, в условиях полного использования сцепления удельная тормозная сила автомобиля равна коэффициенту сцепления:
Тг= ср.
Полное использование сцепления возможно, когда тормозные силы на колесах мостов пропорциональны нормальным реакциям дороги:
Fxl/Fxi = RzJRzi-
Характер распределения тормозных сил между мостами автомобиля, не имеющего специальных регулирующих устройств, является постоянным и определяется конструкцией тормозных механизмов и привода. Его принято оценивать коэффициентом распределения тормозных сил
——Pr = Fxl/FX2.
Из соотношений (4.3) следует, что оптимальный коэффициент распределения тормозных сил
₽r = (b + cp/ig)/(a — cp/ig), (4.4) т. е. для обеспечения полного использования сцепного веса автомобиля при аварийном торможении необходимо, чтобы соотношение между тормозными силами на колесах мостов изменялось в зависимости от состояния дороги (коэффициента сцепления).
На рис. 4.5 показана расчетная зависимость оптимального коэффициента рт от коэффициента сцепления дороги. Зависимости рассчитаны по формуле (4.4) для грузового автомобиля с грузом и без груза, а также для легкового с пассажирами.
Из графика и из выражения (4.4) следует, что у автомобилей, имеющих постоянное соотношение тормозных сил, полное использование сцепного веса автомобиля при торможении возможно только при определенном расчетном коэффициенте сцепления.
График, приведенный на рис. 4.5, позволяет определить, какой мост автомобиля блокируется раньше при аварийном торможении в заданных условиях. Допустим, что грузовой автомобиль имеет тормозную систему, сконструированную таким образом, что тормозные моменты на переднем и заднем мостах одинаковы (рт = 1). Тогда при аварийном торможении груженого автомобиля на дороге с коэффициентом сцепления ср = 0,2 первым начнет блокироваться передний мост, поскольку для одновременной блокировки колес
91
необходимо, чтобы тормозной момент на переднем мосту составлял 65 % тормозного момента на заднем. При торможении на дороге с коэффициентом сцепления 0,6 первым начнет блокироваться задний мост. При выбранном распределении тормозных моментов при торможении автомобиля без груза в любых дорожных условиях первым будет блокироваться задний мост.
Учитывая, что блокировка заднего моста является наиболее опасной, в Правилах № 13 ЕЭК ООН рекомендуется выбирать распределение тормозных сил таким, чтобы передние колеса легковых автомобилей первыми достигали блокировки при значении коэффициента сцепления 0,15...0,7, а грузовых — 0,15...0,3.
Коэффициент распределения тормозных сил рт, при котором обеспечивается выполнение этих условий, может быть найден по рис. 4.5. Например, если провести вертикальную прямую из точки, соответствующей ср = 0,3, до пересечения с линией, характеризующей торможение грузового автомобиля без груза, получим значение = 1,3. Если принять такое распределение тормозных сил, у порожнего автомобиля при ср < <0,3 первыми будут блокироваться передние колеса, при ф = 0,3 — одновременно передние и задние и при ср > 0,3 — первыми блокируются задние. При этом у груженого автомобиля задние колеса будут блокироваться первыми только на дорогах с ср > 0,62. Для обеспечения одновременной блокировки колес легкового автомобиля при ср = 0,7 необходимо, чтобы рт = 2,1. Коэффициент сцепления, при котором одновременно блокируются все колеса автомобиля, в последующем будем называть расчетным (фр).
Максимальное возможное замедление автомобиля достигается в случае, когда на всех его колесах, катящихся с одинаковым скольжением, удельные тормозные силы одновременно стано
вятся равными максимальному кооффи-циенту сцепления сртах. При этом тормозной фактор
= фтах 4~ ^в^4в^а/( 13gffZa)> а замедление
Оттах = g— фтах 4	----4 Фу. (4.5)
Если не учитывать сопротивление воздуха и сопротивление дороги,
От max = ~Г“фтах ~ <ртах. (4-6) °т
Водитель всегда (и при аварийном торможении) стремится тормозить автомобиль так, чтобы не терялась его устойчивость или управляемость. Это может быть достигнуто, если колеса моста, который в данных условиях должен блокироваться первым, катятся со скольжением, соответствующим максимальному коэффициенту сцепления. Колеса же другого моста при этом не будут полностью реализовывать возможную по сцеплению тормозную силу. Допустим, торможение происходит в условиях, когда первым должен блокироваться передний мост. Максимальная тормозная сила на колесах переднего моста
Fti = qRzi, на колесах заднего моста
Ет2 = ^-Ет1,
суммарная тормозная сила
E'r = E'ri4~ET2 = ф7?г[ ^1 4—р—у
Отсюда нормальная составляющая реакции дороги, действующая на колеса переднего моста,
2	<р(1 + 1/₽х) <p(l + l/₽t)'
Приравняв правые части выражений (4.3) и (4.7), после преобразований получим
ЧЧ-Рг) Ут = Ф---'-------.
4₽T-qAg(l + ₽T)
(4-8)
92
Рис. 4.6. Зависимость коэффициента использования сцепления от удельной тормозной силы грузового автомобиля:
1 — с грузом; 2 — без груза
Если торможение происходит на дороге с коэффициентом сцепления больше <рр, во избежание заноса автомобиля увеличение тормозной силы прекращается, когда на колесах заднего моста тормозная сила будет максимальной по сцеплению. В этом случае суммарная тормозная сила может быть таким же методом найдена через тормозную силу на колесах заднего моста:
Fx — Fxl + Р т2’> F х2 = tyRz2> Fxl — = РгЕТ2 = <pPiT?z2> Fx = <p/?z2 (1 + Pr);
YTgma
<P (1 + Pr)
(4-9)

Приравняв правые части выражений (4.3) и (4.9), после преобразований
имеем:
а(1 + Рг) YT = CD ----i.
L + <рЛё (1 + рт) Выражения (4.6), (4.8) и можно представить в виде:
(4.Ю)
(4.Ю)
ах = gmayx = crg-cp, (4.11) где сх — коэффициент использования сцепления дороги, который зависит от коэффициента сцепления ср, параметров автомобиля и расчетного коэффициента
сцепления срр.
При ср = срр сх — 1,
при ср < срр сх =
при ср > срр Ст =
Ь (1 + Рг)
LPT — <p/ig(l + Рт)’
Д(1 +Рт)
L + <P^g (1 + Рт)
Рис. 4.6 показывает зависимость коэффициента сх от ср применительно к грузовому автомобилю типа МАЗ при <рр=0,3, что соответствует |3т= 1,3. График, приведенный на рис. 4.6, позволяет определить максимальную удельную тормозную силу, а соответственно, и замедление автомобиля при торможении на поверхностях с любым коэффициентом сцепления.
Выше было установлено, что тормозные системы автомобилей проектируются таким образом, что при максимальном торможении по дороге с хорошим сцеплением (ср>срР) первым блокируется задний мост автомобиля. Исходя из этого условия, найдем максимальные тормозные моменты, которые должны развивать тормозные механизмы мостов автомобиля.
Максимальный момент, развиваемый тормозами заднего моста, Мт2тах= Гт2тах^0 = фтахРггГо- (4-12)
Значения T?Z2 в этих условиях определяются по выражениям (4.9) и (4.10). Подставив их в формулу (4.12), после преобразований получим:
.Т"*'  (4J3)
i + ^gTmax (1 Рт)
Тормозной момент на колесах переднего моста
Ж Imax — ₽гЖ 2шах* (4-14)
Рабочую тормозную систему всегда стремятся спроектировать таким образом, чтобы максимальные тормозные моменты колесных тормозных механизмов были бы большими, чем возможные по условиям сцепления. Поэтому при определении максимальных тормозных моментов мостов легковых автомобилей следует принимать фтах = = 0,85...!, если в тормозном приводе ус
93
тановлен усилитель, если он отсутствует, принимают ершах = 0,75...0,85. При этом усилие на тормозной педали не должно превышать 250...300 Н. У грузовых автомобилей в связи с трудностями компоновки тормоза внутри колеса расчет ведется применительно к дороге со сцеплением 0,6...0,65.
Тормозной момент, подводимый к колесам от вспомогательной тормозной системы, должен быть таким, чтобы без применения других тормозных устройств обеспечивалось движение автотранспортного средства с установленной постоянной скоростью на дороге с заданным уклоном. В этих условиях движущей силой является продольная составляющая силы тяжести автомобиля, а сопротивление движению достигается за счет тормозных моментов, создаваемых вспомогательной тормозной системой и двигателем, работающим в тормозном режиме, а также сил сопротивления качению и воздуха.
Уравнение тягового баланса при движении автомобиля (автопоезда) под уклон:
Ga sin а = —— +	fGa /гвДви2;
го го
Л4тв — iGa.r0 ' Alex' //'(jGa	&в-АвГ()Ц2,
где'Мд, /Иет— тормозной момент, подведенный к колесам автомобиля соответственно от двигателя и вспомогательной тормозной системы. При определении Л4гт коэффициент сопротивления качению принимают соответствующим движению по дороге с твердым ровным покрытием; Мтв находят по тормозным характеристикам, получаемым при стендовых испытаниях двигателя.
По существующим нормативам вспомогательная тормозная система должна обеспечивать постоянную скорость движения 30 ±2 км/ч на уклоне крутизной i = 0,07. Проверка эффективности системы производится на уклоне протяженностью 6 км, причем для ав
тотранспортных средств, у которых в качестве вспомогательной тормозной системы используется только двигатель без применения специальных тормозных устройств, скорость должна быть постоянной (30±5 км/ч).
Эффективность стояночной тормозной системы должна быть такой, чтобы суммарная тормозная сила, развиваемая механизмами этой системы, обеспечивала удержание автотранспортного средства на уклоне (подъеме и спуске), заданном техническими условиями. При этом крутизна уклона должна быть не менее 25 % для автомобилей и автопоездов, перевозящих людей, 20 — для грузовых автомобилей и 18 % —для автопоездов. При расчетах необходимого момента стояночной тормозной системы сопротивление качению не учитывается.
4.3.	Оценка тормозных свойств автомобилей
Тормозные свойства автотранспортных средств в значительной степени определяют безопасность движения на автомобильных дорогах. Поэтому к эффективности и надежности тормозных систем предъявляют особо жесткие требования.
Оценка эффективности рабочей и тормозной систем осуществляется по длине тормозного пути и установившемуся замедлению, а стояночной и вспомогательной — по суммарной тормозной силе, развиваемой этими системами. Под тормозным путем понимается расстояние, проходимое автомобилем от начала торможения до его полной остановки. За начало торможения принимают момент, в который водитель устанавливает ногу на тормозную педаль.
Поскольку при оценке тормозных систем торможение осуществляется с максимальной интенсивностью, на основном участке тормозного пути замедление примерно одинаково. Это замед
94
ление принято называть установившимся.
Эффективность тормозных систем определяется во время проведения дорожных испытаний. Перед их проведением автотранспортное средство должно пройти обкатку в соответствии с инструкцией завода-изготовителя, нагрузка и ее распределение по мостам должны соответствовать техническим условиям. Агрегаты трансмиссии и ходовой части (кроме тормозов) должны быть предварительно прогреты. Износ рисунка протектора шин должен быть равномерным и не превышать 50 %. Участок дороги, на котором проводятся испытания основной и запасной тормозных систем, и погодные условия должны удовлетворять тем же требованиям, которые к ним предъявляются при оценке скоростных свойств автотранспортного подвижного состава.
Поскольку эффективность тормозных механизмов в сильной степени зависит от температуры трущихся пар, тормозные испытания проводятся при различных тепловых состояниях тормозных механизмов.
По принятым в настоящее время стандартам испытания по определению эффективности рабочей тормозной системы делят на три типа: испытания «ноль», испытания I и испытания II. Испытания «ноль» предназначены для оценки эффективности рабочей тормозной системы при холодных тормозных механизмах. При испытаниях I определяют эффективность рабочей тормозной системы при нагретых путем предварительных торможений тормозных механизмах, а при испытаниях II — при механизмах, нагретых путем торможения на затяжном спуске.
В ГОСТе определены начальные скорости, с которых должно производиться торможение, установившиеся замедления и тормозные пути в зависимости от типа транспортных средств. Регламентируются также усилия на тормозных педалях: педаль легковых
автомобилей должна нажиматься с силой 500 Н, грузовых — 700 Н.
Начальные скорости торможения устанавливаются в зависимости от типа транспортного средства: от и0=’ = 80 км/ч (легковые автомобили) до Уо = 4О км/ч (грузовые автомобили и автопоезда с полной массой свыше 12 т). Установившиеся замедления должны быть не менее: легковых автомобилей — 7 м/с2, автобусов — 6, грузовых автомобилей и автопоездов — 5,5 м/с2.
Расчет нормативной длины тормозного пути (м) при испытаниях «ноль» можно производить по формуле
STo = А1Уа0 "Г уао/(26йуст), (4.15) где А — коэффициент, зависящий от типа транспортного средства: для легковых автомобилей — 0,1, для автобусов и грузовых автомобилей'—0,15, для автопоездов — 0,18; пао — начальная скорость, км/ч; ауст — установившееся замедление.
Установившееся замедление при испытаниях типа I и II должно составлять соответственно не менее 0,75 и 0,67 от замедлений при испытаниях типа «ноль».
Начальные скорости, при которых испытывают запасные тормозные системы, соответствуют начальным скоростям при испытаниях рабочих систем. При этом необходимо посредством запасных тормозных систем обеспечивать замедление легковых автомобилей не менее 2,9 м/с2, автобусов — 2,5, а грузовых автомобилей и автопоездов — 2,2 м/с2. Тормозной путь можно рассчитывать по формуле (4.15). Коэффициенты А принимаются такими же, как и для рабочей тормозной системы.
Методы оценки тормозных свойств автотранспортных средств, находящихся в эксплуатации, обычно определяются правилами дорожного движения. В правилах оговариваются условия испытаний (сухая горизонтальная дорога с твердым покрытием), а так-
95
Рис. 4.7. Принципиальная схема моделирования процесса движения автомобиля при торможении
Рис. 4.8. Блок-схема моделирования на АВМ процесса движения автомобиля при торможении
же начальная скорость, принимаемая одинаковой для всех транспортных средств. Оценочными критериями являются установившееся замедление и тормозной путь. Минимальные установившиеся замедления автомобилей, находящихся в эксплуатации, обычно допускают несколько меньшими (на 10... 12 %), чем у новых.
При расчетах остановочного пути учитывают, что в течение промежутка времени t = tp+t3 скорость автомобиля не изменяется. Поэтому путь, проходимый за это время, находят по выражению: Sp.3 = U o(tp+.t3).
Скорость автомобиля в процессе торможения может быть получена интегрированием по времени замедления автомобиля, а тормозной путь st — интегрированием скорости:
t	t
Vi = v0 — C axdt\ sT = f vxdt.
6	b
В процессе торможения замедление автомобиля меняется: изменяется сила сопротивления воздуха, коэффициент сцепления, дорожное сопротивление. Расчеты тормозного пути при переменном замедлении целесообразно выполнять на цифровых или аналоговых вычислительных машинах. Принципиальная схема расчета тормозного пути двухосного автомобиля показана на рис. 4.7.
Схема включает три системы моделирования: две — тормозящих мостов, аналогичных схемам моделирования движения тормозящего колеса, но рассчитанных по параметрам мостов, и одна —движения массы автомобиля. Моделированием движения массы рассчитываются тормозные моменты A4Tj и Mf2, нормальные составляющие реакции дороги Rzi И Т?г2 И СКОрОСТЬ ЭВТО-мобиля V. Эти параметры используются в системах моделирования движения тормозящих мостов, а получаемые в последних силы Fx< и Fx2 — в системе моделирования движения массы автомобиля.
Движение массы описывается системой уравнений:
а)	Мп = а^пед!	1
б)	Л4т2 — Апед,
в)	ах —	(Fxi + F х2 FBj+ Fi)>
г)	Rzi = А + Сах,	'
д)	7?й = В — Сах, t
е)	v = v0 — f axdt-,
6 t
Ж) ST = [ vdt, 0
где = ai/a2; A = gm^lL, В = gtn&a/L, C = mJiglL.
На рис. 4.8 показана блок-схема моделирования на АВМ процесса торможения автомобиля. Приведенные формулы соответствуют схемам на рисунке.
Схемы а и б обеспечивают заданное соотношение между тормозными момен-
96
тами Af-ri и ЛД2 при любых значениях силы нажатия на тормозную педаль ЕПСд. Если расчеты проводятся при меняющемся (по заданному закону) усилии на тормозной педали, для определения Епед можно применять специальные схемы.
Если расчет ведется для случая движения автомобиля по горизонтальному участку с небольшой начальной скоростью (не выше 80 км/ч), силы сопротивления подъему Fi и сопротивления воздуха Ев можно не учитывать.
При расчете на цифровых вычислительных машинах определяют те же параметры, что и на аналоговых. Тормозной путь sT находят как сумму элементарных тормозных путей, проходимых автомобилем за время AZ, считая замедление его постоянным. Показано, что достаточно высокая точность расчетов обеспечивается при шаге AZ = = 0,01 с.
Практический интерес представляет методика расчета остановочного пути автомобиля при торможении с постоянным замедлением.
Наиболее близко таким условиям соответствует аварийное торможение с начальных скоростей 30...60 км/ч. При расчете остановочного пути в этом случае принимают допущение, что замедление нарастает скачкообразно до аттах в момент времени 0,54, как это показано на рис. 4.1 пунктирной линией. При таком допущении уменьшение скорости начинается через промежуток времени 4 = tv + t3 4- 0,54 с момента возникновения необходимости торможения. Из рис. 4.1, а видно, что при таком методе расчета площадь между осью абсцисс и линией изменения скорости автомобиля, пропорциональная остановочному пути, будет несколько большей, чем получаемая при точном расчете. Но так как время нарастания замедления очень мало, погрешность оказывается небольшой, и ею можно пренебречь.
Остановочный путь может быть найден непосредственно по площади между линией абсцисс и линией изменения скорости по графику рис. 4.1, б: So — Vo (4 4-4 4- 0,54)4-0,5у0(0,54 4-4).
(4-16)
Время tx + 0,54, в течение которого скорость автомобиля уменьшается от vq до нуля при замедлении аттах определяется выражением
0,54 4- 4 = ^о/^т,
и формула (4.16) принимает вид:
So = Vq (tp 4-4 4- 0,54) 4- Уо/(2от).
Замедление ах определяется по формуле (4.11).
Для оценки влияния дорожных условий на остановочный путь автомобиля иногда используют упрощенные методы. Проф. Д. П. Великанов предложил рассчитывать замедление при аварийных торможениях исходя из сцепных свойств дороги с учетом поправочного коэффициента, характеризующего эффективность работы тормозов:
аг = ЕфДэ,
где кэ — коэффициент эффективности действия тормозов, являющийся практически величиной, обратной коэффициенту использования сцепления дороги сх. На основании опытных данных принимают: при <р 0,4 для легковых автомобилей k3 — 1,2; для грузовых k3 = = 1,3...1,4; при ф <4 0,4 для всех автомобилей k3 = 1.
С учетом изложенного формула для расчета остановочного пути может быть представлена в виде:
s0 = (^ао/3,6) (4>4-44-0,54) 4-0,004/гэХ X (И2ао/ф)-
Тормозной путь автомобиля sTo в соответствии с выражением (4.15) может быть найден по формуле
StO —
(44-0,54)
3,6
Vlo
Иа0+ 2&Tmax
(4-17)
4 А. И. Гришкевич
97
Сравнивая формулы (4.15) и (4.16), видим, что коэффициент Аг в выражении (4.15) представляет собой (£3+ + 0,5£н)/3,6.
4.4.	Регулирование тормозных сил
Повысить эффективность торможения при одновременном улучшении устойчивости автомобиля можно путем установки в тормозной системе регуляторов тормозных сил. Регуляторы обеспечивают распределение тормозных сил между колесами мостов, приближающееся к оптимальному, при аварийном торможении в различных дорожных условиях вне зависимости от степени загруженности автомобиля. Все существующие регуляторы делятся на две группы: регуляторы без обратной связи и с обратной связью.
Регуляторы первой группы изменяют соотношения между тормозными силами в зависимости от интенсивности торможения и нагрузки автомобиля. Максимальные же тормозные моменты в этом случае определяются силой, с которой водитель нажимает на тормозную педаль. Поэтому такие регуляторы, обеспечивая распределение сил, более или менее близкое к оптимальному, не исключают блокировки колес, а соответственно, и заноса автомобиля.
Режим работы регулятора с обратной связью зависит от характера качения колеса. В начале блокировки специальные автоматические устройства уменьшают тормозной момент так, чтобы его среднее значение поддерживалось примерно на уровне максимально возможного по сцеплению при данной нагрузке на колесо.
Для уяснения принципа работы регуляторов без обратной связи рассмотрим график (рис. 4.9), на котором показаны оптимальные соотношения между тормозными силами на колесах переднего и заднего мостов грузового автомобиля с полной нагрузкой (100 %),
Рис. 4.9. Оптимальные соотношения между тормозными силами в зависимости от нагрузки и сцепления
с половинной (50 %) и без груза. Штрих-пунктирные линии соединяют точки, соответствующие одинаковым сцеплениям. Из графика видно, например, что для обеспечения одновременной блокировки всех колес при торможении полностью загруженного автомобиля на дороге с коэффициентом сцепления <р = = 0,5 тормозная сила на колесах переднего моста должна быть равна 37 кН, а заднего — 35 кН. Если же в этих условиях тормозится порожний автомобиль, то тормозные силы должны соответственно составлять 21 кН и 13 кН. Таким образом, оптимальное соотношение тормозных сил у груженого автомобиля будет рт = 1, а у порожнего рт = 1,6. Привод без регулятора в рассматриваемом случае обеспечивает соотношение рт = 1,2 (прямая линия на графике). При таком распределении тормозных сил, если водитель чрезмерно сильно нажмет на тормозную педаль груженого автомобиля, первым начне! блокироваться передний мост, а у автомобиля без груза — задний. Как показано в параграфе 4.3, в этих условиях сцепной вес автомобиля не может быть использован полностью.
Поскольку тормозные силы и соот ветствующие им тормозные моменть пропорциональны давлению в тормоз
98
ных контурах мостов, график, показанный на рис. 4.9, можно представить в других координатах. Давление в контурах тормозного привода р\ и р% связано с тормозной силой:
pi =
pi = Г0/42/Й2 = CzFtz-
График, показывающий связь давления в переднем и заднем контурах тормозного привода, будем называть рабочей характеристикой регулятора. У систем, не имеющих регулятора, рабочая характеристика представляет прямую линию, выходящую из начала координат под углом 45° (Р1=Рг).
Обычно регулятор устанавливают в контуре привода тормозов заднего моста. Он изменяет по установленному закону давление в этом контуре в зависимости от давления в контуре переднего моста и нагрузки, приходящейся на задний мост. О нагрузке, приходящейся на задний мост, можно судить по деформации рессоры. Поэтому те регуляторы, которые реагируют на нагрузку, имеют устройства, изменяющие регулируемые параметры в зависимости от деформации упругих элементов подвески.
Идеальный регулятор должен обеспечивать регулирование давления в заднем контуре так, чтобы при всех режимах торможения соблюдались оптимальные соотношения между тормозными силами, как, например, показано на рис. 4.9. Однако такой регулятор оказался бы неоправданно сложным. Практическое регулирование осуществляется по более простым законам. Рассмотрим некоторые из них.
1.	Регулирование путем изменения коэффициента передачи регулятора. В общем виде давления-в переднем и заднем контурах привода можно связать соотношением Р2 = а pi, где а — коэффициент передачи регулятора. Можно построить такой регулятор, который при изменении нагрузки на мост (деформации рессоры) будет изменять
Рис. 4.10. Рабочие характеристики регуляторов
свой коэффициент передачи. Рабочие характеристики такого регулятора и их сравнение с идеальными показаны на рис. 4.10, а. При наличии регулятора повышается эффективность торможения автомобиля при движении с неполной нагрузкой и без груза, но в то же время не исключается блокировка заднего моста. Такие регуляторы применяют при пневматическом тормозном приводе. Они получили название лучевых регуляторов.
2.	Регулирование путем ограничения давления в заднем контуре. Рабочая характеристика такого регулятора показана на рис. 4.10, б. Давление, при котором изменяется характеристика регулятора, будем называть точкой срабатывания регулятора р0. Такие регуляторы иногда применяют на автомобилях с малоизменяющимися весовыми характеристиками. Основной недостаток регулятора — малая эффективность торможения при больших коэффициентах сцепления вследствие неполного использования сцепного веса, приходящегося на задний мост. Лучшая характеристика присуща регуля
4*
99
тору, у которого в точке срабатывания меняется коэффициент передачи. Он называется регулятором с пропорциональным клапаном. Характеристика такого регулятора показана на рис. 4.10,6 пунктирной линией. При наличии в приводе регулятора с пропорциональным клапаном повышается эффективность торможения, но при неполной нагрузке автомобиля не исключена блокировка колес заднего моста.
3.	Регулирование с изменяющейся точкой срабатывания. На рис. 4.10, в показана характеристика регулятора, у которого в зависимости от нагрузки, приходящейся на задний мост, меняется положение точки срабатывания. Характеристика регулятора определяется коэффициентом передачи а и законом изменения положения точки срабатывания в зависимости от нагрузки, приходящейся на задний мост. Применяются регуляторы с такой характеристикой в системах с гидравлическим приводом.
На рис. 4.10,г показана схема регулятора, у которого в зависимости от нагрузки на задний мост меняется положение точки срабатывания и коэффициент передачи а. Эти регуляторы наиболее полно удовлетворяют требованиям оптимального регулирования тормозных сил и применяются в тормозных системах с пневматическим приводом.
При подборе характеристик регулятора для конкретного автомобиля необходимо учитывать предполагаемый тип тормозного привода и условия эксплуатации. Регуляторы должны обеспечивать при любой степени загрузки автомобиля и аварийном торможении на дорогах с коэффициентами сцепления 0,15...0,8 максимально возможное замедление при одновременной блокировке всех колес автомобиля или опережающей блокировке колес переднего моста. Для выполнения последнего условия необходимо, чтобы линия оптимальных давлений совпадала или
Рис. 4.11. Принципиальная схема противобло-кировочной системы:
1 — тормозной цилиндр; 2 — пневматические магистрали; 3 — модулятор;	4<.— ресивер;	5 — главный
тормозной кран; 6— тормозная педаль; 7 •—соединение с атмосферой; 8 — электронный блок управления; 9.—электрические магистрали; 10 — датчик скорости
была выше рабочей характеристики регулятора.
На начальном участке характеристики регулятор обычной конструкции (кроме лучевых регуляторов) не работает и давления в контурах переднего и заднего мостов одинаковы. Поэтому исходными данными для проектирования регуляторов являются: лучевого типа — зависимость коэффициента передачи а от нагрузки, приходящейся на задний мост; с клапаном-ограничителем — точка срабатывания р0 и коэффициент передачи а; с переменной точкой срабатывания — зависимость точки срабатывания р0 от нагрузки, приходящейся на задний мост, и коэффициент передачи а (гидравлический привод) или зависимости точки срабатывания р0 и коэффициента передачи а от нагрузки (пневматический привод).
При применении регуляторов коэффициент распределения тормозных сил рт для участка характеристики, на котором регулятор не работает, подбирают обычно так, чтобы у автомобиля с грузом одновременная блокировка колес происходила при торможении на дороге со сцеплением рт = 0,35...0,45.
Регуляторами тормозных сил улуч-
100
Рис. 4.12. Диаграмма работы антиблокировочной системы:
а— изменение усилия на педали и давления в тормозном цилиндре во времени; б — изменение углового замедления колеса во времени; в— зависимость коэффициента скольжения колеса от удельной тормозной силы
шаются тормозные свойства автомобилей, однако наличие их не исключает возможности потери устойчивости автомобиля вследствие его заноса.
Регуляторы с обратной связью, или противоблокировочные системы (ПБС), предназначены для обеспечения эффективного торможения автомобиля в любых условиях при сохранении им устойчивости. Принципиальная схема современной ПБС показана на рис. 4.11. Система включает электронный блок управления, регулятор давления (модулятор) и датчик угловой скорости колеса. ПБС.могут работать по различным алгоритмам. Основная идея большинства алгоритмов основывается на том, что при превышении скольжения, соответствующего максимальному сцеплению, скорость вращения колеса резко уменьшается.
Рассмотрим работу ПБС по одному из возможных алгоритмов. При нажатии на тормозную педаль и дальнейшем увеличении усилия давление в приводе возрастает (рис. 4.12, а). При возрастании давления увеличиваются тормозная сила и угловое замедление колеса. Угловое замедление колеса увеличивается по двум причинам: вследствие торможения уменьшается скорость автомобиля, а при увеличении удельной тормозной силы увеличивается коэффициент скольжения.
На рис. 4.12, в показана зависимость коэффициента скольжения от удельной тормозной силы. Эта зависи
мость аналогична приведенной на рис. 1.16, но построена в других координатах. В момент достижения удельной тормозной силой максимального значения, равного утах, начинается процесс блокировки колеса и его угловое замедление резко возрастает. Этот момент на графиках рис. 4.12 отмечен точкой 1. Сигнал с датчика угловой скорости колеса передается в управляющий блок, который анализирует угловое замедление колеса. В момент резкого возрастания замедления управляющим блоком подается сигнал в модулятор, которым соединяется полость тормозного цилиндра с атмосферой. При этом в ячейках памяти фиксируется давление в тормозном цилиндре рх. Уменьшение давления в тормозном цилиндре вследствие наличия неизбежного запаздывания срабатывания модулятора начинается в точке 2. В промежутке 1—2 давление в тормозном цилиндре и угловое замедление колеса возрастают, а удельная тормозная сила несколько уменьшается. В момент, соответствующий точке 2, начинается снижение давления в тормозном цилиндре, а также углового замедления колеса и скольжения. Управляющий блок настраивается таким образом, чтобы уменьшение давления происходило до значения р2 (точка 5), несколько меньшего, чем давление pi. Когда давление достигает значения р2, может начаться увеличение давления (следующий
101
цикл) или же оно в течение некоторого промежутка времени (точка 4) будет поддерживаться равным р2. После чего начинается новый цикл работы АБС. '
Противоблокировочные системы, имеющие фазу выдержки, называются трехфазовыми (в отличие от двухфазовых, имеющих только фазы увеличения и уменьшения давления).
Таким образом, антиблокировочная система создает пульсирующий тормозной момент, обеспечивающий качение колеса со скольжением, близким к оптимальному. Использование ПБС
в тормозных приводах позволяет существенно улучшить тормозные свойства автомобиля и обеспечить его устойчивость при торможении с максимальной эффективностью. Испытания показывают, что тормозные системы, имеющие ПБС с правильно выбранными параметрами, позволяют уменьшить тормозной путь (особенно при торможении с высоких начальных скоростей на дорогах с пониженным коэффициентом сцепления) на 20...35 %. При этом устойчивость и управляемость автомобиля сохраняются.
ПЛАВНОСТЬ ХОДА
5.1.	Основные характеристики подвески
Плавность хода — это эксплуатационное свойство автомобиля, характеризующее его способность двигаться в заданном интервале скоростей по дорогам с неровной поверхностью без значительных вибрационных и ударных воздействий на водителя, пассажиров или перевозимый груз. Результаты исследований показывают, что возникающие при движении автомобиля колебания, вызванные неровностями дороги, оказывают существенное влияние не только на плавность хода, но и на ряд других эксплуатационно-технических свойств автомобиля. Так, при эксплуатации грузовых автомобилей на дорогах с неровной поверхностью средняя скорость движения уменьшается на 40...50 %, межремонтный пробег — на 35...40 %, расход топлива увеличивается на 50... 70 %, а себестоимость перевозок — на 50...60 %•
Интенсивность колебаний масс автомобиля при его движении по дорогам с неровной поверхностью зависит от компоновочных характеристик автомобиля, параметров подвесок и шин.
При проектировании в большинстве случаев компоновка автомобиля определяется его назначением и особенностями предполагаемых условий эксплуатации, а параметры шин — тяговым расчетом. Поэтому основной задачей конструктора является разра
ботка подвески, которая обеспечивала бы максимальную производительность автомобиля в наиболее характерных условиях эксплуатации. Поскольку производительность автомобиля непосредственно связана со скоростью движения, задача заключается в разработке подвески, обеспечивающей возможность длительного движения автомобиля по дорогам с неровной поверхностью в интервале эксплуатационных скоростей, без быстрой утомляемости водителя и пассажиров или повреждения перевозимого груза. Конструкция подвески влияет и на другие эксплуатационные свойства автомобиля, в первую очередь на его устойчивость и управляемость.
Проектирование подвески автомобиля ведется в такой последовательности:
1)	по результатам эскизной проработки и анализа параметров подвесок автомобилей данного типа предварительно определяются их основные параметры;
2)	рассчитываются колебания автомобиля с целью определения соответствия плавности хода проектируемого автомобиля в заданных дорожных условиях плавности хода, установленной действующей нормативно-технической документацией. В случае несоответствия корректируют характеристики подвески автомобиля с целью обеспечения требуемой плавности хода;
3)	производится конструктивная
юз
Рис. 5.1. Схема определения упругих характеристик подвески и шин: 1— ладометр; 2 — устройство, подтягивающее кузов вверх; 3 — то же, вниз
разработка подвески с необходимыми расчетами на прочность и усталость.
В «Теории автомобиля» рассматриваются первые два этапа.
Все расчеты плавности хода носят условный характер. Связано это с тем, что по дорогам с неровной поверхностью автомобиль движется неравномерно: водитель увеличивает скорость движения на относительно ровных участках и резко снижает ее перед значительными неровностями, не допуская больших динамических воздействий на автомобиль. При расчетах плавности хода, как и при испытаниях, скорость движения принимают постоянной, что не соответствует реальным режимам движения автомобиля. Однако такой метод в настоящее время является единственно приемлемым, поскольку изменение скорости движения определяется не только характеристиками подвески, но и особенностями вождения автомобиля. Испытания и расчеты при постоянных скоростях движения позволяют получать хотя и сравнительную, но достаточно объективную оценку качеств подвески автомобилей.
К подвескам относят все узлы и детали, соединяющие мосты автомобиля с рамой или кузовом. В них различают три группы элементов: направляю
щие устройства; упругие элементы; гасящие устройства.
Направляющие устройства определяют закон, по которому происходит перемещение колес относительно рамы, и обеспечивают передачу усилий между мостами и рамой (кузовом) автомобиля.
Упругие элементы предназначены для преобразования энергии толчков и ударов, возникающих на неровностях дороги, в потенциальную энергию упругих элементов.
Гасящие устройства обеспечивают рассеивание энергии при колебаниях масс автомобиля.
В некоторых случаях один и тот же элемент подвески может выполнять различные функции.
Конструкции подвесок различаются по типам направляющих и гасящих устройств, упругих элементов. При расчетах плавности хода условно считают, что упругие и гасящие устройства установлены в плоскости колеса и создают вертикальные силы, приложенные к его центру. Такие устройства и их характеристики называются приведенными.
Под приведенной характеристикой упругого элемента понимается зависимость приращения нормальной со-
104
Рис. 5.2. Типовая характеристика упругого элемента подвески:
1 — нагружение; 2 — разгрузка
ставляющей реакции дороги, действующей на колесо, при медленном изменении расстояния между осью колеса и кузовом, которое замеряется в плоскости колеса. Приведенные характеристики определяются экспериментально или расчетным путем по кинематике направляющего устройства подвески и характеристике упругого элемента.
На рис. 5.1 показана принципиальная схема определения приведенной характеристики подвески. Колеса моста автомобиля устанавливаются на весовые устройства (ладометры). Нагрузку на кузов автомобиля можно создавать дополнительными грузами или, что более часто делается, путем подтягивания с помощью тросов и лебедки кузова вниз или вверх. При каждом положении кузова снимается показание ладометра, равное нормальной составляющей реакции дороги, и расстояние hi между осью колеса и некоторой точкой кузова, которое замеряется в вертикальной плоскости, проходящей через центр колеса. Измерение производят при загрузке и разгрузке кузова. Вследствие неизбежного гистерезиса кривые нагружения и разгрузки не совпадают. За характеристику подвески принимается сред
няя между кривыми нагружения и разгрузки, как показано на рис. 5.2. При построении характеристики началом отсчета может быть точка, соответствующая нулевой нагрузке на упругий элемент (значение нормальной реакции опорной поверхности равно доле веса моста, приходящейся на ладо-метр) , или положение, соответствующее статической нагрузке. Последние характеристики являются предпочтительными, так как они без перестроений могут использоваться в расчетах плавности хода автомобиля. Основным параметром, определяющим свойства подвески, является полный ход (полный прогиб), равный перемещению оси колеса относительно кузова по вертикали от нижнего до верхнего ограничителей хода. Полный ход подвески делят на ход отбоя ДОт и ход сжатия Асж. Ход отбоя — перемещение оси колеса от нижнего ограничителя до положения, соответствующего статической нагрузке. Ход сжатия — перемещение оси колеса от статического положения до верхнего ограничителя. Прогибы измеряются в плоскости колеса. При максимальной деформации упругого элемента через подвеску на мост передается максимальная нагрузка Fmax-
Одним из параметров характеристики является приведенный коэффициент жесткости ср — производная нагрузки по перемещению:
dF , ср = — = 1g а.
а А
Если ср= const, упругая характеристика называется линейной (рис. 5.3, а), если жесткость зависит от деформации— нелинейной (рис. 5.3, б). Для линейных характеристик целесообразно рассматривать статический прогиб ACt = F ст/Ср.
—'"Если тгет-ограпичитсля хода отбоя, ход отбоя линейных подвесок равен статическому ходу.
К оценочным параметрам подвески
105
Рис. 5.3. Приведенные характеристики подвески
Л ---
Рис. 5.4. Упругая характеристика шины 7,50—20
относится также коэффициент ее динамичности kn, представляющий отношение максимальной нагрузки, которая передается через подвеску, к статической:
kK=Fmax/Fст.
Этот коэффициент характеризует степень вероятности движения автомобиля по неровным дорогам без ударов в ограничители хода.
Для линейных подвесок:
Ад='(Дст + Ася^)/Аст== 1 + Асж/Аст.
У таких подвесок иногда степень безударного движения оценивают по отношению ходов сжатия и отбоя:
'Ид = Асж/Аот’, ^д=1+'У]д.
Характеристика шины (рис. 5.4) представляет зависимость нормальной составляющей реакции опорной поверхности от деформации шины при изме
Рис. 5.5. Экспериментальная зависимость жесткости шины, установленной на вершине косинусоидальной неровности постоянной высоты от ее длины
нении действующей на нее нагрузки и определяется на специальных установках. Характеристика шины может быть найдена одновременно с приведенной характеристикой подвески путем измерения расстояния hi (см. рис. 5.1). При этом следует иметь в виду, что нормальная реакция, действующая на шину, равна показанию ладометра, а на подвеску — показанию ладометра за вычетом доли веса моста, приходящейся на рассматриваемое колесо. Характеристики шин близки к линейным, поэтому основным параметром характеристики является жесткость, определяемая в зоне статической нагрузки.
При расчетах плавности хода шину представляют в виде пружины, нижний конец которой контактирует с опорной поверхностью в одной точке.
Жесткость шины (радиальная) зависит от ее конструкции, размеров и давления воздуха в ней, а также от формы опорной поверхности. На выпуклых поверхностях жесткость уменьшается, а на вогнутых —• возрастает. Экспериментальная зависимость коэффициента жесткости шины от формы опорной поверхности показана на рис. 5.5.
В реальных условиях шина контактирует с опорной поверхностью на определенной площади. При этом неровности, длина которых соизмерима
106
Рис. 5.6. Характеристика гидравлического амортизатора
с длиной контактной поверхности, сглаживаются. Происходит это вследствие того, что радиус колеса значительно превосходит размеры неровности, а также из-за упругости и гибкости шины. Поскольку жесткость шины зависит от формы опорной поверхности, представление шины в виде пружины, контактирующей с неровностями опорной поверхности в одной точке, может привести к погрешностям, особенно при анализе воздействия на автомобиль коротких неровностей. В связи с этим в расчетных моделях должна учитываться «сглаживающая» способность шин. Наиболее часто сглаживающую способность моделируют путем уменьшения по определенному закону высот неровностей, длины которых соизмеримы с длиной контактной поверхности шины.
Рассеивание энергии при колебаниях автомобиля обеспечивается специальными устройствами (амортизаторами) .
Наибольшее распространение в настоящее время получили гидравлические телескопические амортизаторы двустороннего действия.
Сила сопротивления Fa, создаваемая гидравлическим амортизатором, зависит от скорости деформации подвески:
Fа=&рДр,
где /гр — коэффициент сопротивления амортизатора.
Когда йр=const, амортизатор считается линейным. Зависимость силы сопротивления амортизатора Ка от скорости деформации Др называется характеристикой амортизатора. При расчетах плавности хода используют приведенные характеристики амортизаторов.
На рис. 5.6 показана характеристика гидравлического амортизатора. Обычно коэффициент сопротивления амортизатора при ходе сжатия &р.сж меньше, чем коэффициент сопротивления при ходе отбоя &p.0T: &Р.сж = (0,1... 0,25)£р.от.
Для предохранения амортизаторов от разрушения в полостях с высоким давлением устанавливают разгрузочные клапаны, уменьшающие коэффициенты сопротивления йр.сж и &р.от при скоростях деформации, больших ДСж.к и Дот.к соответственно. Как правило, скорости включения разгрузочных клапанов превосходят максимальные скорости деформаций подвесок при эксплуатационных режимах движения.
Рассеивание энергии при колебаниях масс автомобиля происходит также за счет неизбежного трения между элементами подвески, гистерезисных потерь в деформируемом материале, при вертикальных деформациях катящейся шины.
Сила трения в элементах подвески Может рассматриваться как постоянная. Она определяется главным образом типом и конструкцией упругого элемента и направляющего устройства. При деформации пружин, торсионов, баллонов пневматических подвесок трение практически отсутствует. Трение в рычажной подвеске определяется числом шарниров и их конструкцией. При этом большее трение создают шарниры с гладкими пальцами, меньшее — шарниры с резьбовыми пальцами, а у шарниров с шариковыми, роликовыми или
107
Рис. 5.7. Свободные колебания массы, подрессоренной:
а — на неподвижной шине; б—катящейся
Рис. 5.8. Экспериментальная зависимость относительного коэффициента затухания массы, подрессоренной на катящейся шине, от скорости качения
резиновыми опорами оно практически отсутствует.
Большая сила трения в подвеске имеет место при рессорных упругих элементах (межлистовое трение). При конструировании подвески для ее уменьшения предусматривают установку специальных антифрикционных прокладок между листами, надежное межлистовое смазывание. Уменьшение числа листов у рессор способствует уменьшению трения. Силу трения, возникающую при вертикальной деформации шины, можно рассматривать как зависящую от скорости деформации:
Fin — &1пДш.
Внутреннее трение в шине зависит от ее конструкции, главным образом от числа слоев и материала корда, внутреннего давления, размеров шины и ее деформации. Как правило, оно не является значительным и уменьшается при увеличении скорости качения колеса.
На рис. 5.7 показано, как затухают свободные колебания груза, подрессоренного на шине, катящейся по гладкому барабану, а на рис. 5.8 представлена зависимость относительного коэффициента затухания ф от скорости качения. Относительный коэффициент затухания оценивается по отношению амплитуд колеблющейся массы. Уменьшение рассеивания энергии при вертикальных колебаниях быстро катящейся шиной обусловлено тем, что скорость ее деформации при качении существенно больше скорости деформаций от вертикальных колебаний.
5.2.	Характеристики дорожных неровностей
Основной из причин, вызывающих колебания масс автомобиля, является взаимодействие колес автомобиля с дорожными неровностями. Поверхность даже хорошей дороги не является идеально ровной. С течением времени она изнашивается и разрушается, а количество неровностей и их высота увеличиваются. Интенсивность изнашивания и разрушения поверхности дороги зависит от вида и качества покрытия, атмосферных и температурных условий, воздействия автотранспорта.
В простейшем виде дорожную неровность можно представить в виде косинусоидального выступа (рис. 5.9). В этом случае профиль неровности q может быть описан выражением вида:
<7 = </о[1 — cos (2лх//)],
где <?о — амплитуда высоты неровности; х — абсцисса неровности; I — ее длина.
При движении автомобиля со ско-
108
Рис. 5.9. Профиль косинусоидальной неровности
ростью v абсцисса неровности изменяется по закону x=vt, а возмущение, передаваемое от неровности на динамическую систему автомобиля, по закону
<7 = <?о[1 — cos (W)],
где v — частота возмущения, связанная со скоростью движения автомобиля и длиной неровности соотношением v= —2nvll.
Поскольку характеристики дорожных неровностей не связаны со скоростью движения автомобиля, для оценки их состава по длине используют понятия путевой и циклической частоты.
Под циклической частотой понимают количество неровностей, расположенных на участке дороги длиной 1 м: A=l/Z.
Путевая частота связана с циклической соотношением: = 2,пЛ = 2,п//.
Путевую и циклическую частоты можно представить как частоты возмущений, передаваемых на автомобиль от неровностей дороги при его движении со скоростью 1 м/с: путевую — в радианах в секунду, циклическую — в герцах.
Из теории колебаний известно, что степень воздействия возмущения на динамическую систему зависит от соотношения частот возмущений и собственных колебаний системы. Если частоты возмущения и собственных колебаний близки между собой, реакция динамической системы на возмущение будет наибольшей. При значительном различии этих частот действие возмущения
можно рассматривать как статическое. В частности, если частота собственных колебаний динамической системы превосходит частоту возмущений в 5... 10 раз, можно считать, что перемещения масс в динамической системе будут такими же, как при статическом внешнем воздействии. Если частота собственных колебаний будет во столько же раз ниже частоты возмущения, массы динамической системы не будут перемещаться.
Применительно к автомобилю это положение указывает на то, что если он движется по неровностям, создающим возмущения, частота которых значительно ниже наименьшей частоты собственных колебаний масс автомобиля, имеющиеся в динамической системе автомобиля упругие элементы не будут деформироваться. Это значит, что движение автомобиля в этом случае можно рассматривать как движение жесткого тела. Если же частота возмущений значительно выше наибольшей частоты собственных колебаний автомобиля, его массы не будут совершать колебания. Под воздействием неровностей будут деформироваться только шины.
Соответственно, в зависимости от характера воздействия на автомобиль все дорожные неровности принято делить на три группы: неровности макропрофиля, неровности микропрофиля и шероховатости. Неровности первой группы не оказывают динамического воздействия на автомобиль, а последней — не влияют на плавность его хода. Шероховатости обусловливают шум при движении автомобиля, изнашивание шин, от них также зависит расход топлива и .др. Неровности микропрофиля оказывают динамическое воздействие на автомобиль и поэтому рассматриваются при изучении плавности хода автомобилей.
Проведенные исследования профилей автомобильных дорог позволяют сформулировать некоторые наиболее
109
Рис. 5.10. Типичная кривая спектральной плотности микропрофиля автомобильной дороги
общие закономерности распределения неровностей на поверхности дорожного покрытия.
В реальных условиях неровности дороги имеют беспорядочный характер: различный профиль, разную длину, они могут налагаться друг на друга или следовать одна за другой. С позиций математической статистики изменение ординат продольного профиля дороги (продольного сечения дороги по колее автомобиля) можно рассматривать как случайный процесс. Случайность здесь проявляется в том, что, зная характер неровностей на одном участке дороги, невозможно предсказать их характер / на последующем.
\ В общем случае ординаты профиля -I можно рассматривать как нестационарную случайную функцию пути <7=/:(s). Под нестационарностыо понимается переменность основных статистических параметров, обусловленную тем, что отдельные участки дорог имеют различный характер неровностей. Как правило, на дорогах происходит чередование различных по длине относительно ровных и неровных участков. В то же время измерения микропрофиля на достаточно большом отрезке пути показывают, что статистические характеристики определенной дороги стабильны. Это позволяет считать ординаты продольного профиля конкретных
дорог стационарной эргодической случайной функцией, а относительно короткие участки — представительными, если их статистические характеристики такие же, как и всей дороги. Проведенные измерения высот неровностей показали, что ординаты микропрофиля подчиняются нормальному закону распределения.
При этих допущениях статистические характеристики микропрофиля дороги можно полностью описать спектральной плотностью распределения дисперсий ординат микропрофиля (спектральная плотность микропрофиля) по путевой (циклической) частоте Sg(%).
. Многочисленными измерениями «установлено, что спектральная плот-юность микропрофиля — это монотонно убывающая с ростом X функция, на графике которой возможно появление одной или двух выпуклостей (рис. 5.10). Появление этих максимумов объясняется направленным воздействием автомобилей на полотно дороги при образовании неровностей. Возникновение периодических неровностей может быть объяснено следующим образом. После проезда автомобилем какой-либо неровности вследствие колебаний масс автомобиля возникает переменное давление на дорожное покрытие. Так как частоты собственных колебаний всех автомобилей, как и эскплуатационные скорости их движения, близки, все автомобили в одних и тех же местах создают повышенное или пониженное давление. Это в конечном итоге приводит к появлению периодических неровностей: длинных и коротких, соответствующих двум частотам собственных колебаний масс автомобиля — низким и высоким. На цементобетонных дорогах длина периодических волн может определяться длиной плит.
Длина участков с периодическими неровностями обычно небольшая — две-три волны. Это объясняется тем, что водитель на таком участке, резко
110
Рис. 5.11. Изображение спектральной плотности микропрофиля
изменяя скорость движения, выводит автомобиль из режима интенсивных колебаний. Поэтому большие экстремальные значения спектральной плотности микропрофиля имеют место для коротких участков дорог. С увеличением протяженности измеренных участков доля периодических неровностей уменьшается и кривая спектральной плотности принимает более плавное очертание.
В общем виде кривая спектральной плотности микропрофиля дороги может быть аппроксимирована дробнорациональной функцией вида:
<? С1Л ^0
(5-1)
где Ко, hi — константы.
Учитывая то обстоятельство, что функция (5.1)—монотонно убывающая, ее можно представить кривой, состоящей из нескольких участков с различной скоростью изменения спектральной плотности. Каждый участок может быть аппроксимирован выражением вида:
5?1(1)=5(Ч(^о)И/,	(5.2)
где А,о — характерная для данного типа дорог путевая частота, при которой происходит изменение интенсивности убывания спектральной плотности; 5(Ло) —уровень спектральной плотно
сти при характерной путевой частоте; Wi — показатель степени.
Для аппроксимирования спектральной плотности реальной автомобильной дороги оказывается достаточным ее кривую разбить на два участка. Большие значения показателя указывают на то, что дорога имеет большую долю длинных неровностей, причем их высоты с увеличением длины неровностей значительно возрастают, малые значения показателя w2 — что для данной дороги характерна большая доля коротких неровностей.
Принято спектральные плотности микропрофиля изображать в логарифмической системе координат. При этом функция (5.2) представляется в виде двух прямых, пересекающихся в точке с координатами А,о и 5(Ло) (рис. 5.11).
Имеющиеся данные по характеристикам микропрофилей автомобильных дорог позволяют определить область расположения значений спектральных плотностей микропрофилей различных типов дорог. На рис. 5.12 показаны области расположения кривых спектральных плотностей микропрофилей цементобетонных, булыжно-щебеночных и грунтовых дорог. Из графика видно, что спектральные плотности микропрофиля цементобетонных дорог находятся в относительно узкой зоне, а грунтовых дорог — очень широкой. Верхняя граница соответствует микропрофилю местности, по которой движение автомобилей невозможно, а нижняя граница — практически достижимому уровню ровности цементобетонных дорог.
Функция (5.1) полностью определяет статистические характеристики микропрофиля автомобильных дорог. Интеграл в пределах от Ка до Кь равен дисперсии высот неровностей в диапазоне ДЛИН 1ь — 1а (1ь= 1 AbJ /а=1Да):
Dab = .[ sq(k)d%. (5.3)
111
Рис. 5.12. Области расположения спектральных плотностей микропрофилей автомобильных дорог:
1 — с цементобетонным покрытием; 2 — булыжнощебеночным; 3 — грунтовых
^тах
Рис. 5.13. Определение максимального перепада высот
Среднеквадратическое отклонение высот неровностей в этом диапазоне
<Уаь = V~Dab ,	(5.4)
максимально возможный перепад высот (рис. 5.13)
/lmax = 2утах = 2 • ЗсГай = бсГаЬ-
Циклическая (путевая) частота Л, соответствует частоте возмущений при скорости автомобиля 1 м/с. Если автомобиль движется со скоростью V, час-
Рис. 5.14. Спектральные плотности возмущений, создаваемых микропрофилем грунтовой накатанной дороги при движении автомобиля со скоростями:
/ —1 м/с; 2 — 5; .<3—10; 4 — 20 м/с; Д —диапазон частот, в котором оценивается плавность хода
тота возмущения v при тех же длинах неровностей увеличивается в v раз. В общем виде v=Kv, что равносильно удлинению оси абсцисс графика и площади под кривой спектральной плотности, равной дисперсии высот неровностей, в v раз. Поскольку дисперсия ординат микропрофиля не зависит от скорости автомобиля, то для того чтобы оставить ее неизменной, необходимо в соответствующее число раз уменьшить масштаб по оси ординат. Таким образом, связь между спектральными плотностями микропрофиля и возмущений устанавливается соотношением
s?(v) = -Ls?W.
V \ V /
Например, если задана функция

спектральная плотность возмущения
е zvl = Ко> [(у/Ф2 + ^]
V 1(v/v)2 + ^[v/v2)+X22]
112
или
С /1 Ч /.	(v2 + V])
= ^(v2 + v2) (v2 + <
где v0 = пЛ0; vi = v2 = У^г-
Если спектральная плотность микропрофиля задана выражением (5.2),
S?(v) = J-S?(b0)hj-r
или
5?М = -5?(М(-^Н v \ vo;
где v0 = nA,0.
На рис. 5.14 показан график спектральной плотности распределения высот микронеровностей грунтовой накатанной дороги, описываемой функцией Sg(l) = 6-10“5(Z.2 + 72)/[(V + 0,12)Х X (Z.2 + l)]. На этом же графике приведены спектральные плотности возмущений при движении автомобиля по этой дороге с различными скоростями.
5.3. Критерии оценки плавности хода
Оценочные параметры плавности хода автомобиля должны характеризовать воздействие колебаний на водителя и на перевозимый груз. Допустимый уровень колебаний для организма человека ограничен. Это значит, что если нет специальных ограничений по допустимой интенсивности колебаний для перевозимого груза, то оценочные критерии плавности хода должны основываться на восприятии колебаний человеком.
Разработкой критериев интенсивности колебаний, допустимой для организма человека, занимались многие советские и зарубежные ученые. В большинстве случаев при экспериментальных исследованиях человек находился в различных положениях (сидя, стоя, лежа) на платформе, которой задавались гармонические или случайные колебания. Ощущения его оцени
вались субъективно или по объективным показателям (давление крови, температура тела, время реакции и др.). В результате проведенных исследований было установлено, что человек воспринимает колебания вестибулярным аппаратом, глазами, суставами и мышцами, кожей. Колебания передаются через костную ткань и могут действовать непосредственно на внутренние органы. Человеческий организм воспринимает колебания по-разному в зависимости от их частоты. В зоне низких частот восприятие колебаний пропорционально ускорениям, в зоне средних частот — скоростям, а в зоне высоких частот — перемещениям. Хотя граничные значения частот различными исследователями получены разные, однако все они отмечают, что человеческий организм наиболее чувствителен к вертикальным колебаниям в диапазоне частот 4...8 Гц и горизонтальным — 1...2 Гц.
В связи с вредным воздействием длительных вибраций на организм человека выработаны нормативы на допустимые уровни вибронагруженности человека. При разработке норм учитывалось, что реакция организма человека на вибрации зависит от частоты воздействий, частотный состав которых принято делить на октавы. Октава — это полоса частот, в которой конечная граничная частота в два раза выше начальной. Каждая октава имеет номер и среднегеометрическую частоту октавной полосы. В табл. 5.1 приведены частотные характеристики первых пяти октав.
Каждая октава может быть также разделена на полосы.
Допустимый уровень вибраций, действующих на водителя или пассажира, определяется ГОСТ 12.1.012—78 «Вибрация. Общие требования безопасности» и стандартом 2631 международной организации по стандартизации (ISO) «Вибрация, передаваемая человеческому телу».
из
Табл. 5,1. Частотные характеристики октав вибраций
Номер октавы
Среднегеомет-рическая частота, Гц
Начальная
граничная частота, Гц
Конечная гра-
ничная частота, Гц
I	1	0,7	1,4
II	2	2,4	2,8
III	4	2,8	5,6
IV	8	5,6	11,2
V	16	11,2	22,4
Рис. 5.15. Среднеквадратические значения ускорений, соответствующие пределу «производительного труда» при вертикальных (—) и горизонтальных (- - -) колебаниях продолжительности:
1 —*.8 ч; 2 — 2,5; 3 — 1 ч
Согласно ГОСТу, нормируемыми параметрами являются среднеквадратические значения виброскорости в октавных полосах частот. Уровень вибро-нагруженности L оценивается в децибелах по формуле
L = 201g(<W5-10-8),
где — среднеквадратическое значение виброскорости в октавной полосе частот; 5-10~8 — виброскорость, с которой проводится сравнение, условно принятая за границу ощущений.
ГОСТ устанавливает значения вертикальных и горизонтальных среднеквадратических виброскоростей в октавных полосах частот, действующих на человека непрерывно в течение 8 ч. Стандарт 2631 устанавливает допусти-
мые значения вертикальных и горизонтальных среднеквадратических виброускорений, дифференцированные по длительности воздействия. Колебания рассматриваются в диапазоне частот 1...80 Гц, который разбит на двадцать 1/3-октавных полос. Для каждой полосы дается весовой коэффициент для приведения значений среднеквадратических ускорений в ней к полосе частот, при которой организм человека наиболее чувствителен к колебаниям (4...8 Гц для вертикальных и 1...2 Гц — для горизонтальных). Допустимые значения виброускорений даются с учетом обеспечения производительной работы человека (уровень «производительной работы»). Кроме того, для каждой полосы частот приводятся уровни допустимых для здоровья человека ускорений (уровень «безопасности здоровья») и уровень, при котором не нарушаются условия комфорта (уровень «комфорта»), Допустимые ускорения первого уровня в 2 раза выше, чем уровня «производительной работы», а второго — в 3,15 раза ниже.
На рис. 5.15 показаны среднеквадратические ускорения, соответствующие уровню производительной работы человека при вертикальных и горизонтальных колебаниях.
С учетом указанных выше нормативных документов разработан порядок оценки автомобилей по плавности хода. Для экспериментальной оценки выбираются прямолинейные, горизонтальные участки дорог различного типа и состояния с однородным микропрофилем. Измерения оценочных параметров производятся при постоянной скорости движения автомобиля. Регистрируются вертикальные и горизонтальные ускорения в месте расположения водителя и других точках автомобиля, определенных в специальных методиках. Характер микропрофиля и скорость движения регламентируются руководящими материалами по испытаниям. Оценка плавности хода о'су-
114
Среднегеометрическая частота
Рис. 5.16. Результаты испытаний автомобиля на плавность хода:
1 — результаты испытаний или расчетов; 2 — предельно допустимые вертикальные ускорения при продолжительности воздействия 1 ч; -3 — то же, 8 ч
ществляется по среднеквадратическим значениям вертикальных и горизонтальных ускорений, воздействующих на водителя или пассажира. Оценку плавности хода обычно проводят по ускорениям, частоты которых соответствуют первым пяти октавным полосам частот.
Результаты испытаний или расчетов изображают графически в виде ломаной линии, соединяющей точки, ординаты которых равны значениям среднеквадратических ускорений в октавных полосах, а абсциссы — среднегеометрическим частотам. На эти же графики обычно наносят предельно допустимые ускорения (рис. 5.16). Сопоставление расчетных или экспериментальных ускорений с допустимыми позволяет судить о плавности хода автомобиля, а также выявить наиболее неблагоприятные диапазоны частот колебаний для дальнейшего совершенствования конструкции подвески.
В некоторых случаях, особенно при сравнительной оценке плавности хода автомобилей, удобно пользоваться одним показателем — эквивалентным среднеквадратическим ускорением, определяемым по формуле
Табл. 5.2. Весовые коэффициенты чувствительности человека к ускорениям
Номер октавной полосы частот	Весовой коэффициент при колебаниях	
	вертикальных} горизонтальных	
1	0,5	1
2	0,71	1 .
3	I	0,5
4	1	0,25
5	0,5	0,125
где п—число октавных полос частот; ki—весовой коэффициент чувствительности человека к ускорениям в различных октавных полосах частот (табл. 5.2); ° гг — среднеквадратическое ускорение в t-й октавной полосе частот колебаний.
5.4. Расчетные схемы, применяемые при анализе плавности хода автомобилей
Автомобиль представляет собой сложную динамическую систему, включающую большое количество масс, соединённых различного рода упругими связями. При движении все массы автомобиля совершают более или менее интенсивные линейные и угловые колебания в различных плоскостях. Возбуждение колебаний происходит в результате взаимодействия автомобиля с дорогой, а также из-за неравномерности работы двигателя и агрегатов трансмиссий.
Исследованиями установлено, что ускорения элементов автомобиля при его движении имеют широкий спектр частот (свыше 500 Гц). Весь спектр частот ускорений можно разделить на два диапазона: низкочастотный (0... 25 Гц) и высокочастотный (свыше 25 Гц).
Низкочастотные колебания в основном вызываются взаимодействием ав
115
томобиля с дорогой. Их уровень зависит от условий движения, параметров автомобиля и его подвески. Высокочастотные колебания обусловлены неравномерностью работы двигателя и агрегатов трансмиссии. Они зависят от скорости движения (частоты вращения и нагрузки двигателя и трансмиссии), степени удаленности рассматриваемого элемента от источника возмущения и конструкции элементов, передающих вибрации. Колебания в высокочастотном диапазоне практически не зависят от микропрофиля дороги и параметров подвески.
Сопоставление расчетных и экспериментальных спектров ускорений показывает, что они достаточно близки только в низкочастотном диапазоне. Это объясняется тем, что уровни вибраций в высокочастотном диапазоне определяются факторами, обычно не учитываемыми в расчетных схемах: вибрациями двигателя, трансмиссии, жесткостью элементов конструкции рамы и кузова.
При анализе плавности хода принимают конкретные расчетные схемы, которые эквивалентны с точки зрения колебаний реальному автомобилю. Вид расчетной схемы зависит от диапазона частот, в котором производится анализ колебаний.
Любая расчетная схема включает инерционные элементы (массы), соединенные упругими элементами, а также элементы, обеспечивающие рассеивание энергии при колебаниях масс.
Все массы элементов, имеющихся в автомобиле, можно разделить на две группы; подрессоренные и неподрессо-ренные.
К подрессоренным относятся массы всех элементов автомобиля, вес которых передается на упругие устройства подвески, к неподрессоренным — элементов, вес которых не воспринимается упругими устройствами подвески автомобиля (колеса, мосты). Массы элементов, связывающих подрессорен
ные и неподрессоренные части (упругие элементы, рычаги направляющего устройства, амортизаторы, тяги рулевого привода и карданный вал), относят частично к подрессоренным и неподрессоренным массам.
Исследованиями установлено, что при расчетах колебаний в низкочастотном диапазоне (до 25 Гц) все подрессоренные массы могут быть объединены в одну массу т0 с моментом инерции 1У относительно поперечной оси, проходящей через центр масс, и 1Х — относительно продольной.
Исключение составляют случаи, когда на автомобиле перевозятся специальные грузы, собственные колебания которых находятся в низкочастотном диапазоне, а масса их соизмерима с другими подрессоренными массами (например, лесовозный автомобиль, перевозящий пакеты леса). Сюда же следует отнести и случай, когда вес транспортных средств соизмерим с весом водителя и пассажиров. При расчетах колебаний таких транспортных средств (малые легковые автомобили, мотоциклы) в расчетных схемах необходимо учитывать систему подрессорива-ния человека и самого человека как динамическую систему.
Неподрессоренная масса каждого моста тг рассматривается отдельно и считается сосредоточенной.
Основными упругими элементами в расчетных схемах являются рессоры подвесок и шины. При расчетах принимается, что все эти элементы расположены в плоскостях колес, а их упругие свойства оцениваются приведенными характеристиками. На схемах упругие элементы изображаются в виде пружинок.
Трение, за счет которого рассеивается энергия при колебаниях систем, бывает двух видов: со смазочным материалом и без смазочного материала. В первом случае сила трения и ее направление зависят от скорости деформации элемента, во втором — сила тре-
116
Рис. 5.17. Расчетные схемы, применяемые при анализе плавности хода автомобилей
ния постоянна, а ее направление противоположно скорости деформации. На схемах элементы с трением первого вида изображаются условным телескопическим амортизатором, а элементы с трением второго вида — двумя трущимися пластинами (в некоторых случаях эти элементы на схемах не показывают, хотя и учитывают при математическом описании).
В процессе движения по дороге с неровностями массы автомобиля совершают сложные колебания в продольной и поперечной плоскостях. В силу симметрии автомобиля относительно продольной плоскости колебания в продольной и поперечной плоскостях являются независимыми друг от друга (если рассматриваются колебания в какой-либо определенной плоскости, индекс при моменте инерции обычно не ставится).
Учитывая, что в наибольшей степе
ни плавность хода определяется колебаниями в продольной плоскости, в ряде случаев при ее анализе для упрощения расчетов рассматривают только эти колебания. При этом пространственная модель автомобиля заменяется плоской, в которой совмещаются правые и левые подвески и колеса мостов, а высоты неровностей дороги q считают равными полусумме высот неровностей, находящихся в определенный момент времени под правым и левым колесами моста:
qi — 0,5 (^прг + q^t),
где 7npi, <7лг — высота неровностей дороги соответственно под правым и левым колесами i-ro моста.
Расчетная схема двухосного автомобиля для исследования его колебаний в продольной плоскости приведена на рис. 5.17, а. На схеме показаны: подрессоренная масса т0 с моментом
117
инерции 1У относительно поперечной оси; неподрессоренные массы т\ и т2; упругие элементы подвесок с жесткостями 2ср1 и 2ср2; амортизаторы с сопротивлениями 2йР1 и 2йр2; силы трения КТ1 и Ft2; упругие элементы с жесткостями 2сШ1 и 2сш2 и условные амортизаторы с сопротивлениями 2/гш1 и 2йш2, моделирующие шины. На шины действуют неровности дороги высотой и q2.
Считается, что автомобиль движется с постоянной скоростью. Поэтому массы автомобиля в продольном направлении не имеют ускорений. В про-дольно-вертикальной плоскости подрессоренная масса совершает перемещение по координатам ср и Z, а неподрессоренные — по координатам £i и £2-Перемещение подрессоренной массы можно рассматривать и в других координатах, например в координатах Z]и Z2 (перемещения точек подрессоренной массы, которые лежат над передним и задним мостом соответственно).
В системе координат Z—ср вертикальное перемещение точки А, находящейся на расстоянии х от центра масс,
Z А ~ Z -f- х ср.
Это же перемещение в системе координат Z\ —Z2 запишется следующим образом:
~F- X	। <2 X rj Z EX EX S
2Л = —-Zj---------— ^2'	(5'5)
Расчетная схема для анализа поперечных колебаний автомобиля показана на рис. 5.17, б. В этом случае упругие элементы, амортизаторы, неподрессоренные массы объединяются по бортам (индексы: л — левый, п — правый). За расчетную высоту неровности дороги принимают среднеарифметические значения высот неровностей вдоль каждого борта автомобиля.
В соответствии с расчетной схемой составляют уравнения движения системы, обычно с помощью уравнения Лагранжа
d /	\	, d£p t дЕг _
dt дхг /	<Эх; ‘ <Эхг dyt,i
где Eh — кинетическая энергия системы; Ер — потенциальная энергия системы; Ег—функция рассеивания энергии; — обобщенная координата; Qi — сила, действующая вдоль координатной ОСИ Иг-
Кинетическая энергия системы является однородной квадратичной функцией скоростей масс:
Ek = O,5moZ2 + 0,5Ap2 + 0,5zniti + + 0,5m2ij;
потенциальная энергия — квадратичной функцией деформаций:
Ер = 0,5 (2сР1 АР1 + 2ср2Др2	2сш;Дш1 4~
Ч~ 2сш2ДШ2) >
где Дрь Др2, Дшь Дш2 деформации рессор и шин первого и второго моста соответственно.
Приняв допущение, что рассеивание энергии осуществляется только амортизаторами с силой сопротивления, пропорциональной скорости деформации, получаем следующее выражение для функции рассеивания:
Ег = 0,5 (2йр1Др! + 2йр2Др2 + 2/%Ш1Дш1 + + 2Йш2Дш2)-
В обобщенных координатах Z; и Z2:
Ek = 0,5 \(bZi + aZtf + р2 (Zi -А2
— Z2)2] + 0,5 (mi Л + т2$);
Ер = Cpi (Zr - £,)2 + ср2 (Z2 - :2)2 + + сШ1 (£1 — 7i)2 + сШ2 (£г	7г)2!
Ег = kpl (Zi - S1)2 + kp2 (Z2-ЦЧ Ч~ ^ш1 (tl 71) 4“ &Ш2 (^2	72) >
где p — радиус инерции подрессоренной массы. Для записи этих выражений использованы уравнения связей:
<p = -b(Z1-Z2); Z = Azi + ^-Z2;
ДР1 — 2] — Др2 = 22 — t,2, Дш1 = £1 — 7ь Аш2 = £2 — 72-
118
Произведя дифференцирование по обобщенным координатам и подставив полученные производные в уравнения Лагранжа, после преобразований получим следующую систему дифференциальных уравнений, описывающих движение масс рассматриваемой динамической системы:
,2 ।	2
-J- 2cpiZj +
,	9
, ао— 0	л
+ Y------------Z? — 2йР1^1 —
— 2cpl^i = 0;
д2 I п2 ..
/Ио ---------^2 + 2Йр2^2 + 2ср2^2 +
+ Шоа2_Р121 _	- 2ср2?2 =0;
(5-6)
+ 2 (йР1 йШ1) + 2 (сР1 + ~т Сщ1) £i — 2&piZi — 2cpiZi = = 2йР1^1 + 2сШ1^1;
^2 ^2 + 2 (Йр2 + Йшг) Ь т 2 (сР2 + + Сцй) ?2 — 2kp2%2 — 2cP2Z2 = = 2Йр2<?2 + 2сШ272-
при
Из уравнений (5.6) видно, что ab = p2 система четырех уравнений распадается на две самостоятельные стемы из двух уравнений вида:
moiZ£ -ф- 2kpiZ[ -f- 2cpiZ[ — 2kpit,i — 2cp^i = 0;
+ 2 (kpi kuii) Zi + 2 (Cpi +
~Ь £шг) 2kpiZi 2cp[Zi =
= 2kmiqt + 2сШ1-^,
где mOi =	m02 = y- m0.
си-
К5
•7)
)
Колебательная система, эквивалентная автомобилю при ab — p2, изображена на рис. 5.18, а. Она состоит из двух независимых двухмассовых систем, соединенных безынерционной связью. Координатами Zj и Z2 описываются перемещения точек подрессоренной массы, расположенной над мостами. Перемещение же любой точки подрессорен
ной массы может быть найдено по соотношению (5.5).
Компоновки современных автомобилей таковы, что для большинства конструкций условие а& = р2 соблюдается с погрешностью не более 10 %. Это позволяет рассматривать колебания передней и задней частей автомобиля независимо друг от друга. Поэтому в ряде случаев, особенно когда необходимо проследить влияние характеристик отдельных элементов подвески на интенсивность колебаний, можно использовать расчетную схему, приведенную на рис. 5.18, б, моделирующую переднюю или заднюю часть автомобиля.
Расчетные схемы многоосных автомобилей отличаются от рассмотренных только наличием большего количества мостов. Если на автомобиле применяется балансирная рессорная подвеска, необходимо в расчетных схемах учитывать момент инерции балансира. Возможно представление балансирной подвески тремя практически равнозначными схемами, показанными на рис. 5.19. На первой схеме упругий элемент, соответствующий рессоре балансира, устанавливается между подрессоренной массой и жестким балансиром, момент инерции которого относительно оси качения равен моменту инерции реального балансира. По второй схеме жесткий балансир соединяется шарнирно с подрессоренной массой, а с неподрессоренной — упругими элементами с жесткостью, составляющей 0,5 жесткости рессоры балансира. По третьей схеме колеса связываются жестким безынерционным балансиром, а масса балансира распределяется между подрессоренной и неподрессо-ренными массами так, чтобы моменты инерции реальных и расчетных непод-рессоренных масс и балансира относительно оси качания были одинаковы.
В некоторых случаях при исследовании низкочастотных колебаний подрессорных масс в диапазоне ниже 5...
119
Рис. 5.Id. Расчетные схемы двухосного автомобиля при р =ab
б
Рис. 5.19. Моделирование балансирной подвески
6 Гц можно не учитывать инерционные воздействия неподрессоренных масс. В этом случае расчетная схема двухосного автомобиля может быть представлена в виде балки, установленной на двух пружинах с амортизаторами (см. рис. 5.17, в). Жесткость пружины определяется суммарной жесткостью рессор и шин:
= CpiCnii/ (Cpi + Cjjii),
а коэффициент сопротивления амортизатора
ki — kaiCmi/ (Сщг 4~ Ср,) .
Все параметры элементов, входящих в расчетные схемы, определяются по технической документации, а для готового автомобиля — экспериментально (см. ОН 025-305—67 «Методы определения параметров, влияющих на плавность хода автомобиля»).
Если возникающие при движении автомобиля колебания человека оказывают существенное влияние на колебания подрессоренной массы или появляется необходимость синтеза дополнительной системы амортизации человека, целесообразно рассматривать его как колебательную систему. Многочисленные исследования советских и зарубежных ученых позволяют рекомендовать некоторые расчетные биодинамические модели человека.
В одномассовой модели человек представляется в виде сосредоточенной массы, находящейся на упругом основании. Жесткость упругого основания и рассеивание энергии в системе определяются жесткостью и затуханием колебаний в элементах, предназначенных для сидения (подушки, системы под-рессоривания сиденья). Доля массы тела человека, приходящаяся на сиденье, принимается равной 55 кг
120
Рис. 5.20. Биодинамические модели человека: а — двухмассовая; б — трехмассовая
(при общей массе человека 75 кг). Существующие подушки сидений имеют жесткость 7,8...11,8 кН/м у легковых автомобилей и 14,7... 19,6 кН/м у грузовых. Коэффициент относительного затухания при отсутствии специального амортизатора сиденья составляет в среднем 0,06...0,18. Такие модели целесообразно использовать при расчетах плавности хода транспортных средств с малой подрессоренной массой или при оценке плавности хода автомобиля по интенсивности колебаний человека на сиденье.
При исследовании параметров сиденья целесообразно использовать более сложные биодинамические модели человека: двух- и трехмассовые (рис. 5.20). В первой из них масса mi включает массу таза и нижних конечностей (/«1 = 29,5 кг), а масса т2— массу груди, плеч, верхних конечностей и головы (т2=27,5). Первая масса находится на упругом основании, характеристики которого соответствуют характеристикам сиденья, а вторая — на упругом элементе, имитирующем параметры упругости тела человека. Для расчетов принимают с2 = 22...24 кН/м, А2 = 320... 400 Н с/м. В некоторых случаях из т2 выделяют массу головы человека, при
нимая ее равной 5 кг, и оценку плавности хода проводят по интенсивности колебаний головы. При этом принимают с3 = 1ОО...2ОО кН/м и £3=150... 250 Н с/м. Приведенные данные являются ориентировочными, расчетными. Фактические параметры колебаний человека могут значительно отличаться от приведенных. Обусловлено это индивидуальными особенностями каждого человека, а также особенностями человека как динамической системы. Установлено, что костно-мышечные связи человеческого тела имеют нелинейные характеристики, обладающие свойством авторегуляции, т. е. способностью изменяться в зависимости от особенностей воздействующих колебаний.
Основными характеристиками любой колебательной системы являются частоты собственных колебаний и коэффициенты их относительного затухания. Они определяют частотный диапазон возмущений, при которых систему следует рассматривать как динамическую.
Известно, что если затухание в системе таково, что ее свободные колебания не являются апериодическими, то рассеивание энергии практически не оказывает влияния на их частоты. Это позволяет частоты собственных колебаний автомобиля определять по расчетным динамическим схемам, в которых отсутствуют элементы, рассеивающие энергию, и нет возмущений.
Нахождение частот собственных колебаний целесообразно проводить в такой последовательности: составить уравнения движения системы (по схемам без затухания и возмущений), разделить каждое уравнение на инерционный коэффициент, записать уравнения в операторной форме; составить определитель системы, заменив в нем оператор дифференцирования s на мнимую частоту iQ, и приравнять его нулю; раскрыть определитель и решить его относительно й2.
121
Вычисление определителя для системы с п степенями свободы сводится к решению уравнения, имеющего п корней (значений квадратов частот собственных колебаний).
Уравнения (5.6) без членов, характеризующих затухание и возмущения в системе, в операторной форме будут иметь вид:
(s2 -|-	) Z, -|- Лг^2 — Л^/ = 0;
(s2 Л- со|2) Z2 + Л/21 —	= 0;
(s2 Л- cogj £1 — YzjZi = 0;
(s2 + COj2) £2 — YZ2^2 = 0,
2	2cpl^	2	2cp2^^
где = 7.2/ 2',	;	= 7—-— ’
(&J + p2)m0	(
ab — p2 r. 2 2(cpi + ~L’ “E'=—
2cp/2
2
; =
_ 2 (СР2 + сш2) .
। 'I?!
mQ (b'2 + р2) ’ 2ср1 . ..
т.
m2
9r I2 zcp2b
--- —,,2 , m0(&2 +
г.	2ср2
; Yz, = —yz2 = —
"	т2
После замены оператора дифференцирования на мнимую частоту получаем следующий определить системы, вычислением которого могут быть получены частоты собственных колебаний ситемы:
4, —Й2 Л/	—ле.	о
Лг <-Й2 , 0
0	(4-Й2	о
0	-?z2	0	4-Й2
= 0.
После аналогичных преобразований определитель системы уравнений (5.7)
k>z — й2 —Лг
—л? 4 — Й2
- 0,
(5.8)
где 4 = 2cp/m01-; cog = 2 (ср + ст)1тс, Лг = 2cp/m0Z; т]£ = 2c^lmi.
Решая уравнение (5.8), получаем частоты собственных колебаний системы:
Й2 = 0,5 [(4 + 4 +
+ V (®z — 42+ 4л/ле]-
Рис. 5.21. Парциальные системы двухосного автомобиля при p2=ab
Если принять перед корнем знак плюс, имеем более высокую частоту:
Йв —	0,5 (со/ -|- cog) +
+ ]/(4 — 42+4Л/Ле] > (5.9) при знаке минус — низкую:
Йн = j/" 0,5 (coz + 4 —
— V (coz— cog)2 + 4лгЛе] • (5.10)
Нетрудно показать, что если коэффициенты связи rjz и Ле равны нулю, йн = = ®z и Йв = cog. При этом вместо связанной двухмассовой системы можно рассматривать две одномассовые парциальные, как это показано на рис. 5.21. Парциальную систему можно представить как многомассовую, в которой все массы закреплены, кроме одной, которая может совершать движение по одной координате.
Частота собственных колебаний парциальных систем называется парциальной. Из выражений (5.9), (5.10) видно, что при наличии связи меняется частота собственных колебаний — увеличивается более высокая и уменьшается низкая. Для конструкций реальных автомобилей коэффициенты связи невелики. Поэтому в ряде случаев для сравнительной оценки параметров подвески можно рассматривать не частоты собственных колебаний системы в целом, а парциальные частоты.
Аналогичным образом можно рас-
122
рматривать относительные коэффициенты затухания парциальных систем
Фх = «z/wz и
где nz = Лр/w: п = (kP + k^ltni.
Исходными данными для конструктивной разработки подвески являются приведенные характеристики упругих элементов и амортизаторов. При их выборе следует учитывать, что возможный полный ход подвески ограничен по компоновочным соображениям. Предельный ход зависимой подвески грузовых автомобилей составляет 0,16...0,22 м у переднего моста и 0,20... 0,24 м у заднего. Если применяются независимые подвески неведущих мостов, их предельный ход может быть принят несколько большим. У легковых автомобилей полный ход подвесок составляет 0,18...0,50 м.
Принятый полный ход подвески необходимо разделить на ход отбоя и ход сжатия. Деление производится в зависимости от назначения автомобиля, его компоновки и др. При выборе хода отбоя следует учитывать, что скорость автомобиля при его движении по дорогам с неровной поверхностью может ограничиваться высокой интенсивностью колебаний, передающихся водителю и пассажирам, и наличием частых ударов в ограничители хода. При правильно сконструированной подвеске ограничения скорости движения автомобиля в наиболее характерных дорожных условиях, вызванные обеими причинами, должны быть одинаковыми.
В первом приближении можно считать, что при линейной подвеске ускорение (в долях g), передающееся подрессоренной массе при полном прогибе, равно отношению ходов сжатия и отбоя т]д. Это вытекает из следующих соображений. Сила, передающаяся через рессору при полном прогибе, равна произведению жесткости подвески на ход сжатия: Epi = 2CpiAC!K. Ускорение
подрессоренной массы Z= (2cpi/moi) X ХАОж, а поскольку	= 2cpjACt,
Z=g(Асж/Аот), где moi — часть подрессоренной массы, приходящейся на i-й мост. Следовательно, если динамический ход равен статическому, удары в ограничители возможны только в том случае, когда ускорение подрессоренной массы превысит g. При этом среднеквадратическое ускорение будет примерно 3 м/с2. Обычно даже в тяжелых условиях движения редко имеют место одиночные максимальные ускорения подрессоренной массы более 7,5 м/с2. Поэтому при АСж/Аст~1 в этих условиях обеспечивается движение без ударов в ограничители хода.
При таком соотношении ходов жесткость подвески при ограниченном общем прогибе высока, и плавность хода автомобиля при движении с большими скоростями по дорогам даже с неровностями малой высоты будет низкой. Если сделать динамический ход значительно меньшим, такой автомобиль при движении по дорогам с большими неровностями будет иметь малую скорость вследствие частых ударов в ограничители, и только при движении по хорошим дорогам плавность его хода будет высокой. Поэтому для автомобилей, к которым предъявляется требование высокой подвижности в любых дорожных условиях, т]д принимается близким к единице, а для автомобилей, предназначенных для движения только по хорошим дорогам,— меньше единицы, причем, чем выше требования к комфортабельности автомобиля, тем меньше т]д.
Статический прогиб подвески передних колес современных легковых автомобилей составляет 0,15...0,25 м при независимой подвеске, задних — 0,12...0,18 м. По данным испытаний, у лучших по плавности хода легковых автомобилей передняя подвеска на 10... 30 % «мягче» задней. Статические прогибы передних подвесок грузовых
123
Рис. 5.22. Приведенная характеристика рессоры с подрессорником
автомобилей составляют 0,06...0,1 м, а задних — 0,07...0,1 м.
Общей тенденцией является стремление к увеличению прогибов подвесок. Однако это, помимо затруднений в компоновке, приводит к следующим нежелательным явлениям: а) изменению высоты автомобиля при колебаниях и при изменении нагрузки; при независимой подвеске может значительно изменяться дорожный просвет; б) затруднению согласования кинематики подвески и рулевого привода; в) увеличению продольных наклонов кузова автомобиля при торможениях и крена на поворотах.
Требуемая жесткость подвески может быть определена также исходя из парциальных частот собственных колебаний, которые для современных автомобилей имеют следующие значения: легковых — со- = 0,8... 1,3 Гц, грузовых— сог= 1,2...1,8 Гц. Обычно плавность хода автомобилей тем выше, чем меньше парциальная частота собственных колебаний.
Необходимость обеспечения малой частоты собственных колебаний при
ограниченном прогибе подвесок привела к созданию подвесок с нелинейными характеристиками (см. рис. 5.3,6). У таких подвесок при статической нагрузке жесткость относительно мала и резко возрастает при деформации подвески. Это и обусловливает высокие коэффициенты динамичности и низкую частоту собственных колебаний. В большинстве случаев при применении металлических упругих элементов нелинейность подвески создается за счет установки резиновых буферов таким образом, что они начинают деформироваться при прогибах, составляющих (0,25...0,5) Асж-
Для получения приемлемой плавности хода грузовых автомобилей при различной степени их загрузки в задней подвеске устанавливается дополнительная рессора (подрессорник). При этом предполагается, что без груза подрессоренная масса совершает колебания на основной рессоре с коэффициентом жесткости ср, а с грузом — на основной и дополнительной с коэффициентом жесткости сп.
Исходными данными при выборе характеристики рессоры с подрессорником являются: Ап — полный прогиб подвески (рис. 5.22); иГ2— парциальная частота собственных колебаний подрессоренной массы с грузом; т02— подрессоренная масса автомобиля без груза, создающая нормальную нагрузку на заднюю подвеску; тГ2 — масса груза, создающая нормальную нагрузку на заднюю подвеску; кя2— коэффициент динамичности задней подвески; а — коэффициент, определяющий, при какой части груза включается подрессорник. Обычно принимают Лд=1,8... 2,2; а = 0,5...0,75.
Требуемый коэффициент жесткости рессоры ср и подрессорника сп находят из соотношений:
2	2 (Ср + сп) г-	,	,	,	,
“2г = т Л_т ’ Fms* =	+ тг2);
ш02 Шг2
124
л	^(«02 + amr2) ,
^СТ.Г - "	Г
2ср , fmax-g(m02 + «^r2)
2(Ср + Сп)
Коэффициент относительного затухания колебаний в подвесках современных легковых автомобилей ф = 0,2... 0,35, грузовых — 0,15...0,25. Если нет сведений о характеристиках амортизаторов, последние можно определить по соотношению: &p0 = 2i|V {с^тйг)1/2,. где йр.с — среднее значение сопротивления амортизатора.
Значение £р.с можно использовать непосредственно при расчетах по линейным моделям. Если расчет проводится по нелинейным моделям, необходимо определить коэффициенты сопротивления амортизаторов при ходах сжатия и отбоя: &р.с = 0,5(&Сж + &от), &сж= (0,1...0,25) &от.
5.5. Расчетные методы оценки плавности хода автомобилей
Реальные характеристики подвесок автомобилей всегда нелинейны. Это обусловлено наличием трения в подвесках, ограничителей прогибов и отрывом колес от поверхности дороги. Упругие характеристики рессор, тор-сионов и пружин с учетом кинематики направляющих устройств обычно близки к линейным. Изучение степени влияния нелинейных элементов, имеющихся в подвесках автомобилей, на точность расчетов показало, что в ряде случаев представляется возможным для анализа плавности хода использовать линеаризованные модели. К таким случаям относятся расчеты колебаний автомобиля в эксплуатационных условиях движения, когда максимальный прогиб подвески составляет не более 0,75...0,8 от хода сжатия, некоторые сравнительные расчеты плавности хода автомобиля, а также связанные с выбором базовой жесткости упругих элементов, мощности аморти
заторов. Когда изучаются предельные режимы колебаний или влияние тех или иных характеристик элементов подвески на интенсивность колебаний, расчеты необходимо проводить по нелинейным моделям.
Таким образом, выбор расчетной схемы, типа модели (линейной или нелинейной) и методики расчета полностью определяется характером поставленной задачи. Методы расчета оценочных показателей плавности хода автомобиля по линейным и нелинейным моделям принципиально различны.
Основной задачей расчета плавности хода по линейным моделям является нахождение комплексной частотной характеристики (частотной характеристики) автомобиля как динамической системы. Зная ее, можно определить характеристики колебаний при детерминированном и случайном возмущениях.
Частотная характеристика определяется в такой последовательности: 1) составляют дифференциальные уравнения движения системы и записывают их в операторной форме; 2) делят изображение по Лапласу функции координат на изображение функции неровности; полученные отношения являются передаточными функциями системы по координатам; 3) заменяют оператор дифференцирования s на мнимую частоту iv и определяют частотные характеристики системы, передающей возмущения по координатам (координатные частотные характеристики); 4) исходя из геометрических соображений, находят комплексную частотную характеристику системы, передающей возмущения от неровностей дороги до точки автомобиля, в которой оценивается интенсивность колебаний.
Определим частотную характеристику системы, движение масс которой описывалось уравнением (5.7). Неупругое сопротивление в шинах учитывать не будем.
125
Рис. 5.23. Амплитудно-частотная характеристика двухмассовой динамической системы:
1 — относительные перемещения подрессоренной массы; 2 — то же, неподрессореииой; 3 — относительные ускорения подрессоренной массы
Произведя преобразования по Лапласу и заменив оператор дифференцирования на мнимую частоту iv, имеем следующую систему уравнений для определения координатных частотных характеристик:
(со| — v2 + i2nzv'\ Kz — (i2nzv +
+ coz) Ag = 0;
—a (i2nzv + cof) Ez +	— v2 +
4" i2n.'cy} K^ — ®o>
гдеа=т01-М;2пг =2kp/m0i; co2z =2cp/m0i;
®o = 2ст/гП(-, 2n^ = 2kvlmi, cog = 2 (ep 4-4" сш)Imt,
Kz к Kt, — комплексные частотные характеристики систем, передающих возмущения по координатам Z и £: Kz =
= 2/7; Kt = t/ч-
Определитель системы
А=
(со| — v2 + i2nzv); —(i2nzv-|-coz)
— (i2nzv -ф coz) a; —v24-i2ngv) = Co -|- iD0,
где Co = v4 — v2 [co| + cog 4- 4nz (ng —
— nza} ] — aaz 4- cozcog; Do = —2 [v3(nz + + nJ — v (nzcog 4- ngCDz — 2ап^г) ].
Част отные характеристики
Kz = Az/A; Kg = Ag/A;
Az — Ct 4~ iD[', Ag — C2 -|- 1D2, где Ci = cdzcdo; Di = 2nzcoov; C2 = X X (coz— v2); D2 = 2nzo)J-.
Допустим, что в результате расчета найдено
Kz = E + iF.	(5.11)
Тогда амплитуда перемещений точки А, расположенной над мостом, при вынужденных колебаниях автомобиля, движущегося по дороге с синусоидальными неровностями,
ZA = q0V Е2Л- F2 , где <7о — амплитуда синусоидальной неровности.
Амплитуда ускорений точки А
Za = qov2ZA.
Сдвиг фаз между неровностью, воздействующей на колесо, и перемещением точки А определяется выражением: tg Q — F/E.
На рис. 5.23 показана амплитудно-частотная характеристика, построенная для динамической системы, имеющей следующие параметры: moi = 4300 кг; mi = 570 кг; ср = 160 кН/м; сш = = 500 кН/м; kp = 10 кН • с/м. Частоты собственных колебаний и парциальные: QH = 7,9 рад/с; QB = 48,4 рад/с; az = = 8,6 рад/с; cog = 48,3 рад/с.
Из графика видно, что при малых частотах возмущений перемещения масс практически равны высотам неровностей. Наибольшие перемещения наблюдаются при частоте возмущений, близкой к частоте собственных колебаний системы. При этом наибольшие перемещения подрессоренной массы имеют место при частоте возмущений, близкой к низшей частоте собственных колебаний. Поэтому условно принято считать, что низкочастотный резонанс соответствует резонансным колебаниям подрессоренных масс, а высокочастотный — неподрессоренных. Резонансные
126
колебания характеризуются также наибольшими ускорениями масс.
Интенсивность колебаний автомобиля, движущегося по дороге со случайным микропрофилем, определяется квадратом модуля частотной характеристики системы. Для рассматриваемого случая
I Kz I2 = Е2 4- F2 = (С? + Z)?)/(C02:+ Z<
Если функция возмущений задана спектральной плотностью Sq(y), спектральные плотности распределения перемещений и ускорений точки А
SzA = I Кг \2Sq; S7-a = | Кг l2v459.
Деформация упругого элемента подвески: Ар = § — z. Соответственно для частотной характеристики деформации подвески
С0 и0
Квадрат модуля частотной характеристики системы (см. рис. 5.17), передающей возмущения от неровностей, воздействующих на колесо первого моста, до точки А, в соответствии с выражением (5.5) будет:
КА=1±ДК'1)+Д^К<1>. (5.12)
Индекс (1) означает, что частотную характеристику следует определять по отношению к неровности, действующей на колесо первого моста.
Выражения частотных характеристик систем, передающих возмущения к точкам, расположенным над осями переднего и заднего мостов, имеют одинаковый вид.
Обозначим:

ts(i)	Zi	си +	. >г<2)_ ^2
KZi ~ qx~ CQI + iDQ1 ’
= - T ‘31..	(5.13)
c02 + id02
Высоты неровностей дорожной поверхности qi и 72 связаны временной связью:
^2<^) ==^1 (^ —Т),
где т — время проезда автомобилем расстояния, равного базе автомобиля: x = L/v.
Рассмотрим движение автомобиля по дороге, изменение ординат микропрофиля которой происходит по гармоническому закону: q=qo sin(vO- В этом случае: <?! = <70sin (vz1); <72=t7osin[v(^— — т]. Найдем отношение изображений по Лапласу гармонических возмущений 72 и 7ь
?2
91
?osin[vq-T)] = cos(vT)_
7о sin (vZ)
cos (vZ) . , ,
-------—2-Sin (vx);
sin (vZ)
X sin (vx) = cos (vx)--------— sin (vx).
На комплексной плоскости:
= COS (vx)-----— sin (vx) = cos (vx) —
qi	v
— isin(vx).	(5.14)
Поскольку периодическое возмущение можно рассматривать как сумму гармонических возмущений различной частоты, соотношение (5.14) справедливо при любом таком возмущении. Это соотношение сохраняется и когда возмущение является случайным.
Подставив значения 72 в выражение (5.13), имеем:
7	7
= 3 = __________-___________=
2 q2 [cos (vx) — i sin (vx)]
cos (vx) — i sin (vx)
или
Kzl = Kzl [COS (vx) — i sin (vx)];
= [(C12 cos vx 4- P12sin vx ) -H i(O12 cos vx— C12 sin vx)]/( C02 4- >7*02) •
127
После подстановки значений Kz, и Kzl в выражение (5.12) и преобразований имеем:
|Ка|2 = {{₽1 (С11С02-М1Р02) + + р2 [С01С12 cos (vr) — DmDl2 cos (vr) + + CmDl2 sin (vr) + C12D01 sin (vr)]}2 + + {Pi (Cq2Di\ + CnD02) + p2 [D0ICI2 x
X cos (vt) + CmDl2 cos (vt) -|-
+ £>01^2sin(vr) — C0iC12sin(vT)]}2} x
X[(CoiCo2 — DmD02)2	(C02Dm -|-
+ CoiDo2)2]-\	(5.15)
где pt= (b+x)/L- p2= (a — x)/L.
По выражению (5.15) могут быть найдены частотные характеристики системы, передающей возмущения к любой точке кузова, расположенной на продольной оси автомобиля, и соответственно спектральные плотности перемещений и ускорений этой точки. По данной формуле расчеты могут быть выполнены на небольших вычислительных машинах. При анализе более сложных динамических систем для определения частотных характеристик необходимо раскрывать определители высокого порядка с комплексными числами, что целесообразно делать на более крупных вычислительных машинах.
На рис. 5.24 показаны квадраты модулей частотных характеристик и спектральные плотности перемещений и ускорений масс, а также деформаций упругих элементов динамической системы, изображенной на рис. 5.18,6. Параметры ее соответствуют системе с амплитудно-частотной характеристикой, показанной на рис. 5.23, а спектральные плотности возмущений — рис. 5.15.
Из сравнения графиков (см. рис. 5.23, 5.24) видно, что квадрат модуля частотной характеристики соответствует квадрату ординат амплитудно-частотной характеристики. На кривых спектральных плотностей перемещений
и ускорений при различных скоростях движения наблюдаются максимумы при тех же частотах, что и на амплитудно-частотных характеристиках, но максимум в зоне высокочастотных колебаний значительно меньше, чем в зоне низкочастотных. Объясняется это тем, что короткие неровности реальной дороги, обусловливающие высокочастотные колебания автомобиля, обычно меньшей высоты, чем длинные.
Для оценки плавности хода по выражениям вида (5.3) и (5.4) определяют дисперсии и среднеквадратические значения ускорений подрессоренной массы в октавных полосах частот. Результаты расчетов оформляют графически, как это было показано на рис. 5.16.
Расчет по нелинейным моделям проводится в основном методом статистических испытаний. При этом предполагается, что динамическая система, эквивалентная автомобилю, «движется» с определенной скоростью по дороге с заданными статистическими характеристиками микропрофиля. Во время «движения» модели непрерывно регистрируются показатели интенсивности колебаний: ускорения, перемещения, деформации. С помощью статистической обработки их получают оценочные характеристики плавности хода или другие необходимые параметры.
Методом статистических испытаний решать нелинейные дифференциальные уравнения можно на цифровых или аналоговых вычислительных машинах. Ниже приводятся основные положения методики расчета применительно к аналоговым вычислительным машинам, позволяющим более наглядно представить взаимосвязь параметров динамической системы.
Уравнения, описывающие движения масс системы, изображенной на рис. 5.16,
128
•• 1 z „ 1
<P=y-(aFpl + aFzX — &Fp2 — &Fa2);
— m (Fpi + Fal — Fp2—Fa2);
•• i	}(5.16)
-----mT^"2 + F&~	Fa2), 1 )
где FPj и Fai — силы в подвеске при ее деформации, являющиеся нелинейными функциями от деформации и скоро-
Рис. 5.24. Спектральные характеристики колебаний двухмассовой динамической системы при движении по грунтовой дороге со скоростью 10 м/с:
а — квадраты модулей частотных характеристик: 1— |2К^|2; 2— l^)2; 3 — /Ад|2;
б — спектральные плотности: 1 —'S?; 2—rS^; 3— S^; 4 —
стей деформации упругих элементов; Fgi, Fgi — вертикальные составляющие реакции дороги, зависящие от деформации и скорости деформации шины.
При моделировании системы на аналоговых вычислительных машинах целесообразно за начало координат принимать положения масс, соответствующие ее статическому равновесию. В этом случае под силами, действующими в подвеске, будут пониматься приращения сил вследствие отклоне
ния масс от положения статического равновесия. Вертикальные составляющие реакции дороги определяются зависимостями:
qt (	0
F- = К (Vz — 6)
ql I 0
при qt— — fcF, при qt— t< — /ст’,
при qt —	/„;
при qt </ /ст,
где /ст — статическая деформация
шины.
5 А. И. Гришкевич
129
Рис. 5.25. Блок-схемы набора на АВМ задачи по оценке плавности хода двухосного автомобиля
Блок-схемы для набора модели составляются по общим правилам. Масштаб времени (отношение реального времени к машинному) зависит от характера задачи и типа вычислительного устройства. В случае решения задач с детерминированным возмущением наиболее часто применяют масштаб времени ц( = 0,1, а при случайном возмущении цг= 1.
На рис. 5.25 показаны блок-схемы набора задачи в соответствии с уравне
ниями (5.16). Ускорения масс системы получают суммированием сил, действующих на массы. Последующим интегрированием находят скорости и перемещения. На схеме показано, что силы, действующие на массы, набраны на блоках нелинейности, что в общем случае не является обязательным.
Для моделирования сил могут применяться линейные блоки, а также специальные схемы, разрабатываемые
130-
Рис. 5.26. Схема генерации синусоидальных колебаний
в соответствии с конструктивными особенностями подвески.
Возмущение при анализе нелинейных колебаний может задаваться в виде гармонического или случайного сигнала.
В первом случае в качестве источника возмущения целесообразно использовать генератор синусоидальных колебаний (рис. 5.26). Для имитации возмущения, действующего на первый мост, используется выходное напряжение интегратора 2. Возмущение под вторым и последующим мостами получается суммированием выходных напряжений интеграторов 1 и 2 исходя из соотношений:
sin [v(^—Ti)] = sin(vOcos('VTi) — — cos (W)sin(vri),
где Tj — смещение во времени воздействий неровностей дороги на первый и i-й мост: Ti = /i/u; li — расстояние между первым и t-м мостом; v — скорость движения автомобиля.
В начальный момент целесообразно использовать реле времени, включающее цепь возмущения i-ro моста через промежуток времени п с момента включения машины.
При случайных возмущениях принципиально возможны два способа задания сигнала, соответствующего микропрофилю дороги. При первом способе замеряются микронеровности на конкретных участках дорог, которые при расчете в виде электрических сигналов вводятся в машину. При втором
способе возмущение задается в виде случайного сигнала, спектральная плотность которого соответствует определенным дорожным условиям. Случайные сигналы, имеющие заданную спектральную плотность, получают с помощью генератора белого шума. Белый шум — это стационарный случайный сигнал, имеющий постоянный уровень спектральной плотности в заданном диапазоне частот и представляющий собой обобщенный телеграфный сигнал со случайной длительностью импульсов. Сигнал, снимаемый с генератора белого шума, пропускается через формирующий фильтр, набранный из блоков аналоговой вычислительной машины, или через цифровой фильтр при решении на цифровой машине.
Формирование случайного сигнала с заданной спектральной плотностью распределения Sg(v) можно рассматривать как процесс прохождения стационарного сигнала с постоянным уровнем спектральной плотности Sg(v) = = Кб через определенную динамическую систему, т. е.
S9(v) = ] 77ф|25е(х,),
где I/Уф |2 — квадрат модуля передаточной функции формирующего фильтра:
|ЯФ|2 = S9(v)/S6(v).
Учитывая, что спектральная плотность распределения сигналов генератора белого шума в заданном диапазоне частот является постоянной, имеем:
i7/(i)|2= 1 S9(v),
Лб
где Кб — уровень спектральной плотности распределения сигналов генератора белого шума, В • с/рад.
Например, сигнал со спектральной плотностью

ko (У + Vl) vV-H)
можно представить как сигнал со спектральной плотностью Se (v) = Кб, про-
5*
131
Рис. 5.27. Блок-схема формирующего фильтра для получения случайных возмущений
ходящий через динамическую систему, для которой
kQ S2 4- V?
|Нфр	Чу
s (s ф-ту
Передаточная функция:
5 + V1
Kg s (s + v2) ’
следовательно,
,=81/2Г-Ц±л_.
’	|/ Kt s(s+v.)
Произведя преобразования, получим:
X—6-v2<7.	(5.17)
s J
Блок-схема формирующего фильтра, составленная по уравнению (5.17), показана на рис. 5.27.
При описанном методе задания возмущений для обеспечения стационарности оценочных параметров плавности хода автомобиля требуется большое машинное время для решения на ЭВМ каждого варианта. Поэтому на практике обычно при решении задач, связанных с нелинейными колебаниями, в качестве функции возмущений используют запись ординат микропрофиля конкретных дорог, наиболее же часто тех дорог, на которых проводят испытания автомобиля на плавность хода.
6 УПРАВЛЯЕМОСТЬ И УСТОЙЧИВОСТЬ АВТОМОБИЛЯ
6.1.	Основные определения
Траекторию движения любого автотранспортного средства в общем случае можно рассматривать как криволинейную с непрерывно изменяющейся кривизной. Если кривизна траектории близка к нулю, такое движение условно принято считать прямолинейным.
Криволинейность движения обусловлена необходимостью совершать повороты в соответствии с задаваемой водителем траекторией, а также неизбежным отклонением автомобиля от заданной траектории вследствие действия внешних возмущений.
Криволинейное движение автомобиля характеризуется изменением во времени положения его продольной и вертикальной осей, а также наличием продольных и главным образом поперечных ускорений. Способность автомобиля совершать криволинейное движение оценивается двумя свойствами: управляемостью и устойчивостью.
Управляемость — свойство управляемого водителем автомобиля сохранять в определенной дорожноклиматической обстановке заданное направление движения или изменять его в соответствии с воздействием на рулевое управление.
Устойчивость — свойство автомобиля, характеризующее его способность сохранять заданное направление движения при воздействии внешних сил, стремящихся отклонить его от
этого направления. В экстремальных условиях недостаточная устойчивость автомобиля может привести к его заносу и опрокидыванию.
Принципиальное различие между понятиями управляемость и устойчивость заключается в том, что устойчивость охватывает ряд свойств автомобиля, обеспечивающих его движение по заданной траектории без воздействия водителя, а управляемость — при его воздействии.
При движении автомобиль может иметь траекторные и курсовые отклонения. Траекторное отклонение — это отклонение вектора скорости автомобиля от заданного направления. Курсовое отклонение — отклонение продольной оси автомобиля от направления траектории движения. В соответствии с этим принято различать его траекторную и курсовую управляемость и устойчивость. Криволинейное движение автомобиля может совершаться вследствие воздействия водителя на рулевое управление или при фиксированных управляемых колесах. В первом случае управляемость и устойчивость автомобиля условно считаются динамическими свойствами, а во втором — статическими.
Устойчивость автомобиля по ориентации вертикальной оси в продольной и поперечной плоскостях зависит от продольной и поперечной устойчивости.
Понятия управляемость и устойчи-
133
Рис. 6.1. Схема поворота автомобиля:
а — с задними ведущими колесами; б —• с передними
вость автомобиля взаимосвязаны, поскольку они определяются в основном одними и теми же конструктивными параметрами автомобиля: компоновкой, особенностями рулевого управления, характеристиками шин, параметрами подвесок. В то же время влияние параметров автомобиля на его управляемость и устойчивость может быть различным. Например, с увеличением момента инерции автомобиля относительно вертикальной оси, проходящей через центр тяжести, улучшается устойчивость автомобиля при прямолинейном движении и в то же время ухудшается управляемость: для изменения направления движения к рулевому управлению необходимо приложить большие усилия. Поэтому выбор параметров автомобиля, обеспечивающих наилучшие характеристики устойчивости и управляемости, является задачей оптимизации.
Колесные транспортные средства могут поворачиваться за счет: 1) поворота управляемых колес; 2) притормаживания неуправляемых колес одного борта (поворот «по-гусеничному»); 3) поворота звеньев машины относи
тельно друг друга (двухзвенные ил многозвенные сочлененные машины
Для автомобилей наиболее xapai терен первый способ. Управляемые к< леса при этом поворачиваются вокр) некоторых вертикальных осей (шкво{ ней).
На рис. 6.1 изображена схема си. действующих на автомобиль с пере) ними ведомыми управляемыми колесг ми при движении по круговой Tpaei тории с постоянной малой скоросты (инерционные силы отсутствуют).
От ведущих колес на раму автомс биля передаются силы тяги FT и FT, pai нодействующая которых FT в перво приближении считается направленно вдоль продольной оси автомобиля. Эт сила через раму автомобиля передаете на передний мост. В точках контакт управляемых колес с поверхностью дс роги возникают реакции, равнодейс: вующая которых Rxl также может сш таться направленной вдоль продольно оси автомобиля. Так как отсутствую другие силы, равнодействующая F; равна FT.
Реакция Fxi может быть разложен на две составляющие Ff и RyV, напраг ленные соответственно вдоль и перпен дикулярно к плоскости колес.
Составляющая Ff определяется мо ментом сопротивления качению (civ гл. 2):
Ff=Mf/r0 = fRz.
Соответственно, сила тяги на веду щем мосту при равномерном поворот автомобиля может быть найдена п< выражению:
FT = Fxi = Ff/cos 0, где 0—угол поворота управляемы: колес.
Из рассмотрения суммы моменто; относительно точки D, лежащей посе редине заднего моста, видно, что Ff со здает момент сопротивления повороту a Rvi — поворачивающий момент, ко
134
торый при равномерном движении равен моменту сопротивления повороту:
RyiL cos Q = FfL sin 0.
Поскольку значение Rxi ограничено сцеплением (Rximax = <f>Rzi), a Rvi — = 7?xlsin0, в предельном случае
<pRziCos 0 = Mf/ro,	(6.1)
где Mf — момент сопротивления вращению колес, обусловленный как сопротивлением качению, так и другими сопротивлениями.
Если имеет место только сопротивление качению, условие (6.1) записывается в виде:
qp ^sfcos 0; qp cos 0^f.	(6.2)
Из выражения (6.2) следует, что поворот автомобиля будет осуществляться в том случае, если коэффициент сопротивления качению управляемых колес будет меньше, чем произведение коэффициента сцепления на косинус угла поворота управляемых колес. Если это условие не будет соблюдено, управляемые колеса будут двигаться юзом и поворот автомобиля не произойдет.
Максимальные углы поворота управляемых колес автомобилей обычно не превышают 35...45°. Коэффициент сцепления на твердой и сухой дороге во много раз превышает коэффициент сопротивления качению. Поэтому управляемость автомобиля в указанных дорожных условиях обеспечивается всегда. Однако на мягких и скользких поверхностях различие в коэффициентах ф и f значительно уменьшается, вследствие чего управляемость автомобиля ухудшается. Это же происходит и при торможении автомобиля: тормозная сила суммируется с силой сопротивления качению колес. При интенсивном торможении, когда полностью используются сцепные свойства дороги, поворот автомобиля становится невозможным.
На рис. 6.1, б показана схема сил
при повороте автомобиля с передними ведущими и управляемыми колесами. В данном случае поворачивающий момент создается не боковой реакцией, как это имело место в случае с ведомыми управляемыми колесами, а силой тяги: Afn=ETLsin 0. Поэтому у автомобилей с передними ведущими и управляемыми колесами этот момент всегда будет создаваться, если ведущие колеса создают силу тяги. Этим и объясняется, что такие автомобили обладают лучшей управляемостью, чем автомобили с управляемыми ведомыми колесами, особенно при движении по скользким дорожным поверхностям, когда боковые реакции дороги ограничиваются сцеплением.
6.2.	Увод автомобильного колеса
Автомобильное колесо обладает радиальной, тангенциальной и боковой эластичностью. Управляемость и устойчивость автомобиля в значительной степени зависят от боковой эластичности автомобильного колеса.
Если на катящееся, жесткое в боковом направлении колесо действует боковая сила, траектория качения колеса будет оставаться в его продольной плоскости до тех пор, пока боковая сила не станет больше силы сцепления колеса с дорогой. После этого начинается скольжение колеса в боковом направлении. При действии же боковой силы на катящееся эластичное колесо траектория качения колеса отклонится от плоскости колеса на угол, называемый углом бокового увода.
Сущность происходящих процессов поясним на схеме, изображенной на рис. 6.2.
На рис. 6.2, а показана схема качения эластичного колеса, когда боковые силы отсутствуют. Линия ОА проходит посередине протектора. При качении колеса его точки В и С, находящиеся на этой линии, касаются дороги соответственно в точках Bi и Ci,
135
Рис. 6.2. Схема качения эластичного колеса с
уводом
и траектория качения колеса будет располагаться в плоскости симметрии колеса. При действии на колесо боковой силы Fy вертикальная плоскость, проходящая через центр колеса, сместится относительно центра отпечатка на Д (рис. 6.2, б), а линия ОА, проходящая посередине протектора, будет изогнутой. Вследствие этого при повороте колеса на некоторый угол точка В войдет в контакт с дорогой в точке В2, а точка С — в Сг- При дальнейшем качении колеса все точки, лежащие на середине протектора, будут иметь контакт с дорогой на линии ОК, и траектория колеса (линия ОК) отклонится от плоскости колеса на угол 6.
Деформация элементов шины в боковом направлении по длине контакта разная: впереди элементы шины деформированы в боковом направлении меньше, чем в задней части, так как входящие в контакт с дорогой элементы шины в начальный момент практически не воспринимают боковые реакции. По мере поворота колеса эти точки перемещаются к задней части отпечатка. При этом увеличивается деформация элементов шины и, соответственно, возрастает доля боковой силы, воспринимаемой этими элементами. Вследствие этого продольная ось площадки, по которой шина контактирует с опорной поверхностью, оказыва-
з
24
Рис. 6.3. Зависимость угла увода от боковой силы
ется повернутой относительно продольной плоскости колеса на некоторый угол (рис. 6.2, в). Так как боковая деформация элементов, находящихся в задней части контакта, больше, чем в передней, эпюра боковых давлений будет треугольной формы. Это приводит к тому, что равнодействующая В,. элементарных поперечных реакций, равная силе Fy, оказывается смещенной от центра отпечатка назад на расстояние е. В результате этого создается момент Mc = eRy, стремящийся повернуть колесо в сторону действия боковой силы Fy, называемый стабилизирующим моментом.
Результаты исследований, проведенных в различных странах, позволили установить, что угол увода колеса для определенного состояния шины является функцией боковой силы. В общем случае зависимость между углами увода и боковыми силами нелинейна.
На рис. 6.3 показана характерная зависимость угла увода от боковой силы. На этой зависимости можно отметить три характерных участка: 0—1— угол увода зависит линейно от боковой силы; 2—3— угол увода неограниченно возрастает без увеличения боковой силы; участок 1—2— переходной.
На участке 0—1 увод автомобильного колеса происходит только за счет упругой деформации элементов шины. По мере увеличения боковой силы элементы шины, расположенные в задней
136
Рис. 6.4. Принципиальная схема определения характеристик увода шин на стенде
части контакта и являющиеся наиболее нагруженными в боковом направлении, начинают проскальзывать. Это приводит к нарушению пропорциональной зависимости между боковой силой и углом увода (участок 1—2). При дальнейшем увеличении боковой силы начинается полное скольжение шины в боковом направлении (участок 2—3).
Отношение боковой силы к углу увода, определенное на линейном участке (0—7), называется коэффициентом сопротивления уводу колеса ky:
ky = Fv/8.	(6.3)
Коэффициент сопротивления уводу зависит от ряда факторов, основными из которых являются: размеры и конструкция колеса, давление воздуха в шине, тип и состояние дорожного покрытия, нормальная нагрузка колеса и его окружная сила.
Значения коэффициента ky у шин легковых автомобилей составляют 15...40 кН/рад, а у шин грузовых автомобилей и автобусов 60... 120 кН/рад.
Коэффициенты сопротивления боковому уводу находят экспериментально путем испытания шин на стендах или определением углов увода осей автомобилей в процессе их движения. На рис. 6.4 показана принципиальная схема стенда для определения зависимости боковой силы от углов увода колеса. Испытываемое колесо 1 устанавливается на барабан стенда 2 так, что его ось и ось стенда располагаются под углом 6. При вращении барабана и колеса этот угол соответствует углу увода, поскольку траектория движения колеса относительно барабана лежит в плоскости барабана, а плоскость колеса повернута к плоскости барабана под углом 6.
В процессе испытаний замеряют боковую силу Fv, действующую на колесо, и угол 6. По этим данным строят зависимости Fy=f(8), аналогичные показанным на рис. 6.3. На стендах колесо может испытываться в ведущем, ведомом, нейтральном и тормозном режиме в зависимости от того, какой из электрических двигателей (двигатель барабана 3 или колеса 4) является ведущим. Нагружение колеса обеспечивается грузом 5. Коэффициенты сопротивления уводу, получаемые при испытаниях на таком стенде, вследствие кривизны контактной площадки имеют обычно несколько меньшее значение, чем получаемые при испытаниях на плоских поверхностях.
Ориентировочные значения коэффициентов сопротивления уводу для шин с диагональным расположением нитей корда могут быть определены по эмпирической формуле, полученной в НАМИ:
ky = 5ОО.Во (£> -|-2В0) (рв +1), где Во, Do — ширина и диаметр обода колеса, м; рв — давление воздуха в шине, МПа.
Если шина передает окружную силу (ведущее или тормозящее колесо), коэффициент сопротивления уводу
137
Рис. 6.5. Увод автомобильного колеса при наклоне
уменьшается и ориентировочно может быть подсчитан по выражению:
,	. V1 - [^/(<Р*?г)]2
йу.т - Ry j + 0,375	•
Приведенное выражение справедливо при условии
Если это условие не выполняется, для расчетов требуются дополнительные данные, а коэффициент сопротивления боковому уводу может быть найден методами нелинейной теории бокового увода, разработанными Д. А, Антоновым.
Зависимость коэффициента сопротивления боковому уводу от нормальной нагрузки колеса определяется двумя противоположными закономерностями. С ростом нагрузки повышается давление в контакте. Это обусловливает увеличение силы, необходимой для бокового смещения колеса. С другой стороны, при возрастании нагрузки увеличивается деформация профиля шины. При этом шина становится более склонной к боковому смещению. Максимальное сопротивление боковому уводу соответствует нагрузке, которую будем называть оптимальной. Обычно оптимальная нагрузка близка к номинальной. Приближенно коэффи
циент сопротивления боковому уводу при нагрузке, отличающейся от оптимальной,
^yz= &у[2,4 (Kz/KzOUt) - 1,8 (Кх/Кгопт)2 +
+ 0,4 (Kz/Кгопт) 3],
где R
ZOJIT, Rz — нормальные реакции дороги соответственно при оптимальной и отличающейся от оптимальной нагрузках.
Увод автомобильного колеса происходит также в том случае, когда плоскость колеса отклонена от вертикали. Установлено, что колесо, имеющее наклон % (рис. 6.5), движется с уводом в сторону наклона колеса под углом бх. В зависимости от типа и конструкции шины при наклоне плоскости колеса на один градус угол увода составляет 10'... 15'. Аналогично выражению (6.3) можно записать:
бх = %//гх, где /гх— коэффициент сопротивления уводу от наклона колеса k% = 4...6.
Угол увода колеса, нагруженного боковой силой и имеющего развал, определяется как сумма углов увода от боковой силы и от развала:
б = Fy/ky +	(6-4)
При качении шины с боковым уводом, помимо радиальной деформации элементов шины, находящихся в контакте с дорогой, имеет место также их деформация в боковом направлении. Вследствие этого сопротивление качению шины при боковом уводе увеличивается.
Коэффициент сопротивления качению шины, катящейся с уводом /а, определяется по эмпирическим формулам. Проф В. А. Иларионов предложил следующую:
fe = fo + ky^lRz, а проф. Ю. А. Брянский
fe = f0 exp (5,458Rz/RZH), где Rz/Rzh — отношение действительной нагрузки на шину к номинальной.
138
Рис. 6.6. Прибор «пятое колесо» для определения угла увода мостов:
1 — противовес; 2 — кронштейн крепления колеса;
3 — колесо; 4— прижимная пружина; 5 — потенциометр
Устойчивость и управляемость автомобиля в значительной степени зависят от углов увода мостов, которые определяются уводом шин и кинематикой подвески. Обычно углы увода мостов определяют экспериментально при движении автомобиля с различными скоростями по кругу с закрепленным рулевым колесом. Угол увода моста фиксируется с помощью «пятого колеса» специальной конструкции (рис. 6.6). «Пятое колесо» крепится по оси симметрии автомобиля так, чтобы точка его контакта с дорогой находилась под задним мостом автомобиля (под осью тележки у трехосного автомобиля). При движении по кругу «пятое колесо» катится без бокового увода, поскольку инерционные силы, действующие на него, уравновешиваются противовесом. Поэтому угол между продольной осью автомобиля и плоскостью, в которой расположено «пятое колесо», является углом увода. При этом виде испытаний боковыми являются центробежные силы, которые находятся расчетом по параметрам движения автомобиля или непосредственно замеряются датчиками ускорений.
6.3.	Кинематика поворота автомобиля
Способность автомобиля совершать повороты характеризуется свойством, называемым поворотливостью. Проведенные исследования и опыт эксплуатации автомобилей показывают, что
Рис. 6.7. Схема поворота автомобиля при качении шин без бокового увода
хорошая поворотливость автомобиля возможна, если выполняется ряд условий: управляемые колеса автомобиля катятся без бокового скольжения; рулевой привод обеспечивает правильное соотношение углов поворота управляемых колес; компоновка автомобиля, подвеска и шины обеспечивают оптимальное соотношение между углами увода передних и задних мостов; рулевое управление сконструировано таким образом, что водитель может судить о силах, действующих со стороны дороги на управляемые колеса.
Поворотливость автомобиля изучают в двух характерных режимах движения: поворот с малыми радиусами при малой скорости; с большими радиусами при большой скорости. Первый режим движения характеризуется малыми ускорениями и практическим отсутствием бокового увода шин. Иногда этот режим рассматривают как движение автомобиля при жестких в боковом направлении шинах. При втором режиме на автомобиль действуют значительные боковые силы, а его поворотливость в большой степени определяется уводом мостов.
На рис. 6.7 показана схема поворо
139
та автомобиля при качении колес без бокового увода. Чтобы при повороте колеса катились без бокового скольжения, их оси должны пересекаться в одной точке, называемой полюсом поворота (точка О на рис. 6.7).
Соотношение между углами поворота управляемых колес, при котором обеспечивается их качение без скольжения, определяется из треугольников ONM и ОРК: ctg 6s=0N/NM; ctg0B = = OP IP К. Поскольку MN = PK=L; NP = MK=l0, имеем:
ctg 0H-ctg 0B = /O/L,	(6.5)
где 0н, 0в — угол поворота соответственно наружного и внутреннего колеса; 1о — расстояние между осями шкворней поворотных цапф автомобиля.
Поворот управляемых колес совершается при помощи рулевой трапеции, которая не может в точности обеспечить условие (6.5) при изменении радиуса поворота в широких пределах. Однако при соответствующем выборе геометрических параметров рулевой трапеции можно получить удовлетворительные результаты. Наиболее просто это осуществляется выбором таких углов наклона поворотных рычагов, чтобы в положении, соответствующем прямолинейному движению автомобиля, их осевые линии пересекались в некоторой точке Е (рис. 6.8). При этом значение х принимают в пределах (0,7...0,9)L.
Точность кинематики трапеции проверяется графическим или аналитическим способом. При этом определяют зависимость между углами поворотов наружного и внутреннего колес при выбранных параметрах трапеции и полученные зависимости сравнивают с рассчитанными по формуле (6.5). Если получаются большие расхождения, корректируют положение точки Е. Схема графической проверки параметров рулевой трапеции показана на рис. 6.9. Наиболее часто применяемые схемы
Рис. 6.8. Схема выбора параметров рулевой трапеции
Рис. 6.9. Схема проверки кинематики рулевой трапеции
рулевых трапеций изображены на рис. 6.10.
При расчетах поворотливости автомобиля под радиусом поворота понимается расстояние от мгновенного центра поворота до продольной оси автомобиля. На схеме, изображенной на рис. 6.7, радиус поворота R равен расстоянию OD.
Из геометрических соотношений
ctg 0H+ctg 0B = 2/?/L; R = L/tge, где 0 — средний угол поворота управляемых колес;
ctg 0 = 0,5 (ctg 0Н + ctg 0В).
Движение автомобиля на повороте характеризуется радиусами траекторий
140
Рис. 6.10. Схемы рулевых трапеций
наружного переднего колеса 7?н и внутреннего заднего RB.
Радиус окружности, соответствующий следу переднего наружного колеса при .максимальном угле поворота управляемых колес, называется минимальным радиусом поворота Rmin- Поскольку он не зависит от действий водителя, этот параметр относят к одной из характеристик, по которым оценивают статическую поворотливость автомобиля. Экспериментально минимальный радиус поворота определяется на ровной, горизонтальной, чистой и сухой асфальтобетонной или цементобетонной площадке. След колеса автомобиля с повернутыми до упора колесами, движущегося с малой скоростью, отмечается на площадке меловой чертой, наносимой на середину протектора шины. Автомобиль проезжает полный круг. По диаметру следа определяют минимальный радиус поворота.
В оценочные характеристики управляемости автомобиля входят внешний и внутренний габаритные радиусы поворота /?габ и Кгаб, а также габаритная ширина коридора поворота А. Эти параметры характеризуют способность ав
томобиля или автомобильного поезда совершать повороты при ограниченной проезжей части.
Габаритные радиусы определяются одновременно с минимальным радиусом поворота автомобиля по следу наружного колеса. С этой целью на площадке отмечаются с помощью отвесов наиболее удаленная от центра и наиболее близкая к центру точки автомобиля. Замеряется их удаление А7 и А" по радиусу от оси следа, оставленного передним внешним колесом (рис. 6.11):
Rra6 — Rmin "Ь A j Rra6 ~ Rmin А j А — Rra6 Rra6-
При проектировании автомобиля (автопоезда) минимальные и габаритные радиусы обычно определяются графическим путем. На рис. 6.12 показаны схемы поворота, автопоезда с двухосным прицепом и одноосным полуприцепом. Центр поворота автомобиля находится как точка пересечения осей задних и передних колес. Приближенно можно считать, что ось, на которой лежит центр поворота трехосного автомобиля, располагается посередине базы тележки. Положение прицепа (полуприцепа) устанавливается следующим образом: из центра в точке сцепки проводят дугу окружности радиусом о, равным расстоянию от точки сцепки до оси поворотной тележки прицепа или задней оси полуприцепа. К этой дуге из центра поворота автомобиля проводят касательные. Точка касания А является центром переднего моста прицепа или моста полуприцепа соответственно. Для нахождения положения заднего моста прицепа проводится дуга окружности радиусом г2 (база прицепа). К этой дуге из центра поворота проводится касательная, точка касания В определит положение середины задней оси прицепа. Если автопоезд имеет несколько звеньев, их положения при повороте определяются последовательно аналогичным образом.
141
о
Рис. 6.11. Габаритные радиусы поворота автомобиля
Для уменьшения габаритов поворота длинных автопоездов, а также для улучшения в некоторых случаях их проходимости управляемыми делают колеса полуприцепа. Схема поворота такого автопоезда показана на рис. 6.12, в.
Управление колесами полуприцепа наиболее часто осуществляется посредством специального механизма, поворачивающего колеса в зависимости от угла а между продольными осями тягача и полуприцепа. Положение полуприцепа при повороте зависит от передаточного числа этого механизма. Передаточное число механизма поворота управляемых колес полуприцепа стремятся подобрать таким образом, чтобы колеса полуприцепа двигались по следу задних колес тягача. При построении схемы поворота автопоезда с разными радиусами поворота находят требуемые соотношения между углами а и р и тем самым определяют требуе
мую зависимость передаточного числа механизма поворота управляемых колес полуприцепа.
Для уменьшения габаритов поворота некоторых специальных поездов с прицепами управляемыми делают все колеса прицепов. С этой же целью у некоторых автомобилей делают управляемыми передние и задние колеса.
При движении автомобиля на повороте с высокими скоростями возникают инерционные силы, вследствие чего мосты автомобиля начинают двигаться с боковым уводом. Это приводит к тому, что векторы мгновенных скоростей центров мостов не перпендикулярны к их осям, а отклоняются на углы, равные углам увода 61 и 62. Вследствие этого мгновенный центр поворота перемещается из точки О в точку О' (рис. 6.13), а радиус поворота Д становится равным расстоянию O'D.
142
Рис. 6.12. Схемы поворота автопоездов с: а — двухосным прицепом; б — полуприцепом; в — полуприцепом с управляемыми колесами
Из геометрических соотношений
R tg 62 + /? tg(6 — 61) = L;
7? = L/[tg(0-6I)+tg62],
Поскольку углы увода невелики (5... 10°), а углы поворота управляемых колес при высоких скоростях движения, когда увод существенно влияет на управляемость и устойчивость автомобиля, также не являются большими, приближенно можно считать
r=l/[q+ (б2- 61)].	(6.6)
В зависимости от соотношения углов увода переднего и заднего мостов ра-
Рис. 6.13. Схема поворота автомобиля при наличии увода колес
диус поворота автомобиля может быть равным радиусу поворота при движении без увода (61 = 62), меньше (62< <61) или больше его (<3i>62)-
Смещение центра поворота С всегда происходит внутрь базы автомобиля: C = R'ig 82s^R'82.
Оценка поворотливости автомобиля при высоких скоростях движения производится по характеристике статической траекторной устойчивости, представляющей собой зависимость отношения угловой скорости автомобиля со к его линейной скорости v от углов поворота рулевого колеса ар при постоянном боковом ускорении 4 м/с2. При испытаниях обеспечивается постоянное боковое ускорение путем регулирования скорости движения автомобиля. При установившемся режиме движения отношение co/и равно кривизне траектории К.
143
Рис. 6.14. Характеристика статической траекторной устойчивости автомобиля:
А — зона допустимых значений;----’Пример экспе-
риментальной зависимости
Установлено, что автомобиль обладает приемлемой поворотливостью, если график зависимости K=f(a>/v) располагается в пределах площади, заштрихованной на рис. 6.14, а угол наклона касательной в любой точке этого графика находится в пределах, ограниченных углами наклона границ этой площади. Если указанные характеристики располагаются правее заштрихованной части, поворот автомобиля при высокой скорости будет затруднен (при объезде препятствия или обгоне необходимо перехватывать рулевое колесо), если левее, такой автомобиль будет излишне чувствителен к рулевому управлению.
6.4.	Силы, действующие на автомобиль при криволинейном движении
Силы, действующие на автомобиль при криволинейном движении, можно разделить на четыре группы: окружные силы на ведущих колесах, силы сопротивления движению, инерционные силы и реакции дороги.
Окружная сила на ведущих колесах автомобиля равна сумме окружных сил на наружном FK и внутреннем F"K колесах:
FK == FK 4- FK.
Вследствие наличия в дифферен
циале трения FK > FK. Можно считать, что
Ек = k„FK, Fk — (1 — ^д) FK, где kn — коэффициент распределения окружной силы по ведущим колесам (коэффициент блокировки дифференциала), зависящий от конструкции дифференциала. Он может иметь значения от /гд=0,5 (шестеренчатый дифференциал с малым трением) до /гд= = 1 (дифференциал с муфтами свободного хода).
Трение в дифференциале обусловливает наличие момента, препятствующего повороту автомобиля:
Л4с = К - Fk) В = Fk (2&д - 1) В, где В — колея ведущего моста.
Силами сопротивления движению являются: сила сопротивления качению автомобиля Ff&, сила сопротивления воздуха FB и сила сопротивления подъему El. Эти силы могут определяться по тем же зависимостям, что и для случая прямолинейного движения. Исключение составляет сила сопротивления качению, при определении которой необходимо учитывать увеличение сопротивления вследствие увода колес автомобиля.
Инерционные силы и моменты пропорциональны соответствующим ускорениям. Для нахождения последних рассмотрим общий случай криволинейного движения автомобиля.
Будем считать автомобиль плоским телом, совершающим криволинейное движение в неподвижной системе координат X и Y (рис. 6.15, а). Подвижную систему координат х — у примем с началом в центре масс автомобиля. При этом ось х совпадает с продольной осью автомобиля, а ось у направлена перпендикулярно к ней.
Если мгновенный центр поворота находится в точке О, вектор скорости центра масс автомобиля будет отклоняться от продольной оси на угол ср: tg(p = Z)C/E; DC=b — 7?tg 62, где b — расстояние от центра масс до оси задне-
144
Yi.
о
Рис. 6.15. Схема для расчета ускорений автомобиля при повороте
го моста автомобиля. Считая углы малыми, имеем ф = &//? — б2.
Проекции вектора скорости vc центра масс на оси подвижной системы координат:
^x=^cCOS(p; Цу = Цс8Шф.
Проекции составляющих скорости vG на оси неподвижной системы координат:
<Ух = щсо5 у —uysin у;
vY = vxsin у+vy cos у.
Произведя дифференцирование по времени скоростей их и vY, получаем ускорения центра масс автомобиля в неподвижной системе координат:
dv
ах= —cosy — i^siny — dvy 
----^siny —yycosy;
tdvx •
aY = sin у + vx sin у + dv
+ ~~dT cos^~ vysiny.
Для нахождения ускорений центра масс автомобиля в подвижной системе координат спроецируем векторы уско
рений ах и aY на оси х и у. В соответствии со схемой рис. 6.15, б имеем:
ак = ay cos у + axsin у;
ау = ay cos у — ax sin y.
С учетом соотношений (6.7) после преобразований получим:
dvx dy	dy , dv
ax = — — vv —; av = vx — -1------
dt y dt y dt dt
(6.8)
где vx — поступательная скорость авто-dvy
мобиля; —-dt
рение:
его поступательное уско-
dvx  dv . dt	dt ’
dy
— — угловая скорость курсового пово-dt
рота автомобиля:
dy	v
—T- = ft) = --
dt У P
vy — скорость бокового смещения центра масс автомобиля:
vy = vx tg <Р = v	(0 ~
— 61) —а62];
6 А. И. Гришкевич
145
Рис. 6.16. Силы и моменты, действующие на автомобиль при повороте
!> — ускорение бокового смещения dt
центра масс автомобиля:
(0 - S’) - а62]+a[b(-g-
d6[ \ do2 dt j а dt
Подставив полученные соотношения в (6.8), после преобразований имеем:
v2 ( ь о \
ay = + v (4 —	+ -77 [& (9 —
— 61) — a62].
Угловое ускорение автомобиля: '"т-т|т<8-!' + ф = —[у (0 — 6[ 4~ 62) + v (ё — 6[ 4" 6г)]-
Продольные и поперечные составляющие сил инерции равны произведению массы автомобиля на соответствующие ускорения. Для продольной составляющей инерционной силы необходимо учесть вращающиеся массы:
Fx = 6maax; Fy = maay.
Инерционный момент:
М j = Ize, где Iz — момент инерции автомобиля относительно вертикальной оси, проходящей через его центр масс.
Боковые реакции дороги, действующие на мосты автомобиля, можно опре
делить из схемы сил, изображенной на рис. 6.16. Предполагается, что результирующие боковые реакции Ryi и Ry,, действующие на передний и задний мосты автомобиля, приложены к середине мостов перпендикулярно к плоскостям колес, момент сопротивления повороту Л1С мал, а все другие силы действуют вдоль продольной оси автомобиля. Тогда
R^-^-tFyb + Mfr
L cos 0
Ryz = ±-(Fya —Mj). (6.9)
После подстановки значений Fy и Mj в уравнения (6.9) получим следующие выражения для вычисления боковых реакций, действующих на колеса автомобиля при его повороте:
Ryi =	+ ^77 {[^ (0 — 61) + аД0—
— 61)](b2 -j- pz) 4- (у62 4- flx62)(pz —ab}} j; Ryz = /«a2{-£—^-{[u(0 —61) + ax(Q — — 61)] (P2 — ab) + (f62 + ax62) (a2+Pz)}L
где mai и ma2 — массы, создающие нагрузку на передний и задний мосты соответственно; pz — радиус инерции автомобиля относительно вертикальной оси, 2
проходящей через центр масс: р2 = = Izhna. Для автомобилей современных компоновок р2 л; ab.
В этом случае боковые реакции
(6.10)
Их можно представить в виде трех составляющих:
Ryi = Ryi + Rayl + Reyi, Ry, = Ry, 4-
+ Ry2 4" RyZ,
где Ryi = maiv2/R; Ry, = ma2v2/R;
146
Ryi — mai — [(б — 81) (b2	Pz) +
+ 62 (p2 — ab)];
Ryi = ma2~ [(0 — 5i)(pi — ab) + aL
+ s2 (°2 + pl)];
^, = ^±[(0-6.) (62 + Pi) +
+ 62 (pi —ezb)];
^2 = /na2^-[(0-61)(pi-ab) + + 82 (a2 + pi)].
Первые составляющие обусловлены возникновением при круговом движении центробежной силы. Она непосредственно не зависит от углов поворота управляемых колес и углов увода, а только от скорости движения автомобиля и радиуса поворота. Распределяется центробежная сила между мостами пропорционально распределению веса автомобиля.
Вторые составляющие связаны с угловыми скоростями поворота векторов скоростей середин мостов автомобиля, они определяются как скоростью поворота управляемых колес, так и скоростью увода. При входе в поворот составляющая Ray\ всегда положительна. Направление же составляющей может быть положительным или отрицательным в зависимости от отношения pi/(ab) и соотношения скоростей поворота колес и увода мостов автомобиля. Так как в большинстве случаев pi/(ab)i>
1, составляющая как правило, является отрицательной, т. е. уменьшает боковую реакцию на заднем мосту автомобиля при входе в поворот.
Составляющие и обусловлены поступательным ускорением автомобиля. При повороте с ускорением за счет их увеличиваются боковые реакции, а при повороте с уменьшением скорости—уменьшаются. Исключением является случай, когда движение про
исходит при малых углах поворота управляемых колес, но больших углах увода переднего моста.
Выполненные расчеты показывают, что в большинстве случаев составляющая от центробежной силы примерно на порядок выше остальных. Исключением является момент входа автомобиля в поворот, когда слагаемые, обусловленные центробежной силой и силой, зависящей от скорости поворота управляемых колес и скорости увода мостов, оказываются соизмеримыми. Так как обычно в начале входа автомобиля в поворот боковые силы невелики, можно практически оценивать устойчивость автомобиля при его круговом движении с установившейся скоростью.
В некоторых случаях при больших скоростях движения и резком повороте управляемых колес, например при объезде внезапно появившегося препятствия, роль и Ry2 может оказаться решающей. Поэтому в программу испытаний автомобилей на устойчивость включают определение критической скорости, при которой автомобиль не выходит за пределы заданного коридора движения при его резком переходе на соседнюю полосу.
Распределение боковых реакций между колесами мостов автомобиля зависит от многих факторов, главными из которых являются различия нормальных реакций, коэффициентов сцепления и окружных сил. Так как колеса мостов должны иметь одинаковые углы увода, отношение боковых реакций между наружным Ryi и внутренним Ryi колесами моста равно отношению коэффициентов сопротивления боковому уводу:
Ryl/Ryl = kyl/kyi, Ry'jRtfZ = kyl/kip-
(6.И)
Если известна зависимость коэффициентов сопротивления боковому уводу от вышеперечисленных факторов, соотношения (6.11) позволяют определить
6*
147
а	б	в
Рис. 6.17. Определение положения центров крена по кинематике подвески
боковые реакции, действующие на колеса моста, при известных их суммарных значениях.
При криволинейном движении автомобиля вследствие действия инерционной силы Fy происходит перераспределение нормальных реакций между колесами мостов автомобиля. При этом нормальные реакции под внутренними по отношению к центру поворота колесами уменьшаются, а под наружными — увеличиваются.
На перераспределение реакций существенное влияние оказывает крен кузова — поворот подрессоренной массы относительно неподрессоренных. Поворот кузова происходит относительно оси, называемой осью крена. Положение оси крена определяется кинематикой направляющих устройств передней и задней подвесок. Точки, относительно которых поворачиваются передняя или задняя части кузова при крене, называются центрами крена. Осью крена является линия, проходящая через его центры. Для определения положения центров крена необходимо рассмотреть положение мгновенных центров поворота кузова при крене. Приведем некоторые способы определения положений центров крена кузова при различных типах подвески.
Если имеется двухрычажная подвеска с поперечным качанием рычагов, для определения центра крена необходимо найти точку пересечения осевых линий рычагов (точка k, рис. 6.17,6). Центр крена (точка 7И) располагается на пересечении оси симметрии автомобиля с линией, соединяющей точку k и точку контакта колеса с дорогой (точка Д). Если направляющее устройство подвески обеспечивает вертикальное перемещение колеса без наклона (точка k удалена в бесконечность), центр крена располагается на пересечении оси симметрии автомобиля с плоскостью дороги (свечная подвеска, параллелограммная, с качанием рычагов в продольной плоскости). У однорычажных подвесок с поперечным качанием центр крена располагается на пересечении осей рычагов с осью симметрии (рис. 6.17, в). При неразрезной оси с подвеской колес на продольных листовых рессорах центр крена находится в плоскости L —‘L, проходящей через ушки рессор (рис. 6.17, а).
Поперечная сила приложенная в центре масс кузова, создает момент относительно оси крена (плечо крена /гД, вызывающий поперечный наклон кузова.
В соответствии с рис. 6.18 плечо
148
внутренние колеса автомобиля. Сумма моментов относительно точки М, являющейся центром крена,
F^hK cos X + GKh sin X = щХ,
где GK = mKg; тк — подрессорная масса; X — угол поворота кузова; щ — угловая жесткость подвески.
Считая угол X малым (sin Х=Х; cos Х= 1), имеем:
Рис. 6.19. Силы, действующие на автомобиль при повороте с креном кузова
крена hk определяется из соотношений: hk = hi + т 4- п; n/aK = (h2 — hi)/L;
h.JL = mil-,
l = V +
— (aJiJL + bJiJL).
Определим крен кузова при движении автомобиля по горизонтальной дороге в случае, когда на кузов автомобиля действует боковая сила Еу.
На схеме (рис. 6.19) объединены передний и задний мосты автомобиля. Соответственно реакции и являются суммарными нормальными реакциями, действующими на наружные и
Х = Г^/(сЛ-ад. (6.12)
При повороте кузова на угол X центр масс кузова переместится из точки С в точку С'. Для нахождения суммарной реакции под внутренними колесами составим уравнение моментов относительно точки контакта наружных колес с дорогой (точки А'):
RzB - Gh + FayhH - GK [д- - hG. j + + F*hK = 0,
где GH, hs — соответственно вес мостов и высота центра их масс.
Если принять, что поперечные ускорения центров масс кузова и мостов одинаковы,
F®/iH + F^hK = Fy(mKhK + aymahgt тогда
Rz = g ------ayma gmKX (6.13)
' ma
Rz = g — + аутй gmKh
(6.14)
Из приведенных выражений видно, что изменение нормальных реакций обусловлено моментом, вызванным инерционной силой аут&Нё, и креном кузова. Первый момент распределяется между мостами автомобиля в соответствии с приведенными массами, а второй— обратно пропорционально угловым жесткостям подвесок. Следовательно, нормальные реакции при криво
149
линейном движении двухосного автомобиля
/?zi = (jy + as + , Г. cKl
^21 = ~ m& \ Д ay ~
ck B
Rz2 = ftla (~fF + ay ~.§") + , Л CZ2 Д
+ A, —gmK —;
cz B
r," a ! s ^g\ Rzl — -jjtna ( —g	Cly —g-]
(6.15)
Угловая жесткость подвески определяется по следующим формулам: для зависимых подвесок
Г/ ~ 0,6т]рсрйр,
где Вр — расстояние между серединами упругих элементов, м; ср — вертикальная жесткость упругих элементов; т]р — коэффициент, учитывающий увеличение жесткости упругих элементов при их скручивании в поперечном направлении (для листовых рессор т]р = = 1,05...1,25);
для независимых подвесок
z=z 0,5В2спр,
где В — колея моста, м; спр — приведенная жесткость упругого элемента.
Угловая жесткость подвесок всех мостов
с1. ~ См + Смг,-
6.5. Траекторная и курсовая устойчивость автомобиля
Статическая поворачиваемость автомобиля. Траекторная и курсовая устойчивость автомобиля зависит в первую очередь от увода мостов, степени стаби
лизации управляемых колес и их склонности к колебаниям и автоколебаниям.
Для оценки влияния увода мостов автомобиля на его устойчивость рассмотрим движение автомобиля по кругу большого радиуса с постоянной скоростью. В данном случае в центре масс автомобиля действует боковая сила, определяемая центростремительным ускорением. Боковые реакции дороги в соответствии с выражением (6.10):
V2	V2
Ryi = Ry2 = ma2^-- (6.16)
Углы увода мостов:
feyi	ky^R.	ky^R
(6.17)
Из формул (6.6), (6.16) и (6.17) после преобразования находим
/ т_,	/и „ \ „2
R = R.+	-------- U-, (6.18)
\ «у1	«у2 J У
где RK — кинематический радиус поворота автомобиля, равный радиусу поворота автомобиля при качении шин без бокового увода: /?к=Л/0; feyI и fey2— коэффициенты сопротивления ' уводу мостов, зависящие от коэффициентов сопротивления уводу шин и кинематики подвески.
Из выражения (6.18) следует, что в общем случае радиус поворота автомобиля зависит не только от угла поворота управляемых колес, но и от скорости движения.
Свойство автомобиля изменять кривизну траектории при изменении скорости называется статической поворачиваемостью.
Если mai/ky[ = niaz/kyz (61 = 62), радиус поворота автомобиля с эластичными колесами будет тот же, что и автомобиля с жесткими колесами. При переменной скорости движения, но неизменном положении управляемых колес радиус поворота такого автомобиля будет оставаться постоянным (автомобиль с нейтральной
150
Рис. 6.20. Зависимость радиуса кругового движения от скорости автомобиля с закрепленными управляемыми колесами при:
/ — нейтральной поворачиваемости; 2 — недостаточной; 3 —1 избыточной
(статической) поворачиваемостью).
Если ma.-ilk1i<ma.2lk-S2 (61<6г), радиус поворота автомобиля с эластичными колесами будет меньше, чем автомобиля с жесткими колесами, и с увеличением скорости будет уменьшаться. Это автомобиль с избыточной поворачиваемостью.
В случае, когда mai/^yl>«a2/^y2 (61>6г), радиус поворота автомобиля с эластичными колесами будет больше, чем автомобиля с жесткими колесами, и при увеличении скорости будет возрастать (автомобиль с недостаточной поворачиваемостью).
На рис. 6.20 приведен график, показывающий зависимость радиусов поворота от скорости движения различных автомобилей по кругу с закрепленным рулевым управлением.
Исследуем влияние поворачиваемости автомобиля на его траекторию и курсовую устойчивость. Если на движущийся прямолинейно автомобиль, имеющий жесткие в боковом направлении колеса, действует поперечная сила Ее, он будет продолжать двигаться прямолинейно до тех пор, пока эта сила не увеличится настолько, что начнется скольжение колес.
Автомобиль с нейтральной поворачиваемостью будет также двигаться прямолинейно, но под углом 6 к прежнему направлению, т. е. получит смещение в боковом направлении (рис. 6.21,а). Под действием поперечной силы автомобиль с излишней поворачиваемостью начнет поворачиваться относительно центра О (рис. 6.21, б). При этом возникает центробежная сила Fj, нормальная составляющая которой Fy по направлению совпадает с поперечной силой, вызвавшей поворот автомобиля. Это приводит к уменьшению радиуса поворота и нарастанию поперечной силы. Чтобы сохранить направление прямолинейного движения, водителю необходимо повернуть колеса так, чтобы мгновенный центр поворота переместился из точки О в точку, расположенную на противоположной стороне автомобиля. Поскольку при движении автомобиля поперечные силы действуют практически непрерывно, водителю приходится постоянно воздействовать на рулевое управление, для того чтобы удержать автомобиль на заданной траектории.
Если автомобиль обладает недостаточной поворачиваемостью, поперечная составляющая центробежной силы направлена в сторону, противоположную возмущающей силе (рис. 6.21,8). В результате этого увод быстро уменьшается и автомобиль практически сохраняет прямолинейное направление движения.
Таким образом, автомобиль с недостаточной поворачиваемостью более устойчив и лучше сохраняет направление движения, чем автомобиль с излишней поворачиваемостью. Сложность управления автомобилем с излишней поворачиваемостью возрастает с увеличением скорости движения, и при некоторой скорости, называемой критической по условиям увода Увкр, автомобиль теряет управляемость, т. е. при незначительном боковом толчке и нейтральном положении управляемых ко-
151
Рис. 6.21. Движение автомобиля при действии боковой силы при: а — нейтральной поворачиваемости; б — избыточной; в — недостаточной
лес возникает быстро нарастающий увод, приводящий к заносу автомобиля (А?->0).
Для определения критической скорости умножим правую и левую части выражения (6.18) на 0. Учитывая, что RKG = L, имеем:
/ /ио,	т„ \
Д0 = £+ -Д-----------Д- У2.
\ &у!	/гу2 /
При критической скорости 0 = 0, R—>0,	поэтому,	приравняв	правую
часть последнего	выражения	нулю,	по-
лучаем:
Г I /	mo9 m...	\
п6кр=1/ L -Д----------. (6.19)
V I \	/ь’у2 /гу1	/
Критическую по условиям увода скорость можно определить только для автомобилей с излишней поворачиваемостью. У автомобилей с нейтральной поворачиваемостью она равна бесконечности, а у автомобилей с недостаточной поворачиваемостью — отсутствует (подкоренное выражение в формуле (6.19) отрицательное). Движение автомобиля со скоростью, близкой к критической, затруднительно, так как при незначительных возмущающих силах автомобиль стремится войти в поворот. Поэтому для удержания его на заданной траектории водитель должен непрерывно воздействовать на рулевое управление.
Недостаточная поворачиваемость достигается рядом конструктивных мероприятий: подбором давления воздуха в шинах, распределением масс между передними и задними мостами и выбором направляющих устройств подвески.
Чтобы увеличить углы увода передних мостов, давление водуха в шинах передних колес устанавливают обычно меньшим, чем в задних. Это обусловливает уменьшение коэффициента сопротивления уводу переднего моста. У легковых автомобилей центр масс рекомендуется располагать ближе к передней части, чтобы на передние колеса приходилась большая часть поперечной силы.
Устойчивость автомобиля в значительной степени зависит от конструкции направляющего устройства подвески. При действии на автомобиль поперечной силы происходит крен кузова, причем в зависимости от типа направляющего устройства ось моста может повернуться в горизонтальной плоскости или измениться угол наклона плоскости колес к вертикали.
На рис. 6.17, а показан задний мост автомобиля с рессорной подвеской. Геометрическое место точек центров моста в месте крепления рессор при деформации подвески показано линией
152
NN. При крене кузова на повороте внутренняя рессора, расположенная со стороны центра поворота, распрямляется и центр моста в месте крепления рессоры перемещается в точку А. Центр же моста в месте крепления рессоры с наружной по отношению к центру поворота стороны перемещается в точку В. Это приводит к тому, что ось моста поворачивается в горизонтальной плоскости на угол р, за счет чего увеличивается угол увода моста. При другом наклоне рессоры или изменении положения серьги можно обеспечить поворот моста относительно кузова в противоположную сторону, т. е. уменьшить его угол увода.
Угол увода колеса зависит и от его наклона. На рис. 6.17 показано, как изменяется наклон колес при крене кузовов, закрепленных на подвесках двух типов: независимой двухрычажной и однорычажной с качанием рычагов в поперечной плоскости.
Из схемы видно, что при независимой двухрычажной подвеске колесо наклоняется в сторону от центра поворота (увод моста увеличивается), а при независимой однорычажной — к центру поворота (увод моста уменьшается). Крен кузова при зависимой подвеске практически не вызывает изменения угла наклона колеса (изменение угла наклона плоскости колес за счет различия деформаций шин мало). Этим и объясняется, что в легковых автомобилях наиболее часто используется передняя подвеска на двух поперечных рычагах, а задняя — зависимая или независимая однорычажная с поперечным качанием.
Недостаточная поворачиваемость автомобиля способствует повышению его траекторной и курсовой устойчивости. Однако слишком большой увод колес переднего моста обусловливает ухудшение динамической поворачиваемости автомобиля, т. е. его способности изменять направление движения в соответствии с поворотом рулевого коле
са. Плохая динамическая поворачиваемость автомобиля затрудняет работу водителя, так как для изменения направления необходимо затратить больше энергии. Кроме того, при слишком большом уводе управляемых колес происходит заметное запаздывание поворота автомобиля относительно поворота рулевого колеса.
Оценочными критериями статической поворачиваемости автомобиля являются разность углов увода его переднего и заднего мостов при нормированном боковом ускорении и запас статической устойчивости.
Под запасом статической устойчивости автомобиля понимается отношение расстояния от центра его масс до линии нейтральной поворачиваемости, замеренного на высоте центра масс автомобиля, к колесной базе.
Линия нейтральной поворачиваемости — геометрическое место точек в плоскости симметрии автомобиля, приложение боковой силы в которых не вызывает поворота движущегося автомобиля относительно вертикальной оси.
Если в какой-либо точке движущегося прямолинейно автомобиля с нейтральной, избыточной или недостаточной поворачиваемостью действует поперечная хила, будет иметь место увод мостов. Если точка приложения поперечной силы располагается вблизи переднего моста, угол его увода будет больше, чем заднего, и наоборот. Очевидно, что внутри базы автомобиля можно найти такую точку (точку нейтральной поворачиваемости), при приложении к которой поперечной силы углы увода заднего и переднего мостов будут равны. Если автомобиль обладает нейтральной поворачиваемостью, эта точка совпадает с центром масс, если недостаточной — она будет располагаться позади центра масс, а избыточной — впереди. Поскольку углы увода зависят от крена кузова, расстояние от точки нейтральной поворачиваемости до вертикальной оси, проходящей через
153
Рис. 6.22. Положение линии нейтральной поворачиваемости
центр масс автомобиля, зависит от высоты приложения поперечной силы. Если, например, подвеска автомобиля сконструирована таким образом, что при крене кузова увод переднего моста увеличивается в большей степени, чем заднего, при увеличении высоты приложения поперечной силы точка нейтральной поворачиваемости будет смещаться назад. Геометрическое место этих точек и является линией нейтральной поворачиваемости.
На рис. 6.22 показано положение этой линии для автомобиля с недостаточной поворачиваемостью в случае, когда при крене кузова одинаково изменяются углы увода мостов (линия 1—1), угол увода переднего моста увеличивается в большей степени, чем заднего (или угол увода заднего моста уменьшается, линия 2—2), и угол увода заднего моста увеличивается в большей степени, чем переднего (линия 3—3). Отношение расстояния АС к базе автомобиля L и является запасом статической устойчивости Zc. Запас статической устойчивости считается положительным, если точка нейтральной поворачиваемости располагается позади центра масс автомобиля.
Расстояние AC = d может быть найдено из следующих соображений: для обеспечения нейтральной поворачиваемости автомобиля поперечная сила Fy должна распределяться пропорционально коэффициентам сопротивления уводу: FyilFy2 = kyxlky2-- Отсюда следует feyi/fey2 = mai62/(ma26i) =6б2/(аб1). Для
обеспечения заданного распределения поперечной силы необходимо, чтобы:
Fyr (d + а) = F,ft (b - d\, FyJFyz = = (b — d)l(d + a);
b — d  b 62	__ &262 — a26x
d а	и ф	abi
Зависимость запаса статической устойчивости автомобиля от центробежного ускорения определяется расчетным путем по результатам измерения углов увода автомобиля при движении его по кругу с различными скоростями.
Автомобили общего назначения с хорошей поворачиваемостью должны иметь положительный запас статической устойчивости при всех скоростях движения.
Стабилизация управляемых колес. При движении автомобиля на управляемые колеса всегда действуют силы, стремящиеся отклонить их от заданного положения. В силу наличия зазоров и упругости деталей колеса отклоняются даже при фиксированном положении рулевого механизма. Это может явиться одной из причин неустойчивого движения автомобиля. Устойчивость движения автомобиля обеспечивается стабилизацией управляемых колес, т. е. способностью управляемых колес возвращаться в нейтральное положение (положение, соответствующее прямолинейному движению автомобиля) без помощи водителя.
Стабилизация управляемых колес достигается за счет установки шкворней с наклоном в поперечной и продольной плоскостях и стабилизирующего момента эластичных шин при их качении с боковым уводом.
Оси шкворней управляемых колес устанавливают в поперечной плоскости под некоторым углом а к вертикали. Поэтому при повороте управляемых колес происходит подъем передней части автомобиля. Например, если повернуть колесо на угол 0 (рис. 6.23), точ-
154
Рис. 6.23. Схема стабилизации управляемых колес автомобиля за счет наклона шкворня в поперечной плоскости
ка контакта колеса с дорогой должна была бы переместиться по дуге АА1 радиуса с и опуститься на h ниже опорной поверхности. Так как в действительности этого произойти не может, поворот колеса вызовет подъем части автомобиля, связанной с управляемыми колесами, на эту величину. При этом элементарная работа, совершаемая при подъеме одним колесом передней части автомобиля: dAi= G^dh, где Gi,i—доля веса автомобиля, приходящаяся на колесо. Работа, совершаемая при повороте управляемого колеса: dA2=McrdG, где AfCT — момент сопротивления повороту, равный, если пренебречь силами трения, стабилизирующему моменту колеса.
Из равенства dAi и dA2 имеем:
<т= -^Gu.
at)
Стабилизирующий момент моста равен сумме стабилизирующих момен
тов правого и левого колес. Если пренебречь различием углов поворота управляемых колес,
= Gx
dh dO ’
где 0 — средний угол поворота управляемых колес.
Согласно рис. 6.23,
/i = xsinct; х —с—ccos0;
h = c(\ — cos 0)sin a;
= c sin 0 sin a; M?T=GiC sin a sin 0. de
Так как стабилизирующий момент обусловлен наклоном шкворня в поперечной плоскости и пропорционален синусу угла поворота управляемых колес, он значителен лишь при движении автомобиля с малыми радиусами поворота. Поскольку такие повороты совершаются только при малых скоростях движения автомобилей, можно считать, что наклон шкворня в поперечной плоскости обеспечивает стабилизацию управляемых колес при малых скоростях движения автомобилей. В некоторых случаях, в основном у автомобилей высокой проходимости, по конструктивным соображениям шкворень в поперечной плоскости устанавливают без наклона.
Шкворни управляемых колес устанавливаются в продольной плоскости под углом у к вертикали (наклон назад). Возникающие при повороте автомобиля боковые реакции дороги приложены у жесткого в поперечном направлении колеса на вертикальной оси, проходящей через его центр (рис. 6.24). Вследствие наклона шкворня боковая реакция Ry в точке контакта колеса с дорогой и боковая сила Fg, приложенная к центру колеса, создают момент, стремящийся повернуть колесо в направлении, показанном стрелкой, т. е. возвратить управляемые колеса в нейтральное положение.
155
Рис. 6.24. Стабилизация управляемых колес автомобиля:
а — за счет наклона шкворня в продольной плоскости; б — то же, и стабилизирующего момента эластичных шин
скорости. Поэтому его называют скоростным стабилизирующим моментом.
При исследовании бокового увода эластичного колеса было установлено, что при действии на него боковой силы точка приложения равнодействующей боковых реакций смещается назад на расстояние е. При этом, как видно из рис. 6.24, б, возрастает стабилизирующий момент, так как увеличивается плечо силы Ry\. Суммарный стабилизирующий момент
Муст + <т = Ryi (rAsin у + ecosу).
Смещение е, а соответственно, и момент Л4ст зависят от угла увода колес. При увеличении угла увода (рис. 6.25) стабилизирующий момент возрастает сначала практически линейно, а затем уменьшается. Это объясняется тем, что
Рис. 6.25. Стабилизирующий момент шины 9,00—21:
1 — GK=27,S кН; 2 — Ок=20 кН
качение колеса при больших углах увода сопровождается проскальзыванием в зоне контакта с дорогой задних элементов шины и, следовательно, уменьшением смещения е равнодействующей боковых реакций Ry\.
Максимальное значение стабилизирующего момента зависит от ряда факторов. Он возрастает при увеличении размеров шины, нагрузки на шину и уменьшении давления воздуха в ней. Ориентировочно максимальные значения стабилизирующего момента, соответствующие углу увода около 6°, могут быть найдены по эмпирической зависимости
Л'1сТ
max — (0,015...0,025)GZK,
для
Стабилизирующий момент управляемого моста
Л'1ст = Ry\a = RyirR&\ny.
При движении по кругу постоянного радиуса
ллУ b	v2r
/ИсТ = — та----=— sin у.
L	RcosQ	х
При малой скорости движения стабилизирующий момент незначителен и сильно возрастает при увеличении
где GZK— номинальная нагрузка на шину, кН; Меттах-СТабиЛИЗИруЮЩИЙ МО-
мент, кН • м. Большие значения МсТтах относятся к более эластичным шинам.
В связи с тем что угол увода определяется поперечной силой, действующей на колесо, которая в свою очередь зависит от радиуса поворота и квадрата скорости движения автомобиля, стабилизирующий момент эластичной шины, как и момент, обусловленный
156
Рис. 6.26. Развал (а) и схождение (б) управляемых колес
наклоном шкворня в продольной плоскости, проявляется при высоких скоростях движения. Большой стабилизирующий момент затрудняет управление автомобилем, поэтому у некоторых легковых автомобилей, имеющих высокоэластичные шины, углы наклона шкворней в продольной плоскости делают нулевыми или даже отрицательными.
Кроме стабилизирующего момента, на рулевую трапецию действует момент, обусловленный трением в рулевом управлении. Момент трения противодействует повороту колес. При прямолинейном движении автомобиля стабилизирующий момент равен нулю и удержание колес в нейтральном положении обеспечивается почти исключительно трением. При выходе автомобиля из поворота момент трения препятствует возвращению управляемых колес в нейтральное положение, в результате чего ухудшается их стабилизация. Поэтому при конструировании рулевого управления целесообразно обеспечивать условия достаточно вы
сокого трения в нем при нейтральном положении управляемых колес и малого — при больших углах поворота.
Плоскость управляемых колес автомобиля устанавливается под углом % к вертикали, называемым углом развала колес (рис. 6.26). Целесообразность установки управляемых колес с развалом диктуется следующим: 1) при качении управляемого колеса на него действует сила сопротивления качению. Эта сила создает с плечом с момент сопротивления повороту. При наличии развала это плечо уменьшается и тем самым облегчается управление автомобилем; 2) колесо поджимается к внутреннему подшипнику ступицы, что предотвращает виляние колеса в случае появления зазоров в подшипниках ступицы; 3) при износе поворотных цапф обратный развал не появляется.
Поскольку колесо, плоскость которого отклонена от вертикали, катится с боковым уводом, для его компенсации управляемым колесам, установленным с развалом, придается схождение в горизонтальной плоскости. Обычно схождение замеряется в миллиметрах, как разность расстояний В и А (см. рис. 6.26,6). При наличии зазоров в рулевой трапеции касательные и боковые реакции дороги, а также удары, действующие на колеса, стремятся вызвать их отрицательное схождение. Во избежание этого управляемым колесам часто придается схождение несколько большее, чем необходимо для компенсации развала.
Оценка стабилизирующих свойств управляемых колес производится по усилию Fp, прикладываемому к рулевому управлению при движении автомобиля по кругу с постоянной скоростью. Стабилизация считается нормальной, если для удержания автомобиля на круговой траектории при боковом ускорении ау = 4 м/с2 и скорости движения 40 и 80 км/ч к рулевому колесу необходимо прилагать
157
Рис. 6.27. Динамическая система «управляемый мост»
усилие 60... 120 Н. С увеличением скорости усилие не должно уменьшаться.
Колебания и автоколебания управляемых колес. Управляемый мост автомобиля представляет собой динамическую систему, включающую массы, связанные упругими элементами: шинами, рессорами, рулевыми тягами (рис. 6.27). При движении автомобиля возможны следующие перемещения масс моста: £ — вертикальное перемещение в вертикально-поперечной плоскости, ф — угловое перемещение в вертикально-поперечной плоскости, 0 — угловое перемещение колес относительно шкворней в горизонтальной плоскости. При независимой подвеске моста в вертикально-поперечной плоскости возможна одна форма его колебаний, обусловленная кинематикой подвески. Наибольшее влияние на управляемость и устойчивость автомобиля оказывают угловые колебания колес моста по координате ф и угловые колебания по координате 0.
Одной из характеристик динамических систем являются частоты собственных колебаний. Частота собствен
ных угловых колебаний моста в вертикально-поперечной плоскости
®Ф = У ,	(6.20)
где (оф — частота собственных колебаний, рад/с; Сф — коэффициент приведенной угловой жесткости; /ф — момент инерции моста относительно оси, проходящей через центр его масс.
Коэффициент угловой жесткости подвески моста в вертикально-поперечной плоскости
Сф = 0,5 (Ср/р где ср, сш — коэффициенты линейной жесткости соответственно рессоры и шины; /р, /ш— соответственно рессорная база и колея моста.
Отсюда
= /о,5 (ср/2р + сш/УЛф-
Следовательно, при снижении жесткости рессор и шин, а также увеличении момента инерции переднего моста частота собственных колебаний моста в вертикально-поперечной плоскости уменьшается.
Частота собственных колебаний колес относительно осей шкворней (виляние) может быть найдена по выражению (6.20). В данном случае под I нужно понимать момент инерции колес и связанных с ними деталей относительно осей шкворней. Коэффициент угловой жесткости привода Сд может быть определен как отношение момента Мд, необходимого для поворота колес на угол 0, к этому углу. Момент Мд зависит не только от упругости тяг, но и от стабилизирующего момента, обусловленного наклоном шкворня и уводом шин. Поскольку последний зависит от скорости движения, частота собственных колебаний колес в продольной плоскости также зависит от скорости автомобиля.
Угловые колебания моста в вертикальной и горизонтальной плоскостях взаимосвязаны. Эта связь обу-
158
Рис. 6.28. Принципиальная схема гироскопа
словлена гироскопическим эффектом колес.
Гироскоп — быстро вращающийся маховик, заключенный в рамку, с которой связаны цапфы, позволяющие ей вращаться вокруг вертикальной оси (рис. 6.28). Гироскоп характеризуется кинематическим моментом, равным произведению момента инерции маховика /к относительно оси собственного вращения и угловой скорости
вращения ®к.
Если, приложив внешний момент Мг
поворачивать рамку с гироскопом с угловой скоростью ®пр, как это пока-
зано на рисунке, гироскоп начнет поворачиваться вокруг вертикальной оси „	dtp
с угловой скоростью —. Это движение dt
носит название прецессии и совершается под действием гироскопического момента:
М2 = /к®к dt
Передние колеса движущегося автомобиля представляют собой гироскопы и реагируют на всякое угловое перемещение их осей. Например, если вследствие наезда на неровность ось моста в вертикальной плоскости повернулась на угол ф, возникает гироскопический момент, стремящийся повернуть колеса в горизонтальной пло
скости. Этот момент зависит от скорости автомобиля, момента инерции колеса и угловой скорости поворота оси колеса. Аналогично при повороте колес в горизонтальной плоскости возникает гироскопический момент, поворачивающий мост в вертикальной плоскости.
Таким образом, связь между угловыми колебаниями управляемых колес в вертикальной и горизонтальной плоскостях зависит от скорости движения автомобиля и кинематики подвески. С увеличением скорости движения автомобиля она возрастает и будет тем больше, чем больше отклоняются плоскости колес от вертикальной плоскости при их перемещениях. Если кинематика подвески обеспечивает вертикальное перемещение колес без изменения углового положения их плоскостей в пространстве (например, свечная подвеска), колебания в вертикальной и горизонтальной плоскостях будут независимыми. Независимыми их можно считать и при малых скоростях движения, когда гироскопические моменты колес малы.
Вследствие того что мост автомобиля является колебательной системой, при действии на него периодических или случайных возмущений возникают колебания его масс. Амплитуда колебаний зависит от амплитуды возмущения, соотношения частот возмущения и собственных колебаний и характера затухания колебаний в системе. Наибольшая интенсивность колебаний имеет место в случае, когда частота возмущения близка к частоте собственных колебаний (резонансная зона).
При движении автомобиля колебания управляемых колес обусловлены наличием дорожных неровностей и неуравновешенностью колес. В первом случае имеют место вертикальные колебания управляемых колес, методы расчета которых приведены в гл. 5. Непосредственно вертикальные колебания колес на управляемость и устой-
159
Рис. 6.29. Реакции дороги, действующие на колесо автомобиля при проезде неровностей
Рис. 6.30. Несоответствие кинематики подвески и рулевого привода
чивость автомобиля оказывает малое влияние. Однако они могут вызвать угловые колебания управляемых колес в горизонтальной плоскости, отрицательно влияющие на устойчивость и управляемость автомобиля. Угловые колебания управляемых колес могут возникнуть при вертикальных колебаниях управляемого моста вследствие появления переменных касательных реакций и при несоответствии кинематики подвески и рулевого привода.
При движении колеса по неровности результирующая реакция R (рис. 6.29) отклоняется от вертикали на угол а, который для ведомого колеса может быть приблизительно определен из выражения
tg a = dq[ds,
где <7 = f(s) —функция микропрофиля дороги; s — путь, проходимый колесом.
Результирующая реакция R может быть разложена на две составляющие: вертикальную Rz и горизонтальную Rx. Поскольку реакция R и производная — являются переменными, Rx будет ds также переменной. Она может иметь разное направление при наезде колеса на неровность и при съезде.
На неровной дороге угловые колебания управляемых колес могут возникнуть, если их двойная связь с подрессоренной массой автомобиля через подвеску и рулевой привод не согласована. Например, согласно схеме, показанной на рис. 6.30, при относительном перемещении подрессоренной и непод-рессоренной масс автомобиля шарнир на конце рычага поворотной цапфы должен качаться, с одной стороны, в соответствии с кинематикой рессоры по траектории А А, а с другой — по дуге ВВ, радиус которой равен длине продольной тяги. Расхождение дуг АА и ВВ приводит к тому, что управляемые колеса при их вертикальных перемещениях относительно подрессоренной массы автомобиля поворачиваются вокруг шкворней. Поэтому при выборе кинематики подвески и рулевого привода всегда стремятся расположить как можно ближе центры качания направляющих элементов подвески и рулевого привода.
Если вынужденные колебания управляемых колес вызваны их неуравновешенностью, то возникающие периодические силы меняются с частотой, равной угловой скорости вращения колес, и имеют амплитуду, пропорциональную квадрату скорости движения автомобиля. Поворачивающие моменты на обоих колесах в случае их неуравновешенности могут действовать в одном или разных направлениях, причем их сумма будет максимальна, если неуравновешенные массы (тн) окажутся с противоположных сторон оси, как показано на рис. 6.31.
Интенсивные колебания управляе-
мо
Рис. 6.31. Возбуждение колебаний при неуравновешенности колес автомобиля
мых колес, обусловленные их неуравновешенностью, могут возникнуть в том случае, когда при достаточно высокой скорости движения автомобиля частота возмущений (угловая скорость вращения колес) станет близкой к частоте собственных колебаний управляемых колес в горизонтальной плоскости. Такие условия возможны для легковых автомобилей, имеющих колеса малого диаметра и относительно низкую частоту собственных колебаний управляемых колес. Поэтому колеса легковых автомобилей в сборе с шиной подвергают балансировке, а на изготовление шин установлены жесткие допуски по неуравновешенности (5... 10 Н-см в зависимости от размеров шин).
У грузовых автомобилей частота возмущений от неуравновешенности колес ниже, чем у легковых, так как они имеют меньшие скорости движения и большие радиусы качения колес. Частоты же собственных колебаний колес в горизонтальной плоскости обычно выше, чем у легковых автомобилей. В связи с этим у грузовых автомобилей при эксплуатационных скоростях движения не наблюдаются резонансные колебания управляемых колес.
Амплитуда колебаний управляемых колес в значительной степени зависит от трения в динамической системе «управляемый мост»: от трения в шар
нирах, шинах и гистерезиса в металле. Для увеличения трения и уменьшения тем самым амплитуды колебаний колес в рулевом приводе некоторых высокоскоростных автомобилей устанавливают специальные амортизаторы.
Автоколебания управляемых колес. Вынужденные колебания масс в динамической системе возникают в случае, когда на нее действует периодическое внешнее возмущение. У автоколебательных или самовозбуждающихся систем внешнее возмущение становится периодическим только при наличии колебаний в системе. Если же в автоколебательной системе колебания не возникают, внешнее возмущение будет оставаться постоянным.
В 30-х годах в конструкциях легковых автомобилей в связи с повышением скоростей движения начали применять подвеску с мягкими рессорами, шины низкого давления, тормоза стали устанавливать не только на задние колеса, но и на передние. После введения этих усовершенствований при движении автомобиля с высокими скоростями появились особого вида колебания управляемых колес, получившие название «шимми». Они включали угловые колебания переднего моста в вертикально-поперечной плоскости и колебания колес вокруг шкворней. Автоколебания вызывают большие динамические нагрузки на детали рулевого управления, интенсивное изнашивание шин и приводят к потере автомобилем управляемости и устойчивости. Одной из основных причин возникновения автоколебаний управляемых колес является наличие гироскопической связи между угловыми колебаниями управляемого моста автомобиля в поперечной плоскости и поворотом колес этого моста относительно шкворней.
Рассмотрим физическую сущность процессов, происходящих при автоколебаниях управляемых колес. При высокой скорости движения колеса автомобиля можно рассматривать как бы-
161
Рис. 6.32. Перемещение колес и моста при автоколебаниях
стро вращающиеся гироскопы. При случайном повороте управляемых колес вокруг шкворней на угол 0 (рис. 6.32) возникает гироскопический момент Мг1 = 2/к<Вк0 (/к, <ок — момент инерции и угловая скорость вращения колеса). Под действием этого момента управляемый мост повернется в вертикальной плоскости на угол гр, а в горизонтальной плоскости появится гироскопический момент Л1г2, увеличивающий угол поворота управляемых колес: •Мг2 = 27к(Пк'ф. Таким образом, поворот управляемых колес вызовет перекос переднего моста, который в свою очередь увеличивает поворот управляемых колес.
Вследствие поворота моста в вертикальной плоскости динамический радиус одного из колес уменьшится, а другого —увеличится. В первом случае продольная реакция дороги увеличивается, поскольку возрастает сила сопротивления качению и уменьшается радиус качения колеса. Увеличение продольной реакции при уменьшении радиуса качения колеса объясняется тем, что при постоянной скорости движения автомобиля с уменьшением радиуса качения ведомого колеса должна
увеличиться угловая скорость его вращения, т. е. оно должно получить угловое ускорение. Изменение касательных реакций дороги приводит к появлению дополнительного момента, который поворачивает управляемые колеса в горизонтальной, а вследствие гироскопической связи и в вертикальной плоскостях на некоторый угол. При этом происходит дополнительная деформация рулевого привода, подвески и шин. Когда поворачивающий момент становится равным моменту сопротивления, угловая скорость вращения моста равна нулю и колеса начинают движение в сторону положения равновесия. Поскольку в упругих элементах подвески и рулевого привода произошло накопление потенциальной энергии, мост проходит положение равновесия и происходит поворот колеса в противоположную сторону при одновременном уменьшении его радиуса. Это в свою очередь приводит к появлению момента сопротивления, «доворачивающего» в эту же сторону управляемый мост. После того как момент сопротивления становится равным моменту упругих сил в подвеске, шинах и рулевом приводе, процесс повторяется. Таким образом, при автоколебаниях управляемых колес возникает переменное по значению и направлению сопротивление, поддерживающее колебания колес на определенном уровне. При расчетных исследованиях автоколебаний принимают следующие допущения: 1) подрессоренная масса автомобиля колебаний не совершает, а перемещается по координате х с постоянной скоростью; 2) вертикальные и угловые перемещения моста в вертикальной плоскости не связаны; 3) рулевое колесо в процессе колебаний неподвижно, а колебания вокруг шкворней происходят в силу упругости рулевого управления.
Проведенные исследования показывают, что при уменьшении жесткости подвески, шин и привода, увеличении масс колес, а также гироскопиче-
162
Рис. 6.33. Параллелограммная независимая подвеска
ской связи (увеличении скорости движения автомобиля) возрастет амплитуда колебаний колес.
Поскольку явление автоколебаний управляемых колес вызвано гироскопической связью угловых колебаний моста в вертикально-поперечной плоскости и колес в горизонтальной плоскости, устранение этих колебаний обеспечивается применением таких типов подвесок, в которых деформация упругих элементов не приводит к изменению положения плоскости вращения колес. На рис. 6.33 показана схема такой подвески. Каждое колесо связано с рамой двумя равными по длине рычагами. Если соединить центры шарниров, получится параллелограмм. При таком устройстве вертикальное перемещение колеса не будет сопровождаться наклоном его плоскости. Поэтому гироскопический момент не возникает, и при вертикальных перемещениях колеса не будет его виляния. В настоящее время получили наибольшее распространение подвески передних колес, имеющие рычаги неодинаковой длины. Это обстоятельство приводит к тому, что при вертикальном перемещении переднего колеса угол наклона его плоскости относительно плоскости дороги несколько меняется. Однако пределы изменения этого угла ограничены, ввиду чего гироскопический момент практически не оказывает влияния на движение колеса.
Комплексным оценочным параметром, характеризующим устойчивость автомобиля при прямолинейном движении, служит средняя угловая скорость поворота рулевого колеса
сорт = 2а0у,
где а0 — средний угол поворота рулевого колеса, рад:
а0 =----- | а | ей;
ti — to J
to
ti~t0—рассматриваемый промежуток времени; а — угол поворота рулевого колеса относительно среднего положения; у — частота поворота рулевого колеса, с-1:
? = p/[2(^-t0)];
р — число экстремумов функции a=f(t), превышающих 3°.
Измерения проводятся при скорости автомобиля 60 и 100 км/ч. При скорости 60 км/ч средняя угловая скорость поворота рулевого колеса не должна превышать 0,1 рад/с, а при 100 км/ч — 0,15 рад/с.
6.6. Занос и опрокидывание автомобиля
Предельным случаем потери устойчивости является занос и опрокидывание автомобиля. Занос автомобиля происходит, когда силы, действующие в плоскости контакта колеса с дорогой, больше сил сцепления. Поскольку в зоне контакта продольные и поперечные силы равны соответствующим реакциям дороги, условие движения моста автомобиля без заноса
<рТ?2<Ю^ + ^, где Rz, Rx, Ry •— вертикальная, тангенциальная и боковая реакции дороги, действующие на мост автомобиля.
Опрокидывание автомобиля может произойти в результате его заноса после удара о препятствие, а также без предварительного заноса. В свою оче-
163
б
Рис. 6.34. Силы, действующие на автомобиль при повороте на косогоре
редь занос автомобиля не обязательно приводит к его опрокидыванию.
При движении на автомобиль действуют различные по природе боковые силы, приводящие к заносу или опрокидыванию, например инерционные, которые возникают при повороте автомобиля, сила тяжести — при движении по косогору или возможно их совместное действие.
Для определения условий, при которых возможны занос или опрокидывание автомобиля, рассмотрим его поворот при движении по дороге, имеющий поперечный уклон. Схема сил, действующих на автомобиль, когда инерционная сила и сила тяжести создают моменты противоположного направления, изображена на рис. 6.34, а, действующие в одну сторону — на рис. 6.34, б. Опрокидывание автомобиля произойдет тогда, когда линия действия равнодействующей N инерционной силы и силы тяжести окажется с внешней стороны контакта с опорной поверхностью колес борта, относительно которого происходит опрокидывание. Обозначим: р0 — угол между нормальной к опорной поверхности плоскостью и плоскостью, проходящей через центр масс автомобиля и точки контакта ко
лес с опорной поверхностью, а — угол между нормальной плоскостью и равнодействующей инерционной силы и силы тяжести автомобиля. При а<р0 опрокидывание не произойдет; а>р0 — произойдет; а = р — начнется опрокидывание автомобиля.
Если обозначить tg y = FyIG3.=avlg, из схемы сил рис. 6.34, б следует, что а=у + Р- Тогда условие начала опрокидывания относительно точки А запишется в виде: у + Р = Ро- Из схемы на рис. 6.34, а видно, что а = у —р. В этом случае условие начала опрокидывания относительно точки А будет: а —р = р0; Приняв угол р положительным в том случае, когда момент от инерционных сил противоположен моменту от силы тяжести, условие движения без опрокидывания можно представить в виде: tg(y + p)<tgp0.	(6.21)
Сползание автомобиля начнется в том случае, если сила, действующая вдоль склона, будет равна силе сцепления автомобиля с опорной поверхностью (рис. 6.34, а):
Wsina= (A7cosa)<p; tga = <p.
Условие движения автомобиля без сползания:
tg(y + ₽)<<p.	(6.22)
164
Табл. 6.1. Показатели поперечной устойчивости автомобилей
Тип автомобиля	40	₽0’ гРаД
Легковые	0,9... 1,2	42... 50 Грузовые	0,55...0,8	29...40 Автобусы	0,50... 0,65	27... 33		
Табл. 6.2. Поперечные уклоны виража
Радиус	кривой, м	Поперечный уклон виража	
Менее 600		0,1	
600.	..650	0,06.	.0,05
650.	. .700	0,05.	.0,04
700.	..1000	0,04.	.0,03
1000.	..2000	0,03.	.0,02
Поскольку сползание или занос автомобиля не всегда приводят к его опрокидыванию — наиболее тяжелому случаю потери устойчивости, нужно стремиться конструировать автомобиль таким образом, чтобы потеря устойчивости начиналась с заноса. Сопоставляя выражения (6.21) и (6.22), можно сделать вывод, что это условие будет соблюдаться, если tg Ро^ср.
Рассмотрим некоторые частные случаи. При движении автомобиля по косогору Fy = 0 и у = 0. Начало опрокидывания tgp = tgpo. В соответствии с рис. 6.34,	______________
tg Ро = B/(2ftg) = Tip.
Угол ро называется углом поперечной устойчивости, а его тангенс — коэффициентом поперечной устойчивости т]р. Для того чтобы сползание автомобиля произошло раньше опрокидывания, необходимо, чтобы коэффициент его поперечной устойчивости был больше коэффициента сцепления. Поскольку коэффициент поперечной устойчивости автомобиля зависит от высоты центра масс и размера колеи, для уменьшения вероятности его опрокидывания нужно стремиться при конструировании располагать центр масс возможно ниже при максимальном использовании допустимой колеи.
В табл. 6.1 приведены показатели поперечной устойчивости, характерные для различных типов автомобилей.
Поперечная устойчивость прицепов обычно хуже поперечной устойчивости тягачей. Поэтому поперечная устойчи
вость автопоезда в целом определяется поперечной устойчивостью прицепа.
При повороте автомобиля на гори-зонтальнфй дороге р = 0. Условие движения. /без опрокидывания будет tgT = a^f<tgp0. Условие движения без заноса tgy<<p.
Если осуществляется поворот автомобиля на дороге с поперечным уклоном, условие движения без опрокидывания у<Ро + Р или avlg<Xg(р0 + Р), а условие движения без заноса y<;arctg((p+ip). Следовательно, при наличии на горизонтальных кривых поперечных уклонов (виражей) увеличивается устойчивость автомобилей на повороте по опрокидыванию и заносу: угол наклона виража суммируется с углом поперечной устойчивости автомобиля. Рекомендуемые поперечные уклоны (виражи) для дорог в районах с небольшой продолжительностью сохранения снежного покрова показаны в табл. 6.2.
В районах с продолжительным снежным покровом и частым гололедом поперечный уклон дорог не должен превышать 0,04 независимо от крутизны поворота, так как на скользкой дороге автомобили, движущиеся с малой скоростью, могут сползать вниз по крутому склону виража. В ряде государств виражи рассматривают как обязательный элемент всех закруглений дороги.
Определение коэффициента поперечной устойчивости велось в предположении, что при действии поперечных сил массы автомобиля не меняют сво-
165
Рис. 6.35. Влияние крена кузова на коэффициент поперечной устойчивости автомобиля
его относительного положения. В действительности при действии поперечной силы имеют место поворот кузова автомобиля относительно неподрессо-ренных масс, разные нормальные деформации шин по бортам, а также смещение точек приложения нормальных реакций дороги относительно серединной плоскости колес. Это обусловливает уменьшение угла между плоскостью, нормальной к опорной поверхности, и плоскостью, проходящей через центр масс и точки приложения нормальных реакций дороги. Угол поперечной устойчивости с учетом этих факторов может быть найден в соответствии со схемой, представленной на рис. 6.35:
tg Р/. = (0,5В — h-R. — /ig% — Дш)/йё, (6.23) гДе X — угол крена автомобиля вследствие различной радиальной деформации шин:
Х = сш(Вг— Rz)/B;
Дш — смещение нормальной реакции вследствие боковой деформации шин:
Дш ==z СщуВ sin а,
сш, сшу — соответственно коэффициенты нормальной и боковой жесткостей шин; Rz, Rz— нормальные реакции, вычисляемые по формулам (6.13), (6.14); F — составляющая равнодействующей силы
тяжести автомобиля и внешних сил, приложенных в центре его масс, направленная параллельно опорной поверхности (на схеме рис. 6.35 не показана).
У грузовых автомобилей и автобусов, имеющих сравнительно высокую жесткость шин, основное влияние на поперечную устойчивость оказывает крен кузова за счет деформации подвески.
При изучении устойчивости автомобиля как жесткого тела было установлено, что боковое ускорение (в долях g), при котором начинается опрокидывание при круговом движении по горизонтальной поверхности, равно коэффициенту поперечной устойчивости. Очевидно, такое же условие можно принять для оценки устойчивости автомобиля по опрокидыванию с учетом крена кузова. Таким образом, за коэффициент поперечной устойчивости с учетом крена кузова примем значение центростремительного ускорения ау (в долях g), при котором начинается опрокидывание автомобиля при его движении по круговой траектории:
W = Uy/g.
Если в Х = Лш = 0, лить из выражения (6.12), получим
Т) — аУ — ( В h	)
— — — I —- — Пх ---------
б \ 4
выражении (6.23) принять а угол крена кузова опреде-
с\~Четк I
(6.24) где Рук — ШкОу; тк — подрессоренная масса.
После преобразований выражение (6.24) можно представить в виде:
В ПР* =-----------------------.
тк
21г, + 2------
g «а cx/(g/72K) - hK
Приведенные соотношения показывают, что крен кузова существенно влияет на поперечную устойчивость автомобиля. Она в наибольшей степени за
висит от таких конструктивных параметров автомобиля, как плечо крена и
166
Рис. 6.36. Занос заднего (а) и переднего (б) мостов автомобиля
угловая жесткость подвески. Для увеличения угловой жесткости в подвеску вводят стабилизаторы, представляющие собой торсионные валы, которые закручиваются при крене кузова. При наезде колесами одной из сторон автомобиля на неровности дороги на кузов передаются возмущения, вызывающие его поперечно-угловые колебания. Эти колебания тем больше, чем выше угловая жесткость подвески. Поэтому жесткость стабилизатора не должна быть излишне большой. Ее подбирают таким образом, чтобы при установке стабилизатора крен уменьшался на 20...40 %.
Занос автомобиля, как правило, начинается с заноса переднего или заднего мостов. Поэтому при изучении устойчивости автомобиля рассматривают устойчивость движения каждого моста.
Поскольку, как это следует из формул (6.10), при повороте автомобиля боковые реакции дороги распределяются пропорционально нагрузке, приходящейся на мосты, наиболее вероятным является занос заднего моста. Это происходит вследствие того, что задний мост передает силу тяги, умень
шающую боковую реакцию, реализуемую по сцеплению.
Занос заднего моста у большинства автомобилей не только более вероятен, но и более опасен (рис. 6.36). Допустим, что автомобиль движется прямолинейно со скоростью и. С этой скоростью перемещаются центры передних и задних мостов. При возникновении заноса центр моста, совершающего занос, приобретает скорость v3, вектор которой направлен перпендикулярно к продольной оси автомобиля. Вектор результирующей скорости Dp составляет некоторый угол с продольной осью автомобиля. Это приводит к повороту автомобиля относительно мгновенного центра О и возникновению центробежной силы Fj. В случае заноса заднего моста центробежная сила создает момент, стремящийся увеличить занос. При заносе переднего моста центробежная сила создает момент, противодействующий повороту передней части автомобиля в сторону заноса. Поэтому занос переднего моста гасится автоматически. Для гашения начавшегося заноса заднего моста обычно рекомендуют поворачивать управляемые колеса в сторону заноса так, чтобы центр поворота автомобиля оказался бы на той стороне автомобиля, в которую начался занос заднего моста. Возникающая при этом центробежная сила будет направлена в сторону, противоположную заносу, и занос прекратится.
Поэтому с точки зрения устойчивости по заносу на повороте и лучшей поворотливости предпочтительно создавать автомобили с передними ведущими и управляемыми колесами.
ПРОХОДИМОСТЬ АВТОМОБИЛЯ
7.1.	Основные определения
Под проходимостью понимается способность автомобиля перевозить с высокой средней скоростью груз, пассажиров или специальное оборудование в тяжелых дорожных или внедорожных условиях. Проходимость автомобиля — комплексное свойство, характеризующее его подвижность и экономичность. Оно неразрывно связано со способностью автомобиля наиболее эффективно выполнять транспортную работу в заданных дорожных условиях.
По уровню проходимости автомобили принято делить на три категории: ограниченной, повышенной и высокой проходимости.
Автомобили ограниченной проходимости (дорожные автомобили) предназначены для эксплуатации на дорогах с твердым покрытием и грунтовых дорогах в сухое время года. При использовании дополнительных средств (цепи противоскольжения, арочные шины) они могут работать и в более сложных условиях. Сюда относятся неполноприводные автомобили типа 4X2, 6X2, 6x4, 8X4.
Автомобили повышенной проходимости конструктивно незначительно отличаются от дорожных. Как правило, такие автомобили создаются на базе дорожных, а повышение проходимости обеспечивается приводом на все колеса, постановкой
дополнительной раздаточной коробки, использованием шин с пониженным или регулируемым давлением воздуха. В некоторых случаях устанавливают блокируемые дифференциалы или дифференциалы повышенного трения, лебедки и другие приспособления для преодоления препятствий.
Автомобили высокой проходимости создаются специально для работы в условиях бездорожья, они должны обладать способностью преодолевать встречающиеся на местности препятствия: канавы, вертикальные уступы, подъемы и др.
В отдельную группу по проходимости выделяются специальные автомобили. Они создаются для эксплуатации в определенных условиях: Крайнего Севера, на заболоченной или песчаной местности и др. Такие автомобили имеют особую компоновку и, как правило, специальные типы движителей.
Автомобиль или автопоезд может потерять подвижность вследствие: задевания выступающими частями за неровности дорожной поверхности, опасности опрокидывания или невозможности преодоления подъемов или из-за недостаточной окружной силы на ведущих колесах для преодоления сопротивления движению на поверхностях со слабой несущей способностью.
В соответствии с этим различают препятствия, обусловленные профилем местности и вызванные слабой несущей способностью опорной поверхно
168
сти. Способность автомобиля преодолевать названные препятствия оценивается профильной и опорно-сцепной проходимостью. На труднопроходимых маршрутах встречаются те и другие виды препятствий. Поэтому проходимость автомобиля в целом зависит от его профильной и опорно-сцепной проходимости.
7.2.	Профильная проходимость
Профильная проходимость зависит от компоновки автомобиля и оценивается геометрическими параметрами проходимости, которые определяют по компоновочным чертежам или путем измерения натурных образцов. Все измерения проводятся при полной нагрузке автомобиля на горизонтальной площадке с твердым и ровным покрытием. Геометрические параметры проходимости автомобиля показаны на рис. 7.1.
Дорожный просвет (й) — расстояние от опорной поверхности до
наиболее низкой точки автомобиля, расположенной между колесами. Обычно это точки под картерами главных передач ведущих мостов и в местах расположения рессор. В технических характеристиках автомобилей могут приводиться несколько значений дорожного просвета. Например, дорожный просвет под передним й] и задним й2 мостами. У современных легковых автомобилей дорожный просвет составляет 150...220 мм, автобусов — 220...300 мм, а у грузовых автомобилей ограниченной и повышенной проходимости — 240...300 мм. В нормативах СЭВ рекомендуется для грузовых автомобилей обеспечивать дорожный просвет не менее 270 мм. У автомобилей высокой проходимости за счет применения колесных передач и крупноразмерных шин дорожный просвет достигает 400...500 мм.
Передним (yi) и задним (у2) углами свеса ограничивается проходимость автомобиля при проезде через канавы, пороги, крутые
Рис. 7.1. Геометрические параметры проходимости автомобиля
169
Табл. 7.1. Углы свеса и радиусы проходимости дорожных автомобилей
Тип автомобиля
Угол свеса передний, град.
Угол свеса задний, град.
Радиус проходимости, м
Легковые Грузовые Автобусы
15...20
45
6...20
3...8
2,5...6
4...9
20...30
40...60 25
10...40
Рис. 7.1. Схема определения углов перекоса мостов автомобиля
переломы. Углы свеса — это углы между плоскостью опорной поверхности и плоскостью, касающейся колес и наиболее выступающей точки автомобиля. Большие углы свеса обеспечивают возможность преодоления автомобилем крутых препятствий, не задевая их. Наибольшие углы свеса имеют автомобили высокой проходимости: передний 60...70° и задний 50...60°.
Продольный радиус проходимости —радиус условной цилиндрической неровности, через которую автомобиль может проехать, не задевая ее наинизшей точкой, расположенной в его средней части. Чем меньше RL, тем более крутые неровности может автомобиль преодолеть. Продольный радиус проходимости может быть определен по компоновочному чертежу или экспериментально. При этом можно использовать формулы:
Rl = 0,5Е + V 0,25Е2 + Н
Е= (0,25 L2+/i2-«.2-2r/i)/(2/i);
H = n2(h-r)/(2h).
Смысл величин этих формул показан на рис. 7.1.
Характерные радиусы продольной проходимости и углы свеса дорожных автомобилей приведены в табл. 7.1.
В некоторых случаях для оценки проходимости автомобилей через препятствия, соизмеримые с колеей автомобиля, используют понятие поперечный радиус проходимости (Яв) (см. рис. 7.1).
Способность автомобиля приспосабливаться к неровностям местности без потери контакта колес с дорогой зависит от возможных углов перекоса мостов. Угол перекоса находится как сумма углов перекоса переднего и заднего мостов относительно горизонтальной плоскости (рис. 7.2). У автомобилей, имеющих ведущие мосты, которые сгруппированы в балансирную тележку, определяют также возмож
ные углы перекоса мостов тележки.
Способность автопоезда двигаться по пересеченной местности оценивается углами гибкости в вертикальной плоскости. Схема их определения показана на рис. 7.3. По существующим нормативам угол гибкости g у автопоезда с двухосным прицепом должен быть не менее ±62°, а у седельного автопоезда — ±8°.
Способность автомобиля или автопоезда маневрировать в ограниченном пространстве характеризуется минимальным радиусом поворота и шириной габаритного коридора поворота. Методы нахождения этих характеристик приводились в параграфе 6.1. Для автопоездов дополнительно определяют углы гибкости в горизонтальной плоскости. Они должны быть не менее 55° у автопоездов с двухосными прицепами и 90° — у седельных автопоездов.
Профильная проходимость автомобилей в значительной мере определяется их способностью преодолевать отдельные препятствия.
Максимальный подъем, который
170
Рис. 7.3. Схема определения углов гибкости автопоезда в вертикальной плоскости
автомобиль может преодолеть, зависит от окружной силы, развиваемой ведущими колесами, и от угла его продольной устойчивости — угла между плоскостью, нормальной к опорной поверхности и проходящей через центр масс, и плоскостью, проходящей через центр масс и точки контакта задних колес с дорогой. Этот угол определяет возможность опрокидывания автомобиля относительно задней оси. У автомобилей обычной компоновки он всегда больше угла максимального подъема, преодолеваемого ими, и поэтому опрокидывание относительно задней оси оказывается практически невозможным. Только для автомобилей специальной компоновки с очень высоким расположением центра масс следует анализировать устойчивость при преодолении максимальных подъемов. Максимальная окружная сила, развиваемая ведущими колесами автомобиля, как правило, ограничена сцеплением ведущих колес с опорной поверхностью. Иногда у дорожных автомобильных поездов она ограничивается вследствие недостаточного крутящего момента, передаваемого через трансмиссию к • ведущим колесам. В этом случае максимальный преодолеваемый подъем может быть найден из соотношения imax = Dmax. Найдем максимальный угол подъема, преодолеваемого автопоездом с тягачом 4X2, при условии, что его значение ограничено сцеплением ведущих колес с опорной поверхностью. Примем, что
Рис. 7.4. Силы и моменты, действующие на автомобиль-тягач при преодолении максимальных подъемов
сцепление под обоими колесами моста одинаково. Ввиду малой скорости автопоезда при преодолении максимальных подъемов Fa = Fj=Q. Схема сил и моментов, действующих на тягач, показана на рис. 7.4.
Сумма проекций всех сил на опорную плоскость:
FK=g7nasin а+Л®.	(7.1)
Сумма моментов относительно оси, проходящей через точки контакта передних колес с опорной поверхностью:
Rz2L = Mfi 4- Af/2 + gmahgsm а 4-
+ gmao,cos а + Т^крйкр. .(7-2)
Решая совместно уравнения (7.1) и (7.2) и учитывая, что FK шах — фТ?г2 и FKP=g'mnsin a + fgmncos а, получаем
одиночного автомобиля
Для
(Ткр = 0)
171
Если тягач имеет привод на все мосты (FK=q>magcosa),
/	. т„ \ // т„ \
tg amax = I <р — f-\	1 4----.
\	ma // \ ma /
Для одиночного полноприводного автомобиля tgamax = <p.
Автомобили и автопоезда способны преодолевать подъемы по твердым склонам (<р = 0,6...0,75) следующей крутизны: автопоезда с неполноприводными тягачами— 11...13°; одиночные неполноприводные автомобили — 20...25; автопоезда с полноприводными тягачами — 15...20; полноприводные одиночные автомобили — 27...35°.
Нормативными документами определено, что автомобильные поезда должны преодолевать подъемы с твердой опорной поверхностью крутизной не менее 18 % (10,2°), а одиночные автомобили — 25 % (14°).
Спуск опасен тем, что на нем возможно опрокидывание автомобиля относительно передних колес. У автомобилей обычной компоновки при равномерной скорости движения потеря устойчивости вследствие опрокидывания может произойти лишь на спусках крутизной более 45°. Если же автомобиль на спуске встречает препятствие, возникает инерционная сила, направление которой совпадает с направлением движения автомобиля. В силу увеличения опрокидывающего момента вероятность опрокидывания возрастает. Аналогичные явления происходят при резком торможении на спуске. Опрокидывание автомобиля может произойти также и в конце спуска, когда сопротивление движению в момент перехода с наклонного участка на горизонтальный резко возрастает. При опрокидывании автомобиля в рассматриваемых условиях затрачивается энергия на подъем центра масс за счет кинетической энергии автомобиля. Поэтому для уменьшения вероятности опрокидывания скорость спуска не должна быть большой. Расчеты пока
зывают, что для автомобилей обычной компоновки при предельных углах спуска до 30° скорость движения во избежание опрокидывания не должна превышать 10 км/ч.
Условия движения автомобилей по косогору были рассмотрены в параграфе 6.6. Потеря устойчивости движения может произойти вследствие опрокидывания автомобиля (tg р > или сползания (tg р > <р).
Возможность преодоления рва определяется числом и расположением мостов, размером колес и положением центра масс автомобиля по базе. Для двухосных и трехосных автомобилей' (если центр масс расположен не над средним мостом) ширина преодолеваемого рва зависит от размеров колес. Испытания показывают, что такие автомобили способны преодолеть ров с прочными кромками шириной до 1... 1,3 радиуса колеса (большие значения относятся к автомобилям со всеми ведущими колесами).
Для трехосных автомобилей с равномерным расположением мостов и четырехосных ширина преодолеваемого рва может быть значительной и определяется базой автомобиля, расстановкой колес и положением центра масс по длине. Схема проезда рва многоосным автомобилем показана на рис. 7.5.
Высота йп преодолеваемого автомобилем порогового препятствия (рис. 7.6) зависит главным образом от размера колеса и жесткости кромки порога. Максимальная высота преодолеваемого неполноприводными автомобилями порога составляет 0,3...0,5 радиуса колеса, а полноприводными — 0,5...0,8.
Максимальная глубина преодолеваемого брода зависит от конструкции автомобиля. Лимитирующими элементами при твердом основании брода являются уровни расположения лопастей вентилятора, всасывающего патрубка, аккумулятора, генератора, системы зажигания, воздухосоединитель-
172
Рис. 7.5. Проезд рва многоосным автомобилем
Рис. 7.6. Преодоление автомобилем порогового препятствия
ных отверстий картеров механизмов трансмиссии. Для увеличения глубины преодолеваемого брода у автомобилей повышенной и высокой проходимости выходы всасывающих и выхлопных патрубков стремятся расположить высоко, вентилятор изготовляют с отключающимся приводом, а генератор, систему зажигания, картеры мостов и колесные тормоза — герметичными. При таком конструктивном выполнении автомобили могут преодолевать брод глубиной до 1,6...1,8 м.
7.3.	Опорно-сцепная проходимость
Опорно-сцепная проходимость автомобиля зависит от эффективности использования несущих свойств грунта и определяется главным образом конструкцией движителя и трансмиссии автомобиля. Опорно-сцепная проходимость зависит также от формы корпуса, типа подвески, удельной мощности автомобиля и др.
Грунты и снег относятся к диспер
сным средам, основным отличием которых от сплошных является то, что находящиеся в них твердые частицы не образуют сплошной массы, а занимают лишь часть объема. При этом прочность связи между отдельными частицами значительно меньше прочности материала этих частиц. При действии внешней нагрузки происходят перемещения, сдвиги отдельных твердых частиц относительно друг друга.
По составу различают минеральные грунты и грунты органического происхождения. Минеральные грунты подразделяются на ряд категорий. В основу такого деления положены размеры и соотношение частиц двух фракций: глинистой и песчаной. Классификация по этим признакам называется гранулометрической. В зависимости от относительного содержания глинистых и песчаных фракций минеральные грунты делятся на глины (содержание глинистых частиц по массе более 30 %), суглинистые грунты — (10...30 %), супесчаные (3...10 %) и песчаные (менее 3 %).
Грунты, состоящие из отложений частиц органического вещества, занимают особое место. К ним относятся различные виды торфяно-болотных и илистых грунтов, которые различаются по влажности, составу и происхождению.
Механические свойства грунтов в большой степени зависят от их влажности. При незначительном увлажнении связных грунтов вода находится в них в виде тонких пленок или заполняет тончайшие волосяные промежутки между частицами. В таком состоянии она малоподвижна, слабо испаряется и способствует повышению связности грунта.
С повышением содержания воды заполняются более крупные поры грунта и увеличивается толщина водяных пленок на его частицах. Превышение определенных пределов влажности, характерных для каждого грунта,
173
ведет к резкому изменению некоторых его свойств. Поэтому состояние связных грунтов характеризуется степенью их влажности, которая оценивается относительной влажностью W — отношением массы воды, содержащейся в грунте, к массе сухого грунта:
W— (т—т0)/т0,
где т — масса пробы грунта в естественном состоянии; т0 — масса высушенной пробы.
В зависимости от влажности грунт может находиться в трех состояниях: твердом, пластичном и текучем. Самые неблагоприятные условия для движения автомобилей создаются при текучем состоянии грунта. Такое переувлажненное состояние характерно для весенней и осенней распутицы и в периоды сильных дождей. Глубина переувлажненного слоя весной (в конце периода оттаивания грунта) доходит до 30...50 см, осенью (в период длительных дождей) — до 20...30 см.
Свойства песчаных (несвязных) грунтов мало зависят от влажности. С увеличением влажности их сопротивляемость внешним нагрузкам несколько возрастает, а затем при достижении предела текучести вновь уменьшается. Состояние песчаных грунтов характеризуется их плотностью, оказывающей наибольшее влияние на механические свойства.
Механические свойства заболоченных грунтов определяются прочностью и толщиной дернового слоя.
При воздействии движителя транспортной машины на грунт в нем возникают деформации. Размеры и характер деформаций обусловлены действием внешних и внутренних сил, а также изменением среднего расстояния между частицами. Если после устранения внешнего воздействия частицы грунта вернутся в первоначальное положение, деформация считается упругой, если положение частиц отличается от первоначального, имеет место остаточная
Рис. 7.7. Характерная зависимость давления на грунт от глубины погружения штампа
деформация. Если остаточная деформация равна общей, такую деформацию называют пластической.
В наибольшей степени проходимость автомобилей зависит от механических свойств грунтов — сопротивления сжатию, а также сдвигу и срезу.
Сопротивление грунта сжатию определяют экспериментально путем вдавливания в грунт специальных штампов. При этом измеряют нагрузку, приходящуюся на штамп, и его осадку — глубину погружения. По результатам измерений строят зависимости нормального напряжения <т, равного давлению q, передаваемому от штампа на грунт, от осадки штампа h. Характерная зависимость между глубиной погружения штампа и нагрузкой показана на рис. 7.7. При относительно малых нагрузках деформация грунта при уплотнении практически линейно зависит от нагрузки (участок 0—1). Второй участок (/—2) характеризуется не только уплотнением грунта, но и сдвигом его частиц. При нагрузках, соответствующих этому участку, сопротивление уплотнению больше, чем сопротивление боковому сдвигу. По мере повышения нагрузки увеличивается объем грунта, сдвигаемый в стороны. Это приводит к прогрессирующему увеличению осадки штампа. На третьем участке погружение штампа происходит исключительно за счет развития деформаций сдвига. Штамп резко по-
174
Рис. 7.8. Экспериментальная зависимость несущей способности грунтов от их относительной влажности:
глина; 2— суглинок; 3 — супесь; 4 — песок
гружается в грунт. При этом наблюдается выпирание грунта сбоку от штампа. Напряжение или соответствующее ему давление условно характеризует начало текучести грунта и называется пределом несущей способности </т. Несущая способность грунта в сильной степени зависит от его влажности (рис. 7.8).
Из большого числа формул, описывающих связь деформации и давления (напряжения), широко известна следующая:
q = С№,
Сиц — параметры, зависящие от состава грунта, его влажности и размеров штампа.
Проф. В. В. Кацыгиным предложена зависимость:
о = o0th —h,
По
где По — несущая способность грунта, соответствующая пределу текучести 7Т; к0—коэффициент объемного смятия грунта, численно равный тангенсу угла наклона касательной к кривой деформации грунта в начале координат (см. рис. 7.7).
Несущая способность глинистых грунтов в зависимости от влажности
Рис. 7.9. Схема определения сопротивления грунта сдвигу (а) и характерная зависимость сопротивления сдвигу от деформации грунта (б):
1 — глина; 2 — песок
может изменяться в пределах 0,01... 1 МПа, а у песчаных — 0,03...0,1 МПа.
Сопротивление грунта сдвигу можно определить экспериментально, если к штампу, нагруженному вертикальной силой Fz, приложить горизонтальную силу Т (рис. 7.9).
Сопротивление грунта сдвигу определяется силами сцепления частиц, обусловленными молекулярным и капиллярным взаимодействием воды, и силами трения между частицами. Силы сцепления частиц зависят от влажности грунта и практически не зависят от давления, а силы трения обусловлены сцеплением частиц между собой и могут возникать только при наличии внешней нагрузки.
Таким образом, в общем случае сопротивление грунта сдвигу
T=c0A + fBFz,	(7.3)
где с0 — удельная характеристика
175
Табл. 7.2. Характеристики грунтов
Вид грунта	Несущая способность б0, МПа	Внутреннее сцепление с0> МПа	Коэффициент внутреннего трения
Супе- счаный 0,25...0,5 0,035...0,07 0,4...0,45 Сугли- нистый 0,35...0,6 0,04...0,08 0,3.-.0,4 Глина 0,35...0,7 0,05.. .0,1	0,2. ..0,3			
сцепления между частицами грунта; А — площадь сдвига грунта, равная площади штампа; fB — коэффициент внутреннего трения грунта; Fz— нормальная сила, действующая на штамп.
Разделив все члены выражения (7.3) на А, получим:
т^Со+qfs,	(7-4)
где т — удельное сопротивление сдвигу; q — давление на грунт.
Сопротивление сдвигу зависит от гранулометрического состава и влажности грунта. Так, для песков сопротивление сдвигу практически определяется только внутренним трением, поэтому оно пропорционально давлению. Для глин, наоборот, сопротивление сдвигу в основном определяется сцеплением, которое резко уменьшается с увеличением их влажности.
На рис. 7.9, б показана характерная зависимость деформации грунта от сдвигающего усилия. В первый момент происходит уплотнение грунта и сопротивление возрастает до максимального значения, равного сумме сил сцепления Тс и внутреннего трения Tf. При дальнейшем увеличении деформаций начинается относительное перемещение частиц грунта и его сопротивление становится равным силе внутреннего трения.
В табл. 7.2 показаны некоторые характеристики связных грунтов при влажности, близкой к пределу пластичности.
Песчаные грунты в зависимости от зернистости имеют /в = 0,6...0,8 и с0 =
= (0,001...0,008) МПа. Если штамп углублен в грунт на глубину Н, помимо сдвига грунта происходит его срез по боковым граням. Усилие (Я), необходимое для среза грунта:
Fcp=TcpH,	(7.5)
где Тер — удельное сопротивление срезу, Н/м.
Суглинистые грунты имеют сопротивление срезу 1,2...2 кН/м, а супесчаные— 1,5...2,6 кН/м.
Сопротивление качению колеса по деформируемым грунтам обусловлено затратами энергии на деформацию и перемещение грунтовой массы и гистерезисными потерями при деформировании резины. У недеформируемого колеса сопротивление качению определяется только объемом деформируемого и перемещаемого грунта. Сила сопротивления качению жесткого колеса
Ff^0,5kzbh2,	(7.6)
где h — глубина колеи; b — ширина колеи; kz — коэффициент объемного сжатия грунта, приведенный к размерам колеса: kz = O,O\ko(bD)~42; k0 — коэффициент объемного сжатия грунта, найденный с помощью плотномера малой площади; D — диаметр жесткого колеса.
Глубина следа колеса з /	^2
Л = ]/ <7-7>
С учетом выражения (7.7) преобразуем формулу (7.6):
Ff = 0,5 |/ГЖ&Д2);	(7.8)
f = 0,5^FJ(kzbD2).
Эксперименты показывают, что сопротивление качению колеса с пневматической шиной по деформируемым грунтам на 40...70 % меньше сопротивления качению жесткого колеса равного диаметра, так как при качении пневматического колеса по мягкому грунту происходит деформация шины
176
Рис. 7.10. Схема определения приведенного радиуса жесткого колеса
и колесо контактирует с грунтом на большей площади. Это позволяет рассматривать качение пневматического колеса по деформируемому грунту как качение жесткого колеса, радиус которого соответствует радиусу кривизны поверхности контакта деформируемого колеса. Радиус жесткого колеса, эквивалентного деформируемому, в соответствии с рис. 7.10 можно определить из соотношений:
АВ = У ^ — {ro — h — h^ =
— У гпр — (/пр F)2 ,
Гпр = ro(l-M/i). (7.9)
Сопротивление качению пневматического колеса может быть найдено по выражениям (7.6) и (7.8), если в них вместо диаметра колеса поставить приведенный диаметр, определенный по формуле (7.9). Сопротивление качению, найденное указанным методом, будет меньше реального, поскольку при выводе формул не учитывались затраты энергии на радиальную и тангенциальную деформацию шины. Аналитически учесть влияние этих факторов трудно. Поэтому обычно сопротивление качению колеса определяют экспериментально и по результатам опытов находят эмпирические формулы, связывающие сопротивление качению и основные
параметры колеса и грунта. Одна из наиболее часто употребляемых зависимостей имеет вид:
з / f з / п
F'-C'V 7>+cq/	(7-10)
где Ff — сопротивление качению, кН; С] и С2 — опытные коэффициенты, зависящие от конструкции шины; их средние значения С'1 = 0,0031, 02=0,0425; рв — давление воздуха в шинах, МПа; Fz—нагрузка на колесо, кН; D — наружный диаметр колеса, м; <т0 — несущая способность грунта, МПа.
Первое слагаемое в этой формуле определяет сопротивление качению, обусловленное деформацией колеса, а второе — грунта. При плотных грунтах основную роль играет первое слагаемое, а при мягких — второе.
Окружное усилие, которое может реализовать колесо на деформируемом грунте, определяется сопротивлением грунта смятию и срезу. В соответствии с выражениями (7.3) и (7.5) окружная сила на ведущем колесе
F.-., — Fuf + Fcp + Fem где FKf — сила, обусловленная внутренним трением в грунте: FKf=f3Fz; Fcp — сила сопротивления грунта срезу: 7?Ср = тЯ; Fcm — сила, определяемая сцеплением частиц грунта: FCM=CoA.
Сцепление колеса со связным грунтом осуществляется главным образом за счет сопротивления частиц грунта сдвигу и срезу. Поэтому окружная сила определяется площадью контакта колеса с опорной поверхностью и высотой грунтозацепов. При движении по несвязным грунтам максимальная окружная сила зависит от внутреннего трения частиц грунта, так как сопротивление сдвигу у таких грунтов незначительное. Грунтозацепы при этом оказывают отрицательное влияние: они разрушают поверхностный слой, а при пробуксовке колеса выгребают грунт, увеличивая глубину колеи.
Потеря проходимости автомобилем произойдет в том случае, если окруж-
7 А. И. Гришкевич
177
б
Рис. 7.11. Арочная шина (а) и пневмокаток (б)
ная сила на ведущих колесах окажется меньше силы сопротивления качению. Сопротивление качению, а также реализуемая окружная сила при качении колеса по определенной поверхности зависит от характеристик шин.
Основными параметрами шин, определяющими характер их взаимодействия с опорной поверхностью, являются наружный диаметр и форма поперечного сечения шины. Шины в зависимости от отношения ширины профиля В к его высоте Н делят на четыре типа: тороидные (В/Я=0,9...1,1), широкопрофильные (В/Н= 1,1...1,6), арочные (В/Н= 1,6...2,5), пневмокатки (В/Я=2,5...1О).
Тороидные шины с нерегулируемым давлением устанавливают обычно на дорожных автомобилях. Радиальная деформация их под номинальной нагрузкой не превышает 12... 15 % высоты профиля. Поэтому опорная площадь небольшая и соответственно давление относительно высокое. Рисунок протектора, как правило, дорожный, мелкий. Такие шины на деформируемых грунтах не обеспечивают высокой проходимости автомобиля.
В настоящее время изготовляют тороидные шины, способные работать при переменном давлении (шины с ре
гулируемым давлением). Эти шины, установленные на автомобилях повышенной проходимости, обеспечивают их движение по грунтам со слабой несущей способностью.
Широкопрофильные шины первоначально создавались как специальные шины для автомобилей повышенной и высокой проходимости. При нормальном давлении воздуха опорная площадь у широкопрофильных шин на 30...35 % больше, чем у тороидных такой же грузоподъемности. При понижении давления опорная площадь увеличивается более чем в два раза. Рисунок протектора характерен для шин высокой проходимости. В последнее время широкопрофильные шины применяются также и для дорожных легковых и грузовых автомобилей. Такие шины работают при постоянном давлении воздуха в них. Рисунок протектора — дорожный.
Арочные шины (рис. 7.11) имеют профиль в виде арки и сильно развитые грунтозацепы. Работают при постоянном давлении воздуха 0,05...0,15 МПа. Это позволяет обеспечить относительно низкое давление на грунт и хорошее сцепление колес. Скорость движения автомобилей по твердым дорогам ограничена. Такие шины приме
178
няют в основном как средство для повышения проходимости автомобилей в определенные сезоны года, устанавливая их вместо сдвоенных колес.
Пневмокатки (см. рис. 7.11) —специальные шины, имеющие тонкую резинокордную оболочку и работающие при малом внутреннем давлении воздуха (0,02...0,1 МПа). Применяются только на специальных машинах, предназначенных для движения в особо трудных условиях.
Наиболее труднопроходимые для автомобиля грунтовые и заснеженные поверхности в первом приближении могут быть сведены к четырем видам, различным по физико-механическим свойствам и характеру взаимодействия с движителем: переувлажненный грунт, болото, сухой песок, снег.
Движение по переувлажненному грунту сопровождается образованием колеи, глубина которой оказывает непосредственное влияние на сопротивление качению. Из формулы (7.7) следует, что глубина колеи зависит от диаметра колеса D, ширины профиля В и нагрузки на колесо Fz. Этими параметрами определяется среднее давление колеса на грунт. Если бы шина была абсолютно эластичной, давление колеса на грунт определялось бы давлением воздуха в шине. Поскольку часть нагрузки передается через каркас шины, давление на грунт зависит от соотношения жесткости шины и грунта.
Если жесткость шины больше, чем жесткость грунта, она будет погружаться в грунт не деформируясь, т. е. пневматическая шина будет работать как жесткое колесо. Если же жесткость шины меньше жесткости грунта, шина деформируется. Это приведет к увеличению поверхности контакта шины с грунтом, уменьшению на него давления и сопротивления качению. На деформируемых грунтах площадь опорной поверхности может быть увеличена за счет увеличения ширины шины и ее диаметра и уменьшения давления воз
7*
духа в ней. Наиболее предпочтительным является увеличение диаметра колеса и снижение внутреннего давления в шине, так как с увеличением ее ширины растет объем деформируемого грунта и тем самым увеличивается сопротивление качению. Поскольку при уменьшении давления воздуха в шине площадь контакта растет в большей степени по длине, для повышения проходимости автомобиля целесообразно применять шины, давление воздуха в которых можно уменьшать при движении по деформируемым поверхностям.
Как следует из формулы (7.10), коэффициент сопротивления качению по деформируемым грунтам определяется гистерезисными потерями энергии в шине и затратами ее на перемещение и деформацию грунта. На рис. 7.12 показана зависимость коэффициента сопротивления качению колес по деформируемым грунтам от внутреннего давления в шине. Минимальное сопротивление качению соответствует определенному давлению воздуха в шине. При увеличении давления воздуха в шине свыше этого значения сопротивление качению возрастает из-за увеличения глубины следа (колеи), а при уменьшении — из-за большой деформации шины.
Очевидно, что для каждого типа и состояния грунта может быть найдено оптимальное давление воздуха в шине, при котором сопротивление качению будет минимальным. Оптимальное давление обеспечивается при установке на автомобилях повышенной и высокой проходимости систем регулирования давления воздуха в шинах.
Возможность движения по деформируемым грунтам определяется также реализуемой окружной силой, максимальное значение которой по аналогии со случаем качения колеса по недеформируемой поверхности будем характеризовать коэффициентом сцепления
ф = Ек(ртах/^г-
179
Рис. 7.12. Зависимость коэффициента сопротивления качению от давления воздуха в шине: 1 — сухой песок; 2 — снег зернистый; 3 — разрыхленный влажный песок; 4 — переувлажненная грунтовая дорога
Рис. 7.13. Рисунки протектора шин для автомобилей высокой и повышенной проходимости: а — прямая елка; б, в—косая; г — расчлененная
При движении по связным грунтам коэффициент сцепления в значительной степени зависит от давления воздуха в шине, размеров и формы грунтозацепов. С уменьшением давления в шине увеличивается площадь контакта и большее число грунтозацепов вступает в работу. Форма грунтозацепов оказывает влияние на сцепление, самоочи-щаемость и эластичность шины. На рис. 7.13 показаны наиболее распространенные формы протектора шин автомобилей, эксплуатируемых на мягких
грунтах. При грунтозацепах с наклонной упорной поверхностью повышается уплотнение грунта между ними, вследствие чего возрастает сопротивление грунта срезу. Сужение грунтозацепа к вершине, а также расположение грунтозацепов под углом 45° к продольной оси шины способствует самоочищаемо-сти протектора и обеспечивает хорошее сцепление ее с грунтом во всех направлениях.
При качении шины с сильно расчлененным протектором по твердой дороге возникают вибрации колеса при ударах грунтозацепов о поверхность дороги. Для устранения этого явления у автомобилей, предназначенных для работы по бездорожью и твердым дорогам, применяются шины с универсальным протектором, у которых безударное качение обеспечивается за счет применения сплошного пояса в средней части беговой дорожки.
Если толщина слоя переувлажненного грунта невелика, иногда целесообразно увеличивать давление воздуха в шинах. При этом колесо прорезает переувлажненный слой и входит в контакт с твердым основанием. Это обеспечивает возможность создания большой окружной силы колеса.
Песок и сухой кристаллический снег относятся к несвязным грунтам. Несущая способность их определяется в основном коэффициентом внутреннего трения. Низкая проходимость автомобиля наблюдается только при достаточно большой толщине слоя песка или снега. Если слой песка или снега небольшой толщины лежит на прочном основании, сопротивление качению незначительно. Уменьшить сопротивление качению по слою несвязного • грунта большой толщины можно главным образом за счет уменьшения давления воздуха в шинах. На рис. 7.14 показана зависимость сопротивления качению колеса по сухому песку от давления воздуха в шине при различных нагрузках на колесо.
180
Рис. 7.14. Зависимость коэффициента сопротивления качению по песку от давления воздуха в шине:
I —Рв=0,6 МПа; 2 — рв=0,4 МПа; 3—рв=0,2МПа
Сцепление колес с песчаным грунтом также определяется в основном внутренним трением в грунте. В зависимости от давления на грунт коэффициент сцепления шин с сухим песком Ф=0,2...0,7.
С началом буксования колеса происходит сдвиг песка. Это приводит к увеличению глубины колеи. В этом случае наличие грунтозацепов обусловливает разрыхление верхнего слоя грунта и увеличение глубины колеи. Поэтому наилучшей проходимостью по песку обладают машины, оборудованные пневмокатками с малым давлением воздуха в них и грунтозацепами малой высоты. При преодолении участков сыпучих песков из-за опасности их разрыхления не рекомендуется переключать передачи, маневрировать и останавливаться. Трогание автомобиля с места должно осуществляться плавно, без пробуксовывания колес.
Сыпучий снег характеризуется очень малым коэффициентом внутреннего трения. В связи с этим преодоление участков глубокого сыпучего снега возможно только при специальных конструкциях колесных движителей, обеспечивающих давление на грунт не
более 0,01 МПа. При движении по уплотняющемуся снегу проходимость автомобиля обеспечивается теми же способами, что и при движении по уплотняющимся грунтам.
Особую трудность представляют для автомобилей заболоченные участки. Обычно преодоление таких участков возможно, если колеса автомобиля не прорезают верхний слой, связанный корнями растений. Поэтому при проезде таких участков давление от ходовой части на опорную поверхность должно быть минимальным, а окружное усилие на ведущих колесах — постоянным или плавно изменяющимся.
Опорно-сцепная проходимость автомобиля зависит от схемы и типа трансмиссии. Тип трансмиссии определяет плавность передачи крутящего момента от двигателя к ведущим колесам. С этой точки зрения наиболее неблагоприятной является механическая трансмиссия, при которой возможны разрывы потока мощности при переключении передач, резкие колебания и броски крутящего момента при трогании с места. Гидродинамические, гидрообъемные и электрические трансмиссии обеспечивают плавную передачу крутящего момента к ведущим колесам. Это способствует уменьшению динамических воздействий на грунт и тем самым повышению проходимости автомобиля. У автомобилей повышенной и высокой проходимости все колеса являются ведущими. В приводе к ведущим колесам обычно используют межколесные и межосевые дифференциалы. При наличии межколесного дифференциала максимальное окружное усилие, развиваемое колесами моста, ограничивается сцеплением колеса, находящегося на поверхности с наименьшим коэффициентом сцепления. Допустим, что колеса ведущего моста автомобиля располагаются на поверхностях с коэффициентами сцепления cpi и ср2 (ф1<ф2)- Тогда максимальное окружное усилие, развиваемое колеса-
181
Рис. 7.15. Схема привода к ведущим колесам автомобиля 4X4:
/—двигатель; 2— раздаточная коробка; 3 — главная передача;-/ — карданная передача
ми моста автомобиля при блокировке межколесного дифференциала.
Fk<p = 0,5 (Ф1 + ф2) Fz, (7.11) где Fz — нагрузка на мост.
Если межколесный дифференциал имеет коэффициент блокировки йд, окружное усилие, развиваемое колесом, которое находится на участке с меньшим коэффициентом сцепления, FKl = = 0,5ф1Д.
Усилие, развиваемое колесами моста автомобиля, определяется из соотношений:
FKq> = FKi + Fk2; йд = Fk2/Fk<p;
FK(p = 0,5?lFz/(l-^).	(7.12)
Усилие, найденное по формуле (7.12), не может быть больше определенного по формуле (7.11).
При установке межосевых дифференциалов суммарное окружное усилие, развиваемое всеми колесами автомобиля, будет определяться максимальным окружным усилием колеса, находящегося в наиболее неблагоприятном с точки зрения сцепления положении, и коэффициентами блокировки дифференциалов. При блокированных же межосевых и межколесных дифференциалах максимальное окружное усилие колес автомобиля будет равно сумме окружных усилий всех ведущих колес. Поэтому в трудных условиях движения при блокированном приводе проходимость автомобиля будет, как правило, лучшей, чем при дифференциальном.
В случае движения автомобиля с блокированным приводом по дороге с малым сопротивлением привод к ве-з дущим колесам нагружается дополнительным моментом. Для уяснения этого рассмотрим движение автомобиля 4Х Х4, схема которого представлена на рис. 7.15. Как установлено в гл. 2, радиус качения колеса связан с передаваемым моментом зависимостью, которую можно представить в виде:
Гк — /"о ATF к,
где А-р — Ат/*о»
Допустим, что в силу ряда обстоятельств (неодинаковый износ протектора, разное давление воздуха в шинах, разная нагрузка) радиус качения без скольжения колес переднего моста rOi будет больше, чем заднего Г02, тогда
Гк1 = Гм — ATiFKi;	1	(7.13)
Гк2 = Р)2 — At2Fk2; Гог > Г02- J
С другой стороны,
FkI + Fk2 = Fs,
где F2— суммарное сопротивление движению автомобиля.
Поскольку колеса автомобиля блокированы, они должны вращаться с одинаковой угловой скоростью. Линейная скорость центров колес тоже одинаковая. Отсюда следует, что гк1=гк2 и roi — ATiFKl = Г02 — At2Fk2; 1 FKi + Fk2 = Fj.	J
Решая полученную систему уравнений, находим:
р AT2F2-|-Ar	AT1f2 —Аг
Гк1 — ---7---7--5	------7-,
ati + at2	ат1+ат2
где Дг=г Qi -г 02.
На рис. 7.16 графически изображены зависимости (7.13). Поскольку при движении автомобиля радиусы качения колес переднего и заднего мостов одинаковы, прямая, параллельная оси абсцисс, при пересечении с наклонными, которые соответствуют уравнениям (7.13), отсекает отрезки, пропорцио-
182
Рис. 7.16. Связь радиусов качения и окружных сил колес автомобиля с блокированным приводом:
1 — движение при малом сопротивлении — циркуляция мощности; 2 — граничный случай — передний мост ведущий, окружная сила на заднем мосту равна нулю; 3 — движение при большом сопротивлении — оба моста ведущие
нальные окружным силам колес. При этом окружная сила на колесах большего радиуса (в рассматриваемом случае колеса переднего моста) будет всегда положительной. Окружная сила на колесе меньшего диаметра будет ПОЛОЖИТеЛЬНОЙ ТОЛЬКО ПрИ Гк<Го2- При /"к>го2, как это видно из графика, сила Fk2 будет отрицательной (тормозной). Эта сила создает момент M2 = Fi:2r.32, который передается через трансмиссию к колесам переднего моста и суммируется с моментом, передаваемым к этому мосту от двигателя. Таким образом, в замкнутом контуре (колеса заднего моста — главная передача и карданный вал заднего моста — вал раздаточной коробки — карданный вал переднего моста — главная передача и колеса переднего моста) все элементы, передающие крутящий момент, оказываются нагруженными дополнительным крутящим моментом. Появление дополнительного момента в замкнутом силовом контуре в технической литературе называют циркуляцией мощности: в контуре как бы появляется дополнительная мощность. Из рис. 7.16 следует, что циркуляция мощности отсутствует
при FK2>0, т. е. в случае, когда соблюдается условие
F% Дг/А.Т1.
Движение автомобиля при наличии циркуляции мощности сопровождается повышенным изнашиванием шин и механизмов трансмиссии, а также дополнительным сопротивлением движению автомобиля. Поэтому при движении автомобиля в легких условиях мощность должна подводиться только к одному мосту или в приводе устанавливаются дифференциальные механизмы, позволяющие колесам автомобиля катиться с различной угловой скоростью. Следует отметить, что циркуляция мощности может возникать не только при различных радиусах колес, но и когда колеса автомобиля за один и тот же промежуток времени проходят разный путь, например при движении по криволинейной траектории или по дороге с неровностями.
В настоящее время еще нет единых методов оценки проходимости автомобилей. Наиболее часто она оценивается путем определения характеристик движения по эталонным маршрутам, а также путем сравнительной оценки способности автомобилей преодолевать труднопроходимые участки и отдельные препятствия.
Эталонный маршрут — это специальный маршрут, в который в зависимости от назначения автомобиля включают трудные для движения автомобиля участки: песчаные и заболоченные, броды, лесные и горные дороги, а также булыжные и грунтовые. Он включает также участки дорог с хорошим покрытием. При длительных испытаниях маршруты подбирают таким образом, чтобы они проходили по основным районам страны и включали все виды дорог. Оценку проходимости автомобиля проводят по производительности, средней скорости движения, расходу топлива. Дополнительными показателями могут быть число застре
183
ваний, средняя скорость прохождения особо трудных участков и др.
Способность автомобиля преодолевать труднопроходимые участки можно оценить по тягово-скоростной характеристике при движении на заданном участке и зависимости мощности сопротивления качению от скорости движения. Тягово-скоростную характеристику определяют при движении по размокшей грунтовой дороге или связным грунтовым поверхностям, сыпучему песку и снежной целине. Для этого к испытываемому автомобилю присоединяется динамометрический прицеп, который позволяет регистрировать и плавно менять нагрузку на крюке испытываемого автомобиля.
Для получения одной точки на кривой характеристики автомобиль с прицепом проезжает участок дороги или местности с полной подачей топлива при определенной ступени в коробке передач. Сила тяги, развиваемая автомобилем, и скорость движения фиксируются с помощью аппаратуры динамометрического прицепа.
Изменяя сопротивление движению динамометрического прицепа, находят зависимость силы тяги автомобиля от его скорости. Мощность сопротивления качению определяется как разность мощности, подведенной к ведущим колесам, и мощности на крюке. Мощность, подведенная к ведущим колесам, находится как произведение крутящего момента на ведущих колесах на их угловую скорость. Мощность на крюке равна произведению силы тяги автомобиля на его скорость.
Предельный уровень проходимости автомобиля находят путем испытаний его на особо труднопроходимых участках: по размокшей грунтовой поверхности (суглинок или чернозем), заболоченному лугу, снежному бездорожью.
Все испытания автомобилей на проходимость являются сравнительными. Обычно проходимость испытываемого автомобиля сравнивается с известной из опыта эксплуатации проходимостью одного или группы автомобилей.
8 МОДЕЛИРОВАНИЕ ПРОЦЕССА ДВИЖЕНИЯ АВТОМОБИЛЯ
8.1.	Общие принципы моделирования
Соответствие выбранных параметров автомобиля его назначению устанавливается на основании пробеговых испытаний в характерных для данного автомобиля условиях. Оценочными параметрами обычно являются средняя скорость и расход топлива, определяющие производительность и экономичность автомобиля. Проведение пробеговых испытаний является трудоемким процессом, а изменение параметров спроектированного и изготовленного в опытных образцах автомобиля связано с большими затратами средств и времени. Поэтому на стадии проектирования желательно иметь максимальный объем информации о предполагаемом поведении автомобиля в реальных условиях эксплуатации. Разработанные в последнее десятилетие методы моделирования процесса движения автомобиля на вычислительных машинах позволяют получить объективные данные о его режимах движения в заданных эксплуатационных условиях.
Под моделированием понимается способ изучения системы или явления путем замены реальной системы ее физической или математической моделью, более удобной для изучения, но сохраняющей все существенные черты оригинала. В частности, в модели системы водитель — автомобиль — дорога должны быть три подсистемы (водитель, автомобиль, дорога), а также определены условия их взаимодействия.
Разработаны методики моделирования процесса движения автомобиля применительно к цифровым и аналоговым вычислительным машинам, а также аналогово-цифровым комплексам.
Принципиальная схема моделирования (рис. 8.1) не зависит от типа вычислительного устройства. В схему включены три вышеназванные подсистемы и определена взаимосвязь между ними. Кроме того, в схему обычно включают подсистему регистрации режимов движения.
В общем виде дорожные условия характеризуются макропрофилем, коэффициентом сцепления, ровностью покрытия, извилистостью трассы, шириной проезжей части дороги, интенсивностью движения и ограничениями скоростей, обусловленными регулированием движения и наличием на дорогах помех различного рода. С точки зрения влияния этих условий на режим движения автомобиля их характеристики сводятся к двум случайным процессам, описывающим изменение уклонов (коэффициентов сопротивления подъему i) и максимально допустимой скорости движения ца в функции пути. Подсистема «дорога» предназначена для моделирования этих процессов. Процессы могут генерироваться как случайные сигналы с заданными вероятностными характеристиками или представлять собой конкретные функциональные зависимости. В первом случае модель дороги считается вероятностной, а во втором — детерминиро-
185
Рис. 8.1. Принципиальная схема моделирования процесса движения автомобиля
ванной, поскольку ее параметры соответствуют конкретной реальной или условной дороге, принятой за типовую.
Принципиально методика создания вероятностной модели дороги не отличается от общей методики получения случайного процесса с заданными статистическими характеристиками. В рассматриваемом случае модель состоит из двух генераторов случайных процессов (генераторов случайных чисел при моделировании на цифровой вычислительной машине) и двух формирующих фильтров с заданными передаточными характеристиками. Одна из систем — генератор с формирующим фильтром — обеспечивает случайный процесс, соответствующий изменению уклонов дороги, а вторая — случайный процесс, описывающий ограничения скоростей движения. На реальных дорогах ограничения скоростей движения связаны с профилем дороги и ее кривизной в плане. Поэтому при организации вероятностной модели дороги возникают определенные трудности учета этих связей. Принципиально вероятностная модель может дать более объективные характеристики поведения автомобиля в исследуемых условиях эксплуатации. Однако при расчетах режимов движения автомобиля такие модели применяются в настоящее время редко, так как решение по ним находится методом статистических испытаний, требующим для получения установившихся оценок значительного машинного времени. Кроме того, в настоящее время не накоплен еще достаточ
ный экспериментальный материал по вероятностным характеристикам дорог и ограничениям скоростей движения и их корреляционной связи.
Поэтому более часто используют детерминированную модель, по которой для каждой координаты пути sn определяются дорожный уклон in, кривизна дороги в плане kn, допустимая скорость движения удп, расстояние Ln до точки с такой координатой пути, в которой скорость автомобиля должна быть меньше, чем в точке с координатой sn, а также допустимая скорость в этой точке одЬ.
При построении детерминированной модели используют экспериментальные данные, полученные при проезде автомобилем по типовой дороге, или данные, рассчитываемые по технической документации. Для построения модели дороги по экспериментальным данным автомобиль, близкий по своим характеристикам к проектируемому, оборудуют измерительной аппаратурой и совершают несколько заездов по выбранному участку дороги. В процессе движения регистрируют путь, углы подъемов и спусков, ограничения скоростей движения. После обработки измеренных параметров составляют модель дороги в виде таблицы, в которой указываются координаты пути и соответствующие им уклоны и ограничения скоростей движения.
В процессе решения координаты пути и соответствующие им дорожные уклоны передаются в подсистему моделирования динамики автомобиля и действий водителя, а ограничения скорости — в подсистему моделирования действий водителя.
В подсистеме моделирования динамики автомобиля интегрированием дифференциального уравнения движения определяются затрачиваемая двигателем мощность, скорость и ускорение автомобиля, пройденный путь, текущий расход топлива. Пройденный автомобилем за шаг интегрирования
186
путь передается в подсистему моделирования дороги, где определяется координата пути для последующего шага интегрирования. Текущие значения скорости и ускорения автомобиля передаются в подсистему моделирования действий водителя.
В подсистеме моделирования действий водителя производится сравнение текущей скорости автомобиля с допустимой, а также оценивается режим работы двигателя. По результатам сравнения путем логических операций определяется для последующего шага интегрирования режим работы автомобиля: сохраняется или изменяется подача топлива,! происходит ли переключение ступеней в коробке передач или возникает необходимость изменения скорости автомобиля торможением.
Таким образом, приведенная схема моделирования в принципе позволяет учесть все основные факторы, от которых зависит режим движения автомобиля. Конечными результатами моделирования являются параметры, характеризующие производительность автомобиля и его топливную экономичность. В некоторых случаях результаты моделирования используются для нахождения нагрузочных режимов работы трансмиссии, двигателя или ходовой части.
8.2.	Основные характеристики автомобильных дорог
Условия эксплуатации автомобилей. Автомобили создаются для определенных условий эксплуатации, поэтому совершенство их конструкции должно рассматриваться применительно к этим условиям.
Условия эксплуатации подразделяются на транспортные, природно-климатические и дорожные.
Транспортные условия характеризуются особенностями перевозимого груза и организацией перевозок, включая организацию погрузочно-раз
грузочных работ. Этими условиями определяются такие характеристики автомобиля, как грузоподъемность,, вместимость кузова, приспособленность для погрузочно-разгрузочных работ, запас хода и др.
Природно-климатические условия характеризуются температурой воздуха и ее сезонными и суточными изменениями, влажностью и скоростью ветра. По этим факторам различают зоны умеренного, холодного (арктического) и жаркого климата.
Дорожные условия определяются типом и состоянием дорожного покрытия и дорожных сооружений (узлов, мостов, путепроводов), рельефом местности и интенсивностью движения. От дорожных условий зависит максимальная нагрузка на мост автомобиля и основные эксплуатационные характеристики, методы обеспечения которых изучаются в теории автомобиля: тягово-динамические, экономические и тормозные характеристики, устойчивость и управляемость, плавность хода и проходимость.
В реальных условиях автомобили движутся неравномерно — циклично. Цикл движения состоит из участков разгона, равномерного движения и торможения. Степень неравномерности движения может быть охарактеризована средней частотой разгонов, которая определяется в основном двумя факторами: дорожными условиями и удельной мощностью автомобиля (для нормальных условий составляет 20...80 разгонов за 1 ч).
Необходимость снижения скорости автомобиля обусловливается помехами движению, природа которых различна. На дорогах с асфальтобетонным покрытием наиболее характерны помехи, вызванные наличием большого количества движущихся транспортных средств и пешеходов, перекрестков, зон ограничения скорости и зон с ограниченной видимостью; на грунтовых и булыжно-щебеночных дорогах —
187
Рис. 8.2. Участок трассы в плане:
/ — прямолинейный; II— переходная кривая; III — участок постоянной кривизны
наличием неровностей, крутых поворотов. Помехи движению от другого транспорта вследствие малой интенсивности движения на этих дорогах несущественны.
При увеличении сопротивления движению уменьшается интенсивность разгонов и, естественно, их средняя частота. Она зависит не столько от сопротивления движению, сколько от имеющегося у автомобиля резерва мощности, который может быть использован для разгона: чем больше этот резерв, тем выше частота разгонов.
Основные элементы дорог и дорожные сооружения. На автомобильных дорогах имеются дорожные устройства и комплексы основных и вспомогательных сооружений. К основным относятся сооружения, обеспечивающие организацию движения транспорта, а к вспомогательным —предназначенные для обслуживания транспорта и основных устройств: заправочные пункты, станции технического обслуживания, здания дорожно-ремонтной службы и т. д. Комплекс основных и вспомогательных сооружений зависит от назначения дороги.
Полосу местности, на которой размещаются основные и вспомогательные сооружения, а также дорожные устройства, называют полосой отвода. Расположение оси дороги на местности называют трассой. В общем случае это пространственная линия, имеющая
повороты в горизонтальной и вертикальной плоскостях. Дорогу, как правило, проектируют по кратчайшему расстоянию между пунктами, которое называют воздушной линией. На местности всегда имеются естественные и искусственные препятствия, поэтому реальная дорога оказывается длиннее воздушной линии. Степень удлинения реальной дороги по сравнению с воздушной линией называется коэффициентом развития трассы: kp=LIL0, где L — длина трассы дороги; Lo — длина воздушной линии.
В плане трасса состоит из прямых участков и участков с постоянной кривизной (круговых кривых), соединенных переходными кривыми (рис. 8.2). Наименьший допустимый радиус круговых кривых зависит от расчетной скорости движения автомобилей и регламентируется строительными нормами и правилами. Переходные кривые, представляющие собой кривые переменного радиуса, строят обычно при соединении прямых участков с круговыми, имеющими радиус кривизны менее 2000 м. Длина переходных кривых составляет 30... 120 м и зависит от радиуса кривизны кругового участка. Переходные кривые делают более длинными, когда соединяют прямолинейные участки с круговыми малого радиуса. Наличие переходных кривых обеспечивает плавное изменение центробежной силы при движении автомобиля, а также возможность плавного поворота управляемых колес автомобиля.
На автомобильных дорогах переходные кривые очерчиваются в основном по радоиде (клотоиде), кубической параболе, лемнискате. Кривизна переходной кривой в точке (точка А, рис. 8.3) зависит от удаления последней от начала переходной кривой: р = = Ci/s — радоида (клотоида); р = Сз/х— кубическая парабола; р = с3/а— лемниската, где р — радиус кривизны в точке А-, Ci, с2, с3 — постоянные вели-
188
Рис. 8.3. Переходная кривая:
I— прямолинейный участок; II — участок переменной кривизны; III —^участок постоянной кривизны. Расстояние от точки О до точки А: а — по прямой, s — по переходной кривой; х — по оси прямолинейного участка
Рис. 8.4. Участок продольного профиля дороги: / — прямой; Л—'выпуклая кривая; III — вогнутая кривая
чины; s, х, а •— расстояние от точки О до точки А.
Наиболее часто переходные кривые на автомобильных дорогах делают по радоиде. При этом в случае движения автомобиля с постоянной скоростью переход от прямолинейного движения к круговому обеспечивается равномерным вращением управляемых колес. Кривые, описанные по кубической параболе, выполняют при небольших углах поворота переходной кривой, а по лемнискате — при малых радиусах и больших углах поворота.
Проекцию трассы на вертикальную плоскость называют продольным профилем дороги. Продольный профиль включает прямые участки и вертикальные кривые, обеспечивающие плавный переход между прямыми участками, имеющими различную крутизну (рис. 8.4).
Радиусы выпуклых кривых выбирают таким образом, чтобы обеспечить видимость дороги водителем на длине пути торможения автомобиля. При расчетах высоту зрения (возвышение глаза водителя над поверхностью дороги) принимают равной 1,2 м, что
соответствует высоте зрения водителя легкового автомобиля.
Вогнутые кривые делают для смягчения толчка на соответствующем переломе профиля, при проезде которого возникает центробежная сила, дополнительно нагружающая мосты автомобиля. Радиус вогнутой кривой рассчитывают таким образом, чтобы дополнительная нагрузка не превосходила 5 % статической нагрузки, приходящейся на мост при движении автомобиля с расчетной скоростью.
Конструкции дорог. Характерное поперечное сечение дороги показано на рис. 8.5. Дорога сооружается на з е-мляном полотне, представляющем отсыпанную и спланированную полосу грунта. Для создания земляного полотна в зависимости от рельефа местности устраиваются насыпи или выемки. К земляному полотну также относят боковые канавы и резервы, из которых берут грунт при строительстве. Земляное полотно сооружается из прочных грунтов, предусматривается отвод от него поверхностных и грунтовых вод. Конструкция земляного полотна зависит от гидрогеологических условий местности.
Основными элементами дороги являются: проезжая часть, обочины и боковые канавы (кюветы). Проезжая часть предназначена для движения автомобилей. К проезжей части примыкают обочины. Их используют для остановок автомобилей, для складывания дорожно-строительных материалов во время строительства и ремонта дорог, а также для расширения проезжей части при реконструкции дороги. Расположенные за обочинами канавы, или кюветы, служат для отвода воды от дороги и прилегающих участков.
Прочность проезжей части зависит от материалов дорожной одеж-д ы, которая воспринимает усилия от транспортных средств и передает их на земляное полотно. Дорожная одежда
189
Рис. 8.5. Поперечное сечение дороги: 1 —земляное полотно; 2— обочина; 3 — проезжая часть; 4 — боковая канава (кювет)
является важнейшим и дорогостоящим элементом автомобильной дороги, затраты на ее устройство достигают 50...60 % сметной стоимости дороги.
Дорожная одежда состоит из нескольких конструктивных слоев, уложенных на земляное полотно. Основными требованиями, которым должна удовлетворять конструкция дорожной одежды, являются: высокая прочность и долговечность, ровность поверхности покрытия, хорошая сцеп-ляемость шины с дорогой при любых погодных условиях, малое сопротивление движению автомобиля. Движение автомобиля не должно сопровождаться сильным шумом и запылением воздуха. Верхний слой дорожной одежды должен легко и минимальными затратами восстанавливаться при ремонте, по возможности без прекращения движения. Дорожную одежду проектируют в комплексе с земляным полотном.
По способности воспринимать растягивающие напряжения и накапливать пластические деформации дорожные одежды подразделяют на жесткие и нежесткие. К жестким относятся дорожные одежды, устраиваемые из бетона или железобетона. Они хорошо сопротивляются изгибу, и в них не накапливаются пластические деформации. К нежестким дорожным одеждам относят все остальные конструкции из щебня, гравия и других материалов. В таких конструкциях при многократном воздействии нагрузок накапливаются пластические деформации, что приводит к появлению волнистости на дорожной поверхности.
В конструкции дорожной одежды
различают два основных слоя: покрытие и дорожное основание.
Покрытие — верхняя часть дорожной одежды, непосредственно воспринимающая механические усилия от транспортных средств и атмосферные воздействия. Покрытие должно быть прочным, износостойким, устойчивым к пластическим деформациям, водонепроницаемым, ровным, шероховатым и беспыльным. Оно может состоять из одного или нескольких конструктивных слоев. Верхний слой покрытия, периодически восстанавливаемый в процессе эксплуатации дороги, называют слоем изнашивания.
Дорожные покрытия подразделяют на усовершенствованные капитальные, усовершенствованные облегченные, переходные и низшие. Качество покрытия и определяет в основном транспортно-эксплуатационные свойства дороги.
К покрытиям усовершенствованного капитального типа относятся цементо-и асфальтобетонные покрытия. Наиболее прочными и долговечными являются цементобетонные покрытия, механические свойства которых мало зависят от температуры и влажности воздуха. Асфальтобетонные покрытия склонны к размягчению при высоких температурах и к хрупкости — при низких.
Цементобетонные покрытия могут быть монолитными из бетонной смеси, которую привозят или готовят непосредственно на месте работ, или сборными из плит, изготовленных на заводах.
Жесткие бетонные покрытия чувствительны к деформациям основания, поэтому их устраивают только на достаточно прочных и жестких основаниях. Толщина бетонных покрытий в зависимости от категории дороги и жесткости основания должна быть 18...24 см.
Для предотвращения образования в покрытии трещин, возникающих при
190
колебаниях температуры воздуха, усадке бетона при твердении и неравномерной осадке основания, в процессе строительства делают продольные и поперечные деформационные швы, делящие монолитное покрытие на отдельные плиты. Для того чтобы в деформационные швы не попадали вода, песок, грязь, их заполняют герметизирующими материалами: битумной или резино-битумной мастикой, полимерными герметиками и др.
Покрытия усовершенствованного облегченного типа устраивают с применением прочного щебня, гравия или минеральных смесей различной зернистости, обработанных органическими вяжущими материалами. В качестве,1 вяжущих материалов применяют различные типы битумов.
Покрытия усовершенствованного облегченного типа обладают достаточ-i. ной прочностью в условиях переменных влажности и температуры.
Покрытия переходного типа изготовляют из щебня, гравия, шлака без обработки вяжущими материалами. Эти покрытия обладают малым сопротивлением изнашиванию, так как касательные силы, действующие на покрытие при движении автомобиля, оказывают разрушительное действие на верхний слой вследствие слабого сцепления между каменными частицами, из которых состоит этот слой. К этой же группе покрытий относятся мостовые, устраиваемые из отдельных, уложенных впритык друг к другу, естественных или искусственных камней соответствующей формы.
Покрытие низшего типа устраивают из грунтов, укрепленных различными материалами (песок, гравий и др.). При добавке этих материалов в глинистые, суглинистые, пылеватые грунты увеличивается сопротивление изнашиванию таких покрытий, особенно во влажном состоянии. Для повышения связности песчаных грунтов применяют глинистые или суглинистые добавки.
Покрытие укладывается на д о-рожное основание — нижнюю часть дорожной одежды. Оно служит для передачи усилий от покрытия на земляное полотно. Основание, как правило, устраивают из нескольких слоев. Для устройства верхних слоев используют более прочные и морозостойкие материалы с обработкой или без обработки их вяжущими материалами (битумом, цементом). Для нижних слоев используют более слабые и менее морозоустойчивые материалы. Уменьшения толщины и обеспечения хороших дренирующих и морозозащитных свойств дорожного основания достигают устройством дополнительных нижних слоев основания из песка, гравийно-песчаных смесей и других материалов.
Ширину проезжей части дороги принимают с учетом количества полос и расчетной скорости движения. Строительными нормами и правилами установлены требуемое количество полос движения и ширина проезжей части в зависимости от категории дорог. На дорогах с большой интенсивностью движения для обеспечения его безопасности устраивают разделительные полосы, ширина которых принимается не менее 5 м.
Поперечный профиль проезжей части проектируют так, чтобы обеспечить сток воды с поверхности дорожного покрытия, безопасное движение и снизить интенсивность изнашивания шин1 автомобилей. Поперечный профиль бывает односкатным, двускатным и параболическим. В большинстве случаев на дорогах с твердым покрытием применяют двускатный профиль (см. рис. 1.4). Односкатный профиль имеют дороги на закруглениях (виражах) и при раздельных проезжих частях. Параболический профиль устраивается на широких проезжих частях городских улиц. Такой же профиль обычно имеют грунтовые и щебеночно-гравийные дороги.
Поперечный уклон на прямых уча-
191
Табл. 8.1. Характеристики автомобильных дорог
Категория	Назначение	Ир, км/ч	Н, т	Я» авт./с	В/г	rmax’ 7оо	м	Тип покрытия
Общегосудар-	150	з 75	30	1000 I ственного зна-	щ Более 7000 			ЦБ, АБ чения, основные (80... 120)	Не менее 4 (60)	(250) республиканские	120	3,75	40	600 II	10	3000...7000	— 		ЦБ, АБ (60... 100)	2	(70) (125) III	Республика»-	100	ЮОО...ЗООО	5°	4°° ЦБ, АБ ские, областные (50...80)	2	(80)	(100) Об пястные	80	3,0	60	250 IV иоластные,	6 10	200... 1000			—	Гр, Б районные	(40...60)	2	(90)	(60) 60	„	„	2,25	70	125 V	Местные	6,10 До 200	I р, Гн (30...40)	1	(100)	(30) Примечание: ор— расчетная скорость; Н — допустимая масса, создающая нагрузку на								
одиночный мост автомобиля; И—интенсивность движения; В—ширина полосы движения; г — число полос на дороге; imax — максимальный допустимый уклон; ^min— минимальный допустимый радиус кривой в плане ((в скобках — для горных дорог); ЦБ — цементобетонное покрытие; АБ — асфальтобетонное; Гр — гравийное; Б — булыжное; Гн—грунтовое.
стках дороги зависит от типа покрытия. На дорогах с асфальтобетонным и цементобетонным покрытиями уклон делают 15...20 %0, у щебеночно-гравийных дорог — 2О...ЗО°/оо, а на грунтовых — З0...40°/оо- Поперечные уклоны обочин делают на 10...30 %о большими, чем уклоны проезжей части.
По народнохозяйственному значению автомобильные дороги в СССР делятся на общегосударственные, республиканские, областные и краевые, местные (районные и сельскохозяйственные) и ведомственные (промышленные, лесхозные и др.). Выделяют также курортные дороги, используемые преимущественно для пассажирских сообщений в курортных районах.
В зависимости от степени технического совершенства автомобильные дороги бывают пяти технических категорий. При отнесении дороги к той или иной категории учитывают ее народнохозяйственное значение и перспективную расчетную интенсивность движе
ния, которая рассчитывается на 20 лет вперед от года ввода дороги в эксплуатацию.
Для каждой категории дорог строительными нормами и правилами установлены определенные технические нормативы (табл. 8.1), на основе которых проектируют и строят дороги и искусственные сооружения на них.
Автомобильные дороги с большой интенсивностью движения, предназначенные исключительно для автомобильного движения, называют автомагистралями.
Транспортно-эксплуатационные характеристики дорог. Основными транспортно-эксплуатационными характеристиками автомобильных дорог являются: расчетная скорость, расчетная нагрузка, габариты мостов и тоннелей, пропускная способность и показатели безопасности движения.
Расчетная скорость — наибольшая скорость, с которой может двигаться одиночный легковой автомо-
192
биль при нормальном состоянии дороги в наиболее стесненных местах. По расчетной скорости определяют геометрические элементы дороги. К стесненным участкам относят участки на подъемах и в местах с ограниченной видимостью. Расчетную скорость устанавливают в зависимости от технической категории дороги.
Расчетная нагрузка — наибольшая нагрузка, которую должны выдержать дорога и искусственные сооружения при движении по ним транспортных средств. Она характеризуется классом нагрузки, обозначаемым буквой Н, соответствующей цифрой, показывающей массу автомобилей (в тоннах), находящихся в колонне (Н-10, Н-15, Н-25). Класс нагрузки устанавливается в зависимости от технической категории дороги и долговечности искусственного сооружения (моста, путепровода, дорожной одежды).
Габарит моста или тоннеля — контур пространства, внутрь которого не должны вдаваться никакие элементы конструкции. Соблюдение габаритов обеспечивает беспрепятственный пропуск транспортных средств и пешеходов. Габарит по ширине обозначают буквой Г и числом, соответствующим ширине (в метрах) проезжей части (Г-7, Г-10). Ширину габарита принимают с учетом категории дороги, длины моста и его долговечности.
Пропускная способность— наибольшее количество транспортных средств, которые могут пройти по дороге за 1 ч. Она зависит от числа полос и скорости движения.
Пропускная способность одной полосы определяется по формуле:
n = s/Z.min,
где s — длина пути, проходимого автомобилем за 1 ч; Гтп1п — минимальное расстояние между следующими друг за другом транспортными средствами, включая длину транспортных средств
(равно минимальному расстоянию между осями передних мостов движущихся друг за другом автомобилей).
Пропускная способность дороги
N=nzka,
где z — число полос движения; ka — коэффициент полосности, зависящий от числа полос.
Безопасность движения оценивается коэффициентом безопасности движения &без — отношением скорости на стесненном (опасном) участке дороги пс к скорости на примыкающем свободном	^без“^с/^вх* При ^без^э0,8
участок дороги считается безопасным, при Абез = 0,6...0,8 — малоопасным, при &без = 0,4...0,6— опасным И при ^без< <0,4— очень опасным.
Приведенные характеристики являются расчетными и служат для оценки возможностей дороги.
Режим эксплуатации дороги и ее эксплуатационные показатели характеризуются транспортно-эксплуатационными параметрами: объемом перевозок — массой груза (в тоннах) или количеством пассажиров, перевозимых за год; годовым грузооборотом; грузонапряженностью—массой груза (в тоннах), провозимого в определенный промежуток времени (сутки, год); интенсивностью движения — количеством транспортных средств, проезжающих в данный промежуток времени (час, сутки); коэффициентом аварийности — отношением числа дорожно-транспортных происшествий на данном участке дороги к их числу за тот же промежуток времени на эталонном (благоприятном) участке дороги.
Безопасность элементов дороги в процессе эксплуатации может быть также оценена экспериментально: коэффициент безопасности находится как отношение экспериментально найденных средних скоростей движения на оцениваемом элементе дороги и при подъезде к нему.
193
8.3.	Методика построения модели автомобильной дороги
Как уже отмечалось, модель автомобильной дороги представляет собой функциональную зависимость ее уклонов, кривизны в плане и допустимых скоростей движения от координат трассы. Наиболее часто расчет параметров движения проводят на цифровых вычислительных машинах с использованием детерминированной модели дороги. В этом случае модель представляют в виде таблицы координат трассы, в которых происходит изменение характеристик дорожных условий (уклона, кривизны дороги в плане или допустимой скорости движения). Данные таблицы заносятся в память вычислительной машины.
Основным документом, по которому можно определить характеристики дороги, является чертеж продольного профиля. Продольный профиль оформляется в соответствии с требованиями, принятыми в дорожных проектных организациях. Для наглядности при построении продольного профиля дорог равнинной местности вертикальные расстояния откладываются в масштабе 1 : 500, а горизонтальные — в масштабе 1 : 5000. Для профилей горных дорог используют более крупные масштабы — 1 : 200 и 1 : 2000.
На продольном профиле изображают поверхность земли, линию бровки дороги (красную линию), а также разрез грунтовой толщи по оси дороги, выемки и насыпи. Для облегчения чтения чертежа грунтовый разрез на чертеже смещают на 2 см вниз. На продольном профиле специальными условными знаками (рис. 8.6) показывают места расположения переездов через железные и автомобильные дороги, мостов, труб и других сооружений.
Под продольным профилем в горизонтальных графах указывают основные характеристики дороги. В графе «Уклоны и вертикальные кривые» при-
1
2
-----1 У2 32°45 I____
Т 146,92
Б 21,14
R 500
К 285,80
6998,45
С 37°57
Рис. 8.6. Основные условные обозначения на продольных профилях дороги:
/—линия поверхности дороги; 2—'.линия поверхности земли; 3 — участок дороги с уклоном 45 %0 на протяжении 270 м; 4 — восходящая ветвь выпуклой кривой радиусом 8000 м, длиной 400 м; 5 — вогнутая вертикальная кривая (нисходящая и восходящая ветвь) радиусом 6000 м, длиной 380 м; 6 — охраняемые и неохраняемые железнодорожные переезды; 7 — поворот дороги вправо и характеристики поворота (угол, тангенс, биссектриса, радиус, длина кривой); 8 — длина прямого участка между смежными кривыми и его направлением относительно стран света; 9 — съезд с дороги вправо в 65 м от пикета;
10—километры (7) и пикеты (1 и 2)
водятся сведения о направлении, размерах и длине уклонов, радиусах и длине вертикальных кривых. Наклонной чертой показывается направление уклона в направлении счета километров. Цифра над чертой показывает значение уклона в тысячных (промилле), а цифра под чертой — протяженность участка в метрах. В этой же графе помещают сведения о вертикальных кривых: направление кривой (выпуклая или вогнутая), радиус, начало кривой и ее протяженность. В отдельной графе показываются координаты начала поворота дороги в плане и его характеристики.
Для удобства ориентации на чертеже трассу по длине делят на километровые и стометровые участки-пикеты, которые нумеруют последовательно от
194
Рис. 8.7. Соединения автомобильных дорог:
а —* пересечение;	б — примыкание; в — раз-
ветвление
Табл. S.2. Снижение скорости при проезде перекрестков
Интенсивность движения, авт./ч		Снижение скорости на перекрестке, %
по главной дороге	по второстепенной дороге	
400...450	40...50	6,5
	100...НО	20
600...650	30...35	13
	80...90	30
	200...220	40...45
800...870	40...50	30
	150	40
	280...300	50
1000...1100	20...25	30
	60...100	40

начала трассы. Промежуточные расстояния между пикетами, например расстояние 45.353 м от начала трассы, обозначают ПК 453 + 53 (пикет № 453 плюс 53 м).
Таким образом, используя чертеж продольного профиля, можно составить числовую модель профиля дороги, по которой для каждого шага интегрирования рассчитываются уклоны и радиусы кривизны дороги в плане.
Для составления полной модели дороги необходимо определить участки, на которых исследуемый автомобиль должен двигаться с ограниченной скоростью.
Факторы, вызывающие необходимость ограничения скоростей движения на автомобильных дорогах, могут быть разделены на три группы: зависящие от конструкции дороги и системы регулирования движения; неровности дорожной поверхности; помехи со стороны попутного и встречного транспорта.
Расчет допустимых скоростей движения с учетом влияния первой группы факторов может быть выполнен по технической документации на дорогу. Прежде всего выявляется максимально допустимая скорость на дороге, а также местные ограничения ее дорожными знаками. Скорость движения
ограничивается также в населенных пунктах, пересечениях (узлах), на поворотах, уклонах большой протяженности, участках с необеспеченной видимостью. Наблюдениями установлены закономерности влияния перечисленных факторов на скорость движения автомобилей.
В населенных пунктах н при подъездах к ним скорость обычно регулируется дорожными знаками. Когда скорость в населенных пунктах не ограничивается правилами дорожного движения, при расчетах ее принимают на 10...12 км/ч меиъшей, чем при движении вне населенного пункта.
Соединения автомобильных дорог (узлы) в зависимости от взаимного расположения дорог делят на пересечения, примыкания и разветвления (рис. 8.7). Узлы могут иметь пересечения в одной или двух плоскостях. Пересечения автомобильных дорог влияют на скорость движения в том случае, если они выполнены в одном уровне. Скорость движения автомобилей по главной дороге снижается за 300...400 м до пересечения и становится наименьшей на самом пересечении. Снижение скорости на перекрестке зависит от интенсивности пересекающихся транспортных потоков. В табл. 8.2 приведены обобщенные результаты
195
Рис. 8.8. Зависимость коэффициентов конечной скорости грузовых автомобилей от длины спуска с условиями в конце:
/—подъем; 2 — поворот в плане; 3— сужение проезжей части (имеется встречный транспорт); 4 — сужение проезжей части (встречный транспорт отсутствует); 5 — малый мост; 6 — большой мост
наблюдения за движением автомобилей на перекрестках.
Максимальная скорость движения автомобиля по горизонтальной кривой зависит от поперечной силы, действующей на автомобиль. Установлено, что при поворотах водители стремятся поддерживать такую скорость, чтобы поперечная сила не превосходила 0,15... 0,25 от максимальной поперечной силы по условиям сцепления. При этом большие значения поперечной силы имеют место на кривых малых радиусов.
Для расчетов максимальной допустимой скорости на повороте может быть принята эмпирическая зависимость:
Цц.к=ао—1,05 • 103fe, где v0, цд.к •— соответственно скорость на прямолинейном участке и допустимая скорость на повороте, км/ч; k — кривизна траектории, м-1.
При подъезде к криволинейному участку скорость движения должна быть такой, чтобы обеспечивалась возможность, используя служебное торможение, установить допустимую скорость к моменту перехода автомобиля на участок трассы с постоянным радиусом кривизны.
Скорость движения, особенно автомобилей с малой удельной мощностью, в значительной степени зависит от наличия на дороге уклонов. На подъеме скорость уменьшается вследствие уве
личения дорожного сопротивления. На спусках скорость ограничивается по условиям безопасности движения. Скорость автомобиля в конце спуска зависит от характера дорожного участка после спуска. Если участок спуска переходит в горизонтальный прямолинейный, скорость в конце спуска обычно соответствует скорости движения автомобиля по горизонтальному участку. Если за участком спуска начинается участок подъема, скорость в конце спуска будет большей, чем на горизонтальном участке (но не больше максимальной допустимой на трассе). Если после участка спуска следует участок со стесненным движением (поворот, сужение, мост), скорость в конце спуска будет меньше скорости движения по горизонтальному участку. На рис. 8.8 показана зависимость коэффициентов конечной скорости грузовых автомобилей от длины спуска, которая может быть принята при установлении ограничений скорости на спусках (под коэффициентом конечной скорости понимается отношение скорости в конце спуска в случае перехода спуска к участку со стесненным движением к скорости на прямом горизонтальном участке) .
Придорожные сооружения, переломы профиля в вертикальной плоскости и в плане, лесонасаждения могут ограничивать видимую водителем зону. В этих условиях водитель стремится установить такую скорость, при которой возможно остановиться или сманеврировать в пределах зоны видимости. Скорость движения, поддерживаемая водителем, зависит от коэффициента сцепления и расстояния видимости. На рис. 8.9 приведен график, построенный по данным Бел-дорНИИ, иллюстрирующий зависимость допустимой скорости движения от расстояния видимости. Наблюдения показывают, что водители устанавливают допустимую скорость движения к началу участка с ограниченной види-
196
Видимость
Рис. 8.9. Зависимость допустимой скорости от расстояния видимости:
1 — <р=о,6; 2 — ф =0,4; 3 — ф =0,2
мостью, причем замедление автомобиля происходит с интенсивностью, соответствующей служебным торможениям.
Скорость движения автомобиля зависит от состояния дорожного покрытия: ровности и скользкости, характеризуемой коэффициентом сцепления. Сцепление учитывается при определении допустимых скоростей в стесненных условиях движения. Оно также оказывает влияние на скорость при свободном прямолинейном движении. Однако достаточного объема экспериментально-статистических или расчетных данных для установления соответствующих закономерностей не имеется. Поэтому характеристики сцепления в расчетах скоростных режимов автомобиля при свободном прямолинейном движении не учитываются.
При движении по неровным дорогам средняя скорость автомобиля определяется иногда не его тягово-динамическими качествами, а параметрами подвески. Это объясняется тем, что при подъезде к неровностям водитель снижает скорость движения, для того чтобы избежать чрезмерно высоких ускорений и ударов в ограничитель деформации подвески. Проведенные измерения вертикальных ускорений в зоне расположения водителя и прогибов
подвесок при эксплуатационных режимах движения различных автомобилей показали, что предельные ускорения в диапазоне частот колебаний 0...5 Гц оказались наиболее стабильными. При движении в условиях, когда скорость ограничивалась интенсивностью колебаний масс автомобиля, значения среднеквадратических ускорений в этом диапазоне, как правило, близки к 2,5 м/с2, а максимальное-—не превышает 7,5 м/с2.
Исходя из этого, можно сделать вывод, что во всех случаях вне зависимости от типа машины и условий движения стремятся, изменяя скорость автомобиля, вести его таким образом, чтобы среднеквадратическое ускорение водителя не превышало 2,5 м/с2 (максимальное — не более 7,5 м/с2). Максимальный наблюдаемый прогиб передних подвесок обычно не превосходит 0,7...0,75 максимального хода сжатия, а среднеквадратический составляет его четверть. Это значит, что водитель всегда стремится иметь некоторый запас динамического хода, чтобы обеспечить движение автомобиля без ударов в ограничитель прогибов подвески.
Таким образом, максимальная скорость движения автомобиля по дорогам с неровностями должна быть такой, чтобы выдерживались следующие характеристики интенсивности колебаний: 1) ускорение водителя в частотном диапазоне 0...5 Гц не превосходило 7,5 м/с2; 2) прогиб передней подвески составлял не более 3/4 от полного хода сжатия; 3) среднеквадратическое ускорение водителя было не более 2,5 м/с2.
Ускорения подрессоренных частей автомобилей с линейными подвесками подчиняются нормальному закону распределения. Поэтому, если соблюдается первое условие, не нарушается и третье.
Ускорение (в долях g) подрессоренной массы в точке над осью переднего моста двухосных автомобилей и трех
197
осных с балансирной подвеской задних мостов в низкочастотном диапазоне колебаний примерно равно отношению текущего динамического и статического прогибов. Например, если в определенный момент времени динамический прогиб подвески составляет 5 см при статическом прогибе 10 см, в этот момент на подрессоренную массу будет действовать ускорение 0,5g (5 м/с2). У грузовых автомобилей отношение максимального динамического и статического прогибов подвесок близко к единице (максимальный динамический ход принимают равным или близким к статическому). В этом случае, если место расположения водителя находится вблизи оси переднего колеса, можно считать, что первое и второе ограничения действуют одновременно — ускорение 7,5 м/м2 будет в том случае, когда прогиб подвески составит 0,75 от максимального динамического хода. У легковых автомобилей статический ход делают больше динамического. Кроме того, в легковых автомобилях место водителя обычно располагается внутри базы. Поэтому при движении их по дорогам с неровностями ограничения по прогибам подвесок всегда предшествуют ограничениям по ускорениям.
Из приведенного следует, что для всех типов автомобилей, имеющих близкие к линейным подвески, для определения максимальной допустимой скорости движения по дорогам с неровностями достаточно проанализировать зависимость прогибов подвески от скорости движения при заданных характеристиках микропрофиля дороги. Расчет этой зависимости можно выполнить способами, изложенными в гл. 5. Допустимой будет скорость, при которой прогиб подвески не превосходит 3/4 от максимального прогиба.
Допустимая скорость движения и длительность действия ограничений, вызванных указанными выше факторами, могут быть непосредственно связа
ны с координатами трассы и внесены в модель дороги.
Другая группа ограничений скоростей обусловлена взаимодействием рассматриваемого автомобиля с другими машинами, движущимися в общем транспортном потоке. Исследованиями закономерностей транспортных потоков, выполненными советскими и зарубежными учеными, установлено, что транспортный поток с интенсивностью движения в одном направлении до 400...500 авт./ч можно считать пуассоновским. Движение автомобиля (объекта) в потоке можно рассматривать состоящим из трех этапов: а) свободное движение; б) стесненное, когда объект движется за более тихоходной транспортной машиной со скоростью этой машины; в) обгон.
Длительность свободного движения является случайной величиной и определяется интенсивностью попутного потока, состоящего только из тихоходных автомобилей. Когда расстояние между объектом и попутным тихоходным автомобилем становится равным динамическому габариту объекта, возникает необходимость обгона. Под динамическим габаритом понимается сумма длины автомобиля (автопоезда) и расстояния, на котором обеспечивается его остановка в случае внезапного появления препятствия.
Обгон с ходу является также случайным событием, которое возможно, если: выезду на обгон не мешает впереди идущий обгоняющий автомобиль из-этого потока; на полосе встречного движения во время обгона нет попутного или встречного автомобиля; в попутном потоке перед обгоняемым автомобилем есть интервал, достаточный для возвращения обгоняющего на свою полосу.
Длительность обгона зависит от ряда факторов, основными из которых являются: размеры и соотношение скоростей обгоняющего и обгоняемого автомобилей, динамические качества
198
Рис. 8.10. Принципиальная схема моделирования ограничений скорости в транспортном потоке:
хсв;—время свободного движения; р(и)— обгон с ходу; t»T—скорость тихоходных транспортных средств; —время ожидания безопасных условий для обгона
обгоняющего автомобиля. По экспериментальным наблюдениям наиболее часто обгон совершается за 10... 15 с.
Если обгон с ходу не совершен, автомобиль в течение некоторого времени следует за тихоходным автомобилем с его скоростью. Таким образом, процесс движения автомобиля в транспортном потоке может рассматриваться как случайный процесс, определяемый вероятностями свободного движения, обгона с ходу, вероятной длительностью ожидания условий для обгона и скоростью тихоходного транспорта.
Принципиальная схема моделирования ограничений скорости при движении автомобиля в транспортном потоке показана на рис. 8.10. При трога
нии автомобиля (начало движения) определяется случайная величина — время свободного движения. В этот период автомобиль движется с максимально возможной для данных условий скоростью. По окончании свободного движения (автомобиль догнал более тихоходный) определяется возможность обгона с ходу. Если обгон с ходу возможен, автомобиль совершает его, и после завершения обгона цикл повторяется, т. е. определяется время свободного движения, и т. д. Если после анализа ситуации окажется, что обгон с ходу невозможен, определяются случайные величины: скорость тихоходного транспорта и время ожидания безопасных условий для обгона. По окончании ожидания безопасных условий автомобиль совершает обгон, и затем цикл повторяется. Таким образом, моделирование ограничений скорости при движении автомобиля в транспортном потоке сводится к моделированию дискретных случайных величин при заданных вероятности и законах распределения.
Установлено, что в первом приближении можно считать распределение обгонов с ходу, скоростей автомобилей в транспортном потоке и время ожидания благоприятных условий для обгона подчиненными нормальному закону распределения. Характеристики распределений зависят от интенсивности и состава транспортного потока. В специальной литературе рекомендуются числовые значения характеристик, позволяющие моделировать помехи от транспортного потока.
Из изложенного следует, что в общем виде модель дороги включает две части: таблицу, в которой приведены координаты трассы с указанием уклонов, радиусов кривых в плане и допустимых скоростей, зависящих от конструкции дороги и системы регулирования дорожного движения, и вероятностную модель помех от транспортного потока. Вероятностная модель
199
помех получается достаточно сложной. Поэтому в тех случаях, когда в модель закладываются характеристики реальной дороги, помехи от транспортного потока определяют экспериментально путем проезда по дороге на автомобиле и регистрации помех от транспортного потока. В этом случае помехи «привязывают» к определенным координатам дороги. Для получения достоверных данных об уровне, количестве и продолжительности помех необходимо, чтобы основные характеристики автомобиля, на котором совершается пробег, были близки к характеристикам проектируемого.
8.4.	Моделирование динамики автомобиля и логики действий водителя
При моделировании в соответствии с уравнением тягового баланса ускорение автомобиля находится по выражению:
где FK — окружная сила на ведущих колесах; F%-—суммарное сопротивление движению автомобиля.
Окружная сила на ведущих колесах положительна в случае движения автомобиля в тяговом режиме, равна нулю при движении накатом и отрицательна — при движении в тормозном режиме. Коэффициент учета вращающихся масс определяется номером ступени в коробке передач. При движении накатом или торможении колесными тормозами 6= 1,03...1,05.
Суммарное сопротивление движению складывается из сопротивления подъему Ft, качению F/ и сопротивления воздуха FB. Для каждой координаты дороги сопротивление подъему может быть подсчитано по данным модели дороги, а сопротивление качению и воздуха — по скорости автомобиля методами, изложенными в предыдущих
разделах. Если автомобиль находится на криволинейном в плане участке дороги, необходимо учитывать увеличение сопротивления качению вследствие увода шин.
На каждом цикле расчета интегрированием выражения (8.1) определяется текущая скорость автомобиля, интегрированием которой находится координата пути:
v = J axdt + ц0; s = J vdt + s0, где vo и s0 — начальные скорость и координата пути, полученные в результате предыдущего цикла расчета.
В процессе движения водитель регулирует скорость автомобиля, управляя подачей топлива, переключает ступени в коробке передач, осуществляя торможение. Действия водителя зависят от принятого режима движения. При моделировании обычно рассматривают два режима: режим максимальной производительности, когда наиболее полно используются динамические свойства автомобиля, и режим его максимальной топливной экономичности.
Процесс движения автомобиля в общем случае включает следующие этапы.
1.	Движение с постоянной скоростью без переключения ступеней в коробке передач. Этот случай соответствует движению по участку трассы с ограничением скорости (yR). Предполагается, что тягово-скоростные свойства автомобиля обеспечивают его движение с такой скоростью. Для ее поддержания водитель регулирует подачу топлива таким образом, чтобы в каждый момент времени соблюдалось равенство окружной силы на ведущих колесах и суммарной силы сопротивления движению (Ек = Е2). Движение возможно при работе двигателя на частичном режиме. Крутящий момент двигателя и частота его вращения находятся по формулам:
А1д — ЕкГо/ (Цк^оЛт); Щ = 2,6оЩ|Щ.Цо/Д 
200
2.	Разгон при определенной ступени в коробке передач. Происходит в случае, если скорость автомобиля меньше допустимой на данном участке дороги, а возможная окружная сила на ведущих колесах больше силы сопротивления. При моделировании режима движения, при котором обеспечивается максимальная производительность автомобиля, окружная сила определяется из условия работы двигателя по внешней характеристике, а при моделировании движения автомобиля с наибольшей топливной экономичностью — по характеристике наибольшей экономичности (см. рис. 2.30). Возможны и другие варианты.
3.	Движение с заданной подачей топлива на высшей или промежуточной ступени в коробке передач. На этом этапе автомобиль может двигаться ускоренно (FK> F-F), замедленно (FK < Fx) или с постоянной скоростью (FK = Fv).
4.	Переключение на высшую ступень в коробке передач. При моделировании движения с наибольшей производительностью переключение должно произойти, если будут соблюдаться следующие условия: а) достигнута максимально возможная скорость на низшей передаче (двигатель развил максимальную частоту вращения); б) сопротивление движению автомобиля меньше максимальной окружной силы на высшей передаче (уменьшение сопротивления не должно быть вызвано случайными короткими неровностями покрытия); в) допустимая скорость движения выше минимальной устойчивой скорости на высшей передаче; г) за время переключения скорость движения не должна стать меньше минимальной устойчивой на высшей передаче.
На режиме наибольшей топливной экономичности автомобиля переключение должно происходить как можно раньше, т. е. при скорости, с которой возможно устойчивое движение на высшей передаче при работе двигателя
по характеристике наибольшей топливной экономичности.
5.	Переключение на низшую ступень в коробке передач. Производится в случае, если: сила сопротивления оказывается выше развиваемой окружной силы на высшей передаче; частота вращения двигателя становится близкой к минимальной устойчивой.
При моделировании движения из условия наибольшей производительности автомобиля переключение вследствие повышения сопротивления следует производить при скорости, меньшей, чем скорость, при которой происходило переключение на высшую ступень. Это делается во избежание «зацикли-нивания», т. е. чрезмерно частого переключения с низшей ступени на высшую и обратно. На режиме же максимальной топливной экономичности автомобиля переключение следует производить при частоте- вращения двигателя, близкой к минимальной устойчивой.
При любых условиях движения переключение на низшую ступень должно происходить, если допустимая скорость движения будет ниже минимальной устойчивой скорости на высшей ступени.
Переключение ступеней вверх и вниз осуществляется через нейтраль, включаемую на предварительно установленное время переключения ta. Движение автомобиля на этапе переключения описывается выражением (8.1), в котором FK = 0.
6.	Движение накатом. Происходит на длительных спусках, имеющих протяженность, большую, чем оговаривается в условиях. При движении накатом принимается FK=0. Движение накатом может быть также использовано для уменьшения скорости автомобиля.
7.	Торможение. При движении в реальных условиях водитель оценивает допустимую скорость на основании анализа дорожной ситуации. Очевидно, что погрешность оценки допустимой скорости на значительный период вре-
201
Рис. 8.11. Влияние интенсивности использования тормозов на режим движения грузового автомобиля:
"от—средняя скорость движения; — средняя мощность; лт — частота использования тормоза;------------нормальный уровень помех; - -----высокий уровень помех
мени будет больше, а на малый период (или расстояние) — оценка будет точнее. Таким образом, водитель проводит как «долгосрочный» прогноз, так и возможную оценку скорости непосредственно перед препятствием. Если препятствие еще далеко, а скорость автомобиля велика, водитель уменьшает только подачу топлива или переходит на движение накатом так, чтобы автомобиль мог подъехать к возможному препятствию со скоростью, обеспечивающей безопасность движения (т. е. возможность снижения скорости при помощи тормозов до минимальной или даже до полной остановки). Расстояние до препятствия, при котором водитель начинает сбрасывать скорость, зависит от многих факторов, наиболее важными из которых являются: индивидуальные особенности водителя, скорость движения, характер препятствия, видимость. В соответствии с этим при моделировании торможения необходимо предусматривать возможность снижения скорости за счет наката, торможения двигателем или колесными тормозами.
Частота и интенсивность использования колесных тормозов зависит от стиля вождения. По методу снижения скорости можно выделить два резко различающихся стиля вождения автомобиля: в первом случае водитель не использует колесные тормоза, а снижает скорость за счет движения накатом или путем торможения двигателем; во втором — не изменяя скорости автомобиля, подъезжает к препятствию на расстояние, позволяющее интенсивным торможением снизить скорость до допускаемой. Реальный стиль вождения является промежуточным между указанными.
На рис. 8.11 приведены расчетные графики, показывающие зависимость некоторых показателей режимов движения от метода использования тормозов. Показатель а характеризует частоту использования тормозов. При а = 0 замедление осуществляется только за счет торможения двигателем. При а=1 для замедления используются только колесные тормоза. Из графика видно, что стиль торможения оказывает некоторое влияние на среднюю скорость
202
Рис. 8.12. Блок-схема моделирования процесса движения автомобиля:
/—^расчет окружной силы и силы суммарного сопротивления движению; 2 — оценка необходимости переключения ступеней вверх; 3 — расчет параметров движения автомобиля при переключении ступеней вверх; 4 — оценка необходимости переключения ступеней вниз; 5 — расчет параметров движения автомобиля при переключении ступеней вниз; 6 — оценка необходимости торможения; 7 — расчет параметров движения автомобиля при торможении; 8 — расчет параметров свободного движения автомобиля; 9 — статистическая обработка результатов и вывод их на печать
автомобиля только при большом уровне помех.
На магистральных дорогах, особенно при небольшой интенсивности движения, колесные тормоза используются крайне редко. При движении в условиях города торможение в большинстве случаев осуществляется с использованием колесных тормозов. Из приведенного следует, что при моделировании движения по загородным маршрутам можно принимать режим торможения двигателем как основной. При этом интенсивность торможения не должна превосходить интенсивность служебного торможения. Торможение накатом можно осуществить в условиях повышенного дорожного сопротивления (подъема), а торможение колесными тормозами — при необходимости снижения скорости на спусках или когда текущая скорость автомобиля не может быть снижена до допустимой на задан
ном расстоянии путем торможения только двигателем.
На режимах торможения окружная сила на ведущих колесах:
а)	при торможении двигателем Fk = Л1етИкИо/ (Г оЛт)>
где Мет—тормозной момент двигателя. Определяется экспериментально и обычно аппроксимируется выражениями вида:
Мет = а + Ьа? или Мет = с + da>2e, где а, Ь, с, d — постоянные коэффициенты, зависящие от типа и мощности двигателя;
б)	при заданной интенсивности торможения ах
Fk = — (aT8ma — F2).
При заданном расстоянии sT(-, на котором скорость автомобиля должна снизиться с и0 до Од;,	,г
FK = — 0,5ma (оо — v\i}lsu +
В приведенных формулах знак минус указывает, что окружная сила действует в сторону, противоположную направлению движения автомобиля.
Укрупненная схема алгоритма моделирования движения автомобиля приведена на рис. 8.12. Исходными данными для моделирования являются: параметры автомобиля (масса, характеристики двигателя и трансмиссии); параметры, определяющие моменты переключения передач; зависимости сопротивлений качению и воздуха от скорости движения; зависимость сопротивления качению от кривизны траектории и скорости движения; характеристики тормозных режимов и таблица данных, составляющих модель дороги. Поскольку режим трогания автомобиля не моделируется, в исходные данные включается начальная скорость автомобиля.
Рассмотрим последовательность операций при моделировании режима максимальной производительности автомобиля. Будем считать, что в момент вре
203
мени ti автомобиль, находясь на дороге в точке с координатой sf, имеет скорость Vt при включенной в коробке передач ступени с номером tit. Эти данные позволяют рассчитать для координаты st сопротивление движению и окружную силу на ведущих колесах Fk (блок 1). Если на предыдущем шаге интегрирования не было ограничений скорости автомобиля, FK рассчитывается из условия работы двигателя по внешней характеристике. Если же автомобиль двигался с ограниченной скоростью v^i, FK принимается равным
На следующем шаге моделирования проверяется целесообразность переключения ступеней в коробке передач путем сравнения текущей скорости, суммарного сопротивления и окружной силы на ведущих колесах со скоростью и суммарным сопротивлением, определяющим точки переключения (блоки 2 и 4). При этом учитывается допустимая скорость движения автомобиля. Например, переключение на высшую ступень должно произойти при соблюдении условий: Fu < Fn.B; vt уп.в; о» < Здесь Еп.в и уп.в — константы, определяющие дорожное сопротивление и скорость, при которых возможно переключение на высшую ступень. Если эти условия соблюдаются, в блоке 3 моделируется движение автомобиля в процессе переключения на высшую ступень. В результате моделирования определяется номер высшей ступени и соответствующее ей передаточное число трансмиссии, скорость автомобиля и координата пути в момент окончания процесса переключения. После этого процесс решения повторяется: находятся суммарные сопротивления, окружная сила на ведущих колесах и т. д.
Если же в результате проверки устанавливается, что переключение на высшую ступень нецелесообразно, проверяется необходимость переключения на низшую ступень. Если есть такая необходимость, рассчитывается движение
автомобиля в процессе переключения на низшую передачу (блок 5).
После проверки целесообразности переключения ступеней в коробке передач проверяется необходимость торможения (блок 6). С этой целью, сравнивается текущая скорость Vi с допустимой в рассматриваемой координате Si и с допустимой в ближайшей координате sK, где скорость ограничивается Цд.к. Торможение должно происходить, если Уг>Удг или тормозной путь, необходимый для снижения скорости с Vi до Уд.к, не будет превышать расстояния между координатами sK и Si. Характеристики движения автомобиля при торможении определяются в блоке 7. Если торможение не производится, в блоке 8 рассчитываются параметры свободного движения автомобиля. При моделировании шаг счета, зависит от требуемой точности решения и быстродействия вычислительной машины. Интегрирование может производиться по времени или по пути. Последнее в некоторых случаях представляется более удобным.
Блок 9 предназначен для статистической обработки результатов счета и подготовки их к выдаче на печать.
В зависимости от задач, решаемых в ходе исследований, возможны различные оценочные параметры режимов движения. При оценке тягово-скоростных свойств и топливной экономичности автомобилей обычно определяют среднюю скорость движения и закономерности ее распределения, среднее значение используемой мощности, путевой расход топлива. Последний находят по значениям используемой мощности в соответствии с методикой, изложенной в параграфе 2.7. В тех случаях, когда оценивают нагрузочные режимы работы трансмиссии, дополнительно определяют число включений различных ступеней в коробке передач и путь, проходимый автомобилей при соответствующих включенных ступенях.
204
ЛИТЕРАТУРА
Автомобильные транспортные средства/Под ред. Д, П. Великанова.— М.: Транспорт, 1977.— 326 с.
Агейкин Я. С. Вездеходные колесные и комбинированные движители.— М.: Машиностроение, 1972.— 184 с.
Антонов Д. А. Теория устойчивости движения многоосных автомобилей.— М.: Машиностроение, 1978.— 216 с.
Вонг Дж. Теория наземных транспортных средств: Пер. с англ.— М.: Машиностроение, 1982.— 282 с.
Грузовые автомобили/М. С. Высоцкий, Ю. Ю. Беленький, Л. X. Гилелес и др.— М.: Машиностроение, 1979.— 384 с.
Гуревич Л. В., Меламуд Р. А. Тормозное управление автомобиля.— М.: Транспорт, 1978,— 150 с.
Динамика системы дорога — шина — автомобиль — водитель/Под ред. А. А. Хачатурова.— М.: Машиностроение, 1976.— 535 с.
Зимелев Г. В. Теория автомобиля.— М.: Машгиз, 1959.— 312 с.
Литвинов А. С. Управляемость и устойчивость автомобиля.— М.: Машиностроение, 1971,—416 с.
Михайловский Е. В. Аэродинамика автомобиля.— М.: Машиностроение, 1973.— 222 с.
Осепчугов В. В. Автобусы.— М.: Машиностроение, 1971.— 312 с.
Островцев А. Н. Основы проектирования автомобилей.— М.: Машиностроение, 1968.— 204 с.
Петрушов В. А., Шуклин С. А., Москвин В. В. Сопротивление качению автомобилей и автопоездов.— М.: Машиностроение 1975.— 223 с.
Применение ЭВМ при конструировании и расчете автомобиля/Под ред. А. И. Гришкевича.— Мн.: Выш. шк., 1978.— 264 с.
Проектирование трансмиссий автомобилей: Справочник/Под ред. А. И. Гришкевича.— М.: Машиностроение, 1984.— 272 с.
Работа автомобильной шины/Под ред.
В. И. Кнороза.— М.: Транспорт, 1976.— 237 с.
Расчет эксплуатационных параметров движения автомобиля и автопоезда/А. А. Хачатуров, В. П. Афанасьев, В. С. Васильев и др.— М.: Транспорт, 1982.— 264 с.
Родионов В. Ф., Фиттерман Б. Н. Проектирование легковых автомобилей.— М.: Машиностроение, 1980.— 477 с.
Ротенберг Р. В. Подвеска автомобиля.— М.: Машиностроение, 1972,—392 с.
Силаев А. А. Спектральная теория подрес-соривания транспортных машин.— М.: Машгиз, 1963,— 167 с.
Сильянов В. В. Транспортно-эксплуатационные качества автомобильных дорог.— М.: МАДИ, 1978,— 103 с.
Смирнов Г. А. Теория движения колесных машин.— М.: Машиностроение, 1981.— 269 с.
Стесин С. П., Яковенко Е. А. Гидродинамические передачи.— М.: Машиностроение, 1973.— 348 с.
Фаробин Я. Е. Теория поворота транспортных машин.— М.: Машиностроение, 1970.— 176 с.
Фаробин Я. Е., Овчаров В. А., Кравцов В. А. Теория движения специализированного подвижного состава.— Воронеж: Воронеж, ун-т, 1981.— 158 с.
Чудаков Е. А. Теория автомобиля.— М.: Машгиз, 1950.— 343 с.
Эллис Д. Р. Управляемость автомобиля.— М.: Машиностроение, 1975,—214 с.
Чцепко Н. Н., Прутчиков О. К- Плавность хода грузовых автомобилей.— М.: Машиностроение, 1969.— 220 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ*
Автоколебания управляемых колес 161
Аквапланирование 24
Влажность относительная 174
Время запаздывания тормозного привода 87
—	нарастания замедления 88
—	реакции водителя 87
—	срабатывания тормозного привода 88
Габарит динамический 188
Деформация грунта остаточная 174
--- пластическая 174
--- упругая 174
Диапазон гидротрансформатора рабочий 79
—	передаточных чисел коробки передач 73
Замедление при торможении 88, 92
—	установившееся 95
Занос автомобиля 163
Запас устойчивости статической 153
Категория дороги 192
Коэффициент безопасности движения 193
—	блокировки дифференциала 144
—	высшей передачи 72
—	грузоподъемности 64
—	динамичности подвески 106
—	жесткости упругого элемента 105
--- шины 106
—	затухания относительный 108,123
—	конечной скорости 196
—	массы прицепа 67
—	насоса 78
—	обтекаемости 38	х—
—	объемного сжатия грунта 178
—	передачи регулятора 99
—	перераспределения нормальных реакций 43
—	полезного действия гидротрансформатора 77
------- трансмиссии 33
—	продольной силы колеса 20
—	прозрачности гидродинамической передачи 79
—	развития трассы 188
Составлен проф. А. Н. Гришкевичем. ,
—	распределения тормозных сил 91
— снаряженной массы 61
— сопротивления амортизатора 107
---- воздуха 40
---- дороги 38
----качению 17
---- подъему 37
---- уводу 137
—	сцепления 19, 21
—	сцепного веса 46
—	трансформации 77
—	учета вращающихся масс 43
—	• эффективности тормозов 77
Крен кузова 148
Линия воздушная 188
—	поворачиваемости нейтральной 153
Масса автомобиля полная 65
----снаряженная 65
---- сухая 65
Микропрофиль 109
Моделирование 185
Модель дороги 185
Момент двигателя крутящий 29
—	тормозной 20, 93
—	сопротивления качению 15, 18
—	стабилизирующий 136
Мощность автомобиля удельная 59
—	двигателя 59, 68
Нагрузка нормальная 15
— расчетная 193
Одежда дорожная 189
Основание дорожное 190
Ось крена 148
Отношение передаточное кинематическое 71
Плечо крена 148
Плотность микропрофиля спектральная 110
Поворачиваемость автомобиля динамическая 153
---- статическая 150
Подъем преодолеваемый максимальный 50, 170
Покрытие дороги 190
Полотно земляное 189
206
Полоса отвода 188
—	частот октавная 177
Полюс поворота 140
Прозрачность гидропередачи 79
Просвет дорожный 169
Проскальзывание упругое 13
Профиль дороги продольный 189, 194
Проходимость опорио-сцепная 169
	— профильная 169 .
Путь остановочный 88
—	тормозной 94
Радиус качения 12
— колеса динамический 11
----свободный 11
---- статический 11
Радиус поворота 140
----габаритный 141
---- кинематический 150
— — минимальный 141
— проходимости 170
Развал колес 157
Расход топлива путевой 54
---- средний 54
----удельный 57
Реакция боковая 146
— нормальная 15, 42
Связь гироскопическая 159
Сила колеса инерционная 20
----окружная 17, 33
—	— продольная 16
—	сопротивления воздуха 38
	дороги 38
----качению 17,	35
----	подъему 37
----поступательному разгону автомобиля 41
—	—	прицепа 41
---- разгону колеса 17
—	тяги 19
---- свободная 45
Система парциальная 122
—	противоблокировочная 101
—	тормозная вспомогательная 86
---- запасная 86
— — рабочая 86
---- стояночная 86
Скольжение колеса 13
Скорость автомобиля кинематическая 72
----критическая по условиям увода 151
---максимальная 49
—--------	условная 49
•---расчетная 192
	— — средняя 48
Способность дороги пропускная 139
Стабилизация колес управляемых 154
Схождение колес 157
Торможение аварийное 87
—	служебное 87
Точка срабатывания регулятора 99
Трасса 188
Тяговый баланс автомобиля 43
Увод колеса 135
Угол свеса 169
—	поперечной устойчивости 165
Управляемость 133
Условия дорожные 187
—	природно-климатические 187
—	транспортные 187
—	эксплуатационные 187
Устойчивость курсовая 133, 150
—	траекторная 133, 150
--- статическая 143
—	поперечная 133
—	продольная 133
Фактор динамический 45
—	обтекаемости 40
—	тормозной 89
Характеристика амортизатора приведенная 107
— гидродинамической передачи безразмерная 78
—	двигателя скоростная 28
—	динамическая 46
— подвески приведенная 106
— регулятора рабочая 99
—	топливная установившегося движения 55
---циклического движения 56
—	тяговая 44
—	частотная комплексная 125
—	шины упругая 106
Частота возмущения 109
— колебаний собственных 121
Число передаточное главной передачи 72
--- первой передачи 73
---промежуточной передачи 74
--- раздаточной коробки 76
Центр крена 148
—	парусности 41
—	поворота мгновенный 140
Аркадий Иванович Гришкевич
АВТОМОБИЛИ. Теория
Зав. редакцией В. Г. Самарина
Редактор Ж. И. Васюк
Мл. редакторы А. П. Берлина, Н. В. Валишева
Оформление и худож. редактирование В. Н. Ва-лентовича
Графическое исполнение В. М. Шмидова
Техн, редактор М. Н. Кислякова
Корректор Т. К- Хвалъ
ИБ Ng 1966
Сдано в набор 29.10.85. Подписано в печать 10. АТ 13718. Формат 70X90’/i6. Бумага тип. Гарнитура литературная. Высокая печать, печ. л. 15,21. Усл. кр.-отт. 15,21. Уч.-изд. л.
Тираж 9300 экз. Заказ 1898. Цена 1 р.
Издательство «Вышэйшая школа» Государе ного комитета БССР по делам издательств лиграфии и книжной торговли. 220048, М проспект Машерова, II.
Минский ордена Трудового Красного Знамен лиграфкомбинат МППО им. Я. Коласа. 2: Минск, ул. Красная, 23.