Text
Г. П. ГАВРИЛОВ, А. А. САПОЖЕНКО
СБОРНИК ЗАДАЧ
ПО ДИСКРЕТНОЙ
МАТЕМАТИКЕ
Допущено Министерством Высшего и среднего
специального образования СССР в качестве учеб-
ного пособия для студентов вузов, обучающихся
по специальности «Прикладная математика»
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1977
518
Г 12
УДК 519.95
Сборник задач по дискретной мате-
матике, Г. П. Гаврилов, А. А. С а-
п о ж е н к о. Главная редакция физико-
математической литературы изд-ва
«Наука», М., 1977 г.
Сборник возник как пособие для
практических занятий по курсу дис-
кретной математики. Он содержит как
упражнения, предназначенные для
первоначального ознакомления с основ-
ными понятиями и фактами дискретной
математики, так и задачи повышенной
трудности, рассчитанные на такого
читателя, который обладает достаточ-
ной математической культурой и спе-
циальной подготовкой.
Книга будет полезна студентам
университетов и других вузов, в кото-
рых изучаются дискретная математика
и математическая логика.
Гарий Петрович Гаврилов
Александр Антонович Сапоженко
СБОРНИК ЗАДАЧ
ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
М., 1977 г., 368 стр. с илл.
Редактор Е. 10. Ходан
Технический редактор В. Н. Кондакова
Корректор Г. В. Подволъская
Сдано в набор 12.07.1976 г. Подписано
к печати 18.02.1977 г. Бумага 84хЮ8’/32- Физ.
печ. л. 11,5. Усл. печ. л. 19,32. Уч.-изд. л. 19,94.
Тираж 27000 8кз. Цена книги^л коп.
Заказ 1393
Издательство «Наука»
Главная редакция
физико-математической литера?}ры
117071, Москва, В-71, Ленинский проспект, 15
1-я типография издательства «Наука».
199034, Ленинград, В-34, 9-я линия, д. 12.
Отпечатано с готовых матриц в ордена Трудового Красного Знамени
тип. им. Володарского Лениздата. 191023, Ленинград, Фонтанка, 57.
_ 20204-045 © Главная редакция
053(021—77 физико-математической литературы
' ' издательства «Наука», 1977
ОГЛАВЛЕНИЕ
Предисловие ....<>* >> <<>>>>>>> 5
Глаза I. Булевы функции, способы их задания и ос-
новные свойства ............................... 9
§ 1. Булевы векторы и единичный n-мерный куб . . 9
§ 2. Способы задания булевых функций. Элементар-
ные функции. Формулы. Операция суперпозиции 20
§ 3. Специальные виды формул. Дизъюнктивные и
конъюнктивные нормальные формы. Полиномы 30
§ 4. Минимизация булевых функций.............. , 38
§ 5. Существенные и фиктивные переменные , « . 44
Глава II. Замкнутые классы и полнота . । > 50
§ 1. Операция замыкания. Замкнутые классы ... 50
§ 2. Двойственность и класс самодвойственных функ»
цпй............................................ 54
§ 3. Линейность и класс линейных функций . , , , 59
§ 4. Классы функций, сохраняющих константы , , 62
§ 5. Монотонность и класс монотонных функций , 65
§ 6. Полнота и замкнутые классы , , , , , , , , , 71
Глава III. fc-значнуе логики .,>,•>>>>» 77
§ 1. Представление функций й-зпачпых логик фор-
мулами специального вцда....................... 77
§ 2. Замкнутые классы /с-значноп логики...... 86
§ 3. Исследование систем функций /с-значной логики
на полноту .................................. 95
Глава IV. Графы и сети . . , , . , , , , , , , , 101
§ 1. Основные понятия теории графов.......... 101
§ 2. Планарпость, связность, числовые характерис-
тики градов....................................111
§ 3. Ориентированные графы 117
§ 4. Деревья и двухполюсные сети , 124
§ 5. Оценки в теории графов и сетей............. 137
§ 6. Реализация булевых функций контактными схе-
мами и формулами 148
1» 3
Глава V. Элементы теории кодирования >>«>> 159
§ 1. Коды с исправлением ошибок , , , . , , , . , 159
§ 2. Линейные коды 164
§ 3. Алфавитное кодирование ,........... , , , 168
Глава VI. Конечные автоматы , . . 178
§ 1. Детерминированные и ограниченно-детерминиро-
ванные функции.................................... 178
§ 2. Представление детерминированных функций диа-
граммами Мура, каноническими уравнениями,
таблицами и схемами. Операции над детерминиро-
ванными функциями................................. 190
§ 3. Замкнутые классы и полнота в множествах детер-
минированных и ограпиченпо-детерминирован-
пых функций ..................................... 208
Глава VII. Элементы теории алгоритмов................. 213
§ 1. Машины Тьюринга и операции над ними. Функ-
ции, вычислимые на машинах Тьюринга . . . 213
§ 2. Классы вычислимых и рекурсивных функций 234
§ 3. Вычислимость и сложность вычислений . . . ( 242
Глава VIII. Элементы комбинаторики , , а , , ( ( 249
§ 1. Перестановки и сочетания. Свойства биномиаль-
ных коэффициентов................................. 249
§ 2. Формула включений и исключений .............. 259
§ 3. Возвратные последовательности, производящие
функции, рекуррентные соотношения , , , ( 263
§ 4. Асимптотические оценки и неравенства > ( « 273
Решения, ответы, указания • • • е 281
Литература .*••*>«*• । > । >« t » * « 358
Предметный указатель................................. 360
Указатель обозначений 365
ПРЕДИСЛОВИЕ
Предлагаемый читателю сборник задач задуман как
пособие для упражнений по курсу дискретной мате-
матики и предназначен в основном для студентов млад-
ших курсов университетов. Сборник может быть поле-
зен также студентам старших курсов и аспирантам,
специализирующимся в области математической ки-
бернетики. Преподаватели могут использовать эту
книгу для подготовки упражнений и семинарских за-
нятий.
Книга базируется на курсе дискретной математики,
читавшемся в течение ряда лет сначала на механико-
математическом факультете, а затем на факультете
вычислительной математики и кибернетики Москов-
ского государственного университета.
Сборник состоит из восьми глав. Первые две главы
посвящены алгебре логики. Раздел «Алгебра логики»
является основополагающим при изучении дискретной
математики. В лекционном курсе и на практических
занятиях на факультете ВМиК МГУ ему отводится
около четверти всего времени. На материале этого раз-
дела учащийся получает первоначальные представле-
ния о таких понятиях, как дискретная функция, опе-
рация суперпозиции, функционально полная система;
знакомится с различными способами задания дискрет-
ных функций (табличный способ, представление поли-
номами и нормальными формами, геометрическое пред-
5
ставление с использованием н-мерного единичного
куба); изучает приемы исследования полноты и замкну-
тости систем функций.
Третья глава посвящена А-значным логикам. Пред-
ставленные здесь задачи имеют целью познакомить чи-
тателя с каноническими разложениями А-значных функ-
ций, с эквивалентными преобразованиями формул,
с основными замкнутыми классами функций А'-значной
логики и методами исследования систем функций на
полноту и замкнутость. В ряде задач иллюстрируются
отличия между А-значными логиками (А: > 2) и алгеб-
рой логики.
В четвертой главе содержатся задачи по теории гра-
фов (ориентированных и неориентированных), теории
сетей и схем. Целью этого раздела является ознакомле-
ние студента с основными понятиями, методами и язы-
ком теории графов, которые весьма широко использу-
ются при описании п исследовании структурных свойств
объектов в самых различных областях науки и техники.
В этом разделе приводятся задачи, предназначенные
для закрепления основных понятий теории графов;
задачи, иллюстрирующие применение теории графов
и сетей к синтезу схем, реализующих булевы функции;
задачи на подсчет объектов с заданной геометрической
структурой и т. п. Авторы надеются, что преподаватель
найдет здесь также задачи, с помощью которых можно
обучить студента математически строгому доказатель-
ству геометрически «очевидных» утверждений.
Пятая глава посвящена теории кодирования. Пред-
ставлены задачи на свойства кодов, исправляющих
ошибки; алфавитных кодов; кодов с минимальной из-
быточностью.
В шестой главе содержатся задачи, демонстрирую-
щие различные подходы к описанию дискретных преоб-
разователей (автоматов). Приведены задачи на выявление
детерминированности и ограниченной детермини-
6
рованности автоматов; на различные способы представ-
ления автоматов — диаграммами, каноническими урав-
нениями, схемами; на исследование функциональной
полноты и замкнутости систем автоматных отображе-
ний; на изучение свойств различных операций над та-
кими отображениями.
Седьмая глава, посвященная элементам теории алго-
ритмов, имеет целью дать представление об эффектив-
ной вычислимости и сложности вычислений, о некото-
рых конкретных формах определения алгоритма —
машинах Тьюринга и рекурсивных функциях.
Восьмая глава носит вспомогательный характер и
посвящена комбинаторике. Этот раздел выходит за
рамки программы университетского курса дискретной
математики. Однако изучающему дискретную матема-
тику часто приходится сталкиваться с вопросами суще*
ствования, подсчета и оценки различных комбинатор-
ных объектов. Поэтому авторы сочли полезным поме-
стить задачи по комбинаторике.
В настоящее время отсутствует учебник, который бы
полностью охватывал теоретический материал про-
граммы университетского курса «дискретной матема-
тики». Первый том монографии «Дискретная матема-
тика и математические вопросы кибернетики», М.,
«Наука», 1974, являющийся основным учебным посо-
бием, охватывает теоретический материал, соответ-
ствующий первым пяти главам задачника. Литература,
соответствующая остальным главам, разбросана по
различным монографиям. Поэтому авторам данного
задачника приходилось предварять каждый параграф
теоретическими справками, иногда более подробными,
чем это обычно принято в пособиях такого рода.
На многие (но не все) задачи даны указания и ответы.
Решения изложены по возможности кратко, в конспек-
тивном стиле, тривиальные заключения опущены.
В некоторых случаях дается лишь набросок решения.
7
По происхождению материал задачника весьма
разнообразен. Значительная часть задач носит «фольк-
лорный» характер. Такие задачи хорошо известны
специалистам по дискретной математике, однако уста-
новить авторство задач подобного сорта почти невоз-
можно. Основная часть задач была придумана авто-
рами в процессе ведения упражнений и семинаров,
приема экзаменов по дискретной математике, а также
во время подготовки данного сборника. Некоторая часть
задач возникла в результате обработки журнальных
статей. Некоторые задачи заимствованы нами из дру-
гих руководств. Ряд задач был сообщен нам сотрудни-
ками кафедры математической кибернетики МГУ и
другими нашими коллегами. Большой запас задач
предоставил в распоряжение авторов О. Б. Лупанов.
Отдельные задачи предложены С. В. Яблонским,
В. Б. Алексеевым, А. А. Евдокимовым, В. К. Леонтье-
вым, Ал. А. Марковым. Всем им мы выражаем ис-
креннюю благодарность.
Авторы весьма признательны С. В. Яблонскому за
внимание к нашей работе над книгой. Его советы и
рекомендации в значительной мере определили струк-
туру и тематическую направленность сборника.
Авторы глубоко обязаны О. Б. Лупанову, прочи-
тавшему всю рукопись и уделившему много времени
для обсуждения с авторами ее содержания.
Мы искренне благодарны С. С. Марченкову, весьма
тщательно прочитавшему главу «Элементы теории алго-
ритмов», В. И. Левенштейну, прочитавшему главу
«Элементы теории кодирования» и сделавшему ряд
ценных замечаний, а также рецензентам книги
В. В. Глаголеву и Ал. А. Маркову за критические за-
мечания и соображения по улучшению сборника.
Г. П. Гаврилов, А. А. Сапоженко
Глава I
БУЛЕВЫ ФУНКЦИИ,
СПОСОБЫ ИХ ЗАДАНИЯ
И ОСНОВНЫЕ СВОЙСТВА
§ 1. Булевы векторы и единичный
n-мерный куб L)
Вектор (а1, а2, . . ая), координаты которого прини-
мают значения из множества {0, 1}, называется двоич-
ным или булевым вектором (набором). Для краткости
такой вектор будем обозначать через а” или а. Число п
называется длиной вектора. Множество всех булевых
векторов длины п называется единичным п-мерным ку-
бом и обозначается через Вп. Сами векторы а” назы-
ваются вершинами куба В”. Весом ||ая|| или нормой век-
тора а" называется число его координат, равных еди-
п
нице, т. е. || а" || = 2 а,- Множество всех вершин куба В",
•=1
имеющих вес к, будем называть к-м слоем куба Вп и
обозначать через В"к. Каждому булеву вектору а” можно
п
сопоставить число v (а”) = 2 называемое номером
•-1
вектора ап. Набор ап является, очевидно, двоичным раз-
ложением числа v(a"). Расстоянием (Хэмминга) между
вершинами а и р куба В" называется число р(а, р) =
п
= 2 | а< — |> равное числу координат, в которых они
>=i
*) Этот параграф является вспомогательным. В дальнейшем
используются лишь задачи 1.1—1.6; 1.11; 1.14; 1.15; 1,31; 1.34;
1,35; 1.44.
9
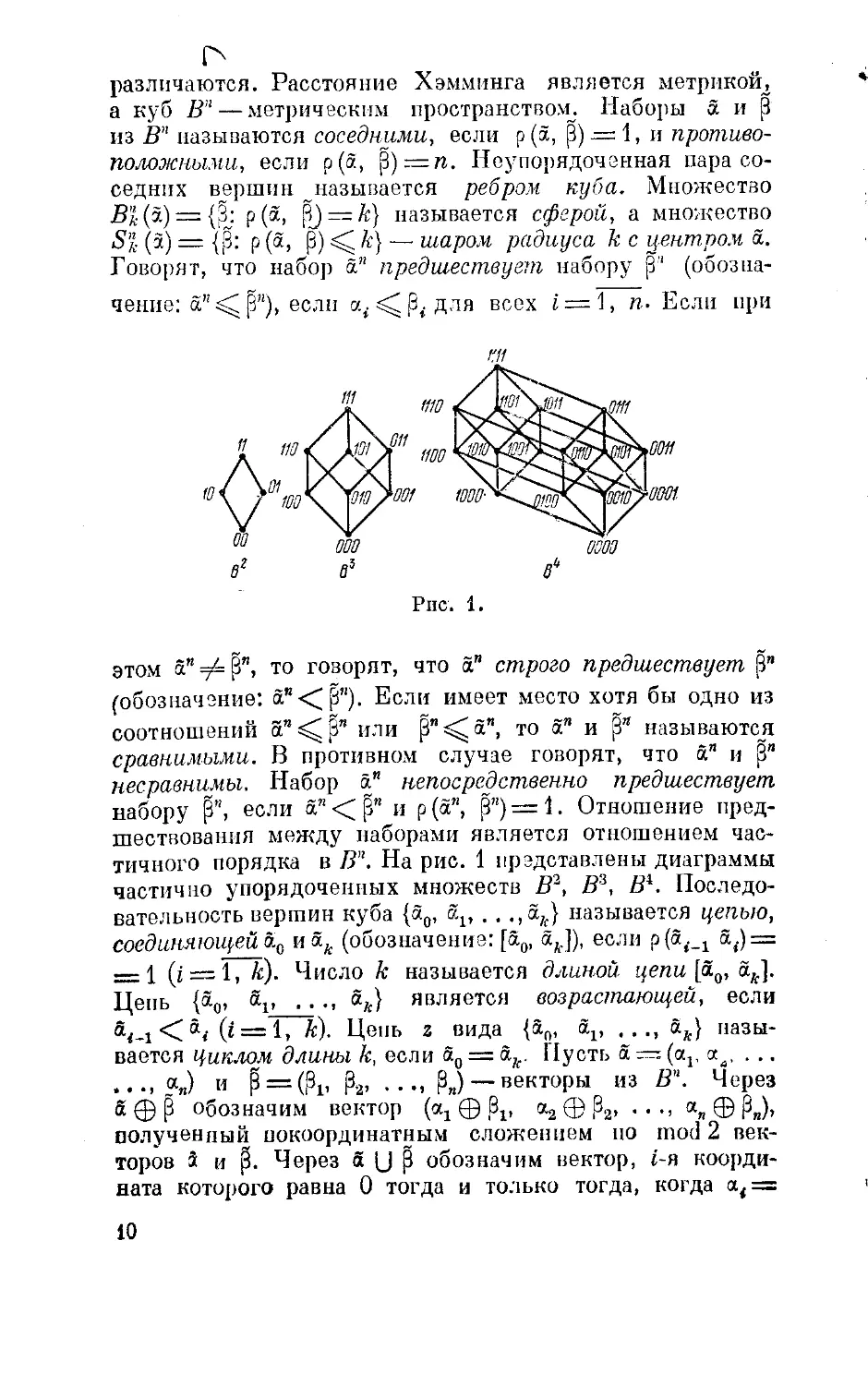
различаются. Расстояние Хэмминга является метрикой^
а куб В’1—метрическим пространством. Наборы аир
из В" называются соседними, если р (5, р) — 1, и противо-
положными, если р(а, р) — п. Неупорядоченная пара со-
седних вершин ^называется ребром куба. Множество
Bl (a) = {pj р(а, fy — k} называется сферой, а множество
Si (5)={.3: р(а, PXJ&} — шаром радиуса к с центром 3,.
Говорят, что набор а” предшествует набору р'' (обозна-
чение: а'г<^ря), если а. для всех i = i, п. Если при
этом а" Р”, то говорят, что а" строго предшествует р”
(обозначение: ав<р"). Если имеет место хотя бы одно из
соотношений а"^Р" или ря^а”, то а” и р” называются
сравнимыми. В противном случае говорят, что а” и рм
несравнимы. Набор а" непосредственно предшествует
набору рч, если а” <( р” и р (ак, р”) = 1. Отношение пред-
шествования между наборами является отношением час-
тичного порядка в В". На рис. 1 представлены диаграммы
частично упорядоченных множеств В2, В3, В1. Последо-
вательность вершин куба {й0, ар. . .,a;f} называется цепью,
соединяющей й0 иак (обозначение: fa0, aj), если р (5<_1 at.) =
— 1 (г = 1, &). Число к называется длиной цепи [a0, аА].
Цепь {а0, ар .... &к} является возрастающей, если
(г = 1, к). Цепь z вида {3Q, a1, ..., Зк} назы-
вается Циклом длины к, если Зо = Зк. Пусть а = (аГ ал, . ..
и р = (РГ, р2, ..рп) — векторы из В". Через
«ФР обозначим вектор (04 ф РР 04 ф ₽а, ..., а„ ф 0B),
полученный покоординатным сложением по mod 2 век-
торов 3 и р. Через a (J р обозначим вектор, l-я коорди-
ната которого равна 0 тогда и только тогда, когда at =
10
= 8{ = 0. Через a QB обозначим вектор, г-я координата
которого равна 1 тогда и только тогда, когда а,. = (3^ = 1.
Через 2 обозначим вектор (противоположный к а), j-я
координата которого принимает значение 0, если а/ = 1,
и значение 1, если а,. = 0. Если з £ (0, 1}, то положим
оа = (за1, аа2, . .., зад). Символом 0 обозначим вектор
(0, 0, . . ., 0), а символом 1 —вектор (1, 1, ..., 1).
Множество Б”1 всех наборов (ар ..ад) из Вп,
у которых а^ = з. (/ = 1, к), называется гранью куба В”.
Множество I = {z\.....ik} называется направлением
грани, число к — рангом грани, а п—к — размерностью
грани.
1.1. 1) Найти число | Б* | наборов а” веса к.
2) Чему равно число всех вершин куба Б!!?
1.2. 1) Найти номера наборов (1001), (01101), (110010).
2) Найти вектор длины 6, являющийся двоичным
разложением числа 19.
1.3. Чему равно число наборов а £ Б*, удовлетворяю-
щих условию 2"*1 ^v(a)<2'?
1.4. Показать, что для любых а, у из В" справед-
ливы соотношения:
1) р(5, Т)<р(а, ₽) + p(3>j);
2) р(«. Т) = р(а ф Ч Ф
3) р(а, Р)Н1Ч+Я-2НПё1|;
4) р(5, (->) = ||я©р||.
1.5. 1) Найти число неупорядоченных пар соседних
вершин Б”.
2) Найти число неупорядоченных пар наборов (а”, р"),
таких, что р(а", $п) = к.
1.6. Пусть а, р — вершины куба Б", р(а, $) = т.
Найти число вершин f, удовлетворяющих условию:
1) р& ч) + р(ъ Р)=р(5> ₽);
2) р(а, Ч) = к’ рф, Ч)~г>
3) Р(а, Т)<Л рф, т) = г;
4) р(а, у) <А, р(3, 7)>г.
1.7. Доказать несовместность следующих систем соот-
ношений для а, р и *7 из В”, п 2:
1) р(а, р) Д> 2лг/3, р(;3, ^)^>2я/3, р(у, а)>2га/3;
. 2) v(a)<v(p©7), »ф)<»(тфа), v(7)< v(а ф р);
11
з) и>ити. цр||>и© ч imi>uwii.
|1аПфПт)1| = 0;
4) II a®>® 711=0, ||Sфр® I\\ = п-1.
1.8. Пусть а, р, у — вершины из В”. Показать, что:
1) а^р равносильно аПр = 0;
2) a U 3 = 1 равносильно р а;
3) аП(аиЗ) = а;
4) а U (а П р) —а;
5) (auP)n(PUi) = (ariT)UP;
6) ((5П'7)ир)П7 = («Пт)и(РПт);
7) из a <7 7 вытекает, что а (J (Р П 7) (а U Р) П Т?
8) a=Cl равносильно a |J (Р П т) (а U Р) П 7I
9) (5ПР)и(рП7)и(тпа) = (aUР)П(РU7)П(7Uа).
1.9. Каково число векторов (а1, а2, . . ., а12) из В™,
таких, что 2 Оч^т/2 для всех щ = 1, 12?
1<Сг т
1.10. Найти число векторов а из Вк, таких, что между
двумя единичными координатами существуют ио край-
ней мере г нулевых.
1.11. 1) Показать, что в Вп существует множество,
состоящее из (|геу2|) попаРно несравнимых векторов.
2) Показать, что всякое подмножество, содержащее не
менее п 2 векторов, содержит пару несравнимых век-
торов.
1.12. Пусть и Л (а) — множество всех
векторов из В", сравнимых с а. Найти мощность мно-
жества С:
1) С = Л(а)П5г, И£В];
2)С = Л(а)ПВ?,
3)С = Л(а), а^В^.
1.13. Пусть А С B’j, а В — множество всех наборов
из Вк, сравнимых хотя бы с одним набором из Л. До-
казать, что
1.14. 1) Показать, что в В” существует nl попарно
различных возрастающих цепей длины п.
2) Показать, что число попарно различных возрастаю-
щих цепей длины п, содержащих фиксированную вер-
шину а из Вк, равно к\ (п — к) I.
12
1.15*. 1) Показать, что мощность любого подмножества
попарно несравнимых наборов куба Вп не превосходит
(h/2|)-
2) Показать, что если подмножество А С Вп состоит
из попарно несравнимых наборов и ||а ||к для всякого
а £ А, то | А | при & .
1.16. Пусть pv р.,, .. ., рп — попарно различные про-
стые числа, a N — множество всех чисел, представимых
в виде р'‘‘рЬ ... /?’», где а. £ {0, 1), г = 1, п. Пусть под-
множество А С N таково, что никакое число a f А не яв-
ляется делителем никакого числа b £ А, отличного от а.
Доказать, что | А |
~ \ [ 72,2- ] /
1.17. Пусть а, В — такие вершины куба Вп, что а р,
р(а, р) — к. Показать, что число наборов у, таких, что
а у р, равно 2\
1.18* . Доказать, что куб Вп можно представить в виде
объединения попарно непересекающихся возрастающих
цепей, обладающих следующими свойствами:
1) число цепей длины п — 2к равно —(^2.1)’
к—0, [п/2], при этом минимальный набор каждой такой
цепи имеет вес к, а максимальный — вес п — к’,
2) если а,., а<+1, а<+2 — три последовательные вершины
возрастающей цепи, имеющей длину п — 2к, то вер-
шина р, такая, что а,- <С Р ®»+2> Р 7^ ®<+1> пРинаДлежит
некоторой цепи длины п — 2к—2.
1.19. Пусть а, р — такие вершины куба В”, что
р(а, р) = к, а С (а, р)—множество всех вершин у, для
которых существует цепь [а, р] длины к-\-2г, содержа-
щая эту вершину. Чему равна мощность множества
С(а, Р)?
1.20. Множество А С В” называется полным в В”,
если любой вектор p^S" однозначно восстанавливается
при условии, что для каждого а £ А известно расстоя-
ние р(а, Р). Полное в Вп множество называется базис-
ным, если для любого вектора а из Л множество 4\{а}
не является полным.
Ь'4) Показать, что любая возрастающая цепь а0, а1,
..., в В” образует базисное множество.
13
2) Показать, что множества В* и являются пол-
ными в В'! при п^>2. Указать такое п^>2, что Б" не
является базисным.
3) При каких п и к множество Вк не является пол-
ным в В”?-?
4) Доказать, что всякое базисное множество А в Вп
удовлетворяет условию - < | А |<га.
5) Доказать, что никакая грань размерности п — 2 не
является полным в В“ множеством.
6) Показать, что число 'Г„ базисных множеств в Вп
/2,г\
удовлетворяет неравенствам 2 • (и !) ЧД ).
1.21. Пусть ф— взаимно однозначное отображение В”
на себя. Говорят, что отображение ф сохраняет расстоя-
ние между вершинами, если р(а, р) = р(<р(а), <р(р)) для
всех а, р из В”. Доказать, что отображение ср сохраняет
расстояние тогда и только тогда, когда оно может быть
получено с помощью:
1) некоторой перестановки координат одновременно
во всех наборах из В”',
2) заменой 0 на 1 и 1 на 0 в некоторых координа-
тах всех векторов.
1. 22. Отображение <р множества Вп в себя называется
монотонным, если из v (а) v (р) вытекает, что v (ф (а)) «Д
^v(-p(p)). Найти число монотонных отображений куба В”.
1. 23. Пусть а£В*. Множество Л/£ (а) = {у: v(y)^
<^v(a), ^QB’k} называется начальным отрезком слоя Вк.
Пусть А С. Вп; обозначим через Z?(A) множество набо-
ров р Q В’}, для которых существует такое a Q А, что р «Д а.
1) Пусть а£В1 и i1, i2, . . ., ik (1<Д1<Да<...
... <Ak^ri) — номера координат вектора а, равных еди-
нице. Показать, что
/п — t'A (п — i„\ /п — 1,-\
= Щ к )+(,_, )+ ... +( , *).
2) Показать, что если Z /с и А — начальный отре-
зок слоя Вк, то множество Z”(A) является начальным
отрезком слоя В",
3) Пусть а £ В* и iv i2, . . ., ik (1 ij < i2 < ...
... <Z ik — номера координат вектора а, равных еди-
нице. Пусть А = Мк(а) и I к. Показать, что
/п — i,\ . In — i, \ (n — i,\
= 1 + 1 z )+(j-i)+ +( i )•
14
4 *) Пусть Доказать, что минимум ве-
личины [Zk~i(A)l по всем таким А С Вк, что |Л| = ттг,
достигается на начальном отрезке слоя Вк.
5) Пусть 1 и I к. Доказать, что минимум
величины |Z"(/)| по всем таким А С Вк, что | X | = ??г>
достигается на начальном отрезке слоя Вк.
6) Пусть а0, av . . ., ап — заданные числа, для кото-
рых существует такое множество А попарно несравни-
мых наборов, что | Л П Вк\ — ак (к~0, тг). Тогда мини-
мум величины |Z?(M)|, взятый по всем таким множе-
ствам А, достигается в том случае, когда для любого
i Д> I множество Z’/ (Л) является начальным отрезком
слоя В}.
1.24*. Пусть А С Б" —такое множество наборов, что
не существует наборов а, р, j из А, для которых ар[3 = 0,
а аОЭ = т- Пусть ак = | Л р| В’к |. Показать, что
для любых натуральных к, тп, не превосходящих п.
1.25. Множество Г(Л) = {а: а£5"\Л, р(а, Л) = 1}
называется границей подмножества A Q В”. Пусть 1
rC h 1-2 'С • • • ijc п- Обозначим через Ллуе>ч
множество всех тех наборов из Л, у которых координата
с номером ij равна (/ = 1, к).
Центром множества А будем называть такой на-
бор, у которого i-я координата равна 0, если | Ло -у | А |,
и равна 1 в противном случае. Обозначим через а’3> '» •••> •*
набор, полученный из а заменой координат с номерами
iv i2, .. ik на противоположные.
1) Показать, что для всякого А С Вп существует
А' С В", такое, что | А' | = | Л |, | Г (Л') | — | Г (Л) |, и цен-
тром А1 является вершина 0 = (0, 0, . .., 0).
2) Будем говорить, что множество Л С В" обладает
свойством 1, если для всякого i — 1, тг из а^Л|: выте-
кает, что а’ ^Л. Показать, что для всякого А С В" су-
ществует множество А' с центром 0, такое, что | А’ | =
= |Л|, Л' обладает свойством 1 и | Г (Л') | <11 Г (Л) |.
3) Будем говорить, что множество Л С В'1 обладает
свойством И, если для любых i, j из
15
аел вытекает, что А. Показать, что для вся-
кого А с центром 0, обладающего свойством I, суще-
ствует А' с центром в 0, обладающее свойствами 1, II
и такое, что |Л| = |Л'|, | Г (Л') | Г (Л) |.
4 *) Показать, что min | Г (Л) | по всем A (Z В”, таким,
fc-l 1с
что2С)<|л1 Д0СТ1|Гается на множестве
»=0 »=0
А = S’}.-! (б) U М”к (а), где Мк (а) — некоторый начальный
отрезок слоя В’к (см. задачу 1.23).
1.26. Пусть ср (га) (ср'(га))—максимальная мощность
множества A С В", такого, что ||арВ||= 1 (соответственно
||аПР||>1) для любых двух различных векторов из А.
Показать, что:
1) ср (га) = га; 2) ср'(га) = 2|!-1.
1.27. Пусть F (п, к)—семейство подмножеств А мно-
жества В”, таких, что || а Пр || к для любых а, р из А.
Пусть ср (га, к)— max \А |. Доказать следующие
лел»,
утверждения:
1)2 О-
2) Пусть А С F (га, к); тогда | А П B*l | Д-1А П #U+»-i1 <
<0-
3) При / > п+М_1 равенство | А И В", | Д-1А П #«-/+*-11 =
= 0 Д°стигается лишь в случае, когда ЛП^я-г+й-1 = 0-
W
4) ср (га, к) — 2 ПРИ нечетном гаД-А,
n+fc+1
в _
1.28. Пусть Fr (и) — семейство подмножеств А С В”,
таких, что р(а, Р)<^2г для любых а, р из А. Пусть
cpr(ra)= max [Л|.
16
1*) Показать, что максимум |Л| ио всем A(*Fr(n)
достигается на множествах вида S" (а) и равен .
fc=0
п__I
2) Для нечетного п и г — —^— привести пример мно-
жества AfcFr(n), не являющегося шаром радиуса г, для
которого | А | = <?г (п).
1. 29*. Будем говорить, что подмножество Л С В" об-
ладает свойством 1, если любые два вектора из А имеют
общую единичную координату, обладает свойством II,
если для любого 5. £ Л противоположный вектор а не ле-
жит в А, и, наконец, обладает свойством 111, если из
а£ А и вытекает, что Пусть — число
подмножеств А С В”, обладающих одновременно свой-
ствами 1 и П, а ср (и) — число подмножеств В С Вп, обла-
дающих свойством 1U. Показать, что:
1) Ф(н)>2<'!(’,“1)'2|\ 2) ф(и)<ср2(ге —1).
1.30. Пусть А С В", В. (А) — число таких ребер (а, р),
что 5.QA, $£В'!\А. Показать, что | В (Л) | min {[ А |,
2" — |Л |).
1.31. Доказать следующие утверждения:
1) Число различных граней фиксированного направ-
ления {iv i2, .. ., ik} равно 2ft.
2) Две различные грани одного направления не пере-
секаются.
3) Объединение всех граней куба Вп, имеющих за-
данное направление, дает весь куб.
4) Число всех граней ранга к куба Вп равно
5) Общее число граней куба В" равно 3".
6) Число граней размерности к, содержащих задан-
ную вершину а, равно
7) Число граней размерности к, содержащих задан-
ную грань размерности I, равно Q _
8) Число й-мерных граней, пересекающихся с задан-
ной Z-мерной гранью куба В", равно 2/_JQ _ .
1.32. Интервалом куба Вп называется множество
вида {?: я t ’С где Р — некоторые такие вершины,
17
что 5<р. Число р(й, р) называется размерностью ин-
тервала. Показать, что грань размерности к является
интервалом размерности к.
1.33. Пусть g2, g3—грани куба Вп. Показать, что
из gjP0, £2Пёз¥= 0, вытекает, что
(^гшп^о-
1.34. Пусть nv nv . ,у, na — такие целые неотрица-
тельные числа, что 22В1'^2В. Тогда в Вп существуют
попарно ненересекающиеся грани gv g2, ..., gs, размер-
ности которых соответственно равны nv п2, ..., ns.
1.35. Грани gY и g2 куба В" называются несравнимыми,
если не выполняется ни одно из включений g± С g2,
gtQgl-
1) Показать, что существует множество граней куба В”,
f п \(:г— [ге/З] \
состоящее из <,гдз|Д [п/3] ) 1ЮпаРн0 несравнимых
граней.
2) Показать, что мощность всякого множества попарно
несравнимых граней куба В" не превосходит
1.36. Пусть L (п, к)—минимальное число таких вер-
шин из В", что в каждой А-мерной грани находится
хотя бы одна из этих вершин. Доказать, что;
1) L (п, 1) = 2""1;
2) L(n, п — 1) = 2;
3) L(n, 2) <[2'73]:
4*)m<L(ra, п — 2)<m-|-2, где т — наименьшее
целое, для которого ([^2])^ п>
[я/*]
5)
»=0
6) L (п, к) 2rL (г, к).
1.37. Показать, что наборы из В” можно расположить
в последовательность оД а2, ..., а2«, являющуюся циклом.
1.38. Показать, что в Вп нет циклов нечетной длины.
1.39. Двоичный вектор (а0, otv ..., ал’-i) будем назы-
вать п-универсальным, если для всякого вектора (30, РР ...
,из В” существует такой номер к, что р< = аА.ф<
18
(i = 0, n — 1), где k@i—k-\-i (mod/V). Выяснить,
является ли вектор а «-универсальным, если:
1) « = (0011), « = 2;
2) а ~(01011), « = 2;
3) а = (00110), « = 2;
4) а = (00011101), « = 3.
1.40. Доказать, что для всякого натурального п су-
ществует «-универсальный вектор длины 2“ и не суще-
ствует «-универсальных векторов длины, меньшей 2".
1.41. Цикл Z куба В" называется 2й-ц«кло.л, если
[ZDS’) (5.) | == 2d Д- 1 для всех a^Z, т. е. если для лю-
бой вершины а цикла Z множество вершин цикла, на-
ходящихся па расстоянии, не превосходящем d (но кубу),
совпадает с множеством вершин, находящихся на рас-
стоянии, не большем d «вдоль цикла».
1 ) Пусть Z («)—максимальная длина 2-цикла в В".
Найти I («) для п = 2, 5.
2 ) Пусть Z — цикл в Вп. Показать, что в любой
грани размерности 4 имеется не более восьми вершин
цикла Z.
3 *) Показать, что максимальная длина цикла в В" не
превосходит 2”"1, « Д> 3.
1 .42. Нара (а,., а,(1), составленная из двух последо-
вательных вершин цикла Z куба В'\ называется ребром
цикла. Показать, что в В3 существует цикл длины 32,
любые четыре последовательные ребра которого имеют
попарно различные направления.
1 .43. Пусть щ, . .., ап — такие числа, что а,О 2
п
(г=1, «). Показать, что число сумм 2(—3,С {0> 1}»
1=1, п, удовлетворяющих условию
2<— i)s,ai
С-1
не превосходит (|ге,2|)-
1 .44 Пусть А С Вп, |И|>2’,‘|. Показать, что суще
ствует не менее « ребер куба, целиком содержащихся в Л.
§ 2 Способы задания булевых функций.
Элементарные функции. Формулы.
Операция суперпозиции
Набор символов переменных (х1; ж2, ..., жя) будем
обозначать через х“ (или х), а множество тех же сим-
волов переменных — через Хп- Функция / (ж"), опреде-
ленная на множестве Вп ^и принимающая значения из
множества (0, 1}, называется функцией алгебры логики
или булевой функцией. Множество всех булевых функ-
ций от переменных xv х2, ..., хп будем обозначать
через Р2(Х”).
Булеву функцию / (х") можно задать таблицей Т (f)
(см. табл. 1). Здесь наборы 8 расположены в порядке
возрастания их номеров. В дальнейшем, предполагая такое
стандартное расположение наборов, будем задавать функ-
цию fix”) вектором й2" = (а0, а1; ..., в котором
координата и. представляет собой значение функции / (£”)
на наборе 3 с номером 1(1 = 0, 1,..., 2” — 1).
ТАБЛИЦА 1
*2 .... Х„_1 «п f (яс,, х2,. . . 1» *^я)
0 0 ... о 0 /(0, 0,.. , 0, 0)
0 0 ... 0 1 7(0, 0... , о, 1)
0 0 ... 1 0 7(0, 0,.. , 1, 0)
1 1 ... 1 1 7(1, 1... ., 1, 1)
Символом Nj будем обозначать множество {3: (3 £ В”) &
Булева функция / (£”) может быть задана также пря-
моугольной таблицей Пл K_fc (/) (см. табл. 2), в которой
значение / (а1, з2, ..., ая) функции / помещается на пере-
сечении «строки» (alt а2, ..., □,.) и «столбца» (зЛ(1,
...» =и). о ,
Булевы функции, заданные табл. 3, 4, будут счи-
таться элементарными.
Приведем обозначения и названия этих функций.
1) Функции 0 и 1 называются соответственно тож-
дественным нулем и тождественной единицей.
20
ТАБЛИЦА 2
0 0... ал+1 , . . 1
0 0... afc+2 . . . 1
*fc+l
п
X] #2 • • •
о о ... о
О 0 ... 1
’I . °л- ............ /(®)
1 1 . . . 1
2) Функция /t называется тождественной функцией
и обозначается через х.
3) Функция /2 называется отрицанием х, обозна-
4) Функция /з называется конъюнкцией хг и xit
обозначается хг& х2 или х1-х2, или хрх2, или min (xlt
х2) и часто читается и ж2».
21
5) Функция fi называется дизъюнкцией хг и х2, обо-
значается хг V х2 или хг-(-х2, или max (х1г х2) и часто
читается «хг или х2».
6) Функция /5 называется суммой по модулю 2 xt
и х2, обозначается x1Q)x2 и часто читается «хг плюс х2».
7) Функция fs называется эквивалентностью xt
и х2, обозначается т,1~а:2 или хг ++ х2, или xt~x2 и
часто читается «тх эквивалентно х2».
8) Функция /7 называется импликацией хг и х2,
обозначается хг -> х2 или х} Z) х2 и часто читается
имплицирует х2».
9) Функция /8 называется штрихом Шеффера xt
и х2, обозначается хг | х2 и часто читается «не х± и х2».
10) Функция /9 называется стрелкой Пирса хг и х2,
обозначается хг | х2 и часто читается «не хг или х2».
Иногда функции 0 рассматриваются как функции,
зависящие от пустого множества переменных.
Символы , &, \/> Ф> ~ ИТ' Дч участвующие в обо-
значениях элементарных функций, называются ло-
гическими связками.
Зафиксируем некоторый алфавит переменных X
(конечный или счетно-бесконечный). Пусть Ф=
= {/(’г>), флн\ ...}— множество функциональных сим-
волов, где верхние индексы указывают местность
(арность) символов. Иногда верхние индексы опуска-
ются, но при этом арности функциональных символов
предполагаются известными.
Определение 1. Формулой над множеством
Ф называется всякое (и только такое) выражение вида:
1) Л и fj&b, xilt..., Xi„), где fk — нуль-местный,
a fj — n-местный функциональные символы и Хц, Xt2, ...
,..,Х{п — переменные из множества X;
2) /тСЯр 212, ..., 21,), где fm — s-местный функцио-
нальный символ и 21,- — либо формула над Ф, либо пере-
менная из X, 1=1, s.
Для акцентирования внимания на том, что в фор-
муле 21 используются только переменные из X (или
только функциональные символы из Ф), будем писать 21 (X)
(соответственно 21 [Ф]).
Иногда формулы вида / (х, у) записывают либо как
(xfy), либо как xfy, а формулу / (х) — как (fx) или fx.
При этом символы / называют связками.
22
Обычно в качестве связок употребляются символы из
множества <5 = {~, &, V> ®> I, 11-
Определение 2. Формулой над (5 называется
всякое (и только такое) выражение вида:
1) х— любая переменная из множества X;
2) (~]2l), (21&23), (21V93), (21ф93), (21-93),
(21->23), (QI 1923), (211 23), где 21, 23 —формулы над (3.
Обычно принимаются следующие соглашения для со-
кращения записи формул над множеством связок в;
а) внешние скобки у формул опускаются;
б) формула (П21) записывается в виде 21;
в) формула (21 & 23) записывается в виде (21 • 23) или
(2123);
г) считается, что связка сильнее любой двухмест-
ной связки из (5;
д) связка & считается сильнее, чем любая из связок
V, Ф> ~, “*> I, I-
Эти соглашения позволяют, например, формулу
((П^) -* ((* &*/) V 2)) записать в виде X (ху \/ z).
Употребляется и «смешанная» запись формул, на-
пример, х ф f (у, z) или xj (za, 0, z3) V 7j/ (1, х2, хя).
Пусть каждому функциональному символу /("•> из
множества Ф сопоставлена некоторая функция F.: В”< -*
—»В. Понятие функции реализуемой формулой 21
над множеством Ф, определяется по индукции;
1) если 21 = /^я<)(ф,, • • •> т0 Для всякого
набора (а1, а2, . .., а„.) значений переменных xJx, xJz, .,.
.Xj значение функции равно F((p.v а2, ..ая<);
2) если 21 = /(21Р 21а,. .., 2IJ, где / £ Ф, 21* =
= 21* (ykv ук2, уке ) —формула над Ф или перемен-
ная из X и на всяком наборе а*2, . . ukS/J значе-
ний переменных ук1, ук2, .,у функция ср равна р*
{к — 1, т), то
?21 (аИ- а12..аЫ,> . . •, а*г а*2> • • •> 7/ге > • • •
. .. а .. а . .. я F (Зо .... В,..... 8 I
• • •» Wil’ 7п2’ ♦ • ” т(}п) \1 1> ’ ! fc» • • •» Г W?/
(здесь F— функция, сопоставленная функциональному
символу /).
Если 21 = f{”‘} (xjit хFin-)' To 'fgi 0<"’03Ha4 b
етсн обычно через F^x^, Xj2,..,, xJn^. Если же
23
21 = /(21p 212, .... 21m), to <f>2| обозначается через
F (?211(Уп> У12’ • • ’ Uls^j.?<2lm Ут2’ • •’ Утвт))-
Понятие функции ср^, реализуемой формулой 21 над
множеством связок <3, вводится следующим образом:
1) формуле 21 = х, где х^Х, сопоставляется тожде-
ственная функция cpQ|(a;)=a:;
2) если 21 = (П 23) (или 21 = (23 О (Е), где о 6 {&> V»
ф, ~, |, I)), то ср2[ — ?Q3 (соответственно <f>Q[ =
= tpgj О 'f’g, где символ О надо понимать уже как обо-
значение для соответствующей элементарной булевой
функции; см. табл. 3, 4).
Пусть (ж1; х2,..., хп}—множество тех переменных,
которые встречаются хотя бы в одной из формул 21
или 23- Формулы 2! и 23 называются эквивалентными
(обозначение: 21 = 23 ил+г^ 21 23), если на всяком на-
боре (ар а2, . .., ая) значений переменных xv х2, ..., хп
значения функций и реализуемых соответственно
формулами 21 и 23, совпадают.
Пусть Ф — множество функциональных символов
(или логических связок), а Р — множество соответ-
ствующих им функций. Суперпозицией над множеством
Р называется всякая функция F, которую можно реали-
зовать формулой над множеством Ф.
2.1. Каково число функций в Р2 (Хп), принимающих
на противоположных наборах одинаковые значения?
2.2. Найти число функций в Р2 (Хп), которые на
любой паре соседних наборов принимают противополож-
ные значения.
2.3. Каково число функций в Р2 (X”), принимаю-
щих^зщачение 1 менее чем на к наборах из В"?
2.4. По функциям / (ж4, х2) и g (х3, ж4), заданным
вйкторно, построить векторное задание функции ft:
1) a/ = (l0l1), а? = (1001),
к (^2> ^З’ ^l) == / С^З’ ^l)’ ^2)’
2) az = (1011), а, = (1001),
к(£*)={(Х1, x2)\/g(x3, х4);
3) ах = (1000), ар=(0111),
/г(54)=/(хр x2)&g(x3, xj.
2.5. Пусть — число, двоичное разложение, ко-
торого есть набор (xlt х2), a v2 — число, двоичное раз-
24
ложение которого есть (х3, ж4). Пусть (£4) — i-й раз-
ряд двоичного разложения числа |vx—v2|, i=l, 2.
Построить прямоугольную таблицу П22 функций
/1 (И и /2 (.г1).
2.6. 1) Функция / (f3) определяется следующим об-
разом: она равна 1 либо при жх=1, либо если перемен-
ные х2 и х3 принимают разные значения, а значение
переменной хх меньше значения переменной х3; в про-
тивном случае функция обращается в нуль. Составить
таблицы Т (/) и Пх 2 (/) функции / (Ж3) и выписать на-
боры множества Nf.
2) Функция / (я1) задается так: она равна нулю
только на таких наборах а2, а3, а4), для которых
справедливо неравенство ах+ ct2 > аз+2а4. Построить
таблицу Т (/) и выписать наборы множества N ? этой
функции.
2.7. Функция /(£”) называется симметрической, если
f (x v х2, ..., хп)=/(х{', xit.xin) при любой подста-
1) Показать, что если / (х") — симметрическая функ-
ция, то из равенства || а" || = || р" || следует равенство
/(«")=/(Ю-
2) Найти число симметрических функций в Рг (X”).
2.8. Пусть f(xn)—произвольная функция алгебры
логики (га^>1). Сопоставим ей симметрическую функцию
S (yv ут), где т — 2я — 1: S (а.т) — / (Д'), если
Доказать, что
S (х^, ..., х^,
2"-1 раз
2W~2 раз 2W”* раз 2 раза
= /(хх, х2, . . ., X., . .., x„_v х„).
2.9. Выяснить, какие из нижеперечисленных выра-
жений являются формулами над множеством логических
связок {Д, &, V,
\)х-+у; 5) (ж-»(р&(Дх)));
2) (х &) ] у; 6) (х & у) Д г;
3) (х у); 7) (Дж — z).
2.10. Выяснить, сколькими способами можно рас-
ставить скобки в выражении А, чтобы всякий раз
25
получалась формула над множеством логических свя-
зок { ’ , если:
1) А = ~]х-+у &х;
2) А = х & у & Д Д z V х;
3) A=x-+~]y-^z&—\x.
2.11. Сложностью формулы над множеством логи-
ческих связок <3 назовем число связок в ней. Индукцией
по сложности формулы доказать, что в формуле
1) ненулевой сложности содержится хотя бы одна
пара скобок;
2) число левых скобок равно числу правых;
3) нет дгух связок, стоящих рядом;
4) нет двух символов переменных, стоящих рядом.
2.12. Индексом связки в формуле будем называть
разность между числом левых скобок, предшествующих
рассматриваемой связке выданной формуле, и числом
правых скобок, предшествующих этой связке. Дока-
зать, что всякая формула ненулевой сложности над
множеством { Д, &, \/, ->}
1) содержит единственную связку индекса 1;
2) может быть единственным образом представлена
в одном из следующих видов: (Д 21), (21&23), (21 \/ 23),
(21 -» 23), где 21 и 23—формулы над множеством {Д,
&, V, ->}•
2.13. Рассмотрим бесскобочную запись формул над
множеством связок { Д, &, \/, ->}, вместо ( Да:),
(х&у), (х\/у) и (х-*у) будем писать Д х, & ху, \/ ху,
-> ху. Например, формула ((Д я)-> (*/V (Д z)) будет
иметь вид-> Д х\/у~\г. Доказать, что если каждую
из связок &, \/, -> оценить числом +1, каждый символ
переменной — числом —1, а связку Д — нулем, то
в бесскобочной записи выражение А будет формулой
тогда и только тогда, когда сумма оценок всех вхожде-
ний символов в А равна —1 и в каждом начальном
отрезке выражения А эта сумма неотрицательна.
2.14. Выяснить, является ли выражение А форму-
лой над множеством Ф, если:
1) А = f,2> (g<2> (х, у), f(2>(x)), Ф = {/(2’, g(2), <рш};
2) А =)а:(<р,1\ Ф = {gfl>, <p’1J);
3) А = ср(11(/(2|(1, х)), Ф = {/(2’, ср(1));
4) A =g'2>(?(1', f(3> (х, у, <р(1>)), Ф = {/(3), g'21, <р(11};
5) Л = (?(1’(/(2)(z, ?(1> (х)))), Ф = (/(2‘, <р(1)).
26
2.15. Найти вектор а функции <р, реализуемой фор-
мулой 21 над множеством Ф = {/р\ /р), g(2)), если
функциональным символам g(2) сопоставлены
булевы функции, определяемые соответственно векто-
рами (10), (1011) и (1000):
1) 21-WR^2’^ /Ry))). у);
2) 2l=g(2,(/)1)(/P)(^ у)), g‘2,& /Р(у)));
3) 21 = (/<*) (х, g<2) (/(2) (х, у), /(1) (у)))).
2.16. Построить таблицы функций, реализуемых сле-
дующими формулами (над множеством связок S):
' 1) С* -» У) ® ((У -* z) ф (z х));
2) (х V у) V (* • z) | (х ~ у);
3) £-> (г ~ (у ф xz));
4) (((x|y)|z)|y)|z.
2.17. Формула над множеством 6 называется тожде-
ственно истинной (тождественно ложной), если реали-
зуемая ею функция равна 1 (соответственно нулю)
на всяком наборе значений переменных. Выяснить,
какие из нижеприводимых формул являются тожде-
ственно истинными или тождественно ложными:
1) (« -* У) -* ((* V 2) -* (У V z));
2) ((х ф у) ~ z) (х yz);__
3) ((x\Jy)\(x®y))®(x-^y^(x\/у));
4) ((х V у) z -> ((ж ~ z) © у)) (х (yz)).
2.18. Эквивалентны ли формулы 21 и 23?
1) 21 = ((ж V у) V г)-» ((ж V у) (ж V z)), 23 = ж~г;
2) 21 = (х -> у) -> г, 23 = ж (у -* г);
13) 21 = ((х ф у) -> (ж у у)) ((х у) -* (х ф у)), 23 = х | у;
4) 21 = (ж -* у) V ((ж -> г) у), 23 = (жу)(у-> xz).
2.19. Найти все функции, зависящие только от пере-
менных из множества {х, у) и являющиеся суперпози-
циями над множеством Р:
1) Р = {н1Ф^, 1);
2) p={»a®(«iV«2));
3) P — {f(uv u2) —(1101), g(uv u8) =
= (10010110)} l).
*) Здесь и в дальнейшем при векторном задании функций
вместо записи ау=р будет употребляться запись f = р.
27
2.20. Глубина формулы QI над множеством Ф (обо-
значение: <1ерф (21)) определяется по индукции:
(I) если 21 — символ переменной или 0-местный функ-
циональный символ, то <1ерф 21 = 0;
(II) если 21 = /<я) (2IV ..., 21J, где £ Ф, то
dePj, (21) = max <1ерф (21,) + 1.
Найти формулу 21 над множеством {|}, имеющую
минимальную глубину и реализующую функцию:
1) f—x\/y, 2) f = x®y, 3) f = xy.
2.21. Выяснить, можно ли реализовать функцию /
формулой 21 глубины к над множеством связок 5, когда:
1) f=zxy, к —2, 5 = {|);
2) f=x->y, к = 3, S — {\/, ~);
3) f=x® у® z, к = 2, S = {-+, &}.
2.22. Доказать, что функцию / нельзя реализовать
формулой над множеством связок 5, когда:
1) f = x®y, S = {&};
2)f=x-y, 5 = {->);
3) f = x\Jyy $ = {-).
2.23. Можно ли реализовать функцию / формулой
глубины /с-|-1 над множеством S, если она реализуема
формулой глубины к над тем же множеством 5?
2.24. Функция / из Р2 реализуема формулой глу-
бины к над множеством S. Показать, что функция /
может быть реализована над тем же множеством S
некоторой формулой, глубина которой больше к.
При оперировании с функциями алгебры логики
часто бываютуполезными следующие эквивалентности
(которые в дальнейшем будут называться основными
эквивалентностями):
х О У = уОх (коммутативность связки О, где сим-
вол О является общим обозначением для связок &, \/,
Ф- ). I);
(х О у) О z = х О (у О z) (ассоциативность связки О»
где о — общее обозначение для &, V, ф, ~);
х&у = х\/у и х V у = х&у (правила де Моргана);
х V (.г & у) = х и х & (х \/ у) = х (правила поглощения);
x\J (х&у)=х\/у н х &(х\/ у) = х& у;
28
x &(y\J z) = (х & у)\/ (х & z) (дистрибутивность конъ-
юнкции относительно дизъюнкции);
х \/ {у & z) — (х \/ у) & (х V z) (дистрибутивность дизъ-
юнкции относительно конъюнкции);
х & (у ф z) = (х & у) ф (х & z) (дистрибутивность конъ-
юнкции относительно сложения по mod 2);
i—x\/x = x\/ 1 = ж ~ х;
x — x = x\/x = x& x = x& i= x\/O;
ж = жф1, х ~ у — (х ф у) ф 1;
® ф У~(х&у)\/ (х&у), х-+ у=^((х&!/) ф х) ф 1.
2.25. Проверить, справедливы ли следующие соот-
ношения:
1) х\/ (у ~ z) = (x\/ у) ~(х\/ z);
2) х — (у ~ z) = (х -+ у) ~ (х z);
3) а: & (г/ ~ г) = (х & у) ~ (х & г);
4) «-»(? V г) = (г-*У) V (* -* z);
5) х (у & г) == (х — у) & (х -> z);
6) X ф (у — г) = (х ф у) (х ф z);
7) ®-»(г/ —z) = (a:->?/) —(z—z).
2.26. Реализовать функцию f с] ормулой над мно-
жеством связок S, если:
t)f=x-+y, 5 = {-|, V);
2)f = x\fy, £ = {-};
3) f = x~y, 5 = {&, -»};
4) f = x\y, S' = U).
2.27. Используя основные эквивалентности, доказать
эквивалентность формул 21 и Q3> когда:
1) <%==(х&г)\/(х&у)У(х&z), ^ — х &.у &.z\JX & z;
2) 21 = (х -* у) ((ж & у) ф (ж ~ у)),
<&=(х\!у)&(хуу);
3) 21 = ж-»(ж&г/-* ((ж-> г/)-» у) & г),
23 = у -> (ж -* г).
2.28. Показать, что формула 21 эквивалентна фор-
муле 23 тогда и только тогда, когда тождественно
истинна ровно одна из формул
(21-*23)->23, 21-(23-1(21-21)).
29
2.29. Доказать, что формула 21, содержащая только
связку —, тождественно истинна тогда и только тогда,
когда любая переменная, содержащаяся в формуле 21,
входит в нее четное число раз.
2.30. Через -Sg211 обозначается формула, получаю-
щаяся из формулы 21 одновременной заменой каждого
вхождения переменной х на формулу (£. Если х не вхо-
дит в формулу 21, то (по определению) полагают
Sg21| = 2l.
1) Доказать, что 21 — тождественно истинная формула
тогда и только тогда, когда тождественно истинна фор-
мула 5^_>г/1211, где и у2 — какие-либо переменные, не
входящие в формулу 21.
2) Можно ли в 1) отбросить условие, что ух и не
входят в формулу 21?
2.31. 1) Пусть функция f(x, у) из Р2 удовлетворяет
соотношению _
/(Ж НУ< z)), /(/'(ж, у), f(x, z)))==l.
Доказать, что тогда справедливы следующие эквивалент-
ности:
a) f (х, х)~ 1;
б) f\x, f(y, ж)) = 1;
в) /(/(Ж у), f(x, z)), f(x, f(y, z))) = i;
г) f(f(x, у), f(f(x, f(y, z)), f(x, z))) = l;
Д) f(y, z)), f(y, f(x, z)))==l.
2) Вытекают ли эквивалентности б), в) и г) из д)?
§ 3. Специальные виды формул. Дизъюнктивные
и конъюнктивные нормальные формы. Полиномы
Формула х°' & хр& ... & х°г (формула хЬ \/ хЬ\/ ...
„Vty где ste{0, 1), = Ж = i*G
£ {1, 2, . . ., и) для всех к=], г, называется конъюнк-
цией (соответственно дизъюнкцией) над множеством
переменных Хп—{хг хг, . . ., хп]. Конъюнкция (дизъ-
юнкция) называется элементарной (сокращенно э. к.
и э. д. соответственно), если xt =^х щт j=^=k. Сим-
волы & в э. к. будут для краткости опускаться. Выра-
30
жения вида х°* будут называться буквами. Число букв
в э. к. (в э. д.) называется, рангом э. к. (э. д.). Кон-
станта 1 будет считаться э. к. нулевого ранга, а нуль —
э. д. нулевого ранга.
Формула вида
(I)
(8 \ __
краткая запись \/ К. I, где К. {i = 1, з)— конъюнкции,
»=1 >
называется дизъюнктивной нормальной формой (сокра-
щенно д. н. ф.).
Формула вида
Q^’==Z»1&D2&... &DS (2)
^краткая запись & D.J, где D. (i = 1, s)—дизъюнкции,
называется конъюнктивной нормальной формой (со-
кращенно к. н. ф.). Число s называется длиной д. н. ф.
{длиной к. н. ф.). Сумма рангов конъюнкций (дизъюнк-
ций) называется сложностью д. н. ф. {сложностью
к. н. ф.). Дизъюнктивная нормальная форма (конъюнк-
тивная нормальная форма) над множеством перемен-
ных Хп={х1, хг, . . ., хп} называется совершенной,
если она составлена из попарно различных элементар-
ных конъюнкций (элементарных дизъюнкций) ранга п.
Пусть / {хп)— булева функция, и пусть 1 <(
<Z i2 • • • <С h п- Через ^{хп) или иногда
через **/ {хп) | будем обозначать функцию, полу-
ченную из / {х”) подстановкой на места переменных
х., х.,..., х. соответственно констант а,, а.,,..., з,.
Функция Д” *2’ *’* {хп) называется х’.'хъ .,. х^-компо-
нентой функции f {£”) или подфункцией функции / {£”).
Подфункция /й;'2’ {х”) называется собственной, если
к =ф= п, к 7^=0. Подфункции функции f {х”) различны, если
они отличаются как функции переменных xv х2, , .., х .
Пусть 1 < г2 < ... <( ik п, тогда справедливо
представление
/(f«)= V (3)
(».. »и .... »») к ' 2 *
где дизъюнкция берется по всем векторам (зх, з2, ..., з&)
31
из Вк. При к = п это представление имеет вид
/(«”) = V х^ ... x'n*f <з2,ая). (4)
(»1> »2,.... »п)
Представление (4) можно записать в виде
/ (хп) - V х^хр ... х°п. (5)
/(9)=1
Правая часть формулы (5) представляет собой совершен-
ную д. н. ф. функции f(x’r). Аналогично, справедливы
представления
Ж)= & (6)
(®1> ’г, 3Л)
/ (£п) = & (яр \/ 42 V • • • V К”)- (7)
5п:/(зи)=о
Элементарная конъюнкция называется монотонной,
если она не содержит отрицаний переменных. Формула
Р (£")=; К, ... ®KS, (8)
где А((г—1, з)—попарно различные монотонные эле-
ментарные конъюнкции над множеством X”, называется
полиномом Жегалкина или полиномом по модулю 2.
Наибольший из рангов элементарных конъюнкций,
входящих в полином, называется степенью этого по-
линома. Число s называется длиной полинома (8).
При s=0 полагаем Р (я”)=0.
3.1, С помощью эквивалентных преобразований при-
вести к д. н. ф. формулу:
1) F — (х^ \у х2Хо) (х^ \у я3),
2) F = ((^i V х2х2х^) ((я, \/ х4) —» ХтГрХ^ \у х%с^
V (^1 V Ж4)>
3) F = ((.Zj —» я2я3) (я2я4 ф я3) —»• х^т,^) \/
3.2. Представить в виде совершенной д. н. ф.
следующие функции:
1) / (Xя) = (яг ф х2) — я2я3;
2) ((я3) = (01101100);
3) / (.г3) = (10001110).
3.3. С помощью преобразований вида А = Ах\/Ах,
/1 \/ -1 -- /1 иер >йти от заданной д. н. ф. D (х3) к совер-
III если:
I) !) (г ) = \/ x^Xgi
2) D (x ) — ^'1'^2 \/
3) D (x3) = xl\/ T1x2 V я2ж3.
3.4. С помощью соотношений вида x\J yz=(x\J y)(x\J z)
преобразовать д. н. ф. из предыдущей задачи в к. н. ф.
3.5. Построить совершенную к. н. ф. для каждой
из функций задачи 3.3.
3.6. Подсчитать число функций / (ж*1), для которых
совершенная к. н. ф. является одновременно и д. н. ф.
3.7. Найти длину совершенной д. н. ф. функции
/(«"):
1) /(гс’^^ф^ф ... фхя;
2) / (хп) — V х2 v • • • V xt!) (^i V ^2 V • • • V хпУ>
3) / (2я) = V Х2 V Хз) (Ж1 V Х2 V Жз) Ф
Фт» ЛЛ т ЛЛ Л^ т
•^4 ф ^5 W • • • 47
3.8. Пусть множества Xa = {xv х2,...,хп} и Ym =
= {yv у2,...,Уя} не пересекаются. Пусть совершенные
д. н. ф. функций / (хп) и g (ут) имеют соответственно к
й I слагаемых. Найти длину совершенной д. н. ф. сле-
дующих функций:
1) / (хп) & g (у“); 2) / (хп) V g П 3) f (хп) ф g (у”).
3.9. Выразить ху-, х2- и ЯрЕд-компоненты функции / (х3)
с помощью д. н. ф. минимальной сложности для:
1) / (ж3) = (01101101);
2) / (я3) = (хг —> х2) ф ж2я3;
3) / (х3) = -* ж2я3) ф х2.
3.10. Среди функций, зависящих от переменных хг
и х2, найти те, которые имеют наибольшее число по-
парно различных подфункций.
3.11. Подсчитать число булевых функций /(#”),
которые переходят в себя после перестановки хг и х2.
3.12. Две функции / (хп), g (£”) перестановочно эквива-
лентны, если существует перестановка к чисел
такая, что f (xv .. ., х„) — g (х*11у жя(я)). Найти число
классов перестановочно эквивалентных функций из Р2 (X2).
3.13* . Функция fn(x") определяется рекуррентно сле-
дующими соотношениями:
fikX) Xr^2 (Х3 V Xi) \/ Х2 (,Х1Х3 V Х1Х1) V
fn+1 (^+1) = f„ fo, Я2, ..., Хп) гв+1 V х2х2 ... жва:я+1 (га > 4).
2 Г, П. Гаврилов, А. А, Сапоженко 33
Для каждой функции из последовательности {/„} найти
число различных подфункций вида f' («”), i — 1, п, □ £ {0, 1},
никакие две из которых не являются перестановочно
эквивалентными.
3.14. Доказать, что число различных функций / («”),
для которых данная функция g является подфунк-
цией, не меньше 22"—(22'г—1уп~к
3.15. Пусть /j(хп) = fi (хп) для всякого
Доказать, что /(«“)— константа.
3.16. Найти число таких функций / (хп), что ДД («”) =
= /{У (х”) для всех 1 i < / п.
3.17. Пусть /г («”)=/(gx («"), . .., g^x”), #,(£"),
g.^1(xn'),...,gn{xn'j), и при всяком 1 = 1, 2,,..,п
и а£{0, 1} выполняется соотношение
5j/i(«'')| = /(5ig1(«’,)|, ..., Slg^tx”^, 3, S^g.+1 («”)[, ...
т. е. что «J-компонента суперпозиции функций /, gv ...
..., g{_v g., g{ v .. ., g„ равна суперпозиции «’-компонент
функций /, gv ...,g{_v gitl, ..., g„. Пусть, кроме того,
для всех /, к (1^7<&<^п) и любых Зу, з/г из {0, 1}
«у«^-компонента функции g. («") совпадает с «’/«^-ком-
понентой той же самой функции g. («”), i = l, п. Пока-
зать, что й(«")—константа.
3.18. Найти число монотонных элементарных конъ-
юнкций ранга г над множеством Хп.
3.19. Найти число полиномов степени г над множе-
ством переменных Хп.—
3.20. Найти число различных полиномов длины к
над множеством X", обращающихся в нуль на наборах
б и 1. (Полиномы считаются различными, если они
различаются составом о. к.)
Примем следующую нумерацию монотонных элемен-
тарных конъюнкций над множеством переменных Х"=
= {«х, «2, ...,«„}. Каждой монотонной э. к. К сопоста-
вим вектор 3(К) = (зх, а2,.. ., ая) из Вп, в котором а( = 1
тогда и только тогда, когда «< входит в К. Номером э. к.
п
К будем называть число v (3 (КХ) = 2 3<2М~*. Константа 1
<=i
будет иметь в этой нумерации номер нуль. Таким обра-
34
зом, каждый полином Р(х”) можно записать в виде
Р (Г)=р0 • 1 ф ф ₽.д2 Ф ... Ф (9?
где К{— э. к. с номером i(j = 0, 2“ — 1). Вектор рг =
= (Р0, Pi’ • • •> ?2я-1) будем называть вектором коэффициен
тов полинома Р (хп).
Метод неопределенных коэффициентов для построе-
ния полинома Жегалкина, реализующего функщ ю
/ (хг‘), состоит в следующем. Рассматривается политом
в виде (9) и для каждого составляется уравне-
ние / (5.) = Р (а). Решение этих уравнений дает коэф
фищппты п элинома Р (хп).
I ’ Р мер. / (г2) ~ xt -> х2, Р (х2) — 3() ф ргг2 ф р^ ф
Зф.
1 ‘/(О, 0) = 1 = р0 ф Рх • 0 ф р2 • 0 ф Р3 • 0;
/(О, 1) = 1=₽офР1.1ф8а.Оф₽8.О;
/(1, 0) = О = ро ф рх • 0 ф Р2 • 1 ф рз • 0;
/(1, 1) = 1 = ро ф рх • 1 ф р2. 1 ф р3 • 1.
Находим р0 = Р2 = Рз = 1, Р1 = 0. Таким образом,
xi х2 = 1 © xi Ф хгх2.
3.21. Методом неопределенных коэффициентов
найти полиномы Жегалкина для функций:
1) / (3?) = (1001);
2) / (ж3) = (01101000);
3) /(ж3) = (11111000).
3.22. Введем операцию Т над векторами из В2”. Если
п = 1 и а = (а0, otj), то 7’(а) = (а0, адф^). Пусть для
каждого 3 £ Б2’1 вектор Т (3) определен и вектор а из B'2”+l
имеет вид & = (р0, рх, ..., р^, у0, Т1,..., у2П_г) и пусть
(Ро> Pi’ • • •> Рг,!-1) ~ ^о> °1’ • • •> ^и-1),
Т (То- То . • •> Т2В_1) = (®0. е1, • • •>
Тогда Т (а) = (30, ох, ,,82п-1> ф г0, 8Х ф %, ..., ф
фе2»-1). Например, если а = (1011), то Т (а) = (1101).
Доказать, что вектор значений функции / (хп) связан
с вектором Рр коэффициентов полинома Р (хп), реализую-
щего функцию /(#“)> следующим образом; а/ = 7’(рр),
рг=Т(5/).
35
3.23. Для такой функции /(ж4), что fiy = (10110010
00101101), найти вектор рг коэффициентов полинома
Жегалкина.
Один из способов построения по-
линома Жегалкина по формуле F состоит в следующем:
сначала строят эквивалентную формулу над множе-
ством связок {&, — }, затем заменяют везде X на жф1,
раскрывают скобки, пользуясь дистрибутивным зако-
ном (жфу) z=xz®yz, и приводят подобные члены.
Пример. х -* х2 = х1х2 = хг (х2 ф 1) ф 1 = х1х2 ф
Ф^ф 1.
3.24. Построить полиномы для функций:
1) / (У!) = (жх | ж.,) | х3,
2) f (ж3) = (хг —> х2) (х2 | х3);
3) / (х3) = ((хг -> х2) V х3) | xv
3.25. Всякую булеву функцию f можно записать
в виде полинома, используя обычные арифметические
операции умножения, сложения и вычитания. Для этого
достаточно выразить / через конъюнкцию и отрицание,
а затем заменить подформулы вида А на 1—А и раскрыть
скобки. Выразить с помощью арифметических опера-
ций следующие функции:
1) / (ж2) = хг ф х2;
2) / ’ (’'l ~* ^2) -* ®з>
3) /(ж3) = (10000001).
3.26. Указать функцию / (жя), у которой длина поли-
нома в 2я раз превосходит длину ее совершенной д. н. ф.
3.27. Доказать справедливость следующей формулы
разложения по к переменным:
7(Л =
— х1'Х22 ... X^f а2, ,.<зк, Хку1,..жя).
(»„»... »*) efi4r
3.28. Доказать, что:
1) / (Я=Ш (П Ф fl (^ Ф fl
2) f (хп\ = (хг V (fl (Хп) ~ fl (ж"))) ~ /} (х”).
3.29. Показать, что функция / (х"), реализуемая много-
членом степени к 0, обращается в 1 не менее чем на
2я-* векторах из В”.
3.30. На скольких наборах из Вп обращается в еди-
ницу полином Р(х”)'.
36
1) Р (х”)----хг . . • хк ф Хм . . . хп",
2) Р (хп) = 1 ф хх ф хгх2 ф ... ф хгх2 ...х„.
3.3 Д Показать, что для всякого I (Z 2я) существует
полином Р (хп) длины, не большей, чем п, для которого
| I — I-
3.32. Доказать, что всякая функция f(xn) может быть
8 ______
представлена в виде /(£”) = К., где К{ (Z = l, s) —
•=i
элементарные конъюнкции, содержащие не более одного
отрицания переменной, а $ 2я*1.
3.33. Показать, что если в совершенной д. н. ф.
знак V везде заменить на знак ф, то получится фор-
мула, эквивалентная исходной. Справедливо ли ана-
логичное утверждение для произвольной д. н. ф.?
Производной булевой функции f(xn) по совокупности
переменных х^, xifi, ,.Xik (или булевой разностью) на-
зывается функция
д(х{г xi,’ xik) = ^ ” ” Ж<1’ ” ” Xik....®
ф / • • •> • • •> • • •> *^я)*
^При Л = 1 применяется обозначение
3.34. Доказать следующие свойства производной:
d л /д/оих.
' dxj \ dx( J dX{ \ dxj ) ’
2) df
' d(xit.....xik) d(xie •xik) ’
3) df(x«) dg{x”)
d (x<t....xik) d {XIC • - xik) W d .......xik) ’
4) ы (, (I.) v g (»» = z (Л fe£) , (n gg)
df (xn) dg (Ж”) _
dx; dx( •
df (xn) dg (xn).
® dx{ dx{ ’
°) ~d3.{ = 0 тогда и только тогда, когда xt не вхо-
дит явно в полином Жегалкина функции / (х”);
37
7) если f (£”) = xg (x2, xs, ..xn) ф h(x2, x3,...,x„),
df(*") < x
T0 dx, —^a’ x& ’ ' xn)-
3.35. Если g(xv .. .,xm) и h (xmJrV — булевы
функции и 1 iy m для всех j — 1, к, то:
1) (g © M __ д?____________
2) -fe dJ
' д(х.,,..,х,Д d (x,, dx{,\*
3) = h----------------
' о (x......d (x.. ..dx.,\
X *1’ • ’ *k) X *1’ *k)
§ 4. Минимизация булевых функций
Допустимой конъюнкцией или импликантом функ-
ции / (хп) называется такая элементарная конъюнкция
К над множеством переменных {а^, х2, . . ., жп}, что
К V / (x”)=f (£"), Импликант К функции / называется
простым импликантом, если после отбрасывания любой
буквы из К получается элементарная конъюнкция, не
являющаяся импликантом функции /. Дизъюнкция
всех простых импликантов функции / называется
сокращенной д. н. ф. функции /.
Дизъюнктивная нормальная форма называется:
минимальной, если она имеет наименьшее число
букв среди всех эквивалентных ей д. н. ф.;
кратчайшей, если она имеет наименьшую длину
среди всех эквивалентных ей д. н. ф.;
тупиковой, если отбрасывание любого слагаемого
или буквы приводит к неэквивалентной д. н. ф.;
д. н. ф. функции /, если она реализует функцию /.
Если элементарная конъюнкция К является пмпли-
каптом функции / (я”), то множество N& таких векторов
а из Вп, что К (х)=1, образует грань, содержащуюся
в множестве N Эта грайь называется интервалом
функции / (х”), соответствующем импликанту К. Ин-
тервал функции /, не содержащийся ни в каком другом
интервале функции /, называется максимальным ин-
тервалом. Максимальные интервалы соответствуют
простым импликантам функции /.
38
4 J. Из заданного множества элементарных конъюнк-
ций выделить простые импликанты функции / (5я),
если:
1) — {^i, £3, ^1-г2, я^з}’ / (я3) = (00101111);
2) = \xxxv х2х3, xv х-^х^, f (f3) — (01111110);
0) Q/^T--- {*^1’ '^4’ *^2^'3» »
/(f4)=: (1010111001011110).
Метод Блейка получения сокращенной
д. н. ф. из произвольной д. н. ф. состоит в применении
правил обобщенного склеивания хКг \/ хК2=хКг \/
\/хК2 \/ КгК2 и поглощения Кг \/ KXK2=KV Подразу-
мевается, что правила применяются слева направо.
На первом этапе производятся операции обобщенного
склеивания до тех пор, пока это возможно. На втором —
операции поглощения. .
Пример. Получить сокращенную д. н. ф, для
@) (ж3) =хгх2 V xrx3 \J Х2Ха.
После первого этапа получим
--*^1^2 \J ^т^з V *^2*^3 V Я'З^'З V *^3 V
После второго —
<^2--®1®2 V
4.2. С помощью метода Блейка построить сокра-
щенную д. н. ф. по заданной д. н. ф. Ж'
1) — Х]Х2 \/ х^Т'^х^ \у х2ХзХ^
2) — х^х^з V хгх2х^ V х3х^,
3) — х±х2 ХуХз \/ х^х,^ \у х^х2х3х^.
Сокращенную д. н. ф. функции / (хп), заданной
в виде к. н. ф., можно получить следующим образом.
Сначала раскрыть скобки, пользуясь законом дистри-
бутивности, затем вычеркнуть из получившейся д. н. ф.
буквы и слагаемые, используя правила хх=0, хх=х,
х \/ х—х, Kr V
Пример. Получить сокращенную д. н. ф. для
f С^3)== (^i V ^2) (^1V ^2 V ^з) •
После раскрытия скобок имеем
= Х1хг V х^ \/ хкх3 V х.^ V х2х2 V х2х3.
Применяя указанные выше правила, получим
— ХуХ3 у/ х2<
39
4.3. Построить сокращенную д. н. ф. по заданной
к. н. ф.:
1) СП V ^"2 V *8) (^1 V Х2 V ^з) (*^2 V ^з)’
2) (Х1 V Ж4) (Х2 V ^3 V (^1 V ^2 V *3)>'
3) (-Л V ^2 V *з) (^1 V ^4) (^"2 V *3 V Xl)’
4.4. Пусть TVy — множество таких векторов а £ В”,
что /(а) = 1, а Г (/) — длина сокращенной д. н. ф. функ-
ции /. Показать, что /° (/)<4-|ЛМ (| ЛМЧ-1).
4.5. Найти длину сокращенной д. н. ф. следующих
функций:
1) ф х2 ф ... ф жя;
2) (^-1 V Х2 V *з) (^1 V ^2 V ®з) Ф ^4 Ф ХЬ Ф * • • Ф
3) ОН V Ж2 V ^з) ('^1 V Ж2 V ®з) (®4 Ф ^5 Ф • • • Ф хя)>
4) (*!ф ... Ф хк) \хкл ф ... ф х„),
5) V • • • V3-») (xi V • • • V хк V xk+i V • • • V ^я)>
1 к п.
4.6. Пусть / (5я) такая, что N, = {а: к ф || а || ф к ф т},
и кфI фкфт, « G В1}.
1) Найти число слагаемых сокращенной д. н. ф. функ-
ции /, которые обращаются в единицу на наборе а.
2) Показать, что длина сокращенной д. н. ф. функ-
ции /(5я) равна (£)("“*).
4.7. Пусть функции / (5я) и g (ут) не имеют общих
переменных, К — простой импликант функции /, a L —
простой импликант функции g. Показать, что К & L —
простой импликант функции f & g.
Каждой элементарной конъюнкции над множеством
переменных {zj, х2, . . ., хп} взаимно однозначно со-
ответствует грань куба Вп, составленная из тех вершин
й, на которых э. к. обращается в единицу. Это позво-
ляет строить сокращенную д. н. ф., исходя из геометри-
ческого изображения булевой функции. На кубе Вп
отмечаются вершины множества Nj, функции /. Выпи-
сываются грани, содержащиеся в и не содержа-
щиеся в других гранях, составленных из вершин мно-
жества Nj,. Каждой из полученных граней сопостав-
ляется простой импликант.
40
Пример. Пусть функция / (ж3) задана вектором
^=(11111000). Требуется найти ее сокращенную д. н. ф.
Решение. Множество Nf есть {(ООО), (001),
(010), (011), (100)}. Грани имеют вид gi={(000), (001),
(010), (011)}, g2={(000), (100)}. Грани gv соответствует
э. к. хг, а грани g2 — х2х3. Сокращенная д. н. ф. есть
\/ х2х3 (см. рис. 2).
4.8. Построить сокращенную д. н. ф. функции /(£"):
1) / (ж4) = (1111100001001100);
2) /(я4) = (0000001111111101); %
3) /(^)=(ооо1101 и 101 юн).
4.9. Подсчитать число функций / (яГ), |/\_Xj
для которых данная элементарная
конъюнкция ранга г является: ^4/
1) имиликантом;
2) простым имиликантом. Р*1С- 2.
4.10. Пусть tr (/) — число импликан-
тов ранга г функции / (х”), a sr (/) — число простых им-
пликантов ранга г. Пусть Рп — множество булевых
функций переменных xv х2, ...,хя;
U/)J
/егя
sr(«) = -^r 2
Показать, что:
1)
2) sr («) = (" ) 2r-^n~r (1 — 2-2”-r)r.
Для небольших значений n сокращенную д. н. ф.
функции / (хп) можно находить с помощью прямоуголь-
ной таблицы (минимизирующей карты). Например,
пусть функция / (±4) задана с помощью табл. 5. Объеди-
няя клетки, соответствующие единичным значениям
функции /, в максимальные интервалы, как показано
в табл. 5, и сопоставляя им э. к., получим сокращенную
Д. н. ф.
XpCgXg \/ •^3^'4 \/ ^2*^4 \/ •^'П'2'^3 \/
41
ТАБЛИЦА 5
&3 0 0 0 1 1 / > О
0 0 0. 1 о 1
0 1 0 ' / 1 О
/ t (/ /) 1 ; 0
1 О 0 0 0
4.11. Построить сокращенные д. н. ф. для функций,
заданных следующими таблицами:
Простой импликант называется ядровым, если уда-
ление его из сокращенной д. н. ф. приводит к д. н. ф.,
которая не эквивалентна исходной. Для каждого
ядрового импликанта К существует такой набор зна-
чений переменных, который обращает К в единицу,
а остальные слагаемые сокращенной д. н. ф. — в нуль.
Такой набор называется собственным набором ядро-
вого импликанта.
4.12. Выделить из сокращенных д. н. ф. ядровые
импликанты:
42
1) 7 рс, у/ x.x3 v zrr2 у у ж2х3ж4 у хгхлх^
2) Хр^'^з V Х^Х2Х3 V ^3^4 V *^2*^4 V •^1‘^2^'s V *^2^4 V ‘^'1^4’
3) Я^з V Х.2Х3 V #1#2 V Х1ХЛ \/ Х3Х4 V Х2Х4 V Х1ГГ
4.13. Показать, что число ядровых импликантов про-
извольной функции f (х") не превосходит 2"-1.
4.14. Найти число ядровых импликантов у функций
из задачи 4.5.
4.15. Найти число булевых функций f (£”), для кото-
рых э. к. хг ... хг является ядровым имнлпкантом.
4.16. Пусть К, Kv К2—конъюнкции из сокращен-
ной д. н. ф., а г, rv г2 — ранги этих конъюнкций. Пусть
К \/ Кг \/ К2 = Kv \/ К2. Показать, что гх Д- г2 г Д- 2.
4.17. Построить все тупиковые д. н. ф. следующих
функций;
1) /(ж3) = (01И И10);
2) / (ж4) = (1110011000010101);
3) / (я4) = (0110101111011110).
4.18. Подсчитать число тупиковых и минимальных
д. н. ф. у функций из задачи 4.5.
4.19. Показать, что число тупиковых д. н. ф.
у произвольной булевой функции f (жл) не превосхо-
/3"\
Дит у.
4.20. Сколько тупиковых д. и. ф. у функции,
имеющей 2,!“1 ядровых импликантов?
4.21. Выяснить, являются ли тупиковыми, крат-
чайшими или минимальными следующие д. и. ф.:
1) ^ = х1х2\/х2;
2) V x^Xi V x^Xg,
3) Q) — х-$х2 \/ х^х3 \у Х2х3х^ \у х.х3.
4.22. Пусть L (/) — сложность минимальной, a 1(f) —
длина кратчайшей д. н. ф. функции /. Показать, что
L (f (5я)) nl (f (£")) для произвольной функции / (хп).
4.23. Показать, что I (f (х”)) 2'!-1, L (/ (хп)) н2л'1
для всякой функции f(x’!).
4.24. Для скольких функций / (х'г) справедливы соот-
ношения:
1) L (f (хп)) == п2п~1-,
2) L (f (хп)) = 712й-1 — п?
43
4.25. Привести пример числа к (0 <( к z?2"), та-
кого, что не существует / (х"), имеющей минимальную
д. н. ф. сложности к.
4.26. Для функций задачи 4.5 найти сложность
минимальных и длину кратчайших д. н. ф.
4.27. Рассмотрим семейство поясковых функций,
т. е. функций / (хя), для которых существуют числа к
и т, такие, что
Nj, = {а: к || а || к -J- т}.
1) Каково число ядровых имплпкантов у пояско-
вой функции / (хп) при различных к и т?
2) На скольких поясковых функциях / (хп) дости-
гается максимум числа ядровых имплпкантов?
4.28. Функция / (ж") называется цепной (цикличе-
ской), если множество N f можно расположить в после-
довательность. являющуюся 2-цепью (соответственно
2-циклом).
1) Найти число тупиковых и минимальных д. н. ф.
цепной функции /(ж"), если pVz|==lZ.
2) То же для циклической функции / (хп), такой,
что \Nf |=2zra (т > 2).
§ 5. Существенные и фиктивные переменные
Переменная х. функции f(xv х2,...,хп) называется
существенной, если найдутся такие наборы а и р, что
а = (ар . . ., a._v 1, a.+J, .. ., ая), р = (ар .. ., а(_р О,
аг+1, • • •> а») и /(а)=^=/(р). В противном случае перемен-
ная х( называется фиктивной (несущественной) перемен-
ной функции / (хп). Две функции / (х,г) и g (хп) назы-
ваются равными, если множества их существенных
переменных совпадают и на любых двух наборах, разли-
чающихся, быть может, только значениями несуществен-
ных переменных, значения функций одинаковы. Пусть
1 ij <) i2 О ... <Д* и. Будем говорить, что функ-
ция ср (а;р , . ., 1, X, . ., Xj2-ir . . .,
xik+i, . .., x„) получается из f (xn) путем отождествления
переменных xit, х{„, .. -,xik, если <р получается из / путем
подстановки х на места переменных х{,, ж,-2, ..., x(k.
В качестве х может быть взята любая переменная, не
принадлежащая множеству Xn/(xil, Xi,, ..., xik).
44
5.1. Показать, что утверждение «х( является суще-
ственной переменной функции / (£”)» равносильно каждому
из следующих утверждений:
1) /Ж); _____
2) существуют переменные х^,..., xik (ij^i, j — 1> к)
и константы ar ...,aft, такие, что функция /4’•••’,** (^*)
существенно зависит от х(.
5.2. Перечислить существенные переменные следую-
щих функций:
1) / (£3) = (*х -» (^i V хъ)) х&
2) /(^2)=(х1
3) / (ж4) = х3 \у £3хз \/ xv
4) f (ж3) =' (X± V ^2 \/ ^g) (^i V -^2 V Хз) (^1 V ^"2 V
V Х3 (*^*1 \/ Х2 \/ Хз) •
5.3. Показать, что хг является фиктивной перемен-
ной функции / (выразив / формулой, в которую xt не
входит явно):
1) /(®2) = (^1© ЯГ2) (Х1 I Xi)’
2j / (ж3) = (((ж3 —» ж2) \/ х^ (х2 —» агх) х3х^ ф х3,
3) / С®3) = (fcl V Xj (Х1 V Хз) -* (% -* Х2Жз)) Х2-
5.4. Указать фиктивные переменные функции /:
1) / (а-3) = (11110000):;
2) /(ж3) = (00110011);
3) /(я3) = (00111100).
5.5. Пусть функция f (х”) задана вектором а/=(а0,
ах, ..., аг"-!). Доказать, что если хк является фиктивной
переменной, то а. = a2«-fc+< для всех i из отрезка
[я2л-*+1, (2s-f-l)2n-ft —1], s = 0, 2fc-1 —1.
5.6. Показать, что если среди переменных функции
f(xn), п^1, имеются фиктивные, то функция прини-
мает значение 1 на четном числе наборов. Верно ли
обратное утверждение?
5.7. Пусть функция / (5") такова, что | Nf | = 2’” (21 — 1).
Каково максимально возможное число фиктивных пере-
менных у функции /?
5.8. Опираясь па результаты задач 5.5 и 5.6, вы-
яснить, от каких переменных функция / зависит су-
щественно.
1) / (я4) = (1011100111001010);
2) /(^) = (0011110011000011);
45
3) /(^) = (0111011101110111);
4) /(х4) = (0101111100001010).
5.9. Для каждой функции из задачи 5.8 построить
равную ей и зависящую существенно от всех своих
переменных.
5.10. Выяснить, для каких п (ге 2) зависят су-
щественно от всех своих переменных следующие функ-
ции:
1) /(Г) = (л:1 V ж2) © (х2 V ж8) © ... ф V х„) ©
© V ж1);
2) / (я:”) = (я?! —> я:2) (ж2 —> х^ © (х2 —> х3) (х3 —» х2) ф...
3) f (х”) = (.. .(fo | жа) | Xj) | | x„) ->
—> | (x21 {x31 ... | xn)...));
f (X)~ (#1 X2> (X2 ~* Жз) ' • 1 (Xn-1 -* Xn) (Xn “* Ж1) “*
-* (^i © x2 © ... ф xn © 1);
5) / (a*) = ( V хчх<г • • • ®<[Я/2Л &
\/ xi.xi2 ... * (^1©^2© . . . ©#„)•
\1<*1<4<...<*[и/2]^и V
5.11. Пусть функции f (£”) и g{ym) существенно
зависят от всех своих переменных, а переменные xv ...
..., хп, yv . . ., ут попарно различны. Показать, что функ-
ция f (xv ..., x„_v g(yv ..., ym)) существенно зависит
от всех своих переменных.
5.12. Пусть Р: (X")— множество всех функций ал-
гебры логики, зависящих от переменных xv х2,...,хп
и притом существенно.
1) Перечислить все функции из Р° (X2).
2) Найти число | Р° (X3) |.
vп (п\
3) Показать, что | Р= (Xй) I = 2 (—1)* t 22"'*-
4) Показать, что lim 2’2” | Р” (Xй) | = 1.
5.13. Пусть а, ,3, 7—такие наборы из Бп, что
а р у, и пусть функция f (хп) такова, что / (а) =
= Показать, что / (ж") зависит существенно
не менее чем от двух переменных.
5.14* . Показать, что xi является существенной
переменной функции / тогда и только тогда, когда эта
46
переменная явно входит в сокращенную д. н. ф. функ-
ции /.
5.15. Показать, что х{ является существенной пере-
менной функции / тогда и только тогда, когда х. явно
входит в полином Жегалкина функции /.
д f (хпУ
5.16. Пусть -у--—— --г —О для любого непу-
с/ (х., ..., xik, Xj)
стого множества {ж,г, ..., ж<й} переменных, отличных
от Xj. Верно ли, что / {х”} фиктивно зависит от Жу?
5.17. Показать, что всякая симметрическая функ-
ция / (ж"), отличная от константы, существенно зависит
от всех своих переменных.
5.18. Пусть в вершинах цепи a,
соединяющей такие вершины а, р куба Вп, что р (а, р) — к,
функция f (хп) изменяет свое значение т раз. Пока-
зать, что / (ж") существенно зависит не менее чем от т
переменных.
5.19. Пусть / (хп) существенно зависит не менее чем
от двух переменных. Показать, что существуют три
вершины а, р, р куба В", удовлетворяющие условиям
р(а, р) = р(р, т) = 1, /(а) =/(?)=£/$).
5.20. Пусть / (ж") существенно зависит от всех своих
переменных. Доказать, что для любого i (1 <1 i п)
найдется такое /, что при некоторой подстановке кон-
стант вместо переменных, отличных от xt и Жу, полу-
чится функция, существенно зависящая от х. и ж..
5.21. Доказать, что для всякой функции / (ж”),
существенно зависящей от п переменных, найдется
такая переменная х{ и такая константа а, что функция
/* (ж") = / (жр ..., ж,.,], а, ж/+1, ...,жя) существенно за-
висит от п — 1 переменных.
5.22. Пусть / (ж") существенно зависит от всех своих
переменных. Справедливы ли следующие утверждения?
1) Существует такое г, что для всякого j найдутся
константы, подставляя которые в f (£п) на места пере-
менных, отличных от х. и Жу, можно получить функцию,
существенно зависящую от х{ и Жу.
2) Для любых двух переменных х. и Жу существуют
константы, подставляя которые в / (ж") на места пере-
менных, отличных от х( и Жу, можно получить функцию,
существенно зависящую от xf и х{.
47
5.23. Перечислить функции из Р2 (X2), которые
могут быть получены отождествлением переменных
из следующих функций:
1) / (f3) = (10010110);
2) /(.г!) = (11111101);
3) /(г3)=ед\/а:л7гл;
--^'l^'2'^'З Ф ^3 ® Х3Х1 ф х2 ф 1 •
5.24. Показать, что из функции / (ж") можно с по-
мощью операции отождествления получить константу
тогда и только тогда, когда / (б)=/ (1).
5.25. Найти число функций / (52), из которых ото-
ждествлением переменных нельзя получить функцию,
существенно зависящую от одной переменной.
5.26. Можно ли из симметрической функции / (хп)
с помощью операции отождествления получить функ-
цию, существенно зависящую от всех своих перемен-
ных и не являющуюся симметрической?
5.27. Пусть а, р, у — три такие вершины из £п,
что a fix”) такая, что / (а) = / (у) =^= / ф).
Показать, что можно отождествить некоторые перемен-
ные функции / так, что в результате получится функ-
ция, существенно зависящая не менее чем от двух и
не более чем от трех переменных.
5.28* . Показать, что у функции / (ж"), п 4, реа-
лизуемой полиномом Жегалкина степени не ниже 2,
можно найти две такие переменные, отождествление
которых уменьшает число существенных переменных
на единицу.
5.29. Перечислить все функции / (£3), существенно
зависящие от трех переменных, такие, что отождествле-
ние любых двух переменных приводит к функции,
существенно зависящей в точности от одной перемен-
ной.
5.30. Пусть функция / (5") Существенно зависит
от всех своих переменных и | )> 2я-1. Показать, что
при отождествлении любых двух ее переменных полу-
чается функция, не равная тождественно нулю.
5.31. Показать, что число функций j (хх, х2, ...,хпП),
из которых путем отождествления переменных можно
получить данную функцию g (xv х2, ..., хп), при п -> со
асимптотически равно п22”.
48
5.32. Показать, что если / (£") фиктивно зависит от
х{, то отождествление этой переменной с любой другой
приводит к функции, существенно зависящей от тех же
переменных, что и / (хп).
5.33. Пусть 1 и функции / (хп) и g (оТ) таковы,
что | N| = 1. Показать, что для всякого 1—1, п по
меньшей мере одна из функций / или g существенно
зависит от xt.
5.34. Показать, что если | {5К) | нечетно,
то функция ср, полученная из / (х”) отождествлением
переменных х( и х^, существенно зависит от п — 1
переменных.
5.35* . Пусть функция / (Ж") существенно зависит от
п переменных. Пусть vf (а) — число тех вершин р, для
которых / (а) =И= / (В) И р (а, Р) = 1. Пусть и (/) — max vf (а).
1) Показать, что ] \/п (/)
2) Указать функции g(£”) и h(x”), такие, что v(g) —
= ]^п[, v (h) — п.
Глава II
ЗАМКНУТЫЕ КЛАССЫ И ПОЛНОТА
§ 1. Операция замыкания. Замкнутые классы
Пусть М — некоторое множество функций алгебры
логики. Замыканием [М] множества М называется со-
вокупность всех функций из Р2, являющихся суперпо-
зициями функций из множества М. Операция по-
лучения множества [ЛИ из М называется операцией
замыкания. Множество М называется функционально
замкнутым классом (короче, замкнутым классом),
если {М\=М.
Пусть М — замкнутый класс в Р2. Подмножество
из М называется функционально полной системой
(короче, полной системой) в М, если [qT]=M. Множе-
ство & функций алгебры логики называется неприво-
димой системой, если замыкание любого собственного
подмножества из оГ отлично от замыкания всего
множества т. е. [<^'[ с I#1] и Неприводи-
мая, полная в замкнутом классе М система называется
базисом класса М. Множество М', содержащееся в зам-
кнутом классе М (в частности, содержащееся во всем
множество Р^, называется предполиым классом в М,
если оно не является полной системой в М, но для
всякой функции / £ М\М' выполняется равенство
[ЛГ U {/}J = м.
Функции /, и /2 будут называться конгруентными,
если одна из них может быть получена из другой заме-
ной переменных (без отождествления). Например,
функции х-у и у -z — конгруентные, а функции х-у
и z-г не являются конгруентными. При рассмотрении
50
вопросов, связанных с замкнутыми классами, бывает
удобно указывать по одному представителю из множе-
ства попарно конгруентных функций. Например, класс
{х, у, z, . . ., х1У х2, . . .состоящий из всех тожде-
ственных функций, будет обозначаться через {х}.
Если М — некоторое множество функций, то через
М (X’1') (или через М”) будет обозначаться подмноже-
ство всех тех функций из М, которые зависят только
от переменных a?lt х2, . . хп.
1.1. Обосновать следующие свойства замыкания:
1) Р/]] = [Л/];
2) если С М2, то С [Л/2];
3) □ [AfjutAfJ;
4) [0] = 0.
1.2. Вытекает ли соотношение 4) из соотношений 1)—
3) задачи 1.1?
1.3. Является ли множество оР замкнутым классом?
Предполагается, что вместе с каждой функцией /
из оР множеству qP принадлежат и все функции из Р2,
конгруентные /.
1) ^ = {0, 1}; 2) <^ = {х}; 3) ^° = {1, 4;
4) * ^2* * *^2 * *^3* • • * > * ^2 * • • • * • * • }»
,5) <^ = {0, хг\/ х2 \/...\/хв, п>1};
6) #> = ф х2 ф ... фхп, 1};
7) £р = {0, агх ф х2 ф... ф ж2я, n > 1}.
1.4. Выписать все зависящие только от перемен-
ных хг, х2, х3 и попарно неконгруентные функции из
замыкания множества оР.
1) = 1);
2) # = {0, х}-,
3) <^ = {х\/у};
4) ^ = {^};
5) <^ = {жф,!/фг};
6) ^ = {(00000001)}.
1.5. Доказать, что если замкнутый класс в Р2
содержит функцию, существенно зависящую от п 2
переменных, то он содержит бесконечно много попарно
неконгруентных функций.
51
1.6. Перечислить все такие замкнутые классы в Р2,
которые содержат лишь конечное число попарно не-
конгруентных функций.
1.7. Всегда ли в Р2
1) пересечение замкнутых классов является замкну-
тым классом;
2) разность замкнутых классов есть замкнутый
класс;
3) дополнение замкнутого класса не является зам-
кнутым классом?
1.8. Сведением к заведомо полным системам в Р2
показать, что множество оР является полной системой
в Р2, где:
1) ^—{х\ у};
2) # = {х • у ф z, (х ~ у) ф z}; .
3) «F = {х у, x®y®z}\
4) (1100001100111100)};
5) <^ = {0, т(х, у, z), а^фг}1);
6) <^ = {(1011), (1111110011000000)}.
1.9. Выяснить, какое из отношений D, С, 2, С
=, выполняется для множеств2) Кг и К2 (отноше.
ние означает, что ни одно из отношений ZD, С, 2
С, = не выполняется).
1) Я1 = ЖГЖ],
2) ^=Ж\^2],
з) /г^жжпед
4) ^жПЖкЖ)],
5) ^=Ж\ЖГЖ)]>
Я2 = Ж]ПЖ];
*2=Ж]\Ж];
#2 = Ж1Ж2]ПЖ1Ж];
#2 = ЖГЖ]иЖГЖ];
/Г2 = Ж]\ЖГЖ].
1.10. Пусть Мх и М2— такие замкнутые в Р2 классы,
что М^\М2 76 0. Привести примеры конкретных клас-
сов Мх и М2, которые удовлетворяли бы еще следую-
щим условиям:
1) МхПМ2 = 0, М2\М±^0, ЖUМ2] = М,UМ2;
2) PI^M.^0, М2\М^0, ж и М,\ = М^М2.
3) м^м2, ж\Ш^\Д;
0 Через т (х, у, z) (или h2 (х, у, г)) обозначается функция
xy\/xz\/yz, которая называется медианой (или функцией голо-
сования).
2) Множества берутся из Р2.
52
4) М, Г) М2 <Z, Л/2\М. 0, [ A/j\М2] = Мх \М2,
5) 0, Л/2\Л/1^=0, — М^М2.
1.11. Из системы <^®, полной для замкнутого класса
М = [<^], выделить базис.
1) ^° = {0, 1, х, х},
2) ^ = {1, x®y®z® 1};
3) <^ = {х V У, X • у • Z, х \J у • Z, (х V У) • 2};
4*) ^>={х®1, x®y®z, т(х, у, z)j;
5) & = {х V у V z, x-y-z, (x-*y)-+z, (x\/y)—>z}j
6) ^={(x-^y)-^(y-^z), х V у \/ (у ф z)};
7) = {х • у, х V у, х -» у, х ф у ф z ф и}.
1.12. Доказать, что всякий предполный класс в Р2
является замкнутым классом.
1.13. Пусть Мг и М2 — различные предполные
классы в одном и том же замкнутом классе М1). Дока-
зать, что если М\=^М\ то М\=/=М\ (т. е. классы Мх и М2
«различаются» уже на множестве функций, зависящих
от одной переменной).
1.14. Перечислить все предполные классы в замк-
нутом классе М.
1) 2И = [0, г]; 4) М = [0, х\/у];
2) Л/ = [0, 1]; 5) М = [0, х • у • г].
3) М ==[«• у];
1.15. Проверить, является ли замкнутым классом
в Р%
1) множество всех симметрических функций;
2) множество всех функций / (ж’1'), п^О, удовлетво-
ряющих условию / (6я) — / (Iм) = 02);
3) множество всех функций / (х”), п^1, у которых
| Nf | = 2м-1.
1.16. Доказать, что если М — замкнутый класс в Р2,
то [Л/и{х)] —
1.17. Доказать, что множество Р2 всех функций
алгебры логики не представимо в виде объединения
0 Предполагаем, что М С Р^-
2) Если п = 0, то / есть константа 0, рассматриваемая как
0-местная функция.
53
U М< (s^2) попарно непересекающихся замкнутых
«=1
классов в Р2.
1.18. Доказать, что всякий замкнутый класс в Р2,
содержащий функцию, отличную от константы, со-
держит и функцию х.
1.19. Доказать, что если замкнутый класс в Р2
имеет конечный базис, то всякий базис этого класса
конечен.
1.20. Оценить сверху мощность множества всех
замкнутых классов в Р2, имеющих конечные полные
системы.
1.21. Доказать, что если непустой замкнутый класс
в Р2 отличен от множеств {0}, {1} и {0, 1}, то его
невозможно расширить до базиса в Р2.
1.22. Пусть М — замкнутый класс в Р2, имеющий
конечное число предполных (в М) классов. Предполо-
жим, что любой замкнутый класс в М расширяется до
предполного класса в М. Доказать, что число функций
в любом базисе класса М не превосходит числа пред-
полных (в М) классов.
1.23. Доказать, что в замкнутом классе [х -> у]
содержатся только такие функции из Р2, которые могут
быть представлены (с точностью до обозначения пере-
менных) в виде х. \/ f (хг,х2, . . ., жД, где f (х”) (5 -^2-
1.24. Пусть функция / (ж") принадлежит замкнутому
классу [а: —> у] и зависит существенно не менее чем от
двух переменных. Доказать, что 1АД | > 2,;~1.
1.25. Доказать (не опираясь на задачу 1.12), что
каждый предполный в Р2 класс содержит тождествен-
ную функцию.
§ 2. Двойственность и класс самодвойственных
функций
Функция g (хг, х2, . . ., хя) называется двойственной
к функции f (з\, ж2, . . ., жД, если g (жп ж,, . . ., х„) =
—] (ж15 х2, . . ., жД. По определению, функцией, двой-
ственной к константе 0, является константа 1 и, наобо-
рот, константа 0 является функцией, двойственной
к константе 1. Функция, двойственная к функции
/ {хх, х2, . . ., жД, обозначается через /* (жх, х2, . . ., жД.
54
Справедливо следующее утверждение, называемое
принципом двойственности: если Ф (хг, х2, . . хп) =
=f (Л (*1, *г. • • •, *я)..1т (*1. *2, • • м *„)), то
Ф* (хг, х2, . . жя)==/* (/* (а?!, х2, . . хп), . . fm (zj,
а:2, . . х„)).
Пусть М — некоторое множество функций алгебры
логики. Через М* будет обозначаться множество всех
функций, двойственных к функциям из множества М.
Множество М* будет называться двойственным к мно-
жеству М. Если М*=М, то множество М называется
самодвойственным.
Функция / (xlt ж2, . . хп) называется самодвой-
ственной, если /* («J, х2, . . ., #„)=/ («х, х2, . . ., хк).
Множество всех самодвойственных функций обозна-
чается через S.
Из определения самодвойственности следует, что
функция самодвойственна тогда и только тогда, когда
На любых двух противоположных наборах значений
переменных она принимает противоположные значения.
Справедливо следующее утверждение, называемое
обычно леммой о несамодвойственной функции: если
функция / (5я) несамодвойственная, то, подставляя на
места ее переменных функции х и х, можно получить
константу.
2.1. Является ли функция g двойственной к функ-
ции /, если:
1) /—g = x~y,
2) / = ж-*у, g = y-+x',
3) f=xy\/xz\/yz, g = xy®xz®yz;
4) f = x®y®z, g — x®y®z;
5) f = xyz \/x(y ~z), g(x, y, z) = (01101101).
2.2. Пусть функция / (5я) задана вектором ау =
= (ар а2, ...,«2»). Доказать, что функция f*(xn) задается
вектором («2В> . . ., «2>
2.3. Пользуясь принципом двойственности, по-
строить формулу, реализующую функцию, двойствен-
ную к функции /. Полученное выражение упростить
(записав в д. н. ф. или в виде полинома Жегалкина).
1) / = ху V yz V xt V
2) / = х • 1 V У (zt V °) V ХУ2''
55
3) f — (x -* и) Ф (О I у) | {% ~ yz));
Д f = ^\/y V(yz©l))^l.
2.4. Пусть функция f (xn) реализуется формулой QI
над множеством {0, 1, ~|, &, \/). Доказать, что функ-
ция /*(#") реализуется формулой 21*, называемой двой-
ственной к формуле 21 и получаемой из 21 заменой
каждого вхождения символа & на символ \/, символа
\/ — на &, символа 0 — на 1 и символа 1 — на 0.
2.5. Доказать, что если формулы 21 и 23 над мно-
жеством {0, 1, Д, &, V} эквивалентны, то формулы
21* и 23* также эквивалентны.
2.6. Доказать, что если функция / (ж”) существенно
зависит от переменной х. (1 i и), то функция
f* (хп) также зависит существенно от х{.
2.7. Доказать, что:
1) множество, двойственное к М*, совпадает с М;
2) множество М является замкнутым классом тогда
и только тогда, когда замкнутым классом является
множество М*;
3) если множество Мг является полной системой
(или базисом) в замкнутом классе М, то двойственное
множество М* образует полную систему (соответственно
базис) в замкнутом классе М*;
4) если Л/х 2 М2, то М* ZD М2.
2.8. Подсчитать число функций, зависящих от пере-
менных xv х2, . . ., хп, в множестве
1) М = {0, х}; 2)М = {х®у}; 3)М = {ху, х^у, 1).
2.9. Самодвойственна ли функция /?
1) f — m(x, у, г);
2) / = (а; —> у) —> xz —> (у —> z);
3) f = {z\Jy\/zj t V xyz;
4) / = (0001001001100111);
5) / = хх ф х2 ф... фх2и1+1 ф а, где а£{0, 1).
2.10. Доказать, что функция / {£”) самодвойственна
тогда и только тогда, когда ее ^-компонента /} (х”)
двойственна к ее ^-компоненте fl(xn).
2.11. Доказать, что если / (ж”)— самодвойственная
функция, то | Nj. | = 2”*1.
2.12. Показать, что не существует самодвойствен-
ных функций, существенно зависящих от двух пере-
менных.
56
2.13. Подсчитать число самодвойственных функций,
зависящих существенно от переменных xlt хг, . . хп.
2.14. Перечислить все самодвойственные функции,
существенно зависящие от переменных х, у, z, и пока-
зать, что каждая из этих функций представима либо
в виде т (ха, у$, z"1), либо в виде жфуфгфа, где а, 0,т,о
принадлежат множеству {0, 1}.
2.15. При каких значениях п~^2 функция f (х”)
является самодвойственной?
1) / (£*) = хг (х2\ух3\/ ... (жз\/ • • • V4)V • • •
• • '\/Хп-2 (Хп-1^Х.)\/Хп-1Хп’
2) / (И = Х1 <Л® Х3 © • • • ®Х„)®Х2 (.Х3 © • • • ©*„)© • • •
• « • ф^и-г (Хп~1 © Хп) ® Хп-1Хп',
3) / (И = -* х2) ф (хг х3) ф ... ф (х^ -» Z„) ф
© (Х„ -* Xl)’
4) Ж)= V
где (дизъюнкция берется по всем монотонным конъюнк-
циям длины ]п/2[, составленным из переменных xv
х2, ..хп).
2.16. Пусть / (И = хг ф х2 ф ... ф х„, g\ (.«’") =
= £я_<+1(Ёт), i = l, 2,...,n. Самодвойственна ли функ-
ция /(^(х”), .. .,gn(xm))?
2.17. Доказать, что если
1) / («к xv • • •> х„) € s> то / (х, х,...,х)£ {х, X};
2) f£S, то т (агр /, х2 ф xs ф /) ф х3 ф xi £ S;
3) / £ S, то ф ж2х, ф хгх3 ф xj ф ф хъ £ S.
2.18. Пусть функции /(хп) и fix”), п^1, удовле-
творяют условию 1^1 = |2V/»|. Доказать, что:
1) если /\//* = consC то f^S;
2) если f ф /•/* = const, то f£S.
2.19. Из самодвойственной функции / с помощью
подстановки на места переменных функций х и X по-
лучить константу.
1) / = (00111001); 3) f = (x\y)-+(x®zY
2) f = (x\/y\/z)t \J xyz-, 4) f=xy\/xz\/yt\/zt.
2.20. Доказать, что если несамодвойственная функ-
ция существенно зависит не менее чем от трех перемен-
57
ных, то, отождествляя некоторые ее переменные,
можно получить функцию, существенно зависящую
от двух переменных.
2.21. Доказать, что если с помощью отождествления
переменных из функции / (ж"), п 3, нельзя получить
функцию, зависящую существенно от двух переменных,
то функция / — самодвойственная.
2.22. Пусть / (х, г/, z)=m (Ф1, г/3, zr), где а, (3, у
принадлежат множеству {0, 1}. Доказать, что для вся-
кого 11^4 из функции / можно получить (с помощью
операции суперпозиции) функцию, существенно за-
висящую от п переменных.
2.23. Доказать следующие эквивалентности:
1) х ф у ф 2 — т (т (ж, у, 2), т (х, у, z), т (х, у, z)) =
т (х, т (х, у, z), т (х, у, г)) = т (т (х, у, г), т (£, у, z), z);
2) (x\/y\Jz) t\Jxyz = m (т (у, z, t), х, t) =
= т(т(х, у, t), т(х, z, Г), т{у, z, t));
3) т(х, у, z} = m(m(x, у, z), у, z).
2.24. Пусть f(xn')^P2 и Доказать следующее
соотношение:
/ (.Ху х2, х3, xit ..., хя) =
= f (xv т (xv х2, х3), т (xv х2, х3), xt,..., хп) ф
®f(m(xv х2, х3), х2, m(xv х2, х3), xv ..х„) ф
Ф / (т (xv х2, х3), т (xv х2, х3), хя, xit ..., х„).
2.25. 1) Используя задачи 2.12, 2.14, 2.23, 1) и
2.24, доказать, что [ т (х, у, z)] = [m(x, у, z)] = S.
2) Доказать, что любой базис класса S всех само-
двойственных функций содержит не более двух функций.
2.26. Можно ли из функции / с помощью операции
суперпозиции получить функцию g, если:
1) / = (10110010), g- = (1000);
2) / = (1111011100010000), g = (00010111);
3) / = (11001100), g = (00110011).
2.27. Функция / (z"), п 2, обладает следующими
свойствами: / (х’г) (£ S и при отождествлении в ней
любых 2 [\Ztz] переменных получается функция из класса
S. Какое наибольшее число существенных переменных
может быть у функции / (жи)?
2.28. Перечислить все такие функции, существенно
вависящие от переменных хх, х2, х3, х4, у которых вся-
58
кая яр-компонента является самодвойственной функ-
цией.
2.29. Является ли самодвойственным множество М?
1) M = {x®y®z, т{х®у, x~z, у~г)};
2) М = {х-у, х\/у, xQy®m(x, у, г)};
3) М = {{х->у)->у, {х\у у) фжф у, {x\/y\/z)t\/xyz}',
4) М = S\{ х ф у ф z, т{х, у, г)}.
§ 3. Линейность и класс линейных функций
Функция / (ж") называется линейной, если она пред-
ставляется в виде
/ (ж") = а0 ф ® ад ф ... © апХп,
где а( £ {0, 1}, 0 г п. Множество всех линейных
функций обозначается через L, а множество всех линей-
ных функций, зависящих от переменных жь х2, . . .
..., хп, — через Ln. Множество L является замкнутым и
предполным в Р2 классом. Справедливо утверждение
{лемма о нелинейной функции)’.
Если / (f L, то, подставляя на места ее переменных
функции 0, 1, х, у, X, у, можно получить либо ху,
либо ху-
Если / © L, то f называется нелинейной.
3.1. Разлагая функцию / в полином Жегалкина,
выяснить, является ли опа линейной.
1) /(ж3) = {х^х^х/ х^х^ фж3,
2) / (ж2) = хгх2 {xt ф х2);
3) / (xi) = x1x2\/x.ixsi\/xixi\/xixl;
4) f {хЛ) '=: (Ж| —» Ж2) (^2 ~-> •’'1) Pl’
3.2. Доказать, что если функция / {хп) на любых
двух соседних вершинах i п из В” принимает проти-
воположные значения, то она линейная. Верно ли об-
ратное утверждение?
3.3. Доказать, что если / (ж") — линейная функ-
ция, отличная от константы, то \N^ |=2Я-1. Верно ли
обратное?
3.4. Выяснить, является ли линейной функция /.
1) /(ж‘) = (1010 1010 0110 1000);
2) / (ж4) = (1001 ОНО 1001 ОНО);
59
3) /(5J) = (1001 0110 01101001);
4) / (54) = (0110 1001 1010 0101).
3.5. Показать, что число линейных функций /(5я),
существенно зависящих в точности от к переменных
из множества {х1, ж2, ..., жя), равно 2^.
3.6. Найти число самодвойственных функций, при-
надлежащих множеству L”.
3.7. Показать, что функцию х -> у нельзя получить
из функций xQyQjz, а?ф1, х@у с помощью операции
суперпозиции.
3.8. Выяснить, можно ли из функции / с помощью
подстановки на места ее переменных функций 0, 1,
х, у, X, у получить ху.
1) / (5’) = (1110 1000);
2) / (53) = (0111 1111);
3) /(53) = (1001 1001);
4) / С® )== (•*! -* —* ^i) ® ~> ^з) (^з —Ф • • •
•••
3.9. Выяснить, можно ли функцию х -> у реализо-
вать формулой над множеством Ф, где:
1) ® = L{J{xy\/xz\/zy}-,
2) Ф = А\5;
3) Ф = {L (J {ху\/yz\/zx})\S;
4) Ф = (Ли(л:г/})\5.
3.10* . Доказать, что функция / (5”), существенно
зависящая от всех своих переменных, является линей-
ной тогда и только тогда, когда при замещении любого
подмножества переменных любым набором констант
получается функция, существенно зависящая от всех
остальных переменных.
3.11* . Показать, что из полинома степени к 3
можно с помощью отождествления переменных получить
полином степени к—1.
3.12* . Показать, что из нелинейной функции
/ (5я), п 4, с помощью отождествления переменных
можно получить нелинейную функцию, зависящую
не более чем от трех переменных. Перечислить все
нелинейные функции / (53), из которых путем отождест-
60
вления переменных нельзя получить нелинейную функ-
цию.
3.13. Показать, что из нелинейной функции с по-
мощью отождествления переменных можно получить
функцию, конгруептную либо ху®1 (х, у), либо
хуфугфггф/ (ж, у, z), где I (х, у) и I (х, у, z) — линей-
ные функции.
3.14. Показать, что если / (xn)§L, то в В” найдется
такая двумерная грань, ровно в трех вершинах ко-
торой функция / (£”) принимает одно и то же зна-
чение.
3.15. Пусть функция /(£*) такова, что для всех
i, у (1 i < / п) (хп) = (х?‘). Показать, что
3.16. Выяснить, какие из нижеперечисленных си-
стем образуют базис в L.
1) {1, х®у}\ '4) {0, жфуфгф!};
2) {х ~ у, х ф у © z}; 5) {1 ф х ф у ф z, яфуфг}.
3) \х~у, а: фу, 0);
3.17. Из полной в L системы выделить все базисы.
1) {0, 1, хф1, х~у, x®y®z}-,
2) {ж ~ у, (х~у)~ z, x®y®z, x®y©z@t}-,
3) {0, (х ~ у) ~ z, х ф 1, х ф у}.
3.18. Доказать, что всякая полная в L система
содержит не менее двух функций.
3.19. Доказать, что всякий базис в L содержит
не более трех функций.
3.20. Доказать, что существует лишь конечное
число замкнутых классов, состоящих только из линей-
ных функций. Перечислить все эти классы.
3.21. Показать, что всякий замкнутый класс, со-
стоящий из конечного числа попарно неконгруентных
функций, содержится в L.
3.22. Функция / (я*), п 1, удовлетворяет усло-
виям:
1) | Nf | = 2й-1; 2) /ф/* — константа.
Показать, что / (£") £ L U S при п =С 3. Привести
пример функции /, удовлетворяющей условиям 1), 2) и
не принадлежащей множеству L U S.
3.23. Доказать, что ЛГ|5' = [а:фуфгф1].
3.24. Показать, что L*=L.
61
3.25. Перечислить все попарно неконгруентпые
функции /, удовлетворяющие следующим условиям:
1) / (Г L-
2) любая (собственная) подфункция функции / ли-
нейна.
3.26. Подсчитать число самодвойственных линей-
ных функции / (Г'), существенно зависящих от всех
своих переменных.
3.27. Сколькими способами можно расставить
скобки в выражении ад —> ж2 -> ад —> ад -> xv, чтобы
получилась линейная функция?
3.28. Пусть / (х”) ( L П S, /(О, 0, . ..,0) = /(0, 0, ...
,..,0, 1) и f (av <z2, . . ., ая) = 0. Чему равно / (dCj, а2, ...
. О?
3.29. При каких п существует линейная функция
f(x”), удовлетворяющая условию / (0, 0, ..., 0) =/=f (1,
1, . . ., 1) и являющаяся симметрической?
3.30. Пусть /(ж") такова, что
-in4:: г ’п (£,г)=xix2 и /об 4,_: о ’” (*”)=х-г-
Показать, что f (x'')§L\jS.
3.31* . Перечислить все попарно неконгруентные
нелинейные функции /, такие, что любое отождествле-
ние переменных приводит к функции из L.
3.32* . Перечислить все попарно неконгруентные функ-
ции / $ L П S, из которых при любом отождествлении
переменных получается функция из L П S.
3.33. Пусть (?={0, ж, Л, /2, /3}, где /х, /2, /3 — по-
парно различные функции, существенно зависящие от п
переменных (п > 1). Доказать, что система Q полна в Р2.
§ 4. Классы функций, сохраняющих константы
Говорят, что функция / (£”) сохраняет константу 0
(константу 1), если / (0, 0, . . ., 0)=0 (соответственно,
если/(1, 1, . . ., 1) = 1). Множество всех функций ал-
гебры логики, сохраняющих константу 0, обозначается
через То, а сохраняющих 1 — через Tv Множество
всех функций алгебры логики, зависящих от перемен-
ных хг, х2, . . ., хп и сохраняющих константу 0 (кон-
станту 1), будет обозначаться через (соответственно
через 71"). Каждое из множеств То, Тг является замкну-
тым и предполным в Р2 классом.
62
4.1. Выяснить, каким из множеств То (J 7\, ТГ\Т6
принадлежат перечисленные ниже функции:
1) ((ж V у) — (•* I У2')') I ((у ~ Z) -» х);
2) {ху -> z) | {{х -> у) | (z ф Ту))-,
3) (* У) & {У I z) V (z -* у).
4.2. Выяснить, при каких п функция f {х”) принад-
лежит множеству Т1\Т0.
1) / (^") — Х1 ф Х2 Ф • • • Ф Х„ Ф 1 >
2) Ж) = (• • • ((*i -* ъ) -* xs) -* • • • *„);
3) / (х”) — (• • Ж -> х2) -» ^з) “> • • • "*х«) Ф
©((••• ((*2 -* Ж3) -> Х4) «я) ф .. .
•••©(••• ((^-*^1)^ ®г)-> • • •
4) / {х") = 1 ф х^х^х^.
i i<Zi 2<Z^^n
4.3. Выяснить, при каких п функция /„ {х"), задан-
ная рекуррентно, принадлежит множеству (ГД/ф U
U (Л\Л>).
1) /2 (х2) = xi Ф х»
fn {£”) = {х, -> Ж1)) {х„ \/ («-’)), п > 2;
2) /1 {х1) == Xv f2(XV Xi) =~ Х1 Ф Х2’
Л (X”) = Хп-1Х,: Ф /«-2 (^'’!'2), « > 3;
3) /1 (^1) = Xl’ t-2 (XV Х2) — Х1 V Х2’
fn («") = /„-1 (^’) ф XKfn-2 («И’2). « > 3.
4.4. Сколькими способами можно расставить скобки
в выражении xr -> х2 -> xt -> х2 -> х±, чтобы получи-
лась формула, реализующая функцию из То?
4.5. Подсчитать число функций, зависящих от пере-
менных xlt х2, . . ., хп, в каждом из следующих мно-
жеств:
1) тй П т1; 5) £,\(ГО П Л); 9) 5 П {То и Л);
2) т0 U Л; 6) L\{Tn U Л); 10) 5 п (ЖЛ);
з)твп£; 7)W; и) 5\(гоиЛ);
4) Т. U L-, 8) Го\5; 12) (S\f0) П Л;
13) L n s п Л;
14) L\(T0 U (Л П S));
15) {L U S)\(T0 U Т^.
63
4.6. Найти функцию j{x, х, .,ж), если:
1) /(хг г2, ..., х^ е ЛХЛ;
2) f(xv z2, .... о:„)€Ь\(Гг Q S');
3) j{xv х2, x,)QS\T0.
4.7. Выяснить, можно ли получить функцию / с по-
мощью операции суперпозиции над множеством Ф, если:
^)f = x®y, Ф = {х ->у};
2) f = x^y, 9={ху, х\/у};
3)f = xyy, Ф=гои($\т»;
4) f = xy, ® = (7’1\L)U
4.8. Доказать, что
1) Т0 = [ху, х ф у] = [ж V у„ xQy];
2) Л — 1хУу, х~у] = [ху, х~у];
3) Т0Г\Т1 = [ху, x®y®z].
4.9* . Доказать, что любой базис в То содержит не
более трех функций. Привести примеры базисов класса
То, состоящих из одной, двух и трех функций.
4.10* . .Доказать, что любой базис в То f| Тх со-
держит не более двух функций. Привести пример ба-
зиса, состоящего из одной функции.
4.11. Существует ли в классе Тй Q 7\ функция, за-
висящая от трех переменных и образующая в нем базис?
4.12. Доказать, что
1) L П ^^[хфр];
2) ЬГ\Тх = [х~у];
з*) s П Тй — \хуУ yz V ZX, Жф!/ф2] =
— [ху V у z V Z^L
4.13. Не всюду определенная функция / (г3) равна
нулю на наборах (ООО), (001) и равна единице на на-
борах (011), (100), (НО). Доопределить функцию / (х3)
на остальных наборах так, чтобы полученная функция
образовывала базис в То.
4.14* . Доказать, что если функция / существенно
зависит не менее чем от двух переменных и / (£ То (J Тх,
то L П S С [/].
4.15. Выяснить, являются ли базисами в То сле-
дующие системы:
1) {ху У yz\J zx, х ф у ф z);
2) {ху, zQy&z, ху у};
64
3) {xy<&z};
4) {я ф у ф 2, ху, x\J у \/ z}.
4.16. Привести пример симметрической функции
/ (ж4), образующей полную в То систему.
4.17. Доказать, что
L П То П = L П 5 П То = АП П7\ = ЬП5 ПЛ>П Л-
4.18* . Доказать, что классы То П L, То Г| 5, То П Тх
являются предполными в То.
4.19. Доказать, что система функций {1}U(7’O\(7’1U
(J L U S)) полна в Р2.
4.20. Доказать, что:
П П = 7’р
2) (гои Л)*=тои Л;
3) (То и Л и S и L)* = То и Тх и S и L;
4) ((7’оП7’1)и5)* = (ТоП7’1)и5;
5) (7’0\S)* = T1\5;
6) (5\Т0)* = 5\Г1.
4.21. Пусть /(54)65ПАПГ0, /(1, 1, 0, 1) = 1 и /(f4)
существенно зависит не менее чем от двух переменных.
Найти /(ж4).
4.22* . Доказать, что классы L Тп, L Г| 7\, L (~| S,
[0, г], и только они, являются предполными в L.
4.23. Доказать, что / £ (То Г) Тх) U S тогда и
только тогда, когда из / с помощью операции суперпо-
зиции нельзя получить ни одной из констант.
§ 5. Монотонность и класс монотонных функций
Булева функция / (ж”) называется монотонной,
если для любых двух наборов а и р из В”, таких, что
а имеет место неравенство f (а) / ф). В про-
тивном случае / (ж”) будет называться немонотонной.
Множество всех монотонных булевых функций обозна-
чается через М, а множество всех монотонных функ-
ций, зависящих от переменных жь х2, . . ., хп, — через
Мп. Множество М является замкнутым и предполным
в Рг классом. Справедливо утверждение (лемма о не-
монотонной функции}-, если / $ М, то, подставляя на
места ее переменных функции 0, 1, х, можно получить
функцию х.
3 Г, П. Гаврилов, А. А. Сапоженко 65
Вершина а куба В" называется нижней единицей
(верхним нулем) монотонной функции / (£”), если / (а) = 1
(соответственно /(а) = 0) и для всякой вершины р из
р<^а вытекает, что /(р) = 0 (соответственно из а<р
вытекает, что /(р) = 1).
5.1. Какие из перечисленных ниже функций являются
монотонными?
1) х^(х->у);
2) х-+(у-+х);
3) ху(х$)у);
5) / (х3) = (00110111);
6) / (ж3) = (01100111);
7) f (я4) == (0001010101010111);
4) ху ф yz © zx ф z; 8) / (я4) = (0000000010111111).
5.2. Выяснить, при каких п функция / (х”) монотонна.
1) f (хп) — ¥, х.ху,
2) / (х”) = хЛ ... _♦ (Х1 ф х2 ф ... ф xj;
3) / (Xя) — xtx2 ... хп ф хх ... ...х„.
5.3. Доказать, что для монотонных функций / (5”)
справедливы следующие формулы разложения:
/ (Л=(*”) V п (П / (П=V К СП) & /1 (П
5.4. Доказать, что для каждой монотонной функ-
ции /, отличной от константы, существуют д. н. ф.
и к. и. ф., не содержащие отрицаний переменных и
реализующие /.
5.5. Сколько существует таких монотонных функ-
ций / (f3), что f (0, 1, 1)=/ (1, 0, 1) = 1, / (0, 0, 1)=0?
Сколько таких функций принадлежит множеству M\S?
Есть ли среди них функции с фиктивными переменными?
5.6. Пусть /(х4)е5Г)Л/, /(0, 0, 1, !) = /(!, 1, 1,0)=1,
/ (г4) существенно зависит от всех своих переменных.
Найти /(f4).
5.7. Доказать, что если / не является константой,
а / V Г — константа, то / (f М (J £.
5,8. 1) Верно ли, что если f (х”) монотонна, то из
условия
Ре Д’. v(P)>v(5). Ш>||П /(«) = !»
вытекает равенство / (р) = 1?
66
2*) Пусть для всякого к (0 к < п) из условий
/(ая) = 1, v (ая) 2я'1 — 2*, v (ря) = v (а”) 4-2* следует,
что /(ря) = 1. Доказать, что f(xn}£M.
5.9. Перечислить все функции /(54)£Л/, удовлетво-
ряющие следующим условиям:
1)/(1, 0, 0, 0) = 1, /(0, 1, 1, 1) = 0;
2) /(1, о, о, 0) = 1, /(54)gz,;
3) /(0, 1, 0, 0)=4=/(1, 0, 1, 1), / (54)— симметриче-
ская;
4) /(1, 0, 0, 1) = 0, /е S.
5.10. Показать, что если fix") немонотонна, то суще-
ствуют такие два вектора а, р из В", различающиеся
ровно в одной координате, что но / (а)> f (?)•
5.11. Показать, что функция /, существенно зави-
сящая не менее чем от двух переменных, монотонна
тогда и только тогда, когда всякая (собственная) под-
функция функции / монотонна.
5.12. Привести пример немонотонной функции
/ (х"), у которой каждая подфункция вида Д (5я), 4 = 1, п,
а£{0, 1), монотонна. Каково число таких функций,
зависящих от переменных xlt х2, . . ., xn?
5.13. Показать, что функция f (5я) монотонна тогда
и только тогда, когда для любого к (к = 1, и — 1),
любого непустого подмножества {41; . .., ifc}C{l, ...
. . ., п} и любых таких наборов 5= (alt . . ., а*) и t =
=(т1, . . ., т ), что 3 t, выполняется соотношение
(*") V /ir.r.v* ** =К”. "ч*
5.14. Доказать, что никакой простой импликапт мо-
нотонной функции не содержит отрицаний переменных.
5.15. Будем говорить, что монотонная э. к. К над
множеством переменных хг, х,, . . ., хп соответствует
вектору (аг, а2, ..., а„) из Вп, если для всякого 4 = 1, п
а{ = 1 тогда и только тогда, когда xt входит в К. Дока-
зать, что если вектор а является нижней единицей
монотонной функции / (5я), то полином Жегалкина
содержит в качестве слагаемого конъюнкцию К, со-
ответствующую вектору а.
5.16* . Пусть /(5я) такая монотонная симметрическая
функция, что Nf={i; S Е Вп}. При каких п
67
и Л ее полином Жегалкина содержит в качестве слагае-
мого хотя бы одну э. к. ранга A-f-2?
5.17. Показать, что не существует монотонных са-
модвойственных функций, имеющих ровно две нижние
единицы.
5.18. Существуют ли монотонные самодвойствен-
ные функции с тремя нижними единицами, зависящие
существенно
1) от трех переменных;
2) более чем от трех переменных?
5.19*. 1) Показать, что максимальное число нижних
(га \
у.
2) Сколько существует монотонных функций /(£"),
(га \
[п/2]) нижних единиц?
5.20. Показать, что если произвольным образом
заменить значения монотонной функции в некоторых
ее нижних единицах на нули, то полученная функция
также будет монотонной.
5.2'*. Показать, что | Мп | 2
5.22. Подсчитать
дующих множеств:
1) Мп\(Т’[ П Т”)-
2) г\(^‘иа
3) АГПЬЯ;
5.23 *. Показать, что:
число функций в каждом из сле-
4) Мп П Ln П S'1;
5) Ln\(Mn U Sn).
1) |5" П Л/“ | < | АР-* |
2) | Л7" ] < | Л/""113
3) I М” I < I Л/”-213 22"-2
при
при
при
га>1;
1;
2.
5.24 . Пусть тга(га) — число монотонных функций, зави-
сящих от переменных xv х2, . .., хп. Показать, что
т(1)—-3, ш (2) =6, гаг(3) = 20, тга(4) = 186.
5.25 . Подсчитать число ш,. (га) монотонных функ-
ций /(£''), существенно зависящих от п переменных,
для га = 1, 4.
5.26 *. Доказать, что | Мп | <Z | S’ | при га 4.
5.27 . Каково число монотонных самодвойственных
функций / (х1), существенно зависящих от всех своих
переменных?
68
5.28 *. Используя то (см. задачу 1.1.18), что куб Я*
(п \
[п/2] /
щих цепей, показать, что:
непересекающихся возрастаю-
п
( ” )
щ ! 2) |Л/"|<(п-1) г"/2] 4-2.
( ” )
5.29*. Доказать, опираясь на 1.1.18, что |ЛГ,|^3''1”.
5.30. Доказать, что число монотонных функций / (хп),
у которых каждая нижняя единица имеет вес, не пре-
вышающий к (0^/с^п/2), не превосходит 1 4-&'4 •
5.31 . Пусть (Л, — частично упорядоченное мно-
жество. Функция /, определенная на множестве А
и принимающая значения из множества {0, 1}, назы-
вается монотонной, если для любых а и р из А, тайих,
что а $4 р, выполнено соотношение f (а) / (Р). Пусть
т (А, — число различных монотонных функций,
определенных на А. Найти min т(А, <^), тахт (И, <С)
|J|=n |.4j-n
и указать, на каких частично упорядоченных множе-
ствах с п элементами достигаются эти минимальные и
максимальные значения.
5.32 *. Привести пример такой последовательности
монотонных функций /в (я2”), п=1, 2, . . ., что число
нижних единиц функции /„ (я2") в 2”/п раз превышает
число верхних нулей.
5.33 . Доказать, что если число нижних единиц
монотонной функции / (х”) не меньше 2, то функция
зависит существенно по меньшей мере от двух пере-
менных.
5.34 *. Пусть t (/) — число нижних единиц монотон-
ной функции /, а р (/) — число ее существенных пере-
менных. Доказать, что р (/) log2 t (/) — log2log2 t (/).
5.35 . Пусть f^Mn, mk(f)— число векторов а из Bk,
таких, что / (а) = 1, <7* (/) = т* (/)/( V Показать, что
fffc-l(/)<?*(/), *=1, п.
5.36 *. Функция (х"), определенная на Вп и прини-
мающая произвольные действительные значения, на-
зывается обобщенной монотонной функцией, если из
.69
fi P вытекает, что <f (a) <p (P). Доказать, что обоб-
щенная монотонная функция может быть представлена
линейной комбинацией монотонных булевых функций
следующего вида:
?(Л=:С +
2
Я/ • / (£”).
где с — действительное, af 0.
5.37 *. Пусть <р(а;м)—обобщенная монотонная функция,
а ?*('?) = (б) Показать’ что (?)<?*(?)’
____
к — 1, п.
5.38 *. Показать, что если / (х”) М (га 4), то,
отождествляя переменные, из нее можно получить не-
монотонную функцию, зависящую не более чем от трех
переменных.
5.39 . Можно ли из функции xyz \/ t (ху -» z) по-
лучить X
1) отождествлением переменных;
2) отождествлением переменных и подстановкой
константы 0 на места некоторых переменных;
3) отождествлением переменных и подстановкой
констант?
5.40* . Показать, что если / (хп) (jjМ (J S (га 3),
то, отождествляя переменные, из нее можно получить
немонотонную несамодвойственную функцию, суще-
ственно зависящую от двух переменных.
5.41. Показать, что если / £ М, то /* £
5.42. Показать, что всякая монотонная функция
содержится не менее чем в двух классах из То,
Л, L.
5.43. Показать, что М не содержится ни в одном
из классов То, 1\, S, L.
5.44. Можно ли из функции zx\J yz\J zx получить
с помощью операции суперпозиции функцию ху!
5.45. Можно ли с помощью функций ху, х \/ у,
1 получить 0?
5.46. Показать, что множество {0, 1, ху, х\/у}
образует базис в М.
5.47. Из множества {0, 1, ху, х \/ у, ху \/ z, ху \/
\Jyz \/ zx} выделить все подмножества, являющиеся
базисами в М.
70
5.48* . Показать, что всякий базис в М содержит
не более четырех и не менее трех функций.
5.49. Показать, что всякий базис в М, состоящий
из трех функций, содержит функцию, существенно за-
висящую от трех или более переменных.
5.50. Привести примеры базисов в следующих клас-
сах:
1) Та П М; 2) 7\ П М; 3) L П М.
5.51. Пусть (и ^>4). Доказать справедли-
вость представления
/(Г) = щ(/(ж1, xv х3, xv ..., хп),
f(xv х2, х2, xv ..., х„), /(аг3, х2, х8, xit ..., х„)),
где m (х, у, z) = xy\/ уz V zx.
5.52. Показать, что:
1) ху \/ yz \/ zx образует базис в М 5;
2) любая функция из М Г) S, существенно завися-
щая более чем от одной переменной, образует базис
в М Q S.
5.53* . Пусть — множество, состоящее из всех
монотонных элементарных дизъюнкций, а — множе-
ство всех монотонных элементарных конъюнкций. Пока-
зать, что множества U (0, 1}, U {0, 1}, М П Тй,
М П 1\, и только они, являются предполными в М.
п—1 2»—2*—1
5.54* . Пусть / (у2") = & & (у( -> у,ч2л-). Доказать,
fc=0 1=0
что 1^1 = 1 Л/”|.
5.55. Пусть f монотонна и существенно зависит от п
переменных. Доказать, что либо ее сокращенная д. н. ф.
имеет слагаемое ранга больше, чем \/п — 1, либо ее сокра-
щенная к. н. ф. имеет сомножитель ранга больше, чем
— 1.
§ 6. Полнота и замкнутые классы
В Р2 справедлив следующий критерий полноты.
Теорема (Пост). Система полна в Р2 тогда
и только тогда, когда она целиком не содержится ни
в одном из классов То, Tv L, S и М.
Функция f (£"') называется шефферовой (или функцией
Шеффера), если она образует базис в Р2.
71
Пусть функция / (хп) существенно зависит от всех
своих переменных. Через 91 (/ {£”)) обозначают множество
всех таких функций, которые получаются из функ-
ции / (хп) отождествлением переменных, причем сама
функция f множеству 91 (/) не принадлежит. Если п<^2,
то, по определению, 91 (/(#”)) = 0. Множество 91 (/(#))
называется наследственной системой функции / (#).
Функция / называется неприводимой, если [91 (/)]#= [/]•
Базис 23 замкнутого класса К называется простым, если
после замены произвольной функции / из 23 ее наслед-
ственной системой получается система, неполная в К.
Функция /, не принадлежащая замкнутому классу К,
называется простой относительно К, если ее наслед-
ственная система 91 (/) содержится в К.
6.1. Показать, что в Р2 не существует предполных
классов, отличных от классов То, Tv L, S, М.
6.2. Используя критерий полноты, выяснить, полна ли
система #.
1) {х-> у, ху • z};
2) — • у, х ~ yz};
3) #={0, 1,
4) {(01101001), (10001101), (00011100)};
5) #={(0010), (1010110111110011)};
6) # = (5\А/) и (^\(^0 и Л));
7) # = (5 П Л1) U (^\/V) U (W):
8) # = (Л\(7’0 П Л)) U (£\S).
6.3. Доказать, что если функция / существенно зави-
сит не менее чем от двух переменных и принадлежит
классу 5 П А/, то система {0, /} полна в Р2.
6.4. Полна ли система # = {/1(f"), /2(5”)}, если:
1) Л 6 5\Л/,
2) Аегои£,
з)
/2 е l и 5,
м s,
Л-*/2 = 1;
6.5. Является ли полной система #={/#?”), /2(^”)>
/3(^л)}, если известно, что Д $ £ U (Т’оПЛ)» /2 6 3/\£,
А^/2=1 и av/3 = i?
72
6.6. Из полной в Р2 системы & выделить всевозмож-
ные базисы.
1) ^={(х\/у)(х\/у), xyQz, (x®y)~z,
т(х, у, z)};
2) <^° = {1, х, xy(y~z), у, z)};
3) — {0, х ф у, (х -> у) | (у ~ z), (х | (ху)) -> z};
4) = {ж V (х Ф У) V z> (х ~ У) ~ z> ХУ Ф z,!>
т(х, у, z)}.
6.7. Привести по три примера базисов в Р2, содер-
жащих одну, две, три и четыре функции.
6.8. Перечислить все различные базисы в Р2, со-
держащие только функции, существенно зависящие от
двух переменных х, у (базисы считаются различными,
если один не сводится к другому с помощью операции
переименования переменных).
6.9. Выяснить, можно ли расширить до базиса
в Р2 множество “21.
1) 21 = {жфу, т(х, у, z)}; 3) 21 = Л/\(Гои Л)!
2)<21 = {х~у, х\/ yz}; 4) 21 = ^Г|Л/.
6.10* . Существует ли базис в Р2, состоящий из таких
четырех функций fv f2, f3, Д, что То, f2 $ Tv
5?
6.11. Используя теоретико-множественные опера-
ции, выразить через известные замкнутые классы То, Tlf
L, S, М и Р2 замыкание множества 21.
1) 2i=p2\(7’oU/’iU^u5u^);
2) 21 = Л/\(Г0 U L); 6) 21 =
3) 21 = Л/\(Г0 П TJ-, 7) 21 = Л\(Т0 и т\);
4) 21 = M\L; 8) 21 = 7’О\7’1;
5) 21 = То П (£\S); 9) 21 = (То П 7\)\М.
6.12. Выяснить, какое из отношений D, С, С,
=, имеет место для классов Кх и К2 (отношение
означает, что ни одно из остальных пяти отношений
не выполняется).
1) К. = [х\/ (х®У)У z\,
2) Кх = [х ~ у, х \/ yz],
3) = [ху, х © р],
К2 = [х\/ У, х ф у];
^2 = Iх Фуг];
К2 = [х-^у, х — у];
73,
4) Л\ = [1, х у у], К2 = [х®у, х\/yz];
5) = x~yz], К2 = [т(х, у, z), x®y(Q
фгф1, ач/фг];
6) X\ = [г-> у], К2 = [х®у, т(х, у, г)].
6.13. 1) Доказать, что в Р2 (X2) существует в точно-
сти две функции Шеффера.
2) Подсчитать число функций Шеффера в Р2 (Xs).
6.14. 1) Доказать, что если / ff То (J Тг U <$» то
f — функция Шеффера.
2*) Подсчитать число функций Шеффера в Р2 (Xй).
6.15. Доказать, что из функции Шеффера, завися-
щей существенно не менее чем от трех переменных,
можно путем отождествления переменных получить
функцию Шеффера, существенно зависящую от двух
переменных.
6.16. При каких п (п > 2) является шефферовой
функция /?
2) / = 1 ф хгх2 ф ^з Ф • • • Ф Я„-Л Ф х„х»
3) f = (xi~* х2) ф (х2-+х3) ф ...
4) f = CH I «г) © I *з) Ф • • • Ф (x„-i I х„) Ф (х„ I *1);
5) / = 1 Ф (х2 -> х2) (х2 -* х3)... (хп_2 -> хп) (ха xj;
6.17. Функция / не принадлежит множеству 7\ (J М
и принимает в точности одно значение, равное нулю.
Доказать, что она либо является шефферовой функцией,
либо существенно зависит от одной переменной.
6.18. Привести пример функции Шеффера, завися-
щей существенно от возможно меньшего числа перемен-
ных и принимающей значение единица ровно на поло-
вине всех наборов значений переменных.
6.19. Привести пример такой функции / (я"), что
для всякого k (l^k^n— 2) и любого подмножества
ix, i2, . . ., ik из {1, 2, . . ., ?г} функция
является шефферовой.
74
6.20. Пусть функция / — монотонная и имеет ровно
две нижние единицы. Доказать, что / — шефферова.
6.21. Доказать, что всякая самодвойственная функ-
ция, не принадлежащая множеству Уо U U U ЛГ,
образует базис в классе S.
6.22. 1) Доказать, что любая функция из класса L
принадлежит хотя бы одному из классов ?'о, Tlt S и М.
2) Привести примеры линейных функций, содержа-
щихся ровно в одном из классов То, Тх и S.
6.23* . Привести пример функции из класса То,
не образующей базиса в То и не принадлежащей мно-
жеству Т\ U L и S и м.
6.24. Привести пример нелинейной функции / (5"),
зависящей существенно от возможно меньшего числа
переменных и удовлетворяющей условию: для всякого
номера I каждая из функций /о(£") и Д(хп)
принимает значение единица в точности на 2"^ наборах
значений переменных.
6.25* . Доказать, что из нелинейной функции, за-
висящей существенно от п 4 переменных, можно
получить путем отождествления переменных нелиней-
ную функцию, зависящую существенно от п—1 пере-
менных.
6.26* . Доказать, что если функция / не принадле-
жит множеству L U S и зависит существенно от п 4
переменных, то, отождествляя в ней переменные, можно
получить несамодвойственную нелинейную функцию,
зависящую существенно от п — 1 переменных. Верно ли
это утверждение для и=3?
6.27* . Доказать, что из шефферовой функции / (х”),
существенно зависящей от п 3 переменных, можно
получить путем отождествления переменных шеффе-
рову функцию, зависящую существенно от и — 1 пере-
менных.
6.28. Верно ли следование:
1) И (Л) и 7\)\S=>/6 L[)M;
2) / (Е То U 7\ U М =>f — функция Шеффера;
3) / € То U 5 U М б П (5\Л/);
4) / б L (J S U Л/ => / — функция Шеффера?
6.29. Пусть подмножество 21 из Р2 (X") содержит
более чем 22"'1 функций. Доказать, что при п~^2 21 —
полная в Р2 система.
75
6.30. Доказать, что каждая функция из простого
базиса в Р2 является простой относительно некоторого
предполного класса в Р2.
6.31. Найти все попарно неконгруентные функции,
простые относительно класса К.
1) К = Т0\ 3) ЛГ==[О, 1, х];
2*) K = L ПЗ; 4) К = [0, 1, х, х].
6.32. Доказать, что функции, простые относительно
класса К и попарно неконгруентные между собой,
исчерпываются функциями множества ЭД.
1)Х = Т0ПГ1, ЭД = {0, 1, г};
2) К = Т0 runs, ЭД = {0, 1, х, ху, х\/у,
т(х, у, г), т{х, у, z)}.
6.33. Доказать, что в Р2 существуют:
1 ) только два простых базиса, состоящих из одной
функции, — {х [у) и {г | у}-,
2*) только три простых базиса, состоящих из че-
тырех функций {0, 1, x^y($z, /}, где f£{xy, х\/ у,
т {х, у, z)}.
Глава III
fc-ЗНАЧНЫЕ ЛОГИКИ
§ 1. Представление функций Л-значных логик
формулами специального вида
Всюду в этой главе число к предполагается натураль-
ным и большим двух. Через Ек обозначается множество
{О, 1, . . ., к— 1}. Функция / (xn)=f (хг, х2, . . хг)
называется функцией к-значной логики, если на всяком
наборе а = (а17 а2, . . ая) значений переменных xlf
х2, хп, где а,. £ Ек, значение / (а) также принад-
лежит множеству Ек. Совокупность всех функций к-
значной логики обозначается через Рк. Понятия фиктив-
ной и существенной переменных, равных и конгруент-
ных функций, формулы над множеством функций
(и связок), операций суперпозиции и замыкания, зам-
кнутого класса, базиса и другие в Zc-значных логиках
определяются так же, как соответствующие понятия
в алгебре логики. Поэтому в дальнейшем приводятся
определения лишь таких понятий, которые чем-то
существенным отличаются от аналогичных понятий
в Р2.
Следующие функции А-значной логики считаются
элементарными:
константы 0, 1, . . ., к — 1; эти функции будут рас-
сматриваться как функции, зависящие от произволь-
ного конечного числа (включая и нуль) перемен-
ных;
отрицание Поста: x+t (mod к), обозначение: ж;
отрицание Лукасевича: (к — 1) — х, обозначением
~х или Nx;
77
характеристическая функция числа г: ]{(х), i = 0,
( 1, если x = i,
1, ..k~ 1; ]({х) = \
I 0, если х =/= г,
характеристическая функция (второго рода) числа I:
(к — 1, если х = 1,
JAx), z = О, 1....к— 1; J.(x) = { n
*4 ' *' ( 0, если х =^= i;
минимум х и у: min (х, у);
максимум х и у; шах (х, у);
сумма по модулю к: х -j- j/(mod/i), читается: «х плюс у
по модулю к»
произведение по модулю к-, х • у (mod к), читается:
«произведение х на у по модулю к» 1);
усеченная разность:
f 0, если 0 х < у к—1,
х — у=\ п .
I х — у, если О у я /с — 1;
импликация:
Г к — 1, если О х <( у к — 1,
X-*V ((&—1) — з:-\-у, если О^у^г^/г—1;
функция Вебба: max (х, у) -|- 1 (mod к), обозначе-
ние: ик(х, у)-,
разность по модулю к:
Г х — у, если 0 у х к — 1,
Х (/г—(у—х), если 0 х < у к — 1.
Функции (операции) min, max, 4- и • обладают свой-
ствами коммутативности и ассоциативности. Кроме
того, справедливы соотношения:
(л:4-у).г = (ж.г)4-(у -г)
— дистрибутивность умножения относительно сло-
жения;
max (min (х, у), z) — min (max {х, z), max (у, z))
— дистрибутивность операции max относительно опе-
рации min;
min (max (x, у), z) — max (min (x, z), min(y, z))
') Всюду в этой главе, если пе оговаривается противное,
знаки + и • понимаются как знаки сложения и умножения по
mod к.
78
— дистрибутивность операции min относительно опе-
рации max;
max (х, х) = х, min (х, х) = х
— идемпотентность операций max и min.
Следующие равенства вводятся по определению!
max (xv ..., xn_v хп) = max (max (Xj.x^), xn), n^3;
min (xlt . .xn_v xn) == min (min (xp .... ar^), arj, n~^ 3;
[ 0, если x = 0,
X | к — x, если x 0.
Принимая во внимание ассоциативность умноже-
ния по mod к, произведение х-х-. . .-х(1 сомножителей,
I 1) часто записывают в виде степени х1.
Любую функцию / (хг, х2, . . хп) из Рк можно
представить в так называемой первой форме, являю-
щейся аналогом совершенной д. н. ф. для функций
алгебры логики:
/(агр х2, . .а:„) =
= шах {min (/(ар а2, . .а„), J.JarJ, J'^xJ, ..Л„(а:„))},
3
где максимум берется по всем наборам 5=(а1, <з2, . . ,
. . од) значений переменных хг, х2, . . хп.
Справедливо еще одно представление для функций
А:-значной логики, называемое второй формой'.
j {хп) = 2 / (5) • (a-J (*„),
где суммирование ведется по всем наборам 5=(alt ..,
. . ад) значений переменных xt, . . хп (сумма и про-
изведение берутся по модулю к).
Многочленом Q (а^, х2, . . а?я) по модулю к от пе-
ременных хи х2, . . хл называется выражение вида
«о + «Л + • • • + атХт,
где коэффициенты а{ принадлежат множеству Ек и
есть либо некоторая переменная из {тр а‘2, . . хл},
либо произведение переменных из этого множества.
Говорят, что некоторая функция из Рк представима
(или реализуется) многочленом по mod к, если суще-
ствует многочлен по mod к, равный этой функции.
В Рк имеет место следующая
79
Теорема. Любая функция из Рк представима
многочленом по mod к тогда и только тогда, когда к —
простое число.
1.1. Доказать следующие соотношения:
1) —(г) = ~аг;
2) ж-5-(а; —у) = min (z, у);
3) (ж Z) у) D У = max (х, у);
4) (х^> y)~l~x = min(x, у);
5) х-^-у — х — min (х, у);
6) (~ж) —(~у) = у — х;
7) (~ж) —(у —ж) = ~тах(ж, у).
1.2. Доказать нижеследующие равенства, в которых
сумма и разность — обычные (а не по mod к} и при взя-
тии минимума значения аргументов не приводятся
по mod к.
1) хпу — min (А — 1, (~ж) Д-у);
2) х ~ у = ~min (0, у—ж);
3) (ж Dy) — (у 3^)=-min (0, х — у).
1.3. Представить функцию 1к_2(х) в виде суперпози-
ции функций к—1, х-1-2 и х — у.
1.4* . При каких значениях а-£.Ек любая функция
(ж), к — 2, представима в виде суперпозиции
над множествохМ {ж-|-а> Ar-ifa)}?
1.5* . Используя только функции из множества {0, 1,...
.к — 1, ж-=-2у}, построить с помощью операции су-
перпозиции какую-нибудь из функций ]{(х).
1.6. Пусть кг(х)=.—х, hM(x)=x3ht(x), i^l.
Доказать, что Jk_1 (х) = ~кк_1 (х).
1.7. Сколько различных функций из Рк, зависящих
только от переменной х, можно представить в форме
х1 (Z 1), где степень берется по mod Zc?
Рассмотреть случаи, когда к=3, 4, . . ., 10.
1.8. При каких значениях к (к 3) функции х2, я?
и xi попарно различны?
1.9* . Пусть Рр обозначает множество всех функ-
ций Л-значной логики, зависящих от одной перемен-
ной. Доказать, что Р^ С [1, Jk_r (ж), ж+у], где квад-
ратные скобки служат для обозначения замыкания
соответствующего множества функций.
80
1.10. Доказать справедливость следующих со-
отношений:
1) + У) = (~*) + (~у);
2) ~(ж-у) = (~ж)-у;
3) х — у — шах (х, у) —у;
4) X у = (ж у) 4- х . ]к_х (у) 4- у • (ж);
5) х = max ((ж 4~ 2) 1, Jк_2 (ж));
6) х= т!п(~7А._1(ж), (к — 2)2)ж);
7) max (х, у) = vk (х, у) 4- х • jk_k (у) 4~ у • (ж);
8) max (ж, у) = max (ж, у) 4- у0 (у — *) 4" Д-i (ж) ’ У>
9) min (ж, у) = min (ж, у) 4- 70 (у — ж) — jk^ (ж) • у.
1.11. Выяснить, имеет ли место «аналог» совершен-
ной конъюнктивной нормальной формы для функций
из Рк, а именно, выполняется ли для всякой функции
/ (ж") £ Рк равенство
f (ж”) = min (max (/ (ar а2...................<з„), ~ 7а, (жх),
J °, • • •> (*„))}•
1.12. Для заданного к представить функцию /
в первой и второй формах.
1) / = 71(^)> * = 3, 4;
2) / = ~ж, к = 5;
3) / = 70 (ж2 — ж), к = 6, 7;
4) / = лмп(ж, у), к = 3;
5) / = ж2 у, к = к;
6) / = а:2 • у2, к= 4.
1.13. Разложить в многочлен по mod к функцию /
из Рк.
1) i=Jk_2 (ж), к — произвольное простое число;
2) /=7j (ж2—ж), к — произвольное простое число;
3) / = ж — ж2, к =. 5;
4) / = Зж — (ж — 2ж), к = Р,
5) / = т!п(ж, у), & = 3;
6)/ = жэу, к —5;
7) / = тах(ж, /2(у)), * = 7.
81
1.14. Доказать, что при составном к перечисленные
ниже функции из Рк не представимы многочленами
по mod к.
1) Л 0 i к — 1; 4) max (х, у);
2) х-*-у; 5) min (х, у);
3) х э у, 6) (z — у) — г;
7) любая функция Шеффера (т. е. функция, образую-
щая в Рк полную систему).
1.15*. Подобрав для функции / (х, у) соответствую-
щим образом такие многочлены Qo (х), (х) и Q2 (х),
чтобы хотя бы одна из функций Qn (j ((\ (ж), Q2 (у)))
или Qo (J (<?! (х), Q2 (х))) заведомо не была разложима
в многочлен по mod к, доказать, что при /;=4, 6 ниже-
перечисленные функции не представимы многочленами
по mod к.
1) / = (2 — а:3) • у;
2) / = ((~^) +</)-(.?-1);
3) f — min(~x, у) (1 — х);
4) / = max (х, у)-^-(х-!- 2).
1.16*. Проверить, представима ли многочленом по
mod к функция / из Рк.
1)/ = (х~У)^-У к = 4;
2)f = 3ju(x), к = 6;
3) / = (тах(а:, у)—min (а:, у))2, к = 4.
1.17. Функции /х (х) и /2 (z) из ?з удовлетворяют
условиям
/i (*) const, /х (Е3) =£ Е3
и
/2 (Е3) = Е3.
Доказать, что функция g (x)=f1 (ж)+/2 (х)> где сумма
берется по mod 3, выпускает хотя бы одно значение
из Е3, т. е. g (Е3)^Е3.
1.18. Функция / (х)=а0х2+а1х-}-а2 из Р3, где а( £ Е3,
а сумма и произведение берутся по модулю 3, выпускает
хотя бы одно значенпе из Е3 (т. е. / (Е3)=£Е3\ Какие
значения могут принимать коэффициенты а0, ах, а2?
82
Функция /(5я) из Рк называется линейной по пере-
менной х{ (l^i^n), если справедливо представление
/ (^") = Xi • ? (ху • • м Xf-v Xiil< • • > Хп) “Ь
+ Ф(хг, ..., x^v xia, .... х„).
где ср и ф — некоторые функции из Рк и сумма и про
изведение берутся по mod к.
Функция / (Ж”) из Рк называется сильно зависящей
от переменной х{ (1 i п), если на всяких двух
наборах значений переменных, отличающихся только
i-й компонентой, функция / (5П) принимает разные
значения.
1.19*. 1) Функция / (х”) принадлежит Р3 и сильно
зависит от каждой переменной. Доказать, что / (х”) —
линейная по всякой своей переменной xf (1 i п).
2) При тех же предположениях о функции / (5я)
доказать, что / (5я) — линейная функция, т. е. что ее
можно представить в виде Яо+а^Ч-. • -Ч-ав^я. гДе
ai £ Е3, а сумма и произведение берутся по mod 3.
1.20*. 1) Функция / (5я) принадлежит Рк (где к —
простое число), отлична от константы и линейна по
любой своей переменной. Доказать, что существует
такой набор значений переменных, на котором функ-
ция / (5”) обращается в нуль.
2) Справедливо ли аналогичное утверждение при
составном к!
1.21. Пусть функция / (5") £ Рк (где к— простое
число) линейна по переменной и сильно зависит от
этой переменной. Доказать, что функция / (5я) пред-
ставима в виде Я’^Ч-? (х2, . . ., жя), где а £ Ек, а^О,
а сумма и произведение берутся по mod к.
1.22. 1) Доказать, что функция 2}( (х) из Pt при
любом i=0, 1, 2, 3 представима многочленом по mod 4.
2) Доказать, что если функция из Р4, зависящая
от одной переменной, принимает значения либо только
из множества {0, 2}, либо только из множества {1, 3},
то она представима многочленом по mod 4.
3*) Привести пример функции из Pt, зависящей
существенно от двух переменных, принимающей только
значения 0 и 2 и не разложимой в многочлен по mod 4.
1.23* . Доказать, что если функция / (х) £ Pt, не
представима многочленом по mod 4, то при любом
83
т 2 функция (/ (х))т, равная zn-й степени функ-
ции / (х), также не представима многочленом по
mod 4.
1.24* . Найти число функций из Р4, которые за-
висят только от переменной х и реализуемы многочле-
нами по mod 4.
1.25. 1) Пусть функция / (х) £ Р6 представима
многочленом по mod 6. Доказать, что / (х) можно реали-
зовать многочленом по mod 6, имеющим вид а0+Я1Ж+«3^.
2*) Доказать, что в Р6 число функций, зависящих
от переменной х и представимых многочленами по
mod 6, равно 108.
1.26. * Перечислить все функции / (х) из Ре, имеющие
вид a-J-bJo U) (здесь а и b принадлежат Ес), не реали-
зуемые многочленами по mod 6 и такие, что (/ (ж))2
представимы многочленами по mod 6.
1.27. 1) Пусть функция ср (х, у) £ Рк удовлетво-
ряет условиям:
а) ?(*, г/)=<р(г/> *);
б) ср (х, ср (у, z)) = ср (ср (х, у), z);
в) каковы бы ни были а и Ъ из множества Ек, суще-
ствует единственное х, такое (зависящее от а и Ь), что
ср (а, х) = Ь.
Через 0а обозначим такой элемент из Ек, что
ср (а, 0а)=а. Доказать, что 0я=04 при любых а и Ъ
из Ек (т. е. Оо=О1= . . . = 0^).
Замечание. Этот «общий элемент» (для всех
а £ Ек) назовем нулем функции <р и обозначим 0 .
2) Доказать, что если Л=3, то в качестве функций
ср (х, у) можно взять только одну из следующих функций
множества Р3: х+у, ж+у+1, х+у+2.
3*) Пусть функция ср (х, у) £ Рк и удовлетворяет
требованиям, перечисленным в и. 1). Функция / (а^,
х2, . . ., хп) £ Рк называется квазилинейной относи-
тельно ср, если для любых аг, а2, . . ., ая, blt b2, . . ., Ьп,
принадлежащих Ек, выполняется равенство
(/ (? («1, ^1). ¥ («2» b2~), • •f («„> &»)). / (0r 0<p, • • > 0,)) =
= ср(/(ар a2, ..., a„), f(bv b2, .. .,b„)).
Доказать, что функция / (ж") Р3 квазилинейна отно-
сительно ac+y-j-г (при произвольном фиксированном
84
г=0, 1, 2) тогда и только тогда, когда / (f") — линей-
ная функция.
1.28. 1) Пусть функция sp (х, у) £ Рк удовлетворяет
условиям а) — в) задачи 1.27, 1). Показать, что функ-
ция <р (х, у) является квазилинейной относительно самой
себя.
2) Доказать, что в Тэ4 существует нелинейная функ-
ция <р (х, у), которая является квазилинейной отно-
сительно самой себя и представима в виде х+у+аху
(где а £ Е±, а сумма и произведение берутся по mod 4).
1.29. Пусть s (х) — разнозначная х) функция из Рк,
зависящая от одной переменной. Функция g (х) £ Рк
называется обратной к функции s (х) и обозначается
через s-1 (х), если g (s (х))=х (тогда справедливо также
тождество s (g (х))=х). Функция /s(a7) (хг, х2, . . ., хп) =
= s-1 (/ (s (x^, s (x2), . . s (z„))) называется двой-
ственной к функции / (жц хг, . . ., хя) относительно
s (х). Если функция / (х") двойственна к самой себе
относительно s (х), то она называется самодвойственной
относительно s (х).
1) Над множеством {1, к — i,xy, х-\-у, min (х, у)}
построить формулу, реализующую функцию, двой-
ственную к / относительно s (х).
a) f = vk(x, у), s(x)=~2:;
б) / = min (х, у) /0 (х) • Д (у) + Д (х) • /0 (у),
s(x) = x-\-j0(x)-^-J1(xy,
в) f = (x-«-y)-]-z + z. ЦуНуЦх), s(x) = X;
г) / = х4-(у-^-z)4-x-y-z —y-/o(z), s(x) = —x.
2) Доказать, что если функция / (х") £ Рк
а) принимает I разных значений (1 I к) или
б) зависит существенно от т переменных (0 т п),
то двойственная к ней функция/*(х) (£”) обладает та-
кими же свойствами.
3) Пусть s (х)=х. Выяснить, при каких значениях к
и параметра а (из множества Ек) функция / (ж, у) яв-
ляется самодвойственной относительно s (х).
a) f(x, у) — х2у22а • х • уу;
б) / (х. у) — шах (х, у) + а • (х у) + 2х — 2у;
в) /(* У)=х + А, (* + аУ}-
9 Функция одной переменной из Рк называется разно-
значной, если она принимает все к значений.
85
4) Выяснить, какие из приводимых ниже функций
самодвойственны относительно s (ж) =—х.
а) г;
б) ~ж;
в)
г) х + у,
Д) (х-±-у) + у,
е) х* 2 * • г/2 • г;
ж) х • у • г 4- у . J[А/2] (z) 4- Z • JW2] (у).
5) Доказать, что если функция / (5) самодвойственна
относительно функций sx (х) и з2 (х), то она само-
двойственна и относительно функций sx (з2 (х)) и
«4 (х).
1.30. Разнозначная функция s(x)£-Pk называется
циклом (или циклической подстановкой), если s' (0)
sj (0) J) для любых I, j, удовлетворяющих условиям
1 <( 7(s* (^) есть сокращенная запись выражения
s(з (... з (х) ...))). Доказать, что если з (х) — циклическая
» раз
подстановка из Рк, то число функций в Рк, самодвой-
ственных относительно з (х) и зависящих от переменных
xv х2, . . хп, равно к11”'1.
1.31. Пусть г — такое наименьшее положительное
число2), что sr(x) = x. Доказать, что если s(x)^x и
г — простой делитель числа к, то число функций в Рк,
самодвойственных относительно з(.г) и зависящих от
переменных xv х2, хп, равно кк,‘>г.
1.32. Доказать, что если функция квази-
линейна относительно ср (х, у)£Рк (см. задачу 1.27, 3)),
то функция /8(х) (хп), двойственная к / (х”) относительно
з (х), является квазилинейной относительно ср®*^ (г, у).
§ 2. Замкнутые классы /г-значной логики
Функция R (xv х2, . .., хп), п'^1, отображающая
n-ю декартову степень Е";: = Ек'/[ ... X Ек множества ЕК
п раз
*) Вместо 0 в этом неравенстве можно взять любой другой
элемент из множества Ек.
2) Это число обычно называют порядком функции (подста-
новки).
86
в множество (0, 1} *), называется п-местным предика-
том, определенным на множестве Ек.
Пусть / (xv . . х., . . хт) — функция из Рк
(т 1), a R (хг, . . Xj, . . х^ —//-местный пре-
дикат, определенный на Ек. Говорят, что функция f
сохраняет предикат R, если, каковы бы ни были эле-
менты
ап.....а1р • • а1п> • • •> а»1> • • aip • • •> ain’ • • •
• • •> aml’ • • •> amjf • • •> amn
из множества Ek, равенства
R(aa, ..., йу, ..., а,.я) = 1 (для всех 1 = 1, ..., т)
влекут соотношение
(/(ан> • • •> аа> ' • •> ami)> • • •> / (агр • • •> aij> • • > amjh • • •
.... /(«1л.......................«<»» «тЯ)) = 1-
Если функция / — константа (например, /=«), то, по
определению, функция / сохраняет предикат R (xlt ...
. . ., хп), если R (а, . . ., а) = 1.
Через Н (R (xt, . . ., хп)) будем обозначать множе-
ство всех функций из Рк, сохраняющих предикат
R (з\, . . хп), определенный на множестве Ек.
2.1. Доказать, что множество H(R(xv ..., хп)) при
любом предикате R является замкнутым классом.
2.2. Пусть <§ — подмножество множества Ек. Говорят,
что функция f(xx, ..., хт) сохраняет множество <§, если
на любом таком наборе а = (а1, .. ., ат), что
(i= 1, ..., т), функция принимает значение /(а), также
принадлежащее множеству <§. Множество всех функций Рк,
сохраняющих множество <§, обозначается через Т (<§) и
называется классом сохранения множества <§.
1) Доказать, что Т (§) = Н (R (х)), если предикат R (х)
равен единице на множестве <§ и равен нулю на мно-
жестве Ек\<§.
2) Доказать, что Т {<§) Рк тогда и только тогда,
когда § отлично от пустого множества и всего множе-
ства Ек.
1) Вместо множества {0, 1 } рассматривают также множества
{И, Л} пли (г, /}, где И (соответственно t) означает «истину»,
а Л (соответственно <f) — «ложь».
87
3) Сколько существует различных замкнутых классов
в Рк, являющихся классами сохранения множеств?
4) Подсчитать число функций из Рк, содержащихся
в классе Т (<§) и зависящих от переменных xv х2, .. .,х„
(п>0).
5) Доказать, что при <§ 0 и §=£=Ек класс Т (<§)—
предполный в Рк.
2.3. Пусть D = (gv g2, — разбиение мно-
жества Ек, т. е. Ек = <§гUU ••• U£s> £,-т^0 пРи
i = l, 2, ..., s и <Sin<Sj= 0 при i=^=j. Говорят, что
элементы а и b из Ек эквивалентны относительно раз-
биения D (обозначение: а — b(modD)), если а и Ъ при-
надлежат некоторому подмножеству <§^ разбиения D.
Два набора a. = (av а2, . . ., аи) и р = (?х, д2.₽от)
называются эквивалентными относительно разбиения D
(обозначение: а ~ р (mod D)), если а.. — pf (mod D) при
i=l, 2, . . ., т. Говорят, что функция f(xm) из Рк со-
храняет разбиение D, если для любых наборов а.т и рт
из эквивалентности а™ — (mod D) следует эквивалент-
ность f (ат) ~ / (pm) (mod Z>). Множество всех функций
из Рк, сохраняющих разбиение D=^{SV <S2, ,
обозначается через U (D) или U (gv §2, ..., <§г) и назы-
вается классом сохранения разбиения D.
1*) Доказать, что U (<§v <§2, .. gs) = H (R(x, у)),
если предикат R (х, у) равен единице на таких и только
таких парах (а, Ь), которые состоят из элементов, экви-
валентных относительно разбиения {«S’x, ё2, .... £в).
2) Доказать, что U (D)=Pk тогда и только тогда,
когда разбиение Z) = {(§’1, <§2, . . ., gs] — тривиальное,
т. е. либо D индуцируется отношением равенства
(в этом случае s=k), либо D задается двухместным
универсальным (или полным) отношением (это соот-
ветствует s=l).
3) Для к=3, 4, 5 подсчитать число различных зам-
кнутых классов в Рк, являющихся классами сохране-
ния разбиений.
4*) Подсчитать число функций из Рк, содержащихся
в классе U (Slt <§2, . . ., <§s) и зависящих от перемен-
ных xv х2, . . хп (п~^ 0).
2.4. Пусть g — непустое подмножество из Ек, от-
личное от всего Ек, &D={g, Ek\g}, Подсчитать число
88
функций из Рк, зависящих от переменных ад, х2, . . .
.. xJ(n~^0) и содержащихся в множестве
1) T(<g)\U(D); 2) U(D)\T(<§); 3) Т (£)U U (D).
2.5. Пусть R (яд, . . ., xn), n 2, — предикат,
определенный на множестве Ек. Его называют вполне
рефлексивным предикатом, если на всяком наборе зна-
чений переменных, содержащем хотя бы две одинаковые
компоненты, он обращается в единицу. Предикат
R (х") называется вполне симметричным, если при
любой перестановке переменных в R (xlt . . ., xt) по-
лучается предикат R (xit, . . ., х<п), совпадающий с ис-
ходным предикатом R (х”). Одноместные предикаты
считаются (по определению) и вполне рефлексивными,
и вполне симметричными. Вполне симметричный и
вполне рефлексивный предикат R (ад, . . ., хг) назы-
вается центральным, если существует такой элемент
с £ Ек, что R (с, ад, . . ., xj = l при любых значениях
переменных х2, . . ., х„ (элемент с, удовлетворяющий
указанному условию, называется центральным, а все
такие элементы предиката R образуют его центр.)
1*) Доказать, что существует ровно
к—2
2 + (-1)*(к-
различных двухместных центральных предикатов, опре-
деленных на множестве Ек.
2) Проверить, что при каждом п 'дух к существует
только один ге-местнып центральный предикат, опре-
деленный на множестве Ек.
3) Перечислить все центральные, определенные на
множестве Ек предикаты, центры которых содержат
ровно к — 1 элементов.
4*) Доказать, что если R (ад, . . ., яд) — централь-
ный предикат, определенный на множестве Ек, то
Н (R (яд, . . ., хг)) = Рк тогда и только тогда, когда
центр предиката R совпадает с Ек.
2.6. Пусть £ С и se{ l......к}. Через Т (£, s)
обозначим подмножество из Рк, состоящее из всех кон-
стант и всех функций / (ад, .. ., хт), т.дх 1, удовлетво-
ряющих условию: для любой системы {4Р ..., -4т) иод-
89
множеств множества Ек, каждое из которых содержит
ровно з элементов, найдется множество Ао С Ек, также
содержащее з элементов и такое, что /(&LMi> •••
£LMm)csiM0.
1) Доказать, что множество Т (<§, .5) является замк-
нутым классом в Рк.
2) Показать, что Т (<§, s) = Pk тогда и только тогда,
когда либо S 0 w s^k — | |, либо g = 0 и s = 1
или к.
3*) Доказать, что Т(0, 2)сГ(0, 3) с ...
...СГ(0, к — 1) и Т (0, к — 1) — предполный класс
в Рк-
4) Показать, что число различных замкнутых клас-
сов в Рк, являющихся классами типа I з), где
1 <1 s к, равно 14-2&-1 (к—2).
5*) Доказать, что при g=^=0 справедливо равенство
Т (<§, s)=H (R (xlt . . ., xtil)), где R — (з-|-1)-местный
центральный предикат с центром g, удовлетворяющий
условию: R (alt . . ., а>+1)=0 лишь тогда, когда ком-
поненты набора (alt . . ., <z4+1) разные и ни одна из них
не принадлежит центру.
6) Найти число функций Л-значной логики Рк,
зависящих от переменной х и принадлежащих мно-
жеству Т ({0}, 1).
2.7. Через Sk обозначается множество всех разно-
значных функций из Рк, зависящих от одной переменной
(т. е. g (ж) принадлежит Sk тогда и только тогда, когда
g(Ek)=Ek). Обозначим через Pft множество всех
функций к-значной логики Рк, зависящих от одной
переменной. Пусть CSk=P$ \ Sk.
1) Показать, что множества Sk и CSk являются зам-
кнутыми классами.
2) Найти число функций, зависящих от перемен-
ной х и принадлежащих классу Sk П U ({0, к — 2},
{1, . . ., к — 3}, {к — 1}).
2.8. Пусть s (х) £ Sk. Через Z (з (х)) обозначим
множество всех таких функций из Рк, которые само-
двойственны относительно s (х) (определение само-
двойственной функции см. в § 1 этой главы).
1) Доказать, что Z (s (х)) — замкнутый класс.
2) Показать, что Z (s (x))=Pk тогда и только тогда,
когда з (х)=х.
90
3) Доказать, что Z (s (z)) С Z (s' (z)) при всяком i О
(s°(z) по определению полагается равной x).
2.9. Пусть s (x) £ Sk. Обозначим через Z (s (x)) мно-
жество всех таких функций / (z") из Pk (п 1), кото-
рые удовлетворяют условию: каковы бы ни были целые
числа iv i2, ..., in, найдется такое целое число i (для
каждой функции — свое), что /(s’>(z), s‘2(z), ..., s’» (z)) =
=«'(4
1) Показать, что Z (s (z)) — замкнутый класс.
2) Показать, что Z (s (г))^=РЛ при любой функции
s (z).
3) Доказать, что Z (s (z))=Z (s (z)) тогда п только
тогда, когда s (z) — циклическая подстановка (см. за-
дачу 1.30).
2.10. Опровергнуть утверждение: при всякой функ-
ции s (z) из Sk выполняется равенство Z (s2 (z)) =
=Z (s’1 (z)).
2.11. Рассмотрим функцию tp (z, у) из Pk, удовлет-
воряющую всем требованиям, перечисленным в задаче
1.27, 1). Обозначим через L (у> (х, у)) множество всех
функций из Рк, квазилинейных относительно <р (z, у).
Если <р (z, y)=z+y, то множество L (<р (z, у)) иногда
обозначается через L и его элементы называются
линейными функциями.
1) Доказать, что L (<р (z, у)) — замкнутый класс.
2) Показать, что L (<р (z, у))т^=Рй при любой функ-
ции <р (z, у).
3*) Справедливо ли утверждение: в Pi при всякой
функции s(x)£Si классы £(<p(z, у)) и L(yl*'(x, у))
совпадают?
Пусть на множестве Ек задано некоторое отношение р
нестрогого частичного порядка. Говорят, что набор
а = (а1... ад) предшествует набору р — (рг .. ., jBJ1)
при упорядочении р (обозначение: Spjj), если для всякого
; = п выполняется соотношение а^. Наборы
а и р называются сравнимыми относительно р, если
либо арр, либо рра. Отношению р соответствует естествен-
ным образом двухместный предикат /?р (z, у), равный 1
на тех и только тех парах (а, Ь) £ Ек X Ек, для которых
справедливо соотношение apb. Функция /(z)£/Jt назы-
Или набор р следует за набором а.
91
вается монотонной ^относительно рл если для любых
наборов аир из арр следует /(а)р/(3). Другими словами,
функция / (х) монотонна относительно р, если она сохра-
няет предикат R?, соответствующий отношению р. Мно-
жество Н (R? (х, у)), т. е. множество всех функций из Рк,
монотонных относительно р, будем обозначать через М (р).
2.12. 1) Рассмотрим два отношения нестрогого частич-
ного порядка, определенные на множестве Ек:
Аг—1 Аг—1
P1=U {(1. 0} и {(0, 0)} и U {(о, 0} и
1=0 »=2
fc-1
U и {(i, i), (i, i + 1)...(j, к -1)},
•=2
A--1
P2=U {(0, 0) и {(1. 1)- (2, 2)} U
i=0
fc—1
и и {0, i). (г. *4-1)....(*. *-!)}•
•=3
Выяснить, какие из приводимых ниже функций при-
надлежат множествам М (рх) или М (р2).
а) ж; д) шах (х, у);
б) Щх); е) х-^-у;
В) Ш ж) 2х-Н*-1 (у)-
г) X + /0 (х) + Щх);
2) Не пользуясь понятием класса сохранения пре-
диката R? (х, у), доказать, что М (р) — замкнутый
класс.
3) Показать, что М (р)—Рк тогда и только тогда,
когда отношение р является отношением равенства
( к-1 \
1т. е. когда р= (J {(7, г)}).
' »=о 7
2.13. Подобрав подходящий класс типа Т (g) или
U (D), доказать, что система А не полна в Рк.
1) А = {~ж, min (х, у), х • у2};
2) А = {2, /0 (ж), х + /0 (х) -|- Zx (х) -ф-1к_х (х), min (х, у)};
3) А = {2z3, 2х-+-у, х2-у, ж •/0(у), ж-4-(~у)};
4) А = {У2 (х), s-Hofr), х -|- /0(х) + /х (х), max (х, у)};
5) А = (1, 2, ж-=-/2(ж), max (ж, у)};
6) А — {/2 (ж), ж -|- /0 (ж) -j- Jk (ж), ж • у, х — у, min (ж, у)}.
92
2.14. Выяснить, при каких значениях к для дока-
зательства неполноты (в Рк) системы А недостаточно
рассматривать только классы типа Т (<§), U (D) и
М (р), а нужно еще использовать классы типа Т $).
1) А = {2]0(х), х. jQ(y)};
2) Л = {1, ~х, j0(x), max (х, у)};
3) А — {0, 1, .. к — 2, J к_г (х), max (х, у), min (ж, у)};
4) Л = {~х, [А/2] • /0 (х - [(А: -1)/2]), Jo (х) (х - 1),
min (я, у)}.
2.15. Можно ли доказать неполноту (в Рк) системы
А, используя только классы L и Z (s (z))?
1) А —{я, 2х — у, тах(х, у) — (х — у)};
2) Я={0, 1, —х, 2х-\-у, ^4-(~г/)};
3) я = {Д (х) 4- J к_г (х), X — у, X • у ’ z};
4) А = {х, — х-±-2у, Xj) + i0(x — у)};
5) А = {~х, min (ж, у), х • у}.
2.16* . Две функции в Рк называются конгруентп-
ными, если одна из них может быть получена из другой
заменой переменных без отождествления (ср. § 1 гл. II).
Пусть функция / (х, y)—2j1 (x)-j2 (у) £ Р3. Доказать,
что замкнутый класс If (х, у)] содержит конечное число
попарно неконгруентных функций (ср. с задачей
1.5 гл. II).
2.17. Пусть А — непустое множество одноместных
функций Zc-значной логики, отличное от всего множе-
ства Р^1 и удовлетворяющее условию: существует
такой предполный класс В в Рк, что В /Э(Д=Л.
Доказать, что он единствен.
2.18* . Доказать, что число предполных классов
в Рк, каждый из которых не содержит целиком мно-
жество /*£>, меньше 2fc/c.
2.19. Доказать, что если замкнутый класс в Рк
имеет конечную полную (в нем) систему, то у него
множество всех (различных) базисов не более чем
счетно.
2.20* . Справедливо ли следующее утверждение?
Всякий замкнутый класс в Рк (к 3), содержащий
функцию, отличную от константы, содержит также
функцию, существенно зависящую от одной перемен-
ной.
93
2.21* . Верно ли, что если замкнутому классу
в Рк {к 3) принадлежит функция, существенно за-
висящая не менее чем от двух переменных, то в этом
классе содержится либо функция х, либо константа?
2.22. Пусть s (х) — разнозначная функция из Рк.
Через As № будем обозначать множество тех и только
тех функций из Рк, для которых в множестве А име-
ются двойственные относительно s (х) функции. Мно-
жество Л’(г> называется двойственным кА относительно
s (д'). Доказать следующие утверждения:
1) Множество (Л5‘(*))8ДЛ), двойственное к ЛМ*) отно-
сительно s2 (х), совпадает с множеством А тогда и только
тогда, когда sx (s2 {х))=х или когда оно двойственно
к самому себе относительно каждой из подстановок
sx (х) и s2 (х).
2) Множество А является замкнутым классом тогда
и только тогда, когда — замкнутый класс.
3) Если множество В образует полную систему
(или базис) в замкнутом классе А, то множество 5в(л)
является полной системой (соответственно базисом)
в классе Л’<Л>.
4) Если то 2 А5'*’.
2. 23*. Как известно, в Рк при к 3 существуют
замкнутые классы, не имеющие базисов, и замкнутые
классы со счетными базисами. Одним из замкнутых
классов, обладающих счетным базисом, является сле-
дующий класс:
= .... •••].
где
1 при xt = ... = д,._1 == х.и == ...
fm (Ч’
•> Ч) = < ••• = Ч. = 2, 4 = 1 (z = 1...............
О в остальных случаях,
т^2. Базисом в Ак является множество {/2....fm, ...}.
Используя класс Ак, доказать, что в Рк (4-^3) суще-
ствует континуальное множество {Ву}, у £• Г, замкнутых
классов, образующих (по включению) цепь, т. е. для
любых двух классов Z?,. и Bh из множества {В^} спра-
ведливо одно из включений:
Вь С Вь или Вь С Вь.
94
§ 3. Исследование систем функций
fc-значпой логики на полноту
В А-значных логиках исследование произвольной
системы функций на полноту сопряжено с большими
техническими трудностями: использование критерия
полноты, основанного на рассмотрении совокупности
всех предполных классов в Рк, даже при к=3, 4 тре-
бует проверки весьма значительного чпсла условий
(так как в Р3 существует ровно 18, а в Pi — 82 предпол-
ных классов). Доказательства полноты конкретных
систем в Рк проводятся обычно с помощью метода све-
дения к заведомо полным системам (таким, например,
как система Россера — Туркетта —
{О, 1, к — 1, Z0(x), J^x), ..., ^(х), min(z, у),
шах (я, у)}
или система Поста — {х, шах (х, у)}). Существует,
кроме того, ряд признаков полноты, в которых рас-
сматриваются множества функций, содержащих не-
которые совокупности функций от одной переменной и
еще только одну функцию, существенно зависящую
не менее чем от двух переменных. Сформулируем наи-
более важные из такпх признаков. Напомним, что Sk —
это множество всех разнозначных функций из Рк,
зависящих от одной переменной, a CSk=P^\Sk, где
/-’’Д — множество всех одноместных функций из Рк.
Функция / (х) £ Рк называется существенной, если она
зависит существенно не менее чем от двух переменных
и принимает все к значений из множества Ек.
Теорема 1 (критерий Слупецкого). Система
Р^ U {/ (я)} полна в Рк (при к 3) тогда и только
тогда, когда / (х) — существенная функция.
Теорема 2 (критерий Яблонского). Система
{/ (я)} полна в Рк (при к^З) тогда и только тог-
да, когда f (х)—существенная функция.
Теорема 3 (критерий Саломаа). Система
Sk U {/ (ж)} полна в Рк (при к ^5) тогда и только
тогда, когда функция / (х) — существенная.
При использовании этих теорем полезными являются
утверждения, дающие разнообразные критерии пол-
ноты систем функций в множествах РФ, Sk, CSk.
95
Приведем один из таких результатов. Пусть функция
hif (х) (где 0 i < j к—1) определяется так:
М*)=
I, если х = j,
], если x = i,
х в остальных случаях.
Теорема 4 (G. Пикар). Каждая из систем (х, h01 (х),
х /0 (ж)} и {h01 (х), h02 (х), ....
^0(7с-1) (ж), x + i0(x)}
полна в PjP.
3.1. Как известно (см. § 1), система
Л — {0, 1, ..., к — 1, /0(ж), jk(x), . .., /^(х), х у, х • у}
полна в Рк.
1*) Доказать, что из системы А можно выделить
полную в Рк подсистему, состоящую из двух функций.
2) Показать, что любая подсистема системы А,
состоящая из одной функции, не полна в Рк.
3.2. Система Россера — Туркетта
А1 — (0, 1,.. ., к — 1, 70 (х), Jj (z),. .., J к_к (х), min (х, у),
max (х, у)},
как известно, полна в Рк (см. § 1).
1) Показать, что
Лг \ {min (х, у}} С Т{2>1,
/IjXJmaxCr, у}} с Т{0, ...,к-з),1
(следовательно, после удаления из системы Аг любой
из функций min (х, у) и max (х, у) получается неполная
в Рк система).
2) Проверить, что, удаляя из Аг любую из констант,
отличную от 0 и к—1, получаем подсистему содер-
жащуюся в некотором классе типа Т (<§), где 0=£<§^Ек
(и, значит, неполную в Рк).
3) Убедиться в справедливости равенств:
а) А| С2-) = ^1 (InaX (1, Jy^x), . . ., 7^-2 (•£)> Л'))>
б) Л-2 (*)))•
4) Выделить из системы Россера — Туркетта пол-
ную в Рк подсистему, состоящую из 2к—2 функций.
S6
3.3. Выяснить., полны ли в Р3 следующие под-
системы системы Россера—Туркетта:
1) {1, 70(ж), 72(х), min (х, у), max (х, у)},
2) {1, 2, J2(x), min (ж, у), max (х, у)}.
3.4. Исследовать на полноту следующие подси-
стемы системы Россера—Туркетта в Р4:
1) {Ь 2, J0(x), Щх), min (ж, у), max{х, у)};
2) {!> 2> -М*), Л(*)> */). max (х, у)}.
3.5. Доказать, что приводимые ниже системы полны
в Рк тогда и только тогда, когда к — простое число.
1) {1, х -J- y + xz}',
2) {х — 1, х 4- У, х2-у}-,
3*) {1 4- xt — х2 4- ххх2... хк}.
3.6. Используя метод сведения к заведомо полным
системам, доказать полноту (в Pfc) следующих систем:
1) {1, ж2 — у, min (ж, у)};
2) {к — 1, х-*-у, ж 4-у};
3) {~ж, х 4- 2, х — у};
4) {к — 2, х 4- у, (~х) 2у};
5) {1, 2х 4- у, х2-^-у};
6) {—х, 1—ж2, х — у};
7) {£ ’ /о (^)- min (х, у)}.
3.7. Используя критерий Слупецкого, доказать пол-
ноту в Рк нижеприводимых систем.
1) {Ж £/)}> где
X 4“ 1 при X = у,
х ври х 2 и у = О,
fix, у) = ’ п .
7 у при х — 0 и у 1,
О в остальных случаях;
2) {1г(х), х 4- у2, х -у 4-1};
3) {% • /о (г/) + у • /о (*)};
4) {к — 1, 2х — у, х2-^- г/}.
4 Г. 1Д. Гаврилов, А, А, Сапоженко
97
3.8. Исследовать на полноту в Рк следующие си-
стемы:
1) {к — 2, х у, min (я, у)};
2) {0, 1, я-(~у)};
3) {1, 2, х^у}-,
4) {2, 2х-|-у, х2— у}',;
5) {1, 2, max (г, у)};
6) {2 —х, max (х, у), х • у);
7) {~х, 2/0(х), Ц(х), х->-у}.
3.9. Доказать, что каждая из приводимых ниже
систем полна в Sk.
1) {^01 С1")’ ^02 С3")’ • • •’ ^O(Jt-l) С3')}’
2) {А)1 (£)’ ^12 (•*•)> • • •> (х), . . ., (Г)}>
3) {х, hol(x)}.
3.10. Доказать, что система {/г01 (х), Ло2 (х).^^Дх),
х-]~70(х)} полна в Р1к1'.
3.11. Доказать, что в Рк существует только один
предполный класс, содержащий целиком множество
Р%>, и таким классом является Т (0, к—1) (см. за-
дачу 2.6, 3)).
3.12. Пусть А — некоторая конечная система функ-
ций из Рк. Рассмотрим следующую процедуру:
1) отождествляем во всех функциях из А перемен-
ные, заменяя их на х (получаем множество Л!);
2) на места переменных в функции из А всевозмож-
ными способами подставляем функции из множества
Аг U {%} (получаем множество А2 из Р^); затем
3) в функции из А на места переменных подстав-
ляем функции из множества Л2 (J U и т> 3«
Доказать, что:
а) на некотором шаге процесс стабилизируется, т. е.
г
при i^i0 будет выполняться равенство {х} U U Aj —
j=i
<ы
== {х} (J U Л, (и равенство Л< = Л<+1);
>=i
б) система А полна в Рк тогда и только тогда, когда
io
найдется такое г0, что {х} (J (J Л, = Р*’, и в Л содер-
/-1
жится существенная функция.
98
3.13. Используя алгоритм, описанный в задаче
3.12, доказать, что:
1) система {я24-г/+2} не полна в Р3;
2) система {z2y+l} полна в Р3.
3.14*. Доказать полноту системы А, преобразовав
ее с помощью подходящей подстановки s (ж) к заведомо
полной системе As^.
1) {х— 1, min (ж, у)};
2) я + у+1};
3) {1 + (у) +У h-1 (я) + гаах (х> у)}-
3.15 *. Опровергнуть следующее утверждение: при
фиксированном к в й-значной логике всегда найдется
базис, состоящий из сколь угодно большого (конеч-
ного) числа функций.
3.16 . Привести пример функции / (х, у) из мно-
жества Р3, удовлетворяющей условию: / — функция
Шеффера, но хА-f не является шефферовой.
3.17 *. Пусть / (х”) — функция из Рк, существенно
зависящая не менее чем от двух переменных и прини-
мающая I разных значений (2 I к). Доказать, что,
подставляя на места ее переменных функции из мно-
жества CSk, можно получить функцию, существенно
зависящую от двух переменных и принимающую I
разных значений.
3.18 . При каких значениях к квадрат всякой су-
щественной функции из Рк является существенной
функцией?
3.19 *. Подсчитать число существенных функций
в Рк, зависящих от переменных х1г х2, . . ., хп (и^> 2).
3.20 . Пусть R (xv ..., хп)—предикат, определенный
на множестве Ек. Он называется сильным предикатом,
если существует такой набор а" = (а1, . .., ая) значений
переменных . . ., хп, что для каждого набора {? =
= (₽х ₽„), на котором предикат R(xv ..., хп) равен 1,
найдется в Н(R(xv . . хп)') функция fix'), удовлетво-
ряющая условию: для любого i = l, ..., п
(другими словами, функция /(я) «переводит» набор а"
в набор Р'1). Предположим, что R(x) — сильный преди-
кат, определенный на множестве Ек, и что И (R (£)) Рк.
Доказать, что если при любой функции g (х), зависящей
от одной переменной и не принадлежащей классу
99
Я(Я(х)), система Я (Я (х)) U {g (ж)} полна в Рк, то класс
Я(Я(х)) является предполным в Рк.
3.21 . Пусть R((£”), — га-местные преди-
каты, определенные на множестве Ек. Положим R(xn) —
= Rr (х") & ... & Я, (х”). Доказать, что П Я (Я,. (х”)) С
С Я (Я (5я)).
3.22 *. Доказать, что в Рк при к 3 множество
всех замкнутых классов, каждый из которых содержит
конечное несло попарно неконгруентных функций,
является счетно-бесконечным.
3.23 *. Доказать, что каждый замкнутый класс
в Рк имеет не более чем счетное множество предполных
в нем классов.
3.24 *. Привести пример замкнутого класса в Рк,
содержащего бесконечно много попарно не конгруентных
функций и не имеющего предполных в нем классов.
3.25 *. Выделить базис из полной в Рк системы А.
1) А = {к — 1, /0 (х), R (х), jk_k (х), х • у, х — у}',
2) А = {х — 2, Jo (х), max (х, у), х у2, х2 • у};
3) А = {~х, min (х, у), х-у, хД-у);
4) Д = {/ъ— 1, хД-2, max (х, у), х-=-у};
5) Л = {2, /0(х), хД-у2, х2->-у, x-y-z}.
3.26 . Доказать, что в любом базисе, выделенном из
системы Россера—Туркетта, обязательно будет со-
держаться хотя бы одна из функций Jt (х), 1 i
—2, но не будет констант 0 и к—1.
Глава IV
ГРАФЫ И СЕТИ
§ 1. Основные понятия теории графов ’)
Пусть V — конечное непустое множество, X —
некоторый набор пар элементов из V. В наборе X мо-
гут встречаться пары с одинаковыми элементами,
а также одинаковые пары. Множество V и набор X
определяют граф с кратными ребрами и петлями
(или, короче, псевдограф) G=(V, X). Элементы мно-
жества V называются вершинами, а элементы набора
X — ребрами псевдографа. Ребра вида (р, v) (и £ V)
называются петлями. Псевдограф без петель назы-
вается графом с кратными ребрами (или, короче,
мулътиграфом). Если в наборе X ни одна пара не встре-
чается более одного раза, то мультиграф G=(V, X)
называется графом * 2). Если пары в наборе X являются
упорядоченными, то граф называется ориентирован-
ным. Ребра ориентированного графа часто называются
дугами. Если пары в наборе X являются неупорядочен-
ными, то граф называется неориентированным графом
или просто графом. Если х=(и, и) — ребро графа,
то вершины и и v называются концами ребра х. Если
вершина и является концом ребра х, то говорят, что
v и х инцидентны. Вершины и и и графа G называются
*) Определения, даваемые ниже, совпадают пли близки
к тем, которые даны в разделе «Графы и сети» книги [10] или
в книге [33].
2) Ниже все определения даются для графов. Как правило,
эти определения очевидным образом переносятся па мульти-
графы и псевдографы. В тех случаях, когда различия в опреде-
лениях существенны, даются определения и для псевдографов.
101
смежными, если существует ребро графа G, соединяю-
щее и и и. Два ребра называются смежными, если они
имеют общую вершину. Степенью вершины и называется
число d (v) ребер графа, инцидентных вершине и.
В псевдографе степень вершины и равна общему числу
ребер, инцидентных этой вершине, сложенному с числом
петель, инцидентных ей. Вершина графа, имеющая
степень 0, называется изолированной, а вершина, имею-
щая степень 1, — висячей.
Последовательность
. хп_^рп (п 2), (1)
в которой чередуются вершины и ребра и при этом для
каждого t = l, п— 1 ребро х( имеет вид п<+1), на-
зывается маршрутом, соединяющим вершины v±, vn.
Число ребер в маршруте называется длиной маршрута.
Маршрутом длины нуль называется последователь-
ность, состоящая из единственной вершины. Маршрут,
в котором все ребра попарно различны, называется
цепью. Маршрут, в котором все вершины попарно раз-
личны, называется простой цепью. Маршрут (1) на-
зывается замкнутым, если Замкнутый маршрут,
в котором все ребра попарно различны, называется
циклом. Цикл, в котором все вершины, кроме первой и
последней, попарно различны, называется простым
циклом. Граф называется связным, если для любых
двух его вершин существует цепь, соединяющая эти
вершины. Расстоянием между вершинами связного
графа называется длина кратчайшей цепи, связываю-
щей эти вершины. Диаметром связного графа назы-
вается расстояние между двумя наиболее удаленными
друг от друга вершпнами. Диаметр графа G будет
обозначаться через D (G). Подграфом графа G назы-
вается граф, все вершины и ребра которого содержатся
среди вершин и ребер графа G. Подграф называется
собственным, если он отличен от самого графа. Компо-
нентой связности графа G называется его связный под-
граф, не являющийся собственным подграфом ппкакого
другого связного подграфа графа G. Остовным назы-
вается подграф, содержащий все вершины графа.
Подграфом графа G=(V, X), порожденным подмно-
жеством U С V, называется граф H=(U, У), множе-
102
ство ребер которого состоит из тех и только тех ребер
графа G, оба конца которых лежат в U. Графы (псевдо-
графы) G=(V, X) и H—(U, Y) изоморфны, если суще-
ствуют такие два взаимно однозначных соответствия
V «-» U и ф: X <+ Y, что для всякого ребра х=(и, и)
из X справедливо <[> (#) = (<р (и), q> (*>))• В случае графов
можно дать следующее определение. Графы G=(V, X)
и H~(U, Y) изоморфны, если существует такое взаимно
однозначное отображение <р! V «-> U, что (и, и) £ X
тогда и только тогда, когда (<р(и), <р (и)) £ У. Такое
отображение <р называется изоморфным. Автоморфиз-
мом называется изоморфное отображение графа на себя.
Под операцией удаления вершины из графа G будет
пониматься операция, заключающаяся в удалении не-
которой вершины вместе с инцидентными ей ребрами.
Операция удаления ребра из графа G=-(V, X) заключа-
ется в удалении соответствующей пары из X. При этом,
если не оговорено противное, все вершины сохраняются.
Дополнение G графа G — это граф, в котором две вер-
щины смежны тогда и только тогда, когда они несмежны
в G. Операция подразбиения ребра (и, и) в графе G=
?= (У, X) состоит в удалении из X ребра (и, и), добавле-
нии к V новой вершины w и добавлении к Х\{(и, у)}
двух ребер (и, w) и (w, и). Граф G называется подраз-
биением графа Н, если G может быть получен из Н
путем последовательного применения операции под-
разбиения ребер. Графы G и Н гомеоморфны, если су-
ществуют такие их подразбиения, которые изоморфны.
Пусть G=(V, X) и H=(U, У) — два графа. Через
G^H будет обозначаться граф, называемый симметри-
ческой разностью графов G л Н с множеством вершин
W=V(JU и множеством ребер Z=X@)Y, состоящим
из тех и только тех ребер, которые входят ровно в одно
из множеств X или У. Через GxH будет обозначаться
декартово произведение графов G=(F, X) и II = (U, У),
т. е. граф, вершинами которого являются пары вида
(и, и) (и £ V, и f U) ив котором вершины (сц, uj
и (и2, и2) смежны тогда и только тогда, когда смежна
хотя бы одна из пар vlt и2 (в графе G) Или ult и2
(в графе Н). Объединением графов G=(V,' X) и Н=
—(U, У) называется граф E=(V (J U, X |J У).
Деревом называется связный граф без циклов. Граф
без циклов называется лесом. Полным называется граф,
103
в котором каждые две различные вершины соединены
ребром. Полный граф с п вершинами обозначается через
Кп. Пустым (вполне несвязным) называется граф без
ребер. Одновершинный граф без ребер называется
'тривиальным. Двудольным называется граф, множе-
ство вершин которого можно разбить на два подмно-
жества (две доли) Vr и Е2 таким образом, что каждое
ребро графа соединяет вершины из разных долей.
Двудольный граф с долями и F2 и множеством ребер
X будет обозначаться через (Elt Е2, X). Если каждая
вершина из V1 соединена ребром с каждой вершиной
из V2, то граф называется полным двудольным графом.
Полный двудольный граф (Vj, V2, X), такой, что
| Е4 | = nv | V21 = n2, обозначается через K„^ Bj. Граф
называется k-связным, если при удалении любых к—1
его вершин получается связный граф, отличный от
тривиального. Вершина графа, удаление которой уве-
личивает число компонент связности, называется раз-
деляющей или точкой сочленения. Граф называется
регулярным графом степени d, если все его вершины
имеют степень d. Регулярный граф степени 1 называется
паросочетанием. Регулярный граф степени 3 называется
кубическим, k-фактором графа называется его остовный
регулярный подграф степени к. Совершенным паро-
сочетанием называется 1-фактор. Максимальным паро-
сочетанием графа G называется паросочетание, содер-
жащее наибольшее число ребер. Гамильтоновым цик-
лом графа называется простой цикл, содержащий все
вершины графа. Гамильтоновой цепью называется про-
стая цепь, содержащая все вершины графа. Единич-
ным п-мерным кубом называется граф Вп, вершинами
которого являются булевы векторы длины п, а реб-
рами — одномерные грани (см. гл. I, § 1).
1.1. Показать, что для произвольного графа G = (Е, X)
справедливо равенство 2 | X | = 2 (у)>
«е у
'1.2. Пусть ik (G) — число вершин степени к
в графе G. Найти число попарно неизоморфных гра-
фов G, у которых:
1) i2 (G) = i3 (G) = (G) = 2, ik (G) = 0 при к 2, 3, 4;
2) i2 (G) = i3 (G) = i4 (G) = 3, ik (G) = 0 при к 2, 3, 4.
104
1.3. Показать, что в любом графе, имеющем не
менее двух вершин, найдутся две вершины с одинако-
выми степенями.
1.4. Доказать, что для любого набора неотрица-
тельных целых чисел (й0, kv ...), такого, что 2^.-==
•
=2т, существует псевдограф с т ребрами, имеющий
для каждого 1=0, 1, ... в точности к. вершин сте-
пени I.
• 1.5. Пусть d0 (G) — минимальная из степеней вершин
графа G, имеющего п вершин.
д — 1
1) Доказать, что если —> т0 граф связен.
’ 2) Можно ли в предыдущем утверждении заменить
1.6. Доказать, что всякий замкнутый маршрут
нечетной длины содержит простой цикл. Верно ли ана-
логичное утверждение для маршрутов четной длины?
* 1.7. Показать, что связный граф с п вершинами
содержит не менее п—1 ребер.
1.8. Показать, что в графе с п вершинами и с ком-
понентами связности число ребер не более у (« — с) X
X (п — с4-1).
1.9. Доказать, что всякий нетривиальный связный
граф содержит вершину, не являющуюся разделяющей.
1.10. Доказать, что в связном графе любые две
простые цепи максимальной длины имеют по крайней
мере одну общую вершину. Верно ли, что они всегда
имеют общее ребро?
1.11. Доказать, что если из связного графа удалить
произвольное ребро, содержащееся в некотором простом
цикле, то граф останется связным.
1.12. Показать, что если в графе с п вершинами
отсутствуют циклы нечетной длины и число ребер
(п —1\2 х
превышает (—— } , то граф связен.
1.13. Найти число рк («), при котором любой «-вер-
шинный граф, имеющий рк (п) циклов длины к, связен.
1.14. Пусть графы би Н изоморфны. Показать, что!
• 1) для каждого d 0 число вершин степени d
в графах G и Н одинаково;
105
2) для каждого I число простых циклов длины I
в графах G л Н одинаково.
1.15. Показать, что условия 1), 2) задачи 1.14 не-
достаточны для того, чтобы графы G и Н были изо-
морфны.
-1.16. Среди пар графов, представленных на рис. 3—
6, указать пары изоморфных и пары неизоморфных
графов. Ответ обосновать.
1.17. Пусть графы виН двухсвязны, имеют шесть
вершин и восемь ребер каждый. Граф G имеет ровно
две вершины степени 2, а граф Н имеет ровно четыре
вершины степени 3. Можно ли утверждать, что графы G
и Н
1) изоморфны; 2) не изоморфны.
1.18. Графы G и Я двухсвязны, имеют шесть вершин
и десять ребер каждый. Одна вершина в каждом из гра-
фов имеет степень d (1 d 5), а остальные имеют
степень dt (dr < d). Показать, что графы G и Н изо-
морфны.
1.19. Показать, что в графе, не имеющем нетри-
виальных автоморфизмов,
1) расстояние между любыми двумя вершинами сте-
пени 1 больше двух;
2) существует вершина степени 3 или выше.
1.20. Каково число автоморфизмов графа, являю-
щегося циклом длины р?
1.21. Построить граф без циклов, не имеющий не-
тривиальных автоморфизмов и содержащий минимально
возможное число ребер.
1.22. Какое наименьшее число п (п>1) вершин может
быть у графа, не имеющего нетривиальных автоморфиз-
мов?
1.23. Пусть в двухсвязном графе с шестью верши-
нами и девятью ребрами степени всех вершин одина-
ковы, а число простых циклов длины 3 равно двум.
Восстановить граф. Найти число его автоморфизмов.
1.24. Пусть О (и) — множество всех вершин, смеж-
ных с v, а О' (v)=O (у) U {и}. Пусть Rn — множество
всех графов Gen вершинами, обладающих следующими
свойствами: для любых двух несмежных вершин и и и
либо О (и) СО (и), либо О (и)С0 (у), а для любых
смежных вершин и и v либо О'(и)С.О'(и), либо
О\и)С.О'(у). Доказать следующие утверждения;
106
Рис. 6.
1) В графе G из Rn вершины одной степени или все
попарно смежны, или все попарно несмежны.
2) В графе G из Rn существует хотя бы одна вершина
степени п—1.
3) Если для некоторого d вершины степени d по-
парно смежны в графе G из Rn, то и вершины степени,
большей, чем d, также попарно смежны.
4) Граф G из Rn однозначно с точностью до изомор-
физма определяется заданием степеней вершин.
5) Удаление вершины из графа GQ RK приводит
к графу из R„^.
1.25. Пусть п 2, и пусть задано семейство F (G) =
= {Я1, Я2, . . ., Нп} графов, в котором граф Я,. получен
из n-вершинного графа G удалением вершины с номе-
ром i (i = l, п). Отметим, что в графах Я,, вершины не
помечены. Доказать, что по семейству F (G) можно
1) найти число ребер графа G;
2) найти для каждого Я,, степень той вершины,
удалением которой из G получен граф Н.\
3) определить для произвольного графа L, имеющего
не более п—1 вершин, является ли он подграфом
графа G;
4) определить, является ли граф G связным;
5) восстановить граф G, если он не является связным.
1.26. Пусть D (G) — диаметр графа G, a G — граф,
дополнительный к G. Показать, что D (G) 3, если
граф G несвязен или если D (G) 3.
1.27. Граф G называется самодополнителъным, если
графы G и G изоморфны.
1) Найти самодополнительный граф с наименьшим
числом вершин.
2) Показать, что самодополнительный граф связен.
3) Показать, что если G — самодополнительный
граф, то 2 D (G) 3.
1.28. Сколько существует попарно неизоморфных
графов с 20 вершинами и 188 ребрами?
1.29. Показать, что если графы G и Я гомео-
морфны, то:
1) для каждого d=£2 число вершин степени d в обоих
графах одинаково;
2) существует взаимно однозначное отображение
множества простых циклов графа G на множество про-
108
стых циклов графа Н, при котором число вершин сте-
пени d в соответствующих циклах одинаково для всех
d=^2.
1.30. Установить, существуют ли в графах, изо-
браженных на рис. 7, подграфы, гомеоморфные графу G.
1) G—K4 (см. рис. 8, а);
2) G=K3 (см. рис. 8, б);
3) G=K3 з (см. рис. 8, e)J
1.31. Операция надразбиения заключается в замене
двух смежных ребер (и, v) и (и, w), общая вершина и
которых имеет степень 2, одним ребром (и, w). Применяя
S)
Рис. 7.
шаг за шагом операцию надразбиения, можно получить
из произвольного графа G, содержащего вершины сте-
пени 2, псевдограф, не содержащий вершин степени 2.
Этот псевдограф будет называться полным надразбие-
нием графа G.
1) Показать, что полное надразбиение графа G
не зависит от того, в каком порядке применялась опера-
ция надразбиения к парам смежных ребер графа G.
2) Показать, что графы G и Н гомеоморфны тогда
и только тогда, когда их полные надразбиения изо-
морфны (как псевдографы).
1.32. Доказать, что в графе Петерсена (рис. 7, а)
нет гамильтонова цикла, но в графе, полученном из
109
него удалением одпой вершины, имеется гамильтонов
цикл.
1.33. Доказать, что в каждом из графов Кк, К*. я, В”
имеется гамильтонов цикл.
1.34. Пусть п нечетно, В" —подмножество вершин
куба Вп, состоящее из вершин веса к. Пусть G — под-
граф куба В\ порожденный множеством U^"+1’
1) Существует ли в графе G совершенное паросоче-
тание?
2) Существует ли в графе G гамильтонов цикл?
1.35. В графе G имеется гамильтонов цикл, а в
графе Н — гамильтонова цепь. Верно ли, что в гра-
фе GXH существует гамильтонов цикл?
1.36. Доказать, что если для любых двух вершин и
и v связного n-вершинного графа выполняется d (u)+
+d (f) n, то граф имеет гамильтонов цикл.
1.37. Показать, что любой граф с п вершинами,
имеющий не менее % 4“ ребер, имеет гамильто-
нов цикл.
1.38. Показать, что граф, у которого имеются две
несмежные вершины третьей степени, а остальные вер-
шины имеют степень, не большую, чем 2, не обладает
гамильтоновым циклом.
1.39. 1) Показать, что D (GxH) (G)+Z) (Н)-
2) Верно ли, что D (GxH) max {D (G), D (Я)}?
1.40* . Доказать, что каждый регулярный связный
граф степени 2d представим в виде объединения непере-
секающихся 2-факторов.
1.41* . Показать, что граф К2п представим в виде
объединения некоторого 1-фактора и п—1 гамильтоно-
вых циклов.
1.42. Показать, что граф Я2я+1 можно представить
в виде объединения п гамильтоновых циклов.
1.43. Показать, что в графе Кп с нумерованными
вершинами имеется in 2 ' различных гамильтоновых
циклов.
1.44. Показать, что число различных совершенных
паросочетаний графа К2п с нумерованными вершинами
(2га) I
₽аВН0 2"raT*
§ 2. Планарность, связность, числовые
характеристики графов
Граф называется планарным, если он может быть
нарисован на плоскости так, что дуги кривых, изобра-
жающие ребра, пересекаются лишь в точках, соответ-
ствующих вершинам графа; причем в любой точке
пересечения сходятся только дуги, сопоставленные
ребрам, идцидентным именно той вершине, которой
соответствует данная точка. Такая геометрическая фи-
гура, являющаяся изображением планарного графа,
называется плоским графом. Внутренней гранью пло-
ского связного графа называется конечная область
плоскости, ограниченная замкнутым маршрутом и не
содержащая внутри себя ни вершин, ни ребер графа.
Маршрут, ограничивающий грань, называется грани-
цей грани. Часть плоскости, состоящая из точек, не
принадлежащих ни графу и ни одной из его внутрен-
них граней, называется внешней гранью. Для двухсвяз-
ных плоских графов (мультиграфов), имеющих п вер-
шин, т ребер и г граней, выполняется формула Эйлера
п—т-\-г=2. Справедлив следующий критерий планар-
ности.
Теорема (Понтрягин—Куратовский). Граф пла-
нарен тогда и только тогда, когда он не содержит
подграфов, гомеоморфных графам К6 и К3 3 (рис. 8, б, в).
Толщиной графа G называется наименьшее число
t (G) его планарных подграфов, объединение которых
равно G. Каждому нетривиальному связному плоскому
псевдографу G можно сопоставить двойственный псевдо-
граф G* следующим образом. Внутри каждой грани
псевдографа G выбирается по вершине графа G*. Если
х — ребро графа G, лежащее на границе граней gr и g2,
a vY и и2 — вершины псевдографа G*, взятые в этих
гранях, то вершины и и2 соединяются ребром в G*.
Плоский псевдограф (граф), изоморфный своему двой-
ственному псевдографу, называется самодвойственным.
Циклы Zlt Z2, . . ., Zk графа G называются линейно за-
висимыми, если для некоторых it, i2, . . ., is (1
«С Ч < h <С • • • < Ч выполняется соотношение
Z^ Ф Z,2 ф ... ф Z. =0, где 0 — граф без ребер,
Z ф Y — симметрическая разность графов Z и Y. В про-
тивном случае циклы Zlt Z2, .. ., Zk называются линейно
111
независимыми. Наибольшее число 5 (G) циклов в сово-
купности линейно независимых циклов графа G назы-
вается цикломатическим числом графа G. Раскраска
вершин (ребер) графа называется правильной, если
смежные вершины (ребра) окрашены в разные цвета.
Наименьшее число /(G), для которого существует
правильная раскраска вершин графа G, называется
хроматическим числом графа G. Наименьшее число
X' (G), для которого существует правильная раскраска
ребер графа G, называется реберным хроматическим
числом графа G. Подмножество U вершин (ребер) на-
зывается покрытием множества вершин (или ребер)
а) 6)
Рис. 9.
графа G, если каждая вершина (каждое ребро) графа
либо совпадает с некоторым элементом множества U,
либо смежна с некоторым элементом из U (соответ-
ственно инцидентно некоторому элементу из U). Покры-
тие называется тупиковым, если после отбрасывания
любого элемента оно перестает быть покрытием. Мини-
мальная мощность такого подмножества U вершин
графа G, что всякое ребро графа инцидентно хотя бы
одной вершине из U, обозначается через а0 (G) и назы-
вается числом вершинного покрытия. Минимальная
мощность подмножества У ребер графа G, такого, что
каждая вершина графа инцидентна хотя бы одному
ребру из У, обозначается через ах (G) и называется
числом реберного покрытия графа G. Множество
вершин (ребер) графа G называется независимым, если
никакие два его элемента несмежны. Через Se (G) (со-
ответственно (G)) обозначается максимальная мощ-
ность независимого множества вершин (ребер) графа G.
Число Ро (G) (число рх (G)) называется вершинным
(реберным) числом независимости графа G. Через а00 (G)
обозначается минимальная мощность такого подмно-
жества вершин U, что каждая вершина графа G, не вхо-
дящая в U, смежна хотя бы с одной вершиной из U.
112
2.1. Являются ли плоскими графы, изображенные
на рис. 6, а, б, 7, а, б, в?
2.2. При каких га 2 графы, изображенные на
рис. 9, а, б, являются плоскими?
2.3. Пусть GK=(V1> V2, X) — двудольный граф,
V2 = {bv b2,...,bn},
X = {xv х2, ..., хп, уL, у2, ..., уп, zv z2, ..z„},
где
х. = (а^ b{), i = l, га;
^ = (аР 6<+1), г = 1, га -1, уя = (га„, ^);
z. — (a., bi+2), i = 1, га — 2,
Z»-1=(«H-V &1)> z„ = («n> b2)-
Определить, при каких га >• 2 граф Gn является
плоским.
2.4. 1) Какое минимальное число ребер необходимо
удалить из куба В1, чтобы полученный граф был пло-
ским?
2) Какое минимальное число вершин нужно удалить
из В1, чтобы полученный граф был плоским?
2.5* . Пусть G — двухсвязный плоский граф, обла-
дающий не менее чем двумя внутренними гранями.
Доказать, что существует такая простая цепь, принад-
лежащая границе внешней грани, удаление которой
приводит к двухсвязному плоскому графу с меньшим
числом граней.
Примечание. При удалении цепи удаляются
все ее ребра и внутренние вершины, а концевые вершины
цепи остаются в графе.
2.6. Используя результат задачи 2.5, доказать
по индукции, что в плоском двухсвязном графе с га вер-
шинами и т ребрами число внутренних граней равно
т—га+1.
2.7. Доказать индукцией по числу ребер, что цик-
ломатическое число £ (G) псевдографа с га верши-
нами, т ребрами и с компонентами связности равно
гаг—га+с.
113
2.8. Для графов, изображенных на рис. 5, а, 6, а,
7, а, найти дипломатическое число £ (G) и выделить
систему из 5 (G) линейно независимых циклов.
2.9. Доказать, что в любом планарном графе суще-
ствует вершина степени, не большей, чем 5.
2.10. Доказать, что в любом планарном графе,
имеющем не менее четырех вершин, найдутся по мень-
шей мере четыре вершины степени не выше 5.
2.11. Доказать, что если у связного планарного
графа с п вершинами и т ребрами каждый простой цикл
7 к й (я — 2)
содержит не менее к ребер, то m к —2 '
2.12. Плоский связный граф, каждая грань кото-
рого, включая и внешнюю, ограничена циклом длины
три, называется триангуляцией.
Показать, что всякая триангуляция с п 3 верши-
нами имеет Зп—6 ребер и 2п—4 граней.
2.13. Пусть t (G) — толщина графа G. Показать, что:
1)
2)
3)
2.14* . Используя формулу Эйлера, доказать, что
графы К3 3 и К3 не являются планарными.
2.15* . Доказать, что из двухсвязного графа с дипло-
матическим числом Ц? > 1) путем удаления цепи
можно получить двухсвязный граф с дипломатическим
числом, равным ?—1.
2.16. Построить граф, двойственный к графу, изо-
браженному на рис. 5, а.
2.17. Показать, что псевдограф, двойственный к связ-
ному плоскому графу, является связным и плоским.
2.18. Показать, что дипломатическое число двой-
ственного графа совпадает с цикломатическим числом
исходного графа.
2.19. Показать, что если G имеет разделяющую
вершину, то и G* имеет разделяющую вершину.
2.20. Показать, что псевдограф G*, двойственный
к трехсвязному плоскому графу G, не имеет петель
и кратных ребер.
114
2.21. Сколько существует попарно неизоморфных
самодвойственных плоских двухсвязных графов с шестью
вершинами?
2.22. Показать, что не существует шестисвязных
планарных графов.
2.23. Показать, что граф, двойственный к «-вер-
шинной (« > 3) триангуляции, является двухсвязным
плоским кубическим графом.
2.24. 1) Показать, что плоский кубический граф,
каждая грань которого имеет не менее пяти вершин,
содержит не менее двенадцати вершин.
2) Показать, что если г. — число граней плоского
кубического графа, ограниченных i ребрами, то
2(б-о^=12.
2.25. Найти хроматические числа графов, представ-
ленных на рис. 4—8.
2.26. Найти реберные хроматические числа графов,
представленных на рис. 3—7.
2.27. Найти хроматическое и реберное хроматиче-
ское число
1) графа Кп;
2) графа Кпп;
3) графа Вп.
2.28. Сколько существует правильных раскрасок
вершин куба Вп в минимальное число цветов?
2.29. Показать, что реберное хроматическое число
графа Петерсена, представленного на рис. 7, а, равно
четырем, но у любого его подграфа G с восемью верши-
нами (G) 3. Верно ли неравенство (G) 3 для
произвольного собственного подграфа графа Петерсена,
полученного после удаления одной вершины?
2.30. Показать, что для раскраски ребер всякого
кубического псевдографа достаточно четырех цветов.
2.31. Показать, что ребра плоского кубического
графа можно раскрасить в два цвета а и Ь так, что каж-
дая вершина будет инцидентна одному ребру цвета а
и. двум ребрам цвета Ъ.
2.32. Доказать, что вершины всякого плоского
графа можно правильно окрасить в 6 цветов.
2.33. Доказать индукцией по числу вершин, что
для плоского графа G справедливо неравенство
X(G)<5.
115
2.34. Построить плоский граф G с минимальным чис-
лом вершин, такой, что (б?) — 4.
2.35. Вершины графа G пронумерованы в порядке
возрастания их степеней. Доказать, что если к — наи-
большее число, такое, что к d (pj + l, то / (G) к.
2.36. Операция стягивания заключается в удалении
из графа двух его смежных вершин и добавлении новой
вершины, которая смежна с теми из оставшихся вер-
шин, с которыми была смежна хотя бы одна из удален-
ных вершин. Показать, что граф, получающийся в ре-
зультате применения операции стягивания к планар-
ному графу, является планарным.
2.37. Пусть I — длина самой длинной простой цепи
в графе G. Показать, что / (G) Z-J-1.
2.38. Пусть d — максимальная степень вершины
графа G. Показать, что:
2) х' (G)
2.39. Пусть р — наибольшее число, для которого
в графе G существует подграф, изоморфный графу Кр.
Показать, что /_ (G) р.
2.40. Показать, что для графа Gen вершинами
1) т-х (£)<«;
2) X (G) • X (G) > п-
2.41. Каково наименьшее га, при котором существует
га-вершинный неплоский граф с неплоским дополнением.
2.42. Найти толщину графа Ks.
2.43. Доказать, что для произвольного связного
графа G с п (га > 1) вершинами
«О (Wo (<?)=«! (<?)+₽! (&)=П.
2.44. 1) Привести пример, опровергающий следую-
щее утверждение: всякое вершинное покрытие содержит
минимальное вершинное покрытие.
2) Доказать, что всякое вершинное покрытие содер-
жит тупиковое вершинное покрытие.
2.45. Найти число тупиковых и минимальных ребер-
ных покрытий
1) цепи длины гаг;
2) цикла длины га;
3) графа Петерсена (рис. 7, а).
116
2.46. Доказать, что для любого графа G справедливы
неравенства а0 (G) (G), (G) pj (G).
2.47. Доказать, что для любого графа G выполня-
ется неравенство а00 (G) оу, (G).
2.48. Доказать или опровергнуть неравенство
Ро (Q < Опп (G).
2.49. Пусть 77CZF — некоторое подмножество вер-
шин графа G=(V, X), a v (U) — число тех вершин
pf V\t7, которые несмежны ни с одной вершиной из U.
Пусть
МС) = 7Г7
\ *
5 ><у)'
PCV, | U |=4
1) Показать, что ао0 (G) (G).
2) Пусть d0 — минимальная из степеней вершин
графа G. Показать, что
4-1
3) Показать, что для регулярного графа G степени d,
имеющего п вершин,
|<«oo(Q<i+7(1+ind).
2.50. Показать, что если d0 — минимальная из сте-
пеней вершин графа G, то оу (G) d0.
2.51* . Если G — двудольный граф, ат — число
его ребер, то т ^ з0 (G) • [% (G). Показать, что равенство
достигается лишь для полных двудольных графов.
§ 3. Ориентированные графы
Ориентированный псевдограф D=D (V, X) опреде-
ляется заданием непустого (конечного) множества V
и набора X упорядоченных пар элементов из V. Эле-
менты множества V называются вершинами, а элементы
набора X — дугами (или ориентированными ребрами)
ориентированного псевдографа D (V, X). В наборе X
могут встречаться и пары вида (и, и), называемые пет-
лями, и одинаковые пары, называемые кратными
(или параллельными) дугами. Пары (и, и) и (и, и) счи-
117
таются одинаковыми лишь в том случае, когда и—и.
Ориентированным мулътиграфом называется ориенти-
рованный псевдограф, не содержащий петель. Если
в ориентированном псевдографе нет ни петель, ни крат-
ных дуг, то он называется ориентированным графом
(или, короче, орграфом). Направленным графом назы-
вается такой орграф, который не имеет симметричных
пар ориентированных ребер, т. е. множество X не может
содержать одновременно и дугу (и, и), и противоположно
направленную дугу (и, и).
Пусть х=(и, и) — дуга ориентированного псевдо-
графа. Тогда вершина и называется начальной вершиной
(или началом), а и — конечной вершиной (или концом)
дуги х; в этом случае говорят также, что дуга х исходит
из вершины и и заходит в вершину и. Если вершина v
является началом или концом дуги х, то говорят, что v
и х инцидентны. Полустепенъю исхода вершины v
(псевдографа D) называется число дуг псевдографа D,
исходящих из вершины и. Полустепень исхода вер-
шины v обозначается через od (и) или d+ (v). Анало-
гично, полустепенъю захода вершины и (обозначение:
id (v) и d~ (v)) называется число дуг псевдографа, захо-
дящих в вершину и.
Заменяя каждую упорядоченную пару (и, v) из на-
бора X ориентированного псевдографа D (V, X) неупо-
рядоченной парой {и, п), состоящей из тех же элемен-
тов и и и, получаем ассоциированный с D (V, X) псевдо-
граф G=(V, Х°).
Ориентированные псевдографы (Vlr Хх) и
D2 (V2, Х2) называются изоморфными, если существуют
два таких взаимно однозначных соответствия f. Vx V2
и ф: Хг Х2, что для всякой дуги х=(и, и) £ Хг спра-
ведливо соотношение ф (*)=(<p (и), (и)). Изоморфное
отображение ориентированного псевдографа на себя
называется автоморфизмом псевдографа. Совокупность
всех автоморфизмов ориентированного псевдографа
образует группу относительно операции умножения
(последовательного выполнения) автоморфизмов. Эта
группа называется группой (автоморфизмов) ориенти-
рованного псевдографа.
Операции удаления вершины и дуги, а также поня-
тия подграфа, остовного подграфа и порожденного
подграфа определяются для ориентированных псевдо
118
графов подобно тому, как это делалось в случае неориен-
тированных псевдографов.
При определении ориентированных маршрута, зам-
кнутого маршрута, цепи, цикла, простой цепи и про-
стого цикла требуется (в отличие от определения со-
ответствующих «неориентированных понятий»), чтобы
последовательность (вершин и дуг) рх, xr, v2, х2, . . .
. . хп_2, pB_u x„_t, ип (п 2) удовлетворяла условию:
каждая дуга х{ (1 i п—1) имеет вид (р,., р<+1),
т. е. вершина и. является началом дуги х(, а вер-
шина pf+1 — концом. Считается, что ориентированный
(и—р)-маршрут ориентирован от своей первой вер-
шины и к своей последней вершине и. Длиной маршрута
называется число дуг в нем. Расстоянием р (и, и)
от вершины и до вершины v называется длина кратчай-
шего (и—р)-маршрута. Ориентированный маршрут
часто называется путем, а ориентированный простой
цикл — контуром.
Ориентированная простая остовная цепь называется
гамильтоновым путем {гамильтоновой цепью). Гамиль-
тоновым контуром называется остовный контур ориен-
тированного псевдографа. Если ориентированный псев-
дограф содержит гамильтонов контур, то сам псевдограф
тоже называется гамильтоновым.
Говорят, что вершина v ориентированного псевдо-
графа достижима из вершины и, если в псевдографе
существует {и—р)-путь, т. е. путь, исходящий из вер-
шины и и заходящий в вершину и.
Ориентированный псевдограф называется сильно
связным (или сильным), если любая вершина в нем до-
стижима из всякой другой его вершины. Ориентиро-
ванный псевдограф называется односторонне связным
(или односторонним), если для любых двух вершин
по крайней мере одна достижима из другой. Ориенти-
рованный псевдограф D (V, X) называется слабо связ-
ным (или слабым), если ассоциированный с ним псевдо-
граф (7, Х°) является связным. Если ориентированный
псевдограф не является даже слабо связным, то он на-
зывается несвязным. Тривиальный орграф, состоящий
лишь из одной вершины, считается (по определению)
сильно связным.
Сильной компонентой орграфа D называется любой
его ориентированный подграф, являющийся сильным
119
орграфом и не содержащийся ни в каком другом сильно
связном ориентированном подграфе орграфа D. Ана-
логично, односторонняя компонента представляет собой
максимальный односторонний подграф орграфа D,
а слабая компонента — максимальный слабый подграф.
Понятия сильной, односторонней и слабой компонент
естественным образом обобщаются и на случай ориен-
тированного псевдографа.
Пусть т={51, S2, . . ., 5П} — множество всех силь-
ных компонент орграфа D. Конденсацией D* орграфа D
называется такой орграф, у которого множеством вер-
шин является у, а дуга (5,., Sимеется в орграфе D*
тогда и только тогда, когда в орграфе D существует
хотя бы одна дуга, исходящая из некоторой вершины
компоненты S, и заходящая в какую-нибудь вершину
компоненты Sj.
Если D=D (V, X) — орграф, то обратный к нему
орграф D' задается тем же множеством вершин V и та-
ким множеством дуг X', что дуга (и, v) принадлежит X'
тогда и только тогда, когда дуга (и, и) принадле-
жит X.
Вершина v орграфа D называется источником,
если из нее достижима любая другая вершина
. орграфа D. Стоком орграфа D называется всякая его
вершина и, являющаяся источником в обратном
(к орграфу D) орграфе D'.
Пусть D — орграф, для которого ассоциированный
с ним граф является деревом. Тогда орграф D назы-
вается растущим деревом, если он имеет источник.
Ориентированный псевдограф называется полным, если
в нем любые две различные вершины соединены хотя бы
одной дугой.
Турниром называется полный направленный
граф.
Пусть D—n-вершинный орграф и его множество
вершин У={щ, и2, . . ., ип}. Матрицей смежности
орграфа D называется (n X и)-матрица A (D) = 11^ -11, у ко-
торой а<у=1, если дуга (vf, принадлежит орграфу D,
и а,-у=0 — в противном случае. Предположим еще, что
множество всех дуг орграфа D тоже упорядочено:
Х—^ац, х2, . . ., х^. Матрицей инцидентности (или
матрицей инциденций) орграфа D называется (nXm)-
120
матрица В (Z>) = 11^-11, у которой
ьч=
1, если вершина у, является концом дуги Xj.
—1, если вершина vf является началом дуги Жу,
О, если вершина v( не инцидентна дуге х^.
3.1. Опровергнуть утверждение: если полустепени
исхода и захода любой вершины орграфа—положитель-
ные и четные, то для каждой вершины орграфа найдется
контур, содержащий ее.
3.2. Пусть орграф D (7, X) является по крайней
мере слабо связным, У={у1, v2, . . ., п 2, и
d+ (v^—d- (pj) = 1, d+ (v2)—d~ (y2) =—1, d+ (v^=d~ (y?)
при 7=3, . . ., n. Доказать, что тогда в орграфе D су-
ществует ориентированная —р2)-цепь, содержащая
все дуги орграфа.
3.3. Доказать, что орграф сильно связен тогда
и только тогда, когда в нем существует ориентированный
остовный цикл.
3.4. Доказать, что слабый орграф является сильно
связным тогда и только тогда, когда в нем существует
ориентированный замкнутый маршрут, содержащий
каждую дугу орграфа хотя бы один раз.
3.5. Пусть орграф D можно представить в виде
объединения некоторых его ориентированных замкну-
тых маршрутов Dk, О2, . . ., Dk (к'^у 1), удовлетворяю-
щих условию: каждые два соседних маршрута
и DJ+1 к—1) имеют хотя бы одну общую вер-
шину. Доказать, что тогда орграф D сильно связен.
3.6. Доказать, что в любом турнире существует
гамильтонов путь.
3.7. Доказать, что турнир Т является сильным
орграфом тогда и только тогда, когда Т имеет остовный
контур (т. е. является гамильтоновым турниром).
3.8. Пусть {ур ;л2, ..., ун}—множество вершин тур-
п п
нира. Доказать, что У, (dv (t>,.))2 = 2 (ге — ('-\))2-
i=i <=1
3.9. Пусть у вершины v турнира Т полустепень
исхода не меньше чем полустепень исхода каждой другой
вершины турнира. Доказать, что расстояние от вер-
шины v до любой вершины турнира не превосходит 2.
3.10* . Обозначим через S некоторое множество дуг
турнира Т. Дуги множества S называются согласован-
121
ными, если можно так перенумеровать вершины тур-
нира Т, что из принадлежности дуги (v{, vj) множе-
ству S будет вытекать неравенство i < j. Пусть / (п)
есть такое наибольшее целое число, что каждый п-вер-
шинный турнир (п 3) содержит множество S, со-
стоящее из / (п) согласованных дуг. Доказать, что / (п)
>й'т-
3.11* . Доказать, что число ориентированных цик-
лов длины 3 в «-вершинном турнире не превосходит
t(n) =
п (и2 — 1)
24
п (п2 — 4)
24
если п — нечетное,
если п — четное.
3.12. Доказать, что группа автоморфизмов любого
турнира имеет нечетный порядок (т. е. состоит из не-
четного числа элементов).
3.13. Показать, что в конденсации D* произволь-
ного орграфа контуры отсутствуют.
3.14. Доказать, что орграф D является односторон-
ним тогда и только тогда, когда его конденсация D*
имеет единственную ориентированную остовную цепь.
3.15. Орграф D (У, X) называется транзитивным,
если из принадлежности дуг (и, v) и (у, w) множеству X
следует принадлежность множеству X дуги (u, w).
Доказать, что конденсация всякого турнира является
транзитивным турниром.
3.16. Бесконтурным орграфом называется орграф,
не содержащий контуров. Доказать, что в бесконтур-
ном орграфе существует вершина с нулевой полусте-
пеныо исхода.
3.17. Доказать, что орграф изоморфен своей кон-
денсации тогда и только тогда, когда он бесконтурный.
3.18. Пусть орграф D — слабо связный, но не одно-
сторонний. Доказать, что в D не существует такой вер-
шины, удаление которой дает сильный орграф.
3.19. Доказать, что слабый орграф является расту-
щим деревом тогда и только тогда, когда лишь одна
его вершина имеет нулевую полустепень захода, а полу-
степень захода любой из остальных вершин равна 1.
3.20. Пусть Sn — симметрическая группа подстано-
вок, действующая на множестве {1, 2, . . ., п}, п^2.
122
Рассмотрим произвольную совокупность Т транспози-
ций из группы Sn. Множеству Т сопоставим орграф
D (V, Хт), у которого V = {1, 2, . . ., п] и дуга (г, /) при-
надлежит Хт только в том случае, когда i< j и транс-
позиция (iy) содержится в множестве Т. Доказать, что
множество Т образует базис в Sn (или, другими сло-
вами, множество Т есть неприводимая система образую-
щих группы 5Я) тогда и только тогда, когда орграф
D (V, Хт) является растущим деревом.
3.21. Доказать, что полный сильно связный орграф
является гамильтоновым.
3.22. Показать, что в полном орграфе существует
источник.
3.23. Убедиться в том, что любой транзитивный
турнир имеет единственный гамильтонов путь.
3.24. Доказать, что в каждом турнире число всех
различных гамильтоновых путей — нечетное.
3.25. Пусть полный сильно связный орграф имеет п
вершин (п 3). Доказать, что, каково бы ни было к
(3 < /с < п), для всякой вершины орграфа найдется
контур длины к, содержащий эту вершину.
3.26. Пусть D (V, X) — полный сильно связный
орграф, у которого |V| 4. Показать, что в орграфе D
существуют две различные вершины и2 и v2, удовлетво-
ряющие условию: орграфы D2 и D.2, получающиеся
из орграфа D после удаления вершин v2 и и2 (соответ-
ственно), являются сильно связными.
3.27. Через А9 обозначается q-я степень матрицы
смежности А (D) = l|a,-JI орграфа D. Доказать, что
(г, Д-й элемент aW матрицы А9 равен числу всех —и^)-
маршрутов длины q (в орграфе D).
3.28. Пусть В — матрица инциденций орграфа
D (7, X). Показать, что подмножество Х2 дуг орграфа
D (Х2С1Х) порождает простой цикл (не обязательно
ориентированный) тогда и только тогда, когда множе-
ство соответствующих этим дугам столбцов (в матрице В)
является линейно зависимым, а всякое его собственное
подмножество таким свойством не обладает.
3.29. Доказать, что определитель всякой квадрат-
ной подматрицы матрицы инциденций В (D) орграфа D
равен либо 0, либо 4-1, либо —1.
3.30. Пусть В — матрица инциденций слабо связ-
ного п-вершинного орграфа D и матрица В получена
123
из В вычеркиванием любой (одной) строки. Доказать,
что существует взаимно однозначное соответствие между
различными *) ориентированными деревьями орграфа D
(рассматриваемыми как ориентированные подграфы
орграфа D) и невырожденными подматрицами порядка
п—1 матрицы В.
3.31. Пусть матрица В — подматрица матрицы
инциденций В слабо связного орграфа D, описанная
в предыдущей задаче. Через В' обозначается матрица,
транспонированная к матрице В. Доказать, что число
различных ориентированных деревьев в орграфе D
равно значению определителя матрицы В'В'.
§ 4. Деревья и двухполюсные сети
Псевдограф G=(V, X), в котором выделено к вер-
шин, называемых полюсами, называется к-полюсной
сетью. Псевдограф G будет называться графом соответ-
ствующей к-полюсной сети. Сеть Г с множеством полю-
сов Р и графом G=(F, X) будет обозначаться через (Р;
V, X). Две /с-полюсные сети изоморфны, если их графы
изоморфны и при этом полюсы одной сети взаимно
a) f) 6) О 0)
Рис. 10.
однозначно соответствуют полюсам другой. Однополюс-
ная сеть, граф которой есть дерево, называется корне-
вым деревом. Единственный полюс такой сети назы-
вается корнем. Плоским корневым деревом называется
изображение графа на плоскости. Это понятие можно
определить по индукции следующим образом. Сеть,
представленная на рис. 10, а, есть плоское корневое
дерево. Если А и В (см. рис. 10, б) — плоские корневые
деревья, то фигуры C,D, Е (рис. 10, в, г) также являются
0 Здесь считается, что два дерева различны, если они не-
изоморфные ориентированные деревья с помеченными (зануме-
рованными) вершинами,
124
плоскими корневыми деревьями. Будем считать, что
произвольное плоское корневое дерево изображается
на плоскости с разрезом, представляющим собой полу-
прямую, исходящую из корня (см. рис. 10, д). При этом
можно предполагать, что ребра, инцидентные корню,
пронумерованы по часовой стрелке числами 1, . . ., т,
где т — степень корня. Если удалить из такого пло-
ского корневого дерева ребро с номером i, то получится
граф с двумя компонентами связности. Ту из компонент,
которая не содержит корня, назовем г-й ветвью исход-
ного корневого дерева. Корнем i-й ветви будем считать
вершину, инцидентную г-му ребру (в исходном дереве).
Для произвольного корневого дерева А обозначим
через d0 (4) степень его корня. Плоские корневые де-
ревья А и В называются одинаковыми, если либо (4) =
—d0 (В)=0, либо <70 (A)—d0 (В)=т >0 и для всякого
i=l, т i-e ветви деревьев А и В — одинаковые. Два
дерева, не являющиеся одинаковыми, называются раз-
личными. Таким образом, деревья D и Е (см. рис. 10, г)
являются различными, если деревья А и В (см. рис. 10,
б) различны. Каждому плоскому корневому дереву Т
с т ребрами можно однозначно сопоставить двоичный
вектор длины 2т, называемый кодом дерева. Дереву
с одним ребром сопоставляется вектор 01. Если де;
ревьям А и В (рис. 10, б) сопоставлены векторы й и р
соответственно, то дереву С (рис. 10, в) сопоставляется
вектор 0а1, а деревьям D тз. Е (рис. 10, г) — векторы сф
и [За.
В дальнейшем, если не оговорено противное, под
сетью понимается 2-полюсная сеть. Сеть Г ({а, 6}; V, X)
будет обозначаться кратко через Г (а, Ь). Подграфом
такой сети будет называться подграф графа (Ё, X).
Вершина подграфа G сети Г называется граничной,
если она либо является полюсом, либо инцидентна не-
которому ребру сети, не принадлежащему подграфу G.
Подграф сети называется отростком, если он обладает
единственной граничной вершиной. Подсетью 2-полюс-
ной сети называется ее подграф, имеющий ровно две
граничные вершины. Эти вершины являются полюсами
подсети. Сеть называется связной, если ее граф является
связным. Тривиальной называется связная сеть (или
подсеть), имеющая одно ребро. Связная сеть называется
сильно связной, если через каждое ребро проходит
125
простая цепь, соединяющая полюсы сети. Сильно связ-
ная сеть называется разложимой, если она обладает
хотя бы одной нетривиальной подсетью. В противном
случае она называется неразложимой. Пусть Г (а, Ь) —
разложимая сеть, G (с, d) — нетривиальная ее подсеть,
а Гх (а, Ь) — сеть, полученная из Г (а, Ъ) заменой под-
сети G (с, d) одним ребром (с, d). Тогда в свою очередь
сеть Г (а, Ь) может быть получена подстановкой сети
G (с, d) вместо ребра (с, d) сети Гх (а, Ь). Таким образом,
разложимая сеть Г (а, Ь) может быть задана указанием
сети Tj (а, Ь), ребра (с, tZ) сети 1\ (а, Ь) и сети G (а, Ь).
Такое задание называется разложением сети Г (а, Ь).
Сеть Tj (а, Ь) называется внешней, а сеть G (с, d) —
внутренней сетями разложения. Сеть Г (а, Ь) назы-
вается суперпозицией сетей Гх (а, Ь) и G (с, d). Сеть,
состоящая из т параллельных ребер, соединяющих
полюсы а, Ь, обозначается через Гг(а, Ь) или, короче, Г₽.
Сеть, граф которой есть простая цепь длины т, соеди-
няющая полюсы а, Ь, обозначается через Г*, (а, Ь) или,
короче, Г^. Сеть, которая может быть получена из се-
тей и Г| применением конечного числа операций
подстановки сети вместо ребра, называется параллельно-
последовательной сетью или, короче, г.-сетью. Нетри-
виальная неразложимая сеть Г (а, Ь), отличная
от Г? (а, Ь) и Г|(а, Ь), называется Н-сетъю.
Разложимая сеть называется р-разложимой (соответ-
ственно s-разложимой), если некоторая внешняя сеть
разложения имеет вид Г£ (соответственно Г“л), т 2.
Если некоторая внешняя сеть разложения сети Г явля-
ется //-сетью, то Г называется Н-разложимой. Справед-
ливо утверждение о том, что всякая разложимая сеть
является либо р-, либо S-, либо //-разложимой. Кано-
ническим р-разложением сети называется р-разложение,
при котором внутренние сети разложения отличны
от сетей вида Г? и сетей, являющихся р-разложимыми.
Аналогично определяется каноническое s-разложение.
Каноническим Н-разложением называется разложение,
внешней сетью которого является //-сеть. Каждой тс-
сети Г с т 1 ребрами можно сопоставить плоское
корневое дерево Т (Г) с т висячими вершинами, такое,
что а) каждая вершина дерева Т (Г), отличная от вися-
чей, помечена символом р или s; б) на каждой цепи,
идущей от корня к висячей вершине, отметки pas че-
126
редуются; в) вершины, отличные от корня, имеют сте-
пень, не равную 2. Висячие вершины дерева Т (Г)
не помечены. Дерево Т (Г) определяется по индукции.
Если Г имеет'вид Г£ (или Г^), то Т (Г) есть дерево, корень
которого помечен символом р (соответственно симво-
лом s), а остальные m вершин являются висячими,
смежными с корнем, и не имеют пометок. Если сеть Г
разложима и отлична от сетей указанного вида и внеш-
няя сеть разложения имеет вид Г£ (или Г£), а внутренние
сети суть Gr, G2, . . ., Gk, то дерево Т (Г) строится сле-
дующим образом. Пусть Т (Gj), Т (б2), . . ., Т (Gk) —
деревья, соответствующие внутренним сетям разложе-
ния. Тогда в качестве корня Т (Г) берется вершина
степени к, помеченная символом р (соответственно сим-
волом s). Вершины, смежные с корнем, помечаются сим-
волом s (соответственно символом р). Вершины vlt
v2, . . ., vk, смежные с корнем, отождествляются с кор-
нями деревьев Т (GJ, Т (С2), . . ., Т (Gk). Например,
п-сети, изображенной на рис. И, а, соответствует де-
рево, изображенное на рис. И, б. Дерево Т (Г) назы-
вается диаграммой канонического разложения "-сети Г.
Отметим, что если внешняя сеть разложения сети Г
имеет вид (а, Ъ), а внутренние сети Gj (а, к1),
G2 (ult u2), . . ., Gk (uk_r, Ъ) подставляются соответственно
вместо ребер (a, itj), (un u2), ..., (uk_r, b), то в дереве
Т (Г) вершины v2, . . ., vk, отождествляемые с кор-
нями плоских корневых деревьев Т (GJ, Т (G2), . . .
..., Т (GJ, следуют друг за другом слева направо в по-
рядке возрастания номеров. Таким образом, дерево Т’(Г'),
изображенное на рис. 12, б, является диаграммой ка-
нонического разложения сети Г' (рис. 12, а), но не
является диаграммой сети Г (см. рис. 11, а).
127
Вершина сети, отличная от полюса, называется
. ’внутренней. Вершина v зависит от вершины и, если
•, всякая простая цепь, соединяющая полюсы и проходя-
I щая через у, проходит и через и. Вершины ели эквива-
' лентны, если v зависит от ни и зависит от и. Вершина v
слабее вершины и, а вершина и сильнее вершины и,
если v зависит от и, но не эквивалентна ей. Вершина v
называется минимальной, если она не слабее никакой
другой внутренней вершины сети. Цепью сети в даль-
нейшем будет называться простая цепь, соединяющая
Рис. 12.
полюсы сети. Случаи, когда термин «цепь» употреб-
ляется в ином смысле, будут всякий раз оговари-
ваться. Цепь сети называется кратчайшей, если она
имеет минимально возможную длину. Длиной сети
называется длина ее кратчайшей цепи. Разрезом назы-
вается множество ребер сети, удаление которых разру-
шает все цепи. Разрез называется тупиковым, если
никакое его подмножество не является разрезом.
Разрез называется минимальным, если он имеет мини-
мально возможное число ребер. Число ребер в мини-
мальном разрезе называется шириной сети.
4.1. Пусть G — граф с п 2 вершинами. Дока-
зать эквивалентность следующих утверждений:
1) G — связный граф с п—1 ребрами.
2) G — связный граф, но после удаления любого
ребра становится несвязным.
3) Любая пара различных вершин графа G соединена
единственной цепью.
128
4) G — граф без циклов, но добавление ребра,
соединяющего любые две вершины, приводит к появле-
нию цикла.
4.2. Доказать, что в любом дереве с п 2 верши-
нами имеется не менее двух висячих вершин.
4.3. Доказать, что если в графе G, имеющем не ме-
нее трех вершин, число висячих вершин равно числу
ребер, то G либо не связен, либо является деревом.
4.4. Пусть F (G) = {HV Н2,...,Нп}—семейство гра-
фов, в котором граф Н. получен из n-вершинного графа
G удалением вершины с номером г (г==1, и). Вершины
в графах Н{ не помечены. Доказать, что:
1) по семейству F (G) можно выяснить, является ли
граф G деревом;
2) если G — дерево, то по F (G) можно однозначно
(с точностью до изоморфизма) восстановить G.
4.5. Пересечением двух графов G и Н называется
граф GftH, все вершины и все ребра которого принадле-
жат как G так и Н. Показать, что непустое пересече-
ние двух поддеревьев одного дерева является деревом.
Пусть Pg[(p, и) — расстояние между вершинами v, и
в графе G=(V, X). Вершина н0, для которой
max pG (и0, v) — min max pG (и, v),
F «6^
называется центром графа, а число R (G) = max рс (и0, и)
ICV
называется радиусом графа.
4.6. 1) Найти число центров в графе
a) G (см. рис. 6, а);
б) G (см. рис. 6, б);
в) G = K„st „2.
2) Доказать, что в любом дереве имеется не более
двух центров.
4.7. Доказать, что дерево обладает единственным
центром в случае, когда его диаметр есть число четное,
и обладает двумя центрами, когда диаметр есть число
нечетное.
4.8. 1) Пусть D (G) — диаметр, a R (G) — радиус
графа G. Показать, что R (G)< D (G) < 2R (G).
2) Показать, что если G— дерево, то R (G) =
3) Привести пример графа G, для которого Rtfi) —
= D{G).
5 Г. И. Гаврилов, А. А. Сапоженко
129
4.9* . Доказать, что дерево однозначно с точностью
до изоморфизма восстанавливается, если заданы по-
парные расстояния между его висячими вершинами.
4.10. Показать, что в дереве с нечетным диаметром
любые две простые цепи наибольшей длины имеют
хотя бы одно общее ребро.
4.11. Бесконечным деревом будет называться граф
со счетным множеством вершин, удовлетворяющий
условию: для любых двух вершин и, и графа суще-
ствует единственная простая (и—к)-цепь, причем длина
этой цени — конечная. Доказать, что если степень
каждой вершины бесконечного дерева конечна, то для
всякой вершины существует простая цепь бесконечной
длины, содержащая эту вершину.
4.12. Пусть Н={г;1, и2, . . .} — бесконечная про-
стая цепь. Пусть G = K2'X.P. Какова мощность множе-
ства всех остовных деревьев графа (Р.
Пусть G = (V, X) — мультиграф с множеством вер-
шин К={р1, к2, . . ., vn}, а М ((?) = ||а<у|| — квадратная
матрица порядка п, где
d (к,.) при i — j,
—1 при (и., и.)£Х;
0 при кД (f X.
Известно [33], что число попарно различных остовных
деревьев графа равно минору любого из элементов
главной диагонали матрицы М (G).
4.13. Найти число остовных деревьев графов, изо-
браженных на рис. 4, а, б, 8, а, б, предварительно
пронумеровав вершины этих графов.
4.14. Каково хроматическое число дерева с п 2
вершинами?
4.15. Верно ли, что если диаметр графа G равен
к (к > 2), то существует остовное дерево, диаметр ко-
торого равен к?
4.16. Доказать, что при п 3 число попарно не-
изоморфных корневых деревьев с п вершинами не менее
чем в два раза превосходит число попарно непзоморф-
ных деревьев с п вершинами, не имеющих корня.
4.17. Пусть корневое дерево с п (п 2) висячими
вершинами не имеет вершин степени 2, отличных
1Э0
от корня. Показать, что общее число вершин дерева
не превосходит 2п—1.
4.18. Построить коды плоских корневых деревьев,
изображенных на рис. 13, а, б.
4.19. По заданному коду а построить плоское кор-
невое дерево.
1) а=(001010011011);
2) «=(0100011001101011);
3) «=(0001010110011011).
4.20. 1) Выяснить, сколько существует попарно не-
изоморфных корневых деревьев с четырьмя ребрами.
2) Сколько существует
попарно различных пло-
ских корневых деревьев
с четырьмя ребрами?
4.21. Множество векто-
ров {«!, а2, а3, а4, а5} раз-
бить на классы эквива-
лентности так, чтобы век-
торы из одного класса яв-
лялись кодами попарно рпс_ 1з_
изоморфных деревьев:
а1=(0010Ю1Ю1), а2=(0100101Ю1), а3=(010100Ю11),
а4=(0100101011), а5=(0010110101).
4.22. Доказать, что код а = (ап а2, . . ., а2л) плоского
корневого дерева с п ребрами удовлетворяет следую-
щим свойствам:
2в
1) 2 а,- = га;
1=1
2) для любого к(1 ^к^2п) справедливо неравен-
ft
ство 2 а<
>=1
4.23. Показать, что всякий двоичный вектор а
длины 2п, удовлетворяющий условиям 1) и 2) предыду-
щей задачи, является кодом плоского корневого дерева
с п ребрами.
4.24. 1) Показать, что для числа ф (л) векторов
а£В2в, удовлетворяющих условиям 1), 2) задачи 4.22,
справедливо рекуррентное соотношение
ф(«) = 2 Ф(г~ 1)ф(« — о> где ф (0) = ф (1) = 1.
5*
131
2*) Найти аналитическое выражение для ф (п).
4.25. Пусть G — связный плоский граф. Исходя
из некоторой вершины и, принадлежащей внешней
грани, будем обходить эту границу так, чтобы она
оставалась все время справа относительно направления
обхода. В некоторый момент мы вновь придем в исход-
ную вершину V. Обход будет продолжаться, если
имеются пепройденные ребра, инцидентные вершине v
и принадлежащие границе внешней грани. В противном
случае обход заканчивается.
1) Доказать, что G — дерево тогда и только тогда,
когда при обходе каждое ребро проходится дважды.
2) Пусть G — дерево с корнем и. В соответствии
с описанным выше обходом дереву G можно сопоставить
двоичный вектор. Последовательно проходя одно ребро
за другим, будем при обходе очередного ребра выписы-
вать 0, если ребро проходится в первый раз, и 1, если
ребро проходится во второй раз. Показать, что полу-
ченный таким образом вектор является кодом дерева G.
4.26. Пусть G — граф с п вершинами и т ребрами.
Граф называется сбалансированным, если никакой его
подграф не имеет вершин степени, большей, чем 2т/п.
1) Показать, что дерево при п>2—несбалансиро-
ванный граф.
2) Привести пример сбалансированного графа, у ко-
торого т = п -|- 3.
4.27. Пусть G — граф, каждому ребру которого
приписан вес — действительное неотрицательное число.
Весом подграфа графа G называется сумма весов ребер
этого подграфа. Минимальным покрывающим деревом
графа G называется его остовное дерево, имеющее
наименьший вес. Доказать, что минимальное покрываю-
щее дерево можно получить с помощью следующего
алгоритма. На первом шаге алгоритма выбирается ребро
наименьшего веса. Затем на очередном шаге выбирается
ребро, имеющее наименьший вес среди всех ребер,
не образующих цикла с ранее выбранными ребрами.
Алгоритм заканчивает работу, если такого ребра
не существует.
4.28. Верно ли, что всякая подсеть сильно связной
сети является сильно связной?
4.29. Пусть в связной сети имеется единственный
отросток с к вершинами, не содержащийся в другом
132
отростке с большим числом вершин. Показать, что до-
статочно провести к—1 дополнительных ребер, чтобы
сделать сеть сильно связной. Можно ли всегда обойтись
меньшим числом дополнительных ребер?
4.30. Верно ли, что для любых п и т (гп п 3)
существуют разложимые сети с п вершинами и т реб-
рами?
4.31. Верно ли, что граф сильно связной сети
является 2-связным?
выбрать в произвольном
две несмежные вершины
в качестве полюсов,
то получится нераз-
ложимая сеть?
4.32. Верно ли, что если
2-связном кубическом графе
Рис. 15.
4.33. Сколько попарно неизоморфных неразложи-
мых сетей можно получить, выбирая в «-мерном кубе
две вершины в качестве полюсов?
4.34. 1) Показать, что если неразложимая сеть
имеет п > 2 вершин и т ребер, то
3« 2zn+2 п (п—1).
2) Показать, что для любых т и п, таких, что
з
-^п — 1, существует неразложимая сеть
с п вершинами и т ребрами.
4.35. Для сетей, представленных на рис. 14, а, б, в,
1) определить тип разложения;
2) найти внешние сети канонического разложения.
4.36. Пусть Г — сеть, изображенная на рис. 15.
1) Указать все минимальные вершины сети.
2) Разбить все внутренние вершины сети Г на классы,
состоящие из попарно эквивалентных вершин.
3) Проверить, существует ли в этой сети вершина,
которая слабее всех остальных.
133
4.37. Доказать, что для каждой вершины v сильно
связной сети существует цепь, содержащая все вершины,
которые сильнее ее или эквивалентны ей.
4.38. Пусть S (Г) — множество всех таких вер-
шин v сети Г, которые не являются минимальными.
1) Верно ли, что если Г является Я-разложимой
сетью без кратных ребер, то после соединения каждой
вершины uQS (Г) ребрами с каждым из тех полюсов,
с которым v несмежна, получится неразложимая
сеть?
2) Достаточно ли для получения неразложимой сети
соединить каждую вершину и из S (Г) ровно с одним
из тех полюсов, с которыми v несмежна?
4.39. 1) Показать, что всякая разделяющая вер-
шина минимальна.
2) Показать, что всякая вершина, смежная с обоими
полюсами, минимальна.
4.40. Пусть все вершины сильно связной сети Г ми-
нимальны.
1) Выяснить, может ли сеть Г быть
а) р-разложпмоп;
б) s-разложимой;
в) Я-разложимой.
2) Пусть сеть Г является s-разложпмой. Показать,
что каждая внутренняя вершина является разделяющей.
3) Пусть сеть Г является Я-разложимой. Про-
верить, может ли какая-либо из внутренних сетей быть
а) Я-сетью;
б) Я-разложимой сетью;
в) сетью, отличной от сетей Гр (т 1).
4.41. Пусть сильно связная сеть Г с 8 ребрами
не является ни р-, ни s-разложимой и не имеет под-
сетей вида Гр, Ггт (пг > 1). Показать, что Г — неразло-
жимая сеть.
4.42. Пусть G=(71, V2, X) —связный двудольный
граф, степень каждой вершины которого больше или
равна 2. Показать, что если построить сеть Г (а, Ь),
соединив ребром полюс а с каждой вершиной мно-
жества Vlt а полюс b — с каждой вершиной мно-
жества Г2> т0 эта сеть окажется Я-сетью.
4.43. Существует ли р-разложимая сеть, у которой
всякая подсеть, имеющая не менее трех ребер, р-раз-
ложпма?
134
4.44. Для сетей, изображенных на рис. 16, а, б,
построить диаграммы канонического разложения.
4.45. Построить к-сети, имеющие диаграммы кано-
нического разложения, изображенные на рис. 17, а, б.
4.46. Доказать, что если п-сети Tj и Г2 не изо-
морфны, то они имеют различные диаграммы канони-
ческого разложения.
4.47. Пусть А и В — две цепи сети Г (а, Ь), и пусть
вершина и принадлежит цепи А, но не принадлежит
цепи В, а вершина и принадлежит цепи В, но не при-
надлежит цепи А. Пусть, далее, [и, и] — простая цепь,
соединяющая и и и, и не пересекающаяся с цепями А
и В нигде, кроме своих концов.
1) Доказать, что существуют по крайней мере две
цепи сети Г, вершины которых принадлежат объедине-
нию цепей Л, В и [и, к| и которые содержат цепь [и, р].
Существуют ли всегда хотя бы три такие цепи?
2) Показать, что если цепи А п В имеют общие
внутренние вершины, но не имеют общих ребер, то су-
ществует не менее четырех цепей сети, содержащихся
в объединении цепей А, В и [и, р], удовлетворяющих
условиям п. 1).
4.48. Доказать эквивалентность следующих двух
определений к-сети.
135
1) Сеть Г (д, Ь) называется п-сетью, если ее ребра
можно ориентировать так, что в каждой простой цепи,
соединяющей полюсы а и Ъ, все ребра направлены
от а к Ъ.
2) л-сетями являются те и только те сети, которые
получаются следующим индуктивным процессом:
а) Сети Г₽ и Г| (рис. 18, а) суть к-сети.
б) Если сети А и В (рис. 18, 6) суть тс-сети, то и сети,
представленные на рис. 18, в, являются ^-сетями.
Рис. 18.
4.49. Показать, что среди всех п-сетей с т (т 4)
ребрами наибольшее число кратчайших цепей имеют
s-разложимые сети.
4.50. 1) Указать вид к-сетей, имеющих максималь-
ное число простых цепей, соединяющих полюсы.
2) Указать вид л-сетей, имеющих максимальное
число тупиковых разрезов.
4.51. Пусть (ш) — максимальное число цепей
л-сети с т ребрами. Показать, что:
1) ? (1)=1;
2) <р (Зд)=Зи (n > 1);
3) <р (Зп+1)=4-Зи (п 1);
4) у (Зп+2)=2-Зл (п 1).
4.52. Верно ли, что максимальное число простых
цепей среди всех сетей с т ребрами имеют п-сети?
4.53. Для каждого п 5 указать Я-сеть с п вер-
шинами, имеющую максимальное число цепей, соеди-
няющих полюсы. Подсчитать для каждого к (1 к п)
число цепей длины к между полюсами.
4.54. Доказать, что для сети с гп ребрами, име-
ющей длину I и ширину t, справедливо неравенство
l-t.
136
4.55. Доказать, что в л-сети пересечение любой
простой цепи между полюсами и любого тупикового
сечения содержит ровно одно ребро.
4.56* . Множество цепей сети Г называется опреде-
ляющим для вершины к, если пересечение множеств
внутренних вершин этих цепей есть {у}. Доказать или
опровергнуть следующее утверждение: для того чтобы
сеть без кратных ребер, не являющаяся р-разложимой,
была неразложимой, необходимо и достаточно, чтобы
для любой внутренней вершины существовало опреде-
ляющее множество цепей.
4.57. Доказать следующее утверждение. Для того
чтобы разложимую сеть Г можно было добавлением
ребер сделать неразложимой, необходимо и достаточно,
чтобы Г не имела кратных ребер и обладала по крайней
мере четырьмя вершинами.
4.58. Построить разложимую сеть с наименьшим
числом ребер и числом вершин п (та 4), которую
нельзя сделать неразложимой последовательной заме-
ной подсетей вида Г’ и Г? на ребра.
§ 5. Оценки в теории графов и сетей
Помеченным (или нумерованным) называется такой
граф (орграф, псевдограф и т. д.), вершинам которого
Приписаны пометки (номера). Через $п будет обозна-
чаться совокупность всех n-вершинных графов (короче,
n-графов), в каждом из которых вершины пронумеро-
ваны числами 1, 2, . . ., п. Через обозначается под-
множество всех графов из $п, каждый из которых имеет
ровно т ребер. Граф с п вершинами и т ребрами будет
называться кратко (та, т)-графом. Графы G и Н из
считаются различными, если существуют две вершины /
и к, смежные в одном из графов, но не смежные в
другом.
Пусть (рл (Р) обозначает число всех графов из $И,
обладающих свойством Р. Говорят, что почти все
п-графы обладают свойством Р,
если lini = 1.
,^=0 I
Пусть т=т (п) — целочисленная неотрицательная
функция, а :ря> и (Р) — число всех графов и.»
обладающих свойством Р. Говорят, что почти все
137
(п, т (п))-графы обладают свойством Р, если
.. <РЯ,т(4 .
,|тт»—г = 1-
«>оо I &н,т I
Группа автоморфизмов графа G (или, короче, группа
графа G) представляет собой множество всех автомор-
физмов графа G с обычной операцией умножения
(последовательного выполнения) автоморфизмов.
Группа графа G обозначается через Г (G). Аналогично
определяется группа псевдографа (орграфа и т. д.).
Группа и-вершиппого графа обычно отождествляется
с изоморфной ей подгруппой симметрической группы 5Я.
Если л — подстановка, определенная на множестве
из п элементов, то ее можно разложить в произведение
непересекающихся циклов. Пусть р. (л),
обозначает число циклов длины к у подстановки л
в ее разложении на непересекающиеся циклы. Набор
О') = (Л< 4 • •, гДе 7*=7fc(тс)> называется вектором
циклосой структуры подстановки к. Если А — не-
которая группа подстановок тг-й степени, то выражение
Z И; tv t2.Q = M|-> 2П^(”
А к=Л
называется цикловым индексом группы А и кратко
обозначается через Z (А). Здесь t2, . . ., tn — так
называемые формальные переменные.
Пусть А — группа подстановок, действующая
на множестве М. Элементы 1ц и Ъ2 из М называются
А-экви валентными, если существует подстановка
переводящая один из этих элементов в другой, т. е.
г. ( Ьр)-- Ь , пли к (Ъ^) = Ъ1. Множество М разбивается
отношением А-эквивалентности на непересекающиеся
классы, называемые орбитами. Справедливо следую-
щее утверждение.
Лемма (Бернсайд). Число орбит А (Л) в мно-
жестве М, определяемых группой А, дается равенством
А(Л) = |/1Г 2 71(4
1L £ А
Пусть на множестве действует группа подстано-
вок А, а на множестве М2 — группа подстановок В.
Степенная группа ВЛ состоит из всевозможных элемен-
138
тов вида (л; о), где л^ А, о £ В, и действует она на мно-
жестве (всех функций, отображающих в Мф
по следующему правилу: (л; °) / (ж) = а (/(п (j))) для
любой функции / (х) из М^. Будем предполагать, что
множество Мг конечное, множество М2 — не более
чем счетное и \Мк | 2 (Л=1, 2). Пусть w. Л/2 —>
—> {0, 1, 2, . . .} — весовая функция, заданная на мно-
жестве М2 п удовлетворяющая условию: при всяком
i=0, 1,2, ... мощность с( подмножества всех элемен-
тов из М2, имеющих вес I, конечна J). Производящая
СО
функция с (х) = 2 сгг'‘ называется перечисляющим ря-
|=о
дом для фигур. Вес (функции f из множества опре-
деляется с помощью равенства w (/) = 2 1У(/(^))- Если
ьем,
группа В равна единичной группе Е, действующей
на множестве М2, то вес w (F) орбиты F в множе-
стве М2', определяемой группой ЕА, равен весу любой
функции / из орбиты F. Число С. орбит веса 1 2) i в мно-
жестве М2' является конечным при всяком I 0. Про-
СО
изводящая функция С (ж) = 2 называется перечи-
сляющим рядом для функций (или перечисляющим ря-
дом для конфигураций). Справедливо следующее утвер-
ждение.
Теорема (Пойа).
С (ж) = Z (Л; с (ж), с (ж2), . .., с (ж”)),
где п — число элементов в множестве (степень
группы Л) и с (ж*) подставляется в цикловой индекс
Z (Л; Ч, • •, Q только на места всех вхожде-
ний переменной tk (1 k п).
5.1. Показать, что:
1) Ш=2©; W„,J = O.
\ т /
1) Часто говорят, что с,- — число «фигур веса 1>> (в мно-
жестве Л/2).
2) Иногда С( называют числом «конфигураций веса I» в мно-
жестве
139
5.2. 1) Найти число различных турниров с п верши-
нами, пронумерованными числами 1, 2, . . ., п.
2) Найти число ориентированных псевдографов
с п нумерованными вершинами и т дугами.
5.3. 1) Показать, что число графов в <^и, у которых
заданные к вершин являются изолированными, равно
2("f)
2) Показать, что число графов без изолированных
вершим в равно
п /п—к\
2 (-irgW 2 Л
к=о /
3) Показать, что почти все га-графы не имеют изоли-
рованных вершин.
5.4. Пусть подмножество состоит из N по-
парно различных графов. Показать, что число попарно
неизоморфных графов в $ не меньше чем Nln\.
5.5. Пусть ф (т) — число попарно неизоморфных
связных графов с т ребрами. Показать, что:
1) ф (т)
2
2) ф при т-*со.
5.6. Показать, что число попарно неизоморфных
псевдографов, не имеющих изолированных вершин
и обладающих т ребрами, не превосходит (стп)”‘, где
с — константа, не зависящая от т и к.
5.7. Показать, что число попарно неизоморфных
/с-полюспых сетей с т ребрами без петель и без изолиро-
ванных вершин не превосходит (2m)*(cm)2’", где с — кон-
станта, не зависящая от т и к.
5.8. Доказать, что число попарно неизоморфных де-
ревьев с т ребрами не превышает числа попарно различ-
ных плоских корневых деревьев с т ребрами.
5.9. 1) Показать, что число попарно различных
плоских корневых деревьев с т ребрами не превосхо-
/2т\
дити)-
140
2) Найти асимптотическое поведение числа q (т)
плоских корневых деревьев с т ребрами при т оо.
5.10. Используя теорему Кэли, утверждающую,
что число попарно различных деревьев с п нумерован-
ными вершинами равно п”~2, показать, что число по-
парно неизоморфных деревьев с п вершинами не меньше
чем cnrTlfien, где Пшся = \/2к.
я->со
5.11. Показать, что число попарно различных де-
ревьев с п нумерованными вершинами, у которых вер-
шина с номером 1 имеет степень к, равно Q _ ^(п—
5.12. Найти число графов в <^я, являющихся ле-
сами.
5.13* . Показать, что число тех лесов в <^я, у кото-
рых заданные вершины / и к принадлежат разным ком-
понентам связности, равно 2пп~3.
5.14. Пусть tf> (п) — число попарно различных кор-
невых деревьев с п висячими вершинами, таких, что
степень корня равна двум, а степень каждой вершины,
отличной от корня и от висячей вершины, равна трем.
1) Показать, что число (я) равно числу способов,
которыми можно расставить скобки в выражении
: Ъ2 : . . . : Ъп, чтобы вновь полученное выражение
имело смысл.
2) Показать, что ср (га)=-^-^2” ~
5.15. 1) Показать, что число попарно неизоморфных
двухполюсных л-сетей с т ребрами не превосходит
удвоенного числа попарно различных плоских корне-
вых деревьев с т висячими вершинами.
2) Показать, что число попарно неизоморфных
л-сетеи с т реорами не превосходит 21 ).
5.16. Найти число попарно нейзоморфных сетей
Г (а, Ь) с п вершинами и т ребрами, обладающих сле-
дующими свойствами:
1) сеть Г (а, Ь) является s-разложимой;
2) все вершины сети Г (а, Ь) минимальны.
Примечание. Полюсы а и b сети Г (а, Ь)
считаются неравноправными; первый из них является
входом, а второй выходом сети. При изоморфном отобра-
жении сети Г на сеть G вход (выход) сети Г должен
соответствовать входу (выходу) сети G.
141
5.17. Пусть Ф (n, т)—число различных формул
над множеством связок {&, \/} и множеством перемен-
ных {гг, х2, . . ., х„} с т вхождениями символов связок.
1) Показать, что Ф (ге, т) равно числу попарно раз-
личных корневых деревьев, у которых каждая висячая
вершина помечена некоторым символом из множества
{хп х2, . . ., хп}, а каждая вершина, отличная от вися-
чей, помечена одним из символов &, \/.
2) Показать, что Ф (п, т) =—-—2ипт+1.
' ' т -j- 1 \ т J
Примечание. Формулы считаются различ-
ными, если они представляют собой различные слова
в алфавите {&, (,), ^1, • • •, Тп}-
5.18. Пусть Ф (м, т, к) — число различных формул
над множеством связок {&, \Д —} и множеством пере-
менных {л-j, х2, . . ., хп} с т вхождениями символов
переменных и к вхождениями символа —. Показать, что
Ф (п, т, А)<- (2т ~ 2>) Зт^пт.
' 7 т \ т—1 /
5.19. Показать, что число несвязных графов в m
не превосходит
С"/2] [(п\ \
Л—1 \ /
5.20. Показать, что число графов в имеющих
ровно две компоненты связности, не превосходит
5.21. Показать, что число Л-связпых графов в
не являющихся (&-{- 1)-связными (к^п — 2), не превос-
ходит
[n-fel
m ffk\ \ t 2 J
0 2 2 (’7>
/ (п — к\ \
X
— г (п — к — г)
ш—/
142
Указание. При к п—2 в графе, не являю-
щемся (&4-1)-связным, существует к вершин, удаление
которых приводит к несвязному графу.
5.22. Показать, что число попарно различных связ-
ных подграфов куба Вп, порожденных подмножествами
из к вершин, не превосходит 2” (Считать, что
вершины куба Вп пронумерованы числами от 1 до 2").
5.23. Показать, что у почти всех n-графов радиус
больше единицы, оценив сверху число графов в $п,
имеющих вершину степени п—1.
Пусть p(G)— некоторый числовой параметр графа G.
Пусть р(п) — 2 W 2 p(G) — среднее значение пара-
6
метра р, a Dp(rc) = 2 2 (p(G)— pin))2— дисперсия
параметра р. Аналогично можно определить среднее зна-
чение и дисперсию параметров графов из Пусть
6 > 0, 8„ (0) — доля тех графов G из $п, для которых
p(G)J>0, а Дя(б)— доля таких графов G из $н, что
|p(G) — Для различных оценок и доказатель-
ства свойств почти всех графов часто используются
следующие неравенства (Чебышев):
О)
Дв(0)<-^.
(2)
Пусть, например, р (G)— число изолированных вер-
шин графа G. Требуется показать, что р (G) — 0 для
почти всех n-графов. Пусть gn (г) — число графов из <^я,
у которых вершина с номером I является изолирован-
ной. Тогда
/>(«) = 2"© 2 P(G) = 2'®2?,(O-
•'=!
____
Очевидно, что gn(i) = 2^ 2 / для всех 1 = 1, п. Отсюда
р(п) = п 2~г‘. Полагая в (1) 0=1/2, получим, что доля
графов G из $я, для которых p(G))>l/2, не превосхо-
143
дит п2 кН. Но limn • 2 к+1 = 0. Следовательно, для почти
w->co
всех n-графов p(G)<^l/2, т. е. p(G) — 0.
Пусть теперь p(G)— число ребер в графе G. Пока-
жем, что у почти всех n-графов p(G)=yQ)(l -ф-ея),
где limsn = 0. Имеем /3(п) = 2 © 2 Р(^) = 2 © X
м->со
X 2 £>(*> f)> г«е Sn^> /) = 2\2/ — число графов, уко-
(•,>)
торых пара вершин (г, /) соединена ребром. Таким об-
разом, p(n)=yQ). Подсчитаем дисперсию:
Dp (n) = 2'0 2 (P(G)-P« =
G
= 2’© 2 Z>2(G)-(/>«.
Пронумеруем все пары вида (г, /), 1 i < j n,
числами от 1 до и пусть gB(v, р) —число графов
G из о^„, у которых пары с номерами чир. являются
ребрами. Тогда
2 p2(G)=2 2 р)=2 §п(у> v) + 2 2 &(*> г)-
Ge®1» •»=! Ц=1 »=! v<n
Но p) = 2W , если v=4=p.. Поэтому
ожЧ(3+4Ш-9-ШЧ(Э-
Полагая в (2) 9 = \/гар(п), получим, что доля тех гра-
фов G£<^„, для которых |p(G) — yQ)! (2) ’ не
превосходит 1/п. Отсюда вытекает, что для почти всех
графов p(G) = yg\(l 4-ея), где lime„ = 0.
/ »->оэ
5.24. Пусть p(G) — число пар различных вершин
графа G из <^я, для которых не существует цепи длины,
144
меньшей, чем 3, соединяющей эти вершины. Пусть
^(га) = 2-© 2 p(G).
1) Показать, что р (га) — yQX^)” *
2) Показать, что у почти всех га-графов отсутствуют
вершины, расстояние между которыми больше двух.
3) Используя результаты задач 5.23 и 5.24, 2), по-
казать, что у почти всех га-графов радиус и диаметр
равны двум.
5.25. Показать, что среднее число гамильтоновых
циклов в графах G из $п равно ^2,i+11 '.
5.26. Найти среднее число циклов длины три в гра-
фах С_из ^П:т.
5.27* . Используя неравенство Чебышева (2), по-
казать, что у почти всех (и, т (га))-графов, где т (га) =
=[ra/ln (п In га)], число изолированных вершин равно
п (1 — s (га)), где lim е (га) = 0.
и->оэ
5.28* . Пусть к — целое и к'^2. Доказать, что
2-А
если т — т (п) = ср (га) • га *-1(где<р(га)-> оопри га-> со),
то почти все (га, /га)-графы содержат полный подграф
с к вершинами.
5.29. Найти среднее число /с-вершинных независи-
мых множеств в графах G из <^я.
5.30. Пусть к — натуральное число. Подсчитать
среднее число
&„.т-
5.31. Пусть
вершин степени к в графах G из
р (G) — целочисленный неотрицатель-
ный параметр, а р (га) — его среднее значение для
графов G из [§п. Показать, что если lim р (га) = О, то
для почти всех графов p(G) = 0.
5.32. Найти цикловой индекс группы автоморфиз-
мов графа G.
1) G — цикл длины 4;
2) G=K2> 3;
3) G—K5—{я}, где х — произвольное ребро гра-
фа Къ.
5.33. Пусть (j) = (ji, 72’ • • •> 7Я) — произвольное
разбиение числа /?, т. е. 7i+2/2+. . .+га/„=га, где jk —
145
целые неотрицательные числа (1 к п). Через h (/)
обозначается число всех таких подстановок симме-
трической группы Sn, у которых векторы цикловой
структуры совпадают с (j).
1) Доказать, что h (/) - —-——------,
П . 11с I
к=1
2) Доказать, что
w А_1
где сумма борется по всевозможным разбиениям (у)
числа п.
3) Показать, что цикловой индекс Z (Дн) равен
коэффициенту при х“ в разложении функции
/, 1 *24
exp Up: —j
I м*
г к
в ряд по степеням х.
4) Убедиться в справедливости рекуррентного соотно-
И
шепия Z (S„) = — tkZ (Sri_!;), где (по определению)
* = 1
положено Z (50) — 1.
5.34. Пусть Ап — знакопеременная группа степени
п (т. е. Ап — подгруппа группы Sn (п 2), состоящая
из всех четных подстановок). Доказать, что
(‘'lя’ ^2> • • •> ^п) =
= Z(SU; tv t2.....tn) + Z(S- tv -t2.......(-1ГЧ).
5.35. Перечислить все орбиты в множестве вершин
графа G, определяемые группой Г(С), если:
1) G = К2 3 — (а-), где х— произвольное ребро графа
^2,3;
2) G = К2 х С4.
5.36. Пусть на n-элементяом множестве Л/1 дей-
ствует группа Л, а на конечном множестве М2 действует
единичная группа Е. Доказать, что число орбит в мно-
1-i‘j
жестве М%*, определяемых степенной группой Ел,
«вдается формулой
я раз
N(EA)=.Z (А\ |М2|, \М2\, .. ,,\М2\),
где правая часть представляет собой результат под-
становки числа |Л/21 в цикловой индекс Z (A; t2,...
. . tK) па места всех вхождений переменных
h (1 < к < п).
5.37. Пусть на тг-элементном множестве М действует
группа А. Рассмотрим два произвольных г-подмноже-
ства множества М\ М1={а1, . . ., ar}, M2~{b1, . . -,br},
1 г п—1. Они называются А-эквивалентпными,
если существует такая подстановка к в группе А,
что к (а..) = Ь/у, где / = 1, . . ., г. Отношение Л-экви-
валентпости разбивает все r-подмпожества из М на
классы А-эквивалентных подмножеств. Доказать, что
коэффициент при хг в выражении Z (И; Ц-х, 1 Д-а?2,
. . ., l+xw) (получающемся из циклового индекса
Z(A; i1( i2,.. tn) заменой каждого вхождения переменной
tk на 1+хД равен числу классов Л-эквивалентных г-
подмножеств в множестве М.
СО
5.38. Пусть Т(х) = 2 Tkxk — производящая функция
Г=1
для корневых деревьев; здесь Тк означает число
всех попарно неизоморфных корневых деревьев с к
вершинами, включая корень. Возьмем гг произвольных
корневых деревьев (п 1) и корень каждого из пих
соединим ребром с новой вершиной у0. Будем считать
вершину v0 (и только ее) корнем нового дерева. Степень
корня v0 равна п. Используя описанную конструкцию
порождения корневых деревьев, доказать, что
00
Т (х) = х 4- х 2 Z (5„; Т (х), Т (х3), ..., Т (х")).
5.39. Доказать следующее рекуррентное соотношение: -
-7 2 2 гТ'т-‘*
к=1 г I к
IsJrsS*
147
здесь п 1 и Tj равно числу всех попарно неизоморф-
ных корневых деревьев с j вершинами, считая и корень
(Л = 1).
со
5.40. Пусть g(x) = 2 Snx” — производящая функция
п=1
со
для графов и I (х) — 2 1пхП — производящая функция
П=1
для связных графов. Коэффициент gn (соответственно Zn)
равен числу всех попарно неизоморфных га-вершинных
графов (соответственно связных графов). Доказать, что
СО
g И = 2 Z (5я; I (х), I (х2), ...,1 (хв)).
5.41. Пусть на re-элементном множестве Мг действует
группа А и на r-элементном множестве М2 действует
группа В. Найти число орбит в множестве опре-
деляемых степенной группой ВА.
1) А — Еп, В — Ег (т. е. Л — единичная группа сте-
пени п, а В — единичная группа степени г);
2) А = Еп, B = Sr;
3) 4 = S„, B = Er;
4*)4 = 52, B = Ss.
5.42. Пусть t(x) и s(x)—производящие функции для
турниров и сильных турниров соответственно, т. е.
СО со
Z (х) = 2 1пх” и s (х) = 2 Snxn, где tn — число всех по-
Я=1 Я=1
парно неизоморфных турниров с п вершинами, a sn—
число всех попарно неизоморфных сильных турниров
с п вершинами. Доказать, что t (х) = 2 (ж)>
§ 6. Реализация булевых функций
контактными схемами и формулами
Сеть Г с А: полюсами, в которой каждое ребро поме-
чено буквой из алфавита {хп х2, . . ., хп, xlt х2, . . ., хя},
называется к-полюсной контактной схемой, реализующей
булевы функции переменных х1,х2,. . .,хя, или, короче,
<к, щ>-схемой. <2, и>-схемы будут называться Хп-схемами.
148
Сеть Г называется сетью контактной схемы. Контакт-
ная схема является связной (сильно связной, параллельно-
последовательной и т. д.,) если таковой является ее сеть.
Параллельно-последовательная контактная схема на-
зывается кратко ^-схемой. Ребра схемы, помеченные
символами переменных или их отрицаний, называются
контактами. Контакт называется замыкающим, если
он помечен символом переменной, и размыкающим,
если он помечен символом отрицания переменной.
Пусть Ех и Е2 — две /с-полюсные контактные схемы,
полюсы каждой из которых помечены буквами at, ,а2,
. . ., ак. Схемы Ег и Е2 называются изоморфными,
если их сети изоморфны и при этом а) соответствующие
ребра помечены одинаково; б) соответствующие полю-
сы помечены одинаково. Пусть а и Ь — два полюса
контактной схемы Е, [а, — некоторая цепь, соединя-
ющая а и Ь, и К 1а Ь} — конъюнкция букв, приписанных
ребрам цепи [а, &]. Функция /а4 (ж"), определяемая
формулой
= (3)
[а, 6]
в которой дизъюнкция берется по всем простым цепям
схемы, соединяющим полюсы а и Ъ, называется функ-
цией проводимости между полюсами а, Ъ схемы Е.
Говорят, что схема Е реализует функцию g (хп), если
в ней существуют полюсы а и Ъ, такие, что g (jc")=fab (£")
Контактная схема с Zc-pl полюсами называется
(1, к)-полюсником, если один из ее полюсов выделен
(он будет обозначаться буквой а), а остальные равно-
правны между собой (они будут обозначаться через
b. (i = 1, /с)). Говорят, что функция g(xw) реализуется
(1, &)-полюсником, если существует такой полюс
М1 &), что tabi (£n)=g В тех случаях,
когда число полюсов схемы не указывается, речь всегда
будет идти о двухполюсных контактных схемах. Две
контактные схемы называются эквивалентными, если
они реализуют одну и ту же булеву функцию. Слож-
ностью контактной схемы называется число ее контак-
тов. Контактная схема, имеющая наименьшую слож-
ность среди всех эквивалентных ей схем, называется
минимальной. Сложностью булевой функции / в классе
контактных схем (обозначение: Lk (/)) называется слож-
149
ность минимальной контактной схемы, реализующей /.
Сложностью булевой функции f в классе ~-схем назы-
вается число контактов в минимальной к-схеме, реали-
зующей / (обозначение: LK (/)). Сложностью булевой
функции / в классе формул над множеством связок
{\/, &, } будет называться число вхождений симво-
лов переменных. Сложность функции / в этом классе
формул обозначается через L® (/).
Схемой из функциональных элементов называется ори-
ентированная бесконтурная сеть, полюсы которой де-
лятся на входные и выходные. Входные полюсы поме-
чаются символами переменных. Выходные полюсы
называются выходами схемы. Каждая вершина, от-
личная от входного полюса, помечена функциональным
символом (или символом логической связки). При этом
должны выполняться следующие условия: 1° Степень
захода каждого входного полюса равна нулю. 2° Сте-
пень захода каждой вершины, отличной от входного
полюса, равна числу мест функционального символа
(или связки), которым эта вершина помечена.
Понятие функции f 4, реализуемой в вершине i схемы Е,
определяется следующим образом. Если вершина i
совпадает с входным полюсом, который помечен сим-
волом х. то f(—x. Пусть вершина i помечена г-ме-
стным функциональным СИМВОЛОМ и пусть <f>15 . . .
— функции, реализуемые в вершинах, из которых
исходят дуги, заходящие в вершину I. Тогда /, = <р (<Рц . ..
. . ., <рг). Говорят, что функция / реализуется схемой Е,
если существует выход схемы, в котором она реали-
зуется. Схемы из функциональных элементов с одним
выходом, у которых входные полюсы помечены симво-
лами хг, . . ., хп, а вершины, отличные от входных полю-
сов — символами V, , будут называться здесь Ха-
функционалъными схемами. Сложностью схемы из функ-
циональных элементов называется число ее вершин,
отличных от входных полюсов. Х"-функциональная
схема Е, реализующая функцию /, называется мини-
мальной, если всякая другая ^’-функциональная
схема, реализующая /, имеет сложность, не меньшую,
чем сложность схемы Е. Под сложностью булевой функ-
ции / в классе схем из функциональных элементов здесь
понимается сложность минимальной Х'-функцио-
нальной схемы, реализующей функцию /. Сложность
150
функции / в этом классе схем будет обозначаться через
L(f).
6.1. Пусть / (5^)=х1фжа. Показать, что L (J (£2))=4.
6.2. Показать, что для булевой функции, отличной
от константы, минимальная контактная схема, реали-
зующая эту функцию, является сильно связной.
6.3. Найти число булевых функций / (л?!, х2), реали-
зуемых контактными схемами сложности 3.
• 6.4. 1) Показать, что для каждого натурального т
существует минимальная контактная схема слож-
ности т.
2) Показать, что не существует минимальных кон-
тактных схем сложности 4, содержащих только замы-
кающие контакты с пометками из множества {a?lt х2, х3}.
6.5. Показать, что если тп>«-2"-1, то ни одна
из .¥"-схем сложности т не является минимальной.
6.6. Показать, что функция / тогда и только тогда
зависит существенно от переменной х, когда в мини-
мальной схеме, реализующей /, присутствует контакт,
помеченный переменной х или ее отрицанием.
6.7. Для контактных схем, изображенных на
рис. 19, а, б, в, 20, а, б, в, найти функции проводи-
мости fal.
6.8. Построить контактные схемы, реализующие
функцию /.
1) / (£3)=(х. V Х2 V ъ) (^V V *»);
2) / (г3) = хгх2 ф х^с3 ф х^,
3) / (£®) = (00011111);
4) /(£®) = (1Ю10001);
5) /(£3)=Я1 фХгфЖз.
6.9. Для каждой из функций предыдущей задачи
построить ^-функциональные схемы.
6.10. Для функции / построить контактную схему
сложности не выше L, упростив предварительно фор-
мулу, с помощью которой / задана.
1) (^1 V ®2^'з) ((^"1 V ^2) (^2 V ^4) V ("^3 V ^4) V
V ==
2) (г1 V Жг) ((^А V ^2®з) Х6 V (^2 V V's) (^2 V ^3) V
\/ (*^1^2 \/ ^1^2 \/ x^j х3 \/ х^х2 \/ x^x^j L — 5,
3) ^^2^-3 (С^4 \/ ’^1^'5) (*^6 V V (^G*^7 \/
& (х^ъ \/ TgXgX?) \/ (хг \/ х2) \/ х3) (х5 \/ х7У), L — 6.
6.11. Для каждой из функций .предыдущей зада-
чи построить схему из функциональных элементов
сложности, не превышающей 6, реализующую эту
функцию.
п
6.12. Пусть v (а) =2 2’a<—номер набора а==(а1(
»=i
а2, . • •! «„)• Построить контактную схему с не более чем
десятью контактами, реализующую функцию
I 11 если v(ai’ a2’ аз) < 7 (а4> аз> аб)»
/ (а6) = 1 „
( 0 в противном случае.
6.13. Построить контактную схему, реализующую
функцию / (ж6), равную единице тогда и только тогда,
когда (хх, х2, х3) (х4, х5, х6).
6.14. Построить контактную схему, реализующую
сложение двухразрядных двоижых чисел. Точнее,
построить контактную схему с полюсами а, Ьо, &х, Ь2,
в которой для каждого i=0,l,2 функция проводи-
мости fabf (ж4) равна z,-, где z,. £ {0, 1} и определяется
из равенства 4zx -f- 2z2 z3 = 2 (xL -|~ x2) -|- x2 x±.
6.15*. Построить схему из функциональных эле-
ментов, удовлетворяющую следующим условиям.
1° Схема реализует три функции хг, х2, х3.
2° Вершины, отличные от входных полюсов, поме-
чены символами \/, &, —.
3° Имеется не более двух вершин, помеченных симво- 1
лом отрицания.
6.16. Показать, что (f) Lk (/) для любой бу-
левой функции /, отличной от константы.
152
6.17* . Привести пример функции / (я3), для которой
Указание. Рассмотреть функцию, реализуе-
мую схемой, изображенной на рис. 19, а.
Пусть двухсвязная двухполюсная контактная схема
2 является плоской (т. е. ее сеть Г (а, 6) является пло-
ской) и ее полюсы а и b лежат в одной грани. Проведем
в ’этой грани ребро (а, Ь) так, чтобы сеть Г', получен-
ная из Г добавлением ребра (а, Ь), осталась плоской.
Выберем в каждой грани сетй Г' по одной вершине.
Рис. 20,
Построим на выбранных вершинах граф G*, двойствен-
ный к графу G сети Г'. Каждое отличное от (а, Ь) ребро
графа G* пересекает некоторый контакт схемы 2. По-
метим это ребро той буквой, которой помечен пересе-
каемый им контакт. Вершины графа G*, расположенные
в гранях сети Г', разделенных ребром (а, Ь), обозна-
чим через а*, Ъ* и назовем полюсами. Удалим ребро
(а*, Ь*) из G*. В результате получится двухсвязная
схема 2* с полюсами а* и Ь*. Схема 2* называется
схемой, двойственной к 2.
6.18* . Показать, что схема 2*, двойственная к пло-
ской двухсвязной схеме 2, реализует булеву функцию,
двойственную к функции, реализуемой схемой 2.
Указание. Установить взаимно однозначное
соответствие между цепями схемы 2 п разрезами схе-
мы 2*.
153
6.19. Построить схемы, двойственные к схемам,
изображенным на рис. 19, а, б, 20, а.
6.20. Доказать, что для всякой булевой функции /
выполняется равенство LK (f)=LT (/*).
6.21. Показать, что если Lk (/) ^7, то Lк (/)=Lk (/).
Контактная схема называется бесповторной, если
из того, что некоторое ребро помечено буквой х или ж,
вытекает, что всякое другое ребро имеет пометку,
отличную от х и ж.
6.22. Показать, что сильно связная бесповторная
контактная схема реализует функцию, существенно
зависящую от всех перемен-
ил*-—-—-/s. ных, встречающихся в схеме.
6.23. Показать, что сильно
/С связная бесповторная схема
минимальна.
~в 6.24. Показать, что если
рнс> 21. к минимальной схеме при-
соединить контакт, помечен-
ный новой переменной, так,
чтобы получилась сильно связная схема, то построен-
ная схема также будет минимальной.
6.25* . Пусть / — функция, реализуемая схемой,
указанной на рис. 21. Доказать, что функция, двой-
ственная к /, не может быть реализована бесповторной
схемой.
6.26* . Верно ли, что для всех булевых функций /
выполняется соотношение Lk (j)=Lk (/)?
6.27. Пусть /ai и fad — функции проводимости трех-
полюсной контактной схемы 2Р a f и feh — функции
проводимости трехполюсной контактной схемы 22. Пусть
2 — схема с полюсами а и е, полученная из схем 2t
и 22 отождествлением полюса Ь с полюсом g и полюса
d с полюсом е. Верно ли, что схема 2 реализует функцию
6.28. 1) Доказать, что функция / монотонна тогда
и только тогда, когда существует контактная схема,
реализующая / и не содержащая размыкающих кон-
тактов.
2) Верно ли, что минимальная контактная схема,
реализующая монотонную функцию, не содержит раз-
мыкающих контактов?
154
Булева функция / (£") называется монотонной по
переменной хи если ее можно представить в виде
/ С® ) == S (^2> ^з» • • • > *„) V С^г» З'З’ • • • > ф)1
Функция / (хп) — квазимонотонна по переменной хъ
если она монотонна по xv или становится монотонной
по хх после замены хх на £х. Аналогично определяется
монотонность н квазпмонотонность по
6.29. Доказать, что функция / (хп) квазимонотонна
по х2 тогда и только тогда, когда существует контакт-
ная схема, реализующая функцию / (5") и не содержа-
щая либо замыкающих, либо размыкающих контактов.
6.30. 1) Доказать, что минимальная контактная
схема, реализующая функцию жхфж2, содержит 4 кон-
такта.
2*) Доказать минимальность схемы, изображенной
на рис. 20, в.
6.31* . Построить минимальную контактную схему
для функции /.
1) f (^) — (Л V Х.2 V Хя) Ху V ХуХ2Х2,
2) / (х )-ХуХ2Х^ (ф ХуХгХу ф ХуХ.уХу ф Х2Х2Ху,
3) /(i4) = (0001011101111111).
6.32, Показать, что число S (ге, т) связных попарно
неизоморфных контактных Х”-схем сложности, не боль-
шей т, не превосходит {спт)т, где с — константа, не
зависящая от п и т.
6.33. Показать, что число Р (п, т) связных попарно
неизоморфных к-схем сложности, не большей т, реа-
лизующих булевы функции переменных жх, х2, . . ., хя,
не превосходит (сп)т, где с — константа, не зависящая
от п и т.
6 .34. Показать, что число Ф (п, т) попарно различ-
ных формул сложности т над множеством связок
(V, &, —) и множеством переменных xlt х2, .... хп
не превосходит (сп)т, где с — константа, не зависящая
от п и т.
При получении нижних оценок сложности реализа-
ции различных классов функций схемами и формулами
часто используются так называемые «мощностные со-
ображения». Примером может служить следующее
утверждение.
155
Пусть S (п, т) — число схем из некоторого класса К,
каждая из которых реализует булеву функцию, зави-
сящую от переменных xlt ж2, . . .,ж„, и имеет слож-
ность, не большую, чем т. Пусть <р (п) — число буле-
вых функций / (ж'г) в некотором множестве?!)?. Тогда,
если S (п, т) < (п), то в 50? найдется функция Дж"),
не реализуемая в классе К схемой сложности, мень-
шей или равной т.
6.35. Показать, что для всякого s >Ои достаточно
больших п существует самодвойственная f (х"), для
которой одновременно выполняются неравенства:
о«-1
a) б)ЛЛ/)>^(1-е).
6.36. Показать, что для всякого s >Ои достаточно
больших п существует функция / (хп), являющаяся
суперпозицией функции (р (х, у, z)=xy V z и такая, что
6.37. Пусть Л (/г) = max Л (/). Показать, что для
/er?
всякой самодвойственной функции / (£") справедливо
неравенство L (j (хп)) ^.Цп — 1) 4п.
6.38. Булева функция F (у”1) обладает свойством Un,
если любую булеву функцию / (х") можно получить из
F (ут) посредством подстановки констант и переобо-
значения переменных (допускаются отождествления).
1) Показать, что функция уху2 обладает свой-
ством U1.
2) Найти функцию с минимально возможным числом
переменных, обладающую свойством U2.
3) Пусть т (п) — минимально возможное число
переменных у функции, обладающей свойством U .
2” ”
Показать, что т (п) 3 • 2”-1.
log2(n + 2) v
6.39. Показать, что существует Х”-функцио-
нальная схема сложности 22'!—п, реализующая все
функции, зависящие от переменных xL, . . ., хп.
При построении двухполюсных контактных схем,
реализующих функции алгебры логики, широко ис-
156
пользуется так называемый метод каскадов. Опишем
его. Пусть / (xlt х2, . . хп), п 2, — функция алгебры
логики, которую нужно реализовать контактной схемой.
Через = п — 1) обозначим множество всех таких
функций алгебры логики, каждая из которых зависит
только от переменных х<+1, а:,-+2, . . ., хп и может быть
получена из функции / (ж”) в результате подходящей
подстановки нулей и единиц на места переменных
хх,-х2, . . ., х{. Каждому множеству 2^ взаимно одно-
значно сопоставим множество Vt, элементами которого
являются точки плоскости, называемые вершинами
i-ro ранга. Добавим еще два полюса: входной полюс а
и выходной полюс Ъ. Полюс а является вершиной ну-
левого ранга, полюс Ь — вершиной n-го ранга. Мно-
жество вершин схемы Е, реализующей функцию / (£”),
Я—1
будет совпадать с {a} (J {b} U L) V(. Множество контак-
•=i
тов схемы S можно описать так: пусть vf —
произвольная вершина i-ro ранга (п—2 i 0), и
пусть ей соответствует функция <р (а:<41, #,Ч2, • • •> жп)
из множества 21^ (при i=0 функция <р совпадает с функ-
цией/ (£")). Функции <р (0, х,.+2, . . ., хп) и <р (1, х.+2, . ..
. ..,хп) принадлежат множеству 2(<+1 и им отвечают
некоторые вершины у'+1 и <л+1 соответственно (если
функции <р(0, xi+2, ...,х„) и <р(1, ж<+2,.. .,жв) равны, то
вершины и l>"+1 совпадают). Вершина соединена
в схеме Е контактом 2<+1 с вершиной к'+1 и контактом
я:<+1 с вершиной о"+1. Наконец, вершины (п — 1)-го
ранга соединяются с вершиной re-го ранга (полюсом Ь)
в соответствии со следующим правилом:
1) если вершина v из отвечает функции хп,
то она соединяется с полюсом Ъ контактом жя;
2) если вершина v отвечает функции хп, то опа соеди-
няется с Ь контактом 5?я;
3) если вершина и сопоставлена функции, тождест-
венно равной единице, то она соединяется с Ъ двумя
параллельными контактами хп и
4) если вершина и сопоставлена тождественному
нулю, то вершина v с полюсом Ь не соединяется.
6.40. Используя метод каскадов, построить схему,
реализующую функцию /.
1) / (х3) — Х1х2 ф х.л;
2) / (±‘) = ххх2 \J х2х3 V x1Xi;
157
3) /(«")=«1©®2© ••• ©*»;
4) / (x”) = x1xa ... x„ V • • • XJ
5) / (^") — V X1 • • • X(-1X4+1 • • • Xn’
•=1
6.41. 1) Показать, что если / (x“)^0, то при построе-
нии по методу каскадов контактной схемы, реализую-
щей функцию /, можно исключить из всех множеств 21,
функции, тождественно равные нулю.
2) Показать, что контактная схема, получаемая при
таком построении, является сильно связной.
6.42. 1) Пусть функция / (х"), п 2, существенно
зависит от всех своих переменных. Доказать, что схема,
реализующая функцию / и построенная по методу кас-
кадов, является сильно связной и не содержит парал-
лельных контактов вида xjy х^ тогда и только тогда,
когда / — линейная функция.
2) Привести пример нелинейной функции / (х"),
п 2, существенно зависящей от всех своих перемен-
ных и такой, что схема, реализующая ее и построенная
по методу каскадов, не содержит параллельных контак-
тов вида Xj, Xj.
6.43. Справедливо ли следующее утверждение: если
функция / (fn), п > 2, существенно зависит от всех
своих переменных и контактная схема, реализующая /
и построенная по модифицированному методу каскадов,
указанному в задаче 6.41,1), содержит п контактов,
то / = х°>хр... х?« (где а, £{0, 1})?
6.44. Опровергнуть следующее утверждение: если
функция / такова, что при некотором i множества 21,
и 21,+1, используемые в методе каскадов, не содержат
функций, тождественно равных нулю и единице, но
в каждом из них не менее трех функций, то схема, реа-
лизующая / и построенная по методу каскадов, яв-
ляется неплоской J).
6.45. Привести пример функции /, для которой
реализующая ее схема, построенная по методу каскадов,
является неплоской.
*) Имеются в впду схемы без источникового ребра, т, е.
без дополнительного ребра, соединяющею полюсы.
Г л а в а V
ЭЛЕМЕНТЫ ТЕОРИИ КОДИРОВАНИЯ
§ 1. Коды с исправлением ошибок
Пусть А и В — два конечных алфавита и R — не-
которое множество конечных слов в алфавите А.
Однозначное отображение ср множества R в некоторое
множество слов в алфавите В называется кодирова-
нием множества R. Образ С множества R при ото-
бражении ср называется кодом множества R. Слова из С
называются кодовыми словами-, при этом, если слово w
из R отображается в слово и из С, то и называется кодом
слова w. Слова из R называются сообщениями, алфавит
А — алфавитом сообщений, алфавит В — кодирующим
алфавитом. Если кодирующий алфавит В состоит из
двух букв (в этом случае будем полагать, что В =
= {0, 1}), то кодирование ср и соответствующий код С
называется двоичным. Код называется равномерным
или блочным, если все кодовые слова имеют одинаковую
длину. Блочный двоичный код, в котором каждое
кодовое слово имеет длину п, представляет собой под-
множество вершин единичного и-мерного куба. Булева
функция /с (сгл), равная единице па множестве С и
нулю вне С, называется характеристической функцией
двоичного блочного кода С. Пусть р (а, j-i) — обычное
расстояние Хэмминга между вершинами а и р из В”,
равное числу координат, в которых а и р различаются.
Величина d (C)=min р (5, Р), где минимум берется по
всем парам различных вершин, принадлежащих коду
С С Вп, называется кодовым расстоянием кода С.
Код С С й” с кодовым расстоянием d будет называться
159
кратко <.n,d>-KodoM. Максимально возможная мощ-
ность <п,й>-кода обозначается через т (n,d),
а <ге, й>-код, мощность которого равна т (n, d), назы-
вается максимальным. Плотно упакованным назы-
вается <н, 2с/+1>-код, удовлетворяющий следующему
условию: для всякой вершины а £ Вп существует ко-
довое слово р, для которого р (а, р) d. Блочный двоич-
ный код называется эквидистантным, если расстояние
между любыми двумя кодовыми словами одинаковое.
Код С С В" называется равновесным, если всякое
кодовое слово имеет один и тот же вес, т. е. если суще-
ствует такое целое к (0 к п), что С С В%. Это число
к называется весом равновесного кода. Величина шах |С |,
где максимум берется по всем <п, й>-кодам веса к,
обозначается через т (п, к, d).
Пусть слова блочного двоичного кода С передаются
по каналу связи, в котором могут происходить искаже-
ния передаваемого слова. Передачу по такому каналу
можно рассматривать как некоторые преобразования
передаваемых слов. Здесь будут рассматриваться только
такие преобразования двоичных слов, которые не ме-
няют длину слова и состоят в замене некоторых букв
на противоположные, т. е. в замене 0 на 1 и 1 на 0.
Если слово а при передаче преобразовалось в слово р,
отличное от а, то говорят, что в канале произошли
ошибки. Если i-я буква переданного слова а отличается
от i-й буквы полученного слова р, то говорят, что про-
изошла ошибка в i-м разряде. Если полученное слово
отличается от переданного в i разрядах, то говорят,
что произошло t ошибок. Очевидно, что число ошибок,
имевших место при передаче, равно расстоянию Хэм-
минга между переданным и принятым словами.
Пусть С С.Вп — двоичный код. Произвольное одно-
значное отображение ф множества В" на множество С
называется декодированием. Пусть а £ С, a _ф-1 (а) — мно-
жество всех таких вершин р из В", что ф (р) = а. Пусть
S" (а) — множество всех слов, которые получаются из
кодового слова а в результате не более чем t ошибок
(очевидно, что S" (а) есть шар радиуса t с центром а).
Говорят, что код С исправляет t ошибок, если сущест-
вует такое декодирование ф, что Sr‘ (a) CZ ф~* (а) для каж-
дого а£С. Код С обнаруживает t ошибок, если любое
слово, которое можно получить из произвольного кодового
160
слова а в результате не более t ошибок, отлично от любою
слова из С\{а}.
1.1. Показать, что код С С Вп исправляет t ошибок
тогда и только тогда, когда р (v, w) 2i+l для лю-
бых двух различных кодовых слов и и w из С.
1.2. Верно ли, что код С CZ Вп, исправляющий t
ошибок, обнаруживает
1) не менее 2i+l ошибок;
2) не менее 2t ошибок;
3) не более 2t ошибок?
1.3. Показать, что из всякого подмножества С С В"
можно получить код, обнаруживающий одну ошибку,
удалив из С не более половины вершин.
1.4. Определить, сколько ошибок исправляет и
сколько обнаруживает код с характеристической функ-
цией /.
1) / (хп) — хг ф х2 ф ... ф ж„;
2) / (£’!) = Х)Х2 ...xn\J хгх2 ... хп;
3) / (х3'1') = ХгХ2 . . . Ж3я \/ Х±Х2 . . . ^2яЖ2и+1‘^2я+2 • • * ^Зя V
V Х1Х2 ‘ • • ХЛ+1Хп+2 • • • Х3п V Х1Х2 • • • Х3п’
i) f (£”) = Х1х2 ... я^фа^ ... хя_2хяф ... фх2х3...
• • • Хп-
1.5. Пусть слова двоичного кода С передаются по
каналу связи. При передаче кодового слова может
произойти не более одной ошибки. Для каждого ко-
дового слова а построить множество тех слов, которые
могут быть получены после передачи а по каналу.
1) С= {01100, 00111, 11010, 10001};
2) С —{11110, 10100, 01011, 11001}.
Пусть вероятность того, что при передаче по каналу
связи произвольного слова w из Вп произойдет ошибка
в г-м разряде, равна р для всех 1=1, п. Пусть С С В” —
некоторый код мощности т, а ф: В“ -» С — декодиро-
вание. Величина
0=^-2 2 ₽p<e’w,(i—р)"-ри,’“о
«еф-* (»)
называется достоверностью декодирования Ф при ко-
де С.
6 Г, П, Гаврилов, А. А, Сапоженко
161
1.6. Показать, что при 0 < р < 1/2 максимум ве-
личины (р, С) по всевозможным декодированиям при
фиксированном С достигается при условии, что для
каждого w^B" выполняется равенство р (w, ф (w)) =
= min р (m, n).
с 6 6’
1.7. 1) Для кода С из задачи 1.5, 1) построить
декодирование ф с максимальной достоверностью
Qi, (р, С), 0 < р < 1/2, указав для каждого w £ С
множество ф-1(т). Найти шах (/(1/4, С).
ф
2) Сколько существует различных декодирований ф
с максимальной достоверностью при коде С из
задачи 1.5, 1) и 0 < р < 1/2?
1.8. Найти максимально возможную мощность кода
С С Вп, обладающего свойством: для любых а и р из
С р (а, р) — четные.
1.9. Сколько существует максимальных <и, 2>-
кодов?
1.10. Пусть п=?>к. Показать, что т (п, 2н/3)=4.
1.11. Показать, что мощность плотно упакованного
d
<п, 2d 1)-кода равна 2Н/ 20’
<=о
1.12. Существует ли плотно упакованный <н, 3>-код
при п = 147?
1.13. Показать, что при тг > 7 не существует плотно
упакованных <ге, 7>-кодов.
1.14. Доказать, что код С С В" не является мак-
симальным, если |С |=3.
1.15. Показать, что если в В" существует плотно
упакованный </г,3>-код, то существует разбиение
куба на непересекающиеся сферы радиуса 1.
1.16. Пусть С — плотно упакованный (п, 2d-|-l)>-
код. Показать,
что
тогда
делится без остатка
1.17. Показать, что не существует эквидистантных
<п, 2с/+1>-кодов мощности больше 2.
1.18. Показать, что при четном d существует экви-
дистантный код мощности [2n/d|.
1.19. Показать, что т (п, d) — неубывающая функ-
ция параметра п.
162
1.20. Показать, что:
1) ni(n-\-d, d)^ 2т(п, d);
2) т (2п, d) (т (п, d))2;
3) т (п, d)^Z2m(n — 1, d).
а '
1.21. Доказать, что т (n, 2t 1) 2"/'^ |
1=0
1.22. Доказать, что
©
m(n, 4, .
2©("7‘)
1=0
1.23. Доказать, что при n<^2d справедливо неравен-
ство
/ л\ 2d
т<П’ ^<2d—n'
1.24. Доказать, что
т(п, к, d) <7 Г—у."|,
' ' — п (2к — d)J
i если 2k2 — п (2к — d)^>0.
1.25. Показать, что:
1) т(п, к, d)^ ^-т(п— — 1)];
2)М»,
3) т(п, к, d) Г 2: & т^п — 1’ ^)]’
1.26. Пусть q(n, d) — максимальное число вершин,
в В”, попарные расстояния между которыми не превос- '
ходят d. Доказать, что
т(п, d-{-l)g(n, d)<^2".
1.27. Доказать, что т(п, d)^.2n d+1.
1.28. Показать, что из всякого множества С С В",
такого, что j С | 2й, можно выделить подмножество
D мощности, не меньшей 2-йн | С ], являющееся
<п, d^-кодом.
163
§ 2. Линейные коды
Выражение вида
Mi Ф ^2®3 Ф • • • Ф (1)
где л(£Вп, Х,.е{0, 1), j = l,s, называется линейной
комбинацией векторов ах, а2, . . ., а>. Линейная комби-
нация (1) называется тривиальной, если Х1 = Х2 = . . .=
= Xg=0, и нетривиальной в противном случае. Всякая
линейная комбинация х) векторов из Вп является,
очевидно, вектором из В”. Векторы alt a2, . . ., a.t
из В” называются линейно независимыми, если любая
их нетривиальная линейная комбинация отлична от
0=(0, 0, . . 0). В противном случае говорят, что
векторы S.1, а2, . . ай линейно зависимы. Подмно-
жество G С В" называется группой, если G замкнуто
относительно операции сложения по модулю 2, т. е.
если для любых а, р из G вектор Йф^ принадлежит G.
Из замкнутости G относительно операции ф вытекает,
что всякая линейная комбинация векторов из G также
принадлежит G (в частности, б £ G). Таким образом,
всякая группа G в В” является линейным векторным
пространством над полем /'2=<{0, 1}, ф, •>. Наиболь-
шее число k=k {G), для которого в группе (в линейном
пространстве) G существует к линейно независимых
векторов, называется размерностью G. Совокупность
из к линейно независимых векторов линейного простран-
ства, имеющего размерность к, называется базисом
этого пространства. Если код G С Вп образует группу,
то он называется линейным или групповым. Если ли-
нейный код в Вп имеет размерность к, то он называется
(п, к)-кодом. Двоичный линейный код, исправляющий
одну ошибку, называется кодом Хэмминга.
Линейные коды удобно задавать с помощью матриц.
Матрица Н (С), строками которой являются кодовые
слова кода С С Вп, называется матрицей кода С.
Матрица М (С), составленная из произвольных к
линейно независимых векторов, являющихся кодовыми
х) Определение операций сложения векторов по модулю 2
и умножения скаляра на вектор дано в параграфе «Булевы век-
торы и единичный га-мерный куб».
164
словами (п, /г)-кода С, называется порождающей мат-
рицей кода С. Если Н — произвольная матрица из
нулей и единиц с п столбцами, то множество С (Я)
всех вершин куба В”, являющихся линейными комби-
нациями строк матрицы Н, называется кодом, порож-
денным матрицей Н. Векторы а = (аг, а2, . . ., ап) и
P = (Pi, • • • , Ря) называются ортогональными, если
aiPi®«2p2® • Множество V (Я) всех век-
торов из В“, ортогональных к каждой из строк матрицы
Я, называется нулевым пространством матрицы Н.
Пусть С — двоичный код, каждое слово которого орто-
гонально каждой строке некоторой матрицы Я. Если
С является (п, /с)-кодом, а матрица Я состоит из п—к
линейно независимых строк, то Я называется прове-
рочной матрицей кода С. Множество С* всех векторов,
представимых в виде линейной комбинации строк
проверочной матрицы (п, /с)-кода С, называется ко-
дом, двойственным к коду С. Через g (и, d) будет обо-
значаться шах |С |, где максимум берется по всем
линейным кодам С С Вп с кодовым расстоянием d.
2.1. Пусть множество ССВ" состоит из к линейно
независимых векторов. Показать, что любые две ли-
нейные комбинации векторов множества С, различаю-
щиеся коэффициентами, представляют собой различные
вершины куба Вп.
2.2. Показать, что в Вп существует система из п
линейно независимых векторов, но не существует си-
стемы из п+1 линейно независимых векторов.
2.3. Показать, что число векторов из Вп, представи-
мых линейными комбинациями вида (1), в которых
8 t
У, не превосходит 2
2.4. Показать, что всякий (п,к)-коц, имеет мощ-
ность 2/с.
2.5. Показать, что в двоичном линейном коде
либо каждый кодовый вектор имеет четный вес, либо
половина кодовых векторов имеет четные веса и по-
ловина — нечетные.
2.6. Показать, что число различных базисов в Вп
равно
(2я — 1) (2я— 2) ... (2" — 2"~1)
п I ’
165
2.7. Показать, что число различных (п, /i)-кодов
в В” равно
(2» —J)(2B—2) ... (2n —2fe~!)
(2/с - 1) (2» — 2) ... (2fc — 2*-1) *
2.8. Найти число векторов из Вп, ортогональных
к данному вектору а из В%.
2.9. Показать, что множество всех векторов из
В", ортогональных к каждой из строк двоичной мат-
рицы Н размерности кхп, образует линейное простран-
ство. Всегда ли это пространство имеет размерность
п—к?
2.10. Верно ли что для каждого линейного кода
можно указать матрицу Н, являющуюся
1) порождающей;
2) проверочной?
2.11. По заданной матрице Н указать мощность
т (С (Н)) порожденного ею кода С (Н) и кодовое рас-
стояние d (С (Я)).
/1 0 0 1 1\
1) Н = 1 1 10 0 1;
\1 1 1 00/'
/0010 1\
/111001
2) Н = I О 1 О 1 О )'•
\1 0 О 1 1/
/1 1 00 ... 00
/ О 1 1 О ... 0 о
I О О 1 1 ... о о
Я= ..................
о 0 о 0 ... 0 1
,1 0 0 0 ... 0 0
здесь матрица Н имеет размерность пХЩ
4) Н = (1кР), где 1к — единичная матрица размер-
ности к\к, а Р — произвольная двоичная матрица
размерности кХ(п—к), каждая строка которой содер-
жит по меньшей мере две единицы, к п—log., («+1);
5) где /5 — единичная матрица, размер-
ности 5x5, а
(11101100104
01111001011
11011011101,
01100111111*
1101011101/
166
2.12. Пусть V С В№ — пространство, состоящее из
линейных комбинаций строк матрицы Н~(1кР), где
1к — единичная матрица размерности кхк, а Р —
матрица из нулей и единиц размерности кх{п—к).
Доказать, что V является нулевым пространством
матрицы G—(PTIn_k), где 1п,к — единичная матрица
размерности (п—к)Х(п—к), а Рт — матрица, транспо-
нированная к матрице Р.
2.13. Для кода, порожденного матрицей Н из за-
дачи 2.11, 1), построить проверочную матрицу.
2.14. Показать, что если С С В” является (и, к)-
кодом, то двойственный к С код является (п, п—к)~
кодом.
2.15. Пусть Н (С) — матрица (и, А:)-кода С С Вп,
не содержащая нулевых столбцов. Показать, что:
1) каждый столбец матрицы Н (С) имеет 2*'1 еди-
ниц и столько же нулей;
2) сумма весов строк матрицы Н (С) равна п-2к~\
2.16. Показать, что кодовое расстояние линейного
кода С С Вп равно минимальному из весов его нену-
левых векторов.
2.17. Показать, что кодовое расстояние (га, &)-кода
не превосходит [ra2*_1/(2fc—1)1.
2.18. Показать, что при n=2d—1 мощность линей-
ного <га, й>-кода не превосходит 2d.
2.19. 1) Показать, что максимально возможная
мощность g (га, d) линейного <га, <Ъ-кода удовлетворяет
неравенству g (га, d) 2g (и—1, d).
2) Используя результат задачи 2.18, показать, что
g (п, d) < d-2s’2d+2.
2.20. Пусть код С является нулевым пространством
матрицы Н. Показать, что кодовое расстояние кода С
тогда и только тогда не меньше d, когда любая совокуп-
ность из d—1 или меньшего числа столбцов матрицы Н
является линейно независимой.
<4—2
2.21. Показать, что если У 'С т0 сУщест~
вует матрица из нулей и единиц размерности к х п,
в которой любые d — 1 столбцов линейно независимы
и, следовательно, существует (га, га—&)-код с кодовым
расстоянием d или большим, чем d.
167
2.22. Пусть Нк К — матрица размерности где
fc=]log2 в которой столбец с номером i пред-
ставляет собой двоичное разложение числа t (i=l, п).
Например, при га=6 матрица Н36 имеет вид
/О 0 0 1 1 1\
Н = 1 о 1 1 О О 1 I
\1 0 1 0 1 о/
1) Показать, что нулевое пространство матрицы
является кодом Хэмминга, т. е. линейным кодом,
исправляющим одну ошибку.
2) Построить код, являющийся нулевым простран-
ством матрицы Н8 в.
3) Сколько ошибок исправляет код, порожденный
матрицей НкД
2.23. Спектром множества С С Вп называется век-
тор s=(s0, sB), где sr есть число пар вершин из С,
расстояние между которыми равно г. Показать, что
для всякого (га, &)-кода С существует (га, Л)-код С',
имеющий тот же Спектр и обладающий порождающей
матрицей вида (IkP), где 1к — единичная матрица
размерности кХк, а Р — некоторая йатрица из нулей
и единиц размерности кХ. (п—к).
2.24. 1) Показать, что g (9, 5)=4.
2) Показать, что т (9, 5) 5.
2.25. Пусть существует (га, /с)-код с кодовым рас-
стоянием d. Верно ли, что тогда существует (га, А)-код
с кодовым расстоянием d—1?
§ 3. Алфавитное кодирование
Пусть А — алфавит, тогда А* — множество всех
конечных слов в алфавите А, включая и пустое. Длина
(число букв) слова w обозначается через X (га?). Пустое
слово обозначается через Л. Соединение слов wr и w2,
получающееся приписыванием слова т2 справа к слову
юг, обозначается через Слово wr называется пре-
фиксом слова а слово т2 — суффиксом слова wpv2.
Префикс и\ (суффикс ш2) слова w1w2 называется соб-
ственным, если одновременно и г«2=4Л. Слово v
называется подсловом слова ю, если существуют такие
слова Uj и и2, что w—UjVU2.
168
Пусть A = {alt а2, .... ат} — алфавит сообщений,
а В — кодирующий алфавит. Пусть (р — однозначное
отображение букв алфавита А в В*. Кодирование слов
в алфавите А, при котором каждому слову (сообщению)
. a.ik ставится в соответствие слово <р («,;) ср (а,2) ...
... ср (а,к), называется алфавитным (или побуквенным)
кодированием. Алфавитное кодирование полностью
определяется порождающим его отображением ср и
обозначается через K,f. Множество (ср (а): а £ А}
называется алфавитным кодом и обозначается через
ср (А). Алфавитное кодирование K,f и соответствующий
код ср (А) называются однозначно декодируемыми, или
разделимыми, если из каждого равенства вида
ср (Hi,) <Р (««,) • • • Т («<*) = ? (ал) ? (ал) • • • <Р («//)
— между словами в кодирующем алфавите В — сле-
дует, что l = k и jt~ it (t=l,k). Код ср (А) называется
префиксным, если никакое слово из ср (А) не является
началом никакого другого слова из ср (А). Разделимый
алфавитный код ср (А) называется полнцм, если для
каждого слова w в кодирующем алфавите В справедливо
утверждение: либо w является собственным префиксом
некоторого слова из ср (А), либо некоторое слово из
ср (А) является префиксом (не обязательно собственным)
слова w.
Один из алгоритмов распознавания разделимости
алфавитного кода заключается в следующем. Пусть
<р (А)= {шх, w2,. .., wm] — алфавитный код. Пусть 5Х —
множество всех собственных суффиксов кодовых слов,
a S2 — множество всех слов, каждое из которых яв-
лясется префиксом какого-либо кодового слова. Рас-
смотрим ориентированный мультиграф вершинами
которого являются элементы множества 5=(5Х (") S2)U
U {А}. Пусть о и t — две различные вершины из S.
Дуга, ведущая из а в т, в графе существует тогда и
только тогда, когда существуют кодовое слово w и
последовательность P = w(i, ш,-3...wik кодовых слов,
такие, что слова w и awitwfj ... wikt равны как слова
в кодирующем алфавите. При этом, если <з=^=А, то
последовательность Р может быть пустой. Дуге, веду-
щей из а в т, приписывается слово w^Wi,...
Петли в мультиграфе отсутствуют. Мультиграф
169
называется графом алфавитного кода ср. Справедлива
следующая
Теорема 1 (Ал. А. Марков). Код ср является раз-
делимым тогда и только тогда, когда в графе отсут-
ствуют контуры, проходящие через вершину А.
Пример 1. Пусть ср (А)={сс, сса, Ъсса, аа, аЪ}.
Тогда S = {Л, с, сса, а, 6}. Граф Go изображен на
рис. 22, а. В существует контур, проходящий через
вершины Л, а, Ь. Выписывая слова, приписанные вер-
шинам и дугам этого контура, находим слово, которое
декодируется двумя способами:
ccabcca — (сса) (bcca) = (сс) (ab) (сса).
Пример 2. Пусть <р (А) —{а, ab, асЪЪ, ЪЬ, ЬЬасс}.
Тогда S= {Л, Ъ, ЪЪ}. В графе G, показанном на
рис. 22, б, контуры, проходящие через Л, отсутствуют.
Код является разделимым.
Пусть имеется источник сообщений, который слу-
чайным образом последовательно порождает буквы
алфавита A — {alt а2, . . ., ат). Предполагается,
что появления букв алфавита А статистически неза-
висимы и подчинены распределению вероятностей /’=
гп
= {Др р2, ..?„}, Pi > 0, 2 Pi = 1- Всякому двоичному
»=1
алфавитному коду C = (wv можно сопоста-
вить число
т
^С(Р)=2М(^).
<=1
называемое стоимостью кода С при распределении Р.
170
Число Хс (Р) равно среднему числу букв кодирующего
алфавита, приходящихся на одну букву алфавита А.
Префиксный код Со называется оптимальным при рас-
пределении Р, если ^с0 (Р) = inf r£c (Р), где нижняя
с
грань берется по множеству префиксных двоичных
кодов, состоящих из т слов.
Метод Хаффмена для построения оптимального
кода опирается на следующую теорему.
Т е о р е м а 2. Если С = wz, . . ., — оптималь-
ный двоичный код при распределении Р — \pv р2,. . ., рт}
и р. = q2, причем р^ р.г'^ ... > р}_г Pj
• • •> Рт^: т0 К0д С' = {WV W2, . •
... Wy_v Wj}V..,wm, wjO, является оптимальным,
при распределении
р = (pv Рг> ’ Pj-V P/,1> ’ Pm> 9i> 921-
Код С будет называться расширением оптимального
кода С. Метод Хаффмена состоит в следующем. Пусть
в исходном упорядоченном по невозрастанию списке
вероятностей две последние вероятности рт_х и р,п.
Эти вероятности из списка исключаются, а их сумма
вставляется в список таким образом, чтобы в получив-
шемся новом списке вероятности не возрастали. Эта
процедура повторяется до тех пор, пока не получится
список из двух вероятностей. После получения списка
из двух вероятностей одной из них приписывается
символ 0, а другой — символ 1 (оптимальный код
для двухбуквенного алфавита сообщений при любом
распределении вероятностей). Затем в соответствии
с теоремой строится оптимальный код для трех букв
при соответствующем списке вероятностей и т. д.
до тех пор, пока не получится оптимальный код при
исходном списке вероятностей. Метод Хаффмена иллю-
стрируется таким примером:
171
При данном распределении вероятностей существуют
и другие оптимальные коды, например,
Т ,\ В Л И НА 6
Pi wi Pi U’i ''i
¥ 0,4 1 00 4 0,1 0010 110
2 0,2 01 01 5 0,1 ООП 111
3 0,2 000 10
Метод Фано построения кодов, близких к оптималь-
ным, состоит в следующем. Упорядоченный по невоз-
растанию список вероятностей делится на две (после-
довательные) части так, чтобы суммы вероятностей,
входящих в эти части, различались как можно меньше.
Каждой букве алфавита сообщений, соответствующей
вероятности из первой части, сопоставляется символ О
(или 1), а остальным буквам — символ 1 (соответ-
ственно 0). Далее точно так же поступают с каждой
из частей, если она содержит по крайней мере две
вероятности. Процесс продолжается до тех пор, пока
весь список не разобьется на части, содержащие по
одной вероятности. Примеры кодов, построенных по
методу Фано, приведены в таблице 6.
3.1. По заданному алфавитному коду <р (Л) построить
граф и выяснить, является ли код разделимым.
1) tp (Л) = {ab, de, a, bcadd, са}, Л = {ц 1 = 1, 5};
2) ®{A) = {ddac, dd, eddab, a, eddd, b], A = {i, i =
= 1Гб};
3) <р(Л) = {а, ab, aebb, abb, bbacc}, A = {i, i = l, 5);
4) ср (Л) = {abc, bbc, beb, caa, aebb, ebeb, bccabb,
abcacbbb}, Л = {{, i = l, 8};
5) ср (Л) = {abc, abb, bcc, ccaa, bcabbbcc, bbccaaabca,
abcabbabbbcca}, A = {i, i = l, 7};
6) ср(Л) = {а&, bb, ca, cba, abb, bac, aabc, cabba},
Л = {1, i = l, 8}.
3.2. Пусть числа 1, 2, 4, 17, 98 кодируются своими
двоичными разложениями минимально возможной
172
длины. Например, код единицы есть 1, код двойки
есть 10, код четверки есть 100. Является ли это коди-
рование разделимым?
3.3. По заданному неразделимому коду <р (Л) =
= {аа, ab, сс, сса, Ъсса} и слову w в кодирующем алфа-
вите В={а, Ь, с] выяснить, является ли слово w ко-
дом некоторого сообщения. Если да, то выяснить,
является ли слово w кодом ровно одного сообщения.
* 1) w = ccabccabccabcc,
2) w = bccaccabccabccacabcca;
3) w = abbccaccabccaabab.
3.4. Пусть <p (Л) — алфавитный код, a — граф
этого кода. Пусть граф G' получен из графа G^ удале-
нием всех вершин, являющихся кодовыми словами.
Останется ли в силе теорема 1, если заменить на G'Ji
3.5. Пусть <р (Л) — алфавитный код, a G? — граф этого
кода. Пусть граф G? получен из удалением всех дуг
с пометками Л, ведущими в вершину Л. Останется ли
в силе теорема 1, если заменить G^ на G^>?
3.6. Для данного разделимого кода <р (Л) построить
префиксный код с тем же набором длин кодовых слов.
1) <р(Л) = {01, 10, 100, 111, 011};
2) <р(Л) = {1, 10, 00, 0100};
3) <р(Л) = {10, 101, 111, 1011}.
3.7. Пусть <р (Л) — алфавитный код мощности т,
в котором сумма длин кодовых слов равна N, а мак-
симальная из длин кодовых слов равна I. Используя
теорему 1, доказать, что код (р (Л) является раздели-
мым тогда и только тогда, когда каждое слово в ко-
дирующем алфавите, имеющее длину не более чем
(Z—1)(N—иг-|-1), либо является кодом ровно одного
слова, составленного из букв алфавита сообщений Л,
либо вообще не является кодом никакого слова из А*.
3.8. Пусть к — наименьшая, а I — наибольшая из
длин кодовых слов алфавитного кода <р (Л), a N —
сумма длин кодовых слов. Показать, что для установ-
ления разделимости кода <р (Л) достаточно проверить
на однозначную декодируемость не более чем NUk
слов в кодирующем алфавите.
3.9. Будем считать, что два слова w и и в алфавите
{0, 1} эквивалентны, если существует такое слово и,
173
которое может быть получено как из w, так и из v
с помощью следующих операций, примененных в ко-
нечном числе:
а) вычеркивание подслов вида 10 и 1001;
б) вставка в промежутки между буквами :) слов
вида 10 и 1001.
Эквивалентны ли следующие пары слов w и и:
1) №=1010101, с?=0101010;
2) №=10010010, i>=010010010;
3) №=11011010, гл=01101101?
3.10. Пусть М — множество, состоящее из т не-
пустых слов в алфавите А, имеющем к букв. Показать,
что:
1) в М найдется слово, длина которого не меньше
log* (1+ш (к—1));
2) для всякого ® > 0 доля тех слов из М, длина ко-
торых меньше чем (1—е) log к (1 -|- т (к — 1)), не пре-
восходит ’пГ при т 2, к ^>2.
3.11. Пусть в алфавитном двоичном коде С мощности
2п+1 каждое кодовое слово имеет длину, не превы-
шающую п.
1) Доказать, что код С не является префиксным.
2) Может ли код С быть разделимым?
3.12. Для заданных распределений вероятностей
появления букв построить оптимальные коды по ме-
тоду Хаффмена.
1) / = (0,34; 0,18; 0,17; 0,16; 0,15);
2) />=(0,6; 0,1; 0,09; 0,08; 0,07; 0,06);
3) /=(0,4; 0,4; 0,1; 0,03; 0,03; 0,02; 0,02);
4) /=(0,3; 0,2; 0,2; 0,1; 0,1; 0,05; 0,05).
3.13. 1) Для распределений вероятностей из пре-
дыдущей задачи построить коды по методу Фано.
2) Привести пример распределения вероятностей,
при котором код, построенный по методу Фано, не
является оптимальным.
3.14. Пусть C={wlt и>2, . . ., №от) — оптимальный
двоичный код, отвечающий распределению /= (р1(
р2, • • Рт), Pi> Рг> • • • > Рт- Показать, что:
*) Разрешается также приписывание слов 10 и 1001 слева
и справа к преобразуемому слову.
174
1) (w;)’ если Pt > Рр
2) Код С является полным.
3) Существует два кодовых слова длины X
имеющих одинаковые префиксы длины X (ш,я)—1.
3.15. Показать, что если т не является степенью
двойки, то при любом распределении вероятностей
P=(pt, Р^ • • •, РпЬ в оптимальном коде найдутся два
слова, имеющих разную длину.
3.16. Опираясь на задачи 3.14, 3.15 и определение
оптимального кода, объяснить, почему нижеследую-
щие коды не являются оптимальными при заданных
распределениях вероятностей.
1) 2) 3)
Pi Wf
0,6 0
0,2 10
0,1 и
о,1 01
Pi
0,6 1
0,2 01
0,15 001
0,05 0001
Pi
0,2 000
0,2 001
0,2 010
0,2 011
0,2 100
3.17. Найти наименьшее т и такое распределение
вероятностей Р = (р1, р2, . . ., рт), при которых суще-
ствуют оптимальные коды, различающиеся наборами
длин кодовых слов.
3.18. 1) Показать, что максимальная длпна кодо-
вого слова в оптимальном коде мощности т не превос-
ходит т—1.
2) Показать, что для всякого целого т {т 2)
найдется распределение вероятностей Р — (pv рг, • • , р„,),
удовлетворяющее j условию: существует оптималь-
ный код, отвечающий распределению Р и такой, что
максимальная длина кодового слова в нем равна т—1.
т ) П0Л"
ных префиксных двоичных кодов мощности т.
3.20. Код называется почти равномерным, если
длины его кодовых слов различаются не более чем на
единицу. Показать, что для всякого натурального т
175
' почти равномерный код является оптимальным при
/1 1 1 \
распределении Р = (— , — . Верно ли обратное?
3.21. 1) Показать (индукцией по т), что сумма
длин кодовых слов оптимального кода с т сообщениями
не превосходит (т 2) (т. — 1).
2) Показать, что для каждого целого т 2 оценка,
указанная в предыдущей задаче, является достижимой.
3.22. Пусть glf g2, . . ., gm — произвольные по-
парно непересекающиеся грани куба Вп размерностей
г1( г2, • • м гт соответственно.
т
1) Используя очевидное неравенство 2 2Г< 2”, по-
»=1
казать, что длины X (wj, X (w2), ..., X (wm) слов произволь-
ного двоичного префиксного кода C = {ivlt w2,...,wm}
т
удовлетворяют условию 2 2"1.
•=i
2) Показать, что для полного префиксного кода спра-
9П
ведливо равенство 2 = 1.
»=i
3) Показать, что если 2 2-х<^1, где Х<— натураль-
_______________ <=1
ные числа, г = 1, т, то существует префиксный код с
длинами слов, равными Хр Х2, ..., Хт.
3.23. 1) Верно ли, что в оптимальном двоичном коде
число кодовых слов максимальной длины четно?
2) Верно ли, что это число является степенью двойки?
3.24. Пусть C = {w1, w2, ...,и>т}—полный префикс-
ный двоичный код, и пусть X (uij X (w<+1) для всех
i = l, щ — 1. Показать, что при т'^2 для всех г =
= 1, т — 1 справедливо неравенство X — X (w.)
^log2m —1.
3.25* . Пусть Lm — наименьшее целое, для кото-
рого существует двоичный префиксный код мощности т
и суммой длин кодовых слов, равной Lm. Доказать,
что Lm т [log2 т] при т~^ 2.
3.26. Показать, что длины кодовых слов Х(ш1),
Х(ш2), . .., X(wm) двоичного оптимального кода C = {wv
т
w2, • • •> подчиняются условию 2 2~Н«ч) =1.
176
3.27. Пусть P — (pv р2,..рт) — распределение ве-
роятностей i — i, т), а X (Р) = inf Хс (Р), где
с
нижняя грань берется по всем двоичным префиксным
кодам мощности т (т 3).
1) Показать, что X (Р) > 1.
2) Доказать, что для любого е > 0 и любого це-
лого т 1 существует распределение вероятностей
P^(Pi, Рг, • • •, Рт), такое, что ^’(7’) < 14-s.
Метод Шеннона для построения кодов, близких
к оптимальным, состоит в следующем,
m
Пусть Р = (рх, р2, ...,рт), Л >0,2 = Pt>
•=i
> р<+1, i=l, т — 1 — распределение вероятностей появ-
ления букв алфавита сообщений А = {av а2, ..., ат}.
Тогда букве а( сопоставляется кодовое слово длины
lt = J log ~~ £, составленное из первых (после запятой)
‘ «—1
1( цифр разложения числа = 2 Pj в бесконечную
У=1
двоичную дробь (с недостатком).
Например, если Р=(0,4; 0,3; 0,3), то код буквы а,
есть 00, код а2—,01, код а3 — 10.
3.28. Построить по методу Шеннона коды для рас-
пределений вероятностей из задач 3.12, 1), 2).
3.29. Указать наименьшее т, при котором суще-
ствует распределение вероятностей Р=(рг, р2, . . ., рт),
такое, что код, построенный по методу Шеннона для
данного распределения вероятностей, не является оп-
тимальным.
3.30. Доказать, что код, построенный по методу
Шеннона, является префиксным.
3.31. Пусть <5?* (m) = sup inf ,2с (Р), где верхняя грань
р с
берется по всем распределениям P = (pv р2, ...,рт), та-
т
ким, что pf^>0, i = l, m, =
•=i
1) Доказать, что (т) [log2 т].
2) Доказать, что <2?* (иг) ^[log2wi]-|-1.
177
Глава VI
КОНЕЧНЫЕ АВТОМАТЫ
§ 1. Детерминированные и ограниченно-
детерминированные функции
Пусть А — непустой конечный алфавит. Элементы
алфавита называются буквами (или символами). Сло-
вом в алфавите А называется последовательность,
составленная из букв алфавита А. Длина (число букв)
в слове w обозначается через л (гг). Множество всех
слов xs=х (1) х (2). . . х (s) длины s (s 1) в алфавите
А будет обозначаться через As. Слово длины 0 {пустое
слово') обозначается символом А. Через А* обозначается
множество {A} (J U А’, а через Аш — множество всех
слов £ш=х (1)х (2). . где х (£) £ А, 1=1, 2, . . .
Слова из Аш называются бесконечными словами в алфа-
вите А.
Слово iv, получающееся приписыванием слова w2
справа к конечному (или пустому) слову иц, называется
соединением слов и\ и т2 и обозначается через и\ш2.
При этом слово иц называется началом {префиксом),
а слово w2 — окончанием {суффиксом) слова ш.
Пусть А а В — конечные непустые алфавиты. Ото-
бражение (р: Л“ -> Вш называется детерминированной
функцией, или детерминированным оператором (со-
кращенно — д. функцией, или д. оператором), если оно
удовлетворяет следующим условиям:
(а) для всякого s 1 s-й символ у (х).слова?/и>=р>(жш)
является однозначной функцией первых s символов
х (1), х (2), . . х (s) слова Xю;
178
(б) если у слов х™ и префиксы длины s(s^l)
совпадают, то совпадают также префиксы длины s
у слов у“ = у(х“) и у? == ср (f£).
Через Фл, в будет обозначаться множество всех д.
функций вида <р : Аш Вш.
Если Л — 4jX Л2Х ... X Ля и В = В1хВ2Х ... ХВт,
то отображение у:А’‘^-В" индуцирует т функций
ср< = <р,. (Хр Х2, . . ., Хн), г = 1, 2, ..., т, каждая из кото-
рых зависит от п переменных, причем переменная X
пробегает множество Л“! (j = l, 2, .. ., га). Эти функции
определяются так. Пусть х“ = х (1) х (2) ... х (Z)...—
слово из Лш и ут = <р (хш) = у (1) у (2) ... у (t) ... Тогда
х(0 = (0- х-г (0- • • • > х„ (О), = xj (' )*у (2)• • •
...х .(I).. .,хш = (х“, х“, ...,££); y(Z) = (y1(Z), ^(0- •••
• •-О))- у- = у((1)у^2)...у({1) ...,у^ =
= (.УЛ Уг> О <?{ («“, х%, . . ., х”) = у*.
Можно поступать наоборот — исходя из функций ср(.,
строить отображение у.
Понятие д. функции от п аргументов возникает
естественным образом при рассмотрении д. функций
вида ?:(Л1хЛ2Х...ХЛ„)ш^5ш.
Переменная Xj функции <р (Х1( Х’2, . .., Хя): (At X
X Л2 х ••• X Л„)ш —» В11 называется существенной, если най-
дутся два набора (£“, £^) и (ff2, 5“ , . . ., £“)
значений переменных Хр Х2, ..., Хя, отличающиеся
только первой компонентой и такие, что ® (£“, ...
. . ., £“) =?= ср (ж“, Если переменная А\ не
является существенной, то она называется фиктивной
(или несущественной). Аналогично определяется суще-
ственность и фиктивность любой другой переменной X,.,
от которой зависит данная функция.
Говорят, что функция ср (Xj, Х2, . . ., Х„) за-
висит существенно (несущественно) от переменной
Х( (1 I п), если эта переменная является суще-
ственной (соответственно фиктивной) переменной функ-
ции ср.
Если Л есть множество всех векторов длины п
с элементами из Ek, а В — множество всех векторов
длины т с элементами из Et, то вместо Фл,д будет
применяться обозначение Ф^”. При п — т — \ верхние
индексы у Фу будут опускаться; если к = 1, то внизу
будем писать только один индекс: Ф”’т.
179
Иногда бывает удобно считать, что д. функция <р
из Фл,е реализуется некоторым дискретным устрой-
ством (автоматом) работающим в дискретные
моменты времени £=1,2,... На вход этого устройства
в каждый момент t подается сигнал х (£), а на выходе
появляется сигнал у (£) (рис. 23). Слова хш называют
входными, слова уш — выходными, А называют вход-
ным, В — выходным алфавитами автомата 21 . Если
Д=Л1ХЛ2Х. . .ХИяи В=ВхХВ2Х. • -ХВт, то можно
считать, что автомат 21? реали-
зует иг детерминированных функ-
ций, каждая из которых зависит
от п переменных.
Любые две функции <рх и <?2
Рис. 23. из Фл,в называются различимыми,
если существует входное слово Хд,
перерабатываемое ими в разные выходные слова, т. е.
<₽i (^) =7^= <f2 (^“)- Если же равенство <рх (хт) = <р2 (х“)
выполняется при всяком входном слове хш, то <рх и ср2
называются эквивалентными, или неразличимыми д.
функциями.
Пусть ср £ Фд в и ф £ в- Если существует такое
слово ж® £ Л*, что ср (xsoxa!) = ср (ж®) ф (£")J) для любого
слова £ Л“, то оператор ф называется остаточным
оператором оператора ср, порожденным словом xs0, и обо-
значается через ср.,. Множество Q (ср, ж®) всех остаточ-
ных операторов оператора ср, эквивалентных оператору
ср.,, образует класс эквивалентности, называемый со-
стоя наем оператора ср, содержащим остаточный опе-
ратор ср.,. Состояние, содержащее оператор ср, назы-
вается начальным. Если х$, то будем говорить,
что оператор ф реализуется состоянием Q (ср, х§ опера-
тора <р. Оператор ср называется ограниченно-детерми-
нированным (сокращенно — о.-д. оператором, или
о.-д. функцией), если он имеет конечное число попарно
различных состояний. Число различных состояний
о.-д. функции называется ее весом. Если множество
попарно различных состояний оператора ср — беско-
нечное, то будем считать, что вес оператора ср равен оо.
*) Здесь через <f (xj) обозначен префикс длины s выходного
слова f (xjx“).
180
Через Фл, я обозначим множество всех функций из Ф.|.в,
являющихся о.-д. функциями.
При рассмотрении д. функций удобно пользоваться
графическим изображением их в виде бесконечных ин-
формативных деревьев. Пусть А — алфавит из п букв.
Через Da обозначим бесконечное ориентированное
корневое дерево, удовлетворяющее условиям:
(а) полустепень исхода каждой вершины, включая и
корень, равна и;
(б) полустепень захода корня равна 0, а всякой
другой вершины — 1;
(в) каждой дуге дерева DA приписана некоторая
буква алфавита А, причем разным дугам, исходящим
Рис. 24.
Рис. 25.
из одной и той же вершины дерева (в частности, из
корня), приписаны разные буквы. Корень дерева будем
считать вершиной нулевого ранга', если вершина v яв-
ляется концом дуги, исходящей из вершины i-го ранга
(i 0), то v называется вершиной (i-f-l)-ao ранга.
Дугой j-го яруса (j 1) называется дуга, исходящая
из вершины (у—1)-го ранга. Всякой бесконечной ориен-
тированной цепи в деревеDA соответствует слово из Л“.
На рис. 24 изображен фрагмент дерева DA, Л = {0, 1),
состоящий из трех первых ярусов этого дерева (мы
предполагаем здесь и в дальнейшем, что символу 0
соответствует левая дуга, исходящая из вершины,
а символу 1 — правая); жирными дугами выделена
цепь, соответствующая слову 101.
Нагруженное дерево DAtB получается из дерева DA
путем приписывания каждой дуге некоторой буквы
из алфавита В. Всякой ориентированной бесконечной
цепи в дереве DAiB отвечает слово из В“, составленное
из букв, приписанных дугам этой цепи. Поэтому можно
18*
считать, что нагруженное дерево DA, в задает (реали-
зует) отображение ср; Аю -> Вш, являющееся д. функ-
цией. На рис. 25 изображен фрагмент некоторого на-
груженного дерева DA, в, где А = {0, 1} и В= {0, 1,2};
д. функция, соответствующая этому дереву, перера-
батывает, например, слово 1010 в слово 2012.
Пусть DAt в — нагруженное дерево, реализующее
д. функцию ср. Остаточному оператору (s 0)
оператора ср отвечает поддерево DAtB (.Го), растущее
из такой вершины и (х°) s-ro ранга, в которой оканчи-
вается цепь, исходящая из корня и содержащая
ровно s дуг, причем этой цепи в г-м ярусе принадле-
жит дуга, помеченная буквой х0 (i) £ А.
Если остаточные операторы ср S1 и <f>.S2 эквивалентны;
то соответствующие им вершины v (х^) и а (т?2) и рас-
тущие из этих вершин поддеревья также называются
эквивалентными. Вес дерева, реализующего д. функ-
цию, равен весу этой функции, а следовательно, мак-
симальному числу попарно неэквивалентных вершин
(или поддеревьев) данного дерева.
1.1. Выяснить, является ли д. функцией отображе-
ние (0, 1}“-» {0, 1}“.
1) ср (х (1) х (2) ,..) — х (2) х (3). . . ,т. е. у (t) — х (t 1),
1,-
2) ср (xw) = 10100100010 ... 010 ... 010 при любом
п раз
входном слове хш\
3) <р (х (1) х (2) х (3).-. .) = х (Ip? (2) х (1) х (2) х (3). . .,
т. е. у (1)=2 (1), у (2) =х (2) и у (t)=x (t—2) при t 3;
4) ср (х (1) х (2) . . .)=0 х (1+х (2))х (1-[-2 (3)). . .,
т. е. у (1)=0, у (t)=x (1-}-2 (£)) при t 2.
1.2. Является ли детерминированной функция
ср: {0, 1 }ш -> {0, 1}“, заданная следующим словесным
описанием?
1) Слово Xs— х (1).т (2) ... перерабатывается в слово
0ш = 000 ... 0. .., если существует такое t, что х (t) — 0;
в противном случае ср(2Ш) = 1“= 111 ... 1 ...
2) s-я буква у (s) в слове у“=ср (х“) равна 0, если при
некотором t s выполняется неравенство х (t) <
<2 (Л-1)+ж (i+2); в противном случае у (s) = l.
182
3) s-я буква у (s) в слове у“=<р (ж“) равна 0, если
существует t s, такое, что х (i) х (s); в противном
случае у (s)=l.
4) У (1)=0 и ПРП s^2 число нулей в префиксе
у (1) у (2). . . j/(s) слова #"=<? (гш) на единицу больше
числа нулей в слове х (1)я(2). . . х (s).
Каждому слову хт—х (1)х (2). . .х (t). . . из {0, 1}“
соответствует некоторое число v (хт) из отрезка
[0,-1], двоичное разложение которого имеет вид
0, х (1) х (2). . . х (Z). . . Если a 0 [0, 1], то его двоич-
ное разложение1) 0, . at. . . порождает слово
<а->=х (1)х (2). . . х (t) . . где х (t)=a1 (7 1).
1.3. Выяснить, является ли детерминированной функ-
ция ср: (0, 1}“-» {0, 1}“
1) <f (Г) = ; 4) ср .
2) = 5)
3) =
1.4. Является ли детерминированной функция <р(Х
Х2,...,Х„):{0, 1}“х{0, 1}“х...Х{0, 1}”?
1) ср(^“ £?) =
2) ? (£?, %) =
3) ? (^, %) =
я раз
1“, если v v (й?),
0“ в ином случае;
ff, если v (х“) v (;££) 1 /2,
£$ в ином случае;
1Ш, если v (f'j') v (х%),
в ином случае;
(<4^)v(^)>, если v(^) = l,
11 2 а ( 0 в ином случае.
1.5. Приводимые ниже частичные функции <р : {0, 1}“ —»
-» {0, 1}“ не определены только на слове 0w = 00.. .0...
Выяснить, какие из этих функций можно доопределить
до детерминированных, а какие — нельзя.
*) Если а = р/2" (и. > 1), то рассматривается такое двоич-
ное разложение, которое содержит бесконечно много нулей.
183
(
ф(П = <
I
1)
х°, если в каждом префиксе слова хш
число нулей не меньше числа единиц,
1Ш в ином случае;
2) ?(Л = г/(1)У(2)...у(0---.где
( 0, если 3s (($ /) & (х (s) — 1)),
у (I) = { .
( 1 в ином случае;
3) <р (£“) = у (1) р (2)... г/(£)..., где
1,если для некоторого в префиксе х (1) х (2)...
— ' . х (s) число нулей больше числа единиц,
x(t) в ином случае;
4) <р (ж") = у (1) у (2) ... у (Z)..где
Г 1, если v (х (1) х (2) ... х (t) 00 ... 0 ...) <11/2,
у (t) = { „
' ' I 0 в ином случае.
1.6. 1) Опровергнуть следующее утверждение: если
функция <р (Хр Х2): {0, 1}“Х{0,1}ш-> {0, 1}" существенно
зависит от переменной и при всяком (фиксированном)
слове £“£{0, 1}ш ср(Хх, £“)— д. функция, то и сама
функция <р (Xv Х2) является детерминированной.
2*) Пусть функция ф (Хр Х2): (0, 1}“х {0, 1}ш -> {0,1}м
удовлетворяет условию: каковы бы ни были слова £'" и
х% из {0, 1}“, функции <р(Хр ж") и ср (ж™, Х2)— детерми-
нированные. Является ли тогда детерминированной и
функция Х2)?
1.7. Для функции уш = ср(жш), принадлежащей мно-
жеству Ф2, построить фрагмент нагруженного дерева,
содержащий s первых ярусов.
1) у (1) = 1 и y(t) = x(t — 1) при t~^2, s = 3;
2) у(1) = 0 и y(t)=x(t) ® y(t— 1) при £>2, $ = 4;
3) ?(Г) = /1\, $ = 3;
4) ?(Г) = /^р\, s = 4.
1. 8. По заданной функции ср(£“)£Ф2 изобразить
в нагруженном дереве цепь, соответствующую префиксу
х3 входного слова хш, и написать префикс у3 выходного
слова у".
1) ? (Г) = 10100100010... (т. е. y(t) = l лишь для
*=(2), »=2, 3, х’ = 0101001;
184
2) ср («“) , (a) «* = 1111101, (б) 0 = 1O1O11O;
/л / 1. если ж(1) + л(2)4-...+x(«)>^/2,
3) у (I) = { _
[ О в ином случае,
(а) «10 = 0101010110, (б) «10 = 1100101110.
1.9. Нагруженное дерево, соответствующее некото-
рой функции ср(«ш)6 Ф2, имеет следующий вид: левой
дуге, исходящей из корня, приписан 0, правой — 1;
если’у — вершина i-го ранга (i 1) и дуге i-го яруса,
заходящей в вершину у, приписан символ а £ {0, 1},
то левой дуге, исходящей из у, приписан тот же символ
а, а правой дуге — символ 3 (отрицание а).
1) Верно ли, что для этой функции s-я буква вы-
ходного слова уш=^ («“) находится из соотношения:
(а) У(!)=«(!)» y(s) — x(s — 1)фя($) при з>2;
(б) у(1)=ж(1), y(2)=j(l)®i(2),y(s)=j(s-2)®
ф х ($) при s^>3;
(в) у (s) = х (1) ф х (2) ф ... ф х ($)?
2) Найти вес функции <р.
1.10. Эквивалентны ли остаточные операторы ср., и
<ргг д. функции ® £ Ф2?
1) ср (Г) = 10100100010 ... (т. е. у(£) = 1 только для
t = fy, i = 2, 3, ...), = 101, ^з==010;
2) = «<1 = 10, «5 = 00101;
3) <р («“) = , «J = 1, «? = 001;
4) <р(Г) = у(1)у(2) ... и
[ 0, если х (1) х (2) -ф- ... х (t)<Z t/2,
I 1 в ином случае,
«2 = 10, «5 = 010110.
1.11. Выяснить, является ли cpj остаточным операто-
ром функции ср £ Ф2.
. р(1) = о,
I У (t) = X (t) Ф У (t — 1), Z > 2,
Tr \y(t)=y(t-l), t^2-,
185
’ f' I y(l) = y(l-^, 7>2,
I 7/(1) = 0,
ь: I y(7) = y(/-l), «>2;
. f 7/(1) = 0,
<F' I у (0 = x (0 • £<J —1) V 7 (0 • xlJ — 1). 7 >2,
. ( y(l) = O,
?1‘ \ y(t) = x(t)Qy(t — 1), t^2;
.. ._ш. /13\ /1\
4) ?(л ) = (O, ) = \i5/-
1.12. Выяснить, является ли функция ср^Ф”’”* о.-д.
функцией, и найти ее вес.
1) ?(*"): { у(1) = у(2) = 1, у(7)=х(7— 2), 7^3;
2) <р(Г): | у (21) —х (7-}~ 1)> tZ^A, y(2t— 1) = г(7), 7^>1; у(1) = 1,
3) <Р(Г): у (27 -1)==® (27—1) ®у (27-3), 7>2, у (27) = х (27 — 1), 7^1; О). У1(7) = Х1(7)фа:2(7) © у2(7 —1), 7>2,
4) ?(Г): • У2 (0 = Х1 (1 ) ’ Х2 (1)> у2 (7) = хх (7) • х2 (7) © хг (7) • у2 (7 — 1) ф фа:г(7).у2(7-1), 7 > 2; г/1(1) = 1,
5) т(П: 7/1(0 =0-1). «>2, 7/2(1) = 0, Уз (0 = 0 —1). *>2.
1.13. Пусть — нагруженное дерево, реализую-
щее о.-д. функцию <р : Ат -* Вш. Каждой вершине дерева
Da, в припишем число, равное весу поддерева, расту-
щего из нее. Получим новое дерево Da, в-
186
1) Для всякого привести пример такой о.-д,
функции tp, чтобы каждая вершина в дереве Da, в, со-
ответствующем функции ср, была помечена числом г.
2) Для всякого г 2 привести пример такой о.-д.
функции <р, чтобы при /=0, 1, . . г—1 каждая вер-
шина J-го ранга в дереве Da, в, соответствующем функ-
ции ср, была помечена числом г—/.
1.14. 1) Доказать, что дерево Da, в, построенное
в соответствии с условием задачи 1,13, обладает сле-
дующим свойством: последовательность чисел v (yj,
v (у2), . . ., приписанных вершинам ориентированной
цепи plt (ух, р2), у2, (v2, р3), и3, . . . (конечной или беско-
нечной), является монотонно невозрастающей и, в слу-
чае бесконечной цепи, эта последовательность стабили-
зируется.
2) Показать, что любой остаточный оператор функ-
ции ср £ Фд, в имеет вес, не превосходящий веса функ-
ции ср.
1.15. Дерево, реализующее функцию ср0 (жш) £ Ф2,
имеет следующий вид: символ 1 приписан только тем
дугам, которые принадлежат ориентированной цепи,
исходящей из корня и соответствующей входному слову
10100100010 ... (здесь ж (£)=:! лишь для Z = I —
= 2,3,. . .); остальным дугам приписан символ 0. До-
казать, что функция ср0 имеет бесконечный вес и, следова-
тельно, не является ограниченно-детерминированной.
1.16. Для каждого г^2 построить пример такой
о.-д. функции веса г, которая удовлетворяет условию:
в реализующем эту функцию нагруженном дереве сим-
вол 1 приписан только дугам некоторой одной беско-
нечной ориентированной цепи Z, исходящей из корня;
остальным дугам (не принадлежащим цепи Z) приписан
символ 0.
Слово £ю Q Аш называется квазипериодическим, если
существуют такие целые числа п0 и Т, что п0 1,
Т 1 и х (п-\-Т')—х (п) при п п0. При этом префикс
х (1) х (2) ... х (,пй—1) слова ж10 называется предпериодом,
число н0—1 —длиной предпериода, словож(ге0)ж(п04-1). ..
... х (пд~гТ—1) —периодом слова х“, а число Т —
.длиной периода. Такое квазипериодическое слово удобно
записывать в виде
х (1) х (2) ... х (п0 — 1) [ж (п0) х (п0Д-1) ... х (п0 Д- Т —1)]“
187
1.17. 1) Доказать, что если функция в,
то всякое квазипериодическое слово из Аш преобра-
зуется функцией tp в квазипериодическое слово из 5“.
2) Показать, не выходя за пределы множества Ф2,
что утверждение, обратное к сформулированному
в 1), неверно.
У Казани е. См. задачу 1.15.
1.18. Опровергнуть следующее утверждение: если
д. функция ср (Хх, Х2): (0, 1}“х{0, 1}ш {О, 1}ш суще-
ственно зависит от переменной Хх и при всяком (фикси-
рованном) слове £££ {0, 1}“ <р (Хр £“)—о.-д. функция,
то функция <р (Хр Х2) также является ограниченно-детер-
минированной.
1.19. Пусть все вершины нагруженного дерева раз-
биты обычным образом на классы эквивалентности.
Доказать, что, каков бы ни был класс эквивалентности,
в нем существует некоторая вершина и, удовлетворяю-
щая условию: все вершины в ориентированной цепи,
исходящей из корня дерева и оканчивающейся в вер-
шине и, попарно не эквивалентны.
1.20. 1) Доказать, что для каждой вершины нагру-
женного дерева, имеющего вес г, найдется эквивалент-
ная ей вершина ранга не выше г—1.
2) Можно ли в предыдущей задаче заменить г—1
на г—2, если г 2?
Пусть /х (жх, х2, ..., хп), f2 (;Гр х2, ..., хп), ..., fm (xv
х2, ..., xt) — функции вида ЕкхЕк X .. X#ft -* Е,, где
п раз
к и I не меньше 2. Оператор из ФДР назы-
вается оператором, порожденным функциями fv f2,.. .,/m,
если для всякого t1
(0 = Л (^1(0» ....*„(£)), j = 2......т.
1.21. Показать, что оператор из Ф$’ | является порожден-
ным (некоторой функцией вида ЕкхЕкХ ... ХЕк -+Et)
п раз
тогда и только тогда, когда его вес равен 1.
1.22. Выяснить, является ли порожденным оператор
<р £ Ф):2, задаваемый следующими соотношениями:
y1(t) = x(t — 1) © y2(t — 1), i>2,
yz(t)=x(t).
188
1.23. Частичный оператор <р : {0, 1 }” —> {0, 1}“ задан
только на входных словах О” и 1“. Доопределить его
так, чтобы получился оператор с минимально возмож-
ньш весом.
1) ?(0“) = 0101 [100]“, с? (1“) = 11 [10]“;
2) <р(б“) = 01 [011]“, <р (Г) = 1010010031000010...
(т. е. y(t) = l только для Z = Q^, 1 = 2, 3, ...^.
1.24. 1) Доказать, что если | А | > 1 и |5|^> 1, то
мощность множества Фа, в равна с (мощности конти-
нуума).
2) Найти мощность множества Фа, в в тех случаях,
когда либо | А | = 1, либо | В | = 1.
1.25. Слова и из Аш называются s-эквивалент-
ными (обозначение: x'f ~ ж“), если равны их префиксы
длины s (s 1). Отношение — является отношением
эквивалентности и разбивает множество Ат на классы
Kj(s) s-эквивалентных слов.
1) Какова мощность каждого класса Kj (s) (s — фикси-
рованное число)?
2) Сколько существует различных классов Кi (s)
(при фиксированном $)?
3) Сколько существует различных классов К($ Z)
в каждом классе K}.(s) (здесь /^>1)?
4) Доказать, что отображение ср; 4“->5“ является
д. функцией тогда и только тогда, когда для всякого s 1
и любых слов х^ и f“, принадлежащих множеству 4“,
соотношение ~ влечет соотношение ср (х?) у <р (£“).
1. 26. 1) Доказать, что если | В | 2, то множество
Фл, в — счетно-бесконечное.
2) Чему равна мощность множества Фл, в, если
]5| = 1?
1.27. Пусть Da, в — нагруженное дерево, реализую-
щее о.-д. функцию <р : 4“ -» Вт веса г. Изменим выход-
ной символ у какой-либо дуги /-го яруса дерева DA, в
(считаем, что | В | 2). Получим дерево D'a, в, реали-
зующее некоторую (новую) о.-д. функцию ср' веса г'.
1) Показать, что l^r'^r-]-/.
2) Привести пример такой о.-д. функции ср, на кото-
рой достигается верхняя оценка, т. е. г1 = г /.
189
£ 2. Представление детерминированных функций
диаграммами Мура, каноническими уравнениями,
таблицами и схемами. Операции
над детерминированными функциями
Пусть Q — {Qa, Qv . .<2ю-1} — множество всех со-
стояний функции у из Фл, в- Сопоставим функции <р
орграф Г?:
1) множеством вершин орграфа Г? является мно-
жество Ew = {0, — 1}, причем считается, что
вершина у соответствует состоянию Qs,
2) если f1*’ и tp'-71 —остаточные операторы функции <р,
реализуемые соответственно состояниями Q{ и Qj (при-
чем в1''1 является также остаточным оператором опера-
тора ср”1, соответствующим префиксу х1 = а, и <р”’ (aiF) —
= by<J> (х"У), то в орграфе Г? имеется дуга (Z, у) и ей
приписывается выражение а (Ь);
3) дуга (i, у) существует в Г только при выполне-
нии условий п. 2).
Вершина из Г?, соответствующая начальному со-
стоянию функции ср, обычно отмечается звездочкой.
Пусть из вершины i в вершину у идут т дуг, кото-
рым приписаны выражения а^Ь^), ат(Ьт)
(здесь обязательно ар =^= aq при p^=q, но некоторые или
все из символов bg могут совпадать друг с другом);
тогда будем соединять i с j только одной дугой (i, у)
и будем приписывать ей все выражения ар (Ьр), р = 1, т-
Орграф Г? называется диаграммой Мура функции <р.
С Г? можно связать две функции:
a) F: A x Q —> В — функция выходов,
б) G: А XQ -*Q — функция переходов.
Функции F и G по Г? определяются так: по паре
(а, у) находим вершину у и такую дугу, исходящую
из у, которой приписан входной символ а (пусть эта
дуга имеет вид (у, г)); значением функции F на паре (а, у)
является выходной символ, приписанный дуге (у, г)
и стоящий в скобках за символом а; значение функции
G на паре (a, j) совпадает с г, т. е. равно «номеру» того
состояния, которое «является концом» дуги (у, г).
Система уравнений
y(t) = F(x(t),
q(f) = G(x(t), q(t-l)), (1)
9(0) = ?o>
190
где х (i) £ А, у (t) £ В, q (t) £ Q (t=l, 2, . . .) и
q0 € Q, называется каноническими уравнениями опе-
ратора с начальным условием q0.
С помощью диаграммы Мура и канонических урав-
нений можно задавать и такие детерминированные
операторы, которые не являются ограниченно-детер-
минированными. Множество вершин орграфа 1Д, со-
ответствующего такому д. оператору, совпадает с на-
туральным рядом /V={0, 1, 2, . . .}.
Если <р — ограниченно-детерминировапный опера-
тор, то функции F (х (/), q (£—1)) и G (х (Z), q (t—1))
(см. систему (1)) и аргументы, от которых зависят
эти функции, принимают конечное число значений;
поэтому возможно табличное задание о.-д. оператора <р
с помощью так называемой канонической таблицы.
ТАБЛ И ЦА 7
»(1| ч (1 - 1)
• •
• •
•
а /
• •
• •
• «
У (О Q (0
• •
• •
F (о, ]) G(a, Л
• •
• •
* •
Вместо канонических уравнений (1) бывает удобно
рассматривать такие канонические уравнения, в кото-
рых функции выходов и переходов являются функ-
циями й-значной логики Рк {к 2). Для получения
соответствующего представления оператора -f алфавиты
А, В и Q кодируются векторами, координаты которых
принадлежат множеству Ек (к 2). Если — о.-д. опе-
ратор и H=]logft |Л |[, m=] logft \В | [, r=]logj<?|[,
то для кодирования букв из алфавитов А, В и Q до-
статочно взять векторы (с координатами, принадлежа-
щими Е^, имеющие длины п, т и г соответственно х).
*) Если д. оператор у не является о.-д. оператором, то
г = со.
191
Система (1) преобразуется тогда в следующую:
У1(О (xi (0..........х« (О» 91 (« — 1), • • qr (t — 1)),
Ут (О = Fm (*i (0. • • •>хп (0> 9i(f — 1), • 9,(« — 1)).
9i(0 = Gi(a:i(i:)...жя(^), 9Х,9r(i — l)), (2)
9Г (0 = Gr (xi (*)> •••.*„ (t), qt (t— 1),
9i (O) = 9oi> ••-9r(0) = 90r-
9r(^-l)).
В дальнейшем используется также «векторная запись»
систем, аналогичных системе (2). При такой записи
система (2) выглядит следующим образом:
1/(В” (Z)( e(r)
qm (f) = G-(r> (х( к> (*), q(rl (t — 1)), (3)
q^ (Q)—q(G.
Функции F. и Gt в системе (2) являются, вообще
говоря, частичными, т. е. не всюду определенными.
Обычно их доопределяют так, чтобы правые части урав-
нений в (2) имели по возможности более простой вид.
Каноническая таблица, задающая о.-д. оператор ср,
соответствующий системе (2), имеет т-}-п-^2г столб-
цов и кп+г строк.
Уравнения системы (2) называются каноническими
уравнениями в скалярной форме, а уравнения из системы
(1) — каноническими уравнениями в векторной форме.
Можно считать, что система (2) определяет оператор
из множества
Пусть д. оператор <р задан системой (2) и каждая
из функций Ft и Gt — всюду определенная функция
Л--значной логики Pk (к^ 2). Будем рассматривать
оператор ср как элемент множества Ф£' “. Схема S?
оператора <р определяется следующим образом: Ц,
представляет собой сеть, полюсам которой приписаны
символы входных и выходных переменных, а некото-
рым вершинам, отличным от полюсов, приписаны сим-
(СО СО \
из множества (J □ Ф’’*'1.
8=1 «'=1 '
Схему оператора ср из Ф£> т будем изображать в виде
192
прямоугольника (рис. 26) с п входными и т выходными
каналами. Входные каналы изображаются в виде стре-
лок, исходящих из входных полюсов, а выходные —
в виде стрелок, заходящих в выходные полюсы. По-
люсы изображаются в виде кружочков. Если тп=1,
то схему Е? оператора ср иногда будем изображать в виде
треугольника (рис. 27) с п входными и одним выход-
ным полюсами.
Считаем, что в каждый момент времени £=1,2,...
на г-й вход xt «поступает» входной символ х. (t) £ Ek,
а на j-м выходе у, «выдается» (реализуется) значение
Уу (xi (0» • • •> хп 91 (t— 1), . • ., qr (t—1)).
Говорят, что выход уj зависит с запаздыванием от входа
Рис, 26. Рис. 27.
х{, если функция Fj (рс(п> (£), q'r> (t—1)) не зависит
существенно от переменной х{ (t).
Понятие зависимости с запаздыванием можно ввести
иначе. Рассмотрим, например, случай д. функции вида
ср (Х1( Х2, . . ., Хп): Л1Х-42Х- • - ХА„ -> В и опреде-
лим зависимость с запаздыванием от переменной Х2.
Функция ср зависит с запаздыванием от Xlt если при
любых входных словах ...,£“ (х^А™, ]=Л,п)
s-я буква выходного слова j?“ = cp(5“, х%, ...,х%) одно-
значно определяется s первыми символами слов £“,...
..., х'"’ и s — 1 первыми символами слова
Пусть д. функция ср задана системой (2) и Е — схема
этой функции. Определим три операции над функцией
<р и схемой Е .
1) Операция Ог — отождествление двух или боль-
шего числа входных переменных в функции <р и отожде-
ствление в схеме Е? соответствующих этим переменным
входных полюсов. Отождествленные полюсы рассматри-
ваются как один полюс новой схемы. На рис. 28 по-
казана схема E^, которая получена из Е^ отождествле-
нием полюсов хг и х2.
7 Г. П. Гаврилов, А. А. Сапожевко
193
2) Операция 02 — удаление некоторой выходной пере-
менной Pj у функции <р (что эквивалентно выбрасыва-
нию из системы (2) уравнения уу (i) = Fy (acw (f),
<7(г) (2 — 1))) и удаление из схемы Е выходного канала
и полюса, соответствующих выходной переменной уу
Рис. 28,
(см. рис. 29, на котором изображена схема Еф, полу-
чающаяся из Ер после удаления выходного канала и
полюса ух).
Замечание. Если тп=1, то, удаляя перемен-
ную У1 (единственную выходную переменную), полу-
чаем автомат без выхода.
3) Операция О3 — введение обратной связи по одной
входной и одной выходной переменным. Пусть в ка-
честве входной переменной взята переменная xt, а в ка-
честве выходной — уу. Операцию О3 можно применять
(к функции <р и схеме Е?) лишь в *-том случае, когда
выход Уу зависит с запаздыванием от входа xf. Канони-
ческие уравнения для новой функции ф получаются
исключением из системы (2) уравненияуу (t)=Fj (х(я) (/),
194
5{r) (t—1)) и заменой переменной х{ (t) в каждой функ-
ции Ft (q^j) и G, на функцию Fj (^(t), . . (<),
ж4ч1 (0, (0. 91 (*—1). • • •. Чг С*—1)), получаю-
щуюся из функции Fj (хи> (t), qm (t—1)) отбрасыванием
несущественной переменной х{ (£). Начальные условия
остаются прежними. Схема Еф получается из схемы Е?
в результате отождествления выхода у^ с входом х{\
прй этом отождествленные полюсы объявляются вну-
тренней вершиной схемы Еф. На рис. 30 показана схема
которая получена из Е? введением обратной связи
по переменным xt и ух.
lV-
£ ф
Рис. 30,
Замечание 1. Если п=1, то, вводя обратную
связь по переменной хг (и любой выходной переменной),
получаем автомат без входа.
Замечание 2. Применяя перечисленные выше
операции, удобно указывать в скобках (за обозначе-
ниями этих операций) те каналы (полюсы и перемен-
ные), к которым операции применяются. Например,
Ог (xlt х3), О2 (z/5), О3 (xw, у2).
Определим еще две операции над д. функциями.
4) Операция Ot — операция объединения двух (или
большего числа) функций. Пусть £ Ф^’ ”•> и <р2 £ Ф}ч>т».
Будем предполагать, что эти функции имеют в качестве
входных переменных х[, х2, ..., х'П{ и x"v х2, ..., х"П1 со-
ответственно, а в качестве выходных — у'и y'2,...,y'mi и
у”, У™,- Считаем, что все эти переменные попарно
различны. Пусть ЕТ1 и ЕТ1 — схемы функций и <р2
соответственно. Тогда схема Еф функции ф, равной
объединению функций <рх и <р2, будет выглядеть так,
195
как показано на рис. 31; при этом выходными (вход-?
ними) полюсами схемы являются все выходные
(входные) полюсы исходных схем S?1 и ETj. Система
канонических уравнений (и начальных условий) функции <[»
получается простым объе-
динением соответствующих
систем функций <рх и <ра
(при этом, естественно,
предполагается, что множе-
ства 0а) и Q'2' всех со-
стояний функций и <р2
не пересекаются).
5) Операция S — опера-
ция суперпозиции. Пусть
Рис. 31,
€ Фа, в и Фд, с- Су-
перпозицией <pj (<р2) операто-
ров <р2 и ?i называется такой оператор ф £ Фа, с, что ф(ж“) =
— <рх (<р2 (Г)) при любом входном слове из Лш. Пусть
операторы (Е Ф**’ (» = 1, 2) и им отвечают схемы
ЕТ| и Е<р, (считаем, что входные и выходные переменные
и состояния функций и <р2 такие же, как в преды-
дущем абзаце). Тогда можно рассматривать «иную»
суперпозицию этих операторов: отождествим, например,
входной полюс x'i схемы с выходным полюсом у'м
схемы ЕТ1, полюс а:''— с полюсом yj+a и т. д., наконец,
196
полюс x"„rj — с полюсом y'mi; получим схему Еф (рис. 32),
у которой: а) входными полюсами будут все входные
полюсы схемы Е?1 и входные полюсы схемы Ет>, не
участвовавшие в указанной выше процедуре отожде-
ствления; б) выходными полюсами являются все выход-
ные полюсы схемы £¥1 и те выходные полюсы схемы
Е?1, которые не были отождествлены ни с одним вход-
ным полюсом схемы Е?2. Отождествленные полюсы
объявляются внутренними вершинами схемы Е^. Схема
называется суперпозицией схем Ет, и Efi (по пере-
менным ж’ — у'м, x” — y'l+2,...,x"mt.i—y’mi). Если опе-
ратор задается системой
y'i W=^(O). 0 — 1). ...
...,q'ri (f —1)),
Ут, (0 = F'm, (х{ (f), ..., 4, (0. Ql (* — 1), • • •
>& (t — 1)),
ч\ (О = Gi (0> • •> (0. О — 1). •••
...,<o-i)),
(0 = Gr, (x\ (/), ..4, (t), q\ (t — 1), q’rt (f — 1)),
. 9r, (0) = •••,?;, (°) = 9or.,
а оператор <p2 — системой
yj (0=^(0). ...,<(«), O-i). •••
....O-i)).
y"mAt) = F';ni(x’’l(t), ...,<(o, O-i).
....?;(«-!)),
y';(0=<?;(^W,....<(0. O-i). ••• (4,z)
Q", (0 = <?;, (xt (0, ...,x"ni (t), q{ (t -1), ...
<i'Aty = q’n,....O°)=O
197
то оператору ф, реализуемому схемой соответствует
такая система:
у! (о—f{ (*; w,.... (о. я! (^—1), •••
У, (0 = Fi М (Z), ..., < (Z), д[ (Z — 1), ...
y'[(t) = F"l(F'M,...,F'mt, ^,_;+1(Z), ...
..х„г (Z), 91 (Z — 1), ..qr2(t — 1)),
Ут, (Z) = F™, (F'uv • • •> F’mi, x'„t_M (Z), ...
• • 42(Z), <?i(Z — 1)...^(Z —1)),
Q\ W — G'i«(Z), .. .,4, (Z), q't (Z — 1), ...
....gUz-l)), (5)
?r, (z) = G', (x[ (I), ...,x’„t (I), q[ (t — 1), ...
?i (Z)= Gi (F(41, ..Fmi, a:mi_/+1 (Z), ...
.... 4JZ), ?1(Z —1), ...,grj(Z —1)),
qrt (t) = G’r, (F’M, ..., F'mt, x’mi..l+1 (Z), ...
.. .,x^(Z),gi(Z —1), ..., qri(t— 1)),
Ql (0) — Qn.....Qi (°) == 9or„ ?! (0) = 5м, ...
где F'j = Fj(x't (Z), ..., x'„t (t),q{ (t — 1)...q^ (Z — 1)),
7 = Z4-1, .... mv
Элементом единичной задержки (в множестве ФЛ)
называется о.-д. оператор <ра, задаваемый системой
y(t) = q(t — 1),
9(Z)=x(Z), (6)
lff(0) = 0.
198
Пример. Оператор ср из Ф2 задан с помощью
диаграммы Мура, изображенной на рис. 33. Канониче-
ская таблица (см. табл. 8), канонические уравнения
и начальное условие для него выглядят так:
таблица 8
я (t) а « -1) v (0 9(0
0 0 1 1
0 1 0 1
1 0 0 1
1 1 0 0
y(t) = x(t)-q(t — 1),
q(t)=z(t)Vq(t-V), (7)
9(0) = 0.
На рис. 34 изображена схема, реализующая этот опера-
тор и построенная с использованием элемента единич-
ной задержки и оператора из Ф1*1, порожденного
стрелкой Пирса х\ у. Здесь
стрелкой Пирса, реализуется
оператор, порожденный
схемой
199
а элемент единичной задержки — схемой
K:o-L_l
Известно, что всякий о.-д. оператор из Ф^" может
быть реализован схемой над таким множеством, которое
содержит: 1) схемы, реализующие элемент единичной
задержки; 2) схемы, реализующие операторы, порож-
денные функциями из некоторой полной в Рк системы.
Другими словами, множество о.-д. операторов, состоя-
щее из элемента <ра и операторов, порожденных функ-
циями из некоторой полной в Рк системы, образует
полную в (J Ф^’”1 систему относительно операций Ov
О2, Os, и S.
Замечание. В дальнейшем, говоря о построе-
нии схемы какого-либо о.-д. оператора <рнад некоторым
заданным множеством М о.-д. операторов, мы будем
понимать это следующим образом: схема Е оператора (р
строится с использованием только одновыходных схем,
реализующих операторы из множества М (при этом
разрешается применять лишь операции Ог, 0.2, О3, Ол
и S, если нет других указаний).
2.1. Построить диаграмму Мура, каноническую таб-
лицу и канонические уравнения для функции <р £ Фа.
.. ( у (2t — 1)=х (2t — 1), t^l,
ч ? <х)- \ У (2t)=x(2t) ф у (2t - 1), Z> 1;
2) ?(Г): I y(t) = x(t-i)®x(t), t^2-
у (3Z — 2) = х (3Z — 2), Z > 1,
3) <p (Г): у (3t — 1) —х (3Z — 2), Z > 1,
у (31) = x (3Z) • у (3t — 1), Z 1;
4) Т(Г) = <2/3>;
5) T(r) = <v(O8>.
2.2. Доопределив некоторым образом частичный
оператор <р: {0, 1 }ш -> {0, 1причем так, чтобы по-
лучился о.-д. оператор, построить для нового опера-
тора диаграмму Мура, каноническую таблицу и ка-
нонические уравнения.
200
1) <р ([011010]") = [0111]", <Р (0[1]"> = 0[1]";
2) т(б") = 1", <p(l[0]") = [10]";
3) ? (1 [Ю]") = [01]", <р ([001]") = 1[10]";
J y(3«-l) = a:(3i-l), <>1,
> ( y(3t) = x(3t — 1), />1.
2.3. Найти вес о.-д. оператора <р из Ф2, заданного
каноническими уравнениями.
y(t) = x (t) • qt (t — 1)V® (0 • q2 (t — 1),
9i (0 = x (0 • (t — 1)\/X (0 • q2 (t — 1),
92 (0=x(t)q2(t 1)V* (0 ’?i(£ 1) ‘Q2(t —1)>
?i(0) = g2(0) = 0;
y(t)=x(t) © q^t— l)®g,(J — 1),
9i(0 = *(0~9i(* —1),
q2 (0 = (x (0 -» 9i (t — 1)) -» * (0 • 9i (t — 1),
9i(0) = 9a(0) = l;
3) <p задается каноническими уравнениями из пре-
дыдущей задачи, но с измененными начальными усло-
виями: qx (0) = 0, q2 (0) = 1;
4) <р:
У (0 = (ж(0-» 92 (i — 1))91 (^ — 1),
91 (0 = 9i (t — 1) -» (х (0 -> 9а (t — 1)),
92(0 = 92^ —1) — а;(0>
91(0) = д2(0) = 0.
2.4. Пусть ($».»; Х2,...,Х„; Ур У2,...,У„)
обозначает множество всех функций из Ф^> “, у кото-
рых входными переменными являются переменные Xlt
Х2, ..., Хп, а выходными — Ур У2, ..., Ym. Показать,
что в множестве (Ф”- т; Xlt Х2, ..., Хя, Yv У2, ..Ут)
число функций веса w не больше чем (ш • кт)а’кП.
2.5. Пусть оператор tp из Ф^т задан системой (2)
и функции Gv G2, ...,Gr связаны соотношением ф
ф G2 ф ... ф Gr = 0. Показать, что вес оператора у
не превосходит 2Г-1.
201
2.6. Реализовать оператор <р £ Ф"’ т схемой над мно-
жеством, состоящим из элемента единичной задержки и
оператора, порожденного штрихом Шеффера.
1) ?:
У (t) = Q (t — 1),
q(t) — x(t),
g(0) = l;
2)
9i (0 =x(t)-> q2 (I — 1),
q2 (0=^i (г — W& (t — !)>
91(0) = 0, ?a(0) = l;
10(110]*°, если r = 6m,
1“ в ином случае;
4) оператор ср задается диаграммой Мура, изобра-
женной на рис. 35;
5) ?:
г/i (t)=x(t)-^q1(t — 1),
У2 (0 = ?i (^ — 1) • 9а — 1)>
92(«) = (9i(f-l)V92(«-l))^(0>
9i(0) = 92(0) = 0.
2.7. По схеме оператора ср £ Ф^т построить кано-
нические уравнения, каноническую таблицу и диаграмму
Мура.
1) см. рис. 36, а; 2) см. рис. 36, б; 3) см. рис. 36, в.
2.8. Для суперпозиции ф = ср* (ср2) операторов ср2 и срг
из Ф2 построить канонические уравнения, диаграмму
Мура и зхему Еф. Схема Еф должна быть построена
202
импликацией х—>у
над множеством, состоящим из элемента единичной за-
держки и операторов, порожденных
и отрицанием х.
1) ?г
z/i(Z) = o:1(i)-91^—1).
9i (0 = ffi (^ — 1) (О,
91(0) = о,
у2 (<) = (/) ф q2(t— 1),
92 (0 — х2 (О V9г 1)>
92(0) = 1;
?2:
l(t)
0)
Рис. 36.
нам
О
0(0)
но
Рис. 37.
диаграммой Мура,
изображенной
оператор <р2 задается
на рис. 37;
z-ок р(1) = 0,
/ Н1) = 1.
Iх Л | у (z) = х (/) -» х (f — 1), t 2;
203
( у (1) = 1,
4) ?1(И- { y(f) = y(<—1)^х(0, f>2,
?2(Г) = <1/7>.
2.9. Построить канонические уравнения и диа-
грамму Мура о.-д. оператора, получающегося из опе-
ратора ср введением обратной связи по переменным ж2, ух.
У1 (0 — Q 1) —(О (0>
Уз (0 = х2 (О V (t) -+q(t — 1)),
q(t) = z2(t)®q(t — 1),
g(0) = 0;
' У1 (0 = У (f — 1) — xt (t) xs (t),
y2(o=(^(o i ?a-i))v x2(t),
q(t) = x2(t) ©g(i-l),
g(0)=o.
1)
2)
2.10. Найти вес о.-д. оператора, получающегося из
о.-д. оператора ср введением обратной связи по перемен-
ным х3, у2.
1) ?:
2)
у —^i (0 -* (^s (f) -* q(f
У2(/)=х2(/)-*а:1 (t),
q (f)=(f) -* (xi (0 «з (0 -* (xi (О -* q !)))>
д(0) = 0;
y1(t)=Xi (t) xs (t)q (t — 1),
у2 (0=«2 (t)q(t — 1),
q(t)=x2(t) vi,(ov
g(0) = 0.
2.11. Пусть оператор ф получается из оператора ср
с помощью операции Ог (отождествление входных пере-
менных).
1) Привести пример такой пары операторов ср и ф,
для которой справедливо неравенство: вес оператора <р
больше веса оператора ф.
2) Возможно ли, чтобы вес оператора ср был меньше
веса оператора ф?
2.12. Пусть ср — о.-д. оператор веса гиф — опера-
тор веса г', получающийся из ср введением обратной
связи по некоторой паре переменных. Верно ли, что
всегда
1) г > г'; 2) г=г'\ 3) г г'?
204
2.13. Пусть о.-д. операторы <рх и ср2 имеют веса гх
и г2 соответственно. Чему равен вес оператора ф, полу-
чающегося из <pi и <р2 с помощью операции (объедине-
ния)?
2.14. О.-д. операторы <рх и <р2 имеют веса, равные гг
и г2 соответственно. Может ли вес суперпозиции срх (ср2)
быть
1) больше Гр 4) больше г±-г2;
’ 2) больше г2; 5) меньше 1\;
3) больше Г!-|-г2; 6) меньше г2?
2.15. Найти вес суперпозиции <рх (<р2), если:
1) операторы срх и ср2 задаются диаграммами Мура,
изображенными на рис. 38, а, б",
Рис. 38.
Рис. 39.
2) операторы <рх и <р2 задаются диаграммами Мура,
изображенными на рис. 39, а, б;
3) ср,:
(t)=xt (0 qt (t — 1),
q< (0={t — 1) -»(0.
g((0) = 0,
4=1, 2.
Оператор ср из Фл, в называется автономным (констант-
ным, оператором без входа), если при любом входном
слове 5“ значение оператора ср на хш равно одному
и тому же (выходному) слову из
205
2.16. Является ли автономным оператор <р£Ф2?
1)
у(1) = у(2) = 1,
ry(t) = y (t — 1) ф у (t — 2),
*>3;
3) <p:
y(t) = x(t)-+q(t — 1),
q(t)—x(t)\/ q(t— 1),
<7(0)=l;
’ у (t) = x (t)-* q (t — 1),
q(t) = x(i) Vq(t — 1),
<?(0)=0;
4) <p(f“):
y(l) = 0,
y(2t-l) = y(2t-2),
у (2Z) = | cos у 11,
f>2,
«>1.
2.17. Пусть <p — автономный оператор веса г (г < оо).
1) Показать, что выходное слово оператора <р
является квазипериодическим.
2) Доказать, что сумма длин периода и предпериода
выходного слова оператора <р не превосходит г.
2.18. 1) Над множеством
w-
о-4~П-х> ,
2) <?:
построить такую схему которая содержит ровно
четыре элемента из М и реализует какой-либо автоном-
ный оператор <р из Ф2.
2) Можно ли построить (над множеством М) схему
Е , реализующую некоторый автономный оператор у
из Ф2 и содержащую менее четырех элементов?
Операцию Оъ — операцию разветвления (некото-
рого выхода о.-д. функции) можно определить так.
Пусть <р — оператор из Ф*-m и Е — реализующая
его схема. В результате применения операции Оъ к вы-
ходу yj функции <р получается оператор ф, реализуемый
такой схемой Е^, у которой вместо одного канала
(и полюса) yj появятся несколько «одинаково работаю-
щих» каналов у^р, . . у^р (s 2), каждый из кото-
рых реализует ту же функцию, что и у^ в схеме Е?.
206
2.19. 1) Какие изменения надо внести в систему
канонических уравнений и начальных условий, задаю-
щую функцию <р, чтобы получить соответствующую си-
стему для функции ф, являющейся результатом приме-
нения операции О& к выходу функции <р?
2) Можно ли, используя операции Ог—Оъ и S,
построить над множеством М (см. задачу 2.18) такую
схему 2 которая содержала бы не более трех элемен-
тов и реализовала автономный оператор из Ф2?
2.20. Пусть оператор ф получен из ср £ т в Ре'
зультате применения операции О5 к некоторому выходу
оператора ср. Показать, что оператор ф можно реализо-
вать над множеством {ср} (т. е. используя несколько
экземпляров оператора ср) с помощью операций Olt Оа
и <Л-
2.21. Операторы срх и <р2 из Ф2 имеют веса, равные 2,
и задаются следующими каноническими уравнениями:
У( (О—(ж< (0» (^ 0)>
(О = (0> (^ 1))> i = 11 2,
91(0)=0,
причем Gt (х, q)=G2 (х, q). Известно, что если в диа-
грамме Мура оператора <рх заменить нули, приписанные
дугам, на единицы, а единицы — на нули, то получится
диаграмма Мура оператора ср2. Доказать, что если вы-
ходные значения операторов <рх и ср2 совпадают на некото-
ром префиксе длины 2 (т. е. срх (о1а2) = ср2 (°1сз2) при не-
которых ап о2), то эти операторы тождественно равны.
2.22. Подсчитать число всех таких о.-д. функций
в Ф2, которые удовлетворяют следующим условиям:
а) функция зависит от входной переменной X; б) вес
функции равен трем; в) в диаграмме Мура, задающей
функцию, полустепень захода каждой вершины одна
и та же и равна полустепени исхода.
2.23. Для каждого г 2 привести пример такого
оператора ср из Ф2, чтобы вес суперпозиции ср (ср) был
равен г. Можно ли это сделать для неавтономных опера-
торов?
2.24. Вес функции ср £ Ф2 равен г, а вес суперпози-
ции <Р (?) равен 2г. Верно ли, что вес суперпозиции
<р (<р (ср)) равен Зг?
207
§ 3. Замкнутые классы и полнота
в множествах детерминированных
и ограниченно-детерминированных функций
Пусть М — некоторое множество д. функций (или
о.-д. функций) и б — какая-либо совокупность опера-
ций, не выводящих за пределы множества всех д. функ-
ций (или о.-д. функций). Другими словами, если (г£0,
то, применяя а к произвольным (или допустимым) д.
(или о.-д.) функциям, мы получаем снова д. (или о.-д.)
функции. Замыканием [Afb множества М относительно
совокупности операций 0 называется множество всех д.
(или о.-д.) функций, которые могут быть получены
из функций множества М с помощью операций из 0,
причем операции можно применять любое конечное
число раз. Обычно считают, что В дальней-
шем мы почти всегда будем предполагать, что это вклю-
чение выполняется (в противном случае будут делаться
специальные оговорки). Операция получения множе-
ства [Aflff из М называется операцией замыкания.
Множество М называется (функционально) замкнутым
классом относительно совокупности операций 0, если
\M]s=M. Пусть М — замкнутый относительно сово-
купности операций 0 класс д. (или о.-д.) функций.
Подмножество из М называется (функционально)
полной системой в М относительно совокупности опе-
раций 0, если Множество & д. (или о.-д.)
функций называется неприводимой системой относи-
тельно совокупности операций 0, если, каково бы
ни было собственное подмножество из
(включение строгое!). Базисом замкнутого класса М
относительно совокупности операций 0 называется вся-
кая полная и неприводимая система из М. Множе-
ство М', содержащееся в замкнутом классе М, назы-
вается предполным классом в М, если оно не является
полной системой в М, но при всякой функции £ М\М'
выполняется равенство [M'U {<р}]^=Л/.
Замечание 1. В дальнейшем, когда ясно, отно-
сительно какой совокупности 0 рассматриваются замы-
кание, полные системы, базисы и т. д., слова «относи-
тельно совокупности операций 0» будут опускаться.
Замечание 2. Обычно в качестве 0 мы будем
брать множество {б\, О2, О3, Oit S }, состоящее из опера-
ций, описанных в § 2 данной главы.
208
Как указывалось в § 2, множество о.-д. функций,
содержащее элемент единичной задержки <р3 и опера-
торы, порожденные функциями из некоторой полной
в Рк (к 2) системы, образует полную систему в мно-
СО со
жестве и и относительно операций Ov О2, О3,
n=Q т—0
Oia S (т. е. в множестве всех к-значных о.-д. функций).
СО со
Оказывается, что в множестве U |J Ф^т (к^2)
Я=0 0 -
существуют базисы относительно {О1, О2, О3, ov S},
состоящие из одной функции. Примером такого базиса
является множество (ср0 (Хх, Х2, Х3, ьВД}, где
элемент единичной задержки из а <р0 — оператор
из !, порожденный функцией max (хх • xi -|- х2 (1 — х^,
х3) -|-1 (сумма, разность и произведение по mod к).
Всюду в данном параграфе мы будем применять
символ Ф(А.) (соответственно Ф(4.,) для обозначения мно-
жества всех А-значных о.-д. (соответственно д.) функ-
ций, включая и функции без входов, или без выходов,
или без входов и без выходов, т. е.
ф(4)= и и Фг (и Ф<*)= и и Ф2’т).
к=0 м=0 ' я=0 w=0 '
3.1. Является ли множество М замкнутым классом
относительно совокупности операций 01
1) М состоит из всех А-значных о.-д. функций, не
имеющих выходов, а также из всех таких функций <р,
со со
принадлежащих (J U которые «сохраняют 0">,
я=0 w?—1
т. е. <р (б“..О”) = (бш, ..., 0“); 0 = {О„ О6, S}.
п раз т раз
2) М состоит из всех таких А-значных о.-д. функций,
которые принадлежат множеству (J Ф^’т и имеют вес,
т=0
кратный к; 0—{S}.
3) М состоит из всех Лг-значных д. функций, принад-
лежащих множеству U U Ф*’т и имеющих четный или
n=l >?i=l
бесконечный вес; 0 = {Ov О2, Ov ОБ}.
4) м = j U (Ф?-от \ Ф?’и); 0=ЛО3, 5}.
м=0 »г==0
209
3.2. 1) Пусть сра — элемент единичной задержки из
множества Ф2 и б = (О3, ОБ, 5}. Доказать, что класс [cp,]ff
содержит лишь функции, тождественно равные 0 (т. е. опе-
раторы, на каждом выходе которых «выдается» слово бш),
и функции, имеющие четный вес.
2) Привести пример функции из Ф2, имеющей четный
вес и не принадлежащей классу [сра]₽, описанному в за-
даче 3.2, 1).
3.3. Пусть <р0 (Хр Х2)—оператор из Ф{2), порожден-
ный штрихом Шеффера х2 | х2, а ср3 — элемент единич-
ной задержки из Ф2. Доказать, что оператор ср(£ш) =
= <1/3> из Ф2 не принадлежит классу [ср0, если
0 = {S}.
3.4. На вход о.-д. оператора ф £ Ф2 подается периоди-
ческое слово хш периода 3. Найти максимальный период
выходного слова (максимум берется по всем входным
периодическим словам периода 3).
1) ср:
У (0 = (t) ® ?i (f — 1)) • q2 (t — 1),
41 (t) — x (t) • q2 (t — 1) • q2 (t — 1) \/ X (/) • q2(t — 1),
qi(t) = x(tyq1(t—i)-q2{t—\)\/x{t)-q2(t — l),
9i (0) = ?2 (0) = 0;
2) ?=
y(0 = a:(0-91^ — 1),
ffi (0 = (i) • q2 (t 1) V q2 (t — 1),
= —1).
?i(0)=<?2(0)=0.
3.5. Пусть <p — о.-д. функция веса г, принадлежащая
множеству Фл,в.
1) Показать, что если входное слово хш является квази-
периодическим с периодом Т, то выходное слово <р (хш)
также является квазипериодическим и его период не пре-
восходит числа г • Т.
2) Оценить сверху длину преднериода выходного
слова ср (ж1"), если известно, что длина предпериода слова
равна р.
3.6. Пусть функции <р0, ср, и ср такие же, как в за-
даче 3.3. Существует ли некоторое 1, удовлетворяю-
щее условию ? (<pf (X)) е [ср0, где 6 = {S}t (Здесь
РО = ?.(?»(•• •'Р.(Х) •••)) — суперпозиция s «штук»
функций <ра.)
210
Если f(x”)£Pk, то через ср/(гВ) (Х1( ..Хв) будем обо-
значать о.-д. оператор (из х)> порожденный функ-
цией f(xn).
3.7. Являются ли полными в Ф(Л:) относительно сово-
купности операций {О1, О2, О3, Ov S] следующие си-
стемы о.-д. функций?
1) Х2), <?,(Х)}, Л>2;
Х2), (X), Х2),
?=1(X), ?=Cft_2) (X)}, (здесь <р=у(Х) —о.-д. опера-
тор, порожденный функцией из Рк, тождественно рав-
ной у);
3) {?Ж+1(Х), ?,(?.(Х)), ?х^(?.(Х), х2)}.
3.8. Из системы полной в Ф()и относительно сово-
купности операций {Ov О2, О3, Ov S}, выделить хотя бы
один базис.
1) ^={?.(Х), ?s0(X), Tsa(X), ^.„(Хр Х2),
Тоех.ех/Хр Х2, Х3)}, Л=2;
2) ^ = {?.(Х), ?=0(Х), ?S1(X), ? (X),
^(ХрХ,)}, Л>3;
3) ^={?^(Х), ср (?,(Х), Х2), <рх+1(Х),
'Р.пЫ^/Хр *>3-
3.9* . Существует ли в Ф(2) базис относительно сово-
купности операций {О1, О2, О3, Ov S}, содержащий пять
функций?
3.10* . Доказать, что в Ф(й) любой замкнутый класс,
отличный от всего множества Ф(Л), расширяется до пред-
полного класса *).
3.11* . Используя задачи 3.8, 1) и 3.10, показать,
что в Ф(2) существует не менее 4 нредполных классов.
3.12. Пусть <ра £ Ф2- Перечислить все классы, пред-
полные в [<ра](о3, оь, в} относительно совокупности опера-
ций {ОБ, 5}.
3.13. Пусть <рх = <рх (X) — о.-д. оператор из Ф(Л),
порожденный функцией х. Доказать, что, каков бы ни
был замкнутый класс1) М из Ф(4.;, всегда выполняется
равенство [Л/и{-ра.}] — (здесь, как обычно, вместе
J) Замкнутость и предполнота берутся относительно сово-
купности операций {Оь Ог, О3, Ог, S}.
211
с функцией берутся и все равные, и все конгруентные
ей функции).
3.14. Существует ли функция, которая принадлежит
каждому предполному в 4(fc) классу?
3.15. Можно ли представить множество Ф(Я;) в виде
8
объединения (J Mt (s 2) попарно непересекающихся
•=i
замкнутых1) в Ф(й) классов?
3.16* . Доказать, что в Ф(4) мощность множества всех
замкнутых классов континуальна.
3.17. Какова мощность множества всех замкнутых
в Ф(Л.) классов1), имеющих конечные полные системы?
3.18* . Доказать, что в Ф(Л., мощность множества всех
замкнутых1) классов равна 2е (мощность гиперконти-
нуума).
3.19* . Найти мощность множества всех замкнутых
в Ф(Л) классов:), обладающих конечными базисами.
3.20. Опровергнуть следующие утверждения:
1) множество Ф(й) образует предполный класс в Ф(Ю;
2) в множестве Ф(А;) существует функция, образую-
щая совместно с множеством полную в Ф(Л:) систему»
3.21. Пусть Мо—множество, состоящее из всех
А-значных д. функций, не имеющих выходов, а также
СО со
из всех таких функций <р, принадлежащих (J U Ф£>т,
я=0 »п=1
которые принимают значение 0 при t—i, т. е. <р (я“, ...
•••>«“) = (у?, •••>#“) и ys.(1) = 0 при j =
1) Является ли Мо предполным в Ф(П классом?
2) Образует ли предполный класс в Ф. пересечение
3.22. 1) Является ли предполным классом в Ф(к) мно-
1 со
жество (J (J Ф»>т?
я=0 т=0
2) Образует ли предполный в Ф(Л) класс множество
U U ®2’ro?
я=0 т=0
х) См, сноску на стр. 211,
Глава VII
ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ
§ 1. Машины Тьюринга и операции над ними.
Функции, вычислимые на машинах Тьюринга
Машина Тьюринга представляет собой (абстрактное)
устройство, состоящее из ленты, управляющего устрой-
ства и считывающей головки.
Лента разбита на ячейки. Во всякой ячейке в каждый
(дискретный) момент времени находится в точности один
символ из внешнего алфавита А = {а0, ах, . . ., ап^},
п > 2. Некоторый символ алфавита А называется
пустым, а любая ячейка, содержащая в данный момент
пустой символ, называется пустой ячейкой (в этот мо-
мент). В качестве пустого символа обычно используют О
(нуль). Лента предполагается потенциально неограни-
ченной в обе стороны х).
Управляющее устройство в каждый момент времени
находится в некотором состоянии q^, принадлежащем
множеству <2={<7о, <71, • • •, 7r-i}> !• Множество Q
называется внутренним алфавитом (или множеством
внутренних состояний). Иногда из Q выделяются
непересекающиеся подмножества и Qo начальных
и заключительных состояний соответственно.
Замечание. В дальнейшем, если не будет ого-
вариваться противное, мы считаем, что | 2, и в ка-
честве начального берем только одно состояние qr. За-
ключительным, как правило, будет состояние q0.
’) Эго следует понимать так: в каждый момент времени
лента конечна (содержит конечное число ячеек), но «размеры»
ленты (число ячеек на ней) можно (при необходимости) увели-
чивать.
213
Считывающая (или печатающая) головка переме-
щается вдоль ленты так, что в каждый момент времени
она обозревает ровно одну ячейку ленты. Головка
может считывать содержимое обозреваемой ячейки
и записывать в нее (печатать в ней) вместо обозревае-
мого символа некоторый новый символ из внешнего
алфавита. «Засылаемый» в ячейку символ может,
в частности, совпадать с тем, который обозревался
(в данный момент).
В процессе работы управляющее устройство в зави-
симости от состояния, в котором оно находится, и сим-
вола, обозреваемого головкой, изменяет свое (внутрен-
нее) состояние (может остаться в прежнем состоянии),
выдает головке приказ напечатать в обозреваемой
ячейке определенный символ из внешнего алфавита и
«приказывает» головке либо остаться на месте, Либо
сдвинуться на одну ячейку влево, либо сдвинуться
на одну ячейку вправо.
Работа управляющего устройства характеризуется
тремя функциями:
G: Q х A -+Q,
F: QXA^ А,
D: QxA-*{S, L, R}.
Функция G называется функцией переходов, функ-
ция F — функцией выходов и D — функцией движения
(головки). Символы S, L и R обозначают соответственно
отсутствие движения головки, сдвиг головки на одну
ячейку влево и сдвиг на ячейку вправо.
Функции G, F и D можно задать списком пятерок
вида
QfijG (q(, aj)F(q{, aj)D(q{, aj) (1)
или, короче, Эти пятерки называются ко-
мандами. Функции G, F и D являются, вообще говоря,
частичными (не всюду определенными). Это значит,
что не для всякой пары (q(, а^) определена соответствую-
щая пятерка вида (1). Список всех пятерок, определяю-
щих работу машины Тьюринга, называется программой
этой машины. Программу машины часто задают в виде
таблицы (см. табл. 9).
214
ТАБЛИЦА 9
Если в программе машины для пары (q{, dj) пятерка
вида (1) отсутствует, то в таблице на пересечении
строки dy и столбца q{ ставится прочерк.
Работу машины Тьюринга бывает удобно описывать
на «языке конфигураций».
Пусть в момент времени t самая левая непустая
ячейка Сг ленты содержит символ Яу,, а самая правая
непустая ячейка С, (s 2) содержит символ яу, (между
ячейками Сг и С, находятся s—2 ячеек). В этом случае
будем говорить, что в момент t на ленте записано
слово Р = а. aJp ... aJs, где Яур — символ, содер-
жащийся в момент t в ячейке Cp(l^p^s). Приа=1,
т. е. когда на ленте только один непустой символ,
Р = а^. Пусть в этот момент времени управляющее
устройство находится в состоянии q( и головка обозре-
вает символ Яу; слова Р (I 2). Тогда слово
а . ... а . q.a . ... а . (2)
J, Jl-t1* л Лв ' '
называется конфигурацией машины (в данный момент t).
При 2=1 конфигурация имеет вид qia^. . .aJe. Если
в момент t головка обозревает пустую ячейку, находя-
щуюся слева (или справа) от слова Р, и между этой
ячейкой и первой (соответственно последней) ячейкой
слова Р расположено и 0 пустых ячеек, то конфигу-
рацией машины в момент t называется слово
qtA, ,.. Аду, ... Ду, (3)
ч 4- 1 раз
(соответственно слово Яу, ... Яу,Л ... Л^Л), где че-
> раз
рез Л обозначен пустой символ алфавита А. Если в мо-
215
мент t лента пуста, т. е. на ней записано пустое слово,
состоящее лишь из пустых символов внешнего алфавита,
то конфигурацией машины в момент t будет слово ^Л.
Пусть в момент t конфигурация машины имеет
вид (2) и в программе машины содержится команда
тогда при dijt=L в следующий момент времени конфигу-
рацией машины будет слово:
a) qij^aijflj* ... aJs, если I = 1;
б) • • • «л. если I — 2>’
в) аЛ... • • • «/,» если 1 > 2.
Случаи, когда dtj(=R или dij=S, или конфигура-
ция машины соответствует головке, находящейся вне
слова Р (как в слове (3)), или слово Р — пустое, опи-
сываются аналогично.
Если в программе машины нет пятерки вида (1)
для пары (g<, или «новое» состояние qtj является
заключительным, то машина прекращает работу, а «ре-
зультирующая» конфигурация называется заключитель-
ной. Конфигурация, соответствующая началу работы
машины, называется начальной.
Пусть в некоторый момент времени конфигурация
машины была К, а в следующий момент — К'. Тогда
конфигурация К' называется непосредственно выводи-
мой из К (обозначение: АГ|=ЛГ'). Если — начальная
конфигурация, то последовательность Кг, К2, . . ., Кт,
где Kip=KM при 1 г т—1, называется тьюринго-
вым вычислением. При этом говорят, что конфигурация
Кт выводима из конфигурации Кх, и пишут А\|— Кт.
Если Кт является к тому же заключительной конфигу-
рацией, то говорят, что Кт заключительно выводима
из Кх, и применяют запись: К^-Кт.
Пусть машина Тьюринга Т начинает работать в не-
который (начальный) момент времени. Слово, записан-
ное в этот момент на ленте, называется исходным,
или начальным. Чтобы машина Т действительно начала
работать, необходимо поместить считывающую головку
против какой-либо ячейки на ленте и указать, в каком
состоянии машина Т находится в начальный момент.
Если Pt — исходное слово, то машина Т, начав ра-
боту «на слове» Ри либо остановится через определен-
216
ное число шагов, либо никогда не остановится. В пер-
вом случае говорят, что машина Т применима к слову Рг
и результатом применения машины Т к слову Рг
является слово Р, соответствующее заключительной
конфигурации (обозначение: Р=Т (PJ). Во втором слу-
чае говорят, что машина Т не применима к слову Рг.
В дальнейшем мы будем предполагать, если не ого-
варивается противное, что 1) исходное слово — непу-
стое, 2) в начальный момент головка находится против
самой левой непустой ячейки на ленте и 3) машина
начинает работу, находясь в состоянии qv
Зоной работы машины Т (на слове Рг) называется
множество всех ячеек, которые за время работы машины
хотя бы один раз обозреваются головкой.
Часто будет использоваться обозначение [Р]’” для
слов вида РР. . .Р (т раз); если Р~а — слово длины 1,
то вместо аа. . .а (т раз) и [а]” будем писать ат.
Через W будем обозначать произвольное конечное
слово во внешнем алфавите машины Тьюринга (в част-
ности, пустое, т. е. состоящее из пустых символов
внешнего алфавита).
При описании работы машины Тьюринга «на языке
конфигураций» будут использоваться выражения, ана-
логичные такому:
1 и у 1. Приведенное выражение надо понимать
так: машина «стирает» слово Iх и останавливается
на первой букве слова W; если же W — пустое слово,
то «останов» происходит на втором 0 (нуле) после слова 1А
Машины Тьюринга Тг и Т2 называются эквивалент-
ными (в алфавите Л), если для всякого входного слова Р
(в алфавите Л) выполняется соотношение Тг (Р)=^Т2 (Р),
означающее следующее: (Р) и Т2 (Р) определены или
не определены одновременно т), и если они определены,
то 1\ (Р) — Т2 (Р). Символ называется знаком услов-
ного равенства.
Пусть машины Тг и 7\ имеют соответственно про-
граммы П1 и П2. Предположим, что внутренние алфа-
виты этих машин не пересекаются и что q{ — некоторое
*) Т (Р) определено (не определено), если машина Т при-
менима (не применима) к слову Р.
217
заключительное состояние машины Тг, a q2 — какое-
либо начальное состояние машины Т2. Заменим всюду
в программе состояние q[ на состояние q2 и получен-
ную программу объединим с программой П2. Новая
программа П определяет машину Т, называемую ком-
позицией машин Т± и Т2 (по паре состояний (q{, q2))
и обозначаемую через ТгоТ2 или ТГТ2 (более подробно:
Т=Т (Т\, Т2, (q{, g'))). Внешний алфавит компози-
ции ТгТ2 является объединением внешних алфавитов
машин Тг и Т2.
Пусть q' — некоторое заключительное состояние
машины Т, a q" — какое-либо состояние машины Т,
не являющееся заключительным. Заменим всюду в про-
грамме П машины Т символ q' на q". Получим про-
грамму П’, определяющую машину Т' (q', q"). Ма-
шина Т' называется итерацией машины Т (по паре
состояний (q', g")).
Пусть машины Тьюринга Т\, Т2 и Т3 задаются про-
граммами 7Zlt П2 и П3 соответственно. Предполагаем,
что внутренние алфавиты этих машин попарно не пере-
секаются. Пусть q[ и q[ — какие-либо различные
заключительные состояния машины Заменим всюду
в программе Пг состояние q[ некоторым начальным со-
стоянием д' машины Т2, а состояние д'' — некоторым
начальным состоянием q'3 машины Т3. Затем новую
программу объединим с программами П2 и П3. Получим
программу П, задающую машину Тьюринга Т =
= Т (Тv (q'lt q2), Т2, (д’, д'), Т3). Эта машина называется
разветвлением машин Т2 и Т3, управляемым машиной Тг.
При задании сложных машин Тьюринга часто при-
меняют так называемую операторную запись алгоритма,
которая представляет собой строку, состоящую из сим-
волов машин, символов
/ ч
перехода(вида —и
а также
символов а и ®, служащих для обозначения соответ-
ственно начала и окончания работы алгоритма. В опе-
раторной записи (некоторого алгоритма) выражение
Т{ Ц’2’ -^-1 Т„ обозначает разветвление ма-
шин Ти Тп, управляемое машиной Т{, причем заклю-
чительное состояние д<0 машины Т( заменяется началь-
ным состоянием дя1 машины Тп, а всякое другое заклю-
чительное состояние машины Ti заменяется начальным
218
состоянием машины Tj (одним и тем же!). Если ма-
шина Т( имеет одно заключительное состояние, то сим-
волы | и дя1 [ служат для обозначения безусловного
перехода. Там, где не могут возникнуть недоразумения,
символы qi0 и qnl опускаются.
Пример. Операторная схема
J J ^lg^2 1*720 Л |?30
2 1 12
описывает следующий «процесс вычисления». Начинает
работу машина Т2. Если она заканчивает работу в со-
стоянии <72о, т0 начинает работать машина 7\, а по окон-
чании работы машины вновь «выполняет работу»
машина Т2. Если же машина Т2 останавливается в не-
котором заключительном состоянии, отличном от q2(i,
то «работу продолжает» машина Т3. Если Т3 приходит
в заключительное состояние q30, то начинает работу
машина Т\‘, если же Та заканчивает работу в некотором
заключительном состоянии, отличном от q30, то «работу
продолжает» машина Tt. Если машина когда-либо
остановится, то процесс вычисления на этом заканчи-
вается.
Пусть а = (а1, а2,..., ая), п"^ 1, — произвольный набор
целых неотрицательных чисел. Слово 1а>+101“’+10 ... 01“м+1
называется основным машинным кодом (или просто кодом)
набора S. (в алфавите {0, 1}) и обозначается к (а). В част-
ности, слово 1“+1 является основным машинным кодом
числа а.
В дальнейшем рассматриваются в основном лишь
частичные числовые функции. Функция / (xt, х2, . . ., жя),
га 1, называется частичной числовой функцией, если
переменные xt принимают значения из натурального
ряда 2V={0, 1, 2, . . ., т, . . .} и в том случае, когда
на наборе а=(ах, 02,..., а„) функция / определена,
/(а)€^.
Частичная числовая функция называется вычисли-
мой (по Тьюрингу), если существует машина Тью-
ринга Тj, обладающая следующими свойствами:
а) если /(Ж) определено, то Tf (к (а)) = к (f (%));
б) если /(а) не определено, то либо Tf (к(&)) не яв-
ляется кодом никакого числа из N, либо машина Тf не
применима к слову к (i).
219
Замечание. В дальнейшем предполагаем, что
в начальный момент головка машины обозревает самую
левую единицу слова к (а). Известно, что это ограниче-
ние не сужает класса вычислимых функций.
Если функция / вычислима по Тьюрингу с помощью
машины Tf, то мы будем говорить, что машина Тf вы-
числяет функцию /.
1.1. Выяснить, применима ли машина Тьюринга Т,
задаваемая программой П, к слову Р. Если применима,
то найти результат применения машины Т к слову Р.
Предполагается, что qr — начальное состояние, д0 —
заключительное и в начальный момент головка машины
обозревает самую левую единицу на ленте.
1) П:
g20g30T?
92^1^
g,l?2lZ?
2) П:
910921Я
£,Og3lZ,
g21?2l5
7?
3) II:
910911Я
9il 930Я
9209j1 R
g309ilL
a) P=l302l2,
6) P = l8013,
в) P = 10[01]2l.
a) P=l401,
6) P = l3012,
в) P = l6.
a) P —1012,
6) P = l202l,
в) P = 11O]21.
1.2. Построить в алфавите {0, 1} машину Тьюринга,
обладающую следующим свойством (в качестве пустого
символа берется 0):
1) машина применима к любому непустому слову
в алфавите {0, 1};
2) машина не применима ни к какому слову в алфа-
вите {0, 1 }, и зона работы на каждом слове — беско-
нечная;
220
3) машина не применима ни к какому слову в алфа-
вите {0, 1}, и зона работы на любом слове ограничена
одним и тем же числом ячеек, не зависящим от выбран-
ного слова;
4) машина применима к словам вида I3" (п 1)
и не применима ни к одному из слов вида 13я+“, где
а=1, 2 и п^1;
5) машина применима к словам вида где
а^1, и не применима к словам если а=^=₽
(а^> 1 и Р 1).
1.3. По заданной машине Тьюринга Т и начальной
конфигурации Кг найти заключительную конфигурацию
(д0 — заключительное состояние).
Qi «2
0 SoiS giOi?
1 qt0R g.,lL
a) б)
Qi 01 Q3
0 goO5 goli
1 да1Л д30Я g^OR
a) ff^l^l5, б) АГх = д11801, в) 2^ = lO^l*.
1.4. Построить в алфавите {0, 1) машину Тьюринга,
переводящую конфигурацию Кг в конфигурацию Ко.
1) ^=*1",
2) Л'1 = д1О"1я,
3) K1 = i”qfi,
4) К^Г^ОГ”,
Kt=9llW
K0=q0W
Ко = Яо^
Яо = 1’401”
(«>!);
1, п
>1).
221
1.5. 1) Показать, что для всякой машины Тьюринга
существует эквивалентная ей машина, программа кото-
рой не содержит символа S.
2) Показать, что по всякой машине Тьюринга можно
построить эквивалентную ей машину, в программе ко-
торой не содержатся заключительные состояния.
1.6. Программа машины Тьюринга Т имеет вид
91 Qi <7з «4
0 д31Я <ц2£ д2ЗЯ
1 д21Я д31Л
2 312L gfiR —
3 — д2ЗЯ д302?
(пустой символ — 0, начальное состояние — <7Х).
1) Показать, что, начиная работу с пустой ленты,
машина Т за t (re) шагов построит слово вида Рп=
= 110102103. . .10"! (ге — произвольное целое положи-
тельное число), причем в любой момент времени t t (п)
(для ге 3) головка машины будет находиться правее
слова Рп_2.
2) Построить машину, обладающую таким же свой-
ством и имеющую в качестве внешнего алфавита мно-
жество {0, 1}.
3) Доказать, что если в программе машины Тью-
ринга не встречается символ L (но могут встречаться,
естественно, символы S и R), то эта машина, начиная
работу с пустой ленты, не может построить сколь угодно
длинный префикс слова 1101021031. . .0"10"+11. . .
1.7. Показать, что для всякой машины Тьюринга Т
(в алфавите А) существует счетное количество эквива-
лентных ей машин 1\, Тг, . . ., 7’П), ... (в алфавите Л),
отличающихся друг от друга своими программами.
1.8. Пусть Л = {а0, ах, . . ., ап_1} — некоторый алфа-
вит, содержащий не менее двух букв. Закодируем его
буквы следующим образом; кодом символа at явля-
222
ется слово 10<+11 в алфавите {0, 1}. В соответствии
с этим кодированием код произвольного слова
P=aiflit. . (s > 1) в алфавите А будет иметь вид
10,>+1110’»+11 ... IO*»44!. Доказать, что, какова бы
ни была машина Тьюринга Т с внешним алфавитом А,
существует машина Тьюринга Ро с внешним алфави-
том {0, 1}, удовлетворяющая условию: при любом
слове Р (в алфавите Л) машина То применима к коду
втого слова тогда и только тогда, когда машина Т при-
менима к слову Р, причем, если Т (Р) определено,
то код слова Т (Р) совпадает со словом, являющимся
результатом применения машины То к коду слова Р.
1.9. Построить композицию ^^2 машин Тью-
ринга 7\ и Т2 (по паре состояний (д10, q21)) и найти ре-
зультат применения композиции к слову Р (qtn —
заключительное состояние машины Т2).
911 Qu
0 gijOi? 9ю^
1 9isl-R 9ц02?
Qn Qu
0 7211Л
1 ?210£
a) P = iso2l2, б) Р = 1401.
«11 9ia 913
0 91зОЛ 9ц02?
1 912^ 9nl^ 91,02?
Qai Qu
0
1 922^ 9210£
а) Р = 140213012, б) Р = 12010Р.
Он Qi? Qu
0 91*02? 9ц02? 9ю^
1 gn12? дп1/? —
01. 0». Qk
0 9230L
1 9211£ §22^ £ 9гз^
а) Р = 1201’012, Р = 120120212.
223
1.10. Найти результат применения итерации ма-
шины Т (по паре состояний (g0, qt)) к слову Р (заключи-
тельными состояниями являются q0 и q'o).
1) i = 1, Т:
71 Qi Q* «5
0 qfiS ?40S <7505 9*1 Я
1 g20J? g307? ?10Я — —
а) Р = 1з*, б) Р = 13*+1, в) Р = 13*+а,
2) i = l, T: Qi Qt Q3 Qi Qs
0 q'rPR q.OR q^L q$R
i g20/? q3QR д31Я q^R q^L
a) P = l2*, 6) P = la»+1, X > 1.
3) 1 = 3, T: 9i Qt «3 Qt q5 Qg
0 g20L — 9’<02? q3iL ge0£ q'^R
1 9127? q2lR — q^R q3iL q^L
2 — q3^R — — qolR
/> = 1*01* (х > 1, у 1).
1.11. Найти результат применения машины Т = 7’(711,
(?!«, (Q"o> 9si)> 7'з) к слову Р (^—заключитель-
ное состояние машины Т2, а <?30 — заключительное со-
стояние машины Т3).
224
Чз1
0 ?32^ 9зо1^
1 —
a) P = 1013. 6) P=-P01.
Qu «2м
0 922^^
1 ^22^
a) P = HO21 (x > 1),
б) P = 1*0101 (x > 1, у > 1, z > 1).
1.12. Используя машины 7\, T2, T3, Tt и T6, по-
строить операторную^ схему алгоритма 21 (здесь q10,
£io’ £20’ 9зо’ ?4о и ?5о — заключительные состояния со-
ответствующих машин).
Ql» Qi2
0 71207?
1 <?IoO-R ?u15
(h< Qt.
0 ?2зОЯ QtoOS
1 ?22^ ^23^
8 Г. П. Гаврилов, А. А, Сапоженко
225
Замечание. Если х=0, то 1* считается пустым
словом.
1.13. По операторной схеме алгоритма 21 и описа-
нию машин, входящих в схему алгоритма, построить
программу машины и найти результат применения
машины, задаваемой этой схемой, к слову Р.
1) 2i=«r1j7V3j2iifia>,
1
0» ?н Яи
0 9230А 9го^
1 Jail-Я — ?231Я
2 ?22^ — —
4u
0 JioOL
1 ?ц2-Я
2 —
?31 ?32
0 Q32OL дзоОЯ
1 ?31^
2 — qsoiR
Р = 1»01*' (х > 1, у > 1).
(Начальные состояния машин — qu, q21 и j31, а заклю-
чительные — ?10, 920, 9зо и q’3O.)
21 — «_] Т.Т21^20^ s 1?зо_Iю»
2 12 1
Qu <7i> ?13
0 — 51зОЯ guOZ, —
1 ?120Я ?121Л ?131Я
?2t Qn 4»
0 ?2о15
1 ?20^ ?зз1Ь ?231-^
226
<Ь 9г.
0 <7ззО^ 9зо^ 9з(Д-^
1 9з4^ — 934^
Р = 1*021* (г > 1, у > 1).
(Начальные состояния машин — qn, q21 и q31, а заклю-
чительные Qjq, q2o, q23, q33 и q3o-)
1.14. Построить машину Тьюринга, вычисляющую
функцию /.
1) / (я) = sg а: = / °’
I 1,
если
если
О,
не
3) 7 (*)=[|] =
х = 0,
х~^ 1;
если
если
определено, если
если х = 2т
х= 1,
х~^ 2,
х = 0;
или
х = 2т~]-1,
т^О;
,, ,, . 0, если
4) f(x, у) — х — у — 1
(я — у, если
5) Ж У)=х— у,
6) Ж У} = ^А.
х
х
Замечание. Здесь (и в дальнейшем) при «ана-
литическом» задании числовых функций часто исполь-
зуются широко известные «элементарные» функции
(из математического анализа). При этом «аналитически»
заданная функция считается определенной только на та-
ких целочисленных наборах значений переменных (при-
надлежащих натуральному ряду N), на которых опреде-
лены и принимают целые неотрицательные значения
все «элементарные» функции, входящие в данное «фор-
мульное задание» определяемой функции. Например,
у
функция-----определена лишь тогда, когда — целое
З-Т
227
неотрицательное число и 3 — у — целое положитель-
хг
ное число, и-------целое неотрицательное число.
3-Т
Говорят, что машина Тьюринга Т правильно вычис-
ляет функцию f (ЗУ), если:
1) в том случае, когда / (ая) определено, Т (к (£*))=
~к (j (ак)) и головка машины в заключительной кон-
фигурации обозревает левую единицу кода к (f (а"));
2) в случае, когда / (а”) не определено, машина Т,
начиная работу с левой единицы кода к (а”), не оста-
навливается.
1.15. Доказать, что для всякой вычислимой функ-
ции существует машина Тьюринга, правильно вычис-
ляющая эту функцию.
1.16. Построить машину Тьюринга, правильно вы-
числяющую функцию /.
1) f(x) = xy~l; 4) f(x, у) = х-]-у;
2) f(x) = sgx = l—sgx; 5) —,
1.17. По программе машины Тьюринга Т написать
аналитическое выражение для функций / (х) и / (х, у),
вычисляемых машиной Т. (Всюду в качестве началь-
ного состояния берется qx, а в качестве заключитель-
ного — q0.)
?! ?2
0 g2lL qfiR
1 gilJ? q^L
Qi Q3 Qs Qi 9s
0 g2OT? 5iOL g40L q$R
1 911Я g30fl gs0Z? q^L q^L
Qa Qa Q& 9« «7 ?8 9s
0 g20/J g30B golS gs0K g30£ g7OL — ge0£ giOB
1 520Я g4lfl g3l£ g4U? q^R gelfl g80Z, g8l£ g,!L
228
1.18. Какие одноместные функции вычисляются
всеми такими машинами Тьюринга (в алфавите {О, 1}),
программы которых содержат лишь по одной ко-
манде?
1.19. Справедливо ли утверждение: две различные
вычислимые функции Д (£") и /2 (я") можно вычислить
на одной машине Тьюринга тогда и только тогда,
когда т^=п1
1.20. Пусть М — счетное множество каких-то вы-
числимых функций и Т (М) — такое минимально воз-
можное множество машин Тьюринга, что для всякой
функции / из М существует машина в множестве Т (М),
вычисляющая функцию /.
1) Показать, что если для некоторого в мно-
жестве М существует бесконечное подмножество, со-
стоящее из n-местных функций, то в Т (М) найдется
машина со сколь угодно большим числом состояний
(т. е. для всякого l0 1 можно указать в Т (М) машину
с числом состояний, большим Zo).
2) Каково необходимое и достаточное условие ко-
нечности множества Т
1.21. Построить операторную схему машины Тью-
ринга, вычисляющей функцию /; в качестве элемен-
тарных операторов используйте машины Т{ (i=4, 5, 6,
7, 8). В задачах 1) и 2) сначала постройте операторную
схему, используя только машины 1\, Т2, Т3, а затем
каждую из машин Ти Т2, Т3 представьте операторной
схемой, использующей машины Tt, Тъ, . . ., Та. Началь-
ными состояниями в рассматриваемых здесь машинах
являются qn, g.2V ..д81, а заключительными — </10,
?10’ ?20’ 9-20’ <7зо> 710’ • •> 7so’ 7*0’
Qu
0 в
1
4si
0
1
Ч«1
?6005
7в11Л
229
0 57о05
1 ?711Л
т •
1 8*
Qbi
0
1
1) /(ж, у) = х-\-у (mod 2),
031
0
1 д311Л
т J 9111 Ь 9ю12.
21‘ {?ц1*+1|-г 101*0д'о12 при х>0;
(1-010^1^920^.
/ 2: | ро*ню^21р |_ 1*+101'0%1* при
здесь х > 0, у > 0, t > 0;
Г3: W0g31P«H ЖО?8012^, у>0;
Z
>0;
3) /(ж)==3а:;
4) /(*> У) = Х'У,
5) /(ж, у) — х— у.
Расстояние между двумя ячейками С и С' ленты
равно увеличенному на единицу числу ячеек, располо-
женных между С и С". В частности, соседние ячейки
ленты находятся друг от друга на расстоянии 1. Пусть
I — целое положительное число. Подмножество всех
таких ячеек ленты, каждые две из которых расположены
друг от друга на расстоянии, кратном I, называется
решеткой с шагом I. Таким образом, ленту можно рас-
сматривать как объединение I решеток с шагом I.
230
Пусть R(n — решетка с шагом I. Две ячейки этой ре-
шетки будем называть соседними, если расстояние
между ними (рассматриваемое относительно всей ленты)
равно I. Говорят, что слово Р=ах а2 . . . ат записано
на решетке R(n, если:
1) символ ах записан в некоторой ячейке Сг этой ре-
шетки;
2) символ а2 записан в ячейке С2, которая является
соседней к Сх на решетке Л(П и расположена справа
от ячейки С\, и т. д.
т) символ ат записан в ячейке Ст, отстоящей
от ячейки Сх на расстоянии {т—1)4 и расположенной
справа от *) Сх.
Будем говорить, что машина Тьюринга Тх модели-
рует машину Тьюринга Т на решетке RU) (с шагом Z),
если, каково бы ни было слово Р (в алфавите Л), выпол-
няется следующее условие: пусть на решетке R(l) за-
писано слово Р и в начальный момент времени головка
машины Тх обозревает самую левую букву слова Р\
машина Тх останавливается тогда и только тогда, когда
машина Т применима к слову Р\ при этом, если Т (Р)
определено, то после окончания работы машины Тх
на решетке Н(П будет записано слово Т (Р).
1.22. На решетке с шагом I смоделировать работу
машины Т, вычисляющей функцию /.
2) /(х, y) = ^-, Z = 3;
3) /(*> y)—x-\-y, / = з.
1.23. Показать, что для любой машины Тьюринга Т
и всякого целого I 2 существует машина Т', модели-
рующая машину Т на решетке с шагом I.
Будем называть 1-кратным кодом набора а" = (а1,
«г,..., «„) слово в алфавите {0, 1), имеющее вид
j j(°4+1)qZ Qi|Kan+l) (/>2)
1.24. 1) Доказать, что машину, преобразующую основ-
ной код набора 2" в Z-кратный код этого набора (Z 2),
Считаем, что вне ячеек Сх, Сг, . . ., Ст на решетке Л(П
расположены лишь пустые символы внешнего алфавита.
231
можно задать следующей операторной схемой:
а7\ _| Тг |?гою1
11
где:
а) 7\ имеет начальное состояние qu, заключитель-
ное — g10 и
. ОГ”*1 И- ?10Г,+102l’,+101as+10 ...
...
б) Т2 имеет начальное состояние g2J и два заключи-
тельных состояния — q№ и q'№ и
д211^021“<+1+10Г^+10 оГ”иО'+11'(а,+1)О'1/С”’+1)О'
Q/j /(«<+!-«)
Oi®«+1oz+iiz(“i+1)o/+1l/(°4+1) o' ... O'l't’>+2~*) при
я>0,
д21102Г'+1+101аж+10 ... 01’”+10'ul'(ei+1)0'...
... 0'1'(а<+1) h- g;„l“<+,+102 r>+’+101’i+3+10 ...
0ia"+10'+4'^a'+1^0'. 0'1 '(a<+1)0'1'
g2110'+1l'(a,+1)0'l'(a,+1)0'.. .0'1,(ая+1)|-г g2ol,(“‘+1)O'l'l’*+1)O'...
QI jz(aH+l)>
2) По словесному описанию машин Т3, Tit . . ., Ти
построить их программы.
Т3 — машина, начав работу с последней единицы
массива из единиц, «сдвигает» его на одну ячейку влево
(не изменяя «остального содержимого» лентых)); го-
ловка останавливается на первой единице «перенесен-
ного» массива;
Ti — при заданном I 1 головка машины, начав
работу с произвольной ячейки, содержащей единицу,
движется вправо до тех пор, пока не пройдет массив
из I -|- 1 нулей; головка останавливается в первой ячейке
за этим массивом, напечатав в ней 1;
Ть — при заданном Z 1 головка машины, начав
работу с какой-то ячейки и двигаясь вправо, ставит
подряд I единиц и останавливается на последней из них;
*) Иными словами, считаем, что ни одной «новой» единицы
не появилось и изменения в исходном куске ленты коснулись
только указанного массива.
232
Tt — мащина начинает работу с самой левой непу-
стой ячейки; при заданном I 1 «отыскивается» первый
слева массив из /+1 нулей и головка останавливается
на последнем из этих нулей («содержимое исходного
куска ленты» не меняется);
Т1 — начав работу с самой левой непустой ячейки,
машина отыскивает единицу, примыкающую с левой
стороны к первому слева массиву из трех нулей,
«окаймленному» единицами; головка останавливается
на найденной единице («содержимое исходного куска
ленты» не меняется);
Ts — в исходной ячейке печатается 0 и головка,
сдвинувшись на одну ячейку влево, останавливается;
Т9 — головка сдвигается на две ячейки вправо
от «начальной» ячейки, и машина останавливается
в состоянии д90, если новая ячейка содержит символ О,
и в состоянии если в «новой» ячейке — 1 (содержи-
мое ленты остается прежним);
Т10 — головка передвигается на одну ячейку влево
(после чего машина останавливается; на ленте никаких
изменений не происходит);
Тп — головка, начав двигаться вправо от какой-то
«начальной» ячейки, «находит» первую (при таком пе-
ремещении) единицу и, сделав еще один шаг, останав-
ливается на ячейке, расположенной справа от «найден-
ной» единицы х) (содержимое ленты не меняется).
3) Взяв в качестве исходных машины Т3, Ту, . . .,
Ти, построить операторную схему для машин Ту и Т2
и для машины, преобразующей основной код набора
в /-кратный.
1.25. Построить операторную схему машины Тью-
ринга, преобразующей /-кратный код набора 3" в основ-
ной код этого набора. В качестве исходных машин,
соответствующих элементарным операторам, исполь-
зуйте машины 7\, Tg, . . ., Ts из задачи 1.21 и еще такие
три машины:
Ту — при заданном / ^ 1 головка машины, двигаясь
вправо от какой-либо пустой ячейки, находит первый
(при таком перемещении головки) массив, содержащий
не менее / единиц, затем в этом массиве стирает первые
1) Если в «начальной» ячейке записана единица, то головка
останавливается на соседней справа ячейке.
233
I единиц и останавливается на ячейке, в которой была
последняя стертая единица («остальное содержимое»
ленты не меняется);
Т2 — головка из «начального положения» сдви-
гается влево на I ячеек (I задано), после чего машина
останавливается на Z-й ячейке; содержимое ленты
при этом не меняется;
Т3 — работает аналогично машине Т2, но «сдвиг»
происходит вправо.
Решетчатым кодом набора а"=(я1, а2, . . ., ая) на-
зывается слово в алфавите {0, 1}, записанное на п ре-
шетках с шагом п, причем так, что на первой решетке
записано слово 1“>+1, на второй — сло'во l’,+1 и т. д.,
на п-й — слово l’»+1; начала слов на решетках должны
быть согласованы, т. е. самая левая единица на первой
решетке непосредственно предшествует (на ленте) самой
левой единице на второй решетке, а эта единица не-
посредственно предшествует самой левой единице
на третьей решетке и т. д.
1.26. 1) Построить операторную схему машины Тью-
ринга, преобразующей основной код набора а” в решет-
чатый код этого набора. В качестве исходных машин,
соответствующих элементарным операторам, исполь-
зуйте машины Т\, Тъ, . . ., Т3 из задачи 1.21 и еще две
машины:
— головка из «начального положения» сдвигается
на п ячеек вправо, после чего машина останавливается
(на n-й ячейке); содержимое ленты при этом не меняется;
Т2 — работает аналогично машине Tlt но головка
передвигается влево.
2) Используя те же машины, что и в предыдущей
задаче, построить операторную схему машины Тью-
ринга, преобразующей решетчатый код набора ®я
в основной код этого набора.
§ 2. Классы вычислимых и рекурсивных функций
Функции, рассматриваемые в этом параграфе, яв-
ляются частичными числовыми функциями.
Функция F (xv ..., хп) = f (gx (xv ..., х„) gm (xv ...
..., xn)) называется суперпозицией функций f и gv ..gm
и обозначается через S g[n\ .. ..gjf5). При этом функ-
ция F определена на наборе ая и F (a") =/(gx(a*), ...
234
• • т°гда и только тогда, когда каждая функция
определена на наборе а” и, кроме того,
функция / определена на наборе (^(а”),..., gm (а")).
Пусть g(xv х^) и h(xv..., xK_v хп, жя+1) — какие-
либо две функции, причем п 2. Определим третью
функцию f\xv ..., xn_v хя) с помощью следующей схемы:
f(x1,...,xn_v0)=g(xL,.,.,x„_1),
г/4-1)= (1)
= /г(а:р...,хя_р у, f(xv ...,2^, у)), у>0.
Схема (1) называется схемой примитивной рекурсии для
функции / (х") по переменным хп и жя+1 и задает прими-
тивно рекурсивное описание функции f (ж") с помощью
функций g и h. Говорят также, что функция / получена
из функций g и h с помощью операции примитивной
рекурсии по переменным хп тз. жя+1. В этом случае исполь-
зуют такое обозначение: f~R (g, h) (и указывают от-
дельно, по каким переменным ведется рекурсия).
При задании примитивно рекурсивного описания
функции / (х), зависящей от одной переменной, схема
примитивной рекурсии имеет вид
/(0) = а,
/(y + l)=fe(y, /(у)), у>0,
(2)
где а — константа (число из натурального ряда N =
= {0, 1, 2, ...}).
Пусть / (жр ..xn_v х„), п 1, — некоторая функция.
Определим функцию g(xv .. ^х^, хя) следующим обра-
зом: пусть а = (яр . .., ая_р ая)—произвольный набор
целых неотрицательных чисел; рассмотрим уравнение
/(«i> •••»«_!, У) = ав,
(3)
а) если уравнение (3) имеет решение у0 f N и при
всех у £ N, таких, что О^у<уо, функция / (ар ..., а^р у)
определена и ее значения отличны от ая, то полагаем
g(a)='/0;
б) если уравнение (3) не имеет решений в целых
неотрицательных числах, то считаем, что g (а) не опре-
делено;
в) если у0 — наименьшее целое неотрицательное реше-
ние уравнения (3) и при некотором y^N и меньшем
235
р0 значение / (ар ..., а„_р уг)не определено, то полагаем:
g (5) не определено. ь
О функции glx"), построенной указанным способом
из функции / (хп), говорят, что она получена из функции
f (а:1, .. ., хя_1, хп) с помощью операции минимизации по
переменной хп (или короче: с помощью минимизации
по хп). В этом случае используются следующие обозна-
чения: g — Mf или g (х”) = МХп (J (ж”)), или g(x’tj =
= (/ жя-1> У) = или S (Л = !**„(/ (Л):
Замечание. Операции примитивной рекурсии и
минимизации можно применять по любым переменным,
входящим в функции /, g и h (но всегда нужно указы-
вать, по каким переменным эти операции проводятся).
Простейшими будем называть в дальнейшем сле-
дующие функции:
a) s (х)—х~\~1 — функция следования;
б) о (х)=0 — нулевая функция;
в) Z« (жр . . . , хг)=хт (1 < т < п; п=1, 2, . . .) —
селекторная функция, или функция выбора аргумента.
Класс К„р всех примитивно рекурсивных функций
представляет собой множество всех функций, которые
могут быть получены из простейших функций с помощью
операций суперпозиции и примитивной рекурсии.
Классом Кчр всех частично рекурсивных функций
называется множество всех функций, которые могут
быть получены из простейших функций с помощью
операций суперпозиции, примитивной рекурсии и ми-
нимизации.
Замечание. При определении классов /Гпр и
Кчр предполагается, что при построении каждой кон-
кретной функции соответствующие операции приме-
няются не более чем конечное число раз (некоторые
или все операции могут вообще не применяться).
Класс Кй,. всех общгрекурсивных функций представ-
ляет собой множество всех всюду определенных ча-
стично рекурсивных функций.
Нетрудно показать, что КчрТ)Кор (включение стро-
гое!). Справедливо также и следующее строгое включе-
ние: KBpZ)Kn!>.
Через Кв будем обозначать класс всех частичных
числовых функций, вычислимых на машинах Тьюринга.
236
Справедливо следующее утверждение: классы и
Кв совпадают.
Теорема (Р. Робинсон). Все одноместные при-
митивно рекурсивные функции, и только они, могут
быть получены из функций х 1 и sg (х (д/х}2)
с помощью конечнократного применения следующих трех
операций:
а) абсолютная разность — f (х) = |/х (х)—/2 (х)
б) композиция — / (x)=/i (/2 (х));
. ( /(0) = 0,
в) итерация — J '
2 F 1/(х + 1) = А(/(х)).
2.1. Применить операцию примитивной рекурсии
к функциям g (xj и Л (хь х2, х3) по переменным х2 и х3.
Функцию / (хп х2)=Д (g, h) записать в «аналитической»
форме.
1) S ("^i)=: xv h(x\, х2, х3) = х1-|-х8;
2) g(xi)—xv h(xv> xv жз) = + *2!
3) g(x1) = 2iC>, Л(хр х2, x3)=x^i (полагаем 0° = 1);
4) g fo) = 1, h (хр х2, х3) = х3 (1 sg | хг 4- 2 — 2х3|);
5) g{x^ — xu h[xv х2, x3) = (x34-l)sg(l 4-
2.2. Доказать примитивную рекурсивность функ-
ции / (Г).
1) / (®i> х2) = Xj х|;
2)/(х1) = Зх‘;
3) / (Хр х2, x3) = xfx2® х3 (сумма по модулю 2).
2.3. Доказать справедливость соотношения f = R(g, h).
1) /(хр x2) = rest(Xp х2) =
__( xv если х2 = О,
[ остаток от деления хг на х2, если х2 0;
g(x2)==0, h(xv х2, х3) = (х3 4~ 1) sg | х2 (х3-1- 1)|,
рекурсия ведется по переменным xv х3.
2) / {xv хз)= [тг] =
( xv если ж2 = 0,
(целая часть от деления хг на х2, если х2 0;
g (х2)== 0» h {хг, х2, Жд) =
— X34-Sg|Xi4-l — (x34-l)x2|4-sgxa,
рекурсия ведется по переменным хх, х3.
237
3)/(*!) = *!
g = 0, h fo, х2) = (х2 +1) sg (4х, ~ (xj + 4х2)).
4) / C*i) — _
g = O, h(xv a:2)=a:24-sg((z34-l)2-»-(x14-l)).
2.4. Показать, что если функции g (у), (х), <р2 (х)
и <р3(а:) примитивно рекурсивны, то функция
/(*, У) =
?i (г), если g (у) < а,
ср2(а;), если a<g(y)^b,
<р3(х), если g(y)>b,
где О^а^Ь, также примитивно рекурсивна1).
2.5. Пусть g1(y'), g2(x) и g3(x, у) — примитивно ре-
курсивные функции. Доказать, что тогда примитивно
рекурсивна и f (х, у), определяемая следующей схемой:
[/(0. y)=gi(y'),
/(ж + 1, 0)=ga(x),
Ц(х-|-1, у4-1)=?3(л!, у)
(здесь х^О и у^О).
2.6. Пусть функции g(xv ..x^v xj, hr(xv...
..., xn_v хв) и h2(xv ..., x„_v xtt), п^>1, примитивно
рекурсивны. Доказать, что тогда примитивно рекурсивны
и следующие функции:
*я
1) / (а'1» • • •» Хп-1’ Хп) == 2 g (Х1> • • •> Xn-V ty
(=0
2) / (л> • • •> Хп-1> Хп) = П g (XV • • •> Xn-V ty
>=0
3) f{xv...,xn_1,y, z) —
g
♦=i/
0 приу<г,
при yj>z;
4) f(x1,...,xB_1,y,z) =
> Xn-V 0 ПРИ У<&
5) f(xt;. ..,x,
1
...» Ля—u *я)
2 g(x1(..., жя_р i)
J) Условия, наложенные на функцию g (у), надо понимать
так: рассматриваются все такие значения у, при которых функ-
ция g (у) удовлетворяет указанному соотношению.
238
(здесь, как обычно, считается, что если верхний предел
суммирования меньше нижнего, то сумма равна 0);
®) / (*С1» • -> Хп-1< Хп) = П S (х1> • • •> Хя-1> 0
(в том случае, когда верхний предел у произведения
меньше нижнего, произведение полагается равным 1).
2.7. Применить операцию минимизации к функ-
ции / по переменной xt. Результирующую функцию
представить в «аналитической» форме.
1)/(Ж1) = 3, » = 1;
2) /fo)=[-§-], i = l;
3) /(жР ж2) = /2(а:1. х2)> i = 2;
4) /(хр х2) = хгх2, i = l, 2;
5) /(*i> ж2) = ж1 —i = l, 2;
6) / (xv х2) = 2х- (2х2 + 1), i = 1, 2.
2.8. Применив операцию минимизации к подходя-
щей примитивно рекурсивной функции, доказать, что
функция / является частично рекурсивной.
1) / (xi)== 2 3) / (х^, х2)=х^ 2z2;
2) /(^) = 4; 4) /(^1- =
2.9. Верно ли утверждение: если хотя бы одна из
частично рекурсивных функций g и h не является
всюду определенной, то f—R (g, h) Ко^
2.10. 1) Можно ли с помощью однократного при-
менения операции минимизации ко всюду определен-
ной функции получить нигде неопределенную функцию?
2) Привести пример Примитивно рекурсивной функ-
ции, из которой двукратным применением операции
минимизации можно получить нигде неопределенную
функцию.
2.11. Доказать вычислимость следующих функций:
1) f(x, у, 2) = [^](х_^(2*-у))-(х + 1)';
2) f(x, у, z)=(^ + 2™)tf^xzy,
239
3) f(x, У,
4) f(x, у, 1)=^£.2<гЧм^'\
2.12. Каковы мощности классов Кпр, Кор, K4f и ЛГ„?
Функция <р (х, у), определяемая схемой
ср(О, у)=у+1,
<р(жД-1, О) = ср(ж, 1),
<р(ж-|-1, у-|-1) = т(ж, <р(жД-1, у)),
где х 0 и у 0, обычно называется функцией Аккер-
мана.
2.13. Показать, что функция Аккермана удовлетво-
ряет следующим условиям:
а) ? (ж> У) > У при любых х и у,
б) <р (х, у) строго монотонна по обеим переменным;
в) <р (ж+1, у) ср (ж, у+1) при любых хиу.
2.14. Используя задачу 2.13 и теорему Р. Робин-
сона (о том, что система {ж-|-1, SS (х ~~ Ia^Т)} полна
относительно операций композиции, итерации и абсо-
лютной разности в классе всех одноместных примитивно
рекурсивных функций), доказать, что, какова бы ни
была одноместная примитивно рекурсивная функция
/ (у), найдется такое х, для которого / (у) < <р (х, у) при
любом значении переменной у.
2.15. Показать, что функция Аккермана общере-
курсивна, но не примитивно рекурсивна.
2.16* . Обозначим через К1^ и К^> соответственно
множества всех одноместных примитивно рекурсивных
и всех одноместных общерекурсивных функций. Дока-
зать, что система U {х у} полна относительно опе-
рации суперпозиции в классе Аир, а система КД1 J
U {х + У} — в классе КОр.
2.17. Пусть машина Тьюринга Т вычисляет функ-
цию /л (ж) £ ЛГор\^ир. Верно ли всегда, что функция
/2 (ж, у), вычислимая на этой же машине, не принадле-
жит А'„р?
2.18. 1) Пусть машины Тьюринга Тг и Т2 вычис-
ляют примитивно рекурсивные функции /х (ж) и /2
соответственно. Верно ли всегда, что композиция ТгТг
также вычисляет некоторую примитивно рекурсивную
240
функцию f (г)? А если машины Тг и Т2 правильно
вычисляют функции /х и /2?
2) Пусть машина Т вычисляет примитивно рекур-
сивную функцию / (х). Всегда ли справедливо утвержде-
ние: если итерация машины Т вычисляет некоторую
всюду определенную функцию g (х), то эта функция
обязательно примитивно рекурсивна?
2.19. Справедливы ли следующие соотношения?
1) рДа:--2) = (1хЛ(а:--1))--1.
2) (Х1 + (Ж2 *1)) = ((®1 " + XJ'
з) р^ЧОб^-
4) М*—(лМ2)б#.гР-
5)
2.20* . Пусть функции f1(x) и f2(x) принадлежат мно-
жеству КОр \К пр. Могут ли быть верными следующие
утверждения?
1) А(/2(а:))6Апр, но /2 (Д (х)) ft К^.
2) ноЕМгЖ.
3) /1 (ж) + /2 (ж) б Kav, но /х (х) + 2/2 (ж) б А„р.
2.21* . Пусть / (ж) б Кор \ Кпр. Всегда ли справедливо
следующее соотношение?
1) /(2^)6^. 4) 1-/(ж)бАир.
2) /(я + ^б^пр- 5) f(x-*-у)б^пр-
3)
2.22. 1) У функции / (х, у) из Кав обе перемен-
ные — существенные. Предположим, что yj (х, у) и
ру/ (ж, У) — всюду определенные функции. Может ли
хотя бы одна из этих двух функций зависеть существенно
только от одной переменной?
2) Функция / (х, у) б КОв имеет одну фиктивную
переменную. Могут ли быть у функции yj (х, у) суще-
ственными обе переменные, если предположить допол-
нительно, что она общерекурсивная функция?
2.23. Сформулировать условие, необходимое и до-
статочное для того, чтобы функция рЛ/ (х) была нигде
неопределенной.
2.24. 1) Каково необходимое и достаточное условие
выполнимости соотношения (х) б Ков?
241
2) Может ли хотя бы одна из функций р^/ (х, у) или
(х> У) быть общерекурсивной, если / (х, у) £ К.^ \ЛГОр?
2.25*. Пусть / (х)£Кор\Кпр. Может ли быть вер-
ным соотношение pxf (х) £
2.26. Известно, что / (x)f*Kov и что f (2х+1)=/ (х)
и / (2х)=/(х+1) при всех х X 0. Верно ли, что
/ (х)е^„Р?
2.27. Выяснить, полна ли система К0^\К^ относи-
тельно операции суперпозиции в классе
2.28. Образует ли множество М полную систему
относительно совокупности операций 0 в классе K4J
1) м=кчр\к„9, 6={R, р}.
2) M = K4f\KOf, 8 = {S}.
3) M=KOf\Kne, 0={S, p).
4) M = K^, 0 = {p>-
2.29. Пусть общерекурсивная функция / (x) та-
кова, что У (N) = {f (х) x^N} является бесконечным
собственным подмножеством множества N. Будет ли
при этом условии выполняться равенство:
те и {>(*»]
где К(^ и К™ — соответственно множества всех одно-
местных частично рекурсивных и всех одноместных
общерекурсивных функций и замыкание берется от-
носительно операций суперпозиции и минимизации.
§ 3. Вычислимость и сложность вычислений
Частичная функция F (х0, хх, . . . , яя) называется
универсальной wlr семейства $ n-местных функций,
если выполнены следующие два условия:
а) для каждого i (i=0, 1, . . .) n-местная функция
F (i, . . . , жя) принадлежит
б) для каждой функции / (хх, . . . , хп) из $ суще-
ствует такое число i, что для всех значений перемен-
ных хъ . . . , хп
F(i, xv xK) — f(xlt..„ х„).
Число г называется номером функции / (xlt . . . , хя),
а полученная таким образом нумерация функций се-
242
мейства $ называется нумерацией, отвечающей уни-
версальной функции F (ж0, хг, . . . , хп). Обратно, если
задана нумерация системы т. е. если задано какое-
нибудь отображение <р: i -* f{ натурального ряда на
то функция F (х0, xlt ... , хп), определенная формулой
^(®0> Х1» • • •> Xn)==fx„(xl.жя)>
является' универсальной для <§. Каждой примитивно
(частично) рекурсивной функции / (xlf . . . , хв) можно
сопоставить терм, отражающий способ выражения
функции / ......х„) через функции /” (жх, . . . , хп) =
=хт, s (х)=ж+1 и о (х)=0 с помощью операций супер-
позиции, примитивной рекурсии (и минимизации).
Пронумеровав все термы, можно получить нумерацию
всех примитивно (частично) рекурсивных функций.
Нумерации такого сорта принято называть геделев-
скими х). В дальнейшем мы будем считать, что зафикси-
рована некоторая геделевская нумерация. Частично
рекурсивная n-местная функция, имеющая номер х
в этой нумерации, будет обозначаться через <р£я). Верх-
ний индекс будет опускаться, если не имеется других
указаний на число переменных функции ^п).
Справедливы следующие утверждения.
Теорема 1 (о функции, универсальной для
совокупности всех n-местных примитивно рекурсивных
функций). Класс всех примитивно рекурсивных п-ме-
стных функций имеет общерекурсивную универсальную
функцию.
Эта универсальная функция (соответствующая вы-
бранной геделевской нумерации) будет обозначаться
через D (х0, xlt . . . , хп).
Теорема 2 (об универсальной функции). Суще-
ствует частично рекурсивная функция U (х0, хг, . . . , хп),
универсальная для совокупности всех п-местных частично
рекурсивных функций.
Понятие универсальной функции часто используется
для проведения доказательств с помощью так называе-
мой «диагонализации». Примером может служить сле-
дующее доказательство существования общерекурсив-
Формальное определение геделевской нумерации можно
найти в книге А. И. Мальцева «Алгоритмы и рекурсивные функ-
ции»,
243
ной функции, не являющейся примитивно рекурсивной.
Пусть D (х0, Ху) — универсальная функция для класса
одноместных примитивно рекурсивных функций. Из п. а)
определения универсальной функции следует, что
D (х0,Ху) всюду определена. Рассмотрим g (х)~
= D (х, z)+1. Функция g (х) не является примитивно ре-
курсивной. В самом деле, если бы g (х) была примитивно
рекурсивной, то для некоторого j и для всех х выпол-
нялось бы равенство D (j, x)=g (х). Но при x=j это
равенство обращается в противоречивое соотношение
D(j, j)=g(]) — D(j, /)4-1.
Важную роль играет так называемая (s—m—n)-
теорема, принадлежащая Клини.
Теорема 3. Для любых т, п 1 существует
примитивно рекурсивная функция такая, что
для всяких х, у у, . . . , ут
(р(^т+и) . #> у^ zp . # t (zp . . ., z„).
Пусть T — машина Тьюринга, а К — некоторая
конфигурация. Временная сложность процесса вычисле-
ния tr (К) определяется как число шагов, который
сделает машина Т при переходе от К к заключительной
конфигурации, если Т применима к К. Функция ti (К)
не определена, если Т не применима к К. Зоной про-
цесса вычисления называется минимальная часть ленты,
содержащая все ячейки ленты, входящие хотя бы в одну
конфигурацию, встречающуюся в процессе вычисления.
Емкостная сложность s? (К) определяется как длина
зоны процесса вычисления с начальной конфигурацией
К, если Т применима к конфигурации К. Функция
Sr (К) не определена, если Т не применима к К. Через
<ог (К) обозначается число изменений направления дви-
жения головки, а через гт (К) — максимальное число
прохождений головки через границу между двумя со-
седними ячейками зоны в процессе вычисления (макси-
мум берется по всем парам соседних ячеек). Функции
<1>т (К) и гт (К) не определены, если Т не применим^
к К. Если в качестве конфигурации К берется началь-
ная конфигурация для слова Р, то функции сложности
обозначаются соответственно через ti (Р), st (Р), ®т (Р)
и гт (Р). Если Цт — некоторая функция сложности, то
Цт (п)= max qT(P).
р; Х(Р)<»
244
3.1. Доказать, что функция, универсальная для
одноместных примитивно рекурсивных функций
а) принимает все значения;
б) принимает каждое значение бесконечное число
раз.
3.2. Показать, что в геделевской нумераций каж-
дая одноместная примитивно рекурсивная функция
имеет счетное число номеров.
3.3. Доказать, что не существует частично рекур-
сивной универсальной функции для семейства всех
n-местных общерекурсивных функций.
3.4. Доказать, что существуют частичные числовые
функции, не являющиеся частично рекурсивными. Дать
два доказательства, одно из которых основано на
Сравнении мощностей множества частично рекурсивных
функций и множества всех частичных числовых функ-
ций, а другое — на «диагонализации».
3.5. Привести пример частичной числовой функции,
принимающей ровно одно значение и не являющейся
Частично рекурсивной.
3.6. Доказать, что функция / не является частично
рекурсивной.
. . ___11, если значение <?х (у) определено,
' ' ’ ’ |0 в противно.м случае.
2) /(ж) = .р’ еСЛИ определено,
' ' 0 в противном случае.
3) j <х = I (у)- если (У) определено,
' J \ ' У) j 0 в противном случае.
4) f(x и 2) = Р’ если чЛУ) = г,
' 1 v ' |0 в противном случае.
{1, если существует у, при котором
(у) = z.
О в противном случае.
3.7. Выяснить, является ли функция / частично ре-
курсивной.
1) = еСЛИ =
' к ' |0 в противном случае.
{не определено, если ф,(ж) определено,
л
1 в противном случае.
245
(1,
3) /(*) =
lo
если единица принадлежит множеству
значений функции
в противном случае.
4) /(х) =
5) f(x) =
1, если <?х является примитивно рекурсив-
ной,
О в противном случае.
1, если в десятичном разложении числа к
имеется бесконечное число нулей,
О в противном случае.
3.8. Пусть и (х0, хг, . . . , хв) — частично рекурсив-
ная функция, универсальная для некоторого непустого
подмножества М общерекурсивных функций, такого
что Кор\М бесконечно. Путем «диагонализации» ука-
зать счетное множество общерекурсивных функций, не
принадлежащих М.
3.9. Показать, что если функция / (х) частично ре-
курсивна, то и всякая функция, отличающаяся от / (х)
на конечном множестве значений аргумента, является
частично рекурсивной.
3.10. Пусть U (х, у) — функция, универсальная для
множества всех одноместных частично рекурсивных
функций. Доказать, что функция f (x) — U (х, х)+1
не имеет рекурсивных доопределений (иными словами,
всякая всюду определенная функция, совпадающая
с / (х) везде, где / (х) определена, а в остальном произ-
вольная, не является частично рекурсивной).
3.11. Пусть частично рекурсивная функция / (х)
такова, что функция h (я), определяемая условием!
h (х) =
0 в тех точках, где / (х) определена,
1 в точках, где / (а:) не определена,
рекурсивна. Показать, что функция / (х) имеет рекур-
сивное доопределение.
3.12. Привести пример двоичной последовательно-
сти а0, ая, . . . , которая порождается под-
ходящим автономным детерминированным оператором
и удовлетворяет следующему условию: функция / (ж),
определяемая при всяком и 0 равенством / (и) — а.п,
не является общерекурсивной.
3.13. 1) Показать, что если последовательность oq,
ах, . . . , «»»•••» является выходной для некоторого
246
автономного о.-д. оператора, то функция / (х), задавае-
мая при всяком га О соотношением / (га)= а„, является
общерекурсивной.
2) Всегда ли такая функция является примитивно
рекурсивной?
3.14. Построить пример бесконечной двоичной по-
следовательности а= «о, ах, . . . , ая, . . . , удовлетво-
ряющей следующим условиям:
1) не существует автономного о.-д. оператора, для
которого а является выходной последовательностью;
2) существует машина Тьюринга, которая, начиная
работу на пустой ленте, строит последовательность а;
при этом для каждого п существует такой момент вре-
мени t0=t0 (га), что для всякого t t0 головка машины
не посещает ячейки ленты, расположенные левее той,
в которой записан символ ав.
3.15. Привести пример преобразования конечных
слов, которое может быть совершено подходящей ма-
шиной Тьюринга, но не может быть совершено ни-
каким детерминированным оператором.
3.16. Для заданной функции / построить машину
Тьюринга Т, правильно вычисляющую /, с верхней
оценкой для ее временной функции сложности и оце-
нить сверху остальные функции сложности. Входные
данные заданы в унарной форме. Внешний алфавит
Л = {0, 1}.
1) /(*» у)=^ + у>
2) f(x) = 2x,
3) /(х) = |х — у|,
4) f{x, У)=[у],
5) /(*) = ]Iog2x[,
(га) сп-,
tT (га) era2;
(га) era2;
(га) era2;
G'(ra) сп2-
3.17. Построить машину Тьюринга Т, осуществляю-
щую перевод унарной записи числа в двоичную с задан-
ными ограничениями на функции сложности: 7т (га)
СхП2, st (и) ~ га, wT (га) с2 га, гт (га) с3га, где
сх, с2, с3 — некоторые константы.
3.18. Построить такую машину Тьюринга Т, осуще-
ствляющую перевод из двоичной записи в унарную, что
tT (n) "С cin2", sT (га) ~ с2га+2", (га) с3га2м, гт (га) с4га2",
где cv с2, с3, с4 — некоторые константы.
247
3.19. Построить машину Тьюринга Т- с входным ал-
фавитом А из т букв, преобразующую слово Р в словр
Р * Р, где символ * не входит в Р, и такую, что tT (га)
sy(ra)^c2ra, u)y (га) с3га, гг(га)^с4га.
3.20. 1) Построить машину Т, распознающую линей-
ность произвольной булевой функции / (ж”). Функция
/ (ж") задается двоичным вектором длины N = 2м. Вход-
ной алфавит машины есть А = {0, 1, А}. Функции tT(N)
и sT (А) должны удовлетворять неравенствам (А)
<С1№, sr(A)<c2A.
2) Построить машину Т, распознающую самодвой-
ственность произвольной булевой функции / (ж”), и такую,
что tr(/V)<C1№, sp(N)^c2N.
3) Построить машину Т, распознающую монотонность
произвольной булевой функции / (ж") и такую, что tT (А)
<С1№, st(N)^c2N.
3.21. Показать, что для любой машины Тьюринга Т
и любого слова Р
1) ^(Р)<^(Р).
2) Существует константа с, такая, что tT (Р) с‘^.
3.22. Пусть sT (га) > п -|- с при любом га. Доказать,
что для любого cx<Zc существует машина Tv такая, что
для всякого слова Р выполняется равенство Т (Р) =
= Г1(Р) и при этом sTi (га) (га) — сх.
г) Машина, распознающая некоторое свойство входного
слова, имеет два заключительных состояния q$ и q'f,. Машина
должна останавливаться в состоянии q'o, если свойство выпол-
нено, и в состоянии gj, если свойство не выполнено.
Глава VIII
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
§ 1. Перестановки и сочетания. Свойства
биномиальных коэффициентов
Набор элементов ati, . . . , а,г из множества U=
= {аг, . . . , ап} называется выборкой объема г из п
элементов или (л, г)-выборкой. Выборка называется
упорядоченной, если порядок следования элементов
в ней задан. Две упорядоченные выборки, различаю-
щиеся лишь порядком следования элементов, считаются
различными. Если порядок следования элементов не
является существенным, то выборка называется не-
упорядоченной. В выборках могут допускаться или
не допускаться повторения элементов. Упорядоченная
(га, г)-выборка, в которой элементы могут повторяться,
называется перестановкой с повторениями из п элемен-
тов по г или (га, ^-перестановкой с повторениями.
Если элементы упорядоченной (га, г)-выборки попарно
различны, то она называется (га, г)-перестановкой без
повторений или просто (га, ^-перестановкой. Число
(га, ^-перестановок будет обозначаться символом Р (га, г),
а число (и, ^-перестановок с повторениями — через
Р (га, г). Неупорядоченная (га, г)-выборка, в которой
элементы могут повторяться, называется сочетанием
с повторениями из п элементов по г или, короче, (га, г)-
сочетанием с повторениями. Если элементы неупорядо-
ченной выборки попарно различны, то она называется
сочетанием (без повторений) из га элементов по г или
(га, г)-сочетанием. Каждое такое сочетание представляет
собой подмножество мощности г множества U. Число
249
сочетаний из п элементов по г будет обозначаться
через С (п, г) *). Число сочетаний с повторениями из п
элементов по г будет обозначаться через С (п, г).
Пример. Пусть U = {а, Ъ, с }, г—2. Тогда имеются:
девять перестановок с повторениями — аа, ab, ас,
Ъа, ЪЪ, Ъс, са, cb, сс;
шесть перестановок без повторений — ab, ас, Ъа,
be, са, сЪ',
шесть сочетаний с повторениями — аа, аЪ, ас, ЬЬ,
Ъс, сс\
три сочетания без повторений — аЪ, ас, Ъс.
Произведение п (п—1) . . . (п—г+1), где п — дей-
ствительное, аг — целое положительное, будет обозна-
чаться через (п)г. По определению положим (п)0=1.
Если п — натуральное, то (п)в обозначается симво-
лом ?г! и называется п-факториалом. При п=0 полагаем
01=1. Для любого действительного п и целого неотри-
цательного г величина называется биномиальным
коэффициентом и обозначается символом (")• Пусть
rx, г2,..., rk— целые неотрицательные числа и гх +
+ г, + ... + г* = п. Величина—:—Д! г называется
121 1 К Г, 1га I ... rk I
полиномиальным коэффициентом и обозначается через
( п Y
Vi. г2..rj
При подсчете числа различных комбинаций исполь-
зуются следующие два правила.
Правило суммы. Если объект А может быть
выбран т способами, а объект В другими п способами,
то выбор «либо А, либо В» может быть осуществлен
т+п способами.
Правило произведения. Если объект А
может быть выбран т способами и после каждого из
таких выборов объект В в свою очередь может быть
выбран п способами, то выбор «А и В» в указанном по-
рядке может быть осуществлен тп способами.
) В литературе встречаются также обозначения С', пСг,
250
1.1. Показать, что:
1) Р(п, г) = пг; 3) С (п, г) = ^пг^;
2) P(n, г) = (п)г; 4) С (п, г) = ("+27 7
1.2. Найти число векторов а=( alt . . . , а„), коорди-
наты которых удовлетворяют условиям:
1) {О,..., к — 1}, 1 = 1, п;
2) а,. £ {0,..., к( — 1}, i = l, и;
3) ^£{0, 1}, 1 = 1, п, 2а< = г-
»=i
1.3. 1) Каково число матриц из п строк и тп столб-
цов с элементами из множества {0, 1)?
2) То же при условии, что строки матрицы попарно
различны.
1.4. Сколько и каких цифр понадобится, чтобы
записать все натуральные числа, меньшие, чем 10"?
1.5. Коалиции А и В ведут войну между собой;
п нейтральных государств находятся в нерешитель-
ности, причем р из них не присоединятся к А, а к не
присоединятся к В. Сколько новых положений может
оказаться в этой войне в зависимости от дальней-
шего поведения нейтральных государств?
1.6. Применяя правило суммы и правило произве-
дения, решить следующие задачи.
Я1) Сколькими способами из 28 костей домино можно
выбрать две кости так, чтобы их можно было приложить
друг к другу (т. е. некоторое число очков встретилось
на обеих костях).
2) Бросают три игральные кости (с шестью гранями
каждая). Сколькими способами они могут упасть так,
что либо все оказавшиеся вверху грани одинаковы,
либо все попарно различны?
3) У англичан принято давать детям несколько имен.
Сколькими способами можно назвать ребенка, если ему
дают не более трех имен, а общее число имен равно 300.
(Два способа, различающиеся лишь порядком имен,
считаются различными.)
1.7. Дано m предметов одного сорта и п другого.
Найти число выборок, составленных из г предметов
одного сорта и s — другого.
251
1.8. Пусть п=р*< ... р*г — разложение числа и
в произведение простых попарно различных между
собой чисел. Найти:
1) число всех натуральных делителей числа п;
2) число всех делителей, не делящихся на квадрат
никакого целого числа, отличного от единицы;
3) сумму делителей числа п.
1.9. 1) Из п букв, среди которых а встречается
а раз, буква b — [J раз, а остальные буквы попарно
различны, составляются сочетания с повторениями
по г элементов. Сколько среди них будет таких, которые
содержат h раз букву а и к раз букву i?
2) Сколько различных слов, содержащих г букв,
можно составить из этих п букв?
1.10. Сколькими способами можно число п пред-
ставить в виде суммы к слагаемых (представления, от-
личающиеся лишь порядком слагаемых, Считаются
различными), если:
1) каждое слагаемое является целым неотрицатель-
ным числом;
2) каждое слагаемое — натуральное число?
1.11. 1) Сколькими способами можно расставить
п нулей и к единиц так, чтобы никакие две единицы
не стояли рядом?
2) Сколько существует целых положительных чи-
сел, не превышающих кп, цифры которых расположены
в неубывающем порядке?
3) Город имеет вид прямоугольника, разделенного
улицами на квадраты. Таких квадратов в направлении
с севера на юг п, а в направлении с востока на запад к.
Сколько имеется кратчайших дорог от одной из вершин
прямоугольника до противоположной?
1.12. 1) Сколькими способами число И” можно
представить в виде трех сомножителей (представления,
отличающиеся лишь порядком сомножителей, считаются
различными)?
2) Та же задача, но представления, отличающиеся
лишь порядком сомножителей, не различаются, a n^=3s.
1.13. Сколькими способами можно расставить к ла-
дей на «шахматной» доске размером мХп так, чтобы
они не угрожали друг другу, т. е. так, чтобы никакие
две из них не стояли на одной вертикали или гори-
зонтали? Рассмотреть случаи:
252
1) к=п=т, все ладьи одного цвета;
2) к=п=т, имеется р белых и к—р черных ладей;
3) к п т, все ладьи окрашены в разные цвета;
4) к п т, имеется kt ладей цвета i (i = 1, s),
+ ^2 + • • • + — к-
1.14. Имеется колода в 4п карт (п 5), которая
содержит четыре масти по п карт в каждой масти,
занумерованных числами 1, 2, . . . , п. Подсчитать,
сколькими способами можно выбрать пять карт так,
что среди них окажутся:
1) пять последовательных карт одной масти;
2) четыре карты из пяти с одинаковыми номерами;
3) три карты с одним номером и две карты с другим;
4) пять карт одной масти;
5) пять последовательно занумерованных карт;
°. 6) три карты из пяти с одним и тем же номером;
7) две карты из пяти с одинаковыми, а остальные
с разными номерами.
1.15. Доказать следующие свойства биномиальных
коэффициентов:
к
‘>G)=U*); 5>
г=0
2> 6>
s> G)=("7‘)+(ri);
г=Л
1.16. Доказать, что:
1) еозрастает по п при фиксированном к;
2) Убывает по г при фиксированных п и к‘,
3) если п фиксировано, то возрастает по к при
А <Цга/2] и убывает при А: та/2 [2);
*) Здесь и в дальнейшем символом [6] обозначается целая
часть действительного числа Ь, а символом ]&[ — наименьшее
целое, которое не меньше Ь. Символом {fe} обозначается дроб-
ная часть числа Ь,
253
4) max (ПЛ=(Г"^;
5) минимальное значение
суммы ("*)+©+
..•+Q*) при условии, что ^raf = ra, равно
(‘-ОСП
где g = [ra/3], г = га— s [ra/s];
6) максимальное значение суммы
. . . ) ПРИ условии,
1 s п -j- 1, равно
©+©+•••
что 0 kL < ... < к, п,
7) Показать, что при простом р и любом р>к~^Л
кратно р.
8) Показать, что Ц где произведение
п<р,<2» \ ге /
берется по всем простым числам р{ (п < р( 2га).
1.17. 1) Пусть т — целое неотрицательное, а га =
= га (гаг) есть минимальное целое, такое, что т<^п\.
Показать, что можно, и притом единственным образом,
сопоставить числу т такой вектор а (гаг) = (а1, а2, ...
• • > а»-1)> что = <+«2» 2 ! + ... 4-а^ (га — 1)!,
где 0 а( i (i = 1, га — 1).
2) Найти вектор а (гаг) для гаг=15, 23, 37.
3) Каким числам сопоставлены векторы й1=(0,1,
0,23), а2=(1,0, 2,4)?
4) Предложить алгоритм бесповторного перечисле-
ния всех (га, га)-перестановок чисел 1, 2, . . . , га.
1.18. 1) Пусть к, га — натуральные числа. Доказать,
что любому целому гаг (в гаг <( ( можно сопоставить,
и притом единственным образом, вектор р (гаг) = (0V р2, ...
..., рА), удовлетворяющий условию
™=6)+(Л)+-••+&)•
254
2) Построить число т по заданному вектору В (т}~
=(6, 3, 0).
3) Построить вектор р (т) для лг=19, п—7, к=4.
4) Опираясь на задачу 1), дать способ бесповтор-
ного перечисления всех векторов длины и, у которых к
координат равны единице, а остальные — нулю.
1.19. Индукцией поп с использованием соотношения
* 1 j) Д°казать тождество
а+<г=2(0Л
к=0
(1)
1.20. Пусть п и т — целые положительные числа.
Используя тождество (1), или иным способом доказать
следующие равенства:
к=о
8> 2Ч0='!2’“;
*=2
5) 2 (2Л+!)(*) = (« +1) 2";
Л=0
6> 2гтт(0=Нп<2“-1):
fc=0
я
255
®> 2(Х:,)=("Г);
r=?0
ks=Q
ln V (2«) I _/2nV
’ Z1 (Л I)2 ((«-*) !)a \n) •
k=0
n n—k
12>55(0("7‘)=3';
fcs=O r=0
13) 2 (-irr(rre)=2(-1)'"1‘r(r);
r=fc r=0
14> 2(4Ж-^
При м e p. Доказать тождество
Первый способ. Число fc-элементных подмно-
жеств множества {1, 2, ..п} равно а число всех
подмножеств — 2”. Отсюда и вытекает тождество.
Второй способ. Положить £ = 1 в тождестве (1).
1.21. Доказать, что:
3) если 0 г < т, то
1 2itirv / 2it»An
’ где z2=-1;
к v=0
256
4> Ж + >т(2'+2'"<:«7!’‘-М' °<г<3:
к
5) если 0 г <С то, т~^Л, то
— (1—(т — 1) cos"—
т \ ' ' т / \тк -|- г/
к
Указание. В пп. 4) и 5) воспользоваться тожде-
ством из п. 3).
1.22. Доказать, что
и с помощью доказанного тождества вычислить:
’)S3‘Q): 2>S<-1>‘2‘(«”+1):
к к
з) Sc-vsV+iXV1)-
к
1.23. Доказать, что при целых т^О, п^О спра-
ведливы равенства:
1) V (”)<— та + 1 т^п.
' 21 (т)к т — п + 1’ ’
2) У
' 2^ \« — V/\«/ (т — п) (т — п + 1)
fc=O
3) (n + fe - l)fc
fc=l fc=L
1.24. Пусть a, b — действительные, к, m, n, r — целые
неотрицательные числа. Доказать, что:
»(ПЧ1<)=СГ);
2>(1+<Г=2(0'’’ |,|<1;
Л=о
3 Г, П. Гаврилов, А, А. Сапоженко 257
2(“7>ОЧ;Г):
k=Q
5) 2 ( к )G - к )=С t *) (теорема сложения);
ks=Q
6) 2(-1)-(0=С7‘):
*=0
’)2('+::r*)C+r,)=C+it”_1
Л=0
8> 2 ю(ос-'*->с+:+е):
ос*» ГСЯ
8)2(-1>‘(?)(Я=/4=
к=0
Л=0
т~1 2кй-у / 2кй\а
ii)m2U+r)d"*'=2e’" u+fe-jjsKt.
Л »=0
1.25. 1) Найти число всех таких слов длины тп
в n-буквенном алфавите, в которых каждая буква
алфавита встречается т раз.
2) Сколькими способами множество из п элементов
может быть разбито на s подмножеств, из которых пер-
вое содержит kt элементов, второе — к2 элементов
и т. д.?
3) Исходя из комбинаторных соображений, показать,
что для любых целых неотрицательных кг, к2, . . .
. . ., к,, п, таких, что . .-\-kt=n, справедливо
равенство
(n\fn — кл (п — — Аа — ... — Л,_Л ______п I____
*1 ) \ к2 )’ * * \ к, J ... к, I *
258
4) Индукцией по s доказать тождество
(*i + *2 Н---+ = 2 Лх I *а7. .. I ’ *•
^1» • • •> ^8
*1+ ... +^«=»
§ 2. Формула включении и исключений
Пусть 'Имеется N предметов и п свойств av . .ап.
Каждый из этих предметов может обладать или не обла-
дать любым из этих свойств. Обозначим через N (а*,, ...
..а!А.) число предметов, обладающих свойствами а(1, ...
..а,> (и, быть может, некоторыми другими). Тогда
число $0 предметов, не обладающих ни одним из свойств
«1,..., а„> определяется равенством
Ч = «о - + S2 - •'. + (-1)’ s„, (2)
где So — N, а
Sk= 5 TV (a,-, ..., afjfc), k — 1, n.
Формула (2) называется формулой включений и исклю-
чений.
Пример применения формулы включений и
исключений. Пусть колода состоит из п карт, пронуме-
рованных числами 1, .... п. Сколькими способами
можно расположить карты в колоде так, что ни для
одного i (1 i п) карта с номером i не занимает
i-е место?
Решение. Имеется п свойств а< вида: «i-я карта
занимает в колоде г-е место». Число всевозможных
расположений карт в колоде равно п!. Число N (а,-,, . ..
..а»*) расположений, при которых карта с номером
занимает место i, (v = l, к), равно (п — к) I Тогда
So == п !, Sk = 2 N (ач........a<>) =
W|<...«10
=G>-щ=£г-
Используя формулу (2), получаем, что число TV0 рас-
положений, при которых ни одно из свойств at не
9* 259
выполняется, равно
я п
2<-1№='!|5<-1>‘й-
Л=0 к=0
2. 1*. 1) Доказать по индукции формулу (2).
2) Пусть $т — число предметов, обладающих в точ-
ности т свойствами из п. Доказать, что
я—т
^.=2 <-<)•("»<з)
к=0
3) Пусть Nm — число предметов, обладающих не
менее чем т свойствами из п. Доказать, что
я—m
• (4>
4=0
4) Показать, что
s*=S(")sr- <5>
т=Ж
<e>
5) Показать, что
5т-(^+1)5т+1<^ю<^- (7)
(8)
2.2. Четыре человека сдают свои шляпы в гарде-
роб. В предположения, что шляпы возвращаются
наугад, найти вероятность того, что в точности к чело-
век получат свои шляпы назад. Рассмотреть все зна-
чения к (0 к 4).
2.3. Пусть Е (г, п, т) — число способов располо-
жения г предметов по п ящикам, при которых имеется
ровно т пустых ящиков, a F (г, п, т) — число тех рас-
положений, при которых не менее т ящиков оказы-
ваются пустыми. Показать, что:
260
п
1)Е(г, п. 0) = 2 С-1)*©
л=о
п—т
2) Е(г, п, ™) = (")2 H)f
&=о
3) F(r,'n,
я—т
Л=0
2.4. При обследовании читательских вкусов студен-
тов оказалось, что 60% студентов читает журнал А,
50% — журнал В, 50% — журнал С, 30% — жур-
налы А и В, 20% — журналы В и С, 40% — журналы
А и С, 10% — журналы А, В и С. Сколько процентов
студентов
1) не читает ни один из журналов;
2) читает в точности два журнала;
3) читает не менее двух журналов?
2.5. На одной из кафедр университета работают
тринадцать человек, причем каждый из них знает
хотя бы один иностранный язык. Десять человек знают
английский, семеро — немецкий, шестеро — француз-
ский. Пятеро знают английский и немецкий, четверо —
английский и французский, трое — немецкий и фран-
цузский.
1) Сколько человек знают все три языка?
2) Сколько человек знают ровно два языка?
3) Сколько человек знают только английский
язык?
2.6. 1) Показать, что количество натуральных чи-
сел, делящихся на п и не превосходящих х, равно
[х/п].
2) Найти число целых положительных чисел, не
превосходящих 1000 и не делящихся ни на одно из
чисел 3, 5 и 7.
3) Найти число целых положительных чисел, не
превосходящих 1000 и не делящихся ни на одно из
чисел 6, 10 и 15.
261
4) Показать, что если п=30пг, то число целых,
не превосходящих п и не делящихся ни на одно из чи-
сел 6, 10, 15, равно 22m.
5) Пусть рр ...,рг — все простые числа, не превос-
ходящие Показать, что число простых чисел р, таких,
Г
что \1п <р^п, равно п — 1—2(—!)*£*> гДе сумма
к=1
берется по всевозможным
наборам
показателей ах,...
..., аг, в которых ровно к из показателей равны 1, а осталь-
ные — нулю.
6) Найти число простых чисел, не превосходящих
250.
2.7. Пусть U — множество из п (п 3) эле-
ментов.
1) Найти число пар (X, У) таких подмножеств мно-
жества U, что Х("]У = 0.
2) Найти число таких пар (X, У), что X С U, Y CZU,
l(x\y)U(r\x)| = i.
3) Найти число таких троек (X, У, Z), что X С U,
YCU, ZCU, X\J(Yf)Z) = X\jY.
4) Найти число таких пар (X, У) подмножеств мно-
жества U, что XftY = 0, |Х|>2, |У|>3.
5) Найти число таких пар (X, У), что X С U, У С U,
|(Х\У)С/(У\Х)| = 1, |Х|>2, 1У|>2.
6) Найти число таких троек (л, У, Z), что X С U,
YCU, ZCU, XU(Yr\Z) = XUY, |Х|>2, |У|>2,
|Z|<1.
2.8. Задача мажордома. К обеду за круг-
лым столом приглашены п пар враждующих рыцарей
(п 2). Требуется рассадить их так, чтобы никакие
два врага не сидели рядом. Показать, что это можно
сделать 2 (—1)* 2* (2п — к) I способами.
л=о '*'
2.9. Задача о супружеских парах.
Сколькими способами можно расположить за круглым
столом п супружеских пар так, чтобы мужчины и жен-
щины чередовались и никакие двое супругов не сидели
рядом?
262
§ 3. Возвратные последовательности,
производящие функции,
рекуррентные соотношения
Последовательность д0, , ап, . . . называется
возвратной, если для некоторого к и всех п выполняется
соотношение вида
* ап+к + + • • • + РЛ = 0, (9)
где коэффициенты р{, i = 1, к, не зависят от п. Многочлен
Ра(Ж) = хй + Р1^-1+...+р4 (10)
называется характеристическим для возвратной после-
довательности {ав}.
3.1. 1) Доказать, что возвратная последователь-
ность полностью определяется заданием ее первых
к членов.
2) Пусть X является корнем характеристического
многочлена. Показать, что последовательность {сХв},
где с — произвольная константа, удовлетворяет соот-
ношению (9).
3) Доказать, что если Хх, . . . , \ — простые (не
являющиеся кратными) корни характеристического мно-
гочлена (10), то общее решение рекуррентного соотно-
шения (9) имеет вид ап = схХв -}-••• Ч" сл/**
4) Пусть Xf является корнем кратности г{ (г=1, s)
характеристического многочлена (10). Доказать, что
тогда общее решение рекуррентного* соотношения (9)
имеет вид
= 2 (С<1 Ч- С{2П Ч" • • • Ч" X",
•=1
где c{j(i = l, s; / = 1, rj— произвольные константы.
3.2. Найти общие решения рекуррентных соотношений:
1) ая+а — Ч+1 + За. = 0;
2) ая+а Ч" = 0;
3) ая+2 — «я+1 — ая = 0;
4) а»+2Ч*2ая+1ч-ая=0;
5) ®я+з 4“ Ч~ 32ая+1 -|- 32а„ = 0;
6) ая+зЧ"Зая+а4-Заяи-|-ая==0.
263
3.3. Найти ав по рекуррентным соотношениям и на-
чальным условиям:
1) ая+2-Ч+1 + За„ = 0,
^ = 10, аа = 16;
2) «я+з Зав+а ов+1 — Зап = 0,
aj = 3, а2 = 7, а3 = 27;
3) «я+з Зав+1 2ав = 0,
а1 = а, а2 = Ь, а3 = с;
4) «я+2 — 2 cos аавН 4- а„ = 0,
ах = cos а, а2 = cos 2а.
3.4. Доказать, что:
1) если х = 1 не является корнем многочлена жа4~
4-p^4*9’ т0 частным решением рекуррентного соотно-
шения
an^ + Pan+i + 9a» = an + P> (11)
где а, р, р, q — данные числа, является последователь-
ность. а*=ап-\-Ь; найти а и Ь;
2) если х=1 — простой корень многочлена х2-}-
+рх4-<?, то частное решение может быть найдено
в виде а*=ге (ап-\-Ь)‘, найти а и Ъ;
3) если х=1 — кратный корень многочлена х24-
-f-px-f-g, то частное решение может быть найдено
в виде а*=п2 (ап-[-Ь)', найти а и й;
4) в каждом из предыдущих случаев найти общее
решение соотношения (11).
3.5. Решить рекуррентные соотношения:
1) «я+1 —«1 = 1;
2) «в+2 4“ 2«„+i — 8«„ = 27 -5",
ах = —9, аа = 45;
3) «я+з — 6«я+2 + 11«я+1 — 6«я = 6«а — 4га -17,
^ = 3, 02 = 15, а3 = 41.
3.6. 1) Пусть {а„} и {Ьп}—две последовательности,
члены которых связаны соотношениями
«я и — Pian ”Ь
^я+1 = РА ?2^я>
4 = Р1& — Р-А^О,
где plt qv р2, q2 — данные числа. Найти выражения
для а, и Ь„, считая, что аг и Ь1 заданы.
264
2) Найти решение системы рекуррентных соотно-
шений
йя+1 = ^ап + Ч
^Я41 =--ая + ^я>
at = 14, Ъг——6.
3) Найти общее решение системы рекуррентных
соотношеГний
°я+1 = 4- 5. &я+1 =-ап + 3-
3.7. Последовательность Фибоначчи {FB} задается ре-
куррентным соотношением FB+a = Гя+1 -|- Fn и начальными
условиями F1 = /'2 = l. Доказать, что:
1) для любых натуральных т и п FB+Bl = Fn_xFm-|-
2) для любых т и п=кт число Fn делится на Fm;
3) два соседних числа Fn и Fn+1 взаимно просты;
4) всякое натуральное число TV (N > 1) может быть
однозначно представлено в виде суммы чисел Фибо-
наччи, такой, что каждое число входит в сумму не более
одного раза и никакие два соседние числа не входят
вместе;
5> '.=Ч(Ч4ЧЧЧ]>
6) Л + Fa 4- ... 4- F2e+1 = F2tl+2;
7) 14-F24-F44-... 4-F2b = F2b+1;
8) ^»+iЧ F”-i — ^3n‘
С каждой последовательностью a0,'ai, . . .
можно связать ряд А (<)=а04-а4Ч. • •+aBi”+. . ., на-
зываемый производящей функцией для последователь-
ности {ав}. В тех случаях, когда ряд A (t) сходится
к некоторой функции / (t), функцию / (Z) также на-
зывают производящей для {а„}. Экспоненциальной про-
изводящей функцией для {ав} называется ряд Е (t)—
а tn
=аа 4~ аф 4" • • '• 4“ Ч • • • Можно определить операции
сложения, умножения и умножения на константу для
производящих функций, рассматривая их как формаль-
ные ряды. Пусть A(t) и В (t) — производящие функции
для последовательностей {ая} и {&в} соответственно,
265
a a, ₽ — константы. Тогда
аЛ (/) 4~ P# (0 = аа0 Н- Р^о + (aai + P^i) * + • • •
...+(аая + ₽Ья)«"+...,
A (<) • В (i) = аД+ (аД + аА) * + • • •
• • • +(a06« + aA-i+- • • + «,&)*" + •• •
Если Еа (i) и Еь (t) — экспоненциальные произво-
дящие функции соответственно для последовательно-
стей {ап} и {&„}, то сложение и умножение на константу
определяются так же, как для обычных производящих
функций, а их произведение определяется как
зд-ад=со+^+---+Й’+---’
где cn = «(A, + (1)aiVi+ ••• + (*)аД-» + ••• +аД-
3.8. Показать, что функция A (I) (соответственно
Е (t)) является производящей (экспоненциальной про-
изводящей) функцией для последовательности {а,},
если:
1) ап = a", A (f) = (1 — at)~l, Е (Z) = exp (at);
2) а„ = п, A (t) = t (1 — t)~\ E(t) = t exp t;
3) a„ -= n (n — 1), A (t) — 2i2 (1 —t)~2,
E (t) = t2 exp t;
4)a„ = n2, A (t) = t(t-\-i)(l ~t)~3,
E (t) = t (t 1) exp f;
5) «»=(;). 4 (*)=(!+0";
6) a„ = («)„, ^(Q = (l+0’".
3.9. Пусть A (t) и E (t) являются соответственно обыч-
ной и экспоненциальной производящими функциями по-
следовательности {а,}.
СО
1) Используя равенство п 1 = j e-xx"dx, показать, что
о
A (t) = j е~*Е (xt) dx. (*)
о
266
2) Убедиться, что формула (*) справедлива для произ-
водящих функций Л(/) = (1—t)~l и = последо-
вательности а0 — ях = а2 = ... = 1.
3) То же для последовательности с общим членом
j 0, п <Z. j,
Л" l(n)y,
3.10. 1) Пусть (а)п = а(а — 1).. .(а — n-|- 1). Доказать,
используя, экспоненциальные производящие функции, что
п
(«+&)л=2СМ-л-
' s=o
Указание. Использовать тождество (1 t)aib =
= (1+<)“(1+Z)\
2) Пусть (а)я, h = а (а Д- h)... (а — h{n — 1)). Показать,
что
я
Л—0
3.11. Пусть {ая}, {Ь„}—последовательности, A (f) и
B(t) — соответствующие производящие функции. Показать,
что:
1) если а„ = bn — bn_v то A (Z) = В (Z) (1 — Z);
2) если ап = ЬпП — Ья, то A = Ь0Гг;
3) если а„ = Ья+1 + Ья+2 +.... то A (Z) = .
4) если ап = nbn, то A (Z) = t В (Z);
5) если ап = п2Ь„, то A (Z) = t ±(t £ В (Z)};
6) если определить операцию S*(&^0) над последо-
вательностью {Ьп} с помощью соотношения
(^я)-Ьп + ( 1) Ьп-1 +•••+,
, Гй + /-л,
+ \ i )b«-j
(к 4- п — 1\
+ •••+( » )Ь0
и положить an = Sk (Ь^, то Л (/) = (!—Z)*”5(Z);
267
7) если ап — b2n, то А (£) = у (5 (ГА) В (—Г А));
8) если ая=А + \+---+ь»-р то A(t) =
= В (<)/(! — i)*1.
3.12. Пусть A (t) uB(t)—производящие функции по-
следовательностей {ая} и {Ая} соответственно, и пусть
A (t) • B(t) == 1. Найти {Ьп} и B(t) по заданной последо-
вательности {дя}.
О «„ = (“); 4) а0 = а2 = 1> а„ = 0 при п=И=0, 2;
2) ап = а”; 5‘) ап = (-1)" ;
3)а„ = п4-1; 6) а„ = (—1)”(2")4-«.
3.13. С помощью тождеств, связывающих произво-
дящие функции, вывести следующие тождества для
биномиальных коэффициентов:
1) (1 4. t)n (1 4- f)m == (1 t)"* m;
к
2(Х-.)=(’П;
5=0
2) (1 — Z)-i-*(l — Z)'1-W==(l — t)-2~n~m;
к
+ m + к + e
e=0
3) (1 ty (1 _p t)~m = (1 +
к
2<-'ГС)(”+4‘ГГ *)=("-/);
5=0
4) (1 _ f)-i-« (I 4-1)-1-” = (1 — t2)-'-”;
2k
2(-D-(“r)(’+r-)=("t‘);
»==0
5) (i 4- t)n (i — t2)-”=(1 — t)'”;
l*/2]
5=0
268
6) (i+*)"(i—*)"=(i—*2)";
2 (—!)*(*” )(ra) = ^—1^/2G/2)> к четно»
»=о I 0, к нечетно.
3.14. Найти общий член ап последовательности, для
которой функция A (Z) является производящей.
1) л(г)=(9+р0’в;
2) Л(о=(1-О’*;
3) Л(*) = \0 — К
4) A(f) = tm(l — t)m;
5) Л(0 = (^ + /2+...+ГГ;
6) Л(0=(1+4)””;
7) 4 (Z) = (l-|-2Z)~'/»(1 —-Ly*”.
8) А (Z) = Z2(1 — 0(1 + 2*)-"’;
9) А (/) = In (1 —J—Z);
10) 4(z) = arctgZ;
И) A (Z) = arc sin t;
12) А (Z) = e~2P;
t
13) 4(Z) = j e-x'dx-
о
3.15. Вывести тождества *):
Ч 2<-irC)(”4t1’)=(.-1):
8
2i V1/_Г 0 при т=/=п,
> I \sj\n) {(-jy. при т==п.
3) 2(-<Л+.)("Г)=ГГ ’):
4> 22©(г»12.)=(Й)+<-1’’С):
8
г) Суммирование ведется по всем s, для которых рассматри-
ваемые выражения имеют смысл.
2&
j-. q / n -|- 2s \ fn 4~ 2w — 2s _f%Ti 4* 2w 4“ 2\
b) 2A "A n /“V 2n 4~ 1
в)2<-i)-'4-c+:+i)=»+i.
4=0
3.16. Пусть последовательность {ая} удовлетворяет
рекуррентному соотношению ая+2 -f- рап^ qan — 0.
1) Показать, что A (i) = \+-р, *
2) Пусть 1 р/д«2 = (1 — Хг0(1 — Х20, Х1=^Х2.
Показать, что
, . . Х? —ХЗ , XJ+1 —Х?«
ап = («1 + М) + ао Х.-Х, ' •
3) Выразить ап в случае, когда 1+р£+<#2=(1—X/)2.
4) Найти производящие функции для последователь-
ностей, заданных рекуррентными соотношениями из
задач 3.2, 1)—4).
3.17. Пусть
п Я—1
«.=2CV).
у=о у=о
n = 0, 1, 2,...,
и A (t), В (Z) — соответствующие производящие функции.
1) Показать, что ап и Ьп связаны соотношениями вида
ая+1 = ап + ^я+1>
&я+1 = ая + &я, «0 = 1> 60 = °-
2) Показать, что A (Z) и В (i) удовлетворяют системе
уравнений
A(t) — l=tA (f)4-B(<),
3) Найти A (Z) и В (f).
4) Показать, что
270
3.18. Пусть члены последовательности {ая} удовлетво-
ряют соотношению
а» — аиа»-1 + аЛ-а + • • • + ап-А> ао — 1 •
1) Показать, что производящая функция А(1) =
00
— 2 удовлетворяет равенству tA2 (/) = A (t) — а0 или,
я=0 _____
' л 1 — ~ 4г
с учетом начального условия, A (t) =----.
2) Разлагая A (/) в ряд по степеням t, показать, что
1 (2п\
a" п -|- 1 \ п ) *
3.19. Вывести рекуррентное соотношение для после-
довательности чисел ал и разрешить это соотношение,
если:
1) ап — число способов разбиения выпуклого (w-f-2)-
угольника на треугольники диагоналями, не пересе-
кающимися внутри этого многоугольника;
2) ап — число таких способов расстановки скобок
в выражении : Ъ2 i . . . : Ья+1, при которых получаю-
щиеся выражения имеют смысл.
3.20. Найти последовательность {ая}, члены которой
удовлетворяют соотношениям:
1) ¥. + а А-1 + • • • + = 2Ч> ао = «1 = 1;
2) aB+2 = (« + l)(a» + a„+i)> ао = 1> ai = °;
3) (н4-2)(н-4-1)ая+а—п2а, = 0, ао = О, а1 = 1;
4) (п 2)2ая+а 4- ая = 0, а0 = 1, а1==0.
00
3.21. Пусть 4(i) = 2 а(п, k)tk—производящая функ-
fc=O
ция для последовательности, удовлетворяющей соотноше-
нию а(п, к) = а (п, к—!)-{-«(« — 1> к) с начальным
условием а(п, 0) = 1. Показать, что;
1) {i-t^A^^A^ty,
2) Ая (t) = (!-/)-;
„ , In 4- к — 1\
3) а(п, к) = {. к
271
3.22. 1) Функция А (£) = JJ(1 — g“Z), |д|<1, раз-
СО
лагается в ряд A (t) = 2 Найти коэффициенты ая.
п=0
Указание. Воспользоваться тем, что A(t) = (1 —
— qt) A (qt). Сравнить коэффициенты в левой и правой
частях этого уравнения.
СО
2) Найти коэффициенты^ ряда В (f) = 2 V, где
п=0
B(t)=л-1 (0.
3.23. Пусть ап — число решений в целых неотрица-
тельных числах уравнения 2х5у7z — п. Доказать,
что
2 a„t” = (1 -12)-1 (1 — *Т’ (1 — *7)'1-
п=0
3.24. Пусть ап — количество представлений числа п в
виде суммы
Х1 + Х2 + Зжз + ж<6{0< 1}> 1 = 17’4.
СО
Найти производящую функцию Л(/) = 2а>А
я=0
3.25. Пусть
П(1+^)=2«Л
&=0 и =4)
Доказать, что an = qbn, где Ья — число единиц в двоичном
разложении числа п.
3.26. Пусть
S(n, к, 0 = i(-i)"”C)(v + 0*.
Доказать, что:
1) 5(га4-1, к, l) = S{n, к, — к, Z);
2) S (п, к, l-\-l) = S(n, к, r) — S(n + i, к, I);
3) 5 (ге, к-]-1, Г) = (п-\-Г) S (п, к, (re — 1, к, /).
4) S (re, к, 1)= 0 при п^> к;
5) S (п, п, l) = n I;
272
6) S (n, к, Z) > О при n к;
7) S(n,.k, I) — возрастающая функция параметров к и I
при п к;
8) S(n, «4-1, /)=Ц^(«4-1)!;
9) 5(1, к, 0) = 1 при 1^/с.
3.27. Пусть
S<n, k) = S(n, к, 0) = 2(-1)Я”С)/
и ая (Z) = 2 $ (га> tytk. Показать, что при ]£|<1
fc=0
.. ..._ nit"
И 3»W-(i-t)(i—24)...(1-и«)’
2) ая(0 = *2(-1Г* 4Э-.
k=l 1 ~ kt
§ 4. Асимптотические оценки и неравенства
При оценке роста функций употребляются следующие
обозначения. Запись <р (х) = О (ф (х)) при х Q X означает,
что существует константа С, такая, что | <р (х) | С | ф (х)|
для х (< X. Если р (х) = О (ф (х)) и <р (х)=О (р (х)) при х £ X,
то пишут р(х)хф(х) при х^Х. Запись р(х) = о(ф(х))
при х-*а означает, что iim^-^ = 0. Говорят, что функ-
ции <р (х) и ф (х) асимптотически равны (обозначение:
р(х)~ф(х)) при х->а, если р (х) = ф (х) -|- о (ф (х)) при
х -» а. При разного рода оценках полезна формула Стир
линга
п I ~ \/2пп ппе~*.
(12)
Для более точных оценок используются неравенства
^2пп п” ехр(—п
12л 360л8) < П| <
<V2wn"exp(—«4-^. (13)
273
4.1. Доказать неравенства1):
1) п”12 < n I < (~у~) п₽и п 2»
2) (2/г)! <[»(«+1)]’;
3)(‘ + 1)"<3!
5)(„!)2<(11±+Яу, га>1;
я(м+1)
6) 1 • 22 • З3 • ... 2 .
7\ <2ге~1)'1 <- 1 .
' (2п) I! ^'V3a+1’
8) (2п — 1)!! < п”, п > 1; 9) п ! > е~япя.
4.2. Доказать неравенства:
»<(;)<©*’ »>*>*;
2>(т)‘<С)<й(^Ег.’ п>л>0:
4Л '(2п\^ 4м . ,
3)—-=<( I С » П>1.
2 Vn \п ) У^Зп -|- 1
4.3. Используя формулу Стирлинга, показать, что
при п —» оо справедливы асимптотические равенства:
1) (2п — 1) II ~ \/2(2п)яе'п;
2) 2")~?1=4’’;
\п / Упп
([Й')*(’-2Ю' 2”
(m + 1) (от + 2) ... (тп + га)
> (4+!)(* +2) ... (Zc-j-от)
5. (2n) II ]/
(2п -1)11 V 2 П-
к I т-к
'^~[п Дл» Целых
неотрицательных к и т;
*) Символом (2п — 1)11 обозначается число 1 >3.5.,,
,,, • (2я — 1), а (2п)!1 = 2.4.6..,,. (2м).
274
4.4. Доказать, что при п -> оо справедливы следую-
щие асимптотические равенства:
fc=l
3> 2(г + ь)а'“'~^1 + “)"’ °<Г<*'
*>244")-^ 5)ЖУ~^4-
*=1 fc=l
4.5. Пусть b0, bv ..., Ьп — такие числа, что
Выяснить, верно ли, что:
я
1) (1 +сГ;
/с=0
я
2) (1 ~а^
к=0
4.6. 1) Доказать неравенство Чебышева в следующей
форме. Пусть А = {аг а2, ..ая} — совокупность чисел,
п я
а= Ва = — й)2, Тогда Доля В, тех а,-,
»-i «=1
1 -1 . Da
для которых |at — a\^t, не превышает -р-.
2) Используя неравенство Чебышева, показать, что
2 ©+ 2
0^Л<”-tVn ^-+t
2 2
3 ) Показать, что 21G) ~ ^7Г •
4. 7. G помощью формулы Стирлинга показать, что:
1) если к-* со и к—~=о(п’'<) при п—► оо, то
А
2Я+1
____ g 2»
V2itra
275
2*) если а }> О, к—* со и к
п —» со, то
рх 4 = (ь^е-Е^)’,1+ Л
\к/ ^2т.па \ V
an
(к (а + 1) — п
п*
3*) если а>0, к<Гт, А:-» со и к,
при п-»оо, то
7га=_тт+°(71’/’)
а +1 1 ' '
(«4-1)” Гм,
v'iS
((а+1)т-ал)д
е~ ”а
т (а -|- 1) — па
((а+1)к-ап)г \
е~ ”я j.
к (a -f-1) — па) •
4*) если
п -» со, то
а>0,
и к-----^-=о(пг/>) при
о (n’ty при
У («у ‘ Л
Xj _W yt2Kt
. Vna
v>»a+/—-
a+1
4. 8. Пусть 0 < X < 1, Xn—целое, p. = l—X, и пусть
G (n, X) =-—. . G помощью формул (12) и (13)
показать, что:
i) (x”)~^(n’ п1,и ге->°°;
2) С(», Х).хр(-2;(4+1))<(«)<0(„. X);
/|J (х«) < 2 G) < 2Х — 1 (in) ПрН
fc=>n
п
5> 2G)<vV” -р" *>|.
к=\п
4. 9. Пусть к и п — натуральные числа (к<Г,п). По-
казать, что:
(оо к—1 \
~2 Л 2Г);
v*=l »=4 /
2) если при п^-со к = о(у)п), то (n)s ~ п*;
276
3) если А —о(п) при п-»оо, то для всякого т^>1
(т-1 X
-2^+Oh
V=1 /
4) при 71 —> со и к = о (п3/<)
. (”)* = "* ехР(—Ё-ЙН-^1))-
4.10. 1) Пусть к=.к(п) и s = s(n) таковы, что при
п -> со s = o(^k). Показать, 4toQ _ ~ .
2) Показать, что если s — o (&r+1), то
fn— s\!fn\ fk\> I V s’*4 /1 1
U-s)l\k)~\n) exp( 2’(’ + W’ n’) •
\ v=l /
4.11. Пусть s = s(n) и k = k(n) — целочисленные
неотрицательные функции натурального аргумента. Пока-
зать, что:
1) если s-\-k — o(n) при п-*оо, то
(00
sk s*k + sk* VT ' ( к V
~й----2n*---S2VU)-
v=3
v=3 /
4.12. Пусть / (x) — непрерывная, монотонно возрастаю-
щая на отрезке (п, т] функция. Показать, что
г
/(«)<2 / №- /(*)dx</(^)-
к~п “
277
4.13. Используя предыдущую задачу, показать, что
при т -> оо справедливы следующие соотношения:
т
1) 2 1п ~ т • т — т + О (In т);
*=1
т
2) = п>1;
т
3) 'V , . —7—j- = 1 n In 1 п т -1- с -1- О ( —j-,
' к In к • In In к 1 \m In т In In mJ
k=2
c — константа;
m
, 4) = у l°g3 m 4~ re"") ’ C — KOiICTanTa>‘
fc=i
in
5) "V , A , = c 4-г-—l-0(—4-s—Y c — константа;
' к In2 к 1 In m 1 In2 m J ’ ’
Л=1
m
lt-n
4.14. Последовательность {pn} определяется рекуррент-
ным соотношением pn = pn_t — pQ t= 1, 0 a < 1,
P J> 1. Показать, что:
1) 0 <p„< 1, n~^ 1;
2) pn монотонно убывает с ростом п;
1 .
3*) р„ ~ (а (,3 — 1) и)!-н, п->со.
Указание. Воспользоваться неравенствами
п рп к+1
2 Pit — Рк-1 С V1 Рк — Рк-1 _
—“Pl-t j — ах^ 1
Л-1 К 1 1 Л=1 * 1
« + 1.
4.15*. Пусть производящая функция A (t) последо-
вательности {ап} имеет вид где Q (t) и
Р (t)—многочлены с действительными коэффициентами.
Пусть Aj—наименьший по абсолютной величине корень
многочлена P(t). Доказать, что:
278
1) если Хх — простой (не являющийся кратным) дей-
ствительный'корень, то при п—>оо
о.---/>'А)=5Р«|,.,;
2) если Хх — действительный корень кратности г, то
при п -*• оо
• (-1)' г ! <? (X,) (г + п - IV П" ”•
а~ \ г-i ди ’
где Р(г) (Хх) есть производная порядка г от P(t) в точке
t = Хх.
4.16. Пусть Л(«)— производящая функция последо-
вательности {ая). Найти асимптотическое поведение ая
при п -> со.
1) Л (t) = 3(2 _ 4t ; 5) Л (£)=6t4 _ j 7t2 + 35Р _ 22t + 4 ’
2) Л (t)=6<3 5f _ 6; 6) Л («)=(8f3 _ j);
3) Л (t) = 6/2 _ §; 7) Л (f) = _ 2)г ;
f (3_ 1
4) Л (/) = 4f2_|_ j ; 8) A (t) — (2t2+i)(ia + l,4t-f-0,49) •
4.17. По заданному рекуррентному соотношению и
начальным условиям найти асимптотическое поведение ая
при п —» ао.
1) а«+2 + ЗаяП2ая = 0, а0 = 1, ах = 2;
2) ал = дая-1 + р(1 «о=1. Р + ? = 1.
Р> ?>0;
3) а,н2 + 2а„+1 + 4а„ = 0, ао = О> <4 = 2;
4) а»+з ~ 9а«+2 + 26ая+1 — 24ая = 0, а0 = ах = 1,
а2 = —3;
5) ая+4-Ч+2 + Ч = 2". «о = 1. «1 = 0. «2 = 2,
а, = 0.
4.18. 1) Показать, что решение уравнения xex = t
имеет вид
aJ = lni-lnlni+^4-6?((^)2), «->00.
2) Показать, что решение уравнения ел-{~1па: = ^
при t -* оо имеет вид
. , In In t , In t\2\
I==lnZ-----—))’.
279
4.19. Пусть /(«)>0 и e^’ = /(Z)-p4-0(l),
0<^t <Z co. Показать, что f — (t~2) при t-* co.
4.20. Пусть an удовлетворяет соотношениям
ая > 2”-1 + (га — 1) • 4-®-1, (14)
«,+2<2-»-3 + (п + 1).4--« +
+«я((т)"2+(п + 2)-2я+2 + Ч)» (15)
«1 = 0, аа = ^.
Показать, что:
1) а„<1/8;
2) «„<9(3/4)";
3) а„ = 2-^ (14-0 ((3/4)”)).
4.21. Пусть к, п — целые. С точностью до 1 вычис-
лить к = к(п), при котором функция f (п, к) принимает
максимальное значение.
1) /(«. *)=(Э2’2*;
2) /(га, A) = (")2"~fc-2ft(l — 2-2*)яЛ
4.22. Найти минимальное и максимальное значения
выражения
как функции от г (0<г<А:<га; г, к, га — целые).
4.23. Найти асимптотическое поведение при га-> оо
величины g(ra)= min / (га, к), к—целое, если:
1) /(«, А) = 2’-*4-22*;
2) / (га, Л) = /с.2‘4-122яЛ
РЕШЕНИЯ, ОТВЕТЫ, УКАЗАНИЯ
ГЛАВА I
§ 1
1.1. 1)(£); 2) 2». 1.2. 1) 9, 13, 50; 2) (010011). 1.3. (*Z1)‘
1.5. 1) П2»-1; 2)Q)2«-1. 1.6. 1) 2*»; 2) *) (л + тп-г ) p-m + r j!
\ 2 / \ 2 J
1.9. Указание. Показать, что число ф (л) векторов a g B„n
таких, что т/2 ‘1ЛЯ всех w= 1, 2п, удовлетворяет
рекуррентному соотношению ф (”) — 2"=1 ф (Z — 1) ф (« — Z),
ф(0) = ф(1) = 1. Используя это соотношение, найти, что
ф(6) = 132.
1.11. 1) Указание. Рассмотреть слой В^я/2]; 2) Ука-
зание. Среди п. -|- 2 наборов из Вп всегда найдутся два на-
бора одного веса.
; 3) 2fc + 2”-* —1.
1.13. Полагая, чтоО < Z< к < п, подсчитаем число р (л, к, I)
пар (5, р) таких, что 5^4, С одной стороны, р (п, к, Z) =
*) При а, не являющихся целыми, здесь полагается
равным 0.
281
[п — l\ (к\
= ] А |(ь _ И, а с другой — р (п, к, I) < | В 11 j. Используя
/П\(П-1\ [п\/к\
тождество = ( JLIi получаем треоуемое неравен-
ство. В случае I > к имеем тот же результат.
1.14. 1) Возрастающая цепь длины п содержит в каждом
слое по одной вершине. Выбрать вершину в слое Bf можно
п способами. После того, как вершина цепи, лежащая в BJ,
выбрана, вершину цепи, лежащую во втором слое, можно вы-
брать п — 1 способами и т. д.
1.15. 1) Пусть А—множество попарно несравнимых на-
боров из Вп, и пусть Л( = ЛПЙ“, a Z (а)—множество возра-
стающих цепей длины п, содержащих вершину 5. Имеем
я
п ! > I и z (а) 1= У I Z (а) I = У I I i 1 (я — i) 1 >
Не-4 I а 6 А »=0
П
♦=0
Отсюда | А | < ([n'/aj) ' Указание. При i < к < п/2 спра-
ведливо i I (п — i) I > к ! (п — к) !
1.16. Указание. Каждому числу вида Pj’p? ... Рпя со-
поставим вектор (ап а2, ..., а„) из Вп. Тогда множеству А
будет соответствовать множество А’С.Вп, состоящее из по-
парно несравнимых наборов. Применяя результат задачи
1.15, 1), получим утверждение.
1.17. Пусть «!, i.2.1к — номера тех координат, в кото-
рых аир различаются. Всякий вектор у такой, что а < j < р,
может быть получен из а заменой в некоторых из перечис-
ленных координат 0 на 1. Число способов произвести такую
замену равно 2к.
1.18. Для В1 разбиение состоит из единственной цепи
Z = {(0, 1)}. Для В2 в качестве цепей разбиения можно
взять Z1 = {(1, 0)} и Z2={(00), (01), (И)}. Свойства I9 и 2Q
выполнены для этих разбиений. Предположим, что утвержде-
ние доказано для кубов размерности < п, и докажем его
для Вя+1. В силу предположения существует разбиение гра-
ней B^+1-h+1 и B’+i. »+! на цепи, удовлетворяющее условиям
1° и 2°. Разбиения в Вя+1’п+1 и BJ+1>”+1 можно выбрать изо-
морфными, т. е. такими, что цепь Z0={a1, а2, .... 5л} тогда
и только тогда принадлежит разбиению куба BJ+1>*+1, когда
282
цепь Z1 = {5{, <i2, .... а',}, полученная из Zo заменой в каждом
наборе а{ из Za нуля в (п-|-1)-й координате на единицу, при-
надлежит разбиению грани В«+1> "+1. Пусть 20={5|, 32, ...
.... 5,} и Z1 = {a[, а2, .... й'} —две такие изоморфные цепи
из разбиений граней Bj+1, ”+1 и BJ+1> я+1. Построим две новые
цепи 20={а1, а2....а,, И’г} а 2^ = {а{, а2, .Цепь 20
получена из Zo присоединением вершины a^Zlt а цепь
получена из Z] отбрасыванием вершины а'. Поступим так
с каждой парой изоморфных цепей. Получим разбиение
куба В№+1 на непересекающиеся цепи. Выполнение условий
1° и 2° легко проверяется.
1.19.
1.20. 2) Покажем, что слой В^— полное множество при
п>2. Пусть — вектор из Bf, у которого t-я координата
равна единице. Пусть заданы расстояния р (а,-, р) = г<1 i = 1,
Покажем, как восстановить р. Если ||р|| = А:>0, то, очевидно,
r^g {Zc — 1, Л + 1). Пусть шах > 2, и пусть А (р) = fi : г( =
1<»^я _ I
= min г Л. Тогда i-я координата вектора р равна единице,
если i g А (р), и равна нулю в противном случае. Если шах г,- =
= 1, то р = 0. При га = 5 слой Bjf не является базисным мно-
жеством, поскольку множество {(00001), (00010), (00100),
(01000)} является полным. 3) При п четном и Л = п/2, при
любом п>1 и к = 0, п. 4) Пусть 4 = {alt ..., ак] — полная
система. Рассмотрим систему равенств р (5,-, p) = rit 4 = 1, к.
Очевидно, что г, g {0, 1,.. .,ге), 1 = 1, к. Каждый набор (rlt г2,...
..., гк), при котором система имеет решение, однозначно опре-
деляет некоторый вектор pg Ва. Отсюда вытекает, что (?г + 1)* <
< 2". Указание. Верхняя оценка для числа векторов в ба-
зисной системе может быть получена из того, что система
уравнений р (а0 р)=г<1 4 = 1, к, может быть сведена к обыч-
ной линейной системе. При Л > и некоторые уравнения этой
системы выражаются в виде линейной комбинации через
остальные. Такие уравнения, а следовательно, и соответствую-
щие им векторы можно удалить.
1.21. Достаточность. Перестановка координат всех
векторов из Вп, а также инвертирование координат ilt i2, ...
..., tk всех векторов из Ва не меняет взаимных расстояний
между вершинами. Необходимость. Пусть <р — отображе-
ние куба В” на себя такое, что для любых 5, р справедливо
Р (?(“), f(₽)) = p(a, ₽)• Рассмотрим множество £> = Sg(J-S’>
' 283
являющееся полным в Вп (см. предыдущую задачу). Пусть
<р (£)) = {у> (0), <р (5]).<р(зл)} — образ множества D, а а,- — век-
тор из В?, у которого i-я координата равна единице. Поло-
жим р,- = tp (б) ©?(“<), i = 1, п• Имеем || ji,-1| = р (б, Р,-) = р (<р (б) ©
@?(б), <p(6)©?(5J)=p (?(б), <p(5j))=p (б, а<) = 1. Пусть
j (i)—номер той координаты вектора р;, которая равна еди-
нице, i = l,n- Тогда отображение л: есть переста-
новка на множестве {1,2.....................п). Для произвольного 5 = (а,, ...
..., а.,.) из Вп положим л (а) = (ак(1), .... агЛ,г)). Покажем, что
для всякого т£Вп справедливо ? (у) = л (у © <р (б)). Тем самым
необходимость будет доказана. В самом деле, р (® (у), (б)) =
= р(у, б), р(?(у), ?(“»))= ?(Ъ “>)• С другой стороны,
р (л (7©5р(б)), ?(б)) = р(7, б), ₽(п(т©т(б)), ?(й<)) = р(т, аД.
Очевидно, множество <р(В) является полным в В”, как и D.
Отсюда вытекает, что ? (?) и л (у ©у>(б)) совпадают.
/2"н — 1\
1.22. 2я — 1)‘
1.23. 1) Для га = 1 и к = 0, 1 утверждение справедливо.
^Мы полагаем, 4toQ.^ = 0 при всех к = 0, 1, . ..). Пусть
утверждение доказано для размерностей, меньших или рав-
ных п — 1, и для всех й = 0, 1.....Пусть а = (а,...а„),
и пусть 5' = (а{..а'_1) = (а2, ..., аД. Если а! = 0, то, оче-
видно, |М£(а) | = |М£~1 (а') | = 1 -|-(Л 1 к'* 4- ...
“1 = 1, ТО |^(а)| = (га 1) + |M^11(a')l = (” д. !) + 1 +
М —l-(i2-l)\ /П —1—(ifc— 1)\ (П — 1Л
+1 к-i ;+•••+( 1 ;=1+1 к )+
(П <л\ гт
। 1.2) Для произвольных к и а£В% число pfc (а) =
= | М). (а) | будем называть номером набора 5 в слое Z?£. Пусть
af В^ — вектор, единичные координаты которого есть ..it,
1 < В < ... < 1* < п. Тогда в силу предыдущего pfc(a) =
(п — (п —
к у+...+^ । ) . Пусть далее набор ^Bf по-
лучен из 5 заменой последних к — I единичных координат на
нули. Покажем, что (5)) = Mnt (ji) или, что то же самое,1
что Z’j (а)) = {7: рг (7) < р, ф)). Покажем сначала, что
для всякого yfS; такого, что р-/ (?) < Р-/ (₽), существует набор
284
8gB% такой, что 7<8 и (8) < (5). Выберем в качестве 3
набор, полученный из'7 заменой последних к — I нулевых ко~
ординат на единицы. Требуется показать, что (8) < (5).
Если (8) > p.fc (а), то существует такое t, что а,- = 3,. при
i<t, а,=0, 8/ = 1. Рассматривая наборы 5' и 8', получен-
ные из i и 8 соответственно заменой последних к — I единич-
ных координат на нули, имеем р.г (5') < (8'), 5' = р, и., (8')
< Р; (7). Получаем противоречие с неравенством Р/(₽) > Р/(7).
Аналогично можно показать, что для всякого 7gB(? такого,
что рг (7) >р; (₽) не существует набора 8gM^(a) такого, что
7 <8. 3) Вытекает из 1) и 2). 4). Пусть А С В% и А не яв-
ляется начальным отрезком слоя В%. Укажем способ построе-
ния такого множества fCBj, что |В| = |Л|,
< Saeav (“)» I z*-i (Л I =S I zl-i M)|. Тем самым утверждение
будет доказано. Обозначим через К (а) множество номеров
единичных координат набора а. Пусть agBg\A и pg Л— те
наборы, на которых достигается min | К (а) \ К (а) |, где мини-
мум берется по всем парам (а, а) таким, что а£Д$\Л, ^Л,
v(3) <>(*). Пусть М= К (а) \ К (р), N = К (р) \ К (i). Оче-
видно, Л/Г)^=0. |4f| = |7V|. Для произвольных а, а из Вп
обозначим через а \ а набор вида а© (a(~)i), и пусть а' =а\р,
р' = р\а. Ясно, что v (а') < v (р'). Положим
о = {7й6л. “'П7=0> ^'<7; (7\Р’) U а'€Л},
£={8;8 = (7\р') U а', 7СО},
В = £'и(Л \D).
Очевидно, что FCB%, |В| = |Л | и по“
скольку к ((7 \ p')U“') < 4 (7) Для всех Остается дока-
зать, что | (F) | < | Z^-j (Л) |. Ограничимся указанием.
Сначала следует показать, что если 8g Z^_j (F) \ ZjjLj (Л), то
аПР'=б и а' < а. Затем показать, что набор a = (a\a')UP'
содержится в Z£_t (Л) \ Zg-y (В). 5) Указание. Провести
индукцию по к — I, 6) Пусть к — максимальное целое, при
котором aft>0. Тогда при 1 = 4-1 утверждение сводится
к пункту 4). При проведении индуктивного шага (индукция
/ к \
ведется по к — I) положим А( = Л Г) В?, Aj = А (J BJ) и за-
метим, что
z?(A) = z? (ZF+1 (л;+1))ил;.
Ясно, что
min | Zj (С) | < min | Z? (С) |.
CQB’}, |C|-m CCIBy, |С|>т *
285
В силу индуктивного предположения min | Z?+1 (4,+1) | дости-
гается в случав, когда каждое Z$(A), 1-^-1, является на-
чальным отрезком слоя В}. Но тогда в силу 2) множество
Zfc, W+t) является начальным отрезком. Тогда выбором 4/+1
множество (А) = ZJ+1 (AJ+1)U-4z+i можно сделать началь-
ным отрезком слоя By. Отсюда и вытекает утверждение.
1.24. Для каждого 1 = 0, п пусть 4г = 4ПВу. Число
t(n, т, к) пар (а, р) таких, что а£Ат, р(~]а = (5, pgB^(J^m+ft-
Из условия вытекает, что pg4. С одной стороны, t (п, т, к) =
= а«С к т\ С ДРУГО“ стороны, t (п, т, к) < - am+kj X
fm-\-k\ ffn\ \(п—к\
т )~'\\к)~а,с)\ т )’ Отсюда и вытекает утвер-
ждение.
1.25. 1) Пусть а — центр множества А; тогда 4' = {а©р,
pg А} является искомым множеством. 2) Можно считать
в силу 1), что 0 является центром А. Для построения А'
достаточно для каждого 1 = 1, п заменить каждый набор а
из А(, для которого а* g А, набором а*. 3) Указание. Пусть
Л СВ' имеет центр 0 и обладает свойством 1°. Пусть i —
преобразование, состоящее в том, что для каждого ag4<>/
такого, что а*> g4, набор 5 заменяется на а{> i. Упорядочим
пары (1, /) такие, что 1 < 1</< п, следующим образом:
(1, п), (1, п-1), .... (1, 2), (2, п),
(2, п-1), ..., (2, 3), .... (п-1, п).
Применив к А последовательно все преобразования S'< 1, на-
чиная с (1, ;) = (!, п) и кончая (1, /) = (п —1, п), получим
искомое А'. 4) Пусть А С Вя удовлетворяет условиям задачи.
Тогда можно считать, что G является центром 4 и 4 удовле-
творяет свойствам 1°, 2°, Если для всякого ag4 ||a|| < fc, то
утверждение верно, так как в силу свойства 2° для каждого 1
множество А{ = А(~]Ву является начальным отрезком слоя В;.
Пусть существует agA такое, что || 5|| >&. Пусть s — наиболь-
шее число, для которого А, не пусто, а 1 — наименьшее число
такое, что 4/эЬВ?. Пусть а — набор с наибольшим номером
в 4,, а р — набор с наименьшим номером в By\At. Пусть
В = (А \{5})U{P}- Для доказательства утверждения достаточно
показать, что | Г (4) | > | Г (В) |. Пусть А'(5) = {7 : 7 g Г (А),
Г(4\{а})} и lV(pj = {7:7gr(Z?), ?(ЕГ(В\{р}}}. Ясно,
что Г (В) = (Г(4)иЛ1 (P)U{5}) \ (N (“)□{₽)). Таким образом,
нужно показать, что | N (а) | > | N (р) |. Пусть S g В” —
286
произвольный набор, обозначим через q (8) число — 1, где
— наименьший номер единичной координаты набора 5. Тогда
| N (5) | = q (а), | N (р) | = q (р). Пусть 7 g В?— набор, получен-
ный из а заменой последних s — t единичных координат на
нули. Тогда q (а) > q (у). Но из ч (7) > v (р)'следует, что q (7) >
> q (р). Отсюда и вытекает утверждение.
1.26. 2) В качестве А такого, что | А\ = 2?~1, можно взять
любую (п — 1)-мерную грань, содержащую I, а при нечетном п
можно взять Множество {а: 1] й ]| > («+ 1)/2}. С Другой стороны,
если | А | > 2”~*, то в Л найдутся два противоположных на-
бора, пересечение которых есть 0.
1.27. 1) Указание. Рассмотреть множество 15; ||5||>
>1 '-2-'- г.
1.28. 1) Аналогично 1.25. 2) А = {5: 5 g Вп, || 51| — четное}.
1.31. 1) Каждой грани В”’ iu^" 'к направления I == {ilt . ..
.... 4а} можно взаимно однозначно сопоставить ее код — вектор
(Тп •••• ~!п) ° координатами 7,- g {0, 1, —}, 1 = 1, п, такой, что
74 =01, ..., 7,-а.= °jt> а в остальных координатах стоят прочерки.
Заполнить фиксированные к мест нулями и единицам и можно 2*
способами. 4) Искомое число равно числу векторов (7Х, ..., 7Я)
с к координатами из множества {0, 1} и п — к прочерками.
Выбрать к мест из п рдя значащих символов, т. е. для 0 и 1,
можно способами, заполнить фиксированные к мест ну-
лями и единицами можно 2* способами. 6) Код A-мерной грани,
содержащей заданную вершину (щ, .... ая), можно задать,
расставив к прочерков вместо некоторых к координат вектора
(“1, .... “«). 8) Пересечение двух граней есть грань. Выбрать
грань размерности / в грани размерности I можно 2l~J спо-
собами. Тем самым в коде грани размерности к уже зафикси-
рованы I координат. Среди остальных п—I координат необхо-
г. (п —
димо расставить к — J прочерков. Это можно сделать _______\
способами.
1.33. Пусть 7ц 72, 73 — коды граней g2, g3 соответственно.
Две грани не пересекаются тогда и только тогда, когда суще-
ствует координата, в которой коды этих граней имеют значащие
символы, причем эти символы противоположны. Если же грани
gx, g2 пересекаются, то код их пересечения содержит значащие
•w
символы в тех координатах, где хотя бы один из кодов 7Х, ъ
имеет значащую координату, причем значащие координаты кода
пересечения совпадают с соответствующими координатами хотя
бы одного из кодов 7а. Если § — код пересечения гра-
ней и g2 и грань g3 не имеет общих вершин с этим пересечением,
то найдется i такое, что i-е координаты векторов 5 и р3 являются
значащими и не совпадают. Но тогда i-я координата вектора 73 не
совпадает со значащей i-й координатой одного из векторов р,
или р2. Это означает, что соответствующие грани не пересекаются.
Противоречие.
1.34. Задача легко сводится к случаю, когда ^EL,2”* = 2”.
Проведем доказательство для этого случая индукцией по га.
Для га = О, 1 утверждение, очевидно, справедливо. Переход
га->га-|-1. Пусть min п{ > 1. Положим nJ = га, —1. Тогда
J^i^s
п'{ — неотрицательные числа и 2*=12"‘ «=2Я. По индуктивному
предположению существует разбиение каждой из граней
2?g+i. я+1 и BJ+1’ л+1 куба В“+1 на грани размерностей nJ, ..., п'я.
Выберем эти разбиения одинаковыми, т. е. такими, что для
каждого 1 = 1, s объединение граней размерности raj. образует
грань gt размерности га,-. Получим нужное разбиение. Если
min га< = 0, то пусть гаг — число тех i, для которых nf = 0.
Из условия 2”‘ = 2"+1 вытекает, что т — четно. Рассмо-
трим новую совокупность nJ, га3, ..., nJ._m,2, полученную из
прежней путем замены т нулей на гаг/2 единиц. Построим,
как в предыдущем случае, разбиение куба В"+1 на грани,
а затем некоторые т/2 граней размерности 1 разобьем на т
граней размерности 0.
1.36. 1) Верхняя оценка. Указание. Рассмотреть
N = {а: af-B”, || а ||—четное}. Нижняя оценка. Пусть Л СВп,
| Л' | < 2"~1. Существует (см. 131, 134) разбиение куба Вп на
непересекающиеся грани размерности 1. Число граней в таком
разбиении равно 2”'1. Отсюда следует, что хотя бы одна из
граней не содержит вершин из N. 3). Указание. Рассмо-
треть N = (5; af-B”, ||а || = 0 (mod 3)} или /Vj = (а: а£Вп,
v (а) = 3 (mod 4)}. 4) Нижняя оценка. Заметим, что для
того чтобы вершина 5 = (а,...а„) содержалась в (га — 2)-мер-
ной грани с кодом р = (7,....р„) (см. решение задачи 1.31),
имеющим значащие координаты в разрядах i и ], нужно, чтобы
= !<• aj = 1j- Пусть /V CZ. Вя, | /V | = т, — множество такое, что
в каждой (га — 2)-мерной грани содержится вершина а из N.
288
Равсмотрим двоичную матрицу М, строками которой являются
векторы из N. Из предыдущего замечания вытекает, что для
каждой пары чисел (i, /), 1 < i < j < га, и любой пары (о, т),
а, xg{0, 1}, должна найтись строка a = (alt ...,а„) такая, что
я,-=а, ау = т. Отсюда вытекает, что любые два столбца мат-
рицы М попарно несравнимы. Число попарно несравнимых
([гаг/2]) Верхняя оценка. Пусть т — наименьшее
целое такое, что ( т 1 > п. Построим двоичную матрицу М
\[ml2]J
с п строками и т попарно несравнимыми столбцами. Добавим
к матрице М строки 0 и 1. Тогда полученная совокупность
векторов-строк будет «протыкающей» для множества всех
(га — 2)-мерных граней куба В”.
1.37. Для га = 1, 2 утверждение очевидно. Пусть аь а2, ...
dg» является циклом в В”. Пусть р<з, где fig В", ag{0, 1},
обозначает вектор длины га + 1, первые га координат которого со-
впадают с соответствующими координатами набора р, а (га + 1)-я
координата равна а. Тогда последовательность а,0, а20, ...
..., а2„0, а2Я 1. “it “J является циклом в Вя+1, содер-
жащим все его вершины.
1.39. 1) Да. 2) Нет. 3) Да. 4) Да.
1.43. У Казани е. Заметить, что если наборы а = (оь.. .,а„) и
а' = (о[,.. сравнимы, то одна из сумм 2 (—2 t *а<
•=1
больше единицы по абсолютной величине.
§ 2
2.1. 2а” 1 (га > 1). 2.2. 2(га> 1). 2.3. . . + С*т~1,
где т = 2"(га > 1, к > 1). 2.7. 2) 2В'Н (га > 1). 2.10. 1) 5 спосо-
бами. 2) 9 способами.
2.12. 1) Базис индукции Если сложность формулы равна
единице (над множеством связок Л/ = {~], &, V, -*}), то ата
формула имеет один из следующих видов: ( "] z), (х & у), (х V у),
(х-ьу) (с точностью до обозначения переменных). Поэтому
утверждение очевидно для формул сложности 1. Индуктивный
шаг. Пусть утверждение справедливо для всех формул (над
множеством связок М), имеющих сложность, не превосходящую
числа I (Z > 1). Возьмем произвольную формулу 21 (над Л/),
Ю Г. П. Гаврилов, А. А. Сапоженио
289
сложность которой равна I + 1. Будем считать, для определен-
ности, что 91 = С® V £) (остальные случаи рассматриваются
аналогичным образом). Очевидно, что связка V. стоящая
между формулами 23 и £, имеет индекс, равный 1. Далее,
если связка в формуле 23 (или £), рассматриваемая как
связка формулы 23 (соответственно, £), имеет индекс больше,
чем 1, то в формуле 21 индекс этой связки уменьшиться не
может. Если же связка в 23 (или £) имеет индекс, равный 1,
то в формуле 21 ее индекс будет равен 2 (индекс увеличи-
вается потому, что в формуле 21 перед подформулой 23 есть
левая скобка).
2.15. 3) (0 1 0 0). 2.18. 3) 21 ~ 23. 2.19. 2) (х, с/) = 0,
/»(г, У) = х< у)=у, h(x, у) = х®у. 2.20. 1) ((фН
|(х|у)). 2) ((х ф у) | ((х |х) | (у^ у))). 2.21. 1) ((х | у) | (х | у)).
2) ((х V (я V V)) ~У)‘ 3) Нельзя.
2.22. 2) Функция, реализуемая формулой над множеством
(->}, принимает значение 1 не менее чем на половине набо-
ров значений аргументов. Этому условию функция ху не удов-
летворяет.
2.23. Вообще говоря, нельзя. Пример: S={1 }, функциях
не реализуема над S формулой четной глубины.
2.24. Если над множеством S реализуются только констант-
ные функции, то утверждение очевидно. Пусть над S реализу-
ема некоторая функция / (Xй) const. Отождествляя в функции
/ (х«) и в реализующей ее формуле все переменные, получаем
функцию ? (х) (и соответствующую ей формулу 21 (х)). Надо рас-
смотреть следующие три случая: а) <р (х) — константа, б) ср (х)=
—х и в) ср (х)=Х. Получив (в случаях а) и в)) формулу, реа-
лизующую функцию х (и имеющую глубину не меньше 1), мы
сможем строить для каждой конкретной функции, реализуемой
формулой над S, формулу сколь угодно большой глубины.
Пусть ср (х)=0. Тогда найдется набор а=(а1, а2,. . ., ая), на ко-
тором функция / равна 1. Заменим все х{, соответствующие а<=1.
на х, а остальные х< — на <р (г)=0. Получим функцию ф (х)=х
Если же ср (х)=1, то аналогичным способом получаем функ-
цию х.
2.26. 2) х V У — (х~>- У) ~>У- 3) х~;/ = (х-»у) & (у->х).
2.30. 2) Вообще говоря, нельзя. Пример: 21 = уа-»х— фор-
мула, не являющаяся тождественно истинной; однако формула
S*.^yj2l |= (J/i Ух) — тождественно истинная.
2.31. 1) Если предположить, что / (0, 0)=0, то, беря х=
=y=z=0, имеем / (/ (0, / (0, 0)), / (/ (0, 0), / (0, 0)))=/ (/ (0, 0),
/ (0,0))=0, что противоречит условию задачи. Итак, / (0,0)= 1
290
Полагая затем / (0, 1)=0, имеем (при x=y=z=0) / (f (0, / (О, О)),
f U (°, 0). / (°> °)))=/ (/ (°. 1). / (1. 1))=/ (0. / (1. 1)) и, в силу ус-
ловия задачи, должно выполняться соотношение / (1, 1)=0.
Но, рассматривая затем х=0, j/=z=l, видим, что / (J (0, / (1,1)),
f (j (0,1), / (0, !)))=/ (/ (0, 0), / (0,<0))=0, а это противоречит ус-
ловию задачи. Таким образом, / (0, 1)=1. Наконец, предполо-
жим, что f (1, 1)=0. Полагая х=у=О и z=l, получаем
/ (/ (0, f (0, 1)), / (/ (0,0), / (0, 1)))=/ (/ (0, 1), / (1, 1))=/ (1, 0).
Принимая во внимание условие задачи, имеем f (1, 0)=1. Но
тогда f (/ (1, f (1. 1)), f (f (1, 1), / (1, 1)))=/ (/ (1, 0), / (0, 0))==
=/ (1, l)=0 — что противоречит условию задачи. Следовательно,
и / (1, 1)=1. Итак, / (0, 0)=/ (0,1)=/ (1,1)=1. Значит,
f (х, у)=х —> у или / (х, y)=i. Далее эквивалентности а)—д)
проверяются непосредственно (например, с использованием ос-
новных эквивалентностей). 2) Нет, не вытекают. Достаточно рас-
смотреть функцию / (х. и)=х — у.
§ 3
3.6. 2я. 3.7. 1) 2”-1; 2) 2я — 2; 3) 2”-1. 3.8. 1) к-1; 2) 4-2’’ +
4-/-2я — к-1; 3) к (2т — I) + Ц2п — к). 3.9.2) ft — xtx„
^(£3)=5!1, /1р(1’) = ха. 3.11. 2<3/4)-2И. 3.12. 12. 3.16. 4.
3.18. 3.19. 2S”-^, где 3’2°‘ °’ вСЛИ *
»=о
нечетно,
/2я — 1
\ к
I, если к — четно. 3.23. = (1101111011100111).
3.26. / (хя) = £t£2 ...£„.
3.29. Указание. Заметить, что при 4 = 1 многочлен
обращается в единицу на 2я-1 наборах. Используя формулу
разложения, провести доказательство индукцией по к.
1
3.30. 1) 2я-*4-2* —1; 2) у (2я — (—1)я).
3.31. Для в = 1 утверждение очевидно. Индуктивный пере-
ход от п — 1 кп. Если I < 2я-1, то по индуктивному предпо-
ложению существует полином Р (х”'1) длины <n —1, для
которого |1Ур|»=1. Тогда полином хвР(2я-1) обращается в 1
в I вершинах куба Вп. Если 2я'1 < I < 2я, то рассмотрим
полином Р (2я*1), обращающийся в единицу на 2я — I вер-
шинах куба В"*1. Тогда полином хя.Р(хя_1)©1 является
искомым.
10»
291
$ 4
4.4. У Казани в. Пусть К == xj' ... z®B, L = х}< ... а£” и
K*L есть э. к., полученная из К вычеркиванием тех букв х*{,
для которых а,- ;3р Заметить, что каждый импликант функ-
ции / (2я) можно представить в виде KCL, где К и L — под-
ходящие в. к. из совершенной д. н. ф. функции / (£”), быть
может совпадающие.
4.5. 1) 2я*1; 2) 2я-1; 3) 3.2*-»; 4) 2Я~»; 5) * + (» — Л) X
X (»-*-!)•
4.6. 1)П( П~1 \.
4.8. 2) ®i*»V ViV хахгха.
Г
4.9. 1)22Я-2Я-г; 2) г2”"8** (—D* 2<‘2‘“".
•=о '
4.11. 1) £2£3 \/ £1xi у xtxs \/ xxxt.
4.12. 1) xtxa, хгха, x1r2z1, 2jXsz4.
4.13. Указание. Показать, что никакие два собственных
набора двух различных ядровых импликантов не являются
соседними, и использовать тот факт, что множество W г~ В",
такое что |/V|>2”-1, всегда содержит ребро (см. 1.44).
4.14. 1) 2”-1; 2) 2я-»; 3) 0; 4) 2я-»; 5) к.
4.15. 22'!-2Я-г(1-(1-2-П2”_Г).
4.18. 1) 1; 2) 52Я-Г; 3) б2”-4; 4) 1.
4.20. Одна. Показать, что все простые импликанты яв-
ляются ядровыми.
4,23. Указание. Провести индукцию по в, используя
разложение (3) функции по переменным.
4.24. 1) У двух функций. 2) У 2Я+1 функций.
и4.25. Например, 4 = л2’ — 1.
4.27. 1) 0, если к 0, Л-|-7в<п; f\ если Л = 0;
если к -f- т = п.
2) На двух при четном п и на четырех
при нечетном в.
§5
5.2. 1) х2; 2) х1( х2; 3) х4; 4) 5.4. 1) х2, ха; 2) х2;
3) xt. 5.7. т. 5.8. 1) xlt х2, хг, х4; 2) xit х2, ха; 3) xt, ж4;
4) хи х2, х4.
292
5.10. 1) n > 3; 2) ни при каком п; 3) м > 3; 4) при чет»
ных п; 5) при га = 4Л— 2, к = 1, 2, ...
5.12. 2) |Pg (Xs) | = 218.
5.13. У к а з а н и е. Из условия задачи вывести, что суще-
ствуют наборы а', р', у' такие, что р (а', р') = р(р', ^') = 1.
Пусть 5' и р' различаются в i-м, ар' и f - в /-м разряде.
Тогда переменные х{ и xj являются существенными.
5.14. Указание. Достаточно показать, что если xt
или входит в некоторый простой импликант К функции /,
то х( — существенная переменная. Вычеркивание xj и*
К приводит к э, к. К', не являющейся импликантом.
Отсюда вытекает существование набора a=(aj, .... а,-_ъ в,
а<+1, .... такого, что К'(а) = 1, но /(а)=0. В то же
время /(а*) = 1, поскольку Х(а’) = 1. Отсюда и вытекает
существенность х(.
5.15. У Казани е. Если х{ входит явно в полином Р (£"),
то последний можно записать в виде x(Q@R, где Q и R—
полиномы, не зависящие от х( и Q^O. Пусть набор й =
= (Я1, .. ., a<_i, af+i, . . ., ап) такой, что (>(а) = 1; тогда
Р(а1,..., a{_lt Х{, а<+1, ..., a„) = xi@R(i). Утверждение
вытекает теперь из задачи 5.1, 1).
5.16. Неверно. У Казани е. Рассмотреть / (хп) = xt ©
© х3 @ ... © х„.
5.17. У к а з а ни е. Пусть f (хп) удовлетворяет условию.
Тогда существует такое целое i (1 < i < п), что для любых а, р
таких, что а £ В”, ptB"_p /(5)^/(р). Утверждение вытекает
теперь из того, что для всякого i в В”_iljB” имеются ребра
любого из i направлений.
5.18. Указание. См. 5.13.
5.19. Если f (хп) выражается полиномом степени больше
единицы, то без ограничения общности ее можно представить
в виде © хгР3 © а:гР8 © Р4, где Р} 0 и Ри Р2, Pt, Р3
зависят от переменных xs, ..., х„. Пусть а = (as, . . ., а„) — такой
набор, что Р](й) = 1. Тогда компонента /2’(хп) имеет вид
© XjZ, © \tx2 © X, и, следовательно, эта компонента суще-
ственно зависит от г, и х2. Отсюда вытекает, что искомые
три набора найдутся в грани В”’ 3’ •'” ”. Если f(x”) выражается
полиномом первой степени и существенно зависит от и х4,
то для всякого набора (<ха, .. ., ая) любые три вершины
в грани являются искомыми.
293
5.21. Предположим противное. Без ограничения общности
можно считать, что среди всех компонент вида f* (2я) наи-
большее число существенных переменных имеет компонента
/} (2я). Тогда предположение эквивалентно тому, что /} (2я)
фиктивно зависит от некоторой переменной, например от *2,
т. е. /1=/п2==/1(Л Поскольку *t — существенная перемен-
ная, то выполнено хотя бы одно из соотношений /}’о2^/оо2»
/н2'?ь /от2. Пусть, например, /ij2 ¥= /о)2- Тогда функция
^ = «i/oi2V *i/ii2
существенно зависит от х, и от всех существенных пере-
менных подфункции /];'2 = /}. Это противоречит тому, что/}
имеет максимальное число существенных переменных.
5.22. 1) Верно. Вытекает из предыдущей задачи. 2) Не-
верно. Указание. Рассмотреть / (2s) = х,х3 \/ х2х3 и пере-
менные *ь х2.
5.23. 1) 2|,'£2; 2) 1; 3) *1( хг; 4) x2-^xlt xt— х2, 1.
5.25. 6. 5.26. Можно. У Казани е. Рассмотреть функцию
V *1*2*4 V *1*1*4 V *2*3*4-
5.27. Номера координат наборов 5, р, можно разбить на
следующие четыре группы:
Ai = {i: ^ = 3^ = ^}, A2 = {i: а{ = ${,
A3 = {i: ,8,= ь}, At={i: а{ = <^ = -ц = 1}.
Пусть /(5) = /(7) = з, //ф)=9. Тогда, если / (0) —
= /(1)=а, то полагаема, = *, если if^jLIXj, х( = у, если
if4,(J-44- Если/(б)=а, /(1)=а, то полагаем *< = * при
If41( xf = y при if42, *,=2 при if Л8иЛ4. Если / (0) = ст,
то полагаем xi — x при tf-^LMa, Х4 = У при *€4а, *» =2
при i f 2I4. Существенная зависимость полученных функций
вытекает из задачи 5.13.
5.29. *! © *2 ©...©*„© о, of {0, 1} при п > 2; *’’*22 V
у г’’*’3 V *з3*?> o,f{0, !}- i = 1, 3 при п = 3; *’*’, *’\/*’
при п = 2.
5.30. Функция, полученная из / (2я) отождествлением пере-
менных if, Xj, имеет вид x(f{\J \/ Из условия вытекает,
что по меньшей мере одна из компонент /};А /*о не равна
тождественно нулю.
5.33. Указание. По меньшей мере одна из функций /, g
обращается в единицу на нечетном числе наборов.
5.34. Указание. См..5.30.
ГЛАВА II
§ 1
1.2. Нет, не вытекает. Можно положить (по определению)
для любого множества М из Р2 (в том числе и пустого) [Af]=P2,
т. е. ввести такую операцию замыкания. Тогда соотношения
1)—3) из задачи 1.1 будут, очевидно, выполняться, а соотноше-
ние 4) выполняться не будет.
1.3. 1) Да. 2) Нет. 3) Нет. 4) Да. 5) Да. 6) Нет. 7) Нет.
1.4. 1) {1}. 2) {0, 1, fj}. 3) {Z], Zj V z2, Zj V z2 V z3).
4) {1, *1, 2j~Z2, Zj (J) z2 © z3}.
1.5. Пусть / (z“) — функция из замкнутого класса, суще-
ственно зависящая от всех своих переменных (п > 2). Тогда
функция
/1 (!6> Уг, . • .. !/„. 22.z„) =
= /(/(К1. У....... Уп)> хг....хп)
существенно зависит от всех 2п—1 переменных (здесь {уп у2,. . .
. . ., у„} Г) {хъ,- •, 2Я}=0). Затем в функцию fa на место
переменной у2 можно подставить функцию / (z, , z21. . ., zK) и полу-
чить функцию, существенно зависящую от Зп—2 переменных
и т. д.
1.6. [0], [1], [z], [0, 11, [0, zj, 11, zj, [z, Я], [0, 1, z], [0, l,z, «].
1.7. 1) Да. 2) Нет, не всегда. 3) Нет, н* всегда (исключе-
нием являются только все Р2 и его дополнение — пустой зам-
кнутый класс 0).
1.8. 3) (z -> у) -»у = х V у, z = z©z@z. 4) Из второй
функции с помощью отождествления всех переменных получа-
ется отрицание. 5) т (z, у, 0)=zy, z° © 0=£.
1.9. 1) А] С К2, но может быть и строгое включение:
Ki С Кг. 2) Aj g А2; например, при Мх — {ху, х} и Мг = {£}
имеем Ai = [zy], a A2 = P2\[z]. 5) См. 1.9, 2).
1.10. 2) Л/! = [2, 0], Л/2 = |х, 1|. 3) A/i = lz, 0], Л/2 = [0).
5) См. 1.10. 2).
1.11. 1) {0, z). 2) {1, х © у}. 3) {х \/ у, х • у • ?}. 4) {z@l,
т (х, у, г)}, так как z @ у © z — т (т (z, у, г), т (z, у, z),
т (z, у, z)) и в замкнутом классе [т (х, у, z)| любая функция,
зависящая существенно от одного аргумента, равна тожде-
ственной функции.
1.12. Пусть М — предполный класс (в Р2). Это значит, что
|Af] g Pt, но при всякой функции ]£Р.1\М имеем |A/U{/}|e
295
= Ра. Если то найдется функция g ив [Л/] такая,
что [Л/] = [ЛУ[_){#}] = Рг- Получили противоречие.
1.13. Если М^ = М1, то утверждение очевидно. Пусть
М1. Предположим, что ЛУ} = Л/|. Так как и М2 —
замкнутые классы и ЛГ}С-^1 и M\(zM2, то, какова бы
ни была функция / из М2 (или из М2), подставляя на места
ее переменных функции из М{ (=Д/|), зависящие от одной и
той же переменной х, получаем снова функции из Л/}. Но это
значит, что, добавляя к М2 произвольную функцию g из
М2\М1 (=/= 0), мы имеем [ЛЛиСгЛП^1 = ¥= Л/1, а это
противоречит предполноте класса в классе Л/.
1.14. 1) [0, 1, х], [г]. 2) [0], [1]. 4) [0, х], [arVid-
1.15. 1) Нет, не является. 3) Нет, не является.
1.16. Если я f М, то утверждение очевидно. Пусть х ( М.
В силу определения операции суперпозиции подстановка тож-
дественной функции может рассматриваться как преобразование,
совершаемое только в множестве М и проводимое в соответствии
с операцией суперпозиции. Значит, [М U {х}] С М |J {х}. Об-
ратное включение следует из свойств операции замыкания.
1.17. Утверждение следует из того, что функция х |у образует
в Р2 полную систему.
1.18. Пусть / (хв) gfe const. Если отождествляя все пере-
менные в функции / (хя), получаем тождественную функцию или
отрицание, то утверждение очевидно. Пусть у (х,. . ., х) =
= const. Для определенности положим, что / (х,. . х) = 0.
Так как / (хя) ф const, то существует такой набор а=(а15. . ., aj,
что У (а)=1. Положим х<=х, если а—1, и х<=у, если 0^=0.
Тогда из функции у получим функцию g (х, у), удовлетворяющую
условиям: g (0, 0)=g (1, 1)=0, g (1, 0)=1. Если g (0, 1)=1, то
g (х, у)—х © у; если g (0, 1)=0, то g (х, у)—х -> у. Очевидно,
что |х@ у]Эх и [х-»у]Эх.
1.20. Так как множество Р2 — счетно-бесконечное, то мно-
жество всех его конечных подмножеств тоже счетно-бесконечное.
Поэтому мощность всех замкнутых классов в Р2, имеющих ко-
нечные полные системы, не более чем счетная.
1.21. Если замкнутый класс в Р2 отличен от множеств {0},
{1}, {0, 1}, то он содержит тождественную функцию (см задачу
1.18); следовательно, его нельзя расширить до базиса.
1.22. Пусть tF — полная система в М. Возьмем в произ-
вольную функцию f2. Она не принадлежит каким-то предполным
в М классам Klt. . ., Кг. Затем выберем в функцию f2, не
принадлежащую хотя бы одному из оставшихся предполных
296
классов, и т. д. Число функций в получающейся при такой
процессе системе «У' не больше числа предполных классов в М.
Система полна в Af, так как в противном случае она бы рас-
ширялась до какого-нибудь предполного класса, а по построе-
нию система <£“' целиком не содержится ни в одном из предпол-
ных в М классов. Если <£• — базис, то при построении со-
ответствующей системы а?1' должны быть использованы вен
функции из <У, иначе бы мы пришли к противоречию с непри-
водимостью системы «5°.
1.23. Доказательство можно провести индукцией по числу
вхождений связки -> в формулы, реализующие функции из
замкнутого класса [я -> у]. Если в формуле одно вхождение
связки -> , то формула (о точностью до обозначения переменных)
имеет один из следующих видов: х -> а: и я -» у. В этом случае
утверждение очевидно. Далее, если 21=Л -*• f2, то нужно рас-
смотреть две возможности.
(а) Формула, соответствующая функции уа, имеет хотя бы
одно вхождение связки Тогда f2=yj\/<f2 (ут) и <21=/1\//2=
=»/V (/iVTs)-
(б) Формула, отвечающая функции /а, представляет собой
переменную (скажем, у}. Тогда
1.24. Применим индукцию по числу вхождений связки ->.
Если связка -> входит один раз, то имеем х->у, и утвержде-
ние очевидно. Пусть 21 = 71 (2я) ->>7а (хп) и функция /, отвечаю-
щая формуле 21, существенно зависит не менее чем от двух
переменных. Если 7а удовлетворяет условию задачи, то [ N | >
>2Н-1 и | ZVy| > | TVyJ >2”~1. Пусть'теперь /а зависит суще-
ственно от одной переменной. [Предположим, для определен-
ности, что f2 = x1 (f2 не может быть равно отрицанию пере-
менной, так как х (f При таком предположении
Очевидно, что /(1, х2, ..., «„) = !. Если бы
7(0, х2, . . ., а:в)=0, то / (х1( х2, . . ., х„) = xlt а это противо-
речит тому, что функция / (2я) существенно зависит не менее
чем от двух переменных. Следовательно, 7(0, х2, .... х„) =& О
и | Nj | > 2я*1. Наконец, если функция }2 зависит от всех
переменных xlt ..., хп несущественно, то Уа=1, но тогда
7 = 1, т. е. тоже зависит несущественно от всех переменных
Х1.....хп-
1.25. Пусть К — какой-либо предполный класс в Р2. Пред-
положим, что х £ К. В силу задачи 1.16 добавление к классу К
функции х не приводит к полной системе в Ра (ибо [К(J {я}] =
= йГи{х} J х|у). Это противоречит предполноте класса К.
297
§2
2.1. 2) Нет. 5) Да. 2.3. 1) xz\/yt. 3) ху © у © 1.
2.4. Применить индукцию по числу вхождений связок из
'множества {0, 1, 1, V) в формулу 21.
2.6. Пусть i = l, т. е. функция / (хя) существенно зависит
от переменной х,. Тогда найдутся наборы 5= (О, а2, ..., а„)
и i' = (l, а2, .... ая) такие, что /(а)^/(а'). Так как
/*(1, а2, ..., ая) = /(0, а2...а„) и /*(0, а.......а„) =
= 7 (1> а2, . .., яя), то f* (1, а2, .. ая) j* (0, а2, ..., ая),
т. е. Xj — существенная переменная функции /* (£”).
2.8. 1) 0. 2) 0. 3) 1. 2.9. 1) Да. 4) Нет. 5) Да. 2.10. Исполь-
зовать разложение: f(xn] — xj(0, х2, . . ., x„)Vxi/(l> xz> • • хп)-
2.11. Если / (хп) — самодвойственная функция, то на лю-
бых двух противоположных наборах значений переменных она
принимает противоположные значения. Следовательно, число
наборов, на которых самодвойственная функция / (ха) принимает
значение 1, равно числу пар противоположных наборов (длины
п), т. е. |Л'у|=2в*1.
2.13. 2 (-I)1'Q22'‘—’, п > 1.
♦=о
2.14. x©y©z, x©p@z©l, тп. (х, у, г), т (х, у, г)©1,
т(х, у, z)@x®y, т (х, у, z)©x©j/©1, т (х, у, z)@x@z,
т (х, у, z) © х© z © 1, т (х, у, z)®y ©z, m (х, у, z) © у ©
©z©l. Легко проверяется, что т (х, у, г) = т (х, у, г)@х©р,
т (х, у, 1)=т (х, у, z) © у © z © 1, т (£, у, г)=т (х, у, z)©l.
2.15. 1) При п = 3. 2) При л = 4т-|-3, т = 0, 1, 2, .. .
3) Ни при каком п > 2 функция не является самодвойствен-
ной, ибо / (б) =/(!). 4) При нечетных п > 3.
2.16. Только при нечетных п.
2-17. 3) g{yi} — y1®y2@y3®yi®yt^S, т(хъ х3, f)£S
и т (х2, xs, если f(*S. Подставляя в g (у*) вместо у2
функцию т (хп х3, /) = © х3/© ххх3, вместо у2 функцию
т(х2, х3, /) = х2/©х3/©х2х3, вместо переменной у3 перемен-
ную х2 и вместо у3 и у3 соответственно переменные х3 и х3,
получаем xj © x3f © x^ @ x2f © x3f © x2x3 © x2 © x3 © xs =
= xlf © «1X3 © x2f © x2x3 © x* © x5.
2.18. 1) Имеем } (xn) f* (xn) = f (xlt . . ., x„) • f(£lt .. ., £n)=
= const. Эта константа не может быть 0, так как в противном
случае должно выполняться соотношение / (хя) = 1. Поэтому
/ (Xj, . . ., х„) • / (xlt .... хя) = 0. Исходя из равенства 12Vy | =
= [ .ZVy» |, заключаем, что у каждой из функций / (хя), /* (£")
298
и/'(£”)=/(£j......£„) число нулей равно числу единиц,
т. е. |7Vy| = |2V^.| = | Nj,, | = 2Я-1. Следовательно, в силу
соотношения / • f = 0, / (ая) = 0 тогда и только тогда, когда
/' (5я) = 1. Значит, / (хя) = f (хя).
2.19. 3) (xjx)->(x©£) = l.
2.20. Пусть / (2я) — несамодвойственная функция и все ее
п переменных (п > 3) — существенные. Из несамодвойствен-
ности / следует, что существуют два противоположных набора
а=(а1 ая) и а' = (а,, ..., ак), на которых функция /
принимает одинаковые значения. Сначала предположим, что
/ (0я) / (Iя), а следовательно, 5^0” и 5 =/= Iя. Рассмотрим
функцию g (х, у), которая получается из / (2я) в результате
замены на х всякой переменной х( такой, что а( = 0, и замены
на у каждой из оставшихся переменных. Имеем g (0, 0)
^g(l, 1) и g(0, l) = g(l, 0). Очевидно, что g (х, у) { S.
Пусть теперь /(0я) =/(!”). Так как / (хя) ф const (ибо зависит
существенно не менее чем от трех переменных), то найдется
набор р=({Зх, ..., ря) такой, что / (р) ^/(0”). Исходя из на-
бора р, строим функцию Л(х, у)-. если ^ = 0, то заменяем
в f (хя) переменную xt на х, если же Э» = 1, то заменяем х{
на у. Функция h (х, у) удовлетворяет следующим соотноше-
ниям: h (О, 0)=А(1, 1) h (0, 1). Очевидно, что Л (х, у) суще-
ственно зависит от двух переменных и несамодвойственна.
2.21. См. предыдущую задачу.
2.22. Нетрудно показать (см. задачу 2.14), что т (х*, х\
rT) = хт<а, 0, Р. Если т (a, р, y)=0, то т (х“, хР, хТ) = £. Сле-
довательно, подставляя в т (х“, у\ zT) вместо х, у и z эту же
функцию т (хя, у\ zt), получим либо т (х, у, z), либо одну
из функций т (х, у, z) © х © у, т (х, у, z) © х © z, т (х, у, z) ф
© у © z. Если имеем одну из трех последних функций, то легко
строим функцию т (х, у, z). Например, т (х, у, т(х,у, z) ф
@ х © у) © х © у = т (х, у, z). Теперь покажем, что из функ-
ции т (х, у, z) можно получить функцию, существенно зави-
сящую от п (> 4) переменных. Если п — нечетное и п > 5, то
имеем g6 (х») =т (хъ х2, т (х3, х4, х6)).... gil+1 (xa,+1) =
= гг, .... xM_2I т (x2Z_j, х2/, ха;+1)), ... Легко дока-
зать (индукцией по Г), что каждая из этих функций существенно
зависит от всех своих аргументов. Для четного п=21 > 4 со-
ответствующая функция получается, например, из функции
g2i+1, если положить х2/_1=х2. При доказательстве существенной
зависимости функций g„ (хя) от всех входящих в них аргументов
полезно иметь в виду, что медиана т (х, у, z) равна 1 только на
тех наборах, которые содержат не менее двух единиц.
299
2.24. Надо взять произвольный набор (04, а„. . ., ая) зна-
чений переменных х1г z21. . х„ и сравнить на этом наборе зна-
чение левой и правой частей данного в условии задачи соотноше-
ния. Полезно различать два случая : (1) среди значений ах, а2
и а3 не менее двух нулей, (2) среди а15 а„ и а3 имеются по крайней
мере две единицы.
2.25. 1) В решении задачи 2.22 было показано, как ив
т (х, у, z) или из т (х, у, z) строится медиана т (z, у, z).
Далее, т (z, z, х)~т (z, z, z) = z, и поэтому (см. задачу 2.23,
1)) из т (z, у, z) (или из т (х, у, 2)) можно построить функцию
х © у © z. Одноместные самодвойственные функции (z и х),
очевидно, содержатся в [т (z, у, г)] (и в [m (z, у, z)|). Как
следует иг задачи 2.12, не существует самодвойственных функ-
ций, существенно зависящих от двух переменных. Наконец,
используя предыдущую задачу, заключаем, что для построе-
ния любой самодвойственной функции от га > 3 переменных
достаточно иметь все самодвойственные функции от п — 1 пере-
менных (а также функции т (z, у, z) и x@y@z, если га = 3).
Если п = 3, то можно воспользоваться тем результатом, кото-
рый сформулирован в задаче 2.14. (Замечание. Задачу 2.14
можно решить, используя результат задачи 2.24 и функции Л,
z©y©z и m(z, у, г).) 2) Пусть / (z”) — произвольная само-
двойственная функция и все ее переменные — существенные
(п > 3). Покажем, что если га >4 и / (zn) не является линей-
ной функцией (т. е. не представима в виде xi @ z2 © ...
... ©£„©=. где в 6 {0, 1}), то из f (х”) с помощью операции
отождествления переменных можно получить нелинейную само-
двойственную функцию, существенно зависящую от трех пере-
менных, (Если f — линейная самодвойственная функция, то
для нее аналогичное утверждение—очевидно.) Итак, пусть
/(5я) — нелинейная функция, существенно зависящая от га > 4
переменных. Из нелинейности функции / следует, что в поли-
номе Жегалкина, представляющем эту функцию, найдется
хотя бы один нелинейный член. Пусть, для определенности,
в этот нелинейный член входит переменная zp Тогда / =
= z,^1 (z3, ..., х„) © (Zg, ..., х„) и <pi ф const. Возьмем набор
(а2......ак), на котором обращается в 0. Имеем / (0, а3, ...
а„)=/(1, аг,...,а„). Рассмотрим два случая. Сначала
предположим, что а2 = ... = ая=1. Так как хг — существен-
ная переменная функции f, то найдутся два набора j и со-
седних по первой компоненте и таких, что / (р) / (?)• О40*
видно, что оба эти набора отличны от наборов 1 и (0, 1.1).
300
Заменим те переменные xit которым в наборах р И д отвечают
нули, на переменную у, а все остальные переменные, кроме
Xj, —на г. Получим функцию g (хг, у, z), удовлетворяющую
соотношениям: g (0, 0, 1) =а, g(l, 0, 1) = з и, в силу само-
двойственности функции g, g (1, 1, 0) = 8и g (О, 1, 0)=з. Если
g (1, 1, 1) =а (ag(O, 1, 1)=а), то g (xit у, у, z) ©о;
если же g(l, 1, l) = 8 = g(0, 1, 1), то g (zj, у, z) = m(x1,
у, z) © а. Рассмотрим теперь случай, когда не все а2, ..., ая
равны 1. При этом, в силу самодвойственности функции /, не
все а( равны 0. Возьмем наборы i и 5=(0, 1, ..., 1). Если
/(!)=/(§), то упомянутые выше наборы р и у отличны и от §,
и от I, и все сводится к первому случаю. Если же /(!)¥=/ (§),
то отождествление переменных в функции / (хп) производим,
исходя из наборов (0, а...ая) и (1, я3,ая). Получаем не-
которую самодвойственную функцию h (хи у, z), удовлетво-
ряющую соотношениям h (I) = а, Л (0, 1, 1) = а, Л (0, 0, 1) =
= Л(1, 0, 1). Если Л (0, 0, 1) = а, то A(zj, у, z) = m(z1, у,
г) © 3; если же h (0, 0, 1) = з, то Л (zlt у, z)—m (xlt у, z) © а.
Так как из линейной функции с помощью операции супер-
позиции можно получить лишь линейные функции, то любая
полная система & в S должна содержать нелинейную само-
двойственную функцию /(хя), из которой, как мы показали,
строится функция вида т(х*, у&, zl}, где а, 3 и д принадлежат
множеству {0, 1}. Если j (х, х..х)=х, то (/(хя)| содержит
т (х, у, z) (см. задачу 2.14), а поэтому [/ (хя)| = S (см. пре-
дыдущую задачу). Пусть теперь f(x, х, ..., х)—х, т. е. / со-
храняет 0 (и 1). Тогда в должна найтись функция Д (хт),
не сохраняющая 0. Если Д — нелинейная функция, то [Д] = S.
Если же Д — линейная функция, то [/, Д] = S и {/, Д} — базис
в S (функция / порождает только функции, сохраняющие О,
а Д — только линейные функции).
2.26. 1) Нельзя, так как f£S, agftS, 2) Можно.
2.27. Наибольшее п равно 4.
2.28. Таких функций две: хг © х2 © х3 © xt © а, где ag
€{0, 1}.
2.29. 1) Нет. 2) Да. 3) Нет. 4) Да.
§ 3
3.2. Пусть / (хя) принимает противоположные значения на
любых двух соседних наборах. Пусть / (б) — о, тогда / (а) = з,
если число || а || нечетно, / (а) = а, если Ц а || четно. Пусть
Ах (г") = *1 ® *»©•••© хя© а- Тогда К;=1У1я. В силу
301
единственности представления функций полиномами / = /,
и, следовательно, f^L. Обратное неверно. См., например,
/(£’) = х1©х3.
3.6. 2". Решение. Пусть f (2я) = ... @ сЛ © ся+1.
В силу /GS имеем с, (гг © 1) © ... © ся(хя© 1) © ся+1 © 1 ==
п
— fix”). Отсюда S с( = 1, т. е. число коэффициентов c<t
________ >=1
i = l, п, равных единице, нечетно. Число векторов (q..., ся)
нечетного веса в В” равно 2я-1. Коэффициент ся+1 можно вы-
брать произвольно. Отсюда и вытекает утверждение.
3.10. Если /(хя)^Ь и У (хя) существенно зависит от всех
своих переменных, то / (хя) = хг @ ... © хя© а, где а £ (0, 1}.
Отсюда легко вытекает необходимость утверждения. Доста-
точность. Пусть f^L. Тогда существуют два соседних на-
бора аир таких, что / (S) = / (^) (см. 3.2). Пусть i — номер
координаты, в которой аир различаются. Тогда / (а,, . . .
.... a(_i, х(, а,+1.а„) фиктивно зависит от xt.
3.11. Пусть Р (хп)— полином степени к > 3. Без ограни-
чения общности можно считать, что э. к. А=сх1хг ... хк яв-
ляется слагаемым полинома Р. Полагая хк = xfc+1 = .., = х„,
нолучим полином Q, в котором А — единственная э. к. ранга к.
Возможны несколько случаев, а) Все э. к. ранга к — 1 над
множеством Хк входят в полином Q. Положим xfc_)=xA..
б) Существуют такие i, У (1 < < к), что э. к. X] ...
... х^гх^+, ... хк и хг ... х^х^ ... хк отсутствуют в Q. Тогда
полагаем х, = х^. в) Число слагаемых ранга к — 1 равно к — 1.
Пусть в Q отсутствует э. к. xL... хк_г. Тогда отождествим
переменные хг и хк. Во всех случаях получаем полином сте-
пени к — 1.
3.12. Рассмотрим полином Р, реализующий функцию /,
Если степень полинома Р больше 2. то с помощью отождествле-
ния переменных из него можно получить полином Q степени 2
(см. 3.11). Без ограничения общности можно считать, что х^.
входит в Q. Отождествив все переменные, отличные от т, и х„.
получим нелинейную функцию трех переменных.
3.13. Из 3.12 вытекает, что, отождествив некоторые перемен-
ные функции /, можно получить функцию трех переменных,
реализуемую полиномом второй степени. Нужно лишь показать,
что если в этом полиноме ровно два слагаемых второй степени
то отождествлением переменных можно уменьшить это число на
единицу. Если, например, в Р входят и хгх^, но не входит
х2х3, то положим Ху=хя.
302
3.14. Если f(3”)QL, то существуют t, / такие, что / (хя) =
= XfXjPi © xtP2 © XjP3 © Pt, где P, — функции, не завися-
щие от х( и Xj-, и 7*1 г£ 0. Положим, что 1 = 1, / = 2.
Пусть а=(аа.....а„) — набор значений переменных х3.........хп
такой, что Р1(а) = 1. Тогда «р (хь х2) =f(x1, х2, а3, .... а„) =
= х1х2©1(х1, х2), где I (хг, х2)— некоторая линейная функ-
ция. Функция <р (£j, х2) обращается в единицу на нечетном
числе наборов. Отсюда вытекает, что грань 31 •;*’" яв-
ляется искомой.
3.18. Пусть ] £ L. Если образует базис > L, то / (0) 0
и / (1) Ф 1, следовательно, / существенно зависит от нечетного
числа переменных. Но тогда она самодвойственна и не может
образовывать базис в L.
3.19. Если Ф — полная в L система функций, то в Ф суще-
ствует ф S, т. е. функция, существенно зависящая от четного
числа переменных. Тогда из нее можно получить константу.
Пусть эта константа есть а. В Ф должна быть также функция
/2 (f То. Подставляя константу о на места переменных функции
/2, получим а. В Ф имеется также функция /3, существенно за-
висящая более чем от одной переменной. Легко видеть, что
[0, 1, /з]=Ь. Таким образом, из всякой полной в L системы всегда
можно выделить полную подсистему, состоящую из трех функций
Отсюда и вытекает утверждение.
3.20. Имеются три класса {0}, {1} и {0, 1}, состоящих
только из констант, два класса {х} и {х, х}, состоящих из функ-
ций, существенно зависящих ровно от одной переменной, че-
тыре класса, состоящих из функций не более чем одной перемен-
ной и содержащих константы и функции, отличные от констант:
[0, х], [1, х], [0, 1, х], [0, 1, х, х]. Если класс линейных функ-
ций содержит функцию, существенно зависящую более чем от
одной переменной, то либо он содержит функцию четного числа
переменных, либо не содержит, либо содержит функцию, не со-
храняющую 0, либо нет. Отсюда вытекает, что классы [х © у ©
Z © 1], [ж © у © z], [х © у], [х © у © 1], L и только они яв-
ляются замкнутыми классами линейных функций, содержащих
функцию, существенно зависящую более чем от одной пере-
менной.
3.22. Указание. Если / (х3) удовлетворяет условию и
не является самодвойственной, то для всякого а £ В3 / (а)=
=/ (3), следовательно, / можно задать полностью, задав ее значе-
ния на наборах вида (ai,a2, 0). Из условия 1), кроме того, выте-
кает, что функция обращается в единицу ровно на двух
303
наборах такого вида. Таким образом, существует яе более
шести несамодвойственных функций, удовлетворяющих усло-
виям 1) и 2). Легко’проверить, что все они линейны.
3.25. При п =/= 2 таких функций не существует. Все функции
вида xtx2 © <zx1 © рх2 © у (а, 0, у f {0, 1 }) и только они удов-
летворяют условиям 1) и 2).
3.26. Две при нечетном п, 0 цри четном. 3.27. Пятью спо-
собами. 3.28. / (а1(. . а„)=1. 3.29. При нечетном п.
3.30. См. 3.14. 3.31, См. 3.13. 3.32. ху, х\/у, xfy, хфу.
3.33. У Казани е. Хотя бы одна из функций /1( /2, /3 не
является линейной.
§ 4
4.2. 2) При четных п. 4) При п =£ ik— 1, fc = l, 2,...
4.3. 1) При всех га > 2. 3) При га = 3к, к = 1, 2, ... 4.4. 7 спо-
собов. 4.5. 2) 3.22”-2; 5) 3 • 2я’1; 8) (22” — 22"“')/2; 12)0;
15) 22" *. 4.7. 1) Нельзя, так как xQpfT’i, а x-^yf~T1.
4.8. 1) Если /f Тд, то ее полином не содержит 1 в каче-
стве слагаемого. Поэтому / можно выразить через \ху и х © у.
Равенство Тд = \х \/ у, л:@у| вытекает из предыдущего и из
того, что х \/ у = ху © х © у,
4.9. Пусть Ф — базис в То. Тогда существует
Отождествляя все ее переменные, получим константу 0. В Ф
существует также функция /2, не являющаяся монотонной.
Функция /, является, очевидно, и нелинейной. С помощью
отождествления переменных и подстановки 0 из /2 можно по-
лучить функцию у] (х, у) вида ху@ах@ту, а, rf{0, 1}
(см. 3.13). Поскольку /2 не является монотонной, то суще-
ствуют наборы i и j такие, что 5 < 0 и / (5) > /(0). Пусть А
(соответственно В) — множество координат набора 5 (0), кото-
рые равны единице. Рассмотрим функцию у2 (х, у, г), полу-
чаемую из /2, если положить в ней х( — х при if* А, х< = у
при if В, х( = z при if В. Имеем у2 (0- 0, 0)=у2(1, 1, 0)=0,
у2 (1, 0, 0)=1. Если при этом у2— самодвойственная функ-
ция, то либо y2 = x@y©z, либо у2 = ху \/ XZ \/ yz. В обоих
.случаях имеем [0, уп у2] = Т'о. Если у2 не является самодвой-
ственной, то рассмотрим функцию у3 (г, у) = у2 (х, у, 0). Имеем
либо Уз = х © у, либо у3 = ху. Если уз = х © у, то [у], у2| = То.
В случае, когда y3 = zy, а у] =£х\/у, все полученные функ-
ции 0, уп у3 принадлежат одному замкнутому классу, а именно,
классу С, состоящему из всех функций / таких, что для лю-
бых двух наборов 5 — (а,......ая), и ₽== (3,....3„) таких, что
304
/(а)=/(р), существует i, для которого а( = ^ = 1. В силу
полноты Ф в То существует функция /3, не принадлежащая
классу G. Функция /3 обладает тем свойством, что существуют
наборы аир такие, что / (5) —/(р), и в а и р нет общих еди-
ничных координат. Пусть А (В) — множество единичных коор-
динат набора а (соответственно, р). Пусть <р4 (х, у) — функция,
получающаяся из /3 подстановкой х вместо х( при igA,
у вместо х(, если i£B, 0 вместо х{ при igA |JB. Тогда есть
либо х\/ у, либо х © у. В обоих случаях имеем [ху, = То.
Таким образом, из полноты системы Ф в То вытекает, что
в ней существует подсистема, содержащая не более трех функ-
ций. Отсюда и вытекает утверждение.
4.11. Аналогично предыдущей задаче. Использовать то, что
в полной системе существуют немонотонная функция и одна
из функцийa g (0, 1), не принадлежащих соответственно
классам G,, состоящим из всех функций / таких, что для лю-
бых двух наборов аир таких, что / (а) = / (р)=а, существует
такое I, что i-e координаты наборов аир равны а. Примером
базиса из одной функции является множество {ху © z © и}.
4.12. Указание. Рассмотреть функцию xy@y@z.
4.13. 3) Проведем доказательство полноты системы Ф =
= {ху V xz V У2, х @ У ®2} В То П s по индукции. Функции
из Т0П5, зависящие не более чем от двух переменных, полу-
чаются путем отождествления переменных у функций из Ф.
Пусть все функции из То|~] 5, зависящие менее чем от п (п > 3)
переменных, являются суперпозициями функций из Ф. Пусть
f{xn) gTofl S- Тогда / (хп xlt x3, xit .... x„), /(x3, x2, x3, x4, ...
.... x„), /(xx, x2, x2, x4, ..., x„) зависят менее чем от п пере-
менных. Воспользуемся теперь результатом задачи 2.24.
4.13. /(1, 1, 1) =0, ибо /(1, 0, 1)=0, поскольку
/gM, /(1, 0, 1) =/(0, 1, 0)=0, поскольку /gS.
4.14. Если / gL, то существует А > 1 такое, что / конгру-
ентна xj © х2 © ... © x2ft+1 © 1. Если / g L, то с помощью ото-
ждествления переменных можно получить либо функцию <р
вида Xi/© в (х © р) © 1, о g {0, 1}, либо ху © xz © yz © 1.
В обоих случаях L П S С [?].
4.18. Покажем, например, что ТдПЬ является предполным
в То классом. Пусть f^T0\L. Отождествляя переменные из /,
можно получить функцию <₽, либо имеющую вид ху@1 (х, у),
либо имеющую вид ху © xz © yz @ I (х, у, г). В обоих случаях
система {х © у, полна в То, т. е. [(То Г)Ь) U {/}] = То.
4.19. Указание, ху © zgT0\(7’1 (JL U s) и {1 > ХУ®2} —
полная в Рг система.
11 Г. П, Гаврилов, А. А, Сапоженко
305
4.21. Xj @ x2 (+) z4. 4.22. Указание. См. 3.20.
4.23. Докажем, что если / (£ (То П Тх) (J 5, то из нее можно
получить константу. Если f£T0\T1 или j£Ti\T0, то, ото-
ждествляя все переменные у функции /, получим константу.
Пусть /(Е^оиЛ- Так как f$S, то / зависит существенно
более чем от одной переменной и можно так отождествить
переменные, что получится функция, существенно зависящая
от двух переменных, именно одна из функций iy или £\/у.
В обоих случаях можно получить константу.
§ 5
5.2. 1) п=2, 3. 2) При четных п. 3) При нечетных га.
5.4. Воспользоваться разложением из 5.3.
5.5. Две функции, среди которых одна имеет фиктивную
переменную.
5.8. 1) Неверно. Рассмотреть / (а!3) = х3 и наборы (110),
(001).
5.12. £, п функций.
5.14. Предположим, что простой импликант I функции
/ (ж") содержит отрицание переменной. Пусть, например, I—
где 1> — некоторая э. к. Рассмотрим {a: L (5)=!}
и произвольный набор 0, с^,. . ., ап из NL. В силу монотонности
/ (1, ах,. . ., а„)=1. Отсюда вытекает, что xL, а следовательно,
и L являются импликантами функции /. Это противоречит тому,
что I — простой импликант.
5.16. При к == М -ф 2 % < I < ~4~^) и ПРИ А = 41 + 1
(^<is^).
5.18. 1) Существует. 2) Не существует. Указание.
Сокращенная д. н. ф. функции / имеет длину три. Формула
®*, двойственная к &>, есть сокращенная к. н. ф. функции /♦.
Сокращенная д. н. ф. функции / получается из раскрытием
скобок и применением правил АА=А, А \/ А=А, А V АВ=А.
Рассмотреть все случаи, когда сокращенная д. н. ф. функции
/♦ имеет длину 3.
5.19. 1) Все нижние единицы монотонной функции попарно
несравнимы. Максимальное число попарно несравнимых набо-
ров в В” равно (ом- 1-15).
5.21. Все функции /(£*) такие, что f(a) = l при || а || > га/2,
/(а)=0 при ||SJ< [(га — 1)/2], являются монотонными.
306
5.22. 1) 2; 3) п 4- 2; 5) 2Я+1 — 2п — 2.
5.23. 1) Пусть / (2”) С Л/П $. Рассмотрим разложение
f — £„fo\/Поскольку f самодвойственна, то (/?)* =/g.
В силу монотонности / имеем f”£M, f$\/ = Таким
образом, если задана функция /J из М, то функция / также
задана. Остается лишь убедиться в том, что при n > 1 суще-
ствует функция такая, что f\/f=£t. Можно взять,
например, функцию f(xlt х2, .... V!) = 0. 3) Пусть /(£")£ Л/.
Если задана компонента /Ь2, то / определена по монотонности
по меньшей мере еще на 2п~2 наборах: если (я3, ..ая) — не-
который набор и /Jo2(l, 0, as, .... а„)=0, то /(0, 0, а3
..., я„) = 0, если же /fo2 (1, 0, а3, ..., ая) == 1, то / (1, 1, а3, . . .
..., ак) = 1. Таким образом, чтобы задать достаточно
задать компоненты /}j2, /Jj 2 и доопределить функцию по моно-
тонности, тогда / останется неопределенной не более чем на
2я-2 наборах.
5.25. ш0(1) = 1, т0(2) = 2, те (3) = 12, те (4) = 126.
5.26. Имеем | Л/11 = 186 (см. 5.24). | S* | = 256. Далее утвер-
ждение доказывается по индукции с учетом того, что | 8я | =
= | 8я-112, | Мп | < | М”'112. 5.27. Четыре.
5.28. Пусть Для каждой возрастающей цепи
Z (• Вп либо /(й)=0 для всех a f В", либо существует набор
flfcZ такой, что /(Р)==1 и /(5)=0 при a£Z, а < ji. Пусть за-
/ га \
\|га/2]/ возрастающих
дано разбиение В” на
цепей. Тогда для
задания функции / (2я) f М достаточно для каждой цепи из
разбиения указать, есть ли в ней вершина а такая, что
/(а) = 1, и если есть, то задать ту ее вершину ji, для которой
f (р) — 1 и / (5) = 0 для всех i f Z таких, что а < ₽. Поскольку
длина каждой возрастающей цепи не превосходит «4-1.
имеется не более га 4- 2 возможностей для каждой цепи.
5.29. Рассмотрим разбиение куба Вя на непересекающиеся
возрастающие цепи, указанное в решении задачи I. 1.18. Это раз-
биение обладает следующими свойствами. 1°) Цепи наименьшей
длины имеют не более двух вершин. 2°) Для каждой двумерной
грани, содержащей три вершины цепи, имеющей fc-j-2 вершин,
четвертая вершина грани содержится в цепи разбиения, имею-
щей к вершин. Из 1°) вытекает, что на каждой цепи минимальной
длины монотонная функция может быть задана не более чем
тремя способами. Из 2°) вытекает, что если монотонная (частич-
ная) функция определена на всех цепях, имеющих к единиц,
то на каждой цепи длины к-f-2 эта функция определена по мо-
11*
307
нотонности везде, кроме, может быть, двух вершин. Следова-
тельно, имеется не более трех способов доопределить ее на каж-
дой такой цепи. Учитывая, что число цепей равно
имеем | Мп | < s'-W2!/.
5.32. (хг V Ж2) (х3 \/ х4,) • • • (х2п-1 V х2п)‘
5.33, Всякая функция, существенно зависящая не более
чем от одной переменной, имеет не более одной нижней единицы.
5.34. Указание. См. решение задачи 1.1.36, 4).
5.39. 1) Нельзя. 2) Нельзя. 3) Можно.
5.40. Утверждение о том, что всякая функция / (Ж”) £ М
представима с помощью суперпозиций над функциями множества
{О, 1, ху, х\/ у}, можно доказать индукцией по п, используя
5.3. Далее утверждение вытекает из того, что {1, ху, х \/ у} С
CZ 7\, {0, ху, х V у} С То, и из того, что из множества {0, 1, х V
V У} нельзя получить функцию ху, а из {0, 1, ху} нельзя полу-
чить функцию х V у. 5.44. Нельзя. 5.45. Нельзя.
5.48. Всякий базис в М содержит константы, а также функ-
цию, существенно зависящую не менее чем от двух переменных.
С другой стороны, пусть Ф — базис в М, содержащий более
четырех функций. Тогда по меньшей мере три из них зависят
более чем от одной переменной. Среди этих функций найдется
функция /15 которая не является элементарной конъюнкцией.
Тогда с помощью подстановки констант получим x\J у. Имеет-
ся также /2, не являющаяся элементарной дизъюнкцией, из
нее получим ху. Тогда {0, 1, Д, /2} — подсистема, полная в М.
5.49. См. 5.48. 5.50. 2) {1, ху \/>}. 5.51. См. 2.24.
5.53. Покажем, например, что МП То является предпол-
ным. Единственная функция есть константа 1.
В М П Та имеются функции 0, ху, х\/ у, которые вместе с 1
составляют полную в М систему. Пусть существует еще один
замкнутый класс Q, не содержащийся ни в одном из перечи-
сленных в условии. Тогда существуют Л(£МГ|Т0, /г^^ПЛ.
/з€®и {0, 1}, 1}. Тогда Л = 1, /2 ==0, из /3 с по-
мощью подстановки констант и отождествления получаем ху,
а из /4- функцию х V У-
§ 6
6.1. Предположить противное и воспользоваться критерием
полноты.
6.2, 4) Полна. 6) Не полна. 7) Полна. 8) Не полна.
308
6.3. Показать, что / g Тв (J 7\ (J L (J М,
6.4. 1) Может быть и неполной, например, Д (2“) =
— m (х1( хг, х3) © Xj © ха, f2 (£*) = (xj -w xa) \/ x„ и полной,
например, Д (£’) =т(хн ха, ха), Д (£*) = хг V xzxz- 2) Полна.
3) Не полна.
6.5. Полна. Покажите, что Д g Тг U^U & UЛ/ и Д g Го.
6.6. 1) {xy@z, (x©y)~z), {(x\/y)(*V?)> (*©?) — *»
m(x, у, z)J. 3)'{0, (x|(xy))->2}, {x©y, (x | (xp))-»Z}, {(x->
6.7. {x|y}, {x|p}, {x©pz@z@l}; {«, xy}, {X, x\/y},
{«, x-*p); {1, x@y, xy}, {1, x@y, x\/y}, {0, 1, x@y@yz};
{0, 1, x@y®z, xy}, {0, 1, X © у © z, x\/y}, {0, 1, X@y@z,
m(x, y, z)}.
6.8. Таких базисов 7: два из них содержат по одной функции,
три содержат по две функции и еще два базиса, содержащие по
три функции, можно выделить из полной системы {ху, х\/ у,
х@у, х~у).
6.9. 1)—3) Можно. 4) Нельзя.
6.10. Не существует. Пусть Д ф 1. Тогда Д g М и либо
Д g Гь либо'Д S. В первом случае можно «удалить» функцию
Д, а во втором — функцию Д. Аналогично исследуется воз-
можность, связанная с соотношением Д ф 0. Предположим
теперь, что Д = 1 и Д = 0. Если Д g М, то система (Д, Д, Д} —
полная. Пусть Д g М\ тогда функция Д должна не принадле-
жать классу М. Если Д g L, то система {Д, Д, Д) — полная.
Осталось рассмотреть случай, когда Д g L\M. Так как Д g
g S U М и Д g L, то Д зависит существенно от четного числа пе-
ременных (и отлична от констант 0 и 1). Следовательно, либо
fi 5 ^1, либо Д g То. Поэтому обязательно будет полной одна
из систем {Д, Д, Д) или {Д, Д, Д}.
6.11. 1) Ра. 2) Л7\(Тои£) = 0. 3) Л/\(ГоПЛ) = {0, 1}.
4) ЛГОТоПЛ. 5) Т0П£. 6) S. 7) £П$. 8) Та. 9) Г0Л7\.
6.12.1) К^К3. 2) К,^К2. 3) К^К3. i) К^К2.
5) К, = К2. 6) К2
6.13. 2) 56.
6.14. 1) Если /(£ T’oUT'iUS, то const и / (б) = 1,
а /(1)=0. Значит, /$ М. Если бы f^L, то, в силу соотно-
шения /g T0U Tj, функция / должна была бы зависеть су-
щественно от нечетного числа переменных (и иметь свободный
член, равный 1). Однако тогда f^S. 2) Число функций Шеф-
фера в множестве Р2 (Хп) равно разности между числом всех
функций / (хя), удовлетворяющих условию: j (б) = 1 и f (I) =0,
и числом самодвойственных функций, подчиняющихся тому же
809
условию. Таким образом, в Р2 (Xя) содержится З2”-2— 22"-1-1
функций Шеффера (га > 2).
6.15. Пусть /(г")— функция Шеффера (здесь га>3 и все
переменные — существенные). Так как f(xn)$S, то найдутся
два противоположных набора 4 = (а,..а„) и а'= (5], ..., ая),
на которых функция / принимает одинаковые значения: f (3) =
= /(i') = a. Очевидно, что а б и ? =£ I (ибо /(б) = 1 и
/(1) = 0). Заменим те переменные г<1 которым отвечают в на-
боре а нулевые компоненты, на х, а остальные переменные за-
меним па у. Получим функцию g (х, у), удовлетворяющую со-
отношениям g (0, 0)=1. g (1, 1)=0, g (0, l)=g (1, 0)=<з. Если
о=0, то g (х, у)=х^у, а если в=1, то g (х, у)=х\у.
6.16. 1) При га=4т-|-2, /га=0, 1, 2,. . . 2)—5) Ни цри ка-
ких п. 6) При всех п > 2.
6.18. Функции, обладающие указанными в условии задачи
свойствами, зависят существенно не менее чем от трех пере-
менных.
6.21. См. решение задачи 2.25, 2).
6.23. ху. Из нее нельзя получить, например, функцию
г \/ у. Вообще, в классе [гр] нет функций, принимающих зна-
чение 1 более чем на половине наборов значений переменных.
6.24. Функции, удовлетворяющие указанному в условии
задачи требованию, зависят существенно не менее чем от четырех
переменных. Пример такой функции: гх © х2 © г2г3 © г3г4.
6.25. Доказательство можно провести индукцией по га.
Базис индукции: п=4 (см. задачу 3.12). Индуктивный шаг.
Предположим, что утверждение справедливо для ra=s > 4, и
докажем его для ra=s-)-l. Пусть функция (ж*+1) существенно за-
висит от всех своих аргументов и не принадлежит классу Б.
ПредставимJфункцию / в следующем^виде: g (г*) © x,+1h (Z*).
Так как г,+1 — существенная переменная функции /, то h (г1) ф
ф 0. Рассмотрим несколько возможностей, (а) В функции g
фиктивной переменной является некоторая переменная г4,
а в функции^ — переменная xj (г ;)• Тогда достаточно по-
ложить xt=Xj. (б) Фиктивных переменных нет ни в g, ни в 7г.
Если h g Б, то применяем индуктивное предположение к функ-
ции h. Если h (j’L, BO’g J L, то индуктивное предположение
применяем к функции g. Если (g, h} с Б, то /= (г4 © . . .
• £»+i 11 можно, например, отождествить х, с г,+1.
(в) В h фиктивных переменных нет, а в g имеются фиктив-
ные переменные. Пусть одна из них — xt. Если h (£ Б, то при-
меняем индуктивное предположение к h. Если h g Б, то отожде-
ствляем х( с г,+1. (г) Предположим, наконец, что в g фиктивных
310
переменных нет, а в / фиктивные переменные существуют.
Пусть хк — одна из них. Если g £ L (а значит, h 1), то ото-
ждествляем х, с той переменной, от которой h зависит сущест-
венно (положим для определенно ч, что тако пер мепной явля-
ется х2). Получим/(х2, х2, х3, ..., хж+1) = х3© . .. ©х,©
© ^Ж+1Л (хг> Х21 г31 • • 1 XJ- Очевидно, эта функция нелинейная и
в ней х2>. . ., хж+1 — существенные переменные. Рассмотрим те-
перь случай, когда g L. По индуктивному предположению
в g найдутся две пер-мэнные х{ i ху, отождествляя которые мы
из функции g получаем нелинейную функцию, существенно за-
висящую от s—1 переменных. Если при отождествлении х{ и ху
функция h не вырождается в тождественный 0, то хж+1 остается
существенной переменной и в новой функции. Пусть теперь при
отождествлении х{ с ху функция h превращается в тождествен-
ный 0. Тогда обе переменные х( и ху — существенные в h. Для
определенности положим, что х<=х2 и ху=х3. Имеем h (х’)=
=х2х3Л1 (х4,. . ., хж) © х2Л2 (х4). . хж) © x3h3 (х4>. . ., х,), при-
чем h3 = \ © h2. Положим хх=хж+1 в функции /. Если при этом
получается функция у, существенно зависящая от s аргумен-
тов, то все доказано. (Нелинейность у очевидна, так как
<Р (хг, Х2, Х2, Х4,. . ., x,)=g (хх, х2, х2, х41. ., X.) $ L). Оц-
нако может случиться, что при хх—х,+1 какая-то переменная
в функции f станет фиктивной. Такой переменной может быть
лишь одна из переменных х2 или х3 (ибо, отождествляя в пе-
ременные х2 и х3, мы должны получить функцию g (хх, х2, х2,
х4). . ., хж), существенно зависящую от s—1 переменных). Пусть
у функции ? фиктивной переменной является х2. Так как /=
= Хх (x2x3gx © X2g2 © X3g3 © g4) © x2x3g6 © x2ge © x3gj ©
©*<+i (адА © xJh © xaha)> гйе каждая из функций gx>. . glt
hi, h2, Лз зависит от переменных х41. . ., х, и Л3 = © й2, то, при
сделанном предположении о фиктивности переменной х2 в функ-
ции ?, имеем <р=/ (хх, -2,. . ., хж, хх)= xx(x3g3 © gj @ x3g, ©
©x^fe-, т. е. gx -= hlt g.-^h^ и g5 = g, = 0. Следовательно,
/ (x”) = Z2 (®i ® z,+1) (x3/ix © h2) © xxx3g3 © xxg4 ©x3g7 ©
©хж+1х3/г3. Положим х2=хж+1. Получим функцию ф=/ (xx, x2, x3,
x41. . ., x„ -,)= (xx © 1) x3 (x3\ © h.) © xLx3g3 © xxgt ©
@x3g, © х2х3Л3. Так как функция f (xx, x2, x2, x4,. . хж, x2)-—
=g (xx, x2, x2, x4l. . ., x,) зависи. существенно от всех своих аргу-
ментов, то у функции ф фиктивной может быть только одиа из
переменных х2 и х3. Но это возможно лишь при (и каких-то
дополнительных условиях). Тогда Л3=/гг и f ~x.2 (х4 © х#11/ ht ©
©ЗЛЙЗ © © хз£1 © х^гХ3Ья. Так как h 0, то при Лх = О
функция Ьг не может «вырождаться» в 0, т. е. ht 0. Следова-
311
тельно, дажеприЛ1 = О функция ty = xt (xi© 1)
®xigi@x3g1®x2xihi существенно зависит и otz2, и от х3. Таким
образом, если ни одно из отождествлений жа = х3 или х1 = х,+1
не дает требуемой функции, то достаточно положить i2 = z<+1.
Этим ваканчивается рассмотрение всех возможностей. Выпол-
нимость индуктивного шага установлена.
6.28. 1)—4) Нет, неверно. В задаче 4) можно взять f (х, у)=
=®-* у.
6.29. Так как | Г” | = | г” | = 22"-1, | L» | =. 21*1 < 22”-1 (при
п > 2), | S" | = 22”-1 и | М* | < 22”-2 + 2 < 22"-1 (при п > 2), то
множество 21 не содержится целиком ни в одном ив классов То,
1\, S, L, М.
6.30. Тождественная функция не содержится ни в каком ба-
зисе в Pt (см. задачу 1.18). Любая из остальных одноместных и
нуль-местных функций алгебры логики не принадлежит какому-
нибудь предполному классу в Р2. В то же время наследственная
система всякой такой функции является пустым множеством,
а значит, содержится в каждом предполном классе (в Р2). Пусть
теперь / (хп) — какая-нибудь функция из некоторого простого
базиса 23 и п > 2 (все переменные — существенные). В силу
определения простого базиса система S= (23\ {/ }) □?((/) пе полна
в Ра, т. е. содержится целиком хотя бы в одном предполном классе
К. Если бы / £ К, то система 23 (G &U {/}) не была бы полной.
6.31. 1) 1, £. 2) 0, 1, ху, х\/у, х^у, я|у, m (х, у, л),
т(х, у, г), m (х, у, i), тп(£, у, Z). 3) £, х@у, х@у@1, ху,
х\/ у, х-+у, х-*у, х © у © г, m (х, у, z), m (х, у, «). 4) х © у,
х~у, XV> х\/ V, Х~*У, х-*у, х±у, х | у, х © у © в, х@у ©з»
m (х, у, г), m (х, у, I), m (х, у, г), m (2, у, 4). При решении
задач 2)—4) полезно использовать результаты, сформулиро-
ванные в задачах 2.14, 2.20 и 3.12.
6.33. 2) Принимая во внимание задачи 2.20, 3.12 и 5.38,
заключаем, что любой простой базис в Р2 состоит только из
функций, существенно зависящих не более чем от трех перемен-
ных. Рассмотрим сначала функции, которые существенно за-
висят от двух аргументов и не являются шефферовыми: а © у,
х — у, х->у, х-+у, ху, х\/у. Выясним, какие ив них могут
входить в четырехэлементный базис в Р2. Видим, что х©у $ T1U
(J S U М, х~У в r0LJSU^, х-+у { T0USUil|Al и ®->у{
€ Pi U S U U Аб. Следовательно, все эти функции для наших
целей не подходят. Предположим, что есть четырехэлемент-
ный простой базис, содержащий ху. Так как ху £
g (То П 7\ f~] ДР) \ (£U s)> то ТРИ остальные функции в базисе
312
должны быть таковы: Л 4 (Л П ЛЛ \ Лн /а € (То П М) \ Т\
и /з€ (Л>П Тг)\М. Очевидно, что h==l, f2 = 0. Если бы
/3 4 L, то система {Л, /2, /3) была бы полной. Следовательно,
/з 4 L, а значит, l3 = x@y@z. Случай с функцией х\/ у
рассматривается аналогично. Теперь выясним, какие нелиней-
ные функции, зависящие существенно от трех аргументов, могут
содержаться в четырехэлементном простом базисе. Если
f (х, у, в) 4 L JJ S, то, отождествляя в / переменные, можно
получить несамодвойственную функцию, существенно завися-
щую от двух аргументов (см. задачу 2.20). Но тогда / (х, у, z)
не может входить в простой четырехэлементный базис (см. рас-
смотренные выше возможности с функциями, зависящими от
двух аргументов). Осталось рассмотреть случай, когда
/ (х, у, z) 4 S\L. Если / 4 Г, П а значит, f 4 М, то при
всякой функции g 4 S система {/, g} полна в Р2. Поэтому пред-
положим, что / 4 П Л- Если / 4 М, то (° точностью до пе-
реименования переменных) f=m (х, у, *){ если же f £ М, то
f=m {х, у, z). В первом подслучае /4 (Те Л Л Л S)\(£ (J М),
а следовательно, в соответствующем четырехэлементном простом
базисе (если он существует) три остальные функции должны
удовлетворять условиям Д 4 (Гх |"| 5)\Т0, /2 4 (Л> Л s)\7’i и
h 4 (То П Тх)\$. Однако (Гх П 5)\Г.= (7’ОГ|5)\7’1=0! т. е.
не существует ни функции Д, ни функции ft в указанными свой-
ствами. Значит, первый подслучай невозможен. Во втором
подслучае / 4 (ro Л Л П 5 П M)\L. Следовательно, три
остальные функции в базисе должны быть линейными (иначе бы
функцию / из базиса можно было удалить). Линейные функции
существенно зависящие от четного числа переменных и отличные
от констант, не могут принадлежать такому базису, ибо каждая
такая функция не содержится либо в множестве Та (J $ (J -W,
либо в множестве Tr (J S (J М. Линейная функция, существенно
зависящая от нечетного числа переменных, может принадлежать
такому базису лишь тогда, когда она сохраняет 0 и 1. Значит,
это может быть только функция х © у @ z. И остались еще кон-
станты.
ГЛАВА III
§ 1
1.3. Надо из к—1 «вычесть» (с помощью функции х — у)
определенное число раз функцию х -|- 2.
1.4. Тогда и только тогда, когда а и к взаимно простые.
313
1.5. Если к—2т > 4, то можно взять у=т—1. При 6=
= 2т-|-1 > 3 рассмотреть функцию 1—2х.
1.7. При к—А, 6, 8, 9, 10 число различных функций требуе-
мого вида равно соответственно 3. 2, 5, 3, 4.
1.8. При к 3, 4, 6, 12. Сначала сравнить значения этих
функций при х=2.
1.9. Имеем: функция J к^ (х) Ц- ... + J к_х (х) (к — Сла-
гаемых) равна (х); Jt (х) =jk^ (х — i — 1), 0<is£fc —2.
Если g (х) С то g (х) = g (0) • 70 (х) + ... + g (i) • J( (х) +
+ ... +g(k — 1) •/*_! (х) (здесь I • (х) = /,.(х)+ ... +;,.(х)—
I слагаемых).
1.14. 2) Функция 1—х=/0 (х) не представима полиномом
по mod к при составном к. 4) {max (х, у), х-j-l} — полная си-
стема при любом к. Следовательно, если бы функция max (х, у)
была представима полиномом по mod к при составном к, то система
полиномов была бы полной при всех к > 3.
1.16. 1) Непредставима. 2) Непредставима. 3) Предста-
вима.
1.18. Либо ^=0, либо <z0 0 и 0.
1.20. 2) Нет, несправедливо. Пример: х2)=
=Зх]Х2-|-1, к=б.
1.22. 2) Если g (х) f Р, и принимает значения только из
множества {0, 2}, то ее можно представить в виде суммы (по
mod 4) соответствующим образом подобранных функций 2j{ (х).
Если g (Я4) С {1, 3}, то функция h (x)=g (х)-{-1 принимает зна-
чения только из множества {0, 2}.
1.24. При подсчете полезно учесть, что 2х3=2х2=2х и Зх3=
=2x4-х3.
1.26. Либо 6=0 и а=0, 1, 2, 3, 4, 5, либо 6=2 и а=2, 5,
либо 6=4 и а=1, 4.
1.29. 3) а) Если 7с=2тп-{-1 > 3, то функция / самодвой-
ственна только при а—2т. Если 6=2ш > 4, то имеются две
возможности: а=2т—1 и а—т—1.
1.30. Если функция t (2") из Рк самодвойственна относи-
тельно циклической подстановки s (х), то она однозначно опре-
деляется своей подфункцией / (0, х2,. . ., хя).
1.31. Все наборы значений переменных х1т. . ., х„ можно
специальным образом разбить на fc"/r непересекающихся под-
множеств. При этом в каждом из подмножеств разбиения суще-
ствует набор а=(а1>. . , ая), удовлетворяющий условию: ка-
ков бы ни был набор 9=(3i,. . ., Ви), отличный от набора 5 и
принадлежащий рассматриваемому подмножеству разбиения,
найдется такое 1 (1 < t < г—1), что®* (сту) = / = 1, п. Функция
314
f (2я), самодвойственная относительно подстановки s (г), одно-
значно определяется заданием / на одном «выделенном» наборе
а из каждого подмножества разбиения.
§ 2
2.2. 3) 2* — 1. 4) тт”кк”-тП (в > О, 1 < т = | 8 | < к - 1).
2.3. 2) Если D — нетривиальное разбиение множества Ек,
то 1 < s < к. Следовательно, найдется такое подмножество <Sit
в котором не менее двух элементов, и еще некоторое подмно-
жество 8j, отличное от <S(. Пусть 5lt Ьг — два каких-то эле-
мента из <J<,ac— какой-нибудь элемент из Тогда функция
g(x), равная с при z = bi и равная bt при х blt не при-
надлежит классу U (D), так как ЬХ~Ь2 (modZJ), с не эквива-
лентно 6j (по mod О) и g(6i)=c, ^(6а) = 61. 4) Пусть (ilt . . .
..., i„) — набор чисел из множества {1, 2, ..., «}. Всего таких
наборов s”. Упорядочим их в лексикографическом порядке и
перенумеруем, приписав номера от 1 до s". Набор (1, 1.1,1)
будет иметь номер 1, набор (1, 1, ..., 1, 2) — номер 2, набор
(1, 1, .. ., 2, 1) —номер s -)-1 и т. д. Если набор (iu ..., *„)
имеет номер т, то число | | • ... • | обозначим через dm.
Число функций в множестве Рк (Xя), сохраняющих разбиение
D = {Si, 8..... 8,}, равно 2 ‘
(>!>••. /г)
• ..-1^1 Г’ гдв r = s" и сумма берется по всевозможным
наборам длины s”, состоящим из чисел, принадлежащих мно-
жеству {1, 2, ..«}.
2.4. 2) Обозначим множество 8 через 8и Ек\8 через <£„
и, как в задаче 2.3, 4), d„ будет обозначать число | <S< |...
• ••|^< |i ГД0 (hi • ••• i*) — набор длины в, состоящий из
чисел, принадлежащих множеству {1, 2}, причем т — номер
набора в лексикографическом упорядочении. Число функций
из Рк(Хп), содержащихся в множестве U (D)\T (<£), равно
2 IW'-И//’•••••!*>/'.
ji
U,...Jr)
где г—2я и сумма берется по таким наборам длин, Iя которые
состоят из чисел, принадлежащих множеству {1, Z |, и у кото-
рых первая компонента равна 2. Приведенная формула спра-
ведлива для 1. Если же п=0, то в множество U \Т (<£)
будут входить все те константы, которые не содержатся в классе
Т (8), т. е. в этом случае число функций равно |£fc\<S|.
315
2.5. 3) Это только одноместные предикаты вида х i
(i = 0, 1 А —1).
2.6. 3) Воспользоваться основной леммой о существенных
функциях (см. лемму 7 в [10] на стр. 47) и показать, что при
2 < s < к — 1 класс Т (0, s) состоит из всех функций, сущест-
венно зависящих не более чем от одной переменной, и всех
функций, принимающих не более s разных значений.
2.7. 2) 2 {к — 3) I. 2.10. Рассмотреть, например, функцию
s (я) = х -|-/0 (я) — (я) при к = 3. 2.12. 1) б) Ц (х) £
(ра) \ М (₽1). г) я -Но (*) + Л W (Pi) \А/ (ра). е) я—j/G
еЛ£(₽а)\М(Р1). 2.13. 1) Т({0, А —1}). 2) U «0, 1), {2, ...
.... Л-1}). 5) Т({1, 2}).
2.14. 2) При А>4 можно рассмотреть разбиение D =
— {0, 1} U {2..Л — 3} J {Л — 2, к — 1}. При Л = 3 подходящее
разбиение найти нельзя. 3) При всяком к > 3 достаточно огра-
ничиться классом типа М (р).
2.15. 1) Можно. 2) Можно. 5) Нельзя; достаточно рас-
смотреть случай А = 3.
2.17. Доказательство проводится аналогично тому, как до-
казывалась вторая часть утверждения, сформулированного
в задаче II.1.13.
2.20. Нет, неверно. Можно рассмотреть, например, класс
(Л (®) • /а (У)] в Ра.
2.21. Нет, неверно. Достаточно взять в Ра замкнутый класс,
порожденный функцией я2у2.
2.23. Установим какое-либо взаимно однозначное соот-
ветствие между всеми рациональными числами из отрезка [0, 1J
и множеством функций {/2, /8, .}. Возьмем произволь-
ное действительное число 7 £ [0, 1] и обозначим через под-
множество всех таких функций из {/2, /а, ...}, которые
при указанном выше соответствии отвечают всем рациональным
числам, меньшим числа 7. При 7Х < 72 имеем с (вклю-
чение строгое!). Пусть 7^=[С'Т]. Очевидно, что В^ при
71<7а-
$ 3
3.1. 1) Такой системой является множество {/0(я), х-|~У}
(см. задачу 1.9 и воспользуйтесь критерием Слупецкого).
3.2. 4) Можно удалить функции 0, Л—1, Ja (я) и J (я).
3.5. 3) Пусть к — простое число, не меньшее 3. Так как
хк = х, то 1-|-я — я-|-як=1 -j-я. Далее, имеем 1-|-я — (я-|-1)-|-
4-Я (я + 1) (я + 2).. .(я + Л — 1) = 0. Значит, можно построить и
316
любую из констант 1, 2,. . к—1. Затем положим z2=z4=. . .
. . .=zfc=l, х± — х и х3=у. Тогда l-|-z—1 -J-rr-1 -у-1. . .l=z-(-zy=
=х (у-И). Полагая здесь y-z-\-k—1, получаем произведение
xz. Осталось построить сумму двух слагаемых. Берем zx=A—1,
х3—х и х3=. . .=xk=Q. Имеем 1-]-(А—1)—z-j-(A—l)-z-0=
= —х. Потом полагаем Zj=z-]-A—1, z2=—у, z3=. . ,=zA=0
и получаем сумму l-|-(z4-A—l)-|-y-]-(z4-A—1) (—у) 0=z+y.
3.6. 2) z — (z — у) = min (z, у); —x = (к — l)-“-z;
max (z, y)=~min(~z, ~y); (A—1)(A — 1) = 1
(к — 1 слагаемых); следовательно, приходим к заведомо пол-
ной системе {z-|-l, max (z, у)}, б) z — z = 0; 1— 02 = 1;
—1=А— 1; (А — 1)-=-г =—х; х — (z — у) = min (z, у);
—min (—z, ~у) = max (z, у); с помощью А — 1, 1 и z — у полу-
чаем константы А — 2, А — 3, ..., 2; ((((А — 1) — z) z) ...
... — z) = Jj.j (z) (здесь z вычитается A —1 раз); /0 (z) =
= (x) — ((^ 2) — z) — (z); ^j._s(z) =
t=/0((A — 3) — z) — Ja ((A — 2) — z) и т. д. Таким образом,
можно построить все функции из системы Россера—Тур-
кетта.
3.7. 3) Очевидно, что функция ? (z, у) = £ja {у) -|- yja (z)
принимает все А значений из Ек. Имеем <р (z, z)=/0(z),
/о (Л> (*)) = ! — /о(г). ?(/о(*). 1— /о (*)) = ! +/о (®). io U +
+ /oM)sO, ф(0, z) = z + /о (z), <f(x, 0)=z + l, f (/#(«),
z + io (x)) = z + /o (z) — Л (z). В силу теоремы С. Пикар си-
стема {х + /о (z), z -|- 1, z + /о (*) ~ ii (*)} полна в Нужно
еще применить критерий Слупецкого.
3.8. 1) При А=2ш > 4 система не полна. При А=2тп-|-1 >
> 3 система полна. 2) Система не полна. 3) Система не полна.
6) Система не полна.
3.9. 1) Полноту (в 5fe) данной системы можно доказать так:
индукцией по i (i > 1) устанавливаем, что любая функция g из
Зк, удовлетворяющая условию: g (z) = z при х > i, порожда-
ется функциями из множества {/fa (z), (z),. . ., h0{ (z)}.
Тогда, полагая i=k—1, получаем требуемое. Индуктивный шаг
осуществляется следующим образом. Пусть g (z) = z при
z > г-|-1 и g (г-f-l) =/, g (Z)= i—|—1 (здесь j i-J-1 и 0 < I < i).
Возьмем функцию h (z), совпадающую с g (z) всюду, кроме х=1
и z=i-J-l, а при этих двух значениях аргумента функция А
такова: h (l)=j и h (i4-l)=i-f-l. Очевидно, что функция A (z)
уже построена (в силу индуктивного предположения). Нетрудно
убедиться в том, что g (z) = А (Ао(<+1) (Аог (AoU+n (z)))). 2) и 3)
Свести эти системы к системе из предыдущей задачи.
317
3.10. Как следует из задачи 3.9, 1), данная система порож-
дает множество Sk. Используя функцию .-г-|-70 (ж), нетрудно по-
строить любую функцию, выпускающую ровно одно значение
(из Ек). После этого, предполагая, что имеются все функции,
выпускающие не более I значений (1 < I < к—2), нужно про-
демонстрировать, как можно построить произвольную функ-
цию из выпускающую г-}-1 значений. Пусть g (ж) —про-
извольная функция, выпускающая только одно значение. Тогда
существуют ровно два значения аргумента — и et, на которых
значения функции g (ж) равны, г. е. g (ea)=g (ex). Элементы из
множества Ек\{еи, е}} обозначим через е2, е3,. . ., ек_г. Возьмем
две функции gx (г) и g2 (г) из множества Sk : gx er)=r, r=0, 1,. . .
. . к—1; gs («)=g (et„ s=l, 2,. . ., к—1, a g2 (0)=e 6 Ek\g (Ek).
Обозначим функцию ж-|-у0 (ж) через h0 (ж). Имеем g (ж)=
=g2 (ha (gj (г))). Берем теперь произвольную функцию g' (ж),
выпускающую гф-1 значений (1 < 1 < к—2). Пусть одно из этих
значений — е'о. Предположим, что g' (60)=g' (6j). Рассмотрим
функцию /г (ж), совпадающую с g' (ж) всюду, кроме ж=60, а
fi (.Ъо)=е'о. Очевидно, что функция / (ж) у нас уже построена
(по индуктивному предположению). Пусть alt. . ., а, — все
разные значения, принимаемые функцией g' (г) (здесь в —
=к—I—1 > 1), и E^fa^. . ., а, }—{<?(>, е{,. . ., е'}. Возьмем
функцию ft (ж), имеющую следующий вид:
{х, если х е’а,
-Г- 0.
g' (Ьо), если х = е0.
Легко видеть, что функция /2 (ж) выпускает только одно значе-
ние, а значит, ее мы умеем строить. Имеем g' (ж)=У2 (А. (х))-
3.14. 1) s(x)=~x. 2) s(x)=~x. 3) * (х)=х—1.
3.15. Это утверждение противоречит тому, что в Рк число
предполных классов не больше чем 2fc* (см. задачи 2.17 и 3.11).
3.16. / (ж, у}=з?у—хуг-^-ху—х2—х—у—1 —функция Шеффера,
а/ Z/)+x € Р ({1 })• Для доказательства того, что [/ (ж, у)]=Р3,
достаточно построить три функции: ж-}-1, ж4-/0 (ж) и ж-фУ0 (ж)—
—h («) — и воспользоваться теоремами С. Пикар и Е. Слунецкого.
Пусть ?(ж)=/(ж, ж), тогда <р (<р (ж))=ж-ф1, g (ж)=У (ж, ж-ф1)=
=ж+Уо (х), / (g (ж), g (ж))=ж2— (ж), g (ж2—/i (ж)) = 1, У (ж, 1) =
=X+Jo (*)—/1 («)•
3.18. Ни при каких значениях к > 3.
3.22. Это множество не более чем счетно. В то же
время существует счетно-бесконечное множество } замкну-
тых классов, каждый из которых содержит конечное число
318
попарно пеконгруентных функций: Аи=[/Л(х1, х,,. . ., х„)],
п=2, 3,. . где /я (хх, х2,. . z,,)=7i (xj)j2 (х2) /2 (х3). . . /2 (х„).
3.24. Таким классом является, например, класс К=
= [/з (Хц Х2), (хх, Х2, Х3), (Хц Х2>. . ., Хя),. . .], где
/я («1» ®2>- • •> *я)=/1 (x^iz (х2)/2 (х3). . . /2 (х„).
3.25. 1) B = {k — 1, /0 (х), х — у}. В самом деле,
[B]Z){0, 1...........к-2, к-1}, (x)=/0((ft —1) - х),
ik-2 (х) = /0 ((к — 2) х) (х), jk_3 (х) = /0 ((ft — 3) — х) —
— it {(к — 2) — х), ...
Далее, любую функцию g (х) из Р^ можно построить так. Сна-
чала строим функцию g0 (х) = ((((ft — 1) — /0 (х)) — j0 (х)) — . . .
...—/о(х)), гДв /о (х) вычитается из ft — 1 такое число раз г0,
чтобы g0 (0) = g (0), т. е. ra = k— 1— g(0). Затем из g0 (х) вы-
читаем rx = k — 1— g(l) раз функцию Д (х) и т. д. В част-
ности, можно построить х. Для доказательства полноты си-
стемы В остается вспомнить, что min(x, у) = х — (х-^у),
max(x, y)=~min(—х, ~у) и что система {х, шах (х, у)}
полна в Рк. Далее, очевидно, что функцию х — у из В уда-
лить нельзя (ибо тогда останутся только функции, существенно
зависящие не более чем от одной переменной). Заметим еще,
что {/0(х), х— у}сТ ({0, 1}), a {ft — 1, х — у} С Т ({0, ft —1)).
3) {—х, min(x, у), х-}-у}. Полезно учесть, что {~х,
min(x, у))сУ((0, ft —1}), {~х, x4-g}CZ£ и {min (х, у),
х-|-у} с Т ({0}). 5) {/0(х), x + j/2}. Здесь стоит иметь в виду,
что /0 (/0 (х)) + (/о (х))2 = 1 и что х-}-уа можно использовать
для построения всех одноместных функций (с помощью /0 (х),
/1 (х), .... i (х))—почти так же, как использовалась в за-
даче 1.9 функция х -|- у.
ГЛАВА IV
§ 1
1.1. Вытекает из подсчета пар вида (у, х), где и f V, х £ X,
v и х инцидентны.
1.2. 2) Ни одного. 1.3. Индукция по числу ребер.
1.5. 1) Пусть О (у)—множество вершин, смежных с v,
а О' (y)={v) U О (у). По условию |О' (н)| > (п-}-1)/2 и
|F\O' (г)| < (п—1)/2. Отсюда вытекает, что каждая вершина из
7\0' (у) смежна с некоторой вершиной из О' (у), следовательно,
граф связен. 2) При четпом п нельзя, при нечетном — можно.
319
1.10. Пусть [р, и], [w, t] —две цепи максимальной длины,
не имеющие общих вершин в G. Граф G связен. Следовательно,
существует цепь Z, соединяющая, например, вершины v и и>.
Пусть — последняя вершина цепи [у, и], встречающаяся на
пути от v к w вдоль цепи Z, a — первая вершина цепи [u>, t],
встречающаяся на этом пути после vx. Вершина vx из цепи [у, и]
делит ее на две части: [г, Uj] и [ц1; и]. Пусть цепь [р, nJ не короче,
чем [рц и]. Аналогично, вершина uij делит цепь [ш, t] на две
части. Пусть [ш, не короче, чем [iz^, i]. Тогда цепь [р, рг;
1РП ip] длиннее каждой из цепей [р, и] и [и>, £]. Противоречие.
1.18. У Казани е. Рассмотреть дополнения графов G
и Н. 1.20. 2р. 1.22. Шесть.
1.24. 1) Пусть v, и, w — три вершины одинаковой степени
некоторого графа G из R„. Предположим, что v и и смежны,
а р и ip не смежны. Для вершин и и ip справедливо хотя бы одно
из включений О (u) С О (ip) или О (ip) С О (и). Отсюда и из
равенства |О (u) |= |О (ip) | вытекает, что О (и)=О (ip), и, следо-
вательно, р f О (ip). Рассмотрим теперь пару р и ip. По доказан-
ному р и ip смежны. Но включение О' (р) С О' (ip) не имеет места,
так как и £ О’ (р)\О (ip). Неверно также и О' (ip) с О' (р),
так как \О' (ip)|= \О' (р)|. Получаем противоречие.
1.26. 1) Число ребер графа G равно сумме чисел ребер гра-
фов Н{, деленной на п—1. 2) Вытекает из 1). 1.28. Два.
1.34. 1) Существует. 2) Не существует. 1.35. Верно.
1.39. 2) Неверно.
§ 2
2.5. Пусть G — плоский двухсвязный граф не менее чем
с двумя внутренними гранями. Если существует внутренняя
грань, отделенная от внешней грани единственной простой цепью
то, удаляя эту цепь, получим двухсвязный граф (доказать это
утверждение). Пусть такой грани не существует. Тогда всякая
внутренняя грань, имеющая общую цепь с внешней гранью, имеет
с ней еще хотя бы одну общую вершину, не лежащую на этой
цепи. Покажем, что этот случай невозможен. Пронумеруем все
внутренние грани. Связные куски границы внешней грани,
принадлежащие одновременно внутренней грани с номером г,
пометим индексом I. Тогда найдутся такие индексы 1, /, которые
встречаются при обходе границы внешней грани в порядке
I, j, I, j. Обозначим соответствующие куски границы через Гп,
Гуп Г<2> Гу2. Выберем на этих кусках по одной точке плоскости:
320
a^, bv аг, b2. Тогда точки аг в а2 можно соединить кривой, все
точки которой, за исключением и а.,, являются внутренними
точками грани с номером г, а точки Ь± и ;>2 можно соединить кри-
вой, внутренняя часть которой лежит в грани с номером I. Кри-
вые пересекаются в некоторой точке d, которая, таким образом,
оказывается внутренней точкой двух различных граней. Полу-
чили противоречие.
2.9. Пусть G — двухсвязный планарный граф, a G' — его
плоская реализация. Пусть п — число вершин, т — число ре-
бер, г — число граней графа G' (включая и внешнюю). В силу
задачи 2.6 имеем г=т—п-}-2. Число пар вида (у, х), где v —
вершина, инцидентная ребру х, равно 2m. С другой стороны,
это число равно сумме степеней вершин графа. Поскольку каж-
дая степень по условию не меньше чем 6, то 2m > 6п, т. е.
т Зп. Граница каждой грани имеет не менее трех ребер,
а каждое ребро принадлежит границе не более двух граней.
Отсюда Зг < 2m. Нетрудно убедиться, что система г=т—п-ф2,
m > Зга, Зг < 2m несовместна.
2.14. Предположим, что граф А. является планарным.
Пусть КБ — его плоская реализация. Тогда число г граней графа
К’Б равно т=т—n-j-2, где т — число ребер, п — число вершин.
Аналогично тому, как в задаче 2.9, имеем Зг < 2m. Отсюда
т < Зп—6. Но т=10, п=5. Получили противоречие. При до-
казательстве непланарности графа K3S заметить, что каждый
его цикл содержит не менее четырех ребер, и, предположив, что
К3 j планарный, воспользоваться 2.11.
2.22. Каждая вершина шестисвязного графа имеет степень
не меньше 6 (см. 2.9).
2.27. 3) х СВ”)=2, х' (5л)=п.
2.28. Две.
2.45. 1) Пусть t (т) — число тупиковых покрытий цепи
длины т. Тогда т (т)= t (т—2)-|-t (т—3), t (1)= т (2)= т (3).
Решение рекуррентных соотношений такого вида см. в § 3
гл. VIII.
2.49. 1) vk (G) равно среднему числу вершин, не смежных
с вершинами подмножества U CZ V мощности к. Следовательно,
существует такое подмножество UQ, |t70| = fc, что v (Z70) < чк (fl).
Если W — множество вершин, не смежных с вершинами из UQ,
то И7 U — вершинное покрытие мощности, не превосходящей
(G). 2) Пусть е (v, u)=l, если вершины г и и не смежны, и
е (г, и)=0, если v и и смежны. Пусть Sk (у) — количество под-
множеств U С V, составленных из к вершин, ни одна из
321
которых не смежна с г, a d (v) — степень вершины v. Тогда
5 '|(С7) = 2 2 е^< “> =
гсМИ=* cqr,|rj = i ,ет
=2^)=2ГЛ‘|<Гл)-
• е? »е>'
Отсюда
I^Lr1/ da \
MGXIVI П (1—Пй|Ът)-
♦=0 11 '
§ 3
3.2. Доказательство можно провести индукцией по числу
вершин орграфа. На индуктивном шаге полезно удалить из
орграфа одну из вершин v± или р2.
3.5. Применить индукцию по числу к.
3.8. Утверждение можно доказать индукцией по числу
вершин в турнире.
3.10. Неравенство очевидно при л=1. Пусть оно справед-
ливо для таких п, что 1 < п < т. Рассмотрим турнир Т с zn-j-l
вершинами. Так как во всяком турнире с m-J-l вершинами ровно
Gm+i ДУГ> найдется вершина р0 с полустепенью исхода
> [(т-}-1)/2]. Удалив из Т вершину v0, получаем турнир Т',
который имеет m вершин и содержит множество S, состоящее
не менее чем из / (тп) согласованных дуг. Дуги, исходящие из
рс, и дуги, принадлежащие 8, согласованы. Воспользовавшись
индуктивным предположением, имеем
^Г7п + 1’1л_Г'ге1Г'” + 11 Ги + 11Гт + 21
/(« + !)>[ 2 j + [2 JL 2 J-[. 2 JL-2J-
3.12. Всякая группа четного порядка содержит хотя бы один
элемент, обратный к самому себе и отличный от единичного эле-
мента группы. Если бы группа турнира Т была четной, то в ней
нашелся бы элемент а, удовлетворяющий указанному выше свой-
ству. Так как а — не единичный элемент, то существуют две
вершины Pj и а2 такие, что а (р1)=р„ и а (р2)=р1. Пусть Т содер-
жит дугу (pj, г2). Тогда дуга (a (fj), а (г2)) тоже должна была бы
принадлежать Т. Получили противоречие.
3.15, Доказательство можно провести индукцией по числу
сильных компонент турнира. Если в конденсации либо только
одна вершина, либо две вершины, то она является транзитивным
орграфом по определению.
3.19, Применить индукцию по числу вершин в орграфе.
Па индуктивном шаге надо удалить одну из вершин с пулевой
322
полустепеныо исхода, установив предварительно существование
такой вершины в данном орграфе.
3.21. Доказательство можно осуществить индукцией по
числу вершин орграфа.
3.25. Применить индукцию по длине контура.
3.29. Доказательство можно провести индукцией по по-
рядку определителя
{ 4
4.2. Исходя из произвольной вершины дерева, будем строить
цепь, присоединяя па каждом шаге по одной новой вершине,
пока это возможно. В тот момент, когда этого сделать нельзя,
концевые вершины цепи окажутся висячими вершинами дерева.
Процесс построения цепи обрывается в силу конечности множе-
ства вершин и отсутствия циклов в дереве.
4.4.1) В силу задачи 1.26 по системе F (G) можно восста-
новить число ребер графа G и его связность.
4.9. Можно провести индукцию по величине радиуса дерева.
4.12, Мощность — континуальная. 4.14. 2. 4.23, Провести
доказательство индукцией по длине вектора. 4.28. Верно.
4.30. Верно. 4,31. Вообще говоря, неверно. 4.32. Вообще
говоря, неверно. 4.33. п—1.
4.34. Неразложимая сеть не имеет параллельных ребер и
не является р-равложимой. Отсюда лг< — 1. В неразложимой
сети каждая внутренняя вершина имеет степень не ниже 3,
а полюсы — не ниже 2 при п > 2.
4.40. 1) а), б), в). Может. 3) а), б) Не может. 4.43. Рас-
смотреть Г£, т > 3. 4.52. Неверно.
§ 5
(*') (паХ
5.2. 1) 2'2Л 2) I L 5.3. 2) Использовать формулу «вклю-
\м /
чений и исключений». 5.5. 1) Использовать то, что в связном
графе m < и m > п — 1. 2) В связном графе о т ребрами
не более т 4-1 вершин. Число пар неодинаковых вершин,
([т. -4- 1\\
I 9 ) I
\ * / I.
т /
Далее применяется формула Стирлинга.
323
5.6. Отметить, что число вершин в графе не превосходит
2т. Далее — аналогично задаче 5.5, 2).
5.7. См. 5.5, 2) и 5.6.
5.9. 1) Код дерева с т ребрами есть двоичный вектор
длины 2т с т единичными координатами. 2) См. 4.24.
5.10. Использовать 5.4 и формулу Стирлинга. 5.14. См.
VIII. 3.18 и VIII. 3.19.
5.16. Сеть Г (а, Ь), обладающая свойствами I и II, является
результатом подстановки сетей типа Г£, Л = 1, т-|-1, вместо
ребер сети (а, 6). Число таких сетей равно числу разме-
щений т предметов по п — 1 ящикам так, чтобы ни один из
(т — 1
п — 2
5.17. 2) Использовать 5.14.
5.19. Если граф не связен, то множество его вершин можно
разбить на две доли такие, что не существует ребер, соединяю-
щих вершины разных долей. Одна из долей имеет число вершин,
заключенное в пределах от 1 до [п/2]. Граф с нумерованными вер-
шинами полностью определяется выбором ребер. Число ребер,
которые запрещено при этом выбирать, равно к (п—к), где к —
число вершин в одной из долей.
5.22. Всякий подграф куба В” полностью определяется
заданием множества вершин. Множество вершин связного под-
графа определяется заданием некоторого его остова (дерева,
содержащего все вершины). Чтобы задать дерево, являющееся
подграфом куба Вп, можно выбрать какую-либо вершину куба,
принадлежащую дереву (имеется не более 2я способов), дерево
с к вершинами (не более 4*-1 способов). Для каждого ребра де-
рева указать направление его как ребра куба Вп можно не более
чем п способами. Отсюда и вытекает оценка.
5.31. Пусть 8 (п) — доля тех графов, у которых р (G) > 1.
В силу неравенства (1) имеем: 8 (n) <р(л)->0 при в-» со.
Отсюда и вытекает результат.
5.32. 2) Z (Г (7^jt а), t2, ?a)
=“ 2 13 1 + 2ta).
324
5.33. 1) Возьмем произвольную перестановку агаг. . .а„ чи-
сел множества {1, 2,..., п} и расставим в ней скобки так, чтобы по-
лучилась подстановка с цикловой структурой j2,. . ., /„);
при этом сначала будут идти ]\ циклов длины 1, затем /2
циклов длины 2 и т. д. (т. е. подстановка будет иметь следующий
вид: (а,) (а2) ... (a?.J (a/1+iay +г) • • •)• Предположим теперь, что из
двух различных перестановок элементов множества {1, 2,. . п}
построены по описанному выше способу две подстановки и
я2 с цикловой структурой (/). Спрашивается, когда 14 совпадает
с я2? Совпадение может быть по двум причинам: (1) одинаковые
циклы в подстановках 14 и п2 стоят на разных местах, (2) циклы
хотя и равны (как циклы подстановки), но при указанном выше
построении они начинаются с разных элементов (например,
(123) и (231)). Первая причина приводит к повторению одной и
п
той же подстановки I раз, а вторая — к повторению
fc=i
я
JJ kJlt раз, причем эти причины действуют независимо друг
Л=1
от друга. 4) Доказательство можно провести индукцией по га с
использованием соотношений из пунктов 1) и 2) данной
задачи.
5.34. Полезно воспользоваться следующим очевидным фак-
том: цикл является четной подстановкой тогда и только тогда,
когда его длина нечетная.
5.36. Следует из перечислительной теоремы Пойа.
5.37. Проинтерпретировать подходящим образом коэффи-
циенты бинома l-t-ж и воспользоваться перечислительной тео-
ремой Пойа.
5.40. Каждому графу сопоставить набор связных графов —
набор всех его компонент связности. Затем применить пере-
числительную теорему Пойа.
5.42. Всякий турнир однозначно определяется своей кон-
денсацией (о нумерованными вершинами) и набором сильных
компонент. Нумерация вершин нужна только для сопоставления
им соответствующих сильных компонент турнира.
§ 6
6.3. Четырнадцать. 6.4. См. 6.2. 6.6. Вытекает из того, что
всякая функция / (я") имеет д. н. ф. сложности не выше га2я-1.
6.16. См. 6.15,
325
6.20. Вытекает из того, что сложность схемы, двойственной
к данной, равна сложности исходной схемы, и из 6.18.
6.21. Если схема содержит не более семи контактов, то ее
так можно нарисовать на плоскости, что добавление ребра между
полюсами оставляет ее плоской. Следовательно, существует
двойственная к ней схема. Замена в последней всех контактов
вида х” на х° приводит к схеме, реализующей отрицание той
функции, которая реализуется исходной схемой.
6.22. Выберем произвольный контакт бесповторной схемы,
реализующей булеву функцию /, и рассмотрим цепь, проходящую
через этот контакт. Можно так зафиксировать значения перемен-
ных, отличных от тех, что входят в выбранную цепь, что все
контакты, не входящие в цепь, окажутся разомкнутыми. Полу-
ченная схема реализует э. к., зависящую от выбранной перемен-
ной. Таким образом, оказывается, что некоторая компонента
функции /, а значит и сама /, существенно зависит от выбранной
переменной.
6.25. Схема 2, указанная на рис. 21, имеет среди своих се-
чений множества {х, у}, {г, u>}, {х, г, v, z} и {х, w, t, и}. Тогда,
если существует бесповторная схема 2П реализующая функцию
/*, то в ней имеются цепи с проводимостями ху, rw, xrvz, xwtu.
Без ограничения общности можно считать, что контакт х при-
мыкает к полюсу а сети Sj. Тогда к этому полюсу примыкает
также или контакт г, или контакт w. В первом случае в не
существует цепи xrvz, а во втором — цепи xwtu.
6.26. Неверно. Воспользоваться тем, что / (хг,. . ., х„)=
=/* (£ц« • • > х„), и результатом задачи 6.25.
ГЛАВА V
§ 1
1.1. Пусть р (у, w) < 2t для некоторых v и w и» С. Тогда
S” (1>)Г]|9" (ш) Ф 0. Следовательно, любое отображение
ф:В"->С такое, что S” (и) CZ (и) для всякого и^С, неодно-
еначно.
1.2. 1) Вообще говоря, неверно. 2) Верно. 3) Вообще
говоря, неверно.
1.3. Множества С0 = {а£С, || а || четно} и Ci = {afC, ||ос[|
нечетно} являются кодами, обнаруживающими одну ошибку.
Хотя бы одно из них содержит не менее половины слов из С.
1.4. 1) Обнаруживает одну и исправляет 0 ошибок. 2) Обна-
руживает п — 1 и исправляет |(п—1)/2] ошибок.
326
1.7. 2) 16. 1.8. 2”-1. 1.9. 2. 1.12. Не существует.
1.13. Пусть для некоторого я >7 существует плотно упа-
кованный <п, 3>-код. Тогда в силу 1.11 для этого п число
2<=о Q ) является степенью двойки. Следовательно, для некото-
рого к выполняется равенство (я 1) (я2 — п — 6) = 3 • 2к. Тогда
либо п 4- 1 является степенью двойки, либо п 4* 1 имеет вид
3 • 2Г для некоторого натурального г. Если л4-1=2г, то
я2 — п 4- 6 = 3• 2к~г. Подставляя в последнее равенство га =
=2Г — 1, имеем 22г~3 — 3 • 2Г-3 4-1=3- 2к~г~3. При г > 3 левая
часть есть нечетное число, превышающее 3, а справа — либо
четное число, либо 3. Аналогично рассматривается второй
случай.
1.14. Пусть вершины а=(а!, . . ., ая), ^ = (^, . . ., ^я),
7 = (7!, .. ., 7„) образуют <ге, й>-код. Без ограничения общ-
ности 5=0 и р (a, fi) = d. Положим А„ = {i: = а, 7< = т},
о, tf{0, 1}. Рассмотрим вершину 8 такую, что 8<=0 при
1€АИ, 5f = l при igAji. Имеем р_(а,_В) =|| 8|| = | A01U A10U
U-^oo I > | A01U410 I = Р (Р, 7) > d, p (8, p)>nil>d, p (8, 7) >
> IIPll = *
1.16. Без ограничения общности считаем, что Of С. Для
каждого а£В%+1 существует и притом единственная вершина
7^ С такая, что р (5, 7) < d. Поскольку вес всякого ненулевого
кодового слова не меньше 2d 4-1, то 7GB"rf+1. Пусть А (7) =
= {i: atBjt-p ₽(“. 7) = d}- Тогда (J А (7)= #3+1 и Для
T!6Cf|B"rf+l
любых 71( 7а из имеем А (71)Г)4 (7а) = 0.
1.17. Кодовое расстояние всякого эквидистантного кода,
имеющего мощность, большую, чем 2, четно.
1.20. 1) В каждой из граней B^+d’d и B"+d’^’ ’d
построим коды Са и Ci мощности т(п, d). Тогда ColjCi есть
(n-\-d, <1>-код мощности 2т (п, d). 3) Указание. Если С
есть <я, d^-код в Вп, то для каждой (л — 1)-мерной грани g
множество СП? является (п — 1, <1>-кодом.
1.23. Пусть я < 2d и С — произвольный <я, й>-код мощ-
ности т > 2. Составим матрицу М, строками которой являются
кодовые слова. Пусть В. — сумма попарных расстояний между
(неупорядоченными) парами кодовых слов. С одной стороны,
(т. »
Id. С другой стороны, Я = 2 Л<). где —
2 / tel
327
число единиц в i-м столбце матрицы М. Поскольку h (иг — Л) <
т2 т (т — 1) тг 2d
< ~ , то ------7j---< п • Отсюда т < 2d — п '
1.25. 3) Пусть С — максимальный <n, к, <1>-код. Тогда
множество С<={5: agC, я4 = 0) является (п— 1, к, <1)-кодом.
Число пар вида (i, р) таких, что 1 < I < п, не превос-
ходит п шах | С{ | < п • т (п — 1, к, d). С другой стороны,
i
каждый вектор 5 g С порождает п — к таких пар. Отсюда
(и — к) т (п, к, d) < пт (п — 1, к, d).
1.26. Пусть a QB”, С С В”, и пусть С5 = {7: 7 = i©ji, [5gС}.
Тогда, если С является <п, <1>-кодом и р (a, < d, то
СаПСр= 0. В самом деле, пусть и S' = S©p,
7'= 7© 5. Тогда р_(7, §) = р (5©7'.?©^) = 11а©7'©3©^11 =
= || (я © ₽) © (7'© §') || =/= О, так как в противном случае я©р =
= 7'©5' и, следовательно, р (я, р) = р (7', S'). Но р (а, p)<d,
а Р (Y. §') > <*, поскольку 7', Отсюда и вытекает утвер-
ждение.
1.27. Вытекает из 1.26 о учетом того, что в любой (d—1)-
мерной грани куба В” попарные расстояния между вершинами
не превосходят d—1, а число вершин равно 2й *1.
§ 2
2.2. Линейно независимой системой является, например,
В\. Если s векторов из В” линейно независимы, то все их комби-
нации вида (1) представляют собой попарно различные векторы.
Если бы нашлось подмножество, состоящее из ra-j-l линейно не-
зависимых векторов, то имели бы равенство |Б”|=2"+1.
2.4. Вытекает из того, что (п, Ь)-код является ft-мерным
подпространством В”, т. е. максимальное число линейно неза-
висимых векторов в нем равно к и всякая линейная комбинация
кодовых векторов принадлежит коду.
2.5. Если в коде существует вектор нечетного веса, то по-
ловина кодовых слов имеет нечетный вес, а другая половина —
четный. В противном случае все векторы имеют четный вес.
Первое утверждение вытекает из того, что число линейных ком-
бинаций, в которые входит заданный вектор нечетного веса,
равно числу тех комбинаций, в которых он отсутствует. Все
комбинации разбиваются на пары, в которых ровно одна имеет
нечетный вес.
2.6. Выбрать ненулевой вектор в В” можно 2я—1 способами.
Если выбраны i линейно независимых векторов, то соответствую-
328
щее подпространство имеет 2* векторов. Всякий вектор из до-
полнения к этому подпространству составляет с i выбранными
векторами линейно независимое множество, а всякий вектор из
подпространства выражается линейной комбинацией выбранных
векторов. Таким образом, выбрать (г-[-1)-й вектор можно 2я—2*
способами.
2.7. См. 2.6. 2.8. 2я-1. 2.10. Вэрно.
2.11. 1) т (С (Я))=8, d (С (Я))=2; 5) т (С (Я))=32,
d (С (Я))=7.
2.14. Порождающую матрицу М (С) (я, Л)-кода С можно
привести к виду (I^P) путем замены строк их линейными комбина*
циями и перестановки столбцов. Если вектор а ортогонален
каждой строке матрицы М (С), то вектор р, полученный из а
соответствующей перестановкой координат, ортогонален каждой
строке матрицы М (С), и обратно. Одна из порождающих матриц
кода С*, двойственного к коду С, порожденному матрицей
(7fcP), имеет вид (рТ1п-ь), т. е. С* является (п, п — /с)-кодом. От-
сюда вытекает, что и код С*, двойственный к С, является (п,п—к)-
кодом.
2.15. Аналогично 2.5.
2.16. Очевидно, что кодовое расстояние d не меньше мини-
мального веса кодового вектора. Если р (а, Р) < d для неко-
торых кодовых слов а, р, то, поскольку а © р также является
кодовым вектором и р (б, а © р)< d, приходим к противоречию
о условием.
2.17. Вытекает из 2.15 и 2.16.
1
2.18. Число единиц в матрице кода С равно | С | п;
с другой стороны, это число не меньше d (| С[ — 1).
2.20. Пусть a=(alt. . ., а„) — вектор веса d, ортогональный
к матрице Я. Обозначим i-й столбец матрицы Я через h{. Из ор-
тогональности а к каждой строке матрицы Я вытекает, что
»
g Отсюда вытекает соотношение линейной зависимости
<=1
между теми столбцами h{, которые входят в линейную комбина-
цию. Следовательно, каждому а веса d из нулевого пространства
матрицы Я соответствует совокупность d линейно зависимых
столбцов этой матрицы. Таким образом, если каждые d—1 столб-
цов матрицы Я линейно независимы, то минимальный вес кодо-
вого вектора не меньше d, и обратно, если существует множество
из d—1 линейно зависимых строк, то существует вектор веса
меньше d в ортогональном подпространстве.
329
2.21. Следствие 2.20.
2.24. 1) Из 2.18 вытекает, что g (9, 5) 10. Нетрудно по-
строить линейный <9, 5>-код мощности 4. Отсюда g (9, 5) £
f {4, 8 }. Предположим, что С — линейный <9, б^код мощности 8.
Тогда четыре кодовых вектора имеют нечетный вес. Никакие
два из этих четырех не лежат вне Bf. Но среди трех векторов из
В1 всегда существуют два, расстояние между которыми не
больше 4.
§ 3
3.4. Рассмотреть код {а, ааЬЪ, ЪЪ}.
3.8. См. 3.7.
3.10. Число слов длины, меньшей чем I, в fc-буквенном ал-
2i-i к1________________1
( Отсюда, если к1 — 1<т (к—1),
то в М. существует слово длины, не меньшей logt(l-|-m (Zc—1)).
3.11. 1) Провести доказательство индукцией по п. 2) Для
всякого разделимого кода существует префиксный код с тем же
набором длин кодовых слов (см. [10], раздел 5).
3.18. 1) Провести доказательство индукцией по т.
3.19. Вытекает из 3.18.
3.22. 1) Пусть С= {»!,. . ., } — двоичный префиксный
код и максимальная длина кодового слова равна п. Пусть ю=
=«!> . . аХ(ю) — слово из С. Пусть 7=(yi,. - Тя) — вектор,
в котором т< = а<, 1 = 1, Х(ю), а в остальных координатах стоят
прочерки. Тогда вектор 7 является кодом (n—X (ш))-мерной
грани куба В. Из префиксности кода вытекает, что грани, со-
ответствующие различным кодовым словам, не пересекаются.
т
Отсюда 2 2Я-Х^“’У) < 2я. 2) Из полноты кода вытекает, что для
/=1
каждого а £ В” существует кодовое слово и>, являющееся пре-
фиксом а. Это означает, что набор а содержится в грани, соот-
ветствующей слову w. Из префиксности кода вытекает, что грани,
соответствующие различным кодовым словам, не пересекаются.
Таким образом, совокупность граней, соответствующих словам
полного префиксного кода, задают разбиение куба В” на непе-
ресекающиеся грани. Отсюда вытекает равенство. 3) Доказатель-
ство аналогично 1.1.34.
3.23. 1) Верно. Утверждение вытекает из того, что вся-
кий оптимальный код является полным префиксным кодом.
3.24. Индукция по т.
830
3.25. Префиксный код с длинами кодовых слов ..., Хм
существует тогда и только тогда, когда Sjli 2-Х< < 1 (см. 3.22).
т
Отсюда Zm=min2 ГД® минимум берется по всем сово-
купностям {X,, . .Xffl} натуральных чисел, удовлетворяющих
m т
условию 2~х* < !• Минимум 2 *< достигается на таких
•=i i=i
совокупностях {Хп . . Хт}, что |Х( —Ху|<1, 1 < I, ] < т.
В самом деле, если существуют такие X,-, Xу, что X,- — Ху > 2,
т
то после замены X,- на — 1 и Kj на Ху + 1 величина 2
»=1
т
не изменяется, а условие У 2-х< 1 остается выполненным.
•=1
Пусть {Xlt .. ., Xm} — совокупность чисел такая, что Х^ = Х
при i = l, т — г, Х< = Х-ф1 при m — г < г < m, X — целое,
m
Тогда 2 + г> а условие принимает вид пг2~х — r2**-1 < 1.
*=1
Из условия вытекает, что k > (log2 т) — 1, и, следовательно,
т
2 > т 11о£а т1-
4=1
3.27. 1) Для т = 3, полагая, что ру > рг > ра > 0, имеем
L (Р) = Pi + 2р3 -|-2р3= 1 4- р2 + р3 > 1. Далее утверждение
вытекает из того, что при операции расширения стоимость
кода не уменьшается. 2) Для заданных е>0 и т>2 рас-
7 8 6 \
смотреть распределение Р = (1—о, , . . ., w ), где
е
° = ] log3 m | •
ГЛАВА VI
§ 1
1.1. 1) Не является, гак как выходной сигнал в момент
времени t зависит от входного сигнала в следующий момент вре-
мени. 3) Является.
1.2, 3) Не является. 4) Является.
1.3. 2) Является. 3) Является. 5) Является: выход в мо-
мент времени t равен отрицанию входа в этот же момент времени.
1.4. 2) Не является. 4) Не является.
331
1.5. 1) Доопределить до детерминированной функции
нельзя. 2) Функция ср допускает доопределение до детермини-
рованной функции. 4) Доопределение возможно.
1.6. 1) Достаточно рассмотреть функцию
„ .fi". если Х2 = б“,
? *’ 2 [xf, если Х2^б“ и Х1 = £~.
1.9. 2) Вес функции ср равен 2. 1.10. 1) Эквивалентны.
2) Не эквивалентны. 1.11. 2) Является. Например,
при s = 1 и 2* = 0. 3) Не является. 1.12.1) Является. Вес равен4.
3) Является. Вес равен 7. 1.13. 2) Если г=3, то в качестве под-
ходящей функции можно взять <р (х“)=<3/4>.
1.16. При г=3 в качестве такой функции можно взять
v («) = Iх (0 © х К — 1)) V К — 1), * > 2.
1.18. См. указание к задаче 1.6, 1).
1.20. 2) Для получения ответа достаточно рассмотреть функ-
цию
ср (£ш) =00а; (2) х (3).. ,х (£) •..
1.22. Является порожденным оператором.
1.24. 2) Если | А | = 1 и | В | > 2, то | Фх< в | = с. Если | В | =
— 1 и | А | > 1, то | Ф4, я | = 1.
1.25. 1) Если | А | > 1, то каждый класс Кj (s) имеет мощ-
ность с. 2) Число различных классов равно | А |*.
1.26. 2) Если | В | = 1 и | А | > 1, то | Ф4 в | = 1.
§ 2
2.1. 4) Канонические уравнения имеют следующий вид:
, у (t) = (x(t) V -1),
I Я (t) = (х (t) £ (t)) д (t — 1),
I g(0)=0;
входной сигнал x (f) можно опустить, так как функция р зависит
от него несущественно.
2.2. 1) Оператор можно доопределить так, что получится
о.-д. оператор веса 4, описываемый такими каноническими урав-
нениями:
y(t} — £ (4) g, (t — 1) g2 (t — 1) ©дг (t — 1) © g2 (t — 1),
gi(t)=m (x(t), ?i(t —1), g2 (t —1)) ©*(0©3i (« — !),
g2 (t)=~£ (t) (fr (t - 1) V <h (t - 1)) © 3i (t - 1) © g, (t - 1),
3i (°) “ Si (°) " °-
332
2.3. 4) Вес оператора равен 3 (состояния, отвечающие па-
рам (qlt g2)=(l, 0) и (gn g2)=(l, 1), можно отождествить).
2.4. Каждой функции веса и> (из указанного множества
о.-д. функций) соответствует каноническая таблица, содержащая
и-]-1 «входных» столбцов (включается также столбец, описываю-
щий состояние функции) и т-|-1 «выходных» столбцов (здесь тоже
учитывается функция переходов). «Входных» наборов в этой
таблице u’/с’1. На «выходе» в таблице должны быть какие-то на-
боры из множества, содержащего элементов («выходных»
наборов). Для получения требуемой верхней оценки надо счи-
тать, что каждому «входному» набору можно сопоставить любой
«выходной» набор.
2.8. 3) Канонические уравнения оператора ф имеют вид
y(t)=q(t — 1),
g («)=?(« — !),
g (0)=0,
т. е. оператор ф — автономный.
2.9. 1) Канонические уравнения оператора, полученного
из оператора введением обратной связи по переменным xi и
ylt выглядят так:
У' (С =1>
g' (t) = xl (t)r3 (t)q’(t —1),
(0) = 0-
2.10. 1) Вес оператора равен 2.
2.11. 1) В качестве <р можно взять следующий о.-д. опе-
ратор:
y(t) = zi (t) V5(t —1).
g(t) = Xl (t) ©x2 («),
g(0)=0.
2.14. 1) и 2) Рассмотреть оператор «,(^3). 5) Полезно ис-
следовать оператор <р8(?=о)’ ГД0 ?=о ~ оператор, порожденный
константой 0.
2.15. 3) Вес суперпозиции равен 4. 2.16. 2) Оператор —
автономный. 3) Оператор не является автономным. 2.19. 2) Та-
кая схема существует.
2.22. Изобразите сначала всевозможные трехвершинные
орграфы с нумерованными вершинами, удовлетворяющие ус-
ловию в) и такие, что полустепень исхода каждой вершины в них
равна 2. В качестве номеров для вершин орграфов можно взять
333
цифры О, 1, 2. Вершину, помеченную цифрой 0, удобно считать
начальной. Затем надо «нагрузить» всевозможными допустимыми
способами дуги каждого из построенных орграфов — так, чтобы
получались диаграммы Мура каких-то о.-д. операторов.
§ 3
3.1. 1) М — замкнутый класс. 2) Множество М не является
замкнутым классом.
3.3. Индукцией по числу задержек можно показать, что
любой оператор ф из [<?0, <ра]^ имеющий один вход, преобразу-
ет слово 0“ либо в слово вида у (1).. .у (п9) [0|ш, либо в слово
вида у (1) ... у (п0) [1 Г, ГД0 ио — Длина предпериода (зависящая
от выбора оператора ф).
3.7. 1) Система не полна. 2) и 3) Системы — полные.
3.8. 2) {?3(Х), ?Л(х)(Х), XJ}.
3.10. Доказательство этого утверждения можно провести
так. Пусть М— замкнутый класс в Ф(й), отличный от всего
множества Ф(й.). Предположим, что М — непредполный класс,
и рассмотрим совокупность всех таких подмножеств М' из
Ф(А}\Л/, которые удовлетворяют условию: \с Фtkv
Эта совокупность не пуста. Выберем в ней какую-либо макси-
мальную цепь (по включению), существование которой можно
установить либо с помощью аксиомы Цермело, либо, учитывая
счетность множества Ф(А),— непосредственно (упорядочив по
типу натурального ряда множество Ф(Й)\Л/). Объединение
всех множеств выбранной максимальной цепи обозначим через
Мо. Тогда М(JМо — предполный класс вФ(/г). При доказатель-
стве существенно используется тот факт, что в множестве
существует конечная полная система относительно совокупно-
сти операций 6 = {ОХ, О2, О3, О4, 5},
3.13. Этот факт можно доказать почти так же, как уста-
навливалась справедливость аналогичного утверждения в ал-
гебре логики (см. задачу II. 1.16).
3.14. Да, существует (см. задачу 3.13 и П.1.25). 3.15. Ср.
с задачей И.1.17,
3.16. При к > 3 утверждение непосредственно следует из
соответствующего результата в Рк. В общем случае (при к > 2)
можно использовать подмножества автономных операторов
3.17. Счетная. 3.19. Эта мощность — континуальная.
3.20. Полезно использовать «мощностные соображения» —
сравнить мощности соответствующих множеств.
334
ГЛАВА VII
§ 1
1.1. 1) а) Т (Р)=130212. б) Машина Т не применима
к слову 13013. в) Т (Р)=10 [01]21.
1.2. 4) Программа одной из возможных машин имеет вид
1.4. 3) Одна из машин Тьюринга, переводящая конфигура-
цию Кх в Ко, задается следующей программой:
qfiqfiR q^iq^L
д»Одвоя
ga0gs17? дБ1дгБ1Ь
д21д21Я gelg70P
gsOg4l£ g7Og0Ofl
g4OgBOL g7lgilH
1.5. 1) Можно поступить так: в программе машины Тьюрин-
га заменить каждую команду вида q^q^S (где а и Р принад-
лежат внешнему алфавиту А) на | А Ц- 1 команд: q^q'^R,
q'^q^L ("t пробегает весь алфавит 4); д', —новое состояние
(для каждого состояния qj — свое).
1.7. Для построения машины Тт достаточно добавить т до-
полнительных (новых) состояний gj, ..., q'm и «пополнить» про-
грамму машины Т, например, такими командами: q^aq^aS, ...
• • •, q'ma9ma^> ГДО а — какой-то фиксированный символ из внеш-
него алфавита.
1.9. 1) а) Композиция ТгТ2 к слову 130212 не применима,
б) TiTj применима к слову 1*01, и результат применения есть
10103!2.
1.10. 1) а) Указанная итерация к словам вида I3* (k > 1)
не применима, б) Не применима она и к словам вида 1зА+1 (к >
> 1). в) Итерация применима к любому слову вида 13*+а (к > 1),
и в результате получается слово 1.
1,11. 1) а) Г (Р) —10*1. б) Т(Р) = 1»01.
335
1.14. 3) Одна из возможных машин Тьюринга:
?10?о0Я ?40?61£
?iigaO-R ?41?41Д
?20?01S ?s0g30L
?21?»0Я ?5i?4il
?30?40Л ?в0?10Я
1.16. 3) Вот одна из возможных машин:
gjOgol£ ?31?40Я
gjlgaOfl ?40?40S
g,Og3O5 ?41?40Я
g2lg30fl ?60711Л
?a0?30S ?61?41S
1.17. 1) f (x}=x+l, f (x, y)=x-f-y-}-2.
1.18. Если считать, как обычно, что машины начинают ра-
ботать в состоянии ?! и в начальный момент обозревается самая
левая единица кода числа х, то указанные в условии задачи ма-
шины могут вычислять только одну из следующих трех функций:
х, х—1 и нигде не определенную функцию.
1.19. Да, это утверждение истинно.
1.20. 1) При фиксированном (конечном!) множестве состоя-
ний существует только конечное число попарно неэквивалент-
ных машин Тьюринга (с заданным внешним алфавитом). 2) Суще-
ствует такое I, что, каково бы ни было п > 1, подмножество
всех n-местных функций в М содержит не более чем I элементов.
§ 2
2.1. 2) x^-j-x2—sgx2.
2.2. 1) Можно доказать сначала примитивную рекурсив-
ность функций х1—хг и х2, а затем применить операцию супер-
позиции. «Прямое доказательство» примитивной рекурсивности
функции g (х)-х2 выглядит так:
р(0) = 0,
I g + !) = (х, g (*)) = х2 + 2х + 1,
т. е. Aj (х, у) = 2х + у + 1;
1 Aj (х, 0) = 2х + 1 = g} (х),
I *1 (х, У + 1) = « (х, у)) = (2х 4- у + 1) -J- 1;
( ?,(0)-1,
I gi (х + 1) = (х, gi (х)) = 2х + 3,
336
т. е. Л2 (х, у) = у + 2;
( h2 (х, 0) = 2,
( Л2 (х, у + 1) = s (fe2 (х, у)) = (у 2) 4- 1.
2.5. / (х, у) = sg x.g](j»)4-^2(x-^l).sgx-sg^4-
+ ё'з(г— 1. 1/ — 1) • sgx • sgy.
2-7. 2) Ря,{^1/21) = 2х1. 4) p.Xi (х, хг) = (х, 4- х2) sg х„
Р-л, (xi *а) — *1 — ха-
2.8. 4) /(х1( х2) = х, (1 -1- х2).
2.9. Нет, неверно. 2.10. 1) Нельзя. 2) l-|-sgx. 2.12. Все
эти классы счетно-бесконечные. 2.17. Нет, неверно: функция
f2 (х, у) может быть даже тождественно равна 0. 2.18. 1) Нет,
неверно. 2.19. 3) Справедливо. 4) Справедливо.
2.20. 1) Да, может быть верным. 2) Это утверждение ложно
при всякой функции Л из Aop\Anp. 3) Утверждение спра-
ведливо для некоторых функций и /2 из множества
*оР \ ^пр*
2.21. 1) Нет, не всегда. 2) Это включение ложно при вся-
кой функции / (х) из КОр\7СПр. 3) Да, соотношение справед-
ливо для любой функции / (х) из Кор \ А1|р.
2.24. 2) Да, может. Пример. / (х, у) = х — у. 2.26. Да,
верно.
§3
3.1. а) Вытекает из того, что в 7Гпр существует функция,
принимающая все значения.
3.2. Всякой примитивно рекурсивной функции можно со-
поставить бесконечное множество термов, отражающих способ
получения функции из простейших функций.
3.3. Если существует частично рекурсивная универсальная
функция F (х0, хи. . ., х„), то она всюду определена. Тогда функ-
ция F (х1( хп х2,. . ., хп)-|-1 общерекурсивна и имеет некоторый
номер у в нумерации, отвечающей универсальной функции
/чл+1). Но тогда F (у, у,. . .. y)=F (у, у,. . ., у)4-1.
3.6. Провести доказательство методом «диагонализации».
3.7. 1)—4) Нет. 5) Да. 3.8. Аналогично 3.3.
3.11. Рассмотреть функцию
{/ (х), если Л (х) = 0,
12 г- П. Гаврилов, А. А. Сапоженко 337
312. Рассмотреть последовательность а0, а„. . такую,
что а,= 1, если <f( (i) определено, а;=0, если (г) не определено,
1=0, 1,. . .
3.13. Для всякого автономного конечного автомата его
выходная последовательность является квазипериодической.
3.15. Например, инвертирование слова. )
3.21. 2) Вытекает, из того, что существует не более cSl^P
различных конфигураций длины ST(P) для некоторого с, за-
висящего от алфавита состояний и внешнего алфавита машины Т.
Если какая-то конфигурация повторяется, то машина Т работает
бесконечное время.
ГЛАВА VIII
§ 1
1.1. 1) Каждый из членов перестановки с повторениями
может быть выбран независимо от других п способами. Поэтому
Р (л, т)=лг. 2) Первый из членов (л, ^-перестановки можно вы-
брать п способами. Если i элементов уже выбраны, то (г-|-1)-й
элемент можно выбрать п—I способами. Применяя несколько
раз правило произведения, получим Р (л, г)=(л)г, п > г.
3) Достаточно заметить, что из каждого (л, г)-сочетания путем
г! перестановок его членов можно получить г! различных (л, г)-
перестановок и каждая (п, ^-перестановка может быть получена
таким путем. 4) Каждому (п, г)-сочотаншо А с повторениями, со-
ставленному из элементов множества U— {ап . . ., а,,}, поставим
в соответствие вектор 5 (А) длины n-f-r-. l из г нулей и п—1 еди-
ниц, такой, что число нулей, находящихся между ((—1)-й и
г-й единицами, равно числу элементов а,, входящих в сочета-
ние A, i = 2, п — 1, а число нулей, стоящих перед первой едини-
цей (после (л—1)-й единицы), равно числу элементов ал (соот-
ветственно элементов а„), входящих я сочетание А. Это соот-
ветствие между сочетаниями и векторами взаимно однозначно.
С другой стороны, число векторов с л—1 единицами и г нулями
равно числу (л—1)-элементных подмножеств (и-|-г—1)-элемент-
/п -|- г — 1\
ного множества. Это число равно I у*
1.2. 1) Л»; 2) к. к,...к„; 3)^. 1.3. 1) 2«"; 2) (2М)Я.
1.4. Для каждого л > 1 понадобится п • 10я*1 цифр для каждой от-
личной от нуля цифры и (л — 1) • 10”*1 нулей. 1,5. 2Р+*3П~*'-* — 1.
338
1.6. 1) 147; 2) 126; 3) 300 + 300 • 299 + 300 • 299 • 298 =
= 26820600, если имена различаются, и 300 + 3002 + 3003, если
имена не обязательно различны.
1.7,
1.8. 1) (1 + (1 + я2) ... (1 + аг). Каждому делителю pj1...
... р?г, i — 1, г, можно сопостапить вектор (Рп ...
г 1 _ pVc-l
...,РГ); 2) 2Г; 3) ТТ —:----. Раскрыв скобки в выражении
fc=i 1 Рк
(1 + Pi + • • • + Р?) • • • (1 + Рг + • • + Ргг)> убедиться, что каж-
дый делитель присутствует в сумме ровно один раз.
1.9.1)
\р— h — к) h 1 к ! \р— h — к)
1.10. 1) [П Число способов равно числу двоичных
векторов длипы п-}-к—1 с п единицами и к—1 нулями. Соответ-
ствие устанавливается так: каждой сумме сопоставляется век-
тор, такой, что первое слагаемое в сумме равно числу единиц,
стоящих перед первым нулем в векторе, второе слагаемое —
числу единиц, стоящих между первым и вторым нулями, и т. д.
2) । j. Поместим к единиц в промежутки между нулями, по
одной единице в каждый промежуток (места левее первого нуля
и правее последнего тоже считаются промежутками). Остальные
п—к единиц распределяются произвольно. Задача свелась к пре
дыдущей.
I, см. задачу 1.10, 2);
, свести
свести задачу
к 1.10, 1).
1.12.
,2
1.14.
1) к !; 2) ( ) . к !; 3) (n)* (m)fc; 4)
\PJ Aj I. . . ti9\
1) 4 (га — 4); 2) 4 (га - 1) га; 3) 24га (га — 1); 4) 4
/4га — 4\ /п -
5) 45 (га — 4); 6) 4га [ ); 7) 6 • 43 • га I V
\ 2 / \ 3 /
12*
339
1.15. 5) Использовать 3).
/п\
\k J ___ п — + 1
1.16. 3) Рассмотреть отношение ----г-----------• Это
(л-1)
Гп1 , - ЪГ
отношение больше 1 при к < и меньше 1 при к > 1 .
5) Если в сумме присутствуют два биномиальных коэффициента
(П{\ (пЛ <
I , и I J , такие, что п{ — п.->1, то, заменив их на
\«/ \k ) J
I j и I ' I соответственно, получим сумму, меньшую,
чем исходная.
[т 1
_ 1) ; J- Пусть
уже определены коэффициенты а-п-г, • тогда
“я-(1+1) =
Гт — (zz — 1) ! — (п — 2) ! — — а^( (п — t) |~|
“L („_/_!) I ]•
Единственность представления докажем от противного. Пусть
некоторому т соответствуют два вектора 5 (т) = (а^ ..., а^)
и f)(m) = (31, Пусть / — наибольший из номеров раз-
рядов, в которых векторы различаются. Без ограничения общ-
ности можно считать, что Имеем
0=2 ₽<* 1 — 2 “i1' 1 > (?/—“/)/• —
«=1 *=1
У-1 /-1
— 2 а*г * > j'— S1 ’11 > °*
•=1 »=1
Пришли к противоречию. 2) (1,1,2), (1,2,3), (1, 0, 2, 1).
3) at — никакому, й2 соответствует числу 109. 4) Сопоставим каж-
дому целому числу т (0 < т <Г п !) перестановку г.т чисел 1, ...
...,и. С помощью вектора 5 (m) = (ctj, ..., a„_i) укажем места
чисел 1...п в перестановке ят. Число 1 поставим на место
с номером 1 + a„_t. Пусть числа 1, .... I, 1=1, п — 1 уже рас-
ставлены. Остается свободными п — i мест. Пронумеруем сво-
бодные места числами 1, 2, ...,п — I. Число «-(-1 поставим на
место с номером 1 + После того как числа 1, 2,,.,
340
п — 1 расставлены, место числа п в г.т определяется одно-
значно. П р и м е р. т =» 15, п = 4, a (m) = (1, 1,2),пт = (4, 2, 1,3).
Алгоритм бесповторного перечисления всех перестановок заклю-
чается в последовательном порождении чисел т (0 < т < п !)
и соответствующих им перестановок r.m.
1.18. 1) Координаты вектора 3 (т) = (31..3*) определя-
ются следующим образом: 31 — наибольшее целое, такое, что
т Р*\ Если 3], ..., 3,- уже определены, то 3<+1 — наибольшее
целое, такое, что т
>
\ Единственность доказывается так же, как в 1.17,
i /
1) . 2) 23. 3) (6,4, 1,0). 4) Сопоставим каждому целому числу
двоичный вектор «т = (ах, ..., а„) с помощью
вектора р (т) = (31. Зг.3fc) (см- !))• Пусть единицы в 5т
стоят в координатах с номерами 314-1, За + 1 • • • > 3fc + 1 • При-
мер: т = 17, п = 6, к = 3, 3 (т) = (5, 4, 1), ат = (010011). Алго-
ритм заключается в порождении чисел т и соответствующих
им векторов. Другой алгоритм. Начнем перечисление с вектора
(!,...,!, 0, ...,0), первые к координат которого равны 1, ос-
тальные— нулю. Рассмотрим произвольный двоичный вектор
а = (а,, ..., ап) и укажем следующий за ним в процессе перечис-
ления вектор а' = (aj, ..., а'). Найдем наименьшее число ], такое,
что ау = 1, a?+i = 0. Тогда положим а' =0, = 1 (сдвигаем
единицу вправо), а все единицы, расположенные в координатах
с номерами, меньшими, чем /, сдвинем влево, насколько это
возможно. Пример. а=(001Ю1), / = 4, а'= (100011).
1.20. 2) Положить в (1) 1 = —1. 3) Продифференцировать
и положить t — 1. 6) Проинтегрировать тождество (1) от 0
1. 7) См. 6). 8) Провести индукцию по п с использованием
(1)
ДО
7);
f 1 — (1 — 1)”
другой спосоо: рассмотреть 1 ----j----dt. 9) Сравнить ко-
fl
эффициенты при tk в левой и правой частях тождества (1 + t)n X
X (1 + t)m= (1 t)n+,n. 10) В 9) положить т = п. 13) Исполь-
зовать тождество
|. 14) Сводится к 9).
(1 + 1)" + (1 — 1)я = 2";
к
341
в последнем случав использовано тождество
“Г1 2к.’Я
2^
v=0
т, если п кратно т,
О в противном случае.
1.22. 1) у[(1 + V3 )’+(!- vd)"].
2) (1 + 7=2)" + 1 (1 +1 7~~^)” - (1 - /=2)” - 1 (1 - 1 7=2)"
4^=2
3) Решение. Используя тождество задачи 1.15, 2), пре-
образуем исходное выражение к
г—1 __ 2&+1—г . .
Рассмотрим случай, когда г четно (случай нечетного г аналоги-
чен). Положим 2м — 2k — г. Тогда придем к выражению
= (.jfv ("j (i + v^^-d-^r^
342
1.24. 2) При |4 | < 1 ряд сходится. Тождество устанавли-
вается путем разложения функции / (4) = (1 + 4)“ по степеням 4.
г * fik} (°) (а\
Следует убедиться в том, что —— = 11
(— а\ (—в) (—а —!)...(—а —Л + 1)
3)UJ= *1
а + к — 1
. к
тождество
_/в+Ц_/в п\ 5) Воспользоваться тождеством (1 + 4)SX
\г + 1 / \г + 1 / *
X (1 + t)b = (1 + 4)а+д. 6) Вытекает из 5), если положить 6 =
= — 1. 7) Следствие тождеств задач 3) и 5). 9) Использовать
/2к\ (__1/2\
-4)fc I ) = ( |. 10) и 11) См. задачу 1.22.
\ к ) \ к )
(тп) I n! „
1.25. (т I)”’* 2) к~I Fl’ 3) ПОД0™™11 ДВУМЯ спосо-
бами число Ля(й1.....к,) упорядочений п предметов, среди
которых кг предметов первого типа, к2 предметов второго типа и
т. д., наконец, к, предметов типа «.Первый способ. Выберем
сначала среди п мест к2 мест для расположения предметов первого
(ге \
, | способами. Затем выберем к2 мест
kiJ
для расположения предметов второго типа. Это можно сделать
(п — кл .
I способами и т. д. Пользуясь «правилом произведения»,
получим, что
А„(ки
п — кг — ... — к.
к,
Второй способ. Подсчитаем число упорядочений га попарно
различных предметов. Будем считать, что предметы разбиты
на s групп так, что в i-й группе А,-предметов (4 = 1, s). Выбор
к2 мест для предметов первой группы, к2 мест для второй и
т. д. можно осуществить A„(klt ...,kt) способами. В группе 4
предметы можно расположить к( способами (4 = 1, s). Отсюда
А„ (klt ..., к,) Ajl ... к, 1 = п I
343
§2
2.1. 1) Доказательство. Прип=1 = N — N (otj) =
= So — Sj и формула (2), очевидно, справедлива. Пусть формула
справедлива для п — 1 свойств и пусть Д' (а,, ..., a„_j) — число
предметов, не обладающих ни одним из свойств ....ап-1-
Имеем:
Я—1
^о=^(«1. = Л^-2 ^(“4)4- 2 «/)-
•=i
— 2 N aJ’ “*) — ••• —
....а^). (♦)
Эта фор мула справедлива и для совокупности предметов, обла-
дающих свойством ап:
N (а1...“я-1> ая) = Л' (аи) — 2 а») + • • • +
+ уу (а1....а^, а„), (**)
где N (а1г ..., а^, а„) — число предметов, обладающих свойством
ап, но не обладающих ни одним из свойств Ясно,
что
(31....ая-1, ая) = W (alt ..., a„_,) - N (an ..., a^u a„).
Вычитая формулу (**) из (*), получаем формулу (2). 2) Дока-
зательство индукцией по числу свойств. 3) Заметив, что ftk+i =
провести индукцию по к. 4) Выведем, например,
(5) из (3). Полагая в (3) т = п, получим $„= S„ в соответствии
с (5). Пусть формула (5) верна для всех к п — 1, v > 1.
Заменим в (3) т на п — ч и, пользуясь индуктивным предпо-
ложением, подставим вместо 5„_,+s для любого й > 1 правую
часть равенства (5), в которой к заменено на п — v-\-k. Тогда
2 ( “К-
\ п — у 1 \п — v-4-к/
к=1 ' т=я—*+* 4 ‘ '
п т—я-j-v
л X? / т \ zv X? +
2i (-1) ( к )=
»я=я—v+l Л=1 '
- 2 (.2>
т=я—v
344
Тем самым формула (5) доказана. Формула (6) доказывается
аналогично (5). Докажем (7). Для этого достаточно убедиться
п
в том, что R (п, г) = 2(-1М j Sk > 0 для всех г. Вос-
к=г ''т
пользуемся формулой (5). Имеем
k=r ?==* ' '
2.2. Для к = 0, 1, 2, 3, 4 вероятности соответственно равны
2 £ £ £
8 ’ 3 ’ 4 ’ °’ 24"
2.3. 1) Число распределений предметов, при которых дан-
ные к ящиков остаются пустыми, равно (п — к)г, $к
X
%(п~к)г. Остается применить формулу (2). 2) Использовать
результат задачи 2.1,2). 3) Использовать формулу (4) из 2.1,3).
2.4. 1).20%; 2) 60%; 3) 70%.
2.5. 1) Решение. 50=13, St:=23, S2 = 12, 7^ = 0. По
формуле (2) 0=13 — 2312—S3, откуда 53 = 2; 2) 6; 3) 3.
2.6. 2) 542; 3) 734; 6) 53.
2.7. 1) 3я. Решение. Рассмотрим диаграмму Венна. Каж-
дый из п элементов множества U может принадлежать или не
X X
У
У
принадлежать каждому из множеств X, У, причем по условию
ХПУ = 0. Отсюда следует, что число искомых пар (X, У)
равно числу расположений п различных предметов но трем ящи-
кам (роль ящиков играют ячейки ХУ, ХУ, ХУ диаграммы).
Но число таких расположений равно, очевидно, 3я. 2) п2п.
345
3)3”. Указание. Заметить, что из условия следует, что
rnyn2u*nwuxnw = tf.
Таким образом, задача сводится к подсчету числа расположе-
ний элементов множества U по трем клеткам XYZ, XYZ и
XYZ соответствующей диаграммы.
4) 3._ п‘ + 7”+]б.2. + HjLta + ,
Решение. Из общего числа 3я пар (X, У), удовлетво-
ряющих условию задачи 1), следует исключить пары, при-
надлежащие множеству С = где Ло =
= {(Х, У): |Х| = 0}, Л1 = {(Х, У):
X------- \ |Х| = 1}, В0={(Х, У): | У | = 0}, В.=
(/Л /Л С\) ={(Х’ У): = Вз = «Х- у):
f—1 \ |У|=2}. Очевидно, что Ло[~)41 = 0,
I | j I 4? I В<ПВ/==0 (0<i</<2). Поэтому
А \ V7\ + + +
< А 47 ) +1в2|-М0ПВ0|-М0пв1|-МоПВ2|-
х-----------' -|Л1ЛВ0|-|41ПВ1|-Л1ПВ2| (ОМ. ри-
сунок). Нетрудно видеть, что | Л0|=2я
(га элементов множества U распределяются по клеткам ХУ иХУ.
Клетки ХУ и ХУ пусты так, как Х=0). Аналогично, | Л2 |=п-2',_*,
|B0|=2B,|Bi |=га.2я*1, | B2|=Q^2”_2. Имеем далее |Л0ПВ0|=1,
= *("-!). МоПВг| =
=(2)’1Л1ПВ2| = т1^ге 2 ^.Отсюда |С|=(п-|-2)2я+п(71—1)2я-»—
п (га2 + 3) „„ ,
—----2----— 1, а число искомых пар равно 3я — |С|.
5) 2га (2я—1). 6) (га + 2) 2я-1 — 4га — 2.
2.8. Подсчитаем число N„jJfc способов рассадки, при кото-
рых к данных враждующих пар не разъединены. Объединим
каждую из к заданных враждующих пар в один «объект».
Тогда имеется 2га — к объектов, которые можно расположить
(2га—А)! способами. В каждой из к заданных пар врагов
можно поменять местами. Таким образом, (V„ л = 2* (2га — А)1,
a Sk = (nk) NnJe. Применяя формулу (2), получим, что иско-
Я
мое число равно 2(-i)4*)2S(2"~a)I
fc=0
я
2.9. 2 (-1)* (2) (2« - к)к [(га - к) I]3.
/с=0
346
§ 3
3.2. 1) q + с23я; 2) q (/=3)" + (-1)” q (^=3)”; 3) q y-) +
(1 _ VFX”
+ <Ц----’’ 4)(-1)Я(с1 + с2ге); 5)(q + C2n)(-4)” + q(-2)”;
6) (—1)" (q + qn + c3n2).
3.3. 1) Общее решение имеет вид a„=q + q3”. Из на-
чальных условий имеем q-|-3c2 = 10, q-|-9c2 = 16, откуда
Ci = 7, с2 = 1. Таким образом, ап = 7 -|- 3я. 2) 3я 4-i” 4-(—’)”•
14 — Ь — 4с Ъ + с — 2а
3) <?i + с2п + с3 (—2)я, где q =--§------> с2 =---у---->
26 — с — а
q =-----jg--. 4) cos an.
о , , (!+₽ + ?)₽ —“(2+p) . m
0.4. l)a = i—:---:—, 0 ==------71—i---: Г5-----! 2) a =
' 1+p + 9 (1 + p + 9)2 ’ '
a a (—P — 4) 4- 2^ (p + 2) _ __a_ , ft ~ »
“2p+4’6~ 2 (2 4~ P)2 , d) a— 6 , 2
ft „ n (n — 1)
3.5. 1) 14----5--. Частное решение уравнения a^ —
•— an = n ищем в виде a* = n (an -f- 6). Подставив а* в исходное
n (n — 1)
соотношение, найдем, что a* =-----%--- Сделаем замену
n(n — 1)
an—-----2---+ ья> т0ГДа ьм-1 —ья = °- Отсюда ья=с> гДе
п(п — 1)
с—константа, и ап =------2--+ с- Из начальных условии
находим, что с=1. 2) —2 (—4)” +3 • 2я4-5".
Указание. Частное решение ищем в виде а* = с> 5я.
3) 0,5 4- 50 • 2я 4- 6,5 • 3я - 4п3 — 13п2 — 50л.
3.6. 1) Невырожденным является случай, когда либо
?i=/=0, либо р2 4= 0. Если ffi=p2 = 0, то, очевидно, аи=с1р'11,
1
6Я=М”. Пусть gj^O. Тогда bn= — (а^ — qaj, 6„+1 =
— ?1 Т1ап+1) •
Подставляя 6и+1 и Ь„ во второе соотноше-
ние, получим а^.2-]~ (—Р1 —q2) а„+1 +(р^ —p2q^ а„ = 0. За-
дача сведена к задаче 3.1. 2) а„= (5 4- 2п) 2я, 6Я= — (I 4- 2п) 2я.
3) а„= q 4- (— f)B+1 с2 + 5,5л, b„ = q 4- 0,5 4- (—1)” с2 4- 5,5».
3.7. 1) Индукция по п. При ге = 2 соотношение
F2+m = FiFm + верно для всех т > 1. Ин-
дуктивный переход п -> п 4- 1: Ея+1+т = Ея+т 4- Fn+m^ =
+ + F„^1Fm^1 — FnFm-}- F„+iFm+1. 2) Провести
347
индукцию по к с использованием 1). 4) Способ пред-
ставления. Выбираем наибольшее п1г такое, что f„ < N;
затем наибольшее пг, такое, что F п < N — Fп , и т. д. Одно"
значность и другие свойства представления доказываются
непосредственно или по индукции. 5) Указание. Найти
решение соотношения Fn+2 = F„+1 -f- Fn с начальными усло-
виями Fi = /?2=1. 6), 7), 8) Доказать индукцией по п.
3.8. 1) Производящей функцией последовательности ап
СО
является ряд 2 а^я. Если | at | < 1, то ряд сходится к функ-
я=0
ции A (£). Следовательно, при | at | < 1 функция A (t) является
производящей для (а”}. Экспоненциальной производящей
2Ш (“0" г.
. Этот
я=0
00
ряд сходится к функции eai при всех t. 2) Ряд 2 ntn, являю-
Я—1
щийся производящей функцией для а„=я, получается по-
00
членным дифференцированием ряда 2 tn и последующим
я=0
умножением на t. При 111 < 1 применение этих операций
допустимо и приводит к функции t (1 — t)-a. Экспоненциаль-
со со
2ntn V <я
гёТ ~ 1 '' тГГ = * ехР4 ‘
я=0 я=0
СО СО 00
3.9. 1) 4 (f) = 2 ant” = 2 И S e~Xxndx =
я=0 О
СО 00 со
= j (xt)n dx = j е~хЕ (xt) dx\
О я=0 О
со со
2) j e~xextdx = ~ j j e~uda = (1 — t)“x.
о о
3.11. 1) Умножим равенство а„ = Ь„ — Ь„_] на i" и про-
00
суммируем по п. В области сходимости рядов 2 ап*п и
я=0
348
co co co
2 bntn справедливы тождества 2 v = 2 (^-Vi)/n=
я=0 я=0 я=0
= 2 b”tn ~ 2 b«-itn== В <f) (1 — *)• 3) Заметить, что Ь„ —
п=0 я=1
= ая_! — а„. Отсюда В (/) = —А (() (1 — г) + а0, ад = В (1).
3.12. 1) Первый способ. Пусть С (<) — производящая
функция последовательности 1, 0, 0, ... По условию С (<) =
= 4(/)В(£). Следовательно, должны выполняться равенства
п
1 = а0Ь0, 0 = адЬ1 + а,Ьв, ..., О = 2 a«-ibi< ... Поскольку а„ =
•=о
6,=0, а для
п
(т\
= 11, то для всех п—1, 2, .
•=0
га = 0 о) Ь0 = 1. Последовательно находим &0 = 1, bt = —т,
гаг (т + 1) (гаг-|-2)
fe2 =----2---» ьз = —---------§--------• Индукцией по п не-
трудно показать, чтоЬя = ^ п ). Таким образом, В (Z)=(14-t)-m.
Второй способ. А (г) = (1 + £)”*, В (г) = [4 (г)]*1 = U + t)~m.
Отсюда 6Я = ^ 2) В (£) = 1—at, Ьо=1, bt = a, b„ = 0
при п > 2. 3) В (г) = (1 — Z)2, Ьй = й2 = 1, bt = —2, b„ = 0 при
н>3. 4) B(t) = (l +«2)'1. Ь2И=(-1)Я. Ь2„+1 = 0. 5) В(«) =
t 1 п (—1)ЯВ“
= ei । > bo : 11 = — -д > ^ги+1 = 0» » > Ъ Ь2п — п [ >
где В„—число Бернулли с номером га. 6) В (i) = Vl -j- t,
‘=(,“2)'.
3.14. р"; 2) 1; 3) (-Ц-С'2); 4)
5) о(._-„"_ь); <4Г(;;)»р"
*
(—m \ (—т\
п — 2J ~ \л — 3J 2Я*3’
1 (_ 1)»-1
9) (—Ю) ~2га — 1 * Указание- Воспользоваться
t
Sdx
I д.2 = arc tg t; И)
о
1 • 3 ..... (2га- 1) 1
2 • 4 ..... 2га ’ 2га + 1 ‘
349
Jdx 1
= arc sin t; 12) (-—2)я/- y„y2) ~l ПРИ
о —
n (-1)”'2
четном n, 0 — при нечетном n; 13) _|_ i'j~| ПРИ четном n,
re I (n — 1 \
0 — при нечетном re; 14) (—1)" _ 1 )•
3.15. 1) Сравним коэффициенты при t"'1 в тождество
(1 4- t)n (1 + t)~m~3 = (1 -)- с одной стороны, этот коэф-
фициент равен 2(relS)(-s-~2) = 2(_1)”1C)C + l)’
8 8
(п— т — 2\ . , ( т \ л ,т
ге — 1 ; = (—!) Vre — !/ Указание-
(?) (ге) = (ге )(”-")• 3) Рассмотреть тождество (1 - X
(—1)т
X (1 — f)-”-1 = tm (1 — t)”-"-1. 4) Рассмотреть тождество
[(1 4- t)n 4- (1 — 0я]2 = (14- О2" + (1 — О2" 4-2(1 — t2)”. 5) Рас-
смотреть тождество ((1 4- 0" 4- (1—1(1 + 0я — (1 — <)я1 =
= (1-Н)2к— (1 — t)2". 6) Рассмотреть тождество 2 (14-20я+**1Х
л==о
(1 4- 2t)w+1_(_£Z)*K
х (—t2)”*S: = (1 4-2i)”+1 1----ц --------и сравнить коэф-
фициенты при t2B+1.
3.16. 1) Умножая на «я+а и суммируя, получим A (t) =
= a2t — я0 4- pt A (t) — paot 4- qA (t) t3. 2) Представим A (t) в виде
+ Г=Т^ • Найдя c> и Сз' получим- что А (0 = X
( 4~ рвп 4“ ^1яв ®1 “1“ Ра0 "4“ ^-2^0 \ тт - хх
XI-----л—т—:------ —---<----------) • Найдя коэффициент при
\ 1 — 1 ~~ Л-2* /
t” в разложении А (г) в ряд по степеням t, получим выраже-
„ С1 С2
ние для ап. 3) Представим А (() в виде + ц___________Xt)2*
_ с, , с2 ао 4- (а1 — 2Х<г0) t
Из равенства (i_uF---------(1 - kt)2 найдем,
что Cj = — j- 4- 2<z0, с2 = — а0. Разлагая A (t) в ряд, получим
СО
Л(«) = 2 (c1V’4-c!(re4-1)W <2я = (ао + п(т-ао))^-
350
1 — t t
3.17. 3) A (/) =! _ 3f + p» в (t) = j-_ 3t + ta; 4) вывести
из 3), что
1 vT ( з + VF — 1 ( 3 — V5"\"
°я== 2V5 к 2 ) + 2V5' \ 2 ) •
i /з + v's’Y’ i /з - v'sY
bn~ \ 2 ) - v'H 2 ) •
3.18. 1) Умножая на t” и суммируя исходное соотношение,
получим A (t) — а0 = г Л2 (г).
3.19. 1) Пронумеруем вершины <п + 2)-угольника числами
1, 2, ...,«4-2 по часовой стрелке. Возможны два случая.
Первый случай. Через вершину п -|- 2 не проходит ни
одна диагональ. Тогда должна существовать диагональ между
вершинами 1 и п-j-l, а число способов разбиения равно а^.
Второй случай. Существует диагональ, исходящая из
вершины п -|- 2. Пусть к — наименьший номер, такой, что
вершина к -f- 1 соединена диагональю с вершиной n-f-2. Если
А > 2, то существует диагональ вида (1, к 4-1). Тогда число
разбиений исходного (п 4- 2)-угольника равно числу разбиений
(к 4- 1)-угольника с вершинами 1, 2,..., к 4- 1, умноженному на
число разбиений (п — к -|-2)-угольника с вершинами A-J- 1»
к 4- 2, ..., п 4- 2, т. е. равно ак~1ап-1с {2^к^п). Естественно
п
считать, что а0 = 1. Тогда имеем ап= У Так же, как
ь=1
1 Z2zi\ 1 (2п\
в задаче 3.18, находим, что а« = \ u / ’ а« = «+”1 \ п/
Решается аналогично задаче 1).
3.20. 1) Умножая на tn и Суммируя по п, получим для
СО
производящей функции А (г) = У, antn функциональное урав-
я=0
нение A2 (г) = А (2г). Будем искать его решение в виде
Л(г) = еа/. Эта функция, очевидно, удовлетворяет функцио-
нальному уравнению. Учитывая, что в] = 1, находим, что
1
д=1, откуда ая = ^-р. Единственность решения вытекает из
исходных соотношений. 4) с2и+1
(—1)”
= о. «г»=щр- («=0, 1,
3.22. 1) Из А (г) = (1 — qt) A (qt) вытекает, что a„ = anqn —
»(я+1) „
— откуда аи — д 2 Ц (s* —I)'1, 1, 2, ...,о0 = 1.
*=1
351
3.26. 1) и 2) S (п. к. I + 1) = 2(-1)"-’[С i !)-G+l)]X
я-f-l я
х (v+1+о*=^ (-i)"+i-’ (n t +n*+2(-1 )в*’ С)х
X (v + Z)ft= S (п 4* 1, Л, I) S (п, к, I). 4) Доказательство
индукцией по к с использованием 3). Для любых I и п>0
п
S (п, О, Z) = ^ (—l)’(v) = 0. Предположим, что утверждение
»=о
верно для некоторого к > 0, любых n >fc и любых I. Пусть
А + 1<п. Из 3) имеем S (п, Л 4-1, I) = (п1) S (п, к, I) 4*
4-п5(л—1, к, I). Поскольку A<n—1, то, в силу индук-
ционного предположения, S (п, к, l) = S(n— 1, к, Z)=0 и,
следовательно, S (п, A-f-l, Z)=0. 5) Использовать 3) и 4).
6) Использовать 3) и 5). 7) Следствие 2), 3) и 6).
3.27.1) Показать, что (Z) = t (1 — t)-1 и что (1 — nt) ая (Z) =
= (О •
§4
4.1. 1) Вытекает из того, что при п>2 и0<1<п
/л + 1\а
справедливы неравенства п < (i + 1) (n — Z) <1—л .
з)(1+1У=2©'‘-^21т<2+22-*<з- 4) п₽°-
fc=0 к=0 к=1
вести индукцию по п с использованием 3). 6) Использовать
. к. - о, 4- Яч 4“ • • • "4* п
неравенство Коши: у ... ак <-----------, af > О,
и тот факт, что среднее арифметическое множителей, стоящих
Я
в левой части неравенства, равно —
2п + 1
3
п (2и — 1) И ✓Зп 4-1
7) Положить ап=-----------------
:1
а показать, что!----
\ ая
(2п) П
пп
п I ’
к=0
4.2. 1) Использовать 4.1, 1) и 4.1, 4). 2) При доказатель-
пп
стве второго неравенства положить ак = и
{к)кк (п-к)«-*
«1
Л
352
( 1 у-*-1
, ак+1 v ‘ п — А — 1)
показать, что а, = 1, —— =------------------->1 при к <
n~i (2 (" + *>\ _ 2я + 1 (2п\ 2(2пЦ-1)4»
2 * 'К п +1 J n + 1 к« ./> 2 Vn (n-Н )/л + 1
4”+1
> - _=•; для второго неравенства использовать 4.1- 7).
4.4. 5) 2*G) = t(2«)* 4>5> Да‘ 2) Нет-
fc=l
4.6. 1) Da=^'^l(a{ — a)i>^ (а< —«)’>
«=1 а<: |<ч — а | > t
> btt\ 2) Указание. Оценить долю тех двоичных векторов
длины п, у которых число координат, равных единице,
I n I /- m 2B+1 — 1
удовлетворяет неравенству л — -у | > i vn . 3) п =
-2тттС)<2тС)< 2 i©<
k=° k—1 fc: |Л—я/2|< (10g,n)
1 fn\ 2n¥1
< (n/2)-V71ogan 2i \kj = n — 2 Vn Jog2 n • C“- 4Л’ 1} И 4>6, 2>‘
k—0
4.7. 1) Используя формулу (13), получим
©'fn nn (1 +O(l/n))
V2tA (n — k) kk (n — k)n~k
, , Yl 9
Положим ж = £-— А; тогда полученное выражение можно
переписать в виде
(П\ =__________ (1 +О(1/п))2”^________________
\kj « п *
Имеем далее
353
Отсюда
W ^Гп
. 2), 3) Переформулировка тео-
ремы Муавра—Лапласа. См. например: В. Феллер, Введе-
ние в теорию вероятностей и ее приложение, т. I,'«Мир», М.,
1967.
4.8. 2) Оценка сверху. Используя неравенства (13),
получаем
п 1 1 1 fl
(Хл) I ([хл) I < ^Х>Г" ехр(12л
_ —-—4-
12Хл 12[хл
1 1 I
360 (Хл)? + 360 ([xn)3J
Без ограничения общности можно считать, что X > ц. Тогда
1 ! 1 , 1 1 1
12л < 12Хл ’ 360 (Хл)3 + 360 (рл)3 180[х3п3 < 12(хл’ ОтеюДа
("„)< G (л, X). Нижняя оценка доказывается аналогично.
3) Используем нижнюю оценку из задачи 2). Если Хл > 3
1 1111 f 1 1
или р»>3, то ш^+12^<12 + зб = У’ но exp|~Tj>
> ~2~ • Если Хл < 3 и рл < 3, то 1 sg рл Хл < 2 и неравенство
проверяется непосредственно. При Хл = [хл = 1 имеем =
= G (л, X).
4) Оценка сверху Q) < (х”)2= 2Т^Т ("„)•
А'=г)л *=0
S-1 . к~г
4.9. 1) (n)k = nk Ц (1 — -0 = л*ехр 1н(1 — > но
•=° V=1
к—1 /с—1 со со к—1
24-4)-22Ш-
•=) •=! V=1 »=! j=l
*—1
2ki+1
v* = - -j-0 (к*). См.
>=i
4.13, 2).
354
4.12. Указание. Сумма 2 Цк) является верхней,
fc=n-J-l
a f (к) нижней интегральной суммой для j
Л=п „
4.15. 1) Разложим A (t) на простые дроби: A (t) =
С1
X! — t
4-т——;+i—:-|-B(£)> где В (I) — многочлен. Для
нахождения коэффициента сх умножим А (<) на Xt — t. Тогда
—Q (t)
(Xj — t)4 = — ... П₽и i==k*
—<? (Xi)
равна сь а правая — • p, у
Таким образом,
левая часть
—Q (М
с*- Р'^) •
Аналогично можно вычислить и коэффициенты c,-(i = 2, т).
Дробь 1 — ti ~k можно разложить в геометрическую прогрес-
оо т оо
сию С - $1=2 ОЭ" •Получаем 4 (°=2 й 2Ю’+
я=0 *=1 п=0
+ В (t). Отсюда для больших п а, ~ -рт + уи + ... + — ~
~ CiXf" *.
4.16. 1) ая~2«3”; 2) ап ~(- (у; 3)
х(у) 4) «2я = °> а2л+1~(—1)К2п+3; 5) Указание.
61* — 17г3 + 35i2 — 22t + 4 = 6 (t — — у) (f — 1 + i /з) X
X(t-l-i'/T), ав~Дз«.
4.17. 1) an — (— 3 (—2)”). 2) Пусть A (t) — ^a^n. Умно-
«=о
жая обе части соотношения на ta и складывая, получим
A (Z) — 1 = qtA (t) -f- pt (1 — i)"1 — ptA («)• Отсюда A (t) =
1 1 1 (q — p)n
= у (1 — t)-1 4- у (1 — (q — p) t)-1, ая= у — ------g------ll2‘
2n+1 / 2кп 4кц\
3) ая = 4^у (sin sia~)- 4) йя~Зя. 5) а„~л22я-8.
4.18. 1) Перепишем уравнение в виде x = lnt — In x (*).
Поскольку t->a>, то можно считать, что t >e и, следова-
355
тельно, х>1. Тогда из (») вытекает, что х < In t, т. е.
1 </ х < In t. Отсюда In х= О (In In t). Таким образом, x = lnt-{-
4- О (In Ini) при 1-»со. Логарифмируя, находим, что 1пх =
, / „71п1п1\\ , /lnlni\
= In In t + In 4- О t J J = In In t 4- О ln f J • Подстав-
ляя в (*), получим новое приближение: z=lni — In In t 4-
/ln In i\
Ч-О1- 1 1. Вновь логарифмируя и подставляя результат
в правую часть (*), получим еще одно приближение, дающее
требуемую точность (см. Н. Г. де Брейн, Асимптотические
методы в анализе, М., ИЛ, 1961).
4.19. Указание. Показать сначала, что /(i)=o(i) при
оо. Тогда исходное равенство можно будет записать в виде
— t 4- о (1) 4- О (1). Пользуясь этим равенством, показать,
что / (1) = о (1), и преобразовать исходное равенство в e*f(n =
In t f 1 \
= 14-0(1). Наконец, доказать, что f (t) = -у- 4- ОI I.
4.20. 1) G помощью соотношений (14) и (15) получаем, что
9 11
a3=i2g, a4 При n > 3 неравенство (15) можно пере-
17 / 323 \
писать в виде аи+а + ал ( ) • Отсюда вытекает,
что если ап < 1/8, то и anvi < 1/8 при п > 3. Пользуясь тем,
1
что ап < 1/8, выведем из (15) новое неравенство: а^.2 <2я+з4_
п 4- 1 1 {( 3 \и+2 п 4- 2 , \ /3 \в+2 1
4- 4»+i + 8 \\ 4 / 2В+2 / ^ \ 4 / 2 °я’ Отсюда
/3\”
по индукции а„ < 9(у 1 • Используя это новое приближение,
1 I 3 \в+2
выведем из (15) неравенство ап+2 < 2»+з 4~ 66аи ( 1 . Поль-
зуясь последним, получим, что ап = 2"*1 ^1 -|- О У}-
4.21. 1)
_ П~к -)-2*
— /с + 1 •
> [log2 Iog2 n],
чение f (п, к)
к = [log2 log2 п| -|- 1- 2) Тот же результат, что и в 1).
р /(», *4-1)
Рассмотрим отношение ак = —т~,--------гт—
1 \П, К)
Если к < [log2 log2 nJ, то если же к >
то ak<^i. Следовательно, максимальное зна-
достигается либо при к = [log2 log2 nJ, либо при
4.22. шах/(п, г, к) = 2~к^, min/(n, г, к) =2^j.
356
4.23. 1) Функция 2п~к + 22* как функция действительного
аргумента к выпукла вниз, причем минимум достигается при
& = log2(re— 2 log2 п) + ")» Отсюда вытекает, что при
целых к и достаточно больших п минимум f (п, к) достигается
либо при fc = |Iog2re|, либо при /c = [log2 re]— 1. Рассмотрим
функцию ф (ге) = ге — 2[108’я1. Ясно, что ф (ге) < ге/2. Рассмо-
трим несколько случаев, а) ф(ге) = сге, 0 < с < 1/2; тогда
on on
on —[10g2nJ_____f____________f____
re — ф (re) (1 — c) re
22[!Og1n] __2n-<p(4) = 2ll~e>n,
g(n) = f(n, [log2 re]) ~ c) „;
б) ф (re) = log2 re + ? (re), где f (re) = o (re), при re-»a>;
2”
тогда g (re) =/(re, Jlog2 re]) ~ —; в) ф (re) = log2 re + c, c>0;
2” (1 -f- 2~e)
тогда g(re)=/(re, [log2re])------------------; г) ф(ге)<^2ге;
2”+i
тогда g (re) = f (re, ]log2 re] — 1) ~ .
ЛИТЕРАТУРА1)
1. Автоматы, сб. статей под ред. К. Э. Шеннона и Дж. Мак-
карти, М., ИЛ, 1956.
2. Алферов а 3. В., Теория алгоритмов, М., «Статистика»,
1973 (VII).
3. А р б и б М., Мозг, машина и математика, М., «Наука»,
1968 (VI, VII).
4. Б е р ж К., Теория графов и ее применение, М., ИЛ, 1962
(IV).
5. Б е р л е к э м п Э., Алгебраическая теория кодирования,
М., «Мир», 1971 (V).
6. Виленкин Н. Я., Комбинаторика, М., «Наука», 1969
(VIII).
7. Гилл А., Введение в теорию конечных автоматов, М.,
«Наука», 1966 (VI).
8. Г и н д и к и и С. Г., Алгебра логики в задачах, М., «Наука»,
1972 (I—IV, VI, VII).
9. Глушков В. М., Синтез цифровых автоматов, М., Физ-
матгиз, 1962 (VI).
10. Дискретная математика и математические вопросы киберне-
тики, т. I, М., «Наука», 1974 (I—V).
11. Захарова Е. Ю., Критерий полноты систем функций
из Рк, Сб. Проблемы кибернетики, вып. 18, М., «Наука»,
1967, 5—10 (III).
12. Захарова Е. ТО., Я б л о н с к и й С. В., О некоторых!
свойствах существенных функций из Рк, Сб. Проблемы ки-
бернетики, вып. 12, М., «Наука», 1964, 247—252 (III).
13. Зыков А. А., Теория конечных графов, т. I, Новосибирск,
«Наука», 1969 (IV).
14. К е м е н и Дж., Снелл Дж., Томпсон Дж., Введе-
ние в конечную математику, М., «Мир», 1965 (IV, VIII).
15. К о б р и и с к и й Н. Е., Трахтенброт Б. А., Вве-
дение в теорию конечных автоматов, М., Физматгиз, 1962 (VI).
16. К о ф м а п А., Введение в прикладную комбинаторику,
М., «Наука», 1975 (IV, VIII).
') Римские цифры, стоящие после названия, указывают
главы задачника, при работе над которыми эта литература мо-
жет оказаться полезной.
358
17. Лавров И. А., Максимова Л. Л., Задачи по теории
множеств, математической логике и теории алгоритмов, М ,
«Наука», 1975 (I, II, VII).
18. Л е о н т ь е в В. К., Задачи по вычислительным системам
(ч. III. Дискретный анализ), МФТИ, 1975 (V, VIII).
19. Л у п а н о в О. Б., О синтезе некоторых классов управляю-
щих систем, Сб. Проблемы кибернетики, вып. 10, М., Физ-
матгиз, 1963, 63—97 (I, IV).
20. М а л ь ц е в А. И., Алгоритмы и рекурсивные функции,
М., «Наука», 1965 (VII).
21. Марков Ал. А., Нерекуррентное кодирование, Сб. Проб-
лемы кибернетики, вып. 8, М., Физматгиз, 1962, 169—186
(V).
22. Мендельсон Э., Введение в математическую логику,
М., «Наука», 1971 (I, VII).
23. Минский М., Вычисления и автоматы, М., «Мир», 1971
(VI, VII).
24. Мощенский В. А., Лекции по математической логике,
Минск, Изд-во БГУ, 1973 (I, II, VII).
25. О р е О., Теория графов, М., «Наука», 1968 (IV).
26. Питерсон У., Коды, исправляющие ошибки, М.,
«Мир», 1964 (V).
27. Риордан Дж., Введение в комбинаторный анализ,
М., ИЛ, 1963 (IV, VIII).
28. Роджерс X., Теория рекурсивных функций и эффектив-
ная вычислимость, М., «Мир», 1972 (VII).
29. Р ы б н и к о в К. А., Введение в комбинаторный анализ,
М., Изд-во МГУ, 1972 (IV, VIII).
30. Т р а х т е н б р о т Б. А., Алгоритмы и вычислительные
автоматы, М., «Советское радио», 1974 (VI, VIII).
31. Трахтенброт Б. А., Барздинь Я. М., Конечные
автоматы, М., «Наука», 1970 (VI).
32. Ф е л л е р В., Введение в теорию вероятностей и ее при-
ложение, т. 1, М., «Мир», 1967 (VIII).
33. Харари Ф., Теория графов, М., «Мир» 1973 (IV).
34. Холл М., Комбинаторика, М., «Мир», 1970 (IV, VIII).
35. Яблонский С. В., Функциональные построения в к-
значной логике, Труды матем. ин-та им. В. А. Стеклова,
т. 51, М., Изд-во АН СССР, 1958, 5-142 (I—IV).
36. Я б л о н с к и й С. В., Г а в р и л о в Г. П., К у д р я в-
це в В. Б., Функции алгебры логики и классы Поста, М.,
«Наука», 1966 (1, II).
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомат 180
— без входа 195
--- выхода 194
Автоморфизм графа 103
— псевдографа 118
Алфавит автомата входной 180
— — выходной 180
— машины Тьюринга внешний 213
— — — внутренний 213
— переменных 22
Арность функционального символа
22
Асимптотическое равенство функ-
ций 273
Базис замкнутого класса 50, 208
— — — простой 72
— линейного пространства 164
Биномиальный коэффициент 250
Буква 30
— (символ) алфавита 178
Булева разность 37
Вектор булев 9
— булевой функции 20
— двоичный 9
— коэффициентов полинома 35
— предшествующий 10
— цикловой структуры подста-
новки 138
Векторы несравнимые 10
— ортогональные 165
— противоположные 10
— соседние 9
— сравнимые 10
Вершина висячая 102
— , достижимая из другой вершины
119
— изолированная 102
— конечная 118
— куба 9
— начальная 118
— разделяющая 105
— сети внутренняя 128
— — минимальная 128
— i-ro ранга 181
Вершины сети эквивалентные 128
— смежные 102
Вес вектора 9
— дерева 181
Вес о.-д. функции 180
— орбиты 139
— равновесного кода 160
— функции 139
Ветвь корневого дерева 125
Внешняя сеть разложения 126
Внутренняя сеть разложения 126
Временная сложность процесса вы-
числения 244
Вторая форма А-значной функции
79
Выборка неупорядоченная 249
— объема г 249
— упорядоченная 249
Выход д. функции, зависящий
с запаздыванием от входа 193
Глубина формулы 28
Гомеоморфизм графов 103
Грань плоского графа 111
---— внешняя 111
— n-мерного куба И
Граф 101
— алфавитного кода 17Q
— вполне несвязный 104
— двудольный 105
---полный 105
— кубический 105
— направленный 118
— неориентированный 101
— нумерованный 137
— ориентированный 118
— планарный 111
— плоский 111
— полный 103
— помеченный 137
— пустой 104
— регулярный 105
— с кратными ребрами 101
— — — — и петлями 101
— связный 102
— тривиальный 105
— А-связный 105
Графы изоморфные 103
— почти все 137
— различные 137
Группа автоморфизмов графа 138
— — ориентированного псевдо-
графа 118
— графа 138
степенная 138
360
Декартово произведение графов 103
Дерево 103
— бесконечное информативное 181
— корневое 124
— нагруженное 181
— плоское корневое 124
— растущее 120
—, реализующее отображение (д.
функцию) 182
Деревья одинаковые 125
Детерминированная функция 178
— —, зависящая с запаздыванием
от переменной .193
---от п аргументов 179
Детерминированные функции раз-
личимые 180
— — эквивалентные (неразличи-
мые) 180
Детерминированный оператор 178
— — автономный 205
— — без выхода 205
---константный 205
Диагонализация 243
Диаграмма канонического разло-
жения %-сети 127
— Мура 190
Диаметр графа 102
Дизъюнктивная нормальная форма
(д. н. ф.) 31
-------кратчайшая 38
— — — минимальная 38
---— совершенная 31
-------сокращенная 38
— — — тупиковая 38
Дизъюнкция 22
— над множеством переменных 30
— элементарная 30
Дискретное устройство, реализую-
щее д. функцию 180
Длина вектора 9
— д. н. ф. 31
— к. н. ф. 31
— маршрута 102
— периода 187
— предпериода 187
— сети 128
— слова 168, 178
— цепи 10
Дополнение графа 103
Достоверность декодирования 161
Дуга 101
—, заходящая в вершину 118
— , исходящая из вершины 118
— орграфа 117
— j-ro яруса 181
Дуги кратные (параллельные) 117
Емкостная сложность • 244
Замыкание множества 50
Знак условного равенства 217
Зона процесса вычисления 244
— работы машины Тьюринга 217
Изоморфные ориентированные псев-
дографы 118
Импликант 38
— простой 38
Импликант ядровый 42
Импликация 22, 78
Индекс связки в формуле 26
Интервал булевой функции 38
— максимальный 38
Инцидентность вершины и дуги 118
— — — ребра 101
Источник орграфа 120
Итерация машины Тьюринга 218
Каноническая таблица о,-д. опе-
ратора 191
Канонические уравнения в вектор-
ной форме 192
— — — скалярной форме 192
--- д. оператора 191
Класс вычислимых функций 236
— общерекурсивных функций 236
— предполпый 50, 208
примитивно рекурсивных функ-
ций 236
— самодвойственных булевых функ-
ций 55
— сохранения множества 87
— — предиката 87
— — разбиения 88
— функций, монотонных относи-
тельно р 92
— функционально замкнутый 50,
208
— частично рекурсивных функ-
ций 236
— A-эквивалентных подмножеств
147
Код 159
— алфавитный 169
— блочный 159
— групповой 164
— двоичный 159
—, двойственный к данному 165
— дерева 125
— , исправляющий t ошибок 160
— линейный 164
— максимальный 160
I— множества 160
— набора основной машинный 219
— — решетчатый 234
---(-кратный 231
— , обнаруживающий ( ошибок 160
> — однозначно декодируемый 169
— оптимальный 171
— плотно упакованный 160
— полный 169
— , порожденный матрицей 165
— префиксный 169
— равновесный 160
— равномерный 159
— разделимый 169
— слова 159
— Хэмминга 164
— эквидистантный 160
Кодирование 159
— алфавитное 169
Кодовое расстояние 159
Команда в машине Тьюринга 214
Композиция машин Тьюринга 218
Компонента односторонняя 120
— связности графа 102
— сильная 119
— слабая 120
361
Конденсация орграфа 120
Константы в ft-значной логике 77
Контакт замыкающий 149
— размыкающий 149
Контактная схема ft-полюсная 148
Контур 119
гамильтонов 119
Конфигурация, выводимая из дру-
гой конфигурации 216
> — заключительная 216
, заключительно выводимая из
другой конфигурации 216
• — машины Тьюринга 215
— начальная 216
Конъюнктивная нормальная форма
31
Конъюнкция 21
> — допустимая 38
— монотонная 32
— над множеством переменных 30
— элементарная 30
Критерий полноты в алгебре ло-
гики 71
1— Саломаа 95
— Слупецкого 95
— Яблонского 95
Куб единичный п-мерный 9
Многочлен по модулю ft 79
— характеристический 263
Множество, двойственное к дан-
ному множеству 55, 94
— , замкнутое относительно сово-
купности операций 208
— самодвойственное 55
— функциональных символов 22
Мультиграф 101
— ориентированный 117
Набор 9
— , предшествующий набору 8 10
— , соседний с а 10
— , строго предшествующий на-
бору 8 10
Наборы несравнимые 10
— сравнимые 10
— , — относительно р 91
Направление грани И
Наследственная система функции
72
Номер вектора 9
Норма вектора 9
Нулевое пространство матрицы 165
Нумерация гёделевская 243
Лемма Бернсайда 138
— о нелинейной функции 59
— — немонотонной функции 65
— — несамодвойственной функ-
ции 55
Лента машины Тьюринга 213
Лес 103
Линейная комбинация векторов 164
Линейно независимая система век-
торов 164
Линейное векторное пространство
164
Логическая связка 22
Максимум х и у 78
Маршрут 102
— замкнутый 102
— ориентированный 119
— — замкнутый 119
Матрица инциденций (инцидентно-
сти) 122
— кода 164
— — порождающая 165
--- проверочная 165
— смежности 122
Машина Тьюринга 213
— —, вычисляющая функцию /
220
— —, моделирующая работу дру-
гой машины Тьюринга на решетке
— —, не применимая к слову Р
217
— —, правильно вычисляющая
функцию f 220
— —, применимая к слову Р 217
Медиана 52
Метод каскадов 157
— неопределенных коэффициен-
тов 35
Минимум х и у 78
Объединение графов 103
Ограниченно-детерминированная
функция 180
Ограниченно-детерминированный
оператор 180
Оператор детерминированный 178
—, порожденный совокупностью
функций 188
— , реализуемый данным состоя-
нием 180
Операторная запись алгоритма 218
Операция введения обратной связи
194
— замыкания 50, 208
— минимизации 236
— объединения д. функций 195
— отождествления переменных 44
--------УД. функции и отожде-
ствления полюсов в схеме 193
— примитивной рекурсии 235
— разветвления 206
— суперпозиции для д. функций
196
— удаления выхода у д. функции
и выходного канала и полюса
у схемы 194
Орбита 138
Орграф 118
— бесконтурный 122
— несвязный 119
— односторонний (односторонне
связный) 119
— сильный (сильно связный) 119
— слабый (слабо связный) 119
— транзитивный 119
— тривиальный 122
Основные эквивалентности 28
Остаточный оператор, порожден-
ный словом 180
Отрицание Лукасевича 77
— Поста 77
— х 21
362
Отросток сети 125
Ошибка в канале связи 1С0
Паросочетание 105
— максимальное 105
— совершенное 105
Первая форма fe-значной функции
79
Переменная существенная 44
— фиктивная 44
Перестановка без повторений 249
— с повторениями 249
Перечисляющий ряд для фигур
-------функций (конфигураций)
139
Период слова 187
Петля 117
Подграф 102
— остовный 102
— , порожденный подмножеством
вершин 102
— сети 125
— собственный 102
Подразбиение ребра 103
Подсеть 125
Подслово 168
Подфункция 31
— собственная 31
Покрытие множества вершин 112
— тупиковое 112
Полином Жегалкина (по модулю 2)
32
Полинома длина 32
— степень 32
Полиномиальный коэффициент 250
Полустепень захода 118
— исхода 118
Полюс 124
Порожденный о.-д. оператор 188
Последовательность возвратная 263
Предикат вполне рефлексивный 89
симметричный 89
— сильный 99
— центральный 89
— п-местный 87
Предпериод слова 187
Префикс (начало) слова 168, 178
Примитивно рекурсивное описание
функции 235
Принцип двойственности 55
Произведение по модулю к 78
Производная булевой функции 37
Псевдограф 101
— , ассоциированный с ориентиро-
ванным псевдографом 118
— гамильтонов 119
— , двойственный к данному 111
— ориентированный 117
— — полный 120
— самодвойственный 111
Пустая ячейка на ленте 213
Пустое слово 168
Пустой символ алфавита 213
Путь 119
— гамильтонов 119
Равные булевы функции 44
Разветвление машин Тьюринга 218
Разложение сети 126
'— — каноническое 126
Размерность грани И
— линейного пространства 164
Разность по модулю к 78
Разрез 128
— минимальный 128
— сети тупиковый 128
Ранг грани 11
• — дизъюнкции 31
< — конъюнкции 31
Расстояние между вершинами графа
102
--------ориентированного псев-
дографа 119
---двумя ячейками ленты 230
— Хэмминга 9
Расширение оптимального кода 171
Ребро графа 101
— источниковое 158
> — куба 10
।— ориентированное 117
< — псевдографа 101
Решетка с шагом I 230
Сеть 124
• — контактной схемы 146
• — неразложимая 126
ч- параллельно-последовательная
126
разложимая 126
1— связная 125
»— сильно связная 125
> — тривиальная 125
• — Н-разложимая 126
• — fe-полюсная 124
> — р-разложимая 126
• — s-разложимая 126
Симметрическая разность графов
103
Симметричная пара дуг 118
Система неприводимая 50
1— Поста 95
> — Россера—Туркетта 95
— функционально полная 50, 208
Слово бесконечное 178
— в некотором алфавите 178
> — входное 180
> — выходное 180
, записанное на решетке 231
• — квазипериодическое 187
> — начальное (исходное) 216
— пустое 178
Сложность булевой функции 149,
150
— д. н. ф. (к. н. ф.) 31
— схемы 149, 150
— формулы 26
Слой п-мерного куба 9
Собственный набор ядрового имп-
ликанта 42
Соединение слов 168, 178
Соседние ячейки ленты 230
Состояние д. оператора 180
— заключительное 213
> — машины Тьюринга 213
— начальное 213
Сочетание без повторений 249
।— с повторениями 249
Степень вершины графа 102
363
Стоимость кода 171
Сток орграфа 120
Стрелка Пирса 22
Сумма по модулю 2 22
-------h 78
Суперпозиция над множеством
функций 24
— сетей 126
— схем 197
— функций 234
Суффикс (окончание) слова 168,
178
Существенная переменная д. функ-
ции 179
Сфера в n-мерном кубе 10
Схема 148
>— бесповторная 154
—, двойственная к данной схеме
153
>— из функциональных элементов
150
I— минимальная 150
> — оператора 192
,— примитивной рекурсии 235
• —, реализующая булеву функ-
цию 148
— Хк-функциональная 150
Считывающая (печатающая) го-
ловка машины Тьюринга 213
Теорема Пойа 139
.— Поста 71
— Р. Робинсона 237
— С. Пикар 96
Тождественная единица 20
Тождественный нуль 20
Толщина графа 111
Точка сочленения 105
Турнир 120
Тьюрингово вычисление 216
Удаление вершины 103
— ребра 103
Универсальная частично рекурсив-
ная функция 242
Управляющее устройство машины
Тьюринга 213
Усеченная разность 78
Функция булева, двойственная
к данной функции 54
— — линейная 59
— — монотонная 65
— — нелинейная 59
— — самодвойственная 55
— — симметрическая 25 ।
-----, сохраняющая константу 62
— — элементарная 20
— Вебба 78
— выбора аргумента 236 >
— выходов 190, 214
— , вычислимая по Тьюрингу 219
— голосования 52
— движения головки 214
— , двойственная к / относительно
s (х) 85
— , квазилинейная относительно
функции ip 84
• — линейная 91
— , монотонная относительно р 92
— , — по переменной х< 155
— неприводимая 72
— нулевая 236
— переходов 190, 214
— , представимая многочленом по
модулю h 79
— проводимости 149 »
— производящая 265
— — экспоненциальная 265
— , простая относительно замкну-
того класса 72
— простейшая 236
—, реализуемая схемой 149, 150
— , — формулой над множеством
связок 24 I
, — — — — функциональных
символов 23
• —, самодвойственная относительно
s (х) 85
— селекторная 236
— следования 236
— , сохраняющая множество 87
— , — предикат 87
— , — разбиение 88
— существенная 95
— тождественная 21
— Шеффера 71, 82
— fe-значной логики 77
— — — элементарная 77
Фиктивная (несущественная) пере-
менная д. функции 179
Формула включений и исключений
259
—, двойственная к данной 56
— над множеством связок 23
— — — функциональных симво-
лов 22
• — Стирлинга 273
— тождественно истинная 27
— — ложная 27
— Эйлера 111
Формулы эквивалентные 24
Фрагмент дерева 181
Функции конгруентные 56, 93
Функция Аккермана 240
— алгебры логики 20
— булева 20
Характеристическая функция вто-
рого рода числа i 78
— — числа i 78
I
Центр предиката 89
Цепь в графе 102
— — n-мерном кубе 10
— — — — возрастающая 10
— гамильтонова 105, 119
— замкнутая 102
— простая 102
— сети 128
— — кратчайшая 128
—, соединяющая вершины 10, 102
Цикл в графе 102 ,
-------- простой 102 ’
-----n-мерном кубе 10
364
Цикл гамильтонов 105
— длины k в В” 10
— подстановки 86
Циклическая подстановка (цикл)
86
Цикловой индекс группы 138
Циклы графа линейно зависимые
111
--------независимые 111
Число вершинного покрытия 112
— независимости 112
— реберного покрытия 112
— реберное хроматическое 112
— хроматическое 112
— цикломатическое 112
Шар в n-мерном кубе 10
Ширина сети 128
Штрих Шеффера 22
Эквивалентность 22
Эквивалентные машины Тьюринга
217
— поддеревья 182
Элемент единичной задержки 198
A-эквивалентные подмножества 147
— элементы множества 138
й-фактор 105
п-факториал 250
<й, п>-схема 148
<п, й>-код 160
(п, й)-код 164
(1, (г)-полюсник 149
а. ад.
х,-‘. • • Xj^-компоиента булевой
функции 31
2Св-схема 148
х-сеть 126
х-схема 149
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
А*, В* 168, 178
А (О, В (I) 265
A (D), В (D) 120
А», А® 178
ат 217
ВА 138
В», В» 9
Bj <“) 10
С 159
С* 165
С(Н) 165
С (п, г) 250
С (п, г), GJ 250
С (х), с (х) 139
CSic 90, 95
В, G, F, L, S, В 214
D*, D' 120
dA, В 181
В (G) 102
Da, В (^) 182
Dp (п) 143
D (Хц, х,, . хя) 243
d (С) 159
d0 (G) 105
d(t>) 102
d+ (г), d~ (®) 118 '
Я 3t
о/ (Д”) „
8 (жч- Ч........х'ч)
Е (t) 265
77
В’(т) (х(п) (1), 9(г’ (1 — 1)) 192
t (хя) 20
/* (х,, х,, .. ., хя) 54
ic (£") 159
•••’** (хя) 31
(х„ х2, .... х„) 85
G 101
G* 111
Gf 169
G ф Н 103
G X И 103
G П Н 129
G(п, X) 276
G<r) (^(и) (()j 9Гг) (<_])) 192
g (n, d) 165
Н (В (х„ х2, ..., хи)) 87
Я (йр (х, р)) 92
Н/с, п 183
й,у (х) 96
(х, у, г) 52
365
3%, (x") 236 id (s) 118 ir (/). ir (n) 4t o (»), O’ (t>) 107 о (Ф (x)), о (ф (X)) 273 C 203
(x) 7ч S* (x) 138 U) 133 (x) 78 P2 (Xя) 20 P (£n) 32, 35 Pn 41 Pc (Xя) 46 Pk 77
К 38 K«' Knt, n, 404 Hi, Pop, ifnp 236 K, ® K, © . .. ф K, 32 K<D 240 л up ' op K,,p 236, 242 K<p 169 йг 31 PJf.1 > 80, 90, 95 P (n, r), P (n, r) 249 P (G), P (nl 143 Q 213 <?ф (p, C) 161 Q (?, x«) 180 g. 213 «(>)(() 192
L 59 L (/) 43, 151 L (<p (x, {/)) 91 g(r) 192 9T (n) 244
Lk (/) 149 Ьф (/), LK (/) 150 I U) 43 Z° (/) 40 2 (P) 177 2* (m) 177 ^C(P) 170 R (G) 129 R (I) 230 Pp (x, y) 9t R (g, h) 234 rT (К), rT (P) 244 S 55, 196
M 65 M” 50, 65 M (Xя) 50 M* 55 M (p) 92 M j 233 МХя(/(хя)) 236 M (C) 164 m (n, d), m (n, h, d) 160 m (x, y, z) 52 Sic 90, 259 S%(«) 10 S (/On), g(»>, gin)} 234 S^*2l | 30 S^2’.2’.:;” |31 s (x) 236 sr (/)> sr (n) 41 SyCK), sr(P) 244
N (A) 138 NK 38 Nf 20 260 N (% "<*) 259 T6, Tr Tg, Tn 62 T (S) 87 T (d, s) 89 Tf 219 T, О T2, Г,Т2 218 T (/) 20
0, 193 O2, O3 194 O, 195 0. 206 T (Г) 126 t (G) 111 tT (If) 244 tl(P) 244
366
0 (D) 88 n*, n-k (/) 20
V (<f„ g„ .. и (.Хш я,, .... V(H) 165 («. У) 78 Х« 20 х, х» 20 х‘ 178 Я 21, 77 хР, х», х' 30 х у (mod ft) х + у (mod ft) x(t) 178 x“, S'-0 178 х» (1) 192 S<mJ (1) 192 Z (A) 138 Z (s (x)) 90 Z(s (x)) 91 2 (A; tn t., ,, #,) 88 , «») 243 78 1 78 .t«) 138 P («, 3) 9 p (u, c) 119 fG («. ®) I29 2 153 192 a a 11 ФЛ, В 179 «Я, В (SI «Ъ «’*, I 179 Фк т‘ фк Т 179 *<*>• ф,к> 209 Г (А) 169 ’tn (₽)> tn, т (Р) 137 <р<п) 243 fL 180 <р (хш) 178 <р(Х„ Л-„ Х„) 179 f8 138
а, 3, in 9 a” < io а» < ря io a ®₽ io a и 3 io an Mt а и a2” 20 «о (G), «, (G), h (G), (G) Г (G) 138 Г (a, 6) 125 ГР, Г' 126 Tn’ m r₽(a, b), 4 Г,, 190 A 168, 215 * (ic) 168, 178 V-y (t (xt, x,, ., ’ (а") 9 » (i“) 183 «00(G) 112 112 (a, b) 126 • м яп—1> 1/) = 236 X (G), Г (О И2 (K)f ШТ (Р) 21* 56 21? 180 21 (X) 22 21 [Ф] 22 9J (/ (х«)) 72 0(х) 236 0, I И II «я II 9 V К, 31 <=1 & Di 31 <=1 Е Ki 32, 37 <=1 [М] 50
367
[M]ff as
~х 77
(V„ V„ X) 104
(a)n, (®)n, h 267
<a> 183
[b], ]b[ 253
{6} 254
(n)r 249
n! 249
2n!I, (2n — 1)1! 273
t] 227
-21-1 237
L J
rest (x>, Xj) 237
sg x, sg x 227
I P),n, [a]”1 217
И 218
k k
- 21, 273
O. 217
X 273
<, < 9
® 10, 29
U 10
n 11
1. &, V. 4.1 21
dxf ’ 6 (xfi> x<2, ..х<й)
+ , • 78
— 78, 227
min, max 78
1=> h, h- 216