Similar
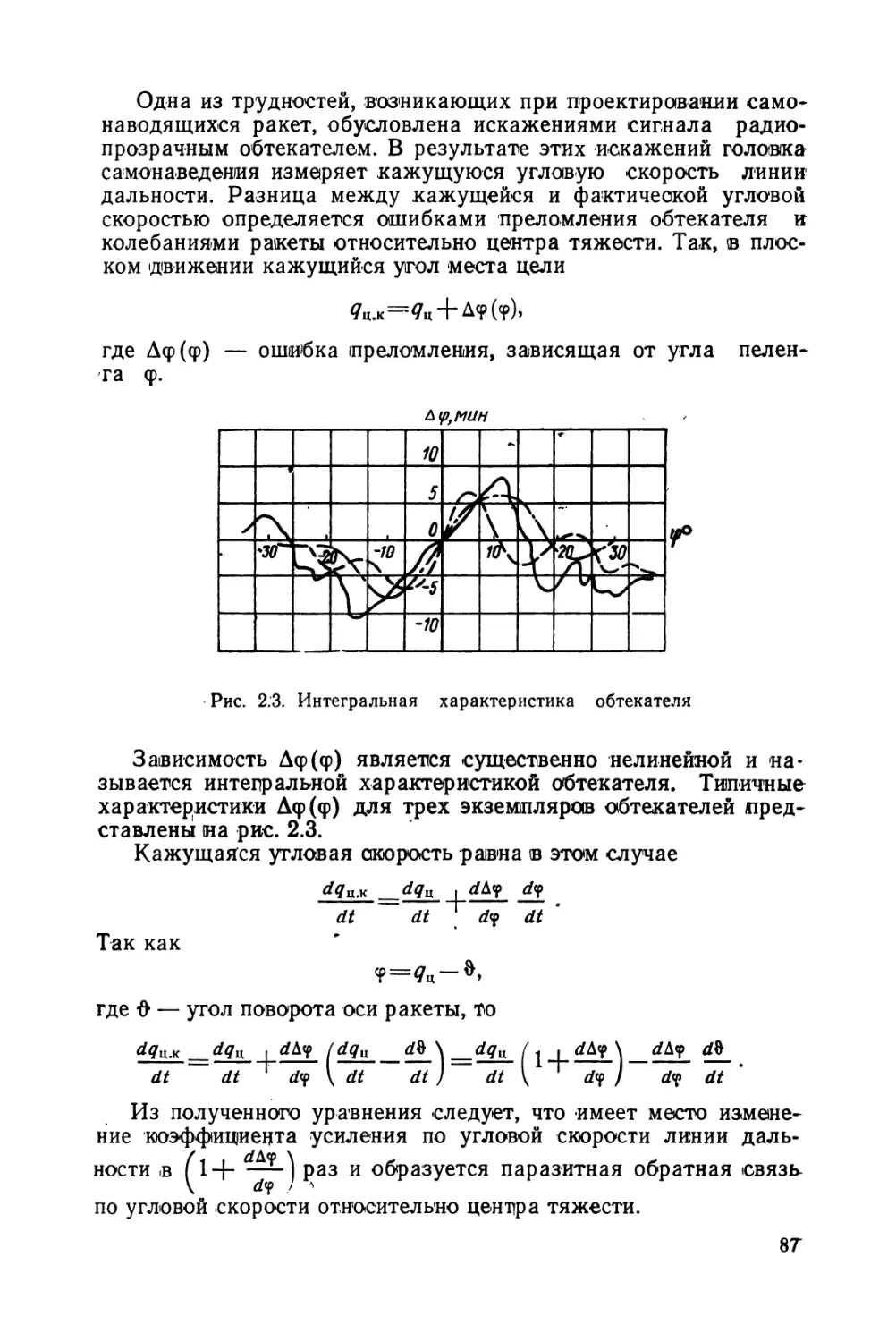
Text
ПРОЕКТИРОВАНИЕ
СИСТЕМ
НАВЕДЕНИЯ
Под ред. д-ра техн, наук
Е. А. ФЕДОСОВА
Москва
«МАШИНОСТРОЕНИЕ»
1975
П68
УДК 629.7.05.001.2
А в т о р ы: А. М. БАТКОВ, А. А. ГОРСКИЙ, В. Ф. ЛЕВИТИН
Г. Г. СЕБРЯКОВ, Е. А. ФЕДОСОВ, Б. Е. ФЕДУНОВ
Рецензент чл.-кор. АН СССР, д-р техн, наук Е. П. Попов
Проектирование систем- наведения. Под ред. д-ра техн,
наук Е. А. Федосова. М., «Машиностроение», 1975, 296 с.
В книге изложены современные математические методы,
применяемые при проектировании систем наведения ракет, и
показан способ их использования. Описан ряд аналитических
и численных методов анализа и синтеза законов управления
линейных и нелинейных систем.
Книга предназначена для инженеров и научных работни-
ков, занимающихся вопросами проектирования систем наведе-
ния.
Табл. 5, ил. 89, список лит. 44 назв.
„ 31305-222
П -------------
038(01)-75
222-75
© Издательство «Машиностроение», 1975 г.
ПРЕДИСЛОВИЕ
Система наведения ракет представляет собой замкнутую
единую систему, состоящую из аппаратуры визирования цели,
датчиков измерения параметров движения ракеты, различных
счетно-вычислительных приборов для выработки команд наве-
дения и сервомеханизмов, приводящих в движение аэродинами-
ческие или газодинамические устройства управления. Весь этот
сложный комплекс аппаратуры объединен в единую систему
процессом прохождения сигналов наведения. Такая сложная ди-
намическая система помимо аппаратуры наведения включает
в себя и собственно динамические звенья управляемого объек-
та — ракеты и кинематические связи его с целью.
Формализация процесса наведения ракеты на цель представ-
ляет собой классическую задачу теории управления с рядом
особенностей.
Первая особенность заключается в резко выраженной неста-
ционарное™ процесса наведения. Эта нестационарность вызвана
тем, что два движущихся объекта в пространстве каких-либо ко-
ординат связаны самим процессом относительного движения
определенными кинематическими связями. Обычно эти связи
формализуются дифференциальными уравнениями, отражающи-
ми движение вектора дальности между целью и ракетой в про-
странстве и во времени. Отдельные параметры этого движения
могут быть измерены аппаратурой визирования цели и использо-
ваны в выработке команд наведения. В связи с тем, что вектор
дальности при сближении с целью стремится к нулю, в контуре
регулирования оказывается сложное нелинейное, нестационар-
ное кинематическое звено, существенным образом определяю-
щее весь процесс наведения.
Вторая особенность связана с динамикой движения лета-
тельного аппарата в пространстве под действием управляющих
сил и всего комплекса мешающих этому движению возмущений.
Эта динамика описывается системой нелинейных дифференци-
альных уравнений, которые линеаризуются при определенных
допущениях. Однако как исходные линейные уравнения, так и
линеаризованные уравнения имеют специфический вид.
3
Третья особенность определяется критериями, по которым
идет проектирование ракетной системы. Это могут быть крите-
рии устойчивости и качества переходных процессов при анализе
и синтезе сйстемы стабилизации, критерии точности или бое-
вой эффективности при анализе и синтезе самого контура наве-
дения ракеты. В отдельных случаях может использоваться кри-
терий эффективность — стоимость.
Эти особенности позволили выделить теорию наведения как
самостоятельную дисциплину из теории управления динамичес-
кими системами.
В последние годы в научно-технической литературе появи-
лось многа публикаций по общей теории наведения. В данной
книге читатель найдет описание некоторых математических ме-
тодов проектирования систем наведения и познакомится со спо-
собами их использования. Здесь изложена методика проектиро-
вания систем наведения, основанная на теории линейных
управляемых систем. Приведены методы исследования таких
математических моделей, которые позволяют учитывать неста-
бильность параметров объекта и производственные допуски.
В книге показано, как, используя современную математическую
теорию оптимального управления и численные методы оптими-
зации, можно устанавливать структуры законов управления и
выбирать их параметры.
Цель данной книги — изложить современные математические
методы проектирования систем наведения ракет. Книга освеща-
ет отдельные фрагменты теории наведения, имеющие внутрен-
нюю общность и связь и являющиеся, по мнению авторов, цент-
ральными на данном этапе развития систем наведения.
Авторы ’приносят благодарность рецензенту книги чл.кор.
АН СССР Е. П. Попову за полезные замечания., способствовав-
шие ее улучшению. Авторы будут весьма признательны читате-
лям, которые сочтут возможным прислать свои замечания по
адресу: Москва, Б-78, 1-й Басманный пер., 3, изд-во «Машино-
строение».
ВВЕДЕНИЕ
Современная ракета —это комплекс сложных технических
устройств, предназначенных для обеспечения ее движения при
выполнении той или иной целевой функции.
При создании сложных ракетных систем инженеры решают
проблемы аэродинамики, газовой динамики, гидродинамики,
электродинамики, материаловедения и другие не менее сложные
физические или химические проблемы. Это определяется физи-
ческими процессами, протекающими в самой ракете и ее элемен-
тах. Ракетная техника наиболее остро из всех других направле-
ний современной техники выдвинула проблемы, связанные с так
называемыми информационными процессами.
Понятие информационных процессов возникает при рассмот-
рении управления движением летательного аппарата, когда для
выработки управляющего сигнала используется та или иная ин-
формация о параметрах движения самой ракеты или преследуе-
мой ею цели. При этом образуется упорядоченная передача тех
или иных сигналов по элементам ракетной системы в форме тех
или иных физических процессов. Однако современная наука об
управлении рекомендует создать модель передачи сигнала по
цепям системы, абстрагируясь от физической сущности самого
физического содержания процесса передачи. Такая модель явле-
ния вскрывает новое качество физического процесса — его ин-
формационное содержание, а сам процесс в такой модели стано-
вится информационным.
Изучением информационных процессов занимается теория
управления. Одним из направлений этой общей теории управле-
ния является теория управления движением, которая иногда
называется теорией наведения. В настоящее время еще не за-
вершено. создание законченной теории наведения ракетных сис-
5
тем. Это обстоятельство объясняется несколько своеобразным
процессом проектирования таких систем. Сложность динамичес-
ких процессов, описывающих движение ракетной системы, с пер-
вых же шагов проектирования требует решения систем нелиней-
ных дифференциальных уравнений высокого порядка. Столкнув-
шись с подобными трудностями в первые годы зарождения
управляемых- ракет, инженеры и ученые обратились к машинной
математике, к вычислительным машинам, особенно аналоговым
вычислительным машинам.
Обойдя таким образом математические трудности, инженеры-
ракетчики стали создавать моделирующие комплексы из аналого-
вых решающих элементов. Появилось целое направление в тех-
нике проектирования и исследования — имитационное модели-
рование. Преимущество аналогового моделирования заключалось
в том, что процессы в аналоговой модели протекают в так
называемом реальном масштабе времени, что позволяет иногда
включать в модель реальные конструкции приборов и элементов
систем управления, выполненных в макетном или опытном ис-
полнении. В настоящее время с ростом быстродействия цифро-
вых машин они все более заменяют аналоговые в моделирующих
комплексах.
Используя мощный аппарат моделирования, инженер полу-
чает все ответы на вопросы, которые возникают при проектиро-
вании. Именно это обстоятельство и привело к тому парадоксу,
когда создаются очень совершенные конструкции ракет при до-
вольно скромных достижениях в аналитической теории систем
наведения. Это обычно компенсируется хорошей оснащенностью
современного конструкторского коллектива вычислительными
машинами, моделирующими комплексами и динамическими
стендами.
Однако моделирование остается только экспериментом, иног-
да математическим экспериментом. Только теория способна
дать нужное обобщение и параметрические зависимости, необ-
ходимые инженеру при проектировании. Авторы глубоко убеж-
дены, что только сочетание моделирования с аналитическими
расчетами и исследованиями позволяет наиболее гармонично
построить процесс современного проектирования систем управле-
ния ракет.
Задачи математического исследования процессов наведения
ракет рассматривались рядом отечественных и зарубежных ав-
6
торов. В книге представлены математические исследования от-
дельных вопросов теории наведения.
Одним из них является методика проектирования системы
наведения, основанная на теории линейных управляемых систем,
достаточно хорошо развитой в настоящее время.
Однако при создании линейной системы управления не всег-
да удается учесть ряд факторов, имеющих большое значение
для повышения эффективности системы управления. Таковыми
являются производственные допуски, нестабильность парамет-
ров, жесткие ограничения на управление, на отклонение органов
управления или на их прочность, ограничения на различные па-
раметры, характеризующие движения объекта (фазовые коор-
динаты). Учет этих факторов либо части из них является настоя-
тельно необходимым при создании системы управления для ра-
боты ракеты в предельных условиях, т. е. при максимальном
использовании ее возможностей.
Работа ракет в широком диапазоне условий и стремление
максимально использовать предельные возможности вынуждают
учитывать при создании системы управления ряд ограничений
на управление (ограничение максимальной величины управля-
ющего усилия, по прочности и возможности отклонения рулей,
углов встречи ракеты с целью и др.).
При этом вначале необходимо получить математическую
модель, учитывающую главную специфику рассматриваемой
задачи и поддающуюся математическому анализу. На основа-
нии условий оптимальности управления в этой математической
модели устанавливаются основные принципиальные особенности
закона управления — определяется его оптимальная структура.
Установление структуры закона управления, обеспечивающей
максимальную эффективность в рамках основных ограничений,
крайне важно для получения совершенной системы управления.
Полученная структура управления должна обеспечивать ра-
ботоспособность реального объекта, математическое описание
которого гораздо сложнее той модели, на которой выбиралась
структура. Сама структура содержит параметры, подлежащие
выбору при создании реального закона управления на основе
этой структуры. Оптимальный выбор параметров при рассмот-
рении сложного объекта возможно производить только с исполь-
зованием вычислительных машин. Все эти вопросы нашли отра-
жение в предлагаемой книге.
7
В книге не отражены вопросы проектирования контуров ста-
билизации, предназначенных для ракет с широким диапазоном
условия их применения. Использование в этих задачах хорошо
развитой в настоящее время теории марковских случайных про-
цессов позволяет получить эффективные технические решения.
Необходимо отметить, что поскольку основное внимание в
данной книге обращается на выявление общих качественных
закономерностей, все приведенные примеры демонстрируют
приемы применения математических теорий в конкретных ситуа-
циях проектирования систем наведения и носят методический
характер, а все численные результаты являются только иллюст-
ративными.
ГЛАВА 1
МЕТОДИКА ПРОЕКТИРОВАНИЯ СИСТЕМ НАВЕДЕНИЯ
НА ОСНОВЕ ТЕОРИИ ЛИНЕЙНЫХ СИСТЕМ
УПРАВЛЕНИЯ
Задачей первой главы является создание единого методичес-
кого подхода к анализу и синтезу линейных (линеаризованных)
систем наведения, использующих различные источники инфор-
мации.
В этой главе дается понятие пролета как меры текущей точ-
ности наведения; угловой скорости линии дальности и линейного
рассогласования, измерение которых позволяет оценить пролет
и сформировать управление.
Линеаризация кинематических зависимостей, связывающих
пролет, линейное рассогласование, угловую скорость линии
дальности с относительным ускорением ракеты и цели, приво-
дит к единой структурной схеме системы наведения с выходом
по пролету и двумя входами: по ускорению цели и по ошибке
измерения относительных координат.
С помощью аппарата весовых и параметрических передаточ-
ных функций формируется подход к исследованию точности
линейной системы в один момент времени наблюдения, вводится
понятие эквивалентных по точности систем.
Для конкретных методов наведения формируются выраже-
ния, связывающие передаточную функцию системы (контура
стабилизации, фильтра, измерителя относительных координат)
с параметрической передаточной функцией замкнутой системы.
Понятие эквивалентности по точности позволило применить
для оптимизации нестационарной системы наведения широко
распространенную задачу Винера, разработанную для стацио-
нарных систем.
1.1. ЗАДАЧА, ПРОЦЕСС И СИСТЕМА НАВЕДЕНИЯ
Относительное движение ракеты и цели в каждый момент
времени удобно характеризовать векторами: дальности Я_(0»
относительной скорости 7(/) и относительного ускорения J(t)
(рис. 1.1).
9
Независимо от того, каким образом формируются начальные
условия этого относительного движения и вектор /(/), предопре-
деляющий изменение векторов V(t) и !?(/), в каждом полете
ракеты модуль дальности имеет минимум, представляющий со-
бой кратчайшее расстояние между ракетой и целью. Задачей
наведения ракеты на цель является минимизация кратчайшего
расстояния 7?к- Естественно, что это возможно только при усло-
вии, что за некоторое время до момента пролета ракеты мимо
цели начнется прогнозирование величины 7?к и на основе этого
Рис. 1.1. Взаимное располо-
жение векторов дальности
R относительной скорос-
ти У(/) и относительного ус-
корения /(О
прогноза будет формироваться соот-
ветствующее управление.
Процессом наведения назовем
прогнозирование кратчайшего рас-
стояния 2?к между ракетой и целью
и управление ракетой, т. е. создание
ускорения 7, обеспечивающего
уменьшение этого расстояния. Век-
тор J представляет собой разность
J = J р J ц,
где 7р(0 и 7ц(0 —векторы ускоре-
ния ракеты и цели.
Обычно наведение осуществляется только с помощью уско-
рения Jp. Ускорение цели /ц всегда ограничено по модулю и мо-
жет произвольно изменяться. В частном случае цель может стре-
миться увеличить кратчайшее расстояние /?к-
Системой наведения назовем всю совокупность устройств,
обеспечивающих управление кратчайшим расстоянием /?к в
каждой реализации процесса наведения. В систему наведения
входят:
информационные устройства, изменяющие текущие парамет-
ры относительного движения ракеты и цели;
вычислительные и корректирующие устройства, прогнозиру-
ющие текущую оценку кратчайшего расстояния между ракетой
и целью в данной реализации процесса наведения и формирую-
щие заданное управление;
контур стабилизации ракеты, обеспечивающий реализацию
заданного управления. Контур стабилизации включает в себя
ракету и автопилот, которые выполняют здесь функции исполни-
тельного устройства и регулятора соответственно.
1.2. ПРОЛЕТ —ТЕКУЩАЯ МЕРА ТОЧНОСТИ НАВЕДЕНИЯ
Текущей мерой точности наведения, т. е. величиной, прогно-
зирующей наименьшее значение модуля дальности принято
считать дальность, на которой ракета пролетит мимо цели, если
с данного момента времени t ракета и цель в относительном дви-
10
жении будут перемещаться прямолинейно (рис. 1.2), т. е. по ка-
сательной к относительной траектории. Эту дальность называют
пролетом (или промахом). Обозначим ее индексом h(t), или Л,
причем аргумент t указывает здесь на то, что величина пролета
может изменяться во времени, так как реальное относительное
движение непрямолинейно’* *. _ _
По определению векторы R,_V и h лежат в одной плоскости
(плоскости Q), причем вектор h перпендикулярен вектору У.
В момент времени в который вектор пролета совпадает с
вектором дальности, расстояние между ракетой и целью мини-
мально, так как вектор дальности
/?&) = *&)
нормален к относительной траек-
тории. Для простоты принимает-
Рис. 1.3. Пример изменения проле-
та при криволинейном относитель-
ном движении (h(tK)—конечный
пролет)
Рис. 1.2. Текущий пролет
ся, что на всей относительной траектории это происходит толь-
ко однажды (рис. 1.3). Момент времени /к будем называть мо-
ментом встречи.
Скалярная величина пролета может быть записана как
A = /?sin X, (1. 1)
где % — угол между векторами R и F, отсчитанный от направ-
ления вектора R.
Из (1.1) следует, что полет ракеты с нулевым текущим про-
летом (Л(/)=0) предполагает относительное движение вдоль
линии дальности (рис. 1.4). К этому случаю применяют обычно
термин — полет в упрежденную точку встречи.
Векторное выражение для пролета будет
А=7?-К0(7?70). (1.2)
* Возможны и другие меры текущей точности, например расстояние, на
котором ракета пролетит мимо цели, если с данного момента ускорение будет
постоянным.
11
Здесь и ниже индексом «О» обозначены соответствующие еди-
ничные векторы [1].
В выражении (1.2) пролет Я представляется в виде катета
прямоугольного треугольника (см. рис. 1.2), в котором гипоте-
нузой служит дальность Л, а вторым катетом — проекция даль-
ности на направление относительной скорости.
Рис. 1.4. Взаимное расположение векторов
дальности и относительной скорости при
пролете, равном нулю
Приняв пролет Я в качестве меры текущей точности наведе-
ния, можно определить возможность управления пролетом. Для
этой цели продифференцируем (1.2) по времени
h=R-^0 (Wo) -170 (£Й0) - Йо (Я70). (1-3)
Учитывая, что R=V и, следовательно,
, Г0(£Р0)=Й0 (Тйо)=й,
получим
h=-V^RVa)-V.(RVoy. (1.4)
Умножим и разделим первое слагаемое выражения (1.4) на
величину относительной скорости V
-V0(RV0) = V0V
(ЯУ0)
V
Произведение VqV представляет собой нормальную со-
ставляющую вектора относительного ускорения. Эта составля-
ющая JH (рис. 1.5) равна проекции вектора относительного
ускорения J на плоскость Н, перпендикулярную вектору относи-
тельной скорости и содержащую вектор пролета.
Выражение в квадратных скобках имеет размерность време-
ни и может быть истолковано как время, оставшееся до момента
встречи /к = ^о при условии, что с данного момента относитель-
ное движение прямолинейно и равномерно.
12
Момент времени /0 назовем прогнозированным моментом
пролета, а разность /у = /о—t— упрежденным временем.
Таким образом, введем обозначение
_ _(W_
у~ V ‘
Первое слагаемое в (1.4) может быть представлено в виде
(1-5)
Вектор JH может быть разложен в плоскости Н на два: по
направлению пролета и перпендикулярно к пролету. Первую
проекцию обозначим А,
вторую —/а , тогда
(1-6)
Второе слагаемое в выра-
жении (1. 4) умножим и раз-
делим на V. При этом ска-
лярное произведение можно
будет преобразовать так:
(^С)=(Ш|=
Рис. 1.5. Составляющие относительно-
го ускорения и скорости изменения
пролета
(1-7)
Учитывая, что векторы R, V й Л лежат в одной плоскости и, сле-
довательно, вектор /а, перпендикулярный h и V, перпендикуля-
рен вектору R, получим
(%)=(ед. (1.8)
Если принять, что положительно направленный вектор А
вращает вектор относительной скорости V в положительном на-
правлении, то угол между R и Jh согласно рис. 1.5 равен Л+-^.
Тогда, с учетом (1.1), (1.7) и (1.8) второе слагаемое может быть
записано в виде
- И0(/?1>0) = -1/0/?/А.соз (*+y) =
= V0R sin X^-=V0h<ohQ.
(1-9)
13
Индексом (dhQ обозначена величина , характеризующая ско-
рость разворота вектора V и, следовательно, перпендикулярного
ему вектора h в плоскости Q.
Из (1.9) следует, что второе слагаемое выражения (1.4)
представляет собой нормальную составляющую скорости из-
менения вектора пролета в плоскости Q, отличную от нуля толь-
ко тогда, когда отлична от нуля проекция вектора относитель-
ного ускорения Jh. Иными словами, выражение (1.9) определяет
составляющую скорости, изменяющую направление пролета в
связи с изменением его скалярной величины. Естественно, что
эта составляющая так же, как и составляющая J^ty, не изменяет
скалярной величины пролета. Итак, производная вектора проле-
та h может быть представлена в виде суммы трех ортогональ-
ных составляющих:
h=Jhty -p/s/y (1. 10)
где Jhty — скорость изменения скалярной величины пролета;
. _ Ja/y — скорость разворота пролета в плоскости Я;
Vohc^hQ — скорость изменения направления пролета в плоскости
Q при изменении его скалярной величины.
На скорость изменения пролета влияет только проекция век-
тора относительного ускорения на плоскость Н (вектор 7н).
Проекция на направление относительной скорости /у оказы-
вает косвенное влияние на скорость изменения пролета вслед-
ствие изменения скалярной величины относительной скорости и,
следовательно, изменения упрежденного времени /у.
Из этого следует, что наибольшей скорости уменьшения про-
лета при заданном по модулю векторе ускорения можно добить-
ся, если направить полный вектор относительного ускорения по
вектору пролета. Идеальная система наведения, таким образом,
должна обеспечить измерение вектора пролета и направить век-
тор относительного ускорения J навстречу вектору пролета.
Увеличение текущего пролета достигается таким маневром цели,
при котором проекция ускорения J на направление пролета по-
ложительна.
Итак, вектор пролета h позволяет прогнозировать кратчай-
шее расстояние между ракетой и целью /?к и указывает, как
ориентировать вектор относительного ускорения, чтобы добить-
ся максимальной скорости изменения этого кратчайшего рас-
стояния.
На практике непосредственное измерение пролета представ-
ляет значительные трудности. Однако существует большое чис-
ло координат, характеризующих относительное движение раке-
ты и цели, которые позволяют при определенных допущениях
оценить пролет. Относительно просто это достигается при не-
14
подвижной цели, так как в этом случае относительная скорость
совпадает со скоростью ракеты.
Измеряя дальность и углы пеленга, можно с точностью до
угла атаки и ошибки, вносимой скоростью ветра, определить
пролет по формуле (1.1), где Х = л—<р (<р — полный угол пелен-
га цели). Для правильной ориентации вектора ускорения знание
дальности необязательно.
В случае подвижной цели для оценки пролета часто исполь-
зуется измерение линейного рассогласования или угловой-ско-
рости линии дальности ракета — цель.
Рассмотрим связь этих координат с пролетом.
1.3. ЛИНЕЙНОЕ РАССОГЛАСОВАНИЕ
Линейным рассогласованием I называют вектор, характери-
зующий расстояние между целью и линией, проведенной через
ракету в заданном направлении й0.
Рис. 1.6. Изменение линейного рассогласования в про-
цессе относительного движения
В прямолинейном относительном движении последователь-
ным положениям вектора дальности R(t) соответствуют векто-
ры линейного рассогласования /(/), лежащие в плоскости L,
перпендикулярной заданному направлению (рис. 1.6).
Вектор ?(/), лежащий в той же плоскости, является проек-
цией вектора относительной скорости на плоскость L. При рав-
номерном прямолинейном относительном движении линейное
15
рассогласование в момент t2 может быть выражено через линей-
ное рассогласование в момент ti формулой
/&)=/(/,)+7
Аналогично
п)
Z(/z) =Z(Z1)+t(/1)«-/1).
Здесь t(ii)—вектор линейного рассогласования в момент, ког-
да вектор дальности R(t) оказывается лежащим в плоскости L.
Рис. 1.7; Взаимная ориентация векторов дальности R(t), отно-
сительной скорости V(f) и опорного направления ио
Согласно рис. 1.6 скалярные величины векторов /(/0), l(ti) и
й(Л) удовлетворяют неравенству
/(^>Л(^)>/(/0). , (1.12)
Действительно, пролет h(ti)—катет в прямоугольном тре-
угольнике, гипотенузой которого является /(^). В то же время
пролет h(/i) может рассматриваться в качестве гипотенузы пря-
моугольного треугольника, в котором /(/о) является катетом.
Докажем, что при определенных условиях из (1.12) ‘следует
Приближенное равенство
~z (/0М&) +7&)(/0-4). (1.13)
Модуль разности верхней и нижней оценок пролета, как это
следует из (1.11), равен величине'
11 (ZJ (ti /0)|,
совпадающей с длиной отрезка bd на рис. 1.6, 1.7.
Для того чтобы сопоставить Э1у величину с величиной про-
лета, введем следующие углы: т) — между вектором й0 и обрат-
16
ным направлением вектора дальности R, % —между векторами
«о и V и v, равный л—X (см. рис. 1.7).
Длина отрезка fd может быть представлена в виде
Р COS71
cos х ’
длина отрезка fa —
cos v.
. Их разность (длина отрезка ad) равна
г» / COS ТП \
cos V -----— -----1 .
\ COS X COS V /
С другой стороны, длина отрезка ad может быть выражена че-
рез длину отрезка bd. Согласно (1.11) и рис. 1.7 длина от-
резка ad равна
Приравнивая последние выражения, получим разность оце-
нок в виде
1 Pi) Рф- Q=R tg х (COS П — cos x cos v). (1.14)
Если направить вектор й0 по вектору У(% = 0), разность оценок
обращается в нуль, так как при этом вектор_ линейного рассо-
гласования I совпадает с вектором пролета h. Кроме того, раз-
ность оценок обращается в нуль, если пролет равен нулю, так
как в этом случае v = 0 и, как следует из рис. 1.7,
'П=Х.
При фиксированных значениях v#=0 и %=#0 величина разнос-
ти оценок (1.14) достигает максимального значения при мини-
мальном т], а минимального значения — при максимальном т].
Такими максимальными и минимальными значениями согласно
рис. 1.7 являются
П=|х| + М и П=1%—v|, (1-15)
что соответствует расположению вектора й0 в плоскости, содер-
жащей V и h. При этом максимальному значению л соответст-
вует ti—^о<О, а минимальному — ti—/0>0. Воспользовавшись
тем, что h = R sin v, из (1.14) для этих случаев получим
*Pi)Pz — /0)=— Asinxtgx при tt—/о<0,
/(/1)й—/0)=Asinxtgx при tt—/о>0.
17
Учитывая, что при (1.15) разность (1.14) максимальна»
имеем
/(^l^-ZoK/t sin xtgx-
Таким образом, относительная величина разности оценок
скалярной величины пролета удовлетворяет неравенству
I (<i) Ю — *pl_, sjn fg
h(f) Л Л
Угол между вектором пролета 7г (6) и его оценками l(t0)
может быть выражен через тангенс углов аЦЬ и aUd (см.
рис. 1.7). Так,
tg(A(^i)JO<sin х,
tgtl&M^Xtgx.
Как следует из рис. 1.7, при малых углах % ошибка в опреде-
лении пролета в основном ориентирована вдоль вектора относи-
тельной скорости,_ поэтому, _направив вектор ускорения J на-
встречу вектору Z(/o)-или /(Л), в соответствии с (1.3) — (1.10)
получим следующие составляющие:
Как следует из (1.13), точность оценки пролета существенно
зависит от точности определения упрежденного времени /у =
= /о—Л- Обычно упрежденное время рассчитывают по прибли-
женной формуле
, Я (6)
У-1*(Л)Г
дающей приемлемую точность только при условии
(1.16)
В связи с тем, что определить положение вектора относи-
тельной скорости довольно трудно, опорное направление выби-
рают близким к обратному направлению вектора дальности
(т. е. задаются малым углом т]). При этом угол % может быть
малым только при малых v, что соответствует выполнению усло-
вия (1.16). Таким образом, использование линейного рассогла-
сования / (/о) в качестве приближения вектора пролета h (6)
допустимо, если выполняется условие (1.16) и угол ц мал.
Обычно в начале процесса наведения условие (1.16) выпол-
няется. В зенитных ракетах это обеспечивается разворотом пус-
ковой установки и этапом вывода, в ракетах «воздух—воздух»—
этапом самонаведения носителя, а в некоторых случаях еще и
автономным управлением на стартовом участке траектории. В
18
процессе сближения ракеты с целью при уменьшении дальности
это условие выполняется тем дольше, чем успешнее происходит
процесс наведения. Однако всегда, в конце концов, дальность
оказывается равной пролету, поэтому, естественно, что в некото-
рой окрестности точки встречи угол v становится большим,
а оценка упрежденного времени неверной. При этом оценка про-
лета с помощью неравенства (1.12) будет неточной. Практичес-
ки чем выше относительная скорость ракеты и пели, тем менее
существенно увеличение угла v. При большой относительной
Рис. 1.8. Траектория ракеты «воздух — воздух»
при управлении по линейному рассогласованию
(истребитель наводится в «собственную» точку
встречи с целью)
скорости условие (1.16) выполняется до малого времени /о—/ь
когда согласно (1.10) пролет уже не может существенно изме-
ниться. Таким образом, положение вектора uq можно выбирать
достаточно произвольно, но так, чтобы угол т] не был большим.
Согласно (1.13) скалярную величину линейного рассогласо-
вания можно рассматривать как решение дифференциального
уравнения первого порядка с h(t) в правой части. Произволь-
ный выбор вектора й0 соответствует произвольному выбору на-
чальных условий по /(0) и компенсируется соответствующим
изменением 1(0).
Вектор й0 может быть, например, выбран так, чтобы линия
заданного направления совпадала с линией дальности ракета—
цель в момент начала наведения. В этом случае угол *n = 0, угол
z=v, /(0)=0, а/~—Л(0).
В качестве примера рассмотрим вариант построения системы
телеуправления ракеты «воздух — воздух» (рис. 1.8).
Положим, что истребитель осуществляет самонаведение в
упрежденную точку встречи с целью. При этом линия дальности
19
истребитель — цель остается параллельной самой себе. Она и
выбирается в качестве опорного направления. После пуска ра-
кеты истребитель с помощью бортовой радиолокационной стан-
ции измеряет дальность до ракеты и угол между линиями
дальности истребитель — ракета и истребитель — цель. Этих
данных достаточно для того, чтобы вычислить линейное рассо-
гласование, т. е. расстояние между ракетой и линией дальности
истребитель — цель. На рис. 1.8,а показано абсолютное, а на
рис. 1.8,6 — относительное движение цели, ракеты и истреби-
теля.
При формировании контура наведения по линейному рассо-
гласованию необходимо знать, как связаны между собой векто-
ры J и I. I — проекция относительной скорости V на плоскость
Л, перпендикулярную плоскости чертежа, I — проекция вектора
относительного ускорения J на ту же плоскость
T=JL. (1.17)
При малых углах у проекция jLc^JHi поэтому согласно (1.10) и
(1.13), направив JL по обратному направлению вектора I (to) 9
можно обеспечить совпадение вектора JHc обратным направле-
нием h и, следовательно, уменьшить пролет.
Таким образом, система наведения по линейному рассогласо-
ванию должна включать в себя:
устройство, измеряющее линейное рассогласование, его про-
изводную и время, оставшееся до встречи ракеты с целью;
вычислитель, который так формирует команды на контур
стабилизации, чтобы проекция полного вектора ускорения раке-
ты на плоскость L была направлена навстречу вектору
(Если имеется информация о проекции ускорения цели на плос-
кость L, естественно так сформировать команду на контур ста-
билизации, чтобы навстречу вектору Z(/o) была направлена про-
екция полного вектора относительного ускорения JLj.
Системы наведения, использующие линейное рассогласова
ние, применяются при телеуправлении, т. е. тогда, когда коор-
динаты ракеты и цели измеряются с поверхности Земли или с
подвижного объекта и сформированные команды транслируют-
ся по линии связи на ракету.
В отличие от описанной схемы на практике для простоты ре
ализации иногда применяют подвижный вектор й0. Так, при
управлении по методу трех точек вектор й0 направляют по даль-
ности станция — цель (имеется в виду, например, радиолокаци-
онная станция, ведущая измерение координат цели и ракеты).
Наличие угловой скорости вектора в первом приближении экви-
валентно маневру цели и приводит к дополнительным затратам
маневра ракеты, однако в ряде случаев это оказывается пелесо-
20 -'
образным, так как отпадает необходимость в точном измерении
дальности до цели (рис. 1.9).
Часто не производят измерения упрежденного времени /у —
= to—tt необходимого для правильного учета производной ли-
нейного рассогласования. При этом команда на контур стаби-
лизациии формируется в соответ-
Рис. 1.9. Траектория ракеты
при наведении по методу
трех точек
ствии с формулой
/(/)+?(/) г,
где Т — константа.
Такой выбор способа управле-
ния основан на том, что для огра-
ничения текущего пролета доста-
Рис. 1.10. Траектория ракеты при вы-
воде на высоту цели при управлении
по линейному рассогласованию
точно ограничения линейного рассогласования и его производи
ной. Важной особенностью здесь является стремление ракеты
совместить дальность с линией заданного направления. В неко-
торых случаях этим пользуются для придания определенных
свойств траектории ракеты*. Так, для того чтобы удержать раке-
ту на высоте, равной высоте полета цели, опорное направление
может быть выбрано горизонтальным (рис. 1. 10).
1.4. УГЛОВАЯ СКОРОСТЬ ЛИНИИ ДАЛЬНОСТИ
Вектор угловой скорости линии дальности со является —Нор-
малью к плоскости Q, в которой лежат векторы R, V и Я
(рис. 1.11). Скалярная величина вектора угловой скорости мо-
жет быть определена из соотношения
V sin К, (1.18)-
характеризующего тангенциальную составляющую относитель-
ной скорости.
Учитывая (1.1), из (1.18) получим
В соответствии с рис. 1.11 выражение для пролета можно
записать в векторной форме
• (1-19>
V V i
2t
Если векторы V, ш и К заданы своими проекциями на оси
так называемой лучевой системы координат Хл, Ул, 7Л, где ось
Хл совпадает с отрицательным направлением вектора дальнос-
Рис. 1.11. Взаимное_расположение плоскости Q, со-
держащей векторы R и V, плоскости S, перпендику-
лярной вектору дальности, и плоскости Н, перпенди-
кулярной вектору относительной скорости
ти, а ось Хл горизонтальна. Составляющие пролета выражают-
ся формулами:
у2 + ^2 +V2^
лл г л л
Равенство нулю проекций /?гл и а>хл определено выбо-
ром системы координат. При малых по сравнению с Vx проек-
циях Уул и Угл (что соответствует условию (1.16))
ll у (1) 7
Г Л ^Л
Л2Х
лл
лл
*х
лл
Vxn'
h 7 ц)у
^л гл
а сам пролет
h ~ |Ллгл4-л1л.
22
Учитывая, что #хл——R и Кхл = |/?|, получим
. Л2
h^-~u%,-^р
h - * (1,20>
Ч-“гл^г-
Из соотношений (1.18) — (1.20) следует, что угловая скорость
линии дальности характеризует текущее значение пролета. Угло-
вая скорость как бы позволяет измерять пролет с переменным
масштабом: чем ближе ракета к цели, тем крупнее масштаб.
Рассмотрим вопрос, как, зная вектор угловой скорости сог
ориентировать вектор ускорения J. Вектор со перпендикуляре»
плоскости Q, поэтому для того, чтобы Ja в (1.6) был равен ну-
лю, потребуем, чтобы
(7ш)=0.
При этом в проекциях на лучевую систему
«Z ТГ (Оу ~I- J Ч (1)7 - О,
1 л г Л 1
откуда
7 г л. Jz„
“у ’
где К — коэффициент.
Тогда и
л=Jгл = К<*ул- (1 • 21)
Для того чтобы скалярная величина пролета уменьшалась,
в соответствии с (1.10) потребуем выполнения неравенства
(JA)<0.
В проекциях на лучевую систему координат это условие имеет
вид
J у hy —J у hy —I— J у h у 0.
лл лл 1 7л 1Л 1 ^л 4л
Подставив /ул и 1гл из (1.21), a hY л и hZ/i из (1.20), получим
неравенство
+4.) j^<o.
из которого следует, что в (1.21) коэффициент пропорциональ-
ности /С должен быть положительным. (Произведение 1хл Ьхл
обычно мало по сравнению с другими слагаемыми, так как при
выполнении (1. 16) hx л«/4л+а1л, а ]Хп либо мал, либо име-
23
ет тот же порядок, что и /уд, /zj- Таким образом, зная проек-
ции угловой скорости в лучевой системе координат, можно,
воспользовавшись (1.21), сформировать ускорения /ул и JZji,
обеспечивающие уменьшение скалярной величины пролета без
изменения его направления.
Полезно знать, как угловая скорость линии дальности связа-
на с вектором относительного ускорения. Рассмотрим вектор-
ную форму выражения (1.18)
^Х^=^оХ(^Х^о)-
_ Раскрывая двойное векторное произведение и учитывая, что
<Яо^о) = 1. получим
шХ^=й-^0(^0Г).
Продифференцируем левую и правую части последнего ра-
венства
-Ro(kov)-Ro(Rov). (1.22)
<умму первого и последнего членов правой части выражения
(1.22) можно представить в виде
7-^0(^07)=7-7л=75, (1.23)
где Jr — проекция вектора относительного ускорения J на даль-
ность;
Js — проекция того же вектора J на плоскость S, перпенди-
кулярную дальности.
Перенесем член Йо (Я0Г) в левую часть выражения (1.22)
л рассмотрим показанный на рис. 1.12 вектор
д=шХ^+^о(Йог). (1.24)
Первое слагаемое в (1.24)
Бго скалярная величина равна соК Скалярная величина второго
слагаемого равна coVsinX, так как (Й0)=со, а угол между век-
торами Ro и V составляет X——
Угол, измеренный от второго
слагаемого к первому в положительном направлении, равен
Вектор А, равный сумме слагаемых (1.24) и, следовательно,
лежащий в плоскости Q, может быть представлен в виде сторо-
ны треугольника, в котором две другие стороны (слагаемые
24
в (1.24)) относятся друг к другу, как sinZ, а угол между ними
X—Такое представление
равен
возможно только, если век-
тор А перпендикулярен меньшей из сторон, откуда следует, что
вектор А перпендикулярен В. и его скалярная величина
o)IZ sin IX-— ] = — u)lZ cos X.
\ 2 )
Учитывая, что V cosX = R, получим
A = — /?0Х^=
(1.25)
. Произведение назовем вектором скорости сближения
и обозначим R. Тогда окончательно
' (1.26)
Второе слагаемое в правой части (1.22)
-Шй)
может быть представлено в виде
-А -“X А
Таким образом, из соотношений (1.22) — (1.26) получим диффе-
ренциальное уравнение
^Х^+2со"ХЛ=75, (1.27)
связывающее векторы w, R и Jg.
Заметим, что при *
7s=O)Ux^) (1.28)
25
все члены уравнения (1.27) коллинеарны и, следовательно, век-
тор со изменяется только по величине. Вектор Js при этом лежит
в плоскости Q и дает такую проекцию на плоскость Н, при ко-
торой нормальная составляющая относительного ускорения
J в равна нулю и вектор пролета не вращается (точнее, не вра-
щается его проекция на плоскость Н, см. разд. 1.2).
В проекциях на оси лучевой системы координат с учетом то-
го, что Кхл =—R и #хл=—R, уравнение (1.27) можно предста-
вить в виде
u)z R 2a)ZjiA? = — Jул,
(1-29)
о)Гл R 2соуЛЙ—Jгл-
1.5. УПРАВЛЕНИЕ ВЕКТОРОМ УСКОРЕНИЯ РАКЕТЫ
Из изложенного ясно, что скорость изменения пролета зави-
сит только от проекции вектора относительного ускорения раке-
ты и цели на плоскость Н, В наиболее часто встречающихся
случаях в системе управления ракеты ускорение цели измерить
непосредственно невозможно, и ракета «парирует» его только
после того, как возникает пролет. Поэтому естественно рассмот-
реть отдельно проекцию ускорения ракеты на плоскость Н.
Как известно, маневренные возможности ракеты ограничены.
Обычная ракета с аэродинамическим управлением способна
создать вдоль связанных с нею осей У1 и Zi ускорения, предель-
ные значения которых колеблются от сотен м/с2 на режимах мак-
симальных скоростных напоров до десятков м/с2 на режимах,
минимальных скоростных напоров. Создание аэродинамических
сил вдоль осей У1 и Z\ сопровождается возникновением силы ло-
бового сопротивления, которая вызывает торможение ракеты
вдоль оси Хь \
В настоящее время реактивные силы для создания линейно-
го ускорения еще не нашли широкого использования в ракетах,
применяющихся в атмосфере. Поэтому ускорение, создаваемое
двигателем и действующее обычно вдоль связанной с ракетой
оси Хь так же, как и лобовое сопротивление, следует рассмат-
ривать как возмущение. Продольное ускорение ракеты, вызван-
ное тягой двигателя, может достигать нескольких сот м/с2. Кроме
перечисленных сил на ракету действуют сила тяжести и ветер.
Если известно, что траектория цели близка к баллистической,
сила тяжести вообще не учитывается, так как в этом случае
она не влияет на относительное ускорение. Воздействие ветра в
основном сводится к изменению направления движения набега-
ющего потока воздуха и появлению дополнительного угла
атаки.
Из изложенного следует, что в обычной аэродинамической ра-
кете возможно управление только проекциями полного вектора
26
ускорения ракеты на связанные оси У) и Zb Проекция ускорения
Jxt при этом изменяется самым произвольным образом. Поэтому
полный вектор ускорения ракеты, как правило, не удается на-
править по пролету. Однако учитывая, что проекция ускорения
на относительную скорость не оказывает вредного влияния на
процесс наведения (если, естественно, при этом не происходит
чрезмерного роста или убывания относительной скорости), сос-
тавляющие Jyf и Jzi следует выбирать таким образом, чтобы
направить по пролету проекцию вектора ускорения на плоскость
Н (см. стр. 14). Это, естественно, возможно только при условии,
что между связанной осью Xi и вектором относительной скорости
угол фу не слишком велик. Для того чтобы скомпенсировать про-
дольное ускорение ракеты , требуется боковое ускорение
tg фу.
Рассмотрим с этой позиции построение системы наведения
по линейному рассогласованию и угловой скорости линии даль-
ности.
В системе наведения по линейному рассогласованию целесо-
образно на ракете установить гироскопическую платформу*
стабилизированную относительно линии заданного направле-
ния Йо.
В частности, такой платформой может быть гиростабилизи-
рованная головка самонаведения, которая с момента пуска ра-
кеты до захвата цели сохраняет положение оси Ад (так называ-
емого равносигнального направления диаграммы направлен-
ности головки самонаведения).
Измеряя проекции ускорения ракеты на плоскость (Ул, 2Л),
перпендикулярную стабилизируемому направлению (рис. 1.13),
и сравнивая их с заданными ускорениями, соответствующими
измеренному с помощью линейного рассогласования пролету»
можно сформировать команды на рули ракеты. Такое построе-
ние бортовой системы управления позволяет непосредственно на
ракете компенсировать проекции возмущающих воздействий на
плоскость, перпендикулярную заданному направлению.
На практике для простоты бортовой системы ракеты сигна-
лы заданных ускорений JYjl и Jz* ракеты, вычисленные в соот-
ветствии с ориентацией измеренного пролета, подают на вход
каналов управления контура стабилизации. В результате срав-
нения этих сигналов с ускорением ракеты по связанным осям
/у, и Jzt формируются команды на рули ракеты. В ситуациях,
отличных от чисто «встречных» или чисто «догонных», когда ось
ракеты повернута относительно линии заданного направления,
возмущения, действующие на ракету, и ошибка в ориентации
вектора JYt +Jzt относительно J ул+Тгл воздействуют на кон-
тур наведения так же, как неизвестный на борту ракеты маневр
цели.
27
При управлении по угловой скорости линии дальности пра-
вильная ориентация полного вектора ускорения может быть до-
стигнута, если рассматривать соотношение (1.21) как выражение
для заданных ускорений в лучевой системе координат:
а команды на рули ракеты формировать как результат сравне-
ния этих заданных ускорений с измеренными 7ул и /ял. И в этом
случае возмущения, действующие вдоль оси Хл, не окажут су-
Рис. 1.13. Проекции вектора относи-
тельного ускорения на лучевые и свя-
занные оси
Рис. 1.14. Связанная, антенная и луче-
вая системы координат
щественного влияния на процесс наведения, если они не приве-
дут к чрезмерно большим или чрезмерно малым скоростям сбли-
жения. При самонаведении измерение составляющих угловой
скорости, заданного ускорения и ускорения ракеты производит-
ся не в лучевой системе координат, а в системе координатора
цели (так называемой антенной системе координат Ха, Уа, Za),
повернутой относительно ракеты на два угла пеленга <ру и q>z.
При нулевых ошибках слежения за целью антенная система ко-
ординат развернута относительно лучевой только в плоскости,
перпендикулярной линии дальности, т. е. оси Хп (рис. 1.14).
В большинстве реальных систем угловая скорость линии
дальности, измеренная в виде проекций <дуа и coza на оси Уа и
Za антенной системы координат, используется для формирова-
ния заданных ускорений ракеты в связанной системе
Jyi=K^z&;
Jzt — —
В этих системах проекция вектора ускорения ракеты на
плоскость, перпендикулярную вектору дальности, может сущест-
ве
венно отличаться от ускорения, соответствующего измеренным
значениям угловой скорости линии дальности. Так же, как и в
случае управления по линейному рассогласованию, эта разница
между заданным и реализованным ускорением воспринимается
контуром-наведения как маневр цели.
Необходимо отметить, что везде выше, говоря об ускорении
ракеты или его -проекциях, имелось в виду,, что это ускорение
включает в себя и соответственно направленное ускорение силы
тяжести. Фактически установленные на ракете датчики линей-
ных ускорений измеряют проекции векторной суммы J^+g. При
свободном падении ракеты и полном отсутствии аэродинамичес-
ких и газодинамических сил эти датчики выдают нулевой сиг-
нал. Поэтому для компенсации ускорения силы тяжести показа-
ния датчиков должны быть скорректированы на величину про-
екций ускорения силы тяжести.
1.6. ЛИНЕАРИЗОВАННЫЕ ЗАВИСИМОСТИ,
СВЯЗЫВАЮЩИЕ ПРОЛЕТ, ЛИНЕЙНОЕ РАССОГЛАСОВАНИЕ
И УГЛОВУЮ СКОРОСТЬ
При исследовании динамики наведения удобно пользоваться
линейными приближениями зависимостей, характеризующих
связь между пролетом, линейным рассогласованием и угловой
скоростью.
Основой для линеаризации является условие малости углов
г] и v (см. рис. 1.7), характеризующих взаимное расположение
нормалей к плоскостям Я, L и S (см. рис. 1.5, 1.6 и 1.П). V — нор-
маль к плоскости Я; й0 — нормаль к плоскости L; R — нормаль
к плоскости S. При этом приближенно можно считать, что про-
екции вектора относительного ускорения ня эти плоскости равны
друг другу
j L — J S — J н-
Если положить, что const (7v~7r~0), дальность мож-
но записать так:
(/) = |^|(/0—/). (1.30)
Тогда, учитывая, что в данном случае |7?| = —R, в проекциях
на оси Ул и 2Л лучевой системы координат имеем
0,гл (^о—0 — 2(Огл = — »
JZ (1-31)
(Z0 — — 2(% — -^7- •
29
Но согласно (1.20), подставляя в (1.31) выражение для дальнос*
ти, находим
hY
и, =----ГН—-----.
|*|(t0-t)2
hz - (1.32)
Гл 1*1 (to-О2
и, следовательно,
hv hv
w —_________La____2 л
z* 1*1 (to- t)2 1*1 (to-t)3 ’
Ч lL33)
l*|(to-t)2 +2 l*l(to-t)3 ‘
Подставив (1.32) и (ЕЗЗ) в соотношения (1.31), после упроще-
ний получим
ч =(/о-*)ч =(^о-0Лл. (1-34)
что соответствует точной формуле (1.10).
Рассмотрим (1.11) в проекциях на оси Ул и Хл:
hY*=1уЛ ~j 35)
Адл=<гл+(гл(А>—0-
Продифференцировав соотношения (1.35), определим
^гл=^гл (А)—^)» ^гл=А?л (^о““^)‘
Учитывая, что
/— J L^J н,
получим
^ул = (zo ^гл» hzn = (^о “
Как уже указывалось в разд. 1.3, линейное рассогласо-
вание можно рассматривать как решение дифференциаль-
ного уравнения (1.13) с произвольным значением начального
условия /(0). Задавшись начальными значениями lYjl (0) и
lz л(0), можно согласно (1.35) выразить /ул(0 и lz л (0 как ре-
шения уравнений:
30
Для дальнейшего удобно представить
'г,(')=8'г,(')+'2л(0).
где ЫУя (/) — вариация величины /Гл(/);
Ц,л(0) = В/2д(0)=0;
1у (0)—const, lZn (0)=const.
При этом
8/ул Р) + (4>- *) Щл У)=Ьуй W - 1ул (0);
+ (1' }
Следовательно, при сделанных допущениях пролет, линейное
рассогласование и угловая скорость связаны между собой и с от-
носительным ускорением линейно.
1.7. СТРУКТУРНЫЕ СХЕМЫ ЗВЕНА
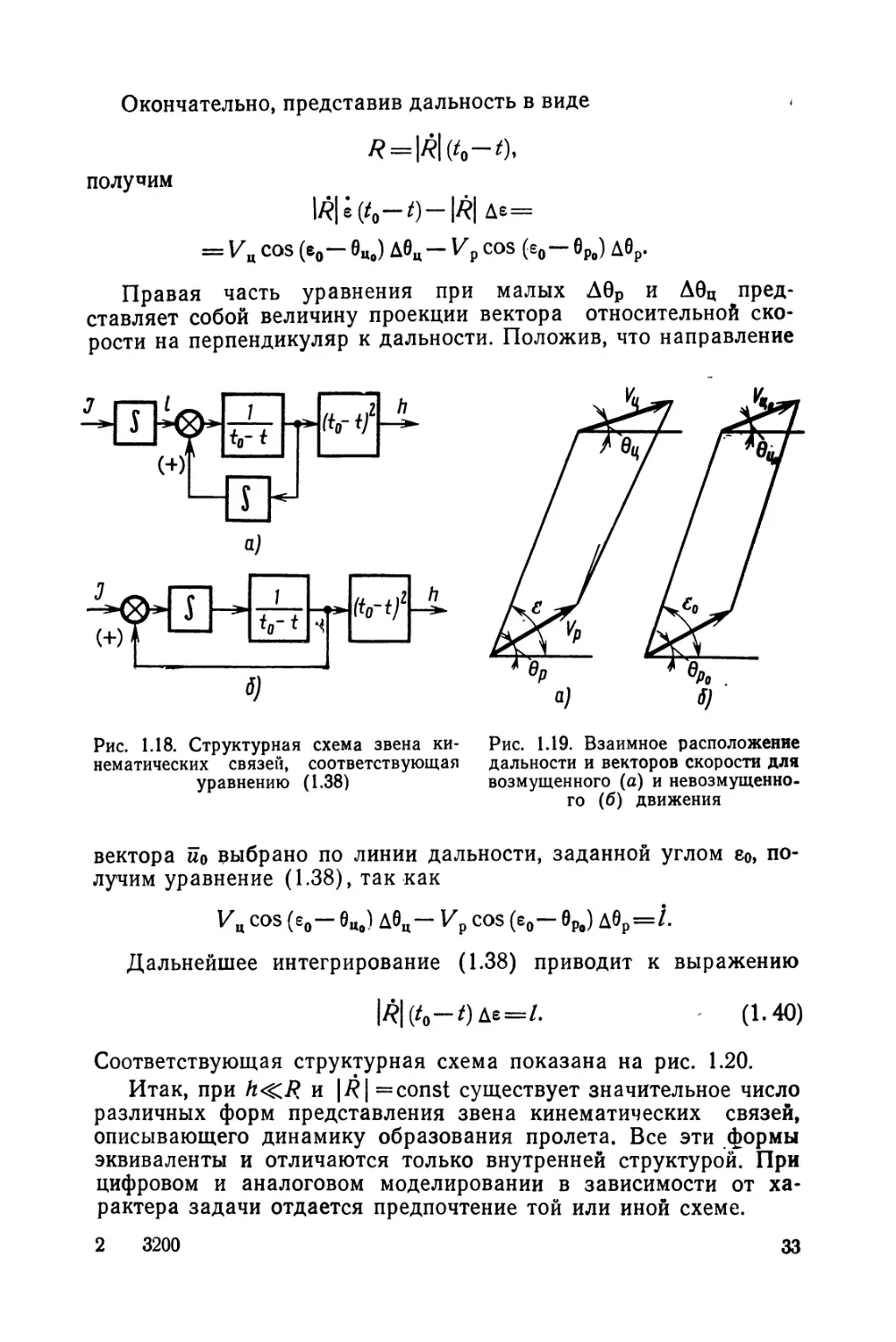
КИНЕМАТИЧЕСКИХ СВЯЗЕЙ
Точные (1.10), (1.11), (1.17), (1.19), (1.27) и приближенные
(1.31), (1.33), (1.34), (1.35), (1.36) уравнения, связывающие
пролет, линейное рассогласование и угловую скорость линии
дальности с относительным ускорением ракеты, называют урав-
нениями кинематических связей или кинематическими соотно-
шениями (фактически эта тер-
минология не точна, так как
связь между этими величинами
носит динамический характер).
Рис. 1.16. Структурная схема
звена кинематических связей,
соответствующая уравнению
(1.35)
Рис. 1.15. Структурная
схема звена кинематичес
ких связей, соответствую-
щая уравнению (1.34)
С целью изучения динамики наведения для представления
контура наведения в виде системы автоматического регулирова-
ния в соответствие линеаризованным уравнениям удобно поста-
вить структурные схемы так называемых звеньев кинематичес-
ких связей.
Согласно соотношениям (1.31) — (1.34) и (1.35) звено кине-
матических связей может быть представлено в виде, показанном
31
на рис. 1.15—1.17. При сделанных в разд. 1.6 допущениях из со-
отношений (1.31) следует
IW (4>-*)]'-1£1 “>=•/•
Проинтегрировав левую и правую части последнего выраже-
ния в предположении |7?| = const, получим
|$| ё (/0—/) — |Д?| де =/, (1.38)
где е=аз;
/ _ *
Де = zdu 4- де (0); I = j* J du 4-/ (0).
о b
Соответствующая схема звена кинематических связей пока-
зана на рис. 1.18, а. Переносом точки суммирования схема пре-
образуется к виду, приведенному на рис. 1.18,6.
Рис. 1.17. Структурная схема звена кинема-
тических связей, соответствующая уравне-
нию (1.31)
Выражение (1.38) может быть получено и непосредственно
при линеаризации уравнений проекций векторов скорости раке-
ты и цели на линию дальности и перпендикуляр к ней (рис.
1.19,а)
Л= cos (е — 0Ц) — Ир cos (е — 0р),
y?s = Vpsin (е —0р) —Vusin (е—0Ц). (1.39)
Положив Vp = const и Vu=const, получим
е = е0 + Де> ®р=®р«_1_Д®р> 0ц=вцо 4“ Д0ц>
где е0, 0Ро, Оц, —константы, удовлетворяющие уравнению
l/psin (е0— 0Р,) — H„sin (е0 — 0Цо)=О(см. рис. 1.19,6), а Де, д0р и
Д0Ц—малые вариации. После отбрасывания членов высших по-
рядков малости получим
Л= Иц COS (е0 — 0цо) — IZp cos (е0 — 6Ро),
/?е‘ = — [Иц cos (е0 — 0Цо) — Ир cos (е0 — 0Ро)] Де 4~
4-Иц cos (е0 — 0ц#) Д0Ц — 1/р cos (е0— 0Ро) Д0р.
32
Окончательно, представив дальность в виде <
Z?=|Z?|(/O—С»
получим
|£|в(/0-/)-|7?| Де=
= Кд cos (е0— 0И<() Д0Ц — Кр cos (е0— 0Ро) Д0р.
Правая часть уравнения при малых Д0Р и Д0Ц пред-
ставляет собой величину проекции вектора относительной ско-
рости на перпендикуляр к дальности. Положив, что направление
Рис. 1.18. Структурная схема звена ки-
нематических связей, соответствующая
уравнению (1.38)
Рис. 1.19. Взаимное расположение
дальности и векторов скорости для
возмущенного (а) и невозмущенно-
го (б) движения
вектора «о выбрано по линии дальности, заданной углом ео, по-
лучим уравнение (1.38), так как
Кц cos (е0— 0Ио) Д0Ц— Кр cos (е0— 0Ро) Д0р=/.
Дальнейшее интегрирование (1.38) приводит к выражению
1Ш~1) (1.40)
Соответствующая структурная схема показана на рис. 1.20.
Итак, при йс/? и |7?| =const существует значительное число
различных форм представления звена кинематических связей,
описывающего динамику образования пролета. Все эти формы
эквиваленты и отличаются только внутренней структурой. При
цифровом и аналоговом моделировании в зависимости от ха-
рактера задачи отдается предпочтение той или иной схеме.
2 3200
33
Для дальнейшего изложения удобно ввести в рассмотрение
звенья, которые преобразуют пролет в величину, измеряемую в
системе наведения. Будем называть такое звено звеном форми-
рования измеряемой величины (ФИВ).
Рис. 1.20. Структурная схема звена кинематических свя-
зей, соответствующая уравнениям (1.40)
Для случая, когда система наведения строится на базе изме-
рения угловой скорости линии дальности, звено ФИВ описыва-
ется выражением
h
Uo —02|Л|
В структурной схеме
ный коэффициент.
это звено представляет собой перемен-
Рис. 1.21. Структурная схема звена, преобразую-
щего пролет в линейные рассогласования
X
Как следует из уравнения (1.37), структурная схема звена
ФИВ в случае использования линейного рассогласования имеет
вид, показанный на рис. 1.21.
1.8. СТРУКТУРНАЯ СХЕМА КОНТУРА НАВЕДЕНИЯ
В разд. 1.1 было введено понятие системы наведения, состоя-
щей из информационных устройств, контура стабилизации вы-
числительных и корректирующих устройств.
Совместно с рассмотренными в предыдущем разделе
звеньями кинематических связей и формирования измеряемой
величины система наведения образует так называемый контур
наведения, представляющий собой замкнутую систему.
Структурная схема типового контура наведения показана на
рис. 1.22.
В теории автоматического регулирования контур наве-
дения представляется системой стабилизации, в которой на
объект регулирования (звено кинематических связей) воздейст-
34
вует возмущение (ускорение цели /ц) и управление (ускорение
ракеты /р); стабилизируемая координата (пролет) измеряется
через звено ФИВ с ошибками ф, свойственными информацион-
ным устройствам; корректирующее устройство (вычислительное
и корректирующее звенья) формирует управляющее воздействие
(заданное ускорение /*) и через исполнительное устройство
(контур стабилизации) подает его на объект регулирования.
Рис. 1.22. Структурная схема кон-
тура наведения
Рис. 1.23. Структурная схема кон-
тура наведения с указанием весо-
вых функций
Контур стабилизации, задачей которого является воспроиз-
ведение с наилучшей точностью заданного ускорения /*, под-
вержен действию возмущений, приложенных к ракете или авто-
пилоту. Та часть возмущений, которая не подавляется автопи-
лотом, является «ложной составляющей» в ускорении ракеты
7 л и воздействует на систему подобно маневру цели.
Для удобства введем весовые функции [4—8] звеньев, обра-
зующих контур наведения: WK(t, т)—весовая функция звена
кинематических связей со входом по /=/ц—/р и выходом по h
(здесь /ц и Jp — проекции соответствующих ускорений на ось
Ул или 7Л лучевой системы координат); в соответствии с (1.34)
' ^К(Л т)=1(/-т)(/0-т); (1.41)
ГФИВ (£ т) — весовая функция звена формирования измеряе-
мой величины со входом по h й выходом по линейному рассо-
гласованию, угловой скорости или другой доступной для изме-
рения координате, характеризующей текущую точность наведе-
ния. В конкретных случаях эта весовая функция будет обозна-
чаться как Wih (t, т), или W (t, т). Индексы I и со указывают,
какая величина измеряется.
Источник информации, вычислительное и корректирующее
звенья, контур стабилизации объединим в одно звено со входом
2*
35
по измерениям (измеряемая величина плюс ошибки измерения
ф) и выходом по /р. Это звено условно назовем автономным
контуром. Оно, по существу, объединяет все, что выше было наз-
вано системой наведения. Весовую функцию автономного кон-
тура назовем W^tr т).
С учетом введенных обозначений структурная схема контура
наведения представлена на рис. 1.23.
В зависимости от типа задачи наведения структурная схема
может несколько изменяться,' однако в основных чертах она
сохраняется практически для всех ситуаций.
1.9. СТРУКТУРНАЯ СХЕМА КОНТУРА НАВЕДЕНИЯ
ПО УГЛОВОЙ СКОРОСТИ ЛИНИИ ДАЛЬНОСТИ
В соответствии с изложенным в разд. 1.4 и 1.6 структурная
схема контура наведения по угловой скорости линии дальности
отличается тем, что звено формирования измеряемой величины
представляется в виде коэффициента
со ______1___
Т—(/0-о2|я1 ’
Как будет показано в разд. 1.11, удобно использовать не
саму угловую скорость «о, а произведение | <о, поэтому в даль-
нейшем будем считать измеряемой величиной |^|ш, соответст-
вующее звено примем в виде коэффициента --------. При этом
Go — О2
весовая функция звена будет
Рис. 1.24. Структурная схема
наведения по угловой скорости
линии дальности
(1Л2>
Обычно в системах наведения по
угловой скорости стремятся к то-
му, чтобы .автономный контур был
стационарен. Этого достигают
применением стационарного кор-
ректирующего фильтра й автопи-
лота, стабилизирующего динами-
ческие характеристики контура
стабилизации, несмотря на су-
щественное изменение коэффици-
ентов ракеты.
Для стационарного автономного контура
W^t, r)=W^t-x). (1.43)
С учетом соотношений (1.41) — (1.43) структурная схема кон-
тура наведения по угловой скорости линии дальности может
быть представлена в виде, приведенном на рис. 1.24.
36
Поскольку контур наведения по угловой скорости включает
в себя нестационарные звенья (их последовательное соединение
имеет весовую функцию 1 —<)), замкнутый контур на-
(4) — О2
ведения нестационарен. Это создает определенные трудности в
синтезе и анализе линеаризованных систем подобного вида.
Подробно эти вопросы изложены ниже.
1.10. СТРУКТУРНАЯ СХЕМА КОНТУРА НАВЕДЕНИЯ
ПО ЛИНЕЙНОМУ РАССОГЛАСОВАНИЮ
Структурная схема, приведенная на рис. 1.21, и уравнение
(1.37) позволяют получить весовую функцию от пролета h до
линейного рассогласования I
т)=^Ц-1(/-т). (1.44)
(z0—т)2 •
При выводе весовой функции следу-
ет положить /(0) = 0 и h(t) =д(/—т).
Рассмотрим системы, в которых
автономный контур от измеренного
значения линейного рассогласова-
ния до ускорения ракеты стациона-
рен. В связи с этим интересно рас-
смотреть в структурной схеме кон-
тура весовую функцию последо-
вательного соединения звеньев
1Fk(/,t) и Wlh(t,r).
Учитывая соотношения (1.41) и
Рис. 1.25. Структурная схе-
ма наведения по линейному
рассогласованию
с весовыми функциями
(1.44), запишем
t t
\ Wlh (t, и) WK (и, x) du = \
J J Ho — uy
t т
(/0— i)du =
du
(<o~«)2
=(*o - (*0 -1) [т-Ц- - —У 1 (/ -1)=(/ - т) 1 (/ - т). (1.45)
L‘o~ t tQ—nJ
Полученное выражение зависит от разности аргументов t и
х и представляет собой весовую функцию двойного интегриру-
ющего звена.
Выражение (1.45) совместное (1.35) позволяет видоизменить
структурную схему контура, приведенную на рис. 1.25, в струк-
турную схему на рис. 1.26, состоящую из замкнутого стационар-
37
ного контура с выходом по I и нестационарного звена, преобра-
зующего I в h. Согласно (1.35) его весовая функция
Whl(t, T) = 8(/-r) + (Z0-/)8<’(Z-f). (1.46)
Естественно, что весовая функция Whi(t, т) обратна весовой
функции Wih(t, т). Для проверки этого факта достаточно убе-
диться в том, что
t
u)Whl(u, x)du=*(i—x).
t
Действительно,
t
\ 1 (/ - «) [8 (« - T) + (/0 - я) 8' (и - t)] =
=y^Lb(t—x)=i(t—x).
(4) — *)
Возможность представления контура наведения по линейному
рассогласованию в виде последовательного соединения стацио-
Рис. 1.26. Структурная схема наведения по ли-
нейному рассогласованию, представленная в
виде последовательного соединения стационар-
ной и нестационарной частей
парной и простейшей нестационарной частей существенно упро-
щает анализ и синтез такой системы.
В ряде случаев стационарность контура наведения по I
явилась причиной того, что именно этому способу построения
системы наведения отдавалось предпочтение. Материалы, свя-
занные с расчетом стационарных систем наведения по линейно-
му рассогласованию, содержатся в последующих разделах на-
стоящей главы.
1.11. ПРОСТЕЙШИЕ СИСТЕМЫ НАВЕДЕНИЯ
ПО УГЛОВОЙ СКОРОСТИ И ЛИНЕЙНОМУ РАССОГЛАСОВАНИЮ
Простейшей моделью системы наведения по угловой скорости
линии дальности является модель, в которой оператор автоном-
ного контура заменяется постоянным коэффициентом усиления.
38
Для этой модели удается получить аналитические зависимости
угловой скорости линии дальности и ускорения ракеты от вре-
мени. Как показывают приближенные расчеты и моделирование,
при времени самонаведения, в 10—20 раз большем эквивалент-
ной постоянной времени автономного контура, эти зависимости
дают достаточно хорошее представление о процессах в реаль-
ной системе.
Итак, уравнение автономного контура имеет вид Jp = Kcd.
Положим К=/Са| /?|, откуда
/P=/C.P?k (1.47)
Контур наведения при этом описывается согласно соотношениям
(1.31) и (1.47) системой уравнений
(/0 /)<о 2и> =-рг|-,
J = Ja~Jv,
откуда
(/0-/); + (^а-2)«>=/ц, (1.48)
где /ц=-гп—приведенный маневр цели.
|Я|
Уравнение (1.48) при f4=const имеет решение вида
2j+-(°) (L49)
Аа \ V / V
Соответствующее приведенное значение ускорения ракеты
(<07Са~2)+<о(О)/Са и-50
Ла— \ а J (0а
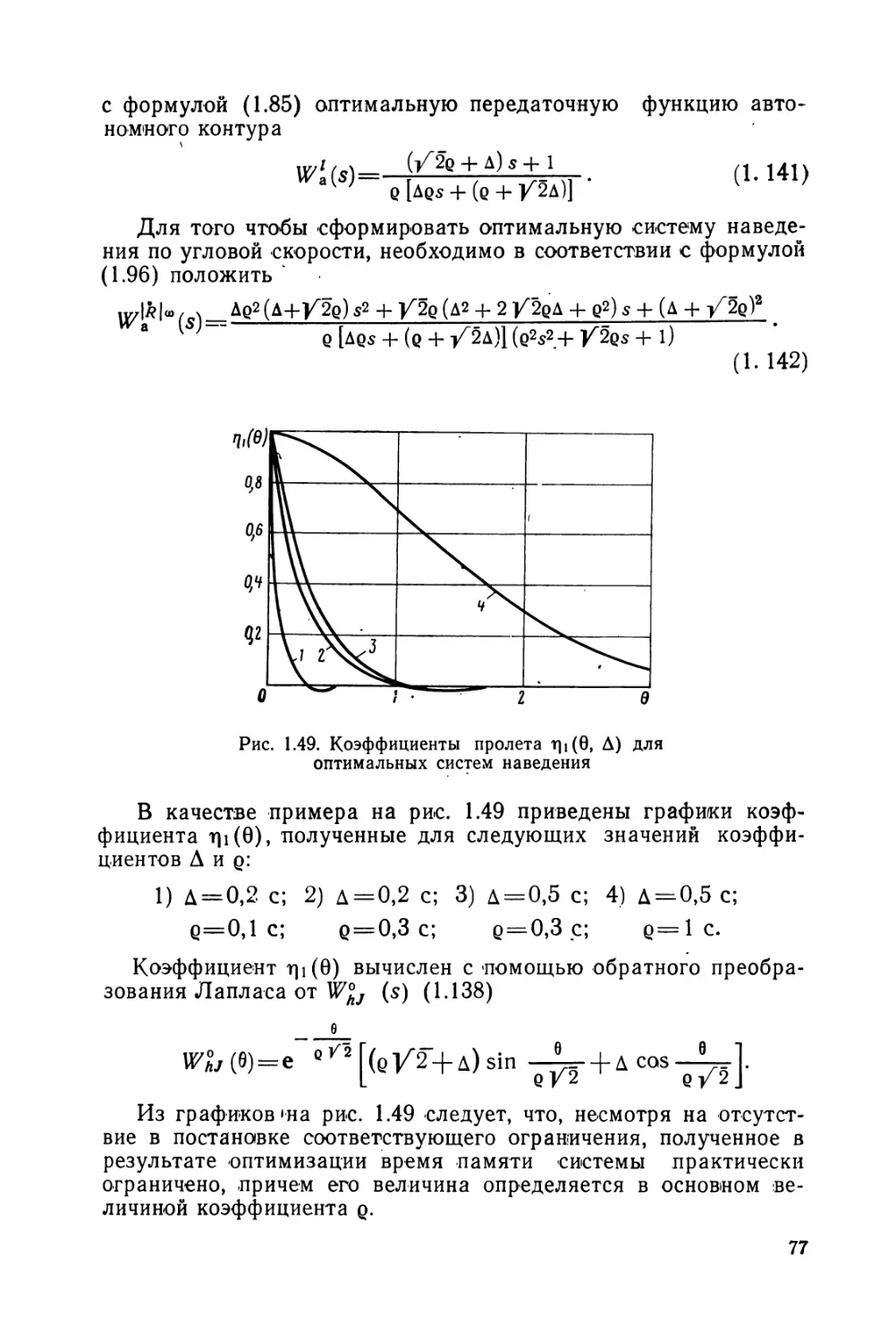
Из соотношений (1.49) и (1.50) следует, что вид кривых «(/)
и /р(0 (рис. 1.27—1.30) зависит не от полного коэффициента К
между со и /р, а от относительного коэффициента На практи-
ке, там, где это представляется возможным, скорость сближе-
ния |Л| измеряется и управление ведется по произведению
]/?|<о. В остальных случаях коэффициент К выбирается так,
чтобы с учетом прогнозируемого на момент встречи значения
|Л| получить определенное значение /Са.
Зависимости процессов изменения со(/) и fp(t) от Ка показа-
ны на рис. 1.27—1.30, из которых видно, что если отсутствует
маневр цели (/ц=0, (о(0)#=0), угловая скорость ©(/) и ускоре-
ние fp(/) не возрастают только в случае Ка>2.
39
Когда Ka^l ИЛИ Ка=2, или Ка=3, угловая скорость и уско-
рение ракеты соответственно растут неограниченно либо посто-
янны, либо изменяются линейно от начального значения до
Рис. 1.27. Угловая скорость ли-
нии дальности при различных
значениях коэффициента Ка
(маневр цели отсутствует)
Рис. 1.28. Ускорение ракеты при
различных значениях коэффициен-
та (маневр цели отсутствует)
нуля. При отсутствии начальных условий и воздействии маневра
(ф(0)=0, J(/)=/=0) угловая скорость и ускорение ограничены
только при Ка>2. Если Ка=3, скорость и ускорение ракеты воз-
Рис. 1.29. Угловая скорость линии
дальности при различных значени-
ях коэффициента усиления К& (на-
чальный пролет отсутствует)
Рис. 1.30. Ускорение ракеты при
различных значениях коэффициен-
та усиления /Са (начальный пролет
отсутствует)
растают линейно от нуля, причем ускорение ракеты достигает
максимального значения, в три раза превышающего ускорение
40
цели. Максимальное ускорение ракеты может быть равно уско-
рению цели только при бесконечно большом коэффициенте уси-
ления. С помощью соотношения (1.32) пролет может быть выра-
жен через угловую скорость
А=(0^(/о_/)2> (1.51)
откуда, учитывая (1.49),
где Л(0) —начальный пролет.
Рис. 1.31. Пролет при различных
значениях коэффициента усиления
Ла (маневр цели отсутствует)
Рис. 1.32. Пролет при различных
значениях коэффициента усиления
Ла (начальный пролет отсутствует)
Естественно, что при Уц=0 пролет не возрастает при любом
неотрицательном значении Ка, так как согласно (1.34) в этих
условиях й^О (см. рис. 1.31, 1.32).
В соответствии с рис. 1.26 структурная схема контура наве-
дения по линейному рассогласованию со стационарным авто-
номным контуром может быть представлена в виде последова-
тельного соединения стационарного и нестационарного звеньев.
При этом автономный контур включен в качестве обратной свя-
зи к, звену, связывающему относительное ускорение и линейное
рассогласование и представляющему собой два последовательно
включенных интегратора. Естественно, что оператор автоном-
ного контура в такой системе не может быть коэффициентом
усиления, так как совместно с двойным интегрирующим звеном
он образует консервативное звено. Простейший автономный кон-
тур системы наведения по линейному рассогласованию харак-
теризуется уравнением
Jp=K(l+Tl). (1.53)
41
В этом случае система уравнений контура наведения имеет
вид
/=./„—ЯГ (Z4-77),
Для постоянного ускорения цели 7Ц из (1.54) следует
(1.54)
1 Т-+ е~“' (— Р (°) +Р(°)- 4Н “Pin »/ +
Л I ш L \ л / J
Л (/)=/(0) e-e/ — [sin tot — (Zo—t) (a sin a7— a>cosa>/]-|-
CO
+/(0) e-®' f— [sin u>/ — (i0 —t) (a sin a7 —w cos<o/)] Ц-
[cos w/ — (/0—t) (acos<i>/-|-<i> sin <o/)]j +
-f- — [1 —e~“z (— [sin wt — (t0 — t) (a sin u>t — <o cos co/)] 4-
К I I
-|-[cos a>/ — (/0 — /) (a cos sin
где
KT
a=— .
2
Стационарность контура наведения от /ц до I и некоторые
свойства последовательного соединения стационарных и неста-
ционарных звеньев (см. разд. 1.13) позволяют проводить иссле-
дование подобных систем методом частотных характеристик,
поэтому усложнение выражения (1.53) не оказывает существен-
ного влияния на методику расчета.
1.12. ТОЧНОСТЬ СИСТЕМЫ НАВЕДЕНИЯ
И КОЭФФИЦИЕНТЫ ПРОЛЕТА
Для удобства исследования точности линейной системы на-
ведения представим текущий пролет в момент t в виде суммы
четырех составляющих
А(*)=2М). (1-55)
/—1
где Й1 (/) — пролет из-за начальной ошибки прицеливания, изме-
ряемой начальным пролетом й(т), т. е. пролетом в момент вклю-
42
чения системы; /г2(0 —пролет из-за маневра цели; Лз(/) и й<(/)—
пролеты из-за случайных ошибок измерения относительных ко-
ординат ракеты и цели.
Поскольку система наведения, как правило, нестационарна
или подвержена воздействию нестационарных входных сигналов,
естественно при исследовании точности воспользоваться аппа-
ратом весовых и параметрических передаточных функций [4, б,
7]. Начальный пролет й(т) является начальным условием в диф-
ференциальном уравнении (1.34). (й(т) равен h(t) при /=т,
Рис. 1.33. Преобразование структурной схемы при замене
начального пролета эквивалентным входным воздейст-
вием
здесь и далее индексом т обозначен момент приложения того или
иного воздействия). Для получения пролета hi удобно заменить
начальное условие й(т) (рис. 1.33,а) эквивалентным входным
сигналом x(t).
Выбирая х(/), будем считать, что начальный пролет подается
на вход системы управления только в момент начала наведения.
Тогда эквивалентный входной сигнал можно выбирать для
звена кинематических связей без учета весовых функций, замы-
кающих контур наведения. Выберем x(t) таким образом, чтобы
выполнялось условие
'+
J U7K(/, u)x(u)jdu=h (г) при /=т.
—00
Учитывая (1.41), получим
х (/)=-* ^—^(т). (1.56)
/0 — и
Тогда пролет hi (/) из-за начальной ошибки может быть записан
в виде
t
К (/) = f (/, в) x (и) du = т) h (т). (1.57)
43
Пх(Л t)
Здесь Whj(t, г)—весовая функция замкнутого контура наведе-
ния со входом по ускорению цели /ц и выходом по пролету Л
(см. рис. 1.33,в). Введем понятие коэффициента пролета
_М0 т)
Л ("И) <0—'®
Как следует из соотношения (1.58), коэффициент пролета ха-
рактеризует относительную величину конечного пролета в зави-
симости от момента т, для которого задано начальное условие
Л(т), и момента наблюдения t.
Для разомкнутой системы, когда весовая функция автоном-
ного контура 1Га(С т)=0 и Whj(t, x) = WK(t, т), коэффициент
пролета гл (/, т) = 1 (/—т).
При выполнении условия физической осуществимости сис-
темы наведения, когда весовая функция звеньев от координаты
fi до Jp (т. е. обратной связи в структурной схеме рис. 1.33,в) не
содержит S-функций и ее производных, должно удовлетворяться
равенство
^АДЛт)=1Гк(/, т) при t=r,
из которого следует, что
ЛДЛ т) = 1 при t=r.
Пролет из-за маневра цели выражается формулой
t
h2 (/)=j WhJ (/, «) 7Ц («) du. (1.59)
В предположении, что
Л0=7ц1(/-Т),
где Zu=const, вторая составляющая пролета в выражении (1.55)
равна
t
h^t)=Ja^WhJ(t,u)du. (1.60)
Коэффициентом пролета из-за маневра цели назовем вели-
чину
t
Л2(Л WhJ(t,u)du. (1.61)
7 ц J
т
Для разомкнутой системы
t t
(А т)=^Гк(/, u)du^ (t0—u)du =</о-'в>2-(/ог2>2. (1.62)
44
Эта формула характеризует приращение пролета в разомкну-
той системе при постоянном ускорении цели (или ракеты) за
время с момента т до момента /.
Для замкнутой системы переменная т в (1.57) трактуется
как момент начала процесса наведения. В (1.60) т — момент
начала маневра цели. Если маневр цели начался до начала
процесса наведения, его с помощью (1.62) следует учесть в на-
чальных условиях, а в (1.60) переменную т принять той же, что
и в (1.57). Если маневр начался позже начала процесса самона-
ведения, значения переменной т в (1.57) и (1.60) окажутся раз-
ными.
Пролет из-за случайной ошибки измерения относительных
координат ракеты и цели можно записать в виде
М0=л8(/)+л4(/)= jrA(1,(/, к)ф(В)4/к. , (1.63)
—00
Здесь Wh<i (t, т) — весовая функция контура наведения с вхо-
дом по ошибке измерения ф (см. рис. 1.33,в).
Как следует из разд. 1.6, ошибка измерения пролета должна
характеризоваться в основном ошибками измерения проекций
координат и скоростей на плоскость, перпендикулярную линии
дальности. Эти ошибки обычно с достаточной степенью точнос-
ти удается аппроксимировать двумя некоррелированными про-
цессами: стационарным случайным процессом по угловому пе-
ремещению линии дальности ракета — цель и стационарным
случайным процессом по изменению линейной координаты цели
в плоскости, перпендикулярной линии дальности. Источником
ошибок, близких к стационарному процессу по угловому пере-
мещению, являются в основном угломерные устройства, установ-
ленные на ракете (так называемые головки самонаведения);
источником ошибок, близких к стационарному процессу по ли-
нейной координате, являются флюктуации центра отражения
цели, устройства измерения углов и дальностей, не совмещенные
с ракетой, бортовые устройства для измерения собственных ли-
нейных координат ракеты.
И те и другие ошибки, как правило, имеют близкую к равно-
мерной спектральную плотность в полосе частот, большей, чем
полоса пропускания реальной системы наведения. Поэтому
естественной аппроксимацией ошибок являются случайные про-
цессы в виде «белого шума».
Корреляционная функция ошибки в определении линейной
координаты ц(/) при этом имеет вид суммы стационарной и не-
стационарной (изменяющейся с изменением дальности ракета—
цель) составляющих
Ml- (^1-4). (1. 64)
45
где Gi — уровень спектральной плотности ошибки, стационарной
по углу, рад2 с; G2— уровень спектральной плотности ошибки,
стационарной по линейной координате, м2-с.
При управлении по линейному рассогласованию 1(f) коорди-
ната ф(/) в соотношении (1.63) и на рис. 1.33,в совпадает с
ошибкой измерения линейной координаты
ф(/)=p.(f).
При управлении по произведению угловой скорости линии
дальности о на скорость сближения |/?| (см. разд. 1.11), считая
|/?| = const, будем иметь
<]»(/) = |£| 6ш,
где бы — ошибка измерения угловой скорости.
Учитывая, что бы является производной ошибки измерения
углового положения цели бе, соответствующую ошибку измере-
ния линейной координаты запишем в виде
В предположении, что |/?|=const и R •7) = |А*| (/0—/), [*(/) =
= |/?|(/0—/)8г(/) = (/0 — /)Х(/), где X (/) = |£|3s, откуда корреля-
ционные функции сигналов (*(/) и Х(/) равны соответственно
(^1, ^2) = [|Л| 01 (to — ^1) (to t2) 4- О2] 8 — /2),
Яхх(ti, ^=№1+.. м] 8 (ti-tj. U‘65)
L U0—П)по—ш J
Выражение, связывающее между собой ошибки ц(/) и
позволяет получить весовую функцию т), преобразующую
гт dl d / ц (t) \
одну ошибку в другую. Поскольку —=— ,
dt dt \ /д — t J
\Y7 <4 t\— d ib(t—*)\_ — + —
VfU ’ м t0-t ) Go-02
Согласно соотношениям (1.42) и (1.46) весовая функция зве-
на, преобразующего линейное рассогласование в произведение
угловой скорости линии дальности на скорость сближения, имеет
точно такой же вид. Таким образом,
_ t) ъ' (t — t) + В (t — Т)
« (,о_0;—- с1-бб)
Использование в системе наведения других кинематических
параметров, характеризующих текущий пролет и линейно с ним
связанных, должно изменить как весовую функцию формирова-
46
Рис. 1.34. Структурная схема
контура наведения
ния измеряемой величины 1ГФИВ (t, т), так и корреляционную
функцию ошибки измерения ф(/) (см. разд. 1.8 и рис. 1.33,в).
При этом, очевидно, можно ожидать, что и новая измеряемая
величина и новая ошибка измерения будут связаны с линейным
рассогласованием /(/) и ошибкой измерения линейной координа-
ты ц(/) одинаковыми операторами. Следовательно, при задании
исходных ошибок корреляционной
функцией (1.64) независимо от вида
измеряемой величины пролет из-за
случайных ошибок измерения Лс(0
можно характеризовать весовой функ-
цией Why. (/, т), связывающей ошибки
измерения линейного рассогласования
с величиной пролета.
Такой подход эквивалентен пред-
ставлению структурной схемы контура
наведения (рис. 1.34), при котором
звено формирования измеряемой вели-
чины разбивается на два последова-
тельно соединенных звена, первое из
которых преобразует пролет в линей-
ное рассогласование [весовая функция
Wih(t, т), см- соотношение (1.44)],
а второе — линейное рассогласование в
измеряемую величину, по которой соб-
ственно и производится управление,
причем ошибка измерения ц(/) всегда
рого звена и имеет корреляционную функцию (1.64). В общем
случае весовую функцию второго звена обозначим №фИВ(^, т).
В случае управления по I
Г^ив = 8(/-т).
Как следует из (1.66), при управлении по | R | со
Гкв(Л т)=^|ш_/(Л т).
приложена к входу вто-
Итак, из-за случайной ошибки измерения относительных ко-
ординат ракеты и цели пролет
Лс W = h3 (t) = [ (f, и) (1 («) du.
Здесь нижний предел т характеризует момент подачи на вход
системы воздействия ц(/) и совпадает с моментом начала наве-
дения. Величину А3 (/) будем считать пролетом из-за стационар-
ной угловой ошибки, а величину Л4(/)—из-за стационарной
ошибки по линейной координате.
47
Считая, что корреляционная функция сигнала ц(/) имеет
вид (1.65), получим выражение для дисперсии пролета из-за
случайных ошибок измерения
Dftc(A т)=ОА,(/, t)+Da<(A т), (1.67)
где
Dh, (А г)=|Л|2 Gi J (/, и) (t0 - и? du,
t
Dhi(i, t)=G2 jwzt(^. и) du.
aj 6)
Рис. 1.35. Структурные преобразования сигнала ц(0 на вход и
выход замкнутой системы наведения:
а — первая фаза преобразования
б — вторая » »
Введем понятие коэффициентов пролетов из-за ошибок изме-
рения т)з (Л т) и т)4 (t, т):
Т)8(/, т)=^у u)(t0-u)2du;
п4(/, т)=^Р^’ Т) ]/jwl(/, u)du.
Полученные выражения показывают, что дисперсия пролета
является неубывающей функцией времени от момента начала
наведения т до момента наблюдения I.
48
Весовые функции Whj(t, т) и (t, т), характеризующие
точность системы наведения, могут быть выражены одна через
другую. Перенесем воздействие ц.(/) к точке приложения сигна-
ла Уц(0 и к выходу системы. Сначала сигнал ц(/) (см. рис. 1.34)
переносится так, как это показано на рис. 1.35,а. Затем преобра-
зование следует в соответствии с рис. 1.35,6. При этом естествен-
но потребовать, чтобы выполнялись следующие условия:
j WhJ(t, u)Wx (и, x)du-Wy(t, x)=W^(t, т),
т
t
u)Wx(u, x)da-We(t, T)=o,
Wy (/, x)=WTb(t, t).
Первое следует.непосредственно из структурной схемы, вто-
рое— из того, что при размыкании контура наведения
(U^a(t т)=0) ошибки не воздействуют на пролет, третье — из
первой фазы переноса воздействия (см. рис. 1.35,а).
В результате вычитания второго условия из первого получим
^,T) = Ju)\wx(u, x)du. (1.68)
Кроме того,
t _ _
Wx(t, T) = jlF,c x)du. (1.69)
Выражение для Wx(t, т) получено в результате подстановки
Wv(t, т) во второе условие и воздействия слева обратной весо-
вой функции (t,x).
Вместо того чтобы определять Wx(t, т) по (1.69), вычислим
обратную весовую функцию
г; (Л т) = J u)WK(u, x)du.
Согласно (1.41) и (1.44) получим
t
НМЛ т)=(/0-/)(/0-т) \ -^-=(/-т) 1 (/-т).
J Го — а
т
Таким образом, Wx (t, т) — весовая функция двойного интегри-
рующего звена (это следует непосредственно из того, что вход
49
последовательного соединения звеньев — относительное ускоре-
ние J, а выход — линейное рассогласование /), и, следовательно,
wx(t,T)= ~ (Е70>
at£
весовая функция двойного дифференцирующего звена.
Подставив соотношение (1.70) в (1.68)), окончательно по-
лучим
t
x)=\[WbAt, u)-WK(t, «)] ^2~т) du=
X
=^]«W>*)-^> т)]. (1.71)
at2
Из выражений (1.70) и (1.71) следует
t
J 1ГАрЛ, u)(.u-T)dti=Whj{t, т)
и, следовательно,
t) = JuzA(1(A u){u-x)du^-WK(t, т). (1.72)
Выражения (1.71) и (1.72) позволяют по заданной весовой
функции Whj( t, т) вычислить И7Ар.(/, т) и наоборот.
Итак, для определения коэффициентов пролетов, характери-
зующих совместно с параметрами .входных воздействий (Л(т),
/ц, G2) точность системы наведения, достаточно знать
весовую функцию замкнутого контура наведения с входом по
маневру цели UZAj(A т) или по ошибке измерения линейной ко-
ординаты (t, т).
1.13. ПАРАМЕТРИЧЕСКИЕ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ
СИСТЕМ НАВЕДЕНИЯ
Понятие параметрической передаточной функции нестацио-
нарной линейной системы было введено Заде [7]. Параметричес-
кая передаточная функция W(s, t) определяется как преобразо-
вание Лапласа от весовой функции W(t, т) по разности аргумен-
тов t—т (где t — параметр)
t
W (s, t)=L {Ц7 (/, т)},_х= J x)fTs(t~^dx. (1.73)
— оо
Соответственно обратное преобразование
W (t, т)=— W(s, ds. (1.74)
2л/ J
c—joo
50
Для стационарных систем, свойством которых является зависи-
мость весовой функции от разности аргументов:
W(t, т)=Г(/-т),
получим
t 00
W(s, t) = j U/(/-t)e-;f(<“’)rfr=JU7(0)e-iW9=UZ(s).
—oo 0
Таким образом, соотношение (1.73), являющееся обобщением
понятия передаточной функции на нестационарные системы, в
случае стационарной системы сводится к обычному преобразо-
ванию Лапласа. Все свойства преобразований Лапласа спра-
ведливы для выражений (1.73) и (1.78), если в качестве вре-
менной переменной рассматривать разность t—т. Сделаем сле-
дующие преобразования, которые будут полезны в дальнейшем:
£ [dW (Л т)) = - l fdW (t' = - sW (s, /);
( ) t—x (d (t — }t—t
L{xW(t, x)}t^=-L{(i-x)W(i, x) — fW(t, T)}z_x=
=dW{s' ° Н-/Г (s, t). (1.75)
ds
Важными являются свойства параметрической передаточной
функции двух последовательно соединенных звеньев с весовы-
ми функциями 1Г1(/, т) и 1Г2(/, т). Звено с весовой функцией
1Г1(/, т) будем считать входным. Параметрическая передаточ-
ная функция
t t
/)= J dx
—co
После замены порядка интегрирования получим
t и
W (s, /)= J Г2 (Л и) du J (и, т) dx.
— СО —00
Если входное звено стационарно, т. е. Wi(t,x) = Wi(t—т), ИН'
теграл
J W^u, dx=W1(s).
—со
В этом случае параметрическая передаточная функция после-
довательного соединения равна
t
w (s, t)=(s) j W2 (t, u) du=UZ2 (s, /) (s). (1.76)
j W2(t, u^-^-^W^u, x) e~s(tt~x’du.
51
При нестационарном входном звене представить параметри-
ческую передаточную функцию последовательного соединения в
виде произведения передаточных функций можно лишь тогда,
когда оператор выходного звена является коэффициентом уси-
ления. Так, если
М72(Л т)=л(/)8(/ —т),
то
* t
т)=jU72(f, x)dti=a(i) W^t, t),
T
При -ЭТОМ
U7(s,/) = a(/)U71(s,/). (1.77)
Воспользуемся понятием параметрической передаточной
функции для описания динамических свойств контуров наве-
дения. Для произвольного контура параметрические передаточ-
ные функции
UZw(s, t')=L{WkJ(t, x)\t-z,
Whb(s, f)=L{Whv.(t,
связаны между собой выражением, которое может быть получе-
но из (1.72) с помощью (1.76). Учитывая, что
L {(/-т)1р-т))г-х=4 ,
находим
t) 4+^(5, t), (1.78)
где согласно (1.41) параметрическая передаточная функция
кинематического звена
lTK(s, t)=L {WK(t, x)}t_,=L {(/0—т) 1 p-r)h_=
=L ((f0-t) 1 (/-1)+Z ((/ — t) 1 (/—т)}г_.
Учитывая соотношение (1.77), имеем
U7K ($, f)=<A4L4-±.=(lo-()A+ 1 . (i. 79)
Из соотношений (1.78) и (1.79) получим
UZ., (s, П- + .
U7ft|l(s, /)=U/W(s, /)s2 —(/0—/)s — 1.
52
Для конкретных законов наведения, когда задана весовая
функция звена формирования измеряемой величины И7фив т),
а автономный контур стационарен, может быть получено вы-
ражение, связывающее передаточную функцию автономного
контура с параметрической передаточной функцией замкнутого
контура наведения.
В случае наведения по линейному рассогласованию в соот-
ветствии с рис. 1.26 и формулами (1.46) и (1.76) параметричес-
кая передаточная функция
/)=Z{(/o-O8;(/-T) + 8(/-T)h_TUZv(s). (1.81)
Первый сомножитель в (1.81)—параметрическая передаточная
функция нестационарного звена равна
Z{(/0- 0 в; (/- т) + 8(/- Т))/_Х=(/„-1) s +1,
откуда
whj.(s, (1-82)
Учитывая, что в прямой цепи замкнутого стационарного кон-
тура (см. рис. 1.26) стоит двойное интетрирующее звено, а в об-
ратной — автономный контур, получим
1
W tJ ($) = = 1 . (1.83) 1+Za(£) «2 + ^(5) К S2
Таким образом, (s, , (1.84) ' s2 + ;ra(s) ’ v '
откуда Wa(д)=(4)-0 * + 0 . (1.85) t)
Сравнивая (1 1.85) с выражением (1.80), находим ^.M=- '* (1-86)
Поскольку вь онарного автоно! ная функция lFa представив Whn ( 1ражение (1.83) справедливо только для стаци- лного контура, определенная из него передаточ- (s) не зависит от t. Это можно проследить, s, t) в виде
где Wm (s, t) — передаточная функция замкнутого контура на-
ведения с входом по ц.(/) и выходом по /(/) (см. рис. 1.26).
53.
При стационарном автономном контуре и управлении по /(/)
1М.0=«Ш
Подставив Whj(s, t) из (1.82) и Wh^fs, t) в (1.86), получим
UZa(s) = -^^-.
17„(S)
Другие виды законов наведения, когда измеряемые величины
отличны от линейного рассогласования, могут быть получены
из зависимостей, аналогичных (1.85), однако здесь встречаются
значительные трудности, так как контур наведения оказывается
нестационарным. Чтобы найти эти зависимости, воспользуемся
выражением для весовых функций взаимно обратных систем
J u,)Whj{u, x)du=l(t—r).
(1.87)
Весовая функция системы, обратной замкнутому контуру на-
ведения (см. рис. 1.23), может быть представлена в виде
^M^T)=rK(/,T) + Jra(/, а)1ГФИв(и, x)du. (1.88)
Подставив соотношение (1.88) в (1.87), получим
t _ t и
u)WK («,r)d« + J W^ujdu JuZa(«-O)X
X 1^фив(»,т)^=8(/-г). (1.89)
Учитывая, что все слагаемые в соотношении (1.89) представ-
ляют собой весовые функции некоторых систем, подадим на их
вход весовую функцию ТГфив (А т). При этом выражение (1.89)
преобразуется к виду
/ и _ _
у WhJ (A и) du у Г к (и - 0) 1ГфИв (», т) d§ +
+ j WhJ (t, u) UZa (и -$)du=1ГФИВ (A t).
(1.90)
Выражение (1.90) связывает между собой весовые функции
Whj(t, т) и 1Га(А т). Для стационарного автономного контура
аналогично (1.81) удобно перейти к преобразованиям Лапласа
L J (А и) rfw [ у Гк (и, &)1ГфИВ(&, т)дЮ] +
+ rft7(s, /)1Га(5)=ГФив(5, /).
(1-91)
34
Подстановкой в (1.90) и (1.91) вместо И7фИВ (t, т) весовой
функции
т)=ГА/(/, т)
можно согласно формулам (1.46), (1.69), (1.70) получить выра-
жение, тождественное (1.85):
« «) 7^8(«-T)rfa. + U7w(s, /)ra(s) = (/0-/)s+l,
J all*
откуда
irA/(s, f) (s2 + U7a(S)) = (/0_/)s+l.
Воспользуемся соотношением (1.91) для исследования связи
между параметрической передаточной функцией замкнутой сис-
темы наведения и стационарным автономным контуром в случае
управления по произведению угловой скорости линии дальнос-
ти и скорости сближения.
В этом случае весовая функция звена формирования измеря-
емой величины имеет вид (1.42), и, следовательно, обратная ве-
совая функция
Гфив(Л r)=r^|ffl_A(Z, т)=ГА_|Л|т(/, т)=8(/ —т)(/0 —/)2. (1.92)
Весовая функция звена, обратного звену кинематических
связей (1.41),
ГГ(/,т)=^1, (1.93)
что следует из структурной схемы, приведенной на рис. 1.15.
Последовательное соединение звеньев с весовыми функциями
(1.92) и (1.93) имеет весовую функцию
* / >
f W7(/, 0)Гфив(0, т)de = С 8'(*~9) (/0-0)25(0-т)de=
J J *0 — *
т т
= —4 [&-W-') V('-*)“2*('-4 (1-94)
(to— t) at
Подставляя соотношения (1.92) и (1.94) в (1.91) и учитывая
(1.75) и (1.76), получим
(1.95)
as
Формула (1.95) является неоднородным линейным дифференци-
альным уравнением относительно параметрической передаточ-
ной ФУНКЦИИ Whj (s, t).
55
В общем случае решение уравнения (1.95) не удается довес-
ти до конца, так как оно сводится, как правило, к интегральным
показательным функциям.
С помощью (1.95) можно получить формулу для вычисления
передаточной функции автономного контура по параметрической
передаточной функции замкнутой системы:
d
(io - О2 + [2 - (to-0 s) Wfu (s, t) + s — W^j (s, t)
<•’ = ---------------^-7-7------------------- (1 96)
w/u(S, t)
Воспользовавшись соотношением (1.80), можно найти ана-
логичную зависимость 1Га($) от ($):
О
—т;-------Whlt[(s, t)(to-t)
Выражения (1.96) и (1.97) получены в предположении, что
автономный контур стационарен, поэтому так же, как и в (1.86),
правые части этих выражений не зависят от t.
1.14. ТОЧНОСТЬ В ЗАДАННЫЙ момент времени.
ЭКВИВАЛЕНТНЫЕ ПО ТОЧНОСТИ СИСТЕМЫ
Точность систем наведения существенна не на всем интер-
вале времени наведения. Так, например, для систем наземного
наведения ракет, в которых на конечном этапе используется ре-
жим самонаведения, т. е. наведения по информации, вырабаты-
ваемой бортовыми устройствами (головкой самонаведения или
бортовой радиолокационной станцией), важна точность в мо-
мент захвата цели. Для этапа самонаведения или телеуправле-
ния ракеты важна точность вблизи точки подрыва боевой части.
Таким образом, условно мо&но принять, что точность наведения
существенна только в один момент времени. Этот момент t\ либо
соответствует началу последующего этапа, как в случае пере-
хода на самонаведение или пуска ракет, либо вообще концу про-
цесса наведения. В последнем случае для того, чтобы иметь
право использовать линейные уравнения кинематических связей,
момент t\ выбирается таким, чтобы еще выполнялось условие
(1.16). При этом пролет определяется с ошибкой, не превы-
шающей
Jraax. (1.98)
Это соотношение может быть получено из (1.62) в предположе-
нии, что с момента Л до /0 действует постоянное максимально
возможное относительное ускорение ракеты и цели Утах- Если
56
потребовать, чтобы ошибка в определении пролета не превосхо-
дила 2 м, и предположить, что максимальное относительное ус-
корение /Шах составляет 100 м/с2, момент наблюдения t\ должен
удовлетворять неравенству
*о-О.2 с.
С другой стороны, если величина пролета равна 10 м, необходи-
мо, чтобы
>?(/)~|Я|(/0-/,)» 10 м.
Когда |^|=200 м/с, дальность /?(/)=40 м. Этого достаточно,
чтобы считать условие (1.16) выполненным и, следовательно,
целесообразно принять Л = /о—0,2 с.
При больших пролетах следует пойти на увеличение допус-
тимой ошибки АЛ и за счет этого увеличить время /0—Л-
Анализ формул (1.58), (1.60), (1.67) показывает, что динами-
ческие и случайные ошибки наведения в момент t\ определяются
только одним сечением весовых функций Whj(t, т) и т),
которые связаны друг с другом формулой (1.72). Аналогич-
ную картину будем иметь, рассматривая параметрические пере-
даточные функции Whj(sf t) и Whp.(s, t) и формулы, связываю-
щие их с передаточной функцией автономного контура для раз-
личных весовых функций звена ФИВ (1.91), (1.96), (1.97).
Это свойство контуров наведения существенно упрощает
задачу анализа точности линейных систем и синтеза оптималь-
ных по точности систем. В первом случае для получения дина-
мических и случайных ошибок достаточно определить лишь одно
сечение весовой функции замкнутой системы или, что по су-
ществу эквивалентно, параметрическую передаточную функ-
цию при одном значении параметра t=t\. Задача синтеза опти-
мальной по точности системы наведения сводится к определению
оптимального сечения весовой функции замкнутой системы или
параметрической передаточной функции при одном значении
параметра t=t\. В этой связи удобно ввести понятие эквивалент-
ных по точности систем, т. е. систем, точность которых в задан-
ный момент времени при произвольных, но одних и тех же вход^
ных воздействиях одинакова. Из выражения
И*х)= x)x(x)dx
—00
следует, что эквивалентными в момент t=it являются такие
системы, весовые функции которых в момент t—t\ равны. Естест-
венно, что у каждой системы может быть бесчисленное множест-
во эквивалентных по точности систем. Геометрически это озна-
чает, что через данное сечение весовой функции можно провести
бесчисленное множество поверхностей, обращающихся в нуль
при /<т (рис. 1.36).
57
Для одного и того же входного сигнала выходные сигналы
эквивалентных систем могут быть различными при а их
производные могут отличаться в момент t=ti.
Для равенства первых п производных выходных сигналов
при первые п производных от весовых функций по t при
/=/1 должны быть равны друг другу.
Рис. 1.36. Весовые функции эквивалентных по точности в момент
t=ti нестационарной (а) и стационарной (б) систем
Поскольку через любое сечение W(t, т) можно провести
цилиндрическую поверхность с направляющей, параллельной
биссектрисе координатного угла t=x (рис. 1.36,6), среди всех
эквивалентных данной системе систем всегда есть стационар-
ная. Из этого не следует, впрочем, что всегда эта стационарная
система имеет дробно-рациональную передаточную функцию,
однако с заданной степенью точности сечение всегда может быть
аппроксимировано суммой экспонент и, следовательно, прибли-
женная передаточная функция будет дробно-рациональной.
В этом случае параметрическую передаточную функцию не-
стационарной системы удобно трактовать как передаточную
функцию стационарной эквивалентной системы, параметрически
зависящую от момента наблюдения /. .
1.15. ТОЧНОСТЬ КОНТУРА НАВЕДЕНИЯ
ПРИ БЕСКОНЕЧНОМ ВРЕМЕНИ УПРАВЛЕНИЯ.
ПОНЯТИЕ ВРЕМЕНИ ПАМЯТИ
НЕСТАЦИОНАРНОЙ СИСТЕМЫ
Анализируя точность контура наведения, можно воспользо-
ваться его стационарным эквивалентом, имеющим передаточ-
ную функцию Whj(s, Zi). В этом случае, используя теорему о
58
начальном и конечном значениях, согласно (1.57) и (1.60) по-
лучим
lim t) (/0—T)] = lim sWhJ (s, /х),
tf— т->оо S-*0
lim T)2(/p t)=lim)FA/(s, /J.
G—X->OO 5->0
На основании (1.64)
00
Hm Dht(tv x)=^-\
ti— т—*-oo Л J
0
(1.99)
(1. 100)
2
^i) d&.
Точно так же, как и в случае стационарных систем, формулы
(1.99) и (1.100) представляют ценность только потому, что ре-
альные системы имеют практически конечное время памяти.
Для стационарной системы с весовой функцией №(9), где
9=/—т, под временем памяти обычно понимают минимальный
интервал времени Т; на котором выполняется условие
т
U7(9)x(/-0) d9=^ W(9)x(t—9)d9
О
для произвольных x(t). Это возможно, если при Q>T, 1Г(0)=С.
Здесь время памяти обычно трактуется как время затухания ре~
акции системы. Однако эквивалентная запись
t t
W(t — x)x(x) dx= f W(t-x)x(x)dx
. t-T
при произвольных х(т) позволяет говорить о времени памяти
как о времени, в течение которого система еще «помнит» входное
воздействие.
Для времени памяти нестационарной системы правильно
только второе толкование
t t
j W (t, т) X (t) dx= J W (t, т) X (t) dx.
—00 t—T
Согласно рис. 1.37 под временем памяти нестационарной сис-
темы в момент наблюдения t\ будем понимать время Т, при ко-
тором выполняется условие W(t, т)«0, если t\—х>Т._ Время
памяти нестационарной системы удобно трактовать как время
памяти стационарного эквивалента. Здесь уже нет сколько-
нибудь четкой зависимости между временем переходного про-
цесса и времением, в течение которого нестационарная система
59
«помнит» входные воздействия. Часто бывает невоз-
можно определить, что такое время переходного процесса,
хотя время памяти системы можно указать всегда, если толь-
ко стационарный эквивалент
устойчив. «
Понятие эквивалентных си-
стем позволяет определить
устойчивость нестационарной
Рис. 1.37. Весовая функция нестацио-
нарной системы
системы как устойчивость ста-
ционарного эквивалента. Для
анализа точности нестационар-
ного контура наведения можно
воспользоваться его стационар-
ным эквивалентом. Задавшись
сечением весовой функции
замкнутой системы или стацио-
нарным эквивалентом системы,
с помощью (1.85) и (1.96)
можно определить передаточ-
ные функции автономных кон-
туров систем наведения по I и
|Л| со. Получившиеся при этом
контуры наведения будут экви-
валентны по точности заданной
системе и между собой.
Подстановка заданного стационарного эквивалента в (1.85)
и (1.96) делает передаточные функции автономных контуров
параметрически зависящими от того, на какой момент времени
задана точность.
1.16. СВОЙСТВА КОЭФФИЦИЕНТОВ полиномов
ПАРАМЕТРИЧЕСКИХ ПЕРЕДАТОЧНЫХ ФУНКЦИИ
ЗАМКНУТОГО КОНТУРА НАВЕДЕНИЯ
В' настоящем разделе рассматриваются контуры наведения
по | R | со. Аналогичные результаты для наведения по линейному
рассогласованию могут быть легко получены. При выборе ха-
рактеристик замкнутого контура наведения важно знать, как
связаны между собой коэффициенты полиномов передаточных
функций WhJ(s, t), Wh^s, t) и ITa(s).
Представим Whj(s, t) в виде
n(s)
где
/-о ;-о
60
Коэффициенты полиномов и Ь, являются функциями пара-
метра t=ti. Подставив соотношение (1.101) в (1.96) и положив
/0_/1=д, (1.102)
получим
w , } №B2s + A(s)B(s)(2—bs) + s[A'(s)B(s)-B'(s)A(s)]
(1.103)
Как следует из формулы (1.103), характеристическим урав-
нением автономного контура является
А($)Д($)=0.
Таким образом, для устойчивости автономного контура дос-
таточно, чтобы полиномы А(з) и B(s) не имели корней с поло-
жительной вещественной частью. Иными словами, замкнутый
контур наведения должен быть минимально-фазовой системой.
Из формулы (1.99) следует, что при ао=О и &о#=О выполня-
ется условие
Игл [П1(/1, т)(/0 —т)]=0,
из которого следует
lira П1(/1, т)=0. (1.104)
/1—1-*00
Для коэффициента пролета
П2 -оо) = Urn П 2, (4, т)= . (1.105)
/1—т-*оо Dq
Анализ соотношения (1.103) показывает, что коэффициент
усиления автономного контура (отношение свободных членов
числителя и знаменателя)
__№Ь1 + 2аъЬ0 Д2
ао4о «о/^о
откуда с учетом соотношения (1.105)
/Са=2 +-----------
12О1, -«)
(1.106)
Этот же результат, но для безынерционной системы, может
быть получен из соотношения (1.52), если положить там Л(0) =
= 0, tQ—t=A при что в данном случае соответствует бес-
конечному времени самонаведения, так как при выводе соотно-
61
шения (1.52) считалось, что начало наведения соответствует
/ = 0. В результате имеем
откуда с учетом соотношения (1.61) непосредственно получим
(1.106), из которого следует, что
— 00)=—^—. ‘ (1.107)
А а
Формально из соотношения (1.107) вытекает, что в случае, ког-
да наведение продолжается до Д = 0, пролет из-за маневра цели
может быть ликвидирован полностью, если только Ка#=2. Одна-
ко, как следует из рис. 1.27—1.32 для безынерционного автоном-
ного контура и из многочисленных расчетов для реальных сис-
тем, потребные ускорения ракеты ограничены только при Ка>2,.
причем даже и в этом случае приходится ограничиваться зна-
чениями Д порядка 0,2 с для определения пролета с точностно
~2 м. При Ка<2 весовая функция Whj(t, т) не стремится к ну-
лю с ростом времени Л—т и коэффициент т)2 неограниченно воз-
растает.
Соотношение (1.105) выражает свойство низкочастотной
асимптоты передаточной функции замкнутого контура Whj(s, ti).
При а0 = 0 передаточная функция Whj(s, в области низких
частот обладает свойствами дифференциатора и коэффициент
пролета г]2(Л, —оо) =0.
Более подробно вопрос о характере динамических ошибок
в функции времени наведения 9=/]—т и времени, оставшегося
до встречи от момента наблюдения Д = /о—Л, рассматривается
в разд. 1.17.
Рассмотрим свойства высокочастотной асимптоты передаточ-
ной функции Whj(s, t). Формула (1.103) позволяет получить
зависимость разности порядков т—п полиномов В ($) и A (s) от
вида И7а(з). В дальнейшем будем рассматривать только физи-
чески реализуемые передаточные функции №а($), для которых
разность порядков полиномов знаменателя и числителя состав-
ляет величину
v + l>0. (1.108)
В соответствии с (1.103) порядок полинома знаменателя в 1Га(з)
равен п+т. Числитель в (1.103)
Д2Я2(з)+Л(5)ад(2-дз)+$[ДЧз)ад-Л (s)5<(s)] (1.109)
должен иметь порядок п+т—v—1.
Как следует из формулы (1.109), порядок первого слагае-
мого— 2т, порядок второго т 4-п4-1, порядок третьего —
т+п. Предположение, что п~>т, неверно, так как в этом слу-
62
чае наибольший порядок, равный n + m+1, в (1.109) имеет вто-
рое слагаемое (старший член — anbrnAsn+rn+1) и, следовательно,
разность порядков полиномов знаменателя и числителя оказы-
вается отрицательной, что противоречит соотношению (1.108).
Предположение, что n<(m—1), также неверно, так как в
этом случае наибольший порядок имеет первое слагаемое (стар-
ший член — A2bm2s2rn) и порядок полинома числителя переда-
точной функции U^a(s) выше порядка полинома знаменателя,
что противоречит условию (1.108). При п = т—1 условие (1.108)
выполняется, если обращаются в нуль соответствующие комби-
нации коэффициентов полиномов A(s) и B(s). Эти комбинации
могут быть получены непосредственно из соотношения (1.109),
однако существует более простой путь,
несколько позже.
Итак, для физически реализуемой передаточной функции
Wa(s) порядок полинома А($) всегда на единицу ниже по-
рядка полинома В (s). Параметрическая передаточная функция
Whp.(s, /1) в соответствии с формулами (1.80) и (1.102) может
быть представлена в виде
Whft(s, -.(As-l)B(s) + ^(s) =-£gL , (1.110)
которым воспользуемся
B(s)
где
Л-0
Подставив Wh* (s, ty) из формулы (1.110) в (1.97), получим
ург 5 [ (5) В ($) + С' (s) B(s) — С (s) В9 ($)] 111)
[B(s) (As + 1) 4- c (s)] В (s)
Аналогичный проведенному анализ показывает, что для вы-
полнения (1.108) порядок полинома С($) должен быть ниже
порядка полинома В($), таким образом
Кт.
Последнее позволяет утверждать, что порядок полинома чис-
лителя в U^a(s) определяется членом AC(s)B(s)s и всегда равен
m + l+1, а знаменателя — членом В2Д$ и равен 2/п+1. Учиты-
вая это, получим
m —Z=v4~l, l = m —V— 1.
"Кроме того, высокочастотные асимптоты передаточных функ-
ций оказываются равными с точностью до знака, так как
ПтГа(s)=-^-=--££=-lim (1.112)
s'*00 От $->оо
63
Из соотношения (1.110) следует выражение, связывающее меж-
ду собой коэффициенты полиномов Л($), B(s) и C(sO,
С/—2 — 6/—1Д — bi.
(1.113)
Выражение (1.113) позволяет определить старшие v+1 коэффи-
циенты полинома Л($). Действительно, поскольку п=т—1, /=
=т—v—1, получим
bm^-\-am^i 0,
ст = “ ^-1А “ Ьт+ат_2=0,
^т—1= Ьт—2& Ьт—1 -р Я/п—3 =
£/п—v = — Ьт_1 —- Ьт—ч Я/п—2 = 0»
£/п—»—1= Ьт_ зД Ьт—V—j 4“Лт__<>_з= Сц
откуда
а п = Л/л—1= Д ’
ап-1 = ат— 2 = Ьт—1Д 4“ Ьт.
^п—г = ат—Ъ = ^т—2 Д 4" Ьт_ 1,
#л—* — 1=#т—э—Ч==ЬТП—»—1Д 4“ bm—'tt
dn— » — 2 = dm—•»—3 = Ьт—v—2 Д 4" Ьт—ч—1 4“ “
= ’»-2Д4~^/п-»— 1 — fbm*
(1.115)
где f=----—коэффициент высокочастотной асимптоты переда-
точной функции ITa(s). Система (1.115) определяет v+З стар-
ших коэффициента полинома А ($).
Учитывая (1.105), получим v+4 условия, которым должны
удовлетворять коэффициенты полинома Д(«) для того, чтобы
обеспечить:
заданную динамическую точность при бесконечном (большем
времени памяти) времени действия маневра цели;
разность порядков, равную v+1, полиномов передаточной
функции автономного контура 1Га($) и заданный коэффициент
ее высокочастотной асимптоты f.
64
Естественно, что выполнение всех этих требований возмож-
но, если n>v + 3 и, следовательно, m>v + 4. Что касается поли-
нома C(s), то согласно соотношениям (1.113) для него получим
С1 — ----fbm,
С2—cLq &2д b2—Л2 00)^0 ^.Д— ^2»
^i= M — ^1»
b0.
(1.116)
В качестве примера приведем передаточные функции Whj(s, t)
и Wh?.(s, t) при минимально возможном т для двух случаев:
1) задается r)2^i, — оо)=т]2, v=0, / = Л;
2) задается только П2^1» — оо)=т]2 и v=0.
В первом случае
Wft (s t )_____4- IM s + [M + ^2—^о'Пг] s2 4- /164s3
bo + b]S 4- b2s2 4- b^s3 4- b$s*
fyp)2 4- [Д62 4-^3— b$f] s 4- [Л63 4- M s2 4- Д&4$3
bo 4- b]S 4- b2s2 4- b^s3 4- b^s*
Во втором случае
ц/ / )= 4- ^1] s 4- [61Д 4-^2 — ^о'Пг] s2
bo 4" b]S 4- b^s2 4- btfP
W (s t) — ^31 5 a^3s2
’ 1 б0 + М + ^2 + Ы3
(Ы17)
при этом
— #1Д4-^2—b$f\2
(1.118)
Приведенные примеры дают представление о том, как, за-
давшись полиномом В($), порядок которого m = v4-4, с по-
мощью (1.105), (1.115) и (1.116) сформировать полиномы А($)
и С($) передаточных функций замкнутого контура наведения
Whj(srt\) и Wh?.(sf /1), обеспечивающих заданный коэффициент
пролета т]2, заданную разность порядков v4-l полиномов-пере-
даточной функции Wa(s) и заданный коэффициент ее высоко-
частотной асимптоты f.
Если m>v + 4, то коэффициенты а\, a2t... 9 и Сз, ...,
гт_,_2 оказываются произвольными.
3 3200 65
1.17. КАЧЕСТВЕННОЕ СРАВНЕНИЕ ВЕСОВЫХ, ПЕРЕДАТОЧНЫХ
ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ НАВЕДЕНИЯ
И КОЭФФИЦИЕНТОВ ПРОЛЕТОВ
Воспользуемся материалом, приведенным в разд. 1.12—1.16,
для того чтобы проследить связь между характеристиками авто-
номного контура и замкнутой системы.
х На рис. 1.38 приведены примеры амплитудно-фазовых лога-
рифмических характеристик автономного контура системы на-
ведения по произведению |/?|со. Соответствующие характери-
стики автономного контура при управлении по линейному
рассогласованию показаны на рис. Е39.
Рис. 1.38. Логарифмические амплитудные и фа-
зовые частотные характеристики автономного
контура систем наведения при управлении по
Автономные контуры 1 и 2 имеют одинаковый коэффи- -
циент усиления, но полоса пропускания контура 2
шире вдвое. Автономный контур 3 отличается от кон-
тура 1 только меньшим коэффициентом усиления
Частотные характеристики автономного контура отличаются
шириной полосы пропускания частот и коэффициентом уси-
ления.
На рис. 1.40—1.42 приведены амплитудно-фазовые частотные
характеристики передаточных функций Whj(s) и Whn(s), весо-
вая функция' Whj(®, А) и коэффициент пролета (исходная сис-
тема— /, система с увеличенной полосой пропускания частот —
2 и система с малым коэффициентом усиления — 3; везде А =
= 0,25). Сравнение характеристик подтверждает приведенные в
разд. 1.16 свойства, связывающие высокочастотную асимптоту
lFa(s) с W%i(s), а низкочастотную асимптоту 1Га($) с Whj(s).
Частотные характеристики W\j(/co) и (i<o) в области частот,
где фазовая характеристика существенно отличается от
66
Рис. 1.39. Логарифмические амплитудные и фазовые час-
тотные характеристики автономного контура систем на-
ведения при управлении по линейному рассогласованию
Рис. 1.40. Логарифмические амплитудные характе-
ристики контура наведения с входом по ошибке
измерения линейной координаты цели
Рис. 1.41. Логарифмические амплитудные характеристики
замкнутых систем наведения с входом по ускорению
цели
3*
67
нуля, но амплитудная еще достаточно велика, нс совпадают ни
с высокочастотной, ни с низкочастотной асимптотами.
Максимум амплитудной характеристики WhJ(s) тем ниже,
чем шире полоса пропускания частот автономного контура. Его
величина характеризует пролет при наихудшем по частоте и фа-
зе синусоидальном маневре цели.
Сравнение этого максимума с максимумом коэффициента
'П2 = 'П2тах показывает, что реакция на наихудшее синусоидаль-
ное воздействие мало отличается от реакции на маневр цели
Рис. 1.42. Весовые функции Whj (О, Д) и коэффициенты
пролета т]2(0, Д) замкнутых систем наведения
с одной наихудшей по времени сменой знака ускорения. Такое
воздействие может быть представлено в виде разности удвоен-
ного по величине ускорения цели /ц, приложенного в момент
смены знака и 'постоянного ускорения, действующего бесконечно
долго. При этом пролет равен
AlHmax- *12 (ОО)]. (1.П9)
Близкий результат дает интеграл
Zy = f (1-120)
о
характеризующий пролет при наихудшем по форме, ограничен-
ном по модулю маневре цели.
Максимум амплитудной характеристики растет с уве-
личением коэффициента усиления автономного контура, точнее,
с увеличением амплитудной характеристики автономного кон-
тура на частотах, где фазовая характеристика автономного кон-
тура существенно отличается от нуля. Этот максимум характе-
ризует пролет при наихудшем по частоте и фазе синусоидальном
68
изменении ошибки в определении линейной координаты цели.
Близкий результат дает наихудшее по форме, ограниченное по
модулю изменение ошибки измерения линейной координаты цели
I^\Wh^(u)\du. (1.121)
Сравнение характеристик исходной и широкополосной систем
подтверждает, что время памяти системы наведения обратно
пропорционально полосе пропускания частот автономного кон-
тура.
1.18. ВЫБОР ПЕРЕДАТОЧНОЙ ФУНКЦИИ
ЗАМКНУТОГО КОНТУРА НАВЕДЕНИЯ
Приведенные в данной главе свойства параметрических пере-
даточных функций замкнутого контура наведения по 17? | со поз-
воляют проектировать систему, обеспечивающую заданное ка-
чество.
Проектирование сводится к:
а) заданию желаемых значений v, f, 132(^1, —00) и времени
памяти замкнутого контура Т (см. разд. 1.15 и 1.16);
б) выбору подходящего полинома B(s);
в) определению коэффициентов полиномов 4(s) и B(s) [см.
формулы (1.114) — (1.116)];
г) вычислению по формулам (1.97) или (1.98) передаточной
функции автономного контура.
Разность порядков полиномов передаточной функции авто-
номного контура v+1 задается в результате подсчета числа на-
иболее инерционных звеньев, образующих прямую цепь автоном-
ного контура (контур автосопровождения головки самонаведе-
ния, фильтр, рулевой привод, ракета). Обычно в полосе частот,
влияющих на точность наведения, принимают v = 44-5.
Коэффициент высокочастотной асимптоты f назначается для
ограничения полосы пропускания автономного контура. Основ-
ной задачей такого ограничения является обеспечение устойчи-
вости контуров, образованных так называемыми «паразитными»
связями через ошибки радиопрозрачного обтекателя и систему
гиростабилизации головки. Следует помнить, что частотная ха-
рактеристика автономного контура может подходить к своей
высокочастотной асимптоте произвольным образом, поэтому не
следует переоценивать эффективности введенных ограничений
полосы пропускания.
Время памяти Т обычно назначают таким, чтобы удовлетво-
рялись следующие противоречивые требования:
1) время памяти должно быть максимально возможным, так
как это уменьшает пролет из-за случайной ошибки, стационар-
69
ной по линейной координате, и снижает флюктуационную пере-
грузку ракеты из-за обеих составляющих ошибки;
2) время памяти должно быть минимально возможным, так
как при этом уменьшается пролет из-за наихудшего маневра
цели (см. формулы (1.119), (1.120)]; время памяти должно быть
не более минимального времени наведения ракеты.
Величина коэффициента пролета из-за маневра т]2(/ь —°°)
назначается малой, если имеется основание принять его постоян-
ным. Если предположить, что цель стремится создать наихудший
маневр, коэффициент пролета согласно формуле (1.119) следует
Принимать блИЗКИМ К Т)2тах-
В соответствии с материалом, изложенным в разд. 1.16, поря-
док полинома B(s) должен быть равен или больше v + 3.
Полином B(s) удобно-выбирать таким, чтобы среди его кор-
ней находились два комплексно сопряженных корня с вещест-
венной частью, приблизительно равной —4/Т, и мнимой частью,,
равной . Остальные корни выбираются кратными вещест-
венными. Влияние этих корней сводится к тому, что с их увели-
чением сужается полоса пропускания автономного контура, что,
в свою очередь, сопровождается повышением максимального
значения т]2тах> увеличением времени памяти-и некоторым воз-
растанием коэффициента т]з-
Приведенное выше представление полинома B(s) эквива-
лентно заданию сечений весовых функций т) и Why. (Л, т)
в виде
U7 (^ - т) = W (9) = Аsin (D0 +
v+3
+ ^2e-a0cos(D0 + 2A0/“3e“pe- (1- 122>
1=3
1.19. ОБЩАЯ ХАРАКТЕРИСТИКА ЗАДАЧИ ОПТИМИЗАЦИИ
СИСТЕМЫ НАВЕДЕНИЯ ПО ТОЧНОСТИ
Как было показано, точность системы наведения в один мо-
мент времени t = t\ определяется сечением весовой функции
замкнутой системы т) или Whu. (Л, т). Этот факт сущест-
венно расширяет возможности по привлечению различных мето-
дов статистической динамики для оптимизации точности систем
наведения.
Независимо от того, стационарной или нестационарной по-
лучается оптимальная весовая функция, используется только
одно ее сечение, причем так, чтобы через него прошла весовая
функция системы наведения, реализованная с помощью одного
из возможных способов измерения текущей точности наведения
и стационарного автономного контура. Иными словами, система
наведения делается эквивалентной по точности (см. разд. 1.14)
оптимальной системе в заданный момент времени t = th
70
С точки зрения статистической динамики наведение рас-
сматривается как обычная задача наилучшего приближения
преобразования заданным оператором полезного сигнала при
измерении его со случайными ошибками. Тот факт, что здесь
имеет место фиксированный момент наблюдения, не вносит ка-
ких-либо особенностей, так как рассматривается конечный или
бесконечный интервал времени наблюдения входных сигналов,
заканчивающийся к моменту t=t\ (см. разд. 1.15).
Рис. 1.43. Структурная схема формирования пролета
Рассмотрим структурную схему (рис. 1.43), реализующую
выражение (1.72), связывающее между собой весовые функции
Wh»(t,x) nWhJ(tfr).
Схема имеет два входа: по ускорению цели 7ц(0 и по ошиб-
ке измерения линейной координаты р(/). В соответствии с фор-
мулой (1.56) на первый вход подается еще и начальный пролет
в виде сигнала
^0 —и
Выходом структурной схемы является текущий пролет. Если
перенести ошибку р(/) на вход двойного интегрирующего звена,
Рис. 1.44. Структурная схема формирования пролета,
преобразованная к стандартному виду задачи оптими-
зации
структурная схема приобретет вид, свойственный обычной зада-
че оптимизации (рис. 1.44).
Здесь верхнюю ветвь (обозначим ее весовую функцию
W°(t, т)) можно рассматривать как оптимизируемое звено, ниж-
71
нюю ветвь — звено кинематики — как оператор заданного пре-
образования полезного сигнала
^0— 13
гт - (О
Дополнительный сигнал ~ на входе оптимизируемого
dfl
звена — ошибка измерения полезного сигнала. Пролет h(t) —
ошибка воспроизведения полезного сигнала.
Выбор того или иного метода оптимизации определяется
критерием точности и характеристиками входных воздействий.
Так, задача Винера [5, 8] может быть использована для оптими-
зации системы наведения, если входные воздействия заданы в
виде стационарных случайных процессов, причем время памяти
системы наведения не ограничивается искусственно, например,
минимальным временем наведения.
В случае существенно ограниченного времени наведения при
стационарных и нестационарных воздействиях целесообразна
использовать метод, близкий к методу Заде — Рагацини [8].
1.20. ПРИМЕНЕНИЕ ЗАДАЧИ ВИНЕРА К РАСЧЕТУ
ОПТИМАЛЬНОЙ СИСТЕМЫ НАВЕДЕНИЯ
Как уже отмечалось, применение задачи Винера возможно
при условии, что входные воздействия представляются в виде
стационарных случайных процессов, а время памяти системы на-
ведения не ограничено искусственно. Положим, что маневр це-
ли задан спектральной плотностью Sjj(s), а ошибка измерения
полезного сигнала п (г) = — спектральной плотностью*
dfl '
Snn (s) •
Начальный пролет учитывать при оптимизации не будем.
Тот факт, что точность (и оптимальность по точности) пред-
ставляет интерес только для момента t = t\, позволяет заменить
заданный оператор — звено кинематики — его стационарным
эквивалентом (см. разд. 1.14) с передаточной функцией
F(s)=-^±1. (1.123)
S2
Если принять, что оптимальная передаточная функция
r°(s) = 4 /)
sz
обеспечивает минимум дисперсии суммарного пролета, получим
обычную постановку задачи Винера.
Определенные трудности здесь вызывает вид передаточной
функции заданного оператора. Дело в том, что произведение
спектральной плотности полезного сигнала на передаточную.
72
функцию заданного оператора F(s) входит в выражение для
оптимальной передаточной функции в качестве взаимной спект-
ральной плотности входного сигнала системы и заданного опе-
ратора от полезного сигнала.
Строго говоря, в случае, если спектральная плотность Sjj(s)
не содержит s2 в качестве сомножителя, то произведение
S77(s)F(s)=Syj(s)
не может рассматриваться в качестве спектральной плотности,
так как спектральная плотность не должна иметь полюсов в
Рис. 1.45. Преобразование структурной схемы, обеспечи-
вающее возможность применения оптимизации по Винеру
начале координат. (Понятие спектральной плотности определено
для стационарных случайных процессов. Полученный на выходе
интегрирующего звена сигнал при подаче на его вход сигнала,
спектральная плотность которого отлична от нуля на нулевых
частотах, нестационарен; его дисперсия растет с течением вре-
мени).
По существу, это означает лишь то, что из условия конечнос-
ти дисперсии пролета h(t) оптимальная передаточная функция
так же, как и заданная, должна содержать 1/s2 в качестве со-
множителя. Однако непосредственное применение задачи Вине-
ра здесь невозможно. Существуют два пути выхода из этого
положения.
Первый [5] состоит в том, чтобы передаточную функцию
77 / ч As 4- 1 As 4- 1
г ($) =----— заменить на ------— , а после оптимизации
s2 (s 4- ?)2
коэффициент р в выражении для оптимальной передаточной
функции положить равным нулю.
Второй, более простой, путь состоит в преобразовании струк-
турной схемы к виду, приведенному на рис. 1.45. В этом случае
в качестве полезного сигнала выступает шум д(/)=-^- со
73
Рис. 1.46. Структурная схема, све-
денная к задаче Винера
спектральной плотностью Snn(s), маневр цели со спектральной
плотностью Sjj(s) выполняет роль шума (рис. 1.46).
Заданный оператор имеет передаточную функцию (1.123),
а оптимизируемая система — передаточную функцию W.hj(s),
соответствующую параметрической передаточной функции зам-
кнутого контура наведения со входом по /ц(0-
Учитывая, что
5„„(s)=^(s), (1.124)
получим, что произведение F(s) Snn(s) не имеет полюсов в на-
чале координат.
Следуя обычной процедуре ре-
шения задачи Винера, оптималь-
ную функцию получим в виде
[Y^~, (1-125)
Ф(«)
где фС?) —результат представле-
ния суммы спектральных плотно-
стей Snn(s) и Sj/(s) в виде
5ял(®)+5//(«)=Ф('5)Ф( -«);
(1.126)
[у($)]+— результат факторизации выражения
Y(s)= - ^)5-ля-(5)- (1.127)
ф(—S)
(т. е. выделения преобразования Лапласа от функции у(/), взя-
той при [4]) .
В соответствии с формулой (1.64) рассмотрим случай, когда
^W=^(s)=Z*s<, ' (1.128)
здесь /4 = G2 — уровень спектральной плотности ошибки изме-
рения, стационарной по линейной координате.
Маневр цели, не знающей момента встречи с ракетой, естест-
венно представить в виде стационарного случайного процесса,
некоррелированного с сигналом ц(/).
Наиболее естественно представление маневра цели в виде
бинарного случайного процесса с пуассоновским распределени-
ем длительности интервалов постоянства знака [5]. Соответству-
ющая спектральная плотность может быть записана в виде
SJJ (*)=---ГТ------ (1. 129)
— s2a2 +1 k '
где а — математическое ожидание интервалов постоянства зна-
ка маневра;
т4=2аа, (1.130)
где а — дисперсия ускорения маневра цели, м2/с4.
74
Для того чтобы получить решение в аналитическом виде, по-
ложим, что
— »а. (1.131)
т
При этом сумма спектральных плотностей
(1.132)
Рис. 1.47. Сумма спектральных плотностей Snn($) +
+*Sjj(s) в случае выполнения неравенства (1.131)
Допустимость такого приближения следует из рис.' 1.47 и
1.48, на которых показаны спектральные плотности Snn(co),
Sjj(oj) и их суммы для двух условий: (1.131) выполняется (см.
рис. 1.47), (1.131) не выполняется (см. рис. 1.48).
Спектральную плотность
Sjj(s)=zn4 можно рассматри-
вать как спектральное пред-
ставление 6-функции [5]. По-
этому, учитывая (1.56), дан-
ную задачу можно трактовать
как оптимизацию по критерию
минимума интегральной квад-
ратической оценки при отра-
ботке начальных условий по
пролету. С учетом формулы
(1. 132) выражение (1. 126)
имеет вид
дам
Рис. 1.48. Сумма спектральных плот-
ностей Snn (s) +Sjj(s) в случае не-
выполнения неравенства (1.131)
<|> ($) <|» (- s) =/4$4+т*=(Z2s2 + V2lms + m2)\l2s2- У 2lms + m2)•
(1.133)
Выражение (1.127) при этом можно записать
у (5)=-^5"я^ =------/<Д$3_+---- л 134)
ф(— s) l2s2—V2lms + m2
75
В результате факторизации у($) представляется в виде
Y (s) = [Y («)]- +[Y («)]+.
где
[у ($)]=________jl---------
J 12$2—у 21ms + m2 (1.135)
[Y(s)]+=£>s + C,
(1.136)
(1.137)
А, В, С и D — постоянные коэффициенты.
Полином Ds + C отнесен к {у(«)1+ потому, что он представля-
ет собой преобразование Лапласа от суммы б-функции и ее про-
изводных, отличных от нуля только при />0.
Коэффициенты D и С равны:
Z?=д/а,
С=/2-|-д//п /2.
Таким образом, оптимальная передаточная функция
= [Y(s)]+ Д/2$ + (р +/2/тД)
’ <p(s) /2«2 + у 21ms + m2
Положив 1!т = §, преобразуем оптимальную передаточную
функцию к виду
W°hj (s)=.
V ’ q2s2 -I- /2QS + 1
Учитывая, что по смыслу структурной схемы (см. рис. 1.46)
передаточная функция W^j (s) представляет собой оптимальную
параметрическую передаточную функцию контура наведения,
получим с помощью соотношения (1.80) оптимальную передаточ-
ную функцию
го Ф = (/2_е+_д) s + 1_.
' e2s2+/2Qs+i
Соответствующие дисперсии пролета из-за маневра цели и
ошибки ц равны:
(1.138)
(1.139)
_ q2 + 2/2qA + 3A2
2/2 V ’
3q2 + 2/2(>Д + Д2
2/2 U
(1. 140)
Эти дисперсии получены в соответствии с таблицами, приве-
денными в [5].
Задавшись целью сформировать оптимальную систему наве-
дения по линейному рассогласованию, получим в соответствии
76
с формулой (1.85) оптимальную передаточную функцию авто-
номного контура
U7i(s)= г(/2е+,А)*>Л1 • U-141)
е [де« + (е + 1^2д)]
Для того чтобы сформировать оптимальную систему наведе-
ния по угловой скорости, необходимо в соответствии с формулой
(1.96) положить '
/-чAQ2(a+/2q) s2 + /2q(д2 + 2 /2qA + q2) s + (Д + /2q)2 .
a ' ’ Q[Aes + (e + /2A)l(e2s2-i-K2es+1)
(1. 142)
Рис. 1.49. Коэффициенты пролета rji (О, А) для
оптимальных систем наведения
В качестве примера на рис. 1.49 приведены графики коэф-
фициента т|1 (0), полученные для следующих значений коэффи-
циентов Лид:
1) д = 0,2 с; 2) д=0,2 с; 3) д = 0,5 с; 4) Д = 0,5 с;
q=0,1 с; q = 0,3 с; q—0,3 с; q=1 с.
Коэффициент т|1 (0) вычислен с помощью обратного преобра-
зования Лапласа от WQhJ (s) (1.138)
__е
С(Ч = е 0<2 [(e/f+д) sin _±=- + acos-®-‘.
L СУ2 су 2 J
Из графиков'на рис. 1.49 следует, что, несмотря на отсутст-
вие в постановке соответствующего ограничения, полученное в
результате оптимизации время памяти системы практически
ограничено, причем его величина определяется в основном ве-
личиной коэффициента q.
77
Упрощающее предположение (1.131) позволило разложить
сумму спектральных плотностей (1.133) на множители в общем
видо и выразить передаточные функции системы и автономных
контуров через параметры входных воздействий.
Рис. 1.50. Логарифмические амплитудные и фа-
зовые частотные характеристики оптимальной
замкнутой системы наведения со входом по
маневру цели
На рис. 1.50—1.58 приведены примеры оптимальных пере-
даточных и весовых функций для спектральной плотности
Q ___ /п4
JJ~ — S2O2 _|_ 1
Для того чтобы ограничить полосу пропускания автономного
контура, что необходимо для облегчения реализации оптималь-
Рис. 1.51 Логарифмические амплитудные и фазовые
частотные характеристики оптимальной замкнутой ’
системы наведения со входом по ошибке измерения
линейного рассогласования
ной системы, в спектральную плотность Snn(s) введено допол-
нительное слагаемое r®s6. При этом
S„„ (s)=Z‘s<(1.143)
78
Это слагаемое повышает уровень спектральной плотности
«полезного сигнала» в области высоких частот. В результате
расширяется полоса частот, .в которой выполняется неравенство
Рис. 1.52. Логарифмические амплитудные и фазо-
вые частотные характеристики автономного конту-
ра оптимальной системы наведения при управле-
нии по линейному рассогласованию
Рис. 1.53. Логарифмические амплитудные и фазо-
вые частотные характеристики автономного конту-
ра оптимальной системы наведения при управле-
нии по угловой скорости линии дальности
что» естественно, сопровождается расширением области частот,
в которой разница между передаточными функциями W^j ($)
и F(s) мала.
Но согласно структурной схеме, 1приведенной на рис. 1.33, в,
контур (наведения представляет собой замкнутую систему, в
79
прямой цепи которой стоит звено кинематических -связей, а в об-
ратной — автономный контур. Учитывая эквивалентность меж-
ду заданным оператором и звеном кинематических связей, при-
Рис. 1.54. Коэффициенты пролетов
оптимальной системы наведения
(вариант 1)
}ис. 1.55. Коэффициенты пролетов
оптимальной системы наведения
(вариант 1')
ходим к выводу, что область частот, на которых совпадают пе-
редаточные функции W^j (s) h*F(s), тем шире (точнее, про-
стирается тем дальше в область малых частот), чем уже полоса
пропускания автономного контура.
Ограничение полосы пропускания автономного контура при
оптимизации приводит к некоторому увеличению дисперсии сум-
Рис. 1.56. Логарифмические амплитудные и фазовые час-
тотные характеристики автономных контуров оптимальных
систем наведения (варианты 1, 2, 3 и 4)
марного пролета системы наведения. (Сравнение оптимальных
систем с ограничением и без ограничения полосы пропускания
должно проводиться при одних и тех же входных воздействиях,
причем естественно положить, что г6 = 0).
80
Предложенный способ воздействия на полосу пропускания
автономного контура не отличается строгостью, так как, во-пер-
вых, заранее не ясно, как сильно повлияет слагаемое — г6^6 на
полосу пропускания, и, во-вторых, невозможно предсказать за-
ранее, нельзя ли достичь того же ограничения полосы пропуска-
ния с меньшим ухудшением точности системы.
Рис. 1.58. Коэффициент пролета
T]i(О, Д) оптимальных систем наве-
дения (вариант 1, 2, 3 и 4)
Рис. 1.57. Коэффициент пролета Д>
оптимальных систем наведения (вариан-
ты Ц 2, 3, и 4).
Расчеты оптимальных систем при входных воздействиях
(1.129) и (1.143) проведены для параметров, показанных в
табл. 1.1.
Таблица 1.1
Вариант 1 1' 2 3 4
/и4, м2/с3 4000 4000 2000 5000 5000
Z4, м2*с 3 3 3 1 10
а, с £ 1,25 1,25 10 25 25
г, м3 -с 0,005 0,05 0,1 0,1 0,1
Д, с 0,5 0,5 0,5 0,5 0,5
а2, м2/с4 1600 1600 100 100 100
На рис. 1.50—1.53 для вариантов 1 (пунктир) и Г (сплош-
ная линия) приведены амплитудные и фазовые логарифмиче-
ские характеристики оптимальной замкнутой системы W\j(Zco)
и (/со) и соответствующих автономных контуров (/со) и
UZa (Z<o). Соответствующие коэффициенты пролета показаны на
рис. 1.54 и 1.55. В данном случае система рассчитана на дина-
мично изменяющийся маневр цели. Выбор коэффициента г=
= 0,05 в варианте Г несущественно повысил ошибки, однако
существенно снизил требования к реализации автономного кон-
тура на частотах, больших со= 10 1/с.
81
На рис. 1.56—1.58 приведены результаты оптимизации для
вариантов 2, 3 и 4, в которых цель маневрирует с меньшим ус-
корением и сравнительно редкими -сменами знака маневра. Су-
жение спектра маневра, цели привело к увеличению памяти оп-
тимальной системы и уменьшению установившегося значения
коэффициента пролета Последнее достигается повыше-
нием амплитудной частотной характеристики автономного кон-
тура №а(ко) в области низких частот. Интересно, что для всех
рассмотренных примеров частотная характеристика автономно-
го контура при управлении по |/?|со обязательно имеет участок
длиной около декады, на котором амплитудная характеристика
равна 3.
ГЛАВА 2
МЕТОДЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ,
ПОЗВОЛЯЮЩИЕ УЧИТЫВАТЬ
СЛУЧАЙНЫЕ разбросы параметров
Трудно -себе представить реальную динамическую систему,
параметры которой в той или иной мере не подвергались бы
случайному разбросу.
Совершенствование систем автоматического управления (при-
вело к появлению таких систем, в которых случайность пара-
метров обусловлена самим принципом построения системы.
Примером этого могут служить различные адаптивные и радио-
технические системы с модуляцией параметров.
Случайные изменения параметров наблюдаются также в эле-
ментах систем управления, подверженных механическим воз-
действиям в виде случайных вибраций и акустических шумов, а
также при эксплуатации систем в условиях изменения темпера-
туры, влажности, радиации и т. д.
При изготовлении элементов системы управления неизбежно
имеет место технологический разброс параметров. Так что в со-
вокупности одинаковых систем параметры отдельных экземпля-
ров всегда будут несколько различаться. Поэтому в процессе
проектирования и при исследовании систем данного типа неза-
висимо от выбора конкретного экземпляра параметры следует
считать случайными, заданными их распределениями внутри
поля допуска. Подобная картина наблюдается также, в резуль-
тате старения различных элементов систем в условиях хранения
и нормальной эксплуатации.
Требования к точности и работоспособности автоматических
систем постоянно повышаются. Это привело к тому, что в нас-
тоящее время учет перечисленных факторов (а также многих
других, обусловленных либо случайностью среды, в которой
происходит движение системы, либо изменением ее собственных
динамических свойств и приводящих к (случайным изменениям
параметров) является необходимым при проектировании и
оценке качества функционирования системы.
83
Общность целого ряда понятий и методов, выработанных
при решении вопросов, связанных со случайным изменением па-
раметров, дает возможность рассматривать эти понятия и мето-
ды как основу складывающегося <в настоящее время раздела
теории автоматического управления — теории стохастических
систем.
Математической моделью процессов, протекающих в стоха-
стических системах автоматического управления, являются сис-
темы обыкновенных дифференциальных уравнений со случайны-
ми коэффициентами. Наиболее строгие и законченные результа-
ты по исследованию таких систем получены для сравнительно
частного случая линейных систем, когда изменения коэффици-
ентов — гауссовы белые шумы [8].
При произвольных спектрах случайных процессов в стоха-
стических системах точное решение задачи анализа не получено.
В работах [3, 6] излагаются приближенные методы анализа, ос-
нованные на структурном представлении линейных стохастиче-
ских систем. Исследование ограничено рамками корреляцион-
ной теории.
В данной главе излагаются некоторые методы анализа ли-
нейных и нелинейных стохастических систем. Вопросы, рассмот-
ренные здесь, далеко не исчерпывают всех задач, связанных с
исследованием стохастических систем. Тем не менее решение
многих задач, возникающих в процессе проектирования, может
быть получено на основе методов, изложенных в этой главе.
2.1. ВОЗДЕЙСТВИЯ СЛУЧАЙНЫХ ВИБРАЦИЙ
НА ДАТЧИКИ ЛИНЕЙНЫХ УСКОРЕНИЙ
При полете ракеты с работающим двигателем *на посадочных
местах приборов в приборных отсеках возникают случайные
вибрации. Одновременно с вибрацией посадочного места прибо-
ра возникает акустическое воздействие, которое создает вокруг
аппаратуры случайное поле давлений. Все это приводит к слу-
чайной модуляции параметров электромеханических цепей.
Диапазон частот вибровозмущений обычно, достаточно широк,
чтобы вызвать модуляционные явления в любой аппаратуре,
установленной на ракете. Эффект модуляции проявляется в
каждом звене системы управления по-разному. Ниже будет рас-
смотрено влияние вибраций на работу датчиков линейных ус-
корений.
Датчики линейных ускорений, или навигационные акселеро-
метрические устройства являются наиболее чувствительными
элементами системы управления, призванными измерять пара-
метры движения ракеты на траектории для выработки коррек-
тирующих сигналов.
Анализ динамических свойств акселерометров при действии
вибраций особенно важен потому, что они являются датчиками
84
первичной информации, и погрешности, возникающие в них, не-
посредственно сказываются на работе системы.
Рассмотрим акселерометры, не имеющие силовой коррекции
и выполненные по двум различным конструктивным схемам: с
вращательным (типа маятника) и поступательным движением
инерционного элемента.
Акселерометр маятникового типа (рис. 2.1) представляет со-
бой инерционный неуравновешенный груз, способный повора-
Рис. 2.1. Акселерометр маятниково-
го липа:
/—токосъемное устройство; 2—корпус;
3— ось подвеса; 4—неуравновешенный
груз
чиваться вокруг оси, укреплен-
ной в корпусе прибора.
С подвижным грузом с по-
мощью шарнирного соединения
связано токосъемное устройст-
во, укрепленное на корпусе
плоскими пружинами.
Акселерометр с поступа-
тельным движением чувстви-
Рис. 2.2. Схема акселеромет-
ра с поступательным движе-
нием чувствительного эле-
мента
тельного элемента представляет собой инерционную массу, под-
вешенную с помощью нескольких плоских пружин к корпусу. На
рис. 2. 2 показана принципиальная схема акселерометра.
При действии вибрационных ускорений, приложенных к кор-
пусу акселерометра, уравнение движения чувствительного эле-
мента маятникового типа можно записать ib виде
[(i-Fg) sin ср —Л COS ср] =0,
где J — момент инерции маятника; В — коэффициент демпфи-
рования; т — масса подвижной системы; I — расстояние от
центра тяжести до оси подвеса; ф — угол отклонения от верти-
кали; х и z — составляющие вектора вибрационных ускорений
в проекциях на соответствующие оси.
Для малых углов отклонения маятника с учетом дополни-
тельных обозначений
/у — в . д //> zml . /• xml
аг = —, Дх(/)=—; /(/) = —
85-
уравнение движения можно записать в виде
?+a2? + l#i +Д1W] <?=/ W-
Из этого уравнения следует, что наличие случайной вибрации
по оси г приводит к появлению случайного коэффициента А± (/)
в левой части уравнения движения.
Процессы 1в акселерометре с поступательным перемещением
чувствительного элемента в условиях вибраций из-за наличия
двух промежуточных стоек должны описываться системой диф-
ференциальных уравнений, которая связывает движение трех
масс. Однако, если учесть, что конструкция датчика обычно
симметричная и влияние движения промежуточных стоек по оси
измерений на положение чувствительного элемента можно пред-
ставить в виде дополнительных внешних воздействий, то урав-
нение движения акселерометра можно приближенно предста-
вить в виде
тх + 2Ах + k [ 1 + pF (/)] х = Р (/),
где k — суммарная жесткость системы; т — масса чувствитель-
ного элемента; h — коэффициент демпфирования; ц — коэффи-
циент относительного изменения жесткости; F(t) — силы, дей-
ствующие в направлении, перпендикулярном оси измерения;
P(t) — силы, действующие в направлении оси измерения.
Таким образом, приближенное уравнение движения акселе-
рометра с поступательным движением чувствительного элемента
имеет вид, аналогичный уравнению для акселерометра маятни-
кового типа.
Акселерометры рассчитаны на вполне определенный диапа-
зон замеряемых ускорений, поэтому в их конструкции предус-
мотрены упоры, ограничивающие перемещения чувствительного
элемента.
Сочетание больших ускорений ракеты с виброускорениями
может привести к тому, что измеряемое ускорение выйдет за
пределы диапазона линейности акселерометра и произойдет уп-
ругий отскок чувствительного элемента от упора. В этих усло-
виях датчик линейных ускорений следует рассматривать как не-
линейную систему со стохастической линейной частью.
2.2. ПРОХОЖДЕНИЕ СИГНАЛА
ЧЕРЕЗ ОБТЕКАТЕЛЬ АНТЕННЫ ГОЛОВКИ САМОНАВЕДЕНИЯ
При использовании различных информационных подсистем
для определения координат целей (например, оптических и ра-
диолокационных головок самонаведения) часто имеет место про-
хождение электромагнитных сигналов через среды, обладающие
случайными свойствами. Особенно ярко это проявляется в ра-
диолокационных головках самонаведения.
«б
Одна из трудностей, возникающих при проектировании само-
наводящихся ракет, обусловлена искажениями сигнала радио-
прозрачным обтекателем. В результате этих искажений головка
самонаведения измеряет кажущуюся угловую скорость линии
дальности. Разница между кажущейся и фактической угловой
скоростью определяется ошибками преломления обтекателя и
колебаниями ракеты относительно центра тяжести. Так, в плос-
ком движении кажущийся угол места цели
где Д<р(ф) — ошибка преломления, зависящая от угла пелен-
га ф.
Рис. 2.3. Интегральная характеристика обтекателя
Зависимость Дф(ф) является существенно нелинейной и на-
зывается интегральной характеристикой обтекателя. Типичные
характеристики Дф(ф) для трех экземпляров обтекателей пред-
ставлены на рис. 2.3.
Кажущаяся угловая скорость равна в этом случае
dqax — d4a I d<f
dt dt "J" df dt'
Так как
? = <7ц —
где О — угол поворота оси ракеты, то
dq^x__dqu , rfAy tdqa___________dqu /1 rfAy \ dfaf db
dt dt d<f \ dt dt) dt \ d<f / d<? dt
Из полученного уравнения следует, что имеет место измене-
ние коэффициента усиления по угловой скорости линии даль-
ности в fl-|- раз и образуется паразитная обратная связь
по угловой скорости относительно центра тяжести.
87
Контур, образованный паразитной обратной связью,'содержит
в прямой цепи значительный коэффициент усиления, в резуль-
тате, несмотря на малость производной —— , -при полетах, осо-
бенно на больших высотах, -имеют место значительные ошибки
системы наведения.
Причина угловых ошибок определения пеленга цели заклю-
чается в деформации диаграммы направленности антенны, кото-
рая ,в свою очередь является следствием фазовых искажений
электромагнитного поля, падающего на обтекатель, и переотра-
жений от внутренних стенок. Величина ошибок зависит от ди-
электрических свойств материала, геометрии обтекателя и угла
падения пришедшей волны. В обтекателях всегда имеет место
локальная неоднородность материала, которая приводит к появ-
лению изрезанное™ характеристики ошибок (см. рис. 2.3).
Вид функции Дф(ф) существенным образом изменяется в за-
висимости от того, через какое сечение обтекателя проходит
падающая волна, и, -следовательно, зависит от движений раке-
ты относительно центра тяжести. Поскольку относительно цент-
ра тяжести ракета движется по случайному закону, в полете
характеристика ошибок обтекателя претерпевает случайные из-
менения.
Помимо этого, в результате ошибок -производства и случай-
ного характера локальной неоднородности материала обтекате-
ля характеристика Аср(ср) для каждого экземпляра обтекателя
имеет различный вид.
Таким образом, искажения, вносимые обтекателем, приводят
к появлению в контуре управления нелинейности Дф(ф), пара-
метры которой случайны как во времени, так и в 'совокупности
одинаковых систем. ' ч
2.3. МОДУЛЯЦИЯ ПАРАМЕТРОВ СЕРВОМЕХАНИЗМОВ РУЛЕЙ
СЛУЧАЙНОЙ НАГРУЗКОЙ
Обладая ограниченной мощностью, сервоприводы органов
управления ракет имеют статические характеристики, парамет-
ры которых существенно зависят от величин нагрузочных мо-
ментов.
На рис. 2.4 показана типичная характеристика, отражаю-
щая зависимость максимальной скорости сервомотора (Отах от
величины момента нагрузки М,— нагрузочная характеристика
сервомотора.
Точка А соответствует режиму «холостого хода», а точка В —
режиму «короткого замыкания». Из рисунка видно, что измене-
ние нагрузочного момента в диапазоне ДЛ4 вызывает измене-
ние максимальной скорости в диапазоне Дсотах. Эти изменения
существенным образом сказываются на виде статических ха-
рактеристик, которые определяют зависимость частоты враще-
ния привода со от величины управляющего сигнала Нуцр.
«8
На рис. 2.5 приведено семейство статических характеристик
сервомотора, управляемого отсечным золотником, для различ-
ных нагрузок на выходном валу.
Рис. 2.4. Нагрузочная харак-
теристика сервомотора
Рис. 2.5. Статические характе-
ристики сервомотора при раз-
личных значениях нагрузки на
выходном валу
На рис. 2.6 показаны статические характеристики сервомо-
тора, управляемого струйной трубкой, которые соответствуют
различным величинам моментов сухого трения Л4тр.
На рис. 2.7 изображены статические характеристики серво-
мотора, управляемого струйной трубкой, при изменении нагруз-
ки и величины сухого трения.
Рис. 2.6. Статические характерис-
тики сервомотора при изменении
величины сухого трения
Рис. 2.7. Статические характеристики
сервомотора при изменении нагрузки
и величины сухого трения
В процессе полета ракеты органы управления (рули, элеро-
ны, поворотные крылья и др.) находятся в возмущенном потоке,
который вызывает 'случайные изменения шарнирного момента.
Изменение шарнирного момента изменяет статические характе-
ристики сервомеханизма. Поскольку шарнирный момент в про-
89
цеосе полета представляет собой случайный процесс, то и пара-
метры зависимости скорости сервомотора от управляющего сиг-
нала (коэффициент усиления линейного участка, зона насыще-
ния, зона нечувствительности и т. д.) являются случайными.
2.4. АНАЛИЗ СТОХАСТИЧЕСКИХ СИСТЕМ
Математической моделью процессов, протекающих в динами-
ческих системах со случайными параметрами, является следую-
щее дифференциальное уравнение:
y=Q{t)f(y, /)+/>(/) Z (/), (2.1)
где у=Цу/111 х т — вектор выходных коор-
динат;
z = Ikzlhxm—вектор аддитивных
входных воздействий;
f (Уу *)=||// (У> ^)||1хл1 — нелинейная вектор-
функция;
О (^) = l|g’/y Wllmxm И P(/) = ||p0(/)||mXm — матрицы КОЭффиЦИ-
ентов.
Относительно элементов матрицы G и компонент вектора
воздействий z будем предполагать, что они являются коррели-
рованными стационарными нормальными случайными процес-
сами с дробно-рациональными спектральными плотностями.
Если функция f(y, t) линейно зависит от у, то уравнения
(2.1) описывают процессы в линейной системе со случайными
параметрами.
Используя идею многомерных формирующих фильтров и рас-
ширив за счет них размерность пространства состояний, систе-
му уравнений (2.1) можно привести к следующему виду:
*=F<>(х) + Л (/) F1 г (/), (2. 2)
где x = |xz| 1Хл — вектор состояния системы;
г~ |г/|1хл — вектор аддитивных воздейст-
вий;
F»=||F?||1X„; F1=IlF/Hixn — нелинейные векторные функ-
ции;
(*) = НМлхл; U (/)=||й/у(/)||лхл —матрицы коэффициентов.
Элементы матрицы и компоненты вектора г представля-
ют собой коррелированные белые шумы со следующими стати-
стическими характеристиками:
М [lt) (/)] =/?/ (0; М [rz (/)]=тЧ (/);
7И [aZy (/) aftZ (Zj)] = С/у^/8 t)\
(2. Uj
Af [azj (t) rk (/x)] = Cijtk% (/j_ /);
Л1 [r* (/) г'? О=8 (4-t) Cr=Z^t) ||с/у||лХл, .
90
где a/y=Z/y —/?/, г*(/) = г(/) — cijtkr, си — постоян-
ные величины.
Появление нелинейной функции F° обусловлено тем, что при
добавлении к системе (2.1) уравнений формирующих фильтров
в правой части образуются слагаемые, представляющие собой
произведения новых фазовых координат на функции f(y, t). Та-
ким образом, даже если исходная система была линейной, сис-
тема (2.2) нелинейна всегда, когда процессы gij(t) не являются
белыми шумами.
Матрица коэффициентов Ц представляет собой сумму де-
терминированной £°=||/?у || и случайной L = ||aij|| составляющих.
Обозначив-
/=’(x) = F0(x) + Z0F1 (х),
перепишем систему (2.2) в следующей форме:
х=F (х) + L (/) F1 (х) + U (/) г (/). (2. 4)
При сделанных предположениях о статистических характери-
стиках вектора воздействий r(t) и элементов матрицы L(t) век-
тор состояния системы (2.4) представляет собой непрерывный
Ипмерный марковский процесс. Для непрерывных марковских
процессов закон распределения вероятностей является решени-
ем уравнения Фоккера — Планка — Колмогорова '
df(xt t)
dt
- S '>1 + vS
Z—l /,>1
d2
dxi dx j
(2.5)
где f(x, t) — вероятность того, что в момент времени система
будет находиться в дифференциальном элементе пространства
состояний.
Вектор коэффициентов сноса А = ||Лг-||1Хп и матрица коэффи-
циентов диффузии B = ||BiJ|n п в уравнении (2.5) определяются
как условные статистические характеристики по формулам:
Л = Ит [Ах/х (/) = х] .
Д/->0 А/
Нп1 М \ьхьх4х (t) = х]
Д/-И) А/
Выражения для А и В могут быть получены из системы
уравнений, описывающих рассматриваемый марковский про-
цесс.
Интегрируя систему (5.4) на интервале времени (t, /4), на-
ходим
х(/х)=х (/) + J/7 [х (т)] dx-\r j Z(t)/71 [x(r)rfr +J U (t) r (x)dx.
91
Воспользуемся следующим соотношением:
т
Fi [х (т)]=F»[x W] + dx (о).
t
Согласно уравнению (2.4)
dx=F (х) dt + L (/) F1 (х) dt+U (/) г (/) dt,
поэтому можем написать
т
F* [х (т)] =F' [х (/)]+ f F [х (a)] dt +
J ох
+ \ L (о) F1 [х (a)] rfa + U (а) г (а) dt.
J dx dx
о t
После этого получим следующее (выражение для вектора со-
стояния:
х (/х) =х (/) -|- J F [х (г)] dx -|- J L (т) F1 [х (/)] dx -|-
(2.6)
t t t
Обозначим
FW=F[x(/)]; ^1=^11
ox dx Lr-r(o
Как уже отмечалось, вектор состояния x(t) является непре-
рывной функцией времени. В силу свойств нелинейных функций
F и F1 они и их производные также непрерывно зависят от вре-
мени. Следует заметить, что по отношению к элементам матри-
цы L и вектора r(t) эти утверждения несправедливы. Можно
написать
tl t tl
\L(x)\ dF'{a}- F (a) dtdx =\{x-t)L (r) dx dF1 (П F (t*),
j J dx J dx
t t t
где /* — внутренняя точка интервала \t, т].
Из непрерывности нелинейных функций следует
dx dx
«2
Приведенные рассуждения применимы и к остальным интег-
ралам в выражении (2.6), поэтому оно может быть преобразо-
вано в следующее выражение:
/1
л(/1)=х(/)+ j F(T)rfT+f L(x)Fl (/) dr+f(r-/)£(T)X
t t t
F dx+HL d-^ L & F1 w d° dx+
OX J ox
t t
U (3) r(3) dadx \ U {x)r {x)dx-\-o(tl—t) =
dx J
dadx-{-
(0 + F (T) dx + L (t) dxF1 (t) + (r-/) L (r) dxd-^±
t t
t t j,ka^l 7
P г ^1(0
+ j V -^-U}l(a)allt(x) rz(a) dadx-\-
(2.7)
Ha основе полученного выражения ^вычислим условное мате-
матическое ожидание приращения вектора состояния M[x(ti) —
—x(t)/x(t) =х]
М [дх/х Р)=х] = f F (т) dx + J М [L (т)] dxF* (f) +
t t
+ ^(т-/)Л4[£
t
F^+ S
X M l“z* (T) aii (°)] rfe dx +
____ dxt
tl
x M l^ik (T) ri (a)l dx 4- f U (т) M [r (t)] dx-\-o (/x — t)
93
Учитывая, что М[L(t)]=0, а также соотношения (2.3) и ис-
пользуя свойства 6-функций, из последнего выражения находим
М [дх/х (/)=х] =F
(Л)д/+т X
4”
dFlk(x)
dxj
ил Wcib,i W яг2(/) д/+о(д/);
1
здесь Д/=/1—I.
Поделив правую и левую части на Д£ и переходя к пределу
при Д/—>-0, получим формулы для вектора сноса
Д=Г(х)+-^-
Ж dXj
1^1 (X) clklii+u}l(t)
-\-U
(2-8)
Чтобы получить выражения для матрицы коэффициентов
диффузии, запишем следующее уравнение для транспонирован-
ного вектора состояния:
h t
х' (/х)=хт (/) + J F’ (т) dx + [ F1 {t) L\x) dx +
t t
t 1
+ j Гт(г) £/т(т)</т4-О(Л—^)-
t
(2.9)
Далее вычислим ДхДхт. Перемножив выражения (2.7) и
(2.9) и применив к произведению операцию условного матема-
тического ожидания, получим в правой части Л4[ДхДхт/х(/) =х]
тридцать шесть слагаемых, из которых тридцать два будут
иметь второй порядок малости относительно Д/ и не войдут в
выражения для коэффициентов диффузии. Лишь условные ма-
тематические ожидания взаимных произведений вторых и шес-
94
тых слагаемых в формулах (2.7) и (2.9) имеют порядок АЛ По-
этому
(tt h
В=lim М U [L (tJ F* (/) Г (т2) + L (тх) Fl (f) rT(t2) £7Т (т2) +
д/->0 А/ J J
ч t
+и (Тх) Г (Тх) гт (т2) UT (T2)+t/ (Тх) г (т2) Fu(t) Г(т2)] dx^dxjx (t)=х}=
=lim — М
Д/->0 А/
ri(t)F}(t) aift(ti)ayz(r2)4-
+ Р) u-ji (*2) a/* Oi) rt (t2)+az* (Tx) F\ (/) ayz (t2) rfe (ti) +
4-И/л Oi) Иц (t2) rk (tx) rz (r2)|| dx^dx^x (/)=*}.
Учитывая соотношения (2.3) и используя свойства д-функ-
ций, находим
5 =
2 ?l W F\ (х) Cikji+ Fl (х) tiji (!) cZft>z +
M-l
+fJ (X) uik (t) c}l,k +utk (/) Ид (/) cftiZ||.
(2.10)
В частном случае, когда исходная система (2.1) линейна, то
F1(x)=x. Пр>и этом матрица---- является единичной и выра-
жения для коэффициентов уравнения Фоккера — Планка —
Колмогорова имеют вид
A=F
п
к, 1-1
Х1С1к,М~\гак1С1к,1 -\-U
п »
У -Wzmi+хЛИд(/)cik4 +xtulk (f) сп>к-\-и1к(/)Ид (/) ск,t .
(2-11)
В этом случае несмотря на линейность Fx(x) функция F(x) —
нелинейна, поскольку содержит произведения, фазовых коорди-
нат системы.
Из выражений (2.8) ,(2.10) и (2.11) видно, что. коэффициен-
ты уравнения Фоккера — Планка — Колмогорова для динами-
ческой системы со случайными параметрами зависят от вида
нелинейных функций, входящих в правые части дифференци-
альных уравнений, и от статистических характеристик случай-
95
ных параметров и воздействий. Само уравнение Фоккера —
Планка — Колмогорова записывается следующим образом:
д/(х, 0
dt
(Fi (х) Cvkji +
п -1 Ч п
+М0<^}7(х,0 +4” V -тА?
I I ОХ £ ох,
;-1 j j
х {[^1 (X) Fl (х) с1Ы + F* (х) (/) с1к4+ F} (х) и1к (/) с,м +
+М)М^»,Ж ф.
Получить точное решение уравнения Фоккера — Планка —
Колмогорова удается лишь в некоторых, не представляющих
практического интереса, случаях. Однако оно с успехом может
быть использовано для получения систем уравнений относитель-
но статистических моментов исследуемых процессов.
Пусть
U* =М Г*?1, Лоа,..., х*л1 —
^klik2t...,kn [ 1 ’ 2 ’ J
смешанный момент порядка /г=Л1+&2+ ... + &п-
Умножим правую и левую части уравнения (2.5) на х*1
х2а • • • хпП и 'проинтегрируем по всем компонентам в бесконеч-
ных пределах
\ ? xi'x*2 •• - х*” - -) dxx dx2... dxn =
J .) dt
— oo —00
V Г ... \ x?*X22... X*" [Д/ (x) f (x)] dx^Xj,... rfx„+
J J dxt
Z—1 —oo —oo
n oo oo
\ ч « • x> [b" w/(x' x
l,j — l—oo —oo
x dxx dx2... dxn.
В левой части последнего выражения операцию дифференциро-
вания можно вынести за знак интеграла, в правой — интегра-
96
лы легко вычисляются, если воспользоваться интегрИрование^м
по частям. В результате будем иметь
п
ki {kt ~1} м [в“{х) х*‘х* ••• • х^~2) • • • л*л]+
kik>M [Bi> w **'**’ * х*лЬ
1 w
klt k2,..., £л=бД; ^+^4-...+^=^ (2.12)
Соотношения (2.12) позволяют получить системы дифферен-
циальных уравнений относительно статистических моментов лю-
бого порядка. Видно, что в общем случае, когда коэффициенты
Ai и Bij нелинейно зависят от вектора состояния, эта система
является разомкнутой, поскольку правая часть содержит мо-
менты, порядок которых выше чем k.
Для того чтобы система (2.12) была замкнутой, т. е. чтобы
она содержала моменты порядка не выше k, коэффициенты Д,
должны линейно, а Вц — квадратично зависеть от вектора сос-
тояния. Из формул (2.8) и (2.10) видно, что это имеет место
лишь тогда, когда функции F(x) и Г1^) линейны, т. е. когда
математическая модель исходной динамической -системы (2.1) —
линейна и случайные параметры — белые шумы. Лишь в этом
случае можно получить точное решение системы моментных
уравнений (2.12).
Полагая в формулах (2.8) и (2.10)
F(x) = jV(/)x, F1(x)=x,
где N(t) = ||Пг,||пхп — матрица, элементы которой — заданные
функции времени, на основании (2.12) будем иметь
4 3200
97
+ Ulj tt) Cil.jXl -YUij Ю 4il (0 2 • • • +
n
Cik,jlXkXl~\~U'jl (0 Cik,lXk +
+ «/»W Cji.bxi + Uih иЛ (0 cft./lx*' • • • • • • xI',h
После осреднения правой части окончательно получим
п
^^^...к = VJ ki +
п
i^a
n
+ ИJI W Cij,№*,-<*i~!)•••»„] H (ki~ 1) X
С/Л/р.*7\(й;_2),..(Лу+1)...Лл+
4-И/; (^) cii,jV‘li,.. ,(й.-2).,.(й/+1)...йл +И;/ (^) И/z (0 cJ,l X
n
X^r2.(^-2)...»n] +-£- M;X
Ji'^j -1
X 1)...(*?-1)...(Л, + i)...(*z+i)...ftn +
+ «д (t) c<4!iftr!.(ft1-i)...(ft>-i)...(ft,+i)...ft,I +
-|-И/, (/) (/) c,,iX
\Z ,?-2 b
x H'ft,...(ft/-i)...(»y-i)...ftj.
^ = 6Д; i=TTn; ^ki=k. (2.13)
Z»1
Система (2.13) (представляет собой систему обыкновенных
дифференциальных уравнений с детерминированными правыми
частями. Если исходная система (2.1) или случайные внешние
воздействия, которые к ней приложены, нестационарны, то и си-
стема моментных уравнений (2.13) получается нестационарной
98
Легко заметить, что уравнения (2.13) содержат .моменты по-
рядка не выше k и, кроме того, имеется столько уравнений;
сколько моментов &-го порядка. Эту систему дифференциальных
уравнений относительно статистических моментов компонент
вектора состояния можно решать обычными методами, но для
определения моментов порядка k необходимо сначала найти мо-
менты более низкого порядка, поскольку они участвуют как не-
однородные члены в правых частях уравнений.
Как уже отмечалось, интегрированием системы (2.13) могут
быть вычислены моменты любого порядка. По известным ста-
тистическим моментам методами теории случайных функций
можно восстановить законы распределения вектора состояния
х(/) или отдельных его компонент. Для систем со 'случайными
параметрами законы распределения координат всегда отличны
от нормальных.
Однако часто задача исследования ограничивается определе-
нием лишь двух первых моментов, а именно, математического
ожидания и дисперсии решения.
Пусть
= [xJ = Hoo...fcz=i...o-
На основании соотношений (2.13) находим
п
Д0|1у+«,7(/) /Пу(/) +
1=1, П. (2.14)
/,v = l
Введем следующие обозначения:
az W = llaz/ WILxi-стРока матрицы Z;
az (/) = ||ап(/)||1Хл —/-й столбец матрицы L;
£>аа$ (^2 ^1)--^ll«Z (^1) а^2)||лХп-
п
2 Cik,kj
Л-1
S (t2
лХл
матрица, зависящая от взаимных интенсивностей случайных па-
раметров;
Dar8(/-/1) = ZW ||az г (/)||1ХЛ=
Уф (^) Cij^ v & (/ ^1)
м-1 1ХЛ
— вектор-столбец, зависящий от взаимных интенсивностей век-
тора воздействия и случайных параметров.
4*
99
Теперь система (2.14) может быть записана в матричной
форме
+ (2.15)
В отсутствие случайных параметров математическое ожидание
вектора состояния определяется следующим уравнением:
^-=N (2.16)
at
Из сравнения уравнений (2.15) и (2.16) следует, что слу-
чайные изменения параметров динамической системы оказыва-
ют влияние на величину регулярной составляющей вектора со-
стояния, т. е. вносят регулярные погрешности в работу системы.
Величина этих погрешностей определяется интенсивностями
процессов, характеризующих изменения параметров, и степенью
коррелированности этих процессов с компонентами вектора воз-
действий r(t).
Выходной сигнал системы содержит регулярную составляю-
щую, зависящую от Dar даже в том 'случае, когда отсутствует
математическое ожидание входного сигнала, т. е. mr(7)=0.
Систему, эквивалентную исходной динамической системе в
смысле преобразования регулярной составляющей, можно запи-
сать в следующей форме:
-^ = АГ8(/)н+£7(/)/пИа (2.17)
где
N9 (/) = N (/) + -±- тгэ (/) = тг (/) + U~* (/) D„ (/).
Видно, что наличие случайных параметров изменяет коэф-
фициенты эквивалентной системы по сравнению с коэффициен-
тами исходной. Кроме того, коррелированность 'между случай-
ными параметрами и аддитивными внешними воздействиями
приводит к появлению ложных детерминированных составляю-
щих на входе системы
Гложи(^)=4-г/"1(С^аг(/)-.
Если обозначить матрицу вторых моментов
6=М [л, л1] = II - Но.. .4,-1...0 II
100
и в уравнениях (2.13) положить 6 = 2, получим систему диффе-
ренциальных уравнений для вычисления статистических момен- ,
тов второго порядка
Csj,jPlp W Csjd +
4" 2 4"^sz Ю cp*,zPv +
v,Z—l
+ p, s=l, n, (2.18)
Система '(2. 18) содержит n2 дифференциальных уравнений
для определения элементов матрицы вторых статистических мо-
ментов. Поскольку матрица 0 симметрична, порядок системы
(2.18) может быть понижен до (L^Lzhll.
Обозначим
nxi $-ю строку матрицы U (/);
Dr^ 8 (/,—f)—М || Ui (/) г {f) aj (/z) p> (^)||лхл —
п
Ъ/-1
nxn & (A—
DaeaB (/,-/) =M ||az (/) 6 (/) a)
n
ji ®vZ
v,Z—l
^лХл (A ^)*
Запишем систему (2.18) в матричной форме
ё = ЛГе-[-9ЛГт -^[jCrUT-]-UmY^mrTUT +
+-L (D„0 + D„pT + 9DL+pDrar) + Da0a + Drra + D,Te(l. (2. 19)
Принимая во внимание, что
0=2 4“WJ'T; в=4~p,p,t+
где 2=— Р)(хТ~11,1)]лхл —матрица дисперсий, для
можно записать следующее матричное уравнение:
+^4-^+^; (2.20)
здесь обозначено Da(l8(f —/1)=Af||az(/)p.|ATa}(Z1)||„xn.
101
Если в системе отсутствуют случайные параметры, то
2= ^2+2 NT+UCrU\ ' (2.21)
Сравнивая уравнения (2.20) и (2.21), приходим к выводу,
что при определенных статистических характеристиках r(t) и
L(t) влияние случайных изменений параметров на уровень дис-
персии выходных координат динамической -системы может быть
весьма-существенным.
Частным случаем рассматриваемых систем являются дина-
мические системы, процессы в которых описываются линейными
дифференциальными уравнениями п-го порядка
+ К (')+Дп W] + • • + (/) + Д2 (/)] ^ +
til III Cl I
+ [а1(/) + Д1(/)]х = /(/), (2.22),
где ai(t) — детерминированные функции времени; АДО — про-
цессы типа белого шума, характеризующие случайные измене-
ния параметров; f(t) — возмущающее воздействие, представ-
ляющее собой сумму детерминированной и случайной
/*(/) (типа белого шума) составляющих:
f^ = mf (/) + /*(/).
Уравнению (2.22) соответствует система уравнений первого
порядка следующего.вида:
y = Ny-\-Ly+Ur, (2.23)
причем в данном 'случае
= 0
У1 =
У =
/=1, га—1
L =
Z=l, га Ц1ХЛ
rn=f(t)
IXn
az/=0
z=l, га— 1
raZy=0 z = l, га—1
га,-, , = 1
N =
i = 1, га — 1
anj------Д/
nXn
j= 1. га
102
Согласно выражениям (2.11) коэффициенты уравнения Фок-
кера — Планка — Колмогорова для 'системы (2.23) имеют вид
Л=^+1. /=1, 1;
— X? а)У} Н-------У1спп,п1-----------Слл.л + /П/;
7=1
Ду=0, Z=l, га — 1, I, /=1, га; (2.24)
Д.л = 2 УкУ1Сп1,.П1 + 2 УцСп^Л Сп.п-
Л,1—1 Ы
Для статистических моментов имеет место система дифференци-
альных уравнений
п
— Нм....*я=.2 & (P'M1...(»V-I)...(ft,+1+I)...»n —
1-1
п
— (4,^...(*,-!)...(*„+!) + (a, — Спп,П^ X
4
X НМ,...(Ч-1)...(^+1)..Ля + (-^^л.л —Нм!..1 5л} +
+ *л (*л-1)
1 ..к~2 I
— СллР*1й»...(*л-2>‘т
,* _ „ft-1
k*,*« • • .(*/+!)• • (fty+1). • (*n-2) ^•,Л11Л1й2...(Л/ + 1)...(Лл-2)
l-l
(2. 25)
В частности, математические ожидания и вторые статисти-
ческие моменты являются (решениями следующих уравнений:
Hz=i*z+i. /=1> «-1;
п
V-n = - 2 («у - уХл,л/) И/ спп,п + mf;
= 7=L я — 1;
п
+ ®л.;+1>
/=1, га— 1;
ЮЗ
п п
2 + + 2 Cnk^kfikl- (2- 26)
Z-l k,l-l
Система (2.26) представляет собой систему обыкновенных
дифференциальных уравнений с переменными в общем случае
коэффициентами. Решение системы может быть осуществлено
обычными методами.
Учитывая, что
уравнения, описывающие поведение математического ожидания»
можно привести к виду
-j^n + enn,nnJ ^п—1 1 Спп,п(п—1)^Х
j/i—2 Г 1 1 1
+ -— сял>Л1] —-с„п>п. (2.27)
Отсюда следует, что на поведение математического ожидания
выходной координаты рассматриваемой системы со случайны-
ми параметрами существенно влияет ’случайная составляющая
коэффициента при (и—1)-й производной/ Наличие ап(0 и ее
коррелированность со «случайными составляющими других пара-
метров изменяет коэффициенты эквивалентного уравнения
(2.27) для математического ожидания по сравнению со средни-
ми значениями коэффициентов исходного уравнения (2.22).
Коррелированность ап(0 с внешним воздействием приводит
к появлению ложных детерминированных составляющих на
1 .
входе системы mf ложн= —— спп>п, что обуславливает дополни-
тельные регулярные ошибки, характерные для систем со слу-
чайными параметрами.
Пример. В качестве примера рассмотрим задачу вычисления математи-
ческого ожидания и дисперсии процесса на выходе системы, описываемой
дифференциальным уравнением второго порядка со случайным коэффициентом
демпфирования
х 4- [а2 4- Д2 (0] х 4- ахх = /.
Пусть f = mf 4- /*; mf = 0; М [/* (Zj) /♦ (z?2)] = с22Ъ (t2 - 6);
M [Д2 (0] = 0; М [ Д2 (6) Д2 (/2)] = с22>22 Ь (t2 - 6);
Л1[Д2 (/!)/* (/2)] = с22>2В (^2 — ^1).
104
На основании уравнения (2.27) для среднего значения выходной коорди
паты имеем
.. / 1 „ \ . 1 „
+ ( а2 “ ~ С22,22 1 р-1 + Л1М-1 = — ~с22,2-
Если система стационарна (ai = const и a2=const) и устойчива,
t-+<x> производные асимптотически будут стремиться к нулю,
то при
случаи-
системы
Вследствие этого в установившемся режиме получим
<?22,2
Таким образом, если аддитивное воздействие f(t) коррелирован© со
ной составляющей коэффициента демпфирования, среднее положение
не совпадает с ее положением равновесия, несмотря на 'io, что воздействие
f(t) центрировано, т. е. не имеет регулярных составляющих.
Для вторых и смешанных вторых моментов процесса и его производной
согласно системе (2.27) имеем следующие дифференциальные уравнения:
0ц = 202Г»
' 1 \ о 1
&2 — ~ ^22,22 I 021 — С22,2^Г,
021 = 622 —
622 = — 2 Л1О21 — 2 ^2 — ^22,22 j ^22^22,2^2 4“ с2,2 4" ^22,22®22 — 2С22,2Н2 =
= С2,2 — 2 (Л1021 + ^2^22) 4" 3 (^22,22®22 — ^22,2^2)-
Если система стационарна, то в установившемся режиме производные по
времени можно приравнять нулю. Учитывая, что в этом случае
Н1 =
^22,2
2^!
р.2 = О,
находим
д С22
”22 =
. п Л А 022 2
2а2 — Зс22122 ’^21 = °’ 91, =
Из последних выражений видно, что случайные изменения коэффициента
демпфирования увеличивают уровень флюктуаций на выходе системы.
2.5. АНАЛИЗ СТОХАСТИЧЕСКОЙ СИСТЕМЫ
ПЕРВОГО ПОРЯДКА
Из результатов предыдущего раздела следует, что в общем
случае, когда параметры системы ’возбуждаются процессами,
которые по спектральным характеристикам отличны от белых
шумов, исследование систем представляет -собой нелинейную
задачу, не имеющую точного решения. Такое решение может
быть получено лишь для систем .первого порядка.
Рассмотрим простейшую параметрическую систему, которая
описывается линейным дифференциальным уравнением первого
порядка вида
х + а (/) х = g (/), (2.28)
105
где a(t) и g(t) — стационарные гауссовы случайные процессы;
в дальнейшем будем предполагать их коррелированными-с из-
вестными статистическими характеристиками
М {a(/)} = /nx; М {g(/)) = m2;
Af{[a(/) — mJ [а(/+т) —/п1))=7?«а(т);
Ж ([а(/) — /пх] [g (t-j-т) — mJ] =#ag(т);
M {[g lg(/ + r)-/n2))=/??ff(T).
При начальных условиях x = 0, / = 0 решение уравнения
(2.28) имеет вид
t
х (/) = J g(tf) exp {— z (u, /)} du, (2. 29)
где
t
z(u,t) = ^ a (r) dx. (2.30)
Так как процесс а(т) является гауссовым, то процесс z(t) так-
же гауссов. Причем
М {z (u, f)) = m1(/ — и);
02(a, f)=M [[z (и, t)— m^t — a)]2) = J J/?««(Tx — r2) dxxdx2.
a и
Используя выражение (2.29), вычислим математическое ожи-
дание и корреляционную функцию процесса x(t). Имеем
t
Af {х (/)} = J [g(tf)exp[ — z(u, /)} du.
Подынтегральное выражение может быть представлено • в сле-
дующем виде:
М {g(a)exp[ — z(u, /)]}= J j gexp{— z] f2(g, z)dgdz, (2.32)
' —oo —oo
где /г(^ — двумерная функция распределения гауссовых
случайных процессов.
106
Для вычисления интеграла (2.32) воспользуемся известным
разложением двумерной нормальной функции распределения в
ряд по многочленам Чебышева — Эрмита [4]
A (£. *)= —— ехр [ —у- (g°2 + z°2)l X
оо
ХУ(2.33)
Л=0
где
go = £z2^; 2o = £^k; Qgz==M (2.34)
Qg QZ
Нп(х) — полином Чебышева — Эрмита Айго порядка.
Взаимный корреляционный момент Qgz легко получить
q^(«. = —Л1(к(/)-т2]Х
к agQz agaz
t t
X a (T) ^T) = —— R*gtf — T) ^T- (2- 35)
J J
U V
После подстановки разложения (2.33) в (2.32) можем написать
ОО h ОО 00
М {g(a) ехр [-z(ц, /)]) = —5— V\ Hk(z°)X
ft=O —oo—oo
X^exp {—г|exp { —i- (g°2 + z°2)| dgdz.
В последнем выражении двойной интеграл распадается на
произведение одинарных. Принимая во внимание (2.34), полу-
чим
оо й Г 00
М {g(a)exp[-z(a, вД ^л(^)Х
2Л R\ J
Л-0 L -оо
X ехр
ОС
х //Л(г°)ехр| — у- (z°24-2azz° + 2mj| dzP.
ОО—
107
В аилу ортогональности многочленов Чебышева — Эрмита пер-
вый интеграл в квадратных скобках равен нулю для всех зна-
чений Л=/=1; второй — для всех ^#=0. Поэтому
оо
М {g (а) ехр[ - z(«, /))} =^gQgz (z°) exp {- тг X
—oo
oo
xexp {—г (2°+°*)2}dz"+5exp {“ т*°*} X
—oo
Xexp{-----^(2° + oz)2}^20-
Используя формулу
oo
j /7(z) exp { - -i- (z -1/)2j dz = yk, (2.36)
—oo
находим
M (Л (/)] = J [tn2-<3gaz (u, t) Qgz (U, Z)X
X exp | — mx (t — и) -]—a2 (a, /)j du. (2.37)
Полученное выражение указывает на появление дополни-
тельных регулярных ошибок в системе, вызванных коррелиро-
ванностью входного воздействия g(i) и случайной составляю-
щей параметра a(t).
Корреляционная функция x(t) равна
Rit^ Q=M {x(/x)}Af {л(/х)).
Согласно выражению (2.29) можем написать
/, t,
М {x(/x)x(/x)|=J j М {g(rx)g(T2)exp[-z (тх,/х)-
— z(t2, /2)1) dtjdr^.
Математическое ожидание подынтегральной функции вычис-
лим с помощью четырехмерной нормальной плотности вероят-
ности
М (£(т1)g(*2)exp [-z (тх, /х)-z (т2, /2)]} =
= J j j j «Ха2ехр{ —и3—a4}/(«х, u2, иг, a4) tZ«x<Zu2 tZ«s da4,
— OO —00 —oo —oo
(2.38)
где
«i=g(*i); »2=gW; «з=г(тз> ^i); «4=z(t2, q.
108
Четырехмерная нормальная плотность вероятности имеет
следующее разложение ото многочленам Чебышева — Эрмита [4]:
г , \ 1 ( 1 / О* I 02 I 02 I \ х
/ («1, я2, а3, и4) = —-------------ехр —— («1 +«2 4-Яз +^4) X
47Wia2°304 I * J
% 1 Q12Q13Q14Q23Q24Q34
k\! k2 ! #3 !.. . Л4 !
Л4,Л3,... ,Л
Hk,+ka+k,
(2.39)
X («?) !+Л4+Л5 («§) нка + Л4 + Лв (#з) ^Л3+Л5 + Лв (#4)-
После подстановки разложения (2.39) в (2.38) четырехкрат-
ный интеграл распадается на (произведение однократных, кото-
рые легко вычисляются благодаря ортогональности многочле-
нов Чебышева — Эрмита.
Окончательное выражение для корреляционной функции про-
цесса x(t) имеет вид
R Q — f J {ow(Ti - т2) +og2 (0) [6gz (т2- tx)+
6 о
+егг (°)1 +egz (Ti - т2) [егг (*2 - ь) +egz (0)1} X
X ехр | (/х, тх) — mA exp {у-(/2, т2) — mA X
тх ~~ т2) dx^dx^
(2. 40)
Л-1
где/?«(т) — корреляционная функция процесса z(t).
Аналогичным образом, используя разложения многомерных
плотностей вероятности, можно вычислить статистический мо-
мент x(t) любого порядка.
Однако связанные с этим выкладки и конечные формулы
оказываются громоздкими и здесь не приводятся.
В заключение рассмотрим частный случай уравнения (2.28)
при g(t) =0 и начальных условиях х=х0, /о = О
^ + а(/)х=0. (2.41)
Решение уравнения (2.41) имеет вид
х=хоехр ( — mJ — z(t)}\ (2.42)
где
z(/) = Jа(т)t/т; a(t)—a(t} — mv
о
109
Откуда находим
M{z(t)}=0;
t t
£(t)=M {z2(/)| = j j M (ci (Тл)а(т2)} dXydx^.
Процесс ct(/) является стационарным, следовательно,
Af { Ct (Ti) Ct (T2)} == ^?aa (^i ^2)*
Выразим корреляционную функцию через спектральную
плотность
/?«« (т) = 2 J Saa (ш) cos vsxdw.
О
В результате получим
оо t t
a|(/)=2 J j* J 5aa(a))C0Sa)(T1 —T2)rfT1rfT2rf(o.
обо
Произведя интегрирование, находим
£ (/) = 2 J Saa (ш) [1 — cos ш/j <0-2</a>. (2.43)
0
Для моментов решения имеем следующее выражение:
М {х^} = J (хр (z) f^z) dz.
—00
где функция плотности вероятности /(z) задается формулой
Лм“-й^ехр (2-44)
На основании (2.42) и (2.44) получим
м = rka, J *оехр|-/> [/n^z] \dz —
— ОО '
=хр0 ехр | — р (mJ — -j- J • (2.45)
Формула (2.45) позволяет вычислить статистический момент
любого порядка.
В частном случае, когда процесс a(t) — белый шум, вычис-
ление по формуле (2.43) дает
где с2 — уровень спектральной плотности шума.
по
Выражение (2.45) принимает вид
7И {лт>} = xS exp | — pt —i- pc2)} . (2.46)
Этот результат совпадает с (полученным ранее в работе [8]. Из
формулы (2.46) следует, что каков бы ни был уровень случай-
ного процесса а(/) статистические моменты реакции системы
(2.41) порядка/? 'будут возрастающими функциями вре-
с2
мени.
2.6. АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ
СО СТОХАСТИЧЕСКОЙ ЛИНЕЙНОЙ ЧАСТЬЮ
Задача анализа динамической точности систем автоматиче-
ского управления часто приводит к необходимости исследования
нелинейных (систем со случайными параметрами, при этом слу-
чайными 'свойствами могут обладать параметры как линейных,
так и нелинейных элементов системы.
Рассмотрим нелинейную систему, динамика которой описы-
вается следующим уравнением:
Zx+F(x)=g, (2.47)
где L — линейный дифференциальный оператор; F(x) — нели-
нейная функция; g=g(t) — случайный процесс.
Пусть оператор L имеет вид
Lx=an(t) *2Zk+...+ao(/)x, (2.48)
dt dt*-1
причем an(t), ao(O —случайные функции.
Для простоты изложения рассмотрим частный 'случай опе-
ратора L, а именно, положим an(t) =an=const,
ал__х (/)=ал_1=const,..., a1(t)=a1=const, а0(/)=а0+ <*(/).
Здесь a0=ioonst, a a(t) — стационарный центрированный слу-
чайный процесс с нормальным распределением. Тогда
Lx=an ^—г+ап-1 ——- + ...+<м + ал=£ х4-ах.
dtn. dt"-1
Ha рис. 2.8 представлена структурная схема системы, опи-
сываемой в рассматриваемом случае уравнением (2.47).
Здесь k{x) и Н(р) являются импульсной переходной и пе-
редаточной функциями, соответствующими оператору L*.
К такой схеме приводится, например, схема датчиков уско-
рений в условиях кососимметричных вибраций с учетом ограни-
чения хода чувствительного элемента и упругого отскока от
упоров.
Ill
Трудности, возникающие при анализе нелинейных систем
вообще, обусловлены искажениями законов распределения, ко-
торые являются следствием нелинейных преобразований. Одна-
ко при прохождении через линейные звенья процесс нормализу-
ется, так что закон распределения процесса на выходе линей-
ного звена всегда ближе к нормальному, чем на его входе.
Причем эффект нормализации тем значительнее, чем инерцион-
нее линейное звено. Поэтому в ряде случаев, встречающихся на
практике, можно предположить, что закон распределения вход-
ных сигналов нелинейных преобразований близок к нормаль-
ному.
Рис. 2.8. Структурная схема нелинейной системы
со стохастической линейной частью
На основе предположения о нормальности закона распреде-
ления можно осуществить приближенный анализ рассматривае-
мой нелинейной системы со случайными параметрами.
Пусть
где mg=const, a gQ(t) — центрированный нормальный случай-
ный процесс.
Согласно структурной схеме (см. рис. 2.8) для реакции сис-
темы имеем выражение
X (/) = J k (о) [g (/ — а) — U (t — — а (/ — а) X (t — о)] rfs. (2. 49)
о
Далее для каждого из звеньев цепи составим уравнения»
связывающие статистические характеристики выходных сигна-
лов с соответствующими характеристиками входов.
Измерительный элемент производит сравнение входного сиг-
нала -системы с сигналами цепей обратной связи
112
Уравнение для спектральной плотности ошибки имеет вид
S" (<»)—(“») 4-Sn (0)) (<о) — SgT (<о) — STg (u>) — SUg (<i>) —
^gu (ш)—Siu (“)—(o)=Sgg (ш) + $Tt (ш) + $ии С10)—
- 2 Re (ш)+SugH+SU7 « (2.50)
Корреляционная функция на выходе блока умножения бу-
дет иметь вид
R-n (*)=Y(OyO!+*) =a(t)x (/) а (/ -j-т) х (*+*).
Центрируя процессы и пренебрегая моментами нечетного поряд-
ка, находим
Атт (т) = tnx (?) + Rxa (x)R ах (?)+RM (?) RXx (?),
откуда, переходя к спектральным плотностям, 'получим
»$П (со) = ГЛх^аа (w) Н- ~\ $ха (v) Sax (<О—v) dv -|-
ч 2л •)
—оо
оо
4~ \ 5.e(v)Sxx(<o-v)i/v. (2.51)
2Л J
—оо
Выражение (2.51) содержит взаимную спектральную плот-
ность Зя» (о). Для ее получения воспользуемся интегральным
соотношением <
Rx<z (г)=х(/)а(*-|-?),
яли 7J
Rx<i(t'j—^ k(a) [g(/ — a)— u(t — а) — а(/ — а)х(/ — а)] а(/-|-Т)_//а =
=J k (а) [/??e (Т + а) — RM (t + а) — mxRM (Т + а)] da.
Возьмем преобразование Фурье от обеих частей равенства
Зха (ш) = Н ( — /'«>) [3g« (u>) — Зцо(<») — ТПxSaa (<*>)] • (2. 52)
Аналогично получим
' 3jrr(«>)=/Z(-/«>)[S„(a>)-Sv(tt>)-/nxSag(<o)]. (2.53)
Взаимные спектральные плотности Sua (со) и Sug(w) будут вы-
числены при рассмотрении нелинейного элемента.
113
Для взаимной корреляционной функции входного воздейст-
вия процессов на выходе блока умножения имеем
Rig (*)=Y (О g° (t + т)=а Ю х (/) g° (t+т) = mxRag (т).
Выражение длй спектральной плотности имеет вид
(2. 54)
Процесс на выходе нелинейного преобразования может быть
представлен ортогональным рядом
(2.55)
Для корреляционной функции выходного процесса имеем
выражение
^вв(т)=2Л!а*е^т)- (2.56)
fe=l
Используя понятие эквивалентной передаточной функции, вы-
ражение для спектральной плотности можно представить в виде
SUU (“>) = k3 О) k3 ( — /<°) SXX (<°)- (2- 57)
Эквивалентная передаточная функция &э(/(о) определяется сле-
дующим образом:
оо
ks О) k3 (~ k! a^bk
где
bk (a)) = o(i) , у » S^XX (w) = Qxx (t).
Функция &э(/(о) зависит как от вида нелинейности,.так и от
статистических характеристик входного процесса. Факт нали-
чия этих зависимостей отражает существенно нелинейные осо-
бенности преобразования.
Теперь вычислим взаимную спектральную плотность Sug(co).
По определению имеем
#ugW=«W£r0(z + *)-
Переходя к осреднению по совокупности, получим
W = J J F 0Pi(x, g) dx dg, (2.58)
— 00 —00
где Pi(x, g) — совместная плотность вероятности процессов
х(0 и g(t).
114
Для вычисления интеграла (2.58) воспользуемся разложени-
ем для нормальной плотности вероятности и ортогональным
представлением (2.55). Подставив в (2.58) вместо F(x) и
Р2(х, g) их разложения и интегрируя, находим
Rug (*) = WgQxg (*) = Rxg W-
х. °-*’
Уравнение для спектральной плотности имеет вид
(“>)=—^(“>)- (2.59)
°х
Аналогичным способом может быть получена взаимная
спектральная плотность Sua(co). Окончательные выражения бу-
дут
ах
(2.60)
•£»« (<*>) =—— 5xa(w).
°х
Подстановка формул (2.59) и (2.60) в (2.52) и (2.53) дает
^-Н
Saa (<о) =----------- [Sg-a (a>) — тх Sax (u>)] J (2.61)
°x
(—»
Sug W = ——-----------(<°)—(2. 62)
1+—//(-»
Остается вычислить взаимную спектральную плотность процес-
сов на выходе нелинейного звена и блока умножения. Для это-
го воспользуемся выражением для взаимной корреляционной
функции
/?ит (т) = н° (/)у(/ + т) = тxRua (т) + н(/)л°(/ + т)а(/ + т).
Момент третьего порядка в последнем выражении определяется
следующим образом
и (/) х° (t -[-г) a (t -(-г) =
00
= J J J F (хх) (ха — тх) ара (лгх, х2, a) dx1 dxzda. (2.63)
—oo
Здесь *i = x(0; Х2=х(/+т); рз(х > а) — трехмерная совме-
стная плотность вероятности.
115
Разложение трехмерной нормальной плотности вероятности
по полиномам Чебышева — Эрмита согласно [4] имеет вид
Рз (•*!’ ^2» ^з)
' х3— т3 \21'| % Л Q12Q23Q13
’з / JJ jZj И mini
I, т, л=0
1 руп (___________________L 17 *1—V I / -У2—т2\г
(2 л)3/2 О1а2азеХР I 2 К 01 /"Ц о2 )
(2. 64)
где Qu — коэффициент взаимной корреляции между Xi и х,.
Воспользуемся этим разложением для вычисления интегра-
ла (2.63). Подставляя в подынтегральное выражение (2.55) и
(2.64) и переходя к почленному интегрированию, получим
( 1 ( Х<1— тх \2) ,
X ехр | -----—j j ахг.
Последнее выражение в силу ортогональности полиномов Че-
бышева — Эрмита отлично от нуля в том случае, если выпол-
няются следующие условия:
/Ц-л=А, 1-\-т=19 т-\-п = 1.
Находим значения переменных суммирования, при которых
интегралы не равны нулю,
a) k=2; 1=п = 1; пг=0;
б) k=0; 1=п=0; т = \.
Окончательно получим
Rm (*) = mxRua (т) + 2а^^хх (т) (т)
ИЛИ
/?ит (т) = mxRuet (т)+Rxx (г) Rxa (т). (2.65>
116
Для определения спектральной плотности применим к выра-
жению (2.65) преобразование Фурье:
оо
SaT (<1>)=тх8ил (о>)+'i Sxx (v) Sxa (o> — v) dv. (2.66)
Ла* J
—oo
Соотношение между спектральными плотностями ’Процессов
на входе и выходе линейного стационарного звена имеет вид
Sxx («,) = Н (/<0) И (- /Ш) 5.. (ш). (2. 67).
Выражения (2.50) 4- (2.52), (2.57), (2.61), (2.62), (2.66) и
(2.67) определяют связь между спектрами входных и выходных
сигналов отдельных элементов системы. Объединяя их между
собой, получим (интегральное уравнение для спектральной плот-
ности процесса на выходе системы
Sxx («>)=-------Я (/<>)//(-/<*)-------
1+*э(Л)М-/®)Я(/»)Я(->) ееК
---------х
х 2л J си
-оо1 + — Н (—jv) 1+—
ах °х
X [Sg-a (v) — (v)] (w — v) — MjcS™ (® — v)] dv +
— H
+2m x Re Sag (a>) — 2Re ——-------------------[S (<*>) — mxSga (w) —
1 + -J- H (- »
a\
— mxH (— y<o)
- 2Re M - m xSaa («>)] +
1 + —Я(-/ш)
+-M $xx(v) «Mco-vJ-^Re
^Л J о'jp
ffUv-M
\+ — H (Jv— Jto)
X [Sga(oj —v) —mx5aa(<U —v)]}rfv),
или короче
S„(«)=---------------------------
!-*.<>)«• <-/»>« (» « (-/“>
w — v, <зх, mx)dv , (2.68)
117
лде А и В — функции, зависящие от заданных ‘статистических
характеристик воздействий и от неизвестных характеристик вы-
ходного процесса.
Таким образом, для спектральной (плотности сигнала на вы-
ходе нелинейной системы с параметрически возмущенной ли-
нейной частью имеем интегральное уравнение типа (2.68). Ре-
шение этого уравнения осложняется тем, что функции А и В
зависят от вида искомой спектральной плотности. Перейдем к
вычислению среднего значения выходного сигнала. Для этого
произведем осреднение выражения (2.49)
tnx=°^k (т) [mg—mu — ^xa\dx. (2.69)
О
Согласно (2.55) для математического ожидания процесса на
выходе нелинейного преобразования имеем
mu=aQ.
Взаимная дисперсия может быть получена интегрированием
соответствующей спектральной плотности (см. формулу (2.52)).
Уравнения (2.68) и (2.69) позволяют определить статистиче-
ские характеристики сигнала на выходе нелинейной стохастиче-
ской системы. Решать эти уравнения следует совместно, так как
спектральная плотность зависит от математического ожидания
и наоборот. Наиболее разумным способом решения является
метод последовательных приближений. При этом для получе-
ния нулевого приближения можно положить а(/) =0.
Анализ уравнений (2.68) и (2.69) позволяет сделать некото-
рые качественные выводы о поведении рассматриваемой систе-
мы. Как видно, среднее значение сигнала на выходе системы
определяется не только величиной управляющего сигнала и ре-
гулярной составляющей входа нелинейного преобразования, но
и степенью корреляций между случайным параметрическим
возбуждением и выходным процессом. Наличие этой корреля-
ции приводит к появлению дополнительных установившихся
ошибок на выходе системы.
Анализ уравнения (2.68) показывает, что спектральные свой-
ства выходного сигнала в основном определяются спектраль-
ными свойствами стационарной части системы. Однако’наличие
случайного коэффициента и нелинейности приводит к значи-
тельному росту уровня флюктуационных ошибок системы.
2.7. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ
СО СЛУЧАЙНЫМИ ПАРАМЕТРАМИ
Как отмечалось в разд. 2.1, анализ динамической точности
систем наведения часто представляет собой задачу исследова-
ния замкнутых структур, включающих в себя нелинейные бло-
ки со случайными свойствами. В качестве примера рассматри-
Л18
вался процесс деформации статических характеристик сервоме-
ханизмов в зависимости от изменений моментов нагрузки.
Если нагрузочный момент изменяется во времени случай-
ным образом, то и изменения параметров нелинейной зависи-
мости скорости сервомотора от управляющего сигнала (зона на-
сыщения, зона нечувствительности, наклон линейного участка
и т. д.) будут характеризоваться случайными процессами. При-
чем в первом случае (см. рис. 2.5) нерегулярный характер на-
грузки обуславливает случайную деформацию нелинейной зави-
симости между управляющим сигналов и скоростью сервомото-
ра вдоль оси ординат. Такое преобразование можно описать
следующим уравнением:
i/(/)=a(/)F[x(/)]. (2.70),
Здесь F(x) — детерминированная нелинейная функция, со-
ответствующая статической характеристике сервомотора при
фиксированном ’значении нагрузки, а а(/) — случайный про-
цесс, отражающий случайный характер изменения нагрузки.
Простейшим преобразованием такого вида является усили-
тельное звено со случайным коэффициентом усиления. К числу
подобных преобразований могут быть также отнесены преобра-
зования, осуществляемые нелинейными элементами релейного
типа со 'случайным уровнем выходного сигнала, типа ограниче-
ния со случайным наклоном линейной зоны и случайным уров-
нем ограничения и другие.
Поле характеристик на рис. 2.6 порождается случайной де-
формацией нелинейной зависимости вдоль оси абсцисс. При
этом уравнение, описывающее преобразование, имеет вид
y(t}=F[a(t)x{t)\. (2.71}
К таким нелинейностям могут быть отнесены, например, эле-
менты со случайной зоной нечувствительности, нелинейности
типа ограничения со случайной линейной зоной. Наконец, в наи-
более общем случае (см. рис. 2.7) случайный характер нелиней-
ного преобразования проявляется в деформации статической
характеристики как вдоль оси абсцисс, так и вдоль оси ординат.
При этом преобразованию соответствует уравнение вида
!/W=a1(/f)F[a2(Z)A:(/)]. (2.72);
Нелинейные преобразования, характеристики которых являются
случайными функциями времени, в дальнейшем будем называть-
стохастическими нелинейностями.
При анализе систем автоматического управления, содержа-
щих стохастические нелинейности, исследователь сталкивается
с трудностями, которые неизбежно возникают при статистиче-
ском анализе замкнутых нелинейных систем. Основная труд-
ность обусловлена невозможностью заранее предсказать харак-
тер законов распределения координат системы.
11»
Существующие методы исследования нелинейных -систем ли-
бо очень громоздки, либо являются приближенными, основан-
ными на предположении о том, что закон распределения сигна-
ла на входе нелинейного преобразования близок к нормаль-
ному. Это предположение оправдывается эффектом нормализа-
ции при прохождении сигнала через линейную часть системы.
Подобное же предположение может быть положено в основу
наследования замкнутых динамических систем, содержащих
стохастические нелинейности.
Из изложенного следует, что. стохастические нелинейности
представляют собой многомерные нелинейные преобразования.
Поэтому ниже будут рассмотрены общие вопросы, связанные с
нелинейным преобразованием векторных случайных сигналов.
Пусть нелинейное преобразование имеет вид
y(f) = f ]г(0], (2.73)
где f — нелинейная функция; r(t) — векторная случайная функ-
ция;
r(f) = ||Xi(/), х2 х„(/)||.
Аппроксимируем преобразование (2.73) его разложением по
многомерным ортогональным многочленам. Выбор той или иной
системы ортогональных многочленов во многом зависит от за-
кона распределения, которому подчиняются входные сигналы.
В частности, если закон распределения вектора r(t) — нормаль-
ный, то для аппроксимации выходного сигнала наиболее рацио-
нально использовать систему многомерных полиномов Эрмита.
Многочлены Эрмита от многих переменных являются обобще-
нием классических многочленов Эрмита одного переменного и
определяются следующим образом [5].
Пусть С — фиксированная положительно определенная мат-
рица с вещественными элементами. С матрицей С связана по-
ложительно определенная квадратичная форма
<р(г) = (Сг, г) = 2 cijXiXj
i,i-i
и взаимная форма
ф(г)=ср(С-1г) = (С-1г, г),
где r= (xi, х2, ..., хп) — вещественный вектор.
Определим две системы многочленов
= Х2, . . . , Хл);
Х2, . . . , Хл)
120
с помощью (производящих функций
ехр (Са, г) - 4- <₽ (а) = V -2- ... Нт (г);
L 2 j Ш\ I тпп I
ехр [(а, г)—1_ф(а)] = Оот(г). .(2.74)
L J т11 mni
Используя разложение Тейлора и (приравнивая коэффициен-
ты при а"*' ... а™Л, получим формулы
W,(r)-(-l)"exp[4-T(r)] ix.,d" дх.п ехр[-4- , (г)]; _
Г 1 1 дт Г 1 1
Gm(C-1r) = (-l)mexp -U(r) ---т-^- ехр [—1- ф(г)1.
|_ 2 J OXj 1 . . . ОХ пп 2 J
Выражения (2.74) или (2.75) определяют многочлены Эрми-
та от многих переменных. При п=1 и Сц = 2 получим классиче-
ские полиномы Эрмита.
Наиболее важным свойством многочленов Эрмита является
свойство биортогональности
J Ge (г) Нт (г)«) (г) dx=blimi... I... т„I (2.76)
и ортогональности многочленов различных порядков
Gm(r)u>(r)rfx=0,
Ht(r) Hm(r)w(r)dx=0 при тф1, (2.77)
где и (г) —весовая функция, определяемая формулой
1 п
(0('') = |С|2 (2л) 2 ехр[-^р],
причем
J 0>(r)tZx= 1.
Произвольная функция /(xi, ..., хп) имеет следующие раз-
ложения по многочленам Эрмита:
(2 78)
Ш=^ЬтНт(г).
При этом
mJ.-./nJ ат=[^(r)f(r)Hm(r)dx;
/nj.../п,! &m = j<i>(r)/(r)Gm(r)rfx.
121
В дальнейшем разложения вида (2.78) будем называть орто-
гональными.
В качестве весовой функции разложения следует использо-
вать закон распределения случайного вектора г(/). В этом слу
чае свойство биортогональности (2.76) будет отражать факт
статистической независимости процессов
= И gmf) = Gm [Г (/)].
Последнее обстоятельство значительно упрощает процедуру
вычисления статистических характеристик процесса на выходе
преобразования.
Проиллюстрируем сказанное на примере вычисления корре-
ляционной функции
Ry (/1( Q = M {у (/,) у (/2)) =М {fir (/,)] / [г (/,)]) =
= И f (^i) / (гг) Pi Г2) drYdr^
где Р2(Л, г2) — совместный закон распределения векторов
ri = r(/i) и r2—r(t2).
Пусть нелинейное преобразование разложено ,в ряд по мно-
гочленам Gm(r)
/(r)=2flA(r). (2.80)
Закон распределения p2(rlt г2) имеет формальное разложе-
ние по многочленам Нт(г)
/!)=«>(г1)«>(г!)2сй//4(г1)Я/(г!). (2.81)
Это разложение представляет собой обобщение на многомер-
ный случай известного разложения Крамера. После подстанов-
ки рядов (2.80) и (2.81) интеграл распадается на сумму сла-
гаемых следующего вида:
amancki j °т (Г1) nk (rx) «) (г J drY J Gn (r2) Hl (r2) <0 (r2) dr2.
Вычисление интегралов, входящих в эти слагаемые, в силу
свойства биортогональности не представляет труда.
Другое не менее важное свойство ортогональных разложе-
ний с законом распределения в качестве весовой функции сос-
тоит в том, что коэффициенты аппроксимации ат или Ьт явля-
ются определенными статистическими мерами процессов. Их ве-
личины зависят как от вида нелинейного преобразования, так
и от статистических характеристик вектора входных процессов.
Таким образом, аппроксимирующее преобразование строится с
учетом статистики входных сигналов, что позволяет использо-
вать понятие средней квадратичной аппроксимации. Это озна-
122
чает, что выход нелинейного преобразования может быть с лю-
бой степенью точности аппроксимирован конечной суммой ряда.
Возможность подобной аппроксимации представляется сле-
дующей теоремой: для всякой измеримой функции f(xlt ..хп),
заданной в области D многомерного пространства и принадле-
жащей классу т. е. такой, что интеграл
[ ... j //(хр ..., хл)/?<р(х1, ... ,x„)dXi ...dxn
b
сходится, -существует последовательность многочленов
(*^1» • • • > Х п) ==
/,=0/2=0 /л=0
удовлетворяющих соотношению
J • • • J If (Л, *2» • • • ’ Хп> - ФМ2...ЛЯ (*1> *2. • • • , ХпУЧ X
ь
X? (*1, х2> • • • хп) dx±dx2.. .dxn —> 0 при k-J^,..., kn—>оо.
Особый интерес представляет случай, когда q = 2 и
<р(х1э х2,..., хЛ)=р(хр х2,..., хл), где р — функция плотности
вероятности случайного вектора r= (xh х2, .., хп).
При этом рассматриваемый интеграл определяет операцию
статистического усреднения. В данном случае из приведенной
теоремы вытекает утверждение, что для любого нелинейного
преобразования, имеющего при рассматриваемых входных сиг-
налах конечное среднее квадратичное значение, существует по-
следовательность многочленов Ф^.,.^ такая, что средний
квадрат ошибок аппроксимации стремится к нулю с ростом по-
рядка аппроксимирующего многочлена.
Поскольку Gm(r) — многочлены, всякая конечная -сумма ря-
да (2.80) также будет многочленом относительно х2, ..., хп-
Может быть поставлена задача нахождения многочлена наи-
лучшего приближения среди всех многочленов Фт(г) степени ап.
Эта задача является частным случаем более общей задачи
наилучшего среднего квадратичного приближения процесса
i/(O=Hr(OL имеющего конечное среднее квадратичное значе-
ние, с помощью линейной комбинации процессов G^r(/)]„
Gi[r(/)], G2[r(0],Gm[r(t)], т. e. задачи минимизации вы-
ражения
123
подбором коэффициентов аг-. Введем обозначение
£(«/) =
т “12
/м-^^ад •
/=0
где черта сверху означает операцию статистического усредне-
ния, определенную выражением (2.82). Раскрывая скобки и диф-
ференцируя по а;, находим
т
^L=-27o;+2Va,oS, > = 0, 1............т.
Необходимое условие минимума E(ai)
дЕ (аЛ г. • п 1
—l_"=o для всех i=0, 1,..., т.
dai
Учитывая свойство ортогональности полиномов различных
порядков, получим следующую систему алгебраических уравне-
ний:
f(r)Gt(r) = 2 afit (r)Gk (г), i=0,1..., т, (2.83)
здесь суммирование производится по всем fe = fei + fe2 + ... +kn = t.
Для различных i имеем независимые системы уравнений, реше-
ние которых дает значения коэффициентов при полиномах
f-го порядка, обеспечивающих (минимум выражения (2.82). Та-
ким образом, при увеличении порядка аппроксимирующего мно-
гочлена коэффициенты разложения будут неизменными.
Рассмотрим нелинейные преобразования двух стационарных
случайных процессов Xf(f) и x2(t), имеющих нормальный совме-
стный закон распределения p2(xif х2),
w.-адь (2.84)
Следует заметить, что требование стационарности не явля-
ется обязательным. Анализ преобразований нестационарных
процессов не вызывает принципиальных трудностей и отлича-
ется лишь наличием зависимости коэффициентов ортогональных
разложений от времени. Так что результаты этого раздела без
труда Обобщаются на нестационарный случай.
Будем раскладывать нелинейное преобразование в ряды по
полиномам Эрмита с весовой функцией p2(%i, х2).
Нормальному закону распределения р2(хь х2) соответству-
ет следующая симметричная квадратная матрица коэффи-
циентов
Г 1 . -2 1
- 1 — Q2 ’ 1 — q2 .
124
С матрицей С связана /положительно определенная квадра-
тичная форма
+ — 20*1*2
ср (Хр Х2) — -- — .
С помощью весовой функции
/ а 1 [
^(х,х2)=2яу1_о2ехр[
xf +х22— 2QX1X2
(1 — Q2)
где q — взаимный корреляционный момент,
.Xi = —--- —нормированный процесс, могут быть определе-
ны две системы многочленов:
11 1 П к ,
Х";]т^х
Хехр[----хг)] ;
v Г 1 1 дт +п
Om„(xv х2)=(- 1)т+лехр [ТФ(^1. *2)]
ехр.
где
z2)j ,
x = C~1z, т. е. x1 = z14-qz2, x2=Qz1Jrz2
а ф(2ь г2) — квадратичная форма, соответствующая матри-
це С~\
ф(гр z2)=zI-]-zI-]-2qz1z2.
Важнейшими свойствами многочленов Нтп и Gwn, которые
используются в дальнейшем, являются свойства биортого-
нальности
оо
J j* Нтп (^1» ^2) ^kl (-^1’ *^2) Рг («^1» -^2) = • (2* 85)
—оо
и ортогональности полиномов Gmn различных порядков
J J (хр х2) Qki (Хр х2) р2 (Хр х2) =
О, если k-\-l ф i-\- j
mIn(Z’/> /П ос\
4!ZI S (Х/ис!"+,""₽и‘+/=,'+;
/я—О
125
Справедливы следующие рекуррентные формулы:
@1+1,Х2) ^@n—l,k^l^ **2) b$@n,k-l (•*!’ ^2)’
(2.87)
°1,}+Л*» х2)=х2О,7(Хр х2)-пеОл_1>й (xlt x2)-kOn,ll_1(xl, x2),
причем Goo=l.
Последовательно применяя формулы (2.87), нетрудно убе-
диться, что Gij является полиномом i-й степени относительно
Xi и /-й относительно х2 с коэффициентом при высшем члене
Х1г'х2Л равном единице.
Для некоторых значений i и / многочлены имеют следующий
вид:
@00 = 1» ^10 = ^1’ ^20 = -^1 1» ^01=='^2» ^02= -^2 1,
= Q, G2i = X]X2— Х2 — 2qXj,
G22=х\х2—Xi—X2 — 4qx^2 + 2q2.
Легко видеть, что при q = 0
о и (A, ^2)=^z(^i)^W;
@IQ ^2) ~ НI (^1)»
<4(*1> АГ2) = (А72),
где Hi — классические одномерные полиномы Чебышева — Эр-
мита г-го порядка.
Полиномы Нтп имеют следующее интегральное представ-
ление:
^(xx, х2) = (-1)'п+л(2я)-1 УТ^ехр[-Г<р(Хр х2)]х
X^^exP
—00
Перейдем теперь непосредственно к задаче вычисления мо-
ментов нелинейного преобразования.
Пусть три случайных процесса связаны соотношением
(2.84). Процесс на выходе нелинейного преобразования предста-
вим в виде ряда
у(/)= 2 atiGSJ [х?(/), х^)], (2.89)
Д ф (Хр X,) - i (Х^+Х^) 1 d\ d\ (2.88)
а
оо
а‘’=TTyT JJ (Х1’ ^х°'х^ Pi (Х1’ х^ dx^dx^- (2- 9°)
126
Математическое ожидание ту находится непосредственно
осреднением ряда (2.89) ’
/И у-Uqq.
Таким образом, (первый член ортогонального разложения
определяет среднее значение процесса на выходе нелинейного
преобразования (2.89).
Для вычисления (корреляционной функции имеем интеграл
Ry (/1» ^2) -JJ f CVll» -^21) f (*^12’ ^22) Pi 0^11» -^12» -^21» ^22) X
—00
X dxlr .. dx22 — my (/J my (/2), (2.91)
где xn=xi^2\ '*=1, 2;
Pi (xii» xi2» x2i» x22) — четырехмерная нормальная плотность
вероятности.
Чтобы вычислить интеграл (2.91), разложим р4 в ряд по
двумерным (полиномам Нц. Плотность вероятности -связана с
характеристической функцией 0 следующим интегральным -соот-
ношением:
оо
Рп (Х1» Х2> • • • ’ Хл) = /пгг\П \ • • • \ Р1’ • • • ’ ^л) X
(2Л) J J
—оо
X exp [ - i (Х^ +... +Х„х„] А... d\n.
Характеристическая функция нормального четырехмерного
вектора имеет вид
04(+ + + X4)=exp[Z(/n1X14-m2X2 + /nsX34-m4X4) —
—у (^1 + ^2 + /?э3Х2з + ^ + 2/?12Х1Х2 +
+ 2/?i3X1X3 2/?14Х1Х4 + 2/?23Х2Хз 2/?24Х2Х4 2/?34Х3Х4)];
здесь через Ra обозначены корреляционные моменты между
Xi и Xj. Подставив последнее выражение в интегральное -соот-
ношение и произведя соответствующие выкладки, получим
оо
А(Л. х2, х3, х4) = -^_ J ... ехр [—X
—00
X exp Г —i-<|> (Xg, х4)1 exp [ - (q^XjXj +q14X1X4 H-q^Xj -f-
+624X2X4)] exp
d\ ... rfk4;
здесь являются нормированными корреляционными мо-
ментами.
127
Разложим третью экспоненту подынтегральной функции в
степенной ряд
/?4 (Хр х2,
ОО ОО 00 / / ъ 1
1 Г* v <1 013614623624
(2л)4 J • • J Z1/1AI/I
—оо- —об
X (-1),+>+й+г k'1+^+%+ftx{+zехр[—i--|»(Xlt
X exp J —1- <|» (Х4, X,)] exp [ -1 (XjX? Н-Х^Ч-
4“ ^3-*-3 4“ ^4-*4)] d\r... dkt.
Выполняя почленное интегрирование и принимая во внима-
ние интегральное -представление (2.88), находим следующее
разложение:
/^<(•^1» «^2» -^8’ ^4) = Р2(^1» ^2) Pl (-^8’ *^4)>С
оо I j k I
X У (2.92)
I I 1 1 R I I I
I
Воспользуемся полученным разложением для вычисления
интеграла (2.91). В результате подстановки (2.92) в подынтег-
ральную функцию интеграл распадается на сумму следующего
вида:
z ,;,лд-о
,х,«1. ^)е{,хг(Л, <2)o*lX1(/i, <2) Q1,X,«1, <2)
i I /I k I I !
X J J f (-^12» -^22) HZ4-*»/+z(^12» *22) Ръ («^12» ^22) dx^x^
(^1) ^00 (^2)*
Интегрирование дает
(f + /)!(fe + /)t(/ + fe)I (/ + /)Г
/IjI* llI
(^1» ^2)*
(2.93)
128
Для стационарных процессов, переходя от корреляционных
функций к спектральным плотностям, получим
VI (Z + /)!(* + Z)!(Z + *)!(./ + Z)!
Jj ZiylAjlZ!
/ч-л+z-i
X ai + j,k + lai+k,j+lSljkl W> (2- 94)
где
Sijkl ((0) (tyQxiXi (*) QXaJfi (*) Qx2X2(^)i T = /2—^1-
Полученные ряды имеют следующий смысл. Первые
члены, для которых выполняется условие Z+/ + fe4-/=l, соответ-
ствуют линейной зависимости между входными и выходными
сигналами. Остальные члены характеризуют нелинейные иска-
жения, вносимые нелинейным преобразованием. Легко видеть,
что эти искажения наиболее существенны при малых т, что со-
ответствует области больших со в спектральной (плотности.
На основании полученных формул может быть введено поня-
тие эквивалентного частотного коэффициента усиления fe3(/(o)
или эквивалентной передаточной функции Нэ(р) безынерцион-
ного нелинейного элемента по каждому из входных воздействий.
Эквивалентный частотный 'коэффициент по воздействию хг- оп-
ределяется следующим -соотношением:
= yi (т + и)! (k + Z)l (m + *)!(л-Н)!
Sx. (о) m\n\k\l\ X
где
(<o)=
",лМ
Таким образом, использование ортогональных разложений
нелинейной характеристики при нормальном совместном рас-
пределении входных сигналов позволяет выразить статистиче-
ские характеристики выходного сигнала в виде рядов по степе-
ням нормированных кросс- и автокорреляционных функций
входных сигналов и построить эквивалентную передаточную
функцию нелинейного преобразования по каждому из входных
воздействий. Бели заданы статистические характер/истики вход-
ных сигналов, корреляционная функция или спектральная плот-
ность выходного сигнала могут быть с любой степенью точно-,
сти вычислены по формулам (2.93) и (2.94).
Рассмотрим задачу средней квадратичной аппроксимации
применительно к двумерным преобразованиям (2.84). В этом
случае система уравнений для коэффициентов аппроксимации,
обеспечивающих минимум среднего квадрата разности между
5 3200
129
исходным и аппроксимирующим /преобразованиями, в соответст-
вии с формулами (2.83) имеет-'Следующий вид:
f°ij= 2 *+*=*+/=const. (2.95)
k+l-l+J
Полиномы G(xb x2) одинакового порядка линейно независи-
мы, т. е. ни один из них не имеет (выражения через линейную
комбинацию других. Это означает, что
D=
О pfip. Gpfpp—1,1 • • • ЧЛ
Gp-lifiр0 ^р-Ы^р-ЬГ 7 . . . ч • • • г4 * * * 1 . . . О. о • • •
^Ор^рО ^Ор^р—1,1 • • • ^рО
/0.
Таким образом, определитель системы £>=/=0, поэтому она
имеет решение и это решение единственное.
Конечная сумма ряда (2.89), аппроксимирующая нелинейное
преобразование, необязательно должна содержать полный на-
бор из (р+1)-го Двумерного полинома Эрмита порядка р.
В этом случае в 'системе (2.95) все не участвующие в аппрокси-
мации полиномы Gp следует заменить нулями.
Решение системы (2.95) имеет следующий вид:
atj=, l-\-j=p= const; (2.96)
здесь A [J — алгебраическое дополнение элемента 6ц6ы в оп-
ределителе D.
Двумерные /полиномы Нр(хь х2) и Gp(xb х2) одного и того
же порядка р связаны между собой соотношением
2 <?м (X1X2) Alk{
(ХР x2)=k+t-i+1 D---------. (2.97)
Сопоставляя (2.96), (2.97) и (2.90), приходим к выводу, что
в том случае, когда для аппроксимации нелинейного преобразо-
вания используется полный набор полиномов G(%i, х2) какого-
либо порядка, коэффициенты ац при этих полиномах, обеспечи-
вающие наилучшую среднюю квадратичную аппроксимацию,
совпадают с коэффициентами ортогональных разложений.
Метод средней квадратичной аппроксимации нелинейных
преобразований можно использовать, чтобы получить прибли-
женные решения технических задач в тех случаях, когда приме-
нение* точных методов не имеет успеха.
130
Если в разложениях (2.80) или (2.89) ограничиться лишь
полиномами Эрмита первого (порядка, то аппроксимирующее
преобразование будет линейным и на его основе может быть
произведена линеаризация 'системы. В этом (случае оптимальные
коэффициенты аппроксимации, вычисленные по формулам
(2.79) и (2.80), совпадают с коэффициентами статистической
линеаризации многомерных нелинейностей.
Подводя итоги изложенному в этом разделе, можно утверж-
дать, что при известном распределении входных сигналов нели-
нейного преобразования выходной сигнал в пределах допусти-
мой ошибки может быть приближен конечным отрезком ортого-
нального разложения. Коэффициенты, обеспечивающие минимум
средней квадратичной ошибки приближения, вычисляются из
системы уравнений (2.83) или (2.95). Величина оптимальных
коэффициентов при полиномах определенного порядка зависит
от количества этих полиномов, используемых для аппроксима-
ции. Если набор используемых полиномов какого-либо порядка
полный, то оптимальные коэффициенты совпадают с коэффици-
ентами ортогональных разложений и вычисляются по формулам
(2.80). Изменение количества аппроксимирующих многочленов
какого-либо порядка не сказывается на величине оптимальных
коэффициентов при полиномах других порядков.
Пример. Проиллюстрируем сказанное простым примером.
Пусть исходное нелинейное преобразование имеет вид
t/ = /(Xi, х2).
Входные процессы Xi и Х2 имеют нормальный совместный закон распре-
деления. Аппроксимирующее преобразование запишем в виде
« = «00 + «10^01 (xi-ty + «10^10 (*1< *°) + «20°20 (*?. *2) +
+ «цОц (-*?, + «02^02 (хр х§). (а)
Определим коэффициенты ац, обеспечивающие минимум выражению
Е=М[у—и]2. Согласно (2.90) имеем
Лоо- *2); (О
/Стю = дю^ю^ю + aoi^oi^oi; 1 Xе)
/GOi = а\o^oi^oi + Ло1б1об1о; J
/^2о = а<#р20^20 + Л11<72о(7п 4- 092620602»
fG\\ = а2о6 1 iO20 + ацОцОц + 002611602;
/Gq2 в Л20<702^20 4- Л116q2611 + 02602 • '
(<0
5*
131
Для вычисления коэффициентов при полиномах каждого порядка имеем
свою систему алгебраических уравнений. Коэффициенты при полиномах пер-
вого порядка имеют вид
X! — РХ2 —-
л ю =/ ; ~ = /^ю»
1— р2
Л ~ Р*1 + ——
*oi =/~:----------— = /#oi-
1 — р^
Из системы (d) находим коэффициенты при полиномах второго порядка
Тогда
«20 =
/</20 + P2/Qq2 —2р/^и
*1 — рх2 \2
1-Р2 /
1
1 — р2
= i ///20-
Аналогично получим
«11 = /Иц;
«02 *= fHw-
Как и следовало ожидать, коэффициенты совпадают с коэффициентами орто-
гональных разложений.
Пусть теперь аппроксимирующее преобразование имеет вид
« ~ «00 + «Ю<Ло (•*?♦ + д01<Л)1 (.«*?» *2) “Ь 1^11 (-*2* **2)*
Здесь использован неполный набор многочленов второго порядка (в ап-
проксимации не участвуют многочлены (по и G02). Поэтому в соответствии с
изложенным ранее система алгебраических уравнений для коэффициентов при
полиномах первого порядка остается неизменной, а для коэффициента аи
при полиноме второго порядка имеем
«iigh(/ii =/</ц»
т. е. ___
/</ц
«н = •
С/ц(/11
Это выражение отлично от полученного ранее для преобразования («)
132
2.8. НЕОДНОЗНАЧНЫЕ ПРЕОБРАЗОВАНИЯ
ГИСТЕРЕЗИСНОГО ТИПА
Преобразования гистерезисного типа широко распространены
в технике (рис. 2.9). Нелинейная характеристика этих (преобра-
зований состоит из двух различных ветвей, одна из «которых со-
ответствует возрастанию выходной величины, другая — убьь
ванию. В данном случае с большой степенью точности можно
утверждать, что выходной сигнал является результатом нели-
нейного преобразования двух сигналов: входного сигнала и его
производной y=F(x,x).
Рис.' 2.9. Неоднозначные преобразования гисте-
резисного типа
Пусть входная величина неоднозначного преобразования яв-
ляется стационарным случайным процессом с нормальным зако-
ном распределения. Тогда, используя ортогональные разложе-
ния, на основании выведенных ранее соотношений (2.90) и
(2.93) можем написать
/п£—ар°
^УУ (т)=
z+y+Sz-i
(< + 7)1 (fe +/)!(/+*)!(/ + /)!
ZljUUl
Xaz+/>s+A+ft,/+iQ.rx (t) (t) (T)Q^ (*)>
(2.98)
где Qxx(t) — нормированная кросскорреляционная функция
x(t) и a(j — коэффициенты ортогонального разложения
преобразования.
Известно, что стационарный процесс ® совпадающие момен-
ты времени не коррелирован со своей производной.
В связи с этим, полагая >в уравнении (2.98) т = 0, находим
выражение для дисперсии сигнала на выходе
= 2 (2.99)
/+/-1
Остановимся несколько подробнее на,вычислении коэффици-
ентов aij. Как уже отмечалось, при QatJJt(O) =0 имеет место ра-
венство
x) = Hi(x) Hj(x\
133
где Hk(x) — одномерные 'полиномы Чебышева — Эрмита k-ro
порядка. Вследствие этого формулы для коэффициентов разло-
жения aij принимают вид
ОО
a‘i\ \ F (-*’ X Hi (Л°>нi
7 2лН/!аЛа^ JJ
—оо
Хехр | [х0>+х0>]1 dxdx.
(2.100)
Неоднозначное нелинейное преобразование состоит из двух вет-
вей, соответствующих возрастанию и убыванию входной вели-
чины
Г(х, л) = (ХИ <<°
(F2(x) х>0.
Функции Ft(x) и F2(x) обычно представляют собой однознач-
ные нелинейные зависимости, симметрично сдвинутые вдоль
оси х на величину, равную половине ширины петли гистерезиса
(см. рис. 2.9), т. е.
ЛМ=/(^.+а);
Учитывая сказанное, интеграл (2.100) можно разбить на два
следующим образом:
aij
1
2л/!
Г 0
//yG^expf
--оо
£)<Ф<
.02
Л 02
0
*02
dx.
(2.101)
Следствием ортогональности полиномов Чебышева — Эрми-
та является равенство
г ( Х2\ (/2л /=0
J „,(х)ехр{-—о .
—оо
НО
оо 0
/7у(х)ехр{—J ///Wexp{—+
—оо —оо
оо оо
+ //;(х)ехр{—[//Дх)+/7у(-х)]ехр|—dx.
о о
134
Полиномы Чебышева — Эрмита четного 'порядка являются
четными функциями аргумента, а нечетного порядка — нечет-
ными. Таким образом, можно написать
оо
Hin (х)ехр{
О
оо
Ий (х)ехр
О
О оо
(*) еХР {---dX = \ 2л+1 W еХР {---------f~) d Х‘
—оо О
Принимая во внимание последние соотношения, из (2.101)
находим
аМя—О при «>0; (2.102
а/»2л+1 = ^2л+1 [а/2' ’
здесь обозначено
1 Г • f х0’ 1 • 1 .
^2л+1= f— ' 1 ^2л+1 еХР | „ ( dx = ~^~ а2п+1'
/2л(2п+1)!а; J ( 2 J 2
(2. 103)
а2л+х —коэффициенты разложения в ряд однозначной нелиней-
ности типа идеального реле. Эти коэффициенты посто-
янны и не зависят от статистических свойств входного
процесса;
1 г ( х°* 1
а(1>=——------ 1 /(x-|-A)//z(x —х°)ехр{------\dx—
/2лЛ«; J I 2 J
Х —00
=а,(/пж + д, °х):
ар=а/(/пж-Д, ах);
щ — коэффициенты разложения функции fi(x).
При Д = 0 нелинейная характеристика однозначна. Легко ви-
деть, что в этом случае все коэффициенты, кроме аго, обраща-
ются в нуль. А коэффициенты аг0 совпадают с коэффициентами
разложения f(x). Выражение (2.98) можно значительно упрос-
тить, исходя из следующих соображений. Для нормированных
корреляционных функций всегда имеют место соотношения:
е^(т)<1; (т)<1.
135
Поэтому члены ряда (2.98) быстро убывают с увеличени-
ем i, j, k и /. Кроме того, при т=0, когда значения автокорре-
ляционных функций максимальны, кроюскорреляционные функ-
ции Qxx(r) и Qxx(t) равны нулю, и наоборот, кросскорреляци-
онные функции достигают наибольших значений при таких тг
при которых автокорреляционные функции уже незначительны.
Вследствие этого вес слагаемых в сумме (2.98), содержащих
произведения кро<сс- и автокорреляционных функций, будет не-
существенным. Если этими -слагаемыми пренебречь, то, прини-
мая во внимание (2.102), формулу (2.98) можно записать в сле-
дующем виде:
^уу W=2,! [alo+ah (т)+3!а?,зХ
Z-1
Хе*. (т)+ 5!а?>5е*. (T) + -]ei,(*)• (2.104)
На основании этой формулы может быть получена эквива-
лентная передаточная функция неоднозначного нелинейного
элемента. Она определяется следующим образом:
со
= 2 Л(2п + 1)!а2(2я+/-^!±^), (2.105)
где Sift((o)=eJrx(T)e;i(r).
В выражениях (2.104) и (2.105) коэффициенты а,2л+1 ПРИ
изменении п изменяются пропорционально квадрату коэффици-
ентов &2n+i (это следует из формулы (2.102)). Вычисление по
формуле (2.103) дает
£2=0,16; £2=-0,004; £2=о?ооо1.
Отсюда видно, что для приближенных расчетов можно учи-
тывать лишь два, а иногда и одно первое слагаемое в квадрат-
ных скобках выражения (2.104). В последнем случае эквива-
лентная передаточная функция определяется следующим соот-
ношением:
92
2.9. ПАРАМЕТРИЧЕСКАЯ АППРОКСИМАЦИЯ
СТОХАСТИЧЕСКИХ НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАНИИ
Полученные в 'предыдущих разделах 'соотношения для стати-
стических моментов процессов на выходе многомерных нелиней-
ных преобразований непосредственно могут быть использованы
136
для доследования замкнутых динамических систем, содержа-
щих стохастические нелинейности, три условии, что процессы в
этих системах эффективно нормализуются линейной частью.
Однако (практическое применение этих соотношений сопряжено
с определенными вычислительными трудностями. Часто требо-
вания, (предъявляемые к точности вычислений, или специфика
самой задачи позволяют исходное нелинейное преобразование
заменить более простым преобразованием, в некотором смысле
эквивалентным исходному. На этом принципе основаны извест-
ные методы статистической линеаризации, состоящие в замене
нелинейного преобразования эквивалентным линейным.
Рис. 2.10. Структурные представления стохастических нелиней
ных преобразований
Непосредственное применение статистической линеаризации к
стохастическим нелинейностям недопустимо, так «как в ряде
случаев оно может привести к результатам, не соответствую-
щим даже качественной картине (процесса управления. Дело
в том, что системы, содержащие стохастические нелинейности,
по своей сущности являются параметрическими. Действительно,
элемент со случайными свойствами можно (представить различ-
ными сочетаниями блоков умножения и детерминированных не-
линейностей. Например, стохастическое преобразование вида
(2.70) можно представить следующей цепочкой (рис. 2.10, а).
Аналогичные цепочки для нелинейностей вида (2.71) и (2.72)
приведены на рис. 2.10, б и в. Таким образом, характерным для
систем, содержащих стохастические нелинейности, является на-
личие в их структуре блоков умножения. Вследствие этого им
присущи все специфические свойства параметрических систем,
такие как явление параметрического резонанса и различные мо-
дуляционные явления, обуславливающие появление дополни-
тельных ошибок системы [6].
При линеаризации нелинейной зависимости исключается вся-
кая возможность учета параметрических явлений. Чтобы сохра-
нить параметрическую сущность задачи, систему, в статистиче-
ском смысле эквивалентную исходной нелинейной, в данном
случае следует искать в классе линейных параметрических си-
стем. Другими словами, преобразование, аппроксимирующее
исходную стохастическую нелинейность, 'следует искать не в
137
классе линейных преобразований, а в «классе преобразований
вида
w=<Po4_Aiao4-^2xo+^aozo (2.106)
для стохастических преобразований (2.70) и (2.71) и
U = ?0 + М? + ^2а2 + М° + А4а?а2 + k^x0 + kea%xQ (2.107)
для преобразований (2.72). Здесь a0, щ0, аг° — центрированные
параметрические возмущения (нагрузка на валу, момент сухого*
трения и т. д.); х° — центрированный входной сигнал.
Аппроксимацию типа (2.106) и (2.107) в дальнейшем будем
называть параметрической аппроксимацией стохастической не-
линейности. Задача построения аппроксимирующего преобразо-
вания сводится к определению коэффициентов передачи <ро, klr
k2 и т. д., обеспечивающих при заданных статистических ха-
рактеристиках входа и параметрических возмущений выполне-
ние следующего условия:
a2=M {[f/(/)-«(/)]2}=min. (2.108)
Нетрудно видеть, что преобразование
«=«oo+<z10C?10(a:, a)+<z01G01(x, a)+auGu(x, a)
принадлежит к классу преобразований .вида (2.106). В соответ-
ствии с изложенным в разд. 2.7 коэффициенты, удовлетворяю-
щие условию (2.108), определяются следующими выражениями:
а„=---------!-------- f ( /<*
J J I 2(1-4’) I
® —oo—oo
oo oo
«io=-' r f a°)X
X/ I x0’+ a°‘— 2px0a0 )
XexPI----------------г------« dxda,',
I 2(1 —Q2) j
OO oo
«01=---- * -— f [/(•*. a)//01(x®, a°) X
2Л ~У 1 — Q2°xaa J
— OO—00
__x°2 + a0* — 2QxOgo|
~ 2(1 —Q2) f
dxda\
=---------!------ f ? ftx. a) °« X
2л У1 — Q2°a-o J J 1 + q2
“ —oo—oo
\x I x°2 + a°2 — 2Qx0a0 1 , ,
XexP----------—------------} dxda.
I 2(1-q2) J
138
Таким образом, для того чтобы осуществить параметрическую
аппроксимацию стохастической нелинейности, достаточно в ее
ортогональном представлении
члена.
Параметрическая аппрок-
симация означает замену не-
линейного элемента со случай-
ными свойствами эквивалент-
ным в смысле минимума
среднего квадрата ошибки ли-
нейным звеном со случайным
коэффициентом усиления (рис.
2.11). Параметры аю, Доь 0ц
эквивалентного звена зависят
учесть лишь четыре первых
Рис. 2.11. Эквивалентное линейное сто-
хастическое звено
от статистических характерис-
тик входных процессов х(1) и а(/). Наличие этой зависимости
позволяет уловить существенно нелинейные особенности преоб-
разования.
Применение параметрической аппроксимации стохастическо-
го нелинейного преобразования сводит задачу анализа исход-
ной нелинейной системы к рассмотрению эквивалентной линей-
ной системы со случайными параметрами [6].
2.10. АНАЛИЗ СИСТЕМ УПРАВЛЕНИЯ С УЧЕТОМ
ТЕХНОЛОГИЧЕСКИХ РАЗБРОСОВ ПАРАМЕТРОВ*
Неизбежные технологические ошибки производства приводят
к тому, что значения параметров реальных систем всегда от-
личны от их номинальных значений, выбранных в процессе про-
ектирования. Технологические разбросы параметров обуславли-
вают различие выходных характеристик (показателей точности,
устойчивости, надежности и т. д.) для различных экземпляров
однотипных систем. В связи с этим возникает необходимость
рассмотрения выходных характеристик всей совокупности сис-
тем, получаемых в результате одного производственного про-
цесса, и оценки влияния технологического разброса парамет-
ров на эти характеристики.
Возможность (подобных оценок является весьма важной при
проектировании систем, поскольку позволяет обоснованно по-
дойти к задаче назначения допустимых разбросов на параметры
системы, исходя из требований к ее выходным характеристи-
кам.
Уменьшение поля допусков для гарантии заданного качества
системы неизбежно влечет за собой неоправданные экономиче-
ские затраты (более точное и дорогое оборудование, более
сложную конструкцию элементов, организацию более сложного
технологического процесса и т. д.). С другой стороны, не обос-
* При написании разд. 2.10 и 2.11 использованы материалы, предостав-
ленные авторам инж. Ж- В. Бовиной.
139
нованное расчетом ослабление требований к точности произ-
водства .приводит к снижению надежности системы и ухудше-
нию качества ее функционирования.
Причины, вызывающие технологические ошибки производст-
ва, весьма разнообразны и случайны по своей природе, поэтому и
сами ошибки, выражающиеся в отклонениях значений парамет-
ров от их номиналов, также носят случайный характер. Таким
образом", оценивая качество функционирования совокупности од-
нотипных систем, исследователь имеет дело с множеством сис-
тем, параметры которых случайным образом распределены в
пределах полей допусков.
Похожая картина имеет место и при флюктуациях пара-
метров, обусловленных износом, старением, изменениями в про-
цессе длительного хранения и т. д.
Исчерпывающей характеристикой случайных ошибок произ-
водства так же, как и всякой случайной последовательности,
являются законы распределения параметров внутри полей до-
пусков. С теоретической и практической точек зрения наиболее
правильным является задание отклонений, допускаемых по
точностным и конструктивным соображениям, именно в виде
требующегося распределения, а не только в виде интервала их
возможных значений. Дело в том, что влияние разброса пара-
метров на качество функционирования совокупности систем
нельзя характеризовать лишь величиной этого разброса. На-
пример, естественно предположить, что три одинаковых допус-
ках множество систем, параметры которых сосредоточены в
центре поля допуска, будет обладать иными точностными ха-
рактеристиками, чем аналогичное множество, фактические зна-
чения параметров которого сосредоточены у границ поля до-
пуска. Поэтому, для того чтобы получить правильную оценку
влияния технологических ошибок на качество функционирова-
ния системы, необходимо знать законы распределения этих
ошибок. Характер этих законов однозначно определяется видом
и качеством технологического процесса [2].
Как показывают исследования, в подавляющем большинст-
ве случаев, когда технологический процесс отлажен и выполня-
ется хорошо, ошибки производства подчиняются нормальному
закону распределения. В том случае, когда помимо многих, труд-’
но устранимых, но малых по своей значимости причин, вызываю-
щих погрешности, имеются некие доминирующие систематиче-
ские погрешности, закон распределения ошибок в большей
или меньшей степени Может отличаться от нормального.
Можно назвать целый ряд факторов, приводящих к всевоз-
можным искажениям (по сравнению с гауссовыми) законов
распределения погрешностей. Это эксцентриситет и биение
станков, колебания параметров технологического процесса, сме-
шение нескольких партий однотипных элементов с разными ха-
рактеристиками разбросов и т. д.
140
Истинные кривые распределения -погрешностей производства
могут быть получены лишь на основании статистических дан-
ных, которые имеются на любом современном предприятии.
В ряде случаев (это относится в основном к этапу проектиро-
вания системы, когда статистические данные о разбросах пара-
метров отсутствуют) подробный анализ технологического про-
цесса позволяет построить так называемые теоретические кри-
вые -распределения погрешностей, которыми можно достаточно
хорошо аппроксимировать истинные распределения параметров
в пределах полей допусков [2].
Задача статистического анализа систем управления в усло-
виях случайного технологического разброса параметров заклю-
чается в вычислении некоторых показателей, характеризующих
качество функционирования всей совокупности этих систем, и в
получении зависимости показателей качества от характеристик
разбросов.
Пусть динамику системы автоматического управления мож-
но описать дифференциальными уравнениями следующего вида:
х = р, g, f); /£[т, Г]; (2.109)
х(/)|/.т=х(т),
где х(/) = ||х1(/), х2(/), ..., xn(t) ||1хл —вектор состояния систе-
мы;
? = НР1, •» llixz—вектор параметров сис-
темы, подверженных тех-
нологическому разбросу;
^W = l|g*iW» £2^), £л(/)||1Хл—векторный процесс, мо-
дели р у ющи й вн еш н-и е
воздействия;
ф=||?1> ?2» •••, ?л||1хл—нелинейная вектор-функ-
ция;
х(т) = ||х1(т), х2(т,)..., хл(т)|(1Хл—вектор начального сос-
тояния системы.
Указанная совокупность систем управления образуется мно-
жеством реализаций вектора 0 внутри области допустимых зна-
чений параметров. Поскольку вектор параметров р входит в
правую часть системы (2.109) нелинейно, то в самом общем
случае можно считать, что его компоненты являются независи-
мыми, распределенными по нормальному закону, случайными
величинами.
Будем исходить из того, что наиболее полной характеристи-
кой качества системы наведения может служить вероятность по-
падания вектора состояния x(t) (или отдельных его компо-
нент) в заданную область для произвольно выбранного момен-
та времени. Величина вероятности попадания зависит от ста-
тистических характеристик внешних воздействий и от значений
вектора параметров 0. Считаем, что условия применения, т- е.
141
статистические характеристики векторов начального состояния
системы и внешних воздействий, являются одинаковыми для
всей совокупности рассматриваемых систем. Тогда каждой реа-
лизации вектора 0, т. е. каждому конкретному экземпляру сис-
темы соответствует определенное значение вероятности попада-
ния. Эти значения образуют случайное множество, статистиче-
ские характеристики которого могут быть использованы для
оценки качества функционирования всей совокупности систем и
для оценки «ожидаемого» качества каждого конкретного экзем-
пляра системы. Таким образом, рассматриваемая задача ана-
лиза сводится к исследованию статистических свойств решения
системы (2.109) со случайными параметрами.
В настоящее время не существует методов, позволяющих в
явном аналитическом виде вычислить вероятность попадания
или закон распределения вектора фазовых координат системы
общего вида. Однако в ряде важных для приложений случаев
удается получить приближенные решения как для линейных, так
и для нелинейных систем управления. В частности, весьма эф-
фективным методом исследования системы (2.109) в случае, ког-
да компоненты вектора внешних воздействий g(t) — детерми-
нированные функции, является интерполяционный метод [7].
Сущность этого метода заключается в следующем.
Решение системы (2.109), т. е. вектор состояния x(t) при
детерминированном векторе g(t) представляет собой некоторую
также детерминированную функцию времени, зависящую от
компонент случайного вектора параметров 0.
Предположим, что необходимо вычислить некоторую стати-
стическую характеристику вектора состояния, например,
Л = ЛЯ/(х)] = у/[х(ЭД/7(РШ ч (2.110)
в
где интегрирование ведется по всей области В возможных зна-
чений вектора 0, а р(Р) — плотность вероятности р.
В частности, если
то В=Р[х1<^а1, х2<а2, ..., хл<ал],
т. е. F определяет интегральный закон вероятности вектора сос-
тояния х. Это следует из того, что функция f (х) принимает зна-
чения или 1, или 0 в зависимости от выполнения или невыпол-
нения условий
<az, / = 1, 2, ..., п.
Для вычисления кратного интеграла (2.110) используется
интерполяционный метод (7]. В результате чего получим приб-
142
лиженное выражение для искомой характеристики в следую-
щем виде:
2 ...
Xf j j ^2 j • • • >
(2.111)
где fjf1, ft**) — узловая точка интерполирования;
См^-чнслз Кристоффеля.
Числа Кристоффеля зависят от значений вектора 0 в узло-
вой точке и вычисляются следующим образом:
В j~l
здесь
“«j (₽/)
-ЖОМ?)
•.,ВД = (|Н)(»Н;НМ'')
есть полином степени qi относительно fo,
ki= 1, 2, ..4=1, 2, .., I.
Обоснование и оценка интерполяционного метода подробно
рассм-атриваться здесь не будут. Достаточно полное изложение
этих вопросов дано в книге В. М. Чернецкого [7]. Отметим толь-
ко, что точность интерполяционной формулы (2.111) существен-
но зависит от количества и выбора узлов интерполирования. Из
формулы (2.111) следует, что искомые статические характерна
стик могут быть выражены через значения вектора состояния,
соответствующие фиксированным значениям вектора 0. Иначе
говоря, поставленная задача решается путем интегрирования
системы (2.109) при вполне определенных величинах парамет-
ров, равных их значениям в узлах интерполирования.
Общее количество узлов интерполирования, а -следователь-
но, и количество необходимых интегрирований системы равно
АГ=П<7*
I “1
Оно зависит от того, с какой точностью требуется вычислять
интеграл (2.110), и от количества случайных параметров в сис-
теме. Несмотря на то, что интерполяционные формулы облада-
ют очень хорошей сходимостью, при большой размерности век-
тора р объем вычислительной работы весьма значителен. По
этой причине интерполяционный метод практически не может
быть использован, когда среди компонент вектора воздействий
g(t) имеются случайные функции времени. Принципиально пу-
тем канонических или неканонических разложений случайных
функций задачу можно свести к раоомотренной (7]. Однако ис-
143
пользование канонических разложений существенно увеличи-
вает размерность вектора 0, а неканонические разложения, из-
за того, что они не обеспечивают совпадения законов распре-
деления исходной и аппроксимирующей функций, вносят з
метод погрешности, которые невозможно учесть.
Ниже будет изложен способ, который позволяет решать за-
дачу статистического анализа системы (2.109) при случайных
воздействиях, не прибегая к каноническим или неканоническим
разложениям.
Пусть вновь требуется вычислить некие статистические ха-
рактеристики вектора состояния системы
F=M[f(x)\.
Если известен совместный закон распределения вектора сос-
тояний и случайных параметров р(х, 0), то для вычисления F
имеем следующее выражение:
И/(х)р(х, $)d'xd$,
BQ
где Q — некоторая область пространства состояний системы.
Воспользуемся известной формулой теории вероятностей
Р)=/2(Х/?)/>(?),
где р(х/0) — условный закон распределения.
В результате интеграл преобразуется в следующий
F=П Jf w р ш dx] р (₽) <2112)
Очевидно, что внутренний интеграл определяет условную стати-
стическую характеристику вектора состояния. Обозначим ее че-
рез Fx(0), тогда
F = ^Fx^p^)d^.
В
Если для В вычисления этого интеграла попользовать интер-
поляционный метод, то окончательное выражение для искомой
характеристики F будет иметь вид
2 F*^"k'................*г (2-113)
Таким образом, задача свелась к вычислениям условных стати-
стических характеристик вектора состояния при значениях па-
раметров, соответствующих узловым точкам интерполирования.
Эти вычисления в зависимости от конкретной формы системы
уравнений (2.109) могут быть осуществлены теми или иными
.144
методами статистического анализа систем с детерминирован-
ными 1параметрам1и.
В частности, если система (2.109) линейна, то она может
быть записана в следующей форме:
x(t) = Ax(t) + Bg(tY (2.114)
y{t)—Cx(t)\ х(О)=хо,
где х—n-мерный вектор состояния системы; g—n-мерный вектор
управлений; у—n-мерный вектор выхода;
А = 11 aijНлхл и £ = Нfy/Нлхл— матрицы коэффициентов; С =
=||С/уЦлхщ— детерминированная постоянная матрица.
Относительно коэффициентов системы ац и Ьц будем пред-
полагать, что они нелинейно зависят от компонент нормально
распределенной векторной случайной величины 0 (вектор пара-
метров) :
ла=ам(р, /); Ьи = Ьи$, /), Z, /=1, 2, п.
Вектор управлений представляет собой сумму детерминирован-
ной g°(t) и случайной g* (t) составляющих: .
Без ограничения общности можно считать, что компоненты
g* (t) — независимые белые шумы со следующими характерис-
тиками:
[£*(/)] = О Г(/х, /2)=УИ (/1)g-*-(/2)]=8^1_/2)/,
где 6(/) — 6-функция; I — единичная матрица пХп.
Как известно, полный статистический анализ линейных сис-
тем с детерминированными параметрами состоит в вычислении
математического ожидания и корреляционной матрицы, зная
которые, можно определить любые статистические характеристи-
ки вектора выхода.
Поэтому любая условная характеристика выхода системы
(2.114) может быть найдена, если известны его условные мате-
матическое ожидание и корреляционная матрица. Часто для
этого достаточно знать условное математическое ожидание и
матрицу условных дисперсий. Введем следующие обозначения:
р!,=М [у/?], = М [х/ЭД — условные математические ожидания;
У = М[(у - НУ) (У - ^)7?],У = М [(х - ^) (х - -
— матрицы условных дисперсий.
Уравнения, необходимые для вычисления условных момен-
тов вектора состояния, можно получить непосредственно из си-
стемы (2.114).
145
Осредняя (правые и левые части (2.114), получим систему
уравнений для условных математических ожиданий
1^=0*,; |»(O)=xo. (2.115)
Для случайной составляющей вектора состояния х* = х—
имеем систему уравнений
х* = Дх* + 5^*; (2.116)
х*(/о)=О.
Используя правила дифференцирования произведения, мо-
жем написать
— (х*х*т)=х*х*г 4- х*х*т.
dt
Транспонированный вектор состояния подчиняется следую-
щей системе уравнений:
xT=xMT + gT5T.
В результате получим
— (х*х*т) = Дх*х*т-|-5^*х*т-|-х*х*тДт4-х*^*т5т. (2.117)
dt
Решение линейной системы (2.116) имеет следующий вид:
t
= x}Bg(x]dx\
*0
здесь Ф(/, 70) — переходная матрица состояний системы; она
удовлетворяет условию Ф(/о, to)=I- (2.118)
Иопользуя эту формулу, преобразуем последнее слагаемое в
выражении (2.117)
t
x*g*Tfft = J ф 7) Qg* (t) g*T (/)
^0
Для транспонированной случайной составляющей имеем
t
х*т(/) = J (т) £ТФТ (/, r)dr.
*0
Отсюда находим
t
Bg*x*T= j Bg* (f) g*r (т) Фт (f, t) dr.
to
146
Полученные формулы позволяют написать
— (х*. х*т) = Д(х*. х*’)+(х*, х*т)Дт +
dt
t Г
4- j Ф (t, t) Bg* (r)g*T (/) B'dx + j Bg* (/) g** (г) ЯТФТ (/, t) dx.
to - ^0
Осреднив правую и левую части последнего выражения,
получим
Хх w=А Хх +2хх & Ат+Jф т) 5гх
*0
t
х (A t) B'dx + J ЯГ (г, /) 5ТФТ (А т) dx = А 2жхХ
to
ХЮ +2хх(/) Лт + J 8 (/ — г) Ф (/, г) BB'dx +
to
t
4-j££T8(r-/)®T(/, x)dx.
Откуда, учитывая свойства 6 функций, а также свойство
{2.118) переходной матрицы, получим систему дифференциаль-
ных уравнений для матрицы условных дисперсий вектора сос-
тояния и вектора выхода
У.. И=А (')+2„ И Л’ + ВВ-.
2,/')=с2,,<'>Ст; 2,,<«=а <2-119>
Эта система имеет порядок п2, однако вследствие симметрич-
п п (и + 1)
ности матрицы SXx порядок может быть понижен до———•
Интегрирование систем (2.115) и (2.119) позволяет найти
«статистические моменты выхода, по которым определяются ис-
комые условные статистические характеристики. Вычисление
абсолютных характеристик производится согласно формуле
(2.115).
Для рассматриваемых линейных -систем со случайным раз-
оренном параметров может быть поставлена наиболее общая
задача -статистического анализа, а именно задача вычисления
закона распределения вектора выхода.
147
Закон распределения вектора выхода выражается через ус-
ловный закон распределения вектора выхода и закон распреде-
ления вектора параметров следующим образом
(2.120)
В
где р(у/Р) — условный закон распределения.
В линейных системах, очевидно, условный закон распределе-
ния является нормальным и полностью определяется условными
математическим ожиданием и дисперсией:
Р (.У ft) = (2л) 2 2 .ехр I” —(у - ^)т (у - I*i,)j.
Если для вычисления интеграла (2.120) применить интер-
поляционные формулы, то задача сведется к интегрированию в
узловых точках систем моментных дифференциальных уравне-
ний (2.15) и (2.119).
Зная закон распределения, нетрудно вычислить вероятность
попадания координаты вектора выхода в заданную область.
Излагаемый метод применим к анализу нелинейных систем в
том случае, если для исследуемой системы каким-либо образом
могут быть получены уравнения условных статистических мо-
ментов. Эти уравнения можно получить, используя, например,
метод статистической линеаризации или метод вычисления се-
миинвариантов.
Для нелинейной системы, имеющей вид
х, ?)+«(/) g(/);
at
где о(/) — матрица пХл, а случайные компоненты вектора
воздействий g(t) — некоррелированные белые шумы, используя
гипотезу о нормальности закона распределения вектора состоя-
ния и осуществив многомерную статистическую линеаризацию
нелинейностей, можно получить следующую систему условных
моментных уравнений:
-^-=?о(а МО)=*о;
^=п(<. и,. 2J 2„+2,л1 ('• 2„)+
2Х.((°)=°.
где
?.(<. !>„. 2,.)=/И |м'’ р)/я;
148
2.11. МЕТОДЫ ОПТИМАЛЬНОГО ВЫБОРА НАСТРОЕК
И ДОПУСКОВ НА ПАРАМЕТРЫ СИСТЕМ
Задача выбора оптимальных настроек и допусков на пара-
метры систем автоматического управления возникает в связи с
тем, что никакое производство не в состоянии изготовить систе-
му, значения 'параметров которой в точности соответствовали
бы запроектированным. Если система синтезирована оптималь-
ным образом, но без учета неизбежного технологического раз-
броса, то параметры каждого конкретного экземпляра этой
системы будут отличаться от оптимальных. Следовательно,
ошибки производства приведут к ухудшению качества функцио-
нирования системы. Поскольку значения параметров в пределах
поля допуска являются случайными, то и отличия показателей
качества отдельных систем от показателя качества оптималь-
ной будут иметь случайный характер. В связи с этим возникает
необходимость рассматривать характеристики качества всей со-
вокупности систем, получаемых в результате одного производ-
ственного процесса и отличающихся друг от друга вследствие
технологического разброса, параметров.
Устанавливая достаточно малые допуски, можно, разумеется,
добиться малого изменения показателя качества каждого экземп-
ляра системы, т. е. добиться близкого к оптимальному
качества функционирования всей совокупности. Однако
уменьшение поля допусков означает повышение требований к
точности производства и всегда приводит к увеличению эконо-
мических затрат. Таким образом, с одной стороны, исходя из
условий качества функционирования системы необходимо су-
жать поле допустимых разбросов параметров, с другой стороны,
максимально расширять для снижения экономических затрат
производства. Поэтому приходится искать компромиссное реше-
ние, которое в той или иной мере удовлетворяло этим двум тре-
бованиям.
Пусть динамика системы автоматического управления опи-
сывается системой дифференциальных уравнений (2.109).. Со-
вокупность систем будет порождаться совокупностью реализа-
ций случайного вектора 0. Предположим, что качество функ-
ционирования каждого конкретного экземпляра системы можно
характеризовать некоторой векторной функцией
ф2В ...» ФИВ
Компоненты вектора ф представляют собой значения различ-
ных критериев качества системы, определяемых техниче-
скими условиями. Это могут быть показатели точности, устой-
чивости, надежности, и т. д. Тогда условия нормальной работы
системы выражаются в виде неравенства
Ф(?)>а, (2. 121}
где а = (щ, а2, . . ctk) — вектор технических условий.
149?
Можно потребовать, чтобы условия (2.121) выполнялись для
всей совокупности систем с некоторой доверительной вероятно-
стью Р, в частности можно положить Р=1. В этом случае в про-
странстве Bi параметров системы, подверженных технологиче-
скому разбросу, неравенства (2.121) выделяют некоторую
область В, в пределах которой с вероятностью Р должен на-
ходиться вектор р. Область В в дальнейшем будем называть об-
ластью работоспособности системы. Часто качество системы
можно характеризовать обобщенным критерием качества /<(0),
зависящим от компонент вектора гр,
К(?)=ЛГ||Ф1. .... ФА||1ХА- (2.122)
В частном случае /С(Р) может иметь следующий вид:
А'(Р)=(а, ф)=2аЖ’
/-1
где а — весовой вектор, отражающий факт неравноценности
показателей *фг.
При использовании обобщенного критерия /С(Р) область ра-
ботоспособности системы В задается неравенством
где с=const.
В условиях технологического разброса параметров значения
показателей качества систем ф(р) и /<(Р) будут случайными.
В связи с этим показателем ^качества всей 'совокупности рас-
сматриваемых систем ф или К может служить некоторая стати-
стическая характеристика -случайных величин лр(Р) или /С(Р).
Например, можно принять
ф=т!пР{фу(р)>ау}; Л=Р{/С(р)>с),
или ф = М [ф (р)]; К = М [Д' (0)] и т. д.
Назначить допуски на параметры системы, это значит в об-
ласти В выделить некоторый брус, внутрь которого с довери-
тельной вероятностью Ро^Р должны попадать все реализации
вектора 0.
Под номиналами параметров при симметричном распределе-
нии вектора 0 будем понимать координаты центра бруса 0О =
= ||0ю, 020. • • •> 0z||ixJ- При несимметричном распределении номи-
нальные значения параметров будем определять как их матема-
тические ожидания 0о=Л1[0] и показатели качества являются
функциями 0о, у и X.
Если поле допуска симметрично относительно номинала, то
Д/=5/==Х.р/0, / = 1, 2, ..., I. (2.123)
150
Введем в рассмотрение функцию стоимости
С = С(д, В).
Функция стоимости характеризует экономические затраты
производства на выдерживание параметров в заданных полях
допусков. Значения функции стоимости определяются техноло-
гическим процессом, который будем считать общим для всех
экземпляров систем из рассматриваемой совокупности.
Вопрос нахождения зависимости функции стоимости от до-
пусков чрезвычайно важен. Представим функцию стоимости сис-
темы как сумму стоимостей обеспечения отдельных параметров
в пределах полей допусков:
С(Д, 8)=2
/=1
Вид функции Ci (Дг-, 6г) существенно зависит от условий про-
изводства. Так, стоимость одного и того же элемента при оди-
наковой величине допуска различна в зависимости от техноло-
гии, квалификации рабочих, характера производства (серийное,
массовое, конвейерное), оборудования и т. д. Только вся сово-
купность таких условий определяет вид функции СДАг, 6$). Эту
зависимость можно получить эмпирически.
Для определения стоимостей элементов массового произ-
водства (резисторов, конденсаторов и др.) можно использовать
прейскурантные справочники.
Очевидно, что функция стоимости является невозрастающеГв
функцией параметров А и б, т. е.
дС < 0; дС^’ 8)<о, Z=l, 2,
d^i дЪ[
причем функция С (А, 6) должна быть положительной, кусочно-
гладкой и удовлетворять условиям:
СДд,, 8J—>оо;
'Д.-+8;-0.
В дальнейшем в целях упрощения формулировок будем счи-
тать, что поля допусков являются симметричными относительно
номиналов, и характеризовать допуск единственным парамет-
ром 6.
Из изложенного следует, что изменения допусков на пара-
метры приводят к изменениям показателей качества функциони-
рования системы и функции стоимости. Причем уменьшение до-
пусков улучшает качество, но увеличивает экономические за-
траты на изготовление системы.
Это оправдывает постановку задач обоснованного выбора
допусков на параметры отдельных элементов системы с целью
151
обеспечения наилучниего качества функционирования и умень-
шения стоимости систем управления. С (практической точки зре-
ния наибольший интерес представляют следующие задачи.
1. Пусть •величина поля допуска пропорциональна номиналу
* = Л
причем значения параметров заданы. Определить значения
номиналов рг0, при которых показатель качества К достигает
максимума.
Необходимость постановки задачи в таком виде объясняется
следующим. Пусть значения параметров р^0 обеспечивают мак-
симум показателя качества системы К. Вследствие ошибок про-
изводства параметры реальных систем будут отличаться от pz°0.
Это значит, что показатель качества совокупности систем К
будет меньше, чем /С Оказывается, что в условиях технологиче-
ского разброса качество систем можно повысить, приблизив
значение К к оптимальному К, если заранее задаться некоторы-
ми смещениями значений параметров относительно номиналов
х во=р?о+д%.
2. Определить оптимальные значения номиналов параметров
fio и допусков 6г так, чтобы функция стоимости С(6) достигала
минимума, а показатель качества /С(Ро, 6) удовлетворял ограни-
чению К(ро, 6)^/Со, где KQ — некоторая постоянная.
3. Определить значения номиналов и параметров допусков,
обеспечивающих максимум показателя качества /С(р0, 6) при
условии С (6)^ Со.
Перечисленные задачи весьма характерны, но они не охва-
тывают всех задач, возникающих при проектировании систем
управления в связи с выбором допусков на их параметры.
Необходимо обратить внимание на следующее. Технологиче-
ский разброс параметров характеризуется не только величиной
допусков, но и законами распределения внутри полей допусков.
Поэтому задачи оптимизации могут 'быть решены лишь при ус-
ловии, что характер распределения технологических разбросов
известен заранее и что допуски 6г- могут быть выражены через
статистические параметры этих распределений.
В основу методов решения экстремальных задач можно по-
ложить результаты предыдущего раздела. В этом случае задача
выбора значений номиналов и допусков разбивается на три са-
мостоятельных части, а именно: на задачу вычисления услов-
ных вероятностных характеристик, т. е. задачу статистического
анализа систем с детерминированными параметрами; задачу
вычисления кратных интегралов вида С К (Р)р(?)аф; задачу на-
152
хождения максимума функции многих переменных при ограни*
чениях типа неравенств, т. е. задачу нелинейного программи-
рования. Существуют различные методы решения этих задач,
обладающие каждый своими достоинствами и недостатками.
Объединение их в одну предъявляет свои требования к выби-
раемым методам. Остановимся кратко на особенностях сформу-
лированных задач оптимизации.
Характерным для первой задачи так же, как, впрочем, и для
остальных, являются большие вычислительные затраты для на-
хождения максимизируемой функции. Поэтому первостепенное
значение имеет скорость сходимости используемого итерацион-
ного процесса оптимизации.
Наиболее быстросходящимся методом решения системы
трансцендентных уравнений, получаемых из необходимых усло-
вий экстремума, является метод Ньютона. Для системы F(x)=O
итерационная схема имеет вид
*я+1=*я-л-1(*яИ Ы
где
"* 11 dF^
Л(*я)=
дх^ F- X.
Необходимость на каждом шаге 'считать обратную матрицу,
т. е. решать систему линейных алгебраических уравнений, яв-
ляется определенным недостатком метода Ньютона; впрочем,
этот недостаток вполне окупается быстротой сходимости. Серь-
езной трудностью при применении 'метода Ньютона является
необходимость попадания нулевого приближения в достаточно
малую окрестность корня. Как показывают исследования [4],
сходимость метода Ньютона обеспечивается'лишь в этом слу-
чае. Для увеличения области притяжения корня применима мо-
дификация, уменьшающая, однако, скорость сходимости
xn+1=xn-^nA-l(xn)F (хп\
где х — скалярный множитель, не /превосходящий единицы.
Однако решение задачи затрудняет наличие локальных экст-
ремумов у максимизируемой функции. В этом 'случае значение
удачного начального приближения особенно возрастает. Полез-
но также априорное представление о величине искомого мак-
симума.
В большинстве случаев удачным начальным приближением
является оптимальное значение вектора параметров, полученное
из оптимизации системы с детерминированными параметрами
(6г=0, z=l, 2,..., /).
153
Если разбросы параметров подчиняются нормальному зако-
ну распределения, то для нахождения экстремума показателя
качества Л(Ро) целесообразно использовать методы, оперирую-
щие с (производными высших порядков.
В этом случае
/?(₽)=(2л; 2 П°Г1ехР
Z-1
поэтому вычисление производных К. не требует дополнительных
интегрирований системы моментных уравнений. Действительно,
°*PZO J a?
В 1
(2. 124)
&>K
ДЛ ,a. <₽/0 — ₽f) (₽Д)— ?>) ,й, ,r.
О)----------—2-------и T. Д,
°z°y
т. e. при вычислении производных используются значения /С(Р)
в тех же узлах, что и при вычислении самого показателя ка-
чества.
Перейдем ко второй задаче. В силу отмеченной монотонно-
сти функции стоимости ее минимум может быть лишь на гра-
нице, определяемой равенством К(Ро, 6) = Ко. Укажем -на -сле-
дующую важную особенность: минимизируемая функция зави-
сит от I переменных, в то время как ограничение — от 2/. Для
каждого набора <Poi, Р02, ...» Рог} минимум стоимости С(6Ь...,
дг) -будет, вообще говоря, различным и достигается при различ-
ных Si* ..6Z*. Иными словами, хотя -=0, но ф 0.
Формальный выход таков: считаем С функцией п величин рог и
решаем обычную задачу поиска относительного экстремума.
Можно доказать, что в этом случае задача решается примене-
нием правила множителей Лагранжа. Относительный минимум
С(6) при условии К(Ро, д)=Ко соответствует абсолютйомуэкс-
тремуму функции Лагранжа
₽02, •••» ₽0Z> &2> •••, az) = C(Si, 8z)-(-
+e(K(₽ov •••> .... ^-Ко].
154
Для нахождения экстремума no-лрежнему наиболее предпоч-
тительным является решение методом Ньютона системы урав-
нений, полученных .из необходимых условий:
-^=0; (2.125)
<7Р01
К (Рох» •••> &1» •••» 8;) = /С0’
Трудности, связанные с выбором нулевого (приближения и
сходимостью метода, те же, что и в (предыдущей задаче.
Заметим, что точки недифференцируемости функции стои-
мости подозрительны на экстремум и требуют специального ис-
следования.
Третья задача является типичной задачей нелинейного про-
граммирования. Из прямых методов наиболее часто в настоя-
щее время применяются метод проектирования градиента и ме-
тод /возможных (йаправлений.
Остановимся несколько подробнее на задачах оптимизации
применительно к системам, процессы в которых можно описать
линейными дифференциальными уравнениями в форме (2.114).
Как уже отмечалось, в достаточно общем случае компоненты
вектора параметров, подверженных технологическому разбросу,
можно считать независимыми величинами, распределенными по
нормальному закону, т. е. можно положить, что
i i
/7(Р) = (2л) 2 П Of1 exp j - у (-^
Z-l
При этом параметр поля допуска принято выражать через
средние квадратичные значения. Например, часто поле допус-
ков задают следующими соотношениями:
^9-¥А<₽,-<Р/о.+ У/’г> Y/>0, * = 1, 2, I,
т. е. полагают
Задача оптимизации в этом случае заключается в определе-
нии оптимальных значений математического ожидания и сред-
него квадратичного отклонения вектора.
Производные нормальной плотности распределения по мате-
матическому ожиданию и среднему квадратичному отклонению
представляют собой произведения некоторых полиномов на гу
же самую плотность. Это позволяет получить удобные для ор-
ганизации итерационного процесса выражения для соответст-
155
вующих 'производных (показателя качества. В частности, наряду
с формулами (2.124) ’нетрудно (получить следующие:
f к (Ю d?= (у /С(Р) ^-в<о)2-а< у, (Р) rffj.
дя‘ i dai J «?
В результате, например, для второй задачи необходимые усло-
вия оптимальности (2.125) могут быть записаны в таком виде:
da/ J 47 я
В *1
U(P) Pf0TPf р(Р)^=О; (2.126)
i °?
^(р)р(р)^=^, / = 1, 2, ..., I.
Решая (первую задачу оптимизации, следует считать, что в
этом случае средние квадратичные отклонения (пропорциональ-
ны математическим ожиданиям
_ ^zPzo
Yz
поэтому плотность распределения вектора параметров будет
зависеть только от математических ожиданий
Р |?1= (2«р П ехр . —1- (-bfM-
. i ^zPzo 2 X, \ Poz /
При этом необходимые условия оптимальности имеют следую-
щий вид:
Y<P'~Y^°~X,Pw р(р)^ = О, / = 1, 2...I. (2.127)
j
Системы уравнений (2.126), или (2.127) целесообразно решать
методом Ньютона, используя для вычисления интегралов интер-
поляционные формулы. Значения условных показателей качест-
ва в узловых точках интерполирования находятся путем интег-
рирования систем моментных уравнений (2.115) и (2.119).
ГЛАВA 3
МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ В ЗАДАЧАХ ПРОЕКТИРОВАНИЯ
СИСТЕМ НАВЕДЕНИЯ
При проектировании 'систем управления современных ракет
наблюдается тенденция к максимальному использованию всех
возможностей ракеты.
Математическими моделями, которыми пользуются при этом,
являются задачи «понтрягинского» типа, т. е. задачи оптималь-
ного управления, в которых объект описывается обыкновенными
дифференциальными уравнениями (детермйнированными или
стохастическими), а на его фазовые координаты и управление
наложены ограничения. Управляющее воздействие при этом ча-
ще всего определяется как оператор от фазовых координат
объекта [6].
На начальной стадии проектирования часто бывает необхо-
димо на основании условий оптимальности и специфики рас-
сматриваемой задачи провести исследования для получения
сведений о свойствах и особенностях искомого оптимального
управления. Такие сведения, которые описывают с точностью до
параметров алгоритм определения управления, называют струк-
турой оптимального управления.
Наиболее развитой математической теорией оптимального
управления, позволяющей решать самые разнообразные задачи
проектирования систем наведения, является принцип максиму-
ма. Основные математические результаты по принципу макси-
мума изложены в работах [1, 5].
В настоящей главе показывается, как, используя результаты
[1, 5], можно установить условия оптимальности управления в
ряде стохастических задач с ограничениями и как на их основе
строить синтез управления.
В разд. 3.1 дается краткое описание способа получения прин-
ципа максимума задач управления с ограничениями на управ-
ление и на фазовые координаты. Излагается схема Дубовицко-
го— Милютина (1, 4], как наиболее приспособленная к получе-
нию условий оптимальности в задачах с различными типами и
157
количествами ограничений на управление и фазовые координа-
ты объекта.
В разд. 3.2 (показывается, как в детерминированных задачах
на основании условий оптимальности могут устанавливаться
свойства искомого управления; находится структура оптималь-
ного по быстродействию управления разворотом ракеты с уче-
том ограничений, свойственных рулевому тракту.
Построение законов управления с учетом случайных воздей-
ствий требует предварительной работы по установлению на ос-
нове принципа максимума условий оптимальности (разд. 3.3) и
преобразованию их к виду (разд. 3.4), удобному для построения
управления. Использование этих результатов для построения
синтеза управления демонстрируется на двух примерах в
разд. 3.5. В первом примере (наведение ракеты на маневри-
рующую цель с учетом ограничений на угол подхода) подробно
описывается способ установления структуры управления, но
определяются только общие свойства оптимального управления^
а параметры его структуры не устанавливаются. Во втором при-
мере (наведение ракеты на маневрирующую цель с учетом ог-
раничений на запас топлива, предназначенного для управле-
ния) процесс 'определения структуры управления описан конс-
пективно. Основное внимание в примере уделено методу
получения параметров структуры.
Рассмотренные примеры указывают метод определения
структуры законов управления.
3.1. МЕТОД ПОЛУЧЕНИЯ УСЛОВИИ ОПТИМАЛЬНОСТИ УПРАВЛЕНИЯ
Кратко изложим, следуя работам А. Я. Дубовицкого и
А. А. Милютина, схему получения необходимых условий опти-
мальности управления в детерминированных задачах с целью
использования этих методов и для стохастических задач управ-
ления. Покажем особенности метода Дубовицкого — Милютина
на примере разбираемой в разд. 3.2 задачи «рулевого тракта».
Летательный аппарат необходимо развернуть на заданный
угол за минимальное время. Рулевой тракт выбран так, что ог-
раничения по угловой скорости отклонения руля и по углу его
отклонения являются на таком развороте существенными. Кро-
ме того, важно при развороте не нарушить прочностные ограни-
чения на рули (силовая нагрузка на руль должна быть меньше
допустимой). Эта задача сводится к следующей задаче опти-
мального управления [1, 4]. Объект описывается системой обык-
новенных дифференциальных уравнений:
= #(/), /), х(0)=х°, х(1)=л1,
dt
где x(t) —фазовое состояние объекта в момент времени
и.(/) —управление,
158
и системой ограничений:
<р(н)^0 — ограничение типа неравенства на управление;
g(x) <0— ограничение типа неравенства на фазовые координа-
ты *.
Необходимо выбрать среди допустимого класа функций
u(t) функцию ц°(0, чтобы функционал
1
J (#(/), х(/)) = J F (х(/), u(f))dt
о
принимал минимальное значение.
Рассмотрим пару функций u(t), x(t). Среди всех таких пар
найдем такую uQ(t), х°(/), которая удовлетворяет всем ограни-
чениям задачи и обеспечивает минимум функционала
J(u(0,x(0).
Найдем необходимые условия оптимальности пары функций
х°(/). Следуя классическому методу, будем -сравнивать
значения функционала J на всех функциях вида
обеспечивающих для достаточно малого е выполнение всех ог-
раничений задачи.
При этом -в отличие от классического метода производится
вначале изолированное определение множества {bu(t), dx(t) },
на котором при достаточно малом е выполняется данное огра-
ничение. Функционал, который минимизируется в задаче, для
однотипности рассмотрения также представляется в виде огра-
ничения типа неравенства
У(я°(/) + е8я(/), х°(/) + е8х(/))<0.
Множества {6u(t)> 6x(t)}, отвечающие соответствующим огра-
ничениям задачи, имеют вид
1) 2^ =|8х(/), 8а(/): ^~= Л8х + 8х(0)= о|;
это множество описывается в виде, включающем информацию
об оптимальной паре «°(£)„ л°(/); так как производные
u(t), t) и /2= -у- f u(t), /) берутся на
л ах аи
оптимальной паре;
2) 2Х(1) = (8x(if), 8«(/):8х(1)=0};
3) 2¥={8х(/), 8«(/) :ср(Ио(/)) + е(ро8и<_8},
* Задача включает в себя только ограничения типа неравенства несме-
шанного типа. Теория Дубовицкого — Милютина касается более широкого
круга задач.
159
где 8>0 и производная берется
“ ди
на оптимальной паре;
4) 2,= {Вх(/),
где 8>0и производная g^=-^ берется на оптимальной паре;
1
5) 27 = {&%(/), bu(t): J —множество
запрещенных вариаций.
Объединение множеств 2j и 2Л(1) обозначим
^ = 2* П 2X(i).
Оптимальная пара должна обладать следующим свойством:
не должно быть общего элемента у всех введенных множеств.
В самом деле, наличие такого элемента было бы эквивалентно
тому, что, не нарушая ограничений, «можно было бы найти та-
кую пару функций w°(/)+edu(/), x°(t) +е6х(0, которая обеспе-
чивала бы меньшее значение функционала.
В случае выпуклости введенных множеств (существование
используемых производных предполагалось) можно воспользо-
ваться следующей теоремой функционального анализа. Если
введенные множества не пересекаются, то существуют такие
линейные функционалы, определенные на пространстве функ-
ций u(t), x(t) и неотрицательные каждый на своем множестве
вариаций, что их сумма (уравнение Эйлера) равна нулю на лю-
бом элементе пространства функций x(t), u(t).
Чтобы воспользоваться этой теоремой, необходимо уметь оп-
ределять общий вид линейного функционала [1, 2, 4], неотрица-
тельного на рассматриваемом множестве вариаций.
Общий вид линейного функционала, неотрицательного на
множестве Q?, можно установить только следующих терми-.
нах (свойствах). Функционал имеет вид —/i(<pu°, i>u). Функцио-
нал /J...) — положительный, т. е. при <pu°6w>0, Л(. ..)^0 и
изменяется только на функциях вида фи°ди, отличающихся
друг от друга на множестве моментов времени t, для которых
ф(«»(О)=о.
Общий вид линейного функционала, неотрицательного на
множестве Qg, будет —higx^x) со свойствами, описанными для
Л(...) с соответствующей заменой: £у06х>0 и =0. На
непрерывных функциях из этого множества функционал при-
нимает вид
1
где мера сосредоточена на множестве тех t, для кото-
рых g(x°(0) =0.
160
Для множества Qj общий вид линейного функционала будет
1
о
а для множеств Q
Z3(&x-8x) + C, 8х(1),
где /3(...) — произвольный линейный функционал; С — произ-
вольный вектор; дх — произвольная функция; 6х — функция,
входящая в множество Qi.
Рассматривая «сразу уравнение Эйлера на множестве функ-
ций из Qi, получим
1
— «о J +^U8«) dt 4-Z1 (— <Р»8«) +
о
1
+j - (/) + С, (1) = 0.
Обычно выбираются для уравнения Эйлера функционалы, обес-
печивающие нормировку
1
Выразим функционалы, зависящие от 6х, через функцию du(Z),
подлежащую «свободному выбору. Для этого используем диффе-
ренциальную связь вариаций:
^=/о8х + /о8а> 8х(0)=0,
и тот факт, что введенные функционалы от 6x(t) являются ли-
нейными функционалами от правой части fu°&u этого диффе-
ренциального уравнения.
Воспользовавшись общим видом такого функционала, «будем
иметь
- s0 j (F06x)rf/ + j -Lg08x^ + Ci 8x(l) = p(Z),
0 0 0
6 3200
161
Справа записан линейный функционал, функцию ф(^) которого
надлежит выбрать так, чтобы равенство
1 1
0 °.
Г dbx
[ dt
fxZx
8x+ф(/), /»8хр/ =
1
=ф(1), 8х(1)-ф(0), 8х(0)-Ц-^- + /°тЖ
О
превращалось в тождество. Для этого необходимо, чтобы
ф(1)=С; _^-=/отф_^о.
Тогда уравнение Эйлера имеет вид
1 1
— s« j Ffiudt — l'i (?28“) + J Ф (z)> fftudt =0.
Отсюда следует, что /i(<pu°6u) можно представлять в виде
• 1
Jxp), tfpudt.
Q
Учитывая произвольность выбора функции получим
уравнение, позволяющее изучать свойства оптимального ре-
шения
_^-х(/\ т2+ж д=о,
где s0>0; Х(/)<р(и»(/))=О; Х(/)>0;
Ф(0 — удовлетворяет приведенной выше системе дифференци-
альных уравнений.
Выше описана довольно общая схема получения условий оп-
тимальности для того, чтобы был понятен путь получения усло-
вий оптимальности управления при исследовании структур уп-
равления в задачах, учитывающих случайные воздействия.
3.2. ЗАДАЧА ТИПА «РУЛЕВОГО ТРАКТА»
Продемонстрируем применение условий оптимального управ-
ления в задаче, к которой сводится исследование по выбору па-
раметров рулевых трактов в- некоторых видах летательных ап-
паратов и в ряде технических устройств. Применительно к лета-
162
тельным аппаратам рассматривается программное управление
разворотом при учете ограничений по углу и угловой скорости
отклонения руля (6, и) и по силе F, возникающей на руле.
В общем виде эта задача формулируется следующим обра-
зом [7].
Объект описывается дифференциальными уравнениями с по-
стоянными коэффициентами *
dF г? . । *
---= и, = а2г
dt-dt
d*
dt
1»
dt
и ограничениями
F2<F2.
(3.1)
(3. 2)
Коэффициенты системы (3.1) связаны соотношениями
kf а = ——, Тч Тч 1! го II "ila- to Io II
Величины z/o, do, Fq постоянны и положительны. Предполагает-
ся, что
а2<0, *4<0, Л>Г2>0, А0>0, ^>0.
Найти измеримую функцию uQ(t) (оптимальное управление),
переводящую объект с максимальным быстродействием из на-
чального состояния д = /7 = б' ='©1 = 0 в конечное состояние
6 = /7 = 0'i = 0, 0' = ^ и обеспечивающую выполнение ограничений
(3.2).
Условия оптимальности. Исследуем эту задачу, используя
результаты работы [1]. Пусть d°(/), ^°(0> ^(О. <h°(0. ы°(0 —
оптимальное решение. Запишем принцип максимума
и° (/) = aosign (Фх+афг),
где
-^-0.
dt dt dt
dt dt dt
(3.3)
(3.4)
(3-5)
^-[(8°W)2-^]=0, ^>0,
[(F<W-F2] = 0, -^->0.
* Постановка задачи принадлежит инж. Н. П. Дергунову.
6*
163
Выражение для функции ф1+#ф2 получим из решения диф-
ференциальных уравнений (3.4):
Ф1^)Ч-«фа(О=(ф1+«фа)я.Ч-<2(^). (3-6)
где
(Фх +«ф2)р. = + Д2е-а1' + AJ + Ал,
t
Q (/) = Ц 28« (0 + 2aFo (Z) Д^_1 dt _
J |_ at at J
о
t т
— -|-aa2) \ e~a,t J 2F° CH)-—- ea>Vri,
о о
Д (gl ^2 Q
a2—b4
л ____#1 + aa2 p
'-^2 —--------------'-'г»
^2
a2b^ 3
Л4 = С4 (Cp C2, C3, C4 —произвольные постоянные).
Используя соотношения на коэффициенты системы диффе-
ренциальных уравнений (3.1), получим Л1 = 0.
Структура оптимальных решений. Оптимальные решения в
рассматриваемой задаче в зависимости от начальных условий
могут «выходить» на фазовые ограничения или «не выходить»
на них.
Пусть оптимальное решение таково, что меры d\iildt = Q (где
f=l, 2), т: е. оно не «выходит» на фазовое ограничение и будет
совпадать -с оптимальным по быстродействию решением (соответ-
ствующей задачи без фазовых ограничений. Из функции (3.6)
следует, что в этом 'случае оптимальное управление имеет два
переключения и представляет собой кусочно-постоянную функ-
цию времени.
Фазовые траектории системы при u = ±uo на плоскости
= Д2-а1-8> ^ = F + ai 8
а2 а2
определяются выражением
2
± аа2~Д1 “о= с ехР —-— У1, (3.7)
а% ± (а2 — а1) ио
где С — произвольная постоянная.
На рис. 3.1 пунктирные кривые дают представление об обо-
их типах фазовых траекторий. Предельные прямые /71 и П2 (см.
164
рис. 3.1) определяются зависимостями (3.7) при у—>-±оо для
u = ±uq соответственно. Замкнутая кривая соответствует типич-
ной оптимальной траектории.
Рис. .3.1. Типы фазовых траекторий и фазовые ограничения системы
Пусть оптимальное решение таково, что хотя бы одна из
мер d^jdt, d\i2ldt не равна тождественно нулю (есть «выход»
на фазовые ограничения). Изучи]
(ф1 + офг) pl имеет не более двух ну-
лей, а ее производная — не более
одного нуля. На рис. 3.2. показан
вид этой функции, функций Q(Z),
ф1(0+яф2(0 и расположение
скачков мер . Заметим, что
на рис. 3.2. указан и ниже разби-
рается случай, когда при / = 0
функция ф1(/) + оф2(0 положи-
тельна. Для другого случая рас-
суждения аналогичны.
Вернемся к рис. 3.1. В коорди-
натах у\, у2 фазовые ограничения
F=±Fq преобразуются в прямые
±Fo, определяемые выражением
а фазовые ограничения S = ±6o —
в соответствующие прямые
функцию (3.6). Функция
Рис. 3.2. Расположение скачков
мер d\bildt (г=1, 2)
6*
3200
165
zfcdo* На фазовые ограничения 4-f’o, 4-до, (—Ль — до) (ом. рис.
3.1, где фазовые ограничения заштрихованы) система 1может
выходить только с /положительным (отрицательным) управле-
нием. Так как а>0 и ai+aa2<0, то из выражения (3.6) легко
видеть, что в момент выхода на фазовое ограничение ни мера
deleft, ни мера d^ldt скачков иметь не может, т. е. в момент
выхода ф1(/)Н-аф2(0 =0. Отметим также, что при нахождении
на фазовой границе ф1 (t) + афг(0 =0 и в момент схода с фазо-
вого ограничения мера не может иметь скачков. Из всего этого
следует (для одного случая это показано на рис. 3.2), что сход
с ограничений +F0 или -j-до может быть осуществлен только в
моменты, когда ^(ф1+аф2) p./dt<0, ибо в противном случае фа-
зовое ограничение будет нарушено (сход с —FQ, —до, когда
d(tyi + aty2)iJdt>0). Таким образом, в случае, когда в началь-
ный момент / = 0 (ф1 + афг) = (^i + fltp2)ix>0, оптимальная тра-
ектория может только один раз выходить на фазовые ограниче-
ния + Л), +6о и только один раз на ограничения —7%,
-до.
Замечание. 1. Каждое решение дифференциальных уравнений (3. 1)
удовлетворяет уравнению
Г1 (Т2& 1 4- — kokfb)+(T2&i 4- — k$kfl) = 0.
Отсюда, учитывая, что в конечной точке 6,i=F=d=0, получим
Замечание 2. Рассмотрим участки оптимальной траектории, лежащие
на фазовых ограничениях. При \F°(t)\=FQ, например при F°(t)=F0, из (3.1)
находим, что функция u°(f), непрерывно дифференцируемая, равна
ц0 (/) = — + fl2^° ехр [ — — Л)^-1], (3 8)
а
где 6 — момент выхода на фазовое ограничение.
При этом координата
80 (t) = j В (/0 + FO1 ехр [ - a, (t - *,) а-1] - Fo (3.9)
L 01 J 0i
и, монотонно возрастая, стремится к д(«>)=—а2Р^а~х.Это следует из aia-1>
>0, равенства (3.7) и ai&+a2F=kf(Т2—Т\)Т2-’[1—е“"^ГаИ°]<0. При |д°(01 =
= д0, например д°=+д0, управление u°(f)«0. Координата F°(t), монотонно
убывая, стремится к F(ж) =—ai60a2~l>().
Таким Образом, оптимальная траектория выходит на фазовые ограниче-
ния только в следующем порядке +Fo, +до, —Fo, —до, хотя при этом может
и не выходить на некоторые из них.
Синтез оптимального управления. При построении синтеза
управления ограничимся наиболее часто встречающимся на
практике случаем, когда фазовая траектория с и = ±и0, проходя-
щая через начало координат, вначале пересекает фазовое огра-
ничение F = 4zF0. Другой возможный случай, когда вначале пе-
ресекается ограничение д = ±до, рассматривается аналогично.
166
Ис-следуем оптимальное решение с управлением на -началь-
ном участке uQ(t) =±Uq. Можно показать [5], что если началь-
ный участок оптимальной траектории заканчивается внутри фа-
зовых ограничений, то вся траектория лежит внутри фазовых ог-
раничений. Задачей синтеза в этом -случае является определение
с помощью текущих фазовых координат объекта двух моментов
переключения.
Рис. 3.3. Оптимальные фазовые траектории системы
Рассмотрим 'случай, когда начальный участок траектории за-
канчивается на фазовом ограничении F = ±F0. Здесь задача син-
теза состоит в определении момента времени t3 схода с фазово-
го ограничения (ограничения F = ±F0 или следующего за ним
d = ±So) и различения после этого двух возможных видов кон-
цевых участков оптимальной траектории:
первый вид — концевой участок целиком находится внутри
фазовых ограничений (рис. 3.3, траектория, проходящая через
точки 2,1,0);
второй вид — концевой участок выходит на фазовое огра-
ничение F°(/)==FFo (рис. 3.3, траектория, проходящая через
точки 3, 4, 5, 0).
Для траекторий с концевым участком первого вида синтез
управления будет осуществлен, если момент t3 и момент /5 —
момент -перехода на участок траектории с и = ±ио, проходящей
через начало координат (см. рис. 3.3), будут выражены через
фазовые координаты системы. Изменение * фазового состояния
6+*
167
объекта на концевом участке описывается при учете формулы
(3.7) следующими уравнениями:
--= и\ ——=a2VUJ;
dt dt 2 i I 3 *
4 . z,
dt 1 3
М/
(3. 10)
Фазовые траектории этой системы .при и = ио в координатах
8= — &1== —_^М —
(22 #2
описываются уравнением
[2
--------8
a3tf0
(3.11)
(3. 12)
где С — параметр.
Выразим фазовые координаты системы в момент (им при-
своим индекс (5), а на рис. 3.3 ему соответствует точка 1) че-
рез координаты в момент /3 (с индексом (3)) перехода на кон-
цевой участок оптимальной траектории. Используя уравнение
(3.12), получим
Здесь и ниже верхние знаки соответствуют траектории, начи-
нающейся с u=+uo, а нижние — траектории, начинающейся с
и = —и0. Проинтегрировав уравнения (3.11) от концевой точки
g = f’ = '&1=0, 'O' = '0iK в обратном порядке соответственно до точки
/5 с u—±Uq, а от точки t5 до t3 с и = =РШ), получим
8(3)_ _ [»(15) + Т Дэиря-Г2] |-e_e,x(3)_ lj _|_
’, ‘ ‘ #2 „
J Т _ 44] +8Ю, (3. 15)
#2 у 2^2 ^2 /
где
. 8(3) _8(5) б(5)
- т'3> —--------•; 5) =---------;
’ "F и0
168
&(5>=±
Дз«0
а2
е-а,т(5) ±
0(5) = т 23ffo [e-e„(5)_ i] ±
д| L 2в2
Подставляя соотношения (3.13), (3.14) и (3.11) в (3.15), по-
лучим
ОО) =0(3) (ВО), 0(3), 0к). (3.16)
Отсюда следует, что момент t3 определяется из- условия равен-
ства нулю функции
../1(8, 0п 0, 0к) = 0(/)-0(±з)(8(/), М). U (3- 17)
Для траекторий с (концевым участком второго вида, кроме
моментов /3, ^5, через текущие фазовые координаты нужно вы-
разить еще один характерный момент времени t4 — момент вы-
хода на фазовое ограничение f’ = zFiFo. При движении по этому
ограничению семейство фазовых траекторий системы описыва-
ется зависимостями:
в плоскости Ф,
&=±Zo_ln »i + ±.fI + (»1 + Af0)2_+C; (3.18)
04 U4 I \ О4 J и<1
В ПЛОСКОСТИ d,
8 + ро =-----------------------------2------. (3.19)
п ^2 ~
Т — Л)
д4
Двигаясь из конечной точки в точку 5, получим зависимость
$)(5) (б(5)), ^5) (§(5))ф Используя первую зависимость, с помощью
(3.7) при F = +Fo определим д<5>:
+ 7\k0F - - (Т2 - Л) (8(5)) = 0.
Из формул (3.18), (3.19) находим, что в точке 4, соответст-
вующей Ц,
&«)= + In I &<4> + Fo
- «4 I 1 *4
+(9"’ +
)4г+с)Ч;
/ D2
8(4) ± -^Fo ---------------------ь--------,
(3.20)
(3.21)
где постоянные С^5>(&к), С^5>(&к) легко находятся из условия
прохождения этих фазовых траекторий через точку 8<5), ^<5),
&(5), +^о-
169
При движении ib открытой области, когда u—const = Тио, из
системы (3.1) можно получить
d (»i — М— b2a2 XF + ab2a2 *8)
— = ——* о,
db О'ОЦъ
что соответствует
_ g2«o(»i.—. М) £ _«о_ р а“о а=с«)гЗ. 22)
Д14г Д1 «1 2
Из условия прохождения фазовой траектории (3.22) через
точку 6<4>, -б/4), -Of4), TFo находим
С<4)=:р_£22о.р(4)_Й4&(4)) + Jf2-F0 + 1^!. (3.23)
С ’Помощью зависимости (3.7) и замечания 1 получим урав-
нение, определяющее 6<4>:
й(4)
+ Л0+-^8<4> + £^±^-«0=с<3)е “° , (3.24)
fl2 aj
где
СО)= F<3>-|-
Д1 g(3) т; аа2 + а1
а2 д|
±£’/3)
е “° ;
ГЛ^(3) - 7\W(3) - (Л - Л) Т=0.
Таким образом, получим
из (3.24) 6<4>=S<4) (8<з>, 0(з>);
из (3.20) 0<4>(8(3), &(3));
ИЗ (3.21) &(4) = &<4) (8<3), &(3));
из (3.23) С(4)=С<4) (8<з), &(3), &к). (3.25)
Переход оптимальной фазовой траектории на концевой уча-
сток, т. е. определение момента времени t$ при синтезе опти-
мального управления, происходит тогда, когда текущие фазовые
координаты системы 6, О удовлетворяют уравнению
Л (8, »к)=+-^
«1
+ -£ifo.8-C(4>(8(3), »(3), &K)-|_2L=o, (3.26)
CL\ 2
где С<4) (...) определяется из соотношения (3.25), F — через Очй
из формулы (3.7).
170
Синтез управления строится следующим образом. В процес-
се движения объекта вычисляются определенные выше [см.фор:
мулы (3.17), (3.26)] функции текущих фазовых координат и
требуемого конечного бк: /<(...), /г(. •.) и проверяются условия
F(О =+Л>(—Fo) и д(0 = +бо(—бо). Вначале движение объек-
та происходит по начальной траектории (см. рис. 3.3) с u°(t) =
= ±uo. Выбор того или другого начала определяется правилом
и°(0)0к>0. Правило обосновывается в {5]. В момент F(t) =
= +Fo(—Fo) траектория выходит на фазовое ограничение по F
и движение продолжается с u°(t), определяемым в соответствии
с формулой (3.8). При этом координата |б(0 | монотонно возра-
стает. В момент б(/) = +б0(—бо) траектория выходит на фазо-
вое ограничение по б и движение продолжается с а°(/)==0.
Траектория сразу же сходит с фазового ограничения по F, так
как координата |F| монотонно убывает.
Описанное движение осуществляется объектом полностью ли-
бо частично в зависимости от того, когда наступит момент /3
схода с фазовых ограничений. Этот момент совпадает с момен-
том выполнения одного из равенств:
Л(*. »к) = 0, /2(8, &, &к)=0.
При выполнении первого равенства оптимальная траектория
имеет «концевой участок .первого вида. Движение объекта с мо-
мента /3 происходит с uQ(t) =h=Uo до момента /5 (на рис. 3.3 он
соответствует в этом случае точке /); при этом Л(б(/), 01(0,
Момент /5 определяется как первый после t3 мо-
мент, когда функция fi(...) -снова становится отличной от нуля.
Начиная с момента t5 управление uQ(t)—±u0 -и «сохраняется та-
ковым до конца процесса, которое определяется равенством
Л(0=«к.
При выполнении второго -равенства оптимальная траектория
имеет концевой участок второго вида. Движение объекта с мо-
мента /3 продолжается с до момента и при этом
/г1б(О, 01(0, ^(0, ^к]=0. Момент /4 определяется из условия
F(f) =—Fo(+Fo).. Начиная с момента f4 и до момента /5 движе-
ние происходит с ц°(/), определяемым .в соответствии с форму-
лой (3.8). Момент определяется условием Д(Л(О, Oi(0> ^(0»
f>K] = 0. Заметим, что до этого момента времени, начиная с на-
чала движения, эта функция знака не меняла. С момента t* и
до конца процесса движение происходит с uQ(t)= ±и0.
Замечание 3. Здесь не устанавливается явная зависимость оптималь-
ного управления и°(...) от текущих фазовых координат объекта. Получение
этой зависимости ввиду ее громоздкости вряд ли целесообразно. Приведенные
выражения для определения характерных моментов времени (£з, /5 и т. д.)
через текущие фазовые координаты и выражения для определения оптималь-
ного управления в промежуточные моменты времени даюг полную информа-
цию для практической реализации искомого синтеза.
171
3.3. УСЛОВИЯ ОПТИМАЛЬНОСТИ УПРАВЛЕНИЯ
В ЗАДАЧАХ С ОГРАНИЧЕНИЯМИ
ПРИ НАЛИЧИИ случайных воздействий
Широкий круг задач определения рациональной структуры
закона управления объектами может математически формули-
роваться как статистические задачи оптимального управления с
осредненными и неосредненными ограничениями на фазовые
координаты.
Условия оптимальности управления в таких задачах получа-
ются на основании .использования подхода Дубовицкого — Ми-
лютина [1].
В этом случае рассматривается задача минимизации некото-
рого функционала при наличии следующих ограничений:
1) дифференциальных уравнений со случайными воздейст-
виями, описывающих поведение объекта;
2) ограничений на фазовые координаты объекта, имеющих
интегральный или неинтегральный вид;
3) ограничений на управление.
Кроме этих ограничений, накладываются ограничения на
информацию, на основании которой выбирается управление.
Общая тенденция решения задач на экстремум функциона-
ла — локальное варьирование. Однако не все задачи допуска-
ют такое варьирование сразу. Иногда необходимо предваритель-
но преобразовать задачу к виду, удобному для локального варь-
ирования, т. е. предварительно «организовать» задачу. Методы
такой организации задач описаны в работах А. Я. Дубовицкого
и А. А. Милютина [1, 4].
Рассматриваемая в работе задача исследуется по следующей
схеме:
1) . проводится преобразование задачи к задаче, удобной для
локального варьирования;
2) устанавливается связь исходной и преобразованной задач;
3) проводится локальное варьирование преобразованной за-
дачи, на основании которого получаются необходимые и доста-
точные условия оптимальности управления исследуемой задачи.
Прежде чем сформулировать задачу, ощишем класс прило-
женных к объекту случайных воздействий и класс используемых
управлений.
Случайные воздействия. g(£ со) — случайный процесс на
следующей природы. Отрезок [О, Г] разбит на п час-
тей:
О = <С 4 • • • < 1 л =
На интервале аргумент со принадлежит некоторому
множеству Qi+i. На множестве Qz+t введена непрерывная веро-
ятностная мера dcDf+v На множествах QiX ... и QjX
172
XQj+iX ... XQn мера определяется как .прямое (произведение
мер dan ... dtoi и . duj+i... соответственно при
i, j= 1, 2,..., n.
Класс управлений. В начале каждого интервала [fy, /<+1] в
момент t=ti наблюдается (Oi+i€Qi+i- На основании этого наб-
людения и наблюдений, проведенных на предыдущих интерва-
лах, выбирается управление
u(t, (01, . . ., (Oi+l)
как измеримая ограниченная функция переменных
Таким образом, управление u(t, со), имеющее на каждом интер-
вале описанный выше вид, есть функция растущего числа пере-
менных. Всякую такую функцию будем в дальнейшем называть
функцией с требуемой структурой. Введем следующие обозна-
чения:
при /€(Л-, ti+\)
/(Х(/, (Dp ..., 0)/+1), И (/, (Dp ..., (oz+1), 5 (/, (о/+1)) =
= /(х(/, со), «(/, (о), !•(/, (о));
J О(Х(/, (Dp ..., (Dz+1))rf(D1...rf(D/+1= J О(х(/, (o))d(D,
С|Х...о/+1 . а
где G(x(...)) обозначает любую из функций F(x(T, о)),
g2(x(t, ш)).
Рассмотрим следующую задачу.
Задача Ло. Среди функций u(t, со) с требуемой структу-
рой найти функцию (управление), минимизирующую функцио-
нал
fF(x(7, <o))rf®
fi
при следующих ограничениях на конечномерные вектор-функции
x(t, <о), u(t, со):
1) ш), а(Л ш), $(/, со)), [0, Г], х(О)=хо;
2) x(t, <o)€D;
3) =
4> u(t,
Предположения на функции и множества:
F(x(T, со)) — абсолютно интегрируемая по со функция;
f(x, и, i), i(t, со), u(t, ®) — такие функции, что решение диф-
ференциального уравнения x(t, со) существует, непрерывно по t
173
для почти ®cex шив любой достаточно малой окрестности точки
^€[0, Г] функция x(t, со) равномерно ограничена по со;
gz(x) —.непрерывная функция;
множества D и U — (произвольны.
Проведем исследование задачи Ло. Будем рассматривать ла-
ры функций ql (Л а)) = {л/ (/, со), (/, <о)}, где функции xl (t, <о).
(о) имеют требуемую структуру, связаны дифференци-
альным уравнением и удовлетворяют неосредненным ограниче-
ниям
xz(Z, о))С£>, (n)€t/.
Назовем эти пары допустимыми парами. В дальнейшем пред-
полагаем, что существует хотя бы одна допустимая пара функ-
ций задачи Ао.
Пустыпара q°(t, со) будет оптимальным решением задачи Ло;
{q'tt, со)}, 1=0, 1, ..., т — некоторый набор допустимых пар.
Построим на этом наборе множество решений следующим об-
разом.
Из множества всевозможных пар, полученных линейной ком-
бинацией из элементов набора
и-о
выделим подмножество пар, которые будут допустимыми. Най-
дем условия на аг((о), достаточные для того, чтобы пара
т
ai (“>) Я1 (А (Ъ) была допустимой,
/-о
Каждой паре пар q°(t, со); </’(/, <о), i = 0, 1,..., tn, поставим в
соответствие число ш), co))=rt-, равное номеру того
интервала разбиения отрезка [0, Г], на котором они впервые
начиная с интервала [й>, не совпадают. Рассмотрим такие ли-
т
нейные комбинации at (^q1 (t, u>), у которых коэффициенты
/-о
обладают следующими свойствами:
1) а^)(о>) = а</...,
2) a{*)(u>) принимает значения либо 0, либо 1;
т
3) 2а/*)((0) = 1' где номер i соответствует номе-
1-0
(3. 27)
ру пары ql (/, a>)€ \ql (t, «>)}•
174
Установим, что если ^°(/, ш), о>), .... q‘ (t, «>),
.... qm(t, ш) —функции с требуемой структурой,
(^(«oj,ajuij.........а>Г1), ..., а, (со,, ..., а»Г/). am (юр ...,a>rm) — •
произвольные скалярные ограниченные измеримые функции и
т
2а'(ш1’ •••• ‘*>г/)= 1,
Z-0
то
т
q(t, 1о)=2а/(ш1’ •••> шг)я1{^ «>)—функция с требуемой струк-
/-о
турой.
Достаточно показать, что функция q(t, со) на произвольном
зависит только от (о1; <0j. Слагаемые аДам,......
соГ/)<?’(£ со), у которых зависят только от требуемого чис-
ла <0. Остальные слагаемые (г,->/) зависят от большего числа
со, однако все они на рассматриваемом интервале обладают
свойством
az(u>i, ..., a>) = az(a>1, ..., <оГ/)^0(/, о>).
Сгруппируем слагаемые
<7 (Л ®)= 2 “/(“v •••> "‘r.'iq'tt, и>)+^°(/, ю) 2 ai (ш1> •••> 0)rzA
Так как
2 а> (“i- %)= 2 <°r? +
Z-0 l.r^j
+ 2 <b'J=1’
/:rz>/
TO
2 al — ,®rz)=l— 2 a^“>1’
Z:rz>7
зависит только от coi, ..ojj. Отсюда следует, что q(t, со) имеет
требуемую структуру.
Если (коэффициенты линейной комбинации
Я (Л о) = 2 а</°
с=о
составленной из набора допустимых пар со)}, удовлетво-
ряют условиям (3.27), то пара q(t, со) будет допустимой парой.
175
Рассмотрим задачу Ао на множестве допустимых пар
?(Л о>)=2 (Л
Z-0
порожденном некоторым фиксированным набором {?’(£, со)}.
Непосредственно ясно, что
f f [ 2 а1Л) (ш) х‘ (г> •®)) rfu>= f 2 а<'А) fu)) F (х/(Г’ю)- а<°'
а \1-о / a 1-0
Убедимся, что если пара qa(t, <о) была оптимальной в зада-
че Ло, то точка а^Л)(о>)=1, а^*>(<о) = 0, /=1, 2, т будет оп-
тимальным решением в следующей задаче.
Задача At.
min Г V а(*> («>,,) F (х‘ (Г, о>)) d<o
при ограничениях:
1) (юГ/) — принимает значение либо 0, либо 1;
2) 2 <4‘>(%) = 1;
Z-0
3) С(0=J2 ч))^<0,
2 Z=0
где
а/ (ШГ/) = а/ (Ш1» <°2» •••» <%)• '
В самом деле, если бы это было не так, то нашлась бы дру-
гая точка аоЛ)(«)), а1Л)(ю), (ю), удовлетворяющая всем
ограничениям задачи Alf для которой выполнялось бы
[ 2 ^ft) (u)) F ^xi ш)) rfu)= fF (2 а^Л) xl to))
2 Z-0 2 \z-l
&
g2 f 2 а^Л) wxi у* «о)< °-
2 V-0 /
Так как
2 а/Л) (<*>)х' (А <«); 2 а^,Л) W ul
z=o z=o
будет допустимой парой, то это противоречит (предположению ог*
оптимальности пары gQ(tf w).
176
Задача Ai определена на множестве функций а}Л)(соГ/), ко-
торые могут принимать только два значения: либо 0, либо 1.
Расширим задачу Д1 так, чтобы получить задачу, удобную для
локального варьирования.
Пусть — пространство ограниченных измеримых
(m-Н)-мерных вектор-функций
«oW = “o(">l- •••', “л)
(Wr |) == (*°1» •••’
а(<о) = ' ’ ' ’ ’ ’ ‘ ........ ’
а/ (^Г/) — а/ • • •»
> am(urm) = am^v (DrJ
и С[0, Г] — пространство непрерывных функций
На прямом произведении пространств Л4т+1хС{0, Г] рас-
смотрим задачу А2.
Задача А2.
' min С V az ((ог.) F (х* (Г, co)) с/о
при ограничениях:
1) 0<az(cof/);
2) 2 a/ = 1’
/-0
3) C(/)<Q;
4) 4Z) — f 2 (*z =
2 /-0
Назовем задачу A2 «задачей для варьирования, соответст-
вующей выбранному набору допустимых пар {^l(t со) }». Ее бу-
дем исследовать методами локального варьирования [1]. Уста-
новим связь задач Ао и А2.
Докажем, что если qQ(tf со) — оптимальное решение задачи
До, то для любого набора допустимых пар {?*(/, со)}, / = 0,
1, ..., т, в соответствующей этому набору задаче для варьиро-
вания Д2 точка
а0 (<о) = {а° (<оЛ) = 1, а?(%) = 0, Z = 1, 2, tn],
2
будет стационарным решением.
Для доказательства этого понадобится следующее утверж-
дение [8]:
177
всякое непустое множество Я (а) функций а(<о) €Afm+l, опре-
деляемое условиями:
1) а, (io,z) 0, i = 0, 1, т;
2) 2 «/(%•)=!;
Z-0
3) J 2 rfto=A’A=0- Ь-Л
S 1—0
содержит точки, состоящие из 0 и 1.
Приступим к доказательству. Пусть а (со), — произволь-
ная вариация из Мт+}ХС[О, Т]. Выпишем множества запре-
щенных вариаций Q° и допустимых Q* по г-му ограничению за-
дачи А2:
2° =
т
С 2 а/ («%)Л*' (Л «>))*«»< О
Q 1—0
— выпуклый открытый конус (предполагаем, что он не пуст);
2Х= [а((<nr.)^ez^>0, Z=l, ..., т; а0 («>„) —любая функция]
— выпуклый открытый конус;
[т т __
2’а,К()=0; С(/)-J2a/(%.)^(^(A «>))^ = 0
Z-0 б Z-0
— подпространство ('выпуклый конус);
Q3=[g(/)<0 на том множестве t, где £a(f)=0, £(0 произволь-
ная на дополнение к этому множеству] — выпуклый, открытый
конус.
Пусть точка ао(<о), £°(/) не будет стационарным решением в
задаче Л2. Тогда приведенные выше конусы будут иметь непус-
тое пересечение [1]. Пусть а°((о), £°(/) — одна из точек этого пе-
ресечения. Составим вектор-функцию
(а, (<оГ/)=а? (<о,.) + еа° (<d,z) ),
С(/)=С»(/)+еС’(/)
и подберем е>0 так^чтобы выполнялись все ограничения зада-
чи Л2 и ограничение £(/)<0, а значение функционала
_ _ т
У («(<*>), £(/)) = J 2 [а?(а>Г/)+еа?(шГ/)]^(хЧЛ a>))da> =
2 Z-0
= £ J а? (<%•) F (0)) “h J (х° (^» (0))
2 Z-0 б
< J F (х° (Г, <»)) d^=J (а0 (а>), С°(/)).
в
178
Покажем, что это противоречит предположению об оптималь-
ности решения qQ(t, со) ® задаче Ло. Для этого установим, что
можно подобрать такую функцию <a(ft)(co), состоящую из 0 и 1,
что вектор-функция (<о), (/)= С а/й) (<%) ёъ (Ъ “>))
2 Z-0
удовлетворяет всем ограничениям задачи Л2 и
С<*> (/))=/(а (ю), С(/)).
Так как С(/) = j* | g2(*z (^» при /=0,
s
_и непрерывны на [О, Г], то существует такое ео>0, что
1(0 <—ео<О. В силу равномерной непрерывности £г(0, £(0 на
интервале [0, Т] последний можно разбить на такие непересе-
кающиеся .интервалы (/>, О+iL на каждом из которых колебание
функций будет меньше ео/2(т+1). Пусть это достигается на
разбиении
Рассмотрим множество функций а(со), для которых
1) 0 az (av.), i — 0, 1, m;
m
2) 2 az (<.>,,)=!;
Z-0
3) J 2 ai Si (x‘ (tj, u>))rfa>=C(/7), j = 0, 1, s;
2 Z-0
4) j 2 ai (%)F (x‘ (T’ °’))dts>=J («W’ w)-
2 Z=0
Из приведенного выше утверждения следует, что это множе-
ство имеет точку
а<»>(а>)={<>(»„), а«*)К,), .... a^>(«>rjb
состоящую из 0 и 1. Непосредственно устанавливается, что
с<») w=j 2 a<ft> g2 (%/ < °-
2 Z-0
Таким образом, точка a(fc)(co), удовлетворяет всем огра-
ничениям задачи Л2 <и
С<»)(/))=/с(/))</(а®(ш), :•(/)).
179
Но пара функций
Я (А <*>)=2 а/Л) <*’
z=o
будет удовлетворять всем ограничениям задачи Ло, и на этой
паре
Л? (Л «)))=./(«(*)(«)), С<Л) (/)) < У (^° (Л со)) = /(а°Н);
что противоречит оптимальности решения q°(t, со). Следователь-
но, точка а°(со), £°(/) = [&2(*°(^ <о))Ло будет стационарной точ-
s
кой задачи Л2.
На основании этого получим условия оптимальности реше-
ния 9°( t, <о) в задаче Ло. Запишем уравнение Эйлера задачи
Л[1].
Конус (Q0)*, -сопряженный конусу Q0, состоит из функционал
лов вида
— s° j 2 az (шг.) У7. (xz (Г, s0>0.
2 Z=0
Конус (Q1)*, сопряженный конусу Q1, состоит из функцио-
налов вида
Z-1
где Хг(...) — позитивный функционал в пространстве £«> функ-
ций ОТ (01, .., соп.
Выпишем общий вид функционала из конуса (Q2’4)*, сопря-
женного подпространству Q2»4.
Из [1] следует, что каждый функционал из конуса (Q24)*
можно записать в виде
(т \ ( _ т __________________ \
2 +Z 40 — J 2 О/ (<*>rz) g2 (/, w)) doy ,
i-Q / \ 2 / —0 J
где o(...) — произвольный линейный функционал из множест-
ва (Л11)*;
Z(...) — произвольный линейный функционал из множест-
ва (С[0, Т])*.
Конус (Q3) *, сопряженный конусу Q3, состоит из функционалов
вида
_ J 40^(0.
о
180
где dn(t)^O — мера, сосредоточенная на множестве тех t, на
которых £°(f) = J(o))d<o = 0.
s
Уравнение Эйлера [1] имеет следующий вид:
т т _
— s° j 2 а‘ (xZ С7’’ <o))rf<o + 2xz(az(«>rP)-
2 /=0 Z = 1
Т / т _ \
_ с с (/) (/)+з 2 а‘ ы + W) -
о V-1 /
т ,
<*>))^)=0, (3.28)
2 Z-0
где |$0, НМ» ^14^1 #О» т- е- не все функционалы нулевые.
I 1 J
Рассматривая это уравнение на подпространстве Q^4 и учи-
тывая, что выбор функции ai(cor/ ), /=1, 2, ..т независим и
что из условия $о = О, d|i(f)=O следует 2||Хг|| = 0 (что противо-
речит условию (3.28), получим для любого i\
— $о j* aZ (WrZ) (Т» <°)) — ? (Х° (Г/ U) ))] rfw +
2
_ _ Г
+ К (ai (*%)) — ai (“г,-) dt>i J [^2 (•*' (Л «>)) —
2 0
— ^(-^(Л <•>))] rfj* (/)=0;
(«о, ^1/0-
(3. 29)
Из_рассмотрения этого .уравнения на положительных функ-
циях ai(co,z ) можно заключить, что для произвольной функции
а<(юп)
s0 j* а, («>г.) [F (xz {Т, ш)) — F (х° (Г, ш)))d<o Ц-
2
+ f “z (<%) du> J [g2 (xz (Л (о)) — g2 (x° (/, to)) ] dy. (f) > 0;
2 0
(s0. /0-
181
Таким образом, для любой пары функций со) из выб-
ранного ранее набора должно быть справедливым следующее
неравенство *:
> J р0Г(х°(Л to)) + Jg2(x°(/,
L о
dw
(3.30)
для почти ®сех со,, а>г,.., i=l,2,..т.
Обозначим рассматриваемый набор допустимых пар через
т, а множество постоянных so^O и мер dp^O, [dp][£°(/)]=O,
удовлетворяющих неравенству (3.30) и условиям нормировки
г
so+^t1(^) = l, через Кт- Отметим, что это множество опре-
6
деляется т (выбранным набором пар).
Рассмотрим два набора допустимых пар mi и гпг задачи Ло.
Если набор т2 включает набор /п1( то, как следует из. (3.30),
Кт^Кть- Если наборы разные, то рассмотрим новый набор
(mt U mz), состоящий из объединения наборов mi и т2. Для это-
го набора Km^KmiU т, И Кт^Кт, um,- Такая система имеет
непустое пересечение К= П Кт [8].
т
Итак, можно найти единую для всех наборов допустимых пар
постоянную $о^О и меру dp с нужными свойствами, при этом
неравенство (3.30) будет выполняться для любой допустимой
пары q(t, со).
Пусть выбраны такие «о, dpe/C
а) Пусть Зо>0. Полагаем s0= 1 и покажем, что необходимые
условия (3.30) оптимальности решения x°(t со), u°(t, со) задачи
Ло будут достаточными.
В самом деле, пусть q°(t, со) есть решение задачи Ао, удов-
летворяющее неравенству (3.30), a q*(t, со) — произвольное ре-
шение. Под решением здесь понимается допустимая пара, удов-
* Здесь и ниже использовано обозначение
У [... ] dar+I У [...]da>.
ач+1Х-хая е/аг
182
летворяющая всем ограничениям задачи Ло. Условия (3.30) для
решения <?°(/, ©) и q*(t, и) дают
F(x*(r, а>)) + f g2 (л* (t, u>)) rfp. (/) rfu>
г T
j* F(№(T, ®)) + J g2 (л® (/, «>)) </(»(/) dw
0/2;.» L 0
для почти любого ..., (Hr* Проинтегрируем это неравенство
по всем © и отметим, что
т т
\ dp(t) { g2(x°(t, <й))</<о = О, a g2(x*(t, u)))rfa><0.
) 2 0 2
Тогда
j* F(X*(T, <о))Жо,
а 2
т. е. 9°(t со) — оптимальное решение.
Итак, сформулируем условия оптимальности решения
qQ(t, (о) = {х°(/,(о), и0(Л о))}
задачи До-
Для того, чтобы пара 9°(/, со) была оптимальным решением,
необходимо (а при s0>0 и достаточно), чтобы для любой пары
q(t, со) = {х(/, о), u(t, со)}, удовлетворяющей дифференциаль-
ным уравнениям и 1неосредненным ограничениям задачи и совпа-
дающей с парой qQ(t, со) на интервале [/0, ^r-iL для почти всех
cot, сог, ..сог выполнялось следующее неравенство:
sqF(x(T, (о)) + Сg2(х(/, (o))cW)
т
s0F (л° (Г, «>)).+ f g2 (л (/,. «>)) (/)
о
с/о),
где
s0>0; б/р, (/) g2 (х°(/, io))4/<o = 0, 4/р.(/)>0.
2
Замечание. Отсюда следует, что вместо задачи До можно исследовать
задачу на минимум некоторого нового функционала при прежних дифферен-
циальных уравнениях и неосредненных ограничениях. Осредненные фазовые
ограничения задачи До «переносятся» в этот новый функционал.
1ВЗ
б) Пусть $о = О. При $о=О мера и из условия (3.30)
для произвольной допустимой шары q(i, со) получим
т т
J d^g2(x(t, <о))4/|1> J <*<ojg2(x®(/, w))<Z|». (3.31)
2/аг О 2/2f о
Из условия (3.31) следует
т т
о = J dp (/) j* g2 (х® (/, <о)) dw < j dp. (t) j* g2 (x (t, «>)) d<o.
0 2, 0 2
Так как тахД^С*0^» <o))dco = 0, то для любой допустимой
пары q(t, со) -существует такая точка /*е[0, Г], что
max (g2(x°(^ f £2(*(**»
o<c<rJ J
<imax Cg2(x(Z, w))cZo).
o</ <r J
Таким образом, условия (3.31) будут необходимыми и дос-
таточными условиями оптимальности решения 9° (Л (о) = [х°(/, со),
я0(/, со)} в задаче на минимум функционала
max fg2(^ <o))rfco.
при ограничениях 1, 2 и 4 задачи Ло.
3.4. ПРЕОБРАЗОВАНИЕ УСЛОВИИ ОПТИМАЛЬНОСТИ
В ЗАДАЧАХ УПРАВЛЕНИЯ
ПРИ НАЛИЧИИ /СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ
В предыдущем разделе было установлено, что задача опти-
мального управления с осредненными и неосредненными фазо-
выми ограничениями эквивалентна задаче только с неосреднен-
ными ограничениями, но с некоторым новым функционалом. По-
этому особенность задач с фазовыми ограничениями с точки
зрения использования необходимых условий оптимальности бу-
дет проявляться и в задачах с неосредненными ограничениями.
Приведем вычислительную процедуру получения оптимального
управления для одного типа статистических задач с неосреднен-
ными фазовыми ограничениями [9].
Задача Af. Найти управление u(tt со), минимизирующее
функционал
J F (х (Г, (о)) с/о)
2
184
при следующих ограничениях:
1) «)) + /(«(/, о>), /Ж (Л ш),
х(О)=хо, /€[0, Г];
2) x(th w)€A, Z = 0, 1, ...» п\
3) и (/, <o)€t/,
где F(x) — выпуклая функция; A(t), f(u, t) — ограниченные
измеримые функции и f(u, t)=B(t) u(t, (d);Di — выпуклые зам-
кнутые множества; U — произвольное замкнутое множество;
£(t, со) — векторный случайный (процесс следующей природы.
Отрезок [0, Т] разбит на п частей с точками деления
0—Ч <^1 tn-1 ’ж ^п. = Т.
На любом интервале 1АЛ+1] аргумент coeQi+i может изме-
няться только при t = ti. На множествах Qi, *=1, 2,..., п, вве-
дена вероятностная мера Лог-. Управление u(t, со) должно при-
надлежать множеству функций -с растущим числом переменных:
на [/г-, /i+i] функция и(/, со)=и(/, ом,..., coi+i), где соь...
coi+i^QiX ... XQi+i. На множествах QiX...XQi+i
мера определяется как прямое произведение мер dcoi,...
... , C?(0i+i.
Предполагается, что хотя бы одно решение задачи сущест-
вует. Из предыдущего раздела следуют условия оптимальности
решения задачи среди множества Q пар функций q(t, со) =
= {u(t, со); со)}, удовлетворяющих всем ограничениям за-
дачи _оптимальная пара qQ(t, со) обладает следующими свой-
ствами: Gi(x°(/i, coi)) ^G\(х(Л, col)i) почти для всех coi и для
всех q(t, co)^Q,
GZ(X°(/Z, (Op ... (0/))<G/(x(//,a)n ...» «)/))
почти для всех coi,..., coi и для всех q(t, co)eQ, совпадающих
с оптимальной парой на интервале [/0, /ж];
<Зл(х°(/я, ®р ... <•>„))<Оп(х(/„, «>!, ..., «>„))
почти для всех coi, сог, .., соп и для всех q(t, co)eQ, совпадаю-
щих е оптимальной парой qQ(t, со) на интервале [4, tn-il
При этом
<»))=F(X(T, (Op ..., «>„));
<*>i, •••, «/))= f min X
X Gi+1(q (t, Wp ..., Wi+i))dw{+1,
7 3200
185
где выражение {q(t, со), |7о, /<]} обозначает множество тех пар
функций q(t, со), которые совпадают на интервале [/о, Л] с фик-
сированной парой q(t, coi, .. .,(ог).
Заметим, что если лары q'ft, со); q2(t, co)eQ для каждой
фиксированной точки coi, ..., cot-eQiX .. .ХЙг обладают свойст-
вом
X1 (ti—1, to) = Х2(^_ 1, со) = XZ_ 1 (со),
а на интервале i, tn] пара qx(t, со) =92(t со), то для них спра-
ведливо
j юр <ол)) д?а>/+1...дГюя=
e/+1x...xo„
= j F(X2(T, (Op .... <Ол))4/(0/+1...4/(Ол.
ex.+1x...xo„
Любые пары с такими свойствами не будут различаться при
проверке свойств. Тогда каждому классу пар {q(t, coi, ..., со<),
[/о, М} можно для почти всех точек coi, ..., сог- взаимно однознач-
но сопоставить точку х(/г-, со±, :.сог) и для каждого класса оп-
ределить функцию
Gz(x(/z, Юр (0z)) = Oz (?(/, wz))
и управление
u(t. x(th (Op (OZ), (Oz+p (0л)=«(/, (Op ..., (OZ, (OZ+P (0л).
Покажем, что в задаче At все функции ^(...) выпуклы и за-
дачи, которые нужно решать на каждом интервале для опреде-
ления оптимального решения, являются однотипными.
Рассмотрим интервал [^n-i, tn]. Определим область допусти-
мых начальных точек Xn-i = x(/n-i)^Dn-u как совокупность то-
чек, для которых выполняются следующие свойства:
1) xn^Dn^
2) для любой точки соп^йп найдется такое управление
U(t, Хп-и что
xn=H(tn)H-^tn_1)xn_1+ J Я(/Л)Я-Ч/)Х
XI/(й.
где H(t) — фундаментальная матрица решений • однородного
дифференциального уравнения из задачи At.
Обозначим результат преобразования точки xn-t в силу диф-
ференциальных уравнений с управлением u(t, xn_if (оп) и
0)п^йп Через Хп = Хп ( и (t, Xn—t, (On), (On, xn—1).
186
Заметим, что в силу теоремы Ляпунова [3] при каждой фик-
сированной паре точек xn-i, соп, произвольном замкнутом мно-
жестве U и измеримых по t функций u(t,'xn-i, (£>n)^U множест-
во S(xn-1, (On) = {xn : Xn(u(t, Xn-1, (Dn), (On, *n-l) } будет выпук-
лым. Назовем множество S(xn_i, шп)_ образом точки (xn-i, <оп).
Укажем путь построения множества Dn-i. Фиксируем произволь-
ную пару точек хп-ь соп, где xn-i^Dn_iy (on^Qn. Введем в рас-
смотрение множество векторов ZeX, ||Z|| = 1, где X — простран-
ство векторов х. Из условий:
С //(/„)/У-1 (/)[/(«, /)-Ь
min
uey
«6(7 , ,
гл-1
I, f f) +
*л-1
определим функции u~(...) и u+(...) соответственно. В этих
условиях только второе слагаемое зависит от и. Это слагаемое
принимает экстремальное значение, когда в каждый момент t
подынтегральная функция экстремальна. Эквивалентные усло-
вия принимают следующий вид:
minZ, Н (/л) Н~~1 (/) f (ц, 1)—+и,~(19 t);
u£U
maxZ, H f (a, t)-+u+ (/, /).
u£U
Заметим, что функции u~, u+ зависят только от переменных
I, t. С помощью функций u~(l, t), u+(l, t) можно получить все
граничные точки множества S(xn_i, соп) для любой точки xn_l9
u)n. Каждую точку отрезка, соединяющего две граничные точки,
которые отвечают одной паре функций u-(l, t), Z), можно
определить из выпуклой комбинации
(1 —?)*л(и-(Л *), xn-i)+$xn(u+ (I, t), а>я, хя_х),
где 1.
Любую точку множества S(xn-i, (оп) можно получить, изме-
няя I и 0. _
Чтобы построить множество Dn-\, нужно среди всех точек
xn_teZ)n_i оставить такие точки, у которых множество S(xn-i,
(On) ПРп яри всех шлейп — непустое. Множество S(xn_i, (оп) П
П Ьп — выпуклое. Для каждого I выделим такое множество 0,
что 0^0^ 1 и
(1 — 0) хя (и-(Z, /), 0>я, Хя_1) + 0хя («+(/, /), <оя,
Обозначим это множество xn-i, (On) }n-i-
7'
187
Ясно, что точки xn-i^Dn-i, для (которых при всех <on^Q?i
хотя бы для одного I множество {р(/, xn-i, (on) }n-f — непустое,
принадлежат множеству Z)n-i. Описанным путем можно постро-
ить это множество. Покажем, что для любой тройки (/, хп-ь
соп), где
1^Х, ||/||=1, xn_^Dn^, юл^2л,
множество {0(/, xn_i, (on) }n-i (если оно непустое) — выпук-
лое.
Докажем это. Пусть точки рь р2е {₽(/, xn-i, (on) }n-i, тогда
для будет выполняться включение
*«(«"('. О, *я-1)+№ -Н1-Х) MX
Х^Л (#+ (Л ^), Хп — 1)=М(1 Р1) (Ц ^)» ШЛ» ^п—1)
+ ?1^Л(«+(/, /), <ОЛ, Хл_1)]+(1-Л) [(1-р2)хл.(я-(/, /), «)л, Хя_1) +
- + ?2*л (я+ (Л *), <*>„, *л-1)] € Dn.
Это следует из того, что каждое из выражений, стоящих множи-
телем при Л, и (1—Л,) принадлежит выпуклому множеству Dn.
Таким образом, для определения множества {$(1, xn-if
(On) }n-t нужно найти его максимальный 0maxG, xn-i, (оп) и ми-
нимальный pminU xn-i, (On) элементы. Докажем, что множество
Dn-i — выпуклое. Пусть
—1 1» Хп— 1 £ Dn—j.
Покажем, что точка xX-i + (l — X)X-iC^!-i,
где 0<Х< 1.
Для этого нужно проверить, что
1) хх;_1+(1-х)х;_1€Пл_1;
2) для всех (On найдется такое управление
«(Л +
что хп(иu;_,+(i-x)x;_p «»„)€£>«.
Первое условие выполняется ввиду выпуклости Dn-i. Для
проверки второго условия, обозначим
^л
j t), t)dt=a+ {I)-,
гл-1
j Я(/л)Я-1(0/(й-(/, /), t)dt=a-(iy
188
fn-l
‘n
//(/„)//-4^-1) <_j+ J H (/„) h~* (/) 5 (/, ^dt=x’n_x (<oj.
*л-1
. В силу предположений о принадлежности точек Хл-ь хл-1
для всех (On^Qn найдутся такие
^1» Хп— 1’ ^лИл—1 И ^2» Рг€ )?(^2» Хп— 1* а)л)}л—1»
ЧТО
+ (1 - W а- (ZJ + (ZJ € Dn;
+ (1 - Р2) а- (Z2) + fW € Dn.
1 / - '•
Так как множество Dn — выпуклое, то выпуклой будет комби-
нация
\Х’п_х 4- м-1 - w a- (Zx)+хмл+ (/1)+(1 - X) Х"п_х +
+ (1 - X) (1 - ?2) «7 (Z2) + (1 - X) Мл+ (Z2) е Dn.
Для каждой точки xn-i, <оп множества S(xn-i, соп) —
—Xn-i(o)n) — выпуклые и не зависят от точки xn-i, con- В эти
множества входят векторы £±(/1), a±(Z2) и их выпуклые комби-
нации. Поэтому
Ш - ?1) «7 (Z1) + ХМЯ+ (/1) + (1 - Х)( 1 - w а- (Z2) +
+(1-х)М+О5(Х<_1-(1-х)х;_1, «„)-
Так как при этом вся выпуклая комбинация принадлежала мно-
жеству Dn, то для точки Ьс^ + и^М-^л-^ДЛЯ всех (i)neQM мож-
но подобрать такие /хи (Jx, что
^-, + (1 - + (1 - Рх) + РхДл+ (Zx) € Dn.
Таким образом, точка лхл-1 + (1 — М хп-\ б £\-i и множество
Dn-i — выпуклое.
В рассматриваемой задаче минимизируемый функционал
F(x(7\ ©I, con)) на интервале [Zn-i, tn] зависит только от ко-
нечной точки. Оптимальную точку х°(7\ coi, ..wn), в которую
должна переходить точка хп-ь соп (где xn-^Dn-\, (oneQn)
можно найти из условия
X* = Хп-х («>„) + (1 - ?опт) а~ (/опт) + ?0I1Ta+ (Z0UT).
189
В последнем условии оптимальные /ОПТ^АГ, ||/опт||=1
и L(L- хп-ъ «>я)€ (?(ZonT> *л-1.“>л)}л-1 получим из выражения
min min F (Х„^ (<оя) + (1 - ?)<(/)+
1 $mln(l,xn—1’®л)<₽<₽тах (1,хп—Ршя)
+ ^+(Z))=O„(x„_1, шя).
Отсюда видно, что оптимальное управление на интервале
[fn-i, Zn] при нахождении системы в точке xn-i, (лп можно также
получить из условия попадания из точки xn-i в точку
*п
хл=хл._1+(1-₽опт(/опт, x„_x, <»„))+ j //(/„)
*л-1
* п
Х/(«~(/ ОПТ» /),/)л+₽опт(/
опт» 1» ^д)
*л-1
*л
X/(«+(U> '). 0^+ j //(z„)//-i(/)e(A <%) л
в силу дифференциальных уравнений
at
и при ограничении на управление weU.
В двух частных случаях оптимальное управление находится
тривиально:
Ропт = 0 И ₽0,„=1.
Ясно, что G„ (X(/„_!, ...))= f <ол)дЧ-
ил
Докажем, что функция Gn(xn_i) — выпуклая. Достаточно
показать выпуклость функции Gn(Xn-i, (оп), так как если пос-
ледняя выпуклая, то и функция
<?л (^л—1) = J ^л (-^л—1» шл) ^шл
Сл
будет также выпуклая.
В самом деле, пусть функция Gn(xn-i, (On) — выпуклая по
Xn-i, тогда для любых точек x”n-i и любых о)п
+ ХХ-1. «-р + “>л)>
где 0 1.
190
Проинтегрировав это неравенство по множеству Qn с поло-
жительной мерой d(on, получим
J G -|" ( 1 М Л'л—Р У а)л)^а)л4"
2л 2л
+(1 -к) Jo
Sn
<xo„(x'_1)+(i -yon «_t).
Покажем выпуклость функции Gn(xn_i, (on). Сохраняя обоз-
начения, введенные выше, запишем
Х<?л«-Г “>л)+(1 — Х)ОЯ(<-1. “>л) =
— Xmin min F(^_1 + (l-?)a7(Z) + ?a;(Z)) +
+ (1-X)min min F(X;t_1+(l-P)a7(Z) + ?a+(Z))= .
1 ’ФК.-»)),-.
= Xf’ 4-(l — p'IIT) a~ +P'nTa+ (Z'nT)) +
+(I - X) F +(1 - о а- о+е;пта+ (z;nT)) >
> ^X'^+(1 - X) X’n_,+X (1 - о a- (z;nT) +
+^'пЛл+ (О +(1 -м (1 -O<0+(1 -х) Р>л+ (О-
Было доказано, что точка
+(1 -X) х;_,+Х [1 -и а- (/;„)(/;„> +
+(i-«и-о<о+(1- х)р;,а+ю
принадлежит множеству 5(x'_j-|-(1 — Х)х’_р (on)nZDn.
Поэтому найдутся такие
1^Х-, || Z^||=1 и ^(?(Z, Xx^ + U-X)
что точка XAT'_j + (1 — X) Х'^ -|- (1 — рх) а~ (Zx) рха+ (Zx) будет
совпадать с названной выше точкой. Отсюда
F ах'_,+(1 - X) 4-х (I - р;пт) а~ (z;nT) 4- х₽;пта+ (ZOTt) +
. 4- (1—М (1—о а- о 4- (1 - X) (z;nT)) =
=^- (xx;_t+(1 -X) ах)+?ч+
>min min ^(kyV'_i+(i_x)^;_i + (l-₽)X
1 ?€{₽(/, Ч-1+(1-Х><-Г“в)1
Х<(04-К (0)=<?л(Ч-1+(1-хХ-1’ и)")-
191
Таким образом, Gn(xn-i) — выпуклая функция.
Для того чтобы решение задачи существовало на интервале
[/n-2, tn], необходимо, чтобы конечная точка хп-л интервала
[/п-2, /п-i] принадлежала множеству Dn-i, так как в противном
случае при 'некоторых соп фазовое ограничение Dn будет нару-
шено. Поэтому множество Dn-z допустимых начальных условий
для интервала [/n_2,_/n-i] будем определять следующими усло-
виями: точка xn-2^Dn-2, если
1) ХП—2'€ ^п—2»
2) для всех con-i^Qn-i найдется такое управление
К (/, Хл—2> ШЛ—1) € U,
что _
хп—1 (# (/’ хп—2» шл—1)> 1» Хп—2) € D^.
Так как множество Dn-i — выпуклое, то для интервала
[/п-2, /п-i] справедливы все предыдущие рассуждения.
Итак, оптимальное решение q°(t, со) задачи определяется
из последовательного решения на каждом интервале {/<_ь /J, / =
= 1, 2, ..., п для каждой точки coi, .. coy^QiX ... Хйг сле-
дующей задачи.
Найти min Gz(x(/z, и)1? ..., <dz))
при ограничениях:
<о)=Л(/)л.(л ш) + /(и(Л ш)> /Ж(Л ю);
dt '
х (fl—1) = х° fi—1» ш1> •••» 1)»
2) x(/z, сор ..., coz)€£)z;
3) я(/, x^/z-x), <vz)€47,
где х°( ti-л, coi, ..., сог-i) — значение функции х°(/, соь ..сог—±),
определенной в результате решения этой задачи на предыдущем
Интервале [/г—2, /г-1], 'В ТОЧКе /г--1, (01, . . (рг-1.
Для интервала [/о, /1] точка х(/0) = хо-
Из доказанного выше все (7г(х(/г, coi, .. .,(0с)) — выпуклые
функции, a Di — выпуклые множества. Таким образом, на каж-
дом интервале решаются однотипные задачи.
Заметим, что в случае дифференциальных уравнений, у ко-
торых есть решение на интервале [О, Т] для любого из рассмат-
риваемых управлений^ решение задачи существует, если:
а) все множества Di (при / = 0, 1, ..., и) — непустые;
б) Xq^Dq.
192
3.5. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ
СТРУКТУР ЗАКОНОВ УПРАВЛЕНИЯ
НА ОСНОВАНИИ УСЛОВИИ ОПТИМАЛЬНОСТИ
встречи) был не
Рис. 3.4. Физическая интерпретация за-
дачи
В настоящем разделе рассматриваются два примера, из ко-
торых видно, как на основании полученных условий оптималь-
ности можно установить структуры законов управления.
Наведение на маневрирующую цель при ограничении на угол
встречи. В некоторых случаях необходимо навести ракету на
маневрирующую цель так, чтобы угол межщу векторами скорос-
тей ракеты и цели в момент встречи (угол
больше заданного. Если
можно пренебречь ошиб-
ками измерений и пред-
положить, что цель манев-
рирует независмым от
поведения ракеты обра-
зом, а управление ракетой
и маневр цели слабо вли-
яют на скорость их сбли-
жения, то исследование
можно свести к решению
задачи, физическая интер-
претация которой дана на
рис. 3.4.
На этом рисунке Vi и
V2 обозначают соответст-
венно векторы скорости
ракеты и. цели, a Ур и
Уц—их проекции на заранее фиксированную и ' неизменную
в процессе наведения стартовую линию. В.обозначениях рис. 3.4
задача формулируется следующим образом.
’Найти такое управление ракетой u(t, ...), которое миними-
зирует функционал
2
при ограничениях:
1)
2)
3)
-^=и; te [О, Г];
dt
dx2
dt
—х2; хх(0); х2(0); х8(0);
dt
|ах1(7’) + х2 (Т)|<?’;
|« К Ио-
со;
193
Здесь Xi — отклонение ракеты от линии дальности; х2 — откло-
нение цели от линии дальности; (ог- — независимые случайные
величины, с помощью которых описывается маневр цели.
Наблюдения фазовых координат производятся в моменты
удовлетворяющие условию
0 = /о<Л<...</г<...</п = Г.
Вместо непрерывных уравнений рассмотрим разностные:
ЛЛ-1)+ J
•^2 fl) == -%2 i) 4“ J ^idt\
• Х3 ft) = Х3 (^/—1) 4“ [•*! 1) (fl—1)] &t.
Приступим к определению оптимального управления. Рас-
сматриваемая задача принадлежит к типу задач, изученных в
предыдущем разделе. Применим результаты этих исследований.
На интервале [/n-i, tn]
*л
(fn) =*i (tn-i) 4- J и 04 dt\
fn-\
*п %
x2(/„)=x2(/„_i)+ j
*л-1
•^3 (fn)=X3 fn—1) 4“ [•*! (fn—1) X2 (fn—1)]
При этом должны выполняться условия:
min | х9 (Jf„)| и |ах1(/п+х2(/л)|<<р°,
и
которые через фазовые координаты в начале интервала можно
выразить следующим образом:
min | х9 (/я_х) + [*! (/„.J — х2 (/„«J] д/|;
и
^п
а J и (/) Л+ахх (/„_!)+x2 (/„-J+<ояд/
fn-l
194
4~ а у и (/) dt 4-/2, L>n______р
Введем обозначения:
ах1 (41-1) +Л2 04-1) ?л-1 4-шлД^ — ?л-1’
Х9 (^л—1).4" 1-*Г (41—1) х2 04—1)1 Д^ — ^л—1> ^п—1 — ^л—1’
'л
?;_!+* J u{t)dt=^, L*n_v = Ln.
*п—\
При случайном воздействии <оп точка <pn-i, £n-i преобразу-
ется в точку фл-i» 2.я_ь которая, в свою очередь, при управле-
нии | u(t) | переходит в точку <pn, Ln. Граничные точки мно-
жества образов точки <рл-ь ^л-i, которые (образы) получаются
в результате управления, определяются из следующих соотно-
шений:
max/,, с₽* ,
|лк«о [л-1
«+(/)=«0 sign/х;
?л=^-1+Р(-«оДО+(1 -М«0Д4 0< 1;
- <Р° < <Рл < ?°-
Образы точки фп-i, Ln-i при случайном воздействии <оп
(случайный сдвиг) и образы точки фл-ь ^л-i при управлении
(управляемый сдвиг) даны на рис. 3.5.
Проведем синтез управления по интервалам.
На интервале [/n-i. ^п] по известным координатам Xi(/n-i).
x2(tn-1), Хз(/п—1) и воздействию con определяем фл-i; если
| ср„_ 1 ±аиоД£| =^ф°, то управление — произвольное (область I на
рис. 3.5); если <рл-1 + аиоД/>ф° или фп-1—au0&t<—ф*. но
| срл-i | ^ф°, то выбор управления ограничивается необходимо-
II на
— ¥°-К-1
стью выполнения условия: —ф°^фп=Сф° (области
рис. 3.5);
если ср*_14>?0 или — ?°> то
«в11Т=-----------, или аопт
<",т аД/ опт аМ
Область Допустимых значений фп-ь £n-i при этом
ляется следующими соотношениями:
?я-1 — aU0^t < <f>°—>?’_! < <р°4-а“оД^
4-а«оД' > - - <р° - аиом < ср;_г
опреде-
195
Область допустимых Xi(/n-i), *2(^-1), x3(/n-i), т. е. множе-
ство Dn-t удобно определять в координатах <pn-i, £n-i:
max - au^t < < <f>° +(au0 - Д/;
O)
min <p*_1+au^t > — <f>°—<pn_j > — <p° — (au0 — $0) д/.
На интервале [4»-2, ^n-i] следует рассматривать задачу мини-
мизации функции <?л-1= f |^_1|^‘*>л=Кл-11 'при фазовом огра-
ил
и#рйзы точек
Образы точек
-1 Линия уровня &п-1
<Р°1<Ргн
Cuhme.f управлении
I
&rH~~Ln-i Gn-i°Ln.j {
I
I
' I
Синтез управления' I
tt
-ч»4*г лГ
Чмт-iU' 2
-tf/" I’
Рис. 3.5. Образы точек фг, Li и ф<*, Рис. 3.6. Построение оптимального уп-
Li* и синтез управления на интервале равления на интервале>[^п_2, £n_i]
[£п— 1, М •
ничении |фп-1| =Сф°+ (а«о—£о)Д/. С учетом этих соотношений и
дифференциальных уравнений задачи удобно ввести следующие
обозначения: /
?л—2 — ах1 (^Л—2) “F Х2 (^п—0 ’?п--2 — ?л—2 шл—1
Н96
Ln—2 — -^3 2) 4" [-^1 (^л—2) «^2 (^л—2)] 2 Д/ >^'л—2 ~
= Ln—2 ^П—1’
Zn-1 *л-1
?л-1=?^_2+а J u(t)dt’, Z„_2=Z*_2+ Д/ J ii(t)dt.
Граница
жения
max lv
|tt|<«0
*п-2 fn-2
образа точки ср*_2, Z*_2 определяется из выра-
гл-1
тГ2+« f
л—1
J и (/) dt
п-2
>u+ = uQ sign (Zxa +12 АП •
Образы точки фп-2, Ln-2 при случайном воздействии (on-i и
образы точки <р*_2, Z*_2 при управлении даны на рис. 3.6.
Область допустимых точек <р*_2, £*_2 определяется следую-
щими соотношениями:
?л-2 “ < ?° + (^0 ~ %) А^?л-2 < <Р° + (2ай0 - U
?л—2 4” Яйо Д/ ?° (CLU^ $q) Д/ *?л_2 £(/) Д^.
Область Dn-2 определяется из выражений:
max ср*_2 — аиод/ < ср°+(auQ — £0) Д/-^
л-1
2 ?° 4г (^«0 U
min ?*_2+ <ш<Д* > — ?° - (auQ — £0) Д^—?л-2 > — ?° - (я«о “ U А*-
'°л-1
Из изложенного следует, что оптимальное управление иопт
на этом интервале, которое определяется только для допусти-
мых точек ср*_2, £*_2, находится из следующего * соотношения:
«опт = Ропт ( - «о) + (1 - Ропт) «о.
где Ропт = Ропт (^опт) получаем как точку, в которой достигается
min min |£л-1=^_2+Д^(- «0) + (1 — Р)«о Д*|-
I РФтШ-Ртах!
Отсюда следует; что и01ГГ не зависит от t- на рассматриваемом
интервале.
Оптимальное управление можно найти также из -следующих
соображений: управление должно смещать точку <р*_2, £*_2 так,
чтобы значение функции Gn-i в смещенной точке было возмож-
но меньшим и фазовое ограничение не нарушалось. Другими
197
словами, нужно перевести эту точку на линию уровня функции
Gn-i с возможно меньшим значением этой функции на ней.
Определим область всех точек <р*_2, Z*_2, которые нельзя да-
же с предельным значением управления перевести в область аб-
солютного минимума Gn-i'
ПРИ £л-2<0
^/1—2 “Ь#оЛ^2 С 0 г < и0д/2;
?Л-2 + ?° + (««О — So) < ?° — SflA^
ПРИ £’-2>°
^л—2 т «О А^2 0 ‘^л—2 ®оД^2’
- ср0 - (аи0 - и д* < ?‘_2 - «и0Д^_2 > - ?°+SoAt
При нарушении фазовых ограничений в случае предельных
управлений оптимальное управление для тех точек, которые не
смещаются в область абсолютного минимума функции Gn-i, на-
ходится из условия:
при £;_2<0 <р;_2+ааоптд/=ф»+(а«0-ео)Д<;
при Z*_2 > 0 ?*_2 +а«оптД/ = - ?° - (<ш0 - ДД
Синтез управления представлен на рис. 3.6. Уравнения гра-
ниц будут
?:_2+««оптД^=<Р° + (««о - So) д^;
. ^_2 + «оПТД'г=0, или 0=£;_2 + ( *°+ (аа° ~ Д/;
?:_2 +^«опТД^ = - ?° - (««0 - S0M
7* I tt л и птл П 7* I / Ч-(аир Со) м —з\.,
(£п-2 + иоптАг — °, «ли 0 = £л_2-Ц------------------
Оптимальное управление и значение функции Gn_2(L*_2,
<рл-2 ) в областях I—IV, I' (см. рис. 3.6) следующие:
уо + (ам0—е0) Д<—у*_2 .
[г. I У° + ’(в«0— Со)Д<— <tn-2 д /.
°л-2- -|_£„-2 Н--------------------- Д*]’
(II) “опт= ®0> ^л—2 = ^'л—2 ^оД^2’
(Hi) «о„т=+“о; <Зл-2 = -1^_2+«оА^];
198
(IV) оптимальное управление определяется из условия сдвига
точки <р*__2, ^л-2 ® область абсолютного минимума функции
Gn-2, т. е. на линию Ln-i=0:
«о,п = -^Г-; °Я-2 = 1°:
п -уО-(аио-6о)А<-«Р^2 .
п г» I Л,
С/л_2 — ^п-2 । ~
На интервале [/п-з, ^n-г] для определения оптимального уп-
равления необходимо предварительно построить функцию
Оп—2 (^л—2» ?л-г) — J <?л-2 (?л—2’ ^л—2) ^П—1-
-Но
Полное построение функции Gn-i(Ln-i, фп-г) ДЛЯ i = 2, 3, ...
затруднительно. Однако определение структуры управления
можно осуществить, зная лишь некоторые ее особенности.
Из рассмотрения на предыдущих интервалах следует, что и
на этом интервале задачу удобно рассматривать в координатах
<рг-, Ц, которые зависят от координат
•^1 (^/)> *^2 (^/)» ^3 &)•
Отметим следующее свойство оптимального управления, ко-
торым неоднократно будем пользоваться ниже. Точки <рг*, Li*, яв-
ляющиеся образами точки фг, Li при всех <х>г-ыeQi+i, лежат на
прямой. Также на прямой лежат образы точки фД Li* при раз-
личных u^U. Уравнения этих прямых будут представлены
ниже.
Так как минимизируемая функция на каждом интервале вы-
пуклая, то ее линии уровня будут выпуклыми функциями. Опти-
мальное управление должно переводить точку <рД Li* на такую
линию уровня, к которой прямая, содержащая образы точки
ср*, L*, будет опорной (в точках образа) или, если таковой нет,
то на линию уровня, расположенную ближе к области абсолют-
ного минимума минимизируемой функции.
Покажем, что обозначения ср, L действительно удобно вво-
дить на каждом интервале.
Пусть для произвольного интервала [/п-г, нУжно ми-
нимизировать функцию Gn-(i-i) переменных
срл_(/__1) = ах1 -|-х2 (^л—.(z—1));
Ln— (1—1) —^3 (^л—(Z—1)) “г [Х1 (^л—(Z—1)’) (/л_(Z—1))] (Z 1) Д/
199
и удовлетворить .в момент фазовым ограничениям
| фл-(/-1> К ?° + (««о - Во) / — 1) Дл
В силу дифференциальных уравнений задачи получим
{п-(1-1) л
u{t)dt +х2(^_/)+«>л_(/_1)Д/;
<?n-(l-l)=a
n—l J
Ln(l—1) = /п—i) + [•*! /п— l) X2 / n—f)] д^ [-V1 /п—i) “F
<«-(/-!) j
-|- f «(/)rf/ —X2(/„_,) —а>л_(/_1)Д/ (Z— 1) Д/.
n—i J
Отсюда видно, что удобно ввести следующие обозначения:
<Pn-i.—axi /п-i) + л2 ^я-/);1?л_/—?л-;+шл-('-1)Д^
^п—I =Х3 /п—l) [Х1 /п—l) —Х2 /п—;)]
^*n—i = ^n—i <°n—(i—i)/ 1) Д^2;
<л—(Z—1)
J и (Z) dt;
n—i
*п-(1-1)
— +(*— 1) Д^
Граница образов точки А*_;, <р*_г
ниях определяется из выражения
/ Г <Л-(/-1)
n—i
три различных управле-
max U
|u|<«0
n—i
n-(l-l)
C a (/) dt
•«+=«0 sign {l^a -j-12 / — 1) Д/] •
* n—l J'
Любой образ точки L*n_t, <p*_z (без учета фазовых ограни-
чений) можно получить на основании равенств:
<рл-( z-i >=?);_/+# [₽(—«о)+(i ~ Р)(+ио)]
1.)[₽(-«о) + (1-?)(+«о)]Д^ при 0<р<1.
Образы точки Ln-i, <pn_t при случайном воздействии (случай-
ный сдвиг) и образы точки <рл_/ ПРИ управлении (управ-
ляемый сдвиг) даны на рис. 3.7.
200
Область допустимых начальных условий Dn-i описывается
неравенствами
<f*-i — < <р° + (аи0 - U — 1) М-+
< <р°+«мод/+(а«о- ?о) («— 1) ;
— <р° — (ая0 — £0) (4 — 1) д/ < 4- аиодг!->
— — <р° — а440Д/ — (а«0 — U (4 — 1) Д/ <
или
max <f>*_. < <f>° + «44ОД/ + (а«0 — ?о) (* — 1) -
<“«-(<-!)
—<?„_{<?°+(аав-%)4д!;
min ср*_. — <р° —4444ОД/ —(а440 —$0)(4 — 1) Д/—»
шл-(/-1)
—><рл_/ — <р° (аи0 $0) / Д/,
т. е. ^л-/ = (1?л-/К?° + (айо — fcoW}-
После определения оптимального управления получим функ-
ции ч _
Ол_/(ср*_р И ^n-iY
Рис. 3.7. Образы точек Тл_р ^п-1
'Рл-п Ln-i
Таким образом, на любом интервале /п-J нужно ми-
нимизировать функцию Gn-i переменных
^n-i = ax1 (tn~i)+x2 {tn^\
L'n—i== (^л— i) Н~ 1^1 (^л—/) ^2 (^л—
8 3200
201
и удовлетворить в момент tn-i фазовым ограничениям
| ?л_,|< <?° + (аи0 - е0) 1Д/.
Внутри интервала иопт не зависит от времени.
Для существования решения задачи необходимо, чтобы на-
чальная точка каждого интервала лежала в допустимой облас-
ти, т. е. удовлетворяла полученным выше фазовым ограниче-
ниям.
Если то для любого i область |фп-г| ^Ф°+(aWo—
—go)iAf не будет пустой, т. е. решение задачи будет существо-
вать для любого Г. Если же аио<£о, то при i, удовлетворяющем
равенству
<Р° + (ам0—^о)/д/=0, т. е. i*M=---——,
0 — £о
множество допустимых начальных условий будет пустым.
ПриГ^>/*д/=-------—— решения этой задачи не существует.
_ Далее рассмотрим случай Исследование функции
Gn-i будем проводить по областям.
Внешняя область функции Gn-iФп-i). Об-
ластью, «.внешней» по отношению к области минимума функции
Gn-i, назовем множество тех точек фп-ъ Ln-i, на котором вид
линий уровня Gn-i = const не изменяется с ростом значения ко-
ординаты Ln-t. Ниже установим, что эта область состоит из
двух подобластей, расположенных
левее линии
Ln^=—(ио-Но) М2 (левая подобласть);
правее линии
Ln_i= (ио-Но) А/2 (правая подобласть).
Ординаты обеих подобластей удовлетворяют неравенству
|<ср° + Ца«0-е0)д/.
Построим эту область и проведем синтез оптимального уп-
равления в ней. Процесс проведем для левой подобласти. Те
же рассуждения можно провести и для правой подобласти.
Сначала предположим, что аио = £о. Случай аио>& исследу-
ется после этого рассмотрения. На интервале [tn-2, /n-i] синтез
управления во внешней области дан на рис. 3.6. Из рисунка сле-
дует, что если для всех
$ 2п-1
£„_2 — <оп_хд^2 < — «0Д/2, Х т. е. £л_2 < — (14-а) «0Д^.
202
го точка (|фп-2|^Ф°, Ln-г) будет принадлежать «внешней» об-
ласти. В этой области функция Gn-2 задается двумя аналитиче-
скими зависимостями. Если фп-г+^п-гД/^Ф0—аооД/ хотя бы
для некоторых (on-i^£2n-i,
т. е. сря_а > ср0 — 2а«0д/,
то в
л—2 = “7; \ 1^-2 4” й0^2] d&n—l
-So
' *° г ♦ Л
[£"-2 + Д/—
В
где 1—<Рл-2 + =?° ~ 000^;
Gn-2 = ^л—2 + ^л-2 СРл—г)*
Определение функции Гп-2(фп-г) ясно из выписанного выра-
жения.
Функция
^л-2(?л-2) =^«оД'2(Жо] + [У°27а2~г]2 -°
имеет на верхней границе области фп-2 = ф° следующие свой-
ства:
1) ^-2(?°)=0;
2) п—2 I __ М
dVn-2 1<РЛ_2-‘Р0 а
Если <рл_2+<*>л—ХД^ <ф°—au,Qbt при любых
«>л-1€ 2л-!> т. е. ?я_2<?°—2аа0д/, то
О п-2 = "пГ"1 ' \ [^л-2 + йоД/2] d^n-Х — [Ln-2 + й0Д^2]-
Производная dLn-2ldqn-2 на линии уровня Gn-2 = const воз-
растает от нуля до своего максимального значения на верхней
границе
^Дл-2 А/
d4n—2 Ун-}-?0 а
(Линия уровня выпуклой функции — выпуклая кривая. Про-
изводная на линии уровня — опорная ’прямая к этой линии).
На интервале [^п-з, tn-^ управляемые образы точки ср*_3, L*__3
располагаются на прямой с углом наклона б/£п-2/^фп-2=2Д//а.
8*
203
Максимальный же наклон касательной к линии уровня Gn-2 =
' . д/ 2дг о .
= const будет --. Поэтому линия управляемых обра*
а а
зов не может быть опорной /к линиям уровня Gn-2 в диапазоне
|фп-г| <ф° (концы отрезка не включены). Поэтому оптимальное
управление будет либо предельным иОПт = ^о> либо должно обес-
печивать выход на фазовое ограничение фп-2=Ф°. Такой резуль-
тат будет для любого А*_3-р2я0д/2 —(1 ^a)u,Qkt, т. е.
< — (3-ра)я0д/2.
В этой области построим функцию </л_3 (А*_3, <р*_3).
Если <р° —а^од/< <р*_3 + ай0д/< <р°, т. е.
и
ср0 -2ая0д/ то «опт = «0
О„_3= - [£’_-3+2й0д/2] +/?л_2(?;_3+ан0д/).
Если <р*_3+а«0Д/> <р°, т. е. <р*_3 <р° — а«0ДЛ т0
<р°- т*_з, „ ,,
-----—; Ол_3= — Z.
^опт . ,
аМ
л—3
’л-3
У° ~ Ул-з
а
2д/ +Fn_2(?o).
Замечание. Так как производная dLn—'ildqn—z к линии уровня Gn—а
растет с увеличением срл-з, то для оценки ее максимального значения нужно
найти функцию Ол--з только вблизи верхней границы ср л—з = Ф°. Функция
6п_з была построена в диапазоне ср0—2аи0Д/<^ф*п_з^ф0 + а^0Д^ который
вмещает все случайным образом сдвинутые точки, находящиеся при ол—2=0
на фл—з = ф°. Поэтому дальнейшего построения функции Gn—з не требуется.
Это замечание будем иметь в виду при рассмотрении других интервалов.
Во внешнюю область включены те точки с |фп-2|^Ф°, кото-
рые для любого соп-2^Нп-2 удовлетворяют неравенству Ап_3 —
— <%_22д/2 < —(З + а) яод/, т. е. Ln_3 < — 3 (1 -|-а) д/.
Отыщем функцию вблизи верхней границы
Е
Gn-S = ~ \ (-[^_3 + 2«0Д/2]+/;-л_2(<р:_3 + аМод/))й<ол_2 +
—Ео
^_3 + — 2Д/ + (?°)1 ^л-2.
a J J
где ' j—>Фл_3 + и^=т° — <ш0М;
О п-3— ~ Д>-з+^л-3 (?л-з) +
Е
^л-г(?л_3 +
2«о J
—Ео
—р —2'
204
Введенная функция
рп-. (<?„-,) = - 2 а0Д/г [ё + $0] + 2
на границе области фп-з = ф() имеет следующие свойства:
Fn_a (ср») = 0;
л-3
= 2—.
а
2)
^?л-3 ^-3=?°
Для удобства записи обозначим
I
Fп—2 (^л—з) —
CLU^t) cl^n.—2*
—Йо
Производная функции имеет вид
^я 2(Уя 3)-1 г^я 2(у;з+аЫод<)^
d<fn-3
<*Рл-3
2fco
'л-
-Но
+ 2?0 Я-21Т>„_3 26О 3
— £о
В точке <рп-з=Ф° производная
dFn-i (?„-з)
С ^л-2
*Рл-2 'Рп-з-^з
^л-2’
+ аи0М
^Рл-3
= 0<
<Рл_3-<Р°
Производная dLn-zldqn_s на линии уровня Gn-3 = const воз-
растает от нуля до своего максимального значения на верхней
границе
1
d ^п~з
= 2 —.
^?л-3 ?Л_2“'Р° а
Функция Gn-3 найдена при этом для тех значений фп-з^ф°>
у которых хотя бы для некоторых значений
<оя_2€2я-2 и <ря_34-<оя_2 д/>ср°—а«од/,'
т. е. для значений фп-з^ф°—2аи0Д/.
Проведем рассуждения для произвольного интервала [/п-г,
/п—(г—1)]« Пусть на предыдущем интервале было получено, что ле-
вая подобласть внешней области располагается в полуплоскости
О'- ПО-2-).. а0д/2
Ln—(i—1)
2
205
и в районе верхней границы области <р°—2auoA/^<pn-(i-i)^<p0
функция
_ 1~2
Оя-а-1)= — Ln-(i-V) + Fn-(i-i) (?«-</-!)) +2 ^л-ДТл-(/-!))•
;-2
где обозначено
(<?„_(,_„) = - (i - 2) [f+ej +
^5.0
+(,_2)
/^я_о_1)(<р0) = 0; -^n-(Z-1) =(/_2)_Д£.
а
»<p«_(z—1) -|-ВД/==<р0—аийМ
i—2
и где функция -(/-1)) обладает следующими свойст-
ва
вами:
1) 2\-/(<р°)*=°;
/-2
1—2
2) —---------------- =0.
dVn-(l-l) <ро
Проведем синтез управления на этом интервале. Управляе-
мые образы точки <р*_р L*nl располагаются на прямой с углом
наклона
dLn-(l-l) (i — 1) м
Максимальное значение .производной dLn-(i-i)/d^n-(i-i) на
линии уровня Gn-a-i) = const, которое достигается при фп_(г-1) =
= Ф°, будет Д^(/—2)/а и оно меньше (I—l)At/a. Поэтому опти-
мальное управление либо предельно иОПт=4-^о, либо обеспечи-
вает-выход на фазовое ограничение фп_г = ф°. Это справедливо
для любой точки
i?:_z|<?o+««*a^
206
В этой области построим функцию ОЯ_/(^*_Р <p*_z).
Если 4-Д«оД^<?0. то «опт=«0 и
<?л-/= — \^{ "И* — 1) иоД^1 + ^л-(*-1) (?л-1+аиоД^) +
+ 2 ? n~i 1 ”t” вИ°Д
J-2
Если <р*_; +аа0Д/>-ср°, т. е. <р*_, > ср0 — аи0М, то
Во внешнюю область на этом интервале 'будут включаться
те точки с |фп-2|^ф°, которые для любого значения con-(»-i)e
удовлетворяют условию
-<»„_(z_n (Z -1) д/2 < —'г ~-1-)2°--2) (1 +а)«оД*2 -
— (« — 1)«0Д*2,
£п_г<—^Ц^-(1+а)иод/2.
Построим функцию вблизи верхней границы (рп-г=Ф°:
е
л~/ = №n-i + (* “ 1) я0Д^2] + Fn-(i-i) (ф*_/ + ащД/) +
-Но
(Фл-Z +яя0Д/)}
У° - Ул-/
а
(/ —1)д/ ?^0)л_(/-1),
где
+(д/=<р° —а«од/;
On-i—n-i (?Л-/)4
1
2fco
1-2 »
“ЬаИ0Д/)+2 Fп-у (?я-/“Ь^оД^)
)-2 . )
207
Введенная функция
имеет следующие свойства:
1) Л.-ч(?°)=0;
2) dP"-№«-A_
dtn-i fn-i-f9 а
Обозначая
1) (?n-Z “Ь
1—2
+ 2^л“/ (?д_/+ай0^)?^а)л(/-1)1
/=2 J
находим, что
2 Л,-/(<?*)=°, так как $=—ая0= — £0>
и
Z—1
j-г____________
d^n-i
Х^л-(/-1) + тг
2 so
i—2
^2
dj
d<fn-
CL
Функция Gn-i построена в диапазоне
Пусть теперь ащ>^. Для этого случая аналогичными раг-
суждениями для интервала [tn-i, устанавливаем, что оп-
тимальное управление будет либо предельным ^Опт=+^о> либо
будет обеспечивать выход на фазовое ограничение
| <рл_( z-1) I < <Р° + (Z - 1) (аи0 - 5о) AZ.
Синтез оптимального управления во внешней области для
интервала [tn-i, /п-о-ц] показан на рис. 3.8.
В области I
<р° + (i - 1) (ац0 - е0)д/ -
208
В области II
— <р0 — (/ — 1) (ан0 — £0) М —
^опт
aAt
Область абсолютного минимума Gn-i(Ln-i, фп-z)•
Назовем областью абсолютного минимума то множество точек
<рп_г- Ln-г, на котором функция Сп-г(...) принимает нулевое
значение. У функций Ъп и (7n-i(£n-i, фп-i) области абсолютно-
Рис. 3.8. Синтез управления для интер-
вала tn_(г__п] во внешней обла-
сти функции Gn— (Z—1) (azzo>go)
Рис. 3.9. Область абсолютного ми-
нимума функции Gn_2((Pn_2, Ln-2)
го минимума одинаковы и представляют собой отрезок оси ф, точки
которого отвечают неравенствам |фп| Ф° и |фп-11 =^ф° + (auo—
—go) А/ соответственно.
Область абсолютного минимума функции Ол_2(?л_2» ^л-г) да"
на на рис. 3.6 (область IV). Для функции Сп-г(фп-2, Ln-z) об-
ласть абсолютного минимума будем искать из условия, что -слу-
чайное преобразование точки фп-2, Ln-2 не выводит ее из облас-
ти абсолютного минимума:
Z„_2 - + <Р0 + (а“о-^о)Д<-(?л-2 + МО д/ 0
а
209
• В этом случае границы области будут следующие:
верхняя
Ln-2 - («О + Во) + уО + 2(аЦо ~-е°2----^2- Д/ = 0;
а
£я-2 + («о+Во)Д/2+ -у°-2(дцо-^^-у^ д/<0;
и
нижняя
Ln-2. + («0 + Во) & + -У°~'2(<щ»~ео) А<~Уя~2 Д/ = 0;
а
левая
— «0Д/2 < £„-2 — £оД/2— — («о — Во) Д^ < £Я-2?
правая
^л—2 "Ь Я0Д^2 >^'л—2 (#о — ?о) Д*2.
Область абсолютного минимума функции (7п-2(фп-2, Ln-г)
представлена на рис. 3.9.
Рассмотрим произвольный f-й интервал tn-(г-ij. Пока-
жем, что граница области абсолютного минимума состоит из
(i—1) линейных участков в своей верхней части, такого же ко-
личества участков в нижней и левой и правой вертикальных
•прямых.
Уравнение /-го участка верхней границы, где отсчет номе-
ров производится слева направо l^/^(f—’1), для i^2 будет
иметь вид
£я-/ - {(«о- в») Д'2 [ - U-1)]} -%- Ь-/-
- (?о + (2/ - 1) (аи9 - Во) Д/ - 2£0д/ [(Z — 1) — (/— 1) (1 — а)] ]].
/*-й участок верхней границы располагается на интервале
(«0 - и д/2 [ - + j и -1)] < («о - Во) Д^2Х
Х[-21£^-+/(/ + 1)]-
Левая ордината области абсолютного минимума
(?я-/)л=?° + (2 - *) (аи0 - и Д/ - (Z - 1) 2$0д/.
На каждом линейном участке приращение по ср постоянно и
равно
&L = j2 («о — Во) Д*2=2а («о — Во) Д£
210
Всего на верхней границе (t—4) участков. Тогда правая ор-
дината области абсолютного минимума будет
(?л-/)пр=?° + * (лИо-U Д/-2аео(/-1) Д/.
v
Подтвердим справедливость этого уравнения границы мето-
дом математической индукции.
Рассмотрим интервал [/я_(<+1), /„_J. Так как наклон
= прямой, на которой лежат управляемые
образы точки <р*_(;+1), больше, чем наклон
1) любого линейного участка
верхней границы области абсолютного минимума, то прй опти-
мальном управлении ы0пт=+ио точки сдвигаются на границу
области абсолютного минимума. Тогда для участков
—1) имеем
^п_(/+1)“Н^2мо . ид^* 2[ ^ 2 j U l)j| —
=/ -^-[?;_(/+1)+ла°Д/-{<р0 + (2/-0 [а«0-%] Д^~
— 2%д/[(Z—1) —(/—1) (1 —а)]}],
Ln—(i+V) —|(Кр $о) Д^2 £-=
= J -%- [<?n-(t+i) - {<?° + (2/- (i + 1)) (а«0 - $0) М -
-2$0д^-с/-1)(1-«ШЬ
Уравнение i-ro участка определяется из условия прохожде-
ния прямой управляемых образов точки через верхнюю правую
точку области абсолютного минимума £n-i(-.
£л-и+1)—[<“0 —5о>д/2 ^2 ш
[?° + / (а«о-бо) M-2al0(i- 1) Д/] а
или
£„_(Z+1)- («о-U д/2 Ь-(/+1> -
2 а
- (?»+ (/- 1) (а«0-U М-2ВоД/ (1 4-а (/-1))}].
211
Правая абсцисса последнего участка удовлетворяет уело-
5о) ’ ^ 2 ~ (z+i)
£„_(Z+1)+*W</и0Д'2 + («0-и М*
Ln-v+i) -С («о - W •
Проводя аналогичные рассуждения, устанавливаем, что ниж-
няя граница области абсолютного минимума состоит из j ли-
нейных участков, где 1^/^(/—1) и отсчет номеров j произво-
дится справа налево:
Уравнение /-го участка для /^2 имеет вид:
Ln_t - [ - («0 - $0) ( - f-(<2 ° + j (j - 1 )j ] = j -У- -
_ {_ ?o _ (2/ - Z) (a«0 - $0) AZ + 2$0AZ [(Z - 1) - (/ - 1) (1 - a)]) ].
Рис. 3.10. Область абсолютного мини-
мума Gn_i(...) при i<i*
Таким образом, область аб-
солютного минимума функции
Сп-г(фп-г, ^n-г) СОСТОИТ (рИС.
3.10) из: верхней границы, со-
стоящей из (/—1) линейных
участков; нижней границы, со-
стоящей также из (/—1) линей-
ных участков, и двух верти-
кальных прямых
Ln-l = ± (^0 — U & li<l +
При увеличении номера ин-
тервала i концы верхней и ниж-
ней границ сближаются. Оце-
ним расстояние между точками
этих границ на правой верти-
кальной граничной прямой (по
верхней границе — участок / =
=^1—1, по нижней границе —
участок / = 1):
<р° + Z (а«0 — е0) AZ — 2a$0 (Z — 1) Д/ — [ — <р° — (2 — Z) (а«0 —
— £ о) AZ -j-2$0AZ (Z — 1)] — 2<р° 2 [<zu0 — £0] AZ 2;0 (Z 1) AZ (1 4~
Касание границ произойдет, когда
I < <р° + (дц0 — W AZ I ! =
S0(l + a)AZ Г
212
При дальнейшем увеличении значения i -происходит сближе-
ние границ и уменьшение области абсолютного минимума. Верх-
няя и нижняя границы сливаются. Номер интервала /**, на ко-
тором границы заведомо слились, можно получить из условия
прохождения (i—1) участка верхней границы области абсолют-
ного минимума через точку фп_г=0, £п_г = 0:
- {(«о- Ео) + (* - 1) (‘ - 2) ]} =
= (Z-l)-^[-{?» + (Z-2)(a«0-te) Д/-2$ОД/ [(/-1)-
_(г_2)(1-а)])].
То значение i, начиная с которого эта линия проходит ниже
начала координат, будет /**. Значение /** можно определить из
приведенного выше уравнения.
Таким образом, начиная -с некоторого значения где /*<
область абсолютного минимума функции Gn-i пропа-
дает. _
Так как функция Gn-i выпуклая, то область абсолютного ми-
нимума вырождается в точку. Линии уровня этой функции бу-
дут выпуклыми линиями. В силу изложенного прямая управ-
ляемого сдвига будет касаться линий уровня только в одной
точке. Все такие точки касания в пределах допустимого управ-
ляемого сдвига будут лежать на некоторой кривой переключе-
ния. Поэтому оптимальное управление будет определяться из
условия максимального приближения к этой кривой.
Изучим кривую переключения вблизи верхней точки области
абсолютного минимума функции Gn-i- При /</* получим вид
линий уровня функции Gn-i вблизи области абсолютного мини-
мума там, где возможно касание управляемой прямой.
Из рассмотрения рис. 3.6 имеем
Сп-2=-----~
" 2?0
“1“ “777 \ Ил-2 И0Д/2]
^0 J
-Ео
где
5 — Ч_2 4--------------------Д/ = О,
1*_2-^оД/2 = О;
5л~2 = 2.2£оД/2(1 +а-1) [£"-г~'°Д/2 +
। ?о + (ацо-2£о)Д<-Уя_2 t ]2 (£л-2 + 60Д/2-М<2)2
“* a J ' 2-2с0Д<2
•°[z* I ?°+ So) М — Ч*п-2
\ Ln-2
а
213
Производная на линии уровня (?n_2 = const будет равна
О=--------2------[L„ 2-U'2 + (Po + (aao-2So)^-?n-2 х
2-260Д^(1+а-*) L а 74
ХД/] (^_^\ + ^^[£л_2+$оД/2_ИоД/2]^-2..
\<*рл-2 а / 2-250Д/2 Лчп-ч
Найдем те точки <рп-г, Вп-г на линиях уровня, 'которых мо-
жет касаться прямая управляемого сдвига, получаемая на ин-
тервале (tn-з, tn-г]. На этой (прямой dLn-2Mpn-2=2AZ/a. От-
[z„_2-+ .JLo_+(.a“o-2So)^-^-2 дЛ =
L a J
= -2(1+ а-i) (Z„_2 + $0д/2 - я0д/2).
Обозначим В2 = 2(1-|-а_1). Методом математической индук-
ции установим, что «при f<Z* кривая линии переключения прохо-
дит через верхнюю точку области абсолютного .минимума и име-
ет линейный участок, определяемый для интервала
tn-i] формулой
fl] = — В2 [2],
где = °~lyi [1 + (t - 1) Я,-!]'”2 (1 +<z-x) (i - 2)"1 для Z>2;
(«0-u[-+++(Z-1)(£— 2)]-(Z- 1)X
X-y- {?„-/ - (?° +' i - 2) (a«0 ~ So) M ~ 2SoA' [1 +«(‘- 2)]} ];
Для нижней полуплоскости можно провести аналогичные
рассуждения (см. рис. 3.10).
После _<<смыкания» границ область абсолютного минимума
функции Gn-i пропадает. В этом случае на фазовой плоскости
оптимальное управление, кроме границ
К <р°+/(л«о-?о)ДЛ
определяется только «линией переключения», т. е. линией, при
переходе через которую оптимальное управление изменяем
знак.
Аналитический вид этой линии получить затруднительно. Для
ее определения следует воспользоваться численными методами
с привлечением ЦВМ.
Подведем итоги исследования. На произвольном интервале
[/п_г, /n_(i_i)], где 1=1, 2, ..., п, оптимальнее управление
^опт(^п-г) постоянно и зависит только от следующих линейных
214
комбинаций фазовых координат xif Хз, со и оставшегося вре-
мени /0СТ = /Д/:
= аХ1 (Лг-i) +х2 (^л-z)
^n—l =^3 n—l) 4“ [•*! /п—l) *^2 /п—/)] ^n-(l-l) (/ 1) Д^2*
Назовем ф* и L* достаточными координатами. Физически
они обозначают прогнозируемый угол встречи и прогнозируемый
пролет соответственно.
Прежде чем охарактеризовать вид оптимального управле-
ния в данной задаче, рассмотрим задачу без фазового ограни-
Рис. 3.11. Синтез управления без фазового ограничения (угол
встречи не ограничивается)
чения |аХ1(Г)+х2(Т) | ^фтах = Ф°,. т. е. задачу на минимум про-
маха. Найдем вид оптимального решения в ней. Известно, что
в этой задаче управление зависит только от £* и t0CT. Эта за-
висимость на плоскости L*, ф* изображена на рис. 3.11.
В зоне I управление принимает экстремальные значения
Иопт = ±и0. Зона II — зона линейной зависимости управления
от L*. Оптимальное управление в этой зоне должно «сдвигать»
точку ф*, L* (находящуюся вне зоны абсолютного минимума)
на границу области абсолютного минимума и будет определять-
ся в «соответствии с формулой
Zn_(z_i) = Z*_z -]-(/— 1)
Зона III — зона нулевого управления цОпт = 0, или зона абсо-
лютного минимума (ЗАМ) функционала. ЗАМ ограничивается
прямыми L*_l = ±L^ip и с увеличением t0CT увеличивается.
При наличии фазового ограничения, т. е. в исходной задаче,
картина синтеза управления резко изменяется. На плоскости
L*, ф* выделяются следующие эоны (рис. 3.12).
215
Зона I (заштрихованная редко) — зона, где оптимальное
управление принимает свои предельные значения и0пт = ±^о.
Зона II (заштрихованная часто)—зона, где оптимальное
управление линейно зависит от координат <р*, L*. Эта зона го-
раздо сложнее описанной выше линейной зоны и состоит из двух
подобластей: в одной, идущей параллельно линиям <£*_,=
= ±Фтах±(аи0—управление определяется из условия вы-
Углах* (auo
У’огр^’Ртах-^о-^^
л
-i
w* Vozp^max-^o-KoY^
т n-l z**«s£
^Опт~~ U о
иопт ~ +
n-i.
Uonr = ~U-o
Рис. 3.12. Синтез управления при наличии фазового ограни
чения (угол встречи ограничивается)
216
держивания фазового ограничения (здесь управление выбира-
ется таким, чтобы точка «сдвигалась» на эти линии);
в другой — из условия минимума функционала (здесь управле-
ние выбирается таким, чтобы «сдвигать» точку ф*_р Z*_z на гра-
ницу ЗАМ либо на линию раздела положительного и отрица-
тельного управления — линию переключения).
Зона III (незаштрихованная) — зона нулевого оптималь-
ного управления иО1ГГ = 0, или ЗАМ.
Границы ЗАМ при
- 6о(1+л)Д^ +1
находятся аналитически и -состоят из вертикальных прямых
£*_z = ±Lnp(f), верхней и нижней выпуклых ломаных линий,
каждая из которых -содержит /, где 1^/^ (I—I), линейных уча-
стков (порядок номеров участков верхней и нижней кривой ука-
зан на рис. 3.12). Каждый /-й участок располагается на интер-
вале
(«о- и д^-2£=д+7(7_1)] < («о- и а*2х
и описывается здесь уравнением вида
/0-1)
2
- {?° + (2/ - /) (аи0 - U А/ - 2ЕоМ [(/ - 1) - (J - 1) (1 - а)]} ].
Криволинейный участок линии переключения (сплошная ли-
ния) в зоне II не удается определить аналитически, хотя началь-
ный ее наклон (вблизи ЗАМ) легко можно найти: [1] = —Bi [2],
где [1] — уравнение последнего участка верхней (нижней) гра-
ницы ЗАМ; [2] — уравнение вертикальной границы ЗАМ; Bi —
коэффициент, определяемый из рекуррентного соотношения
1 +(/-!)£;-!
‘-1/ (1+Д-1Н
у 1 + (/- Ин
при
Z > 2;
Z?2 = 2(l+a-i).
С увеличением I ЗАМ «расширяется» по оси L* и «сжимает-
ся» по оси <р*. На интервале / = /*, т. е. верхняя
и нижняя границы ЗАМ касаются (пропадают вертикальные
217
участки). Начиная с этого интервала, ЗАМ «сжимается» по
обеим координатам и с интервала
i > =___________________________
— ?о(1 + a)M-a(uo-to)M/2
исчезает совсем. Линию переключения линейной области (а
после Z^z** остается вместо границы ЗАМ только она) можно
найти численными методами, используя ЦВМ.
Из рис. 3.12. видно, что введение фазового ограничения на
угол встречи резко изменяет привычную -структуру управления
(в задаче на минимум промаха): во-первых, управление зави-
сит теперь от большего числа переменных <р*, L*, ^ост; во-вто-
рых, с увеличением ^Ост ЗАМ уменьшается и, начиная с некото-
рого интервала, пропадает совсем.
♦ Каким же образом строится оптимальное управление? По
координатам цели и ракеты и по текущей перегрузке цели в спе-
циальном блоке достаточных координат (рис. 3.13) должны оп-
ределяться упрежденный угол встречи ср*, упрежденный промах
L* и время f0CT, оставшееся до встречи.
Оптимальное управление определяется либо по цепи учета
фазового ограничения (верхняя или нижняя цепь), либо по це-
пи минимума промаха (средняя цепь). Сложность цепи мини-
мизации промаха и логики переключения на ту либо на другую
цепь зависит от принятой аппроксимации границ ЗАМ и линии
переключения в переменных L*, <р*, «Л
Анализ полученного алгоритма приводит к следующим вы-
водам.
1. Применение полученного алгоритма управления для задан-
ного класса целей (a, g0) и маневренных возможностей ракеты
(ио) целесообразно ограничить только некоторой4 частью зоны
поражения. Вне отмеченной части оптимальное управление целе-
сообразно находить только из условия минимума промаха.
2. Структура алгоритма управления ракетой, предложенно-
го для работы во всей зоне поражения, должна быть преобра-
зуемой.
В связи с этим отметим, что. приведенная на рис. 3.13 струк-
тура оптимального управления может просто преобразовывать-
ся в новую структуру (управление без ограничения на угол
встречи). Для точек зоны, в которых управление должно нахо-
диться только из условия минимума промаха, достаточно в пол-
ной структуре заблокировать верхнюю и нижнюю цепи, а в сред-
ней цепи использовать алгоритм, построенный только по пара-
метрам —ЛПр, Апр на рис. 3. 13. Это и будет структура, соответ-
ствующая рис. 3. 11.
Наведение на маневрирующую цель при ограничениях на
запас и текущий расход топлива*. Пусть управление ракетой
* В этом примере использованы материалы, предоставленные авторам
инж. Н. А. Соловкиной.
218
происходит с помощью сил, изменение которых производится пу-
тем регулирования расхода |и| «управляющего» топлива, запас
которого ограничен. Необходимо найти управление, обес-
печивающее минимальный ооредненный промах ракеты
AflXifT)! в заданный момент времени Т с учетом ограничений
на суммарный запас топлива и текущий его расход
Рис. 3.13. Блок-схема структуры оптимального управления
Сохраняя принятые в предыдущем примере допущения, за-
дачу можно сформулировать в следующем виде.
Пусть объект управления описывается на заданном интерва-
ле времени [О, Г] следующей системой дифференциальных урав-
нений:
-^2-=^(/)+х4 + А(/)д;
dt dt 1V ’ 1 4 1 v 7 dt 1 1 dt
где
219
li(t)—регулярный маневр цели (перегрузка), известная
функция;
| со | ^<о0; здесь <о — случайная величина, распределенная по
равномерному закону, определенная в каждый момент времени
ti и не зависящая от случайных величин в другие моменты вре-
мени. Это случайный маневр цели. Моменты времени Л удов-
летворяют условию
О—А) <^1 < ••• —т.
Расстояние между любыми соседними моментами времени пос-
тоянно и равно Д/;
|u|^u0, где и(...) — управление ракеты, зависящее от те-
кущих кбординат объекта, которые известны точно и измеряют-
ся только в моменты времени
На объект наложено фазовое ограничение
х8(Т)<ЛГ»(Г).
Необходимо определить управление и(...), минимизирующее
функционал
2
где через Q обозначено пространство всех реализаций процесса
(01, (02, ..(оп, a d(o — вероятностная мера на этом простран-
стве.
Используя результаты, приведенные в разд. 3-4, найдем, что
для определения оптимального управления нужно на каждом
произвольном интервале [tn-m, tn-(m-i] на основании измерений
в момент tn-m вычислить
~ т— 1
+ т{т2 - °
^m = Ln-m + К”»-1)^-2) <ол..(т_1)Д/з.
В координатах L*_m , x3(^n_rn) получена структура управле-
ния, которая показана на рис. 3.14. Из рисунка видно, что плос-
кость L*, х3 разбита на области, в каждой из которых управле-
ние строится по своему правилу. В области и = 0 управление ну-
левое, в области u = ±uo оно максимально <по абсолютной вели-
220
чине. В заштрихованной области управление линейна
зависит от L* и отыскивается из условия попадания точки
Ln_(m_^L*n_m + (zn - ),
•^3 ^3»Л—т + | й (•••)! &
Рис. ’3.14. Структура оптималь-
ного управления для интервала
[ti, ti+l]:
1—граница области абсолютного ми-
нимума; 2—линия переключения
L, х3 приходится задавать
на ближайшую из границ; 1, 2, х3 = № (см. рис. 3.14).
Оптимальное управление находится следующим образом:
после проведения измерения в начале интервала [tn-m,
определяется разбиение плоскости Ln-m, x3(tn^m) на области;
выделяется та область, в которую попадает’ точка L*_m г
полученная на основании проведенных текущих изме-
рений; управление определя-
ется по зависимости, соответствую-
щей выделенной области. Структура
оптимального управления определя-
ется в результате построения функ-
ции Grn_n(L*n_rn, Осред-
няя ее по- случайньш величинам
con-m, получим функцию
Gn—т тп, X3(tn_m).
Эта процедура проделывается
аналитически до интервала {/п_4,
/п-з). Начиная же с интервала
[/п-5, /п_4), точнее с самого построе-
ния функции Gn_4(Ln_4, Х3(/П-4)),
провести 'полное аналитическое ис-
следование не удается. Трудности
возникают в связи £тем, что анали-
тически функцию Gi на плоскости
большим числом зависимостей, каждая из которых относится
только к определенному множеству точек L, х3. Уравнение гра-
ниц этих множеств определять все труднее, да_и число таких мно-
жество резко возрастает. Так, для функции Gn-4(...), которую
удается определить, таких множеств 14.
Несмотря на это, построить синтез управления все же мож-
но. Из анализа задачи по приведенному выше методу можно
заключить, что для определения' оптимального управления ог
минимизируемой функции G требуется только следующая ин-
формация:
1)_описание границы области абсолютного минимума функ-
ции Gn-m,
2) описание на плоскости Ln-m, Хз, п-т геометрического мес-
та точек, для_которых производная dLn_mldx3t п-т на линии уров-
ня функции Gn-m равна коэффициенту наклона траектории уп-
равляемого сдвига точки L*n_m_v х3\п-т-\ (сдвига за счет наз-
начаемого управления un_rn_i(L*_m_1, x3,n-m-i)Y Выше это гео-
221
метрическое место было названо линией переключения (кривая
2 на р;ис. 3.14).
Область абсолютного минимума функции Оп-т можно опре-
делить аналитически. Для интервала tn-(m-i)] граница об-
ластв^абсолютного минимума (кривая / на рис. 3.14) состоит из
т линейных участков. Приведем уравнения участков (ввиду
симметрии картины относительно оси х3 результаты даются
только для положительной полуплоскости Ln-m>0):
Лля 0 < х3 — — 1)
Ln~m = ik и°^3 ~ ш°д /3;
для № — (m — 1) иод/ < х3 ^№ — (tn — 2) и0М
Ln_m = [№ — х3 — (т — 2) и0М] &tk (tn_3) +
+ ik «0Д/3 - V Юод/з;
для № - (т - 2) аод/ < х3 < N (tл_3) - (m - 3) «од/
^п—т ~ 1-^° х8 (in—m) (т 2) И0Д/| 2Д/£ (tn—3) 4~
+2 ik (tn-x-i) «0Д^3- у <»oA's-
Z=2 /?Л
Крайняя правая точка области абсолютного минимума нахо-
дится из рекуррентного соотношения
N (tn_m) = N ’
где jV(/n_1) = W„_2) = №(r);
N (in_3) = № (T)------.
Общий вид линейного участка границы области абсолютного
минимума не приводится, так как нахождение такого важного
элемента структуры, как линии переключения, возможно только
на ЦВМ. В этом случае описание области абсолютного мини-
мума используется только для контроля правильности вычисле-
ний.
Функцию Оп-т можно вычислить следующим образом. В про-
цессе счета на ЦВМ определяются функции
(^л» •*з(^л)) = ^л—1 (^л—1> хз №п—1))“*ОЯ—т Хз(?п—тУ)
в узлах сетки поля > О, /V0 > х8 > 0.
222
Моменты времени /<е[0, Г] и удовлетворяют неравенствам!
0 = t0<ti< . . . <tf< ... </п_!</п = Г.
Функция Gn(...) известна. Последующая функция Gn_m
строится по значениям предыдущей функции Gn_(m_D по следую-
щим этапам.
А. Построение функции Gn-m в узле L=Ln-m, xs=x3(tn^m).
Узлы выбираются только такие, у которых L^L”ax . Задается,
ряд значений со:
СО =5шДсо,
где
с°0
Дсо
•Sai
с°0
Дю
3°
СО
Для каждого со определяется минимальное значение функции:
Qn-m (s<°) (алгоритмы управляемого сдвига) и затем по квад-
ратурной формуле Ньютона находится Gn-m(Ln-m, Хз(^п-т))-
Б. Алгоритм управляемого сдвига (УС). Управляемый сдвиг
фазовой точки Хз(^п-т). L*n-m (s°>) осуществляется в соответ-
ствии со следующими формулами:
^п— (т—i) = Ln—m (tn 1) д/2£ (tn_и (/л_ m);
•^з (tn— (т—1)) = Х3 -|-1 и (/л_^)| Д/.
По зависимости
Gn-(m-l) (L*n_m - (tn - 1) д/2£ (tn_m) su№,\ х3 (tn_m)+s^uM)
для каждого значения su с и,спользо,ванием:
алгоритма интерполяции рассчитывается значение функции
Gn-(m-i) и выбирается наименьшее среди достижимых при управ-
ляемом сдвиге.
Для расчета значений функции Gn-(m-i) вне узловой точки
проводится интерполяция по окружающим ее узлам на основа-
нии интерполяционной формулы Бесселя.
В. Изменение поля. Максимальные размеры поля (его гра-
ницы), на котором задана функция G(...), выбираются из сле-
дующих соображений:
1) обеспечить вычисление наиболее характерных участков-
области определения функции G(...);
2) обеспечить заданное количество интервалов (количество-
функций Gf, где i = n—1, ..., 1) при изменении функции G.
Максимальное значение £™ах в начале интервала т опреде-
ляется по формуле
Lm = £я,-1 _[(?-.ОС?-.2) д£_д£,
max тах L 2Д£ Jii.4
где [.. .]ц.ч — целая часть выражения в скобках;
Д£, Д/ — шаг сетки по L и шаг по времени.
22&
Для вычисления функции G(...) и определения линии пере-
ключения необходимы расчеты на ЦВМ. Расчеты показали, что
как область абсолютного минимума, так и линия переключения
определяются неоднозначно. Это связано с малым изменением
функции G(...) в этих районах. Сравнительно легко определя-
ется «коридор», в котором лежат линии переключения и грани-
ца области абсолютного минимума. Это свойство структуры поз-
воляет в известных пределах упрощать вид линий, что значи-
тельно облегчает их реализацию в технических устройствах.
Опыт проведения вычисления и построения линий переклю-
чения позволил выделить ряд особенностей этого процесса.
Так, моделирование при начальных условиях
^о=4О; £(/) = 1; ц)о = 2О; 2V° = 5O
и параметрах
/л = 15; д/= 1; дя=4; Zmax = 7500;
дЛ=500; До)=5; дх3 = 5
показало, что для построения линии переключения необходимо
точнее строить линии уровня функции G. Для этого функции
^п-т нужно определять,на поле с возможно меньшим шагом
по L. Так, при Д£=500 точка касания находится на участке
кривой, где ошибки определения ее положения по L достигают
ж&ЬЦ. Это потребовало уменьшить шаг по L до Д£=100. При
этом время счета соответственно увеличилось приблизительно в
четыре раза. При расчетах с шагами Ди=4 и Д<о = 5 обнаружи-
лось значительное «колебание» (изломы) функции Gn_m(L, х3).
Уменьшение шага по и и <о вдвое приводит к тому, что функции
сглаживаются. Это объясняется тем, что при изменении со (где
О^со^соо) и и (где при различных т (где т=1,...,
..., 13) неравномерно используется поле, на котором определена
функция Gn_m+\. Управляемая точка x3(/n_(rn_i)) при
смещении вследствие изменения и и <о (при Ди = 4, Д<о = 5) при
т^б два раза попадает в каждую ячейку поля, на котором оп-
ределена функция Gn-m+i (через которые проходит отрезок уп-
равляемого сдвига), при ди = 7,8 — только один раз, а при т^9
попадаются ячейки, в которые управляемая точка не попадает.
Для равномерного использования поля и экономного расхода
машинного времени оказалось целесообразным считать до т^б
с До) = 5, а при всех остальных т брать Дсо = 2,5. Уменьшение
Дсо вдвое приводит к увеличению времени счета соответственно
в два раза.
Как отмечалось выше, линия переключения является геомет-
рическим местом точек касания к линиям уровня функции
Gn-m-i линий управляемого сдвига точки L*n_m , х3,п-т- Так как
линию переключения точно построить нельзя, то на каждом ин-
224
Рис. 3.15. Области возможного положения ли-
нии переключения
Рис. 3.16. Метод построения области возможных положений линии пере-
ключения:
о—построение линии уровня; б—построение коридора
225
тервале был построен «коридор», в котором она должна нахо-
диться.
На рис. 3.15 показаны области возможного положения линии
переключения (коридор), полученные путем расчета на ЦВМ
для приведенных выше начальных условий.
Для построения коридора (см. рис. 3.16, а, б) проводились
касательные к линиям уровня Gn =const и прямые, параллель-
ные им и сдвинутые в сторону меньших х3 на величину 0,1 Дх3,
что допустимо ввиду малого изменения функции Gn при таком
сдвиге.
Точки пересечения линии уровня со сдвинутыми касательны-
ми определили границу коридора (для т=6 такой коридор по-
казан на рис. 3.16, б).
В заключение отметим, что на рассмотренных примерах бы-
ли продемонстрированы способы определения структуры опти-
мального управления (см. пример наведения при ограничениях
на угол встречи) и параметров этой структуры путем использо-
вания аналитических и численных исследований (см. пример на-
ведения при ограничениях на запас и расход топлива).
ГЛABA 4
ПРИМЕНЕНИЕ МЕТОДОВ
СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
К АНАЛИЗУ И ОПТИМИЗАЦИИ
СИСТЕМ УПРАВЛЕНИЯ
В практике проектирования летательных аппаратов и систем
управления ими широкое применение нашли ЦВМ. С их по-
мощью удается проанализировать, не прибегая к натурным экс-
периментам, поведение системы в целом или отдельных ее час-
тей и, таким образом, оценить эффективность системы и выб-
рать наилучшее конструктивное решение с приемлемыми
затратами времени и средств.
Моделирование систем управления летательными аппарата-
ми должно учитывать различного рода случайные воздействия:
шумы в информационных устройствах, разброс параметров»
случайные маневры цели и др. Наличие случайных воздействий
значительно замедляет исследование системы. В связи с этим
одним из главных критериев, по которому сравнивается эффек-
тивность тех или иных методов исследования с помощью ЦВМ»
являются затраты машинного времени.
Целью анализа системы является вычисление характеристик»
определяющих степень выполнения поставленных перед маши-
ной задач — критерия качества. Критерием качества может
быть функция, определяющая точность системы, ее стоимость»
вес и т. д. При любых определениях качества математическая
сторона остается одной и той же — критерий является функци-
ей или функционалом от фазовых координат системы и ее па-
раметров. Поэтому рассмотрение методов анализа целесообраз-
но проводить с обобщенной точки зрения, не конкретизируя
критерий качества.
Одной из наиболее часто встречающихся проблем, решаемых
в процессе проектирования, является оптимизация отдельных
блоков или системы в целом. В связи с усложнением условий
функционирования и повышением требований к системе вопро-
227
сы оптимизации систем управления летательными аппаратами
приобретают все более важное значение.
Известные методы оптимизации можно разбить на две груп-
пы. К первой относятся методы, использующие для расчета оп-
тимальных управлений и параметров необходимые условия экс-
тремума, записанные в той или иной форме. Эти методы пред-
полагают аналитическое или численное решение условий
•оптимальности и могут быть доведены до конца только в случае
достаточно простых уравнений оптимизируемого объекта. Боль-
шим их достоинством является возможность получения не толь-
ко количественных соотношений, но и структуры оптимальных
законов управления, используемой в постановке задач парамет-
рической оптимизации. Рассмотрению некоторых методов первой
группы посвящена третья глава настоящей книги.
Вторую группу составляют прямые методы, сводящие задачу
оптимизации к выбору числовых параметров из условия мини-
мума заданного критерия качества при ограничениях на значе-
ния некоторых функций параметров — ik задаче нелинейного
программирования. Эти методы пригодны для оптимизации
сложных систем и применение их ограничено в основном только
объемом вычислений.
Оптимальные системы зачастую очень чувствительны к точ-
ности, определения их параметров и условий функционирования.
Поэтому использование упрощенных моделей системы в задачах
оптимизации не всегда оправдано и, во всяком случае, должно
сопровождаться проверкой результатов на полной модели сис-
темы.
Поскольку процессы в системах управления летательными
аппаратами описываются дифференциальными уравнениями вы-
сокого порядка, применение к ним первой группы методов целе-
сообразно на первых этапах проектирования системы для выяс-
нения структуры законов управления. Если структура системы
известна, проектирование ее заключается в выборе параметров
отдельных элементов, который целесообразно проводить исполь-
зуя прямые методы оптимизации.
Процесс оптимизации системы с помощью прямых методов
состоит в расчете критерия качества системы при различных
значениях выбираемых параметров и движении к новым значе-
ниям параметров таким образом, чтобы значение минимизируе-
мого критерия убывало. Таким образом, анализ системы, пони-
маемый как расчет ее критерия качества при заданных значе-
ниях выбираемых параметров, является составной частью алго-
ритмов оптимизации прямыми методами.
Существует две группы методов анализа динамических сис-
тем, зависящих от случайных воздействий. Методы первой груп-
пы используют полученные по дифференциальным уравнениям
анализируемой системы уравнения для статистических характе-
ристик, решая которые можно найти искомый критерий качества.
228
К ним относятся статистическая линеаризация [7], [И], методы,
связанные с решением уравнения для плотности распределе-
ния вероятностей значений фазовых координат и вытекающих
из него систем обыкновенных дифференциальных уравнений от-
носительно моментов и семиинвариантов [6] и некоторые другие.
Методы первой группы представляют мощный математический
аппарат качественного, а в некоторых случаях и количественно-
го исследования динамических систем, однако их применение
связано либо со сравнительной малой точностью расчетов (ме-
тод статистической линеаризации), либо с необходимостью ре-
шения систем дифференциальных уравнений, порядок которых
значительно превышает порядок дифференциальных уравнений
исследуемого объекта. Поэтому в большинстве случаев методы
первой группы целесообразно применять при решении модель-
ных задач исследования систем управления летательными ап-
паратами, когда необходимо определить качественную картину
поведения системы.
В методах второй группы для расчета критерия качества си-
стемы используется обработка результатов многократного реше-
ния дифференциальных уравнений системы при различных реа-
лизациях случайных воздействий. Их математическую основу
составляет теория численного интегрирования и метод статисти-
ческих испытаний (метод Монте-Карло).
На практике возможности методов второй группы ограниче-
ны имеющимся ресурсом машинного времени, отведенного для
решения данной задачи. Однако в принципе они позволяют ана-
лизировать системы любой степени сложности и с любой необ-
ходимой степенью точности. Их можно рекомендовать для ис-
пользования на заключительных этапах проектирования, когда
необходимо учитывать все особенности исследуемой системы,
влияющие на её эффективность.
Ввиду того, что для применения методов второй группы не
требуется решения специальных вспомогательных уравнений, а
можно использовать готовые математические модели исследуе-
мых систем, сроки выполнения работ по анализу при использо-
вании методов второй группы могут быть значительно сокра-
щены.
Содержание настоящей главы составляют методы анализа
динамических систем, зависящих от случайных воздействий, ко-
торые основаны на обработке результатов решения уравнений
системы, и их применение при решении задач оптимального
проектирования с помощью алгоритмов нелинейного программи-
рования. Особое внимание уделяется методам исследования си-
стем, зависящих от случайных процессов. Критерием выбора
методов анализа и оптимизации являлась возможность их ис-
пользования на заключительных этапах проектирования при
учете всех особенностей исследуемого объекта.
229
4.1. ПОСТАНОВКА ЗАДАЧИ
СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
Поведение систем управления летательными аппаратами мо-
жет быть описано системой обыкновенных дифференциальных
уравнений
У1. У» xv .... хту, у1(0)=у°1, (4.1)
где уг — фазовые координаты системы; хг- — параметры систе-
мы и сигналы входных воздействий.
Величины Xi могут быть постоянными и функциями време-
ни, фазовых координат и т. п. В большинстве реальных прило-
жений часть или все величины Xi являются случайными. Во мно-
гих задачах начальные условия для системы (4.1) также явля-
ются случайными величинами. Если ввести случайный вектор
x=(xp xm„y°v r/0) = (xp хт), (4.2)
уравнения системы (4.1) можно записать в виде
= У1, ..., ys, xlt ..., xm,);
dt
yt(Q)=xmi+r, i=\, ..., s, (4.3)
где вектор x содержит все случайные величины и процессы, от
которых зависит наведение системы. Среди компонент вектора
х могут быть и детерминированные величины, но в этом случае
они трактуются как случайные, имеющие плотность распределе-
ния в виде 6-функции. При фиксированных реализациях слу-
чайных воздействий и начальных условий фазовые координаты
системы могут быть найдены путем решения дифференциальных
уравнений (4.3)
У1 — Vt (Л х). (4.4)
Сравнение различных, но предназначенных для одной и той
же цели систем 'производится <по заданному критерию эффектив-
ности, характеризующему поведение системы в различных усло-
виях. Степень удовлетворения системой .предъявленных к ней
требований выражается некоторой функцией (или функциона-
лом) качества. Вид этой функции определяется целью, для ко-
торой система предназначена. Она должна быть такой, чтобы
имелась возможность вычислить ее значение для каждого испы-
тания исследуемой системы.
В роли критерия эффективности естественно использовать
границы области изменения функции качества при всех воз-
можных изменениях параметров системы и среды, в которой она
находится. Однако такой критерий не нашел широкого приме-
нения, поскольку большинство реальных систем ему не удовлет-
230
воряет. Обычно существует практически маловероятное сочета-
ние параметров системы и внешних воздействий, для которых
значение функции качества выходит за допустимые пределы. По
критерию границ изменения функции качества система должна
быть отвергнута, хотя для большинства случаев она может да-
вать удовлетворительные результаты.’
Поэтому обычно применяются различные вероятностные кри-
терии эффективности систем. Наиболее общим видом вероятно-
стного критерия является математическое ожидание некоторого
функционала Ф(у^ ..., ys, ..., хт) от фазовых координат и
случайных воздействий, представляющего либо функцию качест-
ва системы, либо функцию от функции качества
}=МФ(у1гys, , хт). (4. 5)
Задача статистического моделирования заключается в опре-
делении J.
Обозначим через f(x)=/(xb ..., хт) функционал, получен-
ный из функцирнала Ф(г/1, ..у3, *1, ..хт), участвующего в
определении критерия эффективности (4.5) подстановкой реше-
ний системы (4.3),
J=Mf(x1,..., хт).
Временно предположим, что среди компонент вектора х есть
только случайные величины. Тогда функционал f будет в дейст-
вительности функцией т случайных величин ..., хт.
Допустим, что плотность распределения компонент векторах
равна p(xi, ..., хт). Тогда для критерия эффективности J спра-
ведливо соотношение
7==1 ....Xm)dx1... dxm. (4.6)
Таким образом, когда среди компонент вектора х нет случай-
ных процессов, решение задачи анализа системы эквивалентно
вычислению интеграла (4.6).
При выполнении экспериментов с системой или ее моделью
можно определить значение функции качества только в отдель-
ных точках области изменения параметров xif ..., хт. 'Задачи
оценки эффективности системы сводится поэтому к определению
интеграла от некоторой функции по ее значениям в отдельных
точках. Это хорошо известная в вычислительной математике за-
дача численного интегрирования.
Другой подход к задаче анализа основан на статистической
трактовке интеграла J как математического ожидания случай-
ной величины /(xi, ..., хт). Используя N независимых реализа-
231
ций случайной величины f, в качестве оценки интеграла можно
принять оценку математического ожидания
где fk — независимые реализации f.
При моделировании системы на ЦВМ независимые реализа-
ции f можно получить, решая систему при N различных незави-
симых реализациях случайного вектора х. В результате в каче-
стве приближенного значения интеграла будет принято выраже-
ние
(4. 7)
Л k 1
где xi, ..., хт—й-я независимая реализация вектора х.
Формула (4.7) представляет оценку интеграла J методом
Монте-Карло. В то же время это не что иное, как квадратурная
формула для вычисления интеграла J по значениям функции
f(xi,...,xm) в узлах-хД..., xmk. Единственной ее особенностью
является то, что выбор узлов интегрирования является случай-
ным, т. е. различным для каждого случая применения формулы.
В силу общности детерминированных методов исследования
эффективности, основанных на формулах численного интегриро-
вания, и методов математической статистики задача оценки ин-
теграла J может быть названа «задачей статистйческого модели-
рования».
4.2. ФОРМУЛИРОВКА ЗАДАЧИ
ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Задачей теории численного интегрирования является вычис-
ление определенного интеграла по значениям подынтегральной
функции в отдельных точках.
Пусть требуется вычислить многомерный интеграл
x^dx^-‘- dx™ (4'8>
где Q — заданная область интегрирования;
р — известная положительная функция, называемая обычно
функцией веса;
/ — функция, подлежащая интегрированию с весом р.
232
Тогда квадратурной формулой называется равенство
(4.9)
Л-1
где аи — постоянные величины, коэффициенты квадратурной
формулы; Xik,..., xmk— точки /n-мерного пространства — узлы
квадратурной формулы; /?(/)—остаточный член квадратурной
формула.
Коэффициенты аь и узлы квадратурной формулы х\к,..., хтк
подбирают таким -образом, чтобы остаточный член R(f) обра-
щался в нуль или был мал для класса функций, которому при-
надлежит /(Xi, ..хт). Если это условие выполнено, то из фор-
мулы (4.9) следует приближенное равенство
-4). (4.10)
Л-1
позволяющее вычислить величину интеграла (4.8) по значениям
подынтегральной функции в узлах хЛ..., хтк, k=l,...,N.
Соотношение (4.9) не является самым общим видом форму-
лы численного интегрирования; существуют квадратурные фор-
мулы, использующие для подсчета интегралов не только значе-
ния подынтегральной функции, но и ее производные. Однако
практического применения в задаче статистического анализа си-
стем они до сих пор не нашли вследствие трудностей, связан-
ных с вычислением производных.
Основная задача теории численного интегрирования состоит
в определении коэффициентов и узлов квадратурных формул,
обеспечивающих удовлетворительную точность численного ин-
тегрирования при заданном числе узлов N. Получение квадра-
турных формул основано на идее интерполяции. По значениям
подынтегральной функции в узлах строится интерполяционная
формула, аппроксимирующая заданную функцию в промежуточ-
ьых точках. Затем производится точное интегрирование интер-
полирующей функции, результат которого принимается за при-
ближенное значение интеграла (4.8).
Поскольку интерполирующая функция зависит от значений
функции в узлах линейно, полученная формула численного ин-
тегрирования также зависит от них линейно, что отражено в со-
отношениях (4.9) и (4.10). Остаточный член формулы (4.9) по-
лучается вследствие того, что интерполирующая функция ап-
проксимирует функцию в промежуточных точках с ошибками.
Поскольку интерполирующую формулу, хорошо приближаю-
цую любые функции, построить невозможно, также невозмож-
о получить квадратурную формулу, дающую хорошую точность
’нтегрирования во всех случаях В зависимости от конкретного
3200
233
типа интегрируемой функции должна выбираться та квадратур-
ная формула, которая дает наибольшую точность при заданном
числе узлов интегрирования.
4.3. ИНТЕРПОЛИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
В ОДНОМЕРНОМ СЛУЧАЕ
Как известно, интерполяционный многочлен Лагранжа, сов-
падающий с функцией f(x) скалярного аргумента х и п точках
х1, ..., хп, имеет стёпень п—1 и может быть записан в виде
п
(х_Х(л.) (410
где
о) (х) = (х — х1) (х — х2)... (х —хл). (4. 12)
Тогда справедливо равенство
/(х) = £„_1(х)+Тл_1(х), (4.13)
где Tn-i(x) — остаточный член формулы интерполирования. Он
может быть оценен. Например, если функция f(x)- имеет про-
изводную до порядка п, для остаточного члена справедлива сле-
дующая формула [1]:
= (4.14)
П ! '
где £ — некоторая точка внутри отрезка x}^.x^Zxn.
Предположим, что нужно вычислить интеграл
ь
[ /(Х)Р (аг)^х, (4.15)
а
зная значения функции f (х) в п точках х1, .:., хп. Используя
формулу (4.13), подставим в интеграл выражение f(x) . через ее
интерполирующий полином
ъ ь
j f (x)p(x)rfx = J
а а
b
Ln-i (х) р (х) dx + J Tn_Y (х) р (х) dx=
а
р (х) dx.
234
Если ввести обозначения
ь
<№=\-(------p(x)dx-, (4. 16)
J (х — Xя) Ц>п [Xя)
а
= (4.17)
а
получим квадратурную формулу для вычисления интеграла
(4.15)
Ь п
\f(x)p (х) dx=^ a^f (х*) +/?„ (/). (4.18)
а Л-1
Коэффициенты квадратурной формулы могут быть вы-
числены заранее по формулам (4.16), остаточный член квадра-
турной формулы Rn(f) может быть оценен согласно (4.17), если
дана оценка остаточного члена формулы интерполяции 7\-i(*).
Перейдем к рассмотрению некоторых, наиболее употреби-
тельных квадратурных формул [1].
Формулы Ньютона — Котеса выведены для случая, когда
р(х) = 1, т. е. для вычисления интеграла
ь
J f (х) dx.
а
и получаются путем замены подынтегральной функции интер-
поляционным многочленом Лагранжа с узлами, разбивающими
промежуток интегрирования на равные части. Таблицы весовых
коэффициентов аьп и множителей при производных в формуле
остаточного члена можно найти в книге [1].
Формулы трапеций и Симпсона. Недостатком формул Нью-
тона — Котеса является громоздкость выражений для весовых
коэффициентов. Кроме того, весовые коэффициенты, принимая
большие по модулю значения, могут иметь разные знаки, что
может привести к большим погрешностям при использовании
приближенных вычислений. Поэтому на практике формулами
Ньютона — Котеса для больших значений п предпочитают не
пользоваться, а разбивают интервал интегрирования на ряд
подынтервалов, вычисление интегралов для которых -произво-
дится с помощью этих формул для малых значений п. Именно
таким способом получаются известные квадратурные формулы
трапеций и Симпсона.
Формула трапеций получается путем разбиения отрезка инте-
грирования [а, 6] на т равных частей длиной й=-=—, на каж-
дой из которых интегрирование проводится с помощью форму-
9* 235
лы Ньютона — Котеса, соответствующей числу узлов и, рав-
ному 2.
Формула трапеций имеет вид
f (х) dx=у + 2/(л1) + • • • + 2/(х->)+/(х-)] + R,
т
(4.19)
где
= /; / = 0, 1,..., т.
т
Остаточный член формулы трапеций может быть вычислен
через вторую производную подынтегральной функции
/?ТР
_ (*-а)3 f',
12/n2 J
где I — некоторая точка внутри интервала а<х<Ь.
Если отрезок интегрирования [а, 6] разбить на 2т равных ча-
стей и к каждой из них применить формулы Ньютона — Коте-
са с тремя узлами, получится квадратурная формула Симпсона
ь
\ f (х) dx=^~\f (х«) + 4/ (х‘) + 2/ (х2) +4/ (Xs) -j-
J o/n
a
+ ...+4/(x2m-1) + /(-v2m)]. (4.20)
где
Остаточный член формулы Симпсона
d = flY /(4) Сп)
с V 2 ) 90т4 ’
где rj — точка, принадлежащая интервалу а<х<Ь.
Формулы численного интегрирования Гаусса. В общем слу-
чае квадратурные формулы Гаусса, полученные с использова-
нием интерполяционного многочлена Лагранжа степени п—1,
производят интегрирование без ошибки произвольного полинома
степени п—1. Рассмотрение выражения для квадратурной фор-
мулы (4. 18) показывает, что при п узлах интерполирования она
зависит от 2п параметров — узлов интерполирования х\...,хп л
коэффициентов а^п\ ..., ап(п).
Можно поставить задачу — так подобрать эти 2п парамет-
ров, чтобы полученная формула численного интегрирования поз-
воляла вычислять без ошибки интеграл от полинома наивысшей
степени.
236
Условием интегрирования без ошибки полинома степени т
является требование, чтобы квадратурная формула была точной
при интегрировании /п+1 функций 1, х, (%)2, ..(х)т. Записы-
вая условие равенства нулю остаточного члена при интегриро-
вании этих функций, получим /п+1 уравнений относительно 2п
неизвестных. Из требований их разрешимости можно найти т:
/п = 2п-1 , (4.21)
— максимальную степень полинома, интеграл от которого можно
вычислить точно, используя квадратурную формулу с п узлами
интегрирования.
Непосредственное разрешение системы для определения а/п)
и х* возможно, но громоздко. Однако узлы интерполирования
могут быть найдены с помощью искусственного приема доста-
точно просто. Пусть искомыми узлами являются абсциссы
х1,..., х+ Рассмотрим многочлен
<оя (х) = (х — л1) (х — х2)... (х — хл). (4. 22)
Этот многочлен удовлетворяет следующему необходимому и до-
статочному условию, из которого можно найти узлы х\ Пока-
жем, что
ь
J Р W (х) Я (*) =0, - (4. 23)
а
если q(x) — произвольный многочлен степени не выше п—1.
Условие (4.23) необходимо, поскольку функция f(x) =
= (оп(х)^(х) является полиномом степени не выше 2п—1 и дол-
жна поэтому интегрироваться численно без ошибки. Но значе-
ния f(x) в точках xk равны нулю, поэтому интеграл (4.23) сог-
ласно формуле (4.18) равен нулю.
Пусть многочлен f(x) имеет степень не выше 2п—1. Тогда
f(x)=^n (x)<?(x)-]-r (х), (4.24)
где q(x) и г(х) — многочлены степени не выше п—1. Поэтому
ь ъ
j /(x)p(x)rfx = j <o„(x)?(x)p(x) dx-\-
а а
b b
J г (х) р (х) dx = J г (х) р (х) dx.
а а
Но
Ь п
J Г (х)р (х) dx =2 4л)г(хй),
а Л=1
поскольку г(х) как полином степени п—1 совпадает со своим
интерполяционным многочленом Лагранжа, построенным по уз-
237
лам xl, ..хп и, следовательно, интегрируется квадратурной
формулой (4.18) без ошибки. Поэтому
J / (х) р (х) 4я)г (х*) =2 а*л) / (•**)»
a Л-1 Л-1
поскольку f(xk) = г(xk) согласно формуле (4.24).
Определив многочлен <оп (х) из условия (4.23) и вычислив
его корни, можно найти искомые узлы квадратурной формулы.
Коэффициенты можно определить по формулам (4.16).
В результате получим квадратурную формулу, которая называ-
ется квадратурной формулой Гаусса. Коэффициенты квадратур-
ной формулы Гаусса называются числами Кристоффеля, они
обозначаются обычно Q^n)-
Для остаточного члена формулы Гаусса можно получить сле-
дующее выражение:
W = Сл!0 \ Рdx-
(2л)! J
а
Практически многочлен <оп(х) определяется следующим об-
разом. При любом весе р(х) можно построить ортонормиро-
ванную последовательность многочленов Рп(х) степени п (п =
=0, 1, ...), удовлетворяющих условиям
J рп W Рт (*) Р (*) Их=8ОТЯ, ч (4.25)
а
где
> _Р ПРИ
• 0 при tnfn.
Тогда, как известно, любой многочлен степени т может быть
представлен в виде линейной комбинации ортонормированных
многочленов PQ(x), ..., Рт(х). Учитывая равенство (4.25), най-
дем
JP„(x)<7(x)rfx=0, (4.26)
а
если q(x) — произвольный полином степени не выше п—1.
Сопоставляя (4.26) и (4.23), получим, что в качестве <оп(*)
можно взять ортогональный полином Рп(х). Числа Кристоффе-
ля выражаются через полином Рп{х) по формуле
, (4-27)
238
Подробные таблицы узлов и весовых коэффициентов квадра-
турных формул Гаусса для весов
_ х*
р (х}= е 2 —оо<Гх<оо,
7 /2л
р(х)=е-х, 0<х<оо
имеются в [20]. В табл. 4.1—4.3 приводятся взятые из [20] значе-
ния для наиболее употребительных в практике -статистического
моделирования случаев использования квадратурных формул
Гаусса.
Таблица 4.1
Узлы и весовые коэффициенты формул Гаусса
1
% для расчета интегралов вида f (х) — dx
-1
Число узлов
2
xi= — х2 = 0,5773503
gj = q2 = 0,5000000
х1 = 0,0000000 Q! =0,4444444
х2 = — х3 = 0,7745967 q2 = Оз = 0,2777778
х, = —х2 = 0,3399810 01 = 02 = 0,3260726
х3=-х4 = 0,8611363 q3=Q4 = 0,1739274
х1= 0,0000000
х2 = —х3 = 0,5384693
х4 = —х5 = 0,9061798
0, =0,2844444
02 =s 03 == 0,2393143
05 = 06 = 0,1184634
Квадратурные формулы Гаусса целесообразно использовать
в тех случаях, когда для вычисления интеграла с высокой точ-
ностью можно использовать значения подынтегральной функции
в небольшом числе точек. Недостатком их по сравнению с фор-
мулами трапеций и Симпсона является сложность вычисления
узлов и весовых коэффициентов. По сравнению же с формула-
ми Ньютона — Котеса формулы Гаусса обладают несомнен-
ными преимуществами ввиду большей точности.
232
Таблица 4.2
Узлы и весовые коэффициенты формул Гаусса
/(*) 7Ге 2 dx
J /к
для расчета интегралов вида
Число узлов xk
2 *1 = —*2 = 0,9999999 21 = @2 = 0,5
3 xi = 0 х2 = х3 = 1,7320508 q1 = 0,6666667 Q2 = Оз — 0,1666667,
4 Xi= — *2 = 0,7419638 *з = -*4 = 2,3344142 21 = 22 = 0,4541241 23 = 24 = 0,0458758
5 *1 = 0 х2 = — х3 = 1,3556261 Х4 = — х5 = 2,8569693 21 = 0,5333333' 22 = 23 = 0,2220759 24 = 25 = 0,01125741
Таблица 4.3
Узлы и весовые коэффициенты формул Гаусса
оо
для расчета интегралов вида f / (x)e—xdx
Число узлов xk
2 *1= 0,5857864 *2= 3,4142135 Q1 =0,8535533 q2 = 0,1464466
3 *1= 0,4157745 *2= 2,2942803 *з= 6,2899450 21 =0,7110930 22 = 0,2785177 2з = 0,0103893
4 *1 = 0,3225476 *2= 1,7457611 *з= 4,5366202 *4 = 9,3950709 21 = 0,6031541 22 = 0,3574186 2з = 0,0388879 24 = 0,0005393
240
Продолжение
Число узлов xk «Л
5 х, = 0,2635603 х2 = 1,4134030 х3 = 3,5964257 х4 = 7,0858100 х5 = 12,6408008 б! = 0,5217556 02 = 0,3986668 0з = 0,0759424 04 = 0,0036118 05 = 0,0000234
4.4. МНОГОМЕРНЫЕ ФОРМУЛЫ
ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Для вычисления многомерных интегралов, как и в одномер-
ном случае, теория численного интегрирования может быть раз-
вита на основе формул интерполяции. Существенной особенно-
стью многомерных интегралов по сравнению с одномерными яв-
ляется то, что для их вычисления необходимо знать значения
подынтегральной функции в большем числе узлов, а сами узлы
распределяются *в /гг-мерном пространстве. Поэтому при выводе
многомерных квадратурных формул для упрощения расчетов за-
частую используют различные искусственные приемы, хотя при
желании эти же формулы можно получить на основе теории ин-
терполяции многомерных функций.
Значительно менее разработанным в многомерном случае яв-
ляется вопрос об оценке остаточного члена. Объясняется это
двумя обстоятельствами: во-первых, тем, что формула остаточ-
ного члена в многомерном случае более громоздка и получение
ее связано со сложными расчетами; во-вторых, даже в тех слу-
чаях, когда выражение для остаточного члена получено, им не
всегда удается воспользоваться, поскольку величины, входящие
в выражение для остаточного члена (производные высокого по-
рядка интегрируемой функции), обычно неизвестны.
Перейдем к рассмотрению конкретных типов многомерных
квадратурных формул.
Метод вычисления многомерных интегралов,
основанный на повторном применении квадратурных формул
Известно, что любой многократный интеграл может быть
Вычислен путем последовательного применения однократного
интегрирования по каждой из переменных. Производя одно-
кратное интегрирование с помощью одной из ранее описанных
квадратурных формул, можно вычислить многомерный интег-
рал.
241
Для примера предположим, что нужно определить значение
двумерного интеграла
y}dxdy, (4.28)
где область интегрирования Q изображена на рис. 4.1.
Обычным, излагаемым в математическом анализе, способом
интеграл (4.28) можно привести к виду
ъ ₽(Р)
J dy J f (х, у) dx. (4. 29)
а л(у')
Применяя какую-нибудь одномерную формулу к внешнему
интегралу (4.29), можно записать
ь к и) N,
\dy j f (x, у) dx = '2ial j /(x, yl)dx-\-R0. (4.30)
fl a(//) 1-1 Л\У[)
Интегралы, стоящие под знаком суммы, представим в виде
₽(?)
J f (X, у1) rfx=2 bi}f (х", (4.31)
•X?)
Подставляя (4.31) в формулу (4.30), получим квадратурную
формулу для вычисления интеграла (4.28)
лг, ni N,
уj/(x, z/)rfx^=22aA//(^. ю+^о-к2aiRi- (4-32)
*0 Z-4/-1 /-1
Остаточный член ее может «быть определен, если известны
остаточные члены формул одномерного численного интегриро-
вания
Nt
R=R.+^iRi-
i-i
Общее число узлов квадратурной формулы (4.32) будет
jv,
ЛГ = 2Л/- (4.33)
/ — 1
Отсюда видно, что с ростом размерности интеграла число
узлов квадратурной формулы растет очень быстро. Например,
если принять, что каждое однократное интегрирование требует
N{ узлов, всего для подсчета /гг-кратного интеграла в этом слу-
чае понадобится Nim узлов. Поэтому при вычислении многомер-
ных интегралов вопрос уменьшения числа узлов квадратурных
формул стоит особенно остро.
242
Для того чтобы уменьшить число узлов ;в квадратурной фор-
муле (4.32) без ущерба в точности, следует применять наиболее
точные одномерные квадратурные формулы, например, форму-
лы Гаусса.
Метод повторного применения одномерных квадратурных
формул в отличие от -стандартных формул численного интегри-
рования неудобен тем, что для у
каждого случая использования
все формулы нужно переписы-
вать заново. Вместе с тем этот
метод имеет и большие пре-
имущества: пригоден для лю-
бых областей интегрирования,
позволяет в широких пределах
изменять используемые одно-
кратные формулы для повыше-
ния точности при фиксирован-
ном числе узлов интегрирова-
ния.
Стандартный многомерные
квадратурные формулы выво-
Рис. 4.1. Область интегрирования дву-
мерной функции
дятся для вполне определен-
ных областей, что позволяет применять одну и ту же форму-
лу много раз. Однако при этом должно быть предварительно
проведено путем соответствующей замены переменных сведение
области интегрирования к виду, для которого выведена стан-
дартная формула.
Многомерная интерполяционная формула Лагранжа.
Метод получения квадратурных формул путем замены
подынтегральной функции интерполяционным многочленом
Интерполяционный полином, значения которого совпадают
со значениями гтг-мерной функции f(xly ..., хт) в точках
х29 > • • •, прямоугольной сетки, образованной всевозможны-
ми комбинациями координат хД ..., хЦ по каждой из осей х<
(/= 1, ..., т), имеет вид
л, л2 пт
Lnin2 ...nm(Xv • • • i Хт) = 2”’ 2
й1в1й2-1
х п (4. 34)
где
- *}) (xi - %2)... (X, - х*,). (4. 35)
243
Точно так же, как и в одномерном случае, может быть вы-
числен остаточный член многомерной формулы интерполяции
/(хр • • • , Х/в) = £Л1Ла...л^ (Хх, . . . , (4.36)
Поскольку выражение для него получается чрезмерно гро-
моздким и зависит от производных высокого порядка, оценить
его практически не удается. Однако можно утверждать, что ес-
ли интерполируемая функция представляет полином степени не
выше Пг—1 по %г, то остаточный член формулы интерполяции
равен нулю.
Предположим, что требуется вычислить интеграл
J ... р/(хр ..., хт) fl Pj(^j)dXi...., dxm. (4.37)
* ат /-1
Заменим подынтегральную функцию f(xi9 хт) ее интер-
поляционным многочленом (4.34). В результате получим следую-
щую квадратурную формулу для вычисления интеграла (4.37),
использующую узлы %2Я, • • • , Хтт-
j • • • \тf (*1, • • •, хт) П Pj(xj)dx1... dxm=
а‘ ' ат
пл пт т
= 2 2--2 П </(*;•••• *>)+«•
Л,- 1Л2-1 A^-lZ-1
где
(4.38)
(4.39)
Остаточный член квадратурной формулы (4.40) обращается
в нуль, если f(xi, ..., хт) есть полином степени не выше nk—1
по каждой из переменных xh. .
< Сравнение формул (4.39) и (4.16) показывает, что весовые
коэффициенты многомерной квадратурной формулы (4.38) пред-
ставляют произведения весовых коэффициентов соответствую-
щих одномерных. Для получения многомерной квадратурной
формулы Гаусса следует взять сумму значений функции
f(xi,..., хт) в точках, координатами которых являются всевоз-
можные комбинации узлов одномерных формул, помноженных на
произведения соответствующих весовых коэффициентов одномер-
ных формул. При этом одномерные квадратурные формулы мо-
гут быть самыми различными, лишь бы они были получены на
основе интерполяционных многочленов.
244
Многомерная формула Гаусса
Подбирая соответствующим образом узлы интерполирования
при получении квадратурной формулы (4.40), можно значитель-
но повысить ее точность. Возьмем .в качестве узлов интерполи-
рования значения координат, соответствующие одномерным фор-
мулам Гаусса.
Абсциссы х^ в этом случае являются корнями ортогональ-
ного полинома Рп. (%г). При таком выборе узлов квадратурная
формула (4.38) примет вид
j • •• J" f (*i. •••.•*«) П pAx^dxj=
а‘ ат > = 1
л, Ла пт т
= 2 2--- 2 П .....................•>:*-) + «. ' (4-40)
Л = 1 Z = 1 1
, 1 * т
где координаты узлов интерполирования являются корнями ор-
тогональных полиномов Рп. (хг), а коэффициенты представ-
ляют коэффициенты Кристоффеля
(х?о p‘^dx‘- (4i4I)
а1 1
Остаточный член многомерной формулы Гаусса обращается
в нуль, если подынтегральная функция f(xb . .., хт) представ-
ляет полином степени не выше 2«г—1 по каждой из перемен-
ных Xi.
Доказательство этого факта проводится так же, как и в од-
номерном случае.
Применение многомерных формул Гаусса к анализу систем
автоматического регулирования подробно рассмотрено в рабо-
те [20]. В ней приводятся значения узлов и весовых коэффициен-
тов Кристоффеля для различных типов весовых функций Pk(Xk),
а также расчетные формулы для определения статистических
характеристик исследуемой величины.
Пример. Рассмотрим применение квадратурных формул Гаусса к вычис-
лению интеграла
а ~ _ (х2-|i)2
/= f f (xi — е^2)2—-----—— е 2а2 dxxdx^ (4.42)
-a Joo 2Д /2ла
который представляет математическое ожидание функции (%i—ехг)2 случай-
ных величин Xi и х2, распределенных по равномерному и нормальному зако-
нам соответственно. В данном случае интеграл может быть легко вычислен
I = аз + е2(|1+а2). (4.43)
245
Интеграл (4.42) является частным случаем интеграла
а оо j j _ (*>—р-)1
/ = f f / (*1. *2) 75------72Г- е 2l* (4.44)
Для применения формул Гаусса (4.44) целесообразно преобразовать к ви-
ду, в котором весовые функции соответствуют табличным (из табл. 3.1 и 3.2).
X] Х2—
Положим 61 =-----, 62 =---------» в результате интеграл (4.44) примет вид
а о
Л
10° 11 - —
/= f f ое2+ Ю-т-----------------2^i^2- (4-45)
Ji J» 2 /2л
Согласно квадратурной формуле Гаусса (4.40) оценка интеграла (4.45) по
ад узлам имеет вид
rtj л2
= 22 f И1 - я& + >х)' (4-46)
й1=1 *,«1
где числа pjj и 6?1 берутся из табл. 4.1, a pJJ1 и ~ из дабл. 4.2.
Если П1=п2=2, то по формуле (4.40)
/22 = 0,25/(0,5774а, а 4- р.) 4- 0,25/ ( — 0,5774а, а 4-ц)4- (4.47)
4- 0,25/(0,5774а, — а 4- и) 4- 0,25/ ( — 0,5774а, а 4- ц).
Если Л1=2, л2 = 3, то
/2з = 0,3333/ (6,5774а, р.) 4- 0,3333/ (— 0,5774а, р.) 4- (4.48)
4-0,0833/(0,5774а, 1,732а 4- и) 4- 0,0833/ (0,5774а, 1,732а 4-и) +
4-0,0833/(0,5774а, — 1,732а 4- и) 4- 0,0833/ (0,5774а, — 1,732а 4-и)*
Если, например, положить а3 = 3, р. = 0, а = 0,5, £то из (4.43) и (4.47)
(448)’при / (х, у) = (х— е^)2 получим / = 4,649; /22 = 4,543; /23 = 4,634.
4.5. ОСНОВНЫЕ ПРИНЦИПЫ ПОДСЧЕТА ИНТЕГРАЛОВ
МЕТОДОМ МОНТЕ-КАРЛО
Рассмотрим интеграл
ь
J = J f (х) р (х) dxy (4.49)
а
где функция р(х) не отрицательна и удовлетворяет условию
ъ
J p(x)dx=l. (4.50)
а
Интеграл (4.49) представляет формулу для определения ма-
тематического ожидания функции f(x), зависящей от случайной
величины х, с плотностью распределения вероятностей р(х).
246
Поэтому в качестве значения интеграла можно взять оценку ма-
тематического ожидания функции f(x). Если произвести п неза-
висимых испытаний случайной величины х и для каждого зна-
чения х' вычислить /(%*), то оценкой математического ожидания
явится величина
п
J*=-^g/(x'), (4’51)
которую и примем за приближенное значение интеграла (4.49).
Погрешность интегрирования в этом случае будет равна
Ъ п
R=J—J* — ^ f (х) p(x)dx —f (xl). (4. 52)
При использовании метода статистических испытаний точ-
ность формулы (4.51) уже не может быть оценена так же, как в
детерминированном случае, величиной остаточного члена. Пос-
ледняя зависит от реализаций случайной величины х: х\..., хп
и, следовательно, сама является величиной случайной. Полно-
стью охарактеризовать величину остаточного члена можно, оп-
ределив функцию распределения.
Однако практически такая задача трудно выполнима. По-
этому в качестве характеристик остаточного члена (4.52) исполь-
зуются его первые два момента: математическое ожидание и
дисперсия.
Производя осреднение в формуле (4.52), получим, что мате-
матическое ожидание остаточного члена равно нулю:
f(x)p(x)dx—Л1/(х;)= J7 = 0.
а / -1 / = 1
(4. 53)
Поскольку случайные величины /(х*) независимы, дисперсия
может быть найдена следующим образом:
п
DR=±-X\Df(x^
I = 1
или DR= — Df, (4.54)
п
b
где Df = J f '2 (x) p (x) dx — J2. (4. 55)
247
Доверительный интервал для остаточного члена определяет-
ся соотношением
Р (|7?|>еК^7}== 1 — 2Ф(е /й), (4.56)
где Ф(ы) — функция Лапласа:
Ф(«)=^=-Се 2 dt. (4.57)
V 2л J
о
Совершенно аналогично производится вычисление многомер-
ных интегралов методом Монте-Карло. Если необходимо вычис-
лить интеграл
J=='\ - xm)P{xv ..., xm) dxt... dxm, (4.58)
где
P(xv •••• J-- - j>(Xi, ...xm)dXi... dxm=\,
с помощью n независимых реализаций ди-мерной случайной ве-
личины *1, ..хт с плотностью распределения вероятностей
p(xi, ..хт), то он принимается равным величине
п
....<4И>
Дисперсия остаточного члена
R=J — J* (4.60)
по-прежнему определяется формулой (4.54) с единственным от-
личием, что в многомерной квадратурной формуле дисперсия
подынтегральной функции f (хь ..., хт) определяется из соотно-
шения
-2-- xm)dx1.. .dxm—J2. (4.61)
Оценка ошибки интегрирования методом статистических ис-
пытаний (4.56) показывает, что с ростом п точность повышает-
ся медленно, порядок убывания остаточного члена равен .
Практически это означает, что для того, чтобы повысить точ-
ность вычислений на порядок, необходимо увеличить число ис-
пытаний на два порядка. Из-за этого при использовании метода
Монте-Карло не удается добиться точности выше, чем две-три
значащие цифры. Метод статистических испытаний целесообраз-
но применять в тех случаях, когда необходимая точность вычис-
лений невелика, а построение регулярных формул численного
интегрирования затруднительно.
248
Формулы (4.51) и (4.59) представляют частный случай квад-
ратурных формул, когда весовые коэффициенты аьп все одина-
ковы, а узлы выбраны случайным образом. Естественно поэто-
му, что они не могут дать большую точность, чем квадратурные
формулы, специально построенные с учетом требования Умень-
шения ошибок. Распределение узлов квадратурных формул
(4.51) и (4.59) случайно и регулируется только законом рас-
пределения величины* х. Поскольку имеется определенная ко-
нечная вероятность получения нетипичных выборок -случайных
величин х или . .., хт, при использовании квадратурных фор-
мул (4.51) и (4.59) возможно 'появление значительных ошибок.
Это один из основных недостатков метода Монте-Карло.
Существующие способы улучшения сходимости метода Мон-
те-Карло в большинстве своем представляют попытку повысить
детерминированность распределения узлов квадратурных фор-
мул (4.51) и (4.59). Естественно, что наивысшая степень опре-
деленности будет при использовании детерминированных квад-
ратурных формул. Поэтому, если их применение не связано с
большими затратами, детерминированным методам численного
интегрирования всегда следует отдавать предпочтение по срав-
нению с методом статистических испытаний.
В некоторых случаях может оказаться целесообразным ис-
пользование обобщенного метода Монте-Карло для вычисления
интегралов (4.49) или (4.58). В одномерном случае -соответст-
вующая оценка математического ожидания имеет вид
п
= (4.62)
Л = 1
где ak — положительные постоянные, удовлетворяющие ус-
ловию
п
2а*=1-
А —1
Легко показать, что формула (4.62) дает несмещенную оцен-
л
ку интеграла (4.49) с дисперсией, равной Df При ис-
Л=1
пользовании оценки (4.62) дисперсия остаточного' члена будет
иметь минимальное значение, если выполнено условие
ak = —, 1, 2,..., п,
п
т. е. когда используется стандартный метод Монте-Карло.
249
Аналогично записывается формула интегрирования обобщен-
ным методом Монте-Карло функции нескольких переменных:
п
.... <4-63>
Л-1
Обобщенный метод Монте-Карло отличается от обычного
тем, что вычисленным значениям функции f(x) придается нерав-
ный вес. Это повышает дисперсию остаточного члена, но может
оказаться полезным, если точность вычисления функции f(x) в
разных точках изменяется. Подбором весовых коэффициентов х
можно уменьшить инструментальную погрешность оценки (4.62).
4.6. СПОСОБЫ ПОВЫШЕНИЯ ТОЧНОСТИ ИНТЕГРИРОВАНИЯ
МЕТОДОМ МОНТЕ-КАРЛО
Подробное описание методов повышения интегрирования с
помощью статистических испытаний можно найти в книге [2].
Поскольку эти методы при оценке эффективности систем имеют
весьма ограниченное применение, то в настоящей работе они
будут изложены кратко. Основной целью рассмотрения будет
оценка возможностей различных методов понижения ошибки
интегрирования.
Метод выделения главной части. Предположим, что требу-
ется вычислить интеграл (4.49), кроме того, имеется некоторая
функция g(x), близкая к /(х):
g(x)?s/(x), (4.64)
значение интеграла от которой определяется легко
ь
I = J g (х) р (х) dx. • (4. 65)
а
Тогда выгодно вместо определения интеграла (4.49) мето-
дом Монте-Карло вычислить интеграл
ь
J—I = ^\f(x) — g(x)\p[x)dx (4.66)
а
и к результату добавить интеграл /.
Дисперсия разности f(x) — g(x) равна
ь
D{f-g] = \\f (х) - g(x)]2 р (х) dx - (J - Z)2. (4. 67)
a
Если функция g(x) близка f(x), то дисперсия разности (4.67)
меньше дисперсии функции f(x) (4.55). Поэтому при заданном п
дисперсия остаточного члена квадратурной формулы интегриро-
250
вания f(x) — g(x) методом Монте-Карло будет меньше диспер-
сии остаточного члена для f(x).
Особенностью метода выделения главной части по сравне-
нию с другими является отсутствие необходимости регулиро-
вать распределение случайной величины х. Повышение точности
интегрирования достигается путем изменения подынтегральной
функции. Это делает метод выделения главной части пригодным
и в том случае, когда распределение случайной величины х не-
известно, например, при исследовании реальной системы, а так-
же в случае оценки эффективности системы, подверженной воз-
действию случайных процессов.
Существенная выборка. Выборка по группам. Предположим,
что нужно сосчитать интеграл
*
ь
J = j f(x)dx. (4.68)
а
Его можно представить в виде
ь
J=\1SZL p<x)dx, (4.69)
J Р(х)
где р(х) — произвольная функция, удовлетворяющая условиям:
-ъ
p(x)>0, J p(x}dx— 1. •
а
Интеграл (4.69) можно считать методом Монте-Карло, ис-
пользуя случайную величину х с плотностью распределения ве-
роятностей р(х). Согласно результатам предыдущего раздела
величина остаточного члена будет определяеться дисперсией
f (х\
функции ——!. Подбором р(х) ее можно уменьшить. Очевид-
р(х) .
но, дисперсия будет тем меньше, чем ближе отношение—к
постоянной величине. Поскольку f(x) может иметь разные зна-
ки, для ускорения счета желательно выбирать р(х) таким, что-
бы выполнялось соотношение
const. (4. 70)
Р (*)
Условие (4.70) означает, что распределение случайной вели-
чины х должно быть таким, чтобы вероятность попадания случай-
ной величины х в область, где f(x) велика до модулю, была
также большой. Способ существенной выборки в применении к
определению интеграла (4.68) методом Монте-Карло состоит в
подборе плотности распределения величины в соответствии с со-
отношение^ (4.70).
251
Выборка по группам, по существу, представляет частный слу-
чай способа существенной выборки, когда р(х) принимается
ступенчатой функцией. По форме метод выборки по группам за-
ключается в разбиении интервала интегрирования на ряд под-
ынтервалов, для каждого из которых применяется своя форму-
ла интегрирования, в отдельности. Число узлов в каждом подын-
тервале берется таким, чтобы общая плотность распределения
величины х на всем интервале интегрирования удовлетворяла
соотношению (4.70).
Изложенные методы понижения дисперсии не исчерпывают
всех существующих, однако являются типичными. Они без тру-
да обобщаются на случай многомерных интегралов. Специфиче-
ским методом уменьшения дисперсии остаточного члена при
счете многомерного интеграла является правило, согласно ко-
торому, если выполнить интегрирование аналитически по части
переменных, дисперсия уменьшается. Доказать это легко пря-
мым подсчетом дисперсий [2].
4.7. ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОСТИ СИСТЕМ,
ПОДВЕРЖЕННЫХ ВОЗДЕЙСТВИЮ СЛУЧАЙНЫХ ПРОЦЕССОВ
Практически все случайные процессы, встречающиеся в
практике исследования управляемых систем, могут быть интер-
претированы как результат прохождения белого шума через
линейные или нелинейные формирующие фильтры. Поэтому,
добавляя к уравнениям системы уравнения формирующего
фильтра, можно всегда считать, что исследуемая система под-
вержена воздействию стационарного случайного процесса в виде
белого шума.
Для конкретности изложения будем предполагать, что на ис-
следуемую систему действует стационарный случайный процесс,
в частном случае белый шум.
Исследование эффективности систем, находящихся под воз-
действием случайных процессов, точно так же, как и случайных
параметров, можно проводить с помощью детерминированных
методов и метода статистических испытаний.
Как известно [14], случайный процесс u(t) всегда может быть
представлен с какой угодно степенью точности каноническим
разложением
< п
w(/) = mu+2 (4.71)
Л = 1
где ти — математическое ожидание и(/);
q)k(t) —детерминированные, линейно независимые, образую-
щие ортогональную систему функции;
Vh — взаимно некоррелированные случайные величины.
252
Если процесс u(t) нормален, величины Vk независимы. Плот-
ность распределения Vk в этом случае будем обозначать через
Pk(Vk).
Точность аппроксимации процесса u(t) суммой (4.71) за-
висит от числа членов п. Для получения точного равенства,
когда это возможно три данном выборе функций <?&(/) , требует-
ся обычно бесконечное и даже несчетное число членов. В послед-
нем случае сумма (4.71) переходит в интеграл.
В качестве функций <?&(/) часто используются, например,
гармонические функции sinw^t cosco^/, белый шум удобно ап-
проксимировать суммой импульсов фь(0=6(^—6t) и т- Д-
Функция качества f системы является функционалом от слу-
чайного процесса u(t), следовательно, функцией случайных ве-
личин Vk. Поэтому оценка эффективности системы состоит в
вычислении интеграла
п
(...(/ (Уп ..., Г„) П Рк (^) dV.... dV п, (4. 72)
где область интегрирования Q определяется границами изме-
нения случайных величин Vk.
Таким образом, задача исследования эффективности сис-
тем, подверженных воздействию случайных процессов, может
быть сведена к задаче численного интегрирования. Следует, од-
нако, отметить два обстоятельства, заставляющих рассматри-
вать эту задачу отдельно. Во-первых, интеграл (4.72) определя-
ет эффективность приближенно. Для точного ее определения
следует взять бесконечное (в некоторых случаях несчетное)
число членов в формуле (4.71) и, следовательно, произвести
бесконечное число интегрирований в формуле (4.72). Во-вторых,
для достижения нужной точности оценки эффективности число
членов в (4.71) обычно приходится брать большим. Если ис-
следуемая система подвержена воздействию случайных процес-
сов, то для оценки ее эффективности необходимо вычислить
интеграл высокого, в некоторых случаях бесконечного порядка.
Эта особенность сильно усложняет задачу анализа эффективно-
сти систем при случайных воздействиях. Для некоторых част-
ных систем и случайных воздействий имеются специальные ме-
тоды оценки эффективности, однако их применение ограничено.
При исследовании линейных систем автоматического управ-
ления задача исследования систем существенно упрощается при
применении теории сопряженных систем [17], [9].
Другой метод оценки эффективности нелинейных систем, по-
ведение которых описывается нелинейными обыкновенными
дифференциальными уравнениями, заключается в сведении этой
задачи к исследованию уравнения Фоккера — Планка [10].
Однако этот способ малоэффективен, поскольку решение урав-
нения Фоккера — Планка в случае мало-мальски сложных сис-
253
тем представляет трудную задачу, ничуть не легче вычисления
интеграла (4.72).
Поскольку число интегрирований в формуле (4.72) велико,
применение детерминированных формул численного интегриро-
вания потребует большого числа узлов для вычисления интег-
рала. Поэтому основным методом изучения систем, зависящих
от случайных процессов, остается метод Монте-Карло.
При использовании детерминированных формул должны
быть решены два вопроса: во-первых, определено каноническое
разложение, аппроксимирующее процесс u(t) с необходимой
точностью; во-вторых, определен рациональный выбор узлов
квадратурной формулы для подсчета интеграла (4.72).
Метод статистических испытаний может применяться непос-
редственно, т. е. без предварительного установления свойств
входного сигнала или разложения (4.72). Недостатком этого ме-
тода и в данном случае является медленная сходимость. Несмот-
ря на это, часто применять метод Монте-Карло выгоднее, чем
детерминированные методы, использующие канонические раз-
ложения, поскольку число необходимых испытаний оказывается
имеющим одинаковый порядок, а реализация исследований с
помощью метода Монте-Карло значительно проще.
В следующих разделах рассмотрены два метода анализа сис-
тем, которые можно применить к исследованию систем, завися-
щих от случайных процессов; эти методы обладают повышенной
точностью по сравнению с методом Монте-Карло.
4.8. ИСПОЛЬЗОВАНИЕ КОМБИНИРОВАННЫХ ФОРМУЛ
ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
ДЛЯ АНАЛИЗА ДИНАМИЧЕСКИХ СИСТЕМ
Часто случайные воздействия ..., хт неравноценны, и их
можно разбить на две группы. В первую группу входят компо-
ненты вектора х=(хь ..., хт), существенно влияющие на пове-
дение системы и, следовательно, на величину подынтегральной
функции. Во вторую группу — остальные. Тогда, если построить
детерминированную формулу для интегрирования по перемен-
ным первой группы и при ее. использовании остальные перемен-
ные выбирать случайным образом, полученная квадратурная
формула будет давать значения вычисляемого интеграла с нуж-
ной степенью точности при меньшем числе узлов по сравнению
с методом Монте-Карло.
В дальнейшем предполагается, что сильновлияющими явля-
ются первые г компонент вектора х.
Разделение переменных интегрирования на две группы яв-
ляется весьма условным. Сходимость полученных квадратурных
формул может быть гарантирована всегда, если соответствую-
щие детерминированные формулы сходятся. От разбиения на
группы зависит только скорость сходимости.
254
Комбинированные квадратурные формулы могут применять-
ся для исследования систем, зависящих от случайных парамет-
ров и случайных процессов одновременно. Случайные парамет-
ры или их часть следует отнести к первой группе переменных,
а составляющие канонических разложений случайных процес-
сов — ко второй. При этом фактического знания канонических
разложений не требуется.
Обозначим через v вектор, состоящий из г первых компонент
вектора х, а через w — вектор, содержащий остальные компо-
ненты,
v=Cv!,т»г) = (х1,..., хг);
w=(w1,...» Wm_r) = (xr+1,..., хт).
Для простоты 'будем считать, что векторы v и w статистиче-
ски независимы. Тогда анализ системы (4. 1) сводится к вычис-
лению интеграла по векторным переменным v и w
/=J f(x)p(x)dx= [ f /(v, w) pT(v) pv (w)dvdw, (4.73)
.2 2, 22
где интегрирование по векторным переменным понимается как
интегрирование по всем компонентам соответствующего векто-
ра; р(*)> Рг (у)> Р* (w) — плотности распределения соответст-
вующих случайных векторов; й, йь Й2 — области определения
векторов х, v и w.
Комбинированная квадратурная формула для вычисления
интеграла J получается следующим образом. Построим обыч-
ную детерминированную квадратурную формулу для вычисле-
ния интеграла
J <Р (V) pv (V) dv
®v
от некоторой функции
п
. f<p(v) pT(y)dv =24л) <p(v*) + Z?, - (4.74)
s7 *-i
тогда комбинированная квадратурная формула для вычисления
интеграла (4.73) имеет вид
[ f /(v, w)pv(v)pw (w)dvdw = f (v*, w*) + R, (4. 75)
либо
J n
/(V, w) pr (v) pw (w) dv dw = а?*/ (Vй, w«) + /?.
su sT 1=1 Л-1
(4. 76)
255
В обеих формулах (4.75) и (4.76) vk —узлы из формулы
(4.74), wft в формуле (4.75) и whl в формуле (4.76) — независи-
мые реализации случайного вектора w.
Дадим обоснование формул (4.75) и (4.76). Введем следую-
щие обозначения для условных математического ожидания и
дисперсии функции f(v, w) при фиксированном значении век-
тора v:
<p(v)=Af |/(v, w)|v] = J /(v, w) pv (w) dw;
»u
<|»(v)==£>[/(v, w)|v] = j /2(v, w)pw(w)rfw — <p2(v).
Пусть функция f(v, w) удовлетворяет следующим обычно вы-
полняющимся на практике условиям:
1) (p(v) дифференцируема до порядка и и имеет ограничен-
ную производную п-го порядка:
2) ф(у) ограничена равномерно по всем v:
|Ф(у)|<6/.
Рассмотрим следующую формулу
/=24”/^. (4.77)
Й = 1
Эта формула включает в себя как частные случаи комбини-
рованную квадратурную формулу, если координаты vk опреде-
ляются из формулы (4.74), a wh — -случайные, и формулу обоб-
щенного метода Монте-Карло, если и vft и — случайные реа-
лизации векторов v и w.
Математическое ожидание квадрата остаточного члена фор-
мулы (4.77) выражается через его условные математическое
ожидание и дисперсии с помощью формулы
_ MR1 — WAf^lv1,vn] = M .. ., vnl2} +
..., Vя]. (4.78)
Подсчет отдельных членов, входящих в (4.78), дает
М ...» Vя] — M[J — w*)lvl, • • • » Vя] =
=J-^c№M\f (v*, w*)|vft]=J-24n)<p(v*); (4.79)
fe-1
256
.... vn] = 7W {[/?—MR (v1,..., v")]2^1,..., v"} =
— M
2 akn)(/(v*, w*) —^v*))^1,
s-i
. , V2] =
= 2 c&nrM [f (v\ w*) - <P (v»)|v*] = 2 4Л)* ф (Vft). (4. .80)
Лй-l Z-l
Подставляя формулы (4.79) и (4.80) в (4.78), получим
MR* = M
j - 2 4л) ? (уЛ)2+м 2 (v*}’
Л = 1 J ы
(4.81)
Если узлы Nh взяты из квадратурной формулы (4.74), то в
силу выполнения функцией f(v, w) условия 1) справедливо не-
равенство
п
(4.82)
где величины С и а определяются типом квадратурной формулы
(4.74) и получаются из оценки ее остаточного члена. Для квад-
ратурных формул, построенных с помощью интерполяционных
полиномов, аЗ>1. С учетом соотношения (4.82) и условия 2), на-
ложенного на функцию f(v, w), из формулы (4.81) следует не-
равенство
п
(4.83)
п
Если узлы vh независимы, разность J ¥ (V*J пред-
л-i
ставляет оценку интеграла
J cpfv) pv (v) dv
®V
обобщенным методом Монте-Карло и, следовательно,
п
I2
М J-2 <№?(?*)
п
Л-1
(4. 84)
Ы
Второй член формулы (4.81) оценивается так же, как и раньше:
м 2 4Л)’ Ф (Vй)=2 4л)‘УИф (V) < 4/2 а*л)а- <4-85)
Л»1 Jfe-1
257
Подставляя соотношения (4.84) и (4.85) в (4.81), получим
п п
(4.86)
fe-1 Л=1
Вторые члены в правых частях формул (4.83) и (4.86) совпада-
I*
ют. Первый член в формуле (4.86) убывает не быстрее, чем —.
п
Поэтому первый член в формуле (4.83) убывает значительно
быстрее, чем в формуле (4.86). Обычно первый член в формуле
(4.83) бывает настолько мал, что им можно пренебречь. По-
грешность комбинированной квадратурной формулы определяет-
ся в основном вторым членом формулы (4.83) и, если d неве-
лико, что бывает, когда w содержит слабовлияющие параметры,
будет малой. Повышение точности комбинированной квадратур-
ной формулы объясняется резким уменьшением первого слагае-
мого в неравенстве (4.83) по сравнению с (4.86). Естественно,
преимущество комбинированной квадратурной формулы тем
значительнее, чем большую роль в неравенстве для математиче-
ского ожидания остаточного члена интегрирования играет пер-
вое слагаемое в правой части формулы (4.86).
Неравенства (4.83) и (4.86) позволяют сравнивать точность
комбинированной квадратурной формулы (4.75) и обобщенного
метода Монте-Карло. Но если коэффициенты akn мало отлича-
ются друг от друга, качественные выводы остаются справедли-
выми и для обыкновенного метода Монте-Карло, поскольку в
этом случае сумма квадратов коэффициентов а^п) будет мало
отличаться от своего минимального значения.
Обычно на практике уже при сравнительно небольшом чис-
ле узлов квадратурной формулы (4.74) первый член справа в
формуле (4.83) мал, а основную роль играет второй член.
В этом случае можно в формуле (4.75) вместо f(v\ wfe) исполь-
зовать величины
f (yk, Vlkl),
осреднения функции f (v\ w) 'no s независи-
вектора w (для каждого k — различным).
полученные путем
мым реализациям
В результате получается формула (4.76). Оценка остаточного
члена квадратурной формулы (4.76) имеет вид
п
__________ Л = 1
* Сумма коэффициентов должна быть равна 1 (условие интегрируе-
мости без ошибки постоянной величины). В этом случае сумма квадратов
коэффициентов принимает минимальное значение, если все коэффициенты
,_х I 1
одинаковы, т. е. } = —, равное —.
п п
(4.87)
258
Первый член справа в формуле (4.87) по сравнению с (4.83)
на изменяется, а второй уменьшается в s раз.
На практике процедура построения комбинированных квад-
ратурных формул состоит в следующем. После разбиения слу-
чайных воздействий на сильновлияющие и слабовлияющие стро-
ится квадратурная формула для оценки математического ожи-
дания функции f(x), учитывающая только воздействие первой
группы. Затем в правой части при вычислении значений f(x) в
узлах воздействия второй группы заменяются независимыми
Рис. 4.2. Структурная схема системы самонаведения в плоскости
случайными реализациями сектора w. В результате получается
формула (4.75). Если такие расчеты проделать 5 раз, каждый
раз используя свои реализации вектора w, и взять среднее ариф-
метическое полученных результатов, получится формула (4.76).
Проиллюстрируем методику статистического моделирования с использо-
ванием комбинированных квадратурных формул на примере анализа статис-
тических характеристик точности самонаведения ракеты с двумя управляю-
щими органами: рулями и крыльями. Структурная схема контура наведения
в плоскости представлена на рис. 4.2.
Параметры автопилота kit Z?2, &з, предполагаются случайными и рас-
пределенными по равномерному закону в диапазоне
ki max, i—1, 2, 3, 4.
Внешними воздействиями на систему являются шум на выходе головки
самонаведения о)ш(/) и маневры цели. Требуется оценить математическое
ожидание и дисперсию промаха
£>2 (/Осл) ш (^осл)
fl =-----------;-----------
где /осл — момент ослепления.
259
Математическое ожидание промаха в рассматриваемом случае равно
ъ k b k
imax 2max Зтах 4max
Mh = —---------------------- j J J J *2. *3. x
П (fymax ^zmln) *lmin ^2min ^3min ^4min
Л-1
X dk\dk4dk3dk^t (4.88)
где AJ[Zi|Azi, k2, ks, kb]— условное математическое ожидание промаха как
функционала от шума сош (/) при фиксированных значениях параметров ku
k2, #з, kb. Использование в формуле (4.88) условного математического ожида-
ния позволяет избежать необходимости применять канонические разложения
для выражения зависимости математического ожидания от шума сош(О-
Средний квадрат промаха определяется формулой
ъ ъ ъ ь
Imax 2 max Зтах 4тах
М№ = —-----------‘----------- J J J J М *2, *3. *4] X
П (^Zmax ^zmin) min ^2mln *3mln *4min
Ы
X dk\dk2dk3dk^ (4.89)
Дисперсия промаха определяется по формулам (4.88) и (4.89) обычным спо-
собом: Dh=Mh2—(Mh)2.
Предварительный анализ динамических свойств системы, приведенной на
рис. 4.2, показывает, что параметры кз и kb слабо влияют на величину про-
маха. Поэтому в комбинированных квадратурных формулах детерминирован-
но будут задаваться только значения коэффициентов k[ и k2.
Путем линейного преобразования переменных
ki
2
^zmax ^z'min
^zmax kimjn
^zmax ^zmln
i= h 2, 3, 4
осуществляется переход от переменных ki к переменным ki, изменяющимся в
диапазоне Г—1, +1]. Если обозначить
h(k, kz, k3t £4, <ош) = А(^1, k3, k4, <ош),
то выражения для математического ожидания и среднего квадрата промаха
примут вид
1111
Mh = — у у (£], г2> ?з. *4, ®ш)1*Ь *2. *з. Л4]х
-1 _’l -1 _’1
X dk\dk2dk3d~kc (4.90)
1111
МЛ2 = -^- у у [л1[л2(^, ki, k3, ki, <ошМ, k3, k3, ГЧ)]х
-1 -i _‘i _li
X dkidk^k^iki.
(4-91)
260
Применяя квадратурные формулы Гаусса с четырьмя узлами для интег-
рирования по каждому из переменных ki и получим следующие формулы
для оценок интегралов (4.90), (4.91):
4 4
M*h = 22 (4.92)
/-1 >1
4 4
Л1*Л2 = 2 2 Р/р(~k№y~k1^), (4.93)
i-1 /-=1
где ’ k\ = — = —#2 —0,8611;
—^=11= —'12 = 0,34;
P1 = p4 = 0,1739; р2=Рз = 0,3261,
a k™n, —независимые реализации случайных величин и процесса. Эти
величины наряду с k{ и k подставляются в дифференциальные уравнения
системы, на основании решения которых определяется величина h.
Точность, даваемая формулами (4.92), (4.93) при значительных уровнях
шума, недостаточна ввиду слабого эффекта осреднения случайных отклоне-
ний, вызванных шумом. Для повышения точности следует проводить много-
кратные вычисления по формулам (4.92), (4.93) каждый раз с новыми реали-
зациями параметров Хгз, и шума, а затем полученные результаты осреднить.
В результате фактически получается формула интегрирования типа (4.76).
Расчеты по формулам (4.92) (4.93) и обычным методом Монте-Карло,
когда используются оценки
п
<-к Л = -±- У Л ( , (4.94)
1^1
п
М*п.к Л2 = V . (4.95)
I = 1
показали, что в широком диапазоне изменения параметров системы и условий
наведения применение комбинированных квадратурных формул к рассматри-
ваемой задаче позволяет снизить необходимое число интегрирований диффе-
ренциальных уравнений системы по сравнению с методом Монте-Карло в не-
сколько раз. Количество интегрирований определялось после достижения с
помощью формул (4.92) (4.93) и (4.94) (4.95) одинаковой точности расчетов.
4.9. ПРИМЕНЕНИЕ МЕТОДА ВЫДЕЛЕНИЯ ГЛАВНОЙ ЧАСТИ
К АНАЛИЗУ ТОЧНОСТИ СЛОЖНЫХ СИСТЕМ
Пусть имеется некоторая система F, подверженная учиты-
ваемому случайному воздействию х и неучитываемому и. Вы-
ходным параметром системы является величина у. В задаче ана-
лиза динамических систем, подверженных случайным воздейст-
виям, величина у совпадает с функцией /. Будем считать, что
выходная величина однозначно определяется входными воздей-
261
ствиями. Величины х, и, у могут быть скалярными, векторными
любой размерности или иметь более сложную природу. В нас-
тоящем разделе будем считать величины х, и, у, а также опреде-
ленные ниже V. и z случайными величинами с известными зако-
нами распределения. Распространение на общий случай прово-
дится без труда; достаточно, например, -считать рассматривае-
мые величины элементами соответствующих вероятностных про-
странств. Все полученные при этом формулы будут аналогичны
используемым.
Задачей статистического исследования является вычисление
математического ожидания U выходной величины системы.
При использовании метода Монте-Карло производится N не-
зависимых испытаний систем F и в качестве U используется
величина
N
= у1, (4.96)
где yi — значение у, полученное в Л-м испытании.
Как следует из общих положений теории вероятностей, мате-
матическое ожидание оценки U* совпадает с U. Точность опре-
деления U зависит от дисперсии оценки I/*, которая равна
DU*—-^-Dy, (4.97)
где Dy — дисперсия случайной величины у.
Предположим, что наряду с системой F имеется другая сис-
тема G, близкая к F по метрике, которая будет уточнена ниже.
Входными величинами системы G являются х и vf выходная ве-
личина z. Особенностью системы является возможность вычис-
ления математического ожидания V выходной координаты ка-
ким-либо нетрудоемким способом.
Согласно методу выделения главной части следует на осно-
вании Ni независимых испытаний обеих систем F и G одновре-
менно получить оценку математического ожидания разности
Nt
М* (У — z)=^- (У1 — zl). (4.98)
Каждое испытание систем F и G должно проводиться таким
образом, чтобы на обе системы воздействовали одни и те же
реализации учитываемой входной величины х, в силу чего ве-
личины у* и z\ имеющие одинаковый индекс, являются зави-
симыми.
262
Добавляя к формуле (4.98) значение V, вычисленное одним
из методов, описанных ниже, получим новую оценку математи-
ческого ожидания сигнала у
V(z/'-z') + V. (4.99)
i = 1
Легко показать, что оценка (4.98) является несмещенной, а
ее дисперсия
DU* = — D(y —z), (4.100)
где D(y—z) — дисперсия разности у—z.,
1 Если системы F и G таковы, что дисперсия разности D(y—z)
меньше дисперсии выходной величины первой системы, то при
одинаковом числе испытаний оценка (4.99) дает большую точ-
ность по сравнению с (4.96).
Из формул (4.97) и (4.100) следует, что одна и та же точ-
ность определения U при использовании оценок (4.96) и (4.99)
получается, если выполнено условие
£>У —
N
или
N.
Dy
А
Следует учесть, что в методе выделения главной части каж-
дое испытание состоит в параллельном испытании двух систем
F и G. Поэтому общее число испытаний систем, необходимое для
получения оценки (4.99), фактически равно 2AG, не считая за-
трат на определение математического ожидания выходной вели-
чины системы G. Использование метода выделения главной час-
ти будет эффективным только при условии, что экономия машин-
ного времени, вызванная уменьшением дисперсии D(y—z) по
сравнению с Dy, превышает затраты на анализ системы G.
' Метод выделения главной части особенно удобен при исполь-
зовании цифровых вычислительных машин. В них легко осуще-
ствляется запоминание реализаций случайных процессов, вслед-
ствие чего моделирование систем F и G может производиться в
разное время. Если используются псевдослучайные последова-
тельности, то необходимое повторение реализаций достигается
путем повторения счета обеих систем, начиная с одной и той же
точки псевдослучайной последовательности. При использовании
аналоговой модели обе системы должны моделироваться одно-
временно либо необходимо предусмотреть устройство для запи-
си и воспроизведения случайных процессов.
263
Исследуем требования к степени близости систем F и G.
С этой целью преобразуем выражения для дисперсий Dy и
D(y-z)-.
Dy = M(y — Му)2 = ММ [(у - Му)2\х\ =
=ММ [у2|х] - 2МуМ [у\х] -]-(Му)2 = М {М [у2\х] —
— (Л4 [у\х]?} +(Л1 [у\х])2 — 2МуМ [у\х] + [Му]2=
=М [М [у2\х] — (М [z/|x])2{ +М [М [у\х] - (Му)2} =
= М {D [y\x]}+D {М [у\х]}. (4.101)
Аналогичными преобразованиями получим
D (у - z) = М {D [у|х]} + М {D [z\x\} +
+ £> (М [уЩ-М [z|x]}. (4.102)
Член Л1{£)[у|х]} в формуле (4.101) и члены М(D[y|х]} и
М {D[z| х]} в формуле (4.102) вызвано воздействиями на системы
неучитываемых входных величин и и v. Подбором системы G
можно добиться уменьшения последнего члена в формуле
(4.102). Из рассмотрения формул (4.101) и (4.102) следует, что
применение метода выделения главной части эффективно в том
случае, когда учитываемая входная величина является домини-
рующей, т. е. члены. Л4{£)(#|х]} и Af{D[z|x]} малы, а система G
подобрана таким образом, что условное математическое ожида-
ние разности выходных координат слабо зависит от х.
На практике дисперсии Dy и D(y—z) априори неизвестны, и
заранее с достоверностью установить эффективность метода вы-
деления главной части не удается. Можно рекомендовать сле-
дующий способ. В процессе моделирования наряду с оценками
математических ожиданий производятся оценки дисперсий по
формулам:
п / п \ 2
:4'103’
п р /» "2
D*(y — z) =—Ц-V} У1 — z‘ — — — zi)
п— 1 п
7-1 J
(4. 104)
Применение метода выделения главной части признается це-
D*(y— z} ,
лесообразным, если отношение оценок дисперсии -----------
полученных при небольшом п, меньше заданной величины. На-
D* (у—z) 1
пример, если ---—---— <Z—: > то можно утверждать, что при
D*y 4
одинаковой сложности систем F и G метод выделения главкой
части позволяет снизить затраты машинного времени при ста-
264
тистическом исследовании при помощи ЦВМ в два раза (необ-
ходимое число испытаний уменьшается в четыре раза, но каж-
дое испытание состоит в моделировании двух систем). В зависи-
мости от результатов сравнения оценок дисперсий принимается
решение: либо продолжать исследование методом выделения
главной части, либо исследовать систему F обычным способом
Монте-Карло.
Рассмотрим некоторые конкретные случаи применения мето-
да выделения главной части.
Определение моментных характеристик
выходной величины нелинейной системы;
на вход которой поступает случайный процесс
Широкое распространение для исследования линейных сис-
тем, находящихся под воздействием случайных процессов, по-
лучил метод сопряженных систем [17]. При его помощи вычисле-
ние моментных характеристик любого порядка выходной вели-
чины системы сводится к определению сечения весовой функции,
которое может быть найдено путем однократного, моделирова-
ния сопряженной системы. Это позволяет использовать линейные
системы в методе выделения главной части в качестве прибли-
жающих исследуемую нелинейную систему.
Предположим, что на вход нелинейной системы F начиная с
момента поступает случайный процесс x(t) с известными
статистическими свойствами. Требуется определить моментные
характеристики закона распределения выходной величины сис-
темы y(t\) в заданный момент времени t\. Для определенности
рассмотрим наиболее часто встречающийся на практике случай
определения математического ожидания и среднего квадрата
выходной величины. Вычисление моментов более высокого по-
рядка проводится аналогично.
Проведем линеаризацию системы F, в результате получится
линейная система G, связывающая случайный процесс x(t) с
процессом на выходе z(t). Способ линеаризации может быть
любым. Простейший вариант состоит в исключении всех нели-
нейных функций, входящих в систему. В некоторых случаях це-
лесообразно применение статистической или иной линеаризации.
Линейная модель может быть упрощена за счет замены отдель-
ных инерционных блоков коэффициентами усиления.
Пусть G(t, т) — функция веса системы G. Предположим,
что случайный процесс x(t) получается из белого шума единич-
ного уровня путем пропускания последнего через линейны?!
фильтр с весовой функцией Ф(/, т). Функцию веса последова-
тельного соединения формирующего фильтра и системы G обоз-
начим через Gi(t, т),
t
G± (t, Т) = С G (t, а) Ф (о, т) б/з.
10 3200
265
В этом случае математическое ожидание и средний квадрат
выходной величины системы G -в момент ti определяются фор-
мулами
М2 (/J = j* G т) Мх (т) dx,
о
Afz2(/i)= С G?(/1? x)dx.
(4. 105)
(4. 106)
Сечения весовых функций G(t\, т) и Gi(/b т) могут быть най-
дены путем однократного моделирования сопряженных систем
G* и Gi*. Затем по формулам (4.105) и (4.106) определяются
начальные моменты выходной величины системы G.
В процессе -статистического анализа нелинейной системы F
методом выделения главной части на основании результатов па-
раллельного испытания систем F и G строятся оценки момен-
тов
п
"••у Л)=Т^У. Is’ft)-**(У| +Мг(1,1. (4. 107)
М**у* [У** о +M^X). (4.108)
Одновременно для установления точности оценок (4.107) и
(4.108) и решения вопроса о целесообразности применения ме-
тода выделения главной части по стандартным формулам вы-
числяются оценки дисперсий
D* [г/(У-[t/2^)-г2 (/,)].
Моделирование проводится до.тех пор, пока точность оценок
(4.107) и (4.108), определяемая на основании оценок дисперсий
формулами типа (4.97), (4.100), не окажется в допустимых
пределах.
Определение моментных характеристик
выходной величины системы,
зависящей от случайных параметров
Обобщая задачу, рассмотренную в предыдущем разделе,
предположим, что нелинейная система F, подверженная воздей-
ствию случайного процесса x(t), зависит также от случайных
параметров. Для простоты 'предположим, что такой параметр
266
только один Л. В этом «случае первые начальные моменты вы-
ходной величины системы F выражаются в виде интегралов
Му (/J = J М [у (/х)|Х] р (X) rfX; (4. 109)
—оо
Му* (^) = J М \у* (<)|Х) р (X) d\, (4. 110)
— оо
где р(Х) — плотность распределения параметра X.
Применяя соответствующие квадратурные формулы, интег-
ралы (4.109) и (4.110) можно представить в виде
<s
Му ^=^акМ [г/ (/х)|Х*] +/?1: (4.111)
Му* &) = 2 акМ [у* + R2, (4. 112)
где остаточные члены и Т?2 могут быть сделаны сколь угодно
малым путем соответствующего подбора квадратурных формул
и узлов интегрирования V.
Условные математические ожидания, входящие в суммы
(4.111) и (4.112), представляют собой моментные характеристи-
ки выходных величин детерминированных нелинейных систем,
соответствующих фиксированным значениям 'случайного пара-
метра к при входной величине в виде случайного процесса x(t).
Для их подсчета может применяться процедура, рассмотренная
выше.
Ввиду дополнительного осреднения, осуществляемого квад-
ратурными формулами, точность определения условных мате-,
матичбских ожиданий может быть сравнительно невысокой, что
позволяет ограничиться небольшим числом испытаний системы
F. В некоторых случаях, когда число узлов формул (4.111),
(4.112) достаточно велико, при расчете условного математиче-
ского ожидания по формулам типа (4. 107), (4.108) можно поло-
жить Ni= 1.
Статистический анализ систем
с использованием упрощенной нелинейной модели
Одним из основных ограничивающих факторов при статисти-
ческом исследовании сложных систем является продолжитель-
ность расчета одного испытания системы на ЦВМ, вследствие
чего не удается выполнить необходимого согласно методу Мон-
те-Карло числа испытаний. Попытки упрощения системы для
уменьшения затрат машинного времени приводят к тому, что
10*
267
достоверность полученных результатов снижается, поскольку они
будут относиться .к упрощенной модели, а обоснование допус-
тимости упрощений не всегда осуществимо.
В этом случае для анализа системы можно воспользоваться
методом выделения главной части, а определение необходимых
характеристик выходной .величины упрощенной модели произво-
дить методом Монте-Карло. Все исследование будет состоять в
выполненйи большого числа испытаний упрощенной модели для
получения оценок методом Монте-Карло и ограниченного числа
испытаний 'системы и модели одновременно для их уточнения.
В некоторых конкретных случаях такая методика позволит
уменьшить затраты машинного времени-. В качестве простейше-
го варианта упрощенной нелинейной модели можно взять про-
грамму основной системы, просчитываемую при увеличенном
шаге счета.
Анализ эффективности метода выделения главной части при
использовании нелинейной модели G можно выполнить следую-
щим образом. Поскольку оценка математического ожидания
упрощенной нелинейной модели производится методом Монте-
Карло, последний член в формуле (4.99) является также слу-
чайным и дисперсия оценки (4.99) равна
(4.113)
Mi М2
где М2—число испытаний системы G, использованных для
оценки математического ожидания ее выходной величины по
формуле типа (4.96). Условием одинаковой точности вычислений
с использованием метода выделения главной части и обычного
метода Монте-Карло является равенство дисперсий оценок
(4.96) и (4.99)
Е>У D(y~z) । Я* /4 114)
М Mi м2
Пусть %F и %g — затраты машинного времени на одно испы-
тание систем F и G соответственно. Если обозначить tQ=Nxp —
полное время счета системы F для получения оценки (4.96),
/1 = Mi(tf + tg) — полное время счета систем F и G одновремен-
но для получения первого члена в оценке (4.99), t2=N2XG — пол-
ное время счета системы G для получения второго члена в оцен-
ке (4.99), то условие (4.114) можно записать в. следующем ви-
де:
Dyvp D(y-z')pP + ^ Р^о (4 115)
to , <1 t2
268
Из формулы (4.115) можно вычислить отношение затрат
машинного времени /1 + /2 и /0 «а получение оценок (4.99)
и (4.96)
6 + <2/2 ! £>(у-*)(у + *0) 11б)
^0 1 ГЛ ГЛ 1
Dy.xp-D^0 —
При соответствующих соотношениях между дисперсиями Dy,
Dz, D(y—z) и временами xF и rG для систем F и G отношение
(4.116) меньше единицы, что свидетельствует о целесообразно-
сти применения метода выделения главной части. Например, ес-
ли D(у—z)=0,25Dy, Dy = Dz, tg = 0,1tf, то, положив /V2 = 2/Vb
т. е. /2 = О,2/о, получим (^ + ^)/^о = 0,75. Заметим, что отношение
(ti + tzj/to зависит от величины ^2//o=W2tg//Vtf. Оптимальное зна^
чение tz/tOt обеспечивающее минимум отношения (/1 + /2) /t0, мож-
но получить, приравняв нулю производную выражения (4.116).
В рассмотренном примере
(=0,266; (^2) =0,706.
\ *0 /опт
Поскольку дисперсии выходных сигналов систем F и G неиз-
вестны, при применении формулы (4.116) следует воспользо-
ваться их оценками.
Экономия машинного времени, достигаемая при использова-
нии метода выделения главной части, в значительной степени
определяется выбором системы G. Поскольку на поиски подхо-
дящей системы также необходимо затратить некоторые усилия,
приходится идти на определенный компромисс между желанием
выбрать систему G, хорошо аппроксимирующую исследуемую
систему, и затратами на ее поиски. В некоторых случаях удает-
ся осуществить корректировку системы G в процессе статисти-
ческого исследования, используя результаты предшествующих
испытаний.
Однако даже при данной системе G путем надлежащей об-
работки результатов моделирования можно увеличить точность
оценок. Это тем более важно, что при анализе сложных систем
время, затраченное на статистическую обработку, бывает значи-
тельно меньше машинного времени, связанного с проведением
испытаний.
Предположим, что выходная величина системы G умножает-
ся на некоторый постоянный множитель k и полученная при
этом величина z'=kz используется в методе выделения главной
части. Исследуем влияние коэффициента k на точность получен-
ных оценок. Точность метода Монте-Карло определяется дис-
269
Персией Dy, точность метода выделения главной части —* дис-
персией разности
D (у — z')=D (у — kz).
Но
D (y-kz)=Dy — 2kz YDyDz^-k2Dz, (4. 117)
где г — коэффициент корреляции сигналов у и z.
Найдем значение k, при котором дисперсия разности мини-
мальна. Приравнивая нулю, получим
rz,
ь =У2У-г z -VDy
опт /D? ’ • опт VDi
DrQm=r*Dy, D(y — zonT) = (1 - г2) Dy.
(4.118)
Поскольку коэффициент корреляции г всегда меньше едини-
цы, из формул (4.118) следует, что для ускорения сходимости
всегда целесообразно добиваться, чтобы дисперсия выходной
величины системы G была меньше дисперсии выходной величи-
ны исследуемой системы F. Оптимальным будет случай, когда
Dz в г2 раз меньше Dy.
На практике значение коэффициента корреляции г и диспер-
сий Dy и Dz неизвестно, поэтому при образовании величины
2опт, участвующей в вычислении оценки Му по методу выделе-
ния главной части, следует воспользоваться их оценками.
4.10. ПОСТАНОВКА ЗАДАЧИ
ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ
Многие задачи оптимального проектирования систем управ-
ления летательными аппаратами заключаются в выборе пара-
метров исходя из экстремума заданного критерия эффективно-
сти и могут быть сформулированы следующим образом.
Поведение системы определяется векторным нелинейным
дифференциальным уравнением
~“=F(y, t, z, х), (4.119)
at
где у = (z/i, ..., ys) — вектор фазовых координат системы; z =
= (zr, ..., zn) — вектор параметров системы, подлежащих выбо-
ру в процессе проектирования; х=(хь..., хт)—вектор слу-
чайных воздействий; F=(F1, .. ., Fs) — векторная нелинейная
функция, удовлетворяющая условиям существования и единст-
венности решения системы (4. 19) при фиксированных z и х.
Критерием эффективности системы является математическое
ожидание функционала Фо (у, z, х). Вектор z должен быть выб-
ран таким образом, чтобы выполнялись условия типа равенств
270
и неравенств, наложенные на математические ожидания функ-
ционалов Фг
ТИФ,,(у, z, х)<0, /= 1,..., р\ МФ1 (у, z, х)=0, i=p -\~ 1,..., q,
и, кроме того, математическое ожидание функционала Фо при-
нимало минимальное значение.
К рассмотренной схеме на практике зачастую сводится так-
же задача расчета оптимальных законов управления. С этой
целью искомые управляющие функции аппроксимируются ко-
нечными суммами заданных функций с неизвестными коэффици-
ентами, и задача определения оптимального управления форму-
лируется как задача определения этих коэффициентов.
Фазовые координаты системы в силу уравнений (4.119) яв-
ляются функциями параметров z. Поэтому функционалы Фг
представляют случайные функции вектора z. Введем обозначе-
ния:
//(г) = 7ИФ/(у, z, х), / = 0, 1,..., (4.120)
тогда выбор оптимальных параметров системы сведется к зада-
че нелинейного программирования:
/0(z°)=min/0(z) (4.121)
260
В качестве примера рассмотрим в упрощенной постановке задачу выбора
оптимальных параметров автопилота, обеспечивающего автоматическое сбли-
жение летающего аппарата с неманеврирующим объектом в' безвоздушном
пространстве. Сближение происходит за счет работы поворотного двигателя
постоянной тяги, смещенного относительно центра масс, по сигналам гироста-
билизированного радиопеленгатора (рис. 4.3).
Уравнения сближения в плоскости имеют следующий вид.
1. Уравнения движения летательного аппарата
1 Р х .
”»'-7rbrFsin
W
d(Jiz
dt
= <DZ.
-------Fa sin
/ (0
d<tz
dt
2. Кинематические соотношения
D<a 4- = — Wy\
D — Z)2(o = — wx\
wx = wXi cos (<p — <Pz) + sin (<p — <fz);
Wy = — wXi sin (<p — <pz) + wyt sin (<p — fz).
271
3. Уравнение радиопеленгатора
1
т^2 + 2е|Т1Р+1
<D + - 4- n (t) 4- <dc
T2p2 4- SfoT*2P + 1
4. Уравнения автопилота и сервопривода управления поворотным двига-
телем
ь 1 *1 при | ЬП < 5тах,
J Ьтах sign В] при | 51| > 5тах,
dZy
dt
dZ
dt
dZ I
ПРИ — <
dt |
’max»
8тах sign 8
при
dZ
dt
•max»
Ay
1
5 =
i ^2
~9----------------I —ГТ Шизм +--------Ш2
7^2 4-2e3T3p 4“ 1 L 74p+l p
Обозначения в уравнениях системы ясны из рис. 4.3.
Входным воздействием на систему является белый шум n(t) и эквива-
лентное постоянное смещение сос
Рис. 4.3. Геометрия системы уп-
равляемого сближения с по-
мощью радиопеленгатора
на входе пеленгатора. Задачей управления
является уменьшение начальной дальности
до .минимального значения. Постоянное сме-
щение и начальная дальность представляют
нормально распределенные случайные ве-
личины.
Минимизируемым критерием качества
системы является средний квадрат прома-
ха — минимальной дальности, достигнутой
в данной реализации сближения. Его мини-
мизация должна осуществляться путем вы-
бора параметров автопилота Аи Д2, А3 и
Дополнительные ограничения в рассматри-
ваемой задаче отсутствуют.
Указанный пример иллюстрирует
особенности рассматриваемых за-
дач оптимального проектирования
систем управления. Система, при-
веденная на рис. 4.3, представляет
упрощенную модель реальной сис-
темы; она моделирует сближение
только в одном канале пространст-
венного движения. Но даже в таком
виде система настолько сложна, что
применить к ней вариационные
методы, не задаваясь структурой
в явном „ виде закон управления,
автопилота, а разыскивая
крайне сложно. Применение методов вариационного исчисления,
принципа максимума, динамического программирования для ре-
шения задач оптимизации систем управления летательных аппа-
ратов затруднительно ввиду сложности уравнений (4.119). По-
этому задача оптимизации, приведенная к задаче нелинейного
272
программирования (4.121), решается численными методами поис-
ка экстремума. Обзор этих методов составляет содержание сле-
дующего раздела.
Неотъемлемой частью прямых численных методов поиска
экстремума является многократное вычисление критерия качест-
ва и ограничений. Поскольку, как было показано выше, расчет
функций fi(z) чрезвычайно трудоемок и практически выполня-
ется приближенно, в реальных ситуациях вместо задачи (4.121)
на самом деле решается задача
cp0(z*) = min<p0(z),
r:|Ti(z)<0, /=1,..., р; <pt (z)=0, z = q},
(4.122)
где <Pi(z), f = 0, 1, ..., q являются оценками соответствующих
функций fi(z). Очевидно, решения задач (4.121) и (4J22) не
совпадают, z°=/=z*. В результате использования z* вместо z°
будут, во-первых, нарушены ограничения, а, во-вторых, критерий
качества будет принимать неоптимальное значение. Потери при-
ближенной оптимизации можно оценить ^+1 числами: fo(z*)—
—fo(z°) и fi(z*y i= 1,..., q. Оценкам этих потерь посвящен за-
ключительный раздел настоящей главы.
4.11. ОБЗОР ЧИСЛЕННЫХ МЕТОДОВ ОПТИМИЗАЦИИ
Основу всех численных методов решения задач нелинейного
программирования составляет решение задачи минимизации
критерия качества без ограничений. Как будет показано ниже,
общая задача нелинейного программирования может быть све-
дена к задаче без ограничений либо в процессе решения общей
задачи учет ограничений только слегка изменяет процедуру ми-
нимизации критерия качества. Вследствие этого вначале целесо-
образно рассмотреть методы минимизации функций многих пе-
ременных без ограничений.
Минимизация функций без ограничений
Пусть требуется минимизировать функцию
/(z) = /(z1,..., z„). (4.123)
Практически все методы поиска, за исключением, возможно,
перебора, предполагают отсутствие локальных экстремумов в
области изменения оптимизируемых параметров. Различные спо-
собы поиска глобального экстремума, известные в литературе,
связаны с принятием тех или иных гипотез о свойствах функ-
ции качества. В дальнейшем будем предполагать, что функция
f(z) не имеет локальных минимумов.
Согласно [13] классификацию методов поиска целесообразно
проводить по способам аппроксимации функции качества в ок-
рестности исследуемой точки (линейный, квадратичный) и по-
273
рядку — наивысшему 'порядку производных функции качества,
участвующих в вычислениях.
Простейший ме^год поиска, не требующий никаких сведений
о свойствах функции качества,— перебор, он гарантирует сходи-
мость в случае, когда область определения функции качества
содержит конечное число точек, в общем же случае применение
его невозможно без привлечения дополнительных сведений о
свойствах функции качества. Недостатком метода перебора яв-
ляется медленная сходимость, особенно в случае большой раз-
мерности вектора z. Однако в одномерном случае перебор ус-
пешно применяется и для него разработаны оптимальные проце-
дуры, позволяющие локализовать минимум функции в отрезке
наименьшей длины за заданное число шагов [13]. Одномерный
перебор зачастую входит как составная часть процесса мини-
мизации по многомерному вектору z, для чего процедура поис-
ка сводится к последовательной минимизации по каждой из
компонент вектора z (метод Гаусса — Зейделя).,
Важное значение имеет метод случайного поиска, теория ко-
торого подробно рассмотрена в книге [16]. Случайный поиск яв-
ляется частным случаем перебора и отличается тем, что назна-
чение точек z, в которых сравниваются значения f(z), произво-
дится с использованием стохастической процедуры. Например,
пусть текущая точка поиска zh. Точка zft+1 получается из zh до-
бавлением n-мерного-вектора Az, полученного как реализации
случайного вектора g с законом распределения, обладающим
определенными свойствами. Затем числа f(zk+') и f(zk) сравни-
ваются. Если /(zfe+1) <f(zh), осуществляется переход в точку
zh+x и производится следующий шаг. Если f(zh+i)^f (zk), к век-
тору zk добавляется новая реализация вектора £ и процесс по-
вторяется снова.
Основными достоинствами случайного поиска является прос-
тота реализации и возможность использования при любых раз-
мерностях вектора z. Недостатком является сравнительно мед-
ленная его сходимость. Существует много модификаций случай-
ного поиска, повышающих его сходимость, все они связаны с по-
вышением детерминированности метода.
Поиск экстремума симплексным методом производится сле-
дующим образом (10]. В n-мерном пространстве оптимизируемых
параметров строится (п+1)-мерный правильный симплекс (мно-
гоугольник), в вершинах которого производится вычисление
функции качества. Среди п+1 вершин симплекса выбирается та,
значение функции качества в которой максимально, а взамен ее
строится новая, симметричная относительно гиперплоскости,
проходящей через п оставшихся вершин. Как показало экспери-
ментальное исследование, симплексный метод сходится бы-
стрее случайного поиска, однако, если функция качества носит
выраженный «овражный» характер, то эффективность симплекс-
ного метода снижается.
274
Перебор, случайный 'поиск и симплексный метод являются
методами нулевого порядка — для реализации требуется вы-
числение только функции f(z) и не используются никакие гипо-
тезы о форме f(z).
Большое распространение в практике получили 'линейные
методы поиска, использующие аппроксимацию функции качест-
ва в окрестности исследуемой точки поверхностью первого по-
рядка. Линейными методами являются, например, градиентный
и метод наискорейшего спуска.
Общая формула градиентного метода имеет вид
где Zih — i-я координата k-й итерации поиска.
Градиентный метод имеет первый порядок, поскольку для
его использования необходимо вычисление производных первого
порядка функции f(z). Однако он может быть реализован и без
вычисления производных, если последние заменить разностями
df(z) ^f(z^.,,t ZZ +А,..., гя)—/(Z1,..., zn) .
dzt b
Различные модификации градиентного метода получаются
путем задания коэффициентов а&. В простом градиентном мето-
де ak — постоянная. В методе наискорейшего спуска аь выби-
рается из условия, чтобы точка zfe+1 соответствовала минимуму
f(z) по направлению градиента. В этом случае, например, ис-
пользуется аппроксимация вдоль линии градиента параболой по
значениям ее в трех точках. >
Иногда применяется градиентный метод с постоянным ша-
гом
X
k ||grad / (z)||
где -
Л п
V (^7)2-
Доказано, что если в окрестности точки экстремума f(z) мо-
жет быть аппроксимирована поверхностью второго порядка, гра-
диентный метод сходится со скоростью геометрической прогрес-
сии. Знаменатель прогрессии q вычисляется следующим об-
разом:
<7=-^- ’ (4-125)
М 4- т
где М — наибольшее собственное значение матрицы вторых про-
изводных функции f(z)> т — наименьшее.
275
Из формулы (4.145) видно, что градиентный метод является
эффективным только в случае, когда все собственные значения
матрицы вторых производных примерно одинаковы.
Если функция f(z) имеет «овражный» характер (в аппрок-
симации f(z) поверхностью второго порядка это проявляется
в большом разбросе собственных значений), сходимость гради-
ентного метода резко ухудшается. Некоторого улучшения сходи-
мости в этом случае можно добиться, если применять,различные
значения коэффициентов f(z) по каждой координате гг-. Так, в
градиентном методе с подбором масштабов делается преобразо-
вание координат
В этом случае поверхность второго порядка, аппроксимирую-
щая f(z), переходит в сферу. В старых координатах уравнение
метода имеет вид
z»+i=z»_aftXz^)| 1=1,:.., п.
OZ[ \z - z
Однако для реализации такой процедуры поиска требуется рас-
чет на каждом шагу матрицы вторых производных, что резко
замедляет поиск.
Примерно такой же степенью эффективности; как и градиент-
ный, обладает метод покоординатного спуска Гаусса — Зейде-
ля, в котором производится последовательное движение в сто-
рону уменьшения по каждому из переменных Zi. При соответст-
вующем преобразовании переменных метод покоординатного
спуска совпадает с градиентным.
Специально для оптимизации изрезанных функций разрабо-
тан метод «оврагов» (3]. В некоторых случаях эффективным
может оказаться метод «тяжелого шарика», задаваемый урав-
нением
dzi lz = z
Большое количество других модификаций градиентного ме-
тода имеется в работе [13].
Методы, основанные на аппроксимации f(z) поверхностью
второго порядка, имеют квадратичную скорость сходимости, но
сходятся только при достаточно жестких ограничениях на по-
ведение функции f(z). Простейшим вариантом метода, исполь-
зующего аппроксимацию второго порядка, является метод Нью-
тона. Он получается из алгоритма Ньютона решения системы
нелинейных уравнений вида
grad/(z)=0.
Недостатком метода Ньютона является необходимость вычисле-
ния вторых производных. Поэтому имеется большое число ра-
276
бот, в которых рассматриваются методы первого и нулевого по-
рядка, использующие аппроксимацию f(z) поверхностью второ-
го порядка. Примером таких методов является метод сопряжен-
ных градиентов и его модификации [13].
Для проектирования систем управления летательных аппара-
тов применение методов поиска экстремума, использующих ап-
проксимацию поверхностью второго порядка, в большинстве слу-
чаев нецелесообразно. Дело в том, что с увеличением порядка
аппроксимации увеличивается скорость сходимости метода, но
одновременно уменьшается область сходимости и увеличивается
его критичность к выполнению используемых гипотез о функ-
ции f(z). Критерии эффективности динамических систем имеют
обычно сложную форму и даже могут быть разрывными. В этом
случае методы, использующие аппроксимацию функциями вы-
сокого, порядка, расходятся или сходятся очень медленно. По-
этому, как правило, при расчете систем, зависящих от случай-
ных воздействий, следует пользоваться градиентным методом
или даже методами нулевого порядка.
Вообще говоря, сравнение эффективности различных мето-
дов поиска экстремума является достаточно условным. Эффек-
тивность метода определяется для класса минимизируемых
функций, а поскольку мы обычно не знаем, к какому классу при-
надлежит рассматриваемая функция, результаты сравнения ме-
тодов не могут быть приняты без экспериментальной проверки
на интересующей нас функции. Практически выбор метода по-
иска экстремума достаточно случаен и определяется наличием
соответствующих стандартных программ на ЦВМ.
Методы решения задач на условный экстремум
Самым простым методом решения задач на условный экстре-
мум является сведение их к безусловному путем разрешения
дополнительных условий. Такую операцию удается выполнить
не всегда, но в тех случаях, когда можно разрешить хотя бы
часть дополнительных условий, это нужно сделать.
Предположим, что в задаче (4.121) в качестве дополнитель-
ных фигурируют условия, которые разрешить не удается.
Метод проекции градиента может применяться как в задачах
вариационного исчисления, так и в задачах нелинейного про-
граммирования. Он заключается в следующем. Вместо формулы
градиентного метода
zft+1=z* —a^grad / (z*) (4. 126)
используется формула
zft+1 = P0[zs —aft grad(4.127)
277
где PG — оператор проектирования на множество G. Он опре-
деляется из условия
||P0(z)-z||=Jin/||v-z||.
v£Q
Метод условного градиента использует линеаризацию fi(z)
в окрестности текущей точки и решение задачи нелинейного про-
граммирования для определения приращения zft+1—z\ миними-
зирующего fo(z) при выполнении всех ограничений.
Общим методом решения задач на условный экстремум яв-
ляется метод штрафных функций [16]. С его помощью задача
(4.121) сводится к задаче на 'безусловный экстремум функции
f(z), совпадающей с fo(z)f если z принадлежит G, и принимаю-
щей очень большие значения, если z находится вне области G.
Обычно замена происходит следующим образом. Ограничения
типа равенств заменяются двумя ограничениями типа нера-
венств по формулам.
Вместо ограничения fi(z) =0 два ограничения:
/z(z)<0 и — /,(z)<0.
В дальнейшем изложении предполагается, что такая замена
уже сделана и в задаче (4.121) присутствуют только ограниче-
ния типа неравенств.
Задача (4.121) заменяется задачей на безусловный минимум
функции
/(z)=/0(z)+2^(7(A(z)), ' (4.128)
Z-1
где G(u) — функция, равная нулю при и<0 ;и возрастающая
положительная функция при а>0. При выполнении определен-
ных условий на вид функции G(u) и коэффициентах Ait стре-
мящихся к бесконечности, решение задачи минимизации f(z)
совпадаете решением задачи (4.121).
Недостатком метода штрафных функций является то, что при
больших значениях коэффициентов Лг- вдоль границ области
функция (4.128) имеет «овражный» характер, вследствие чего
сходимость методов численного поиска при минимизации функ-
ции (4.128) может оказаться медленной.
Для исключения этого недостатка может быть предложена
модификация метода штрафных функций, позволяющая в неко-
торых случаях ускорить сходимость процедуры поиска миниму-
ма благодаря сглаживанию оптимизируемой функции в окрест-
ности границы области G. Она заключается в следующем. Зада-
278
ча (4.121) заменяется задачей на безусловный минимум функ-
ции
/о(2)+2«(Л(2)-М, (4.129)
/=1
где G(u) — строго выпуклая при и>0 непрерывная функция,
обращающаяся в нуль при и<0; — постоянная величина.
Обозначим через zx, Л=(ЛЬ..., Лр), решение задачи (4.129).
Пусть fi(z\) = Цг(1). Тогда zx является одновременно решением
задачи [4]
/о (Zx) = min /0 (z); (4.130)
Оу. = (z) Oz (1), i=\,...,p}.
Для задач выпуклого программирования функции цДМ не-
прерывны. Если зафиксировать все Лг-, кроме Л&, то ць(Х) как
функция кь является неубывающей до некоторого значения
Х™ах, а затем остается постоянной. Существует такой набор пе-
ременных Хг» возможно, неединственный, при котором все числа
Цг(1) обращаются в нуль или отрицательны.
С использованием (4.129) процедура решения задачи (4.121)
заключается в следующем. Задаваясь произвольными значения-
ми Хг-, можно определить минимум функции (4.129) и вычислить
fi(zx) =Цг(Л). Если функции Цг (1) не обращаются в нуль, выби-
раются новые значения Л1 и процедура поиска минимума по-
вторяется снова до тех пор, пока либо все значения цДЛ) не ста-
нут отрицательными и меньшими Ль либо все значения цг(Л)
не станут отрицательными или равными нулю. Выбор новых
значений Л; можно производить, используя любой способ числен-
ного решения системы нелинейных уравнений
sup(0, f (zx)) = O, Z=l,...,p. (4.131)
В функции (4.129) штрафной член отличен от нуля не толь-
ко вне области, но и вблизи ее границ. Расстояние от границы,
начиная с которого добавляется штраф, подбирается таким, что-
бы решения задач (4.129) и (4.121) совпадали.
Функция (4.129) носит заметно менее выраженный «овраж-
ный» характер, чем функция (4.128). Процесс поиска ее мини-
мума занимает значительно меньше машинного времени, чем ре-
шение задачи (4.128), поэтому, даже несмотря на то, что для
определения значений Лг- удовлетворяющих уравнениям (4.131),
приходится задачу (4.129) решать несколько раз, суммарные за-
траты машинного времени на решение задачи (4.121) с по-
мощью (4.129) могут оказаться меньшими, чем при использова-
нии (4.128). К этому следует добавить, что при применении
обычного метода штрафных функций в общем случае миними-
зацию функции (4.128) приходится производить несколько раз
279
при различных коэффициентах Аь, пока полученное решение не
окажется в области G.
Другим важным преимуществом модификации метода штраф-
ных функций является возможность оценки влияния отдельных
ограничений на решение задачи (4.121). В процессе минимиза-
ции функции (4.129) и решения уравнения (4.131) будут найде-
ны решения задачи (4.129) для нескольких значений Хг-, которые
являются решениями задачи (4.130) для |1г- (1). Анализ зависи-
мостей fo(zx) и Цг(М позволяет становить степень влияния ог-
раничений на оптимальное значение функции fo(z).
Можно применять другой вариант рассмотренного метода,
позволяющий обойтись только одним параметром X и, соответ-
ственно, решать только одно нелинейное уравнение. Введем
функцию
/Jz) = max{/1(z),/p(z)}. (4.132)
Если функции fi(z) выпуклы, то функция f*(z) также выпук-
ла. Ограничения Д(г)^0, f=l, ..., р эквивалентны одному ог-
раничению (z)^0. Поэтому, если zx — решение задачи мини-
мизации функции
/o(z)+G(A(z)-k) (4.133)
и выполняется условие f*(zx)=O, то zx является решением за-*
дачи (4.121). Значение X, для которого функция f*(zxj обра-
щается в нуль, разыскивается путем численного решения урав-
нения
sup(0, A(zx))=0. (4.134)
Можно показать, что решение системы (4.131) существует, а
величины Цг(Х) =Д(2х) при фиксированных Х&, £=/=/, представ-
ляют неубывающие функции обращающиеся в нуль в един-
ственной точке или на целом отрезке. В остальном характер
уравнений (4.131) произволен. В связи с этим решение системы
(4.131) представляет известные трудности и, если нет особых
оснований выделять отдельные ограничения, целесообразно ис-
пользовать вариант минимизации функции (4.133), для которого
левая часть нелинейного уравнения (4.134) является неубываю-
щей функцией скалярного аргумента X, вследствие чего реше-
ние уравнения (4.134) не представляет затруднений.
Опыт решения задачи оптимизации нелинейных динамиче-
ских систем, зависящих от случайных воздействий, путем сведе-
ния к задаче нелинейного программирования показывает, что
трудоемкость решения задачи мало зависит от выбора метода
оптимизации. Обычно минимизируемый критерий качества та-
ких систем является нелинейной функцией сложной формы, за-
частую многоэкстремальной. Методы оптимизации достигают
280
высокой эффективности за счет использования особенностей ми-
нимизируемой функции. Поскольку обычно свойства минимизи-
руемых функций неизвестны, отдавать предпочтение определен-
ным методам оптимизации нет оснований. На практике вопрос
о выборе метода оптимизации решается в основном исходя из
наличия стандартных программ оптимизации, имеющихся в биб-
лиотеке ЭВМ.
Более важным является вопрос о назначении параметров ме-
тода оптимизации (число искомых переменных, шаг поиска, ко-
эффициенты пригпроизводных и т. д.) и общей 'стратегии реше-
ния задачи.
Поскольку оптимизируемая функция может оказаться много-
экстремальной, необходимо выделить область изменения иско-
мых параметров, в которой отсутствуют локальные минимумы.
Кроме того, при физической постановке задачи в искомые пара-
метры часто включаются величины, слабо влияющие на величину
критерия качества. Это выражается в появлении «оврага» ми-
нимизируемой функции вдоль оси координат, соответствующей
слабовлияющему параметру. Желательно слабовлияющие пара-
метры из рассмотрения исключить, так как -с ростом размер-
ности вектора z время решения задачи оптимизации резко воз-
растает.
Все эти вопросы можно решить, вводя специальный пред-
варительный этап исследования, во время которого путем рас-
смотрения задачи, в упрощенной постановке и вычисления кри-
терия качества в отдельных точках исследуются особенности по-
ставленной задачи, выбирается метод поиска и уточняется мно-
жество искомых параметров.
Само решение задачи также целесообразно проводить по-
этапно. Вначале, когда ничего о свойствах оптимального реше-
ния неизвестно, проводится оптимизация с использованием уп-
рощенной модели системы при сравнительно неточном вычисле-
нии критерия качества и ограничений. В результате без боль-
ших затрат удается попасть в окрестность оптимальной точки.
Затем с использованием полных уравнений при возможно более
точном вычислении критерия качества и ограничений оконча-
тельно определяется оптимальное решение.
Задачи оптимизации с ограничениями проще всего решать
методом штрафных функций, используя эквивалентность задач
(4.129) и (4.130).
При решении примера из 4.10 расчет критерия качества проводился с по-
мощью. комбинированной квадратурной формулы с 16 узлами и занимал
до 10 мин машинного времени, поскольку ввиду наличия малых постоянных
времени уравнения системы считались с очень малым шагом. Поэтому была
принята двухэтапная процедура. Вначале оптимальные параметры выбирались
для системы, полученной из исходной выбрасыванием звеньев с малыми по-
стоянными времени. Счет дифференциальных уравнений проводился с укруп-
ненным шагом, в результате чего расчет критерия качества занимал менее
минуты. Результат оптимизации упрощенной задачи использовался в качестве
281
начальных условий для основной. Оптимизация проводилась методом, пред-
ставляющим комбинацию метода симплексов и покоординатного спуска. Все
иешение задачи занимало два-три часа машинного времени.
4.12. ОЦЕНКА ТОЧНОСТИ ПРИБЛИЖЕННОГО РЕШЕНИЯ
ЗАДАЧИ ОПТИМИЗАЦИИ ПРИ ИСПОЛЬЗОВАНИИ
СТАТИСТИЧЕСКИХ ОЦЕНОК ОПТИМИЗИРУЕМОЙ ФУНКЦИИ
Предположим, что целью проектирования системы является
минимизация функции качества f(z)f представляющей математи-
ческое ожидание функционала Ф(у, z, х). При использовании
для оценки функции f(z) метода Монте-Карло функция qp(z),
приближающая /(z) к фактически используемой пр.и оптимиза-
ции, имеет вид
' /С
?JV(z)=^S0(y*’z’Х*х (4,135)
или 4
(z) = 2 ak® (У*, x*)> (4.136)
если для оценки функции f(z) используются комбинированные
квадратурные формулы.
В формулах (4.135), (4.136) xk — k-я реализация вектора
случайных воздействий, yh — решение системы (4.119), получен-
ное при х = х* и z, индекс N при функции <р (z) означает, что она
вычислена с использованием N решений системы^ (4.119).
Особенность использования методов Монте-Карло и комби-
нированных квадратурных формул для вычисления критерия ка-
чества при оптимизации заключается в том, что полученные с их
помощью оценки являются случайными. Это, с одной стороны,
затрудняет оценку точности приближенного решения задачи оп-
тимизаций и, с другой стороны, ухудшает сам процесс поиска
экстремума.
Обычно при подсчете значений функции <p(z) в разных точ-
ках z в формулах (4.135) и (4.136) используются различные
наборы реализаций случайных воздействий х. Это приводит к
тому, что погрешность определения функции f(z), выражаемая
разностью
(Z) =<рЛ’ (z) — /(z),
является случайной и может трактоваться как случайный про-
цесс по векторной переменной z. Функция <pN (z) при этом мо-
жет содержать дополнительные локальные минимумы, тормозя-
щие решение задачи. Действительно, пусть в процессе реализа-
282
ции поисковой процедуры сравниваются значения функций
c?n (z) в точках zk и zft+1. Пусть в этих точках выполняется не-
равенство
/(zfe+1) —/(z*)<0,
тогда, если бы значение функции f(z) при минимизации вычис-
лялось точно, из точки zk необходимо было бы перейти в точку
zfe+1 и дальше продолжать поиск или, если в точке zft+1 выпол-
няются условия минимума, считать задачу решенной. Но по-
скольку в процессе минимизации вместо функции /(z) исполь-
зуется (pN (z) решение о переходе из точки zk в точку zft+1 при-
нимается на основании разности
= /(zft+1)-/(zft)+^lzft+1)-tp;v(zft). (4. 137)
Если разность (z/l+h)^-t|)yv(zA) получается положительной
и большей первых двух членов в (4.138), будет принято непра-
вильное решение о том, что точка zh является точкой минимума.
Вероятность неправильного решения зависит от статистических'
свойств разности
ф^ (z*+1)—-ф^ (zfe).
Обычно математическое ожидание фЛГ (z) равно или близко
к нулю, а закон распределения близок к нормальному. Поэтому
вероятность принятия неправильного решения определяется дис-
персией разности
D НА (z**1) - ф* (z*)] = D^N (z**1) + DtyN (z*) -
- 2r )/£h|A(z*+1) Z>]A(z*),'
где r — коэффициент корреляции между ip;v(zft+1) и 4A(zfe).
Если для подсчета <p7V (z) используются независимые реализации
случайных воздействий, г=0.
Естественным способом уменьшения дисперсии Df-ijA (zfe+1) —
—ipyv(zfe)], а значит, и вероятности неправильного решения яв-
ляется увеличение числа членов в формулах (4.135) и (4.136),но
при этом возрастают затраты машинного времени на поиск. Од-
нако есть и другой способ, состоящий в организации расчетов
таким образом, чтобы погрешности (zk) и t|?iV(z/l+1) были за-
висимы с положительным коэффициентом корреляции. Этого
можно добиться, например, если использовать одни и те же реа-
лизации случайных воздействий при подсчете q)7V(z) в точках zk
и zft+1. По-видимому, впервые этот факт был отмечен в статье
А. С. Фролова и Н. Н. Ченцова {18] и применен к задачам чис-
ленного поиска Ю. Г. Полляком [12].
В статье [5] доказано, что использование одних и тех же
реализаций случайных воздействий х в течение всего процесса
поиска не ухудшает окончательной точности определения экст-
ремума. Получена оценка точности решения задачи минимиза-
283
ции функции /(z) при использовании вместо /(z) ее оценки ме-
тодом Монте-Карло или комбинированными квадратурными
формулами. Эти оценки, являясь достижимыми, для большин-
ства практических задач предъявляют завышенные требования
к точности аппроксимацйи f(z).
В связи с этим представляет интерес получение оценок по-
грешностей оптимизации, имеющих негарантированный харак-
тер, но позволяющих определить потери приближенного реше-
ния задачи оптимизации достаточно точно при сохранении удов-
летворительной степени достоверности.
Потери приближенной оптимизации ограничены неравен-
ством
/ (z*) - / (z) < [/ (z*) - <? (z*)] - [/ (z°) - <р (z®)]. (4.138)
Предположим, что в процессе решения задачи поиска ис-
пользовалась конкретная функция q)yv(z), так что точка z* фик-
сирована. Точка z° определяется исходной задачей, следователь-
но, тоже фиксирована.
Проведем оценку отдельных членов в правой части уравне-
ния (4.132). Разность f(z*)—q>N(z*) при фиксированной точке
z* является реализацией случайной величины, имеющей нулевое
математическое ожидание и дисперсию DqN(z*).
Разность f(z°)—(py(z°) также имеет нулевое математическое
ожидание и дисперсию DqN(zQ). Следовательно, вся правая
часть неравенства (4.138) имеет нулевое математическое ожи-
дание и дисперсию, не превышающую 2[Dq)N(z*) +DqN (zQ)].
Следовательно, с доверительной вероятностью р выполняется
неравенство
[/ (z*) - <р" (z*)]-[/ (z°) - <рЛг (ZO)]^ ар у2 [D^ (г*)+£)<[Л(г0)],
(4. 139)
где ар — корень уравнения
Для р = 0,95 ар = 2, для р = 0,99 ар = 3.
Объединяя (4.138) и (4.139), получим
P{/(z*)-/(z°J <ар]/2 [D^ (z*) +Z)^(z°)]}>p. (4. 140)
Поскольку точка z* известна, дисперсия DyN (z*) может быть
сосчитана по обычным формулам оценки дисперсий
D*^(z*)
Ni Г
Л = 1 L
2
, (4. 141)
где <p^(z*) — k-я независимая реализация функции фдг(г*).
284
Если функция <рА (z) определяется формулой (4.135), то ее
дисперсия может быть вычислена и другим способОхМ — через
дисперсию функционала Ф по формуле
ОФ (у*, z*, х), (4. 142)
а дисперсия функционала Ф оценивается формулой
ЛГ г N 42
£>*Ф=——V1 фь—-Уф, ,
N — l^j ь N J
k-1 L J
где
ФЛ = Ф(у\ z*, Xй).
Оценка DqN (з!*) по формулам (4.142) требует N решений
уравнений оптимизируемой -системы, а по формуле (4.141) —
MAf решений.
Принимая гипотезу, что статистические характеристики фун-
кции (z) мало изменяются с изменением z, для оценки
Дф(г°) можно принять значение оценки дисперсии функции ф(г)
в некоторой точке z1. В частности, в качестве точки z1 можно
принять точку z*, формула (4.140) в этом случае примет вид
P{/(z*)-/(z°)<2ap/Z>p(z)) (4.143)
При наличии соответствующих возможностей желательно
проверить гипотезу слабой зависимости дисперсии DyN (z) от z,
для чего нужно построить оценку ее по формуле (4.141) или
(4.142) в нескольких точках z. В этом случае в формуле (4.140)
вместо /)ф(г°) используется максимальная из полученных оце-
нок.
Формулы (4.140) /и (4.143) являются приближенными по сле-
дующим причинам. Во-первых, строго говоря, случайная величи-
на фЛГ(г*) распределена по закону, отличному от полученного в
предположении фиксированности точки z*, поскольку точка z*
зависит от реализации фЛГ(г). Поэтому сделанные предположе-
ния о характере распределения фЛГ(г*) справедливы только, ес-
ли наличие зависимости z* от фЛГ(г) не сильно изменяет харак-
тер распределения. Во-вторых, как уже указывалось, дисперсия
ОфЛГ(г°) неизвестна и заменяется дисперсией в некоторой точке
z1, отличной от z°. Наконец, формулы (4.140) и (4.143) получе-
ны в предположении, что правая часть неравенства (4.138) рас-
пределена по нормальному закону, что, строго говоря, неверно,
поскольку она не может быть отрицательной. Однако, если чис-
ло N членов в формуле (4.135) или (4.136) достаточно велико,
закон распределения правой части неравенства (4.138) можно
считать близким к нормальному.
Формула (4.140) и следующая из нее формула (4.143) дают
также завышенную оценку приращения функции f(z), поскольку
285
они не учитывают корреляционной зависимости разностей
f(z)—cp/v(z*) и f(z°)—(рЛ'(2°)- Если функция cpy(z) прибли-
жает f(z) достаточно точно, точки z* и z° мало отличаются друг
от друга и значения обеих разностей статистически связаны с
большим положительным коэффициентом корреляции. В этом
случае дисперсия правой части неравенства (4.138) меньше дис-
персий отдельных членов.
Если дисперсия разности [f(z*)—q)/v(z*)]—{f(z°)—<py(z0)] из-
вестна, неравенство, оценивающее приращение f(z) с 'вероятно-
стью, большей р, имеет вид
(z°)<ap VD ([f (z*) - «Л (z*)] -D\f (z°)- <?"(z0)]}} >p.
(4. 144)
Для практического его использования можно предположить,
что дисперсия разности if(z*)—^(z*)]—[f(z°)—qAfz0)] не
больше дисперсии разности ff(z*)—<p'v(z*)]—Iffz1)—<pN(z1)].
Точка z1 выбирается, например, путем оценки дисперсии раз-
ности по формуле
£>* [/ (z*) - <?" (z*) - / (z) - (z)] =
N, /V,
-хА У W <*•) - и] - У ww-tf и]!
1ST
в нескольких произвольных точках z и использования в качест-
ве z1 той из них, для которой оценка дисперсии максимальна.
При этом важно обследовать всю область изменения z, в кото-
рой возможно появление точки z°. В противном случае диспер-
сия разности tf(z*)—(p^fz*)]—[f(zl)—tp^fz1)] ]^ожет оказаться
малой не вследствие малости приращения f(z*)—f(z°), а из-за
близости точек z* и z1, и оценка приращения по формуле
(4.144) будет заниженной.
На практике встречаются задачи, в которых точность вы-
числения функции f(z) уменьшается по мере увеличения /(z).
Так, например, если f(z) при фиксированном z представляет
средний’ квадрат центрированной нормально распределенной
случайной величины, дисперсия ее оценки по формуле (4.135)
может быть подсчитана следующим образом.
Пусть Ф(у, z, х)=и2, где и — центрированная нормально
распределенная случайная величина. Тогда, поскольку
(z)=-j^- £>Ф (у, z, х)=-“" 1ф(У» х)]2— [ТИФ (у, z, х)2} —
= _L [Ми* - (Ми2)2] = -1- [3 (Ми2)2 - (Ми2)2] =
28 6
Следовательно, в этом случае погрешность вычисления f(z) по
формуле (4.135) при фиксированном z -прямо пропорциональна
значению/(z).
Аналогичная ситуация будет во всех случаях, когда критери-
ем качества системы является математическое ожидание квад-
рата центрированной случайной величины, распределение кото-
рой близко к нормальному.
Для таких задач использованное выше предположение о сла-
бой зависимости статистических характеристик функции qN (z)
от z несправедливо. Однако и в этом случае формулой (4.144)
можно пользоваться. Действительно, внутри окрестности опти-
Рис. 4.4. Структурная схема системы самонаведения в плос-
кости
мальвой точки z°, где функция f(z) мало отличается от /(z°),
оценка точности, определенная по формуле (4.144), справедли-
ва. Вне этой области, несмотря на большую погрешность вычис-
ления f(z), вследствие того, что f(z) велико, ср(У) также прини-
мает большие значения, и следовательно, точка z* должна на-
ходиться в окрестности точки z°. Поэтому весь вывод формул
для потерь приближенной оптимизации можно повторить, огра-
ничиваясь рассмотрением указанной окрестности точки z°. При
этом, разумеется, оценка f(z) >по формуле (4.135) должна быть
все-таки настолько точной, чтобы глобальные свойства функций
f(z) и ф(г) совпадали.
Пример. В модели процесса самонаведения методом пропорциональной
навигации с линеаризованным кинематическим соотношением, изображенной
на рис. 4.4, выбираются навигационный коэффициент k и постоянная времени
Тф фильтра, минимизирующие средний квадрат промаха с учетом шума n(t),
постоянного маневра цели, начального значения промаха и разброса времени
самонаведения ; г о — —;— •
D
Расчет критерия оптимальности проводился с помощью комбинированной
квадратурной формулы, полученной на основе формул Гаусса с двумя узлами
по каждому из трех случайных переменных: начальному промаху Ао, маневру
цели /ц и времени самонаведения
8
Ч8(к, Уф) = 2о‘Л(Ло> 4 nl(t)),
( = 1
287
где ho — реализации промаха при соответствующим образом подобранных
значениях начального промаха, маневра цели и времени самонаведения и не-
зависимой случайной реализации шума n(t).
В результате решения задачи поиска методом Гаусса-Зейделя с постоян-
ным шагом были найдены оценки оптимальных значений искомых параметров
Л*=5,2; ТФ* = 0,2 с.
После десятикратного вычисления ф8(&*, Тф*) с различными реализаци-
ями шума n(t) была подсчитана по формуле (4.141) дисперсия ф8(/г*, Тф*),
которая оказалась равной 0,032 м4. Следовательно, согласно формуле (4.143)
с доверительной вероятностью р=0,99 (ар = 3) выполняется неравенство
МЛ2(£*. Г*) — Mh^(k0, Т°) < 6 ]/0Т032 = 1,08 м2.
В табл. 4.4 для различных значений k построены значения ф8(£, 7)=M/i2,
f(k, T)=Mh2 и У£)ф8(&, Т). Предполагается, что функция, полученная путем
осреднения десяти независимых реализаций ф8(&, Т), совпадает с f(k, Т). Ана*
лиз данных таблицы показывает, что оценка потерь приближенной оптимиза-
ции, даваемая формулой (4.143), справедлива.
Таблица 4.4
k 3 4,2 5,2 7
Тф) 977 14,9 0,35 0,58
f(k, Тф) 1029 12,7 0,39 1,21
У^щ.Тф) 85 2,54 0,178 0,68
При решении задач на условный экстремум возможная сте-
пень нарушения ограничений задачи (4.121) в точке z* оцени-
вается непосредственно подстановкой.
Приращение критерия качества /о(х*)—/о(х°) вычисляется по
оценкам потерь, вызванных приближенным вычислением крите-
рия качества в задаче «а безусловный экстремум, полученной
из исходной задачи методом штрафных функций, и оценкам зна-
чений функций fi(z), i=l, . •Я в точке z*. Например, если z*
найдено из решения задачи минимизации функции
Q
<Р (z) =<р0 (z)+2 ° (?/ (z) -
Z — 1
288
то согласно формуле (4.143) с вероятностью р
Z-l Z-1
откуда с той же вероятностью
/о (Z*) - /о (z°) < 2ар ]/d7(F)+2 О (ft (z°) - X,)—
Z-0
- 2 О (ft (z *) - Xz)<2ap VD^i - 2 O(ft(z*) - M +
i — 1 i — 1
+2
Z-l
СПИСОК ЛИТЕРАТУРЫ
К главе 1
1. Дубнов Я. С. Основы векторного исчисления. Ч. I. ГИТТЛ, 1952, 368 с.
2. Кринецкий Е. И. Системы самонаведения. М., «Машиностроение».
1970, 235 с.
3. Лебедев А. А., Карабанов В. А. Динамика систем управления беспи-
лотными летательными аппаратами. М., «Машиностроение», 1965. 528 с.
4. Лэнинг Дж. X., Бэттин Ф. Г. Случайные процессы в задачах автомати-
ческого управления. М., ИЛ, 1958, 387 с.
5. Ньютон Дж. К., Гулд Л.А., Кайзер Дж. Ф. Теория линейных следя-
щих систем. М., Физматгиз, 1960, 407 с.
6. Пугачев В. С. Теория случайных функций- и ее применение к задачам
автоматического управления. М., Физматгиз, 1962, 883 с.
7. Солодов А. В. Линейные системы автоматического управления с пере-
менными параметрами. М., Физматгиз, 1962, 224 с.
8. Солодовников В. В. Статистическая динамика линейных систем авто-
матического управления. М., Физматгиз, 1960, 655 с.
К г л а в е 2
1. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. М., «Наука»,
1966, 296 с.
2. Бородачев Н. А. Основные вопросы точности производства. М., Изд-во
АН СССР, 1950, 416 с.
3. Матвеев П. С., Синицын А. С. Динамическая точность систем автома-
тического управления со случайно изменяющимися параметрами. — В сб.:
Автоматическое управление и вычислительная техника. М., «Машинострое-
ние», 1967, вып. 7, с. 232—305.
4. Моисеев Н. Н. Численные методы в теории оптимальных систем. М.,
«Наука», 1971, 157 с.
5. Пупков К. А., Себряков Г. Г. Ортогональный метод исследования не-
линейных САУ при случайных воздействиях. — «Известия АН СССР. Техни-
ческая кибернетика», 1967, № 2, с. 157—167.
6. Федосов Е. А., Себряков Г. Г. Спектральный анализ систем управления
со случайно изменяющимися параметрами. — В сб.: Автоматическое управле-
ние и вычислительная техника. М., «Машиностроение», 1967, вып. 7, с. 207—
239.
7. Чернецкий В. И. Анализ точности нелинейных систем управления. М.,
«Машиностроение», 1968, 248 с.
8. Caughey Т., Dienes. The behavior of linear systems with random
parametrie excitation, Journ. Phys. 1962. No 41, pp. 300—318.
К г л а в e 3
1. Дубовицкий А. Я., Милютин А. А. Задачи на экстремум при наличии
ограничений. —ЖВМ и МФ‘, 1965, т. 5, № 3, с. 395—493.
2. Люстерник Л. А., Соболев В. И. Элементы функционального анализа.
М., «Наука», 1966, с. 180—196.
3. Ляпунов А. А. О вполне аддитивных вектор-функциях. — «Известия
АН СССР. Сер. математическая», 1940, т. 4, № 6, с. 465—478.
4. Милютин А. А. Задачи на экстремум при наличии ограничений. Диссер-
тация на соискание ученой степени д-ра физ.-мат. наук. № 66—ТПЫ (ГБиЛ).
Институт химической физики АН СССР, 1966, с. 1—63.
5. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе Р. В. и др. Матема-
тическая теория оптимального управления. М., Физматгиз, 1961, 391 с.
290
6. Федосов Е. А., Батков А. М., Левитин В., Ф. и др. Общие вопросы те-
ории наведения. IV Конгресс ИФАК. Краткое содержание докладов. Варша-
ва, 1969, 312 с.
7. Федунов Б. Е. Синтез управления в задаче с фазовыми ограничения-
ми.— «Прикладная математика и механика», 1973, т. 37, вып. 1, с. 23—31.
8. Федунов Б. Е. Условия оптимальности в некоторых задачах управле-
ния со случайными воздействиями. — ЖВМ и МФ, 1971, т. 11, № 4, с. 894—
909.
9. Федунов Б. Е. Использование условий оптимальности в некоторых за-
дачах управления с неосредненными фазовыми ограничениями при случайном
воздействии. Доклады II Всесоюзного совещания по статистическим методам
теории управления (Ташкент, 1970). Дополнительный сборник. М., АН СССР,
АН Уз. ССР. Институт проблем управления (автоматики и телемеханики),
1972, с. 114—130.
К г л а в е 4 '
1 Березин* И. С., Жидков Н. П. Методы вычислений, т. 1, М., Физматгиз,
1959, 464 с.
2. Бусленко Н. П., Голенко Д. И., Соболь И. М. и др. Метод статисти-
ческих испытаний (метод Монте-Карло). М., Физматгиз, 1962, 331 с.
3. Гельфанд И. М., Цетлин М. Л. Принцип нелокального поиска в систе-
мах автоматической оптимизации. АН СССР, 1961, т. 137, № 2, с. 295—299.
4. Горский А. А. Модификация метода штрафных функций для решения
задач выпуклого программирования — «Известия АН СССР. Техническая ки-
бернетика», 1971, №'6, с. 21—29.
5. Горский А. А. О машинной оптимизации нелинейных динамических сис-
тем. — «Автоматика и телемеханика», 1970, № 8, с. 24—31.
6. Демух В. И. Приближенные методы анализа точности нелинейных сис-
тем.— «Автоматика и телемеханика», 1965, № 6, с. 1021—1025.
7. Казаков И. Е., Доступов Б. Г. Статистическая динамика нелинейных
автоматических систем. М., Физматгиз, 1962, 332 с.
8. Левитин Е. С., Поляк Б. Т. Методы минимизации при наличии ограни-
чений. —ЖВМ и МФ, 1966, т. 6, № 5, с. 787—823.
9. Лэнинг Дж. X, Бэттин Р. Г. Случайные процессы в задачах автомати-
ческого управления. М., ИЛ, 1958, 387 с.
10. Налимов В. В., Чернова Н. А. Статистические методы планиоования
экстремальных экспериментов. М., «Наука», 1965, 340 с.
11. Первозванский А. А. Случайные процессы в нелинейных автоматичес-
ких системах. М., Физматгиз, 1962, 351 с.
12. Полляк Ю. Г. Вероятностное моделирование на электронных вычисли-
тельных машинах. М., «Советское радио», 1971, 400 с.
13. Поляк Б. Т. Методы минимизации функций многих переменных —
«Экономика и математические методы», 1967, т. 3, вып. 6, с. 881—902.
14. Пугачев В. С. Теория случайных функций и ее применение к задачам
автоматического управления. М., Физматгиз, 1960, 600 с.
15. Пугачев В. С. Применение теории марковских процессов к анализу
точности нелинейных систем. — «Известия АН СССР. Энергетика и автома-
тика», 1961, № 3, с. 47—57.
16. Растригин Л. А. Статистические методы поиска. М., «Наука», 1J968,
376 с.
17. Солодов А. В., Петров Ф. С. Линейные системы с переменными пара-
метрами. М., «Наука», 1971, 620 с.
18. Фролов А. С., Ченцов Н. Н. О вычислении методом Монте-Карло интег-
ралов, зависящих от параметров.— ЖВМ и МФ, 1962, т. 2, № 4, с. 714—717.
19. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы
г оследовательной безусловной оптимизации. М., «Мир», 1972, 240 с.
20. Чернецкий В. И. Анализ точности нелинейных систем управления. М.»
Машиностроение, 1963, 248 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Акселерометр маятникового типа 85
— с поступательным движением чув
ствительного элемента 85
Аппроксимация параметрическая 136
— средняя квадратичная 122, 129
Воздействия случайные 172
Время упрежденное 18
Головка самонаведения гиростабили-
зированная 27
Датчики линейных ускорений 84
Звено кинематических связей 32
— формирования измеряемой вели-
чины 34
Класс управления 173
Контур автономный 36
— стабилизации ракеты 10
Координатор цели 28
Критерий качества обобщенный 150
Коэффициент усиления частотный
эквивалентный 129
Маневр ракеты 20
— цели 20
Метод Дубовицкого—Милютина 158
— интерполяционный 142
— Ньютона 153
— семиинвариантов 148
— статической минеаризации 148
— трех точек 20
Многочлен Лагранжа интерполяцион-
ный 234, 243
Многочлены многомерные ортогональ-
ные 120
— Эрмита 120
Момент захвата цели 56
Наведение (процесс) 10, 11
Напор скоростной (максимальный и
минимальный) 26
Направление опорное 21
292
Область абсолютного минимума функ-
ции 209
— работоспособности системы 150
Обтекатель антенны 86
Параметры (номинальные значения)
150
Платформа гироскопическая 27
Поле допуска 140, 149
Полет в упрежденную точку встре-
чи 11
Преобразование гистерезисного типа
133
Программирование нелинейное 271
Пролет 10
Разброс параметров технологический
139, 150
Разложение плотности распределения
нормальной двумерной 107
---------четырехмерной 108
Разложения канонические 144
Ракета с аэродинамическим управле-
нием 26
Рассогласование линейное 20
Рули ракеты 28
Сервомеханизм 88
Сила лобового сопротивления 26
Синтез оптимального управления 166
Система бортовая 27
— наведения 9
— координат антенная 28
---- лучевая 28
---- связанная 28
стохастическая 90
Скорость линии дальности угловая 15
Соотношение кинематическое 31
Станция радиолокационная борто-
вая 20
Траектория, баллистическая траекто-
рия 27
— стартовый участок 18
Угол пёлинга 15
Управление автономное 18
Уравнение Фоккера—Планка—Колмо-
горова 95
— Эйлера'160
Уравнения кинематических связей 31
Ускорение «ложное» 35
— продольное 28
Устройства вычислительные и коррек-
тирующие 10
— информационные 10
Флюктуации центра отражения 45
Функция передаточная эквивалент-
ная 129
Функция стоимости 151
Формула квадратурная Гаусса 236,
244
----Симпсона 236
---- трапеций 235
Функционал линейный (общий вид)
160
Этап вывода ракеты 18
Этап самонаведения носителя 18
содержание
Стр.
Предисловие......................................................... 3
Введение ........................................................... 5
Глава 1. Методика проектирования систем наведения на основе те-
ории линейных систем управления .................................... 9
1.1. Задача, процесс и система наведения........................ 9
1.2. Пролет — текущая мера точности наведения.................. 10
1.3. Линейное рассогласование.................................. 15
1.4. Угловая скорость линии дальности.......................... 21
1.5. Управление вектором ускорения ракеты.................. . 26
1.6. Линеаризованные зависимости, связывающие полет, линейное
рассогласование и угловую скорость............................. 29
1.7. Структурные схемы звена кинематических связей .... 31
1.8. Структурная схема контура наведения....................... 34
1.9. Структурная схема контура наведения по угловой скорости
линии дальности.................................".............. 36
1.10. Структурная схема контура наведения по линейному рассо-
гласованию .................................................... 37
1.11. Простейшие системы наведения,по угловой скорости и линей-
ному рассогласованию........................................... 38
1.12. Точность системы наведения и коэффициенты пролета ... 42
1.13. Параметрические передаточные функции систем наведения . 50
1.14. Точность в заданный момент времени. Эквивалентные по точ-
ности системы.................................................. 56
1.15. Точность контура наведения при бесконечном времени управ-
ления. Понятие времени памяти нестационарной системы . . 58
1.16. Свойства коэффициентов полиномов параметрических переда-
точных функций замкнутого контура наведения ................... 60
1.17. Качественное сравнение весовых, передаточных функций замк-
нутой системы наведения и коэффициентов пролетов ... 66
1.18. Выбор передаточной функции замкнутого контура наведения 69
1.19. Общая характеристика задачи оптимизации системы наведе-
ния по точности................................................ 70
1.20. Применение задачи Винера к расчету оптимальной системы
наведения..................................................... 72
Глава 2. Методы исследования процессов, позволяющие учитывать
случайные разбросы параметров................................. 83
2.1. Воздействия случайных вибраций на датчики линейных уско-
рений ......................................................... 84
2.2. Прохождение сигнала через обтекатель антенны головки са-
монаведения . ,................................................ 86
2.3. Модуляция параметров сервомеханизмов рулей случайной на-
грузкой ..................................... <................ 88
294
Стр.
2.4. Анализ стохастических систем............................... 90
2.5. Анализ стохастической системы первого порядка............. 105
2.6. Анализ нелинейных систем со стохастической линейной частью 111
2.7. Прохождение сигналов через нелинейные элементы со случай-
ными параметрами............................................... 118
2.8. Неоднозначные преобразования гистерезисного типа .... 133
2.9. Параметрическая аппроксимация стохастических нелинейных
преобразований ................................................ 136
2.10. Анализ систем управления с учетом технологических разбро-
сов параметров............................................... 139
2.11. Методы оптимального выбора настроек и допусков на пара-
метры систем................................................... 149
Глава 3. Математическая теория оптимального управления в зада-
чах проектирования систем наведения . . . .»....................... 157
3.1. Метод получения условий оптимальности управления .... 158
3.2. Задача типа «рулевого тракта»............................. 162
3.3. Условия оптимальности управления в задачах с ограничения-
ми при наличии случайных воздействий........................... 172
3.4. Преобразование условий оптимальности в задачах управления
при наличии случайных воздействий............................. 184
3.5. Примеры определения структур законов управления на осно-
вании условий оптимальности.................................... 193
Глава 4. Применение методов статистического моделирования к ана-
лизу и оптимизации систем управления........................... . 227
4.1. Постановка задачи статистического моделирования .... 230
4.2. Формулировка задачи численного интегрирования..............232
4.3. Интерполирование и интегрирование в одномерном случае . . 234
.4.4. Многомерные формулы численного интегрирования.............241
4.5. Основные принципы подсчета интегралов .методом Монте-Карло 246
4.6. Способы повышения точности интегрирования методом Монте-
Карло ......................................................... 250
4.7. Определение эффективности систем, подверженных воздейст-
вию случайных процессов........................'............... 252
4.8. Использование комбинированных формул численного интегри-
рования для анализа динамических систем........................ 254
4.9. Применение метода выделения главной части к анализу точ-
ности сложных систем........................................... 261
4.10. Постановка задачи оптимального проектирования .... 270
4.11. Обзор численных методов оптимизации...................... 273
4.12. Оценка точности приближенного решения задачи оптимиза-
ции при использовании статистических оценок оптимизируе-
мой функции.................................................. 282
Список литературы.................................................. 290
Предметный указатель............................................... 292
Батков Александр Михайлович, Горский Александр Антонович,
Левитин Вилен Финеесович, Себряков Герман Георгиевич,
Федосов Евгений Александрович, Федунов Борис Евгеньевич
ПРОЕКТИРОВАНИЕ СИСТЕМ НАВЕДЕНИЯ
Редактор издательства Л. Ф. Ермилова
Техн, редактор Т. С. Старых
Художник А. Я. Михайлов
Корректор А. И. Карамышкина
Сдано в набор 30/IV-1975 г. Подписано к печати 31/VI 1-1975^г. Т-13416
Формат 60X 90716 Бумага № 2 Печ. л. 18,5 Уч.-изд. л. 16,7 Тираж 3000 экз.
Изд. зак. 3476 , Цена I р. 08 к.
Издательство «Машиностроение», 107885, Москва, Б-78, 1-й Басманный пер., 3.
Московская типография №‘8 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли
Хохловский пер., 7. Тип. зак. 3200