БИБЛИОТЕЧКА МАТЕМАТИЧЕСКОГО КРУЖКА
ВЫПУСК 17
ЗАРУБЕЖНЫЕ
МАТЕМАТИЧЕСКИЕ
ОЛИМПИАДЫ
Под редакцией И. Н, СЕРГЕЕВА
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 8 7

ББК22.1
3-35
УДК 51 (023)
КОЛЛЕКТИВ АВТОРОВ!
С. В. КОНЯГИН, Г. А. ТОНОЯН, И. Ф. ШАРЫГИН,
И. А. КОПЫЛОВ, М. Б. СЕВРЮК, М. Л. СИТНИКОВ,
О. А. БАЙБОРОДИН, В. П. БУРИЧЕНКО, Г. В. ГОЛОВИН,
Д. О. ОРЛОВ, Л. Б. ПАРНОВСКИЙ, Т. А. СОКОВА,
И. В. СТЕЦЕНКО, В. В. ТИТЕНКО, С. А. ФИЛИППОВ
Зарубежные математические олимпиады./Конягин С. В., То-
ноя н Г. А., Шарыгин И. Ф. и др.; Под ред. И. Н. Сергеева. —М.:
Наука. Гл. ред. физ.-мат. лит., 1987. — (Б-ка мат. кружка). — 416 с.
Книгу можно рассматривать как продолжение серии «Задачи и
олимпиады», начатой издательством «Мир» в 1975 г.
В сборнике представлены наиболее интересные задачи националь¬
ных олимпиад 19 стран и ряда международных соревнований. Оии
разбиты на 7 глав по тематическому признаку. Все задачи (а их бо¬
лее 500) снабжены решениями.
Для учащихся старших классов, учителей, проводящих различ¬
ные математические конкурсы, а также для всех любителей матема¬
тики.
Рецензенты:
кандидат педагогических наук А. М. Абрамов,
доктор физико-математических наук Ю. В. Нестеренко
_ 1702010000-151 с_
3' 053 (02)-87	 4°'87
<g) Издательство ♦Наука».
Главная редакция
физико-математической
литературы, 1987

СОДЕРЖАНИЕ
Предисловие	   5
Структура книги 	 ,	  .......	9
Задачи Решения
Глава I. Арифметика	11	80
§ 1. Делимость. Простые и составные числа .... 11	80
§ 2. Уравнения в целых и рациональных числах . .14	92
§ 3. Факториалы и биномиальные коэффициенты . .17	107
§ 4. Числовые множества 	19	116
§ 5. Различные свойства чисел	22	132
Глава 2. Уравнения и неравенства	24	145
§ 6. Уравнения и системы	24	145
§ 7. Неравенства 	26	152
§ 8. Задачи с целой частью 	29	162
Глава 3. Планиметрия	31	171
§ 9. Треугольники	31	171
§ 10. Окружности и круги	34	185
§11. Многоугольники	37	203
§ 12. Точки, отрезки и прямые	39	215
§ 13. Геометрические неравенства 	42	227
§ 14. Геометрические задачи на экстремум	45	244
Глава 4. Стереометрия	47	255
§ 15. Тетраэдры	47	255
§ 16. Многогранники, сферы и другие множества . .49	266
Глава 5. Анализ	53	284
§ 17. Последовательности 	53	284
§ 18. Экстремумы	56	294
§ 19. Различные свойства функций	57	300
§ 20. Функциональные уравнения	59	304
Глава 6. Многочлены	62	316
§ 21. Корни многочленов	62	316
§ 22. Делимость и равенство многочленов	65	325
§ 23. Различные свойства многочленов 	68	334
Глава 7. Комбинаторика 	70	342
§ 24. Множества и подмножества	70	342
§ 25. Задачи с использованием графов 	72	348
3

§ 26. Различные комбинаторные задачи	 74	352
§ 27. Элементы теории вероятностей 	 77	362
Приложения	367
Приложение А. Комментарии к условиям задач	367
Приложение Б. Математические соревнования
в разных странах	369
Приложение В. Основные библиографические
источники 	386
Приложение Г. Вспомогательные сведения	.	.	388
Приложение Д. Список рекомендуемой литера¬
туры 	412
Приложение Е. Список обозначений	413

ПРЕДИСЛОВИЕ
В целях популяризации математики среди учащихся
средних учебных заведений во многих странах регулярно
проводятся математические олимпиады школьников. Олим¬
пиады в целом доказали свою эффективность в пропаганде
математических знаний среди молодежи. Кроме того, про¬
ведение международных олимпиад является одной из форм
сотрудничества ученых разных стран. Поэтому олимпиад-
ное движение в настоящее время получило очень большое
развитие во всем мире.
С каждым годом растет число стран, которые проводят
национальные олимпиады, а с 1959 г. проводятся и между¬
народные математические олимпиады. Количество участ¬
вующих в них стран увеличилось с 5—7 на первых олим¬
пиадах до 30 и более в настоящее время. За последнее
десятилетие получили распространение различные регио¬
нальные международные математические соревнования
школьников. Математические олимпиады проводятся и раз¬
личными учебными заведениями, а также некоторыми
математическими журналами.
В нашей стране сложились богатые традиции как в про¬
ведении школьных олимпиад разного уровня, так и в обес¬
печении их соответствующей литературой. Представители
СССР, как правило, успешно выступают на международ¬
ных математических олимпиадах.
В связи с быстрым накоплением опыта проведения
национальных олимпиад и постоянным ростом числа стран,
участвующих в международных олимпиадах, все более
актуальной становится задача широкого ознакомления
интересующихся математикой советских школьников с луч¬
шими достижениями олимпиадного движения за рубежом.
В 1976 г. был выпущен сборник венгерских математиче¬
ских олимпиад [I]1), в 1978 г.—• польских математических
олимпиад [2]. Задачи некоторых национальных олимпиад
J) Здесь и далее указаны ссылки на литературу из приложения Д.
5

(10 стран) и небольшая часть материалов жюри между- i
народных математических олимпиад опубликованы в 1976 г. i
в сборнике международных математических олимпиад [3]. i
Зарубежным математическим соревнованиям школьни- i
ков посвящена и настоящая книга, в которую вошли (
наиболее интересные (по мнению авторов) или наиболее i
типичные задачи различных олимпиад. Книга отличается i
большим числом представленных задач. В ней использо- •
ваны задачи национальных олимпиад 19 стран, а также <
материалы жюри международных математических олим- i
пиад 1976—1977, 1979, 1981—1983 гг., задачи между- i
народных соревнований в Люксембурге и Финляндии,
олимпиады стран Балканского полуострова (так называе- i
мой Балканиады) 1984 г., традиционных олимпиад «Авст- (
рия—Польша». Очень широко представлены материалы ]
олимпиад Болгарии, Великобритании, Румынии, США, i
ЧССР и Югославии. Включены задачи венгерских и поль- i
ских олимпиад последних лет, не вошедшие в сборники
[1] и [2]. Большинство представленных в книге задач (
относится к последним турам соответствующих националь-1
ных олимпиад. Некоторые из задач сначала предлагались (
на олимпиадах нашей страны и только после этого были <
использованы в зарубежных математических соревнованиях, г
Сборник адресован прежде всего интересующимся |
математикой старшеклассникам, и его основной целью J
является повышение математической культуры школьни¬
ков. Большинство задач в книге не слишком сложны, hoi
в совокупности они представляют почти все основные идеи,;
встречавшиеся в олимпиадной практике. Поэтому авторы (
надеются, что школьник, не имеющий достаточного опыта i
участия в олимпиадах, ознакомится со сборником с боль-г
шой пользой для себя. Более подготовленный читатель С
испытает значительное удовольствие при решении более!
сложных задач (нескольких последних задач каждого с
параграфа, отмеченных звездочками), а также получит!
довольно полное представление об олимпиадном движении)
за рубежом. Особый интерес могут вызвать задачи из тех i
разделов математики, которые недостаточно полно пред-т
ставлены или вовсе отсутствуют в программе общеобразо-i
вательных школ нашей страны.	<
Материал книги может быть использован для занятий}
математических кружков или специализированных физико-г
математических школ.	I
Все задачи снабжены решениями; некоторые из них.
представляют собой перевод на русский язык решений,
6

опубликованных организаторами соответствующих олим¬
пиад, а другие (особенно решения геометрических задач)
написаны авторами заново. Однако, книга рассчитана
прежде всего на активного читателя. Лучший способ глу¬
боко разобраться в той или иной математической идее —
это решить задачу, в которой используется эта идея, или
по крайней мере прочесть ее решение только после доста¬
точно настойчивых попыток справиться с задачей само¬
стоятельно. При этом читателю придется восстанавливать
недостающие детали в тех решениях, которые написаны
недостаточно подробно.
Внутри каждого параграфа авторы старались по мере
возможности располагать задачи так, чтобы близкие по
своей тематике задачи находились рядом. Поэтому при
решении какой-либо задачи желательно обращать внима¬
ние и на ее окружение, где часто в несколько иной ситуа¬
ции представлена та же идея.
При отборе задач авторы стремились в значительно
большей степени помочь читателю овладеть часто встре¬
чающимися приемами решения нестандартных задач и выра¬
ботать у него необходимую дисциплину мышления, нежели
сообщить новые математические факты. Тем не менее в ряде
задач используются сведения, несколько выходящие за
рамки школьной программы. Эти сведения собраны в при¬
ложении Г.
Для работы над настоящим сборником весной 1984 г.
на механико-математическом факультете Московского госу¬
дарственного университета им. М. В. Ломоносова был
создан специальный студенческий научный отряд «Олим¬
пия» в составе 13 человек. Командиром этого отряда был
ассистент механико-математического факультета МГУ
,С. В. Конягин, комиссаром—аспирант И. А. Копылов.
:В отряд входили аспиранты механико-математического
I факультета М. Б. Севрюк и М. Л. Ситников, студенты
О. А. Байбородин, В. П. Буриченко, Г. В. Головин,
[Д. О. Орлов, Л. Б. Парновский, Т. А. Сокова, И. В. Сте-
;ценко и В. В. Титенко. Летом 1984 г. в отряде работал
■также десятиклассник из школы № 14 г. Белорецка (Баш¬
кирская АССР) С. А. Филиппов. Кроме бойцов отряда
«Олимпия», авторами сборника являются заведущий кафед-
!рой Ереванского государственного университета Г. А. То-
■ноян и старший научный сотрудник НИИ СиМО1)
АПН СССР И. Ф. Шарыгин.
с
,	*) Содержания и методов обучения.
7

Почетным бойцом отряда «Олимпия» состоял выдаю¬
щийся советский математик академик А. Н. Колмогоров,
уделяющий большое внимание работе со школьниками.
Летом 1984 г. отряд «Олимпия» работал в здании
ФМШ № 18 при МГУ, и авторы искренне признательны
И. Т. Тропину, который в то время являлся директором
этого интерната. Авторы выражают сердечную благодар¬
ность старшему научному сотруднику механико-математи¬
ческого факультета МГУ, заместителю главного редактора
журнала «Квант» Ю. П. Соловьеву за большое участие
в организации отряда и постоянный интерес к работе над
книгой.
Тексты задач национальных и других зарубежных
олимпиад (на языках соответствующих стран) авторам
предоставили старший научный сотрудник НИИ СиМО
А. М. Абрамов, член редколлегии журнала «Квант»
Н.	Б. Васильев, доцент механико-математического факуль¬
тета МГУ Е. А. Морозова, член редколлегии журнала
«Математика в школе» И. С. Петраков, младший научный
сотрудник ВНИИ геофизики В. В. Прасолов, югославский
математик Д. Реповш, доцент МФТИ, член редколлегии
журнала «Квант» А. П. Савин, старший научный сотрудник
Института математики АН НРБ И. Табов, доцент МГПИ
А. А. Фомин. Аспирант механико-математического факуль¬
тета МГУ И. В. Мустяца оказал помощь «Олимпии» в
переводе задач с румынского языка, а студенты Н. Н. Оси¬
пов и Т. Фиммель (ГДР)—с французского и немецкого.
Ценные замечания, способствовавшие улучшению ру¬
кописи, были внесены редактором книги А. Ф. Лапко
и рецензентами А. М. Абрамовым и доцентом механико¬
математического факультета МГУ Ю. В. Нестеренко. Всем
названным товарищам авторы выражают большую при¬
знательность.
Авторы глубоко благодарны титульному редактору
сборника ассистенту механико-математического факуль¬
тета МГУ И. Н. Сергееву за огромную работу по совер¬
шенствованию рукописи.

структура книги
Сборник состоит из трех частей.
В первой части приведены условия задач. Она состоит
из семи глав, а каждая глава — из нескольких парагра¬
фов. Разбиение на главы и параграфы проводилось по
тематическому принципу. Оно достаточно условно, по¬
скольку некоторые задачи с равным успехом могли быть
помещены в несколько параграфов книги.
В начале каждого параграфа даются ссылки на те из
сведений (помещенных в приложении Г), которые исполь¬
зованы в условиях и решениях задач данного параграфа.
После номера каждой задачи указано, в каких извест¬
ных авторам зарубежных олимпиадах она предлагалась.
Номера более трудных задач отмечены звездочками. Боль¬
шинство задач книги предлагались на национальных
олимпиадах, ссылки на которые состоят из названия
страны, проводившей олимпиаду, и года ее проведения.
«Пекин» означает ссылку на Пекинскую олимпиаду, а «Нью-
Йорк»—на издававшийся в Нью-Йорке журнал для уча¬
щихся двухлетних колледжей. Задачи международных
соревнований обозначаются следующим образом: ((Авст¬
рия—ПНР»—совместные соревнования школьников Авст¬
рии и Польши, «Балканиада»—соревнования учащихся
Балканских стран, «ММС»—международные математи¬
ческие соревнования 1980 г. Наконец, ссылка на мате¬
риалы жюри международных математических олимпиад
начинается словом «Жюри», далее указана страна, пред¬
ложившая задачу, и год ее обсуждения. К сожалению,
авторам неизвестно, какие страны предлагали задачи на
международную олимпиаду 1981 г.
Во второй части приводятся решения задач первой
части книги. Третья часть содержит различные прило¬
жения.
Условия некоторых помещенных в книге задач отли¬
чаются от оригинальных. Эти изменения, за которые
9

авторы несут полную ответственность, отражены в при¬
ложении А.
В приложении Б даны краткие сведения о зарубежных
математических соревнованиях школьников, а также усло¬
вия задач тех олимпиад 1985—1986 г., которые оказались
в распоряжении авторов. Решения этих задач не при¬
водятся, читателям предлагается решить их самостоятельно.
В приложении В указаны основные книги и журналы,
использованные авторами при составлении настоящего
сборника. В приложении Г перечислены основные понятия
и факты, необходимые для правильного восприятия мате¬
риала первой и второй частей.
Для более серьезного изучения соответствующих раз¬
делов математики читателю предложена литература, при¬
веденная в приложении Д. Наконец, приложение Е содер¬
жит список используемых в книге обозначений.

ЗАДАЧ И
Глава 1
АРИФМЕТИКА
§ 1. Делимость. Простые и составные числа
(см. Приложение Г: определения 11—16, 19;
теоремы 1, 4, 9—12, 14, 18, 19, 21, 23, 25)
1.1. (Англия, 68). Пусть alt а2, ..., а7—целые числа,
а Ьи Ь2, ..., Ь7—те же самые числа, взятые в другом
порядке. Доказать, что число
(«1—М (а2—Ь2) ... (а7—Ь7)
является четным.
1.2. (Нью-Йорк, 76). Пусть а, щ, аи ..., ап—произ¬
вольные целые числа. Верно ли, что целое число
П
2 (а2 + l)3ft«*
*=о
делится на а2-\-а-\- 1 (или на а2—а-\- 1) тогда и только
тогда, когда число
2 (-!)*«*
к= 0
делится на а2 + а-\- 1 (или соответственно на а2—а-\- 1)?
1.3. (ЧССР, 52; Англия, 65). В бесконечной «треуголь¬
ной» таблице
«1,0
«2, ■
-1 «2,0
«2,1
«3,
-1 «з,о
«3,1
«3,2
, «i,
-1 «4,
0 «4,1
«4,2 «4,3
ali0 = l, а каждое число ап< k, стоящее в л-й строке
(лС1М, л> 1) на k-u месте (k£Z, \k\<,ri), равно сумме
11

an-t, ft-1 + ап-1, fe + G„-1, ft+i Трех чисел предыдущей строки
(если какое-либо из этих чисел отсутствует в таблице, то
в сумме оно заменяется нулем). Доказать, что в каждой
строке, начиная с. третьей, содержится хотя бы одно чет¬
ное число.
1.4. (ЧССР, 71). Доказать, что для любого простого
числа р > 2 числитель т дроби
-7Г=1 +Т + Т+ +	(m.nCN)
делится на р.
1.5. (Нью-Йорк, 75). Доказать, что для каждого целого
значения п > 1 число л"—п2 + п — 1 делится на (п — I)2.
1.6. (НРБ, 65). Доказать, что только одна тройка
натуральных чисел, больших единицы, обладает тем свой¬
ством, что произведение любых двух из этих чисел, увели¬
ченное на 1, делится на третье.
1.7. (Англия, 76). Доказать, что при любом значении
п число 19 - 8" 4-17 является составным.
1.8. (Канада, 83). Доказать, что для любого простого
числа р существует бесконечно много чисел вида 2"—п
(где п £ N), делящихся на р.
1.9. (ЧССР, 73). Доказать, что существует бесконечно
много значений N, для которых любое число вида
m4 + п (т € N) является составным.
1.10. (ЧССР, 79). Найти все натуральные числа п > 2,
не превосходящие числа 10 ООО ООО и обладающие следую¬
щим свойством: любое число т, взаимно простое с п
и удовлетворяющее неравенствам 1 < т < п, является
простым.
1.11. (ФРГ, 77). Пусть а> 1—натуральное число.
Найти все числа, являющиеся делителями хотя бы одного
из чисел
П
ап = 2	п С N.
к = о
1.12. (Нью-Йорк, 74). Для заданной пары натураль¬
ных чисел т < п определить, любое ли множество из п
последовательных целых чисел содержит два различных
числа, произведение которых делится на тп.
1.13. (Нью-Йорк, 76). Пусть f(ri)£ N—наименьшее
И п)
число, для которого сумма 2 ^ делится на п. Доказать,
k= 1
что равенство f(n) = 2n—1 справедливо для чисел вида
n = 2'”(m£Z+) и только для них.
12

1.14. (Жюри, ФРГ, 79; НРБ, 81). Доказать, что если
число 1 + 2" -н 4" при некотором значении п £ N является
простым, то п — 3ft, где &£Z+.
1.15. (СРР, 78). Пусть числа т, л £ N таковы, что для
любого значения k £ N наибольшие общие делители пары
чисел \\k—1, т и пары чисел \\k—1, л совпадают.
Доказать, что для некоторого значения I £ Z справедливо
равенство т=\\1п.
1.16. (Нью-Йорк, 75). Пусть наибольший общий дели¬
тель чисел а, Ь, с, d£Z равен 1. Верно ли, что любой
простой делитель числа ad—be является делителем чисел
а п с тогда и только тогда, когда при каждом значении
п 6: Z числа ап-\-Ь и сп -f d взаимно просты?
1.17*. (США, 82). Доказать, что существует такое число
&£N, что при любом значении п (Е N число k-2n-\-\ яв¬
ляется составным.
1.18*. (СРР, 78). Доказать, что для любого значения
с £ N, большего 2, существует бесконечно много чисел
n£N таких, что число ап—1 делится на п. Верно ли
аналогичное утверждение для а = 2?
1.19.	(Жюри, Бельгия, 83). Доказать, что существует
бесконечно много чисел ngN, удовлетворяющих для всех
значений k—\, 2, ..., п — 1 неравенствам
р(п) - о (Щ
п	к	3
где через о (п) обозначена сумма всех делителей числа л.
1.20*. (ВНР, 82). Для заданного натурального числа
&>1 через Q(n), п С N. обозначено наименьшее общее
кратное чисел п, п -f 1, ..., n + k. Доказать, что сущест¬
вует бесконечно много значений л £ N, удовлетворяющих
неравенству Q(n) > Q(n-f 1).
1.21*. (Австрия, 73). Доказать, что для любого зна¬
чения п £ N справедливы неравенства
0<У
и ^ k 3^3’
Л=1
где через g(k) обозначен наибольший нечетный делитель
числа k.
1.22*. (Жюри, СФРЮ, 79). Пусть через Л (л) обозначен
наибольший простой делитель числа л С N (л ^ 2). Является
ли бесконечным множество значений л, удовлетворяющих
условию
Л (л) < h (л -f 1) < Л (л + 2)?
13

1.23*. (Жюри, СФРЮ, 79). Пусть через w(n) обозна¬
чено количество простых делителей натурального числа
п > 1. Доказать, что для бесконечного множества зна¬
чений п выполняются неравенства
w (л) < w (п -f 1) < w (л -f 2).
§ 2. Уравнения в целых и рациональных числах
(см. Приложение Г: определения 11, 12, 14—16;
теоремы 2, 4, 5, 8, 10, 12, 16, 18, 21—23, 25, 60, 61)
2.1. (Нью-Йорк, 77). Решить уравнение 2*4 1=у2
в натуральных числах.
2.2. (Англия, 72). Доказать, что для любых значе¬
ний а, Ь, с, d£ Z, афЬ, уравнение
(х 4 ау 4 с) (х + by + d) = 2
в целых числах имеет не более четырех решений. Опре¬
делить, при каких значениях о, Ь, с, d имеется ровно
четыре различных решения.
2.3. (ГДР, 73). Решить уравнение
х(х+ l)(x + 7)(x+8 ) = у2
в целых числах.
2.4. (СРР, 81). Решить уравнение
Xе 4 За3 + 1 —у1
в целых числах.
2.5. (СФРЮ, 74). Решить уравнение
х* + ху + у* = х*у*
в целых числах.
2.6. (ГДР, 74). Решить уравнение
(х + 2)4 —х* = уэ
в целых числах.
2.7. (США, 79). Решить уравнение
4 х\ 4 ■ • ■ 4 а^4 = 1599
в целых числах.
2.8. (ГДР, 70; СРР, 80). Доказать, что для любых
нечетных значений a, b, c£Z уравнение оа'24йа4с=>0
в рациональных числах не имеет решений.
2.9. (Англия, 70). Решить уравнение
V2V^—i = \Ti^%—Vy\rb
в рациональных числах.
14

2.10. (Бразилия, 83). Доказать, что уравнение
1+1 +±=J_
х ~ у ~ z 1983
в натуральных числах имеет лишь конечное множество
решений.
2.11. (СФРЮ, 81). Доказать, что для любых значений
a,b£ Z, удовлетворяющих неравенствам 5а^7Ь^0,
система
fx-h 2у + 3z+ 7ы = а,
\ у + 2z + 5и — Ь
в целых неотрицательных числах имеет решение.
2.12. (ГДР, 77). Сколько существует пар значений
р,	не превосходящих 100, для которых уравнение
х6 + рх + q = 0
в рациональных числах имеет решения?
2.13. (ЧССР, 76). Решить уравнение х2 + у2—3z2 в целых
числах.
2.14. (ВНР, 83). Доказать, что уравнение
х3 + 3 у3 + 9z3—9 xyz — 0
в рациональных числах имеет единственное решение х =«
= y = z = 0.
2.15. (США, 76). Решить уравнение
X2 -1- у2 + Z2 = х2у2
в целых числах.
2.16. (Англия, 70). Для каждого значения ngN обо¬
значим через an£Z+ количество решений уравнения
п2 + х2 = у2
в натуральных числах, больших п.
а) Доказать, что для любого числа М неравенство
а„ > М справедливо хотя бы при одном значении п € N.
б) Верно ли, что Нщ ап = оо?
П —*■ <Х
2.17. (ВНР, 77). Доказать, что для любого простого
числа р > 5 уравнение
х* + 4 х — р
в целых числах не имеет решений.

2.18. (ГДР, 80). Доказать, что уравнение
(2х)2ж— 1 = yz+1
в натуральных числах не имеет решений.
2.19. (ГДР, 81). Доказать, что для любого значения
п (Е N уравнение
х\ + ... + xft = y*
в натуральных числах имеет решение.
2.20. (Жюри, СРР, 77). Пусть заданы числа
а± ап, o„+i€N. причем для каждого значения
"1=1, ..., п числа а, и о„+1 взаимно просты. Доказать,
что уравнение
, Л ,	,	von   ап +1
*1 Т *2 Т ■ . . Т лп   лп+1
в натуральных числах имеет бесконечно много решений.
2.21. (Жюри, Франция, 79). Доказать, что для любых
взаимно простых чисел а, b £ N и любого натурального
значения с^(о—l)(b—1) уравнение с = ах + Ьу в целых
неотрицательных числах имеет решение.
2.22. (ВНР, 78). Доказать, что для любых значений
я. 6€Q уравнение ах2-f by* = 1 в рациональных числах
либо не имеет решений, либо имеет бесконечно много
решений.
2.23. (Жюри, СРР, 79). Доказать, что для любых
взаимно простых чисел a, b£ Z уравнение ах*-\-Ьу* = z3
в целых числах имеет бесконечно много решений, удовле¬
творяющих условию (х, у) = 1.
2.24. (Англия, 80). Доказать, что ни при каком зна¬
чении пС N. большем 1, уравнение х"4- у" = гп в нату¬
ральных числах не имеет решений, удовлетворяющих усло¬
виям x^Ln, у^п.
2.25*. (Австрия, 72). Доказать, что при любом зна¬
чении ngN, большем 2, уравнение
хп + (х-f 1)" = (х + 2)"
в натуральных числах не имеет решений.
2.26*. (Нью-Йорк, 81). Решить уравнение
Хх+У = (х + y)v
в положительных рациональных числах.
2.27*. (ВНР, 80; НРБ, 81). Доказать, что если число
/г С N нечетное, то уравнение

в натуральных числах имеет решение тогда и только
тогда, когда
n = m(4k — 1) при т,
2.28*. (Жюри, Канада, 82). Доказать, что множество
всех значений n£N, для которых уравнение
в натуральных числах не имеет решений, не может быть
представлено в виде объединения конечного множества
арифметических прогрессий (как конечных, так и беско¬
нечных).
2.29*. (НРБ, 79). Доказать, что уравнение x2-f 5=#3
в целых числах не имеет решений.
§ 3. Факториалы и биномиальные коэффициенты
(см. Приложение Г: определения II, 12, 14—18;
теоремы 2, 4, 8, 12, 13, 16—17, 20, 21, 96)
3.1. (Голландия, 82). Что больше;
(17091982!)а или 17091982170в,ввг?
3.2. (СФРЮ, 74). Найти все числа n£N, для которых
при каком-либо значении
&€ {1; 2; ...; /г—1}
имеет место равенство
в натуральных числах.
3.4.	(Жюри, США, 82). Доказать, что для любого зна¬
чения п £ N справедливо равенство
3.5. (Жюри, Австралия, 82). Для заданного значения
т £ N:
П
а) доказать, что число т^\ С^п является натуральным;
17

б) найти наименьшее значение k£N, для которого
k
число	С%т	является натуральным при каждом
натуральном значении п^т.
3.6. (Нью-Йорк, 74). Доказать, что для любых нату¬
ральных значений ti^k наибольший общий делитель
чисел Ск„,Скп+1, ..., Скпл.к равен 1.
3.7. (Англия, 81). Доказать, что для любых значе¬
ний т, п € N число
т
S =* 1 + Y (— 1)* (" + 6+1)! .
1	fcTi	n\(n	+	k)
делится на ml, но при некоторых значениях т, л 6 N число
Sm ri не делится на m\(ti + 1).
3.8. (СФРЮ, 70). Доказать, что если число р простое,
го число С%р—2 делится на р2.
3.9. (СФРЮ, 75). Решить уравнение
11+21 + ... +(х + 1)! =yz+%
в натуральных числах.
3.10. (НРБ, 82; Австралия, 83). Решить уравнение
(y+l)x—l=yl
в натуральных числах.
3.11. (Австрия, 73; СФРЮ, 77; ГДР, 79). Для задан¬
ного значения ngN, большего 1, обозначено
mk = nl + k, k£N.
Доказать, что для любого значения &€{1; ...; п} суще¬
ствует простое число р, на которое делится число тк и
не делится ни одно из остальных чисел
тл, mk_t, mk+i, ..., m„.
3.12*. (НРБ, 68). Доказать, что число нечетно
тогда и только тогда, когда числа п,	удовлетворяют
условию: если в каком-либо разряде двоичной записи
числа k стоит 1, то в том же разряде двоичной записи
числа п также стоит 1.
3.13*. (ММС, Люксембург, 80). Доказать, что для лю¬
бого значения n^N и простого числа р следующие усло¬
вия эквивалентны:
а) ни одно из чисел С* при k = 0, 1, ..., п не делится
на р.
б) n = psm—1, где s€Z+, m£N, т < р.
18

3.14*. (Жюри, СССР, 83). Пусть через hn обозначена
последняя ненулевая цифра десятичной записи числа п\.
Доказать, что бесконечная десятичная дробь
to,hji2ha...
представляет собой иррациональное число.
§ 4. Числовые множества
(см. Приложение Г: определения 1, 2, 11, 12;
теоремы 1,2, 10, 13, 18, 23, 55, 95, 96)
4.1. (СРР, 78). Доказать, что при любом разбиении
множества
Х={1; 2; 3; 4; 5; 6; 7; 8; 9}
на два подмножества хотя бы одно из полученных под¬
множеств содержит 3 таких числа, что сумма двух из
них равна удвоенному третьему.
4.2. (Бельгия, 79). Найти сумму всех 7! чисел, кото¬
рые можно получить всевозможными перестановками цифр
в числе 1234567.
4.3. (Англия, 66). Доказать, что из любых 52 целых
чисел всегда можно выбрать 2 числа, сумма или разность
которых делится на 100.
4.4. (Англия, 70). Доказать, что в любом множестве
из п натуральных чисел можно выделить (непустое) под¬
множество чисел, сумма которых делится на п.
4.5. (ПНР, 79). Натуральные числа аи а2, ..., а„ при
делении на некоторое число m£N дают разные остатки,
причем п > т/2. Доказать, что для каждого числа k 6 Z
существуют такие номера
/ € {1; • • •; п)
(не обязательно различные), что число а( + а/—k делится
на т.
4.6. (СФРЮ, 77). Даны 20 натуральных чисел а2 <
< а2 < ... < а2В, не превосходящих 70. Доказать, что среди
разностей ау—ak (j > k) найдутся хотя бы 4 одинаковых
числа.
4.7. (СФРЮ, 81). Множество чисел 1, 2, ..., 100 раз¬
бито на 7 подмножеств. Доказать, что хотя бы в одном
из этих подмножеств найдутся или 4 числа а, Ь, с, d,
для которых a + b = c + d, или 3 числа е, f, g, для кото¬
рых e + f = 2g.
19

4.8. (США, 83). На числовой оси взят интервал длины
1/п (л С N). Доказать, что в этом интервале содержится
не более (п-1-1)/2 несократимых дробей вида plq, где
p,q£ Z, 1
4.9. (СФРЮ, 77). Для заданного значения n С N опре¬
делить, сколько существует троек натуральных чисел,
сумма которых равна 6л.
4.10. (НРБ, 80). Доказать, что число способов, кото¬
рыми из набора 1, 2, ..., 49 можно выбрать шестерку
различных чисел так, чтобы хотя бы два из них были
последовательными, равно
С6	Г*Ъ
49	'-'44е
4.11. (Австрия—ПНР, 78). Для заданного положи¬
тельного рационального значения с Ф 1 доказать, что мно¬
жество натуральных чисел можно представить в виде
объединения двух непересекающихся подмножеств А н В
так, чтобы отношение любых двух чисел из множества А,
а также отношение любых двух чисел из множества В
не равнялось числу с.
4.12. (Жюри, Испания, 77). Сумма целых чисел а1у
а2 ап равна единице. Доказать, что тогда среди чисел
Ь,- = я,- + 2л1+1 + За1+2 + ... + (л—i + 1) ап + (л—i-f-2) ai-f-
+ (п—i + 3) а2 + ... -|- па{_г (i = 1, 2 л)
нет одинаковых.
4.13. (Жюри, СССР, 82). Найти все значения л(Е1М,
для каждого из которых существует строка из 2л чисел,
обладающая следующим свойством: для любого значения
k=\, ..., л в строке имеются 2 числа, равных k, между
которыми находится ровно k чисел.
4.14. (Австрия, 75). Для непустого множества McQ
выполнены два условия:
1) если	и	Ь£М,	то	л +	и ab£M;
2) если г С Q, то верно ровно одно из трех следую¬
щих утверждений: г£Л4, —г (ЕМ, г = 0.
Доказать, что множество М совпадает с множеством
всех положительных рациональных чисел.
4.15. (Нью-Йорк, 73). Конечное множество BczR на¬
зовем базисом для множества Mcz R, если каждое число
из множества М может быть единственным образом пред¬
ставлено в виде произведения целых степеней чисел из
множества В. Верно ли, что для любого конечного мно¬
жества положительных чисел существует базис?
20

4.16.	(Австрия—ПНР, 80). Доказать, что для любого
значения п £ N имеет место равенство
£
1^1
где суммирование ведется по всем возможным наборам
чисел
li < 12 < • • • < Н' k=l,2 п,
из множества {1; 2; ..	п}.
4.17*. (НРБ, 83). Найти все значения N, для каж¬
дого из которых существует такая перестановка
(at; а,; ...; ап)
чисел 0, 1, ..., п—1, что все числа
аи аха2, а^а2аг, ..., а^. . .ап
дают разные остатки при делении на п.
4.18*. (Жюри, Швеция, 83). Доказать, что если число
N не является целой степенью простого числа, то
существует перестановка
(^1» ^2* * ‘	^п)
чисел 1, 2, ..., п, для которой справедливо равенство
П
2 k cos (2nik/ri) = 0.
fe=i
4.19*. (Жюри, Финляндия, 82). Определить сумму всех
натуральных чисел, в десятичной записи каждого из ко¬
торых цифры образуют возрастающую или убывающую
последовательность.
4.20*. (Жюри, Финляндия, 79). Набор (аг; ...; ап)
натуральных чисел, удовлетворяющих равенству
аг + 2аг + ... + па„ = 1979,
назовем четным, если число п четно, и назовем нечетным,
если число п нечетно. Доказать, что четных наборов су¬
ществует столько же, сколько нечетных.
4.21*. Доказать, что для любых чисел о^, .... nmgN:
а)	(Жюри, ПНР, 79) существует такой набор из п < 2т
чисел, в котором все подмножества имеют разные суммы
чисел, причем среди этих сумм содержатся все числа
йу, • • • , CLm,
21

б) существует такой набор из л<т чисел, в котором
все подмножества имеют разные суммы чисел, причем среди
этих сумм содержатся все числа а, ат.
4.22*. (Жюри, ПНР, 83). Существует ли множество
McN, удовлетворяющее следующим двум условиям:
1) любое число я £ N, большее 1, представимо в виде
пва + 6, где a, b£M;
2) если каждое из чисел а, Ь, с, d£M больше 10, то
равенство а + b — с + d возможно лишь в случае а = с или
c = d?
§ 5. Различные свойства чисел
(см. Приложение Г: определения 11—19;
теоремы 1, 2, 4, 10, 13, 18, 23, 55, 95, 96)
Б.1. (ЧССР, 52). Доказать, что если положительные
числа_а, b,j: £ Q удовлетворяют равенству	а + У b *= с,
то Vа, V b£Q.
5.2. (СРР, 75). Доказать, что существуют положитель¬
ные иррациональные числа а и Ь, для которых число аь
является натуральным.
5.3. (Бразилия, 83). Доказать, что сумма
1 + — + — 4-	+	—
* 2 ‘ 3 +••• + п
не является целым числом ни при каком значении п£ N,
большем 1.
5.4. (США, 78). Доказать, что любое число гс С N,
большее 32, представимо в виде суммы нескольких нату¬
ральных чисел, сумма обратных величин которых равна 1.
Указание. Значения п = 33, 34, 35, ..., 73 требуе¬
мому условию удовлетворяют.
5.5. (Англия, 82). Запись числа л£1М, кратного 17,
в двоичной системе счисления содержит ровно 3 цифры 1.
Доказать, что в этой записи содержится не менее 6 цифр 0,
а если их ровно 7, то число п является четным.
5.6. (СФРЮ, 83). Найти все значения ngN, обладаю¬
щие следующим свойством: если записать рядом числа п3
и л4 (в десятичной системе счисления), то в полученной
записи каждая из 10 цифр 0, 1, ..., 9 встретится ровно
1 раз.
5.7. (СФРЮ, 77). Найти все значения п£ N, обладаю¬
щие следующим свойством: пятая степень суммы цифр
десятичной записи числа п равна п2.
22

5.8. (Англия, 78). Доказать, что если знаменатель
правильной дроби не превосходит 100, то в десятичной
записи этой дроби не могут встретиться три цифры 1, 6,
7, идущие подряд в указанном порядке.
5.9. (Нью-Йорк, 78). Доказать, что любое простое
число вида
22" + 1 (п б N)
не представимо в виде разности пятых степеней двух на¬
туральных чисел.
5.10. (Нью-Йорк, 77). Существует ли значение n£N,
при котором числа
2n+1— 1 и 2п~1(2й— 1)
одновременно являются кубами целых чисел?
5.11. (СРР, 78). Доказать, что если числа т, n£N
удовлетворяют неравенству V 7—т/п > 0, то VI —т/п >
> \'тп.
5.12. (ММС, Финляндия, 80). Определить, какие цифры
в разрядах единиц и десятых стоят в десятичной записи
числа
(V3+V2)16eo-
5.13. (СРР, 80). Доказать, что для любых значений
m, п б N существует число k б N, удовлетворяющее равенству
(Vm + Vrn—\)n = Vk + Vk—i.
5.14. (Жюри, ПНР, 77). Доказать, что для любых зна¬
чений a, fc б R и е>0 существуют числа k, m£Z и n£ti,
удовлетворяющие неравенствам
| па—&|<е и | nb—т | < е.
5.15. (Жюри, СРВ, 76). Доказать, что существует
бесконечно много чисел вида
5" (пб N),
в десятичной записи каждого из которых можно выделить
не менее 1976 цифр 0, идущих подряд.
5.16*. (Жюри, Англия, 77). Доказать, что для любого
значения ш б N существует бесконечно много чисел вида
5" (п б N),
у которых каждая из т последних цифр десятичной записи
имеет четность, отличную от четности соседних с ней цифр.
23

5.17*. (СФРЮ, 73). Доказать, что если длины сторон
прямоугольника — нечетные числа, то внутри этого прямо¬
угольника нет точки, расстояние от которой до любой из
четырех его вершин является целым числом.
5.18*. (Жюри, ВНР, 79). Доказать, что не существует
правильной четырехугольной пирамиды, у которой длины
всех ребер, полная поверхность и объем являются целыми
числами.
5.19*. (Англия, 81). Для заданных различных чисел
оь о2, ..., ап С N (п > 1) и каждого значения i= 1,2,...
..., п обозначено
Pi= II («/—«у)-
1 <i<n
i=ti
Доказать, что при любом значении k С N число
2 aVpi
»=1
является целым.
Глава 2
УРАВНЕНИЯ И НЕРАВЕНСТВА
§ 6. Уравнения и системы
(см. Приложение Г: определения 2, 19; теоремы 6, 7, 18, 55, 56)
6.1. (Нью-Йорк, 78). Решить уравнение 8*(Зх+1)=4.
6.2. (Австрия, 74). Доказать, что для любых значений
а, Ь, с С R уравнение
(х—а) (х—b) + (х—Ь) (х—с) -f (х—с) (х—а) = О
имеет хотя бы одно решение.
6.3. (ГДР, 83). Доказать, что уравнение
х4 + 5х3 + 6х2—4х—16 = 0
имеет ровно два решения.
6.4. (Нью-Йорк, 80). Найти все пары чисел а>1,
b > 0, для которых уравнение а* = х6 имеет ровно одно
положительное решение. Указать это решение для каж¬
дой пары найденных значений а, Ь.
6.5. (СФРЮ, 72). При каждом значении a g R решить
уравнение
— 1) f—!—|—!—н—г! W
'	'	\ Sin X 1 COS X ' sin X COS X }
24

6.6. (Нью-Йорк, 73). Найти все значения х£[0, п/2],
удовлетворяющие уравнению cosBx + sin8х— 97/128.
6.7. (Нью-Йорк, 78). Найти все пары натуральных
чисел А Ф В, для которых система
J cos Ах + cos Вх= О,
(A sin Ах + В sin Вх = О
имеет решение.
6.8. (ЧССР, 56). Найти все пары чисел х, у С (0, п,'2),
удовлетворяющие системе
Г COS X г, „
   2 cos2 у,
cos у	и
sin х о-s
-— = 2 sin2 и.
sin у	и
6.9. (ГДР, 66). Решить уравнение
(sin (х—у) + I) (2 cos (2х—у) -f 1) = 6.
6.10. (СРР, 78). При каждом значении n£N решить
уравнение
sinxsin2x.. .sin nx-f cosxcos2x.. .cosnx— 1.
6.11. (ГДР, 66). При каждом значении n£N решить
уравнение (х + у)" = хп + у".
6.12. (ГДР, 78). Решить систему
1х + ху+У = 2 + 31^2,
\х2 + у2 = 6.
6.13. (Англия, 75). Доказать, что для любого значе¬
ния п С N существует ровно один набор чисел хи ..., а„,
удовлетворяющий уравнению
(1 —Xi)2 + (xt—х2)2 + ... -f (xn_i—х,,)2 + х2 = 1 /(п + 1).
6.14. (НРБ, 68). Найти все значения n£N, для кото¬
рых существует набор положительных чисел xlt ..., х„,
удовлетворяющий системе
(X1 + х2 + ... + х„ = 9,
1т+зг+---+-]г=1-
Х\ -л 2	*п
Указать все такие наборы при каждом из найденных
значений п.
25

6.15*. (ЧССР, 82). Для каждой пары значений
найти все наборы неотрицательных чисел хг, х2, .хп,
удовлетворяющие системе
6.17*. (Австрия—ПНР, 79). Для любых значений ng N
и а С R решить систему
§ 7. Неравенства
(см. Приложение Г: определения 18, 30, 32; теоремы 2, 4—7, 34, 55, 56)
7.1. (ГДР, 74). Что больше: |/ 4-f )/7—4-/7—У 2
или 0?
7.2. (Бельгия, 79). Расставить числа
в порядке возрастания, если известно, что а < b < с < d.
7.3. (СФРЮ, 76). Доказать, что если произведение
трех чисел равно 1, а их сумма больше суммы их обрат¬
ных величин, то ровно одно из этих чисел больше 1.
7.4. (Нью-Йорк, 75). Доказать, что для среднего ариф¬
метического А = (а-\-Ь)/2 и среднего геометрического
B — Vab любых положительных чисел а^=Ь справедливы
оценки
[ л£ + 4 + ...+х*=1,
\ (1 + *i) (1 + я») • • ■ (1 + Х„) = 2.
6.16*. (ГДР, 80). Решить систему
{
'2 х + х*у = у,
2y + !fz=z,
2 г + г2х = х.
х = (а-ТЬ) (с + d),
y=(a + c)(b + d);
z = (a + d)(b + c)
26

7.5. (СФРЮ, 76). Доказать, что для любых чисел а,
Ь, с, больших 1, справедливо неравенство
9 / bgb a	logc Ь Ioga с \ ^	9
\ а-\-Ь	Ь-\-с ' с+о /а+Ь+с"
7.6. (Австрия, 71). Доказать, что для любых положи¬
тельных чисел а, Ь, с справедливо неравенство
а2 (b + с—a) -f bz (а + с—Ь) + с2 (а + b—с) ^ 3abc.
7.7. (США, 80). Доказать, что для любых чисел
a, b, с£[0; 1] справедливо неравенство
ттЬт+-г+!+г+7рг+г+<1-'-> (•-») <>-с> <
7.8. (ЧССР, 59). Доказать, что если числа а, Ь, с £ R
удовлетворяют неравенствам
а + b + с > 0, ab + Ьс + га > 0, abc > 0,
то эти числа положительные.
7.9. (Бельгия, 76). Доказать, что при всех а £ R вы¬
полнено неравенство
sin (cos а) < cos (sin а).
7.10. (Балканиада, 84). Доказать, что для любых
положительных чисел cq, ..., а„ (п ^ 2), сумма которых
равна 1, справедливо неравенство
п
Eat ^ п
Ч-щ ^ 2п — 1'
7.11. (ГДР, 67; Англия, 76). Доказать, что для любых
положительных чисел а, а„ (п ^ 2) справедливо не¬
равенство
" а ■	п п
/. -	где обозначено s= 2 ai-
(=1 s—п 1	i=i
7.12. (Нью-Йорк, 75). Верно ли, что для любых поло¬
жительных чисел ait а2, ..., ап и a,l+1 = ai справедливо
неравенство

7.13. (Жюри, Канада, 82). Доказать, что для любых
положительных чисел х Ф 1, а < 1 справедливо неравенство
1 уа
7^-<(1 +хУ~К
7.14. (Жюри, СССР, 82). Доказать, что для любого
значения а<1 и любых чисел xit ..., х„, удовлетворяю¬
щих условиям 1 ^ хх ^ х2 ^^хп > 0, справедливо
неравенство
(1 +Xt + xa+ ... + *я)“<1 + 1“-1дЗЧ-2а-1*“+. •. +па~1х%.
7.15. (НРБ, 82). Доказать, что для любых чисел
fli ап С [0; 2] (п ^ 2) справедливо неравенство
2 2 I «I—о, К л8.
i = i / = 1
Определить, при каких значениях аи .... ап достигается
равенство.
7.16. (СФРЮ, 72). Доказать, что если число М и набор
чисел
Д|1» ^12* * * ' *
^21» ^22» • • • » ^2/1»
^«2»	•	•	•	» ^/1Г»
удовлетворяют неравенствам
л
2 | Я/Л + aj2x2 + ... + а/пхп | < М
/ = <
при любых значениях хи ..., х„€{—1; 1}, то справед¬
лива оценка
I «и | + | a2i ( + ... + | апп |<Л4.
7.17.	(Жюри, США, 82). Доказать, что для любого
набора чисел ..., ап С R можно подобрать такое зна¬
чение ££{1; ...; я), чтобы любые неотрицательные числа
bi^Ь.г^.. .^b„, не превосходящие 1, удовлетворяли
неравенству
2 biai
t= 1
с
k
2 Щ
i=i
7.18*. (НРБ, 84). Доказать, что для любых значений
m.ftg N и любых чисел xt хп, ух У„£[0; П>
удовлетворяющих условиям x{ + yt=l при t = l, ..., п,
28

справедливо неравенство
(1 -	.	.*„)* + (1 -у?). .. (1 -Ifri) > 1.
7.19*. (Жюри, США, 77). Доказать, что для любых
положительных чисел а <1 b ^ с <1 d справедливо неравен¬
ство
abbcc^da ^ bacbdcad.
7.20*. (ГДР, 80). Доказать,	что	для	любых	чисел
N, больших 1, справедливо	неравенство
п*	п
/= 2 /= 2
7.21*. (Жюри, Франция, 82). Доказать, что для любых
положительных чисел аи .... ап справедливо неравенство
П	  П
2 \/ах.. .aft<e 2 ak,
k—l	*=i
где е—основание натуральных логарифмов.
7.22*. (США, 77). Доказать,	что	если	фиксированы
два положительных числа р < q, то	для	любых	чисел
а, р, у, б, е £ [р\ q\ справедливо неравенство
(« + е + т + 6 + е)(1 + { + ± + 1+1)< _
Определить, при каких значениях а, Р, у, б, е достигается
равенство.
7.23*. (ГДР, 70). Доказать, что для любых положи¬
тельных чисел а, Ь, с, d справедливо неравенство
Kabc+abd + acd + bed	abас-\-adbc-\- bd-\- cd
4	^ V	6	•
Определить, при каких значениях а, Ь, с, d достигается
равенство.
§ 8. Задачи с целой частью
(см. Приложение Г: определения 11, 15, 18, 19; теоремы 2,6,8, 18,20)
8.1.	(Австрия, 73). Решить уравнение
1 I „ , 1 I [*] —*

8.2. (Англия, 75). Решить уравнение
[VT]+ 11/2]+...+[У^1] = 400
в натуральных числах.
8.3. (Канада, 81). Доказать, что уравнение
[а] + [2х] + [4х] + [8а] -f [ 1 6а] + [32а] = 12 345
не имеет решений.
8.4. (Швеция, 82). Для каждого значения п g N опре¬
делить, сколько решений имеет уравнение а2—[а2] = {а}2
на отрезке [1; п].
8.5. (Австрия, 74). Доказать, что для любого значе¬
ния п С N справедливо равенство
[Vn + ]ЛГ+Т] = [l^W+2],
8.6. (Жюри, Бельгия, 79). Какие натуральные числа
нельзя представить в виде \ti-\-\rn + 1/2], где ng N?
8.7. (СФРЮ, 83). Доказать, что среди членов после¬
довательности {а,,}, заданной соотношениями
а^ = 2, п„+1 = [(3/2) а„] при ng N,
имеется бесконечно много четных и бесконечно много не¬
четных чисел.
8.8. (Австрия—ПНР, 79). Для каждого значения п g N
найти наибольшее значение fcgZ+, при котором число
[(3 + ]/1 1)2"-г| делится на 2к.
8.9. (Жюри, СРР, 79). Доказать, что для любого зна¬
чения п g N имеет место оценка
{nV2}> H(2nV2),
причем для любого е>0 найдется число п g N, удовлет¬
воряющее неравенству
{пУ2}<(1 + е)1(2п V2).
8.10*. (США, 75). а) Доказать, что для любых не¬
отрицательных чисел а, у справедливо неравенство
[5а] + [5у] > [За + у] + [3у + а].
б) Доказать, что число
 (5т)! (5п)!
т\п\ (Зт-\-п)! (Зл + т)!
является целым при всех значениях т, п g N.
30

8.11*. (США, 81). Доказать, что для любых чисел
х^О и ngN справедливо неравенство
[м]>И+^! + ...+М.
8.12*. (НРБ, 83). Доказать, что если числа а, Ь, с при
каждом значении п g N удовлетворяют равенству [па\ -f-
-f [nb] — [пс], то хотя бы одно из чисел а, b является
целым.
Глава 3
ПЛАНИМЕТРИЯ
§ 9. Треугольники
(см. Приложение Г: определения 36, 40, 41 \
теоремы 64, 67, 74, 75, 77, 82, 83)
9.1. (СФРЮ, 81). В остроугольном неравностороннем
треугольнике через одну вершину проведена высота,
через другую—медиана, а через третью—биссектриса.
Доказать, что если проведенные линии, пересекаясь,
образуют треугольник, то он не может быть равносторонним.
9.2. (Бельгия, 77). Доказать, что если заданы поло¬
жительные числа а, Ь, с g R и для каждого значения
ng N существует треугольник со сторонами о", Ьп,сп со¬
ответственно, то все эти треугольники равнобедренные.
9.3. (Швеция, 82). Найти все значения ngN, для
каждого из которых существуют число mg N, треугольник
ABC со сторонами АВ = 33, АС — 21, ВС — п и точки D,
Е на сторонах АВ, АС соответственно, удовлетворяющие
условиям AD = DE — ЕС = т.
9.4. (Жюри, СРВ, 79). Найти все тройки чисел
a, b, cgN, являющихся длинами сторон треугольника с
диаметром описанной окружности, равным 6,25.
9.5. (Нью-Йорк, 78). Треугольники ABC и DEF впи¬
саны в одну и ту же окружность. Доказать, что равенство
их периметров равносильно условию
sin /_ А + sin /_ В -f sin /_С = sin /_D-f sin /_ Е-\-sin /_F.
9.6. (СФРЮ, 81). Прямая делит треугольник на две
части равных площадей и периметров. Доказать, что
центр вписанной окружности лежит на этой прямой.
9.7. (Австрия, 83). В треугольнике ABC на сторонах
АВ, АС и ВС взяты точки С', В' я А’ так, что отрезки
31

АА', ВВ' и СС' пересекаются в одной точке. Точки А",-
В" и С" симметричны точкам А, В и С соответственно
относительно точек А', В’ и С'. Доказать, что	I
Sa”b"C" = 3 SABc + ^ Sa-b’C'-
9.8. (Австрия, 71). Медианы треугольника ABC пере¬
секаются в точке О. Доказать, что
АВ2 + ВС2 + СА2 = 3(ОА2 + О В2 + ОС2).
9.9. (Нью-Йорк, 79). Доказать, что если центр тя¬
жести треугольника совпадает с центром тяжести его
границы, то треугольник равносторонний.
9.10. (Англия, 83). Пусть О—центр окружности, опи¬
санной около треугольника ABC, D—середина стороны
АВ, а Е—точка пересечения медиан треугольника ACD.
Доказать, что если АВ = АС, то OEj_CD.
9.11. (ЧССР, 72). Найти все пары положительных I
чисел a, b € R, для которых существуют прямоугольный
треугольник CDE и точки А, В на его гипотенузе DE, 1
удовлетворяющие условиям DA—AB = BE и АС = о, I
ВС = Ь.	|
9.12. (Нью-Йорк, 76). Найти хотя бы один прямо¬
угольный треугольник с целочисленными сторонами, j
каждый угол которого можно разделить на три равные
части с помощью циркуля и линейки.	!
9.13. (Финляндия, 80). Перпендикуляры, проведенные!
через середины сторон АВ и АС треугольника ABC, пе¬
ресекают прямую ВС в точках X и Y соответственно.;
Доказать, что равенство ВС = XY: а) выполнено, если
Ч/.В-Ч ZC = 3;
б)	может также выполняться и при условии
tgZB-Ъ АСФЗ;
I
найти множество McR, для которого указанное равен¬
ство равносильно условию
tgZB-tgZCcM.
9.14. (Нью-Йорк, 76). Высоты остроугольного тре-!
угольника ABC пересекаются в точке О, а на отрезках'
ОВ и ОС выбраны точки Bt и Сг, для которых	'
Z АВ£ = Z АСгВ ~ 90°.
Доказать, что АВ1 = АС1.
32

9.15. (Англия, 81). Высоты треугольника ЛВС пере¬
секаются в точке О, а точки At, Вг, С* являются сере¬
динами сторон ВС, СА, А В соответственно. Окружность
с центром О пересекает прямую В1С1 в точках Dlt D2,
прямую СуАг — в точках Еи Е2, а прямую AyBt — в точ¬
ках Ft,F2. Доказать, что
ADt = AD2 = ВЕг = ВЕ2 = CFt = CF2.
9.16. (СФРЮ, 83). Внутри треугольника ABC взята
точка Р, а на сторонах АС и ВС взяты соответственно
точки М и L, для которых
/_РАС = /_РВС, /_PLC = /_PMC = 90°.
Доказать, что если D—середина стороны АВ, го DM = DL.
9.17. (СРР, 78). Найти геометрическое место точек М,
лежащих внутри равностороннего треугольника ABC и
удовлетворяющих условию
/_МАВ + /_МВС + /_МСА=Ж.
9.18. (НРБ, 82). Через Bif (i, /€{1; 2; 3}) обозначена
точка, симметричная вершине Af данного неравнобедрен¬
ного треугольника AlA2As относительно его биссектрисы,
проходящей через вершину Ау-. Доказать, что прямые
Bl2B2l, B13B3i и В23В32 параллельны.
9.19. (НРБ, 81). Биссектрисы внутреннего и внешнего
углов С треугольника ЛВС пересекают прямую АВ в
точках L и М соответственно. Доказать, что если
CL = CM, то
АС2 + ВС2 = 4Я2,
где R — радиус описанной окружности.
9.20. (СФРЮ, 83). Внутри треугольника ЛВС взята
точка М, для которой MBA = 30°, //МАВ= 10°.
Найти Z АМС, если /_АСВ = 80° и АС = ВС.
9.21. (Англия, 70). На сторонах ВС и АС треуголь¬
ника ЛВС выбраны точки D и Е соответственно так,
что Z BAD = 50°, /_ ABE = 30°. Найти /_ BED, если
Zabc=z ACB = 50°.
9.22. (ГДР, 64). На стороне ВС треугольника ЛВС
взята точка Р, для которой PC = 2ВР. Найти / АСВ,
если ,/ЛВС = 45°, АРС = 60°.
9.23*. (Жюри, Голландия, 79). Внутри равносторон¬
него треугольника ЛВС взяты точки К, L, М, для ко¬
торых /_КАВ — ^_LBA — 15°,	/_ МВС = /_ КС В = 20°,
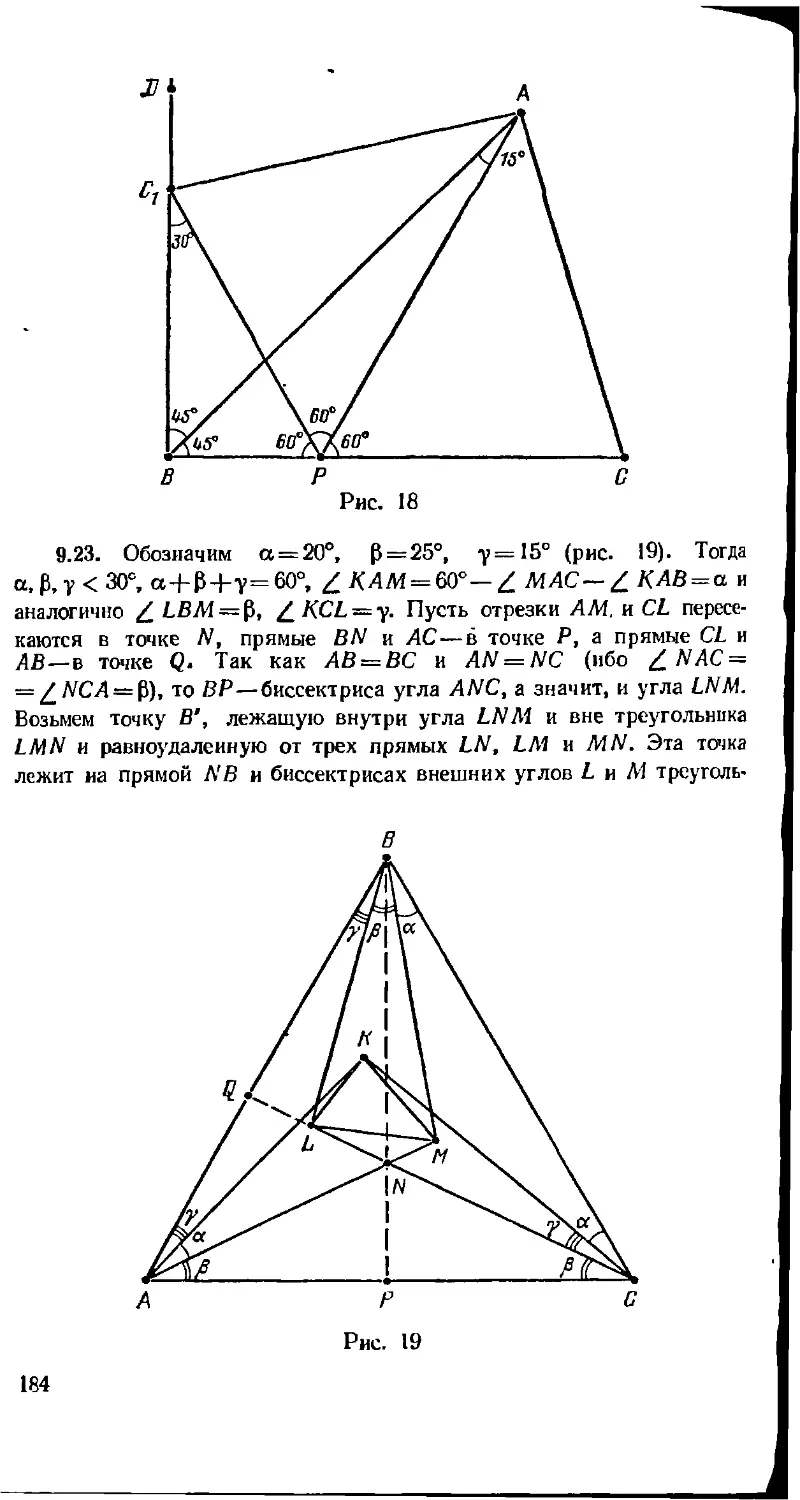
/_LCA — /_МАС — 25°. Найти углы треугольника KLM.
2 Под ред. И. Н. Сергеева	^3

§ 10. Окружности и круги
(см. Приложение Г: определения 35, 36; теоремы 66 — 75, 79)
10.1. (Бразилия, 83). Доказать, что все точки окруж¬
ности можно разбить на два множества так, чтобы среди
вершин любого вписанного прямоугольного треугольника
присутствовали точки обоих множеств.
10.2. (Нью-Йорк, 75). Доказать, что четыре рассто¬
яния от точки окружности до вершин вписанного в нее
квадрата не могут одновременно быть рациональными
числами.
10.3. (Жюри, Бельгия, 76). Биссектрисы AAlr ВВ1г
ССг треугольника ABC пересекаются в точке М. Дока¬
зать, что если радиусы окружностей, вписанных в тре¬
угольники MBiA, МСгА, МСгВ, МА^В, MAfi и МВ^С,
равны, то треугольник ABC равносторонний.
10.4. (Англия, 75). Семь точек в круге . единичного
радиуса расположены так, что расстояние между любыми
двумя из них не меньше 1. Доказать, что одна из точек
совпадает с центром круга.
10.5. (Пекин, 62). Шесть кругов на плоскости распо¬
ложены так, что центр каждого из них лежит вне осталь¬
ных кругов. Доказать, что все шесть кругов не имеют
общей точки.
10.6. (Австрия—ПНР, 78). На плоскости располо¬
жены непересекающиеся круги, каждый из которых ка¬
сается по меньшей мере шести из остальных кругов.
Доказать, что множество кругов бесконечно.
10.7. (НРБ, 84). Доказать, что для любого треуголь-1
ника ABC существуют 3 окружности одинакового радиуса, I
одна из которых касается сторон АВ и ВС, другая—'
сторон ВС и АС, третья—сторон АС и АВ, а все 3
окружности имеют ровно одну общую точку.
10.8. (ММС, Люксембург, 80). Две окружности ка-1
саются друг друга в точке Р. Прямая, касающаяся одной 1
из них в точке А, пересекает другую в точках В и С.
Доказать, что прямая РА является биссектрисой угла
ВРС или смежного с ним.
10.9. (Жюри, США, 79). Окружность, центр которой
лежит на стороне ВС равнобедренного треугольника ABC,
касается его равных сторон АВ и АС. Доказать, что
отрезок с концами Р и Q, лежащими на сторонах АВ и
ВС соответственно, касается окружности тогда и только
тогда, когда BP-CQ = BC2/4.
10.10. (Англия, 80). На диаметре АВ полуокружности
34

взяты точки К и L, а на полуокружности—точки М, N
и С так, что четырехугольник KLMN является квадратом,
площадь которого равна площади треугольника ABC.
Доказать, что центр вписанной в треугольник ЛВС окруж¬
ности совпадает с точкой пересечения одной из сторон
квадрата и одной из прямых, соединяющих вершину N
или М с вершиной А или В.
10.11. (Жюри, СРВ, 79). Точка М лежит на окруж¬
ности, описанной около данного равностороннего тре¬
угольника ЛВС. Доказать, что величина МЛ4 + MB1 + MCi
не зависит от выбора точки М.
10.12. (ГДР, 73). Дан- выпуклый четырехугольник
ABCD, в котором AB = AD и CB = CD. Доказать, что;
а) в него можно вписать окружность;
б) около него можно описать окружность тогда и
только тогда, когда ЛВДВС;
в) если ABJ_BC, то квадрат расстояния между центром
вписанной окружности (радиуса г) и центром описанной
окружности (радиуса R) равен
Я2 + г2—rVV + 4tf2.
10.13. (СРР, 78). Доказать, что четыре вершины
квадрата не могут быть расположены соответственно на
четырех концентрических окружностях, радиусы которых
образуют арифметическую прогрессию.
10.14. (СФРЮ, 83). На дуге АВ описанной около
прямоугольника ABCD окружности взята точка М, от¬
личная от вершин Л, В. Точки Р, Q, R и S являются
проекциями точки М на прямые AD, АВ, ВС и CD
соответственно. Доказать, что прямые PQ и RS перпен¬
дикулярны и пересекаются на одной из диагоналей пря¬
моугольника.
10.15. (Англия, 77). Сторона ВС треугольника ЛВС
касается вписанной в него окружности в точке D. Дока¬
зать, что центр окружности лежит на прямой, проходя¬
щей через середины отрезков ВС и AD.
10.16. (Австрия, 72). Две окружности касаются друг
друга. В большую окружность вписан равносторонний
треугольник, из вершин которого проведены касательные
к меньшей окружности. Доказать, что длина одной из
трех касательных равна сумме длин двух других.
10.17. (Жюри, США, 79). Из точки Р, лежащей на
дуге ВС окружности, описанной около треугольника ЛВС,
опущены перпендикуляры РК, РВ и РМ на прямые ВС,
2*	35

АС и АВ соответственно. Доказать, что
ВС АС АВ
РК~ PL+ РМ'
10.18.	(ГДР, 70; СФРЮ, 72). а) Пусть точка О—центр
вписанной в треугольник АБС окружности, а точка D —
отличная от А точка пересечения прямой АО с описанной
около треугольника АБС окружностью. Доказать, что
DB = DC = DO.
б) Доказать, что если A BCD—вписанный четырех¬
угольник, то центры Blt Си Я, окружностей, впи¬
санных в треугольники BCD, CD A, DAB, АБС соответ¬
ственно, являются вершинами прямоугольника.
10.19*. (Балканиада, 84). Доказать, что вписанный
четырехугольник А1А2А3А4 равен четырехугольнику,
вершины которого Я,, Я2, Яэ, Я4 являются точками пе¬
ресечения высот треугольников
А2А3А4, AlA3Ai, АуА2АА±А2А3
соответственно.
10.20*. а) (Жюри, США, 82). Диагональ данного впи¬
санного четырехугольника делит его на два треугольника.
Доказать, что сумма радиусов окружностей, вписанных
в эти треугольники, не зависит от выбора диагонали.
б) (ВНР, 78). Доказать, что наибольшая высота не¬
тупоугольного треугольника не меньше суммы радиусов
вписанной и описанной окружностей. Определить, когда
достигается равенство.
10.21*. (СФРЮ, 77). На плоскости расположены 100
точек. Доказать, что существует конечное множество
кругов, удовлетворяющее следующим трем условиям:
1)	любая из данных точек лежит внутри одного из кру¬
гов; 2) любые две точки разных кругов удалены друг от
друга более чем на 1; 3) сумма диаметров всех кругов
меньше 100.
10.22*. (Пекин, 63). На плоскости расположены
2п+3 точки, из которых никакие три не лежат на одной
прямой и никакие четыре не лежат на одной окружности.
Существует ли окружность, проходящая через какие-либо
три из этих точек и ограничивающая круг, внутри ко¬
торого лежит ровно половина остальных точек?
10.23*. (НРБ, 78). Доказать, что у любого выпуклого
многоугольника найдется такая тройка соседних вершин,
что проходящая через них окружность ограничивает круг,
покрывающий весь многоугольник.
36

10.24*. (Финляндия, 80). Среди п > 1 пар противо¬
положных сторон вписанного 2п-угольника выбрана п—1
пара параллельных сторон. Найти все значения п, для
которых стороны оставшейся при этом пары обязательно
параллельны.
10.25*. (НРБ, 82). На плоскости расположены п раз¬
личных окружностей радиуса 1 каждая. Доказать, что
хотя бы одна из них содержит дугу, не пересекающуюся
ни с одной из остальных окружностей и имеющую длину
не меньше 2л/п.
§ 11. Многоугольники
(см. Приложение Г: определения 1, 2, 35, 37;
теоремы 2, 65, 70, 73, 74, 80)
11.1. (СФРЮ, 81; Швеция, 82). Доказать, что если
для некоторой точки О, лежащей внутри четырехуголь¬
ника A BCD площади треугольников А ВО, ВСО, С DO,
DAO одинаковы, то эта точка лежит хотя бы на одной
из диагоналей АС или BD.
11.2. (Канада, 82). Площади четырехугольников ABCD
и A'B'C'D' равны S и S' соответственно. Доказать, что
если внутри четырехугольника ABCD существует точка
О, для которой
СМ = Л7В', ОВ = В7С', ОС^СТУ, (Ю — ЁУА’,
то S = 2S'.
11.3. (СФРЮ, 72). Восемь прямых, соединяющих
вершины параллелограмма с серединами несмежных сто¬
рон, пересекаясь, образовали восьмиугольник. Доказать,
что его площадь составляет шестую часть площади па¬
раллелограмма.
11.4. (СФРЮ, 70). Диагонали выпуклого пятиуголь¬
ника ABCDE, пересекаясь, образуют пятиугольник
A1B1C1D1El и пятиконечную звезду.
а) Найти сумму углов этой звезды при вершинах А,
В, С, D, Е.
б) Найти отношение площади пятиугольника Л1В,СгО,£1
к площади пятиугольника ABCDE при условии правиль¬
ности последнего.
11.5. (Жюри, Франция, 79). Соответственные стороны
четырехугольников ABCD и A’B'C'D’ равны. Доказать,
что имеет место одно из следующих двух утверждений;
a)	BD± AC и B'D'±A'C’-,
37

б)	точки М и ЛГ пересечения прямых АС и А'С' с
перпендикулярами, проходящими через середины отрезков
BD и B'D' соответственно, удовлетворяют равенству
МА-М'С' = МС-М'А' и либо одновременно лежат на от¬
резках АС и А'С' соответственно, либо одновременно
лежат на их продолжениях.
11.6. (Австрия, 73). Доказать, что если все углы вы¬
пуклого восьмиугольника равны, а отношение длин любых
его соседних сторон рационально, то противоположные
стороны этого восьмиугольника равны.
11.7. (СФРЮ, 76). На плоскости нарисован правиль¬
ный шестиугольник со стороной а. Для любого значения
я £ N, большего 1, построить с помощью одной линейки
отрезок длины а/п.
11.8. (Жюри, 81). Доказать, что если для углов рав¬
ностороннего выпуклого пятиугольника ABCDE выполнены
неравенства /_ А~^/_В~^ /_С~^/_D~^ /_Е, то этот
пятиугольник правильный.
11.9. (ГДР, 74; ГДР, 79). а) Доказать, что если вер¬
шины одного выпуклого л-угольника лежат в другом
равном ему л-угольнике, то вершины этих л-угольников
совпадают.
б) Верно ли утверждение а) для невыпуклых много¬
угольников?
в) Для любого ли невыпуклого многоугольника утвер¬
ждение а) неверно?
11.10. (Жюри, Бельгия, 79). Любой ли правильный
2л-угольник можно разбить на ромбы?
11.11. (ГДР, 64). Вне ромба ABCD с заданной сто¬
роной а берется точка О, удаленная от каждой из вершин
Л и С на заданное расстояние b > а. Доказать,
что произведение OB-OD не зависит от величины уг¬
ла BAD.
11.12. (ВНР, 76). Вне параллелограмма ABCD взята
точка Р так, что /_РАВ — /_РСВ, причем вершины А
и С лежат в разных полуплоскостях относительно пря¬
мой РВ. Доказать, что /_ АР В — /_ DPC.
11.13. (Жюри, Бельгия, 83). В шестиугольнике
ABCDEF углы при вершинах А, С, Е равны и не пре¬
восходят'180°, причем
/_ ABF = CBD, /_AFB = /_ EFD.
Доказать, что если точка А' симметрична вершине А
относительно диагонали BF и не лежит на прямой СЕ,
то четырехугольник A'CDE — параллелограмм.
38

11.14. (НРБ, 79). Вершины выпуклого пятиугольника
ABCDE расположены так, что треугольники ABC и CDE
равносторонние. Доказать, что если точка О—центр тре¬
угольника ABC, а точки М и N — середины сторон BD
и АЕ соответственно, то треугольники ОМЕ и OND
подобны.
11.15. (Жюри, СССР, 82). В выпуклом пятиугольнике
ABCDE углы при вершинах В, Е прямые и /_ВАС=
= /_EAD. Доказать, что если диагонали BD и СЕ пе¬
ресекаются в точке О, то прямые АО и BE перпендику¬
лярны.
11.16. (Англия, 66). Найти число сторон правильного
многоугольника, если для четырех его последовательных
вершин А, В, С, D выполнено равенство
11.17*. (Англия, 71). На окружности, вписанной в
правильный 2л-угольник, взяты точки А и В. Доказать,
что если диагонали, соединяющие противоположные вер¬
шины 2п-угольника, видны из точки А под углами
а*, ..., an, а из точки В под углами Рл Р„ соот¬
ветственно, то
tg2ai+ ••• + ^2а„ = ^2Рх+ ••• + *g2P„-
11.18*. (ВНР, 78). Вершины выпуклого многоуголь¬
ника с нечетным числом сторон окрашены так, что любые
две соседние вершины имеют разный цвет. Доказать, что
для всякой раскраски, удовлетворяющей этому условию,
многоугольник можно разбить непересекающимися диа¬
гоналями на треугольники так, чтобы концы каждой
диагонали имели разный цвет.
§ 12. Точки, отрезки и прямые
(см. Приложение Г: определения 1—3, 18, 34, 35, 37;
теоремы 1, 2, 64, 65, 96)
12.1.	(Нью-Йорк, 80). Средние линии равностороннего
треугольника ABC делят его на четыре треугольника
ADE, BDF, DEF и CEF, на сторонах которых отмечены
середины К, Е, М, N, О, Р, Q, R, S. Каждая из 15 по¬
лученных точек окрашена в один из двух цветов. Дока¬
зать, что найдутся 3 точки одного цвета, являющиеся
вершинами равностороннего треугольника.
39

12.2. (США, 81). На плоскости нарисован угол вели¬
чиной 180°/п, где число ngN не делится на 3. Доказать,
что с помощью циркуля и линейки этот угол можно раз¬
делить на 3 равных угла.
12.3. (СФРЮ, 72). Доказать, что любые два диаметра
выпуклого множества на плоскости имеют хотя бы одну
общую точку.
12.4. (ГДР, 82). Любой ли выпуклый четырехуголь- ,
ник можно разбить ломаной на две части, диаметр каж¬
дой из которых меньше диаметра исходного четырехуголь¬
ника?
12.5. (ГДР, 72). Доказать, что если п точек на плос¬
кости расположены так, что любая прямая, проходящая
через две из них, содержит хотя бы еще одну из точек,
то все они лежат на одной прямой.
12.6. (ЧССР, 68). Отрезки АВ и CD равны и не па¬
раллельны. Найти геометрическое место точек О, обла¬
дающих следующим свойством: отрезок, симметричный
отрезку АВ относительно точки О, симметричен отрезку '
CD относительно некоторой прямой.
12.7. (Бельгия, 77). Доказать, что если множество на
плоскости имеет более одного центра симметрии, то оно
имеет их бесконечно много.
12.8. (Бельгия, 78). Доказать, что объединение L осей
симметрии множества М на плоскости содержится в объ¬
единении осей симметрии множества L.
12.9. (Жюри, ГДР, 79). Множество на плоскости имеет
две оси симметрии, пересекающиеся под углом а, где чис¬
ло а/л иррационально. Доказать, что если это множество
содержит более одной точки, то оно содержит бесконечно
много точек.
12.10. (СФРЮ, 76). Найти все значения л € N, боль¬
шие 2, для которых на плоскости можно выбрать п то¬
чек так, чтобы любые две из них являлись вершинами
равностороннего треугольника, третьей вершиной кото¬
рого служит также одна из выбранных точек.
12.11. (ЧССР, 80). Множество М получено из
плоскости выбрасыванием трех различных точек Л, В и
С. Найти наименьшее число выпуклых множеств, объеди¬
нением которых является множество М.
12.12. (Жюри, СРР, 79). Доказать, что для любого
значения ngN, большего некоторого числа па, всю плос¬
кость можно разбить на п частей, проведя несколько пря¬
мых, среди которых обязательно есть пересекающиеся.
Найти наименьшее из таких значений па.
1

12.13. (ЧССР, 82). На координатной плоскости найти
выпуклое множество, которое содержит бесконечно много
точек с обеими целочисленными координатами, но в пере¬
сечении с любой прямой содержит лишь конечное (или
пустое) множество таких точек.
12.14. (ГДР, 74). Найти все пары ненулевых векторов
х, у, для которых последовательность чисел
а„ = \х—пу\ (п£ N)
является: а) возрастающей; б) убывающей.
12.15. (СФРЮ, 73). Несколько точек на плоскости рас¬
положены так, что расстояние между любыми двумя из
них больше 2. Доказать, что любое множество площади
меньше л можно параллельно перенести по плоскости на
вектор длины меньше 1 так, чтобы оно не содержало ни
одной из точек.
12.16. (Бельгия, 77). Внутри круга радиуса	рас¬
положены 4п отрезков длины 1 каждый. Доказать, что
если задана некоторая прямая, то найдется другая пря¬
мая, либо параллельная, либо перпендикулярная ей и
пересекающая по крайней мере два отрезка.
12.17*. (ЧССР, 73). В квадрате со стороной 50 распо¬
ложена ломаная. Доказать, что е^ли расстояние от любой
точки квадрата хотя бы до одной точки ломаной не больше
1, то длина ломаной больше 1248.
12.18*. (Жюри, ЧССР, 79). На - прямой расположены
л2-)- 1 (п € N) отрезков. Доказать, что либо среди них
можно выбрать непересекающиеся друг с другом п + 1
отрезков, либо найдется общая для некоторых п + 1 от¬
резков точка.
12.19*. (США, 83). На прямой расположены несколь¬
ко множеств, каждое из которых является объединением
двух отрезков. Доказать, что если любые три из этих
множеств имеют общую точку, то существует точка,
принадлежащая по мецьшей мере половине всех . мно¬
жеств.
12.20*. (СФРЮ, 75). На плоскости отмечены п + 4 точ¬
ки, четыре из которых расположены в вершинах квад¬
рата, а остальные п лежат внутри этого квадрата. Любые
из отмеченных точек разрешается соединять отрезками,
лишь бы при этом никакой построенный отрезок не со¬
держал отмеченных точек, отличных от его концов, и
никакие два из построенных отрезков не имели общих
точек, кроме, возможно, концов. Найти наибольшее число
отрезков, которые можно построить таким образом.
41

§ 13. Геометрические неравенства
(см. Приложение Г: определения 1, 35, 38;
теоремы I, 6, 64, 69, 70, 74, 75, 77, 80)
13.1. (Англия, 67). Длины а и b двух сторон тре¬
угольника удовлетворяют условию а > Ь, а длины соответ¬
ствующих им высот равны ha и hb. Доказать неравенство
а + ha ^ b + hb.
Определить, когда достигается равенство.
13.2. (ЧССР, 76). Доказать, что если один выпуклый
многоугольник лежит внутри другого (также выпуклого),,
то периметр внутреннего многоугольника меньше пери-i
метра внешнего.	I
13.3. (СФРЮ, 75). Доказать, что если последователь¬
но соединить середины сторон выпуклого п-угольника
(где п'^ 4), то площадь полученного многоугольника будет
не меньше половины площади исходного.
13.4. (Австрия—ПНР, 78). В правильный шестиуголь¬
ник вписан параллелограмм, центр симметрии которого
совпадает с центром шестиугольника. Доказать что пло¬
щадь параллелограмма не превосходит 2/3 площади шес¬
тиугольника.
13.5. (СФРЮ, 77). Доказать, что площадь любого квад¬
рата, лежащего в треугольнике, не превосходит половины
площади этого треугольника.
13.6. (Пекин, 64). В треугольник ABC, в котором угол
при вершине А не является острым, вписывается квад¬
рат BiC^DE (сторона DE которого лежит на отрезке ВС,
а вершины Bt и С* — на отрезках АВ и АС соответст¬
венно). Затем в треугольник ABjC* аналогичным образом
вписывается квадрат BiC2DlEl и т. д. Это построение
проводится несколько раз. Доказать, что сумма площадей
всех вписанных квадратов меньше половины площади тре¬
угольника ABC.
13.7. (ЧССР, 75). Доказать, что любой остроугольный
треугольник площади 1 можно поместить в прямоуголь¬
ный треугольник площади не больше У3.
13.8. (Жюри, 81). Доказать, что если на полуокруж¬
ности радиуса 1 последовательно расположены точки А,
В, С, D, Е, то справедливо неравенство
АВ2 + ВС2 + CD2 + DE2 + AB BC CD + BC CD DE < 4.
13.9. (ЧССР, 83). Доказать, что для любой точки О,
лежащей на стороне АВ треугольника ABC и не совпа-
42

дающей с его вершинами, справедливо неравенство
ОС АВ < ОА ВС + ОВ АС.
13.10. (ГДР, 62). Доказать, что для любого выпуклого
четырехугольника отношение наибольшего из расстояний
между его вершинами к наименьшему из них не мень¬
ше V 2.
13.11. (Австрия, 75). Доказать, что если на плоскости
расположены 6 различных точек, то отношение наиболь¬
шего из расстояний между этими точками к наименьшему
из них не меньше V3.
13.12. (Нью-Йорк, 77—79). Доказать, что если а, Ь,
с—длины сторон треугольника, Р—его периметр, a S —
его площадь, то справедливы неравенства:
' а Ь с — Р
2) а2 + Ь2 + с2 > Р2/3.
3)P2>12K"3S.	_
4) а2 + If + с2 > 4 V 3S.
5) а3 + Ь3 + с3 ^ P3J9.
6) а3 -f Ь3 + с3	SP.
7) o4 + fc4 + c4> 16S2.
13.13. (СФРЮ, 75). Доказать, что для любой точки О,
лежащей внутри треугольника ABC с полупериметром р,
справедливо неравенство
пл /ВАС , „ п /ЛВС ,	/АСВ^
О А ■ cos 	(- О В • cos =~2 h ОС • cos	р.
Определить, когда достигается равенство.
13.14. (ГДР, 65). Доказать, что для углов а, Р, у лю¬
бого треугольника справедливо неравенство
cos а + cos р + cos у ^ 3/2-
Определить, когда достигается равенство.
13.15. (Англия, 67). Доказать, что для углов а, р, у
любого треугольника справедливо неравенство'
cos2 а + cos2 р + cos2 у 3/4.
Определить, когда достигается равенство. Доказать, что
величина cos2 a -f cos2 р + cos2 у не принимает наибольшего
значения.
43

13.16.	(СФРЮ, 76). Доказать, что для углов а, р, у!
любого нетупоугольного треугольника справедливо нера¬
венство
sina-Ь siriP+ siriy > cos а + cos Р-Ь cos у-
13.17.	(Жюри, СРВ, 77). Доказать, что для любого
треугольника с длинами сторон а, Ь, с и площадью S
справедливо неравенство
ab-\ ас-\-Ьс
45	•э-
13.18.	(ЧССР, 74). Доказать, что если стороны впи¬
санного шестиугольника ABCDEF удовлетворяют равен¬
ствам
АВ — ВС, CD = DE, EF^FA,
то площадь треугольника АСЕ не превосходит площади
треугольника BDF.
13.19. (Австралия, 82). Доказать, что если продолже-
ния биссектрис углов А, В а С треугольника ABC пере¬
секают описанную около него окружность в точках Аь
Bt и Ct соответственно, то справедливо неравенство
AAt + BBt + СС, > АВ + ВС + АС.
13.20. (ГДР, 81). Доказать, что если AD, BE и CF—
биссектрисы треугольника ABC, то площадь треугольни¬
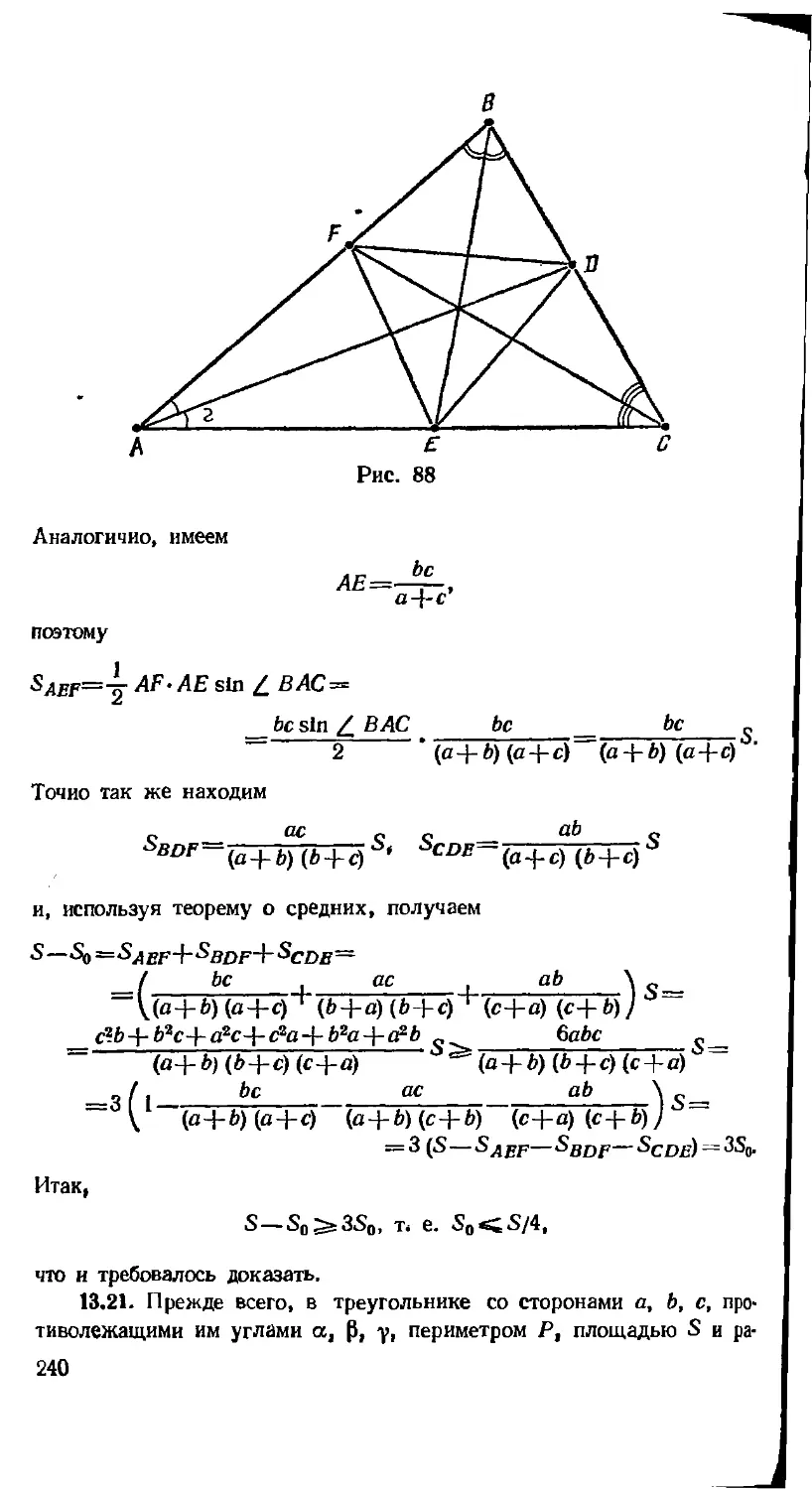
ка DEF не превосходит четверти площади треугольника
ABC.
13.21. (США, 82). Внутри правильного треугольника
ABC взята точка At, а внутри треугольника АХВС—точ¬
ка А2. Доказать,- что
-Sf
р2 > р| ,
где Slt S2 и Pf, Р2—площади и периметры треугольни¬
ков АгВС, А2ВС соответственно.
13.22. (Англия, 83). Доказать, что если 10 точек рас¬
положены в круге диаметра 5, то расстояние между не
которыми двумя из них меньше 2.
13.23. (Жюри, Польша, 82). Точки Alt А2, ..., А,
на окружности с центром О и радиусом 1 расположенн

так, что
ОЛх -J- ОЛ2 + ... + ОАп = 0.
Доказать, что для любой точки В справедливо неравен¬
ство
ВАг “Ь ВА2 -Ь • • • -Ь ЕАп ^ п.
13.24*. (ВНР, 81). Доказать, что для любых точек А,
В, С, D, Е на плоскости справедливо неравенство
AB + CD + DE + EC^AC+ AD + АЕ + ВС + BD + BE.
§ 14. Геометрические задачи на экстремум
(см. Приложение Г: определения 35, 37; теоремы I, 6, 64, 75)
14.1. (ЧССР, 80). Длина наибольшей стороны равно¬
бедренной трапеции равна 13, а периметр — 28.
а) Найти стороны трапеции, если ее площадь равна 27.
б) Может ли площадь такой трапеции равняться 27,001?
14.2. (Жюри, Бельгия, 82). Из всех треугольников
заданного периметра найти такой, у которого радиус впи¬
санной окружности максимален.
14.3. (Жюри, США, 77). Через точку, находящуюся
на расстоянии k < 1 от центра окружности радиуса 1,
проводится пара перпендикулярных хорд. Найти наиболь¬
шее и наименьшее значения суммы их длин.
14.4. (СФРЮ, 73). Доказать, что сумма расстояний
между серединами противоположных сторон четырехуголь¬
ника равна его полупериметру тогда и только тогда, ког¬
да этот четырехугольник — параллелограмм.
14.5. (Англия, 82). Доказать, что если для точки О,
лежащей внутри четырехугольника ABCD площади S,
справедливо равенство
2 S = О А2 + ОВ2 + ОС2 4- OD2,
то четырехугольник ABCD — квадрат, а точка О—его центр.
14.6. (Нью-Йорк, 80). Пусть AiHi (г = 1, 2, 3)—высоты
треугольника АлАгАъ, площадь которого равна S. Дока¬
зать, что треугольник ЛХЛ2Л3 равносторонний тогда и
только тогда, когда
3
S = -^I4AiAiTl-AiHi (Л4 = ЛХ).
i- 1
45

14.7. (НРБ, 68). Найти соотношения между сторонами
треугольника, удовлетворяющего равенству
a cos а +6 cos |3 | с cos у	Р
а sin Р + 6 sin у | с sin а 9R'
где а, Ь, с—стороны треугольника, а, р, у—величины
противолежащих углов, Р—периметр, R—радиус опи¬
санной окружности.
14.8. (Нью-Йорк, 79). Доказать, что вершины наи¬
меньшего по площади правильного п-угольника (п > 3),
вписанного в данный правильный n-угольник, совпадают
с серединами сторон последнего.
14.9. (СФРЮ, 74). Для произвольных 3 точек Аи
А2, ..., Ап на плоскости, никакие 3 из которых не ле¬
жат на одной прямой, через а обозначен наименьший из
углов /_ AtAjAk, образованных тройками Ait AJt Ak раз¬
личных точек. При каждом значении п найти наибольшее
значение а. Определить, при каких расположениях точек
это значение достигается.
14.10. (НРБ, 83). Найти квадрат наименьших раз¬
меров, в котором можно расположить 5 кругов радиуса
1 каждый так, чтобы никакие два из них не имели общих
внутренних точек.
14.11. (Жюри, ГДР, 82). Доказать, что если радиус
окружности, вписанной в треугольник, вдвое меньше ра¬
диуса окружности, описанной около него, то этот тре¬
угольник является равносторонним.
14.12. (США, 79). На плоскости нарисован угол, внутри
которого отмечена точка О. Провести через точку О такой
отрезок ВС с концами на сторонах угла, для которого
величина
во^ со
принимает наибольшее значение.
14.13*. Для каждой точки Т заданного треугольника
ABC через m (Т) и М (Т) обозначены наименьшая и со¬
ответственно наибольшая из длин отрезков ТА, ТВ, ТС.
а) (ЧССР, 74). Найти все точки Т треугольника ABC,
для которых величина т(Т) принимает наибольшее значение.
б) (СРР, 82). Доказать, что если /_ ВАС ^ 90°, то
для любой точки Т треугольника ABC справедливы не¬
равенства

Глапа 4
СТЕРЕОМЕТРИЯ
§ 15. Тетраэдры
(см. Приложение Г: определения 10, 42;
теоремы 6, 64, 84, 86—89, 91, 92)
15.1. (НРБ, 66). Доказать, что для любого тетраэдра
можно построить треугольник, сторонами которого слу¬
жат 3 ребра тетраэдра, выходящие из одной его вершины.
15.2. (ЧССР, 67). Доказать, что если ребра тетраэдра
ABCD удовлетворяют равенствам
АВ2 + CD2 = АС2 + BD2 = AD2 + ВС2,
то по крайней мере одна из его граней является остро¬
угольным треугольником.
15.3. (Канада, 83). Верно ли, что если площади четы¬
рех граней одного тетраэдра равны площадям соответст¬
вующих граней другого, то объемы этих тетраэдров равны?
15.4. (ЧССР, 71). Доказать, что существует тетраэдр
ABCD, все грани которого являются подобными прямо¬
угольными треугольниками с острыми углами при вер¬
шинах А и В. Определить, какое из ребер этого тетра¬
эдра наибольшее, а какое—наименьшее, и найти длину
наименьшего ребра, если длина наибольшего равна 1.
15.5. (ГДР, 74). Определить, на сколько частей раз¬
бивают правильный тетраэдр шесть плоскостей, каждая
из которых проходит через одно из ребер и середину
противоположного ребра тетраэдра. Найти объем каждой
из частей, если объем тетраэдра равен 1.
15.6. (ЧССР, 76). Тетраэдры ABCD и A'B'C'D' рас¬
положены так, что прямые АА', ВВ', СС' и DD' парал¬
лельны, грани ABC и А'В'С' не имеют общих точек, а
вершины D	и	D'	лежат	в плоскостях А'В'С'	и	ABC	со¬
ответственно.	Доказать,	что	объемы этих	тетраэдров	оди¬
наковы.
15.7. (НРБ, 68). Внутри тетраэдра ABCD расположена
точка О так, что прямые АО, ВО, СО, DO пересекают
грани BCD, ACD, ABD, ABC тетраэдра в точках Аи В„
Си Dj соответственно, причем отношения
АО	ВО	СО DO
Ах0 '	ВгО	’ СгО ’ D,0
равны одному и тому же числу. Найти все значения, ко¬
торые может принимать это число.
47

15.8. (НРБ, 66). На ребрах АВ, AC, AD заданного
тетраэдра ABCD для каждого значения п (Е N выбираются
точки К„, Ln, Мп соответственно так, что
АВ = пАКп, AC = (n+l)ALH, ЛП = (п + 2)ЛМ„.
Доказать, что все плоскости KnLnMn проходят через
одну и ту же прямую.
15.9. (ПНР, 79). Доказать, что четыре прямые, соеди¬
няющие вершины тетраэдра с центрами окружностей, впи¬
санных в противоположные грани, пересекаются в одной
точке тогда и только тогда, когда три произведения длин
противоположных ребер равны между собой.
15.10. (НРБ, 76). Плоскость пересекает три ребра тет¬
раэдра, выходящие из одной вершины. Доказать, что эта
плоскость разбивает поверхность тетраэдра на части, про¬
порциональные объемам соответствующих частей тетра¬
эдра, тогда и только тогда, когда она проходит через
центр сферы, вписанной в тетраэдр.
15.11. (ЧССР, 68). Доказать, что если в тетраэдре
имеются две пары противоположных взаимно перпендику¬
лярных ребер, то середины всех его ребер лежат на одной
сфере.
15.12. (Жюри, Греция, 79). Доказать, что если пра¬
вильный тетраэдр с ребром а вписан в правильный тет¬
раэдр с ребром b так, что на каждой грани последнего
лежит ровно одна вершина вписанного тетраэдра, то 3а^Ь.
15.13. (ГДР, 83). В тетраэдре ABCD ребра AD, BD и
CD взаимно перпендикулярны, а их длины равны а, Ь, с
соответственно. Доказать, что для любой точки М, лежащей
на одной из сторон треугольника ABC, сумма S расстоя¬
ний от вершин Л, В и С до прямой DM удовлетворяет
неравенству
S < (/2 (а2 + Ь2 -Ь с2).
Определить, когда достигается равенство.
15.14. (СФРЮ, 73; Австрия — ПНР, 80). Доказать, что
для любой точки, лежащей внутри тетраэдра, сумма уг¬
лов, под которыми из этой точки видны его ребра, боль¬
ше 540°.
15.15. (НРБ, 76). Доказать, что расстояния от неко¬
торой точки пространства до каждой из четырех вершин
правильного тетраэдра с ребром 2 являются одновремен¬
но целыми числами тогда и только тогда, когда эта точка
совпадает с одной из вершин тетраэдра.
48

15.16.	(ЧССР, 73). Доказать, что для высот Л,- (*=*1,
2, 3, 4) любого тетраэдра и радиусов г{ вневписанных
сфер справедливо равенство
2 (^ + ^ + /i + i) = i+^ + i + i-
15.17*. (ПНР, 78). Доказать, что для высот hu h2, hs,
h4 любого тетраэдра и расстояний dL, d2, d3 между парами
его противоположных ребер справедливо равенство
hVK^hi + hi df + dj + dj-
15.18*. (Жюри, НРБ, 81). Сфера касается ребер АВ,
ВС, CD, DA тетраэдра ABCD в четырех точках, являю¬
щихся вершинами квадрата. Доказать, что если эта сфе¬
ра, кроме того, касается ребра АС, то она касается и
ребра BD.
15.19*. (НРБ, 81). Плоскости а, |3, у, б касаются опи¬
санной около тетраэдра ABCD сферы в точках А, В, С,
D соответственно. Доказать, что если линия пересечения
плоскостей а и Р лежит в одной плоскости с прямой CD,
то линия пересечения плоскостей у и 6 лежит в одной
плоскости с прямой АВ.
§ 16. Многогранники, сферы и другие множества
(см. Приложение Г: определения 11, 16;
теоремы 2, 10, 85, 87—89)
16.1. (ЧССР, 79). Рассматриваются кубы, центры ко¬
торых совпадают с центром симметрии заданного прямо¬
угольного параллелепипеда с ребрами а < b < с, а грани
параллельны граням последнего. Найти ребро куба, имею¬
щего наименьшую разность между объемами объединения
и пересечения с этим параллелепипедом.
16.2. (ГДР, 83). Доказать, что внутри куба с ребром
а можно разместить два правильных тетраэдра с ребром
а, не имеющих общих точек.
16.3. (СФРЮ, 73). В пространстве расположены 5 то¬
чек так, что никакие 4 из них не лежат в одной плос¬
кости. Доказать, что некоторая прямая, проходящая через
2 из них, пересекает плоскость, содержащую остальные
Зточки, внутри треугольника с вершинами в этих 3 точках.
16.4. (ВНР, 80). Пространство разбито на 5 непере-
секающихся непустых множеств. Доказать, что некоторая
49

пЛоскость имеет общие точки по крайней мере с 4 мно¬
жествами.
16.5. (Жюри, СССР, 83). Доказать, что при любом
разбиении пространства на 3 множества хотя бы одно из
множеств отличается тем, что в нем для каждого значе¬
ния а>0 можно выбрать 2 точки, расстояние между
которыми равно а.
16.6. (СРР, 80). Доказать, что для любых векторов
а1г а2, а3 справедливо равенство
з
У (е^! Н г2а2 + е3а3)2 = 8 2 «I.
в котором сумма слева берется по всем 8 различным на¬
борам чисел е,, е2, е3£{—1; 1}. Обобщить это утвержде¬
ние на случай любого числа n£N векторов а1,а2,
16.7. (ЧССР, 62). Через концы Л и В отрезка дли¬
ны а проведены прямые, перпендикулярные друг другу
и отрезку АВ. На этих прямых берутся точки С и D
соответственно так, чтобы точка пересечения отрезка CD
с плоскостью, проходящей через середину О отрезка АВ
перпендикулярно ему, была удалена от точки О на рас¬
стояние г. Доказать, что длина отрезка CD определяется
значениями а и г. Найти геометрическое место точек С.
16.8. (НРБ, 82). Сфера s радиуса г проходит через
центр сферы S радиуса R. Доказать, что если хорда АВ
сферы S касается сферы s в точке С, то
АС2 -f- ВС2 2R2 + г2.
16.9. (США, 82). Каждая из двух несовпадающих сфер
радиусов т! и г2 касается внутренним образом сферы S
радиуса R и проходит через точки А, В, С, расположен¬
ные так, что перпендикуляр к плоскости ЛВС, проходя¬
щий через точку Л, проходит и через центр сферы S.
Доказать, что rt + r2 = R. .
16.10. (СРР, 58). Через S и V обозначены площадь
поверхности и объем правильной /г-угольной пирамиды.
а) Для заданных значений п и S найти наибольшее
значение V.
б) Найти стороны оснований и высоты всех пирамид,
для которых п = 4, S=144, V = 64.
16.11. (НРБ, 82). Доказать, что при любом значении
п £ N, большем 1, среди всех правильных 2/г-угольных
призм Л1...Л2„Л;...Л'„ с фиксированным радиусом R
окружности, описанной около основания, наибольший
угол между диагональю АгАп+1 и плоскостью Л1Л3Л^+2
50

имеет призма, для которой
A1A[ = 2R cos (180°/2о).
16.12. (ВНР, 79). Доказать, что если в пирамиде
с равными боковыми ребрами любые соседние боковые
грани образуют равные двугранные углы, а основанием
служит многоугольник с нечетным числом сторон, то этот
многоугольник правильный.
16.13. (НРБ, 84). Основанием пирамиды SABCD слу¬
жит параллелограмм ABCD. Плоскость а пересекает пря¬
мые AD, SA и SC в точках Р, Q, R соответственно так,
что
АР	SQ	RC
AD	Si4	SC ’
причем все три точки A, S и С либо одновременно при¬
надлежат отрезкам PD, QA и SR соответственно, либо
одновременно им не принадлежат. Точка N является
серединой отрезка CD, а точка М на прямой SB распо¬
ложена так, что прямая MN параллельна плоскости сс.
Доказать, что геометрическим местом точек М при все¬
возможных положениях плоскости а является некоторый
отрезок длины (К5/2) SB.
16.14. (НРБ, 77). Площади оснований усеченной пира¬
миды равны Sx и S2, а площадь боковой поверхности
равна S. Доказать, что если некоторая плоскость, парал¬
лельная основаниям, делит пирамиду на две усеченные
пирамиды, в каждую из которых можно вписать сферу,
то
s=(Vs;+VX) (УХ+ УХУ-
16.15. (Англия, 68). Найти наибольшее число точек,
которые можно расположить на сфере радиуса 1 так,
чтобы расстояние между любыми двумя из них было:
а)	не меньше V 2; б) больше V2.
16.16. (ЧССР, 70). Найти все значения n£N, боль¬
шие 1, и гп > 0, для которых на сфере радиуса 1 можно
расположить непересекающиеся окружности С0, С*, ..., С„
радиуса гп каждая так, чтобы при любом значении
г = 1, .. -, п окружность Сt касалась окружностей С0 и
Pi+i	+ 1 —Cj).
16.17. (США, 79). Три окружности, лежащие на сфере
и имеющие общий с ней центр О, проходят через точку
51

А. На этих окружностях выбраны точки В, С, D соот¬
ветственно так, что /_ АОВ — 90°, а прямая ОВ является
биссектрисой угла COD. Доказать, что если лучи АВ',
AC, AD' касаются дуг АВ, AC, AD соответствующих
окружностей, то луч АВ' является биссектрисой угла
CAD'.
16.18. (Жюри, СССР, 82). На окружности одного
основания прямого кругового цилиндра взяты диамет¬
рально противоположные точки Л и В, а на окружности
другого основания—точка С, не лежащая на. плоскости
АВО. где О—середина оси цилиндра. Доказать, что сумма
двугранных углов трехгранного угла с вершиной О и
ребрами ОА, ОВ, ОС равна 360°.
16.19. (США, 81). Сумма величин плоских углов вы¬
пуклого многогранного угла равна сумме величин его
двугранных углов. Доказать, что этот угол является трех¬
гранным.
16.20. (Жюри, Бельгия, 79). Можно ли разбить
пространство на 1979 равных непересекающихся под¬
множеств?
16.21. (Англия, 70). Найти наименьшее число плоско¬
стей, разбивающих куб не менее чем на 300 частей.
16.22*. (СРР, 78). На плоскостях а и а', пересекаю¬
щихся по прямой I, выбрано по три точки: А, В, С и
А', В', С' соответственно. Плоскость ct'вращается вокруг
прямой /. Доказать, что если прямые АА', ВВ', СС
пересекаются в одной точке при некотором положении
плоскости а , то и при любом ее положении, отличном
от плоскости а, они также пересекаются в одной точке.
Найти геометрическое место этих точек пересечения.
16.23*. (ЧССР, 73). Рассматриваются повороты вокруг
различных осей в пространстве, переводящие вершину А
куба ABCDA'B'C’D'- в вершину В. Найти геометрическое
место точек поверхности этого куба, являющихся обра¬
зами вершины С при таких поворотах.
16.24*. (ВНР, 82). Куб в пространстве с прямоуголь¬
ной системой координат расположен так, что координаты
некоторых 4 его вершин, не лежащих в одной плоскости,
являются целыми числами. Доказать, что все вершины
куба имеют целые координаты.
16.25*. (Жюри, СФРЮ, 79). Доказать, что если прямо¬
угольный параллелепипед можно разбить на прямоуголь¬
ные параллелепипеды, каждый из которых имеет ребро
целочисленной длины, то и исходный параллелепипед
тоже имеет такое ребро.
52

Глава 5
АНАЛИЗ
§ 17. Последовательности
(см. Приложение Г: определения 2, 12, 14, 15, 18, 19;
теоремы 1, 2, 10, 16, 18, 21)
17.1.	(СФРЮ, 76). Вычислить сумму а1 + о2+ • • ■ +а99.
где обозначено
"	(n-fl)jC п _f_n \f п+1
17.2. (ЧССР, 72). Доказать, что существуют числа А
и В, удовлетворяющие при любом значении п С N равен¬
ству
ai-\-a2+ ■■■+ап = А tgn + Bn,
где обозначено
= (k — 1).
17.3. (Нью-Йорк, 74). Пусть
1-3-5 ... (2п— 1)	..
°п~	2-4-6	... 2n ’ n^N.
Найти lim ап.
п —*■ ес
17.4. (Нью-Йорк, 74). В последовательности положи¬
тельных чисел а„, а*, ... каждый из членов ап (п £ N)
равен либо ап_*/2, либо а„_,. Может ли эта последо¬
вательность иметь предел, принадлежащий интервалу
(0; 1)?
17.5. (США, 80; СФРЮ, 81). Для заданного натураль¬
ного значения п ^ 3 найти наибольшее возможное число
возрастающих арифметических прогрессий, состоящих из
трех членов, которые могут быть выбраны из какого-либо
набора, содержащего ровно п различных чисел.
17.6. (СФРЮ, 81). Числа 1, 9, 8, 1 являются соответ¬
ственно четырьмя первыми членами последовательности,
в которой каждый из последующих членов равен послед¬
ней цифре суммы четырех предшествующих ему членов.
Могут ли в этой последовательности встретиться числа 1,
2, 3, 4 идущими подряд?
17.7. (Австрия—ПНР, 80). Последовательность нату¬
ральных чисел at < а2 < а3 < ... удовлетворяет условиям
а!=1 и с„+1^2п при я £14. Доказать, что для любого
53

значения п £ N существуют члены ар и aq этой последо¬
вательности, для которых справедливо равенство ар—а=п.
17.8-. (ПНР, 79). Даны числа А > 1 и В > 1 и после¬
довательность [ап] (п £ N) чисел из отрезка [1; АВ].
Доказать, что существует такая последовательность {Ь„}
чисел из отрезка [1; А], что для любых т, п£ N выпол¬
нена оценка ат/а„^ВЬт/Ьп.
17.9. (Жюри, Франция, 82). Пусть все члены последо¬
вательностей {«„} и [Ьп\ —натуральные числа. Доказать,
что существует пара номеров р < q, для которых справед¬
ливы неравенства ap^.aq и Ьр ^ Ьд.
17.10. (Пекин, 64). Последовательность положительных
чисел Gi, а2, ... удовлетворяет неравенствам а* ^ ап—an+i
при л (Ё N. Доказать, что для любого значения n£N
имеет место оценка ап < 1/п.
17.11. (ММС, Финляндия, 80). Последовательность
чисел а0, а,, ..., ап задана следующим образом:
а0=1/2, Gft = aft_1+(l/n)al_1	(k=l,...,n).
Доказать, что 1 — 1/л < ап < 1.
17.12. (Австрия—ПНР, 80). Дана числовая последо¬
вательность {«„}, удовлетворяющая • неравенствам
|ак+т — ah—am|^l при k, т£ N. Доказать, что для
любых p,q £ N выполнено неравенство
10E-——L1	* I *
I Р 9 I Р ч'
17.13. (ПНР. 78). Для заданного числа а* £ R опреде¬
лим последовательность at, а2, — следующим образом:
I (1/2) (а„— 1/g„), если а„=^0,
0	,	если	а„ = 0,
при n£N. Доказать, что в этой последовательности
имеется бесконечно много неположительных членов.
17.14. (Англия, 80). Найти все значения c0€R. для
которых последовательность а0, ait ..., определенная
равенствами an+t = 2n—3ап при п £ Z+, возрастает.
17.15. (Австрия, 72; НРБ, 78). Доказать, что после¬
довательность ненулевых чисел щ, а2, ..., удовлетворяю¬
щая для некоторого числа а условиям
аи а2е Z, (af + al + a)/(a1a2)€Z, an+2 = (a*n+1-\-a)Jan
при n£N, состоит из целых чисел.
54

17.16. (ЧССР, 68). Доказать, что каждый член после¬
довательности
a„=((2 + /3)"-(2-K3)n)/(2/3)	(«С	Z)
является целым числом. Найти все значения п С Z, при
каждом из которых число ап делится на 3.
17.17. (ЧССР, 78). Доказать, что каждый член после¬
довательности
(5±р)" + (ЦР)"_2 (eeN)
является натуральным числом и представляется в' виде
5/п2 или т2 (т С N) при четном или нечетном п соответ¬
ственно.
17.18*. (Жюри, Англия, 82). Последовательность
о0, а,, ... удовлетворяет для некоторого параметра а С N
соотношениям
а0 = 0, «1=1, an+1 = 2an+(a—l)an_i
при n£N. Для фиксированного простого числа р0 > 2
найти наименьшее значение а, при котором верны два
утверждения: а) если р—простое число и р^р0, то число
ар делится на р; б) если р—простое число и р > р0, то
число ар не делится на р.
17.19*. (Англия, 78). Доказать, что существует ровно
одна последовательность целых чисел аи а2 удовлет¬
воряющая условиям
«! = 1, «2 > 1, «£+1 + 1 = апап+2 при п G N.
17.20*. (ЧССР, 70). Для заданного простого числа р
найти количество различных последовательностей натураль¬
ных чисел а0, аи ..., удовлетворяющих равенствам
Ж + Ж+-"+^ + Ж£- = 1 ПРИ n £ N-
а1 а2	ап	ап	+1
17.21*. (Англия, 83). Доказать, что для последователь¬
ности чисел (Фибоначчи) а1у а2, ..., заданной соотноше¬
ниями
«1 = а2=!. g«+2 = g«+i + g« ПРИ «CN,
существует единственная тройка чисел а, Ь, с С N, удов¬
летворяющая условиям: b < а, с < с и для любого зна¬
чения N число ап—nbcn делится на а.
55

§ 18. Экстремумы
(см. Приложение Г: определения 9, 15, 16; теоремы 10, 12, 14, 36)
18.1. (ГДР, 73). Найти все пары (х; у) положитель¬
ных чисел, на которых достигается наименьшее значение
функции
,,	. X* , у*	X2	У2 1 X . у
/(*> у)--£Г + -5Г—+7+Т*
и найти это наименьшее значение.
18.2. (Жюри, Швеция, 79). Найти наибольшее значе¬
ние произведения x2y2z2u при условии, что х, г/, z, и^Ои
2х + ху + z yzw = 1.
18.3. (ГДР, 78; ЧССР, 80). Для заданных чисел
«1 < «2 < • • • < ап определить, существуют ли точки х£ R,
в которых функция
/(*) = 2 I*—Я/1
1 = 1
принимает наименьшее значение. Если существуют, то
найти все такие точки, а также наименьшее значение
функции / (х).
18.4. (Жюри, ГДР, 79). Для заданного числа п ^2
найти наибольшее и наименьшее значения произведения
*1*2 • • • *«
при условии, ЧТО X,- ^ 1/п (* = 1,2, ..., я) и xf + x§ + ■ • •
■ • • + хп — Г
18.5. (Жюри, Швеция, 79). Для заданных чисел п ^ 2
П — 1
и а > 0 найти наибольшее значение суммы 2 *,*,+i при
1 = 1
условии, что х,^0 (1 = 1 п) и Xj-j- .. . +х„ = а.
18.6. (СРР, 79). Даны положительные числа п1<о2<...
... < ап. Для какой перестановки (Ьх; Ь2; ...; Ьп) этих
чисел произведение
II (ai+ Vb.)
i=l
максимально?
18.7. (ЧССР, 63). Для каждого значения k С N пред¬
ставить число 2k в виде суммы двух взаимно простых
чисел х и у так, чтобы произведение ху было наибольшим.
18.8. (ЧССР, 83). Для заданных чисел п С N и а С [0; п]
наити наиоольшее значение выражения
56
2 sin2x1-
i = i
при

условии, что
п
2 sin*xf = a.
1 = 1
18.9.	(СФРЮ, 74). Для каждого числа я £ N найти
наибольшее значение, которое принимает произведение
натуральных чисел с фиксированной суммой п.
18.10*. (Англия, 81). Найти наименьшее значение
величины | 12“—5й | при т,п£ N.
§ 19. Различные свойства функций
(см. Приложение Г: определения 2, 3, 6;
теоремы 27, 28, 30, 33, 34)
19.1. (ГДР, 83). Даны два положительных числа х*,
х2, а про функцию /: R—*■ R, заданную формулой
/ (х) = ах* + Ьх2 + с (где a, b, c£R, афО),
известно, что / (0) = / (хх) = 1 и /' (х2) = 0. Найти коэффи¬
циенты а, Ь, с.
19.2. (СРР, 81). Существует ли функция /: R—► R,
удовлетворяющая для всех х С R' неравенству
/(x*)-tf(x))*> 1/4
и не принимающая никакое значение более чем в одной
точке?
19.3. (ВНР, 79; Жюри, США, 79). Доказать, что если
функция /; R —R удовлетворяет для всех х, у С R нера¬
венствам
f(x)<x, /(х + yXf(x) + f(y),
то справедливо тождество
/ (х) = х, х С R.
19.4. (ГДР, 72). Дана функция
J 0	при	х = л/2 + &л, k£Z,
f(x) — | l/(2-f-tg2x) при остальных значениях х.
Доказать, что функция g (х) == / (х) + / (ах) периодична
тогда и только тогда, когда а С Q.
19.5. (Канада, 81). Пусть непрерывные функции /(х)
и g (х) удовлетворяют тождеству
/(£(*)) = £(/(*)). ХС R-
57

Доказать, что если уравнение f(x)=*g (х) не имеет дейст¬
вительных решений, то их не имеет также и уравнение
f(f (x)) = g(g(x)).
19.6. (СРР, 81). Пусть f: [0; + оо)—>-[0; + оо) — не¬
прерывная функция. Доказать, что
а) если lim /(/ (*))=» + со, то lirn f (х) = + со;
X —► + со	X	<х>
б) результат пункта а) не верен для функции
Ь (0; +оо)—v(0; +оо).
19.7. (СРР, 79). Доказать, что не существует непре¬
рывной функции /■ R—>- R, обладающей следующим свой¬
ством: число f (х) рационально при тех и только тех зна¬
чениях x£R, при которых Число f (х + 1) иррационально.
19.8. (Нью-Йорк, 79). Существует ли не равная кон¬
станте функция /: R —>- R, удовлетворяющая для всех
х, у С R неравенству
(f{x)-f(y))*^\x-y\s?
19.9. (Нью-Йорк, 76). Пусть непрерывная функция
fi [0; 1] —► [0; 1]
дифференцируема на интервале (0; 1), причем /(0) = 0,
/" (1) = 1. Доказать, что существуют такие числа a, b£ (0; 1),
что
афЬ и f' (a)f (b) = l.	I
19.10*. (Австралия, 82). Найти все числа d£(0; 1], !
обладающие следующим свойством: если f(x)—произволь- |
ная непрерывная функция, определенная при х£[0; 1],
причем /(0) = /(1), то сущертвует число хо£[0; 1—й],
для которого
f(x0) = f(x0 + d).	|
19.11*. (СРР, 78). Пусть функция fi R—>-R опреде- i
лена следующим образом: / (х) = 0, если х иррационально;
f (p/q) = l/q3, если р £Z, (Е N и дробь plq несократима.
Доказать, что эта функция дифференцируема в каждой
точке x^Vk, где k—натуральное число, не являющееся I
квадратом целого числа.
19.12*. (Жюри, ПНР, 76). Пусть / = (0; 1]. Для за¬
данного значения а £ (0; 1) определим функцию /: I—>-/
следующим образом:
( х + (1—а) для 0<х^а,

Доказать, что для любого интервала Jczl существует
такое число n£N, что пересечение fn(J)r\J не пусто.
19.13*. (Жюри, Швейцария, 77). Для заданной воз¬
растающей функции /: R —>R определим функциюg(х, у)
формулой
Пусть для всех у> 0 при л: = 0 и для всех у£(0; |л:|]
при хфО выполнены неравенства
2-1 <g(x, у) < 2.
Доказать, что при всех х £ R, у> 0 справедливы оценки
14-*<g(*, у)< 14.
§ 20. Функциональные уравнения
(см. Приложение Г: определения 5, 6, 18, 20;
теоремы 1, 3, 7, 16, 27, 28)
20.1. (Нью-Йорк, 78). Функция /: R—*-R удовлетво¬
ряет тождеству
X, yeR, х+у=£ 0.
Существует ли такое значение х£ R, для которого f (а) Ф0?
20.2. (НРБ, 68). Найти все функции f: R—>-R, удов¬
летворяющие тождеству
xf(y) + yf(x)z=(x + y)f{x)f{y),	х, у£ R.
20.3. (Жюри, ГДР, 82). Пусть М—множество функ¬
ций ft Z—>R, удовлетворяющих условию / (0)	0	и	тож¬
деству
f (п) f (т) = / (ti -j- т) -f / (п—т),	п,т£ Z.
Найти: а) все функции	для	которых	/	(1)	=	5/2;
б)	все функции f(n)£M, для которых /(l^J/S.
20.4. (Австрия — ПНР, 79). Найти все функции
f: Z+ —► R, удовлетворяющие тождеству
f (п + т) + f (п—т) = f (Зп),	n,m£Z+,	п	^	га.
20.5. (Нью-Йорк, 76). Функции f, g: R—»■ R непо¬
стоянны и удовлетворяют двум тождествам
f(x + y) = f{x)g (У) + g(x)f (у),
g(x + y) = g(x)g (у) f (х) / {у),
х, у С R. Найти все возможные значения / (0) и g (0).
69

20.6. (ММС, Люксембург, 80). Найти все функции
f; Q—>-Q, удовлетворяющие условию / (1) — 2 и тождеству
f(xy) = f(x)f{y)—f(x + y)+l,	х,у£ Q.
20.7. (СФРЮ, 83). Функция f: Z —*- R удовлетворяет
условиям
при n£Z. Доказать, что для любого значения я <100
справедливо равенство /(я) = 91.
20.8. (СРР, 79). Функции f,g,h: N —*- N удовлетво¬
ряют следующим трем условиям:
а)	функция h (я) не принимает никакое значение
более чем в одной точке я С N;
б) множество значений функции g(ti) есть N;
В) / («) = g (n)—h (я) + 1, я с N.
Доказать, что справедливо тождество /(я)= 1, я€ N.
20.9. (СРР, 78). Доказать, что существует функция
f: N —► N, удовлетворяющая тождеству
20.10.	(СРР, 78). Рассматриваются непостоянные функ¬
ции f (я, яг), определенные на множестве всех пар целых
чисел, принимающие целочисленные значения и удовлет¬
воряющие тождеству
/(я, m) = ^(f(n — 1, m) + f(n+ 1, m) + f(n, яг—1) +
ti,m£Z. Доказать, что: а) такие функции существуют;
б)	для любого значения k С Z каждая такая функция при¬
нимает значения как большие k, так и меньшие k.
20.11.	(Австрия—ПНР, 78). Для заданного подмно¬
жества S множества пар целых чисел назовем функцию
f: S—>S универсальной, если она обратима и для любой
пары (я; яг) С S удовлетворяет условию
f(n, яг)С {(я— 1; яг); (я+1; яг); (я; яг—1); (я; ягД- I)}.
Доказать, что если существует хотя бы одна универсаль¬
ная функция, то существует универсальная функция
f(n, яг), удовлетворяющая тождеству
я—10,	если	я> 100,
/ (f (n-f 11)), если я <100,
+ f(n, яг+1)),
/ (f («» т)) = («; т)>	(,«;	т)	€	s-
6°.

20.12*. (США, 82). Найти все пары ненулевых целых
значений т^п, удовлетворяющих неравенству т-\-пф 0
и тождеству
fm(x,y)fn(x,y) = fm+«(X'У), х, у £ R, ху (х + у) ф 0,
где обозначено
/* (*. У) = (**+ Ун + (-1)* (х + y)k)/k.
Указание. Пары т — 2, п = 3 и т — 2, ц = 5 тре¬
буемым условиям удовлетворяют.
20.13*. (Жюри, ПНР, 77). Доказать, что если функ¬
ция f(x, у), определенная на множестве всех пар рацио¬
нальных чисел и принимающая только положительные
значения, удовлетворяет трем тождествам
f(xy, z) = f(x, z)f(y, z),
f(z, xy) = f(z, x)f(z, y),
f(x, 1—x)= 1, x, y, z£ Q,
то справедливы тождества
f(x, x)ss 1, f(x, —x)= 1, f(x, y)f(y, X)= 1, x, y£Q.
20.14*. (Жюри, СФРЮ, 79). Доказать, что любая
функция f: R—> R, удовлетворяющая одному из тождеств
f(x + y) = f(x) + f(y), х, у£ R,
f(xy + x + y) = f(xy) + f(x) + f(y), х, у£ R,
удовлетворяет и другому.
20.15.	(Австрия, 75). Найти все непрерывные функ¬
ции /: (1; + оо)—> R, удовлетворяющие тождеству
f (ху) = xf (у) + yf (х), х, у > 1.
20.16*. (СРР, 82). а) Доказать, что если непрерывная
функция f: R—»-R удовлетворяет тождеству
f(f(f{x))) = x, x£R,
то при любом значении x£R справедливо равенство
f(x) = x.
б)	Привести пример (разрывной) функции g: R —<• R,
удовлетворяющей условиям
g(х)фх и §(§ (g(x))) = *, x£R.
20.17*. (Жюри, Франция, 79). Найти все монотонные
обратимые функции /: R—»• R, удовлетворяющие тождеству
!(x)-\-f~1(x) — 2x, x£R.
61

20.18*. (Нью-Йорк, 77). Найти все дифференцируемые
функции /: R —»- R, удовлетворяющие тождеству
20.19.	(Бельгия, 77). Найти все бесконечно дифферен¬
цируемые функции /: R —>- R, удовлетворяющие тождеству
20.20.	(Англия, 69). Доказать, что если не равная
тождественно 0 функция /: R —>- R удовлетворяет тожде¬
ству
и дифференцируема в точке х = 0, то она бесконечно
дифференцируема в любой точке х 6 R.
§ 21. Корни многочленов
(см. Приложение Г: определения 18, 20, 22 — 24, 26, 28 — 30, 32;
теоремы 2, 6, 28, 35, 38, 40, 41, 45—51, 53, 55—57, 59 —61, 63)
21.1.	(НРБ, 80). Доказать, что для корней xlt х2
многочлена
выполнено неравенство xf + xf ^ 2 +2.
21.2. (НРБ, 61). Найти все пары действительных чи¬
сел р, q, для которых многочлен х4 + рх2 + q имеет 4
действительных корня, образующих арифметическую про¬
грессию.
21.3. (Англия, 67). Доказать, что если корнями мно¬
гочлена х2 + рх-1-1 являются числа а и Р, а корнями
многочлена x2-\-qx-1- 1 — числа у и 6, то справедливо ра¬
венство
21.4.	(ГДР, 70). Доказать, что для любых ненулевых
значений а, |3 корни хи х2, х3 многочлена
f(x + y) = f(x) + f(y) + 2xy, х, у€ R.
f{x)f{y) = f(x + y), х, у£ R,
Глава 6
МНОГОЧЛЕНЫ
х2 + рх—р-,	где R, РФ 0,
(а—у)(Р—у)(а + 8) (|3 + 6) = <72—р2.
62

г
удовлетворяют равенству
(хг + х2 + х3) ( J- + -±- + ■-j- ) = — 1.
21.5. (Австрия, 83). Найти все значения а, при кото¬
рых корни х,, х2, х3 многочлена х3—6х2-\-ах-\-а удов¬
летворяют равенству
(*i — З)3 + (х2-— З)3 + (х3—З)3 = 0.
21.6. (Жюри, Канада, 82). Пусть один из корней мно¬
гочлена
Р (х) = x3 + ax2 + bx + c, где a,b,c£ Z,
равен произведению двух других. Доказать, что число
2Р(—1) делится на число Р(1) + Р(—1)—2(1+Р(0)).
21.7. (США, 77). Пусть а и b—два из четырех кор¬
ней многочлена х* + х3— 1. Доказать, что ab—корень
многочлена хв + х4 + х3—х2—1.
21.8. (СФРЮ, 81). Про целые числа а, Ь, с известно,
что а > 0, а многочлен ах2 + Ьх -]- с имеет два различных
корня на интервале (0; 1). Доказать, что а ^5. Найти
хотя бы одну пару чисел Ь, с при а = 5.
21.9. (ЧССР, 67). Числа а, Ь, с являются тремя из
четырех корней многочлена х4—ах3—bx + с. Найти все
такие тройки чисел а, Ь, с.
21.10. (ЧССР, 54). Доказать, что комплексные числа
а и b удовлетворяют условию а3 — 2ЬфО тогда и только
тогда, когда корни многочлена x2-j-ах + Ь образуют на
комплексной плоскости две вершины равнобедренного
прямоугольного треугольника, у которого вершина пря-
I мого угла расположена в начале координат.
21.11. (ВНР, 83). Многочлен
I	Р	(х) = х" + aiXn~x + ... + ап_1х + 1
с неотрицательными коэффициентами аи ..., ап_f имеет
п действительных корней. Доказать, что
Р (2) > Зп.
21.12. (НРБ, 84). Многочлен
I
^	ахп—ахп~г + с2хп~2 + . .. + си_2х2—n2bx + b
имеет ровно п положительных корней. Доказать, что все
. эти корни равны между собой.
63

21.13. (НРБ, 83). Могут ли многочлены
хъ—х—1 и х2 + ах-\-Ь, где а, b£Q,
иметь общие комплексные корни?
21.14. (Сингапур, 78). Для некоторого многочлена
Р (х) степени п и некоторых чисел а < Ь выполнены не¬
равенства
Р (а) <0,	—Р’ (а) < 0, Р" (а)< 0	(—1)"	Р<"> (а) < О,
Р(Ь)> 0, Р'(Ь)>0, Р"(Ь)>0, ..., Рм ф) > 0.
Доказать, что все действительные корни многочлена Р (х)
принадлежат интервалу (а; Ь).
21.15. (ГДР, 70). Доказать, что для любого значения
/z£Z + многочлен
/п(л:)=1+-': + '2Г+* - *
не может иметь более одного действительного корня.
21.16*. (ГДР, 69; ГДР, 71). Доказать, что если мно¬
гочлен Р (х) степени п с действительными коэффициен¬
тами не имеет действительных корней, то многочлен
Q(x) = P (х) + аР' (х) + ... + апР1п) (х)
при любом значении а£ R тоже не имеет действительных
корней.
21.17*. (ПНР, 79). Доказать, что для любого много¬
члена Р (х) степени п > 1, имеющего п различных дей¬
ствительных корней Xi, х2,- ..., х„, справедливо равенство
 !	|	! l _]	!— = о.
21.18*. (Нью-Йорк, 75). Пусть Р (х) — многочлен с
действительными коэффициентами, все корни которого
являются чисто мнимыми числами. Доказать, что все
корни многочлена Р' (х), кроме одного, являются также
чисто мнимыми.
21.19*. (СРР, 78). Доказать, что ненулевые многочле¬
ны Р и Q с комплексными коэффициентами имеют оди¬
наковые корни (одинаковой кратности) тогда и только
тогда, когда функция ) (z) = | Р (z) |—| Q (z) | имеет посто¬
янный знак во всех точках z С С, в которых она отлична
от нуля.

§ 22. Делимость и равенство многочленов
(см. Приложение Г: определения II, 22—33;
теоремы 2, 4, 24, 35 — 47, 49 — 55, 57, 68, 63)
22.1. (Нью-Йорк, 73; Бельгия, 81). Доказать, что для
любого значения n£Z+ многочлен (х+l)2,,+l 4-х"+* де¬
лится на многочлен х2-Ьх+1.
22.2. (СРР, 62). Доказать, что при любых значениях
«€ N и а б R, удовлетворяющих условиям пф 1 и sin а Ф
Ф 0, многочлен
Р (x) = x”sina—xsin/ia + sin(п — 1)а
делится на многочлен
Q (х) = х2—2х cos a + 1.
22.3. (СРР, 66). Найти все многочлены R(x) степени
меньше 4, для каждого из которых существует много¬
член Р (х), удовлетворяющий тождеству
7 sinsi / + 8 sin18 i — 5 sin61 cos41—10 sin71 + 5 sin51—2 ss
esP (sin t) (sin41—(1 +sin t) (cos21—2)) + R (sin t),	/€ R-
22.4. (США, 77). Найти все пары чисел т, п£М,для
которых многочлен 1 + хп + х2" + ... 4- хтп делится на
многочлен 1 + х + х2 + ... + хт.
22.5. (США, 76). Пусть многочлены Р (х), Q(x), R (х)
и S (х) удовлетворяют тождеству
Р (х5) + xQ (х6) + x2R (X6) S3 (х4 + X3 + х2 4- х + 1) S (х).
Доказать, что многочлен Р (х) делится на многочлен
х—1.
22.6. (Нью-Йорк, 75). Найти все многочлены Р(х),
удовлетворяющие условию Р(0) = 0 и тождеству
P(Jt) = i.(P(x+1)4-P(x— 1)), x6R.
22.7. (ГДР, 77). Найти все многочлены Р (х), удов¬
летворяющие тождеству
хР (х—1) = (х—2)Р(х),	xgR.
22.8. (Нью-Йорк, 76). Найти все многочлены Р(х),
удовлетворяющие тождеству
(X— 1)Р(х+ 1)—(х4-2)Р(х) = 01 x€R.
3 Под ред. И. Н. Сергеева	65

22.9. (СРР, 80). Найти все ненулевые многочлены
Р(х), удовлетворяющие тождеству
Р (X*) ^ (Р (х)У,	*<Е R
22.10. (НРБ, 76). Найти все ненулевые многочлены
Р (х), удовлетворяющие тождеству
Р(х*—2х) = (Р{х—2))2,	x€R
22.11. (Жюри, НРБ, 79). Найти все ненулевые мно¬
гочлены Р(х) с действительными коэффициентами, удов¬
летворяющие тождеству
Р(х)Р(2х3)^Р(2ха + х),	*€R.
22.12. (СРР, 78). Доказать, что для любого много¬
члена Р (х) ф х и любого числа п 6 N многочлен
Q„W = P^M>(x)...))-x
П
делится на многочлен Qx (х) = Р (х)—х.
22.13. (СРР, 78). Доказать, что если многочлены
Р(х), Q (х), R (х) третьей степени с действительными ко¬
эффициентами удовлетворяют неравенствам Р (x)^LQ (х) ^
^ R (х) при всех значениях х С R и хотя бы в одной
точке x0 6 R выполнено равенство Р (х0) = R (х0), то для
некоторого числа &€[0; 1] справедливо тождество
Q (x)==kP (x) + (l—k)R (х), х€ R.
Можно ли утверждать то же самое для многочленов чет¬
вертой степени?
22.14. (Жюри, ВНР, 79). Дан многочлен Р (х) — ax2 +
-\-bx-\-c, где афО. Доказать, что для любого числа
п € N не может существовать более одного многочлена
Q (х) степени п, удовлетворяющего тождеству Q(P(x)) ^
^P(Q(x)),	*€R.
22.15. (СРР, 79). Доказать, что многочлен Р (г) пред¬
ставляет собой четную функцию от z£C тогда и только
тогда, когда существует многочлен Q (г), удовлетворяю¬
щий тождеству
P(z) = Q(z)Q(—2),	z€C.
22.16. (Жюри, ВНР, 79). Доказать, что если много¬
член Р(х) с действительными коэффициентами принимает
при всех х С R только неотрицательные значения, то он
66

представим в виде
/>(х) = <й(*)+...+<й(*),
где Qi(jc) Qn (х)— некоторые многочлены с действи¬
тельными коэффициентами.
22.17*. (ВНР, 76; Жюри, Швеция, 76). Пусть много¬
член Р (х) с действительными коэффициентами удовлет¬
воряет неравенству Р (х) > 0 при всех значениях х > 0.
Доказать, что существуют многочлены Q (х) и R (х) с не¬
отрицательными коэффициентами, для которых справед¬
ливо тождество
P(x) = Q(x)/R(x).
22.18*. (Жюри, ГДР, 83). Пусть А (л)—множество
многочленов вида
Р (х) = а0 + afx+ - • • + апхп,
где 0 < су, = ап < а± = а„_г < ... <afn/2] = сц(п+1)/2]. До¬
казать, что если Р (х) (Е А (л) и Q (х) € А (т), то многочлен
Р (х) Q (х) принадлежит множеству А (т + п).
22.19*. (Жюри, ВНР, 77). Для каких' значений n£N
существуют ненулевые многочлены Р и Q от л перемен¬
ных с целыми коэффициентами, удовлетворяющие тож¬
деству
(Xj х2 ... Xn) Р (Xj, х%, . •., Хи) — Q (xi, х2, I *., хй),
Xi, х2, ... л хп ^ R?
22.20*. (Жюри, 81). Пусть для многочленов Р(х),
Q(x) степени больше 0 обозначено
Рс = {г€С|Р(г) = с}, Q, = {z<EC|Q(z)=c}.
Доказать, что если P0 = Qo и Pi = Qu то P(x)=Q(x),
x^R.
22.21*. (ПНР, 78). Доказать, что если многочлены
Р(х, у), Q (х, у), R (х, у) степени меньше m £ N удовлет¬
воряют тождеству
х2тР(х, y) + yzmQ(x, у) = (х + у)2т R (х, у), х, R,
то
Р(х, y) = Q(x, y)~R(x, у) = 0.
3*	67

§ 23. Различные свойства многочленов
(см. Приложение Г: определения 10, 18— 20, 28 — 32;
теоремы 2, 4, 17, 18, 27, 45—50, 52, 62)
23.1. (СРР, 62). При каких ограничениях на целые
числа р и q:
а) многочлен P(x) — x* + px + q принимает при всех
x£Z четные (нечетные) значения;
б) многочлен Q (х) = х3 -\- рх + q принимает при всех
x£Z значения, делящиеся на 3?
23.2. (ГДР, 83). Доказать, что многочлен
п / \	1 «	I _ , 13 -	82 . , 32
^(х)~630*	21	Х ^ЗО’*'"	63 "^ЗБ*
при всех x£Z принимает целые значения.
23.3. (ЧССР, 62). Найти все значения x£Z, при ко¬
торых многочлен 2х*—х—36 принимает значения, рав¬
ные квадратам простых чисел.
23.4. (СРР, 75). Для заданных чисел р, q £ R найти
все значения, которые многочлен Р (х) — х2 +рх+q при¬
нимает при х^(—1; 1].
23.5. (Пекин, 63). Многочлен Р(х) с целыми коэффи¬
циентами принимает значение 2 при четырех различных
значениях x£Z. Доказать, что ни при каких x£Z этот
многочлен не принимает значений 1, 3, 5, 7 и 9.
23.6. (Англия, 80). Найти хотя бы одно множество
М, состоящее из 7 последовательных натуральных чисел,
для которого существует многочлен Р (х) пятой степени
со следующими свойствами!
а) все коэффициенты многочлена Р (х)—целые числа;
б) для пяти чисел k£M, включая наименьшее и наи¬
большее числа, выполнено равенство Р (k) = k;
в) P(k) — 0 для одного числа k(tM.
23.7. (ГДР, 74). а) Доказать, что не существует мно¬
гочлена Р (х), для которого при любом xgR выполнены
неравенства; 1) Р' (х) > Р" (х) и 2) Р (х) > Р" (х).
б) Будет ли верно утверждение а), если неравенство
1)	заменить неравенством 1') Р (х) > Р' (х)?
23.8. (СРР, 82). Пусть заданы многочлены Рв (х),
Pi (х), ..., Рп (х) с действительными коэффициентами и
числа ai, ..., a„6R. Доказать, что если функция
/(*) = *•(*)+ 2 ak [ Pk (х) |
*=i
68

не принимает никакое значение более чем в одной точке
x£R, то множество всех ее значений есть R.
23.9. (Жюри, СРР, 83). Пусть {ап} — последователь¬
ность чисел (Фибоначчи), определяемая равенствами щ =
— а2— 1, an+2 = an+i + ап (п € N). Доказать, что если
многочлен Р (х) степени 990 удовлетворяет условиям
Р (6) = ak при 6 = 992, ..., 1982, то Р (1983) = йшз— 1.
23.10. (Англия, 78). Доказать, что:
а) для любого п g N существует многочлен Рп (х) сте¬
пени п с целыми коэффициентами, удовлетворяющий
тождеству
2 cos nt = Рп (2 cos /), /CR;
б) для любого «CQ число cosan либо совпадает с
одним из чисел 0, ±1/2, ±1, либо иррационально.
23.11. (Финляндия, 80). Пусть на координатной пло¬
скости задана кривая, являющаяся графиком некоторого
многочлена
P(x) = x* + px? + qx3-\-rx + s (р, q, г, s£R).
Прямую на этой плоскости назовем горизонтальной, если
она параллельна оси абсцисс и пересекает кривую в че¬
тырех точках А, В, С, D (перечисленных по порядку
слева направо). Если, кроме того, длины отрезков АВ,
АС и AD могут являться длинами сторон некоторого
треугольника, то такую прямую назовем триангулярной.
Доказать, что возможны только два случая: либо все
горизонтальные прямые триангулярны, либо все они не
являются триангулярными.
23.12. (НРБ, 77). Пусть Q(x)—ненулевой многочлен.
Доказать, что для каждого ngZ+ многочлен Р (х) =
= (х—1)'! Q (х) имеет не менее п + 1 ненулевых коэффи¬
циентов.
23.13*. (ЧССР, 74). Пусть М — множество всех мно¬
гочленов вида
Р (х) = йх3 + fcx2 + сх + d (а, Ь, с, dgR),
удовлетворяющих неравенству |Р(х)|^1 при х£ [—1; 1].
Доказать, что некоторое число k осуществляет оценку
|aj^6 для всех многочленов Р(х)£М. Найти наимень¬
шее значение k.
23.14*. (Жюри, Финляндия, 83). Пусть р и q—про¬
извольные натуральные числа. Доказать, что существует
такой многочлен Р (х) с целыми коэффициентами, что для
69

всех значений из некоторого интервала /cR длины l/q
выполнено неравенство |Р(*)—p/q |< l/q2.
23.15. (ГДР, 80). Найти все пары многочленов Р (х),
Q (х) третьей степени с действительными коэффициентами,
удовлетворяющие четырем условиям:
а) оба многочлена в каждой из точек х=1, 2, 3, 4
принимают значение 0 или 1;
б) если	Р (1) = 0	или Р(2)=1,	то	Q(1) = Q(3)=1;
в) если	Р (2) = 0	или Р (4) = 0,	то	Q (2) = Q (4) = 0;
г) если	Р (3) = 1	илиР(4)=1,	то	Q(1) = 0.
23.16. (США, 75). Многочлен	Р (х) степени п удов¬
летворяет равенствам Р (k) = h/(k-\- 1) при k = 0, 1, п.
Найти Р(п + 1).
23.17. (Жюри, 81). Многочлен Р (х) степени п удов¬
летворяет равенствам Р (&) = 1/С*+1 при k — 0, 1, ..., п.
Найти Р (n+ 1).
23.18*. (Жюри, СРВ, 77). Пусть заданы целые числа
хв < *i < .. • < хп. Доказать, что среди значений много¬
члена хп + а1хп~1 + ... + ап в точках х0, хи ..., хп най¬
дется такое число, которое по модулю не меньше
чем п\/2".
23.19*. (Жюри, ВНР, 79). Многочлен Р (х) имеет сте¬
пень, не большую 2п. Известно, что для каждого целого
££[—п\ п\ выполнено неравенство |Р(^)|^1. Доказать,
что для любого числа х£[—п\ п] справедлива оценка
|Р(х)|<22п.
Г лава 7
КОМБИНАТОРИКА
§ 24. Множества и подмножества
(см. Приложение Г: определения 1—4, 11; теоремы I, 97)
24.1. (ЧССР, 73). Сколько различных пар непересе-
кающихся подмножеств имеет множество, состоящее из п
элементов?
24.2. (ПНР, 78). Множество X состоит из п элемен¬
тов. Для двух подмножеств Аи Л2<=Х сосчитано число
элементов множества А1П А2. Доказать, что сумма всех
полученных чисел равна п-4п~г.
24.3. (Нью-Йорк, 78). Про числа п > 3, k =
= j^-g-n(n+ l)j и множество Хп, состоящее из п(п+ 1)/2
элементов, известно, что k элементов этого множества

имеют синий цвет, k элементов—красный цвет, а все
остальные элементы—белый цвет. Доказать, что множе¬
ство Хп можно разбить на п попарно непересекающихся
подмножеств Alt ..., А„ так, чтобы для любого значе¬
ния т = 1, ..., п подмножество Ат имело ровно т эле¬
ментов и причем одного цвета.
24.4. (СФРЮ, 72). Для каждого значения п g N найти
наибольшее число /г £ N, обладающее следующим свойст¬
вом: в множестве, состоящем из п элементов, можно вы¬
брать k различных подмножеств, любые два из которых
имеют непустое пересечение.
24.5. (Англия, 76). Пусть в конечном множестве X
выбрано 50 подмножеств Аи ..., As0, каждое из кото¬
рых содержит больше половины элементов множества X.
Доказать, что можно найти подмножество ВаХ, содер¬
жащее не более 5 элементов и имеющее хотя бы один
элемент, общий с каждым из множеств Аи ..., ЛБ0.
24.6. (Австрия—ПНР, 78). Дано 1978 множеств, каж¬
дое из которых имеет по 40 элементов. Известно, что
любые два из этих множеств имеют ровно один общий эле¬
мент. Доказать, что существует элемент, принадлежащий
всем 1978 множествам.
24.7. (Пекин, 63). Множество из 2" элементов разбито
на попарно непересекающиеся подмножества. Рассматри¬
вается операция, состоящая в переводе некоторых эле¬
ментов из одного подмножества в другое, причем число
переводимых элементов должно совпадать с числом эле¬
ментов во втором множестве (которое должно содержать
элементов не больше, чем первое). Доказать, что с по¬
мощью конечного числа таких операций можно получить
подмножество, совпадающее с исходным множеством.
24.8. (Жюри, ЧССР, 79). Пусть М—подмножество
множества всех пар натуральных чисел i < k, не пре¬
восходящих заданного натурального числа п ^2. При
этом, если пара t < k принадлежит множеству М, то ни¬
какая пара k < m ему не принадлежит. Какое наиболь¬
шее число пар может быть в множестве Л4?
24.9*. (Жюри, Бельгия, 79). Множество X состоит из
п элементов. Какое наибольшее число трехэлементных
подмножеств можно выбрать в X так, чтобы любые два
из них имели ровно один общий элемент?
24.10*. (США, 79). В множестве, состоящем из п^5
элементов, выбрано n+ 1 различных трех элементных под¬
множеств. Доказать, что найдутся два выбранных под¬
множества, имеющих ровно один общий элемент.
71

24.11*. (СРР, 78). Множество X разбито на попарно
непересекакяциеся подмножества Alt ..., Ап, а также
разбито на попарно непересекающиеся подмножества
В,, ..., В„. Известно, что объединение А ,■ и Вt любых
непересекающихся подмножеств Л,-, Bf (1	^ п, 1
^Ljk^n) содержит не менее п элементов. Доказать, что
число элементов множества X не меньше п*/2. Может ли
оно быть равным п2/2?
§ 25. Задачи с использованием графов
(см. Приложение Г: определение 43; теоремы 1, 2)
25.1. (Англия, 72). На множестве S введено отноше¬
ние —f, которое выполнено для пар элементов из мно¬
жества S и обладает следующими свойствами: 1) для
любых различных элементов a, b£S выполнено ровно
одно из отношений а—>-Ь или b—*а\ 2) для любых трех
различных элементов a, b, c$S выполнение отношений
а—+Ь и b—>с влечет за собой выполнение отношения
с—*а. Каково наибольшее число элементов, которое мо¬
жет содержать множество S?
25.2. (США, 82). В обществе, состоящем из 1982 че¬
ловек, среди любых четырех человек можно выбрать по
крайней мере одного, знакомого с остальными тремя. Ка¬
ково минимально возможное количество людей, которые
знакомы со всеми?
25.3. (НРБ, 78). В компании, состоящей из пяти че¬
ловек, среди любых трех человек найдутся двое, кото¬
рые знают друг друга, и двое, незнакомых друг с дру¬
гом. Доказать, что компанию можно рассадить за круглым
столом так, чтобы по обе стороны от каждого человека
сидели его знакомые.
25.4. (США, 78). Девять математиков встретились на
международной конференции и обнаружили, что среди
любых трех из них по меньшей мере двое говорят на
одном языке. Кроме того, каждый математик может го¬
ворить не более чем на трех языках. Доказать, что хотя
бы три из них говорят на одном и том же языке.
25.5. а) (Англия, 80). В комнате находится 10 человек,
причем среди любых трех из них есть двое знакомых
между собой. Доказать, что найдутся четыре человека,
любые два из которых знакомы друг с другом.
б)	(Жюри, ПНР, 77). Останется ли верным утвержде¬
ние п.а), если в нем число 10 заменить на 9?
72

25.6. (НРБ, 81; США, 81). В некоторой стране любые
два города связаны друг с другом непосредственно одним
из следующих средств сообщения: автобусом, поездом или
самолетом. Известно, что не существует города, обеспе¬
ченного всеми тремя видами транспорта, и в то же время
не существует таких трех городов, любые два из которых
связаны одним и тем же средством сообщения. Найти
наибольшее возможное количество городов в этой
стране.
25.7. (СФРЮ, 75). В некотором обществе любые два
знакомых не имеют общих знакомых, а любые два незна¬
комых имеют ровно двух общих знакомых. Доказать,
что в этом обществе все имеют одинаковое число зна¬
комых.
25.8. (ВНР, 77). В каждой из трех школ учится по
п человек. Любой ученик имеет в сумме п + 1 знакомых
учеников из двух других школ. Доказать, что можно
выбрать по одному ученику из каждой школы так, чтобы
все трое выбранных учеников были знакомы друг с другом.
25.9*. (Австрия, 73). В пространстве даны 2п различ¬
ных точек Аи Аг, ..., Л2л(п> 1). Никакие три из них
не лежат на одной прямой. Пусть М—множество из (п24-1)
отрезков, концами которых являются данные точки. До¬
казать, что существует хотя бы один треугольник с верши¬
нами в некоторых точках Аг, As, At, все стороны кото¬
рого принадлежат множеству М. Доказать, что если число
элементов множества М не превосходит п2, то такого тре¬
угольника может и не существовать.
25.10*. (СРР, 78). На вечере собралось несколько
юношей и девушек. При этом оказалось, что если выбрать
любую группу юношей, то число девушек, знакомых по
крайней мере с одним из юношей этой группы, будет не
меньше числа юношей в группе. Доказать, что все юноши
одновременно смогут танцевать каждый в паре со знако¬
мой девушкой.
25.11*. (Жюри, Австралия, 83). Некоторые из городов
Pi, • • •. Асйз соединены попарно некоторыми авиалиниями,
принадлежащими компаниям Alf ..., А1В. Известно только,
что из любого города можно перелететь в любой другой
без пересадок и что каждая авиалиния действует в обоих
направлениях. Доказать, что (как бы ни были города
соединены авиалиниями) существует хотя бы одна компа¬
ния, которая может обеспечить путешествие с началом
и концом в одном и том же городе и с нечетным числом
используемых авиалиний.
73

§ 26. Различные комбинаторные задачи
(см. Приложение Г: определения 16, 18, 35, 43, 44;
теоремы 1, 2, 6, 10, 93—97)
26.1. (СФРЮ, 75). Г1о кругу написаны в произвольном
порядке четыре единицы и пять нулей. Над ними произ¬
водится следующая операция: между одинаковыми цифрами
пишется нуль, а между разными—единица, после чего
первоначальные цифры стираются. Затем такая же опе¬
рация производится над полученными цифрами и т. д.
Доказать, что после нескольких таких операций невоз¬
можно получить 9 нулей.
26.2. (Жюри, НРБ, 79). На клетчатой бумаге отмечены
произвольные п клеток. Доказать, что из них всегда
можно выбрать не менее чем п/4 клеток, попарно не со¬
прикасающихся друг с другом (соприкасающимися счи¬
таются клетки, имеющие хотя бы одну общую вершину).
26.3. (СФРЮ, 81). Мышка грызет куб сыра с ребром 3,
разбитый на 27 единичных кубиков. Когда мышка съедает
какой-либо кубик, она переходит к другому кубику, имею¬
щему общую грань с предыдущим. Может ли мышка съесть
весь куб, кроме центрального кубика?
26.4. (ЧССР, 77). На прямой отмечены п различных
точек Ait А2, Ап(п^4). Каждая из этих точек по¬
крашена в один из четырех цветов, причем все четыре
цвета присутствуют. Доказать, что существует отрезок
прямой, содержащий ровно по одной точке двух цветов
и по крайней мере по одной точке двух оставшихся цветов.
26.5. (СРР, 78). На плоскости дано множество М, со¬
стоящее из п точек, никакие три из которых не лежат
на одной прямой. Каждому отрезку с концами из М постав¬
лено в соответствие либо число +1, либо число — I, причем
число отрезков, которым соответствует число —1, равно т.
Треугольник с вершинами из М назовем отрицательным,
если произведение трех чисел, соответствующих его сто¬
ронам, равно —1. Доказать, что число отрицательных
треугольников имеет ту же четность, что и произведение пт.
26.6. (Пекин, 64). На кольцевой дороге расположены п
заправочных станций, содержащие вместе такое количе¬
ство бензина, которого хватает для поездки одного авто¬
мобиля по всему кругу ровно один раз. Доказать, что
автомобиль с пустым баком (неограниченной вместимости)
может начать движение с одной из заправочных станций
(предварительно заправившись на ней) и совершить пол¬
ную поездку по кругу.
74

26.7. (СФРЮ, 74). На шахматной доске размером 8x8
стоят 8 белых фишек на первой горизонтали и 8 черных —
на восьмой. Игроки по очереди (начинают белые) делают
ходы, состоящие в перемещении одной из своих фишек
по вертикали на одну или несколько клеток вперед или
назад. Запрещается снимать фишки с доски, ставить фишку
на клетку, занятую фишкой противника, или перепрыги¬
вать через нее. Проигрывает тот, кто не может сделать
очередного хода. Доказать, что черные могут ходить так,
чтобы наверняка выиграть.
26.8. (СФРЮ, 83). Прямоугольная полоса размером
1Хп(п^4) составлена из единичных полей, занумерован¬
ных числами 1, 2, ..., п. На полях с номерами п—2,
п—1, п стоит по одной фишке. Двое играют в следующую
игру: каждый игрок своим ходом может перенести любую
фишку на любое свободное поле с меньшим номером.
Проигрывает тот, кто не может сделать очередного хода.
Доказать, что начинающий может ходить так, чтобы на¬
верняка выиграть.
26.9. (СФРЮ, 83). «Дельфин»—фигура, которая ходит
на одно поле вверх, вправо или по диагонали налево
Рис. 1
вниз, как показано на рис. 1. Может ли «дельфин», на¬
чиная из левого нижнего угла доски размером 8x8,
обойти всю эту доску, побывав в каждой клетке ровно
по одному разу?
75

26.10. (Жюри, ПНР, 82). На бесконечной во все сто¬
роны клетчатой доске, на которой первоначально расстав¬
лены фишки, заполняющие 'в точности прямоугольник
размером 3kxn, происходит игра по следующим прави¬
лам: любой фишкой можно перепрыгнуть через любую
соседнюю (по вертикали или по горизонтали) фишку, за I
которой следует незанятая клетка, после чего фишка,
через которую перепрыгнули, должна быть убрана с доски.
Доказать, что на доске никогда не останется ровно одна
фишка.
26.11. (СРР, 78). Дан выпуклый многограннике п ^5
гранями, из каждой вершины которого выходит ровно по I
три ребра. Двое играют в следующую игру: каждый по I
очереди пишет свое имя на одной из свободных граней. I
Для победы игрок должен написать свое имя на трех I
гранях, имеющих общую вершину. Доказать, что сущест- I
вует выигрышная стратегия для первого игрока.	I
26.12. (Жюри, СРР, 77). Пусть Л=(й1; ...; ат)— I
набор из т = 2" (п € N) чисел а,- € {1;—1}, t == 1,2,	I
Операция S определяется формулой	I
S {А) = (ata2; а2а3; ...; атаг).	I
Доказать, что для любого набора А в последовательности г
A, S (A), S(S(A)), ... имеется набор из т единиц. I
26.13. (Нью-Йорк, 76). Доказать, что квадратную доску I
размером 2пх2п, где п не делится на 3, из которой I
удалена одна произвольная клетка, можно покрыть пра- I
вильными тримино. (Правильное тримино—это квадрат I
размером 2x2, из которого удалена одна клетка.)	I
26.14. (США, 76). а) Пусть каждая клетка прямоуголь- I
ной доски размером 4x7 окрашена в белый или черный I
цвет. Доказать, что на доске обязательно найдется пря- I
моугольник, образованный горизонтальными и вертикаль- L
ными линиями доски, все четыре угловые клетки которого I
окрашены в одинаковый цвет.	[
б)	Привести пример раскраски прямоугольной доски 1
размером 4x6, для которой указанного в п. а) прямо- К
угольника не существует.	I
26.15. (Швеция, 82). На плоскости с прямоугольной Е
системой координат рассматривается множество А1 точек I
(х, у), где х, у£ N, причем 12, у ^12. Каждая из I
этих 144 точек окрашена либо в красный, либо в белый, К
либо в синий цвет. Доказать, что существует прямоуголь-1
ник (со сторонами, параллельными осям), все вершины I
76

которого принадлежат множеству М и одинаково окра¬
шены.
26.16.	а) (Жюри, СРВ, 77). На координатной плоскости
отмечены п ^ 3 точек с целочисленными координатами
так, что любые три из них образуют треугольник, медианы
которого не пересекаются в точке с целочисленными ко¬
ординатами. Найти наибольшее число п, при кото¬
ром это возможно.
б)	(Жюри, СРР, 77). В пространстве отмечены 37 раз¬
личных точек с целочисленными координатами, никакие
три из которых не лежат на одной прямой. Доказать,
что из них можно выбрать такие 3 точки, что коорди¬
наты точки пересечения медиан образованного ими тре¬
угольника являются целыми числами.
26.17*. (СФРЮ, 75). Какое наибольшее число ладей
можно расставить на шахматной доске размером ЗлхЗп
так, чтобы каждая из них находилась под ударом не
более одной из остальных?
26.18*. (ВНР, 81). Клетки шахматной доски размером
пхп, где п—четное число, большее 2, раскрашены п2/2
красками так, что каждой краской окрашены ровно две
клетки. Доказать, что на доске можно расставить п ла¬
дей так, чтобы они стояли на клетках разного цвета и
не били друг друга.
26.19*. (ВНР, 79; Австралия, 82). На каждом поле
таблицы размером пхп(п>2) стоит некоторая буква.
Известно, что все строки таблицы различны. Доказать,
что в ней имеется столбец, после стирания которого оста¬
нется таблица, также не имеющая совпадающих строк.
26.20*. (Жюри, Люксембург, 83). В пространстве
с прямоугольной системой координат рассматривается
множество Е точек с целочисленными координатами, при¬
нимающими значения от 0 до 1982. Каждая из этих точек
окрашена либо в красный, либо в синий цвет. Сколько
существует раскрасок, обладающих следующим свойством:
число красных вершин у любого параллелепипеда (с вер¬
шинами из £ и ребрами, параллельными осям) делится на 4?
§ 27. Элементы теории вероятностей
(см. Приложение Г: определения 18, 46—49)
теоремы 95, 96, 98—100)
27.1.	(Бельгия, 80). Каждая из двух урн содержит
белые и черные шары, причем общее число шаров в обеих
урнах равно 25. Из каждой урны наугад вынимают по
77

одному шару. Зная, что вероятность того, что оба выну¬
тых шара окажутся белыми, равна 0,54, найти вероят¬
ность того, что оба вынутых шара окажутся черными.
27.2. (Англия, 73). Учителю и учащимся некоторого
класса задаются вопросы. Вероятность того, что ответ
учителя будет правильным, равна а, а вероятность пра¬
вильного ответа учащегося равна Р или у в зависимости
оттого, кто отвечал—мальчик или девочка соответственно.
Вероятность того, что ответ случайно выбранного учащегося
совпадет с ответом учителя, равна 1/2. Найти отношение
числа мальчиков к числу девочек в классе.
27.3. (США, 83). Из вершин правильного я-угольника
(я >6) наугад выбираются две тройки различных точек.
Какова вероятность того, что два треугольника, верши¬
нами которых являются выбранные тройки, не пересе¬
каются?
27.4. (ГДР, 78). Вокруг правильного 2/г-угольника
описана окружность. Тройка различных его вершин на¬
зывается односторонней, если существует полуокружность,
на которой лежат эти вершины (концы полуокружности
принадлежат ей). Какова вероятность того, что случайно
выбранная тройка вершин окажется односторонней?
27.5. (Жюри, Бразилия, 82; Австралия, 83). В урне
находятся п белых и т черных шаров, рядом сурной —
ящик с достаточно большим количеством черных шаров.
Производится следующая операция: из урны наугад вы¬
нимается пара шаров; если они оказались одноцветными,
то черный шар из ящика перекладывается в урну; если
же они оказались разноцветными, то белый шар возвра¬
щается в урну. Операция повторяется до тех пор, пока
в урне останется один шар. С какой вероятностью он
будет белым?
27.6. (Австралия, 82). Игрок А бросает монету и+1
раз, а игрок В — я раз. Какова вероятность того,
что в итоге у игрока А выпадет больше «орлов», чем у иг¬
рока В?
27.7. (Нью-Йорк, 76). Строка (it; t2; ...; i„) состав¬
лена из я > 3 первых натуральных чисел, расположенных
в случайном порядке. Какова вероятность того, что при
всех k=\, 2, ..., я справедливо неравенство ik~^k—3?
27.8. (США, 75). Колода из я различных игральных
карт, расположенных в случайном порядке, содержит
три туза. Верхние карты колоды одна за другой снимаются,
пока не будет снят второй туз. Доказать, что среднее
число снятых карт равно (я + 1)/2.
78

27.9. (Нью-Йорк, 81). Строка (t^ i2; ...; in) состав¬
лена из п первых натуральных чисел, расположенных
в случайном порядке. Найти среднее число инверсий (бес¬
порядков) в этой строке, если инверсией называть каж¬
дую пару чисел if > ik, для которой j < k.
27.10. (Бельгия, 81). Два игрока А и В наблюдают
за мальчиком, который без остановки подбрасывает мо¬
нету. Результаты подбрасываний записываются последо¬
вательно с помощью букв: на k-м месте последователь¬
ности ставится буква О или буква Р в зависимости от
того, что выпадает при k-u подбрасывании—«орел» или
«решка» соответственно. Игрок А утверждает, что тройка
ООО встретится в записи раньше, чем тройка ОРО. Игрок В
поспорил, что произойдет обратное. Кто из игроков имеет
больше шансов выиграть в этом споре?
27.11. (Бельгия, 77). Три стрелка А, В, С решили
одновременно драться на дуэли. Они расположились
в вершинах равностороннего треугольника и условились
о следующем: первый выстрел делает А, второй — В,
третий—С и т. д. по кругу; если один из стрелков выбы¬
вает, то дуэль продолжается между двумя оставшимися.
Известно, что стрелок А поражает цель с вероятностью 0,3,
стрелок С—с вероятностью 0,5, а стрелок В вообще ни¬
когда не промахивается. Каждый стреляет в одного из
двух других или в воздух с таким расчетом, чтобы с на¬
ибольшей вероятностью выиграть дуэль. Куда должен
направить свой первый выстрел стрелок А: 1) в стрелка С;
2)	в стрелка В; 3) в воздух?
27.12*. (Бельгия, 78). Точка движется по ребрам
куба ABCDA'B'C'D'. Из любой вершины она может дви¬
гаться по одному из трех ребер (выходящих из этой вер¬
шины) наугад с одинаковой вероятностью, равной 1/3.
Вершины В' и С' отличаются тем, что, попав в любую
из них, точка уже никуда не движется. Если точка на¬
чинает движение из вершины Л, то с какой вероятностью
она: 1) остановится в вершине В’; 2) остановится в вер¬
шине С'; 3) никогда не попадет ни в вершину В', ни
в вершину С'?
27.13*. (Бельгия, 82). На внутренней обертке каждой
шоколадки серии «Великий Математик» изображен один
из я выдающихся математиков, причем портрет каждого
из них встречается с одинаковой вероятностью, равной 1/я.
Сколько в среднем надо купить шоколадок, чтобы собрать
полную коллекцию портретов?

РЕШЕНИЯ
Глава 1
АРИФМЕТИКА
§ 1. Делимость. Простые и составные числа
1.1. Произведение чисел су=д,—6,-,/=], 2, ..., 7, является чет¬
ным, так как хотя бы одно из них четно (если бы каждое из чисел с,-
было нечетным, то нечетной была бы и их сумма, равная
Cl+f2"b • • •	=	(°1	—	^l)4~(a2 — Ь2) + • ■ • + (fl7 —Ь7) =
= (0\ -f- 4 +... -f- <Jj) — (fcj + b2 + . ■. -J- 67) = 0).
1.2. Обозначим ЬЕ — аг.-\-т-\-1, где е*=1. Тогда из равенств
(о2 + I)3 = (Ь£—во)3 еа3 (mod be),
— ео3 = — еоЬе+а2 + еа =Ье(— еа+ 1)— 1=-1 (mob b£)
вытекает соотношение
(а2-}-1)3==—1 (mod fc£).
Таким образом,
2 Ч (а2+ 1)ЗА	« 2	(-П* Ч (mod (о2	± а+1)),
к —0	Л — 0
т. е. ответ на вопрос задачи положителен.
1.3. Рассмотрим функцию, определенную на множестве целых
чисел:
(0, если т четно,
/ Кт)	( 1,	если	т нечетно,
и построим таблицу чисел,	заданных	формулами	Ь„,	* = / (о„, к)- То-
тда при п > 1 имеем
bn,k — f (°п, *) = / (Ч-и k-i-han-i, ft + «n-x, ft+i) =
= f fl (°n-it д-i) + / (Ч-i, k) ~h l (йя-1> Jt+i)) =
= / (bn-i. ft-l + bn-1, ft+bn_i S+J;
при этом отсутствующее в таблице число заменяется нулем. Прямой
подсчет показывает, что набор первых четырех чисел b„t
Ь0

b,i,t-ni fcn, з-n. bn,4-n л-й строки однозначно определяет набор
первых четырех чисел (п+1)-й строки, причем в восьмой и четвертой
троках эти наборы совпадают. Следовательно, эти наборы совпадают
в девятой и пятой отроках, в десятой и шестой строках и т. д. По¬
скольку в каждой строке, начиная с третьей, эти наборы содержат
нули, то в этих же строках исходной таблицы содержатся четные
числа, что и требовалось доказать.
1.4.	Заметим, что число р—1 четное, и преобразуем дробь т/л
к виду
■1-+4-+4+.- • 1
-(т+7^)+(т+7^2)+(т+7=:з)+-‘1
...V	1	•	1
-I ^ Р+\ у 1 (р-1) ' 2 (р — 2)
2 2 /
Р it Р
3 (/) -— 3)	‘	р—	1	/7+1
2 2
1.1.1
I (Р—О + 2 07—2) + 3 (р— 3) +•••+ р-1р+1 У
Приводя полученное выражение к общему знаменателю
1 (р- 1)-2 (р—2)-3 (р—3)... £=l! £+i = (р_ i)|f
лолучаем соотношение
“=р(р—1)1
из которого вытекает равенство т (р—1)! = рря. Поскольку ни одно
из чисел 1, 2, 3, ..., р—1 не делится на простое „числор, то послед¬
нее равенство возможно лишь в случае, если m : р. Утверждение за¬
дачи доказано.
1.5.	Пусть л > 2, тогда по теореме 4 справедливы равенства
а»—л2 + я— 1=(лп-?— 1) я2 + (л—1) =
= (л-1)(я"-3 + ... + 1)л? + (л— 1) л° = (л— 1) №«-* + ..•+л2 + л°).
Поскольку nsl (mod (я—1)), то для каждого значения k — 0, 2,
..., я—1 имеем
л* = 1 (mod (я— 1)),
а значит,
nn_I+,,,+n2+fl°sO(mod (я—1))
(количество слагаемых в левой части этого соотношения равно л — 1).
Поэтому число
(я— 1) (я«-1+... + я2+я°)
81

1
делится на (п— I)2. Для завершения доказательства достаточно заме¬
тить, что при п=2 число п" — и2 -|- я —1 = 1 также делится на
(п—1)*= 1-
1.6. Пусть тройка чисел а, b, N удовлетворяет условиям
(оЬ+1) ; с, (ас+1) ■ 6, и (6с+1) : а.
Заметим, что числа а, Ь, с попарно взаимно просты (если, например,
(а, 6) > 1, то (ас, b) = d > 1 и число ас-{-1 не делится на d, а тем
более на 6), следовательно, все они различны. 4hc.ios—аЬ-рос+йс |-1
делится на каждое из чисел а, Ь, с, а в силу взаимной простоты этих
чисел—делится и на их произведение, поэтому s^abc. Без ограни¬
чения общности можно считать, что 2 < а < Ь < с. Предположим,
что 4, тогда 5, a6c>2.4-5 = 40 и
, .	.	,	. . обе . abc abc ,
s*=ab-\-ac-\-bc+1 <-g—1* —^—1—g—Ъ =
abc , ,	,	40	,	.
= abc 2б"+1 ^	20^	<
Полученное противоречие означает, что Ь < 4, поэтому а = 2, 6=3.
Поскольку число а6+1 =7 делится на с, то с= 7, а значит, условию
задачи удовлетворяет единственная тройка чисел 2, 3, 7.
1.7. Если n = 2k (здесь всюду k£Z+), то
19-82й + 17= 18-82*+ 1-(1 + 63)* + (18—l)sa0 (mod 3).
Если я = 4й-}-1. то
19.84*+1 + 17=13-84й+1 + 6-8-642* + 17 =
= 13-84й+1+39.64?* + 9.(1— 65)2* + (13 + 4)зз0(то<1 13).
Если же п = 4й+3, то
19.84й+3+17= 15-84й+*+4-83-642й+17 =
= 15 • 84*+3+4 • 510 • 642й + 4 • 2 • (1 — 65)2* + (25—8) = 0 (mod 5).
Таким образом, число 19-8”+ 17 при любом значении л£Z+ делится
хотя бы на одно из чисел 3, 13 или 5.
1.8. Если р = 2, то каждое из чисел 2<?*>— (2k), где N, делится
на р. Пусть р > 2, тогда, учитывая малую теорему Ферма (теорема 25),
получаем
2р~1 з=э 1 (mod р), 2т <Р-1) sas 1 (mod р),	/n£N<
Если же тзз— 1 (mod р), то имеем
2m(/j-i) — т (р—j) = 2m (p-i)_|-/n—щр sa 0 (mod р).
Таким образом, если р > 2, то каждое из чисел
2"—л, где n = (fep—1) (р~1),
делится на р.
82

1.0.	Пусть пас4£4, где k — 2, 3,	Тогда для любого значения
т 6N число
m4+n = /n4+464= (m4 + 4m262+464)—4m262 =
= (т3+2/г*)* — (2т£)а=(т2+2mA + 2£2) (яг2 - Чтк+262) =
= ((яг -f 6)2+А2) ((т—6)2+К1)
является составным, поскольку каждый из сомножителей (яг ± 6)2+А2
больше единицы (ибо k > 1).
1.10. Пусть число п обладает требуемым в задаче свойством.
Если оно не делится на 2, то я<22 (иначе число я»=4, взаимно
простое с я и меньшее его, было бы простым). Поэтому я = 3. Если
п делится на два, но не делится иа 3, то по аналогичным соображе¬
ниям я<32, т. е. я £{4; 8}. Если я делится на 2 и 3, но не делится
на 5, то я < 5? и я • 6, т. е.
я£{6; 12: 18; 24}.
Если же п делится на 2, 3 и 5, но не делится на 7, то я<7! и
я- 30, т. е. я=30. Пусть для некоторого значения 6 5= 4 число я
делится на каждое из чисел р*, рг,	рд, но не делится на Pft+i,
где 2 = р^ < р2 < ,, ,< рь < р*+1 — последовательные простые числа.
Тогда
n<pl+1 и п\ PiPa...pfti
Из оценки
piPa-. .р^ <я < 10 000 000
получаем, что 8. Наконец, замечаем, что при каждом значении
6=4, Б, 6, 7, 8 справедливо неравенство
PiPi., .pft > pi+i>
которое противоречит необходимому условию
PiPa. *. Pft ^7 я ^ pk +!•
Полученное противоречие показывает, что рассматриваемый случай
невозможен. Таким образом, доказано, что все возможные значения я
принадлежат множеству
{3; 4; в; 8; 12; 18; 24; 30}.
Проверка показывает, что каждое число из этого множества обладает
свойством, указанным в условии задачи.
1.11. Докажем, что искомое множество М состоит из всех чисел
т €N, взаимно простых с числом а. Если некоторое число m£N имеет
общий делитель d. > I с числом а, то т (fc М. Действительно, для
любого я £ N имеем
(с„, а)=( 2 я*. а)=( 1+а 2
\fe=o J \	к= о
83
ой, а )=(1, о) = 1,

т
поэтому число ап не делится на d, а значит, и на т. Пусть теперь
т> I и (т, а)=1. Среди чисел су, .... ат, am+t найдутся две
числа о,- и су (i > /), которые имеют одинаковые остатки от деления
на т, так как количество возможных равличных оетатков меньше
количества чисел. Тогда разность этих чисел
£	/	£	£-/-1
а,-—ау = 2	—2 °й=а 2	c*=“fi^+1	2	с*
ft=0	fc=0	k=i+1	fc=0
делится иа т. Но число с/+1 взаимно просто с т, поэтому число
£-/-1
c/_y_i= 2 а*	I
А=о	|
делится на т (случай I—/—1=0 невозможен, ибо т Ф I). Поэтому
т£М. Наконец, замечаем также, что I £ М.	'
1.12. Докажем, что ответ на вопрос задачи положительный. Пусть '
заданы п последовательных целых чисел су, о2,	а„.	Тогда из не¬
равенств т < п < ап — (ay—1) следует, что среди иих обязательно
найдется число щ, кратное п, и число Су, кратное т. Если i Ф /. то |
произведение с/су делится иа тп. Рассмотрим случай, когда 1=1. |
Обозначим d=(m, п), q = [m, я], тогда
mn = dq, с,-; d и о,- ; q.
Докажем, что хотя бы одно из чисел a/-\-d или в,-—d, кратных d,
принадлежит множеству {ах; с2;	а„). Если это не так, то '
o,'-i-d > а„, ai—d < ay, откуда i+d^n + l, I—d <1 и 2d > я, но
я • d, поэтому d = я > т, что противоречит условию т ; d. Итак, ,
ai и a,-+d (или соответственно щ—d) являются искомыми, так как I
произведение а,- (а,- ± d) делится на dq—mn.	|
1.13. Докажем сначала, что если л = 2“, где /м £Z+, то [ (л) =
= 2я—1. Действительно, с одной стороны, сумма
2'*-^^==(2я+1-1).2я
fc=i
делится на 2я = п. С другой стороны, если /<2л—2, то сумма
£
2 k = t{l + \)/2
fc=l
не делится на 2я, так как одно из чисел /, / I нечетно, а другое
не превосходит числа 2л—1 = 2Я+*—1 и, следовательно, не делится
иа 2m+1. Пусть теперь число я не является степенью двойки, тогда
п=2яр, где m£Z+, а число р > 1 нечетно. Докажем, что существует'
натуральное число I <2п—1, удовлетворяющее условиям I ■ 2я+1 и I
(f-f-1) ■ р (тогда сумма
2 k = Ц1-{-1)/2
1 |
84
i

делится на 2тр — п, откуда ( (п) < 2п—I). Поскольку числа 2m+L и р
взаимно просты, то, согласно китайской теореме об остатках (тео¬
рема 23) существует число I, удовлетворяющее условиям
I es 0 (mod 2m+1), l = p—I(modp),
О < /*г2“+1-р = 2я.
В действительности же это число удовлетворяет более сильному ус¬
ловию I <2п—i. В самом деле, если
(=2л— 1 =2т+1р— I,
то I не делится иа 2т+1, а если
1л=2п = 2т+1р,
то (+1 не делится на р > I. Поэтому I < 2л—I, что и требовалось
доказать.
1.14. Пусть я = Зйг, где fe£Z+, а число г£N не делится на 3.
Докажем, что число
р=1+2« + 4"
делится на число
9= 1+23* + 48*.
Рассмотрим два возможных случая.
1-й случай: r = 3s+l, s£Z+. Применяя теорему 11, имеем
р-? = ( 2" —28*) + (4«—4ЗЙ) =
= 23ft(23fc-3S-l)+43,! (23*'es— l) ==0 (mod (23*'3-1)).
Так как
2з*-з_ 1 = (23ft— 1) (l +23*+43*) = (23*- 1) q,
то число р—q делится на q, откуда р q.
2-й случай: /-=3s + 2f s£Z+. Применяя теорему II, имеем
р- q = (4я — 23*) + (2" - 43*) =
= 23ft (2з*.з<и+1)_ i)+22'3fc (23ft-3S- 1) s0 (mod (23* 3- 1)),
откуда так же, как и в 1-м случае, получаем р ; q.
Итак, если число р простое, то оно совпадает со своим делителем
q> 1, т. е. я = 3й, что и требовалось доказать.
1.15. Пусть Я1=11'р, n—\Uq, где «,/£ Z + , а числа p,q£ N не
делятся на 11. Докажем, что p=q (откуда будет следовать, что
m= ll'-Zn). Предположим, что это ие так, причем р > q (случай
p<q рассматривается аналогично). Поскольку числа р и II взаимно
просты, то в силу китайской ?еоремы об остатках (теорема 23) су¬
ществует число а > 0, удовлетворяющее условиям
0(mod р), as—1 (mod 11).
Тогда имеем
а— 1 Ik— 1 (fegN),
(life—1, /я) = (а, lUp)~ p,
(life—I, я) = (a, lUq)<q < p,
85

что противоречит условию
(lift—1, m) = (llft—1, п).
Доказательство закончено.
1.16. Докажем, что утверждение верно. Пусть каждый простой
делитель числа ad.— be является делителем чисел а н с, однако,
вопреки утверждению, для некоторого значения л£ Z числа an-\-b и
cn-f-d делятся на простое число р. Тогда число
ad—bc=a{cn-\-d) — с (ап-{- Ь),
в следовательно, и числа а и с, делятся на р. Поэтому числа
b = (an-\-Ь)—ап и d = (cn-\-d) — сп
также делятся на р, т. е.
(с, Ь, с, d)Ssp > 1,
что противоречит условию задачи. Пусть теперь
(art-j-b, crt-j-d) = l
для каждого значения Z, однако, вопреки утверждению, для не¬
которого простого числа р выполнены соотношения
cd—0 (mod р), c^O(modp)
(случай c^O(modp) рассматривается аналогично). Тогда в силу ки¬
тайской теоремы об остатках (теорема 23) существует число л£ Z,
удовлетворяющее условию
ап =—b (mod р),
откуда получаем
ап-\- 6 = 0 (mod р),
а (сп -j-d) — с (ап + b) + {ad — be) = 0 (mod р).
Поскольку (а, р) = 1, то
cn+ds=0(mod р) и (an-\-b, c/i+d) Р > 1-
Полученное противоречие завершает доказательство утверждения.
1.17. Заметим, что числа am=21m-{-l при m = 0, 1, 2, 3, 4 яв¬
ляются простыми, а число
23a -J-1 = (232 — 1) +2 =
= (2« +1) (2® +1) (2* +1) (2? +1) (2 +1) (2 -1) + 2 =
= а0а1а2а3аА+2 ^ 2 (mod а,п)
взаимно просто с каждым из нечетных чисел а0, а*, а2, а3, а4 и
делится на простое число 641 = аъ, но не делится на его квадрат,
т. е. число ав = (23?+1)/641 не делится на аъ. Таким образом, все
числа Со, at, а2, а3, <з4, а6, ав попарно взаимно просты. Согласно
китайской теореме об остатках (теорема 23) существует целое число
k > max{а0; аг\ Og},
86

удовлетворяющее соотношениям
k^l (mod Од,) при м = 0, I, 2, 3, 4, 5,
ft =—I (mod Of).
Докажем, что любое число вида k-2n-\-\, где л £ N, является со¬
ставным. Пусть п=2тр, где m£{0; 1; 2; 3; 4}, а число р нечетное.
Тогда имеем соотношения
A.2" + I^2«+I(mod am),
2" + I = 2*т Р+I = (ат - \)Р +1 ^ (- \)Р +1 (mod ат),
k-2n + 1е0 (mod ат).
Пусть я = 26р, где число р нечетное, тогда
ft-2n-f- 1 s2"-(-1 (mod йц),
2” +1 = (2за)я +1 = (— 1)Р + 1 (mod c5),
ft- 2n -f-1 es 0 (mod ce).
Пусть, наконец, я = 2вр, где р £ N, тогда
ft-2"	1	=—2П+ 1 (mod ов),
2п — I = 2ЫР— I s= (— I)2^— I (mod а,),
k-2n-\- \	0 (mod aj).
Поскольку число ft-2n-}-I > ft больше любого из простых чисел а0,
ai, ..., ав и делится хотя бы на одно из них, то оно является со¬
ставным.
1.18.	Пусть задано натуральное число а^З. Докажем индукцией
no ft£N, что последовательность {я*}, заданная соотношениями
щ=1, пк+1 = апк— I, ftgN,
удовлетворяет условию — 1 • щ. При ft=l имеем а—1 ; 1. Пусть
для некоторого значения ft £ N уже доказано, что a 'h—1 ; яд, т. е.
а"*— 1=Яй<7,
где	Тогда	в	силу	теоремы	11 число
a"*+i— 1 =e"*9— I
делится на яа+1 = й"й — 1. Поскольку последовательность {яЛ} мо¬
нотонно возрастает, то все полученные значения я—я^ различны, а
значит, утверждение задачи доказано.
Докажем, что аналогичное утверждение для а--2 неверно, и
более того, ни прн каком натуральном значении я> 1 число 2”—1
не делится на я. Предположим противное, т. е. 2” — 1 ■ я для неко¬
торого я > 1. Тогда я нечетно (ибо 2п — 1 нечетно) и наименьший
простой делитель р числа я также нечетен, поэтому, согласно малой
теореме Ферма, удовлетворяет соотношению 2Р~х—1 ; р. Обозначим
через d £ N наименьшее число, для которого 2d— 1 : р, и докажем,
что для любого m £ N из условия 2т — 1 \ р вытекает условие т ■ d.
87

Действительно, пусть m = dq-{-r, где q,r£Z+, г < d, тогда в силу
теоремы 11 число
(2т — 1) — (2r— 1) = 2Г (2*0— 1)э0 (mod (2а— 1))
делится на р. Следовательно, если 2т — 1 ■ р, то 2Г—1 ; р, откуда
г=0 (в силу выбора числа d и неравенства d > г). Таким образом,
из условий 2”— 1 : р и 2Р~1 — 1 ; р имеем л : d и р—1 : d. Но
(я, р—1) = I, так как число я не имеет делителей, меньшнх р и
отличных от 1. Поэтому d = 1, откуда получаем, что число 21—1= 1
делится на р > 2. Полученное противоречие означает, что на вопрос
задачи следует дать отрицательный ответ.
1.19. Предположим, что, вопреки утверждению задачи, лишь
конечное - множество значений n£N удовлетворяет неравенствам
ап > а/, при А=1, 2, ..., я—1, где обозначено а„ — о(п)/п. Пусть
N—наибольшее из таких значений л. Тогда последовательность
чисел
Ап = max {а,-}
1 < i < п
ограничена сверху числом Ад, так как At <	и для
каждого числа л > N имеем
i4n = max{i4„_t;
(ибо для некоторого числа ££{1; 2; ...; л—1} выполняется нера¬
венство	откуда Ад-= Адг+j = Адг+2 = .. Следовательно,
последовательность {ап} также ограничена сверху числом А дг, равным
числу Сдг, так как а; < од- при i — 1 N—1. С другой стороны,
среди делителей числа 2N есть все числа вида 2d, где л j d, и число 1,
поэтому
a(21V)3i2a(/V)-H.
2а(Л0 + 1	,	1
Qs;v3s > адг= Atf.
Полученное противоречие доказывает справедливость утверждения
задачи
1.20. Докажем, что неравенству Q (л) > Q (л+1) удовлетворяет
любое число
я = г-£!— 1, где r£N, г^З.
Обозначим
т = [л -j-1, •.., л k\.
При 1=1, k имеем яs—l(mod/), откуда
(л, /) = 1 и (л, я-)-/) = 1.
Следовательно,
(л, т)= 1 и Q (я) = [л, я + 1, л + £] = [л, т] =пт, ^
С другой стороны, число
п+£+1 =r-k\ +k

г
делится на k. Число т делится на и-j-1 = r-k\, а значит, и на k.
Поэтому число m(n-\-k-\-l)lk делится как на т, так и на n+ft-f-l-
Значит,
Q О = 1п~ЬI» я-f-A, я11 =
= [т, n + k-\-1] < т (я+£+ l)/k.
Отсюда, учитывая оценки k^2; г 3, получаем
что и требовалось доказать.
1.21.	Обозначим через т (k) показатель двойки в разложении
числа	на простые множители, тогда k=2m'-m g (k) н
П	”	I
<?— v &Ш— v 1
Z- k Z* 2й	'
к— 1	feal
Заметим, что среди чисел 1,2, .... я содержится ровно [л/2] четных
чисел, [я/22] чисел, кратных четырем, [я/23]	чисел,	кратных	восьми,
и, вообще, [п/2т] чисел, делящихся на 2™	(здесь	величина	m	про¬
бегает значения 0, 1, 2, ..., а начиная с некоторого числа Л1, удов¬
летворяющего условию 2Л> > я, будут выполнены равенства [я/2Л1] =
= [Я/2-ЛГ+1J = ... =0). Поэтому количество	чисел	& £{1; 2;	я},
для которых величина т (k) принимает значение т, равно [п/2т] —
— [я/2/я+1]; следовательно, имеем
так как [я/2Л*+1]=0. Учитывая, что для любого значения x£R имеет
место неравенство [х] < х, получаем первую оценку
м	м
S>n~X 2^’JZ=n-n £
msl	m=l
n f I \	2	, я 2
= rt-y41-4Afj=Tn+3^	“3	n‘
Для доказательства другой оценки заметим, что для любых значений
P. 9€N выполнено неравенство
[*]**?-'■
89
I

Действительно, пусть [piq] = r\ тогда
p = rq+s, где s£{0; 1; 2; q— I},
откуда имеем
Г р	1 _г	Гр—s]	(<?—О _р + 1 ,
I я	J	I.	? J	9	q
Используя доказанное неравенство, получаем соотношения
m=l	т—	I
-»-(»+■> £ i+f ^=«-4i('-j»)+('-sii)-
m= 1	т= I
2	2	л-fl	1
— 3 я'' 3 + 3-4Л1 pi'
Поскольку
2М > л > («+1)/3, то (п + 1)/(3-4Л1) < 1/2Л1,
откуда получаем вторую из требуемых оценок
0.2	2
<	3 П^~ 3	‘
Утверждение доказано.
1.22.	Пусть выбрано простое нечетное число р. Докажем, что
любые два числа из возрастающей последовательности четных чисел
ат=1 (m£Z+) не имеют общих делителей, больших двойки.
Действительно, если т > 1^0, то число
р2"_ 1 г-(рг™-* -f-1) (рг»"-*— 1) = ...
,.. = (р»"-+ 1) (р*—+1).. .0»»*+ 1) (р*1-1)
делится на p2*+1, поэтому
(в«, аг) = (2 + (р2т_1), p.i+i) = (2, р^+1) = 2.
Рассмотрим множество тех членов последовательности, которые де¬
лятся хотя бы на одно простое число, большее р. Это множество
не пусто, так как вследствие доказанного выше свойства последо¬
вательности {а,„} лишь конечное множество ее членов может не иметь
делителей, больших р. Пусть ат — наименьшее число в этом множе¬
стве. Тогда имеем
h(am) >р, h (ат — I) =Л (рвет) — р,
h (ат—2) = h (p2m— 1) = тах {Л (р2“-‘+ 1), Л (р2т~,_1)}= ,
... =тах{ft (р2ОТ-1+ 1), h(p2m-‘+ 1)	Л(р+1), Л(р—1)} =
— max {ft (cm_i), h(am-г) Л(а0), Л(р—1)} < р,
поскольку h (р—1) < р и при каждом значении /=0, 1 т—2,
т— 1 согласно выбору числа т имеем Л(а/)<р, а кроме того,
90

щ = 1 (mod р), откуда /; (сг) < р. Таким образом, для заданного не¬
четного простого числа р указано число вида ri = рът—1, удовлетво¬
ряющее неравенствам
h(n) <h (л + 1) < h (я+2).
Поскольку при разных числах р будут получаться разные значения л,
то множество таких значений бесконечно.
1.23. Докажем прежде всего, что среди чисел вида л = 2*, где
A£N, имеется бесконечно много таких, которые удовлетворяют нера¬
венству w (л) <ц)(л-|-1). Предположим, что для некоторого значения
я=2* выполняется противоположное неравенство w(n)^w (я+1).
Тогда имеем
1=ш(2*)>ю(2*+1);э= 1,
откуда
iti(2A-f 1) = 1 и 2*-fl=pCT, где m^N,
а р — простое число. Если т = 21, то получаем
2* = р\1 — 1 = (р* — 1) (рг + 1),
а значит, оба числа pl -f 1 и р*— 1 являются степенями двойки, что
возможно лишь в случае рг + 1=4, р1 —1=2, т. е. при /7 = 3, 1=1
и к-=3. Если же число т нечетно, то /я=1 (поскольку в случае
т > 1 в силу разложения
2* = р» —1 = (р-1) (Ри-1+...+Р+1)
нечетное число
/7п>-1'+,1.+/7+1 > 1
было бы одновременно и степенью двойки). Однако равенство 2А+1 =р
возможно лишь в случае k = 24, где q£Z+. Действительно, если
к — 2чг, где число г > 1 нечетно, то получаем, что простое число
(см. теорему 11)
р = 2* + 1 = 2*7 -г + 1 == O(mod (22<! +1))
делится на число 2*г +1 < р. Итак, доказано, что для бесконечного
множества значений Р (; N (отличных от трех и степени двойки) спра¬
ведливо неравенство
w (2*) < w (2*+ 1).
Предположим, что утверждение задачи неверно. Тогда среди значе¬
ний к, удовлетворяющих неравенству
w (2к) < w (2A-f-1),
лишь конечное множество удовлетворяет также и неравенству
и>(2*+1) < ю(2* + 2).
Поэтому найдется такое (достаточно большое) число ка = 2ч« > 5, что
для всех значений
k = k0 + \, ко+2,	2*0—1	<	2?о+*

справедливы соотношения
ю(2я+1) Эгю (2я+2) = ю (2 (2А-1+ I)) = 1 + и) (2я_1-|-1),
из которых получаем неравенства
W (2?яо-1+1) з» 1 +ш (22яо-2 + 1) SS. .	(k0— I) +Ш (2яо + 1) Зг к0.
Следовательно, если обозначить через Pi < Ра < Рз < • ■ * последова¬
тельные простые числа, то будут выполнены оценки
2«o-*+l &plPa...pfto= (2.3.5-7-П) (рв...рАо) > 4°-4я„-* =
= 2“яо > 22йо-*-|-1.
Полученное противоречие доказывает утверждение задачи.
§ 2. Уравнения в целых и рациональных числах
2.1. Перепишем уравнение в виде
2* = <?-1) Q/+I),
тогда для искомых значений х, N имеем, что числа у— 1, //+1 £Z+
являются делителями числа 2х, т. е. у—1=2Р и 1 = 2^, где
р, ?£Z+, р <q. Поэтому
29—2/'=(р+1) — (у— 1)=2, т.е. 2Р(29~Р —1) = 2.
Заметим, что q—р<1 (иначе нечетное число 2я~р—1 > 1 было бы
делителем числа 2), поэтому q — p-\-1 и 2Р (2—1) = 2, т.е. р 1,
9 = 2. Наконец, проверка показывает, что единственно возможное
значение у—3 удовлетворяет уравнению только при ж = 3.
2.2. Поскольку х, у, а, Ь, с, d£ Z, то уравнение
(х+ау+с) (x+by+d) = 2
равносильно совокупности всех систем вида
1*+ау + с=Р.
\x+by + d = q,
где числа р, q£Z удовлетворяют равенству pq = 2. Каждая из таких
систем не может иметь более одного решения, так как значения не¬
известных определяются из системы однозначно (напомним, что по
условию а Ф by.
iy~(P—Q-\-d—c)l(a— b),
\x=p—q—ay.
Заметим, что различных целочисленных пар (р; q) имеется всего
четыре: (1; 2), (—1; —2), (2; 1), (—2; —1), причем разным парам
чисел р, q соответствуют разные пары неизвестных х, у. Таким обра¬
зом, исходное уравнение не может иметь б алее четырех решений,
причем количество этих решений равно четырем в том и только в том
случае, если каждое из чисел вида (р—q-\-d — с)/(а— Ь) является
целым, т.е. если (±l + d — c)j(a — b) £Z. Для этого необходимо, чтобы
02

разность
1+d—с	—1+^—с  2
а— b	а—b	а—Ь
была целым числом, т. е. 2: (а — Ь). Если а—6= ± 1, то
(±14-d—с)/(о—b)£Z. Если жеа—& — ±2, то числа"(± 1-f-d — с)/(а—6)
являются целыми тогда и только тогда, когда число d—с нечетно.
Итак, уравнение имеет ровно четыре решения в следующих случаях:
либо |а—51 = 1, либо |а — 61 =2 и с—d=2& + 1, где k£Z.
2.3. Пусть числа ж, y£Z удовлетворяют уравнению, тогда
У2 = (*(ж+8)) ((ж +1) (х+7)) = (жа + 8х) (ж3 + 8ж + 7) = г2 + 7г,
где обозначено г=ж3 + 8ж. Если г > 9, то
(г+3)2 = г? + 6г+9 < гг+7г = ф < г2 + 8г + 16 = (г + 4)3,
а значит, число у1. заключено между квадратами двух последователь¬
ных натуральных чисел, что невозможно. Поэтому ж2 + 8ж = г < 9,
откуда —9 <ж<; 1. Перебирая последовательно значения
ж = —9, —8, .... 1,
находим, что число ж (ж + 1) (ж+ 7) (ж+8) является квадратом целого
числа только при ж, равном —9, —8, —7, —4, —1, 0 и 1. Таким
образом, получаем все решения исходного уравнения: (—9; 12),
(-9; -12), (-8; 0); (-7; 0), (-4; 12), (-4; -12), (—1; 0), (0; 0),
(1; 12), (1; -12).
2.4. Пусть уравнению удовлетворяет некоторая пара чисел ж, y^Z.
Предположим, что ж > 0. Тогда имеем
(ж3+1)2 = ж® + 2ж3-1-1 < ж6 + 3xs + 1 = {/* < жв + 4ж3 + 4 = (ж3+2)2,
откуда получаем, что число у2 не может быть целым, так как
ж3+1 <у2 <ж3+2.
Аналогичное противоречие получаем и при ж «С—2. Действительно,
в этом случае х3 3 < 0, а значит, имеем
(ж3+2)^ =ж6 + 4ж3 + 4 < ж6+Зж3+1 =j/4 < ж6+2ж3+1 = (ж*+1)*,
откуда получаем соотношения
_(ж3 + 2) = |ж3 + 2| <у*. < |ж3 + 1| = -(ж3+1),
не выполняющиеся ни при каком целом значении у. Далее, при ж = —1
уравнение преобразуется в равенство —1=#4, которое невозможно.
Наконец, при ж==0 имеем равенство 1 —= у*. Таким образом, получаем
ответ: ж = 0, у=±1.
2.5. Пусть пара чисел ж, //£ Z удовлетворяет уравнению, тогда
х2 + 2ху+ф=х2уг + ху, т. е. (х+у)2 — ху {хуф 1).
Если ху > О, то
1 > Vxyixy+X) > ху.
93

В этом случае число
|*+Pl = Vxy(xy+l)
лежит между двумя последовательными целыми числами ху и xy-j-l,
а значит, не может быть целым. Аналогично, если ху <—1, то
—ху— 1 < У ху (ху -[- I) <—ху,
а значит, число \x-\-y\ снова не может быть целым. Итак, имеем
либо ху=0, либо ху=—1. В обоих случаях уравнение равносильно
равенству х-\-у—0,. поэтому либо х=у=0, либо х = — р=±1 соот¬
ветственно. Таким образом, получаем ответ: (0; 0), (1;—I), (—1; I).
2.6. Пусть пара чисел х, у £ Z удовлетворяет уравнению. Пред¬
положим, что *5=0, тогда
,/=8х*+24*2 + 32*+-16 = 8 (х3 +	+4х+2),
Поэтому у=2г (z^Z) и
г3 = х3 -f- Зх2 + 4х -f- 2i
Заметим, что
(x+I)3=x3+3x3 + 3x+l < zs < х3+6*2+12х+8 = (х + 2)3,
поэтому х-\~ 1 < г < х+2, что невозможно. Предположим, что x«s;—2,
тогда пара чисел дсг =— х—2^0, у± = —у также удовлетворяет
исходному уравнению, так как
(*х+2)4 - (*г)4 = х4 - (х+2)*=- tf = Ы3-
Но, как было, доказано выше, неравенство лгу Q приводит к проти¬
воречию. Таким образом, имеем оценки —2 < х < 0, из которых
получаем единственное решение х——1, у=0.
2.7. Заметим, что если число л четное, то n = 2k и
л4 = 16^ = 0 (mod 16);
если же л нечетно, то число
л4— 1 = (я— I) (П+ 1) (ла+1)
делится на 16 (так как каждое из чисел п — 1, л + 1, я2-|-1 является
четным, а одно из чисел л—1 или л + 1 делится на 4), т. е.
л4 = 1 (mod 16).
Следовательно, остаток от деления на 16 левой части уравнения
Х1+Х2+ • ■ • -\-x\ti равен количеству нечетных чисел н наборе хг,
х2, ..., ДС14, т. е. не превосходит 14. С другой'стороны, имеем
1599=1600—1 = 15 (mod 16),
а значит, равенство левой и правой частей уравнения невозможно ни
при каких целых значениях неизвестных.
2.8. Пусть хотя бы одно из возможных решений
—Ь± У 6‘2—4яс
2а
94

исходного уравнения является рациональным числом. Тогда число
УЬг — 4ас рационально, а значит (см. теорему 61), число Ы — 4ас
является квадратом некоторого числа d£ Z. Поскольку числа а, Ь, с
нечетны, то число d также нечетно, а кроме того,
ас = 1 (mod 2), —4ас =s 4 (mod 8)
и
Ьг = 1 (mod 8), d2E3 I (mod 8)
(ибо (2/г + 1)? = 4rA +4я 4-1 = 4п (я +1) +1 )• Таким образом, имеем
б? — 4ос = 5 (mod 8),
а значит, равенство d2—№—4ас невозможно.
2.9. Пусть числа х, //£Q удовлетворяют уравнению. Тогда спра¬
ведливы равенства
2У~3—3=«У~3+уУ"Ъ—2УЗху,
(х+у-2) У~Ъ = 2УЗху-8.
Поскольку
(*+j,_2)?-3 = 9 + 12ху-12Уз^,
то число У 3ху рационально, а значит, справедливы равенства
х-{-у—2=0,
2УЗху—3 = 0
(в противном случае число У 3 = {2У Зху—3)/(*+{/—2) было бы
рациональным). Поэтому числа х, у удовлетворяют равенствам х+у—2,
ху—3/4, т.е. являются корнями уравнения
<2—2/+3/4 = 0.
Так как х > у, то исходное уравнение может иметь только одно ре¬
шение х=3/2, у= 1/2, которое, как показывает проверка, действи¬
тельно удовлетворяет уравнению.
2.10. Заметим, что данное уравнение имеет решение: например,
х=у — г = 3-1983. Докажем теперь, что существует лишь конечное
множество наборов чисел х, у, z£N, удовлетворяющих исходному
уравнению и неравенствам дc<^<z. Действительно, для любого
такого набора выполнены соотношения
1	1	11	1	1.1.1	3
г	у	хх	1983	х у г	х
из которых вытекают неравенства 1983 < x<L 3-1983. Поэтому неиз¬
вестная величина х принимает не более 2-1983 значений. Для каж¬
дого из значений х получаем
111.12
■ ^ т»
1983 х у г у
95

откуда
и неизвестная величина у принимает ие более 2г-1983г значений!
Наконец, если значения к и у уже заданы, то неизвестная величина г
определяется уравнением однозначно. Таким образом, существует не
более 2М9833 решений, удовлетворяющих условию //<; г. По¬
скольку к решениям такого вида с помощью перестановок неизвест¬
ных приводятся все остальные решения исходного уравнения, то
общее число решений не превосходит 6-23-19833.
2.II.	Пусть числа a, 6£Z удовлетворяют неравенствам 5а 76	0.
Положим u = [6/5], тогда величина v=b—5u может принимать лишь
значения из множества
{0; 1; 2; 3; 4}.
Используя равенства
76 = 7 (5м + о) = 35м + 7v,
получаем соотношения
76	„	7v
а—7м ^2——7 M=-jr*
В случае о=0 положим
р = г = 0, х=а—7и,
тогда хГЭ=7о/5 = 0. В случае V — 1 положим
у= 1, 2 = 0, лс=а—7м—2,
тогда жЗг7/5—2 > — I, т. е. дсЗгО (ибо x£Z). В случае о = 2 положим
$/ = 0, 2=1, х = а — 7и—3,
тогда 14/5—3 > — 1, т. е. *Э=0. В случае а = 3 положим
у = г— I, х—а — 7и — 5,
тогда л:21/5—5 > — I, т. е. х^0. Наконец, в случае о = 4 положим
у = 0, 2 = 2, х=а—7м—6,
тогда *5=28/5—6 > — I, т. е. дс^О. Таким образом, в каждом из
разобранных случаев числа
*. У, г, м£Z+
удовлетворяют равенствам
х=а—7м — Зг—2у, Бм = 6 — о = 6 — 2г—I/,
а значит, и исходной системе.
2.12.	Пусть для некоторых значений
р, ?€{!; 2;	100}
число *£Q удовлетворяет уравнению
x?-\-px-\-q = 0.
86

Так как все коэффициенты многочлена, стоящего в левой части урав¬
нения* являются целыми, а его коэффициент при старшем члене
равен 1, то в силу теоремы 60 любой рациональный корень этого
многочлена, в том числе и число х, является целым. Докажем, что
— 3 < х < 0. Действительно, если х^О, то
x6 + px-j-q^q^ 1 > 0,
а если — 3, то
лсв + рх+9<—3е—3р+^<—3е—3+100 < 0.
Итак, возможны лишь два случая: х =— 1 или х =—2. Подставляя
в уравнение значение х — —1, получаем соотношение для коэффици¬
ентов 9=р + 1, которое выполняется ровно для 99 пар чисел р, q,
удовлетворяющих заданным ограничениям. Аналогично, при *=■—2
имеем условие <? = 2р+32, которое выполняется для 34 пар чисел
р, q. Поскольку условия ij = p+ 1 и <? = 2р+32 ие могут выполняться
одновременно (ибо р > 0), то все полученные пары будут различны,
а их число равно 99+34=133.
2.13. Набор чисел ж=р=г = 0 является решением уравнения.
Предположим, что уравнение имеет и другие решения. Выберем среди
них тот набор чисел х, у, г, для которого величина
«=м+ы+м
принимает наименьшее (натуральное) значение. Заметим, что для
любого значения п$г справедливо следующее: либо rt = 2ft(ft£ Z),
тогда
л? = 4ft? 0 (mod 4),
либо n = 2fc+1, тогда
n? = 4ft?+4ft + l з= 1 (mod 4),
Поэтому остаток от деления на 4 числа х?+р? (равный либо 0, либо 1,
либо 2) совпадает с остатком от деления на 4 числа 3z2 (равным
либо 0, либо 3) только в том случае, если каждое из чисел х, у, г
является четным, т. е.
х = 2хь у = 2уь z = 2zj, где xit yit Z^Z.
Так как
**+!/- = 3z2, то x?+p?=3zf(
причем величина
«i = I *i 1 +1У11 +1 *i I
удовлетворяет условиям 0<ai = a/2<a, что противоречит выбору
набора чисел х, у, г. Таким образом, исходное уравнение имеет един-
ственное решение х—у — г — 0.
2.14. Заметим, что если набор чисел х, у, г является решением
исходного уравнения, то любой набор чисел tx, ty, tz, где <£Q,
также является решением. Поэтому, если некоторый ненулевой набор
4 Под ред. И. Н. Сергеева	97

(т. e. ие совпадающий с набором x = y=z=0) рациональных чисел
х=m/л, у = 1/к, г = p/q,
где т, I, p£Z и п, к, g£N, удовлетворяет уравнению, то ненулевой
набор целых чисел
Х\ — t\X, yi = tiy, Zi = tiZ, где ti — nkq,
также удовлетворяет уравнению. Пусть d — наибольший общий дели¬
тель чисел ху, yi, Zi, тогда набор целых чисел
x2—t2Xi, у2 = l2yi,	где	t2=l/d,
также удовлетворяет уравнению, причем наибольший общий делитель
этих чисел равен 1. Из уравнения получаем, что число
Х-2 = 3 (— у 2 — Зл2 -]- Зх2// 2z3)
делится на 3, поэтому ха = Зх3 (x3£Z). Далее,
{/2+3za+9x1—9у&зХц == О,
т. е. набор значений х=у2, у = г2, г = х3 также удовлетворяет урав¬
нению. Поэтому у2 — 3//з (у3£ Z) и набор значений x = z2, у = х3, z=ys
также удовлетворяет уравнению, откуда za = 3z3 (z3£ Z). Таким обра¬
зом, каждое из чисел х2, у2, г2 делится на 3, что противоречит выбору
этих чисел. Утверждение задачи доказано.
2.15.	Набор чисел x0 = y0 = z0 — 0 является решением уравнения.
Предположим, что уравнение имеет еще одно решение (х; у; г). Тогда
правая часть уравнения х*у2 делится на 4 (в противном случае х
и у—нечетные числа, откуда
х?г= 1 (mod 4), i/? = 1 (mod 4), х2у2 = 1 (mod 4)
и либо
х2.+У^+ Z? = 2 (mod 4)
при четном z, либо
х*. + У* + z? = 3 (mod 4)
при нечетном г, т. е. равенство х? + tj* + z? = x2yi невозможно). Заме¬
тим, что левая часть уравнения х? \-y2-\-z2 делится на 4 только
в случае, если каждое из чисел х, у, г является четным (ибо остаток
от деления на 4 левой части равен количеству нечетных чисел в на¬
боре х, у, г). Поэтому х = 2ху, у~2у±, z = 2zi, причем
xt+yi+zl = 4xlyl
Правая часть последнего уравнения также делится на 4, откуда с по¬
мощью аналогичных рассуждений получаем, что ху = 2х2, yt = 2y2l
Zi=2z2 и
+	*1=	шьл
Продолжая подобные рассуждения и далее, получаем последователь¬
ность наборов целых чисел
xft=x/2* Уь=у12*, г* = г/2* где k£N,

Однако никакое целое число, отличное от нуля, не может делиться
на любую степень двойки, поэтому каждое из чисел х, у, г равно
нулю. Следовательно, нулевой набор представляет собой единственное
решение исходного уравнения.
2.16. Каждой паре чисел х, у£N, удовлетворяющих уравнению
л2=у2—х2, соответствует пара чисел р=у-\-х, q=y—х, произведе¬
ние которых равно п2. Поэтому количество ап этих пар не превос¬
ходит количества различных натуральных делителей числа п2. Следо¬
вательно, для всех простых чисел п имеет место неравенство в„ < 3,
поскольку при таких значениях я число «5 имеет ровно 3 натураль¬
ных делителя. Таким образом, на вопрос п. б) ответ отрицательный.
Далее, каждой паре чисел р, q, имеющих одинаковую четность и удо¬
влетворяющих равенству рщ=п2, соответствует пара чисел
Р=(Р+9)/2, х=(р—?)/2,
причем неравенство х > п имеет место в том и только в том случае,
если
2x — p—q = n2/q—q>2n, т. е. g<n/(l-f}/" 2).
Для всех значений n = 3l (I£ N) число q имеет вид 31 (j£Z+), а число
р=ЗР1~‘ имеет ту же четность. При этом неравенство 3* < 3z/(l -f- V 2)
выполняется для значений i=0, 1, ,.I— 1, поэтому -ап = 1, откуда
вытекает справедливость утверждения п. а).
2.17. Докажем, что если для некоторого значения x£Z число
Ж = **+4*
является целым, то это число либо не превосходит пяти, либо яв¬
ляется составным. Действительно, если х < 0, то число f (х) не целое*
Далее, при х—0 и х= 1 имеем
/(0) = 04+4° < 5, /(1)=14+4* = 5.
Если x=2k	то число
/ (х) = 24*4+42*=24 (Л*-f4? <*-'»)
является составным. Наконец, если x=2£-f-l (£(; N), то число
/(х)=х4 + 4.42* = (х4+4х2 (2*)? + 4(2*)4)—4х2 (2*)2 =
= (х? + 2 (2*)?)*— (2х2*)2 =
= (х?+2х2А+2(2*)?) (xS—2x2*+2<2*)?) =
= ((х+2*)2+2?*) ((х—2»)?+2**)
также является составным, поскольку каждый из сомножителей
(х± 2Й)?+2?Л больше 1 (ибо 2?Л > 1 при k > 0)* Таким образом, если
число р > 5 простое, то равенство х4+4х — р не выполняется ни при
каких значениях х €Z,
2.18. Предположим, что тройка чисел х, у, г£М удовлетворяет
уравнению. Тогда имеем разложение
((2х}*+1) mx~l)=y*+if

причем числа
к = (2х)*+\ и т = (2х)х—\
взаимно просты, ибо они нечетны и
(к, т) = (к, к—т) = (к, 2) = 1.
Поэтому в силу теоремы 22 найдутся числа р, q£ N, удовлетворяю¬
щие равенствам
k = pz+1, m = qz+1,
откуда имеем
2 = р*+‘—9*-и = (р—q) (p* + pz-1<7+. ..+9г).	1.
Поэтому
2^pz+pz~1q+.,.+qz^pz+qt^P + q > 2q^2.
Полученное противоречие доказывает утверждение задачи.
2.19. Докажем индукцией по п более сильное утверждение: для
любого значения n£N существуют числа
*1. .... *n€N
и нечетное число уп > 1, удовлетворяющие уравнению
*!+..-+*л=Рл.
При п=1 утверждение справедливо (достаточно положить xf —#{=3).
Пусть утверждение доказано для некоторого значения 1. Рас¬
смотрим соответствующий набор чисел Xi, хл, уп и положим
Хп+1={Уп—0/2, Уп+i — О/л-ЬО/2.
Так как число уп нечетно и уп > 1, то xn+t, J6,+i€N и Уп+1 > I-
Тогда набор
  *л» ^п+£» Уп + t
удовлетворяет условиям
*! + ••• + *л + *л+1==0п+*л+1==Ул+ — — =* (Vn + l)a>
Уп+i = (Уп + 0/2 =3 1 (mod 2)
(так как {/?!= 1 (mod 4)), т. е. утверждение справедливо н для зна¬
чения я+1.
2.20. Если п= 1, то при каждом значении z^N пара чисел
xi = zai, — zai
удовлетворяет уравнению. Пусть теперь п > I. Тогда, согласно китай¬
ской теореме об остатках (теорема 23), существует бесконечно много
натуральных чисел г, удовлетворяющих двум условиям:
zssO (mod а*,. ,ап) и г s—l(moda„+i).
Каждому из таких значений г соответствуют натуральные числа
У1 = Фи .У„ = г/а„, уп+Т = (г+1)/а„+1,
100

по которым в свою очередь строится набор .неизвестных
Xj = ny'£N, i=l, n, п+1.
Каждый из полученных наборов удовлетворяет уравнению, так как
+ ... +*£" = (ny‘)ai + ... +(пУп)ап = п2+... +/!* =
= п-п2 — nz+l = (n^'n+,)aп+, = Jc“^+, .
Поскольку при каждом значении n£N разным значениям г соответ¬
ствуют разные наборы неизвестных, то исходное уравнение в нату¬
ральных числах имеет бесконечно много решений.
2.21. Согласно китайской теореме об остатках (теорема 23) суще¬
ствует целое число n£(0; ab), удовлетворяющее условиям
п^=0 (mod b) и л Ess с (mod о).
Поэтому п = Ьу—с—ах для некоторых значений х, i/£Z, Так как
0^,by < at, то
y<La—1 и л<(а—1)Ь.
Наконец, из неравенств
с—ax<(a—1 )b, cSs (а— 1) (Ь—1)
получаем
ах^э; (а — 1) (Ь— 1) — (а — 1) b— 1 —а > — а,
т. е. х > —1. Таким образом, пара значений х, у^1+ представляет
собой решение исходного уравнения.
2.22. Пусть пара чисел х0, y0£Q является решением исходного
уравнения, а число k£Q удовлетворяет условию ак3.-\-Ь Ф 0 (таких
значений к бесконечно много, так как а? -\-Ь2 > 0, а значит, равен¬
ству ak3-\-b = 0 может удовлетворять не более двух из бесконечного
множества значений k£Q). Тогда числа
(Ь—ак3) х0—2bky0	(b—ак2) уй-^-2акх0
Х*~	ак3-\-Ь	’	Ук~~	ак3+Ь
также удовлетворяют уравнению, поскольку
...г , u..2 (b—ak3)3(axn+btj)+4abk3(axl+byl) ,2 , L..2_t
axk+byk =	(aiW+t)»	 axo+byo=	1.
Заметим, что если пара чисел	у к может быть получена с помощью
указанных выше формул, то это возможно не более чем при двух
значениях к, удовлетворяющих системе
/ а (хк+*e)	+2by0k+Ь (х/, — xe) = О,
I а(Ук+Уо) &—2ах0к-\-Ь (Ук—Уа) =0
(поскольку ax*+Ьуо = 1, то хотя бы в одном из этих равенств коэф¬
фициент при к отличен от нуля, и, следовательно, этому равенству
не могут удовлетворять более двух значений к), Таким образом, ис-
101

ходное уравнение имеет бесконечно много решений. Действительно,
если бы всего решений было п, то различных значений k£Q, удов¬
летворяющих условию ак2.-\-Ь ф 0, было бы не более 2п, что неверно.
Утверждение доказано.
Замечание. Приведенное решение задачи имеет наглядный
геометрический смысл: на координатной плоскости точки (xe; у0) и
(**'> Ук)—эт0 точки пересечения прямой х—х0 = к(у—у0) и кривой
ах2 + by2 = 1. То, что значения хц и рациональны, можно доказать,
не вычисляя самих значений: действительно, при ак2-\-Ь ф 0 числа
Ув и Ук являются корнями квадратного уравнения (относительно у)
а(х0+к (у—у0))2+Ьу?=1
с рациональными коэффициентами. По теореме Виета УоЛ~Уи—рацио¬
нальное число. Значит,
yk£Q и x„=x0-\-k{yk— y0)€Q.
2.23.	Для любых чисел k, т, а, Ь справедливо равенство
(ак2 + Ьт2)3 = а (ак3—3bkm2)2 + Ь (Зак2т—Ьт3)2.
Поэтому, если положить
x = ak3—3bkm2, у = Зак2т—Ьт3, г = ак2-\-Ьт2,
то будет выполнено равенство
ах2 ~^~Ьу2 = z®.
Докажем, что существует бесконечно много пар чисел к, т£Z, кото¬
рым	соответствуют различные тройки чисел х, у, z£Z,	удовлетворяю¬
щие	условию	(х,	у) = \. Заметим, что если все числа	к,	т,	а,	b
попарно взаимно просты (числа а и b взаимно просты по условию),
причем ровно одно из них четно и нн одно из чисел к, т не делится
на 3, то числа х и у взаимно просты. Действительно, при указан¬
ных условиях имеем
(к,	у) = (к, 3ак2т—Ьт3) = (к, Ьт3) — 1,
(т,	х) = (т, ak3—3bkm2) = (m, ак3) = 1,
причем хотя бы одно из чисел а или Ь, например Ь, не делится на 3
(случай, когда о не делится на 3, рассматривается аналогично; слу¬
чай, когда оба числа а и Ь делятся на 3, невозможен, ибо (о, fc)=l).
Тогда справедливы соотношения
(*> y) = (k (а* - — 3Ьт2), т (3ак2 — Ьт2)) =
= (ak2—3bm2, Зак2 — Ьт2) < (3ak2—9bm2, 3ak2—bm2) =
= (8Ьт2, 3ак2—Ьт2) = (Ьт2, 3ak2 — Ьт2) = (Ьт2, ЗаЛа) = 1,
так как число 3ак2—Ьт2 нечетно, а число Ьт2. не делится на 3.
Пусть оба числа а и Ь ненулевые. Положим
k = 3 | o6|-fl,
102

Тогда каждому значению
т= (61 ab | + 1)г при /£N
соответствует набор чисел х, у, г, удовлетворяющий условию задачи
(поскольку для чисел k, т, а, Ь выполнены указанные выше усло¬
вия). При этом все полученные наборы различны, так как все полу¬
ченные значения
различны. Пусть, наконец, одно из чисел а или Ь, например Ь, равно
нулю (случай а — 0 рассматривается аналогично). Тогда, если поло¬
жить х — г = а, а в качестве у брать различные числа, взаимно про¬
стые с числом а, то будут выполнены равенства
Задача решена.
2.24.	Предположим, что тройка чисел х, у, z£N удовлетворяет
уравнению при я > 1 и неравенствам х<^п, у<^п. При этом без
ограничения общности можно считать, что х^у. Тогда, используя
бином Ньютона, получаем
(у+1)" — у" -\-пуп~г •. • +1 > уп+хуп~1^:уп-\-хп = гп >уп.
Поэтому у +1 > z > у, что невозможно ни при каких значениях
2.25.	Пусть при некоторых значениях х, n£N, я > 2, исходное
уравнение превращается в верное равенство. Обозначим у=х-{-1^2,
тогда имеем равенство
из которого получаем
0= (у +1)”—у" - (у — 1)” зз 1 - (-1)» (mod у).
Поэтому число я четно, так как при нечетном я > 2 получилось бы
Os 2 (mod у), откуда
что невозможно. Далее, согласно биному Ньютона, при четном я
справедливы сравнения
(у ± 1)”^ П ’ ■ Уа ± пу + 1 (mod у3),
0=(у+1)п—уп — (у— 1 )п = 2пу (mod у3),
следовательно, 2я = 0 (mod у2), откуда 2n=si/2. Деля исходное равен¬
ство для у на у", получаем соотношения
z=ak2.-\-bm2.
ах? + by* = а- а2+0-i/2 = а3 = z3.
У, zgZ.
G/—«)"+</" = Q/+l)n,
z/= 2 и 0 = 3n — 1 — 2п > 0,
103

С другой стороны, в силу неравенства Бернулли (теорема 5) имеем
(4-7)" > 1+7=1+1)-^1+%==1+т^2-
Полученное противоречие означает, что исходное уравнение не может
иметь решений.
2.26.	Пусть положительные х, y£Q удовлетворяют исходному
уравнению. Докажем, что тогда положительное число
является натуральным. Из уравнения получаем
хх+хг = (х-\-хг)хг, т. е. дс1+г = лсг (1 +*)*,
поэтому имеем равенство
х=(1+г)*.
Обозначая
z—plq, х = т 'п,
где	I
р, q, т, n£N и (р, q) = (т, п) = 1,
получаем соотношение
(m/n)4 = ((p-\-q)/q)P, т. е. m4qP = n4 (p+q)P.
Поскольку (тЧ, пЧ) = 1, то qP : пЧ. С другой стороны,
((Р+Ч)р. ?я) = (Р+9. Ч)р = (р. 9)^=1.
поэтому пЧ-qP. Таким образом, имеет место равенство qP-пЧ, из
которого следует, что если q > 1, то в разложении числа qP на про¬
стые множители каждый из простых делителей имеет степень, крат¬
ную как числу р, так и числу q, а значит, и их произведению pq
(так как числа р и q взаимно просты). Следовательно, в разложении
числа q на простые множители каждый из простых делителей имеет
степень, кратную q, что невозможно (ибо q <24 при любом ?£N).
Итак, доказано, что 9=1. Поэтому получаем
x = (l-fz)*, y = z(\+z)z при z£N,
а проверка показывает, что все полученные пары значений х,
удовлетворяют исходному уравнению.
2.27.	Если
п = т (4k— 1)	(т, k£N),
то выполнено равенство
J .	1	=	4	4
km ' km (4k— 1)	т (4k— 1)	п’
т. е, уравнение имеет решение
x = km, у—km (4k— 1).
Пусть теперь числа
x=24xit у=2гщ, где q, r£Z+,

*i, yi — нечетны, удовлетворяют уравнению. Тогда, если q < г, то
число
  4ху   29+г+2лс1(/(
П~х + у~ 24 (*i+2'~чУ1)
является нечетным только в случае q-\-r-\-2 = q, что невозможно.
Аналогично доказывается, что невозможен случай q > г. Таким обра¬
зом, q=r и число
24+
п—	;——
нечетно. Поэтому сумма нечетных чисел Xi и у\ делится на 4, а зна¬
чит, они дают разные остатки при делении на 4. Заметим, что если
бы все простые числа вида 4k—1 при N входили в разложения
чисел х н у на простые множители с одинаковыми степенями (воз¬
можно, нулевыми), то выполнялось бы соотношение	(mod 4),
что неверно. Следовательно, существует простое числор—Лк—1 (fe£ N),
удовлетворяющее условиям
*1 = Р"*2. г/1 = Рг'{/2. «. v^Z+, ифь,
где числа xa, у2 не делятся на р. Пусть и < v (случай и > v рассмат¬
ривается аналогично), тогда ы+о > и и число
_ 24+2р“+*хгу2
п ри (*2+рг,-“г/2)
делится на р, т. е. имеет вид
ti = mp = m(4k— 1).
Доказательство закончено.
2.28.	Обозначим описанное в задаче множество чисел через М и
допустим, что оно представимо в виде объединения конечного мно¬
жества арифметических прогрессий. Докажем, что среди этих про¬
грессий нет ни одной бесконечной. Действительно, пусть для некото¬
рых значений a, d£N множество М содержит все числа вида a-\-jd
при /£Z+. Заметим, что 3d—1 ф М, так как при n — 3d—1, x=d,
y — d (3d—1) имеют место равенства
3	3	1.	1	1	.	1
п ~3d— 1 ~ d+d {3d— l)^ х + у '
Далее, если пф М, то тп ф М для любого значения m£N, так как
из равенства
п~ х ' у
вытекает равенство

Выберем число т, удовлетворяющее условиям
/лее—a (mod d), т 3= aj(3d— 1),
тогда число
т (3d — 1) a (mod d),
с одной стороны, имеет вид a-\-jd (j(£ Z+). С другой стороны, оно не
содержится в множестве М. Полученное противоречие доказывает, что
множество М является объединением конечного множества конечных
арифметических прогрессий, т. е. это множество конечно. Докажем,
что и это невозможно. Для этого проверим, что любое число вида
п— 7к (6£Z+) принадлежит множеству М. Предположим, что это не
так, т. е. равенство
выполняется для некоторых значений х, г/£N, A£Z+. Обозначим
?=(*. У), т°гДа имеем x=qxx, у=ду±, (хь t/i) = 1 и
3 ^.x+y^xj+yt
7й ху qxyyt ’
т. е.
7*(Jfi+4'i)=3?x1i/1.
Заметим, что (xx-f-j/х, ХхУх) = 1, так как если произведение хху± делится
на какое-либо простое число р, то одно из чисел xit ух делится на р,
а другое нет (ибо (хх, ух)—1), а значит, сумма хх-f-yx также не
делится на р. Но число 7ft(xx+ti) делится на ххух, поэтому имеем
соотношения
Xi = 7", yi = 7v (и, v£Z+),
Xi = (2-3 + l)“=l (mod 3), w = (2-3-f 1)»^ 1 (mod 3),
xx-j-yxsEs 2 (mod 3).
Таким образом, число 7*(xx+j/x) ие делится на 3, что противоречит
равенству
7* (xi -j-yi) = 3qxxyi
н завершает доказательство утверждения задачи.
2.29.	Предположим, что, вопреки утверждению задачи, некоторая
пара чисел х, у£Z удовлетворяет уравнению. Тогда число х четно.
Действительно, в противном случае
x? = (2ft+l)? = 4*(ft+l) + ls=l (mod 4),
откуда
у* = х? + 5 ее 2 (mod 4),
что невозможно (поскольку в этом случае у четно, а значит,
у3 = О (mod 4)). Из четности числа х следует, что
у3 = х?+5 ее 1 (mod 4),
поэтому
уагш 1 (mod 4)
106

(если у ез—1 (mod 4), то у3 —1 (mod 4)). Обозначим
х = 2я, y = 4m-\-l	(т, n£Z),
тогда из уравнения получаем
4 (««+1) = x2+4=p8-1 = {у- 1) {у*+у+1) = 4т (16т* + 12/я+З),
откуда
ti2-\-\—md, где d— l6/ns+ 12m+3 аЗ (mod 4).
Заметим, что хотя бы один из простых делителей числа d должен
иметь вид р = 4/+3, где l(£ Z+, Действительно, так как число d не¬
четно, то все его простые делители нечетны. Если бы все они были
сравнимы с единицей по модулю 4, то и число d (равное произведе¬
нию этих делителей, взятых в некоторых степенях) было бы также
сравнимо с единицей по модулю 4. Итак, имеем
л? +1 = md as 0 (mod р),
поэтому
л2 = —1 (mod р) и пР~1 = я4'+? = (л2)2/+1 “ —1 (mod р),
что противоречит малой теореме Ферма (теорема 25), согласно кото¬
рой
пР~г 1 (mod р).
Утверждение задачи доказано.
§ 3. Факториалы и биномиальные коэффициенты
3.1. Докажем, что для любого значения я£N, большего 2, спра¬
ведливо неравенство
(л!)2 > л".
Действительно, имеем
я'-я! = (1 -2.. .я) (я (я— 1)... 1) = (1-я) (2 (я— 1)).. .(я-1) > я",
так как
1-я = я< 1 — я и к{п—Л1) = (я—к) (к—1)+я>я
при к — 2, ..., л— 1. Положив в доказанном неравенстве
я =17091982,
получим ответ:
(17091982!)2 > 17091982170НВ82.
3.2. Поскольку для каждого значения £=1, 2, ,.я— 1 выпол¬
нены соотношения
/-'к—х /~'к к	-| 1 ..ft Я к ^ [ /\
с" =c"'n_ft+i‘' Ln	с"^0'
то равенство
2С* = Сп-'+С£+1
107

равносильно равенству
2=jrniqpi+Sr или (п-2^ = "+2-
Следовательно, искомые значения N обязаны иметь вид я = Я12—2,
где га = 2, 3, ... Однако если га = 2, то я = 2 и равенство (и—2k)2=
= n-f-2 не выполняется при единственно возможном в этом случае
значении k= 1. Если же га > 2, то это равенство справедливо, напри¬
мер, при k—m(m—1)/2—1 (указанное значение k является целыми
удовлетворяет неравенствам 0 < k < л, так как одно из чисел га или
га— 1 является четным и при га > 2 имеют место оценки
О < га (га— 1)/2— 1 < га2 — 2).
Таким образом, искомые значения я— это все числа вида п — т2—2,
где га = 3, 4, ...
3.3. Пусть числа х, у, г, u£N удовлетворяют исходному уравне¬
нию, а через v обозначено наибольшее из чисел х, у, г. Тогда
1 <v < и и
ш>\ < и (и— 1)1 = н1 = х! +J/I + z! < 3ul,
откуда uv\ «s; Зи!, а значит, u«S 3. При ы = 3 имеем равенства
31 = Зо! = х! -\-yl +г1,
которые справедливы только в случае x = y=z = v = 2. При ы=2
уравнение решений ие имеет, так как в этом случае
ul = 2 < 3«i xI+j/1 + г!.
Таким образом, исходное уравнение имеет единственное решение
х=у—г=2, и = 3.
3.4. Из тождества
(1+х)2" = (1+х)'»(1+х)«,
пользуясь биномом Ньютона, получаем
Сап + С|п* + • • • + СгпХ2" =
— (Сп ] Спх + ... +СпХ") (Сп СлХ -)-,., +Спдс”).
Приравнивая коэффициенты при хп и учитывая равенства
СЙ=СЙ“\ * = 0, 1 я,
получаем соотношение
сЪ = (с?,)2+(сА)2+... + (ей)2.
Поэтому
V (2л)!	(2п)!	V	(«О2
(*1)2 ((«—*)!)» — я!я! (ft!)2 ((я— Л)!)2
= Саг, [(С°)2 + (С‘)2+ ... + (Сй)2] = (Сй„)2,
что и требовалось доказать.
108

г
3.5.	а) Положительное число
1	,-т	^т \ /^т пт	(2/п)!	/^т-1
_ С2т _	~^pi)	^чт Cam (т — 1)! (т -f-l)i Ш
является целым, ибо Cam, С^'£N при m£N.
б)	Пусть задано число т£N. Так как при л = т число
fe рп+т	fe
я -1- т +1 2П	2т+1
должно быть натуральным, то искомое значение N должно делиться
па 2m-]-1, поэтому k^2m-\-\. Пусть Л=2т+1. Тогда при я = т
положительное число
k ,-п+т
п+т-И
является натуральным, а при я > т оно равно
2т 4-1 /wi+m (, я—m \ пп+т
п+т+ I м ~Л л+m+l/ _
(2я)!
(л + т + I)! (л—т— 1)!
wi ьт /^п+т+1
:(-<2П	—»
т. е. является целым, ибо С^т, C^m+1 £N. Таким образом, искомое
наименьшее значение k равно 2т +1.
3.6. Пусть числа С%, Cm+i Сп+к имеют общий делитель d £ N.
Тогда числа
/".fc — 1 /^к	r^h	fk—\ />k r> k	/^fc-1	/>k	/А
t-n =Ln+i —L/I, t>n + l = '-'n + 2 — '-'Л + tf •••* ^я+ft— 1—
также имеют общий делитель d. Аналогично получаем, что числа
dr2
имеют общий делитель d. Продолжая аналогичные рассуждения и да¬
лее, получим в итоге, что число (?„ — 1 делится иа d. Следовательно,
d—l.
3.7. При каждом значении л £ N докажем индукцией по m£N
справедливость равенства
(я+т)!
При т = 1 имеем верное утверждение
л!
S, „= 1- (И^}' ^1-(л+2) = --(п-+т^!,
л! (я -j-1)	'	1	л!
109

Пусть для некоторого значения m£N равенство уже доказано, тогда
имеем
s f =s	I /	1V»+1 (» + m+2)! _
*m+i, „=->», n+(	*)	n!(n+m+l)	—
c,_,« (»+m) 1 . ,	1>M+i	(<i	+	m)!(n+m+2)_
i	u	nl -i-i	Ч	я)
= (_1)<т.+1 (” + m)' (_ \+n+m+2) = (— l)m+1 ("+ n|+1)!’
т. e. утверждение справедливо и для значения m+1. Таким образом,
число
Sm, „=(-!)“	mi	=	(-1)* C?+mm!
делится на ml,	ибо C”+m£N.	Наконец, заметим,	что	при л=2,	т = 3
число Srai„=—60 не делится	на т! (и +1)= 18.	Задача	решена.
3.8. Рассмотрим простое число р > 2 (при р = 2 утверждение за¬
дачи верно, так как число С|—2 = 4 делится на 2? = 4). Прежде всего,
имеем равенства
пР	(2Р) I _ 2р (2р — 1) I	0^р-1	.
С2" - -Ш-р{р-\)\р\ -
Из соотношения
(2р—ft) (p+k) Е= ft (р—ft) (mod р2),
выполненного при каждом значении ft=l, 2, ,,., (р—1)/2 (число
р— 1 четное), получаем, что произведение
(2р-1)(2р-2)...(р+1) =
= ((2р— 1) (р+ 1)) ((2р—2) (р+2))... ( (Яр-fi^-J (p+^J ) -
»(1-(р-1))(2.(р-2))...	(modp2)
сравнимо с числом (р—1)1 по модулю р2. Следовательно, для некото¬
рого числа т£ Z справедливы равенства
^р-1	(2р—	1)(2р—2) ... (р+1)_тр2 + (р— 1)1 _ тр2 ,,
гр~г~	(р—1)1	[Р-1)1 (Р—1)1
Поскольку число тр*Цр—1)1 = Cap-i— 1 является целым и
(р2. (Р- 1)0 =1. то т = I (р—1)1, где Z. Поэтому имеем соотношения
С?А = /(gl1)i||P-+1 = /р2 + 1 ^ 1 (mod р2),
C?p = 2Cfpi1^2(modp2),
откуда вытекает справедливость утверждения задачи,
3.9. Обозначим
/(*)= 11+2!+ ,.•+(*+1)1,
110

тогда
/ (I) =3. / (2) = 9 = 31+1, /(3> = 33=3-ll.
При x > 3 получаем, что величина
/(*) = /(3) + 5! + ... + (*+ 1)! ^ 3 (mod 5)
не является квадратом целого числа, так как при любом 6£Z имеем
(56)2 = 2562 = 0 (mod 5),
(56 ± 1)? = 2562 ± 106+1	1	(mod 5)
и
(56 ± 2)? = 256? ± 206 + 4 зз 4 (mod 5).
Следовательно, значение г — 1 ни при каких натуральных числах х Ф 2
и у не удовлетворяет равенству f (х) =уг+1. Докажем, что при осталь¬
ных значениях г >2 это равенство также не выполняется. Непосред¬
ственная проверка показывает, что каждое из чисел f (х) при х= 1, 2,
3, 4, 5, 7 делится на 3, но не делится на 27, а значит, не может быть
представлено в виде
f(x) = y*+1, г 3*2.
■ч.
Такой же вывод можно сделать н при х > 7, так как в этом случае
/ (*) = / (7)+91 + . .. + (*+ 1)- = f U) (mod 27).
Наконец, при х=6 также получаем, что число
f (6)=5913 = 34-73
не представимо в указанном виде. Итак, уравнению удовлетворяет
единственный набор значений х=2, у=3, г=1.
3.10.	Пусть пара чисел х, p£N удовлетворяет уравнению. Заме¬
тим, что число р—у-\-1 простое. Действительно, если существует дели¬
тель d числа р, удовлетворяющий условию 1 < d < у-\-1, то имеем
у\ : d и
1 = (У+ 0*—г/1 = 0 (mod d),
что невозможно. Поэтому имеем уравнение
рх— 1=(Р— 1)1,
из которого вытекает, что р < 7. Действительно, предположим, что
р^-7. Тогда, сокращая обе части уравнения на р—1, получаем ра¬
венство
Рх-1+ ■ ■ • + 1 = (р—2)1,
в котором правая часть делится на 2-(р—1)/2 = р—1 (так как 2<
< (р — 1)/2 р—2 при рз* 7 и (р— 1)/2£Z), а левая часть представ¬
ляет собой сумму х чисел вида
р'= К га 1 (mod(p— 1)), 1=0, I,- х— 1,
Следовательно, 0 (mod (р— 1)), а значит, *3= р~- Ь Но это невоз¬
можно, так как
р*-1 < р*-*+... +1 = (р—2)1 < (р-2)*-* < р*-\

т. е. х < р— 1. Итак, простое число р < 7 может принимать только
значения 2, 3 или 5. Если р = 2, то
2*—1=1 и х= 1, у = 1.
Если р=3, то
3*—1=2 и х= 1, i/= 2.
Если же р— 5, то
5*—1 = 24 и х=2, р= 4.
Таким образом, получаем, что исходному уравнению удовлетворяют
только три пары натуральных чисел (х; у): (1; 1), (1; 2) и (2; 4).
3.11. Пусть
h=THr+1 (*=1< •••. п).
Докажем, что если р—простой делитель числа /*, то число р не делит
ни ©Дно из чисел my, j Ф к. Так как при этом число р делнт число
mfc = /ftA, то оно будет искомым. Предположим, что /ь : р и ту \ р при
некоторых значениях k Ф /. Тогда /у : р или / • р. Случай / ■ р невоз¬
можен, так как число / является одним из сомножителей в произведении
1-2.. .(к— 1) (ft-f- 1).. .« = /*— 1
и, значит, (/*— 1) : / и
(i. /ь) = (/. 1)=1.
Остается рассмотреть случай lk : р, /у : р (к Ф [). Пусть р < я. Тогда,
если р Ф к, то число р взаимно просто с числом /* (доказательство
этого факта подобно проведенному выше для чясла /), а если р Ф j,
то число р взаимно просто с числом /у (доказательство аналогично).
Следовательно, в любом случае число р взаимно просто хотя бы
с одним из чисел /* или /у. Поэтому неравенство р<я невозможно.
Пусть р > я. Тогда имеем
й—/=mfc—my = A/fc—//у в® О (mod р),
т. е. (А—У) • р, что невозможно, так как
0< | А—/| < я <р.
Утверждение доказано.
3.12. Показатель степени, в которой двойка входит в разложение
числа IX на простые множители, равен
Й+М+М+-
см. теорему 20), Поэтому число С* = щ^—^ является нечетным
тогда и только тогда, когда наибольшая степень двойки, на которую
112

делится число Сп, имеет показатель
чш-т-мми-ш-м)+
+([4Н4]-М)+--
равный нулю (при достаточно больших значениях m £ N каждое из
чисел [л/2т], [Л/2™], [(л—ft)/2ra] равно нулю). Из равенств
я _ ft n-k_ Г ft 1 Гя-ftl ,1*1, /я~*\
2m 2m 2m L J L J \ 2m j \ 2m f
вытекает, что каждое из чисел
[^ЫтМт^НФ+М]
при m£N неотрицательно. Поэтому равенство d = 0 возможно в том
и только в том случае, если для всех значений	выполнены	нера¬
венства
[kl2-»}+{(n—k)/2“} < 1.
Докажем, что последнее . условие равносильно условию для двоичных
записей чисел я и ft, сформулированному в задаче. Предположим, что
в любом разряде двоичной записи числа л стоит не меньшая цифра,
чем в том же разряде числа ft. Тогда для каждого m£N имеем
{n/2m}3*{ft/2m}, поэтому
Предположим теперь, что в некотором разряде числа я стоит меньшая
цифра, чем в том же рааряде числа ft (это могут быть только цифры
О и 1 соответственно). Тогда для некоторого значения m£N имеем
(л/2я) < {ft/2™}, поэтому
М-{-*М±}+,>,-{±}-
Итак, равносильность указанных выше двух условий доказана. Задача
решена.
3.13.	Докажем, что условие б) эквивалентно следующему условию:
в)	n=p1l + (pt— 1), где /gZ+, /gN, I < p.
Действительно, из условия б) имеем
п=р*т—1 =ps (т— 1)+(р*— 1),
где sgZ+, mgN, m < р. Если m > I. то положим
t = s, l — (m— 1) > 0.
Если же m= 1, то s > 0, так как иначе п—р°< 1 — 1 =0 £ N. Поэтому
n = pi~l-p~l—pi~i (p— l)-f
,113

и можно положить t — s—1^0, 1— р—1 < р. В обоих случаях ус»
вие в) выполнено. С другой стороны, из условия в) имеем
n = p4 + (pt-l) = pt (/-hi) — Ь
Если 1 -(-1 < р, то
m = l+1, s = t,
а если /+1 =р, то
т= 1, s=l+l.
Для заданного числа n£N найдется такое t£Z+, что
Р*<п < р'+\
откуда
п = рЧ-\-г, где 0<г<р<, 1</<р.
Поскольку наибольший показатель степени простого числа р, на кото¬
рую делится число q\, равен
[р]+й+И+-г
то наибольшая степень числа р, на которую делится число
nk п\
я I
~k\ (п— А)!’
имеет показатель
(при i > t каждое из чисел [п/p'J, [А/p'], [(п—*)/р*‘] равно нулю). №
соотношений
вытекает, что d* = 0 тогда и только тогда, когда имеют место
ства
1=0, 1, 1,
Докажем, что это возможно лишь в случае г=р* — 1, т. е. при усло¬
вии в). Действительно, если г<р*—2, то положим А=р*—1, i=t,
Тогда имеем
следовательно, указанное выше равенство, а с ним и условие а) к
выполняются, Пусть теперь выполнено условие в), тогда для всех
114

шчений *х= О, I, / и k — O, 1, .п имеем
k = pi +q, О <.q<pl,
поскольку 0*Ср' — (?+1) < р*. Поэтому d* = 0 при ft = 0, I, я,
а значит, условие а) выполнено. Доказательство закончено.
3.14.	Предположим, что число
O.ftiMs-.-
рационально. Тогда существуют числа N, 7"£ N, для которых выпол¬
нены равенства й0+г=й„ при всех N. Докажем, что существует
число Ti, которое делится на Т и имеет последнюю ненулевую цифру,
равную 1. Действительно, пусть
Т=2“-5^ .р, где a, F£Z+,
а число р не делится нн на 2, ни на 5. Тогда последняя ненулевая
цифра числа
Г„ = 2Р-5аГ= 2“+<,-5а+Р.р = 10“+Рр
нечетна и отлична от 5. Если она равна 1, то положим 7у= Тв, если
она равна 3, то положим Ti — 7Te, если она равна 7, то положим
Tt=3Tt и, наконец, если она равна 9, то положим Т1 = 9ТЛ. В этих
случаях последняя ненулевая цифра числа 7\ совладает с последней
цифрой числа 1, 21, 21 и 81 соответственно. Итак, найдено число
Tf= 10« (10д +1)	(m,	a£Z+),
удовлетворяющее равенствам ha+Tt=h„ при N. Докажем, что
Л„ jfc5 для любого значения л£ N. Действительно, показатель степени,
в которой входит двойка в разложение числа п! на простые множи¬
тели, равен
у = [п/2] + [п/22] + [п/23] + ...,
а соответствующий показатель для пятерки равен
б=[п/5] + [п/52] + [л/53] +...
(см. теорему 20). Поскольку справедливы оценки [л/2'] ^ [л/5‘] при
i£N, то ySs6 и
nl = 2V -5е .0= 10е • 2y~6-q,
где число q не делится ни на 2, ни на 5, а значит, последняя нену¬
левая цифра числа nl совпадает с последней пифрой числа 2v-e-q,
отличной от 5, Выберем число N таким большим, чтобы выполня¬
лось неравенство М= 10*" (1СЦ>+1) > N, и обозначим Йд|_е=А. Тогда
(/И—1)1= 10*(10с4-й), где й, c£Z+,
118

откуда получаем равенства
М1 = (М— I)! М = 10я (Юс+А)-10"» (10&+-1) ==
= 10*+»>(10(106c+ft6+c)+/i)l
поэтому hM = h. Далее, hM_i+Tt =hM_f — h, откуда имеем равенство
(М —1+Гх)! = 10'(1ад+Л). где I, d£Z+.
Следовательно, получаем соотношения
(М + Г,)! = (М- 1 + 7\)! (М + Ту) =
= 10' (10d+ft) (10»» (106+1) + 10я» (10а + 1)) =
= 10»» +' (lOd + h) (10 (а + 6) + 2) =
= 10»» +' (10 {lOad + 106d +аЛ + bh + 2d) +21),
т. е. величина +Tt совпадает с последней цифрой числа 2h (отлично!
от нуля, ибо Н ф Он Н ф 5). С другой стороны, эта цифра должш
равняться hfii—h, чего не может быть ни для одного из значений
6=1, 2, 3, 4, 6, 7, 8, 9. Полученное противоречие доказывает спра-
ведливость утверждения задачи.
§ 4. Числовые множества
4.1. Пусть Х = А[)В и для определенности 5£А. Предположим,
что ни в каком из множеств А и В нет тройки чисел, сумма двух из
которых равна удвоенному третьему. Если 3£ А, то 1 £В, 4£В и7£й,
что противоречит предположению, так как 1+7 = 2-4. Аналогично
доказывается, что 7 £ А. Поэтому 3£В и 7£ В. Заметим, что хотя
бы одно из чисел 4, 6 принадлежит множеству В (иначе числа 4,5,6
образовали бы недопустимую тройку). Пусть,4gB (случай 6£В ана¬
логичен), тогда
2£А	(иначе	{2;	3;	4} с В),
8£В	(иначе	{2;	5;	8} С А),
6(иначе {4; 6; 8) с S),
9£А	(иначе	{7;	8;	9} с В).
Если 1 £А, то
{1; 5; 9} с А.
Если 1£В, то
{1; 4; 7} С В.
Получили противоречие с предположением,
4.2. Для любых значений i, /€(1; •••: 7> количество чисел,
в которых на (-м месте стоит цифра /, равно 61, Поэтому сумма всех
чисел равна
(61-1 +... + 6!-7) + (61-1 + ... + 61-7) 10+
+ (61-1 +... +6! -7) 102+ +(6! • 1 + ... + 61-7) 10® =
=6! (1 +2+... +7) (1 +10+.. .+10®)=720-28-1111111 =22399997760.

4.3. Разобьем все возможные остатки от деления на 100 на сле¬
дующие группы:
{0}, {1; 99}, {2; 98}, ..., {49; 51}, {50}.
Так	как	всего групп 51, а чисел 52, то по принципу Дирихле	(тео¬
рема 1) среди них обязательно найдутся 2 числа, остатки от деления
которых на 100 попадают в одну группу. Эти числа и будут иско¬
мыми (если их остатки совпадают, то на 100 делится разность чисел,
а если различаются, то их сумма).
4.4. Пусть для некоторого множества, состоящего из чисел
а,, аа,	..., ап, утверждение задачи неверно. Тогда ни одно из л	чисел
Si = alt S2 = a»+a2 S„ = a1 + a2+... +ап
не делится на п. Поскольку количество возможных ненулевых остат-
. ков от деления на л равно л—1, то по принципу Дирихле (теоре¬
ма !) найдутся два числа Sj и Sy (1 <1 < /<л), имеющие одинако¬
вые остатки. Следовательно, разность
•Sy—S,- = a,-+i -f-... +Яу
делится на л, что противоречит сделанному предположению н дока¬
зывает утверждение задачи.
4.5. Рассмотрим 2я чисел
^1»	к—а2,	A—oni
Так как 2л > т, то хотя бы два из них дают при делении на т оди¬
наковые остатки. По условию задачи числа at, с2, ..., ап имеют раз¬
ные остатки от деления на т, откуда получаем, что числа
А—aj, А—а2, .... А—а„
также имеют разные остатки. Поэтому пару чисел с одинаковыми
остатками могут образовывать только числа вида а,-, А—ау (для неко¬
торых номеров », /). Тогда разность этих чисел а,-+fly—А делится
на т, что и требовалось доказать.
4.6. Предположим, что утверждение задачи неверно. Тогда среди
19 натуральных чисел
азо—ai»t aiu—fli8, •••» ва—ai
нет 4 одинаковых чисел. Поэтому среди них ни одно из чисел 1, 2,
3, 4, 5, 6 не может встретиться более 3 раз. Следовательно, хотя бы
одно из этих 19 чисел больше 6 (иначе чисел, не превосходящих 6,
было бы более 18), хотя бы 3 из оставшихся 18 чисел больше 5, хотя
бы 3 из оставшихся 15 чисел больше 4 и т. д. Поэтому их сумма
(а10—<Тц) +(йТв—ais) + — + (й2—ai) Si
^7+(6+6+6) + (5+5+5) + ...+(1 + 1 + 1) = 70
не'может быть равна числу aw—a* <70—1 = 69. Полученное про¬
тиворечие доказывает требуемое утверждение!
117

4.7. Заметим, что хотя бы в одном из 7 подмножеств содержится
не менее 15 чисел (в противном случае во всех подмножествах вместе
содержалось бы не более 7-14 = 98 чисел). Каждой паре чисел а>Ь
нз этого подмножества поставим в соответствие разность а—Ь. Тогда
всего получится не менее
Си =15-14/2 = 105
разностей, среди которых обязательно найдутся одинаковые (так как
величина разности может принимать не более 99 значений 1,2, ...,99).
Пусть оказалось, что для двух пар чисел а > Ь и с > d выполнено
равенство а—b = c—d (откуда а ф с, Ь Ф d), тогда a + d = fc+c.
Если же при этом a = d (или 6 = с; других совпадений быть не может),
то Ь-\-с=2а (илн a+d = 26). Утверждение задачи доказано.
4.8. Предположим, что, вопреки утверждению задачи, в некотором
интервале длины 1/я содержится более (л+1)/2 несократимых дробей
вида p/q, где q£{ 1; 2;	л}.	Докажем, что среди знаменателей
этих дробей найдутся два, один из которых делится на другой. Дей¬
ствительно, представим каждый из знаменателей в виде 2rs, где s —
нечетное число, rg z+. Количество различных нечетных чисел среди
чисел 1, 2, ..., л равно [(л	1)/2]	(т. е. меньше, чем количество рас¬
сматриваемых знаменателей), следовательно, найдутся два знаменателя
q = 2r-s и qi = 2ri-Si,
для которых в—Si и г<г(. Тогда одни из них делится на другой,
т. е. 9] = kq. Таким образом, среди дробей можно выбрать два раз¬
личных числа вида m/q и l/kq, где kq^n. Тогда
\ т	/ I _1_
I q	kq I	^ л ’
так как оба числа лежат в интервале длины 1/л. Поэтому km—I—О,
ибо в противном случае
I т 1\  | fern—/1	1	_1_
I q kq I	kq	kq	n	‘
Итак,
km = l и l/kq = km/kq = m/q,
т. e. оба выбранных числа совпадают. Полученное противоречие дока¬
зывает утверждение задачи.
4.В. Найдем количество троек натуральных чисел
составляющих в сумме 6л. При каждом значении k— 1, 2, ..., п
выпишем все тройки, для которых x=2ft—1 и соответственнох=2k:
(2k—1; 2k—1; 6л —4ft+2),
(2k—1; 2k;	6л—4ft+l),
	  t	i »	•	■	•
| (2ft—1; Зя—ft; 3n—ft-j-1),
118

и соответственно
(2k; 2k; 6л — 4k),
(2k; 2fe+l; 6л —4ft—1),
(2k; 3n — ft; 3n—ft).
Поэтому количество всех выписанных троек равно
Sk = (Зп—k) — (2 k—2) + (Зя—k) — (2ft — 1) = 6я—6k + 3,
а количество всех троек, удовлетворяющих условию задачи, равно
£	=	(6n-6fe+3)	=	^~3l+j.n	=	3n?.
*=i	*=i
4.10. Каждому набору из 6 различных натуральных чисел от 1
до 49 (без ограничения общности считаем их расположенными в по¬
рядке возрастания)
ах < яа < as < я4 < я6 < я»
поставим в соответствие набор вида
ои —1» а3—2, я4—3, Й5 — 4, йд — 5,
Числа в последнем наборе различны в том и только в том случае,
если в исходном наборе не было последовательных чисел, и всегда
расположены в порядке неубывания. Таким образом, мы установили
взаимно однозначное соответствие между множеством наборов из 6 раз¬
личных чисел от 1 до 49, среди которых нет последовательных чисел,
и множеством всех наборов из 6 различных чисел от 1 до 44. Коли¬
те
чество элементов в каждом из этих множеств равно Си, а количество
всех наборов из 6 различных чисел от 1 до 49 равно С'3. Таким обра¬
зом, количество наборов, в которых есть последовательные числа,
равно См—С*4-
4.11. Будем строить множества А и В индукцией по л £ N. Поло¬
жим 1 £ А, Пусть числа 1, .... я—1 уже распределены по подмно¬
жествам А и В, Рассмотрим число п. Если найдется число
; л 1),
удовлетворяющее равенству kx/n = c, то отнесем число я в то под¬
множество, которое не содержит числа kx. Если же для некоторого
числа
...; л—1}
выполнено равенство n/k^ = с, то отнесем число л в подмножество,
ие содержащее числа k2. Заметим, что равенства kjn = c и n/ft2 = с
одновременно выполняться не могут, поскольку иначе было бы верно
равенство ki/n = n/kt, т. е. kxft2=n2, что невозможно. Наконец, если
чисел kx и йд нет ни в одном из подмножеств, то положим п£А.
119

Полученное в итоге разбиение множества N на два подмножества
будет удовлетворять условию задачи.
4.12. Поскольку
bi—b/+t = (l —л) +	-+а(-+2+ ...
.. ■ Ojj -f- flj -f- ... -f- Д/= 1 —nfl/ = 1 (mod я)
при каждом значении I—I я—1, то
bn-i^b„ + l (modn),
6n-a^ 6„_x + l (mod n),
(mod я).
Следовательно, числа
/>„_; = bn + t (mod n), i'=0, I,..., n—I,
дают при делении на я различные остатки, а значит, не могут
совпадать.
4.13. Допустим, что для некоторого значения я существует строка
из 2я чисел, обладающая требуемым свойством. Обозначим через т/,
номер того из двух чисел, равных к, которое идет в строке первым
(слева). Тогда второе из этих чисел имеет номер т^ + к +1, а сумма
номеров всех 2я чисел в строке равна
2 (ть + (тк + к +1))=2 2 mk+n(n + 3)/2.
*=|	k=I
С другой стороны, сумма тех же 2п номеров равна
2 п
2 /=я(2я + 1).
i = 1
Поэтому
П
2 2 пгк—п (2п + 1)—я(я + 3)/2=я(Зя-1)/2,
k=\
следовательно, число я (Зя—1)/4 является целым. Поскольку лишь
одно из чисел я и Зя—1 может быть четным," то оно же должно
делиться и на 4, а значит, возможны только два случая: либо я = 4/,
либо Зя —1=4/', т. е.
я = 4Ш-1=4/—1.	где /, /'gN.
О
Докажем, что любое число я указанного вида удовлетворяет условию
задачи. При я = 4/, /^ 2, требуемым свойством обладает, например,
строка
(4/—4;...; 2/; 4/—2; 2/—3;1; 4/—1; 1;...;2/—3;
2/;...; 4/—4; 41; 4/—3;...; 2/+1; 4/—2; 21—2;...; 2;
21—1; 4/^1; 2;	21—2;	21+1;...;	41—3;	21—1;	41),
120

в которой каждое многоточие обозначает арифметическую прогрессию
с разностью 2 или —2, начинающуюся числом перед этим многоточием
и кончающуюся числом после него. Аналогично, прип = 4/—1,1^2,
подходит, например, строка
(4/—4; .21; 41—2; 21—3; I; 41— I; I; 21—3;
21; ...; 4/—4; 21— I; 41—3;	2/+1;	4/-2;	21—2; ...,2;
2/— I; 4/— 1; 2;	21—2; 2Z+I;	4/—3).
Наконец, для п=4 и п = 3 имеем строки (2, 3, 4, 2, I, 3, I, 4)
и (2, 3, I, 2, I, 3) соответственно. Таким образом, условию задачи
удовлетворяют числа вида n — 4l, п = 41—I (/£N) и только они.
4.14. Из условия 2) следует, что либо 1 £Л1, либо (—1)£Л1. Но
(—1) ф М, так как иначе в силу условия 1)
(—1) (—1) = 1 €Л4,
что противоречит условию 2). Поэтому 1 £/И. Из условия 1) следует,
что 1 + 1£М, 2+1£/И и т. д., т. е. /ИZD N. Если теперь(—1 /т)£Л4
(где т£ N), то, согласно условию 1),
(—1/т) т = {— 1)£М,
что неверно. Поэтому (—1/т) £ М и l/m£ А/ для любого m£N. Из
условия 1) далее следует, что
п (1/т) —п/т^М для любых п, m£N.
Тогда
(—п/т)£ М	(п, mgN),
а кроме того, из условия 2) имеем 0 (fc М. Утверждение доказано.
4.15. Докажем, что для конечного множества М положитель¬
ных чисел существует базис В. Назовем подмножество S положитель¬
ных чисел надбазисом для М, если каждое число из М представимо
в виде произведения
а'*	где	о^,	am£S,	if /,„£Z.
Например, само множество М является надбазисом для М. Среди
всех надбазисов для М выберем множество
So =	•	Р«}>
содержащее минимальное число элементов. Докажем, что если п^>2,
то S0—базис для М. Допустим, что некоторый элемент и £ Л1 допускает
различные представления в виде произведения целых степеней эле¬
ментов из S0:
В = Р|*...Р'» = Р'‘...Р'П. т.е. Р5*...р*»=1
для целых чисел kt = it—j[t не равных одновременно при всех
1=1, ..., п нулю. Без ограничения общности можно считать, что
k„ ф 0. Пусть
Sr = {Yi, Yn-i}. где Yf = P//ft" при 1=1, ..., п — 1.
121

Тогда каждый элемент множества S0 представляется в виде произве¬
дения целых степеней элементов из
& = ■#» при 1=1	п-1;	=	•••	Уп-г~1‘
Поэтому множество Si является надбазисом для М, содержащимп—1
элементов, что противоречит выбору S0. Значит, 50—базис для М.
Если существует надбазис S0 для М, содержащий единственный эле¬
мент $Ф 1, то S0 также является базисом для М, так как равен¬
ство Р‘ = В^ невозможно при i ф /. Наконец, если множество S0 = {1}
является надбазисом для М, то М = 0} и множество Si = {2} будет
базисом для М.
4.16.	Первое решение. Рассмотрим многочлен
который по теореме Виета имеет вид
Р (х) = xn-\-a1xn~l + а&п~i +... + ап,
где обозначено
01=^-Х’ °2=	^	VT	С"=Т2...п *
«, = 1	1	I	<	fi < г, ^ п
Тогда указанная в условии задачи сумма равна
Ci+e»+ •• • + G;»=P (1)— 1 =
-('+1)('+т)-('+4)-'=24й^-'-
= (« + !) —1=«,
что и требовалось доказать,	-ч
Второе решение. Обозначим
“	It	...	lb
1 < h < ... < tk < п	*
через S„ и докажем индукцией по п, что S„ = n. Прип = 1 это верно:
Sj= 1. Пусть пз»2 и S„_i = n— 1, тогда
ii • • • tb
1 <н < - <*fc = п	*
1 ,	V	1	_	1	.	S„-1
ii ... ifn n n '
-T+... £
1 <U< •••
т. e*
122

4.17.	При я«= I перестановка (fli) = (0) удовлетворяет условию
задачи. При л = 4 требуемым свойством обладает перестановка
(fli; я2; я3; я4) = (1; 3; 2; 0).
Пусть л— простое число. Согласно китайской 'теореме об остатках
(теорема 23) для каждого значения fe=2, ..., я существует число 6*,
удовлетворяющее условиям
bk = 0 (mod k— 1), 6* ss fe (mod л).
Обозначим через я* остаток от деления на п числа Сд= bk/(k—1),
тогда
ьк = ck (k— 0 = ak (ft—1) (mod л).
Положим	fli=l	и докажем, что все числа а^, я2, ...,	я„	различны.
Действительно,	имеем я„ = 0 и с* Ф ап при k= 1, ...,	п—I	(так	как
с„(п— I) = 0 (mod n), fli=I, я* (ft— I) k (modn) при ft=2 л— 1).
Далее, если выполнено равенство я* = яд = я, где 1 < ( < ft < л, то
имеем
я (kl—ft) = a4 (I— I) fc== Ik (mod л),
с {kl—l) — ak (k— I) (= kl (mod n).
Тогда
a (k — l) = a (kl—I) — я (kl—ft) s= 0 (mod n),
что невозможно, так как
(я, n) — (k—l, n) = I.
Наконец, в случае Яд = я*, где 1 < k < л, также получаем противоречие
k— I =Яд (k— I) г k (mod n).
Таким образом, множество
{я,; я2; ...; я„}
состоит из л различных чисел, лежащих в множестве
{0; I; ...; п-1},
а значит, совпадает с этим множеством. Докажем, что полученная
перестановка
(fll! ^2i • • • 5 ®п)
удовлетворяет условию задачи. Действительно, имеем равенства
fli= 1, я,я2 ... я„ = 0,
а при fe=2 я—I получаем, что числа
Я1Я2я3 ... Яд, 1 -я2я3 ... яд, 2я3 ... ад (ft— 1) Яд, k
дают одинаковые остатки от деления на п, т. е.
flifl3 ... Ojsfc(modn).
Следовательно, множество остатков от деления на л чисел Я{, ага^,
о,о2я3> ..., fljflg ... я„ совпадает с множеством
{I; 2; ...; л—1; 0},
123

Докажем, что никакое составное число п > 4 не удовлетворяет усло¬
вию задачи. Если п = р2, то положим q — 2p < п, а в противном слу¬
чае число п представимо в виде произведения pq, где I < р < q < п.
В обоих случаях
pq^sO (mod'n).
Предположим, что существует перестановка (Ох; а2;	о„),	удовлетво¬
ряющая условию задачи. Тогда
а* Ф 0 при 1, ..., п— I,
так как иначе
ах ... а* = 0 (modп)
и
Of ... fl*eft+i^0 (modft),
Возьмем такие значения k, I < п, для которых ah=р, at = q. Обо¬
значим
m = max (k, /),
тогда
.°1°2 ■ ■ ■ am '■ akai>
поэтому
...	=	0	(modn)
и
Oifl2 ... amam+1 ^ 0 (mod n),
что противоречит предположению. Итак, условию задачи удовлетво¬
ряют числа 1, 4, а также все простые числа.
4.18.	Число п представимо в виде произведения p-q взаимно
простых чисел р > 1 и q > 1. Для каждого k=l, 2, ..., п подберем
числа
«€{0; 1;...; р-1}, /£{1; 2;...; ?},
для которых выполнено равенство k—mq+l, и положим /д =	1,
где т—остаток от деления числа (mq-\-lp—1) на п. Таким образом,
получен набор чисел
if. ^2» •••»	*">
Докажем, что среди них нет одинаковых. Пусть, напротив, нашлись
два различных номера
ki = tti\q -f- (f, k2 — tn2q +12,
для которых выполнено равенство	Тогда	число
(mrf+liP) — (m2q + l2p) = (mi—m2) ff+((,—/а) P
делится на n — pq, но числа p, q взаимно просты, поэтому число
(mi—m2) делится иа р, а число [1г—(2) — на q. Поскольку
\mi—m2\<p,	\li—l2\<q,
то справедливы равенства гтц—т2 = /,—/2=0, откуда ki = ka, что
противоречит сделанному выше предположению. Таким образом, набор
(*"li 'а, • • • >
124

представляет собой перестановку чисел 1,2 п. Пользуясь пе¬
риодичностью функций sin х, cos х и группируя специальным обра¬
зом слагаемые в сумме
п
S = 2 k cos (2nik/n),
k=\
получаем
p	2я	{mq	-f-	Ip)
(m<7 + 0cos w
m=0l= I
v'1 Z' 2jim i 2jI*\ i V4 f V'1'	( 2lTm i 2л*\
=£	^	cos(—+Tj+£ /X cos(_+Tj =
m=0	1=	1	1=	1	m=0
p ~1	^ 2лт
p-i /
4
cos
m = 0
Я
\ p
+£»(■
1=1 \
2л/
cos
9
Я
£
2п/
cos
q
, 2л т
s,n р L
, .
■Vr
/= 1
(=i
/
Р-1
£
2л т
cos
Р
2л/ г-i
■ s,% S
1 2лт \
sin	 1 =
Р / ’
т = 0
m = l
j /
r-i 2л/ yi . 2л/ n
> cos—=> Sin—=0
Xa q L* q
1=1	t=	1
P — I	л	P“	1	_
2irm	v''	* 2лт л
\ cos => sin = 0
p	ЛшЛ	p
m=0	m=0
(для доказательства последних равенств достаточно заметить, что,
согласно теореме Виета, суммы комплексных чисел
2л/	. .	2п/	.
Xi = cos ——sin— , 1=1 q,
и
2лm . . , 2лт	п	,
ут = cos—-—sin—у ,	т = О,	р—1,
являющихся корнями многочленов Xя—1 и хР—I соответственно,
равны нулю; более элементарное доказательство этих равенств со¬
стоит в том, что если на плоскости ввести систему координат, то
точки
(cos (2rtj/N); sin (2л///V)),	/ = 1, 2,	N,
где N^2, суть вершины правильного /V-угольннка с центром в на¬
чале координат, а сумма всех N векторов, проведенных из центра
правильного Л'-уголышка к его вершинам, будучи инвариантной от-
125

носительно поворота плоскости вокруг этого центра на угол 2n/N,
равна нулевому вектору). Итак, доказано, что определенная выше
перестановка (гх; «2;	i„)	удовлетворяет	требуемому равенству.
4.19.	Обозначим через А и В множества натуральных чисел со
строго возрастающими и соответственно со строго убывающими циф¬
рами. Сумму всех чисел из какого-либо множества М будем обозна¬
чать через S(M). Множество В разобьем на два непересекающнхся
подмножества В0 и Вх чисел, которые оканчиваются цифрой 0 и со¬
ответственно не оканчиваются цифрой 0; при этом
S(B)=S(B0)+S(B1).
Если сопоставить друг другу числа Ь£Вх и (10Ь)£Вп, то получится
взаимно однозначнее соответствие между множествами Вi и Вс; при
этом
S(B0) = 10S(B1),
а значит,
S(B) = IIS(Bi).
Далее, если сопоставить друг другу числа
а = ах. ..ак£А и 6 = (10—flj.. .(10 — ак)£Вх
(при этом
" я+6 = (10/9) (10*-1)),
то получится также взаимно однозначное соответствие между мно¬
жествами А и Вх. Поскольку каждое число, принадлежащее множе¬
ству А, получено из числа 123456789 выбрасыванием каких-либо
цифр и при каждом значении k—l, 2, ..., 9 в множестве А име¬
ется ровно С* fe-значных чисел, то
9
l=S(/4)+S(B1)= 2 C£(10/9)(10*-1) =
*=1
= (10/9)( 2 С* 10*-2 С»)= (Ю/9) «1 + 1С)»-(1+ !)•)=»
\fe= о	*=0	)
= (10/9) (11в—2е).
Обозначим через В2 подмножество чисел из множества В, начинаю¬
щихся цифрой 9, а множество всех остальных #исел из множества
В вместе с числом 0 обозначим через В3 (при этом S (В) —S (Bs) +
+ S (В3)). Тогда между числами
а=ах...ак£А и b—(9—a1)...(9—ak)^Bs
существует взаимно однозначное соответствие, при котором а-\-Ь =
= 10*—1. Следовательно,
9
m — S (-4)+S (Bs)= 2 Св (10*— 1) = ll9 — 2®.
k= 1
126

Наконец, если каждому числу
b=9&i. •. bfc ^ В2
поставить в соответствие число
а = (9-Ь1)...(9-Ьк)£А
при	и число 0 при k = 0, то получится взаимно однозначное
соответствие между множествами В2 и A U{0}, при котором а-\-Ь =
= 10Л+1—I. Следовательно,
9
n = S(,4)+S(B2)= 2 С9 (10*+1— I) = 10- II9 — 29
fc=0
и
т +п = S (Л) + S (Bs) + S (Л) + S (В2) = 2S (Л) + S (В).
Итак, получаем систему
Г S(/4) + (l/ll)S (-В) = 7 = (10/9) (ll9 — 29),
\ 2S (Л)+S (В) = m+n= II10—210,
из которой находим
S (Л) = (1/9) (Ш—т—п), S (В) = (11/9) (m+n—21).
В множествах Л и В есть 9 общих элементов, а именно, однознач¬
ные числа, сумма которых равна 45. Поэтому вся искомая сумма
равна
SH)+S(B)-45=-^(m+n)~/-45 =
=-^(11Ю_210)™ • П10+|у ' 2“-45=§у • И10—• 210—45.
4.20.	Каждому набору (flj; ап) соответствует набор Ь =
— фх, Ьп) натуральных чисел, определяемых равенствами
б; = С|при / — 1 п.
Таким образом, существует взаимно однозначное соответствие между
множеством исходных наборов и множеством В наборов Ь, удовлет¬
воряющих условиям
bi> ba> ... bn9
bi+ba+...+b„=m9.
Обозначим через п ф) последнее число Ьп в наборе Ь, а через о (6)—
наибольшее число s, для которого выполнено равенство
b$=b\—s+1
(заметим, что 1 < s < п), а значит, и равенства
1, ba=^ba 1, • • •, b$ = bg—j - I.
Определим в множестве В операции а и р, результатами действия
которых на набор Ь£В будут некоторые новые наборы а ф) и f> ф)
127

из множества В. Пусть я (Ь) < о (ft). Тогда Ьп < я— 1 (в противном
случае
я— 1 < ft,, «Sо (6) «с я, т. е. о (ft) = ft„ = я,
а значит,
I979 = ftn + ft„_i-f... +/>1 = п + (я+ 1) + ... + (2я— 1) = я (Зп-1)/2,
чего не может быть ни при каком значении n£N), следовательно,
возможна операция
o(*i; bn)=(bi+h &2+1» • ftnito + i; bn(b)+i; • ••» b„~i).
При этом
я (а (6)) = 6„_i > Ьп = я (Ь) = о (а (6)).
Пусть я (ft) > о (6). Тогда зададим операцию
P(fti; bn)=(bi—I; b2—1;	60(&>—1; fcatbi+il bn; a(b)).
Заметим, что в случае о (ft) = я будет выполнено необходимое нера¬
венство Ьп — 1 > о (Ь) (иначе n = o (ft) < ft„ (ft) +1 =П-Н> т. е.
Ь„ = я+1. fcn-i = n + 2 &т = 2я, а значит,
1979 = 6„ +6„_i + ... +6* = п (Зп + 1)/2,
чего не может быть ни при каком значении n£N). При этом
я ф(Ь)) = о(Ь)<оф(Ь».
Множество В разобьем иа пары элементов: с каждым набором b свя¬
жем набор Ь', равный набору а (6) или Р (b) в зависимости от того,
какое из неравенств я (ft) < о (Ь) или я (ft) > <т (ft) имеет место (при
этом выполнено условие
P(a(ft)) = ft или a(P(fc))=ft-
соответственно, гарантирующее, что набор ft' образует ту же самую
пару наборов ft, ft'). Поскольку в каждой паре один из наборов чет¬
ный, а другой — нечетный (под действием каждой из операций а или
Р четность набора, определенная четностью числа п, меняется иа
противоположную), то во множестве В содержится одинаковое коли¬
чество четных и нечетных наборов. Следовательно, то же самое мож¬
но утверждать и о множестве исходных наборов (fli; ...; а„).
4.21.	а) Рассмотрим двоичные записи чисел  	  и	допол¬
ним некоторые из них' спереди цифрами 0 так, чтобы все записи
имели равную длину к. Образуем прямоугольную таблицу размером
тХк из нулей и единиц, в которой для каждого значения i = I, ...
..., т 1-я строка представляет собой полученную выше запись чис¬
ла о,-. Поскольку каждый столбец этой таблицы состоит из т цифр,
то число я различных ненулевых столбцов в ней не превосходит
21* — 1. Каждому из этих я столбцов поставим в соответствие число,
двоичная запись которого содержит цифру I в тех и только тех раз¬
рядах, в которых таблица содержит столбцы, совпадающие с дай-
128

ным. Полученный набор чисел Ь\, Ьп удовлетворяет условию
задачи. Действительно, так как в любом из k разрядов цифру 1 со¬
держит не более чем одно число из набора
Фа • • •* б„),
то любое подмножество чисел из этого набора однозначно определя¬
ется двоичной записью их суммы. Следовательно, различные подмно¬
жества из полученного набора имеют различные суммы. Наконец,
если для какого-либо значения
»'€{!; •••; «}
сложить все числа из набора
(^li • • • » б„) I
содержащие цифры 1 только в тех разрядах, в которых их содержит
число о,-, то сумма совпадает с этим числом (заметим, что во всех
разрядах, в которых некоторое число из этого набора содержит
цифру I, число о,- содержит либо только цифры I, либо только
цифры 0). Так как п < 2т, то утверждение доказано полностью.
б) Докажем утверждение индукцией по сумме данных чисел N =
= а1+...+ост. Если (V=l, то m= I, аг=1, и можно положить
Пусть утверждение верно для всех наборов, сумма элементов
которых меньше N, и (о^; ...; ат) — произвольный набор такой, что
а1 + — + ат = N-
Будем называть набор (Ьг; ...; Ьп) допустимым для набора
(а1;...; ат), если n < т, все подмножества множества
{&i; ...; Ь„]
имеют разные суммы чисел, причем среди этих сумм содержатся все
числа а%, ..., ат. Нужно доказать существование хотя бы одного
допустимого набора. Если все числа аг, .... ат являются четными,
то рассмотрим новый набор а[, ..., а'т, где
a'l = fl(72	(i—	I	m).
Так как
flI+...+flm = W/2< N,
то по предположению индукции существует допустимый набор
(Ь[\
• • • I ^п),
допустимый для набора
(о!;
• • •; от).
Тогда набор
(2&;:
...; 2Ьп)
будет допустимым для набора
(2al;
.. •; 2dm)’
5 Под ред. И. Н. Сергеева

Пусть теперь набор (at; ат) содержит хотя бы одно нечетное
число. Рассмотрим наименьшее среди нечетных чисел этого набора.
Так как набор (в,; ...; ат) не изменится при перенумерации его
элементов, то можно считать, что это число равно ат. Рассмотрим
набор, состоящий из всех чисел вида а} (t = 1, ..., т—1), где
/ о,/2,	если а,- четно,
с‘=(с,-—ат)/2, если а,- нечетно.
Набор {щ} содержит не более т—I элементов (число его элементов
может быть меньше т—1, если а\ = а/ при некоторых i ф /). Заме¬
тим, что все элементы О;— натуральные числа. Сумма чисел набора
{й;} не превосходит
“1 + • • ■ +G/H-1	—Ь- • -Н	"2 ^ ^ ci + • • • +°m-i < N.
Поэтому к нему применимо предположение индукции, согласно ко¬
торому существует набор (61; ...; bk), допустимый для набора {щ}.
Докажем, что набор
(&!; ...; fcft+i),
где bj=2b'i при i=l, ..., k и Ь/г+1 = ат, является допустимым для
набора
(fll, . . ., Он)-	'
Количество элементов набора (bt; ...; Ь/г+1) не превосходит fe-j-laS
sS m— 1 +1 =т. Далее, заметим, что Ьк+\—единственное нечетное
число в наборе (bt; ...; Ьк+1). Все подмножества набора
(61; ...; bh+1)
имеют разные суммы чисел. Действительно, пусть суммы чисел ка¬
ких-либо двух подмножеств одинаковы. Если они равны четному
числу, то оба этих подмножества не содержат элемента bk+i, и, раз¬
делив все элементы этих подмножеств на 2, мы получим два подмно¬
жества множества
{61;
имеющих одинаковые суммы чисел, что противоречит допустимости
набора
(Ь[; ...; b'k).
Если же суммы чисел двух подмножеств набора
(Ь\, ...; bk+1)
равны нечетному числу, то оба этих подмножества содержат элемент
bk+i, и, удалив его из этих подмножеств, мы получим два подмно¬
жества набора
Ф1', ...; Ь^)
130

г
с одинаковой четной суммой чисел, т. е. придем к уже разобранному
случаю. Остается проверить, что каждое число Я/ (1 eSLi е^т) пред¬
ставимо в виде суммы различных элементов набора
(6|,	•	•	•;	6/е) .
Число ат само является элементом этого набора. Если I < т и щ
четно, то
о,72 — cii — bi ... -\-bp
для некоторых элементов 6/, ..., b'p из набора
(^i» • • • * ftft) •
Поэтому
а,- = 2 bi -J-... 4-2 bp=bj -}-... -j-bp
Если же i < т и я,- нечетно, то
ai = am-\-^ai — &Л+1 + 2 (&/ + •■• +&p) = 6ft+l + fy + ■ • •
для некоторых элементов 6г, Ьр из набора
(fti, . •. j bff).
Утверждение задачи доказано.
4.22.	Предположим, что описанное в задаче множество Ж суще^
ствует. Обозначим через т* количество чисел из множества Ж, не
превосходящих числа ft£N. Тогда количество чисел я£ Ж, удовлет¬
воряющих неравенствам 10 < a<:ft, равно ш*—ш10, а количество
различных пар таких чисел равно
Cmk-mLO = (mk—™io) (mA—ш10 —1)/2.
Если каждой такой паре чисел я > Ь поставить в соответствие их
разность я—Ь, то все полученные разности будут различны. Дейст¬
вительно, пусть для пар я > b и с > d справедливо равенство я—Ь =
= с—d, тогда a-\-d = c-\-b и, согласно, условию 2), либо я=6 (что
неверно, ибо я > Ь), либо а —с (откуда 6 = d, т. е. пары совпадают).
Поскольку все полученные разности меньше ft, то имеем неравенства
k > Cmk-m10 > (m»-mie-l)*/2.
Но ml0 < 10, поэтому
m* < 2ft+nixo+ 1 < У 2k11
для любого значения ft=ll, 12, ... Далее, любое число
п£{2; 3; ...; 2ft}
представимо, согласно условию 1), в виде суммы двух чисел из мно¬
жества Ж, причем либо оба этих числа не превосходят ft, либо ровно
одно из них больше ft, но меньше 2ft. Поэтому количество таких пар
чисел, с одной стороны, не меньше 2ft—1, а с другой стороны, не
5*	131

больше чем
—- + mh(m2k—m*)= ^ (2m2k—mh— 1) < ^ (2т2к —mt).
Таким образом, при любом значении ft > 10 имеем неравенство
тк (2т2к—тк) & 4fc— 2,
а учитывая, что
m2fc < V^4fe+ll = o и тк<}/~2ft+M=P < а,
получаем
4ft—2<^тк (2а—тк) = (а—(а—тк)) (а+ (а—тк)) =
— а2— (о—mi,)2 < 4ft-(-44 У k -(-121—ft (2 — У 2 )2.
Следовательно, при всех значениях ft > 10 квадратный трехчлен
/ (y^ft) = ft(2— У~2)2— 44 >^ft — 123
принимает только неположительные значения, что неверно. Получен¬
ное противоречие доказывает, что множества М, удовлетворяющего
условиям задачи, не существует.
§ 5. Различные свойства чисел
Б.1. Так как а, Ь, с £ Q, то число
d a-b_(Va+Vl)(Va_-Vb)__v-	^
с	уа+УЬ
рационально, следовательно, рациональны и числа
У a =(c-(-d)/2, УЪ = (с—d)/2.
5.2. Возьмем положительные числа
а=У2 и b=iogv— 3,
тогда число
log,/-3
аь = у 2 V2 =3
является натуральным. Число а иррационально. Докажем, что число
b также иррационально. Действительно, в противном случае имеем
b=p/q, где p.	откуда
Plq — 2 logs 3, т. е. 2Р = 3?0,
что невозможно.
5.3. Обозначив через ft натуральное число, удовлетворяющее
условию
2*<п<2*+\
а через М—произведение всех нечетных чисел, не превосходящих л,
умиожим каждое слагаемое суммы
1,1, ,1

на произведение 2/!~1М. Любое число mgN представимо в виде
m=2P-q, где pgZ+, q— нечетное число. При этом, если m<;t, то
9<л (ибо <? = т/2Я < и), а если, кроме того, тф 2й, то p<k
(действительно, в случае р > k имеем
т = 2Р ■ q 5s 2Й+1 > п,
а в случае p = k имеем
q Ф 1 и m=f2P-q^ 2й.3 > 2Й+1 > п). \
Поэтому число
ат = — . 2Й~»М
m
является целым при любом значении т= 1, 2, п, кроме одного
(равного 2й), следовательно, число
5*2Й~* - Af = zZi-J-/Za +n„
не является целым. Таким образом, сумма S также не может быть
целым числом.	—
5.4.	Заметим, что если число п удовлетворяет условию задачи,
то числа 2/г+2 и 2п+9 тоже ему удовлетворяют. Действительно,
если
п = а1 + а2 + • • • + ak>
где
аь аг, ..., aftgN и ±+± + ...+1=1,
ТО
2п-\~2 = 2аг + 2а2-\-2aft-\-2r
причем
i +(^Г +• • ■u
и
2 п -}- 9 = 2oi	2 dfi -j- 3 -J- 6,
причем
i+---+2Hi+T+T=y(i+',‘+i)+'§'+^=
=Т+Т+¥=!-
Теперь докажем по индукции, что все числа п 33 удовлетворяют
условию задачи. Числа 33	 73 обладают нужным свойством.
Пусть уже известно, что этим свойством обладают все числа от 33
до п—1, где п > 73. Если число п четно, то оно представимо в виде
2т+2, а если нечетно—то в виде 2/тт+9, где mgN, /i>m5t
>(74—9)/2 > 32. В обоих случаях, согласно доказанному выше,
число п удовлетворяет условию задачи, поскольку число т этому
условию удовлетворяет. Утверждение доказано.
133

5.5. Поскольку двоичная запись числа п, делящегося на 17, со¬
держит ровно 3 цифры 1 (а остальные цифры—0), то это число
представляется в виде суммы
п = 2*+2* + 2«>,
где числа к, I, т£ Z+ удовлетворяют неравенствам к < I < т. Пусть
рассматриваемая двоичная запись содержит менее 6 цифр 0. Тогда
т<7 и соотношение
п = 0 (mod 17)
не может быть выполнено, поскольку числа вида 2' при i = 0, 1, 2,
3, 4, 5, 6, 7 сравнимы по модулю 17 с числами 1, 2, 4, 8, —1, —2,
—4, —8 соответственно, и несложный перебор показывает, что сумма
любых 3 [различных чисел из последнего набора не делится на 17.
Поэтому в двоичной записи числа « имеется по меньшей мере 6
цифр 0. Если же их ровно 7, то т — 9. Тогда число п не может
быть нечетным, так как иначе k = 0 и
2«+2CT s 3 (mod 17),
в то время как соотношение
21 = — 3 (mod 17)
не выполнено ни при каких значениях
/€{'; 8}.
Следовательно, в этом случае число п является четным (оно дейст¬
вительно может делиться на 17, например, если й=1, 1— 6, т = Щ.
5.6. Обозначим через f (т) число цифр в десятичной записи числа
N, тогда для искомого числа п имеем
/(«*)+/(«*)= ю.
Кроме того, f (п3)	4, так как в противном случае были бы выпол¬
нены соотношения п3 < 1000, п < 10 и ft4 < 10 000, откуда
/(л3)+/(п4) < 4+5 < 10.
С другой стороны, если f (п3) >4, то п > 10, п4 > 10п3, откуда
/(«*)> 5, /(n4)Ss/(n9) +1
и
Hn3)+f(n4)Ss 5 + 6 > 10.
Таким образом, /(п3) = 4 и /(ft4) = 6. Далее, из неравенства п3 <
< 10000 имеем оценку п <22, так как 223 > 10 000. Аналогично, из
неравенства п45* 100 000 имеем оценку п > 17, так как 174 < 100 ООО.
Итак, I8<n«g2I. Поскольку любое натуральное число сравнимо по
модулю 9 с суммой своих цифр, то
п3+п4 = (0+1 + ... +9) (mod 9),
откуда
ft3 (п+ 1) s 0 (mod 9).
134

Последнему условию не удовлетворяют значения л =19 и л = 20, а
значение л = 21 не обладает требуемым в задаче свойством, так как
оба числа 213 и 214 оканчиваются цифрой 1. Наконец, проверка по¬
казывает, что единственно возможное значение л =18 удовлетворяет
условию задачи (183 = 5832, 184= 104 976).
6.7.	Пусть л — искомое число, s—сумма цифр его десятичной
записи, a ft—количество этих цифр. Тогда имеют место соотношения
s6 = n?, s< 9ft, nSslO*-1,
из которых получаем, что
96ft5	s5 = л2 Эг 102ft_2.
Обозначим
a* = 95ft5/102*-?,
тогда из соотношении
9E(fe+ 1)5	_(fc+l)»	10»	«»+*>-»
95ft5	ft3	^	ш	—	Ю2Й-2	’
выполненных при каждом значении ft£N, получаем оценку ак+\ < «s.
т. е. последовательность чисел ак убывает. Поскольку ав < 1, то при
всех ft Ss 6 имеем неравенства
95ftB < 102*-?,"
а значит, число ft не может принимать значений, больших 5. По¬
этому s<9-5 = 45. Из равенства sr> = л2 заключаем, что число s
должно быть квадратом какого-либо натурального числа, так как все
простые делители в разложении числа s5 (а значит, и числа s) на
простые множители должны иметь четные степени. Поэтому число s
может принимать лишь следующие значения: 1, 4, 9, 16, 25, 36.
Проверка показывает, что лишь для двух значений s=l н s- 9
число л= У s5 имеет сумму цифр, равную s. Поэтому условию задачи
удовлетворяют два значения л=1 и л = 243.
6.8.	Предположим, что существует дробь m/л, где т, л £ Z и
т< л< 100, причем десятичная запись этой дроби имеет вид
т/п~0, ака2.. .akl67ak+i..
где Oi, а2,..., а/,, ak+4, ...—некоторые цифры. Тогда для числа
р=10*т/л имеем
поэтому
Р—[р] = 0,167а*+4....
0,167	—	[Pi"	<	о,168.
Обозначим
тогда имеем
q— 10ftm—[р] n£Z,
1,002<6<?/л < 1,008.
Следовательно, справедливы соотношения
0 < 0,002 < 6д/л — 1 = (6?—л)/л < 0,008 < 1/100,
135

из которых вытекают оценки 0 < 6q—п < п/100<; 1, т. е. число л
ие может быть целым. Полученное противоречие доказывает требуе¬
мое утверждение.
5.9. Пусть, вопреки утверждению задачи, существуют числа
п, т, ft£N, удовлетворяющие равенству
22" + l = m5—ft3,
причем число
тъ—ft3 = (m—k) (m4 -\- m3k-\-m2k2 tnk3 к4)
является простым. Тогда m—k= 1 и
22" + 1 = (к + I)5— ft5 = 5ft4 + 10ft3 + 10ft? + 5ft + 1,
поэтому число
22" = 5 (ft4 + 2ft3+2ft2 + ft)
делится на 5. Полученное противоречие доказывает справедливость
требуемого утверждения.
5.10. Предположим, что при некотором значении п £ N число
2«-i(2«—1)
является кубом целого числа. Заметим, что двойка входит в это про¬
изведение с показателем п—1 (ибо второй сомножитель 2" — 1 не
делится на 2), поэтому п—I = 3ft, т. е. п — 3ft-(-1, где ft£Z+. Но
тогда число
2«+4— 1 - 23s+2— 1 = 4 (7+ 1)*— 1 = 3 (mod 7)
не может быть кубом целого числа, так как куб любого целого
числа при делении на 7 может давать остаток 0, 1 или 6 (действи¬
тельно,
(7т)3 = 0 (mod 7), (7m ± I)3 = ± 1 (mod 7),
(7m±2)3^±l (mod 7), (7m±3)3=Tl (mod 7)).
Таким образом, ни при каком значении	числа	2n+1	— 1 и
2»-i(2n— 1) не могут одновременно быть кубами целых чисел.
5.11. Требуется доказать, что из неравенства п Y7 — m > 0, где
п, т 6N, вытекает неравенство п Y7 —т > 1/т. Если п Y7 — т>1,
то тем более п У~Т—m > 1/m. Рассмотрим случай 0 < п Y7 —m< 1
(равенство п Y7—т=1 невозможно, так как иначе число Y7 —
=(l -\-m)jn было бы рациональным). Заметим, что натуральное число
7n2—m2 = (n YT—m) (п YT + m)
не может быть равно 1 или 2, так как число т? не может давать
при делении на 7 остаток 6 или 5 (действительно,
(7ft)2 = 0 (mod 7), (7ft±l)2=l (mod 7),
(7ft±2)2 = 4 (mod 7), (7ft±3)2 = 2 (mod 7)).

Поэтому 7п2—т2Э=3 и, следовательно,
nY? —т Si 3 l(n Y 7 +т) > 1/т,
поскольку
Зт ;э= 2т + 1 > 2m + (n Y7 — т) = п V 7 +т.
Утверждение доказано.
Б. 12. Докажем, что число
m = (У^З + /2 )1880 + (VS— у^2")1880
является целым, и определим его последнюю цифру. Обозначим
о„ = (у^З + Y2 )2" + {\ГЗ - V2)*n = (5+2 Y&)n + (5-2 у^б)”-
Тогда при любом значении n£Z+ справедливо равенство
ап+а=^ 10ал+1	а„.
Действительно, пусть
(5+2^6)" = а, (5-2у^б)” = р,
тогда
fl/i = o+P, ои+1 = (52 "|/"6) а + (5—2 у/"б)Р,	^
«,,+а = (5+2 V^6)2a+(5-2 /'6)2P = (49-[-20 У^Т) a +
+(49- 20 ^6 ) Р = (50+20 Y 6 ) а+(50 — 20 У^б ) Р— (о+Р)=» -
= 10ля + 1 йпш
Так как числа а0 = 2, 0^=10 целые, то ап£Ъ при Z+ и, кроме
того, каждое из чисел
ап +a«+2= 10a„+f
делится на 10. Поэтому каждое из чисел
я«+4—ап = (аи+4+ап+а) — (ал+а+ап)
также делится- на 10, а значит, числа
а2, ав, аю, ..., a»eo
дают одинаковые остатки при делении на 10. Поскольку аа = 98, де¬
сятичная запись числа m = a880 оканчивается цифрой 8. Наконец, из
оценок
m = (у^З"+ yAlT)1880 + (уАз" — Y2")1880 > (lA3 +Y2)1™0 >
> т — (0,5)1в80 > т—0,1
t
получим, что в десятичной записи числа (уАз + у^2 )1880 в разряде
единиц стоит цифра 7, а в разряде десятых—9.
5.13.	Для заданных чисел m, n £N, пользуясь биномом Ньютона,
получаем
(Yin ± Yт— 0” = 2 С‘п (Yin)n~‘ (± Ym— l)A
1 = 0
137

В случае л = 2/ (/ £ N) имеем
(У in ± У'т— 1)" =
1 = 0
± 2 с%~1(\Лп)г/~г,’+г (УлГ^т)2<’~1=
»= 1
/   /
= 2	(т-1У ± Ут(т— 1) 2	(/л-l)/-i =
1= О	‘	=	1
= о ± Ь У tn(m — I),
где a, 6£Z+. В случае я=2/—1 (/£N) имеем
(f^m ± У"т—1)" =
= 2 с» (Ут)2'-1-* (У^Г ±
1=0
± 2 с«-1(ую*'-"(у;г=1)*'-1=
1= 1
/-1   /
= Ут 2 CttmJ-l-1 (т-\)1 ± Ут—\ 2 С11~1т/-‘ (т- 1V--i =
1 = 0	i=l
= с Уга ± d У т—1,
где с, dgZ+i В обоих случаях имеют место равенства
(Ут ± У7^1Г=Ук ± ут,
где k, l£Z+, причем	I
к-1=(Ук+уТХУ£-УТ)=
= (Ут-\-Ут— 1)"(Ут — Ут— 1)” = ((Ут)2 —(Ут~ l)2)" = l.
Поэтому
l=k— 1 и (Ут-\- Ут^-\)п = У k -fy~k^\,
что и требовалось доказать.
5.14.	Выберем целое число N > 1/е и каждой паре значений
*. ШО; 1)
поставим в соответствие пару чисел и, о, определяемых формулами |
u = [Nx], ц= [Ny\.	I
Тогда, если двум парам (л^; уд, (х2; уд соответствует одна и та же
пара (и; v), то
I ху- х21 = | jj- (и + {NxJ) _ 1 (и+{N х.г)) [=
= ^г I	{W*a}| < i- < е
138

н аналогично | у\—у2 \ < е. Поскольку
и, og{0; ...; ЛГ-1},
то всего различных пар (u; v) имеется №. Рассмотрим множество из
1)	пар значений
х = {1а}г у—{Щ при / = О, I, №.
По принципу Дирихле (теорема 1) хотя бы двум парам (скажем, при
/—i и / = /, где с > /) из этого множества соответствует одна и та же
пара (и; и). Поэтому, обозначив
n = i—/, k = [ia] — \ja], m = [ib]~[jb],
получаем требуемые неравенства
| па—k | = | (ш — [iaj) — (ja—[/а]) | = | {ш}—{/а} | < е,
\nb—m\=\(ib — [ib]) — (jb—ljb\)\ = \{ib}—{jb} | < е.
Замечание. Решение допускает наглядную геометрическую
интерпретацию. Пусть квадрат
К = {(ж; У) I 0<х < 1, 0<у < 1}
на координатной плоскости разбит на № квадратиков со стороной
1 /N каждый. Тогда, согласно решению, двум парам значений xlt у±
и хг, соответствует одна и та же пара целых чисел и, v в том и
только в том случае, если точки (лг^; уг) и (х2; у2) попадают в одчн
и тот же квадратик.
б. 16. Докажем, что для любого значения к £ N существует беско¬
нечно много чисел т £ N, удовлетворяющих условию
5m = 1 (mod 2й).
Действительно, среди чисел
5°, 5\ 52	 52*
найдутся два числа 5Р и 5(/ (р > q), дающие при делении на 2* оди¬
наковые остатки. Тогда их разность
5Р — 5Ч — 5ч (5р-ч— 1)
делится на 2й, а значит, число 5Р~Ч—1 и все числа вида
5мд>-в>_1 (,-gN)
делятся иа 2й. Таким образом, для каждого значения m=r(p—q),
r£N, имеем
5m = 1 (mod 2й),
откуда
51л+л== 5* (mod 10й),
т. е. последние к цифр числа 5“+й образуют десятичную запись числа
5й. Пусть число к удовлетворяет неравенству 2й > Ю1876, тогда деся¬
тичная запись числа
5й = 10й/2й < 10й-1878
139

содержит не более k—1976 цифр. Следовательно, среди последних к
цифр числа 5т+й ненулевыми могут быть только последние к—1976
цифр, а остальные 1976 цифр (идущие подряд) являются нулями.
Утверждение доказано.
5.16. Прежде всего индукцией по /£Z+ докажем, что число
52^—1 делится на 27+2, но не делится на 27+®. При / = 0 имеем
55°—1=4,
т. е. утверждение верно. Далее, пусть для некоторого /	0 число
5?;— 1 делится на 27+2, но не делится на 27+3, тогда число
—1 =(52; — 1) (5?^-|-1)
делится на 27+®, но не делится на 27+4, так как
5?'+1 = (4 +1)2/ +1 es 2 (mod 4),
Докажем теперь утверждение задачи индукцией по т£ N. При т = 1
получаем верное утверждение, так как последняя нечетная цифра 5
(десятичной записи) числа 5” при п > 1 всегда соседствует с пред¬
последней четной цифрой 2. Пусть утверждение справедливо для не¬
которого значения т^1, т. е. существует бесконечно много чисел
ngN. для каждого из которых’ число 5" оканчивается т +1 циф¬
рами чередующейся четности. Пусть 5"—одно из таких чисел, причем
5п > Ют+2. Построим число 5й, оканчивающееся m-f-2 цифрами
чередующейся четности. Если (яг+2)-я и (т + 1)-я цифры (считая
справа) числа 5” имеют разную четность, то положим к —п. В про¬
тивном случае положим k=n-\-2m~l, тогда имеем
5/г-(т+2)_5л-(т+2)==5п-ш+2> (52m-I_ j) s 2m+1' (mod 2т+2),
поскольку число 55т 1 — 1 делится на 2m+1, но не делится на 2га+!,
Поэтому
5«—5n = 5.10m+1- (mod 10m+2),
т. е. последние т-\-1 цифр чисел 5й и 5” просто совпадают, а
(m-f-2)-e цифры этих чисел имеют разную четность. Таким образом,
число 5й построено (причем, поскольку 5й ^ 5”, таких чисел беско¬
нечно много), а значит, утверждение справедливо и для значения
т-\-1. Задача решена.
5.17. Обозначим через *г и х2 расстояния от некоторой точки
внутри прямоугольника до двух его противоположных сторон, а через
W и Уг — расстояния до двух других его сторон. Тогда по условию
стороны прямоугольника
А=х±-{-х2 и В — у^-\-у2
являются нечетными числами. Предположим, что найдутся числа
Пц, о 12, Оа1, Й22 ez,
140

удовлетворяющие условиям
а , г а
Х1~\~У] — °И
(здесь и ниже /, /=1, 2). Обозначим
Uj — XjAB, Vj = yjAB.
Тогда имеем
ui и% — (*х х2) АВ — (xi—хз)В = ((дсх + «/i) — (*2 у\)) В =
= (On-fllx)fl = C,
Ui + «8 = (*1 +jc2) AB = A2B = D.
Аналогично получаем
V\ — ^а = (он — «12) А — Е, Vi-\-v2 = AB2 = F,
Наконец, имеем
и! + н? = (*?+W) А2В2 = 4'Л2В2 = Ь2ц.
При этом числа С, Е и А,у целые, a D и f нечетные. Предположим,
что все числа iy целые. Тогда одно из чисел Hj, и2 является не¬
четным (ибо их сумма нечетна) и одно из чисел vu va также нечетно.
Обозначая эти два числа через и и о, а сумму их квадратов через
№, имеем:
и2 1 (mod 4), v2 = 1 (mod 4),
и равенство
и1. + о? = М
невозможно, так как
b202 (mod 4).
Полученное противоречие доказывает, что не все числа и,-, iу явля¬
ются целыми. Поэтому хотя бы одно из целых чисел
(У,- = 2ц,-, Vf = 2vj (2uj — D ±С, 2vj = F ± Е)
является нечетным. Пусть нечетным оказалось, например, число Ui
(остальные случаи рассматриваются аналогично). Тогда из равенства
получаем равенство
U\+V\*=Ab\u
которое невозможно, так как
U\ = 1 (mod 4), Ab'n = 0 (mod 4), но Vt Ф 3 (mod 4).
Доказательство закончено.
5.18.	Предположим, что указанная в задаче пирамида существует.
Обозначим через g длину стороны квадрата, служащего ее основанием,
а через h — высоту пирамиды. Тогда длина бокового ребра пирамиды,
ее полная поверхность и объем равны соответственно
f — VЛ2 + 2(g/2)2, s^g* + 2gVM + m*- и v — g2h/3.
141

Поскольку g, f, s, tig N, то числа
*=g3. y = &>, z—g(s—g2), “ = 2g2f
являются натуральными, причем справедливы соотношения
x2+p3-=g«+Збо2 = 4g* ((я/2)2 + Л2) = g2 (s—ga)2 = г2,
а:2 + г2 «= я» + 4я* (Л2+(я/2)2) = 4я4 (« + 2 (я/2)2) = и2.
Таким образом, система уравнений в натуральных числах
( x2+i/2-=»z2,	*
\ х2 z2 = и2
имеет решения. Выберем среди иих решение (х0; уа; га; ив), для ко¬
торого величина xgN принимает наименьшее возможное значение х0.
Тогда числа х0; ув; гв\ щ попарно взаимно просты. Действительно,
если какие-либо два из них одновременно делятся на некоторое
простое число р, то из равенств
2 * 2	2	2.2	2	2.2	г» 2
*о + £/о=£о» Xo-\-Zo = Uo, ^/о4~^о = 2го
следует, что и два других числа также делятся на р. Но тогда набор
(*о/р; Уо/Р', zB/p; «о/Р) представляет собой решение системы, причем
*о/Р < *0, что противоречит выбору значения х0. Кроме того, число
х0 четно, а значит, числа у0, гв, и0 нечетны. Действительно, если х0
нечетно, то
Хо = 1 (mod 4),
а число и2 = 2х2 + я2 при делении на 4 дает остаток 2 или 3 (в зави¬
симости от четности числа у0), чего не может быть. Из равенства
Xo = zjS—уо получаем равенство
( *о У_ го+Ро	го—У о
\ 2 J 2	’	2
причем натуральные числа (г0+Яо)/2 и (г0—г/0)/2 взаимно просты,
так как в противном случае выполнялись бы соотношения
(го> У в) = (zo> 2о—Уо) S-
т. е. числа г0 и ув не были бы взаимно простыми. Следовательно,
числа (г0+Яо)/2, (го—Ро)/2 являются квадратами некоторых взаимно
простых чисел k, ZgN соответственно, поэтому
xB = 2td. ув = № — Р, г0 = й+/2.
Аналогично, из равенства
в а 2
*0 = «о— Zo
вытекают соотношения
хв — 2тп, гв — т2—л2, п0 = т2 + л2
142

для некоторых чисел т, п £ N. Таким образом, получаем систему
J	kl = mn,
Обозначим (k, т)~а, тогда
k=ab, т = ас, где a, b, eg N и (Ь, с)=1.
Равенство kl = mn записывается в виде аЫ = асп, откуда Ы = сп и
l—cd, где d gN (ибо Ы I с, но (Ъ, с) = 1)* Следовательно, bed = сп,
откуда n = bd, причем из условия
\ = (k, I) = (ab, cd)
вытекает соотношение (a, d) = 1. Далее, имеем равенство
a2M+c2d2 = oV? — b2d2,
из которого получаем условие
(о2+d2) (Ь2+с2) = 2о2с*.
Поскольку
(a2+d2,	a2) = (d2, с2) = 1 и (fc2	+ c2, еа) = (Ь2,	с2)= 1,
то последнее условие выполнимо лишь	в следующих	двух	случаях:
( a? + d2 = 2с2, иди (	a2+d2 = c2,
( 62 + c2 = a2	\	fc2 + c2 = 2o2,
В этих случаях соответственно имеем
I	№ + d2 = c2,	I d2 + fc2 = a2,
\	Ь2 + с2 = о?	\ d2 + a2 = c*,
откуда получаем, что один из наборов
ф; d; с; а) или (d; b; а; с)
удовлетворяет исходной системе наряду с набором
(*о; Уо; г0; и0).
Так как x0 = 2mn — 2mbd, то Ъ < х0 и d < х0, что противоречит вы¬
бору значения х0. Утверждение доказано.
5.19.	Докажем требуемое утверждение сначала для значений
k = 0, 1 п— 1.
Построим многочлен степени не выше (л — 1), который в каждой точке
с,- (/=1, 2 п) принимает значение af. Согласно формуле Лаг¬
ранжа (см. теорему 62) этот многочлен имеет вид
Р(х)=21а‘ П а, —a,	П	(x-aj)t
i=i i < j < n ‘	1 i=i К j < n
j Ф I	j	Ф I
n
а коэффициент при хп~г равен 2 Щ/Pi- С другой стороны, многочлен
i= 1
Р(х) совпадает с многочленом хн, поэтому при k < п—1 указанный

коэффициент равен нулю, а при k = n—1—единице. Таким образом,
п
доказано, что число 2 ai/Pi является целым при каждом значении
i=i
fc=0, 1, ..., п—1. Докажем теперь, что если для некоторого числа
и чисел bt, Ь2, ...,	£Z выполнены равенства
то число
of-1
1 ^
J	Л
Pi
1-2
ai
Pi
, «5-
1 1
4- .-I
Pn
at2
Pi
Pi
r	r
Pn
Jt—n
fll
k—n
1 02
k —n
" -1
Pi
Pa
Pn
*0
=—+■
Pi
fi+.
Pa
A
Pn
^2.
(1)
является целым. Тогда, согласно принципу математической индукции,
требуемое утверждение будет доказано для любого fe£N. Рассмотрим
многочлен
xn-\-clxn~l-\-cixn-i-\-... +с„,
корнями которого являются числа at, а  ап, В силу теоремы
Виета коэффициенты Сх, с2, с„ этого многочлена являются целыми
числами, при этом для каждого / = 1, 2, п выполнены равенства
п VI .. п—<
«/=—2j Ci°i ‘
Умножая первое равенство выписанной системы (1) на С(, второе —
на с2, ..., последнее—на сп, а затем складывая все полученные ра¬
венства, имеем
/ = 1 J <= 1
*=I/=i
т. е. число
(Г,"'
б0=— 2 c‘bt
i=i
является целым, что и требовалось доказать.
144

УРАВНЕНИЯ И НЕРАВЕНСТВА
§6. Уравнения и системы
6.1. Число х==1/3 является решением данного уравнения. Дока¬
жем, что других решений нет. При х>— 1/3 функции yt(x) = 8x и
у2(х)=Зх-|-1 принимают положительные значения и возрастают, сле¬
довательно, их произведение (левая часть уравнения) также является
возрастающей функцией. Поэтому на промежутке (—1/3; +оо) урав¬
нение не может иметь более одного решения. Далее, при х<—1/3
имеем yi (х) > 0, у2 (х) <0, а значит, уг (х) у2 (х) < 0. Поэтому на
промежутке (—оо; —1/3] уравнение не имеет решений. Таким образом,
получаем ответ: 1 /3.
6.2. Обозначим
/(х) = (х—а) (х—Ь) -f- (х—Ь) (х—с) + (х—с) (х—а).
Без ограничения общности можно считать, что a<fc<c. Если а — Ь
или Ь — с, то f (Ь) = (Ь — а) (b—с) =0. Если же а < Ь < с, то f (b) < 0
и /(а) = (а—Ь) (а — с) > 0. Так как функция f (х) непрерывна, то су¬
ществует такое число х0 £ (а; Ь), что f (х0) = 0.
6.3. Докажем, что функция
f (х) = лг4+5х3+6л;® — 4х—16
принимает значение 0 ровно в двух точках. Для этого исследуем
производную этой функции
f' (х) = 4х3 + 15х? +12х—4 = (х+2)2 (4* — 1).
При х < —2 и при —2 < х <V4 имеет место неравенство /' (х) < 0, а
при х > х/4—неравенство f (х) > 0. Поэтому функция f (х) убывает
на интервале (—оо; */4) и возрастает на интервале (г/4; +оо).
Поскольку f (—10) > 0, f (10) > 0 и f (1/l) < f (0) < 0, то на каждом
нз двух указанных интервалов функция f (х) однажды принимает зна¬
чение 0, а уравнение f (х) = 0 имеет ровно два решения.
6.4. Уравнение ах = хь равносильно уравнению сх = х, где
с=а}!ь > 1. Так как производная функции f (х) = с*—х, равная
/'(х) = с*1пс—1, положительна при сх > logce и отрицательна при
сх < logc е, то функция f (х) имеет минимум в точке х0 > 0, удовлет¬
воряющей равенству схо = logc е. Если f (х0) > 0, то исходное уравне¬
ние не имеет решений; если /(х0)=0, то уравнение имеет единствен¬
ное положительное решение х = х0; если же f (х0) < 0, то уравнение
имеет два положительных решения (по одному решению на интервалах
(0; х0) и (х0; .оо) соответственно, поскольку f (0) > 0 и limf (х) = оо).
Итак, исходное уравнение удовлетворяет требованиям задачи тогда
и только тогда, когда х0 = с*о = logcе, т. е. x0 — cioece—e и с = е1*е-

Таким образом, искомые значения а, b (и только они) удовлетворяют
равенству ае = еь, где Ь > О, т. е. a—t, b = e\nt, где /£ (1; оо) при
этом единственное положительное решение уравнения есть х=е.
6.5. Преобразовывая левую часть уравнения, получаем
(а_,) (JL +_L+^J U(a_ и /sosx+sinx+jv
9 \ SU1X Cos X 1 Sin X COS X J	\ sin X COS X j
G(a_1)/J^smjx±£V^x т> e вЫЧх+п1А)ф^
sin? (x+n/4) — J J
Следовательно,
, 2(a—1)	_2(	или	sin	(х+я/4)	= о/|^2 ф ± 1/^2.
Y 2 sin (x+я/4) — 1
Последнее соотношение не имеет решений при | а | > Y 2 или
при | а| = 1, а при остальных значениях а имеет решение. Таким
образом, в случае Mcminn 2; + оо) исходное уравнение ре¬
шений не имеет. Если же |a|£[0; 1)U0‘> Y^]> то исходное уравне¬
ние имеет решения
х=(—1)" arcsin (a Y 2/2) — я/4-)-яп,
где ngZ при |с|0О; l)U(l; Y4 и п/2£Z при |а| = |/~2.
6.6. Преобразовывая левую часть уравнения, получаем
cos8 х+sin8 х
_ ^ l+cos2x^* ^ ^1—cos2x\*
=-4 (2+12 cos? 2х+2 cos4 2х) = ~ (4+12 (1+cos 4x)+(l+cos 4х)2)=
lo	OL
—Jz (cos2 4х+14 cos 4х+ 17)i
оХ
Поэтому имеем (равносильное исходному) уравнение
cos2 4х+ 14 cos 4х=97/4— 17 = 29/4,
т. е.
(cos 4х+29/2) (cos 4х— 1/2) = 0, или cos 4х= 1/2.
Учитывая, что 4л+[0; 2я], имеем 4х£{я/3; Бя/3}. Таким образом,
получаем ответ: я/12, 5я/12.
6.7.	Пусть заданная система при некоторых искомых значениях
А, В имеет решение х. Из первого уравнения системы получаем, что
cos Вх=—cos Ах, поэтому sin Вх—г sin Ах, где е+{ — 1; 1}. Тогда
из второго уравнения системы получаем
(Л + еВ) sin Ах=0.
Так как А, В£N и А ф В, то А+еВ ф 0. Итак, sin Ax = B = s\nBx,
откуда
Ax—kn, Вх=пп (k, n£Z).
146

Подставляя эти значения Ах и Вх в первое уравнение системы, нахо¬
дим, что числа k и п имеют разную четность. Исключая переменную х,
получаем условие Bk = An. Так как четность чисел k и п различна,
то в разложении чисел А, В £ N на простые множители число 2 имеет
различные показатели. Обратно, если А=21р, В = 2mq, где I, m£Z+,
/ Ф т, /),<?£ N и p. q нечетны, то исходная система имеет решение
х=я/2*, где s = min (/; т).
6.8.	Сложив уравнения исходной системы, получаем для любого
решения системы
а поскольку х, у £ (0; я/2), то либо х — у, либо х+3у = я. Далее,
рассмотрев разность двух исходных уравнений, имеем
Если х—у, то sin 4у = 0, откуда i/ = n/4 (ибо у £(0; п/2)). Отсюда
следует, чтох = #=я/4. Если же х = я—3у, то sin (4{/—я) sin 4у,
илн — sin4y=-i- sin 4у, значит, sin4r/ = 0. Поэтому опять получаем
у=я/4, х=я—Зя/4 = я/4. Таким образом, имеем х = у = я/4. Про¬
веркой убеждаемся, что значения х = у — я/4 действительно удовлет¬
воряют исходной системе.
6.9.	В силу оценок —l^sina^l, —l^cosa^l имеем нера¬
венство
cos xsin j/+ sin х cos у g
cos у sin у
т. е.
sin (x-j-y)
sin 2у
Следовательно,
sin (и—х)	_	,	.	.	1	,	.
 е-тг—- = cos2ц, т. е. sin (у—х)=-гг sin 4о.
sin 2ц	w '	2 я
(sin (х—у) + 1) (2 cos (2 х—у) + 1)< 6,
в котором равенство возможно лишь в случае, когда
sin (х—у) = 1 и cos (2х—у) = 1.
Поэтому уравнение равносильно системе
1 sin (х- у) = 1,
\ cos (2х—у) = 1,
{
т. е. системе
147
L

Таким образом, имеем
*=—■J+2(n-m)n = 2nft~ (*€Z),
у = (2(л—2m)— 1) я= (2 (А—т)— 1) я= (2/-J- 1) л (/gZ).
6.1ft. Пусть п=1, тогда
1 = sin x-|-cos х — j/'2 cos (х—я/4),
т. е.
х = 2лт или х=я/'2 + 2яА (от, k£7).
Пусть п=2, тогда
1 = sin х sin 2х + cos х cos 2х = cos (2х— х) = cos х,
т. е.
х=2пт (m£Z).
Пусть, наконец, п > 2, тогда
l = sinxsin2x ... sinnx+cosxcos2x ... cos nx<
< | sin * sin 2* ... sin nx | +1 c°s x cos 2x ... cos nx (^
< | sin x sin 2x | +1 cos * cos 2x | =
= max (| sin * sin 2x+cos x cos 2x |, | sin x sin 2x—cos x cos 2x\ )—
= max(|cosx|, |cos3x|),
Поэтому, если некоторое значение х является решением исходного
уравнения, то либо | cos Зх | = 1, либо | cos х | = 1. Однако если
|cos3x| = l, то sln3x=0, откуда cosx ... cosnx=l, и |cosx| —1,
Поэтому достаточно рассмотреть случай |cosx| = l. Проверка пока¬
зывает, что все значения х = 2ят (m£Z) удовлетворяют исходному
уравнению при любом п^З. Если же х = (2/г+ 1) я (6£Z), то
sin/-x=0, cosrx=(—I)1- при r=l, ..., п.
Поэтому значения x—(2k-}-l)n(k£Z) удовлетворяют исходному урав¬
нению лишь в случае
l=sinxsln2x ... sinnx+cosxcos2x ... cosлх = (—i)n(n+1i/2,
т. e. при четном n(n+l)/2. Но число n(n+l)/2 четно тогда и только
тогда, когда одно из чисел п или /г+1 делится на 4. Итак, оконча¬
тельный ответ имеет вид:
если п=1, то х=2ят или x=nj2-\-2nk (т, &£Z),
если п=41—2 или п = 41-\-1 (l^N), то х = 2лт (m£Z),
если п=4/ или rt = 4l—1 (1£N), то х = яот (m£Z).
6.11.	Если п=1, то х и у—любые. Далее, для любого ngN
имеем: если х=0, то уравнение выполняется при любом у, если же
у~ 0, то уравнение выполняется при любом х. Пары (х; у), для кото¬
рых ху Ф 0 и х-\-у=0, удовлетворяют уравнению при нечетных зна¬
чениях п (и только при них). Докажем, что при 2 никакая пара
(х; у), для которой
ху (х+р) Ф О,
148

не удовлетворяет уравнению. Пусть для определенности |х|^|{/|,
обозначим г=у/х Ф—1, тогда | z | £ (0; 1], а уравнение принимает вид
(l+z)"=l+zn.
Если г > 0, то
(l+z)"=l+nz+...+zn > \+гп.
Если же г < 0, то
(l+z)« = (l-|z|)" < 1—|z| < 1- Izl^l+z".
В обоих случаях
(l+z)n ф l + zn.
Таким образом, имеем следующий ответ:
если п = 1, то
(х;
если п = 2k (k£ N), то
(*; у)е{(0; 0l'€R}U{(<; 0)|/€R},
если n = 2ft+l (ft£N), то
(*; !/)6{(°; 0l*€R}U{(<; 0)|/gR}u{(^; —/)I#€■«}-
6.12. Умножив первое уравнение на 2 и сложив его со вторым,
получаем для любого решения системы
х*+2ху+у* + 2(х+у) = (х+уУ+2{х+у) = 10+6 У 2,
т.е. (х+{/+1)2 = (3+1А2)а, а значит, х+р+ 1 = ± (3+ У 2). Если
х-|-у=—4—У 2, то хр=6+4 У 2 и (х—р)? = (х-)-р)2— 4ху =
= (4+ y~2f — 4(6 + 4 У~2) = —6—8 У 2 < 0, что невозможно. Сле¬
довательно, х -1- у = 2 4-1/" 2, ху — 2 У2, откуда получаем две пары
*х=2, у! = У 2 и х2 = У 2, уъ = 2, каждая из которых (как пока¬
зывает проверка) удовлетворяет исходной системе.
6.13. По теореме о средних (теорема 6) имеем
(1 - х^2+ (х, — хг)2 + ... + (х„ _ 1 — х„)2 + *2 5г
j ((1 — xj +(хх — х2) + •••+(*..,_х —*л) + *л)2=^р-у .
причем равенство достигается лишь в случае
1— Х1 = *1 — *2= ...=Х„_1 — Х„=Х„=1/(Л+1),
т.е. когда х,- = 1 — i/(n |-1). Следовательно, существует единственный
набор чисел xlf ..., хп, удовлетворяющих указанному в задаче урав¬
нению.
6.14. Обозначим R= \/хх ... хп, где (Хх; ...; хп) — решение
системы. Применяя теорему о средних, получаем
1=-—|--—(-..^ -п > 9 = xx+xg-f- ... -|-х„ Зал/?,
Хх х*	х„	к
149

откуда /?3*я и Ж 9/я. Поэтому я2 <<9 и я«£3. При этом, если
п — 3, то все написанные неравенства обращаются в равенства, а это
возможно (и действительно имеет место) только в случае хг = х2 =
— Хз = R = 3. Значит, значение я = 3 удовлетворяет условию задачи
и при этом значении я система имеет единственное решение в поло¬
жительных числах (3; 3; 3). Поскольку при я=1 получаем несов¬
местную систему, остается рассмотреть случай я = 2. В этом случае
имеем систему
которая в силу равенства
*1 + *2=9,
—+—=1,
*1 *2
равносильна системе
_J j j *1 + *2
*1 *2 *1*2
I *l+*2 = 9,
\	*1*2 = 9.
*■
По теореме, обратной теореме Виета, значения х^, х2 образуют пару
корней многочлена /2—9/ + 9, имеющих вид <i, 2 = (9 ± 3 УТ)/2.
Таким образом, имеем два решения (/х; /2)> (t2\ М- Так как t\, t2> О,
то значение я = 2 удовлетворяет условию задачи.
6.15.	Заметим, что для любого номера i£{l; ...; я} набор неиз¬
вестных *
*/=1.	*i=	... = */_i=*,+1= ... =*„ = 0
удовлетворяет исходной системе. Докажем, что других наборов из л
неотрицательных чисел, удовлетворяющих этой системе, не существует.
Заметим, что если x,-S=0 при »=1, 2 я и *i+x2 + • ■ • +*л=1.
то *,-00; 1]. Следовательно, для искомых значений неизвестных имеем
2= (1 +*i) (1 + *а) • • • (1 +*«) =
:=1+(*1 + *2 + + *п) +	2	*1+/+	•	•	■+*1*2 • • • *л=&
I <£ < /<п
■ •+(*?+•. ■+**)+ 2 x‘xs—2
Х:Х
1ЛР
1<£</<п	1	<£</<л
поэтому 2	*j*y = 0. Отсюда следует, что все значения неизвест-
I <£</<я
ных, кроме, быть может, одного, должны быть равны нулю (если бы
нашлась пара неизвестных хр, х(р отличных от нуля, с номерами
р < Q, то выполнялись бы неравенства 2	*/*/S* xpxq > 0). На-
1 <к/<п
конец, если для некоторого номера (£{1; 2; ...; я} все переменные
*i xi-1, */+i, ..., *„ равны нулю, то в силу системы имеем
*,- = 1.
150

6.16. Пусть набор (*; у; г) удовлетворяет исходной системе.
Если обозначить x = tg а, где а£( —я/2; я/2), то из первого уравне¬
ния системы получаем
у = 2х/(1 — x2) = tg 2а,
из второго—
z = tg 4а,
а из третьего —
x=tg 8а.
Отсюда
tga = lg8a, т.е. 7a=nk (&£Z)<
Следовательно, а = я/г/7. При этом
х —tg (nk/7), y = tg (2nk/7), z = tg (4nk/7).
Проверка показывает, что при k£{—3; —2; —1; 0; 1; 2; 3} полу¬
ченные 7 наборов чисел х, у, г различны и действительно удовлетво¬
ряют исходной системе.
6.17. Заметим, что для любого номера «£{1; ...; п] набор неиз¬
вестных
Xi = a, *■!=...=*■,■_!=*7+1 =...=*„ = 0
удовлетворяет исходной системе. Докажем, что других решений эта
система не имеет.
1) При п=1 получаем единственное условие х1 = а.
2) При п = 2 имеем систему
f Xi+x2 = a,
\ xt+xl = a*,
из которой получаем условие
(*i+х2)*—(х?+х*) = 2X1*2 = 0*
Поэтому либо Xi = a, х2 = 0, либо Xi = 0, x2 = a.
3) Пусть п 3, тогда для любого решения системы имеем по
меньшей мере два условия:
( х?-|- ... -J-xn = a2,
\ х? +... +х3 = а3.
Если а=0, то из первого условия получаем xi=... = x„ = 0. Если
жеа^сО, то (х1/а)2+ ... +(х„/а)2= 1, поэтому для всех *=1, ..., п
имеем | х,-/а	1, а значит, (х,-/а)3 < (х,-/а)2. Далее,
П
1= 2 to/a)3< 2 to/a)2='•
t=l	i	=	l
следовательно, при всех значениях i справедливы равенства
ШтНЬ
151
I

т. е. либо Xi — 0, либо х,- = а. С другой стороны, если для некоторого
номера	...; п) оказалось, что х,-=а, то в силу системы все
остальные переменные Xi, ..., x/_i, x,-+i, ..., х„ равны нулю, и
наоборот. Таким образом, во всех трех случаях описанные выше
наборы и только они удовлетворяют системе. (Попутно доказано, что
при л^З из второго и третьего уравнений исходной системы выте¬
кают все остальные ее уравнения.)
§ 7. Неравенства
7.1. Пользуясь теоремой 4, получаем
V4+V1 - V4— VI -V~2 =
т. е. заданные числа равны друг другу.
7.2. Так как a < Ь < с < d, то
у—x=ab-\-cd— ас—bd — (a—d) (Ь—с) > О
и
z—y=ac-\~bd—ad—bc—(a—b) (с—d) > О,
Таким образом, х < у < г.
7.3. Пусть числа а, Ь, с удовлетворяют условиям задачи:
abc= 1 и а+й+с > —-4—гЧ—-•
а Ь с
Тогда
(а—1) (6—1) (с— 1) = оЬс—ab—ас—бс+а+б+с— 1 =»
= (аЬс—1) + (а+*+с)—=
= (а+6+С)-(7Г+!+!) >°-
Итак, произведение трех сомножителей (а—1) (6—1)(с—1) положи¬
тельно, а значит, либо ровно один из этих сомножителей положите¬
лен, либо положительны все три числа а—1, 6—1, с—I. Но послед¬
ний случай невозможен, так как если а>1,6>1,с>1, то аЬс> 1,
что противоречит условию abc— 1.
7.4. Требуемые оценки вытекают из неравенств В < (А + В)/2 < А
(поскольку В < А) и соотношений
(а — 6)г ^ (У~а2— Y~b2Y	(Y~a-\-Y~b)*	Л + В
В (А —В)	4(V"b-V"b)2	4	2
152

7.5.	Применяя теорему о средних и учитывая, что числа logb а,
1оgcb, logo с положительны, а их произведение равно единице, по¬
лучим
| *0gcb ■ logo с „ logb a logc 6 logfl с _
a+b'*'b+c~^~ a+c V (a + ft) (ft + c) (a + c)
3	9	19
Y(a+b)(b + c)(a+c)	(a+й)+(6+c) + (a+c)	2	a	+	b+c’
откуда вытекает требуемое неравенство.
7.6. Без ограничения общности можно считать, что аЗэ с > 0.
Преобразуем разность между правой и левой частями неравенства
и виду
Зобс+а2 (а—Ь—с) + 62 (Ь—а—с)+с2 (с—а— Ь) =
=Забс+о3 -f- б3+С3—а2 6—Ь'1а—агс— 62с—<?а—с26=
=а2 (а — Ь) + б2 (6 — а) + с (2аЬ — а2 — б2) -}- с (с2 — Ьс-\-аЬ—ас) —
= (а—Ь) (а2—б2) — с (а—fc)2+c (с—а) (с—Ь) =
— {а—б)2 (а + б—c) + c(6—с) (а—с).
Теперь для доказательства требуемого неравенства остается заметить,
что полученное выражение неотрицательно, так как
а + б > с, б 5: с, а 3» с, с > 0.
7.7. Если а=б = с = 0, то неравенство справедливо. Пусть
s^a+6-t-c > 0, тогда
+НТЯП+(1-fl) (1 -й) (1-с) =
_а а (1—о) .6	6(1 —б)  с	с (1 — с) .
"I s(64 с+1) s	s(a + c+ I)	s s (а + 6+I)-**
-H>-4 0-4(1-4	+7)-
-“^(гетт-о-к'-о)-
_£*V^(s+1+T_(174('_0|)s'.
так как
7+Т+Т""1' iilff!!(T+T+1-('-t)(1-e|):s0'
У!га(гтт+т-"-“)('-е))а'0'
Для доказательства первого из трех последних неравенств достаточно
153

заметить, что
-(1-“Чо,
S
I	^b)(l^ib+^-(b + c+J)bc_
fr+c+1	fc+c+l
^ (6 + с)2— 3be (b — c)2-|-ftc__ .
г>4-с+1	“	b-rc+l s'
Аналогично доказываются и два других неравенства.
7.8. Пусть р==а + 6 + с>0, q-=ab-\-bc+ac > 0, r—abc> 0.
Тогда многочлен Р (х) = х3—рх*+qx—г принимает отрицательные
значения при дг<0. Следовательно, все корни этого многочлена, рав¬
ные по теореме, обратной теореме Виета, числам а, Ь, с, являются
положительными.
7.9. Пусть ех£[0; я/2). Тогда, во-первых, подставляя х=cos а
в неравенство sin х < х, справедливое прн х > 0, получаем оценку
sin (cos а) < cos а. Во-вторых, из неравенства а ^ sin а имеем оценку
cos а < cos (sin а), так как функция cos х убывает при *£[0; л/2).
Таким образом, sin (cos а) < cos а cos (sin а), т. е. требуемое нера¬
венство доказано при а £ [0; я/2). Далее, при а£[я/2; я] имеем
sin (cos а)<0 < cos (sin а), т. е. неравенство выполняется и при
а£[я/2, я]. Учитывая четность функций sin (cos х) и cos (sin х),
получаем требуемое неравенство для а£[—я; я], а поскольку число
2я является периодом этих функций, то неравенство справедливо при
всех а £ R.
7.10. Обозначим Р,- = 2—а; > 0 (1=1, .... л). Тогда, учитывая
П
равенство 2 Pi = 2л—1 и теорему о средних, получаем
(=1
п	2л2	2 я2	я
^ п/рг^'л&р1+-+Р" n~2n-1 п~~2п-г
что и требовалось доказать.
7.11. Обозначим b,- = s—а; > 0 (1=1, ..., л). Тогда, учитывая
равенство 2 й,- = (л—1) s и теорему о средних, получаем
i= 1
1т?И:№+')—ii—i*-*
i=i	i=i	i=i	i=i
л	л2	л2	л
S& S   	— nSsS-r—:	Г-7	Л = ; Я =
т/ьг...Ь„	b!+...+b„	л —1	л-1
что и требовалось доказать.
154

7.12. Обозначим a,/a/+i=fc/ («= 1, ..., л) и положим frn+i=l.
n+ 1
Тогда имеем	и,	пользуясь	теоремой о средних, получаем
i= 1
соотношения
п+1	П+1	п+1 ,	я+1
ЕтгЕ	)=Е*
£= I	(= 1 1 =*= * i= 1 \ /чЧ	(= I
П	п
из которых вытекает справедливость неравенства
i=i £ = 1
Таким образом, на поставленный в задаче вопрос следует дать утвер¬
дительный ответ.
7.13. Введем обозначение 1—а — Ь. Рассмотрим сначала случай,
когда 0 < х < 1. По неравенству Бернулли (теорема 5), учитывая,
что 0 < Ь < 1, имеем (1+х)ь 1+ Ьх, следовательно, (1+х)-6^
3;1/(1 + 6х). Снова применяя неравенство Бернулли, получаем
(I + i)x*=(l + ft)(l-(l-x))*<(l + ft)(l-ft(l-x)) =
= l + bx+b2.(x— 1) < 1+Ьх,
откуда
1 +bx > (IЬ) х11, или xa-{-bxa+1 > (1-J- А>) дс.
Теперь имеем
„ , ч ь	Ха	1	1— Ха
(1 +^)—ь ; S- • j—г	:	=
1 — х	1 + Ь* 1—х
1— x+(xfl-^l)(l + fcx)_xa+fexa+1 — (1 + Ь)*	0
(1+йх)(1—X)	—	(1	+	6х)(1—х)
(мы воспользовались тем, что (1+Лх)(1—х) >0). Итак, (1—х)_ь>
1— ха
> -—— при 0 < х < 1, что и требовалось доказать. Случай х > 1
сводится к предыдущему подстановкой х= 1//. Тогда 0 < / < 1 и
,-ь
I х° \-\Ца ь
1-х	1	—	1	jt
1	/а	/1	\-Ь
—j </b(l+/)-«- = ^7+lj =(1 + х)-ь,
что и требовалось доказать.
7.14.	Доказательство проведем индукцией по n£Z+. При л = 0
получаем верное неравенство 1“<1. Допустим, что неравенство
справедливо для числа л, и докажем его для числа л + 1- Имеем
(1 +Хх -J- . . . +X„-j-Xn + i)a ■— (1 +Xl+ . . . +x„)a =
)--')<
<0 Н“Х1+ ... + x„)a_1-xu+i < ((л + 1) xn + i)a~1-x„+1 =
= («+!)“ 1,Xn+i
•	155

(справедливость неравенства	,ч
0+*Н	+*/;)а-1-*л+1<	(("+	О	*«+i)“_1	••*■«+!
ытекает из условий 1 +*1+ ... +*„ Эг (л + 1) хп + 1 и а—1<|0). Из
доказанного неравенства и предположения индукции получаем
(1 +*i+ • • • +*«+i)a.< (1 +-*1+ • • • +*«)“ + (я+ 1)“-1*“+1<
< I + I®"1 *?+2е-1	*“+ (л +	1)а_1^+1,
что и требовалось доказать.
7.15. Без ограничения общности считаем, что
Тогда
5= 2 2K-flyl =	2	l°i—flyl+ 2 К—и/1 =
i=l/=l	)<<</<л	I	</<«<«
=2	2	| а,-—ау |=2	2	а'»-2	2	а-»	=
1<К/<п	1<т</<п
п
=2	2	(2т—п — 1)ат.
т— 1
Сумма S принимает наибольшее значение в том и только в том слу¬
чае, если для номеров т, удовлетворяющих неравенству 2т—п—1 > О,
каждое из чисел ат равно двум, а для номеров т, удовлетворяющих
неравенству 2т—п—1 < 0, все числа ат равны нулю. Поэтому спра¬
ведливо неравенство
S<4	2	(2m—n—1).
(л+1)/2 < т <л
Пусть n — 2k-\-\ (ft£N), тогда
2*+1
S<4 2	(2m~	2k—?) = 8(1+2+ . ..+ft)=4ft(ft+l)=.
m=A+2
= (2*-h l)*— 1 < n\
причем равенство 5=л? невозможно. Пусть n = 2k (ft£N), тогда
2k
5<4	2 (2/n_ 2k~ l) = 4(l+3 +	h(2*—	1)) = 4#> = л?..
m=ik+1	4
При этом равенство S=л? .выполняется тогда и только тогда, когда
среди чисел alt а2, .... а2д ровно k чисел равны двум, а остальные ft
чисел равны нулю.
7.16. Поскольку
П
2 I	•	•	•	+а/л*л	I	<	Л4
/ = 1
для любого набора чисел xlt .... хп£{—1; 1}, то имеем неравенство
( "	4
577 L (	I a/i*T +	•	+а/пхп	I	)	< М,
{*•:... ;*„Л/= 1	'
156

которое можно переписать так:
;м.
X	X	\a/iXi+---+a/nXn\)
i= 1 \ {х,;.. .;х„}	/
Для каждого фиксированного значения /^{1; п) в сумме
Sj= 2 I aj\x\-\- ** •+<*/»*« I
разобьем все 2" слагаемых на 2”-1 пар так, что в каждой паре зна¬
чения xt, Xy_i, Ху+1, х„ совпадают, а значения Ху различны.
Тогда сумма слагаемых в каждой паре имеет вид \ A-\-ajj\-\-\A—ауу I,
где
■^ = аУ1ж1+ • • • +аУ,(/-1)^/-1 + аУ,(У + 1)^/+1+ • • -
Но
| +ауу | +1 Д — ауу | ^ | (У1+ауу) — (Л—оуу) | = 2 | а/7 |,
поэтому Sy^2n_1-2| ауу |=2“ | ауу |. Таким образом, получаем
|anl + ..i+|om,l = X(i-2"lfl//l'HX
/= i '	'	/	=	1
что и требовалось доказать.
п
7.17.	Заметим, что сумму S = 2 Ь,а,- можно представить в виде
i=l
S= fctai + 2 bi (ал + ... +0/)— 2 (ai “Ь • • • +ai-i) —
1=2	i=2
n	n—	1
*= 2(0i+*--	— 2(ai+--‘ “ba') ®i+i=
i= 1	(=	1
= 2 (“*+••• +a') №,■—i>/+i),
i= 1
где считаем fc,i+j = 0. Далее, среди чисел А;=\ аг-\-...	о,-1
(1=1, ..., п) выберем наибольшее число Ак. Тогда для этого зна¬
чения k имеем
isi<2 I■ ■ ■ "Ь0'i‘i
i=i
п	п
^ 2 А» (hi */+0 = ^*2	®i + i)= Ak №1	6,1+|)^y4j,
i= l	i=	l
что и требовалось доказать.
7.18.	Доказательство проведем индукцией по и £ N. Поскольку
{i-x^+(i-v4,)=yT+(i-yT) = i,
157

то при n = 1 утверждение верно. Пусть оно верно для числа п—
тогда имеем
(1— Xi ... x„)m + (l —pf) ... (l —£«) =
= (I -Xi ... *„_! (I - у„)Г +(1 -й*) ... (1 -sff-,) (1 -9Й*)
Э*(1 —Xi ... x„_i+*i • • •	+	(1 — (1 — *i ■ ■ • x„-i)m)U —Уп)=
= (а+ (1 -a) ir„)<* + (1 - o'») (1 -/fo ) = (а+6—а6)“ +(1 -o'") (1—№»),
где обозначено а = 1—x1...x„_i и Ь—уп. Докажем индукцией по
mgN, что для любых чисел a, fcg[0; 1] справедливо неравенство
(а-|-6—ab)m ^ат-\-Ьт—атЬт.
При m= 1 это неравенство обращается в равенство. Пусть для числа
т— 1 неравенство также верно, т. е.
(а_|- ь — ab)™ ~15= ат ~1 + Ьт -1—ат-гЬт ~г.
Тогда (учитывая к тому же, что a+6—afrSsO) получаем справедли¬
вость этого неравенства для числа т. Действительно,
(a+Л—ab)m—ат — Ьт-\-атЬт^
7^5 (ат~1 -f bm~1'—am~lbm~1) (а+ Ь—ab)—ат — Ьт -\-атЬт =
— 2 ambm	Ьат~1 — атЬт~1— Ьтат~1—атЬ— Ьта =
= (bm~1 — bm) (а—ат)-\-(ат~1~~ат) (Ь—Ьт)^0,
так как а5=ат_15=ат, b ^ Ьт~1 ^ Ьт. Итак, доказано, что для
любого числа mg N справедливо неравенство, которое можно пе¬
реписать в виде
(a+fc—ab)m + {l— ат) —	1.
Из него, согласно принятым выше обозначениям, вытекает справед¬
ливость требуемого в задаче неравенства для числа п. На этом индук¬
тивный переход закончен. Утверждение доказано.
7.19.	Сделаем замену b = ax, с = ау, d = az, тогда в силу условия
задачи имеем 1<;х<7р<;г, а требуемое неравенство можно записать
следующим образом:
апх (ах)°У (ау)аг (аг)а 5г (ах)а (ау)ах (аг)аУапг.
Далее, после сокращения на аааахааУааг и возведения обеих (поло¬
жительных) частей неравенства в степень 1/а получаем равносильное
неравенство
хУугг^2 хухгУ,
Положим y=xs, z — xt, тогда	(так как x<7p<z) и y'Szs
(так как х^ 1), а неравенство имеет вид
Xxsyxtxt з- Хух (xt)xs.
158

После сокращения на xxsyxxt и возведения обеих частей неравен¬
ства в степень l/х имеем равносильное неравенство
Если у— 1, то неравенство верно, так как в этом случае
х— 1, s—у/х — 1, у<-1 = 1 = t1~1= 1.
Если t = 1, то неравенство также справедливо: yt-1=y°=I — Is 1 ',*= 1.
Пусть у > 1 и t > 1. Тогда, возводя обе части неравенства в степень
1 у
> 0, получаем равносильное неравенство
t-\ у-1
уУЛу-D^fS/U-i) ^где	s^y).
Рассмотрим два случая.
а)	Пусть	Докажем,	что	функция	(а)	=	аа'/(сг_1)	воз¬
растает при а > 1. Имеем
(а) = (е(а/(а_1)) 1п = е(“/(«-1)) in а ^ !	!ИЕ_^	=
= а'?/(а~1)-а_1_ 1)2 (tx— 1 — In ос) >0
(последняя оценка вытекает из неравенства g 1(а) = а—1 — 1па>0,
выполненного при а > 1, поскольку gi (а) = 1 — 1 /а > 0 и gt (1) = 0).
Поэтому требуемое неравенство следует из соотношений
yy/W-И = fl (у) ^ fi {t) =	-1) ^ f/Ч -1).
б) Пусть у < t. Докажем, что функция /2 (а) = а1/<а-1) убывает
при а > 1. Имеем
f' £fvl = (e<1/(a-l)) In ол'	(i/(a-i)) In а ( j	!E£L_V
() K	’	\a (a— 1) (o-l)*J-
* (a— 1 —a In a) < 0
a (a — 1)?
(последняя оценка вытекает из неравенства g2 (a) = a—1—a In a < О,
выполненного при a> 1, поскольку g2(a)=l—In a—1< 0 и й(1)=0).
Следовательно, и в этом случае неравенство выполнено, так как
уУПУ-D=(ft {у))у ^ (/а {t))y = (У/и-1) ^ ,*/</-«
7-20. Преобразуем левую часть неравенства к виду
/=2
159

и заметим, что для любого «б N выполнены соотношения
1	I.	1	»	|	,	1	\	|
п}~1-1-1	п‘	2п‘~1	)
=Y, (	!-Л>	£	-
о \ (т— 1) к‘-1+1	mn'-1/	A	mn‘~l	J	,т
т=2	'	1	'	т=2	'	'	т=2
Отсюда следует требуемое неравенство
п*	ft	п
2т>1(т+“+7Кг
/=2	г=1	4	1=2
7.21. Обозначим
6Й = (*+ 1)*/АЛ-1 = Л: (1 + 1/А)Л	(fc=l л).
Учитывая соотношения 6* <; 6е (см. теорему 7) и
bi ... 6ft = (*+!)*,
а также теорему о средних, имеем
pAit... ah =^-j- V (“i6i) ■ • ■ («ft6ftX
R
<*(F+ij- <aibl + • • • +а*г’*) = (t ~ Fp) Z a'bi-
Далее,
-S(*AS(™))-
=(тА)^а|й2т4*
w ^ //=1 /=1 /=1
что и требовалось доказать.
7.22. Будем считать, что пятерка чисел a, Р, у. 6. 6 совпадает
(с точностью до порядка) с пятеркой чисел
Тогда
(* + *+* + * + *) (-^+1"+^-+^Г+^-) =
160

где сумма берется по всем С| = 10 парам индексов- 1 ^ С < / < 5.
Далее, имеем
Докажем, что для положительных чисел	справедливо	нера¬
венство f (х, y)+f(y, z) < f (х, z), т. е.
так как х/у <|1 и 1 Зг у!г. Аналогично получаем оценку
которая в сумме с предыдущей дает необходимое неравенство. Кроме
того, равенство достигается тогда й только тогда, когда либо х=у,
либо у=г. Пользуясь доказанным соотношением, получаем следующий
ряд неравенств
l(Pi *х)+ /(*!>	*2)+f(Xi,	x3)+f(x3,	Xi)+f (x4,	x5)+/ (x6, q)*Zf(p, q),
fiP,	xi) + f(xlf	x3)+f(x3,	x3)+f(x3,	qXf (p,	q),
f(P. *i)+/4*i. xt)+f(x4, <?X/(p, q),
f(P,	x2)+f (x2,	x5)+f(x6,	q)*if (p,	q),
f(p.	x2)+f (x2>	*4)+f(x4,	qXf(p,	q),
f (P, *i)+/(*г, xB)+/(x6, q)<,f (p, q),
сложив которые и отбросив положительные слагаемые вида f (р, х,)
и/(xl< q)> получим требуемое неравенство. Теперь определим, когда
имеет место равенство. Заметим, что если р < х2 или х, < q, то ра¬
венство не достигается, поскольку тогда среди отброшенных выше
слагаемых / (р, х2) или f (х4, q) есть ненулевое. Поэтому для равенства
необходимо выполнение соотношений xi = х2 = р и х4=х5 = 9- Тогда
из второго среди выписанных выше шести неравенств получаем
Поскольку и в этом неравенстве должно быть выполнено равенство,
то либо р = хз, либо x3 = q. Переходя к исходной формулировке,
получаем, что равенство достигается, в том и только в том случае.
2 f (*'■ X]) < 6/ (р, q).
Kl
Заметим, что
fiP. x3)+f(xa, q)<f(p, q).
6 Под ред. И. И. Сергеева
161

когда два числа из пятерки чисел а, (5, у, б, е совпадают с одним
концом отрезка [р; q\, а остальные три числа—с другим его концом.
7.23.	Будем считать, что четверка чисел а, Ь, с, d совпадает
(с точностью до порядка) с четверкой чисел	хз<*4-	Найдем
производную многочлена
Р (х) = (х—хг) (*—*2) (*—*3) (*—*4).
С одной стороны, по теореме Виета
**—^23*/^*®+
+(	2	*/*/V2-(	2	*/*/*ftJ*+(*i*s*3*4)J =
\l<i</<4	)	\i<i	<i<k< 4	j	J
= 4x3—("з 2*A*2+f2	2	2	x‘xjxb'
\ i=l J \ l<i</<4 J I<i</<fe<4
С другой стороны, по теореме Ролля, если	для	некоторого
значения i е{1; 2; 3}, то производная Р' (х) равна нулю в некоторой
точке у£ (*,-; x,+i). Если же многочлен Р (х) имеет кратный корень,
то многочлен Р' (х) имеет тот же корень на единицу меньшей крат¬
ности. Таким образом, многочлен Р' (х) третьей степени имеет корни
Уй f/г, Уз, удовлетворяющие неравенствам *1^г/1<х2«£г/2^*з<
^(/3^*4, следовательно,
Р' (х) - 4 (х—г/i) (х— г/г) (х—Уз) =
= 4х3—4 (ух+г/г+г/з) jc2+4 (г/1^2+ут -! г/1//з) х—4у1у!у3.
По теореме о средних имеем
Уш^ё < w+sf+M*.,
откуда У А^\Гв, где обозначено
А = У1У2УЯ =	(*1*2*3 +XiX2Xi + *1*3*4 + *2*3*4).
5 = {УгУз+УзУз +Ут) = -g- (*1*2 Т-*1*3+*1*4 + *2*3 + *2*4 +*3*4)-
Итак, требуемое неравенство доказано, причем равенство имеет место
тогда и только тогда, когда У1У2 = у2Уз = У1Уа, т. е. когда у1 = у2=у3.
Последнее условие выполняется в том и только в том случае, если
*! = *2 — *з — *4, т. е. если a — b = c=d.
§ 8. Задачи с целой частью
8.1.	Исходное уравнение равносильно уравнению
I*— 1 |(|х+11— 1) = {*} при хф 1.
Рассмотрим следующие случаи: *>1, —1<х< 1 и х< — 1. При
х > 1 уравнение записывается в виде х(х—•) = {*) и не имеет реше-
162
Р'(*)-

иий, так как х (х— 1) > х— 1	{*}- При — I ^х < 1 имеем урав¬
нение
х(1 — х) = {х}.
Так как (х}^0 и 1—х > 0, то х:&0. Но при 0«£х< 1 справедливо
равенство (х} = х. Следовательно, в этом случае получаем уравнение
х(1—х) = х, т. е. х = 0. При х< — 1 получаем уравнение
(2+х)(х-1) = {х>.
Так как х—1 <0 и (х}^0, то 2+х^0, т. е. х*^—2. Число
х=—2 удовлетворяет уравнению. Если —3<х < —2, то {х}=х+3,
а уравнение принимает вид
(2-f-х) (х— 1) = 3-(-х
и имеет решение —У 5g[—3; —2). Наконец, нн одно значение
х<—3 не удовлетворяет уравнению, ибо при х < —3 имеем
|(24-х)(1-х)| = |24-х|.| l—xl > 1-4 > |{х}|.
Таким образом, получаем ответ: 0; —2; —У 5.
8.2. Заметим, что соотношение \\Ут] = 6, где т, 6gN, равно¬
сильно неравенству 63<т<(6-]-1)3—•• Количество натуральных
чисел т, удовлетворяющих этому условию (прн фиксированном 6),
равно (64- О3—ft3 = 3ft? 4-3fc-|-1* Следовательно, левая часть уравне-
х-1
ния равна 2 S^, где обозначено
fe=i
Sk = к (36? -J-364-1).
Так как S* > О при 6gN, Si=l-7 = 7, S2 = 2-19 = 38, 53 = 3-37=1П,
S4=4.61=244 и 5x4-52 4-53 4-54 = 400, то исходное уравнение
имеет единственное решение в натуральных числах: х=5.
8.3. Докажем, что для любого 6gN справедливы оценки
6[х]^[6х]с6[х]4-6_1.
Действительно, обозначим т — [х\, а = {х}, тогда получаем x = m-f-a,
mgZ, 0<а < 1 и
6m = [6m] < [6х] = [6m4-6а] < 6m -f-6а < 6m4-6.
Таким образом, имеем
S=[х] 4- [2х] 4- [4х] 4- [8х] 4- [16х] 4- [32х] <
^63 [xj4-(14-34-74-154-31) = 63 [х]-(-57 и SSa63[x],
т. е. для некоторого mgZ имеют место оценки
63т S	63т 4- 57.
С другой стороны, 12345 = 63-1954-60, поэтому равенство S = 12345
невозможно ни прн каком значении х.
Ь*	163

8.4. Положим m=M, a=\xV Тогда х= tn+a и исходное урав¬
нение будет иметь вид
(т + а)? — [т2 +2та + а2] = а2,
откуда
mi 2та = [mi -j- 2 та + a2].
Но m2£Z, поэтому
2та = [2та+а2].
Последнее равенство при 0<а< 1 равносильно условию 2ma£Z,
следовательно a = k/(2m), где &£{0; 1; 2т—1}. Таким обраэ
при каждом из значений т= 1 п—1 (при л=1 таких значений!
нет) величина а может принимать ровно 2т значений, а при т=Л
имеем а = 0 (так как х<я), а значит, количество решений равно]
2+4+...+2 (я— 1) + 1=я (я— 1) + 1=я2 — я+1.
8.5. Докажем, что для любого я£ N выполнено неравенство]
v«+v л +1 < у 4и + 2. Действительно, поскольку 4я(я+1)<|
< (2л+ 1)2, то 2 Yп (я + 1) < 2л + 1. Поэтому
(Г я+Гя + 1)2 = 2я+1+2^я(я + 1) < 4л+2,
откуда вытекает требуемое неравенство, а значит, и неравенство
[V71+^^Г+Т] <; [>^Г+2].
Предположим, что для некоторого /i£N имеет место строгое иера* |
веиство
[\Гп+}Гп + 1]< [УАп+2].
Тогда существует такое N, что
\Гп +>/Гл+1 <	>^4л+2.
Отсюда имеем
2 \Гп (п+1) < т* — (2я+1)<2я + 1,
а значит,
4л (л+1) < (от2 — (2л + 1))2<4я (л+1) + Ь
Поскольку число (от? — (2я+1))? является натуральным, то ш2-
— (2л + 1) = 2я+1. Следовательно, число т2. — 2(2п + 1) делится иа ?_J
но не делится на 4, что невозможно. Таким образом, требуемое рь]
венство справедливо при любом я £ N.
8.6. Обозначим
/(n) = [n+Vrn + 1/2], ngN,
тогда разность
/ (Я+ 1) — / (я)= [я+ 1 + \Гп-![- 1 + V2] — [я + У п +х/2] =
= i+[/п+т+vJ-[/n +‘/,1]
больше единицы в том и только в том случае, если
[/TT+I+Vs] > [Vn+V*],
164

г. е. если 1гл -f V* < тс У/г +1 + V* для некоторого
Последнее неравенство равносильно неравенству
п < /л?—n-J-1,
т. е. условию n = m2— m. С другой стороны, для любого n£ N имеем
оценку
/(в+1)=п + 2 + [У"М:Т-1/.]«гя + [/я+1/*]+2 = /(я) + 2.
так как	—Vs < Vп Л-1/2- Таким образом, получаем
/(„ + 1)_/(„)=J 2при„ = т2-ш, т = 2, 3
1 1 при остальных n£N.
Следовательно, величина f (п) принимает все натуральные значения,
кроме чисел вида
f {т2—т)-\-\=пЛ-\-\\Гт2—т-1г11^—т-\-\—т2.
(последнее равенство вытекает из оценок т—1 < У т2 — пт+1/2 < т,
справедливых при т ^2) и чисел, меньших числа / (1) =2. Итак, дока¬
зано, что натуральное число не представимо в виде \п-\~Уti +V2]>
n£N, в том и только том случае, если оно является квадратом
какого-либо натурального числа.
8.7. Предположим, что среди членов последовательности {а }
имеется лишь конечное множество нечетных чисел. Тогда, выбрав
н'четное число ат с наибольшим номером т, получим, что все числа
°а+п, fi£N, являются четными. Пусть am+1 = 2pq, где q нечетно и
r;£N (am+1 Ф 0, так как последовательность возрастает и > 0);
тогда
°-т + 2 ~ j^'2' ат + 1J =2Р 1-3q.
Аналогично получаем, что am+s—2’>~2-32q и т. д., наконец, ат+р+1—
= 3°?—нечетное число, что противоречит выбору номера т. Предпо-
лэжим теперь, что среди членов последовательности имеется лишь
инечное множество четных чисел. Пусть ат — четное число с наиболь¬
шим номером т, тогда число ат+1 является нечетным и am+, — 1 =
= 2pq, где q нечетно и p£N. Имеем
йт + 2 = J ~2 am + l j — (am + i— U Ч—2" J =2Р 1-3g-(- 1,
г. е.
am + 2-l=2p~1.3q.
Аналогично получаем, что ат+3— 1 =2p~2-32q и т. д., наконец,
“я+р+i — l=3pq. Поэтому am+p+1 = 3pq-{-l — четное число, что про¬
тиворечит выбору номера т. Утверждение задачи доказано.
8.8. Обозначим
а„ = (3+/П)" + (3-|/17П

тогда имеет место равенство
a„+2 = 6a„+i +2а„,	n£Z+.
Действительно, пусть а= (3 -}- У1l)", Р = (3—У ll)n, тогда
о„ = а-\- Р,	_
_ ая+1 = (3+2'‘П)о + (3-УТГ)Р.
о,+. = (3 + 1/' ll)2a + (3— У ll)2p = (20+6Vr ll)a + (20—бУ 11)р=
= (18+6 V^iT)a + (l8 — 6 VTi) Р + (2а+2Р) = 6а„+1+2а„.
Отсюда и из равенств а0 = 2,	=-.	6 следует, что число ап является
целым для любого n£ Z+. Поскольку —1 < 3— У И < 0, то при
п £ N имеем
о21-1 = (3 + >АП)2п"1 + (3-^П)2"-1 < (3 +/7Г)2"-1 <a1(I_i+l,
а*,-ж = [(3+УТТ)*"_13-
Теперь докажем индукцией по n£N следующее утверждение: число
о2 ,_2 делится на 2п, а число a2i-i делится на 2", но не делится
на 2П+1. При п=1 утверждение верно, поскольку а0 = 2, ai=6.
Пусть оно верно для некоторого значения п £ N. Тогда число с21 =
= 6а2,г_1+2о2.;_2 делится на 2п+1, так как оба числа a2«-i и с2„
делятся на 2". Далее, число o2n + i = 6a2,J + 2a2n_1 делится на 2П+1
(поскольку оба числа а2п и а2п-\ делятся на 2П), но не делится иа
22,,+2 (поскольку число a2l делится на 2П+1, а число a2„_i —не де¬
лится). Утверждение доказано. Таким образом, наибольшая степень
двойки, на которую делится число a2„-i, равна 2П, т. е. k — n.
8.9.	Для заданного значения п £ N обозначим т=\пУ 2]. Так
как т Ф п У2 (иначе число У 2 =т/п было бы рациональным), то
т< п У 2 и т2 < 2п2. Поэтому
1 sj2пЯ—т?-—{п У 2 —т) (п У2 +т) =
= {п У2 } (п У2 +т) < {п У2 } 2п j/T,
откуда вытекает требуемая оценка. Пусть задано число с > 0. Рас¬
смотрим последовательности {п,} и {т,-}, определенные следующим
образом: nj —т2= 1,
п,-+1 = 3п/+2т/, т/+1 = 4п,-+3т,-, i£N.
Тогда 2п\—т\= 1 для всех /£ N. Действительно, при t=l имеем
верное равенство 2п\ — m2 = 1. Если же это равенство верно для
некоторого значения i £ N, то
2«i+i—m2i+i = 2 (9гц + 12n;m;+4mf) —
— (16п2+24п,/п,- + 9 mf) = 2гц—m2 = 1,
т. е. оно верно и для значения t+1. Так как последовательность
{п,-} возрастает, то можно выбрать такое значение п = п,-0, чтобы вы-
166

поднялось неравенство
п > (1/(2 У 2)) (1 + 1/с).
Тогда справедливы оценки
е(2п У 2 — l) > 1, (1 +с) (2п У 2 — 1) > 2n Y~W,
кз которых при m = miQ вытекают соотношения
■ +Д- >	)=	>	—уЛ	= п У~2-т = {п	У2},
2п\2	2п	У2	— 1 пУ2+т
поскольку 0 < п У 2 —т—1/(п У2 + m) < 1. Задача решена*
8.10.	а) Рассмотрим функцию
/ (х, у) = [5х] + [5у\ - [Зх+у] - [Ъу+х] - [х] - [у]
и докажем, что f (х, у) 3= 0 при х, y£R- Пусть для некоторых значе¬
ний х, «/£[0; 1) имеет место неравенство
fix. У) = f5*!+[%] — [Зх+у] — f Зу+х] < 0.
При этом без ограничения общности можно считать, что x<iy. Тогда
/(*. У)<—1 (ибо f (х, y)£Z) и
t(x,y) > (5х—1) + (5^— 1) — (Зх+у) — (Зу+х) = х-\-у—2,
т. е. х-\-у—2 < —1, или х-\-у < 1. Так как
(51/] - [3у+х] 3= [5у] - [4у] 3, О,
то
[5*] — [3x-\-y] = f (х, у) — ([5t/] — [3{/+х]) < — 1,
С другой стороны,
[5х]— [Зх-J-у\ 3= [5х] — [Зх+1—х] = [5х]— [2х+1].
Значит, [5х] < [2х+ 1], откуда следует, что 5х < 2х+ I, или х < 1/3.
Но тогда
[2х+1]<ф.-1+1] = 1,
т. е. [5х] < 1, или х < 1/5. Так как
[3*+#]&1+(5*]=1,
то у^ 1—Зх > 2/5 и [Ъу\^2. Заметим, что
[з*+{/1 < f 3 • -=-+11 - -1.
3	1
Если у< 3/5, то Зу+х < 3--g—J--g- = 2, [Зу+х]«с1 и
f (*. У) = (5*1 + (5у] — [Зх-\-у\ — [3{/+х] 3= 0+2—1 — 1=0,
Если же у Зг 3/5, то [Ъу\ 3 3,
[3{/+х] = \у+х-\-2у\ < [//+х] +2 <2,
/(*, У) 5=0+3- 1-2=0.
167

Итак, неравенство f (х, у)^ 0 доказано при х, у£ [0; J). Но так как
число 1 является периодом функции f (х, у) по каждому из аргумен¬
тов х, у, то это неравенство можно считать доказанным при всех
х,	Наконец, прн х, y^sO имеем
[5х| + |5р] = / (х, {/) + [Зх+^] + [%+х] + [х] + [(/] S3 [Зх+(/] + [3у+х],
что и требовалось доказать.
б)	Докажем, что степень, с которой произвольное простое число р
входит в разложение знаменателя т\п\ (Зп-{-т)\ (п-\-Зт)\ на простые
множители, не превосходит соответствующей степени для числителя
(5т)1 (5п)! Поскольку число р входит в разложение числа q\ в сте¬
пени, равной [qlp] + fa/p2] -f- •. •, то в числитель оно входит в степени
[5т/р]-]-[5т/р?]-(-*«» + [5я/р]-|-[5я/р2]+.*.. а в знаменатель — в сте¬
пени
I т/р\ + [m/p2] Н	+ [п/р] + [п/р2] + ...+[ (3 т+п)/р] +
+ [(Зт+n)/p?] -J- . . . +1(3« + т)/р] + [(3п+т)/р2] +...
Обозначим m/p^ — Xk, п/р* = ук, где ££ N. В силу доказанной выше
(в п. а)) оценки имеем неравенства
[5х*] + [5ук\ S3 [xk] -f [yk] + (Зхд, + yk] + [xfc+3yh\,
суммируя которые по всем значениям N (при достаточно больших
к обе части неравенств равны нулю), получим требуемое неравенство.
8.11.	Так как х=т-\-а, где т — \х\, а = {х), то при любом *£N
имеем
[,kx] = [km-\-k а] = km + Ika].
Поэтому исходное неравенство имеет вид
«/»+[««]	 -f	j,
а значит, равносильно неравенству
г * [al I [2сс1 ,	,	[на]
[па] 2з	^+... +-Lj-i.
Следовательно, достаточно • рассмотреть случай 0<х<1. Левая и
правая части неравенства при х£[0; 1) представляют собой неубы¬
вающие кусочно-постоянные функции, которые могут менять свои зна¬
чения только при переходе через точки вида x—p/q, где числа
р, N взаимно простые, т.е. (р, ?)=1, н	1<р<9—	1.
Поэтому достаточно доказать неравенство лишь в точках такого вида
(а также в точке х=0, где оно, разумеется, выполнено). При этом,
если обозначить [k {pjq)\ = ak, q {к (p/q)) = bk, k=\, ...,я, to
0 *S.bh<q, kp = akq+bk,
а неравенство, которое требуется доказать, имеет вид
168

Заметим, что числа 6Х, Ьд-± отличны от нуля и попарно раз¬
личны (если b; — bj при * > /, то ip—ЩЦ = ]р—ajq, откуда
(» — 1) Р = (о/—aj) q, 0 < i—j < q,
что невозможно, так как (р, q) = 1). Поэтому
{Ьй b9_i}={l; q—1},
а из теоремы о средних имеем
bi,b*+...+bJLZl
1	2	1	•"	1	q-l.
q— 1
\ f blb* ■' ■ V-»~ J (q- !)!_
У 1-2... («7-1) V (9-1)!	*•
откуда
bi ,	,	b„	^	b,
Таким образом,
_ i?-k„ . b„_np _p ,2p , яр _
on “I	^ Си -j--——— — — “Нп—~T" • • • i —
q	q q q 2q	nq
. °i_La2 i	I	I 1 (b\ .	i	°2	I	I	an	I	q	t
-т+т+---+т+7(,т+---+7г; ^а1+-2+;‘-+тг+“-’
что и требовалось доказать.
8.12.	Заметим, что из условий задачи вытекает равенство с —
= а-\-Ь, так как в противном случае при достаточно больших значе¬
ниях л£ N равенства	*
[<т] + [Ъп] = [СП]
не могут выполняться. Действительно, если с > а+6 и л ^
^1/(с —а—Ь), то
[яс] > пс— 1 fe; па -f-nb & [яа] + [nb],
а если с<а-]-Ь и яЭ*2/(а+Ь—с), то
[лс]<яс<;яа—l-f-nfc— 1 < [na]-\-[nb].
Кроме того, при л=1 получаем [а] + [&] = [с]. Далее, без ограниче¬
ния общности можно считать, что 0<a < 1, 0<6< 1 и c=a+b< 1
(действительно, если обозначить a = [a] + a, fc = [fc]-f-P, с = [с] -}- у,
то для чисел a, Р, у^[0; 1) из равенств
[ал] + [Ьп] = ([а] п [ап]) + ([b] п + [Р«]) =
= ([а] + И)« + [««] + [ Р«] = [с] « + [уп]
вытекает условие [an] -}-[Рл] = [уя]). Предположим, что а ф О, Ь Ф О,
и рассмотрим два случая.
а)	Пусть а, Ь — рациональные числа, т. е. а = к/т, Ь = 1,т, с =
= ф-\.1)/т, где k, I, т£ N и к-\-1 < т. Тогда если п=т— 1, то
[an \ = [k{m~ 1 )/m] = [к —- kjm] = [к —■ и ] = к — 1;
169

аналогично,
[fcn] = l—1 и [cn\ = k-{-l—1,
следовательно, равенство [an]-{-[bn] — [cn] не выполняется при этом
значении я.
б)	Пусть хотя бы одно из чисел а, Ь, скажем число а, является
иррациональным. Выберем число p^N, удовлетворяющее неравенствам
а+рЬ < 1 <а+(р+1) Ь,
и докажем, что для некоторого числа n£ N выполнены оценки a-\-pb<
< {ла}. Действительно, обозначим е= t — (а \-pb) и рассмотрим числа
{а}, {2а}, {За} {<а}, где t > 1/B-J-1. Поскольку все эти числа
принадлежат интервалу (0; 1), то среди них обязательно найдутся по
меньшей мере два числа {га} и {qa} (г < q), отличающиеся друг от
друга менее чем на в (в противном случае наименьшее и наибольшее
из этих чисел различаются не менее чем на е (/—1) > е(1/е) = 1).
Поэтому имеются две возможности: либо {(q—г)а}>1—с, либо
{(^—г) а} < е. В первом случае положим n — q—г и получим a-\-pb —
= 1 — е < {па}. Во втором случае обозначим б={(?—г) а) < е и вы¬
берем число s^N, удовлетворяющее оценкам 6s < l<6(s+l). Тогда
положим n = s(q—г) и получим
{na}~s{(q—r)a} = 6s > 1—е.
Поэтому и во втором случае имеем a-{-pb < {па}. Для найденного
значения п должны выполняться равенства
[яа] + [пЬ] = (пс],
{па} + {nb} = п (a -J- b) — ([па] + [nb]) = {пс}.
Таким образом, имеем оценки
{па} > а,
{яс} = {па} + {пй}3г{яа} > а+р&3га+й = с,
{nfc}={nc}—{па} < 1 — (а+рй) = 1 — (а + (р+1) b—Ь) с
<1 —(1 —6) = 6,
из которых получаем, что n > 1 и
[(я—1)а] = [па], [(п— 1)с] = [яс],
[(п-1) й] = [пй]-1,
а значит, равенство
[(„_ 1) а] + [(я-1) fc] = [(л-1) с]
не выполняется. Итак, доказано, что хотя бы одио из чисел а или b
должно быть равно нулю. Полученное противоречие завершает дока-
эательство утверждения задачи.
170

Г лава 3
ПЛАНИМЕТРИЯ
§ 9. Треугольники
9.1.	Предположим противное, т. е. высота АН, медиана ВМ и
биссектриса CL остроугольного неравностороннего треугольника ABC
(рис. 2), пересекаясь, образуют правильный треугольник. Точки пе¬
ресечения отрезков АН и
ВМ, ВМ и CL, CL и АН
обозначим соответственно Р,
Q, R. Тогда в треугольни¬
ке CRH имеем CHR — 90°,
CRH = 60°,	откуда
/_ RCH = 30°. Далее, в тре¬
угольнике CMQ имеем
£ QCM = ^ RCH = 30°,
£MQC = 60° (равенство
/_BQC = 60° невозможно,
так как иначе ABC >
> £ QBC= 180°— BQC—
— £ QCB = 90°, т. е. тре¬
угольник ABC тупоугольный), откуда ВМ\_АС. Таким образом,
медиана ВМ является одновременно высотой треугольника ABC,
поэтому
ВАС= / ВС А = £ ACL + / BCL = 60°,
т. е. треугольник ABC правильный, что противоречит условию задачи.
9.2.	Без ограничения общности можно считать, что
Если с > Ь, то
Ьп
lim
Г„ = °.
lim ^=0
СП
и при достаточно больших значениях n£N не выполняется неравен¬
ство an-j-bn > с", необходимое для существования треугольника со
сторонами а", Ьп, сп. Следовательно, Ь = с и все треугольники рав¬
нобедренные.
9.3.	Пусть числа т, n£N удовлетворяют условию задачи. Тогда
т = СЕ < ЛС = 21 и из треугольника ADE (рис. 3) имеем 21—т =
= АЕ < AD-\-DE = 2m, т. е.
7 < т. < 21,
Далее, поскольку AD — DE, то для угла а = ^ ВАС находим
cos а = AE/(2-AD) = (21 —т)/2т.
171

Наконец, по теореме косинусов
для треугольника ABC полу¬
чаем
п? = ВС? = ЛВ? + ЛС? —
—2ЛВ-АС •со^а,—
21—т
=33?+212—2-33-21
= 2223 —
2т
27-49-11
т
откуда следует, что число т
является делителем числа
27-49-11. Из двух возможных
значений т= 9 и т= 11 пер¬
вое не подходит (так как гЛ ф 606), а второе дает равенство п2 =
= 900, т. е. п=30. Проверка показывает, что все условия задачи
при найденном значении п выполняются.
9.4.	Пусть a, й, с£ N—-длины сторон треугольника с диаметром
27? = 6,25 описанной окружности, площадью -S и полупериметром
р=(а+й+<7)/2. Так как a, й, c<2R, то
а, й, с€{1; 2; 3; 4; 5; 6}.
Далее, имеем равенства
(айс)? = (4ВД)2 = р (р—а) (р—Ь) (р—с) (4Rf,
откуда получаем
64а?6?с? = 625 (а + й+с) (с + й—а) (а+с—й) (а+й—с).
Следовательно, число 64а? й2с? делится иа 625, а значит, по крайней
мере два из трех чисел а, й, с равны 5. Пусть, например, а = й=5,
тогда
64с? = (10+с)с? (10—с),
т. е. 64=100—с?, откуда с=6. Итак, искомая тройка может состоять
только из чисел 5, 5, 6, которые, как показывает проверка, удовлет¬
воряют условию задачи.
9.5.	Пусть R — радиус окружности, в которую вписаны треуголь¬
ники ABC и DEF. Тогда по теореме синусов имеем
ВС+АС+ АВ рх
sin ^ A+sln ^ fl+sln Z.C =
2R ~~2R’
где р{—периметр треугольника ABC. Аналогично,
sin B+sIn ^ Z)+stn ^ F=p2/(2R),
где р2—периметр треугольника DEF. Поэтому равенства
sin / A-j-sln B-J-sln Z. С=sin / Д-j-sin ^ D-j-sin ^ F
равносильны.
172
P1 — P2

9.6.	Пусть прямая пересекает стороны треугольника ЛВС в точ¬
ках К и М, лежащих для определенности иа сторонах АВ и АС
соответственно (рис. 4). Докажем, что равенство
Sakm	АК + АМ
Sabc	АВ + АС+ВС
имеет место тогда и только тогда, когда прямая КМ проходит через
центр вписанной в треугольник ABC окружности. Утверждение
В
Рис. 4
еадачи является частным случаем этого факта при дополнительном
условии
Sакм — (I/2) Sabc
(ибо последнее условие равносильно равенству £>акм—$квсМ’ а условие
ЛД + ЛМ = (1/2) (ЛВ+ЛС+ВС)
— равенству
АК + АМ+КМ = КВ + МС+ВС + КМ),
Пусть г— радиус окружности, вписанной в треугольник ЛВС. Тогда
2$авс = г (А В + ЛС+ ВС).
С другой стороны, пусть р — радиус окружности с центром на пря¬
мой КМ, касающейся сторон Л К и AM. Тогда
2$Акм = Р (АК + AM).
Следовательно, сформулированное выше равенство равносильно равен¬
ству г = р, которое справедливо тогда и только тогда, когда центры
обеих окружностей совпадают.
9.7.	Пусть отрезки ЛЛ', ВВ', СС' пересекаются в точке О (рис. 5)
и АОВ = ц>. Тогда имеем равенства
2Saor= АО-ВО sin ф,
2SaoB' — АО-В'О sin <р,
2Sboa, = ВО-А'О sin <р,
2Sa-ob< = Л'О-В'О sin ф,
откгла
A"0-B"0 sin ф=у (Л0+2Л'0)(В0+2В'0) sin ф =
= §аов + 2S^oB' + 2 Suva' +	'ОВ<-
173

Аналогично доказываются равенства
5д"0С~ = Sa ос+2 Saoc + 25ссм' + 45д юс,
Sb"OC" = Sboc+2 SboC'+2Sqob• + 4 Sb -ос-.
С"
Таким образом, получаем
■SA»B"C" = Sa«ob"+^ос" + Sb"OC" =
=5двс+2 (SA ол'+5в-ос+5сол'+5/1'ОВ+5воС'-1-5с'Ол)+45л.;в.С' =
= 35хвс+45д-в-С'.
что и требовалось доказать.
9.8. Положим АВ = с, ВС = а, С А = &, тогда
Л0=1(с-6), 1ю=-^(а-с),С0=±(Ь-а)
И
(Ш + ВС2+СА2) —3 (ОЛ2 + ОВ2 + ОС2) =
= аа + 6? + с2—j ((а — *>)* + (& —с)2 + (с — а)2) =
=-^(а2+Ь2+с2+2аЬ+2&е+2ас)=-^-(а + &+с)2=0,
что и требовалось доказать.
9.9. Пусть центр тяжести границы треугольника ABC совпадает
с центром тяжести самого треугольника, т. е. с точкой О пересечения
его медиан. Обозначим через а, Ь, с длины сторон ВС, СА, АВ со¬
ответственно, а через /Ц, В1р Cj —их середины (которые являются
их центрами тяжести). Тогда
а.0А1 + Ь-ОВ1+с-"0Сх = 0.
Поскольку
^C1==i.^C1=l (СЛ_|_СВ)= —g (AB + AC)-^r (BA +ВС) =

мы получаем
(а—с) ОЛ1 + (Ь—с)~OB1=aOAi+bOBi + cOCi = О,
откуда в силу иеколлинеарности векторов О Ах н 06* имеем а=с — Ь,
т. е. треугольник ABC правильный.
А
9.10. Из соотношений (рис. 6)
^ = 1 (^+Н + OD) == 1 ^ ОС+1 ОЛ+1 Об ) ,
(СЛ+СВ) = у (ОЛ+ ОВ—20Q,
АВ = АС, АО^ВС
попучаем
1206- CD = (20?-1- ЗОЛ + 06)-(О Л + OB — 20С) =
= ЗОЛ?+06?—40С? + 40Л •'0В—40С-'0А=.
= ЗЯ? + Я?—46? +40Л-(06 — ОС) = 40Л • СВ = О,
где R = OA = OB — OC—радиус окружности, описанной около тре¬
угольника Л6С, и, значит, ОЕ J_ CD.
9.11. Обозначим СЛ = х, СВ=у, тогда (рис. 7)
~DA = ВЕ — ~АВ ~у—х, СЕ = 2у — х, CD = 2x—y,
а условие CD J_ СЕ равносильно равенству
(2х— у) (2у—х) — 0, или 5(х— >)?=х?+>?.
Последнее условие означает, что стороны ВС = а, АС=Ь, АВ = с
треугольника ABC удовлетворяют равенству 5с? = а?+Й. Такой
175

треугольник существует при тех и только тех значениях а, Ь, при
которых выполнены неравенства треугольника
I a-b\<Y( a2+fc2)/5 < a-\rb,
Т' е'	5	(а—ft)? < а2+6? < 5 (а+Ь)2.
Правое неравенство выполнено при всех а, b > 0, а левое равносильно
С
условию (2а—b) (2ft—а) >0. Таким образом, получаем ответ: 1/2 <
< а/Ь < 2.
9.12.	Выберем угол а, удовлетворяющий условиям 6а < 90° и
tg Q (годится, например, значение tg а = 1/4). Тогда каждое из
чисел
tg2a=-r^-, tg3a =‘82й + 'В“
1 —tg2a ’	1—tg2atga’
0	1—	tg2	a'	2	tg	a
cos 2a=T . . a—, sin 2a—
1+tg2 a’	1	+	tg2a ’
1—tg23a	, „	2	tg	3a
cos 6a =. . , „ , , sin 6a—
1+tg2 3a ’	1+tg2	3a
является рациональным. Поэтому у прямоугольного треуготь-
ника AjBiCi, удовлетворяющего условиям
^Ci=90°, ^ A2 = 6a, A2Bj = 1, A1Ci = cos6a, BxCi = sln6a,
длины всех сторон рациональны, следовательно, он подобен некото¬
рому треугольнику ABC с целочисленными сторонами (например, при
tga=l/4 стороны треугольника ABC могут быть равны АВ=4913,
АС = 495, ВС = 4888). С другой стороны, у прямоугольного тре¬
угольника А2В2С2, удовлетворяющего условиям
^С2 = 90°, ^А2 = 2а, А2В2=1, A2C2 = cos2a, B2C2 = sin2a,
длины всех сторон также рациональны. Поэтому можно построить
с помощью циркуля и линейки угол 2а = (1/3) £_ А1( т. е. разделить
на три равные части угол А треугольника ABC. Поскольку угол,
равный 30°, также можно построить и
176

ю каждый угол треугольника ABC можно разделить на три равные
части с помощью циркуля и линейки. Итак, треугольник ABC удов¬
летворяет требованиям задачи.
9.13.	В треугольнике ABC обозначим
а =£А, P = ZB. Y =ZC, а —ВС, Ь = АС, с=АВ,
R—радиус описанной окружности. Равенство BC — XY выполнено
в том и только в том случае, если BC = YX или BC—XY, что
А
в силу равенств
|ХК± ВС| = |ХВ + ВС + СГ ± ВС| =
с I	Ь , I „I sin у sin Р	,	I
= — „ в*Га—5	±	а	 5*	t-+2(l±l)	slna	,
2 cos Р 2 cos у I I cos P C03 y	I
равносильно условию
о/i I i \ i sin y , Sin p
2(1 ± 1) slna= 5--J	—
'	cos P 1 cos у
(знак «плюс» соответствует случаю, изображенному на рис. 8, а знак
«минус»—случаю, изображенному на рнс. 9), Учитывая, что
sin у | sin Р  sin у cos y+sin р cos Р sin 2y-|-sin 2p
cos (i cos у	cos P cos у	2 cos P cos у
 sin (y+p) cos (у—P) sin a (cos у cos P+sin у sin P)
Cos P cos у	cos	p	cosy
= sln a (1 + tg у tg P),
177

получаем равносильное условие
2(l±l)=l+tgytg Р,
которое выполнено в том и только в том случае, если tgptgY*=3
или tg р tg v =—1- Таким образом, М = {— 1; 3} и утверждение п. а)
доказано, а для доказательства п. б) достаточно заметить, что случай
tgptg-y=—1 реализуется, например, при а = Р=30°, у=120°.
9.14.	Обозначим через В2 и Са основания высот, опущенных на
стороны АС и АВ соответственно (рис. 10). Тогда из соотношений
AABtC оо &АВ2Ви ДАВВ2 оо ДЛССа, ДЛС^б оо АЛСаС1
(каждая из указанных пар прямоугольных треугольников имеет
В
общий острый угол) имеем
ЛВ? = Лба-ЛС=ЛС2.ЛВ=ЛС?,
откуда получаем требуемое равенство ABt — AC
9.15.	Обозначим через Л2, ба, Са основания высот, опущенных
на стороны ВС, СА, АВ соответственно. Тогда справедливы равенства
А0.А20 = В0'В20 = С0.С30
(первое равенство следует из подобия прямоугольных треугольников
АОВг и ВОА2, а второе — из подобия прямоугольных треугольников
С0В2 и В0С2), Далее, поскольку В1С1—средняя линия треуголь¬
ника ABC, то точка Q ее пересечения с высотой ЛЛа делит послед¬
нюю пополам, причем OQ J_ DiD2, и по теореме Пифагора имеем
AD)==AQ?+(/?2-OQ?) = tf2+(AQ.-OQ)HQ+OQ)(t = i, 2),
где R—радиус окружности. Перебор различных случаев расположе¬
ния точки О на прямой ЛЛа показывает, что справедливо равенство
AD\ = R2 ± А0.Л20,
178

причем если точка О лежит внутри треугольника ЛЕС, то в этом
равенстве стоит знак «плюс», а если вне его, то «минус» (например,
А
Рнс. 11
в случае, изображенном на рис. 11, имеем AQ—0Q==^2Q — OQ = AtO,
dQ-)-OQ = АО). Аналогично устанавливаются равенства
В£; = Я? ± B0-B20, CF\=.R2 ±С0-С20,
из которых вытекает доказываемое утверждение.
9.18.	Пусть Е и F—середины отрезков АР и ВР соответственно.
Тогда, так как DE и DF—средние линии треугольника АРВ, то
В
четырехугольник DFPE — параллелограмм, и из прямоугольных тре¬
угольников АРМ и BPL имеем	я
ME = -i- АР = DF, LF=~ BP = DEi
179
1

Далее,
РЕМ = 2 £ ЕАМ = 2 £ FBL=£ PEL, £_ PED=£ PFD.
Таким образом, треугольники DEM и DFL равны по двум сторонам
и углу между ними (равному величине
а= РЕМ + Z. PED= £ PFL+ £ PFD,
если, как изображено иа рис. 12, а < 180°, и равному 360°—а,
если а > 180°; если а= 180°, то сразу имеем
DM — ME-\-DE—DF-\-LF — DL),
откуда вытекает равенство DM = DL.
9.17.	Приведенное в задаче условие выполняется для всея точек,
лежащих иа рысотах правильного треугольника ABC. Например,
В
Рис. 13
если Mi—точка на высоте, выходящей из вершины А (рис. 13), то
I MtAB + £ MtBC+£MiCA= £ МхЛВ + Z МфС + ^ ЛДВЛ =
= ^ МХАВ + £ ABC=90°,
Докажем, что других таких точек нет. Пусть, напротив, условию
задачи удовлетворяет точка М, не лежащая ни на одной из высот
треугольника. Тогда прямая ВМ пересекает высоты, проведенные из
вершин Л и С, в некоторых точках Mi и М2 соответственно. Если
бы для всех трех (непременно различных) точек М, Мг, Ма было
выполнено условие задачи, то имели бы место соотношения
£ МЛМ1= Z. МСМи £ МЛМ„ = £ МСМ2.
Но тогда точка С', симметричная точке С относительно прямой ВМ,
лежала бы как на окружности, описанной около треугольника ЛММ1,
180

г
так и иа окружности, описанной около треугольника АММ2. Поэтому
обе эти окружности, проходя через три различные точки А, М, С'
(С' Ф А, ибо прямая ВМ не перпендикулярна стороне АС), совпа¬
дали бы, что невозможно, так как точки М, Mi, М2 не могут ле¬
жать на одной окружности.
9.18.	Пусть AjCi—биссектриса треугольника АХА2А3 (рис. 14).
Так как образ отрезка А2А3 при преобразовании симметрии относи¬
тельно прямой /4iCi есть отрезок В21ВЯ1, то прямые А2АЯ и В21ВЯ1
пересекаются в точке Сх. По свойству биссектрисы имеем
AiA2   С\А2
А1А3 С1А3 ’
откуда получаем
Bi2Ci  ^12^2 CiA2   А\А2 CjA2 AiA2
В13С1 В13А3—С1А3	А1А3—С1А3	А1А3 '
поскольку B12A2 = AiA2, В13А3 = А1/43. Аналогично устанавливается
равенство
B2iCf А\А2
В31С1 A1A3
Таким образом, треугольники Bl2CiB2i и SisCiAm гомотетичны,
откуда В12В21Ц В13В31. Аналогично доказывается, что В2ЯВ32\\ BiaB3i.
Замечание. Можно доказать, что прямые Bi2B2i, B13B3i,
В23В33 перпендикулярны прямой, проходящей через центры вписан¬
ной и описанной окружностей треугольника А^зАз.
9.19.	Пусть точки A, L, В, М расположены на прямой АВ
в указанном порядке (рис. 15; случай их расположения в порядке
М, A, L, В рассматривается аналогично), тогда
z LCM=y * 180°=90° и Z CLM — 45ч
’ 181

(ибо CL —СМ). Поэтому
2 £ BAC+ £BCA = 2{£ LAC + £ LCA) — 2 ^ CLM = 9 0°
и
^ 6ЛС + ^ 6СЛ = 180°— £ ABC,
откуда
£ BAC= ABC—90°.
Поскольку угол ABC тупой, то диаметр AD описанной около тре¬
угольника ABC окружности лежит вне этого треугольника, а значит,
£DAC = (m°~£ADC)—£ACD = £ ABC—90°= ВАС
(ибо ^ ABC и £ ADC—противоположные углы вписанного четырех¬
угольника ABCD). Поэтому DC = BC и
AR2 = AD2 = AC2. +CD2 = АС2 + ВС2,
что и требовалось доказать.
9.20.	Пусть высота СН треугольника ABC пересекается с пря-
С
182

койВМ в точке Е (рис. 16). Тогда АЕ = BE и
^ £ЛЖ = ^Ш-^ШЙ=30о-10о=20о1
^ ЛСЕ = ( 1/2) ^ ЛСВ = 40°,
^ ЕАС = £ САН—£ ЕЛВ = (90°—40е)— 30° = 20о,
^ ЛМЕ = £ МАВ + £ МВА= 10°+30° = 40°,
а значит, треугольники АМЕ и ЛСЕ равны по общей стороне й двум
углам. Поэтому -
АМ = АС, £АМС=£ ЛС7И = (1/2) (180°— ^ С А М) = 70°,
9.21. Пусть О—точка пере¬
сечения прямых AD и BE
(рис. 17), тогда
^ ЛОВ = 180°—30°—50°=100°,
IBDA = 180°—50°—50°= 80°,
/ СВЕ=50°—30°=20°,
1АЕВ=£ С BE + ^ £Сб=70°,
ICAD — 180°— ^ АСВ —
— £ ABC— £ BAD = 30°.
По теореме синусов имеем
OD sin 20° OB sin 50°
Ш ~~ sin 80° ’ О A ~*sin 30°’
О A	sin 70°
ОЕ sin 30°’
откуда получаем	Рис.	17
OD OD ОВ О A sin 20° sin 50° sin 70°
0Е~~ OB ‘ О А ' ОЕ~ sin 80° sin3 30°	—
4 sin 20° cos 40° cos 20°	2	sin	40°	cos	40°	sin 80°
sin 80°	sln86°	sin 80°
т. e. OD = ОЕ и
£ BED=£ ODE=y (180°— ^EOD)=~ (180°— 100°) = 40°.
9.22. Если точка Ci симметрична точке С относительно прямой АР
(рнс. 18), то С1Р = СР = 2ВР и £CiPB=m°—£APC—£APC1 =
= 180°—60°—60° = 60°. Поэтому ^CiBP — 90° (ибо треугольник CjPB
подобен прямоугольному треугольнику с гипотенузой 2 и катетом 1),
а значит, В А — биссектриса угла CtBP. Таким образом, точка Л,
равноудаленная от прямых СгР, PC, С1В, лежит на биссектрисе
угла PCiD (где точка D лежит на продолжении отрезка ВС1 за точку Cj).
Поэтому	•
Z АСВ = £ ЛС[Р = у (180п— ^ ВСгР) = Y (180°—30°) = 75°.
С
А	В
183

Рис. 18
9.23.	Обозначим а = 20°, Р = 25°,	7= 15° (рис. 19). Тогда
а,р,у<30°, а+Р+у=60°, ^ КАМ = 60°— Z MAC— £ КАВ = а и
аналогично LBM = Р, /_ KCL — 7. Пусть отрезки AM, и CL пересе¬
каются в точке N, прямые BN и АС—в точке Р, а прямые CL и
АВ—в точке Q. Так как АВ — ВС и AN = NC (ибо £NAC =
= NCA = р), то ВР—биссектриса угла ANC, а значит, и угла LNM.
Возьмем точку В', лежащую внутри угла LNМ и вне треугольника
LMN и равноудаленную от трех прямых LN, LM и MN. Эта точка
лежит иа прямой Л'В и биссектрисах внешних углов L и М треуголь-
В
Рис. 19
184
J

ника СЛШ, поэтому
ILB'M= 180°— ^ B’LM—£B'ML =
1Спо	180°—£NLM	180 °—£NML £NLM + /NML
= 180 ^ 2 = 2
W°-£LNM £NAC+£NCA p
Следовательно, B'=B и
£BLM — BLQ— 180°—^ CQB—^ ABL —
= £ABC + £ BCQ — £ ЛВ/. = 60°+а+у—у = 60°+а.
Поскольку
^ BLC= 180°— Z LBC— ZLCB = 180°— (P+a) — (a+y) = 120°—a,
TO
I MLC = </ BLC— BLM = 120°—a—(60° + a) = 60°—2a
(напомним, что a < 30°). Подобным же образом доказывается, что
^ /(LB = 60°—2а.
Итак, имеем
IKLM = £ BLC— £ KLB— £ MLC =
= ( 120° - a) - (60° - 2a) - (60°—2a) = 3a,
т. e.
^ KLM = 3a = 60°.
Аналогично доказываются равенства
^ LKM = 3P = 75° и ^ KML = 3y = 45°.
§ 10. Окружности и круги
10.1. Разобьем все точки окружности на пары диаметрально про¬
тивоположных точек и в каждой паре одну точку (любую) отнесем к
крвому множеству, а другую—
ко второму. Так как гипотенуза
любого вписанного прямоуголь¬
ного треугольника является диа¬
метром окружности, то верши¬
ны острых углов такого тре¬
угольника будут принадлежать
разным множествам.
10.2. Пусть квадрат ABCD
клисан в окружность диаметра
L а точка Р лежит на дуге
■AD (рис. 20). Обозначим а =
= £ АСР. Тогда, если числа
A/^dsina и CP = d cos а	Рис.	20
185

являются рациональными, то число
BP = d sin ^ PDB = d sin (Z AD В + £ ADP) =
= d sin (45°-f-a) —d (sin a + cos oc) (|^2/2) = (|A2 /2) (AP-\-CP)
иррационально.
10.3.	Рассмотрим равные окружности с центрами 0г и 02, вписан¬
ные в треугольники АСгМ и АВгМ соответственно. Пусть они ка-
В
Рис. 21
саются отрезка AM в точках Ki и К2 (рис. 21). Тогда прямоуголь¬
ные треугольники AOiKi и А02К2 раЬны, поскольку
0iKi = 02K. и £0tAKi = \ £CiAM=*^ £BiAM= £OtAK*
Поэтому Ki — Ki и прямоугольные треугольники ОлК\М и 02КгМ
также равны (по двум катетам), откуда
£01MKi=£OiMK2 и
^ СгМА = £ BiMA.
V2
Следовательно,	имеем	Z ACtC =
= Z ABiB (из треугольников ACtM
и ABiM, имеющих по два соответст¬
венно равных	угла),	Z АВВ{ =
г= £ ACCi (из треугольников ABBi
и ACCi) и Z ABC — Z АСВ. Аналогич¬
но доказывается равенство Z ^СВ =
= ^ ВАС.
10.4.	Пусть, вопреки утвержде¬
нию задачи, ни одна из точек Оь ...
• -■» 0„ расположенных в порядке об¬
хода вокруг центра О данного круга по
часовой стрелке (рис. 22), ие совпадает
с точкой О. Так как сумма углов
£Охоог, zо2оо3, ..., zovoo,
186

равна 360°, то хотя бы одни из них меньше 60°. Пусть, например,
l_ 0fiO2 < 60°, а угол 00]02—больший из двух оставшихся углов
треугольника 00j02 (если 04002 = 0, то сразу 0t02 < 1). Тогда
/_ 00|02 > 60° > ^ 0i002, откуда 0iO2 < 020< 1, что противоречит
условию задачи.
10.5. Пусть, вопреки утверждению задачи, существует точка О,
принадлежащая всем шести кругам. Обозначим через (Д, 02, 03, 04,
0Ъ, 0в центры этих кругов в порядке обхода вокруг точки О по
часовой стрелке (см. рис. 22; согласно условию точка О ие может
Сыть центром ни одного из кругов). Так как сумма углов ^ 0j002,
(_ 02003 OgOOx равна 360°, то хотя бы один из них не пре¬
восходит 60°. Пусть, например, £_ 0j002<: 60°. а угол 00t02 —
больший из двух оставшихся углов треугольника 00102 (если
£01002 = 0, то сразу 020 ^ О20{). Тогда £ 00х02^ 60'Si £ 01002,
откуда 020	020ь Поэтому круг с центром 02, содержащий точку О,
содержит и центр 04 другого круга, что противоречит условию за¬
дачи.
10.6. Допустим, что множество кругов конечно. Тогда круг
с центром О и наименьшим радиусом г касается шести кругов с цент¬
рами Оь ..., Ов (расположенными в порядке обхода вокруг точки О
по часовой стрелке; см. рис. 22) и радиусами п, • ••, г,, соответственно.
В треугольнике 0г002 сторона 0jO2 = t\ -|- г2 наибольшая, откуда
£0i002~s:60°. Аналогично получаем, что 02003^60°,..., О,.00^
5>60 . Но сумма перечисленных шести углов равна 360°, поэтому
каждый из них равен 60° и каждый из остальных углов треуголь¬
ников 0j002, 02003	 01.001	(не превосходящий 60°) также
равен 60°, т. е. все эти треугольники равносторонние, откуда г —
= п =	Поскольку круг с центром Oj, например, также имеет
наименьший радиус, то к нему применимы те же рассуждения, в силу
которых он касается некоторого круга того же радиуса с центром
0- А О, лежащим иа прямой 0О1ш Аналогично, последний круг также
кусается некоторого круга того же радиуса с центром Ов Ф Оь лежа¬
щим на той же прямой, и т. д. Таким образом, множество кругов
бесконечно, а утверждение задачи верно.
10.7. Пусть дан треугольник ABC. Построим подобный ему тре¬
угольник А'В'С', для которого существуют указанные в задаче
т.ружности (тогда существование соответствующих окружностей для
исходного треугольника ABC также будет доказано). Для этого про¬
ведем 3 окружности с центрами соответственно в точках А, В, С
и радиусом, равным радиусу описанной около треугольника ABC
окружности. Тогда эти окружности имеют единственную общую точку
(I авноудаленную от вершин А, В, С). Три общие касательные к па¬
рам проведенных окружностей образуют искомый треугольник А'В'С,
подобный Tpeyi ельнику ЛВС (ибо A'B'jAB, В’С' || ВС, А'С' Ц АС;
см. рис. 23).
187

в
/
с'
Рис. 23
10.8. Рассмотрим гомотетию с центром Р, при которой окруж¬
ность, содержащая точки б и С, переходит в другую окружность.
При этой гомотетии точки б и С переходят в некоторые точки В’
и С', лежащие иа прямых ВР и СР соответственно, а прямая ВС —
в параллельную ей прямую б'С*. Следовательно, дуги В’А и С1 А
равны, а значит, вписанные углы В’РА и С'РА либо равны (в слу¬
чае внутреннего касания, изображенного на рис. 24), либо состав- I
ляют в сумме 180° (в случае внешнего касания, изображенного на I
рис. 25), т. е. равными являются углы ВРА и С'РА. В обоих слу¬
чаях прямая РА является биссектрисой одного из углов В PC или ВРС'.
10.9. Пусть отрезок PQ касается указанной в задаче окружности
с центром О (совпадающим с серединой основания ВС равнобедрен¬
ного треугольника ABC). Обозначим
£PBO=£QCO = a, £BPO=£QPO = р, ^CQO=^PQO=y
(рис. 26), тогда, рассматривая четырехугольник CBPQ, имеем
следовательно, треугольники ВРО и COQ подобны (по трем углам).
Поэтому получаем
BP-CQ =ВО-ОС = бС?/4,
Допустим теперь, что отрезок P'Q’ не касается указанной окруж¬
ности. Построим отрезок с концами Р и Q на сторонах АВ и АС
соответственно, параллельный отрезку P'Q' и касающийся окруж-
2а+2Р+2у=360°, т. е. а + Р+у=180°,
188

с
А
Рис. 26
189

иости. Тогда, согласно доказанному выше, имеем
ВС*/4 = BP-CQ ф BP’-CQ’.
Утверждение полностью доказано.
10.10.	Пусть а—сторона квадрата, R — радиус полуокружности
с центром О, г—радиус вписанной в треугольник ABC окружности,
а= ^ AON < 90° и ^ СОВ < 90°
(рис. 27). Тогда
а2 = NK* = ОЛ'2—КО2 = Д2— (а/2)2,
откуда a = 2R/\r5, Из равенства площадей квадрата и треуголь¬
ника ABC получаем, что высота СН последнего равна 4R/5. Дока-
Рис. 27
жем, что ON—биссектриса угла АОС. Действительно, так как
sin а = 2/1/"5 (откуда а> 45°), то имеем
2	1	4
sin 2а=2 sin а cos а =2 • —r?=-. ——^=—=sin / СОВ — sin / АОС,
]А5	]А5	5	с-
где 2а > 90°, АОС > 90°, Следовательно, ^ АОС = 2а и ^ AON =
= ^ CON. Поскольку вписанные углы ABN и CBN опираются на
равные дуги, то BN—биссектриса угла ABC (равного а) и иа ней
лежит центр вписанной в прямоугольный треугольник ABC окруж¬
ности, радиус которой равен
г=(1/2)(ЛС+ЙС— Дб) = (1/2).2/? (slna+cosa—1) = Д(3/уг5-|).
Но тогда точка Р пересечения прямых BN ■ и LM является центром
этой окружности, так как из подобных треугольников N КВ и PLB
имеем
NK-LB п (2/^5)(1-1/^5)
КВ К 1 + 1/^5
10.11.	Без ограничения общности можно считать, что точка М
лежит на дуге АВ (рис. 28) описанной окружности с центром 0 и
190

в
Рис. 28
радиусом R. Обозначим АОМ = а, тогда
MA = 2R sin (а/2),
MB =2tf-sin-i(Z АОВ— £ АОМ) = 2R sin (60°—а/2),
MC = 2R sin-i(</ ЛОС + / ЛОМ) = 2Р sin (60°+а/2).
Поэтому величина
AM +МЙ +/ИС = 1б ^sin4 (а/2)-f-sin4 (60°—а/2) + sin4 (60°+а/2))=
= 4 ((1 — cos а)2 + (1 — cos (120°—а))2 + (I — cos (120°+а))2) =
= 12 — 8 (cos а +(cos (120°—а) +cos (I20°-j-a)))-j-
+ 4 (cos2 a+cos2 (120°—a) + cos2 (I20°+a)) = 12—8 cos a—
-8-2 cos a cos 120°+2 ((1 —cos 2a) + (I — cos (240°—2a)) +
+(1 — cos (240°+2a))) = 12—8 cos a+8 cos a + 6 —2 cos 2a—
-2-2 cos 2a cos240°= 18—2 cos2a+2 cos2a= 18
не зависит от выбора точки М.
10.12.	а) По условию задачи
AB+CD = AD + BC,
поэтому в четырехугольник ABCD можно вписать окружность.
б) Из равенства треугольникоз ABC и ADC следует, что
LB= L П- Поэтому около четырехугольника ABCD можно описать
окружность тогда и только тогда, когда
В —(1/2) (^ б + / П)= 18072 = 90°,
т. е. когда В = 90° и АВ _[_ ВС.
в) Пусть вписанная окружность с центром N касается сторон
АВ и ВС в точках Л\ и Д'2 соответственно, а проекциями центра М
т

описанной окружности на стороны АВ и ВС являются их середины
Рис. 29
, т. е. ху = г(х+у).
у ВС
Далее, учитывая равенства лг?-[— t/? — AB'i-\- ВС'- = ACi = (2Д)?, по¬
лучаем
(x+y)? = x*+2xy+y*=4R* + 2r (х+у),
откуда
х+у — r+У Д- + 4Д?.
Наконец, из свойств проекций имеем
NM2 = NtMl+N2Ml = (ВЛ/j —ИВ/2)? + (B/V2 — ВС/2)? =
Mi и М2 (рис, 29; заметим, что точки N и М лежат на оси симмет- I
В	I
рии АС четырехугольника ABCD). Обозначим АВ=х, ВС = у, тогда
из подобия треугольников ANiN и ABC имеем
х АВ ANi х—г
= (г—х/2)? + (г—р/2)? = (** +у?)/4 — г (х+у) + 2г% =
= /?? — /• (r+jAr?+4B?)+2r? = /?? + /•? — г Vг? + 4Я2,
что и требовалось доказать.
Замечание. Равенство п. в) справедливо для любого четы¬
рехугольника, являющегося одновременно вписанным и описанным,
10.13.	Если бы вершины квадрата располагались на концентри¬
ческих окружностях радиусов a, a+d, a+2d, a+3d соответствен ни,
то в силу теоремы 79 выполнялось бы одно из равенств
а? + (а+d)? = (а+2d)? + (а+3d)?,
а? + (a+2d)? = (а+d)? + (а+3d)?,
(a+d)* + (a+2d)* = a?- + (a+3d)*,
у которых левые части меньше правых при любых значениях a, d > О,
(92

10.14.	Обозначим через L отличную от М точку пересечения
окружности с прямой QS (рис. 30). Тогда
'RS==MS — MR = QL—QBi PQ=?AQ+M<$,
откуда, используя теорему 71, получаем
PQ • RS=~AQ - QL—MQ • QB + MQ - QL-AQ - QB = а■ Ь—с■ d = 0,
где обозначено MQ=a, QL=b, AQ=c, QB = d. Итак, доказано,
что PQ JL RS. Пусть прямая RS пересекает прямые PQ и BD в точ¬
ках Т и Е соответственно, a F—’Точка пересечения прямых BD и QS.
Тогда из подобия различных
треугольников имеем
QF-
BQ-AD d (b—а)
BA c+d *
FS = QS-QF = (b-a) —
d(b—а) с (b—а)
с-| d c+d '
RE^RB^ a (c+d)
ES FS c(b—a)
С другой стороны, получаем
RT-RS — RM-RP,
TS-RS^QS-MS,
Рис. 30
откуда
RT RM-RP
TS MS-QS
d(c+d)	a (c+d) RE f	d_^ a_\
b(b—a)	c(b—a) ES \	b с )'
Таким образом, точки Т и Е делят отрезок RS в равных отношениях,
а значит, совпадают. А это означает, что прямые PQ, RS, BD пере¬
секаются в одной точке.
10.15.	Пусть вписанная окружность касается сторон АВ и АС
в точках Е и F соответственно, а вневписанная окружность касается
стороны СВ в точке L и продолжений сторон АВ и АС в точках
/Ии N соответственно (рис. 31). Тогда имеем
2DB—DB + BE = CB—CD + AB — АЕ — СВ + АВ — CF — AF^=
= СВ + АВ — АС,
2CL=CL+CN = CB—LB+AN—AC = CB — BM+AM — AC =
= СВ + АВ — АС,
откуда
DB = (CB+AB — АС)!2 = CL,
7 Под ред. И. Н. Сергеева

А а значит, середина отрезка ВС совпадает
’ с серединой отрезка LD. Пусть точка D'
диаметрально противоположна точке D на
вписанной окружности, а прямая С'В' ка-
В сается этой окружности в точке D'. Рас¬
смотрим гомотетию с центром А, переводя-
£ щую вневписаиную окружность во вписанную.
При этой гомотетии точка L переходит в точ-
® ку D'. Следовательно, точки L, D' и А ле¬
жат на одной прямой, поэтому середины
отрезков LD, D'D и AD также лежат на
А одной прямой — средней линии треуголь¬
ника ADL (параллельной стороне AL), что и
требовалось доказать.
10.16.	Пусть D — точка касания окруж¬
ностей, a ABC—правильный треугольник,
вписанный	в большую	из них. Без ограни¬
чения общности	можно	считать, что точка
D лежит на дуге АВ (рис. 32). Докажем, что DC = DA -\-DB. Для
этого на отрезке DC возьмем точку М, для которой AD = DM
(заметим, что DC 5: BC=AB^AD). Тогда треугольник ADM пра¬
вильный,	ибо	он	равнобедренный	и	ADM= £ ABC —■ 60°. Сле¬
довательно,	при	повороте на угол	60°	вокруг	точки А точка D
переходит в точку М, а точка В—в точку С, поэтому BD = MC к
DC — DM-\-MC = AD-\-DB. Пусть R и г—радиусы большей и
меньшей окружностей соответственно, 1д, Ig, 1С — длины касатель¬
ных к меньшей окружности, проведенных из точек А, В, С соот¬
ветственно, а А' — отличная от D (если А Ф D; в противном слу¬
чае A' = D) точка пересечения прямой AD с меньшей окружно-
А
194

сгью. Точка А' получается из точки А в результате гомотетии с
центром D и коэффициентом ± r/R (если окружности касаются
внешним образом, то берется знак «минус», а если внутренним—то
«плюс»). Поэтому
АА’ = AD ± DA' = AD (1 ± r/R)
и по теореме о касательной и секущей имеем
1А = УAD-AA' = AD У1 ± r/R.
Аналогично доказываются равенства
lB = BD У1 ± r/R, lc = CD У1 ± r/R.
Отсюда вытекает требуемое равенство !<; —
10.17.	На отрезке ВС существует точка N, для которой РЫВ=
«= £ PC А (ибо PC В < Z РСА = 180°—^ РВА < 180°—/ РВС,
см. рис. 33). Тогда имеем
&BPNco/\APC и	р
Д СРА/оо Д АРВ,
так как
Z РВС=£ РАС
и
1РСВ = £РАВ, £РЫС =
= 180°— / РЫВ = ^ РВА.
О
Учитывая, что РК—высота
треугольников BPN и С'РА',
а РА и РМ — высоты подоб¬
ных им треугольников АРС
и АРВ, получаем
АС	ВЫ	АВ _СЫ
PL	РК ' РМ~РК'
откуда
АС , АВ
_ВЫ+СЫ ВС
PL РМ
РК
РК
что и требовалось доказать.
10.18.	а) В условиях задачи обозначим ^ ВАС —а, ABC = f>,
£ ВС А—у (рис. 34) тогда имеем ,/ DAB—£ DAC = а/2, откуда
BD = DC. Поскольку
ODC = £ ЛВС = Р,
Z = / OCB + £BCD = -j I ACB + £BAD = (a+y)/2,
то
COD=180°—P —(a+Y)/2 = ct+Y—(а+у)/2 = (аф-у)/2=^ OCD,
так что DO = DC, Равенства доказаны,
7*	195

в
б) В условиях задачи обозначим ,40 = 2а, АВ — 2р, ВС=2у,
CD = 26, а через М и N обозначим середины дуг ВС и CD соответ¬
ственно. Тогда точки Df и В* лежат на отрезках AM и И/V соответ¬
ственно, a есть точка пересечения отрезков BN и DM (рис. 35).
Согласно п. а) имеем
MDi = МВ = МС = MAt,
поэтому треугольник DxMAi равнобедренный и
I D1A1M = ( 1/2) (180°—/ AMD) = 90°—а/2.
196
I
	J

Аналогично получаем
Так как
. £ BXAXN = 90°— р/2.
£ DAXN = £ ВАхМ = (у+6)/2,
L DXAXBX = 180°— / DxAxM — ({_ BXAXN — £ DAXN) —
= 180° — (90°—a /2) — (90° — Р/ 2) + (у+б) /2 = (сг + p + у + 6) /2 90°,
Аналогично доказывается, что и остальные 3 угла четырехугольника
AXBXCXDX прямые.
10.19. Докажем сначала, что середины отрезков АХНХ и А2Н2
совпадают. Для этого через точку Ая проведем прямую, перпендику¬
лярную стороне А3А1г и обозначим через К отличную от А3 точку
пересечения этой прямой с
окружностью, описанной око¬
ло	четырехугольника
AxA2A3At (рис. 36). Тогда
А,НХ1КА3 (ибо А2НЛ | /4g/44)
кА3НхЩА2 (ибо А3НХ}_
1ЛА, и / АЛ2А4 = 90°,
так как КAt~ диаметр),
поэтому КА2НХА3— парал¬
лелограмм, откуда А2Нх —
= КА3. Аналогично доказы¬
вается, что АхН2А3К—па¬
раллелограмм,	откуда
А\Н2=КА3. Итак, А2Нх =
=АхН2 и отрезки АХНХ, А2Н2
являются диагоналями парал¬
лелограмма АХН2НХА2, т. е.
делятся в точке их пересечения пополам. Подобным же образом до¬
казывается, что середина отрезка А2Н2 совпадает с серединой отрезка
А3Нз, которая в свою очередь совпадает с серединой отрезка АХН
Следовательно, при центральной симметрии относительно этой общей
для всех 4 отрезков середины четырехугольник AxA2A3At переходит
в четырехугольник НХН2Н3Н& из чего вытекает утверждение задачи.
10.20. а) Пусть четырехугольник АХА2А3А4 вписан в окружность
с центром О и радиусом R, а проекциями точки О на хорды АХА3,
АхА2, А2А3, A3Ait AtAx являются нх середины Н0, Нх, Н2, Н3, Н1
соответственно. Обозначим
hi=OH{ (« = 0.	4),
пусть Sx, S2 и pj, р2 — площади и полу периметры треугольников
АхА2Аз, А3АХАХ, а гх, г2 — радиусы вписанных в них окружностей.
Рассмотрим треугольник, содержащий точку О (если такой сущест¬
197

вует, т. е. если О лежит в исходном четырехугольнике). Предполо¬
жим для определенности, что точка О лежит в треугольнике АгА2А3
(рис. 37). Используя теорему Птолемея (теорема 69) для вписанных
четырехугольников A3HBOH2, AiHtOH„, A2H2OHi и тот факт, что
НВН2, Н0Н1, НгН2—средние линии треугольника АгА2А3, получаем
(R-]-r{) pi = R• Н0Н%-\-R'Htfix~\'R,Hiflа+=
= Ф0' H2As +Л2-H0A3) + (h0 • НхА i+hi • HBA{)-\-(h2 • H\A2-f-hi ■ //2j42) +
—f-(I/2) (hi‘AiA2-)-h2‘A2As-\-Iib-AsAj) = (hi-\-h2-j-hB)plt
Теперь рассмотрим случай, когда центр О описанной окружности
лежит вне треугольника. В этом случае ровно одна из его вершин
лежит с точкой О в разных полуплоскостях относительно противоле¬
жащей стороны. Пусть для определенности такой вершиной является
вершина Л4 треугольника A3AtAi (см. рис. 37). Тогда четырехуголь¬
ники /4i#4//0O, А3Н3НвО, А3Н1ОН3 являются вписанными, поэтому
получаем
(/?-]-г2) р3 = R-HBHi-\-R-H0H3-\-R-H3Ht-\-S2 =
={hi'HBAi—7i0-Н tA{)(h3-Н ВА3—hB - H 3A3) -\- (hf H 3At-\-h3 - H ^Aq)
+ (1/2) (h3- AsA^-j-hi-AtAi—hB-AiA3) = (/i2-f-ft4—ft0) p2,
Рис. 37
откуда
R + rj — h±+ft2 +Л0.

а в общем случае искомая сумма радиусов вписанных окружностей
равна сумме величии hi, h2, ha, /i4, 2R, взятых с определенными зна¬
ками, зависящими лишь от расположения точки О относительно че¬
тырехугольника AiA2A3At. Следовательно, эта сумма не зависит от
того, какая диагональ проведена.
б) Пусть AiA2As—данный нетупоугольный треугольник, a klt k2,
Аз—длины высот, опущенных из вершин А1ш А2, А3 соответственно.
Все обозначения для остальных элементов и параметров треугольника
AiA2A3 сохраним такими же, как и в решении п. а). Без ограниче¬
ния общности считаем, что ^a k3, а так как
ki • А2А3 = k2- А±А3 = k3' Ai А 2 = 2S1(
то A2A3^s AiA3~ss AiA2. Итак, имеем
2Sj Н2'А2А3-\-к3' AiA3-\-hi' AiA2
кз AiA2~
AiA
1^2
^ h2-AtA^+hp^iAf + b- Ai_Az==h. + h2+ho = R+ri
AiA2
(последнее равенство установлено в п. а)). Требуемое неравенство,
таким образом, доказано. При этом, если треугольник АгА2А3 остро¬
угольный, то точка О лежит внутри него, откуда Л2 > 0, а равен¬
ство достигается прн kl — k3, т. е. для равностороннего треугольника.
Если же треугольник AiA2A2 прямоугольный, то ^ Лх = 90°, h2=0,
hi > 0, а равенство достигается при k2 = k3, т. е. для равнобед¬
ренного прямоугольного треугольника.
10.21.	Рассмотрим следующую процедуру, заключающуюся в вы¬
полнении некоторого числа шагов. На первом шаге покроем каждую
из данных точек кругом диамет¬
ра 1/200. Пусть после k-то шага
N) существуют два круга,
удаленные друг от друга не бо¬
лее, чем иа I. Через Ot и 02
обозначим центры этих кругов,
а через Af, А2, Аа, At—точки
пересечения прямой Ог02 с ок¬
ружностями, ограничивающими
эти круги (точки А2 и А3
лежат между точками Af и Ait
причем А2А3а£^ 1; рис. 38). Тогда
(Л-|-1)-й шаг заключается в том,
что указанные два круга заменя¬
ются кругом, построенным иа от¬
резке AiA4, как иа диаметре. Описанная процедура продолжается до тех
пор, пока это возможно, т. е. пока не будет выполнено условие 2).
Так как после первого шага число кругов было равно 100, а на
каждом последующем шаге их число уменьшается на 1, то общее
199
Рис. 38

. число шагов ие превосходит 100. Поэтому процедура обязательно закон¬
чится, а условие 1), выполненное на каждом шаге, будет выполнен!< и по
окончании процедуры. Поскольку после первого шага сумма диамет¬
ров равнялась 100/200 = 0,5, а иа каждом последующем шаге она
может увеличиваться не более чем на 1, то итоговая сумма диамет¬
ров не будет превосходить числа 0,5+99 < 100, т. е. условие 3)
также будет выполнено.
10.22. Возьмем прямую, относительно которой все точки лежат в
одной полуплоскости, и будем ее параллельно передвигать до тех
пор, пока она не пройдет через первую точку Аг. Затем будем пово¬
рачивать полученную прямую вокруг точки Аг до тех пор, пока она
не пройдет впервые через другую точку А2. Тогда все остальные
точки лежат в одной полуплоскости относительно прямой АгА2. Зану¬
меруем эти точки Аа А2п+з так, чтобы выполнялись неравен¬
ства Z AiAlA2^ AtAl+1A2 при i=3,	2л + 2. При этом равен¬
ство	A1A/A2 = A±Ai+iA2 невозможно ни при каком значении!
(ибо точки Ай А[, A/+f, А2 не лежат на одной окружности). Поэтому
неравенство ^ AiA„+3A2 < ^ A1AiA2 выполнено ровно для п точек
А[ = A,l+i /2,г+3, которые (и только они) лежат внутри круга,
ограниченного	окружностью,	проходящей через точки А1ш Ап+3, А2.
10.23.	Среди	всех	окружностей,	проходящих через какие-либо три
вершины данного многоугольника, две из которых являются сосед¬
ними, а соединяющая их сторона видна из третьей вершины под
углом, не превосходящим 90°
(множество таких троек вершин
не пусто, ибо оно содержит лю¬
бую тройку соседних вершин),
выберем окружность Г наиболь¬
шего радиуса R. Пусть для оп¬
ределенности она проходит че¬
рез соседние вершины Ait А2
В и некоторую вершину А много¬
угольника, причем
<90° (рнс. 39). Пусть какая-
либо вершина В данного много¬
угольника лежит вне круга,
ограниченного выбранной ок¬
ружностью Г. Поскольку точка
В лежит в той же полуплоско¬
сти относительно прямой AiA2,
что и точка А, то
Рис. 39
^ А\ВА2 < ^ i41i4i42<90°
и (по теореме синусов) радиус описанной около треугольника А^Аф
окружности больше R, что противоречит выбору исходной окруж¬
200

ности. Итак, выбранная окружность ограничивает круг, покрывающий
весь многоугольник. Докажем, что вершина А3, соседняя с верши¬
ной А2 и отличная от А^, также лежит на выбранной окружности.
Допустим, что это не так, т. е. точка А3 Ф А лежит внутри сегмента
круга, соответствующего хорде А2А (рис. 39). Тогда А2А3А >
> 180°—A2AiA ^ 90° и (по теореме синусов) снова радиус описан¬
ной около треугольника А2А3А окружности больше R, что противо¬
речит выбору исходной окружности. Таким образом, тройка вершин
Af, А2, А3 удовлетворяет условию задачи.
10.24.	Докажем, что искомые значения п—это все нечетные чис¬
ла п > 1. Пусть п нечетно и в 2п-угольнике Ai...A2n все пары про¬
тивоположных сторон, кроме, быть может, пары АхА2п, А„Ап+1,
откуда AnAn+i\\AiA2n. Теперь докажем, что при том же (нечетном)
значении п существует 2 (п—1)-угольник, для которого требуемое в
задаче условие не выполнено. Возьмем какой-либо 2п-угольник
А\...А2п, для которого противоположные стороны параллельны, но
AiA2An+i Ф 180°. Для этого достаточно дугу AlA,1+i < 180° разбить
на п равных дуг точками А2 Ап и провести последовательно
хорды
после чего, согласно доказанному выше, будет выполнено условие
А3пАЛАпАп+1, причем
АзА„+2Ап+3—180°-)-се,
Поэтому
„ИЯ+1Л2П= 180°+(-l)"+ice = 180°+а.
^П + 1^П + 2 ]| ^1^2» ■ *	^2n~	1^2n	II	^П	—	Х^Пу

Поэтому
А2А2Ап ^2n^2n—iAn+2~A2An+iAn+2 A2nAn+iAn===A2An+iAn^.2
- (360°-Л^4ТЛО Ф 0.
т. е. отрезки А2А2п и АпАп+2 не параллельны и 2 (п—1)-угольннк
Аа.. .А„Ап+4.. .А2п имеет ровно п—2 пары противоположных па¬
раллельных сторон.
10.25.	При п— 1 полная дуга единственной окружности имеет
длину 2л Js 2л/п, т. е. утверждение задачи верно. Пусть п ^2. Пред¬
положим сначала, что центры всех п окружностей лежат на одной
прямой. Выберем тот из центров, относительно которого все ocfaflb-
ные центры лежат на одной полупрямой. Тогда перпендикуляр к этой
прямой, проходящий через выбранный центр, отсекает от соответст¬
вующей окружности дугу длины я^2л/п, которая не пересекается
ни с одной из остальных окружностей. Рассмотрим теперь случай,
когда центры окружностей не лежат на одной прямой. Из всех вы¬
пуклых многоугольников с вершинами в центрах (множество таких
многоугольников не пусто, ибо оно содержит хотя бы один треуголь¬
ник) выберем тот, вне которого лежит наименьшее число этих точек.
Докажем, что вне выбранного многоугольника нет ни одной из точек.
Действительно, если некоторая точка О лежит вне выбранного мно¬
гоугольника, то проведем через нее прямую, не пересекающую его, и
будем поворачивать ее вокруг точки О до тех пор, пока она не прой¬
дет сначала через первую вершину А, а затем через последнюю вер¬
шину В многоугольника (если их оказалось несколько, то выберем
наиболее удаленную от точки О; рис. 41). Наконец, все вершины
многоугольника, лежащие в треугольнике АОВ, заменим лишь тремя
вершинами А, О, В, тогда вне полученного многоугольника будет
содержаться меньше точек, чем вне выбранного. Полученное проти¬
202
/

воречие означает, что существует выпуклый А-уголышк (k^n) с
вершинами в центрах, в котором содержатся все центры. Так как
сумма внешних углов А-угольника равна 360°, то найдется внешний
угол, не меньший 360°/А Зг 360°/п. Пусть им оказался внешний угол
BfiA угла О А-угольника (см. рис. 41). Тогда перпендикуляры OL и
ОМ к сторонам ОВ и О А соответственно отсекают на внешней дуге
окружности с центром О дугу LM длины не меньше 2л/п, так как
£L0M= B-fiA. Докажем, что эта дуга не пересекается с другими
окружностями. В самом деле, пусть N — произвольная точка дуги LM.
Поскольку
NOA > 90° и Z NOB > 90°,
то окружность с центром N и радиусом 1 имеет с А-угольником
единственную общую точку О. Это значит, что центр любой из дан¬
ных окружностей, проходящих через точку N, должен совпадать с
точкой О. Утверждение доказано.
§ 11. Многоугольники
11.1.	Пусть диагональ АС пересекает прямые ОВ и OD в точ¬
ках Р и Q соответственно (рис. 42). Так как площади треугольников
АОВ и СОВ равны, то равны и их высоты к общей стороне ОВ, а
Рис. 42
значит, АР —PC. Аналогично, имеем AQ = QC, откуда P=Q. По¬
этому, если О ф Р, то точки В, Р, О, D лежат на одной прямой,
т. е. точка О лежит на диагонали BD; если же 0 = Р, то точка О
лежит на диагонали АС.
11.2.	Параллелограммы ОАМВ и A'B'C'N, построенные на век¬
торах ОА, ОВ и А'В', В'С' (рис. 43), равны, поэтому имеем
SaOB~(1№)SoAMB=(M2) Sa.B'C'N — SА'В'С’.
Аналогично получаем
SbOC = SB'C'D’, Scod = SC'D'A’< ^DOA — ^D'А'В',
203

откуда
S=Si40B+Saoc+ScOD + SD0A = ($A 'B'G'-\-Sa'D 'C')+(Sb 'C'D '+
—IS'.
что и требовалось доказать.
11.3.	Обозначим через At, Bi, Ct, Dj середины сторон АВ, ВС,
CD, DA параллелограмма ABCD площади S, через Л, Ль Ла—точки
пересечения прямой АС\ с прямыми BDt, AtD, CD± соответственно.
Аналогично получим точки L,Li,L2,M, Mi, М2, N, Ni, N2 (рис. 44).
Так как параллелограмм AAfCCi (АЛ1ЦСС1, AAi = CCt) имеет ту же
Рис. 44
высоту, что и параллелограмм ABCD и вдвое меньшее основание
ААх — АВ12, то его площадь равна S/2. Далее, параллелограмм KLMN
(LMIKN, KL || MN) имеет ту же высоту, что и параллелограмм AAtCCi
и основание ЛЛ'= (2/5) АСг (ибо ЛЛ = ЛЛ' из подобия треугольников
204

AKDi, AND и KN — LM = MC = 2NCi), поэтому
Sklmn — (2/5) Saa,cc, = (2/5). (S/2) = S/5.
Точка Ki является точкой пересечения диагоналей ACi и DAi парал¬
лелограмма AAiCtD, поэтому АК^ = К^С^. Точка К2 является точкой
пересечения медиан CDj и АС\ треугольника ACD, поэтому АК.2=2К2Сх.
Таким образом, имеем
KKi=AKi-AK=(i/2) ACt-(2/5) ЛС* = (1/10) ACt = (1/4) KN,
NК2 = Cl/Си — C\N = (1/3) ACi — (1/5) ACi = (2/15) ACi = KN/3.
Аналогично получаем
KL2 = KL/3,
откуда
Z K\KL2 —
=0/2)-(l/4)A:/V.(l/3)/(L.slnZ/V/(L=(l/12)S^i=(l/24)S^7V=S/l20.
Подобным же способом доказывается, что
SLLiM, = S«AliAr» = SNN,K, = S/120,
следовательно,
SK,L>L,MiM,WiN,K, = S/5 — 4 - (S/120) -= S/6,
что и требовалось доказать.
11.4.	а) Сумма внутренних углов пятиугольника	и
десятиугольника AAiBBiCCiDD1EE1 равны соответственно 3.180° и
8-180°. Кроме того, каждый из углов этого пятиугольника в сумме
с углом десятиугольника при той же вершине составляет 360°
(рис. 45). Поэтому имеем
Z AiBBi + Z BiCCi -f- Z C^DDi -f-
+Z DiEEi -f- Z EiAAi =
x=8.180° + 3-180°—5-360°== 180°.
б)	Если ABCDE—правильный
пятиугольник, то из соображений
симметрии (относительно биссектри¬
сы любого из его углов) имеем
AA1 = AEi = EE1, AC\\ED,
откуда
z ЛЛХ£= Z AiED = Z СЕЛ =
== £ЕААи	Рис.	45
т. e. треугольник Л£ЛХ равнобедренный. Обозначим а = АЕ, х=Лх£х,
тогда из подобия равнобедренных треугольников ЛХЛЕХ и ЛХ£Л (по
общему углу при основании) получаем
ЛЛХ/ЛХ£Х = Лх£/ЛЛх, т. е. (а—х)/х=а/(а—х),
205

откуда
Поэтому
х2 — 3ах -]- а2 = 0.
х/а=(3 — Y 5)/2 (ибо х < а)
Sa,b,c,d,b,/Sabcdb= (*/& = №- V 5)/2)2 = (7-3 ^ 5)/2.
11.5.	Пусть в четырехугольнике ABCD точка О—середина от¬
резка BD, а точки К и L—проекции на прямую BD вершин А и С
соответственно; при этом OK — xBD, OL = yBD (соответствующие
элементы в четырехугольнике A' B'C'D' будем помечать знаком «штрих»).
Тогда имеем (рис. 46)
Jb=Jk+kb, AD = AK + KD,
AB2-AD2 = AK2 + КВ*-Am-KD2 = (KB +KD) (KB-KD) =
= ((KB + BO) + ^<b + D6)) (DK+KB) = 2/CO - DB = 2xBD2
и аналогично
СВ2—CD2 = 2yBD2,
2x'B'D'1 = A'B'sl — A'D'* = 2xBD2,
2 yB’D'2 = C'B’t—C’D’2 = 2yBD2.
Если x = y, то x’=y’ к K = L, K’ = D,
т. e. имеет место утверждение а). Если
же х ф. у, то одно из чисел х, у, на¬
пример число х, не равно 0, поэтому
МС=(у/х) AM и
ЛГС' = (у'/х') ММ' = (р/х)/ГМ',
откуда следует утверждение б) задачи.
11.6.	Без ограничения общности можно считать, что длины сто¬
рон данного восьмиугольника AiA2..,As являются рациональными
числами (в противном случае докажем требуемое утверждение для
подобного восьмиугольника И'И'... И', у которого И'И'= 1, а зна¬
чит, остальные стороны рациональны; в результате утверждение будет
доказано и для исходного восьмиугольника). Рассмотрим векторы
а, = И,И/+1	(1=1,	«.., 8; А2=Аг),
сумма которых равна 0. Так как все углы восьмиугольника равны и
в сумме составляют 6-180°, то каждый из углов равен (3/4)-180°,
углы между векторами щ и а,-+1 (а9 = ах) равны (1/4)-180°=45°
(рис. 47). Спроектируем все векторы на ось, параллельную, например,
206

г
вектору аи и через х обозначим длину проекции суммы aj+a5, а
через //—длину проекции суммы a2 + a4 + ae + a8. Так как проекция
суммы a3 + a7 равна 0 (ибо a3 J_ ai, а7_]_ах), то х—у=0. С другой
стороны, длина проекции каждого из векторов а2, а4, ав, а8 равна
некоторому рациональному числу, умноженному на cos 45°= ]/"2/2.
Рис. 47
Поэтому имеем х—у=гУ 2, где х, г£0, откуда дг=0 и а5=—ау.
Аналогично доказывается, что
ав = —а2, а7 = —а3, Ое ==—
Следовательно, получаем
А{Аа = AsAg, А2А3 — А8А2, АдА^ = А2А8, AtA2 = AeAi,
что и требовалось доказать.
11.7.	По заданному правильному шестиугольнику A0AiB2C2CiB0
(рис. 48) построим с помощью линейки следующие точки: А2 и As —
на пересечении прямой A0Ai с прямыми С2В2 и CiB2 соответственно,
Рис. 48
Ся— на пересечении прямых CiC2 и А^В2, В, и В3—на пересечении
прямой BqB2 с прямыми AiCi и И3С8 соответственно. Тогда имеем
AiA2 =■ СгС2 — а

(ибо AiA2C3C1 — параллелограмм),
ЛаЛ3 = CiCg=о
(ибо Д A2AsB2 — Д
СгСв— >4	=	л
(ибо Д C2CsB2 = Д Л2Л1В2) и, наконец,
BiB3 = B2Bs=a
(ибо /1, Л2С2С1, И2И8С3Са—параллелограммы и В0В9|| Л0ЛХ). Теперь
проведем аналогичные построения для правильного шестиугольника
И1И2В3С3С2В1, являющегося результатом параллельного переноса
исходного шестиугольника на вектор ЛХЛ2, добавив 1 к индексу у каж¬
дой буквы (при этом часть точек уже построена). Получим точки Atl Bt,
С4, затем аналогично точки Л5, В5, Cs и т. д. Когда будет построена
точка Вп, найдем точку О пересечения прямых А0Вп и ЛХВХ. Из
подобия треугольников Л0ЛхО и А0АпВп имеем отрезок
Л„В„-Л0ЛХ а-а а
ЛхО =
АоАп
что и требовалось построить.
Замечание. Справедливо следующее общее утверждение: если
дан отрезок и прямая, ему
параллельная, то с помощью одной ли¬
нейки можно разделить этот отрезок
на п равных частей.
11.8.	Так как
ЛС = 2-Л В sin (Z В/2) 3s
С	^2-CD	sin (Z D/2) = CE
(рис. 49), то из треугольника АСЕ
имеем Z АЕС ^ Z ЕАС. С другой
стороны, получаем
Z ЕАС = Z Л — (180° — Z В)/2 =
= Z А + Z В/2—90° S=ZB+Z В/2—
—90° = Z Е— (180° — Z О)/2 = Z ЛЕС.
Следовательно, имеет место равенство
Рис. 49
Z£’ЛC=Z ЛВС, которое возможно лишь в случае
Z Л = Z В, Z В/2-Z В/2,
^ л = zв = zc=zв = zв■
Таким образом, пятиугольник ABCDE правильный.
11.9.	а) Если вершины первого многоугольника лежат во втором,
равном ему выпуклом многоугольнике, то первый многоугольник
полностью лежит во втором. Из равенства их площадей следует, что
они совпадают.

б)
б) Неверно (см. рис. 50, на котором изображены равные невы¬
пуклые четырехугольники А ВСЕ и ACDE).
в) Рассмотрим невыпуклый четырехугольник ABCD, в котором
вершина С является центром равностороннего треугольника ABD
(рис. 51). Тогда, если вершины равного ему четырехугольника
Рис. 50
A'B'C'D' лежат в четырехугольнике ABCD, то вершины равносто¬
роннего треугольника A'B’D' лежат в треугольнике ABD. Согласно
утверждению п. а) вершины этих треугольников совпадают, следователь¬
но, совпадают и вершины С'и С. Таким образом, ответ на вопрос п. в)
отрицателен.
11.10.	Докажем более общее утверждение: любой равносторонний
2«-угольннк, противоположные стороны которого параллельны, можно
разбить на ромбы. При п — 2 утверж-
.дение справедливо, ибо равносто¬
ронний четырехугольник уже есть
ромб. Пусть утверждение доказано
для некоторого значения nS* 2 и
дан 2 (п+ 1)-угольник
AiA2.. .An + iBi.. .„„+у
указанного вида. Пусть точки Су =
^л+ъ С2 Сп и Сл+у = яв¬
ляются результатом параллельного
переноса точек Вг Вп и Вп+1 на
(рис. 52). Тогда
Рис. 52
вектор В„+уИу
имеем равенства
В/Су = Bn+iAi = B;Bj+у
при i= 1, .,п,
из которых в силу параллельности всех прямых В,-С/ вытекает, что
все четырехугольники С/В/В/+1Су+у—ромбы, причем
AnCi — CiC2= ..I =СпА% и С,С,-+х|| В|В,+11| И/Л/+у.

Следовательно, 2/1 -угольник А\... А пС\.. .СГ1 также имеет указанный
вид и его, согласно индукционному предположению, можно разбить
на ромбы. Утверждение доказано. Таким образом, на вопрос задачи
следует дать утвердительный ответ.
11.11.	Так как каждая из точек О, D, В равноудалена от вер¬
шин А и С, то эти точки лежат на одной прямой. Рассмотрим ок¬
ружность с центром А и радиусом а (рис. 53). По теореме 73 произ¬
ведение OB-OD равно квадрату длины касательной ОЕ, проведенной
Рис. 53
из точки О к этой окружности, т. е. величине Ь2 — а2, не зависящей
от угла BAD.
11.12. Возьмем точку Q, для которой четырехугольник QPAB —
параллелограмм (рис. 54). Тогда QPDC—тоже параллелограмм, ибо
CD = BA = QP, CD ЦДЛ || QP.
Так как вершины равных углов PQB и PC В лежат по одну сторону
относительно прямой РВ, то точки Q, Р, В, С лежат на одной ок¬
ружности, откуда получаем
APB=£PBQ = £PCQ = £ DPC,
что и требовалось доказать.
11.13. Заметим, что треугольники A'EF и BDF подобны. Дей¬
ствительно, имеем (рис. 55)
£EFD = £ BFA = l_BFA', £_ FED = £ FAB= £ FA'B,
210

Рис. 54
Л
Рис. 55
211

поэтому
^ A'FE=\£EFB — £ A'FB\ = \£ EFB— £ EFD |= £ DFB,
а из подобия треугольников EDF и A'BF получаем .
EF/DF = A'F/BF.
Таким же образом доказывается подобие треугольников А'СВ и BDF.
Следовательно, получаем
ДЛ'££с/з ДВС/Г,
откуда
А'С А'В DE
EF	A'F	EF ’ Т’ е‘ C-DE‘
Аналогично, A’E = CD, поэтому A'CDE—параллелограмм.
11.14. Обозначим через Р и Q середины отрезков ВС и АС со¬
ответственно. Заметим, что если треугольник ОРМ повернуть вокруг
точки О на 60е (по часовой стрелке; рис. 56), а затем применить к
нему гомотетию с центром О и коэффициентом 2, то он перейдет в
треугольник ОСЕ. Действительно, так как
^ СОР = 60° и СО = 2-ОР
(ибо точка О—центр правильного треугольника ABC), то точка Р в
результате указанных преобразований перейдет в точку С. Далее,
так как
РМ ||DC,	DCE — 60° и EC = DC = 2-PM
(ибо РМ—средняя линия треугольника BCD), то отрезок РМ пе¬
рейдет в отрезок СЕ, а треугольник ОРМ — в треугольник ОСЕ.
Таким образом, имеем
^ ЕОМ = 60° и £0=2* МО.
Аналогично доказывается, что в результате поворота вокруг точки
О на 60° (против часовой стрелки) и гомотетии с центром О и коэф¬
фициентом 2 треугольник OQN перейдет в треугольник OCD, откуда
£ NOD = 60° и DO = 2-NO.
Поэтому
Д NOD оо Д МОЕ,
что и требовалось доказать.
11.15. Пусть продолжение перпендикуляра АН к прямой BE пе¬
ресекает прямые СЕ и BD в точках Р и Q соответственно. Докажем,
что AP = AQ, откуда будут следовать равенства Po=Q = 0. Опустим
перпендикуляр СК к прямой BE (рис. 57), тогда из подобия прямо¬
угольных треугольников СКВ, ВНА (с попарно перпендикулярными
сторонами АВ ] ВС, СК_\_ВН) имеем
CK-M=BC „/ВАС
ВН~ АН АВ
212

в
Рис. 57
а из подобия прямоугольных треугольников ЕНР, ЕКС получаем
ЕН-СК ЕН■ ВН• tg ^ ВАС	EH-BHAg £ ВАС
ЕК ~ ЕВ — ВК	ЕВ—AHAg £ ВАС'
Аналогично доказывается равенство
BH-EHAg £EAD
4 ЕВ —AH-lg £EAD ’
откуда с учетом равенства l_BAC=£_EAD получаем PH = QH.
Утверждение доказано.
11.16.	Пусть около многоугольника описана окружность с центром
О и радиусом R (рис. 58). Обозначим а = ^ АОВ, тогда 0 < а <
< 120° и	В
AB = 2R sin (се/2), AC=2R sin а,
AD = 2R sin (За/2),
откуда имеем
1 1 , »
sin (а/2) sin a sin (За/2) *
Следовательно, получаем
0 = sin a sin у-— ^slna+siny-^ х
v . a 1 / a 5a\	\	(	a	3a	\
X siny=y ^ cosy — COS -yj _y ^cosy —cos—J —
—-g- (cos a—cos 2a) = у ^ cos ^y-+ cos 2a j — ^ cos a -J- cos у	=
7a / a 3a \	„ 7a , a	a
= cos-y ^ cos у - cos y-J =2 cos y-sin у sin у ,
213

откуда
7а/4 = 90° и а = 360°/7,
т. е- исходный многоугольник имеет семь сторон.
11.17.	Пусть точка О—центр	правильного 2п-угольника
C0Ci.. .Са„—j, a R— радиус описанной около него окружности. Возьмем
Рис. 59
произвольную точку А на расстоянии т Ф R от точки О и обозначим
ct/i= £ Ck ACfyj.n, \k — £ AOCft
при ft=0, 1, ,.n — 1. Тогда по теореме косинусов имеем (рис. 59)
АС% — PS + г?—2Rr cos у*,
ACk+n = PS-f-r2+2Рг cos уь,
ACt + ACl+n~CkCl+n	г2— Р2
COS CLfo —	 Ar> 	=	—	 ■	■	.
Z* AL k'ACk+n	у	(/??	+	г2)2—4R2r2 cos2 y*
откуда получаем
tg? a*——J	1 =
- я cos2 a*
1	; ((P? + Г2)2 — (P2 — r2)2 — 4PV2 cos2 V*) =
(P2—r2)?'
4яа'а	.
— (P2 — Г2)2	T*'
Без ограничения общности можно считать, что
Yft = Vo+*n/n
(при этом, возможно, потребуется лишь перенумеровать вершины
исходного 2п-угольника в другом порядке). Поэтому имеем
. „ 2PV ^	ч	2R2r2n
X-l ®'а* (ра Г2)2^,| ^ C0S^Yft) —(^2 г2\2*
ft=0	ft=0
П — 1
ибо 2 cos2yft = 0. Для доказательства последнего равенства рас-
k= о
смотрим векторы d* единичной длины с координатами
(sln2y*; cos2yA) при k=0, 1, и—1
214

и заметим, что углы между векторами и dk+i (dn = d0) равны
2л/л. Следовательно, существует правильный я-угольник D0Dl..
для которого
DkDk+i = dk	(Dn = D0),
а значит, сумма векторов d0, dy, dk, равно как и сумма их
проекций на любую ось, равна 0. Итак, доказано, что для любых
точек А и В, удаленных от точки О на расстояние, не равное R,
рассматриваемая сумма одинакова, откуда вытекает утверждение за¬
дачи (ибо радиусы вписанной и описанной окружностей не совпадают).
11.18.	Доказательство проведем индукцией по числу я сторон
многоугольника. При я = 3 утверждение верно, ибо треугольник не
имеет диагоналей. Пусть оно уже доказано для некоторого нечетного
значения п^З и дан выпуклый (я+2)-угольник, вершины которого
окрашены указанным в задаче способом. Тогда найдется такая вер¬
шина А, что две соседние с ней вершины имеют разный цвет. Дей¬
ствительно, в противном случае любые две вершины, расположенные
через одну, имели бы одинаковый цвет, а в силу нечетности числа
п+2 все вершины оказались бы одного цвета, что противоречило бы
условию задачи. Тогда диагональ, соединяющая две вершины, сосед¬
ние с вершиной А, делит (п + 2)-угольник на треугольник и (л+1)-
угольник. Если в этом (л + 1)-угольнике также найдется вершина,
соседние с которой имеют разный цвет, то соединим эти две разно¬
цветные вершины диагональю, после чего образуется еще один тре¬
угольник и л-угольник, для которого, по предположению индукции,
существует требуемое разбиение. Если же такой вершины в (я+1)-
угольнике нет, то любые его вершины, расположенные через одну,
имеют одинаковый цвет, т. е. все его вершины раскрашены в два
цвета в чередующемся порядке. Поскольку цвет вершины А отличен
от цветов соседних с ней вершин, то он отличен от цветов и всех
остальных вершин исходного (л+2)-угольника. Следовательно, если
с самого начала из точки А провести все выходящие из нее диагонали
(л-(-2)-угольиика, то получится требуемое разбиение. Таким образом,
утверждение доказано и для следующего за числом л нечетного зна¬
чения п+2.
§ 12. Точки, отрезки и прямые
12.1.	Докажем более сильное утверждение: среди 10 точек А,
D, Е, К, L, М, N, О, Р, Q, расположенных, как показано на
рис. 60, найдутся 3 точки одного цвета, являющиеся вершинами пра¬
вильного треугольника. Пусть это не так. Тогда точку О без ограни¬
чения общности считаем черной, причем хотя бы одна из точек Р,
E, L, скажем Р, также является черной. Далее, черной является
хотя бы одна из точек Q, D, М, но точки Q и D обязаны быть бе¬
215

лыми (они образуют правильные треугольники OPQ и OPD соответ¬
ственно). Итак, точка М черная, а точки Q и D белые. Аналогию
получаем, что точки Е и L также являются белыми (из треугольников
ОМЕ и OML соответственно). Наконец, рассмотрев треугольники
Рис. 60
DEA, QLN и DLK, получим, что вершины правильного треугольника
AKN являются черными. Из полученного противоречия вытекает
справедливость требуемого утверждения.
12.2. Если n = 3ft+l (fc£Z+), то с помощью циркуля и линейки
строим угол
60° к 180°^(3fe + !)• 180°—3k-180°	1_ 180^
п	Зи	3	п ’
а если n=3k—1 (fc^N), то строим угол
. 180° _по 3k-180° — (3k— 1). 180°	1 180°
к • 	—	OU	= ■ ■	■	•	-	.
п	3 п	3	п
В обоих случаях	строится	угол	втрое	меньший	исходного.
12.3. Предположим противное. Пусть два непересекающихся от¬
резка являются диаметрами выпуклого множества. Возможны два
случая:	1)	никакой из	отрезков	не	пересекается	с продолжением
другого; 2) один из отрезков пересекается с продолжением другого.
В первом случае рассмотрим выпуклый четырехугольник A BCD, сто¬
роны АВ и CD которого являются диаметрами (рис. 61). Так как
хотя бы один из его углов, например угол D, не меньше 90°, то
имеем АС > CD, т. е. CD — не диаметр. Во втором случае рассмотрим
точку О пересечения диаметра АВ с продолжением диаметра CD за
точку D (рис. 62). Так как хотя бы один из углов АОС или ВОС,
216

г
Рис. 61
Рис. 62
скажем первый, не меньше 90°, то имеем АС > ОС > CD, т. е. CD —
не диаметр. Итак, в обоих случаях получено противоречие.
12.4. Ответ на вопрос задачи отрицателен. В самом деле, рас¬
смотрим выпуклый четырехугольник ABCD, в котором АВ = АС =
= BC=d, BD < d (рис. 63). Его диаметр равен d. С другой стороны,
хотя бы две из трех вершин А, В, С попадают в одну из двух ча¬
стей, на которые ломаная разбивает этот четырехугольник. Тогда
диаметр этой части равен d.
Замечание. Можно доказать, что если среди вершин данного
выпуклого четырехугольника нельзя выбрать три вершины, попарные
расстояния между которыми равны его диаметру, то указанное в
задаче разбиение возможно, причем достаточно использовать не ло¬
маную, а прямую.
12.5. Допустим, что не все точки лежат на одной прямой. Про¬
ведем всевозможные прямые через все пары точек и рассмотрим все
не равные нулю расстояния между точками и проведенными пря¬
мыми. Так как этих расстояний конечное число, то найдется точка
А и прямая I, расстояние между которыми минимально. Опустим
перпендикуляр АН на прямую I (рис. 64). Поскольку прямая I
В
/
И В
с\
Рис. 63
Рис. 64
217

содержит по меньшей мере три из данных точек, то хотя бы две из
них лежат на прямой I с одной стороны от точки Н. Пусть ими
оказались точки В к С, причем точка В лежит между точками Н и
С. Тогда, если ВК и НМ— перпендикуляры к прямой АС, то из
подобия треугольников ВКС и НМС имеем
НМ-ВС
В/С=
НС
-<АШ < НА
(если А = М, то АС Ц НС, что неверно), т. е. расстояние, от точки А
до прямой I не является наименьшим. Полученное противоречие до¬
казывает, что все точки лежат на одной прямой.
12.6.	Обозначим через А'В' образ отрезка АВ при симметрии
относительно искомой точки О. Рассмотрим произвольную прямую 1
такую, что образ C'D' от¬
резка	CD при симметрии
относительно I параллелен
А'В'. Так как C'D'|M'B'||
|| АВ, то прямая I парал¬
лельна одной из взаимно
перпендикулярных биссект¬
рис илн /а между прямы¬
ми А В и CD (рис. 65). Обо¬
значим образ отрезка CD при
симметрии относительно пря¬
мой I через CiDx в слу чае
11| /( и через С'г'Са в слу¬
чае	11| 1а. Поскольку
CiD1 = — CaDa, то один из
двух векторов CiDlt или
CaDa, скажем первый, ра¬
вен вектору АВ. В этом
случае отрезки А'В' и CiD[ совпадают (при соответствующем выборе
прямой / }| /i) тогда и только тогда, когда точка 0 = 0т лежит на
прямой mxAJu равноудаленной от точек А и D. Аналогично, отрезки
А'В' и CaDa совпадают (при соответствующем выборе прямой /1| /2)1
когда точка 0=0а лежит на прямой maJ_/a, равноудаленной от точек
А и С. Таким образом, искомое геометрическое место точек О есть
объединение указанных прямых mt и та.
12.7.	Пусть множество М имеет два различных центра симметрии
Ох и Оа. Тогда точка 03, симметричная точке Ot относительно точки
0а, также является центром симметрии множества М. Действительно,
218

если через С о (А) обозначить точку, симметричную точке А относи¬
тельно точки О, то из симметричности точек А и Со, (А), а также
точек 03 и 04 относительно точки Оа вытекает (рис. 66) симметрич¬
ность точек Cq, (А) и Со, (Со, (А)) относительно той же точки 0„.
№%<*»	А
\ ч	/	\
\ ч	/	\
' Чч /	\
-А V
/	и 2.	Ч
V/
/
Ч
Ч
]{J
\
Он
с0ш
ч
Рис. 66
Поэтому для любой точки А справедливо равенство
Со, (А) = Со, (С0, (С0, (А))),
откуда имеем
Со, (Щ = С0, (Со, (С0, (Щ) = Со, (Со, (Щ = Со, (М) = М.
Аналогично, точки
04 = Со3(02), 05 = COl (О,-,) и т. д.
являются центрами симметрии множества /И. Так как
0,02 = 0а03 = 0304 — ...,
то все полученные центры симметрии различны, а значит, их беско¬
нечно много.
12.8.	Пусть множество М имеет оси симметрии /0 и 14 (не обя¬
зательно различные). Тогда прямая /2, симметричная прямой I, отно-
219

сительно прямой /0, также является осью симметрии множества М.
Действительно, если через St (Л) обозначить точку, симметричную
точке А относительно прямой I, то из симметричности тонк А и
Si0 (Л), а также прямых 12 и h относительно прямой (0 вытекает
(рис. 67) симметричность точек S (А) и (S^ (У1)) относительно той
же прямой /0- Поэтому для любой точки А справедливо равенство
S|1M)-=S,0(S|I№.(i4))).
откуда имеем
su (М) = St. (S,. (S2o (М))) = S/o (S,, (М)) = S,0 (М) = м.
Таким образом, любая ось симметрии /0 множества М является осью
симметрии множества L, откуда вытекает утверждение задачи.
12.9.	Пусть оси симметрии 10 и множества М пересекаются в
в точке О, причем ось 1а при вращении по _ часовой стрелке вокрут
точки О на угол а переходит в ось /2. Тогда, если обозначить черн
St (i4) точку, симметричную точке А относительно прямой I, то при
вращении по часовой стрелке вокруг точки О на угол 2а любая
точка А переходит в точку R (A) = Stl (Sto (И)). Действительно, рас¬
стояние от точки О до любой из точек Л. si„ И). st, (sin И) одина¬
ковы (см. рис. 67), и если ориентированный по часовой стрелке угол
между прямыми О А и 10 равен Р (А ф О), то угол между прямы*»
ОА и OStl (Slo (/1)) равен 2|3—2 (|3—а) = 2а. Поскольку множество М
содержит более одной точки, то оно содержит точку А0 ф О. Итак, имеем
R (M) = Sh (Slo (Af)) = Stt (AQ = M,
поэтому каждая из точек А0, At — R (А0), A2 = R (У^), /4S=/?(/),)
и т. д. содержится в множестве М. При этом все указанные точки
различны, так как если бы при не
которых значениях i > / точки Л,- и
A j совпали, то выполнялось бы равен¬
ство
2а (i—/) = 2nft	(fcgN),
т. е. число а/я = &/(/—/) было бы
рациональным. Таким образом, мно¬
жество М бесконечно.
12.10.	Докажем, что условию а-
С,ВГдачи удовлетворяет лишь значение
п = 3 (при котором точки достаточно
расположить в вершинах правильного
треугольника). В самом деле, пусть
указанным в задаче образом можно
расположить п ^ 4 точек. Выберем из
них две точки А к В, расстояние меж¬
ду которыми максимально, и третью
точку С, для которой треугольник ABC
правильный. Тогда все остальные
220
Рис. 68
t

гочки лежат в фигуре М, являющейся пересечением трех кругов
радиуса АВ с центрами в точках А, В и С (рис. 68). Если точка
О—центр треугольника ABC, то Отрезки АО, ВО и СО делят мно¬
жество М на три равные части, ни в одной из которых не может
располагаться ни одна из п точек, кроме уже названных. Действи¬
тельно, пусть, например, в части Мвс> составленной из треугольника
ВОС и сегмента круга с центром А и дугой ВС, находится еще одна
точка D. Тогда существует точка D', для которой треугольник ADD'
правильный. Следовательно, при повороте (в определенном направле¬
нии) вокруг точки А на угол 60° точка D переходит в точку D',
лежащую, таким образом, одновременно и в образе Мвс части Мдс
при этом повороте, и [в множестве М. Но так как £ ВАС — 60°, то
либо С' —В, либо В' = С. Предположим для определенности, что
В'=С. Тогда множества Мвс И М лежат в разных полуплоскостях-
относительно прямой В'О', ибо
^ ВВ'0' = £ ВСА + £ ЛВ'0' = 600+300 = 90°,
т, е. прямая В'О' касается дуги АС, Поэтому Мвс и М имеют
только одну общую точку В', откуда £)' = б' и D = B, что противо¬
речит выбору точки D. Утверждение доказано.
12.11.	Пусть вначале точки А, В и С расположены на одной
прямой. Тогда эти точки делят прямую иа 4 интервала, причем ни¬
какие точки разных интервалов не могут лежать в одном выпуклом
Рис. 69
множестве. Поэтому число искомых множеств не может быть меньше 4.
Число 4 достигается, если разбить множество М иа части так, как
показано на рис. 69. Пусть теперь точки А, В н С не лежат на
одной прямой. Тогда точки В и С делят прямую ВС на 3 интервала,
причем точки разных интервалов должны лежать в разных выпуклых
множествах. Поэтому число искомых множеств не может быть меньше 3,
а 3 множества можно выбрать так, как показано на рис. 70.
12.12.	Среди проведенных прямых по условию обязательно есть
две пересекающиеся, которые уже делят плоскость на 4 части. Если
провести еще одну прямую, то, как показывает несложный перебор
случаев ее расположения, число частей увеличится по крайней мере
на 2. Поэтому ровно 5 частей получиться не может, откуда п<, ^ 5.
С другой стороны, любое число п > 5 частей можно получить тре¬
буемым способом: если n = 2k N), то разбиение плоскости можно
построить так, как показано иа рис. 71, если же n = 4k-{-3, то см.
221

2 параллель -
пых прямых

ряс. 72, а если n = 4А+5, то см. рис. 73. Таким образом, наимень¬
шее значение я„ равно 5.
12.18.	Условию задачи удовлетворяет, например, множество на
координатной плоскости, представляющее собой полосу
М = {{х\
В самом деле, это множество содержит бесконечно много целочислен¬
ных точек вида (х; [У 2 х]) при x£Z. С другой стороны, любая пря¬
мая y=tkx-\-b в случае к = У? содержит не более одной целочислен¬
ной точки (иначе число
|(У 2~ху + Ь) - (У 5"х2 + 6)1 = У 21 Хт-х* I
было бы целым прн | ху—х2 |£ N, что противоречило бы иррацио¬
нальности числа У 2), а в случае кф~\Г 2 пересекает множество М по
некоторому отрезку, который не может содержать бесконечно много
целочисленных точек.
Замечание. Можно доказать, что полоса, лежащая между
любыми двумя параллельными прямыми y = kx-\-bt и у — кх-\-Ьг
с иррациональным значением к, всегда содержит бесконечно много
целочисленных точек (какой бы малой ни была разность |	—	621).
Таким образом, любая такая полоса удовлетворяет условию задачи.
12.14. Так как ап^0 при всех значениях п, то возрастание или
убывание последовательности {а„} равносильно возрастанию или убы¬
ванию последовательности чисел
а% — (х—/у»)2 == х2—2пху+п2у2,
которая представляет собой последовательность значений квадратного
трехчлена с положительным старшим коэффициентом в точках n£N.
Из свойств квадратных трехчленов вытекает, что такая последова¬
тельность не может быть убывающей, а возрастающей она является
тогда н только тогда, когда а\ < at, или
ха—2ху+у? < ха—4ху+4у2.
Таким образом, условие а) равносильно условию
Зу? > 2ху, т. е. 3 | у | > 2 | х | cos ер,
где ф—угол между “векторами х и у, а условие б) не выполняется
никогда.
12.15. Пусть Л1 — множество площади меньше я, б/у, ..., U„ —
круги единичного радиуса с центрами в данных точках Ау, ..., А„
соответственно,
У,= и,Г)М (1=1	п).
Поскольку расстояния между центрами кругов больше 2, то круги
не пересекаются, а значит, не пересекаются и множества Еу Vn.
С другой стороны, имеем V, с Л4, следовательно, площадь множества
^iU^aU ■ - ■ U С М меньше я. Поэтому, если мысленно с помощью
параллельного переноса совместить все круги (У/ (вместе с содержа¬
223

щимися в них множествами Vj) в один круг с центром О, то внутри
него найдется точка В, не принадлежащая ни одному нз образов
множеств Vf. Тогда после параллельного переноса множества М на
вектор ВО длины меньше 1 центры Л,- всех кругов (У,- уже не будут
принадлежать этому множеству.
12.16. Заметим, что сумма длин двух проекций каждого отрезка
на заданную прямую I и прямую Г, ей перпендикулярную, не мень¬
ше 1. В самом деле, если вектор а длины 1 параллелен некоторому
отрезку, а векторы х и у являются проекциями вектора а на пря¬
мые I и то а==х~\у, откуда
1*| + |Яг&|а|=1.
Но длины проекций отрезка равны |дс| и |у |, поэтому их сумма
также не меньше 1. Следовательно, сумма длин проекций всех отрез¬
ков не меньше 4п. Поэтому нз двух прямых I и Г можно выбрать
прямую, сумма длин проекций отрезков на которую не меньше 2л.
Так как все отрезки расположены внутри круга радиуса я, то объе¬
динение нх проекций на любую прямую имеет длину меньше 2л.
Следовательно, на выбранной прямой найдется точка, принадлежа¬
щая проекциям хотя бы двух отрезков. Прямая, проходящая через
эту точку перпендикулярно выбранной прямой, пересекает по край¬
ней мере эти два отрезка. Так как эта прямая либо перпендикулярна,
либо параллельна прямой I, то она удовлетворяет условиям задачи.
12.17. Обозначим U (М) объединение всех кругов радиуса 1,
центры которых принадлежат множеству М на плоскости. Докажем
индукцией по я 6N. что для любой ломаной Л0Л^...Л„ справедливо
неравенство
п
At-iAi + n.
i=1
При я = 1 множество U (A0A^) разбивается на два полукруга радиу¬
са 1 и прямоугольник со сторонами A0Ai и 2, поэтому
1А0АЦ = 2 - Л„/4 i + я,
т. е. утверждение справедливо. Пусть оно уже доказано для некото¬
рого значения я— 1£N. Обозначим
Х=(/(Л0...Л„-1). К = (/(Л„_,Л„), Z = X{\Y,
тогда	(нбо	Zd(/(4„_i))	и,	учитывая	предположение	индук¬
ции, имеем
SUiA0-■■An_1An) = Sxur = SX\Z+ SY\Z + Sz =
f n-1	\	n
<[2 2 А(^\А[ +я ) + (2Л„_1Дп +я) — я = 2^
\ 1=1	/	1=1
224

что и завершает доказательство неравенства. Для данной в условии
задачи ломаной множество U (Л„ ... Ап) содержит весь квадрат со
стороной 50, поэтому ее длина не меньше чем
(%М0 ■ • • Л„>-*)/2 > (50?-4)/2= 1248.
что и требовалось доказать.
12.18. Выберем на прямой левое направление и будем говорить,
что один отрезок находится левее другого, если левый конец первого
отрезка расположен левее (точнее, не правее) левого конца второго.
Каждому отрезку поставим в соответствие один из п номеров 1, 2, ...
п следующим образом. На первом шаге самому левому из всех
отрезковх) поставим в соответствие номер 1. Затем на каждом после¬
дующем шаге найдем самый левый нз еще незанумерованных отрез¬
ков 1) и поставим ему в соответствие номер, отличный от номеров
пересекающихся с ним отрезков (уже занумерованных). Если на ка¬
ком-то шаге выбран некоторый отрезок, но для него не удается по¬
добрать очередной номер, то это означает, что он пересекается с п
отрезками, расположенными левее его и имеющими разные номера.
В этом случае левый конец выбранного отрезка принадлежит п +1
отрезкам. Если же на каком-то шаге занумерован последний отрезок,
то по принципу Дирихле (теорема I) хотя бы одни из п номеров
соответствует более чем п отрезкам, которые, согласно описанному
порядку нумерации, не пересекаются. Доказательство закончено.
12.19. Каждому множеству А{ (/=1, ..., п), представляющему
собой объединение двух отрезков прямой (где выделены левое и пра¬
вое направления), поставим в соответствие отрезок В,-, левый конец
которого совпадает с самой левой точкой множества А,-, а правый —
с самой правой. Так как В,- Z3 Л,-, то любые два (и даже три) из
отрезков Blt ..., В„ имеют общую точку. Докажем, что существуют
отрезки Bf, и Вт (возможно, k = т), пересечение С которых содер¬
жится в любом нз отрезков В,-. Действительно, пусть левый конец
отрезка В/, является самым правым из всех левых концов отрезков
Ва правый конец отрезка Вт—самым левым из всех правых кон¬
цов. Тогда пересечение
c=Bfcnsm
лежит не левее левого конца любого нз отрезков В,- и не правее
правого его конца, т. е. С с В,-. Заметим, что
C[\Ai = Bk[\Bm[\Ai гэ Akf]Amf]Ai ф 0.
Поэтому каждое множество Л/ содержит либо самую левую точку а
множества С, либо самую правую его точку Ь (возможно, а = Ь).
В самом деле, в противном случае имеем
о, 6£В/\Л,- и С cz В,\Д,.
*) Если таких отрезков несколько, то выбираем любой из них.
8 Под ред. И. Н. CepieeBa	225

откуда
СПЛ; = 0,
что неверно. По принципу Дирихле (теорема 1) хотя бы одна из то¬
чек а илн Ь принадлежит по меньшей мере половине 'Множеств А-„
что и требовалось доказать.
12.20.	Предположим, что по данным п~\-4 точкам уже построена
некоторая сеть отрезков, удовлетворяющих условию задачи, причем
больше ни одного отрезка провести нельзя (такие сети, называемые
в дальнейшем максимальными, обязательно существуют, так как ко¬
личество всех возможных отрезков ограничено числом Сл+а). Много¬
угольник, вершинами которого служат данные точки, а каждая сто¬
рона есть либо отрезок сети, либо объединение нескольких отрезков
сети, лежащих на одной прямой, будем называть сетевым. Стороны
квадрата К с вершинами в 4 отмеченных точках, внутри которого
лежат остальные п точек, всегда принадлежат максимальной сети,
так что этот квадрат является сете¬
вым многоугольником. Докажем, что
максимальная сеть разбивает квадрат
К на сетевые треугольники, каждый
из которых содержит ровно три дан¬
ные точки, а именно его вершины. Рас¬
смотрим произвольную точку О квад¬
рата. Среди всех сетевых многоуголь¬
ников, содержащих эту точку (мно¬
жество таких многоугольников не пус¬
то, ибо содержит квадрат К), выберем j
m-угольник М наименьшей площади. |
Так как сумма углов многоугольника L
М равна 180°(т—2), то среди его
вершин найдется такая вершина А,
угол при которой меньше 180°. На
каждой из двух сторон этого угла вы¬
берем ближайшую к вершине А данную
точку, получим тем самым точки В и С
(рис. 74). Отметим, что треугольник ABC
содержит данные точки, отличные от Л и В, например точку С. Возьмем
ту из них—точку D,—для которой угол ABD минимален (если та¬
ких точек несколько, то выберем из них ближайшую к точке В).
Тогда	в	треугольнике	ABD	нет данных точек, отличных от вершин
Л,	В,	D,	а	значит,	ни	один	из отрезков сети не имеет общих точек
со сторонами AD и BD, кроме, возможно, этих вершин. В силу мак¬
симальности сети отрезки AD и BD ей принадлежат. Таким образом,
треугольник ABD сетевой. Если он не совпадает с многоугольником
М, то последний разбивается на две части, каждая из которых так¬
же является сетевым многоугольником, что противоречит выбору

многоугольника М. Поэтому треугольник ABD и есть многоуголь¬
ник М. Итак, точка О лежит в сетевом треугольнике ABD, не содер¬
жащем данных точек, отличных от его вершин. Теперь сосчитаем ко¬
личество k отрезков в максимальной сети. Для этого найдем сумму
всех углов всех треугольников, на которые квадрат К разбит этой
сетью. С одной стороны, она равна 180°- /, где I—число треугольни¬
ков. С другой стороны, она составлена из суммы углов при верши¬
нах квадрата н всех полных углов с вершинами в данных точках
внутри квадрата, т. е. равна 360° (п -(-1). Поэтому имеем
180М = 360°.(п + 1),
откуда / = 2(п + 1). Наконец, каждая сторона квадрата К является
одной стороной одного треугольника, а каждый отрезок сети, отлич¬
ный от стороны этого квадрата, является общей стороной двух тре¬
угольников. Следовательно, получаем равенство 4 + 2 (А—А) =31,
откуда
А-=-|-/+2 = Зл+5.
§ 13. Геометрические неравенства
13.1. Заметим, что
2S = ab sin	аб,
где S—площадь треугольника, а у—угол между данными сторонами.
Поэтому если а > Ъ, то
(а+йа)-(<>+йб) = (а+^)-(б+^) = (а-<>)(1-^)э=0,
причем равенство достигается тогда и только тогда, когда 2S=ab,
т. е. когда угол между данными сторонами прямой.
13.2. Пусть выпуклый многоугольник
М0 = AfAi ... Ап
лежит внутри выпуклого многоугольника М. Тогда прямая АгА2 де¬
лит многоугольник М на две части, одна из которых представляет
собой выпуклый многоугольник Mi, содержащий многоугольник М0
(рис. 75), причем сторона BiBs многоугольника Mi, содержащая от¬
резок AiA2, не является стороной многоугольника М, откуда имеем
PMi < Рм (ибо отрезок ВгВ2 короче любой ломаной, соединяющей
его концы). Прямая А2А3 отсекает от многоугольника Mi выпуклый
многоугольник М2, содержащий многоугольник Мв, причем
Рмг<Р\1,- Рассуждая подобным образом и далее, получаем после¬
довательность многоугольников
8*
м z> Mi Z2 м2 э.. .э м„,
227

последний из которых совпадает с многоугольником М0, причем вы¬
полнены неравенства
рм >	•	•	•	&	?мп	—	РМш.
откуда следует требуемое неравенство.
13.3.	Пусть точки Bi, Ва, , В„ являются соответственно се¬
рединами сторон AiA2, A2As,	АпАх	выпуклого	я-угольннка
Л
223

AiAz ... Л„ площади S. Положим An+l = Alt Лп+а _= Л2, тогда лю¬
бой треугольник
^/^/ + 1^1 + 2	(1=1. п)
не имеет общих внутренних точек ни с одним из других таких тре¬
угольников, кроме двух из них, имеющих своей вершиной точку Л1+ь
причем два последних треугольника не имеют общих внутренних то¬
чек (рис. 76). Поэтому любая точка п-угольника является внутренней
не более чем для двух из таких треугольников, откуда имеем
2S^2 ‘^Л,ч4/ + 1Н/ + а.
1=1
Поскольку каждый отрезок В/В/+1 (6n+i = Bi) является средней ли¬
нией треугольника Л,Л,-+1 Л/+а, то
^/?|Л/ + 1®1 + 1	^ SAjAj + iAj+x »
а значит, справедливы соотношения
П
Sbld, ... я„ = «-1Ха-+1Я,-+1 =
( = 1
П
=S-TH S^,.+H,.+a^S-l5 = l S,
i=i
из которых вытекает требуемое неравенство.
13.4.	Пусть параллелограмм A BCD вписан в правильный шести¬
угольник М, центр О которого является точкой пересечения диаго¬
налей параллелограмма. Выберем вершины Е и F шестиугольника,
лежащие в одной полуплоскости
с точкой В относительно прямой
ОА и удовлетворяющие неравен¬
ствам £АОЕ < 60°, /_АОЕ <
< 120° (рис. 77; заметим, что
этими условиями вершины Е
и F определяются однозначно).
Тогда имеем
60°« Z.AOF < 120°,
так что остальные вершины Е и
С шестиугольника (а с ними и
точка В), лежащие в этой полу¬
плоскости, удалены от прямой
АО не дальше вершины F. По¬
этому	Рис. 77
Saob^SAof=SEOf,
так как точки А к Е лежат на одной стороне шестиугольника, па¬
раллельной прямой OF, т. е. равноудалены от этой прямой. Из свойств
229

параллелограмма и правильного шестиугольника вытекают равенства
Saob=sboc = scod = sdoa = (1/4) Saecd
и
shof=(*/6)
следовательно, справедливо неравенство
(*/4) ^abcd 0/6) 5д1,
откуда
Sabcd ^ (2/3) SM,
что и требовалось доказать.
13.5.	Докажем более общее утверждение: площадь любого па¬
раллелограмма KLMN, лежащего в треугольнике ABC, не превосхо¬
дит половины площади этого треугольника. Заметим, что каждая из
д	прямых KL и MN- пересекает
две стороны треугольника ABC
(возможно, в его вершинах), а
значит, хотя бы две из четы¬
рех точек пересечения по прин¬
ципу Дирихле (теорема 1) при¬
надлежат одной стороне. Пусть,
например, сторона ВС пересека¬
ет прямые KL и MN в точках
и Nx соответственно. На сто¬
ронах АВ, АС и ВС выберем
соответственно точки D, Е и F
' так, чтобы для точек Li н Mi
пересечения прямых KL н MN
с отрезком DE выполнялись ус¬
ловия
' KiU=KL, LiMiWKiNi,
Рис. 78
причем EF\BD (рис. 78). Тогда параллелограммы KLMN и
имеют равные высоты к равным основаниям, а в параллелограммах
BDEF и KiLiMiNi основание DE не меньше основания LiMu в то
время как высоты к ним равны. Поэтому имеем
SKLMN — SKiL iA!1A'1 < SBDEF-
Пусть AE = x-AC, тогда EC = (1—x) AC, и нз подобия треугольников
ABC, ADE и EFC получаем
3fiD£F= $АВС — $ADE—SfEC = $ABC — x2$ABC — (1 — *)2 SABC =
— 2x (1 — x) SABC < (1/2) SABC,
ибо x(l— x)s£l/4 при любом x. Поэтому
SKLMN< (1/2) SABC,
что и требовалось доказать.
230

13.6.	Так как по условию £ВАС90°, то точка А лежит в
круге с диаметром ВС и центром О на нем. Поэтому для высоты АН
треугольника ABC имеем
АН<АО<ВО = ВС12
(рис. 79), т. е. ВС^2АН. Отсюда и из подобия треугольников BBLE
и ВАН, а также треугольников CCjD и САН, получаем
sbb,c,c_sb,c,de , ^вд,е , SCC,D  ^ ^ BE CD _
SB,CtDE SBlC1DE SBlc,DE SBlC1DE	2ВгЕ	2	CtD
=1+^+™=I+^2,
2 AH ' 2AH
т. e. SBtCtDE <SBBjCtC/2. Аналогично, имеем
2 АН'
SB,CtD,El< 2" SB1B,CJCl> •••• SBnCnD„_iEn_1<YSBn-lBnCnCn-t<
где n — число построенных квадратов. Складывая эти неравенства,
получаем, что сумма площадей квадратов не превосходит половины
площади четырехугольника ВВ„СпС, а значит, меньше половины
площади треугольника ABC.
13.7.	Пусть в остроугольном треугольнике ABC площади I угол
при вершине А наибольший. Проведем окружность с центром в се¬
редине М стороны ВС и радиусом R = MA, которая пересекает пря¬
мую ВС в точках D и Е (рис. 80). Тогда угол DAE прямой и
а = МВ = МС < R
231

(иначе MB^MD, MC^zME, откуда £BAC^s £DAE — 90°, что
противоречит остроугольное™ треугольника ABC). Хотя бы один .'з
углов АМС или АМВ не является острым, например £АМВ = а^
5»90°. Так как АВ *5 ВС = 2а (ибо £ВАС £АСВ), то по теореме
косинусов имеем
№+а2 = МА* + МВ?^МА? + МВ?—2МА-MB cos а = АВ?<4а\
откуда R < ]/" 3 а н
SADB=(l/2)DE-AH = R.AH<zy~3a-AH=}r3-(\/2) ВС-АН^ |/”з
(где АН—перпендикуляр к прямой ВС). Утверждение доказано.
13.8.	Обозначим АВ — а, ВС = b, CD = c, DE = d, АС — х, СЕ- у,
/_САЕ = а, £АЕС = р. Без ограничения общности можно считать,
что точки Л и £ являются концами диаметра, стягивающего полу-
Рис. 81
окружность (рис. 81), ибо в противном случае их можно переместить
в указанные концы, после чего выражение
я2 + Ь2 + с?+d2- + abc + bed.
только увеличится. Так как £АСЕ = 90°, то хг-\-уг — 4. Далее,
£АВС= 180°~£АЕС= 180°—р, £CDE= 180°- ЦЕАЕ= 180°-а;
232

следовательно, по теореме косинусов
х2 — а2-\-Ь2—2ab cos £ А ВС = а2 -\-b2 -\-2ab cos Р,
р? = с2 + d2 — 2cd cos £CDE = с2+d2 +2cd cos a.
Наконец, из соотношений
2 cos a = x > b, 2 cos P=у > с
получаем
4=x2 -f p2 = a2 + fe?+ofcp+с2 + d?+cdx > a?+fcB+c?+d?+a6c+6cd,
что и требовалось доказать.
13.9. Поскольку	С
~АО=х-~АВ и ОВ = (1— х)-АВ,
где х£ (0; 1), то имеем (рис. 82)
0С=| СЛ +ЛО | = | cl+x (СВ — с7)| =
= |(1—х) СЛ + хСВ | < С А (1— х) + СВх
(ибо векторы С А и СВ не параллельны), от¬
куда получаем
ОС-АВ < СА (1— х) АВ-\-СВх АВ —
= СА .ОВ+СВ-ОА,	в
,	Рис.	82
что и требовалось доказать.
13.10. Пусть М— наибольшее, а т — наименьшее из расстояний
между вершинами четырехугольника. Поскольку хотя бы один из его
углов, скажем угол ABC, ие является острым, то по теореме коси¬
нусов имеем
М2 Si AC2 3s А В2 + ВС2 S& /п2+т2 = 2т2,
откуда
М	У 2 т, или М/т Эг	У 2 ,
что и требовалось доказать.
13.11. Заметим прежде всего, что если среди данных точек всегда
можно выбрать три точки А, В, С, для которых 120°ABC, то
утверждение задачи выполнено. Действительно, пусть М — наиболь¬
шее, а т—наименьшее из расстояний между точками, тогда по тео¬
реме косинусов (справедливой и в случае £ ABC —180°) имеем
М? 3: ACi = АВ2 -f- ВС2—2АВ • ВС cos £ ABC s*
Эг /н2 + /н2+2/п2-(1/2) =3т2,
откуда М^У3 т. Если 6 точек расположены в вершинах выпук¬
лого шестиугольника, то хотя бы один из его внутренних углов (со¬
ставляющих в сумме 180°-4= 120°-6) не меньше 120°. Если же это не
так, то хотя бы одна точка О обладает следующим свойством: отно-
233

сительио любой прямой, проходящей через точку О и еще одну из
точек, все остальные точки не лежат внутри одной полуплоскости.
Тогда возьмем еще одиу точку А ив каждой из двух полуплоскос¬
тей относительно прямой ОА выберем точки В и С соответственно,
для которых углы АО В и АОС максимальны (рис. 83). Тогда
^ АОВ + £АОС^5 180°
(иначе все точки лежат внутри одной полуплоскости относительно
, g	прямой	О	В), поэтому возможны три
случая: либо
^ АОВ Ss 120°,
/ АОС120°,
/ ВОС = 360°—/ АОВ — £ АОС >
> 120°.
Итак, в любом из случаев расположе¬
ния точек существуют три точки, образующие угол не меньше 120°,
следовательно, утверждение задачи справедливо.
13.12.	1) По теореме о средних имеем
Сab-{-bc-{-ca) (a-f-ft+c) =а?й+6?а-)-с2а+а2с-1- Ь2сс2 b-j-ЗаЬс
6abc-\-3abc=9abc,
откуда вытекает неравенство
с ^ Р
2) Неравенство
а2 + />2+с2ггР?/3
вытекает из цепочки соотношений
РЗ = (а + b+с)? = а? + йЗ -f- с?+2аЬ + 2ас+2 Ьс <
< а? + йЗ+с?+(аЗ + В2) + (a3 + с2) + (й2+с2) = 3 (а2 + В2 + с2).
3) По формуле Героиа и теореме о средних получаем
27S3 = 27 (Р/2) (Р/2—а) (Р/2— В) (Р/2—с) <
.	^27 (Р/2) ^/^)+^у) + (Р/2-С)
т. е. Р35& 12 [Аз S.
4) Согласно неравенствам 2) и 3) имеем
а?-|- йЗ+с2 э- РЗ/З Дг 4 [A3 S.
5) Неравенство
а3 +й3 + с35гР3/9

следует из цепочки соотношений
Р3=(о-|-6-1-с)3 = а3 + 63 + с3+6а6с+За6 (« -J- 6) 36с (6-|-с) +
+ 3 са (c+tz) <а3+ 63+с3+2 (а3 + й3 + с3)+3 (a*—ab+ Ь*) (а + Ь) +
+ 3 (а2 —ас+с2) (а + с)+3(6?— Ьс+с2) (Ь + с) = 9 (а3-)-*;3-)-*?).
6) Согласно неравенствам 3) и 5) имеем
а3 + 63 + с3>Р3/9> 12 ]АЗ SP/9 = (4 |АЗ /3) SP.
7) Из неравенства 4) получаем
l6S=<^+^±^ =
fl4+fc4 + c4 + 2c2fc2 + 2a2c2 + 2fc2c3 ^ ^ | ^ | ^
13.13.	Положим сц= £ОАС, а2 — £ОАВ, $i= /.ОБА,
P2=ZO®^> Чг= £ОСВ, у2=£0СА, а = ах+а2, P = Pi + p2>
В
Рис. 84
V=yi4-T2 (рис. 84). Тогда требуемое неравенство вытекает из сле¬
дующей цепочки соотношений:
p=£i^if== .2. joe cos ух+ОС cos y2+0B cos рх + ОВ cos р2 +
-j-ОA cos а±-\-ОА cos а2) = ОС cos cos ^ ^ ^2-f~
-J-OBcos cos	cos у c°s gl g И2<
< (M cos -^--f-OB cos y+OC cos
При этом равенство достигается при
ссх = сс2, Pi = Рг» Vi = T2.
т. е. когда точка О является точкой пересечения биссектрис тре¬
угольника АБС.
13.14.	Заметим, что при а = Р = у = С0° требуемое неравенство
обращается в равенство. Пусть хотя бы два угла треугольника,
235

скажем та и (3, не равны, тогда
cos та + cos P + cos 7=003 та + cos Р— cos (та + Р) =
„ та + Р та—В ,	, о, п та + Р _ „та + Р . .
=2 cos ■ cos ——cos (та + Р) < 2 cos —^	2	cos*	—^—(-1 =
• (п « + Р , V , 3^3
—	2 V	0S 2	/ "*■ 2 < 2’
т. е. требуемое неравенство также выполнено, но является строгим.
Таким образом, равенство имеет место только для правильного
треугольника.
13.15. Обозначим
/(a, Р, у) = cos2 a + cos2 Р+cos2 у,
где a, Р, 7—углы треугольника. Тогда та + Р+7= 180°, следова¬
тельно,
„1*, а ч 3\	„/^l + cos2ct , I+cos2P , 1+COS27	3\
4(М«. P. V)—4 j=4^ g +	2	+	2 Tj =
= 2 cos 2a+2 cos 2p+2 cos 27+3 = 4 cos (a+P) cos (та—P) +
+4 cos2 (та+Р) + 1 = (2 cos (a + P) + cos (та—f))2 + 1 —cos2 (a—P)feO,
откуда вытекает требуемое неравенство
f (a, P, 7) Ss 3/4.
При этом равенство достигается тогда и только тогда, когда
cos (та—Р) = 1, cos(a + P) = —1/2, т. е. при та = Р = у=60°.
Заметим, что величина f (та, Р, у) не принимает наибольшего значе¬
ния, так как для любого набора углов та, Р, у треугольника при
достаточно малом положительном значении е выполнены оценки
е < та,Р,у < 180°—2е,
из которых получаем
| cos та | < cos е, | cos Р | < cos е, | cos 71 < cos е
и
f (a, Р, 7) < / (в, е, 180°.— 2е).
13.16. Для углов та, Р, у <90° треугольника имеем
о ,	та + Р a—Р . та+у та—у .
cosa+cosP+cosy=cos —~~ cos —g-^+cos —j—1 cos —^+
+cos ^cos ^	<	2	sln-g-	cos	-jr+2	sin	cos	~+
+2 sincos -^-=sln y+sln P+sina,
при этом использованы неравенства
cos ((a—Р)/2) < 2 cos (у/2),
cos ((та—y)/2) < 2 cos (P/2),
cos ((P — y)/2) < 2 cos (та/2)
236
J

(для доказательства, например,
первого из иих достаточно заме¬
тить, что у/2 < 60°, откуда
cos ((ос—Р)/2) «S 1 =
= 2 cos 60° < 2 cos (у/2);
остальные неравенства доказы¬
ваются аналогично).
13.17.	Пусть в треугольнике
ABC выполнены равенства
АВ — с, АС = Ь, ВС = а и
^ ВАС = а.
Рассмотрим опирающуюся на сто¬
рону ВС дугу ВАС окружности,
Рис. 85
описанной около треугольника ABC (рис. 85). Так как середина
D этой дуги является наиболее удаленной от хорды ВС точкой
дуги, то для высот АН=Л и DK треугольников ABC и DBC спра¬
ведливы соотношения
A«£D* = fi*.ctg(i- £ В£>с) = |-ctg
Согласно теореме о средних имеем
4 V (I
а?ЬЧ2
3 з
((1/2) be sin а)? ((1 /2) ah) 2 V h sin? а
±\f
2 V sin? а (
; ctg (а/2) •
Снова применяя теорему о средних и обозначая cos а=х, получаем
Y sin? a ctg -^- = sln а cos2	sin	а	(1 +cos а) =
=1 }ГТГ^(1+ж)=1. у(i+j)a (!_*) =
-«))'-
ай+пс+ be.
45	=
что и требовалось доказать.
V 3
-Уз,
237

А
Рис. 86
13.18.	Если точка О—центр описанной около данного шести¬
угольника ABCDEF окружности радиуса R (рис. 86) и
а =£САЕ, $ = £АЕС, у = £ АСЕ,
то из равенств сторон, указанных в условии, имеем
/АОВ=/ВОС=$, COD = £ DOE = а,
£ EOF=£FOA = y.
Отсюда находим площадь
Sacb=EC‘ 4к AE=R 81П K'2*4t Sln Г=2т Sln ° S,n P sln v
и аналогично
SBDF= 2Я? sln 2+Ё sinsin
Из соотношений
sin? a sln? p sln? у = (sln a sin p) (sin a sln y) (sln P sin y) =
=i- (cos (a—P)— cos (a+ P)) - -i- (cos (a—y) — cos (a + y)) X
X y (cos (P—y) — cos (P+y)) <
<-i-(l — cos(a+P)) --|-(1 — cos (a+y)) ■ -^-(1—cos (P+y)) =
==sine^+Psin2P + Vsln2^+1
справедливых для любых положительных значений а, р, у, удовлет¬
воряющих условию
ct-J-p-[-■у = 180°, ■
238

откуда вытекает требуемое неравенство.
13.19.	Докажем, что ААХ > (АВ + АС)/2. Действительно, по тес
реме Птолемея (теорема 69) имеем
АА1-ВС = АВ-А1С + АС-А1В
(рис. 87j и, учитывая равенство вписанных углов ВААи СААХ
В
Рис. 87
получаем А\В=АхС — х и
2ААх — 2 --В'Х+сАС'Х=(АВ + АС) • ^ > АВ + АС,
ибо
2х = АхВ + АхС > ВС.
Аналогично доказываются неравенства
BBi > (ВА + ВС)!2, CCi > (СА + СВ)/2,
складывая которые, получаем требуемое неравенство
ААХ + В Bi+ССХ > (А В + АС + А В + ВС+АС+ВС) /2= АВ+ВС+ АС
13.20.	Обозначим
а = ВС, Ь = АС, с=АВ, S = Sjibc> S0 = S£,Ep.
Тогда по свойству биссектрисы треугольника (рис. 88) имеем
AF _BF AF+BF __ с
b а 6 + а а-\-Ь’
откуда
.Ьс

Аналогично, имеем
£
Рис. 88
Л£=-^-,
а+с
поэтому
Saef— ^ AF-AE sin ВАС-
Ьс sin ^ ВАС  йс  Ьс
S.
2	(о+й)	(c-f с) (а + Ь) (а+с)
Точно так же находим
с  	^	с	с	 с
ВОР ~{а + Ь) (й + с)’	CDE {а+с) (й+с)
и, используя теорему о средних, получаем
5—S0=SAEF+SBDF+SC£)B—
( be	ас	аЬ \ „
“^(в+й)(а+0+(й+^(й+1»+(с+а) (с+й)/ ~
с2й+й2с+а2с+с2а + 62я + а2й „^	ёаЬс	_	_
(а+й) (й + с) (с+й)	-"(в	+ й)(й + с)(с+с) —
/ .	йс	ас	ab	\
~ \	(а+Ь)	(а+с)	(а	+	й)	(с+й) (с+а)(с+й)/
= 3 (S—SAEF—SBDF—SCDE) = 3S0.
Итак,
S—S„^3S0, т< е. S0<S/4,
что и требовалось доказать.
13.21.	Прежде всего, в треугольнике со сторонами а, б, с, про¬
тиволежащими им углами а, Р, у, периметром Р, площадью S и ра¬
240
J

диусом г вписанной окружности имеем соотношения
а=г (ctg (Р/2) + ctg (у/2)), Ъ = г (ctg (а/2)+ctg (у/2)),
С—г (ctg (а/2) + ctg (Р/2)),
g=2g=2 (a+_b+C)=4 (ctg (a/2)+ctg (р/2)-f-ctg (у/2)).
Следовательно, для решения задачи достаточно доказать, что
ctg(ai/2)4-ctg (Pi/2)4-ctg (y,/2) < ctg (a2/2)4-ctg (PB/2)4~ctg (y2/2),
где обозиачеио
aj=£BAfi, f>j=£AjBC, уj=£AjCB.
Рассмотрим точку A3, лежащую на одной из сторон треугольника
АгВС, скажем на пересечении прямой ВА2 со стороной АгС (рис. 89).
Тогда ух=уз=у и соответствующее неравенство для треугольни¬
ков AtBC и АаВС примет вид
dg (ai/2)4-ctg (Pi/2) <
< ctg (as/2) -fctg (Ps/2).
Для его доказательства заметим,
что
ctg («у/2) + ctg (fly/2) =
_ sin (ay/2-f-Py/2)
sin (ay/2) sin (Py/2)
 	2	cos	(y/2)
—cos (ay/2—Py/2) — sin (y/2) ’
поэтому из неравенства	А	С
cos ((ai—PJ/2) > cos ((a3—Ps)/2)	Рис.	89
(вытекающего из оценок a8> at > п/3 > Pi > Ps, 0 < (ai —pt)/2 <
< («я—Ps)/2 < л/2) получаем
- Si/Pi > Sa/Pl
где Sj и Pj—площадь и периметр треугольника AjBC. Применяя
доказанный факт еще раз к паре треугольников АаВС и А2ВС (за¬
метим, что точка А2 лежит на стороне А3В треугольника АаВС),
получаем неравенство
S3/P2 > S2/P\,
а с ним и требуемое в задаче неравенство.
13.22.	Выделим в данном круге с центром О концентрический
с ним круг диаметра 2. Тогда, если внутри круга лежат некоторые
две из данных точек, то расстояние между ними меньше 2, и утверж¬
дение задачи справедливо. В противном случае в оставшемся кольце

данного круга расположены по меньшей мере 9 точек. Разобьем это
кольцо	лучами, выходящими	из	точки О, на 8 равных кольцевых
секторов	(углы между	соседними	лучами равны 45°; рис. 90) ,'огда
хотя бы две данные точки А н
В находятся в одном кольцевой
секторе CDEF. На радиуса*
ОС и OD возьмем точки и
В1 соответственно, для кото¬
рых OAi = OA, OBi= OB, а
значит, АВ eg AtBi (по теореж
косинусов, так как
< ,/ AiOBi). Заметим, что
y4xBi<max{y4x£); »х£}.
Действительно, точка Вх лежит
на прямой DE между проев-
цией Н (на эту прямую) точки
Рис. 90	Лх	и хотя бы одной из точек
D, Е, например точкой D. По¬
этому проекция HD наклонной A%D не меньше проекции НВ1
наклонной AiBf, т. е.
AiBi ^ AtD.
По той же причине имеем
£)>4x<max{DF; DC}, ДЛх^шах {££; ЕС}.
Из оценок
EF? < CD? = ОС? + OD?—20С • OD cos 45° =
4	4
ЕС? = FD? = OF? + OD?—2 OF -OD cos 45° =
, . 25	5	fTT
„2.	“£1=3,75<,.
5-1 4
< 7,25— —i—=3,75 < 4
получаем
ЛхВх<шах{£)£; DC; EF; EC} < 2,
Утверждение доказано.
13.23.	Обозначим
OAi — ai, OB = b (1=1,	n),
тогда имеем
242
(a,-|=l, BAi = OAi — OB = ai—b

1=1
2 BAt= 21 ei-»i= 2 ie/-»i-ie/is»
■	i=l	i=	I
n	n	П
Ss	2 (“i — b)a«= 2 ar~b 2	of = «-&.0 = n,
i= l	t= l	«= l
что и требовалось доказать.
13.24.	Заметим,	что если точки А, В, С, D, Е	глежат на одной
прямой, то	неравенство выполнено. Действительно,	пусть для опре¬
деленности точка Е лежит между
точками С и D, тогда имеем
\AC+AD) +
+(BC+BD + AE+BE)3*
SsCD+CD + AB =
= (CE+ED) +CD + AB,
Фиксируем некоторую прямую
на плоскости и точку О на ней.
Обозначим через /ф образ прямой
/0 при повороте на угол <р против
часовой стрелки вокруг точки О, а
п'рез Хф —проекцию произволь¬
ной точки X на прямую /ф. Тогда
для любого отрезка XY, параллельного некоторой прямой /ф, имеет
место равенство
ХфКф = ХК-| cos (if—ф) |
(рис. 91), из которого получаем
^ХфТф£/ф = ХУ	cos (ip—if) | d<p = XY J | cos x MX —
о	о	-ip
я	Я/2
= ХУ J I cosxMx= 2XY j cos%d% = 2XY
(ибо интеграл л-периодической функции | cos % I на отрезке длины л
не зависит от расположения этого отрезка на числовой оси). Следо¬
вательно, интегрируя по ф в пределах от 0 до л обе части установ¬
ленного выше иеравеиства для проекций У1Ф, ВФ,СФ, £>ф, £ф данных
точек на прямую /ф
^фйф+СфДф -f-ДфДф | £'фСф AfpCfp -f- AfpDfp -f-Иф/зф -[-ВфСф -f-
-|- бф£)ф -(-Вф^ф,
получаем неравенство
2АВ+2CD+2DE+2ЕС < 2AC+2 AD -f 2AE+2BC+2BD+2BEt
равносильное требуемому.
£43

§ 14. Геометрические задачи на экстремум
14.1.	Пусть AD—большее основание, а ВН—высота данной тра¬
пеции ABCD (рис. 92). Тогда
AD= 13
(в противном случае AB — CD= 13, AD-\-BC = 2&— 2-13 = 2 и S/bcd=
= BH.(AD+BC)/2< 13-(2/2)= 13 < 27),
АВ = х,
ВС= 28-13-2*= 15—2х, Л/7=13~(1|~~2^—х—18
ВН = У АВ?—АШ = У 2х— 1.
В	С
АН	В
Рис. 92
Применяя теорему о средних, получаем
SABCD= ]Г2^1-(28-2х)/2= У(2х-1) (14—х)2 <
< /(g»-') + (l4-,) + 1H-4y=1/-
причем равенство SABBB)=27 возможно лишь в случае
2х—1 = 14—х, т. е. х = 5,
• и AB — BC=CD—5, а равенство
5лясв=27>001
невозможно.
14.2. Пусть о, Ь, с—стороны треугольника с заданным полупе-
риметром р, S—его площадь, а г — радиус вписанной окружности.
Тогда по теореме о средних имеем
(rp)?=S2.=p(p—a) (р—Ь) (p—t) s;
^ _ ((Р—а) + (Р— *) + (Р—c)V_ Р4
^РI,	3	)	27	’
откуда г < р/У27, причем наибольшее значение величина г прини¬
мает в случае р—а = р—Ь = р—с, т. е. когда треугольник правиль¬
ный.
14.3. Пусть через точку А, находящуюся иа расстоянии k от
центра О окружности, проведены перпендикулярные хорды KL и MN.
Опустим перпендикуляры ОВ и ОС на хорды KL и MN соответст-
244

венно и обозначим </ ЛОВ = а (рис. 93). Тогда
KL = 2В£ = 2 У1— k2 cos2 а,
MN—2МС = 2 У\—k2 sin? а
(KL-\-MN)2 = 8—Ak2 (cos2 а+sln? a)-f-
+8 У l—k2 (cos? сс + sin2 a) + № cos? a sin2 a =
=8—4*2+4	4—4k2+k* sin2 2a.
Последнее выражение максимально при sin2a=l, т. е. при а = 45°,
и минимально при sin 2a = 0, т. е. при а = 0° или а = 90°, Поэтому
наибольшее значение величины KL -\- М.N равно
У 8—4£?+4 (2—k2) = 2 У A —2k2,
а наименьшее—равно
|/'8_4fe2+8 УТ^к2 = 2(\ + УТ^к2)-
14.4.	Пусть К, М, N—середины сторон АВ, ВС, CD, DA
четырехугольника ABCD (рис. 94). Тогда имеем
М4=у (KA+AD+DM) + у (Ш + ВС+СМ) = у (Л£> +ВС)
и аналогично
Поэтому
Н=у(лв+пс).
КМ=i-1 AD + ВС I < i- (AD + ВС)
| ЛВ+DC |< 1 (ЛВ + ВС).
245

и справедливо неравенство
КМ +LN < у {АВ + ВС + CD+DA),
в котором равенство достигается тогда и только тогда, когда векторы
AD, ВС коллииеарны и векторы АВ, DC также коллинеарны, т. е.
когда ABCD—параллелограмм.
14.5. Поскольку имеют место соотношения (рис. 95)
ОЛ?4-ОВ?+ОС24-ОП? =
= ^ {О А2 + ОВ2) +-1 (ОВ?+ОС2)	(ОС? +0D2) +-1 (ОО?+О А2)
SsOA-OB + OB-OC+OC-OD + OD.OA^s
^ 2S/ ов 4~ 2Sb о с 4~ 2Sc od 4~ 2Sdcm = 2S,
причем равенства достигаются только при
0у4 = 0В = 0С = 0О и £AOB = £BOC=£COD = £DOA,
то диагонали АС и BD данного четырехугольника ABCD перпенди¬
кулярны и делятся в точке О их- пересечения пополам, т, е. ABCD —
квадрат с центром О.
14.6. Положим
о1 = Л2Л3, о2 = Л1Лд, а3 = А1А2,
hi = A\Hf, й2=Л2//2, ha=A3H3,
тогда справедливы равенства
os^i4" 0j/i2 4~ a2h3 =
= «Л %-+а*. f-=2S(?-+-^+^)-
Oi	^2	с3	\	G1	°2	с3	/
По теореме о средних имеем оценку ——3, в которой
Ol 02 Og
246

равенство достигается тогда и только тогда, когда
03	п2
-Т-=ТГ=-7Г • т- е- Ci = «2 = os.
Ci	С2 С3
Поэтому условие
csfti -f"Ci/i2 “ I с2й3 = 65
равносильно условию с1 = о2 = Оз, что и требовалось доказать.
С
14.7. Пусть ha, hi,, hc—высоты треугольника, удовлетворяющего
указанному в условии задачи равенству, a S—его площадь, тогда
(рис. 96)
aslnP=hc, bsiny~ha, csina — hi,,
и исходное равенство равносильно условию
Р (Лд+ЛС) = 9R (a cos а + b cos р -j- с cos у).
С одной стороны, согласно теореме 75, имеем
9 R (a cos а + 6 cos Р+с cos у) =
= 9R (2R sin а cos а + 27? sin р cos Р +27? sin Y cos Y) =
= 97?? (sin 2а+sin 2p+sln 2y)= 18S.
С другой стороны, пользуясь теоремой о средних, получаем
^(Йд + Й|>+Йс) = (а + Ь + С) (Йд + Йь+Йд)^
^9 abc \/йдй|,йс = 9 {УahabhbChc =9 {У(2S)3= 18S.
При этом равенство достигается тогда и только тогда, когда
а —^ b с, йд—й6 — йд,
т. е. когда треугольник равносторонний.
14.8. Пусть правильный л-угольиик В±...Вп площади Sg вписаи
в правильный л-угольник А±...Ап площади S/. Тогда, если они не
совпадают, то на каждой стороне A,-A,-+i при 1=1, ..., п (Ап+1 =
= А{) лежит ровно одна вершина, для определенности В,-. Действи¬
тельно, в противном случае по принципу Дирихле (теорема 1) хотя
247

бы на одной стороне, скажем А±А2, лежат две точки В1 и В2 (для оп¬
ределенности АгВ2 > AiBi), тогда вершина Ва (лежащая в треуголь¬
нике AiA2Aa, подобном треугольнику BtB2Ba) и вершина Вп (в тре¬
угольнике AzAiAn) могут лежать только на сторонах А2Аа и АгАп
Рис. 97
соответственно (ввиду п > 3 отрезки А2Аа и А2Ап являются диаго¬
налями, а не сторонами л-угольника А±... Ап), а значит, Bt = Аг и
В2 = А2. Докажем, что
AiBf = АаВа — • • • — А„Вп.
В самом деле, треугольники BiA2B2 и В2АаВа равны (рис. 97), по¬
скольку
Z BiA2B2 — Z В2АаВа — Z ВгВ2Ва = 180°-(я — 2)/я,
Z А2В±В2=\Ш— £ BiA2B2- £ A2B2Bi =
— 180°— Z BiB2Ba—Z A2B2Bi= £ AaB2Ba,	ВХВ2 = В2В3.
Поэтому j42B2 = j4sBs; аналогично доказываются остальные равенства.
Величина
SB~SA — SBtA,Bt — SB,A,Вг~~ • • • ~SB„AtBi ~SA~п5ВгА,В,
принимает наименьшее значение, когда площадь треугольника ВгА2В2
максимальна. Пусть
у41у42 = о,	А1В1 = х,
тогда величина
^в,Агвг~~2 &iA2'A2B2 sin Z В2А2В2 —
= Y (о—-*) х sin Z BtA2B2 = Y ^	(*~t) ) slnZ ВИ2В2
принимает наибольшее значение при х=а/2, т. е. когда •41B1 = Bi/42.
Утверждение доказано.
14.9.	Докажем, что наибольшее значение а равно 180°/л. Дейст¬
вительно, пусть некоторому расположению точек на плоскости соот-
248

ветствует значение а. Рассмотрим такую прямую, скажем A[A'2i от¬
носительно которой все точки расположены в одной полуплоскости,
и выберем точку А3, для которой угол AtA2A3 максимален
(рис. 98). Тогда все остальные
точки лежат внутри этого угла и
ЛхЛгЛз^а (л—2),
так как каждый из л — 2 углов
между соседними лучами А2А{
(Л,- Ф Л2) не меньше «. Далее,
выберем точку Ai> для которой
угол £_ А2А3А3 максимален.
Тогда все точки
Л/6{Лг; Лз; Л4}
лежат внутри этого угла и
^ А2А3А3^ а (п—2).
Если Л4 Ф Ai и А\ ф А2, то вы¬
берем аналогично точку А3 и т. д. Так как число точек равно л,
то одна из точек в последовательности А[, А2, А3, ... обязательно
первый раз повторится. Пусть это произошло после выбора точки
Л*, т. е. угол £_ Ak-\AkAj максимален для некоторой точки
Л/=Л|£{Л|; —; Л*_2}»
Тогда, если i ?£ 1, то точка А\ лежит внутри угла £ Л*_1Л*Л/, а
значит, и внутри выпуклого многоугольника А\А\+\.. .Л*_1Л*, что
противоречит ее выбору. Поэтому /=1 и выпуклый k-угольник
AiA2...Ak имеет сумму углов
откуда
а ё:
180°(fe—2)3вй.сс(л—2),
180° (k — 2)	180°
  180° /	2 \ 180°	/	2 \	180°
(л — 2) k л— 2 \	k )^п — 2	\	п )	л
При этом равенство а=180°/я возможно лишь в случае, если А = я,
А\А2А3 = ^ Л2ЛзЛ4= .•• = £, АкА\А2 = а (л— 2),
и все диагонали, исходящие из любого угла л-угольника А\.. .Ап,
Делят его на равные углы а. Такой я-угольник может быть только
правильным, поскольку для любого значения /= 1, ..., л имеем
Z AiAi+zAi+i— £ Ai+2AiAi+i, т.е. AiAi+1 — Ai+iAi+2
(считаем A„+i— Ах, /1,1+2 = А2) (рис. 98), следовательно, л-угольник
249

должен иметь не только равные углы, но и равные стороны. Наконец,
вершины правильного я-угольника действительно удовлетворяют усло¬
вию а=180°/л. Это становится ясным, если описать около «-уголь¬
ника окружность и заметить, что все углы между соседними диаго¬
налями, исходящими из любой вер¬
шины, опираются на дуги 360°/п,
а значит, равны 180°/л.
14.10. Пусть ABCD—квадрат
с центром О и стороной а, содер¬
жащий 5 непересекающихея кругов
радиуса 1.	Тогда центры кругов
лежат во	внутреннем квадрате
AlB1C1Di с центром О и стороной
а—2 (где y41fil||J4fi; рис. 99). Пря¬
мые, соединяющие середины про¬
тивоположных сторби квадрата
AiB1C1D1, разбивают его на четыре
маленьких квадрата, в одном из ко¬
торых (по принципу Дирихле (тео¬
рема 1)) расположено по крайней мере два из центров кругов. Тогда
расстояние между	ними,	с	одной	стороны, не	превосходит диагонали
маленького квадрата,	а	с	другой стороны,	не меньше 2. Поэтому
имеем
2*sCMi =
AiBt
V~2 =—п—Уг2,
откуда
as=2 У2 +2,
Наконец, если a = 2J^2+2 и
центры кругов лежат в точках О,
Ai, В±, Ci, Du то все требуемые
условия выполнены. Таким образом,
искомый квадрат имеет сторону
2 J/T+2.
14.11. Пусть точки Ai, Blt Ci
являются соответственно середи¬
нами сторон ВС, АС, АВ данного
треугольника ABC, для которого
радиусы R и г описанной и впи¬
санной окружностей соответственно
удовлетворяют равенству R = 2r. Тогда радиус р окружности, опи¬
санной вокруг треугольника	подобного треугольнику ABC
(с коэффициентом подобия 1/2), вдвое меньше радиуса R. Если эта
250

окружность не касается некоторых сторон треугольника ABC, то
проведем касательные, параллельные этим сторонам, к соответствую¬
щим дугам этой окружности, выходящим за пределы треугольника
(рис. 100). Тогда окружность радиуса р вписана в получившийся
треугольник А2В2С2, подобный треугольнику ABC и имеющий боль¬
шую площадь. Следовательно, имеем г < р= RJ2, что противоречит
условию задачи. Таким образом, указанная окружность касается
сторон АВ, ВС, АС, откуда по свойству касательных получаем
АВ\ = ACi, BCi = BAi, поэтому АС~ АВ = ВС, т. е. треугольник
ABC равносторонний.
14.12.	Докажем, что если через точку О проведены отрезки В1С1
и В2С2, концы Bi и В2 которых лежат на стороне АВ данного угла
В
Рис. 101
ВАС, а концы Cj и С2 — на стороне АС, причем
АОВ2 > AOBi ^ 90°
(рис. 101), то
J 	1_ J 1
/ДО+CiO > В20^С20 *
Обозначим через В3 и Са точки пересечения прямой ВгСi с прямыми,
проходящими через точки В2 и С2 соответственно параллельно пря¬
мой АО. Так как
£ В2В30=£ АОВ3^ 90°,
ТО ОВ2 > ОВ3 и
1	1	B20—Bi0	ВзО—ВгО Вф3 _ В2В3
BiP В20~ BiP-B20 > BjO-B20 ~в1о-в2р'~ ао-в2о
251

(ибо Д бхб3б2 счз Д В)ОА). Аналогично получаем
J	1	' С2С3
CjO С20 > А0-С20'
Складывая полученные в итоге неравенства и учитывая подобие тре¬
угольников баб30 и СаС30, имеем
JL . J (Л „ б2б3	с2с3
\в2о'~с2о)	А0*б20	ло-с2о
  1	( б2б3 С2С3	\
б20 СаО	/	'
Если прямая, проходящая через точку О перпендикулярно прямой
АО, пересекает лучи АВ и АС в точках б, и С, соответственно, то
отрезок В1С1 искомый. Действительно, для любого другого отрезка
б2С2, проходящего через точку	О, имеет место	одно из	неравенств
£ АОВ2> Ж	или ^ ДОС2 >	90°
(для определенности можно считать, что точки	б2 и Са	лежат	на
лучах АВ и АС соответственно	и выполнено, например,	первое	из
неравенств). Тогда справедливо доказанное выше неравенство. Если
же прямая, проходящая через точку О перпендикулярно прямой АО,
не пересекает одну из сторон угла ВАС, скажем сторону АС, то ис¬
комый отрезок построить	нельзя.	Допустим,	что искомым является
некоторый отрезок б2С2,	концы б2	и	Са	которого лежат на	лучах
А В и АС соответственно	Тогда
£ АОВ2> 90°,
а значит, если выбрать точку С1 на продолжении отрезка АС2 за
точку С2 и провести еще один отрезок С1В1 через точку О, то снова
90° < £_ AOBi < ^ ЛОба
и в силу доказанного выше неравенства отрезок б2С2 ие удовлетво¬
ряет требуемому условию.
14.13.	а) Пусть треугольник АБС нетупоугольный. Тогда иско¬
мая точка Т есть центр О описанной около треугольника окружно¬
сти радиуса R. Действительно, перпендикуляры ОНъ ОН2, ОН3,
опущенные из точки О иа стороны АВ, ВС, АС соответственно, раз¬
бивают треугольник ABC иа три четырехугольника
OHiAHa, ОНгВН2, ОН2СИ3 (рис. 102).
Если точка Т ф. О лежит, например, в первом из четырехугольников,
то
m (Т) ^ АТ < A0 = R — m(0),
ибо точка Т лежит в круге с диаметром АО (содержащем весь че¬
тырехугольник ОД1АД3: вследствие равенств
^ ОН1А = £ОН3А = Ж
252

этот четырехугольник вписан в окружность с диаметром АО). Пусть
теперь в треугольнике ABC угол при вершине А тупой и ^ С<; В.
Через середины D, Е сторон АВ, АС проведем перпендикуляры к
этим сторонам до пересечения их в точках F, G соответственно со
В
стороной ВС и обозначим BF=b, СО = с. Заметим, что Ь ^ с, при¬
чем равенство Ь = с имеет место лишь в случае /. С = £ В. В самом
деле, из треугольников BDF, CEG и ABC (по теореме синусов) имеем
b BD	cos ^ С АВ cos ^ С sin С cos ^ С
с	costs’	СЕ	AC cos ^ В sin ^ В cos ^ б
sin (2^ С)
sin (2 / В)
так как 0 < 2	С<2 ^ б < 180°—2 ^ С. Заметим далее, что
BG > с (а тем более FC > £>), поскольку
Z B+ZC < 90° < Z еле,
а значит,
</В< £ВАС—£С=£ BAG и BG>AG = GC = c.
Наконец, высота АН треугольника ЛВС разбивает его на два тре¬
угольника АВН и АСН. Если точка Т ф. F лежит в треугольнике
АВН, то
m (Т) < m (F) = b,
ибо она лежит либо в круге с диаметром BF, либо в круге с диа¬
метром AF (рис. 103 и рис. 104, на которых изображены случаи
253

В < 45° и Z. В > 45° соответственно). Аналогично, если точка
Т фй лежит в треугольнике АСН, то m (Т) < m (G) = с. Таким
образом, если треугольник ABC равнобедренный, то искомыми являются
обе точки F и G, а если он неравнобедренный, то
m(F) < m (С)
и искомая точка совпадает с точкой G.
б) Для любой точки Т треугольника ABC имеем
М (Г) S& ТВ, М(Т)^ ТС,
откуда
2/И (Г) ^ ТВ + ГС Ss ВС, т. е. ВС/2 < /И (Г).
Наконец, согласно утверждению, доказанному в п. а), величина m (Т)
в случае А > 90° достигает наибольшего значения в некоторой
точке G отрезка ВС. Поэтому для любой точки Т треугольника ABC
имеем
m (Г) < m (G) min {GB; GC} < ВС/2.
254

Глава 4
СТЕРЕОМЕТРИЯ
§ 15. Тетраэдры
15.1.	Пусть АВ — наибольшее ребро тетраэдра ABCD. Тогда
имеем (рис. 105)
{AC+AD — AB) + (BC + BD—ВА) =
= (AC + CB — AB) + (AD + DB — AB) > 0,
поэтому справедливо хотя бы одно из неравенств ACAD > АВ или
BC-\-BD > В А, гарантирующих, что из ребер AC, AD, АВ или соот-
Л
Рис. 105
ветственно из ребер ВС, BD, В А можно соста¬
вить треугольник (остальные неравенства
треугольника вытекают из выбора ребра АВ).
15.2. Для данного в задаче тетраэдра
ABCD по теореме косинусов имеем (см.
рис. 105)
2АВ-АС cos Z ВАС=АВ*. + АС? — ВС? =
= AB2- + AD2—BD? = 2AB.AD cos	BAD,
откуда следует, что
sign cos Bv4C = sign cos ^ BAD,
т. e. углы ВАС и BAD либо одновременно острые, либо одновременно
неострые. То же самое можно утверждать (доказательство аналогично)
и про любые плоские углы этого тетраэдра, имеющие общую вершину.
Если все плоские углы тетраэдра ABCD острые, то любая его грань
является остроугольным треугольником. Если же хотя бы один из
плоских углов, скажем при вершине А, не является острым, то все
три плоских угла при этой вершине неострые, а значит, все осталь¬
ные плоские углы тетраэдра острые (ибо любая грань имеет по мень¬
шей мере два острых угла). В этом случае треугольник BCD остро¬
угольный.
15.3. Пусть через концы отрезка АВ длины d проведены прямые,
перпендикулярные друг другу и отрезку АВ. На этих прямых рас¬
положены по одному отрезку длины а с серединами А и В соответст¬
венно. Концы этих отрезков являются вершинами тетраэдра, у которого
каждая грань имеет площадь
(1/2) а V(a/2)2 + d?= (1/4) aVа2 + 4d2,
а объем равен a2d/6. Поэтому два тетраэдра, соответствующие значе¬
ниям Qj = 3, di — 2 и соответственно а2=1, 4г—У56, имеют оди¬
наковые площади граней (ибо Ci Va\-{-4d\= 15= а2a%-\-4d.t) •
но разные объемы (ибо	18	ф y56 = ald2). Итак, ответ иа
вопрос задачи отрицателен.
255

в
15.4. Предположим, что указанный в условии задачи тетраэдр
ABCD существует, и докажем, что ребро А В является наибольшим,
а ребро CD —наименьшим. Из условия задачи следует, что каждый
из углов АСВ, ADB, а также один из углов ACD или A DC, скажем
угол ACD, прямой (рис. 106). Положим ^ ВАС — ф. Тогда /_ ABD = rp,
поскольку в противном случае ^ BAD — ф и AC—AD, что невоз¬
можно (ибо AD—гипотенуза треуголь¬
ника ACD). Аналогично, £CDA = tр
(иначе £CAD = ф и AB = AD, что не¬
возможно). Поэтому имеем равенства
BD—АС =* АВ совф,
ВС = AD = АВ sln ф,
CD — AD cos ф = АВ sin ф cos ф,
AC = AD sln ф = АВ sln2 ф,
откуда, в частности, получаем, что
cos ф = sin2 ф = 1 — cos2 ф,
т. е.
Рис. 106	ф = агссоэ((У 5—l)/2).
Таким образом, наибольшее ребро А В имеет длину 1, а наименьшее
ребро CD—длину sin ф cos ф= ^"cos ф cos ф = [(У 5—l)/2)3^2. Для
доказательства существования такого тетраэдра достаточно заметить,
что если рассмотреть тетраэдр ABCD с ребрами
СА = (У~5— 1 )/2, СВ = ((УЪ—\)/2)1/2, CD — ((У~5— 1 )/2)3/2
и плоскими углами
^ ВС А =	DC А = 90°,	BCD = arccos (( У~5 — 1 )/2),
то
AB=l, AD — CB, BD = AC, £САВ=£ BCD,
откуда вытекают равенства
ДА5П = ДВАС, ДС5П = ДОАС
и подобие всех граней тетраэдра.
15.5. Поскольку любая из проведенных плоскостей содержит один
из отрезков, соединяющих середины противоположных ребер тетраэдра,
то все плоскости проходят через точку пересечения этих отрезков,
лежащую внутри тетраэдра (см. теорему 92). Поэтому шесть проведен¬
ных плоскостей разбивают все пространство иа многогранные углы
с общей вершиной, а значит, любая из частей тетраэдра имеет хотя
бы одну грань, принадлежащую грани тетраэдра. С другой стороны,
никакие две грани тетраэдра не могут служить границей одной и той
же части, так как любые две его грани отделены друг от друга
плоскостью, проходящей через их общее ребро. Таким образом, число
частей тетраэдра равно числу частей, на которые разделена его поверх-
256

иость, а так как каждая грань тетраэдра разделена на 6 частей (в ней
проведены медианы), то всего частей имеется 6-4 = 24. Из соображе¬
ний симметрии (относительно любой из шести плоскостей) следует,
что все части тетраэдра равны между собой, а объем каждой из них
равен J/24.
15.6.	При любом расположении точки D в плоскости треуголь¬
ника А'В'С' хотя бы одна сторона этого треугольника пересекается
с прямой, проходящей через проти¬
воположную ей вершину и точку D.
Пусть для определенности О—точ¬
ка пересечения стороны А 'В' с пря¬
мой C'D, а прямая, проходящая
через точку О параллельно пря¬
мой DD’, пересекает плоскость
ABC в точке О' (рис. 107). Тогда
из параллельности прямых А А’,
ВВ’, СС, DD', 00' вытекает, что
отрезок АВ пересекает в точке О'
прямую CD'. Обозначим через <р
угол между прямой 00' и плоско¬
стью ABC. Тогда имеем
1
DD'
VABCD = 'jSABC'DD'’sla({l = -QQr • -дг SAgC‘00'шsinФ^-qqT УАвсо
и аналогично
DD'
VA'B'C'D' = ~оогУ А'В'С'О»
Далее, пусть а—расстояние между прямыми АА' и ВВ', тогда
5дво=у АВ'ОО'-sin Z. 00'В =i-a-00'
и аналогично
SA'B’0' = у я-00'.
Обозначив через b расстояние между плоскостью АВВ' и прямой СС’,
получаем
Уавсо=-^ Sab0- * = -g SA'B>0’■ b = VA-B'CO't
откуда
vABCD —~00г VABCO-
DD
00
—Va’B’C’O’ = Va’B'O’D' i
что и требовалось доказать.
15.7.	Пусть V—объем тетраэдра ABCD, a ft—искомое число.
Тогда имеем
V AAt АО . OAi
V obcd	OAi AiO OAi
= ft+l
® Под ред. И. H. Сергеева
257

и аналогично
откуда
V
V
VoACD V OAR D Vo ABC
АЧ
W
-=-f7-=4, т. e. k=
-3.
VoBCD + V OACD+V OABD + V О ABC
15.8.	Докажем, что все прямые KnLn при и £ N проходят через
фиксированную точку О, лежащую на прямой, проходящей через вер¬
шину А параллельно прямой ВС. Действительно, если прямая KnLn
пересекает прямую ВС в точке Р (лежащей на луче СВ; рис. 108),
то из подобия соответствующих треугольников имеем
РВ ВКп
О А АКп
1,
PC _CLn
О А — ALn
= п,
откуда получаем
ОА=пОА-
-(п— 1) ОА = РС—РВ = ВС.
Аналогично доказывается, что все прямые LnMn при n£N проходят
через фиксированную точку Q, лежащую на прямой, проходящей
через вершину А параллельно прямой CD. Следовательно, все пло¬
скости KnLnMn при n£N проходят через прямую OQ.
В
Рис. 108
Рис. 109
15.9.	Для того чтобы две прямые, соединяющие точки б и С с цент¬
рами окружностей, вписанных в треугольники ACD и ABD, пере¬
секались, необходимо и достаточно, чтобы они лежали в одной пло¬
скости. А это в свою очередь равносильно тому, что биссектрисы
углов ABD и ACD пересекают ребро AD в одной точке (рис. 109).
Последнее условие, согласно свойству биссектрисы треугольника,
выполняется тогда и только тогда, когда
АВ АС
BD CD ’
258

т. е. когда
AB'CD — AC'BD.
Таким образом, если четыре прямые, о которых говорится в условии
задачи, пересекаются в одной точке, то произведения длин противо¬
положных ребер равны. Обратно, если три указанных произведения
равны, то каждые две из четырех прямых пересекаются, причем никакие
три из них не лежат в одной плоскости, поэтому все прямые пере¬
секаются в одной точке.
15.10. Обозначим через V, S и г объем, площадь поверхности
тетраэдра и радиус вписанной в него сферы. Одна из частей, на
которые плоскость разбивает тетраэдр, есть пирамида с основанием,
лежащим в этой плоскости. Обозначим через Vi, Sj и rj объем, пло¬
щадь боковой поверхности этой пирамиды и радиус сферы с центром
иа ее основании, касающейся ее боковых граней. Основание пирамиды
проходит через центр сферы, вписанной в тетраэдр, тогда и только
тогда, когда г = тг. Последнее равенство, согласно формулам
V=(l/3)Sr, Vi = (l/3)V1(
равносильно равенству
V S	V—Vi	S—St
Vi - Si'T-e- Vt ~	'
что и доказывает утверждение вадачи.
15.11. Пусть ребра тетраэдра ABCD удовлетворяют условиям
АС _|_ BD, AD J_ ВС. Проведем через каждое ребро тетраэдра пло¬
скость, параллельную противоположному ребру. Полученные три пары
в'
Рис. 110
параллельных плоскостей образуют параллелепипед AB’CD’A'BC'D
1рис. 110). Параллелограммы AB'CD' и A’BC'D являются ромбами,
так как их диагонали параллельны взаимно перпендикулярным пря¬
мым АС и BD. Аналогично, AA'DD' и ВССВ'—ромбы, поэтому Beg
9*	259

ребра параллелепипеда равны между собой. Наконец, расстояние от
центра О симметрии параллелепипеда до середины любого ребра тет¬
раэдра равно половине ребра параллелепипеда (например, расстояние
от точки О до середины ребра АВ равно расстоянию от центра сим¬
метрии параллелограмма ABC'D' до середины его стороны АВ, т. е.
половине - ребра AD' параллелепипеда), откуда и следует утверж¬
дение задачи.
15.12.	Пусть правильный тетраэдр Тг вписан в правильный
тетраэдр Т2. Тогда радиус Ri описанной около тетраэдра Тг сферы S
не меньше радиуса г2 сферы, вписанной в тетраэдр Т2. Действительно,
проведя к сфере S касательные плоскости, параллельные граням
тетраэдра Т2, можно получить тетраэдр Та (подобный тетраэдру Т2,
а значит, тоже правильный), описанный около сферы S и содержа¬
щий тетраэдр Т2. Поэтому радиус ra = Ri вписанной в тетраэдр Та
сферы не меньше т2. Так как радиус тг вписанной в правильный
тетраэдр Тх сферы втрое меньше,
чем Ru то Зг1 = /?1^г2, откуда
вытекает требуемое неравенство.
15.13.	Пусть для определенно¬
сти точка М лежит на стороне А В
треугольника ABC и /_ MDB = ф
(рис. 111). Тогда
S = c-j-a cos ф + b sln ф
и, обозначив
d = a cos ф + b sin ф,
ф=агссоэ (а/У а2 + Ь2),
имеем неравенство
d=V"^+Px
X (cos ф cos ф + sin ф sin ф) =
= У гг2 + Ь2. cos (ф—ф)<У а2-\-Ь2,
причем равенство достигается тогда и только тогда, когда ф = ф,
т. е. когда
cosy = AD/AB = cos Z.DAB или DM_]_AB.
Далее, используя теорему о средних (теорема 6), получаем оценку
S = c+d< V2 (c2+d2),
в которой равенство достигается тогда и только тогда, когда c=d.
Таким образом, требуемое неравенство
S<y2{c2+a2+b2)
доказано. Равенство достигается в том и только в том случае, если
ребра AD, BD, CD могут служить тремя сторонами прямоугольного
260
С

треугольника, a DM— высота, опущенная на меньшую из сторон
треугольника ABC.
15.14.	Пусть точка О лежит внутри тетраэдра ABCD. Обозначим
через Р точку пересечения прямой DO с плоскостью ABC, а через Q
В
Рис. 112
точку пересечения прямой ВР со стороной АС (рис. 112). Тогда по
теореме 84 получаем
£АОВ + £ АОС= Z АОВ + Z AOQ + £QOC> Z BOQ + Z QOC =
= Z ВОР+ Z POQ + Z QOC > Z ВОР+ Z РОС =
= 180°— Z BOD +180°— Z COD,
откуда имеем
Z АОВ + ^ ЛОС + / BOD + Z. COD > 360°.
Аналогично получаем неравенства
Z AOB + Z BOC+Z AOD + Z COD > 360°
и
Z AOC+Z BOC + Z. AOD + Z BOD > 360°,
Сложив эти три неравенства и разделив обе части полученного нера¬
венства на два, получим требуемое.
15.15.	Докажем, что если расстояния от точки Л1 до вершин тет¬
раэдра ABCD с ребром 2 являются целыми числами, то хотя бы одно
из расстояний равно 0 (обратное утверждение сомнений не вызывает).
Заметим, что если точка М расположена на прямой, содержащей ребро
тетраэдра, скажем ребро АВ с серединой Н, то, обозначив МН — х,
МС = у, имеем у > *3г0 и x2 + (j^ 3)2=у2, откуда
(у—х)(у+х)= 3 и у—х= 1, у+х = 3,
поэтому х=1, а это значит, что точка М совпадает с одной из вер¬
шин А или В. Если же точка М не лежит ни на одной из таких
261

прямых, то кратчайшее расстояние х > 0 до вершин тетраэдра отли¬
чается от остальных расстояний менее чем на 2, т. е. каждое из рас¬
стояний равно либо х, либо х+1. Рассмотрим четыре случая.
1) Все четыре расстояния равны х. Тогда М—центр описанной
около тетраэдра сферы радиуса У 6/2, что невозможно, ибо х£ N.
2) Три расстояния равны х, а одно— х+1. Пусть для определен¬
ности
МА = МВ = МС = х, MD = x+1,
а точка О—центр треугольника ABC. Тогда точка А1 лежит на лу¬
че DO, причем х^ АО — 2/У 3 > 1, т. е.
DM = x+l >2 >2 Y2/3=DO^DAI—MO = x+l — Yx2—4/3,
откуда
х+1=2 УЩ-\-Ух2 — 4/3 = 2 У 2$ + *л(х—1/2)2+х—19/12 >
> 3/2+х—l/2 = x+1,
что невозможно.
3) Три расстояния равны х + 1, а одно равно х. Аналогично
случаю 2) считаем
MD = x^ 1, МА = МВ = МС = х+1 Ss2.
Тогда точка М лежит на прямой OD, причем точка О не может
находиться между точками М и D, так как иначе
х=2 j/"2/3 + Y(х+1)2—4/3 > 1+х.
Поэтому точка М лежит на луче OD и
2 Y2/3=-OD = OM — MD= К(х+1)2 — 4/3—х < х+1— х=
= 1 < 2 УЩ,
что также невозможно.
4) Два расстояния равны х, а два другие— х+1. Пусть для
определенности
МА = МВ = х^ 1, MC=MD = x+lS&2.
Заметим, что х Ф 1 (поскольку согласно доказанному выше точка
М ие может лежать на прямой АВ), следовательно, х^2. Пусть
точки Е и F —середины отрезков АВ и CD соответственно. Тогда
точка М лежит на луче FE, причем
MF = Y(х+1)2—1 Зг Y~3 > Y~2 = EF,
откуда имеем
Y (х+1)2—1 — Vx*—1 = MF — ME = EF *= У "2,
что невозможно, так как
Y(х+1)2—1 — Y^^i < У”2 при 1 < xgN.
Таким образом, утверждение полностью доказано.
262

15.16.	Обозначим через V и 5 объем и площадь поверхности
тетраэдра, а через S; площадь той его грани, которая соответствует
высоте hi тетраэдра и касается вневписаиной сферы радиуса г/. Тогда
имеем равенства
ЗУ = А454 = Ti (S2 +S3+S4 — S4) = r± (S—2.S,)
и аналогично
3V = hiSi=n(S—2S/)
при остальных значениях i. Поэтому получаем
i	I	I	i	i	oc
'	-(S-2Si-fS-2S2+S-2Ss+S-2S4)=—==
3V
(S1+S2+S3+S4) =2 [-L+-L+-L+-Ly
т. e. равенство справедливо.
15.17.	Пусть в тетраэдре v41/42j4s/44 обозначено: А/—высота, опу¬
щенная из вершины А[, a S,-—площадь соответствующей грани, (14,
cf2, dg—расстояния между ребрами А2А3, AiA3, А\Аг и противопо¬
ложными ребрами тетраэдра соответственно, a Qi, Q2, Q3—площади
параллелограммов с диагоналями, параллельными и равными парам
соответствующих противоположных ребер тетраэдра, ф4, <р2, Фз —
двугранные углы при ребрах А2А3, ALA3, АХА2. Тогда объем тет¬
раэдра равен
V = -g-	=	— dfrQk
(см. теорему 87; здесь н ниже i= 1, 2, 3, 4; А= 1, 2, 3). Далее, имеем
S4 = S4 cos фг+52 cos фг+Ss cos ф3
(см. теорему 90) и, наконец,
Si-}-—2StSk cos фд —Qk*
Последнее равенство можно доказать, если провести плоскость, пер¬
пендикулярную, скажем, ребру А2А3, и заметить, что для длин проек¬
ций а, Ь, с ребер ALA2, А2А4, АХА4 соответственно на эту плоскость
по теореме косинусов имеет место равенство
с2 -f- 6?—2ab cos фх = с2.
Умножая обе части этого равенства на число (Л2Л3/2)2, получаем
требуемое равенство при k—\. Аналогичные рассуждения можно про¬
вести и при остальных значениях к — 2, 3. Таким образом, получаем
Qi-J-Q|-}-Q3 = 3S4-|-Si-|-S2-j-Sa—
— 2S4 (Sj cos ф1+52 cos ф2 +S3 cos фз) = 5|+51+5з+51>
263

откуда
• , 1 _l_L
dl
d\ dl
Qi , Ql , Ql	S\	Si Sl Si
91/2 T QV2 ■ дуг дуг 9V2 ' 9V2 ' 9V2
1
1
1
1
~ h{+ hi + hl + hi '
что и требовалось доказать.
15.18. Обозначим через К, L, М, N точки касания ребер АВ,
ВС, CD, DA соответственно со сферой (рис. 113). Через центр О сферы
проведем прямую I перпендикулярно плоскости квадрата KLMN.
Четыре плоскости, касающиеся сферы в точках К, L, М, N, об¬
разуют равные двугранные углы
с плоскостью квадрата, а значит,
либо параллельны прямой /, либо
пересекаются в некоторой точке S
на прямой I. В последнем случае
оии образуют правильную четырех¬
угольную пирамиду с вершиной S,
основанием, содержащим квадрат
KLMN, н апофемами SK,SL,SM,SN.
Так как ребра АВ, ВС, CD, DA ле¬
жат в соответствующих гранях этой
пирамиды, то точки А, В, С, D лежат
на ее ребрах. Из равенства биссектрис
SK, SL, SM, SN равных углов ASB,
BSC, CSD, DSA вытекает равенство
треугольников ASB, BSC, CSD, DSA,
откуда получаем
S/i = SC, SB — SD, AK=CL = CM =
= AN,
Рис. 113
^ а если ребро AC также касается сфе¬
ры, то
AC = AK+CL = 2AK.
Из подобия равнобедренных треугольников /ISC, BSD по свойству
биссектрисы треугольника имеем
BD/AC = SB/S А = КВ/АК,
откуда
АС
BD=-£r- КВ = 2КВ.
АК
Поэтому для середины Р ребра BD, лежащей на прямой I, справед¬
ливо равенство ОР — ОК (ибо прямоугольные треугольники ВОК и
ВОР с общей гипотенузой ВО имеют равные катеты ВК и ВР), т. е.
ребро BD касается сферы в точке Р. Наконец, в случае, если четыре
264

упомянутые касательные плоскости параллельны прямой /, то и тогда
они пересекают плоскость квадрата KLMN по сторонам некоего квад¬
рата, причем серединами его сторон также служат точки К, L, М,
N. В этом случае
АК = КВ ~BL = LC = СМ = MD = DN»= AN
и центр О, совпадающий с центром квадрата KLMN, равноудален
от ребер АС и BD, а значит, сфера может касаться этих ребер только
одновременно. Утверждение доказано.
15.19. Пусть около тетраэдра ABCD описана сфера с центром О
и радиусом R. Обозначим
a = OA,b — OB, с = ОС, d=OD
• ' ►
н, вообще, х*=ОХ для любой точки X пространства. Тогда
a2 = b2=zc2 = d2 = R2.
Так как а _]_ О А, то точки X, принадлежащие плоскости а, задаются
уравнением
а(х—а) = 0, нли ax = R2.
Аналогично, точки X, принадлежащие плоскостям Р, у, 6, задаются
уравнениями
bx = R2, cx=R2, dx=R‘i
соответственно. Заметим, что уравнение
(Яа + р&)*=(Я+р) R2
для любых значений Я и р, не равных нулю одновременно, задает
плоскость, проходящую через прямую I пересечения плоскостей а и
Р (нбо Яа + р&^О и для любой точки Х£1 имеем ax — bx—R2).
Кроме того, для любой точки X пространства найдутся такие числа
Я и р, не равные нулю одновремеиио, что
Я (ax—R2) + р (Ьх— R2) = О,
т. е. через любую точку X проходит плоскость, задаваемая некото¬
рыми значениями Я и р. Поэтому прямая CD лежит в одной плоско¬
сти с прямой / тогда и только тогда, когда система
( Я (ас—R2) -1- р (be—R2) = О,
\ Я (ad—Я2) + р (bd— R2)=0
имеет ненулевое решение (относительно пары неизвестных Я, р), т. е.
когда
(ac—R2) (bd — R2) = (ad — R2) (bc — R?).
Аналогично доказывается, что линия пересечения плоскостей у и б
лежит в одной плоскости с прямой АВ тогда и только тогда, когда
(ca — R2) (db — R2) = (cb—R2) (da—R2).
Так как два полученных условия равносильны, то утверждение за¬
дачи доказано.
265

§ 16. Многогранники, сферы и другие множества
16.1. Если обозначить через х ребро куба, то указанная в зада¬
че разность объемов равна
abc—Xs
ж=
abc + (х—а) х2—ах2.
x2-\-ab (с—х)— abx
х3 — abc
при
прн
при
при
О < х < а,
а < х < Ь,
Ь < х < с,
с < х.
Заметим, что функция f (х) непрерывна при х > 0, а ее производная
равна
(
—Зх?
, Зх2—4ах
f (х)= j Зх2—2аЬ
I Зх2
при 0 < х < а,
при а < х < Ь,
при Ь < х < с,
при с < х.
Следовательно, эта функция убывает при 0 < х < а, возрастает при
b < х (ибо Зх2—2ab > 36?—2аЬ > 0), а на интервале (с; 6) она либо
убывает, если 6<4с/3 (ибо Зх?—4ах < 36?—4а6<0), либо имеет
минимум в точке х = 4а/3, если 6 > 4а/3. Таким образом, наименьшее
значение функция f (х) принимает либо при х—Ь (если 6<4я/3),
либо при х = 4а/3 (если 6 > 4с/3), а искомое значение х равно
min{6; 4а/3].
16.2.	Проведем через’ центр О данного куба AiAzAsAiA'xAiAsAi
плоскость, перпендикулярную диагонали А4Аз (рис. 114). Эта плос¬
кость проходит через середины ВХ( В2, В3 ребер A^Al, А2Аз, А3А4
соответственно, ибо каждая из то¬
чек Вх, В2, В3 удалена от вершин
At и Аз на одинаковое расстояние
а У5 /2. Поскольку
Вх0 = В20=В30
и
ВХВ2 = В2В3=В3ВХ = а Уз/2 >
> a У 5/2,
то каждая нз двух правильных
пирамид
АффяВз и
(не имеющих общих внутренних точек) содержит правильный тетраэдр
с высотой	_
а\Гъ 12= AiP = AlO
и основанием Вфф^ гомотетичным треугольнику Вфф^ относитель¬
но центра О. Наконец, внутри этих тетраэдров
АхВффз н АзВуВфз
266

лежат искомые правильные тетраэдры, гомотетичные им относительно
их центров с коэффициентом 2	/3 < 1 и имеющие высоту a Y2/3,
а значит, ребро а.
16.3.	Рассмотрим тетраэдр с вершинами в данных точках Аъ А3,
As, At. Тогда пространство разбивается плоскостями его граней на
2 множества. Первое из иих объединяет 4 однотипных области, каж¬
дая из которых составлена из трехграиного угла при какой-либо
вершине тетраэдра и ему симметричного относительно этой вершины.
Если точка А3 лежит, например, в области, соответствующей верши¬
не At, то прямая АЬА4 пересекает треугольник А4А2А3 (рис. 115). Вто¬
рое множество объединяет 6 однотипных областей, каждая из которых
представляет собой пересечение двугранного угла при каком-либо ребре
Рис. 115	Рис.	116
тетраэдра с углом, симметричным двугранному углу при противополож¬
ном ребре относительно этого ребра. Если точка Аь лежит, например,
в области, соответствующей ребру А3А4, то прямая АгАг пересекает
треугольник А3А4Аъ (рис. 116).
16.4. Допустим, что, вопреки утверждению задачи, любая плоско¬
сть пересекает ие более 3 множеств. Выберем точки А, В, С, D, Е
разных множеств. Тогда никакие 4 из них ие лежат в одной плоско¬
сти, и, следовательно, никакие 3 не принадлежат одной прямой.
Далее, через некоторые 3 из иих проходит плоскость, относительно
которой остальные 2 точки расположены в разных полупростран¬
ствах (таким свойством обладает хотя бы одна нз плоскостей А£С,
ABD, АВЕ). Пусть эта плоскость проходит через точки А, В, С.
Точка F пересечения с ней прямой DE принадлежит одному из мно¬
жеств, содержащих точки А, В, С, например множеству, содержащему
точку А. Следовательно, плоскость, проходящая через точки D, Е,
F, В, пересекает не менее четырех множеств. Полученное противоре¬
чие доказывает справедливость утверждения задачи.
16.5. Пусть, вопреки утверждению задачи, пространство разбито
на 3 множества ЛД, М2, М3 и существуют такие положительные
числа	что	при	каждом	значении i= 1, 2, 3 между лю¬
267

быми точками множества Mi не реализуется расстояние с/. Рассмотрим
тетраэдр A BCD с ребрами 1
АВ = а4, АС = ВС — а2, AD = BD = CD = а3
(такой тетраэдр существует, поскольку центр О окружности, описанной
около равнобедренного остроугольного треугольника ABC с нуж¬
ными сторонами, лежит внутри него, а значит,
О А — О В = ОС < а2 < а3
и на перпендикуляре к плоскости ABC, проходящем через точку О,
найдется искомая вершина D) и расположим его в пространстве так,
что
А, В, С ф М3 и А, В ф М2.
Для этого достаточно поместить вершину D в какую-либо точку мно¬
жества Ms (если Мз = 0, то автоматически А, В, С(£М3), а вер¬
шину С в какую-либо точку множества М2, удаленную от точки D
на расстояние а3 (если таких точек не найдется, то автоматически
А, В 0 М2). Тогда получим, что А, В £ Mi и АВ=а4, что противо¬
речит сделанному предположению и доказывает утверждение задачи.
16.6.	Обозначим через Ап множество 2" всевозможных наборов
е = (eij	е„),
состоящих из чисел в,•£{—1; 1} (1=1, ..., л). Введем также обозна¬
чение
п
«е ~ 2
к= 1
где е£А„, а сц, ..., а„—произвольные векторы, и докажем индук¬
цией по n£N следующее равенство:
2 «1=2" 2
ееАп	k=i
При п— 1 равенство верно, так как
2 «I=«г + (—«1) - = 2а? = 21 2 °к‘
ее Л,	к= 1
Пусть равенство уже доказано для некоторого значения п—1 £ N.
Если в наборе
E = (ei>	еп—i!	е„)
выделить набор
е = (Bji ■*., Еп—i)
н обозначить
Л-1
«е' —
ft=i
то, используя справедливое для любых двух векторов Ь н с равен¬
ство
(Ь+с)? + ф—cf. = 2Ы+2d
268

(ср. с равенством параллелограмма), можно получить требуемое ра¬
венство для значения п:
2 «1= X ((ае- + а„)2 + (аЕ- — ап)2) =>
sgA п	е'€^п-1
= X 2 (а1'+Оп) = 2-2"-1 2 а1+2.2«-1а^=-2п 2 «*■
e'e^n-i	fc	=	i	*=i
Утверждение доказано.
16.7.	Пусть отрезок CD пересекает указанную в задаче плоскость
в точке Е, а точки С' и D’ — проекции точек С и D на эту плоскость
(рнс. 117). Из равенства прямоугольных треугольников СС’Е и DD'E
Рис. 117
(где СС' = DD' = а/2, ^ СЕС' = /_ DED') следует, что ОЕ — медиана
прямоугольного треугольника COD', откуда C'D' =20Е = 2г. Поэтому
CD —2 У С'С?+С'£2 = V4г2 + а2,
а точки С заполняют отрезок длины 4г с серединой в точке Л.
16.8.	Проведем плоскость, проходящую через точки А, В и центр
О сферы S. Сечением сферы s будет окружность с центром Of и ра¬
диусом ri<r, касающаяся прямой АВ. Пусть ОН и ОК—перпенди¬
куляры к прямым АВ и 0]С соответственно (рис. 118), тогда, обоз¬
начив
АВ = 2а, ОН = h,
получаем
А С2+6С2 = (с+НС)2. + (а—ЯС)2 = 2с2 + 2 НС =
= 2 (Я2—ОЯ2) + 2 (00\—Ох/С2) = 2 (Л2—А2)+2 (г2 — (rf—Л)2) =
= 2Я2—4А2 + 4Агх = 2Я 2 + г2—(2h — п)2 < 2Я2 + г2.
269

16.9.	Проведем через точку А прямую d, перпендикулярную
плоскости ABC. Тогда центры Ог и 02 сфер, касающихся сферы S,
лежат на прямой I, состоящей из точек, равноудаленных от точек
А, В, С, а значит, параллельной прямой d. Пусть А'—точка, сим¬
метричная точке А относитель¬
но прямой I, a D—точка пере¬
сечения прямых ОА' и I (рис.
119). Точка А (а также точка
А’) принадлежит обеим сферам,
поэтому 04А = Г]- и ОгА — г2-
Из условий касания сфер имеем
OjP = R — r-i н OaO = R — г2, по¬
этому
ОхО+OlA = r = o2o+o2a.
Докажем, что точки Ох и 02
симметричны относительно точ¬
ки D. Действительно, фиксиру¬
ем точку Оь для которой
Рис. 119	ОгО+OiA^R.
Тогда для точки ,02, симметричной точке 0± относительно точки D,
имеем
020+ 02А = Oi А + ОхО = R.
Далее, для любой точки 02, лежащей на прямой 1 между точками D
и 02, имеем
ОгО+ОаЛ = OjO+02Л' < 020-f 02Л'=020+02Л = Я
(нбо периметр внутреннего треугольника меньше периметра внешне¬
го), а для любой точки 02, расположенной на продолжении отрезка
270

DOt за точку 02, аналогично имеем
020 -\-02А > R.
Точно так же рассматриваются точки луча DO^. Таким образом, по¬
лучаем
R — r1 = 010 = 02A = r2,
откуда
ri + r2 —
что и требовалось доказать.
16.10.	Введем дополнительные обозначения: Q — площадь основа¬
ния, h— высота пирамиды, х—косинус двугранного угла между осно¬
ванием и боковой гранью, а—сторона основания, г—радиус окруж¬
ности, вписанной в основание. Тогда справедливы равенства
а = 2г tg (180°/п), Q=n( 1/2) ra = nr2 tg(I80°/n),
h = r tg (arccos x) = г V1 —x2/x, S = Q -j- (l/дс) Q,
откуда
Q=xS/(jc+1), r=	ntg (180o/n) = У n tg (i80°/n) x+T*
1 l n 1 У1—x2 -j^/" S	x xS
V=i-hQ =
3 v—3 x V «tg(l80°/n) x+\	x+\
1 ^ ...
3 Vntg (180°/n) *
где
а) Имеем
/' M =	—~,
2(l + x)2 1^(1—х)
поэтому наибольшее значение функции f (х) при дс£(0; 1) равно
f (1/3) = ]/"2*/4 (ибо /' (дс) > 0 при х < 1/3 и /' (дс) < 0 при дс > 1/3), а
искомое значение объема V равно
j/Y	S'/a
12	' |A„tg (180°/n) '
б) Подставляя в полученное соотношение между величинами V,
S, п, х данные значения п, S, V, получаем уравнение для х
У х (1—дс)/(1 +дс) = 2/9,
имеющее корни дс^ = 1/17 и дса = 4/5. Поэтому Qt — 8 и Qa = 64, откуда
гг = У2 и г2 = 4, следовательно,
аг = 2 У2, hi = 24 и яа=8, ha = 3,
271

16.11.	Обозначим через h высоту призмы. Тогда в тетраэдре
AiA3An^-iAn+2
(рис. 120) угол между противоположными ребрами AiAs и A'n+iAn+2
равен углу
Z А3А\А2 — (1 /2) Z Л3ОЛ2 = 180°/2я
(где	О—центр
многоугольника
.г
Ai...A2n; заметим, что

Рис. 120
An+iAn+il Л1Л2Ц А4А^. Расстояние между ребрами ЛХЛ3 и Лп-цЛ^+!!
равно h, а их длины равны
Л*Л3 = 2/? sin (180°/л), A'n+lA'n+2=2R sin (180°/2я),
поэтому объем указанного тетраэдра равен
(1/6) ;M3. А'п+гАп+2'h sin (180°/2я) = (2/3) R2h sin (180°/я) sin2 (180°/2я).
С другой стороны, если ф—угол между прямой A4An+i и плоскостью
А4А3Ап+2, то тот же объем равен
(1/3) S , .ЛИ; jBlnq),
AtA,ArH-2
где
AiA'n+l =V (iMJ)* + HMn+i)*= Уй*+4Я*,
^а а a' =(^/2)-^i.4з‘Ап+ Н —
Л‘Л»ЛП+2
=(1/2) 2 R sin (180°/я) У hi + (2 R cos2 (180°/2л))2
(А'п+2Н—высота треугольника А4АвАп+2). Таким образом, получаем
равенство
(2/3) R2h sin (180°/я) sin2 (180°/2я) =
= (1/3) R sin (180°/я) У hi+4Ri cos4 (180°/2я) • У hl + 4Ri sin ф,
272

-1/2
поэтому величина
sln(p = 2R sln2 (180°/2n) (h* + 16^4-C-0S^.|.—
-j-4Ri cos4 (180°/2n)+4R2^
максимальна, когда в неравенстве
нг _|_ 16/?1 соs^l 80°/2га) ^ 2 ]/~ 16/?* cos4 (180°/2и)
достигается равенство, т. е. когда
,	16R4	cos4	(180°/2п)	/юп°/о	^
h‘ =	р		—-	, нли h = 2R cos (180 /2n),
что и требовалось доказать.
16.12. Из равенства боковых ребер пирамиды SAx...A„ следует,
что проекция О вершины S на основание пирамиды равноудалена от
вершин Ах, ..., А„, т. е. является центром окружности, описанной
около многоугольника Ах...Ап. Поскольку при каждом значении
k= 1 п пирамида SOAkAk+x (где А,1+х — Ах) симметрична отно¬
сительно биссектральной плоскости двугранного угла при ребре SO,
то ее двугранные углы при ребрах SAk и	равны	одному	и
тому же числу ф*. Так как по условию
ф1' + ф2 = ф2+<Рз= ‘	=ф«-1+фп=фп+ф1.
а число п нечетно, то
ф! = фЗ = . * * = фп=ф2 = • ‘ * = фв-1>
откуда вытекает равенство всех пирамид SOA^A^^ (ибо любые две
соседние пирамиды симметричны друг другу относительно нх общей
грани) и равенство всех углов ^ А^ОА^^х- Таким образом, много¬
угольник Ах...Ап правильный.
16.13. Обозначим
S/1 — a, SB = b, SC = c
(рис. 121), тогда
AD — ВС=с — b, SD = SA-{-AD = a-\-c — b
и если
то
SQ = ха,
SR — (l— х) с, SP = SA-{-xAD = a [-х(с — Ь),
QR = SR — SQ = (1 —х) с—ха,
QP — SP~SQ =(1 —х) а-\-х(с — Ь),
273

причем векторы QR и QP ие параллельны ни при каком значении х
(что следует из их разложений по трем векторам а, Ь, с, не лежа¬
щим в одной плоскости). Так как точка М лежит в плоскости,
проходящей через точку N параллельно плоскости а, то для некото¬
рых значений X и pi имеем
SM = SN +kQR + pQP =
= (1 /2) (SC+SD) + X ((1 — x) с—ха) + p ((1 — x) a + x (c — b)) =
= (1/2—Xx+p(l — x))a + (—1/2—put) b + (l+X(l—х) + цх)с.
Поэтому точка M лежит на прямой SB тогда и только тогда, когда
SM = yb, т. е.
/ 1/2 —Хх+р(1—х) = 0,
\	1	+	Х(1—x) + pjc=0.
Последняя система совместна при любом значении XI
х+1	,	Зх—2
■ •	/,
2(2х?—2х+1)’	2(2х?—2х+1)
(заметим, что 4хг—4х+2 = (2х—1)^+1 > 0). Следовательно, искомые
значения у и только они удовлетворяют равенству
„	1	■	х(х+\)
у	2 '2 (2х?—2х+ 1)
хотя бы при одном значении х. Иными словами, уравнение
(4у+ 1) х*-(4у+3) х+(2у+ 1) = 0
разрешимо относительно х при искомых значениях у, т. е. при
(4у+-4 (4у +.1) (2у +1) = -Щ2 +5 > 0
274

(в том числе и при 4у—1=0, 4^+3 5^0). Таким образом, искомые
значения у заполняют отрезок [— Y 5/4; Y 5/4].
16.14. Пусть большее основание Mt исходной усеченной пирамиды
имеет площадь Si, меньшее основание М2—площадь S2, а общее
основание М0 двух усеченных пирамид, составляющих исходную,—
площадь S„. Продолжим боковые ребра пирамиды до их пересечения
в точке Т и обозначим через Рi,
Р2 и Р0 пирамиды с вершиной Т и
основаниями Мх, М2 н М0 соответ¬
ственно (рис. 122). Гомотетия отно¬
сительно точки Т, переводящая ос¬
нование Mi в основание М0, пере¬
водит сферу, вписанную в пирами¬
ду Pi, в сферу, вписанную в пира¬
миду Р0, а значит, переводит осно¬
вание М0 в основание М2 и сферу,
вписанную в пирамиду Р0, в сферу,
вписанную в пирамиду Р2. Поэтому
для радиусов /?*, Р2, R0 вписан- •'
ных сфер и площадей Qi, Q2, Q0
боковых поверхностей пирамид Pi,
Р2, Ро соответственно имеем про¬
порции
Jk
Ri
Jk
Ro’
02
Qi
*^2
Jk.
Rl
Рис.
Объем пирамиды P2 равен, с одной стороны, (1/3) Р2 (Q2+S2), а с
другой стороны, (1/3) (Qa—S2) (ибо сфера радиуса R0 вневписана
по отношению к пирамиде Р2), поэтому
откуда
Ri (Q2 ~I ^^2)—Ro (Q2—S2),
Q 2 — S2  R2  R2  Y R2
Q2+S2~ Ro ~ YRiR2~ YrI~ {/Si
(Q2—s2) ^YSi—(Qa+SJ yYSs-
Следовательно, получаем
Q2	\Zsi + \Yst
s2 ~
275

и, наконец,	  _
о,	iVSi+ys,
(Si-S^X \ (Sx-Sjд
*2	У Si — у s2
= (У Si+ У S.) (У Si+ у s2)2,
что и требовалось доказать.
16.15.	а)	Докажем,	что	если точки Л/,	А2,	...,	Ап	располо¬
жены	на	сфере с центром О	и	радиусом 1 так,	что	расстояние	между
любыми точками A,-, Aj (1 ф j) не меньше У 2, то п <; 6. В самом деле,
пусть п > 6. По теореме косинусов имеем
Л/Л/= 2—2 cos £ Л,ОЛу^ 2,
откуда Л,ОЛу^ 90° и ОЛ/-ОЛу<0. Выберем в пространстве пря¬
моугольную систему координат с началом в точке О следующим об¬
разом. Заметим прежде всего, что среди векторов ОЛ/ обязательно
найдутся три некомпланарных вектора (в противном случае все п > 4
векторов лежали бы в одной плоскости и, следовательно, угол между
какими-то двумя из них был бы острым). Без ограничения общности
можно считать, что векторы ОАу, ОА2, ОА3, некомпланарны. Ось ОХ
направим вдоль прямой ОЛ/ так, чтобы абсцисса точки Л/ равня¬
лась 1. Далее, ось OY направим так, чтобы точка Л2 лежала в
плоскости XOY и имела положительную ординату. Наконец, ось 07,
направим так, чтобы аппликата точки Л3 была положительной.
Обозначим через дс/, у;, г/ координаты точки Л/. Тогда
ОЛ1 = (1; 0; 0), ОА2 = (х2; у2; 0), 0Л8=(х8; у8\ гя),
где у2 >0, г8 > 0, поэтому для всех значений i > 1 имеем
ОЛ,-ОЛ1 = х/<0;
далее, для всех значений « > 2 имеем
ОАгОА2 = х;х2+у,у2 < 0,
откуда {//«С0 (ибо лг2«С0, х,«СО, у2 > 0); наконец, для всех значе¬
ний i > 3 имеем
ОЛ,-ОЛз = дс/Хз++г,-гз ^ 0,
откуда г,-С0 (ибо х3<;0, х/СО, уя«S0, j//<c0, г3 > 0). Среди четы¬
рех векторов ОЛ4, ОЛ8, ОАе, ОА7 хотя бы два имеют одноименную
отрицательную координату, а значит, их скалярное произведение
положительно. Полученное противоречие доказывает, что п ^6. Так
как 6 точек с координатами
(± 1; 0; 0), (0; ±1; 0), (0; 0; ±1)
удовлетворяют условию п. а), то наибольшее число точек равно 6.
276

б) Докажем, что если точки Аи Аг, .... А„ расположены на той
же сфере так, что расстояние между любыми точками А/, А у (i ф /)
больше Y 2, то л <4. В самом деле, пусть л > 4. Тогда ОА/-ОАу < О,
и если выбрать прямоугольную систему координат так же, как в ре¬
шении п. а), то аналогично при i > 3 будем иметь х,- < 0, щ < О,
z/ < 0. Поэтому скалярное произведение векторов ОЛ4, ОЛ5 будет
положительно. Итак, доказано, что л <; 4. Поскольку 4 точки, рас¬
положенные в вершинах правильного тетраэдра, вписанного в сферу,
удовлетворяют условию п. б), то наибольшее число точек равно 4.
16.16.	Пусть О—центр сферы, О/—центр окружности С/ (i = 0,
1, ...» л), /4/—точка пересечения луча ОО/ со сферой, В—точка
касания окружностей С0 и С/. Обозначим ф = Z Л0ОВ, тогда
sin ф = гп и А0А1 = 2гп,
так как
OB = OA0 = OAi — l, О0В = О1В = гп,
£ОО0В = £ 00/6 = 90°
I
(рис. 123). В правильной пирамиде OAqA^^ плоские углы при вер¬
шине О равны 2ф, а двугранный угол при ребре ОА0 равен 360°/я.
Рис. 123
Если AJ1—перпендикуляр к ребру ОА0, то
AiH = А%Н = sin 2ф = 2 sin ф cos ф = 2г„ Y1 — г®.
Далее, имеем
2г„ == j4OJ4i = у4Иа = 2 • АХН. sin (180» = 4г„ Vl — Гп sin (180°/я).
откуда
2 V1 — гп sin (180°/л) = 1.
277

Поэтому
sin (I80°/n) = 1/(2 VI — r%) > 1/2 и n < 6
(последнее неравенство вытекает также из того факта, что двугран¬
ный угол ^ ЛхЯЛа = ЗС0°/п при боковом ребре ОА0 больше плоского
угла £ AiA0A% = &f основания пирамиды), а для остальных значе¬
ний п = 2, 3, 4, 5 имеем
16.17.	Угол С'АВ' представляет собой линейный угол двугран¬
ного угла с ребром ОА и гранями, проходящими через точки С и В
соответственно, так как лучн АС’ и А В' перпендикулярны общему
радиусу ОА (рис. 124). Аналогично угол D'АВ' является линейным
углом двугранного угла с ребром О А и гранями, проходящими через
точки D и В. Так как указанные двугранные углы симметричны друг
другу относительно прямой ОВ (прямая О А симметрична себе, а точка
С — точке D), то они равны, а значит, равны и их линейные углы
Z C'AB' = £D’AB'.
16.18.	Пусть точка С' симметрична точке С относительно центра
симметрии цилиндра—точки О (рис. 125). Тогда, если у трехгран¬
ного угла ОАВС двугранные углы при ребрах ОА, ОВ, ОС равны
а, Р, у, то у трехгранного угла ОАВС' двугранные углы при ребрах
ОА, ОВ, ОС' равны 180°—а, 180°—Р, у соответственно. Пусть D— >
центр окружности с диаметром АВ. Тогда в пирамиде OADC' дву- Д
грэнные углы при ребрах ОА и ОС' равны (ибо эта пирамида сим-
В
1
Рис. 124
278

метричиа относительно биссектраль-
ной плоскости двугранного угла при
ребре OD), а в пирамиде OBDC' рав¬
ны двугранные углы при ребрах ОВ
и ОС' (по той же причине), откуда
(180°—а) + (180°—Р) ==Yi т.е.
ot-f- Р + у=360°,
что и требовалось доказать.
16.19.	Заметим, что сумма плоских
углов данного угла с вершиной S и
ребрами S/4r, ..., S/4„ меньше 360°,
Возьмем какую-либо внутреннюю точ¬
ку О этого я-гранного угла и опустим
из нее перпендикуляры ОН/ на плос¬
кости SA/Ai+t («'= 1 л; Л„+1 =
= ,4i). Полученный л-гранный угол с
вершиной О н ребрами ОН/ явля-
Рис. 125
ется выпуклым, ибо все его ребра лежат
относительно любой его грани в том же полупространстве, что и
точка S. Каждый его плоский угол £Н/ОН/_/ (Н0 — Нп) в сумме
с линейным углом двугранного угла при ребре SA/ (перпендику¬
лярном плоскости HiOH/_1) составляет 180°, Так как сумма пло¬
ских углов построенного л-гранного угла также менЬше 360°, то
сумма величин двугранных углов исходного л-гранного угла боль¬
ше 180°-л—360° и не может быть меньше 360° ни при каком значе¬
нии л ^4. Следовательно, условию задачи может удовлетворять толь¬
ко трехгранный угол.
16.20.	Введем в пространстве систему координат и для каждого
значения i= 1	 1979 отнесем к t-му множеству все точки, абсциссы
которых удовлетворяют равенству
Построенный пример показывает, что ответ на вопрос задачи поло¬
жителен.
16.21.	Докажем индукцией по л, что л прямых разбивают пло¬
скость не более чем на
частей, причем в точности р (л) частей получается, если никакие
2 прямые не параллельны и никакие 3 прямые ие проходят через
одну точку. Действительно, р (0) = 1, н при любом значении л £ N
имеем неравенство
[jc] = I (mod 1979).
279

причем равенство достигается (n-я прямая, пересекаясь с каждой из
остальных прямых, сама разбивается не более чем иа п-частей, каж¬
дая из которых определяет новую часть плоскости). Аналогично дока¬
жем, что п плоскостей разбивают пространство ие более чем на
частей, причем в точности q (п) частей получается, если никакие 2
плоскости не параллельны, никакие 3 плоскости не проходят через
одну прямую и никакие 4 плоскости не проходят через одну точку.
Действительно, q (0) = I н при любом значении п £ N имеем нера¬
венство
Я (п) < q (и— 1) +р (п — 1) =
(п— 1)3 + 5(л—1)+6 , (п—1)п	я34-5я	+	6
— 6 ^ 2 ' 6 ’
причем равенство достигается (я-я плоскость, пересекаясь с осталь¬
ными плоскостями, сама разбивается не более чем на р (п— 1) частей, |
каждая из которых определяет новую часть пространства). Искомое ,
число плоскостей равно 13, поскольку
Действительно, 12 плоскостей не хватает, а 13 плоскостями можно
разбить все пространство на q (13) частей, затем выбрать внутри каж¬
дой из них по одной точке и взять куб, содержащий все q (13) точек,
после чего останется подвергнуть всю конструкцию преобразованию
подобия с надлежащим коэффициентом.
16.22.	Докажем, что в условиях задачи прямые АА' н В В' пере¬
секаются при любом положении плоскости а'. Так как в начальном
положении эти прямые пересекаются, то точки А, АВ, В' лежат
в одной плоскости. Поэтому прямые АВ и А'В’ либо пересекаются,
q (12) = 299 < 300 < 378 = ? (13).
Рис. 126
280

либо параллельны. В первом случае (рис. 126) точка О их пересече¬
ния лежит на прямой /, причем
ОА-ОВ' ф ОВ-ОА'
(ибо прямые АА' и В В' не параллельны). Так как те же условия
будут выполнены и для других положений а', то прямые АА' и В В'
по-прежнему будут пересекаться. Во втором случае прямые АВ\\А'В'
параллельны прямой I, причем АВ Ф А'В', что сохраняется при вра¬
щении плоскости а'. Следовательно, и в этом случае прямые АА'
и ВВ' пересекаются при любом положении а'. Если прямые АА',
ВВ', СС' в начальный момент не лежат в одной плоскости и пере¬
секаются в одной точке, то при любом положении а', отличном
от а, они также не лежат в одной плоскости и, согласно доказан¬
ному выше, попарно пересекаются, а значит, имеют общую точку
пересечения. Наконец, если прямые АА', ВВ',СС' в начальный момент
лежат в одной плоскости, то рассмотрим четвертую прямую DD’,
проходящую через точку их пересечения, но не лежащую в той же
плоскости. Тогда прямые АА', ВВ', DD' пересекаются в одной точке
и прямые АА', СС', DD' также пересекаются в одной точке, причем
эти точки совпадают с точкой пересечения прямых АА', DD'. Поэтому
прямые АА', ВВ’, СС’ пересекаются в одной точке при любом поло¬
жении а', отличном от а. Через точку Af = Af0 пересечения данных
прямых в начальном положении проведем плоскость Р, перпендику¬
лярную прямой I, и заметим, что точка М не покидает эту плоскость
при вращении плоскости а'. В плоскости Р проведем прямую f, про¬
ходящую через точку М параллельно плоскости а', и докажем, что
точка F ее пересечения с плоскостью а не зависит от положения а,'.
Если в начальном положении — это точка F0, а в другом — Flt то
в последнем положении плоскости а' прямая MF0 (М ф f0, иначе
F0 = M = F1) пересекает плоскость а' в некоторой точке F'. Сле¬
довательно, согласно доказанному выше, в начальном положении
прямая F0F' также проходит через точку М, т. е. совпадает с пря¬
мой /, однако не параллельна плоскости а'. Аналогично доказывается,
что точка G пересечения плоскости а' с прямой g, проходящей через
точку М параллельно плоскости а, поворачивается вместе с пло¬
скостью а, занимая фиксированное положение на ней. Таким образом,
при вращении плоскости а' точка М вращается вокруг точки F,
находясь от нее на постоянном расстоянии (равном расстоянию от
точки G до прямой I) и образуя тот же угол с плоскостью а, что и
плоскость а'. Поэтому искомое множество есть окружность в пло¬
скости Р с центром F и радиусом FMU (возможно, нулевым), из ко¬
торой выброшены две диаметрально противоположные точки, принад¬
лежащие плоскости а.
16.23.	Прямая I может служить осью поворота, переводящего
точку А в точку В тогда и только тогда, когда точки А и В имеют
281

общую проекцию О на эту прямую и равноудалены от нее, т. е. когда
прямая I лежит в плоскости аг, проходящей через середину отрезка АВ
перпендикулярно ему. Поворот вокруг такой прямой I на угол <р
совпадает с результатом последовательного применения симметрий
относительно плоскости оц, а затем относительно плоскости а2, яв¬
ляющейся образом плоскости ai при повороте вокруг прямой I на
угол ф/2 (в том же направлении). Для доказательства этого факта
Bi Следовательно, все образы точки С при рассматриваемых поворотах
можно получить следующим образом: сначала симметрично отразить вер¬
шину С относительно плоскости ar (получив вершину D), а затем —
относительно произвольной плоскости а2, проходящей через точку В
и не параллельной плоскости ai- Поэтому образы точки С заполняют
сферу с центром В и радиусом BD, за исключением точки, симмет¬
ричной точке D относительно плоскости ВСС', а значит, не лежащей
на поверхности куба. Таким образом, искомое множество есть пере¬
сечение этой сферы с гранями куба и состоит из трех дуг DA', А'С’,
C’D окружностей с центрами в точках А, В', С соответственно и
радиусами, равными ребру куба (рис. 127).
16.24.	Предположим сначала, что три из четырех данных вершин
куба
(см. рис. 114) лежат в одной грани. Пусть для определенности ими
являются точки Ait А2, А3, тогда вершина At также имеет целые
координаты, так как координаты вектора АзАц = АзАу являются
целыми. Следовательно, какой бы ни оказалась четвертая из данных
вершин, At, А'2, Аз или А\, координаты всех остальных вершин куба
являются целыми, поскольку
достаточно заметить, что, на¬
пример, в плоскости АВО (ко¬
торая перпендикулярна оси I)
поворот вокруг точки О на угол
Ф совпадает с результатом двух
симметрий:	относительно	пря¬
мых li и /2, лежащих в пересе¬
чении плоскости АВО с пло¬
скостями ai и а2 соответствен¬
но. Поскольку симметрия отно¬
сительно плоскости aj уже пере¬
водит точку А в точку В, то
плоскость а2 для рассматрива¬
емых в задаче поворотов (и толь¬
ко для них) проходит через точку
А
В
Рис. 127
А-уА^АзА^АхА^АзА^

Предположим теперь, что никакие три из данных четырех вершин
не лежат в одной грани. Так как эти вершины по условию не лежат
в одной плоскости, то они являются вершинами правильного тетра¬
эдра, ребра которого—диагонали граней куба. Пусть для определен-
 »-
ности это вершины А1г Л2, Аз, Ац. Докажем, что вектор А\А'Ъ имеет
целые координаты. Действительно, рассмотрим вектор
2А1А3 — А\А2-\~ А\Аз~\~ А\А^,
который имеет целые координаты х, у, г. Обозначим
(аха;) =(ахАз) =(аха;) =в,
AiA2-A1A3 = AiAi-AiAi — А\Аз-AiA\ = a cos 60° = а/2 = b,
тогда a, b£ Z и
х2+у2 + г* = (2А^Аз) =3а + 3-26 = 126 = 0 (mod 4).
Так как квадрат четного числа дает при делении на 4 остаток 0, а
квадрат нечетного числа — остаток 1, то остаток при делении на 4
числа x2 + «/2-f г2 равен количеству нечетных чисел среди чисел х,
 ►
у, г. Таким образом, все координаты х,у,г вектора 2А1АЯ — четные числа,
а координаты вектора AiA3—целые числа. Поэтому точка А3, лежа¬
щая в одной грани с точками А2, А4, имеет целые координаты и,
согласно доказанному вначале утверждению, координаты всех вершин
куба являются целыми.
16.25.	Мысленно разобьем все пространство, в котором лежат
параллелепипеды, на кубики с ребром 1/2 и раскрасим их в белый
и черный цвет в «шахматном» порядке (т. е. так, чтобы любые ку¬
бики с общей гранью имели разный цвет). Докажем, что если какой-
либо параллелепипед имеет целое ребро и все его грани параллельны
граням кубиков, то объем его белой части равен объему его черной
части. Действительно, с помощью разрезов плоскостями, перпендику¬
лярными целому ребру, разобьем весь параллелепипед на слои тол¬
щины 1/2 и заметим, что при параллельном переносе крайнего слоя
до совмещения его с соседним слоем белые части первого совпадают
с черными частями второго и наоборот. То же самое произойдет со
следующей парой соседних слоев и т. д. Следовательно, объем белой
части равен объему черной в каждой паре соседних слоев (которых
всего имеется четное число), а значит, и целиком в параллелепипеде.
Пусть грани исходного параллелепипеда параллельны граням куби¬
ков, причем его вершина А совпадает с вершиной одного из кубиков,
а среди его ребер нет целочисленных. Тогда все параллелепипеды,
на которые он по условию разбит, имеют по целому ребру (а грани
283

их, разумеется, параллельны граням кубиков, так как этих парал¬
лелепипедов конечное множество и их можно последовательно пере¬
брать, если сначала выбросить тот из них, который лежит в углу
исходного параллелепипеда, затем тот, который лежит в углу остав¬
шейся фигуры и т. д.). Следовательно, в силу доказанного выше
утверждения объем белой части каждого из них (а значит, и исход¬
ного параллелепипеда целиком) равен объему черной. В исходном
параллелепипеде тремя плоскостями, параллельными его граням,
можно вырезать параллелепипед с вершиной А, целыми ребрами и
наибольшим объемом. Среди оставшихся семи параллелепипедов, кото¬
рые образуются в результате этих разрезов, шесть имеют по целому
ребру, а один имеет все ребра, меньшие 1, и вершину В, совпадаю¬
щую с вершиной одного из кубиков. Достроим этот параллелепипед
до куба с ребром 1 и той же вершиной В. Три плоскости, вырезаю¬
щие в этом кубе внутренний параллелепипед, разрезают куб на восемь
параллелепипедов, среди которых хотя бы один имеет все ребра, не
превосходящие 1/2, поэтому объемы его белой и черной частей не
равны (ибо один из этих объемов равен 0). То же самое можно ска¬
зать и про три параллелепипеда, имеющих с ним общую грань (каж¬
дый из которых образует с ним параллелепипед с ребром 1), а также
про остальные параллелепипеды, в том числе и про тот из них, кото¬
рый имеет вершину В. Таким образом, исходный параллелепипед
оказался разрезанным на восемь параллелепипедов, в семи из которых
объемы белых и черных частей равны, а в восьмом — нет. Полученное
противоречие показывает, что исходный параллелепипед не может не
иметь целого ребра.
17.1.	Замечая, что при каждом п= 1, 2, ..., 99 справедливы
равенства
Глава 5
АНАЛИЗ
§ 17. Последовательности
1
(п + 1)У п — пУп+ 1
(n + l)?n—яа(и + 1)
1 1
V п Y п+1 ’
для искомой суммы получаем
284

17.2. Пользуясь формулой
tg fe—tg (k— 1)
tg 1 =
1 +tg tg (*— 1)
(заметим, что ввиду иррациональности числа п выражение tg k опре¬
делено при всех k£ N), получаем при любом п £ N равенства
й1-Иг+ ■ ■•+<!„= £, tgMg(*_l)=^ (—^tIt" 1>~11=1
А=1	*=	I	\	/
п	п-1
tgtgn
tg i 2-a tg i	tg	i
(r=l	fc=l
Таким образом, числа = I/tg 1, В — — 1 удовлетворяют требованиям
задачи.
17.3. Так как
г Н.Зг.....(2п—1)2_
°п—	22.4 г.....(2п)а
1-3 3-5	(2л— 1) (2л +1)	1	1
“ 22 ' 42 ’ ’ ’	(2л)2	‘2/1	+	1	2/1 + 1
при любом /t£N, то
О < а„ < 1/^2л + 1 и Игл а„ = 0.
п-*- 00
17.4. Пусть Л£(0; 1) и lima„ = + Тогда найдется такое нату-
П—>-00
ральное число N, что для всех номеров n^N имеют место оценки
2Л/3 < ап < 4А/3. Если для любого п> N выполнено равенство
ап =	a„_i, то, переходя в нем к пределу при л ->■ оо, получаем
A— lira а„ = lim VЧц-\ = -\Г lim a„-i—V А.
П-+ао	Л-*со	У	Л—> оо
Следовательно, Л£{0; 1), что противоречит условию А £ (0; 1). Если
же для некоторого номера п> N равенство an = V~aa~i не выпол¬
нено, то a„ = a„_,/2< (1/2)-4Л/3=:=2Л/3, т. е. а„ < 2Л/3, что противо¬
речит выбору числа N. Поэтому у последовательности {а,,} не может
быть предела, лежащего в интервале (0; 1).
17.5. Рассмотрим число а,- из набора а* < сг < ... < а,. Коли¬
чество трехчленных арифметических прогрессий, в которых это число
является средним членом, не превосходит как i—1, так и л— i, по¬
скольку на месте первого члена может стоять только одно из чисел
Oj, a,-_j, а иа месте последнего—одно из чисел а1 + ь в/+2, •••
..., ап. Поэтому общее число прогрессий не превосходит суммы
2 rnin{i — К n — i) — S.
(= 1
285

Если tt — 21 (/£N4(1}). то
П
i= 1
Если же п = 2/+1 (/£N), то
t=f + 1
п
s=2(«-o+ 2 ("-о=л
£= 1
£=/+ 1
Заметим, наконец, что полученные оценки для количества прогрессий
достигаются в случае последовательности ai = t (i = I л).
17.6.	Пусть а1( а2, о3, ...—указанная в задаче последователь¬
ность. Рассмотрим функцию, определенную на множестве целых чисел:
и зададим последовательность {Ь„} формулами b„ = f (а„), n£N. Тогда
для любого л £ N справедливы соотношения
bn+l — f (an+i)=f (ал + ап + 1'“ba/i + i~ban + ») =
~f(f (°л) +f (a« + i)+f (ал+г) +f (an+»)) — f (bn + ^n + i“b^n+a+^n+s).
поскольку число a„+4 является четным в том и только в том случае,
если четна сумма a„ + fl,i+i+fln+a + an+8- Первые 9 членов после¬
довательности {£>„} равны соответственно 1, 1, 0, 1, 1, 1, 1, 0, 1.
Поэтому be = bi, b-j = b2, fc8 = fc3, bB=bi и, вообще, Ьп+Ъ = bn, а зна¬
чит, в этой последовательности нули стоят только на местах с номе¬
рами вида я = 3 + 5й (k£Z+). Таким образом, в последовательности
{о,,} разность номеров любых двух четных членов делится на 5. Сле¬
довательно, четверка чисел 1, 2, 3, 4 встретиться не может.
17.7. Пусть задано число л £ N, тогда из условия следует, что
каждое из чисел aj, а% a„+j не превосходит 2л. Множество
чисел 1, 2 2л разобьем на л пар: (1; я+1), (2; я+2), ...
..., (л; 2л). Поскольку среди чисел 1, 2, ..., 2л содержится не ме¬
нее (л+1) членов последовательности, то найдутся два разных числа
ар и Од, принадлежащие одной паре. Для завершения доказательства
остается заметить, что разность между числами в каждой из пар
равна п.
17.8. Построим последовательность [Ьп] следующим образом:
и обозначим ап/ЬП через с„. Тогда справедливы оценки 1 <	< Д
для всех n£N. Поэтому для любых m, n£N имеем ст/сп <: В, т. е.
аш/а/1 ВЬт/Ь„.*
17.9.	Построим возрастающую ’ последовательность номеров {/,]}
следующим образом. Пусть а,-, — наименьшее из чисел а%, а2, ... (оно
существует, ибо все члены последовательности {ая} — натуральные
286
0, если х четно,
1, если х нечетно,
{
а„, если а„ «С А,
А, если а„ > А,

числа); я,-а—наименьшее из чисел a/1+i, я/1+2, ...; а,-3—наименьшее
из чисел а,-а+1, о,3+2, ••• и т. д. Тогда бесконечная последователь¬
ность I а{ \ не убывает. Пусть Ь{ — наименьшее из чисел Ь,-, b;v .,.
I "I	к
Тогда if, < ik+1. о,- < a.i , b- <6,	,	т.	e. в качестве искомых
k k+ 1 k k+ 1
номеров p и q можно взять числа i^ и i^+i соответственно.
17.10. Докажем утверждение индукцией по п. При п = 1 имеем
af<ai —а2 < аи откуда я* < 1. Кроме того,
a2	<	1/2,
т. е. ап < 1 In при п = 2. Пусть утверждение уже доказано для неко¬
торого числа п^2. Докажем его для числа п + 1. Так как функция
f (х) = х—хъ возрастает на отрезке [0; 1/2] и ап < 1/л, то
, ч *( М 1	1	1	1	1
an+1<I(an)<t{n)-n	П2~ п+1	„2(п+1) < п + 1 ’
что и требовалось доказать.
17.11. Соотношение	+	a*_i/rt	эквивалентно равенству
_J 1 _	1
a-k-i a*-n+aft_x'
Поскольку l/2 = a0 < fli < ... < a„, то справедливы неравенства
111 ,
< — при R— I, . . ., Л,
ak— 1 ak n
складывая которые, получаем оценку
1 1
          < 1*
flo 0/1
Следовательно, l/an > 2—1 = 1, а значит, ап < 1. Поэтому справед¬
ливы неравенства
1 1 ^ 1 » *
	>	г~Г При «= 1, »... п,
ак л + 1 р	»
складывая которые, получаем оценку
1	1 п
Следовательно,
а значит,
	>	гг •
flj ап п+1
_!_ , 2 п	п+2
ап	п+1	rt +1 ’
а,I > (п+1)/(п+2) > (л- 1)/л.
Утверждение задачи доказано.
17.12.	Из условия имеем неравенства
а*+я>— Ка* + ат<ял+я) + 1,	k, mgN.
287

Докажем индукцией по q£N, что для любых ptq£N выполнены
неравенства
ард — (9—1)« qap < apq + (q — 1).
При q = 1 имеем верные неравенства. Пусть неравенства доказаны
для числа q. Докажем их для числа 9+1. Действительно, для лю¬
бого значения	имеем
(9+1) ap — qap +а/> ^арЛ~ард + (q 1) ^ар+рд~\~Я~ал (д+1)_Ь<7-
Аналогично доказывается, что
(Я + 0 ар ^ ар (?+i)—9-
Поменяв местами р и q, получаем неравенство
аРд—(Р —1)< рач < ард + (р — 1).
Таким образом,
I Р&д q&p I
< max { I apg+(p— 1)—(apg—(q— 1)) |, | apq-\-{q—\)—{apn—(p—\)) |} =
=Р+Я—2 < p+q,
а значит,
I aQ aP I 1	,	1
I q p I q p '
что и требовалось доказать.
17.13. Допустим, что множество неположительных членов конечно.
Тогда найдется такое натуральное число N, чтоа„ > 0 для всех
Но	в	этом	случае	для всех n^sN имеем также а„ > 1 (если ап<1,
то	а„+1 = (1/2)	(а„ — 1/а„)<0). С другой стороны,
аЛг+1 = (1/2) (ajg—1/ajg) < адг/2,
avV+2 = (l/2) (a/g+l — 1/QN+i) < o/v+i/2 < ajg/i
и, вообще,
aN+k < aNftk для всех ££N.
Поэтому адг+*< 1, если 2* > а/д. Полученное противоречие доказы¬
вает утверждение задачи.
17.14. При n£N имеем равенства
ап=2п~1 — Зап_1=2"~1—3*2',-5+9>ап_2 = ...
... =2П~1—31-2П~?+ .,. +(—1)п-1Зп-* + (—1)пЗпа0.
из которых получаем формулу
а„ = (2П + (—l)'i+13")/5 + (—1)яЗпа0,
справедливую также и при п = 0. Далее, находим разность
d„ = а„—а,,-! = (2" + (—1)" +13«)/5 + (- 1)"3"а0-
_(2«-Х + (— l)«3"-i)/5—(—1)"-13"-Ч =
= 2"-1/5 + (— 1)"+1-4.3п-х/5 + (— 1)п.4.3«-1а0 =
«=2п_1/5 + (—l)n+x.4.3n-i (1/5—а0) =
= (2"-»/5) (I + 4-(-1)«+х (3/2)"-х (1 -5а,,)).
288

Если 1—5о0 > 0, то dn < 0 при достаточно больших четных значе¬
ниях я, а если 1— 5с0 <0, то dn < 0 при достаточно больших нечет¬
ных значениях я. Следовательно, если о0 Ф 1/5, то последовательность
{а,,} не является возрастающей. Если же о* = 1 /5, то d„ = 2n~1/5 >0
при всех п £ N, а значит, последовательность [ап] возрастает.
17.15. Заметим, что для указанной в задаче последовательности
справедливы соотношения
Ял+1 Ял+З + Яп+1 = fl«+2 +Д +Дц+1 = Ял+2 + впвп + 21	Л	£	N	,
из которых получаем равенство
(ал + 8 + an + l)/an + 2 = (ал + 2 + ал)/ал + 1'‘
Поэтому, если обозначить Ьп = (ап+г-[-ап)/ап+1, то имеют место
равенства 6Х = b2~ bs = ... = Ь, откуда получаем
(ап+2+о л) 1° п+1 — Ьп== (аз+Cl)/C2 =
= ((fl2“bfl)/al-bal)/a2 = (al +a2“ba)/(°la2) £Z,
т. e. an+i = ban+i—a„, где Z, n£N. Поскольку ai.fl^gZ, to
каждое из чисел a3 = ta3—a1( a4 = fca3—аг, ... является целым.
17.16. Заметим, что a0=0, ах=1, и докажем справедливость
равенства а„+2 = 4а„+х—а„ при каждом n£Z+ (откуда последова¬
тельно получим, что каждое из чисел аг, а3, а4, также является
целым). Действительно, пусть
a = (2+/3)7(2 /3), р = (2-/3)п/(2 /З),
тогда имеем
а„ =а—Р,
a„+1 = (2 + /3)a-(2-/3)p,
Ол+. = (2+/ 3)г a — (2 —/ 3)гр = (7+_4/ 3) а-(7-4 / 3)р =
= (8 + 4/ 3)а-(8-4/ 3) р-(а + р) =4а„н х-ап.
Поскольку
о-п+2 ^ Лл+1 оп (mod 3),
а остатки от деления на 3 первых 8 членов последовательности а0,
аи ^2, ... равны соответственно 0, 1, 1, 0, 2, 2, 0, 1, то
а6 ss о0 (mod 3), a, = ax (mod 3),
и, вообще,
an + e=a„(mod 3).
Таким образом, в этой последовательности остаток 0 при деле¬
нии на 3 дают члены вида д3^, где k£Z+, и только они. Так как
(2 + /1) (2-/3)=1, то имеет место равенство

из которого вытекает, что при отрицательных значениях п числа о„
также целые, причем а„ == 0 (mod 3) тогда и только тогда, когда
л = 0 (mod 3).
17.17.	Обозначим
тогда при л £ N имеем ап > 0 и
4(JW4J^n)(3^+-4pi)-
- (№)■-№)■) ^ •
Индукцией по ££N докажем, что число о2*_1 является целым, а
число a2ft имеет вид тУ 5 при Z. Действительно, при £=1
имеем Oj = 1, о2=	5. Далее, пусть утверждение верно для некото¬
рого значения	Тогда
а2к+1=У 5 a2k — o2fe_i = 5m—c2ft-i,
°2ft+2= У 5 o2t+i—ci2ft= У 5(^+1—m),
т. e. утверждение верно и для значения А+1. Следовательно, ука¬
занное в условии задачи число
является квадратом числа ап £ N при нечетном п и имеет вид
(лг У 5)2 = 5т2	(т £ N)	при четном п.
17.18.	Заметим, что две последовательности
а„ = (1 + У~а)п и a„ = (l— У~а)п
удовлетворяют условию
ап+1 = 2ап + (а—1)ап-и	ng N-
Действительно, имеем
ап+1—2a„ + ( 1—a)a„_1=(l ± У а)2ап_1—2(1 ± У а)а„-1 “h
+ (1 —a)a„_i = 0
при любом значении n£N. Следовательно, любая последовательность
вида	„
ап=А (1+УЪ)п + В{1-Удп
290

также удовлетворяет этому условию. В частности, при А = —В =
- 1/(2 V а) имеем последовательность
я« = (( 1 + |^а)п-(1-/а)п)/(2^с).
которая удовлетворяет заданным в условии задачи соотношениям,
так как а0 = 0, я* = I. Пользуясь биномом Ньютона, для любого
простого числа р, отличного от 2 (а значит, нечетного), получаем
соотношения
lj=r ((1 + Y~а)р-(1 - Y~a)p)=
г 2 у а
—2 СИY~aY- 2 ci(-Y*y)=
2Y a \iiо	tto	J
(p-lJ/2
= 2	Cj,+Vsal',-1>/*(mod	p),
i = 0
так как в последней сумме все слагаете вида Ср,+1а‘ при i =
= 0, 1,	(р—1)/2— I делятся на р (ибо
Cp = p\l(k\ (р—fe)!) = 0 (mod р)
при fc=l, 2, .... р—1), а при i=(p —1)/2 соответствующее слагае¬
мое равно Cpal = dp~1>/а. При р = 2 имеем
V= ((1 + Ya )а- (1- Ya YWYa ) = 2 - 0 (mod р).
Таким образом, для выполнения указанных в задаче утверждений
а)	и б) необходимо и достаточно, чтобы число а делилось на каждое
простое число р, удовлетворяющее неравенствам 2 < р < р0, и не де¬
лилось ни на одно из простых чисел р > р0. Наименьшее значение N,
обладающее этим свойством, равно произведению всех простых чи¬
сел р, удовлетворяющих неравенствам 3 < р < рв.
17.19.	Пусть последовательность {а„} удовлетворяет условию
задачи. Поскольку ^ > 0, аа > 0 и аа +1 = то а3 > 0. Анало¬
гично получаем, что ап > 0 при п=4, 5, ... Поэтому an+a=(a®+1 + 1 )/а„
при ngN, а значит,
Пз = (а^_Ь l)/al = a2+ 1>
^4 = 0*з-f-1 )/п2 = ((лI -Г I )3 —|— I )/й2 = (а®+За2+Зоа+2)/оа =
—1ci2 ! 3^2 "Ь 3fl2 -I 2/аа.
Так как	то	число	оа	>	I	является	делителем двойки, т. е.
02 = 2. Поскольку все остальные члены последовательности однозначно
определяются первыми двумя ее членами, то указанная последова¬
тельность единственна. Докажем индукцией по N, что все члены
этой последовательности—целые числа (т. е. она действительно удов¬
летворяет условиям задачи). Как было уже проверено, числа at, а2, а3,
являются целыми. Далее, пусть для некоторого значения пё=5 до¬
10*	291

казано, что о*, .... o„_i£Z. Тогда имеем
о„ = (ап-i + 0/яп - а = (((ой-а + 0/Оп - з)3 + 0/ап - а =
= (о«-2+Зоп- г+Зоп— -f-1 -| а«-з)/fln — асп—з>
причем числитель полученной дроби делится иа Оп-з. поскольку
число
(о*—. +Зап-г + Зоп_2+1 -Ьая-з)/ая-з = o«-i 4~1
является целым. Этот числитель делится и на дп-а> так как
(аП-2 +3г2„_2 + 30n-2+ 1 +аЛ-з)/ап -2 = ая-2 + Зо„ _г +30п-2 + ав-4-
Докажем, что числа дп_2 и о®_в взаимно просты (откуда будет сле¬
довать, что числитель рассматриваемой дроби делится на произведе¬
ние этих чисел). Действительно, этот факт вытекает из соотношений
(ал-2> ап-з)=((аЛ-3+ l)/an-4i аи-з)< (ал-3+ 1 » ал-з)—(1, ап-з)=1.
Таким образом, число а„ является целым. Утверждение доказано.
17.20.	Обозначим	I
sB= £» + * + ...+£•+_£_;
а1 а2	ап	ап+1
тогда последовательность Sj, S2, .., состоит из одинаковых чисел	(
в том и только в том случае, если для каждого я £ N разность
S  s °° I - Р - р р~а°
П + 1	" ал + 1 ал + 2 ал + 1 а„ + 2 ал + 1
равна нулю, т. е. ап+2 = (р/(р—<2о)) ан+1- Пусть последовательность
ав, Ci, ... удовлетворяет условию задачи, тогда при всех значениях	|
п ^ 3 выполнены равенства	I
ал = (РНР—ас» ал -1 = (Р2/(Р—ао)г) ал - г = * - - = (рп ~ 21(Р — ао)" _ -8) а2*	I
Поскольку ап £ N, а числа р и р—о0 взаимно просты (ибо 0 < р—а0 < р),	!
то число а2 делится на любую степень (с натуральным показателем) I
числа р—До. откуда р—а0— 1. Поэтому имеем равенства
ао = р—1.	-Р„-	+-^-=1.	ап	=	рп~?а2	(ai,	aa€N)
oi а2
при п = 3, 4, ,.,
Выполнение же указанных равенств гарантирует, что последователь¬
ность удовлетворяет условию задачи, так как в этом случае имеем
Si=l, Sn+1 = s„ при ngN.
Итак, задача свелась к нахождению по заданному простому числу р
количества решений уравнения
р—1 р
а1 1 а2
292
-=1

в натуральных числах. Перепишем уравнение в виде
/701 = 05,(0! — (р— 1))
и заметим, что левая часть этого уравнения делится на р. Поэтому
уравнение может иметь решение только при выполнении одного из
двух условий a2 = kp или а1 — (р—\)=тр, где k, т£N (ибо па > О,
Й1 — (р—1) > 0). При этом указанные два условия несовместны,
так как если Ci—(р—1) ^0 (mod р), то аг ^— 1 (mod р), левая часть
уравнения не делится на ра и, стало быть, число а2 не делится на р.
Пусть a2 = kp, тогда исходное уравнение перепишем в виде
ai = k(a1—(р—1)), т. е. р— 1 =(fe— 1) (в!—р + 1).
Поэтому каждое решение в этой серии получается следующим обра¬
зом: в качестве значения Qj—р + 1 нужно взять любой из делителей
числа р—1, а затем положить a2 — kp, где
*=(Р— l)/(Ol—Р+ 1) + I-
Пусть теперь а2—(р—1) = тр, тогда исходное уравнение имеет ре¬
шение в том и только в том случае, если
глр+р—1=а2т, т. е. р—1 = (а-> — р) т.
В этой серии все решения получаются так: в качестве значения гр.
нужно взять любой из делителей числа р — 1, а затем положить
a2 = (p—l)/m+p, а! = тр+р— 1.
Ни одно из полученных решений не может принадлежать обеим
сериям сразу, так как иначе оно удовлетворяло бы двум исключаю¬
щим друг друга условиям. Поэтому количество решений уравнения,
равное количеству искомых последовательностей, совпадает с удвоен¬
ным числом делителей числа р—1.
17.21.	Докажем, что тройка чисел a, b, cgN, где Ь < а, с < а,
удовлетворяет условию задачи тогда и только тогда, когда выпол¬
нены условия
&C£sl(modo),	(1)
nbcn-\-(n—1) 6с"-х=й (п +1) bcn+l (mod а)	при n£N.	(2)
Пусть числа	а,	Ь,	с	удовлетворяют условию	задачи.	Тогда	усло¬
вие (1) вытекает из соотношений
bcss.a1 (mod й), at = 1,
а с учетом соотношений
2Ьс? ;= о2 (mod о), о2 = о/
Получаем и условие (2) при п=1, которое в этом случае выглядит так:
6е=5 2bc2 (mod а).	(3)
293

Наконец, при остальных значениях п > 1 условие (2) также выпол¬
нено, так как
Пусть теперь числа а, 6, с удовлетворяют условиям (1) и (2). Индук¬
цией по я£ N докажем, что каждое из чисел ап—пЪсп делится на а.
При п= 1 и я = 2 утверждение вытекает из условий (I) и (3) (послед¬
нее совпадает с условием (2) при подстановке п= 1), так как о1=о2=1.
Пусть для некоторого значения я> 1 уже доказано, что числа а„—nbcn
и о„_ 1—(я—1) Ьсп~1 делятся на а. Тогда из условий (2) и (4) сле¬
дует, что число
оп+г— (« +1) Ьсп+1 = ((а„—пЬс") + (о„ _г — (я — 1) Ьсп - ■*)) (mod а)
также делится на а. Заметим, что из условия (1) вытекают соотно¬
шения (6, а) = (с, а) = 1. При этом условие (2) равносильно тому,
что каждое из чисел
dB=(n+ 0 с2—яс—(я—1) = (я+1)(сг —с—1) + (с+2)
при п делится иа а, что (в свою очередь) имеет место тогда и
только тогда, когда каждое из двух чисел
с2—с—l=da—«Д и c+2 = dx—2 (с2—с—1)
делится на а. Следовательно, число
(с?- с— 1) — (с+2) (с—3) = 5
должно делиться на а. Поскольку д> I, то а=5, а из соотношений
с+2 = 0 (mod 5),. 1<с<5 и 6c=I(mod5), 1 <6 < 5 имеем с=3,
6 = 2. Для завершения доказательства остается заметить, что полу¬
ченные значения а, 6, с удовлетворяют условию (1) и числа с-(-2 и
с2- — с—1 делятся на а.
18.1.	Наименьшее значение функции f (х, у) при х,у > 0 равно 2,
поскольку имеют место соотношения
а равенство f (х, у) = 2 достигается тогда и только тогда, когда х=</•
18.2.	Используя теорему о средних, имеем
ап — nbcn (mod о),
о„ _ 1 = (я — 1) Ьс" ~* (mod а), а„+1 = (я +1) 6сп+1 (mod а),
ал + ал-1 = ап + 1-
(4)
§18. Экстремумы
/ (X, у)—2 =
£/2х2у2г2и =рг2х-ху-г-уги <
2х+ху-\-г-\-уги  1
4
4 »
294

т. е. Jt2(/2z2« <1/512. Равенство достигается, если 2х = ху = г=уги=\ /4,
т. е. при х=1/8, у = 2, г= 1/4, «=1/2. Итак, наибольшее значение
равно 1/512.
18.3.	Пусть сначала n = 2k, где k£N. По неравенству треуголь¬
ника имеем
\х—fli| + |x—а„|3*	«1,
I х—«аИ-!-*—-11 =& «л-1—«а.
I*—«ftl + l*—«ft+ilS= «ft+i—«ft.
откуда
ж = 2 i*—«/is* 2	ay)'
i= i	y=i
При этом, если	Ofc+i],	то
fe
ж= 2 (“»-/+!—°у)*
/=i
С другой стороны, если [а*: Oft+il. то
\x—ak\ + \x—ak+i\>ak+i—ak
И
k
f(x)> 2 K-y+i—«/)•
/=i
Итак, функция / (х) принимает наименьшее значение, равное
k
2 («в-/+1—«/)» при любом x£[ak; оА+1].
/ = 1
Пусть теперь n = 2k — 1, где fe£N. Имеем
| X «11	1	X - Qn | «п — «1,
I*—аа 1 + 1 *—««-1 l>««-i —«а.
откуда
I* — «ft-l l+l*—«ft-n|Ss«ft + l—«ft-П
I*—«ft IS*0,
n	ft-l
f(x)= 2	2	(««-/+!-“/)•
/=i
t=i
При этом, если x=ait то
ft-l
/(*) = 2 (“«-/+!—«/)•
/ = i
Если же г / ак, то
ft-i	ft-l
/	2	(«я-/+х	—	ay)	4-|	Jf—«ft | > 2 («**—/+1	«/)'
/=1	;=i
295

Итак, функция / (х) принимает наименьшее значение, равное
/?-1
2 (fln-7+i—?у). ПРИ х ah.
/ = 1
18.4.	а) Найдем наименьшее значение произведения х^х2...хп.
Пусть произвольный набор (ж,; ...; хп) удовлетворяет условию за¬
дачи. Рассмотрим новый набор
W1';*?»; ...; *?>),
где
<1>_V	v°> —V
Xj —Xi, X2 —X2, ..., Xfi—2 — *n —2>
*"-1= VXn-1 + X?l— 1 In2, Xn' = I/П.
Этот набор удовлетворяет соотношениям
xf',^im(i=l я), 2 (*i1’)*=b
i- I
Докажем, что
*1*2-• *«3*xi1’ Xj1’ ... *n*.
Действительно, имеем
*,ti xs-(*k"i *;1,,)2=
= x^-i j&— ^4_i+*n —	_=^jcna_i_
Далее, положим
(2)_ (1)	y<2>„ _V<1>
*1 —*1 , ..., Хп-з — *n-3>
*n —2	*£,	=	*“»= l/„
и аналогично получим, что
xp^l/n. 2№l
i = l
И
<D V(D vO) _	(2) (2)	(2)
Л] *2	* * • *fi	aj Л2 • • • Xn •
Повторив эту процедуру (л—1) раз, мы в итоге получим набор
/у<”-1). v<n-l).	.	у(«-1Л
V*1	> *2	,	• . ., *л 1>
где
лГ^^-п-Н/н,	хГ1^... =х"-1>= 1/л,
причем
хГ1’^!/»!. 2 (^1)),= 1
1=1
*,**.. .х„S>xf-1» ... Х?~" = \П^п+Мпп.
296

Значит, для любого набора (*i; хп), удовлетворяющего условию
задачи, справедливо неравенство
*1*2 ... х„ё*Уп2 — л+1/пП,
а при
х1 = Уч'г — я + 1/n, х2= ,,.=х„=\/п	ж
достигается равенство. Итак, наименьшее значение равно
Y п2—n+1/я".
б)	Найдем наибольшее значение произведения XiX2. > ,хп. Приме¬
няя теорему о средних, получаем
*1. • ■ *»< ((*?+ ... +xl)ln)n= 1/п»,
т. е.
Х\Хг...Хп<П~п12‘
Равенство достигается при хг=х2= t,t=xn=l/У п• Итак, наиболь¬
шее значение равно п~п^2.
18.5. Пусть max (Xj	хп) = хк. Тогда
л—1	А—1	* п—1
2 xixi+i =	+1	+1^
is]	i	—	1	i—k
A-1	n
2 xi+xh 2 Xi = xk(a—xk)*z((xk+a—xk)/2)2 = a2/4.
i=l	i=k+l
Равенство достигается, например, при jc1=x2 = o/2, х3 = ... =jc„ = 0
Следовательно, наибольшее значение равно а2/4.
п
18.6. Обозначим А =	о/. Для чисел 0 < а* < .,. < а„ имеем
i = 1
п	п	п
И te + l/6,') = II (№+1)/Ь) = (1/А)Ц (°«А+1)<
i-1	i	=	1	i	=	1
<(>М) nw+1)
i= I
(для доказательства последнего неравенства достаточно заметить, что
(а,-61-+ 1)? = о^+2аА+1 < aff+cq+bj+l = (а?+1) (bf+1),
откуда
П (oA+i)?<n (oi+ow+i)	= П (о?+02)-
1=1 1=1 1=1
Равенство достигается, причем	только если 2a,b/ = ai-j-bi для	всех
1 = 1	п. Таким образом,	указанное в	задаче произведение	ма¬
ксимально только в случае
Ai • • • I Ьп) — (а,; ■!,; ап),
297

18.7. Без ограничения общности можно считать, что х^у. Обо-в
значим p — x—k. Тогда x = k-\-p, y = 2k—x=k—p,	0, и произ-1
ведение
ху = (k+Р) (k—р) = k-5—р?
принимает наибольшее значение при наименьшем возможном значе.
нии р. Пусть р — 0, тогда x=y = k и числа х, у являются взаимно)
простыми лишь при k=l. Пусть р= 1, тогда x = fe-|-l, y = k—I,
Для того чтобы числа х, у были взаимно простыми, необходимо,
чтобы число k было четным (в противном случае	оба	числа	х	и	у
делились бы на 2). Но это же условие является	и	достаточным,	по¬
скольку общими делителями чисел х и у могут быть только делители
их разности х—y=(fe+l) — (k—1) = 2 (т. е. числа 1 или 2), а при.
четном значении k число 2 не является делителем, например числа !
x = fe+l. Пусть р = 2, тогда числа x=k-\-2,y = k—2 при нечетнои|
значении k являются взаимно простыми, так как в этом случае
числа х, у нечетны и не могут иметь общих делителей, отличных от
делителей их разности х—j/ = (fe+2) — (k—2) =4. Итак, искомые чи¬
сла х, у определяются следующим образом:
если fc=l, то х= 1, у— 1;
если k = 2т, m£N, то x=k ± I, y=k Т 1;
если fe = 2m+l, m£N, то x=k ± 2, y = k ^	2,
18.8. Имеем
п	п
а= 2 sln?x/= 2 (1—cos 2xi)[2,
i=i	i=l
т. e>
n
2 cos 2x; = n—2a.
i= 1
Далее, рассмотрим на плоскости векторы
(cos 2хр, sin 2xi)
единичной длины. Их сумма имеет длину не больше п, а значит, вы¬
полнено неравенство
2sin2*,|<;	п¥—^ 2 cos 2х,-
= Уп* — in—2п)? = 2 У a(n—d),
в котором при
Xi = xa= ... =x„ = arcsln У а/п
достигается равенство. Итак, наибольшее значение равно 2 Уа(п—а)•
18.9. Заметим, что любое фиксированное число n£N можно раз¬
ложить в сумму натуральных чисел лишь конечным числом способов^
298

Поэтому среди этих представлений найдется такое (быть может, неедин¬
ственное) разложение п = тг-\-т2-\-... + тк, где тх с лг2< ... <лгь,
для которого произведение т\гп2.. .тк принимает наибольшее значение
/ (и), причем ни одно из чисел т,- (1=1, 2 k) не равно 4 (любую
четверку с самого начала можно заменить двумя двойками, после
чего ни сумма, ни произведение чисел не изменится). Тогда каждое
из чисел /л,- не превосходит 4, так как если тк > 4, то произведение
чисел mi, т2 тк—2, 2 будет больше прежнего (ибо (тк— 2) 2 >
> тк), в то время как их сумма по-прежнему равна п. При л = 1
имеем единственное разложение, поэтому / (1) = 1. Далее, при л > 1
ни одно из чисел /л,- не равно 1, так как если т\= 1, то произведе¬
ние чисел	т3, тк будет больше прежнего (ибо
> mimz), а сумма равна п. Наконец, среди чисел /л,- не может быть
трех (и более) двоек, так как если т± = т2 = ms = 2, то произведение
чисел 3, 3, mt тк будет больше прежнего (ибо 3? > 23) при той
же сумме. Таким образом, если п > 1, то каждое из чисел т; равно 3,
кроме, быть может, одного или двух чисел, равных 2. Этими усло¬
виями набор чисел т, определяется однозначно для каждого значения
п > 1. Поэтому для искомой величины / (л) имеем
/(1)=1, /(3/) = 3*, /(3/-1) = 2-3*-1
и
/(31 + 1) —4-Зг~1 при /£N,
18.10.	Докажем, что наименьшее по модулю значение величины
/ {гп, п) = 12ш — 5"
при ту п равно 7. Прежде всего, имеем равенство /(1,1) =7.
Далее, предположим, что для некоторых чисел т, л£1Ч выполнено
неравенство
| / (т, п) | < 7,
Поскольку число f(m, п) не делится ни иа одно из чисел 2, 3, 5, то
I f (т, л) | = 1. Следовательно, остаток от деления числа / {т, л) на 13
равен либо 1, либо 12. Так как
12“ = (—1)“ (то.1 13),
то остаток от деления числа 12т на 13 равен 1 при четном и и 12
при нечетном т. Пусть л = 4й-|-г, где k£Z+, г£{0; 1; 2; 3). Тогда
5п = 625*.5г= 1*.5г (mod 13),
откуда следует, что остаток от деления числа 5" на 13 равен 1, 5, 12
или 8, если число г равно 0, 1, 2 или 3 соответственно. Таким обра¬
зом, остаток от деления числа 12™ — 5" на 13 не может равняться
Ии 1, ни 12, а значит, неравенство | / (т, л) | < 7 не выполняется ни
при каких значениях m,n£N.
29 9

§ 19. Различные свойства функций
19.1. Условия задачи выполнены тогда и только тогда, когда
f (0) = с=1
и справедливы равенства
t (*i) = ах\ + bxi -{-1 = 1,
/' (х2) — 4ах2 + 2Ьх2 =О,
из которых получаем
Ь =—2ах2 и ах\—2ах2х\ = ах? (xl—2д|) = О,
а значит, Xi = x2 У 2 (так как числа х2, а отличны от нуля). Про¬
верка показывает, что если х2=х2 У 2, то функция
f (х) = ах4—2axlx* -{-1
удовлетворяет условиям задачи. Таким образом, если Х\ Ф х2 У 2,
то указанной функции не существует, а если Хх = х2У 2, то тройка
(а; 6; с) имеет вид (а; —2ах%; О (где а—произвольное ненулевое
число).
19.2. Докажем, что такой функции не существует. Действительно,
в противном случае имеем: / (0) — (/ (0))? ^ 1/4, т. е. (f (0) —1/2)*<0,
откуда / (0) = 1 /2. Аналогично получаем, что /(1) = 1/2, т. е. / (0) =
= /(I), что невозможно.
19.3. Докажем требуемое тождество. Подставляя в неравенство
f (ж+УХ/М +f(y)
значения х=у=0, получаем f (0)<;2/(0), или /(0)^0. Отсюда и из
неравенства /(0)^0 следует, что f (0) = 0. Далее, для любого x£R
имеем
f(x)^f (х+(— х))—/ (—x)= — f(—x)s= х.
Отсюда и из неравенства	вытекает	тождество f (х) = х, х£ R.
19.4. Рассмотрим функцию
g(x)=f(x)+f (ах).
Если a—pjq, где p£Z, <7£N, то Т = qn—период функции g(х), так как
g (x+qn) = / (*+qn)+f (ах+рл),
а л—период функции f(x). Докажем, что если а иррационально, то
функция g (х) непериодична. Заметим, что g (0) = f (0)	/ (0) = 1. Если
же Ё (*о) — 1 Ддя некоторого х„ ф 0, то tg2 х0 =0 и tg?(ax0) —0, т. е.
х0 = лk и ах0=л/ (k, l£Z).
Но Xq Ф 0, значит, а = //£, что противоречит иррациональности числа а.
Итак, функция g(x) принимает значение 1 в единственной точке х —0,
следовательно, она непериодична.
300

19.5. Поскольку уравнение f (х) g(x) не имеет действительных
решений, то функция
h(x) = f{x)~ g(x)
принимает либо только положительные, либо только отрицательные
значения прн всех x£R. Поэтому функция
f if(*))—gigМ) = /(/ М)—gif W)+f ig (*))—gigM) =
= h(fix))+h(g(x))
не принимает нулевых значений ни при каком x£R.
19.6. а) Пусть /: [0; + со)—>• [0;	со) — непрерывная функция и
lim /(/(х)) = -fco.
X -»■ + ос
Предположим, что утверждение неверно. Тогда существует такое зна¬
чение N > 0, что для любого n£N найдется число хп > п, удовлетво¬
ряющее условию /(x„)£[0; N], Так как функция } (х) непрерывна,
а значит, ее значения на отрезке [0; N\ ограничены, то найдется такое
значение М, что если / (х) N, то / (/ (х)) < М. Поэтому для каж¬
дого n£N существует число хп > п, для которого / (/ (х„))< М, что
противоречит условию
lim /(/(*)) = +со.
X —У <Х
Значит,
lim / (х) = +со,
х -+■ + 00
б)	Пусть } (х) = 1/х, тогда /: (0; -f со)—»■ (0; + оо),
/(/(х)) = х, Ит /(/(*))=+05. lim / (х) =~ 0.
X —► + се	Ж->+оо
19.7. Пусть описанная в задаче функция / (х) существует. Рас¬
смотрим непрерывные функции
g(x) = /(x+l) —/(х) и /г(х) = /(х+1) Ь/(х).
Они не могут быть одновременно постоянными, так как иначе функ¬
ция / (х) = (/i (х)— g(x))/2 была бы постоянной. Пусть, например,
h(x) — не постоянная функция, т. е. существуют такие значения хх
и х2, для которых h (хх) < h (х2). Тогда существует рациональное
число г £ [Л (xi); h (x2)J, и в силу непрерывности функции h (х) най¬
дется такое число х0, что /i(x(,) = /’. Итак, / (х0+ >)+/ {Ч) = г- Сле¬
довательно, числа / (х0 + 1) и / (х0) либо одновременно рациональные,
либо одновременно иррациональные. Получили противоречие.
19.8. Из неравенства (/(х) —/{у))2<| х—j/|s при хфу следует, что
\f i*)—fiy)\^, „ .,11/2
откуда
ЦИгШ)*,,-,,.
Ita I'W-fMI 0
Х-*у\ Х-у I
301

(так как lim |х—i/|1/2 = OY Значит, функция f(x) дифференцируема I
V	х-*у	J	I
в каждой точке, причем /' (х) = 0, x£R. Следовательно, она может
быть только константой.
19.9.	Пусть функция / (х) удовлетворяет условию задачи. Рассмот¬
рим функцию g (х) = I (х) + х—1, определенную на отрезке [0; 1]. Так
как она непрерывна (ибо f (х) непрерывна), причем g (0)=—1, g (1) = 1,
то существует такое число с£(0; 1), что g (с) = 0, т. е. / (с) = 1—с.
По теореме Лагранжа найдутся точки а£(0; с), Ь £ (с; 1), для которых
I— С
поэтому
ГШ’(Ь)=~~С=1.
19.10. Дойажем, что любое число d=l/£, где ££N, удовлетво¬
ряет условию задачи. Возьмем произвольную непрерывную функцию
f (х) и число k > 1 (число d = 1 удовлетворяет условию, ибо f (0) =
= f (1)). Рассмотрим функцию
g(x) = { (х+1/fc)—/(х),
определенную на отрезке [0; (k— 1 )/£]. Поскольку сумма чисел
g(0) = /(l/*W(0), gО/*) = /(2/A)-/(1/ft) g((ft-l)/ft) =
= /=(!)—/=((*—1)/*)
равна 0, то среди них есть как неположительные, так и неотрицатель¬
ные числа. Поэтому в силу непрерывности функции g(x) существует
число х0, для которого g (х0) = 0, т. е.
f(xo+\/k) = f(x0).
Пусть теперь дано число d£(0; 1], не равное l/k ни при каком зна¬
чении ££N. Возьмем такое число ££N, для которого kd < 1 < (k-\- l)d,
и рассмотрим произвольную непрерывную функцию f (х), определен¬
ную на отрезке [0; d] и удовлетворяющую равенствам
/ (0) = 0, f(l-kd) = -k, f (d) = 1.
Продолжим эту функцию на отрезок [0; 1] таким образом, чтобы при
каждом x£[d; 1] выполнялось равенство
f (x) = f{x—d) + l.
Полученная функция непрерывна, причем	—d) + l =
= /(1—2d) +2= ...==/(1—kd) -\-k—0 = f (0) и при любом значении
х£[0; 1—d] имеют место соотношения f (x+d) = / (х)+1 Ф f (х).
19.11. Пусть число ££N не нвляется квадратом целого числа.
Покажем, что f (У к) = 0. Так как У fc (£ Q, то f (У k) — 0, н остается
доказать, что предел
lim / (х)/(х— У~к)
■ V~k
302

существует и равен 0. Возьмем произвольное е > 0. Существует лишь
конечное число дробей p/q (всюду ниже p£Z, <?£N), удовлетворяю-
щих условиям
0 < q < Л/е и I p/q — У k | < 1,
Поэтому при некотором 6£(0; 1) в интервале
16=(У1-&;	+
таких дробей нет совсем. Если x=p/q^I(,, где p/q—несократимая
дробь, то
9S* 1/е и \ У~к+рШ\< У~Ь + (У~к+&)<2У~к+\,
причем |*9?—р?|^1 (ибо *9?—p?£Z\{0}), следовательно, имеем
I	I -|	1(Р1Ф_	1	\У~Ь+Р/я\\У к+р/д\
I х У k j I p/q— y~k I 93 | *—P2/9a 1 Я	Iff2*—P2 I
<e(2 У~к +1).
Если же число x €'б\Ю} иррационально, то f(x) = 0
и | / (х)/(х—У к) | = 0. Утверждение доказано.
19.12. Предположим, что существует такой интервал /с/длины d,
для которого
fn(J)()J = 0 при любом n£N.
Тогда для любых т, n£N имеем
Р+и (J) = fa (/" (J)f)J) = fm (0) = 0.
поэтому множества / (J), f-(J), ..., fn (J), ... попарно не пересе¬
каются. С другой стороны, каждое множество fn(J) при л £ N есть
объединение нескольких промежутков суммарной длины d, лежащих
в /. Поэтому все они не могут попарно не пересекаться. Полученное
противоречие доказывает требуемое утверждение.
19.13. Обозначим h (х, y) — f(y)— I (х), тогда функция h (х, у)
возрастает по второму аргументу и убывает по первому, причем
^ ix, у) > 0 для всех у > х и
е (х, у) = h (х, x+y)/h(x—y, х).
Докажем, что при всех x£R, у > 0 справедлива оценка g(x, у) < 14,
Если х—у 0 нлн х+р<0, то по условию уже имеем
ft (х, х+у) < 2ft (х—у, х),
а кроме того, для всех у > 0 выполнено неравенство
/1(0, у) < 2/i (— у, 0).
Поэтому остается рассмотреть два случая: 1) х—у < 0 < х; 2) х <
< 0 < х+у. Заметим, что для всех xS*0, у > 0 справедлива оценка
h(x+y, х-ЬЗу) < б/i(х, х+у).	(1)
303

Действительно, имеем	и
ft (х+у, х+2у) < 2ft (х, х+у),
ft (х+2у, х+3у) < 2ft (х+у, х+2у) < 4Л (х, х+у),
откуда
h(x+y, x+3y) = h (х+у, x+2y)+h(x+2y, х+Зу) <6h(x, х+у).
Рассмотрим случай 1). Если х—у < 0«^х—у/2, то, используя оценку
(1), получаем
h(x, х+у) < 6 Л (х—у 12, х) < б/i (ж—(I, х) < 14 ft (х—у, х).
Если же х—у/2 < 0 < х, то
х < у—х < х+у < 3 (у— х)
и, используя оценку (1), имеем
ft (у—х, х+у) < ft (у—х, 3 (у—х)) < б/i (0, у—х).
Поскольку ft (х, у—х) < h (0, у—х), то снова получаем
h(x, x+y) = h(x, у—х) +h (у—х, х+у) < 7h(0, у—х) <
< 14h(x—y, 0) < 14ft (х—у, х).
В случае 2) имеем
h (х, 0) < 2ft (2х, х) < 2h (х—у, х),
ft (0, х+у) < 2fi(—x—y, 0) < 2h(x—y, 0) =
= 2ft (х—у, x)-t-2ft(x, 0) < 6ft (х—у, х)
поэтому
ft (х, х+у) < 8ft (х—у, х).
Итак, во всех случаях доказано, что
ft (х, х+у) < 14ft (х—у, х),
откуда следует оценка g (х, у) < 14. Докажем теперь, что g (х, у) > 14-1
при всех x£R, у > 0. Рассмотрим возрастающую функцию fi (х) =
=—f (—х) и положим
я (х ,Л h (х+У)~ ft (х)
gl{*' ^С*-!/)'
Так как gi (х, y) = (g(—x, у))~К то 2~l < gl (х, у) <2 для всех
у > 0 прн х=0 и для всех у£(0; | х|] прн х Ф 0. Тогда, по доказан¬
ному выше, для функции gi (х, у) справедлива оценка gl (х, у) < 14
при всех x£R, у > 0, откуда следует, что
g(x, g) = l/gi(—х, у) > 1/14.
Утверждение задачи доказано.
§ 20. Функциональные уравнения
20.1.	Положим у= 1 в тождестве, выполненном для функции / (х).
Тогда имеем тождество
/ М - (/ (х) 4-/ ОМ*+1) (хФ-1),
304

т. е. xf(x) = f( 1). При х=0 получаем /(1) =0, а значит, при х £
$*{—1; 0} имеем f(x) = 0. Далее, подставляя в исходное тождество
значения у = 0, х = 2, получаем / (0) = (/ (2) + / (0))/2, откуда f (0) =
= /(2) = 0. Наконец, подставляя значения у = 0, х——1, получаем
F (0) = — f (— 1)—f (0), откуда ^ (—1) = —2/ (0) = 0. Таким образом,
для функции-f (х) доказано тождество /(х) = 0, x£R.
20.2. Положим в исходном тождестве х — у=1, тогда получим
2f (1) = 2 (/(I))2, т. е. f (1) =0 илн /(1)=1. Рассмотрим каждый из этих
случаев:
а) Если f (1)=0, то, положив в тождестве у=\, получим тож¬
дество / (х) = 0.
б) Если / (I) = 1, то, снова положив у—\, получим тождество
/(*)+*=(*+>)/(*), Т. е. х(/(х) —1) = 0,
откуда при любом х Ф 0 имеем f (х) = 1. Таким образом, для функции
/ (х) имеется две возможности: либо { (х) = 0, либо
= I 1 Прн
' '	\ а при х = 0, где a£R<
Проверка показывает, что любая из этих функций удовлетворяет ус¬
ловию задачи.
20.3. Подставляя в исходное тождество для функции f (п) £ М
значения я=/п = 0, получаем (f (0))i = 2f (0). Но f (0) ф 0, поэтому
f (0) =2. Далее, подставляя в тождество значение т=1, получаем
тождество f (я) f (1) = f (n+ 1) +/ (л— 1). n£Z. Если заданы значения
функции f (и) в точках л=0 н п— 1, то из этого тождества однозначно
определяются значения / (2) н f (—1), а затем f (3) и f (—2) и т. д.,
т. е. все значения / (п) при ngZ. Таким образом, функция } (п) един¬
ственным образом определяется условиями задачи, так как /(0)=2
и / (1) = 5/2 (в п. а)) или /(1)=|/” 3 (в п. б)). Остается'убедиться
в том, что функции
f (п)= 2"+2 “п и f (п) =2 cos (лп/6)
удовлетворяют всем условиям п. а) и б) соответственно. Действительно,
имеем:
а) f (0) =2°+2° Ф 0, /(1)= 21+ 2-1 = 5/2,
Ип)И|”) = (2л+2"")(2Ч2‘“) = (2л + в+2-»-|») + (2”-|+2в-»)=
= /(п + /л)+/ (п—т) при всех п, т£Z;
б) / (0) = 2 cos 0 ф 0, f (1) =2 cos (я/6) = Y 3,
1 (n) f (m) = 2 cos (лп/6)-2 cos (ят/6)=2 cos (л(п+т)/6) +
+2 cos (л (п—т)/6) = / (п + т) + / (п — т)
при всех п,т£ Z.
20.4. Положив т=0 в исходном тождестве, для функции f (п)
получим 2f (п)	/	(3n)	(n£Z+),	а при п=т=0 имеем / (0) =0. Далее,
305
к

положив в тождестве п— т, получим
f (2и) +f (0) = f (Зп), т. е. f (2п) = f (Зп).
Отсюда с одной стороны для любого значения /л£ Z+ имеем равенства
/ (4m) = f (6/и) = f (9т),
а с другой стороны, из тождества при л=3т получаем
/(4m) + /(2m) = /(9m),
что возможно лишь в случае / (2т) = 0. Следовательно, при любом
значении я£ Z+ имеем
/ (я) = (1/2) / (Зл) = (1/2) / (2я) = 0,
т. е. исходному тождеству может удовлетворять (и действительно
удовлетворяет) лишь функция f (п), тождественно равная 0.
20.5. Положив х = у = 0 в каждом из двух тождеств, которым
удовлетворяют непостоянные функции f(x), g(x), получим два равенства
/ (0) = 2/ (0) в (0) и g (0) = (g (0))? - (f (О))2.
Поскольку g (0) ф 1/2 (в противном случае из второго равенства сле¬
довало бы, что (/(О))2 =1/4—1/2 < 0), то из первого равенства имеем
/(0) = 0, а из второго получаем, что либо g(0) = 1, лнбо g (0) = 0.
Однако последний случай невозможен, так как иначе в силу первого
тождества при у = 0 функция
f(x)^f(x)g(0)+g(x)f(0)^0
была бы постоянной. Итак, получены единственно возможные значе¬
ния / (0) = 0, g (0) = 1, которые реализуются, например, для функций
/ (х) = sin х, g (х) = cos х.
20.6. Положив в исходном тождестве у=1, получим тождество
f(x) = f(x)f(l)-f(x+l) + l (x£Q),
f(x+l)^f(x) + l.
Отсюда для всех x£Q, я£Z имеем
f (x+n)=f (х)+п,
поэтому
/(я)=?(1) + л-1=я+1.
Далее, подставляя в исходное тождество значения х=1/я, у = п при
я£ Z, получаем
откуда
2 = / (1/п) (я + 1) — f(l/n) — я+1, т. е. / (1/л) = 1 + 1/л,
Наконец, подставляя значения х — р, y=ljq прн р£Z, q£ N, имеем
306

откуда
f (P/Я) = (Р+1) 0/9+ О—!/?—Р = Р/Я +1.
Таким образом, имеем только одну функцию f(x) = x+l, которая
действительно удовлетворяет всем условиям задачи.
20.7.	Пусть сначала я <100 и я+ 11 > 100, т. е. 90<я<100.
Тогда
Пусть теперь я < 90. Выберем такое число m£N, чтобы выполня¬
лись оценки
Тогда имеем
/ (я) = /?(я +11) = ... = /m+1 (я + 11т) = /т (f(n + llm)) = fm (91) = 91.
Таким образом, требуемое равенство доказано при всех значениях
я <100.
20.8.	Докажем тождество g(n) = ft(n) (n£N), из которого
в силу условия в) будет следовать, что
(ибо / (я) Sa 1). Предположим, что для некоторого значения n£N
равенство g(n)=h(n) не выполнено, тогда ft (л) < g(n) = k. Согласно
условию б) найдутся числа nlt ..., g N, для которых g (я,) =- i
при i=l, ..., k—1. Поэтому каждое из к чисел ft (пг), ..., ft (пд._,),
ft (я) принадлежит множеству {1;	—1}, следовательно, по прин¬
ципу Дирихле (теорема 1) функция ft (я) принимает некоторое зна¬
чение более, одного раза, что противоречит условию а). Утверждение
доказано.
20.9.	Пусть последовательность п± = 2, п2 = 3, я3 = 5, ... пере¬
числяет в порядке возрастания все натуральные числа, не являющиеся
квадратом целого числа. Положим
Тогда %,B+i = (n*, J2, и каждому значению я>1 соответствует
единственная пара чисел к, т, для которых я = я*, т. Определим
Функцию / (я) следующим образом:
^ (я) = f (/ (я + 11)) = / (я +11 — Ю) = / (я +1),
поэтому
f (90) = / (91)= —f (100) = / (101) = 91.
90< n+ 11/л < 100.
f (я)=й(я)—ft(n) + X 1, n£N.
При любом n£N имеем
h{n) = g(n) + l—f (n)Cg(n)
ял, m = (nft)2m, где ft£N, m£Z+.
если k нечетно,
если k четно,
307

20.10.	а) Например, функция
/(л, m) = rt (п, m£Z)
удовлетворяет всем условиям задачи.
б)	Пусть утверждение неверно, т. е. для некоторого числа k£Z
все значения некоторой функции f (п, т), удовлетворяющей условию
задачи, например, не превосходят k. Тогда среди значений / (п, т)
(п.т^Т) найдется наибольшее, равное, скажем, / = /(л0, ,по)- Этому же
значению равны и все числа / (я0 ± 1, m0), f (л0, Щ± 0> так КЕК
в противном случае оказалось бы, что
/(«о. "»<>) =
=■4" (f (по—	то) + / (по +1»	то) + / (яо. та— 1) +/ (по> то + 1)) <
Рассуждая подобным образом, можно получить равенство
/ = /(я0, л?0) = /(л0± 1, л?о) = /(«о ± 2, т0) =•••=/(«о ± «. «о) =
=/(л„ ± л, /я„ ± 1) == / («о ± п, т0± 2) = ...=/ (л0 ± л, т® ± /л)
для любых значений л, m£N. Таким образом, /(л, т) е=/, что про¬
тиворечит условию задачи.
20.11.	Назовем точку (л; m)£S четной или нечетной в зависи¬
мости от того, является ли сумма л+m четной илн нечетной соот¬
ветственно. Пусть существует универсальная функция g(n, т), тогда
функция g~l(n, т) также универсальна. Рассмотрим функцию, задан¬
ную следующим образом:
е, V-. -•-/>	если точка	(л; т) четная,
1 —1 /.. ._■> если точка	/л) нечетная,
I g(n, trt),
I g-1 (л, m).
/!(я, m) = -*
при (л; m)£S. Точки g(л, m) и g~l(n, m) имеют противоположную
с точкой (л; т) четность, поэтому для любой точки (л; m)£S
получаем
g~l(g(n, т)) = (л; га), если точка (л; т) четная,
g (g~l (л, т)) — (п\ т), если точка (я; яг) нечетная.
Таким образом, доказано тождество
/?(л, т) = (я; Я1),	(л;	т)£S,
из которого вытекает обратимость функции f (л, м), а для доказа¬
тельства универсальности этой функции достаточно теперь вспомнить,
что функции g (л, т) .и g-1 (л, т) универсальны.
20.12.	Докажем, что никакие пары искомых значений, кроме
приведенных в указании, не удовлетворяют требуемым условиям.
Предположим, что некоторая целочисленная пара (т; л), отличная
от (2; 3) и (2; 5), удовлетворяет неравенствам т^п, тп (т + л) Ф 0
и тождеству
tm (■*. У) fr, (■*. У)^!т +,, (*. У).	*,	-*«/(•*+</) £ 0»
где
/*(*» У)=1*НУ*-Н—при	МО.
308

Для каждого фиксированного значения у = у0^0 справедливы сле¬
дующие утверждения.	Если k < 0,	то
lim	xk = lim	(*+j/0)* = 0,
X-»-ce
откуда
lim fk (x, y0)=yo/k.
x-m
Если число	четно,	то
/	k	—	\	V
/А 1*. 0=-g'^2**+2i'*+x cw_‘j.
откуда
lim fk(x’	Уо)	2
oo X	k
Наконец, h(xt y)===0, a-если число нечетно и k ф 1, то
k — 1
Ы*. !/)=—Ск*‘Ук~11
1= 1
откуда
i:~ f* (Ж- */0>	f/0	r,k-l
lim	 =	TCk =—Уо-
Рассмотрим несколько случаев.
а)	Пусть числа т, п£ N четны. Тогда, учитывая исходное тож¬
дество, получаем
2	  fm	+	n(X>	Vo)	 fm (•*» 1/p) fn (•*» l/o)  4
Xя* x-»oo xn	m/i	*
откуда (m+n)/2 = mn/4, т. e. (m/2—1) (n/2—1) = 1. Последнее усло¬
вие выполняется лишь при n/2 = m/2 = 2, откуда т = п = 4, что невоз¬
можно, ибо
f*(f. 1)М1. 1) = (2 + 2У/4? = 81/4 ф 129/4 = (2+2в)/8 = /8(1, 1).
б) Пусть числа т, n£N нечетны. Тогда имеем
lim	^	— iim 1 fm(x, Уо) /„(*. "о)_0
Х-r*,	xm	+	rt	xi	xm-1 Xn-L	1
»i fm + n fo* */(0 	^
*»+"	m	+	n	!
что противоречит исходному тождеству.
в) Пусть одно из чисел т, n£N (обозначим его через р) четно,
а другое (обозначим его через q) нечетно. Тогда q > 1, так как если
9=1, то /в(1, 1) = 0, и в силу тождества имеем
о 9 P+Q
fP+e(i. *)= р_=°.
309

что невозможно, ибо p-\-q> 1. Поэтому получаем
fp (х, г/о) ft7 (х, у0)	fp	(х,	у0)	fg	(х,	у0)	2у0
]im 	 =	llm	—Э	FT“=—7Г'
*-»*,	Xй	4	хг	хч	Р
fp+g(x* Уо)
откуда /7=2. Из тождества имеем
3.(2-29)/9 = fa(l, 1)^(1, 1) = /2+9(1, 1) = (2-2*+9)/(2+9),
т. е.
3(2+<?)(1 — 2?-») = 9(1 — 2?+1), или 3+9 = (6—q)2Q~?.
Поэтому q < 6, а так как q нечетно и q > 1, то <?£{3; 5}, что проти¬
воречит сделанному предположению.
г) Пусть т < 0, а число л £ N четно. Так как п > m+я, то неза¬
висимо от знака и четности числа m+л имеем
i;m fm + n{Xt </о) п
}1Ш 	JS 	°*
*-><»	*
в то время как
lim f„ (х, y«)JAx, г/о)= ijm fm (Xt yo) ]im f i (*.,o)	ф	о.
X-+ eo	^	JC-^oo	X-*oo	X	fil/l
д) Пусть m < 0, а число л £ N нечетно. Тогда л ^ 1, так как
если л = 1, то /„(1, 1) = 0, и в силу тождества имеем
„	2 + (—i)w+n2m+n п
Тт+п{ 1, •)	к.
что невозможно, ибо /л+я < 0. Поэтому, с одной стороны, получаем
lim fm {Х'	(Х’ У0)-= lirn f-n (*. Уо) lim fn%yl's]- = ~f+' *0,
С другой стороны, если т <— 1, тол—1>т+я, и независимо от
знака и четности числа m + л имеем
lim f*+« (* ’	=0.
Х-*оо	X
Поэтому число т может быть равным только —1. Тогда число
т+л = л — 1 четно и
lim fm + n (те, Уо) _	2
г"-1	л—1
Итак, при каждом значении уе Ф 0 справедливо равенство 1/г/о =
= 2/(л—1), что невозможно,
е)	Пусть т, я < 0. Тогда
lim fm (х, y0)fn{x, ya) = tfi‘+n/mn,
JC-+CC
I'm fm + n(xi yt>)=ya+,‘/(mi-n)t
*-►00
310

но равенство yal+n/mn = iff+п/(т-f-п) не имеет места, ибо тп > О,
т+л < 0.
Таким образом, условию задачи удовлетворяют только две пары
(т; я): (2; 3) и (2; 5).
20.13. Подставляя в первое исходное тождество для функции
f (х, у) значения х=у = 0 и х=у = 1, получаем равенства f (0, z) = l
и /( 1, г)=1 соответственно. Далее, подставляя х=у = —1, имеем
*)=/(-!. *)/(-!, г) = (/(-1, г))*,
следовательно, f(—1, г) = 1. Аналогично из второго исходного тож¬
дества получаем равенства f (z, 0) =/ (z, 1) = /(z, —1)=1. Отсюда
следует, что
/ (0, 0) = 1 и /(0, z)f(z, 0) = 1.
Остается доказать требуемые тождества для ненулевых значений х
и у. При х Ф 0 имеем
l=f(l, z)=/(x, z)f( 1/х, г),
поэтому
fix, Z) = \lf(l/xt г).
Далее, получаем
1 = /(х, 1-х)	~'Х)^
=	(1—х)/х)/(1/х, х).
Но поскольку
/(1/*, (1-х)/х)=/(1/Х, 1/Х—1).1=/(1/Х, 1/х—1)/(1/х, -1) =
— / (1/Х, 1 — 1/х)=1,
то /(1/х, х)=1. Итак, имеем
1 = /(*. 1)=/(х, 1/х) =/ (х, х) = / (х, х)/(х, — 1)=/(х, —х),
т. е. /(х, х)=/(х, —х)= 1. Наконец, при х Ф 0, уф 0 имеем
/(*, y) — f (х, y)-f(Uy, y)=f(x/y, y)~f (xly, y)-f(x/y, x/y) =
=f (x/y, x) = f(x/y, x)-f (1/x, x)=f (l/y, x)= 1// (y, x).
Следовательно, f (x, y)f(j/, x) = l.
20.14. Если функция f(x) удовлетворяет первому тождеству, то
/(xg+x+g) = /(*#)+/(х —1 г/) за / (хг/) +/ (х) +f (у)
(х, g£R), т. е. второе тождество для нее также выполнено. Пусть
теперь функция f (х) удовлетворяет второму тождеству. Положив
в нем y = u+v-{-uv, получим
f (х+ы+ц+хи+хо+ып+хыо) =
(x)+f (u + v+uv)+f (XU+XV+ xuv),
что можно преобразовать к виду
f (х-|-ы | у-фхн + ху+ио+хып) =
= / М +/ (и) +/ (о) +/ (UV) -]-/ (хп +ХО+XUO).	(1)
311

Поменяв местами переменные х, и в тождестве (1), получим
f (x + M+0 + JW + XO-|-UtJ-f-XUl')s=
^f(x)+f («) +f (v)+f (xv)+f (хи + uv+xuv). (2)
Из тождеств (1) и (2) получаем
f (uv) -f/ (XU + XU -f xuv) Si f (XL1) -f- f (XU + ЫО+ХШ)).	(3)
Положив в тождестве (3) х= 1, имеем
f(uv)+f(u + v+uv)~f (v)-f f (и+2uv)t
ИЛИ
f М +/ («) + f (v) +f (lw) = f(v)+f (u+2uv).
Отсюда
/(и)+2/(«п)^/(«+2ио).	(4)
Положив в тождестве (4) ы = 0, получаем f (0) = 3/ (0), поэтому
f(0) = 0.	(5)
Положив в тождестве (4) v — —1, получаем /(—ц) = /(п)+2/ (—и),
следовательно,
/(_„)—/(«). (6)
Положив в тождестве (4)	—	1/2, получаем
/ (0) = / (к) +2/ (— и/2).
Используя соотношения (5), (6), получаем
/(«)== 2/(и/2) или f (2и) = 2f (и),	(7)
Из тождеств (7), (4) имеем / (п+2пе) ^ / (и)+/ (2uv), и, сделав
в последнем уравнении замену 2п = /, получаем
f(u + ut) = f(u) + f(ut).	(8)
Итак, мы приходим к тождеству f(x-j-у) = f (х)-j-f (у), так как при
х=0 это тождество обращается в равенство (5), а при х Ф 0 имеем
из тождества (8)
I(x+y)*^f	M+f
20.15.	Докажем, что для любого значения k > 0 справедливо
тождество
/ (хй) = &xs_1 / (х) (х > 1).
Доказательство проведем в три этапа.
I)	Пусть	Если	ft=l,	то имеем
/(х»)^ЬхМ(*),
а если тождество справедливо для некоторого значения fc£N, то оно
-справедливо и для значения Л+1. так как
/ (х*+*) в } (х*х) — Xй/ (х) +xf (х*) —
ES Xй/ (х) -j-xfcx*-!/ (х)» (ft4- 1) XRi (х).
312

По принципу математической индукции тождество справедливо для
любого A£N.
2) Пусть fe£Q, k > 0, т. е. k = p/q, где р, q£N. По доказанному
в п. 1) имеем два тождества
(х),
f((xp'T)^<7(*P/T“V(*p'c).
Приравнивая правые части этих тождеств, получаем
f (хл/«)=(p/q) xp!v ~ xf (х),
т. е. тождество справедливо для любого рационального k > 0.
3) Пусть R, k > 0. Тогда выберем такую последовательность
положительных рациональных чисел klt k2 для которой
lim kn = k.
П-* оо
Поскольку функция f (х) непрерывна, то для любого значения х > 1
имеем
/(**)= lim /(/")= lim kn^n~1f{x) = kx»-1f(x).
П—ь 00	п~*-оо
Из доказанного тождества легко найти явный вид функции f (х).
Действительно, обозначив t — 1пх, т. е. х—е*, получим
f(x) = l (е1) = tet-'f (е) = (Inx)~f (е).
С другой стороны, при любом значении с£ R функция f(x) = cx\nx
удовлетворяет условию задачи.
20.16.	а) Из условия задачи следует, что функция f (х) не при¬
нимает никакого значения более чем в одной точке x£R. Действи¬
тельно, если u = f(x) = f(y) для некоторых х, у£ R, то
х = р (х) = I2 (и) = /3 (у) = у.
Отсюда и из непрерывности функции f(x) следует, что она строго
монотонна. В противном случае найдутся числа хх < х% < x3t удов¬
летворяющие неравенствам
/ (*i) < 10*2). 1 (-*2) > 1 (^з)
илн
f (Хх) > I (Xi), I (Xi) < f (Хз),
а значит, некоторое значение и, лежащее как между числами f (хг) и
f (*2), так и между числами / (х2) и f (xs), согласно теореме о про¬
межуточном значении непрерывной функции, будет приниматься функ¬
цией f (х) в двух различных точках х4£ (х,; х2) и х6£(х2; xs), что
невозможно. Итак, функция f (х) либо убывает, либо возрастает на
всей числовой прямой. В первом случае функция /? (х) возрастает,
з функция fs(x) убывает, поэтому тождество /3 (х) = х выполняться
не может. Допустим, что f (х) возрастает и / (х0) Ф х0 при некотором
313

значении х0 €*• Тогда, если f (х0) > хп, то
Р (х0) > f (*o). Р (х0) > р (х0) и Р (х0) > х„,
а если f (х0) < х0, то
Р (Хд> < f (*0)> Р (*о) < Р (л®) и Р (х„) < х„,
В любом случае имеем противоречие с равенством /3(х0) = х0. Таким
образом, доказано тождество /(х)=ах, x£R.
б) Функция
{х, если х£{1; 2; 3},
2, если *=1,
3, если х — 2,
1, если х = 3
удовлетворяет всем требованиям задачи.
20.17.	Рассмотрим функцию g(x)=f(x)—х и докажем, что для
любого значения k£Z справедливо тождество
f(x+kg(x))^x+ (*+l)g(*)	(x£R)-
При k=0 имеем верное тождество / (х) ^x-j-g (х). Пусть для неко¬
торого значения	тождества
f (х + (k — 1) g (х)) = х + kg (x)
И
/ (x—(k— 1) g (x)) = X—kg (x)
уже доказаны. Тогда, используя тождество для функции / (х), задан¬
ное в условии задачи, получаем
f(X±kg (X)) з= 2 (X ± kg (X)) — С1 (X ± kg (X)) S3
= 2(х± kg(x)) — (х± (k— l)g (х)) ^х ± (k+l)g(x),
С помощью установленного тождества докажем, что функция g (х)
постоянна. Пусть, напротив, для некоторых значений xt, x2£R имеет
место неравенство g (хх) < g(x2). Тогда существует такое число N,
что
Xl — kg(X,) > х2 — kg(x2).
Заметим, что функция f (х) является неубывающей (так как в против¬
ном случае функция f~l (х), а с ней и функция / (x)-f-/-1 (х) s= 2х
были бы невозрастающимн, что неверно). Следовательно, при любом
значении л £ N функция /" (х) также является неубывающей. Итак,
имеем неравенство
f" (Xi — kg (xj) V1 (xa—kg (x2)),
из которого в силу равенств
fn (Xi—kg (X,)) = fn~1(xi + (l — k)g (Xi)) = . . . = Xi + (n—k) g(Xi)
(i= 1, 2) получаем неравенство
Xi |- (n—k)g (xO 52 x2 + (л — k) g (x2).
314

Однако при достаточно больших значениях п последнее неравенство
неверно (ибо gW<gW). Таким образом, функция g(x) = c
постоянна, а значит,
f (х) = х + с.
Заметим, что при любом значении c£R функция /(х)==х-|-с удов¬
летворяет всем условиям задачи.
20.18. Поскольку, в силу условия задачи, при любом значении
уф 0 справедливо тождество
(,€щ.
правая часть которого дифференцируема по х, то
г м = Г (*+У)-Г	=
'	2	у
\f(x+2y)-f(x)	f(x-2y)~f(x)]
2У L	2у	(-2у)	\
_ f{x + 2y)+f(x-2y)-2f{x)
4у*
Далее, последнее выражение снова дифференцируемо по х, поэтому
Г" - Г (Х + 2У)+Г (x-2y)-2f (х) _
4у2
_	1	\f(x+4y)—f(x)	f(x—4y)	—	f(x)	f(x+4y) — f(x—4yW
4у* L 4t/	(—4y)	4y	J
Таким образом, искомые функции обязаны удовлетворять тождеству
f" (х) = 0, поэтому
Г М - Г (0), Г М - Г (0) х+Г (0),
f(x) В Г (0) х2/2+Г (0) X + f (0).
Заметим, что любая функция вида
f (x) = cx2 + fcx+c, где я, fc, c£R,
обладает всеми указанными в задаче свойствами.
20.19. Подставив х = у = 0 в исходное тождество, получим f (0) =
= 2f (0), т. е. f(O) — 0. Для любого х£ R из тождества
/(*+40 —/ W*3 f{y)+2xy
имеем
Г(х)= lim т±=Ж = limIM±^ =
£ -> 0	1/	#	-»	0	У
= 2x + lim f{y)~f{0)=2x+f' (0),
j-*» У
поэтому искомые функции обязаны удовлетворять условию
X
/(*) = / (X) — f{0)=\jf' (у) dy = xS +/' (0)х<
о
315

Заметим, что прн любом значении fi£R функция f (х)=х5 + ох удов¬
летворяет требуемому в задаче тождеству.
20.20.	Подставив в исходное тождество для функции {(х) значе¬
ния х=у = 0, получим / (0) (/ (0) —1) = 0, т. е. /(0) = 0 или / (0) = 1.
Но если / (0) = 0, то из тождества
f(0)f(x)^f(x)	(x£R)
следует тождество {(х) = 0, противоречащее условию задачи. Итак,
f (0) = 1. Докажем, что функция f (х) дифференцируема на всей чис¬
ловой прямой. Действительно, для любого х£ R имеем
f(x+y)=Bf(x)f (у)	(у £ R),
отсюда
вп,	ЦтШиШ.
у -*■ ъ	У	у	-+	Q	У
Значит, предел в левой части последнего тождества существует и
равен
Г(х)=Пх)Г(0).
Пусть f' (0) = а, тогда f'(x) — af(\:). Функция f (х) дифференцируема
любое число раз. Действительно,
f" (х) = af (х) = а2/ (х), Г" (х) = a2f- (х) = а3/ (х)
и т. д. Таким образом, при любом n£N имеем
!i,‘> (х) = ап f (х).
Глава 6
МНОГОЧЛЕНЫ
§ 21. Корни многочленов
21.1. Используя теорему Виета (xi+х2 = —р, xtx2 = —1/(2р2))
и неравенство между средним арифметическим и средним геометри¬
ческим двух чисел, получаем
xi -f - Xj — (Xj -f - Х2)4 — 2х,х2 (2 (Xj -(- х2)? -*■ XiX2) =
S.2+2/p. •
= 2 + V 2,
что и требовалось доказать.
21.2. Многочлен х1 ф-рх2 ф- у имеет 4 действительных корня в том
и только в том случае, если многочлен у2+ру+у (относительно
у—х2) имеет два неотрицательных корня, т. е. числа р и q удовлет¬
воряют условиям'р2>4у, уЭ*0, p*S0. Если исходный многочлен
имеет 4 действительных кория (а именно: —xlt —х2, х2, хь где без
ограничения общности считаем, что Xj ^х2 52 0), то они образуют
316

арифметическую прогрессию тогда и только тогда, когда совместна
система
— 2х2= -—Xj4-x2, *?-)-*2=—Р> л3х| — q
(см. теорему Виета и обратную к ней), т. е. когда g=0,09p2. Таким
образом, все искомые пары чисел р, q описываются условиями
P*S 0, q — 0,09р?
(неравенства р2^4^ и	вытекают из последнего равенства).
21.3. По теореме Виета имеем равенства
« + Р=—Р. оф=1, у+6= — q, у6=1,
из которых получаем
(а—у) (Р—у) (а + 6) (Р+6) =
=(«Р — (а + Р) у+у*) (аР + (а + Р) б+б2) = (1 +ру + Vs) (1 — рб+62)=
=(V2 +1 + У2**- + б2) + Р (у - 6 - 6у2 + уб2) - р2уб =
= (у + 6)2+р(у-б)(1-бу)-р2 = <?2-р2,
что и требовалось доказать.
21.4. По теореме Виета для корней х*, х2, xs многочлена
ах3—ах2 + Рх-(-Р имеем
*i + x2+x3= >. *1*2+х2ха + xix3 = P/а, х1х2л'3 — — Р/а.
Поэтому
(х2+Х2 + Хз) ^=
Х!х2х3	«V	а)
21.5. Сделаем замену у=х—3, тогда числа yt = xt — 3, у2 =
= х2—3 и уа = ха—3 являются корнями многочлена
(У + З)8— 6 (у + 3)2+а (у -f 3) + a=у3 + Зр2 + (с — 9) у + 4с—27.
По теореме Виета имеем равенства
УхЛ'УзЛ'Уз^—3,
УН/2 + УхУз +УзУз^а—9,
УТУяУз = 27 — 4а,
а кроме того, должно выполняться соотношение Pi + у\ { Уз 0. Не¬
посредственной проверкой убеждаемся в справедливости тождества
^ (Pi+Рг+Ра)3 — 3 (PiPa + УхУз + РгРз) (Pi + Р2+У а) +ЗрхУаРз.
Иа которого получаем необходимое и достаточное условие для а:
0 = (—З)3—3 (а—9) • (—3) |-3(27 —4а) = —27—За,
т- е. а = —9.
317

21.6.	Для корней и, v и uv многочлена Р (х) по теореме Виета
имеем равенства
и +о+ыо= —а,
uv (1 ф-ы+о) = Ь,
u2v2 = —с,
из которых в случае а Ф 1 получаем
Ь—С— uv (1 ф-иф-1’ф-/д/) = ии (1 —а),
т. е. uv—(b—с)/( 1—а)—рациональное число. Так как число и2и2. =
=—с целое, то и число uv также целое (см. теорему 61). Поэтому из
равенств
Р(1) + Р(-1)-2(1+Р(0)) =
= (1+а + Ь+с) + (-1+а-Ь+с)-2(1+с)=2(а-1) =
=-2(« + о+ио+1) = —2(1+и)(1+и)ф0,
2 Р (—1) = 2 (— 1 — и) (—1 —») (—I — uv) = — 2 (1 + uv) (1 + и) (1 + v)
вытекает, что число
2 Р (-1)
Р(1) + Р(-1)-2(1 + Р(0))
= l-)-uv
является целым. В случае а=1 имеем равенство 0 = u-f-n-f-uo-j-l =
= (w-f-1) (n-f-l), поэтому один из корней равен —1, т.е. число
2 Р(—1) — 0 делится иа любое целое число.
21.7. Пусть о, Ь, с, d—корни многочлена
Р (х)=х4ф-х3 — 1 =(х—а) (х—Ь) (х—с) (x—d).
Докажем равенство
(ab)3 + (cd)s+ab + cd + 1=0
(из которого будет вытекать требуемое
(abf -j- (ob)4 + (ab)3—(abf — 1 =
так как по теореме Виета abed = —1). Действительно, из равенств
Р (а) — Р (Ь) =0 имеем а2= l/(a-f-l), b3=l/(b-)-l), откуда получаем
/ М3	^	^	0	/II	\	/|	I	J\
(ab) ~ (1+а)(1 + b) ~	Р(— 1)	~	(1+c)(1+d>-
Аналогично получаем (cd)3 ——(1+a) (I + b). Следовательно, имеем
(ab)3 + (cd)3 +ab+cd + l = -(l+c) (1 +d)-(1 +a) (1 + b) +
-bab+ci+l =—1—a—b—c—d=0<
так как по теореме Внета a + b-|-c-f-d =—1.
21.8. Поскольку многочлен Р (x) = ax2-j-bx-j-c (а > 0) имеет два
различных корня 0 < х* < х2 < 1, то Ьа > 4ас и в силу теоремы
Виета 0 < с/а < 1, b/а < 0, т.е- а > с > 0, b < 0. Далее, Р(1)==
= а-(-Ь-(-с>0| откуда a-j-c >-=-b. Возводя в квадрат обе (положи*
318

тельные) части последнего неравенства, получаем а2-\-2ас-{-с2 > Ь2,
откуда имеем оценки (а—с)2 > Ь2. — 4ас > 0, из которых вытекает,
что о—с> 2. Если предположить, что а *£4, то возможны лишь три
набора целых коэффициентов а, с:
ai— 4, Cj = 2;	аа = 3, с2= 1; Оз = 4, eg = 1,
а для коэффициента b должны Ьбыть выполнены соответственно три
условия:
4 > Ь\—32 > 0,	4	>	—12 > 0,	9	>	b\—16 > 0.
Но ни одно целое число не удовлетворяет ни одному из этих трех
условий. Следовательно, а 3= 5чНаконец, уравнение 5х2—5х -f 1=0
имеет своими корнями числа (5+]/" 5)/Ю и (5—)/" 5)/Ш, принадле¬
жащие интервалу (0; 1).
21.9.	Предположим, что с = 0. Тогда число с является корнем
уравнения х4—ах3—Ьх = 0, следовательно, отстается найтн все много¬
члены вида х3—ах2—Ь, для которых числа а и b являются корнями.
Если обозначить через d третий корень такого многочлена, то по
теореме Виета будем иметь a-}-b-\-d — a, т. е. d =—b, далее, ab-f-
-\-ad-\-bd = ab—b (a -\-b) ——b2 = 0, т. е. b — 0. Наконец, замечаем,
что любая тройка чисел вида [а; 0; 0) удовлетворяет условию задачи.
Теперь предположим, что с Ф 0. Тогда нн одни из четырех кор¬
ней с, Ъ, с, d многочлена х* — ах3—bx-^-с не равен нулю. По тео¬
реме Внета имеем a-\-b-\-c-{-d = a, т. е. d — —(&+с), далее,
ab+ас-j- be+ad + bd -f- cd —
— ab-\-ac-\-bc—(а + 6+с) (fc+c)= —b2—be—c2 = 0,
abc+abd -f - acd -f- bed = abc—[ab -f- ac -f- be) (b -f-c) =
= —a (M + fcc+c2) — b2c— bci = — be (fc-f-c) = b,
т. e.
b2——c(b-{-c)=l, c2 + fcc+l=0,
наконец,
abed = —abc (b-\-c) = ab = c,
т. e. a=c/b. Поэтому возможны лишь четыре набора чисел а, Ь, с:
-1 ± 1 Г 3	_	_1±1|Аз
°1, 2— •> Cl, 2	2	 ’	2	2	 ’
l±iV~3 .	-1Т*|ЛЗ
°в,4~ — 1. Сэ, 4 =	2	*	3. 4	2	 ’
каждый из которых удовлетворяет условию задачи. Таким образом,
тройка (а; Ь\ с) либо имеет вид (а; 0; 0), где а—любое комплексное
число, либо совпадает с одной из троек:
(^±+iVз , -1+1^3^	,	—1 — / 1/"зЛ
\	2	'	2	/’V	2	2	)'
(z^-iV 3 .	,	1-НГ^	(-l+iV"3	,
V 2	’	2	\	2	1	*	2 /
319

21.10.	Пусть хи х2 — корнн многочлена х2+ах+6. Точки хи
х2, 0 образуют вершины требуемого в задаче треугольника тогда и
только тогда, когда xt ф 0 и число x2/*i равно либо i, либо —I
(
так кая модули чисел Xi и х2 совпадают, а их аргументы отличаются
на величину (-2лп для некоторого числа л£2^ . Это означает, что
либо x2 = ix 1, либо Xx = ix2, т. е. корни исходного уравнения имеют
вид х0, **oi причем хв Ф 0. Согласно теореме Виета последние усло¬
вия эквивалентны системе
(1+1) х0= —а,
(х? — Ь,'
*о ^ °»
которая совместна тогда и только тогда, когда о2 = 26 ф 0 (так как
2{ixl)= ((l+i)*0)2).
21.11. Так как все коэффициенты многочлена Р (х) неотрица¬
тельны, то ни один из его корней «i, ..., а„ не может быть положи¬
тельным. Следовательно, этот многочлен имеет вид
Р(х) = (х+р1)...(х+р„),
где р,- = —щ > 0, 1=1, 2, ,.я. Используя теорему о средних (тео¬
рема 6), получаем неравенства
2 + Р; = 1 +1 + Pi 3 ф 1 • 1 • Р/ = 3 у/Pj, 1= 1, 2, > >., л*
Учитывая, что по теореме Виета Р1Р2*. ip„ = 1, получаем
P(2) = (2 + P1).i.(2 + Pn)^3" J/piP2...pB = 3»,
что и требовалось доказать.
21.12. Так как исходный многочлен имеет л положительных кор¬
ней х1, .... хп, то его степень не меньше п. Поэтому а Ф 0, и но
теореме Виета имеем
*i + *s + • ■ • +*п =
п
(—1)" ^ ХХХ2. . .X/_iXl+i. .	= л2 —,
i = 1
(—1)"*1*2 •«* *п=—,
а
откуда b Ф 0. Учитывая теорему о средних, получаем условие
п!== ь (н!г”6/i-=^+X2+“,+x"} (irbTr+“,+i)3s
ХхХ2 ... Хп) (п лФ— — ... —)=П2|
\ Г Хх х% хп /
которое выполняется лишь в случае, когда
*1 = х,= ... —хп = 1/л.
320

21.13. Допустим, что некоторое число а является решением каж
дого из двух данных уравнений, т. е.
а5 = а + 1 и а2 =—аа—6.
Тогда
а 4-1 = а5 = а (а8)а = а (— аа — 6)а = а (а2 (— аа— 6) f-2a&a-(-6a) =
= (2аЬ—а3) (—аа—6)+ (62 — аг6) а=(а«—Заа64-6?)а4-(а36—2а6а),
следовательно, выполнено условие
(а«—За*Ь + 6? — 1) а = — а3 6+2а62 4-1,
из которого получаем равенства
а*—Заа6 + 6а —1=0,
— a36+2a6a-f 1=0
(в противном случае число а являлось бы рациональным корнем
многочлена х5—х—1, не имеющего в силу теоремы 59 рациональ¬
ных корней). Исключая нз двух последних равенств число
6 = (2а5—2а — 1) /(5а3),
получаем равенство
а104-3ав— 11а5—4аа—4а— 1 =0,
противоречащее рациональности числа а (ибо многочлен х10+3х*—
— Их5—4х2—4х—1 в силу той же теоремы 59 не имеет рацио¬
нальных корней). Следовательно, многочлены х5—х—1 и х'Ц-ах-\-Ь,
где а, 6£ Q не могут иметь общих корней.
21.14. Рассмотрим многочлен
Q (х) = Р(а — х) = а„хп4-...4-а1х4-а0.
Тогда имеем
a„ = Q (0) = P(a) < 0,
a.-Q'(O) = — Р' (а) С 0,
_ Q" (0)	(—I)2 Р" (а) _А
а2=—^	21
Q(n> (0)	(_!)»	Р*»» (в) Л
и!	и!
Поэтому Q (х) < 0 для всех х 3* 0, а значит, многочлен Р (х) не имеет
корней при xg(—оо; а]. Аналогично, для многочлена
R (х) = Я(64-х) = 6„х"4- ... +btx+b0
имеем
bo=R(0)=P(b) > О,
61 = /?'(0) = Р' (6)SsO.
, Я* (0)	Р"(6)	_	0
62 —gj——J}—
ь /?«»> (0) Р(п) (6) ^ Л
я л!	л!	'
^ Под ред. И. Н, Сергеева	321

откуда R (х) > 0 при х^О. Следовательно, многочлен Р (х) не имеет
корней и при х£[6; +оо). Тем самым доказано, что все действи¬
тельные корни многочлена Р (х) лежат на (а; Ь).
21.15. Докажем по индукции, что если _п четно, то многочлен
Рп (х) принимает положительные значения при всех х£ R (следова¬
тельно, он не имеет действительных корней), а если п нечетно, то
многочлен Рп (х) имеет ровно один действительный корень. При
п = 0 имеем Pn (х)= 1 >0 при всех х. Пусть утверждение верно для
всех значений, меньших числа п £ N. Докажем, что оно верно и для
значения п.
а) Пусть п нечетно. Тогда, согласно индукционному предположе¬
нию, Рп (х) — Рп_I (х) > 0 при всех х£ R, поэтому функция Р„ (х)
возрастает и не может обращаться в нуль более одного раза. Так
как Я„(0) = 1 >0 и lim Р„(х) =—оо (т. е. функция Р„(х) прн-
X -* — <ю
нимает отрицательное значение хотя бы в одной точке х), то непре¬
рывная функция Рп (х) хотя бы один раз принимает нулевое зна¬
чение (см. теорему 28).	*
б) Пусть п четно. Тогда многочлен Рп (х) = Р„ (х) имеет ровно
один действительный корень х0 Ф 0. Так как Рп (х) — Р„_2 (х) > О
при всех x£R, то Р'п (х) > 0 при х > хь и Рп(х) < 0 при х< х0. Сле¬
довательно, при всех х£ R имеем
Рп (X)S* Р„ (х„) = Ра_i (Х0)+4=4 > 0.
Утверждение доказано.
21.16. Имеем
Q' (х) = Р' (х) +аР" (х) +... +ап-Ч*п> (х)
(ибо Р<"+1> (х) = 0). Поэтому
Q (х) — aQ'{x) = P (х).
Без ограничения общности считаем, что старший коэффициент мно¬
гочлена Р (х) положителен. Так как этот многочлен не имеет дейст¬
вительных корней, то его степень п — четное число, и для всех x£R
выполнено неравенство Р (х) > 0. Предположим, что многочлен Q (х)
имеет действительные корни xt<x2< ... <х&. Пусть а^гО. Тогда,
так как старший коэффициент многочлена Q (х), равный старшему
коэффициенту многочлена Р (х), положителен, то lim Q (х) = -{- 00 •
*-> + О0
откуда имеем Q (х) > 0 при х > х*. Поэтому Q' (хд)^0 и
Р (хк) = Q (х*) — aQ' (х*)	0.
Если же	а <	0, то	при х < xt имеем Q	(х) >	0 (так как deg Q (х) = п — ,
четное	число).	Поэтому Q'(xj)^0 и	I
Р (xi) = Q fa)—aQ' (xt)	< 0.	I
322	|

В обоих случаях получено противоречие с неравенством Р (х) > 0.
Следовательно, многочлен Q (х) ие имеет действительных корней,
21.17.	Разложим исходный многочлен на множители:
Р (х) = а (x—xi) ... (х—хн), где а Ф 0.
Тогда
P'(*) = P1(*) + ...+P„(*)>
где через /Д (х) (k=l, 2 п) обозначен многочлен степени n— ISsl,
удовлетворяющий тождеству
(х—хк)Рк(х)^Р(х).
Заметим, что Р*(х/) = 0 при k Ф i, а значит,
Р (■*/)= Р{ (xi) ^ 0-
Рассмотрим многочлен
Мх I Рп (*)
Р (ж) = —1 +
Р' WT'"TP'W’
степень которого (если F (х)	0) не превышает числа п—1. Для
каждого »‘=1, 2 п имеем равенства
(*/) д Р/ (Xf) |  Q
а значит, многочлен F (х) имеет п различных корней. Следовательно,
F (х) е= 0. Так как старший коэффициент каждого из многочленов
Р*(х) равен а, то коэффициент многочлена F (х) при хп-1 равен
выражению
+ •■• +
но этот коэффициент равен нулю. Отсюда вытекает утверждение задачи.
21.18.	Согласно теореме 57 многочлен с действительными коэф¬
фициентами может иметь только четное число чисто мнимых корней,
которые разбиваются на пары взаимно сопряженных. Поэтому данный
многочлен Р (х) представляется в виде Р(х) = а(х—ia{i... (х—ia3n) =
= а (х2	а?)... (х3. -\- ап), где а, ах а2п — ненулевые действи¬
тельные числа и а„+й = —а* при k = 1 п. Поскольку у мно¬
гочлена Р (х) коэффициент при х2 отличен от нуля, а при х1 — равен
нулю, то многочлен Р' (х) будет иметь ровно один корень х*=0.
Докажем, что остальные его п—2 кория — чисто мнимые. Пусть
Р' (6-(-tc) = 0, причем Ьа4-<^^0. Если при этом Р(6-|-»с) = 0, то
Ь-|-ic—корень исходного многочлена, а значит, это чисто мнимое
число. Если же P(b-\-ic) ^ 0, то
0 =
2л	2л
Р' (* + fc)__V'	1	 \т	Ь—Цс—ак)
P(b + ic)	Ь+Цс—ак)	+	а*)»
И*	323

так как
2 п
Р'(х)	1
Р (*) _ “ x~ iak '
Поэтому действительная часть выражения Р' (b-\-ic)/P (b-{-ic) равна
2 п
6? + (с_а*)?=0*
а значит, 6 = 0, что и требовалось доказать.
21.19.	Пусть корни многочленов Р и Q совпадают (вместе с крат-
ностями), тогда имеем
Р (г) = a (z—zi)nt (г— г2)п' ... (г—г*)"*,
Q (z) = 6 (г—zt)n‘ (г — z2)"J ... (z—zft)"*,
где a, 6—ненулевые комплексные числа, nlt л2, ..., n*£N. Поэтому
функция
f(z) = \P (z) 1-1 Q (z) I = (| a 1-161) | (z- zx)"- ... (z-z*)"ft I
не может принимать значения разных знаков. Пусть теперь функция
f (z) ие принимает, для определенности, отрицательных значений.
Тогда deg Р ^ deg Q, так как в противном случае для достаточно
больших по модулю значений г было бы выполнено неравенство
| Р (г) | < | Q (г) |, т. е. / (г) < 0. Далее, предположим, что
Р (z) = (z—Zo)"" Ро (г),
где z0£C, n0€N> ро (*) — многочлен, Р0 (г0) ф 0. Пусть Q (г) =•
= (z—Zo)"1» Qo (г), где m06z+. Q0 (z) — многочлен, Q0(z0) ^0. Дока¬
жем, что m0 ^ л0. Действительно, если 0 < т0 < л0, то число
/ (г) = | z—z0 |m« (| (z—г0)п°-'яо-Ро (z) | — I Q0 (z) |)
будет отрицательным для некоторого значения z, достаточно близкого
к z0. Таким образом, если многочлен Р имеет корни   zk крат¬
ностей «1, ..., пк соответственно, то такие же корни не меньших
кратностей  тк соответственно имеет и многочлен Q. Нако¬
нец, из неравенств
«i<mx, ...,пк<тк, nl-\-...+nks»ml-\-...+mk
вытекает, что
т = ть ....	=	deg Я = deg Q
и что других корней, кроме zlt ..., zk у многочлена Q нет, следо¬
вательно, корни многочленов Р и Q совпадают.
324

§ 22. Делимость и равенство многочленов
22.1. Доказательство проведем индукцией по n£Z+. При п=0
утверждение справедливо, так как в этом случае (jtr-f- 1)2п+14-хп+2ээ
==х2-\-х-\-1. Предположим, что для некоторого значения п—1 утверж¬
дение выполняется, т. е. многочлен (х-|-1)2и_1-|-хп+1 делится на
многочлен x2-f-x-|-l. Но тогда многочлен
(*+1)2«+1 + х"+2 = (х+ I)2 (х+ I)2"-1 + х-х"+1 ^
=э(х24-2х+1) (х+1)2и-14х-хп+1зз
^(х2+х+ l)(x+l)2"-i-fx((x+l)2n-l+xn+1)
также делится на многочлен х24х+1, т. е. утверждение верно и
для значения п.
22.2. Обозначим хе = cos a+fe sin а, где eg{—1; 1}. Тогда мно¬
гочлен Q (х) представляется в виде
Q (х) = (х—cosa—isina) (х—cos a4i sin a) = (x—xx)(x—x_x).
По формуле Муавра имеем x?=(cos ea+i sin ea)n ==cos ena+t sin ena=
= cos na + el sin па, поэтому
P (x8) = (cos na + et sin na)n sin a — (cos a 4 ei sin a) sin na +
4 sin (n— 1) a= cos na sin a —cos a sin na + sin (n— 1) a —
= sin (1 —n) a-(-sin (n— 1) a = 0.
Следовательно, по теореме Безу многочлен P (x) делится на каждый
из многочленов х—хх, х—х_х (не равных друг другу, так как
sin а ф 0), а значит, и на их произведение Q (х).
22.3. Сделаем замены cos2/= 1—sin21 и sin I = х. Получим, что
искомый многочлен R (х) степени меньше 4 есть остаток от деления
многочлена S (х) =-7х31 -[-8х13—5х9—2 на многочлен Q (х) = х4 |-х34"
+х2 4 х 4 I > ибо тождество S (х) = Р (х) Q (х) -[- R (х) должно быть вы¬
полнено при всех *€[-1; 1]. а значит, и при всех х£С (см. тео¬
рему 52). Поскольку (х—1) Q (х)=х5—1, то существуют 4 различных
значения переменной х, удовлетворяющих условию Q (х) = 0. Для
каждого из этих значений имеем равенства х5= 1 и
R (х) = S (х) = 7х31 + 8х13—5х8—2 =
= 7х-(-8х3—бх4—2-J-5Q (х) = 13х345х24 12x43.
Итак, многочлены R (х) и 13х345х2412x43, степени которых не
превышают 3, в четырех различных точках принимают одинаковые
значения, следовательно, они совпадают.
22.4. Многочлены Я (х) = 1 4 * 4- • • • + хШ и Q (х) = 1 +х" 4 • • •
-..+хтп не имеют кратных корней, поскольку их не имеют мно¬
гочлены х“ +1 — 1 = (х— 1) Я (х) и хп «“ +D — 1 = (хп -— 1) Q (х). Поэтому,
согласно теореме 54, многочлен Q (х) делится на Я (х) в том и только
в том случае, если каждый корень многочлена Я (х) является корнем
325

многочлена Q (х) или, что то же, если каждый отличный от 1 корень
уравнения хт +1 = 1 (удовлетворяющий автоматически и уравнению
длол + И--!) не является корнем уравнения хп=1. Таким образом,
все искомые пары (и только они) чисел т, п должны быть таковы,
чтобы система
( *т + 1= Jf
\ Хп = 1
имела единственное решение *=1. Если (т+1 ■ n) — d> 1, то
эта система имеет одним из своих решений число х—cos (2n/d) -f-
+ i sin (2jx/d) ф 1. Если же (m+1, я)=1, то в силу теоремы 24
существуют такие целые числа k и I, что	— а значит,
для любого решения х этой системы имеем j( = хк^т + 1)+1п =
=(х,я+1)й(хп)/ = 1. Следовательно,, пара натуральных чисел т, п
тогда и только тогда удовлетворяет условию задачи, когда числа
т +1 ип взаимно просты.
22.5. Пусть «о,	..., s„ — коэффициенты многочлена S (а) =
— s0-}-SiJC... +s„x". Умножая обе части исходного тождества на
многочлен х—1, получаем тождество
(х— 1) (Р (х5) +xQ (х5) + х?/? (х6))	(х5	—	1)	S	(х),
или
Р (хг’) -J - (хг‘ — 1)	(х) £3
= — (х5 — 1) Sa (х) 4- хР (хг>) + (х2 — х) Q (х5) + (х3—х2) R (х5),
где обозначено
Si (x) = so+s8x5+s,ox10-(- ... -hssmX'">,
S2(x)=S(x)—Si (x), m = [n/5].
Поскольку в левую часть последнего тождества переменная х входит
лишь с показателями, кратными пяти, а в правую часть—лишь с по¬
казателями, не кратными пяти, то обе части тождества равны нулю,
откуда имеем
Р (хв) ез— (х5— 1) Sx (х).
Подставляя в последнее тождество значение х = I, получаем Р (1) =0,
следовательно, по теореме Безу многочлен Р (х) делится на х— 1.
22.6. Любой многочлен вида Р(х) = ах, где а — константа, удов¬
летворяет условиям задачи. Докажем индукцией по Z+, что для
каждого искомого многочлена Р (х) выполнены равенства P(n)=/iP(l).
При п = 0 и п — I эти равенства верны. Пусть они уже доказаны для
чисел п—1 и п, где n£N. Тогда P(n + l) = 2P(n) — P(n — 1) =
= (л-(-1) Р (I), а значит, равенство справедливо и для числа n + 1.
Поскольку многочлен Р (х) — Р(1)х имеет бесконечно много корней
х=0, 1, 2, то он равен нулю. Таким образом, искомые мно¬
гочлены имеют вид Р (х) = ах.
22.7. Подставляя в исходное тождество значения х=0; 2, полу¬
чаем, что многочлен Р (х) имеет корни 0 и 1, а значит, делится на

многочлен х3—х. Далее, подставляя в тождество выражение Р (х) =
= (х2—х) Q (х), получаем для многочлена Q (х) тождество Q (х) =
• - Q (х— 1); отсюда имеем Q (0) = Q (— 1) = Q (—2)= ... Поэтому
Q (х) = а — константа, и искомые многочлены имеют вид Р (х) =
= а (х2—х). (Проверка показывает, что все многочлены такого вида
удовлетворяют требуемому тождеству.)
22.8. Подставляя в исходное тождество последовательно значения
х~ 1; —2; 0, получаем, что искомый многочлен Р (х) имеет корни 0,
±1, а значит, делится на многочлен х3—х. Далее, подставляя в тож¬
дество выражение
Р (х) = (х3 — х) Q (х),
получаем для многочлена Q (х) тождество Q (х+ 1) — Q (х)=0, откуда
имеем Q (0) = Q (1) = Q (2) = ... Поэтому Q (х) гз а — константа, и
искомые многочлены имеют вид Р(х) = а(х3—х). (Проверка показы¬
вает, что все многочлены такого вида удовлетворяют требуемому
тождеству.)
22.9. Пусть искомый многочлен имеет вид
Р(х) = а„хп+ап_1хп-1 + ...+а1х+а0. где а„ Ф 0.
Предположим, что хотя бы один из коэффициентов а„_х ах, а0
отличен от нуля. Выберем наибольшее значение k < п, для которого
а^ф 0. Тогда имеем
Р (х2) === апх2п 4 flftX2* 4 • • • 4ai*2 4ао sa
=» (апХп 4	4 • • • 4 сцх4 а0)2 35 (Р (*))*•
Сравнивая коэффициенты при х"+я, получаем равенство 0 = 2а„ад,
которое противоречит условиям ап Ф 0, а^Ф 0. Следовательно,
а„_х= ... = ах = ао — 0 и Р(х) = с„хи. Наконец, из условий а„х2п~
== Р (х2) =$ (Р (х))2 ОпХ2п получаем а„ = 1, т. е. Р(х) = х", где n£ Z+.
22.10. Обозначим у = х—1, Q(y) = P(y—1). Тогда имеем
(Р (х-2))2 = (Р (у- 1))2 = (Q (г/))2,
Р (х2 — 2х) = Р (у2 — 1) = Q (У2),
а исходное тождество записывается в виде
Q (.4) = (Q (у))2. У& R,
т. е. совпадает, с точностью до обозначений, с тождеством зада¬
чи 22.9. Поэтому Q{y) ~уп и Р(у) = (у41)". гДе n£Z+.
22.11. Пусть ненулевой многочлен Р (х) = а„хп 4 - • - 4 aix 4 аи>
где ап Ф 0, удовлетворяет условиям задачи. Тогда, сравнивая в исход¬
ном тождестве коэффициенты при х3п и при х°, получаем равенства
Оп = а„, По — ао. откуда а„ = 1 и аи — 1 (если а0=0, то Р (х) =х-'Рх (х),
где Рх (0) Ф 0, /£N, и из тождества
хгРх (х) • (2х2)г Рх (2х2) = (2х34х)‘ Рх (2х34х)
получаем тождество
2'х2<Рх (х) Рх (2х2) = (2х24 1)' Pi (2Х3 -| х);
327

отсюда Р( (0) = 0—противоречие). Пусть а=р (cos ф +i sin ф)—про¬
извольный корень многочлена Р {х); тогда число 2а3-[- а также явля¬
ется его корнем, так как Р (2a3-J-a) = Р (а) Р (2а2). Далее,
12а3+а | = | а |-| 2а2+1 | ^ | а |-(21 а |a— 1),
поэтому, если |а| = р > 1, то |2а3+а| > |а|, и многочлен Р(х)=£
=£0 имеет бесконечно много различных корней Pj = a, P/+i = 2P|-fPy
при 1=1, 2, ..., что невозможно. Следовательно, любой корепь
многочлена Р (х) по модулю не превосходит 1, но так как произве¬
дение всех корней этого многочлена равно 1 (по теореме Виета), то
ни один из его корней ие может быть по модулю меньше 1. Итак,
р =1 и из цепочки равенств •
1=|2а3+а|а = |2аа +112 = 4 сов2ф-)-5
имеем ф = -^+ят, mgZ, и а=± (. Так как многочлен Р (х) имеет
действительные коэффициенты, то Р (х) = (ха+ l)ft, где £gZ+. Нако¬
нец, проверка показывает, что все многочлены такого вида удовлет¬
воряют условиям задачи.
22.12.	Доказательство проведем индукцией по ngN. Так как
многочлен Qi(x) делится на себя, то при п=1 утверждение справед¬
ливо. Пусть теперь для некоторого значения ngN уже доказано тож¬
дество Qn (х) = Rn (jc) Qj (х), где Rn(x)— многочлен. Тогда имеем
Qn+i W = Р (Qn (*)+*)—*= Р (Rn (х) Qi (*)+*) — *=■
— (р (Rn м Qi to -\~x)—p w)+(R to - 4-
m
Пусть P (x) = 2 о*хд, тогда
k = 0
m
Qn + lto = 2°* W Ql to + *)*~X*) + Ql to —
* = 0
m	/	m	\
^ 2 ад/?п to Qi to sk to+Qi to = Qi to-( 14- 2 akRn to sb to )■
fc=o	\	/
где обозначено
*-i
Sk to = 2 (Rn to Qi to +*)'
1 = 0
(мы воспользовались равенством
fc-i
fls_6« = (a— b) 2
/=o
при a — R„ (x) Qi (x)+x, b = x). Таким образом, утверждение доказано
и для значения и+1.
22.1-3. Заметим, что если многочлен S (х) степени не выше трех
удовлетворяет условию S (х)^0 при всех xg R и равенству 5(х0) = 0,
328

то он представляется в виде S (х) а(х—ж0)2, где с>0. Поэтому
R(x)^P (х)-| а (ж—ж,,)2,
Q (ж) в Р (ж) + Ь (ж—ж0)а =
- ^ р W +4 (Р {Х) +а (*~*о)2) - кР (ж)	(\-k)R (ж),
где	О, ft= 1—[0; 1] (в случае а — 0 имеем R (ж) s Q (ж) =
es Р (ж), поэтому требуемое тождество справедливо, например, при
А=1). Аналогичное утверждение для многочленов четвертой степени
неверно. Например, многочлены Р (ж) =■ ж4, Q (ж) = ж44*2. R (ж) =
я* 2ж4+ж» удовлетворяют соотношениям Р (ж) С Q (ж) С R (ж), ж£ R,
и Р(0) = Р (0), ио тождество х*-\-х2 е=Лж44(1—к) (2х44жа) не выпол¬
няется ни при каком значении k (для константы ft имеем противоре¬
чивые равенства 1 = k4-2 (1 — к) и 1 = 1 — к).
22.14. Если некоторый многочлен Q (ж) =<7„жп 4-• ■ •+<7о удовлет¬
воряет условиям qn 0 и Q (Р (ж)) ее Р (Q (ж)), то, приравнивая стар¬
шие коэффициенты многочленов Q (Р (ж)) и Р (Q (ж)) степени 2п, полу¬
чаем qnan = aijn, т. е. qn — ап~1. Поэтому, если, вопреки утверждению
задачи, для некоторого значения п и многочлена Р (ж) существуют
два разных многочлена Qj (ж) и Q3 (ж) степени п, удовлетворяющих
требуемому тождеству, то многочлен R (ж) ^ Qx (ж) — Q2 (ж) имеет сте¬
пень	к <	п (так как старшие коэффициенты многочленов Qi (ж) и
Qa(ж)	равны одному и тому же числу а"-1) и удовлетворяет тож¬
деству
R (Р (ж)) в Qx (Р (ж)) - Qa (Р (ж)) - P(Qi (ж)) - Р (Qa (ж)) в
= a (Qf (ж) - Q| (ж)) 4 Ь (Qt (ж) - Qa (ж)) в
- (Qx (*>-Q. (*)) (а (Qi (*> + Q. М) 4 Ь) ^ R (Ж) Т (ж),
где обозначено Т (ж) —aQx (ж) + aQa (ж) 4 Ь. Поэтому
2k = deg R (Р (ж)) = deg (R (ж) Т (ж)) = * 4 п,
что противоречит неравенству к < п и, тем самым, доказывает утверж¬
дение задачи.
22.15. Если P(z) = Q (г) Q (— г), то Р (— z) е Q (—z)Q (z) = P(z),
т. е. Р (г) — четная функция. Пусть теперь известно, что ненулевой мно¬
гочлен Р (г) — четная функция (если Р (г) = 0, то положим Q (z)=0).
Докажем индукцией по числу m ненулевых корней многочлена Р (г),
что существует многочлен Q (г), удовлетворяющий тождеству Р (г) ^
в* Q (z) Q (—г). При т— 0 многочлен Р (z) имеет вид P(z) = oz",
причем а 0, и из четности функции Р (z) вытекает, что п — 2ft,
где ft£Z+. Тогда многочлен Q (z)=ftzft, где Ьа = (—1)й а, удовлетво¬
ряет требуемому тождеству, так как агп в 6гй6 (— г)й. Пусть утверж¬
дение доказано для всех значений, меньших m£N. Докажем, что
оно верно и для значения т. Действительно, если а—ненулевой
329

корень многочлена Р (г), го Р (— а) = Р (а) = 0, поэтому
Р (г)	(z—а) (г+а) Я (г),
где многочлен Д(г) — четная функция (ибо R (—г) ((— г)*—а2) =з
=5 Р (—г) s=i Р (г) = R (г) (г2—а2)). Согласно предположению инду¬
кции существует многочлен S (г), удовлетворяющий тождеству Д(г)^=
=sS(z)S(—г). Положим Q(z) = l(z—a)S(z), тогда
Р (г) = 1 (z—a)S (z) i(—z—a)S(—z) = Q (z) Q (— z).
Утверждение доказано.
22.16. Докажем утверждение задачи индукцией по числу т тех
корней ненулевого многочлена Р(х), которые не являются действи¬
тельными числами (если Р (х)	0, то положим п=\ и Qj(x) = 0).
Пусть т = 0 и многочлен Р (х) удовлетворяет условию задачи. Тогда
любой из его корней действителен и имеет четную кратность (если
Р (х) = (х— a)1 R (х), где agR и / нечетно, то Д (х) О при всех
х > а и R (х) < 0 при всех х < а, откуда число а является корнем
многочлена /? (х)). Поэтому имеет место тождество
P(x) = a(x—ai)2il (х—ах)г1‘ ... (х—а*)2\
где а > 0, аь а2, a*gR, 1ь la, .... f*gZ+. Положим п=1 и
Qx (*)= У а (х—а,)'1 (х—аа)'* .. .(х—ай)Ч
тогда Р (х) = Qi (х). Пусть утверждение доказано для всех значений,
меньших mgN. Докажем, что оно верно и для значения т. В самом
деле, если многочлен Р (х), удовлетворяющий условию задачи,
имеет т корней, не являющихся действительными числами, то
он представим в виде Р (х) -- (х2 -\-2px-\-q) R (х), где р3 < q (т. е.
х2 + 2рх4-<7 = (х+р)2 + (д—р2) > 0 при всех *gR), а многочлен
R (х), согласно предположению индукции, для некоторых много¬
членов Q, (х), ..., Qn (х) удовлетворяет тождеству
Д (х) Qi (х) +... + Q*(х).
Тогда из тождества
Р(х)^((х+р)3+с3) (Qi (х)-f Q*(х)),
где с=]Д^ — р1. вытекает, что многочлен Р (х) представим в виде
суммы квадратов некоторых многочленов с действительными коэффи¬
циентами.
22.17. Исходный многочлен представляется в виде (см. теорему 58)
P(x)^aFi(x) ... Fm (x)Gl (х) ...J}k(x),
где многочлены Р,- (х) и Gy (х) имеют вид
F( (х)—х—а;,	0, 1=1, ..., т;
Gy(x) = (x-Py)(x-py), PygC\R, /=1 к,
330

и о > 0. Заметим, что произведение многочленов с неотрицательными
коэффициентами снова является многочленом с неотрицательными
коэффициентами. Поэтому достаточно доказать представимость каж¬
дого из многочленов F, (ж) и Gj (ж) в виде отношения Q (x),'R (ж) мно¬
гочленов с неотрицательными коэффициентами. Для многочлена F (ж)=
= ж— а (а<0) положим Q (ж) = F (ж) = ж + | а |, R(x)=l. Далее,
если Re р<;0, то для многочлена G (ж) = (ж Р) (ж — Р) положим
Q (ж) = G (ж) = ж2+2 | Re Р | ж+1 Р |2, Я(ж)=1. Если >KeReP>0,To
без ограничения общности считаем, что argP£(0; я/2). Выберем такое
я g N, чтобы выполнялись условия 2" arg Р £ [я/2; я) и 2s arg р £ (0; я/2)
при s = 0, 1 п—1. Так как arg(P2r) = 2'-argP (0«£г<;я), то
Re(P2")«CO и Re(p2,I)>0 при s=0, 1, ..., и—1. Таким образом,
имеем
С(ж) = (ж —Р)(ж—р) =
^ (ж2- Р2) (ж2-ffl2) =	(ж4- Р*) (ж4— (р)*)	_	_
(ж+р)(ж+Р)	(ж + Р)	(ж + Р) (ж2 + Р2) (ж2 + (Р)2)
в	(ж2П-р2”)	(ж2"-Р2”)	 Q	(ж)
(ж{-Р)(ж + Р)... (ж2П-1+Р2П~1)(ж2П"1+Р2'!~1)~Я (*)’
где многочлены
<?(ж)=(ж2П-р2")(ж2П-р2И),
Я(ж) = (ж + р)(ж+р)...(ж2П“‘+р2" ') (ж2" ЧР2” ’)
имеют неотрицательные коэффициенты, так как каждый из многочле¬
нов вида (жЧу) (жЧу) = ж2г + (2 Rey) ж* Н Y 1г? ГДе *€N, Rey>0,
имеет неотрицательные коэффициенты.
22.18.	Введем обозначение Rn< ,■ (ж) = жЧ*‘+1+	гДе
i = 0, 1,	[п/2].	Тогда	любой	многочлен	Р	(х)£	А	(п) представим
в виде
Р (Ж) =£!„/?„, 0 (Ж) + (Ох — flo) R„. 1 (X) + . . .
[П/2]
‘••+(а[п/2] — °[n/2]-l) Rft, [П/2] W = 2 bftn,l(x),
i = 0
где fc0 = fl0, fc,- = o; — а/_х (* —1, .... [n/2]) — неотрицательные числа.
Аналогично, если Q (ж) £ А (т), то
[т/2]
Q {х)— 21 j (х)>
/= о
где Су5>0, / — 0, 1	[т/2]. Наконец, если Р (ж) £ А (п) и Q (ж) g А (т),
То многочлен
Р (■*) Q W = 2 ^1с/^п> ‘ W j w
». /
331
к

принадлежит множеству A (m-fn). Для доказательства этого утверж¬
дения достаточно проверить, что R„,(■*) Rm, /	(w	+ «) nP«
любых значениях Kn/2, /<m/2. Действительно, обозначим p—n—2i,
q — tn—2j и предположим для определенности, что р<?. Тогда мно¬
гочлен
Rn, I	/ W s *' (! + * + ‘ • • +Xp) x> (i +X+,,. + хЯ) в
==x‘+./ (Rp+q, о (*)-{~Rp+q, 1 (■*)+• ■ ‘ + ^p+?, p (*)) ™
= Rm + n, /+1 (x) + ^m + n, /+r + f (■*)+ - • - + ^m + n, /+n-r (x)
принадлежит множеству /l(m+n). Утверждение доказано.
22.19.	Обозначим через Ап множество 2П всевозможных наборов
е = (е*; ...; е„), состоящих из чисел е/, каждое из которых равно
либо 1, либо —1. Обозначим также хк = г±х%+ ... +е„х„ и докажем,
что произведение JJ хЕ для каждого n£N представляется в виде
ее Ап
Qn (х? Хп), где Qn — некоторый многочлен с целыми коэффици¬
ентами. Для п— 1 это утверждение верно, так как
[J XessXi (— *i) = Qi (Xl).
ее А,
Пусть теперь п > 1 и ft £{1; 2; ,,,; п}; тогда, если обозначить
e' = (Ei;	е^+1; ...; е„),
то будем иметь
П*- П ((v+**)(*e«-**))“ П (4-*2)-
сб/1 п €'6ЛП_,	е'6 An—t
Вслн в последнем произведении раскрыть все скобки и привести по¬
добные члены, то получится некоторый многочлен (с целыми коэф¬
фициентами) от переменных xt, х2, ..., хп, причем переменная х^
в каждом одночлене будет иметь четную степень. Поскольку индекс k
произвольный, то аналогичное утверждение справедливо для каждой
из переменных xi, ..., хп. Таккм образом, доказано представление
П xe=Q„(x\, .... Хп)-
ее Ап
Заметим, что многочлен Qn ненулевой, так как
I Qn (1. 0	0)1	=	1.
Выделяя в произведении
л
П tei xi+.-- + Bnxn)
ее Ап
сомножитель Xi+.,, + хп, получающийся при е = (1;	1),	и	обо¬
значая многочлен (с целыми коэффициентами от п переменных), рав¬
ный произведению всех остальных сомножителей, через Рп, получаем
332

требуемое тождество
(*1+ • ‘ * +*п) Рп (Xi, ■ • • I ^л) S Qn (Xl, ' *<) Кnj
для любого значения п £ N.
22.20. Если многочлен Р (х) имеет корни aj, as кратностей
A>i, ..., ^соответственно, то многочлен Q (х) имеет те же корни
(но, возможно, других кратностей), так как Po~Qo- Аналогично, если
многочлен Р (х)—1 имеет корни 0Ь ..., Р, кратностей llt ..., /г
соответственно, то многочлен Q (х)—1 имеет те же корни, так как
Pt = Qi. Поэтому каждое из попарно различных чисел alt а^,
flf 0, является корнем многочлена Р (x) — Q (х). Предположим,
что Р(х)— Q (х) ф 0, тогда deg (Р (х)—Q(x))S*s + r. Не уменьшая
общности, считаем, что deg Р (х) ^ deg Q (х)^ 1. Поэтому
deg Р (х) = deg (Р (х) — 1) Ss deg (Р (х) — Q (х)).
Далее, если кратность корня у многочлена Р(х) — с равна т > I, то
многочлен Р' (х) имеет корень у кратности т—1> Поэтому имеем
deg Р' (x)^(ki— 1)+ ,.. -f- (ks—	—	1) + .. i + (/, — 1) =
*= №i+ • ■ ■ +^i) + Ui+ - • ■ lr) — (s+ r) ^
Sa deg P (x) + deg (P (x) — 1) — deg (P (x) — Q (x)) 3* deg P (x),
что противоречит неравенству deg P' (x) < deg P (x). Следовательно,
P (x) = Q (x).
22.21. Допустим, что хотя бы один из многочленов Р, Q, Р,
удовлетворяющих условию задачи, не равен нулю тождественно. Тогда
существуют числа х0 и уоФ 0 такие, что хотя бы одно из чисел
Р (*о> Уо), Q (*о, Уо), R (Хо, Уо) отлично от нуля. Рассмотрим много¬
члены от одной переменной
Pi М = Р (х, уо), Qi (x)—yo'nQ (х, уо), Ri (х) = Р (х, у0)-
По условию задачи имеем
x2mPt (х) + Qi (х) 5= (х+у0)»“ Ri (х),
причем степени многочленов Pi (х), Qi (х) и Рх (х) меньше т. Обо¬
значим
U (х) = х^Рх (х), Т (х) = U (х) + Qi (х) в (x+yo?m Ri (х),
S (х) = Р(га> (х).
Так как многочлен U (х) делится на х2т, то число 0 является его
корнем кратности не меньше 2т, поэтому
(/«"> (0) = (y(m+D (0)= ... = (J&m-l) (0) = о.
Так как degQx(x) < т, то
Q[m} (0) = Q(1m+1) (0) = ... = 0.
Следовательно,
Tim) (0) — гоя+н (0) = ... = Г<аи -« (0)=0,
833
L

Т‘ е'	S(0)	= S'(0)=...=S‘m-»>(0) = 0.
Поскольку число —у0 является корнем многочлена Т (х) =
= (х+Уо)2т Ri W кратности не меньше 2т, то
Т(т> (- Уо) = Т{т * " (- Уо) = ■ ■ • = TV” -« (- jro) = О,
а значит,
S (_ у0)=S' (- уо) = ... = S<«~ » (- уо) = О-
Таким образом, числа 0 и —Уо Ф ® являются корнями многочлена
S (х) кратностей, не меньших т. Следовательно, этот многочлен де¬
лится на многочлен хт (х+уо)'” степени 2т. Но deg Т (х) < Зт, а
значит, deg S (х) < 2т, поэтому S (х) = 0. Отсюда вытекает, что мно¬
гочлен Т (х) имеет степень меньше т, но он делится на многочлен
(х+уо)2®, следовательно, Г(*)эО, откуда Ri (х) = 0. Из тождества
ximPi (х) + Qi (х) ^ Т (х)	0 и неравенства deg Qi (х) < m получим,
что Pj (х) = Q, (х) = 0. Таким образом, Pt (х0) = Qi (х0) == Rt (х0) =0,
что противоречит выбору чисел х0 и у0. Утверждение задачи доказано.
§ 23. Различные свойства многочленов
23.1. а) Значения Р (х) при всех x£Z имеют одинаковую четность
тогда и только тогда, когда каждое из чисел
Р(х+1)— Р(х) = ((х+1)2 + р(х+1) + ?) — (х?+рх+у) = 2х+1+р
делится на 2, т. е. когда р нечетно. При этом четность всех значе¬
ний Р (х) однозначно определяется по четности числа q — P (0). Таким
образом, все значения Р (х) четны (нечетны) при нечетном р и четном
(соответственно нечетном) q.
б) Поскольку Q (х)=х (х2 Тр)+9. то.значения Q (3х)=3х (9х2+РИ'7
при всех x(;Z делятся на 3 тогда и только тогда, когда число q де¬
лится на 3. При этом каждое из значений
Q (Эх ± 1) = (Зх ± 1) (Эх2 ± 6х+1 +р) +у = ± (1 4-р) (mod 3)
делится на 3 в том и только в том случае, когда число 1 -f-р делится
на 3. Таким образом, все значения Q (х) делятся на 3 при условиях
у = 0 (mod 3), р ss 2 (mod 3).
23.2. Заметим, что исходный многочлен можно представить в виде
Р (х) =2 5j7 д(*—4) (х—3) (х—2) (х—1) х (х+1) (х+2) (х+3) (х+4).
Поскольку среди девяти последовательных целых чисел обязательно
найдутся числа, делящиеся на 2, 5, 7, 9, то при любом x£Z произ-
4
ведение JJ (x+t) делится на 2-5-7-9 (произведение взаимно простых
I = - 4
чисел), т. е. число Р (х) является целым.
334

23.3. Пусть 2х2—х—36 = р2, где р—простое число. Тогда р2 =
= (х+4) (2х —9)= ab, где обозначено а- х-|-4, Ь = 2х— 9, причем
о. b£Z и 2о—5=17. Так как о —целое число, на которое делится
ра, то розможны лишь следующие 6 случаев:
1) а = р2, b= 1, тогда 2р*—1 = 17 и р = 3, поэтому х- о—4 =
= /,2 — 4 = 5;
2) С — р, Ь=р, тогда 2р — р— 17 и р=17, поэтому х=а — 4 =
= р —4=13;
3) 0=1, Ь = рг, тогда 2—р? = 17 и р? =—15, что невозможно;
4) а--=—р?, 5 = —1, тогда —2р?-|-1 = 17 и р2 = —8, что не¬
возможно;
5) а=— р, Ь=— р, тогда —2р+р = 17 и р — —17, что невозможно;
6) а = — 1, Ь =— рг, тогда —2 + р? = 17 и р2 = 19, что невоз¬
можно.
Итак, искомыми значениями являются х = 5 и х= 13.
23.4. Функция Я (х) имеет на прямой одну точку минимума
*о = — Я/2. При х < х„ эта функция убывает, а при х > х0 — возра¬
стает. Поэтому для множества А значений функции Р (х) на отрезке
[—1; 1] имеем следующее: если р <—2, то х0 > 1 и
Л = [Я(1); Я(-1)} = [1+р+д; 1 -„ + ?];
если —2 < р < 2, то —1 < х„ < 1 и
Л = [Я(х0); max {Р (—1); Я(1)}],
т. е,
A = [q—p2/4\ 1 —р + 9] при —2s£p<0
и
71 = [g—р2/4; 1+р + ?1 при 0<р<2;
если р > 2, то х0 <—1 и
л = [Р(-1); Я(1)] = [1-/>+?; 1+Я+91-
23.5. Рассмотрим многочлен Q(x) = P(x) — 2 и докажем следую¬
щее утверждение: если многочлен Q (х) с целыми коэффициентами
имеет четыре различных целых корня, то при любом значении x£Z
целое число | Q (х) | либо равно нулю, либо является составным
(в частности, оно не может быть равно 1). Пусть а, Ь, с, d— раз¬
личные целые корни многочлена Q (х). Тогда по теореме Безу имеем
разложение Q (х) = S (х) R (х), где
S (х) = (х—о) (х— Ь) (х—с) (x—d),
a R (х)—некоторый многочлен. Так как старший коэффициент мно¬
гочлена S (х) равен единице, то многочлен R (х) по теореме 48 имеет
целые коэффициенты. Пусть х0 — целое число, отличное от а, Ь, с и d.
Тогда число R (х0) целое, а число Q (х0) делится на произведение
(х„ — а) (х0— Ь) (х0 — с) (х0 — d) четырех различных целых чисел (хотя
бы два из которых отличны от 1 и —1). Поэтому либо Q(x0) -^0,
335

либо число | Q (х0) |—составное. В частности, ни при каком значении
xgZ число Q (ж) не равно ни одному из чисел —1, I, 3, 5 и 7, а
значит, число Р (х) — Q (х) +2 не равно ни одному из чисел 1, 3, 5,
7 и 9.
23.6. Множество М = {25; 26; 27; 28; 29; 30; 31} и многочлен
р (х) = х-\-(х—25) (х—27) (х—28) (х—29) (х—31) удовлетворяют всем
условиям задачи (при этом условие б) выполнено для к = 25, 27. 28,
29, 31, а условие в)—для к = 30).
23.7. а) Если Р (я) — константа, то Р' (х) «з Р" (х) нз 0, и неравен¬
ство 1) не выполнено. Пусть degP(x)=nSs 1, тогда если и нечетно,
то deg (Р (jt) —Р" (х)) = п — нечетное число, откуда Р (х) — Р* (х) < 0
хотя бы в одной точке xg R, если же п четно, то deg (Р' (х)— Р" (х))=
= я—1 — нечетное число, откуда Р' (х)—Р" (х)<0 хотя бы в одной
точке xg R. Таким образом, для любого многочлена Р (х) не выпол¬
нено либо неравенство 2), либо неравенство 1). Утверждение а) до¬
казано.
б) Положим Р(х) = дй + 3. Тогда при всех xg R имеем
Р(х)—Р' (х) = х2—2х+3 > 0, Р(х) —Р"(х) = д? +1 > 0,
т. е. ответ на вопрос п. б) отрицателен.
23.8. Можно считать, что все многочлены Р* (х), ..., Р„(х) нену¬
левые. Выберем какое-либо число х+, большее всех действительных
корней любого из этих многочленов. Тогда при всех х^х+ функция
t (х) совпадает с многочленом
Р+ (х) = Р0 (х) +2 ак (sig“ pk (*+)) pk М.
k=\
поскольку каждый из многочленов Рi (х), ..., Р„ (х) на промежутке
|х+; + оо) имеет постоянный знак. Аналогично, выберем такое число
х-, чтобы при всех х<х~ функция f (х) совпадала с некоторым
многочленом Р~ (х). Так как функция f (х) не принимает дважды ни
одного из своих значений, то многочлены Р+ (х) и Р~ (х) не являются
константами, поэтому
lim |f(x)| = Пт If (х) | = оо.
Х-++ЯЭ	X	-к	— со
Из свойств функции f (х) следует, что есть лишь две возможности:
либо
lim f (х) = —оо, lim }(х) = +оо,
X — со	X -*• + со
либо
lim f(x)=+oo,	lim	f (x) = —oo.
X-*-— a>	X -*■ t CO
В обоих случаях функция f (х) принимает сколь угодно большие по
модулю как положительные, так и отрицательные значения. Покажем,
что она принимает любое значение egR, Действительно, существует
336

точка JTj такая, что f (xt) > с и существует точка ха такая, что
f (х2) < с. Так как f (х)—непрерывная функция, то по теореме о про
межуточном значении существует точка х, лежащая между хг и х2.
для которой f(x) = c. Доказательство закончено.
23.9. Докажем индукцией по я £ N общее утверждение: если мно¬
гочлен Р (х) степени п удовлетворяет условиям Р(к) = аь при к —
= л + 2	2п±-2, то Р (2«-±3) = a2n+s—1. При п = 1 имеем
Р(3) = 2, Р (4) =3, откуда Р (х) s= x—1 и Р (5) = 4 = а6—1. Пусть
теперь утверждение верно для числа п—1. Докажем, что оно верно
и для числа п. Пусть многочлен Р (х) имеет степень п и Р (k) =
для всех к=п+2, ..., 2n-f-2. Рассмотрим многочлен Q (х)=Р (x j-2)—
—Р (х+ 1) степени не выше п— 1. Он удовлетворяет условиям Q (к) — аь
при k=n + l, ..., 2п, так как Q (k) = Р(к-|-2)—B(£-f l)=Gft+a—
— oft+1 = oft. Значит, Q (2п+1) = ог„+1—1 по предположению индук¬
ции. Но Q (2л-±1)=Р(2л-±3) — Р(2п+2) и, следовательно, Р(2л+3)=
= Р (2п + 2) + Q (2n + 1) =о2п+а + Огп +1 — • = «яп+8— 1 • Утвержден ие
доказано.
23.10. а) Обозначим x = 2cos/, <£R. Тогда
2 cos (0■ ()	2	=	Р0	(xj,	2cos (1 • i) = 2cos / s= x = Pi (x).
Полагая в формуле
2 cos nt =—2 cos ((n—2) /) + 2 (cos t) 2 cos ((n— 1) t) ==
=-fn-2W+^n-lW
значение n равным сначала 2, затем Зит. д., находим сначала мно¬
гочлен Р2 (х), затем Р3 (х) и т. д. Заметим, что старший коэффициент
любого из многочленов Р„(х) (n£N) равен 1.
б)	Пусть а = т/п, где т£Z, n£N, и дробь т/п несократима.
Тогда величина 2 cos (пап) — 2 cos (тп) равна либо 2, либо —2. В силу
доказанного выше утверждения а) величину 2 cos (nt) можно пред¬
ставить в виде многочлена Р„ (х) с целыми коэффициентами от пере¬
менной x=2cosf. Тогда число х0 = 2 cos ап является корнем мно¬
гочлена Q (х) = Рп (х) — 2 cos (тп), у которого все коэффициенты целые,
а коэффициент при старшем члене равен 1. Поэтому (см. теорему 60)
число 2 cos (ал) может быть либо целым, либо иррациональным.
Пусть 2 cos (ал)—целое число. Так как |2cosan|<2, то оно равно
одному из чисел 0, ±1, ±2. Получаем, что если число cos (ал)
рационально (где a£Q), то оно равно одному из чисел 0, ±1/2, ±1.
23.11. Пусть произвольная горизонтальная прямая у = у0 пересе¬
кает кривую у = Р(х) в четырех точках А, В, С, D с абсциссами
*i < ха < х3 < х* соответственно. Эта прямая триангулярна тогда
и только тогда, когда |ЛВ| + МС| > | AD |, т. е. когда
(Xa—Xi) + (*s—xj > (х4—Хх),
что эквивалентно неравенству
Ха*—Xi > х4—х8
337

или | АВ | > | CD |. Предположим, что, вопреки утверждению задачи,
существуют две горизонтальные прямые, пересекающие кривую в точ¬
ках Aly Si, С,, Dt и А2, В2, С2, D2 соответственно, причем | AxBi | >
> I СгО, | и | Л2В2 | < | C2D2 |. Из свойств многочленов четвертой сте¬
пени вытекает, что любая прямая, параллельная этим двум прямым
и проходящая между ними, также пересекает эту кривую в четырех
точках. Тогда хотя бы одна из таких прямых пересекает кривую
в точках А, В, С, D, для которых справедливо равенство | Л В | = | CD |.
Пусть середина Е отрезка ВС (она же—середина отрезка AD) имеет
координаты (х0; у0). Тогда многочлен Q (и), графиком которого яв¬
ляется данная кривая в системе координат и = х—хс, v=y—у0, имеет
четыре корня «j, и2, иЙ, н4, являющихся абсциссами точек Л, В, С,
D соответственно, причем Ui = —«4 и и2 ——и3. Уравнение кривой
будет записываться в виде
v=(u—иг) (и—и2) (и—и3) (и—и4) = (и2 — и\) (и2 — ul),
поэтому Q(u) = Q(—и), т.е. кривая симметрична относительно оси
ординат. Следовательно, какой бы горизонтальной прямой ее ни пере¬
секли, для точек пересечения Л, В, С, D будет выполнено равенство
|ЛВ| = |СП|. Из полученного противоречия вытекает справедливость
утверждения задачи.
23.12. Докажем требуемое утверждение индукцией по числу n£Z+.
При п = 0 многочлен Р (х) = Q (х) имеет по крайней мере один нену¬
левой коэффициент, так как Q (х) ^ 0. Пусть для некоторого п ^ 1
уже доказано, что если многочлен R (х) ненулевой, то многочлен
(х—I)”-1 R (х) имеет не менее п ненулевых коэффициентов. Предпо¬
ложим, что для некоторого ненулевого многочлена Q (x) = xrQ„ (х)
(где г g Z+, Q о (0)	0) многочлен
Р (х) = (х- 1)" Q (х) = хг (х- 1)" Qо (х)
имеет, вопреки утверждению задачи, не более п ненулевых коэффи¬
циентов. Тогда многочлен Р0 (х) = (х— 1)" Q0 (х) также имеет не более
п ненулевых коэффициентов, а его производная Ро (х) — не более п — 1
ненулевых коэффициентов. Но
Р'о (х) нз (х- 1)" Qo (х) + п (х- I)”"1 Qo (*) = (*- I)"-1 R М,
где R (х) ф 0 (ибо Р0 (х) не есть константа). Получено противоречие
с индукционным предположением. Утверждение задачи доказано.
23.13. Многочлен Р0(х) = 4х3—Зх принадлежит множеству М,
поскольку Р0 (—1)=—1, Р0 (1) = 1, а в точках его экстремума имеем
Р0(—1/2) = 1, Р0 (1 /2) = — 1. Докажем, что для любого многочлена
Р (х) g М имеет место оценка [ а | <; 4. Пусть, напротив, существует
многочлен Р (х) —сх3 + Ьхг + сх+й, удовлетворяющий неравенствам
| а | > 4 и | Р (х) | sg 1 при | х | < 1. Тогда рассмотрим ненулевой мно¬
гочлен
Q(x) = P0(x)--ip(x),
338

степень которого не превосходит двух. Поскольку | — Я(х) | < 1 при
|x|=sS 1, то Q (—1) < О, Q (—1/2) > О, Q (1/2) < О, Q (1) > 0, а значит,
многочлен Q (х) имеет ие менее трех корней. Полученное противоречие
доказывает, что искомое число k равно 4.
23.14. Если q — 1, то положим Р (х) = р. Пусть q > 1, тогда рас¬
смотрим интервал / = (1/(2д), 3/(2?)) длины l/q. Так как 3/(2q) < 1, то
существует такое число т £ N, что (3/(2q))m < l/q. Обозначим а= 1 —
— (1/(2q))m, тогда имеем неравенства 0< 1 - qxm < а < 1 для всех
к £ /. Выберем число и £ N столь большим, чтобы выполнялось
1
неравенство ап < —, и положим
Р (х) = £- (1 — (1 — qxm)n).
Я
Многочлен Р (х) имеет целые коэффициенты, так как
Р (X) ^ £. (1 - (1 -qxm)) Q (X) I px”Q (X),
а коэффициенты многочлена Q (х)—целые числа. Далее, при х £ /
имеем
| Р(х)-^ 1 = -^-1(1 -qx*y | < -£■ «" < -+■.
что и требовалось доказать.
23.15. Пусть обозначено а^ —Р(k), P*=Q (k), где k=\, 2, 3, 4,
а многочлены Р (х) и Q (х) удовлетворяют условию задачи. Тогда
«четырехзначные» числа а1а2“з«1 и р1р2р3р4 не равны ни одному
из чисел 0000, ОНО, 1001, 1111, так как многочлены Р (х) и Q (х)
имеют третью степень. С другой стороны, число а]а2а3а4 не может
принимать ни одного из видов 0ct2lct4, 0ct2ct3l, at 1 la4 или «ila3l,
так как иначе из пп. б) и г) получаем противоречие: Pi=l и pi — 0.
Отсюда, учитывая п. в), заключаем, что условию задачи удовлетво¬
ряют следующие семь пар чисел (а!С12а3а4; р1ргЭзРа) и только они:
(0100; 1010), (1000; 0010), (1000; 1000), (1000; 1010), (1010; 0010),
(1011; 0010) и (1100; 1010). Заметим, что при этом использованы
всего шесть различных «четырехзначных» чисел, а именно, 0010, 0100,
1000, 1010, 1011 и 1100. Следуя интерполяционной (формуле Лагранжа,
каждому числу ViYaYeY* поставим в соответствие многочлен R (х),
удовлетворяющий равенствам R (k) = уь при fe=*l, 2, 3, 4. Тогда
339

получим соответственно шесть многочленов:
tfi(*) = -Y*3+y*3-7x + 4,
1	19
Я2 М = ■-j х2 — 4*2+у * — 6»
D/ч	I	а	I ® а 13.,,
Rs (х) = — -g- х3+у х2— — х+4,
2	34
Я4 (х) = —— д^+бх2—-g-x + 8,
Л. (X) =•—уX» +4х*- ^х+7,
P6(x)=i-x2-|-x2+^x-2.
Итак, пара многочленов (Р (х); Q (х)) совпадает с одной из пар:
(Р2(Х): #4(х)), (R3(x); Rt(x)), (Rs (х): R3 (х)), (Я3 (х); Rt (х)),
(Я4(х); Ri (х)), (Ps (х);	(x)),	(Re(x);	Rt(x)).
23.16. Заметим, что существует только один многочлен Р (х),
удовлетворяющий условиям задачи, так как если бы существовал
другой многочлен Q (х) ^ Р (х) с такими же свойствами, то многочлен
Р (х) — Q (х) степени, не большей п, имел бы не менее л +1 корней.
Поскольку для многочлена R (х)- х + — * - (0—х) (1—х) ... (л—х)
выполнено условие R(—I) = 0, то по теореме Безу этот многочлен
делится на х+1, т. е. R (x) = S(x) (х+ 1), где S (х) — многочлен сте¬
пени л. Так как R(k)—k и S(k) k/(k-\-l) при * = 0, 1, ..., л, то
S (х) удовлетворяет условиям задачи, а значит, P(x)h==S(x) и
ее+о-^-*-±Ч&!^:
23.17. Используя интерполяционную формулу Лагранжа, получаем
(ниже подразумевается, что 1 < i < л)
л	п	ТТ	(х—О
Р(Х)= У _1_ П ^=У 1фк	-
СЙ+1 ii к (к 0 П'о C*+i (-1)"-* (л - Л)! М
— У / ПП-* (»+! —*). ТТ (х_п
£0‘ 4	(п+1)!	iiV
^(«+1) = Е (-!)-* J П (n + 1-O-
=Е («+1-о=Б (-1)-*.
fc=0	1=0	ftuO
Поэтому Р (я + 1) = 0, если л нечетно, и Р (я + 1) = I, если л четно.
340

23.18.	Согласно интерполяционной формуле Лагранжа много¬
член
Р (х) = х" +я1х"-1+ ... +ап
можно представить в виде (ниже подразумевается, что 0 < t < л)
Р(х) =
Предположим,- что утверждение задачи не выполняется, т. е.
| Р (xj) 1 < nl/2" при / = 0, 1, ..., п. Тогда старший коэффициент
1 многочлена Р (х), равный сумме старших коэффициентов в произве¬
дениях Ц х~х‘., по модулю не превосходит числа
1 =гь / Х] Х‘
п
у JHL ТТ !
2" 41/ I х! Xi I
L П ^
/То ' эь / */ Х‘
 1	1	--	1	V "»	_	1 V с/ = ,
Т)2” П (/-'•)	2“	/!(«-/)!	2"^о "
* < j	‘	>	/
Полученное противоречие доказывает справедливость утверждения
задачи.
23.19.	Согласно интерполяционной формуле Лагранжа имеем ра¬
венство (ниже подразумевается, что —
Я(х)= £ P(k) Д
fe=-n
Так как |P(ft)|<l при k — — п, —п + 1, ..., п, то
Iр(чк £ i'-wi П jfEfh £ п т£тг'
1**1» ч	I* ч
Для каждого действительного числа	—п,	п] справедливо нера¬
венство
Д |x-i|^(2n)!.
i=&k
Действительно, в случае x^k имеем
ТТ I*—*'| = (1 *—(*+!) I ••• |х—nl)(|x—(ft—1)1 ... |х+н|)*£
i Ф к
<.{п — ft)!-((n — ft+1) ... (2п)) = (2н)!-
341

Аналогично рассматривается случай х < к. Таким образом, получаем
,Ц, !*—! ’®12"’1 П -рглт ’* l2'‘,, (*+„)! (я_й, I ■
I'WK £ щ^=щ=Е ж§Вщ"Е
к--п '	’	'	'	Л	=	0	'	'	fc=0
что и требовалось доказать.
Глава 7
КОМБИНАТОРИКА
§ 24. Множества и подмножества
24.1. Найдем количество различных пар непересекающихся под¬
множеств при условии, что в паре выделены первое и второе подмно¬
жества. Для каждого из п элементов есть 3 возможности: его можно
или включить в первое подмножество, или включить во второе под¬
множество, или не включать ни в одно из них. Поэтому количество
указанных пар равно 3". Среди них есть одна пара, в которой оба
подмножества пусты. Оставшиеся (3я — 1) пары в свою очередь разби¬
ваются на двойки совпадающих пар, если разрешить переставлять
в парах местами, первое и второе подмножества. Таким образом, су¬
ществует (3я —1)/2 (неупорядоченных) пар подмножеств, нз которых
хотя бы одно не пусто. Всего же имеется (3я — 1J/2 + 1 = (Зп + 1)/2
различных пар подмножеств, удовлетворяющих условию задачи.
24.2. Так как существует всего 2я различных подмножеств
множества X, то различных упорядоченных пар подмножеств
существует (2Я)2 = 4Я. Разобьем все эти пары на 4я-1 четверок,
включая каждую пару (Ль Л2) в одну четверку с парами (Ль Л2),
(Ль А2), (Ai; А2) (здесь через А обозначено дополнение А\А к под¬
множеству А с X). В результате получим разбиение множества всех
пар на четверки. Действительно, пара (Ль Л2), например, образует
четверку (Ай Л2), (Ль Л2), (Ай Л2), (Ад Л2), которая совпадает
с четверкой, образуемой парой (Ай Л2), ибо Л = Л. Аналогично про¬
веряется, что пары (Ль Л2), (Ай Л2) образуют ту же четверку. Далее,
поскольку каждый элемент множества X принадлежит либо подмно¬
жеству Л, либо его дополнению Л, то он входит в точности в одно
из множеств четверки AiQA2, Aif]Л2, At(]A2, Л2Г)Л2. Следовав
тельно, суммарное количество элементов в любой четверке равно п.
Так как всего четверок 4я-1, то сумма количеств элементов всех
множеств вида ЛiПА12 равна п-4я-1.
342

24.3.	Докажем утверждение индукцией по п > 3. При п — 4, 5,
6, 7, 8, 9 возможные разбиения множества Хп на подмножества
Ai, А„ указаны в таблице, где для каждого значения п и каж¬
дого из трех цветов указаны номера т тех множеств Ат, которые
должны состоять из элементов соответствующего цвета (например.
Таблица I
п
п (11+ 1 )
2
к
Синий
Красный
Белый
4
10
3
1; 2
3
4
5
15
5
1; 4
2; 3
5
6
21
7
1; 6
2; 5
СО
7
28
9
4; 5
3; 6
1; 2; 7
8
36
12
5: 7
4; 8
1; 2; 3; 6
9
45
15
6; 9
7; 8
1; 2; 3; 4; 5
при п=6 элементы множеств А2 и Ав должны быть красными). Пусть
теперь П72 10 и для чисел, меньших и, в частности для числа п — 6,
утверждение доказано. Разбиение множества Хп построим следующим
образом: множества Ах, ..., Л„_в составим из элементов тех же
цветов, что и в разбиении множества Х„_в. Множества Л„_5, Ап
составим из элементов синего цвета, множества Л„_3, Ап_2 — из эле¬
ментов красного цвета, а множества Л„_4, An_t —цд элементов белого
цвета. Полученное разбиение удовлетворяет условию задачи, так как
количество снних, красных и белых элементов (в отдельности) мно¬
жества Хп больше количества соответствующих элементов множества
Х„_в на одну и ту же величину, равную 2л— 5.
24.4. Зафиксируем элемент at множества X- {аь а2; ... ; а,,}
и будем рассматривать только подмножества, содержащие аг. Число
таких подмножеств равно числу подмножеств множества {а2\ ...; а
т.е. числу 2"_1. Следовательно, k^2n~l. С другой стороны, пусть
выбрано более чем 2"-1 подмножеств множества X. Разобьем все воз¬
можные подмножества множества X иа 2П_1 пар, объединяя в пару
подмножество и его дополнение. Тогда по принципу Дирихле (тео¬
рема 1) хотя бы два выбранных подмножества обязательно составляют
пару и, следовательно, не пересекаются. Таким образом, k = 2n~1.
24.5. Пусть количество элементов в множестве X равно п. Каждое
из выбранных подмножеств Ах, ..., Л60 содержит более чем п/2 эле¬
ментов, а значит, сумма количеств элементов всех этих множеств
343

превышает 50-(n/2) = 25/t. По принципу Дирихле существует элемент
множества X, принадлежащий не менее чем 26 выбранным подмно¬
жествам. Аналогично доказывается, что при любом значении k < 50
среди множеств А(, А{ можно выбрать не менее [А,/2]+1 мно-
1	к
жеств, содержащих общий элемент. Возьмем элемент множества X,
который принадлежит не менее чем 26 множествам (этот элемент
будет одним из пяти элементов множества В). Выбросим из рассмот¬
рения какие-либо 26 множеств из числа тех, которым он принадле¬
жит. Тогда найдется элемент, принадлежащий по крайней мере 13
из 24 оставшихся множеств. Выбросим из рассмотрения и эти
13 множеств. Тогда для оставшихся 11 множеств найдется элемент,
принадлежащий по крайней мере шести из этих множеств. Для
остальных пяти множеств существует элемент, принадлежащий по
крайней мере трем из них. И, наконец, существует элемент, принад¬
лежащий последним двум множествам. Таким образом, найдено не
более пяти элементов множества X (возможно, менее пяти, так как
некоторые из выбранных элементов могут совпадать), которые состав¬
ляют множество В. При этом любое из множеств Ai, ..., Аы содер¬
жит хотя бы один из этих элементов.
24.6. Рассмотрим любое множество А из данных 1978 множеств.
Оно пересекается с каждым из остальных 1977 множеств, поэтому
существует элемент а £ А, принадлежащий не менее чем 50 из этих
множеств. (Действительно, если каждый из 40 элементов множества А
принадлежит не более чем 49 множествам, то всего имеется не более
40-49=1960 множеств, отличных от А, что неверно.) Итак, пусть
элемент а принадлежит множествам A, Ait Aa, ..., А60. Докажем,
что тогда он принадлежит и любому другому множеству В из данных
1978 множеств. Действительно, никакие два из множеств А, Аи
Аа, ..., Аьо не имеют общих элементов, отличных от а (так как
любые два множества пересекаются ровно по одному элементу). Пусть
афВ. Тогда множество В имеет с каждым из множеств А, Аи
А2, ..., А60 общие элементы, которые отличны от а, а значит, раз¬
личны. Поэтому множество В содержит не менее 51 элемента, что
невозможно. Следовательно, элемент а принадлежит всем множествам.
24.7. Рассмотрим подмножества (если такие имеются), которые
содержат нечетное количество элементов. Поскольку общее количество
элементов четно, то количество множеств с нечетным числом элементов
также четно. Разобьем эти множества на пары (произвольным обра¬
зом). С множествами из каждой пары произведем операцию, указанную
в условии задачи, т. е. из большего множества переведем в меньшее
столько элементов, сколько содержит меньшее множество. После этого
все множества будут содержать четное число элементов. Рассмотрим
те множества, количество элементов в которых не делится на 4 (при
2, если же п = 1, то элементов всего 2 и оба они уже содержатся
в одном подмножестве). Поскольку общее количество элементов де-
344

лится на 4, то количество таких подмножеств четно. Разобьем эти
множества на пары произвольным образом и над каждой парой про¬
изведем операцию, указанную в условии задачи. После этого коли¬
чество элементов в каждом множестве будет делиться на 4. Анало¬
гично поступаем далее так, чтобы количество элементов в каждом
множестве делилось (последовательно) на 8, !6, ... Когда количестно
элементов в каждом множестве будет делиться на 2", то все 2" эле¬
ментов будут содержаться в одном подмножестве.
24.8. Обозначим через А и В множества всех меиьших и соот¬
ветственно больших чисел, из которых состоят пары множества М.
Тогда по условию задачи ни один элемент из В не содержится
в множестве А, а значит, A f)B = 0. Пусть количества элементов
множеств А и В равны а и Ь соответственно. Тогда a +
и в любой паре из Л1 меньший элемент может принимать не более
чем а значений, а больший—не более чем Ь значений. Поэтому
число элементов в Л1 не превосходит числа
ab<*a(n—а)< ((а + и—а)/2)2 = я2/4.
Так как abg Z, то ай<[л2/4]. Если число п четное, то наибольшее
количество элементов в множестве М достигается в случае
М = {(/'; О I / < п/2; I > п/2}
(тогда М состоит из па/4 элементов). Если же число п нечетное, то
достаточно взять
м = {(/; ОI/ < n/2; i > п/2}
(тогда М состоит из
я — I п + 1  я2 1	 Г 1
2	’	2	~4	4	[4]
элементов).	Таким	образом, и в случае	четного,	и в	случае	нечет¬
ного я	наибольшее	возможное количество	элементов	в	множестве	М
равно [я2/4].
24.9. Обозначим искомое число через кп. Предположим, что
в множестве X выбраны kn трехэлементных подмножеств, любые два
из которых имеют ровно один общий элемент. Возможны три случая.
а) Никакой элемент множества X не входит более чем в два
трехэлементных множества. Пусть одно из множеств есть [а; Ь\ с).
Тогда любое из оставшихся множеств пересекается с множеством
{а; Ь\ с), причем среди этих оставшихся множеств ие более одного
множества содержит элемент а, не более одного—элемент Ь и не
более одного—элемент с. Поэтому всего множеств не более 1+3.1=4,
т. е. £„<4.
б) Существует элемент множества X, входящий в три трехэле¬
ментных множества, но никакой элемент множества X не входит
более чем в три трехэлементных множества. Тогда, если {а; Ь\ с) —
345

одно из множеств, то любое из оставшихся множеств пересекается
с ним, причем не более двух из этих оставшихся множеств содержит
элемент а, не более двух—элемент б и не более двух—элемент с.
Поэтому всего множеств не более 1+3-2 = 7, т. е. kn 7.
в)	Существует элемент а множества X, принадлежащий по край¬
ней мере четырем трехэлементным множествам. Тогда все остальные
элементы этих четырех множеств различны, а любое из оставшихся
множеств также должно содержать элемент а (иначе такое множество
имело бы по одному различному общему элементу с каждым из че¬
тырех множеств, т. е. содержало бы по меньшей мере 4 элемента).
Таким образом, в этом случае имеем 1+2-б„<;п, т. е. £„«s[(n—1)/2].
Для п= 1, 2, 3, 4, 5 имеем k2--0, k3 = kt -А, kb — 2. Пусть
п~ 6. Тогда ни один элемент не принадлежит сразу трем множествам,
иначе их объединение состояло бы из 7 элементов. Поэтому имеет
место случай а) и ka < 4. С другой стороны, существует пример
четырех множеств: если Х = {я; б; с; d; е; f), то трехэлементными
подмножествами могут	быть {а; б; г}, {с; d;	е], (е;	f; a}, {fc; d; /}.
Таким образом, ke	4.	Пусть я£{7; 8; ...;	16}. Тогда, если имеег
место случай в), то количество множеств не превосходит [(16— 1)/2[ =
=7; если же имеет место случай а) или б), то это количество также
не превосходит 7. С другой стороны, если множество X среди своих
элементов содержит 7 элементов а, б, с, d, е, f, g, то существует
пример семи трехэлементных подмножеств: {а; б; с}, {с; d\ е},
{е; f; а},	{б; d; f},	{а;	g\ d}, {6; g\ e}, {с;	g; f}.	Таким образом,
k„ -7 при n — 7, 8	 16. Наконец, если n За	17, то	в любом из слу¬
чаев а), б), в) справедлива оценка £„<;[(«—1)/2], причем эта оценка
достигается при следующем выборе трехэлементных подмножеств:
один из элементов является общим для всех множеств, а остальные
элементы (кроме, быть может, одного в случае четного п) разбиваются
иа пары и образуют с общим элементом требуемые подмножества.
Таким образом,
kn = [(п— 1)/2] при п А 17.
24.10.	Предположим противное. Тогда любые два из выбранных
подмножеств либо не пересекаются, либо имеют ровно два общих
элемента. Если подмножества А к В имеют ровно два общих эле¬
мента, то будем писать А ~ В. Пусть А, В, С—три подмножества.
Докажем, что если А ~ В и В ~ С, то А ~ С. Действительно, пусть
А — {я; б; с}, В {о; б; d}. Так как множество С должно иметь с
множеством В два общих элемента, среди которых обязательно есть
а или б, то С пересекается с ,4, а значит, С ~ А. Таким образом, все
выбранные подмножества разбиваются иа классы, в каждом из кото¬
рых любые два разных множества имеют ровно два общих элемента,
а множества из разных классов не пересекаются. Для каждого клас¬
са множеств возможны 3 случая:
346

1) класс охватывает ровно 3 элемента;
2) класс охватывает ровно 4 элемента;
3) класс охватывает больше 4 элементов.
В первом случае класс состоит ровно из одного множества, во
втором—количество множеств не больше четырех (так как у множе¬
ства из 4 элементов существует всего 4 различных трехэлементных
подмножества). Рассмотрим третий случай. Пусть выбраны два мно¬
жества из рассматриваемого класса: А = [а; Ь\ с} и В — {и; b; d}.
Существует элемент е, отличный от а, Ь, с, d и принадлежащий
некоторому множеству С из этого класса. Из условий А ~ С и В ~С
получаем, что С = {я; Ь; с}. Поэтому и любое множество D из этого
класса в силу условий А ~ D, В ~ D, С ~ D содержит элементы
а и Ь. Тогда количество множеств в классе ровно на 2 меньше коли¬
чества элементов в этом классе (каждому элементу, отличному от а, Ь,
соответствует ровно одно множество, которому он принадлежит).
Таким образом, в каждом классе количество множеств не больше
количества элементов. Однако общее количество множеств больше
общего количества элементов. Противоречие.
24.11.	Пусть к—число элементов в том из множеств Ах, ..., А„,
В1, ..., В„, в котором оно наименьшее. Для определенности считаем,
что множество Ах содержит к элементов. Множества Вх, ..., Вп
между собой не пересекаются. Поэтому условие Ax[\Bj Ф 8 выпол¬
нено не более чем для к из множеств Вь ..., В„. Пусть, например,
это условие выполнено для множеств Вх, ..., Вга,-где т<£. Число
лементов в каждом из множеств Вх, ..., Вт не меньше k (согласно
выбору числа к), следовательно, их объединение содержит не менее
тк элементов. Число же элементов в каждом из множеств Вт+1, ...
..., В„ не меньше п — к (по условию, так как АХ[)Вj = 8 при / =
~т-(-1, .... л), а число таких множеств равно п — т. Поэтому всего
в множестве X = Вх (J ... (JВп не менее чем 1 = кт-\-(п — к)(п—т)
элементов. Если k^nj2, то каждое нз множеств Ах, ..., Ап содер¬
жит не менее п/2 элементов, а всего элементов не менее п-(п/2) =
= п2/2. Если же к < п/2 (напомним, что т^к), то
I- п (п — к) — т (п — 2к) ^ п (п—к) — к (п—2к) =
Теперь приведем пример, когда множество X содержит ровно и2/2
элементов. Пусть п■—четное число и X — AX[J ... (jA„ — разбиение
множества X на п подмножеств (попарно не пересекающихся), каж¬
дое из которых содержит ровно п/2 элементов. Положим В1 = А1, ...
..., Вп= А,„ тогда все условия задачи будут выполнены.
347

§ 25. Задачи с использованием графов
25.1. Предположим, что	в множестве	S найдутся три	элемента
а, Ь, с такие, что а —>■ Ь и	а —-*■ с. Если	b —»• с, то из	а —>- Ь	и
Ь—ус следует с■—> а, что противоречит условию а—>- с. Если же
с—>-6, то из а—»• с и с—► Ь следует b—у а, что противоречит ус¬
ловию а —>■ Ь. Аналогично доказывается, что в S нет элементов а,
d, е таких, что d —► а и е —► а. Если в множестве S имеется 4 или
более элементов (один из которых обозначим через а), то из первого
условия задачи следует, что	в S найдутся	или такие элементы b	и
с, что а—► Ь и а—► с, или	же такие элементы due, что	d—>- а	и
е—у а. В обоих случаях получаем противоречие. Поэтому в множе¬
стве S не более трех элементов. Пример множества S с тремя эле¬
ментами а, Ь, с, удовлетворяющего обоим условиям задачи, может
быть таким: а —>• Ь, Ь —> с, с —у а.
25.2. Если незнакомых людей нет, то количество людей, которые
знакомы со всеми, равно 1982. Пусть А и В не знакомы друг с дру¬
гом. Тогда все остальные люди между собой знакомы (если С не
знаком с D, то в группе А, В, С, D никто не знаком с остальными
тремя). Если А и В знакомы со всеми остальными, то 1980 человек
знакомы со всеми. Если же А не знаком также и с С, где С Ф В,
то и А, и В, и С знакомы со всеми остальными 1979 людьми (так
как в любой группе А, В, С, D только D может быть знакомым с
остальными тремя), которые к тому же знакомы между собой. Таким
образом, минимальное количество людей, знакомых со всеми, равно
1979.
25.3. Заметим, что каждый гость знает ровно дзоих из осталь¬
ных четырех гостей. В самом деле, допустим, что гость А имеет трех
знакомых: В, С и D. Тогда если В и С знают друг друга, то среди
А, В и С нет незнакомых. Поэтому В и С (аналогично В и D, Си
D) незнакомы, и среди В, С, D нет знакомых. Аналогично рассмат¬
ривается случай, когда А имеет трех незнакомых. Пусть теперь зна¬
комые А — гости В и С. Тогда В и С не знакомы, и у В есть зна¬
комый D (D ф A, D ф С). Если D знаком с С, то каждый из гостей
А, В, С, D знаком с двумя гостями внутри этой четверки, поэтому
пятый гость Е не может быть ни с кем знаком. Таким образом, D
не знаком с С, и так как он не знаком с А, а С ие знаком с В, то
С и D знакомы с Е. Следовательно, гостей можно расбадить, напри¬
мер, в таком порядке: Е, D, В, А, С.
25.4. Допустим, что никакие трое из математиков ие говорят на
одном и том же языке. Рассмотрим произвольного математика А. Он
говорит не более чем на трех языках, причем на каждом из этих
языков говорит еще не более чем один из математиков (иначе мы по¬
лучили бы противоречие с допущением). Поэтому найдутся пять ма¬
тематиков, с которыми А не говорит на одном языке. Пусть один
348

из этих пяти — математик В. По той же причине, что и А, матема¬
тик В может говорить на одном языке не более чем с тремя мате¬
матиками. Поэтому среди остальных четырех математиков, ие гово¬
рящих на одном языке с А, найдется математик С, не говорящий на
одном языке с В. Таким образом, в тройке А, В, С никакие двое
не говорят на одном языке, что противоречит условию задачи.
25.5. а) Предположим, что среди любых четырех человек име¬
ются двое незнакомых. Тогда, скажем, человек А не может иметь
более трех незнакомых: если А имеет четырех незнакомых, то, со¬
гласно предположению, среди них найдутся двое незнакомых между
собой, а они образуют вместе с А тройку попарно незнакомых лю¬
дей. Итак, А имеет не более трех незнакомых, а значит, не менее
шести знакомых. Пусть А знаком с Blt В2, ..., Вв. Тогда среди
Si, В2, ..., б8 нет тройки попарно знакомых людей (иначе эта трой¬
ка вместе с А образовывала бы четверку попарно знакомых людей,
что противоречило бы предположению). Значит, среди любых трех
человек из В4, В2, ..., бв есть двое незнакомых. Тогда В4 не мо¬
жет иметь более двух незнакомых среди В2, ..., В2 (если Si не зна¬
ком, например, с В2, В3, В4, то В2, В3 и В4 попарно знакомы). По¬
этому Si имеет по крайней мере троих знакомых среди В2, ..., бв.
Тогда в этой тройке людей найдутся двое знакомых друг с другом,
образующих вместе с В4 и А четверку попарно знакомых, что про¬
тиворечит предположению.
б)	Докажем, что утверждение останется верным. Если какой-ли¬
бо человек знаком по крайней мере с шестью людьми, то доказа¬
тельство аналогично проведенному выше в п. а). Если же каждый
человек знаком ровно с пятью людьми, то общее количество пар
знакомых равно 9-5/2, т. е. не является целым, что невозможно. На¬
конец, если найдется человек, не знакомый по крайней мере с че¬
тырьмя людьми, то -.ти четверо попарно знакомы (иначе нашлась бы
тройка попарно незнакомых людей), т. е. образуют искомую четверку
людей. Утверждение доказано.
25.6. Предположим, что существуют пять городов, соединенных
указанным в задаче образом. Докажем прежде всего, что ни из ка¬
кого города не выходят три линии одного и того же вида транспор¬
та. Пусть город А соединен с городами В, С и D, например, само¬
летом. Тогда по условию ни одна пара из городов В, С и D не мо¬
жет быть соединена самолетом. Пусть В и С соединены, например,
поездом. Города С и D не могут быть соединены автобусом, так как
иначе город С имел бы все три вида транспорта. Поэтому С и D
соединены поездом. По тем же причинам города В и D также сое¬
динены поездом. Получили, что В, С и D попарно соединены поез¬
дом. Противоречие. Итак, из каждого города выходят две транспорт¬
ные линии одного вида и две транспортные линии некоторого дру¬
гого вида. Тогда каждый город обслуживается ровно двумя видами
349

транспорта. Поэтому хотя бы один вид транспорта обслуживает не
более чем три города (иначе всего городов было бы ие менее чем
4-3/2 =6). Если он обслуживает ровно два города, то из каждого
из этих городов выходит только одна транспортная линия такого
вида, что невозможно. Если же он обслуживает ровно три города,
то они должны быть соединены попарно этим видом транспорта, что
также невозможно. Таким образом, мы доказали, что для пяти го¬
родов условие задачи невыполнимо. Тем более оно невыполнимо для
большего числа городов. Если же рассмотреть четыре города А, В,
С и А, которые связаны следующим образом: А с В поездом, С с D
автобусом, а все остальные пары самолетом, то все условия задачи
будут выполнены. Следовательно, наибольшее число городов равно 4.
25.7. Докажем, во-первых, что любые два знакомых имеют оди¬
наковое число знакомых. Действительно, пусть А и В знакомы, а
А\, А2, ..., Ап—все знакомые А, отличные от В. Тогда, согласно
условию задачи, никакие двое среди В, А±, Аа, ..., Ап не знакомы
между собой. Рассмотрим А1ш Поскольку Ау не знаком с В, то он
имеет с В двух общих знакомых: А и, например, В2. Так как В, и
А не знакомы друг с другом, то, кроме В н Alt у них нет общих
знакомых, а значит, не знаком с А2, ..., А„. Аналогично нахо¬
дим В2 — общего знакомого Аа и В (отличного от Ви так как Bi ие
знаком с А2) и т. д. Таким образом, всем знакомым А (отличным
от В) соответствуют разные знакомые В (отличные от А), а значит,
число знакомых А не превосходит числа знакомых В. Аналогично
доказывается, что число знакомых В не превосходит числа знакомых
А. Поэтому А и В имеют одинаковое число знакомых. Во-вторых,
если С и D ие знакомы, то они имеют общего знакомого Е. Тогда
по доказанному выше С и £ имеют одинаковое число знакомых, то
же имеет место и для D и Е. Следовательно, С и D также имеют
одинаковое число знакомых, совпадающее с числом знакомых Е.
25.8. Среди всех Зп учеников выберем такого ученика (точнее,
9Дного из таких учеников), который имеет наибольшее число к зна¬
комых в одной из двух других школ. Пусть для определенности им
оказался ученик А первой школы, который знает k учеников, на¬
пример, из второй школы. Тогда А знает п +1 — к учеников из
третьей школы, причем п+1—k^s 1, так как ке£^п. Рассмотрим
ученика В третьей школы, знакомого с А. Если В знает хотя бы
одного ученика С из k знакомых А во второй школе, то ученики
А, В, С образуют искомую тройку. Если же В не знает никого из
к знакомых А во второй школе, то в этой школе он знаком не более
чем с п — к учениками, а значит, в первой школе он знаком не ме¬
нее чем с п -J-1 — (п—£) = £ +1 учениками, что противоречит выбо¬
ру к. Утверждение доказано.
25.9. Докажем индукцией по л £ N, что если в графе с 2п вер¬
шинами никакие три ребра не образуют треугольника, то число ре¬
350

бер не превосходит я2. Для п = 1 число ребер всегда не превосходит
1=я2. Пусть утверждение доказано для числа п. Докажем его для
числа я+1. Пусть имеется граф с 2 (я + 1) вершинами, никакие три
ребра которого не образуют треугольник. Выберем две вершины, со¬
единенные ребром (если в графе нет ни одного ребра, то все дока¬
зано). Тогда каждая из оставшихся 2п вершин соединена ребром не
более чем с одной из выбранных вершин. Эти 2п вершин соединены
между собой, по предположению индукции, не более чем п2. ребрами.
Тогда общее число ребер ие превосходит я?+2я+1 = (я + 1)2. Ут¬
верждение доказано. Наконец, если 2л вершин разделить на два
множества по я вершин, а затем любые две вершины, лежащие в
разных множествах, соединить ребрами, то получится граф с я2 реб¬
рами, не содержащий ни одного треугольника.
25.10. Будем решать задачу индукцией по я — числу юношей.
Для я=1 утверждение вытекает из того, что для одного юноши
обязательно найдется знакомая девушка. Пусть утверждение доказано
для всех чисел, меньших я. Докажем его для числа я. Рассмотрим
два случая.
1) Найдется такая группа А из k < я юношей, что общее число
всех знакомых с ними девушек равно к. Пусть каждый юноша из
этой группы танцует со знакомой девушкой (это возможно в силу
предположения индукции). Тогда для оставшихся юношей и деву¬
шек условие задачи будет выполнено. Действительно, если имеется
группа В из i не входящих в А юношей, то у юношей из объедине¬
ния множества В с множеством А имеется не менее чем i-\-k знако¬
мых девушек. Юноши, входящие в А, знакомы в общей сложности
не более чем с к девушками. Значит, i юношей из группы В знакомы
по крайней мере с t из оставшихся девушек. Таким образом, по
предположению индукции, каждый из юношей, не входящих в А,
также может танцевать со знакомой ему девушкой.
2) У любой группы из любого количества к < я юношей число
знакомых девушек превышает к. Тогда, если один из юношей будет
танцевать со знакомой ему девушкой, то множество остав нихся юно¬
шей и девушек будет по-прежнему удовлетворять условию задачи.
Действительно, любая группа из й«£я—- 1 оставшихся юношей зна¬
кома ие менее чем с А + 1 девушками (одна из которых, возможно,
уже танцует). Значит, по предположению индукции, каждый из
оставшихся юношей также сможет танцевать со знакомой ему де¬
вушкой.
25.11. Докажем индукцией no n£N, что если есть я компаний
At, ..., А„ и N городов Рх, .... Рдг, причем N > 2П и любые два
города соединены авиалиниями, то хотя бы одна компания сможет
обеспечить круговое путешествие с нечетным числом авиалиний. По¬
скольку 1983 > 1024 = 210, то требуемое в задаче утверждение будет
доказано. Если я=1, то /V3 и Pi/VVi—искомое путешествие.
351

Пусть утверждение доказано для числа п—1. Докажем его для числа
п. Пусть все круговые путешествия компании А„ состоят из четного
числа авиалинии (иначе утверждение можно считать доказанным).
Тогда разобьем города на две группы
Я={Яъ ■ Rk} и Q={Qi'> • ••; От}
следующим образом. Положим Р, £ R. Далее, все города, в которые
можно прилететь иа самолетах компании Ап без пересадок из Р,,
включим в группу Q. Все города, в которые можно прилететь на
самолетах компании Ап из городов, лежащих в Q, без пересадок,
включим в R, и т. д. При этом никогда ие случится .так, что два
города из одной группы (R или Q) связаны авиалинией компании
А„ (иначе появится круговое путешествие с нечетным числом авиа¬
линий). Если мы исчерпали все города, в которые можно прилететь
из Pi на самолетах компании Ап, то включим в R любой из остав¬
шихся городов и продолжим описанные действия (до тех пор, пока
все города не будут распределены по группам). Хотя бы в одной из
групп R или Q находится более чем 2П-1 городов (ибо А+т =
= N > 2П), а внутри каждой из этих групп все перелеты обеспечивают
компании Ах, А2, ..., Л„_г (так как компания Ап соединяет только
города из R с городами нз Q). Остается применить предположение
индукции.
§ 26. Различные комбинаторные задачи
26.1. Допустим, что после нескольких указанных в задаче опера¬
ций получился набор из одних нулей. Пусть это в первый раз про¬
изошло после k-ik операции. Тогда после (k—1)-й операции все цифры
на окружности были одинаковые и не равные нулю, а следовательно,
равные единице. Значит, после (k—2)-й операции любые две сосед¬
ние цифры на окружности были различными. Поэтому нулей было
столько же, сколько и единиц, а общее количество цифр было чет¬
ным, что противоречит условию.
26.2. Разобьем всю плоскость на одинаковые квадраты, состоя¬
щие из четырех клеток каждый. Далее, в каждом из этих квадратов
«левую верхнюю» клетку назовем черной, «правую верхнюю» — белой,
«левую нижнюю» — красной, а «правую нижнюю» — синей. Тогда,
с одной стороны, любые две клетки одного цвета не соприкасаются.
С другой стороны, среди отмеченных клеток можно выбрать не менее
четверти таких, которые имеют одинаковый цвет (в противном слу¬
чае всего клеток было бы менее чем 4-(«/4) = п).
26.3. Каждый из 26 единичных кубиков, отличных от централь¬
ного, будем считать либо черным, либо белым в шахматном порядке:
12 кубиков, имеющих ровно по две грани на поверхности большого
куба, назовем белыми, а остальные 14 кубиков — черными. Заметим,
352

что в любой паре таких кубиков, имеющих общую грань, один ку¬
бик будет белым, а другой—черным. Указанные 26 кубиков мышка
съесть не сможет, поскольку в противном случае их можно было бы
разбить на 13 пар, каждая из которых состояла бы из белого и чер¬
ного кубика, а тогда белых и черных кубиков было бы поровну.
26.4. Без ограничения общности считаем, что At < Аг <...< Ап.
Выберем наименьший номер i, для которого среди точек Ai, ..., А,-
присутствуют точки всех четырех цветов. Тогда цвет А[ отличен от
цветов Ai, A,_t. Теперь выберем наибольший номер / < i, дл'.
которого среди точек Aj, ..., Л; присутствуют точки всех четырех
цветов. Тогда цвет Aj отличен от цветов Л/+1 Ai и отрезок
(Aj\ Л/] — искомый.
26.5. Пусть k—число отрицательных треугольников. Для каж¬
дого треугольника перемножим числа, соответствующие его сторонам,
а затем перемножим все полученные произведения. В итоге получится
число (—1)й. Заметим, что число, соответствующее любому отрезку,
входит в это произведение п—2 раза, так как любой отрезок при¬
надлежит п—2 треугольникам. Следовательно, полученное произве¬
дение равно (—i)cn-s)m> поэтому число к имеет ту же четность, что
и число (п—2) т = пт (mod 2).
26.6. Предположим, что машина имеет запас бензина, достаточ¬
ный для того, чтобы проехать всю дорогу без заправок. Пусть она
начинает движение с любой станции (забирая по дороге весь бензин
на каждой станции) и оканчивает движение в той же точке и с тем
же количеством бензина. Обозначим через Л станцию, подьезжая
к которой, машина имела в баке наименьшее за все время движения
количество бензина. Пусть в этот момент количество бензина в ма¬
шине было равным х. Если машина с количеством бензина, равным
х, начнет движение со станции Л, то в баке всегда будет бензина не
меньше х. Следовательно, если машину с пустым баком заправить на
станции Л, то она сможет, начиная движение с этой станции, совер¬
шить поездку по кругу (так как это количество х бензина можно
с самого начала вылить и совершить путешествие без него).
26.7. Разобьем доску на четыре части по две вертикали в каж¬
дой. Пусть черные в ответ на ход белых в какой-либо части делают
ход в той же части. Тогда, если черные лишат белых возможности
ходить в каждой из частей, то белые не смогут ходить вообще. Итак,
достаточно описать выигрышную стратегию черных для случая, когда
игра происходит в пределах двух вертикалей. Если белые передви¬
гают свою фишку на к клеток вперед, то черные передвигают свою
фишку, стоящую в другой вертикали, на к клеток впере„. Если же
белые передвигают свою фишку на к клеток назад, то черные пере¬
двигают свою фишку, стоящую в той же вертикали, иа к клеток
вперед. Тогда после каждого хода черных расстояния между фиш¬
ками, стоящими в одной вертикали, и qbHiuKaMn, стоящими в другой
12 Под ред. И. И. Сергеева	353

вертикали, становятся одинаковыми. Поэтому на любой ход белых
черные имеют ответный ход, а значит, черные ие могут проиграть.
С другой стороны, черные ходят только вперед, так что игра обяза¬
тельно закончится через конечное число ходов. Таким образом, чер¬
ные выигрывают.
26.8. Разобьем все целые числа, начиная с двух, на непересекаю-
щиеся пары вида (2k; 2ft+l), ££N. Тогда среди трех чисел п,
п—1, п—2 два обязательно образуют пару. Начинающий должен
первым ходом фишку, стоящую на поле с тем номером, который не
попал в пару, переставить иа поле с номером 1. После этого пере¬
ставленная фишка двигаться уже ие будет. Пусть другой игрок своим
ходом переставил одну из фишек на некоторое поле т. Тогда пер¬
вый игрок должен оставшуюся фишку поставить на поле т—1 или
/71+1 в зависимости от того, какое из этих чисел образует пару
с номером т. Это всегда можно сделать, так как пары не пересе¬
каются ни друг с другом, ни с числом 1. Действуя так же и далее,
первый игрок не может проиграть. Поскольку игра обязательно за¬
кончится через конечное число ходов, то проиграет второй игрок.
26.9. Занумеруем горизонтали доски снизу вверх числами
О, 1, ..., 7 н вертикали доски слева направо теми же числами. Каж¬
дой клетке доски поставим в соответствие сумму номеров вертикали
и горизонтали, на пересечении ко¬
торых эта клетка находится. «Дель¬
фин» начинает свой путь в клет¬
ке, которой соответствует число О,
i
ц
Hi
Я
iti
ш
ш
ш
ц
iH
Я
ии
я
Hi
ш
о
ill
1
Рис. 128
Рис. 129
При каждом ходе «дельфина» число х, соответствующее клетке, на
которой он находится, либо увеличивается на 1, либо уменьшается
на 2, поэтому остаток от деления на 3 числа х изменяется в следую¬
щей последовательности: 0, 1, 2, 0, 1, 2,
354
Предположим, что

«дельфии» обошел всю доску, побывав в каждой клетке по одному
разу. Разобьем оставшиеся (после отбрасывания начальной клетки)
63 клетки на 21 тройку клеток, подряд идущих по ходу «дельфина».
Тогда в каждой тройке ровно одной клетке соответствует число,
кратное 3. Однако таких клеток (заштрихованных на рис. 128)
имеется лишь 20. Полученное противоречие доказывает, что «дель¬
фин» не может обойти всю доску.
26.10. Разобьем все клетки бесконечной доски на 3 множества,
как показано на рнс. 129 (разными цифрами обозначены клетки раз¬
ных множеств). Тогта при каждом ходе количество фишек в двух
множествах уменьшается на единицу, а в одном—увеличиваетси на
единицу. При этом четность количества фишек в каждом множестве
меняется на противоположную. Если сначала фишки занимали прямо¬
угольник (3к)Хп, то их количества в каждом множестве были равны.
Следовательно, после каждого хода четности количеств фишек в каждом
из трех множеств должны совпадать. Если бы после какого-то хода
на доске осталась одна фишка, то в двух множествах количество
фишек было бы четно, а в одном—нечетно. Поэтому такая ситуация
возникнуть не может.
26.11. Докажем, что хотя бы одна из граней данного много¬
гранника не является треугольником. Пусть, напротив, все п его гра¬
ни—треугольники. Тогда у этого многогранника Зя/2 ребер (ибо
каждое из трех ребер любой грани принадлежит одновременно двум
граням) и п вершин (ибо каждая из трех вершин любой грани при¬
надлежит одновременно трем граням). По формуле Эйлера (теорема
93) имеем п-\-п—Зп/2 — 2, т. е. п = 4, что противоречит условию за¬
дачи. Покажем, как может играть первый игрок, чтобы наверняка
выиграгь. Первым ходом он должен занять грань Л4, не являю¬
щуюся треугольником. Вторым ходом он должен занять свободную
грань Л2, прилежащую к грани Л4 и имеющую общие ребра с двумя
свободными гранями А3, Л4, также прилежащими к грани Ах (это
можно сделать, поскольку второй игрок мог занять лишь одну грань,
прилежащую к грани Л]). Наконец, третьим ходом первый игрок
может занять одну из граней А3 или Л4, не занятую вторым игро¬
ком. Итак, первый игрок выигрывает на третьем ходу.
26.12. Докажем индукцией по п£Z+, что в результате последо¬
вательного применения 2П операций S получится набор из т = 2п еди¬
ниц. Для я = 0 имеем 5(Л)=^(а,а1) = 1. Пусть утверждение уже до¬
казано для числа п—1. Докажем его для числа п. Заметим, что
в наборе
Т (Л) =S(S(Л)) =S (ata2; а3а3; ...; amax) =
= (а1°з> a2a4; ...; am_xat', amaa)
числа, стоящие на четных местах, совпадают соответственно с чис¬
лами, которые получаются из набора (а2; а4; ...; ат) под действием
12*	355

операции S. Аналогично, числа, стоящие в наборе Т (А) на нечетных
местах, образуют набор
^ (°ii °з'. ■ • ■!
По предположению индукции, после т/2 = 2"-1 операций Т как на
четных, гак и на нечетных местах будут стоять одни единицы. Сле¬
довательно, после m операций S весь набор будет состоять из
единиц.
26.13.	Заметим, что прямоугольник 3x2 можно покрыть три-
мино (рис. 130). Поэтому, если выкинутая клетка не лежит в фи¬
гуре, являющейся объединением полос шириной в шесть клеток, при¬
легающих к двум смежным сторонам квадрата, то мы можем покрыть
Рис. 130	Рис.	131
эту фигуру прямоугольниками 3x2 (рис. 131) и перейти к оставше¬
муся квадрату 2 (п—3)х2 (л—3) с выкинутой клеткой. Так как та¬
кую операцию всегда можно проделать при 7, то без ограниче¬
ния общности можно считать, что л «С 5. Рассмотрим все возмож¬
ные случаи.
1) л= 1. Квадрат 2x2 без одной клетки покрывается одним
тримино (см. определение тримино).
2) п — 2. Выкинутая кле-тка лежит в одном из четырех квадра¬
тов 2x2, три оставшиеся клетки которого покрываются одним три¬
мино (рис. 132).
3) л = 4. Воспользуемся тем, что, как было показано в случае 2),
квадрат 4x4 с любой выкинутой клеткой можно покрыть тримино
(рис. 133).
356

4)	я»=5. Квадрат 10x10 с выкинутой клеткой всегда можно раз¬
бить на два прямоугольника ЗхЮ и один прямоугольник 4x10 так,
чтобы выкинутая клетка лежала в прямоугольнике 4X10. Прямоуголь¬
ник ЗхЮ покрыть тримино можно. Прямоугольник 4хЮ можно
Рис. 132	Рис. 133
разбить иа два прямоугольника 3x4.и один квадрат 4x4 так, чтобы
выкинутая клетка лежала в квадрате 4x4. И прямоугольник 3x4,
и квадрат 4x4 с выкинутой клеткой можно покрыть тримино.
26.14. а) Рассмотрим всевозможные пары одноцветных клеток,
расположенных в одном столбце (считаем, что столбцы имеют высоту 4,
а строки—длину 7). В каждом
столбце имеется не менее двух таких
пар, а значит, всего на доске их по
крайней мере 14. Следовательно,
существует такой цвет, который
имеют не менее 7 из рассматривае¬
мых пар. Так как количество вари¬
антов расположения пары клеток
в столбце равно 6, то существуют
два столбца с одноцветными оди¬
наково расположенными парами,
что и требовалось доказать.
б)	См. рис. 134.
26.15. Естественным образом разобьем все точки из М на 12 строк
(по первой координате) и на 12 столбцов (по второй координате).
Существует цвет, в который окрашено не менее 144/3 = 48 точек.
Выберем из них ровно 48 точек. Число выбранных точек в столбце
со второй координатой, равной 1, 2, ..., 12, обозначим через Оь
о2 а12 соответственно (а1 + а2+ ... + ai2 = 48). Тогда количество
пар выбранных точек в i-м столбце равно «/(а,-—1)/2, а общее коли-
357

чество пар точек, у которых вторые координаты совпадают, равно
, a{(ai—1) , а2(а2—1) ,	■ Oia (<112^— 1)
2 г 2	"Г-'-'Г	2
=—(aJ-|-...-|-aJ2)—g- (flj+...-fcla).
Пользуясь теоремой о средних (теорема 6), получаем оценку
„ ^	1	(Oi	+	.. • + O12)2	1	ч^ ля то
Л^Т 12	"2"	(а1	+ • ■ • +fli*)	~2 ' 12 _Т 7 •
Каждой паре выбранных точек, лежащих в одном столбце, соответст¬
вует пара строк, в которых эти точки находятся. Поскольку количест¬
во различных пар строк, равное С*2 = 66, меньше числа А, то найдутся
две пары выбранных точек, которым соответствует одна и та же
пара строк. Найденные 4 точки являются вершинами искомого пря¬
моугольника.
26.16.	а) Если (*,; yi), (х2; у2), (х3; у8) — координаты вершин тре¬
угольника, то точка пересечения его медиан имеет координаты
(Xi -\-х2-'г х3 „ Kiljfa+j/aX
V 3	з	)	•
Назовем точку (х; у) точкой типа (гг; г2), если г*, г2 — остатки от
деления на 3 чисел х, у соответственно. Восемь точек, удовлетворя¬
ющих условию задачи, существуют. Достаточно взять эти точки такими:
две точки типа (0; 0), две—типа (0; 1), две—типа (1; 0) и две —
типа (Г, 1). Кроме того, никакие три из них не должны лежать на
одной прямой. Этим условиям удовлетворяют, например, следующие
точки: (0; 0), (0; 3), (3; 1), (3; 4), (1; 0), (4; 3), (1; 1), (7; 4). Пред¬
положим теперь, что существуют 9 точек, удовлетворяющих условию
задачи. Разобьем эти 9 точек на группы одного типа. Тогда ни в одной
из групп не содержатся 3 точки (иначе они образовали бы треугольник,
в котором медианы пересекаются в целой точке). Поэтому всего групп
имеется не менее пяти, а значит, среди наших 9 точек найдется 5
точек разного типа. Разобьем эти 5 точек на 3 группы в зависимости
от остатка от деления на 3 первой координаты. Ни в одной из этих
групп не содержатся 3 точки (действительно, если бы такие 3 точки
существовали, то они имели бы соответственно тип (г; 0), (г; 1), (г; 2)
для некоторого г, а значит, образовали бы треугольник с целой
точкой пересечения медиан). Следовательно, в двух из этих групп
находятся по две точки, а в третьей группе—одна точка. Без огра¬
ничения общности можно считать, что эта одна точка имеет тип
(0; 0). Тогда среди наших 5 точек нет точек типа (0; 1) и (0; 2). Кроме
того, среди них одновременно не может быть двух точек типа (1; 1) и
(2; 2) (иначе они вместе с точкой типа (0; 0) образовали бы тре¬
угольник, в котором медианы пересекаются в целой точке). По той
же причине среди них не может быть одновременно двух точек типа
358

(1; 2) и (2; 1), а также двух точек типа (1; 0) и (2; 0). Отсюда получа¬
ем, что всего у иас не более четырех выбранных точек. Противоречие.
б)	Каждой целочисленной точке (х; у\ г) поставим в соответст¬
вие числа g (х), g (у), g (г) — остатки от деления на 3 чисел х, у, г
соответственно. Так как величина g (х) принимает не более 3 значе¬
ний, то по крайней мере 13 из рассматриваемых 37 точек имеют оди¬
наковые значения g (х) (иначе всего точек ие больше 12-3 = 36).
Аналогично, не менее 5 из этих 13 точек имеют одинаковые значе¬
ния g (у). Точка пересечения медиан треугольника с вершинами
{хйУй zj, (х2; i/г; za), (х3; у3\ z3) имеет координаты
При этом, если g (xi) = g (x2);=g (х3) и g (yi) -^g (у2) = g (Уз), то
числа Xg и ;/о целые, а число z„ является целым тогда н только
тогда, когда- Z!+z2+Z3 = 0 (mod 3). В нашем случае отобраны 5
точек, для которых равны все числа g (х) и равны все числа g(y).
Если среди этих точек найдутся три, для которых числа g (г) при¬
нимают значения 0, 1, 2, то для этих точек
Если же таких точек нет, то числа g (г) для отобранных 5 точек
принимают не более 2 значений, поэтому найдутся 3 точки, в кото¬
рых величина g (г) принимает одно и то же значение, и соответству¬
ющее им число г0 является целым.
26.17.	Пусть каждая ладья на доске находится под ударом не
более одной из остальных. Тогда можно выделить несколько пар
ладей так, что ладьи в каждой паре бьют друг друга и не бьют нн
одной из остальных, а все ладьи, не объединенные в пары, вообще
а
Zi + z2-|-Z3 = g (Zi)-j-g (z2)-j-g (z3) ==■ 0-|-1 -j-2 = 0 (mod 3).
■
Puc. 135
359

ничего не бьют. Пусть количество указанных пар ладей равно А,
а количество одиночных ладей равно В. Общее количество горизон¬
талей и вертикалей на доске ЗпхЗп равно 6п. Из иих каждая пара
ладей, бьющих друг друга, занимает три линии (две горизонтали и
вертикаль или две вертикали и горизонталь), на которых уже не
могут стоять никакие другие ладьи, а каждая одиночная ладья зани¬
мает две линии (вертикаль и горизонталь), отсюда ЗА+2В<;6п.
Поэтому для количества ладей справедлива оценка:
2А + В< (2/3) (ЗА + 2 В) ^ (2/3) ■ 6п = 4п.
С другой стороны, Ап ладей на доске расставить можно, например,
так, как показано иа рис. 135 (закрашены в черный цвет те клетки,
в которых должны стоять ладьи). Таким образом, наибольшее коли¬
чество ладей равно 4п.
26.18. Заметим, что на доске размером тХт можно расставить т
не бьющих друг друга ладей ровно т! способами, поскольку на первой
горизонтали ладью можно расположить т способами, затем на второй—
(m—1) способами и т.д., наконец, на последней — единственным
способом. Пусть утверждение задачи неверно. Тогда, если доска рас¬
крашена, как указано в условии задачи, то для любой расстановки
не бьющих друг друга ладей какие-то две из иих стоят на клетках
одного цвета. Следовательно, число п! всех таких расстановок не
превосходит (п2/2) (п — 2) !, поскольку пару ладей можно расставить
на клетках одного цвета не более чем п2/2 способами, а затем осталь¬
ные п — 2 ладьи — (п—2)1 способами. Итак, имеем оценку п!
*S(n2/2) (я—2) I, откуда п—1 «Sn/2, т. е. л С 2, что противоречит
условию.
26.19. Предположим, что утверждение задачи неверно. Тогда для
любого значения с = 1, 2, ..., п найдется пара строк, в которых
различны только i-e элементы. Зафиксируем для каждого I по одной
такой паре и построим следующий граф: каждую строку таблицы
назовем вершиной графа, а пары вершин, соответствующие зафикси¬
рованным парам строк, назовем ребрами. Так как у полученного
графа п вершин и п ребер, то, согласно теореме 94, в нем найдется
цикл, проходящий через некоторые вершины (строки таблицы) а2,
а2, ..., ак, а,. Тогда строки аг и а2 отличаются только в i-м месте
(для некоторого i), в то время как строки о2 и ая, а3 и о4, ..., ак
и й] в i-м месте совпадают. Таким образом, i-e элементы строк а2
и а2 одновременно и различаются, и совпадают. Противоречие.
26.20. Докажем прежде всего, что раскраска точек множества Е
удовлетворяет условию задачи тогда и только тогда, когда любой
прямоугольник с вершинами из £ и сторонами, параллельными осям,
имеет четное число красных вершин. Предположим, что число красных
вершин некоторого прямоугольника П0 нечетно и равно, скажем, 1
(случай, когда их 3, рассматривается аналогично). Рассмотрим два
360

разных параллелепипеда с одной гранью П0 и с противоположными
гранями Пх и П2 соответственно. Тогда, если раскраска удовлетво¬
ряет условию задачи, то каждая из граней Пх и П2 имеет по 3
красных вершины, а параллелепипед с гранями Пх, П2 имеет 6 крас¬
ных вершин, что противоречит предположению. Пусть теперь любой
прямоугольник имеет четное число красных вершин. Рассмотрим про¬
извольный параллелепипед. Если все его вершины одноцветны, то
число красных вершин делится на 4. Если же не все вершины одно¬
цветны, то существует ребро с неодноцветными вершинами и все
параллельные ему ребра также имеют неодноцветные вершины (ибо
каждая грань имеет четное число красных вершин), а число красных
вершин параллелепипеда равно 4. Утверждение доказано. Пусть зада¬
ны цвета (1+3-1982) точек (0; 0; 0), (х; 0; 0), (0; у, 0), (0; 0; г), где
х, у, г пробегают все целые числа от 1 до 1982. Докажем, что су¬
ществует единственная раскраска остальных точек из Е, удовлетво¬
ряющая условию задачи. Для доказательства рассмотрим функцию
,	_	J	0, если точка (х; у, г) красная,
г' I 1, если точка (х; у; г) синяя;
по значению / (х, у, г) однозначно восстанавливается цвет точки
(х; у; г). Зададим операцию аф/> (сложение по модулю 2) следую¬
щим образом:
^,	(0, если число а-\-Ь четно,
a b = <	.	.
j 1, если число а-\-о нечетно.
Теперь положим
/(х, у, г) = / (х, 0, 0)®/(0, у, 0) ф / (0, 0, г),
Проверка показывает, что для ранее заданных точек эта формула
также справедлива и любой прямоугольник с ребрами, параллельными
осям, имеет четное число красных вершин (например,
}(Хи Уъ 2)®/(х2, Уй 2)ф/(хъ у2, 2) ф f (Х2, у2, 2) = 0),
т. е., согласно доказанному выше утверждению, полученная раскраска
удовлетворяет условию задачи. В силу того же утверждения эта
раскраска единственна, так как для нее необходимо выполнение сле¬
дующих условий:
fix, у,	0) = f (0,	0,	0)0/ (х,	0,	0)ф/(0,	у,	0),
fix, 0,	г) = /(0,	0,	0) ф / (х,	0,	0)ф/(0,	0,	г),
fi0. У,	г) — / (0,	0,	0)ф/(0,	у,	0)ф/(0,	0,	г),
fix, у, г) = / (0, 0,	г) ф / (х, 0, г)ф/(0,	у,	г) =
= / (0, о, г)ф(/(0, 0, 0) ф / (х, 0, 0)ф/(0, 0, 2))ф
ф(/(0, 0, 0)ф/(0, У, 0)ф/(0, 0, г)) =
= /(*, 0, 0)ф/(0, р,0)ф/(0, 0, г).
Таким образом, число искомых раскрасок равно
21 +3-1Э82 =_259'17
361

§ 27. Элементы теории вероятностей
27.1. Пусть общее количество шаров в первой и второй урнах
равно тг и т% соответственно (для определенности считаем т, < т2),
а количество белых шаров в этих урнах равно ki и й2 соответствен¬
но. Тогда вероятность того, что оба вынутых шара белые, равна
(ki!m\)'(k%ltnt). Получаем соотношения:
-^-•■^-=0,54=^, т! + т2=25.
тг tn%	ou
Так как 27тгт2 = 50й1й2, то хотя бы одно из чисел тг, т2 делится
на 5. Но сумма mr + m2 тоже делится на 5, поэтому каждое из чисел
тг, т2 делится на 5. Таким образом, имеем всего две возможности:
либо mi = 5, ma = 20, либо mt = 10, т2=15. В случае mi = 5, т2 = 20
получаем
fcx*2 = 54, где 0 < < 5, 0 < кг < 20.
Перебрав все возможные значения ki, найдем *i = 3, к2= 18. Тогда в
первой урне 2 черных шара, во второй тоже 2 черных шара, и вероят¬
ность вытащить два черных шара равна (2/5) • (2/20) =0,04. Аналогично,
в случае /лг = 10, т2=15 находим ki = 9, k3 = 9. Тогда в первой
урне 1 черный шар, во второй—6 черных шаров, и вероятность
вытащить два черных шара снова равна (1/Ю)-(6/15) = 0,04 (в обоих
случаях ответы одинаковы).
27.2. Обозначим через б вероятность того, что случайно выбран¬
ный учащийся даст правильный ответ. Вероятность совпадения отве¬
та случайно выбранного учащегося с ответом учителя равна сумме
вероятности аб правильного ответа обоих и вероятности (1—а)(1—б)
неправильного ответа обоих. Поэтому условие задачи можно записать
в виде
а6+(1—а) (I—6) = 1/2, или (ct—1/2) (6— 1/2) = 0.
Если а =1/2, то это условие выполнено и отношение числа мальчи¬
ков к числу девочек в классе может быть любым. Предположим
теперь, что а Ф 1/2. Тогда 6=1/2. Обозначим через х w у соответст¬
венно число мальчиков и девочек в классе. Вероятность 6 правиль¬
ного ответа случайно выбранного учащегося класса равна сумме веро¬
ятности (хЦх-\-у)) Р того, что будет выбран мальчик и он даст пра¬
вильный ответ, и вероятности (у/(х-\-у)) у того, что будет выбрана
девочка и она даст правильный ответ. Таким образом, условие зада¬
чи имеет вид
-Г=^	или (p-_l^=^_Y^.
Поэтому, если р = у=1/2, то отношение числа мальчиков к числу
девочек в классе может быть любым; если р == 1/2, но у ф 1/2, то
362	’

класс состоит только из одних мальчиков; если же Р Ф 1/2, то отно¬
шение числа мальчиков к числу девочек в классе равно (1—2у)/(2р—1)
(разумеется, при условии, что указанная дробь неотрицательна).
27.3. Разобьем все возможные пары троек вершин на С® групп,
собирая в одной группе те и только те пары троек, которые образуют
одинаковые шестерки вершин. С одной стороны, каждая такая груп¬
па содержит столько элементов, сколькими способами можно разбить
шестерку фиксированных вершин на две тройки, т. е. С« = 20 элемен¬
тов. С другой стороны, существует ровно 6 способов разбить шестерку
на две тройки, удовлетворяющие требуемому в задаче условию. По¬
этому искомая вероятность равна 6/20 = 0,3.
27.4. Если из трех вершин две уже выбраны, то число способов,
которыми можно выбрать третью вершину так, чтобы полученная
тройка оказалась односторонней, зависит от углового расстояния /
между двумя первыми вершинами. (Угловым расстоянием между вер¬
шинами А и В будем называть величину 1 = АОВ-(п/п), где О—центр
2л-угольника; при этом всегда / < л, а угловое расстояние между
соседними вершинами равно 1.) Если I < п, то третью вершину можно
выбрать (/—1) + 2(л— 1) — 2п—1 — I способами; если же 1 — п, то ее
можно выбрать произвольно, т. е. 2л—2 способами. Далее, для каж¬
дого значения /=1,2 л— 1 есть ровно 2п-2 = 4п способов вы¬
брать сначала первую, а затем вторую вершину иа угловом расстоя¬
нии / от первой. Наконец, для 1—п есть только 2п таких способов.
Поэтому общее количество способов последовательного выбора трех
вершин равно
П- 1
4п«2 (2и — 1 — /) + 2 л (2л — 2) =
г = 1
= 4л (2п — 1) (n— 1)—4п (n~1)n-f4n (п- 1) = 6ns (п — 1).
Мы сосчитали количество односторонних троек при условии, что
в каждой тройке выделены первая, вторая и третья вершины. Если
же вершины не упорядочивать, то количество троек будет в 6 раз
меньше. Количество способов произвольным образом выбрать три
вершины равно
cL,=--i- • 2п • (2я — 1) • (2л — 2),
поэтому искомая вероятность равна
п3—п2	  Зп
-i-- 2л-(2л —1)-(2л—2)	2 (2л — 1)
о
27.5. Поскольку четность числа белых шаров, содержащихся в
урне, не меняется после каждой операции, то последний шар бу¬
363

дет белым тогда и только тогда, когда число л нечетно. Поэтому
искомая вероятность равна либо 1 (если л нечетно), либо 0 (если
л четно).
27.6. Пусть у игроков А и В выпадает тик «орлов» соответст¬
венно. Тогда искомая вероятность р события т > к равна .вероят¬
ности q события (п-\-1) — т>п — к, т. е. вероятности того, что у
игрока А выпадает больше «решек», чем у игрока В (так как при
каждом бросании монеты «орел» и «решка» выпадают с равной
вероятностью). С другой стороны, событие т > к имеет место тогда
и только тогда, когда п — т<п — к, т. е. когда (л + 1)—т<я —&
(поскольку п — т и п — к—целые числа). Поэтому р=1— q, откуда
имеем р = <7 = 1/2.
27.7. Найдем количество строк (i'i; ...; «„), для которых ‘ь^к—3
при k= 1, 2, ..., п. Число i„ может принимать четыре значения:
п—1, п — 2, п—3. Число i„_i может принимать пять значений:
п_ п—1, п—2, п—3, п — 4, за исключением того значения, которое
уже занято числом i„. Таким образом, число /„_] также может при¬
нимать 4 значения. Аналогично, каждое из чисел („_*	(4	может
принимать 4 значения. Числа ilt i2, is могут быть выбраны произ¬
вольным образом из трех значений, оставшихся после выбора чисел
ln i4. Таким образом, среди всех л! возможных строк имеется
ровно 4"-3-3! строк, удовлетворяющих требуемому условию. Следо¬
вательно, искомая вероятность равна 4/1_3-3!/«!.
27.8. Разобьем все варианты распределения карт на пары взаимно
«обратных» колод: если в какой-либо колоде карты расположены в
некотором порядке, то в пару к ней подберем колоду карт, идущих
в обратном порядке. Пусть теперь в какой-то колоде второй сверху
туз имеет номер к. Тогда для того, чтобы вытащить второй туз из
этой колоды, нужно снять к карт, а чтобы вытащить второй туз из
«обратной» колоды (это будет тот же самый туз), нужно снять
л-(-1—к карт. Среднее арифметическое чисел к и я + 1—к равно
(л -j- 1)/2 для любой пары взаимно «обратных» колод. Поэтому среднее
число карт, которое нужно снять до появления второго туза, также
равно (л + 1)/2.
27.9. Разобьем все строки на пары взаимно «обратных» строк:
(i4; ...; i„) и (i„; ...; it). Любые два натуральных числа т > I, не
превосходящие л, образуют инверсию ровно в одной из строк каждой
такой пары. Следовательно, в каждой такой паре строк имеется ровно
л (л—1)/2 инверсий (столько, сколько существует способов выбрать
в строке указанные числа т, I). Поэтому среднее число инверсий для
каждой пары строк равно л (л—1)/4. Тому же значению равно и
среднее число инверсий по всем строкам.
27.10. За первой буквой О (с момента начала наблюдения за
мальчиком с вероятностью 1 буква О хотя бы один раз появится)
с одинаковой вероятностью, равной 1/4, может следовать одна из
364

комбинаций:
РО, ОО, РР, ОР.
В первом случае выигрывает игрок В, во втором случае выигрывает
игрок А, в если реализовался третий случай, то после этого игроки
будут иметь такие же шансы, как и в начале игры. В четвертом
случае с вероятностью 1/2 последует буква О и выиграет игрок В,
а с вероятностью 1/2 последует буква Р, после чего игроки будут
иметь такие же шансы, как и в начале игры. Таким образом, с вероят-
■ .	.	1.113
ностью 1/4 выиграет А, с вероятностью ——— - —=— выиграет В
и с вероятностью 3/8 возникнет ситуация, когда игроки будут иметь
такие же шансы, как в начале игры. Поэтому игрок В имеет больше
шансов выиграть, чем игрок А.
27.11. Рассмотрим три события, которые могут наступить после
первого выстрела стрелка А.
1) Поражен С. Тогда с вероятностью 1 стрелок А будет поражен
первым же выстрелом В.
2) Поражен В. Тогда: или с вероятностью 0,5 стрелок С поразит
А своим первым выстрелом, или с вероятностью 0,5.0,3 стрелок А
поразит С своим вторым выстрелом, или с вероятностью 0,5.0,7-0,5
стрелок С поразит А своим вторым выстрелом, или с вероятностью
0,5-0,7-0,5-0,3 стрелок А поразит С своим третьим выстрелом и т.д.
Следовательно, вероятность для А выиграть дуэль в этом случае
равна
0,5.0,3+0,5-0,7-0,5-0,3 + 0.5-0,7-0,5.0,7-0,5-0,3+...=
-0.16 (1+0,35 +0.36-+.. ,)_0.15	.
3) Никто не поражен. После этого В будет стрелять в С (как
в более меткого из своих противников) и поразит его. Затем А с ве¬
роятностью 0,3 поразит В, выиграв дуэль.
Таким образом, самой выгодной для стрелка А является ситуа¬
ция, когда после его выстрела никто не поражен. Значит, он должен
первый раз стрелять в воздух.
27.12. Заметим, что из любой вершины куба с вероятностью не
меньшей чем 1/9 точка попадет в одну из вершин В', С' (ибо для
любой вершины куба, отличной от В' и С', существует маршрут,
проходящий не более чем по двум ребрам и соединяющий ее с В'
или С'). Поэтому вероятность того, что за два хода точка не попа¬
дет ни в В', ни в С', не больше чем 1 — 1 /9 = 8/9, а вероятность
того, что за 2k ходов точка не попадет ни в В', ни в С', не больше
чем (8/9)А. Следовательно, вероятность того, что точка-никогда не
попадет ни в В', ни в С', не превосходит (8/9)* для любого ££N,
а значит, равна 0. Итак, точка с вероятностью 1 попадет в В' или
365

С\ Далее, через р обозначим вероятность того, что из А точка по¬
падет в В' (и, следовательно, с вероятностью 1—р точка попадет
из А в С'), а через q—вероятность того, что из В точка попадет
в В' (и, следовательно, с вероятностью 1— q точка попадет из
В в С')- Из соображений симметрии вытекает, что вероятность того,
что точка попадет из D в В', равна (1—р), из А' в В'— q, а из С
или из D' в В'— (1—q). Если точка находится в А, то с вероят¬
ностью 1/3 она попадет в А', с вероятностью 1/3 она попадет в D и
с вероятностью 1/3 оиа попадет в В. Поэтому вероятность р того,
что точка попадет из А в В', равна
1 „ ч .	1	,	1
у (>-/»)+з-«+з-Ч.
т. е. 4р—2q=\. Аналогично, вероятность q попадания точки из В
в В' равна	(1 —	т‘	е-	4<?—р = 2. Таким образом,
р — 4/7, и искомая вероятность того, что точка остановится в вер¬
шине В', равна 4/7, а в вершине С'—3/7.
27.13.	Назовем особой такую шоколадку, на которой изображен *
портрет, ранее не встречавшийся. Пусть среди купленных шоколадок
имеется ровно k различных. Обозначим через Мк среднее количество
шоколадок, которое надо купить после этого, чтобы последняя из них
оказалась 'особой. Тогда с вероятностью (л— k)/n очередная шоко¬
ладка будет особой, а с вероятностью k/n будет куплена неособая
шоколадка, после чего среднее количество шоколадок, которые по¬
следуют до особой, снова равно Мк. Согласно теореме 100 получаем
уравнение
• 1 + у(1 + Мд).
откуда Mfc = n/(n—k). Тогда в силу теоремы 99 среднее число шоко¬
ладок, которые надо купить, равно
L «.-S гЬ-=»('+т+-+^п+т)-
А = 0	к=0	4	'

ПРИЛОЖЕНИЯ
Приложение А
КОММЕНТАРИИ К УСЛОВИЯМ ЗАДАЧ
1.3. В- задаче олимпиады ЧССР предполагалось, что в первой
строке стоят 3 нечетных числа, и требовалось доказать, что в каж¬
дой строке, начиная со второй, есть четное число.
1.6. В условии явно указывалась требуемая тройка чисел.
1.6. Требовалось указать 5 чисел п, обладающих указанным
в задаче свойством.
2.2. Задача формулировалась в геометрических терминах. Так,
первая часть выглядела следующим образом: доказать, что на кри¬
вой (х+о#+с) (x+ftp+d) = 2 существует не более четырех различ¬
ных точек с целыми координатами.
2.7. Требовалось найти все решения в неотрицательных целых
числах. При этом решения, отличающиеся перестановкой чисел хх,
х2, .... х14, считались одинаковыми.
2.9.	Требовалось найти какие-нибудь рациональные числа X и
К, удовлетворяющие равенству У~2 У 3 —3 = Х1/4 —К1/4. Заметим,
что решение задачи, приведенной в книге, позволяет дать ответ на
этот вопрос, так как Ух УЗ = Х1/4, УуУЗ = К1/4 при X = Зх2,
Y--3y\
2.16.	Задача формулировалась в геометрических терминах. Зна¬
чение о., определялось как число различных прямоугольных тре¬
угольников с целочисленными сторонами и наименьшим катетом,
равным п. В п. а) требоваЛЬсь найти формулу для о„. Пункты б) и в)
по существу соответствовали приведенным в книге пп. а) и б).
2.27. В задаче олимпиады НРБ требовалось доказать утвержде¬
ние «только тогда».
3.14. Требовалось доказать, что последовательность цифр hi,
h2, ... непериодична.
4.21. б) Это утверждение, усиливающее п. а), доказано участни¬
ком международной олимпиады 1985 г. J1. А. Ивановым.
5.14. Задача формулировалась следующим образом. Пусть К —
круг с центром в начале координат. Доказать, что для любого век¬
тора а существует натуральное число п такое, что образ круга К при
переносе на вектор пи содержит точку с целыми координатами. По
существу эта (формулировка равносильна приведенной в книге.
7.3. Числа предполагались положительными.
7.5.	Требовалось доказать утверждение задачи и в случае
О < с < 1, 0 < b < 1, 0<с< 1.
7.13.	Предполагалось, что 0<х<1,0<а<оо, и требовалось
Доказать нестрогое неравенство.
367

7.14.	На а налагалось дополнительное несущественное условие
а^О.
7.17. Требовалось доказать утверждение для произвольных комп¬
лексных чисел Дь ..., д„.
9.9.	Требовалось найти условия, которые надо наложить иа
стороны треугольника и при которых центр тяжести треугольника
совпадает с центром тяжести его границы.
ТО. 18. На олимпиаде ГДР предлагался только п. а) задачи со
следующей формулировкой. Пусть К и К'—две различные окружно¬
сти, проходящие через вершины А и В треугольника А ВС, центры
М и М' которых лежат на окружности, описанной около треуголь¬
ника ABC. Доказать, что центр окружности, вписанной в треуголь¬
ник ABC, лежит на К или на К'.
11.13. Задача была предложена Бельгией со следующей форму¬
лировкой. На сторойах треугольника KLM построены подобные рав¬
нобедренные треугольники KPL (КР PL), LQM (LQ = QM) и KRM
(KR = RM), причем треугольники KPL и RLM лежат по разные сто¬
роны от прямой KL, треугольники LQM и K.LM — по разные стороны
от прямой LM, а треугольник KRM лежит поту же сторону от прямой
КМ, что и треугольник KLM. Доказать, что LPRQ — параллело¬
грамм. Условие равнобедренности треугольников KPL, LQM и KRM
здесь на самом деле излишне.
12.1. Данные в условии задачи 15 точек определялись как центры
соответствующим образом расположенных биллиардных шаров.
12.5. Носит название задачи Сильвестра. На олимпиаде предла¬
галась для значений я <8 и допускала решения, использующие тог
или иной перебор различных случаев расположения малого числа
точек.
12.7. Соответствующее утверждение не формулировалось, а за¬
давался вопрос: что можно сказать о множестве центров симметрии
при условии, что оно содержит более одной точки? Кроме этого,
требовалось привести пример множества, имеющего более одного
центра симметрии.
12.8. Требовалось также найти L в случаях, когда М — квадрат
или правильный треугольник.
12.17. Требовалось доказать, что длина ломаной не меньше 1248.
13.12.	Пункты 6) и 7) предложены в 1977 г., пп. 1) — 5) — в
1978 г. (с исправлениями — в 1979 г.).
14.7. Требовалось определить вид треугольника.
14.8. Условие задачи предполагало, что на каждой стороне боль¬
шего многоугольника лежит вершина меньшего. При этом не требо¬
валось, что я > 3.
15.5. Был дан правильный тетраэдр с ребром а.
15.19.	Предполагалось, что линия пересечения плоскостей а и Р
пересекается с прямой CD.
16.8. На R и г налагалось условие R > 2г.
16.14. Предлагалось решить задачу для треугольной пира¬
миды.
18.3.	В задаче олимпиады ЧССР требовалось найти только ми¬
нимум функции /.
19.1. Задача состояла из двух пунктов. Условие п. б) отличалось
от приведенного в книге тем, что в нем вместо соотношения f’ (х2) =
= 0 предполагалось, что функция f имеет экстремум в точке х2, а
также предполагалось, что х2 < xj. Пункт а) являлся частным слу¬
чаем п. б), соответствовавшим значениям х2=1, х, = у^2.
19.5. Задача формулировалась для многочленов.
368

19.9.	Требовалось найти соответствующие числа а, Ь из отрезка
Id 1]-
20.8.	На функции g и h накладывались излишние ограничения.
Требовалось, чтобы обе они не принимали никакого значения более
чем в одной точке п £ N и чтобы множество их значений совпадало
с N.
20.20.	Требовалось доказать также, что
оо
У, /(0 = Г"-1 /п . если f (1) < 1.
Кроме того, задача содержала второй пункт, в котором требовалось
решить функциональное уравнение
f (х) f(y)^t (x-У), х, у£ R.
Эта часть задачи приведена в книге [3].
21.4.	На числа а и Р накладывалось несущественное условие
а Ф Р-
22.2. В задаче требовалось найти частное R (х) от деления Р (х)
на Q (х) и решить пп. б) и в):
б) Пусть через Е (/) обозначено выражение, которое получается
из R (х) заменой хй на со ski (й=1, 2 п — 2). Решить уравнение
Е (0=0.
в) Определить сумму квадратов коэффициентов многочлена R (х).
23.19.	Требовалось доказать оценку
|Р(х)|<(2П+1)С«„.
Приведенное в книге утверждение является более сильным, так как
^2п =	„	_|_	j • • -2и	k*' п П^И ^ =	*	п
С2«=С1Г* < С2п ПР« *=«+ 1	2п-
а значит,
(2n +1) С", >	+... + С^ + ... + С*}-1+С% = 2*»
(см. теорему 17).
27.3. Предполагалось, что шесть точек распределены на окруж¬
ности равномерно и независимо. Условие такой задачи требовало бы
от читателя существенно большей теоретико-вероятностной подго¬
товки, чем решение задач, приведенных в настоящей книге.
Приложение Б
МАТЕМАТИЧЕСКИЕ СОРЕВНОВАНИЯ В РАЗНЫХ СТРАНАХ
I
МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ ШКОЛЬНИКОВ
В ЗАРУБЕЖНЫХ СОЦИАЛИСТИЧЕСКИХ СТРАНАХ
Венгрия (ВНР)
История математических олимпиад Венгрии берет свое начало
еще в прошлом веке, когда в 1894 г. Венгерское физико-математи¬
ческое общество приняло решение о проведении математических
369

олимпиад для выпускников гимназий. Эти олимпиады, получившие
название соревнований Этвеша по имени президента общества физики
Лоренца Этвеша, проводились ежегодно (с трехлетним перерывом)
до 1943 г. С 1947 г. по инициативе венгерского Математического
общества олимпиады возобновились. В 1949 г. им было присвоено
имя профессора Будапештского университета Йожефа Кюршака.
Олимпиады имени Кюршака проходят в Венгрии ежегодно по на¬
стоящее время. Участникам соревнований Кюршака предлагаются
три задачи, на решение которых отводится 4 часа. В настоящее
время к участию в олимпиадах имени Кюршака допускаются не
только выпускники средних школ, но и учащиеся младших классов.
Кроме соревнований Кюршака, в Венгрии ежегодно проводятся еще
3 олимпиады по математике, из которых можно выделить так назы¬
ваемые национальные соревнования имени Д. Араньи—основателя
математического журнала «Kozepiskolai Matematikai Lapok» для
средних школ, издается с 1894 г. Эти соревнования впервые были
организованы в 1923 г. В настоящее время они проходят в 2 тура
для 9—10 классов и в 4 тура для 7—8 классов. К участию в по¬
следнем туре для 7 класса допускаются шестиклассники.
Задачи всех венгерских математических олимпиад регулярно
публикуются в журнале «Kozepiskolai Matematikai Lapok».
Румыния (СРР)
Первый математический конкурс для учащихся последиих
классов лицеев в Румынии был организован в 1889 г. С 1902 г.
такие конкурсы проводились регулярно журналом «Gazeta Matema-
Бсй», Ser. А, рассчитанным на учителей математики средних школ
(издается с 1895 г.). Форма проведения конкурсов с течением вре¬
мени менялась. До 1948 г. они, как правило, проходили в 2 тура.
С 1950 г. начался второй период проведения математических олим¬
пиад Румынии. С 1961 г. математическими олимпиадами руководит
Министерство просвещения Румынии. В настоящее время олимпиады
проходят в 3 тура. В них участвуют лишь учащиеся 11 класса
средней школы. Задачи олимпиад регулярно публикуются в журнале
«Gazeta Matematiclb.
Польша (ПНР)
Математические олимпиады в Польше проводятся ежегодно
с 1949 г. Польским математическим обществом. Олимпиады проходят
в 3 тура. Первый тур продолжается 3 месяца и носит.заочный ха¬
рактер: в начале каждого месяца участники получают по 4 задачи,
которые они должны решить дома в течение месяца. Второй тур
(уже очный) проводится в течение 2 дней. В каждый из этих дней
участникам дается по 3 задачи на 5 часов. Третий тур, который
проводится в Варшаве, организуется так же, как второй. Таким
образом, во время первого тура участникам предлагается 12 задач
на 3 месяца, а во время второго и третьего туров —по 6 задач
на 10 часов. Задачи и решения польских математических
олимпиад публикуются в журнале «Matematyka», который издает¬
ся с 1948 г.
370

Задачи 3 тура олимпиады ПНР 1986 г.
(2 день)
1. Найти все значения n€N, для каждого из которых сущест¬
вует многочлен степени я с действительными коэффициентами, удов¬
летворяющий неравенству F(x)Szf'(x) прн *£R.
2. В шахматном турнире участвуют 2я (л > I) игроков, причем
любые два из них играют между собой ие более одной партии. До¬
казать, что прн этих условиях турнир, в котором ни одна тройка
игроков не сыграла между собой три партии, возможен в том и
только в том случае, если число всех партий, сыгранных в турнире,
не превосходит я2.
3. Доказать, что если АК, BL, СМ — высоты треугольника ABC,
а точка N—середина стороны ВС, то четыре точки К, L, М, N ле¬
жат на одной окружности.
Болгари я (НРБ)
Математические олимпиады в Болгарии проводятся ежегодно,
начиная с 1950 г. В настоящее время олимпиада проводится в 3 тура
для учащихся 8—II классов общеобразовательных школ и 3—5 кур¬
сов техникумов и в 2 тура для учащихся 5—7 классов школ и I—2
курсов техникумов. Для отбора членов команды на международную
математическую олимпиаду для учащихся 11 класса школы и послед¬
него курса техникумов организуется дополнительный тур. Большую
роль в проведении школьных олимпиад в Болгарии играют журналы
«Обучението по математика» (основан в 1958 г.) н «Математика»
(основан в 1962 г.).
Задачи олимпиады НРБ 1986 г.
1. Найти наименьшее значение я £ N, для которого число
и*—п + П разлагается в произведение четырех простых чисел (не
обязательно различных).
2. Доказать, что если корни многочлена Р (х) второй степени
принадлежат отрезку [—1; I], причем тах|Р(х)| = 1, то справед-
UI < 1
ливо неравенство шах |P'(x)|3il.
1*1 < «
3. Найти наибольшее значение объема куба, который можно раз¬
местить в правильном тетраэдре с ребром I так, чтобы одна из диа¬
гоналей куба лежала на высоте тетраэдра.
4. Найти наименьшее значение "€N. большее 2, для которого
существует такой л-угольник с точкой А внутри него, что на каж¬
дой стороне этого я-угольника можно выбрать точку, которая не
видна из точки А. Доказать, что найденное значение л обладает
следующим свойством: внутри любого л-угольиика найдутся такие
две точки В и С, что любая точка л-угольника видна из точки В
или С.
5. Для заданных значений а > 0, ф£(0; 180°) и точки А, не
лежащей на заданной окружности, найти геометрическое место
точек М, для каждой из которых на окружности можно выбрать
точку В, удовлетворяющую условиям АМ/АВ = а, ВЛ/И = (р.
6. Доказать, что в последовательности чисел аг, а2, удов¬
летворяющей при некотором значении 6^(0; I) неравенствам
a„+i:<(1-1-6/л) ап — 1. л^й!,
существует хотя бы одно отрицательное число,
371
L

Чехословакия (ЧССР)
Математические олимпиады в Чехословакии проходят ежегодно,
начиная с 1951 г. В настоящее время участники олимпиады разби¬
ваются на 4 возрастные группы, так называемые категории А, В,
С, D (18-летние, 17-летние, 16-летние, 14—15-летиие учащиеся соот¬
ветственно). Для категории А олимпиада проходит в 3 тура, а для
остальных трех категорий — в 2 тура. Первый тур является заочным:
его участники дома решают задачи, напечатанные в периодических
изданиях. Второй и третий (для категории А) туры очные. Начиная
с 1951 г. в ЧССР выходит журнал «Matematika ve skole» для учи¬
телей математики средних школ. Кроме того, в Чехословакии изда¬
ется математический журнал для учащихся «Rozledy matematicko—
fyzikolni».
Задачи олимпиады ЧССР 1986 г.
1. Для каждого значения n£N иайти наибольшее возможное
число элементов множества А, состоящего из подмножеств множества
{1; 2; ...; я) и обладающего следующим свойством: для любых двух
множеств В£А, С £ А множество (В (J С)\(В ПО имеет четное число
элементов.
2. Доказать, что если многочлен Р (х) с целыми коэффициентами
степени я 3s 3 удовлетворяет для некоторых т ^ 3 различных чисел
Х\ х,„ £Z равенствам
Р (*i) = Р (х2) = ,..= Р (хт) = 1,
то он не имеет целых корней.
3. Доказать, что все пространст¬
во можно разбить на «кресты», со¬
стоящие из семи единичных кубиков,
расположенных, как указано на рис.
136.
4. В выпуклом ограниченном мно¬
жестве М иа плоскости выбраны три
точки Ci, С2, Са. Непересекающиеся
лучи If, la, /3 с вершинами в точках
Сг, С2, С3 соответственно разбивают
дополнение к множеству Л1 (J^lU^U
на три области D*, D2, D3. Доказать,
что если выпуклые множества А и В удовлетворяют условиям
АГ)// = 0г = ВП//, АП£>/5*0 5*ВП£>/ 0=1, 2,3),
то Af)B Ф 0.
5. Последовательность натуральных чисел аи а2, ... удовлет¬
воряет условиям Oi=l, а„+2 = 2о„+1 — о„+2 прн n£N. Доказать,
что для любого значения n£N существует такое число m£N, что
a„o„+i = Од,.
6. Для любых чисел т, я из некоторого множества McN спра¬
ведливо неравенство \т—я | ^ тп/25. Доказать, что множество М
содержит не более 9 элементов. Определить, может ли такое множе¬
ство М состоять из 9 элементов.
Китай (КНР)
Математические соревнования школьников в Китае впервые про¬
водились в 1956 г. в 4 городах: Пекине, Шанхае, Тяньцзине и
Инкоу. В следующем году они были организованы и во многих дру¬
Рис. 136
372 х

гих городах. Типичными примерами этих соревнований могут слу¬
жить шанхайские олимпиады 1956— 57 г. Они проводились по двум
возрастным группам: для предпоследнего и соответственно для вы¬
пускного классов средней школы (полный срок обучения в средней
школе в КНР—12 лет). На каждом уровне олимпиада проходила
в 3 тура. В последние годы в Китае организуются общенациональ¬
ные математические олимпиады. Содержание задач на этих олимпиа¬
дах весьма своеобразно, и оцениваются они по сложной системе
баллов. В Китае существует рассчитанный на учителей математики
и интересующихся математикой школьников журнал «SHUXUE
TONGXUN». Этот журнал проводит систематический конкурс по
решению задач.
Германская Демократическая Республика
(ГДР)
Отдельные математические соревнования школьников в пределах
одного города в ГДР проводились, начиная с 1956 г. В 1960 г. была
проведена первая олимпиада в Лейпциге, в 1961 г. - первая массо¬
вая олимпиада в Берлине. Первая математическая олимпиада
в масштабах всей страны была организована в 1962 г. С тех пор
математические олимпиады школьников в ГДР проходят в 4 тура
(школьный, районный, окружной и заключительный) для учащихся
II—12 классов, в 3 тура для учащихся 7—10 классов и в 2 тура
для учащихся 5—6 классов. На районных олимпиадах участникам
предлагаются 4 задачи, а на окружных—6 задач. Задачи математи¬
ческих олимпиад ГДР и международных математических олимпиад,
а также их решения регулярно публикуются в рассчитанном на
учащихся 11—12 классов журнале «Alpha», который издается с 1967 г.
Кроме того, журнал «Alpha» проводит конкурс по решению задач,
знакомит читателей с победителями олимпиад. В ГДР также вы¬
ходит предназначенный для учителей средних школ журнал «Mathe-
matik in der Schule».
Югославия (СФРЮ)
Математические олимпиады в Югославии в пределах одного го¬
рода, района или республики проводятся, начиная с 1950 г. С 1960 г.
проводятся Всеюгославские математические соревнования, которые
проходят в 4 тура: школьный, районный, республиканский и все-
югославскнн. Для формирования национальной команды на между¬
народную олимпиаду с 1963 г. проводится дополнительный отбороч¬
ный тур. Задачи математических олимпиад СФРЮ регулярно пуб¬
ликуются в журнале «Matematifko fizitki list», который рассчитан на
учащихся и учителей средних школ.
Задачи олимпиады СФРЮ 1986г.
(Школьникам в зависимости от класса, в котором они обучались,
предлагается один из трех наборов задач: с № 1 по № 4, с № 5 по
№ 8 или с JV« 9 по № 12.)
1. Доказать, что существует бесконечно много значений n(;N, Для
которых каждое из чисел п, п-f-l, л -| 2 представляется в виде сум¬
мы двух квадратов целых чисел.
2. Доказать, что если для выпуклого четырехугольника ABCD
справедливо неравенство АВ -\- BD < AC [-CD, то АВ*С,АС.
373

3. В треугольнике ABC углы при вершинах В и С равны по 40°.
На продолжении стороны АВ за вершину А взята точка D так, что
AD = BC. Найти углы треугольника ADC.
4. В каждой клетке доски размером 5x5 лежит по монете. Раз¬
решается несколько раз проделывать следующую операцию: выбирать
любые две монеты и каждую из них передвигать в любую из сосед¬
них клеток (имеющих с исходной общую сторону). Можно ли в итоге
добиться того, чтобы все 25 монет лежали в одной наперед заданной
клетке?
5. Доказать, что если числа m,n£N удовлетворяют равенству
2/п2+т = Зя*+я, то числа т—я, 2т+2я+1, Зт + Зл-|-1 являются
квадратами целых чисел.
6. Доказать, что для любых чисел а, Ь,с£Н справедливо нера¬
венство
а3/{а2 + aft + 62) + fc3/(fc2 + be +с2) f с31{с2 + со+с2) С (а + 6+с)/3.
7. На окружности с диаметром AD выбрана точка В, а на диа¬
метре AD—точка С так, что AB — CD. Доказать, что в треугольнике
ABC биссектриса, медиана и высота, выходящие соответственно из
вершин А, В ч С, пересекаются в одной точке.
8. Доказать, что из любых пяти различных положительных чисел
можно выбрать два числа, нн сумма, ни разность которых не равны
ни одному из трех оставшихся чисел.
9. Найти все возрастающие функции f: R —► R, удовлетворяю¬
щие тождеству
f(x-l fm ^ !(Х+У) + 1,	х,у£ R.
10. Доказать, что если числа xit х2	хп €R удовлетворяют
равенству
(я— 1) (xi + X2-f- ... + Хп) = (xi Ц-лГгЧ- - - ■ ~\~хп)2<
то они либо все неотрицательны, либо все неположительны.
11. Из середины каждой стороны вписанного четырехугольника
опущен перпендикуляр на противоположную сторону. Доказать, что
все четыре перпендикуляра пересекаются в одной точке.
12. Найти наибольшее число я £ N, обладающее следующим свой¬
ством: для любой нумерации клеток шахматной доски числами 1,
2, ..., 64 существуют две соседние клетки (имеющие общую сторону),
разность номеров которых не меньше я.
Вьетнам (СРВ)
Первая математическая олимпиада в СРВ состоялась в 1962 г.
для учащихся 7- и 10-летних школ. С тех пор олимпиады в СРВ
организовывались ежегодно, а после объединения страны в 1975 г. они
стали проводиться иа всей территории Вьетнама. Средняя школа в
СРВ делится иа 3 ступени: 1—5 классы, 6—9 классы, 10—12 клас¬
сы. Математические олимпиады во Вьетнаме проходят в последнее
время в 4 тура: школьный, уездный, провинциальный и заключи¬
тельный. В уездном и провинциальном турах олимпиады участвуют
школьники всех классов, начиная с пятого. На заключительный
(общевьетнамский) тур приглашаются только учащиеся последнего
класса каждой ступени, т. е. 5-, 9- и 12-клчссники (на олимпиаду
для 12 класса допускаются и 11-классиики). Заключительный тур
проходит в два дня. Каждый день участникам предлагаются 3—4

задачи на 4 часа. Учащиеся 11 н 12 классов — победители заклю¬
чительного этапа олимпиады (около 20 человек) — приглашаются на
отборочные соревнования, по результатам которых формируется ко¬
манда страны на международную олимпиаду. Эти соревнования орга¬
низуются так же, как н заключительный тур олимпиады.
Монголия (МНР)
Математическая олимпиада школьников в Монголии проводится,
начиная с 1963 г., в 4 тура для учащихся 10 классов, в 3 тура для
школьников 7—9 классов и в 2 тура для учеников 1—6 классов. Из
числа 14 десятиклассников—победителей четвертого тура—формиру¬
ется команда страны на Международную олимпиаду.
Куба
Отдельные математические соревнования школьников проводились
на Кубе, начиная с 1962 г. Первая общенациональная математичес¬
кая олимпиада была организована в 1970 г. Математические олим¬
пиады в стране проводятся в 3 тура. На каждом туре участникам
предлагается за 4 часа решить: на первых двух турах по 3 задачи,
на третьем — 4 задачи.
II
МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ ШКОЛЬНИКОВ
В КАПИТАЛИСТИЧЕСКИХ И РАЗВИВАЮЩИХСЯ СТРАНАХ
США
Каждый год в США организуется очень большое число разных
по характеру и целям математических соревнований для учащихся
средних школ. В 1955 г., например, было проведено на менее 60 со¬
ревнований.
Многие из этих соревнований организуются университетами, за¬
интересованными в выявлении талантливых ребят как потенциальных
студентов. Наиболее значительные из таких состязаний — математи¬
ческие конкурсы Стэнфордского университета, которые проводятся
ежегодно начиная с 1946 г. Эти конкурсы были организованы по
инициативе профессора Стэнфордского университета Дж. Пойя. Они
очень похожи на венгерские соревнования Этвеша, в которых в свое
время добился успеха учащийся одной из средних школ Будапешта
Дьердь (Джордж) Пойя.
Другие соревнования организуются Американским математическим
обществом (The American Mathematical Society—AMS) и Математи¬
ческой Ассоциацией Америки (The Mathematical Association of Ame¬
rica—MAA).
Каждый год, начиная с 1958 г., в США проводятся организуемые
МАА и Страховой компанией США так называемые национальные
состязания, в которых участвуют также учащиеся из Канады. На
этих состязаниях школьникам отводится 80 минут на 50 задач, мно¬
гие из которых носят характер вопросов.
Нельзя не упомянуть организованное Нью-Йоркским отделением
МАА в 1950 г. состязание «Нью-Йорк метрополитен»—самое массовое
соревнование этого года, в котором приняли участие школьники не
только из штата Нью-Йорка, но и нз ряда других штатов.
375

С 1972 г. в США проводятся так называемые национальные ма¬
тематические олимпиады, организуемые AMS. К участию в олимпиаде
допускаются старшеклассники, успешно сдавшие экзамены в конце
учебного года, а также победители школьных математических олим¬
пиад. Число участников не превышает 100 человек. Каждый участник
пишет олимпиаду в своей школе. На олимпиаде даются 5 задач, на
решение которых отводится 3 часа. Проверка решений организуется
централизованно. Из числа победителей национальной математической
олимпиады формируется команда США на международную олимпиаду.
Большой популярностью в стране пользуются математические
соревнования отдельных штатов. Например, математические состязания
штата Висконсин проводятся, начиная с 1965 г. На них основное
внимание уделяется скорости решения задач.
В последнее время в США широко известны так называемые
конкурсы Двухлетнего Колледжа.
Вопросы организации математических соревнований в стране
обсуждаются на страницах журналов «The Mathematics Teacher»,
«American Mathematical Monthly», «Mathematics Magazine*.
Швеци я
С 1961 г. Шведское математическое общество и газета «Svenska
Dagbladet* ежегодно проводят математические соревнования для
учащихся старших классов шведских гимназий. Эти соревнования
проходят в 2 тура: аттестационный тур, в котором участвуют 300
гимназистов, и заключительный тур для 12—15 лучших участников.
Задачи олимпиады Швеции 1985 г. (ноябрь)
1. Доказать, что для любых значений а > b > 0 справедливы
неравенства
2. Найти наименьшее натуральное число, обладающее следующим
свойством: если первую цифру его десятичной записи переставить в
конец, то это число увеличится в 7/2 раза.
3. Точки А, В, С на окружности радиуса г и точка D внутри
ограничиваемого ею круга расположены так, что АВ — ВС, а тре¬
угольник BCD равносторонний. Луч AD пересекает окружность в
точке Е. Доказать, что DE—r.
4. Многочлен Р (*) степени п с действительными коэффициентами
удовлетворяет условию Р(х);згО при всех значениях х£ R. Доказать,
что справедливо неравенство
Р (х) + Р' (х) + Р" (*) +•.,. +• Р<л> (х) Зэ 0, х £ R •
Б. В прямоугольной системе координат иа плоскости вершины
треугольника ABC имеют соответственно координаты (а; 0), (0; Ь) и
(с; d), где а, Ь, с, d положительны. Доказать, что справедливо нера¬
венство
АВ + ВС+СА ^2-СО,
где О—начало координат.
6. В городе организовано несколько обществ, каждое из которых
объединяет не менее 3 человек. Для любой пары жителей города есть
376

ровно одно общество, в которое они оба входят. Для любых двух
обществ есть ровно один житель, который входит в каждое из иих.
По крайней мере одно общество имеет ровно 17 членов. Сколько
человек живет в городе?	^
Нидерланды
В Голландии математические олимпиады проводятся с 1962 г.
Они проходят в 2 тура. К участию в первом туре допускаются стар¬
шеклассники из нескольких привилегированных школ. Около 60 по¬
бедителей первого тура проходят на второй тур. Математические
соревнования в стране организуются также журналом «Pythagoras»,
рассчитанным на учащихся средних школ. С 1925 г. в Голландии
издается журнал «Euclid». Отдел задач по элементарной математике
и математическому анализу имеется в журнале «Nieuw tijdschrift voor
Wiskunde», основанном в 1913 г.
Италия
Итальянское математическое общество в 1962—1968 гг. прово¬
дило местные соревнования (в пределах одного города) и в 1963—
1967 гг.— национальные соревнования школьников. Характер задач,
предлагавшихся на этих соревнованиях, колебался от ограниченных
школьной программой задач на олимпиадах гор. Турина до в высшей
степени оригинальных и эксцентричных задач римских олимпиад.
Целесообразность продолжения математических соревнований в стране
обсуждается в журнале «Archimedes».
Испания
С 1964 г. в Испании регулярно проводятся школьные математи¬
ческие олимпиады в 2 тура. На каждом туре участникам в течение
2 дней предлагается по 8 задач. По сложности задачи колеблются
от простейших до довольно сложных, включающих в себя и элементы
математического анализа.
Великобритания
В начале 60-х годов примерно в 300 британских школах прово¬
дились математические тесты, задания для которых заимствовались
с национальных состязаний США, проводимых МАА. В 1965 г. была
организована первая британская математическая олимпиада, задачи
для которой составил ее инициатор профессор Лондонского универ¬
ситета У. К. Хейман вместе с М. Хейман. На решение задач учащим¬
ся было дано 3 часа. С тех пор британские математические олимпиады
проводились регулярно. Проблему математического образования в
стране освещают журналы «The Mathematical Gazette», «Mathematics
in School», «Mathematical Teacher».
Задачи британской математической
олимпиады 1986 г.
I.	Привести к несократимому виду дробь т/п, где
т=2244851485148514627,
« = 8118811881188118000.
377

2. К окружности S проведены две параллельные касательные /|
и 12. Окружность S, радиуса Гу касается окружности S и прямой 1у.
Окружность S2 радиуса г2 касается окружностей S, Sy и прямой /2.
Все окружности касаются друг друга внешним образом. Найти ра¬
диус окружности S.
3. Доказать, что если числа т, п, удовлетворяют равенству
I+/П+Л	=
то число т является квадратом целого числа.
4. Найти наибольшее значение D£R, осуществляющее оценку
Д2 + б2+с2
(а + б+с)?
для сторон а, Ь, с любого тупоугольного треугольника.
б. Найти количество перестановок (at; а2\ ап) набора
(1; 2;	я), удовлетворяющих условиям
а/ < а,-+а при I	—2,
я/ < Я/+з при I	— 3.
6. Пусть АВ, АС и AD—три ребра куба. Точка Е взята иа
луче АС так, что АЕ = 2АС, а точка F взята на луче AD так, что
AF = 3AD. Доказать, что площадь сечения куба любой плоскостью,
параллельной плоскости BCD, равна площади сечения тетраэдра АВЕР
той же плоскостью.
Канада
Учащиеся канадских школ принимают участие в национальных
состязаниях США, организуемых МАА, начиная с 1958 г. Собствен¬
ные математические олимпиады Канады проводятся с 1969 г. Олим-
пиадиые задачи публикуются в журнале «Crux Mathematicorum».
Задачи олимпиады Канады 1986 г.
1. На стороне АС треугольника ABC взята точка D так, что
CD = AB=l,	ABD = 90°, ^CfiD = 30°. Найти AD.
2. Чемпионат между тремя участниками А, В и С состоит нз п
спортивных соревнований. В каждом соревновании за первое место
начисляется mi очков, за второе— т2, а за третье—	т3, где
ту, тг, тх £ N и ту > т2 > т3. В результате чемпионата участник А
набрал 22 очка, а участники В и С—по 9 очков. Участник В вы¬
играл забег на 100 метров. Найти значение п и определить, кто был
вторым по прыжкам в высоту.
3. Хорда CD полуокружности с диаметром АВ имеет заданную
длину. Точка М является серединой хорды CD, а точка Н — основа¬
нием перпендикуляра, опущенного нз точки С на диаметр АВ. До¬
казать, что величина /_ СНМ не зависит от положения хорды CD.
4. Для чисел /п, л£ N обозначено
т
f(m,n)= 2 №п~\
ft=i
Доказать, что для любых значений т, n£N число f (тi п) делится
на число f(m, 1),
378

б.	Доказать, что если последовательность целых чисел ах, а2, .,.
удовлетворяет равенствам ах = 39, о2 = 45 и аи+2 = яД+1— ап при
n€N. то бесконечно много ее членов делятся на 1986.
Австрия
Школьные математические олимпиады проводятся в Австрии с
1970 г. Организация этих олимпиад очень своеобразна: к участию в
олимпиаде (даже в 1 туре) допускаются только школьники, посещаю¬
щие специальные подготовительные курсы. Эти курсы разбиваются
на два уровня:
1) курсы для начинающих, которые школьник имеет право по¬
сещать лишь 1 год. На них принимаются все желающие из 9—11
классов (австрийская средняя школа 12-летняя), а в порядке исклю¬
чения и отдельные школьники младших классов;
2) курсы второй ступени—для учащихся, успешно окончивших
курсы для начинающих. На курсы второй ступени зачисляются после
вступительной беседы и другие учащиеся 11—12 классов.
С 1975 г.. австрийские олимпиады проводятся в 2 тура для курсов
первой ступени и в 3 тура для курсов второй ступени. Роль первого
тура играют курсовые испытания, в которых участвуют все слушатели
подготовительных курсов. Победители курсовых соревнований допус¬
каются на второй тур олимпиады—земельные соревнования для пер¬
вой ступени и областные для второй (Австрия делится на 9 земель,
которые в свою очередь делятся на области). Победившие в област¬
ных соревнованиях слушатели курсов второй ступени (около 30 школь¬
ников) допускаются до' участия в заключительном (всеавстрийском)
туре олимпиады. Вопросы физико-математического образования в
стране обсуждаются в журнале «Mathematisch-physikalische Semester-
bcrichte».
Задачи австрийской олимпиады 1986г.
1 де и ь
1. Доказать, что для любого значения я £ N, большего 2, в пра¬
вильный я-угольник можно вписать квадрат.
2. На координатной плоскости для заданных значений k,l£ N
найти количество ромбов, вершины которых имеют координаты
удовлетворяющие неравенствам x*£,k, y^l, а диагонали
параллельны координатным осям.
3. Найти все значения Oo.OjgR, для которых последовательность
{и,,}, удовлетворяющая равенствам
д"+1=з5;_1-25; при n(EN’
содержит бесконечно много членов, являющихся целыми числами.
2 де н ь
4. Найти наибольшее значение я £ N, для которого существует
я-значное (в десятичной записи) число Oia2- •. все цифры которого
различны, и при каждом значении «=1 я число ata2-. .а,- делится
на *'!, Для найденного значения я указать все такие я-значные числа.
378

5. Доказать, что при каждом значении n£N, большем 3, сред¬
нее арифметическое длин всех сторон любого выпуклого л-угольника
•меньше среднего арифметического длин всех его диагоналей.
6. Для заданного значения	найти все функции f: N —> R,
удовлетворяющие тождеству
f (m-\-k) = f (mk—n), m,k£N,mk>n.
Федеративная Республика
Германии (ФРГ)
Математический конкурс в ФРГ был впервые организован Не¬
мецкой научной ассоциацией в 1970 г. К конкурсу допускались все
учащиеся II—13 классов. Он состоял из 3 туров. В первых 2 турах
предлагалось решить в качестве домашней работы по 4 задачи. Тре¬
тий тур носил характер коллоквиума. Вопросы математического
образозания в ФРГ широко обсуждаются в журналах «Praxis (ler
Mathematik», «Archimedes», «Mathematische und Naturwissenschaftliche
Unterrichts.
Бельгия
В начале 60-х годов в Бельгии для математических соревнований
школьников использовались задачи, предлагаемые в США на состя¬
заниях, организуемых МАА. С 1965 г. в стране для этих соревнова¬
ний используются также контрольные вопросы журнала «L’enseigne-
ments. Собственные бельгийские математические олимпиады прово¬
дятся ежегодно с 1976 г. С 1982 г. олимпиада проводится в 3 тура
(школьный тур, полуфинал, заключительный тур) отдельно для 2
возрастных групп. Организация школьного тура олимпиады весьма
своеобразна: он проходит в виде контрольной работы, где на каждую
задачу дается несколько возможных ответов, из которых нужно вы¬
брать правильный. В Бельгии выходят два рассчитанных на школь¬
ников и учителей математики журнала «Mathesiss и «Nico» (от «Ni¬
colas Bourbaki»). В стране издается также журнал по методике пре¬
подавания математики «Les mathematiques et la pedagogies.
Люксембург
В Люксембурге собственные национальные олимпиады не прово¬
дятся. С 1963 г. ежегодно около 85 учащихся 11—13 классов уча¬
ствуют в соревнованиях, на которых предлагаются задачи с нацио¬
нальных состязаний США, организуемых МАА.
Франция
Математические олимпиады учащихся во Франции не проводятся.
Однако в стране уже в течение столетия организуются заочные со¬
ревнования «Concours general», а в последние годы Франция участ¬
вует в международных математических олимпиадах. Вопросы препо¬
давания математики в стране обсуждаются в «Bulletin association des
professeurs de mathematiques de l’enseignement publics. С 1875 г.
издается ученический математический журнал «Journal de mathema¬
tiques elementaires», a с 1890 г.— учебно-методический журнал «Revue
de mathematiques specialiess. С 1887 г. выходит также журнал
«L’education mathematiques,
380

lit
Задачи соревнований «Concours gёnёгab
1986 г.
1. Дан тетраэдр ABCD.
а) Доказать, что середины ребер АВ, AC, BD и CD лежат в
одной плоскости.
б) Найти в этой плоскости точку, сумма расстояний от которой
до прямых AD и ВС минимальна.
2. На плоскости расположены точки А, В, С и М.
а) Пусть D — точка плоскости, для которой DA «£ С А и DB СВ.
Доказать, что существует точка N, удовлетворяющая неравенствам
NAezMA, NB*ZMB и ND <; МС.
б) Пусть А', В', С' — точки плоскости, для которых А'В' < АВ,
A'C'sZAC, В'С'<ВС. Существует ли точка М', удовлетворяющая
неравенствам М'А' sZMA, М'В' *zMB, M'C'sZMC?
3. а) Для любых ли чисел г,ш£С справедливо неравенство
|г|-||ш|<;|г|ш| + |г—ш|?
б)	Доказать, что для любых значений Zj, г2, г3, г4 £С справед¬
ливо неравенство
4
2izti< 2 \zi+zj\-
Задачи исследовательского характера
I. Для любой последовательности {a,,} (n£N) определим последо¬
вательности {Аая} и {А2а„} следующими формулами:
. Аа„=а„+1 — ап,
А2а„ = Аап+1 — Да„.
Кроме того, при всех значениях я £ N, для которых Ааа„ Ф 0, положим
а-п==а
“	«	Ааа„
1. Для каких последовательностей {а„} последовательность {Даа„}
постоянна?
2. Найти все последовательности {а„}, для которых числа а'п опре¬
делены при всех значениях n£N и последовательность {а«} посто¬
янна (отдельно рассмотреть случай а'п = 0).
3. Пусть последовательность {а„} сходится к числу а = 0, причем
а„ ф а при всех значениях n£N и последовательность <	11-—- >
1 ап~а J
сходится к числу А ф 1.
а) Доказать, что А£[—1; 1).
б) Доказать, что при всех значениях п £ N, начиная с некоторого
номера «о, справедливо неравенство А2а„ Ф 0.
в) Пусть А Ф 0. Для каждого значения k£Z+ исследовать по¬
следовательность •! —— > на сходимость (отдельно рассмотреть случай
,	\an+kf
k = 0).
г) Пусть А = 0. Доказать, что последовательности {aj°п I и
{on/fln+i} сходятся к нулю. Привести пример последовательности {а„},
Для которой последовательность {оя/лп+»} имеет ненулевой предел.
381

4.	Как изменятся результаты п. 3, если снять условие а=0?
II.	Функции f, g: [0; 1]—► R заданы формулами
f (*) = V1—*.	=
а через с обозначен какой-либо корень уравнения x = f(x).
1. а) Исследовать функцию f (х) и нарисовать ее график. Дока¬
зать, что уравнение x=f {х) имеет единственный корень, причем
eg[0,72; 0,73].
б) Исследовать функцию f' (х). Пусть Му и Ма—точки на графике
функции f (х). имеющие разные абсциссы. Как расположена дуга
МуМ2 этого графика относительно отрезка МуМ2?
в) Исследовать функцию g(x) и нарисовать ее график. Как рас¬
положен график этой функции относительно прямой у — х? Найти
касательные к графику в точках с абсциссами 0 и 1.
г) Доказать, что любая последовательность {с„}, удовлетворяющая
условиям flig(0; 1) и an+1 — f (ап) при ngN, сходится (рассмотреть
подпоследовательности {o2n-i}. {«*„} (я gN) и функцию g (х), приду¬
мать графическую иллюстрацию).
2. На графике функции f (х) рассматриваются точки М и М'
с абсциссами х и f (х), где х Ф с.
а) Доказать, что прямая ММ' пересекается с прямой у=х в точке
с абсциссой
h(x)-x	V (*)-*)*
g(x) + x~2f(x)
б) Доказать, что если xg(0; с), то ft (х) g (х; с).
в) Исследовать любую последовательность {а„}, удовлетворяющую
условиям (iy g(0; с) и fln+i = ft (а„) при ngN, на сходимость. Доказать,
]а„+т—с)
что последовательность < - —	> сходится и наити ее предел.
I ап Я J
3. Пусть калькулятор округляет каждое число bg[—2; 2] до
значения й, имеющего р десятичных знаков после запятой. Выполнить
на этом калькуляторе следующую последовательность операций:
1) положить о = 0,72;
2) вычислить б (a)=f (а)—а;
3) если | б (а) | > 0,5- 10-.Р, то вычислить ft (о) и перейти к опера¬
ции 2), придав числу а значение ft (а);
4) если | б (а) | <0,5- 10~р, то закончить вычисление.
Пусть с—последнее из вычисленных значений ft (о). Пользуясь
тем, что для любого значения xg[0,72; 0,73] справедлива оценка
11 (х)—f (х) | < е, определить по величине б (с), с какой точностью (за¬
висящей от е) значение с представляет число с.
4. Пусть последовательность {а„} удовлетворяет условиям at = 0,72
и an+i = /(a„) при /IgN. Найти наименьший номер n0gN, начиная
скоторого при всех значениях ngN справедливо неравенство |а„ — с| <
< ю-6.
Индия
В Индии проводятся ежегодные заочные олимпиады среди аби¬
туриентов математических отделений университетов. В ряде штатов
организуются олимпиады для учащихся старших классов школ (первая
382

такая олимпиада была проведена в 1958 г. в Бенгалии). В стране
также выходит журнал «The mathematical student», который прово¬
дит конкурс по решению задач.
Австралия
Первый математический конкурс в Австралии был проведен в
1976 г. в рамках столицы страны Канберры. Он охватил 33 школы
и 1300 учащихся. Конкурс проходил в виде письменного экзамена по
обычному школьному курсу математики. К 1978 г. этот конкурс пере¬
рос в Австралийский математический конкурс на приз Уэлса, который
проводится в масштабах всей страны. В 1981 г. состоялась первая
Австралийская математическая олимпиада.
Ар гентина
Математические олимпиады в Аргентине не проводятся, но с 1965 г.
Кордобский университет организует соревнования под названием
«Feria de ciencios» («Торжество науки»). В этот университет ежегодно
присылаются оригинальные научные работы, выполненные учащимися
школ страны. Принимаются работы как отдельных учащихся, так и
коллективные. В стране выходит журнал «Buletin matematico», осно¬
ванный в 1928 г.
III
РЕГИОНАЛЬНЫЕ МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ
Австро-польск а я олимпиада
Австро-нольские математические олимпиады проходят с 1982 г.
От каждой страны в олимпиаде принимают участие 6 школьников.
Соревнования продолжаются 3 дня. В первые 2 дня проходит личное
первенство, а в третий день — командное.
Балканская олимпиада
Первая Балканская математическая олимпиада (так называемая
Балканиада) состоялась в 1984 г. В ней приняли участие Болгария,
Греция и Румыния. Организаторами олимпиады являлись Греческое
математическое общество и Министерство спорта Греции. Команда
каждой страны состояла из 6 школьников—учащихся 10 н 11 классов.
Участникам было предложено 4 задачи.
Ill Балканская математическая олимпиада
Бухарест, 1986 г.
1. (Греция). Прямая, проходящая через центр О окружности
радиуса г, вписанной в треугольник ABC, пересекает эту окружность
в точках D и Е, а описанную около треугольника ABC окружность —
в точках f и й, причем точка D лежит между точками О и F. До¬
казать, что DF-EG^r2. Определить, когда достигается равенство.
2. (НРБ). На ребрах АВ, ВС, AC, AD, BD, CD тетраэдра ABCD
выбраны точки Е, F, G, Н, К, L соответственно. Доказать, что если
справедливы равенства
AEBE = BF-CF=AG.CG = AH-DH = BK-DK = CL.DL,
то точки Е, F, G, Н, К, L лежат на одной сфере.
S83

3.	(НРБ). Доказать, что все члены последовательности а1, о2, ..
удовлетворяющей для некоторых значений a, b, с£ R, ab ф 0, с > О,
равенствам
являются целыми числами тогда и только тогда, когда числа а, Ь
4.	(СРР). Точка М в плоскости треугольника ЛВС расположена
так, что треугольники МАВ, МВС и MAC имеют одинаковые пери¬
метры и одинаковые площади. Доказать, что если точка М лежит
внутри треугольника ABC, то этот треугольник равносторонний, а
в противном случае—прямоугольный.
Олимпиада Скандинавских стран
В последние годы проводится заочный математический конкурс
решения задач для учащихся Скандинавских стран. В нем участвуют
школьники Дании, Исландии, Норвегии, Финляндии и Швеции.
Магриб — арабское название территории Африки, расположенной
к западу от Египта (где в настоящее время находятся страны Ливия,
Тунис, Алжир, Марокко). Эти северо-афрнканские страны в начале
80-х годов провели первую математическую олимпиаду учащихся.
Задачи олимпиады стран Магриба 1986 г.
1 день
1.	Найти все тройки цифр х, у, г, для которых при любом зна¬
чении п £ N справедливо равенство
2. Прямая, параллельная диагонали АС выпуклого четырехуголь¬
ника ABCD и проходящая через середину диагонали ВО, пересека¬
ется в точке О с прямой, проходящей через середину АС параллель¬
но BD. Доказать, что четырехугольники ОАВС, OBCD, OCDA, ODAB
имеют равные площади.
3. Доказать, что существует и при том единственная последова¬
тельность чисел аь а2, ..., удовлетворяющая условиям
4. Доказать, что для любых положительных чисел «ь fi2, яя спра
ведливо неравенство
в2 -f- Ьъ + с
и  г
целые.
Олимпиада стран Магриба
хх .. х—уу ... у —гг ... г.
2П цифр п цифр п цифр
2 день
384

5. Две окружности имеют обший центр О. Две прямые, пересе¬
кающиеся в точке О, пересекают окружность большего радиуса в
точках А, В и окружность меньшего радиуса в точках С, D, причем
точка О лежит между точками А и С, а точка D-—между точками
В и О. Доказать, что окружность, описанная около треугольника
ЛОВ, окружность, описанная около треугольника COD, окружность
с диаметром АС и окружность с диаметром BD пересекаются в одной
точке.
6. Решить уравнение
52*—3-2*У-^ЬХ-2У-*-—2У-1—2-5*+1 =0
в целых числах.
IV
МЕЖДУНАРОДНЫЕ МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ
Международные математические олимпиады школьников прово¬
дятся с 1959 г. Об их истории и особенностях подробно рассказано
в [3J.
Задачи международной математической
олимпиады 1986 г.
1 день
1. (ФРГ). Пусть d — натуральное число, отличное от 2, 5 и 13.
Докажите, что во множестве {2; б; 13; d) можно найти два различных
числа а и Ь такие, что число ab—1 не является квадратом целого
числа.
2. (КНР). На плоскости даны треугольник А±А2А„ и точка Р0.
Положим Ал = Ал_3для любого целого s^ 4. Строим последователь
ность точек Р„, Plt Pt, ... так, что точка Рк+£ есть образ Рк при
повороте вокруг точки Ак+$ на угол 120° по часовой стрелке (к = 0,
1, ...). Докажите, что если	то	треугольник AtA2A3 —
равносторонний.
3. (ГДР). Каждой вершине правильного пятиугольника приписа¬
но некоторое целое число так, что сумма всех пяти чисел положи¬
тельна. Если трем последовательным вершинам соответствуют числа
х, у, z и у < 0, то разрешается следующая операция: числа х, у, г
заменяются соответственно на х у, —у, г-\-у. Такие операции по¬
следовательно совершаются, пока хотя бы одно из пяти чисел отри¬
цательно. Определите, обязательно ли этот процесс закончится за
конечное число шагов,
2 день
4. (Исландия). Пусть А и В —соседние вершины данного пра¬
вильного /г-угольника (п ^ 5) с центром О. Треугольник XYZ, равный
треугольнику ОАВ, вначале совпадает с ним, потом движется в плоско¬
сти n-угольника так, что точки Y и Z остаются на границе, а точка
А- внутри данного /г-угольника. Какую фигуру опишет точка X,
когда точки Y и Z вместе совершат полный оборот?
5. (Англия). Найти все функции / (х), определенные на множестве
неотрицательных действительных чисел, принимающие значения в том
множестве и удовлетворяющие следующим условиям:
^3 Под ред. И. Н. Сергеева
385

1) / (tf (y))’f (у) ~f (*+#) Для всех неотрицательных чисел х, у\
2)/(2) = 0;
3)	f (х) Ф 0 для всех 0 < к С 2.
6.	(ГДР). Пусть М — произвольное конечное множество целочис¬
ленных точек на координатной плоскости. Всегда лн можно окрасить
некоторые точки множества М в белый цвет, а остальные в красный
так, чтобы для каждой прямой /, параллельной .любой из координат¬
ных осей, абсолютная величина разности между числом белых и
красных точек на I не превосходила бы единицы? Ответ обосновать.
Приложение В
ОСНОВНЫЕ БИБЛИОГРАФИЧЕСКИЕ ИСТОЧНИКИ
[ЦБ'удуров С. Т. Математически олимпиади.— София! Народна про¬
света, 1972.
[2] Давидов Л., Тонов И. Републиканска олимпиада по математика
за 1977 г. // Математика.— 1977.— Г. 16, № 4. —С. 17—21,
[3] Министерство на народната просвета, Централна комисия за
олнмпнадата по математика. Първите три британски математи¬
чески олимпиади.— София, 1983.
[4] Пешков В., Тонов И. Републиканска олимпиада по математика
за 1976 г. // Математика.— 1976. — Г. 15, № 4.—С. 16 — 20.
[5] Табов Й. Четвърти кръг на олимпиадата по математика // Мате¬
матика.— 1982.—Г. 21, № 7,—С. 22 - 27.
[6] Табов Й. IV кръг на XXVIII национална олимпиада по матема¬
тика 1979 година // Математика.— 1979.— Г. 18, № 4.— С. 24 — 30.
[7] Тонов И. XXX национална олимпиада по математика.— 1981 г.
// Математика.— 1981.— Г. 20, № 8.— С. 28—34.
[8] Централна комисия за провеждане на олимпиадата по матема¬
тика. Решения, на задачите от първия и втория ден на подбор-
ния кръг на XXXII национална олимпиада по математика за
средношколци —14 и 15 май 1983 година.— София, 1983.
[9] Auswahl Е. Aufgaben mit Losungen aus Olympiaden Junger
Mathematiker der DDR, Band 1, —Berlin: Volk und Wissen Volk-
seigener Verlag, 1972.
[10] Auswahl E. Aufgaben mit Losungen aus Olympiaden Junger Ma¬
thematiker der DDR, Band 2. — Berlin: Volk und Wissen Volks-
eigener Verlag, 1975.
[11] Auswahl E. Aufgaben mit L6sungen aus Olympiaden Junger Ma¬
thematiker der DDR, Klassen 5—8.—Berlin: Volk und Wissen
Volkseigener Verlag, 1983.
[12] Chirita М., Maftei I. V. Rezolvarea problemelor date la olimpia-
da de matematicfi, etapa finals, Pitejti, 6—9 april 1979 // Ga-
zeta matematicS.— 1980. — V. LXXXV, № 4. — P. 168—177.
[13] Klamkin M. S. The Olympiad Corner: 21 // Crux Mathematicorum.—
1981, —V. 7, № 1. —P. 11 — 17.
[14] Klamkin M. S. The Olympiad Corner: 22 // Crux Mathematicorum.—
1981,—V. 7, № 2,—P. 42—47.
[15] Klamkin M. S. The Olympiad Corner: 25// Crux Mathematicorum.—
1981,—V. 7, № 5,—P. 139—144.
[16] Klamkin M. S. The Olympiad Corner: 26 // Crux Mathematicorum.—
1981,—V. 7, № 6.— P. 171—177.
[17] Klamkin M. S. The Olympiad Corner: 28//Crux Mathematicorum.—
1981,—V, 7, № 8.—P. 235—237.
386

Klamkin M. S. The Olympiad Corner: 291 j Crux Mathematicorum.—
1981,—V. 7, № 9,—P. 267—273.
Klamkin M. S. The Olympiad Corner: 31 //Crux Mathematicorum.—
1982 —V. 8, № 1,—P. 12—14.
Klamkin M. S. The Olympiad Corner: 35 // Crux Mathematicorum.—
1982.—V. 8, № 5,— P. 133—135.
Klamkin M. S. The Olympiad Corner: 36 // Crux Mathematicorum.—
1982,—V. 8, №6.—P. 164—172.
Klamkin M. S. The Olympiad Corner: 38 // Crux Mathematicorum.—
1982.—V. 8, № 8,—P. 237—244.
Klamkin M. S. The Olympiad Corner: 39 // Crux Mathematicorum.—
1982.—V. 8, № 9,—P. 269—275
Matematicka Olympiada, 1951—1981, Jednota Ceskoslovensk ych
matematlku a fyziku hstfednl vybor matematike olympiady —
Praha, 1983.
Ministerstwo Oswiaty I Wychowanla. Dwudzlesta Dzlewlata Olym¬
piada Matematyczna (1977/1978).—Warszawa: Wydawnictwa szkol-
ne i pedagogiczne, 1978.
Ministerstwo Oswiaty i Wychowania. Trzydziesta Olympiada Mate¬
matyczna (1978/1979).— Warszawa: Wydawnictwa szkolne i peda¬
gogiczne, 1979.
Romania Ministry of Education. 43 problems (Romanian Mathema¬
tical Olympiad — 1978).— Bucharest. 1978.
Savezno takmicenje mladih matematicara // Matematicko-fizicki
list.— 1972—73.—О. XXIII, № I.—S. 21—23.
Savezno takmicenje mladih matematicara // Matematicko-fizicki
list.—1973—74,—G. XXIV, № 1.—S. 20—22.
Savezno takmicenje mladih matematicara // Matematicko-fizicki
list.—1975—76,—G. XXVI, № 1,—S. 19—21.
Solu'tiile unor probleme date la concursul de matematicS, 1975 //
Gazeta matematicS.— 1976.— V. LXXX1, № 7.— P. 367—372.
VIII Olympiade Junger Mathepiatiker der DDR. DDR-Olympiade
(28.3bis 1.4.1969). Aufgaben//Alpha.— 1969.— V. 3, №3.— P. 60.
IX Olympiade Junger Mathematiker der DDR. DDR-Olympiade (22.3
bis 26.3. 1970). Aufgaben // Alpha.— 1970.— V. 4, № 4.— P. 60.
XI Olympiade Junger Mathematiker der DDR. DDR-Olympiade
(28.3. bis 30.3. 1972). Aufgaben // Alpha — 1972— V. 6, № 4,— P.85.
XIII Olympiade Junger Mathematiker der DDR. DDR-Olympiade
(8.4 bis 10.4.1974). Aufgaben // Alpha.— 1974.— V. 8, № 3.— P. 59.
XVI Olympiade Junger Mathematiker der DDR. 4. Stufe (DDR-
Olympiade) // Alpha.— 1977.— V. II, № 4. — P. 84.
XVIII Olympiade Junger Mathematiker der DDR. 4. Stufe (DDR-
Olympiade)//Alpha.— 1979. — V. 13, № 5.— P. 113.
XIX Olympiade Junger Mathematiker der DDR. 4. Stufe (DDR-
Olympiade) // Alpha.— 1980.— V. 14, № 5. — P. 114—117.
XXI Olympiade Junger Mathematiker der DDR. 4. Stufe (DDR-
Olympiade)//Alpha.— 1982.— V. 16, №5.— P. 114—115.
XXII Olympiade Junger Mathematiker der DDR. 4. Stufe (DDR-
Olympiade)//Alpha.—1983,—V. 17, №5.—P. 114—115. _
XVII savezno takmicenje iz matematike ucenika srednjih skola//
MatematiCko-fizickI list.— 1976—77.— G. XXVII, №2.— S. 66—
68.
XVIII savezno takmicenje iz matematike ucenika srednjih Skola//
Matematicko-fizicki list.— 1977—78.— G. XXVIII, № 1.— S. 28—
31,
13*	387

Приложение Г
ВСПОМОГАТЕЛЬНЫЕ СВЕДЕНИЯ
В настоящем приложении собраны наиболее важные для решения
задач понятия и факты (из различных областей математики), иногда
выходящие за рамки школьной программы. Доказательства здесь не
приводятся, но большинство из них заинтересованный читатель может
найти в тех книгах, которые перечислены в списке литературы (при¬
ложение Д). Например, ссылка [19], [20] означает, что доказательство
данной теоремы можно прочесть в учебниках [19] или [20]. Доказа¬
тельства некоторых утверждений содержатся в решениях задач из
сборников [3] и [4], доказательства некоторых других утверждений
содержатся в разделе III сборника [1] (теоретические примечания
к решениям задач). При ссылке на эти сборники в скобках указан
номер задачи, в решении которой (или в примечании к решению
которой, если ссылка делается на [1]) приведено доказательство дан¬
ной теоремы. Например, выражение [3 (83)] означает, что имеется
в виду решение задачи № 83 в сборнике [3]. Отдельные теоремы нз
приведенных ниже представляют собой несложные упражнения для
читателя: В приложении Е дан перечень наиболее часто встре¬
чающихся в книге обозначений, смысл которых, как правило, разъ¬
яснен в определениях (номера определений в этих случаях указаны
в скобках).
# # #
Определение 1. Множество А называется подмножеством
множества В (обозначение А С В), если каждый элемент множества А
принадлежит множеству В.
Определение 2. Объединением A\JB множеств А и В назы¬
вается множество, состоящее из всех элементов, принадлежащих
по крайней мере одному из множеств А к В. Пересечением А(]В
множеств А и В называется множество, состоящее из всех элементов,
принадлежащих как множеству А, так и множеству В♦
Аналогично определяется объединение и пересечение нескольких
множеств.
Определение 3. Разностью А\В множеств А и В назы¬
вается подмножество множества А, состоящее из всех его элементов,
не принадлежащих множеству В. Если В С. А, то разность-А\В
называется дополнением к множеству В в множестве А,
Наборы, состоящие из одних и тех же элементов, но различаю¬
щиеся их порядком, представляют собой одно и то же множество
(например {1; 2; 3} = {2; 3; 1}). Если возникает необходимость не
смешивать также наборы, различающиеся только порядком входящих
в них элементов, то в этом случае наборы называют упорядоченными.
388

Определение 4. Декартовым произведением АXВ множеств
А и В называется множество всех упорядоченных пар (х; у), где
х £ А и у £ В.
Аналогично определяется декартово произведение нескольких
множеств.
Теорема 1 (принцип Дирихле). Если множество, со¬
держащее п элементов, представлено в виде объединения k подмно¬
жеств, то хотя бы одно из этих подмножеств содержит не менее
n/k элементов.
Эта теорема обычно используется в ситуации, когда k < п, а под¬
множества попарно не пересекаются.
Теорема 2 (принцип математической индукции).
Пусть для некоторого утверждения U (п), зависящего от параметра п,
справедливо следующее:	.
а) утверждение U (1) истинно;
б) если при некотором значении п £ N утверждения 0(1), ..., U (и)
истинны, то утверждение U (и+1) также истинно.
Тогда утверждение U (и) истинно для любого значения п £ N.
Через f: А —>■ В обозначается функция с областью определения А
и областью значений В.
Определение 5, Пусть задана функция f: А —>- В. Функция
g: В—>- А называется обратной к функции f (обозначение:	/-1),
если справедливы тождества
g(f (*)) = *, f(g(y))^y, х£А,у€В.
Теорема 3. Функция f: А—V В имеет обратную функцию
тогда и только тогда, когда для любого элемента у £ В существует
элемент х £ А, удовлетворяющий условию f(x)=y, и для любых двух
различных элементов хъ х2 £ А значения f (х{) и f (х2) также раз¬
личны.
Определение 6. Суперпозицией двух функций f: А —»- В и
g: В—>■ С называется функция h: А—>-С, определенная тождеством
h(x) = g{f{x)), х £ А.
Аналогично определяется суперпозиция нескольких функций
fi- А±—► А2, f2. А2—»■ А3, ..., fn: Ап—*■ An+i.
Суперпозиция n совпадающих функций f: А —> А обозначается
через fn. Если задана функция f: R —>■ R, то суперпозицию
fn (*)= f(f (!(■■■ (*)...))>
или обратную функцию /-1 (х) не следует смешивать с функцией,
вначение которой в каждой точке х равно (/ (*))" или (f (х))_ 1 соот-
389

ветственно. Исключение составляют логарифмическая и тригонометри¬
ческие функции (например, выражение sinax равно sin х-sin х, а не
sin (sin (х))).
* * *
Определение 7. Функция /: А—► R называется:
— ограниченной сверху, если некоторое число Л1 £ R осущест¬
вляет оценку f (х) < М при всех х (£ А;
— ограниченной снизу, если некоторое число m(SR осуществляет
оценку f (х) > т при всех х £ А.
Функция f: А —>■ R, ограниченная одновременно как сверху, так
и снизу, называется ограниченной.
Определение 8. Пусть А с. R. Функция /т А—*R назы¬
вается:
возрастающей, если f (х,) < f (х2),
убывающей, если / (хх) > / (х2),
невозрастающей, если f (xj) ^ f (х2),
неубывающей, если f (xt) < f (х2),
где каждое из условий выполнено для любых чисел Xf, х2 £ А,
удовлетворяющих неравенству xt < х2. Функция f: А—► R, обладаю¬
щая одним из этих четырех свойств, называется монотонной. Функ¬
ция, являющаяся либо возрастающей, либо убывающей, называется
строго монотонней.
Частным случаем функций f: А—>■ R, область определения кото¬
рых есть подмножество множества R, являются числовые последова¬
тельности, т. е. отображения о: N—>■ R или a: Z+—> R, значения
которых обозначаются через ап. В соответствии с определениями 7
н 8 говорят об ограниченных сверху или снизу, ограниченных, возра¬
стающих, убывающих, невозрастающих, неубывающих, монотонных
и строго монотонных последовательностях.
Теорема 4. Для любых значений a, ft £ R и л f N справед¬
ливы равенства:
an+l—bn+1 = (a—b) (fl"4-nn-ifc + ... +a6"-*+6'>),
ain+1 _|_ b2n+1 = (а _|_ щ (din—а2" -Ч> +... — ab%n ~ *+Ь2п),
д2« _ Ь2п ^ (а + Ь) (а2п ~1 — а2« ~ 2fc +... + аЬ2„ - 2 _ Ь2„ -
Теорема 5 (неравенство Бернулли) ([I (35)], [9], [21]),
Для любых вначений a, b £ R, удовлетворяющих условиям а > —1,
390
при	b,	Ь	>0.
* * *

г
а Ф О, Ь ф 0, b ?4 1, справедливы неравенства
(1 + с)ь < 1+аЬ, если 0 < Ь < 1
(1 +а)ь >'1 + ab, если Ь ф [0; 1].
Определение 9. Средним арифметическим чисел а\,..., а„ £ R
называется число
flj + • • • 4- Од
п
Средним геометрическим неотрицательных чисел alt ..., ап назы¬
вается число
... а„.
Средним гармоническим положительных чисел at, ..., ап называется
число
Cl	о„
Средним квадратическим чисел	а„ £ R называется число
• f cj + - - - + Сп
V п
Теорема 6 (теорема о средних) ([1 (68, 115)], [9], [21]).
Любые положительные числа ai ап удовлетворяют неравенствам
п	п/~	Ci+...	+с„_,_, / af + ... + 0,1
~Т~	Cl	...	С„<	-	<1/	-	.
■НГ+---+^
причем если среди этих чисел имеются хотя бы два различных, то
все неравенства строгие.
Наиболее употребительным является неравенство между средним
геометрическим и средним арифметическим, верное также и для
неотрицательных чисел.
Теорема 7 ([4 (224, £25)], [9], [19], [20], [21]), Последовательность
чисел	(я € N) является возрастающей и имеет предел,
обозначаемый через е, который удовлетворяет неравенству
ЫУ
<е
для любого значения п £ N.
Логарифм по основанию в называется натуральным и обозна¬
чается через In (logex= lnx, х > 0),
391

* * *
Определение 10. Функция
(	1,	если	х	>	0,
sign (х) = •{	0,	если	х	=	О,
V	—1,	если	х <	О,
называется функцией внака.
определение 11. Целой частью [х] числа х £ R назы¬
вается наибольшее целое значение, не превосходящее числа х.
Дробной частью числа х £ R называется число {х} = х—[х].
Теорема 8. Целая часть является неубывающей функцией, а
дробная часть — периодической функцией с периодом, равным 1.
*	*	*
Определение 12. Пусть даны числа а, b £ Z, причем Ь Ф 0.
Тогда числа q£l и г£{0, 1, ..., | Ь |—1} называются соответственно
частным и остатком от деления числа а на число Ь, если выполнено
равенство
а = qb + г.
При этом, если г = 0, то говорят, что число а делится на Ь, или что
число а кратно числу Ь, или что число Ь является делителем числа а
(обозначение а ■ Ь).
Определение 13. Наименьшим общим кратным ненулевых
чисел аг ап называется наименьшее натуральное число, ко¬
торое делится на каждое из этих чисел (обозначение [clt ..., а„]).
Определение 14. Наибольшим общим делителем чисел
сь ..., ап£Z, из которых хотя бы одно отлично от нуля, называется
наибольшее натуральное число, на которое делится каждое из этих
чисел (обозначение (ау, ..., а,,)).
Теорема 9. Для любых двух натуральных чисел а и b имеет
место равенство
(а, 6)-[a, b] = ab.
Определение 15. Числа а, b£Z называются взаимно про¬
стыми, если (а, Ь)= 1.
Определение 16. Пусть даны числа a,b,c£Z, причем
с Ф 0. Говорят, что число а сравнимо с числом Ь по модулю с (обозна¬
чение: a = (mod с)), если (а—Ь) \ с; в противном случае говорят,
что число а не сравнимо с числом Ь по модулю с (обозначение:
а ф b (mod с)).
Теорема 10. Пусть ваданы числа а, Ь, с, d, т, k£Z, причем
т ф 0, k Ф 0. Тогда справедлиры следующие утверждения:
а) если a = f> (mod т) и b = c (mod т), то а = с (mod т);
б) если а~ Ь (mod т) и c = d (mod т), то a+cs=<>+d (mod т)
и ac = bd (mod т);
392

в) если a^b(mod т), то апаз b" (modт) для любого вначения
п£ N;
г) если a^b (mod т), то ak = bk (mod mk);
д) если аяшЬ (mod т) и а • k, b ■ k, т • k, то
a/k эз b/k (mod m/k).
Теорема 11. Для любых значений а, Ь£1 и п £ N имеют
место следующие утверждения:
а) если а Ф Ь, то (ап—Ьп) • (а—Ь)\
б) если а Ф—Ь, то (а3.п~Я-[-№п-1) • (а+6);
в) если аф — Ь, то (о?" — fc?") ■ (o+fc).
Эта теорема вытекает из теоремы 4 или из теоремы 10 в).
Пусть т—произвольное натуральное число, большее 2. Различ¬
ные целые числа при делении на т могут давать любой	из	остатков
0, 1 т—1. Однако	степени	целых чисел с фиксированным на¬
туральным показателем п > 1 не обязательно снова могут давать
при делении на т любой	из этих	остатков.
Теорема 12. При	делении	на т (3<т<10)	п-е	степени
целых чисел (2<п<5) могут давать те и только те остатки, ко¬
торые указаны в таблице 2.
Таблица 2
ч
2
3
4
Б
3
0; 1
0; 1; 2
0; 1
0; 1; 2
4
0; 1
0; 1; 3
0; 1
0; 1; 3
5
0; 1; 4
0; 1; 2; 3; 4
0; 1
0; 1: 3; 4
6
0; 1; 3; 4
0; 1; 2; 3; 4; 5
0; 1; 3; 4
0; 1; 2; 3; 4; 5
7
0; 1; 2; 4
0; 1; 6
0; 1; 2; 4
0; 1; 2; 3; 4; 5; 6
8
0; 1; 4
0; 1; 3; 5; 7
0; 1
0; 1; 3; 5; 7
9
0; 1; 4; 7
0; 1; 8
0; 1; 4; 7
0; 1; 2; 4; 5; 7; 8
10
0; 1; 4; 5; 6; 9
0; 1; 2; 3; 4; 5;
6; 7; 8; 9
0; 1; 5; 6
0; 1; 2; 3; 4; 5;
6; 7; 8;9
Обычно числа записываются в десятичной системе счисления,
которая допускает следующее обобщение.
Определение 17. Говорят, что число n£N имеет запись
ах ... ат в k-ичной системе счисления (££N, k > 1), если справедливо
393

равенство
n = a1kl”~1 + ...+am_1kL + am№,
где at,	am — целые неотрицательные числа, меньшие ft, причем
«i > 0.
Теорема 13 [14]. Для заданного значения £g N, большего 1,
любое число ngN имеет запись в k-ичной системе счисления, причем
единственную.
Теорема 14. Любое натуральное число сравнимо с суммой
своих цифр в десятичной системе счисления по модулю 9.
Доказательства теорем 10—12 и 14 и другие свойства сравнений
можно найти, например, в [1 (13)], [11], [18], [21], [22].
Определение 18. Пусть т, ngZ;	Биномиальным
коэффициентом С„ называется число
у-т  nj
”	ml (и—/л)! *
где обозначено
ni_f l-2..«n при ngN, •
‘	1	при	п = 0
(л! читается «эн—факториал»).
Теорема 15. Для любых значений т, ngZ+ справедливы сле¬
дующие соотношения:
а) С°, = СЙ = 1;
б) Сп = Сп~т. если п 3» т 5= 0;
в) Сп ^Сп—, если п > т > 0.
Теорема 16 (бином Ньютона) ([1 (25)], [12], [18], [21],
[25], [28]). Для любых значений a,6gR «ngN справедливо равенство
(а + Ь)'‘=Спа'‘ + CW‘~1Ь + ... +Cf?cn~mf>m +... +сГ1с&"-1+0",
Из этой теоремы вытекает следующее утверждение.
Теорема 17. Все биномиальные коэффициенты являются нату¬
ральными числами, причем справедливы равенства:
а) С^+Й+.,.+С” = 2";
б) СЙ-С^+С^-... + (-1)»СЙ = 0.
Соотношение 17 а) получается из тождества теоремы 16 при
подстановке а=Ь= 1, а соотношение 176) — прн а= — 6=1.
Определение 19. Натуральное число, большее 1 и не имею¬
щее натуральных делителей, отличных от 1 и самого себя, называется
простым. Остальные натуральные числа, большие 1, называются
составными. Число 1 не является ни простым, ни составным.
Теорема 18 (основная теорема арифметики)
([1 (7)], [13], [18], [21], [22]). Каждое составное число разлагается
в произведение нескольких простых чисел, не обязательно различных,
причем такое разложение единственно с точностью до порядка со¬
множителейI
394

Теорема 19 ([4 (349)], [11], [18], [21], [29]). Простых чисел
бесконечно много.
Теорема 20 (теорема Лежандра) ([1 (86)], [3 (83)],
[4 (75)], [18], [22]). Простое число р входит в разложение числа я!
на простые множители в степени
[7] + й + й+“
(^при достаточно больших значениях k имеем |^j=0^.
Следующие 3 теоремы описывают свойства взаимно простых чисел.
Теорема 21 ([1 (24)], [18], [22]). Пусть a, b, c^Z и с Ф 0.
Если ab • с и (Ь, с) = 1, то а \ с.
Теорема 22 ([3(241)], [21]). Пусть а,Ь,с,т£N. Если ab = cm
и (с, b)= 1, то a-d? и b = b™, где alt <>i£N, причем (ау, f>i)=l
U 0^1=0.
Теорема 23 (китайская теорема об остатках) ([18]).
Если целые числа /лу т* отличны от нуля ы попарно взаимно
просты, то для любых целых чисел  	 о* существует целое
число х, удовлетворяющее условиям с,- (mod т,-) при всех i=l, ..., k.
При этом число х можно считать принадлежащим любому наперед
ваданному полуинтервалу длины т±т2 ... т*.
Теорема 24 ([11], [13], [18], [22]). Для любых двух чисел
а, Ь£2, йз которых хотя бы одно отлично от нуля, существуют
числа р, q(£2, удовлетворяющие равенству pa-\-qb= (а, Ь).
Теорема 25 (малая теорема Ферма) ([1 (22)], [4(340)],
[11], [18], [21], [22]). Если число a£Z не делится на простое число р,
то число аР~х—1 делится на р.
Непосредственным следствием малой теоремы Ферма является
теорема 26.
Теорема 26. Пусть р—простое число. Тогда для любого зна¬
чения а (£2 имеет место сравнение
аР е= a (mod р),
* • •
Теорема 27 (о промежуточном значении непре¬
рывной функции) ([19], [20], [21]). Пусть функция /: [о; b]—>-R
непрерывна на отрезке [а; 6], причем A = f (а) < f (Ь) — В. Тогда для
любого числа С £ (Л; В) найдется точка с£(а; Ь), для которой выпол¬
нено равенство f (с) = С.
Частным случаем теоремы 27 является следующее утверждение.
Теорема 28 (об обращении в нуль). Если функция
f: [а; Ь\ —>■ R непрерывна на отрезке [с; Ь\ и принимает на его кон¬
цах ненулевые значения разных внаков, то существует точка с £ (с; Ь),
для которой выполнено равенство f (с) = 0.
395

Те рема 29 ([19], [20], [21]). Если функция f: [с; Ь\—> R
непрерывна на отрезке [а; Ь], то существуют такие числа с, d£[a; 6],
что для всех значений х£[а\ Ь\ выполнены неравенства { (с)<
<Lf(x)^f(d).
Из теоремы 29 вытекает следующее утверждение.
Теорема 30. Любая непрерывная на отрезке функция огра¬
ничена.
Ниже через I обозначается некоторый интервал числовой пря¬
мой R.
Рассмотрим некоторую функцию f: I —► R. Предположим, что
эта функция в каждой точке х£/ дифференцируема, т. е. имеет
производную f (х). Тогда возникает новая функция f': I —*■ R,
значением которой в каждой точке х£1 является число f (х). Эта
функция называется первой производной функции f и может в свою
очередь также оказаться дифференцируемой в каждой точке интер¬
вала /. Тогда ее производная называется второй производной исходной
функции f. Аналогичным образом можно определить п-ю производную
функции f (обозначение: /<">) при каждом следующем значении
п = 3, 4, 5, ... Первую, вторую и третью производные функции
обычно обозначают через f', f" и f" соответственно, а иногда записи
/1V, /v, ... используют и для обозначения следующих по порядку
производных функции f.
Определение 20. Функция f: I —► R назйвается:
п раз дифференцируемой, если л £ N и функция f имеет n-ю про¬
изводную в каждой точке интервала /;
п раз непрерывно дифференцируемой, если она п раз дифферен¬
цируема и функция f{n) непрерывна на интервале /;
бесконечно дифференцируемой, если она имеет п-ю производную
для любого значения п £ N.
Теорема 31 (признак монотонности) ([19], [20], [21]).
Пусть функция f: I —► R дифференцируема на интервале I. Тогда
:/>ункция f является неубывающей (соответственно невозрастающей)
тогда и только тогда, когда в каждой точке х£1 выполнено нера¬
венство Г (х)	0 (соответственно f (х) < 0). Если в каждой точке
х£/ выполнено неравенство f (х) > 0 (соответственно f (х) < 0), то
функция f является возрастающей (соответственно убывающей).
Определение 21. Функция f: I—>- R называется выпуклой
вниз на интервале I, если для любых чисел х,у£1 и a£[0; 1]
справедливо неравенство
f (ax+ (1 о:) у) «S af (х) + (1 — a) f (у).
Функция f: / —>■ R называется выпуклой вверх на интервале I, если
функция g (х) = — f (х) является выпуклой вниз на этом интервале.
Теорема 32 (признак выпуклости) ([19], [20]). Пусть
функция f: I —>■ R дважды дифференцируема на ■ интервале [с; 6].
396

Тсгда функция f является сыпуклой вниз (соответственно вверх) на
атом интервале в том и только в том случае, если в каждой точке
х£ I выполнено неравенство f" (х) Зз 0 (соответственно f’(*)<0).
Теорема 33 (теорема Лагранжа) ([19], [20]). Пусть
функция f: [с; b\ —>- R непрерывна на отрезке [с; 6] и дифференци¬
руема на интервале (а; Ь). Тогда существует число с£(а; Ь), уде
влетворяющее равенству
Частным случаем теоремы Лагранжа является следующее
утверждение.
Теорема 34 (теорема Ролл я). Пусть функция f: [с; *]—*- R
непрерывна на отрезке [а; Ь] и дифференцируема на интервале (с; Ь),
причем f (a) = f (Ь). Тогда существует число с£(а; Ь), для котора
Г (с) = 0.
* * *
Материал о комплексных числах подробно изложен в [10], [151,
[16], [17], [20], [21], [23], [24].
Определение 22. Множеством С комплексных чисел назы¬
вается множество упорядоченных пар действительных чисел, на кото¬
ром введены операции сложения и умножения следующим обрг^.
(с; b) + (c\ d) = (a-fc; b-\-d),
(с; Ь) (с; d) = (ас—bd\ ad -j- be),
где a, b, с, d£R.
Отметим, что (a; 0)-)-(&; 0) = (a-\-b\ 0) и (с; 0) (b; 0) = (ab-, 0).
Поэтому комплексное число вида (с; 0) обычно отождествляют
с действительным числом а. Комплексное чисчо (0; 1) называют мни¬
мой единицей и обозначают через i. Мнимая единица удовлетворяет
соотношению
i* = — 1.
Для любого комплексного числа (а; Ь) справедливо равенство (о; Ь)—
— (а; 0) [-(6; 0) (0; 1). Поэтому комплексное число (а; Ь) обычно
записывают как a-\-bi.
Определение 23. Число а£К называется действительной
частью комплексного числа г- a-\-bi (обозначение: а - Re г), а число
fc£R— его мнимой частью (обозначение: b—lmz). Комплексные
числа с нулевой действительной частью (т. е. числа вида Ы) называ¬
ются мнимыми.
Действия над комплексным ислами подчиняются тем же зако¬
нам, что и над действительными числами: коммутативному и ассо¬
циативному для сложения и умножения, а также дистрибутивному
для умножения относительно сложения,
397

Комплексные числа можно изображать точками на плоскости,
считая абсциссой действительную часть, а ординатой—мнимую часть
комплексного числа.
Определение 24. Модулем комплексного числа г = а-\ГЫ
называется число | г |
Теорема 35. Для любого числа г£С справедливо неравенство
| z 13= 0, причем равенство | г | = 0 имеет место тогда и только
тогда, когда г = 0. Для любых чисел z,w£C справедливо равенство
|гю| = |г|-|ш|.
Теорема 36 (неравенство треугольника)! Для лю¬
бых двух чисел z,w£ С справедливо неравенство
|г+ш|<|гЦ-|и;|,
причем равенство имеет место тогда и только тогда, когда либо
г = 0, либо w — кг, где к Зг 0.
Определение 25, Аргументом ненулевого комплексного числа
z = a-\-bi называется определенный с точностью до слагаемого 2пп
(п £ Z) угол <р, удовлетворяющий соотношениям
cosф = с/г, sln<p = f>/r, где r = |z[.
Значение угла <р из промежутка (— я; я], определенное однозначно,
называется главным значением аргумента (запись: ф = arg г).
Модуль и аргумент комплексного числа, изображенного на коор¬
динатной плоскости, показаны на рис. 137.
Теорема 37 (тригонометрическая форма записи
комплексного числа). Любое ненулевое число z£C можно пред¬
ставить в виде
z = r(cos <p + »stnq)), где r = |z|, q) = argz.
О п р е д ел е н и е 26. Комплексное число г —а—bi называется
сопряженным комплексному числу z = a-\-bi.
398

Теорема 38. Для любого числа z£C справедливы равней» а
Rez = Rez, Imz=.—Imz, (z) = z.
Чисю г является:
а) действительным тогда и только тогда, когда ~г= г;
б) мнимым тогда и только тогда, когда г = —г. *
На координатной плоскости сопряженные комплексные числа
расположены симметрично относительно действительной оси (см.
рис. 137).
Теорема 39. Для любых чисел z,w£C справедливы рсгенстм
I г | = | г I, гг = [г|2, z-\-w = z+w, zw = zw,
а если г Ф 0, то arg г = — arg г или если г < 0 arg z = arg г =- я.
Вычитание и деление комплексных чисел определяются как дей¬
ствия, обратные соответственно сложению и умножению.
Теорема 40. Если z = c + W, ш = c-\-di—произвольные комп¬
лексные числа, то уравнение z-f-x—w имеет в комплексных числах
единсг' ■ енное решение (называемое разностью чисел w и г)
x=c—a-\-(d — b) i.
Теорема 41. Если г~a-\-bi, w=c-j-di—произвольные комп¬
лексные числа, причем г Ф 0, то уравнение zx=w имеет в комплекс¬
ных числах единственное решение (называемое частным чисел w и г):
w-z   ac-\-bd , ad—be
| z l2 c2+f>2 lc2+f>2
Теорема 42. Умножение и деление комплексных чисел, заданных
в тригонометрической форме, производятся по следующим формулам:
(/■i (cos фх + i sin cpi)) (r2 (cos ф2 + f sin ф2)) =
= TVa (cos (ф! + фг) + i sin (ф! + фа)),
fl (COS ф! + i Sin фх) £i	sin (ф1_ф2)).
r„ (cos ф2 +1 sin фа) r„
Из этой теоремы вытекают следующие два утверждения.
Теорема 43 (формула Муавра). Возведение в п-ю степень
(я£ N) комплексного числа производится по формуле
(г (cos ф -(- i sin ф))" — rn (cos яф + i sin яф).
Теорема 44. Для любого ненулевого числа г£С и любого зна¬
чения п £ N уравнение хп - г в комплексных числах имеет ровно я
различных решений, называемых корнями п-й степени из числа г.
Корнями ti-й степени из единицы являются числа
2nk	. . 2nk	_.. ,	.,
xft = cos ——|-1 sin —	,	k£{0,	1,	n—	1}.
399

Определение 27. Числовая функция f действительного или
комплексного аргумента х называется четной (нечетной), если она
удовлетворяет тождеству f(—x)ssf (х) (соответственно f (—x)=—f (х)),
x£R или х£С.
$ $ $
Определение 28. Многочленом (от одной переменной) назы¬
вается функция действительного или комплексного аргумента х,
которую можно представить в виде
Р (x) = anxn + an_ixn-i+. *. +Ci#+Go*
где п €z+ I Со* °й ■ • • • ^п €С, причем, если nSi 1, то ап ф О*
Теорема 45. Два многочлена
Р (х) = апХп + ,, . +GiX + G„,
Q (х) = Ьтхт j . I. I ЬуХ+Ь0
равны (т. е. совпадают как функции) тогда и только тогда, когда
п = т и а0 = Ь0, at = bi ап = Ь„.
Определение 29. Числа а0, ai   называются коэф¬
фициентами многочлена
Р (х)—апхп + ... +ai*+a0.
Число а0 называется свободным членом, а число ап — старшим коэф¬
фициентом (или коэффициентом при старшем члене) этого много¬
члена. Если 1, то число п называется степенью многочлена Р (х)
(обозначение deg Р). Степень многочлена Р (х) = о0 равна 0, если
Од Ф 0, и равна —1, если о0 = 0.
Теорема 46. Пусть Р (х) и Q (х)—произвольные многочлены.
Тогда'.
а) функция Т (х) = Р (х) + Q (х) также является многочленом,
причем
deg Т< шах (deg Р, deg Q),
а если deg Р Ф deg Q, mo
deg Т = max (deg P, degQ);
б) функция W (x) — P (x) • Q (x) также является многочленом, при¬
чем, если Р (х)	0	и	Q	(х)	^ 0, то W (х)=Д 0 и
deg W = degP-f- degQ.
Определение 30. Корнем многочлена Р (х) называется ре¬
шение уравнения Р (х) = 0.
Многочлены, так же как и целые числа, можно делить друг на
друга с остатком. Здесь мы изложим основные определения и тео-
оемы, доказательства которых и более подробные сведения можно
найти в [1 (16)], [16], [17], [23], [24].
100

Теорема 47. Пусть даны два проиш/лших мчогочлг.ча Р (х)
и Q (х), причем Q (х) ^ 0. Тогда существуют единственные мносо-
члены S (х) и R (х), удовлетворяющие двум ус~окиям:
а) P(x) = S(x)Q (х) + /?(х);
б) deg R < deg Q.
Определение 31. В условиях теоремы 47 многочлен R (х)
называется остатком от деления многочлена Р (х) на многочлен Q (х).
Если R (х) ss 0, то говорят, что многочлен Р (х) делится на много¬
член Q (х).
Теорема 48. Если коэффициенты многочленов Р и Q в усло¬
виях теоремы 47 действительны, то коэффициенты многочленов S
и R также действительны. Если коэффициенты многочленов Р и Q
рациональны, то коэффициенты многочленов S и R также рацио¬
нальны. Если коэффициенты многочленов Р и Q — целые числа, причем
коэффициент многочлена Q при старшем ччене равен 1 или — 1, то
коэффициенты многочленов S и R—также целые числа.
Теоре'ма 49 (теорема Без у). Остаток от деления много¬
члена Р (х) на многочлен х—х0 равен чиау Р (х0).
Из теоремы Безу вытекает следующее утверждение.
Теорема 50. Многочлен Р (х) делится на многочлен х—х0
тогда и только тогда, когда число х0 является его корнем.
Определение 32. Число х0 называется корнем многочлена
Р(х) кратности k (&£ N), если многочлен Р (х) делится на много¬
член (х—х0)Л, но не делится на многочлен (х—Xo)ft+l-
Говорят, что многочлен Р (х) имеет корни Xi хп, если каж¬
дый из корней многочлена Р (х) повторяется в наборе (Хь ...; хп)
столько раз, какова его кратность, и никакое число, отсутствующее
в наборе, корнем не является.
Теорема 51 (основная теорема алгебры). Любой мно¬
гочлен степени п 1 имеет ровно п комплексных корней.
В качестве следствий получаем теоремы 52—54.
Теорема 52. Если значения двух многочленов степени не выше п
совпадают в п + 1 различных точках, то эти многочлены равны.
Теорема 53. Любой многочлен Р (х) степени л 0 единствен¬
ным образом (с точностью до перестановки сомножителей) предста¬
вим в виде
Р (х) = а„ (х—хх) (х—х2)... (х—х„),
где ап—старший коэффициент многочлена Р (х), а х%, х2, ..., х„ —
его корни.
Теорема 54. Многочлен Р (х) делится на многочлен Q (х) 'ф 0
тогда и только тогда, когда каждый корень многочлена Q (х) явля¬
ется корнем многочлена Р (х), причем не меньшей кратности.
Теорема 55 (теорема Виета) ([1(80)], [23], [24]). Пусть
многочлен
Я(х) = а„хП + ...+а1х-1 а0
401

имеет корни хь х„. Тогда справедливы равенства
Xi+xa+...+x„=—an-i/“n»
XjX2	"Н	• ■ • “Ь*п — I*n = ^n~~z!^n*
1 XiX2x3 -ф- xjx2x4	х„ _ 2х„ _ 4x„ = — ап _ s/fl„,
, *1X2 •. .х„ = (—1)" o0/a;li
Верна и обратная теорема.
Теорема 56. Числа хь • • • ■ х £С, удовлетворяющие системе
из теоремы 55, являются корнями многочлена
Р (х) = апхп +... +QJX+O0.
Теорема 57 ([16], [17], [23], [24]). Если Р (х) — многочлен
с действительными коэффициентами и комплексное число г с. ненуле¬
вой мнимой частью является'его корнем, то сопряженное комплексное
число г также является его корнем, причем той же кратности.
В частности, многочлен Р (х) делится на многочлен
(х—г)*-(х—z)ft = (x2—2x*Rez-]-| г |?)й,
где k—кратность корней гиг.
В качестве следствия получаем аналог теоремы 53 для много¬
членов с действительными коэффициентами.
Теорема 58. Любой многочлен Р (х) с действительными коэф¬
фициентами степени п единственным образом (с точностью до пере¬
становки сомножителей) представим в виде
Р (х) = ап (х—хх).. .(х—хт) (*2+2fijx-| -Cj)...(х3 + 2й*х-;
где т, 0, т \-21 = п, ап—старший коэффициент многочлена Р (х),
хь ..., xmgR —действительные корни Р (х) с учетом их крат¬
ностей, Ьи ..., bt,  	 причем квадратные трехчлены
х2 -'-2biX-\-Ci, .... х?-)-2 btx-\-Ci
не имеют действительных корней (m. е b\ < cf, ..., b\ < сг).
Теорема 59 ([24]). Если рациональное число pjq, где (p,q) — 1,
является корнем многочлена а„х"a4x-\-ав с целыми коэффициен¬
тами, то а0 \ р и an\q.
Из этой теоремы вытекают следующие два утверждения.
Теорема 60 ([1 (40)], [4 (317)], [22], [23], [24]). Каждый корень
многочлена
х" + а„ _ ххп “1 + • • • + ах*+«о
с целыми коэффициентами есть либо целое число, либо иррациональ¬
ное.
Теорема 61. Если a, n£N, то число \/ а является либо
целым, либо иррациональным.
Теорема 62 (интерполяционная формула Ла¬
гранжа) ([23]). Пусть заданы различные числа Ь0, Ьг Ъ,,£С
402

и произвольные	значения	с0, с±, с„£С	(n£Z+).	Тогда	существует
единственный	многочлен	Р (х) степени не	выше п,	удовлетворяющий
равенствам
р(Ьо) = с0, P(bi) = Ci,	P(bn) = cn,
Этот многочлен имеет следующий вид:
Л	тт	Х-Ь,
P(*)=2lC/n Ai '1,— ьг
ыо	°<'<»	bi bj
Укажем связь между коэффициентами многочлена и его произ¬
водными.
Теорема 63. Пусть дан многочлен
P{x) = anxn + ...+aiX-{-a0,
Тогда
Р (0) = а0, Р' (0) = ai, Р" (0) = 2а3.	Я">	(0)	=	п!	ап,
и исходный многочлен можно записать в виде
0!	1	1!	1	Й	    п!
Определение 33.. Пусть n£N. Многочленом от п перемен¬
ных называется конечная сумма функций действительных или комп¬
лексных аргументов хх хп, каждая иэ которых имеет вид
ах,1.. .х*«, где agC, kit ... kn£Z+.
Доказательства изложенных ниже теорем, относящихся к плани¬
метрии и стереометрии, можно найти в [31], [32], [33], [34]. В ка¬
честве дополнительной литературы можно рекомендовать сборники
задач [5], [6], [7], [8].
Теорема 64 (неравенство треугольника). Для
любых точек А, В, С справедливо неравенство
АВ*цАС-{-ВС.
При этом равенство имеет место тогда и только тогда, когда точ¬
ка С лежит на отрезке АВ или все три точки совпадают.
В следующих двух определениях под множеством понимается
произвольное множество точек.
Определение 34. Диаметром множества называется отрезок
наибольшей длины, концы которого принадлежат этому множеству.
Отметим, что произвольное множество может иметь более одного
диаметра или не иметь их вообще.
Определение 35. Множество называется выпуклым, если
вместе с любыми двумя своими точками оно содержит весь отрезок
с концами в этих точках.
403

Под многоугольником в настоящей книге понимается произволь¬
ный (не обязательно выпуклый) многоугольник. Всякий раз, когда
рассматриваются только выпуклые многоугольники, это требование
специально оговаривается.
Теорема 65. С ум Да углов любого п-угольника (я 3) равна
180° (я—2).
Определение 36. Пусть А, В, С — три последовательные вер¬
шины выпуклого многоугольника, a D и Е — произвольные точки
причем многоугольники М/ и Му при i ф j не имеют общих внут¬
ренних точек.
Определение 38. Многоугольник т называется вписанным
в многоугольник М, если все вершины многоугольника т лежат на
сторонах Многоугольника М.
Теорема 67. Выпуклый четырехугольник ABCD можно вписать
в окружность тогда и только тогда, когда
Теорема 68. В выпуклый четырехугольник ABCD можно
вписать окружность тогда и только тогда, когда
Теорема 69 (теорема Птолемея). Если четырехуголь¬
ник ABCD можно вписать в окружность, то
Пусть А и В —две соседние вершины многоугольника, вписанного
в окружность. Тогда под дугой АВ понимается (если не оговорено
противное) та из двух дуг с концами в точках А и В, на которой
не лежат другие вершины многоугольника.
Теорема 70 (теорема о вписанном угле). Для лю¬
бого треугольника ABC, вписанного в окружность, справедливо равенство
на продолжениях сторон АВ и ВС соответ¬
ственно за точку В. Тогда углы АВЕ и
CBD (рис. 138) называются внешними угла¬
ми этого многоугольника при вершине В (в
С отличие от угла ABC, часто называемого
внутренним углом многоугольника).
Теорема 66. Сумма внешних углов
выпуклого многоугольника, взятых по одному
при каждой вершине, равна 360°.
Рис. 138
Определение 37. Говорят, что
многоугольник М разбит на многоугольни¬
ки Mi, ..., М„, если М = Мхи ■ ■ ■ U-M„,
£ ABC + ^ CD А = BAD + £ DCB =180°.
AB+CD = BC + AD.
AB-CD-\-BC-AD = AC-BD.
404

Теорема 71. Пусть диагонали четырехугольника АХА2ВХВ2,
вписанного в окружность, пересекаются в точке Р. Тогда (рис, 139)
справедливы равенства-.
а) АХР-ВХР = А2Р’В2Р\
б) £ АХРА2 =-^-(ахА2-\-В^^)*
Теорема 72. Пусть четырехугольник АХВХВ2А2 вписан в окруж¬
ность. Тогда:
1) прямые АХВХ и А2В2 параллельны в том и только в том слу¬
чае, если АХА2 = ВХВ2\
2) прямые АХВХ и А2В2 пересекаются в точке Р, лежащей в той
же полуплоскости относительно прямой АХА2, что и отрезок ВХВ2,
в том и только в том случае, если АХА2 > ВХВ2. При этом (рис. 140)
справедливы равенства:
а) АХР-ВХР=А2Р-В2Р;
б) z ахра2=-1 (ли^-ва)*
Под длиной касательной, проведенной из точки Р к окружности,
понимается расстояние от точки Р до точки касания. Рассматривая
по теореме 72 касательную как предельное положение секущей, у
которой две точки пересечения с
окружностью сливаются в одну
точку касания, можно получить
следующее утверждение.
Теорема 73. Пусть тре¬
угольник ABC вписан в окружность,
а прямая I касается окружности
в /почке С. Тогда:
1) прямые I и АВ параллель¬
ны в том и только в том случае, если АС = ВС;
2) прямые I и АВ пересекаются в точке Р, лежащей в той же
полуплоскости относительно прямой АС, что и точка В, в том и
405
Рис. 141

только в том случае, если АС > ВС, При этом (рис, 141) справед¬
ливы равенства:
а) АР-ВР = СР2;
б) £АРС==±-(АС-ВС).
Из теорем 70, 71 б), 72.2 6), 73.2 6) вытекает следующее утверж¬
дение.
Теорема 74. Пусть дан отрезок АВ, а а,—одна из двух
полуплоскостей относительно прямой АВ. Тогда, если ф—значение
из интервала (0°; 180°), то множество точек М полуплоскости а,
для которых АМВ = ф, есть дуга некоторой окружности с кон¬
цами А и В. Если точка N £ а лежит внутри круга, ограниченного
втой окружностью, то £ AN В > tp, а если вне—то AN В <-ф.
Теорема 75. Пусть в треугольнике ABC
а^ВС, Ь = АС, с=АВ
— длины сторон,
а=£ВАС, $=£АВС, у = АСВ
— углы, р = (а + £ + с)/2—полупериметр, г—радиус вписанной окруж¬
ности, R—радиус описанной окружности,. ha — длина .высоты, опу¬
щенной на сторону ВС, га—радиус окружности, касающейся сто¬
роны ВС и продолжений сторон АВ и АС. Тогда площадь S тре¬
угольника ABC можно вычислить по любой из следующих формул:
а) S~~T ’
1 %
б) S=-^-bc sln ai
в) S — У р (р — а) (р — Ь) (р — с) (формула Герона)}
abc
Г> AR
д) S = гр\
е) S = y га (Ь + с—а);
ж) S = -i-Д2 (sln 2a-]-sln 2Р-f-sln 2у).
Формула д) справедлива для площади S любого многоугольника с
полупериметром р, описанного около окружности радиуса г.
Теорема 76. Если а и Ь—катеты прямоугольного треугольника,
с—его гипотенуза, г—радиус вписанной окружности, a R—радиус
описанной окружнссти. то
г= (1/2) (а-\-Ь — с), R = c/2.
Теорема 77. Если AL — биссектриса треугольника ABC, то
спра едливо равенство
BL АВ

Теорема 78 (равенство параллелограмма). Для
любого параллелограмма A BCD справедливо равенство
АВ3 + ВС2 + CD3 + /ID2 = AC? + BD3.
Теорема 79. Для любой точки Р и любого прямоугольника
ABCD справедливо равенство
РА*-{-PC3-- PB3-{-PD?.
Все проекции на прямые в настоящей книге предполагаются
ортогональными.
Теорема 80. Если АХВХ—проекция отрезка АВ напрямую,
пересекающуюся с прямой АВ под (нетупьш) углом ф, то
АхВх = АВ cos у.
Теорема 81. Пусть а—ненулевой вектор на плоскости, а
О—точка этой плоскости. Тогда для любого внцчения ££R множе¬
ство точек X плоскости, удовлетворяющих равенству а ■ ОХ = k, есть
прямая.
Теорема 82. Для любого набора точек Ах, ..., Ап и любого
набора чисел ku ..kn £ R, сумма которых не равна нулю, существует
единственная точка О, удовлетворяющая условию
9
2*М=о.
i'= I
При этом для любой точки Р справедливо равенство
( 2	.2	(Л-)-
На этой теореме основаны следующие три определения.
Определение 39. Центром тяжести системы точек Ах, ...
..., Ап называется точка О, удовлетворяющая условию
2®?/=о.
(=1 -
Определение 40. Центром тяжести системы отрезков
АХВХ, ..., АпВп называется точка О, удовлетворяющая условию
2 liOMi = 0,
1*1
где // (1--1, .... п)—длина отрезка Л/В/, а М,-—его середина.
Определение 41. Центром тяжести системы fnpey.ольников
АхВхСх, ..., АпВпСп называется точка О, удовлетворяющая условию
2S^=°>
i— 1
407

где Sj (i- 1, гг) —площадь треугольника AiBfii, а Л4,— точка
пересечения его медиан.
Теорема 83. Если М — точка пересечения медиан треугольника
ABC, то для любой точки Р (не обязательно лежащей в плоскости
ABC) справедливо равенство
PM = (РА + РВН-'Рс)/3.
Для плоских углов двугранного угла имеет место следующий
аналог неравенства треугольника.
Теорема 84. Плоские углы ф, ф, х любого трехгранного угла
удовлетворяют неравенствам ф < ф -|- у.
Теорема 85. Сумма плоских углов произвольного выпуклого
многогранного угла меньше 360°.
Определение 42. Многогранник т называется вписанным в
многогранник’ М, если все вершины многогранника т лежат на гра¬
нях многогранника М.
Теорема 86. Пусть три прямые, не лежащие в одной плоско¬
сти, проходят через точку А. Пусть Bi и В2—две отличные от А
точки на одной прямой, С± и С2 — на другой, Dx и D2—на третьей.
Тогда для отношения объемов Vi и V2 тетраэдров AB1CiD1 и
АВ2С2Е>2 имеет место равенство
Vi АВ±- ACi- AD±
V2~AB2-AC2-AD2'
Теорема 87. Пусть Sj и S2—площади двух граней произволь¬
ного	тетраэдра,	у—величина двугранного угла	между	ними, а—длина
их общего ребра,	Ь—длина	противоположного	ребра,	d—расстояние,
а ф—угол между этими ребрами. Тогда для объема V тетраэдра
справедливы равенства
2SXS2 sin ф 1
V =— -=—abd sin	ф.
За	6	т
Пусть в тетраэдре ABCD точки Е, F, G, Н—середины ребер
АВ, ВС, CD, DA соответственно, S—площадь параллелограмма EFGH,
d—расстояние между ребрами АС и BD. Тогда объем этого тетраэдра
равен
Теорема 88. Объем V пирамиды равен
V=-iftS0,
где S0—площадь основания пирамиды, a h—ее высота. Если суще¬
ствует сфера, касающаяся основания пирамиды и продолжений боко¬
вых граней, то объем такой пирамиды есть
V —~о ro (Q ”-^о)»
408

где г о — радиус этой сферы, a Q—площадь боковой поверхности пи¬
рамиды.
Теорема 89. Объем V многогранника, описанного около сферы
радиуса г, равен
еде S—площадь поверхности этого многогранника.
В частности, все формулы теорем 88 и 89 справедливы для тет¬
раэдра.
Все проекции иа плоскости в настоящей книге предполагаются
ортогональными.
Теорема 90. Пусть плоскости а и Р пересекаются под угл'>м ф
и в плоскости а расположена фигура плсщади S. Тогда площадь про-
■ещии этой фигуры на плоскость Р равна S cos ф.
Теорема 91. Пусть а—ненулевой вектор в пространстве, а
О—произвольная точка. Тогда для любого вначения k£R множество
точек X пространства, удовлетворяющих равенству а-OX~k,. есть
плоскость.
Теорема 92. Три отрезка, соединяющие середины противопо¬
ложных ребер любого тетраэдра ABCD, пересекаются в одной точке М,
являющейся серединой' каждого из этих отрезков, причем для любой
точки Р справедливо равенство
PM=i- (РА-\-РВ-\-РС-\-Ш).
Теорема 93 (формула Эйлера) ([21]), Пусть 1—число
еершин выпуклого многогранника, т — число его ребер, а п^-число его
граней. Тогда имеет место равенство
1—т-\-п = 2.
* * *
Определение 43. Говорят, что задан граф, если, во-первых,
фиксировано некоторое множество А =^{аг; ...; а,,}, элементы кото¬
рого называются вершинами, а, во-вторых, выделено произвольное
множество пар, составленных из элементов множества А и называемых
ребрами. Граф называется ориентированным, если его ребра пред¬
ставляют собой упорядоченные пары вершин.
Примером неориентированного графа может служить граф, мно¬
жеством вершин которого является некоторая группа людей, а реб¬
рами являются пары людей, знакомых друг с другом. При этом
считается, что отношение знакомства симметрично, т. е. если некто
а знаком с Ь, то и Ь знаком с а.
При работе с графом удобно пользоваться его геометрической
моделью, которая строится так: каждой вершине графа сопоставляется
409

точка на плоскости или в пространстве, а каждому ребру—отрезок
или кривая с концами в соответствующих точках (в случае ориенти¬
рованного графа на этих линиях фиксируется направление).
Определение 44. Циклом длины- k 2 в графе с вершинами
аь ..., ап называется последовательность различных ребер вида
(а/1>	(°/а>	ala)’	ali)'
Теорема 94. В графе, имеющем ровно п вершин и п ребер, су¬
ществует по крайней мере один цикл.
Теория графов изложена в [30].
* * *
Основы комбинаторного анализа изложены в [28]. Свойства пе¬
рестановок, разбиений и сочетаний изложены также в [12], [25], [26],
[29].
Определение 45. Если два набора элементов (ах;....; а„) и
(Ьг; ...; Ьп) состоят из одних и тех же элементов и, возможно, раз¬
личаются только порядком, то один из них называется перестановкой
другого.
Теорема 95. Число перестановок набора, состоящего из п раз¬
личных элементов, равно nl
Теорема 96. Число т-элементных подмножеств п-элементного
множества (где 0<т<п) равно С™.
Число Сп называют также числом сочетаний из п по т.
Из теоремы 17 а) и теоремы 96 вытекает следующее утверждение.
Теорема 97. Число всех подмножеств п-элементного множества
равно 2".
* * *
Ниже на наивном уровне определяется, что такое- вероятность и
случайная величина. Начала теории вероятностей изложены в [25],
[26], [29].
В качестве сборника задач по «интуитивной» теории вероятностей
можно рекомендовать [27].
Определение 46. Пусть производится эксперимент, в резуль¬
тате которого из множества A={at\ ...; ап} выбирается наугад, или
случайно, один элемент. Рассматривается событие, заключающееся в
в том, что выбранный элемент является элементом подмножества
ВаА, содержащего ровно т элементов. Тогда вероятность Р (В) этого
события считается равной т/п.
Например, результатом подбрасывания монеты является выбор
элемента из множества А = («герб»; «решка»}, а вероятность выпаде¬
ния, скажем, «герба» при этом равна 1/2. Другими примерами могут
служить вытаскивание шара из урны, выбор тройки точек из мно¬
жества всевозможных троек данных точек, перестановка элементов
410

набора (точнее, выбор такой перестановки из множества всех пере¬
становок элементов данного набора) и т. д.
Если производится- серия (конечная или бесконечная) экспери¬
ментов, то результат очередного эксперимента может зависеть или не
зависеть от результатов предыдущих. В любом случае понятие ве¬
роятности определяется так, что справедливо следующее утверждение.
Теорема 98. Вероятность любого события В удовлетворяет
неравенствам 0 <: Р (В) «£ 1. Вероятность того, что событие В не
произойдет, равна 1 —Р(В). Если события В и С не могут произойти
одновременно, то вероятность того, что произойдет одно из событий
В или С, равна Р (В) + Р (С). Если событие В не зависит от события С,
то вероятность того, что произойдут оба события В и С, равна
Р(В)Р(С).
С экспериментом, описанным в определении 46, может быть свя¬
зана некоторая функция X: А —»■ R, значения которой фактически
зависят от того, какой из элементов множества А выбран в резуль¬
тате этого эксперимента. Такая функция называется случайной, а
среднее арифметическое чисел X (а^ (1=1, ..., и) называется средним
(или математическим ожиданием) этой функции. Например, если
производятся k бросаний монеты, то число выпавших в итоге «гербов»
есть случайная функция, принимающая значения О, I, ...,k взависи-
мости от результатов бросаний.
Определение 47. Случайной величиной называется величина,
все возможные значения которой образуют конечное или бесконечное
множество чисел, причем принятие ею каждого из этих значений есть
случайное событие с определенной вероятностью.
Определение 48. Пусть случайная величина X принимает
конечное множество значений xit х2 хп с вероятностями ръ
Pi, Рп соответственно. Тогда средним величины X называется
число
М(Х)=2 Pk*k-
k=i
Определение 49. Пусть случайная величина X принимает
бесконечное множество неотрицательных значений xlt х2, с ве¬
роятностями plt р2, ■ ■ • соответственно. Тогда средним величины X
называется число М (X), равное пределу
П
lim У №■
п-*а k=l
если этот предел существует.
Теорема 99. Среднее суммы случайных еечтин равно сумме их
средних
т	т
К 2 г 2 м (*')•
\i=i / i=i
411

Предположим, что из всех событий выделено некоторое событие В.
Тогда можно рассматривать вероятность любого другого события при
условии, что произошло событие В. Совсем не обязательно эта ве¬
роятность сохранится прежней (если в урне было, скажем, / белых
шаров и т черных, то вероятность вытащить наугад черный шар
равнялась т/(1-\-т), если же I черный шар вынут из урны, то эта
вероятность равна (ш—l)/(/ + m—1)).
Наравне с другими событиями можно рассматривать и событие,
состоящее в принятии случайной величиной X какого-либо из своих
значений при условии, что произошло событие б. При этом получится,
вообще говоря, другая случайная величина, обозначаемая через Хв.
Т еорема 100. Пусть два события В и С не могут произойти
одновременно, но одно из них непременно происходит. Тогда для любой
случайной величины X справедливо равенство
М (X) = Р (В).М (Хв) + р (С) М (Хс).
Приложение Д
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Й. Кюршак, Д. Нейкомм, Д. Хайош, Я. Шурани. Венгерские
математические олимпиады.— М.: Мир, 1976.
2. С. Страшевич, Е. Бровкин. Польские математические олимпиады.—
М.: Мир, 1978.
3. Е. А. Морозова, И. С. Петраков, В. А. Скворцов. Международ¬
ные математические олимпиады.— М.: Просвещение, 1976.
4. Д. О. Шклярский, П. П. Ченцов, И. М. Делом. Избранные за¬
дачи и теоремы элементарной математики; арифметика и алгебра —
М.: Наука, 1976.
5. Д. О. Шклярский, П. Н. Ченцов, И. М. Делом. Избранные за¬
дачи и теоремы планиметрии.—М.: Наука, 1967.
6. Д. О. Шклярский, П. Н. Ченцов, И. М. Дглом. Избранные за¬
дачи и теоремы элементарной математики; геометрия (стереомет¬
рия).— М.: Гостехиздат, 1954.
7. Д. О. Шклярский, П. П. Ченцов, И. М. Делом. Геометрические
неравенства и задачи на максимум и минимум.— М.: Наука, 1970.
8. Д. О. Шклярский, Н. Н. Ченцов, И. М. Дглом. Геометрические
оценки и задачи из комбинаторной геометрии.— М.: Наука, 1974.
9.	П.	П.	Коровкин. Неравенства.— М.: Наука,	1974.
10.	А.	И.	Маркушевич. Комплексные числа и	конформные отобра¬
жения.— М.: Наука, 1979.
11. Н. Н. Воробьев. Признаки делимости.— М.: Наука, 1974.
12. В. А. Успенский. Треугольник Паскаля.— М.: Наука, 1979.
13. JI. А. Калужнин. Основная теорема арифметики.— М.: Наука,
1969.
14. С. В. Фомин. Системы счисления.— М.: Наука, 1980.
15. Л. С. Понтрягин. Комплексные числа.— Квант, 1983, № 2,
с. 16-19.
16. Л. С. Понтрягин. Основная теорема алгебры.— Квант, 1982,
№ 4, с. 3 — 9.
17.	Л.	С.	Понтрягин. Обобщения чисел.— Квант,	1985, №2, с. 6—12.
18.	Л.	Д.	Савельев (отв. редактор). Олимпиады.	Алгебра. Комбина¬
торика (сборник).— Новосибирск, Наука, 1979.
412

19. О. С. Ивашев-Mt сш пн. Начала математического анализа.— М,I
Наука, 1976.
20. Л. Д. Кудрявцев. Математический анализ. Т, 1.— М.; Высшая
школа, 1981.
21. Р. Курант, Г. Роббинс. Что такое математика?—М.: Просвеще¬
ние, 1968.
22. А. А. Бухштаб. Теория чисел.— М.: Просвещение, 1966.
23. А. Г. Курош. Курс высшей алгебры.— М.: Наука, 1975.
24. Д. К. Фаддеев. Лекции по алгебре.— М.: Наука, 1984.
25. А. Н. Колмогоров, И. Г. Журбенко, А. В. Прохоров. Введение в
теорию вероятностей.— М.: Наука, 1982.
26. Б. В. Гнеденко, А. Д. Хинчин. Элементарное введение в теорию
вероятностей.—М.: Наука, 1976.
27. Ф. Мостеллер. Пятьдесят занимательных вероятностных задач с
решениями.— М.: Наука, 1985.
28.	П.	Д.	Виленкин. Популярная комбинаторика.— М.: Наука,	1975.
29.	Б.	А.	Кордемский. Математика изучает случайности.— М.:	Про¬
свещение, 1975.
30.	О.	Оре. Теория графов.—М.: Наука, 1968.
31.	И.	Ф.	Шарыгин. Задачи по геометрии: Планиметрия.— М.: На¬
ука, 1986 (Б-чка «Квант», вып. 17).
82. И. Ф. Шарыгин. Задачи по геометрии: Стереометрия—М.: Наука,
1984 (Б-чка «Квант», вып. 31).
33. В. В. Прасолов. Задачи по планиметрии. Часть 1.— М.: Наука,
1986.
34. В. В. Прасолов. Задачи по планиметрии. Часть II.— М.: Наука,
1986.
Приложение Е
СПИСОК ОБОЗНАЧЕНИЙ
0—	пустое множество
N — множество натуральных чисел
Z—множество целых чисел	‘
Z+—множество целых неотрицательных чисел
Q — множество рациональных чисел
R —множество действительных чисел
С —множество комплексных чисел
со — символ бесконечности
а£А —элемент а принадлежит множеству А
а(£А—элемент а не принадлежит множеству А
{Сх; ...; с,,} — множество, состоящее из элементов flj, ап
(Сх; ап) — строка (упорядоченный набор) элементов ах ап
{с,,}—последовательность чисел а„ при n£N или п£Z+
{о |а} —множество всех элементов а, обладающих свойством а
BczА — множество В является подмножеством множества А (оп¬
ределение 1)
A\JB—объединение множеств А и В (определение 2)
(J Ва — объединение всех множеств Ва при а £ А
ие А
Af)B — пересечение множеств А и В (определение 2)
413

f) Ва— пересечение всех множеств Ва при ag Л
аел
А\В— разность множеств Л и В (определение 3)
Ах В — (декартово) произведение множеств ЛиВ (определение 4)
[а; Ь] — отрезок числовой прямой с концами а и Ь
(а; Ь) — интервал числовой прямой с концами а и Ь
[а; Ь) — числовой промежуток {х|а<х< Ь)
(с; Ь] — числовой промежуток {х | а < х < Ь)
f: А—► В — функция f с областью определения Л и областью
значений В
— функция, обратная к функции f (определение 6)
fn — суперпозиция п функций f (определение 6)
F — (первая) производная функции f
f"—вторая производная функции f
F"—третья производная функции f
f(n>—п.я производная функции f
deg Р — степень многочлена Р
i—мнимая единица (определение 22, только в главе 6)
я—длина полуокружности радиуса 1
е—основание натуральных логарифмов (теорема 7)
1п—натуральный логарифм (теорема 7)	,
sign—функция знака (определение 10)
м — целая часть числа х (определение II)
{%} — дробная часть числа х (определение 11)
Rez—действительная часть числа г (определение 23)
Imz — мнимая часть числа г (определение 23)
| z I — модуль числа г (определение 24)
arg z—аргумент числа г (определение 25)
г — число, (комплексно) сопряженное числу г (определение 26)
max{хь *„}—наибольшее из чисел хг хп
шах {ха} — наибольшее из всех чисел ха при а£А
ие Л
п
2 XI—сумма чисел х*, ..., хп
i= 1
2 ха —сумма всех чисел ха при а
а € А
п
JJ х/—произведение чисел Xi,
i= I
Д xa—произведение всех чисел ха при а£А
Кб А
п! — факториал числа (определение 18)
Сп'—биномиальный коэффициент (определение 18)
Cx.t.c„ — запись n-значного числа в какой-либо системе счисле¬
ния (определение 17)
414

а ; b—число а делится на число Ь (определение 12)
а 5= b (mod с) — число а сравнимо с числом Ь по модулю с (опре¬
деление 16)
b (modс) — число а не сравнимо с числом b по модулю *
(определение 16)
[fli, .я„] — наименьшее общее кратное чисел  ап (оп¬
ределение 13)
(ах, ап) — наибольший общий делитель чисел ах, ап
(определение 14)
АВ — отрезок с концами А к В или его длина
АВ — прямая, проходящая через точки А и В
АВ—луч, выходящий из точки А и проходящий через точку В
АВ—дуга с концами Л и В или ее величина
ЛВС—плоскость, проходящая через точки Л, В и С
ЛВС—дуга с концами Л и С, содержащая точку В
^ Л—угол с вершиной Л или его величина
^ ЛВС—угол с вершиной В и сторонами ВА, ВС или его величина
ДЛВС—треугольник с вершинами Л, В и С
А1...Ап—многоугольник с вершинами Лх, А„
РЛ1 — периметр многоугольника М
Sfrj — площадь многоугольника М
УЛ1 — объем многогранника М
Мс = Д12 — многоугольники A4i и Л1а равны (конгруэнтны)
Mi оо М2— многоугольники Mj и М2 подобны
Л В —вектор с началом Л и конном В
|а|—длина вектора а
ab~~a-b—скалярное произведение векторов а и 6
Р(А) — вероятность события Л (определение 46)
М(Х) — среднее случайной величины X (определение 48)

Ceprefi Владимирович Конягии, Гарник Агасиевич Тоноян,
Игорь.Федорович Шарыгии, Игорь Анатольевич Копылов,
Михаил Борисович Севрюк, Михаил Леонидович Ситников,
Олег Аркадьевич Байбородин, Владимир Петрович Буричепко.
Григорий Викторович Головин, Дмитрий Олегович Орлов,
Леонид Борисович Парновский, Татьяна Анатольевна Сокова,
Инна Вячеславовна Стецснко, Владимир Викторович Титснко,
Сергей Анатольевич Филиппов
ЗАРУБЕЖНЫЕ МАТЕМАТИЧЕСКИЕ ОЛИМПИАДЫ
Под редакцией И. Н. Сергеева
ери я «Библиотечка математического кружка», выпуск 17
Редактор А. Ф. Лапко
Художественный редактор Г. At. Коровина
Технический редактор С. Я■ Шкляр
Корректор Н. Б. Румянцева
ИБ № 32455
Сдано в набор 23.12.86. Подписано к печати 30.06.87.
Формат 84X108/32. Бумага тип. №3. Гарнитура литера¬
турная. Печать высокая. Уел. печ. л. 21.84. Уел. кр.-отт.
22,05. Уч.-изд. л. 24,52.- Тираж 163000 экз. Заказ 19.
Цена 1 р. 50 к.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция
физико-математической литературы
1 17071 Москва В-71, Ленинский проспект, 15
Ордена Октябрьской Революции и ордена Трудового
Красного Знамени МПО «Первая Образцовая типография»
нм. А. А. Жданова Союзполиграфпрома при Государствен¬
ном комитете СССР по делам издательств, полиграфии и
книжной торговли. 113054 Москва М-54, Валовая, 28