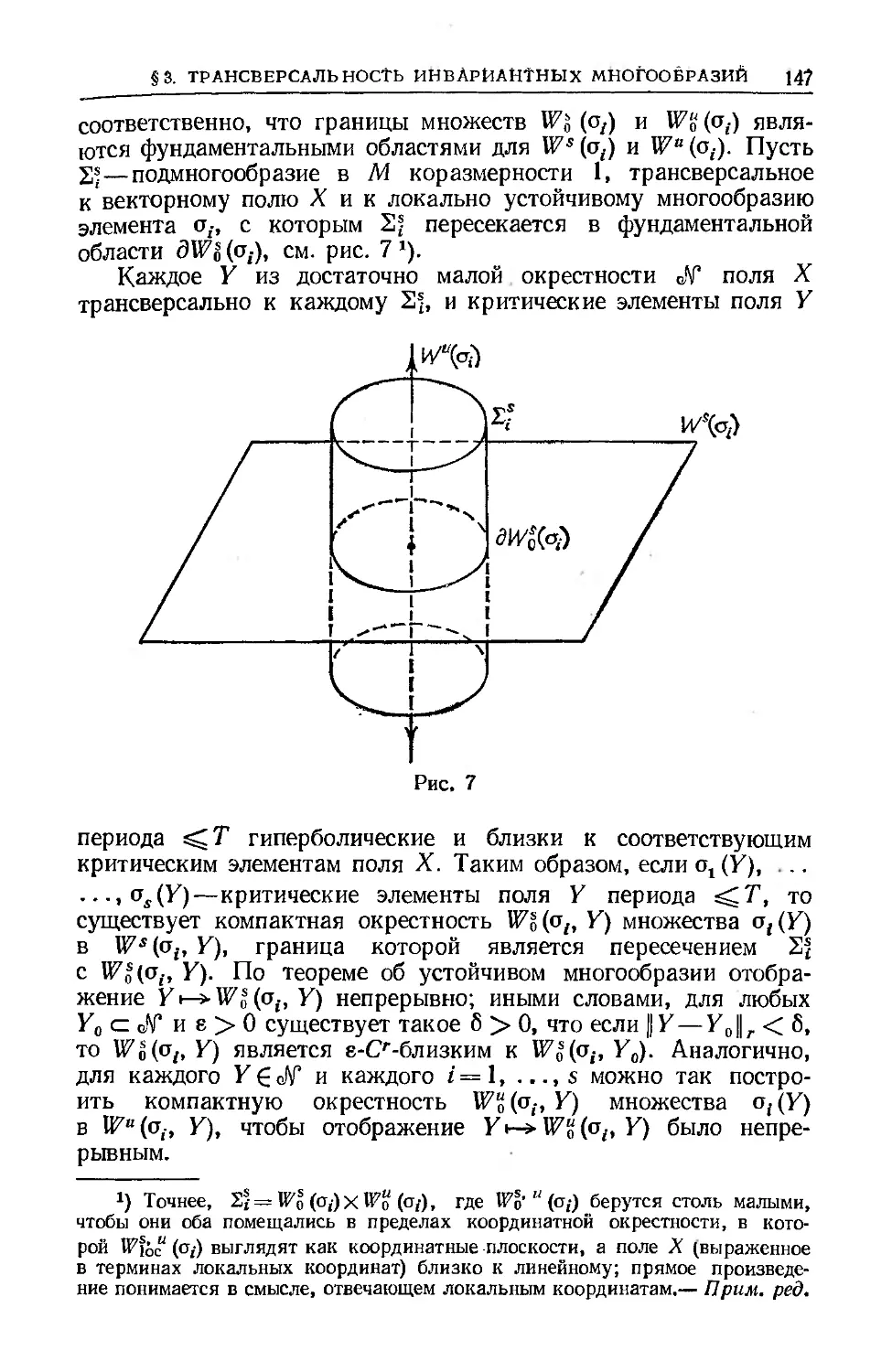
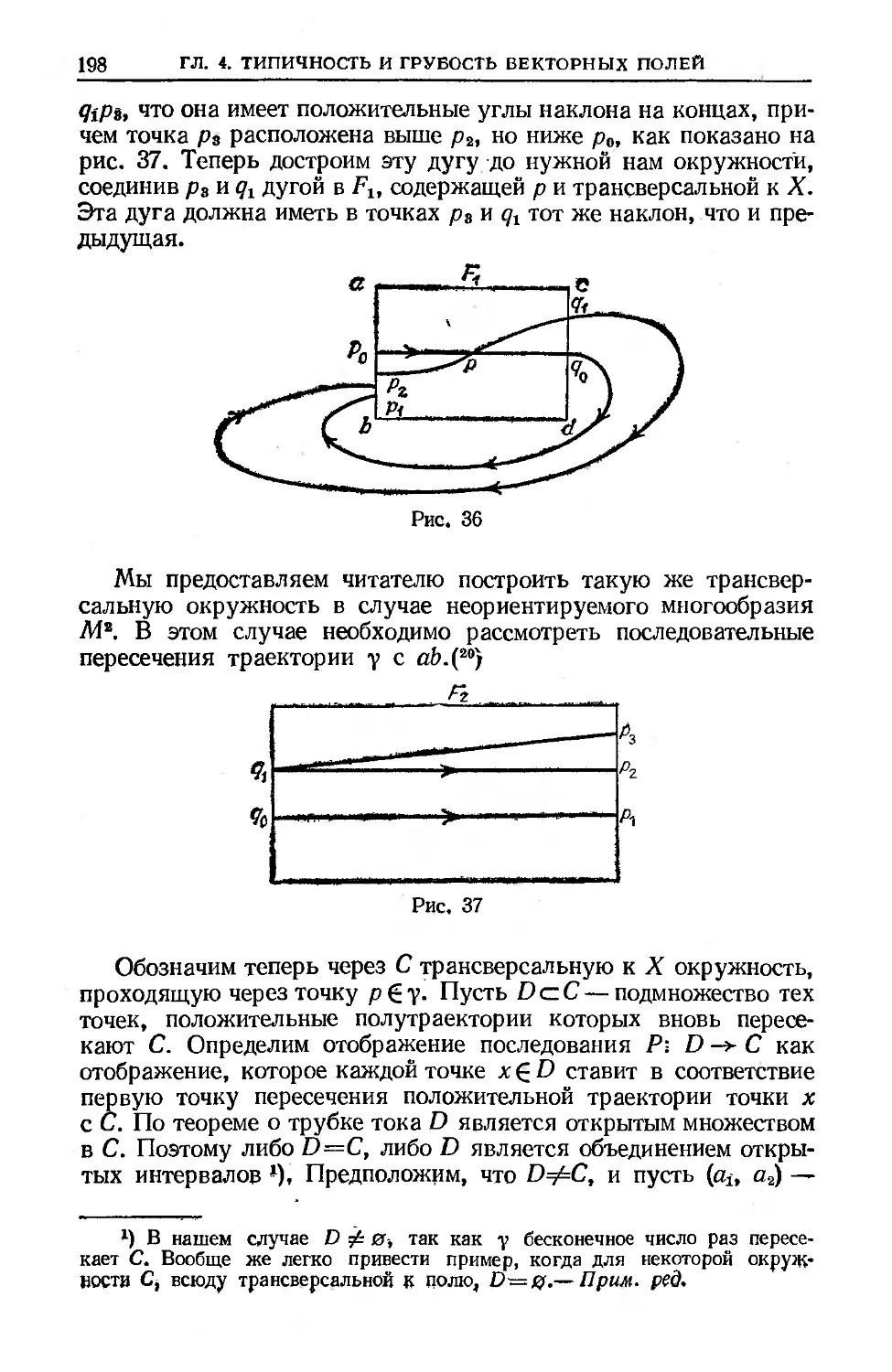
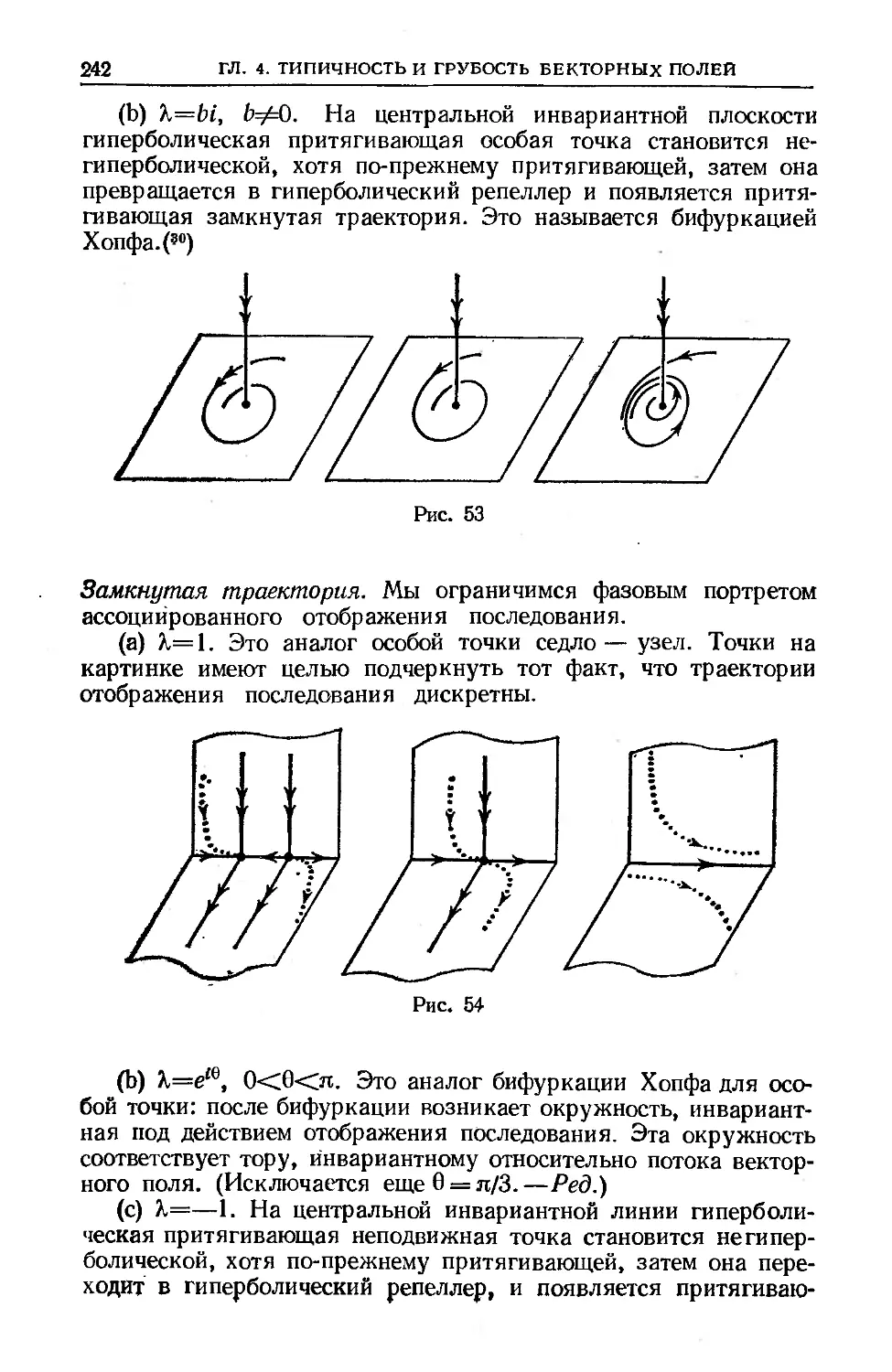
Text
R&C
JACOB PALIS, Jr.
WELINGTON DE MELO
Geometric Theory of
Dynamical Systems
An Introduction
SPRINGER-VERLAG
New York Heidelberg Berlin
1982
СОВРЕМЕННАЯ МАТЕМАТИКА
ВВОДНЫЕ КУРСЫ
Ж.ПАПИСВ.ДИМЕЛУ
ГЕОМЕТРИЧЕСКАЯ
ТЕОРИЯ
ДИНАМИЧЕСКИХ
СИСТЕМ
ВВЕДЕНИЕ
Перевод с английского
В. Н. КОЛОКОЛЬЦОВА
под редакцией и с послесловием
Д. В. АНОСОВА
МОСКВА
«МИР»
1986
ББК 22.161.6
П14
УДК 517.91
Палис Ж-, ди Мелу В.
П14 Геометрическая теория динамических систем: Введение:
Пер. с англ.—М.' Мир, 1986.—301 с, ил.
Доступное введение в теорию гладких динамических систем, написаииое
известными бразильскими математиками. В отличие от имеющихся на русском
языке книг но этой тематике она более элементарна. Изложение в иея начи-
начинается с простых понятий и доводится до более сложных, связанных с много-
многомерным фазовым пространством. Рассмотрены потоки в двумерном случае,
типичные свойства положений равновесия, замкнутые траектории.
Для математиков разных специальностей, аспирантов и студентов универ-
университетов.
1702050000-099 ББК 22.161.6
П 041 @1)-86 20"86> ч* ' 517.2
Редакция литературы по математическим наукам
© 1982 by Springer-Verlag New York Inc.
All rights reserved. Authorized trans-
translation from English language edition
published by Springer-Verlag Berlin
Heidelberg New York Tokyo
© перевод на русский язык, «Мир», 1986
ОТ АВТОРОВ
Эта книга возникла из курса лекций и семинаров, проводимых
в IMPA (Институт чистой и прикладной математики в Рио-де-
Жанейро.— Перев.) и в некоторых других институтах в Брази-
Бразилии и за границей; первый вариант текста был подготовлен для
X Бразильского математического коллоквиума. С некоторыми
дополнениями он был впоследствии издан в виде книги в бра-
бразильской математической серии Projecto Euclides, выходящей
на португальском языке. Ряд улучшений был произведен для
английского перевода.
Мы выражаем благодарность многим коллегам и студентам,
которые внесли полезные предложения и, кроме того, поощрили
нас представить эти вводные идеи по геометрической динамике.
В частности, мы благодарны Пауло Саду и особенно Алсидесу
Линсу Нето за написание части первого конспекта, а также Ан-
тони Мэннингу за английский перевод.
ОТ ИЗДАТЕЛЬСТВА
Теория гладких динамических систем—классическая область
математики, которая вступила сейчас в новый бурный период
развития. На русском языке по этой тематике имеется много
специальной литературы, но нет книги, могущей служить
введением в предмет. Предлагаемая книга, продолжающая
серию «Современная математика. Вводные курсы» призвана
заполнить этот пробел. Для ее чтения достаточно знание на-
начальных курсов анализа и дифференциальной геометрии. По-
Полезно также знакомство с самыми элементарными понятиями,
относящимися к многообразиям; соответствующие формули-
формулировки приведены в книге, но это скорее сводка для напоми-
напоминания.
С любезного согласия авторов русское издание сопровож-
сопровождается значительным числом поясняющих примечаний редактора
перевода, которые помещены как в тексте, так и в конце
книги. Ему же принадлежит послесловие, содержащее обзор
некоторых направлений теории динамических систем, не на-
нашедших отражения в книге.
ВВЕДЕНИЕ
... это качественное изучение (дифференциальных
уравнений) будет иметь первостепенный самостоя-
тельвьш интерес...
А при Пуанкаре, 1881
В этой книге мы предлагаем обзор геометрической теории
динамических систем, который является вводным, но, однако,
дает читателю представление о некоторых основных идеях, от-
относящихся к двум важным темам: грубость и типичность.
Этой теорией занимались многие математики, начиная с Пу-
Пуанкаре, Ляпунова и Биркгофа. В последние годы она была
значительно развита, и определились некоторые ее общие цели.
Более двух десятилетий прошло между двумя важными со-
событиями: работой Андронова и Понтрягина A937), где было вве-
введено основное понятие грубости, и статьями Пейксото A958—
1962), доказавшего плотность грубых векторных полей на по-
поверхностях. Затем Смейл существенно обогатил теорию. Указав,
что ее основной задачей является поиск типичных и грубых
свойств, он получил результаты и предложил проблемы, имею-
имеющие большое значение в этом контексте. В это же время Хартман
и Гробман показали, что локальная грубость является типичным
свойством. Вскоре после этого Купка и Смейл предприняли
успешное изучение задачи о периодических орбитах.
Мы намереваемся дать почувствовать читателю вкус этой
теории, разобрав ряд примеров и дав систематическое доказа-
доказательство теоремы об устойчивом многообразии и теоремы Харт-
мана — Гробмана (гл. 2), теорем Купки — Смейла(гл. 3) и Пейк-
Пейксото (гл. 4). Некоторые из наших доказательств проще ориги-
оригинальных и допускают важные обобщения. В гл. 4 мы также об-
обсуждаем основные примеры грубых диффеоморфизмов с бес-
бесконечным числом периодических траекторий. Мы приводим
общие результаты о грубости динамических систем и делаем
некоторые краткие замечания по другим темам, как, например,
теория бифуркаций. В приложении к гл. 4 мы вводим важное
понятие 'исла вращения и применяем его для описания краси-
красивого примера потока, предложенного Черри.
Для чтения этой книги необходимо предварительно ознако-
ознакомиться лишь с основными курсами по дифференциальным урав-
уравнениям и гладким многообразиям, причем самые нужные нам ре-
результаты этих курсов мы собрали в гл. 1. В гл. 2 требуется лишь
аппарат линейной алгебры, теорема о неявной функции и теорема
ВВЕДЕНИЕ 7
о сжимающих отображениях в банаховых пространствах. Гла-
Глава 3 наименее элементарна, но заведомо не самая трудная. Там
мы систематически используем теоремы трансверсальности. Фор-
Формально гл. 4 зависит от гл. 3, хотя мы используем теорему Куп-
ки — Смейла в наиболее элементарном частном случае двумер-
двумерных поверхностей.
Много важных результатов и различных направлений иссле-
исследований возникло из доказанных здесь теорем. Краткий (и не-
неполный) обзор этих результатов представлен в последней части
книги. Мы надеемся, что эта книга даст читателю начальное
представление о теории и облегчит ему ознакомление с современ-
современной литературой.
Жакоб Палис мл,
Велингтон ди Мелу
Рио-де-Жанейро, сентябрь 1981
СПИСОК ОБОЗНАЧЕНИЙ
R вещественная прямая
R" евклидово n-мерное пространство
С" комплексное n-мерное пространство
С" класс гладкости отображений, имеющих п непре-
непрерывных производных
С°° класс гладкости бесконечно дифференцируемых
отображений
Сы класс гладкости вещественно-аналитических ото-
отображений
df(p), dfp производная отображения / в точке р
или Df (p)
(д/dt) f, df/dt частная производная
D2f(x, у) частная производная по второму аргументу
dnf(p) п-я производная функции / в точке р
L(Rn, Rm) пространство линейных отображений
Lr(Um; Rft) пространство r-линейных отображений
|| | норма
go f композиция отображений g и f
0 пустое множество
/1М ограничение отображения / на подмножество М
U замыкание множества U
ТМр касательное пространство к М в р
ТМ касательное расслоение многообразия М
ЖГ{М) пространство С-векторных полей на М
f«X образ поля X при отображении /
Xt диффеоморфизм, индуцированный потоком по-
поля X в момент времени t
в(р) траектория точки р
со(р) со-предельное множество точки р
а(р) а-предельное множество точки р
СПИСОК ОБОЗНАЧЕНИЯ g
Sn единичная n-мерная сфера
Т2 двумерный тор
grad/ градиентное поле функции /
\f интеграл /
idM тождественное отображение М
<, > риманова метрика
<, >р скалярное произведение в касательном прост-
пространстве точки р, порожденное римановой мет
рикой
С(М, N) пространство С-отображений
II II, С'-норма
Diifr(M) пространство С-диффеоморфизмов
ffaS f трансверсально к S
6Х (р) траектория поля X, проходящая через точку р
6+(р) положительная полутраектория, начинающаяся
в точке р
a' (t) производная в / отображения интервала
Т" n-мерный тор
jg^R") пространство линейных операторов в R"
3 (С") комплексное векторное пространство линейных
операторов в С"
Lk L0L0L0...0L
Exp(L), eL экспонента L
GL(R") группа обратимых линейных операторов в R"
#(Rn) пространство гиперболических линейных изо-
изоморфизмов в R"
ffl(Rn) пространство гиперболических линейных век-
горных полей в R"
Sp(L) спектр L
$0 пространство векторных полей, у которых все
особые точки простые
det(Л) определитель А
$4 пространство векторных полей, у которых все
особые точки гиперболические
Go пространство диффеоморфизмов, у которых все
неподвижные точки элементарны
Gt пространство диффеоморфизмов, у которых все
неподвижные точки гиперболические
Cl(Rm) пространство непрерывных ограниченных ото-
отображений из Rm в Rm
10 СПИСОК ОБОЗНАЧЕНИЙ
dim Ж размерность М
W*(p) устойчивое многообразие точки р
Wa(p) неустойчивое многообразие точки р
№| (р) устойчивое многообразие размера Р
№р(/?) неустойчивое многообразие размера Р
Wfoc @) локально устойчивое многообразие
№"ос @) локально неустойчивое многообразие
<§1 з пространство векторных полей из Ъ^, все замк-
замкнутые траектории которых гиперболичны
Зс(Т) пространство векторных полей из $1г у кото-
которых все замкнутые траектории периода ^7"
гиперболичны
La (X) объединение а-предельных множеств траекторий
поля X
La, (X) объединение ш-преде*льных множеств траекторий
поля X
Q(X) множество неблуждающих точек поля X
М—S множество векторных полей Морса—Смейла
дМ граница М
int А внутренность множества А
От редактора перевода. При ссылках на литературу, приве-
приведенную в конце книги, указывается номер цитируемой работы
в квадратных скобках. Ссылки же вида (*) относятся к моим
примечаниям, вынесенным в конец книги. Знак | указывает
на конец доказательства.
Глава 1
ГЛАДКИЕ МНОГООБРАЗИЯ
И ВЕКТОРНЫЕ ПОЛЯ
В этой главе приводятся понятия и основные факты, необ-
необходимые для понимания дальнейшего.
Прежде всего мы излагаем некоторые классические резуль-
результаты из анализа в R", из теории обыкновенных дифференци-
дифференциальных уравнений и подмногообразий в R". Затем мы опреде-
определяем векторные поля на многообразиях и применяем к этому
случаю локальные результаты теории дифференциальных урав-
уравнений в R". Мы начинаем качественное изучение векторных
полей с понятия а- и со-предельных множеств и доказываем
важную теорему Пуанкаре — Бендиксона.
В § 2 мы определяем Сг-топологию на множестве дифферен-
дифференцируемых отображений многообразий. Мы показываем, что
множество Сг-отображений с Сг-топологией является сепарабель-
ным пространством Бэра и что С-отображения плотны в нем.
Отсюда мы получаем топологии с теми же свойствами для прост-
пространств векторных полей и диффеоморфизмов.
Раздел 3 посвящен теореме трансверсальности, которую мы
часто будем использовать.
В заключение этой главы мы устанавливаем общие цели
геометрической или качественной теории динамических систем.
В частности, мы обсуждаем понятия топологической эквивалент-
эквивалентности и грубости для дифференциальных' уравнений, определен-
определенных на подмногообразиях в R".
§ 0. АНАЛИЗ В R." И ГЛАДКИЕ МНОГООБРАЗИЯ
В этом разделе мы изложим некоторые понятия и основные
результаты анализа в R", теории дифференциальных уравне-
уравнений и гладких многообразий. Доказательства собранных здесь
фактов из анализа в R" можно найти в [46], [48]; из теории
дифференциальных уравнений—в очень рекомендуемых нами
вводных курсах [4], [41], [116] или в более продвинутых [33],
[35] и [47J; из теории гладких многообразий—в [29], [38]
и [49].
Пусть /: UczR —-> Rft—отображение, определенное на откры-
открытом подмножестве U пространства Rm. Будем говорить, что /
12 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
дифференцируемо в точке р из U, если существует такой линей-
линейный оператор Т: R'" —-> Rfc, что для малых v f(p-+v) = f{p) +
+ Т (v) + R (v), где lim (R (»)/IMI) = 0. Линейное отображение Т
называется производной отображения f в точке р и обозначается
df (p) или иногда dfp или Df(p). Из существования производ-
производной f в р следует, в частности, непрерывность / в р. Если /
дифференцируемо в каждой точке из U, то мы имеем отобра-
отображение df: U —+L(Rm, Rk), которое каждой точке рg U сопо-
сопоставляет производную / в р. Здесь L(Rm, Rk) обозначает век-
векторное пространство линейных операторов из R" в Е' с нор-
нормой |T| = sup {|Ту|: 1^11=1}. Если df непрерывно, то мы
говорим, что / принадлежит классу С в (/ (или / класса
С1, /—О-отображение). Хорошо известно, что / принадлежит
классу С1 тогда и только тогда, когда частные производные
координатных функций отображения /, т. е. df'/dXj-: U —> К,
существуют и непрерывны. Матрицей df(p) по отношению
к каноническим базисам Rm и Rk является [(df'/dx^p)]. Ана-
Аналогично мы определяем d2/(p) как производную df в р. Таким
образом, &f(p) принадлежит пространству L(Rm, L(Rm, R.k)),
которое изоморфно пространству L2(Km, Rk) билинейных ото-
отображений из RmxRm в IR*. Норма, индуцируемая в L2(Rm, Rft)
этим изоморфизмом, есть JB| = sup{j|B(«, v)\\: |и|| = ||у||= 1}.
Мы говорим, что f принадлежит классу С2 в и, если d2f: U —>¦
*-+L2(Rm, Rfr) непрерывно. По индукции мы определяем drf(p)
как производную отображения dr~x/ в точке р. Следовательно,
drf (p)(tLr (RCT, Rft), где Lr(R.m, Rft) — пространство г-линейных
отображений с нормой
||С|= sup{||С(Vl vr)l: Ы=... =1^11=1}.
Будем говорить, что / принадлежит классу С в U (или /
класса Cr, f—Сг-отображение), если отображение drf: U—>¦
—> Lr (Rm, Rk) непрерывно. И наконец, / принадлежит классу С°°
в U (/ класса С°°, /—С°°-отображение), если / класса Сг для
всех г^О. Отметим, что / принадлежит классу Сг тогда
и только тогда, когда все частные производные до порядка г
координатных функций / существуют и непрерывны. Пусть
U, V—открытые подмножества в Rm и /: U —> V—сюръектив-
ное отображение класса Сг. Отображение / называется диф-
диффеоморфизмом класса Сг, если существует такое отображение
g: V—>U класса Сг, что gof является тождественным пре-
преобразованием U.
0.0. Предложение. Пусть UczRm—открытое множество и
/„: U—*Rk—последовательность отображений класса С1. Пред-
Предположим, что /„ сходится поточечно к /: U —> R* и что после-
§ 0. АНАЛИЗ В Ri И ГЛАДКИЕ МНОГООБРАЗИЯ 13
довательность dfn сходится равномерно к g: U—+L(Rm, Rft).
Тогда f принадлежит классу С1 и df — g. |
0.1. Предложение (цепное правило). Пусть Uc:Rm и VcR." —
открытые множества. Если /: U —»¦ R" дифференцируемо в p?U,
f (U)czVug\ V—*Rk дифференцируемо вq=f (p), mog о fi U —* R*
дифференцируемо ери
Следствие 1. Если fug принадлежат классу Cr, mo go f при-
принадлежит классу Cr. |
Следствие 2. Если /• U —> Rft дифференцируемо в р g U
и a: (— 1, I)—* U —такая кривая, что а@) = р и (d/dt) a@)=v,
то /оа—кривая, дифференцируемая в нуле и (d/dt)(f оа)@)—
0.2. Теорема (об обратной функции). Пусть /: UсRm —* Rffl
принадлежит классу С, r^l. Если df(p): Rra—>-Rm—изомор-
Rra—>-Rm—изоморфизм, то f является локальным диффеоморфизмом в p?U
класса СГ; это означает, что существуют такие окрестности
VczU точки р и WcRm точки f(p) и такое С-отображение
g: W—*V, что gof = lv и fog=lw, где lyu Iw—тождест-
Iw—тождественные отображения V и W соответственно. |
0.3. Теорема (о неявной функции). Пусть f/cRraxR"—откры-
f/cRraxR"—открытое множество и /: U—>R" принадлежит классу С, г^1.
Пусть гв = (хв, yo)kU " c = /(zo)- Предположим, что частная
производная по второму аргументу DJ(z0): R"—»-R"—изомор-
R"—»-R"—изоморфизм. Тогда существуют открытые множества VcR, содер-
содержащее х0, и WeU, содержащее г„, такие что для каждого
x?V существует единственное ?(х)?R" с (х, ?(д;)) ? W
и f(x, ?(-*:)) = с. Отображение ?: V—>R", определенное таким
образом, принадлежит классу С, и его производные даются
формулой
Замечание. Эти теоремы переносятся на произвольные банаховы
пространстваа).
0.4. Теорема (локальная форма для иммерсий). Пусть
открыто и отображение /¦ U —> Rm+n класса Сг, г ^ 1. Предпо-
Предположим, что для некоторого xo?U производная df (jc0): Rm —»- Rm+»
инъективна. Тогда существуют окрестности VczU точки
хя, WcR" начала координат и ZcRra+" точки f(x0) и Сг-диф~
1) Это используется в дальнейшем, поэтому укажу, что банаховы
варианты этих (нли эквивалентных) теорем имеются в [135, 139].— Прим. ред.
14 ГЛ. !. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
феоморфизм hi Z—*VxW, такие что hof(x) = (x, 0) при всех
V
0.5. Теорема (локальная форма для субмерсий). Пусть UczR.m+n
открыто и отображение /• U—>R" класса Сг, г > 1. Предпо-
Предположим, что для некоторого zo? U производная df (z0) сюръективна.
Тогда существуют окрестности ZcU точки z0, W с IR" точки
c = /(zo) u VczR. начала координат и С-диффеоморфизм
h\ Vx W —*Z, такие что] о h(x, w)—wnpu всех x?V uw? W. |
Пусть /¦ UcR.m—>• R"—Сг-отображение, г~^\. Точка x?U
называется регулярной, если df(x) сюръективно; в противном
случае х называется критической точкой. Точка cgR"—регу-
cgR"—регулярное значение, если каждая х5/~х(с) является регулярной
точкой; в противном случае с—критическое значение. Подмно-
Подмножество в К" называется остаточным, если оно содержит счет-
счетное пересечение открытых плотных подмножеств. По теореме
Бэра каждое остаточное подмножество в R" плотно.
0.6. Теорема (Сард [64]). Если /i UcRm—»R" принадлежит
классу С°°, то множество регулярных значений является оста-
остаточным в R". |
Мы должны здесь отметить, что если /~1(с) = 0, то с—регу-
с—регулярное значение. Для существования регулярной точки x?U
необходимо, чтобы т^п. Если т < п, то все точки U крити-
критические, и, следовательно, f(U)—«тощее» множество в R", т. е.
Rn\f (U) является остаточным.
Мы намереваемся теперь изложить некоторые основные
результаты из теории дифференциальных уравнений. Вектор-
Векторным полем на открытом множестве f/cRm называется отобра-
отображение X; U —* R". Мы будем рассматривать лишь поля класса
Сг, г ^ 1. Интегральной кривой поля X, проходящей через
точку p?U, называется такое дифференцируемое отображение
a: I—+U, где /—открытый интервал, содержащий 0, что
а@) = р и а' (/) = Х(а(/)) при всех fg/. Мы говорим, что а
есть решение дифференциального уравнения dx/dt=X (x) с началь-
начальным условием х@) = р.
0.7. Теорема (существования и единственности решения). Пусть
X—векторное поле класса Сг, г~^\ на открытом множестве
UczR.m, и пусть p?U. Тогда существует интегральная кри-
кривая a: I—+U поля X с а@) — р. Если p: J—+U—другая ин-
интегральная кривая поля X с C @) == /?, то a(t) = $(t) при всех
t?luJ. I
Локальным потоком поля X в точке р € U называется та-
такое отображение <р: (—е, e)xVp—* ?/, где Vp является окре-
окрестностью р в U, что для каждого q?Vp отображение
§ 0. АНАЛИЗ В R« И ГЛАДКИЕ МНОГООБРАЗИЯ 15
Ф9! (—е, е) —»¦ U, определенное равенством ф9@ = ф(^> <?). задает
интегральную кривую, проходящую через q. Иными словами,
ф@, <?) = <? и (d/dt)<p(t, q) = X{(p(t, <?)) при всех (t, q)G
€(—е, e)xVp.
0.8. Теорема. Пусть X—векторное поле класса Сг в U, r^l.
Для всех p(tU существует локальный поток ф.! (—е, е) х
X Vp —>¦ U, принадлежащий классу Сг. Кроме того,
q) = DX(<p(t, q))-D24,(t, q)
и D2y@, q) является тождественным отображением Rm, еде
Dx и D$ обозначают частные производные по первому и вто-
второму аргументам соответственно. |
Можно рассматривать также векторные поля, зависящие
от параметра, и зависимость их решений от параметра. Пусть
Е—банахово пространство и F: ExU-+Rm—отображение
класса С, г~^\. Для каждого е?Е отображение^- LJ—j-Rra,
определяемое равенством Fe(p) = F(e, p), является векторным
полем на U класса Сг. Следующая теорема показывает, что
решения этого поля Fe зависят непрерывно от параметра е ? Е.
0.9. Теорема. Для каждого е?Е и p?U существуют такие
окрестности W точки е в Е и V точки р в U и такое
С-отображение ср: (—е, e)xVxW—>¦ ?/, что
Ф(О, q, %) = q,
q, Я)=Р(Я, ф(*. q, Ц)
при всех (t, q, K)€(—e, e)xVxW. |
Теперь мы введем понятие гладкого многообразия. Для
упрощения изложения мы определим многообразия как под-
подмножества в R*. В конце этого параграфа мы обсудим абст-
абстрактное определение.
Пусть М — подмножество евклидового пространства R*. Мы
будем пользоваться индуцированной топологией на М; иными
словами, AczM считается открытьш, если существует такое откры-
открытое множество А' сR*, что A = A'{)M.Mc:R.li называется гладким
многообразием размерности т, если для каждой точки р?М
существуют такие окрестность UaM точки р и гомеоморфизм
х: 0 —»- UB, где UQ является открытым подмножеством в Rm,
что обратный гомеоморфизм лГ: [/0-+t/cR* является иммер-
иммерсией класса С°°, т.е. для каждой u^U0 производная dx~l(u):
Rm —*¦ R* инъективна. В этом случае U называется координат-
координатной окрестностью точки р, а пара (х, U)—локальной картой
возле р. Если упомянутый выше гомеоморфизм лГ1 принадле-
принадлежит классу С, мы говорим, что М—многообразие класса. С.
16
ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
То, что мы назвали гладким многообразием, есть многообра-
многообразие класса С". Из локальной формы для иммерсии 0.4. следует,
что если (х, U)—локальная карта возле р, то существуют
такие окрестности А точки р в R*, V точки х(р) и W начала
координат в Rft~m и такой диффеоморфизм h; А —*¦ V X W, что
h (q) = (х (q), 0) при всех q ? А П М. В частности, локальная
Л/CR*
Рис. 1
карта—это ограничение С-отображения открытого подмноже-
подмножества R* в R. (рис. 1). Из этого замечания мы получаем сле-
следующее предложение.
0.10. Предложение. Пусть xi U—>Rm и у\ V—<-Rm—локаль-
V—<-Rm—локальные карты в М. Если U[)V=0, то замена координат
yox~li х (U f]V)—*у (U f]V) является С°°-диффеоморфизмом
(рис. 2). |
Теперь мы определим дифференцируемые отображения между
многообразиями. Пусть Мт и N"—многообразия и /: Мт—>
—>¦ N"—отображение. Мы говорим, что / принадлежит классу
СТ, если для каждой точки р g M существуют такие локаль-
локальные карты х: U—*Rm возле р и yt V—>-R." возле f(p), что
f(U)cV и у о fo x-1; x(U)—+y(V)—отображение класса С.
Поскольку замена координат принадлежит классу С°°, это опре-
определение не зависит от выбора карт.
Рассмотрим дифференцируемую кривую а: (—е, е)—j-MctR*
с а@) = /7. Легко видеть, что а дифференцируемо в соответ-
соответствии с данным выше определением тогда и только тогда, когда
§0. АНАЛИЗ В R« И ГЛАДКИЕ МНОГООБРАЗИЯ
17
а дифференцируемо как кривая в Rk. Следовательно, существует
касательный вектор (da/dt) @) = а' @). Множество векторов,
касательных ко всем таким кривым а, называется касательным
пространством- к М в р и обозначается ТМр. Рассмотрим ло-
локальную карту к: U —* R.m, х (р) = 0. Легко видеть, что образ
производной dx~* @) совпадает с ТМр. Таким образом, ТМр
является векторным пространством размерности т.
x(UC\V)
У {Uf\ V)
Рис. 2
Пусть /; М —»¦ N—дифференцируемое отображение и
v^TMp, p?M. Рассмотрим дифференцируемую кривую
а: (—е, е)—>¦ М с а@) = р и а'@) = у. Тогда/о а- (—е, е) —*
—*¦ N—дифференцируемая кривая, так что мы можем опреде-
определить df [p) v = (d/dt) (/ о а) @). Это определение не зависит от
кривой а.
Отображение df(p): TMp-+TNf(P) линейно и называется
производной f в точке р.
Так как гладкие многообразия устроены локально как от-
открытые подмножества в евклидовых пространствах, все тео-
теоремы из анализа, которые мы перечислили ранее, распростра-
распространяются на многообразия.
0.11. Предложение (цепное правило). Пусть /: M—+N и
g: N —»- Р—отображения класса С гладких многообразий. Тогда
go f: M—+P принадлежит классу С и d (g о /) (р) = dg (/ (/?)) о
odf(p). I
Отображение /: М —»- N называется С-диффеоморфизмом,
если оно принадлежит классу С и имеет обратное того же
класса. В этом случае для любого р?М отображение
df(p): TMp—^TNup)—изоморфизм с обратным df~1(f(p)).
В частности, М и N имеют одинаковую размерность. Отобра-
Отображение f:M-^N называется локальным диффеоморфизмом
в р?М, если существуют такие окрестности U (р)сМ и
18
ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
V(f(p))c:N, что ограничение / на U является диффеоморфиз-
диффеоморфизмом U на V.
0.12. Предложение (об обратной функции). Если /: М—* N —
отображение класса С, г^\, и df(p)—изоморфизм для не-
некоторого р?М, то f—локальный диффеоморфизм класса Сг в р.
Рассмотрим теперь подмножество S многообразия М. S на-
называется подмногообразием М класса Сг и размерности s, если
для любого р ? S существуют такие
открытые множества U с М, содержа-
содержащее р, VcR.s, содержащее 0, WczRm~s,
содержащее 0, и такой С-диффео-
С-диффеоморфизм ф: U—у V х W, что ф (S Л U)=
= Ух{0} (рис. 3).
Заметим, что Кй является глад-
гладким многообразием и что если McRk—
многообразие (в смысле данного выше
определения), то М — подмногообра-
подмногообразие в Кй. Подмногообразия много-
многообразия McRk—это те подмногооб-
подмногообразия R*, которые содержатся в М.
0.13. Предложение (локальная форма
для иммерсий). Пусть f:Mm —* Nm+n—
отображение класса Cr, r^l, и
р?М — точка, для которой df(p)
инъективно. Тогда существуют такие
окрестности U (p), V(f(p)), ?/0@) в Rm и Уо@) в R" и такие
диффеоморфизмы q>: U —> 00, я]): V —¦ Uox Vo, что^ о / о ф (х) =
= (*, 0). I
Сг-отображение f: M—+N называется иммерсией, если df(p)
инъективно при всех р?М. Инъективная иммерсия f: M—+N
Рис. 3
Рис. 4
называется вложением, если /: М—* f(M)cN—гомеоморфизм,
где / (М) наделено индуцированной топологией. В этом случае
f(M)—подмногообразие в N. Если f: M—+N является лишь
инъективной иммерсией, мы назовем / (М) иммерсированным
подмногообразием. На рис 4 приведены примеры многообра-
многообразий, которые иммерсированы, до не вложены.
§ 0. АНАЛИЗ В К" И ГЛАДКИЕ МНОГООБРАЗИЯ 19
0.14. Предложение (локальная форма для субмерсий). Пусть
f: Мт+п —»• N"—отображение класса С, г ^ 1, и р ? М—точка,
для которой df(p) сюръективно. Тогда существуют такие ок-
окрестности U(p), V{f(p)), t/0@) в Rm и V0@) в R" и такие
диффеоморфизмы ф! U —- Uux Vo, -ф: V —>¦ Vo, что ty о f о
оф-х(д;, у) = у. |
Точка q ? N называется регулярным значением отображения
/: Мт —г N", где / класса С, г~^ 1, если для всех тех р?М,'
для которых f{p) = q, отображение df{p) сюръективно. Из по-
последнего предложения следует, что f~l (q) является С-подмно-
гообразием М размерности т—п.
0.15. Предложение (Сард). Пусть f\ M —»- N—отображение
класса С". Тогда множество регулярных значений f является
остаточным: в частности, оно плотно в N.
Доказательство предложения 0.15 получается из теоремы
Сарда с использованием локальных карт и того факта, что
каждое открытое покрытие многообразия допускает счетное
подпокрытие. |
Заметим, что если М компактно, то множество регулярных
значений f: M —>¦ N открыто и плотно в N.
Рассмотрим счетное покрытие {Uп) многообразия открытыми
множествами. Это покрытие называется локально конечным,
если для любого р g M существует окрестность V точки р, ко-
которая пересекается лишь с конечным числом элементов покры-
покрытия. Разбиением единицы, подчиненным покрытию \И„\, назы-
называется счетный набор {фп} таких неотрицательных вещественных
функций класса С°°, что:
а) для каждого индекса п носитель фп содержится в Un;
напомним, что носителем фп называется замыкание множества
точек положительности Чрп;
б) 2«Ф« (Р) = 1 Для всех р g M.
0.16. Предложение. Для любого локально конечного счетного
покрытия многообразия М существует подчиненное ему разбие-
разбиение единицы. ¦ |
Следствие 1. Пусть К а М-—замкнутое подмножество. Тогда
существует такое отображение /: М —>¦ R класса С°°, что
П@) = К I
Следствие 2. Пусть f: M—+RS—отображение класса Сг, где
McrR*—многообразие, являющееся замкнутым подмножеством
Rft. Тогда существует такое С-отображение }: Rft —>- Rs, что
I\M f I
20 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
Из этого предложения следует, что если даны открытые
множества U и V в М с UcV, то существует такая С°°-веще-
ственнозначная функция ц>^0, что ф = 1 на U и ф = 0 на
М\У. Эта функция называется «шапочкой».
Теперь мы определим касательное расслоение ТМ многооб-
многообразия. Mm<=Rk. Положим ГУМ = {(р, v)€RkxR.k:p€M,v€TMp\.
Снабдим ТМ индуцированной топологией как подмножество в
RftxRft; тогда естественная проекция л: ТМ—>¦ М, л(р, v) = p
непрерывна. Покажем, что ТМ является гладким многообра-
многообразием и л принадлежит классу С°°. Пусть х: U—>Rm—локаль-
U—>Rm—локальная карта для М. Определим отображение Тх: л'1 (U) —*¦ Rm x Rm
формулой Тх(р, v) — (x(p), dx(p)v). Легко видеть, что
(Тх, п~* (U))— локальная карта для ТМ и, следовательно,
TMcRkxR.k — многообразие Заметим, что выражение для л
в терминах локальных карт (Тх, л'1^))—это просто естест-
естественная проекция К^хК на первый сомножитель; таким обра-
образом, л—отображение класса С°°. Легко также видеть, что если
/: М —г- N принадлежит классу Cr+1, то df: ТМ —>- TN,
df(p, v) = (f(p), df(p)v) принадлежит классу Сг.
Как мы отметили ранее, существует абстрактное определе-
определение многообразий, которое является более общим, чем приве-
приведенное нами. Пусть М — хаусдорфово топологическое прост-
пространство со счетной базой. Локальной картой в /I называется
пара (х, U), где UcM—открытое подмножество и х: U—>¦
—>-UBcR.m—гомеоморфизм на открытое подмножество UocRm.
Будем говорить, что U—параметризованная окрестность в М.
Если (х, U) и (у, V) — локальные карты в М с U[\Уф0, то
замена координат
уох-1: x(U[]V)-*y(Uf]V)
является гомеоморфизмом. Гладким многообразием класса С,
г^1, называется топологическое пространство, снабженное
таким семейством локальных карт, что а) параметризованные
окрестности покрывают М и б) замены координат являются
Сг-диффеоморфизмами. Такое семейство локальных карт назы-
называется Сг-атласом для М.
Используя локальные карты, мы можем определить диффе-
ренцируемость отображений между такими многообразиями
аналогично тому, как мы делали это раньше. В частности,
кривая а: (—е, е) —¦ М дифференцируема, если отображение
л: о а: (—е, e)-^-Rm дифференцируемо, где (х, U)—локальная
карта с а(—е, e)cU. Касательный вектор к а в р = а@)
определяется как множество дифференцируемых кривых
р: (—е, е)-*М, таких, что Р(О) = р и d(xo P)@) = d(xo a)@).
Это определение не зависит от локальной карты (х, U). Каса-
§ 0. АНАЛИЗ В R" И ГЛАДКИЕ МНОГООБРАЗИЯ 21
тельное пространство ТМ„ к М в р—это множество касатель-
касательных векторов ко всем дифференцируемым кривым, проходящим
через р. Отсюда следует, что ТМр обладает естественной струк-
структурой m-мерного векторного пространства. Если /: М —*¦ N —
дифференцируемое отображение с /(/?) = q, то мы определяем
df(p): TMp—*TNq как отображение, которое переводит каса-
касательный вектор в р к кривой а: (—е, е) —*- М в касательный
вектор в q к кривой / о а: (—е, е) —¦ N. Легко видеть, что
это определение не зависит от выбора кривой а и что . df (p)
линейно. Отображение /: М —>¦ N называется иммерсией, если
df(p) инъективно при всех р?М. Вложением называется инъек-
тивная иммерсия f: M —>¦ N, для которой существует непре-
непрерывное обратное отображение/: f(M)cN—>M. Если f: M —*-
—> Rk—вложение класса С°°, то f(M)aRk—подмногообразие в
К* в смысле определения, данного ранее1).
Следующая теорема устанавливает соответствие между аб-
абстрактным определением многообразия и определением подмно-
подмногообразия в евклидовом пространстве.
0.17. Теорема (Уитни). Если N1—гладкое многообразие размер-
размерности т, то существует собственное вложение f: M—+ R2m+1. |
Пусть М — гладкое многообразие и SczM—подмногообра-
SczM—подмногообразие. Трубчатой окрестностью S называется пара (У, я), где
V—окрестность S в М и п:- V—-S—такая субмерсия класса
С°°, что п (р) = р для S
0.18. Теорема. Каждое подмногообразие ScM имеет трубча-
трубчатую окрестность. |
И наконец, каждое многообразие класса Cr, r^l, можно
естественным образом рассматривать как многообразие класса С°°.
0.19. Теорема (Уитни). Пусть М—многообразие класса С,
/•^1. Тогда существует такое С-вложение f: M—*Rim+1, что
f(M)—С"-подмногообразие в Rim+1, являющееся замкнутым
подмножеством R2m+1. I
По теореме 0.17 этот результат эквивалентен следующему:
если А—Сг-атлас на М, то существует такой С°°-атлас Л на
М, что если (х, U) ? Л и (х, О)?А с 11Г\Оф0, то хох~х
и хох~х принадлежит классу Сг
г
1) В дальнейшем кое-где встречаются также многообразия с краем, для
которых тоже имеются понятия гладкого отображения, касательного вектора
и т. д. Их наглядный смысл достаточно очевиден, а необходимые детали
можно найти в соответствующих учебниках, например в 38].— Прим. ред.
22 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
§ 1. ВЕКТОРНЫЕ ПОЛЯ НА МНОГООБРАЗИЯХ
Приступим теперь к качественному изучению дифференци-
дифференциальных уравнений. Так как при этом важны одновременно и
локальные, и глобальные аспекты, естественно рассматривать
такие уравнения на гладких многообразиях. Один из первых
основополагающих результатов, который носит глобальный ха-
характер,—это теорема Пуанкаре—Бендиксона, которой мы за-
заключим этот параграф.
Пусть MmczWt—гладкое многообразие. Векторное поле
класса Сг на М—это отображение, которое каждой точке р € М
сопоставляет вектор X (р) ? ТМр. Иначе говоря, это такое Сг-
отображение X: М—*ТМ, что пХ тождественно на М, где
п—естественная проекция ТМ—» М. Обозначим через ?Г(М)
множество векторных полей на М класса С'.
Интегральная кривая поля X ? ЛЕГ (М), проходящая через
точку р?М,—это такое Cr+1 -отображение а: I —+М, где / —
интервал, содержащий 0, что а @) = р и а' (t) = X (а (t)) при
всех t ? I. Образ интегральной кривой называется траекторией
или орбитой.
Если /: M—-N—это С+1-диффеоморфизм и Х?%Г(М), то
Y — f*X, определенное формулой Y (q) = df (p) (X (р)) при q =
= /(/?), является Сг-векторным полем на N, так как f*X =
^dfoXof-1. Если а: I—* М—интегральная кривая поля X,
то /о а: / —> N — интегральная кривая поля Y. В частности,
/ отображает траектории X на траектории Y. Таким образом,
если х: U—*i70czlRm—локальная карта, то Y = x№X является
Сг-векторным полем в Vo; будем говорить, что Y—это выра-
выражение поля X в локальной карте (а;, И). Ввиду сказанного
локальные теоремы существования, единственности и дифферен-
дифференцируемое™ решений переносятся на векторные поля на мно-
многообразиях, как в следующем предложении.
1.1. Предложение. Пусть Е—банахово пространство и F: Ех
х М —> ТМ —такое С-отображение, г~^\, что nF (Я,, р) = р, где
п: ТМ—*М—естественная проекция. Тогда для каждого
Хо ? Е и каждого ро?М существуют такие окрестности W
точки \ в Е и V точки р0 в М, такое вещественное число
8>0м такое С-отображение ср: (—е, е)х^х W —* М, что
ф@, р,Ц = р и (d/dt)q>(t, p, X) = F(K, q>(t, p, X)) при всех
t?(—е, г), p?V и \?W. Кроме того, если а: (—е, е) —*
—*¦ М—интегральная кривая векторного поля F^ = F(K, ¦) с
а@) = р, то а = ф(-, р, I). I
1.2. Предложение. Пусть I, J —открытые интервалы и а: I —>¦ М,
Р: J—>-M—интегральные кривые поля Х??Г{М), г~^\. Если
§ 1. ВЕКТОРНЫЕ ПОЛЯ НА МНОГООБРАЗИЯХ 23
a{t«) = P(t0) для некоторого tu?lr\J, то a(t) = fi(t) при всех
t?lr\J. Следовательно, существует интегральная кривая
у: I\jJ—*M, которая совпадает caHalucfinaJ. |
Доказательство. Из локальной единственности следует, что»
если сс(^1) = Р(^1), то существует такое е>0, что a(t) — fi(t)t
при \t—*i|<?. Поэтому множество ld(]J, где ее совпадает.'
с Р, открыто. Так как дополнение множества / также открыто
и f(]J связно, то I = I(]J. Щ:
1.3. Предложение. Пусть М—компактное многообразие и
X ? Жг (М). Тогда на М существует глобальный С-поток *)¦
для X. Иными словами, существует такое С-отображение
ф: UxM-^M, что ф@, р) = р и (d/dt)q>(t, p) = X(cp(t, p)).
Доказательство. Рассмотрим произвольную точку р ? М,
Покажем, что существует интегральная кривая, проходящая-
через р, которая определена на всей прямой IR. Пусть (а, Ь) crIR —-
область определения интегральной кривой а: (а, Ь)—*М
с 0 ? (а, Ь) и а @) = р. Будем говорить, что интервал (а, Ь)-
максимален, если для каждого интервала J с тем же свойством:
мы имеем Jcz(a, b). Утверждается, что если (а, Ь) максимален,
то Ь=-\-оо. Если это не так, рассмотрим последовательность
tn —>Ь, tn?(a, b). Так как М компактно, можно считать (пере-
(переходя к подпоследовательности), что a (tn) сходится к некоторой
точке q?M. Пусть ф: (—е, &)xVq—*М—локальный поток
поля X возле q. Выберем такое п0, что Ь—tno < е/2 и а(^„0) €^?-
Определим у: (a, tno + e)—>- М формулой y(t)°—a(t), если t"^tno,
и формулой y(t) = q>(t—<Пп, а(^„0)). если t^tno. Отсюда сле-
следует, что у—интегральная кривая поля X, что приводит к проти-
противоречию, так как (а, ^„о + е)=з(а, Ь]. Тем же способом можно
показать, что а — — <х> и, следовательно, существует интеграль-
интегральная кривая a: IR—>М са@) = р. Согласно предложению 1.2,
эта интегральная кривая единственна. Определим ф(?, p)=a(t).
J) Поток, или динамическая система с непрерывным временем,— это
однопараметрическая группа преобразований {<р^} некоторого «фазового про-
пространства» М, удовлетворяющая (в зависимости от характера рассматри-
рассматриваемых вопросов) тем или иным условиям типа непрерывности, гладкости
или измеримости <pt (дг) =ср (i, дг) по (/, х). В данной книге рассматриваются
только гладкие потоки, которые порождаются гладкими векторными полями,
как описано в книге. В этом случае о тех или иных свойствах потоков
можно с равным основанием говорить как о свойствах соответствующих
полей.
Кроме того, в некомпактном случае (который в книге играет второсте-
второстепенную роль) может случиться, что интегральные кривые t—><р(<, х)
нельзя определить при всех t. Хотя тогда однопараметрической группы
преобразований не возникает, все же обычно и в этом случае позволяют
себе говорить о потоке. (Точная формулировка очевидна; впрочем, она
имеется в [38,.)—Прим, ред.
24 ГЛ. I. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
Ясно, что ф@, р) — р и (d/dt)tp(t, p) = X((p(t, p)). Мы утверж-
утверждаем, что cp(/ + s, p) = y(t, cp(s, p)) для t, sgK и pgM. Дей-
Действительно, пусть P(t) = tp(t-^ s, р) и у(О = ф(<, 4>(s, р)). Мы
видим, что Р и у—интегральные кривые поля X и |3@) = у@) =
= ф (s, p), что доказывает утверждение. Наконец, покажем,
что ф принадлежит классу С. Пусть р?М и -ф: (—гр, гр)х
xVp —* М—локальный поток поля X, который принадлежит
классу С по предложению 1.1. Из единственности решения
следует, что -ф есть ограничение ф на (—ер, &p)xVp. В частно-
частности, (pt = (p(t, •) принадлежит классу С на Vp при \t\<zp-
Вследствие компактности М существует такое е > 0, что q>t
класса С на М при 111 < е. Кроме того, для каждого t?R
можно выбрать такое целое число п, что |?/п|<е и, значит,
ф4 = ф//п о ... о ф//п класса С. При всех i0 ^ К и р0 g M ф клас-
класса С в окрестности пары (t0, рв). Пусть \t— tB\ <Сери p?Vpe.
Тогда ф(?, p) = q>to°4>(t — ^„> р) является отображением клас-
класса С, так как ф(о и ф|(—ept)J гРв)хУРо класса С. Это завер-
завершает доказательство. |
Следствие. Пусть Xgj?r(M) и tp: R.xM—>-M—поток, опре-
определяемый, полем X. Тогда для каждой точки t ? R отображение
Xt: М—*М, Xt(p) = (f(t, p) является С-диффеоморфизмом.
Кроме того, Хв—тождественное отображение и Xt+s = Xt о Xs
при всех t, sglR- I
Пусть X(t?r(M) и Xt, t?R,— поток поля X. Траекторией
поля X, проходящей через точку />g M, называется множество
6{p) = {Xt(p), t?R\. Если Х(р) = 0, то траектория, проходя-
проходящая через р, сводится к точке р. В этом случае мы говорим,
что р—особая точка (или особенность) поля X *). В противном
случае отображение a: IR—> М, a(t) = Xt(p)—иммерсия. Если а
не инъективно, то существует такое ю > 0, что а (ю) = а @) = р
и а(Ь)Фр, когда 0 < t < ю. В этом случае траектория точки р
диффеоморфна окружности S1 и называется замкнутой траек-
траекторией с периодом ю. Если траектория не является ни особен-
особенной, ни замкнутой, то она называется регулярной. Таким обра-
образом, регулярная траектория—это образ инъективной иммерсии
прямой.
Назовем а-предельным множеством ю (р) точки р?М мно-
множество тех точек q 6 М, для которых существует последова-
последовательность /а-»оо с Xtn [р) —>¦ q. Подобным образом определим
а-предельное множество точки р как a(p) = {q?M: Xtn(p)—*q
для некоторой последовательности tn—>• — оо).
2) Название связано с тем фактом, что в такой точке поле не задает
никакого направления. Никакой особенности в аналитическом смысле там
нет. У нас особые точки чаще называются положениями равновесия, но мы
сохранили терминологию авторов,— Прим. ре$,
§1. ВЕКТОРНЫЕ ПОЛЯ НА МНОГООБРАЗИЯХ 25
Отметим, что сс-предельное множество точки р является
io-предельным множеством точки р для векторного поля —X.
Кроме того, (о(/?) = ю (/?), если р лежит на траектории точки р.
Действительно, р — Xt<^ (р), и поэтому если Xtn {p) —»¦ q при
гп—>оо, то Xtn-ta(p)^ qu tn — tB—>- оо. Таким образом, можно
определить ю-предельное множество траектории точки р как
ы(р). Интуитивно, а(р) — это место, где траектория точки р
«рождается», а ю (р)—где она «умирает».
Пример 1. Рассмотрим единичную сферу S2czIR3 с центром
в нуле. Будем использовать стандартные координаты (х, у, г)
в IR3. Точку pN = @, 0, 1) назовем северным полюсом сферы S2,
а точку ps = @, 0, —1)—южным. Определим векторное поле X
на S2 формулой X (х, у, z) = (—хг, —уг, х2 + у2). Ясно, что
X—поле класса С°° и что особые точки X—это pN, ps. Так
как X касается меридианов сферы S2 и направлено вверх, то
®{Р) = Рн и a(P) = Ps> если P€S2\{Pn' Ps\ (Рис- 5)-
Пример 2. Рациональные и иррациональные потоки на то-
торах1). Пусть ф: R2—*T2c=IR3 дается формулой
Ф(ы, v) = (B + cos 2nv) cos 2nu, B + cos 2nv) sin 2nu, sin2no).
Мы видим, что ф—локальный диффеоморфизм, который ото-
отображает горизонтальные прямые из IR2 в параллели на торе,
вертикальные прямые в меридианы и квадрат [0, 1]х[0, 1] на
весь тор Т2. Кроме того, ф (ы, v) = q> (и, v) в том и только том
случае, когда и—-и = т и v—v = n для некоторых целых т
и п. Для каждого a g IR рассмотрим векторное поле в R2, зада-
задаваемое формулой Хгл(и, v) = (l, а). Легко видеть, что Ya=(p*Xrx —
корректно определенное С°-векторное поле на Т2. Траектории
*) У нас чаще говорят о рациональной или иррациональной обмотке
тора. Впрочем, это же название может обозначать и отдельную траекторию
данного потока,— Прим, ред.
26 ГЛ. !. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
Ya—это образы при отображении ср траекторий Ха, которые
являются прямыми в К2 с угловым коэффициентом а. Покажем,
что при рациональном а каждая траектория Vх замкнута, а при
иррациональном а каждая траектория Ya плотна в Т2. Для
каждого с ? К пусть Ае обозначает проходящую через @, с)
прямую в К2 с угловым коэффициентом а; Ас={(и, с+аи): и g R\.
Как мы уже отмечали, ф(Ас)—траектория поля Ya. Если а
рационально, эта траектория замкнута для каждого cgR, так
как если а = п/т, то (т, с -\- (п/т) т) ? Ае и ф (т, с -f- п) = ф @, е).
Предположим теперь, что а иррационально и eg IR. Мы утверж-
утверждаем, что C = {c?R: ф(Ае) = ф(А-)} плотно в IR. Отсюда сле-
следует, что Ue6CAc плотно в К2 и, следовательно, ф(А-) =
= ф(иебСАс) плотно в Т2. Чтобы показать, что С плотно в IR,
достаточно доказать, что G — \ma-\- n: m, n?Z\ плотно в R,
ибо с?С тогда и только тогда, когда с—c?G. Поскольку
G—подгруппа аддитивной группы R, то, как известно, G либо
плотна, либо дискретна. Таким образом, осталось показать,
что G не дискретна. Но для каждого m ? Z существует такое
n(EZ, что um = ma + n принадлежит интервалу [0, 1]. Последо-
Последовательность ит имеет предельную точку, и ее члены различны
в силу иррациональности ее. Значит, G плотна.
Векторное поле Ya, построенное выше, называется рацио-
рациональным или иррациональным полем на Т2 соответственно тому,
рационально а или нет. Если а рационально, то со-предельное
множество всякой траектории—это сама траектория. Если а
иррационально, то со-предельное множество всякой траектории —
это весь тор Г2.
Пример 3 (градиентные векторные поля). Рассмотрим много-
многообразие Mmc:Rk. Для каждой точки р?М возьмем в ТМр
скалярное произведение <, >, индуцированное из IR*. Обо-
Обозначим норму, индуцированную этим скалярным произведением,
через | \\р, или просто || I Если X и Y—векторные поля клас-
класса С°° на М, то функция g: M —IR, g(p) = <X(p), Y (p)>p,
принадлежит классу С°°. Пусть f: M—>IR—это (^""-отображе-
(^""-отображение. При любом р ? М существует единственный вектор X (р) ?
?ТМр, для которого dfpv — <X(p), v>p при всех v?TMp. Это
определяет векторное поле X класса Сг. Оно называется гра-
градиентом функции / и обозначается X=grad /. Укажем некоторые
основные свойства градиентных полей. Во-первых, grad f{p) = О
тогда и только тогда, когда dfp = O. Вдоль неособых траекто-
траекторий поля X = grad/ функция / строго возрастает, так как
dfpX (р) = || X (р) |2. В частности, grad f не имеет замкнутых траек-
траекторий. Более того, ю-предельное множество всякой траектории
состоит из особых точек. Действительно, предположим, что
Х и q€«(/?) для некоторого р?М. Пусть S—пересе-
SI. ВЕКТОРНЫЕ ПОЛЯ НА МНОГООБРАЗИЯХ
27
чение f~1{f(q)) с малой окрестностью точки q. Мы видим, что
S — подмногообразие размерности т—1, ортогональное полю
X = grad/, и в силу непрерывности потока траектория, про-
проходящая через любую точку, достаточно близкую к q, пересе-
пересекает S. Поскольку q ? ю (/?), то существует последовательность рп
точек траектории р, сходящаяся к q. Таким образом, траекто-
траектория р пересекает S более чем в одной точке (в действительно-
действительности в бесконечном числе точек), что приводит к противоречию,
ибо / возрастает вдоль орбит. С другой стороны, ясно, что
,0)
Рис. 7
Рис. 8
если ю-предельное множество траектории градиентного вектор-
векторного поля содержит более одной особой точки, то оно должно
содержать бесконечно много особых точек. Мы собираемся пока-
показать, что это действительно может случиться.
Пусть /: IR2 —* R определяется формулой
еслиг<1;
если г = 1;
_i)_e)t если г > 1.
0,
Пусть X — grad /. Имеем X (г cos б, г sin 6) = 0 в том и только
том случае, когда г = 0 или г=1. Мы собираемся показать,
что существует траектория поля X, у которой ю-предельным
множеством является окружность С с центром в нуле и радиу-
радиусом 1. Заметим, что f'1 @) = С и Ei U Е„ где Ел и ?2—спирали,
задаваемые формулами
?! = {(/• cose, /-sinO). г=1 + 1/(л+6), —я<е<оо},
—2я<в<оо}.
Рассмотрим область
{/ = {(/"cose, rsinG): 1
Пусть / — интервал {{х, 0); Ц-1/Bя)<х<1 + 1/я}. Мы пока-
покажем, что существует точкари 6 Л положительная полутраектория
28 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
которой принадлежат области U. Отсюда будет следовать, что
со-предельным множеством точки р0 является окружность С.
На рис. 8 мы изобразили некоторые кривые уровня функции /
в U. Пересечение кривой уровня, проходящей через точку р ? /,
с I/ — это компактная дуга, концы которой лежат в /. Длина
этой дуги стремится к бесконечности, когда р стремится к концам
интервала /.
Пусть q ? Et. Поскольку X (<?) ортогонально Et и направлено
вовне U (так как f отрицательно в II), мы видим, что отрицатель-
отрицательная полутраектория q пересекает одну из кривых уровня, про-
проходящих через точку из внутренности интервала /. Таким об-
образом, отрицательная полутраектория точки q пересекает /.
Следовательно, множество J={p?l: Xt(p)?U при 0<3<s и
Xs(p)^E1) непусто. Более того, если дано q€Elt то существует
такое р ? J, что положительная полутраектория точки р содержит
q и дуга траектории, заключенная между р и q, лежит в U.
С другой стороны, если q ? Е2, то отрицательная полутраектория
точки q также пересекает /, так что 1ф1.
Пусть рв— нижняя грань J. Мы утверждаем, что положитель-
положительная полутраектория точки р0 принадлежит U. Предположим, что
это не так. Тогда существует такая точка q на положительной
полутраектории точки рв, что дуга траектории, заключенная меж-
между точками р0 и q, содержится в U и Xt(q) (? II для достаточно ма-
малых ?>0. Таким образом, либо q ? Eu либо q ? Е2, либо q^I. Если
q?Eu то каждая положительная полутраектория точки из J
пересекает Ех в некоторой точке отрезка между A + 1/я, 0) и q.
Но это приводит к противоречию, так как отрицательная полу-
траектория, проходящая через всякую точку из Elt пересекает /,
а значит, и J. Если q?E2 или q ? /, то положительная полутраек-
полутраектория каждой близкой к р0 точки выходит из U, не встретившись
с Е1з что опять-таки приводит к противоречию, так как р0 —
нижняя грань J. Таким образом, положительная полутраекто-
полутраектория точки р0 содержится в О, что доказывает наше утверждение.
Отметим, что векторное поле на S2 из примера 1 является
градиентом функции высоты, которая измеряет высоту точки
над плоскостью, касательной к сфере S2 в ps. Другие простые
примеры можно получить, рассматривая функцию на поверх-
поверхности в R3, которая измеряет расстояние от ее точек до некото-
некоторой фиксированной плоскости. Некоторые из этих примеров бу-
будут рассмотрены позднее.
Теперь мы обсудим некоторые общие свойства со-предельных
множеств.
1.4. Предложение. Пусть X g Жг (М), еде М — компактное много-
многообразие, и р?М. Тогда
(а) Ы(р)ф0,
§ I. ВЕКТОРНЫЕ ПОЛЯ НА МНОГООБРАЗИЯХ 29
(b) (о(р)—замкнутое множество,
(c) а(р) инвариантно относительно потока поля X, т. е. яв-
является объединением траекторий X, и
(d) ч>(р)—связное множество.
Доказательство. Пусть tn —> оо и рп = Xtn {р). Поскольку М
компактно, то рп содержит сходящуюся подпоследовательность,
предел которой лежит в ю(/?). Таким образом, а(р)Ф 0. Пред-
Предположим теперь, что <7(?ю(/?). Тогда она имеет окрестность V (q),
которая не пересекается с множеством {Xt(p): f^T) для
некоторого Т > 0. Отсюда следует, что ни одна точка V(q) не
принадлежит ю(/?). Значит, ю(/?) замкнуто. Далее, предположим,
что q?u>(p) и q — Xs(q). Выберем такую последовательность
*„-^-оо, что Xtn(p)—>q. Тогда Xta+s(p) = XsXtn(p) сходится
к Xs(q) = q, а, значит, q?o)(p). Это показывает, что ю(р) инва-
инвариантно относительно потока. Предположим, что (о (р) несвязно.
Тогда можно выбрать такие открытые множества Vt и V2, что
(*{p)czVx\]Vb ы(р)пУ1Ф0, 1п{р)[\У^Ф0 и Р1П^2=0.
Траектория точки р время от времени должна попадать в
Vt и V-2, поэтому при любом Т > 0 найдется такое t > Т, что
Xt (р) € К где К = M\(V1 U V2). Значит, существует такая
последовательность tn—> со, что Х(п(р)?К- Переходя в случае
необходимости к подпоследовательности, имеем Xtn (/?)—>¦ q для
некоторого q?K. Но из этого следует, что q^oj(p)c:V1[jVz,
а это невозможно. 1
. Рис. 9
Замечание. Ясно, что указанными выше свойствами обладают
также и сс-предельные множества. С другой стороны, если много-
многообразие некомпактно, то в предыдущем обсуждении надо огра-
ограничиться тем случаем, когда положительная (или отрицатель-
отрицательная) полутраектория содержится в некотором компактном мно-
множестве. На рис. 9 изображена траектория векторного поля в IR2,
у которой ю-предельное множество несвязно.
Как мы уже видели, ю-предельным множеством всякой траек-
траектории иррационального потока на торе является весь тор.
Существуют более сложные примеры векторных полей на Т2
со значительно более сложными со-предельными множествами,
30
ГЛ. I. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
как в примере 13 гл. 4. Между тем для сферы S2 ситуация
значительно проще из-за следующего топологического факта:
каждая непрерывная замкнутая кривая без самопересечения
разбивает S2 на две области, гомеоморфные кругу (теорема
Жордана). Структура ю-предельного множества векторного поля
на S2 описывается теоремой Пуанкаре—Бендиксона, доказа-
доказательство которой мы сейчас приведем, разбив его на ряд лемм.
Пусть X?Xr(S2), г>1.
1.5. Лемма. Пусть SczS2—дуга, трансвереальная к X. Положи-
Положительная полутраектория 6+ (р) точки р ? S2 может пересекать 2
только по монотонной последовательности точек; иными сло-
словами, если Pi—i-e пересечение б+ (р) с 2, то /?,€[ft-i>
2
Рис. 10
Рис. 11
Доказательство. Рассмотрим дугу траектории между точка-
точками pl_1 и р; вместе с дугой [р/_1, р,-]с=2. Они образуют замк-
замкнутую кривую, ограничивающую круг D. Так как 2 трансвер-
сально полю X, которое направлено внутрь D, положительная
полутраектория точки р( содержится в D. Таким образом,
[ \
Следствие, а-предельное множество траектории у пересекает 2
не более чем в одной точке.
Доказательство. Предположим, что ю (у) содержит две точки
<7i и <7г ДУГИ 2- Пусть рп—последовательность точек пересе-
пересечения у с 2. Тогда существуют подпоследовательности рп, схо-
сходящиеся соответственно к qs и q2, что противоречит свойству
монотонности рп. |
1.6. Лемма. Если а-предельное множество траектории у не
содержит особых точек, то а (у)—замкнутая траектория,
а траектории точек, достаточно близких к точке р€у, имеют
ту же замкнутую траекторию в качестве своего ^-предельного
множества.
(Последнее гарантируется, если у незамкнутая.—Ред.)
§ 1. ВЕКТОРНЫЕ ПОЛЯ НА МНОГООБРАЗИЯХ 31
Доказательство. Пусть q?o)(y). Покажем, что траектория
точки q замкнута. Пусть х? ы(ф. Тогда х не является особой
точкой. Рассмотрим отрезок 2, трансверсальный к полю X и со-
содержащий х. По предыдущей лемме положительная полутраек-
полутраектория точки q пересекает 2 по монотонной последовательности
дп -> х. Поскольку qn 6 со (у), то, учитывая следствие, получаем,
что qn—х при всех п. Таким образом, траектория точки q замк-
замкнута. Беря трансверсальный отрезок, содержащий q, заключаем,
как в лемме 1.5, что со (у) сводится к траектории точки q. Дока-
Доказательство второго утверждения получается непосредственно.
1.7. Лемма. Пусть pt и р2—различные особые точки, лежащие
в (й-предельном множестве точки pftS*. Тогда существует,
самое большее, одна траектория уса(р), для которой «G)==
=*pt и co(v) = p2.
Доказательство. Рассуждая от противного, предположим,
что существуют две такие траектории уи Y2c=co(p), что oc(Y/)=Pf
и соG() = р2 при i—l, 2. Кривая С1У состоящая из траекторий
Yi, Yz и точек pv р2, разбивает S2 на два круга, один из кото-
которых содержит р, как показано на рис. 12. Пусть 2t и 22—
трансверсальные полю X отрезки, проходящие через точки
9i6?i и ^гбТг соответственно. Так как ylt у2са(р), то поло-
положительная полутраектория точки р пересекает 2t- в некоторой
точке а и позднее пересекает Eg в некоторой точке Ь. Рассмот-
Рассмотрим кривую С2, состоящую из дуг abczQ(p), bq2cz'E2, q2p2czyit
Psj^cyi, ^gczEi и точки р2. Мы видим, что С2 разделяет S2
на два круга: Л и б. Положительная полутраектория точки Ъ
остается целиком в А, что приводит к противоречию, ибо
()
1.8. Теорема (Пуанкаре—Бендиксона). Пусть X?3tr{S2)—век-
X?3tr{S2)—векторное поле с конечным числом особых точек. Возьмем p?S2,
и пусть со(р)—(й-предельное множество точки р. Тогда реали-
реализуется одна из следующих возможностей:
A) со(р) —особая точка;
B) со (р) — замкнутая орбита;
C) со (р) состоит из особых точек ри . . . , рп и таких регуляр-
регулярных орбит, что если усв)(р), то a(y)=Pi и u>(y)=pj.
Доказательство. Если со(р) не содержит особых точек, то по
лемме 1.6 со(р) является замкнутой траекторией. Если со(р) не
содержит регулярных точек, то со(р) сводится к одной точке,
которая является особой, так как X имеет лишь конечное число
особых точек, а со(р) связно.
Предположим, что со(р) содержит регулярные точки и особые
точки. Пусть y — регулярная траектория, содержащаяся в со(р).
Мы утверждаем, что co(y) — особая точка. Если co(y) содержит
32 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
некоторую регулярную точку q, возьмем трансверсальный к X
отрезок 2, проходящий через q. Так как ус со (р), то по следствию
леммы 1.5 у пересекает 2 только в одной точке. По лемме 1.6
у — замкнутая траектория и и>(р)=у. Но это приводит к про-
противоречию, потому что со(р) содержит особые точки. Таким
образом, со (у) — особая точка. Аналогично, а (у)—особая точка. |
В следующих примерах мы иллюстрируем некоторые факты,
связанные с этой теоремой.
Пример. Пусть X — векторное поле на S2, изображенное на
рис. 13. Северный и южный полюсы являются особыми точками,
Рис. 12
а экватор — замкнутой траекторией. Другие траектории рож-
рождаются на полюсе и умирают на экваторе.
Пусть ф: S2 ->¦ R — неотрицательная С-функция, обращаю-
обращающаяся в нуль точно на экваторе. Рассмотрим векторное поле
У=фХ. Каждая точка экватора является особенностью поля Y,
а со-предельное множество любой точки, не являющейся полю-
полюсом и не лежащей на экваторе,— это весь экватор. Этот пример
показывает, что теорема Пуанкаре — Бендиксона не выпол-
выполняется без предположения о конечности числа особых точек.
Пример. Пусть X — векторное поле на сфере, изображенное
на рис. 14. Векторное поле X имеет две особые точки рв и pN
и одну замкнутую траекторию у. Для траекторий в северной
полусфере а-предельное множество — это pNi a со-предельное
множество — это траектория у. В южной полусфере мы имеем
особую точку р8, которая является центром розы с бесконечным
числом лепестков, каждый из которых ограничен траекторией,
рождающейся в ps и умирающей в ps. Ситуация внутри любого
лепестка изображена на рис. 15.
§2. топология на Пространстве с-отображений
33
Другие траектории в южной полусфере имеют у своим а-пре-
дельным множеством, а край розы — своим со-предельным мно-
множеством. Таким образом, со-предельное множество траектории
Южная полусфера
Северная полусфера
Рис. 14
Рис. 15
может содержать бесконечно много регулярных траекторий.
Это показывает, что если р±==р%, то лемма 1.7, вообще говоря,
неверна.
§ 2. ТОПОЛОГИЯ НА ПРОСТРАНСТВЕ С-ОТОБРАЖЕНИЙ
Мы введем здесь естественную топологию на пространстве
Жг (М) векторных полей класса Сг на компактном многообра-
многообразии М. В этой топологии два векторных поля X, Y??r(M)
близки, если эти векторные поля и их производные до поряд-
порядка г близки во всех точках многообразия М.
Рассмотрим вначале пространство Cr{M, Rs) отображений
М—»К* класса Cr, Q^.r < оо, определенных на компактном
многообразии М. На Сг (М, Rs) имеется естественная струк-
2 л» ,61
34 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
тура векторного пространства: (f + g)(p)==f(p)-j-g(p), (Ц)(р)
—Ц(р) для /, g?Cr(M, Rs) и X?R. Возьмем такое конечное
покрытие многообразия М открытыми множествами Vly ..., Vk,
что каждое V{ содержится в области определения некоторой
карты (*,., ?/,.), причем ж, (?/,) = В B) и x,{Vt) = B(l), где ВA)
и В B)—шары в Rm радиуса 1 и 2 соответственно с центром
в нуле. Для f?Cr(M, R") пусть f' = foxil: ВB)—*RS. Опре-
Определим
| /||г = max sup {|| f (и) ||, | df (и) ||, ..., | d'/' (и) |: и € В A )}•
2.1. Предложение. | Ц, является полной нормой в С(М, Rs).
Доказательство. Непосредственно ясно, что || ft,—норма в
С (М, Rs). Остается доказать, что каждая последовательность
Коши сходится. Пусть fn. М —» Rs — последовательность Коши
в норме \\ \\г. Если р g М, то /п (р) является последователь-
последовательностью Коши в R5, и поэтому она сходится. Положим f{p)~
=lim /„ (р). В частности, /^ (и) —* /' (ы) для и ? В A) и* = 1, ...,&.
С другой стороны, при каждом «gB(l) последовательность
d/j, (ы) является последовательностью Коши в L (Rm, Rs) и оттого
сходится к некоторому линейному оператору Т'(ы). Мы утверж-
утверждаем, что сходимость dfln —»• Т1 равномерная. Действительно,
заметим, что
II dfk (и) - Т' {и) || < 1 dfln (и) - dfln. (и) || +1| dtn ¦ (и) - Т< (и) |.
Для произвольного фиксированного е > 0 существует такое п0,
что если п, п' ^ п0, то fld/j, (и)—dfln. (и) | < е/2 при всех и ё В A).
С другой стороны, для каждого «gB(l) существует такое
п'^2иг0, зависящее от и, что ||d/n<(w)—Т'(ы) | < е/2. Таким
образом, для п^п0 мы имеем |d%(u)—Т'(ы)|<е при всех
MgB(l). В силу предложения 0.0, /' принадлежит классу С1
и df = Т'. Отсюда следует, что fn~* f в норме || (,. Аналогично
можно по индукции показать, что / принадлежит классу Сг
и /„—>-/ в норме ||г. |
Легко видеть, что топология, определяемая на Cr(M, Rs)
нормой | |г, не зависит от покрытия Vit ..., Vk многообразия М.
Теперь мы опишем некоторые важные свойства пространства
СГ(М, К*) с Сг-топологией.
Подмножество топологического пространства называется
остаточным, если оно содержит счетное пересечение открытых
плотных множеств. Топологическое пространство называется
пространством Бэра, если каждое его остаточное подмножество
является плотным. Поскольку Cr (M, Rs)—полное метрическое
пространство, мы немедленно получаем следующее предложение.
§ 2. ТОПОЛОГИЯ НА ПРОСТРАНСТВЕ С-ОТОБРАЖЕНИЙ 35
2.2. Предложение. Сг (М, Rs) является пространством Бэра. |
Покажем, что О (М, Rs) содержит плотное счетное подмно-
подмножество. При f?Cr(M, Rs) рассмотрим отображение f'=f oxjh
В B) с= Rm —»• Rs. Заметим, что отображение
j'f'i fiB) —BB)xR*xL(R-, R*)x...X.Lr{?Lm, R*) = E,
определенное формулой /г//(и) = (и, /'«, df'iu)^..., drf'(и)), не-
непрерывно. Поэтому множество Jr{f') = jrf'(B(\)) является ком-
компактным подмножеством в Е. Легко видеть, что если W —
окрестность отображения / в Cr (M, Rs), то существует такая
окрестность W множества Jr(f)=Jr(f1)x...xJr{f) в ЕхЕх...
...х?, что если g?Cr(M, Rs) и Jrg=Jrg1X...xJrgkczW, то
5Г
2.3. Предложение. Cr (M, R*) сепарабельно; иными словами, оно
имеет счетную базу открытых множеств.
Доказательство. Поскольку Е* = Ех ... хЕ—открытое мно-
множество в евклидовом пространстве, существует счетная база
открытых множеств Ev ..., Et, ... для топологии вЕк. Пусть
Ёг, ..., Ej, ...—множество тех открытых подмножеств в Ек,
которые являются объединениями конечного числа множеств Et.
Пусть iBj — {g^Cr(M, Rs): Jr(g)aE,\ для каждого /. Ясно, что
Sj открыто в Cr(M, Us). Пусть ж—некоторая окрестность
отображения f в Cr(M, Rs) и W—такая окрестность множе-
множества У(/) в Ек, что если Jr(g)<=W, то g?W. Так как Jr(f)
компактно, то существует конечное покрытие Jr (f) открытыми
множествами Е(, содержащимися в W. Пусть Ej обозначает
объединение этих Et. Ясно, что Jr(f)cEjc:W. Следовательно,
<Bj содержит / и содержится в W. Это показывает, что [Slt ...
..., ?j, ...} является счетной базой для топологии на прост-
пространстве С (М, Rs). |
Теперь мы покажем, что каждое Сг-отображение может быть
аппроксимировано в С-топологии отображением класса С".
2.4. Лемма. Пусть fi UczR.1" —* R.s—отображение класса Сг,
где U—открытое подмножество. Пусть КC-U—компакт. Тогда
для любого е > 0 существует такое СГ-отображение g: R.m —»- R.s,
что lf—g\\r<e на К-
Доказательство. Рассмотрим функцию tp: RCT —*¦ R, которая
принимает значение 1 на К и значение 0 вне некоторой ок-
окрестности множества К, содержащейся в U. Положив h = q>f,
мы будем иметь h = f в К и /г = 0 вне U. Поскольку h класса Сг,
а К—компакт, то существует такое б > 0, что
, И<8}<е,
36 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
где dJ обозначает производную порядка / для / = 1, ..., г. Пусть
фб: Ки—* R такова, что <рс(и) = 0 при ||u||>6, q\. (t>) ^ 0 при
всех v и ^ фб (v) dv = 1. Определим g< Rm —- R.s формулой
g (и) = § Ф0 (у) h (и + v) dv = $ ф0 (г—и) h (г) d2.
Тогда
dJg (и) = $ Ф6 (г>) d/ft (и + v) dv,
dig (и) = (—IK \ <*Лрй (г— и) Л (г) dz.
Из второго выражения следует, что g принадлежит классу С°°.
С другой стороны, из первого выражения мы имеем при всех
К
\d>g(u)—d>h(и)| = | $ Фа(v) d'h(u + v)dv— J ф6(о)d^h(и)cto|=
= | S Фб (») («"Л (и + о)—d>ft (и)) dt;| < в.
Так как h — f на К, то g удовлетворяет требуемьш условиям. |
2.5. Предложение. Подмножество С"-отображений плотно в
Cr(M, Rs).
Доказательство. Пусть (xt, Ut), i = l, ..., k,—такие ло-
локальные карты, что xt (?/,) = В B) и М = U Vt, где Vt = xtrl (В A)).
Возьмем разбиение единицы {ф{: М —»• R}, подчиненное покры-
покрытию {F/}. Пусть /€СГ(М, R*) и е > 0. По предыдущей лемме
для любого б > 0 существует такое С°°-отображение g': iRm —- iRJ,
что \\f' — g'||r<6 на ВA), где ji = foxjl. Беря б достаточно
малым, можно добиться того, чтобы ||ф,/—4>ig'ox{lr < e/k.
Таким образом, g = ^l(pig'°xt принадлежит классу С°° и
I/—ё1 = 1^Ы—Ф|в*«,)|г<е/А+ ... +е/* = е. I
Рассмотрим теперь многообразие iV. По теореме Уитни мы
можем считать, что N—подмногообразие в iR* для некоторого s > О,
замкнутое как подмножество R*. Поскольку N—замкнутое под-
подмножество в Rs, то Cr (M, N) замкнуто в Cr {M, Rs) Следова-
Следовательно, Cr(M, N) является сепарабельным пространством Бэра
в топологии, индуцированной из СГ(М, К*).
Пусть A^jciR5', yV2c=IRSi—многообразия, замкнутые в Rs>, и Ф;
Ni—>-N2—некоторое С-отображение, г^/^оо. Определим Ф»:
СГ{М, Л/,)-*Сг(М, N2) формулой Ф./ = Фо/.
2.6. Предложение. Отображение Ф„ непрерывно.
Доказательство. В силу следствия 2 предложения 0.16 су-
существует такое С-отображение Ф: IRS» —»• R4-, что Ф = Ф на Nv
§2. ТОПОЛОГИЯ НА ПРОСТРАНСТВЕ С"-ОТОБРАЖЕНИЙ 37
Пусть (х{, Uc), 1=1, ..., k,— такие, как и раньше, локальные
карты в М. Легко видеть, что для любого е > 0 существует
такое б > 0, что если ||/.о*Г' —g°x7' ||г < б на ВA), то||(Фо/ —
— <bog)oxr' lr < е на ВA). Следовательно, если ||/ —g\i < б, то
||Фо/ — Фо^|г = ||Фо/—OogK s,
что доказывает непрерывность Ф». |
Пусть теперь М и Л/—абстрактные многообразия, причем
М компактно. Мы можем определить некоторую Сг-топологию
на Cr(M, N). Для этого достаточно вложить N в евклидово
пространство Rs (теорема 0.17). Доказанное выше предложение
показывает, что эта топология не зависит от вложения*).
2.7. Предложение. Подмножество отображений класса С°° плот-
плотно в Cr(M, N).
Доказательство. Предположим, что NcRs. Пусть Vc=R
трубчатая окрестность многообразия N и л: V —>¦ N—соответ-
N—соответствующая проекция Пусть f?Cr(M, N). Согласно предложе-
предложению 2.5, можно аппроксимировать f отображением g) M—*-Rs
класса С". Тогда nog: M—*¦ N класса С" и nog аппроксими-
аппроксимирует /, ибо п» непрерывно.
2.8. Предложение. Множество Diffr(M), состоящее из ^-диф-
^-диффеоморфизмов многообразия М, открыто в Cr(M, M).
Доказательство. Пусть / € Diffr (M). Можно предположить,
что McR*. Если р?М, го по теореме об обратной функции
существуют такие окрестности Vp точки р в М и "^ отобра-
отображения / в Cr(M, M), что если g^f^p, то g\Vp—диффеомор-
g\Vp—диффеоморфизм. Пусть Vpt, ..., Vp —конечное подпокрытие М. Положим
|?/Э=П(=1 "У3р- Если б—число Лебега покрытия, то при d(p, g)<б
и р Ф q обязательно g(p)?=g (а) при всех g 6 СУ3. С другой
стороны, число
p = inf {dtf(p), f(q))i p,q?M, d(p, q)^8\
положительно. Следовательно, можно считать (уменьшив, если
потребуется, "У3), что если g^f3, то g инъективно. Так как
g—локальный диффеоморфизм, получаем, что g—диффеомор-
g—диффеоморфизм. |
х) После этого формулировка предложения 2.6 приобретает смысл и
в том случае, когда Л// не предполагаются подмногообразиями в Rs, а яв-
являются абстрактными многообразиями. Справедливость такого варианта
предложения 2.6 сразу следует из предыдущего, он нередко используется
ниже, начиная с 2.7.— Прим. ред.
38 ГЛ. I. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
Из предыдущего предложения вытекает, что Diffr(M) яв-
является сепарабельным пространством Бэра и что подмножество
С"-диффеоморфизмов плотно в нем.
Рассмотрим, наконец, пространство 3cr {M) векторных полей
класса Сг на компактном многообразии М. Предположив, что
Mc=IRs, легко видеть, что 3?Г{М)—замкнутое подпространство
в С (М, Rs). Значит, 2?Г(М)—сепарабельное пространство Бэра.
Покажем, что каждое векторное поле X?3ir(M) может быть
аппроксимировано С"-векторным полем. Действительно, X может
быть аппроксимировано С°°-отображением У- М—+ ТМ. Пусть
п: ТМ—*М—естественная проекция. Так как я, непрерывно,
то noY является С-близким к лоХ = idM. По предложению 2.8
Ф = поУ—диффеоморфизм. Пусть Z = Yo(p~1. Тогда Z—это С"
векторное поле, ибо Y, ф класса С°° и jtoZ = idw. Кроме того, Z
аппроксимирует X. (См. упражнение 15 в конце этой главы.)
§ 3. ТРАНСВЕРСАЛЬНОСТЬ
Пусть ScN:—С-подмногообразие и /: М —- N—^-отобра-
N—^-отображение, где k, r^l. Будем говорить, что f трансверсально к S
в точке pgM, если либо f(p)^S, либо dfp(TMp) + TSfip) =
— TNf{p), т.е. если образ ТМр под действием отображения dfp
содержит подпространство в TN/(pV дополнительное к TS/lpy
Будем говорить, что / трансверсально к S, ffaS, если оно транс-
трансверсально к S в каждой точке р 6 М. Заметим, что если раз-
размерность многообразия М меньше, чем коразмерность подмно-
подмногообразия S, то / трансверсально к S тогда и только тогда,
когда / (М) П S = 0.
Интересная ситуация складывается, если /: М —»- N—суб-
мерсия. В этом случае / трансверсально каждому подмногооб-
подмногообразию SczN. Определим трансверсальность между двумя под-
подмногообразиями Slt S2cN следующим образом: St трансвер-
трансверсально к S2, если отображение вложения i: St—^N трансвер-
трансверсально к S2.
Напомним, что каждое многообразие локально является
прообразом регулярного значения. Точнее, если q?ScN", то
существует такая окрестность Vg точки q в N и такой диф-
диффеоморфизм ф: Vg —> Rs х R"~s класса Сг, что q>(S{] Vg)=Rs x {0}.
Таким образом, 5п1/9 = (л2оф)-1@), где л2: RsxR"~s-*R"~s —
естественная проекция. Пусть теперь fi M—+N и UpczM —
окрестность точки р с f(Up)cVg, где q=f(p). Рассмотрим ото-
отображение л2офо/|?/,, схематически изображенное на рис. 16.
Следующее предложение получается непосредственно.
§3. ТРАНСВЕРСАЛЬНОСТЬ
39
3.1. Предложение. Отображение f: M —> N тогда и только тогда
трансверсально к S в точке pgf~1(S), когда О является регу-
регулярным значением отображения n2otpof\Up для некоторой ок-
окрестности Uр, такой, как выше. |
Следствие. Пусть f?Ck(M, N") и Ss—С-подмногообразие в N
с k, r^l. Если f трансверсально к S, то f~1(S) либо пусто,
Рис 16
либо является С1-подмногообразием коразмерности п—s, где
1= min (k, r). I
3.2. Предложение. Если М компактно и подмногообразие ScN
является замкнутым подмножеством, то отображения из
Ск(М, N), трансверсальные к S, образуют открытое подмно-
подмножество.
Доказательство. Пусть f^Ck(M, N) трансверсально к S.
Для каждой точки q ? S возьмем такие окрестность V и диф-
диффеоморфизм ц>д\ Vg—>. R^xIR"""*, что ф^(SП^) = IRJх{0}- Для
каждой точки p^f~1{q) рассмотрим такую окрестность U^, что
f(Up)czVg и производная отображения л2о<р9о/ сюръективна
в каждой точке из Vр. Существует такая окрестность f^p(f)cz
czC"(M, N), что то же самое верно для n2oq>gog на Up при
любом g^f^p. Пусть UPt, ..., UPm—конечное покрытие ком-
компактного множества /-U(S) Положим 11 = UPlU • ¦. U ИРт и
<V* (/) = <fvpx n ... П ^рщ ¦ Ясно, что если g 6 IP, то g трансвер-
трансверсально к S во всех точках U. Так как M\U компактно и
f{M\U)(]S = 0, то, уменьшив, если потребуется, "У3, можно
считать, что g(M\U)f\S= 0 при всех g?f™. Тогда каждое
g?<fv трансверсально к S, что доказывает предложение. |
Заметим, что если ScN не замкнуто, то предложение ос-
остается верным для замкнутых подмножеств S. А именно если
SaS замкнуто в N, то множество отображений /: М—*N,
трансверсальных к S на /-1 (S) (т. е. во всех точках /-1 (S)),
открыто в Ch(M, N).
40 ' ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
Пусть Л, М, N — многообразия и F: АхМ —*¦ N—С°°-ото-
бражение. При 'к g Л обозначим через F%: M —>¦ N отображение,
определенное формулой Fk (р) = F (X, р). Пусть Sс= N — С~-под-
многообразие, и пусть TsczA—множество таких точек X, что
Fk трансверсально к S.
3.3. Предложение. Если F:AxM-+N трансверсально к ScN,
то Ts является остаточным множеством в А.
Доказательство. Пусть п: АхМ —*А—естественная проек-
проекция. Так как F трансверсально к S, то S = F~1(S) — подмно-
подмногообразие в ЛхМ и ns — n\S: S —>¦ А—отображение класса С".
Легко видеть, что FA тогда и только тогда трансверсально к S,
когда К—регулярное значение ns. Поэтому предложение вы-
вытекает из теоремы Сарда. |
Следствие 1. Пусть /: М —* R" класса С° и ScR."—подмного-
ScR."—подмногообразие. Множество таких векторов i^IR", что f-\-v транс-
трансверсально к S, является остаточным.
Доказательство. Отображение Fi IR"xM —> К", определенное
формулой F (v, p) = f (p) + v, является субмерсией и, следова-
следовательно, трансверсально к S. Поэтому следствие немедленно
вытекает из предложения. |
Следствие 2. Если М — компактное многообразие, а подмного-
подмногообразие ScR." замкнуто как подмножество К", то множество
TscCk(M, R") отображений, трансверсальных к S, открыто
и плотно в Ch(M, R").
Доказательство. Открытость множества Ts следует из пред-
предложения 3.2, а плотность вытекает из следствия 1 и плотности
С"-отображений в Ck(M, R"). |
Подчеркнем, что многообразия Л, М и N в предложении 3.3
необязательно компактны. Заметим также, что в предложении 3.3
и следствии 1 требуются отображения и подмногообразие класса
С™, потому что при доказательстве мы используем теорему Сарда.
3.4. Теорема (Том). Предположим, что М компактно и что
ScN—подмногообразие, замкнутое ках подмножество N. Тогда
множество отображений f?Ck(M, N), трансверсальных к S,
открыто и плотно в Ck(M, N).
Доказательство. Так как открытость уже доказана, остается
доказать плотность множества отображений, трансверсальных
к S. Возьмем f?Ck(M, N). Надо показать, что для каждого
р 6 М существуют такие окрестности Up точки р в М и 1^>v
отображения f в Ck{M, N), что множество тех g^f^p, которые
трансверсальны к S на V'р, открыто и плотно в "Pp. Действи-
§ 4. ГРУБОСТЬ 41
тельно, если это уже доказано, то пусть UPt, ..., IIРт—конеч-
IIРт—конечное подпокрытие многообразия М окрестностями указанного
типа и Ч/3 (/) = ^р, Л ¦. ¦ Л ^Рт • Тогда множество тех g ? 1^°,
которые трансверсальны к S в каждой точке М, открыто и
плотно. В частности, мы можем аппроксимировать / отображе-
отображением, трансверсальным к S. Итак, займемся построением таких
окрестностей Up и Ч^р. Пусть у: V—»-R"—локальная_ карта
возле f(p). Возьмем такую окрестность Up точки р, что f(U^)cV,
и такую окрестность f^p отображения /, что g(Up)cV при
всех g€f^p. Из доказательства предложения 3.2 следует, что
множество тех gZ^p, которые трансверсальны к S на Up,
открыто. При доказательстве плотности мы можем рассматри-
рассматривать С°°-отображение g ? f^p, ибо С°*-отображения плотны в
Ck(M, N). Легко видеть, что если ogR" мало по норме, то
существует такое gv^!V3l/, близкое к g, что y°gv~y°g-{-v на
Uр и gv = g вне некоторой окрестности множества V'р. По след-
следствию 1 предложения 3.3 существует такое достаточно малое
по норме v g R", что отображение
Up-+R": Xr->y(g(x)) + v
трансверсально к y(S)cRn. Таким образом, gv трансверсально
к S на Up, что завершает доказательство. |
Замечание. В теореме 3.4 мы требовали, чтобы S было С°°-под-
многообразием. Однако результат остается верным, и когда S
класса Сг, г ^ 1. Действительно, достаточно в приведенном выше
доказательстве взять такую локальную карту {у, V) класса Сг,
чтобы у (S) было С°*-подмногообразием в R", и затем аппроксими-
аппроксимировать g отображением g, для которого yog—класса С°° на Vр.
§ 4. ГРУБОСТЬ
Качественное изучение дифференциального уравнения состоит
в геометрическом описании его пространства траекторий. По-
Поэтому естественно спросить: когда два пространства траекторий
имеют одинаковое описание, одинаковые качественные черты?
Требуется, следовательно, установить некоторое отношение эк-
эквивалентности между дифференциальными уравнениями. Ниже
будет определено отношение эквивалентности, которое улавли-
улавливает геометрическую структуру траекторий; оно называется
топологической эквивалентностью.
Пусть ?Г(М)—пространство С'-векторных полей на ком-
компактном многообразии М с С'-топологией, г j> 1. Два вектор-
векторных поля X, Y ? Жг (М) называются топологически эквивалент-
эквивалентными, если существует гомеоморфизм h: М —* М, который пе-
42
ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
реводит траектории поля X в траектории поля У, сохраняя
их ориентации; это последнее условие означает, что если р?М
и б > 0, то существует такое е > 0, что если 0 < t < б, то
hXt(p) = Yr (h(p)) для некоторого t' g @, е). Будем называть Л
топологической эквивалентностью между X и Y Таким образом,
мы определили отношение эквивалентности на 3cr (M). Другим,
более сильным отношением является сопряженность потоков
векторных полей. Два векторных поля X и У называются со-
сопряженными, если существует топологическая эквивалентность Л,
сохраняющая параметр t; это означает, что hXt (р) — Yth (p)
при всех р^М и t?R.
Следующее предложение, доказательство которого получается
непосредственно, отмечает некоторые качественные свойства
пространства траекторий, которые должны быть общими для
двух эквивалентных векторных полей.
4.1. Предложение. Пусть h—топологическая эквивалентность
между полями X, Y ?&r (M). Тогда
(a) pgM—особая точка поля X в том и только том случае,
когда h(p)—особая точка поля Y;
(b) траектория 6Х (р) поля X, проходящая через точку р, замк-
замкнута в том и только том случае, когда 6Y (h (p)) замкнута;
(c) образом аз-предельного множества траектории 6х(р) под
действием h является ы-предельное множество траектории
GY{h(p))\ аналогично для а-предельного множества. |
Рис. 18
Пример 1. Рассмотрим линейные векторные поля X и У на
R2, определенные формулами
xix> У) = {х, у) и Y(x, y) =
§4. ГРУБОСТЬ 43
Соответствующие потоки—это отображения
xt(x, У) = е*(х, у),
Yt(x, y) = et(xcost-{-ysint, —х sin t + у cos t).
Мы построим гомеоморфизм h многообразия R2, сопрягаю-
сопрягающий Xt и Yt. Поскольку 0—это единственная особая точка
как X, так и Y, необходимо h @) = 0. Легко видеть, что еди-
единичная окружность S1 трансверсальна полям X и Y. Кроме
того, все траектории полей X и Y, кроме особой, точки 0, пе-
пересекают S1. Определим h(p) = p для pgS1. Если <7€К2\{0},
то существует единственное t (Е К. такое что Xt (q) = p$ S1.
Положим h(q) = Y_t(p) = Y_tXt(q). Непосредственно видно,
что h непрерывно и имеет непрерывное обратное на R2\{0}.
Непрерывность h и его обратного в нуле может быть прове-
проверена с использованием свойств потоков полей X uY.
Пример 2. Пусть X и Y—линейные векторные поля на R2,
задаваемые в стандартном базисе матрицами
Эти векторные поля неэквивалентны, ибо все траектории поля
Y замкнуты, а для поля X это не так (рис. 19).
Векторное поле грубое, если топологическое поведение его
траекторий не меняется при малом возмущении векторного
поля. Формально поле X g ?r (M) называется грубым, если су-
существует такая окрестность "У3 поля X в j?r (M), что любое
Y g еУэ топологически эквивалентно Xг).
Очевидно, что нулевое векторное поле ни на каком многооб-
многообразии не является грубым. С другой стороны, линейное вектор-
1) В первоначальном определении грубости, данном Андроновым и Понт-
рягиным, требуется еще, чтобы при достаточной малости "У3 гомеоморфизм,
осуществляющий топологическую эквивалентность между X и Y, мог быть
сделан сколь угодно близким к тождественному в С°-топологии (т. е. сколь
угодно мало сдвигал точки М). Вариант без этого требования предложен
Пейксото, поэтому в тех случаях, когда надо уточнить, какой именно ва-
вариант грубости имеется в виду, говорят о грубости по Андронову—Понт-
рягину и о грубости по Пейксото., Однако в настоящее время не ясно,
действительно ли эти варианты различаются между собой и имеет ли один
из них существенное преимущество перед другим.
Приведенное определение зависит от г (^ есть окрестность в Жг {М)),
При необходимости явно указывать на эту зависимость можно говорить о
грубости в классе Сг.
В иностранной литературе грубость часто называют структурной устой-
устойчивостью и ради краткости говорят просто об устойчивости и об устойчи-
устойчивых динамических системах. Как известно, термин «устойчивость» можег
употребляться и в других смыслах, но обычно из контекста ясно, что
именно имеется в виду,—Прим, ред.
44
ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
ное поле Х(р)=р, рассмотренное в примере 1, является грубым
в пространстве линейных векторных полей на R2 *). Чтобы мо-
мотивировать необходимость условий грубости, которые будут даны
в следующих главах, мы рассмотрим теперь некоторые примеры
негрубых векторных полей.
Рис. 19
Пример 3. Рассмотрим рациональное векторное поле на торе,
определенное в примере 2 § 1. Это векторное поле не является
грубым в ?Г(Т2). Действительно, все его траектории замкнуты,
в то время как иррациональное векторное поле, которым его
можно аппроксимировать, не имеет замкнутых траекторий.
В действительности на (компактном) многообразии размерно-
размерности 2 никакое векторное поле с бесконечным числом замкнутых
траекторий не является грубым, поскольку, как будет показано
в гл. 4, его можно аппроксимировать векторным полем, имеющим
лишь конечное число замкнутых траекторий.
Рис. 20
Пример 4. Пусть тор Т2 обычным образом вложен в R3
(рис. 20); он касается горизонтальной плоскости л во всех
точках некоторой «параллели» (горизонтальной окружности),
1) Точный смысл этого утверждения достаточно ясен (см. также § 2
гл. 2), но, строго говоря, оно не укладывается в рамки приведенного оп-
определения грубости, поскольку последнее относится к компактному М.—
Прим. ред.
§4. ГРУБОСТЬ
45
а остальные его точки расположены выше п. Пусть /: Г2 —¦
—»R—функция, которая каждой точке тора Т2 ставит в соот-
соответствие ее расстояние до л. Положим X = grad/. Параллель
тора Г2, содержащаяся в л, целиком состоит из особых точек
поля X. Пусть теперь X'=grad/', где/' — расстояние до плос-
плоскости л', получаемой из л малым вращением. Так как только
4 плоскости, параллельные л', касаются Тг и каждая из них
имеет лишь одну точку касания с тором, то поле X' имеет
лишь 4 особые точки. Поэтому X неэквивалентно X' и, значит,
X не является грубым. В гл. 2 будет показано, что никакое
векторное поле с бесконечным числом особых точек не грубо,
так как его можно приблизить полем с конечным числом осо-
особых точек.
Рис. 2Г
Пример 5. Опишем теперь векторное поле на S2, которое
не грубо, хотя топологически эквивалентно грубому вектор-
векторному полю, направленному вдоль меридианов из южного по-
полюса в северный (см. пример 1 из § 2). Пусть /: R. —* R—отоб-
R—отображение класса С°°, удовлетворяющее следующим условиям:
/@>0 при 1фО; /@=1/*2 при *>1 и
/ @) = dfldt @) = ... = d'fldf @) = ... = 0.
Рассмотрим векторное поле X на R2, определенное формулой
X (г cos9, r sin 9) = (rf (r) cos 9, rf (r) sin 9).
Векторное поле X радиально, и 0 является его единственной
особой точкой, dX@) = 0 и [|Х (р)\]= 1/|/э J, если [|р||^1.
Пусть л: S2\\pN\ —>- R2—стереографическая проекция, по-
показанная на рис. 22. Определим векторное поле X на S2 фор-
формулами X (р) = dn~\p, X (л (р)), если р =?= pN, и X (pN) = 0.
Ясно, что X—векторное поле класса1) С00, имеющее две осо-
особые точки: рА и ps. Отметим, что тождественное отображение
является топологической эквивалентностью между X и вектор-
векторным полем из примера 1^1- Покажем, что существует С-
*) При проверке гладкости X в р^ удобно использовать карту, полу-
получающуюся при тереографической проекции с центром проектирования ps
и плоскостью проекции, касающейся S2 в pjj,—Прим, перев.
46
ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
близкое к X векторное поле, имеющее замкнутую траекторию.
Пусть Y—векторное поле на R*, определенное формулой
Y (/-cosO, rsine) = (r/(r) cos в+ r# (r) sin 6, — rg (r) cosQ +
-f- rl(r) sinЭ), где /, g: R —-R суть отображения класса С°° с гра-
графиками, изображенными на рис. 23.
Z(O) = Z(g) = O; g@) = g@ = 0, если ^
I (f) = Ijt2, если t > 1; g- @ > 0, если 0 < / < с;
/@ < 0, если 0 < t < a; g' (a) = 0;
/ @ > 0, если t > g; g (a) = 6.
Рис. 22
Окружность So радиуса а с центром в нуле является замк-
замкнутой траекторией поля Y, так как Y касается Sa в каждой
Рис. 23
ее точке. Вне круга радиуса 1 Y=X. Таким образом, Y опре-
определяет векторное поле Y на S2, которое имеет северный и юж-
южный полюсы своими «притягивающими» особыми точками и
«отталкивающую» замкнутую траекторию y = n~l(Sa). Если
взять /Сг-близким к / и g-C-близким к нулевой функции, то
У окажется Сг-близким к X. Поскольку X топологически не-
неэквивалентно Y, то X не является грубым в ?r (S2).
Подчеркнем, что из этих примеров только векторное поле
примера 5 эквивалентно грубому векторному полю. Основной
причиной негрубости в этом случае является вырожденность
производной векторного поля в особой точке р8.
§4. ГРУБОСТЬ 47
Доказать грубость векторного поля в общем случае нелегко.
Много таких примеров приводится в гл. 4. Теперь же мы проана-
проанализируем грубость векторных полей на S1. Это очень простой
случай, но он проясняет общие цели теории динамических систем.
Пусть Х°—одно из двух единичных векторных полей на S1.
Любое X ? Jf (S1) может быть записано единственным образом
в виде X{p) = f(p)X'(p), pgS1, где f?C'(&, R). Ясно, что
X (р) = 0 тогда и только тогда, когда / (р) = 0. Как мы уже
отмечали, для любого компактного множества KcS1 сущест-
существует такое f^CiS1, R), что /~1@) = /С. Таким образом, К яв-
Рис. 24
ляется множеством особых точек поля X = fX°. Так как топо-
топологическая эквивалентность сохраняет особые точки, сущест-
существует по крайней мере столько классов эквивалентности векторных
полей, сколько имеется классов гомеоморфных компактных
множеств в S1. Это показывает, что невозможно описать и
классифицировать структуру разбиения на траектории для всех
векторных полей на S1. Естественно поэтому ограничиться
остаточным подмножеством в 3tr (S1) или, еще лучше, откры-
открытым плотным подмножеством.
Особая точка р поля X ? 3Lr (S1) называется невырожденной
(или гиперболической), если йХ (р) Ф 0, т. е. df (р) Ф 0, где X =
= fX\ Если df (р) < 0, то р называется стоком (или притя-
притягивающей особой точкой), а если d/(p)>0—то источником
(или отталкивающей особой точкой). Пусть Gc?r(S1)—под-
Gc?r(S1)—подмножество, состоящее из векторных полей, все особые точки
которых гиперболичны; поскольку такие особые точки изоли-
изолированы, их число конечно (возможно, равно нулю!). Утвер-
Утверждается, что G открыто и плотно. Действительно, пусть X =
= fX°. Ясно, что X ? G тогда и только тогда, когда /: S1 —»- R
трансверсально к {0}. Но множество /gC7"^1, R), трансвер-
сальных к {0}, открыто. Это множество также й плотно, ибо
для любого / множество тех v, для которых f-\-v трансвер-
трансверсально к {0}, остаточное. Итак, всегда можно выбрать сколь
угодно малые и, для которых (/ -f v) X° ? G,
48 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
Если X g G и X = /Х°, то из графика /: S1 —¦ R видно, что
стоки и источники поля X должны располагаться поочередно
на окружности S1. В частности, число особых точек четно.
Из этого следует, что если X, Y g G имеют одинаковое число
особых точек, то X и Y топологически сопряжены. Действи-
Действительно, пусть altbx,g2, Ь2, ..., as, fcs—хтоки и источники поля X,
записанные в порядке их размещения на S1. Аналогично, пусть
Oi, Ь[, а'2, Ь'2, .... a's, b's—стоки и источники поля У, записан-
записанные в порядке их размещения на S1. Положим h(al) — a'i и
h фг) = Ь':. Выберем точки р{ g {a{, bt), q, g ф{, ai+1) и р[ ? (а[, Ъ[),
q'i€{b'i, a'Ul). Положим к(р{) = р1 и h(q{) = q't. Если p€(altb{),
то существует единственное fglR, такое что Xt(p) = pt; поло-
положим h(p) = Y_t(p'i) = Y_thXt(p) и аналогично поступим сточ-
сточками интервалов ф{, а{+1). Теперь ясно, что h—гомеоморфизм,
сопрягающий потоки полей X и Y.
Если X не имеет особых точек, то единственной траекто-
траекторией поля X является вся S1. Если Х = /ГХ°, то либо />0,
либо / < 0 на S1. Если />0, то тождественное отображение
задает топологическую эквивалентность между X и Х°. Если
/ > 0, то в качестве топологической эквивалентности надо взять
гомеоморфизм, обращающий ориентацию. Наконец, мы утвер-
утверждаем, что если поле X g 3Lr (S1) грубо, то X ? G. Заметим
вначале, что число особых точек X конечно. Это следует из
плотности G, так как X должно быть эквивалентно близкому
к X векторному полю Y ? G. Мы оставляем читателю показать,
что эти особые точки гиперболические; если бы это было не
так, мы могли бы возмутить X таким образом, чтобы число
особых точек увеличилось, что противоречило бы грубости X.
Таким образом, X ? ?r (S1) грубо тогда и только тогда, когда
X ? G. Следовательно, грубые векторные поля образуют в Жг (S1)
открытое плотное множество и, как мы видели, их можно
классифицировать.
Развитие геометрической теории дифференциальных урав-
уравнений естественным образом ведет к параллельному изучению
диффеоморфизмов *). Сейчас мы введем некоторые основные по-
1) Итерируя диффеоморфизм <р: М —»¦ М и обратное к нему преобразование
«р-1, получаем группу преобразований {ф"} — динамическую систему с диск-
дискретным временем, или каскад; о тех или иных свойствах каскада {фп}
можно с равным основанием говорить как о свойствах порождающего его
диффеоморфизма ф, что и делают авторы.
Кроме того, иногда рассматриваются итерации отображений ф: М —>• М,
определенных не на всем М, а только на некотором открытом подмноже-
подмножестве NcM (и являющихся—в данной книге—диффеоморфизмами N на
Ф(Л')). Может случиться, что ф" (х) определены не при всех п. Хотя тогда
не получается группы преобразований, все же обычно и в этом случае го-
говорят о каскаде. — Прим. ред.
§4. ГРУБОСТЬ 49
нятия, связанные с изучением структуры траекторий диффео-
диффеоморфизма.
Пусть / € Diff (M). Траекторией точки р?М называется
множество 6(p) = {f"{p): n?Z\. Если 6 (р) конечно, будем го-
говорить, что р—периодическая точка, а наименьшее такое це-
целое п > 0, что /" (р) = р, называется периодом р. Если же
/г(р) = р, будем говорить, что р—неподвижная точка. Далее,
аз-предельным множеством <а{р) точки р называется множество
таких точек q, что существует такая последовательность це-
целых чисел nt—¦ оо, что f"i(p)—*q. Если х$6(р), то ю(х) =
= со(р). Кроме того, и(р) непусто, замкнуто и инвариантно.
Инвариантность означает, что оо(р) является объединением
траекторий диффеоморфизма /. Если р—периодическая точка,
то со (р) = 6 (р), поэтому со (р) несвязно, если период точки р
больше единицы. Аналогично определяется а-предельное мно-
множество а(р) точки р— как со-предельное множество точки р
для f 1. Указанные выше свойства ю(р) выполняются также
и для а(р).
Эквивалентность структуры траекторий двух диффеомор-
диффеоморфизмов определяется через сопряжение. Сопряжение между
f, gg Diff' (M)—это такой гомеоморфизм h: М —» М, что h о f =
= g о h. Отсюда следует, что h о /" == g" о h при любом целом п,
и поэтому hFf (p)) = 6„(<?), если q = h(p). Это означает, что Л
переводит траектории f в траектории g, и в частности, перио-
периодические точки в периодические точки того же периода. Кроме
того, h(faf{p))=&g(q) и h{af(p)) = ag(q).
Пример 6. Рассмотрим два линейных сжатия в R: /(х) =
= A/2)л и g(x) = (l/3)x. Покажем, что / и g сопряжены. Возь-
Возьмем две точки с координатами а > О, Ъ < 0 и рассмотрим
интервалы
такой
что {)
дого х g R, х ф 0, существует такое целое п, что /" (х) g [/ (a), a] U
U [b, f(b)]. Положим h{x) = g-"hfn(x) и Я @) = 0. Легко ви-
видеть, что h корректно определено и является сопряжением
между f a g. С другой стороны, сжатия f(x) — (l/2)x и g(jc) =s
= —A/3)х не сопряжены.
Такими рассуждениями можно также показать, что два ли-
линейных сжатия прямой R сопряжены тогда и только тогда,
когда они оба сохраняют или оба обращают ориентацию IR.
Пример 7. Линейные преобразования R2 / (х, у) = (х/2, 2у),
g (x, у) = (х/3, fy) сопряжены. Построим, как в примере 6, не-
некоторое сопряжение hx между /IRxjOJn g|Rx{0} и некоторое
сопряжение/^ между /({OfxR и g'|{0}xR. Тогда сопряжение
между fug будет задаваться формулой h (х, у) = (hlt (x) \ (у)).
60
ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
Пример 8. Линейные преобразования Хи Yu порождаемые
в момент времени 1 векторными полями X, Y из примера 2, не
сопряжены. Достаточно заметить, что Ух сохраняет семейство
концентрических окружностей, a Xt — нет.
Сопряженность естественным образом приводит к понятию
грубости для диффеоморфизмов: / ? Diff (M) называется грубым,
если существует такая окрестность "У3 диффеоморфизма / в
Diff''(М), что каждый диффеоморфизм g^.'V3 сопряжен с /.
Тождественное отображение, очевидно, не грубо. Диффео-
Диффеоморфизмы, порождаемые в момент времени /==1 векторными
полями X из примеров 3, 4 и 5 этого параграфа, также не грубы.
Pi h
Рис. 25
Пример 9. Возьмем векторное поле X ?Эсг (S1), которое яв-
является грубым и имеет особые точки. Как мы уже видели, X
имеет четное число особых точек, попеременно стоков и источ-
источников, flj, blt a2, b2, ..., as, bs. Выберем точки p{€(ait b{) и
<?i6(bj, a{+1). Рассмотрим теперь диффеоморфизм/Г = Х1, порож-
порожденный полем X в момент t = 1. Докажем, что / g Diffr (S1)
является грубым. Известно, что /—это сжатие на [<?/_!, Pi\
с неподвижной точкой а{ и растяжение на [pt, q{] с непод-
неподвижной точкой Ь{. Если g Cr-близко к /, то g—сжатие на
[<7i-i> Pi] с единственной неподвижной точкой at, близкой к а,-.
К тому же g является растяжением на [pt, qt] с единственной
неподвижной точкой Ь{, близкой к bt. Положим /г(а,-) = йг,
h (bt) = bt, h (pt) = Pt, h (q{) = qlt h (f (pt)) = g (pt), h (f (<?,)) = g (<?,.)•
Пусть h—какой-нибудь гомеоморфизм отрезка [р{, f(p{)] на
[Pi. g(Pi)] и отрезка [<?,, f(q,)] на [<?,-, g(<?,)]. Продолжим h
на [п/, b;] и [&,-_!, fl,-J, как в примере 6. Мы получим сопря-
сопряжение между fag, показывающее, что f является грубым.
§ 4. ГРУБОСТЬ
51
Подчеркнем, что грубые диффеоморфизмы в Diff7" (S1) обра-
образуют открытое плотное множество. Доказательство этого ре-
результата намного более трудоемко и будет дано в § 4 гл. 4.
Укажем также, что в приведенном выше примере мы начали
с грубого векторного поля из j?r(S1) и показали, что порож-
порожденный им в момент времени t = 1 диффеоморфизм является
грубым в Diff7" (S1). Следующий пример показывает, что это не
всегда так.
Рис. 27
Пример 10. Рассмотрим единичное векторное поле Х° на
S1. Тогда S1—замкнутая траектория поля Х° периода 2л.
Диффеоморфизм f = X\, порождаемый в момент времени t=\,
является иррациональным вращением. Траектория Qf (р) плотна
для каждой точки p^S1. Чтобы увидеть, что / не грубо, ап-
аппроксимируем / диффеоморфизмом g = X$, где t близко к еди-
единице и t/{2n) рационально. Каждая траектория 6g(p) перио-
периодична, и поэтому / не сопряжено с g.
Теперь объясним, почему мы определяли сопряжение как
гомеоморфизм, а не как диффеоморфизм. Рассмотрим снова диф-
диффеоморфизм / из примера 9. Как мы видели, / является гру-
грубым: если g CT-близко к /, то существует такой гомеоморфизм
h окружности S1, что h о f = g о h. При построении h мы сперва
заметим, что для каждого стока at диффеоморфизма / сущест-
существует сток al диффеоморфизма g, близкий к а{, и что то же
самое верно и для источников. Мы положили /j(of) = a|-. Легко
видеть, что можно выбрать такой близкий к / диффеоморфизм
g, что а1 = а{, a g' (at)^=f (at). Предположим теперь, что h
является в действительности диффеоморфизмом. Тогда h (at) =
= а, и h' {a{)-f {ай^g' (a,)-hr {а{), откуда /''{а,) = g' {a{), что
противоречит нашей гипотезе. Таким образом, если требовать,
52 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
чтобы сопряжение было диффеоморфизмом, то / не будет гру-
грубым в Diff (S1I). Подобным образом можно показать, что ни-
никакой диффеоморфизм f ?Dillr(M), имеющий неподвижную или
периодическую точку, не будет грубым. Это показывает, что
мы не должны накладывать условие дифференцируемое™ на
сопряжение. Та же идея приложима к топологической эквива-
эквивалентности между векторными полями. Хотя доказательство бо-
более сложно, по-прежнему верно, что никакое векторное поле
с особой точкой или замкнутой траекторией не будет грубым,
если требовать, чтобы отображение эквивалентности было диф-
диффеоморфизмом (см. упражнение 13 гл. 2 или упражнение 5 гл. 3).
УПРАЖНЕНИЯ
1. Покажите, что каждое С1-векторное поле на сфере Sa имеет по край-
крайней мере одну особую точку.
2. Назовем два векторных поля X, У?ЖГ (М) коммутирующими, если
%s (Yt (Р))= Yi Ws (Р)) ПРИ всех Р^М и s, l?R. Покажите, что
если X, F^3?1(S2) коммутируют, то у X и Y имеется общая особая
точка (Е. Лима).
3. Пусть Х = (Р, Q)—векторное поле на R2, где Р и Q—многочлены
степени два. Пусть у—замкнутая траектория поля X и DcRa —
круг, ограниченный у. Покажите, что X имеет единственную особую
точку в D.
4. Пусть Xg3?1(/W2) и FcM*—такая область, гомеоморфная цилиндру,
что Xt (F)cF при всех t ^ 0. Предположим, что X имеет конечное
число особых точек в F. Покажите, что ш-предельное множество
траектории точки p?F либо является замкнутой траекторией, либо
состоит из особых точек и регулярных траекторий, у которых со- и а-
предельные множества являются особыми точками.
5. Пусть FcM2—гомеоморфная листу Мёбиуса область, и пусть Х?
^Зс1 (М2)—такое векторное поле, что Xf(F)cF при всех /^0.
Покажите, что если X имеет конечное число особых точек в F, то
ю-предельное множество траектории точки p?F либо является замк-
замкнутой траекторией, либо состоит из особых точек и регулярных тра-
траекторий, у которых со- и а-предельные множества являются особыми
точками.
6. Пусть у—изолированная замкнутая траектория векторного поля
Х?ЖГ (М2). Покажите, что существует такая окрестность V траекто-
траектории у, что для p?V либо а(р)=у, либо w(p)=y..
7. Замкнутая траектория у поля XgJ^/W2) называется притягиваю-
притягивающей или аттрактором 2), если существует такая окрестность V тра-
!) В приведенном рассуждении подчеркивается, что сопряжение h должно
переводить а/ в п{. Это так, если накладывать дополнительные условия,
что сдвиги точек под действием h малы-(грубость по Андронову — Понтря-
гину). Если же его не накладывать, то можно взять такое g, близкое к /,
чтобы его неподвижные точки были те же, что у f, и чтобы при всех i, j
было g' (aj) Ф Г (о/). Считая, что h переводит сц в некоторое а/, рассуж-
рассуждаем далее как в тексте.—Прим. ред.
2) Компактное инвариантное (т. е. состоящее из целых траекторий)
множество А называется аттрактором, если у него имеется такая окрест-
окрестность V (ее называют поглощающей), что Xt(p)?V при <3=0 и со (p)dA
при всех р^у. Синоним—асимптотически устойчивое множество (формально
УПРАЖНЕНИЯ 53
ектории у, что Xf(p)?V при всех t^:0 и ы(р) — у при всех p?
Покажите, что если X имеет замкнутую траекторию, являющуюся
аттрактором, то каждое векторное поле Y, достаточно близкое к X,
также имеет замкнутую траекторию.
8. Пусть X— векторное поле класса С1 на проективной плоскости.
Покажите, что если X имеет конечное число особых точек, то со-пре-
дельное множество любой траектории либо является замкнутой тра-
траекторией, либо состоит из особых точек и регулярных траекторий,
у которых со- и а-предельные множества являются особыми точками.
9. Пусть X — векторное поле на торе Т2, порождающее иррациональ-
иррациональный поток Xt. Покажите, что для любых п?Й и е > 0 существует
такое векторное поле Y, что оно имеет ровно п замкнутых траекто-
траекторий и ЦК—Х||г < е.
10. Циклом1) векторного поля Х?%Г(М) называется такая последова-
последовательность особых точек plt ..., pj, pj+i = pi и регулярных траек-
траекторий Yi V/. чт0 а(Т;) = Р/ и <b(w = Pi+i- Пусть X??r(S2),
/¦> 1, удовлетворяет следующим условиям:
A) X имеет конечное число особых точек;
B) если p?S2—особая точка поля X, то либо р—отталкивающая
особая точка, либо множество таких траекторий у, что а (у) = р,
конечно.
Покажите, что для любой траектории у:
(a) если (й(у) содержит более одной особой точки, то со (у) содержит
цикл;
(b) если pj и р%—особые точки, содержащиеся в со (у), то сущест-
существует цикл, содержащий рх и р2.
11.А. Пусть GczRn — аддитивная подгруппа. Покажите, что если G замк-
замкнута, то она изоморфна R"XZl при некоторых k и I, где &+'<"•
Указание, (а) Покажите, что если G дискретна, то она изоморфна %1\
иными словами, существуют такие линейно независимые векторы
J±n.v.:ni(zA
Ч, ¦¦-, az€Rn. что
(b) Покажите, что если G не дискретна, то оиа содержит прямую,
проходящую через 0.
(c) Пусть ?crRn — векторное подпространство наибольшей размер-
размерности, содержащееся в G. Пусть Е^-—ортогональное дополнение к Е.
Покажите, что G = ?®(?-LnG) и что E^-{\G—дискретная подгруппа
в ЕК
определение асимптотической устойчивости выглядит несколько иначе, но
оказывается эквивалентным). На протяжении большей части настоящей
книги нужны только случаи, когда А—замкнутая траектория или особая
точка. В этих случаях говорят также о стоке.
Если А является аттрактором для динамической системы, получающейся
из нашей системы при «обращении времени» (поле X заменяется на Y =
= —X, так что движение t-+Yt(p) каждой точки р происходит по той же
траектории, но в обратную сторону), то говорят, что для исходной систе-
системы А является репеллером. Если при этом А сводится к одной точке или
замкнутой траектории, то часто говорят еще об источнике, а также об
отталкивающей или вполне неустойчивой особой точке или замкнутой тра-
траектории.—Прим. ред.
1) Чаще говорят о сепаратрисном контуре. Циклами же Пуанкаре
называл замкнутые траектории, и в двумерном случае этой терминологией
многие пользуются до сих пор,—Прим. ред.
54
ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
11.В. Пусть а = (аь ..., an)?R" и G — {la-\-m: /gZ, m?%,"}. Предполо-
Предположим, что 1 и координаты вектора а линейно независимы над коль-
коль?2 ^Ъп таковы, что
m=0. Пока-
Пока, р р
цом целых чисел; иными словами, если
1щ-\-<.т, а>=0, где <m, a> = 2?=i m«ai» T0 mo =
жите, что G плотна в R".
Указание, (а) Пусть л: R"-»• R"—проекция л (*1, ..
() у р A, „)(!,
Пусть G — замыкание G. Предположим по индукции, что
лС5) = К"-1.
(Ь) Пусть ?crlRn—подпространство наибольшей размерности, содер-
содержащееся в G. Тогда Е содержит вектор а, и либо размерность Е
равна л—1, либо она равна п.
Рис. 28
(с) Пусть Eij={x: xk=0, если k ф i, /}. Покажите, что Е;у(]Е —
прямая в E{j с рациональным угловым коэффициентом. Выведите
отсюда, что Е содержит п—1 линейно независимых векторов с це-
целыми координатами. Векторным произведением этих векторов явля-
является вектор с целыми координатами, перпендикулярный Е.
11.С. Постройте пример векторного поля класса С~ на торе Tn = SxX...
...XS1, все траектории которого плотны в Тп.
12. Пусть X1—векторные поля класса С", определенные в окрестностях
дисков DfdR2, где i = l, 2. Предположим, что X' трансверсалйю
границе С/ диска D/ и что X1 направлено вовне Db a Xi направ-
направлено вовнутрь D2. Покажите, что существуют такое С~-векторное
поле X на многообразии S2 и такие вложения hf. D,--»-S2, что:
A) hi(D1)f)h2(Di) = 0;
B) dhi(p)-Xi(p) = X(hi(p)) при всех p^DC,
C) если p?hi (С{), то w-предельное множество точки р содержится
в Л2 (Dg). ^м. рис. 28.)
¦13, Пусть X1, X2—векторные поля класса С" на многообразиях JHX, M2
одинаковой размерности. Пусть D/cM;—такие диски, что X1 транс-
версально к границе С,- диска D/, i = l, 2, причем X1 направлено
вовне Dlt a Xs направлено вовнутрь D2. Покажите, что существуют
такое С"-векторное поле X на некотором многообразии М и такие
вложения hf. Mf\Di-+ M, что:
A) h1(M1\D1)f\h2(M2\D2) = 0;
B) dht(p).X4p) = Xfri(p));
C) если р^Иг(С), то а-предельное множество точки р содержится
в h2 (MD)
УПРАЖНЕНИЯ 55
14. Пусть X—параллельное поле d/dt на цилиндре S1X[0, 1]. Пусть
М—фактор-пространство S1X[0, 1] по отношению эквивалентности,
отождествляющей 5хХ{0} с SXX{1} с помощью иррационального
поворота R: 5хХ{0}-»-S1X{l}. Пусть л: S1X[0, 1] -> М—естествен-
М—естественная проекция. Покажите, что
(a) существует такая структура многообразия на М, что л является
локальным диффеоморфизмом, а л^Х—векторным полем класса С™
на М\
(b) существует такой диффеоморфизм h: М-*Т3, что если Y=h^X,
то Yf—иррациональный поток.
15. Пусть М, N и Р—многообразия, причем М и N компактны. Пока-
Покажите, что
(a) отображение comp: Cr(M, N)xCr(N, Р)-+&{М, Р), задаваемое
формулой сотр(/, g) = g°f, непрерывно;
(b) отображение i: Diffr (M) -»¦ Diff (M), задаваемое формулой i (/) =
= /-1, непрерывно.
16. Пусть М и N—многообразия, причем М—компактно, и пусть Sc
CMXN—подмногообразие. Рассмотрим множество Ts = {f?Cr (M, N):
graph (/) трансверсален к S}, где graph (f) = {{p, f (p)): p?M}. Пока-
Покажите, что Ts является остаточным подмножеством в Cr (M, N).
17. Для каждого /gCr(Rn, Rm) рассмотрим отображение
jrf: Rn -^R"xRmXL (R«. Rm)X .. .XLrs(Rn; Rm)
xy^{x, f(x), df(x) <Ff(x)).
Пусть E—евклидово пространство RnxRmXL(Rn, Rm)X...
... xLs (Rn; Rm). Для каждого открытого множества UczE определим
подмножество
o?{U) = {f?C>-(Rn; Rm): jrf (Rn)czU}.
(a) Покажите, что множества q/Ц (U) образуют базу для некоторой
топологии на С (Rn; Rm) (топологии Уитни).
(b) Покажите, что С (Rn, Rm) является пространством Бэра в топо-
топологии Уитни.
(c) Покажите, что С°°-отображения образуют плотное подмножество
в С (Rn, R).
(d) Покажите, что если k < г, то отображение
C(Rn, Rm)-yC— *(Rn, RnxRmXL(R", Rm)X .. .XZ-t (Rn; Rm))
непрерывно.
(e) Пусть ScR"XRmXL(Rn, Rm) — подмногообразие. Рассмотрим
множество Ts = {f€Cr(Rn, Rm): Ljb.S}, где r^2. Покажите,что
Ts является остаточным.
18. Пусть X°^3?r(S1) (где г^З)—векторное поле без особых точек.
Пусть 2,i—множество таких векторных полей Х = /Х0?Э?'' (S1), что
особые точки X все не вырождены, кроме одной, в которой вторая
производная / ие равна нулю. Пусть 2^ х—множество таких вектор-
векторных полей X = f Х°, что их особые точки все не вырождены, кроме
двух, в которых вторая производная / не равна нулю. Пусть 2li 2 —
множество таких векторных полей X = fX°, что все их особые точки
не вырождены, кроме одной, в которой вторая производная отобра-
отображения равна нулю, но третья не равна нулюх).
1) Хотя в случае S1 можно условиться, что всегда используются коор-
координаты, связанные с представлением S1 в виде R/Z, все-таки стоит прове-
проверить, что условия, фигурирующие в определениях ?ь 2Х) ь 2lt 2, на самом
деле не зависят от выбора локальных координат. — Прим. ред.'
56 ГЛ. 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ
(a) Покажите, что 2Х является подмногообразием коразмерности 1
в банаховом пространствех) 3tv (S1) и что 2t открыто и плотно
в $r (S1)\G, где G состоит из грубых векторных полей, как в § 4.
(b) Покажите, что 22 = 2Х i(J^i г—подмногообразие коразмерности 2
в ^(S1) и что 22 открыто и' плотно в $r (S^^GU 2Х)
(c) Опишите все классы эквивалентности в окрестности векторного
поля из 2Х и в окрестности векторного поля из 22.
Замечание. Сотомайор [114] рассматривал подобные условия в кон-
контексте теории бифуркаций.
19. (а) Покажите, что если g: R ->• R—диффеоморфизм класса С1, ком-
коммутирующий с /: R -> R, задаваемым формулой f(x) = kx, где
О < Я, < 1, то g линеен.
(b) Покажите, что если g: R2 -» R2—диффеоморфизм класса С1, ком-
коммутирующий с линейным сжатием, собственные значения которого
комплексны, то g линеен.
(c) Покажите, однако, что существует нелинейный С1-диффеоморфизм,
коммутирующий с некоторым линейным сжатием.
20. Компактификация Пуанкаре. Рассмотрим сферу S2=<j у ? R8: 2 ^=' J
I «= 1 )
и плоскость P = {y?R3: «/з=1}> касательную к сфере в северном
полюсе. Пусть Ui={y^Sz: yt > 0}, Vi = {y^S2, y{ < 0}. Пусть л8:
Р-* U3, щ: Р-+Уз—центральные проекции, т. е. щ (х) и Лз (х)—
это пересечения прямой, соединяющей х и 0, с 1/3 и Va соответст-
соответственно. Пусть L—линейное векторное поле на R2. Рассмотрим поля
X1 = (пв)JL на U3 и Ха = (ла)^ на Vs.
(a) Покажите, что X1 и X2 продолжаются до некоторого С"-вектор-
С"-векторного поля X на S2, которое обозначается л(Ц, и что экватор
инвариантен относительно потока, порождаемого полем X.
(b) Опишите траектории полей n(L'), i=\, 2, 3, 4, где U в стан-
стандартном базисе представляются матрицами
(к 0\ к 0\ Д, 0 /о PN
\0 К)г \1 X)' \0 Ъ)' V-P а)'
(c) Покажите, что если L1 и L2=j4Li>4~1—линейные векторные поля
и Л—линейный изоморфизм, то л(/-х) и л (L2) топологически экви-
эквивалентны.
(d) Покажите, что если L—линейное векторное поле, которое имеет
два равных собственных значения или собственное значение с ну-
нулевой вещественной частью, то л (L) не грубо в ЗЁ°° (S8).
Указание. Используйте локальные карты ф,-: t/,--»-R2, ip,-: V/-»-Ra,
х) Определение гладкого подмногообразия MczE банахова простран-
пространства Е почти дословно совпадает с определением гладкого подмногообразия
евклидова пространства (§ 0 гл. 1), только евклидовы пространства всюду
заменяются банаховыми. Здесь, правда, имеется некоторая тонкость. По-
Поскольку у замкнутого линейного подпространства банахова пространства
не всегда существует дополнительное замкнутое линейное подпространство,
то не всегда у точки р?М существует такая окрестность А в Е, что име-
имеется диффеоморфизм h: A-+VXW на прямое произведение двух окрестно-
окрестностей нуля в некоторых банаховых пространствах ?ъ ?2. что Mf\A=h~1X
X(VXO). Требование, чтобы такие А, V, W, h существовали для каждой
р?М, можно положить в основу определения более узкого класса под-
подмногообразий (которого достаточно для многих целей). Однако для под-
подмногообразий конечной коразмерности (она определяется как размерность
ТМ или ?2) различия между этими двумя вариантами нет. — Прим. ред.
УПРАЖНЕНИЯ 5?
определенные формулами ф,- (у) = (yj/yi, yklyi), Ь(У) = (У/1УЬ Ук/Уд,
где j < k.
Замечание. Грубые поля, порождаемые на сфере S" линейными по-
полями, были охарактеризованы Г. Палис в [73].
21. Траектория у поля Х?ЖГ (Мп), г^\, называется а-рекуррентной х),
если yczco(y), и а-рекуррентной, если уса^). Пусть М—ком-
М—компактное многообразие и у—ш-рекуррентная траектория поля X ?ЖГ(М).
Покажите, что если f = Xf=i и Х?У> то точка к является ш-ре-
ш-рекуррентной, т. е. *?шу(я).
Замечание. Центр (в смысле Биркгофа) С(X) поля Х^Ж1(М) опре-
определяется как замыкание множества тех траекторий, которые явля-
являются одновременно со- и а-рекуррентными. То же определение рабо-
работает и для /^Diffr (Ж). Это упражнение показывает, что если f —
диффеоморфизм, порождаемый полем X в момент времени <=1, то
С(Х)=С(/).
х) В другой терминологии такие траектории называются устойчивыми
по Пуассону (в положительном направлении), а название «рекуррентность»
резервируется для других целей. Терминология, принятая в тексте, пред-
предложена Готтшалком и Хедлундом, поэтому при необходимости уточняют:
рекуррентность в смысле Готтшалка — Хедлунда. — Прим. ред.
Глава 2
ЛОКАЛЬНАЯ ГРУБОСТЬ
В этой главе мы будем анализировать локальное топологиче-
топологическое поведение траекторий векторных полей. Мы покажем, что
для векторных полей из некоторого открытого плотного подмно-
подмножества в пространстве Зсг(М) можно описать поведение траекто-
траекторий в окрестности каждой точки многообразия. Кроме того, ло-
локальная структура траекторий не меняется при малых возму-
возмущениях поля. После этого сразу получается полная классифи-
классификация через топологическую сопряженность.
Этот локальный вопрос рассматривается в двух случаях: возле
регулярной точки и возле особой. Первый случай, значительно
более простой, разбирается в § 1. Второй случай изучается
в § 2—5. Параграф 2 посвящен линейным векторным полям и изо-
изоморфизмам, для которых вводится понятие гиперболичности.
В § 3 это понятие распространяется на особые точки линейных
векторных полей и неподвижные точки диффеоморфизмов. Ло-
Локальная грубость для гиперболических особых точек или ги-
гиперболических неподвижных точек доказывается в § 4. Наконец,
в § 5 мы даем локальную топологическую классификацию. Па-
Параграф 6 посвящен другому важному результату — теореме об
устойчивом многообразии. С ней тесно связана Х-лемма (лемма
о наклоне), рассматриваемая в § 7. В качестве ее применений мы
приведем несколько нужных нам результатов и новое доказа-
доказательство теоремы о локальной грубости.
§ 1. ТЕОРЕМА О ТРУБКЕ ТОКА
Определение. Пусть X, Y ??Г(М) и р, q?M. Будем говорить,
что X и Y топологически эквивалентны в р и q соответственно,
если существуют такие окрестности V' и Wq и такой гомео-
гомеоморфизм hi Vp —*¦ Wq, что h(p) = q и h переводит траектории
поля г) X в траектории поля Y, сохраняя их ориентацию.
Пример. Рассмотрим векторные поля X и Y на S2, изобра-
изображенные на рис. 1. X и Y не эквивалентны в P,v, P'N, поскольку
1) Точнее, содержащиеся в Vp дуги траекторий.— Прим. ред.
§ 1. ТЕОРЕМА О ТРУБКЕ ТОКА
59
любая окрестность точки P'N содержит замкнутые траектории
поля Y, но возле точки PN нет замкнутых траекторий поля X.
Определение. Пусть X € 2ir (M) и р € М. Будем говорить, что
поле X локально грубо в р, если для любой окрестности
U (р) сг М существует такая окрестность Жх поля X в Xr (M),
что для каждого У€о1У*х поле X в р топологически эквива-
эквивалентно Y в q для некоторой точки q € U С1)-
Рис. 1
Следующая теорема описывает локальное поведение траек-
траекторий в окрестности регулярной точки.
1.1. Теорема (о трубке тока). Пусть Xg?r(M) и р?М—ре-
р?М—регулярная точка поля X. Пусть С = {{х1, ..., xm)?R.m: |x'|< 1}
и Хс—векторное поле на С, определенное формулой Хс(х) =
— A, 0, ..., 0). Тогда для некоторой окрестности Vp точки р
в М существует диффеоморфизм h: Vp —»¦ С, переводящий тра-
траектории поля X в траекторию поля Хс.
Доказательство. Пусть х: U—>-Uoc:R.m—локальная карта
возле р с х (р) = 0. Пусть х„Х—Сг-векторное поле, индуцирован-
индуцированное полем X в Uo. Так как Х(р)фО, то х*Х @) Ф 0. Пусть
ср: [—т, т]хУ0—* Uв—локальный поток поля х*Х, где V0^0.
Положим Я = {(о^Кт: <>со, х*Х @)> = 0}. И является подпро-
подпространством, изоморфным К1"- Пусть i|}i [—т, x]xS—>-U0 —
ограничение ф на [—т, t]xS, где S = H(]V0. Возьмем такой
базис {ех, еа, ..., ет} в UxH^Um, что ех = A, 0 0) и
е2, ..., ея€{0}хЯ. Тогда
0, 0)е1 = х*Х@) (по определению локального потока),
Q)ej=ej, / = 2, ..., т,
поскольку я]; @, у)—у при всех у ? S.
Таким образом, Di|j(O, 0): Rxff—»-Rra—изоморфизм. По тео-
теореме об обратной функции -ф—диффеоморфизм некоторой окре-
60
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
стности точки @, 0)€[—т, t]xS на^ некоторую окрестность
нуля в IRm. Поэтому если е > 0 достаточно мало, Съ =
= {(*, 4€КхЯ: _|/|<е. 1!*!!<е}, a if: CE -* ^„—ограниче-
^„—ограничение 1]з на СЕ, то ф—диффеоморфизм класса Сг на свой образ,
который открыт в LJ0. Кроме того, tjj переводит траектории
|/0 х (т)
«р
Рис. 2
параллельного поля XCt в СЕ в траектории поля х*Х. Рассмот-
Рассмотрим С~-диффеоморфизм /: С—*-СЕ, fiy) = ey и определим
/i~1 = x~1iJ5/: С-^-УИ. Тогда h: х^ (СЕ) —>С является С-диф-
феоморфизмом, удовлетворяющим требованиям теоремы. |
Замечание. Диффеоморфизм Я: СЕ—>-М, определенный фор-
формулой Л~1 = л:~1^, переводит траектории единичного параллель-
параллельного поля ХсЕ в траектории поля X, сохраняя параметр t.
Следствие 1. Если X, Y € ?r (M), a p,.q ? М —регулярные точки
полей X и Y соответственно, то X эквивалентно Y ври q.
Следствие 2. Если X ^?Г(М) и р?М—регулярная точка поля X,
то X локально грубо в р. |
§ 2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ
Пусть «24IR")—векторное пространство линейных отобра-
отображений из К" в R" с обычной нормой:
Сперва напомним некоторые основные результаты из линейной
алгебры. Если L^<S>(R"), a k—целое положительное число,
будем обозначать через Lh линейное отображение L о ... о L.
По индукции легко показать, что || Lk | <; || L \к. Рассмотрим
последовательность линейных отображений Em = '^(\k\Lk
где L0 означает тождественное отображение.
$2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ 61
2.1. Лемма. Последовательность Ет сходится.
т
Доказательство. Последовательность вещественных чисел
Sm = 2)™=о A/&0 \L |* является последовательностью Коши, схо-
сходящейся к Ф1К С другой стороны,
1т+т' II т+т'
Е WL1< ? 7rrllLl*H|Sm+m<-SJ|.
Это показывает, что {Ет}—последовательность Коши. Так как
^(R") —полное метрическое пространство, отсюда следует, что
последовательность \Ет] сходится. |
Определение. Отображение ехр: 3! (R")—^3(Rn), задаваемое
формулой ехр (L) = eL = 2?=о A/&I) Lk, называется экспоненциаль-
экспоненциальным отображением.
2.2. Лемма. Пусть a: R —> & (R") определяется формулой
a(t) = etL. Тогда а дифференцируемо и a' (t) = Leu.
Доказательство. Пусть am(t) = I+tL+(t2/2\)Lz+...+(tm/ml)Lm.
Ясно, что ат дифференцируемо и
fm—1
ат (t) = L + tl» + • • • + ^гщ L"' = Lam_ г (t).
Поскольку a.m_1(t) сходится к еп равномерно на каждом огра-
ограниченном подмножестве К, отсюда следует, что а'т (t) —*¦ LetL
равномерно. Таким образом, а дифференцируемо и a' (t)=LetL. |
2.3. Предложение. Пусть L—линейное векторное поле на R".
Тогда отображение ф: Rx11?"—>K", определенное формулой
ф (t, x) = etLx, является потоком поля L.
Доказательство. Так как отображение jg7 (К") х К" —•• R",
(L, x)*—>Lx, билинейно, а отображение t—*etL дифференци-
дифференцируемо, то, в силу цепного правила, получаем дифференци-
руемость ф. Кроме того, (d/dt)q>(t, x) = L<v(t, x) по лемме 2.2.
Так как ф @, х) = х при всех х ? К", то предложение дока-
доказано. |
Пусть С"—множество наборов из п комплексных чисел
с обычной структурой векторного пространства. Любой элемент
из С" может быть записан в форме и + iv, где и, v ? R". Если
a-\-ib?C, то (a-\-ib) (u-\-iv) = (au—bv)-\-i(av-{-bu). Пусть
3! (С") обозначает комплексное векторное пространство линей-
линейных отображений из С" в С" с обычной нормой:
|L| = sup{|Lt>|: »€С», М=1}.
Если L G 2 (R"), то можно определить отображение L: С" —<- С"
формулой С (и -j- ш) = L (ы) -f- гХ (&). Легко видеть, что I является
62
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
С-линейным, т. е. L?3(C"). Пусть ехр: 3(С") —*3(С") —
экспоненциальное отображение, определяемое так же, как и
в вещественном случае. Пусть %: 3 (R") —> 3 (С")—отображе-
(С")—отображение, которое каждому оператору L сопоставляет его комплекси-
фикацию L, определенную выше. Следующее предложение вы-
вытекает непосредственно из определений.
2.4. Предложение. Отображение #: 3 (R") —* 3 (С") обладает
следующими свойствами:
A) tf(L + T) = tf (L) + tf (Г),
B) Т
C)
() (p)
при всех L, T?3(R") и а?К- |
Пример. Пусть Lg <5?"(Кг) и {е^, е2}—базис пространства Ка,
по отношению к которому матрица оператора L имеет вид
^J Тогда матрица оператора L = 'e(L) в базисе
/Я 0\
{ех+'щ, ег—te2} пространства С2 есть (
о
0
Поэтому матрица оператора eL в этом базисе—это
С другой стороны,
io (eL) (е1 -J- ie2) = е^ег -\- ieLe2 =
= eL (ех + ie2) = e% (et + ie2).
Поскольку e^ = ea(cosP4-isinP), отсюда следует.
(о
что
eLet =
= ^"^05^—sinPe2) и eie2 = e'x(sinPe1 + cosPe2). Следовательно,
матрицей оператора eL в базисе \е1У е2} является матрица
( cosp sir
\—sinP cosP
2.5. Теорема (вещественная каноническая форма матрицы).
Если L?3(R"), то существует базис пространства R". в ко-
котором матрица оператора L имеет вид
(At О
о
В,
§2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ
63
где
л,.=
*., о
1XJ
i=\, ..., r, %i
о \\{)
о
О / Су)
* / — 11 • • " ) Sj
с,=
а,
Матрицы Л1? ..., Лг, So ..., Bs определены однозначно,
с точностью до перестановки. |
Следствие. Пусть L^_S(R"). Для любого е> 0 существует
такой базис пространства К", в котором матрица оператора L
имеет вид
(At О
О
где
0
О
В.
О/Р/
О
е 0.
0 е . .
е 0 ау (Зу
О 0 е — fy a.
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
2.6. Лемма. Если Л, B???(Rn) таковы, что АВ = ВА, то
еА+в = еАев.
Доказательство. Пусть Sm (/)=/ + tA + ... + (tm/m\) Am.
Поскольку АВ = ВА, имеем AkB = BAk и, значит, Sm(t)B =
= BSm (t). А так как Sm (t) — etA, то etAB = J3eM. Пусть х 6 К".
Рассмотрим кривые a, 0: К—*К", а(/) = е* {A+B)x, §(t)=etAetBx.
По лемме 2.2 имеем а' @ = (Л + B)eUA+B)x = (A + B)a(t) и
Р' AtAw tABtB Л'^<в В^'в (Л ВР
Р@ + ( +)Р(О
поскольку e1AB = BetA. Таким образом, а и Р являются интег-
' ральными кривыми линейного векторного поля Л -f В и удов-
удовлетворяют одинаковым начальным условиям а @) = Р @) = х.
По теореме единственности a(tf) = P(tf) при всех I. В част-
частности, еА+вх = еАевх. Так как это выполнено при всехх^К".
отсюда следует, что еА+в=еАев. |
Если L^^(R"), то спектр оператора L, т.е. множество
собственных значений I, называется комплексным спектром
оператора L. Это множество совпадает с множеством корней
характеристического многочлена оператора L. Каноническая
жорданова форма комплексифицированного оператора L пред-
представляется матрицей
(К О
0
и X;—собственные значения оператора Ъ.
Заметим, что диагональные элементы треугольной комплекс-
комплексной матрицы являются ее собственными значениями, причем
каждый элемент повторяется ровно столько раз, какова его
кратность как собственного значения.
2.7. Предложение. Если L€J?(R.n) и %—собственное значение
оператора L, то ек—собственное значение оператора eL той же
кратности.
Доказательство. Рассмотрим (m x т)-матрицу
, где
Л,=
•
,0
•
1
0 '
'к
о 1 х
§ 2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ НОЛЯ
где
. Имеем
?> =
а о)
о к
где
и /V =
г о
1 О
0 10;
Легко видеть, что Nm — 0 и ND = DN. По лемме 2.6 полу-
получаем, что еА = eDew. Но ew = / + N + /V2/2! + • • • + N^ftm— 1)!,
поскольку /V*==0 при k^m. Поэтому
1 О )
1. 1.
_1_
2.
Далее,
Значит, еА является треугольной матрицей, у которой все
диагональные элементы равны е\ и, следовательно, е%—собст-
е%—собственное значение оператора еА кратности т.
Пусть теперь L ? 2 (R"). По теореме о вещественной кано-
канонической форме матрица оператора С в некотором базисе Р
пространства С" имеет вид
(%, 0)
о
лг>
где Л7 =
Легко видеть, что
1
0 1 а,
-и
при всех k?fi, и поэтому
66
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Это показывает, что собственными значениями оператора еА
являются числа е\ ..., е%г и только они, где "kit ..., "кг —
собственные значения оператора А. Но eL = eL представляется
в базисе р пространства С" матрицей еА, откуда следует, что
е**, ..., е%г—собственные значения комплексификации опера-
оператора eL. I
Определение. Линейное векторное поле Lgj2?(IRn) называется
гиперболическим, если спектр оператора L целиком лежит вне
мнимой оси. Число собственных значений L с отрицательными
вещественными частями называется индексом1) оператора L.
Заметим, что гиперболическое линейное векторное поле имеет
лишь одну особую точку—начало координат.
2.8. Предложение. Если L^.g(Rn) является гиперболическим
векторным полем, то существует единственное разложение
(называемое «расщеплением») пространства R" в прямую сумму
Rn*=EsQ)Ea, где Es и Еп—инвариантные подпространства
для оператора L и для потока, порождаемого полем L, такое
что собственные значения оператора Ls = L\ES имеют отри-
отрицательную вещественную часть, а собственные значения опера-
оператора La = L\Ea имеют положительную вещественную часть.
Доказательство. Пусть е±, .... е„—базис К", в котором
матрица оператора L имеет вещественную каноническую форму
А?
В,
О
о
Си'
х) Последнее название не является общепринятым, но может быть при-
принято по аналогии с индексом квадратичной формы.— Прим. ред.
$2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ
67
Здесь
Гк,
А,=
1 X,
О 1
О
0;
My
I М,
о
и «/ < О;
.0 / М, )
К
1
0 1
'Mt 0)
/ м,
о
, где м,=(_
Пусть Es—подпространство, натянутое на elt ..., es, где
eit ..., es—объединение базисов инвариантных подпространств,
ассоциированных с Ait ..., Ar, Bt Bs». Пусть Еп —
подпространство, порожденное es+i, ..., еп. Ясно, что Es и
Еп инвариантны относительно L и что матрица оператора Ls
в базисе {еи ..., es} имеет вид
'At 0
Bf
О
68
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
а матрица L" в базисе {es+l еп) — вид
и'
0
что показывает существование требуемого разложения. Един-
Единственность получается непосредственно. I
Пусть L?j?(Rn)—гиперболическое векторное поле. Если
обозначить через Lt поток, порожденный полем L, то Ll = eL,
откуда по предложению 2.7 следует, что Lt не имеет собствен-
собственных значений на единичной окружности S1, поскольку L не
имеет собственных значений на мнимой оси. Это мотивирует
следующее определение.
Определение. Линейный изоморфизм А € GL (R") называется
гиперболическим, если спектр оператора А не пересекается
с единичной окружностью S1 с С. В частности, диффеоморфизм,
порождаемый в момент времени t = 1 потоком гиперболического
линейного векторного поля, является гиперболическим изо-
изоморфизмом.
2.9. Предложение. Если A?GL(Rn)—гиперболический изомор-
изоморфизм, то существует единственное разложение Rn = EsQ)Ea,
такое что Es и Еа инвариантны относительно А и собствен-
собственные значения оператора AS=A\ES—это собственные значения
оператора А, которые по модулю меньше чем 1, а собственные
значения оператора Аа = А\Еа—это собственные значения опе-
оператора А, которые по модулю больше чем 1.
Доказательство. Аналогично доказательству предложе-
предложения 2.8. |
2.10. Предложение. Если A?GL(Un)—гиперболический изомор-
изоморфизм, то существует такая норма fl-fl, в R", что |Л5||1<1
и ||(Л°)~1||< 1; иными словами, As является сжатием, а А"—
растяжением.
Доказательство. Рассмотрим каноническую форму для one-
$2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ
69
ратора As =
где
О
1 •
0 1 X, J
о)
в,
•s"J
a,
-P/
1
0
0
P/
o'
Г
•
• •
a •
• •
Г
0
1
•
• •
0 a,
1 — В
о
Для каждого i g R рассмотрим матрицы
а, В,
- В/ «у
/1,@ =
< .
0
. B,(t) =
О . .
о
о
t 0 а,
О t -р,
70
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
О
А, (О
i (9
О
я,-(9
Утверждается, что существует б > 0 со следующим свойством:
если е< 8 и «1, ..., es—ортонормальный базис пространства
Es, а Л-1-линейное преобразование Es, матрица которого
в этом базисе имеет вид М(е), то ||Л||< 1. Действительно,
пусть Л (t)—линейное преобразование пространства Es, матрица
которого в базисе eit ..., es есть М (t). Легко видеть, что
|Л@)|| = тах{|?ч|, УЩ+Щ}. Поэтому |Л@)|]<1. Поскольку
композиция отображений t*-> A(t)t->\A(t)\ непрерывна, то
существует такое 6 > 0, что |]Л(?)|<1 при 0<?<6; это
доказывает утверждение.
Пусть теперь 8 > 0 такое, как выше. По следствию из тео-
теоремы 2.5 существует базис eit , es пространства Es, в ко-
котором матрица Л* есть М (е). Определим новое скалярное
произведение на Es формулой <е,, е7>, = 8//t где 8f/ = 1, если
» = /', и 0, если 1ф\. Пусть \\—норма, порожденная скаляр-
скалярным произведением <, \. Так как наш базис ортонормирован-
ный, то из утверждения следует, что |Л*||1<1. Аналогично
выбирается норма в Е" так, что JM")"!, < 1. Определим
норму || • ||х на К" формулой1) |u|, = max{j|ys|lt Jw"||i}, где vs
и Vй—компоненты разложения вектора v в Es и Е" соответ-
соответственно. Ясно, что эта норма удовлетворяет требованиям пред-
предложения. |
Следствие. Если L—гиперболическое линейное векторное поле
с потоком Lt, aR" = EsQ)Ea—расщепление из предложения 2.8,
то Lt (х) стремится к нулю, если x?Es и t—>• -f oo или если
Еа и t-+—co.
Доказательство. Пусть x^Es. Достаточно показать, что
Ln(x)-+0, где п?Щ и я—>-оо. Действительно, если /€[0, 1],
х) Или ||(|
квадратичной формо
V ||u*(|i+|]^°
ой формой.—
|| если желательно, чтобы квадрат нормы давалед
Прим. ред.
$2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ
то (ввиду непрерывности Lt) для любого е > 0 существует та-
такое 64 > 0, что ||Lt (у) | < е при \у\ < 6t. Так как отрезок [0, 1] —
компакт, то существует такое б > 0, что ||Lt (у)\ < е при \у\ < S
и при всех /?[0, I]1). Если Ln(x)-*0 при п—*оо, то су-
существует такое п0 ? И, что | Ln {х) || < б, если п :> пв. Если
t > п0, то / = п-J- s "с некоторым целым п ^ п0 и s ? [0, 1]. Таким
образом, | Lt (x) || = || LsLn (x) || < е. Итак, достаточно показать, что
||Ln (x) || = L?(j:) сходится к нулю. По предыдущему предложению
существует метрика на Es, в которой Lt—сжатие, т. е. \ЬХ\ < 1.
Тогда Ц^хК^ЦИ^^ГИ. Поскольку |L,|»-*0, полу-
получим, что |LJa;||—j-0, что и требуется. Вторая часть следствия
доказывается аналогично. |
2.И. Предложение. Множество H(Rn) гиперболических изомор-
изоморфизмов пространства R." открыто и плотно в GL(R").
Доказательство, (а) Открытость. Пусть А?Н(R"). Пока-
Покажем, что существует такое б > 0, что если ||Л—Б||<б, то
B$H(Rn). Пусть k?Sl. Так как Я, не является собственным
значением оператора А, то с1е1(Л—К1)ф0, где /—тождест-
/—тождественное отображение пространства С". Далее, deb ?? (С") —*¦ С—
непрерывное отображение. Поэтому существует такое б^ > 0
и такая окрестность V% точки К в С, что если \\В—Л[|<бя
и и€^ь то det(B—ц/)=т^0. Пусть Vx,, ...t Vk —конечное
подпокрытие покрытия {V^i ^gS1} окружности S1. Положим
6 = min{6v, ..., 6^}. Если ||fi—ЛКб и n€Sl, то ^gF^
для некоторого / и, следовательно, det(Z?—[\,1)ф0. Значит,
B?H(Rn), что и требуется.
(Ь) Плотность. Пусть оператор A?GL(Rn) n%it ..., %п—
его собственные значения. Легко видеть, что если ^ g R, то
собственные значения оператора А -{- [х/—это Я,4 + ^, ... Дст + ц.
Пусть Я,,,, ..., Я,, —собственные значения А, не принадлежа-
принадлежащие S1. Рассмотрим следующие числа:
Ч
= min{|a|' a + t'P является собст-
собственным значением оператора А
с а2 + Р2=1 и
Проще сразу использовать
Все равно непрерывность Ltx (использование которой подразумеваетсй
в аргументации с компактностью) доказывается с помощью сходных пера*
венств.—Прим, ред.
72
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Ясно, что 6j > 0, 6г > 0 и 6„ > 0. Если 0 < ^ < min {6t, 6j, 6g}
и X, является собственным значением оператора Л, то 7. +fi^S1,
и поэтому оператор В = А-\-ц/ является гиперболическим. Для
любого данного е > 0 возьмем ц < е и ц < min {6t, 6г, 8,}.
Тогда В—гиперболический оператор и \\В—А || = ||^/|| <е. Это
показывает, что Н (R") плотно в GL (R"). |
2.12. Предложение. Множество W(R") гиперболических линей-
линейных векторных полей в R" открыто и плотно в ^R)
Доказательство, (а) Открытость. Отображение ехрг J)
—* GL (К") непрерывно. По предложению 2.7 получаем, что
55f(IR") = exp-1(^(IR")). Так как Я (R») открыто, то и §V(Rn)
открыто.
(Ь) Плотность. Пусть L g S? (К"), 6, = min{|a|! a+ф —
собственное значение L и а Ф 0}. Для любого е > 0 возьмем
б < min {е, 6,}. Легко видеть, что векторное поле Т = Ь-\-Ы
является гиперболическим и \\Т—L||<e. |
Наша следующая цель — дать необходимое и достаточное
условие топологической эквивалентности двух гиперболических
линейных векторных полей.
2.13. Лемма. Пусть L—гиперболическое линейное векторное
поле на R" индекса п. Тогда существует такая норма ||-| на
R", что если S"'1 = {v € R"! ||ц||=1}, то при всех xt^S"'1 век-
вектор Цх) в х трансверсален к S"~a.
Доказательство. Рассмотрим базив eit
IR", в котором матрица L имеет вид
еп пространства
А =
(Л
Bt{l)
0
с Л|A) и Bj(\) такими, как в предложении 2.10.
Пусть L—линейное векторное поле на IR", матрица кото-
§2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ
73
рого в ортонормированием базисе евть
,@) О
А АО)
В±@)
о бл) ;
Легко видеть, что L трансверсально к S". Так как S" ком-
компактно, то для достаточно малых е > 0 поле L, задаваемое в этом
ортонормированном базисе матрицей
(At{e) О
As>(e)
О Б^о.,
трансверсально к S"~%. G другой стороны, по следствию из
теоремы 2.5 существует базис пространства К", в котором
матрица оператора L есть Л. Определим скалярное произведе-
произведение на R" так, чтобы этот базис стал ортонормированным. Тогда
приведенное выше рассуждение показывает, что L трансвер-
трансверсально к единичной сфере в этой норме. |
2.14. Предложение. Если L и Т—линейные векторные поля на
R." индекса п, то Существует такой гомеоморфизм hi R" —>- R",
что hLt = Tth при всех /gK.
Доказательство. Пусть ||-|| и ||-|2—такие нормы на R", что
сферы S?-1 = {v g R"i I v \\i = 1}, Sg" = {v g K"j || v ^ = 1} транс-
версальны к полям L и Т соответственно. Если х g R"\{0}, то
по следствию из предложения 2.10 получим, что iimt-ю, Lt(x)=0
и Umt-*a>lL_t(x)l = оо, так что траектория Ql{x) обязательно
пересекается с S^1. Поскольку L трансверсально к SJ, отсюда
следует, что 6l(x) пересекает S? в единственной точке.
Пустьh: Sf —* S^'1 —любой гомеоморфизм (например, можно
положить /г (*) = */!*У- Теперь продолжим h на R". Положим
74 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
h@) = 0. Если *6R"\{0}, то существует единственное такое
*0€R, что L-tAtiZ-ST1- Положим h(x) = Tth(L_u{x)). Легко
видеть, что hLt = Tth при всех t?R и что /г имеет обратное.
Остается показать непрерывность h.
Пусть A;gRn\{0} и (дгга)—сходящаяся к х последователь-
последовательность. Возьмем такие tm ? R, что L_,m (xm) g Sf ~1, и такое t0 g R,
что L_to (*) g Sy1. Поскольку поток непрерывен, отсюда сле-
следует, что tm-*tu и L_tm(xJ~* L_u(x). Поэтому ft(*J-
=TtmhL-tm(xm) сходится к Г1()/г1_4()(д;) = /г(д;), что показывает
непрерывность h в точке х. Покажем, что h непрерывно в нуле.
Из предложения 2.10 и компактности сферы S%~1 следует, что
для любого е>0 существует такое /8>0, что ||7\(#I<е ПРИ
всех t > tE и всех у ? Sg-1. С другой стороны, так как L @) = 0,
то существует такое б > 0, что если ||д;|| < б и L_t(x) GS?, to
f > tR. Таким образом, ||/г(д:)|| < е, если |д;|| < б, что показывает
непрерывность h. Аналогично можно показать, что отображе-
отображение /г непрерывно. |
2.15. Предложение. Пусть L и Т—гиперболические линейные
векторные поля. L и Т топологически сопряжены тогда и только
тогда, когда они имеют одинаковый индекс.
Доказательство. Предположим, что L и Т имеют одинаковый
индекс. Пусть ES,ES'—устойчивые подпространства для L и Т
соответственно. Тогда dim?'* = dim.?v. По предложению 2.14
существует гомеоморфизм hs: Es —* Е^, сопрягающий Ls и Ts,
т. е. hJJt = Tsths при всех t € R. Аналогично, существует гомео-
гомеоморфизм hui Eu —>¦ Еи', сопрягающий La и Та. Определим
h: ?*ф?и-+?5'ф?и' формулой h(xs + xtt) = hs{xs) + hu(xa).
Легко видеть, что h—гомеоморфизм, сопрягающий Lt и Tt.
Обратно, пусть h—топологическая эквивалентность между L
и Т. Так как 0—единственная особая точка полей L и Т, то
мы должны иметь /г @) = 0. Если x?Es, то со(л:) = О. Так
как топологическая эквивалентность сохраняет со-предельные
множества траекторий, имеем со (h (х)) = h (со (л:)) = 0. Поэтому
h(x)?Es', так что h(Es)czEs'. Аналогично h^iE^czE*. Сле-
Следовательно, h\Es—гомеоморфизм между Е" и Es'. По тополо-
топологической теореме об инвариантности размерности получаем, что
dim?'s = dim?'s', что и доказывает предложение. |
Теперь мы намереваемся показать, что собственные значе-
значения оператора непрерывно зависят от оператора. Под этим мы
понимаем следующее. Для L6«S?(R") пусть %г, \, ..., \—его
собственные значения кратностей т±, т2,..., mk соответственно.
Рассмотрим шары Ве (kt) с центрами ^, 1 ^ i ^ k, и такого
радиуса е, что все они попарно не пересекаются. Мы хотим
показать, что для любого е > 0 существует такое б > 0, что
§2. ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПОЛЯ
если TgJg^lR") и ЦТ—L||<6, то Т имеет ровно mt собствен-
собственных значений в В?(к{) (с учетом их кратностей) при всех
1 < i < k.
При L^3?(R") пусть Sp(L) обозначает спектр оператора L,
т. е. множество его собственных значений. Следующая лемма
показьюает, что Sp (L) не может сильно измениться при малом
возмущении оператора L.
2.16. Лемма. Пусть L€J?(Rn). Для любого е>0 существует
такое б>0, что если TgJ^IR") и ЦТ—L|]<6, то для каж-
каждого ?t'gSp(T) существует %?Sp(L) с \К~-У\<е.
Доказательство. Если >»gSp(L), то Я,—собственное значе-
значение комплексифицированногооператора ?,так что |7.|^||L|=|L||.
Поэтому если ЦТ—L||< 1, то спектр оператора Т содержится
во внутренности диска D комплексной плоскости С с центром
в нуле и радиуса 1-J-JL]. Пусть Ve—объединение шаров ра-
радиуса е с центрами в точках спектра Sp (L). Если \i (E D\Ve,
то det(L—^/)^=0. Ввиду непрерывности определителя суще-
существует такая окрестность U^ точки \i в С и такое 6^ > 0, что
если ЦТ—?||<8ц и ц' g 1/д, то det(f—ц'/)=^0, так что
(х' (? Sp (f). Из компактности множества D\Ve следует, что
существует такое 6 > 0, что если ЦТ—L||<6 и цё^Х^е» то
det (Т—^,7)^=0. Поскольку Sp(T)cD, отсюда следует, что
Sp(T)cVre, что доказывает лемму. |
Если собственные значения оператора L попарно различны,
то из леммы 2.16 следует, что они непрерывно зависят от опе-
оператора. Пусть Я,—собственное значение оператора L кратности т,
и пусть E(L, Х)сСп—ядро оператора (L—Х1)т. Тогда Е(L, 1)
является подпространством размерности т. Кроме того, если
k^m, то ядро оператора (L—A,/)ft—это E(L, К).
2.17. Лемма. Если Я,—собственное значение оператора L^S? (Кй)
кратности т, то существуют такие е0 > 0 и 6 > 0, что если
ЦТ—L|<8, то сумма кратностей собственных значений опе-
оператора Т, содержащихся в круге радиуса е0 с центром %, не
превышает т.
Доказательство. Рассуждая от противного, предположим,
что при всех е > 0 и б > 0 существует такое Т g S? (Rn)
с ЦТ—L[|<8, что число собственных значений оператора Т,
взятых с их кратностями, которые содержатся в круге ради-
радиуса е и с центром в точке К, больше чем т. Тогда сущест*
вуют такое т' > т и такая последовательность операторов
Lk —у L, что собственные значения Kkl, ..., hk , операторов Lh
сходятся к К. Пусть Ek обозначает ядро оператора (Lh—9^7)о,м
76 i.'i. г. Локальная грубость
...оAй — Kk ,/). Можно считать, что dimEk = m'. Пусть е\, ...
..., е%,.—ортонормированный базис пространства Ек. Так как
|| ^ ||=1 и единичная сфера в С" компактна, то можно предпо-
предположить (переходя, если нужно, к подпоследовательности), что
е) —*¦ е{. Ясно, что система векторов ег, ..., ет- ортонормиро-
ванна и поэтому она порождает подпространство Ё размер-
размерности т'. Поскольку последовательность операторов (Lk—KkJ)o...
...o(Lk—Km-f) сходится к (L—Я7)ш', то по непрерывности мы
получаем, что ядро оператора (L—Я,/)' содержит Е. Но это
приводит к противоречию, так как это ядро должно иметь
размерность т <т'. |
2.18. Предложение. Собственные значения оператора
непрерывно зависят от L.
Доказательство. Пусть Kit ..., Xk — различные собственные
значения оператора L с кратностями соответственно п1г ..., nk.
По лемме 2.16 для любого е>0 существует такое 6>0, что
если ЦТ—L|< 6, то собственные значения оператора Т содер-
содержатся в кругах радиуса е с центрами в точках Кг Остается
показать, что сумма кратностей собственных значений опера-
оператора Т, содержащихся в круге с центром в точке Kj, равна пу.
По лемме 2.17 при некотором е < eD эта сумма меньше или
равна П]. Но если при некотором / эта сумма строго меньше п,-,
то сумма кратностей всех собственных значений оператора Т
строго меньше 2/=in/ — n' что приводит к противоречию. |
Следствие. Если LgJg^lR")—гиперболическое векторное поле,
то существует такая окрестность V а& (R") оператора L, что
все Т g V имеют тот же индекс, что и L. |
Другим следствием этого предложения является тот факт,
что корни многочлена непрерывно зависят от коэффициентов.
2.19. Предложение. Всякое гиперболическое линейное векторное
поле является грубым в пространстве линейных векторных полей.
Доказательство вытекает непосредственно из приведенного
выше следствия и предложения 2.15. |
2.20. Предложение. Пусть L—грубое линейное векторное поле.
Тогда L является гиперболическим.
Доказательство. Пусть L—негиперболическое линейное век-
векторное поле и
6 = min {| а |: а-\- i$ является собственным значением оператора L
и а=^0}.
Если 0</<6, то L + tf и L—tl — гиперболические вектор-
векторные поля с различными индексами, и поэтому они не могут
§ 3. ОСОБЕННОСТИ И ГИПЕРБОЛИЧЕСКИЕ НЕПОДВИЖНЫЕ ТОЧКИ 7?
быть топологически эквивалентными. Это показывает, что в лю-
любой окрестности оператора L существуют два топологически
неэквивалентных векторных поля. Следовательно, L не является
грубым. |
Резюмируя изложенные выше результаты, можно сказать,
что линейное векторное поле является грубым в пространстве
линейных полей тогда и только тогда, когда оно гиперболи-
гиперболическое. Кроме того, грубые линейные поля образуют открытое
и плотное множество в S? (R").
§ 3. ОСОБЕННОСТИ И ГИПЕРБОЛИЧЕСКИЕ
НЕПОДВИЖНЫЕ ТОЧКИ
В этом параграфе мы собираемся определить такое множе-
множество $cz?r(M), что локальная структура траекторий каждого
X ? Ъ является грубой и достаточно простой для классификации.
Следующий пример показывает, что в окрестности особой
точки векторное поле может иметь чрезвычайно сложную струк-
структуру траекторий.
Пример. Если L—линейное векторное поле на R2, имею-
имеющее 0 своим собственным значением, то существует одномерное
Рис. 3
подпространство FcrR2, состоящее из особых точек поля L.
Пусть L—векторное поле, задаваемое в стандартном базисе
матрицей ( i)- в этом случае F = {(/, 0): f?lR}.
Мы покажем, что сколь угодно близко к L существует такое
несчетное множество effl* векторных полей, что при любых X,
Z€b41 поле X неэквивалентно локально полю Z в нуле.
Пусть У—постоянное векторное поле У=A,0). Пусть /С с R—
компактное подмножество. Известно, что существует ограни-
ограниченное С°°-отображение р: R —>- R, обращающееся в нуль точно
в точках множества К- Можно также предположить, что пер-
первые г производных отображения р ограничены. Для любого
е>0 можно выбрать такое п?Н, что ||A/п)р[|г < е. Пусть
Z = L-{-(l/ri)pY. Тогда \Z—Lfl,. <e, и множеством особых точек
78
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
поля 1 является К- Таким образом, если К и К'—два него-
меоморфных компактных множества, получается, что поля Z
и Z'-, построенные так, как указано выше, не являются топо-
топологически эквивалентными. Следовательно, существует по край-
крайней мере столько же классов эквивалентности векторных полей,
сколько существует классов негомеоморфных компактных под-
подмножеств в R1). Этот пример мотивирует следующее опреде-
определение.
Рис. 4
Определение. Будем говорить, что р?М—простая особая
точка векторного поля X ? Жг (М), если 0 не является собст-
собственным значением оператораа) DXr\ ТМр —>- ТМ
р.
3.1. Предложение.Пусть X ?3cr (М). Предположим, что р?
простая особая точка поля X. Тогда Существуют окрестности
off (X)c36r(M), UpczM поля X и точки р соответственно и
непрерывная функция р: <ЛГ (X) —>¦ Up, которая каждому век-
векFV(X) д
() p у
торному полю FgcJV(X) ставит в соответствие единственную
особую точку поля Y в V'р. В частности, простая особая точка
является изолированной.
Доказательство. Воспользуемся теоремой о неявной функции
в банаховом пространстве. Поскольку проблема локальная, то
можно считать, пользуясь локальной картой, что M*=Rm, p = 0
X?(D D {lR |||| 1}
у р p
и что X—векторное поле из ?r(Dm), rfleDro = {xglR'n: ||л:||< 1},
3cr = ?r (Dm) является банаховым пространством, а отображение
q>: Dmx?r -+Rm, задаваемое формулой ф(лг, Y) = Y(x), принад-
г) Такие классы, конечно, образуют несчетное множество, но поскольку
сейчас речь идет о локальной эквивалентности, то следует добавить, что
неэквивалентных ростков компактных подмножеств R тоже несчетное число.—
Прим. ред.
2) Если X (р) = 0, то DXp—корректно определенное линейное преобра-
преобразование в ТМр; в терминах локальных координат оно описывается матри-
матрицей (dx'idxJ). (Заметим сразу же, что при X (р) Ф 0 это не так—при ис-
использовании различных координат получились бы различные операторы.)
Простые особые точки часто называют еще невырожденными,— Прим. ред.
§ 3. ОСОБЕННОСТИ И ГИПЕРБОЛИЧЕСКИЕ НЕПОДВИЖНЫЕ ТОЧКИ 79
лежит классу гладкости С. Имеем ф (О, X) = 0, и по предполо-
предположению D^@, X) = DX@): Rra—¦Rra—изоморфизм. По теореме
о неявной функции существуют окрестности U точки 0 и JV
поля X и однозначно определяемая функция о: JV —»¦ U класа Сг,
такие что <р(р(У), У) = 0 и что если x?U, FgcJV и ф(лг, К) = 0,
то x = p(F). Иными словами, если x?U, то К(д;) = 0 тогда и
только тогда, когда лг = р(К). Кроме того, так как DX@) —
изоморфизм, а множество изоморфизмов открыто, можно счи-
считать, уменьшив в случае необходимости JV и U, что DY(p(Y))
является изоморфизмом, так что p(F)—простая особая точка
поля Y. |
Теперь мы охарактеризуем простые особые точки векторного
поля X в М в терминах трансверсальности. Рассмотрим для
этого касательное расслоение ТМ = \{р, v): р?М, ь&ТМр}, и
пусть М0 = {(р, 0): р€.М)—нулевое сечение. Мо—это подмно-
подмногообразие в ТМ, диффеоморфное М, а векторное поле можно
представлять себе как С-отображение из М в ТМ, которое
мы будем обозначать той же буквой X. Таким образом, р яв-
является особой точкой поля X тогда и только тогда, когда
3.2. Предложение. Пусть X—С-векторное поле (r^z 1) на мно-
многообразии М и ре?М—его особая точка. Тогда р0 является
простой особой точкой поля X в том и только том случае,
когда отображение р ¦—»¦ (р, X (р)) из М в ТМ трансверсально
нулевому сечению Мо в точке р0.
Доказательство. Пусть xi U—*Um—локальная карта g
х (а,)=0. Пусть TU={{p, v) б ТМ: р g Щ. Отображение Тх: TU-^
—>RmxlRm, определенное формулой Тх(р, v) = (x(p), Dxp{v)),
является локальной картой для ТМ. Рассмотрим следующую
диаграмму:
TU
;т х Ш"
где Яг—проекция- я2(х, у) —у.
Положим h~n2TxX. Тогда X трансверсально к Мо в точке р0
тогда и только тогда, когда р0 является регулярной точкой
отображения h, т.е. когда dh(pB): TMp-^-Rm—изоморфизм.
С другой стороны, dh(po) = Dx(po)DX (рв). Следовательно,
dh(pe)—изоморфизм тогда и только тогда, когда DX(p0) —
изоморфизм, что и доказывает предложение. |
Пусть $ос36г(М)—множество векторных полей, у которых
все особые точки простые; иными словами, $0 = {Х gj6M)
80 ГЛ 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Х>. М —* ТМ трансверсально к MJ. Поскольку простые особые
точки изолированы, а М компактно, отсюда следует, что лю-
любое X ? $„ имеет лишь конечное число особых точек.
3.3. Предложение. $„ открыто и плотно t ?r (М).
Доказательство, (а) Открытость. Поскольку множество
С-отображений из М в ТМ, трансверсальных к Мо, открыто,
мы заключаем, что $„ открыто.
(Ь) Плотность. Пусть X ? 3lr (М). По теореме Тома о транс-
трансверсальности существуют сколь угодно близкие к X отобра-
отображения Yi M —>¦ ТМ, трансверсальные к М„. Может случиться,
однако, что Y не будет векторным полем, так как возможно,
что п (Y (р)) ф р при некотором р?М, где л: ТМ —* М обозна-
обозначает проекцию (р, v) I—> р. Но пХ = \йм, и если Y достаточно
близко к X, то ф = лУ близко к idAi, так что ф является диф-
диффеоморфизмом, ибо множество диффеоморфизмов многообразия М
открыто в Сг (М, М). Тогда 2 *= Уф" является векторным по-
полем на М, потому что nZ = яУф~1 = фф" = 1с1Л1. Поскольку Y
трансверсально к Мо, а ф является диффеоморфизмом, отсюда
следует, что Z трансверсально к Мо. Если Y близко к X, то
это же верно и для Z. |
Пример. В этом примере мы рассмотрим линейное векторное
поле на R2 с простой особой точкой и покажем, что его нели-
нелинейное возмущение может дать векторное поле с чрезвычайно
сложной структурой траекторий. Рассмотрим векторное поле,
задаваемое матрицей
— 1 О
Пусть р: R—-R—такая С°°-функция, что р@) = 0 и рш@) = 0
при всех k ? N. Пусть X —векторное поле на R2, определенное
формулой
X (х, у) = (у + Р (г8) х, —х+р (г2) у),
где г2 = х2-\-у2. Легко видеть, что X класса С" и что
DX{0, 0) = .
\—' и/
Таким образом, @, 0)—простая особая точка поля X. Пусть
К—компактное подмножество полупрямой R+, содержащее 0.
Можно так выбрать р, чтобы р (/С) = 0 и чтобы р не обраща-
обращалось в нуль на /\К, где / = (—б, 6) есть интервал, содер-
содержащий К. Для любых е > 0 и г > 0 можно выбрать р так,
что ||X—L||r<e. Если ro?U+ таково, что р(^о) = О» то век-
векторное поле X касается окружности радиуса г0, так что эта
§3. ОСОБЕННОСТИ И ГИПЕРБОЛИЧЕСКИЕ НЕПОДВИЖНЫЕ ТОЧКИ 81
окружность является замкнутой траекторией поля X. С другой
стороны, если (й, 6)cR+—такой интервал, что р(/2)>0 при
t?(a, b) и р(а2) = р(Ь2) = 0, то траектории поля X, проходящие
через точки кольца Db\Da = \г ? Ra: a < | г || < Ь\, не замкнуты,
а именно они являются спиралями, у которых со-предельное
множество—это окружность радиуса Ъ. Это следует из того,
что <(*, у), X (х, у)у = л2р (л2), так что радиальная компонента
поля X есть лр (г2), что положительно при г ? (а, Ь). Анало-
Аналогично, в интервале (а, Ь), где р(а2) — р(Ь2) — 0 и р(/2)<0 при
t ? (а, Ь), траектории в кольце Db\Da будут иметь окружность
Рис. 5
радиуса b в качестве своего а-предельного множества и окруж-
окружность радиуса а в качестве своего со-предельного множества
(рис. 5).
Эта конструкция дает сколь угодно близкое к L векторное
поле X, замкнутые траектории которого пересекают ось абсцисс
точно в точках компактного множества {rgR+; r2?/(j, гомео-
морфного К- Если К и К'—два негомеоморфных компактных
множества, а X и X'—векторные поля, ассоциированные с ними
по этой конструкции, то X и X' топологически неэквивалентны.
Определение. Пусть Х??Г{М) и р?М—особая точка поля X.
Будем говорить, что р—гиперболическая особая точка, если
DXp\ TMp—+TMp—гиперболическое линейное векторное поле,
т. е. DXp не имеет собственных значений на мнимой осих).
Пусть ^1с=^г(М) обозначает множество тех векторных по-
полей, у которых все особые точки гиперболические. Ясно, что
J) Если читателю придется иметь дело со старой литературой по ка-
качественной теории дифференциальных уравнений, то надо иметь в виду, что
тогда особую точку, для которой спектр DXp лежит целиком слева или
целиком справа от мнимой оси, не называли гиперболической.— Прим. ред.
g2 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
3.4. Теорема. <ё1 открыто и плотно в ЖГ(М).
Доказательство. Поскольку $0 открыто и плотно в 3()
а $,с=$0, то достаточно показать, что $, открыто и плотна
в $„. Пусть Xg$0, и пусть р0, ..., рА€М—особые точки
поля X. По предложению 3.1 существуют такие окрестности
off(X) поля X и {/„ ..., ?/ft точек рх, ..., pft соответственно)
и такие непрерывные функции р/ оЛГ —* U/f / = 1, .... &, что.
Pj(Y) является единственной особой точкой поля Y в Uj~
Можно предположить, что эти окрестности попарно не пере-
пересекаются. Если р € M\U*= I i/y, то Х(р)фО. Вследствие ком<-
пактности множества M\U;=1(/y существует такое б>0, что
|] X (р) || > б при всех р € M\yJUj. Следовательно, уменьшив
в случае необходимости JV, можно считать, что любое FgdV
не имеет особых точек в M\UL^. Предположим, что X g 5?х.
Поскольку DXP —гиперболическое линейное векторное поле,
а такие векторные поля образуют открытое множество1), мы
получаем из непрерывности отображений ру (уменьшив, если
потребуется, оЛГ), что DYP (y) — гиперболическое линейное век-
векторное поле при всех Y^Jf- Таким образом, cIVcS,, что дока-
доказывает открытость множества St.
Предположим теперь, что Х?&0. Покажем, что сколь
угодно близко к X существует Y € $, П оЛГ. Заметим, что если
и > 0 достаточно мало, то DXP -f и/ является гиперболическим
линейным векторным полем на ТМР при всех /=1, ..., k.
Поэтому достаточно показать, что в любой окрестности
o)V\c=cJ\P поля X существует такое поле VgolVi, что Y(pj) = 0
и DYP —DXP +ы/. Пусть VjClUj—окрестность точки ру и
я/: Vy—> ВC)c=Rm—локальная карта с х*(р/) = 0, где ВC)
есть шар радиуса 3 с центром в нуле. Пусть ф: Rm —* К —
такая положительная С°°-функция, что ф(ВA)) = 1 и
Ф (Rm\BB)) = 0. Пусть х>» (X) обозначает выражение вектор-
векторного поля X в локальной карте х*\ иными словами,
xiX (q) = Dxf ((xO-1 (q)) X ((j^-i (9)).
Положим У (р) =г X (р), если р € M\UyVy, и
К (/?) = D (xf)'1 {х> (р)) (xt X (х/ (р)) + иф (х/ (р)) Jt/ (p)),
х) В пространстве всевозможш х линейных векторных полей на ТрМ
со всевозможными р?М, снабженном естественной топологией. Впрочем,
далее достаточно рассматривать только p?U/, а ~огда, считая Uj доста-
достаточно малой, можно использовать локальные координаты, и все становится
фчевидным.—Прим. ред.
§ 3. ОСОБЕННОСТИ И ГИПЕРБОЛИЧЕСКИЕ НЕПОДВИЖНЫЕ ТОЧКИ 83
если p?Vj. Легко видеть, что Y—векторное поле класса С0*,
что Y(p/) — 0 и что DYP —DXP -\-uI. Кроме того, выбирая и
достаточно малым, будем иметь Y^Jfi, что завершает дока-
доказательство. |
Теперь мы распространим эти результаты на диффеоморфизмы
компактного многообразия М. Мы опустим доказательства пред-
предложений и теоремы, поскольку они аналогичны тем, которые толь-
только что были даны для векторных полей.
Определение. Пусть р € М—неподвижная точка диффеоморфизма
/€Diff(M). Будем говорить, что р—элементарная неподвиж-
неподвижная точка х), если 1 не является собственным значением опе-
оператора Dfp\ ТМр-+ТМр.
3.5. Предложение. Пусть /?Diffr(M). Предположим, что р—
элементарная неподвижная точка отображения f. Тогда суще-
существуют окрестности dV диффеоморфизма f в Diffr (M) и U
точки р и непрерывное отображение р: Jf —>- U, которое каж-
каждому диффеоморфизму g?c№ сопоставляет его единственную
неподвижную точку в U, и эта неподвижная точка элемен-
элементарна. В частности, элементарная неподвижная точка изоли-
изолирована.
Пусть Д обозначает диагональ {(р, p)?MxMi p?M}, ко-
которая является подмногообразием в МхМ размерности пи
Если f gDiff7"(М), рассмотрим отображение }: М -+МхМ,
задаваемое формулой /(р) = (р, f{p))- Его образ—это график
отображения f.
3.6. Предложение. Пусть f?Dillr(M) и р?М—его неподвиж-
неподвижная точка. Тогда р—элементарная неподвижная точка тогда
и только тогда, когда f трансверсально к А в точке р.
Пусть Goc=Dillr(M) обозначает множество диффеоморфиз-
диффеоморфизмов, все неподвижные точки которых элементарны. Таким
образом, f?G0 тогда и только тогда, когда / трансверсально
к Д. Используя теорему Тома о трансверсальности, получаем
следующее предложение.
3.7. Предложение. E0 открыто и плотно в Diff" (M).
Определение. Пусть р?М—неподвижная точка отображения
/ € Diff7" (M). Будем говорить, что р—гиперболическая непод-
неподвижная точка, если Dfp: TMp —*¦ ТМр является гиперболиче-
1) По другой терминологии—невырожденная.—Прим. ред.
84 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
ским изоморфизмом, иными словами, если Dfp не имеет собст-
собственных значений, равных по модулю I1).
Пусть GlczD\Ur{M) обозначает множество диффеоморфиз-
диффеоморфизмов, все неподвижные точки которых гиперболические.
3.8. Теорема. Gt открыто и плотно в D'\tfr (М). |
В следующем параграфе мы покажем, что диффеоморфизм
/ ? Gj является локально грубым.
§ 4. ЛОКАЛЬНАЯ ГРУБОСТЬ
В этом параграфе мы докажем принадлежащую Хартману
и Гробману теорему, согласно которой диффеоморфизм / локаль-
локально сопряжен своей линейной части в гиперболической неподвиж-
неподвижной точке. Аналогично, векторное поле X локально эквивалентно
своей линейной части в гиперболической особой точке. В качестве
следствия мы получим локальную грубость в гиперболической
неподвижной точке и в гиперболической особой точке. Приве-
Приведенное нами доказательство применимо также в банаховом про-
пространстве [25], [36], [74], [90] Другие обобщения и ссылки
можно найти в [80].
4.1. Теорема. Пусть /gDiff(M) и р?М—его гиперболическая
неподвижная точка. Пусть A=Dfp: ТМр—+ТМр. Тогда суще-
существуют такие окрестности V(p)<zM и U @)<zTMp и такой
гомеоморфизм h: U —»- V, что
Замечание. Поскольку проблема локальная, можно предпола-
предполагать, используя локальную карту, что /: Rm—*IRm—диффео-
Rm—*IRm—диффеоморфизм с гиперболической неподвижной точкой 0. Для дока-
доказательства теоремы 4.1 нам понадобится несколько лемм.
4.2. Лемма. Пусть Е—банахово пространство. Предположим,
что L?2 (E, Е) таково, что||L||<с < 1 и что G^^(E, E)—
изоморфизм с ||G~1|^a< 1. Тогда
(a) 1 + L—изоморфизм и KI + Ly1^ 1/A— а),
(b) I + G—изоморфизм и {A + G)-1\\s^a/(l—a).
Доказательство, (а) Для заданного у € Е определим и: Е—+
-+Е формулой и(х) = у—L(x). Тогда u(xl)—u{x2) = L(x2—xl).
Таким образом, !«(.*;,)—и (я2) || ^ а|| xt—д:2||, так что и является
сжатием. Следовательно, и имеет единственную неподвижную
х) Здесь также произошло изменение терминологии: раньше неподвиж-
неподвижную точку, для которой спектр Dfp расположен целиком внутри или цели-
целиком вне единичной окружности, не называли гиперболической,—Прим. ред.
5 4. ЛОКАЛЬНАЯ ГРУБОСТЬ 85
точку х?Е; это значит, что х = и(х) = у—Lx. Поэтому суще-
существует единственное х?Е, такое что (L -f /) х — у; иными сло-
словами, I + L является биекцией. Пусть у?Е таково, что ||#J=1.
Возьмем такое х?Е, что (I + L)~1y = x. Так как x+Lx — y,
имеем |]л:||—а|л:||^ 1, так что ||лг|^1/A—а). Таким образом,
+ LL< 1/A-а).
(b) Заметим вначале, что I + G = G(f-{-G-1). Поскольку
|G~1||^a<l, то по первой части леммы / + G обратимо.
Следовательно, (I + G)'1 = (I+G~1)~1G~1, и поэтому
что доказывает лемму. |
Так как A—DfB—гиперболический изоморфизм, то суще-
существуют инвариантное расщепление Rm = EsQ)Ea и норма ||-||
на Rm, в которой
1, где AS = A\ES; E*-+Es,
< 1, где Аа = А\Еа: Еи-+Еа.
Пусть Cb(Rm)—банахово пространство ограниченных непре-
непрерывных отображений из Rm в Rm с равномерной нормой: \и\—
= sup {|) и (х) \\: х ? Um). Поскольку Rm = Е* 0 Еа, мы получаем
разложение Q (Rm) = C°b (Rm, Es)@C{,(Rm, Ea), где u = us + ua
cus = nsou и и"=яйой получаются при естественных проек-
проекциях ns: ES@EU-+ES и па: ES@EU-+Ea.
4.3. Лемма. Существует такое е > 0, что если ф,, ф2 g CJ (Rm)
имеют постоянную Липшица, которая меньше или равна е, то
А + 4>i и ^ + Фа сопряжены.
Доказательство. Надо найти гомеоморфизм hi Rm —>¦ Rm,
удовлетворяющий уравнению
/1(Л + ф1) = (Л+ф2)/1. A)
Будем искать решение в виде h — I-\-u с u?C°b(R.m). Тогда
нам необходимо, чтобы
(/ + ")(Л + ф1) = (Л + ф2)(/ + ы), B)
или
что эквивалентно
Аи—«(Л+фО^Ф!—ф2 (/ + «)• C)
Покажем, что существует единственное и ? C°b (Rm), удовлетво-
удовлетворяющее уравнению C). Рассмотрим линейный оператор
g\ Q (Rm) — С% (IRm),
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Мы утверждаем, что S обратим и что fj^!!^! А~гЩ1—а)
Действительно, S— AS*, где S*: Q (Rm) -*¦ C°b (Rm) задается
формулой S* (и) = и—А~1и (Л + ф^ а Л: С% (R">) -* C°b (Кя) -
формулой Л(«) = Лои. Поскольку Л обратим, надо лишь пока-
показать, что S* обратим, так как тогда S~i- = S*~XA~X. Заме-
Заметим, что Cg(Rm, Es) и Cg (Rm, Ea) инвариантны относительно
оператора ??*, потому что Es и Е" инвариантны относительно
А'1. Поэтому можно написать g* = S*s®3*a, где
:?•'¦= J?e|CJ(R«, ?s) и <g>*a = &*\CBb{Rm, E*).
Легко видеть, что если е достаточно мало, то А ~\- фх является
гомеоморфизмом1) и поэтому оператор us —>¦ А ~ lus (Л + фх)
обратим, а его обратный us\-*Asus(A +Ф!) является сжатием
с нормой, ограниченной числом а < 1, упоминаемым в условии
гиперболичности оператора Л. Из части (Ь) леммы 4.2 следует,
что S*s обратим и |(«27**)Ка/A—а). Из части (а) леммы 4.2
мы заключаем, что 2*п также обратим и
Поэтому & обратим и
что доказывает наше утверждение.
Теперь рассмотрим отображение
I*: Cg(R-) — Cg(К»), ц^-
Имеем
При е, достаточно малом, е||Л~1||A.—й) < 1, а тогда ц явля-
является сжатием и поэтому имеет единственную неподвижную
точку и в Cb(Um). Поскольку ugCft(IRm) является решением
уравнения C) тогда и только тогда, когда и—неподвижная
точка отображения \i, то мы заключаем, что C) имеет един-
единственное решение в Q(Rm). Остается доказать, что / + и явля-
является гомеоморфизмом. Для этого заметим вначале, что исполь-
использованный выше метод позволяет также доказать, что уравнение2)
J) Уравнение (Л + Ф1) (x)=y (с заданным у) эквивалентно уравнению
х = А~1у—А~1<р1(х), правая часть которого (при фиксированном у) опре-
определяет сжатне в Rm (если ||Л~Ч|е< 1). — Прим. ред.
2) Оно отличается от B) просто тем, что <j>i и ф2 поменялись местами,
а ведь на них накладывались одни и те же условия.—Прим. ред.
$4. ЛОКАЛЬНАЯ ГРУБОСТЬ 87
также имеет единственное решение v^Cl(Rm). Мы утверждаем,
что
Действительно,
С другой стороны, поскольку (I + u)( ) ( + )
имеет вид I-\-w с w — v + «(/ + v) €Q(Rm), а /(Л + ф2) =
= (Л+Ф2)А то единственность решения уравнения
()A+) (A)(I доказывает, что
Аналогично (/-fi>) (/ + «) = /• Это показывает, что / + « явля-
является гомеоморфизмом, сопрягающим Л-|-ф1 и Л+ф^. Лемма
доказана. |
4.4. Лемма. Для любого е > 0 существуют окрестность U
точки 0 и продолжение отображения f\U на Rm вида А + ф,
где ф € С? (Ки) имеет постоянную Липшица, не превосходящую е.
Доказательство. Пусть a: R —>- К—С°°-функция со следую-
следующими свойствами s
a(R)c=[0, 1];
a(/) = 0, если />1;
а@=1, если ^<у;
при всех t?R |а'(^)|</С, где ^К» ^С> 2—некоторая кон-
константа. Пусть /! = Л+'ф с -ф@) = 0 и D\pv = 0. Пусть Ве—шар
с центром в нуле и радиуса е, такой что || Dtyx \\ < е/2К для
х?Ве. Определим ф: Rm—*Um формулой ф(дг) = а(|дг|/е)-ф(дг).
Ясно, что ф(аг) = О, если \х\~^е. Покажем, что ф удовлетво-
удовлетворяет условиям, указанным в лемме. Действительно, поскольку
(p(x) — ty(x) при || я |[ ^е/2, то мы видим, что Л+ф является
продолжением отображения f\Be/2. С другой стороны, если
хи х2^Ве, то мы имеем
-Ф (х.) 1=I [о (| х, Не) ф (Xl) -a (| xg Це) ф (x2)]| =
ЕСЛИ ^! € ^е И *2 ^ ^е> Т0
B4P(-«i)—Ф(-^)Й
а если xv x2^Be, то Цф(ж,)—ф^Ц^О^в!^—х?||. Таким
88 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
образом, ф имеет постоянную Липшица, не превосходящую 8,
что доказывает лемму. |
Доказательство теоремы 4.1. Пусть е > 0 такое, как в лем-
лемме 4.3. Пусть Л + ф—продолжение отображения f\U(O), где
U @)—окрестность нуля, а ф имеет постоянную Липшица не
больше е. По лемме 4.3 существует такой гомеоморфизм hi
Rm —»¦ Rm, что hA — (Л + ф)h. Следовательно, hA=jh в окрест-
окрестности нуля, что и требуется. |
Замечания. A) Сопряжение между Л + ф] и А-{-щ, построен-
построенное в лемме 4.3, является единственным среди отображений,
находящихся на конечном расстоянии от тождественного отоб-
отображения. Существует, однако, бесконечно много сопряжений,
не удовлетворяющих этому последнему условию. Например,
рассмотрим сжатие ф: К—>-IR с ф@) = 0. Предположим, что
фA) = а>0 и ф(—1) = Ь<0. Возьмем любой гомеоморфизм
h: [—1, b]U[а, 1]—>[—1, b]\j[a, 1] с условиями h(— 1) =
= — 1, h(b) — b, h(a) = a, /i(l) = l. Продолжим h на всю ве-
вещественную прямую, положив h@) = 0 и h(x) = q>nh(p~"(x), где
ngZ выбирается так, чтобы <р~"(х)?[—1, fc]ll[c, 1]. Этим
способом мы находим столько же решений уравнения h(p = q>h,
сколько имеется гомеоморфизмов множества [—1, Ь]и[я, 1]
на себя.
B) Даже если потребовать, чтобы сопряжение между Ли/
было близко к тождественному отображению, оно все равно
не единственно, потому что зависит от продолжения Л + ф
отображения / на все пространство Rm.
Теперь мы покажем, что из теоремы 4.1 вытекает локаль-
локальная грубость гиперболического линейного изоморфизма в 3? (Rm).
В действительности, как мы увидим в следующем параграфе, ги-
гиперболический изоморфизм является глобально грубым в 3 (Кт).
4.5. Предложение. Пусть А — гиперболический изоморфизм.
Тогда существует такое б> 0, что если B?j? (Rm) и || В—Л |)<б,
то В локально сопряжено о А.
Доказательство, Будем искать гомеоморфизм hi Rm —*¦ Rm,
сопрягающий Л и продолжение отображения В \ U, где U —
окрестность нуля.
Пусть а: К—¦ К—С-отображение со следующими свойст-
свойствами:
а@ = 1, если |*|<1;
а@ = 0, если \t\>2;
o(R)<=[0, 1].
Можно записать В в виде А + (В — А). Пусть qp; Rm-* Rm
определено формулой ф(х) = а(|лг||)-(В—А){х). Тогда ц>\Вг =э
§4. ЛОКАЛЬНАЯ^ГРУБОСТЬ
= (В—A)\Blt где Вх—шар с центром в нуле радиуса 1, и
ф(х) = 0, если И|>2. При всех x?Rm ЦОф^К/СЦВ—А|+
+ \\В—Л ||, где /C = sup{|a'(/)|: t ?Щ больше чем 1. Пусть
задано е > 0. Возьмем 6 < е/2/С так, что UDq^fl < е. Отсюда
следует, что ф имеет постоянную Липшица, не превосходя-
превосходящую е. По лемме 4.3 существует такой гомеоморфизм h: Um—*¦
—j-IRm, что
Поскольку Л + ф является продолжением В\ВХ, то/i—локаль-
то/i—локальное сопряжение между А я В. |
4.6. Теорема. Пусть f^DiW(M), r^\, и р?М—гиперболи-
р?М—гиперболическая неподвижная точка отображения f. Тогда f является
локально грубым в р.
Доказательство. По предложению 3.5 существуют окрест-
окрестности |(/) и F(р) и непрерывное отображение р: Л"(/) —¦ W,
которое каждому g € о)\Г (/) ставит в соответствие единственную
неподвижную точку p(g) отображения g в W, и эта неподвиж-
неподвижная точка является и гиперболической. Взяв достаточно малую
окрестность cff(/)c=o)V'(/), получим, что Dfp близко к Dgp{g,,
и поэтому по предложению 4.5 эти линейные изоморфизмы
локально сопряженых). Поскольку / локально сопряжено с Dfp,
а g локально сопряжено с DgPig)> то отсюда следует, что /
локально сопряжено eg. I
Теперь мы распространим эти результаты на векторные
поля. Пусть V—окрестность нуля в R.m и Х\ V—*Rm — Сг-век-
Сг-векторное поле, г~^\. Напомним, что 0 является гиперболиче-
гиперболической особой точкой поля X, если L = DX0—гиперболическое
линейное векторное поле. Мы покажем, что если 0—гипербо-
0—гиперболическая особая точка поля X, то траектории поля X в окрест-
окрестности нуля имеют ту же топологическую структуру, что и
траектории линейного векторного поля L. Для этого нам пона-
понадобится несколько лемм.
4.7. Лемма (неравенство Гронуолла). Пусть и, vi [a, b] —>- К—
такие непрерывные неотрицательные функции, что при неко-
х) Пользуясь подходящей картой (Fs у) многообразия М, мы можем
рассматривать Dfp и Dgp (p) как линейные отображения в Rm. Более фор-
формально, локальная сопряженность fBpngBp(p) следует из локальной
сопряженности в нуле отображений
х Н» у~Чу (*+ У (Р))—У [Р),
y-Jgy (х+ур (р))—ур (р),
производные которых в 0 суть dypoDfpodypl и йуе<
Прим. ред.
90 ГЛ. 2. ЛОКАЛЬНАЯ ГРУЁОСТЬ
тором а ^ 0 выполнено неравенство
t
u{t)^.a-\-\ u(s)v(s)ds у/ ? [с, Ь] .
а
Тогда
Гг 1
и (t) ^ a exp J f (s) ds I.
Доказательство. Пусть со: [а, Ь] —»-R—это отображение
t
to(tf)==a-f- ^ u(s)v(s)ds.
а
Предположим вначале, что a > 0. Имеем со (а) — а и со (t) ^
>а>0 при всех <g[a, 6]. Поскольку со'(*) = р(*)ы(*)<
)(^), то со' (/)/со (/) ^ v (/). Интегрируя от с до t, получим
Отсюда
Uv(s)ds .
Если а = 0, то из рассмотренного случая вытекает, что при
всех «х > 0
и (t) ^ аг ехр
Следовательно, u(t)~0, и неравенство по-прежнему выпол-
выполнено. |
4.8. Лемма. Пусть Y\ Rm—¦ Rm—векторное поле класса Cf
с Y @) = 0, удовлетворяющее условию Липшица с постоянной К.
Тогда поток поля Y определен на RxRm и tYt(x)—Ki(«/)||^
^eKl'l|x—t/fl при всех х, y?Rm.
Доказательство. Пусть xgR'-. Рассуждая от противного,
предположим, что максимальным интервалом, на котором опре-
определена интегральная кривая поля Y, проходящая через точку х,
является (с, Ь) с Ь<оо. Пусть ф: (с, b)—*Rm—интегральная
кривая, проходящая через точку х. Имеем
8 4. ЛОКАЛЬНАЯ ГРУБОСТЬ 91
Поэтому если t^O, то
t t
о о
Из неравенства Гронуолла получим
Пусть tn~+b. Рассмотрим последовательность {ф(^„)}, члены
которой принадлежат шару с центром в нуле и радиуса
М =е**||лс|. Вследствие того что
tn
получаем
Значит, ф(^„) является последовательностью Коши и поэтому
сходится к некоторой точке y?Rm. Локальный поток поля Y
возле точки у позволяет нам продолжить интегральную кри-
кривую ф вправо за точку Ь, что противоречит нашему первона-
первоначальному предположению. Таким образом, поток поля Y
определен на RxRm. Из равенства
t
мы выводим, что при
о
Из неравенства Гронуолла получаем, что
—y\. если
Применяя аналогичные рассуждения к полю —Y, мы получим
такое же неравенство и при *<;0. |
4.9. Лемма. Пусть X: V —¦¦ Rm—векторное поле класса Сг
с X @) = 0. Пусть L = DX0. Тогда для любого е > 0 существует
С-векторное поле Yi Rm —»- Rm со следующими свойствами:
A) поле Y удовлетворяет условию Липшица с некоторой по-
постоянной К, так что поток, порожденный полем Y, опре-
определен на KxR";
B) Y = L вне шара Bt\
C) существует такое открытое множество UcV^ содержа,'
щее 0, что Y = X на U\
92 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
D) если Ft = Lt + <p/, то существует такое М > О, что |ф4|^
при всех t (Е [—2, 2] a q>j имеет постоянную Липшица, кото-
которая не превосходит е. Кроме того, D(9jH = 0 ылн, ч/ио
эквивалентно, D (УгH—eL=Li.
Доказательство. Так как L = DX0, имеем X = L -f- i]), где я];:
V —> Rm—такое Сг-отображение, что г])@) = 0 и D% = 0. Пусть
а: К—»-R—такое С'-отображение, что a(R)c[0, 1], а(*)=1
при |/|<//2 и а(*) = 0 при *>/.
Определим ф- Rm—>R формулой ф (л:) = ct (||л; |)• г|; (л:), если
х € V, и ф (х) — 0, если х g Rm \ V. Для любого б > 0 можно
выбрать такое / > 0, чтобы отображение ф принадлежало
классу С и имело постоянную Липшица, не превосходящую 6.
Ясно, что ф = г]з на В[/2 и ф = 0 вне Bv Пусть Y\ Rm—»• Rm—
векторное поле, задаваемое формулой Y = L-\-tp. Опять-таки
ясно, что Y = X на Б//2, F.= L вне Вг и что У удовлетворяет
условию A). Остается доказать, что выполняется условие D).
П 48 \Y() Y\^\\ Ц—2, 2].
||Л1
у () у
По лемме 4.8 \Yt(x) — Yt{y)\^^\x—y\ при 1Ц ]
Положим (pt — Yt—Lt. Существование такого М, что |ф4|<Л1
при t g [—2, 2], следует из того факта, что Yt и Lt ограничены
на Bt при t?[—2, 2] и K = L вне Вг Имеем также1)
t t
<Pt W-Ф* (Й = S [Ф (У, W)-4> (У,D0)] &+ J
о о
Используя неравенство Гронуолла, мы заключаем, что Vt
€[-2,2]
|] ()
При достаточно малом б первая часть условия D) тем самым
удовлетворена. Наконец, покажем, что С(ф1)(| = 0. Мы соби-
собираемся доказать, что для любого р > 0 существует такое г > О,
что ЦфхМЦ^рЦхЦ при |х||^г. Поскольку (D(p)o = O, то можно
выбрать г таким образом, чтобы ||ф (г)||^ г\||г|| при ||z|<r, где
т] < ре~ке~^L". Аналогично приведенному выше выражению имеем
1 i
Ф1 (х) = $
и
Используя тот факт, что ЦУДдОЦ^е*!*! при O^s^l, полу-
получаем из неравенства Гронуолла
Это завершает доказательство леммы 4.9.
') Поскольку qiv(x) = G при всех х и q>t = Yt— Lj = (i.-j-ф)оК/ — LoLt
= L (K, — Z.t) -J- <}ГсК( = фоУ,, -|- !(},.— Прим. ред.
§4. ЛОКАЛЬНАЯ ГРУБОСТЬ 93
4.10. Теорема. Пусть Х\ V —*Rm—векторное поле класса Сг
и 0—гиперболическая особая точка поля X. Пусть L = DX0.
Тогда X локально эквивалентно полю L в точке 0.
Доказательство. Пусть Y- Кя —> R1"—векторное поле класса
С из леммы 4.9. Поскольку Y — X в окрестности U точки 0,
то тождественное отображение переводит Х-траектории в
F-траектории. Таким образом, Y локально эквивалентно полю X.
Остается доказать, что Y локально сопряжено с L. Мы покажем,
что действительно существует гомеоморфизм многообразия IRm,
сопрягающий потоки Yt и Lt.
По лемме 4.9 Yt = Lt + (pt, и так как DY0 = L, то мы имеем
D(F^o = eL=Li. Поэтому диффеоморфизм Yl = Li-\-^ имеет
точку 0 своей гиперболической неподвижной точкой, а ^ имеет
постоянную Липшица, не превосходящую е. По лемме 4.3 суще-
существует единственный гомеоморфизм hi Rm —+ Rm, находящийся
на конечном расстоянии от тождественного отображения (т. е.
h = I-\-и с u^C°b(R.m)) и удовлетворяющий уравнениюhYl=Llh.
Определим Hi R.m -* fcm формулой
о
Ясно, что Н является непрерывным отображением и по усло-
условию D) леммы 4.9 находится на конечном расстоянии от тож-
тождественного отображения. Покажем теперь, что
LSH = HYS при всех
Для этого достаточно рассмотреть s ? [0, 1]. Имеем
L_thYtdt)Ys= S L
o /o
Полагая ы =
1
[ L h]
0
t-\-s—1, получим
s
-l+s
0
= S L-«L-ihY
S
-f+S
Положив v = и -\-1 в первом слагаемом и v = u ъо втором и
использовав равенство L_1hY^=h, получим отсюда, что
94
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Это показывает, что Н является непрерывным отображением,
находящимся на конечном расстоянии от тождественного ото-
отображения и сопрягающим потоки Lt и Yt. Остается показать,
что Н—гомеоморфизм. Действительно, поскольку L1H = HYI
и L1/i = ftF1, то единственность решения этого уравнения вле-
влечет за собой равенство Н = ft, которое и завершает доказатель-
доказательство теоремы. |
4.11. Теорема. Пусть Х?Эсг(М) и р^М—гиперболическая
особая точка поля X. Тогда X является локально грубым в р.
Доказательство. Мы видели, что существуют такие окрест-
окрестности JV (X) поля X в ?Г(М) и U точки р в М, что каждое
векторное поле Y ? o)f (X) имеет единственную гиперболическую
особую точку ру в U. Кроме того, при достаточно малой oJf (X)
точка ру имеет тот же индекс, что и р. Таким образом, поля
DXp и DY топологически эквивалентны. Так как X локально
эквивалентно полю DXp, a Y локально эквивалентно полю
DYP , то это доказывает теорему. |
§ Б. ЛОКАЛЬНАЯ КЛАССИФИКАЦИЯ
Мы видели, что подмножество $t(M)c:2?.r(М), состоящее из
тех векторных полей, у которых все особые точки гипербо-
гиперболичны, открыто и плотно в ХГ(М). Кроме того, эти векторные
поля являются локально грубыми в каждой точке многообра-
вия М. Мы опишем теперь возможные типы локального топо-
топологического поведения векторных полей из 5^.
Рассмотрим линейные векторные поля Lo, Lt, ..., Lm в Rm,
которые в стандартном базисе представляются матрицами
а
1
0
с
Г—1
1
о
1
Г—1
—1
0 —1
Если L—гиперболическое линейное векторное поле в Rm, то
L сопряжено с Lt, где i—индекс поля L.
Пусть С\ Rm —*¦ Rm—постоянное векторное поле, заданное
формулой С(х) = A, 0, ..., 0). В следующей теореме собраны
результаты, доказанные в предыдущих параграфах.
5.1. Теорема. Пусть XgS,(M). Выберем р?М.
(а) Если р—регулярная точка поля X, то X локально эквива-
эквивалентно в точке р постоянному векторному полю С в moKKfi 0.
$5. ЛОКАЛЬНАЯ КЛАССИФИКАЦИЯ 95
(b) Если р—особая точка поля X, то X локально эквивалентно
полю L,, где i—индекс точки /?B).
Доказательство, (а) Это следует из теоремы о трубке тока.
(Ь) Примените теорему Гробмана—Хартмана и предложе-
предложение 2.15. |
Рассмотрим теперь пространство Diffr(M) диффеоморфизмов
многообразия М класса гладкости Сг. Мы видели, что множе-
множество G1(M)cDUlr(M), состоящее из тех диффеоморфизмов, все
неподвижные точки которых гиперболические, является откры-
открытым и плотным в Diffr(M). Мы опишем теперь возможные
типы топологического поведения траекторий диффеоморфизма
из Gt возле неподвижных точек. Согласно теореме Хартмана
и Гробмана, достаточно классифицировать гиперболические
линейные изоморфизмы.
5.2. Предложение. Пусть A?j?(R.m)—гиперболический линей-
линейный изоморфизм. Тогда существует такое е > 0, что если
B?j?(R.m) удовлетворяет условию |]Л—Б|)<е, то В сопря-
сопряжено с А.
Доказательство. По предложению 4.5 В локально сопря-
сопряжено с Л; иными словами, существует такой гомеоморфизм Ы
V@) —»- U @), что hA=Bh. Пусть Es и Е"—устойчивое и не-
неустойчивое подпространства оператора A, a Es' и Еи'—соот-
Еи'—соответствующие подпространства для В. Пусть Vs = V @)f\Es,
Va = V{0)nE«, Us' = If @) n Es' и U«' = U{0)r\Eu>. Ввиду не-
непрерывности h получаем h(Vs) = Us' и h(Va) = Uu'. Определим
гомеоморфизм hsi ES—*ES', сопрягающий Л* = Л|?* и Bs' =s
= B\ES'. Если x?Vs (а это является окрестностью нуля в Es),
то положим hs(х) = h(x)gEs>. Если x€Es\Vs, то, поскольку
А" (х) —* 0 при п —»- оо, существует такое г € N, что АТ (х) € Vs.
Положим hs(x) = B~rhAr(x). Так как h сопрягает Л и В в У1,
то непосредственно видно, что hs не зависит от выбора г.
Также легко проверить, что hs—гомеоморфизм, сопрягающий
As и Bs'. Аналогично определяется гомеоморфизм h": Еа—>-Еи\
сопрягающий Аа и Ва. Теперь можно определить hi EsQ)Ea—>
— Es' ф Е"' по формуле h (xs + х°) = hs (xs) + ha{xa). Ясно, что h
является гомеоморфизмом, сопрягающим А н В. |
Мы оставляем читателю доказательство следующего пред-
предложения.
Б.З. Предложение. Пусть А и В—гиперболические изоморфизмы
пространства R.m. Пусть Е" и Е"—устойчивое и неустойчи-
неустойчивое подпространства оператора A, a Es', Еи>—соответствую-
Еи>—соответствующие подпространства для В. Утверждается, что А и В сопря-
гл. 2. Локальная грубость
жены тогда и только тогда, когда AS = A\ES сопряжен с Bs'=
¦=B\ES' и Аа = А\Еа сопряжен с Ви' = В\Еи'. |
Мы хотим дать необходимое и достаточное условие сопря-
сопряженности двух гиперболических изоморфизмов.
5.4. Предложение. Пусть Л, и Л2—изоморфизмы простран-
пространства IRm, которые в стандартном базисе представляются
матрицами
п
о
2J
, 2,=
1
о
2)
Пусть А—гиперболический изоморфизм индекса т. Если А
сохраняет ориентацию, т. е. если det^)>0, то А сопряжен
с Лх. Если А обращает ориентацию, т. е. если det (Л) < О,
то А сопряжен с Л2.
Доказательство. Из локальной грубости Л следует, что Л
сопряжен с каждым изоморфизмом из некоторой окрестности
оператора Л. Поэтому можно упростить доказательство, пред-
предположив, что Л диагонализуем.
Пусть {vlt ..., vm\ —базис пространства Rm, в котором Л
представляется матрицей А, имеющей вещественную канони-
каноническую форму!
[ 0)
о
§5. ЛОКАЛЬНАЯ КЛАССИФИКАЦИЯ
97
где —1
0<ц,< 1 и
Uft a
Заметим, что два гиперболических изоморфизма Вв и Sj
сопряжены, если они принадлежат одной и той же компоненте
связности пространства гиперболических изоморфизмов, кото-
которое является открытым множеством в & (Rm). Действительно,
пусть а: [0, 1]—*GL(IRm)—такая непрерывная кривая, что
a (t) является гиперболическим при каждом t g [0, 1] и а @)=В0,
аA) = В1. Из локальной грубости следует, что при каждом
t g [0, 1] a(t) имеет такую открытую окрестность F(cGL(Rm),
что всякий изоморфизм из Vt сопряжен с a (t). Возьмем такие
открытые отрезки Ut с серединой в t, что a,(Ut[)[0, \])aVt.
Так как [0, 1]—компакт, то существуют такие tt = 0 < t2 <...
• ••< k_j < f*= li что Utt[) ... U Utkz>[0, 1]; можно считать,
что ни одно Ut не содержится целиком ни в одном другом Ut
Поскольку тогда все Uit [) Ui{+j Ф 0 и тем более Vi{ П У?/+г Ф0,
то a (tt) сопряжено с а (^+1); таким образом, Ве сопряжено с Bt.
Благодаря этому замечанию достаточно найти такой непре-
непрерывный путь а; [0, 1] —¦ GL (Rm) в пространстве гиперболиче-
гиперболических изоморфизмов, что в базисе vit ..., vm оператор а@)
представляется матрицей А, а оператор аA)—матрицей At или
А2, так как изоморфизмы Аг и Л2 подобны изоморфизмам, пред-
представляемым в базисе {w,, ...,.vm\ матрицами А± и А2 соответ-
соответственно (и, следовательно, сопряжены с этими изоморфизмами).
Мы построим вначале такой непрерывный путь а,! [О, 1] —»¦
—*GL(R/B), что ai@) = i4, ax@ является гиперболическим при
всех t?[0, 1] и
о
Затем мы построим такой непрерывный путь Щ: [0, 1] —*
-*GL(R«»), что ^@)^^A) и а1A) = Л1 или Ай. Положим
98
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
«,@ -
О
'МО
О
где
1 B^—1L-2A—0 /(а?+Р?)/
если
где
]
COS (i CD,) = 0^@! + PJ), Sitl (I CO,) = -yVM+Щ-
Легко видеть, что —1<Х{(^)<0, 0<\it(t) <Cl при всех
?g[0, 1J и что собственные значения оператора Bt(t) по моду-
модулю меньше единицы при /?[0, 1]. Отсюда следует, что at(t)
является гиперболическим при всех I g [О, 1J. Поскольку а±
непрерывно, получаем, что at @) = А сопряжен с «хA), матрица
которого есть
О
О
2
Теперь построим кривую щ. Предположим, что А обращает
ориентацию, иными словами, det(^)<0. Поскольку ах непре-
$5. ЛОКАЛЬНАЯ КЛАССИФИКАЦИЯ
рывно и a, (t) является изоморфизмом при всех t?[0, 1], имеем
det(a,@)<0 при всех ^ ^ [0, 1] и, в частности. detfa^lJX0-
Таким образом, в этом случае число V отрицательных диаго-
диагональных элементов матрицы a^l) нечетно. Положим
О
т.
О
где
c f cos И) sm{p.t)\f—2 ° "\
1 \ — sin(nl) cos{nt))\ о -/
Тогда мы имеем
Су@) = (
4 -
о -i
Кроме того, собственные значения оператора Cj(t) имеют вид
— е±я"/2 и поэтому по модулю меньше единицы при всех
??[0, 1]. Так как а2@) = а, (I), а а2A) представляется матри-
матрицей Лг, получаем, что Л сопряжено с Л2. Аналогично если
det (Л) > 0, то Л сопряжено с Л,. Воспользовавшись теорией
степени в том виде, в каком она представлена в [64] или [38],
можно доказать, что At не сопряжен с Л2. Действительно, если
h—гомеоморфизм, сопрягающий Л, и Л2, то
deg ft — (deg ft) (deg A t) = deg (h A t) =
= deg (A „ft) = (deg Л2) (deg h) = — deg h,
а это приводит к противоречию, так как degft=;±l. |
Замечание. Если Л является гиперболическим изоморфизмом
индекса 0, то Л сопряжен с одним из следующих изоморфизмов:
'2 0^ (—2
2
0
о
100
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
смотря по тому, будет ли det^)>0 или det^)<0. Доказа-
Доказательство этого факта полностью аналогично доказательству
предложения 5.4.
Мы дадим теперь классификацию гиперболических неподвиж-
неподвижных точек диффеоморфизмов, используя локальную сопряжен-
сопряженность в качестве отношения эквивалентности.
А1 = A3—I •*• I Аг — А4- —
5.5. Теорема. Пусть f g Diff (M). Предположим, что р?
гиперболическая неподвижная точка отображения f. Тогда f
доцально сопряжено в точке р одному из перечисленных ниже
S 6. ИНВАРИАНТНЫЕ МНОГООБРАЗИЯ 101
линейных изоморфизмов А{ пространства Rm, где m — dimM.
Эти изоморфизмы А[, 0<i<mu 1 ^ / ^4, имеют индекс il)
и в стандартном базисе пространства Rm представляются
матрицами, приведенными перед формулировкой теоремы.
Доказательство непосредственно следует из теоремы Харт-
мана и Гробмана, предложения 5.3 и предложения 5.4. |
§ 6. ИНВАРИАНТНЫЕ МНОГООБРАЗИЯ
Пусть f?Dillr(М). Предположим, чтор^М—гиперболиче-
чтор^М—гиперболическая неподвижная точка отображения /. Множество Ws(p) тех
точек многообразия М, которые имеют точку р в качестве
своего со-предельного множества, называется устойчивым мно-
многообразием точки р, а множество W" (р) тех точек, которые
имеют точку р в качестве своего а-предельного множества,
называется неустойчивым многообразием точки р. Ясно, что
Ws(p) и Wu(p) инвариантны относительно отображения /.
Пользуясь гиперболичностью точки р, мы опишем в настоящем
параграфе структуру этих множеств и проанализируем их изме-
изменения при возмущениях диффеоморфизма /. Аналогичные опре-
определения и результаты имеют силу и для особых точек вектор-
векторных полей.
Пример 1. Если A?GL(R.m)—гиперболический изоморфизм,
то существует такое инвариантное расщепление Rm = ?* 0 ?°,
что когда q?Es, то An(q)—*0 при п—>• оо, а когда q^Ea,
то A~n(q)—>0 при п—> оо. Кроме того, для всех других q
II ^" (<7) II —* °° одновременно и при п—»-оо, и при п—*—оо.
Таким образом, WS(Q) = ES и W"@) = Ea.
Предположим, что MaRk, и пусть а—метрика, индуциро-
индуцированная на М из IR*. Для |3 > 0 будем обозначать через ВМ
шар радиуса |3 с центром в р.
Определение. Множества
WI{р) = {q €fipi /" (q) б В& V«> 0},
Wl (p) = {q<t Дв: /-»(q) € fip V« > 0}
называются соответственно локальным устойчивым и локальным
неустойчивым многообразиями размера р точки р.
Напомним, что топологической иммерсией многообразия Rs
в М называется такое непрерывное отображение Е: Rs—>М,
что каждая точка х € R* имеет окрестность V со следующим
свойством: ограничение F\V отображения F на окрестность V
J) Такой же индекс имеет и dfp; говорят, что i есть индекс неподвижной
точки р. Здесь тоже можно сделать терминологические замечания, анало-
аналогичные сделанным в случае особой точки-— Прим. рее).
102 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
является гомеоморфизмом на свой образ. В этом случае мы
будем говорить, что F(R*)c:M— иммерсированное топологиче-
топологическое подмногообразие размерности s. Топологическим вложе-
вложением R* в М называется инъективная топологическая иммерсия,
являющаяся гомеоморфизмом на свой образ.
6.1. Предложение. Если Р>0 достаточно мало, то
A) W^(p)cWs(р) и W%{p)cWa {р); иными словами, те точки
в окрестности точки р, у которых положительные {соот-
{соответственно отрицательные) полутраектории остаются в
этой окрестности, имеют в качестве своего w-предельного
{соответственно а-предельного) множества точку р;
B) Wsp{p) {соответственно W%{p))—вложенный в М топологи-
топологический диск, размерность которого равна размерности
устойчивого {соответственно неустойчивого) подпростран-
подпространства оператора А = Dfp;
C) W'(p) = Un>of-«(WW) и W"{p) = Un>of»{WUp)). Сле-
довательно, существует топологическая иммерсия q>s:
Es—»-М(фо: Еа—* М), образом которой является Ws{p)
{соответственно Wa {p))t где Es и Еа—устойчивое и неустой-
чивое подпространства оператора A=Df {p).
Доказательство 1). A) и B): по теореме Гробмана—Хартмана
существуют окрестность U точки 0 в ТМр и гомеоморфизм h:
Bti—>U, сопрягающий / с изоморфизмом А. Из того что А —
гиперболический изоморфизм, следует, что если x?U—такая
точка, что A"{x)?U при всех п^О, то x?Es и поэтому
А"{х)—»-0 при п—*оо. Пусть q€.W\{p). Поскольку ["q^B^
при п^О и hf"{q) = A"h{q), то A"h{q)€.U при n^O, так
что A"h{q)—»-0. Таким образом, f"{q) =h~1A"h{q) сходится к
р = ft-i@), откуда W%{p)dWs{p). Кроме того, h-1{Esr\U) =
= Щ{р), что доказывает часть BJ). Аналогично Wi(p)c:Wa (р)
W%{) h-1(U[)E«)
1) Строго говоря, вместо B) здесь будет доказано; что в Wp содер-
содержится некоторый топологический диск надлежащей размерности, являю-
являющийся окрестностью точки р в Wp. Тогда C) надо понимать с заменой
Ц7р(р) на этот диск. Этого достаточно, чтобы получить основное заключе-
заключение C)—о существовании ф^ и фа. Утверждение же, сформулированное в
тексте, тоже верно—его можно доказать с помощью тех результатов и
методов, которые излагаются далее; при некотором же специальном выборе
метрики на М возле р (a W% (p), очевидно, зависит от метрики) это делается
при доказательстве 6.2.— Прим. ред.
2) Строго говоря, если х?В„ и h(x)?Es, то ведь отсюда еще не сле-
следует, что fx?Bp или (что то же самое) Ah(x)?U. Правильнее сказать4
что в ТрМ имеется такой малый шар VdU с центром в нуле, что все
A" {Esf] V)dU при всех гс>0; тогда h~1(Es(]U)—тот самый диск, о кото-
котором говорилось в предыдущем примечании.— Прим, ред.
§6. ИНВАРИАНТНЫЕ МНОГООБРАЗИЯ ЮЗ
C) Поскольку Ws (р) инвариантно относительно /и W| (р) cz
cWs(p), то f-"(Wl(p))cWs(p) при всех п, так что
U, > оГ" (Щ (р))с W (р). С другой стороны, если q ? W (р),
то limn.» а, р (<7) = р и, значит, существует такое n0 ? N, что
f"(q)?Bti при всех п^п0. Таким образом, [п°(ф€Щ(р), и
поэтому <? б f~"tWl (p). Аналогично можно показать, что Wa (p) =
= Un>o/"l^p(p)- Определим теперь отображение фв: Es—>-M,
образом которого является Ws(p). Если x?Es, то существует
такое nogN, что An°(x)(zU, где U — рассмотренная выше
окрестность нуля. Определим (ps(x) = f~"«h~1A"o(x). Поскольку
h~x сопрягает Л и /, то отсюда следует, что «р, корректно
определено, т. е. не зависит от выбора п0. Легко видеть,
что ф5—инъективная топологическая иммерсия и что qs(Es) =
= Ws (p). Аналогично можно построить инъективную топологи-
топологическую иммерсию фа! Еа—*М, образом которой является
W'{p). I
Замечания. A) Если р?М—неподвижная точка отображения f,
то устойчивое многообразие точки р для / совпадает с неустой-
неустойчивым многообразием точки р для f~l. Эта двойственность
позволяет превращать каждое свойство устойчивого многообра-
многообразия в свойство неустойчивого многообразия.
B) Хотя локальное устойчивое многообразие является вло-
вложенным топологическим диском, но глобальное устойчивое мно-
многообразие может и не быть вложенным подмногообразием в М,
что показывает приведенный ниже пример 2.
C) Важно подчеркнуть, что теорема Гробмана — Хартмана
позволяет наделить W*(p) лишь структурой топологического
подмногообразия, как мы видели в предложении 6.1, в то время
как следующая ниже теорема 6.2, независимая от теоремы Гроб-
Гробмана — Хартмана, показывает, что W*(p) является на самом деле
дифференцируемым иммерсированным подмногообразием того же
класса гладкости, что и диффеоморфизм. Мы привели предло-
предложение 6.1 как мотивировку для основного результата этого
параграфа.
Пример 2. Пусть /; S2-*-S2 — диффеоморфизм, порождае-
порождаемый в момент времени t=\ потоком векторного поля X, имею-
имеющего следующую структуру траекторий: северный полюс pN
является единственной особой точкой в северной полусфере;
южный полюс ps является седлом, устойчивое и неустойчивое
многообразия которого образуют «восьмерку», охватывающую
две другие особые точки (рис. 6). В этом примере устойчивое
многообразие точки ps не является вложенным подмногообра-
подмногообразием в S2.
Пример 3. Пусть f = Yit где Y—векторное поле на S2, струк-
структура траекторий которого показана на рис. 7. В этом примере
104 гл- 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
(Ps) и Wa (ps) являются вложенными подмногообразиями
сферы S8.
Определения. Пусть S и S'— подмногообразия г) в М класса С',
и пусть е > 0. Будем говорить, что S и S' являются еС-близ-
кими, если существует такой С-диффеоморфизм hi S—>S'cM,
что i'h и i являются е-близкими в Сг-топологии. Здесь i: S—*М
и i'i S' —к М обозначают вложения.
Северная полусфера Южная полусфера
Рис. 6
6.2. Теорема (теорема об устойчивом многообразии). Пусть
/ (: Diffr (/И), р—гиперболическая неподвижная точка отображе-
отображения f и Es—устойчивое подпространство оператора A=Dfp.
Тогдах
Северной полусфера Южная полусфера
Рис. 7
A) Ws(p) является Сг-инъективно иммерсированным подмно-
подмногообразием в М и касательное пространство к Ws(p) в
точке р—это Е";
1) Компактные (только для них введена топология в С (S, М)), ноу
как будет видно из формулировки теоремы 6.2, с краем.— Прим. ред.
S 6. ИНВАРИАНТНЫЕ МНОГООБРАЗИЯ 105
B) пусть DaWs(p)—вложенный диск, содержащий точку р.
Рассмотрим такую окрестность off cDiff' (M), что каждый
диффеоморфизм g€<N" имеет единственную гиперболическую
неподвижную точку pg в некоторой окрестности U точки р.
Тогда для любого е > 0 существует такая окрестность
effcrdV, что для каждого g^Jf существует г С-близкий
к D диск Dg<=Ws(pg).
Мы собираемся дать доказательство этой теоремы, исполь-
использующее теорему о неявной функции в банаховых пространствах.
Это доказательство принадлежит М. Ирвину [43]. Наше изло-
изложение основано на ряде заметок Ж. Франкса х).
Мы докажем, что локальное устойчивое многообразие Wg(p)
является графиком некоторого С'-отображения и что точки
многообразия №| (p) имеют р своим со-предельным множеством.
Отсюда следует, что глобальное устойчивое многообразие при-
принадлежит классу Сг, поскольку Ws(p) = Un>of-"W^(p). Следо-
Следовательно, можно ограничиться тем случаем, когда /—диффео-
/—диффеоморфизм, определенный в некоторой окрестности V точки 0 в
Rm, и 0—его гиперболическая неподвижная точка.
Пусть A = Df(O). Рассмотрим Л-инвариантное расщепление
Кет = ?*ф?° и такие нормы ||-|U ||-|о на Es, E", что ||Л*^<а< 1
и || (Л0)!,, < а < 1. На R™ будем использовать норму ||яя©л;о ||===
= max {!>:,]„ ||хп|и}. Для |3 > 0 будем обозначать через Вр
открытый шар радиуса р с центром в нуле. Положим В|=з
= Вр fl Es, Вр = Вр П Е". Выберем |3 так, чтобы в Bg, можно было
написать / = Л+Ф, Ф@) = 0, |?)Ф||<е
с некоторым е, таким что 0 < е < (а—1)/2. Будем также
использовать обозначения f = (fs, f"), A = (AS, Л°) и Ф=*
=(Ф*, Ф°). Для доказательства теоремы 6.2 нам понадобится
следующая лемма.
6.3. Лемма. Если z = (xs, xa) и z' = (xs, x'u) таковы, что
fn(z)^B& и /»(г')€^ при всех /г>0, то z = z'.
Доказательство. Рассмотрим такие две точки y = (ys, ya) и
y' = (y's, У'и) в Вр, что lyt—y's^<ijya—y'ul Мы утверждаем, что
х) Метод доказательства принадлежит О. Перрону (ссылки см. в [3]), а
возможно (хотя бы отчасти), и еще более ранним авторам (заслугой Пер-
Перрона является то, что он нашел удачные условия в неавтономном случае,
который здесь не рассматривается). Ирвин, по-виднмому, самостоятельно
открыл этот метод, но главное—заметил, что его можно оформить с
помощью теоремы о неявной функции в банаховых пространствах. Это
значительно упрощает доказательство гладкости устойчивого многообра-
вия.— Прим. ред.
106 Гл. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
tfs(y)-f4y'n<lfa(y)-fa(y')l
Действительно,
F {y)-fa (У') = А- (у)-А" (у1) + Ф« (у)-Фа (у').
По теореме о среднем значении1) имеем
Поскольку || у—у'\ — \уа—у и}, получаем, что
\faiH)-fa(y')\\>(a-l-z)\ye-yul
Аналогично
|l/s (y)~fs (У') \<а\у,-? | + е \у-у' |.
Так как 1у—у'1 = \уа—уи1>Уа—уЦ, то
I|/J (У)-Р (У') II < (а+е) | #0-/и
Из этих неравенств заключаем, что
Рассмотрим теперь первоначальные точки г, г' и положим
y = fn(z), y' = f"(z') для п > 0. Из приведенных выше рассуж-
рассуждений следует, что
Поскольку с—е> 1, то мы заключаем, что г = г\ так как
в противном случае расстояние между ^"(г) и /"(г') стреми-
стремилось бы к бесконечности при п —»• оо в противоречие с тем
фактом, что /"(г) и fn(z') принадлежат шару Bti при всех n^O. |
Доказательство теоремы 6.2. Мы хотим показать, что мно-
множество тех точек, положительные полутраектории которых
остаются в некоторой окрестности нуля, является С'-подмно-
гообразием. Мы также покажем, что это множество совпадает
с множеством тех точек, положительные полутраектории кото-
которых сходятся к нулю. Вначале мы дадим мотивировку дока-
доказательства. Пусть К—пространство последовательностей у(п),
п ^ 0, в R1", таких что у (п) —*¦ 0, с нормой | у \\ = supn | у (п) |.
Пусть G — подмножество в К, определенное формулой
G {/С ()#р при О}
1) Распространенное название неравенств вроде || Фи (у) — Ф° (г/') || ^
^ sup || ОФ" ||. || у—{/' ||. — Яр/ш. рей.
2) С—открытый шар в К: если у («)—>- 0 и все || -у (п) || < [5, то
| у () |1 < Р-
§6. ИНВАРИАНТНЫЕ МНОГООБРАЗИЯ 10?
Предположим, что y?G и y(n) = fn(z) для некоторого
Тогда
у(п) = А(А + Ф)" (г) + Ф (у (и-1)) =
= Лп(г)+ 2 Ап-
» = 0
Вторая компонента вектора у{п) выражается формулой
(Л«)" [г. + 2 (Л«)"»-'Ф« (y @)] .
В силу того что Аа—растяжение, заключаем, что
@) сходится к —г/).
Это мотивирует введение отображения F: B| x G —»¦ /С, опре-
определяемого формулой
F(x, y)(n) = y(n)-((AT(*) + 2 "
Мы покажем, что F (х, у) 6 /С и что для каждого х существует
такое у ? G, что F (х, у) = 0.
Выберем такое b > 0, что ||Ф(г)||<? для zgflp. Так как
0 < а < 1, то 2о°й^ ограничена и сходится к A —а). Сначала
заметим, что у(п)~*0 и (As)n (х)—*¦ 0, поскольку |(Л*)"|| <а".
Кроме того,
2 (^»)"-1-'Ф« (у (t)) | < A —a)'1 sup || Ф° (у @) •
Поэтому для заданного е > 0 выберем п настолько большим,
чтобы ||Фв(т@)|| < A—Й)е ПРИ »^п. Вторая компонента век-
вектора F (х, у) стремится к нулю. Рассмотрим первую компоненту.
Для 0 ^ т ^ п справедливо неравенство
1= О II
< A — a)-lan-mb + A —a)*1 sup || Ф* {у (t)) fl.
г) Здесь v (n) = (Y* (n)i Yn («)) c фиксированным п играет роль г для
OP
последовательности f _¦ -у Iя +«). Поэтому y* l«) == — 2 ('4а)™~1~' фв iV (('))«—
«=л
Прим. ред.
108 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
При данном е > 0 сделаем т настолько большим, чтобы второй
член стал меньше е/2. Тогда мы можем выбрать п настолько
большим, чтобы первый член был меньше е/2. Следовательно,
F(x, y)€K.
Теперь воспользуемся теоремой о неявной функции. Если
зафиксировать уgG, то отображение x—+F(x, у) из Б| в К
будет аффинным и непрерывным. В частности, оно принадлежит
классу С7". Мы покажем, что при и?К
/и-1
D2F(x, у)(и)(п) = и(п)-( 2 (ЛТ-'
\«=0
_ 2 (ЛТ- w ОФи {у (/)) (ы @)\
Чтобы упростить последующие выражения, обозначим через К
правую часть этого уравнения. Мы хотим доказать, что для
любого заданного 6 > 0
\F(x, y-\-u)(n)—F(x, y)(n)—ЯЦ^бЦыЦ
при малом || и |. Левая часть этого неравенства меньше или равна
2 (ЛО""''[Ф*(у @ + и@)-Ф*(у (i))-DU>*(у @) (и@)] +
i=0
+1.2 {А «)»-*-' [Ф« (у (о + и @) - Ф» (т @) - ^Ф" (т @) («(ОЙ || •
Поскольку DO непрерывно на замыкании множества Вр, то оно
равномерно непрерывно на Вр. Поэтому для любого б' > О
существует такое р > 0, что || D© (z-f м)—DO(z)!|<6',e^H zgB6
и || и | настолько мало, что z-\-u?Bb и ||ы||<р. Применяя тео-
теорему о среднем значении к функции и—>Ф(г-\-и)—О (г),
получим, что1)
||Ф(г + и)—Ф(z)—DCb(г)и||< б'|и|.
Мы заключаем, что каждое слагаемое из сумм, стоящих под
знаком || ||, в приведенном выше выражении меньше чем
A—я)6'[[м||. Поэтому достаточно взять такое 6', чтобы
удовлетворить неравенству 2A—й)~1б'<б. Это показывает,
что K = D2F(x, y)(u)(n). Легко проверить непосредственно,
что DjjF непрерывно по (х, у).
Мы заключаем, что F принадлежит классу С1, так как DXF
и D2F непрерывны. Кроме того, прямой проверкой убеждаемся,
что D2F @, 0) является тождественным отображением / про-
пространства К. По теореме о неявной функции существуют такой
г) Ясно, что и—>-Я=Я [и)— ограниченный линейный оператор в К.—
Прим. ред.
§6. ИНВАРИАНТНЫЕ МНОГООБРАЗИЯ 109
шар Bf в Es и такое Сх-отображение ф: Bbr—+G, что ф@) = 0
и F(x, <p(x)) = 0 при всех x?Bf. Имеем
<р(х) @) = [х, — 2 (Л0)-'©0 (ф(л
\ 1 = 0
Обозначим через ft.» В* —»?и отображение, задаваемое второй
компонентой этого выражения, так что ф (х) @) = (х, h (x)).
Отображение ft класса С*, так как ф класса С1, а отображе-
отображение б- G —»- Rm, переводящее у в у @), является линейным и
непрерывным. Заметим, что Л = я2обоф, где я2- Rm—»-?и —
естественная проекция. Так как F (х, ф (х)) (п) = 0 при всех
п!>0, то
(л*)- (х) + 2 (Л*)»-»-' ф* (ф (х) @),
1 = 0
Отсюда следует, что1)
Ф (х) (п + 1) = (А + Ф) (Ф (х) (п)) = / (Ф (х) (п)).
По индукции получаем, что ф (х) (п) = /" (х, ft (л:)) при всех п > 0.
Это показывает, что если г g graph (h), то р (г) стремится
к нулю при п —>- оо. С другой стороны, если г и ее положи-
положительная полутраектория остаются в малой окрестности нуля,
то лемма 6.3 показывает, что г g graph (ft). Таким образом,
/(graph(ft))с graph (ft) и graph (ft) представляет локальное
устойчивое многообразие точки 0 для отображения /.
Осталось доказать, что касательным пространством к ло-
локально устойчивому многообразию в нуле является Es. Для
этого надо установить, что Dh @) = 0. Так как F (х, ф (х)) = 0,
то DyF (х, ф (х)) + D2F (x, ф (х)) Dtp (x) = 0. Из этого следует, что
?>ф@) = — ZV40, 0), так как A,F@, 0) = /. Если v?Es, то
Dq@)(v)—DtF @, 0)(v) = — и, где ы(п) = ( — (A')"v, 0) при
п^0. Так как к = л^овокр, то Dh@)(v) = n2o6oD((>@)v, по-
поскольку ла и б линейны. Таким образом, Dh @) v=n3 ((As)° v, 0)=0,
что мы и стремились доказать.
Выше было доказано, что устойчивое многообразие принад-
принадлежит классу С1. В действительности оно класса Сг, если /
класса Сг. Это следует из того факта, что использованное выше
1) s-компонента (Л + Ф) (<р (я) (я)) содержит член Ф* (ф (#) (п)), даюший
слагаемое в выражении для ф (л;) (n+l). отвечающее i = n, а при действии
А* на выражение для s-компоненты ф (дг) (гс) получаются остальные слагае-
слагаемые. В «-компоненте член Ф° (ф (я) (п)) сокращается с членом, получаю-
получающимся при действии Аи на первое слагаемое бесконечного ряда (отвечающее
i = n).— Прим. ред.
ПО ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
отображение F класса Сг, мы видели, что DtF класса С',
и можно прямо проверить, что D2F тоже класса С. Непре-
Непрерывная зависимость локального устойчивого многообразия от
возмущения Ф доказывается с помощью аналогичных рассуж-
рассуждений. В этих рассуждениях достаточно считать, что F зависит
от Сг-возмущения Ф, подчиненного все тем же условиям
(Ф@) = 0, ЦГ)ф|<е) на Bf F = F(x, у, Ф). Тогда проверяется,
что DSF принадлежит классу С~1, так что F класса Сг. Осталь-
Остальная часть рассуждений остается прежней. К этому надо только
добавить, что в общем случае неподвижная точка отображения
Л+Ф может изменяться (непрерывно) вместе с Ф. Но это не
очень существенно влияет на рассуждения, поскольку непод-
неподвижную точку можно возвращать обратно в нуль с помощью
С-диффеоморфизма. C) |
Интересно отметить, что приведенное доказательство работает
также для отображений, а не только диффеоморфизмов, т. е. As
может иметь собственные значения, равные нулю. Однако этим
способом можно доказать только существование устойчивого
многообразия (*). Неустойчивое многообразие тоже существует,
что можно показать, используя другое доказательство, так
называемое преобразование графика, объясненное ниже.
Интересно также отметить, что приведенное выше доказатель-
доказательство имеет силу и в банаховых пространствах: надо только
добавить предположение, что локальное отображение / и его
производные равномерно непрерывны в Вр F).
Рассмотрим теперь векторное поле X ? ?r (M), и пусть
р(?М — гиперболическая особая точка поля X. Устойчивое
многообразие Ws(p, X) точки р для векторного поля X—это
множество тех точек многообразия М, со-предельным множест-
множеством которых является р. Пусть f = Xt—это диффеоморфизм,
порождаемый полем в момент времени t=\. Как мы видели,
р—гиперболическая неподвижная точка для f. Если через
Ws(p, f) обозначить устойчивое многообразие точки р для /,
то W'(p, f) = Ws(p, X). Действительно, если x?W*(p, X),
иными словами, если Xt(x) —*р при t —* оо, то ясно, что
Хп (х) = f" (х) —»• р при п—* оо. Следовательно, Ws(p, X)c
cWs(p, f). С другой стороны, пусть U — произвольная окрест-
окрестность точки р. Так как X (р) = 0, то существует такая окрест-
окрестность V точки р, что Xt(V)cU, если 0 < I < 1. Если х ? Ws (p, /),
то существует такое пю ? Н, что /'" (х) ? V при п ^ п0. Следова-
Следовательно, Xt (х) € U, если I ^ п0. Это показывает, что Xt (х) —> р
при *--оо. Поэтому Ws(p, f)c:W'{p, X).
Мы приведем также набросок другого, более геометриче-
геометрического доказательства теоремы 6.2, которое можно найти в [39]
и [77]. Мы опустим детали этого второго доказательства, по-
§6. ИНВАРИАНТНЫЕ МНОГООБРАЗИЯ
111
скольку они технически более сложные. Подчеркнем, однако,
что это доказательство ведет к важным обобщениям, изложен-
изложенным в [40].
Пусть Ш cCr (В%, Bg)— множество Сг-отображений, у которых
постоянная Липшица не больше 1. Тогда ?— замкнутое под-
подмножество в Cr (fig, В") и, следовательно, является простран-
пространством Бэра. Если a?<jF, то график отображения a—это
Рис. 8
Сг-подмногообразие в Rm. Так как А сжимает векторы на Е*
и растягивает векторы из Еп, то отсюда следует, что
А~г (graph (а)) Г)ВР является графиком некоторого Сг-отобра-
жения из В\ в В% которое мы обозначим через Г^(а). Дей-
Действительно, rA(a)(xs) = (Aa)~1a(Asxs). Поскольку постоянная
Липшица отображения Г,, (а) также не превосходит единицы,
то мы определили отображение Гд: ? —*¦ ?, называемое пре-
преобразованием графина, ассоциированным с А. Легко видеть, что
если а??, то последовательность \Гпд (а)\ сходится к нулевому
отображению, график которого—это локальное устойчивое мно-
многообразие оператора А. Поскольку А является производной
отображения / в точке 0, то естественно ожидать, что, беря Р
достаточно малым, можно определить преобразование графика
Г,- ?-*?, ассоциированное с /. Если Tf имеет притягиваю-
притягивающую неподвижную точку а^Ст(В^, В$), иными словами, если
Т/(а/)=а/ и Г?(а)—.-а, для каждого а?$",то /(graph(af))~
= graph (af) и graph (af)—это множество тех точек из Вр, у ко-
которых положительные полутраектории отображения / остаются
в Вр. Таким образом, graph (af) = Wfi@). Другими словами, до-
доказательство теоремы можно разбить на следующие шаги:
A) Г/ корректно определено и имеет притягивающую непод-
неподвижную точку af€Cr(Bf,, ?g);
B) если g близко к / в Сг-топологии, то Г^ корректно опре-
определено и имеет притягивающую неподвижную точку, непре-
непрерывно зависящую от g.
112
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
§ 7. Jl-ЛЕММА (ЛЕММА О НАКЛОНЕ).
ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ЛОКАЛЬНОЙ ГРУБОСТИ
В этом параграфе мы обсудим некоторый локальный факт,
существенный для нескольких результатов теории динамических
систем, и объясним некоторые из них [75] (в). В частности, мы
дадим другое, более геометрическое доказательство теоремы
Гробмана — Хартмана. Снова можно заметить, что тот же ре-
результат (и то же доказательство) имеет силу и в банаховых
пространствах.
Рис. 9
Пусть f—С-диффеоморфизм некоторой окрестности V в Rm
и 0—его гиперболическая неподвижная точка. Рассмотрим ги-
гиперболический изоморфизм A = Df @) и инвариантное расщеп-
расщепление Rffl = ?s0?°. В § 6 мы видели, что локальное устой-
устойчивое многообразие W\cc@) неподвижной точки 0 является
графиком некоторого С'-отображения <р,: Вр —> Еа с фЛ @) = О
и Dtps @) = 0. Здесь Bp@)aEs обозначает шар с центром в нуле
и радиуса р. Аналогично, локальное неустойчивое многообразие
Wfoc @) является графиком некоторого Сг-отображения фв: В% —*¦
—+ES с фп @) = 0 и ?)фп @) = 0. Рассмотрим отображение
у ^ /у гп / У \ У ГП (y W
ли) — \xs Фа \ли) > ха 4>s \xs))'
Ясно, что ф принадлежит классу Сг и что Лф(О)—тождествен-
Лф(О)—тождественное отображение. Поэтому ограничение отображения ф на не-
некоторую окрестность нуля в Rm является диффеоморфизмом.
Рассмотрим диффеоморфизм/ = ф,/ = ф/ф-1. Тогда J—это такой
диффеоморфизм некоторой окрестности нуля, что f@) = 0 и
D]@) = A. Кроме того, локальное устойчивое многообразие
диффеоморфизма f является окрестностью нуля в Es, а локаль-
локальное неустойчивое многообразие—окрестностью нуля в Е". Дру-
Другими словами, всегда можно считать, что локальное устойчивое
(соответственно неустойчивое) многообразие гиперболической
неподвижной точки диффеоморфизма является окрестностью
§7. Я-ЛЕММА. ГЕОМЕТРИЧ. ДОКАЗАТЕЛЬСТВО ЛОКАЛЬН. ГРУБОСТИ 113
неподвижной точки в устойчивом (соответственно неустойчивом)
подпространстве линейной части отображения /.
Пусть ||-||—такая норма на Rm, что ||Л*Ц<а< 1 и Д(Л«)-*||^
<[а< 1, где As и Аа—ограничения А на ?s и Еа соответ-
соответственно. Если Is: Bp-+Es—ограничение отображения / на
Wse(O)ciBlciEs, то Df*@) == Л*. Поскольку Л*—сжатие, то
/*—сжатие при малых р. Следовательно, если BsczBl—откры-
BsczBl—открытый шар с центром в нуле1), то f(dBs)czBs, где dBs = BS\BS —
граница шара Bs. Кольцо Gs@) = Bs—f(Bs) называется фун-
W" @)
Рис. 10
даментальной областью для устойчивого многообразия точки 0.
Ясно, что dGs(O) — dBs[)f(dBs).
Если х? W* @)\{0}, то траектория точки х имеет не меньше
одной и не больше двух точек в фундаментальной области
Gs@), т. е. UneZfn(G*@)) = Ws@)\{0}, а если x?intGs@),
то f"(x)$Gs(Q) при всех n?Z\{0}.
Любая окрестность А^@) множества Gx@), не пересекаю-
пересекающаяся с WfoC@), называется фундаментальной окрестностью
для устойчивого многообразия точки 0. Аналогично опреде-
определяются фундаментальная область G° @) и фундаментальная
окрестность Na @) для неустойчивого многообразия точки 0.
Пусть BsaEs—шар, содержащийся в W\oc@), B°c?°—шар,
содержащийся в №\ж@), и V — BsxBa. Рассмотрим точку
<7€^!ос@) и диск Da размерности и = dim Е", трансверсальный
к Wfoc @) в q.
7.1. Лемма (Х-лемма). Пусть V = BsxBa, q ?WS @)\{0} и Da —
такое, как выше2). Пусть D%—связная компонента множества
fn (D") П V, содержащая f" (q). Тогда для любого е > 0 сущест-
существует такое no€N, что если п\
г-С^-близкими. B)
ущ
п0, то D% и Ва являются
1) Шар не в топологическом смысле, а в смысле метрики.— Прим. ред.
а) На самом деле не исключено, что в ходе доказательства Bs, Ba и V
придется уменьшить. Но во всяком случае, это зависит только от /, а не
от 6 и Du,— Прим. ред,
114
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Доказательство. Выражение для / в окрестности V точки О
дается формулой
f{xs, xa) = (Asxs + <ps(xs, xa), Aaxtt + q>a{xs, xa)),
где
o = (/H, A"), xs?B*, ха?В»
=П
Так как д<р?/длу(О, О) = О при i, / = s, и, то из непрерывности
этих частных производных следует, что существуют такое k,
)я
Рис. II
что a1 = +
и такая окрестность V'cV, что
Можно предположить, «то q?V и 6я, В°сУ = BsxBn. Далее
пишем У вместо V. Пусть о0—единичный вектор в (TDa)q.
В произведении V = BsxBu можно писать vo = (vl, x%). Пусть
Ко выражает наклон вектора vv, Ko = ||oo||//|^cj- Здесь ||fo||?0
так как Da трансверсально к Bs в q. Рассмотрим точки
§7. Я-ЛЕММА. ГЕОМЕТРИЧ. ДОКАЗАТЕЛЬСТВО ЛОКАЛЬН. ГРУБОСТИ Ц5
Для q?dBs
A'
Atf0 + dyjdx, (q) vl + dys!dxa (q) i#\
У
Таким образом,
1 _ 1КД
~ I) vt i ~
I Aavt + д(е»/дх» W vo II
Числитель ограничен сверху выражением
IIЛ Vo I +1 d<ps/dxs (q) vll + l d<pjdxa (q) ifti | <
Знаменатель ограничен снизу выражением
Следовательно,
Так как kjbn—>-0 при n—>co и &/F—1) < (fc—1)/4, то
существует такое nx ^ Z+, что для каждого п > их мы имеем
Я„<F—1)/4. Пусть 0 < kx < min f e-^-, ^)- Поскольку
dq>Jdxa \ви = 0 и В°—компакт, то существует такое б<е, что
для Vl==6BsxB"cV будем иметь
max
Здесь 6BS обозначает шар, радиус которого равен радиусу шара
Bs, умноженному на б. Заметим, что в области Vx под дей-
действием / у любой точки ее s-координата уменьшается в отно-
отношении ^ alt а ы-координата увеличивается не менее чем в b раз;
116
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Действительно,
q>u(xs, 0) = 0,
)—ц>а(х,, 0) К А: |
Поскольку uD можно выбрать так, чтобы Я,о было макси-
максимальным возможным наклоном единичных векторов в G7>)9,
то существует такое п2^п,, что при п^щ все ненулевые
векторы из (Tfn(Du))Qn имеют наклон К^Ф—0/4 и д„^У±.
Следовательно, ввиду непрерывности касательного простран-
пространства к многообразию D^ существует такой вложенный в D? диск
Da с центром в qn^, что наклон X каждого единичного вектора
из (TDa)p, p€.Da, удовлетворяет неравенству К^ф—1)/2.
Пусть v g (TDa)p и р ? Du. В разложении и = (ия, if) вектор
v имеет наклон кПо = J о* |/|| о° |. Посчитаем наклон итераций
вектора и. Имеем
tp {V)
так что
vn0+l"
PvJd*. (P) * + АФ + дуи1дхи (р)
dxs(p)v^+dq>a/dxa(p)v'4
dxs (p) vs-\-Attvu-\-d(pa/dxa (p) f°|)
Vj'
Числитель этого выражения меньше чем а
а знаменатель больше чем
1A «w fl-
Отсюда
(Р) "* I >
—k\tf\—k\v*\.
6-АЯ»,
Пусть ^=-^-F+1),
тогда
— 1
Существует такое п3, что при n^ng правая часть
<.2kiftbi—1) <е. Такая оценка для Хп+Па справедлива в точке
S 7. Я-ЛЕММА ГЕОМЕТРИЧ. ДОКАЗАТЕЛЬСТВО ЛОКАЛЬН. ГРУБОСТИ 117
fnp, pg/5°, если все f'pG.Vi, Os^ts^n. Уменьшив, если по-
потребуется, Dn, можем считать, что все /'D"crVi, O^t^n3-
Тогда все ненулевые касательные векторы из Т (fnDa)jnp с п ^ щ
имеют наклон, меньший е, пока fnp не выйдет из У^.
Сравним норму вектора, касательного к /" (D") Л Vf в точке
fnp, с нормой его образа под действием отображения Df:
ой)
Из выражений для ujj41 и t{ заключаем, что
Поскольку наклоны Кп+1 и Кп сколь угодно малы, то мы видим,
что при итерациях нормы ненулевых векторов, касательных
к /n(D")nVi. увеличиваются в отношении, близком к fc=s
= а'1—ft>l. Можно считать, что при и^п4, где п4^п2,
это отношение > Ьг. А уменьшив еще раз Da, можно считать,
что piPczV! при 0<п<и4.
Множество /"«D0 содержит некоторый шар (во внутренней
метрике) с центром в qnt. Пусть г—радиус этого шара. Тогда
fnt+n?)u СОдержит шар с центром в qni+n радиуса Щг, если
только этот шар не выходит из У,. Проекция этого шара на
Еи содержит шар с центром в 0 радиуса fc^r/^l+e2 и содер-
содержится в шаре радиуса Щг. Существует такое пъ, что Ь""г/2)/Т+??
не больше, a.fcr/Kl+e2 больше радиуса В". Получается, что
при п ^ пг -f «5 некоторая часть f"Da состоит из точек
(х"(хи)> хи)> гДе ха пробегает В°, а х?(.)—^-функция, С°-
норма которой, как и С°-норма ее производной, меньше е. Эту
часть f"Du обозначим через D%. Ясно, что она е СЧ5лизка к Ва.
Она содержится в шаре в f"D" с центром в qn радиуса fcr/V^l 4- е2,
а те точки шара радиуса Ь1'+1г, которые не принадлежат пре-
предыдущему шару, лежат вне V—их «-координаты лежат вне Ва.
(Можно считать, что ]/ 1 -f ?2 < Ь±, а уменьшив предварительно
радиус Ва не более чем в 2 Ь± раз, можем считать, что в 6BS x 2ЪгВа
поведение траекторий и оценки наклонов такие же, как в V1.)
Поэтому связная компонента множества fn (D°) f| Vt совпадает
с Г>п. Это завершает доказательство Я-леммы. |
Замечания. A) к-лемма может быть доказана для семейства
дисков, трансверсальных к Ws@), при условии, что это се-
118
ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
мейство непрерывно в С1-топологии. А именно пусть F: Gs @)—*
—>С1(В", М)—непрерывное отображение, которое каждой точ-
точке q из фундаментальной области Gs@) сопоставляет некото-
некоторый диск D% = F(q)Bu, трансверсальный к Bsl). Пусть V =
= BsxBu—такое, как выше. Тогда для любого е>0 сущест-
существует такое пй ? N, что /" (?>?) Л V при каждом q (Е G* @) и п > п0—
диск, е О-близкий к В".
Рис. 12
B) Хотя это и не является необходимым для большинства
приложений, но можно доказать, что эти диски С-близки к Ви,
г^1, если F—непрерывное семейство Сг-дисков, иными сло-
словами, если мы имеем непрерывное отображение Fi Gs @) —*-
-+С'(В", М).
C) Следующий факт является непосредственным следствием
Х-леммы. Предположим, что D*—маленький s-мерный диск,
трансверсальный к Wa @). Тогда существуют такое п0 > 0 и
такая последовательность точек гп g D°, п ^ п0, что /" (г„) € Ds.
D) Х-лемма (вместе с приведенными вслед за ней замеча-
замечаниями) справедлива и полезна также применительно к локаль-
локальным диффеоморфизмам или даже (^-отображениям в банаховом
пространстве возле гиперболической неподвижной точки. Мы
предполагаем, что частные производные отображения равномер-
равномерно непрерывны и что неустойчивое (устойчивое) многообразие
конечномерно. В связи с этим см. [183].
Следствие 1. Пусть pit p2, pt?M—гиперболические неподвиж-
неподвижные точки диффеоморфизма f € DifP" (M). Если Wa (pt) в неко-
некоторой точке трансверсально пересекает Ws (pa), a W" (р3) в не-
х) Или F: К—«-^(В», М)— непрерывное отображение, которое каждой
точке q из некоторого компакта К С Ws @) сопоставляет некоторый диск
D" = F(q)Btt, трансверсальный к Ws @) в точке q—F (?) О. — Прим, ред.
§ 7. АлЛЕММА. ГЕОМЕТРИЧ. ДОКАЗАТЕЛЬСТВО ЛОКАЛЬН. ГРУБОСТИ 119
которой точке трансверсально пересекает Ws(p3), то Wa(p1)
в некоторой точке трансверсально пересекает Ws(p3).
Доказательство. Пусть q—точка, в которой трансверсально
пересекаются многообразия Wa(p2) и Ws(p3). Рассмотрим замк-
замкнутый диск DczWa(p2), содержащий р2 и q. Поскольку D
имеет точку трансверсального пересечения с Ws (p3), то отсюда
следует, что существует такое е>0, что если D—диск, е С1-
близкий к D, то D также имеет точку трансверсального пе-
V
Рис, 13
ресечения с Ws(p3). Пусть теперь д^—точка трансверсального
пересечения W°(pi) и Ws(p2) и D"cWa(pi)—диск, содержа-
содержащий q2, той же размерности, что и Wa(p2). По Х-лемме суще-
существует такое целое пв, что fn« (?>") содержит диск D, который
е СЧ5лизок к D. Поэтому существует точка q?,Df}Ws(p3).
Поскольку Wa(p1) инвариантно, мы имеем /"«(D")c:W7o(p1), так
что q—точка трансверсального пересечения WlpJ и W* (р3). |
Следствие 2. Пусть р^М—гиперболическая неподвижная точка
диффеоморфизма / € Diff (M), a Ns(p)—фундаментальная
окрестность множества Ws(p). Тогда Un > ofn(Ns(p))^> U\WfOi. (p)
для некоторой окрестности U точки р.
Доказательство. Заметим, во-первых, что итерации фунда-
фундаментальной области Gs(p)czNs (p) под действием / покрывают
Ws(p)\{p\; иными словами, Uns2/"(Gi(p)) = W*(p)\{p}. Кроме
того, по Х-лемме каждая точка из некоторой окрестности U
точки р, не принадлежащая Wfoc, принадлежит некоторой ите-
итерации трансверсального к 0s (p) сечения, содержащегося
Б №(р) (в). |
120 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
Докажем теперь к-лемму для векторных полей. Пусть р g M—
гиперболическая особая точка поля Х?ЭЕГ(М). Пусть Wsloc(p)
и Wfoc (p)—локальное устойчивое и неустойчивое многообразия
точки р. Пусть В*—такой вложенный в №foc(p) диск, что dBs
трансверсальна к полю X в Ws(p). Сфера ?>s (p) = dBs назы-
называется фундаментальной областью для Ws (р). Легко видеть,
что если x?Ws(p)\{p}, то траектория точки х пересекает
%s(p) только в одной точке. Аналогично можно определить
фундаментальную область 3" (р) для W" (р).
Пусть Da—диск, трансверсальный к №foc (p), который содер-
содержит точку q ? Щж (р) и имеет размерность dim Da = dim W{oc (p).
Пусть К.—следующее компактное множество: K—{Xt(q): t ? [0,1]}.
Для каждой точки Xt (q) ? К рассмотрим диск D" (Xt (q))=Xt(Du);
он содержит точку Xt(q) и трансверсален к Wfoc(p), так как Xt—
диффеоморфизм uW\oc(p) инвариантно относительно Xt. Пусть
f = X1—диффеоморфизм, порождаемый потоком в момент времени
<= 1. Тогда р—гиперболическая неподвижная точка для /, аустой-
чивое и неустойчивое многообразия точки р совпадают с устой-
устойчивым и неустойчивым многообразиями точки р для векторного
поля X. Пусть Bs—вложенный в Wfoc (p) диск, содержащий р,
а В"—вложенный в №foc (p) диск, содержащий р, и
V = BsxBu—окрестность точки р. По Х-лемме для диффео-
диффеоморфизмов, для любого е > 0 существует такое n0 g N, что если
п > щ, то D" (х) является е-С1-близким к Ва, где ?% (х) —
связная компонента множества f"(D"(x)) {]V, содержащая
/" (х), и х ? К- Это доказывает следующую лемму.
7.2. Лемма. Для любого е > 0 существует такое t0 > 0, что
если t > t0 и ?>"—связная компонента множества Xt(Da)f\V,
содержащая Xt (q), то Щ и Ва являются г-С1-близкими. |
Приведем теперь другое, более геометрическое доказатель-
доказательство теоремы Гробмана — Хартмана. Мы будем пользоваться %-
леммой и теоремой об устойчивом многообразии, доказательства
которых, как уже отмечалось, не зависят от теоремы Гроб-
Гробмана — Хартмана. Мы изложим доказательство для потоков, но
аналогичные рассуждения применимы и для диффеоморфизмов.
7.3. Лемма. Пусть р?М—гиперболическая особая точка
векторного поля X g ЖГ (М). Тогда существуют окрестность U
точки р и непрерывное отображение ляг U —+ Bs, где Bs =
= ?/Л№?Ос—диск, содержащий р, со следующими свойствами!
A) n^1(p) = Ba = U Г\ Wfodp)—диск, содержащий р;
B) для каждого x?Bs его прообраз nj1 (x) является Сг-под-
Сг-подмногообразием в М, трансверсальным к W\x (p) в точке х;
C) ns является отображением класса Сг всюду в И, за исклю-
исключением, быть может, точек из Ва;
§7. Л-ЛЕЛША. ГЕОДШТРИЧ. ДОКАЗАТЕЛЬСТВО ЛОКАЛЬН. ГРУБОСТИ 121
D) расслоение (8), определяемое отображением ns, инвариантно
относительно действия потока поля X в том смысле, что
если t^O то Xt(n^1(x))=>nj1(Xt(x)).
Доказательство. Можно предполагать, используя локальную
карту, что X—векторное поле, заданное в окрестности V нуля
в Rm = Es(?)Ea, и 0—гиперболическая особая точка. Можно
также предполагать, что Wfoc@)—открытое подмножество в ES,
содержащее 0, и что Wfoc@)—открытое подмножество в Еп,
содержащее 0. Пусть %s @)—фундаментальная область для
Ws@). 4s @) является сферой, содержащейся в Es и трансвер-
сальной к векторному полю X на Es. Пусть ВасЕа—диск,
содержащий 0. Если взять В" достаточно малым, то цилиндр
$5@)х?" будет трансверсален к полю X. В $s@)xfiu опре-
определено Сг-отображение ns: S*@)xfi° —» Wfoc@), являющееся
проекцией на первую компоненту. Слои itj1 {х), содержащие
точки х 6^@),—это диски, трансверсальные к Wfoc@). По
следствию 2 из клеммы, Ut>0 Xt($sxBa)=>U\En, где U —
некоторая окрестность точки р. Если х € U П Еп, то положим
ns ix) — Р- Если х ? U\En, то существует такое t > 0, что
X_t\x)?'3sxBu. Тогда мы полагаем ns(x) = XtnsX_t(x). Ясно,
что ns принадлежит классу Сг в U\Ea. Непрерывность ns
в точках множества Еп следует из ^-леммы. |
Используя построенные выше слои, можно доказать локаль-
локальную грубость гиперболической особой точки. Действительно,
пусть р?М—гиперболическая особая точка поля Х?ЖГ(М).
Пусть N—такая окрестность поля X, что каждое F€ N имеет
особую точку ру возле р и притом того же индекса. Опреде-
Определим гомеоморфизмы А», Щж{р)-+ IFfocOv). ha\ Wfoc(p)-*Wfoc(pK),
сопрягающие потоки полей X и F, задав их вначале на фунда-
фундаментальных областях и продолжив их потом на W\oc(p) и
^foe(p) так же, как в предложении 2.14, т. е. используя по-
122 ГЛ. 2. ЛОКАЛЬНАЯ ГРУБОСТЬ
токи полей X и У. Как и в лемме 7.3, рассмотрим расслое-
расслоения я*! Up->W\x(p), я*: Up-* W'{oc(p), яГ: Vp —WbciPrh
Ж Vpy—W^ipy).
Если q € Up, то положим /i (9) = q, где g таково, что nf (9) =
= hs(n$q) и я% (q) — hu(nXq). Легко видеть, что h—гомеомор-
h—гомеоморфизм, сопрягающий потоки полей X и Y. Заметим, что рас-
рассмотренные выше расслоения определяют непрерывные коорди-
координатные системы, в которых потоки представляются как произ-
произведения1), и, следовательно, гомеоморфизм h—это произведе-
произведение hs и ha.
Доказательство теоремы Гробмана — Хартмана для диффео-
диффеоморфизмов, использующее ^.-лемму, имеется в [75]. Построения
подобны изложенным выше, но более трудоемки.
УПРАЖНЕНИЯ
1. Покажите, что линейное векторное поле L является гиперболическим
тогда и только тогда, когда ш-предельное множество каждой траекто-
траектории—либо точка 0, либо пусто.
2. Покажите, что существуют такое линейное векторное поле L в R4 и
такая траектория у поля L, что ш-предельное множество траектории у
содержит у, но у не является ни особой точкой, ни замкнутой траекто-
траекторией.
3. Скажем, что линейный изоморфизм A: R" —> R" вкладывается в поток?
если существует такое векторное поле Х-, что /4 = Xj, где Xj—поток,
порожденный полем X. Охарактеризуйте канонические формы гипербо-
гиперболических линейных изоморфизмов, вкладывающихся в потоки.
4. Пусть /: М—>.R принадлежит классу Cr, r ^2, и пусть X—gradf.
Покажите, что р?М является гиперболической особой точкой поля X
тогда и только тогда, когда df(p)=O и rf2/(р)—невырожденная били-
билинейная форма.
5. Пусть X = grad/, где f: M—> R принадлежит классу Cr+1, r^zl. По-
Покажите, что если р?М—особая точка поля X, то собственные значе-
значения оператора dXp вещественны.
6. Приведите пример такого векторного поля XgJ''(S2), что Xg^t и
Xf_i$-G1( т. е. Xj_i имеет негиперболическую неподвижную точку.
7. Пусть X = grad/j где f: M—>¦ R класса Cr+1, r^l. Покажите, что
Х?& тогда и только тогда, когда X<=1gGi.
8. Будем говорить, что С'-функция /: М —* R, г Зг2, является функцией
Морса, если grad/ggf, иными словами, если все особые точки поля
grad / гиперболические. Покажите, что множество функций Морса от-
открыто и плотно в Cr (M).
Указание. Пусть ф: R"—>¦ R класса С~. Покажите, что 0—регулярное
значение отображения Ф: R"XL(Rn, R)—*• L (R", Щ, определенного
формулой Ф{х, A)=dq> (x)-{-A.
9. Пусть X и Y—векторные поля класса С1 на Rm. Предположим, что 0—
притягивающая гиперболическая особая точка полей X и Y. Покажите,
*) Например, для X при подходящих W\oc @), W\oc @) в некоторой
окрестности V$0 можно ввести «координаты»
V —> W\oc @)X Wioc @), д i-» (я?./, n?q),
причем Xtq—>{Xtn^q, Xtp?q)> пока Xtq не выйдет из V.—Прим. ред.
УПРАЖНЕНИЯ 123
что существует такой гомеоморфизм h окрестности нуля, который со-
сопрягает диффеоморфизмы Xf=i и Yf-i, но не переводит траектории
поля X в траектории поля Y.
10. Пусть р?М — гиперболическая неподвижная точка диффеоморфизма /.
Пусть {рп}—такая последовательность периодических точек диффеомор-
диффеоморфизма f, что рпФ р и рп —* р. Покажите, что существует последова-
последовательность периодических точек диффеоморфизма /, сходящаяся к неко-
некоторой, отличной от р, точке на неустойчивом многообразии точки р.
11. Покажите, что если /gDiff (M), г ^ 1, является грубым, то все непод-
неподвижные точки диффеоморфизма / гиперболические.
12. Пусть р?М—гиперболическая периодическая точка диффеоморфизма
/gDiff'(ЖI). Покажите, что для любого п ? М существует такая окрест-
окрестность V точки р, что каждая периодическая точка отображения / из'
V\{p} имеет период больше п.
13. Пусть 0?R"—гиперболическая особая точка векторных полей X и
Y?$r(R"). Покажите, что если существует ^-диффеоморфизм f: R" —э-R",-
переводящий траектории поля X в траектории поля К и 0 в 0, то соб-
собственные значения оператора L=DX@) пропорциональны собственным
значениям оператора L—DY @).
Указание. Из условия следует, что существует такая функция К: R"—>-R,
что Df (х)-Х(х) = К (x)Y (f (x)). Покажите, что для каждого v ф 0 су-
существует 1 (у) = lim<_ о "k (t, v) и что Df @) • Lv—\(v) ~LDf @) -v.
14. Пусть f: R»—> R"—^-диффеоморфизм и /@)=0. Пусть Еа и Е° —
инвариантные подпространства для /, такие что Rn = E°Q)Eu. Будем
обозначать через fu: Еа —>- Еа и f°: Е° —>• Ее ограничения отображения
f на Еи и Е° соответственно. Предположим, что собственные значения
оператора dfa @) по модулю > 1 и что собственные значения оператора
df° @) по модулю < 1. Пусть D"cEa—диск, содержащий 0, и D —
такой трансверсальный к Е° и содержащий точку q?E° диск, что
fn(q)—>0 при п—>-оо. Покажите, что существует такая окрестность V
точки 0 в R", что при любом е > 0 найдется в„ ? М" со следующим
свойством: если п^п0, то f"D содержит диск, еО-близкий к Vf]Du.
15. Пусть /: R2_*R2_С3-диффеоморфизм J (л:, y) = (h(x, у), fa(x, у)),
обладающий следующими свойствами:
A) МО, У)=0 при всех
B) f2(x, 0)=0
C)dh/dy@,
h\x, 0)=0 при всех x?R;
D) если a (x)-=h (х, 0), то а' @) = 1, а" @) =0 и а'" @) < 0.
Покажите, что существуют такое а > 0 и такая окрестность V точки
@, 0), что для любого е > 0 и любого отрезка D, трансверсального
к оси * = 0 в своей внутренней точке @, y)?Vi имеется такое no?Af,
что если п > п0, то f~" (D) содержит л отрезок, е ^-близкий к интервалу
Цх, 0): — а<х<а}.
По
16. Покажите, что диффеоморфизм/ из предыдущего упражнения локально
сопряжен с диффеоморфизмом g (х, у) = (х—х3, 2у).
17, Пусть /: R2—*-R2—С2-диффеоморфизм, /(*, y) = (h(x, у), f2 (x, »/)),
обладающий следующими свойствами:
Ы0, «/)=0 при всех y?R;
f2(x, 0)=0 при всех x?R;
1
D если а (х) = h
Покажите, что f локально сопряжен с диффеоморфизмом
ад.
dfi/dy(O, 0) > 1;
если а (дс) =/i (х, 0), то а' @) = 1 и а" @) ф 0.
х) То есть периодическая (с периодом Щ точка, являющаяся гипербо-
гиперболической неподвижной точкой для /*.—Прим. ред.
Глава 3
ТЕОРЕМА КУПКИ—СМЕЙЛА
Пусть М—компактное многообразие размерности т и
2сг (М)—пространство Сг-векторных полей на М, г~^\, с Сг-нор-
мой. В гл. 2 было показано, что множество <Sla Иг {М), со-
состоящее из тех векторных полей, у которых все особые точки
гиперболические, является открытым и плотным в Жг (М). Это
пример типичного свойства, т. е. свойства, которому удовлет-
удовлетворяют почти все векторные поля. В этой главе мы проанали-
проанализируем другие типичные свойства в ?Г(М). Оригинальное
доказательство излагаемых здесь результатов можно найти
в [44], [82] и [107].
Вначале мы вводим понятие гиперболичности для замкнутых
траекторий. Как и в случае особых точек, гиперболическая замк-
замкнутая траектория у выживает при малых возмущениях вектор-
векторного поля. Кроме того, возле нее структура траекторий поля
чрезвычайно проста и является грубой относительно малых
возмущений. В частности, точки, которые имеют у в качестве
своего ю-предельного (а-предельного) множества, образуют глад-
гладкое многообразие, называемое устойчивым (неустойчивым) мно-
многообразием траектории у. В некотором смысле, который будет
уточнен в тексте, компактные части этих многообразий изме-
изменяются лишь немного при слабом возмущении поля.
Рассмотрим две гиперболические особые точки ot и а2. Если
устойчивое многообразие точки ot пересекает неустойчивое
многообразие точки а2, то at и а2 как бы связаны посредством
траектории, рождающейся в а2 и умирающей в ох. Если пересе-
пересечение трансверсально, то слегка возмущенное поле будет иметь
гиперболические особые точки, связанные таким же образом.
Аналогичные понятия и свойства имеют силу и для замкнутых
траекторий, что будет видно из дальнейшего.
Здесь будет показано, что все эти свойства присущи полям
из некоторого остаточного множества в ?Г(М). В конце главы
аналогичные свойства будут установлены для диффеоморфизмов.
§ I. ОТОБРАЖЕНИЕ ПОСЛЕДОВАНИЯ 125
§ 1. ОТОБРАЖЕНИЕ ПОСЛЕДОВАНИЯ
В предыдущей главе мы описали топологическое поведение
траекторий векторного поля в окрестности гиперболической осо-
особой точки. Теперь мы собираемся предпринять аналогичное
исследование для замкнутых траекторий. Как и в случае особых
точек, чтобы получить простое описание структуры траекторий
в окрестности замкнутой траектории, необходимо ограничиться
некоторым подмножеством в пространстве векторных полей.
Пусть у—замкнутая траектория векторного поля X € 2?r (M).
Рассмотрим трансверсальное к полю X сечение1) 2, проходя-
проходящее через точку хо?у.
Траектория, проходящая через х0, вновь пересечет 2 в мо-
момент времени т, где т—период у. Ввиду непрерывности потока
поля X траектория, проходящая через достаточно близкую
к х0 точку х € 2, также пересечет 2 в момент времени, близкий
к та). Таким образом, если V с 2—достаточно малая окрест-
окрестность точки х0, то можно определить отображение Р: V—*2,
которое каждой точке x?V ставит в соответствие точку Р{х),
где траектория точки х впервые вновь пересекает 2. Это отоб-
отображение называется отображением последования (или отобра-
отображением Пуанкаре) для траектории у (и сечения 2). Знание
этого отображения позволяет дать описание траекторий в окрест-
окрестности траектории у. Например, если х?V—неподвижная точка
отображения Р, то траектория точки х замкнута и ее период
приблизительно равен периоду у, если х близка к х0. Аналогично
если х—периодическая точка отображения Р с периодом k,
т. е. если P{x)?V, P2{x)?V, ..., Рк{х)=х, то проходящая
через х траектория является периодической с периодом, при-
приблизительно равным kx.
Если Pk (x) определено при всех k > 0, то положительная
полутраектория точки х содержится в некоторой окрестности
траектории у, а если вдобавок Рк(х)—+х0 при k—» op, то
ю-предельное множество траектории точки х есть у. Можно
также определять траектории, имеющие у в качестве своего
а-предельного множества, используя отображение, обратное к Р,
которое является отображением последования для поля —X.
Из непрерывности потоков полей X и —X следует, что Р —
гомеоморфизм некоторой окрестности точки х0 из 2 в 2. Исполь-
*) Небольшое гладкое подмногообразие коразмерности 1.— Прим. ред-
2) Из непрерывности следует, что точка Х% х близка к х0, а тогда из
теоремы о трубке тока (теорема 1.1, гл. 2), примененной к Р=х0, легко
вывести, что небольшая дуга траектории поля X, проходящая через Ххх,
пересекает 2 в некоторой точке Р (х), которая как раз и является первой
по времени точкой пересечения исходящей из х положительной полутраек-
полутраектории с 2. Это рассуждение делает очевидным и гладкость отображе-
отображения Р,— Прим, ред.
126
ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
зуя информацию о классе гладкости диффеоморфизма из теоремы
о трубке тока, мы покажем позднее, что Р является на самом
деле локальным диффеоморфизмом того же класса гладкости,
что и поле. Тогда мы сможем использовать производную отобра-
отображения Р в х0 для описания структуры траекторий в окрестно-
Рис. 1
сти у. Для этого нам понадобится несколько предварительных
результатов.
Выпрямляюирй картой для поля Х??Г(М) называется
пара (F, /), где F—открытое множество в М и /—Сг-диффео-
морфизм множества F на куб
I"- = Ixlm-1 = {(x, y)^RxR—1: \х\ < 1
и \у{\< 1, t = l, ..., т—\},
переводящий траектории поля X в F в прямые /х {у} с /х 1т~г.
Если обозначить через /SX поле в 1т, индуцированное / и X,
Рис. 2
т. е. f*X(x, у) = D//-.{Xi y)-X{f~1(x, у)), то ftX параллельно
постоянному полю (х, г/)ь-»A, 0).
Открытое множество F называется трубкой тока для поля X.
В предыдущей главе было показано, что если р?М—регу-
р?М—регулярная точка поля X, то существует трубка тока, содержащая р
(теорема о трубке тока).
1.1. Предложение (о длинной трубке тока). Пусть у с М —
компактная дуга траектории, не являющаяся замкнутой кривой.
§ I. ОТОБРАЖЕНИЕ ПОСЛЕДОВАНИЯ 127
Тогда существует такая выпрямляющая карта (F, /) для X,
что F э у.
Доказательство. Пусть a (t) — такая интегральная кривая
поля X, что а ([0, а])—у. Пусть (F0) /0) — такая выпрямляющая
карта возле точки а@), как в замечании к теореме 1.1, гл. 2, т. е.
//0 = С. = {x?R-»i |х,|<е, 1=1 ..., т\, /0(о@)) = @ 0),
и /0 переводит траектории поля X в траектории поля A,0, ..., 0)
с сохранением параметра t. Поскольку дуга у—незамкнутая,
то (уменьшив, если потребуется, е) можно считать, что a (t)=^=
фа{?) при t, <'€[—е, а + е] и 1фГ.
Взяв й^г, обозначим
1Т* = {Ф, y)(tCei \y,\<d, / = 1 т-Ц, S = /0(/r1).
Для каждого р ? у = ос ((— е, а + е)) возьмем такое t g (— е, а-\-е),
что /? = Х,а@), и положим 2Я = Х4B). Проверим, что при
достаточной малости d 2_ п 2= 0 при р=^9-
Прежде всего если р = Xta @), 9 = ¦^«а @), < =^s и | <—s |< 2е,
S ^ б б d Дй
р t () 9 « ) | |
то S_ п ^в = 0 при любом выборе d < e. Действительно, пусть
T==-2-(^ + s), так что \t—т|<е, \s—т|<е. Тогда
A:.x2/, = X/_tS = /0-]{(<-t, y)\ \y,\<d),
X^q = Xs_tS = fr {(s-т, y)i \yj\<d).
Ясно, что fo(X_xEp[)X_TI,(l) = 0, а тогда и 2pn29=0.
Чтобы гарантировать выполнение условия 2р П 2в = 0 в том
случае, когда /? = а(/), 9 = «(s) и \l—s|^2e, может понадо-
понадобиться взять d достаточно малым. Пусть р—какая-нибудь
метрика на М (например, индуцированная вложением М в евкли-
евклидово пространство). Функция (t, s)y->p(a(t), a(s)) непрерывна
и положительна на компактном множестве
{(*, s)€[— е, а + е]х[— е, о + е]: |/—s|>2e},
а потому имеет на нем положительную нижнюю грань б. Возь-
Возьмем d столь малым, чтобы каждое 2р содержалось в б/2-окрест-
ности точки р. (Функция
1?-гх[— в,
непрерывна, и 0х [— е, a-f е] —*¦ 0, поэтому такое d существует.)
Тогда при p~a(t), q = a(s) и |<—s|>2e будет р(р, ^) > о
и 2/,п2в = 0.
Множество ^ = UP€-2/,—открытая окрестность дуги у.
Действительно, F => у, а если р g F, то /? € 2а(<), — е < < < а + е,
т. е. р = Xtplt pt € 2. У /?j имеется окрестность (/ вида
/о^: \У.\<г, \У,-У)\<г\),
128 ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
причем (уменьшив, если потребуется, г) можно считать, что
(t—г, t-\-r)c(—е, а-\-г). Тогда XtU—окрестность точки р
и XtU cf.
В окрестности F з у мы имеем Сг-расслоение с базой у,
слоем которого над точкой р является 1>р. Соответствующая
проекция я^: F—*у сопоставляет точке z?F ту точку р, для
которой г?2р. Это—отображение класса Сг, его гладкость
возле г очевидна, когда г ? f0, а в общем случае некоторое
X~sz?.F0, и тогда в некоторой окрестности точки z имеем
nl — XsnlX_s, причем в правой части отображение n1 = n1\F0—
гладкое. Далее, на F определена другая проекция щ: F—s-Sj
класса Сг; она сопоставляет каждой точке z?F пересечение
с 2 дуги траектории поля X, лежащей в F и проходящей
через г. Точнее, если г^2я и p — a(t), то n2(z) = X^t(z). Взяв
какие-нибудь два диффеоморфизма gti у—>(—1, 1) и g2: 2—>Im~*,
определим /: F—*Ixlm~1 по формуле /(г) = (g^(г), g)
Ясно, что (F, f)—выпрямляющая карта, содержащая у.
Замечание. Построенный выше диффеоморфизм / переводит
траектории поля X (точнее, их дуги, лежащие в F) в траекто-
траектории постоянного векторного поля
С! /х/"-1 — R, С(х, у) = A, 0).
Вообще говоря, / не сохраняет параметр t, т. е. /,Х не совпа-
совпадает с полем С. Однако из доказательства видно, что можно
построить диффеоморфизм /¦ F—>¦(—Ь, Ь)х1т~1 (с некоторым
?>0, именно с ?> = а/2 + е), переводящий X в поле С. Надо
только вместо gt взять диффеоморфизм ^s у—*(—b, b), обрат-
обратный к ti-^-a(t-\-al2).
1.2. Предложение. Пусть у—замкнутая траектория вектор'
ного поля Х??Г(М), а 2—трансверсальное к X сечение, про-
проходящее через точку р?у- Если Р2> U с 2 —*2—отображение
последования, то Р? является Сг-диффеоморфизмом некоторой
окрестности V точки р в 2 на открытое множество в 2.
Доказательство. Пусть (Ft, /j)—выпрямляющая карта, со-
содержащая р, a (Fg, f2)—такая длинная выпрямляющая карта,
что у сг Fi U F§, как показано на рис. 3.
Пусть 2j и 2g—трансверсальные к X компоненты границы
множества Fb т. е. 21 = /2-1({— I\xlm-J) и22:=/2-1({Цх/'я-1I).
а V—малая окрестность точки р в 2. Обозначая через
х) Хотя формально {±l}X^m~l находится вне области определения /г" t
можно без ограничения общности считать, что (F2, f-,) — часть чуть большей
выпрямляющей карты; тогда ясно, что следует понимать под этими прооб-
прообразами.— Прим. ред.
§ 1. ОТОБРАЖЕНИЕ ПОСЛЕДОВАНИЯ
129
nt
V cr 2 —¦ 2lt л2: Б1
й X
и п3: 22
проекции вдоль
й
t 2 1 g 2 р
траекторий поля X (точнее, вдоль дуг траекторий, лежащих
соответственно в Fit F2 и FJ, имеем Р? = п3 о п2 о щ. Из тео-
теоремы о трубке тока легко следует, что щ, щ и п8—отобра-
Рис. 3
жения класса Сг. Таким образом, Р? класса Сг. Поскольку
Р обладает обратным класса Сг, которое является отображе-
отображением последования для поля —X, то отсюда следует, что
Ре—Сг -диффеоморфизм из V на открытое множество в 2. Это
завершает доказательство. I
Рис. 4
|—трансверсальные к X сечения, проходящие
и р2 замкнутой траектории у, как показано
Пусть 2( и
через точки pt
на рис. 4.
Пусть hi 2j —¦ S2—отображение, которое каждой точке
2 сопоставляет первую точку пересечения траектории
[30 ГЛ. 3. ТЕОРЕМА КУПКИ -» СМЁЙЛА
точки q с 22. По теореме о трубке тока h—диффеоморфизм
класса Сг. Если Pz, и Р2г—отображения последования соот-
соответственно для сечений 2t и 22, то P^2 = ho P^o h~x. Таким
образом,
(Л) = Dh (Pl) о DP?l (л) о DA-» (р2),
и, значит, DP^2 (p2) имеет те же собственные значения, что
и DP^t (pi). Это показывает, что следующее определение зави-
зависит только от поля, а не от сечения 2.
Определение. Пусть р€?» где у—замкнутая траектория поля X.
Пусть 2—трансверсальное к X сечение, проходящее через
точку р. Будем говорить, что у—гиперболическая замкнутая
траектория поля X, если р—гиперболическая неподвижная
точка отображения последования Р; Fc2-+S.
Замечание. Поскольку поток векторного поля непрерывно зави-
зависит от поля, то и отображение последования зависит от поля
непрерывно. Точнее, пусть Рх'- V сг 2 —¦ 2—отображение
последования для X. Пусть "И3—такая окрестность поля X
в Зсг(М), что при всех Y из Ч^ гиперповерхность 2 все еще
является трансверсальным к Y сечением и каждая траектория
поля Y, проходящая через точку из V, вновь пересекает 2 *).
Тогда отображение f^—t-C(V, 2), сопоставляющее каждому
у ?<fv ero отображение последования, непрерывно.
Из этого замечания можно заключить, что если у—гипер-
у—гиперболическая замкнутая траектория поля X, то существует такая
окрестность "У3 поля X в Зсг(М), что каждое Y?°Р имеет
близкую к у гиперболическую замкнутую траекторию уу. Это
следует из того, что аналогичное свойство выполнено для ги-
гиперболических неподвижных точек диффеоморфизмов, как мы
видели в предыдущей главе.
Теперь мы покажем, что если у—гиперболическая замкнутая
траектория векторного поля X ^ ?r (M), то X является локально
грубым в у2). Это означает, что для каждого векторного поля У,
принадлежащего некоторой окрестности °Р поля X, существует
гомеоморфизм h: V—+V, где V, V—некоторые окрестности
траектории у, переводящий траектории поля X в траектории
поля У. Как мы уже отмечали, нельзя требовать, чтобы гомео-
гомеоморфизм h сопрягал потоки Xt и Yt, потому что это повлекло
бы за собой, кроме всего прочего, равенство периодов траек-
траекторий yY сг V и у* Между тем ясно, что существует сколь
1) Последнего заведомо можно достичь (при достаточной малости
чуть уменьшив V-— Прим. ред.
?) Говорят также о локальной грубости у,—Прим. ред.
§ 1. ОТОБРАЖЕНИЕ ПОСЛЕДОВАНИЯ 131
угодно близкое к X векторное поле Y, для которого период yY
отличен от периода у: достаточно взять Y(l+n~x)X с доста-
достаточно большим п.
Пусть 2—трансверсалыюе к X сечение, проходящее через
точку р?у. Будем говорить, что 2—инвариантное сечение,
если существует такая окрестность U с 2 точки р, что
Ха (U) с 2, где со—это период траектории у. Следующая лемма
показывает, что можно репараметризовать поле X таким обра-
образом, чтобы сделать данное сечение инвариантным1). Доказа-
Доказательство носит весьма, технический характер, хотя результат
интуитивно ясен.
1.3. Лемма. Пусть Х?ХГ(М) и у—гиперболическая замкнутая
траектория поля X с периодом со. Пусть 2—трансверсальное
к X сечение, проходящее через точку /?€v- Тогда существует
такое непрерывное отображение \х: "У3 —*ЖГ (М), где "У*—окрест-
"У*—окрестность поля X, что
(a) \i(Y) — pY-Y, где ру: M-+R—положительная дифференци-
дифференцируемая функция, принимающая значение 1 всюду вне неко-
некоторой окрестности некоторой точки у;
(b) существует такая окрестность U с: 2 точки р, что
Y^ (U) а 2, где Y* = \i(Y). Иными словами, 2—инвариант-
2—инвариантное сечение поля Y* = n(Y) при всех Y^f^.
Доказательство. Пусть 2' = Х_(О)_<о)B), где 0<?0<со.
Мы имеем Xto(p)=p' ? 2'. Рассмотрим Сг-отображение а: 2 —* К,
сопоставляющее каждому у ? 2 наименьший положительный
момент времени а (у), при котором Xaw)(y) g2'. Заметим, что
если a(y)**=t0 при всех у из некоторой окрестности точки р
в 2, то сечение 2—инвариантное.
Пусть U cz U cz 2—такие окрестности точки р, что U cz U.
Используя функцию-шапочку», принимающую значение 1 на U
и 0 вне 0, построим Сг-отображение |3: 2 —>- R, равное а на U
и принимающее постоянное значение t0 вне 0. С помощью
той же «шапочки» построим для каждого векторного поля Y
из некоторой окрестности поля X такое Сг-отображение
Ркз 2 —»- R, которое совпадает с ау на U и равно t0 вне О.
Здесь через а^: 2 —> R обозначена функция, которая каждому
t/g2 сопоставляет наименьший положительный момент вре-
времени ау(у), при котором Yay {у) (у) € 2'у, где 2к = К_(@_<о)B).
Теперь мы построим желаемую репараметризацию. Пусть
Gi <3^x2xIR—»¦ R—отображение класса СТ, удовлетворяющее
х) Имеется в виду переход к полю К*, векторы которого имеют всюду
то же направление, что и у поля К; точнее см. в лемме- 1.3. «Репарамет-
ризуются» при этом траектории, в связи с чем обычно говорят о замене
времени в потоке,— Прим. ред.
5*
132
ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
Рис, 5
следующему условию; для каждого Y?<2^ и каждого у^
GY (t) — G(Y, у, t) является полиномом по t степени 2/- + 3,
коэффициенты которого определяются из формул
Отсюда GYt y {t) = t
V
det/4
j=\, .... r
A
v i "г lo oj ч> • • *
и Ац обозначает алгебраическое дополнение элемента ai} =
'"'" в Л.
g = l при
Следовательно, HY(y, t) =? dGY< y/dt (t) удовлетворяет следу-
следующим условиям;
(a) HY(у, 0) =
(b) HY(y, 0 = ^
(c) DkH?(y, 0)=Б*//к(г/, д = 0 при всех t/g2 и fe^l г.
Условие (с) легко вытекает из предыдущих равенств.
Поэтому Н12 х [0, t0] продолжается до С'-отображения.
Hi ?xK—*-'R, такого что //=1 вне 2х[0, /0].
§ 1. ОТОБРАЖЕНИЕ ПОСЛЕДОВАНИЯ 133
При малых f3 и U отображение GYty\ [О, t0] —> [0, Рк(/)]
является диффеоморфизмом, поскольку Gy,y—тождественное
отображение при у(^С1)- Отображение (pYi 2х[0, t0] —»¦ М,
определенное формулой q>Y(y, t) = Yt*(y), где t* — GY,g{t), также
диффеоморфизм. Пусть W = (pKBx[0, t0]) cr M. Определим
отображение рк- М —¦ К, принимающее значение 1 вне мно-
множества W, а на W задаваемое композицией отображений
По построению р? принадлежит классу Ст. Рассмотрим
векторное поле Y* = py-Y. Мы утверждаем, что Y"l<t(y)?HY
при каждом у€2. Действительно, пусть y^U и пусть
¦ф: [О, Рк (г/)] —»¦ Л1—интегральная кривая поля Y, проходящая
через точку у. Таким образом, fy(t) = Yt(y) и tyфу(у))?2'Y.
Пусть теперь i|5*i [0, tB]—*M—отображение, задаваемое фор-
формулой г];* = г];о Gyy v2). Проверим, что г]з*—интегральная кривая
поля Y*, проходящая через у. Имеем
Поэтому К; (г/) = ^ (t0) = ф (р
Мы завершим доказательство, положив ц (Y) = Y*. |
Замечание. Пусть Х?ЖГ(М), pv?M и 2—трансверсальное к X
сечение, содержащее точку р0. Пусть 2' = Xti B) и pf = Xtl (p0).
Из доказательства леммы следует, что можно параметризовать
все векторные поля, близкие к X, таким образом, чтобы они
переводили сечение 2 в сечение 2' за время tf. Такая репара-
метризация может быть «сосредоточена» в окрестности дуги,
состоящей из точек Xt (р0), 0 ^ t ^ tf.
1.4. Предложение. Если у—гиперболическая замкнутая траек-
траектория векторного поля Х?ЖГ(М), то X является локально
грубым в у.
Доказательство. Пусть со—период траектории у и 2—транс-
2—трансверсальное к X сечение, проходящее через точку р?у. Тогда
р—гиперболическая неподвижная точка отображения последо-
вания Рх. Для близкого к X поля Y отображение последова-
ния PY является близким к Рх. Следовательно, из локальной
грубости гиперболической неподвижной точки получаем, что
*) Подробнее: если U и <у достаточно малы, то $у {у) при всех
Y g "ръ близко, к tu, а тогда все Су близки к 0.— Прим. ред.
2) Так что q, фигурирующее при определении ру, совпадает с г})* (Q.—¦
Цриц. ред.
134 ГЛ. 3. ТЕОРЕМА КУПКИ = СМЕЙЛА
существуют окрестности "У3 поля X и U с: 2 точки р со сле-
следующим свойством: для каждого Y € У3 можно найти гомеомор-
гомеоморфизм hy окрестности U на некоторую окрестность точки р
в 2, сопрягающий Рх и Ру, т. е. такой, что hYPx = PyhY.
Продолжим hy на некоторую окрестность траектории y- Пусть
\xi f^—*3cr(M)—отображение, построенное в лемме 1.3. Пусть
у—такая окрестность траектории у, что если у$Л/, то сущест-
существует t € [0, со], при котором X* (у) cz U, где Х* = ц(Х). Положим
тогда hy(y) = Yl.lhYX"t {у). Легко видеть, что если V достаточно
мало, то hY корректно определено, является гомеоморфизмом
и сопрягает потоки X," и Y*. Поскольку X* и Y* имеют те же
траектории, что поля X и Y соответственно, то мы заключаем,
что hy переводит траектории поля X в траектории поля Y. |
Если у—гиперболическая замкнутая траектория векторного
поля X € Зсг (М), то можно определить устойчивое и неустой-
неустойчивое многообразия траектории y:
Существует такая окрестность V траектории у, что если
Xt (q) g V при всех t^ 0, то q g Ws (у). Это вытекает из анало-
аналогичного свойства отображения последования траектории y-
Рассмотрим множества
: Xt(y)dV при всех t>0\,
Xt(y)€V при всех *<0}.
Имеем Ws(v) = \Jn^X-nWb(y) и W"{y)~\JnuNXaWt(y). |
1.5. Предложение. Пусть у—гиперболическая замкнутая
траектория векторного поля Xg3tr(M). Если V—малая
окрестность траектории у, то Wsv (у) и W'{, (у) являются С-
подмногообразиями в М. Щ(у) трансверсально к Wy(y) и
n(v)nn(v)=v-
Доказательство. Пусть 2-—трансверсальное к X сечение,
проходящее через точку р?у. Если Uczl.—малая окрестность
точки р, то обозначим через Wsv (p) и Wl(j (p) соответственно
устойчивое и неустойчивое подмногообразия отображения по-
последования Рх- Так как р—гиперболическая неподвижная
точка отображения Рх, то Wsv(p) и Ч?и(р) являются Сг-под-
многообразиями, которые трансверсальны друг к другу в 2, и
Wsu (p) П Wu (p) — {р\. Следовательно, если период траектории y
равен «, то \Jte{0,2et)Xt(Wb(p)) и U/6@,2и)Х_((^(р))-С-
подмногообразия, пересекающиеся трансверсально в точках
траектории y- Если V—малая окрестность траектории у, то
W\ (у) и W4/ (y)—открытые окрестности y в \Jte{Oi 2й) xt (Wv(p))
§ 2. типичность вЕкторНых Полей 135
и в U<€@ 2a>)^-t(Wu{p)) соответственно. Это доказывает
предложение. |
Следствие. Ws (у) и Wa (у) являются иммерсированными С-под-
С-подмногообразиями в М. I
Мы оставляем читателю доказательство следующего утверж-
утверждения. Пусть у—гиперболическая замкнутая траектория век-
векторного поля X g ?r (M). Покажите, что существует такая
окрестность "У3 поля X, что каждому полю Yczf? можно по-
поставить в соответствие некоторую окрестность WYc Ws (yY)
траектории уу таким образом, чтобы отображение Y —*¦ WY было
непрерывно. Это означает, что для любого е > О и Уо ? "У3
существует такое б > 0, что если || Y—Ya\ < 6, то Wy является
е Сг-близким к Wy<).
% 2. ТИПИЧНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
С ГИПЕРБОЛИЧЕСКИМИ ЗАМКНУТЫМИ ТРАЕКТОРИЯМИ
В предыдущей главе мы показали, что множество <S1cz3Lr (M),
состоящее из тех векторных полей, у которых все особые точки
гиперболические, является открытым и плотным в 31Г(М).
В этом параграфе мы покажем, что множество '§licz'&1 тех
векторных полей, у которых все замкнутые траектории гипер-
гиперболические, является остаточным. Для этого достаточно пока-
показать, что если Т > 0—любое целое число, то множество
R{T)cz'S1 тех векторных полей, у которых все замкнутые
траектории периода ^Т1 гиперболические, открыто и плотно.
Поскольку ^12 = Пг>1 ?(Т), то отсюда будет следовать, что
S,2 является остаточным.
2.1. Лемма. Пусть р?М—гиперболическая особая точка
поля X ? ?г (М). Для любого Т > 0 существуют такие окрест-
окрестности UcM точки р и <Ucz3cr(M) поля X и такое непрерыв-
непрерывное отображение р: 41—*U, что:
(i) если Y ?11, то р(У)—единственная особая точка поля Y
в U, и эта особая точка гиперболическая;
(ii) каждая замкнутая траектория поля Y&1L, пересекающая
U, имеет период > Т.
Доказательство. Часть (i) была доказана в предыдущей
главе.
По теореме Гробмана—Хартмана существует такая окрест*
ность V точки р, что любое поле Y^il не имеет замкнутых
траекторий, целиком содержащихся в V. Так как Х(р) = 0, то
можно найти такую окрестность U сV точки р, что еслид€^1
то Xt (q) ? V при t ^ 2T. Уменьшая (в случае необходимости)
136 ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
окрестность 11, получим, что Yt(q)?V при t^lT, если q?U
и K^ii. Поскольку Y не имеет замкнутых траекторий, цели-
целиком содержащихся в V, то лемма доказана. I
2.2. Лемма. Пусть Т > О и у—гиперболическая замкнутая
траектория векторного поля Х?ЖГ(М). Тогда найдутся та-
такие окрестности U сМ траектории у и 'йс^г(М) поля X, что:
(i) каждое Y?il имеет гиперболическую замкнутую траек-
траекторию yyczU u каждая замкнутая траектория поля Y,
которая пересекает V и не совпадает с уу, имеет период
больше Т;
(и) траектория уу непрерывно зависит от поля Y.
Доказательство. Возьмем трансверсальное сечение 2, про-
проходящее через р?у, и пусть Рх: V—> 2 — отображение после-
дования, ассоциированное с X. Пусть т есть период у и
п—такое положительное целое число, что т > 27\ Для доста-
достаточно малого Ус2 отображение Р\ определено на V.
Поскольку отображение исследования непрерывно зависит от
векторного поля, то существует такая окрестность 41 поля X,
что если Y^il, то Ру определено на К. Поскольку р гипербо-
гиперболическая неподвижная точка отображения Рх, то существует
(возможно, для меньших 41 и V) такое непрерывное отображе-
отображение р: %—>V, что р(F)—единственная неподвижная точка
отображения Ру в V, и эта точка гиперболическая. Если
уу—траектория поля Y, проходящая через p(Y), то отсюда
следует, что уу—гиперболическая замкнутая траектория, при
этом ясно, что уу зависит от Y непрерывно. Из теоремы Гроб-
мана —Хартмана для диффеоморфизмов и из непрерывной за-
зависимости отображения последования от векторного поля сле-
следует, что существуют такие окрестности Vс V точки р и %
поля X, что Py(q)€V при всех Y€,Я1, q?V я k—\, ..., п.
Поэтому (для, возможно, меньшего Щ каждая отличная от уу
замкнутая траектория поля Y?4l, проходящая через точку
q?V, имеет период больше Т, так как q не является перио-
периодической точкой отображения Ру с периодом, не превосходя-
превосходящим п. Теперь достаточно взять ^ = и<€[0 т+8] XtV, где е>0
достаточно мало.
Следствие. Пусть X€$ti, т. е. все особые точки и замкнутые
траектории поля X гиперболические. Тогда для любого Т > О
существует лишь конечное число замкнутых траекторий пе-
периода г?^7\ В частности, X имеет не более счетного числа
замкнутых траекторий.
Доказательство. Рассуждая от противного, предположим,
что X имеет бесконечное число замкнутых траекторий периода
5 2. ТИПИЧНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ J37
и пусть уп—последовательность таких траекторий, где
упфуп, при п=Фп'. Рассмотрим последовательность точек
Рп € Уп- Поскольку М компактно, то, переходя в случае необ-
необходимости к подпоследовательности, можно считать, что /?„ схо-
сходится к некоторой точке р. Поэтому траектория точки р лежит
в замыкании множества, состоящего из бесконечного числа
замкнутых траекторий периода ^ Т. По лемме 2.1 р не может
быть особой точкой, а по лемме 2.2 траектория точки р не
замкнута. Следовательно, траектория точки р регулярная.
Рассмотрим точки р' = Х_т(р) и р" = Хг(р). Пусть F—трубка
тока, содержащая дугу р'р" траектории р. Если рп достаточно
близка к р, то Xt (pn) g F при t g [—Т/2, Т/2], так что траек-
траектория точки рп имеет период > Т. Это приводит к противо-
противоречию. |
2.3. Лемма. Пусть Х?ХГ(М) и К<=М—такое компактное
множество, что X не имеет особых точек в К и пересекающие
К замкнутые траектории поля X имеют период больше Т.
Тогда существует такая окрестность cUc:3tr(M) поля X, что
никакое Y g 1L не имеет особых точек в К и пересекающие К
замкнутые траектории поля Y имеют период > Т.
Доказательство. Поскольку К компактно и X Ф О в К, то
существует такая окрестность ЖсЖ.г(М) поля X, что никакое
векторное поле Y g Jf не имеет особых точек в К. Пусть р ? К.
Так как проходящая через р траектория поля X либо регу-
регулярна, либо имеет период больше Т, то существуют та-
такое е > 0 и такая окрестность Ир точки р, что для
q€.Up Xt(q)(?Up при всех t?[e, Т + е]. Поскольку по-
поток непрерывно зависит от векторного поля, то существует
такая окрестность 1LDcz<№' поля X, что этим же свойством
обладают все поля Y?4lp. В частности, каждая замкнутая
траектория поля Y ? 1Lpt пересекающая Uр, имеет период
больше Т. Пусть UPl, ..., Up —конечное покрытие компакт-
компактного множества К- Положим ^ = Пг=1%ь- Ясно, что каждая
пересекающая К замкнутая траектория любого [поля Y?4l
имеет период больше Т. |
Пусть X—С°°-векторное поле на М, у—замкнутая траек-
траектория поля X и 2—трансверсальное сечение, проходящее
через точку р?у. Пусть Ч1с:кг(М)—окрестность поля X и
Vcl.—такая окрестность точки р, что отображение последо-
вания определено на V для всех Y$41.
2.4. Лемма. При этих условиях существует окрестность UczV
точки р на 2 со следующим свойством: для любого е > 0 су-
существует такое С°°-векторное поле Y^IJ,, что ||К—Х||/.<е, а
138
ГЛ. 3. ТЕОРЕМА КУПКИ - СМЕЙЛА
Ру имеет лишь конечное число неподвижных точек в U, и все
они элементарные.
Доказательство. Пусть (F, f)—такая выпрямляющая карта
с центром р, что /(F) = [—b, bjxf'1, /-1({fc}x/'n-1) = 2nF,
a faX является единичным векторным полем С на [—b,Щх 1т~г.
Пусть С—такое определенное на /(F)<=IRm векторное поле
класса С30, что С1 трансверсально к {—Ь^х/1"*1 и Щх!1"'1 и
каждая пересекающая множество]—b\xlm~1 траектория поля
С обязательно пересекает и Щх!'1. Тогда можно опреде-
-1
—
1
г
-?> ib 0 b
2. 2
Рис. 6
лить отображение Lgi {—Ь^х/'1—> \Ь\х 1т~*, которое каж-
каждой точке множества {—^х/1" сопоставляет пересечение ее
траектории с \b\ x Im~l. По теореме о трубке тока Lg явля-
является диффеоморфизмом. Пусть
Л = [-Ь, I] хI*-i и
, Ъ\
х
1 U [ -|,
Мы утверждаем, что для любого е > 0 существует такое
8j > 0, что при каждом v?Rm с ||»Ц<8, можно выбрать такое
векторное поле С класса С30, что \\С—С|,.<е на [—b.fcjx/1"",
С = С на А и L5(—b, y) — (b, y + v), если y^Ifu1. Действи-
Действительно, пусть ¦ф: [—b, b]—>R+—такая С°°-функция, что
ф(/) = 0, если t?[—b,—b/2]\j[b/2, b], и ф(/)>0, если
f(E(—Ь/2, Ь/2). Возьмем также такую функцию <р; Im~l—+R+,
что Ф(«/)== 0, если || #|| > 3/4, и ф(«/)=1, если I^Kl/21).
Положим С (х, #) = A, рф (у) ty (x) v) и найдем такое веществен-
вещественное число р, при котором С обладает указанным свойством.
Ассоциированное с С дифференциальное уравнение может быть
^} Здесь Jj^J)—не евклидова норма, a maxj(/./J,—Прим. перее.
§ 2. ТИПИЧНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ J39
записано следующим образом!
Решение этого уравнения с начальными условиями х @) == — Ь,
'i/4 задается формулой
х(t) = t-b, у(t) = у0 + (\рф(у(s))^(s-fc)dAо
Пусть 1/р = \ ty{s—b)ds. Легко видеть, что если |и|| доста-
достаточно мала, то |]</@1< '/2 при всех ^€[0. 2?>]. Таким обра-
образом, ф(i/(s)) = 1 и y(t) = Уо + [Р \ty(s—b)ds\v. Поэтому
Lg{—b, yo) = (b, yo + v), что доказывает наше утверждение.
Пусть F —векторное поле на М, равное X вне множества
tl{[~-b, bjxl-1) и равное (f~%C на f~l(\—b, bjx/1»-1).
Ясно, что Y принадлежит классу С и ||У—Л\. < е.
Можно считать, что малая окрестность W czV точки
f'1 (b, 0) на 2 и дуга траектории у от f'1 ф, 0) до f~l (—b, 0)
лежат в области определения другой выпрямляющей карты
(F1, /'), причем
(так что Y\F' = X\F'), и можно определить отображение га
U—->/~1({—&}x/m-1), сопоставляющее точке w?W точку
пересечения с /-1({—b\ x I'1) дуги траектории поля V или X,
лежащей в F' и проходящей через w (иными словами, f'w и
f'nw имеют одну и ту же вторую координату). Тогда
Ру = Lg о п, и если
то при и = 1Ф, у) g V получается, что в локальной карте/| 2
отображение Ру выражается формулой
РуФ, у) = Рх(Ь* y) + v-
По предложению 3.3 гл. 1 можно так выбрать i»?!Rm~\
1у1<еи чтобы отображение у—* {у, Ру(у)) было трансвер-
140 ГЛ. 3. ТЕОРЕМА КУПКИ «- СМЕЙЛА
сальным к диагонали в R**~1xlR1B~11. При таком выборе все
неподвижные точки отображения Ру в U элементарны, что
доказьюает лемму. (lfl) I
2.5. Лемма. Пусть у—замкнутая траектория С°°-векторного
поля X. Тогда для любого е > 0 существует такое С"-вектор-
С"-векторное поле Y на М, что JY—Х||г<е и у—гиперболическая
замкнутая траектория поля Y.
Доказательство. Пусть (F, /)—такая выпрямляющая карта
с центром в некоторой точке траектории у, что /*Х—единич-
/*Х—единичное поле С на [—Ъ, Ь\х1т~г. Мы покажем, что для любого
е > 0 существует такое е, > 0, что для каждого 6 ? @, е^
можно найти такое С°°-векторное поле С, что \\С—С||г<е на
[—b, b]xIm-\ С = С на Л и L~(—b, y) = (b, A+6)*/), если
У GPS*1- Будем использовать те же обозначения, что и при до-
доказательстве леммы 2.4.
Действительно, пусть я|з: [—b,b]—*R+—такая С'-функция,
(t 0 [—b, —b/2]\j[b2 b] @
I
что ty(t) = 0, если ^g[—b, —b/2\\j[b/2, b], и ty(t)>0, если
t?(—b/2, b/2), а ф: I1»'1—* R+—такая, что ф(«/) = 0, если
||#j|>3/4, ф(г/)=1, если ft/Kl/2, и ф(г/)>0, если 1/2 <
< |у | < 3/4. Положим C(t, у) = (\, рф (у) ij) (?) t/) и будем искать
такое вещественное р, при котором С обладает указанным свой-
свойством. Непосредственно из определения следует, что С = С
на А. Ассоциированное с С дифференциальное уравнение мо-
может быть записано следующим образом!
( ^-1
Пусть уо? I'1 и '||г/0||^ 1/4 Имеем, что ф(г/0)= 1 и ф(г/)= 1
в окрестности точки у0. Решение написанного выше уравнения
с начальными условиями х@) = —Ь, у@) = уо задается фор-
формулой
t
х (t) = t-b, у (t) = ув + j рф (у (s)) $ (s-b)у (s) ds.
Из непрерывности у (s) следует, что существует такое / > 0,
что ф(г/(s)} = 1 при всех s(E[O, I]. Отсюда y{f) — yux
Ы ехр ( Р^ iJj(s—b)dsjB [0, /]. Это можно проверить дифференци-
а /
$2. ГИПИЧНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ 141
рованием. Пусть (j, (/) = exp f р \ -ф (s—b)ds). Тогда (х @) = 1.
Далее, при 0<p<8j — In 2/J ip(s—b)ds мы получаем, что
р—возрастающая функция, 0< рBЬ)<2 и ||#()||<||#0|K
Следовательно, <p(t/(s)) = l при всех sg[O, 2b], так что y(s)=
=p(s)i/0 и Lg(—6, #„) = (&, ц (Щ у0). Легко видеть, что можно
выбрать р таким образом, чтобы р B6) = 1 -j- б с заданным
б€@. ex), а тогда Ls (—Ь, уа) = (Ь, A+б)#0). Кроме того,
беря р достаточно малым, можно, очевидно, добиться того,
чтобы || С—С||г<е.
Пусть Y—векторное поле на М, равное X вне множества
/-х([—Ь, Щх!1»'1) и равное (f~%C на /-*([—b, b]x Im~l).
Ясно, что Y принадлежит классу С, \\Y—Х||г<е и у—замк-
у—замкнутая траектория поля У. Действительно, пусть2=/~1({Ь}х/*п~1).
В локальной карте /12 отображение последования выражается
формулой
РуФ, у) = A+8)Рх(Ь, у), если |у]<т-
Поэтому D (Ру) (bi 0, = A + б) D (РхIЬч о). При малых б > 0 соб-
собственные значения оператора D(Py\b m по модулю отличны
от 1. ' |
Замечание. В леммах 2.4 и 2.5 мы начинали с векторных полей
класса С" и возмущали их в С-топологии. Нельзя провести
аналогичные доказательства, если X класса Сг, потому что
в этом случае выпрямляющая карта (F, f) класса Сг, а век-
векторное поле (f'\ С только С1. Читатель может, однако,
доказать, что для любого е > 0 существует е С-близкое к X
векторное поле X клаеса С", имеющее близкую к у вамкнутую
траекторию у. Мы вернемся к этому вопросу в конце настоя-
настоящей главы.
2.6. Теорема. Множество $д, состоящее из тех векторных
полей, у которых все критические элементы (т. е. особые точки
и замкнутые траектории) гиперболические, является остаточ-
остаточным (и, следовательно, плотным) в ?Г(М).
Доказательство. Возьмем Т>0 и рассмотрим множество
T = \X?$ii все замкнутые траектории поля X с периодом
^ гиперболические}. Мы покажем, что Ж (Т) открыто и
плотно в 3?r(Af), откуда будет следовать, что $iu является
остаточным, так как оно равно ?(
142 ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
Часть 1. Ж(Т) открыто в &(М).
Пусть X g Ж (Т). По следствию из леммы 2.2 X имеет лишь
конечное число замкнутых траекторий с периодом ^7\ Пусть
р?М. Необходимо рассмотреть три случая:
(a) р—особая точка поля X;
(b) 6(р)—либо регулярная траектория, либо замкнутая с пе-
периодом > Т;
(c) 6(р)—замкнутая траектория с периодом е^Т (и, следова-
следовательно, гиперболическая).
В случае (а) по лемме 2.1 существует такая окрестность
Up точки р в М и такая окрестность dfp поля X в 36Г(М),
что каждое векторное поле Y g сЛГо имеет лишь одну особую
точку p(Y)?U~, причем эта особая точка гиперболическая, и
всякая пересекающая Uр замкнутая траектория поля Y имеет
период > Т.
В случае (Ь) по теореме о трубке тока существует такая
окрестность U р точки р в М, что всякая пересекающая Uр
замкнутая траектория поля X имеет период > Т и X не имеет
особых точек в Up. По лемме 2.3 существует такая окрест-
окрестность <№р поля X в ЖГ(М), что каждое векторное_поле Y ?olfp
не имеет особых точек в Uр и пересекающие Up замкнутые
траектории поля Y имеют период > Т. В случае (с) по лемме
2.2 существуют такая окрестность Uр траектории 6(р) в М и
такая окрестность (№р поля X в ?Г(УИ), что каждое вектор-
векторное поле Y?<№p имеет только одну замкнутую траекторию
в Up, причем эта траектория yY гиперболическая, а все дру-
другие пересекающие Uр замкнутые траектории поля Y имеют
период > Т. Кроме того, Y не имеет особых точек в Uр.
Мы построили, таким образом, открытое покрытие \Up- p g M\
многообразия М. Выберем конечное подпокрытие Ult ..., Ut,
и пусть о)У\, .... о!\Гг—соответствующие окрестности поля X
в Зсг(М). Положим ^ = 0)\Г1п ... DoIVY Теперь легко видеть,
что замкнутые траектории с периодом ^Т всякого векторного
поля Y^4l близки соответствующим замкнутым траекториям
поля X и являются гиперболическими, при этом Y имеет
то же число особых точек, что и X, и все они гиперболиче-
гиперболические. Это доказывает первую часть теоремы.
Часть 2. ?(Т) плотно в 2ЕГ(М).
Достаточно доказать, что X (Т) плотно в $х. Поэтому возь-
возьмем X ? 5?!.
Утверждение 1. Существует такое т>0, что каждая замкнутая
траектория поля X имеет период ~^х.
Рассуждая от противного, предположим, что существует та-
§2. ТИПИЧНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ 143
кая последовательность {уп} замкнутых траекторий, что после-
последовательность {tn) их периодов убывает и стремится к нулю.
Рассмотрим последовательность точек рп € уп- Переходя в случае
необходимости к подпоследовательности, можно считать, что
рп сходится к некоторой точке р ? М. Точка р непременно должна
быть особой точкой поля X, поскольку в противном случае
существовала бы содержащая р трубка тока и пересекающие ее
замкнутые траектории не могли бы иметь сколь угодно малые
периоды. Поскольку Х?$и то р — гиперболическая особая
точка. По лемме 2.1 существует такая окрестность U точки р
в М, что всякая пересекающая U замкнутая траектория поля X
имеет период больше единицы. Это противоречие доказывает
утверждение 1.
Рассмотрим теперь множество Г=Г(т, Зт/2) = {р?М\ 6{р) —
замкнутая траектория с периодом t и т^^Зт/2}.
Утверждение 2. Множество Г компактно.
Достаточно доказать, что Г замкнуто. Пусть рп — последо-
последовательность точек из Г и рп -> р. Как было замечено выше, р
не может быть особой точкой поля X. Если траектория точки р
регулярная или если она замкнута и ее период больше Зт/2, то
всякая замкнутая траектория поля X, проходящая через близ-
близкие к р точки, имеет период больше чем Зт/2. Это приводит к про-
противоречию. Таким образом, 6 (р) является замкнутой траекто-
траекторией с периодом, заключенным между т и Зт/2. Это доказывает
утверждение.
Чтобы завершить доказательство, нам надо для любого
е>0 найти такое Y?3?(T), что \Х—К||, < е. Мы начнем
с того, что набросаем план построения поля У. Представим Т
в виде пт/2 + <7. где O^.q^.r/2. Вначале мы аппроксимируем
X С°° -векторным полем X с ||Х—Х|7.<е/2п. Затем мы
аппроксимируем X С°°-векторным полем У, g 3E (Зт/2) так, чтобы
||X—У,||г<е/2п. Следующим шагом является аппроксимация
Yt С~-полем К2^3?Bт) с \Уг-—У2|]г<е/п. Выполняя п—1
раз операцию, использованную при аппроксимации Yt полем
У2, получим С~-поля Yit F2, ..., Уп с У,- € Х(/т/2 + т) и || Yj+1 —
— Yj || r < e/n. Полагая Y = Yn, получим, что Y g Ж (Т) и
\Y-X\,<b.
Аппроксимация X полем У, ? Зс (Зт/2).
Пусть pi, ...,ps—особые точки поля X. По лемме 2.1
существуют такие окрестности Ult ...,US точек рх, ...,ps и
такая окрестность J\TX с Ч/х поля X в ?r (M), что при всех
У € oWr пересекающие U = U1u ... \J Us замкнутые траектории
поля У имеют период больше чем Т. Кроме того, можно пред-
144 ГЛ. 3. ТЕОРЕМА КУПКИ = СМЕЙЛА
положить, что никакое поле Y g оЛР, не имеет особых точек
в M\U. Отныне мы ограничиваемся полями из o)VV
Пусть у—замкнутая траектория поля X на Г, a Sv—транс-
версальное сечение, проходящее через р?у. Рассмотрим такие
окрестности Vv c= 2V точки р и о)У% поля X, что Р\ опреде-
определено на Vv при всех Y (Е <APV и положительные полутраектории
поля Y, проходящие через точки множества Fv, впервые вновь
пересекают Sv в момент времени t > Зт/4. Рассмотрим также
такую окрестность Wv траектории у, что положительная полу-
полутраектория поля Y, проходящая через любую точку из Wv,
пересекает 2V по крайней мере дважды1).
Открытые множества Wv, построенные по замкнутым траек-
траекториям у cz Г, покрывают компактное множество Г. Пусть
Wlt ..., Wk—конечное подпокрытие, и пусть Xv>, ...,XVft —
соответствующие окрестности поля X. Положим о№2 = оМ\>1 П •••
...fl JVVfc и W = Wt U... U Wk.
Рассмотрим теперь компактное множество К = M\(U U W).
Поскольку X не имеет особых точек в К и каждая замкнутая
траектория поля X, проходящая через точки множества К,
имеет период больше чем Зт/2, то по лемме 2.3 существует
такая окрестность сЛГ3 с: <АГ2 поля X, что проходящие через
точки множества К замкнутые траектории всякого поля K€o№g
имеют период больше чем Зт/2. Далее мы будем рассматривать
поля лишь из окрестности oNV Для каждого / = 1, ...,& и
для каждого Y?df3 рассмотрим отображение Пуанкаре
Pjyi Vj —*¦ Sy. По лемме 2.4 можно аппроксимировать X таким
С°°-полем Fj, что все неподвижные точки отображения PiYt
в Wlf\I.1 элементарные. Как мы видели в предыдущей главе,
каждое поле, достаточно близкое к Ух, обладает тем же свой-
свойством. Поэтому можно аппроксимировать Yt таким полем К§,
что Р,уг и ^2Y, имеют лишь элементарные неподвижные точки
в Wif\ili и W2n22. Повторяя эти рассуждения, мы получим
сколь угодно близкое к X поле Yk, отображение последова-
ния Р .у которого имеет лишь элементарные неподвижные
точки в Wjft'Lj для /=1, ...,^(и). Пусть ц,1г ..., pt—замк-
pt—замкнутые траектории поля Yk, соответствующие неподвижным
х) Странные на первый взгляд условия насчет t > Зт/4, Р\ и двух
пересечений нужны, чтобы периодическая траектория поля Y с периодом
из [т, Зт/2], пересекающая Wy, пересекала Vv Б точке, которая является
неподвижной точкой отображения Ру. (Впрочем, это надо чуть модифици-
модифицировать* как позднее будет объяснено в (w), (u).)—Прим, ред.
§ 3. ТРАНСВЕРСАЛЬНОСТЬ ИНВАРИАНТНЫХ МНОГООБРАЗИЙ 145
точкам этих отображений последования. Другие замкнутые
траектории поля Yk имеют период > Зт/2. Кроме того, су-
существует такая окрестность Jf(Yh), что все замкнутые траек-
траектории периода ^ Зт/2 всякого поля Y ? <ЛГ (Yk) являются эле-
элементарными И бЛИЗКИМИ К Цг, . . ., Ц[.
Последовательно применяя лемму 2.5, мы аппроксимируем
Yk С"-полем Ytr. у которого замкнутые траектории длины
^Зт/2 такие же, как и у Yk, но являются гиперболическими
для Yp Таким образом, Fj g 3? (Зт/2).
Так как 36 (Зт/2) открыто, то существует окрестность <ЛГ4
поля Ylt содержащаяся в .36 (Зт/2). Для всех замкнутых траек-
траекторий поля Yi периода ^Зт/2 рассмотрим окрестности Us+i, ...
...,Us+t из леммы 2.2. Положим t/ == Ufi/1/,-. Тогда всякая
проходящая через точку множества U замкнутая траектория
близкого к Yt поля либо гиперболическая, либо имеет период
больше чем Зт/2.
Аппроксимация Yt полем K2g36Br).
Из компактности множествах) Г = Г (Зт/2, 2т) и лемм 2.4
и 2.5 мы получаем такую окрестность W множества Г, что Yt
может быть аппроксимировано полем У2, у которого замкну-
замкнутые траектории, проходящие через точки множества W, либо
гиперболические, либо имеют период > 2т. Поскольку замкну-
замкнутые траектории поля Yt в компактном множестве К =
= M\(U U W) имеют период > 2т, то отсюда следует, что
можно выбрать С°*-поле У2, так чтобы У2^36Bт). Аналогично
можно получить поля Ya, ..., Yn, и это завершает доказа-
доказательство плотности. ¦
§ 3. ТРАНСВЕРСАЛЬНОСТЬ ИНВАРИАНТНЫХ МНОГООБРАЗИЙ
В этом параграфе мы закончим доказательство теоремы
Купки—Смейла.
Будем говорить, что Xg3?r(M)—векторное поле Купки —
Смейла, если оно удовлетворяет следующим условиям:
(a) критические элементы поля X (т. е. особые точки и замк-
замкнутые траектории) гиперболические, иными словами, X ? ^ 2;
(b) если ах и а2—критические элементы поля X, то инвариант-
инвариантные многообразия Ws(ot) и Wa(o2) трансверсальны.
х) Для поля X множество Г (Зт/2, 2т) не обязательно компактно:
последовательность замкнутых траекторий, периоды которых стремятся
к 2л, может сходиться к траектории с периодом т. Но для поля Yt по-
подобное явление невозможно ввиду гиперболичности всех его замкнутых
траекторий с периодами ^Зт/2. Поэтому для него соответствующее мно-
множество компактно,— Прим. ред.
146 ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
Будем обозначать множество векторных полей Купки —
Смейла через ?т или К—S.
3.1. Теорема (Купки—Смейла). К—S является остаточным
множеством в ?Г(М).
Мы уже показали, что множество 312 является остаточным
в Зсг(М), поэтому осталось только показать, что K—S является
остаточным в ?12. Доказательство этого факта мы разобьем на
несколько лемм.
Для упрощения обозначений условимся считать, что особая
точка поля Х??Г(М)—это критический элемент с нулевым
периодом. Таким образом, если Т > О и X ? ? (Г), то X имеет
лишь конечное число критических элементов периода ^Т и
все они гиперболические. Пусть ЗЕ(Г)—множество тех вектор-
векторных полей Х(Е?(Т), у которых Ws(at) трансверсально к Wa(o2)
для любых критических элементов периода ^Т1.
3.2. Лемма. Если Ж (Г) является остаточным в ?r (M) при всех
Т^О, то множество К—S остаточное.
Доказательство. Так как К—S = р ы&(п) и каждое Ж (п)
остаточное, то К—S тоже остаточное. I
3.3. Лемма. Пусть Е—сепарабельное1) пространство Бэра и
F с= ?—плотное подмножество. Подмножество UczE является
остаточным тогда и только тогда, когда каждое x?F имеет
такую окрестность Vx, что U п Ух—остаточное множество в Vx.
Доказательство. Пусть VXl, ..., VXn, ...—такое счетное
покрытие множества F, что U f]Vx.—остаточное множество
в Vx. при всех /. Тогда U f]Vx. r> p?^ Uи, где Vи открыто и
плотно в VH. Пусть V = U," , Vx. и WU = VU U (V\VX.). Тогда
V и Wи открытые и плотные. Легко видеть, что U содержит
n^ifl/^i^7//- Поэтому U является остаточным. Обратная
импликация очевидна. |
Следствие. Предположим, что при всех Т^О и X g 31 (Т)
существует такая окрестность off поля X, что Зс(Т)—оста-
Зс(Т)—остаточное множество в off. Тогда К—S тоже остаточное.
Доказательство следует из лемм 3.2 и 3.3 и плотности
множества Ж (Т) в ЖГ(М). щ
Пусть Х?Х(Т) и о?, ...,os—критические элементы поля
X периода ^7\ Для каждого i возьмем такие компактные
окрестности W%(Oi) и IF" (о,-) множества а, в Ws(al) и Wa(pt)
*) Т. е. имеющее счетное всюду плотное подмножество.— Прим. ред.
§3. ТРАНСВЕРСАЛЬНОСТЬ ИНВАРИАНТНЫХ МНОГООБРАЗИЙ 147
соответственно, что границы множеств W% (o/) и W& (а,) явля-
являются фундаментальными областями для Ws (о() и W" (о{). Пусть
Sf—подмногообразие в М коразмерности 1, трансверсальное
к векторному полю X и к локально устойчивому многообразию
элемента а,-, с которым 2| пересекается в фундаментальной
области dW% (а;), см. рис. 7 г).
Каждое Y из достаточно малой окрестности JV поля X
трансверсально к каждому 1.% и критические элементы поля Y
Рис. 7
периода ^Т гиперболические и близки к соответствующим
критическим элементам поля X. Таким образом, если ох (У), ..
...,os(Y)—критические элементы поля Y периода ^Г, то
существует компактная окрестность Wo(olt Y) множества ot(Y)
в Ws(o{, Y), граница которой является пересечением 2|
с Wl (a,., Y). По теореме об устойчивом многообразии отобра-
отображение Fi-^- Wo (a,., Y) непрерывно; иными словами, для любых
У„ с= JV и е > 0 существует такое б > 0, что если ЦК—Ко]|, < б,
то Wo(a/. Y) является е-Сг-близким к WHph Yo). Аналогично,
для каждого Y?df и каждого / = 1, ..., s можно так постро-
построить компактную окрестность W%(oit Y) множества o,-(F)
в Wa(oit Y), чтобы отображение Y*->W"(oltY) было непре-
непрерывным.
х) Точнее, 2/= Wo (o,)xW" (Pi), где Wl' " (а,-) берутся столь малыми,
чтобы они оба помещались в пределах координатной окрестности, в кото-
которой H^foc" fa) выглядят как координатные плоскости, а поле X (выраженное
в терминах локальных координат) близко к линейному; прямое произведе-
произведение понимается в смысле, отвечающем локальным координатам,— Прим. ред.
148 ГЛ. 3. ТЕОРЕМА КУПКИ ь- СМЕЙЛА
Для каждого положительного целого п определим
W' (а„ У) = У_„ (Wl (at, Y)), W» (a,, Y) = Yn (W"B (alt Y)).
Ясно, что отображения Ki-»^(a,, К) и Ун-*№?(a/t У) непре-
непрерывны, поскольку Yn и У_„—диффеоморфизмы, непрерывно
зависящие от Y. Кроме того, W%(olt Y) и W%(ot, У)—это ком-
компактные подмногообразия с границей!
W (о„ У) = Un > UW* (о„ У), «7» (а„ У) == Un > ОЙ7« (а„ У).
Пусть ?„ (Г) обозначает множество тех векторных полей У € off,
у которых W% (о{, У) трансверсально к W" (a^, У) при всех i и /х).
3.4. Лемма. Пусть Х??(Т) и JV—рассмотренная выше
окрестность поля X. Если Жп (Т) открыто и плотно в «ЛГ пры
всех n^N, то ?(Т)[)$'—остаточное множество в X.
Доказательство легко следует из формулы
r = n"-.?,(T). ¦
3.5. Лемма. Пусть Х??(Т) и off—рассмотренная выше ок-
окрестность поля X. Тогда ?„(Т) при всех ngN открыто и
плотно в oJf.
Доказательство. Пусть а(, ..., а5—критические элементы
поля X периода ^ Т. Будем обозначать через 3tni /, j (Г) мно-
множество таких векторных полей У g X, что W% (a,., У) транс-
трансверсально к №{j(a,» У). Ясно, что ?„СО = П!,/,=1.?П./,/ (Г).
Поэтому достаточно показать, что каждое ?n,t,j(T) открыто
и плотно в oJf.
Часть 1. Открытость множества 3tn, /t j (T).
Пусть X б Хп ly j (T). Так как Wsn (ot, X) трансверсально
к W»(pf,X) и отображения Yt-^W*(ot,Y) и Y*->WZ(Oj,Y)
непрерывны, то существует такая окрестность JSTц поля Я
в Дг, что ^ (а,, У) трансверсально к №? (oj, У) при всех
^ € «ATj/. Следовательно, gV*// с Зс„% ,, у (Г), что и доказывает от-
открытость множества ЗЕ„, f, у (Г).
Часть 2. Плотность множества Hn%UJiX).
Пусть X g J (Т) п <ЛГ. Мы покажем, что существует такая
окрестность сЛГ поля X в <АГ, что JTn,,, j (T) fj cff открыто и
1) Трансверсальность в точке края понимается как трансверсальность
некоторых окрестностей этой точки на Wst Wa.— Прим, ред.
§ 3. ТРАНСВЕРСАЛЬНОСТЬ ИНВАРИАНТНЫХ МНОГООБРАЗИЙ 149
плотно в #. В частности, X можно сколь угодно близко
аппроксимировать элементами множества Жп^ ,-, t(TI).
Рассмотрим компактное множество К = W% (ct, X) n
П W% {pj, X). Если x € К, то существуют такая выпрямляющая
карта (Fx, /^ *)» содержащая х, и такое положительное число
Ьх, что fj, X(FX)^> [—bx, bjx/1" и векторное поле (/х> x)tX
совпадает с единичным векторным полем на [— Ьх, bx] х 1т~г.
Пусть Ах cz Fx—такая открытая окрестность точки х, что
замыкание множества Ах_ содержится во внутренности множе-
множества (fx. *)~Ч[—&х> bjx/i/l1)- Уменьшив, если потребуется,
Fx, можно считать, что каждое из множеств W\n (ot, X) n Fx
и W"n iPj, X) n Fx имеет только одну компоненту связности2).
Пусть Ait .... At—конечное покрытие множества К такими
открытыми множествами. Через (Fh, /^ k) будем обозначать
соответствующие выпрямляющие карты. Тогда (/j k)~l
([—bk, bftjx/f/l1) содержит Ak. Поскольку отображения
Yi-* W*n(о,, У) и Yt-^-W^iOj, Y) непрерывны, то существует
такая окрестность X поля X в X, что
при всех Kg off. В случае необходимости уменьшая df, можно
даже считать, что для каждого Y?df и k=l, ..., I сущест-
существует такая выпрямляющая карта (FY, ft. / Y, к) Для ^» что
FY, ft =э Лй, /Ki ft (FKi fe) r> [—fcft, Ьл]х Z и внутренность мно-
множества fy) к ([—Ьк, bftJx/i/Г1) содержит замыкание множества
Лй8). Это вытекает из непрерывной зависимости потока от
х) Достаточно было бы доказать только последнее, но аппроксимирую-
аппроксимирующее поле будет строиться в несколько шагов, на каждом из которых
трансверсальность будет обеспечиваться в новой части фазового простран-
пространства путем аппроксимации поля, полученного на предыдущем шаге, неко-
некоторым новым полем. Поэтому и приходится доказывать более сильное
утверждение (а точнее, доказывать, что фигурирующие ниже jfft являются
открытыми и плотными подмножествами некоторой окрестности Jf ^ ^0-
Ситуация аналогична той, из-за которой понадобилась лемма 2.4' из (хо).—
Прим. ред.
*) И что то же самое справедливо для VP%n (о/, Z) П Fх и
W"n (Op Z) П Fx. при всех Z-, достаточно близких к Х-, скажем при Z g jjf",
а также что при q g W%n (о/, Z) П Fx (соответственно при q g W^n (oj, Z)(]
(]FX) положительная (соответственно отрицательная) полутраектория поля Zs
исходящая из точки q, выйдя из Fx, никогда больше не попадает туда.—
Прим. ред.
3) И что при К, 1 g Jf для Wtnfri, Z) П PY,k> W"n(op Z)[\FYt h
справедливы утверждения, сделанные ранее при Y = X,— Прим. ред.
150
ГЛ. 3. ТЕОРЕ MA КУПКИ — СМЕЙЛА
векторного поля. Пусть теперь Хк обозначает множество тех
векторных полей К(Е<$\ У которых №^(р/, Y) трансверсально
к W%(Oj, Y) во всех точках множества Ак. Ясно, что j?ft—от-
j?ft—открытое подмножество в off, и поэтому для наших целей дос-
достаточно показать, что Жк плотно в off, поскольку 3cntl<J(T)f\
nAPnU?
Покажем теперь,- что ?к плотно в Jf. Возьмем фиксирован-
фиксированное С°°-векторное поле Y^Jf. Если ZgJV1, то обозначим через
Рис. 8
.S+ (Z) пересечение множеств /Ki k (W% (olt Z) ft FKt k) и {bk\ x lm~x,
а через U+(Z)—пересечение множеств /Ki k(W^(oj, Z)[)FY%k)
м {b^xl1"'1. Легко видеть, что если S+(Z) трансверсально
:к U+(Y) в {bjx/vl1, то WZ(oly Z) трансверсально к W%(oj,Y)
в Ак (рис. 8).
Аналогично доказательству леммы 2.4 получаем, что для
любого е> 0 и любого v?R.m~x с достаточно малой |у|| можно
найти такое С"-векторное поле Y на М с ||У—У||г<е, что
(a) Y = Y вне множества /р%([ — Ьк, Ьк]х.1т~%
(b) L? (—b, y) = (b, y + v) при всех у € /"д1.
Здесь b~bk, a Lp—отображение из {—Ь}х!т~* в Щх1т~\
которое каждой точке (—Ь, у) ставит в соответствие точку
пересечения проходящей через (— Ь, у) траектории поля
(/к. к)*У с {^Jx/. С другой стороны, по предложению
3.3 гл. 1 можно выбрать такое достаточно малое v, чтобы
S+(Y) было трансверсально к U+(Y) + v. Тогда fy]kE+ (Y))
является пересечением множества W%n (a,, Y) с трансверсзльным
сечением fy]k ({Ьк\ XI1"'1), a fy] b(U+ (Y) + v)~пересечением
множества W\n (о,-, Y) с сечением fy], ({Ьк} х I?/!1)- Поэтому мы
заключаем, что эти два подмногообразия трансверсальны
$3. ТРАНСВЕРСАЛЬНОСТЬ ИНВАРИАНТНЫХ МНОГООБРАЗИЙ 15В
в /""*([—bk, bk]x /Г/71)- Следовательно, Wfl{pl,Y) трансвер*-
сально к W" (oy, Y) на Ак 1). Это показывает, что Y ? Хк-
Таким образом, каждое С"-поле из Jf может быть аппрокси-
аппроксимировано полем из Эск. Поскольку каждое поле из Jf может быть,
аппроксимировано С"-полем, то отсюда следует, что ?к плотно;
в Jf t что завершает доказательство леммы. |]
Теорема 3.1 является теперь непосредственным следствием1,
лемм 3.2, 3.3, 3.4 и 3.5. |!
Замечание. Важно отметить, что К—5 не является открытым:
в ?Г(М). Действительно, рассмотрим иррациональный поток
Xt на торе Т2. Векторное поле X ? К—S, ибо оно не имеет
критических элементов. Однако X можно аппроксимировать
векторными полями Y, для которых Yt—рациональный поток.
Все траектории поля Y замкнуты, но не гиперболические.
Поэтому Y^K—S.
Теперь мы сформулируем теорему Купки — Смейла для диф-
диффеоморфизмов. Доказательство аналогично случаю векторных
полей и будет оставлено читателю в качестве упражнения.
Будут предложены, однако, два независимых наброска доказа-
доказательства.
Диффеоморфизм /?Diffr(M) называется диффеоморфизмом
Купки—Смейла, если
(a) периодические точки диффеоморфизма гиперболические;
(b) если р и q—периодические точки диффеоморфизма /, то
Ws (p) трансверсально к W" (q).
Множество диффеоморфизмов Купки—Смейла будем обоз-
обозначать также через К—S.
3.6. Теорема. К—5 является остаточным множеством в Diffr(M).
Набросок доказательства. A) Если /? Diffr(M) и k?H, та
обозначим через /*¦ М —> МхМ отображение, задаваемое фор-
формулой ]"(р) = {р, fk(p))- Если р—периодическая точка ото-
отображения f периода k, то точка 1к(р) = (р, р) принадлежит
диагонали АаМхМ. Такая точка элементарна тогда и только
тогда, когда /й трансверсально к А в р. Пусть п?Щ и <?>" —
множество таких диффеоморфизмов /gDiffr(M), что ]к транс-
трансверсально к А при fe=l, ..., п. Тогда S>n открыто и плотно.
B) Пусть /?©" и р—периодическая точка отображения /
периода < п. Легко аппроксимировать f таким g ? §Dn, что
1) В силу наших условий о полутраектрриях S+ (F)=S+ (К) ц
U. (?) = t/_ (F).— Прим. ре$,
152 ГЛ. 3. ТЕОРЕМА КУПК И "- СМЕЙЛА
g = f вне некоторой окрестности точки р и р—гиперболическая
периодическая точка диффеоморфизма g. Поэтому множество
S"c@" тех диффеоморфизмов, периодические точки которых"
периода k=l, ..., п гиперболические, открыто и плотно1).
3) Пусть #" обозначает множество тех диффеоморфизмов из
Ш)п, у которых устойчивые и неустойчивые многообразия пе-
периодических точек периода <! п попарно трансверсальны. #" —¦
остаточное множество. Поскольку К—<^ = ПпеМ^"' т0 отсюда
следует, что К—5—остаточное множество. |
Другое доказательство теоремы Купки—Смейла для диф-
диффеоморфизмов может быть получено из соответствующей тео-
теоремы для векторных полей. Для этого нам понадобится кон-
конструкция, позволяющая диффеоморфизмам на многообразии М
соотносить векторные поля на многообразии М, где размер-
размерность многообразия М на единицу больше размерности мно-
многообразия М. Эта конструкция называется надстройкой диф-
диффеоморфизма2).
Пусть Х^ЖГ(М) и ЁсгМ—компактное подмногообразие
коразмерности 1. Будем говорить, что 2—глобальное транс-
трансверсальное сечение для X, если (а) X трансверсально к 2, (Ь)
положительная полутраектория поля X, проходящая через лю-
любую точку сечения Ё, обязательно вновь пересечет его.
Если 2—глобальное трансверсальное сечение для X g ?r (M),
то поток поля X порождает диффеоморфизм }: 2 —»- 2, который
каждой точке /7^2 сопоставляет точку f(p), в которой поло-
положительная полутраектория точки р впервые пересекает 2. Диф-
Диффеоморфизм / называется отображением последования, ассоции-
ассоциированным с 2.
Легко видеть, что если X ? 3tr (M) допускает глобальное
сечение 2, то под действием потока 2 заметает все М, иными
словами, U* 6 RXt B) = М. В частности, X не имеет особых
точек.
1) «Подводный камень»: если р—элементарная неподвижная точка ото-
отображения /*, но у df" (р) имеется такое собственное значение X, что X1 — 1,
то р не будет элементарной неподвижной точкой для отображения /*'.
Поэтому, доказав A) для какого-нибудь k, надо затем доказать B) для
того же k и только после этого переходить к A) с k-\-\.— Прим ред.
2) А также надстройкой Смейла, поскольку 1) Смейл впервые исполь-
использовал ее в контексте теории динамических систем (само же построение М
по М и /, конечно, встречалось в топологии); 2) термины «надстройка» и
даже «надстройка отображения» имеют в топологии другой смысл.— Прим. ред.
§3. ТРАНСВЕРСАЛЬНОСТЬ ИНВАРИАНТНЫХ МНОГООБРАЗИЙ 153
Отметим, наконец, что структура траекторий поля X опре,-
деляется структурой траекторий отображения последования /
и наоборот. Действительно, следующие факты получаются
непосредственно:
(i) /?€^—периодическая точка диффеоморфизма J тогда и
только тогда, когда траектория 6х(р) замкнута;
(ii) р€^—гиперболическая периодическая точка диффеомор-
диффеоморфизма ] тогда и только тогда, когда 6х(р) — гиперболи-
гиперболическая замкнутая траектория;
(Hi) если /?j и р2—гиперболические периодические точки диф-
диффеоморфизма /, то U ]' Ws (pj) тогда и только тогда трансвер-
сально к Uf'Wa(p2), когда WsFx(Pi)) трансверсально к
Р@*(л));
(iv) g €«•(/?) тогда и только тогда, когда 6x(q)c:aFx(p)).
Следующее предложение показывает, что каждый диффео-
диффеоморфизм является отображением последования, ассоциирован-
ассоциированным с глобальным сечением некоторого векторного поля.
3.7. Предложение. Пусть /gDiffr(M), где М—компактное
многообразие. Тогда существуют компактное многообразие М,
векторное поле X^3i.r~1(M), допускающее глобальное транс-
версальное сечение 2, и Сг-диффеоморфизм h: M —*¦ 2, сопря-
сопрягающий f и отображение последования f: S—*-2.
Доказательство. Рассмотрим следующее отношение эквива-
эквивалентности на МхК:
(р, s)~(q, t)&s—t = n<t% и q = f"(p).
Пусть М—факторпространство MxR/~ и я: MxR—>-M —
естественная проекция. Пусть 2сМ обозначает образ множе-
множества Мх{0} под действием я. Для каждого to^R ограничение
отображения л на Mx(t0, to-{-l) задает взаимно однозначное
соответствие между Mx(tB, tB+l) и М\я(Мх\to\). Кроме
того, я(р, 1) = л (f (р), 0). Введем на М топологию, индуциро-
индуцированную проекцией л, иными словами, АаМ будет считаться
открытым тогда и только тогда, когда л (А) открыто.
Покажем, что М имеет естественную структуру гладкого
многообразия и что л является локальным Сг-диффеоморфиз-
мом. Пусть х(. Ui—>-U(jc:Rm, i=l, ..., s,— такие локальные
карты на М, что \Jsl=lUt=~M. Тогда Vt=*n(utx(—j, у
и V{ =^л A/{ х (-7-, -4)) открыты в М. Определим xt: U,,
154 ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
- у* 4") и ^': ^1-^^ох(т> 4)
х,(л(р, t)) = (xt{p), t) и */,(л(р, t)) = (xl(p), t). Ясно, что л, и
yt—гомеоморфизмы. Мы утверждаем, что набор карт \(xt Dt),
(у, Vt); i = l, ..., s\ задает Сг-атлас на М. Действительно,
a-,V(m, t) = (x,xf'{u), t), ytyjl(u, 1) = {хгх^(и), t) и
Uxtxj4u), t), /<e(|, 1),
^/-'(и. 0= /l 5\
[(я,/*/-1 («). '-!). <€(¦§-. т)
являются Сг-диффеоморфизмами, что и доказывает утверждение.
На самом деле /Й можно считать С00-многообразием, по-
поскольку по теореме 0.19 гл. 1 на М существует такая струк-
структура С^-многообразия, что хг и у{ являются (^-диффеомор-
(^-диффеоморфизмами.
Так как Xfono^^xid)—тождественное отображение на
Uox'(—g", -g-J, а у1оло(ХAх{^^тождественное отображение
на ^oxf-j". -г)» т0 0ТСЮДа следует, что it является локаль-
локальным Сг-диффеоморфизмом. Пусть д/dl обозначает единичное
векторное поле на MxIR, траектории которого суть прямые
.линии {p}xR, peM. Пусть Х(п(р, t)) = dn(p, t)(d/dt(p, t)).
Легко видеть, что Х(п(р, t)) = X(л(/(р), t—1)). Поэтому X
:является С1 векторным полем на М. Поле X трансверсально
:к Ё, и его траектория, проходящая через точку р = п(р, 0),—
это л({р}хК). Таким образом, положительная полутраектория
поля X, проходящая через точку р = п(р, 0)?2, впервые вновь
пересечет 2 в точке q = л (р, 1) = л(/(р), 0). Отображение после-
дования: /: 2 —>¦ S, ассоциированное с 2, задается, следовательно,
формулой f(n(pt 0)) = n(f(p), 0). Отображение hi M~»-2, опре-
определяемое формулой h (р) = л (р, 0), является С-диффеоморфиз-
мом, и ~foh = hof, что завершает доказательство. |
Замечание. По предложению 3.7 надстройка С'-диффеомор-
физма—это С'~1-векторное поле. В [80] изложенная выше
конструкция несколько модифицирована и дает Сг-векторное
поле в качестве надстройки Сг-диффеоморфизма. Но мы не
будем пользоваться этим фактом. A2)
Докажем теперь плотность множества диффеоморфизмов
Купки—Смейла, используя надстройку. Пусть /0 € Diffr (M).
Вначале мы аппроксимируем f0 диффеоморфизмом /класса С".
Чтобы аппроксимировать / диффеоморфизмом Купки—Смейла,
УПРАЖНЕНИЯ 155
рассмотрим С°°-векторное поле X на М, полученное как над-
надстройка f, и пусть h: M —* 2 —диффеоморфизм, сопрягающий
f и отображение последования /: 2 —»- 2 поля X. Аппроксими-
Аппроксимируем X в Сг-топологии С^-векторным полем Купки—Смейла
Y и обозначим через g: 2 —* 2 отображение последования
поля F. Так как g является Сг-близким к / диффеоморфизмом
Купки—Смейла, то отсюда следует, что и g = h~1ogch явля-
является Сг-близким к / диффеоморфизмом Купки—Смейла. |
УПРАЖНЕНИЯ
1. Пусть Xf—поток, порожденный векторным полем Х?ЖГ(М). Пусть
у—гиперболическая замкнутая траектория поля X с периодом X. Рас-
Рассмотрим диффеоморфизм f = X), и точку р?у.
(a) Покажите, что ТрМ разлагается в прямую сумму подпространств
Н и Но, инвариантных относительно dfp, так что На имеет размерность 1
и содержит вектор X (р).
(b) Покажите, что если S а М—такое подмногообразие, что его каса-
касательным пространством в р является И, и л: UaS—>-S—отображение
последования, ассоциированное с у, то dn(p) = df(р)\Н.
2. Покажите, что если X—векторное поле Купки—Смейла на S2, то
ш—предельное множество всякой траектории является критическим
элементом.
3. Покажите, что множество векторных полей Купки—Смейла является
открытым в 3Er (S1).
4. Покажите, что множество векторных полей Купки—Смейла является
открытым в ЗЕГ (S2).
5. Пусть у и Y являются замкнутыми траекториями векторных полей X
и X соответственно. Покажите, что если существует гомеоморфизм h
некоторой окрестности траектории у на некоторую окрестность траек-
траектории у, переводящий траектории поля X в траектории поля X с сохра-
сохранением ориентации, то отображения последования, ассоциированные
с замкнутыми траекториями у и у, сопряжены. Если /г—диффеоморфизм, то
отображения последования сопряжены посредством диффеомор-
диффеоморфизма.
6. Покажите, что всякое векторное поле Купки—Смейла на компактном
двумерном многообразии имеет лишь конечное число замкнутых траек-
траекторий.
Указание. Любое компактное двумерное многообразие диффеоморфно
либо сфере с п ручками (в случае ориентированного многообразия),
либо проективной плоскости или бутылке Клейна с п ручками (в случае
неориентируемого многообразия). Бутылка Клейна диффеоморфна проек-
проективной плоскости с вклеенным в нее листом Мёбиуса.
7. Покажите, что грубое векторное поле на компактном двумерном много-
многообразии является полем Купки—Смейла.
8. Нарисуйте векторное поле на S2 с бесконечным числом гиперболических
критических элементов.
9. Пусть CczS2—окружность. Рассмотрим множество $с С! Жг (S2) таких
векторных полей, которые касаются С во всех ее точках.
(a) Покажите, что множество ЗЕсПК—S не является плотным в $с.
(b) Рассмотрим множество KSc a Jс векторных полей со следующими
свойствами: (i) их особые точки и замкнутые траектории гиперболичны-»
156 ГЛ. 3. ТЕОРЕМА КУПКИ — СМЕЙЛА
(ii) если у—такая траектория, что a (v) и ш (у) являются седлами, то
у d С. Покажите, что KSq открыто и плотно в $с.
10. Пусть Gradr (М) С ЭЕГ (М)—множество градиентных векторных полей
на М, иными словами, X?Gradr (M) тогда и только тогда, когда су-
существуют такая функция f?Cr+1 (M) и такая римаиова метрика g, что
X=grad/ в метрике g. Покажите, что множество векторных полей
Купки—Смейла является остаточным в Gradr (М)
Указание. Покажите, что если X=grad/ в метрике g, F—трубка тока
для X и Y—близкое к X векторное поле, совпадающее с X на M\F,
то существует такая метрика g, что Y является градиентом / в ме-
метрике g. Используйте также упражнение 8 из гл. 2.
11. (а) Покажите, что если Х?$Г(Л4)—векторное поле Купки—Смейла,
имеющее глобальное траисверсальное сечение, то ассоциированное ото-
отображение последования является диффеоморфизмом Купки—Смейла.
(Ь) Покажите, что надстройка диффеоморфизма Купки—Смейла—вектор-
Купки—Смейла—векторное поле Купки—Смейла.
12. (а) Покажите, что если /gDiff (M), г^\, является грубым, то его
периодические траектории гиперболические,
(b) Покажите, что если /^DifP (jW) является грубым, то f—диффеомор-
f—диффеоморфизм Купки—Смейла. Отметим здесь, что К. Робинсон доказал в ра-
работе [98] аналогичное утверждение для /gDiffr (M), г>2.
(c) Покажите, что грубое векторное поле Xg-E1^) является полем
Купки—Смейла.
Замечание. Остается открытой проблемой возможность доказательства
того факта, что грубое векторное поле Х?ЖГ{М), г>3, имеет лишь
гиперболические замкнутые траектории.
13. Пусть X?$Lr{M)—векторное поле с замкнутой траекторией. Пусть
Xf—поток, порожденный'полем X. Покажите, что диффеоморфизм Xf
не является грубым.
14. Покажите, что на любом компактном многообразии Мп, п^1, мно-
множество диффеоморфизмов Купки—Смейла не является открытым в
Diff(M), rssl.
Указание. Покажите, что на каждом многообразии существует векторное
поле Купки—Смейла с замкнутыми траекториями.
15. Покажите, что на всяком компактном многообразии Мп, пё=3, мно-
множество векторных полей Купки—Смейла не является открытым
Ж'ЧМ) 1
Глава 4.
ТИПИЧНОСТЬ И ГРУБОСТЬ
ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА
Как мы уже подчеркивали раньше, основной задачей теории
динамических систем является описание структуры траекторий
векторных полей на гладком многообразии. Однако, как пока-
показывает пример из § 3 гл. 2, существуют поля с чрезвычайно слож-
сложной структурой траекторий. Таким образом, стратегия, которую
следует выбрать исходя из данной программы, состоит в том,
чтобы ограничиться изучением некоторого подмножества в прост-
пространстве векторных полей. Желательно, чтобы это подмножество
было открытым и плотным (или настолько обширным, насколько
это возможно) и чтобы его элементы были грубыми и имели до-
достаточно простую структуру траекторий, поддающуюся класси-
классификации. В локальном смысле эта проблема полностью решена,
как было показано в гл. 2.
В настоящей главе, в § 1 и 2, будет показано, что в глобаль-
глобальном смысле намеченная выше программа может быть реализована
для компактных двумерных многообразий. Этот результат, по-
полученный Пейксото [81], [85], является одной из ранних вех
в современном развитии теории. Говоря об истории этого резуль-
результата, кроме предшествовавшей фундаментальной работы Андро-
Андронова — Понтрягина и последовавшей за ней работы Де Баггиса,
изучавшего случай диска D2 и сферы S2 (см. [5], [47]) A?), следует
упомянуть, что Плисе [87] *) получил результат Пейксото для
векторных полей без особенностей на торе Т2.
В высших размерностях множество грубых полей по-преж-
по-прежнему обширно, но не является уже всюду плотным. Здесь сущест-
существуют богатые и более сложные явления, сохраняющиеся при
малых возмущениях первоначального поля. Даже для грубых
полей структура траекторий предельных множеств до конца не
ясна, и ее описание по-прежнему остается областью активного
исследования. Эти факты обсуждаются в § 3 и § 4.
В этом контексте вновь стоило бы подчеркнуть важность изу-
изучения типичных свойств, т. е. свойств, присущих почти всем
векторным полям (т. е. полям, образующим бэровское подмно-
*) И еще раньше А, Г. Майер [141], Подробнее об истории см.
Прим. ред.
158 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
жество в пространстве всех векторных полей). Такому изучению
посвящена как раз теорема Купки — Смейла из предыдущей
главы.
Отметим, наконец, что предложенную выше программу мож-
можно проводить для некоторых подмножеств пространства вектор-
векторных полей, представляющих особый интерес. Одним из наиболее
естественных примеров является множество градиентных век-
векторных полей на компактном многообразии. В этом случае
грубые поля образуют открытое плотное подмножество [79],
[106]. В § 3 мы укажем некоторые основные свойства структуры
траекторий этих полей *).
В § 4 собраны общие результаты о грубости. В частности,
мы продемонстрируем грубые системы с бесконечным числом
периодических траекторий.
§ 1. ВЕКТОРНЫЕ ПОЛЯ МОРСА-СМЕЙЛА;
ГРУБОСТЬ
Здесь мы определяем класс векторных полей, играющий важ-
важную роль в теории динамических систем. Этот класс, называе-
называемый системами Морса — Смейла, образует непустое открытое
подмножество, а его элементы являются грубыми. Хотя эти
результаты верны для компактных многообразий любой размер-
размерности [75], [79], мы изучим в этой главе лишь случай многообра-
многообразий размерности 2, когда системы Морса — Смейла являются
также плотными.
Мы начнем этот параграф с определения векторных полей
Морса — Смейла. Затем будет доказана грубость полей Морса —
Смейла на М2. Проводимое доказательство взято из работы [75].
Оно отлично от оригинального [85] и допускает обобщение на
высшие размерности.
Прежде чем дать формальное определение векторных полей
Морса — Смейла, мы мотивируем его с помощью примеров.
Поскольку мы стремимся найти класс грубых полей, необходимо
потребовать, чтобы в этом классе все особые точки и замкнутые
траектории были гиперболическими. Без этого предположения
поля не были бы даже локально грубыми. Подчеркнем также, что
пересечения устойчивых и неустойчивых многообразий критиче-
критических элементов (особых точек и периодических траекторий) долж-
должны сохраняться при действии любой топологической эквива-
эквивалентности. Поэтому естественно потребовать, чтобы эти пересе-
пересечения были трансверсальны, так как это будет гарантировать,
что они будут устойчивы к малым возмущениям поля.
*) В подобных случаях (когда системы с определенными свойствами
образуют открытое множество) естественно говорить о грубых свойствах
системы; по существу, такая терминология восходит к А. А. Андронову.—
Прим, ред.
§ 1. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ
159
Пример 1. Рассмотрим тор Т2с®?; пусть X=grad/i, где
h — высота точек тора над горизонтальной плоскостью (рис. 1).
Это векторное поле имеет четыре особые точки plt р2, р3, р&
Рис. 1
где pi — сток, рц я р3 — седла и р, — источник. Устойчивое
многообразие точки р2 пересекает неустойчивое многообразие
точки р3 нетрансверсально. Как в гл. 1, малым, возмущением
поля X можно качественно изменить
структуру этого пересечения, так что
полученное поле К не будет эквивалент-
эквивалентно X.
Таким образом, ясно, что поля Мор-
Морса — Смейла следует определить как
подмножество множества полей Купки—
Смейла. На данном этапе необходимо от-
отметить фундаментальный факт, что
принадлежность векторного поля к клас-
классу полей Купки — Смейла не дает ника-
никакой информации об а- и со-предельных
множествах траектории в общем случае.
Поскольку топологическая эквивалент-
эквивалентность между векторными полями сохра-
сохраняет а- и со-предельные множества со-
соответствующих траекторий, то необ-
необходимо наложить некоторые специальные условия на эти пре-
предельные множества.
Пример 2. Рассмотрим векторное поле X, порождающее ир-
иррациональный поток на торе Т2. В этом случае а- и со-предельные
160
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
множества каждой траектории поля X — это весь тор Tz. В част-
частности, X не имеет особых точек и периодических траекторий.
Следовательно, X — это поле Купки — Смейла. Тем не менее X
не является грубым, поскольку оно может быть приближено по-
полем Y, порождающим рациональный поток (см. § 4 гл. 1). Все
траектории поля Y периодические, и поэтому структуры пре-
предельных множеств полей X и Y совершенно различны.
Для определения полей Морса — Смейла необходимо допол-
дополнительно ввести некоторые новые понятия и обозначения.
Пусть X ??Г(М). Рассмотрим множества La (X) = {р 6 М:
р€а(Я) Для некоторого q^M\ и LfJ)(X) = {р?М: р€а(ч) для
некоторого q?M\. Эти множества инвариантны под действием
потока, порожденного X, и траектория каждой точки «рож-
«рождается» в La и «умирает» в La.
Определение. Пусть Х?2ИГ(М). Будем говорить, что р?М —
блуждающая точка для X, если существуют такая окрестность
V точки р и такое число t0 > 0, что Xt (V) (] V— 0 при 111 > t0.
В противном случае точка р—неблуждающая.
Множество неблуждающих точек для X будем обозначать
через О(Х). Следующие свойства вытекают непосредственно из
определения:
(a) ?1(Х) компактно и инвариантно под действием потока, по-
порожденного полем X;
(b) ?l(X)^)La(X)[jLa(X). В частности, Q(X) содержит крити-
критические элементы поля X;
(c) если X, Y??r{M) и h: M—>-M—топологическая эквива-
эквивалентность между X и Y, то h(Q(X)) = Q(Y).
Следующий пример показывает, что, вообще говоря, Q
строго содержит La{]La.
Пример 3. Рассмотрим О-векторное поле X на S2 с двумя
особыми точками, у которого все остальные траектории перио-
периодические (рис. 3). Умножим поле X на неотрицательную
С^-функцию ф! S2 —* К, которая обращается в нуль в одной
$ «. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА: ГРУБОСТЬ
161
лишь точке р, отличной от pt и р-%. Пусть У = фХ. Сш-поле Y
имеет три особые точки рь р2 и р, а все траектории периоди-
периодические, за исключением одной траектории у, у которой а(у) =
z=zw{y) = p. Никакая точка х из у не принадлежит La[jLmj
но x?Q, поскольку в любой ее окрестности находятся точки,
принадлежащие периодическим траекториям поля Y (рис. 4).
Определение. Пусть М—компактное многообразие размерности
п и Х^ЖГ(М). X называется векторным полем Морса —
Смейла, если:
A) X имеет конечное число критических элементов (особых точек
и периодических траекторий) и все они гиперболические;
B) если ot и о2—критические элементы поля X, то Ws(ot)
трансверсально к Wa(a2);
C) Q(X) совпадает с объединением критических элементов
поля X.
Теперь мы дадим несколько примеров полей Морса — Смейла.
В примерах 4, 5, 6 и 7 это будут поля на S2, а в примерах 8 и 9 —
на Т2. Критический элемент называется
притягивающим (аттрактором) или от-
отталкивающим (репеллером), если его ин-
индекс является максимально возможным
или соответственно равен нулю *). В про-
противном случае он называется седлом.
Пример 4. Полем, соединяющим север-
северный и южный полюсы, называется всякое
векторное поле на S2 со следующими свой-
свойствами:
Pn, Ps — гиперболические особые точ-
точки; pn—притягивающая особая точка,
a ps — отталкивающая; если х?52\
{Pn, Psh то a(x) = pN и a(x) = ps-
Пример 5 (рис. 6). Полюса pN, ps являются гиперболиче-
гиперболическими отталкивающими особыми точками, у — гиперболическая
притягивающая замкнутая траектория, и если х? S2s\{pN, ps, у},
то и(л:)=у, а а(х)=рк или ps.
Пример 6 (рис. 7). Особые точки pit p% — гиперболические
притягивающие, а ги г2 — гиперболические отталкивающие,
s1? s2 — гиперболические седла, и Q(X)={pit p2, rit r2, slt sj.
1) В общем случае эти понятия определяются так, как в примечании
на стр. 52. Для гиперболических критических элементов, только о кото-
которыми мы сейчас и имеем дело, определение может быть перефразировано
так, как сделано в тексте,— Прим. ред.
6 Я» 61
Рис. 10
§ 1. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ 163
Пример 7 (рис. 8). Особые точки ru r2, rs — гиперболические
отталкивающие, s — гиперболическое седло, уи у2 — гипербо-
гиперболические притягивающие замкнутые траектории, и ?1(Х)=
— {ги г2, rs, s}UYiUY2- На рис. 9 показаны траектории поля
на цилиндре, ограниченном Yi и Y2-
Пример 8 (рис. 10). Особая точка р — гиперболическая
притягивающая, а г — отталкивающая, st, s2 — гиперболиче-
гиперболические седла, и Q{X)={p, г, su s2}.
Пример 9 (рис. 11). Замкнутая траектория Yi — гиперболи-
гиперболическая притягивающая, у2 — отталкивающая, и ?2(X)=YiUY2-
Множество полей Морса — Смейла будем обозначать через
М — S. Следующее предложение дает простую характеризацию
полей Морса — Смейла на двумерных многообразиях. Траекто-
Траекторией, соединяющей седла г), называется такая траектория, что ее
а- и а)-предельные множества являются седлами.
1.1. Предложение. Пусть М—компактное многообразие раз-
размерности 2. Х??Г(М) является полем Морса—Смейла тогда
и только тогда, когда:
(a) X имеет конечное число критических элементов и все они
гиперболические;
(b) не существует траекторий, соединяющих седла;
(c) каждая траектория имеет единственный критический эле-
элемент в качестве своего а-предельного множества и единствен-
единственный критический элемент в качестве своего ^-предельного
множества.
Доказательство. Ясно, что если XgM—S, то X удовле-
удовлетворяет условиям (а), (Ь), (с), приведенным выше. Докажем
обратное. Возьмем X ? ?r (M), удовлетворяющее (а), (Ь), (с).
Так как устойчивое многообразие стока и неустойчивое мно-
многообразие источника двумерны, то условие трансверсальности
пересечения могло бы нарушиться лишь для устойчивых и
неустойчивых многообразий седел. Но этого не может прои-
произойти вследствие отсутствия траекторий, соединяющих седла.
Таким образом, достаточно доказать, что Q (X) состоит из кри-
критических элементов.
Вначале покажем, что устойчивое многообразие стока со-
состоит из блуждающих точек, за исключением самого стока.
Предположим, что сток—это особая точка р. Как мы уже
видели, существует диск DczWs(p), содержащий р, границей
которого является окружность С, трансверсальная к X. По-
Поскольку Ws (р)\{р} = U< 6 R Xt (С) и множество блуждающих
точек инвариантно, то достаточно показать, что все точки ок-
1) А также сепаратрисой, идущей из седла в седло.— Прим. ред,
6*
164
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
ружности С—блуждающие. Рассмотрим диски Dx = X1(D), со-
содержащийся во внутренности диска D, и D_, = X_,(D), вну-
внутренность которого содержит D. Возьмем точку х € С. Пусть
V—некоторая окрестность точки х, не пересекающаяся с Dt
и M\D_1. Тогда Xt (V) t)V = 0 при | /1 > 2. Эгим доказано,
что х—блуждающая. Предположим теперь, что стоком является
периодическая траектория у. В этом случае также существует
окрестность U траектории у, граница которой 5 трансверсальна
к полю X. Если у расположена на U двустороние, го U го-
меоморфно кольцу, a S—дизъюнктному объединению двух
окружностей. В противном случае U гомеоморфно листу Мё-
Мёбиуса, a S—окружности. Кроме того, Ws (-у)\у = U, 6 R Xt (S).
Так же как и раньше, можно доказать, что 5, а следовательно,
и №^(у)\Т> состоят из блуждающих точек. Аналогично если
о—отталкивающий критический элемент, то Wu {o)\a также
состоит из блуждающих точек И наконец, если х 6 М. не яв-
является особой точкой и не принадлежит периодической траек-
траектории, то либо а(х)—отталкивающий критический элемент,
либо со (х) — притягивающий критический элемент, либо и то
и другое, гак как не существует траекторий, соединяющих
седла. Поэтому х—блуждающая точка, и доказательство тем
самым завершено. I
Пример 10. Полярные поля на кренделе.
Мы приведем несколько примеров полярных полей Морса —
Смейла на кренделе, т. е. векторных полей Морса — Смейла без
а
--г*-
/-Т
ь-л
с -
-7-1
Рис. 12
периодических траектории и имеющих лишь один сток и один
источник. Крендель (или сфера с двумя ручками, или «тор с дву-
двумя дырами») может быть представлен 159] восьмиугольником,
ребра которого попарно отождествлены таким образом, что:
A) два отождествляемых ребра не имеют общей вершины;
B) диффеоморфизм, отождествляющий два ребра, обращает ори-
ориентацию;
§ I. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ
165
C) в результате склеивания сторон все вершины отождествля-
отождествляются в одну точку.
На рис. 12 крендель представлен двумя различными спосо-
способами.
Если задано представление кренделя в виде восьмиугольника,
то можно построить полярное поле Морса — Смейла, поместив
источник в центр восьмиугольника, седло в середину каждого
ребра и сток в вершины. На рис. 13 мы изобразили поля Мор-
19,
У)
.X'
X.
К)
,/4
Рис. 13
са — Смейла на кренделе, соответствующие заданным представ-
представлениям. Обратно, пусть X — полярное поле Морса — Смейла
на кренделе. Разрезав крендель вдоль неустойчивых много-
многообразий седел, мы получим поле, описанное выше.
Аналогично можно построить полярные поля Морса — Смейла
на любом компактном двумерном многообразии.
Определение. Для заданного векторного поля X Морса—Смейла
определим фазовую диаграмму Г поля X как множество кри-
критических элементов со следующим частичным упорядочением:
для аи о2 ? Г считаем, что о, ^ о2, если Wa (ог) n ws (o2) Ф 0,
т. е. если существует траектория, которая идет из о, в о2.
Отношение ^ является частичным порядком, так как не
существует траекторий, соединяющих седла. Следует также от-
отметить, что поскольку dim M=2, то фазовая диаграмма всякого
поля Морса — Смейла имеет, самое большее, три уровня.
Примеры. Фазовые диаграммы примеров 4—9 этого парагра-
параграфа показаны на рис. 14 х).
Определение. Пусть X, X ? М—S и Г, Г — их фазовые диа-
диаграммы. Будем говорить, что Г и Г изоморфны, если сущест-
существует такое взаимно однозначное отображение h: Г —¦¦ Г, что:
г) Фазовая диаграмма рассматривается как некое абстрактное частично
упорядоченное множество, и соответственно на рисунке ее элементы изобра-
изображаются точками, хотя сам по себе такой элемент может быть замкнутой
кривой.— Прим. ред.
166
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
(a) х?Т—особая точка тогда и только тогда, когда h(x)?T —
особая точка;
(b) если хл, х2$Г, то xt^.x2 тогда и только тогда, когда
h()^h{)
Рис. 14
Мы собираемся показать, что при малом возмущении поля
Морса — Смейла получаются поля Морса — Смейла с изоморф-
изоморфными фазовыми диаграммами. Для этого мы воспользуемся
понятием фильтрации, ассоциированной с полем Морса — Смей-
Смейла. Заметим, что это понятие может быть с пользой применимо
к более общим векторным полям [14], [109].
Определение. Пусть XgM—S. Фильтрацией лап X называется
такая последовательность Мо= 0, MtczM2c ... <zMh = M ком-
компактных подмногообразий М, (с границами при 0 < i < k), что:
(a) X трансверсально к границе многообразий М{ и Xt(M{)c
с int M[ при t> 0;
(b) в Mt+l \ int (Mt) максимальным инвариантным подмноже-
подмножеством потока Xt является один критический элемент ot+it
иными словами, r\t6RXt(Mt+1\mtM{) = o{+1.
1.2. Лемма. Пусть Х?Х.Г (М2)—поле Морса—Смейла. Тогда
существует фильтрация, ассоциированная с X.
Доказательство. Пусть alt о2, ..., ау-—притягивающие кри-
критические элементы поля X. Выберем их непересекающиеся
окрестности Vlt V2, ..., Vj с границами, трансверсальными
К X, как и в доказательстве предложения 1.1. Положим M1 = Vi,
§ 1. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ
16?
M2 = MtuV2, .... Af/ = 7H/_1UV/. Пусть o/+i, .... as—седла
поля X. Рассмотрим а/+1 и компоненты множества Wa(oJ+1)\p/+i
(которое пересекает dMf трансверсально). В окрестности
точки а/+1 построим два сечения St и S2, трансверсальные
к Ws (oJ+i) \ оу+1. Если эта окрестность достаточно мала, то
траектории поля X, проходящие через концевые точки сечений
St и S2, пересекают dMf трансверсально1). Вблизи этих дуг
траекторий построим трансверсальные к X кривые с,, са, с„
Рис. 16
и с4, соединяющие концевые точки сечений S± и S2 с
Эти кривые можно построить таким образом, чтобы они каса-
касались подмногообразий Slt 5a и дМу. Это можно сделать, исполь-
используя трубки тока, как это показано на рис. 16.
Пусть У/+1Э°/+1—область, ограниченная кривыми Slt S2, clt
са, с3, с4 и частью дМf. Положим, что M/+l = M} U V/+1. Легко
проверить, что П(ек^<(^/+1) = о/+1 и что M/+i удовлетворяет
требуемым условиям. Повторяя конструкцию для каждого седла,
получим последовательность подмногообразий 0 = МоаМ1с:...
... сМ,+1с... сА{5. Пусть, наконец, as+i, ..., ок—источники
поля X. Как и в случае стоков, рассмотрим окрестности
Vs+1, Vs+2, .... Vk этих источников, границы которых транс-
версальны полю X. Положим
лС = М\(intvZU ... U intVh)
и т. д. до Mh = M. Легко проверить, что 0 — МосМ1а..^
...сМк—фильтрация для X. |
х) Они идут сперва близко к W*(oy+i) (приближаясь к <ty+i)i затец
(удаляясь от Oj+1 и приближаясь к dMj) вдоль Wu{Oj+{jt—upuM. ред.
168
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Следующие две теоремы имеют место и в высших размерностях
[75], [79]. Мы приспособили их доказательства к намного более
простому двумерному случаю.
1.3. Теорема. Пусть XgM—S. Тогда существует такая окре-
окрестность И поля X в ?Г(М2), что если Y ?41, то У?М—S
и его фазовая диаграмма изо-
изоморфна диаграмме поля X.
Доказательство. Так как
критически элементы поля X
гиперболические, то для каждо-
каждого a,- g Q (X) существуют такие
окрестности (Ulc.3iT(Mi) поля
X и U, элемента о{, что всякое
У ? I^i имеет единственный кри-
критический элемент ot(Y)c:U{.
Более того, по теореме Гробма-
на—Хартмана можно считать,
уменьшая в случае необходи-
необходимости окрестности 4L{, U{, что
о, (У) является единственным ин-
инвариантным под действием по-
потока Yt множеством, целиком
принадлежащим Ut. Положим
Рис> 17 И = П; "U-t- Рассмотрим фильт-
фильтрацию 0 = 7Иос=М1с:Л12с:...
.. .сМк — М для X. Мы покажем, что при достаточно малом
% последовательность 0 = Мо с М1 а ... а Мк == М является
также фильтрацией для любого У 611. Из этого будет следо-
Рис. 18
вать, что Q(Y) состоит из определенных выше критических
элементов ot(Y). Прежде всего заметим, что поскольку X
трансверсально к компактному множеству dMt, то это же
верно и для достаточно близкого к X поля Y. Уменьшим
теперь окрестности U{ таким образом, чтобы UlcMt\Mi_x.
Поскольку f\t 6 r Xt (Mt \ int M(_ x) == ot, то существует такое
§ I. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ 169
Т > О, ЧТО
Такое же включение выполнено и для всех У(?41, если %
достаточно малая. Поскольку (~)t e R.Yt (U{) = a{ (У), то отсюда
следует, что
nFt(M{\int7Hi_i)=ai(F).
Поэтому 0 = М0 с М j с ... с: МА = М—фильтрация для всех
Y?4L. Мы утверждаем, что al(Y)=Q{Y)r\(Mi\intMi_1). Дей-
Действительно, всякая отличная от сг,(У) траектория у, прохо-
проходящая через точку из М{\intMt_i, должна пересечь дМ{
или дМ(_г (или и то и другое), так как единственная траек-
траектория, целиком содержащаяся в M/\intM/_1,— это о,(У).
Поскольку YfiMt^cMt^ при <>0и Yt(M \M,)cM \Mt
при t < 0, то у—блуждающая траектория. Таким образом,
о{ (Y)—это единственная траектория из Q(F) в Aft\int М{_4.
Таким образом, Q (Y) = U/°f {У) и точка o{(Y)—гиперболичес-
o{(Y)—гиперболическая при всех /.
Чтобы заключить, что У?%—поле Морса—Смейла, доста-
достаточно показать, что при достаточно малом % не существует
траекторий поля Y, соединяющих седла. Пусть ot = o{(X) —
седло, и предположим, что некоторая компонента у множества
Wa(oi)\ol имеет сток а = о{Х) в качестве своего ю-предель-
ного множества. Пусть V—окрестность точки о, такая же, как
и в конструкции фильтрации. Так как компактные части мно-
множества W" (а, (У)) близки к Wa (а,), то некоторая компонента
множества W"(o{(Y))\at(Y) также пересекает 3V трансвер-
сально. Поэтому ее ю-предельное множество—это o(Y). Ана-
Аналогичные соображения применимы ко всем компонентам устой-
устойчивых и неустойчивых многообразий седел. Таким образом,
при достаточно малом 11, если У?41, то У^М—S и заданное
выше соответствие ot (X) t—> at (У) является изоморфизмом фазо-
фазовых диаграмм. Теорема доказана. |
1.4. Теорема. Если Х??г(Мг) — поле Морса—Смейла, то X
грубо.
Доказательство. Из предыдущей теоремы известно, что суще-
существует такая окрестность % а 2сг {М%) поля X, что если Y^it,
то У^М—S и существует изоморфизм ol(X)*-^-ot(Y) фазовых
диаграмм.
Часть 1. Предположим сначала, что X не имеет замкнутых
траекторий. Рассмотрим сток о поля X и соответствующий
сток о(Y), где Y^H. Пусть V, как и раньше,— такой диск
170
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
в Ws(o), содержащий о, что dV трансверсально к X и ко всем
Y^il. Кроме того, o{Y)?VczWs(a(Y)). Пусть at, o2,...— такие
седла поля X, что о, =^.о, а ри р2,...— те точки, в которых
неустойчивые сепаратрисы седел ot (т. е. компоненты связности
множества №в(<Х{)\а,) пересекают dV. Пусть далее Pi{Y),
p2{Y),...— соответствующие точки для поля Y. Для каждого
о{ рассмотрим сечения St, S{, которые трансверсальны к устой-
устойчивым сепаратрисам точки а, и проходят через точки qt, q{,
как показано на рис. 20.
Рис. 19
Рис, 20
Действуя потоком Xt на сечения S{, S{, получим, как в § 7
гл. 2, трубчатое семейство для W" (ot). Слоями этого семейства
являются множества Xt (S{) и Xt (St) при всех / 6 R, а также
множество Wa (ot). Проекция лг, которая каждому слою / ста-
ставит в соответствие точку / П Ws (ot), является непрерывной.
Кроме того, ограничение п{ на некоторую окрестность /t точки
pt в dV является гомеоморфизмом It на некоторую окрестность
точки о{ в Ws(a{) (l4). Выполним то же построение для поля Y1).
Теперь начнем определять топологическую эквивалентность h
между X и Y. Положим h (о) = о (Y), ft(a,) = a, (F), h(pt) =
«=/»«(V). M<7t)-<7fOO и h{q,) = q,{Y). Продолжим h на W*{ot)
посредством равенств
hXt (qt) = Yth (qt) = Ytqt (Y), hXt (qt) = Ytq, (F).
Далее определим h на /, следующим образом: при х?/{
hx=[nt(Y)\[t]-1hntx.
х) Здесь нужен вариант Л-леммы (§ 7 гл. 2), который относится сразу
ко всем динамическим системам, близким к данной, и заключение которого
включает определенную равномерность по этим системам. Просматривая
с этой точки зрения рассуждения из § 7 гл. 2, нетрудно убедиться, что
они доказывают такой вариант,— Прим. ред.
§ 1. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ
m
Таким образом, h определено на конечном числе попарно не-
непересекающихся интервалов lt в 6V. Заметим, что если окре-
окрестность 4L поля X достаточно мала, то h\It близко к тожде-
тождественному отображению. Поэтому можно продолжить h на всю
окружность DV. Повторим ту же конструкцию для всех сто-
стоков г). Наконец, определим h на всем М2 с помощью уравнения
Рис. 21
Рис. 22
hXtz = Ythz. Из построения легко видеть, что h имеет обрат-
обратное отображение А~\ которое может быть определено анало-
аналогично h, если поменять ролями X и Y.
Таким образом, остается доказать непрерывность h. Она
очевидна в стоках, источниках и на устойчивых многообразиях
1) Если не существует седла а,- с о,- < о, то определим h \dV как, ска-
скажем, тождественное преобразование. Кроме того, определим очевидным обра-
образом h для источников. Теперь h определено во всех особых точках, устой-
устойчивых многообразиях седел и на окружностях dV, транснерсальных к полю
и окружающих стоки,— Прим. ред.
172
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
стоков '). Мы проанализируем случай устойчивых многообразий
седел. Возьмем x€Ws(O[), где о,-—седло. Вспомним, что h
переводит слои трубчатого семейства для ot в слои трубчатого
семейства для a,(F), иными словами, л,- (Y) hz = hnt (X) г2).
Рассмотрим любую последовательность хп —¦* х. Мы хотим
показать, что hxn —>¦ hx. В соответствии со сделанным выше
замечанием слой, проходящий через hxn, приближается к слою,
\
Рис. 23
проходящему через /ис. Иными словами, nt (Y) hxn —*• ftx. Остается
показать, что Лх„ неограниченно приближается к Ws(al(Y)).
Для этого мы построим трубчатые семейства для Ws(oi) и
и Ws (ot {Y)). Это можно сделать, выбрав сегменты Ih It (Y) в dV
и подействовав на них соответственно потоками Xt и Yt. Так
как h(It) = It(Y), то ясно, что ft переводит слои трубча-
трубчатого семейства для Ws (o() в слои трубчатого семейства для
Ws (a{ (Y)). Таким образом, если через nt и л,- (Y) обозначить
проекции соответственно на Wu (cf) и Wa (at (Y)), то hnl (г) =
— nt (Y) h (г). Поскольку nt непрерывно и xn —> x ? Ws (a{), то
*) Непрерывность в источниках не совсем очевидна. Если К'—неболь-
К'—небольшой диск, содержащий источник о' и имеющий границу dV', трансверсаль-
ную к полю, а седла о,-^о', то нужно проверить непрерывность в точках
Ws (O{)[)dV- Но это частный случай нопрсса о непрерывности в точках
Ws (о,-), обсуждаемого далее в тексте.— Прим. ред.
2) На каждой траектории поля X (кроме «входящих» сепаратрис, т. е.
компонент Ws (О/У\а/), проходящей через трубчатое семейство, имеется
точка z^V; для нее по построению л; {у)кг=кщ(Х) г. Для других точек
той же траектории аналогичное равенстно следует из того, что hXt — Yfh
и что ni(Y)Yt=Ytni(Y), itiXt = Xtni, пока соответствующие композиции
отображений определены,— Прим ред.
$ 1. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ
173
П{Хп —»¦ nlx = ol. Кроме того, так как ограничение отображе-
отображения h на Wa (с,) непрерывно, то h (п,хп) —* h (с,) = at (Y). С дру-
другой стороны, h(nl(xn)) — nl(Y)h(xn), и поэтому п? (Y) h (хп) —»-
—yot(Y). Это показывает, что h\xn) неограниченно прибли-
приближается к устойчивому многообразию точки ot(Y) и, следова-
следовательно, h (хп) —»¦ h (x). Доказательство для случая, когда X не
имеет периодических траекторий, завершено.
-—
i
\
"
Рис. 24
Часть 2. Предположим теперь, что X имеет периодические
траектории. Эти периодические траектории обязаны быть либо
притягивающими, либо отталкивающими, поскольку они ги-
гиперболические, a dim M=2. Как мы уже отмечали, существуют
сколь угодно близкие к X поля Y, такие что Xt и Yt не сопря-
сопряжены. Чтобы получить такое поле, достаточно посредством ма-
малого возмущения изменить период одной из периодических
траекторий поля X. Мы избежим этой трудности, определив со-
сопряжение h между потоками Xt и Yt, которые отличаются от
потоков Xt и Yt соответственно лишь другой параметризацией.
Поскольку траектории полей X п X совпадают, так же как и
траектории полей Y и Y, то отсюда будет следовать, что h опре-
определяет топологическую эквивалентность полей X и Y.
Пользуясь леммой 1.3 из гл. 3, можно предполагать с самого
начала, что все периодические траектории полей X и Y имеют
один и тот же период т и допускают инвариантное трансверсаль-
ное сечение. Чтобы упростить изложение, рассмотрим два под-
случая.
Bа) Рассмотрим вначале тот случай, когда все периодиче-
периодические траектории притягивающие. Попробуем построить сопря-
сопряжение аналогично части 1. Вокруг каждой притягивающей осо-
особой точки ot, at (Y) рассмотрим окружность Ct, трансверсаль-
174 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
ную к X и Y. Для каждой замкнутой траектории a/t которая
при малом возмущении переходит в замкнутую траекторию о, (Y)
поля Y, возьмем инвариантное трансверсальное сечение ?, и
в нем фундаментальную область /, для ассоциированного
отображения последования*). Построим, как и раньше, неустой-
неустойчивые трубчатые семейства, ассоциированные с седлами ok,
ак (Y) полей X и Y\ возьмем сечения Sk и Sk, трансверсальные
к Ws(ak) и Ws(ok(Y)) соответственно; тогда слоями семейств
будут множества Xt (Sk), Xt (Sk) и Yt (Sk), Y, {Sk). Гомеомор-
Гомеоморфизм, который мы желаем построить, должен переводить каж-
каждый слой трубчатого семейства для oft в слой трубчатого семей-
семейства для ok (Y). Кроме того, он должен сохранять трансвер-
трансверсальные окружности С,- и трансверсальные сечения 2/. Таким
образом, определив сопряжение между X | Ws(ok) и Y\ Ws (ak {Y))
для каждого седла ak, мы автоматически задаем гомеоморфизм
h на конечном числе подынтервалов, принадлежащих С, и /у.
Эти подынтервалы содержат пересечения неустойчивых много-
многообразий седел с С, и /у. Полученный гомеоморфизм близок
к тождественному, если X и Y близки, и, следовательно может
быть продолжен на все С{ и /у2). Для каждой особой точки ot
определим h (с,) = о, (У), а для каждой периодической траекто-
траектории Gj определим к Bу П <*/) — ^/ П °/ (Y). Наконец, продолжим
h на все М, используя уравнение h — YthX_t, как и в первой
части доказательства. Ясно, что h биективно. Непрерывность h
в особых точках и на устойчивых многообразиях седел прове-
проверяется так же, как и в первой части. Непрерывность h в точ-
точках периодических траекторий вытекает из инвариантности
сечений Бу, как мы видели при доказательстве локальной гру-
грубости гиперболических периодических траекторий (см. § 1 гл. 3).
BЬ) Предположим, наконец, что X имеет некоторую при-
притягивающую периодическую траекторию и некоторую отталки-
отталкивающую периодическую траекторию. Этот случай становится
полностью аналогичным предыдущему после новой замены пара-
параметра в потоках Xt и Yt. Эта новая репараметризация позво-
позволит нам продолжить на отталкивающие периодические траекто-
траектории гомеоморфизм, построенный в Bа). Для этого возьмем
трансверсальные инвариантные сечения 2„ ассоциированные
с отталкивающими периодическими траекториями а,, и пусть
х) Ij состоит из двух отрезков. Можно считать, что их концы не по-
попадают на выходящие сепаратрисы седел поля К, стремящиеся к Оу.—
Прим. ред.
2) В последнем случае так, чтобы образом Ij была некоторая фунда-
фундаментальная область I j (Y) отображения последования для поля Y. Если же
для данной замкнутой траект рии о не имеется седел о,- с о,- < о, то просто
отображаем гомеоморфно /у в близкую lj (К).— Прим. ред.
§ 1. ВЕКТОРНЫЕ ПОЛЯ МОРСА — СМЕЙЛА; ГРУБОСТЬ
175
/,—соответствующие фундаментальные области1). Каждая
область 7j разлагается в объединение замкнутых интервалов,
конпы которых, лежащие внутри /,, являются пересечениями
устойчивых многообразий седел с int /",. Заметим, что все внут-
внутренние точки каждого из этих интервалов имеют один и тот же
притягивающий критический элемент в качестве своего со-пре-
дельного множества. Это изображено на рис. 25. Пусть р?
€ Ws(ak) П /,—одна из концевых точек какого-то из этих интер-
интервалов. Рассмотрим такой маленький сегмент [а, Ь]с/,, содер-
Рис. 25
жащий р в качестве своей внутренней точки, что траектория,
проходящая через всякую точку из [а, Ь], пересекает трансвер-
сальное сечение Sk. Используя рассуждения из доказательства
леммы 1.3 гл. 3, видим, что можно так параметризовать поле X,
чтобы все точки сегмента [а, Ь\ достигали Sk за одно и то же
время /=1. Пусть далее X обозначает это по-новому пара-
параметризованное поле. Пусть [a', b']c(a, b)—сегмент, содержа-
содержащий р. Новой репараметризацией можно добиться того, чтобы
все точки из [Xj(a), X,(a')]c:Sft достигали 2, за время i—\.
Аналогично можно уравнять с 1 время движения всех точек
сегмента [Ххф), Х,(&')] до С,. Таким образом, Х2\а, a'}c'ZJ
и X2[b, b']cCt. Повторим это построение для всех седел,
устойчивые многообразия которых пересекают /,. Наконец,
параметризуем X таким образом, чтобы все точки из /,, не
1) Выбранные так, чтобы концы составляющих f, двух интервалов 7J,
\1 це попадали на W* (о^) с о/ Зг ог,— Прим. ред.
176 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
принадлежащие объединению интервалов типа [а, Ь\, достигали
соответствующих им сечений С, и Е, за одно и то же время
* = 2. (Ч)
Мы произведем такую же репараметризацию для всех близ-
близких к X полей Y. Сопряжение h между Xt и Yt строится
теперь аналогично случаю Bа) с использованием одного допол-
дополнительного требования; h(l.lr\o[) = Illf\al{Y). |
Когда у X нет особых точек, эту конструкцию надо слегка
изменить. Мы не будем требовать, чтобы все точки из 7, до-
достигали С, или 2^ за постоянное время, скажем за время t = 2.
Вместо этого определим гомеоморфизм h\ lt —* 7, (Y) и репа-
репараметризацию поля Y таким образом, чтобы при x^~It точка
Yt (h (x)) попадала бы в С{ или Еу в тот же момент времени,
когда Xt(x) попадает в Сг или Е/.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА
НА ОРИЕНТИРУЕМЫХ ПОВЕРХНОСТЯХ
В этом параграфе мы покажем, что М — S плотно в ?Г(М2)
для ориентируемой поверхности М2. Использование теоремы
Купки — Смейла позволит нам несколько упростить оригиналь-
оригинальное доказательство Пейксото [81], хотя следует отметить, что
работа Пейксото появилась раньше и послужила своего рода
мотивировкой для георемы Купки — Смейла. В § 3 анализи-
анализируется случай неориентируемого многообразия М2, а в § 4 об-
обсуждаются соответствующие результаты для диффеоморфизмов.
Мы начнем этот параграф с доказательства теоремы о плот-
плотности для еферы S2. Этот случай значительно проще общего,
но хорошо иллюстрирует его.
Определение. Пусть у—траектория поля Х?ЖГ(М). Будем
говорить, что у рекуррентная, если со(у)зу или «(у)зу1).
Критический элемент поля X является всегда рекуррентной
траекторией. В этом елучае будем говорить, что рекуррентная
траектория тривиальная. Всякая траектория иррационального
потока на торе является рекуррентной и нетривиальной.
По теореме Пуанкаре—Бендиксона каждая рекуррентная
траектория векторного поля X^3cr(S2) тривиальная. Этот факт
значительно упрощает доказательство плотности множества
М—S в ^(S2).
2.1. Теорема. Если Xg3ir(S2)—векторное поле Купки—Смейла,
то X—поле Морса—Смейла.
1) См, примечание к упр. 21 гл. 1.— Прим. ре§.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА 177
Доказательство. Поскольку X — поле Купки — Смейла, то
оно имеет лишь конечное число особых точек и все они гипербо-
гиперболические. По теореме Пуанкаре — Бендиксона со- и а-предель-
ные множества каждой траектории являются особыми точками
или периодическими траекториями. Действительно, если бы
предельное множество какой-нибудь траектории у содержало
более одной особой точки, то эти точки были бы седлами, а, зна-
значит, о (у) содержало бы регулярную траекторию, соединяющую
седла. Но X не имеет таких траекторий, так как X — поле
Купки — Смейла. Это доказывает высказанное выше утверж-
утверждение. Периодические траектории поля X являются гиперболи-
гиперболическими притягивающими или отталкивающими, поэтому ос-
остается лишь доказать, что их конечное число. Рассуждая от
противного, предположим, что X имеет бесконечное число пе-
периодических траекторий. Пусть х±, дс2> • • • . *п> • • •— последо-
последовательность точек, принадлежащих различным периодическим
траекториям. Переходя к подпоследовательности, можно счи-
считать, что хп сходится к некоторой точке х ? S2. Ясно, что со(х) —
седло, поскольку уетойчивое многообразие притягивающего
критического элемента не может содержать периодической тра-
траектории. Аналогично, а {х) — седло. Поэтому сама точка х
является седлом, так как в противном случае ее траектория была
бы траекторией, соединяющей седла. С другой стороны, опять-
таки в силу отсутствия траекторий, соединяющих седла, со-пре-
дельные множества неустойчивых сепаратрис точки х являются
стоками. Но это приводит к противоречию, поскольку траекто-
траектория всякой точки, которая достаточно близка к седлу х, но не
лежит на его устойчивых сепаратрисах, имеет один из этих сто-
стоков в качестве своего со-предельного множества. Таким образом,
х не принадлежит замыканию множества точек, траектории ко-
которых периодические. Теорема доказана. I
Так как множество полей Купки — Смейла плотно в Зсг(М),
то мы получаем
Следствие. М—S плотно в ?r(S2). |
Мы перенесем на общий случай ориентируемой поверхности
основные этапы изложенного доказательства. При этом, однако,
возникнут дополнительные трудности, связанные с существо-
существованием нетривиальных рекуррентных траекторий. Иррациональ-
Иррациональный поток на торе доставляет простейший пример нетривиальных
рекуррентных траекторий. Мы предлагаем читателю попробо-
попробовать самостоятельно доказать, что векторное поле, порождающее
иррациональный поток, может быть аппроксимировано полями
Морса — Смейла. Рассмотрим некоторые примеры векторных
полей, которые имеют нетривиальные рекуррентные траекто-
траектории, на других двумерных многообразиях.
178
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Пример 11. Построим такое векторное поле на кренделе
(т. е. на сфере с двумя ручками). Обобщение предлагаемой
конструкции позволяет получить примеры векторных полей,
имеющих нетривиальные рекуррентные траектории, и на сфе-
сферах с г ручками при г > 2. Пусть X: R3—>-R3—отражение
Рис. 26
Рис. 27
относительно плоскости \хя = 0\, иными словами, %{xuxs, xs)=
= (х„ х2, —х3). Рассмотрим тор Т2, вложенный в R8 таким обра-
образом, что Х(Т*) = Т2 и T*n{xi xK = 0\ является объединением
двух окружностей.
Пусть X—градиентное поле высоты, измеряемой относи-
относительно плоскости \ха — 0\. Ясно, что X— симметричное поле,
т. е. Х^Х = — X. Особыми точками поля X являются седла
h и &g, источник г и сток с, как показано на рис. 26. Рае-
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА j?g
смотрим окружность С^Т2, которая ортогональна полю X и
ограничивает диск Dlt содержащий сток. Пусть С2 = кС1. Тогда
?J = M^i)—Диск с границей С2. Вследствие симметричности
поля траектория, проходящая через всякую точку р € С2 (не
лежащую на сепаратрисе сёдла), пересекает С, в точке q = к (р).
Пусть h: Cj—*• С2—диффеоморфизм, определяемый форму-
формулой h = Ra°h, где Ra— иррациональное вращение окружно-
окружности С2. Рассмотрим на T2\(Dl (J D2) отношение эквивалентно-
эквивалентности, отождествляющее С1 и С2 посредством h. Пусть М—фак-
тормногообразие и Р: T2\(D, (J D2) —* М — каноническая
проекция. Пусть Y = PmX. Ясно, что М диффеоморфно крен-
кренделю. Кроме того, все траектории поля Y плотны в УМ, за
исключением седел st и s2 (расположенных соответственно ниже
и выше плоскости х3 = 0) и неустойчивой сепаратрисы точки
s, 1). Действительно, все остальные траектории пересекают
Р (С2), так что достаточно показать, чго пересечение каждой
траектории с Р(С2) плотно в Р(С2). Пусть р?Р(С2); возьмем
такую точку q?C2, что P(q) = p. Траектория поля X, прохо-
проходящая через q, пересекает С1 в точке k(q), но эта точка
отождествлена с hh(q) — Ra(q). Таким образом, положительная
полутраектория точки р впервые пересекает Р (С2) в точке
PRa (я)- По индукции получаем, что положительная полутраек-
полутраектория точки р в я-й раз пересекает Р(С2) в точке PRa{q)-
Поскольку а иррационально, то множество \R?,(q): п?Щ
плотно в Cj. Это показывает, что положительная полутраек-
полутраектория точки р плотна в Р(С2) и, следовательно, плотна в
кренделе2).
Пример 12. Теперь мы опишем С"°-векторное поле X на крен-
кренделе со следующими свойствами:
(a) X — поле Купки—Смейла;
(b) X имеет только две особые точки, являющиеся седлами;
(c) каждая регулярная траектория плотна в кренделе8).
В лемме 2.5 этого параграфа будет показано, что X можно
аппроксимировать векторным полем, содержащим траекторию,
соединяющую седла. (Этот факт можно проверить непосредст-
непосредственно.) Следовательно, множество полей Купки—Смейла не
является открытым на кренделе. Аналогичные примеры можно
1) Точнее, в кренделе не плотны только следующие полутраектории:
Sf, s2, полутраектории (положительные и отрицательные) точек из Wa (s^)=
=WS (s2), положительные полутраектории точек из Ws (s{), отрицательные
полутраектории точек из Wa(s2).—Прим. ред.
2) По-видимому, впервые данный пример опубликовал А. А. Блохин,
описавший его несколько иначе [129].— Прим. ред.
s) Точнее, плотна каждая положительная (отрицательная) полутраек-
полутраектория, которая не является ни седлом, ни устойчивой (неустойчивой) сепа-*
ратрисой седла,— Прим. ред.
180
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
построить на сфере с k ручками при любом k ;> 2. Мы начнем
построение с поля Морса—Смейла Y на торе, которое имеет
один сток, один источник и два седла. Вырежем по диску
вокруг стока и источника и затем отождествим границы этих
дисков посредством подходящего диффеоморфизма. Эта опера-
операция эквивалентна приклеиванию ручки к тору Т2. Пусть л:
(?2 __,. 72 обозначает каноническую проекцию. Вначале опишем
поле У на R2, а затем рассмотрим поле Y — n^Y- Для того
Рис. 28
чтобы можно было спроектировать У в поле на Т2, потребуем
выполнения следующего условия: Y(x) — Y(y), если координаты
точек х, у € К2 различаются лишь на целые числа. Поэтому
достаточно определить У на квадрате в R2 с вершинами @, 0),
A, 0), A, 1) и @, 1). Поместим источник поля У в точку
A/2, 1/2), сток —в начало координат и седла—в точки @, 1/2)
и A/2, 0). Пусть С г и С2—окружности радиуса б< 1/4 вокруг
источника и стока соответственно, как показано на рис. 28 ').
х) Из рис. 28 видно также, что устойчивые многообразия этих седел
должны лежать на прямых у =1/2 и дг=1/2, а неустойчивые—на осях у
и х. Потребуем еще, чтобы в маленьких квадратиках, на которые сепарат-
сепаратрисы разбивают плоскость, траектории (как линии без учета направления
движения по ним) были симметричны относительно диагоналей, соединяю-
соединяющих седла,— это обеспечит нужные сеойствэ отображений ф,- ниже. Нако-
Наконец, возле окружностей Q поле Y пусть будет направлено строго по ра-
радиусам этих окружностей (наружу или внутрь) и его векторы пусть будут
иметь одну и ту же длину—это обеспечит, что после производимых отож-
отождествлений на кренделе получится поле класса С".
Дуга С/, состоящая из точек с угловыми координатами из (а. В), обо-
обозначается ниже просто через (а, Р).— Прим. ред.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА ^ СМЕЙЛА
181
Если сс€@, зх/2)сгС1, то положительная траектория точки а
пересекает С2 в точке ф, (а). Таким образом получается диф-
диффеоморфизм фх- @, зх^сС! —(—л, —л/2). Аналогично опре-
определяем ф2: (л/2, л) —(—л/2,0), Фз: (л, Зл/2)->(—2л, — Зл/2)
и ф4: (Зл/2, 2л)—>(—Зл/2, —л).
Построив симметричное поле У, будем иметь ф,(а) =
= —а—л/2, если i = l, 3, и ф,(а) =— а-\-п/2, если i = 2, 4.
Рис 29
Пусть ф: C2-^Cj—диффеоморфизм ф(а) =— а + е, где в/и
иррационально. Пусть D, и D2—открытые диски, границами
которых являются окружности Сх и С2 соответственно. Мы по-
получим крендель Т2, отождествив посредством диффеоморфизма <р
окружности Cj и С2, которые образуют край многообразия
T2\(Dx{jD2). Пусть X—это поле, порожденное на Т2 полем У
в соответствии со сделанным отождествлением. Иными словами,
X = P,Y, где Р: T*\(Dt U D2)-^ Г2 = ^\(DX U D2)/~— проек-
проекция (рис 29).
Мы покажем, что каждая регулярная траектория поля X
плотна в кренделе. В дальнейших рассуждениях Ct будет обо-
обозначать как окружность С, на торе, так и окружность Р (С,)
на кренделе. Так как всякая регулярная траектория пересе-
пересекает окружность С,, то достаточно показать, что пересечение
любой регулярной траектории с Ct плотно в С,. Пусть D=
=ф"(л/2): i = 0, 1, 2, 3}. Положительная полутраектория
поля X, проходящая через некоторую точку к €СЛ\Г>, впер-
впервые вновь пересечет Сх в точке \J> (к), где ty: С, —>¦ Ct опреде-
182 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
ляется формулой 1)
Пусть 6+ (а) = {i])m (a): m ^ 0} — положительная ¦ф-полутраекто-
рия точки а и 6_ (a) = ]i])m (a): т^О}—ее отрицательная
¦ф-полутраектория. Если Q+{a)f]DФ0, то а принадлежит
устойчивому многообразию некоторого седла поля X, а если
F_ (a)\a) П D Ф 0—то одному из неустойчивых многообра-
многообразий. Если 6+ (а) Г) D = 0 и 6+ (а) плотно в Сг, то положитель-
положительная Х-полутраектория точки а плотна в кренделе Т2. Подоб-
Подобным же образом обстоит дело и с отрицательными t]> и Х-по-
лутраекториями. Мы покажем, что все положительные (и
отрицательные) ф-полутраектории плотны, а следовательно,
таковы и X-траектории. В частности, X является примером
поля с нетривиальными рекуррентными траекториями.
Покажем, что положительные ¦ф-полутраектории плотны в
Сг. Заметим прежде всего, что отображение ч]з биективно, тер-
терпит разрыв лишь в конечном множестве D(=CX и сохраняет
длину отрезков (меру Лебега), т. е. образ интервала длины
L—это конечное объединение интервалов, сумма длин которых
равна L. Мы утверждаем также, что у 1]з нет периодических
точек и что всякая траектория отображения яр имеет с мно-
множеством D не более одной общей точки. Действительно, пусть
х б Сх (соответственно х g D) и пусть m Ф 0—такое целое число,
что tym(x) = x (соответственно ipm(x)^D). Но \J)m (х) = х + те +
-г- nmnl2 для некоторого целого пт, 0 ^ пт ^ 3. Следовательно,
x-\-me-{-nmn/2 —
(или х + me + пял/2 = /л/2, / g Z),
что противоречит иррациональности числа е/л.
Теперь мы покажем, следуя идеям из 145], что если if —
отображение окружности в себя с перечисленными выше свой-
свойствами, то каждая положительная (отрицательная) ¦ф-полутра-
') Если a?D, то положительная полутраектория точки а никогда
больше не попадет на С; если a?<p(Z)), то то же относится к отрицатель-
отрицательной полутраектории. Но можно формально определить ip и в точках D, как
написано в тексте. Для этого tp будет доказано, что каждая его полу-
полутраектория плотна на Сх. Отсюда, очевидно, будет следовать доказываемое
утверждение о полутраекториях потока на кренделе.
Преобразование ч?>—частный случай так называемых перекладываний,
которым посвящен ряд работ помимо использованной авторами работы [45].
См, [137J,— Прим. ред.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА J83i
ектория является плотной. Это есть прямое следствие доказы-
доказываемых ниже предложений A) и B).
A) Если FcCt—такое конечное объединение замкнутых
интервалов, что ¦ty(F) = F, то F^C^. Рассуждая от противного,
предположим, что F=^Clt пусть x(tCt— граничная точка F.
Поскольку \J){F) = F, а ограничение отображения 1]з на Сг\В
является гомеоморфизмом, то из этого следует, что i])^) —
либо граничная точка множества F, либо принадлежит D.
Поэтому существует такое целое положительное k, что»
ty~k(x)?D, поскольку F имеет лишь конечное число гранич-
граничных точек, а у \J) нет периодических точек. Аналогично либо,
¦ф {х) является граничной точкой множества F, либо х g D. Сле-
Следовательно, существует такое неотрицательное целое /, что
Ху1 {х) ? D. Как следствие получаем, что tyk+-/ (у) ? D, где
y = ty~k(x)?D. Но это противоречит одному из перечисленных
выше свойств отображения 1]з. Таким образом, получаем, что.
F = Ct.
B) Если /сС, — замкнутый интервал, то существует такое
положительное целое п, что U"_o vj> ' (/) = Сг. В частности»
6+(д:) плотно при всяком x^Ct. (Утверждение, что положи-
положительная полутраектория точки х попадает в отрезок /, экви-
эквивалентно тому, что x^\J^~'{I).) Доказательство плотности
6_ (х) совершенно аналогично.
Поскольку / при необходимости можно уменьшить, то
можно считать, что / Г) D = 0 и что концы / не лежат на
траекториях точек из D. Пусть B = (dl){j D, где д! означает
границу интервала /. При каждом х € В положим
{ +оо, если if:n(x)(?int/ при всех п> О,
\ tnin{n>0i \))"(д:)€ int/} в противном случае.
п
Можно представить / в виде объединения /= U 1}, где/у —
такие замкнутые интервалы с попарно непересекающимися
внутренностями, что
U 61, = (dl) U {i])P <*> (x)i x 6 В, р (х) <оо}.
Для каждого / положим
Утверждается, что п} конечно. Предположим, что это не так.
Тогда i]rm int Ij П i>~" int If = 0 при всех n, m: 0 <; n < m, ибо в
б б 1тв) it/ it/ /
д ] j П i f р , < ,
противном случае было бы ¦ф~1т~в) int/у n int/у =/=0 и, значит, tij
было бы конечно (ведь int/^сint/). Но множества ty~n\ntIj
184 гл. 4. типичность и грубость векторных полей
не могут быть все попарно непересекающимися, так как длина
каждого из этих множеств (представляющих собой конечное
объединение интервалов—открытых, замкнутых или полуот-
полуоткрытых— плюс еще, может быть, конечное число точек) равна
длине интервала lj. Таким образом, п,- конечно. Проведенное
рассуждение позволяет также заключить, что множества
int/,, ijrMnt/,-, •••. ^'"/""int/,
попарно не пересекаются.
Убедимся, что все эти множества лежат на отрезках, на
которых i]) является гомеоморфизмом, так что эти множества
и i])~"/int/y—открытые интервалы. Для int/у это так (все
int / лежит в таком отрезке). Пусть это так для ijr' int lt
с г = 0, ..., h—1, a i]3~*int/y не лежит в таком отрезке
(ls^u<tty). Последнее возможно только в том случае, когда
¦ф~йint 1/ содержит некоторую точку вида ф(d), d?D. Тогда
^(^it/it/p^^l НбР й1
^(^eyp^X Р() +
то строго внутри Ij лежала бы точка i])P <d) (d), что противоре-
противоречит определению интервалов If (любая точка такого вида
является концом некоторого Ik, \k^k^.n, и потому не может
принадлежать int/,). Значит, f5(d)</i+l. Для x — ^h+1{d)
имеем x^'mt If и 1]3P«o-'1-1 (х) = -фр№ (d)€ int/. Но число
п = h + 1 —р (d) таково, что п > 0 и п < п} (ведь h<tij и
P(d)^l), а в то же время ty~"lj Г) int / Ф 0. Это противоре-
противоречит определению nf.
Далее, мы утверждаем, что ф~п/ int/y-c:/. Действительно,
в противном случае в открытом интервале ф~"/ int If имелась бы
точка х?д1, поскольку ф~"/int/у-П I Ф0- Из определения
числа П] вытекает, что i]/(x)(?/ при 0^г<Пу, a i]/1/ (д:) ле-
лежит в int /у с int/. Так как л:?/?> то «у = Р(д:), а это приво-
приводит к противоречию—\J)P(x)(x) не может лежать строго внутри
Ij по той же причине, по какой это невозможно для i])P (d) (d)
выше.
Положим
.". "Г1
F= U U xb-
и докажем, что ty'^cF, т. е. что -ф^"*int/c= T7 при всех
рассматриваемых k, j.
Проверим сперва, что при наших k, j
за исключением того случая, когда правый конец Ij есть
точка вида ^^(d), d?D и /e = f5(d)— 1. В этом случае
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА 185
Действительно, \J)~ftint/y- с k = 0, ..., п,- суть открытые
интервалы, переходящие друг в друга под действием $ гомео-
морфно и с сохранением ориентации. Пусть г]) к int /,- == (х, у),
k<rij: Тогда
iirMjrMnt/, = г)) (х) U г])"* int /; U ijr1 (у).
Но у любой точки имеется такая правая полуокрестность, на
которой if является гомеоморфизмом, сохраняющим ориента-
ориентацию. Поэтому
г)) Мег])-1!*, у) =^=ТШТ/.
Аналогично и г)) *(«/)(= г)) *(х, у), если у у имеется левая полу-
полуокрестность с таким же свойством. Подобной полуокрестности
нет только в том случае, когда y = ty (d), d?D. Тогда правые
концы i])~'int/y с О^л <С k суть $к~'у—они уже не могут
попасть в D—и, в частности, правый конец интервала int /y-
есть z = tyk+1(d). Он не совпадает с правым концом / (кото-
(который не принадлежит Ц1!3' {D)) и оттого лежит в int /. Значит,
. А если бы было P(d) <&+1, то мы имели бы
,фр (rf)-fc-i (Z) = ,j,p № (J) g int /,
причем 0<&-|-1—P(d)<n^. Но это противоречило бы опре-
определению riji поскольку i]) непрерывно в точках \))~1(z),
0^i<^, то в г]}Р№-*-> int/у имеются точки, сколь угодно
близкие к i|>P<d>-fc-1(z).
В обсуждавшемся сейчас случае, когда &+l=P(d) и т. д.,
z не может быть правым концом / и потому является левым
концом некоторого /й. Покажем, что $(d)^nh. Предположим,
что P(d)—пй>0. Мы уже знаем, что г)) *int/ftcr/, а по-
поскольку i]) всюду непрерывно справа, то
Но \]f"ft(z) = \l)PW-"ft(d)$d/, поэтому ^^-"h(d)^ int/, что
противоречит определению P(d).
"л
Из сказанного следует, что dg U ч]5~*int/л и что при
ft=0
ip-^-ftint/ycl U i))-ftint/y и! U \))-ftint/ft .
\fc=o . у \fc=o у
U U г))"* int /; = /=¦ U ( U ijj-"/ int /, ).
/= 1 ft=0 \/=l /
Следовательно,
186
ГЛ. А. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Но ij>
, 1]з /int//(=/, так что ^"
/. Наконец,
/ = U int LcF.
Поэтому ^
Отсюда следует, что FcztyF. А так как F является объеди-
объединением конечного числа замкнутых интервалов, то из свойств t|>
явствует, что tyF—тоже объединение конечного числа интер-
интервалов, быть может не только замкнутых, но и полуоткрытых
или открытых. Значит, если бы tyF\F=?0, то множество
tyF\F имело бы внутренние точки. Но это невозможно, ибо
i|> сохраняет длины интервалов. Следовательно, tyF = F.
В силу A) заключаем, что F = CV Это доказывает B).
Мы предлагаем читателю показать, что построенное вектор-
векторное поле X может быть аппроксимировано полями Морса —
Смейла.
Пример 13. Здесь мы собираемся кратко описать пример
Черри векторного поля класса С°° (или даже аналитического)
Рис. 30
на торе Т2, которое имеет нетривиальные рекуррентные траек-
траектории, а также один источник х). Построение этого поля до-
достаточно нетривиально и будет изложено в конце главы в при-
приложении. Представим тор в виде квадрата, у которого противо-
противоположные стороны отождествлены. Поле Черри X имеет один
источник / и одно седло s. Неустойчивые сепаратрисы yt и у2
этого седла являются со-рекуррентными. В действительности
со-предельное множество траектории yt содержит как уи так
и у г. Кроме того, у X нет периодических траекторий. Таким
образом, X — поле Купки — Смейла. Как будет показано в кон-
конце этого параграфа, X может быть аппроксимировано полем,
J) В приложении строится пример класса С°°, у самого Черри пример
аналитический,— Прим. ред.
$2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА 187
которое обладает траекторией, соединяющей седла. Поле Черри
на Т2 изображено на рис. 30.
Рассмотрим трансверсальную к X окружность С, которая
ограничивает диск D, содержащий источник /. Пусть М — ком-
компактное двумерное многообразие и У — векторное поле на М,
имеющее гиперболическую притягивающую особую точку. Пусть
D — диск, который содержит сток поля Y и граница которого С
трансверсальна к Y. Приклеивая T2\D к M\D посредством
диффеоморфизма h: C-*~~C, получим многообразие М. Векторное
поле X, индуцированное на М полями X, Y и проведенным отож-
отождествлением, имеет нетривиальную рекуррентную траекторию.
Таким способом можно строить векторные поля с нетривиаль-
нетривиальными рекуррентными траекториями на любом двумерном много-
многообразии, кроме сферы, проективной плоскости и бутылки Клей-
Клейна, на которых все рекуррентные траектории тривиальны. По-
Последнее верно для сферы и проективной плоскости в силу теоремы
Пуанкаре — Бендиксона, а для бутылки Клейна доказано в [56],
[126].
Определение. Пусть X ?дсг (М). Будем говорить, что КаМ —
минимальное множество для X, если К замкнуто, непусто и
инвариантно относительно Xt и, кроме того, в К не сущест-
существует собственного подмножества, обладающего такими свой-
свойствами. Если К является критическим элементом поля X, то
будем говорить, что К—тривиальное минимальное множество.
Отметим, что если К минимально и у—траектория, содер-
содержащаяся в К, то у—рекуррентная. Это следует из того факта,
что со (-у) является замкнутым, непустым и инвариантным под
действием Xt множеством и со (у) с/0 Поэтому со (у) = К :э у.
Аналогично a(y)z)y.
2.2. Лемма. Пусть F cr M— замкнутое, непустое и инвариант-
инвариантное под действием Xt множество, где К<=Эсг(М). Тогда суще-
существует минимальное множество KcF.
Доказательство. Пусть ?—множество замкнутых подмно-
подмножеств F, инвариантных под действием Xt. Рассмотрим в W сле-
следующий частичный порядок: если A, B^W, то Л<В в том
случае, когда АсВ. Пусть теперь {Л,-}—линейно упорядочен-
упорядоченное семейство в ?. По теореме Больцано—Вейерштрасса
ПИ,- непусто. Поскольку С\(А{ замкнуто и инвариантно под
действием Xt, то оно принадлежит ? и является, таким обра-
образом, нижней границей семейства \А{}. По лемме Цорна [46]
в W существует минимальный элемент. |
Необходимо упомянуть следующие важные факты о мини-
минимальных множествах, хотя они и не будут использованы в тексте
188 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
(за исключением приложения, где дано полное описание потока
Черри). В [16] Данжуа построил векторное поле класса С1 на
торе Т2 с нетривиальным минимальным множеством, отличным
от Т2. С другой стороны, Данжуа [16] и Шварц [100] показали,
что минимальное множество Сг-поля на Мг либо тривиально,
либо совпадает со всем М2 и в последнем случае М2 является
тором. Следовательно, со-предельное множество всякой траекто-
траектории либо содержит особые точки, либо является замкнутой тра-
траекторией или тором Т2. В [31] читатель сможет найти обращение
теоремы Данжуа — Шварца ').
Определение. Графом г) для поля X ? 3?r (M2) называется такое
связное замкнутое подмножество в М, состоящее из седел и
сепаратрис, что:
A) со- и а-предельные множества всякой сепаратрисы графа
являются седлами;
B) у каждого седла графа по крайней мере одна устойчивая
и одна неустойчивая сепаратрисы принадлежат графу.
Примеры. На рис. 31 и 32 изображено четыре примера графов
для векторных полей на двумерном многообразии.
2.3. Предложение. Пусть Х??Г(М2)—векторное поле, у ко-
которого все особые точки гиперболические. Если поле X обла-
обладает лишь тривиальными рекуррентными траекториями, то
(о-предельное множество каждой траектории является крити-
критическим элементом или графом; аналогично для а-предельного
множества 3).
Доказательство. Рассмотрим сперва тот случай, когда М2
ориентируемо.
Пусть А" — множество всех неустойчивых (выходящих) сепа-
сепаратрис, А5—множество устойчивых сепаратрис. Для каждой
6gAuL)A5 построим локальное сечение 2F), пересекающее б
только в одной точке рF). Зафиксируем ориентацию Мг. Тогда
на каждом ? F) можно различать правую и левую части Епр F)
и ЕлевF), на которые р(б) разбивает Е F). Именно, вектор из
Тр (бJ F), направленный в сторону ?пр F), и вектор X (р F))
*) На русском языке пример Данжуа имеется в [157], теорема Дан-
Данжуа—в [35], [72], теорема Шварца—в [35].— Прим. ред.
2) В русскоязычной литературе чаще употребляется термин сепарат-
рисный контур. При этом в основном имеют в виду тот случай, когда этот
контур является со- или а-предельным множеством какой-нибудь траекто-
траектории. Но и графы в настоящей книге, хотя они определяются более общим
образом, фактически рассматриваются именно в этом случае.— Прим. ред.
3) Из доказательства будет видно, что если особые точки X гипербо-
гиперболические и все рекуррентные траектории, лежащие в со (у) или а (у), три-
тривиальны, то это множество—критический элемент или граф.— Прим. ред.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА 189
Рис. 31
Рис. 32
190 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
образуют (будучи взяты в этом порядке) положительно ориен-
ориентированный базис в Тр ф)Мг.
Пусть б? Д*. Седло о = со(б) имеет две выходящие сепарат-
сепаратрисы. Возьмем в ТОМ* вектор из TCW" (о), направленный в
сторону какой-нибудь из этих сепаратрис б', и вектор из
TaWs (а), направленный в сторону, противоположную 6. Если
эти два вектора образуют положительно ориентированный базис
в ТаМ2, то будем говорить, что сепаратриса б' является пра-
правой выходящей сепаратрисой относительно б, и писать 6' =
= Дгр(б), а вторую выходящую сепаратрису будем называть
левой относительно б и обозначать через Длев (б). (Таким обра-
образом, Дпр и Длев суть некоторые отображения Д* —*¦ Д°.) Без осо-
особого труда доказывается (и достаточно наглядно), что если
точка х?2пр(б) достаточно близка к р(б), то на положительной
полутраектории y = {Xt(x), t^O] имеется дуга, которая начи-
начинается в точке х, кончается в некоторой точке Ф„р(л:) € 2пр(Дпр(б))
и близка к дугам [р(б), а)сб и (о, р(ДпрF))]сДпр(8). Если же
д:^2лев(б), то на этой полутраектории имеется дуга, которая
идет из х в некоторую флев (*) G 2лев (Длев (б) и близка к дугам
[рф), а) с:б и (а, р(ДЛев(б))]<=ДлевF). Указанные дуги траек-
траекторий у, б, Дгр (б) или Длев (б) вместе с о и с отрезками 2 (б)
и 2(Дгр(б)) или 2(Длев(б)) от р(б) до х и от р(ДпрF)) или'
р (Длев (б)) до фпР (х) или Флев М ограничивают некоторую замк-
замкнутую область G (х), близкую к указанным дугам сепаратрис.
Она гомеоморфна квадрату Ixl, / = [0, 1], причем гомеомор-
гомеоморфизм /: / X / —>¦ G (х) можно устроить так, что / (/ X 0) совпадает
с указанной выше дугой 2F), /Aх/)—с дугой у, /(/xl) —
с дугой Е(ДПр(б)) или 2(Длев(б)) и /(Ох/)—с дугой, состоящей
из дуги б от р (б) до о (точнее, из ее замыкания) и дуги Дпр (б)
или Длев(б) от а до соответствующей точки р.
После этих предварительных замечаний возьмем любую
траекторию у = Xt (а) поля X и предположим, что со (у) не
является критическим элементом. Ясно, что множество со (у)
не может содержать притягивающую особую точку или замк-
замкнутую траекторию, ибо в противном случае оно совпадало бы
с одним из этих элементов. С другой стороны, со (у) должно
содержать седло. Это следует из того факта, что минимальное
множество в со (у) должно быть критическим элементом, причем
этот элемент, как указано выше, не может быть аттрактором.
Таким образом, со (у) содержит седло, а следовательно, и сепа-
сепаратрису седла, ибо со (у) не сводится к особой точке. (Если о —
седло и Xtn (a) —* о, то хотя бы одна из сепаратрис этого седла
входит в со (у), иначе со(у)=о.)
Предположим вначале, что каждая сепаратриса из со (у) имеет
единственное седло в качестве своего со-предельного множества,
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА - СМЕЙЛА J91
так что все сепаратрисы из со (у) принадлежат Д° П А*- Покажем,
что со (у) — граф.
Пусть o,gw(Y)—седло, a yt— неустойчивая сепаратриса ох<
входящая в со Су). Значит, имеется такая последовательность
Xfl (а)€2Gг), что Х^ (а) -+ р (yj, t\ —*- оо. Пусть, скажем,
бесконечное число точек X () (а) лежит на 2ni,(Vi); изменив
обозначения, можем считать, что все Xfl (a)€^np(Vi)- Положим
a2 = co(Yi))H Y2 = Anp(Vi)- При достаточно больших п получается,
что на у есть дуга
\Xt(a): *'„<*<?},
расположенная вблизи дуг [р (у,), o2) cr Vt. (о2, Р^гМ^Та и
такая, что ХB (а) € 2np (Y2)> ^* (а) -*¦ р (у2) (в частности,
V2 cr со (v)). Далее берем a3 = co(v2), V3 = AnP(V2) и т. д. Поскольку
имеется лишь конечное число сепаратрис, то этот процесс даст
нам некоторую последовательность у{, yi+1, ¦.., yt — yt сепарат-
сепаратрис из co(y). При этом yj-ФУк при '^/<^</ (но это не
обязательно так для седел oh = a(yh)). Дуги \Xt(a): tin^.t^.tr^i\
расположены вблизи дуг [р(у/), 0/+i)cv/, (o/+1, p(yJ+1)]c:
сТ/+1» xtin (а) € 2nP (Vy)- Отображение Х^ (a) t-> X(i (а) совпа-
¦•дает с действием на первую точку композиции ф^о •.. °ФпР-
Все это так при достаточно больших п—скажем, при n~^zm.
Дуга {Xt(a): tfn^t^Q вместе с отрезком /с:^^),
заключенным между X,i (a) и Xл (а), образует замкнутую кри-
т т
вую L. Траектории пересекают ее только в точках /, причем
все траектории локально пересекают / в одну и ту же сторону.
Кривая L близка к замкнутой кривой Lo, получающейся, если
идти по yt от р(у{) к о/+1, затем пройти всю y*+i» •••¦ У1-1 и,
наконец, пройти по y* = Yj от °i к p(Vj)- Ясно, что Lo—граф.
(В отличие от L, Lo может иметь самопересечения.) Область
A=UljZ\G(Xti (а)) заключена между L и Lo (т. е. ее граница
dA=L[)L0) и целиком содержится в некоторой окрестности
кривой Lo. Ее внутренность А гомеоморфна кольцу. Действи-
Действительно, исходя из упомянутых выше гомеоморфизмов между
G{Xtj (a)) и /х/, легко получить, что А гомеоморфна области,
получающейся из (О, 1)Х@, /—1) при отождествлении @, 1)х
Х{/—1} с некоторой частью @, 1)х{0} (сейчас будет доказано,
что Xл (а) расположен ближе к p(yt), чем Xл (а)). Траектории
т m
пересекают дА только в точках /, причем если X t (а) ближе
т
к p(yt), чем X i (а), то траектории входят в Л, а если Xл (а)
дальше от p(v*)> чем Xfi (а), то траектории выходят из А.
192 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
В частности, у в точке X(t (а) входит в А или выходит из А
т
в зависимости от взаимного расположения Хл (а) и X, (а) на
2nP(Vj)- B первом случае траектория, вошедшая в А, уже не
может оттуда выйти, а во втором—траектория, вышедшая из А,
уже не может туда вернуться. Но в области А имеются точки
Xtl (а) ^V с п > т> так что V не может выходить из А. Значит,
Xtim (а) ближе к р (yt), чем Х^ (a), a Xt (а) ?А при t > t'm.
Следовательно, a)(y)czA, а поскольку область А можно считать
заключенной в е-окрестности Lo с заранее заданным е > 0, то
(x>(y)cL0. В то же время все Y/C@(y)» так что <°(y) = ?o-
Предположим теперь, что существует сепаратриса у1с<л(у),
у которой^ со-предельное множество не сводится к одному седлу.
Тогда co(Yi)c:<o(y) и co(y,) не содержит Yi. ибо все рекуррент-
рекуррентные траектории тривиальны. Если со (y,) содержит лишь такие
сепаратрисы, у которых со-предельные множества являются
седлами, то, как мы видели, co(yx)—граф. Этот граф должен
являться со-предельным множеством также и для Y- (Действи-
(Действительно, построив для Yi такую область А, как выше, получим,
что поскольку Yi имеет точки внутри А и co(y)^Yi> to Y тоже
попадает в область Л и не может оттуда выйти.) Но если co(y)
совпадает с этим графом, то Yi^My)- Таким образом, должна
существовать такая сепаратриса Y2CC0 (Yi)> У которой со-предель-
ное множество не сводится к одной особой точке. Кроме того,
имеют место строгие включения co(y2)c:co(y1)c:co(y). Продолжая
этот процесс, мы построим бесконечную последовательность раз"
личных сепаратрис у{; между тем число сепаратрис конечно.
Наконец, пусть М2 неориентируемо. Рассмотрим ориенти-
ориентируемое двулистное накрытие я: Ма —»¦ Ма и поднимем поле X
на М%, т. е. возьмем такое поле X на М2, что dn(p)Xp =Xn(p)
при всех р?М2. Любая траектория y поля X накрывается
некоторой траекторией y поля X (т. е. пу — у). Тогда kco(y)==
= co(y). Действительно, включение псо(у)с:соG) очевидно.
Если же y = \Xta\, y = \Xta\, па —а и Xtna —* х € со (y), to
выберем из \Xtna\ подпоследовательность, сходящуюся к неко-
некоторой точке х; ясно, что х g со (у) и пх = х.
В нашем случае особые точки поля X — гиперболические
(ведь я устанавливает диффеоморфизм между окрестностью осо-
особой точки она Ми окрестностью особой точки па на М, при
котором X переходит в X), а если бы у X имелась нетриви-
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА ¦= СМЕЙЛА 1дЗ
альная рекуррентная траектория у, то ату по сказанному
была бы нетривиальной рекуррентной траекторией поля X.
Поэтому со (у) для любой траектории у поля X есть граф или
критический элемент. Но тогда то же самое справедливо для
<а(пу). |
Следствие. Если Х?ЖГ(М2)—поле Куши—Смейла, у кото-
которого все рекуррентные траектории тривиальны, то X—поле
Морса—Смейла.
Доказательство. В силу предложения 2.3 каждая траекто-
траектория поля X в качестве своего со-предельного множества имеет
некоторый критический элемент (аналогично для а-предельного
множества), потому что вследствие отсутствия траекторий, сое-
соединяющих седла, поле X не имеет графов. Остается показать,
что существует лишь конечное число замкнутых траекторий. Это
может быть доказано аналогично тому, как это было сделано для
случая M=S2 в теореме 2.1. |
Теперь мы переходим к доказательству плотности множества
полей Морса—Смейла в ЖГ(М2) в том случае, когда многооб-
многообразие М2 ориентируемо. Чтобы аппроксимировать произвольное
поле X полем Морса—Смейла, мы предъявим близкое к X
поле Y, обладающее следующим свойством: существует такая
окрестность cllcz^.r(M2) поля Y, что всякое Z^il имеет лишь
тривиальные рекуррентные траектории. Затем аппроксими-
аппроксимируем Y полем Купки—Смейла Z^il. Из последнего следствия
вытекает, что Z—поле Морса—Смейла.
Ниже будут нужны следующие две леммы. Их доказательство
будет приведено в конце этого параграфа.
2.4. Лемма. Если Х??:(М*)—векторное поле без особых
точек, то X может быть аппроксимировано полем Y, содержа'
щим замкнутую траекторию.
2.5. Лемма. Предположим, что М* ориентируемо. Если X g Xr(M2)
имеет особые точки, которые все гиперболические, и существует
нетривиальная рекуррентная траектория, то X может быть
аппроксимировано полем Y, у которого число траекторий,
соединяющих седла, на единицу больше, чем у X.
2.6. Теорема. Для ориентируемого многообразия М2 множество
полей Морса—Смейла плотно в 3?г(Ма).
Доказательство. Пусть Xg Эсг(М2). Поскольку подмножество
полей, у которых все особые точки гиперболические, плотно в
ХГ(М2), то можно сразу считать, что X принадлежит этому
подмножеству.
194 гл. 4. типичность и грубость векторных Полей
Случай 1. X не имеет особых точек.
Так как М2 ориентируемо, то оно должно быть в этом случае
тором. По лемме 2.4 поле X можно аппроксимировать полем Xlf
имеющим замкнутую траекторию. Согласно лемме 2.5 гл. 3,
Хх можно аппроксимировать полем У, имеющим гиперболиче-
гиперболическую замкнутую траекторию у. Поскольку у поля У нет особых
точек, то у не может ограничивать диск в Т2, а следовательно,
Т2\у является цилиндром. Поэтому У имеет лишь тривиальные
рекуррентные траектории. (") Каждое близкое к У поле обла-
обладает тем же свойством, поскольку оно также имеет замкнутую
траекторию. Возьмем теперь близкое к Y поле Купки — Смей-
ла Z. Согласно следствию из предложения 2.3, Z — поле Мор-
Морса — Смейла.
Случай 2. X имеет особые точки, и все они гиперболические.
Пусть у — неустойчивая сепаратриса седла. Будем говорить,
что у стабилизируется, если ы(у) — гиперболический притяги-
притягивающий критический элемент (особая точка или замкнутая тра-
траектория). Подобным же образом, устойчивая сепаратриса седла
стабилизируется, если ее а-предельное множество является
гиперболическим отталкивающим критическим элементом.
A) Если все сепаратрисы седел поля X стабилизируются, то X
может быть приближено полем Морса—Смейла.
Действительно, существует такая окрестность 11 поля X, что
у всякого Y ? 11 все сепаратрисы также стабилизируются. Таким
образом, в силу леммы 2.5 эти поля могут обладать лишь три-
тривиальными рекуррентными траекториями. Аппроксимируем
теперь X полем Купки—Смейла Y?H. Согласно следствию из
предложения 2.3, У—поле Морса—Смейла.
B) Если X имеет нестабилизирующиеся сепаратрисы, то X
можно аппроксимировать полем Y, у которого число стаби-
стабилизирующихся сепаратрис больше, чем у X.
Доказав это утверждение, мы завершим доказательство тео-
теоремы: существует лишь конечное число сепаратрис, и последо-
последовательно стабилизируя их, придем к ситуации, рассмотренной
в A).
Пусть 11—такая окрестность поля X, что каждое поле
У ? 11 имеет не меньше стабилизирующихся сепаратрис, чем X.
В силу леммы 2.5 поле X можно аппроксимировать полем
У ? 11, имеющим лишь тривиальные рекуррентные траектории,
так как существует лишь конечное число седел, и у них лишь
конечное число сепаратрис.
Следует рассмотреть четыре возможности. A7)
(a) У не имеет траекторий, соединяющих седла. Пусть у —
какая-нибудь нестабилизирующаяся сепаратриса седла для по-
поля У. (У уже удовлетворяет A), если таких у не существует.)
Тогда ш (у) (или а (у)) — негиперболическая периодическая тра-
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА 195
Рис. 33
ектория. Можно аппроксимировать Y полем Z, у которого соот-
соответствующая траектория гиперболическая AS), и таким образом
стабилизировать сепаратрису поля Z, соответствующую у.
(b) Y имеет граф, который является со-предельным (или
а-предельным) множеством некоторой траектории. Рассмотрим
трансверсальное сечение S, проходящее через регулярную
точку р этого графа Траектория у, у которой ю-предельное
(или а-предельное) множество содержит точку р, пересекает S
по последовательности точек ап —> р. При достаточно большом п
дуга траектории у, заключенная между точками ап и ап+1,
сегмент (ап, ап+1) в сечении S и граф ограничивают открытую
область АсМ%, гомеоморфную кольцу Пусть F—малая трубка
тока, содержащая р, и пусть AF—Сг-малое векторное поле
на F, которое трансверсально к У во всех точках внутренности
196
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
множества F, направлено от р к ап+1 (от ап+1 кр)и обращается
в нуль вне /, как показано на рис. 33. Если Z = Y-}-AY, то
Zt(A)czA при />0в случае р?со(у). Сепаратриса точки at
(или а2 в случае р g a (v)), первоначально принадлежавшая
графу, после возмущения проникнет в кольцо. (и) Таким образом,
со-предельное (или а-предельное) множество этой сепаратрисы
превращается в некоторую замкнутую траекторию поля Z, при-
принадлежащую кольцу. Это следует из теоремы Пуанкаре—Бен-
диксона, поскольку Z не имеет особых точек в А. Дальнейшим
Рис. 34
возмущением поля Z превратим эту замкнутую траекторию в
гиперболическую и тем самым стабилизируем рассмотренную
сепаратрису. (Если р?а(\), то рассмотрим Zt при t^.0.)
(c) Y имеет граф, возле которого скапливаются замкнутые
траектории, как показано на рис. 34. Рассмотрение кольца.Л,
ограниченного графом и достаточно близкой к нему замкнутой
траекторией, позволяет провести в случае (с) рассуждения, аб-
абсолютно аналогичные случаю (Ь).
(d) Проанализируем теперь последнюю возможность. Пусть
у — траектория, соединяющая седла, a S — трансверсальное
сечение, проходящее через точку р € У, как показано на рис. 35.
Рассмотрим малый открытый интервал (a, p)aS. Все точки
интервала (а, р) имеют одно и то же ш-предельное множество,
которое является притягивающей особой точкой или замкнутой
траекторией. Отметим, что если это не так для достаточно малого
(а, р), то мы оказываемся в ситуации, рассмотренной в (Ь) или (с).
Действительно, если Y не удовлетворяет условиям, рассмотрен-
рассмотренным в случае (Ь), то со-предельное множество каждой точки из
(а, р) является особой точкой или замкнутой траекторией.
Кроме того, за исключением у, не существует устойчивой сепа-
§2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА
197
ратрисы седла, у которой со-предельное множество содержало бы
точку р, так как а-предельное множество такой сепаратрисы
содержало бы у, и мы попали бы в ситуацию, рассмотренную
в случае (Ь). Итак, со-предельное множество каждой траектории
из (а, р) является притягивающей особой точкой или замкнутой
траекторией. Поскольку р не является точкой накопления
замкнутых траекторий, что соответствовало бы случаю (с), то
отсюда следует, что все точки из (а, р) имеют одно и то же со-пре-
со-предельное множество, которое мы обозначим через а.
Рис. 35
Действуя как и раньше, мы возмутим поле таким образом,
что а станет со-предельным множеством неустойчивой сепаратри-
сепаратрисы точки Cj. Если а — притягивающая особая точка, то мы тем
самым стабилизировали еще одну сепаратрису. Если а — замк-
замкнутая траектория, то мы превратим ее, если потребуется, в ги-
гиперболическую с помощью дальнейшего возмущения и опять-
таки стабилизируем еще одну сепаратрису. Это завершает до-
доказательство теоремы. |
Прежде чем доказывать леммы 2.4 и 2.5, сделаем некоторые
замечания по поводу нетривиальных рекуррентных траекторий.
Пусть Х??Г(М2) и у—нетривиальная со-рекуррентная
траектория. Мы утверждаем, что через любую точку р ? у можно
провести окружность, трансверсальную полю X.
Действительно, рассмотрим трубку тока Fi, содержащую
точку р. Пусть ab и cd — трансверсальные к полю X стороны
трубки Ft. Так как р? со (у), то у пересекает аи бесконечное число
раз. Пусть р^ — первая точка, в которой у вновь пересечет ab.
Возьмем какую-нибудь трубку тока F2, содержащую дугу тра-
траектории qopt. Предположим, что pt -расположена ниже точки р0
в ab, как показано на рис. 36. В обратном случае построение ана-
аналогично. Если М2 ориентируемо, то в F2 можно найти дугу
траектории поля X, начинающуюся в некоторой точке qi?cd,
расположенной выше q0, и пересекающую ab выше рх в некоторой
точке р2- В Ft можно взять такую трансверсальную к X дугу
198
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
что она имеет положительные углы наклона на концах, при-
причем точка ps расположена выше р2, но ниже р0, как показано на
рис. 37. Теперь достроим эту дугу до нужной нам окружности,
соединив р8 и qx дугой в Fu содержащей р и трансверсальной к X.
Эта дуга должна иметь в точках р8 и qt тот же наклон, что и пре-
предыдущая.
Рис. 36
Мы предоставляем читателю построить такую же трансвер-
трансверсальную окружность в случае неориентируемого многообразия
М2. В этом случае необходимо рассмотреть последовательные
пересечения траектории у с оЬ.B0)
Рис. 37
Обозначим теперь через С трансверсальную к X окружность,
проходящую через точку р ? у. Пусть DczC — подмножество тех
точек, положительные полутраектории которых вновь пересе-
пересекают С. Определим отображение последования Pi D ->¦ С как
отображение, которое каждой точке х ? D ставит в соответствие
первую точку пересечения положительной траектории точки х
с С. По теореме о трубке тока D является открытым множеством
в С. Поэтому либо D=C, либо D является объединением откры-
открытых интервалов *), Предположим, что ВфС, и пусть (ait a2) —
1) В нашем случае D ф 0, так как у бесконечное число раз пересе-
пересекает С. Вообще же легко привести пример, когда для некоторой окруж-
окружности С, всюду трансверсальной в полю, Ь-=е/.— Прим. ред.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА -» СМЕЙЛА 199
максимальный интервал в D. Покажем, что и>(а^ является сед-
седлом, так же как и со(а2).
Если бы положительная полутраектория yt точки а* стреми-
стремилась к притягивающему положению равновесия либо навивалась
на замкнутую траекторию или граф (как это описано в доказа-
доказательстве предложения 2.3), то каждая траектория, попавшая
в некоторую окрестность А этого положения равновесия или в
рассматривавшееся ранее кольцо А, примыкающее с одной
стороны к замкнутой траектории или графу, уже не могла бы
после этого отойти от cofo) и, в частности, не могла бы пересе-
пересекать С. Когда точка q достаточно близка к аи точка Xtq долго
остается близкой к XtO-i и в течение этого времени не пересе-
пересекает С, а потом она вместе с Xt^ попадала бы в А. Стало быть,
эти три случая для cofo) исключены, ибо каждая траектория,
проходящая через точки из (аи а2), должна вновь пересечь С.
Согласно предположению 2.3, остается доказать, что ю(аО
не содержит нетривиальных рекуррентных траекторий. Допус-
Допустим, что в (о^) имеется такая траектория у'. Тогда в малой ее
окрестности имеется замкнутая несамопересекающаяся кривая
С, которая всюду трансверсальна к полю и которую у' пересе-
пересекает бесконечное число раз. Значит, и уг пересекает С бесконеч-
бесконечное число раз. С другой стороны, если q g (alt a2), то число N пере-
пересечений дуги траектории qP(q) с С конечно, так как С транс-
трансверсальна к X, a qP (q) компактно. Используя теорему о трубке
тока, получаем, что это число постоянно в некоторой окрест-
окрестности точки q. (Часть С, попадающая в длинную и достаточно
узкую трубку тока, «центральная линия» которой есть qP(q),
представляет собой несколько кривых вида х1=х1(х^.) А по-
поскольку (alt a2) связно, то это число N постоянно на всем интер-
интервале. Применяя же теорему о трубке тока к дуге yi от at до
точки, взятой после n-го пересечения -у* с С*, где n>N, найдем,
что на (а1у а2) имеются точки, у которых положительные полу-
полутраектории пересекают С по крайней мере п раз до своего воз-
возвращения на С. Это противоречит постоянству N. Полученное
противоречие доказывает, что со (с^) — седло. Аналогично и
со (а2) — седло.
Итак, D — это конечное объединение открытых интервалов
в С, концы которых принадлежат устойчивым сепаратрисам
седел. Если мы рассмотрим обратное к Р отображение Р~х
(отображение последования для —X), то его областью опреде-
определения будет конечное объединение открытых интервалов, концы
которых принадлежат неустойчивым сепаратрисам седел.
Отметим, что если отображение последования определено на
всей окружности С, то М2 является тором Т2 или бутылкой
Клейна К*- Действительно, легко видеть, что множество
200 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
U^rX^C), заметаемое траекториями точек из С, открыто и
замкнуто*) и, следовательно, совпадает с М2. Поэтому векторное
поле X не имеет особых точек, что и доказывает наше утверж-
утверждение, и мы получаем, что М2 = Т2 или М2 = К2 в зависимости
от того, сохраняет отображение Р ориентацию окружности С
или обращает ее. Если Р: С —>¦ С обращает ориентацию, то Р
имеет неподвижную точку, которая соответствует замкнутой
траектории у поля X. Эта замкнутая траектория не является
границей диска в К2, и поэтому К2\у—лист Мёбиуса A7).
Следовательно, X имеет лишь тривиальные рекуррентные тра-
траектории.
Доказательство леммы 2.4. Если у поля X есть замкнутая
траектория, то все доказано. Если у X нет замкнутой траек-
траектории, то это поле имеет рекуррентную траекторию у, а М2—Т2.
Возьмем точку р?у, и пусть С—трансверсальная окружность,
проходящая через р. Положим С1 = Х-с,{С) и С2 = Хе(С), где
6 > 0 достаточно малое. Ясно, что Сх и Cg трансверсальны к
полю X. Рассмотрим содержащую точку р трубку тока F, у
которой трансверсальные к X стороны лежат в С4 и С2.
Определим Pi С2 —*¦ Cit сопоставив каждой точке х g C2
первую точку, в которой ее положительная полутраектория
пересечет С(. Как мы видели, Р корректно определено и со-
сохраняет ориентацию. Под этим мы понимаем то обстоятельство,
что при заданной ориентации окружности С2 отображения Р
и X_2ei C2—*Cj индуцируют одну и ту же ориентацию на Сг.
Пусть теперь qo==X6(p), po = X_e(p), Pi = P(qt~i), <7i = **«(/>/)
((^1). Существует такая последовательность пг, что /?„.—>-р0, и
можно предположить, что каждая точка рп лежит ниже р0 на
ab, как показано на рис. 38.
Рассмотрим семейство полей Z(u) — X-\-mY, где е > 0,
O^u^l, a Y—это поле, которое трансверсально к X во
внутренности множества F, направлено там вверх и обращается
в нуль вне F. Если е достаточно мало, то Z(u) близко к X
при всех О^ы^ 1.
Зафиксируем теперь интервал / на ab, для которого точка
рв является внутренней. Для каждой точки xg/ рассмотрим
расстояние по вертикали в F между х^/ и первой точкой пе-
пересечения положительной полутраектории поля Z(\), проходя-
проходящей через х, с окружностью Cj. Поскольку множество / ком-
компактно, то это расстояние достигает на / своего минимума
х) Открытость очевидна. Время, за которое XfX с х(?С возвращается
на С, непрерывно зависит от х и, значит, ограничено сверху некоторым Т.
Поэтому рассматриваемое множество совпадает с образом при отображении
(tg x)*->Xtx компакта [0, Т]ХС— Прим. перев.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА — СМЕЙЛА
201
р > 0. Мы утверждаем, что при некотором и g @, 1] траекто-
траектория поля Z (и), проходящая через qu, замкнута. Действительно,
поскольку при каждом и поле Z(u) совпадает с X вне множе-
множества F, то можно определить рк (и) = Р (^_г («)) при k ^ 1, где
qo(u) = qv и <7ft-i(u) — первая точка пересечения положительной
полутраектории точки Pfc_i(«)€Q: с С2.
Зафиксируем такое число i, что точка pt = Pl (q0) располо-
расположена ниже р0 и ее расстояние до р0 меньше р.
Рис. 38
Отметим, что р{(и) и qt(u) непрерывно зависят от и. При
малом и точка Pi(u) принадлежит /, расположена ниже р„ и
ее высота возрастает вместе с ростом и. Аналогично, <7i(u)
расположена ниже q0 и ее высота возрастает вместе с ростом и.
Таким образом, либо Pi(uo) = po при некотором ио?(О, 1], либо
Р;(")€/ при всех ug@, 1]. В первом случае <?,•(«„) располо-
расположена выше q0, и поэтому существует такое иг < и0, что qi(u1)=qe.
Во втором случае точка qt(l) расположена выше q0, потому
что расстояние от pt(l) до р0 меньше р. Следовательно, суще-
существует такое щ < 1, что qt (ut) = ^о- В обоих случаях траекто-
траектория поля Z(Ui), проходящая через q0, является замкнутой. |
Доказательство леммы 2.5. Прежде всего будет доказано,
что если у—нетривиальная со-рекуррентная траектория, то су-
существует, некоторая устойчивая сепаратриса, точки которой
накапливаются возле у. Иными словами, существует такая
устойчивая сепаратриса у2, что a(y2)z^y. Рассмотрим точку
р ? у и трансверсальную к X окружность С, проходящую через
точку р. Пусть Р: DcC—±C—отображение последования, оп-
определенное на D. Имеем, что йфС, так как в противном слу-
случае X не имело бы особых точек. Рассуждая от противного,
предположим, что у не принадлежит «-предельному множеству
202
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
никакой устойчивой сепаратрисы. Поскольку сепаратрис конечное
число, то это эквивалентно существованию в С такого содер-
содержащего р интервала, который не пересекает ни одна устойчи-
устойчивая сепаратриса. Пусть /сС—максимальный интервал, обла-
обладающий этим свойством. На нем определены все Pk, k > 0.
Поскольку у является со-рекуррентной и р ? у, то Pk (p) ? / при
некотором целом k > 0. Далее, интервал J = Р* (/) содержится
в /. Это вытекает из того, что, во-первых, / Г) J ф 0, поскольку
Рис. 40
Pk(p)?l, и, во-вторых, если бы J(?I, то J содержал бы ин-
интервал, во внутренности которого находилась бы одна из кон-
концевых точек интервала /. Так как / —максимальный интервал,
через который не проходят устойчивые сепаратрисы, то из
этого следовало бы, что J содержит точку устойчивой сепа-
сепаратрисы. В силу инвариантности сепаратрис относительно потока
и, следовательно, относительно отображения Рк, интервал /
тоже должен был бы содержать точку устойчивой сепаратрисы
седла, поскольку J = Pk(I). Но это противоречило бы опреде-
определению интервала /, откуда мы и заключаем, что Pk (/)=>/.
А тогда можно построить гомеоморфную кольцу область, содер-
содержащую точку р и инвариантную относительно потока Xt, /^0
(рис. 40). Это приводит к противоречию, ибо тогда у не мо-
может быть нетривиальной и-рекуррентной траекторией в Л.
§ 2. ПЛОТНОСТЬ ВЕКТОРНЫХ ПОЛЕЙ МОРСА <= СМЕЙЛА 203
Поэтому возле у действительно накапливаются точки некото-
некоторой устойчивой сепаратрисы у2.
Мы утверждаем также, что либо возле у накапливаются
точки некоторой неустойчивой сепаратрисы, либо у сама явля-
является неустойчивой сепаратрисой. Рассуждая от противного,
предположим, что это не так. Если у—не сепаратриса, то
рассмотрим, как и в предыдущем случае, точку р?у и мак-
максимальный открытый интервал IcC, содержащий точку р и не
пересекающийся с неустойчивыми сепаратрисами. Так как у
является со-рекуррентной, то существует такое целое k > 0, что
Рь (/) П / Ф 0• Из этого вытекает, что Р~к (q) корректно опре-
определено при некотором q?l и P~k{q)?l. Необходимо рассмот-
рассмотреть две возможности. Если Р~к не определено на всем интер-
интервале /, то существует точка г g /, отрицательная полутраектория
которой имеет седло в качестве своего а-предельного множе-
множества. В частности, г ? / Г) у для некоторой неустойчивой сепа-
сепаратрисы у, что противоречит определению интервала /. Другая
возможность заключается в том, что Р~ь корректно определено
на всем интервале /. В этом случае, как и раньше, будем
иметь P~fc(/)c/. Мы оставляем читателю завершить доказа-
доказательство утверждения, используя последний факт.
Следует отметить, что доказанное выше утверждение верно
также и для неориентируемых многообразий. Единственное от-
отличие этого случая заключается в том, что использованная
область А может быть листом Мёбиуса, где опять-таки не бывает
нетривиальных рекуррентных траекторий.
Пусть теперь ул—неустойчивая сепаратриса, для которой
либо Yi^Y- либо m^y^zDy, а у2—устойчивая сепаратриса, для
которой cx(y2) = y- Как и при доказательстве леммы 2.4, рас-
рассмотрим трансверсальные к X окружности Cj = X_6(C) и
С2 = Х6(С). Пусть Pi DczC2—»СХ—отображение последования,
a F—трубка тока, содержащая точку р?у. Так как число
седел конечно, то F можно выбрать таким образом, чтобы это
множество не пересекалось с траекториями, соединяющими
седла, которые могут быть у X.
Пусть ах и а2—седла, соответствующие сепаратрисам yt и
Y2, точки которых накапливаются возле у. Рассмотрим семей-
семейство полей Z(u) = X-\-euY, где е > 0, O^u^l, a Y транс-
версально к X во внутренности множества F, направлено вверх
и обращается в нуль вне F. Если брать достаточно малые е,
то Z (и) близко к X при всех и ? [0, 1]. Мы хотим показать,
что при некотором и ? @, 1] у поля Z (и) больше траекторий,
соединяющих седла, чем уХ х).
*) В F направление вверх определяется с помощью локальных коор-
координат (xi, xj), фигурирующих в теореме о трубке тока. Поскольку выбор
204
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Зафиксируем малый замкнутый интервал / в [а, Ь\, содер-
содержащий р0 в качестве своей внутренней точки. Как и раньше,
обозначим через р > 0 минимум по всем х g / вертикальных
расстояний в F между х и первой точки пересечения положи-
положительной полутраектории поля 2A), начинающейся в х, с
окружностью С2. Пусть х0 и г0—первые точки пересечения
Рис. 41
л, е
h
> —
<
V
о
г
%
4
^ \<
Рис. 42
траектории yf с [с, fc] и соответственно траектории уа с [с, d].
Отметим, что дуги сепаратрис а,х0 и а2г0 не изменяются при
произведенном выше возмущении поля X на euY (рис. 42).
Выберем теперь такую близкую к р0 точку я g ух Л / и та-
такую точку z g у2 П С2, что расстояние по вертикали между х; и г
меньше р. Точка х соответствует t-му пересечению траектории
положительного направления оси х% является случайным, то не исключенов
что на самом деле Y надо будет направить вниз. Об этом см. ниже.—
Прим. ред.
3. ОБОБЩЕНИЯ 205
Yj с Q с некоторым целым i > 0. Аналогично, точка г соот-
соответствует /-му пересечению траектории у2 с С2 с некоторым / > 0.
Предположим, что х расположено ниже г в F. Если это не
так, то нам следует взять поле Y направленным вниз.
Рассмотрим отображения, которые каждому и ставят в соот-
соответствие i-e пересечение х(и) сепаратрисы у^и) поля Z(u) с Cit
ее же t-e пересечение у (и) с С2 и /-е пересечение z(u) сепаратрисы
у2(и) поля 2 (и) с С2. Ясно, что х(и) и z(u) корректно определены
при малых и. Так как М2 ориентируемо, то в терминах F точка
х(и) с ростом и поднимается вверх, если только она не выйдет из
F; но и тогда с ростом и она движется по Сх в том же направле-
направлении, которое на попадающей в F части Ct есть направление вверх.
у (и) с ростом и движется по С2 в том же направлении, а г (и) —
в противоположном.
Следует рассмотреть две возможные ситуации. Предположим
вначале, что х(и), у (и) и г(и) корректно определены при всех
wg[0, 1]. Тогда существует такое ыо€(О, 1), что y(uo)—z(uo).
Это видно из следующего: у (и) и г (и) непрерывны; г @) находится
на [с, d] выше г/@) на расстоянии, меньшем р; с ростом и они
движутся навстречу друг другу, причем г/A) находится выше
у@) по крайней мере на р (а то и вовсе у (и) выходит при этом
движении из F); z(l) находится ниже г@) (а то и вовсе z(u)
выходит из F). Следовательно, мы имеем траекторию, соединяю-
соединяющую седла аг(ы0) и о2(и0).
Предположим теперь, что одно из отображений, например
х(и), определено не при всех ы?[0, 1]. Это означает, что при
некотором ио€@,1) траектория "Vi(«o) достигает одной из гранич-
граничных точек области определения Р; иными словами, она дости-
достигает такой точки, у которой со-предельным множеством является
некоторое седло о3. В этом случае мы получим траекторию, сое-
соединяющую седла аи о3. В случае когда г (и) определено не при
всех ug[0, 1], рассуждения аналогичны. Это завершает доказа-
доказательство леммы 2.5 и, следовательно, теоремы 2.6.
В заключение этого параграфа отметим, что из теоремы 2.6
вытекает, что всякое грубое векторное поле Х?ХГ{М2) является
полем Морса — Смейла *).
§ 3. ОБОБЩЕНИЯ
Теперь мы дадим некоторые комментарии к теореме о плот-
плотности полей Морса — Смейла на ориентируемых поверхностях,
а также частичное ее расширение на случай неориентируемых
поверхностей.
См. упр. 20 в конце главы (ср. также с упр. 21, 30).— Прим. ред.
506 гл. 4. типичность и грубость векторных Полей
Здесь также будут сформулированы теоремы об открытости
множества полей Морса — Смейла и их грубости на многообра-
многообразиях любой размерности. В частности, существуют грубые поля
на любом многообразии. Однако поля Морса — Смейла в прост-
пространстве векторных полей на многообразиях размерности 3 и
более уже не составляют плотного множества. Тем не менее
следует отметить одно полезное специальное пространство,
в котором поля Морса — Смейла плотны, а именно пространство
градиентных полей на любом компактном многообразии.
Наше первое замечание заключается в том, что при дока-
доказательстве леммы 2.5 нельзя гарантировать существования
малого возмущения, при котором будут соединены траекторией
те два седла (о1 и с2), которые рассматривались вначале. Это
приводит к формулировке следующей проблемы. Пусть ух—не-
ух—неустойчивая сепаратриса и у2—устойчивая сепаратриса седел
поля X ? J6r (М2). Предположим, что со (yj Л у2 Ф 0 или ю(Тг) П
П сх {уг) ф 0 • Трудно ответить на вопрос, возможно ли «слить»
эти две сепаратрисы посредством Сг-малого возмущения поля X.
Эта проблема является открытой при любом г ]> 1 как для
ориентируемого М2, так и для неориентируемого М%.
Трудность доказательства плотности полей Морса—Смейла
в 3?r (М2), когда Мг неориёнтируемо, заключается в доказа-
доказательстве леммы 2.5. Все остальные факты верны и в этом слу-
случае. В неориентируемом случае вопрос остается открытым. Он
представляет интерес независимо от того, будет ли ответ на
него положительным или отрицательным, хотя отрицательный
ответ был бы неожиданностью. В этом направлении получены
некоторые частичные результаты, а именно:
A) Поля Морса—Смейла плотны в ?г(М2) как для ориен-
ориентируемых, так и для неориентируемых М2. Пью получил этот
результат, используя лемму о замыкании, как и мы сделаем
это ниже. Ограничение С1-топологией вытекает из того факта,
что лемма о замыкании до сих пор доказана только в этом
случае.
B) Легко видеть, что теорема верна для j6r (P2) при любом
1, где Р2—проективная плоскость. Это следует из того, что
векторные поля на Р2, как и на сфере S2, не имеют нетриви-
нетривиальных рекуррентных траекторий. Теорема о плотности верна
также и для бутылки Клейна К.2, как показал в [56] Маркли 1).
Гутиеррес [30] упростил доказательство для /С2 и показал, что
на неориентируемом многообразии L2, род которого на единицу
больше чем у /С2, т. е. на торе с вклеенным в него листом
Мёбиуса, все нетривиальные рекуррентные траектории явля-
*¦) Точнее говоря, Н. Маркли [56] и С. X. Арансон [126] доказали, что
и на бутылке Клейна тоже не бывает нетривиальных рекуррентных траек-
траектории.— Прим. ред.
§3. ОБОБЩЕНИЯ 207
ются «ориентируемыми» BI). Поэтому доказательство, приведен-
приведенное нами для ориентируемого М2, проходит и в этом случае.
Итак, плотность полей Морса—Смейла в ?г (М2) при каждом
г^ 1 доказана в том случае, когда М2 = Р2, К2 или L2
Теперь мы опишем доказательство для Ж1 (М2), используя
лемму о замыкании.
Лемма о замыкании [88]. Пусть М"—компактное п-мерное
многообразие без края. Пусть Х^Х}(Мп)иу—нетривиальная
рекуррентная траектория поля X. При заданных р ? у и е > 0
существует такое Y g X1 (М"), что || Y—X ||Ci < e и траектория
поля Y, проходящая через точку р, является замкнутой.
Доказательство леммы о замыкании чрезвычайно сложно
даже для случая поверхностей. Что же касается аналогичного
утверждения с малым возмущением поля X в j6r (M"), то воп-
вопрос открыт при каждом г ;> 2 и п !> 2.
В случае поверхностей М2 замкнутая траектория, построен-
построенная по нетривиальной рекуррентной траектории, не может огра-
ограничивать диск. Это вытекает из существования трансверсальной
к X окружности, не ограничивающей никакого диска, которая
была построена в § 2 настоящей главых).
3.1. Теорема. Множество векторных полей Морса—Смейла
плотно в J1 (М2) как для ориентируемого, так и для неориен-
тируемого многообразия М2.
Доказательство. Мы покажем, что всякое поле Х^ЗРЩ2)
может быть аппроксимировано полем Купки—Смейла, обла-
обладающим лишь тривиальными рекуррентными траекториями.
Согласно следствию из предложения 2.3, теорема тем самым
будет доказана.
Возьмем близкое к X поле Купки—Смейла X*. Если X*
имеет лишь тривиальные рекуррентные траектории, то дока-
доказательство завершено. В противном случае рассмотрим нетри-
нетривиальную рекуррентную траекторию у, поля X* и точку р ? ух.
В силу леммы о замыкании, существует такое близкое к X*
поле Xj, что его траектория <тх, проходящая через р, замкнута.
Теперь аппроксимируем поле Хх полем Купки—Смейла Х\,
которое имеет близкую к ох гиперболическую замкнутую тра-
траекторию а\. Если Хх имеет лишь тривиальные рекуррентные
траектории, то XJ — поле Морса—Смейла. Если это не так, то
мы повторяем описанный выше процесс, отправляясь от поля
1) Построим трансверсальную к X окружность С, проходящую через р.
При достаточной близости Y к X она трансверсальна и к У, а замкнутая
траектория б поля К, проходящая через р, пересекает эту окружность При
лом все пересечения б с С происходят «в одну сторону» Отсюда легко
вывести, что б не только не ограничивает никакого диска, но и вообще не-
гомодогичиа нулю.— Прим. ред.
208 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Х\, но при этом не изменяя его в окрестности траектории о\.
Мы утверждаем, что число шагов в этом процессе конечно и
ограничено числом 2^, где g—род (число ручек) многообра-
многообразия М. Дело в том, что каждый этап этого процесса по су-
существу приводит к рассмотрению поля Купки—Смейла на
многообразии меньшего рода (или, что эквивалентно, большей
эйлеровой характеристики K(N2), так как К (N2) = 2—2g(N2)
для ориентируемого N2 и К (Nz) — 2—g(N2) для неориентируе-
мого N2 [59], [119]). Так как K(/V2)<2 для всякого N2, то
через конечное число шагов мы придем к полю Купки—Смей-
Купки—Смейла, у которого будут лишь тривиальные рекуррентные траек-
траектории; оно будет полем Морса—Смейла, что и требуется.
Чтобы увидеть, как происходит это понижение рода, разре-
разрежем М вдоль гиперболической замкнутой траектории а\, полу-
получившейся при перестройке нетривиальной рекуррентной тра-
траектории. Здесь возможны два варианта: либо мы получим
многообразие Ми с краем, либо два многообразия Ми и М12 с
краями [59]. В первом случае край многообразия Mi0 состоит
из одного или двух экземпляров aj в зависимости от того,
расположена ли о\ на М односторонне или нет. Во втором
случае края многообразий Ми и Ми являются каждый копи-
копией Cj. В первом случае мы вклеим один или два диска Dx и
D2, так что Mi0\jD1 или M10\jD1\jD2 превратится в многооб-
многообразие без края. Имеем, таким образом,
или
К (М10 U D, U D2) = К (М) + К (Di) + К (Z>J.
Поскольку К {Dt) = 1 при i = 1, 2, то К {М10 и ?>х) или К{М10 и
U Dx и Д.) будет больше К(М). Во втором случае К(М)=К(М11)-\-
+К(М12) и К(Мп)< 1, К{М12)<1, так как иначе о* огра-
ограничивало бы диск. Итак,
К (Ми [)D1) = K (Ми) + 1 > К (М)
и
К (М12 UD2) = K (М12) +1>К (М).
Хотя это и не является необходимым для наших целей, отме-
отметим, что можно доопределить поле Х{, заданное на М10, Mlt
или М12, поместив в Dt и D2 сток или источник, в зависи-
зависимости от того, является траектория а* отталкивающей или
притягивающей.
Продолжим процесс с многообразиями Mtj (j=0, I, 2), полу-
полученными после вклеивания дисков, не изменяя при этом поле
в окрестности этих дисков. Так как эйлерова характеристика
ограничена числом 2 и возрастает при каждой перестройке, то
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 209
количество этих перестроек конечно и ограничено числом 2?,
что и утверждалось. Теорема доказана.
Следует отметить, что классы эквивалентности полей Морса —
Смейла на М2 были описаны Пейксото [83] и Флейтасом [19],
а связные компоненты пространства полей Морса — Смейла были
классифицированы в [32].
Рассмотрим теперь многообразие М произвольной размер-
размерности, наделенное римановой метрикой. Важным вопросом яв-
является вопрос о существовании грубого поля на М. Результаты
из [75], [79], [106] показывают, что на М существует много полей
Морса — Смейла и эти поля являются грубыми; см. также[57].
Эти результаты таковы:
A) множество полей Морса—Смейла является непустым и
открытым в Жг (Мп), г^1;
B) если X g Ит (Мп), г^1, — поле Морса — Смейла, то X
является грубым;
C) множество градиентных полей Морса—Смейла открыто
и плотно в Gradr(M"), r^l.
Здесь Grad' (Mn) обозначает подмножество в j?r (M"), состоя-
состоящее из градиентных полей С'+1-функций М —»- IR по отношению
к некоторой римановой метрике на М. Рассмотрим структуру
траекторий градиентных полей Морса—Смейла. Как мы видели
в § 1 гл. 1, градиентное поле не может иметь замкнутых траек-
траекторий. Кроме того, а- и со-предельные множества каждой
траектории состоят лишь из особых точек. Мы оставляем чи-
читателю доказательство того факта, что неблуждающее мно-
множество для этих полей также состоит лишь из особых точек.
Поэтому градиентные поля Морса—Смейла—это в точности
поля Купки—Смейла, у которых неблуждающее множество —
это конечный набор гиперболических особых точек.
В противовес тому, что происходит в случае пространств
2?г(М2), где г=1, или г^1 и Мг ориентируемо, или в случае
Gradr(M"), поля Морса—Смейла не образуют плотного мно-
множества в J6' (Мп) при п ^ 3. Этот факт будет получен в сле-
следующем параграфе вместе с примерами грубых полей в ХГ(М3),
которые не являются полями Морса—Смейла, поскольку они
имеют бесконечное число периодических траекторий.
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ.
ДРУГИЕ ТЕМЫ
В этом параграфе мы дадим краткое описание диффеоморфиз-
диффеоморфизмов Морса — Смейла и Аносова, а также диффеоморфизмов,
удовлетворяющих аксиоме А и условию трансверсальности.
Первые аналогичны полям Морса — Смейла, исследованным в
предыдущих параграфах. Последние же включают в себя первые
210 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
два класса и являются наиболее общим известным классом гру-
грубых диффеоморфизмов. Мы подробно разберем два знаменитых
примера, которые хорошо иллюстрируют два последних класса:
один из них предложен Томом (диффеоморфизм Аносова на Г2),
а другой — это подкова Смейла.
Помимо самостоятельного значения, которое имеет изучение
диффеоморфизмов, это изучение оказывается чрезвычайно полез-
полезным и для понимания структуры траекторий векторных полей.
Это подчеркивалось уже Пуанкаре и Бикгофом в их пионерских
работах по качественной теории динамических систем. Одним из
примеров является описание поведения траекторий векторного
поля в окрестности замкнутой траектории. Как мы видели в гл. 3,
при этом используется отображение последования (или локаль-
локальный диффеоморфизм), ассоциированное с трансверсальным се-
сечением. В конце гл. 3 мы указали на более широкие возможности
применения этой идеи, описав конструкцию надстройки диффео-
диффеоморфизма. Благодаря этой конструкции, каждый диффеоморфизм
f на многообразии размерности п можно реализовать как отобра-
отображение последования для некоторого поля Xf на многообразии
размерности п+1. Поле Xf называется надстройкой для /, и его
траектории находятся в естественном соответствии с траектория-
траекториями диффеоморфизма /. В частности, Xf в том и только том случае
является полем Купки — Смейла, когда / — диффеоморфизм
Купки — Смейла. Кроме того, Xf — грубое тогда и только тогда,
когда диффеоморфизм / грубый.
Пусть fgDiffr(M). Точка р?М называется неблуждающей
для /, если для каждой окрестности U точки р и каждого
целого п„ > 0 существует такое целое п, что | п | > п0 и
fn(U){]U Ф 0. Множество Q(/) неблуждающих точек замкнуто
и инвариантно, т. е. состоит из полных траекторий диффео-
диффеоморфизма /. Предельные множества <»(<?) и a(q) для каждой
точки q?M принадлежат й(/). В частности, всякая неподвиж-
неподвижная или периодическая точка принадлежит Q(/).
Будем говорить, что / ? Diff (М) является диффеоморфиз-
диффеоморфизмом Морса — Смейла, если
(a) й(/) состоит из конечного числа неподвижных и периоди-
периодических точек, и все эти точки гиперболические;
(b) устойчивое многообразие любой неподвижной или пери-
периодической точки трансверсально неустойчивому многооб-
многообразию любой такой точки.
Теперь мы перечислим некоторые важные факты, относящиеся
к диффеоморфизмам Морса — Смейла.
A) Множество диффеоморфизмов Морса—Смейла открыто
(и не пусто) в Diffr (М) для каждого многообразия М и вся-
всякого г ^ 1 [75].
§4- ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ %\\
B) Если f?Dilir(M)—диффеоморфизм Морса—Смейла, то
/ является грубым [75], [79].
C) Множество диффеоморфизмов Морса — Смейла плотно
в DiffM^1), г ^ 1. Этот результат, принадлежащий Пейксото*),
может быть выведен непосредственно из теоремы Купки —
Смейла для диффеоморфизмов с использованием рассуждений,
близких к тем, которые применялись при доказательстве
леммы 2. 4 этой главы. Но более изящным является следую-
следующее доказательство. Пусть / ? DifP (S1). Возьмем С°°-диффео-
морфизм /, С1"-близкий к /. Рассмотрим надстройку Xj диф-
диффеоморфизма f, которая представляет собой С°°-поле, опреде-
определенное на Т2 или /С2 в зависимости от того, сохраняет ли /
ориентацию S1 или обращает ее. Мы можем считать S1 глобаль-
глобальным трансверсальным сечением поля Х7 на Т2 или /С2, а / —
соответствующим отображением последования. Если Y—Сг-близ-
кое к Xj поле на Т2 или /С2, то S1 является трансверсаль-
трансверсальным сечением также и для Y, а соответствующее полю Y
отображение последования g является Сг-близким к / и, сле-
следовательно, к /. В силу плотности полей Морса—Смейла
в Жг (Г2) или Хг (/С2), можно выбрать Сг-близкое к Xj поле У
так, чтобы оно принадлежало классу Морса—Смейла. Тогда
g будет Сг-близким к f диффеоморфизмом Морса—Смейла.
D) Множество диффеоморфизмов Морса—Смейла не является
плотным в Diffr(M") при п^2. Сейчас мы приведем пример
такого непустого открытого множества 4lcDillr(S2), что
4lf\M\S=0. Подобные примеры можно строить на любом
многообразии размерности п ^ 2. Рассмотрим на S2 поле X
класса С°°, у которого имеется такая траектория, что ее а- и
«-предельным множествами является одно и то же седло. Траек-
Траектории поля изображены на рис. 43; а1 и о2—стоки, о4 —
источник и о3—седло, все эти точки гиперболические. Пусть
Xt—поток, индуцированный полем X и f = X1—это диффео-
диффеоморфизм, отвечающий моменту времени t=\. Тогда о3—гипер-
о3—гиперболическая неподвижная точка для /, и одна из компонент
множества W*(o3)\o3 совпадает с одной из компонент мно-
множества W" (о3)\о3. Возмутим / таким образом, чтобы полу-
получить диффеоморфизм g, для которого о3 по-прежнему является
гиперболической неподвижной точкой, но помимо о3 сущест-
существуют другие точки трансверсального пересечения многообразий
*) Фактически он неявно содержится в [87] и может быть легко вы-
выведен также на основе [191] (хотя я бы уже не сказал, что он там неявно
содержится), а явно был отмечен В. И. Арнольдом в работе, цитирован-
цитированной в [5, 125]. Правда во всех этих работах рассматривались диффеомор-
диффеоморфизмы, сохраняющие ориентацию, но если диффеоморфизм обращает ориен-
ориентацию, то он имеет неподвижную точку, и все сводится к бодее простому
исследованию диффеоморфизмов отрезка,— Прим. редщ
212
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Ws (о3, g) и W (а3, g). С этой целью возьмем точку р g Ws (а3) fl
r\Wu(o3), рфа3, и такую малую окрестность U точки р, что
U [\fU = 0. Пусть t: S2 —* S2—такой Сг -диффеоморфизм с но-
носителем в (/ (в том смысле, что отображение i тождественно
на К = M\U), для которого i (/?) = /? и W = i(Wa (ag)) транс-
версально к Ws (о3) в р. Положим g = i о /. Мы утверждаем,
что ни g, ни какой-либо диффеоморфизм из достаточно малой
окрестности диффеоморфизма g не являются диффеоморфизмами
Морса—Смейла. Поскольку g — f вне множества U, то os —
гиперболическая неподвижная точка для g, и локальные устой-
устойчивое и неустойчивое многообразия точки о3 у диффеоморфиз-
диффеоморфизмов g и / совпадают. Но Wc=WK(a3, g). Действительно, если
x&W, то Г1 (х) g W" (о3), и поэтому
(I о /)-i (х) = /-Ч-» (х) € W7« (a.) П /С-
Так как отображение t тождественно на К, то
(t о /)-»(х) = /""Г1 (ж) 6 W7° (a.) П /С
при n^l. Таким образом, ^6^°(a3t ^J» поскольку g~n(x)==
= (( о /)"" (х) сходится к as при п —»¦ с», и поэтому We W"(aa, g).
С другой стороны, Ws (og) n f/c W* (o3, g). Действительно, если
i/ g №* (o3) n f/, то / (y) k. Ws (o3) п К, и поэтому при n^s 1
в" (У) = (« о /)" (У) = /" (У) € ^' (о,) П /С.
Итак, t/ € ^ (^з! ?f)i так как последовательность g" (г/) сходится
к о3 при /г —»¦ с», а это и показывает, что №*(о3) п UcWs(oe, g).
Таким образом, Ws (o3, g) трансверсально к W" (os, g) в точке
р. Хотя это и не является необходимым, отметим, что за счет
незначительного усложнения конструкции можно добиться того,
$ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ
213
чтобы W* (o3, g) и Wu(a3, g) были трансверсальны во всех
точках пересечения. Это соответствует одному из утверждений
теоремы Купки—Смейла для диффеоморфизмов. Построенная
выше точка р трансверсального пересечения многообразий
Ws (O3, g) и Wa (a3, g) называется трансвереальной гомоклини-
ческой точкой. Читателю предлагается нарисовать рисунок
(грубым наброском которого является рис. 45), изображающий
Рис. 45
пересечения устойчивых и неустойчивых многообразий вдоль
трансверсальной гомоклинической траектории.
Биркгоф показал, что возле р накапливаются точки гипер-
гиперболических периодических траекторий диффеоморфизма g; Смейл
обобщил эти результаты на более высокие размерности ([108];
см. также [66] *)). Здесь нам необходим лишь тот факт, что р
1) Теперь это можно получить как простое следствие из доказанной
позднее теоремы о семействе е-траекторий, о чем вкратце говорится, напри-
214 гл. 4. типичность и Грубость векторных полей
неблуждающая Для доказательства рассмотрим дугу / много-
многообразия Wa(a3, g), соединяющую о3 с р. Для каждой окрест-
окрестности U точки р рассмотрим малую дугу 1г многообразия
W°(as, g), проходящую через точку р и принадлежащую U.
Так как 1Х трансверсально к Ws(os, g), то, согласно Я,-лемме,
g"^) содержит сколь угодно близкую к / дугу при всех
п>п0 с некоторым п0 > 0. Поскольку /jct/и 1(]Оф0, то
g"U[]U?=0 при п>по. Поэтому pk&(g), а поскольку точка
р не является периодической, то g не является диффеоморфиз-
диффеоморфизмом Морса—Смейла. То же самое верно и для всех диффео-
диффеоморфизмов, достаточно близких к g, поскольку они также
имеют трансверсальные гомоклинические точки. Это следует
из того факта, что компактные части устойчивого и неустой-
неустойчивого многообразий седла не сильно изменяются при малом
возмущении диффеоморфизма в Сг-топологии. Поэтому можно
гарантировать, что эти многообразия по-прежнему имеют траек-
траекторию трансверсального пересечения, отличную от возмущен-
возмущенного седла.
Из того что диффеоморфизмы Морса—Смейла не образуют
плотного множества в Diff' (М2), можно вывести, используя
конструкцию надстройки, что поля Морса—Смейла не обра-
образуют плотного подмножества в 2tr (Мп) при п 33s 3.
Теперь мы дадим другой, принадлежащий Тому пример диф-
диффеоморфизма с бесконечным числом периодических траекторий.
Потом мы покажем, что этот диффеоморфизм грубый.
Это был один из примеров, которые послужили мотивировкой
для определения некоторого класса грубых систем с бесконечным
числом периодических точек, предложенного Д. В. Аносовым [3].
В частности, существуют грубые системы, которые не принадле-
принадлежат к классу Морса — Смейла.
Рассмотрим линейный изоморфизм L в IR2, который в стан-
стандартном базисе пространства IR2 представляется гиперболической
матрицей с целыми элементами и единичным определителем.
Легко видеть, что собственные значения оператора L, т. е.
% и 1Д, где |Я,| < 1, иррациональны, а у их собственных под-
подпространств Е* и Еи тангенсы углов наклона к оси абсцисс
иррациональны. Так как detL=l, то L~l обладает такими же
свойствами. Если Z2cIR2—множество точек с целочисленными
координатами, то L(Z2) = Z2. Рассмотрим такую структуру
многообразия на Т2 = IR2/Z2, для которой я: R2 —»¦ Т2 локаль-
локальный диффеоморфизм. Эта структура многообразия может быть
получена посредством отождествления IR2/Z2 с тором вращения,
как в примере 2 из § 1 гл. 1. Напомним, что я (и, ю) — л(и', v')
мер, в [125]; об этой теореме см. [72] (добавление 1 в русском издании),
A24] или [101],— Прим. ред.
§4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 215
в том и только том случае, когда и—u'gZ и v—e'gZ.
Поэтому n(L(u, v)) — n(L(u', v')), что позволяет определить
отображение /: Т2 —»¦ Т2 с помощью формулы / (я (и, v))=nL(u, v).
Поскольку я—локальный диффеоморфизм класса С°\ то и /
принадлежит классу С°°. Аналогичные рассуждения применимы
к L'1, откуда получаем, что / является в действительности
С-диффеоморфизмом.
Для каждого р g Т2 и всякого х € IR2, такого что я (х) = р, кри-
кривая Ws (р)=зх(х+?*) плотна в 7Х Набор множеств {Ws (р), р ? F2}
определяет слоение B2) в Т2, называемое устойчивым слое-
слоением; у него все слои плотны в Т2. Кроме того, это слоение
является инвариантным относительно /, т. е. fWs (p) = WS (/ (р)).
Аналогично определяется неустойчивое слоение {W\(p), p?T*}
посредством формулы W"(p) = n(x-\-Ea). Если обозначить через
Esp и Еир касательные пространства к Ws (p) и соответственно
к W4p) в р, то E°p = dnx(Es), E»p = dnx{E") и Ef(p) = dfp(Ep),
Ef^^dfpiE-).
Рассмотрим на Г2 метрику, индуцированную из IR2 посред-
посредством я, а именно: если wlt w2?T (T2)p=JtiX), то положим
<,wv Wg}p = (dnx1w1, dn^w^y. В этой метрике
, если
|^,^| = |Я.Г11а'1|. если Щ
Из этих формул следует, что если q&Ws(p), то d(f"(q),
f" (Р)) -^Опри п -* с», а если q G Wa (р), то d(/-" (q), f~n (p)) -*. О
при п—^ оо. Следовательно, всякая периодическая точка р
диффеоморфизма / является гиперболической, а устойчивое и
неустойчивое многообразия точки р—это определенные выше
№*(р) и №° (р). Кроме того, Ws(p) трансверсально к Wa(q)
при любых р, q? Т2, и при этом Ws {р) П W^u (q) плотно в Т2.
В частности, /? = зх(О)—гиперболическая неподвижная точка
для /, а ее трансверсальные гомоклинические точки плотны
в Т2. Как и в предыдущем примере, из этого вытекает, что
/ не является диффеоморфизмом Морса—Смейла, равно как и
всякий близкий к / диффеоморфизм. Результат Биркгофа и
свойство плотности трансверсальных гомоклинических точек
влекут за собой плотность множества периодических точек
диффеоморфизма / в Т2. Теперь мы дадим прямое доказатель-
доказательство этого факта.
§ 4.1. Предложение. Периодические точки диффеоморфизма
/: Т2 —> Т2 образуют плотное в Т2 множество.
Доказательство. Пусть 3 — множество точек в R2 с рацио-
рациональными координатами Мы покажем, что u(J?) совпадает
с множеством Per (/) периодических точек диффеоморфизма f.
Поскольку 3? плотно в IR2, то отсюда будет следовать плот*
216 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
ность множества Per (/) в Т2. Если 3„ = {(m^n, mjn): mx, m2 g Z},
то 3 = Un >! 3 n. Так как элементы матрицы L—это целые
числа, то LCn) = 3n. Следовательно, /(яЗп) = пЗ п. А так
как пЗ„ — я {(mjn, mjn): m,, m2gZ, 0<т, <n, 0<m2<n},
то я«5'„—это конечное инвариантное подмножество в Т2, а
значит, все его точки периодические. Следовательно,
nC)cPer(f). С другой стороны, пусть при некотором целом
п точка x?U2 удовлетворяет равенству f"(n(x)) — n(x). Утвер-
Утверждается, что координаты точки х рациональные. Действительно,
точка y = L"x—х имеет целые координаты, так как n(L"x)=n(x).
Поскольку L—это гиперболическая матрица с целыми элемен-
элементами, то L"—/—обратимая матрица с целыми элементами, так
что (L" — /)~*—матрица с рациональными элементами. Следо-
Следовательно, координаты точки x = (Ln—I)'1}/ рациональны, а
значит, Per (f)cnC), что завершает доказательство утвер-
утверждения. |
На первый взгляд может показаться, что доказательство гру-
грубости диффеоморфизма /, имеющего бесконечное число периоди-
периодических точек, должно быть очень сложным. Диффеоморфизм /,
однако, обладает одним полезным свойством: он имеет глобаль-
глобальную гиперболическую структуру и даже индуцирован линейным
изоморфизмом в IR2. В частности, все периодические траектории
диффеоморфизма / — это седла е устойчивыми многообразиями
одинаковой размерности. Диффеоморфизмы Морса — Смейла,
напротив, должны иметь источники и стоки, а обычно также и
седла. Теперь мы дадим принадлежащее Мозеру [65] простое
и элегантное доказательство грубости диффеоморфизма /. Это
доказательство подобно аналитическому доказательству теоремы
Гробмана — Хартмана из гл. 2. Напомним, что / порождено изо-
изоморфизмом L пространства IR2, где L задается гиперболической
матрицей с целочисленными элементами и единичным опреде-
определителем.
4.2. Теорема. Диффеоморфизм fi T2 —>- Га грубый.
Доказательство. Возьмем близкий к / диффеоморфизм
g?Diffr(T2). Мы утверждаем, что существует близкий к L
диффеоморфизм G: IR2 —»- R2, который порождает g на Т2. Дей-
Действительно, для каждого х ? IR2 можно рассмотреть /я (х) = nL (x),
где я—каноническая проекция из IR2 в Т2. Поскольку gn(x)
близко к fn(x), то существует единственная близкая к L(x)
точка y?R, такая что n(y)~gn(x). Положим G{x) = y. Тогда
nG(x) = gn\x). Легко проверить, что G и L являются С-близ-
кими. Теперь представим G в виде суммы G = L-\-O, гдеФ —
Сг-малое отображение пространства R2. Так как L—гипербо-
L—гиперболический изоморфизм, то мы знаем из леммы 4.3 гл. 2, что L
$ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 217
и L-\-O сопряжены. Это означает, что существует такой гомео-
гомеоморфизм Н пространства R2, что HL = GH. Таким образом,
достаточно проверить, что Н порождает гомеоморфизм h на Т2
с лЯ = /1я, потому что это повлечет за собой равенство hf=gh.
Действительно, nHL = hnL = hfn аналогично nGH = gnH — ghn,
а, следовательно, hfn = ghn. Так как я: IR2 —> Г2 сюръективно,
то отсюда следует, что hf = gh. Проверим теперь, что гомео-
гомеоморфизм Н пространства IR2 индуцирует гомеоморфизм h тора
Т2. Для решения уравнения HL — GH мы представляем HnG
в виде # = / + « и G = L + CD и получаем uL = Lu + Ф (/ + и).
Мы ищем решение ы ? СЦ (R2), а для данной теоремы нам нужно,
чтобы / + и проектировалось в отображение на торе Т2. Это
последнее требование эквивалентно следующему: для каждого
х?Ш.2 и каждой точки р с целочисленными координатами су-
существует такое q с целочисленными координатами, что
или, что эквивалентно,
Но для близких к / диффеоморфизмов g норма построенного и
должна быть мала, поэтому из последнего уравнения вытекает,
что и(х+р) = и{х) при каждом xgR2 и каждом р с целочис-
целочисленными координатами. Это приводит нас к рассмотрению под-
подпространства 5*с:С^(К.2), состоящего из периодических функций
«GQ(Ka)t удовлетворяющих уравнению и(х + р) = и(х) при
каждом xgR2 и каждом р с целочисленными координатами.
Непосредственно ясно, что 5s замкнуто в Q (R2) и что .i? Es) с: 5s,
где оператор 3: С% (R2) -* С% (R2) определен формулой 3 (и) =
— uL—L«. Кроме того, 3 обратим, так как оператор L гипер-
гиперболический. С другой стороны, поскольку G = L + d> проекти-
проектируется в отображение тора Т2 и Ф является Сг-малым, то
приведенные выше рассуждения показывают, что Ф g 5s. Следо-
Следовательно, отображение \л: SP—+SP, \i,(u) = J2?~1(<b(/ + «)) кор-
корректно определено и является сжатием. Единственная неподвиж-
неподвижная точка и отображения \л удовлетворяет уравнению uL—Lu=^
— ФA-\-и) или, что эквивалентно, (I-{-u)L = (L + O)(I + u).
Доказательство того факта, что Н = 1-\-и есть гомеоморфизм,
проводится, как в лемме 4.3 гл. 2. Так как и g 5s, то гомео-
гомеоморфизм Н = 1-\-и проектируется в гомеоморфизм h тора Т2,
и hf = gh. Это показывает, что / является грубым в Diffr(r2),
>1 I
Диффеоморфизм /: Т2—*Т2—это характерный пример диф-
диффеоморфизма Аносова, и теперь мы собираемся дать общее опре-
определение.
U\& ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Определение. Пусть М—компактное многообразие. Будем гово-
говорить, что /?Diffr(M), г^\,— диффеоморфизм Аносова, если:
(a) касательное расслоение многообразия М разлагается в
непрерывную прямую сумму *) TM = Es(?)Ea;
(b) подрасслоения Es и Е" инвариантны под действием про-
производной Df отображения /; иными словами,
DfxE^Efw и DfxE« = E?w
при всех х?М;
(c) существует такая риманова метрика на М и такая
постоянная Х?@, 1), что ||D/>|K^||a|| и |Df^u||<X||и|| при
всех х?М, v?Esx и и?Ех.
Грубость этих диффеоморфизмов в Diffr(Al) для М любой
размерности была впервые доказана Аносовым (см. [3], [65],
[144]). Аносов определил также аналогичный класс векторных
полей и доказал их грубость 2). Надстройка диффеоморфизма
Аносова является примером такого векторного поля. В качестве
другого важного примера можно указать геодезический поток на
многообразии отрицательной кривизны [3].
Отметим, что существование диффеоморфизма Аносова на
многообразии налагает строгие ограничения на многообразие.
Например, среди компактных многообразий размерности 2
только тор допускает диффеоморфизмы Аносова. Имеется даже
гипотеза, что диффеоморфизмы Аносова существуют лишь на
очень специальных многообразиях типа тора Т" и нильмногооб-
нильмногообразии [109], [ИЗ]3). Поля Морса — Смейла, напротив, сущест-
существуют на любом многообразии. Известно также, что всякий диф-
диффеоморфизм Аносова на Т" сопряжен с диффеоморфизмом, инду-
индуцированным линейным изоморфизмом пространства R", как в
описанном выше примере [55] *). Есть предположение, что
*) Это значит, что при каждом р?М в ТМр имеются два подпростран-
подпространства Ер и ?р (слои расслоений Е'в Еа), в понятном смысле непрерывно
зависящие от р, причем TMp = ElQ)E%.— Прим. ред.
2) В отличие от случая диффеоморфизмов для потоков Аносова, к со-
сожалению, пока не опубликовано существенно более простых доказательств
грубости, чем в [3]. (В [65] доказательство для потоков неверно. Его, ви-
видимо, можно исправить, но элегантность доказательства в значительной
степени утратится.) Разумеется, теперь грубость этих потоков получается
как частный случай позднейших результатов о грубых системах, упоминае-
упоминаемых далее в основном тексте, но они доказываются не проще.—Прим. ред.
s) Такие диффеоморфизмы построены еще на так называемых инфра-
инфранильмногообразиях (но не на любом (инфра) нильмногообразии существует
диффеоморфизм Аносова). Определение и литературную ссылку см. в [20].
Поэтому в гнпотезе надо говорить об инфранильмногообразиях. Кроме того,
под «тором» (и прочими названными многообразиями) надо понимать мно-
многообразие, гомеоморфное тору (и пр.), но не обязательно диффеоморфное
ему [18].— Прим. ред.
4) Т.е. с гиперболическим автоморфизмом тора Т" = К"/Е"—отобра-
К"/Е"—отображением Тп->Тп, индуцированным гиперболическим изоморфизмом L: RnIR»
§4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 219
периодические траектории всякого диффеоморфизма Аносова
плотны в многообразии. По этим вопросам различные важные
результаты были получены Френксом [20], Мэннингом [55],
Ньюхаусом [67] и Фаррелом — Джонсом [18]. Недавно Френк-
Френксом и Вильямсом [24] был построен один очень интересный класс
потоков Аносова, для этого класса неблуждающее множество не
совпадает со всем объемлющим многообразием. Соответствующий
вопрос для диффеоморфизмов Аносова остается открытым.
Мы имеем, таким образом, два класса грубых диффеомор-
диффеоморфизмов, Морса — Смейла и Аносова, которые, как уже подчер-
подчеркивалось, обладают сильно различающимися свойствами. Смейл
ввел новый класс диффеоморфизмов, включающий предыдущие
два. Эти- диффеоморфизмы, которые мы вскоре определим, яв-
являются грубыми, и есть предположение, что всякий грубый диф-
диффеоморфизм принадлежит к этому классу.
Рассмотрим компактное многообразие М. Пусть /gDiff'(M)
и АаМ—замкнутое инвариантное множество. Л называется
гиперболическим для /, если:
(a) касательное расслоение многообразия М, ограниченное
на Л, разлагается в непрерывную прямую сумму ТАМ =
= ?л®?л х)> причем это разложение инвариантно под дейст-
действием Df\
(b) существует такая риманова метрика на М и такое число
0 1), что HD/^IK^H и ИЛ/т^ЮЦыЦ при всех х?А,
и и?Е».
Рассмотрим теперь множество неблуждающих точек Q = Q (/),
которое замкнуто и инвариантно.
Определение. Будем говорить, что / удовлетворяет аксиоме А,
если Q гиперболическое для / и Q = Per (/), т. е. периодические
точки диффеоморфизма / плотны в Q.
Если / удовлетворяет аксиоме А, то, как показал Смейл,
Q=Q(/) разлагается в конечное дизъюнктное объединение
замкнутых, инвариантных и транзитивных множеств2): Q=
==Q1UQaU. . .UQft. Детали можно найти в [109], [70], [72],
который имеет (в стандартном базисе) матрицу с целочисленными коэффи-
коэффициентами и определителем ± 1. (В предыдущем примере тоже можно было
брать определитель —1.) Читателю стоит проверить, что предложение 4.1
и теорема 4.2 переносятся на гиперболические автоморфизмы и-мерного
тора без изменения доказательств— Прим. ред.
1) Это значит, что при каждом р?Л в ТМр имеются два подпрост-
подпространства Е% и Ер (слои расслоений ESA и ?д), в понятном смысле непрерыв-
непрерывно зависящие от р, причем TMp=Es,,QEp.— Прим. ред.
2) Смейл назвал это утверждение теоремой о спектральном разложении.
Основания для такого названия не кажутся вескими, но оно часто ветре/,
чается В литературе,— Прим. ред.
220 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
[77], [101], [124]1). Множества йг называются базисными множе-
множествами. Транзитивность 2) означает, что в каждом Qt существу-
существуют плотные траектории. В случае диффеоморфизмов Морса —
Смейла базисные множества являются периодическими траекто-
траекториями. В случае диффеоморфизмов Аносова на торе Т2 имеется
лишь одно базисное множество — это весь тор Т2. В общем слу-
случае эти базисные множества могут обладать значительно более
сложной структурой, как мы увидим в примерах. Как и в случае
Морса — Смейла, они могут быть притягивающего, отталкиваю-
отталкивающего и седлового типа. В примерах 3—6 будут представлены
различные интересные непериодические базисные множества,
являющиеся аттракторами, репеллерами и типа седел. Примеры
5 и 6 можно рассматривать как специальные примеры некоторого
достаточно широкого класса аттракторов для диффеоморфизмов
с аксиомой А, структура которых была описана Вильямсом [121].
(См. также [150].— Ред.)
Относительно данного выше определения аксиомы А извест-
известно, что если dimM = 2, то гиперболичность множества Q(f)
влечет за собой равенство Per (/) = Q (/), а в высших размер-
размерностях это неверно [71], [15].
Сделаем одно последнее замечание о требовании транзитив-
транзитивности базисных множеств. Поскольку выполнение этого требо-
требования трудно проверить непосредственно, то, как в разбирае-
разбираемых ниже примерах 4 и 5, может оказаться более полезен
следующий критерий. Если Л—гиперболическое множество
для /, в котором периодические точки плотны, и если
A=>Wll(p)f]Wa(q)^0 при всех р, tfgPer (/) ПЛ, то Л
транзитивно. Действительно, при каждом р g Per (/) Г) Л точки
множества Ws(p) накапливаются возле множества Рег(/)пЛ,
и поэтому W* (р) плотно в Л. Для каждого р g Per (/) fl Л вы-
выберем базу окрестностей U\, Щ, ..., (/?, ... точки р в Л.
Тогда Vf = Uwgg/"^fe открыто и плотно в Л. Поскольку Л
замкнуто, то оно удовлетворяет свойству Бэра, а множество
*) Нужно сказать, что «гиперболическая» теория, которой целиком или
в значительной степени посвящены цитированные сочинения, не сводится
к теореме о спектральном разложении и что в ней многое относится к ги-
гиперболическим множествам, которые не предполагаются совпадающими с О (/)
и Per (/).—Прим. ред.
2) Точнее говорить о топологической транзитивности и определять ее
в общем случае как существование траектории у, для которой ш (у) совпа-
совпадает со всем рассматриваемым компактным инвариантным множеством.
В большинстве интересных случаев (в том числе и для f>,- из теоре-
теоремы о спектральном разложении) это эквивалентно существованию плотной
траектории, но у потока на S1, описываемого в терминах угловой коорди-
координаты х(mod2я) дифференциальным уравнением х=\—cos x, имеется тра-
траектория, плотная в S1, а траектории у с co(v)=S1 нет,—Прим. ред.
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 221
периодических траекторий отображения / в Л счетно, так как
они гиперболические. Итак, D = r\pkVpk (пересечение берется
по всем р € Per (/) П Л и k g N) плотно в Л. Легко видеть, что
траектория каждого x?D плотна в Л. Действительно, если
дано некоторое непустое открытое подмножество ЛсЛ, то
существует ЩаА, а поскольку х€V% = Un/"^. то отсюда
следует, что f~"(x)? U\aA при некотором ngZ.
Имея в виду свойство грубости, мы собираемся обобщить
понятие устойчивого и неустойчивого многообразия на неперио-
непериодические траектории. Пусть /gDiff(M) и х?М. Определим
Ws{x) = {y?Mi d(J"x, fny)—*О при п^-оо},
d(fnx, /"*/) —0 при п—у— оо},
где d обозначает метрику, индуцированную римановой метри-
метрикой на М. Когда Q = Q(f) гиперболическое и x^Q, то Ws(x)
и Wa (х) являются образами Сг-инъективных иммерсий евкли-
евклидовых пространств Rs и R" дополнительной размерности [39] B3).
Это в данном случае оправдывает то, что множества Ws(x) и
W" (х) называются многообразиями. В каждом базисном мно-
множестве Q| диффеоморфизма, удовлетворяющего аксиоме А, ус-
устойчивые многообразия всех траекторий в Q4 имеют одинаковую
размерность. Кроме того, их объединение совпадает с множест-
множеством точек, у которых со-предельное множество содержится в Qit
см. [9]. В частности, если Qt—аттрактор, то объединение устой-
устойчивых многообразий точек из Qt является окрестностью мно-
множества пг. В случае диффеоморфизма Аносова на Т2, индуци-
индуцированного линейным изоморфизмом пространства IR2, устойчи-
устойчивые многообразия—это проекции на Т2 параллельных прямых
в R2. Соответствующие утверждения верны и для неустойчивых
многообразий.
Определение. Пусть /gDiff(M) удовлетворяет аксиоме А.
Будем говорить, что / удовлетворяет условию трансверсальнос-
трансверсальности х), если Ws(x) и W" (у) трансверсальны при всех х, г/€^(/)-
Прежде чем обсуждать грубость диффеоморфизмов, удовле-
удовлетворяющих аксиоме А и условию трансверсальности, мы дадим
некоторые примеры таких диффеоморфизмов.
Пример 1. Диффеоморфизмы Морса — Смейла.
Пример 2. Диффеоморфизмы Аносова на торе Т\ индуци-
индуцированные линейными изоморфизмами пространства Ra. Верно
также, хотя это и не будет здесь доказано, что всякий диффео-
диффеоморфизм Аносова удовлетворяет аксиоме А и условию трансвер-
трансверсальности.
*) Его называют также сильным условием трансверсальности.— Прим.
ред.
222 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
Пример 3. Пусть g: S1—«-S1—диффеоморфизм Морса —
Смейла с двумя неподвижными точками, северный полюс п
является репеллером, а южный s—аттрактором. Пусть /: Та —»•
—>¦ Т2—диффеоморфизм Аносова, индуцированный линейным изо-
изоморфизмом пространства R2. Рассмотрим прямое произведение
диффеоморфизмов gxf: SlхТ2 —> S1 хТ2. Легко видеть, что
множество неблуждающих точек этого диффеоморфизма состоит
из двух частей, Я1 = {п}хТ2 и fi2 = {s}xP, и эти части явля-
являются гиперболическими и транзитивными. Qj здесь является
репеллером, а п2—аттрактором. Проверим условие трансвер-
трансверсальности. Пусть (г, w)?S1xTz—точка пересечения множеств
Ws(x) и Wa(y), где х?Я2 и ^/gQx. Ясно, что Ws(x) является
произведением множеств W\?Sxx{w\ и Wic{z}xT2. Анало-
Аналогично обозначим через W" и W\ факторы множества W" (у) в
S1 х {w} и {г} х Г2. Поскольку Wi=(S1\n) х {w}, a №?=(si\s) X
x{w}, то W\ и W\ трансверсальны в S1x\w}. Кроме того,
Wl и W" трансверсальны в {г}хР, потому что они являются
проекциями прямых линий из R2, параллельных независимым
векторам. Это доказывает, что Ws (х) и W" (у) трансверсальны.
Если х и у одновременно принадлежат одному из множеств
Q, или Qit то трансверсальность многообразий Ws (x) и W (у)
получается еще непосредственнее. Поэтому диффеоморфизм gx
xf: T3 —* Т3 удовлетворяет аксиоме А и условию трансверсаль-
трансверсальности. Ясно, что gxf не является ни диффеоморфизмом Морса—
Смейла, ни диффеоморфизмом Аносова.
Пример 4. В этом примере мы опишем диффеоморфизм /
сферы S2, удовлетворяющий аксиоме А и условию трансверсаль-
трансверсальности. Множество неблуждающих точек Q = Q(/) этого диффео-
диффеоморфизма состоит из трех базисных множеств: fix—отталкиваю-
fix—отталкивающая неподвижная точка, Я3—притягивающая неподвижная
точка, a fi2—канторово множество, в котором периодические
седла образуют плотное подмножество. Важной частью этого
примера является «подкова Смейла». В северном полюсе сферы
помещаем гиперболический источник Qlt а вся северная полу-
полусфера Я+, включая экватор, принадлежит его неустойчивому
многообразию Wa (fix). Таким образом, если через Н_ обозна-
обозначить южную полусферу, то f(H_)cz\n\H_. Теперь опишем /
на Н_ как композицию двух отображений, обозначаемых через /
и g. При этом Н_ считаем вложенной в R2, как показано на
рис. 46, и выделяем в ней три части: D,, прямоугольник Q
и D2. На Q отображение / действует как линейное отображе-
отображение, сжимающее горизонтальные прямые с коэффициентом сжа-
сжатия Xg(O, 1/4) и растягивающее вертикальные прямые с коэф-
коэффициентом растяжения [г>4. НаDt отображение ' также сжи-
сжимает в горизонтальном направлении, а на вертикальных пря-
прямых локальный коэффициент растяжения быстро уменьшается
§ 4. ОЕЩЙЁ ЗАМЕЧАНИЙ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ
223
с удалением от Q, так что образы D{ конгруэнтны тем же Dt,
уменьшенным в 4 раза. Отображение g изгибает прямоугольник Q
в той его части, которая является прямоугольником, занимающим
четверть Q по высоте, а вне ее изометрично, так что из Q получа-
получается подкова; при этом g помещает / (#_) в положение, показан-
показанное на рис. 46. Таким образом, Q n fQ имеет две прямоугольные
компоненты Rt и R2, которые являются образами прямоуголь-
у ч/
Ч
Рис. 46
L-
-fQ
ников i?j и i?2 из Q (рис. 47). В прямоугольниках Rt и R$
диффеоморфизм / аффинный (композиция линейного отображе-
отображения и сдвига), сжимающий горизонтальные прямые с коэффи-
коэффициентом Я и растягивающий вертикальные прямые с коэффи-
коэффициентом [г. Наконец, в центре диска Д — fDt мы помещаем
гиперболическую притягивающую неподвижную точку Qs, и
DcWs(Qa). Проанализируем множество Q = 12(/). Если х?Н+
и не совпадает с северным полюсом, то х—блуждающая точка,
так как она принадлежит неустойчивому многообразию источ-
источника. Если jc^Dj и х=?Я3, то х—блуждающая, ибо она при-
принадлежит устойчивому многообразию стока. Если x?Dlt то
224
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
/(xNDlt и х—блуждающая. Если x?D2, то f(x)^D1, и х
опять-таки является блуждающей точкой. Отсюда заключаем,,
что когда х?Н_ и x=?Qa> т° х может быть неблуждающей
лишь в том случае, когда ее траектория целиком содержится
в Q. Следовательно, если x?Q, но хфп1 и хфЯа, то
щ
i
[
1
1
I
1
1
1
L
Опишем теперь множество Л. Поскольку Qr\fQ имеет две
прямоугольные компоненты, то Q Г) fQ П fzQ имеет 4 прямоуголь-
прямоугольные компоненты и так далее. Схематично имеем: Q; Qn/Q==
=#х U #2; Q П /Q П /2<3 = #11U #12 U #21 U #22. Далее аналогично.
Индексы приписываются прямоугольникам следующим спосо-
способом: fRt Г) Q = Ru U #12 и #и с #,, #12 П #i = 0 • Подобным об-
образом /#2 П Q = #21 U #22 и #21_П#2 = 0, #22<=#а.
В общем случае определим R0l...,Op, где индексы с, равны 1
или 2, как пересечение П?=о/*(#с _fc). Это узкие прямоуголь-
прямоугольники, которые в вертикальном направлении простираются на
всю высоту Q. Из определения видно, что ROl...a f =
= /(#а1...ар)П#ар+1» откуда легко вывести, что все они не-
непусты. Далее, для любых двух прямоугольников ROl... o и
#xi...xi c P^l либо эти прямоугольники дизъюнктны, либо
#xi. ..%i(— ЯО1...оРг причем последнее имеет место в точности
тогда, когда {tt_p+i, ..., т[) = (о1, . ,.,ар). В этом случае будем
говорить, что прямоугольники совместимы. Отметим, что при
любом N > 0 можно найти такое k > N, что /* (#о,...ар) П
f\Roi...op Ф0. Например, можно взять k*=np с таким п, что
§4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 225
пр> N, и тогда
R<st...Op<sl...Op...ol..ap ^— ' (Rat—Op) П Roi...op
(у левого R блок а1...ар повторяется л+1 раз).
Рассмотрим любую такую горизонтальную прямую а, что
af]Q?=0, и пусть [a,b] = af]Q. Тогда [с, 6] П /Q—это
объединение двух замкнутых интервалов, которые остаются на
[с, Ь] после удаления из него трех попарно непересекающихся
отрезков. Из каждого из двух оставшихся мы удаляем еще
три, чтобы образовалось множество [а, Ь\ n fQ Л fzQ, и так
далее. Теперь видно, что [а, Ъ\ Л (fln>o/"Q)—канторово мно-
множество. Взяв вертикальную прямую и проведя те же рассуж-
рассуждения, обнаружим, что пересечение этой прямой с П n<of"Q
также является канторовым множеством. Поскольку отображе-
отображение / аффинное, то A = f|ngz;/nQ—канторово множество, кото-
которое можно представить в виде произведения канторовых мно-
множеств, заданных на вертикальной и горизонтальной пря-
прямых. Гиперболичность множества Л ясна: / переводит
вертикальные отрезки в вертикальные отрезки с коэф-
коэффициентом растяжения больше единицы, а горизонталь-
горизонтальные остаются горизонтальными и сжимаются. Возьмем
теперь точку л:?Л, и пусть R—содержащий х прямоугольник
в Q с двумя вертикальными сторонами той же высоты, что и
Q. Заметим, что как бы ни была мала ширина R, он все
равно содержит один из прямоугольников fea a a . Это сле-
следует из того, что Л содержится в объединении пересечений
всевозможных последовательностей совместимых прямоугольни-
прямоугольников ROi,(js...op. Покажем теперь, что дс?Л—неблуждающая точ-
точка. Пусть Qx с: '. — квадрат, содержащий х в качестве своей
внутренней точки, и пусть N—положительное число. Мы по-
покажем, что f"Qx П О.ХФ0 при некотором n>/V. Так как /
растягивает вертикальные отрезки, то существует такое целое
т ^0, что {mQx П Q содержит прямоугольник Rjm(x), высота
которого равна высоте первоначального квадрата Q. Л инва-
инвариантно относительно /, откуда ]т (х) ? Л. Поэтому существует
прямоугольник R<j,<j2...ap с Rfm(x). Как уже отмечалось, можно
выбрать такое целое &> N -\-т, что
/ RotOf-Op П RoiOr..Op ^ 0'
Отсюда следует, что /*/?/»»w П Rfn{x) Ф0,к поэтому fnQx Г) <2хф
Ф0, где n = k—m>N. Это показывает, что каждая точка
х?Л неблуждающая. Теперь докажем, что периодические точки
диффеоморфизма / плотны в Л. Действительно, по доказанно-
доказанному ранее при каждом дс?Л и каждом квадрате Qx, содержа-
226
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
щем х, существует сколь угодно большое п, для которого
f"Qx Л Qx?=0- Отображение /" сжимает горизонтальные сто-
стороны и растягивает вертикальные стороны квадрата Qx ли-
линейно. Из этого мы заключаем, что существует такой горизон-
горизонтальный отрезок /й в Qx, что fnlhczlh, и такой вертикальный
отрезок lv в Qx, что f"lv^lv. Тогда lh f) /„ — неподвижная
точка отображения f", а значит, пе-
периодическая для / Это показывает,
что периодические точки плотны в
Л. Прежде чем заключить, что Л—
базисное множество, необходимо еще
доказать существование в нем плот-
плотной траектории В соответствии с
критерием, который был дан после
определения базисных множеств, для
доказательства транзитивности мно-
множества Л достаточно показать, что
устойчивое и неустойчивое многооб-
многообразия любых двух периодических
^Q точек из Л имеют непустое пере-
Рис. 48 сечение. Но последнее заведомо
верно в данном примере, потому
что устойчивые многообразия содержат горизонтальные от-
отрезки, а неустойчивые—вертикальные отрезки, которые сое-
соединяют противоположные стороны квадрата Q. Итак, базисные
множества диффеоморфизма /: S2—»-S2—это Qlf Q2 = A, Qa.
Выполнение условия трансверсальности очевидно непосредст-
непосредственно, так как fij—отталкивающая неподвижная точка, a fi3 —
притягивающая неподвижная точках). Поэтому f удовлетворяет
аксиоме А и условию трансверсальности.
Отметим, что конструкция типа подковы может быть пост-
построена и в высших размерностях [108], [66], [70], [72].
Пример 5. Мы опишем здесь другой важный пример С-диф-
феоморфизма тора Т2, который удовлетворяет аксиоме А и
условию трансверсальности. Этот пример предложен Смейлом
(см. [109], [122]) и известен под названием DA-диффеоморфизма
(«derived from Anosov»). Множество неблуждающих точек этого
диффеоморфизма гиперболическое и состоит из двух базисных
множеств: отталкивающей "неподвижной точки и одномерного
•
X
1) Надо проверить еще трансверсальность пересечений Ws (х) с W (у)
в том случае, когда х, J/?A. Из сказанного выше видно, что в точках Л
пересечение трансверсально. Но легко видеть, что если z?Ws (x)f[Wa (у),
то г?Л. Действительно, для такой г ее траектория }пг неограниченно при-
приближается к Л при | п\ -»¦ оо. Значит, {f"z} С Н, — ведь Н+ с: W (Hi). Тогда
{/"г} с Q, ибо из {/"г} Г) №i[}DJ ф 0 следует, что Iim /nz=Q3- А Л
как раз и ^сть {г: {["г) с Q}.
§4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 227
аттрактора, который локально гомеоморфен произведению ин-
интервала на канторово множество. Начнем построение с диффе-
диффеоморфизма Аносова g: Т2 —»• Т2, индуцированного линейным
изоморфизмом L пространства R2 посредством естественной про-
проекции п: R2—*Т2, как в примере 21). Пусть Vs и va—соответ-
va—соответственно сжимающийся и растягивающийся собственный вектор
оператора L. Пусть es и еа — векторные поля на Т2, определен-
определенные формулами es (n(x)) = dn(x)-vs и е°(зх(х)) = с!я(л:)-уо. Рас-
Рассмотрим на Т2 риманову метрику, для которой \es (р), е" (р)\—
ортонормированный базис в Тр(Т2) для каждой точки р?Т2,
Отсюда dg (p) -es (p) = h>s (g (p)) и dg (p) -еа(р) = це" (g (p)), где к
и [л = 1А—собственные значения оператора L. Заметим, что
е" и еа—это векторные поля класса С°\ и их траектории, ко-
которые являются слоями устойчивого и неустойчивого слоений
соответственно, плотны в Т2 Рассмотрим теперь диффеомор-
диффеоморфизм / тора Т2, обладающий следующими свойствами:
A) / совпадает с g в дополнении к малой окрестности U
неподвижной точки ро = зх@) диффеоморфизма g\
B) / сохраняет устойчивое слоение диффеоморфизма g, ин-
индуцируя то же отображение на пространстве слоев2), т. е.
f(Ws(p)) = W*(g(p)) при каждом р?Т2;
C) р0—отталкивающая неподвижная точка для /; кроме нее
у / в U имеется еще ровно две неподвижные точки р, и ра,
которые являются седлами3) и лежат на слое Ц = w's(p0) ==
= Ws(pn, g)—точнее, на содержащем р„ связном отрезке А из
пересечения Ws(p0) n U, причем на каждой половине, на ко-
которые р„ разбивает этот отрезок, лежит по одной из этих то-
точек pi,
D) если определить отображения а, Р: Т2—*R формулами
n dP(f(f
)
то ра<((х2— 1)([х— IJ, где P = sup|P(p)| для р?Т2, и суще-
существует такая окрестность V точки р0 в неустойчивом многооб-
многообразии точки р0, что 0<а(р)<а<1 при некотором а и всех
TV
\
Прежде чем доказывать существование диффеоморфизма,
удовлетворяющего четырем перечисленным свойствам, опишем
его динамику и покажем, что он удовлетворяет аксиоме А.
х) Помимо того что g—гиперболический автоморфизм Т2, авторы сейчас
предполагают, что (как и раньше) определитель L равен 1 и даже что соб-
собственные значения L положительны. Читателю предоставляется посмотреть,
что изменится, если чтих тополнительных предположений не делать.—
Прим. ред.
2) Лучше сказать «на множестве слоев», поскольку никакой специаль-
специальной структурой это множество не снабжается.— Прим. ред.
8) По аналогии с седлом для потока здесь под седлом понимается та-
такая неподвижная точка отображения /, что одно из соответствующих соб-
собственных значений по модулю > 1, а другое < 1,— Прим. ред-
8*
228 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
В каждой связной компоненте множества L0\{p0} отобра-
отображение / имеет неподвижную точку — рх или ра. Других непод-
неподвижных точек в такой компоненте нет. Действительно, подобная
неподвижная точка могла бы лежать только в U, ибо f=g вне U,
а у g на W* (po) нет периодических точек, кроме р0. Но, по B),
в U у / нет неподвижных точек, кроме р0, ри р2-
Рассмотрим теперь действие / на Lo. Рассматриваемый со
своей внутренней метрикой, слой Lo изометричен IR. При ите-
итерациях гомеоморфизма прямой любая траектория либо «уходит
в бесконечность», либо стремится к некоторой неподвижной точ-
точке. В нашем случае последние исчерпываются ри р2 (для f\L0
это аттракторы) и р0 (репеллер). Кроме того, все точки, лежащие
вне Д, под действием / приближаются к р0 (во внутренней мет-
метрике Lo). Действительно это так для точек из L0\U (расстояние
от f(p) до р0 равно умноженному на к расстоянию от р до р0).
Остается еще множество (Lo П ?/)\А, состоящее из открытых
отрезков. У каждого такого отрезка (a, b) концы a, b(^U. Но
тогда
f(\a, b])=lf(a), f(b)]=[g(a), g(b)]^g([a, b])
(это всё отрезки на Lo), а последний отрезок не пересекается
с la, b]*). Так как его конец/(а) лежит во внутренней метрике Lo
ближе к р0, чем с, то f(b) тоже ближе к ре, чем а, а значит, весь
отрезок /([с, Ь]) оказывается ближе к р0. Из сказанного следует,
что компонента L0\{pJ, содержащая рг, совпадает с Ws(pt, /),
и потому Ws (pj, f) плотно на торе (i = 1, 2).
Если положить A = T2\W(p0, /), то, очевидно, Q(f) с
с: {ро\ U Л и Л содержит замыкание неустойчивых многообра-
многообразий точек pt (i=l, 2). Теперь мы докажем, что обратное так-
также верно, а точнее, что W (р0, /) плотно в Та и что Л явля-
является замыканием множества трансверсальных гомоклинических
точек, принадлежащих сепаратрисам точек рг (i=l, 2).
Начнем с замечания, что поскольку Ws(pt) плотно в Та,
то оно пересекает W(pj, f), i, / = 1, 2B4). Поэтому точки
№«(/?,, /) скапливаются вблизи Wa{pt, /), т. е. Wa (p,) zj W (pt)
(^-лемма из § 7 гл. 1).
Пусть теперь р?Л и W—окрестность точки р. Пусть
IcW — какой-нибудь маленький отрезок устойчивого многооб-
многообразия какой-нибудь периодической точки q отображения g. В
силу свойства B) слой /,, = и7*(<7, g) устойчивого слоения пе-
переходит в себя под действием некоторых степеней диффеомор-
диффеоморфизма /—степеней, кратных периоду точки q как периодичес-
периодической точки отображения g. Поскольку f~l растягивает Z,, в до-
х) Довольно очевидно, что это гарантировано при достаточной малости
U; впрочем, это будет совсем уж непосредственно явствовать из постро-
построения /.— Прим, ред.
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 229
полнении к V и Lx плотно, то существует такое целое п, что
f-"(I) nV = 0B6). Значит, l[)Wa(po, ОФ0; это доказывает,
что р принадлежит замыканию множества W" (р0, /). Но р не
принадлежит множеству W» (рь, /), и поэтому либо W" (plt f),
либо Wa (p2, f) пересекается с W B6), а так как каждое из
этих двух многообразий содержится в замыкании другого, то
они оба пересекаются с W. Это доказывает, что Wa(plt f) и
W (р2, /) плотны в Л. Исходя из плотности множества Ws(p{, /),
заключаем, что W содержит трансверсальные гомоклинические
точки, ассоциированные с рг, что и утверждалось. В действи-
действительности ни одна компонента множества Wu (pt, f) f] W не мо-
может содержаться в устойчивом слое. В противном случае, беря
отрицательные итерации, мы получим, что часть локального
неустойчивого многообразия W" (pt, f) расположена вдоль ус-
устойчивого слоя, что, очевидно, невозможно. Таким образом,
гомоклинические траектории, ассоциированные с рх при i=l,
2, плотны в Л. В частности, Q (/) = {/?„} (J Л.
Теперь докажем, что Л имеет гиперболическую структуру.
Для р ? Л и чисел а < О, Ь > 0 рассмотрим конус
Ср (с, Ь) = \хе* (р) + уеа (р)> уфО, а < х/у < Ь\.
Из свойства D) вытекает, что образ конуса Ср (а, Ь) под дейст-
действием dfp—это конус С/{р}(а1, Ь% где
так что
а^аК V<+, o<(ia).
-^ц fJ.' ^ ц ' и' ^Hv '
При с = — Р/0*—1)» ^ = Р/(и—1) получается, что a'
b'^b, т. е.
dfp-Cp(a, b) aCAp}(a, b).
Поэтому в пересечении
П df}-n(p)(Cf-nlP)(a, Ь))
п-й конус содержится в (п— 1)-м, а кроме того, n-й конус
есть конус вида Ср(ап, Ьп), где
К—о„ <
Следовательно, данное пересечение—это одномерное подпро-
подпространство в Т (Тг), которое мы обозначим через Еир. Ясно,
что dfp(E%) — Ef(P). Таким образом, при каждом р?А имеется
разложение ESPQ)E% касательного подпространства к Т2 в р.
230 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
где Е*—подпространство, порожденное вектором es(p). Такое
разложение инвариантно относительно производной отображе-
отображения /, и Es сжимается с коэффициентом а. Остается показать,
что dfp равномерно растягивает векторы из Е%. Чтобы увидеть
это, сперва оценим наклон подпространства Е"р *). Пусть v =
= xes (p) + уеп (р)— вектор в Е%, и пусть
vn = df~nv = х„е* (/-»(р)) + у „е- if-" (p)).
Из определения пространства Е% получаем, что \хп/уп\ рав-
равномерно ограничено при всех п > 0. С другой стороны,
xn-i
Хп ¦
У
Уп-\ U Уп
потому что vn_1 = df (f~"(p))-vn. Таким образом,
*_"=1|<^Ы+1 при всех «>1.
По индукции заключаем, что при всех п ^ 1
_ п-\
P l-
.1 ' м 1-ОЛ*) "
Следовательно, | х/у \ ^ Р/((х—1). Докажем теперь, что dfp рав-
равномерно растягивает векторы из Е%. Пусть v = хе11 (р)-\-уеп (р)—
вектор из Е", a v = x^ (f (p))+ye* (f (p))—его образ под дейст-
действием dfp. Согласно свойству D) и написанному выше выраже-
выражению, имеем
Это доказывает наше утверждение. Мы оставляем читателю до-
доказательство непрерывности расслоений Es и Еа (см. упраж-
упражнение 45).
Покажем, что периодические траектории плотны в Л. Этот
факт вытекает из доказанной выше плотности трансверсальных
гомоклинических траекторий и теоремы Биркгофа, утверждаю-
утверждающей, что гомоклинические траектории аппроксимируются перио-
периодическими. Мы, однако, собираемся изложить чрезвычайно
х) Авторы хотят доказать, что | х/у \ < Р/((д.— 1) для вектора из Е%.
Это сразу следует из того, что E%czCp(a, b) с —a=fc = P/(ji.—1). Но в
оригинале в рассуждении с конусами была допущена ошибка, и в частно-
частности, такой оценки там не получалось. Ниже авторы выводят ее несколько
иначе—ознакомиться с соответствующим простым рассуждением тоже стоит,
хотя, как видно, необходимости в нем нет,—Прим. ред.
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ
231
поучительное доказательство, следуя так называемой лемме
Аносова о замыканиих). Пусть р g Л и W—окрестность точки р.
Пусть R(=W—замкнутый прямоугольник, содержащий р в
качестве своей внутренней точки, граница которого состоит из
четырех интервалов: /х и /„ содержатся в устойчивых слоях,
a J, и Jj трансвереальны к устойчивому слоению. Каждая
связная компонента пересечения устойчивого слоя с /? —это
интервал, который мы называем устойчивым слоем прямоуголь-
R
Рис. 49
ника R. Поскольку p?A=Q(f), то f~n(R) пересекает. R при
бесконечном числе значений п g N. Для достаточно большого п
множество f~n(R)—это очень длинный (в устойчивом направ-
направлении) и очень узкий прямоугольник, расслоенный на интер-
интервалы, содержащиеся в устойчивых слоях. Можно считать, что
/"" (R) П R связно; если это не так, то можно укоротить R в
устойчивом направлении, как показано на рис. 49а). Следова-
Следовательно, можно найти такой прямоугольник R и такое N
х) Я никогда не публиковал той леммы, которая встречается в лите-
литературе под этим названием, но провел сперва соответствующее рассуждение
в частном случае в [3], а потом опубликовал намного более общую теорему
о семействе е-траекторий, упомянутую в подстрочном примечании на с. 213.
Формулировать частный случай последией в виде отдельной леммы, по-моё-
му, незачем. Впрочем, авторы этого и не делают, а только поясняют неко-
некоторые из относящихся сюда идей на примере.— Прим. ред.
а) Нужно еще, чтобы было /-«{J-i)r\R=0, /*П/~Я (#) = #. {=1> 2-
Читатель при желании может проверить, что можно обеспечить выполнение
этих свойств и что этого достаточно для рассуждений, приводимых в основ-
основном тексте (или хотя бы, что это так на рис. 49). Впрочем, при (нежела-
(нежелании читатель вправе рассматривать эти рассуждения как эвристические—в
конце концов, общая теория (излагаемая в цитированной выше литературе)
для того и существует, чтобы не было нужды каждый раз делать все го-
голыми руками.— Прим. ред.
232
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
что для каждого устойчивого слоя IcR множество / "(/) со-
содержит устойчивый слои прямоугольника R. Если через 1Х
обозначить устойчивый слои, содержащий x?Jv то f~n(Ix)
пересекает /^ в точке а (х). Так как отображение a: Jx —* Jt
непрерывно, то оно имеет неподвижную точку у, а, значит,
/""(/) содержит / . Ограничение отображения /" на интервал
/""(/„) является непрерывным отображением интервала f~n(ly)
на 1у и, следовательно, имеет неподвижную точку q. Таким
образом, мы нашли периодическую точку для / в W.
Рис. 50
Пользуясь тем же критерием, что и в разобранном выше
примере 4, читатель может доказать существование плотной
траектории в Л. Заметим, что Л содержит одномерные неус-
неустойчивые многообразия точек pt при t=l, 2 (на самом деле
оно содержит неустойчивые многообразия всех точек из Л).
В сечении вдоль устойчивого слоя Л локально содержит кан-
торово множество. Точнее, пусть р?Л и пусть /—такой со-
содержащий р малый интервал вдоль устойчивого слоя, что
3IczWa (р0, /). Тогда / ПА—канторово множество B!).
Наконец, мы докажем существование диффеоморфизма /з
Тг —>¦ Та, удовлетворяющего четырем перечисленным выше свой-
свойствам. Пусть Uo—окрестность точки р0 и q>: UQ—+R2—локаль-
UQ—+R2—локальная карта, у которой обратное отображение задается формулой
Ф^, xi) = n(x1vs-{-x2t>°), где Vs и ои—единичные собственные
векторы оператора L. Ниже Utt отвечает (xv xz) с |xt|< 1/4.
Очевидно,
пока это имеет смысл, т. е. в области |л^|< 1/4, Ix2| <
Соответствующую область на Га обозначим через и.
§4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 233
Пусть функция ty: R—»-R такова, что \p?Cw, -ф четная,
•ф(К)сг[0, 1], -ф(л:) = 1 при |*|< 1/10ц, ч}з(лг) = 0 при \х\^1/5ц,
ty'(x)^0 прилг^О. Пусть, далее, функция %: R—+R. такова, что
% € С°°.Х нечетная, % @) == 0, х'@) = 2, всюду %> 0, х (х) = to при
\х\^\/5, %'(х) > 1- на некотором отрезке (—г, г), %' не убы-
убывает на @, г), х'М < 1 nPH \х\ >г и
(*) sup | х (х)—%х|• sup |
(Чтобы убедиться в существовании такой %, построим сперва
непрерывную нечетную кусочно-линейную функцию %0, имею-
имеющую «изломы» в точках ±/-т, ±г2, где 0 < гг < г2 < 1/5, и та-
такую, что %0(х) = 2хпри |д;|^г„ %o(x) = hx при \х\~^г%. Ясно,
что
Это > 0, если гх < Хг2/2. Затем «сгладим» %о в малых отрезках
возле точек ±г1У ±г2 так, чтобы у сглаженной функции %
производные в этих отрезках изменялись монотонно. При до-
достаточно малом гг разность %(х)—Кх будет мала, что позволит
обеспечить выполнение (*).) Полагаем теперь f = g в дополне-
дополнении к U и / = ф~1о/гоф в Uo, где
F (Хи Х2) = (F1 (Хг, Х2), F* (Хг, Х2)) = (к
Заметим, что F(q>U)c:U0 и F возле границы (/ совпадает
с отображением (хх, х2) >—> (ixlt цх2), поэтому / корректно оп-
• ределено и является отображением класса Сш. Это диффеомор-
диффеоморфизм, поскольку таковым является
Свойства A) и B) очевидны. Для неподвижной точки отображе-
отображения /, лежащей в И, локальные координаты х2=0 и Xx—F^x^, 0) =
=X(*i)i a последнее уравнение в силу свойств % имеет ровно три
корня. Один из них Хг=0, а два других отличаются только зна-
знаком, и в них x'(*i)<l- Так как '
то начало координат является отталкивающей гиперболической
неподвижной точкой для F, а две другие неподвижные точки—
седла. Тем самым установлено C). Условие P2<(fA2—1J(ц—IJ
следует из (*). Остается доказать существование такой окрест-
окрестности №сф((/) начала координат, что W содержится в не-
234 ГЛ. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
устойчивом многообразии W" (О, F):
(**) sup (dF^dxJ (x) = а < 1.
Действительно, построив указанное W, мы можем взять V=
=Ф~Х (№), и соответствующая часть свойства D) будет выпол-
выполнена.
Обозначим
Jt*={si (dFWxJis, 0>П и /Я1 =
Очевидно, что
Jt = {si X'(s) > [i -a. A -
Последняя дробь с увеличением * от 0 до 1/5 возрастает (точ-
(точнее, не убывает), изменяясь от 1 до оо, так как при этом
г|) (t) убывает от 1 до 0, а функция
убывает на [1, оо). Из свойств % следует, что при й^1 мно-
множество {х: %'(х)^а\ либо пусто, либо является симметричным
относительно точки 0 замкнутым интервалом, а при увеличе-
увеличении о оно, очевидно, не увеличивается. Поэтому JtczJt-, если
t^t'^O. Так как dF1ldxi (хх, х2)^ 1 при всех (хг, х2)?IХг с
фиксированным х2 (т. е. при всех хх€-О и Т7^—xlt xj=
=—F1(xl,x2), то отсюда следует, что F~1(/JCj)—это симмет-
симметричный интервал, длина которого не больше длины интервала
1Хз. Таким образом, F~1(/JCa) содержится в /ц/ю*,. Но ясно,
что
lD = JuX{0\ = [-r,r]x{0\czW°@,F)
(на отрезке [— г, г] оси хх отображение F имеет вид xt ¦—»• %(*i)i
а %(xi)>xi на этом отрезке). Поскольку W"@, F)—открытое
подмножество R2, то и при всех достаточно малых х%
'^^XlxJc/.xMcIT'lF, 0).
Наконец, /Хзсг№о@, F) при всех х$, ибо F'^iJ^czI^-k^. Так
как объединение замкнутых интервалов /Ж1 есть компактное
множество
расположенное строго внутри компактаС = [—1/5, 1/5]х[—1/^,
l/5[i], и так как Wa @, F) открыто, то при достаточно малом
е > 0 открытая е-окрестность W множества К целиком лежит
как в С, так и в №° @, F). Для нее верхняя грань в (**)
совпадает с верхней гранью по компакту C\W, которая < 1.
Итак, / удовлетворяет всем указанным выше условиям
A)—D). Таким образом, мы построили DA-диффеоморфизм на
торе Т», |
$4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ
235
Замечание 1. Пусть рг — другая периодическая точка диффео-
диффеоморфизма Аносова g, рассмотренного выше. Мы можем одновре-
одновременно изменить g в окрестностях точек р0 и рх и получить удов-
удовлетворяющий аксиоме А диффеоморфизм /, у которого множество
неблуждающих точек состоит из трех базисных множеств: от-
отталкивающей неподвижной точки р0, отталкивающей периоди-
периодической траектории 6{pi) и непериодического аттрактора Л.
Выполняя то же построение вдоль различных периодических
траекторий диффеоморфизма g, можно получить несколько при-
примеров несопряженных гиперболических аттракторов (число пе-
периодических траекторий данного периода может быть различ-
различным . . .)•
Замечание 2. Те же методы можно применять и для построения
в высших размерностях аттракторов, удовлетворяющих акси-
аксиоме А. Следует начинать с диффеоморфизмов Аносова, у которых
устойчивые многообразия одномерны, и выполнять построения,
-аналогичные приведенным выше.
В\
MML-,
Рис. 51
Пример 6. Теперь мы покажем, что даже для сферы S воз-
возможно построение удовлетворяющего аксиоме А диффеомор-
диффеоморфизма с непериодическим аттрактором. Этот результат принад-
принадлежит Р. В. Плыкину (см. [5], § 33, или [150], где имеется ссылка
на первую публикацию и выразительная картинка). Пусть Ф:
R2 —*¦ R2—инволюция: Ф (х) = — х. Поскольку Ф (Za) = Z2, то
Ф индуцирует инволюцию г\ на торе T* = Ra/Z*. Заметим, что
т] имеет четыре неподвижные точки: ро = л(О, 0), р1 = п A/2, 0),
р2 = лA/2, 1/2) и р3 = л@, 1/2). Пусть V(—такие малые пря-
прямоугольные окрестности каждой из точек р{, O^t'^3, что
236 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ" ВЕКТОРНЫХ ПОЛЕЙ
T)(V/) = Vt, и пусть N = T2\\jV,. Ограничение т] на /V является
инволюцией без неподвижных точек. Пусть ~—отношение
эквивалентности на N, отождествляющее точки, принадлежащие
одной и той же траектории отображения!]. Пусть М—фактор-
пространство /V/~ и р: N —¦ М—каноническая проекция. На-
Наделив М гладкой структурой, индуцированной из N посредством
р, увидим, что М диффеоморфно дополнению четырех попарно
непересекающихся дисков в S2. М соответствует затемненной
области, показанной на рис. 51, с отождествлением соответст-
соответствующих сторон. Получаем, что р—это двулистное накрытие.
Это означает, что р является локальным диффеоморфизмом, у
которого каждая точка в образе имеет ровно два прообраза.
Следовательно, если /: N —>¦ /V— такое дифференцируемое ото-
отображение, что /т] = т}Д то оно индуцирует такое дифференци-
дифференцируемое отображение /: М—*М, что р/ = /р- Как в примере 5
(см. замечание 1), можно построить DA-диффеоморфизм / на
торе, у которого р0—отталкивающая неподвижная точка, а
\ри р2, ps\—отталкивающая периодическая траектория (перио-
(периода 3). Далее, легко видеть, что можно построить такое f, что
/т} = т}/, поскольку можно начинать построение с диффеомор-
диффеоморфизма Аносова g, который индуцирован линейным изоморфиз-
изоморфизмом и, следовательно, коммутирует с т). Например, начнем с
диффеоморфизма тора Г2, индуцированного линейным изомор-
изоморфизмом пространства R2, заданного в канонических координа-
координатах формулой L(xx, х2) = Bх1-\-х2, хл -\-х2). Возьмем теперь такие
замкнутые окрестности Vt точек р{, что t)(V/) = V/, причем V{
содержится в неустойчивом многообразии W" (р{, [) при 0^ i ^3.
Имеем: / является диффеоморфизмом из Л^ = Т2\и,.^г на f(N)cN
и Л =f)n>0/n(iV)—это DA-аттрактор. Поэтому f индуцирует
диффеоморфизм / многообразия М на f(M)czM. Можно про-
продолжить / на сферу, поместив по источнику в каждый из че-
четырех дисков из дополнения к М, причем один из них будет
периодическим с периодом 3. Теперь нетрудно видеть, чтой(/)
состоит из этих отталкивающих неподвижных или периодичес-
периодических траекторий и множества Л==р(Л), которое является одно-
одномерным притягивающим базисным множеством. Последнее
утверждение следует из того факта, что р—двулистное накрытие
и р/ = /рB8).
Теперь мы изложим результаты, касающиеся грубости диф-
диффеоморфизмов, удовлетворяющих аксиоме А и условию транс-
трансверсальности. Пусть t^''(M)c:Diff''(M)—подмножество таких
диффеоморфизмов, причем М компактно. Первый результат
здесь принадлежит Роббину [92], [93], доказавшему грубость
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 237
всякого диффеоморфизма f?A2(MI). Затем тот же результат
был получен в [61] для 1^ЛХ(М2). Это оставляло открытым
вопрос о грубости диффеоморфизмов / g Л1 (М) для М высшей
размерности. Этот вопрос был положительно решен Робинсоном
[97], а в [95], [96] он доказал соответствующий результат для
векторных полей.
Важной проблемой, до конца еще не решенной, является
обращение перечисленных результатов: если / грубо, то обяза-
обязательно ли оно удовлетворяет аксиоме А и условию трансвер-
трансверсальности? В том частном случае, когда Q (/) конечно, / ? Dif f7" (M)
грубо тогда и только тогда, когда /—диффеоморфизм Морса—
Смейла [79]. В общем случае, когда Q(/) не конечно, некото-
некоторые частные результаты получили Плисе [86], [149] и Мане
[53]. Используя очень оригинальную идею, Мане [54] недавно
решил проблему для двумерных многообразий2). Другой ре-
результат в этом направлении принадлежит Френксу [21], Гу-
кенхеймеру [26] и Мане [52]. Они ввели новый вариант поня-
понятия грубости, определенный ниже, и для этого варианта им
удалось получить характеристику грубости, аналогичную той,
которую мы только что сформулировали. Будем говорить, что
/€ Diffr (M) является абсолютно грубым, если существует такая
окрестность V (/)<=Diff (М) и такое число К > 0, что при каж-
каждом g ? V (/) существует такой гомеоморфизм h многообразия М,
что hf = gh и po(/i, /)^/Cpo(/, g). В этом выражении / обозна-
обозначает тождественное отображение многообразия М, а р0 обозна-
обозначает С°-расстояние, т. е. ро(/, g) = maxp(/(*), g(x)), где р —
метрика в М. Было показано, что если f?Dillr(M) абсолютно
грубо, то / удовлетворяет аксиоме А и условию трансверсаль-
трансверсальности. Френке также выяснил, проследив доказательство гру-
грубости диффеоморфизмов / ? Ar (M), что они являются абсолютно
грубыми. Можно сказать, таким образом, что /?Diffr(M) яв-
является абсолютно грубым тогда и только тогда, когда f ? Ar (M).
При -изучении грубости диффеоморфизмов и потоков специ-
специальное внимание уделялось варианту, когда грубость, так ска-
сказать, ограничена на множества неблуждающих точек. Мотиви-
Мотивировкой для такого изучения послужила идея о том, что динамика
системы в конечном счете (по прошествии большого времени)
концентрируется на множестве неблуждающих точек. Там лежат
все предельные множества и, в частности, все периодические
и рекуррентные траектории. Будем говорить, что / 6 Diff (M)
является Q-грубым, если существует такая окрестность V(f)c
cDUfr(M), что при каждом g?V(/) существует гомеоморфизм
х) Хотя f?A2{M), грубость / понимается в обычном смысле, т. е. от-
относительно возмущений, малых в смысле С1 (а не С2).— Прим. ред.
2) Одновременно несколько более слабый результат (в котором / пред-
предполагается класса С2) опубликовал А. Саниами [179].— Прим. ред.
238 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
h: Q (/)—»¦ Q (g), удовлетворяющий уравнению hf (х) = gh (х) при
всех х ? Q (/). Важным понятием здесь служат циклы в мно-
множестве неблуждающих точек. Пусть / удовлетворяет аксиоме А,
и пусть Q = Q1U-.-U^ft—разложение множества Q = Q(/) на
базисные множества. Циклом в Q называется такая последо-
последовательность точек рх € Qftl, Р2 € Ц,., •¦¦.Pts6 ^ = йй , что
И7* (/>/) П №" (pi+i) =^ 0 при 1 < i < s— 1. В работе [110J Смейл
доказал, что если / удовлетворяет аксиоме А и не имеет циклов
в п (/), то / является Q-грубым. Соответствующие результаты
для векторных полей были получены Пью и Шубом [91].
Позднее Ньюхаус [69] показал, что для выполнения условия
Q-грубости достаточно потребовать гиперболичности и отсут-
отсутствия циклов на предельном множестве. Недавно Мальта [50],
[51] ослабил эту гипотезу до центра Биркгофа, который опре-
определяется как замыкание тех траекторий, которые являются
одновременно а- и ш-рекуррентьыми 1). Относительно обратного
утверждения известно, что если / удовлетворяет аксиоме А и
существуют циклы в Q (/), то / не является Q-грубым [76].
Остается проблема: вытекает ли из Q-грубости диффеоморфиз-
диффеоморфизма / выполнение аксиомы А? Существуют результаты по Q-
грубости, подобные описанным выше для обычной грубости.
Другой естественно возникающей проблемой является вопрос
о том, образуют ли грубые диффеоморфизмы и векторные поля
плотное множество (а следовательно, открытое и плотное) в
Diff'M и ?Г(М). Первый контрпример к предположению об
их плотности был построен Смейлом [111]. Q-грубость также
не является типичной: примеры см. у Абрахама—Смейл а [2],
Ньюхауса [68]2), Шуба и Вильямса [104J и Саймона [105].
Хотя множество грубых систем в DifP(M) и в ?Г(М), вообще
говоря, не является плотным, тем не менее оно достаточно об-
обширно, как мы сейчас укажем. Прежде всего, такие системы су-
существуют на любом многообразии; диффеоморфизмы Морса —
Смейла являются типичными примерами. Более того, Смейл по-
показал [113], что грубые диффеоморфизмы имеются в каждом
изотопическом классе в Diff (M). Иными словами, всякий диффео-
диффеоморфизм может быть соединен с некоторым грубым непрерывной
дугой диффеоморфизмов. Другим интересным фактом является
возможность С-аппроксимации всякого диффеоморфизма грубым
1) Ньюхаус и Мальта доказали также, что при выполнении их усло-
условий предельное множество и центр совпадают с множеством неблуждающих
точек, так что в конечном счете эти формально более слабые условия ока-
оказываются эквивалентными условиям У-грубости, указанным Смейлом.—
Прим. ред.
2) Небольшая неточность, допущ иная в [68], исправлена в [171]. Во-
Вообще же по этой теме имеется еще несколько других работ, см. ссылки в
1125].— Прим. ред.
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 239
(Шуб [102]) Таким образом, в пространстве С'-диффеоморфиз-
С'-диффеоморфизмов, г^1, наделенном С°-топологией, грубые диффеоморфизмы
образуют плотное множество. Изотопические классы в Diff'(M),
содержащие диффеоморфизмы Морса — Смейла, были проана-
проанализированы Шубом — Сулливаном [103], Френксом — Шубом
[23] и, в случае поверхностей, Роха [94]. В последней работе
предложена характеризация в терминах нулевой скорости роста
автоморфизма, индуцированного на фундаментальной группе.
В [22] исследованы возможные типы периодического поведения
для грубых диффеоморфизмов в заданном изотопическом клас-
классе *). Для векторных полей Азимов [8] построил системы Морса —
Смейла без особых точек на любом многообразии с нулевой эй-
эйлеровой характеристикой и размерности больше чем 3. Такие
потоки, конечно, имеются на двумерных поверхностях (торе
и бутылке Клейна). Несколько удивительным оказался резуль-
результат Моргана [60], показавшего, что на некоторых трехмерных
многообразиях с нулевой эйлеровой характеристикой таких
потоков нет. Однако М. Карвальо показал, что каждую си-
систему можно аппроксимировать грубой (Thesis, Univ. Warwick,
1976).
Возможно, самое важное типичное свойство из числа откры-
открытых до сих пор в теории динамических систем принадлежит
Пью. Комбинируя теорему Купки—Смейла со своей леммой о
замыкании, Пью [89] доказал следующую теорему: существует
такое типичное множество ^c:Diff1(M), что для каждого /?#
периодические точки диффеомерфизма / гиперболичны и плотны
в Q(/), а их устойчивые и неустойчивые многообразия транс-
версальны. Важный вопрос состоит в том, чтобы выяснить,
верен ли тот же результат в Diff^M) при г ]> 2. Этот резуль-
результат известен под названием общей теоремы о плотности.
Диффеоморфизмы, удовлетворяющие аксиоме А, и в частности
диффеоморфизмы Аносова, изучались также с использованием
мер, определенных на неблуждающих множествах и инвариант-
инвариантных относительно диффеоморфизмов. Относящаяся к динамиче-
динамическим системам ветвь математики, использующая эту технику для
описания поведения траекторий диффеоморфизма, называется
эргодической теорией. Корни этой теории идут из механики
консервативных систем, где рассматриваемые диффеоморфизмы
обычно сохраняют объем. Эргодическая теория диффеоморфиз-
диффеоморфизмов, удовлетворяющих аксиоме А, начинается с работ Д. В. Ано-
Аносова, Я. Г. Синая и Боуэна. С этой теорией читатель может по-
познакомиться по работам [7], [9], [10], [120], [134].
Другой активно развивающейся областью исследования яв-
является теория бифуркаций, которой занимались многие матема-
математики начиная с Пуанкаре. Грубо говоря, эта теория заключается
*) Об этом см. также в [133].— Прим. ред.
240 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
в описании возможных изменений фазового портрета Bв) (про-
(пространства траекторий) при возмущении первоначальной динами-
динамической системы. Сюда относится, в частности, вопрос об описа-
описании классов эквивалентности систем, лежащих возле некоторой
исходной системы, относительно топологической сопряженности
или топологической эквивалентности и об описании (тоже с точ-
точностью до некоторых естественных эквивалентностей) семейств
систем, зависящих от одного или нескольких параметров.
Родственные вопросы возникают и в других областях матема-
математики, например в теории особенностей отображений х) и в теории
уравнений с частными производными (с этой проблематикой мож-
можно познакомиться в [17], [28], [42], [99], [118]), но мы ограничимся
несколькими замечаниями по поводу бифуркаций векторных
полей и диффеоморфизмов. Как уже говорилось, общая точка
зрения здесь состоит в том, что следует определить, как эволю-
эволюционирует фазовый портрет системы, зависящей от некоторых
параметров, при изменении этих параметров. Точки бифурка-
бифуркации — это те значения параметров, при которых фазовый порт-
портрет претерпевает топологическое изменение. Число результатов,
относящихся к этому направлению, растет, особенно для одно-
параметрических семейств (дуг) векторных полей и диффеомор-
диффеоморфизмов. Чтобы дать читателю представление об этой теме, рас-
расскажем о двух таких результатах, первый из которых имеет
более локальную природу, чем второй.
Пусть / = [0, 1J и М—компактное многообразие без края.
Обозначим через Л пространство С*-дуг векторных полей
\: I —*¦ Зсг (М), наделенное С*-топологией, 1^^л и г ^ 4.
Исходя из того факта, что типичное (т. е. такие поля обра-
образуют остаточное множество) векторное поле является полем
Купки—Смейла, можно ожидать, что для типичной дуги \%.А
поле ? (ц) € J?r (M) принадлежит классу Купки — Смейла при
почти всех значениях \i?l. Если ?(цо) не является полем
Купки—Смейла при некотором цо?1, то либо у поля ?([г0)
есть негиперболическая периодическая траектория, либо суще-
существуют нетранверсально пересекающиеся устойчивое и неустой-
неустойчивое многообразия. Более того, если дуга ? «невырождена»,
то либо у поля |((io) имеется лишь одна негиперболическая
периодическая траектория, либо все его периодические траек-
траектории гиперболические и существует ровно одно устойчивое и
ровно одно неустойчивое многообразие, которые имеют нетранс-
версальное пересечение, только вдоль одной траектории поля
|(|li0). Отсутствие гиперболичности у особой точки р поля
!() связано с тем, что одно собственное значение (или пара
1) Об особенностях дифференцируемых отображений см. также статью
под таким названием в J143J, где можно найти и дальнейшие ссылки,—
Прим. ред.
§4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ
241
комплексно сопряженных собственных значений) оператора
Z)g(fio) в Р имеет нулевую вещественную часть. А отсутствие
гиперболичности у замкнутой траектории у возникает из-за
того, что одно собственное значение (или пара комплексно
сопряженных собственных значений) оператора DP в р?у
имеет единичную абсолютную величину, где Р—отображение
последования некоторого проходящего через р трансверсаль-
ного сечения. Обозначим в обоих случаях это собственное
значение через К.
Теперь дадим описание локального фазового портрета поля
|(|i) для |i, близких к fi0. Для того чтобы это было возможно,
следует дополнительно потребовать выполнения некоторых ус-
условий невырожденности на струи поля ? (ц) высших порядков.
Эти условия здесь не обсуждаются. Решающим моментом в них
является существование для всех |i, близких к fi0, инвариант-
инвариантного относительно | (ц) многообразия, ассоциированного с соб-
собственным значением К. Оно называется центральным многооб-
многообразием и имеет размерность 1 в случае вещественного "к и 2
в противном случае (см. [40]) х). Бифуркации, по существу, про-
происходят на центральном многообразии; перпендикулярно ему
имеет место гиперболичность (см. [80]). В приводимых ниже ри-
рисунках гиперболичность обозначена двойными стрелками.
Особая точка.
(а) Х=0. На центральной инвариантной линии два седла 2)
сливаются и затем исчезают (или наоборот). Это называется би-
бифуркацией седло-узла.
Рис. 52
х) О его использовании при исследовании бифуркаций см. [5], с. 32—34
(где оио называется нейтральным многообразием).— Прим. ред.
2) Собственно говоря, сливаются две гиперболические особые точки,
индексы которых различаются на 1; на рисунке они обе седловые, вообще
же одна из них может (а в двумерном случае должна) быть аттрактором
или репеллером. Этим объясняется н название данной бифуркации: в дву-
двумерном случае особая точка, получающаяся прн бифуркационном значении
параметра, называется седло-узлом. (Узел—это гиперболическая особая
точка, для которой соответствующие собственные значения вещественные и
одного знака),— Прим, ред.
242
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
(Ь) "к=Ы, ЬфО. На центральной инвариантной плоскости
гиперболическая притягивающая особая точка становится не-
негиперболической, хотя по-прежнему притягивающей, затем она
превращается в гиперболический репеллер и появляется притя-
притягивающая замкнутая траектория. Это называется бифуркацией
Хопфа. C0)
Рис. 53
Замкнутая траектория. Мы ограничимся фазовым портретом
ассоциированного отображения последования.
(а) Я,= 1. Это аналог особой точки седло— узел. Точки на
картинке имеют целью подчеркнуть тот факт, что траектории
отображения последования дискретны.
•-
* -
•
1
1
Рис. 54
(b) "k=em, О<0<Сгс. Это аналог бифуркации Хопфа для осо-
особой точки: после бифуркации возникает окружность, инвариант-
инвариантная под действием отображения последования. Эта окружность
соответствует тору, инвариантному относительно потока вектор-
векторного поля. (Исключается еще 6 = я/3.—Ред.)
(c) Я,=—1. На центральной инвариантной линии гиперболи-
гиперболическая притягивающая неподвижная точка становится не гипер-
гиперболической, хотя по-прежнему притягивающей, затем она пере-
переходит в гиперболический репеллер, и появляется притягиваю-
§ 4. ОБЩИЕ ЗАМЕЧАНИЯ О ГРУБОСТИ. ДРУГИЕ ТЕМЫ 243
Рис. 55
Рис. 56
Рис. 57
Щая периодическая точка периода 2. Это называется бифуркацией
удвоения периода 1).
Негиперболическая особая точка или замкнутая траектория,
такая, как выше, называется квазигиперболической.
Для траектории, вдоль которой имеет место нетрансверсаль-
ное пересечение устойчивого и неустойчивого многообразий, мы
требуем, чтобы касание было второго порядка (квадратичное).
На рис. 57 изображено касание второго порядка (происходящее
вдоль траектории, соединяющей седла) между устойчивым и не-
') В оригинале flip bifurcation. А. Пуанкаре, впервые рассматривав-
рассматривавший данную бифуркацию (для гамнльтоновон системы на уровне постоян-
постоянной энергии), говорил о рождающемся периодическом решении как о «пе-
«периодическом решении второго рода»,— Прим. ред.
244
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
i
Рис. 58
Купки — Смейла для всех
устойчивым многообразиями двух особых точек трехмерного
векторного поля. Рисунок 58 относится к аналогичной ситуации
для двух седловых замкнутых траекторий. На рисунке изобра-
изображено двумерное трансверсальное сечение; показаны его пере-
пересечения с этими двумя траекториями и с их инвариантными мно-
многообразиями, два из которых ка-
касаются друг друга в точках траек-
траектории, идущей от одной замкну-
замкнутой траектории к другой (?l).
Теперь мы можем сформули-
сформулировать результат, принадлежа-
принадлежащий главным образом Сотомайе-
ру [115]; некоторые части этого
результата рассматривались нес-
несколькими другими авторами, в
частности Б руновским [11]. Су-
Существует такое остаточное мно-
множество дуг ^ci, что если
Е G SB, то 5 (fi) является полем
у |i?/, за исключением некоторого
счетного набора ц,г, ..., |л„, .... Для каждого п?Щ реализуется
одна из следующих двух возможностей. Либо все периодические
траектории поля ? (jin) гиперболические, за исключением одной,
которая является квазигиперболической, и их устойчивые и
неустойчивые многообразия трансверсальны, либо все периоди-
периодические траектории гиперболичны, а устойчивые и неустойчи-
неустойчивые многообразия трансверсальны, за исключением касания
второго порядка вдоль одной траектории.
Рассмотрим теперь понятие грубости дуг векторных полей
и сформулируем один из недавно полученных б этом направ-
направлении результатов. Две дуги ?, Е' € Л называются эквивалент-
эквивалентными, если имеется такой гомеоморфизм р: / —*¦ /, что при
каждом ц ? / существует гомеоморфизм h^, осуществляющий
эквивалентность между |(fj,) и ?'(p(fj,)). Более того, требуется,
чтобы гомеоморфизм h^ непрерывно зависел от ц?1. Пусть
%аА обозначает подмножество дуг градиентных векторных
полей на М. Следующая, недавно полученная теорема принад-
принадлежит Палису и Такенсу: открытое и плотное подмножество
дуг в •§ грубо [184].
Мы отсылаем читателя к [1], [5], [6], [27], [34], [58], [78],
[84], [117] для более подробного ознакомления с этой темой.
УПРАЖНЕНИЯ
1. Покажите, что каждое поле Морса—Смейла на компактном многообра-
многообразии размерности л имеет по крайней мере один притягивающий кри-
тический элемент и один отталкивающий критический элемент.
упражнения 245
2. Пусть X— векторное поле Купки—Смейла на компактном многообразии
размерности п. Покажите, что если неблуждающее множество поля X
совпадает с объединением его критических элементов, то X—поле
Морса — Смейла.
3. Пусть /: Мп—> R — функция Морса класса С+1, т. е. / имеет конеч-
конечное число невырожденных критических точек. Предположим, что каж-
каждой паре различных критических точек всегда отвечают различные
образы. Покажите, что существует фильтрация для поля X = grad/.
4. Пусть X — градиентное ноле на компактном многообразии размерности
п. Покажите, что X можно аппроксимировать полем Морса — Смейла.
б. Будем говорить, что дифференцируемая функция /: М —> R является
первым интегралом векторного поля X?$r (M), если df (р) о X (р) =0
при всех р^М. Покажите, что если X—поле Морса—Смейла, то вся-
всякий первый интеграл, является константой.
6. Пусть М—компактное многообразие размерности п, а X—векторное
поле класса С на М с двумя гиперболическими особыми точками р и
q, причем точка р притягивающая, a q отталкивающая. Предположим,
что при всех х?М\{р, q} ш-предельное множество точки х—это р, а
а-предельное — это q. Покажите, что М гомеоморфно сфере Sn.
7. Пусть X g36r (М2) — поле Морса—Смейла. Будем говорить, что поле X
полярное, если X имеет лишь один источник н один сток и не имеет
замкнутых траекторий. Пусть X — полярное поле со стоком р, а Су —
окружность, которая трансверсальна к X и ограничивает диск, содер-
содержащий р. Покажите, что на ориентируемом многообразии размерности
2 полярные поля X и Y тогда и только тогда эквивалентны, когда
существует гомеоморфизм h: Сх —»¦ Су со следующим свойством:
х> У^Сх принадлежат неустойчивому многообразию седла поля X в том
и только том случае, когда h (x), h (у) принадлежат неустойчивому
многообразию седла поля Y (Г. Флейтас).
8. Покажите, что любые два полярных поля на торе топологически
эквивалентны.
9. Покажите, что на сфере с двумя ручками (кренделе) существует пара
топологически неэквивалентных полярных полей.
10. Опишите все классы эквивалентности полярных полей на кренделе.
Указание. См. пример 10 в § 1 этой главы.
11. Рассмотрим замкнутый диск DaR2, и пусть С—его граница. Хордо-
Хордовой системой в D называется конечный набор непарно непересекающихся
дуг в D, каждая из которых соединяет две точки окружности С и
трансверсальна к С в этих точках. Покажите, что для каждой хордо-
хордовой системы в D существует трансверсальное к С векторное поле X со
следующими свойствами:
(i) дуги системы содержатся в неустойчивых многообразиях седел
поля X, и каждая дуга содержит ровно одно седло;
(ii) каждая связная компонента дополнения к объединению системы
содержит ровно одни источник;
(Hi) а-предельное множество всякой точки из С—это либо источ-
источник, либо седло.
12. Пусть X и Y—векторные поля на дисках Dx и D2, ассоциированные
с двумя хордовыми системами, как п примере 11. Пусть h: dDt—>dD2 —
такой диффеоморфизм, что если p(^dDx содержится в неустойчивом
многообразии седла поля X, то h (p) содержится в устойчивом много-
многообразии стока поля —Y. Склеивая Ил и D2 посредством h, получим
поле Z на S2, которое совпадает с X на D, не — К на D2. Покажите,
что:
(a) Z — поле Морса—Смейла;
(b) всякое поле Морса—Смейла на S2 без замкнутых траекторий топо-
246
ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
логически эквивалентно некоторому полю, полученному описанной
конструкцией.
13. Пусть X и К—такое поля Морса—Смейла на S2, что они содержат
ровно по одному стоку, н структура траекторий в дополнении к диску,
содержащемуся в устойчивом многообразии стока, такая, как показано
на рис. 59. Покажите, что фазовые диаграммы полей Л и Y изоморфны,
но сами они не являются топологически эквивалентными.
Рис. 59
14. Опишите все классы эквивалентности полей Морса—Смейла на S2, со-
содержащих ровно один сток, три седла и четыре источника и не имею-
имеющих замкнутых траекторий
15. Опишите все классы эквивалентности полей Морса—Смейла на торе Г2,
содержащих ровно одни сток, два источника и три седла и не имею-
имеющих замкнутых траекторий.
16. Рассмотрим векторное поле X, структура траекторий которого показана
на рис. 60. Неблуждающее множество поля состоит из источников d и
f2, седел sj и s2 и стоков pj и р2. Докажите, что поле X можно ап-
аппроксимировать полем, имеющим замкнутую траекторию. Это показы-
показывает, что X не является Й-грубым.
17. Пусть X—поле Купки—Смейла на компактном многообразии размер-
размерности л с конечным числом критических элементов. Покажите, что если
предельное множество поля X совпадает со множеством критических
элементов, то X—векторное поле Морса — Смейла
18. Покажите, что множество полей Купки—Смейла не является открытым
в $Г(Л12), если М2 отлично от сферы, проективной плоскости или бу-
бутылки Клейна.
Указание. Используйте пример Черрн (пример 13 настоящей главы).
19. Пусть Х? Jr (Л12) = поле, все особые точки которого гиперболические.
Если G—граф для поля X и w(p) = G при некотором р^М, то суще-
существует такая окрестность V точки р, что w(<?) = G для каждой точки
q?V.
20. Покажите, что если /И2—ориентируемое многообразие и Х?$Г(М3)
грубое, то X—поле Морса—Смейла. Покажите также, что если М не-
ориентируемо и XgJMM2) грубое, то X — поле Морса—Смейла.
21. Покажите, что если /gDiff1 (M) является грубым и имеет конечное
число периодических точек, то /—диффеоморфизм Морса—Смейла.
22. Пусть 3fr (К2), г Зг 1, — множество векторных полей на R2 с топологией
Уитни (см. упражнение 17 гл, 1), Покажите, что существуют грубые
поля в ?г (R2).
УПРАЖНЕНИЯ
247
Указание Рассмотрите триангуляцию плоскости и постройте поле с осо-
особыми точками в центрах треугольников, в центрах нх ребер и в вер-
вершинах. C2)
Замечание. П. -Мендес показал в [63], что грубые векторные поля и
диффеоморфизмы существуют на любом открытом многообразии.
23. Покажите, что если у — нетривиальная рекуррентная траектория неко-
некоторого поля X на неориентируемом многообразии размерности 2, то
существует трансверсальная к X окружность, проходящяя через любую
фиксированную точку ?
Рис. 60
24. Покажите, что если h: S1—>-Sl—гомеоморфизм, обращающий ориен-
ориентацию, то h имеет неподвижную точку.
25. Покажите, что векторное поле без особых точек на бутылке Клейна
имеет лишь тривиальные рекуррентные траектории.
26. Покажите, что множество диффеоморфизмов Морса—Смейла не является
плотным ни на каком многообразии размерности 2.
27. Покажите, что множество полей Морса—Смейла не является плотным
ни на каком многообразии размерности >3.
28. Покажите, что если предельное множество диффеоморфизма или век-
векторного поля состоит из конечного множества траекторий, то центр
Биркгофа состоит из (конечного числа) неподвижных точек и периоди-
периодических траекторий. (Центр Бнркгофа—это замыкание множества точек
тех траекторий, которые одновременно ш- и а-рекуррентны.)
29. Покажите, что если диффеоморфизм или векторное поле имеют конеч-
конечное число неподвижных точек и периодических траекторий, причем все
они гиперболические, то не существует циклов между этими неподвиж-
неподвижными точками и периодическими траекториями вдоль трансверсальных
пересечений их устойчивых и неустойчивых многообразий.
30. Покажите, что грубый диффеоморфизм или грубое векторное поле, у
которых предельное множество состоит из конечного числа траекторий,
должны принадлежать классу Морса—Смейла.
31. Покажите, что множества диффеоморфизмов Аносова и Морса—Смейла
не пересекаются.
32. Покажите, что единственное компактное двумерное многообразие,
допускающее диффеоморфизм Аносова, — это тор.
33. Покажите, что диффеоморфизм Аносова из предложения 4.1 этой главы
имеет плотную в Т2 траекторию.
248 ГЛ. 4. ТИПИЧНОРТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
34. Постройте пример диффеоморфизма Аносова на торе 7'" = S1X .. . XS1.
35. Используя общую теорему о плотности, покажите, что всякий диффео-
диффеоморфизм Аносова удовлетворяет аксиоме А.
36. Покажите, что на каждом многообразии размерности 2 существует диф-
диффеоморфизм, удовлетворяющий аксиоме А и условию трансверсальности
н обладающий бесконечным числом периодических траекторий.
Указание. Испольчуйте подкову Смейла в S2 и диффеоморфизм Морса —
Смейла на М2.
37. Покажите, что если /j: Мг—» Мг и f2: Мг—>-Мг—два диффеомор-
диффеоморфизма, удовлетворяющие аксиоме А и условию трансверсальности, то
этими же свойствами обладает и диффеоморфизм f:MiXM2—»¦ Мгу.М%,
где /(р, <?) = (Ыр). /,(*))•
38. Пусть /: М—*-М—диффеоморфизм, который является С'-грубым и
удовлетворяет аксиоме А. Докажите, что тогда /должен удовлетворять
условию трансверсальности.
39. Покажите, что всякий диффеоморфизм, который удовлетворяет аксиоме
А, должен непременно иметь притягивающее базисное множество.
40. Покажите, что если диффеоморфизм / компактного многообразия М
удовлетворяет аксиоме А, то объединение устойчивых многообразий
точек, принадлежащих притягивающим базисным множествам диффео-
диффеоморфизма /, открыто и плотно в М.
41. Покажите, что на каждом многообразии существует открытое множество
диффеоморфизмов класса Сг (/¦ :& 1), которые изотопны тождественному,
но не вкладываются в поток.
Напомним, что диффеоморфизм / называется изотопным тождест-
тождественному, если существует непрерывная дуга диффеоморфизмов, соединяю-
соединяющая / с тождественным диффеоморфизмом. Поток С-днффеоморфизмов—
это непрерывная группа гомеоморфизмов <р: (R, -)-)—»- (Diff (M), о).
Мы говорим, что / вкладывается в поток, если /=<р A) для некоторого
потока <р.
42. Покажите, что два коммутирующих векторных поля1) класса Сг (г Зз 1)
на поверхности ненулевого рода имеют общую особую точку (Э. Лима).
Указание. Покажите прежде всего, что всякое векторное поле класса Сг
на поверхности может иметь лишь конечное число нетривиальных мини-
минимальных множеств. Для г 2& 2 это следует нз теоремы Данжуа—Шварца,
так как в этом случае существуют лишь тривиальные минимальные
множества. Заметьте, что в гл. 1 мы поставили аналогичную проблему
для двумерной сферы. Соответствующий-вопрос в высших размерностях
остается, по-видимому, полностью открытым.
43. Покажите, что на ориентируемой поверхности М2 множество векторных
полей с тривиальным централизатором содержит открытое и плотное под-
подмножество пространства Э?°° (М2) (П. Сад). Векторное поле X имеет по
определению тривиальный централизатор, если для каждого коммути-
коммутирующего с X поля Y?Ж°° (М*) выполнено равенство Y=cX при неко-
некотором с^К. Если вместо 3?°° (M) рассматривать пространство вектор-
векторных полей Морса—Смейла (нли, Солее обшим образом, векторных по-
полей, удовлетворяющих аксиоме А), то сформулированный выше результат
верен также и в высших размерностях. Обратите внимание на тот факт,
что пара коммутирующих векторных полей порождает действие R2.
Понятие грубости для К2-действий рассмотрено в [12].
44. Пусть X—векторное поле класса С" на компактном многообразии М.
Предположим, что X обладает первым интегралом, который представ-
представляет собой функцию Морса. Покажите, что существует С°°-аппрокси-
мация поля X векторными полями Морса—Смейла без замкнутых
траекторий.
1) См. упр. 2 к гл. 1.— Прим. ред.
ПРИЛОЖЕНИЕ: ЧИСЛО ВРАЩЕНИЯ И ПОТОК ЧЕРРИ 249
Напомним, что /: М —> R называется функцией Морса, если все
ее критические точки невырождены или, что эквивалентно, если все
особые точки поля grad / гиперболические. Быть первым интегралом
поля X для функции / означает быть постоянной вдоль траекторий
поля X.
45. Пусть /gDiff(/W) н Ас М — замкнутое подмножество, инвариантное
под действием /. Предположим, что существует рнманова метрика на
М, число Х?@, 1) и разложение ТХМ = Е\ ф Е" для каждого х?А,
такие что Djx (?*) =Щ(]а, Dfx (Eux) = Efm, || D/^ | < X || t; [[ при всех
v?Esx и ||Dfxha||<'к||w[[ при всех w?Efm. Покажите, что множество
Л гиперболическое, т. е. что подпространства Ех н Е% в ТХМ зависят
от точки х непрерывным образом.
46. Для всех л 5*2 существует такой диффеоморфизм /: S"—>Sn, удо-
удовлетворяющий аксиоме А и условию трансверсальности, что неблуж-
неблуждающее множество содержит отталкивающую неподвижную точку и
непериодический аттрактор.
Указание. Используйте пример 6 из § 4 гл. 4.
47. Покажите, что заключение упражнения 46 останется верным для всех
многообразий М размерности га ^ 2.
48. Покажите, что множество грубых диффеоморфизмов сферы не является
плотным в Diff1 (S2).
Указание. Используйте упражнение 38 и незначительную модификацию
примера 6 из § 4.
49. Покажите, что для каждого многообразия М размерности яЭ=2 мно-
множество грубых диффеоморфизмов не является плотным в Diff1 (М).
ПРИЛОЖЕНИЕ: ЧИСЛО ВРАЩЕНИЯ
И ПОТОК ЧЕРРИ
Здесь мы дадим подробное изложение построения примера
Черри, который был упомянут в примере 13 этой главы. Прежде
всего мы докажем существование таких С°°-полей на торе, кото-
которые трансверсальны некоторой окружности 2 и имеют ровно две
особые точки: сток и седло, причем обе гиперболические. Отоб-
Отображение последования такого поля определено на дополнении
к замкнутому интервалу в 2 и продолжается до монотонного
эндоморфизма окружности 2 степени 1. Понятие числа враще-
вращения, введенное Пуанкаре для изучения динамики гомеоморфиз-
гомеоморфизмов окружности, можно распространить и на такие эндоморфиз-
эндоморфизмы C3). Мы покажем, что рассматриваемые поля в том и только
том случае имеют нетривиальные рекуррентные траектории,
когда числа вращения индуцированных на 2 эндоморфизмов
иррациональны. Поскольку число вращения непрерывно зави-
зависит от эндоморфизма, то отсюда будет вытекать существование
полей с нетривиальными рекуррентными траекториями.
Пусть я- К2—*Т—накрывающее отображение, введенное в
примере 2 из § 1 гл. 1. Тогда я—локальный диффеоморфизм
класса С°°, л(х, у) = п(хг, у') тогда и только тогда, когда
/Z и y—t/eZ, и я([0, 1)х[0, 1]) = ТК Если X—век-
250 гл. 4. типичность и грубость векторных полей
торное поле класса С°° на торе, то можно определить С°°-поле
Y — n*X на R2, положив У(г) = (^яг)~1^ (я (г)). Ясно, что так
определенное поле Y удовлетворяет условию
V (х, у) € К2, V (п, /и) € Z2 К (х+n; r/+m) = К {х, у). (*)
Наоборот, если Y—векторное поле класса С°° на плоскости,
удовлетворяющее условию (*), то существует единственное та-
такое С°°-пбле X на торе, что Y = n*X. Можно, таким образом,
отождествить векторные поля на торе с векторными полями на
К2, удовлетворяющими условию (*).
Пусть %—множество векторных полей X ? JT° (R2), удовлет-
удовлетворяющих следующим условиям-
@ V(*. У)?№, (т, «)€Z2
Х(х+п, у + т) = Х (х, у);
(ii) X трансверсально к прямой {0} х R и имеет в прямо-
прямоугольнике [0, 1 ] X [0, 1] только две особые точки р, s, где р—
сток, a s—седло, причем обе эти точки гиперболические;
(iii) существуют такие a, b?R, что а<Ь<а+1, и если
у?(Ь, а+1), то положительная полутраектория поля X, про-
проходящая через точку @, у), пересекает прямую {1} х R в точке
A, fx(y))> а если у?(а, V), то положительная полутраектория
точки @, у) идет прямо в сток, не пересекая прямой {1}R
(iv) limy^bf'x (У) — + °° и Ига^о+ \f'x (у) = + оо.
На рис. 61 мы изобразили траектории поля X ? #. Отметим,
что из условия (iii) вытекает, что «-предельные множества
точек @, а) и @, Ь)—это одно и то же седло. Если обозначить
через A, с) точку пересечения неустойчивого многообразия
этого седла с прямой {1}xR, то можно непрерывно продол-
продолжить fy на интервал [а, а+1], положив, что fx{y) = c для
у?[а, Ь\. Условие (i) влечет за собой равенство fx(a-\-l) =
= fx ia) + 1 • поэтому можно непрерывно продолжить fx на R
по формуле fx(y + n) = fx(y) + n для у?[а, а+l] и n?Z.
Обозначим через X векторное поле на торе, индуцированное
полем Х?#, так что Х=л*Х. Тогда X имеет ровно две осо-
особые точки, причем обе гиперболические; л(р)—это сток и
n(s)—седло. Кроме того, X трансверсально к окружности
2 = n({0}xR) и отображение последования Р-%, определенное
на л({0}х (Ь, а+ 1)), может быть непрерывно продолжено на 2.
Отображение fx является поднятием отображения Р-%. Дейст-
Действительно, яг R—•¦?, определенное формулой я(г/)==я@, у) —
накрытие и nofx = Р^оя.
ПРИЛОЖЕНИЕ: ЧИСЛО ВРАЩЕНИЯ И ПОТОК ЧЕРРИ
251
Лемма 1 • "ё не пусто.
Доказательство. Рассмотрим векторное поле Y (х, у) =
= Bх(х-\-2/3), —у). Множество неблуждающих точек поля Y
состоит из двух особых точек: седла @, 0) и стока (—2/3, 0).
Легко проверить, что Y трансверсально к единичной окруж-
окружности во всех точках дуги
С = {(х, у): х* + у*=1, х<1/2}.
(См. рис. 62.) Пусть
Z (х, у) = (ф (х, у) Bх2 + |*) + A—ф (х, у)) (х2 + 1), -у),
где ф—такая С°°-функция, что фA?2)с [0, 1], <р(х, у)=1, если
х > 1/2 или (х, у) 6 U, ф (х, у) = 0, если х < 1/4 и (х, у) 6 K*\V.
Здесь U и V—такие малые окрестности дуги С, что VczV.
Рис. 61
Рис. 62
Если V достаточно мала, то множество неблуждающих точек
поля Z пусто. Возьмем такое Т > 0, что Zt(C)cz{(x, у): х> 1}
при всех t^T. Используя поток поля Z, можно определить
диффеоморфизм Н\ @, 1)х@, 1)—*№ с К2 по формуле Н{х,у)~
—ZxT(h(y)), где ft; [0, 1] —*С—какой-нибудь диффеоморфизм.
Если г 6@, 1)х@, 1), то положим
Поскольку Z = Y в окрестности дуги Сив области {(х, у): х >
> 1/2} х), то Х(г) = A, 0), если г принадлежит малой окрест-
1) И поскольку
Прим. ред.
при всех
, если дг—конец дуги С—
252 гл. 4. типичность и грубость, векторных полей
ности границы прямоугольника [0, 1]х[0, 1] Теперь можно
продолжить X на К2, положив Х(г) = A, 0), если г принадле-
принадлежит границе прямоугольника [0, 1]х[0, 1], и
Х(х+п, у-{-т) = Х(х, у),
если {х, у) 6 [0, 1] х [0, 1] и (п, т) € Z2. Непосредственно про-
проверяется, что X удовлетворяет условиям (i)—(Hi) Условие (iv)
вытекает из того факта, что, как может проверить .читатель,
след оператора dX(s) положителен. (Можно считать, что X
линейно в малой окрестности точки s, хотя это не так уж не-
необходимо *)).
Лемма 2. Существует такое векторное поле Х^'б, что dfx («/)> 1
при всех y€(b, а+1).
Доказательство. Возьмем такое Y^'e, что У (х, у) — A, 0),
если 2/3^x^1 2). Поскольку /V диффеоморфно отображает
интервал (b, о+1) на некоторый интервал длины 1 и, в силу
условия (iv), />(«/)> 1 возле точек Ь и о+1, то отсюда сле-
следует, что существует такой диффеоморфизм /: ф, а-\- 1)—>
—*(/у(&)> /V(«+!)> что ПРИ всех У€(^. а+Ц выполнено нера-
неравенство /' (у) > 1 и / (у) = fY (у), если у расположено либо вбли-
вблизи точки Ь, либо вблизи точки а +1. Остается доказать сущест-
существование такого поля X ? %, что fx — f.
Пусть q>t: (с, с + Г)—*(с, с+ 1) определено формулой ц>г(у)—
=(l — t)y + ty(y), где Ф=/о/р] и c=fv (о). При каждом ^ ё [0, 1]
отображение ф4 является диффеоморфизмом и q>t (г/) = у, если у
близко либо к точке с, либо к точке с + 1. Пусть а! [2/3, 1] —»¦
—>-[0, 1]—такая функция класса С", что а = 0 в окрестности
точки 2/3 и а = 1 в окрестности точки 1. Рассмотрим отобра-
отображение
Hi (|,
задаваемое формулой Н(х, у) = (х, ЧамУ)- Тогда Н—диффео-
Н—диффеоморфизм. Пусть X—векторное поле, определяемое формулой
Х{х, y) = dH(H-i (х, y)).Y(H-i(x, у)),
если {х, у) 6 B/3, 1)х(с, с+1),
Х(х+п, у + т) = Х(х, у),
если {х, у) е B/3, 1)х(с, сЦ-1) и (и, mNZ2,
х) Имеется в виду, что X можно изменить таким образом, что (i)—(iii)
не нарушатся, а возле s поле станет линейным с положительным следом
матрицы коэффициентов; для измененного X проверить (iv) совсем просто.—
Прим. ред.
2) Нетрудно убедиться, что для каждого YC.4S имеется такое Zgyg,
что f z =}y и Z(x, y) = (l, 0) при 2/3<х<1. (Это используется также
а в лемме 4.)— Прим. ред.
ПРИЛОЖЕНИЕ: ЧИСЛО ВРАЩЕНИЯ И ПОТОК ЧЕРРИ 253
Xix, y) = Y(x, у),
если ((х, у) + Z2) П B/3, 1) х (с, с+ 1) = 0.
Легко проверить, что X?g и ^ = фо/у =/. |
Лемма 3. Пусть /, g: R.—>¦ IR—такие монотонные непрерывные
функции, что /(х+1) = /(х)+1 и g(x+ l) = g(x) + l при всех
x^R- Тогда:
(i) p(/) = linw«,(/"@)/n) существует и \(f"(O)/n—p(f)\<
1/
< 1/и;
(ii) Нт„_а>(/"(х)—{х)/п существует при всех x?Ru равен р (/);
(in) p(f) = m/n, где т, n?Z, m~> О, в том и только в том
случае, когда существует такое x?R, что f"(x) = x + m;
(iv) для любого е > 0 существует такое 8 > 0, что если
И/—ё( о = sup*6R|/(*)—?(*) |< 6, то |р(/)—p(g)\<s;
(v) р(/ + л) = р(/) + « лр« любом целом п.
Доказательство. Пусть Mk = mzxx€R(fk(x)—х) и тк—
=minA:e к (/*(*)—-^)- Мы утверждаем, что Mft—/пй < 1. Дейст-
Действительно, поскольку / (х + 1) = / (х) + 1, то f (х + 1) = /* (х) + 1.
Поэтому отображение ф = Р—id периодично с периодом 1.
Следовательно, существуют такие xk, Xk ? К, что 0^xk—Xk <
<1 и ф (xk) = mft, ф (Xfc) = Mk. Поскольку fk также монотонно
не убывает, то fk(Xk)^.fk(xk). Поэтому Mk + Xk ^mk + xk, и
значит, Mk—тк^хк—Xk < 1, что доказывает высказанное
выше утверждение.
Теперь мы собираемся доказать, что V*. у € К
A)
Действительно, fk {у)—у— 1 ^ Мк — 1 < тк <! fk (х)—х <! Мк ^
^ ть + 1 ^ /ft (у)—у+1. Подставив в формулу A) значения
у = 0 и x = fkU~l>@), получим
/* @)— 1 < /S/ @)—Р V-» @) < /* @) +1.
Следовательно,
< 2( V*J @)-/ft V-« @)) < п (^ @) + 1).
Из этого вытекает, что
nfk @)—п < /ft" @) < n/ft @) + п.
Разделив последнее неравенство на kn, получим:
254 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
ИЛИ
Аналогично,
I Р" @)
I fen п I~~"- п
Последовательность /ft @)/& является последовательностью Ко-
ши, потому что \fk(O)/k—f"@)/n\^ \lk-\- l/п, и поэтому она
сходится к некоторому пределу р(/). Устремляя п к оо в не-
неравенстве B), получим, что |р(/)—/fc@)/&|<; l/k. Это доказы-
доказывает (i).
Подставляя у = 0 в A), будем иметь
f*@)—1 < fk(x)—
Поэтому
Отсюда следует, что (fk(x)—x)/k сходится к р(/), и тем самым
(и) тоже доказано.
Приступая к доказательству утверждения (ш), предположим,
что существует такое х € К, что f" (х) = х + т, где т, n?Z,
п > 0. Отсюда легко следует по индукции равенство fhn (x) —
= x + km. Таким образом,
р (/) =,limft^.a, (/*" (x)—x)lkn — limfe^.» km/kn = /я/и.
Пусть теперь р (/) = т/п\ предположим, рассуждая от против-
противного, что $"(х)Фх-{-т при всяком x?R. Таким образом,
V* € К. /" (х)—х > т (или, наоборот, V* € R, f" (х)—х < т).
Так как отображение /"—id периодично, то существует такое
а > 0, что f"(x)—x^m-+-a (или f"(x)—х^.т—а) при всех
x?R. Поэтому fkn(x)—x^km-\-ka (или fkn(x)—x^km—ka),
а значит, p(f)^(m + a)/n (или p(/)^(m—a)/n), что приводит
к противоречию.
Для доказательства (iv) заметим, что
rft@) /*@)
Зафиксируем такое целое &, что 2/k < е/2, и выберем такое
б > 0, что |?*@)-Р@)|< ke/2 при |g—f|j0 < 6. Тогда lp(g)—
— Р (/) | < е, если jg—fju < S. Остается доказать, что р (/ + я)=
= РСО + л» если n^Z. По индукции имеем! (/+п)*(х) =»
ПРИЛОЖЕНИЕ: ЧИСЛО ВРАЩЕНИЯ И ПОТОК ЧЁРРЙ 255
= f%x) + kn. Таким образом,
Лемма 3 позволяет ввести понятие числа вращения для
монотонного эндоморфизма окружности степени 1. Действитель-
Действительно, пусть п: R—* S1—накрытие и л (t) = exp Bnit). Эндомор-
Эндоморфизм a: S1 —»S1 является монотонным и имеет степень 1 в том
и только в том случае, когда он имеет поднятие a: R—«-IR,
которое представляет собой монотонную функцию, удовлетво-
удовлетворяющую уравнению а(х+ \) — а(х) + 1. Определим число вра-
вращения эндоморфизма а посредством формулы р (а) = п (р (а)). Оно
не зависит от выбора поднятия а в силу леммы 3 (v).
Лемма 4. Существует такое Х^'в, что dfx(у) > 1 при всех
у€(Ь, а+1) и число t>(fx) иррационально.
Доказательство. Выберем такое Х° ? %, что dfx° (у) > 1 при
всех у?ф, а+1) и Х°(х, у) = A, 0), если 2/3<х<1. Мы
построим такое семейство векторных полей Хк ? '6, что
fxi=*fxo+l. Пусть Н> B/3, 1)хК—B/3, \)xR определено
формулой Н(х, у) = (х, у + а(х)К), где аг [2/3, 1]—* [0, 1] —
такая функция класса С", что а(д:) = 0, если х расположено
возле точки 2/3, и а(х) — \, если х расположено "возле точки 1.
Определим:
Х*{х, y) = dH(H-i(x, y)).X°(H-*(x, у)),
если (х, у) 6B/3, 1)хК;
Х*-{х+п, у) = Х^(х, у), если х€B/3, 1);
Х*(х, у) = Х»(х, у), если (x+Z)f1B/3, 1)=0.
Поскольку Н (х, у + т) = Н(х, у) + @, т) при всех mgZ, то
Xя €#¦ Отсюда непосредственно следует, что fxi=fxt X
Рассмотрим отображение h: R—»-IR, задаваемое формулой ()
p(fxx). Согласно лемме 3, h непрерывно и АA)=/г@)+1.
Поэтому существует такое А,€[0, 1], что h (К) иррационально.
Теперь достаточно взять Х — Хк. |
Теорема. Существует С"'-векторное поле Y на торе со следую-
следующей структурой траекторий:
A) Y имеет ровно две особые точки, сток Р и седло S,
причем обе гиперболические;
B) Ws (Р) плотно в Т2 и компактное множество А =
= T2\WS(P) транзитивно, а именно, существует такое
q?A\{S\, что w(q) = a(q) = A,
C) если q?T2\(Au{P}), то u>(q) = P и a(q)czA;
256 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
D) существует трансверсальная к У окружность 2, для
которой множество 2 Г) Л является канторовым. C4)
Доказательство. Возьмем такое У 6 ЗЕ~ (Т2), что я*У = X
удовлетворяет условиям из леммы 4. Ясно, что Y удовлетво-
удовлетворяет A) с Р = п(р) и S = n(s). Окружность 2 = jt({0}xlR)
трансверсальна к У и fx является поднятием отображения по-
следования Ру: 2—>-2 1). Если Q—первая точка пересечения
неустойчивого многообразия точки S с 2, то ф = яA, с) и
Py1(Q) = n({0}xfo, Ь\). Если со (Q) = S или co(Q)=P, то суще-
существует такое п ? N, что Р? (Q) = Q. Таким образом, nfx (с) =
= PYn (с) = Ру (Q) = Q = л (с), и поэтому существует такое m ? Z,
что /х(с) = с + /и- Это противоречит иррациональности числа
P(fx)- Следовательно, у поля У нет траекторий, соединяющих
седла, и co(Q) не содержит Р. Аналогичные рассуждения пока-
показывают, что у Y нет замкнутых траекторий.
Теперь мы покажем, что WS(P) плотно в Т2. Для этого
достаточно доказать, что компактное множество /C = 2\W*(P)
имеет пустую внутренность. Рассуждая от противного, предпо-
предположим, что у множества К непустая внутренность, и возьмем
максимальный интервал JcK. Пусть Jn = P'x(J) = Px(^n-i)-
Так как Jf\Ws(P) = 0, то Jn является компактным интерва-
интервалом, длина которого больше длины интервала Jп-±. Поскольку
J—максимальный интервал, а у поля У нет замкнутых траек-
траекторий, то интервалы J„ попарно не пересекаются2). Это про-
противоречие доказывает, что WS(P)—плотное множество.
Согласно теореме Данжуа—Шварца, У имеет лишь триви-
тривиальные минимальные множества. Проверим этот факт непосред-
непосредственно. Предположим, что L—нетривиальное минимальное
множество для У. Тогда L П 2 — компактное множество, не име-
имеющее общих точек ни с устойчивым, ни с неустойчивым мно-
многообразиями седла S, так как в противном случае L содержало
бы седло. Так как множество WS(P) плотное и Lf]Ws(P) = 0,
то LczWs(S). Таким образом, если /—максимальный интервал
в 2\L, то Ру (J) Г) J ф 0 при некотором п C6). Поскольку
концевые точки интервала J принадлежат L, то Py(J)==/,
откуда следует существование замкнутой траектории8). Это
противоречие показывает, что Р и S—единственные минималь-
минимальные множества для У.
х) Далее fx и Ру считаются доопределенными по непрерывности.—
Прим. ред.
2) Если •^n = ^m, то концы / могли бы еще лежать не на замкнутых
траекториях, а на сепаратрисах S. Но это тоже невозможно—тогда у У
была бы замкнутая сепаратриса (т. е. сепаратриса, образующая замкнутую
петлю—исходящая из S и снова возвращающаяся в S),— Прим. ред.
2) Или замкнутой сепаратрисы.— Прим. ред.
ПРИЛОЖЕНИЕ: ЧИСЛО ВРАЩЕНИЯ И ПОТОК ЧЕРРИ 257
Интервалы /п = Ру"(Ф) попарно не пересекаются, к
U~_, int (/„) = Ws (Р) П 2 плотно в 2. Концевые точки интерва-
интервала /„ принадлежат к различным компонентам множества
№*(S)\{S}. Следовательно, W%(S) и Ws (S), оба плотны в
J1\WS(P), где Wi (S) и Wl(S) обозначают компоненты мно-
множества U7*(S)\{S}. Отсюда следует, что W\ (S) и Wl(S) яв-
являются плотными в A = T2\WS (P), и поэтому а-предельное
множество каждой точки из U7*(S)\{S}—это Л. Пусть
д?Т2\(Л[)Р). Поскольку a(q)—компактное инвариантное
множество, а минимальные множества для поля Y—это S и Р,
то получаем, что a(q) содержит S. Поэтому либо a(q) = S,
либо a (q) содержит некоторую точку устойчивого многообразия
точки S, и, следовательно, a(q) = A. Легко видеть, что ЛГJ—
совершенное множество с пустой внутренностью. Таким обра-
образом, Л Г) 2—канторово множество. Наконец, поскольку (Ws (S) U
U W" (S)) Г) 2 счетно, а Л п 2 несчетно, то существует
q€Z\(Ws(S)\J W"(S)), а значит, a (q) = о (q) = Л. |
Замечание. Хотя векторное поле Y из этой теоремы не явля-
является грубым, можно тем не менее полностью классифицировать
все классы топологической эквивалентности векторных полей
в малой окрестности elf поля Y. Действительно, если z^olf и
off достаточно мала, то окружность 2 попрежнему трансвер-
сальна к Z и производная отображения последования Pz боль-
больше единицы во всех точках его определениях). Отсюда следует,
что если ZGoff — поле Морса—Смейла, то Z имеет ровно одну
замкнутую траекторию, и эта траектория является репеллером.
(Поля Морса—Смейла существуют, конечно же, в elf, поскольку
они плотны в 3?°°(Т2)). Если Z не является полем Морса —
Смейла, то имеются две возможности: либо Z имеет траекто-
траекторию, соединяющую седло с ним самим, причем ее замыкание
(топологическая окружность, которая получится, если присо-
присоединить к этой сепаратрисе седло) является репеллером, а мно-
множество неблуждающих точек поля Z сводится к замыканию
этой траектории и стоку, либо число вращения эндоморфизма
окружности 2, индуцированного полем Z, иррационально, и в
этом случае Z удовлетворяет условиям A)—D) теоремы. Можно
показать, что если эндоморфизмы окружности 2, индуцирован-
индуцированные полями Zj и Z2, близкими к Y, имеют одно и то же ирра-
иррациональное число вращения, то. Zt и Z2 топологически эквива-
эквивалентны. Этот результат имеет частичное обращение: если су-
*) Если S\gr—седло поля W на R2, накрывающего поле Z, то след
dW (sw) положителен ввиду близости sw к s=s^ и W к X; это гаранти-
гарантирует, что f'z(y) -*¦ °°i когда у стремится к точкам, аналогичным а и Ь
выше. На некотором расстоянии от них f'z (у) близко к f'x (у) просто из-за
малости возмущения- Поэтому всюду f'z > 1,— Прим. ред.
» М61 '
258 ГЛ. 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
ществует близкая к тождественному отображению эквивалент-
эквивалентность h между Zj и Zj и число вращения поля Zj иррацио-
иррационально, то число вращения поля Z^ равно числу
вращения поля Z*. В действительности, достаточно
потребовать, чтобы h было гомотопно тождественному
отображению. Таким образом, в окрестности поля У мы
имеем ровно один класс эквивалентности грубых полей, содер-
содержащих траекторию, соединяющую седла, и бесконечное число
классов полей с нетривиальными рекуррентными траекториями.
Эти последние характеризуются одним вещественным парамет-
параметром—числом вращения эндоморфизма, индуцированного на 2.
Следует подчеркнуть, что невозможно дать полную класси-
классификацию классов топологической эквивалентности полей в ок-
окрестности поля на торе без особых точек, у которого имеется
нетривиальная рекуррентная траектория. Действительно, если
У — такое поле, то существует трансверсальная к Y окруж-
окружность 2, и отображение последования определено на всей окруж-
окружности 2. Согласно одной важной теореме Эрмана [37], можно ап-
аппроксимировать Y полем X, которое С°-эквивалентно иррацио-
иррациональному потоку (зв). Затем можно аппроксимировать X таким
полем, у которого все траектории замкнуты. Отсюда следует,
что ни в какой окрестности поля Y число замкнутых траекторий
полей Морса — Смейла не ограничено. Таким образом, в каждой
окрестности поля У существует бесконечное число классов экви-
эквивалентности грубых полей (?7).
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
(*) Иными словами, в понятном смысле эквивалентны ростки
семейств траекторий (малых дуг траекторий), определяемые X
в р и Y в q (определения ростка см. в [143], статья «Росток»).
В определении ничего не говорится о зависимости h, Vp и
Wg, фигурирующих в определении топологической эквивалент-
эквивалентности, от Y. Можно дать формально более ограничительное
определение, в котором требуется, чтобы при достаточной ма-
малости clf^ окрестность Vp можно было взять одной и той же
для всех Y^dfx ([125] или [143], статья «Локальная грубость»),
при этом различаются варианты «по Андронову—Понтрягину»
и «по Пейксото». Все эти определения даются для локальной
грубости не только в точке р, но и возле компактного (и обыч-
обычно инвариантного) множества А (при этом говорят короче о
локальной грубости А). В случае А—{р\ различные варианты
в конечном счете оказываются эквивалентными. Различаются
ли они вообще—неизвестно.
B) Т. е. индекс DXP. Для гиперболической особой точки
термин «индекс» уже можно считать установившимся. Однако
имеется и другой объект, тоже называемый индексом особой точ-
точки, или еще индексом векторного поля в этой точке (см. [38],
гл. 5, [64] §6, или [133], статья II, гл. 2, а в двумерном слу-
случае— также [4], гл. 5, [35], гл. VII, или [47], гл. IX). Когда
имеется опасность путаницы, приходится удлинять название:
тот индекс, о котором говорится в этой книге — это индекс
Морса, а другой — индекс Кронекера — Пуанкаре.
C) Очевидно, утверждение B) теоремы непосредственно сле-
следует из непрерывной (вместе с производными) зависимости h
от Ф, если в B) диск D лежит в той малой окрестности точки
р, в которой №foc представляется как график h. В общем слу-
случае возьмем сперва такое k, что f~kD лежит в такой окрест-
окрестности, а затем—такое 6>0 и такую окрестность Jfi3/ в
Diffr(M), что из 6-С-близости диска D' к f~hD и из gzJtf't
следует е-С-близость gkD' к D. Применяя уже доказанную
часть B) к f~kD, найдем такую окрестность J\T. Э/ в DiiirlM\.
9*
260 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
что при ggoffa B W*(pg) имеется 6-С-близкий к f~k(D) диск
D'o. Тогда при g^.Jf1f]Jfz за искомый диск Dg можно взять
Z*D'e
D) Методом Перрона можно непосредственно получить W",
исходя из следующих наводящих соображений. Даже если
отображение необратимо, следует ожидать, что на W" оно об-
обратимо (в конце концов так оно и окажется), так что точка
z?Wa имеет в W$ отрицательную полутраекторию у (—я)?
? №р, п ^ 0, которая обладает такими свойствами:
Ж—п) = у(—
Исходя отсюда, можно составить уравнения для у. На сей раз
zs будет выражаться в виде сходящегося ряда, уравнение же,
выражающее ги через у(—1), ..., у(—п), надо разрешить от-
относительно у" (—п). Остальное ясно.
Упоминаемое далее в тексте преобразование графика — это
другой способ доказательства теоремы 6.2, восходящий к Ж. Ада-
мару (ссылки см. в [3]). Он тоже допускает различные варианты
и, в частности, может непосредственно давать как Ws, так и Wtt.
По сравнению с методом Перрона метод Адамара более нагляден,
но его (ни в одном из вариантов) не удается подвести под теорему
о неявной функции. Поэтому гладкость приходится доказывать
специально, и это не так уж просто. Всего геометричнее это
сделано в [170].
(б) Между прочим, A) можно доказать и без этого добавления.
Равномерная непрерывность / в Bti следует из равномерной огра-
ограниченности Df в Вр, а последняя при достаточной малости р*
следует просто из непрерывности Df(z) при 2=0. Равномерная
непрерывность Df при доказательстве A) нужна фактически
только при доказательстве гладкости отображения у*—^-Фсу
(после этого гладкость F получается автоматически), а здесь мож-
можно воспользоваться компактностью множества {у(п), п^0}[]
U{0}. См. также [43], [165].
(в) Нечто вроде Я,-леммы, о которой сейчас идет речь, исполь-
использовал еще Смейл в [186]. (См. лемму 3.2 из [186]. Стоит отметить,
что в этой работе впервые были введены (еще без специального
названия) системы Морса — Смейла, рассматриваемые в гл. 4
настоящей книги, и появилось упорядочение критических эле-
элементов, используемое в § 2 гл. 4 и, в соответственно обобщенном
виде, играющее заметную роль в «гиперболической» теории, о ко-
которой говорится в § 4 гл. 4). Но в [186] Смейл не привел доказа-
доказательства этой леммы и, главное, не подобрал формулировки,
удобной для более разнообразных приложений (которых тогда
еще не было).
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 261
(') Эта лемма будет использоваться в несколько ином виде.
Отличия состоят в том, что в W @) берется диск В?, содер-
содержащий 0 строго внутри себя, но не обязательно такой малый,
как В", а диск D" предполагается трансверсальным к Ws{0)
в некоторой своей внутренней точке q, не обязательно лежа-
лежащей в пределах того небольшого Ш\ж @), которое строилось в
§ 6. Утверждается существование таких окрестности Уг^Щ и
п0, что при п > п0 связная компонента /" (Du) n Vv содержащая
/"(<?). е-С^-близка к В". Этот вариант сводится к приведенному
в тексте. Если Bs, В", V—такие, как там, то имеется такое к,
что f~k(Bt)czBn, и такое /, что Da = fl(Da) есть диск, трано-
версальный к В!в точке fl(q). Применим лемму к D" Если
соответствующая компонента Dfcfn(Da) достаточно С1-близка
к В", то пересечение D? с некоторой окрестностью W мно-
множества f~kB" в V будет очень О-близко к f~kB", а тогда связ-
связная компонента пересечения /"+*+' (Da) с Vl = fb(W), содержа-
содержащая fn+k+i(q), будет е-С1-близка к Щ.
Очевиден также вариант, в котором говорится, что при
п—> оо прообразы f~n(Ds) трансверсального к Wa@) диска Ds
как бы «прижимаются в своей центральной части» к Ws@).
Он сводится к предыдущему варианту, если вместо / рассмат-
рассматривать Z. Позднее будут упомянуты и другие варианты К-
леммы, которые уже не редуцируются к приведенному в тек*
сте, но получаются при небольшой модификации его доказа-
доказательства.
(8) Эта аргументация непонятна. Ведь из того, что под
действием f трансверсальные к Gs(p) «сечения» (т. е. некие
трансверсальные к Ws(p) диски), содержащиеся в Ns(p), «при-
«прижимаются» к Wfeci еще не следует непосредственно, что они
целиком заполняют некоторую окрестность №fec. Здесь надо
рассуждать иначе, применяя ^-лемму (точнее, ее модификацию,
указанную в замечании A)) не к /, а к /""*. (Кстати, очевидно,
что для необратимых С1-отображений данное следствие, вообще
говоря, неверно; значит, нам действительно необходимо как-то
использовать обратимость /).
Рассмотрим семейство дисков, трансверсальных к W*(p) и
имеющих, в терминах использовавшихся выше локальных ко-
координат, вид Bsx\q\, q?Ba Имеется такое п0, что при п > п0
соответствующие связные компоненты Dsn (q) пересечений
f~"{Bsx{q\)f]V являются е-С1 -близкими к В". При достаточно
малом г диски /""• (В, X {q\) еще не выходят из V. После этого
точка f~"(p), p€.Bs,xBa, со временем выходит из V, если
р ф @, q), но до того она остается на Ц? (q), т. е. очень близко
к Bs. В это время конечный отрезок траектории f~"(p) (фик-
262 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
сированной временной длины) очень близок к своей проекции
на Es, а последняя близка к соответствующему отрезку тра-
траектории любой своей точки. Теперь ясно, что BfxB" можно
принять за U. Действительно, если f~"+1(p)?V, f~"(p)^V, то,
обозначая проекцию на Es через ns, имеем:
где б—малое число (б—>-0 при е—>-0). Из последнего «
следует также, что
Ж -26)/-*
Стало быть, nj-n+1 (р) ? ?*\A—26) f'1 (Bs) (так что эта проек-
проекция «почти содержится» в Gs (/?)). А поскольку f~"+1(p) отстоит
от своей проекции не более чем на е, то при достаточной ма-
малости е и 6 отсюда следует, что f~n+1(p) ?Ns@). Итак, под
действием итераций f-1 каждая точка из U\Ba со временем
попадает в Л^@); это и означает, что Un>efnNs(O)
(") Здесь и кое-где в других местах встречается термин «рас-
«расслоение», который не определялся (за исключением определения
касательного расслоения в § 0 гл. 1). Никаких сведений о рас-
расслоениях в книге не используется. Это относится даже к точному
определению. Достаточно представлять себе, что это слово упо-
употребляется в ситуации, когда имеется некое отображение п:
X-*¦ Y одного пространства (многообразия, области) на другое,
причем X тоже называют расслоением, Y — базой, я — проек-
проекций, n~x{y) — слоем над точкой у? Y; говорят еще о расслоении
над Y. Что еще надо требовать от (X, я, Y), чтобы это было рас-
расслоение, а не просто сюръективное отображение, — этого знать
не нужно (если, конечно, не пытаться самому употреблять этот
термин).
A0) В действительности далее потребуется несколько более
сильное утверждение:
2.4'. Лемма. В тех же предположениях существуют такие
окрестность UcV точки р на 71 и окрестность Ч1'сЧ1 поля
X, что для любого Y^il' и любого е > 0 в %' найдется поле
Z с ||Z—Y\r < е, для которого Pz имеет лишь конечное число
неподвижных точек в V и все они элементарные.
Идея доказательства состоит в том, что при достаточной
малости %' для любого Y ?11'Г\ ?°°(М) найдется выпрямляю-
выпрямляющая карта (FY, fr), в понятном смысле близкая к (F, /), при-
причем fy\{b}'Klm~1 можно считать одним и тем же для всех Y.
С ее помощью проделываем такие же построения, как в дока-
ватедьстве леммы 2.4; надо только проследить, что U можно
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 263
взять одной и той же для всех Y. Поля же из 1l'\3Z°° (M)
сперва аппроксимируем полями класса С".
(и) Лемма 2.4 гарантирует нам существование полей Yj, для
которых Р jYj обладает нужными свойствами не в Wyf] 27, а
лишь в некоторых Uf. Априори размеры этих Uit ..., LIk могли
бы быстро уменьшаться, и тогда ниоткуда не следует, что у
Yk нет замкнутой траектории с периодом <! Зт/2, пересекающей,
скажем, Hjf]Wj вне Uj в неэлементарной неподвижной точке
отображения PjYk- Поэтому надо использовать лемму 2.4'.
Пусть иу и Il'y—такие, как в лемме 2.4', и пусть Wy и
<№уС:Щ—такие окрестности у и X, что любая замкнутая тра-
траектория поля F?eJ\Tv с периодом из [т, Зт/2], пересекающая
Wv, пересекает Uy в неподвижной точке отображения последо-
вания. Далее берем Wy{, dW. eJV, W, К и eJ\T3, как в тексте,
а при аппроксимации поля X полем F1, поля Yt полем Y 2 и
т. д. используем лемму 2.4' из A0).
A2) Аппроксимируем / в С-топологии С°°-диффеоморфизмом
fit и пусть надстройка для последнего приводит к Mit nlt Xt,
2lf hi, это объекты класса С°*. Легко построить в Л^ такое
поле Y класса С, для которого 2Х является глобальным тран-
сверсальным сечением и соответствующее отображение последо-
вания есть hjh^1. Например, можно принять, что Y (лх (р, t)) =
= dn,(p, t)-Z(p, t), где Z—С-поле в Мх(—е, 1 + е). которое
строится так (расшифровка формального определения представ-
представляется читателю). Будем считать М вложенным в некоторое
R." и обозначим через Р: V—»-М проекцию на М некоторой
его трубчатой окрестности (теорема 0.18 гл. 1). Пусть функция
ф: (—е, 1+8)—>К такова, что ф?С™, ф(—е, е) = 0, фA—е,
1 + е) = 1, ф'^0. Рассмотрим
8t (Р) = Р (A -Ф @) Р + Ф @ /Г1/ (Р))-
Если fi достаточно близко к /, то gt корректно определено и
при каждом t является Сг-диффеоморфизмом; gt {p) и gt (p) ==
класса Сг по (р, t). Положим Z(p, t)=(gt(gf-1{p)I 1).
A?) Эти учебники цитируются, видимо, как источники лите-
литературных ссылок,— в остальном же все, что говорится в них о
грубых системах, покрывается настоящей книгой (причем в ней
указаны и упрощения, возникающие для рассматриваемых в [5,
47] потоков на S2). Однако стоит отметить, что в [5] вопрос о ти-
типичных свойствах динамических систем обсуждается не только
в контексте грубых систем, но и в более широком плане. Один
264 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
-- —¦... ¦ ¦¦¦¦ —..I! ., - I— - I— i . iiii.i i т. i.i _.. а
из обсуждаемых там аспектов этого вопроса затронут также в п. 8)
моего послесловия к настоящей книге.
A4) В ситуации, изображенной на рис. 20, подразумевается,
что St или S{ берется за D" из леммы 7.2 гл. 2; точнее, рас-
рассматривается только «верхняя половина» этих St, S{. За фигу-
фигурирующую в этой лемме окрестность V надо взять образ под
действием Хг с достаточно большим г окрестности Bs х Ва точки
Of, описанной перед леммой 7.1 гл. 2 (точнее, «верхней поло-
половины» этой окрестности). Здесь г надо взять таким, чтобы
«верхняя половина» ХГВ"—в данном случае это примыкающая
к а, дуга «выходящей» сепаратрисы седла а, (связной компо-
компоненты Wa (crf)\of), стремящейся к а,—содержала р. Лемма 7.2
гл 2 обеспечивает С1-близость Xt (S{) [) V, Xt (S{) {] V к упомя-
упомянутой дуге при достаточно больших t. Уменьшив, если потре-
потребуется, St и St можно достичь, чтобы только при таких t об-
образы S{, St под действием Xt «дотягивались» до 6V (здесь уже
имеется в виду V из основного текста данного параграфа).
Ср. с Г).
(*5) Этого нельзя достичь для того отрезка Д' из указан-
указанного дополнения, один из концов которого совпадает с бли-
ближайшим к аг концом 7;, и аналогичного отрезка Д"с/;. Ведь
положительная полу траектория, исходящая из указанного кон-
конца 7^, снова попадет на 2, в дальний от аг конец 1\ или Т\ за
время т, а затем у репараметризованного поля она должна
попасть на некое Ct или Sy за время 2.
Другой конец Д* является концом какого-то из рассматри-
рассматривавшихся выше отрезков J вида [а, а'] или [b, b1]. Во изме-
изменение сказанного выше, репараметризуем X так, чтобы точки
J достигали Sk за время 1 и после этого достигали Ct или 2у
8а дополнительное время 1+т (а не 1). После этого при ре-
параметризации X обеспечим, чтобы точки Д' достигали соот-
соответствующего Ct или 2/ за время 2 +т. Аналогично поступим
с Д".
Фундаментальную область 7г(У) отображения последования
для поля Y определим, потребовав, чтобы дальние концы сос-
составляющих ее двух отрезков совпадали с дальними концами
I't, F'l (тогда она определится однозначно). Репараметризацию
Y осуществим так, чтобы выполнялись в точности те же усло-
условия (с теми же а, Ь, а1, Ь'), что и для X.
Если 7' или ?" (или и 7 , и Г) не пересекаются ни с одной
входящей сепаратрисой, то надо действовать, как сказано в
последнем абзаце § 1.
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 265
A6) Цилиндр диффеоморфен кольцу на плоскости и поэтому
предельное поведение траекторий на нем описывается теорией
Пуанкаре — Бендиксона (§ 1 гл. 1). В соответствующих доказа-
доказательствах на самом деле не существенно, определено ли поле на
всей плоскости. В данной книге окончательная формулировка —
теорема 1.8 гл. 1 — дана при условии, что поле имеет конечное
число особых точек (достаточно, чтобы их было конечное число
в рассматриваемой области G и чтобы рассматриваемое предель-
предельное множество было компактно в G). Это не существенно для до-
доказательства теоремы 2.6 гл. 4 хотя бы потому, что в соответст-
соответствующем рассуждении у поля Y и близких к нему полей вообще
нет особых точек на цилиндре, а гиперболичность у гарантирует,
что с ростом t все траектории могут только входить в цилиндр
(если у — репеллер) или только выходить из него (если у — ат-
аттрактор). Но кроме того стоит заметить, что утверждение об от-
отсутствии нетривиальных рекуррентных траекторий следует уже
из леммы 1.5 гл. 1, которая верна независимо от условия об
особых точках (и от условия, что предельное множество траекто-
траектории компактно в G).
Поскольку лист Мебиуса накрывается цилиндром, то и на
нем не может быть нетривиальных рекуррентных траекторий.
A7) Различные случаи лучше выделять чуть иначе;
(а) Существует сепаратриса у, для которой со (у) или а (у) —
негиперболическая замкнутая траектория. Действуем, как в (а)
основного текста.
(б) Существуют траектория у. Для которой со (у) или а (у) —
граф. Это — случай (Ь) основного текста.
(в) Ни (а), ни (б) не выполняется. Поскольку Y удовлетво-
удовлетворяет условиям предложения 2.3, то каждая сепаратриса у либо
стабилизируется, либо идет из седла в седло. Последнее в обо-
обозначениях из доказательства предложения 2.3 означает, что
У € Л" П Д*- При этом такие у действительно существуют, — иначе
нечего доказывать. Сопоставив каждой сепаратрисе у сечение
2 (у) и т. д., как в доказательстве предложения 2.3, возьмем
какую-нибудь у,€ДвГ)А*. Пусть V2 = ^nP(Yi)- Если у2 стабили-
вируется, т. е. стремится к притягивающему критическому эле-
элементу о, то положительные полутраектории достаточно близких
к р (yt) точек 2np (Yi) стремятся к а. В этом случае действуем,
как сказано в (d) основного текста, а именно, возмущаем Y
таким образом, чтобы уг тоже стремилась к а. Если же у2 не ста-
стабилизируется, то у2 g Дп П Д5; рассмотрим у3 = \Пр (у2) и повто-
повторим то же рассуждение. На каждом шаге этого процесса мы
либо строим поле, у которого по сравнению с Y стабилизиру-
стабилизируется еще одна сепаратриса, либо переходим от у,- к у,-+). Если
все получающиеся таким путем у{ не стабилизируются, то рано
266 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
или поздно они начнут повторяться: ус, ..., уг = у(., образуя
граф. В некоторой окрестности p(yt) на 2пр(у;) возникает ото-
отображение исследования ф = Фп'-1°... °Фп{,- Введем на 2пр (у,-) ко-
координату х ^ 0 так, что точка р (у,-) имеет координату 0. Если
бы, в этих терминах, при всех достаточно малых х > 0 было
у(х)Фх, то либо всегда ф(л:) < х, либо всегда ср(х) >л:. Соот-
Соответственно, либо у"(х) —»¦ 0, либо ц>~п(х) —*- 0, а тогда для траек-
траектории у любой точки из 2пр(у(.) (с достаточно малым х > 0) со (у)
либо а (у) было бы графом, вопреки предположению, что (б)
не имеет места. Следовательно, сколь угодно близко к 0 име-
имеются такие х, что <р(х) = х\ им соответствуют замкнутые тра-
траектории поля Y, скапливающиеся к графу. Это—случай (с)
основного текста.
Здесь шла речь об ориентируемом М2, к которому и отно-
относится теорема 2.6. Однако в § 3 обсуждается случай неориенти-
руемого М2. В связи с этим читателю рекомендуется убедиться,
что если бы существовал аналог леммы 2.5 для неориентируе-
мого М2, то можно было бы и в этом случае доказать плотность
полей Морса — Смейла, модифицируя доказательство теоремы
2.6. Хотя в неориентируемом случае нельзя единообразным об-
образом определить для всех сепаратрис, какая часть 2 (у) яв-
является «правой», а какая — «левой», все же построение цепочки
сепаратрис у1г у2, . ¦ ¦ по существу не меняется. Однако теперь
может случиться, что положительные полутраектории, начинаю-
начинающиеся на 2 (yt) с одной стороны от p(yi), сперва возвращаются
на 2 (yt) с другой стороны, а потом — с первоначальной стороны.
Точно так же в (а) сепаратриса может навиваться на односторон-
односторонне расположенную замкнутую траекторию. В подобных случаях
построение возмущения надо производить несколько иначе.
A8) А сепаратриса у стремится к этой траектории. Пусть,
например, у Y замкнутая траектория 8=©(у). Отображение по-
следования для 8 имеет вид х*-^х+Ц>(х), где у(х)=о(х) и ф(л:)<0
при х>0 (считаем, что у попадает на соответствующее сечение 2
в той его части, где хХ)). Малым возмущением отображения, со-
сосредоточенным возле х—0, можно достичь, чтобы в х—0 получи-
получилась гиперболическая неподвижная точка, причем к ней стреми-
стремились траектории точек из 2 П {л:>0}. Затем подбирается такое
возмущение поля Y, которое сосредоточено вблизи 8 и «реали-
«реализует» данное возмущенное отображение последования.
A8) В результате этого возмущения в случае р € со (у) неустой-
неустойчивая сепаратриса аг, войдя в F, пересечет S не в р, а в некото-
некоторой точке р', которая ближе к оп+1. Обойдя возле графа, эта
сепаратриса снова вернется на S в некоторой точке р", которая
еще ближе к а„+1. Кривая, образованная дугой сепаратрисы от
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 267
р' до р" и отрезком S между теми же точками, и рассматривав-
рассматривавшаяся выше кривая, образованная дугой у от ап до йп+1 и соот-
соответствующим отрезком S, ограничивают некоторое кольцо Л',
откуда ни одна траектория не выходит, в котором нет особых
точек и в которое входит сепаратриса. В случае р € а (у) с по-
помощью устойчивой сепаратрисы точки а2 строится другое коль-
кольцо, из которого траектории могут только выходить.
B0) В дальнейшем авторы еще раз предлагают читателю про-
провести соответствующее построение (упражнение 23). Поскольку
это упражнение, то подробные пояснения противоречили бы
замыслу авторов. Ограничусь двумя замечаниями. 1) С помощью
рассуждений типа проведенных в тексте легко получается транс-
версальная окружность, лежащая в малой окрестности заданной
положительной полутраектории у+ траектории у (как множества)
и проходящая через некоторую точку у+, но не обязательно через
заданную точку (нередко этого уже достаточно). 2) Если С —
трансверсальная к X окружность, то и XtC тоже. (Более того,
если т: C-*-R— гладкая функция, то {Ххшх: х?С}— транс-
трансверсальная к X кривая, но только она может иметь самопере-
самопересечения).
B1) Ориентируемость — это то свойство, которое обеспечи-
обеспечивает нужную монотонность х(и), у (и) и z(u) в третьем с конца
абзаце в доказательстве леммы 2.5. Нетривиальная рекуррент-
рекуррентная траектория на М2 называется неориентируемой, если для
любой ее точки р и любого трансверсального сечения S, прохо-
проходящего через р, как в {Xtp: t^.0}, так и в {Xtp: Q>0} найдутся
такие дуги с концами на S, нигде больше не пересекающие S,
что если «замкнуть» такую дугу, соединив ее концы отрезком на S,
то получится односторонне расположенная замкнутая кривая.
К. Гутьеррес показал [162], что на любом компактном неориен-
тируемом двумерном многообразии, род которого больше 3,
могут существовать неориентир уемые нетривиальные рекуррент-
рекуррентные траектории. Для них имеющееся доказательство леммы 2.5
не проходит.
B2) Слоение на n-мерном многообразии М"—это. такое разби-
разбиение М" на линейно связные подмножества, именуемые слоями,
что М" можно покрыть «выпрямляющими картами»—коорди-
картами»—координатными окрестностями Ua с локальными координатами х1а, ...,
х%, в терминах которых локальные слои, т. е. компоненты
связности пересечений слоев с Ua, задаются уравнениями
xg+I= const, .... x'i = const. Более описательно можно сказать,
что локально разбиение М на слои устроено так же, как раз-
разбиение R" на параллельные подпространства R/'x const. Приме-
Примером может служить разбиение многообразия на траектории
векторного поля, если последнее не имеет особых точек. Сле-
26Й ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
дует предупредить, что (в отличие от этого примера) для дру-
других слоений, возникающих в теории динамических систем, может
не существовать гладких выпрямляющих карт (хотя сама сис-
система гладкая).
О слоениях см. [157] или соответствующую статью в [143],
об их применениях в теории динамических систем — в литера-
литературе, цитируемой в § 4 гл. 4. В настоящей книге реально исполь-
используются только два слоения — устойчивое и неустойчивое слое-
слоения для гиперболического автоморфизма двумерного тора. Они
совпадают с разбиениями тора на траектории некоторых ирра-
иррациональных потоков, поэтому их свойства достаточно ясны.
B3) Доказательство можно получить, дословно следуя доказа-
доказательству того же факта для систем Аносова, данному в [3].
По существу же, как подчеркивается в [3], речь идет о неко-
некотором варианте теоремы Адамара—Перрона об инвариантных
многообразиях в неавтономном случае. Строятся (по схеме
Адамара или Перрона) устойчивое и неустойчивое локальные
инвариантные многообразия Wfo, (х) и №"ос (х), затем проходящие
через них траектории неограниченно продолжаются в обе сто-
стороны по времени; проделав это для всех точек данной траек-
траектории у, получаем ее «полные» устойчивое и неустойчивое
многообразия Ws(y), Wa(y), в которых выделяются Ws(x),
W (х). После этого доказывается, что определенные чуть выше
в основном тексте множества совпадают с этими многообрази-
многообразиями. Отличие от работы Перрона состоит в том, что проверя-
проверяется известная равномерность построения по всем траекториям
у из Qt. В [39] вместо этого использован некоторый трюк,
позволяющий свести доказательство существования семейства
локальных многообразий W^ (х), №"ос (х), х € Ц, к бесконечно-
бесконечномерному варианту теоремы 6.2 гл. 3. При осуществлении этой
редукции в [39] допущена ошибка, отмеченная и исправленная
в [160].
Все это делается не только для Qt, но и для любого гипербо-
гиперболического множества Л. Однако при Л=йг оказывается, что
{xi а(х)сЛ}= U W\y), \x- со(х)<=Л}= U W*(y),
usa цел
а в общем случае этого нельзя утверждать. Любые два устой-
устойчивых многообразия либо не пересекаются, либо совпадают;
в частности, если у g Ws(x) П А, го W\х) = W "(у). Аналогично
для неустойчивых многообразий. Если А = М" (случай диф-
диффеоморфизма Аносова), го семейства {№*(х;)} и- ^W"(x)} суть
некие слоения в М" Эти слоения упоминаются в основном
тексте в частном случае гиперболического автоморфизма Т2.
В общем случае эти семейства — уже не обязательно слоения
(ибо входящие в них многообразия уже не обязательно запол-
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 269
няют всё М" или хотя бы какое-нибудь открытое подмножест-
подмножество М"), но все же в какой-то степени напоминают таковые.
B4) Введем на накрывающей плоскости декартовы коорди-
координаты (xlt х2), координатные оси которых суть собственные под-
подпространства оператора L—по оси хх происходит сжатие,
а по оси х2—растяжение. С помощью стандартной проекции
п: R2 —>• Т2 в малой окрестности Up любой точки р тора можно
ввести локальные координаты (xlt x2) как координаты (xlt x2)
в небольшой области VpcR2, для которой n(Vp) — Up и
л | Vp: Vp —s- Up есть диффеоморфизм. В терминах этих локаль-
локальных координат Ws(pt) П &р выглядит как счетная система отрез-
отрезков х2 = const с плотным множеством А значений х2. Дуга
кривой W(pj, /), попадающая в Uр, допускает гладкую пара-
параметризацию, т. е. может быть представлена в виде (хг (s), хг (s)),
где параметр s пробегает некоторый интервал S; х% + х1Ф0
при всех s. Если х2 (s0) ф О, то сколь угодно близко к s0 име-
имеются такие s, что x2(s)?A. При этих s кривая (^(s), x2(s))
пересекает Ws(pi). При близких к s0 значениях s все еще
х\ (s) Ф 0, так что у W (ру, /) имеются не просто пересечения
с Ws (pi), но и трансверсальные пересечения. Наконец, такие
s0, для которых х2 (s0) Ф 0, всюду плотны на S. Действительно,
допустим, что x2(s) = 0 на некотором интервале S'czS. Это озна-
означает, что некоторая дуга J кривой W (pj, f) содержится в неко-
некотором устойчивом слое Ws(q). Применяя к ней отображения /~"
с достаточно большими п, получим, что
Г"(¦/)<= П>с(/>/> f)n№(f-nq),
причем дугу Wfoc (py, f) здесь можно считать сколь угодно малой.
Но Wiocipj, f) трансверсально к Ws(pj) в точке pj. В терми-
терминах локальных координат (хи х2), введенных на сей раз в об-
области U, это означает, что №"ос (pJy f) трансверсально к оси хх.
Значит, это Wioc (если при необходимости его уменьшить) во всех
своих точках трансверсально к прямым х2 = const, т. е. к по-
попадающим в U кускам устойчивых многообразий. Получается,
что f~n(J) состоит из не более чем счетного множества точек,
что невозможно.
Приведенные рассуждения вкратце намечены несколько далее
в основном тексте книги. Простая их модификация показывает,
что в действительности W(p,, f) всюду трансверсально к на-
направлениям es(p), так что, в частности, все пересечения
W" (рр /) с Ws (pi) являются трансверсальными. Если бы кри-
кривая Wa(pj, f) касалась неустойчивого слоя, то, применяя /~"
с достаточно большим п, мы получили бы, что и №"ос(Р/> f)
касается некоторого неустойчивого слоя, т. е. в терминах
270 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
координат (jclf x2) в U, некоторой вертикальной линии, что
невозможно.
Еще дальше в основном тексте доказывается (независимо
от обсуждаемых сейчас свойств Wa (pj, f)) гиперболичность Л
и при этом устанавливается, что касательные к W (pjt f) и вооб-
вообще к неустойчивым многообразиям точек из Л содержатся
в некоторых углах, равномерно отделенных от направлений
векторов es(p). Если принять этот факт, то существование пере-
пересечений Wa {pj, f) с Ws{pi), их плотность на W (pJt f) и их транс-
трансверсальность становятся очевидными. Но в данном месте, как
мы видели, можно обойтись без гиперболичности Л.
B5) Здесь нужна не просто плотность Llt а более сильное
свойство: для любого е > 0 имеется такое т, что любой отре-
отрезок траектории иррационального потока на торе, имеющий вре-
временную длину > т, является е-сетью для тора (т. е. в е-окрест-
ности любой точки тора имеются точки из этого отрезка).
Ведь мы не знаем, где именно на L1 расположены отрезки f~nk(I),
где k—период q и и=1, 2, ...1). С другой стороны, исполь-
используя указанное выше свойство, мы можем взять за / не отрезок
Lu а отрезок на любом слое устойчивого слоения, в частности,
такой отрезок/, что p?lc:W[)Ws(p), и рассматривать /""(/)
со всеми и=1, 2, ... Если предположить, что они не пересе-
пересекаются с V, то это должна быть система отрезков неограниченно
возрастающей длины. То, что они могут находиться на различ-
различных траекториях иррационального потока, ничему не мешает—
указанное выше свойство этого потока гарантирует, что доста-
достаточно длинный отрезок пересекается с V. Отсюда следует, что
W" (А>> /) не просто пересекается со сколь угодно малой окрест-
окрестностью точки р, но что оно пересекается со сколь угодно малой
дугой на Ws(p), содержащей р. Этот факт понадобится в B7).
Правда, если брать / на L1=Ws(q) с периодической q, то
указанное свойство достаточно использовать только для отрезков
фиксированной траектории (нашей Lt). Но это не существенно:
если некоторая траектория потока обладает соответствующим
свойством, то уже нетрудно показать, что обсуждаемое свойство
аппроксимации тора длинными отрезками траекторий выпол-
выполняется в том именно виде, как сформулировано выше (так ска-
сказать, равномерно по всем длинным отрезкам всех траекторий).
*) Положение было бы иным, если бы мы знали, что / содержит перио-
периодическую точку отображения f,—тогда каждый следующий из отрезков
f-nn (/) содержал бы предыдущий строго внутри себя, а для такой после-
последовательности отрезков неограниченно возрастающей длины уже из одной
плотности L] в торе следует, что, начиная с некоторого номера, они должны
пересекаться с V. Но мы пока еще ничего не знаем о периодических точ-
точках / (позднее будет доказано, что они плотны в Л, но в доказательстве
будут использоваться свойства Л, доказываемые сейчас).
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 271
Указанное свойство (с очевидными изменениями, формули-
формулировки) имеет место для всех компактных минимальных множеств
потоков и каскадов. Обратно, если оно выполняется для замкну-
замкнутого инвариантного множества, то последнее минимально. Полу-
Получаемая таким путем характеризация компактных минимальных
множеств посредством свойства равномерной аппроксимации
отрезками траекторий принадлежит Дж. Биркгофу. См. [148],
[153].
Для иррационального потока на торе данное свойство имеет
место, ибо тор является минимальным множеством этого потока.
(В примере 4 § 4 гл. 1 показано, что каждая траектория плотна
на торе, а это, очевидно, и означает минимальность). Впрочем,
для этого потока данное свойство легко получить также из
простых теоретикочисловых соображений или используя почти
периодичность соответствующих функций 11—* Xtx.
B6) Здесь нужно использовать тот факт, что (при подходя-
подходящем выборе /) на / имеется точка, не принадлежащая Wu(p(l, /).
Если, как предложено в (г5), брать / = Wsloc (р), то это очевидно:
такой точкой является сама р. Если же, как предлагают авторы,
брать /cLj, то в качестве точки /, не принадлежащей W(p(l, /),
можно взять точку пересечения №foc (p, f) Л /. Сама воз-
возможность говорить о Щж(р, f) связана с гипербо-
гиперболичностью Л, которая будет доказана далее в основном
тексте. Тот факт, что W?oc (p, f) пересекает достаточ-
достаточно близкие к р отрезки кривой Llf попадающие в W, сле-
следует из того, что Wfoc(p, f) трансверсально к es(p) (это тоже
будет доказано). Так или иначе, /<?№"(/?„, f). Дальше можно
рассуждать так.
Введем в U такие же локальные координаты (xt, x2), как
и в B4), приняв за соответствующий прообраз области U тот
из ее прообразов на плоскости, который является окрестностью
начала координат. В некоторой полоске |х21 < е связная ком-
компонента попадающей в эту полоску части W" (р0, /), содержа-
содержащая р0 (обозначим ее через We), ограничена вертикалями х2 =
= ± е и соединяющими эти вертикали дугами кривых W" (/?,-, /)
(i=l, 2), содержащими pt. При итерациях f~" некоторые точки
отрезка /~" / стремятся к р0 и, значит, попадают в WE, а сам
он (вернее, попадающая в U его часть) выглядит как верти-
вертикальный отрезок или несколько таких отрезков. Поскольку
/¦¦"(/)С?№е, то этот отрезок или тот из этих отрезков, который
содержит точки из WE, выходит из №е и потому пересекается
с W" (pt, f) или Wu (p2, /). Стало быть, соответствующее W" (/?,-, f)
пересекается с IaW.
B7) Точнее, Лп/ — совершенное (замкнутое и не имеющее
изолированных точек) нигде не плотное в / множество. Замк-
272 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
нутость очевидна. Отсутствие изолированных точек следует из
того, что W" (/?,, /) и Wa(p2, f) плотны в Л, откуда в сочета-
сочетании со сказанным в конце (S4) следует, что W" (pt, f) П / и
^° (Ри< /) П / плотны в /. То, что Л п / нигде не плотно, сле-
следует из B6).
Само же Л локально устроено как прямое произведение
канторова множества на отрезок. Такое локальное представле-
представление Л получается, если через каждую точку р ? Л П / провести
небольшую дугу W" (p, f). Конечно, здесь надо доказать, что
в терминах локальных координат из B4) на каждом Wa (p, f)
имеется содержащая р дуга, идущая от лг2 = а2—е дол:2 =
= аг + е, где а2—вторая координата точек /, и что в соответ-
соответствующей области нет никаких других точек Л, кроме лежа-
лежащих на таких дугах.
BS) В этом примере дополнение к аттрактору состоит из че-
четырех связных областей, причем в окрестности каждой точки
аттрактора имеются точки всех четырех областей. Это заметно
сложнее, чем в примере 5 на торе. Оказывается, у любого гипер-
гиперболического одномерного аттрактора диффеоморфизма S2 до-
дополнение состоит не менее чем из четырех областей, так что
проще, чем в примере 6, на S2 нельзя сделать. (Это, кстати, до
некоторой степени объясняет, почему такие аттракторы до сих
пор не встречались в численных экспериментах). О гиперболиче-
гиперболических аттракторах с неустойчивыми многообразиями коразмер-
коразмерности один см. [150].
B9) Всех вообще его изменений или изменений только неко-
некоторых его черт, в частности, изменений локальной фазовой
картины возле некоторой особой точки или замкнутой траек-
траектории.
Выражения «фазовый портрет» и тем более «черты фазового
портрета» являются довольно неопределенными; при исследова-
исследовании различных конкретных вопросов фактически каждый раз
уточняется, о чем именно идет речь, при этом в различных случа-
случаях уточнения бывают различными. Выражение «пространство
траекторий» ничуть не лучше, поскольку никакой структуры
в этом «пространстве» мы не ввели (а как абстрактное множество,
характеризуемое только своей мощностью, оно всегда одно
и то же).
C0) В отечественной литературе эта бифуркация называется
бифуркацией рождения предельного цикла. Она была известна
А. Пуанкаре, хотя он, по-видимому, не выделял специально
«типичных» (в указанном выше или каком-нибудь ином смысле)
бифуркаций и не отмечал, что данная бифуркация — одна из
них. Далее, А. М. Ляпунов, исследуя устойчивость в негипербо-
негиперболическом случае, фактически тоже подготовил необходимый ап-
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 273
парат для исследования бифуркации рождения цикла в много-
многомерном случае, хотя сам, по-видимому, специально ею не зани-
занимался. В явном виде бифуркация рождения цикла была подробно
исследована в двумерном случае А. А. Андроновым и его сотруд-
сотрудниками. Андронов выделил типичные бифуркации на плоскости;
сюда, естественно, вошла и данная бифуркация. (Формально его
определение типичности отличалось от данного в основном тек-
тексте, но в двумерном случае это несущественно). Статья Э. Хопфа
о бифуркации рождения цикла для двумерного потока появи-
появилась позднее (и не содержала столь же четкой формулировки, что
означает типичность бифуркации). Зато Хопф первым опублико-
опубликовал исследование этой бифуркации в многомерном случае,
причем он указал, что стремился дать такое изложение, которое
было бы удобнее с точки зрения возможного в будущем перехода
к бесконечномерному случаю. Публикации горьковских мате-
математиков о 3-х и 4-х-мерном случае задержались из-за войны и с
точки зрения указанной перспективы изложение в них было ме-
менее удобным. Сам же переход к бесконечномерному случаю был
произведен позднее, когда, с одной стороны, подобные задачи
стали реально исследоваться в приложениях (прежде всего в ма-
математической гидродинамике), а с другой — общий уровень
понимания в подобных вопросах настолько вырос (и это стало
настолько распространенным), что этот переход уже не вызвал
серьезных затруднений. Условность названия «бифуркация Хоп-
Хопфа» сознается многими западными авторами, но оно, видимо,
укоренилось. (К тому же название «бифуркация Пуанкаре —
Андронова», которое было бы исторически правильным, требо-
требовало бы пояснений: ведь у них было несколько различных би-
бифуркаций).
(?1) Надо иметь в виду, что в последних двух случаях инва-
инвариантные многообразия могут быть инвариантными многообрази-
многообразиями одного и того же положения равновесия или одной и той же
замкнутой траектории. Кроме того, для потоков в размерности
>2 возможна ситуация, когда нетрансверсально пересекаются
инвариантные многообразия седла и седловой замкнутой тра-
траектории.
Авторы не говорят, какие изменения в качественной картине
происходят при бифуркациях, связанных с касанием инвариант-
инвариантных многообразий. Эти изменения могут быть намного сложнее,
чем в предыдущих случаях, и по сей день исследованы не пол-
полностью. Только для потоков в двумерном случае, когда речь идет
о бифуркациях сепаратрисы, идущей из седла в седло, А. А. Анд-
Андронов и Е. А. Леонтович дали полное и в то же время достаточно
простое описание этих изменений. В частности, если сепаратриса
возвращается в то же самое седло, откуда она выходит, то в ти-
10 а 61
274 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
пичном случае бифуркация приводит к появлению нового пре-
предельного цикла, «рождающегося» из замкнутой петли сепаратри-
сепаратрисы (или исчезновению предельного цикла, сливающегося с этой
петлей,— это по существу то же самое, ибо сводится к предыду-
предыдущему, если изменять параметр в другую сторону).
Список типичных бифуркаций потоков на плоскости (точнее,
сфере) завершается еще одной бифуркацией, связанной с бифур-
бифуркацией седло-узла. У последнего как бы сохраняются три из
четырех сепаратрис седла. Две из них делят малую окрестность
седло-узла на две половины, в одной из которых траектории
ведут себя так же, как возле узла, а в другой — как возле седла.
В последней полуокрестности расположена и третья сепаратриса.
Может случиться, что эта сепарафиса, описав петлю, попадает
в первую полуокрестность и входит в седло-узел. При определен-
определенных «типичных» условиях исчезновение седло-узла сопровож-
сопровождается рождением предельного цикла из этой замкнутой петли.
Здесь мы сталкиваемся с возможностью нелокальных изменений
качественной картины при бифуркации, имеющей, казалось бы,
совершенно локальный характер.
C2) Пример грубого поля на Ч2 можно получить проще —
например, годится поле Х(х)=х. (Здесь к один раз обозначает
точку R2, а другой раз вектор; вК'и вообще в векторных прост-
пространствах на сей счет принимаются (чаще всего молчаливо)
соответствующие соглашения, и запись вроде х=х для диффе-
дифференциальных уравнений является обычной). Построение же, опи-
описанное авторами, годится для любого двумерного многообразия
(если исходить из триангуляции с гладкими сторонами, каковая,
как можно доказать, существует).
О грубых потоках в некомпактном случае см. [166].
(?s) Под монотонным эндоморфизмом окружности авторы по-
понимают непрерывное отображение аз S1 -*¦ S1, удовлетворяющее
условиям, которые формулируются перед леммой 4. Наглядно
эти условия означают, что если точка х делает один оборот по
окружности, двигаясь все время в одну сторону, то и а(х) делает
один оборот по окружности, двигаясь все время в ту же сторону,
но только, может быть, с остановками.
Число вращения, о котором говорят авторы, определяется
ими для монотонного эндоморфизма окружности, а нужный им
эндоморфизм связан с некоторым потоком на торе, так что в ко-
конечном счете число вращения связано в данном случае с потоком
на торе. Число вращения можно непосредственно интерпретиро-
интерпретировать в терминах поведения траекторий накрывающего потока на
накрывающей плоскости (они «уходят в бесконечность» в на-
направлении, угловой коэффициент которого есть число вращения).
Такая точка зрения имеет более широкую область применимости
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 275
[133]. С другой стороны, для непрерывного отображения окруж-
окружности в себя (не обязательно гомеоморфизма или монотонного
эндоморфизма), накрываемого непрерывным отображением /;
R -*¦ R, иногда бывает полезно ввести множество вращения —
совокупность всевозможных предельных точек последователь-
последовательностей f"(x)/n со всевозможными х.
C4) Черри обсуждает также ситуацию, когда при сходном
построении число вращения p(fx) иррационально, но не вы-
выполняется условие dfx {у) > 1 на (Ь, с+1), так что WS(P) не
обязательно плотно на Т2. В частности, у него имеется ана-
аналитический пример, в котором WS(P) плотно на Ts, но это
обеспечивается не за счет того, что dfx(y)> 1 на (Ь, а-\-1),
а за счет других обстоятельств (и посредством более сложных
рассуждений, напоминающих доказательство теоремы Данжуа).
C6) Включение LaWs(S) следует из плотности Ws(P)r\%
на 2 (которая фактически и доказана выше) и из того, что
концы открытых интервалов ft, являющихся компонентами
связности Ws(P)f}?,, суть точки №ff(S)n2 (один конец лежит
на одной сепаратрисе, другой—на другой). Убедимся теперь,
что строго внутри любого максимального интервала / из 2\L
имеются хотя бы два из упомянутых выше интервалов /t. Сколь
угодно близко к любой точке J имеются точки и /j; значит,
J Л h Ф 0 при некотором i\ но концы J не могут принадлежать
1{, поэтому /jc:J. Пусть J'—один из двух связных интерва-
интервалов, составляющих J\If, повторяя предыдущее рассуждение,
находим сперва такое /у, что IjuJ'?z0, а затем доказываем,
что IjcJ'. (Концы J' не могут принадлежать /у—ведь один
из них лежит в L, а другой является концом It. Если бы It
и /у имели общий конец, то получилось бы, что W" (Р) П 2 с
обеих сторон примыкает к я @, с) или я (О, Ъ)\ тогда у S име-
имелась бы замкнутая сепаратриса). Наконец, пусть х, соответст-
соответственно у, —конец lt, соответственно /у, лежащий на входящей
сепаратрисе седла S, проходящей через п (О, Ь), так что РуХ =
= п(О, Ъ) = Pfy при некоторых п, пг^О, пфт. Если теперь,
скажем, п > т, то Ру~тх=у, nPY~mJr\J?:0-
C6) Теорема Эрмана утверждает (в частности), что диффео-
диффеоморфизм а? Diif°* B), который сохраняет ориентацию и для
которого р (а) удовлетворяет некоторому арифметическому усло-
условию, С-сопряжен с «поворотом» 2 (т. е. с преобразованием,
которое при С"*-накрытии R—»-2 накрывается отображением
Xv-^.x-\- const). Об этом условии сейчас достаточно знать, что
удовлетворяющие ему точки образуют всюду плотное множе-
множество А. Если для исходного У отображение последования PY
имеет иррациональное число вращения р(Ру)(т. е. если ирра-
10*
276 ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА
циональны числа, служащие представителями р(Ру) как смеж-
смежного класса, являющегося элементом факторгруппы R/Z), то
сколь угодно близко к Y имеется X с р(Рх)?А. (Рассуждая,
как в лемме 4, или поворачивая во всех точках тора векторы
поля Y в одну и ту же сторону, получим однопараметричес-
кое семейство полей YK с Y° = Y и р (YK) Ф const. Поэтому
имеются сколь угодно малые % с р(УА)?Л). Из СЧопряжен-
ности Рх с поворотом легко вытекает С°°-эквивалентность X
иррациональному потоку.
(s!) Непонятно, почему это свидетельствует о невозможности
полного описания классов топологически эквивалентных систем
в окрестности У. Нет сомнений, что в многомерных случаях
полная классификация (хотя бы только для полей, близких к за-
заданному) в общем случае ни в каком разумном смысле не возмож-
возможна, но в данном примере это не так. В этом примере получается
достаточно полное описание ситуации. Будем ли мы считать, что
оно дает, полную классификацию или нет — это до некоторой
степени зависит от того, что считать полной классификацией
(см. ниже).
В данном примере все сводится к классификации диффео-
диффеоморфизмов а окружности, сохраняющих ориентацию, а она та-
такова. Прежде всего, существенно, рационально или иррацио-
иррационально число вращения р (а) (т. е. рациональны или иррацио-
иррациональны числа, служащие представителями р(а) как смежного
класса, являющегося элементом факторгруппы R/Z).
При рациональном р(а) некоторая (скажем, л-ая) итерация
а" имеет неподвижные точки, образующие некоторое замкну-
замкнутое множество AcS1, а в каждом смежном к А интервале
точки под действием итераций отображения а" движутся от
одного конца интервала к другому. А и направления движе-
движения в этих смежных интервалах не совсем произвольны—в
понятном смысле они переходят в себя под действием а. Пол-
Полный произвол в их выборе имеется только на дуге IaS1, на-
начинающейся в какой-нибудь точке a G А и кончающейся в дру-
другой точке траектории \ака\—той точке, которая является
ближайшей к с в ту или иную сторону по окружности. (При
каком именно k точка ака окажется ближайшей к с и каково
взаимное расположение дуг а'7 на S1—это, как можно пока-
показать, однозначно определяется числом вращения). Задав замк-
замкнутое множество Bel (лишь бы оно содержало концы /) и
направления в смежных интервалах, можно затем построить
подходящее а. Имеется еще произвол в выборе начала а дуги /,
но его можно устранить, «замкнув» эту дугу в окружность.
(Качественная картина на всей исходной окружности восста-
восстанавливается с точностью до гомеоморфизма при л-к ратном на-
ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА 277
крытии). Итак, выбор замкнутого подмножества В окружности,
и, скажем, знаков -f- или — во всех смежных интервалах к В
определяет класс эквивалентности а и сам определяется им с
точностью до гомеоморфизма окружности (так сказать, сохра-
сохраняющего расстановку знаков в смежных интервалах). Этот
объект—В и знаки ± в смежных интервалах, рассматривае-
рассматриваемый с точностью до гомеоморфизма, —есть тот «параметр»,
«значения» которого полностью классифицируют наши а с дан-
данным р(а). Подобный «параметр», конечно, менее «обозрим»,
нежели это было бы в том случае, когда параметром служит
число или набор чисел. Считать ли «полной» классификацию,
зависящую от подобного «параметра»—на этот вопрос едва ли
можно ответить, не договорившись заранее, чего мы ожидаем
от «полной» классификации и что мы намерены с нею делать.
Если р (а) иррационально, а а ? С2, то по теореме Данжуа
а сопряжено с поворотом S1 на соответствующий угол; класс
топологически сопряженных а, стало быть, полностью опреде-
определяется в этом случае заданием р (а). Если р (а) иррационально,
а а ? С1, то различные такие а уже не все сопряжены друг с
другом, но их классификация все же возможна [185].
ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Книга Палиса и ди Мелу посвящена направлению в теории
динамических систем, которое авторы несколько условно назы-
называют геометрической теорией (условность связана с тем, что гео-
геометрические понятия и соображения играют немалую роль и в
других направлениях). За пределами этого направления находят-
находятся многочисленные вопросы аналитического характера, исследо-
исследования специфических свойств систем аналитической механики
(гамильтоновых и других), интегрируемые системы, топологи-
топологические (т. е. не обязательно гладкие) динамические системы,
эргодическая теория. Естественно, здесь я тоже не собираюсь
говорить об этих вещах и ограничусь ссылками на относящуюся
сюда литературу более или менее учебного характера, имею-
имеющуюся на русском языке! [5, 58, 123, 127, 130, 136, 137, 145, 148,
153, 155]. (Литература аналогичного характера по вопросам,
рассматриваемым в данной книге, уже указывалась по ходу из-
изложения, но стоит повторить: [3, 5, 6, 9, 42, 72, 109, 123, 124,
125].) В связи с литературой надо также иметь в виду, что в на-
настоящее время ВИНИТИ издает серию «Современные проблемы
математики. Фундаментальные направления». Несколько первых
ее томов, начиная с [133, 134], посвящены различным вопросам
теории динамических систем. По характеру этого издания по-
помещенные в нем статьи должны представлять нечто среднее меж-
между учебником и обзором. Наконец, обращаю внимание на «Мате-
«Математическую энциклопедию» [143] и имеющиеся в ней литератур-
литературные ссылки.
Что же касается геометрической теории, то в дополнение к об-
обзору, содержащемуся в § 4 гл. 4, стоит указать еще следующее.
1) В данной книге поведение траекторий потоков на поверх-
поверхности рассматривается более или менее систематически только
для грубых систем, если не считать случая S2, к которому отно-
относится теорема Пуанкаре — Бендиксона (гл. 1, § 1). В действи-
действительности и для других замкнутых поверхностей имеется до-
достаточно продвинутая теория, сравнимая по общности и опреде-
определенности своих заключений с теоремой Пуанкаре — Бендиксона.
Некоторая информация об этом имеется Р Ш
ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 279
2) С 60-х годов центральное положение в геометрической тео-
теории занимают вопросы, связанные с гиперболическим поведе-
поведением траекторий (вообще говоря, не отдельных траекторий, а
бесконечных множеств таковых). В §4 гл. 4 говорится о гипер-
гиперболических множествах и аксиоме А. Если бы оказалось (как
надеялись вначале), что системы, удовлетворяющие аксиоме А,
типичны, это давало бы вполне удовлетворительное решение
вопроса о типичных свойствах гладких динамических систем.
Но оказалось, что это не так [2, 40, 68]. Не увенчались успехом
и другие попытки найти такое условие, которое выполнялось бы
для типичной системы и в то же время в значительной степени
определяло бы ее свойства (подобно тому, как это имеет место
для грубости в случае малой размерности). Литературные ссыл-
ссылки см. в [125]. В то же время в соответствующих примерах все-
таки проявляется некоторая гиперболичность, только более
слабая. Быть может, со временем эта ослабленная гиперболич-
гиперболичность найдет отражение в подходящем общем понятии, но пока
что за рамками гиперболических множеств имеется только два
хорошо изученных типа инвариантных множеств, о которых из-
известно, что эти типы сохраняются при малых возмущениях;
оба они имеют довольно специальный характер. Один из них
рассмотрен в [173, 174], а о другом (аттрактор Лоренца) см. в п. 7)
ниже.
Совершенно независимо от вопроса о типичных свойствах
при исследовании ряда систем, о которых говорится далее (не-
(некоторые из них даже не являются гладкими), тоже в той или иной
степени обнаруживается нечто вроде гиперболического поведения
траекторий. (Я не останавливаюсь здесь на неравномерной и час-
частичной гиперболичности, играющей важную роль в эргодической
теории [134].)
3) Рассмотрим класс 3 изотопии диффеоморфизмов (или
гомеоморфизмов) двумерного тора 712=R2/Z2. В каждом таком
классе имеется представитель, индуцируемый линейным преоб-
преобразованием в Rs с целочисленной матрицей коэффициентов, име-
имеющей определитель ±1. Подобные отображения (некоторые из
них рассматривались в § 4 гл. 4) обладают рядом «хороших»
свойств (в том числе выходящих за рамки настоящей книги —
эргодические свойства; дилатация (коэффициент квазиконформ-
квазиконформности) на 3 достигает минимума на указанном представителе).
Помимо того что свойства этих представителей вполне обозримы,
иногда их (и представителей, и их свойства) можно использовать
при решении вопросов, непосредственно относящихся не к ним
самим, а к другим отображениям из 3 (простейший пример:
оценка снизу числа периодических точек).
Если теперь взять класс 3 изотопии диффеоморфизмов или
гомеоморфизмов ориентируемой замкнутой поверхности М2 рода
280 ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
>1, то столь же хорошего представителя найти, вообще говоря,
не удастся. Интуитивно это отчасти связано с тем, что на М2 нет
диффеоморфизмов Аносова, а между тем чувствуется, что для
многих Э искомый представитель должен обладать достаточно
сильной гиперболичностью. Ясно, что чем-то из «хороших»
свойств диффеоморфизмов Аносова надо пожертвовать. У. Тёр-
стен предложил в конечном числе точек пожертвовать глад-
гладкостью. Оказывается, среди таких гомеоморфизмов имеются го-
гомеоморфизмы, очень похожие по своим свойствам на пример § 4
гл. 4. Тёрстен назвал их псевдоаносовскими гомеоморфизмами.
Для других 3 Тёрстен тоже указал хороших представителей.
В действительности еще одна особенность теории Терстена со-
состоит в том, что ее надо с самого начала строить для компактных
поверхностей с краем, потому что даже в том случае, когда М2
замкнута, может случиться, что М2 надо разрезать на несколько
частей, на каждой из которых искомый представитель устроен
по-своему.
О теории Терстена (включающей как построение этих пред-
представителей и исследование их свойств, так и применения к изу-
изучению других гомеоморфизмов) см. [180]. К некоторым из соот-
соответствующих вопросов имеются и другие подходы. Один из них
развивался Я- Нильсеном начиная с 20-х годов, а другой связан
с квазиконформными отображениями и восходит к О. Тейхмюл-
леру. Например, предложенная Тёрстеном классификация клас-
классов изотопии столь же естественно получается и при других
подходах (фактически она уже имелась у Нильсена). Псевдоано-
совские гомеоморфизмы f фактически возникают в теории Тейх-
мюллера, однако цель как его первоначальных набросков, так
и работ Л. Альфорса и Л. Берса (приведших эту теорию в удов-
удовлетворительное состояние) состоит в исследовании конформных
структур на поверхностях, а отображения f являются вспомога-
вспомогательным средством; с этой точки зрения нет причин интересо-
интересоваться итерациями {/ft}. Связь с теорией динамических систем
установил только Тёрстен (естественно, это и можно было сде-
сделать только после того, как в последней возникло и получило
достаточное развитие «гиперболическое» направление).
Удачную теорию со временем оказывается возможным ис-
использовать в таких вопросах, о которых при ее создании не дума-
думали и которые внешне не имеют к ней отношения. Примерами та-
такого использования теории Терстена (отнюдь не сводящегося к ее
автоматическому применению) являются работы [163, 178].
4) Рассматриваемые в настоящей книге динамические сис-
системы с дискретным временем являются обратимыми, т. е. они
порождаются преобразованиями f, имеющими обратные (в соот-
соответствии с этим итерации fk рассматриваются при всех целых k).
Можно рассматривать и динамические системы, порождаемые
ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 281
необратимыми преобразованиями f (тогда /* рассматриваются
только при целых ?>0). Изменения, которые это вносит, иногда
значительны, а иногда совсем очевидны — например, ясно, что
в необратимом случае по-прежнему можно говорить об со-пре-
дельных точках, а об а-предельных точках говорить не прихо-
приходится.
Если f — гомеоморфизм отрезка, то свойства динамической
системы {/*} очевидны и просты. В 60-х годах А. Н. Шарковский
обратил внимание на то, что для необратимых непрерывных отоб-
отображений отрезка ситуация совершенно иная и что в то же время
для них можно развить достаточно содержательную теорию. Вна-
Вначале он был единственным, кто этим занимался, но затем поло-
положение изменилось — теперь имеется много работ (частью в виде
малодоступных препринтов) об отображениях отрезка или ок-
окружности. (При этом рассматриваются и разрывные отображения
достаточно простых типов. Первые примеры такого рода рассмат-
рассматривались в эргодической теории еще до Шарковского, но специ-
специфика одномерного случая оставалась в тени — ведь с чисто
метрической точки зрения, если разрывы никак не ограничива-
ограничиваются, одномерный случай ничем не отличается от многомерного.)
Помимо самостоятельного интереса необратимые одномерные
отображения играют вспомогательную роль при исследовании
некоторых обратимых динамических систем в большей размер-
размерности [156, 128, 158].
На русском языке пока имеется только очень краткая сводка
с преимущественным вниманием к эргодическим вопросам [134].
В иностранной литературе отмечу [187,188]. На Международном
математическом конгрессе в Варшаве A983 г.) одномерным отобра-
отображениям был посвящен доклад М. Мизюревича, с публикацией кото-
которого в Трудах конгресса такой обзор наконец-то появится. Допол-
Дополнительно дам три литературных указания по самым важным во-
вопросам. Сводка результатов Шарковского имеется в [176] (резуль-
(результаты последнего времени там сформулированы неточно). Водно-
мерном случае было обнаружено и исследовано качественно новое
явление — бесконечная последовательность однотипных бифурка-
бифуркаций периодических точек, происходящих при конечном изменении
параметра и приводящих к существенному усложнению движе-
движения. (Кое-что отчасти перенесено и на многомерный случай.)
См. [131]. Наконец, в [156, 189] имеется некоторая информация
о важном нидинг-инварианте Дж. Милнора — У. Тёрстена (ра-
(работа которых пока существует в виде препринта).
5) Другой класс необратимых динамических систем с диск-
дискретным временем получается при итерировании отображений
сферы Римана или плоскости комплексного переменного, опре-
определяемых рациональными или цельши функциями комплексного
переменного. Исследование таких итераций называют конформ-
282 ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
ной (или комплексно-аналитической) динамикой. Оно было на-
начато Г. Жюлиа и П. Фату в конце 10-х годов. Одна из глав
книги [147] содержит сведения о работах того времени. После
долгого перерыва работа в этой области возобновилась около
1970 г. Здесь имеется новый обзор [159].
6) Дифференцируемое отображение f замкнутого многооб-
многообразия М в себя называется растягивающим [177, 20], если под
его действием длины всех касательных векторов (в смысле ка-
какой-нибудь, а тогда и любой римановой метрики) растут с экс-,
поненциальной скоростью, т. е. существуют такие константы
С>0 и Х>0, что для всех X 6 ТМ и всех />0
\df*{X)\>CW\X\.
Примером может служить отображение S^R/Z—«-S1, кото-
которое в терминах угловой координаты х mod 1 задается форму-
формулой як-*2л:. Как и в этом примере, растягивающее отображение
всегда необратимо. Имеется вариант понятия растягивающего
отображения без условий дифференцируемое™, охватывающий,
в частности, многие ранее изучавшиеся одномерные при-
примеры [181].
Свойства растягивающих отображений аналогичны свойст-
свойствам диффеоморфизмов Аносова (в частности, они тоже явля-
являются грубыми), а отчасти даже проще. Так, растягивающее
отображение класса Cr, r ^2, всегда имеет конечную инвари-
инвариантную меру, задаваемую в терминах локальных координат
положительной плотностью (класса С1", а в аналитическом
случае—аналитической) [167, 168, 169]. Любое растягивающее
отображение сопряжено с отображением, получаемым при по-
помощи некоторой алгебраической конструкции [161].
7) Необходимо упомянуть еще о так называемых странных
аттракторах, тем более что их значение выходит за рамки
чистой математики — они доставляют математический образ
стохастических (или, как еще говорят, хаотических) автоколе-
автоколебаний х), само представление о которых сложилось не без влия-
влияния теории динамических систем [140, 151, 152]. (Высказывается
также надежда, что странные аттракторы объясняют природу
турбулентности, но это более проблематично [156, 146, 151,
175]. Реальные достижения, которые с этим связаны, относятся
к исследованиям механизма возникновения турбулентности.
В различных случаях переход от ламинарного течения к турбу-
турбулентному происходит по-разному, и — если интерпретация экс-
экспериментов правильна — здесь реализуются все те возможности,
которые в настоящее время можно представить себе на основа-
г) Тогда как математический образ периодических автоколебаний, как
известно, доставляется асимптотически устойчивыми замкнутыми траекто-
траекториями (А. А. Андронов, 1929 г.}.
ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 283
нии теории динамических систем. См. краткий обзор в [152]
и подробнее [175].)
Не имеется общепринятого точного определения, что такое
странный аттрактор. Прежде всего так называют гиперболиче-
гиперболические аттракторы и во многом сходный с ними аттрактор Лоренца
([156, 128, 158]; между прочим, в [128] и [158] последний пони-
понимается несколько шире, чем в некоторых статьях из [156], но,
как бы то ни было, в обоих случаях речь идет о четко опреде-
определенных объектах). Далее, странными аттракторами называют
также некоторые компактные инвариантные множества, которые,
как и аттрактор Лоренца, были обнаружены в численных экспе-
экспериментах и (по крайней мере на первый взгляд) кажутся во мно-
многом похожими на предыдущие два аттрактора. В подобных
случаях . отмечаются следующие характерные черты:
а) Некоторая гиперболичность (неустойчивость индивидуаль-
индивидуальных траекторий), возможно, более слабая, чем для гиперболи-
гиперболических множеств, но все же приводящая к характерной слоистой
структуре (см. рисунки, представляющие результаты численных
экспериментов, в [140, 156]; надо, впрочем, сказать, что ориги-
оригиналы намного выразительнее репродукций), а также к сложному,
«хаотическому» поведению траекторий и их практической неде-
недетерминированности. Возникает мысль, что поведение соответст-
соответствующих физических систем должно описываться статистически.
В математическом отношении в этом направлении многое сделано
для гиперболических аттракторов и аттрактора Лоренца [9, 154],
но это уже относится к эргодической теории г).
б) Сложная структура (это не многообразие), с чем и связано
название «странный» аттрактор. (Впрочем, в физической лите-
?атуре указывают, что это менее существенно, чем а),— см.
140], прим. ред. на с. 19, 74; [152], с. 368.)
в) Устойчивость относительно возмущения начальных дан-
данных, точнее, даже асимптотическая устойчивость,— оттого и го-
говорят об аттракторе. Кажется, что именно устойчивость и позво-
позволяет его обнаружить по скоплению точек — образов нескольких
исходных точек при итерациях отображения последования (в слу-
случае потока) или отображения, порождающего рассматриваемый
каскад (если время дискретно).
г) Устойчивость относительно возмущений динамической сис-
системы. При таких возмущениях аттрактор сохраняется, хотя не-
*) Системы, рассматриваемые в статистической физике (например, си-
система молекул газа), имеют много степеней свободы и являются консерва-
консервативными (гамильтоновыми). В прошлом казалось, что с этими двумя их
свойствами и связана возможность успешного применения статистических
понятий. Теперь же ясно, что гиперболичность может привести к появле-
появлению статистических свойств в поведении систем иного характера—с не-
небольшим числом степеней свободы и притом как консервативных, так и
существенно неконсервативных.
284 ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
которые «тонкие детали» его структуры могут измениться, так
что он не обязательно является локально грубым. Практически
это свойство означает, что рассматриваемый объект не представ-
представляет собой какую-то случайную патологию, вызванную неудач-
неудачным выбором математической модели физической системы.
д) Всего этого еще мало. Ведь априори могло бы случиться,
что «большинство» траекторий стремится к некоторой части В
нашего аттрактора А. Если мы интерпретируем аттрактор как
математический образ «режима», который «устанавливается в
пределе при / -> <х>» в физической системе, то таковым придется
признать В, а не Л.
Так, в примере 4 § 4 гл. 4 множество -Д =Пл>о/(#_)—
аттрактор. Он содержит асимптотически устойчивую неподвиж-
неподвижную точку Q3, гиперболическое множество A = Q2 и еще мно-
множество.
(U W (х))\А,
хел
образованное траекториями, идущими из Л в Qs. В целом А
определенно имеет слоистую структуру и устроено довольно
сложно (оно является неразложимым континуумом, гомеоморф-
ным первому из примеров таких континуумов, приведенных в
[138], § 48, V). Однако f"x-*~ Q3 при п-> оо для почти всех х ? S2
(исключительные точки образуют замкнутое нигде не плотное
множество, к тому же меры нуль, если f — класса С2). Хотя А
является аттрактором, эксперимент с «наудачу» выбранными на-
начальными точками покажет, что траектории идут из О* в Qs-
Влияние Л будет сказываться в том, что иногда будут попадаться
траектории, которые «по дороге» из Qx в Q3 как бы «временно за-
застревают» где-то возле Л; «поколебавшись» там довольно причуд-
причудливым образом, они наконец (как бы «спохватившись, что им надо
идти в Q3») устремляются к Q3, причем две траектории, вначале
близкие друг к другу и близко подходящие к Л, могут возле Л
далеко отойти друг от друга и могут по-разному уйти от Л к
й3 — одна в одно время и по одному пути, другая в другое
время и по другому пути.
Не имеется общепринятого соглашения, какое дополнитель-
дополнительное свойство, предположительно присущее различным приме-
примерам и исключающее подобные «неприятности», следует доба-
добавить к а)—г). Возможно, годится топологическая транзитив-
транзитивность А (имеется х?А сса(х) = А) или перемешивание областей
в А (для любых двух открытых в А непустых подмножеств U,
VczA имеется такое т, что fkU t\VФ 0 при всех /г>т (если
речь идет о каскаде \fk\) или XtU(]Уф 0 при всех />т
(если речь идет о потоке {Xt\). Иной характер имеет пред-
ПОСЛЕЙЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 285
лагавшееся в этой связи понятие «стохастического аттрактора»
([154, 134]).
Однако в этой области не просто дать теоретически состоя-
состоятельную интерпретацию численных экспериментов хотя бы в по-
порядке догадки, не говоря уже о ее последующей проверке,—
пока что все это удалось проделать только для аттрактора Ло-
Лоренца *) (если говорить о гладких системах; строгий анализ удал-
удался также в некоторых кусочно гладких случаях). Возможно
даже, что некоторые «странные аттракторы» не являются аттрак-
аттракторами в том смысле, как это понимается в настоящей книге.
Строго доказано, что при тех свойствах системы, которые как
будто обнаружены в численных экспериментах, в соответствую-
соответствующей области U (которая на первый взгляд кажется поглощающей
для странного аттрактора) может (а нередко и должно) существо-
существовать бесконечное число асимптотически устойчивых периодиче-
периодических траекторий [70, 172, 182]. Не исключено, что в этих экспе-
экспериментах наблюдались просто траектории, лежащие в «областях
притяжения» Ut (т. е. устойчивых многообразиях) периодиче-
периодических траекторий с очень большими периодами. В U заведомо
имеется и гиперболическое множество Л, аналогичное подкове
Смейла, но; подобно ей, оно не является аттрактором. Образно
выражаясь, к Л (или, быть может, к некоему большему инвари-
инвариантному множеству А) «прилипло много мелких крошек» Uif
и эти-то «прилипшие крошки» и делают видимым Л (или А);
Можно, конечно, высказать и другое предположение — что все-
таки множество ?/\ U Ut не является пренебрежимо малым (ска-
(скажем, имеет положительную меру) и лежащие в нем траектории
стремятся к некоторому сложно устроенному множеству А (это
суррогат в)), причем это так при «многих» значениях параметра,
от которого зависит система (это суррогат г)).
Для гамильтоновых систем возможность и даже типичность 2)
сосуществования «островков устойчивости» (только в этом случае
не асимптотической) с «большим» множеством «хаотических»
движений (быть может, даже с эргодической компонентой поло-
положительной меры) не вызывает сомнений (она достаточно убеди-
убедительно продемонстрирована в численных экспериментах и отча-
отчасти обоснована теоретически). Для неконсервативных систем
ситуация не ясна.
*) Доказано, что при выполнении определенных условий система имеет
аттрактор Лоренца. Достаточно очевидно существование систем, удовлетво-
удовлетворяющих этим условиям (так что аттрактор Лоренца действительно сущест-
существует). При проверке же выполнения этих, условий для той конкретной
системы, которую рассматривал сам Э. Лоренц, приходится использовать
ЭВМ. Как бы то ни было, это сделано достаточно тщательно и не вызы-
вызывает сомнений.
2) Типичность, конечно, не во всем пространстве таких систем, а в не-
некоторых его областях.
286 ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Так или иначе, одни из «странных аттракторов» являются
настоящими аттракторами, а другие, по-видимому, нет. Это не
значит, что последние не заслуживают внимания, но, видимо,
лучше называть их иначе — скажем, квазиаттракторами [158].
8) Наконец, надо отметить, что наряду с топологическим по-
пониманием типичности, типичных свойств и т. д., развиваемым
в настоящей книге, возможна и другая точка зрения — метри-
метрическая (в смысле теории меры). Исследование типичности с мет-
метрической точки зрения пока проведено только в отдельных слу-
случаях, однако в принципе она является столь же законной, как
и топологическая. В теории функций для характеристики под-
подмножеств отрезка (или подмножеств более общих пространств)
используются обе точки зрения. Известно, что они во многом
параллельны, но не совпадают (вплоть до того, что остаточное
множество, которое с топологической точки зрения следует
считать весьма «массивным», вполне может иметь меру нуль,
т. е. с метрической точки зрения быть «малым», «пренебрежи-
мым»). Коллизия между топологической и метрической типич-
типичностью имеет место и в вопросе о типичных свойствах динамиче-
динамических систем.
Остановимся подробнее на метрическом понимании типично-
типичности динамической системы. При попытке непосредственно сфор-
сформулировать метрическую точку зрения в этом вопросе возникает
очевидное препятствие — в бесконечномерных функциональных
пространствах нет столь же естественной меры, как мера Лебега
в R". Нет и естественного класса эквивалентных мер (тогда как
на конечномерных гладких многообразиях таковым является
класс мер, которые в терминах гладких локальных координат
эквивалентны мере Лебега). Поэтому не приходится говорить
о множествах меры нуль (которые с метрической точки зрения
считались бы исключительными) или полной меры («метрически
типичных»). Однако метрическая точка зрения становится осмыс-
осмысленной, если рассматривается не всё функциональное простран-
пространство, а только семейство динамических систем, зависящих от од-
одного или нескольких числовых параметров, ибо в пространстве
параметров уже есть естественная мера (или класс эквивалент-
эквивалентных мер). Если конкретная задача с самого начала относится
к такому семейству, то метрическая постановка вопроса о ти-
типичности, типичных свойствах и т. п. ясна. Если же рассматри-
рассматривать всевозможные семейства, то среди них будут и «вырожден-
«вырожденные» — например, такое семейство, для которого система при
всех значениях параметра одна и та же. Ясно, что такие семей-
семейства надо считать «исключительными» и исключить из рассмот-
рассмотрения. Поэтому представляется целесообразным следующий
подход.
Будем рассматривать семейства гладких динамических сие-
ПОСЛЕСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА 287
тем, гладко зависящих от одного или нескольких числовых
параметров. Такие семейства сами образуют некоторые функцио-
функциональные пространства (можно брать различное число параметров
и требовать различной степени гладкости, поэтому пространств
получается много. Выбор пространства, подходящего для того
или иного конкретного вопроса, отнюдь не очевиден). В таком
пространстве можно воспользоваться топологическим понима-
пониманием типичности, т. е. считать типичными семейства, которые
как элементы этого пространства образуют остаточное множе-
множество. Для каждого же типичного семейства будем рассматривать
меру множества параметров, при котором система имеет те или
иные свойства. Множество Ас?(Мп) будем называть (терми-
(терминология не является стандартной): 1) метрически пренебрежи-
мым, если для типичного семейства {X*} множество {X: Х*?Л}
имеет меру нуль; 2) метрически существенным, если оно не яв-
является метрически пренебрежимым; 3) метрически типичным,
если дополнение к нему метрически пренебрежимо. Аналогично
для A cDiffr(M") (С чисто топологической, точнее, гладкой
точки зрения тоже бывает нужным характеризовать «массив-
«массивность» множества ЛсЖ (М") (или AcDittr(Mn)), рассматривая
для типичного семейства {Х^} множество {К: Х^^А}—только
теперь речь идет не о мере этого множества, а чаще всего просто
о том, пустое оно или нет. См. [5], гл. 6.)
Ввиду теоремы 2 в [114] (с учетом теоремы 2.1 гл. 4) (при
надлежащих уточнениях) грубые потоки на сфере, проективной
плоскости и бутылке Клейна метрически типичны. С другой
стороны, грубые диффеоморфизмы на S1 не являются метрически
типичными (хотя, конечно, множество этих диффеоморфизмов,
как и любое открытое подмножество в пространстве динамиче-
динамических систем, метрически существенно). Именно, в DiffS1 с до-
достаточно большими г диффеоморфизмы, сопряженные с поворотом
на иррациональный угол, оказываются метрически существен-
существенными [5, 37]. Поэтому грубые потоки на торе Т2 тоже не являются
метрически типичными (хотя и являются метрически существен-
существенными). Фактически это относится к потокам без положений
равновесия, имеющим глобальное трансверсальное сечение (в
смысле § 3 гл. 3). Они все принадлежат одной связной компо-
компоненте пространства векторных полей на торе без особых точек
(но не исчерпывают ее). В других компонентах этого простран-
пространства ситуация должна быть такой же, как на сфере. Неизвестно,
какова ситуация при наличии особых точек на торе или для по-
потоков на компактных поверхностях с отрицательной эйлеровой
характеристикой (где рсегда имеются особые точки; специальный
интерес представляет случай, когда все они седла).
ЛИТЕРАТУРА
1. R. Abraham and J. Marsden, Foundations of Mechanics, rev. ed.— Benja-
Benjamin — Cummings, 1978.
2. R. Abraham and S. Smale, Nongenericity of й-stability.— In: Global
Analysis. Proc. Symp. in Pure Math., vol. XIV.— American Math. Soc.,
1970. [Имеется перевод: Абрахам Р., Смейл С. fi-устойчивость не ти-
типична.—В кн.: Сб. пер. Математ., 1969, т. 13, № 2, с. 156—160.]
3. Аносов Д. В. Геодезические потоки на замкнутых римановых многооб-
многообразиях отрицательной кривизны.— В кн.: Труды МИАН, т. 90.— М.:
Наука, 1967, с. 1—210.
4. Арнольд В. И. Обыкновенные дифференциальные уравнения.— М.: Нау-
Наука, 1975, с. 1—239.
5. Арнольд В. И. Дополнительные главы теории обыкновенных дифферен-
дифференциальных уравнений.— М.: Наука, 1978, с. 1—304.
6. Арнольд В. И. Лекции о бифуркациях и версальных семействах.—
Успехи мат. наук, 1972, т. 27, №5, с. 119—184.
7. V. Arnold and A. Avez, Theorie Ergodique des Systemes Dynamiques.—
Gauthier-Villars, 1967.
8. D. Asimov. Round handles and nonsingular Morse — Smale flows.— Ann.
of Math., v. 102, 1975, No. 1, p. 41—54.
9. R. Bowen, Equilibrium States and the Ergodic Theory of Anosov Diffeo-
morphisms.— Lecture Notes in Mathematics, vol. 470, Springer-Verlag,
1975. [Имеется перевод: Боуэн Р. Методы символической динамики.—
М.: Мир, 1979, с. 1—245.]
10. R. Bowen, On Axiom A Diffeomorphisms. Conference Board Math. Scien-
Sciences, 35, American Math. Soc, 1977.
11. P. Brunovsky, On one-parameter families of diffeomorphisms II: generic
branching in higher dimensions.— Comm. Math. Univers. Carolinae, 1971,
v, 12, N4, p. 765—784.
12. C. Camacho, On Я*Х Z'-actions.— In: Dynamical Systems, edited by
M. Peixoto.— Academic Press, 1973, p. 23—74.
13. T. Cherry, Analytic quasi-periodic curves of discontinuous type on a torus.—
Proc. London Math. Soc, 1938, v. 44, № з, р. 175—215.
14. С Conley, Isolated Invariant Sets and the Morse Index, Conference Board
Math. Sciences, 38. Providence: American Math. Soc, 1980, p. 1—90.
15. A. Dankner, On Smale's Axiom A diffeomorphisms.— Ann. of Math., 1978,
v. 107, №3, p. 517—553.
16. A. Denjoy, Sur les courbes definies par les equations differentielles a la
surface du tore.— J. Math. Pure et Appl., 1932, v. 11, ser. 9, p. 333—375.
17. J. Duistermaat, Oscillatory integrals, Lagrange immersions and unfoldings
of singularities.— Commun. Pure and Appl. Math., 1974, v. 27.
18. F. Farrell and L. Jones, Anosov diffeomorphisms constructed from nx Diff
(S«).— Topology, 1978, v. 17, N 3, p. 273—282.
д. G. Fl<"
19. G. Fleitas, Classification of gradient like flows on dimensions two and
three.— Bol. Soc. Brasil. Mat., 1975, v. 6.
20. J.Franks, Anosov diffeomorphisms.—In: Global Analysis. Proc. Symp.
in Pure Math., vol. XIV.— American Math. Soc, 1970. [Имеется перевод:
ЛИТЕРАТУРА 289
Френке Дж. У-диффеоморфизмы.— В кн.: Гладкие динамические сис-
системы.—М.: Мир, 1977, с. 32—86.]
21 J. Franks, Differentiably Q-stable diffeomorphisms.— Topology, 1972,
v. 11, N3, p. 107—113.
22. J. Franks and C. Narasimhan, The periodic behavior of Morse — Smale
diffeomorphisms.— Invent. Math., 1978, v. 48, N 3, p. 279—292.
23. J. Franks and M. Shub, The existence of Morse — Smale diffeomorphisms.—
Topology, 1981, v. 20, N3, p. 273—290.
24. J. Franks and R. Williams, Anomalous Anosov flows.— In: Global Theory
of Dynamical Systems, edited by Z. Nitecki and C. Robinson.— Lecture
Notes in Mathematics, vol. 819. Springer-Verlag, 1980, p. 158—174.
25. Гробман Д. М. О гомеоморфизме систем дифференциальных уравнений.—
Докл. АН СССР, 1959, т. 128, № 5, с. 880—881.
26. J. Guckenheimer, Absolutely й-stable diffeomorphisms.— Topology, 1972,
v. 11, N2, p. 195—197.
27. J. Guckenheimer, Bifurcations of dynamical systems.— In: Dynamical
Systems. CIME Lectures-Bressanone (Italy), Birkhauser, 1980, p. 115—
231.
28. M. Golubitsky and V. Guillemin, Stable Mappings and Their Singulariti-
Singularities.— Graduate Texts in Mathematics, vol. 14. Springer-Verlag, 1974.
[Имеется перевод: Голубицкий М., Гийемин В. Устойчивые отображения
и их особенности.— М.: Мир, 1977, с. 1—290.]
29. V. Guillemin and A. Pollack, Differential Topology. — Prentice-Hall,
1974.
30. С. Gutierrez, Structural stability for flows on the torus with a cross-cap.—
Trans. Amer. Math. Soc, 1978, v. 241, p. 311—320.
31. C. Gutierrez, Smoothing continuous flows and the converse of Denjoy —
Schwartz theorem.—Anais Acad. Brasil. Ciencias, 1979, v. 51.
32. C. Gutierrez and W. Melo. The connected components of Morse — Smale
vector fields on two manifolds, Proc. Illrd Latin American School of Ma-
Mathematics, edited by J. Palis and M. Carmo.— Lecture Notes in Mathe-
Mathematics, vol. 597. Springer-Verlag, 1977, p. 230—251.
33. J. Hale, Ordinary Differential Equations, rev. ed. Robert E. Krieger Publ.
Co., 1980.
34. J. Hale, Topics in Dynamic Bifurcation. Conference Board Math. Scien-
Sciences.— American Math. Soc, 1981.
35. P. Hartman, Ordinary Differential Equations.—Wiley, 1964. [Имеется
перевод: Хартман Ф. Обыкновенные дифференциальные уравнения.—
М.: Мир, 1970, с. 1—720.]
36. P. Hartman, A lemma in the theory of structural stability of differential
equations.—Proc. Amer. Math. Soc, I960, v. 11, p. 610—620.
37. M. Herman, Sur la conjugaison differentiable des diffeomorphismes du
cercle a des rotations.— Publ. Math. Inst. Hautes Etudes Scientifiques,
1979, v. 49, p. 5—234.
38. M. Hirsch, Differential Topology.— Graduate texts in Mathematics, vol.
33.— Springer-Verlag, 1976. [Имеется перевод: Хирш М. Дифференци-
Дифференциальная топология.— М.: Мир, 1979, с. 1—280.]
39. М. Hirsch and С. Pugh, Stable manifolds and hyperbolic sets.— In: Global
Analysis.— Proc. Symp. in Pure Math., vol. XIV.— American Math. Soc,
1970, p. 133—163.
40. M. Hirsch, С Pugh and M. Shub, Invariant Manifolds, Lecture Notes in
Mathematics, vol. 583, Springer-Verlag, 1977.
41. M. Hirsch and S. Smale, Differential Equations, Dynamical Systems and
Linear Algebra.— Academic Press, 1974.
42. G. Iooss and D. Joseph, Elementary Stability and Bifurcation Theory.—
Undergraduate Texts in Mathematics. Springer-Verlag, 1980. [Имеется
перевод: ИоссЖ-, Джозеф Д. Элементарная теория устойчивости и би-
бифуркаций.—М.: Мир, 1983, с. 1—300.]
290 ЛИТЕРАТУРА
43. М. Irwin, On the stable manifold theorem.— Bull. London Math. Soc.,
1970, v. 2, part 2, No. 5, p. 196—198.
44. I. Kupka, Contribution a la theorie des champs generiques.— Contrib.
Diff. Equations, N. Y.: Interscience publ., 1963, v. 2, p. 478—484; 1964,
v. 3, p. 411—420.
45. M. Keane, Interval exchange transformations, Math. Z., 1975, Bd. 141,
№5, S. 25—31.
46. S. Lang, Analysis, vol. I.— Addison-Wesley, 1968.
47. S. Lefschetz, Differential Equations: Geometric Theory. Wiley, 1963.
[Имеется перевод: Лефшец С. Геометрическая теория дифференциальных
уравнений.—М.: ИЛ, 1961, с. 1—387.]
48. Е. Lima, Analise no espaco R».— Univ. Brasilia and Edgard Blucher,
1970.
49. E. Lima, Variedades diferenciaveis, Monogr. de Mat., IMPA, 1973,
v. 15.
50. I. Malta, Hyperbolic Birkhoff centers.— Anais Acad. Brasil Ciencias, 1979,
v. 51; and Trans. Amer. Math. Soc. 1980, v. 262, № 1, p. 181—193.
51. I.Malta, On fi-stability of flows.— Bol. Soc. Brasil. Mat., 1980, v. 11.
Б2. R. Mane, Absolute and infinitesimal stability. On infinitesimal and ab-
absolute stability of diffeomorphisms.— In: Dynamical Systems Warwick
1974, edited by A. Manning.— Lecture Notes in Mathematics, vol. 468.—
Springer-Verlag, 1975, p. 24—26, 151—161.
53. R. Майе, Contributions to the stability conjecture, Topology, 1978, v. 17,
N 4, p. 383—396.
54. R. Майе, An ergodic closing lemma.—Ann. of Math., 1982, v. 116,
N 3, p. 503—540.
55. A. Manning, There are no new Anosov diffeomorphisms on tori, Amer.
J. Math., 1974, v. 96. [Имеется перевод: Мэннинг Э. Отсутствие новых
У-диффеоморфизмов на торах.— В кн.: Гладкие динамические системы.—
М.: Мир, 1977, с. 99—110.1
66. N. Markley, The Poincare — Bendixson theorem for the Klein bottle.—
Trans. Amer. Math. Soc, 1969, v. 135, p. 159—165.
Б7. L. Markus, Lectures in Differentiable Dynamics, rev. ed.— Conference
Board Math. Sciences, 3.— American Math. Soc, 1980. .
Б8. J. Marsden and M. McCracken, The Hopf Bifurcation and Its Applicati-
Applications.— Appl. Math. Sciences, vol. 19.— Springer-Verlag, 1976 [Имеется
перевод: Марсден Дж., Мак-Кракен М. Бифуркация рождения цикла
и ее приложения.—¦ М.: Мир, 1980, с. 1—368.]
69. W. Massey, Algebraic topology: an Introduction.— Harcourt-Brace-World,
1967. [Имеется перевод: Масси У. Алгебраическая топология. Введение.—
В кн.: Масси У., Столлингс Дж. Алгебраическая топология. Введение.—
М.: Мир, 1977, с. 7—278.]
60. J. Morgan, Nonsingular Morse — Smale flows on three-manifolds.— Topo-
Topology, 1979, v. 18, N 1, p. 41—53.
61. W. Melo, Structural stability of diffeomorphisms on two manifolds.—
Invent. Math., 1973, v. 21, N 3, p. 233—246.
62. W. Melo and J.Palis, lntrodu^ao aos Sistemas Dinamicos.— Projeto
Euclides, IMPA-CNPq, 1977.
63. P. Mendes, On stability of dynamical systems on open manifolds.— J. Diff.
Equations, 1974, v. 16, N 1, p. 144—167.
64. J.Milnor, Topology from the Differentiable Viewpoint.—Univ. Press of
Virginia, 1965. [Имеется перевод: Милнор Дж. Топология с дифферен-
дифференциальной точки зрения.— В кн.: Милнор Дж., Уоллес А. Дифференци-
Дифференциальная топология. Начальный курс. — М.: Мир, 1972, с. 177—
277.J
65. J Moser, On a theorem of Anosov, J. Diff. Equations, 1969, v. 5, N 3,
p. 411—440.
ЛИТЕРАТУРА 291
66. J. Moser, Stable and Random Motions in Dynamical Systems with Special
Emphasis on Celestial Mechanics, Princeton Univ. Press, 1973.
67. S. Newhouse, On codimension one Anosov diffeomorphisms, Amer. J. Math.,
1970, v. 92. [Имеется перевод: Ньюхаус Ш. Е. Об У-диффеоморфизмах
коразмерности один.— В кн.: Гладкие динамические системы.— М.:
Мир, 1977, с. 87—98.]
68. S. Newhouse, Nondensity of Axiom A(a) on S2.— In: Global Analysis,
Proc. Symp. in Pure Math., vol. XIV.— American Math. Soc, 1970,
p. 191—202.
69. S. Newhouse, Hyperbolic limit sets.— Trans. Amer. Math. Soc, 1972,
v. 167, p. 125—150.
70. S. Newhouse, Lectures on dynamical systems. In: Dynamical Systems.
CIME Lectures-Bressanone (Italy). Birkhouser, 1980, p. 1—114.
71. S. Newhouse and J. Palis, Hyperbolic nonwandering sets on two-dimensi-
two-dimensional manifolds In: Dynamical Systems, edited by M. Peixoto. Academic
Press, 1973, p. 293—301.
72. Z. Nitecki, Differentiable Dynamics, M. I. T. Press, 1971. [Имеется пере-
перевод: Нитецки 3. Введение в дифференциальную динамику.— М.: Мир,
1975, с. 1—304.]
73. G. Palis, Linearly induced vector fields and factions on spheres.— In:
Dynamical Systems —Warwick, 1974.—Lect. Notes in Math. No. 468.—
Berlin — Halb.— N. Y.: Springer, 1975, p. 13—17.
74. J. Palis, On the local structure of hyperbolic fixed points in Banach
spaces.— Anais Acad. Brasil. Ciencais, 1968, v. 40, No. 3, p. 263—
266.
75. J. Palis, On Morse — Smale dynamical systems.— Topology, 1969, v. 8,
N4, p. 385—404.
76. J. Palis, A note on Q-stability.— In: Global Analysis, Proc. Symp. in
Pure Math., vol. XIV.—American Math. Soc, 1970, p. 221—222.
77. J. Palis (editor). Seminario de Sistemas Dinamicos, Monogr. de Mat.,
IMPA, 1971, v. 4.
78. J. Palis, Moduli of stability and bifurcation theory. Proc. Int. Congress
of Mathematicians, Helsinki, 1978.
79. J. Palis andS. Smale, Structural stability theorems.— In: Global Analysis,
Proc. Symp. in Pure Math. vol. XIV.— American Math. Soc, 1970. [Имеет-
[Имеется перевод: Пали Дж., Смейл С. Теоремы структурной устойчивости.—
Сб. пер. Мат., 1969, т. 13, № 2, с. 145—155.]
80. J. Palis and F. Takens, Topological equivalence of normally hyperbolic
dynamical systems.— Topology, 1977, v. 16, N 4, p. 336—346.
81. M. Peixoto, Structural stability on two-dimensional manifolds.— Topo-
Topology, 1962, v. 1, N 2, p. 101—120. Structural stability on two-dimensional
manifolds — a further remark.— Topology, 1963, v. 2, N 2, p. 179—
180.
82. M. Peixoto, On an approximation theorem of Kupka and Smale.— J. Diff.
Equations, 1967, v. 3, N 2, p. 214—227.
83. M. Peixoto, On the classification of flows on two-manifolds.— In: Dynami-
Dynamical Systems, edited by M. Peixoto.— Academic Press, 1973, p. 389—
419.
84. M. Peixoto, On bifurcations of dynamical systems.— Proc. Int. Congress
of Mathematicians, Vancouver, 1974, v. 2, p. 315—319.
85. M. Peixoto and M. С Peixoto, Structural stability in the plane with en-
enlarged boundary conditions.— Anais Acad. Brasil. Ciencias, 1969, v. 31,
No. 2, p. 135—160.
86. Плисе В. А. Поведение решений периодической системы дифференциаль-
дифференциальных уравнений, имеющей интегральное множество нулевой меры.—
Дифференц. уравнения, 1972, т. 8, № 3, с. 553—555.
87. Плисе В. А. О грубости дифференциальных уравнений, заданных на
торе.— Вестник ЛГУ, 1960, № 13, сер. мат., мех. и астр., вып. 3,
292 ЛИТЕРАТУРА
с. 15—23.
88. С. Pugh, The closing lemma, Amer. J. Math., 1967, v. 89.1Имеется перевод:
Пью Ч. Лемма о замыкании.— Сб. пер. Мат., 1968, т. 12, № 6, с. 80—
135.]
89. С. Pugh, An improved closing lemma and a general density theorem, Amer.
J. Math., 1967, v. 89. [Имеется перевод: Пью Ч. Усиление леммы о замы-
замыкании и теорема о плотности. Сб. пер. Мат., 1968, т. 12, № 6, с. 136—
146.]
90. С. Pugh, On a theorem of P. Hartman, Amer J. Math., 1969, v. 91, N 2,
p. 363—367.
91. С Pugh and M. Shub, The Q-stability theorem for flows, Invent. Math.,
1970, v. 11, N2, p. 150—158.
92. J. Robbin, A structural stability theorem, Ann. of Math., 1971, v. 94.
[Имеется перевод: Роббин Дж. У. Теорема о структурной устойчиво-
устойчивости.— В кн.: Нитецки 3. Введение в дифференциальную динамику.—
М.: Мир, 1975, с. 233—289.]
93. J. Robbin, Topological conjugacy and structural stability for discrete
dynamical systems, Bull. Amer. Math. Soc, 1972, v. 78, N 6, p. 927—
952.
.94. L. Rocha, Characterization of Morse — Smale isotopy classes on two-mani-
two-manifolds, Anais Acad. Brasil. Ciencias, 1978, v. 50, and to appear in J. of Ergo-
dic theory and Dynamical Systeme.
95. С Robinson, Structural stability of vector fields, Ann. of Math., 1974,
v. 99, N 1, p. 99, N 1, p. 154—175; 1975, v. 101, N 2, p. 368.
96. C. Robinson, Structural stability of C1 flows, In: Dynamical Systems War-
Warwick 1974, edited by A. Manning, Lecture Notes in Mathematics, vol. 468.
Springer-Verlag, 1975, p. 262—277.
97. С Robinson, Structural stability of C1 diffeorhorphisms, J. Diff. Equations,
1976, v. 22, N 1, p. 28—73.
98. C. Robinson, С structural stability implies Kupka — Smale.— In: Dyna-
Dynamical Systems, edited by M. Peixoto.— Academic Press, 1973, p. 443—
449.
99. D. Ruelle, Dynamical Systems with Turbulent Behavior.— Lecture Notes
in Physics, vol. 80.— Springer-Verlag, 1978.
100. A. Schwartz, A generalization of a Poincare — Bendixson theorem to closed
two-dimensional manifolds.—Amer. J. Math. 1963, v. 85, N3, p. 453—
458.
101. M. Schub, Stabilite globale des systemes dynamiques, Asteiisque, 1978,
v. 56.— Paris: Soc. math, de France, 1978.
102. M. Shub, Structurally stable diffeomorphisms are dense.— Bull. Amer.
Math. Soc, 1972, v. 78, N 5, p. 817—818.
103. M. Shub and D. Sullivan, Homology theory and dynamical systems.—
Topology, 1975, v. 14. [Имеется перевод: Шуб М., Сулливан Д. Теория
гомологии и динамические системы.— В кн.: Гладкие динамические сис-
системы.—М.: Мир, 1977, с. 140—180.]
104. М. Shub and R. Williams, Future stability is not generic.— Proc. Amer.
Math. Soc, 1969, v. 22, N 2, p. 483—484.
105. С Simon, Instability in Diff (Г8) and the nongenericity of rational zeta
functions.— Trans. Amer. Math. Soc, 1972, v. 174, p. 217—242.
106. S. Smale, On gradient dynamical systems.— Ann. of Math., 1961, v. 74,
N 1, p. 199—206.
107 S. Smale, Stable manifolds for differential equations and diffeomorphisms.—
Ann. Scuela Sup. Piza, 1963, v. 17, N I—II, p. 97—116.
108. S. Smale, Diffeomorphisms with many periodic points. In: Differential and
Combinatorial Topology. Princeton Univ. Press, 1965. [Имеется перевод:
Смейл С. Диффеоморфизмы со многими периодическими точками.— Сб.
пер. Мат., 1967, т. 11, № 4, с. 88—106.]
ЛИТЕРАТУРА 293
109. S. Smale, Differentiable dynamical systems, Bull. Amer. Math. Soc, 1967,
v. 73. [Имеется перевод: Смейл С. Дифференцируемые динамические
системы. Успехи мат. наук, 1970, т. 25, № 1, с. 113—185.]
ПО. S. Smale, The Q-stabi!ity theorem.—In: Global Analysis.—Proc. Symp.
in Pure Math., vol. XIV. American Math. Soc. 1970. [Имеется перевод:
Смейл С. Теорема Q устойчивости.— Сб. пер. Мат., 1969, т. 13, №2,
с. 161—169.]
111. S. Smale, Structurally stable systems are not dense.— Amer. J.Math.,
1966, v. 88. [Имеется перевод: Смейл С. Грубые системы не плотны.—
Сб. пер. Мат., 1967, т. 11, №4, с. 107—112.]
112. S. Smale, Stability and isotopy in discrete dynamical systems.— In: Dy-
Dynamical Systems, edited by M. Peixoto.— Academic Press, 1973, p..527—
530.
113. S. Smale, Essays on dynamical systems, economic processes and related
topics.— In: The Mathematics of Time.— Springer-Verlag, 1980.
114. J. Sotomayor, Generic one parameter families of vector fields on two-
dimensional manifolds.— Publ. Math. Inst. Hautes Etudes Scientifiques,
1973, v. 43, p. 5—46.
115. J. Sotomayor, Generic bifurcations of dynamical systems.— In: Dynamical
Systems, edited by M. Peixoto.— Academic Press, 1973, p. 561—582.
116. J. Sotomayor, Licoes de equacoes Diferenciais Ordinarias, Projeto Euclides,
IMPA-CNPq, 1979.
117. F. Takens, Introduction to Global Analysis, Comm. no. 2.— Math. Inst.
Univ. Utrecht, 1973.
118. R. Thom, Structural Stability and Morphogenesis.— Benjamin — Addison
Wesley, 1975.
119. С Zeeman, Uma introducao informal й topologia das superficies, Monogr.
de Mat., IMPA, 1975, v. 20.
120. P. Walters, An Introduction to Ergodic Theory.— Graduate Texts in Ma-
Mathematics, vol. 79.— Springer-Verlag, 1982.
121. R.Williams, Expanding attractors, Publ. Math. Inst. Hautes Etudes Sci-
Scientifiques, 1973, v. 43, p. 161—203.
122. R. Williams, The «DA» maps of Smale and structural stability.— In:
Global Analysis.— Proc. Symp. in Pure Math., vol. XIV. American Math.
Soc, 1970, p. 329—334.
ЛИТЕРАТУРА, ДОБАВЛЕННАЯ ПРИ ПЕРЕВОДЕ
123. Алексеев В. М. Символическая динамика. (Одиннадцатая математиче-
математическая школа, ч. 1).— Киев: Ин-т матем. АН УССР, 1976, с. 1—210.
124. Алексеев В. М., Каток А. Б., Кушниренко А. Г. Гладкие динамические
системы.— В кн.: Девятая летняя математическая школа.— Киев:
Ин-т матем. АН УССР, 1972, с. 50—348; 2-е изд.— Киев: Наукова думка,
1976, с. 50—348.
125. Аносов Д. В. Грубые системы.— В кн.: Топология, обыкновенные диф-
дифференциальные уравнения, динамические системы. Сборник обзорных
статей к 50-летию Института. 2. Труды МИАН, т. 169.— М.: Наука,
1985.
126. Арансон С. X. Траектории на неориентируемых двумерных многообра-
многообразиях.— Мат. сб., 1969, т. 80, № 3, с. 314—333.
127. Арнольд В. И. Математические методы классической механики.— М.:
Наука, 1974, с. 1—431.
128. Афраймович В. С, Быков В. В., Шильников Л. П. О притягивающих
негрубых предельных множествах типа аттрактора Лоренца.— Труды
Московского мат. общества, 1982, т. 44, с. 150—212.
294 литература
129. Блохин А. А. Гладкие эргодические потоки на поверхностях.— Труды
Московского мат. общества, 1972, т. 27, с. 113—128.
130. Брюно А. Д. Локальный метод нелинейного анализа дифференциальных
уравнений.— М.: Наука, 1979, с. 1—253.
131. Вул Е. Б., Синай Я. Г., Ханин К. М. Универсальность Фейгенбаума
и термодинамический формализм.— Успехи мат. наук, 1984, т. 39, № 3,
с. 3—37.
132. Гробман Д. М. Топологическая классификация окрестностей особой
точки в п-мерном пространстве.— Мат. сб., 1962, т. 56, № 1, с. 77—94.
133. Динамические системы 1. Серия «Итоги науки и техники. Современные
проблемы математики. (Фундаментальные направления)».— М.: ВИ-
ВИНИТИ, 1985.
134. Динамические системы 2. Серия «Итоги науки и техники. Современные
проблемы математики. (Фундаментальные направления)».— М.: ВИ-
ВИНИТИ, 1985.
135. Дьедонне Ж. Основы современного анализа.— М.: Мир, 1964, с. 1—430.
136. Клиигенберг В. Лекции о замкнутых геодезических.— М.: Мир, 1982,
с. 1—414.
137. Корнфельд И. П., Синай Я. Г., Фомин С. В. Эргодическая теория.—
М.: Наука, 1980, с. 1—383.
138. Куратовский К. Топология, т. 2.— М.: Мир, 1969, с. 1—624.
139. Ленг С. Введение в теорию дифференцируемых многообразий.— М.:
Мир, 1967, с. 1—203.
140. Лихтенберг А., Либерман М. Регулярная и стохастическая динамика.—
М.: Мир, 1984, с. 1—528.
141. Майер А. Г. Грубое преобразование окружности в окружность.— Уче-
иые записки Горьковского университета, 1939, вып. 12, с. 215—229.
142. Майер А. Г. О траекториях на ориентируемых поверхностях.— Мат. сб.,
. 1943, т. 12, № 1, с. 71—84.
143. Математическая энциклопедия.— М.: Советская энциклопедия.— Т. 1,
1977, с. 1—1152; т. 2, 1979, с. 1—1104; т. 3, 1982, с. 1—1184; т. 4, 1984,
с. 1—1216; т. 5, 1985, с. 1—1248.
144. Мезер Дж. Диффеоморфизмы Аносова. Сб. пер. Мат., 1969, т. 13, № 2,
с. 142—144.
145. Мозер Ю. Лекции о гамильтоновых системах.— М.: Мир, 1973, с. 1—167.
146. Монин А. О. О природе турбулентности.— Успехи физ. наук, 1978, т. 125,
№ 1, с. 97—122.
147. Монтель П. Нормальные семейства аналитических функций.— М.— Л.:
ОНТИ НКТП СССР, 1936, с. 1—240.
148. Немыцкий В. В., Степанов В. В. Качественная теория дифференциаль-
дифференциальных уравнений.— М.— Л.: Гостехиздат, 1949, с. 1—550.
149. Плисе В. А. Интегральные множества периодических систем дифферен-
дифференциальных уравнений.— М.: Наука, 1977, с. 1—303.
150. Плыкин Р. В. О геометрии гиперболических аттракторов гладких кас-
каскадов.— Успехи мат. наук, .1984, т. 39, №6.
151. Рабинович М. И. Стохастические автоколебания и турбулентность.—
Успехи физ. наук, 1978, т. 125, № 1, с. 123—168.
152. Рабинович М. И., Трубецков Д. И. Введение в теорию колебаний и
волн.—М.: Наука, 1984, с. 1—432.
153. Сибирский К. С. Введение в топологическую динамику.— Кишинев:
АН МССР, 1970, с. 1—144.
154. Синай Я. Г. Стохастичность динамических систем.— В кн.: Нелинейные
волны.—М.: Наука, 1979, с. 192—212.
155. Степин А. М. Интегрируемые гамильтоновы системы.— В кн.: Качест-
Качественные методы исследования нелинейных дифференциальных уравнений
и нелинейных колебаний.— Киев; Ии-т матем. АН УССР, 1981, с. 116—
170.
ЛИТЕРАТУРА
295
156. Странные аттракторы.— М.: Мир, 1981, с. 1—253.
157. Тамура И. Топология слоений.— М.: Мир, 1979, с. 1 317.
158. Afraimovich V. S., ShiFnikov L. P. Strange attractors and quasiattrack-
tors.— In: Nonlinear dynamics and turbulence.— Boston-L.-Melbourne-
Pitsman publ., 1983, p. 1—34.
159. Blanchard P. Complex analytic dynamics on the Riemann sphere. Bull
Amer. Math. Soc, 1984, v. 11, N 1, p. 85—141.
160. Foster M. J. Fibre derivatives and stable manifolds: a note.— Bull. Lond
Math. Soc, 1976, v. 8, p. 3, N 24, p. 286—288.
161. Gromov M. Groups of polynomial growth and expanding maps.— Publ.
math. Inst. Lautes etud. sci., 1981, N 53, p. 53—78.
162. Qutierrez С Smooth nonorientable nontrivial recurrence on two-mani-
two-manifolds.— J. Different. Equat., 1978, v. 29, N 3, p. 388—395.
163. Handel M. The entropy of orientation reversing homeomorphisrns of sur-
surfaces.—Topology, 1982, v. 21, N3, p. 291—296.
164. Hartman Ph. On the local linearization of differential equations.— Proc.
Amer. Math. Soc, 1963, v. 14, N 4, p. 568—573.
165. Irwin M. С On the smoothness of the composition map.— The quarterly J.
Math., 1972, v. 23, N90, p. 1—133.
166. Kotus J., Krych M., Nitecki Z. Global structural stability of flows on open
surfaces.— Memoires of the Amer. Math. Soc, v. 37, N 261.— Providence:
Amer. Math. Soc, 1982, p. 1—108.
167. Krzyzewski K- Some results on expanding mappings.— In: Dynamical
systems, Warszaw A977), II. Asterisque, No. 50.— Paris: Soc. mathem. de
France, 1977, p. 205—218.
168. Krzyzewski K. A remark on expanding mappings.— Colloquium Math.,
1979, v. 41, N 2, p. 291—295.
169.'Krzyzewski K. On analytic invariant measures for expanding mappings.—
Colloquium Math., 1982, v. 46, N 1, p. 59—65.
170. McGehee R. The stable manifold theorem via an isolating block.— In:
Symposium on ordinary differential equations. Lect. notes in math.,
N 312.— Berlin — Hdlb.— N. Y.: Springer, 1973, p. 1-204.
171. Newhouse Sh. E. Diffeomorphisms with infinitely many sinks.— Topology,
1974, v. 13, N 1, p. 9—18.
172. Newhouse Sh. E. The abundance of wild hyperbolic sets and non-smooth
stable sets for diffeomorphisms.— Publ. math. Inst. hautes etud. sci.,
1979, N 50, p. 101—152.
173. Newhouse S. E. Dynamical properties of certain non-commutative skew-
products.— In: Global theory of dynamical systems. Lect. notes in math.j
N819. В.—Hdlb.—N. Y.: Springer, 1980, p. 353—363.
174. Newhouse S. E., Young L.— S. Dynamics of certain skew products.— In:
Geometric dynamics. Lect. notes in math., N 1007.— Berlin — Hdlb.—
N. Y.— Tokyo: Springer, p. 611—629.
175. Nonlinear dynamics and turbulence.— Boston — London — Melbourne:
Pitman publ., 1983, p. 1—356.
176. Sharkovsky A. N. On some properties of discrete dynamical systems.— In:
Sur la theorie de l'iteration et ses applications. Colloq. Internet. deCNRS,
No. 332.— Toulouse: Univ. P. Sabatier, 1983, p. 153—158.
177. Shub M. Endomorphisms of compact differentiable manifolds.— Amer.
J. Math., 1969, v. 91, No. 1, p. 175—199.
178. Smille J. Periodic points of surface homeomorphisms with zero entropy.—
In: Ergodic theory and dynamical systems, 1983, v. 3, N 2, p. 315—334.
179. Sunnami A. The stability theorems for discrete dynamical systems on two-
dimensional manifolds.— Nagoya math. J., 1983, v. 90, p. 1—55.
180. Travaux de Thurston sur les surfaces.— Seminaire Orsay. Asterisque,
No. 66—67. Paris: Soc. Mathem. de France, 1979, p. 1—284.
181. Walters P. Invariant measures and equilibrium states for ^some mappings
296 ЛИТЕРАТУРА
which expand distances.— Trans. Amer. Math. Soc, 1978, v. 236, p. 121—
153.
182. Robinson С Bifurcation to infinitely many sinks.— Commun. Math. Phys.,
1983, v. 90, N3, p. 433—459.
183. Palis J. A note on the inclination lemma (A,-lemma) and Feigenbaum's rate
of approach.— In: Geometric dynamics. Lect. Notes in Math., No. 1007,
p. 630—635.
184. Palis J., Takens F. Stability of parametrized families of gradient vector
fields.—Ann. Math., 1983, v. 118.
185. Markley N. G. Homeomorphisms of the circle without periodic points.—
Proc. Lond. Math. Soc, 1970, v. 20, N 4, p. 688—698.
186. Smale S. Morse inequalities for a dynamical system. Bull. Amer. Math.
Soc, 1960, v. 66, N 1, p. 43—49. [Имеется перевод: Смейл С. Неравенства
Морса для динамических систем.— В кн.: Сб. пер. Мат., 1967, т. 11,
№4, с. 79—87.]
187. Nitecky Z. Topological dynamics on the interval — In: Ergodic Theory
and Dynamical Systems II. Proc. of special year, Mariland, 1979—1980,
ser. Progr. in Math., vol. 21. —Birkhauser, 1982, p. 1—73.
188. Collet P., Eckmann J.-P. Iterated map on the interval as dynamical
system.— Progr. in Physics, vol. 1.—Birkhauser, 1980, 248 p.
189. Misiurewicz M. One-dimentional dynamical systems. In: Proc. Intern.
Congr. Math., 1983, Warsaw, vol. 2. —Warsaw, PWN. —North-Holland,
1984, p. 1277—1281.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
(Стандартные термины, относящиеся к другим разделам математики — ана-
анализу, геометрии и т. д.,— в указатель не включены, равно как и названия,
используемые только временно в ходе отдельных рассуждений.)
абсолютная грубость 237
Адамара метод 260, 268
аксиома А 219, 236, 248
Аносова лемма о замыкании 231
— диффеоморфизм, поток 218
аттрактор 52, 161, 235
базисное множество 220
Биркгофа теорема о гомоклиниче-
ских точках 213
бифуркации 239
— рождения предельного цикла 272
— седло-узла 241, 274
— сепаратрис 273, 274
— удвоения периода 243
блуждающая точка 160
Бэра пространство, теорема 14, 34
векторное поле 14, 22
вложение диффеоморфизма в поток
122, 248
вращения число 249, 255, 274
выпрямляющая карта 126
гиперболическая замкнутая траек-
траектория 130
— неподвижная точка 83
— особая точка 47, 81
— периодическая точка 123
гиперболический линейный изомор-
изоморфизм 68
гиперболическое линейное векторное
поле 66
— множество 219
глобальное трансверсальное сечение
152
глобальный поток 23
гомоклииическая точка, траектория
213
градиентное векторное поле 26, 209,
244
граф 188
графика преобразование 111
Гробмана — Хартмана теорема 84,
120
Гронуолла неравенство 89
грубое свойство 158
грубость 43, 50
грубость дуг векторных полей 244
DA -диффеоморфизм 226
Данжуа поток 188
Данжуа — Шварца теорема
замкнутая траектория 24
188
298
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
инвариантное множество 29, 49
— сечение 131
индекс (Морса) 66, 95, 101, 259
интегральная кривая 14, 22
иррациональный поток, иррациональ-
иррациональное поле на торе 25
источник 47, 53
квазигиперболичность 243
коммутирующие векторные поля 52,
248
конформная (комплексно-аналитиче-
(комплексно-аналитическая) динамика 282
критический элемент 141
Купки — Смейла векторное поле 145
— диффеоморфизм 151
— теорема 146, 151
Ji-лемма 113, 120
лемма о замыкании 207
локальная грубость 59, 259
гиперболической замкнутой
траекто рии 133
локальное неустойчивое (устойчивое)
многообразие 101, 268
.Лоренца аттрактор 283
метрически пренебрежимое (сущест-
(существенное, типичное) множество 287
минимальное множество 187
Морса функция 122
Морса — Смейла векторное поле 161
диффеоморфизм 210
надстройка (Смейла) 152
иеблуждающая точка 160, 210
иеориентируемая рекуррентная тра-
траектория 2'67
неподвижная точка 49
неустойчивое многообразие 101, 134,
221, 268
— слоение 215, 268
fi-грубость 237
обратимая динамическая система 280
общая теорема о плотности 239
ориентируемая рекуррентная траек-
траектория 267
особая точка 24
остаточное множество 14, 34
Пейксото теорема 157, 169, 193, 205
период 24, 49
периодическая точка 49
Перрона метод 105, 260, 268
Плыкина аттрактор 235
поглощающая окрестность 53
последования отображение 125
поток 23
предельное множество 24, 49, 160
простая особая точка 78
псевдоаносовский гомеоморфизм 280
Пуанкаре — Бендиксона теорема 31
растягивающее отображение 282
рациональный поток, рациональное
поле иа торе 25
регулярная траектории 24
рекуррентность 57, 176
репеллер 53, 161
седло 161
сепаратриса 170
—, соединяющая сёдла 163
сепаратрисный контур 53, 188
сечение 125
слоение 267
Смейла подкова 222
сопряжение векторных полей 42
— диффеоморфизмов 49
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
299
сток 47, 53
странный аттрактор 282
теорема об устойчивом многообразии
104, 268
— о спектральном разложении 219
— о трубке тока 59, 126
типичное свойство 124, 155, 239
топологическая эквивалентность 42,
58
траектория 22, 24, 49
транзитивность (топологическая) 220
трансверсальности условие 221
тривиальная рекуррентная траекто-
траектория 176
тривиальное минимальное множество
187
трубка тока 126
фазовая диаграмма 165
фильтрация 166
фундаментальная область диффеомор-
диффеоморфизма (потока) на устойчивом (не-
(неустойчивом) многообразии 113,
120
Хопфа бифуркация 242
центр (Биркгофа) 57, 247
центральное многообразие 241
цикл в множестве неблуждающих
точек 238
цикл для векторного поля 53
Черри поток 186, 249
устойчивое многообразие 101,
221, 268
— слоение 215, 268
134, элементарная неподвижная точка 83
эндоморфизм окружности 249, 274
эргодическая теория 239
ОГЛАВЛЕНИЕ
От авторов . . , 5
От издательства « , , . 5
Введение 6
Список обозначений ... 8
ГЛАВА 1. ГЛАДКИЕ МНОГООБРАЗИЯ И ВЕКТОРНЫЕ ПОЛЯ И
§0. Анализ в R" и гладкие многообразия 11
§ 1. Векторные поля на многообразиях 22
§2. Топология на пространстве С-отображений 33
§3. Трансверсальность 38
§4. Грубость 41
Упражнения ..,..., 52
ГЛАВА 2. ЛОКАЛЬНАЯ ГРУБОСТЬ 58
§ 1. Теорема о трубке тока , , 58
§ 2. Линейные векторные поля 60
§3. Особенности и гиперболические неподвижные точки 77
§ 4. Локальная грубость 84
§ 5. Локальная классификация , 94
§ 6. Инвариантные многообразия 101
§ 7. Я,-лемма (лемма о наклоне). Геометрическое доказа-
тельство локальной грубости 112
Упражнения 122
ГЛАВА 3. ТЕОРЕМА КУВДИ — СМЕЙЛА 124
§ 1. Отображение последоваиия 125
§ 2. Типичность векторных полей с гиперболическими замк-
замкнутыми траекториями 135
§3. Трансверсальность инвариантных многообразий . , , 145
Упражнения 155
ОГЛАВЛЕНИЕ 301
ГЛАВА 4. ТИПИЧНОСТЬ И ГРУБОСТЬ ВЕКТОРНЫХ ПОЛЕЙ
МОРСА — СМЕЙЛА 157
§ 1. Векторные поля Морса—Смейла; грубость 158
§ 2, Плотность векторных полей Морса — Смейла на ори-
ориентируемых поверхностях 176
§3. Обобщения 205
§ 4. Общие замечания о грубости. Другие темы 209
Упражнения 244
Приложение: число вращения и поток Черри 249
Примечания редактора перевода 259
Послесловие редактора перевода 278
Литература 288
Предметный указатель , , 297