Author: Кац М.
Tags: теория вероятностей и математическая статистика физика теория вероятностей
Year: 1965
Text
И ЗДАТЕЛЬСТВО
«МИР»
LECTURES IN APPLIED MATHEMATICS
PROCEEDINGS OF THE SUMMER SEMINAR,
BOULDER, COLORADO, 1957
Volume I
PROBABILITY
AND RELATED TOPICS
IN PHYSICAL SCIENCES
by
MARK KAC
Department of Mathematics,
Cornell University
With Special Lectures
by
G. E. UHLENBECK
Department of Physics,
University of Michigan
A. R. H I В В S
Jet Propulsion Laboratory,
California Institute of Technology
Interscience Publishers, Ltd., London
Interscience Publishers, Inc., New York
М. К а ц
ВЕРОЯТНОСТЬ
И СМЕЖНЫЕ ВОПРОСЫ
В ФИЗИКЕ
ПЕРЕВОД С АНГЛИЙСКОГО
Р. А. МИНЛОСА
ИЗДАТЕЛЬСТВО «МИР»
Москва 1965
УДК 519.2:530.16
Автор знаком советскому читателю по переводу его ра-
работы «Статистическая независимость в теории вероятностей,
анализе и теории чисел» (ИЛ, 1963). Его новая книга в основ-
основном посвящена одной из интереснейших задач физики: опи-
описать, как система из очень большого числа частиц (газ в
сосуде) приходит в состояние равновесия, и объяснить, как
необратимость этого процесса во времени согласуется с обра-
обратимостью во времени исходных уравнений. Наибольшее внима-
внимание уделяется вероятностному аспекту проблемы; рассматри-
рассматриваются статистические модели, имитирующие основные черты
задачи. Две первые главы имеют и самостоятельный интерес —
на удачно подобранных примерах автор показывает, каким
образом понятие вероятности возникает в математических и
физических задачах и какой аналитический аппарат исполь-
использует теория вероятностей.
В данное издание включены статьи Каца и других авто-
авторов, касающиеся затронутых в книге вопросов.
Редакция литературы по математическим наукам
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
В своем предисловии автор ясно очертил как стиль
книги, так и те педагогические и литературные принци-
принципы, которыми он руководствовался. По своей форме и
манере изложения эта книга принадлежит к новому
жанру в математической литературе, изобретенному, по-
видимому, недавно. Эту форму можно наполнить любым
содержанием, и с ее помощью читателя можно вести
почти от «нуля» в самую гущу нерешенных проблем, не
отнимая у него возможности в любом месте с достоин-
достоинством выйти из игры.
Одно замечание относительно содержания книги. Не-
Несмотря на то что она очень фрагментарна и состоит из
большого числа искусно расположенных этюдов, в ней
все-таки центральное место занимает третья глава.
Здесь сделана далеко идущая попытка ввести читателя
в круг вопросов, связанных с кинетическими уравне-
уравнениями. Автор следует в этой главе своей основной тен-
тенденции (впрочем, вполне совпадающей с общим замыс-
замыслом книги)—дать статистическое истолкование кине-
кинетическим уравнениям и тем необратимым процессам,
которые ими описываются. В связи с этим здесь почти
отсутствует упоминание о других аспектах и подходах
к этой проблеме. Этот пробел, правда частично, воспол-
восполняется лекцией Г. Е, Уленбека, помещенной в приложе-
приложениях к книге. Но следует иметь в виду, что книга на-
написана около пяти лет назад, а за последнее время
в этой области появилось много интересных работ.
В конце книги добавлено приложение, которого не
было в оригинальном издании. Это цикл недавних ста-
статей М. Каца, Г. Уленбека и П. Хеммера, где подробно
разбирается одна модель фазового перехода.
В третьей главе, а также в лекции Уленбека трак-
трактуются вопросы неравновесной статистической механи-
механики — каким образом большая система, исходя из произ-
произвольного состояния, приходит к равновесию. Однако уже
в равновесной статистической механике существует очень
важная нерешенная задача — задача о фазовом пере-
переходе. В настоящее время в классической статистической
механике имеется лишь одна модель (двумерная и трех-
трехмерная решетки Изинга), в которой строго установлено
существование фазового перехода. Непрерывной же мо-
модели (модели газа) фазового перехода еще нет, не гово-
говоря уже о том, что отсутствует какое-либо описание тех
систем, где такой переход возможен.
В помещенном нами цикле статей строится модель
одномерного газа с очень малым и очень дальнодей-
ствующим притяжением, в которой обнаруживается фа-
фазовый переход. Хотя этот случай и не улавливает всех
трудностей истинной трехмерной задачи, эти работы
очень интересны. К этим статьям мною написано не-
небольшое добавление, где кратко изложены необходимые
сведения о проблеме конденсации. Читателю, мало зна-
знакомому с вопросом, лучше начать с этого добавления.
Р. А. Минлос
ОТ АМЕРИКАНСКОГО
РЕДАКЦИОННОГО КОМИТЕТА
Эта книга представляет собой первый том трудов
летнего семинара по прикладной математике, организо-
организованного Американским математическим обществом и
проходившего в Колорадском университете в течение
четырех недель с 23 июня 1957 г.
Цель этого семинара состояла в том, чтобы ознако-^
мить квалифицированных математиков с современным
состоянием нескольких областей прикладной математики
и поставить перед ними ряд важных и интересных
задач, которые до сих пор не решены. Такой семинар
можно рассматривать как попытку содействовать раз-
развитию сотрудничества между математиками и физиками.
Труды семинара публикуются для того, чтобы информа-
информация, приобретенная участниками семинара, стала до-
доступной значительно более широкому научному кругу.
В то же время эти книги могут служить справочником
для тех, кто слушал лекции.
Программа семинара была разработана организа-
организационным комитетом Американского математического
общества в составе П. Гарабедяна, А. Хаусхолдера,
М. Каца, Р. Ленгера, Линь Цзя-цзяо, В. Прагера, Дж.
Стокера и М. Мартина (председатель).
Подготовка семинара (составление программ заседа-
заседаний, организация отдыха участников) была осуществле-
осуществлена комитетом Отделения прикладной математики
Колорадского университета в составе Бриттона, Бен
Крига, Рутланда, Снивли, Шталя, Хатчинсона (пред-
(председатель).
Неисчерпаемая энергия и энтузиазм председателя и
других сотрудников университета внесли неизмеримый
вклад в успешное осуществление планов семинара.
Семинар открылся 23 июня вступительным докладом
Р. Фейнмана (Калифорнийский технологический инсти-
институт) на тему «Связь математики и физики». Заседания,
предусмотренные программой, проводились по утрам, с
тем чтобы сохранить свободным послеполуденное время
и предоставить участникам возможность проводить не-
неофициальные дискуссии по отдельным вопросам.
А. Хаусхолдер
13 октября 1958 г.
Памяти моих родителей и моего
брата — невинных жертв войны
ПРЕДИСЛОВИЕ
Эта книга — расширенное изложение двенадцати
лекций, прочитанных на семинаре по прикладной мате-
математике в Колорадском университете летом 1957 года.
Как и лекции, книга представляет собой введе-
введение в теорию вероятностей и предназначена для квали-
квалифицированного читателя, не имеющего почти никаких
предварительных сведений о предмете.
Это не означает, что она может служить учебником;
для этого она слишком фрагментарна и, возможно,
слишком сильно отражает вкусы, наклонности и пред-
предубеждения автора. По сути дела, это скорее обзор неко-
некоторых собственных его исследований и точек зрения.
В теории вероятностей автора больше всего привле-
привлекает необычайное разнообразие ее применений. Немно-
Немногие математические дисциплины имеют такой широкий
диапазон приложений — от теории чисел до физики; еще
меньше среди них тех, которые столь решительно про-
проникают во все наше научное мышление.
Отразить эту многогранность теории вероятностей и
показать широту ее применений — в этом и заключается
цель книги. Чтобы добиться этого, мы сосредоточили
основное внимание в нашем изложении на ряде отдель-
отдельных примеров и задач, не делая при этом никаких серьез-
серьезных попыток вложить их в общие схемы или теории.
Помимо того, что такой стиль изложения весьма
свойствен автору, он кажется нам наиболее ярким, во
всяком случае в педагогическом отношении.
Стремление к общности и абстрактности в курсе лек-
лекций, призванных служить введением в новую область,
выглядело бы, мягко говоря, глупо. Это могло бы
привести к искаженной картине, где все побудительные
мотивы были бы скрыты; да и, кроме того, чтобы спа-
спасти изложение от смертельной скуки, от автора потре-
потребовался бы литературный талант, далекий от его воз-
возможностей.
Книга делится на четыре главы. В первой (теорети-
(теоретико-вероятностный способ рассуждений) показывается,
каким образом вероятностные понятия возникают при
исследовании различных задач и насколько они бывают
плодотворны.
Во второй главе (аналитические средства и приемы
теории вероятностей) мы прежде всего хотели показать,
как подступаются к этим задачам и как их решают. При
этом мы получили возможность обсудить на ряде при-
примеров вопрос о роли переформулировок одного и того
же утверждения и выявить столь свойственную теории
вероятностей связь между комбинаторным и аналитиче-
аналитическим аспектами.
Третья глава (самая длинная) называется «Вероят-
«Вероятность в некоторых задачах классической статистической
механики». Эта глава дополнена двумя лекциями
Г. Е. Уленбека об уравнении Больцмана (приложение I).
Очень удачно, что мы смогли поместить в нашей книге
столь прозрачный обзор физических идей, господствую-
господствующих в этой трудной и важной области, и заручиться
сотрудничеством столь выдающегося авторитета в этих
вопросах. Наша третья глава в значительной степени
является последовательным комментарием к некоторым
вопросам, затронутым в первой лекции Уленбека, и хотя
содержание этой главы независимо, мы очень советуем
читать ее вместе с этой лекцией.
Вторая лекция Уленбека подводит читателя к гра-
границе наших сегодняшних знаний и ставит его перед
обширной областью, где возможности дальнейших от-
открытий почти неограниченны.
Однако я обязан Уленбеку значительно большим.
Почти вся третья глава написана под прямым или кос-
косвенным влиянием наших с ним бесед и переписки, длив-
длившихся в течение почти пятилетней дружбы и научного
сотрудничества. И удовольствие, с которым я приношу
ему благодарность, заставляет меня полностью забыть
те муки, с которыми я писал и переписывал эту главу.
В четвертой главе (интегрирование в функциональ-
функциональных пространствах) излагается действительно новый
способ исследования задач классического анализа и фи-
физики. Эти фундаментальные идеи были выдвинуты в на-
начале двадцатых годов Н. Винером и с несколько другой
точки зрения Р. Фейнманом в 1942 г. Наши собствен-
собственные исследования возникли под сильным влиянием ра-
работ Фейнмана, хотя в чисто математическом плане мы
опирались на строго установленные свойства меры
Винера в пространстве непрерывных функций.
Подход Фейнмана к нерелятивистской квантовой ме-
механике настолько изящен и нагляден, что мы просили
доктора А. Р. Гиббса прочитать специальную лекцию
(приложение II), чтобы ознакомить семинар с этим ме-
методом. Мы крайне признательны А. Р. Гиббсу за по-
помощь. Читатель может подождать появления книги
Фейнмана и Гиббса, целиком посвященной этому важ-
важному и захватывающему предмету.
Со своей стороны мы в четвертой главе сосредото-
чили внимание на выявлении возможностей интегрирова-
интегрирования в функциональных пространствах как метода ре-
решения задач, не имеющих на первый взгляд ничего
общего с вероятностями или мерой в функциональном
пространстве.
Когда в 1948 г. впервые было строго установлено
соответствие между уравнением Шредингера и средним
от некоторого функционала по пространству непрерыв-
непрерывных функций (идея, навеянная работой Фейнмана),
нами была задумана определенная программа. Эта про-
программа состояла в том, чтобы изучить аналитические
свойства некоторого класса дифференциальных и инте-
интегральных операторов, связав их со средними значениями
от определенных функционалов по подходящему про-
пространству функций. Краткое ее изложение дано в на-
нашей статье «On some connections between probability
theory and differential and integral equations» (Proc.
Sec. Berkeley Symp. in Math. Stat. and Prob., 1951). Важ-
Важная часть программы (касающаяся асимптотики собст-
собственных значений уравнения Шредингера) была выпол-
выполнена Д. Рэем в 1953 г. Мы указываем здесь также на
возможности применения метода функционального инте-
интегрирования в классической теории потенциала.
За последние годы появилось много статей различ-
различных авторов, касающихся некоторых вероятностных ас-
аспектов теории потенциала и смежных задач. Эти статьи
следуют другому пути: авторы стремятся главным обра-
образом к окончательной общности вероятностного истолко-
истолкования, а не к использованию вероятностных методов как
руководства к открытию, пониманию и доказательству
определенных фактов из анализа и физики.
Хотя в узком техническом смысле наши результаты
являются, может быть, частными случаями некоторых
более поздних и общих теорий, мы предпочитаем вычис-
вычисления и формулы словесным доводам, основанным на
тонком (но утомительном) использовании теории меры;
потеря же общности с избытком вознаграждается яс-
ясностью и конкретностью.
Эта книга возникла из записи лекций и сохранила
их свободный стиль. То, что научная книга столь ради-
радикально отступает от пресловутого «Введения в теорию
слонов» («Einffihrung in die Elephantenlehre»), произо-
произошло в значительной степени из-за отвращения автора к
увесистым заумным трактатам. Если я слишком пере-
перегнул в другую сторону, то надеюсь, что читателю по
крайней мере будет все понятно.
Многие друзья и коллеги всячески помогали мне в
работе над книгой. А. Иоффе помогал в составлении пер-
первоначальных мимеографических записей; Дж. Риордан
значительно помог мне советами и с выдержкой и тактом
исправлял мои погрешности в английском языке. Наи-
Наибольшую благодарность я приношу Г. Кестену, который
критически просмотрел большую часть рукописи и ис-
исправил там потрясающее количество ошибок.
Я особенно благодарен участникам встречи в Боул-
Боулдере, чье неизменное внимание и неиссякаемый интерес
к предмету служили для меня постоянно ободряющим
источником, и, наконец — но не в последнюю очередь,—
я благодарю сотрудников издательства Interscience Pub-
Publishers за их замечательное содействие.
Марк
Итака, Нью-Йорк
ГЛАВА I
ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ
РАССУЖДЕНИЙ
1. Что превратило теорию вероятностей в особую
науку?
Она, несомненно, является ветвью анализа и в уз-
узком смысле ветвью теории меры. В своей наиболее руди-
рудиментарной (и часто наиболее трудной!) части она свя-
связана с комбинаторикой.
Однако все это далеко не исчерпывает содержания
теории вероятностей, и вряд ли возможно определить
ее точное место и границы.
Поэтому мы не будем даже пытаться установить, что
такое теория вероятностей. Вместо этого мы покажем,
что можно из нее извлечь.
Чтобы облегчить изложение, мы предлагаем очень
общую (и, следовательно, почти тривиальную!) схему,
которая встречается во всех теоретико-вероятностных
рассуждениях.
Эта схема предполагает, что задано некоторое мно-
множество 5 (называемое «выборочным пространством»)
и выделено семейство F его подмножеств (называемых
«элементарными событиями» или «элементарными мно-
множествами»), которым заранее приписаны их меры. Кро-
Кроме того, постулируется ряд правил, с помощью которых
меры (или, что то же самое, «вероятности») могут быть
вычислены для других подмножеств из S.
В классической теории вероятностей приняты сле-
следующие правила:
1. Если обозначить через \х меру, то
@ — пустое множество).
2. Если множества Вп попарно не пересекаются (т. е.
Bi(]Bj = 0, 1ф]) и измеримы (т. е. \х(Вп) определены),
то
Обычно допускаются счетные суммы множеств (впол-
(вполне аддитивная мера), но в некоторых интересных слу-
случаях (замечательный пример дает теория чисел) допу-
допустимы только конечные суммы множеств.
3. Если некоторое множество В измеримо, то и его
дополнение 5\Б измеримо.
4. Если \i(C) =0 и Бс=С, то \х(В) = 0.
Последний постулат не является общепринятым, но
мы не станем здесь это обсуждать.
Само собой разумеется, что первоначальное задание
меры (вероятности) на элементарных множествах (со-
(событиях) должно быть согласовано с перечисленными
правилами.
Может показаться удивительным, что столь «тощая»
схема служит основанием богатой и плодовитой теории,
однако на деле это богатство и плодовитость возникают
в значительной мере за счет выбора специальных мно-
множеств и специальных мер.
Выбор множества S, так же как и выбор в нем се-
семейства элементарных событий и задание меры, зави-
зависит каждый раз от условий рассматриваемой задачи.
Теперь мы хотим на ряде примеров проиллюстриро-
проиллюстрировать способ рассуждений, принятый в теории вероятно-
вероятностей.
2. Пример 1. Рассмотрим одноатомный идеальный
газ, состоящий из N молекул с массой т и находящийся
в тепловом равновесии. Пусть vb v2, ..., Vjy — векторы
скоростей молекул в некоторый момент времени. Мы хо-
хотим найти вероятность того, что значение абсциссы vix
вектора v2- заключено между числами а и Р; обозначим
эту вероятность, как принято,
A.2.1) Р{а<г;,ж<р}.
Сейчас мы переведем эту задачу на точный матема-
математический язык. Под идеальным газом понимают газ, в
котором можно пренебречь силами взаимодействия ме-
жду молекулами. Отсюда, если обозначить полную энер-
энергию такого газа через ?, мы получим соотношение
A.2.2) v? + v2+...+v^ = -^- (V2=Vvy).
Естественно допустить, что энергия Е пропорцио-
пропорциональна iV, т. е.
A.2.3) ? = xjV,
где к не зависит от N.
Состояние газа определяется набором векторов
vv v2, ..., vN и может быть изображено точкой
{vix, viy, ul2, .. ., vix, viy, viZy .. ., vNXi vNy, vNz) на по-
поверхности ЗЛ/-мерной сферы S3n(R) радиуса
A24) Л
Интересующее нас событие a<vix<$ определяет
очень простое множество на поверхности сферы
^злм I ) (такое множество называется сферической
зоной).
Таким образом, выборочным пространством 5 в на-
шем случае служит поверхность сферы ош I
и мы должны теперь задать в этом пространстве меру.
Выбор этой меры продиктован нашим предположением
о тепловом равновесии в газе.
Мы просто примем (это эквивалентно определению
теплового равновесия), что мера \i(B) элементарного
множества В равна отношению
/т о с\ /о\ Площадь множества В
A. Z.O) ц(#) =
Площадь поверхности оОЛ.
«3iv i\ m } J
В качестве элементарных множеств мы можем взять,
например, фигуры, ограниченные дугами больших кру-
кругов (сферические многоугольники).
Семейство элементарных множеств должно быть все-
всегда достаточно богатым, чтобы мы имели возможность,
пользуясь постулатами теории меры, распространить
меру (вероятность) на широкий класс «интересных»
множеств (событий).
В рассматриваемом случае интересным для нас мно-
множеством является сферическая зона a<vix<$.
Итак, задача нахождения вероятности Р{а< vix <P}
сводится к простому геометрическому вычислению пло-
площади сферической зоны. Ответ хорошо известен и выра-
выражается формулой
(I. 2.6) P[oi<vix<$}= -^
dx
\ 2%1V )
-R
В пределе при N->oo получаем
(I. 2.7) lim P {a < vix < p} =
1 3m"
, /1 Зт Г Г
= У2^-ъг J Lexp
Это приводит нас к известной формуле Максвелла, если
положить
A.2.8) %
где k — универсальная постоянная и Г —абсолютная
температура.
С чисто математической точки зрения этот пример
слишком примитивен, поскольку интересующее нас мно-
множество случайно оказалось очень простым. Следующая
задача более тонкая.
Рассмотрим долю, которую составляют молекулы с
абсциссой скорости, заключенной между а и |3. Какова
вероятность того, что эта доля отличается от вычислен-
вычисленной нами вероятности Р {а < vix < p} более чем на е>0?
Если обозначить через г|эа|8 (х) функцию, принимаю-
принимающую значение 1 на интервале а<х<$ и 0 вне этого
интервала, то интересующее нас множество опреде-
ляется неравенством
N
I. 2.9)
Это уже достаточно сложное множество, и вычислить
его меру намного труднее.
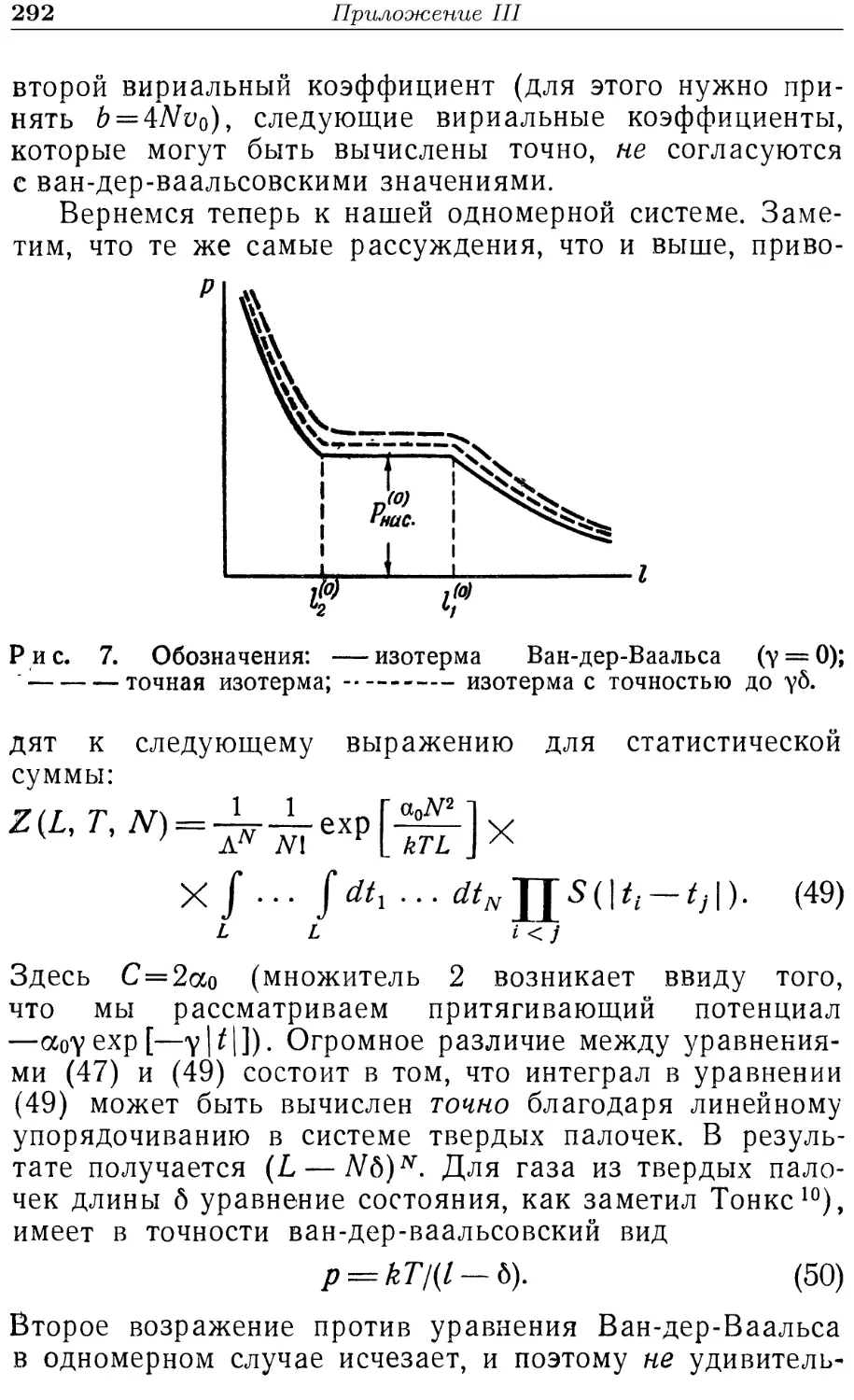
Не вдаваясь в подробности, заметим только, что,
даже не вычисляя точного значения вероятности собы-
события A.2.9), легко доказать, что для любого е>0 она
стремится к нулю при N-+oo (это пример «слабого за-
закона больших чисел»).
Необходимо иметь в виду, что этот вывод следует
пока только из основного предположения A.2.5). Тем
не менее то обстоятельство, что вероятность события
A.2.9) мала, нас радует, поскольку мы придерживаемся
интуитивного истолкования вероятности как частоты, а
сформулированная выше теорема, по-видимому, служит
опорой нашей интуиции.
В сущности, как это ни обидно, в этой теореме не так
уж много содержания. В ней говорится фактически сле-
следующее: если вероятность Р некоторого события вычис-
вычислена в соответствии с определенными допущениями и
правилами, то мала вероятность (снова вычисленная с
помощью тех же допущений и правил) того, что частота,
с которой это событие встречается в большом числе
испытаний, будет значительно отличаться от Р.
Как ни скромно такое утверждение, но в основном
это все, что можно ожидать от чисто математической
теории.
Применима ли такая теория в естественных науках,
в конечном счете решается опытом. Но это в равной
мере относится ко всяким применениям математической
теории за пределами самой математики, и смутное ощу-
ощущение неудобства, которое многие (большей частью фи-
философы) испытывают, впервые сталкиваясь со статисти-
статистическими рассуждениями, следует приписать сравнитель-
сравнительной новизне идей.
Для меня не существует методологического различия
между возможностью применять дифференциальные
уравнения в астрономии и теорию вероятностей в термо-
термодинамике или квантовой механике.
Она работает! И хотя в такой точке зрения много
грубого прагматизма, лучшая еще не найдена.
3. Пример 2. Сколько в среднем вещественных кор-
корней имеет полином
A.3.1) а„ + <М+ ••• +an.lta-1
с вещественными коэффициентами?
Как и раньше, чтобы придать этому вопросу точный
смысл, мы должны установить, как понимать выраже-
выражение «в среднем». Среди необозримого количества воз-
возможных толкований мы выбираем следующее, аналити-
аналитически самое простое.
Каждому полиному вида A.3.1) мы сопоставим точку
(или вектор) я-мерного пространства (а0, аи ..., an_i) =а
и рассмотрим только те полиномы, для которых эта
точка лежит на единичной сфере Sn(l):
A.3.2) ||а||2=2а| = 1.
Число вещественных корней полинома A.3.1) обозна-
обозначим через yV(a) =N(a0, au ... ,an-i).
Условимся теперь для полиномов со свойством A.3.2)
средним числом корней считать
A.3.3) -^ jN(*)do,
Sn(l)
где
A.3.4) \Sn(l)\=(
— площадь поверхности единичной сферы, a da-—эле-
da-—элемент этой поверхности.
Таким образом, выборочным пространством в нашем
случае является сфера 5ПA), а мерой — обычная мера
Лебега (нормированная) на ее поверхности (т. е. та пло-
площадь, которую можно чисто геометрически определить
на поверхности я-мерной сферы).
Мы можем сформулировать задачу несколько более
удобным способом.
Рассмотрим интеграл
A.3.5) Мп =
... dan.x
— оо —оо
и заметим, что для каждого вещественного числа а
мы имеем N (а&) = N (а). Перепишем A.3.5) в виде
N(a)dcAdr
0 \Sn(r)
и заметим, что
J л^а^а^г"-1 J N (a) da.
Sn(r) Sn(l)
Отсюда получим
(I. 3.6)
поскольку
|5Я AI Bк
Формула A.3.5) показывает, что мы могли бы в ка-
качестве выборочного пространства S взять я-мерное ев-
евклидово пространство, а меру произвольного множе*
ства В определить так:
A.3.7) И?) = B*Гл
Такая формулировка в терминах, более привычных
для теории вероятностей, означает, что коэффициенты
полиномов независимы и каждый из них распределен
нормально с нулевым средним и единичной дисперсией.
Обозначим через М^ и Ж(/22) соответственно средние
значения числа вещественных корней, заключенных в
интервале (—1, 1) и лежащих вне этого интервала.
Сначала мы покажем, что
A.3.8)
и, следовательно,
A.3.9)
Для доказательства равенства A.3.8) заметим, что по-
лином ^aktk имеет в интервале (—1,1) столько же
о
я-1
вещественных корней, сколько полином ^dn_l_ktk вне
о
п-} п-\
этого интервала, так как Zjuktk = tn~l Zj^n-i-k \т) *)•
Jmm мят \ I I
О О
Обозначая через ЛП(а0, а4, ..., ап-4), соответственно
N2(a0, au ...,an_i), число вещественных корней поли-
/Z-1
нома ^aktk внутри, соответственно вне, интервала
о
(—1,1), получаем отсюда равенство
N<l>(a0, av ...>an_l) = N^{an_v an_2, ..., a0).
Следовательно,
+ OO +OO
Xexp(— ^-|
X exp (— 11| a ||2) dao... dan-i = M{
l) Здесь, конечно, предполагается, что свободный член полино-
п-\
ма Е aktk отличен от нуля, т. е. среди его корней нет нуля. Поли-
о
номы, у которых ао = О, образуют множество меры нуль. — Прим.
перев.
Теперь мы вычислим М$. Для этого нам понадобится
следующая лемма.
Пусть функция f(t) непрерывна на отрезке a^t^,b,
непрерывно дифференцируема на интервале a<t<b и
имеет конечное число стационарных точек (т. е. таких
точек на (а, Ь), где производная f'(t) обращается в
нуль). Тогда число нулей функции /(/) на интервале
(а, Ь), которое мы обозначим через п(а, Ь\ f), опреде-
определяется формулой
оо Ъ
(I. 3.10) п(а, Ь\ р) = $ъух f dtf cos \%f{t)]\f'(t)\dt.
— оо а
При подсчете п(а, b; f) кратный нуль считается один
раз, а нуль, совпадающий с а или Ь, считается за «пол-
«полнуля» [т. е. дает вклад в п(а, b\ f), равный Х12].
Докажем лемму. Обозначим стационарные точки
функции f(t) через ai, 0&2, ..., &k\ # = ao
= b. Имеем
cos [6/ (t)]\f (t)\dt =
)
± / cos [?/(/)]/'(/) Л =
j = Q a.
;=0
Знак « + » выбирается для участков, где функция /(/)
возрастает, знак «—» — для участков убывания функции
f(t). Таким образом, получаем
оо Ъ
fdifcos[kf(t)]\f'(t)\dt =
= 0 I
;=0
Пусть теперь а = — 1, Ь = \ и
k = 0
Имеем
00 ОО ОО
Ж(л1) = B1г)-"/2 /... / ехр (— -g-llall2) B™)-1 / flf? X
— OO —CO
1
X JcosW(t)}\f (t)\dtda0... dan_x.
-1
Нетрудно показать, что порядок интегрирования
можно изменить1); это дает:
+ 1 ОО
(I. 3.11) М{}] = BъГ1 f dt f dtRn?, t),
-1 -oo
где
ОО ОО
A.3.12)
— ОО —ОО
X cos Wt)]\f (t)\da0 ...dan_v
Чтобы завершить вычисления, мы воспользуемся фор-
формулой
ОО
\y\=TZ~1 Г A C0S7]yO]~2rf7]
и получим
A.3.13) /?
ОО ОО
я /... /ехр(-1||а||2)х
_оо —оо
X {cos [?/ (/)] - cos \%f (t)\ cos {-nf (/)]} do,, ... </ая_,.
!) Доказательство хотя и простое, но не вполне тривиальное.
Мы его опускаем, поскольку для наших целей оно имеет лишь вто-
второстепенное значение,
Заметим теперь, что
cos [if (t)\ cos \r\f (/)] = 1 Re {exp / [;/ (t) + nf' (t)]
+ exp /
и, следовательно,
oo oo
Bл)-"/2 J ...
— 00 —
.. • rfa;!_1--iReBn)-"/2 f ... f exp(- i||a[|2) X
00 00
— 00 —00
X
exp
n-\
0
\da0 .
n-\
-f-exp
Полагая 11 = 0, получаем
Bл)-"'2/...
oo 00
—00 —00
л-1
= exp
Возвращаясь к формуле A.3.13), после нескольких про-
простых преобразований находим
оо Г п — \
A.3.14) #„(!,/) = я-1 JV*
ехр
— ехр
u,
где интеграл понимается в смысле главного значения.
Введем обозначения
А»(') = 2<
О
cn@ = "s>
1
п-1
2k-l.
подставляя выражение A.3.14) в A.3.11), мы придем
после элементарных интегрирований к формуле
п \)
или окончательно
A.3.15, Д-МС-<,
Из этого выражения нетрудно вывести асимптотиче-
асимптотическую формулу
A.3.16) yW/z~2jx-4ogfl, я->оо.
Читателю может быть интересно, насколько резуль-
результат A.3.16) зависит от выбранного нами определения
среднего A.3.5) или A.3.3).
Если Мп определяется формулой
1 1
Мп = 2-п f ... jN(a)dao...dan.1
-1 -1
(в обычной для теории вероятностей терминологии это
соответствует предположению, что коэффициенты много-
многочлена независимы и распределены равномерно на от-
резке [—1, 1]), то снова выполняется асимптотика
A.3.16), однако ее доказательство значительно услож-
усложняется.
Как недавно показали Эрдёш и Оффорд, асимпто-
асимптотика A.3.16) остается в силе, даже если положить
т. е. считать, что коэффициенты принимают лишь два
значения +1 и —1 и что всем последовательностям
±1, ±1, ..., ±1 приписаны равные веса B~п).
Нас радует, что асимптотика A.3.16) так нечувстви-
нечувствительна к изменениям исходных предпосылок; в этом в
известной мере выражается тенденция вещественных
полиномов к относительному уменьшению числа веще-
вещественных корней с возрастанием степени.
Предыдущий пример очень поучителен: он показы-
показывает, какие замечательные возможности таятся в стати-
статистическом подходе к задачам, которые при индивидуаль-
индивидуальном подходе неразрешимы. Определить число вещест-
вещественных корней отдельно взятого вещественного много-
многочлена степени 106 — почти безнадежная задача. Тем не
менее можно высказать содержательные утверждения
относительно совокупности всех вещественных полино-
полиномов степени 106.
Мы видим здесь в миниатюре одну из наиболее пло-
плодотворных научных идей — идею, которая пронизывает
всю современную науку и которая привела к наиболее
поразительным достижениям в статистической механике.
Вернемся снова к нашей первоначальной формули-
формулировке [вектор а=(а0, аи ..., tfn-i) равномерно распре-
распределен на поверхности единичной сферы 5ПA)]; тем же
способом, что и выше, можно показать, что среднее чис-
число вещественных корней, лежащих в промежутке (а, C),
которое мы обозначим (Nn(a, p)), равно
{Nn(a, р)> = я-
где
hn (t) = titn~\\ — t2) A — t2ny\
Отсюда видно, что функцию
можно считать «средней плотностью» вещественных кор-
корней.
График Pn(t) (рис. 1) наглядно показывает, что ве-
вещественные корни с ростом степени резко сгущаются
вблизи +1 и —1. Можно хорошо ощутить, насколько
сильно такое сгущение, если заметить, что
в то время как общая площадь, ограниченная кривой
Рп(/), асимптотически равна 2n~x\ogn.
Это наблюдение полностью согласуется с нашей ин-
интуицией, поскольку в исходных наших определениях
подразумевается, что в среднем все коэффициенты
ah — это величины, грубо говоря, одного и того же по-
порядка и, следовательно, корни многочлена
О0+М+ ... -\-an_xtn~x
должны быть близки к +1 или —1; в противном случае
было бы трудно добиться уничтожения всех членов.
Мы видим здесь убедительное подтверждение давних
слов Лапласа: «Вероятность — это здравый смысл плюс
точность».
4. Пример 3. Пусть со(п) означает число простых
делителей натурального п с учетом их кратностей [т. е.
соB0) =соB2-5) = 2 + 1=3] и v(n) — число простых дели-
делителей без учета кратностей [т. е. vB0) =vB2- 5) =2]. Ка-
Какова «вероятность» р& того, что со (п)—v(n)=k?
Выборочным пространством 5 здесь служит множе-
множество натуральных чисел 1, 2, 3, . . . , а мерой (или вероят-
вероятностью) множества В — его обычная плотность. Плот-
Плотность определяется следующим образом: обозначим
через DN(B) число элементов множества В среди пер-
первых /V целых чисел; плотность D(B) ( = \х(В)) задается
тогда формулой
ц (Я) = ?>(?)= lim DN(B)/N,
разумеется, в предположении, что этот предел суще-
существует.
Плотность не является вполне аддитивной мерой;
это означает, что если В представляется в виде суммы
счетного числа попарно непересекающихся множеств:
оо
В= [JB, (Bit\BJ=09 1Ф]\
то плотность множества В может оказаться и не равной
сумме плотностей множеств В{. [Например, все про-
пространство 5, имеющее плотность 1, является счетным
объединением множеств Ви каждое из которых состоит
из одного целого числа 1(В{ = {1}); ясно, что плотность
любого Вг равна нулю.] Это обстоятельство усложняет
некоторые рассмотрения и требует известной осторожно-
осторожности при применении теоретико-вероятностных методов к
задачам теории чисел.
Пусть pi, р2,... — простые числа (pi = 2, p2 = 3 и т.д.).
Напишем разложение
оно определяет функции ai(n), a2(n)
Рассмотрим теперь множество целых чисел, для ко-
которых одновременно ai(n)=ku a2(ft)=&2, ..., ar(n)=kr.
Все такие числа представимы в виде
где т не делится ни на одно из простых чисел
Ри Рг, ..., Рг.
Для того чтобы узнать, сколько целых чисел, мень-
меньших N, представимо в виде A.4.1), достаточно найти,
сколько целых чисел, меньших чем
N
Pi • • • Pr
не делится ни на одно из pi, ..., рг. Но число целых чи-
чисел, меньших М и не делящихся ни на одно из простых
pi, рг, ..., Рг, асимптотически (при М->оо) равно
М
(это просто доказывается с помощью классического ре-
решета Эратосфена) *). Отсюда вытекает, что
(I. 4.2) D{*l{ri) = kl, ,
Формулу A.4.2), чтобы лучше раскрыть ее смысл, мы
перепишем в виде двух формул:
A.4.3)
PJ
(I. 4.4) D {аг (п) = kl9...9ar (п) = kr) = П D |ау (п) = kf].
; = 1
Представление A.4.4) плотности в виде произведе-
произведения особенно примечательно: оно выражает то обстоя-
обстоятельство, что функции cci(ft), сс2(я), ..., аг(п) статисты-
1) Для читателя, не знакомого с теорией чисел, мы приводим
набросок доказательства. Пусть для простоты у нас три простых
г м - \ Ml Г Ml Г Ml
числа pi, рг, Рз. Среди первых М чисел найдется — , — I , —
1 Р\ I I Р2 i \ Ръ л
чисел, делящихся соответственно на р\, р2 и р3 (Ы — наибольшее
v ^ Г М 1 Г М 1
целое, не превосходящее а). Существует также , ,
L Р\Р2 л L Р\Рз J
Г М 1
чисел, делящихся соответственно на р\р2, pips, P3P2, и,
Г М 1 т
наконец, чисел, делящихся на Р\р2ръ- Таким образом, чис-
L Р\Р2Ръ J
чески независимы; именно в этом заключена возмож-
возможность применения обычных методов теории вероятно-
вероятностей к задачам теории чисел, которые на первый взгляд
никак не связаны со случаем, независимостью и другими
вероятностными понятиями.
Чтобы перейти к нашей задаче, мы введем функции
Ра (я) при помощи формулы
(п) — 1, если аЛ(л)>1,
и заметим, что
A.4.5) »(л)-*(я)
k
Читатель может легко проверить, пользуясь форму-
формулой A.4.4), что функции рл(А1) также независимы, т. е.
A.4.6) О{р1(Л) = А1э...эрг(л) = *Л=Д Я{Ру(л)=*уЬ
Заметим еще, что
2%
BТГ) J ехр (— Щ ехр [й (о> (/г) — v (/г))] d\ =
о
1, если со (/г) — v (#) = ?,
О, если со (/г) — v (/г) Ф k.
ло тех чисел, которые не делятся ни на одно из Рг (/=1, 2, 3), рав-
равно, как нетрудно сообразить,
Р\\ L /?2 J L Ръ J L /?l/?2 J L Р\Ръ
] Г М I
1
J *
L РхРгРъ J *
при М->со имеем —т- h^ —r- (h фиксировано), и, следовательно,
указанное число равно
м\\— --
Р\ Р2 Рг Р\Р2 Р\Ръ Р2Р3 Р1Р2Р3
-— Прим. перев.
Обозначая через Rk(N) число целых чисел, не превос-
превосходящих N, для которых со(п) —v(n)=k, мы видим, что
N
ехр[#(<о(л)
Если мы сможем доказать, что
N
A.4.7) lim ЛГ1 2ехр[«(со(л) — v(/*))]
ЛГ -> со /2=1
существует для каждого вещественного g, то, обозначив
этот предел через F(?), мы получим (используя теорему
Лебега о сходимости ограниченной последовательности
функций)
A.4.8) 9k= lim Rk(N)N~l = Biz)~l Г exp(—
N + oo J
Независимость функций §и{п) [выражаемая форму-
формулой A.4.6)] позволяет ожидать, что
со
lim AT1 2 exp [«(о> (л) —v (/*))] =
N->oo n-l
N
= lim N-1 ЦехрГ/б2рл(лI =
П
и поскольку, как легко проверить,
lim N-'Y ехр[«рА(л)] =
мы могли бы также ожидать, что
Будь плотность вполне аддитивной, равенство
Л'
A.4.10) lim ЛГ1 ^exp №%$fc(n)] =
N-+co /2 = 1 k
-ft Hmyv-'iexpf
k = \ N->oo « = 1
тривиально следовало бы из независимости функций
М/г) [формула A.4.6).]. Но это не так — плотность не
обладает полной аддитивностью, поэтому равенство
A.4.10) следует проверить. К счастью, оно проверяется
совсем легко.
Положим
Lrin)= 2 рЛ(/г)
и заметим, что
п=\ k > г п-\
Вспоминая, что
для тех я, которые делятся на ри и не делятся на pi*1,
мы видим, что
N оо
([х] означает, как обычно, наибольшее целое число, не
превосходящее х), следовательно,
Д рЛ (л) < 2Л^ 1 (/ - 1)/^ = 2Nj(pk - 1J.
Отсюда
/г - 1 ^ > г
И Sf—>0 При Г ~> ОО.
Теперь мы можем написать
A.4.11)
ЛГ N
/z = 1 \ к ) /г=1 \ k ^.г
N N
п=\
и из независимости р& [см. A.4.6)] вытекает, что для
каждого фиксированного г
N _
lim Л^ V ехрЛ'^ ^
k = \ /2=1
Г
Из оценки A.4.11) и из того, что 6г-^0 при г-^оо, сле-
следует, в силу сходимости бесконечного произведения
k=i
равенство A.4.10).
Таким образом, мы обосновали A.4.10), а также
формулу [см. A.4.8)]
A.4.12)
П
0 v=l
Можно переписать A.4.12) в эквивалентной форме
A.4.13) 2jPkzk =
Полагая z = 0, получаем
Последнее равенство хорошо известно и в нашем случае
означает, что плотность чисел, «свободных от квадра-
квадратов» (не делящихся ни на какой квадрат), равна 6/я2.
Полагая 2=1, получаем
2 Р*=
k0
что просто означает полную аддитивность плотности для
множеств
Соображения, основанные на теории вероятностей,
следует применять в подобных задачах с крайней осто-
осторожностью. Следующий пример (воспроизводимый здесь
в назидание физикам, которые известны своим оптимиз-
оптимизмом при использовании эвристических соображений) ил-
иллюстрирует возможную опасность.
Вероятность того, что некоторое целое число не де-
делится ни на одно из простых чисел ри ..., Рл, равна,
как легко показать,
Другими словами, число целых чисел, не превосходя-
превосходящих JV и не делящихся ни на одно из простых чисел
ри • • •, pkt равно приблизительно
A.4.14)
Рассмотрим теперь число целых чисел, не превосхо-
превосходящих N и_не делящихся ни на одно из простых чисел,
меньших YN. Такими числами_могут быть только про-
простые числа, лежащие между YN и N, и их число равно
—k(Yn) [мы пользуемся стандартным обозначе-
нием п(х) для числа простых чисел, не превосходя-
превосходящих х].
Из A.4.14) мы немедленно заключаем, что
A.4.15) *(AO-
Но известно (теорема о числе простых чисел), что
<K(N)~N/\ogN
П _ I1 ~ 7j) ~ ехр (~ т)/l0g V^ = 2 ехр (- T)/log Л/
Pj <Vn
(у — константа Эйлера). Следовательно, из A.4.15)
можно было бы заключить, что
2ехр(-т)=1,
а это заведомо неверно.
Чтобы читатель не чувствовал себя оскорбленным
тем, что его хотят так грубо провести, мы отсылаем его
к ряду писем, появившихся в журнале Nature, 148
A941), 436, 694—695, где несколько авторов были за-
заняты бурным, но бесплодным обсуждением именно этой
проблемы.
5. Пример 4. В нашем последнем примере мы хотим
кратко обсудить теорию игры «герб или решетка».
Выборочное пространство S в этом случае состоит
из всех бесконечных последовательностей вида
A. 0.1) /Ц, /Ц» -^з» • • •»
где каждое Aj может быть одним из двух символов:
Г (герб) или Р (решетка).
Элементарными множествами служат множества по-
последовательностей, в которых k элементов фиксированы
(&=1, 2, 3, ...). Например, элементарное множество со-
составляют последовательности, в которых первые три эле-
элемента— это Г, Р, Г (& = 3), а также последовательности,
в которых 25-м, 27-м и 35-м элементами являются соот-
соответственно Р, Р, Г (снова А = 3),
В классической теории орлянки («правильная» мо-
монета и бросания независимы) мера, приписываемая эле-
элементарному множеству, равна
где k — число фиксированных элементов.
Рассмотрим все BП) последовательности длины п:
Пусть Nn(a) —число тех из них, в которых количе-
количество гербов (Г) отличается от у ft по абсолютной вели-
величине менее чем на а У п. Мера множества таких после-
последовательностей равна
Если обозначить через Нп число гербов (символов Г) в
последовательности Ль Л2, ... , Ап, то можно написать
A.5.2)
Замечая теперь, что Nn(a) легко выражается через би-
биномиальные коэффициенты, мы приходим к формуле
С*.
\*-±«\<aVTT
В качестве упражнения (впрочем, не такого уж лег-
легкого) предлагается доказать, используя формулу Стир-
линга, что
(I. 5.3)
2а
lim <Гп 2 С» = Bll)"I/2 / ехР (— \ x<1) dx-
2 П <"
Сравнивая A.5.2) и A.5.3), мы получаем
A. 5.4)
Нш Р 11Н. — 4- я I < а Уп \ = Bтс)-'/2 Г ехр (— | х2) dx.
—2а
Обе формулы A.5.3) и A.5.4) полностью эквивалент-
эквивалентны, но формула A.5.4) подсказывает возможность эмпи-
эмпирической проверки.
Предположим, что мы подбрасываем нашу монету
тп раз и располагаем результаты наблюдений в т групп
по п наблюдений в каждой. Затем мы подсчитываем в
каждой группе количество гербов Я/г1}, Hf\ ..., Н(пт\
определяем число 1а(т) тех групп, для которых
и сравниваем полученную частоту
с интегралом
Bjt)-1/2 J exp (- i *2) dx.
-2a
Если наша теория применима к описанному опыту,
мы должны ожидать хорошего совпадения двух этих чи-
чисел. Случайно, конечно, расхождение между ними мо-
может оказаться и большим, но это можно приписать
«злой судьбе». Если же большие расхождения возни-
возникают чаще, чем предсказывает теория, то это все еще
может быть и от «злой судьбы», однако при этом воз-
возникают вполне оправданные подозрения, заставляющие
нас пересмотреть исходные предпосылки. Мы можем
обнаружить, что наша монета неправильная или что спо-
способ ее бросаний вызывает сомнения в их независимости.
Читатель, несомненно, заметил, что в формулировке
теоремы A.5.4) мы не использовали нашего выбороч-
выборочного пространства S всех бесконечных последовательно-
последовательностей Аи А2, Л3, ... . На самом деле нам нужно было
только пространство всех конечных последовательностей
Аи ..., Ап. Переход к пределу при п-+оо здесь срав-
сравнительно безобиден: он требует рассмотрения не «бес-
«бесконечномерного» пространства S всех последовательно-
последовательностей, а лишь последовательности «конечномерных» про-
пространств, в каждом из которых теория меры совершенно
тривиальна.
Зачем в таком случае вообще говорить об S? Для
этого имеются вполне убедительные доводы. Мы мо-
можем, например, поставить вопрос, какова вероятность
l/i-юо п
или, другими словами, какова мера множества тех бес-
бесконечных последовательностей, для которых предел
Нп/п существует и равен р.
Чтобы ответить на этот вопрос, мы должны по-
построить меру на множестве S, согласованную с мерами,
заданными на элементарных множествах.
Это можно сделать следующим образом. Если вме-
вместо Г всюду писать 1, а вместо Р ставить 0, то каждая
бесконечная последовательность Аи Л2, ... запишется в
виде последовательности ei, e2, ... из нулей и единиц.
Сопоставим теперь каждой такой последовательности ве-
вещественное число
Тем самым выборочное пространство отобразится на
интервал 0</< 1.
Это отображение не является взаимно однозначным;
так, например, последовательности 1, 0, 0, ... и 0, 1, 1, ...
перейдут в одно и то же число, а именно 1/2. Тем не ме-
менее множество всех таких чисел (соответствующих двум
разным последовательностям) счетно (оно состоит из
двоичного-рациональных чисел, т. е. чисел вида r/2s, где г
и s — целые положительные), и мы можем вообще не
принимать его во внимание. Элементарные множества
отображаются при этом в объединения конечного числа
попарно непересекающихся интервалов с двоично-рацио-
двоично-рациональными концами, и, кроме того, мера каждого эле-
элементарного множества совпадает с суммой длин интер-
интервалов, в которые оно отобразилось.
Таким образом, чтобы построить нужную нам меру
в S, достаточно построить меру на интервале @,1), со-
согласованную с определенной выше мерой элементарных
множеств. Ясно, что такой мерой является обычная мера
Лебега на этом интервале. Теперь мы в состоянии пере-
перевести поставленный вопрос на более привычный язык.
Напишем
и рассмотрим множество тех t [в интервале @,1)], для
которых
Теперь наша задача — найти меру Лебега этого мно-
множества.
Для этого заметим, что функции ei(/), 82@» ••• не'
зависимы, т. е.
v- К @ = ^i» е*2 @ = ^2» • • •» е*г @ = 4} = 2~г =
где ц — обычная мера Лебега и каждое r\j принимает
значение либо нуль, либо единица.
Введем вспомогательные функции гг-(/)
и заметим, что они также независимы; следовательно,
1 , 1
Теперь легко
м
° L
поэтому
видеть, что
п -j4
оо 1
л=1 0
г П
1
т4
<оо.
В силу известной теоремы1) из теории меры Лебега
ряд
оо Г п 14
сходится почти всюду, т. е. всюду, кроме множества
меры нуль. Отсюда a fortiori
i= 0
всюду, кроме множества меры нуль, или, другими сло-
словами,
Мы встретились здесь с простейшим случаем «уси-
«усиленного закона больших чисел».
Выражаясь несколько вольно, мы можем сказать, что
«усиленные законы» относятся к мерам в «бесконечно-
«бесконечномерных» пространствах, в то время как «слабые за-
законы» [например, A.5.4)] формулируются в терминах
«конечномерных» пространств возрастающей , размерно-
размерности. По моему мнению, большинство «усиленных зако-
законов» имеют лишь математический интерес. Как только
мы переходим к применениям теории вероятностей (осо-
(особенно в физике), наиболее интересными и важными
оказываются «слабые законы». В связи с этим в даль-
дальнейшем мы не будем заниматься «усиленными зако-
законами».
1) Здесь имеется в виду следующая теорема, если fn(t)^O и
оо 1 оо
ряд У | /«(*) dt сх°Дится, то функциональный ряд V fn (t)
л=1 0 л=1
сходится почти всюду, т. е. за исключением множества меры нуль.
Читателю должно уже стать ясно, в чем состоит тео-
теоретико-вероятностный способ рассуждений: частные яв-
явления включаются в совокупность подобных им явле-
явлений, и утверждения об этих индивидуальных явлениях
заменяются утверждениями о всей совокупности.
Я не могу не привести еще один пример, простой и
поучительный. Это задача, восходящая, я полагаю, к
Фреше, о нахождении максимума определителя
K=\\4j\U *> У = 1. 2, ..., /г,
где все е^ равны ±1.
Обычная оценка Адамара дает
тах|Д„|</г1/2/\
и задача (до сих пор не решенная!) состоит в том, что-
чтобы определить, когда в действительности достигается
эта верхняя граница.
Статистический метод немедленно приводит к неко-
некоторому результату.
Определим г(х), 0^.х^. 1, так:
+1,
1,
Имеем [полагая e,j =
max|AJ> J...
L
и простое вычисление дает
Отсюда
о о
На самом деле можно продвинуться дальше, используя
неравенство
тах|Дя|>
L0
и получить более точную оценку снизу.
Если перейти от 4 к 6, 8 и т. д., то, возможно, в прин-
принципе и удастся найти тах|Дп| точно, однако вычисления
становятся (безнадежно?) трудными. Тем не менее пре-
преимущества, возникающие от рассмотрения всей сово-
совокупности определителей, очевидны.
ГЛАВА II
НЕКОТОРЫЕ АНАЛИТИЧЕСКИЕ СРЕДСТВА
И ПРИЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1. В этой главе мы подробно разберем несколько за-
задач, с тем чтобы проиллюстрировать ряд аналитических
приемов, используемых в теории вероятностей. Мы нач-
начнем с задачи о случайном блуждании, представляющей
самостоятельный интерес.
Точка, выходя из начала координат, движется по
плоскости шагами длины единица. Направление ft-ro
шага выбирается случайно, причем так, что угол, кото-
который оно образует с направлением предыдущего шага,
распределен с плотностью вероятности р(а) (—я<^а<
<я). В качестве нулевого направления выбирается по-
положительная полуось х, а последовательные углы аь
a2, ... предполагаются выбранными независимо друг от
друга.
Мы хотим найти распределение вероятностей для по-
положения точки через п шагов и в особенности его асимп-
асимптотическое поведение при п -> оо.
Сначала переведем эту задачу на обычный язык ана-
анализа.
Рассмотрим фиксированный набор углов он, аг, .»., an.
С помощью этих углов координаты (хп, уп) блуждаю-
блуждающей точки после п шагов выразятся, очевидно, так:
Хп = COS 04 Н- COS @4 -f a2) + ...
... + cos @4-f ... -f ал),
(ПЛЛ) Уп = sin a1+sin(a1 + <*2)+ •••
... +Sin(a1+ ... -4-aJ.
Мы хотим найти совместную вероятность
Фактически мы определим предел при д-^оо вероят-
вероятности
P{xn<aVn, уп<Ь~\П1).
Выборочным пространством S здесь служит д-мер-
ный куб —я<^а;<я, /=1, 2, ... , п. Наше предположе-
предположение, что все углы щ независимы и каждый из них рас-
распределен с плотностью р(а), означает, что мера, припи-
приписываемая каждому элементарному множеству В, равна
(II. 1.2) J
В
(В качестве элементарных множеств могут быть вы-
выбраны, например, кубы с ребрами, параллельными коор-
координатным осям.)
При этом, очевидно, должны выполняться соотно-
соотношения
p(a)>0 И
Искомая вероятность, таким образом, равна
хп < a VTi, yn<bV~n
Чтобы несколько упростить задачу, отбросим уело-
вие уп < b У п (это означает, что мы полагаем 6 = оо)
и рассмотрим распределение
(II. 1.3) вп (а) =/.-./ Р (а,) • • • р К) da,... dan.
хп < а Уп
Заметим, что оп{а), как функция от а, обладает сле-
следующими свойствами:
1) вп(а)—неубывающая функция;
2) Оп(—оо)=0; а„( + оо)=1;
3) ап{а) непрерывна слева (в нашем случае просто
непрерывна) *).
1) Если бы углы аъ. были распределены не непрерывно с неко-
некоторой плотностью, как мы это предполагаем, а принимали бы, на-
например, лишь два значения +р и —р с вероятностью 72, то ап(а)
Функция о (а), удовлетворяющая условиям 1, 2, 3,
называется функцией распределения.
Вопросам сходимости функций распределения в ма-
математической литературе уделено большое внимание
(мотивированное главным образом нуждами теории ве-
вероятностей).
Следующий результат, принадлежащий Полю Леви,
считается ныне классическим. Пусть
оо
fn (?) = Г ехр (%а) don (а) (? — вещественное число);
— оо
предположим, что
Ит/Л E) = /(&).
п->оо
причем сходимость равномерна в каждом конечном ин-
интервале значений |. Тогда существует единственная
функция распределения о (а), такая, что
/($)= f ехр (Ка) da (а)
оп(а)->о(а)
в каждой точке а, где о (а) непрерывна.
В этой теореме требование равномерной сходимости
fn(l) на каждом конечном интервале значений g может
быть заменено более простым (но эквивалентным) тре-
требованием непрерывности f (?) при ? = 0.
Успехи, достигнутые с помощью этой теоремы в тео-
теории вероятностей (особенно в теории сумм независимых
случайных величин), затмили более раннюю теорему,
которая тем не менее очень полезна и которую часто
определялась бы как сумма и была бы разрывной функцией. Тем
ке менее непрерывность слева сохранялась бы, так как она непо-
непосредственно следует из полной аддитивности меры.
Дискретные и непрерывные распределения (а также смешанные
случаи) можно изучать одновременно, если пользоваться интегра-
интегралом Стильтьеса, но это унылое занятие, которое мы предпочитаем
обойти, отсылая интересующихся читателей к любому стандартному
изложению.
можно применять в тех случаях, когда предыдущая тео-
теорема ничего не дает. Мы говорим о следующей теореме.
Если
оо оо
(II. 1.4) lim fakdon(a)= (akdc(a) (k = 0, 1, 2,...)
— оо —оо
и, кроме тога,
со оо
(II. 1.5) 2(^)-1/fe = oo, где vk= f\a\kdc(a),
k = l -ОО
то снова
(II. 1.6) ап(а)->с(а)
в каждой точке непрерывности функции о (а).
Условие (П.1.5) введено по той причине, что если
оно не выполняется, то может существовать функция
распределения т(а), отличная от о (а) и такая, что
f akdz(a)= f akdo(a).
Отсюда, полагая ап(а)=т(а) для п=1, 2, ... , мы ви-
видим, что утверждение (П.1.6) становится неверным.
Условие (II.1.5) просто гарантирует единственность
функции распределения о(а) с заданными моментами
оо
fa" da (а).
— ОО
Наконец, имеется значительно более слабая теорема
такого же рода, которая тоже часто бывает полезна (мы
применим ее при решении нашей задачи о случайном
блуждании).
Если для всех вещественных х
оо оо
(II. 1.7) lim f exp(xa)dcn(a) = g(x) = Г exp(xa)da(a)
и если g(x)—целая функция [т. е. существует целая
функция g(z), совпадающая с g(x) на вещественной
оси], то
(II. 1.8) оп(а)->о(а)
в каждой точке непрерывности функции о (а).
Поскольку в такой форме эту теорему трудно найти
в литературе, мы дадим набросок ее доказательства.
Положим
оо
gn (*) = f exp (za) dan (a) (z = x + ty)
— oo
и заметим, что
oo oo
\gn{*)\ < /|ехр(гв)|Ля(в)= f exp(xa)don(a).
— OO — Oo
Далее легко видеть, что для каждого /?>0 функции
gn(z) аналитичны в круге |z|</?, если п достаточно
велико.
Поскольку lim gn (x) существует для каждого веще-
/1->оо
ственного я, мы видим, что в круге \z\<R функции gn(z)
равномерно ограничены и поэтому можно выбрать под-
подпоследовательность
равномерно сходящуюся внутри круга \z\<R к аналити-
аналитической функции. Эта аналитическая функция совпадает
с g(z) для —R<x<R и, следовательно, во всем круге
||^ Отсюда вытекает, что интеграл
оо
Г ехр (Ца) donk (а) (% — вещественное число)
равномерно сходится в каждом конечном интервале из-
изменения g к g(ii) и, значит,
Те же рассуждения показывают, что любая беско-
бесконечная подпоследовательность {тк} содержит подпосле-
подпоследовательность \ш\ такую, что
а это и означает, что
° п (<*)-+<*(<*)•
2. Вернемся теперь к нашей исходной задаче о слу-
случайном блуждании и рассмотрим интеграл
оо
Jexp(xfl)flfon(a),
— оо
гдесгп(#) определяется формулой (II.1.3).
Заметим, что
оо
(И. 2.1) gn(x)= fexp(xa)den(a) =
— ОО
к тс
= J ... Jexp(A:A:^-1/2)p(a1) ... p(ajrfa1 ... daiv
где хп определяется формулой (II.1.1).
Рассмотрим теперь вместо gn(x) несколько более об-
общее выражение
(И. 2.2) gm(x,y) =
к п
= f ... J ехр \{ххт 4- уут) п-Ц р (а,) ... р (ат) d^ ... dam
-ж -к
и заметим, что из определения кт и ут следует (если
положить x = rcos6, y = rsin6) соотношение
т
ххт + уут = г 2 COS (a, + ... + ak — 0).
* = i
Полагая
(П. 2.3) ga(x, y)*=hm(9)
(мы считаем здесь г фиксированным и обращаем вни-
внимание лишь на зависимость от 6), мы сразу получаем
(И. 2.4) Ат(в) =
= / Р (ai) ехр [гп~Ч* cos F — аг)] hm^x F — ах) dav
—%
где
АоF) = 1.
Рассматривая р(а) как периодическую функцию с пе-
периодом 2я, мы с помощью простой замены переменных
приходим к формуле
(И. 2.5) hm F) = / Р (9 — а) ехр (гл-V* cos a) AM_! (a) rfa.
Умножая обе части на ехр (у гп-Ч* cos 6J и пола-
полагая
(II. 2.6) ехр (-1 гя-У» cos б) Лт (в) =^т (9),
мы получаем
(И. 2.7) ряф) =
= Г ехр {~2гп~112 cos e) p@"^"a) ехр fy r/z-'^cosa^^.j (a)da
— тс
^0 F) = ехр A гл-Vi cos б)).
Если теперь предположить, что
р(а) = р(— а)
J р2 (a) da < со,
то можно решать нашу задачу с помощью теории воз-
возмущений. (Теперь становится ясно, почему мы решили
работать с интегралом
оо
J exp (ха) dan (a)
— оо
для вещественных х. Таким путем мы приходим к инте-
интегральному уравнению с вещественным симметрическим
ядром.)
Пусть Xi(n), ^(я), ... — собственные значения и
<р[п)(а), ФB/г)(а)> ...— соответствующие им нормиро-
нормированные собственные функции интегрального уравнения
(II. 2.8) J ехр (-g-гй-'А cos б) р F — а) X
— тс
X ехр ij гп-У* cos а) ф (а) da = lq> F).
Мы получаем
(II. 2.9) pm(Q) =
(«) / ехр (i гл-V. cos а) $р (а) da ep<«> (в)
; = 1 -ж
и, следовательно,
(II. 2.10) hn @) = ехр (— i- гл-'А cos б) X
оо тс
х 2 %nj (п) {ехР (y rn~x'2 cos а) ^(а) da^f (е)-
1
Теперь уже совершенно ясно, что произойдет дальше.
Напишем
оо
(II. 2.11) р(а) — Bл) + 2 a, cosуа.
Отсюда
(II. 2.12) р (в — а) ~ Bя)-'Л • Bя)-'/2 +-
оо
2 л^у (л/а cosy'6ji-1/2 cos уа + я-1/* sinyBjt-1/» sinya),
l
и, следовательно, собственные значения невозмущенного
ядра рF — а) равны
Каждое собственное значение nak — двукратное, и
соответствующие нормированные собственные функции
равны n-^coskQy л;-1/* sin ?6. Кроме того,
Собственные значения возмущенного ядра
exp (yr#-V2cos6jpF — а) ехр (угп~1^ cos а)
близки к соответствующим собственным значениям не-
невозмущенного ядра, и, так как в формуле (II.2.10) все
они возводятся в п-ую степень, мы видим, что суще-
существенно лишь собственное значение, близкое к 1. Таким
образом, при п ->- оо
(II. 2.13) Лл@)
X J exp (j rn-Чж cos a) ф("> (a) rfoq/») @).
— тс
Теперь с помощью обычных приемов теории возмуще-
возмущений вычислим Хх (п) и ф^^а). Напишем
AЬ Z-14) <fi» (a) = Bл)-1/, + п-Ч>% (a) + n'% (a) + ...
и подставим эти ряды в интегральное уравнение (П.2.8),
Сравнивая коэффициенты при я~1/а и Д в обеих ча-
частях уравнения, мы приходим к равенствам
тс
(II. 2.15) J p (8-a) [ih (а) + у г Bя)"'/г (cos 9 + cos a)] da =
(II. 2.16) /р(8 —a)[ifc,(a) + -^r*1(a
+ 1 BяГ1/2 (jrj (cos 0 + cos aJ] da =
Поскольку функция ц[п)(а) нормирована, для i|)i(a)
имеем также соотношение
(И. 2.17)
Интегрируя обе части равенства (П.2.15) по 6, мы
получаем
(И. 2.18) |11 = 0.
Отсюда следует также, что
(II. 2.19) % (а) = ^г Bя)~1/2A ~\- яа2)A —па^" cos а.
Интегрируя (Н.2.16) по 6 и принимая во внимание
(Н.2.18) и (И.2.19), мы получаем
|12 = |г2BяГ1 / /р(Э -^[(l+jtaOO-Jta^X
X cos a (cos а + cos 6) + у (cos а + cos 6J1 da dQ.
В силу ограничений, наложенных на р(а), все пре-
предыдущие вычисления, использующие теорию возмуще-
возмущений, могут быть строго обоснованы.
Итак, мы имеем наконец
lim Л/гF) =
где
Ф = Dл)-1 / J р @ - а) [A+ шх) A - па,)-1 X
— 7С — 7С
X cos а (cos а + cos 6) + у (cos а + cos 6J1 da dQ.
Полагая у = 0, получаем
оо
(II. 2.20) lim Г exp (xa) don (а) = ехр (^о2х2) =
Л-»оо J \* I
-оо
оо
= о-1 Bя)"ъ f ехр (ха) ехр (— -^ da.
— оо
Таким образом,
(И. 2.21) an(a) = P{xn<aVn}->
Теорему [см. (II.1.7) ц (II.1.8)], на основании кото-
которой сделан вывод (П.2.21), можно легко обобщить на
случай нескольких переменных и получить таким обра-
образом более содержательный результат:
а
f
— оо —оо
3. Предыдущий пример является упрощенным ва-
вариантом задачи, привлекшей к себе значительное вни-
внимание в связи с молекулярными цепями.
Задача состоит в следующем. В пространстве задана
цепь из п звеньев; каждое звено имеет длину 1 и обра-
образует фиксированный угол (называемый «валентным уг-
углом») с предыдущим звеном; в остальном цепь распо-
располагается произвольно. Требуется найти распределение
вероятностей для «размера» цепи («размером» назы-
называется расстояние между концами цепи).
Обозначим через rh вектор (длины 1), представляю-
представляющий k-e звено, и через U, \% — пару взаимно перпенди-
перпендикулярных единичных векторов, перпендикулярных к rk.
Мы можем написать
гЛ+1 = i,e sin a cos 9Л + h s'm a sin 9* + rk cos a>
где угол Qk выбран подходящим образом из интервала
@,2л).
Мы можем теперь определить 1Л+1 и jh+i при помощи
формул
U+i =sin еЛ — cose j^,
j^+1 = cos бд, cos a \k + sin 0^ cos a \k — sin a rk.
Заметим, что
h+i ' h+i — h+i* rk+i = j*+i * rA;+i =0'
Таким образом, цепь определяется углами
qv e2,..., e^.j @<е^<2я),
и тем самым мы можем считать (п— 1)-мерный куб
0<9?<2я, А = 1, 2, ..., /г —1,
выборочным пространством S,
В качестве меры в S мы можем выбрать обычную
меру Лебега, нормированную таким образом, что мера
всего куба равна 1.
[Пользуясь теоретико-вероятностной терминологией,
мы можем сказать, что все 6^ независимы и распреде-
распределены равномерно на интервале @, 2я).]
Выбирая произвольно гь мы получаем, что «размер»
цепи равен длине вектора
Ъя = гг + т2+ ... +гя.
Легко вычислить среднее значение величины ||Rn||2,
т. е.
2% 2к
Действительно, пусть Ak=A(Qh) — матрица
sin 6^ _cos6^ 0
cosacos6fe cos a sin бд, —sin a
nacos6fe sin a sin бд, cos a
Заметим, что элементы третьей строки матрицы
равны соответственно
R^-ij, Кя - ji и Rn-rv
Отсюда
(П. 3.1) I|RJ!2 = 633,
где Ь3з — элемент матрицы ВпВ'п (В' — транспонирован-
транспонированная матрица В). Далее
и, следовательно,
ВпВп = / + Вп-\А\ -f- A\Bn-\-\-Bn-\B,i-\
(поскольку Ai — ортогональная матрица, A[Ai = I).
Итак,
{ = 1 + Е {{B^Afa№
\ „
Из нашего предположения о том, что углы 6i, ... , 6n-i
независимы и равномерно распределены, следует, что
...+Е{А1\Е[А2}
где
,..E{An^}=M + M* +
0 0 О
О 0 —sin a
О 0 cos a
яП-\
1) Следует, конечно, иметь в виду, что ?n-i является функци-
функцией от 02, ..., Эп-1, в то время как Вп зависит от всех углов
ел г\ *
Ь U2, iг 4 . , t)n~l.
Аналогичный результат получается, конечно, и для
E{A'iB'n-i}. Окончательно мы приходим, используя
(Н.3.1), к рекуррентной формуле
12} = 1 +2cosa
откуда
Эта формула была впервые получена Айрингом. Можно
экспериментально (измеряя рассеяние света) опреде-
определить размер молекулярной цепи и убедиться в том,что
он пропорционален (? {||R||2})I/2. При этом оказывается,
что размер цепи пропорционален УЪ или корню квад-
квадратному из молекулярного веса. Этот простой закон
действительно выполняется при определенных условиях.
Предыдущее рассмотрение неудовлетворительно, по-
поскольку мы полностью пренебрегли весьма существен-
существенным эффектом «исключенного объема». Чтобы учесть
этот эффект, необходимо подчинить цепь дополнитель-
дополнительному ограничению
J
(И. 3.2)
2
/
выражающему то обстоятельство, что атомы, «сидящие»
на концах звеньев, не могут перекрываться.
Пытаясь вычислить fdlRJI2}, мы должны были бы
интегрировать теперь только по той части куба 0 < 9&<
<2я, в которой выполняется неравенство (Н.3.2). Это
крайне сложная и еще не решенная задача.
4. Возвратимся теперь к нашей упрощенной задаче
(в которой мы пренебрегаем эффектом «исключенного
объема»). Мы хотим найти распределение вероятностей
(в пределе при п~>оо) для какой-нибудь компоненты
вектора Кпп~1/2.
В действительности лучше попытаться сразу оты-
отыскать совместное распределение вероятностей для трех
взаимно ортогональных компонент вектора Rn^~1/2.
С этой целью мы рассмотрим
Е {ехр (хп-Щп • & + уп-Щп • Ъ + гп-Щп . с)},
где а, Ь, с — три взаимно ортогональных единичных век-
вектора, или в более общем виде
gm{xn-4*, у/г-1/*, zn-ll*) =
Если принять для простоты
a = i1? to = ji, с = Г!,
то можно заметить, что
хп-Щт • а + ул-Щт • b + гл-V-R^ • с
является третьей компонентой вектора
(
Обозначив через \ вектор с компонентами
уп-^у гп~Цу мы можем написать 1)
О О
2%
= ехр BЯ-'/*) (г^) / ^^ (А F) |) are =
О
= ехр (г/г-!/2) B'к)'1 Jg-^.j (хл-1/! sin в — уп-Ч* cos 9,
о
хп,-1!* cos a cos б -f- у/г-1/» cos а sin 9 — г/г~1/2 sin а,
х/г-1/2 sin а cos Э + Уп~1/2 sin а sin9 + zn~xl% cos а) dQ.
1) Индекс C) означает здесь, что мы берем третью компоненту
вектора.
Для упрощения вычислений рассмотрим частный слу-
случай а = -2" я. Пред
шется теперь так:
чай а = -2" я. Предыдущая рекуррентная формула запи-
запи= ехр (zti-Ц Bя)"! J gm_1 (хп-Ч* sin 9 — уп~^ cos 9,
о
— zn-42, хп-Ч> cos 9 + yn-xl* sin 9) dQ.
Положим
х = A — z2f2 cos р, у = A — z2)Vt sin p;
без ограничения общности мы можем также считать,
что x2 + y2 + z2=l. Отсюда получаем
gm (О — 22)lyV'/2 COS P, A — Z2L' Л/. Sin P, 2/*-V«) =
2тс
= ехр (гл-1/.) Bя)-1 J g^ (A-^2I/2 я-V, sin (9-р), — гп~Ъ,
о
A — z>f n-ll> cos (9 — р)) dQ =
= ехр (гл-1/.) BЯ) J gm_j ((I — z2f n~^ sin 9, — zn~\
о
A— 02)V2^-V2Cos9)rf9.
Из этой формулы видно, что gm не зависит от |3, и мы
можем, следовательно, положить |3 = 0. Это дает
&*((!— *2I/2 ^/2> 0' г"2) = ехр (гл-1/.) BЯ)'1 X
X /gm-i((l— s^/i-usine,— ^-!/«, (l-z^'n-1'*cos
о
Но
gm-l ( 0 — ^2)'/2 Я"'А Sin Э, — 2Я-У«, A — Z2)''2 П-1'* COS0) =
= gm-i(n-4'[\— A— г2)sin2в]'А, 0, (l-22)'/2«-'/2cose);
полагая
^((l-*2)**-1/., 0, zn-lb)=fm(z)9
получаем
fm(z) = exp(zn-1b) Bл)-1 J/in-i(O — ^2)V2cos
о
или, с помощью простых преобразований,
(II. 4.1) /т(г) =
Пусть ядро /((со, z) определено на квадрате —1-^ со,
z < 1 следующей формулой:
?)ГА« если «2 + ^2<Ь
0 в противном случае.
Тогда (И.4.1) можно переписать в виде
1
(И. 4.2) /„ (z) = ехр (zn-Ц f ЛС(о, г) /„,_, (со) dv>.
-1
К сожалению, ядро /((со, 2) сингулярно, и непосред-
непосредственное применение теории возмущений может вызвать
сомнения. Чтобы обойти эту трудность, заметим, что
итерированное ядро
1
КB) (z, <*>)=/ K(zy \х) K(\i, со) d\x
-1
ведет себя уже достаточно хорошо.
Действительно,
1
(И. 4.3) J J /СB) (z, со) ^ rfco < со.
Для того чтобы в этом убедиться, будем исходить из
легко проверяемого равенства *)
1
f Kl2) (Z, @) Р„ (©) flfco = i%Pk (Z),
-1
где Pk (z) — полиномы Лежандра и
2тс
о
Отсюда немедленно вытекает соотношение
со
(г, ю) ~ 2 Я.1 i- Bk +1) Pft @) Я, (о),
а следовательно, и неравенство (Н.4.3).
Переписав теперь рекуррентную формулу (Н.4.2)
в виде
1
мы сможем легко симметризовать наш оператор и снова
применить теорию возмущений (в точности так же, как
в двумерном случае). При этом мы должны будем раз-
различать случаи четного и нечетного п, но это уже совсем
незначительная трудность.
Как и раньше, мы получим
/ Это равенство легче всего проверить, если переписать его в
эквивалентной форме
2к
Bп)~1 j Pk ((I — г2L* sin 0) db = i%Pk (г).
где а=1 для а = я/2. При а Ф я/2 вычисления стано-
становятся более сложными, хотя метод по существу не ме-
меняется.
5. В качестве другой иллюстрации технических прие-
приемов, часто используемых в теории вероятностей, рас-
рассмотрим следующую задачу.
Точка, выходя из начала координат, двигается по
прямой таким образом, что за каждую единицу времени
она смещается на +1 или —1. Предполагая, что оба
смещения равновероятны и что смещения в разные мо-
моменты времени независимы, определим асимптотические
свойства распределения вероятностей числа Nn возвра-
возвращений точки в начало координат за первые п шагов.
Выборочное пространство S состоит из 2П «точек»:
каждая «точка» — это последовательность (Хи ... , Хп)
из +1 и —1. Мера любой такой «точки» равна 2~п;
это просто перефразировка нашего предположения не-
независимости шагов и равновероятности смещений ( + 1
и -1).
Пусть теперь
1, /ю = 0,
Заметим, что
= V(Si)+V(s2)^ ... +V(sn),
где
sk = Xx-\-X2-\- ... -\-Хк.
Вычислим теперь моменты
?{Л^}, ? = 1, 2, ....
При этом надо иметь в виду, что Е {Nn} — просто сумма
Покажем, как проводятся эти вычисления, взяв k = 2.
Имеем
= E{Na} + 2
Далее,
Положим
и рассмотрим
JL 1-У
l<i < j <n j
Заметим теперь, что
,2
1
и, следовательно,
л = 1 1 \ 1
Здесь мы воспользовались очевидным тождеством
оо со "I
Л=1 1 J
В нашем случае
О, если i нечетно,
С™т • 2~2"\ если / = 2т,
или
Pi = B)"!
Отсюда
и, следовательно,
%E{Nl}zn~2(\—zy1(\-z2ry2 при г->1.
1
Простое обобщение предыдущих вычислений дает
или
где мы положили N0 = 0.
Поскольку Nn^>Nn-i, мы имеем Е {Л/*} ^>Е {A/^-i}.
и отсюда с помощью тауберовой теоремы Карамата по-
получаем
или
{*} ^D ) * = 0, 1, 2,
при п->оо.
Теперь легко проверить, что
2Bя)-% /в*ехр (-i-«a) rf« = к!
0
и, следовательно, полагая
получаем
оо
lim (akdan(a)= lim Е{(Ыап-Цк) =
rt->00 J rt->OO
00
= 2 BлГ1/2 J ak ехр (— 1 д2] da.
о
Применяя теорему о моментах, упомянутую в п. 1
этой главы, мы находим
lim оп (а) = lim Р [п~1Шп < а} =
Л->00 /*->ОО
а
= 2 Bя)~1/2 J ехр (— 1 й2) rf«.
о
Читатель может заметить, что предыдущий вывод
легко непосредственно обобщить на случай, когда шаги
Хи Х2у ... по-прежнему независимы, но могут принимать
любые целые значения.
Действительно, пусть
где <?ft>0 и 2^=1; допустим еще ради простоты,
— оо
ЧТО Ck = C-k.
Выборочное пространство состоит теперь из множе*
ства последовательностей
где каждое Xj может принимать любое целое значе-
значение /г. Мера «точки» (Хи ... , Хп) равна
\x{(Xv ..., Xn)}=cXlCx2 •.. схп
(стоящее справа произведение напоминает нам, что
шаги предполагаются независимыми!).
Отличие от предыдущего случая состоит только
в том, что pi задается формулой
2тс
где
Отсюда мы можем получить
Sz*E{(Nan-lt*)k}~k\\ Bл)-1 Г[1 —2:/(еI~1лГе ) ;
V о /
при / @) = cos 0 = -тг ехр (/8) + ~2 ехР (— №) это приво-
дит к предыдущему случаю.
Если
то /''(в) существует (///(8) = —а2) и легко видеть,
что
2тс тс
^t/ [l — ^(l — ±
конечно, в предположении, что f@) не обращается в 1
в полуинтервале 0<6<я. Отсюда, как и выше, мы по-
получаем
(И. 5.1)
a
lim P [Nnn-lb < aa} = 2 Bя)/г J exp (— 1 й2) da.
Ясно, что в нашем первом примере а—1. Если /@)
обращается в 1 где-нибудь в полуинтервале О<0<я,
то те ky для которых ck ф 0, имеют общий делитель. Если
обозначить их наибольший общий делитель через А, то
видно, что а следует заменить на o/h.
6. Читатель, несомненно, уже заметил, что вероят-
вероятностный язык — это всего лишь удобный способ выра-
выражения некоторых математических фактов, касающихся
довольно сложных сумм и интегралов.
Если не пользоваться теоретико-вероятностной тер-
терминологией, то результат (П. 5.1) звучит так: предел
суммы
взятой по тем наборам из п целых чисел (Хи ... , Хп)9
для которых число нулей в последовательности
(Хи Xi+X2, ... , Xi+X2+ ... +Хп) не превосходит
ao~lnxl\ равен
а
2Bя)-1/2|ехр(— \u^du.
о
Это тяжеловесное утверждение, по-видимому, само по
себе лишено всякого интереса.
Становится ли оно более интересным, будучи запи-»
сано в виде (П. 5.1)? Или оно становится только менее
громоздким?
Здесь мы касаемся спорных вопросов, затрагиваю-
затрагивающих отношение математики к нематематическим дисцип-
дисциплинам.
Позвольте мне привести пример из области, связан-
связанной с математикой, но отличной от нее. Я имею в виду
следующее утверждение: при подходящих ограничениях
(гарантирующих существование всех нужных интегра-
интегралов) для четной функции f(x) и для ее преобразова-
преобразования Фурье
оо
Ф (;?):= Bл)" f exp{ipx)f(x)dx
— оо
имеет место неравенство
Это довольно забавное неравенство выводится крайне
просто при помощи равенства Парсеваля и удачного
применения неравенства Шварца.
Тем не менее оно служит математическим выраже-
выражением принципа неопределенности в квантовой механике,
принципа, который, безусловно, лежит в самой основе
наших представлений о физических явлениях.
Нельзя отрицать, что наше восприятие научных вы-
выводов зависит во многом от контекста, в котором мы
их встречаем. Один и тот же факт в одном контексте
выглядит только как некое верное утверждение, и его
присутствие там лишь в слабой степени оправдывается
его истинностью; в другом контексте этот факт, выра-
выраженный подходящим языком, может быть весьма поучи-
поучительным и заманчивым.
Поскольку теория вероятностей обязана своим воз-
возникновением и развитием прежде всего нематематиче-
нематематическим вопросам (например, играм, кинетической теории
вещества и др.), то и на природу ее задач оказали не-
непреодолимое влияние нематематические рассмотрения.
Мы возвратимся к этому вопросу в следующей главе,
где мы проследим роль теории вероятностей в класси-
классической статистической механике.
В заключение этой главы мы обсудим две совер-
совершенно не связанные друг с другом задачи: обе они ил-
иллюстрируют преимущества теоретико-вероятностного
языка.
7. Первая задача связана со случайным блужда-
блужданием, рассмотренным в конце п. 5.
Шаги Хи Х2, .,. , Хп считаются независимыми, и, как
и прежде,
Мы предположим еще, что
с0Ф0
оо
2 kck < оо.
1
Условие со Ф 0 несущественно, но оно избавит нас впо-
впоследствии от лишних оговорок.
Рассмотрим теперь не все выборочное пространство
S (т. е. множество всех наборов из п целых чисел
(Хи X2i ..., Хп))9 а подпространство S*, определенное
условием
Введем меру в S* следующим образом: мера точки
(/i, ... , 1п) из S* равна 1)
(И. 7.1)
/ \ Р {Xj = /ь , Хп = 1п, Х\-\- ,.. -\-Хп = 0}
...,in)— P {X{+ .. ~
• • cin-ich+ - +/л-1 _ chch • • •
P{5n = 0} есть мера (см. начало п. 5) множества, опре-
определенного условием 5п = 0.
Вспомнив, что
мы можем написать
2%
Р [Sn = 0) = BЯ) / Г (в) dQ > с% Ф 0.
о
Эта новая мера в S* известна под названием «услов-
«условная вероятность».
Рассмотрим теперь максимум
max@, sv ..., 5Л_1, sn),
взятый по элементам множества S* [т. е. равный
max@, Su ••• » 5n-i)], и среднее значение этого макси-
максимума на S* [разумеется, по мере (II.7.1)]. Это среднее
(«условное математическое ожидание») мы обозначим
1) Очевидно, что
через
Е {max @, sv ..., 5л)|5я = О};
оно равно сумме
2 max@, lv ..., /2 —(— /2 —|— .
Очень существенно, что \х — симметрическая функция
от /ь /2, ... , /п.
Пусть
1 2 ... л
'1 U2
— некоторая перестановка. Заметим, что
2 max (О,/1Э ...,/!+••• +/rt)n('i>
= 2 тах@,
г + ... +i =о
и, следовательно,
V max@, /j, ...,
/1+...+/я-о
4 S
il+...+tn=o\<,
где внутренняя сумма берется по всем перестановкам а.
Мы докажем теперь следующую лемму, впервые
сформулированную и доказанную Хантом.
Пусть аи . .., ап — вещественные числа и о—некото-
о—некоторая перестановка
1 2 ... п
Пусть далее N(g) —число положительных членов в по-
последовательности
Тогда
max @, аа^ по^ -\~пз , ..., аа + ... -\-аа \ = ^аа N (о).
s
Мы приведем крайне простое доказательство, при-
принадлежащее Дайсону.
Пусть
6 <*>=<>, *<0;
заметим, что
(И. 7.2) max @, av a.
— max (О, #V яц-Ь
-f- max @, аа, а
— max (О, <2V a
Обозначим через
О К, ..., со*)
множество тех перестановок, у которых первые k индек-
индексов (взятые в некотором порядке) равны coi, ... , со^.
Таким образом, множество всех перестановок п элемен-
элементов разбивается на Сп попарно непересекающихся мно-
множеств G(cob ... , cofe). Суммируя обе части равенства
(П. 7.2) сначала по всем перестановкам множества
G(coi, ... , cofe), а затем по всем множествам G, мы по-
получим
(II. 7.3)
— тах@, av ... , а^Ч-
,,
Суммируя равенство (П. 7.3) по k от 1 до п, мы прихо-
приходим, очевидно, к утверждению леммы.
Используя эту лемму и равенство (П.7.1), мы полу-
получаем
max@, 1и ..., /2+ ... -+-/Л)|х(/1Э ..., /„) =
где N (а) обозначает теперь число положительных чле-
членов последовательности
Но
2 (SWi, ..../„)==
S
И ЯСНО, ЧТО
i
k=i il+...+ik
S
o
S
Далее,
Воспользовавшись легко проверяемым равенством
2it
= Bл) J exp (— //9) fk F) db X
0 2,
X Bл) / exp (//6)/*-* @) fife,
мы наконец получаем
P {sn = 0} E {max @, 5l, ..., 5^1)|5, = 0} =
max
@, /j, ..., /j + ... -f ln) ax ci2 ... cin =
п — 1 oo 2тс
k=l 1=1 О
2tc
X Bn)~l f
l) Следует заметить, что
oo
= t, sn = 0] < 2
1=1
<E{\xl+ ...
Так как справедливо тождество
и функция /(9) четна [так что при замене / на —/
в exp (HQ) интеграл не изменится], мы приходим к сле-
следующему любопытному тождеству:
(II. 7.4)
2 max@, lv..., /,+ ..
X BЯ) J/*(8)exp(tfe)</8
X
X
где по-прежнему
Читатель здесь вправе недоумевать, к чему на него
был обрушен весь этот каскад комбинаторных трюков.
Но мы просим еще немного терпения, и ход нашей
мысли станет ясным.
Займемся теперь другой задачей. Рассмотрим
((т+ 1) X (т+1))-матрицу Теплица для функции f@),
т. е. матрицу
Обозначим через Xi(m), ... , %m+i(m) ее собственные
значения. Справедлива следующая теорема:
(П. 7.5)
( т + 1 2к \
lim { У\к" (т) — (т^
W->ool; = l
= —2 J] max(O,
Прежде чем мы перейдем к доказательству (очень
простому) этого утверждения, заметим, что в соедине-
соединении с тождеством (П. 7.4) оно приводит к следующему
замечательному результату Сегё1).
Для достаточно малых действительных | (/ — еди-
единичная матрица) имеем
(II. 7.6)
lim -—
det(/-6Cw)
Г 2тс
т->оо 1
где
Этот чисто аналитический результат (доказанный впер-
впервые Сегё виртуозным использованием ортогональных
полиномов) эквивалентен, таким образом, следующему
факту из теории вероятностей:
(II. 7.7)
Л sv .... sn_x\
я-1
вытекающему в свою очередь из доказанной выше чи-
чисто комбинаторной леммы2).
1) В действительности результат Сегё формулируется в несколь-
несколько иной, но эквивалентной форме.
2) Чтобы соблюсти историческую достоверность и избавить чи-
читателя от подозрений, что в этой области математики прибегают
Здесь мы встречаемся с замечательным примером
того, как из теоретико-вероятностного результата сле-
следует весьма нетривиальный аналитический факт.
В главе IV мы приведем несколько других примеров
совершенно иного происхождения, где из результатов,
мотивированных теорией вероятностей и доказанных ее
методами, следуют факты классического анализа.
Нам осталось доказать теорему (II. 7.5). Мы прове-
проведем доказательство для случая д = 3, тем более что оно
содержит все существенные моменты общего доказа-
доказательства.
Мы имеем
2 I) (т) = Tr [Cl) = 2 cix-ifih-ibcib-ix.
1 0</ /2, /3<га
Полагая if>(/) = l для 0-^i^.m и г|)(/)=0 для осталь-
остальных /, мы можем написать
2
(т) = 2Ф d)Ф (h) Ф(h) ctx-ifii7-ibciz-ix,
где сумма берется теперь по всем значениям iiy i2,
Вводя новые переменные
h == h ^i» /з== ^з
мы получаем
/7Z + 1
2 А (т) = 2 Ф (Л) Ф (Л 4- Л) Ф (Л -I- Л+Л) chcncj2+h.
к «черной магии», мы можем правдиво изложить ход событий. Исходя
из результата Сегё, я смог доказать, что он эквивалентен тожде-
тождеству (П. 7.7). Уже после того, как эта редукция была выполнена
и истинность формулы (II. 7.7) была тем самым твердо установлена,
Хант нашел чисто комбинаторное ее доказательство.
Здесь же я перестроил доказательство с заранее задуманным
намерением достичь определенного «драматического» эффекта
Заметим, однако, что совершенно независимо и лишь немногим
позже Спитцер (частично в сотрудничестве с Боненблюстом) пришел
с помощью теоретико-вероятностных рассмотрений к существенному
обобщению комбинаторной леммы Ханта; свой результат он затем
применил к решению многих задач. Работа Спитцера, по моему мне-
мнению, является одним из наиболее значительных вкладов в теорию
вероятностей за последние годы.
Заметим, что
2 Ф (л) Ф (Л + Л) Ф (Л + Л+Л) =
— {max@, у2, у2 + у3) —min@, у2, у2+у3)Ь
если стоящее справа выражение неотрицательно; в про-
противном случае эта сумма равна нулю.
Мы придем к требуемому ответу, если заметим, что
Wj«u = <M-1 f
и воспользуемся условием симметрии C-j = Cj.
Небольшое видоизменение предыдущего рассужде-
рассуждения дает также оценку
га + 1 2Л
lnj (т) - (т + 1) B*) / Г @)
о
<2 ^ с, ...ct max @Л1,/1
Эта оценка нужна для обоснования некоторых формаль-
формальных шагов, ведущих от формулы (II.7.5) к результату
Сегё.
8. Результаты предыдущего пункта немедленно на-
наводят на мысль об их непрерывном аналоге.
Не вдаваясь в подробности, мы просто сформули-
сформулируем соответствующие факты, предоставив их проверку
читателю.
Пусть функция р(х) такова, что:
оо
3) fP(x)dx=h
— оо
оо
4) J хр (х) dx < со.
Положим
оо
F(ri) = J exp (Jy\x) p (x) dx.
—oo
Предположим, кроме того, что
Рассмотрим интегральное уравнение
(II. 8.1)
и обозначим его собственные значения через Xi(a),
Я2(а),....
Наконец, напишем
оо
р(«) (х) = Bл)-1 f Fn (ti) exp (щх) dry,
— oo
это означает, что р<п)(х) является я-кратной сверткой
функции р(х) с самой собой. Тогда
lim
a->oo
= —2
oo
1
oo
/•¦
(a)-
oo
• /
-2ШГ1
max @,
oo
IF
J
0
" Cn) ^л
—оо —оо
l)dx1 ... dxn_x
[аналог равенства (П.7.5)] и
оо оо
J ... Jmax@, xv
— oo —oo
X p (*i)P(x2). • • p(xn_i)p (jc, +• •. +xn_i)rfjf! • • • dxn_1
OO /2-1
О /г=1
[аналог тождества (II. 7.4)].
Наконец, для достаточно малых ? имеем
lim
ехр
= ехр
Г log A —
Bя) ! / log(l —
dx
[аналог формулы (II.7.6); Da(Q—определитель Фред-
гольма интегрального оператора (II. 8.1)].
Здесь на совсем частном примере мы ясно видим, как
важно уметь по-разному формулировать один и тот же
факт. Ьсли бы мы не сформулировали результат Сегё
на языке теории вероятностей, было бы очень трудно,
а может быть, и невозможно обобщить его на случай
интегральных уравнений.
9. Другой пример, где сказываются преимущества
различных формулировок, мы возьмем из теории чисел.
Рассмотрим функцию \{п) (уже определенную
в третьем примере из гл. I), задающую число простых
делителей числа п (без учета кратности).
Пусть р — простое и
\ )
1, если п делится на /?,
o в противном случае.
Тогда
Функции рР(п) (р пробегает все простые числа) не-
независимы, т. е.
D [9рх (п) =
k
(п) = гк] = Д D {рР. (п) = е,},
где каждое ел равно 0 либо 1 и D{ } обозначает (как и
в примере 3 из гл. I) плотность множества целых чисел,
написанного в фигурных скобках,
Положим теперь
p<pk
Ak= 2 ^
и обозначим через с^(а) плотность тех целых чисел я,
для которых
(vk(n) — Ak)Aull2<a,
т. е.
ok(a) == ?> {(v, (п) — Ак) А?1* < а).
Напишем
оо
f exp (Ца) dak (a) = аМ (ехр [ц (v* (я) - Л) Лj'A]} =
—со
N
= \ш —У. ехр [л (v* (п) — Л*) Л*1А]-
Воспользовавшись независимостью, мы получим (как и
в примере 3 гл. I)
<М {ехр [a (v* (л) - Л*) А* %]} =
АГ1Ар„ (я)]} =
= ехр (- ЛА]@ П [1 -Pll+Pjl exp(^АГ1А)].
Теперь легко проверить, что
lim аМ {ехр [Ц (ук (я) — А*) АпЦ) = ехр f— 112).
Отсюда вытекает, что
а
lim ak (a) = Bя)~'/2 Г ехр (-1и2) rf«.
— оо
Читатель, хорошо знакомый с теорией вероятностей,
несомненно, заметил, что мы здесь доказали очень част*
ный случай центральной предельной теоремы.
Если обозначить теперь через lN,k(a) число целых
чисел я, 1 < п < N, для которых
то доказанный нами результат можно представить
в виде
а
(II. 9.1) lim Vim N-xlN>k (а) = Bл)-ъ fexpf—J-«aW
?->оо 7V->oo J \ Z I
— oo
Это наводит на мысль, что, может быть, справедливо
также и равенство
а
1lNiN(a) = Bn)-'1' fexpf— ±u
lim
или (поскольку /ln = log log N + O(l)) если через off
обозначить число целых чисел, не превосходящих /V и
имеющих простых делителей не более чем
log log N + a (log \ogNI/з, то
а
tf/N -> Bя)-1/2 | ехр (— 1 и2) du.
— oo
В действительности это так, хотя доказательство сложно
и требует сравнительно тонких теоретико-числовых (не
теоретико-вероятностных!) рассуждений.
ГЛАВА III
ВЕРОЯТНОСТЬ В НЕКОТОРЫХ ЗАДАЧАХ
КЛАССИЧЕСКОЙ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
1. Хотя в кинетической теории газов с самого начала
пользовались (особенно Клаузиус) аргументами, заим-
заимствованными из теории вероятностей, только после за-
замечательных работ Максвелла и Больцмана (прибли-
(приблизительно с 1870 г.) был отчетливо поставлен вопрос
о существе и роли теоретико-вероятностных рассужде-
рассуждений в физике.
Чтобы понять и оценить некоторые трудности и за-
задачи, связанные с подходом Максвелла — Больцмана,
мы кратко изложим классический вывод уравнения
Больцмана.
Больцман рассматривает систему из N частиц (кото-
(которые он считал твердыми шариками диаметра 6), заклю-
заключенных в объеме V. В предположении пространственной
однородности он выделяет частицы «А» (скорости кото-
которых равны v с точностью до бесконечно малого эле-
элемента d\) и частицы «В» (скорости которых равны w
с точностью до rfw). Затем он переходит к нахождению
числа столкновений между частицами «А» и «В» в тече-
течение времени dt, при которых линия центров направлена
вдоль единичного вектора 1 с точностью до бесконечно
малого элемента d\ (на поверхности единичной сфе-
сферы) 1). Этот подсчет (который можно найти в любом
учебнике по кинетической теории газов) проводится так.
Для того чтобы частица «А» столкнулась указанным
образом с частицей «В», должно выполняться неравен-
неравенство
(III. 1.1) (w —v).{<0
1) Можно назвать их (v, w, ^-столкновениями.
и центр частицы «В» должен лежать внутри косого ци-
цилиндра («цилиндра столкновений»), опирающегося на
площадку 62dl на поверхности сферы радиуса б, с осью,
направленной вдоль w —v и имеющей длину |w — \\dt
Объем этого цилиндра, если принять во внимание
(III. 1.1), можно записать в виде
(III. 1.2) б21 (|(w — v) • 1| — (w — v) • 1) dldt.
Обозначая через пА и пв соответственно число ча-
частиц класса «А» и «В», мы получаем (предполагая про-
пространственную однородность), что число столкновений
указанного типа равно
(III. 1.3) пАпв(б2/!/) . i(|(W-v). ц —(w - v) • \)dldt.
Кроме того, предполагается, что
(III. 1.4) пА = Nf(v; t) dv, nB = Nf (w; t) dw.
После того как указанное столкновение произойдет, ско-
скорости частиц v и w изменятся и перейдут соответствен-
соответственно 'В
(III. 1.5) v + ((w — v) • 1) 1 и w — ((w — v) • 1) 1
(подсчет основан на законах сохранения энергии и ко-
количества движения при упругом столкновении).
Теперь без труда выводится уравнение
(Ш. 1.6)
где
c=NJV,
5A) —поверхность единичной сферы.
2. Приведенный вывод на первый взгляд кажется
непогрешимым, а окончательное уравнение (III. 1.6)
(уравнение сохранения, выражающее то обстоятельство,
что число пА может уменьшиться за счет (v, w, 1)-
столкновений и увеличиться за счет (v+((w — v) • 1I,
w — ((w — v) -1I,1)-столкновений ')) выглядит очень
естественным. Поэтому кажется удивительным, что урав-
уравнение (III. 1.6) допускает крайне парадоксальное след-
следствие. А именно из него непосредственно следует зна-
знаменитая Я-теорема Больцмана, утверждающая, что
(III. 2.1) -^f dvf(v; t)log/(v,t)<0,
причем равенство достигается только для
/ = const • ехр (— av • v).
Эта теорема замечательна тем, что она перебрасы-
перебрасывает мост между механикой и термодинамикой. Дейст-
Действительно, Больцман видел в ней механическое обосно-
обоснование второго закона термодинамики, где величина
; t)
принята за энтропию с обратным знаком.
3. Однако утверждение Я-теоремы нельзя понимать
буквально, поскольку в таком наивном толковании она
противоречит механике.
В самом деле, все уравнения механики обратимы во
времени (инвариантны относительно преобразования
t-* 1), в то время как Я-теорема выделяет некоторое
направление времени. Это было самым ранним возра-
возражением против подхода Больцмана; его выдвинул впер-
впервые Лошмидт в 1876 г. (оно называется обычно «пара-
«парадоксом обратимости»). Лошмидт просто заметил, что
если газ, находясь в некотором состоянии So, перейдет
по прошествии времени / в состояние S/, то по предпо-
предположению должно быть Ht < Яо. Обратим теперь напра-
направления всех скоростей. Тогда, с одной стороны, за вре-
1) Внимательный читатель заметит, что здесь использован сле-
следующий факт: преобразование
ЛA): (v, w) -> (v-f((w~-v) -1I, w—((w—v)-1I)
совпадает с преобразованием Л(—1).
мя t состояние St должно снова вернуться в So, а, с дру-
другой стороны, больцмановская Я-теорема снова утвер-
утверждает, что Но < Ht. Таким образом, величина Н не
могла бы измениться. (На это возражение Больцман,
говорят, ответил: «Ступайте, поверните их!»)
Более существенное возражение исходило от Цер-
мело и состояло в том, что, согласно теореме Пуанкаре
о возвращаемости (Wiederkehrsatz), замкнутая механи-
механическая система должна (если только она не находилась
в некотором исключительном начальном состоянии) вер*
нуться в конце концов как угодно близко к своему ис-
исходному состоянию. Таким образом, если бы Н была
чисто динамической величиной, она не могла бы всегда
убывать.
Стараясь отвергнуть это возражение, Больцман ука-
указал на то, что промежутки времени между возвраще-
возвращениями (так называемые циклы Пуанкаре) чудовищно
велики (он, как говорят, ответил: «Долго же вам при-
придется ждать!»).
Теорема Пуанкаре настолько проста и настолько
фундаментальна, что мы прервем наше изложение, что-
чтобы доказать и обобщить ее.
4. Состояние физической системы с п степенями сво-
свободы можно изобразить точкой в 2/г-мерном простран-
пространстве (так называемом фазовом пространстве, или Г-про-
странстве). Координатами точки в Г-пространстве слу-
служат
Я\> • • •» Я» Рг> • ••» Рп>
т. е. обобщенные координаты и канонически сопряжен-
сопряженные им импульсы.
Поведение системы определяется функцией Гамиль-
Гамильтона
Н{Я\> •••> Я» Рг> •••» Рп)
(предполагается, что Н не зависит явно от /), а урав-»
нения движения имеют вид
dq. дН dp. дН
Из этих уравнений вытекает, что Н (так мы обозначаем
теперь гамильтониан, и его не следует путать с Я из
п. 2) является постоянной движения (закон сохранения
энергии); мы предположим, что поверхность постоянной
энергии
^( •••> Яп> Р\> -••> Рп) = Е
является ограниченным множеством.
Допустим, что в начальный момент наша система
находится в точке
М) — \Ч\> • • •» Ул» Pv # • •» РпУ
Ее положение в момент времени t задается решением
уравнений движения
л (<> = *,(??..••.&/>!..... # О-
Эти формулы определяют однопараметрическое семей-
семейство Tt преобразований Г-пространства в себя
Преобразование Tt, как это утверждается в извест-
известной теореме Лиувилля, сохраняет обычную меру Лебега
в Г-пространстве: мера Лебега множества Tt(A) равна
мере Лебега множества А.
Если рассматривать нашу систему только на поверх-
поверхности постоянной энергии H(qiy .. ., qn, Ри • • •» Рп) ==Е,
то из теоремы Лиувилля вытекает следующее. Опреде-
Определим меру |л(Л) множества А на поверхности постоян-
постоянной энергии формулой
(мы предполагаем, что llgrad #||>c>0 на этой поверх-
поверхности, так что мера всей поверхности конечна; собствен-
собственно, достаточно ввести только это предположение, не ого-
оговаривая отдельно, что вся поверхность ограничена), где
do — элемент поверхности и
||gradtf|| =
Тогда
После такого введения мы можем описать ситуацию
чисто математически.
На множестве Q (поверхность постоянной энергии)
задана вполне аддитивная мера ji, такая, что ji(Q) = l
(последнее принимается для удобства; важно только,
что ji(Q)<oo). Далее, существует однопараметрическое
семейство взаимно однозначных преобразований Ти со-
сохраняющих меру. (То обстоятельство, что в механике
преобразования Tt взаимно однозначны, тривиально вы-
вытекает из уравнений движения.)
Теорему Пуанкаре о возвращаемости можно теперь
сформулировать так.
Пусть А — такое подмножество в Q, что [х(Л)>0.
Тогда для почти всех со ? А (т. е. за исключением мно-
множества точек со ji-меры нуль) найдется сколь угодно
большое /, такое, что 7\со ? А.
Существует много доказательств этой теоремы, и все
они почти тривиальны1). Мы выбираем одно из них
(совсем не самое простое), удобное для наших целей.
Прежде всего, вместо того чтобы рассматривать не-
непрерывное время, будем считать его дискретным и рас-
рассмотрим лишь последовательность
7\со, Г2ш, ....
Ясно, что
I 2== 1 1, У з= ¦* 1» • • • •
Пусть теперь А\ — множество таких точек со, что
1) Это еще один пример важного и глубокого факта, чисто ма-
математическое содержание которого лежит почти на поверхности.
Обозначим через Л„ множество тех со, для которых
Иначе говоря, имеем
Ап = А п С (ТТгА) П С (ГГ2Л) П • • • П С (Т^А) П П"А,
где через С (В) обозначено дополнение к В (в мно-
множестве Q).
Пусть /(со)—характеристическая функция множе-
множества Л, т. е.
Тогда характеристическая функция множества Ап рав-
равна, очевидно,
/(©)A -/G»)... A -
и, следовательно,
2
Положим
2
и заметим, что
При выводе этой простой формулы мы существенно
пользуемся тем, что преобразование 7\ сохраняет меру.
Действительно, если взять, например, (я(Л3), то можно
написать:
ц (А3) = f f (со) A - / G») A - / (Г?©) ) / (Г?©) 4i =
Поскольку Ti сохраняет меру, два средних интеграла
равны друг другу. Отсюда
Заметим теперь, что
и так как последовательность {шп} не возрастает и огра-
ограничена снизу (нулем), то lim wn существует и, следо-
следовательно,
\\m{wn— дая+1) = 0.
Таким образом,
1
Итак, почти каждая точка со множества А такова, что
по крайней мере одна из ее итераций Ло, Tiw, .. ¦
должна попасть в А.
Отсюда немедленно вытекает, что для почти каждой
точки со из Л бесконечно много ее итераций попадает
в А. В самом деле, пусть DL—множество тех со из Л,
для которых Тпсх) не принадлежит Л при п > /. Приме-
Применяя только что доказанную теорему к преобразованию
Т[ (вместо Ti), мы получаем [х(А)=0 и, следовательно,
также
U
v=i
Таким образом, почти каждая точка из А бесконечно
много раз возвращается в А. Теорема Пуанкаре дока-
доказана.
5. Теперь у нас имеется способ вычислить и среднее
время возвращения (или, как его часто называют, цикл
Пуанкаре). Для дискретных наблюдений (дискретное
время с промежутком единица) среднее время возвра-
возвращения определяется формулой
Выбирая промежуток времени между наблюдениями,
равный т секунд, и заменяя, следовательно, Ti на Гт,
мы получаем
о
Далее,
2
Л1
и поскольку последовательность ^jk[i(Ak) не убывает,
последовательность wn + n(wn — wn+i) не возрастает.
Так как очевидно, что wn + n(wn — ^n+1) ^ 0, то предел
lim [wn + n(wn — wn+l)\
/2->ОО
существует, и поскольку lim wn также существует, мы
заключаем, что существует и предел
lim n{wn — wn+l).
/?->оо
Кроме того, ряд
сходится (это равносильно существованию предела
lim wn) и, следовательно,
lim n(wn — wn+l) = 0.
я->оо
Окончательно,
оо
2 k\x (Ak) =1 — lim wn.
1 /z->oo
Наиболее интересен случай, когда
lim wn = 0.
/г->оо
Это условие, разумеется, не всегда выполняется, но оно
заведомо имеет место, если предположить, что Тх «мет-
«метрически транзитивно» *), т. е. всякое множество, инва-
инвариантное при преобразовании Гх, имеет ^i-меру либо О,
либо 1. Чтобы убедиться в том, что метрическая тран-
транзитивность влечет за собой условие Нтшп = 0, заме-
заметим, что lim wn равен мере множества тех точек со, для
которых
2
Обозначим это множество через В.
Рассмотрим множество ТХВ. Если
то
т. е.
Г,® 6 Я,
и, следовательно, со ? Б, т. е. 7\ В с Б. Аналогично
ГХ2Б сГх? и т. д. Положим
lim
л->оо
и заметим, что ТХС = С. В силу метрической транзитив-
транзитивности мера \i{C) равна либо 0, либо 1. Поскольку
1) В нашей литературе чаще употребляется термин «эргодич-
но». — Прим. перге.
^ (т"В) = ^i (В) и Т'хг+1ВаТ"В, отсюда следует, что
li(C) = ji(B), т. е. мера \х(В) равна либо 0, либо 1; \х(В)
не может равняться 1: это означало бы, что \х(Л)=0
вопреки нашему предположению. Таким образом,
и,(В)=0, т. е. lim wn = 0, и, следовательно, для мет-
/г->оо
рически транзитивного преобразования
(III. 5.1) 0* = тДг(Л).
Как хорошо известно, метрическая транзитивность
играет важную роль в эргодической теории. Однако
узнать, какие гамильтонианы приводят к метрически
транзитивным преобразованиям, — почти неразрешимая
задача.
Таким образом, с точки зрения механики формула
(III. 5.1) сравнительно бесполезна.
Она имеет также тот недостаток, что при стремле-
стремлении т к нулю (т. е. при переходе к непрерывным на-
наблюдениям) мы всегда получаем тривиальный предел 0.
Это легко исправить, если заметить, что такое выро-
вырождение происходит за счет рассмотрения события (о ? Л,
Тхы?А}как возвращения через время т. Для непрерыв-
непрерывного движения «вероятность» этого события, т. е.
должна быть очень близка к единице, и, следовательно,
на долю этого «ложного» возвращения (через время т)
приходится почти весь вес. Следуя Смолуховскому,
определим среднее время возвращения формулой
Мы имеем (предполагая, что Гх метрически транзи-
тивно)
1 1 1
= 1-\1(Аг)~(\л(А)
и окончательно
вх = t [1 - jx (A)]/[\l (А) - ti (со 6 А 7> ? А)].
Этой формулой можно уже пользоваться для пре-
предельного перехода при т->0; все зависит теперь лишь
от существования предела
[i(co? Л, 7
т-»0
Хотя понятие среднего времени возвращения и
играет важную роль при изучении основ статистической
механики, ясно, что это весьма грубое понятие.
Явление выхода и возвращения точек множества Л,
вообще говоря, слишком нерегулярно, чтобы его можно
было адекватно описать с помощью одного только сред-
среднего цикла. К несчастью, средний цикл является един-
единственной количественной характеристикой, применимой
к общей механической системе, но даже и в этом случае
мы должны опираться на почти непроверяемое допущен
ние о метрической транзитивности.
6. Результатам пп. 4 и 5 можно придать другую
форму, которая на вид отличается от предыдущей, хотя
формально ей эквивалентна.
Допустим, что на множестве Q, на котором опреде-
определена вполне аддитивная мера [г, задано однопарамет-*
рическое семейство X(t\ со) (со 6 ^» —оо<^<оо) веще-
вещественных ji-измеримых функций (т. е. для каждого t
множество тех точек со, для которых X{t\ co)<a, р,-из-
меримо при каждом вещественном а).
Такое семейство называется случайным процессом.
Процесс называется стационарным в узком смысле (или
строго стационарным), если
\х [X(tx\ со) < аг, ..., X(tn; со) < ап) =
+ х; Q)<alt ..., X(tn + v, ©)< ап}
для всех наборов t±, t2i ..., tn, t, ai, a2, ..., an.
Поскольку все это может показаться чересчур аб-
абстрактным и ничем не оправданным, мы попытаемся
вкратце объяснить сущность того, что мы стремимся
формализовать,
Когда физик говорит о «смещении X(t) броуновской
частицы за время /», для него это, разумеется, не озна-
означает, что X(t) есть точно определенная функция /; он
имеет в виду, что X(t) зависит не только от t, но и от
чего-то еще, что неопределенно (и вводя до некоторой
степени в заблуждение) называют «случаем».
Опознав «случай», физик обращается к статистиче-
статистической теории, задача которой — предсказывать вероят-
вероятности осуществления или неосуществления некоторых
событий. Чтобы построить такую теорию, он должен
(что мы неоднократно подчеркивали в гл. I) приписать
вероятности некоторым «элементарным» событиям, с по-
помощью которых, по-видимому, могут быть вычислены
остальные нужные вероятности.
Эту ситуацию можно формализовать, определяя слу-
случайный процесс, как это было сделано выше.
Выбор множества Q не имеет существенного значе-
значения; оно играет чисто вспомогательную роль. Мы могли
бы на самом деле выбрать в качестве Q множество всех
допустимых функций X(t) и рассматривать со как обо-
обозначение соответствующей функции.
В связи с этим возникла довольно важная матема-
математическая задача, о которой здесь стоит хотя бы упомя-
упомянуть. Физическая теория доставляет нам множество
функций
o(av tx\ a2, t2\ . . .; ал, tn),
которые, как мы надеемся, будут служить вероятно*
стями
Р {*('.)<«.. .... X{tn)<an),
если вообще такие вероятности могут быть подходящим
образом определены.
Вопрос, таким образом, состоит в следующем: су-
существуют ли множество Q с вполне аддитивной мерой
\х (вероятностью) и семейство измеримых функций
X(t; со) (о f й), такие, что
Р {*(*!)< alf ..., X(tn)<an} =
=\i{X(tx; ®)<av ..., X(tn\ (о)<ая}=а(а1, tx\ ...; аЛ, tn).
Подразумевается, конечно, что функции о удовлетво-
удовлетворяют очевидным условиям согласованности, например
lim a(alf^; ...; ая, tn) = a(avtl; ...; ая-1, tn_x).
Положительный ответ на этот вопрос был дан Колмо-
Колмогоровым и в более общем виде Дубом. Окончательная
теорема, несмотря на свою несомненную важность — в
ней устанавливается существование тех объектов, о ко-
которых пойдет речь, — обычно мало касается более анали-
аналитических аспектов теории вероятностей. Однако имеются
исключения, и в гл. IV мы вернемся к этому вопросу.
Теперь же мы просто перефразируем результаты
пп. 4 и 5 в терминах стационарных случайных про-
процессов.
Предположим, что X(t\ со)—строго стационарный
случайный процесс и Л — такое множество веществен-
вещественных чисел, что множество тех со, для которых X(t\ со) ?
? Л, измеримо и имеет положительную меру [из стацио-
стационарности следует, что вероятность
одна и та же для всех t].
Определим теперь следующие величины:
, A, .... А, А) = Р[Х@; а)?А, X (х; ©)?л
— 1)х; со)(?л, Х(пх;
Р(А\А, .... A, A) = Wr(A, A,..., A, A)/W,(AI).
(Напомним, что Wx (A) = W (А) > 0.) Тогда
со
2Р(А|Д .... А, А) = \
1) Это по определению так называемая условная вероятность
того, что, выходя из множества А в момент времени /=0 и двигаясь
шагами продолжительностью г, мы вернемся первый раз в А через
п шагов.
(III. 6.1) 2ятР(Л|Д ..., A, A) =
/z=l
если предположить, что
(III. 6.2) lim WT(A, Д .... Л) = 0.
(Определения Wx (А, ...,Л) и аналогичных величин
очевидны.)
Аналогом среднего времени возвращения по Смолу-
ховскому является, очевидно, величина
1 — W (А)
<Ш63) » ^^
Эти формулы выводятся при помощи прямого повто-
повторения простых шагов, намеченных в пп. 4 и 5. Если при
этом следить за выкладками, то можно ясно увидеть,
где используется условие строгой стационарности.
Можно было бы также получить эти формулы из анало-
аналогичных формул в пп. 4 и 5, если ввести некоторое искус-
искусственное преобразование Ти сохраняющее меру (так
называемое «преобразование сдвига»).
Обратно, читатель может заметить, что функция
f{Tt(d) в п. 4 задает, в соответствии с нашим определе-
определением, стационарный случайный процесс.
Таким образом, «динамические теоремы» в пп. 4 и 5
и «статистические теоремы» (III. 6.1) и (III. 6.2) этого
пункта с чисто математической точки зрения эквива-
эквивалентны.
Сделаем еще одно замечание относительно (III. 6.2).
Пусть %а(*)—характеристическая функция множества
А (т. е. %а(#) = 1 для х ? А и %а(х) =0 в противном слу-
случае); рассмотрим
Мы имеем
f(±\%A(X(T; «))+ ... +Хд(Л-(ят; со))] - W (А)
где <3„ — множество, на котором X (т; а) (? А,
..., Х(пх; со)(?Л, и, следовательно,
..., 1).
п-\
Теперь легко проверить, что если
(III. 6.4) lim Р{Х@; со)еЛ\ X(лт; со)g Л} = Г2(Л)
/2->ОО
(асимптотическая независимость!), то
;©) I-И7 (Л)J ф=
и, следовательно,
(III. 6.5) lim 1ГХ(Д ..., Л) = 0.
/г->оо
Свойство (III. 6.4) (называемое «сильным перемеши-
перемешиванием») влечет за собой метрическую транзитивность,
и, следовательно, его проверка для динамических си-
систем почти безнадежна. Для многих же «статистиче-
«статистических» систем (III. 6.4) легко проверяется.
7. Возражения Лошмидта и Цермело обнаруживают
несостоятельность наивной формулировки //-теоремы.
Формулу для числа соударений («Stosszahlansatz»)
(III. 1.3), на которой основан вывод уравнения Больц-
мана, нельзя рассматривать как простое следствие урав-
уравнений механики, поэтому необходимо некоторое допол-
нительное истолкование. Сам Больцман предложил ин-
интерпретировать Я-теорему статистическим образом.
Несмотря на блестящее исследование П. и Т. Эрен-
фестов, осветившее местами неясные идеи Больцмана и
значительно подкрепившее их правдоподобность, этот
вопрос даже теперь (через 45 лет после появления ра-
работы Эренфестов!) решен далеко не полностью.
Обсуждаются, говоря в общих чертах (и несколько
расплывчато), две проблемы:
I. Можно ли примирить обратимость во времени и
теорему о возвращаемости с «наблюдаемой» необрати-
необратимостью?
П. Возможно ли такое примирение в рамках клас-
классической механики?
Первая проблема, по существу, логического харак-
характера. Утвердительный ответ может быть получен, если
будет указана модель, обладающая всеми требуемыми
свойствами.
Такая модель была предложена П. и Т. Эренфестами
в 1907 г. Это, вероятно, одна из наиболее поучительных
моделей во всей физике, и хотя это только пример ко-
конечной марковской цепи, она представляет большой са-
самостоятельный интерес.
Модель в первоначальном ее виде можно описать
так1): 2R шаров, занумерованных от 1 до 2R, раскла-
раскладывают по двум ящикам А и В. Затем «случайно» выби-
выбирается целое число между 1 и 2R, и шар с этим номе-
номером перекладывают из коробки, где он лежит, в другую.
Эта процедура затем повторяется много раз.
Интуитивно совершенно ясно, чего хможно ожидать.
Предположим для простоты, что сначала все 2R ша-
шаров находятся в ящике А. Тогда на первом шаге мы
обязательно перенесем шар из Л в В. На втором шаге
мы можем вернуться к начальному состоянию, но ве-
вероятность этого равна BR)~l. Если 2R очень велико
(скажем, порядка 1023, что сравнимо с числом Авогад-
ро), то с подавляющей вероятностью, а именно 1 —
— BR)~\ в коробку В попадет и следующий шар.
В действительности до тех пор, пока пл (число шаров
1) Ее часто называют «моделью пса и блохи».
в А) будет намного больше пв (числа шаров в В), мы
будем наблюдать «перетекание» шаров из Л в В.
Если наше математическое понятие вероятности от-
отражает какую-либо «реальность», то мы должны ожи-
ожидать «почти необратимого» течения в предпочтительном
направлении.
Рис. 2. Ордината на этом графике соответствует значению величины
Мы не можем сказать с определенностью, что nA{s)
(число шаров в А после s шагов) всегда убывает, но
мы можем с уверенностью ожидать, что в некотором
смысле nA(s) убывает «почти всегда»1).
Этот эксперимент был действительно осуществлен
с сорока шарами; получившаяся кривая воспроизведе-
воспроизведена на рис. 2.
Как с помощью этой модели опровергнуть возраже-
возражения Лошмидта и Цермело?
1) Здесь невозможно не привести эпиграф к главе об энтропии
из известной книги Mayer M. G., Mayer J., Statistical Mechanics:
«What never? No never! What never? Well, hardly ever». [Это пере-
переводится приблизительно так: «Этого никогда не бывает? — Никогда!
Совсем никогда? — Ну, вряд ли когда-нибудь». — Прим. ред.] Эта
самая образная и лаконичная формулировка, в которую Джильберт и
Сулливан облекли второй закон термодинамики в его статистиче-
статистическом варианте, поистине великолепна!
Чтобы посмотреть, что происходит при обращении
времени, вычислим вероятности
(III. 7.1) P{nA(s + \) = n\nA(s) = m}
[т. е. условную вероятность того, что nA(s+l) =п, если
пА (s) =m] и
P{nA(s — l) = n\nA(s) = m)
(т. е. условную вероятность того, что nA(s—1)=я,
если nA(s)=m). С помощью довольно простых рассу-
рассуждений мы получаем
[б(/)—символ Кронекера]. Несколько труднее вычис-
вычислить
Чтобы сделать это и отчетливее понять смысл условных
вероятностей, сформулируем нашу задачу более точно.
Если положить пА@)=п0, то выборочным простран-
пространством S будет служить множество бесконечных после-
последовательностей по> пи п2, ... неотрицательных целых чи-
чисел, заключенных между 0 и 2/?, причем
Элементарными событиями служат множества последо-
последовательностей, первые / (/=1, 2, ...) элементов которых
фиксированы. Например, множество всех последователь-
последовательностей, начинающихся с чисел
представляет собой элементарное событие.
Мера на элементарных множествах задается, как это
следует из описания самой модели, следующим образом:
(III. 7.2) Р («„I я,) Р (я,| п2) ... Р (я,.,| я,).
где Р («ft-il/Zft) — вероятность перехода от Щ-i к nk,
определяемая формулой
Рассмотрим теперь вероятность
Р{»Л(*-1) = л; ллE) =
Эта вероятность по определению равна
21
причем суммирование распространяется на все fti, л2,
..., ns-2 [из формулы для Р (n>k-\\ nk) Уже вытекает, что
nk равно либо /zfe_i +1, либо Пк-\. — 1]. Искомая условная
вероятность определяется отношением
Р \пя E — 1) = п, пя (s) = т\
причем условная вероятность (III.7.1) равна (по опре-
определению)
i
Снова используя определение условной вероятности,
мы можем написать
P{nA(s— \) = n, nA(s) = m) =
Наконец,
(III. 7.3) Р {nA(s-\) =
— n)b(m — n — 1)}.
Напомним, что мы положили пА@)=п0. Таким обра-
образом, вероятности Р [пА(s — 1) — п) и Р {nA(s) = m} (и,
следовательно, их отношение) могут зависеть (и в дей-
действительности зависят) от По1). Можно надеяться, что
при s -+ оо существует предел
lim P {nA(s) = m) =W(m) (W(т) не зависит от по1).
5->СО
Физически мы именно этого и ожидали; такое положе-
положение вещей соответствует нашему ощущению (а может
быть, только сильному желанию!), что с течением вре-
времени вероятность обнаружить систему в состоянии т
полностью определена и не зависит от начального со-
состояния. К сожалению, для модели Эренфестов это не
так! Истоки этой трудности неглубоки, но мы несколько
отложим ее обсуждение. А пока мы попробуем выйти
из затруднения с помощью одного простого приема.
Вместо того чтобы фиксировать число п0, мы будем
считать его распределенным с вероятностями
W(n0) ^ W (п0) > 0, 2 W (п0) =
Иными словами, в качестве выборочного пространства S
мы возьмем теперь множество всех последовательностей
(по может принимать любое целое значение между О
и 2/?), а меру элементарного множества будем считать
равной не (III.7.2), а величине
(III. 7.4) W (По) Р(По\пг)...Р (п^г | щ).
Мы получим
Постараемся выяснить, можно ли распределение W(n0)
выбрать так, чтобы для всех 5 выполнялось равенство
Правильнее было бы записать эти вероятности так:
nA(s-l) = n\nA@) = n0) и Р{лЛE) = т|пд@)
Ясно, что этого можно добиться, если система урав-
уравнений
(III. 7.5) W(m) = S ИГ(Ло) Р (*о I "О (т = 0, 1, 2, ..., 2R)
яо=О
имеет решение в неотрицательных числах.
Легко видеть, что единственное ее решение [нормиро-
[нормированное так, что 2 W(m) = l] равно
Выбрав это решение и соответственно определив вероят-
вероятности [см. (III.7.4)], мы найдем
+ BR)'1 BR - п) 6 (п - т + 1)).
Теперь без труда проверяется, что
Р {/гл E — 1) = /г |/гл (s)=/n} = Р {/гд E + 1 )=п \ пА (s)=m).
Таким образом, оказывается, что наша модель (при
подходящем выборе начальных вероятностей) обратима
во времени!
В этом месте мы воспроизведем весьма поучительные
выкладки, принадлежащие Эренфестам.
Рассмотрим условную вероятность
Р [nA(s — l) = m — l, /&дE+1) =/тс — 1 \nA(s) = m},
которая, очевидно, равна
(+ 1) = m - 1}
Р {лд (s — 1) = m — 1} Р (m — 1 | m) P (m | /и — 1)
1 m =
С другой стороны, аналогичные выкладки дают
Р {nA(s — 1) = /и + 1,/гл (s -f- l) = m — 1 |/гАE) = /га}
и, наконец,
Р {nA(s—\) = m + \, nA(s-\-\) =
Отсюда следует, что если т близко к 2R (т. е. мы да-
далеки от равновесия), то чередование
значительно более вероятно, чем остальные располо-
расположения:
Это просто означает, что если из множества всех «кри-
«кривых»
пробегаемых последовательными значениями пА, мы вы-
выбираем подмножество, определенное условием
nA(s) = m,
то в подавляющем большинстве «кривых» этого под-
подмножества осуществляется именно первое чередование.
Этот несложный анализ подводит нас к истолкова-
истолкованию, казалось бы, бессмысленного и парадоксального
утверждения Больцмана, что каждая точка Я-кривой
является максимумом.
Статистическая интерпретация (подобная только что
изложенной) придает смысл этому утверждению и со-
согласуется как с обратимостью во времени, так и с тен-
тенденцией к убыванию.
Чтобы лучше оценить роль распределения
мы обратимся сейчас к возражению Цермело,
Снова рассмотрим выборочное пространство 5 всех
последовательностей
(каждое п$ — целое число, заключенное между 0 и 2/?),
определяя меру элементарных множеств формулой
(III. 7.4). Полагая
со {/г0, /ij, щ, ...}
и
X(s\ a) = ns E = 0, 1, 2, ..О1),
мы можем легко убедиться в том, что X(s;cd) —строго
стационарный процесс (время теперь считается дискрет-
дискретным). Таким образом, применяя «статистический ва-
вариант» теоремы Пуанкаре, мы получаем
(III. 7.6)
где
_
P(no\n
o,
обозначает вероятность того, что если вначале в ко-
коробке А находилось п0 шаров, то первый раз там снова
окажется п0 шаров через k шагов (щ — любое целое
число, отличное от п0).
Другими словами, каждое начальное состояние п0
снова достигается с вероятностью 1.
Можно доказать формулу2), аналогичную (III. 5.1),
и найти тем самым, что среднее время возвращения 0*
равно
(III. 7.7)
1) Нетрудно распространить это определение на отрицатель-
отрицательные s.
2) Мы не делаем здесь этого, потому что ниже мы приведем
другой вывод этой формулы для среднего времени возвращения.
Как мы увидим ниже, формулу (III. 7.7) можно по-
получить непосредственным вычислением, не обращаясь
к понятию строго стационарного процесса.
Однако введение меры с помощью формулы
(III.7.4) — не просто математическое ухищрение.
Распределение
играет ту же роль, что и инвариантная мера (см. п. 4)
в исходной механической задаче, и формула (III. 7.5)
2R
W{m)=
служит аналогом теоремы Лиувилля.
Как бы много нам ни говорили эти аналогии и как
бы сильно мы ни ощущали, что модель Эренфестов ула-
улавливает самую суть спора между Больцманом и его оп-
оппонентами, мы не должны упускать из виду, что фунда-
фундаментальная проблема II (см. стр. 96) остается еще не
выясненной.
Обсуждаемая модель является чисто статистической,
и вероятностный механизм (т. е. случайный выбор
числа) заранее в ней постулируется. Этот вероятностный
механизм, должным образом истолкованный, служит для
того, чтобы примирить необратимое поведение с обра-
обратимостью во времени и возвращаемостью.
8. Возможно, стоит вкратце ознакомиться с точкой
зрения самого Больцмана на то, как примирить наблю-
наблюдаемое необратимое поведение с обратимостью во вре-
времени и возвращаемостью. Мы следуем изложению этого
вопроса в статье Эренфестов в «Enc. Math.Wiss.» A911).
Вместе с фазовым пространством всей системы
(Г-пространством) рассмотрим также фазовое простран-
пространство одной частицы (^-пространство). Для одноатомного
газа это ^-пространство шестимерно (три координаты и
три составляющих импульса).
Разобьем ^-пространство на ячейки Сь С2, ... оди-
одинакового (шестимерного) объема \С\,
Для каждой точки Г-пространства (т. е. для любого
заданного состояния всей системы) мы получим после-
последовательность целых чисел («чисел заполнения»)
пи п2, ... (^i+^2+ ... =# — общее число частиц), ука-
указывающих, сколько частиц находится в соответствующей
ячейке Си С2, .... Обратно, всякий набор чисел
Пи п>2, • • •, удовлетворяющий условию
определяет множество Z (называемое «Z-звездой») то-
точек в Г-пространстве, для которых эти числа служат
числами заполнения. Объем FЛ^-мерный) Z-звезды ра-
равен, очевидно,
п{\п2\ ..
Предположим теперь, что ячейки С* достаточно
малы. Обозначим через ег- энергию частицы, попавшей в
некоторую точку ячейки Сг (важно подчеркнуть, что мы
пренебрегаем энергией взаимодействия между частица-
частицами!). Тогда с большой точностью можно написать
где Е — полная энергия системы.
С другой стороны, ячейки должны быть все-таки та-
такими, чтобы числа rii были достаточно велики.
Больцман находит те значения /гг-, для которых вы-
выражение
пх\п2\ ..
достигает максимума, при дополнительных условиях
(III. 8.1) lini=N,
(III. 8.2) 2 ifit = Е.
Это делается при помощи сомнительного (с матема-
математической точки зрения!) метода замены яг! по формуле
Стирлинга (именно поэтому нужно, чтобы числа п{ были
большими), после чего щ рассматриваются как непре-
непрерывно меняющиеся переменные.
Задача, таким образом, сводится к нахождению ми-
минимума выражения
2 n>t log nt
при дополнительных условиях (III. 8.1) и (III. 8.2). От-
Ответ дается формулой
(III. 8.3) nt = а ехр (— реД
где а и C определяются подстановкой решения (III. 8.3)
в формулы (Ш.8.1) и (Ш.8.2).
Эренфесты дают следующее пояснение к рассужде-
рассуждениям Больцмана.
(а) При числах заполнения
(III. 8.4) л/ = аехр(— ре,)
объем Z-звезды не только достигает максимального зна-
значения, но и становится «подавляюще» большим. Это оз-
означает, что «небольшие» отклонения от (III.8.3) ведут
к «чудовищному» уменьшению объема Z-звезды.
(б) Z-звезда, соответствующая числам заполнения
(III. 8.4), высекает «подавляющую» часть поверхности
постоянной энергии
(в) Как следует из эргодической теоремы, почти все
траектории, описывающие движение системы, проводят
«подавляющую» часть времени в той части поверхности
постоянной энергии, которая высекается максимальной
Z-звездой.
Таким образом, если система не находится в состоя-
состоянии, соответствующем числам заполнения (III.8.4), то
она почти наверняка попадет в это состояние; если же
система уже находится в этом состоянии, то она почти
никогда не выйдет из него.
Хотя это утверждение почти полностью лишено ма-
математической строгости, оно представляется чрезвычайно
правдоподобным.
С физической точки зрения затруднения, связанные
с этим методом, заключаются в том, что в нем совер-
совершенно умалчивается о процессе «приближения к равнове-
равновесию» [т. е. то, каким образом, исходя из произвольных
чисел заполнения, система приходит к «равновесным»
числам заполнения (III. 8.4)]; неясна также его связь
с кинетическим методом (т. е. с уравнением Больцмана).
В частности, неизвестно, монотонно ли приближается си-
система- к равновесию.
9. Какой аналог только что обсуждавшемуся подходу
Больцмана можно найти в модели Эренфестов?
Предположим, что вначале в ящике А находится п0
шаров. В этом случае можно показать, что почти во
всех 1) последовательностях
частота появления фиксированного целого числа т
равна
Это и есть эргодическая теорема для нашей системы
(известная также как «усиленный закон больших чи-
чисел») 2).
Ясно, что наибольшее значение W(m) принимает при
m = R, хотя это значение и не будет «подавляюще» боль-
большим.
Однако, если мы рассмотрим узкий промежуток со-
состояний
R - a {2R)k < т < R + а B/?Д
«вероятность» которого приближенно равна
2а
1/2 Jexp(—^я
-2а
то для а = 5 эта вероятность уже «подавляюще» больше
вероятности дополнительных промежутков.
!) Здесь «почти во всех» означает «за исключением множества
последовательностей меры нуль». Мера строится на основании фор-
формулы (III. 7.4).
2) Это следует из общей эргодической теоремы, но для модели
Эренфестов легко может быть доказано и непосредственно. Можно
также использовать так называемую «эргодическую теорему в сред-
среднем», доказываемую еще проще.
Таким образом, если no>R + 5BR)l/2 или nQ<R —
— 5BR)l/\ то система очень охотно переходит в окрест-
окрестность равновесия и, попав туда однажды, покидает эту
окрестность лишь «ненадолго» 1).
Этот вывод хорошо подтверждается эксперименталь-
экспериментальной кривой на стр. 97.
Здесь вполне уместно привести краткий обзор неко-
некоторых идей Гиббса.
Гиббс с самого начала отказывается от мысли рас-
рассматривать индивидуальную систему и предлагает рас-
рассматривать распределение систем во всем Г-простран-
стве (или еще лучше в области между двумя поверхно-
поверхностями постоянной энергии Е и Е + АЕ).
Если вначале системы распределены с плотностью
D(Pv •••> Ар <?!> '••> Чп> 0),
то уравнения движения позволяют определить плотность
в произвольный момент времени t. Уравнение, управляю-
управляющее изменением D во времени, — это известное уравне-
уравнение Лиувилля
дР __ [Н Пл_\ (дН дР дН дР\
dt — 1^' Ut—2d[dqt dPi dPi dqt)9
1
где Н — гамильтониан системы.
Далее Гиббс пытается доказать, что Dt стремится в
некотором смысле к равномерному распределению в об-
области между поверхностями постоянной энергии Е и
Е + АЕ (микроканоническое распределение).
Впервые Эренфест разъяснил, в каком смысле можно
надеяться доказать это утверждение. Он предложил вве-
ввести понятие «крупнозернистой» плотности («Grobe
Dichte»).
Разобьем область между поверхностями Е и Е-\-АЕ
на конечное число фиксированных кусков Ai, Д2,. .., Ат
и определим «крупнозернистую» плотность Pt таким об-
1) В то время как вероятность покинуть эту окрестность равна 11
разом: если | принадлежит Дг-, то
t(p, q)dPl ... dpndqx ...dqn
(|Д/| — объем Л,-).
Предположим теперь, что при t = 0 плотность Do по-
постоянна в каждом куске (т. е. Do = Po при ^ = 0). Тогда
«теорема» Гиббса утверждает, что
Pt (I) -> const
независимо от куска, где выбрана точка ?.
Пытаться доказать это утверждение почти безнадеж-
безнадежно; оно является более сильным, чем эргодическая тео-
теорема. Известные доводы самого Гиббса (основанные на
аналогиях с перемешиванием жидкостей), даже если от-
отбросить содержащиеся в них существенные ошибки, слу-
служат в лучшем случае указанием на правдоподобность
этой «теоремы».
Тем не менее верна следующая забавная теорема, до-
доказанная Эренфестом (он устранил ошибку Гиббса).
Определим r\t (гиббсовская «энтропия») формулой
(III. 9.0)
i
= fPt\ogPidp1...dpndql ... dqn.
Тогда
4t < %
Крайне простое доказательство основано на неравен-
неравенстве
(III. 9.1) х log х — х log у — х -f у > 0.
Напишем
Л/ — Ло = / Л 1оё Ptdx — j Do\ og Do dx =
= J Dt log Ptdx — fD0 log Do dx =
= dpx ... dpndqx ... dqn.
Из теоремы Лиувилля следует, что
J Do log Dodx = f Dt log Dt dx,
и поскольку
мы получаем
Л, - Ло = / (A log Я, - D, log D, + D, - Pt) dx.
Отсюда в силу неравенства (II 1.9.1) следует, что
Л/ < Ло-
Эта теорема показывает, что гиббсовская энтропия (в
действительности отрицательная энтропия) является
наибольшей при кусочно равномерном 1) распределении,
но ничего не говорит нам о ее поведении во времени.
Идея Гиббса о том, что вероятность следует вводить
в механику только посредством плотности ?>@), ка-
кажется, конечно, очень привлекательной. Но, вообще го-
говоря, эта точка зрения, по-видимому, несостоятельна, и
вероятность в механике должна появляться и разными
другими путями. Мы еще обсудим это в пп. 14 и 15.
Подход Гиббса можно применить к вероятностным
моделям, подобным модели Эренфестов.
Тогда это просто означает, что мы задаемся каким-
либо начальным распределением D(n; 0) 2) и пытаемся
определить D(m; 5), т. е. вероятность найти систему в
состоянии m после 5 шагов.
«Теорема» Гиббса в этом случае означала бы, что
lim D (m\ s) = W(m) = C?R . 2
-2R
S-+00
1) To есть при распределении, плотность которого постоянна на
каждом куске Л/. — Прим. перев.
2R
2) То есть таким набором чисел D(n\ 0) ]>0, что ^D (/г; 0)=1.
Как было замечено на стр. 100, это не так, если
D(n; 0) = l, л = Ло,
D (п\ 0) = 0, п Ф п0.
Причина состоит в том, что такое распределение недо-
недостаточно «крупнозернисто». Мы еще вернемся к этому
вопросу после более детального обсуждения эренфестов-
ской модели, которому посвящены два следующих
пункта.
10. Мы покажем теперь, как вычислить вероятность
(III. 10.1) P{nA(s) = m\nA@) = n}
для эренфестовской модели.
Введем сокращенные обозначения
(III. 10.2) Р \пА(s) = т\пА@) = п) = Р(п\т\ s),
(III. 10.3) Р(п |т\ \) = P(n\m) = Q(n]mI)
и напомним, что
(III. 10.4)
Р (п | т\ s) = 2j Q (п | #j) Q (#! | n2) ... Q {ns_^ | m).
Это следует, конечно, из конструкции самой модели, а
так называемое свойство марковости, т. е. то, что ве-
вероятность конечной цепочки
п, nlf ,.., ns_i, тп,
равна Q(п\п\)Q(ni\n2) .,. Q(ns_i|m), вытекает здесь
из независимости последовательных перекладываний
шаров.
Вероятности перехода Q(n\m) задаются формулой
(III. 10.5) Q(n\m) =
Если обозначить через Q матрицу вероятностей пере-
перехода, т. е. матрицу, в которой элемент с индексом (n, m)
1) Эти обозначения вводятся в соответствии с обозначениями
Уленбека в первой части приложения I.
равен Q(n\mI то, как мы видим из (III. 10.4), элемент
с индексом (я, т) матрицы Qs равен
(III. 10.6)
Р(п\т; s).
Это простое замечание является решающим в теории
марковских процессов и сводит ее к изучению степеней
матриц (или в более общем виде — некоторых линей-
линейных операторов).
Для того чтобы получить явное решение, постараемся
диагонализировать матрицу Q, т. е. найти такую невы-
невырожденную матрицу Т, что
i О
(III. 10.7)
TQT~l =
0
После того как нам удастся это сделать, мы получим
1 0
(III. 10.8)
Qs =
0
7\
и делу конец!
Хорошо известно, что несимметрические матрицы,
вообще говоря, не всегда приводятся к диагональному
виду. Однако в нашем специальном случае такое приве-
приведение можно выполнить в явном виде.
Сначала заметим, что матрица Q выглядит так:
о
1
о
0 2B
0
0
-1
о
о
1-2B/?
r1
. . . 0
. . . 0
. . . 0
..10
Ее левые собственные векторы определяются системой
линейных уравнений:
) X Ях
Рассмотрим теперь бесконечную систему
(III. 10.9)
* = 0, 1, 2, ...,
где х_1 = 0, и заметим, что всякое решение бесконечной
системы, удовлетворяющее условию
(III. 10.10)
автоматически является решением конечной системы и
определяет, следовательно, левый собственный вектор.
Введем производящую функцию
о
и получим с помощью (III. 10.9) уравнение
или
(III. 10.11) f(z) = xo(l— zf{l-l)(l~i-z)
Поскольку f(z) аналитична вблизи нуля, наши формаль-
формальные действия законны. Заметим теперь, что если
(Ш. ю.12) а,=//?-\у = -/?, —/?+i, ...,o,i,..., /?,
то / — полином степени 2R, и, следовательно, условие
(III.10.10) выполняется.
Числа 'k = jR~l служат, таким образом, собственными
значениями матрицы Q, и поскольку их ровно 2^1
они исчерпывают все ее собственные значения.
Компоненты левых собственных векторов
cfc» = i, с(Л (У,..., ей
определяются, как легко видеть, с помощью тождества
(III. 10.13) A —zf-J(l+z)R+J= Ц C(/V.
о
Левые собственные векторы образуют строки матрицы Г,
и нам осталось найти только обратную матрицу Т~1. Для
этого нужно решить уравнение
V C(kj)a(p = b(k, r); k, г = 0, 1 2/? *).
Мы имеем
2R R
= A _г) V (i +z)
2/?
= 0 -^24^.A4
ИЛИ
2/?
Полагая
мы получаем
и
2/?
/=о
Сравнивая это выражение с формулой (III. 10.13), мы
находим
1) Таким способом мы найдем в действительности матрицу, об-
обратную к транспонированной матрице Т, но это не меняет дела.
или
Теперь легко вычислить P(n\m: s) [см. (III. 10.6) и
(III. 10.8)]; мы получаем окончательно
(III. 10.14) P(n\m; s) = (— If2'2i?
11. Решение, изложенное в предыдущем пункте, яв-
является исторически первым A947 г.). Оно проводится
обычным способом теории марковских цепей, хотя и тре-
требует, как читатель мог заметить, некоторого искусства.
Вскоре после его опубликования было предложено не-
несколько других решений. Среди них представляет зна-
значительный интерес решение, найденное независимо Зи-
гертом и Гессом. Мы здесь следуем изложению Гесса.
В рассмотрениях предыдущего пункта состояние си-
системы определялось числом шаров в ящике А. При та-
таком определении состояния наша вероятностная модель
становится марковской цепью; ее вероятности перехода
задаются матрицей Q.
Гесс и Зигерт предложили более сложное определе-
определение состояния системы. При этом весь процесс по-преж-
по-прежнему образует марковскую цепь, однако матрица ве-
вероятностей перехода выглядит крайне просто и может
быть почти сразу приведена к диагональному виду.
По Гессу и Зигерту, состояние системы определяется
указанием точного положения каждого шара1).
Если ввести векторы
1\ /0
и 6 =
то каждое состояние системы можно представить тен-
тензорным произведением
п — р V р V Yp
1) Читатель, знакомый с терминологией статистической механи-
механики, поймет, что здесь мы имеем дело с микросостояниями, в то вре-
время как в предыдущем решении использовались макросостояния.
где каждое Ej принимает значение либо а, либо C; а со-
соответствует ящику Л, р — ящику В.
Так, например, произведение
представляет состояние, при котором все шары, за
исключением второго, находятся в ящике А.
Введем теперь матрицу
О 111
1 о г •
обладающую тем свойством, что
5а = р, 5р = а,
и рассмотрим тензорное произведение
5/ = /Х/Х...Х5Х...Х/
(/—единичная матрица второго порядка).
По определению
*->/Л == ei X ?2 X • • • X *^е/ X • • • X е2/?'
и, таким образом, действие Si на ц эквивалентно пере-
перекладыванию i-ro шара из одного ящика в другой.
Теперь ясно, что
является линейной комбинацией 22Я векторов1), отве-
отвечающих всевозможным состояниям нашей системы (по-
(понимаемым в новом смысле). Коэффициент при r\i в этой
линейной комбинации равен, очевидно, вероятности
того, что, выходя из состояния г), система через s шагов
попадает в состояние г];.
Если, как обычно, определить скалярное произведе-
произведение векторов
1) Точнее тензорных произведений, но мы можем их считать и
просто векторами, не опасаясь недоразумений..
формулой
Л * б = П
то можно написать
Теперь легко убедиться в том, что
где сумма берется по всем С?/? состояниям г], при кото-
которых в ящике А лежит п шаров, и по всем C™R состоя-
состояниям Ц1, при которых в ящике А лежит т шаров.
Теперь ясно, что нужно лишь диагонализировать опе-
оператор
2Д
Матрица S имеет нормированные собственные векторы
Г
И V = - у
(они отвечают собственным значениям соответственно
1 и— 1). Очевидно также, что
а = 2~1/з (\х -f-v), р = 2~1/2(ц—v).
Далее ясно, что выражение
где каждое бг- есть либо (л, либо v, равно
где 2/ равно числу векторов |ш минус число векторов v
в произведении 61Х62Х ... Хб
Таким образом, числа
у//?, —
являются собственными значениями нашего оператора
(кратности Сзд~, соответствующими собственным век-
векторам
содержащим среди множителей ровно R+j векторов \х.
Теперь уже обычным путем снова приходим к фор-
формуле (III. 10.14).
Это решение, помимо своего изящества, замечательно
еще и тем, что оно содержит одну идею, которая может
оказаться весьма важной и общей.
Обычно сложность проблемы возрастает по мере
того, как учитывается все большее и большее число де-
деталей. Более того, слишком детальное описание может,
вообще говоря, оказаться совершенно неприемлемым1).
Метод Гесса — Зигерта показывает, что это не всегда
так. Здесь сокращение в описании (или отбрасывание
части информации) усложняет задачу!
Соотношение между подробным и сокращенным опи-
описанием касается самого существа статистической фи-
физики, но в настоящее время мы все еще далеки от его
правильного понимания.
Последнее замечание. Вообще говоря, если мы объ-
объединим состояния в группы и затем будем рассматри-
рассматривать эти группы в качестве новых состояний, то марков-
марковский характер процесса может нарушиться2). В действи-
действительности мы часто должны производить «разукрупне-
«разукрупнение», чтобы вернуться к исходному марковскому процессу.
12. Вооруженные формулой (III. 10.14), которая дает
полное решение задачи Эренфестов, мы можем вернуть-
вернуться к вопросу, обсуждавшемуся в конце п. 9.
Заметим сначала, что при s-> 00 все члены, кроме
двух, в формуле (III. 10.14) стремятся к нулю. Не исче-
исчезают лишь члены, соответствующие j=R и /= — R. Они
/ В связи с этим см. специальные лекции Уленбека в приложе-
приложении I к этой книге.
2) Если упустить это из виду, то могут возникнуть ошибки. Так,
например, в прекрасной обзорной статье Чандрасекара в Rev. Mod.
Phys. A943) есть несколько таких ошибочных «укрупнений» во мно-
многих местах гл. III.
равны: для j = R
/ л\п 0-2Rr(R)r(R-n) rm 0-2R w/ / ч
(—1) 2 Lm L2R =C2R- 2 =W(m)
и для j= — R
(•_!)*(_1)я 2-w6-R)C{0R~n) = (-\)s+n+m W(m).
Таким образом,
2R
D (m\ s) = ^D{ti\ 0) P(n\m; s)~
n = 0
2R
~W(m)+(— l)m+s W(m)%(—l)nD(n; 0).
Очевидно, что если D(n; 0) меняется медленно, то вто-
второй член мал, особенно при больших /?.
Строго говоря, даже крупнозернистое распределение
D(m\ s) не стремится к W(m), но отклонения имеют
приблизительно порядок R~\ и ими можно спокойно пре-
пренебречь.
С помощью формулы (III. 10.14) можно вычислить
различные средние значения, хотя это можно сделать
также и непосредственно, не используя этой формулы.
Мы получаем
((nA(s)-RJ) = (n0-RJb -2/гТ
Отсюда
({nA(s)-R)*-((nA(s)-R)Y) =
= («0 - Rf [A - 2/Г7 "A - R'T] + 4 [1 -О -2/Г У]
и, наконец,
((nA(s)-R-{nA(s)-R)J)
L
Мы вычислили квадрат так называемой «относительной
флуктуации»; эта величина измеряет устойчивость сред-
среднего значения.
В самом деле, с помощью классического неравенства
Чебышева получаем
ф;
2
>е
и, следовательно,
— 1
nA(s)-R
(nA(s)-R)
Если no = 2R и 5 имеет порядок xR, мы получаем
Ф? ~ (ехр Bх) — 1) B/?) — xR~\
и, таким образом, отношение Ф?/е2 мало, если 82/?^>1.
2 2
Если no = 2R и 5 имеет порядок /? , то ф5 становится
огромным [приблизительно порядка BR)~l ехр 2/?] и пре-
предыдущее неравенство уже бесполезно. В действительно-
действительности можно показать, что в этом случае большие откло-
отклонения от среднего весьма вероятны и «усредненная»
кривая
теряет смысл. С другой стороны, как уже упоминалось в
п. 7, среднее время возвращения в состояние no = 2R
равно 2т и R2 значительно меньше, чем 22Я. Таким об-
образом, вообще говоря, неверно, что в течение всякого
промежутка времени, малого по сравнению с циклом
Пуанкаре, система ведет себя необратимым образом.
Крайне невероятно, что система вернется в состояние
no = 2R за промежуток времени порядка R2, но ожидать,
что в течение всего этого времени поведение системы бу-
будет в каком-то смысле монотонным, было бы верхом оп-
оптимизма!
13. Марковский характер эренфестовской модели [вы-
[выражаемый формулой (III. 10.4)] позволяет существенно
подробнее обсудить задачу о времени возвращения.
Пусть
?'{п\т\ s)
обозначает вероятность того, что после 5 перекладыва-
перекладываний в ящике А впервые окажется га шаров, если вна-
вначале их там было п.
Справедливо следующее соотношение:
(III. 13.1)
5-1
Р(п\т; s) = P'(n\m; s)-f 2 Р'(п\т; k) Р (т\т\ s — k).
*i
Чтобы убедиться в этом, достаточно заметить, что если
вначале в ящике А было п шаров, то прийти к га шарам
за 5 шагов можно следующими взаимно исключающими
друг друга 5 способами:
(а) га достигается впервые после 5 шагов;
(б) т достигается впервые на первом шаге, и затем
через E— 1) шагов мы (начиная уже с га шаров) снова
возвращаемся к га шарам;
(в) га достигается впервые за два шага, и затем че-
через (s — 2) шагов мы снова приходим к га, и т. д.
Каждый из этих способов дает соответствующий
вклад в сумму (III. 13.1). При этом марковский характер
процесса сказывается здесь в том, что вероятность ка-
каждой такой возможности — начиная с п шаров впервые
получить га шаров после k шагов и затем через 5 — k
шагов снова прийти к га шарам — равна произведению
Р'(п\т\ k)P(m\m\ s— k).
Если ввести производящие функции
со
h(n\m\z)= 2 Р'(п|т\ s)zs,
5=1
00
g (п | пг\ z) = 2 Р (п | tn\ s) z\
то видно, что соотношение (III.13.1) эквивалентно равен-
равенствам
(III. 13.2) g(n\m; z) — h(n\m\ z)-\-h(n\m\ z)g(m\m\ z)
или
h(n\m\ z) = g(n\m; z)/(l+g(m]m; z)).
Поскольку вероятность P(n\m;s) известна [см.
(III. 10.14)], мы тем самым знаем g(n\m\z) и, следова-
следовательно, знаем, по крайней мере в принципе, h(n\m\z) и
Р'(я|т; 5). В действительности найти явные формулы
для Р'(п\т\ s) очень трудно.
Однако следующие результаты получаются почти не-
немедленно:
оо
h(n\n; 1)=S P'(n\n; s) = \,
s=l
lim
Эти результаты нам уже известны с более общей точки
зрения. Тем не менее теперь можно пойти дальше и вы-
вычислить, например, дисперсию времени возвращения
2
5=1
Не вдаваясь в подробности, мы упомянем лишь, что для
n = 2R получается
2
Это показывает, что возвращение в состояния, далекие
от равновесия, происходит с такими огромными 'флук-
туациями, что теряет всякий смысл говорить о среднем
времени возвращения.
Это другое выражение того явления, которое мы об-
обсуждали в конце предыдущего пункта.
Рассмотрение эренфестовской модели мы закончим
кратким обсуждением понятия энтропии в применении
к этой модели. Мы следуем изложению М. Дж. Клейна.
Существуют два определения энтропии, принадлежа-
принадлежащие одно Больцману, другое — Гиббсу.
Больцман определял энтропию как логарифм числа
микросостояний, реализующих данное макросостояние
системы (точнее этот логарифм, умноженный на k, где
k — постоянная Больцмана, но это несущественно для
нашей искусственной модели), т. е.
Гиббс определял энтропию через величины Р(га; s)
(т. е. вероятности найти систему в состоянии т в мо-
момент времени s).
Его определение таково:
(III. 13.3) 5г = —
т
где Н^(/я) задается формулой
(III. 13.4)
Заметим, что выражение (III. 13.3) совершенно ана-
аналогично формуле (III. 9.0).
Что означают оба эти определения для равновесного
состояния?
Следует заметить, что равновесие имеет совершенно
разный смысл у Больцмана и у Гиббса. По Больцману,
равновесием называется состояние с наибольшей энтро-
энтропией, т. е.
m = R.
Таким образом,
(если пренебречь членами порядка log/? и выше).
По Гиббсу, равновесным называется не состояние, а
распределение в пространстве состояний. Другими сло-
словами, различные величины, описывающие систему, нахо-
находящуюся в физическом равновесии, Гиббс получает ус-
усреднением по всем состояниям, но при этом усреднение
происходит относительно распределения вероятностей
с наибольшей гиббсовской энтропией. Итак,
5г;Равн, = тах5г,
и можно показать (повторяя рассуждения, проведенные
в конце п. 9), что максимум достигается для
Р(/ю; s)=W(m)
и, следовательно,
Таким образом, в случае равновесия эти два опреде-
определения энтропии совпадают; они различаются только по-
поведением энтропии во времени.
Гиббсовская энтропия возрастает с ростом времени 5.
Это простое следствие выпуклости функции х log x и
того обстоятельства, что Р(га; s+1) • 2-2R/W(m) яв-
является линейной комбинацией
где
Больцмановская энтропия изменяется гораздо более
беспорядочным образом (как это демонстрирует график
на стр. 97), и только среднее ее значение ведет себя
монотонно.
Заметим кстати, что, как мы видели, монотонное из-
изменение 5г не означает, что Р(/п; 5) [или лучше
Р(п\т\ s)] стремится к W(m). В самом деле, мы знаем,
что Р(га; 5) в строгом смысле не приближается к W(m)l
Эти два определения приводят к двум различным
формулировкам второго закона термодинамики.
В одной формулировке (Больцман) понятия состоя-
состояния и энтропии вполне наглядны, но при этом нельзя
прямо утверждать, что энтропия монотонно возрастает.
Во второй формулировке (Гиббс) возрастание энтро-
энтропии строго доказывается, но само понятие энтропии, а
также способ приближения к равновесию очень сложны
и не очевидны.
14. Мы столь подробно обсуждали эренфестовскую
модель, потому что ее рассмотрение является превосход-
превосходным введением в статистическую механику необратимых
процессов. Тем не менее эта модель не может помочь
нам понять более существенную проблему, каким обра-
образом вероятность появляется в классической механике.
Чтобы разобраться в этом вопросе, мы обсудим дру-
другую искусственную модель, которая по своему харак-
характеру значительно ближе к «реальности».
Рассмотрим п равноотстоящих друг от друга точек
на некоторой окружности; отметим т из них и обозна-
чим это множество_через S; остальные п — т точек со-
составят множество 8. В каждую из точек мы положим
белый (б) или черный (ч) шар. Пусть за единицу вре-
времени каждый шар перемещается против часовой стрелки
в ближайшую точку, причем выполняется следующее
правило: если шар находился в точке из S, то при пере-
перемещении его цвет меняется; шары, находящиеся в точ-
точках из 8, сохраняют свой цвет.
Предположим, что сначала все шары были белыми;
спрашивается, что произойдет после многих перемеще-
перемещений.
14а. Аналог классического решения Больцмана.
Пусть NqA) (N4(t)) —общее число белых (черных) ша-
шаров в момент времени t (т. е. после / перемещений,
t принимает целые значения) и Nq(S\ t) '(N4(S; t)) —
число белых (черных) шаров, находящихся в момент
времени t в точках множества S. Мы сразу можем на-
написать следующие соотношения (законы сохранения):
N6(t + l) = N6(t)-N6(S; t) + N4(S; t),
A11. 14.1) лгч(*-|_1) = ли*)-ЛМ5; t)-+N6(S; t).
Теперь, следуя Больцману, мы введем предположение
(«Stosszahlansatz»), что
N6(S; t) = mn-1N6(t),
(III. 14.2) N4(S;t) = mn-W4(t),
и получим
Отсюда
(III. 14.3) rr*[N6(t)-N4(t)] =
= A — 2тп~1У я-> [W6 @) — W4 @)] = A —
и, следовательно, если
(III. 14.4) 2т <п
(что мы в дальнейшем и будем предполагать), то число
черных шаров монотонно приближается к числу белых.
Этот вывод очевидным образом непригоден, посколь-
поскольку наша модель полностью «обратима». Действительно,
начиная с одних белых шаров GV4@) =0), будем дви-
двигать их некоторое время, а затем изменим направление
движения (по часовой стрелке), предварительно повер-
повернув множество S на один шаг против часовой стрелки.
Мы вернемся тогда к начальному состоянию вопреки
формуле (III. 14.3), которая для «обращенной» модели
должна выполняться так же хорошо, как и для исход-
исходной.
Кроме того, эта модель строго периодична с перио-
периодом 2п (цикл Пуанкаре), что опять-таки несовместимо
с (III. 14.3).
146. Теоретико-вероятностное рассмотрение. Совер-
Совершенно ясно, что источником этой трудности являются
формулы (III. 14.2). Они должны быть заново истолко-
истолкованы, и их смысл следует «выяснить более тщательно.
Пусть
+1, если в момент t шар в точке
(IIIЛ 4.5) цМ) =
р(\ </? <я) белый
—1, если в момент /этот шар черный.
Оусть, кроме того,
(Ш. 14.6) гр
Тогда
(III. 14.7) M0 = W-l)?P-i
и, следовательно,
(III. 14.8) х[р (*) = x[p_t @) гр_гер_2 ... ep_t.
(Ясно, что р — к следует брать по модулю п.)
Отсюда
N6 (t) - N4 (t) = 2 л, (*) = 2 Ъ-t (°) гР- i*p-2 • • • е„_„
р р
и в простейшем случае Мч@) = 0 [т. е. "П^, @) = 1 ] имеем
(III. 14.9) tr*[N6(t)-N4(t)] = n-'2viVa ••• W
Если вся информация относительно множества S ис-
исчерпывается тем, что оно содержит т точек (т. е. 2е^ =
р
= п — 2т), то представляется естественным рассматри-
рассматривать величину
(III. 14.10) п-^гр_ггр_2 ... ep_t
Р
статистически.
Если мы предположим, что все возможные располо-
расположения множества S равновероятны, то мы сможем легко
вычислить среднее значение величины (III. 14.10) с по-
помощью очевидной формулы
(III. 14.11) (л^ V)
/ \ 1 V
= <e!e2 ... е/) = -^г2^ г^ * * * 8"
где штрих означает, что суммирование происходит при
дополнительном условии
2 гр = п — 2т.
р
Замечая, что
Bшт1/-
dz
С
z
?ер+1ч
1,. если
р
0, если ^грф п — 2т
(С — простой замкнутый контур, охватывающий начало
координат), мы получаем
z
где суммирование под знаком интеграла происходит уже
по всем возможным наборам е. Итак,
и, используя формулы (III. 14.9) и (III. 14.11), мы по-
получаем
A11.14.12) (l(N6(t)-N4(t))) =
Bm-) f z-1 A - г2У A + *W+ l)nz'2m
с
z'2mdz
~~ BШГ1 f(z2+ l)a z-<2m + V dz
С
Если фиксировать t и устремить п и т к бесконеч-
бесконечности так, чтобы
(III. 14.13) Hm mn~l = \i < j,
то, применяя метод перевала (который в этом простом
случае легко обосновать), можно получить
(III. 14.14) Hm (n-'(N6(t)-N y
что устанавливает справедливость формулы (III. 14.3)
«в среднем».
Чуть более сложное вычисление показывает, что при
указанном предельном переходе дисперсия величины
n-l(Nb(t) —Л/ч@) стремится к нулю (как п~1).
Наконец, можно показать, что
(III. 14.15) Hm </i-W6(S, t)) = \illm{rr1N4(t)).
П-+ОО
Это оправдывает «в среднем» предположение (III. 14.2).
Немного поразмыслим теперь, что это все означает.
Допустим, что мы построили для каждого множе-
множества S график величины n~l(N4(t) —Л^б(О) (как Функ-
Функции t). Мы получим С™ «кривых», начинающихся в еди-
единице при /=0 и имеющих период 2я. Допустим также,
что мы смогли бы взглянуть на все эти кривые в фикси-
фиксированный момент времени /<С п. Можно считать п по-
порядка 1023, a t — порядка 106. При таком t ординаты
всех кривых сосредоточены в очень узкой окрестности
около A — 2\\)г и большие отклонения от A—2\х)г
можно воспринимать как чрезвычайное невезение.
Как ни убедительны эти аргументы, мы должны по-
помнить, что в предположении о равновероятности всех
расположений множества S содержится элемент про-
произвола. Хотя это предположение, несомненно, можно
ослабить, какое-то допущение подобного рода неиз-
неизбежно.
В терминологии Эренфеста кривая A—2\х)г является
кривой Н-теоремы [в то время как каждая индивидуаль-
индивидуальная кривая n~l(N4(t) —Л^б(О) является Я-кривой], или
«Verdichtungskurve».
15. «Круговую модель» из п. 14 можно рассматри-
рассматривать дальше, с тем чтобы лучше понять схему, опи-
описанную в конце первой части приложения 1, принадле-
принадлежащего Уленбеку.
Прежде чем перейти к этому, мы несколько изменим
нашу модель, чтобы облегчить вычисления.
В предыдущей формулировке число m элементов мно-
множества S считалось строго фиксированным. Ослабим те-
теперь это условие, применив следующий прием. Для ка-
каждой из п точек мы произведем испытание (бросание
монеты), имеющее вероятность успеха |^<9"- В соответ-
соответствии с исходом этого испытания мы включим или не
включим эту точку в множество S.
Другими словами, переменные е принимают уже не
фиксированные, а случайные значения с вероятностями
(III. 15.1) Р {еу = — 1} =\х; Р {еу = 1} = 1 — \i.
Мы предположим далее, что испытания (бросания) про-
происходят независимо друг от друга, так что еь е2,..., еп-^
независимые случайные величины.
Число элементов множества S равно, таким образом,
т = тг п —
и также является случайной величиной. Среднее значе-
значение числа элементов равно
дисперсия же этого числа равна
Таким образом, можно считать, что отклонение т от
(in в подавляющем числе случаев имеет порядок У~п, и
мы с уверенностью можем ожидать, что результаты не
изменятся оттого, что мы прибегнем к этому обходному
маневру.
Для такой измененной модели мы получаем
= <еЛ ... е,> = <е,> (е2) ... <е,> = A
в полном согласии с прежним результатом.
Вычисления теперь стали значительно проще, и мы
обошли сложный вывод асимптотической формулы
(Ш.14.19).
Эта уловка хорошо известна в статистической меха-
механике. Читатель, знакомый с обычной терминологией, за-
заметит, что «микроканонический ансамбль» (определен-
(определенный тем жестким ограничением, что число элементов
множества S равняется т) мы заменили «каноническим»
(или точнее «большим каноническим») ансамблем, в ко-
котором это ограничение существенно ослаблено.
Что служит Г-пространством для нашей модели?
Ясно, что это множество всех векторов
4 = 011. % •••> ЛЛ Лу=±Ь
Оно содержит 2П точек.
Если
p(tj; О) = р(ть ..-, r\n; 0)
— начальное распределение
(р(ч;0)>0, 2
и если мы знаем положение множества S, то мы можем
написать уравнение, аналогичное уравнению Лиувилля:
(III. 15.2) p(Th, ri2, ..., цп\ / + l) = p(e1ri2, е2т1з, ..., е^; t).
Мы можем переписать его в виде
где L — «оператор Лиувилля» — является унитарным
оператором.
Мы можем теперь формально написать
и, усредняя по всем положениям множества S, получить
(III..15.3) <p(t)) = (Lt)9@).
Вообще говоря, это очень трудно сделать, поэтому фи-
физики заменяют уравнение (III. 15.3) уравнением
<р (*)> = <?>'Р(О).
Этот другой подход приводит к тому, что мы назы-
называем в настоящее время «основным уравнением». Про-
Проанализируем, что при этом получается.
Мы перейдем от описания в терминах оператора L
к чисто вероятностному описанию.
Если в момент времени t модель находилась в со-
состоянии 6, то может произойти переход в состояние ц
(за единицу времени), где
Вероятность перехода Ь->ц равна вероятности того, что
Поскольку 8i, 82,... ,8П независимы и удовлетворяют
условию (III. 15.1), мы получаем
(III. 15.4)
Заменим теперь уравнение Лиувилля (III. 15.2) «ос-
новным уравнением»
(III. 15.5) «р (Ч; t +1) = 2 Ф E; t) Р (81Ч)
с начальным условием
(III. 15.6) срE; 0) = р(8; 0) = р(8).
Мы обозначаем теперь распределение символом ср вме-
вместо р, потому что ф(т]; /), вообще говоря, не совпадает
с р(ц; t). «Основное уравнение» можно легко решить,
если заметить, что ф(т],* 0) = р(т]) можно единственным
образом представить в виде
(III. 15.6) <p(ij; 0) =
• # • +4 2,..., nW * • ' %•
Далее,
и вообще
(III. 15.7)
Следует заметить, что «основное уравнение» является
полным аналогом уравнения
(III. 15.8) Р(л|/и;$+1) =
которое управляет изменением распределения во вре-
времени для эренфестовской модели.
Основное различие состоит в том, что в эренфестов-
эренфестовской модели уравнение (III. 15.8)—строгое следствие
исходных вероятностных предположений, в то время как
в нашей модели «основное уравнение» является лишь
специальным допущением, подсказанным уравнением
Лиувилля и интуицией.
Основная проблема состоит, таким образом, в том,
чтобы обосновать эту вероятностную трактовку, опи-
опираясь на уравнение Лиувилля (III. 15.2).
К счастью, мы можем выписать решение уравнения
(III. 15.2) в явном виде, а именно
(III. 15.9) p(ijlf ...9fin;t) =
= p(...,e/?, sp+1, ..., ep+i_v 7ip+g, ...; 0) =
= 2~" + S cpnp+fip ... ep+t_1 +
p
Таким образом,
(in. 15.10) ф(Ч; о = (р(ч; 0> = ^{р(ч; 0} =
P<Q
Это не совпадает в точности с тем, что дает решение ос-
основного уравнения. Действительно,
(III. 15.11) {ер ... ep+t^eq .. . s^+/_1) = (l — 2ц)д(/7'*; °.
где
(III. 15.12) &(р> q\ t) = \ ^
\ 2{q —p), q —р < t,
откуда видно различие в некоторых членах.
Чтобы выяснить ситуацию, мы ограничимся лишь
симметрическим начальным распределением, т. е. та-
таким, что
сь = съ
Ck, l==C\,2
и т. д. Формула (III. 15.10) запишется теперь в виде
(III. 15.13)
Кр<ч<п
Мы видим отсюда, что не только возникает различие
в некоторых членах, но даже разрушается исходная сим-
симметричность.
Симметризуем теперь -ф (т|; t). Получим
(II. 15.14) 5 {*Df t)}=2~n+ A-2^
р
+ ^i,2 2 A-2йL(Л';0 2 VW+-
••• +(-1L,2 л---v
Для фиксированного ^ и больших /г имеем
и т. д., что уже явно согласуется с решением основного
уравнения.
Остаются еще члены вида
которые не исчезают даже после симметризации, однако
это несущественно: если начальное распределение до-
достаточно гладко, то в разложении (III. 15.6) отсутствуют
(или почти отсутствуют) «высокие гармоники». Иными
словами, следует рассматривать лишь достаточно «круп-
«крупнозернистые» начальные распределения. Наше рассмо-
рассмотрение выявило еще одну трудность, связанную с «ос-
«основным уравнением».
Очевидно, что при замене
х. 2 (i-
величиной
х
п
A-2IXJ'
возникает ошибка порядка
Аналогично ошибка, возникающая при замене третьего
члена, имеет порядок
г2/г3
и т. д.
Каждая из этих ошибок стремится к нулю при п-+оо,
но это может быть не так для суммарной ошибки, если
только коэффициенты с не убывают достаточно быстро.
Таким образом, мы снова приходим к необходимости
считать начальное распределение достаточно «крупно-
«крупнозернистым».
Следует добавить еще несколько слов, чтобы объяс-
объяснить значение симметризации.
Рассмотрим частичное распределение
(III. 15.15) /(v П,;*) = 2Ч(Ч;').
где два штриха у знака суммы означают, что суммиро-
суммирование происходит по всем щ, кроме k\v и r\q.
Из (III. 15.13) легко получается равенство
(III. 15.16) /(%,%; t) =
= 1
или в другом виде
-f-?12(l — 2\i)^^Ptq;t)(ol(d2 (o)j, со2 равны либо+1, либо —1).
Таким образом, совместное распределение вероятно»
стей для значений в двух фиксированных точках при
t-+oo не стремится к равновесному распределению. Од-
нако совместное распределение вероятностей для значе-
значений в двух (или более) фиксированных точках нам и не
нужно. На самом деле нас интересует совместное рас-
распределение для значений в двух случайно выбранных
точках. Такое совместное распределение дает именно
симметризация f(coi, co2; t) [здесь мы, разумеется, пред-
предполагаем, что все пары (/?, q), p<q, равновероятны]. Мы
приходим, таким образом, к формуле
5 {/К, «2; *)} ==-L + (l_2lx)'c1(ffl1 +
В пределе при д^-оо (^ фиксировано) получаем
± + (\-2\i)'cl(<i>l + <o2) + cl,2(l—2\if<ol(o2,
что согласуется с решением основного уравнения.
Если здесь допустимы аналогии (возможно, очень
натянутые) с кинетической теорией, то мы можем ска-
сказать, что в больцмановской теории функцию f(vu vz\ t)
следует понимать не как совместную вероятность для
значений скоростей двух фиксированных молекул, а
как совместную вероятность для значений скоростей
двух случайно выбранных молекул.
16. Больцмановская теория разреженного одноатом-
одноатомного покоящегося газа (случай пространственной одно-
однородности) также может быть построена с помощью ос-
основного уравнения.
Обозначим через Vi, v2, ... , vn скорости п молекул и
составим из них (Зд-мерный) «основной вектор» R
(III. 16.1) R = (v,, v2, ..., vn).
Рассмотрим теперь процесс, при котором за промежуток
времени dt может произойти «столкновение» /-й и /-й
частиц (i<j), причем направление их линии центров
(т. е. линии, соединяющей центры /-го и /-го шариков в
направлении от I к /) задается вектором I с точностью
до элемента d\. Мы предполагаем, что вероятность та-
такого столкновения представима в виде
(III. 16.2) bjdldt = ^((yj-vi)'l Ivj-vtftdldt.
Для случая твердых шариков
(ш. 1б.з) bj=^\(\(yJ-yt).\\-(y;-vt)-\),
что соответствует больцмановскому предположению
(«Stosszahlansatz»).
Если (/, /, 1)-столкновение произошло, то R перехо-
переходит в Aij(l)R, где
(III. 16.4) Alj(l)R = (vv ..., yl + ({Vj-y.).l)l ...
•••> vy —((vy — v,) • 1I, .... vj,
а остальные компоненты R не меняются.
Таким образом, мы можем сказать, что
R->^/;-(l)R с вероятностью ^tjd\dt,
R->R с вероятностью 1 —dt ^ f dltytJ.
К / < j < п
Поскольку при каждом столкновении сохраняются
импульс и энергия, мы имеем
(III. 16.5) Svy = const1),
п
(III. 16.6) 2 vr vy = const = ш2.
He ограничивая общности, мы можем считать, что по-
постоянная в формуле (III.16.5) равна нулю.
Таким образом, конец вектора R всегда лежит на
(Зп — 3)-мерной сфере Sn(o) радиуса а]/п. Пусть в
момент времени ^ = 0 начальное распределение для то-
точек R задается плотностью cp(R; 0). Легко видеть, что
изменение этого распределения во времени происходит
в соответствии со следующим уравнением:
(Ш. 16.7) W§JL =
= 2 / dl [ф <Ац О) R; 0 - ф (R; *)) Фу
<j <п
1) Это несовместимо с тем, что газ находится в сосуде, так как
при столкновении молекул со стенками импульс не сохраняется.
Однако это досадное обстоятельство можно обойти, если предполо-
предположить, что при каждом столкновении со стенкой молекула вновь по-
попадает куда-нибудь внутрь V с тем же импульсом. Это небольшое
затруднение возникает и при выводе исходного уравнения Больцма-
на; вывод этот не строго обоснован, так как в сосуде действуют
внешние силы.
Это и есть основное уравнение, аналогичное уравне-
уравнению (III. 15.5) для круговой модели, а также уравне-
уравнению (III. 15.8) для эренфестовской модели.
Поскольку при выводе «основного уравнения»
(III. 16.7) предполагалось, что все %j задаются форму-
формулой (III. 16.3), в нем уже содержится главное допуще-
допущение Больцмана («Stosszahlansatz»). Однако уравнение
(III. 16.7) в отличие от больцмановского уравнения
(III. 1.6) линейно. Ясно, что переход от уравнения
(III. 16.7) к уравнению (III. 1.6) требует дополнитель-
дополнительных предположений.
Чтобы обсудить эти предположения, а также более
отчетливо выявить ряд других обстоятельств, мы по-
построим упрощенную математическую модель, обладаю-
обладающую многими (если не всеми) существенными чертами
нашей задачи.
Пусть
(III. 16.8) R = (*!, ..., хп)
удовлетворяет условию
(III. 16.9)
и пусть
(III. 16.10) А/у (в) R = (.*!, ..., xt cos e + jcy sine, ...
..., — xt sin 6 ~f- Xj cos 6, ..., xn).
Пусть далее1)
(III. 16.11) Фу =-5^-= const.
l) Чуть большая общность достигается, если положить
= v/ (е)М где / (— 6) = / F) («микроскопическая обратимость»)
тс
и I / F) dQ = 1,/ F)>0. Вся теория тогда сохраняется без су-
—тг
щественных изменений. Эта более общая теория аналогична теории
максвелловского газа.
«Основное уравнение» теперь принимает вид
(Ш. 10.12) Щ^- =
2тс
=i 2 if ^(Аи@)R;') -
аналогом же уравнения (III.1.6) служит уравнение
(III. 16.13) д/<? ° =
оо 2тс
= v fdy-^f [f(x cos 0 + y sine, <) x
-оо О
Х/(— х sin 9-f-y cos6, t)—f(x, t)f(y, t)}dQ.
Наши упрощения состоят в следующем:
(а) мы отбросили закон сохранения импульса (III. 16.5);
(б) упрОСТИЛИ ВИД tyij\
(в) заменили более сложное шестимерное вращение
Aij(l) двумерным вращением Aij(Q).
Предположим теперь, что q>(R; 0)—симметрическая
функция переменных Хи ..., хп. Отсюда следует, что
cp(R, t) также симметрична.
Введем следующие частичные распределения:
(III. 16.14) /W; t)= f f (R; <)й„
x\\- ... -\-х^г = п-х2
(III. 16.15) An)(x,y,t)= f ф(Я; t)da2
о 9 9 9
и т. д. Интегрирование ведется по сферам, уравнения
которых написаны под знаком интеграла, а свободные
переменные заменяются на х, у и т. д.1)- Функции плот-
плотности /\\ /г , • • • естественно называть сужениями ф;
/kn) образует k-мерное сужение. Легко подсчитать
1) Разумеется, при этом de\, da2, ... определены соответствую-
соответствующим образом.
с помощью (III. 16.12), что
df[n) (х, t)
(III. 16.16) ' д) =
2TZ
/Z-JtT2)V2
J dy±
— л; sin 6 +у cos6, t)-~f2n)(x, у,
Это уравнение очень напоминает уравнение (III. 16.13).
Чтобы получить (III. 16.13), достаточно лишь предполо-
предположить, что
(III. 16.17) /f(jc, у, t)~An)(*> t)fxn)(y, t)
для всех х, i/ в допустимой области. Здесь мы немед-
немедленно сталкиваемся со следующей трудностью: функ-
функция qp(R; t) однозначно определяется распределением
qp(R; 0), и, следовательно, всякие дополнительные пред-
предположения о q>(R); t) должны быть выведены из неко-
некоторых заранее постулированных свойств распределения
q>(R;O).
Размышляя над этим обстоятельством, мы убедимся
в том, что для вывода уравнения (III. 16.13) нужно сна-
сначала доказать следующую теорему.
Основная теорема. Пусть <pn(R; 0)—последователь-
0)—последовательность плотностей вероятности, определенных на сферах
обладающая «больцмановским свойством»
(III. 16.18) lira f[n\xv ..., xk\ 0)= П Hm fT(xp 0).
n -> oo j = 1 n •> oo \ у /
фn(R, 0 [т. е. решение уравнения (III.16.12)] так-
также обладает «больцмановским свойством»
lim f:\xv ..., xk; *)= П Hm
/2"^°° /=1/2->0О
Другими словами, больцмановское свойство сохраняется
во времени!
Таким образом, оказывается, что нелинейность урав-
уравнения Больцмана (III. 16.13) возникает только благо-
благодаря крайне специальному предположению относитель-
относительно начального распределения. Основная теорема прояс-
проясняет, что прежде скрывалось за предположением о мо-
молекулярном хаосе.
Возникает вопрос, существуют ли плотности вероят-
вероятности, обладающие больцмановским свойством. Не вда-
вдаваясь в подробности, укажем, что если с(х)^ О и для
некоторого положительного z функция
с (х) ехр (— zx1)
интегрируема и если с(х) удовлетворяет некоторым сла-
слабым условиям регулярности, то можно показать, что
последовательность
П
/п
обладает больцмановским свойством.
17. Мы приведем теперь доказательство основной
теоремы в предположении, что функция (pn(R; 0) инте-
интегрируема с квадратом по Sn. Это условие гарантирует,
что распределение (pn(R; 0) достаточно «крупнозерни-
«крупнозернисто».
Рассмотрим гильбертово пространство интегрируе-
интегрируемых с квадратом вещественных функций i|)n(R), опреде-
определенных на сфере Sn, IIRII2 = fl, и линейный оператор Q:
(III. 17.1) 2фя =
1
Легко проверить, что
(III. 17.2)
и
(III. 17.3)
1
l < / < ; < п о sn
Оператор Q является, таким образом, самосопряженным
и, очевидно, ограниченным (хотя его норма может зави-
зависеть и в действительности зависит от п).
Итак, можно написать
(Ш. 17.4)
Пусть g(R)=g(xi)—ограниченная функция только од-
одного переменного. Из формул (III. 17.2) и (III. 17.4) мы
имеем
(III. 17.5) («MR; t), g(R)) =
Vn
= f Ф„ (R; t) g (x,) da= f fxn) (x, t) g (x) dx =
sn
Теперь
(III. 17.6)
Полагая
(III. 17.7)
Qg =
n
~ л" ^
; =
g(*>
r=
2n
d ^ J ^
2 0
y) =
2tc
0
-Vn
oo
-
(x} cos 6 -f
(x cos e +
k\
- Xj sin 6) —
у sin 6) —
мы получаем
(III. 17.8)
Далее,
(Ш. 17.9^
И
2тг
(III. 17.10) Qg2(xv x2) = ±±f {g2(xx cos e+*2 sin 6,
о
— хг sin 6 + *2 cos e) — g (*i» ^2)} do +
п 2тс
~^~~п ^J 2тг/ tS*2 (-^i cos в + ^ sin в, х2) —
;=3 О
п 2%
+ ~ ^ -^ J {g (^1э ^2 C3S 6 + л:;- sin 6) — g2 (xv x2)\ dQ.
; = 3 О
Поскольку фn(R; 0) >-0 и
(III. 17.11)
и так как \g(R)\<M, мы имеем |g|<2M и, следова-
следовательно,
(III. 17.12) |(Qg, фя(И; 0))|<2ЛГ.
Кроме того,
(III. 17.13) \Qg2\< 4М/П + 4М • 2(л — 2)/л < 2! • 4Ж
и, следовательно,
(III. 17.14) |Q2g-|<2!-22Af.
Вообще
(III. 17.15) |2*g, фл(К; 0)|<Л!.2^Ж.
Предыдущее доказательство применимо только для
. Однако эта формула остается справедливой и для
k>n, поскольку
\Q*g\ = \Qk~nQng[< n*-nn\2nM<kl- 2kM.
Далее
oo
(III. 17.16) lim ^g",<p«(R;O)) = J J/2(a:, y)g2{x,y)dxdy
где
(III. 17.17) f2(x, y)= lim /s'V, y, 0).
/Z -> OO
И вообще
(III. 17.18) lim (Q*g, фл(R; 0)) =
П -> oo
где gfe+i определяются по индукции следующим образом:
(III. 17.19) ?i (*)
cos 0 + л:Л+1 sin0, ..., хЛ) —
Так как мы предположили, что последовательность
9n(R; 0) обладает больцмановским свойством, мы имеем
(Ш.17,20) lim (Q*g, <pn(R; 0)) =
л ¦> oo
X gk+l (xlt ..., xk+l)dxx ... dxk+1>
где
A11. 17.21) f(x) = f1 (x; 0)= lim /?\х\ 0).
Из (III. 17.5), (III. 17.15) и (III. 17.20) следует, что-для
0<^<l/2v имеем
(III. 17.22) ff(x, t)g{x)dx =
где1)
/(*; f)=*fx{x\ t)= Hm
Начиная теперь с функции уг(*1, -^2) =g"(^i)^(x2) и опре-
определяя Yft(xi» ..., ^fi) по индукции с помощью формулы
(III. 17.19), мы снова получим для 0</<l/2v соотно-
соотношение
оо
(III. 17.23) f ff2 (xu x2;t)g (x,) h (x2) dxx dx2 -
•••> xk+2)dxx ... dxk+2.
Легко проверить, что
(III. 17.24)
(III. 17.25) y4(*i. ^ ^з» x4) = h2(x2, x4)g2(xv x3) -f-
i> x4)h2(x2, хг) +
и т. д.
!) Ясно, что здесь имеется в виду слабый предел в пространстве
L(—00, 00).
Таким образом, мы имеем, например,
оо
(III. 17.26) / / / / / (*i) • • • / (*4) Y4 (xv х2, х3, х4) X
(ОО v
ff(x)h(x)dx\x
-оо /
xlffff(x1)f(x2)f(x3)gz(xv х2У xz)dxxdx2dxA
—оо /
2 (f f f (х:) f (x2) g2 (xv x2) dxx dx2 \ X
X (/ / / (x,) f (x2) h2 (xv x2) dxx dxA
+ ( ff(x)g(x)dx\x
xlffff(xi)f(x2)f(x3)h3(xv х2У x3)dx1dx2dxA
и так как справедливы другие подобные формулы, то
для 0</<l/2v получаем
(III. 17.27) / / /2 (хи х2; t) g (Xl) h (x2) dxx dx2 =
— oo
oo
oo
v t)g(x1)dx1 f f(x2; t)h(x2)dx2.
—oo —oo
Так как g як произвольны, мы получаем для 0<^/<l/2v
(III. 17.28) /2(хи х2\ t)=f(xx; t)f{x2\ t).
Аналогичные, но более утомительные рассуждения при«
водят к формуле
(III. 17.29) fk(xv .. -, хк; t)=f{xx\ t) ... f(xk; t).
Ограничение, наложенное на промежуток времени
t@^,t<l/2v), можно устранить, если заметить, что оно
не зависит от начального распределения. Действительно,
выбирая некоторый момент времени /0. 0</0<Bv), за
начальный, мы можем, повторяя все предыдущие рассу-
рассуждения, доказать, что больцмановское свойство сохра-
сохраняется на интервале /0< t<to + Bv)~*. Продолжая та-
таким способом, мы, очевидно, исчерпаем все значения
/, 0</<оо.
Предыдущее доказательство теряет силу, если огра-
ограничение на промежуток времени зависит от начального
распределения. Оно неприменимо в важном для физи-
физиков случае твердых шариков. Пока не удается получить
общее доказательство того, что больцмановское свойство
сохраняется по времени.
18. Мы изучим теперь Я-теорему и вопрос о прибли-
приближении к равновесию.
Исходя из основного уравнения (III.16.12)
аи. 18.1) 41-=
2тс
= г 2 i / f<р (Аи @) R; 0 - ф (R; *)} м>
мы получим [см. (III.17.3)]
(III. 18.2) ^/
2%
\<i<j<n 0
и, следовательно,
(HI. 18.3) ijV(R; t)do<CO.
Далее, если а>1, мы получаем с помощью неравенства
Гёльдера
(III. 18.4)
< (/ Ф« (R) dof-1)la (/ Ф« (Аи F) R) def* = f Ф« (R) da
и, следовательно,
(III. 18.5) -
Поскольку
(III. 18.6) log q> = lim
>0
мы получаем как следствие из (III. 18.5), что
(III. 18.7) -%- f ф (R; t) log <p (R; t) do < 0.
Равенство в (III.18.3), (III.18.5) и (III.18.7) возможно
только при условии
(III. 18.8) <р (R, t) = const = \/Sn (//Г),
где Sn\\n) — поверхность сферы ||R||2 = fz.
Одномерное сужение распределения (III.18.8), как
легко видеть, равно
(III. 18.9) 141~*~'*2J1 •
Г -1 2 l{n"Z)
В пределе при п->оо получается плотность Максвел-
Максвелла — Больцмана
(III. 18.10) Bя)/2ехр(— \х2У
(См. в связи с этим первый пример из гл. I.) Мы дол-
должны теперь доказать, что х)
(III. 18.11) q)(R; t)->\/Sn(Vn)
при /-^оо, по крайней мере в слабом смысле; это озна-
означает, что для каждой функции x(R) 6 L2(Sn)
(III. 18.12) lim
t->oo
i Это просто эргодическое свойство рассматриваемого здесь
марковского процесса. Однако вместо того, чтобы обращаться к об-
общей теореме, мы предпочитаем придерживаться независимого изло-
изложения и приводим доказательство, в этом случае совсем простое.
Поскольку основное уравнение может быть записано в
виде
(III. 18.13) -J- = 2Ф,
где Q — ограниченный самосопряженный отрицательный
оператор, мы имеем
A11.18.14) (<p,x) /
= fexp(U)dx(E(b)<p(R;O), x (R)),
— схэ
где ЕA)—проекционные операторы, задающие разло-
разложение единицы для оператора Q.
Функция
(Ш. 18.15) r(a,) = (?(b)<p(R, 0), x(R))
имеет ограниченную вариацию, и, поскольку оператор Q
ограничен, г(Х) постоянна для достаточно больших от-
отрицательных X. Таким образом,
(III. 18.16) -^/ф (R; t)i(R)do= fXexp(Xt)dr(D
— со
и, следовательно,
(III. 18Л7) lim-^ f<p(R; t)%(R)da = 0.
/->оо
Из (III. 18.3) следует, что существует такая последова-
последовательность /s->oo, что cp(R; t8) слабо сходятся к функции
<Po(R), т. е.
(III. 18.18) lim Гф(К, ts)%(R)do= [%(R)%(R)do
S -> ОО J J
И
(III. 18.19) lim f(p(R; ts)%(Au(Q)R)do =
S -> CO J
Поскольку
(III. 18.20) -^
2%
[ dQ j do у (R; t) {% (Atj F) R) — % (R)},
Kt<j<n 0
из (III.18.17) следует (если считать, что t -> оо, пробе-
пробегая последовательность /s), что
(III. 18.21)
= S i
2%
2тс
/у @) R) - ф0 (R)}
и поскольку x(R)—произвольная функция, мы полу-
получаем
2%
(III. 18.22) 51 i / ^о Иу (9) R) - Фо (R)} dQ = 0.
Умножая обе части формулы (III.18.22) на cpo(R) и инте-
интегрируя по Sn, мы получаем
2%
(III. 18.23) ^ f
и, следовательно,
(III. 18.24)
для почти всех 9 и почти всех R. Чтобы из формулы
(III.18.24) вывести, что функция cpo(R) постоянна почти
всюду, нам нужно убедиться в том, что Л^F) по-
порождает транзитивную подгруппу в группе всех п-мер-
ных вращений. Это почти тривиально. Действительно,
если взять вектор
(III. 18.25)
то при помощи подходящего выбора Ai2(Q) можно пере-
перевести его в вектор
(III. 18.26) (УЩТЦ, О, ?з, ¦••.?„)¦
Выбрав затем подходящим образом Ai3, мы переведем
вектор (III.18.26) в вектор
(III. 18.27) (УЦ+Щ+Ц, 0, 0, ..., 1п)
и, продолжая таким образом дальше, мы получим, что
подобранное соответствующим образом произведение
(III. 18.28) А1пфп-1)-- А12фг)
переводит вектор (III.18.25) в вектор (]Лг, 0, ..., 0)=
= Ro. Предполагая, что значение <po(Ro) определено,
мы видим, что
(Ш. 18.29) Ф0(Т) = ф0A*0)
при условии, конечно, что выбран вектор Т, для кото-
которого значение фо(Т) определено и углы 6i, ..., 6n-i (ко-
(которые, очевидно, зависят от Т) не принадлежат исклю-
исключительному множеству меры нуль. Ясно, что для почти
каждого Т углы 6i, ..., 6„ не входят в это исключитель-
исключительное множество и, следовательно,
(III. 18.30) ф0 (R) = const = \/Sn (yT)
почти всюду.
Поскольку для любой последовательности ti, ..., ts
получается один и тот же предел фо^), мы имеем
(III. 18.31) lim <p(R; <) = <po(R),
t ->оэ
где предел понимается в слабом смысле.
Все предыдущие рассуждения проходят без каких-
либо изменений для общего основного уравнения
(III.16.7), только доказательство того, что Л^A) по-
порождает транзитивную подгруппу (Зп — 3) -мерной орто-
ортогональной группы, требует некоторых ухищрений.
Итак, мы показали, что «основная» плотность
Ф^; /) приближается при /->оо к равновесной плотно-
плотности
(III. 18.32)
и что такое приближение происходит «необратимо», как
это следует из (III.18.3), (III.18.5) или (III.18.7). Из
того, что «основная» плотность стремится к (III. 18.32)
и одномерное сужение плотности (III. 18.32) равно
(III. 18.9), следует (снова в слабом смысле), что
(III. 18.33) lim /гп)(х, t)= у1Г{
4-(л-3)
/»
~Bn)-'kexp(-±-xA.
-VT
Мы обсудим теперь Я-теорему Больцмана в свете
наших рассмотрений.
Эта теорема утверждает, что
со
(III. 18.34) -J- / / (х, t) log / (х, t) dx < О,
— oo
и легко выводится, как это сделал сам Больцман, из
уравнения (III.16.13). Однако в отличие от утвержде-
утверждений (III.18.3), (Ш.18.5) и (Ш.18.7) [которые можно
обобщить дальше, заменив фа или ф log ф любой вогну-
вогнутой сверху функцией М(ф)] функционал
(III. 18.35) # (/) = ff\ogfdx
является единственным известным до сих пор функцио-
функционалом от f, меняющимся монотонно.
Чтобы прояснить ситуацию, мы должны вспомнить,
что уравнение (III.16.13) применимо только в том слу-
случае, когда распределение обладает больцмановским
свойством. Если бы можно было сказать, что в некото-
некотором смысле
П я*/;')
(III. 18.36) Ф„ (R; t) -! ,
то отсюда мы получили бы
(III. 18.37)
/ t)-\ogCn\do =
= -log Cn + -g-f do log/ (*,; 0 JJ f(x,; t),
где
(III. 18.38) Cn =
и /(х; ^) служит предельным одномерным сужением для
q>n(R; О-
Асимптотически при больших п мы получили бы
(III. 18.39) /ф/г1оёф„</а~
оо
log С„ + я J / (*, 0 log / (х; t) dx,
— оо
и из того, что
(III. 18.40) JcpJogcp^a
убывает со временем, следовало бы, что
оо
(III. 18.41) H(f)= f /\ogfdx
— со
также убывает.
Если все предыдущие шаги сделать строгими, мы по-
получим вполне удовлетворительный вывод Я-теоремы
Больцмана.
19. Как мы уже видели в пп. 16, 17, 18, действи-
действительно возможен теоретико-вероятностный подход к на-
нашим задачам; он основан на представлениях о случайном
блуждании, которые излагаются в первой части прило-
приложения I, принадлежащего Уленбеку. Этот подход при-
приводит к результатам, находящимся в полном согласии
как с прежними нашими знаниями, так и с интуицией.
Остается, однако, существенная задача — обосновать
основное уравнение, исходя из уравнения Лиувилля. Дру-
Другими словами, необходимо исследование, подобное тому,
которое было проведено для круговой модели в послед-
последней части п. 15.
Такое исследование было предпринято Р. Броутом,
о чем также упоминается в первой части приложения 1.
Поскольку я считаю попытку Броута чрезвычайно важ-
важной (хотя мне хорошо известно, что многие места там
требуют дальнейшего прояснения), я постараюсь поды-
подытожить все, что касается главных, по моему мнению,
пунктов предложенного Броутом подхода.
Предупреждаю читателя с самого начала, что мы на
время покидаем надежную почву математики и отпра-
отправляемся на экскурсию в другую область. Не противьтесь
мне! Сами идеи, несомненно, верны, хотя вполне строгое
их обоснование может оказаться очень трудным.
Начнем с нескольких замечаний.
Если мы обозначим через
D(vv ..., Уд,, rlf ..., Гдг; 0)
начальное распределение в Г-пространстве (мы теперь
используем обозначение г,- для положения частицы и Vj
для ее скорости), то
D(vv ..., Удг, rlf ..., Гдг; t)= ^
= 0(vf<, .... v~', гГ<, .... г-'; 0),
где
\r-t V~* V~* V~*
— скорости и положения наших молекул (одноатом-
(одноатомных!) в момент времени —/, если в нулевой момент они
равны
Предположим, что вместо нашей системы мы рас-
рассматриваем систему, в которой межмолекулярные силы
— Tj\) действуют только внутри некоторой вы-
выделенной группы молекул (в которую входят, скажем,
первая, третья и пятая молекулы), в то время как
остальные молекулы не взаимодействуют ни друг с дру-
другом, ни с этой выделенной группой.
Иными словами, потенциальная энергия равна не
2 <p(/v)+S
j
S ?/(г;),
где «звездочка» над знаком суммы означает, что сумми-
суммирование происходит только по тем i и /, которые при-
принадлежат к выделенной группе.
Обозначим через
D(l, ..., /;, ..., Vv ..., Гп, ..., N)
плотность в момент времени t, в которую переходит на-
начальная плотность
D(vv ..., Удг, rv ..., Гдг; 0),
если межмолекулярные силы «включены» только между
частицами t'i, ..., in-
В частности,
r-<; 0)
, 2,..., A0 =
Квадратные скобки, окружающие vt* и гт^, означают,
что /-я частица движется только под действием внеш-
внешней силы — grad U(Tj).
Если же внешние силы отсутствуют, мы получаем
Ь 19.1)
г-л_г _
Конечно, стенки, ограничивающие наш сосуд, со-
создают (сингулярные!) рнешние силы, но мы будем обра-
щаться с ними бесцеремонно, забывая о них при исполь-
использовании формул (III.19.1), но помня о них при интегри-
интегрировании по переменным г,-.
Чтобы быть уверенными, что обозначения понятны,
заметим, что
и, например,
D(l', 2', 3', 4, ..., N)
получается, когда Vf', v^*, v-', T~f, r^K T~f находятся
из точного решения задачи трех тел, в то время как
vj* и гт' (/>3) берутся в квадратных скобках. Дру-
Другими словами,
D(l', 2', 3', 4, ..., N) =
г V Г-* r~t
-vNt; 0).
С0
с}
С?;
^\vl ' V2 ' V3 '
Положим теперь
= 0A, 2, ..., /V),
= 0A, 2, ..., /', .
= 0A, 2, ..., /', .
-0A, 2, .... /', .
— 0A, 2, ..., /, ..
* = 0A, 2,..., /', ..
— 0A, 2, ..., /', .
— 0A, 2, ..., /, ..
— 0A, 2, ..., /', .
+ 0A, 2, ..., /', .
+ 0A, 2, ..., /, ..
+ 0A, 2 /, ..
-0A, 2 ЛП
, v4, ...,
.. Л/) — 1
.., /, ..
... ло-
.,/,...
..,/,...
..,/,..
.., /,...
.,/,...
• , у, •••,
v г-' г-* г-*
vN' 'l ' ' "з
— V4*, . .., Гдг — V
9A, 2, ..., Л0 = '
., ло —
, Л^) + 0A, 2, ...
., k', .... iV) —
., k, .... Л/) —
а' ЛЛ
, fe', .... yV)-f-
k ... /V) -4—
, k, ..., ^V) +-
A', ..., A/) —
и т. д. Теперь при помощи сравнительно простых выкла-
выкладок можно убедиться в том, что
(III. 19.2) Z)(vr<, ..., v^, r,-', ..., г-'; 0) =
= D(Y, 2', ..., N') =
S} 2 с?у+ 2 ?
l<i
Это почти тривиальное равенство, но оно содержит раз-
разложение, в котором каждый член допускает непосред-
непосредственное и очень естественное истолкование.
Рассмотрим, например,
г3
Допустим, что гь г2, г3, Vi, v2, v3 таковы, что в тече-
течение промежутка (—/, 0) частицы 1, 2, 3 не взаимодей-
взаимодействуют. Напомним, что межмолекулярные силы пред-
предполагались близкодействующими, и, таким образом, до-
допустимо, чтобы в течение промежутка (—t, 0) каждая
из этих частиц оставалась вне сферы действия других
частиц. Или предположим, что только первая и вторая
частицы «ощущают» друг друга.
Ясно, что для таких начальных расположений частиц
Ci23 = 0. Действительно, легко показать, что
во всех случаях, когда не все три частицы «ощущают»
друг друга.
Мы ограничимся теперь рассмотрением газа из твер-
твердых шариков и сделаем следующие основные предпо-
предположения:
(а) D(vv ..., Удг, rlf ..., Гд,; 0) =
= <p(vlf ...,
(б) -ф(гх, ..., г^) =
П
/7
// П il-4\ri-rj\))dri-dr
V V l<i<j<N
{1, 0 < х < 6 F — диаметр молекулы),
0 вне этого промежутка.
Допущение (б) означает, что вначале у нас было
равномерное распределение в пространстве. Оба допу-
допущения (а) и (б) сделаны только для t = 0.
Мы хотим теперь вычислить
<p(vlf ..., vN; t) =
= f ... f D(vv ..., Удг, rlf ..., rN\ t)drx ... drN.
V V
Для этой цели мы используем «комбинаторное» разло-
разложение (III.19.2). Заметим, что
J ... fc°dr1...drN = y(vv ..., vN) = y(vv ..., v^O).
V V
Поскольку С] = 0, мы начнем с рассмотрения
f ... f С2и dr, ... drN.
V V
Чтобы упростить запись, мы положим t=l, / = 2 и заме-
заметим, что
Г ... J
V V
= J ... /ф(Г, 2х, 3, 4 TV) —
г v
-D(l, 2 Л^)}*! ... drN =
. М. •••- [r-N'])}drl...drN =
= f ... /{ф(уГ', v2-', v3, .... vN)X
V V
ХЦ*Т'> Ч'> гз г„)-
— 4>(VV V2, .... V/fWiTi, .... Глг)}^ ... drN.
Здесь на последнем шаге мы воспользовались форму-
формулами (III. 19.1). Напоминаю, что как я уже предупреж-
дал, мы бесцеремонно обращаемся со стенками всякий
раз, когда нам это удобно!
Теперь рассмотрим интеграл
л. г2) = J ... J4(i"i, • • -, rN)drs ... drN.
V V
Это хорошо известное двучастичное распределение для
газа из твердых шариков в равновесии. Его точное вы-
вычисление представляет пока еще не решенную проблему,
и в отчаянии физики обращаются к разложению (так
называемому вириальному разложению) по степеням
плотности
C = lV/V=\/v
(v — объем на одну частицу).
В нулевом приближении (идеальный газ) мы имеем
P(rlt r2)~l/V2
и, следовательно,
J ...
V V
= 473- / {<p(vf<, v2-'f v3, ..., vN) —
B(vx, v2)
— <p(vlf v2f ..., v^)}*! dr2,
где B(vu v2)—область в шестимерном пространстве, в
которой Ci2 Ф 0.
Ясно, что Г! (или г2) можно выбирать произвольно
внутри V (здесь мы снова пренебрегаем стенками), и
условие Ci2 Ф 0 означает просто, что г2 должно быть та-
таким, чтобы в промежутке времени (—/, 0) между части-
частицами (гь vi) и (г2, v2) (значения относятся к моменту
/ = 0) произошло ровно одно столкновение.
Для модели твердых шариков, которую мы все время
рассматриваем, получается выражение
J ... J
V V
... drN =
о);
здесь мы пользуемся обозначениями из п. 16.
Мы видим теперь, что
<p(R; t)= f ... fD(vv- .., vN, rv ...,
V V
Xdr, ... dr^ = q>(R; 0) + * S Q,/p(R; 0)+
jN
и если ввести оператор
2=
то мы видим, что он совпадает с основным оператором
(III. 16.7).
Становится совсем весело, когда мы переходим к
рассмотрению
Здесь для данных vt-, v?-, vk мы должны исследовать
те расположения (гг-, Tj, rfe,), для которых все три части-
частицы «ощущают» друг друга в течение промежутка
(-чо).
Сначала следует классифицировать различные типы
«расположений столкновения». Броут заимствовал эту
классификацию у Грина, который провел ее во всех под-
подробностях.
Различают (а) точные тройные столкновения (i, /, k);
(б) последовательность парных столкновений, напри-
например (/, /), (i, k)\ это означает, что сначала i-я частица
сталкивается с /-й, а затем i-я — с k-й [эту последова-
последовательность следует отличать от (i, k), (i, /), где i-я части-
частица сначала сталкивается с й-й, а затем с /-й]; (в) «вир-
«виртуальные» столкновения, например (i, /)Л, (i, k)'\ это оз-
означает, что i-я частица столкнулась бы с й-й, если бы
этому не помешало предшествующее столкновение ее с
/-й частицей; (д) «циклы столкновений», например
(UK (i,k), (j9k).
Столкновениями типа (а) пренебрегают из-за боль-
большой разреженности газа; пренебрегают также столкно-
столкновениями типа (д), считая, что их число сравнительно не-
невелико при больших N.
Вклады от (б) и (в) вычисляются тогда и дают
В добавление к этим членам мы получим вклад от чле-
членов С4
Если объединить все члены второго порядка по /, то
они дадут
причем мы пренебрегаем величиной
Это аргументируют тем, что 2/у соответствует повтор-
повторным столкновениям (i, /), (i, /), которые могут происхо-
происходить только после промежуточного столкновения со
стенкой. Снова считается, что в пределе (jV->oo;
1/->оо) такое пренебрежение законно. (Это место встре-
встречается также в доказательстве распространения хаоса
во времени, приведенном в п. 17.)
Если это все еще недостаточно скверно, то подумаем
о членах высшего порядка Cijki и т. д.!
Помимо чисто комбинаторных трудностей (при клас-
классификации различных конфигураций столкновений), с
которыми можно справиться с помощью диаграмм, по-
подобных введенным Фейнманом в квантовой электроди-
электродинамике, мы сталкиваемся с различными предельными
переходами (ЛГ->оо, V->oo, N/V=c, c->0, ^->oo; ct
остается фиксированным), разобраться в которых по-
поистине немыслимо!
Вы можете понять, почему Уленбек в первой части
приложения I называет попытку Броута отважной. Од-
Однако картина все же начинает проясняться и, может
быть, скоро станет полностью понятной.
20. Главный недостаток метода, использующего ос-
основное уравнение, по крайней мере для кинетической
теории газов, состоит в том, что его трудно (если не
невозможно) обобщить на случай пространственно не-
неоднородного газа.
Поэтому неясно, в каком же смысле полное уравне-
уравнение Больцмана (т. е. вместе с членами, описывающими
течение газа) является вероятностным уравнением.
Можно сказать, что раз мы принимаем во внимание
зависимость от расположения в пространстве, то ситуа-
ситуация становится переопределенной и не остается возмож-
возможности для усреднения.
Здесь уже нет аналога нашему множеству S в кру-
круговой модели, и могут быть только «удачные свойства»
начального распределения D.
Неясно, достаточно ли этого для удовлетворитель-
удовлетворительного вывода полного уравнения Больцмана. Я лично
сомневаюсь.
Подход Боголюбова, подробно изложенный во вто-
второй части приложения I, выглядит (по крайней мере в
настоящее время) чересчур формальным. Он оставляет
без ответа слишком много вопросов, чтобы его можно
было признать окончательным.
Чувствуется (по крайней мере, я так думаю), что не-
некоторое усреднение должно каким-то образом происхо-
происходить в течение короткого времени т (времени столкнове-
столкновения), после которого многочастичное распределение уже
функционально зависит от одночастичного распределе-
распределения.
Эта основная проблема требует выяснения, хотя для
формального применения метода Боголюбова это несу-
несущественно.
21. Оставшиеся пункты этой главы будут посвя-
посвящены обзору теории Смолуховского флуктуации плот-
плотности.
Эта теория сложит прекрасным примером статисти-
статистической теории в физике; она поможет нам лучше понять
многое из того, что уже обсуждалось в других пунктах
этой главы.
Смолуховский развил свою теорию, чтобы объяснить
результаты опытов Сведберга и других с коллоидными
растворами. Позднее эту теорию и экспериментальные
данные, на которые она опиралась, он положил в основу
блестящего и глубокого анализа пределов применимости
второго закона термодинамики.
Сведберг наблюдал через определенные промежутки
времени C9 наблюдений в минуту), сколько коллоид-
коллоидных частиц находится в фиксированной области А внут-
внутри большого сосуда. В результате наблюдений он полу-
получил последовательность из 517 чисел; мы приводим на-
начало этой последовательности:
1,2,0,0Д2,0,0Д2,4,1,2Д1Д2,1,1,1,1Д1,1Д5,1,1,1Л2,ЗД1.
Как следует анализировать эти числа и что поучи-
поучительного мы можем извлечь из такого анализа? Это ти-
типичная задача, которая должна часто вставать перед
естествоиспытателем, и мы постараемся сейчас показать,
как он к ней подходит.
Предположим, что объем сосуда равен V и что в
нем содержится N коллоидных частиц. Сделаем теперь
два допущения: A) каждая частица совершает броунов-
броуновское движение; B) частицы не зависят друг от друга.
Первое допущение для математической теории несу-
несущественно: все, что нам требуется, — это достаточно
полное статистическое описание движения одной части-
частицы. Под этим понимается, что положение г(т) любой
выбранной частицы является реализацией какого-то
случайного процесса (принимающего векторные значе-
значения) , который нам полностью задан.
Чтобы читатель не перескакивал к уже забытому п. 6
этой главы, напомним, что все это означает следующее:
г(т) является однопараметрическим семейством измери-
измеримых функций г(т; со), заданных на некотором множе-
множестве й, снабженном вполне аддитивной мерой \i
(|i(Q) = l); при этом мера ji вводится так, что для лю-
любых трехмерных борелевских множеств Аи Л2, ..., Лп
мы имеем 1)
(III. 21.1) Р{г(^NЛ> г(/2NЛ2, ..., r(tn)?An) =
= v{r(tv coNA> rfe «>)?Л> •••> r(tn; со)? Ап).
1) Физик, редко ощущающий потребность в формализации «оче-
«очевидного», полагает, что случайный процесс полностью определен,
коль скоро он знает, как вычислить вероятности в левой части
Очень существенно допущение B), чрезвычайно
упрощающее задачу. Оно позволяет игнорировать та-
такое важное явление как коагуляция; однако это может
быть обосновано лишь для очень слабых коллоидных
растворов.
Формальный смысл допущения B) следующий: пусть
г,-(т; coj), coj ? Qj, — случайный процесс, описывающий
движение /-й частицы. В предположении, что частицы
неразличимы, мы можем считать, что все Q\,Q2,... ,Qn
тождественны (?2j = Q). При статистическом описании
совместного движения всех частиц мы неизбежно дол-
должны иметь дело с произведением множеств:
^X^X^X — X^•
Предположить независимость — это значит задать меру
в ИХ ... Хй как произведение мер.
Некоторые другие допущения более специального
характера будут сделаны дальше по мере надобности.
22. Пусть г|э(г)—характеристическая функция обла-
области Л, т. е.
GIL 22.1) гИг)
Тогда
(III. 22.2) Лд(*)
есть просто число частиц, попавших в А в момент вре-
времени t.
Очевидно, что nA(t)—случайный процесс и более
последовательно было бы его записать так:
N
(III. 22.3) пА (t) = nA (/; со) = 2 г|) (г; (t; oy)),
(III.21.1). Математик же большую часть времени проводит в обду-
обдумывании того, могут ли эти и более сложные вероятности быть кор-
корректно определены. Существуют ситуации (см., например, пп. 1—3,
гл. IV), когда такие предосторожности оправданы, но в этом и сле-
следующих пунктах они имеют второстепенное значение,
где со — сокращенное обозначение набора (соь ..., )
и coj ? Q (иными словами, со ? Q X й X ... X й). Остается
теперь вычислить вероятности
(III. 22.4) Р [пАЦг) = nv пА (t2) = /г2, ..., пА (tk) = nk].
Мы подробно покажем, как вычисляется вероятность
(III. 22.5) Р{пАуг) = т, nA(t2) = n],
после чего станет ясно, как производить вычисления в
общем случае (III.22.4). Мы исходим из очевидной фор-
формулы
2тс 2%
(III. 22.6) BяГ2 J J exp {i(i
о о
где k и / — целые числа и б — обычный символ Кроне-
кера.
Отсюда немедленно следует, что
Р {n(t1) = m, n(t2) — n} =
2п 2п
= Е {Bя)~2 J f exp [- / (lm + цп)] X
О О
О О
X exp [/ (ЪпА {tj Ч- тa (h))] d\ йц }¦
Здесь символ Е означает интегрирование по произве-
произведению пространств QX ... Хй. Меняя порядок инте-
интегрирования (Фубини!), мы получаем
(III. 22.7) Р {п (t,) = tn, n (t2) = п} =
2тс 2%
-=Bл)-2 J J expl-i(im + m)]X
о о
X Е {ехр [/ (|ти (t,) + т|лд (t2))]} dl dx[.
Остается вычислить
т. е. просто интеграл по произведению мер в простран-
пространстве QX ... Хй от функции
exp [/ (%nA (tx\ со) + щА (t2; w))].
Используя выражение (III.22.2) и предположение о
независимости частиц (т. е. то, что мера в ИХ ... XQ
является произведением мер), мы получаем
(III. 22.8) Е {ехр [/ &пА
= ПЕ {ехр[/ОД,(гуft)) + Л^(tj(t2)))]} =
Второе равенство непосредственно следует из независи-
независимости, в то время как третье равенство есть следствие
того, что частицы неразличимы (и поэтому статистиче-
статистически одинаковы).
Теперь, поскольку ty принимает только значения 0 и
1, имеем
= 1 Ч- [ехр (^) — 1] * (г (/,)) -Ь [ехр (*п) — 1] * (г
+ [ехр (%) - 1 ] [ехр (ft]) - 1 ] Ч> (г &)) $ (г {t2))
и, следовательно,
(III. 22.9)
+ [ехр(Л)-1][ехр(/П)-1]Р{г(<1)бД г(
Комбинируя (III.22.7), (III.22.8) и (III.22.9), мы по-
получаем
(III. 22.10) Р {Яд ft) = от, Яд(/2) = я} =
2ч
= Bя)~2 J J ехр [- / Цт + пя)] X
, r
Эта формула слишком сложна, чтобы с ее помощью
можно было многого добиться, и мы должны теперь
обратиться к некоторым дополнительным соображениям,
позволяющим упростить ответ.
Первая возможность такого упрощения усматривает-
усматривается в том, что оба числа N и V велики. В самом деле,
формула (III. 22.10) нас интересует только в пределе
(III. 22.11) W->oo, V->oo, N/V~>v
(смысл v очевиден: среднее число частиц в единице
объема).
Дальнейшее упрощение возникает из предположения
о «статистическом равновесии». Это предположение в
действительности состоит из двух частей:
(а) вероятность Р {г (tx) 6 Av ..., г (tn) ? Ап)
зависит только от разности моментов времени (/< — tj)
(стационарность);
(б) P{r(t)eA)=\A\/V,
где \А\ — объем области А.
И вот, наконец, третье необходимое нам допущение,
которое на первый взгляд кажется более странным, чем
оно есть на самом деле. Это предположение состоит в
следующем:
(в) P{r(,
= J..
где
Wv{rv /,; .
и предел
lim Pv(rlt tx
h)?Av
¦ !w
An
••; «¦«.
|r2, ^2;
, .... г(О6Л} =
К\Г1» fl» Г2» f2» • ••»
/B)=ir1/>v(r1, /,|
...; г„, tn) = P(rv i
rn, tn)drx
r2, '2! • • • *
^|r2,^2;...
• • • drn,
существует в слабом смысле.
Здесь подразумевается, что при 1/->оо не только
объем сосуда, но и все его размеры стремятся к бесксн
нечности.
Смысл предположения (в) становится более понят-
понятным, если обратиться к броуновскому движению.
Если броуновская частица движется в сосуде с отра-
отражающими стенками, то можно показать, что
= V-lPv{rv tx\r» t2)Pv(r2> /2|r3, /3) ...
где
— фундаментальное решение уравнения диффузии
(III. 22.12) 4r=4AP'
удовлетворяющее граничному условию
дп
на стенках сосуда и начальному условию
(единица измерения выбрана так, чтобы коэффициент
диффузии равнялся 1/2).
Для конечного сосуда Py(r|p; t) зависит как от его
размеров, так и от его формы, но можно опять пока-
показать, что
lim Pv(r, *Jp, t2) =
V
= Я(г, 0|р, t2-tx).
Написанная функция служит фундаментальным реше-
решением уравнения (III. 22.12) во всем пространстве.
Любопытно отметить, что хотя нам с большим тру^
дом удается избавиться от V (устремляя |/к оо), мы не
могли бы никаким естественным образом (во всяком
случае, я не знаю как) действовать сразу во всем про-
пространстве и избежать обременительного предельного пе-
перехода.
Теперь уже все просто!
Переходя к пределу (Ш.22.11) и используя все наши
предположения, мы получим
(III. 22.13) W(m, n\ t2—tl)=W(m, tx; n, t2) =
= lim Р {пА (tx) = т, пА (t2) = n} =
2ъ 2%
= BяГ2 J J ехр[-
о о
где
(III. 22.14) F& 4)
(III. 22.15) |i = v|^|,
(III. 22.16) g(t) = jI1 f /Я(г, 0|р, t)drdp.
A A
Смысл |i и ^(/) очевиден: \i — среднее число частиц в
области А и g(t)—условная вероятность [после пре-
предельного перехода (Ш.22.11)] того, что частица, нахо-^
дящаяся в момент ?=0 в А, вернется в Л к моменту t.
Смолуховский использовал величину
(III. 22.17) Р(/)=1-?(/),
которую он назвал «вероятностью последействия»
(«Wahrscheinlichkeitsnachwirkung»).
Он получил формулы
9 0;
/=o
n
W(m, 0;m-k, 0 = exp(-|i)-g- ^ 4°
i=k
где
Вывести эти формулы из (III. 22.13)—уже простое
упражнение (немного утомительное). Вывод самого Смо-
луховского (чисто комбинаторный) намного проще на-
нашего. Однако наш вывод может быть немедленно рас-
распространен и на вычисление вероятности (III.22.4) в
общем случае, в то время как способ Смолуховского
приводит здесь к сложной комбинаторике.
Несмотря на то что нам потребовалось очень много
разговоров, чтобы получить формулу (III. 22.13), и не-
несмотря на ее довольно сложный вид, чисто математиче-
математическое содержание последних двух пунктов сравнительно
бедно.
«Знаток» теории вероятностей может с легкостью
опустить все это, полагая, что здесь просто «много шума
из ничего», или, еще хуже, перечеркнуть их непререкае-
непререкаемым и, по-видимому, самым уничтожающим словом
«тривиально».
Но попробуем теперь взглянуть на окончательные
формулы с точки зрения физика.
Он мог бы при помощи данных Сведберга вычислить,
скажем, частоту f@, 0; /), с которой нули последова-
последовательно появляются друг за другом через t секунд (t сле-
следовало бы брать кратным 1/39, поскольку Сведберг де-
делал 39 измерений в минуту). Затем он мог бы прирав-
приравнять наблюденную частоту и теоретически вычисленную
вероятность W@, 0; /) и получить численное значение
для g(t). Поскольку в экспериментах Сведберга ча-
частицы были по существу свободными броуновскими ча-
частицами, он мог бы положить
Щ
А А
(мы вернулись теперь к истинному коэффициенту диф-
диффузии D\) и вычислить D. Для сферических частиц D
задается формулой
D = кТ/Fпац) = RT/FNna4),
где R — универсальная газовая постоянная, N — число
Авогадро, а — радиус коллоидной частицы, ц — коэффи-
коэффициент вязкости той жидкости, в которой взвешены кол-
коллоидные частицы.
Отсюда он нашел бы, что число Авогадро приблизи-
приблизительно равно 6,09-1023.
Поистине невероятно, что можно получить число по-
порядка 1023 из чисел Сведберга, каждое из которых не
превосходит 6!
Здесь мы снова видим результат, ценность которого
не может быть определена одними только математиче-
математическими его достоинствами.
23. Из выражения (IH.22.13) для W(m, tx\ n, t2) мы
немедленно получаем формулу для
W(m, tx)= lim P{nA(t1) = m}.
Действительно,
оо
(III. 23.1) IF (яг, t1) = 2 W{m, tx\ n, t2) =
2k
= Bл) J exp (— Цт) F ft, 0) d\ = exp (— \x) \xm/ml
о
Эту формулу, разумеется, можно получить также и не-
непосредственно. Более интересны формулы для
W(nv tx; n2, t2\ ...; nk, tk) =
= lim Pv{nA(t1) = nv nA(t2) = n2, ..., nA{tk) = nk).
Непосредственным обобщением метода из п. 22 мы по-
получаем следующий ответ:
(III. 23.2) W(nv tx\ л2, t2; ...; п» th) =
о о \ ;-i
где
(III. 23.3)
«Звездочка» над знаком произведения означает, что его
нужно понимать в следующем смысле: перемножим все
S"i» g2, ... , gk так, как если бы они были числами, а за-
затем заменим произведение
ёф2 ¦ • • gis
выражением
(III. 23.4)
А А
(если s=l, g, просто заменяется единицей). Напри-
Например,
+ g (t21 <з) (exp (ry - 1) (exp (/y — 1) +
i 1^2. 4) (exp (г&О -1) (exp (/y - 1) (exp (%) -1).
Предположим теперь, что существует процесс г(/) 2)
с вероятностями перехода Р(ги ^|г2, /г, • • •, •"„, tn).
Иными словами, существует такой процесс, что
(III. 23.5) Р{г(^1) =
= J ... f Я(г1э tx |г2, ^2; ...; гл, О^2 • • • dtn.
А2 \
(Например, трехмерное свободное броуновское движе-
движение является именно таким процессом; подробности см.
в гл. IV.)
1) Само собой разумеется, что моменты времени tu ..., h, так
же как и Ux, ..., Us, упорядочены.
2) Мы пользуемся тем же обозначением для другого процесса.
Для согласованности обозначений мы должны были в преды-
предыдущем пункте использовать обозначение г^(/),
С этим процессом мы можем связать процесс nA(t) *),
принимающий лишь неотрицательные целые значения и
определяемый следующим набором вероятностей:
(III. 23.6) Р \пА (tx) = nv ..., пА (tk) = nk) =
= W(nv t{, n2, t2; ...; nk, tk)
[здесь все W задаются формулами (III. 23.2) и
(III. 23.3)].
Определен ли на самом деле формулой (III.23.6) слу-
случайный процесс nA(t)? Почти непосредственно можно
показать, что nA(t) удовлетворяет требованиям согла-
согласованности и непрерывности. Все это следует из соотно-
соотношения
(III. 23.7) Umg(t) = \.
Но будут ли вероятности W неотрицательными? Если
вероятности Р могут быть получены как предельные
значения вероятностей Pv [см. условие (в) из п. 22 этой
главы], то неотрицательность всех W очевидна, так как
они являются пределами неотрицательных величин. Но
можем ли мы быть в этом уверены, если Р — просто
вероятности перехода для процесса г(/)?
Прямое доказательство неотрицательности W должно
получаться из формул (III. 23.2), (III. 23.3), но такое
занятие выглядит непривлекательным и скучным.
Верно ли, что вероятности Р могут всегда быть
получены как пределы вероятностей Pv для подходящим
образом определенного процесса !>(/)?
Почти наверняка это так, но я не знаю доказатель-
доказательства.
Что же нам теперь делать?
Чтобы сэкономить время, мы просто ограничимся
процессами г(/), подобными свободному броуновскому
движению, для которых можно определить процесс
МО-
Добившись согласованности и неотрицательности, мы
обратимся к теореме Колмогорова (п. 6 этой главы) и
приведем наконец все в полный порядок.
1) Мы снова употребляем одинаковые обозначения для разных
вещей. Формально мы должны были бы писать nAV(t).
Определенные так процессы nA(t) мы назовем в честь
их истинного изобретателя процессами Смолуховского.
24. Процесс Смолуховского, полученный с помощью
броуновского движения свободных частиц, служит про-
простейшей статистической моделью, имеющей непосред-
непосредственное отношение к действительности, для которой
можно обсудить некоторые детали, касающиеся обрати-
обратимости и возвращаемости. Конечно, эренфестовская мо-
модель «пса и блохи», подробно рассмотренная в этой
главе, во многом проще. Но сколь она ни остроумна и
полезна, она все же слишком искусственна. Модель
Смолуховского прочно укоренилась в физике, и выте-
вытекающие из нее выводы о реально существующих телах
могут быть сопоставлены с экспериментальными дан-
данными. Мы обсудим вопросы о возвращаемости в сле-
следующих пунктах.
Здесь же мы сделаем несколько замечаний, чтобы
закончить физические рассмотрения.
Сначала определим условные вероятности
P(nv tx \щУ t2] • • •; tik, h)
по обычной формуле
(III. 24.1) Р(л1э tx\ti2, t2; ...; /гЛ, tk) =
W(n>v tv n2> h'> • • • 5 nk> h)=
nv tx\ n2, t2; ...; nk, tk)
~W (пь tx)
и заметим, что
(III. 24.2) P(nv tx\n2, t2\ ...; nk% tk) =
= P(nv 0|/г2, t2 — tx\ ...; nk, tk—tx).
Вычислим теперь
oo
(III. 24.3) E [nA @) = m \ nA (t)} = ^tiP (m, 0 |/i, t),
/г=0
т. е. среднее число частиц в области А при условии, что
в момент времени t = 0 там было m частиц.
Имеем
оо
, 0|я, t) = -~^y ^nW(m, 0; п, t) =
/г=0
2тс 2тс
y
я=0 /г=0
оо 2тс 2тс
f
/г=0 0 0
= w,m) 2nBЯ) J exp(— i
л=0 О
где
^(глГ1 J expC-ft/w)/7^ ц)сЦ.
о
Поскольку
оо 2«
/0D = 2 BЯ) / ехр (- Ил)/©rf? exp (/туг),
мы имеем
' (п) = / 2 "BЯГ1 J ехр (— ?л)/(Е) rfC exp (/туг)
о
и, следовательно,
(III. 24.4) Е{пд@) = т
2тс
ехр (~ilm) (Д
= W^(m) Bя) 1 Г ехр (— ilm) exp (jo, [ехр (/?) — 1 ]) X
о
Эта формула находится в полном согласии с макро-
макроскопической теорией диффузии, если вспомнить, что
А А
В самом деле, \х есть просто нормальное [и предель-
предельное, поскольку g(t) -> О при t-> оо] количество «веще-
«вещества» в Л, в то время как (т — \i)g(t)—это то, что
останется в Л к моменту времени t от дополнительной
части вещества (т — jo,) в начальный момент / = 0 (она
может быть и отрицательной!), если диффузия происхо-
происходит по классическим законам.
Подобным же образом мы найдем, что
(III. 24.5) Е \пА@) = т \(пА(t)-lL-(m-V)g(t))*} =
= mg(t)(\-g(t))
Итак, относительная флуктуация равна
и при больших jo, и т~а имеет порядок |дг1/2; поэтому ею
можно пренебречь. Таким образом, можно обойтись без
вероятностей и пользоваться феноменологической тео-
теорией диффузии. Для малых значений \х (в упомянутом
опыте Сведберга \х^ 1,54) флуктуации перекрывают сред-
среднее, и статистическое рассмотрение становится неизбеж-
неизбежным.
25. Для эренфестовской модели «пса и блохи» мы
имели
(III. 25.1) P(no\nv щ, ..., nk) =
Это есть свойство «марковости», благодаря которому
модель легко поддается математическому исследованию.
Выполняется ли марковость для модели Смолухов-
ского? Иными словами, верно ли, что
(III. 25.2) P(nv /J/i.,, t2; ...; nk, tk) =
^P{nv tx\n2, t2) ... P(/i*_lf tk^\nk, tk)l
Вообще говоря, следует отсветить «нет», и мы должны
будем обратиться к некоторому искусственному при-
примеру, прежде чем получим марковскую модель.
Чтобы разобраться в этом, заметим, что из (III. 25.2)
получается выражение
оо
Р(/ю, 0|/г, 0=2 Р(^. 0|ife, т; /г, 0 =
оо
= 2Р(/и, 0|&, т)Р(Л, 01/г, / —т);
/г =0
другими словами, это означает, что матрица
П@ = ||Р(да, 0|л, 011
удовлетворяет уравнению
(III. 25.3) П(/) = П(т)П(* — тI).
Посмотрим, выполняется ли для нашего процесса хотя
бы условие (III. 25.3).
Напишем
ехр [ц {(ехр (Л) — 1) + (exp (ftO - 1) + g (t) (ехр (Ц) — 1) X
X(exp(in)—1)}] = ехр[|х(ехр(Л)-1Iехр[ц(ехр(|тО—1
Мы видим, что
(III. 25.4) Р(/ю, 0|л, *) =
где
(III. 25.5) xmk=^exp(\x)m\\x-mBnf1 { exp(— i&n)X
о
X ехр [ц (ехр (Л) -1)] (ехр (Л) - \?d\
1) Это уравнение (так называемое уравнение Чгпмена — Кол-
Колмогорова — Смолуховского) часто ошибочно принимают за опреде-
определение марковского процесса. Существует пример, принадлежащий
П. Леви, в котором выполняется условие (III, 25.3), а условие
(III. 25.2) не выполняется.
(III. 25.6) ykn = -i- BЯ) / exp (- 1щ) X
0
X exp \\x (exp (it|) — 1)] (exp (/т|) — 1)* dr\.
Поскольку
Р(яг, 01/г, 0) = 6ш>л
[это следует из того, что #@) = 1], мы получаем
со
(III. 25.7) 2 -ЯдлУл/я = К, ,v
и, следовательно, (III. 25.4) можно рассматривать как
приведение матрицы П(/) к диагональному виду1).
В частности, числа
1 О (t\ eft (i\ о% (t\
служат собственными значениями матрицы П(/).
Теперь ясно, что для справедливости равенства
(III. 25.3) необходимо, чтобы
(III. 25.8) g (t) = g (t) g(t — t),
и поскольку функция g(t) измерима, она должна иметь
вид
(III. 25.9) g (t) = exp (— а/), а > 0.
Так как в опытах с коллоидными частицами g(t) ни-
никогда не получалась в виде экспоненты, то этот процесс
не может быть марковским.
1) В действительности соотношений (III. 25.7) недостаточно,
чтобы утверждать, что (III. 25.4) приводит матрицу Щ/) к диаго-
диагональному виду. Необходимо еще условие
оо
(III. 25.7a) SV,»-»,,,-
m=0
которое для бесконечных матриц не вытекает из (III.25.7J и на
самом деле может оказаться даже неверным. К счастью, в нашем
случае (III. 25.7а) можно получить отдельным вычислением, хотя и
не очень простым. Может быть, читатель ради развлечения сам най-
найдет доказательство.
Возникает вопрос, будет ли процесс, для которого
g(t) представляется в виде экспоненты (III. 25.9), мар-
марковским.
Легко доказать (хотя необходимые для этого вычис-
вычисления слишком утомительны, чтобы их здесь воспроизво-
воспроизводить), что если в дополнение к условию (III. 25.9) мы
имеем также (при /4 )
(III. 25.10)
то условие (III. 25.2) будет выполнено и процесс дей-
действительно марковский.
Несколько раздражает оставшаяся нерешенной сле-
следующая задача: следует ли (III. 25.10) из (III. 25.9)?
Ответ представляется почти наверняка отрицательным,
ибо почему вид g(t\\t2) должен определять последей-
последействие высших порядков?
Пока вопрос остается открытым. Если бы удалось
найти процесс, для которого
= exp(— at)
и в то же время не выполняется условие (III. 25.10), то
мы получили бы другой пример немарковского процесса
(менее искусственный, чем упомянутый выше пример
П. Леви), для которого выполняется (III. 25.3).
26. Существует ли процесс, удовлетворяющий усло-
условию (III. 25.10)?
Ясно, что это условие может выполняться только в
том случае, когда каждая отдельная частица движется
так, что, находясь в Л в моменты времени tt и 4, она
непременно должна находиться там и во все промежу-
промежуточные моменты времени.
Процессы, удовлетворяющие условию (III. 25.10), мы
будем называть устойчивыми.
Простейший устойчивый процесс был впервые изу-
изучен Фюртом. Он рассматривал число nA(t) пешеходов,
проходящих по тротуару в некотором фиксированном
отрезке А. Предполагается, что пешеходы двигаются с
постоянной скоростью \v\ в любом из двух противопо-
противоположных направлений, нигде не меняя направления сво-
своего движения, за исключением двух искусственных
отражающих барьеров, расположенных в —Ьи +L (мы
устремим затем L к оо). Интервал А может быть вы-
выбран равным (—у/, у Л-
Пусть фь(*) определяется следующим образом:
yL{x) = x — 2pL, \x — 2pL\<L, /? —четное,
4>l(x) = — x + ZpL, \x — 2pL\ <?, /? —нечетное.
Мы можем положить
(III. 26.1) riiL(t)
где Xi, ..., xN, 81, 82, ..., 8jv все независимы, каждое л:
равномерно распределено на интервале (—L, L), а каж-
каждое 8 принимает значения +1 или —1 с равными ве-
вероятностями A/2).
В чисто математических терминах это означает, что
наше множество Q является произведением множеств
(III. 26.2) (-L, 1)Х{-1, 1}
и на (—L, L) выбирается обычная (нормированная) ме-
мера Лебега, а мера на {—1, 1} задается приписыванием
равных весов 1/2 для +1 и —L Мера же множества
(III. 26.2) является произведением мер (это математиче-
математическое выражение нашего соглашения о том, что началь-
начальные точки и направления движения независимы). Почти
очевидно, что при L-^oo мы получаем
(III. 26.3) g(t) = \ " '
I 0, t> l\v\ .
Ясно, что этот процесс устойчив.
Если обобщить его, положив
где Vi распределены с одной и той же четной плотностью
распределения f(v) *), мы снов^а получим устойчивый
О Множеством Q является теперь (—L, L)X(—00, со), где
мера на (—со, со) определяется так:
= f f (v) dv.
Е
Все предположения о независимости, разумеется, сохраняются.
процесс, для которого g(t) (опять в пределе при L->oo)
задается формулой
сю
(III. 26.4) g(t) = 2f max(l — rW, 0)f(v)dv =
(l — rlvt)f(v)dv.
Отсюда видно, что не всякая функция g(t) может
служить для определения устойчивого процесса описан-
описанного выше типа.
Ясно, что g(t) должна быть такой, чтобы найденная
с ее помощью функция f(v) была неотрицательной.
Предполагая, что g дважды дифференцируема при
/>0, мы получим дифференцированием формулы
(III. 26.4)
2Г1/ vf(v)dv = -g'(t).
о
Дифференцируя еще раз, получаем
Отсюда, если g"(t)^> 0, мы приходим к решению
(III. 26.5) /И^-^М-УСМ)-
Для того чтобы было
о
мы должны еще ввести предположение
lim tg' (t) = 0.
Очевидно, что
удовлетворяет этим условиям, и, следовательно, с по-
помощью этой функции можно получить устойчивый про-
процесс. Итак, марковский процесс nA(t) может быть
построен, но его распределение скоростей
f(v) = \ Po? J v Г3 exp (—la\v f1)
крайне искусственно.
Читатель должен был заметить, что устойчивость
процессов, рассматриваемых в этом пункте, объясняется
тем, что область А (в нашем случае интервал)
связна.
Будь А объединением двух или большего числа ин-
интервалов, нельзя было бы утверждать, что
(III. 26.6)
Поскольку из опытных данных, подобных данным
Сведберга, можно решить, выполняется ли (III. 26.6),то
тем самым (забавно!) мы имеем возможность опреде-
определить связность (одномерного) множества с помощью
статистического анализа.
Последнее замечание в заключение этого пункта.
С процессом nA(t) мы можем связать процесс e(t)
следующим образом:
(III 26 7) e(t)-lh 6СЛИ n*® = 0'
10, если пА (t) Ф 0.
Ясно, что процесс (III. 26.7) стационарный и
(III. 26.8) Е [е (*)} = Р \пА (t) = 0} = exp (— |х).
Далее,
(III. 26.9) E{e(t1)e(t2)} =
2тс 2тс
Пусть теперь
И, = log 2
и
Мы имеем
E{e(t)}=0
Отсюда следует, что любая функция вида
может служить корреляционной функцией стационарно-
стационарного процесса, который принимает два значения +1 и —1
в предположении, что существует процесс Смолуховско-
го с функцией g(t).
В частности, если
g@) = h ?"(*)> 0, t>0
и
lim tg' (t) = О,
/->о /0
ТО
может быть корреляционной функцией стационарного
процесса со значениями +1 и —1.
27. Формулы (III. 23.2) и (III. 23.3), хотя и имеют
совершенно явный вид, настолько сложны, что их почти
невозможно использовать при обсуждении вопроса о
времени жизни и времени возвращения для различных
состояний.
Однако состояние 0 (в области А нет частиц) может
быть изучено во всех деталях, и это уже достаточно
интересно.
Сначала рассмотрим задачу о времени жизни (на-
(называемом также временем устойчивости) состояния 0.
Задача состоит в том, чтобы вычислить
(III. 27.1) Р@, 0|0, А*; 0, 2Ы\ ...; 0, пА/),
особенно в пределе
(III. 27.2) Д*->0,
Этот предел можно принять за определение вероят-
вероятности того, что время жизни нулевого состояния превос-
превосходит /.
Как следует из нашей основной формулы (III. 23. 2),
Р@, 0|0, М\ О, 2М\ ...; О, пМ) =
/ ) .... ln)dl0 ... dln.
О О
Теперь нужно заметить, что
) П
= 0 -?«) П* [A ~
+ exp (Цп) gn Д* [A - gj) + ^ exp (il
где оба произведения
П* и
;=0
следует понимать символически.
Отсюда вытекает, что
2%
Bл)-1 J>go, .... Urf|n =
= exp [ц A - gn)] Д * [A - gj) + gj exp ад,
и, повторяя эту процедуру, мы получим
Г " 1
(III. 27.3) Р@, 0|0, Л*; ...; О, лД*) = ехр U П A—g/) •
L y-o J
Символическое произведение
можно теперь вычислить по нашим правилам, после чего
получается (если использовать элементарный принцип
«включения и исключения» комбинаторного анализа)
(III. 27.4) П* (!-?,•) =
П-\
==— 2
Эта формула становится особенно простой для устой-
устойчивых процессов, поскольку в этом случае слагаемые
равны
Таким образом, для устойчивых процессов
(III. 27.5) Р@, 0|0, А*; ...; О,
и видно, что ответ получается в точности таким же, как
если бы процесс был марковским. Это, конечно, особен-
особенность нулевого состояния.
В пределе при Д/-*0, nAt = t мы получаем
в предположении, что g'@) существует.
28. Намного интереснее результат, относящийся ко
времени возвращения. Время возвращения в нулевое со-
состояние является временем жизни (временем устойчи-
устойчивости) укрупненного состояния «не нуль» @), и в этом
заключается основная трудность задачи.
Мы должны теперь вычислить
(III. 28.1) Р@, 0|0, А*; 0, 2А*; ...; б, пМ) =
= S P@, 0\kl9 A*; k2, 2M\ ...; kn$
1) В пределе при Af->0, nl^t—t эта вероятность стремится к
нулю. Это та же самая трудность, с которой мы уже сталкивались
в п. 6 этой главы. Чтобы получить разумный предел, мы должны
разделить _ __
Р@, 010", А^; 0, 2Af; ...; 0, пМ)
на Р@,0]0, АО и тогда уже перейти к пределу. Это совпадает с
определением среднего времени возвращения, принадлежащим Смо-
луховскому.
Сумма в (III. 28.1) равна
k^O, .., кпф0 О О
и мы замечаем, что
2*
*>о
= ехр [ц Д* (A - gj) + gf exp (ilj)) J -
^ О — gJ П (A — gj) + g/ ехр
Продолжая таким образом, мы получим
2тс 2п
^ Bя) Г / ехр [- / (*„_,?„_! + U«)J X
jut Д* — ехр \\i A — g^-i) П* —
[л-2 1 Г п-2 1
^ A — ёп) TV н~ ехр I и» A—gn-i) A — ^) П*
и, наконец, заметив, что интегрирование по ^о несколько
отличается от интегрирования по другим переменным,
(III. 28.2) Р @, 0 |б, А*; ...; б, л АО =
п
-go)] —S ехр [цA -
exp[n(l-ga)(l-gf)(l-gy)]-
п
= ехр [ц A - go)] - S exp [ji A -
К / < j < п
Здесь, разумеется, все экспоненты следует понимать сим-
символически.
Используя формулу, аналогичную формуле (III. 27.4),
мы получаем
Р @, 010, А^; ...; 0, п At) =
S
2
1 < j < У < я
Для устойчивых процессов опять можно достичь су-
существенного упрощения.
Полагая
(III. 28.3) h(t) = \
мы получаем (только для устойчивых процессов)
(III. 28.4) Р„ = Р @, 010, Л*; ...; 0, п Ы) =
= 1 —Sexpl—ц*(/Д*)] +
+ 2 ехр [- цА (/ А/)] ехр [- [х (Л (у -1) Щ - ...
Рассмотрим теперь производящую функцию
оо
(III. 28.5) H(z) = 2 ехр [— \ih (i Щ zl
и заметим, что
п
2 ехр [—\xh (i At)]
служит коэффициентом при zn в разложении функции
l) h(t) есть в точности P(t) Смолуховского [см. (III. 22.17)]. Мы
изменили обозначение, полагая, что буква Рг должно быть, устала
от столь частого употребления.,
а сумма
ехр [- \xh (i АО] ехр [- \i (h (j
К*
есть коэффициент при zn в разложении функции
A-гГ1НЦг)
и т. д.
Отсюда следует, что
/Ы1
или
(III. 28.6) A -z) ^ Р„г« = - A -z
Переписывая (III. 28.6) в эквивалентном виде
(III. 28.7)
и полагая
2 = ехр (—5 АО,
мы видим, что
r* pr *+i; z*+1 = exp(— sM) ехр i
Л = 1 О
где
Предполагая, что g'@) существует, мы имеем
Р,==Р(О, 0|0, Ы) = \ — Р@, 0|0, Д*) =
7 @) Д^ = а М (а = цА7 @))
и, следовательно, из (III. 28.7)
оо
а — lim Г ехр (— st) doAt (t) =
Ioo -i-l
а J ехр (— st) ехр (— \xh (t) )dt\ .
Отсюда вытекает, что предел
lim Obt(t) =
существует и что
оо
(III. 28.8) fexp(—st)do(t) =
i-l
= 1 + 5а — Г
а Г ехр (— st) ехр (— \ih (t) )dt\ ¦
о J
Функция a(t) может теперь быть истолкована просто
как распределение интервала времени между «послед-
«последним» мгновением,, когда еще наблюдается состояние
нуль, и «первым» мгновением, когда оно наблюдается
вновь.
Хотя невозможно, по-видимому, обратить преобразо-
преобразование (III. 28.8) с тем, чтобы найти a(t) в явном виде,
некоторые интересные выводы можно получить прямо
отсюда.
Во-первых, устремляя 5 к нулю и замечая, что
оо
J ехр (— \ih (t) )dt = O,
о
мы получаем
III. 28.9)
о
Это есть просто теорема Пуанкаре о возвращаемости.
Затем, допуская, что g(t)->0 при t -> 00 [откуда
I при /->оо], и используя разложение
оо
(III. 28.10) J ехр (— st) exp (— jxA (t)) dt =
о
оо
= 5 ехр (— |х) Ч- / ехр (— st) [exp (— \ih (t)) —
о
— ехр (— |х)] dt = s~l ехр (— fx)-j— /(s),
мы получаем, дифференцируя формулу (III. 28.8) по s и
устремляя 5 к нулю,
(III. 28.11)
Это формула Смолуховского для среднего времени воз-
возвращения в случае непрерывных наблюдений.
Следующие моменты также могут быть вычислены,
но вычисления становятся все более и более утомитель-
утомительными.
Интересный предельный случай может быть получен
из (III. 28.8). Обозначая время возвращения через Г,
мы имеем
(III. 28.12) lim Р {Т > иа~1 (ехр \х — 1)} = ехр (— и).
[Х->ОО
Для доказательства этого равенства достаточно за-
заметить, что
Р {Т > шх-1 (ехр IX — 1)} = 1 —а(шх-1 (ехр \х — 1)),
и показать, что
lim Гехр(— 5и)й?0(иа-> (ехрц — l)) =
H + coJ
ОО
= J exp (— su) exp (— и) da,
о
откуда уже следует (III. 28.1.2).
Интуитивный смысл выражения (III. 28.12) совер-
совершенно очевиден.
Чувствуется, что вероятность
равна приблизительно
(III. 28.13)
Р @,0| 0, Лшх (е* — 1); 0,2 Аиа~1 (е» — 1); ...; О, п Дш (^ — 1))
Р@, 01 б, ДисТ1^ —0)
где пАи = и. Далее, для больших |х снова чувствуется,
что наблюдения в моменты времени
почти независимы, так что предел (III. 28.12) должен
приблизительно равняться
[Р@, 0|0, Лист1 (ехр |i — 1))]я"\
что в пределе при Аи-* 0, пАи = и обращается в
ехр (—и).
Хотя эти рассуждения с математической точки зре-
зрения кажутся грубыми, они удобны и наводят на мысль
о весьма общей теореме: время возвращения, отнесенное
к среднему времени возвращения, распределено экспо-
экспоненциально в пределе, когда среднее время возвращения
становится бесконечно большим.
Это справедливо для эренфестовской модели. При
этом экспоненциальный характер предельного распреде-
распределения объясняет уже замеченное нами явление, что для
большого времени возвращения его относительная
флуктуация равна приблизительно 1 A00%).
Последнее замечание. Если рассматривать газ, на-
настолько разреженный, что столкновениями между моле-
молекулами можно пренебречь (газ Кнудсена), и если А —
выпуклое множество, то мы приходим к реальному устой-
устойчивому процессу nA(t).
Так как скорости в газе подчиняются максвеллов-
скому распределению
(III. 28.14) m^BnkTy3'2 ехр [— т\ • v BkT)'1] =/(v),
то легко показать, что
где if>(r)—характеристическая функция множества А
[см. (III. 22.1)].
Формула (III.28.8) в этом случае применима, и, та-
таким образом, возможно в принципе найти распределение
последовательных интервалов времени, в течение кото-
которых в множестве А нет частиц газа!
г л \ в л IV
ИНТЕГРИРОВАНИЕ В ФУНКЦИОНАЛЬНЫХ
ПРОСТРАНСТВАХ И НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
1. До сих пор в тех задачах, которыми мы занима-
занимались, ссылки на теорию меры были сравнительно три-
тривиальны. Теперь мы переходим к рассмотрениям, опи-
опирающимся на значительно более сложные факты из гео-
рии меры.
Исходной точкой служит для нас результат, впервые
полученный Эйнштейном и Смолуховским, о том, что ве-
вероятность попадания свободной броуновской частицы,
находящейся в начальный момент в точке х = 0, в проме-
промежуток между cci и Pi в момент tu в промежуток между
а2 и р2 в момент t2, и т. д., между ап и р„ в момент tn,
задается формулой
(IV. 1.1) J ... /Р@|х1; Ь)Р(хг\х2; t2 — tj...
•. • Р (¦*„_! 1 ха; tn — tn^) dxx... dxiv
где
(IV. 1.2) 0</1</2< ... <tn
и
(IV. 1.3) Р (jc I у; /) = Bjt/rVlexp[—i(y-^
На самом деле
P (X\y; t) = ± (яД0"/2ехр[-1(у - xf D-l
где коэффициент диффузии D очень просто связан с вяз-
вязкостью и температурой среды, в которой происходит
броуновское движение, и с радиусом частицы (частицы*
считаются шариками). Формула для D содержит также
число Авогадро, входящее в выражение для константы
Больцмана к. Тем самым число Авогадро может быть
определено из опытов с броуновскими частицами. Дей-
Действительно, именно из-за этой возможности теория Эйн-
Эйнштейна—Смолуховского и стала столь привлекательной
для физиков. Однако с чисто математической точки зре-
зрения физический смысл D несуществен, и мы можем вы-
выбрать такие единицы измерения, что
Теперь попытаемся вложить теорию броуновского
движения в общую схему, описанную в п. 1 гл. I.
В качестве выборочного пространства S мы возьмем
сначала все вещественные функции x(t) @<^<oo),
удовлетворяющие условию х@) =0.
Элементарными множествами мы объявим множества
функций, определяемые условиями вида
(IV: 1.4) {a1<^c(/1)<Pi, ¦.., ал<х(О<РлЬ
0</!</2< ... <tn
(Винер называл такие множества «квазиинтервалами»).
Мера, приписываемая таким множествам (мера Ви-
Винера) задается формулой Эйнштейна — Смолуховского
(IV. 1.1).
Легко теперь проверить, что заданная так мера эле-
элементарных множеств удовлетворяет условию согласован-
согласованности.
Действительно, нетрудно видеть, что условие согла-
согласованности вытекает из соотношения
(IV. 1.5)
Как только установлена согласованность, с помощью
общей теоремы Колмогорова (упомянутой в п. 6 гл. III)
можно построить вполне аддитивную меру в простран*
стве всех вещественных функций x(t), (х|0)=0.
Построенная таким образом, эта мера почти беспо-
бесполезна, поскольку многие интересные и нужные нам мно-
множества оказываются неизмеримыми. Например, неизме-
неизмеримым будет множество С всех непрерывных функций.
В самом деле, можно показать, что
(IV. 1.6) [X* (С) = 1, |х, (С) = О,
где [х* и \i* — соответственно внешняя и внутренняя
меры.
Дубом было показано, что если в определении эле-
элементарных множеств (IV. 1.4) ограничиться непрерыв-
непрерывными функциями (т. е. считать, что квазиинтервалы со-
состоят только из непрерывных функций), а их меру по-
прежнему задавать с помощью формулы (IV. 1.1), то
можно получить вполне аддитивную меру, причем
(IV. 1.7) |г(С) = 1.
2. Не вдаваясь в доказательство предыдущих утвер-
утверждений, постараемся объяснить, что из них следует.
Исходя из элементарных множеств, которым заранее
приписаны меры, мы построим новые множества при
помощи объединений (конечных или счетных) элемен-
элементарных множеств и дополнений к уже построенным та-
таким образом множествам.
Этим способом получается запас множеств, который
называется борелевским полем, порожденным заданны-
заданными элементарными множествами.
Теперь по очевидным правилам (см. п. 1 гл. I) мы
можем приписать меру всем множествам борелевского
поля (эту операцию называют продолжением меры).
Трудное место в теории Колмогорова — показать, что
при таком продолжении сохраняется согласованность.
Иными словами, надо показать, что два разных разло-
разложения любого множества В из борелевского поля на
элементарные множества приводит к одному и тому же
значению меры В (в разложении может быть использо-
использовано счетное число операций суммирования и перехода
к дополнению).
Упомянутый выше результат Дуба можно сформули-
сформулировать так: добавим к элементарным множествам
множество С непрерывных функций и припишем ему
меру, равную 1. Снова построим борелевское поле мно-
множеств и, как прежде, продолжим на него меру. Мы по-
получим таким образом новую меру на множестве всех
вещественных функций x(t) (х@) — 0), полностью сосре-
сосредоточенную на пространстве С.
Здесь трудно показать (причем эта трудность мень-
меньшая, чем в доказательстве Колмогорова), что условие
[i(C)=l согласовано с заданием меры на «квазиинтер-
«квазиинтервалах» (IV. 1.4).
Мы можем теперь забыть о пространстве всех веще-
вещественных функций и рассматривать нашу меру, опреде-
определенную только на пространстве непрерывных функций.
Это мера Винера в пространстве непрерывных функций
x(t), нормированных условием х@) =0.
Винер, который первым ввел эту меру в начале 20-х
годов, сделал это гораздо менее абстрактным образом.
Он построил явное отображение пространства С в ин-
интервал @,1) [точнее, в интервал @,1) минус множество
меры нуль], при котором квазиинтервалы (IV. 1.4) пере-
перешли в множества, обычная мера Лебега которых совпа-
совпадала с мерой квазиинтервалов (IV. 1.1).
Метод Винера, несмотря на большую привлекатель-
привлекательность (особенно для аналитика), обладает рядом недо-
недостатков (которые мы укажем в дальнейшем) и в на-
настоящее время вышел из моды.
Тем не менее не следует забывать, что именно Вине-
Винеру первому принадлежит эта идея, и поэтому его вклад
в эти вопросы все еще непревзойден.
3. Поскольку согласованность мер, приписанных ква-
квазиинтервалам (IV. 1.4), следует из соотношения (IV. 1.6)
(уравнения Чепмена — Колмогорова — для математиков,
уравнения Смолуховского — для физиков, причем по-
последнее исторически более справедливо), мы можем
исследовать другие решения этого уравнения, с помощью
которых можно построить меру в подходящем простран-
пространстве функций.
Не вникая в детали классификации решений этого
уравнения, что само по себе составляет обширную тему,
кратко упомянем лишь один интересный класс таких
решений, а именно
(IV. 3.1) P(x\y;t) =
со
-Bл) /ехр[?(у-*)]ехр[—/|&|в?, 0 < а < 2.
Это так называемые «устойчивые плотности с показате-
показателем а».
Случай а = 2 соответствует броуновскому движению
и кратко обсуждался в предыдущих пунктах.
Случай а<2 интересен тем, что вместо (IV. 1.7) здесь
оказывается, что
(IV. 3.2) \f(C) = 0,
и, следовательно, невозможно построить меру в про-
пространстве С с помощью функции (IV. 3.1).
Однако, как показал П. Леви (а позднее Дуб), мож-
можно с помощью (IV. 3.1) ввести меру в пространстве 3)
функций, непрерывных слева (или справа) и имеющих
разрывы лишь первого рода.
Нам кажется, что в этом случае уже нелегко приме-
применить метод Винера (т. е. построить явное отображение
в множество, где мера вводится просто); в этом и за-
заключается основной изъян метода Винера.
4. Как только построена вполне аддитивная мера в
пространстве С, обычным образом определяется инте-
интеграл (интеграл Винера), обладающий всеми основными
свойствами интеграла Лебега 1).
Мы будем пользоваться символом математического
ожидания Е для интегралов и Р — для меры.
Пусть V(x)—непрерывная функция, определенная
на интервале (—со, со), и, кроме того, V(x)^0.
1) Имеется группа математиков, считающих преступлением сна-
сначала вводить меру, а затем уже интеграл. Хотя эта точка зрения
разделяется немногими и вряд ли заслуживает полемики, можно
отметить, что в теории вероятностей, которая является одной из
основных «потребительниц* теории меры и интегрирования, «старо-
«старомодный» порядок (сначала мера, затем интеграл) совершенно есте-
естествен.
Рассмотрим теперь интеграл Винера
t 1
(IV. 4.1)
Е { ехр
-fV(x(x))dx\\.
Существует ли он?
Поскольку подинтегральный функционал ограничен,
достаточно показать, что он измерим.
Так как
/ п
(IV. 4.2) Г V(x(x))dx= lim tn'1 У V{x{ktn^))
о ^°° JTi
[напомним, что х(х)?С и что мы предположили непре-
непрерывность У(#)!] и функционал
2
k=i
V{x{ktn^))
очевидным образом измерим, то тем самым установле-
на измеримость функционала Г V(x (x)) dx, а следова-
о
тельно, и измеримость
Из равенства (IV. 4.2) и теоремы о сходимости огра-
ограниченной последовательности функций следует, что
(IV. 4.3) Е \ ехр
-fV(x(x))dx\\ =
= lim E { ехр
Я-»оо
—/л-» 2
причем здесь заодно утверждается и существование пре-
предела в правой части.
С другой стороны, из (IV. 1.1) ясно видно, что
(IV. 4.4) Е ехр Г— tnr1 ^V(x (ktn-1))] =
X
ОО ОО
= /... /ехр
-оо —оо
-tn-1% V(xk)
k-1
Отсюда мы получаем следующий вывод: предел
оо оо р п -|
(IV. 4.5) llm f ... fexp \-tnr^V(xk) X
X P @1^; ^/г^1) P to |x2; //г)... P (хп_г\xn; tn~l)dxx... dxn
существует и равен
(IV. 4.6) E | ехр I — J У(х(т)) rft
E | ехр I — J
Существование предела (IV. 4.5) следует здесь про-
просто из измеримости некоторого функционала. Это про-
простой, но важный пример тех аналитических возможно-
возможностей, которые таятся в теории меры х).
Можно попытаться определить интеграл (IV. 4.6) как
предел интегралов (IV. 4.5); эту процедуру в действи-
действительности применил Фейнман.
Недостатки такого подхода с математической точки
зрения очевидны, хотя он и имеет формальные основа-
основания.
1) Эти рассуждения напоминают знакомый прием из классиче-
классического анализа, с помощью которого существование предела
/я \
Нт ( У, к--logn)
1
выводится из существования интеграла J (t~x — [t~ ]) dt (в смы-
смысле Римана).
Фейнман записал интеграл (IV. 4.5) в виде (хо =
j ОО ОО г-
п-^п J ... /ехр -/л-'
— ОО —ОО |_
k-\
откуда очевидно, что в экспоненте стоит интегральная
сумма для интеграла
о
Вместо (IV. 4.6) Фейнман пишет
(IV. 4.7)
/ехр Г- J{1 (-?)' + V(x(x))\dx\d (траектория).
Это символическое обозначение физически более нагляд-
наглядно, поскольку
есть функция Гамильтона частицы с массой 1, движу-
движущейся в потенциальном поле V(x).
В действительности Фейнман в своем новом подходе
к нерелятивистской квантовой механике пришел к инте-
интегралу
(IV. 4.8)
)
It -1
ih~l /{ Dт) ~ V(x(x))^dx \d (траектория),
о J
где
?=о1г (h — постоянная Планка)
(IV. 4.9)
является классическим действием вдоль траектории х(т)<
Из-за стоящего в экспоненте i(^Y—0 фейнмановскую
теорию нелегко сделать строгой. С другой стороны, с ин-
интегралами Фейнмана вида (IV.4.7) удобнее обращаться,
если переписать их в форме (IV. 4.6).
5. Мы покажем теперь, что вычисление интеграла Ви-
Винера
(IV. 5.1)
ехр Г-
можно свести к решению дифференциального уравнения,
тесно связанного с уравнением Шредингера.
Ныне такое сведение можно произвести многими спо-
способами, но мы выбираем далеко не самый изящный. Его
основное достоинство в том, что ой требует очень немно-
немного предварительных сведений.
Мы наложим сначала дополнительное ограничение на
V(x), а именно будем считать, что функция V(x) огра-
ограничена также и сверху:
0<
Теперь
ехр
-fV(x(x))dx
и так как
t
(IV. 5.2) 0 < f V(x (т)) dx < Mt,
о
мы получаем
(IV.5.3) ? | ехр Г—/ К(лг(т))<*т 11 =
Рассмотрим теперь моменты
(IV. 5.4)
fV(x{x))dx
и вычислим их для &=1 и fe = 2, с тем чтобы увидеть,
как они себя ведут.
Для k=l мы имеем 1)
t оо
=/ / V® Bят)-'А ехр (-1
О ^с
Для k = 2 вычисления несколько усложняются:
Г г t т2 )
= 2\Е Iff V(x(x1))V(x(x2))dx1dxA =
(о о J
t ъ
= 2\ffE\V{x{xl))V{x{xi))\dxldx2 =
о о
оо оо
J fV(l1)V(l2)Bnx1rl''exp(-^fllx1)x
оо -оо
X [2л (т2 - xj]-'1' ехр [- i (Е2-6,J/(т2—
о о
t х2 оо оо
0 0 -оо -оо
!) Здесь мы обращаемся к теореме Фубишь
Теперь совершенно ясно, как перейти к случаю общего k.
Определим функции Qn(xJ) следующим образом:
(IV. 5.5) Qo (*, t) = Bя/)/2 ехр (- ijc
/ оо
(IV.5.6) Qn+l(x, t) = f f [2я(г-т)-'/2Х
О -оо
X ехр [--i (x-iy/(t~x)] V(l) Qn(l, x)dl dx.
Заметим, что
оо
(IV.5.7) »h(t) = k\ JQk(x,t)dx.
— оо
Далее, так как мы предположили, что 0<V(x) <М,
то по индукции можно показать, что
(IV. 5.8) 0 < Qn (х, t) < Ш- Qo (x, t).
Положим
(IV. 5.9) Q (х, /) = S (-1)" Qk (x* 0;
k = 0
в силу (IV. 5.8) этот ряд сходится для всех х и t ф 0.
Ясно, что
, /)|<exp(M/)Q0(x, /),
и в силу (IV. 5.5) и (IV. 5.6) Q удовлетворяет интеграль-
интегральному уравнению
(IV.5.10) Q(x J
0 -оо
X ехр [- \ (x-lf/(t-x}\ V (I) Q (|, -с) dl dx = Qo (x, t).
Комбинируя формулы (IV. 5.9), (IV. 5.7) и (IV. 5.3),
получим
(IV.5.11) ?<ехр — fV(x(x))dx 1 = f Q {x, t) dx.
Под математическим ожиданием
Л \ Си, <»
ь \ ели I v 1л i II I
I L о
мы понимаем интеграл по всему пространству С.
Если бы мы интегрировали по части пространства С,
определенной условием
a<x(t)<b,
мы пользовались бы очевидным обозначением
t
; a<x(t)<b\.
ехр — f V(x(x))dx
L о
С помощью небольших изменений в наших рассу-
рассуждениях мы получим
(IV. 5.12)
Е \ ехр
I-
-fV(x(x))dx
откуда, в частности, следует, что
(IV. 5.13) Q(x, /)>0.
Мы можем теперь освободиться от условия
V(x) < М.
Действительно, положим
рМ. если V(xL.M,
Уму*) — \ м< если v(x»M,
и обозначим соответствующую функцию Q через
В силу полной аддитивности меры Винера мы имеем
lim Е ехр — Г VM{x(x)) dx ; а < х (t) < b \ =
м+*> [ [ J J J
= Е \exp\~fV(x(x))dx ; a<x{t)<b\,
и, как следует из (IV. 5.12), при М-^оо функции
Q{M)(x, t) образуют убывающую последовательность.
Отсюда далее вытекает, что предел
{M)
lim Q{M)(x, t) = Q(x, t)
f
существует и что Q удовлетворяет основному интеграль-
интегральному уравнению (IV. 5.10).
Из интегрального уравнения (IV. 5.10) следует, что Q
удовлетворяет дифференциальному уравнению
а из (IV. 5.12) немедленно получаются начальные усло-
условия для Q:
(IV. 5.15) Q(x, t)->6(x), t->0,
т. е.
е
lim Г Q(x, t) dx = \.
— s
В действительности проще применить преобразова-
преобразование Лапласа к уравнению (IV. 5.10) и получить
со
(IV. 5.16) г|> (jc) + Bs)~I/2 J ехр (— Bs)'121 х — 11) X
— оо
X V(l) Ф (I) rf& = Bs)/2 ехр (— Bs)V21 x \),
где
оо
(IV. 5.17) ф (jc) = J Q (л, 0 ехр (— «/) Л, s > 0.
— оо
Теперь просто убедиться в том, что
(IV. 5.18) itf'-
и что ур(х) удовлетворяет следующим условиям:
(а) а|)->0, х-> ±оо;
(б) ij/ непрерывна всюду, кроме х — 0;
(в) ^(-0)-^(+0) = 2.
В случае, когда функция V(x) имеет конечное число
разрывов, во все предыдущие рассуждения надо внести
небольшие и очевидные изменения.
6. Поскольку Q(x, t) непрерывна по х [это вытекает
из (IV. 5.10)], мы получаем из формулы (IV. 5.12)
(IV. 6.1)
|Г '
ехр — [V(x(t))dx;
L о
)
\=Q(a, t).
j
Определим условное математическое ожидание
Е ехрГ-
как предел
lim
S->0
ехр \—
; а < х (t) < a -f- ?
Р {а < x(t) < а-+г}
Поскольку
lim i- Р {а < х (/)< а + г} = Bnt)~1/2 ехр (— 1 a1 It)
мы получаем из (IV. 6.1)
(IV. 6.2) Bя/)~1/2 ехр (— \ а2//) X
в\
X Е ехр
-fV(x(x))dx
= Q (a, t).
Допустим теперь, что
(IV. 6.3) V {х) -> оо; х -> ± оо.
Хорошо известно, что при этом предположении соб-
собственные значения задачи
(IV. 6.4) ±ty"~V(x)^ = — АлЬ г|)??2(— оо, оо),
образуют дискретный спектр
им соответствуют нормированные собственные функции
ih С*), ^2 (¦*)>
Известно также, что Q можно записать в следующем
виде:
(IV. 6.5) Q (а, 0=2 ехр (— у) ^ (а) fy @).
Комбинируя формулы (IV. 6.5) и (IV. 6.2), мы полу-
получаем
(IV. 6.6) Bnt)~42 ехр [— 1 a2/t] X
ехр — J V(x(x))di
x(t) = a
и с помощью небольшого обобщения приходим к выра-
выражению
(IV. 6.7) Bя<)~V2 ехр [— 4 (а - ?J/*] X
Итак, мы смогли выразить чисто классическую вели-
величину
2
в терминах интеграла по пространству функций. Заме-
Замечательно, что ряд важных свойств этой величины можно
немедленно вывести из вероятностного представления
(IV. 6.7.)
В самом деле, полагая а=?, мы получаем
(IV. 6.8)
л: @ = 0 =
ехр
и почти очевидно (доказать это очень легко), что
Г г
(IV. 6.9) НтЯ ехр —
~* |_ о
Таким образом, при ?~>0
2 ехр (— Xjt) г|У/ (?) '— Bnt)~^2,
и из классической тауберовой теоремы вытекает, что
(IV. 6.10) ^i f/(y^2 л А, л->оо.
= 0 =1.
Этот в высшей степени нетривиальный аналитиче-
аналитический результат получается здесь как следствие почти
очевидного соотношения (IV.6.9).
Интегрируя равенство (IV. 6.8) по ^ и используя то
обстоятельство, что все г|? нормированы, мы получаем
(iv. 6.И)
= Bnty'h f E ехр
= 0 \d\.
можно рассматривать как интеграл по пространству не
прерывных траекторий, удовлетворяющих условиям
= 0 и
Для малых t естественно считать, что x(t) в проме-
промежутке 0<т<? приблизительно равно 0. Таким обра-
образом, можно ожидать, что
и, точнее, что
°° ( Г '
(IV. 6.12) / El ехр -/
-оо I L 0
dx
ехр [-tV{l)\ dl,
в предположении, конечно, что V(x) растет достаточно
быстро, чтобы гарантировать существование интеграла в
правой части для всех />0.
Строгое обоснование асимптотики (IV. 6.12) было дано
Реем; оно состоит в основном в доказательстве того,
что функции х(х) в интервале @, /) лишь с «малой»
вероятностью принимают «большие» значения.
Таким образом, при t-+0
(IV.6.13)
—со —со
Пусть
N(X)= 2 1
Л2
и В (X) — площадь области -j-+ V(l) <h-
Тогда формула (IV.6.13) может быть переписана в
виде
оо оо
J ехр (— Xt) dN (X) ~ Bл) J ехр (— Xt) dB (X), t -> О,
о о
и можно ожидать, что при подходящих тауберовых усло-
условиях мы получим
(IV. 6.14) М(Х)~Bл)-1 В(Х), Я~>оо.
Это результат фундаментальной важности для кванто-
квантовой механики; он привлекал к себе заметное внимание
и в чисто математической литературе.
Мы с предельной ясностью изложили интуитивное
обоснование формулы (IV.6.14), и строгое рассмотрение
(данное Реем) следует пути, подсказанному предыдущи-
предыдущими эвристическими рассуждениями.
7. В качестве непосредственного применения форму-
формулы (IV. 6.11) рассмотрим вычисление статистической
(квантово-механической) суммы
(IV.7.1) Z=S ехр(-р?я),
/2=1
где
(k — константа Больцмана, Т — абсолютная температу-
температура) и Еп — энергетические уровни кранторо-одеханиче-
ской системы.
В простейшем (одномерном) случае частицы в потен-
потенциальном поле V(x) энергетические уровни являются
собственными значениями уравнения Шредингера
(IV. 7.2)
Полагая
х = h
мы получаем
) = <р
Это совпадает с формулой (IV. 6.4), если в ней заменить
V(x) на V(hm-^x). Таким образом, с помощью (IV. 6.11)
получаем
Z= V ехр (- $Еп) = Bлр)"V2 X
X
exp
или после простри замены переменных
(IV. 7.3) Z = mhhrx Bjtp)/2X
X {Е exp \—
-оо I 1 О
Можно теперь разложить Z в ряд по степеням h, a
именно
и т. д. Напишем
Р
J K
(т)
и, следовательно,
ехр
1
-
= ехр (- pV(i)) I 1 - hm-bV* (I) f x (t) dx +
I
]2
Мы можем теперь вычислить
Мы вычислим только второе среднее
2
предоставив читателю вычислить два остальных
Мы имеем
Г Р ч
= 2Е If f x (x,) x (t2) dxx dx21 jc(P) = (
lo о
о о
и, таким образом, нам осталось вычислить только
Е{х(хг)х(ъ)\х$) = 0}. 0<т1<т2<р.
Согласно определению условного математического
ожидания,
р {__
оо оо е
[
— СХ> — ОО —?
X [2л (р - т2)]~>к ехр [-1 (gZ
: Bяр)-'/2 J ехр (-^
— оо —оо
и, следовательно,
В \ 2
Э т2
= 2 J* J т, A — хф'1) dxx dx2 = рз/12.
о о
Подобным же образом мы найдем, что
Е \fx(x)dx\x($) = 0 =0,
= 0 =р2/б.
Окончательно
f °°
Z=h-lmk Bяр)/2 J exp [
l-
24
Это разложение впервые было получено Вигнером и
Кирквудом.
8. В качестве последней иллюстраций применения ин-
интегрирования в функциональных пространствах мы
кратко рассмотрим некоторые вопросы классической тео-
теории потенциала.
До сих пор мы имели дело лишь с мерой в про-
пространстве С непрерывных функций x(t) (x@) = 0).
Теперь нам понадобится мера в пространстве всех
непрерывных.трехмерных кривых г(т) (г@)=0).
Поскольку г(т) задается просто тройкой непрерыв-
непрерывных функций (х(х), у(т), г(т)), естественно в качестве
меры выбрать произведение мер в СхСхС.
Этот способ задания меры зависит от выбора системы
декартовых координат в трехмерном пространстве, но в
силу свойств нормального распределения наши выводы
от этого выбора не зависят.
Мера строится так, что для любого набора моментов
времени 0<ti<Ct2<.. .<tn и борелевских множеств
Йь ^2, ..., йп в трехмерном евклидовом пространстве
R3 имеем
(IV. 8.1)
XP(ri|r2; t2 — tx)... Р(га_г\гя; tn — tn_
где
(IV. 8.2) P(r|p; ^) =
Здесь Up — r|| обозначает евклидово расстояние ме-
между г и р, dv — элемент объема.
Должно быть ясно, что мы имеем здесь дело просто
с теорией броуновского движения (теорией Эйнштейна —
Смолуховского) в трехмерном евклидовом пространстве.
Пусть Q — ограниченная замкнутая область в R3 и
V(r) — ее характеристическая функция, т. е.
A, ^,
Рассмотрим функционал
(IV. 8.4) Ts(y)
он представляет полное время, которое броуновская
траектория у+г(т), начинающаяся в у, проводит внутри
области Q. Мы имеем
О
оо
= / / Bjtt)-3'2 exp (-1 T-i ||r - у ||2) dv dx =
О 9
и, следовательно, значение Tq (у) конечно для почти
всех траекторий г(т).
Легко вычислить все высшие моменты для Tq (у). По-
Получим
(IV. 8.5)
•••Jr* — Ть-гГЫгг ... dvk.
Формула (IV. 8.5) наводит на мысль рассмотреть ин-
интегральное уравнение
(IV. 8.6)
Его ядро
BпГ1\\?-г\Г1
вполне непрерывно и положительно определено. Если
обозначить через
Ль Л2, •••
его собственные значения и через
— соответствующие нормированные собственные функ-
функции, мы получим
l J<(>j(?)dpBn)-1 f Wp-yW-'cf^dp, k>\.
Рассмотрим выражение (и !> 0)
(IV. 8.7) А (у; и) = Е{ехр[~иТа(у)\\.
Легко подсчитать, что
(IV. 8.8) А (у; и) =
= 1 - 2 я О +М / Ф; (Р)d? Bл) X
Если y?Q, то формула (IV. 8.8) может быть перепи-
переписана в более простом виде
(IV. 8.9) Л (у; и) =
оо
=1 — S h (и~1 + h)~l / Фу (р) ^РФу (У)' У ^ °-
Если у находится внутри области Q, то Га (у)>0
для любой траектории г(т) и, следовательно,
lim Л (у; я)= lim Е {ехр(— иГ0(у))} =0.
Таким образом,
оо
(IV. 8.10) lim V %} F + Xfyx Г фу (р) dp Ф (у) = 1
для каждого у из области Q. Этот аналитический резуль-
результат, выражающий то обстоятельство, что разложение
единицы в ряд Фурье по собственным функциям ф^ сум-
суммируется к 1 некоторым методом суммирования, выте-
вытекает здесь из того тривиального замечания, что
Га(у)>0.
Более тонкое рассуждение показывает, что если об-
область Q удовлетворяет некоторым условиям регулярно-
регулярности (например, если она является локально звездной),
то для у (? Q
lim A—Л (у; #))— lim A—?{ехр[—
и ^ оо и ^ оо
где U(у) —объемный потенциал области Q, т. е. гармо-
гармоническая функция, обращающаяся в нуль на бесконеч-
бесконечности и стремящаяся к 1 при приближении у к регуляр-
регулярным (в смысле теории потенциала) точкам границы.
Кроме того, формула (IV. 8.10) остается верной для
каждой регулярной точки границы, в то время как для
нерегулярных точек этот предел, если он существует,
меньше 1.
Мы приходим, таким образом, к явной формуле
(IV. 8.11) U(y) =
Для объемного потенциала области, удовлетворяющей
некоторым слабым условиям регулярности.
Хотя формула (IV. 8.11) чисто «классическая», впер-
впервые она была установлена и доказана вероятностными
методами; тем самым еще раз подтвердились их сила и
полезность.
ПРИМЕЧАНИЯ И БИБЛИОГРАФИЯ
Глав а I
1. Идея о том, что теория вероятностей может быть формали-
формализована на основе теории меры, появилась впервые в классической
статье Э. Бореля [В о г е 1 Е., Sur les probabilites denombrables et
leurs applications aritmetiques, Rend. Circ. Mat. Palermo, 47 A909),
247—271]. Борелем же был открыт «усиленный закон» больших чи-
чисел (см. п. 5). Впервые значительная часть аксиоматики теории ве-
вероятностей была дана Г. Штейнгаузом в его статье: Stein-
h a u s H., Les probabilites denombrables et leur rapport a la theorie
de la mesure, Fund. Math., 4 A922), 286—310. Наиболее полная
аксиоматика принадлежит А. Н. Колмогорову, и ее можно найти в
его книге «Основные понятия теории вероятностей» (М. — Л., 1936).
Мало кому известно, что аксиоматика теории вероятностей входила
в знаменитый список проблем Гильберта.
2. Вывод, приведенный в этом пункте, принадлежит Максвеллу,
но часто приписывается Борелю. Доказательство «слабого закона»
больших чисел получится, если показать, что
стремится к нулю при N->со (напомним, что R зависит от N1).
3. Изложение этого пункта следует моим статьям «On the ave-
average number of real roots of a random algebraic equation», которые
появились в журналах Bull. Л тег. Math. Soc, 49 A943), 314—320
(и 938) и Proc. London Math. Soc, 50 A948), 390—408. Статья Эр-
дёша и Оффорда появилась в журнале Proc. London Math. Soc,
6 A956), 139—160. Вопрос о нулях случайных функций предста-
представляет значительный интерес и особенно важен в теории случайных
шумов и связанных с ними явлений. Наиболее важный вклад здесь
принадлежит Раису [Rice S. О., Mathematical theory of random
noise, Bell System Tech. Л, 2В A944), 282—332; 25 A945), 46^-156].
4. Изящная формула A.4.13) была открыта Реньи [R ё п у i A.,
On the density of certain sequences of integers. Acad. Serbe. Bull.
Acad. Sci. Mat. Nat., 8 A955), 157—162]. Приведенное здесь дока-
доказательство близко следует моей заметке «A remark on the preceding
paper by A. Renyi» (ibid., 163—165).
Если мы обозначим через M{f(n)} предел (в предположении,
что он существует)
N
lim Гг ,
то наиболее трудное место в нашем доказательстве — это уравнение
( 1} {
2 } { Д
М {ехр [«рл (л)]}.
Оно получается с помощью элементарных вычислений из формулы
A.4.6) и является простым повторением обычных рассуждений, ис-
используемых при доказательстве того, что математическое ожидание
произведения независимых случайных величин равно произведению
их математических ожиданий.
6. Смотри S z e k e r s G., Turan P., Ober ein Extremalproblem
in der Determinantentheorie (венгерск., резюме нем.), Mat. termeszett
Brtes., 56 A937), 796—804.
Глава И
1. Задаче о случайном блуждании из этого пункта для частного
случая р(а) = Bя;) @<а<2я) уделено значительное внимание
в математической литературе. Это особенно простой случай, по-
поскольку здесь последовательные смещения независимы. Рассмотре-
Рассмотрение этого случая можно найти в работах: Чандрасекар С,
Стохастические процессы в физике и астрономии, ИЛ, М., 1947;
Rice S. О., Distribution of а sum of n sine waves, Bell Tel. System
Tech. Publ., Monograph 2365. Теорему Поля Леви (называемую тео-
ремой о непрерывности преобразования Фурье — Стильтьеса) можно
найти в любом стандартном учебнике; см., например, Л о э в М.,
Теория вероятностей, ИЛ., М, 1962.
Теорема о моментах была впервые доказана Чебышевым. Она
была существенно обобщена Марковым (см., например, его книгу
«Исчисление вероятностей», С.-Пб., 1908), которая, по моему мнению,
до сих пор является одной из лучших и наиболее ярких книг по
теории вероятностей). Условие (II. 1.5) было найдено Карлеманом.
2. Насколько мне известно, в доказательстве предельных теорем
теория возмущений используется впервые. Вычисления, использую-
использующие теорию возмущений, не всегда легко строго обосновать, но
для наших целей вполне достаточно сослаться на работу: R е 11 i с h,
Storungstheorie der Spektralzerlegung, I, II, Math. Ann., 113 A937),
600—619; 677—685 (то же самое относится к п. 3).
3. Хотя модель полимерной цепи, которая рассматривается в
этом пункте, принадлежит Айрингу, соответствующая задача о слу-
случайном блуждании была исследована Смолуховским в одной из его
ранних статей по броуновскому движению. Вычисления в этом
пункте в основном принадлежат Смолуховскому.
4. Первое доказательство основного результата этого пункта
было дано Мораном [М о г a n, The statistical distribution of the
length of a rubber molecule, Proc. Cambridge Phil. Soc, 44 A948),
342—344], который воспользовался одной общей теоремой
С. Н. Бернштейна. Наше доказательство (опирающееся на теорию
возмущений) намного более аналитическое, но зато и более прямое.
5. Теоремы этого пункта принадлежат В. Феллеру [Feller W.,
Fluctuation theory of recurrent events, Trans. Amer. Math. Soc, 67
A949), 98—119], но мы следуем изложению Дарлинга и Каца
[Darling D. A., Kac M., On occupation times for Markov proces-
processes, Trans. Amer. Math. Soc, 84 A957), 444—458].
6. Математическая формулировка принципа неопределенности
принадлежит Г. Вейлю.
7. 8. Изложение в этих пунктах следует моей статье «Toeplitz
matrices, translation kernels and a related theorem in probability
theory» [Duke Math. /., 21 A954), 501—509].
Результат Сегё был опубликован в работе l) «On certain hermi-
tian forms associated with the Fourier series of a positive function
(Festskrift Marcel Riesz, Lund, 1952, 228-238). Задача нахождения
предела (II. 7.6) возникла у Онзагера в связи с его работой по
двумерной модели Изинга. Работа Спитцера содержится в основном
в его статье: S p i t z e r, A combinatorial lemma and its application
to probability theory, Trans. Amer. Math. Soc.r 82 A956), 323—339.
Идея использовать чисто комбинаторные методы при исследовании
некоторых вероятностных задач появилась впервые у Андерсена,
чья работа (цитируемая в упомянутой выше статье Спитцера) ока-
оказала сильное влияние на Спитцера.
9. Теорема этого пункта была впервые доказана Эрдёшем и
Кацем. Обзор недавних работ по применению вероятностных мето-
методов в теории чисел можно найти в статье: К у б и л ю с И. П., Ве-
Вероятностные методы в теории чисел, УМН, 11; 2 F8) A956), 31—66.
Глава III
1, 2. Больцман изложил большую часть (но не все) своих ра-
работ в двухтомном трактате «Vorlesungen (iber Gastheorie». Это одна
из величайших книг в истории точных наук, и мы очень советуем
читателю ознакомиться с ней. Полученное удовлетворение оправ-
оправдывает затраченные усилия.
3. Полемика между Больцманом и Цермело изложена в клас-
классической статье П. и Т. Эренфестов (Enc. Math. Wiss., 1911). Этот
знаменитый обзор содержит наиболее глубокий анализ идей, лежа-
лежащих в основании статистической механики; всякий, кто намерен
серьезно изучить предмет, должен прочитать эту статью.
4, 5. Доказательство теоремы Пуанкаре, а также вычисление
среднего времени возвращения следует моей заметке «On the notion
of recurrence in discrete stochastic processes» (Bull. Amer. Math.
Soc, 53 A947), 1002—1010). Впервые доказательство формулы
0 Результат Сегё содержится в книге: Гренадер У. и
Сегё Г., Тёплицевы формы и их приложения, ИЛ, М., 1961.—
Прим. перев.
(II. 5Л) было дано Биркгофом [В i r k h о f f G. D., Proof of a recur-
recurrence theorem for strongly transitive systems, Proc. Nat. Acad. Sci.
USA, 17 A931), 650—655]. Но последовавшее за этим доказатель-
доказательство эргодической теоремы, данное Биркгофом, настолько затмило
эту заметку, что ее потеряли из виду. Работа Смолуховского о сред-
среднем времени возвращения кратко изложена в его прекрасных лек-
лекциях «Drei Vortrage uber Diffusion, Brownsche Molekularbewegung
und Koagulation von Kolioidteilchen» (Phys. Z., 17 A916), 557—571,
587-599).
6. Теорема Колмогорова доказана в его книге, упомянутой
выше.
7. Первоначальное описание этой модели см, в работе: Е h r e п-
f e s t P., E h г е n f e s t Т., Uber zwei bekannte Einwande gegen das
Boltzmannsche //-Theorem, Phys. Z., 8 A907), 311—314.
График взят из второго тома учебника К- Шефера «Теоретиче-
«Теоретическая физика».
8. Изложение в этом пункте следует мимеографическим записям
Хиггинсовских лекций, прочитанных Г. Е. Уленбеком в Принстон-
ском университете осенью 1954 г.
9. Читатель, возможно, заметил, что мы не рассматривали
подробно эргодическую теорему. Роль этой теоремы в статистиче-
статистической механике была чрезвычайно преувеличена, и мы старались
как-нибудь это уменьшить.
Блестящее изложение эргодической теории см. в книге: Хал-
м о ш П. Р., Лекции по эргодической теории, ИЛ, М., 1959. Крат-
Краткое изложение идей Гиббса следует Хиггинсовским лекциям Улен-
бека, упомянутым выше.
10. Вывод этого пункта следует моей статье «Random walk and
the theory of Brpwnian motion» (Amer. Math. Monthly, 54 A947),
369—391).
Любопытно отметить, что если бы мы попытались, используя
тот же самый метод, искать сначала правый собственный вектор,
то мы натолкнулись бы на трудности»
П. Siegert A, J. F., On the approach to statistical equilibrium,
Phys. Rev. 76 A949), 1708—1714.
Hess F. G., Alternative solution to the Ehrenfest problem,Amer.
Math. Monthly, 61 A954), 323—327.
12. Формулы для (пА (s)) и (n\(s)) можно найти, например,
в статье: Wang М. С, Uhlenbeck G. E., On the theory of
Brownian motion, II, Rev. Modern Phys., 17 A945), 323—342.
13. См. цитировавшуюся выше статью «Random walk and the
theory of Brownian motion» и обсуждение энтропии в работе:
Klein M. J., Entropy and the Ehrenfest urn model, Physica, 22
A956), 569—575.
14. В этом пункте почти дословно воспроизводится моя за-
заметка «Some remarks on the use of probability in classical statistical
mechanics» (Acad. Roy. Belgique. Bull. CL Sci., 42 A956),
356—361).
16. 17, 18. Эти пункты почти дословно повторяют часть моей
статьи «Foundations of kinetic theory» (Proc. Third, Berkeley Symp.
on Math. Stat and Prob., v. 3, 171—197).
19. См. В г о u t R., Statistical mechanics of irreversible proces-
processes, Part VII: Boltzmann equation, Physica, 22 A956), 509—524.
В обзорной статье, написанной для нового справочника «Hand-
buch der Physik», Г. Град дает подробную критику работ Броута
и М. С. Грина.
21. Краткое изложение работы Смолуховского можно найти в
его работе «Drei Vortrage...», цитированной выше (п. 5 этой
главы).
Обзор более поздних работ см. в статье Чандрасекара, цитиро-
цитированной в п. 1 гл. II.
22, 23. Содержание этих, а также части последующих пунктов
относится к лету 1946 г., когда автор работал в Мичиганском уни-
университете.
Эти результаты были получены в сотрудничестве с Уленбеком,
который впервые привлек внимание автора к этому комплексу за-
дач. Хотя эти результаты не были ранее опубликованы, они соста-
составили основную часть доклада, сделанного автором в Орегонском
университете в июне 1952 г.
В недавней статье Линдлея [L i n d 1 е у D. V., The estimation
of velocity destributions from counts, Proc. Int. Congress, Amsterdam,
1954, 427—444] содержится вывод формулы (III 23.2), использую-
использующий другой метод, и приводится интересное обсуждение работы
Ротшильда по определению средней скорости сперматозоида. Из-за
недостатка времени материал, изложенный в п. 21—28, не был
представлен на семинаре в Боулдере.
24. Формулы (III. 24.4) и (III. 24.5) были первоначально вы-
выведены Смолуховским сложным путем. Простой и изящный вывод
был дан Чандрасекаром в его обзорной статье, цитированной выше.
26. Ссылка на работу Р. Фюрта содержится в обзорной статье
Чандрасекара.
27. Формулировка и применение принципа «включения и исклю-
исключения» имеется, например, в превосходном учебнике: Ф ел л ер В.,
Введение в теорию вероятностей и ее приложения, М., 1964.
Глава IV
1, 2. Подход Винера можно найти в главе о случайных функ-
функциях из книги: П э л и Р., Винер Н., Преобразования Фурье в
комплексной области, М., 1964. Метод Дуба можно найти в его
книге «Вероятностные процессы» (ИЛ, М., 1956).
Стоит ли столько «возиться» с теорией меры в применений
к теории вероятностей — вопрос вкуса. Я лично предпочитаю огра-
ограничить «волнения» по этому поводу до минимума, потому что я
твердо уверен, что теория вероятностей теснее связана с анализом,
физикой и статистикой, чем с теорией меры как таковой.
3. См. Levy P., Sur les integrates dont les elements sont des
variables aleatoires independantes, Ann. Pisa, 3 A934), 337—366.
4, 5, 6. Эти пункты следуют моей статье «On some connections
between probability theory and differential and integral equations»
(Proceedings of the Second Berkeley Symposium on Mathematical
Statistics and Probability, pp. 189—215). См. также: Ray D., On
spectra of second order differential operators, Trans. Amer. Math.
Soc, 77 A954), 299—321.
7. Это применение было впервые указано Зигертом в его об-
обзоре «Brownian motion theory as a tool in statistical mechanics»
(Phys. Rev., 86 A952), 621). Мы приводим последующий (независи-
(независимый) вывод А. М. Яглома, содержащийся в прекрасной обзорной
статье: Гельфанд И. М. и Яглом А. М., Интегрирование в
функциональных пространствах и его применение в квантовой фи-
физике, УМН, 11; 1 F7) A956), 77—114.
УРАВНЕНИЕ БОЛЬЦМАНА
Г. Е. УЛЕНБЕК
Часть I
1. Введение. Общая тема двух этих лекций — мате-
математическая структура теорий, описывающих так назы-
называемые необратимые процессы типа теплопроводности
(выравнивание разностей температур), вязкости (вы-
(выравнивание разности скоростей) и т. п. Мы знаем, что
практически все процессы в природе имеют опреде-
определенную тенденцию приближаться к состоянию равнове-
равновесия (или состоянию с максимальной энтропией); таким
образом, возникает задача описать это приближение с
молекулярной точки зрения; при этом предполагается,
что структура молекул и законы их взаимодействия нам
известны.
Поскольку все эти вопросы со времени основопола-
основополагающих работ Больцмана, Максвелла, Чепмена, Энскога
и других только недавно стали вновь активно разраба-
разрабатываться, можно различить пока только общие очерта-
очертания математической картины; конкретных же резуль-
результатов получено очень мало. По этой причине, а также
из-за недостатка времени я постараюсь изложить лишь
общие идеи и поставить математические задачи. Я ду-
думаю, что они представляют математический интерес,
так как они являются своего рода обобщением эргоди-
ческой теории и, несомненно, очень быстро приводят к
настоящей terra incognita.
2. Общая задача. Мы будем рассматривать только
молекулярную систему простейшего типа: N точечных
молекул в сосуде (объема V), между которыми действу-
действуют парные силы отталкивания, задаваемые для каждой
пары (i, j) центрально-симметричным монотонным по-
потенциалом ф(г^), имеющим конечный радиус действия г0
и таким, что ф@)-*-+оо, ф(го)=О. Мы будем пользо-
ваться классической механикой. В квантовой механике
появляются некоторые дополнительные особенности и,
возможно, даже упрощения, но основные задачи, как
мне кажется, по существу те же самые.
Движение всей системы молекул можно представить
движением одной точки, Г-точки, в 6Л^-мерном фазовом
пространстве (Г-пространстве) по поверхности постоян-
постоянной энергии Е{хи ..., Xjv)=const [обозначения: Х{^
= (Чг,Рг) —координата и импульс 1-й частицы]. Известно
благодаря Пуанкаре, что это движение квазипериодич-
но: точка, начав двигаться из любой конечной области
на поверхности постоянной энергии, возвращается в эту
область по истечении цикла Пуанкаре. Эта возвращае-
мость во времени является по существу следствием об-
обратимости во времени механических уравнений движе-
движения. Исторически она привела к известному спору между
Больцманом и Цермело1), а также к ошибочному вы-
выводу, что тем самым невозможно объяснить необрати-
необратимые процессы с помощью обратимых механических мо-
моделей. Причина, по которой теорема Пуанкаре не имеет
отношения к теории необратимых процессов, двоякого
рода:
(а) Поскольку N очень велико, время возвращения
для некоторой фиксированной «малой» начальной обла-
области становится огромным, гораздо больше, чем наблю-
наблюдаемое время выравнивания или релаксации. Тот факт,
что для конечной механической модели существует вре-
время возвращения Го, лишен, таким образом, интереса, так
как мы хотим следить за системой только в продолже-
няе времени t<^T0.
(б) Начальное состояние никогда не бывает полно-
полностью определено, так как любое макроскопическое изме-
измерение дает информацию лишь о средних величинах по
большой совокупности молекул. Поэтому мы должны
рассматривать не одну механическую систему, а, по тер-
терминологии Гиббса, ансамбль идентичных систем, отли-
отличающихся только начальной фазой, и следить за тече-
0 См. Ehrenfest P., Ehrenfest Т., Grundlagen der Stati-
Stischen Mechanik, Enz. der Math. Wiss., IV, 32. Это обсуждается
также в книге: Н а а г D. ter, Introduction to Statistical Mechanics.
нием всего этого ансамбля во времени. Иными словами,
следует ввести в Г-пространстве распределение вероят-
вероятностей DN(xu ..., xN, t) и следить за его изменением
во времени. Известно, что изменение DN(xu ..., xN) во
времени определяется теоремой Лиувилля
njr=l". я*Ь A)
где Я—функция Гамильтона, равная в нашем случае
(/-,/) B)
Wi(qi) — потенциал внешних сил, включающий «потен-
«потенциал стенок», т. е. потенциал, создаваемый стенками со-
сосуда; ra = \qi — qj| — расстояние между 1-й и /-й молеку-
молекулами]; фигурные скобки означают скобки Пуассона
) C)
Теорема Лиувилля является непосредственным след-
следствием уравнений движения и позволяет в принципе
найти DN(t), если задано начальное распределение
DN(xu ... , xN, 0). Все наблюдаемые макроскопические
величины системы могут быть выражены как соответ-
соответствующие средние значения по распределению DN. Мож-
Можно ожидать в соответствии с эргодической теорией, что
любое начальное распределение будет с течением вре-
времени приближаться к равновесному распределению, ко-
которое в нашем случае является равномерным распреде-
распределением между соседними поверхностями постоянной
энергии Е и Е + АЕ1) (так называемое микроканониче-
ское распределение). Именно это приближение интерес-
интересно для теории необратимых процессов; оно не противо-
противоречит (но и имеет мало общего) квазипериодичности
движения каждой точки ансамбля.
1) Это приближение здесь понимается в смысле крупнозерни-
крупнозернистой плотности; см. Е h r e n f e s t P., E h r e n f e s t Т., цит. раб.
Только в этом смысле можно придать точное значение рассуждениям
из гл. 12 книги Гиббса. См. также Tolman, Statistical Mechanics,
где проводятся аналогичные рассмотрения в квантовой механике.
Общая задача — найти подходящие законы прибли-
приближения к равновесию. Я говорю «подходящие», потому
что не следует стремиться проследить изменение DN во
всех деталях. Это потребовало бы нахождения точного
решения уравнений движения, что, очевидно, является
непосильной и неинтересной задачей, поскольку необхо-
необходимо проследить за изменением во времени лишь неко-
некоторых средних (или макроскопических величин).
Спрашивается, как нужно выбрать начальное распре-
распределение DN@), чтобы оно было согласовано с нашими
первоначальными макроскопическими сведениями о си-
системе. Рассматриваемая теория не дает общего рецепта
для такого выбора, и я долгое время думал, что это яв-
является существенным пробелом данной теории. Теперь
уже я больше так не думаю по причинам, к которым я
вернусь во второй части.
3. Сравнение с теорией случайных процессов. Сочета-
Сочетание квазипериодического движения индивидуальных то-
точек ансамбля с монотонным приближением начального
распределения вероятностей к равновесному распределе-
распределению является характерной чертой теории стационарных
марковских процессов х).
Допустим сначала, что все переменные принимают
дискретные значения; пусть X — случайная величина
(или совокупность случайных величин), которая можег
принимать дискретное множество значений Х{\ пусть на-
наблюдения делаются в дискретные моменты времени
t8 = sx. Обозначим через V(Xj\Xhs) условную вероят-
вероятность того, что X = Xi в момент времени st, при условии,
что в нулевой момент времени X=Xf, для марковского
процесса эти вероятности удовлетворяют так называе-
называемому уравнению Смолуховского
P(Xt, s) = 2P(**. s-l)P(**|*,, 1), D)
k
в которое, однако, не входит начальное распределение
значений Xj. Назовем Р(Хк\Хи \)==Q(Xky X{) вероятно-
1) См Феллер В., Введение в теорию вероятностей и ее при-
приложения, М., 1964; Wang М. С, Uhlenbeck G. E., The theory
of Brownian motion II, Rev. Mod. Phys., 17 A945), 323; Kac M,
Amer. Math. Monthly, 54 A947), 369.
стями перехода; тогда, поскольку
мы можем переписать уравнение D) в виде
Р(*„ s)-P(Xh s-l) = %[P(Xk, s-l)Q(Xk, Xt)-
k
-Р(Х„ s-\)Q(Xlt Xk)\, E)
где штрих означает, что при суммировании надо опустить
член k = i. Уравнение E) имеет простую интерпретацию:
приращение Р равно «прибыли» (за счет переходов
Xu-^Xi) минус «потери» (за счет переходов Хг-^Хи).
Если все переменные непрерывны, то уравнение E)
превращается в уравнение
X)-P(X, t)Q{X, Y)\. F)
Известно, что при довольно общих предположениях
относительно Q из уравнений D) или E) следует, что
P(Xi,s) монотонно приближается при s->-oo к «равно-
«равновесному» распределению W(Xi), хотя каждая серия на-
наблюдений Х\% Х2,... обнаруживает квазипериодическое
поведение и не выделяет поэтому «направления вре-
времени». По-видимому, то же самое верно и для непрерыв-
непрерывного случая, описываемого уравнением F).
Аналогия между движением газа и некоторым слу-
случайным процессом становится правдоподобной, если по-
попытаться проследить за движением Г-точки по поверх-
поверхности постоянной энергии в Г-пространстве. Очевидно,
что эта поверхность имеет форму некоторого гиперци-
гиперцилиндра; если пренебречь на время межмолекулярными
силами, то поверхность Е = const будет сферической в на-
направлениях импульсов и цилиндрической в координатных
направлениях при условии, что все координаты меняются
в объеме V. Если газ разрежен (ro<cF), то межмолеку-
межмолекулярные силы образуют в этом цилиндре редко располо-
расположенные узкие и глубокие расселины. Движение Г-точки
до столкновения происходит по прямой; после столкнове-
столкновения она очень быстро перескакивает в другое место, дви-
движется по прямой, снова перескакивает и т. д. Движение,
таким образом, напоминает случайное блуждание по ги-
гиперцилиндру; поэтому можно ожидать, что распределе-
распределение DN(X, t), где X = (х\, Х2, ..., xN), изменяется подоб-
подобно тому, как это происходит в марковских процессах,
поскольку случайное блуждание является, так сказать,
классическим примером марковского процесса.
Исходя из представления о случайном блуждании,
М. Кац 1) вместо уравнения Лиувилля предложил другое
уравнение, описывающее изменение DN(X, t) во времени
и похожее на уравнение F). Кац сделал два упрощаю-
упрощающих предположения:
A) DN зависит только от импульсов частиц, так что
Х= (Рь р2, ..., Piv); это предположение делает движе-
движение Г-точки очень похожим на случайное блуждание по
гиперсфере.
B) Газ очень разрежен, так что нужно рассматри-
рассматривать только парные столкновения. Вероятности перехода
для случайных шагов могут быть определены, если мы
умеем решать динамическую задачу о столкновении
двух частиц.
Я не сомневаюсь, что при этих предположениях урав-
уравнение Каца (называемое в настоящее время основным
уравнением) удовлетворительным образом описывает
приближение к микроканоническому распределению.
Точное рассмотрение приводит к ряду интересных ма-
математических задач, особенно когда хотят узнать поведе-
поведение системы при очень больших N. С физической же точ-
точки зрения эти упрощающие предположения являются, к
сожалению, довольно ограничительными, и неясно, как
можно было бы от них освободиться.
Остается нерешенной главная проблема — в каком
смысле основное уравнение служит приближением к
уравнению Лиувилля. Броут2) сделал отважную попыт-
попытку выяснить это, но удовлетворительного ответа, я ду-
думаю, пока еще нет.
4. Уравнения Б-Б-Г-К-И и общие законы сохранения.
Другая линия развития исходит из представления, что в
1) К а с М., Proceedings of the Third Berkeley Conference on
Mathematical Statistics and Probability, v. Ill, 1956, 171 — 197.
2) В rout R., Physica, 22 A956), 509.
большинстве случаев интересующие нас макроскопиче-
макроскопические величины зависят не от всей функции распределения
DN(xu ... , xN, t) в Г-пространстве, а от вероятности
того, что в некотором элементе dpdq фазового простран-
пространства находится одна частица, независимо от положения
других частиц. Я называю это распределение распреде-
распределением в [х-пространстве. Ясно, что оно получается ин-
интегрированием DN по всем переменным xiy кроме одной.
Заметим, что, поскольку все частицы одинаковы, плот-
плотность DN должна быть симметрической функцией от Х\,
... , xN; таким образом, не имеет значения, какую из пе-^
ременных х\ считать фиксированной. Требование симме-
симметричности DN не противоречит уравнению Лиувилля,
поскольку гамильтониан Н также симметричен.
Интегрируя уравнение Лиувилля, мы получаем це-
цепочку уравнений, которые независимо и почти одновре-
одновременно были выведены Боголюбовым, Борном, Грином,
Кирквудом и Ивоном 1) и которые я поэтому буду назы-
называть уравнениями Б-Б-Г-К-И.
Введем частичные функции распределения
VsFs (xl9 ..., xs, t) = /•••/ DN dxs+l ... dxN. G)
Интегрируя уравнение Лиувилля по xs+\, ..., xN, нахо-
находим, что при фиксированном 5 в пределе при jV-^
V-+oo(V/N=v фиксировано)
d-^-={Hs,Fs}+±;fdXs+l
Ф/, J+lf Fs+l , (8)
j
где Hs — функция Гамильтона для группы из 5 частиц:
U(qi) —потенциал внешних сил без потенциала стенок и
') Боголюбов Н. Н., Проблемы динамической теории в
статистической физике, Л., 1946. Статьи М. Борна и Грина собраны
в книге Kinetic theory of Fluids; К i г k w о о d J., /. Che т. Phys., 14
A946), 180; 15 A947), 72.
Уравнение (8) является уравнением Б-Б-Г-К-И. Оно
получается непосредственно, и его вывод поэтому можно
опустить. Особенно интересен случай 5=1, который за-
задает изменение распределения в jui-пространстве. Напи-
Напишем это уравнение более подробно:
К = — Vq f7 — внешняя сила. Первые два члена в правой
части описывают изменение Fu возникающее из-за дви-
движения в (шестимерном) ji-пространстве. Если перенести
эти члены в левую часть, то в комбинации с dFJdt мы
получим полную (или субстанциональную) производную
по времени DFJDt, которая показывает, как изменяется
Fu если вместе с частицей движется элемент dp dq
^-пространства; последний член уравнения A0) описы-
описывает изменение Fu возникающее из-за взаимодействия с
другими молекулами; в него входит парная функция
распределения F2.
Обычное макроскопическое описание состояния газа
получается из Fi (и F2) с помощью дальнейшего усред-
усреднения по импульсам1). Например, плотность р полу-
получается так:
средняя скорость равна
u(q, t) = — -у
Интегрируя уравнение A0), мы получаем уравнение не-
непрерывности (закон сохранения массы)
~ + div (pu) = 0. A1)
Если уравнение A0) сначала умножить на р и затем
проинтегрировать по р, мы получим после ряда манипу-
1) Лучше всего эта часть теории изложена в работе: Kirk-
woo d J., /. Chem. Phys., 14 A946), 180.
ляций уравнения движения (закон сохранения импуль-
импульса) в виде
Тензор напряжений P2J- состоит из двух частей; первая
часть зависит только от F{ и определяется равенством
где Ut = — (pi— mtii) — тепловая скорость; вторая часть
зависит от межмолекулярного потенциала и парной
функции распределения F2\ она задается формулой
где r = qi — q. Полный тензор напряжений, очевидно,
симметричен.
Наконец, из A0) можно вывести уравнение, выра-
выражающее закон сохранения энергии; оно имеет обычную
форму
Правая часть — это работа, производимая тензором на-
напряжений; она содержит также тензор деформаций
dui di
Левая часть дает приращение внутренней энергии, со-
содержащее величину
—q1|)/72(q, qv p, pv t),
и ее уменьшение, возникающее из-за теплового потока
плотности q; последний, так же как Р^ и Q, состоит из
двух частей: одна чисто кинетического происхождения
(выражается через /ч), другая возникает из-за межмо-
межмолекулярных сил и выражается через F2. Я опускаю под-
подробную формулу.
Следует подчеркнуть, что все это чисто формальные
выводы, строго следующие из уравнения Лиувилля в
пределе при N->oo, У->оо, отношение N/V конечно;
они получаются при помощи только интегрирования и
подобающего истолкования средних значений. Никаких
предположений не делается. В результате возникает
общая, но малосодержательная схема. Эта схема мало-
малосодержательна потому, что система уравнений не зам-
замкнута. Уравнение A0) не является уравнением только
относительно Fb оно включает также и F2. Уравнения
A1), A2) и A3) не образуют систему уравнений дви-
движения относительно макроскопических величин р, и и Q,
поскольку они содержат величины Р^ и q, зависимость
которых от макроскопических переменных неизвестна.
Ясно, что нельзя поумнеть только от вычисления ин-
интегралов. Нужны дальнейшие предположения. Они дол-
должны как-то отражать тот факт, что наблюдаемые в
действительности макроскопические изменения состоя-
состояния системы одни и те же для подавляющего большин-
большинства элементов ансамбля, так что среднее значение не-
некоторой величины по ансамблю будет в любой момент
времени представлять значение той же величины для
отдельной системы.
5. Уравнение Больцмана и уравнения гидродина-
гидродинамики. Замкнутая система уравнений, описывающих из-
изменение распределения в ^-пространстве и изменение
макроскопических переменных, конечно, известна, но она
была выведена из интуитивных или феноменологических
предпосылок. Уравнение, задающее изменение Fu — это
известное уравнение Больцмана, на котором основана
кинетическая теория разреженных газов. Чтобы напи-
написать его в обычном виде1), мы будем использовать ско-
скорости вместо импульсов и положим
/(/, х, %) = ^F{t, q, p).
1) В о 11 z m a n п, Vorlesungen tiber Gasiheorie, В. I; см. также.
Chapman, Cowling, Mathematical Theory of Non-uniform Gases.
[Ясно, что f(t, x, I)—число частиц в элементе dxd%
^-пространства.] Тогда уравнение Больцмана примет вид
D/ _ д/ , , д/ , у д/ _
dug/ (g, Э) (/'/; -//,). A4)
Левая часть здесь такая же, как и в уравнении A0) (за-
(заметим, что теперь Х{ — ускорение Kiltri)\ отличие этого
уравнения от уравнения A0) связано с членами, описы-
описывающими столкновение. Здесь штрих и индекс 1 у f от-
относятся только к переменной скорости, так что, напри-
например, /i=/(f, х, gi) и т. д. Буквы |, |ь §', |i обозначают
скорости при парном столкновении
(§, Ц <-> (§', §|); g = | § — gj | = | % — §; I — относительная
скорость;
направление относительной скорости после столкнове-
столкновения изменяется на угол 9 (см. рис. 1). Два члена в пра-
правой части представляют соответственно вклад от обрат-
обратных столкновений (§', §i)->(§» ^) и потери от прямых
столкновений (§, §j)->(^, gj). Чтобы подсчитать число
прямых столкновений, рассмотрим относительное дви-
движение. Все молекулы со скоростями, лежащими внутри
элемента d\\, сталкивающиеся так, что их «параметр
соударения» заключен между Ъ и b + db, и находящиеся
в небольшом цилиндре gb db de dt вне сферы действия
(е — полярный угол), в следующий промежуток времени
dt столкнутся так, что относительная скорость g откло-
отклонится на угол 9. Зависимость между Ь, 9 и g опреде-
определяется динамикой столкновения или, что то же самое,
законом взаимодействия. Больцман далее предполагает,
что число прямых столкновений в единице объема за
единицу времени равно
gbdbdzffxd\d\x, A5)
т. е. он предполагает, что это число пропорционально
произведению числа сталкивающихся частиц. Это пред-
предположение (Stosszahlansatz*)), конечно, правдоподоб-
правдоподобно, но, разумеется, не может быть выведено из исходных
предпосылок нашей механической модели. Аналогично
подсчитывается число обратных столкновений. Подстав-
Подставляя эти числа в формулу A4), окончательно можем на-
написать:
b dbde = I(g,Q)du — дифференциальное сечение расстоя-
расстояния для столкновений внутри телес-
телесного угла dQ = sinQdedQ.
Уравнение Больцмана часто подвергалось критике.
Особенно сомнительным кажется то обстоятельство, что
в допущении A5), несмотря на существование силы
взаимодействия между молекулами, не принимается в
расчет корреляция между направлениями скоростей двух
сталкивающихся частиц, так что вместо F2 появляется
произведение двух F{. Очевидно, что Больцман имел
в виду некоторую схему последовательных приближений.
В нулевом приближении, когда пренебрегают межмоле-
межмолекулярными силами, состояние газа в точности описы-
описывается функцией f(t, х, v); в следующем приближении
при учете только парных столкновений можно еще обхо-
обходиться с помощью f. Только тогда, когда плотность газа
настолько велика, что тройные и более высокого поряд-
порядка столкновения начинают происходить с заметной ча-
1) См. Ehrenfest P., Ehrenfest Т., цит. раб.
стотой, следует уже принимать в расчет корреляцию ме-
между скоростями.
Таким образом, больцмановское уравнение законно
только в том случае, когда плотность газа не слишком
велика. Кроме того, сомнительно, чтобы явления, связан-
связанные с быстрым изменением в пространстве или во
времени, могли бы описываться этим уравнением. Я на-
надеюсь вернуться к этому вопросу во второй лекции.
Замкнутой системой уравнений, описывающей измене-
изменение макроскопических переменных, является хорошо из-
известная гидродинамическая система уравнений Навье—
Стокса. Она состоит из уравнений, имеющих тот же вид,
что и общие уравнения переноса A1), A2) и A3), и,
кроме того, содержит дополнительные уравнения, выра-
выражающие тензор напряжений Pij и плотность теплового
потока q через макроскопические величины. Вот эти
уравнения:
pij = Pbij — 2м- [рИ — \ Daab
q = —a,grad7\ A6)
Они содержат два коэффициента вязкости \х и v и коэф-
коэффициент теплопроводности X; эти параметры характери-
характеризуются уже самим газом и могут зависеть от р и Г, при-
причем зависимость определяется экспериментально. Вместе
с уравнением состояния р(р, Г) и тепловым уравнением
состояния Q(p, T) мы получаем пять уравнений для
пяти макроскопических величин р, и и Т.
6. Выводы. Связь между различными описаниями
состояния газа может быть изображена схемой, приве-
приведенной на стр. 240. В левом столбце стрелки вниз соот-
соответствуют строгому выводу; пунктирные стрелки озна-
означают, что переход связан с некоторой аппроксимацией
и требует дополнительных предположений. Каждая
пунктирная стрелка в действительности представляет
целую теорию, которой должна быть посвящена по
крайней мере одна лекция, тем более что пока боль-
большинство этих связей еще далеко не ясны. Однако су-
существует, как мне думается, одна общая точка зрения,
принадлежащая Боголюбову, которую я и постараюсь
кратко изложить в следующей части,
Описание в
Г-простран-
стве
Описание в
[л-простран-
стве
Макроскопиче-
Макроскопическое описание
Механические процессы Необратимые процессы
Уравнение
Лиувилля
i
Цепочка
уравнений
Б-Б-Г-К-И
i
Уравнения
переноса
(общие
законы
сохранения)
—...->...—
Основное уравнение
(описание с помощью
случайного процесса)
Уравнение Больцмана
для малой плотно-
плотности -f- различные
обобщения
j
Гидродинамические
уравнения Эйлера,
Навье— Стокса
Часть 2
7. Идеи Боголюбова. Наша основная проблема — вы-
выяснить соотношение между левым и правым столбцами
в указанной общей схеме. Поскольку нас главным об-
образом интересует развитие системы во времени, важно
сначала обсудить, какие масштабы времени содержатся
в нашей задаче. Ясно из самой модели, что появляются
следующие характерные промежутки времени, располо-
расположенные в порядке возрастания:
(а) время молекулярного взаимодействия, или время
столкновения:
т = го/т;,
ср.
A)
где vСр. — средняя скорость;
(б) среднее время свободного пробега, или время
между столкновениями:
*o = tytfCp.. B)
где X — средняя длина свободного пробега. Для газа
средней плотности to^x (скажем, в 102 или 103 раз боль-
больше) , для жидкости /0 и т—величины одинакового порядка;
(в) время макроскопической релаксации:
%=L/vep;9 C)
здесь L — макроскопический размер, например расстоя-
расстояние между параллельными стенками, между которыми
течет газ или проходит тепло, или длина звуковой волны,
распространяющейся в газе, и т. д. Вообще L — это рас-
расстояние, на протяжении которого заметно изменяется
какая-нибудь из макроскопических величин р, и или Т.
Для обычных медленно протекающих явлений 6о^>/о; в
исключительных случаях (высокочастотный звук, удар-
ударные волны) 9о может стать одного порядка с t0.
Рассмотрим случай газа средней плотности с мед-
медленно меняющимися макроскопическими величинами,
так что 8о!Э>^о^>т-Из физических соображений можно
ожидать, что развитие распределения DN во времени
проходит различные стадии.
а. Начальная стадия. Для произвольного начального
распределения DN(xu х% . .. , xN; 0) можно ожидать, что
все частичные функции распределения Fs(xi, ..., xs, t)
при s !> 2 меняются очень быстро в течение промежутка
времени порядка т. Способ их изменения зависит от ис-
исходной ситуации, поэтому его нельзя описать в общем
виде. Только первая функция распределения Fi(x, t) не
связана непосредственно с отталкивающим межмолеку-
межмолекулярным взаимодействием и поэтому изменяется мед-
медленно.
б. Кинетическая стадия. Можно ожидать, что по про-
прошествии промежутка времени порядка т развитие си-«
стемы будет управляться изменением во времени функ-
функции F{. Поскольку в положении равновесия высшие
функции распределения FsE>2) зависят от Fi [так как
в этом случае Fs = Fl(xi) .. . Fx(xs) • ехр(—р2<р(г*;-))э по
крайней мере в первом приближении], то можно думать,
что Fs примет вид
Fs (t, х{, ..., xs) = Fs (xl9 ..., xs\ Fx), D)
где зависимость от времени полностью заключена в Fu
каково бы ни было начальное распределение. [Уравне-
[Уравнение D) не является, следовательно, тривиальным утвер-
утверждением, что всегда можно использовать F4 вместо /,
поскольку тогда F8 зависело бы также от начального
распределения для /V] Уравнение для F\ имеет, как
можно ожидать, следующий вид:
^j- = A(x;Fl) E)
(кинетическое уравнение, или общее уравнение Больц-
мана). Это уравнение полностью описывает изменение
состояния газа во времени.
Через промежуток времени т в описании состояния
газа происходит своего рода сужение, или сокращение,
после чего развитие во времени определяется уже го-
гораздо меньшим числом переменных (а именно F{ вместо
всех функций Fs).
Мы можем также сказать, что в течение времени т
происходит первое сглаживание или хаотизация, когда
теряются подробности начальной информации.
в. Гидродинамическая стадия. Через промежуток
времени порядка t0 происходит следующее сглаживание
или хаотизация. Очень быстро (всего через несколько
столкновений, следовательно, в течение времени по-
порядка to) в скоростях почти устанавливается равновесие,
и дальнейшее развитие во времени управляется измене-
изменением макроскопических переменных р, и и Г' (или вну-
внутренней энергии Q). Функция распределения /^ примет
теперь вид (поскольку она имеет такой вид в равновес-
равновесном состоянии):
/Мя, р> 0 = Л(ч. р;р> "> П F)
где зависимость от времени полностью заключена в р,
и, Г, каково бы ни было начальное распределение для
F\. По аналогии с формулой E) можно ожидать, что
уравнения для р, u, T запишутся в виде
-§- = /?(q;P, u, T),
-g- = U(q;P, u, T), G)
^ = 0(q; p, u, T).
Это общие гидродинамические уравнения; они описы-
описывают теперь дальнейшее изменение состояния газа во
времени. Это есть следующее сужение, или сокращение,
описания; р, u, T являются лишь первыми пятью момен-
моментами распределения F\ относительно р, и поэтому раз-
развитие во времени определяется теперь еще меньшим
числом переменных.
Возможно, существует следующая стадия развития
по пути к равновесию, а именно стадия турбулент-
турбулентности. Исследования Тэйлора, Кармана — Ховардаидр.
по изотропной турбулентности с помощью усреднения
уравнений Навье — Стокса напоминают вывод уравне-
уравнений Б-Б-Г-К-И из уравнения Лиувилля. Снова полу-
получается цепочка уравнений, включающая последователь-
последовательно парные, тройные и т. д. корреляционные функции
скоростей. Снова, очевидно, должны быть сделаны даль-
дальнейшие предположения. Следуя точке зрения Боголю-
Боголюбова, сначала надо найти различные масштабы времени
или длины, содержащиеся в самой задаче. Если удастся
расщепить 9о (или L) на два или больше промежутков
времени (или отрезков), то можно ожидать дальней-
дальнейшего сужения описания. Возможно, для изотропной
турбулентности L расщепляется на длину вихрей, обра-
образующих турбулентность, и корреляционную длину, ко-
которая приблизительно раз в десять меньше. Возможно,
в этом случае единственной функцией, которая описы-
описывает развитие во времени, служит парная функция рас-
распределения, и все высшие распределения функциональ-
функционально зависят от нее. Возможно, появившуюся недавно
теорию Чандрасекара *) можно рассматривать как
l) Chandrasekhar S., Proc. Roy. Soc. (London), A229
A955), 1.
первый шаг в этом общем направлении. Заметьте, что
почти каждое предложение я начинаю словом «возможно»!
Все это только предположения, и я ничего не знаю сверх
сказанного.
Следует упомянуть о недавних работах Ван-Хова 1)
и Кона и Латтинджера 2) по квантовой статистической
механике. Эти авторы впервые удовлетворительным об-
образом вывели так называемое уравнение переноса (ко-
(которое в нашей терминологии является квантовомехани-
ческим аналогом основного уравнения) из квантового
уравнения Лиувилля. Существенным моментом их вы-
вывода является то обстоятельство, что внедиагональные
элементы матрицы плотности (которые очень быстро ме-
меняются во времени) выражены через медленно меняю-
меняющиеся диагональные члены. Уравнение переноса (или
основное уравнение) содержит только эти диагональные
члены, так что снова получается сокращение в описа-
описании состояния системы.
Представляется вероятным, что такие последователь-
последовательные сокращения описания являются существенной чер-
чертой теории необратимых процессов. Конечно, возмож-
возможность таких сокращений должна быть заложена в свой-
свойствах исходных уравнений системы. Кроме существова-
существования ряда времен релаксации (таких, как т, /0 и 9о) или
длин релаксации, из свойств исходного уравнения
должно также вытекать, что его решения для практи-
практически всех начальных условий обнаруживают своего
рода кусочно-эргодическое поведение во времени. Ре-
Решения с любыми начальными условиями должны скап-
скапливаться все вместе к кривой (образовывать «Verdich-
tungskurve»), которая описывается уже меньшим чис-
числом переменных и подчиняется следующей системе
уравнений и т. д. Ясно, что при этом возникают две
основные задачи:
1. Показать, что решения исходных уравнений (урав-
(уравнения Лиувилля или уравнений Б-Б-Г-К-И в кинетиче-
кинетической стадии, уравнения Больцмана в гидродинамиче-
0 Van Hove L, Physica, 21 A955), 517; 23 A957), 441.
2) Kohn W., Luttinger J. M., Phys. Rev., 108 A957); 590;
109 A958), 1892.
ской стадии) обладают таким кусочно-эргодическим по-
поведением во времени. Обычно физик это допускает, и
его больше интересует вторая задача.
2. Найти переменные и уравнения, которые описы-
описывают указанную кривую («Verdichtungskurve»), или
асимптотическое поведение решений исходных уравне-
уравнений. Я постараюсь кратко изложить, как предлагает ре-
решать эту задачу Боголюбов.
8. Кинетическая стадия. Существенная черта метода
Боголюбова состоит в том, что сокращение уравнений
сочетается с процедурой последовательных приближе-
приближений или разложения в степенной ряд. В кинетической
стадии это есть хорошо известное вириальное разложе-
разложение в ряд по степеням плотности l/v. Напишем уравне-
уравнения E) и F) в виде
^ ..., (8)
Fs(xv .... x,,t)
, ..., xs; /?,)+ ... (s>2). (9)
В действительности следует разлагать в ряд по степе-
степеням т/to, однако проще использовать l/v. Сравним те-
теперь (8) и (9) с уравнениями Б-Б-Г-К-И:
Положим сначала 5 = 1. Используя разложение (9) для
F2j получаем
оо
Сравнивая это уравнение с уравнением (8) и приравни-
приравнивая члены с одинаковыми степенями l/v, находим
и т. д. Следовательно, Ао описывает течение газа, в то
время как высшие члены А содержат парные функции
распределения, взятые в приближении, на один шаг бо-
более низком. Далее, рассмотрим уравнения Б-Б-Г-К-И
для 5^-2. Производную по времени—г—следует теперь
заменить произведением
dt ~~ б/7! dt '
где 6Fs/6Fi — вариационная производная по Л- Заме-
Заменяя dFJdt выражением (8), a Fs — разложением (9) и
приравнивая одинаковые степени l/vf получаем
{//., F^-DoFl^D^+fdxsJ^^Fful A1)
и т. д., где оператор Dr, действующий на любой функ-
функционал г|)(хь ,.., xs\ F\), определяется так:
Теперь ясно, как вычислять последовательные прибли-
приближения. Первое уравнение A1), куда входят только F{s0)>
содержит Л о, которое уже известно. Решая это уравне-
уравнение относительно F{s\ мы найдем из второго уравнения
A0) Ai(x;Fi). Это полностью определяет правую часть
второго уравнения A1), откуда затем можно найти Т7^.
Это в свою очередь дает А2(х; Fi) и т. д.
Все это, по крайней мере формально, можно проде-
проделать. Чтобы дать представление о характере результа-
результатов, позвольте мне только упомянуть, что в первом при-
приближении
v ..., xs; F1) = UF1(QiisK /?>, /)• A2)
Здесь Р(/>—начальный импульс /-й частицы, при кото-
котором после 5-кратного столкновения (описываемого га-
гамильтонианом #s) через время t достигается конфигу-
конфигурация хи ..., xs; Q{p — положение /-й частицу, которое
она должна была бы занимать через время t, если бы
она двигалась без столкновений с постоянным импуль-
импульсом Р{?\ Как Р{?\ так и Qf являются, следовательно,
функциями от Х\у .. ., xs, которые можно было бы найти,
если бы мы могли проинтегрировать уравнения движе-
движения для 5 частиц. Поскольку Я50) является произведе-
произведением 5 функций Fu мы можем сказать, что в этом при-
приближении 5 точек хи ..., xs не коррелируют друг с дру-
другом [в смысле A2)]. Следует подчеркнуть, что это верно
только для первого приближения; Я61} уже не предста-
представляется более в виде произведения Л. Подставляя вы-
выражение A2) для 5 = 2 в уравнение A0) для Ai(xi\Fl)i
можно доказать, что /li превращается в член уравне-
уравнения Больцмана, задающий число соударений, по край-
крайней мере в том случае, когда в этом члене можно пре-
пренебречь различием положения двух сталкивающихся ча-
частиц.
Как я уже сказал, все это можно действительно про-
проделать. В следующем приближении в кинетическом
уравнении A2(xi\ Fi) зависит от тройных столкновений
и т. д. Тем самым вириальное разложение кинетических
уравнений напоминает обычное вириальное разложение
для величин равновесного газа в том смысле, что ка-
каждый следующий член учитывает взаимодействие все
большего и большего числа молекул.
9. Гидродинамическая стадия. Предварительные ре-
результаты. В гидродинамической стадии основным яв-
является кинетическое уравнение (8). Сокращение в опи-
описании по-прежнему сочетается с разложением в ряд по
степеням некоторого параметра. Таким параметром слу-
служит теперь to/% или X/L\ он измеряет, следовательно,
относительное изменение макроскопических величии на
расстоянии длины свободного пробега, поэтому мы бу-
будем его называть параметром однородности ji. Анало-
Аналогично уравнению (8) гидродинамические уравнения G)
могут быть разложены следующим образом:
-^ = ^D-, р, и, г)+^2/?2(я;р, и, Г)+ ...,
A3)
; Р> и, Т) + №2(Ч; р, и, Г)+
и подобное же уравнение для dT/dt. Разложение начи-
начинается с первой степени ji, поскольку ji = 0 соответствует
равновесному распределению, при котором все макро-
макроскопические переменные не меняются во времени. По
аналогии с разложением (9) можно написать разложе-
разложение для функции F):
q. Р> P. u. T)+.... A4)
Используя кинетическое уравнение, мы можем тогда
последовательно определить функционалы Ri, U2-, 6г- и
последовательные приближения для функции распреде-
распределения Fi.
Если в кинетическом уравнении (8) остановиться на
члене, пропорциональном l/v, так что уравнение (8)
станет по существу уравнением Больцмана (прини-
(принимаются в расчет лишь члены, описывающие течение газа
и парные столкновения молекул), то сокращение в опи-
описании, а именно введение параметра ji, полностью экви-
эквивалентно выводу гидродинамических уравнений методом
Энскога. В этом случае мы знаем, что:
1. В первом порядке по ji получается уравнение Эй-
Эйлера для идеальной жидкости и, кроме того, уравнение
состояния для идеального газа.
2. Во втором порядке по ji мы приходим к уравне-
уравнениям Навье — Стокса, причем для вязкости и коэффи-
коэффициента теплопроводности получается явное выражение
через межмолекулярный потенциал. Эти коэффициенты
не зависят от плотности — классический результат ки-
кинетической теории газов, — и их значения и темпера-
температурная зависимость хорошо согласуются с эксперимен-
экспериментальными данными. Для нашей модели (одноатомный
газ) существует лишь один коэффициент вязкости;
коэффициент v равен нулю. Уравнение состояния такое
же, как для идеального газа. Здесь появляется неболь-
небольшая неувязка, поскольку следовало бы ожидать, что эф-
эффекты парного взаимодействия входят во второй ви-
риальный коэффициент. Неувязка эта возникает потому,
что мы заменяем А\(х; F\) больцмановским оператором
столкновений даже в случае, когда /^ существенно за-
висит от q. Если подходящим образом учесть эту зави-
зависимость, то, как показал Боголюбов, мы получим ожи-
ожидаемое отклонение от закона идеального газа.
3. В третьем порядке по (i получаются так назы-
называемые уравнения Бернетта. Они очень сложны и до
сих пор очень мало применялись к конкретным зада-
задачам. Действительно, в частных случаях обычно проще
пользоваться не разложением Энскога, а исходить не-
непосредственно из уравнения Больцмана. Однако разло-
разложение Энскога во всяком случае верно. Оно только
становится очень сложным в высших порядках по |х, и,
вероятно, это разложение не сходится, а является толь-
только асимптотическим.
Если в кинетическом уравнении (8) оставить только
члены с Л2, Аз и т. д., так что будут учитываться трой-
тройные и более высокого порядка столкновения, то ситуа-
ситуация значительно усложнится. В первом порядке по |i
все еще можно ожидать получить уравнения Эйлера
для идеальной жидкости, но уравнение состояния со-
содержит теперь столько вириальных коэффициентов,
сколько членов Ап(х; Fi) оставлено в кинетическом
уравнении. Это, действительно, было доказано недав-
недавно1), по крайней мере для членов порядка l/vz (чет-
(четвертый вириальный коэффициент); общее доказатель-
доказательство связано с некоторыми еще не решенными комби-
комбинаторными задачами.
Если в кинетическом уравнении оставить члены трой-
тройных столкновений (l/v2)A2(x\ /4), то во втором порядке
по A снова получается уравнение Навье — Стокса1).
Однако теперь вязкость и коэффициент теплопроводно-
теплопроводности зависят от плотности; в самом деле, для этих коэф-
коэффициентов переноса получается вириальное разложе-
разложение в виде
') Choh S. Т., Dissertation, University of Michigan, 1958.
где jio и ко совпадают с выражениями, найденными Чеп-
меном и Энскогом (они зависят от поперечника сече-
сечения двойных столкновений), и jii и h — поправки, воз-
возникающие за счет тройных столкновений. Они сложно
выражаются через динамические характеристики взаи-
взаимодействия трех частиц, и поэтому трудно (но не не-
невозможно!) получить численные результаты. В заключе-
заключение интересно отметить, что теперь появляется также
второй коэффициент вязкости, который в этом прибли-
приближении пропорционален плотности.
КВАНТОВАЯ МЕХАНИКА
Л. Р. ГИББС
Профессор Кац описал различные типы вероятност-
вероятностных мер. Он объяснил также, что в схеме квантовой
механики, предложенной Фейнманом, используется ана-
аналог вероятностной меры, дающий возможность описать
поведение квантовомеханических частиц. Он упомянул,
что эта мера обладает некоторыми особенностями;
в частности, она комплексна.
В этой статье я сообщу некоторые дополнительные
сведения о квантовомеханической мере и коснусь, в част-
частности, следующих трех вопросов. Во-первых, я хочу об-
обсудить вопрос о том, почему для описания поведения
некоторой физической величины необходима эта осо-
особая комплекснозначная мера. Во-вторых, я хочу выяс-
выяснить, что это за мера и как именно она описывает по-
поведение некоторой физической системы. В-третьих,
я хочу показать два различных математических под-
подхода. Один из них дает возможность вычислять так на-
называемые интегралы по траекториям и приводит с их
помощью к более или менее полному описанию движе-
движения квантовомеханической частицы. Второй в действи-
действительности несколько искажает квантовомеханическую
меру, но тем не менее позволяет решать другой тип за-
задач из квантовой механики.
Мы начнем с обсуждения оснований квантовомехани-
квантовомеханической меры. Поскольку это лекция по физике, естествен-
естественно исходить из опыта, быть может, воображаемого, но
все-таки опыта. Представим себе источник, излучаю-
излучающий электроны (спираль в левой части рис. 1); они дви-
движутся к экрану (а), проходят через две щели в нем А
и В, а затем направляются к счетчику электронов, кото-
который может перемещаться вниз и вверх вдоль экрана (б).
Если бы электроны подчинялись законам классиче-
классической физики, то можно было бы ожидать, что счетчик
включается (т. е. отмечает поступление электрона)
только в двух положениях. Одно из этих положений
определяется пересечением с экраном (б) прямой, про-
проведенной от источника через щель Л, другое—пересе-
другое—пересечением прямой, проведенной от источника через щель В.
Однако мы не слишком удивились бы, обнаружив, что
электроны не следуют этим классическим предписаниям.
Поступающие электроны не сосредоточены >в двух раз-
различных местах на экране, а размазаны по нему. В дей-
действительности мы убедимся в том, что невозможно
связать с начальными (источник) и граничными (по-
(положение щели) условиями нашего эксперимента какое-
нибудь определенное место поступления электронов на
экран. Лучшее, что мы можем сделать, ?— это связать
с этими условиями вероятность попадания электрона
в какую-нибудь точку на экране (б).
Для простоты допустим, что электроны, испускаемые
источником, имеют одинаковую энергию. Исследуем те-
теперь вид вероятностных законов, поочередно закрывая
одну из щелей А и В. Когда открыта только щель Л,
распределение электронов, наблюдаемое на экране (б),
выглядит, как показано на рис. 2а; если же открыта
только щель 5, то это распределение выглядит, как по-
показано на рис. 26.
Открывая одновременно обе щели, мы могли бы
ожидать на основе естественных предположений, что
результирующее распределение равно сумме распреде-
распределений, изображенных на рис. 2а и 26. Однако если
действительно произвести такой опыт, то получающееся
распределение выглядит так, как показано на рис. 3.
Это распределение, напоминающее интерференцион-
интерференционную картину, совершенно определенно отличается от
суммы распределений, полученных в отдельности от ще-
щелей А я В. Таким образом, в терминах теории вероят-
вероятностей
А A)
Почему это так? Почему наше привычное представле-
представление о вероятностях и о правилах обращения с ними ока-
оказывается непригодным? Мы могли бы подумать, что
наши допущения неправильны, а именно что прохо-
прохождение через щели Л и Л не определяет отдельных-
событий и, может быть, электрон дробится и одна его
часть проходит сквозь щель Л, а другая — сквозь щель В.
Однако мы можем проверить эту гипотезу, помещая
источник света позади щелей и подстерегая проходящие
через них электроны. Электроны рассеивают свет, так
что мы можем заметить, какая из щелей пропустила
электрон, по тому, в какой точке рассеялся свет. Если
выбрать достаточно слабый источник электронов, испу-
испускающий не более одного электрона в любой момент
времени, то можно обнаружить, что свет рассеивается
только позади какой-нибудь одной из щелей А или 5,
но никогда не рассеивается позади обеих щелей одно-
одновременно. Мы могли бы также измерить заряд, кото-
который проходит через щель А или 5, и обнаружить, что
он совпадает с полным зарядом электрона, проходив-
проходившим в это время через соответствующую щель.
Мы могли бы представить себе другую возможность:
что электроны совершают особого рода движение, про-
проходя сначала через одну щель, затем через другую, по-
потом снова через первую и т. д., прежде чем они окон-
окончательно попадают на экран (б). Мы опять можем про-
проверить эту гипотезу, освещая щели и наблюдая за
рассеянием света. Мы найдем, что если взят источник
электронов достаточно слабой интенсивности, то каждый
раз, когда электрон проходит от источника к счетчику,
свет рассеивается только позади одной щели.
Из этих наблюдений мы вынуждены сделать следую-
следующие заключения:
1. Движение электронов должно описываться неко-
некоторым вероятностным законом, поскольку совокупности
начальных условий мы можем сопоставить лишь рас-
распределение конечного положения электрона.
2. Правила, управляющие «сложением» вероятно-
вероятностей для взаимно исключающих способов движения, от-
отличаются от тех правил, к которым мы привыкли в обыч-
обычной теории вероятности.
Оказывается, что такое движение электронов можно
описать, вводя новое математическое понятие «ампли-
«амплитуды вероятности». Мы обозначим амплитуду вероят-
вероятности через ф и припишем каждому из возможных
способов попадания электрона из источника на экран
свою амплитуду. Таким образом, в нашем опыте есть
две амплитуды, фА и фВ, для каждой из двух щелей.
Правило сложения амплитуд для двух взаимно исклю-
исключающих путей состоит в обычном сложении амплитуд.
Таким образом, общая амплитуда вероятности для элек-
электрона, проходящего от источника к счетчику, при обеих
открытых щелях равна
Ф(Л+?) = ф(Л) + ф(?). B)
Далее постулируется, что вероятность события рав-
равна квадрату модуля амплитуды вероятности этого собы-
события. Итак, всегда
Р=|ф|2- C)
Амплитуда и, таким образом, вероятность зависят от
начальных условий, конечного положения и, разумеется,
от любых ограничений, встречающихся по пути, таких,
как положение щелей А и В.
Используя предыдущие правила, мы можем полу-
получить вероятность того, что электрон попадет в какую-
нибудь выбранную точку экрана (б), когда обе щели
открыты:
. D)
Так как вещественная часть произведения
вообще говоря, не равна нулю, мы видим, что
Р(Л + ?)?=Р(Л) + Р(?). E)
Можно представить себе, что, когда мы обсуждали
основания понятия амплитуды вероятности, мы ввели
возможность парадокса. В самом деле, допустим, что
мы помещаем источник света позади экрана (а) и на-
наблюдаем, какая из щелей рассеивает свет. Мы уже го-
говорили, что таким способом можно сосчитать отдельно
каждый электрон, проходящий через ту или иную щель.
Предположим, что на чистом листе бумаги мы отдельно
для каждого электрона отмечаем его прохождение через
щель А или щель S, а также его конечное положение
на экране (б). Если мы после этого построим кривые
распределения отдельно для этих двух классов электро-
электронов, то получим кривые, изображенные на рис. 2а и
26; однако, сложив эти кривые, мы получим кривую,
не имеющую никакого сходства с интерференционной
картиной. По всей логике вещей эта кривая должна
совпадать с наблюдаемой функцией распределения для
объединенных классов.
Мы можем сравнить эту результирующую кривую,
полученную при помощи листка бумаги, с наблюдаемым
распределением всех электронов. Проделав это, мы
найдем, что они совпадают. Интерференционные явле-
явления исчезли! Как это может быть? В нашем предыду-
предыдущем опыте мы наблюдали интерференционную картину,
изображенную на рис. 3, тогда как теперь мы получили
сравнительно гладкое распределение, совпадающее
с суммой кривых на рис. 2а и 26. Различие этих опы-
опытов только в том, что в последнем случае мы следили
за тем, через какую щель проходит электрон.
Итак, мы открыли другую особенность квантовоме-
ханического поведения. Если мы заглядываем в экспе-
эксперимент, так сказать, в середине, то мы меняем его конеч-
конечный результат. С физической точки зрения мы можем
понять, почему это происходит. В случае электронов
мы имеем дело с очень маленькими и очень легкими ча-
частицами. Они на самом деле настолько легки, что их
движение может существенно измениться от столкнове-
столкновения с квантами света. Каждый световой квант обладает
импульсом, обратно пропорциональным длине его вол-
волны. При взаимодействии с электронами (это взаимо-
взаимодействие и приводит к наблюдаемому рассеянию света)
происходит перераспределение импульсов между све-
световым квантом и электроном. Импульс электрона за-
заметно меняется, причем случайным образом, так что
интерференционная картина в окончательном распреде-
распределении смазывается. Нет уже более интерференционных
пиков и впадин.
Теперь вам может прийти в голову, что существует
способ выиграть эту игру. Можно постараться выбрать
источник света столь слабым, чтобы импульс светового
кванта был слишком мал и не мог заметно повлиять, на
движение электронов. Однако, как я уже говорил, им-
импульс светового кванта не зависит от интенсивности
источника, а зависит лишь от длины световой волны.
Раз так, мы могли бы сильно увеличить длину волны и
тем самым уменьшить импульс каждого кванта. Однако
это возможно лишь до определенного предела. Как хо-
хорошо известно, расстояние между двумя источниками
света невозможно определить с большей точностью,
чем, грубо говоря, длина волны излучаемого ими света.
Этим обстоятельством в действительности и ограничена
разрешающая способность оптических микроскопов.
В нашем эксперименте мы хотим различить щели А
и В. Таким образом, мы должны иметь дело только со
светом, длина волны которого меньше расстояния ме-
между этими щелями. Но как раз тогда импульс, который
несет квант света с такой длиной волны, уже настолько
велик, что смывает интерференционную картину в окон-
окончательном распределении. Мы заключаем, что мы не
в состоянии — по крайней мере используя такие мето-
методы — сказать про каждый электрон, сквозь какую щель
он прошел, с тем чтобы не разрушить интересующую
нас интерференционную картину. Природа нас снова
перехитрила.
На самом деле неизвестна никакая эксперименталь-
экспериментальная техника, которая позволила бы наблюдать ход экс-
эксперимента так, чтобы не изменить его результат. Для
привычных нам больших тел, таких, например, как тет-
тетрадь, карандаш, эти вызываемые наблюдениями возму-
возмущения так ничтожны, что совершенно незаметны в на-
нашем обычном опыте. И только тогда, когда мы обра-
обращаемся к мельчайшим частицам, это обстоятельство
становится существенным. Итак, мы приходим к вол-
волнующему заключению, что в описанном эксперименте,
когда мы получаем функцию распределения, изображен-
изображенную на рис. 3, нам не дано узнать, через какую щель
проходит электрон. Некоторые физики скажут, что
нельзя даже утверждать, что он проходит через какую-
нибудь из щелей, поскольку можно утверждать лишь
то, что поддается наблюдению. Самое большее, что мы
можем сказать, — это то, что электрон имеет некото-
некоторую амплитуду вероятности пройти сквозь каждую из
щелей, и эти амплитуды, интерферируя, дают результи-
результирующее распределение.
То обстоятельство, что технические возможности экс-
эксперимента ограничены, и составляет принцип неопреде-
неопределенности Гейзенберга. Мы можем сформулировать этот
принцип многими способами. Традиционная формули-
формулировка касается неопределенности, возникающей при од-
одновременном измерении положения и импульса частиц.
Утверждается, что положение и импульс частицы нельзя
измерить одновременно с точностью, большей, чем по-
постоянная действия Планка ft, деленная на 2я (эта вели-
величина—постоянная Планка, деленная на 2я, — обычно
обозначается через h). Однако этот принцип можно
выразить другим способом, более близким к нашим
рассмотрениям. Он состоит в следующем. Как только
произведено наблюдение за движением некоторой ча-
частицы, все другие альтернативные возможности этого
движения немедленно исключаются. Это означает, что
если мы наблюдаем за электроном, проходящим сквозь
щель Л, то из наших вычислений следует исключить ам-
амплитуду вероятности этого электрона пройти сквозь
щель В. Мы знаем, что он через нее не прошел. Итак,
каждое наблюдение ограничивает число допустимых
альтернативных способов движения частиц. Оба эти
выражения принципа неопределенности в действитель-
действительности эквивалентны.
В само понятие квантовомеханического поведения мы
включили то утверждение, что результат некоторого экс-
эксперимента может быть получен только с той или иной
вероятностью. Мы ввели понятие амплитуды вероят-
вероятности, квадрат модуля которой дает вероятность или ее
функцию распределения. Возникает очень интересный
вопрос. Верно ли, что такая вероятностная интерпретация
квантовомеханического поведения является единственно
возможной? Может быть, существует более детермини-
детерминированное описание такого поведения? До сих пор ка-
казалось, что только вероятностная точка зрения дает
удовлетворительные результаты. Однако это, конечно,
не доказано.
Несмотря на то что этот вопрос интересен, он, по-
видимому, не очень важен. Вероятностное описание дает
физику адекватное объяснение наблюдаемых им явле-
явлений. В настоящее время важнее понять особенности по-
поведения ядерной материи. Интересно подумать, какие
новые понятия придется ввести, чтобы объяснить пове-
поведение частиц, рождающихся при высоких энергиях
в наших ускорителях.
Теперь мы посмотрим, какой вид имеет амплитуда
вероятности. На самом деле, она имеет очень простой
'ВИД
<p~exp(iS/A), F)
где S — действие вдоль траектории, которой приписы-
приписывается амплитуда ф, т. е.
S= J L(x, х, t) dU G)
где L — функция Лагранжа, равная разности кинетиче-
кинетической и потенциальной энергии, а интеграл берется вдоль
указанной траектории от начального до конечного мо-
моментов опыта. Сама эта траектория является траекто-
траекторией частицы. Мы можем построить ее, если захотим,
обобщая наш воображаемый эксперимент. Допустим,
что мы поставили очень много экранов между источни-
источником и счетчиком и в каждом экране просверлили не-
несколько щелей. Затем, записав последовательность ще-
щелей, через которые проходит электрон, и моменты вре-
времени каждого прохождения, мы получим приближенное
описание его траектории. Мы придем к окончательному
описанию в пределе, когда поставим бесконечное число
экранов между источником и счетчиком и >в каждом из
них проделаем бесконечное число отверстий, так что
фактически никаких экранов уже не останется, а мы по-
получим саму траекторию, т. е. положение электрона как
функцию времени. Тогда полная амплитуда вероятности
пройти от источника к счетчику представится суммой
амплитуд для каждой отдельно взятой траектории по
всем возможным бесконечным траекториям. Считая для
простоты пространство одномерным, мы можем записать,
амплитуду вероятности выхода из точки ха в момент
времени ta и достижения точки хь в момент времени tb
в виде
K(xb, tb\ xa, ta) =
3x(t). (8)
Символ 2) обозначает операцию интегрирования по
траекториям.
Это интегрирование можно определить таким спосо-
способом, который позволит фактически вычислять инте-
интегралы. Интеграл строится по аналогии с обычным инте-
интегралом Римана. Допустим, что траектория разбита на
ряд дискретных шагов по времени. Обозначим точки,
через которые траектория проходит в отмеченные мо-
моменты времени, соответственно через Xi, х2, ..., xiy ...,
как показано на рис. 4.
Между точками деления мы заменим каждую траек-
траекторию отрезком классического пути. Иными словами,
мы вообразим, что частица проходит через точки деле-
деления, а между точками деления движется как классиче-
классическая частица под действием потенциального поля в со-
соответствующих точках пространства и врехмени. Таким
образом, на отрезке пути между точками (#$, ^) и
(Xi+u ti+i) действие равно
¦^класс. CM =
/-I
^ zL \{xt - х^/г, (xt + xt_x)l2\ {tt +1^/2] (9)
и для всякой траектории действие вдоль всей траекто-
траектории приблизительно равно
yv
U[t A0)
2
Теперь полная амплитуда вероятности движения ча-
частицы из начальной точки а в конечную точку b полу-
получается интегрированием по всем значениям х в точках
деления. Таким образом,
оо оо р N -|
lim Г ... Г exp U- У 1класс. dt\dxl ... dxN_v
— оо — оо I l — ^ J
A1)
где начальная и конечная точки х0 и xN фиксированы и
совпадают с ха и х&, а число делений равно Af =
= (tb—ta)le. Для лагранжианов, квадратичных по ско-
скоростям, все интегралы сводятся к гауссовым квадрату-
квадратурам, и, таким образом, их можно вычислить. Однако
при переходе к пределу при е->0 мы с ужасом обна-
обнаружим, что функция, определенная уравнением A1),
расходится. Очевидно, что требуется некоторый норми-
нормирующий множитель.
В определении обычного интеграла Римана мы скла-
складываем ординаты дискретного множества точек и рас-
рассматриваем предел, когда число точек стремится к бес-
бесконечности. Однако мы должны всегда умножить эту
сумму на расстояние между точками, чтобы избежать
расходимости. В случае интеграла по траектории мы
должны умножить кратный интеграл на Bnhie/m)"Nf2.
Вы, возможно, заметили, что в определении инте-
интеграла по траектории молчаливо подразумевается, что
пути могут быть разбиты по времени и результаты по-
последовательно складываются. Иными словами, мы поль-
пользуемся тем принципом, что амплитуда вероятности
событий, происходящих последовательно во времени,
получается как произведение амплитуд для каждого из
двух событий. Отсюда получаем уравнение
оо
K(b,a)= f K{b,c)K(ca)dxc. A2)
—оо
Этот результат справедлив всегда, когда действие само
может быть разделено, т. е. всякий раз, когда действие
вдоль пути от одной точки до другой может быть пред-
представлено как сумма двух действий: от начальной точки
до некоторой промежуточной точки и от этой точки до
конечной. Поскольку действие входит в показатель экс-
экспоненты для амплитуды, мы видим, откуда получается
формула с произведением.
В релятивистской квантовой механике этот результат
так непосредственно не получается. Здесь движение
электрона определяется полем фотонов, сквозь которое
он движется. Кроме того, электроны испускают вирту-
виртуальные фотоны и затем при своем дальнейшем движе-
движении снова их поглощают. Таким образом, полное опи-
описание системы в произвольный момент времени требует
указания не только положения и имлульса электронов,
но также и состояния полного электромагнитного поля,
окружающего электрон; тем самым вводится зависи-
зависимость от предыдущего движения электронна.
Описанный подход к квантовой механике (при по-
помощи интеграла по траекториям) помогает легко по-
понять классическое описание движения больших масс.
Пусть, например, рассматривается движение массы бил-
лиардного шара. Для каждого возможного пути из на-
начальной точки движения в конечную существует ампли-
амплитуда вероятности, пропорциональная экспоненте, где
в показателе стоит действие, умноженное на i и делен-
деленное на Ъ. При очень больших массах действие чрезвы-
чрезвычайно велико по сравнению с Л. Всякое небольшое из-
изменение пути приводит к очень большому изменению
отношения действия к h и тем самым к бешеной осцил-
осцилляции амплитуды между +1 и —1. Таким образом, при
сложении амплитуд всех близких путей эти амплитуды
гасят друг друга, так что в результате получается нуль.
Однако в окрестности одной особой траектории, а имен-
именно в окрестности траектории, где действие экстремаль-
экстремально, дело обстоит иначе. Здесь малое отклонение траек-
траектории приводит к незначительному изменению действия.
В этой области просуммированные амплитуды будут
интерферировать так, что результат окажется ненуле-
ненулевым. Таким образом, только вдоль пути, для которого
действие экстремально, амплитуда будет заметно отли-
отличаться от нуля. Но это есть в точности классический
результат, а именно: всякое тело движется по пути
наименьшего действия.
Вам, возможно, приходилось иногда слышать о ве-
величине, называемой волновой функцией и являющейся
решением волнового уравнения Шредипгера. Оказы-
Оказывается, что амплитуда, которую мы записали в виде (8),
сама является волновой функцией специального типа и
удовлетворяет волновому уравнению Шредингера.
Это уравнение, которое является, возможно, самым
важным сегодня математическим утверждением, было
сведено к виду
Егр = Нг|). A3)
Это операторное уравнение, и его кажущаяся простота
несколько обманчива. Здесь Е — оператор энергии, Н —
оператор Гамильтона. Для частицы, движущейся в од-
одномерном пространстве под действием потенциала
V(x, /), это уравнение принимает вид
Его решением являются волновые функции г|)(х, t), за-
зависящие от х (положение в пространстве) и t (время).
Эта волновая функция представляет собой на самом
деле специального вида амплитуду вероятности, опре-
определенную формулой (8); она получается, когда началь-
начальная точка ха, ta опущена в определении и остается
только конечная точка. Такие амплитуды полезны в тех
случаях, когда прошлая история частицы несущественна
и нам нужно знать лишь некоторую функцию, которая
описывает положение частицы в данный момент и в дан-
данном месте.
То, что амплитуда вероятности, определенная с по-
помощью интеграла по траекториям, удовлетворяет урав-
уравнению Шредингера, можно доказать, исследуя, как ме-
меняется амплитуда за очень короткий промежуток вре-
времени и на очень малых расстояниях в пространстве. Со-
Согласно правилу перемножения амплитуд для событий,
происходящих в последовательные промежутки вре-
времени, мы напишем
К(х2, /2 + е; xv tl) =
оо
= jК(x2J t2-\-z\ x2 — l, t2)K(x2 — l, t2; xv tx)dl. A5)
Первый множитель под знаком интеграла может быть
записан в виде
с точностью до первого порядка по 8 и второго порядка
по ?. Второй множитель может быть разложен в ряд
Тейлора по g, и тогда интегрирование по g даст все не-
необходимые члены.
Если левую часть уравнения A5) разложить в ряд
Тейлора по 8, то можно затем приравнять члены одина-
одинакового порядка по 8.
Приравнивая члены нулевого порядка по 8, мы уви-
увидим, что нормирующая константа, которая вводится,
чтобы обеспечить сходимость выражения A1), действи-
действительно определяется формулой
/т. A7)
Приравнивая члены первого порядка по 8, мы полу-
получим волновое уравнение Шредингера, где все призвод-
ные берутся по переменным, относящимся к конечной
точке. (Несколько изменений знака приводят к урав-
уравнению, связывающему производные по переменным, от-
относящимся к начальной точке.)
Определение интеграла по траектории, записанное
формулой A1), на самом деле довольно неудобно для
практического использования. К счастью, существует
другой технический прием, вполне пригодный для боль-
большинства квантовомеханических задач. Сделаем замену
переменных, полагая х=х + у, где х—траектория, про-
проходящая через заданные конечные точки, вдоль которой
действие S экстремально. Тогда у обращается в нуль
в концах. Сделаем эту замену в лагранжиане L и рас-
рассмотрим его интеграл вдоль какой-нибудь траектории.
Этот интеграл равен, конечно, действию вдоль этой тра-
траектории, и, поскольку х определяется как траектория,
вдоль которой действие S экстремально, все члены, со-
содержащие у в первой степени, должны при интегриро-
интегрировании исчезнуть. Следовательно, в том частном случае,
когда лагранжиан L является квадратичным по про-
пространственным переменным, после интегрирования не
может остаться членов, содержащих смешанные произ-
произведения вида ху. В результате мы получаем, что в этом
случае действие по любой траектории разбивается в сум-
сумму двух действий, а именно
y]. A8)
Здесь 5Класс — действие вдоль траектории, по которой
частица должна была бы двигаться по классическим за-
законам, т. е. классическое действие, a S' — дополнитель-
дополнительное действие, зависящее только от отклонения у от
классической траектории.
Поскольку траектория х фиксирована, при сумми-
суммировании изменяется только у. Таким образом, интеграл
по траекториям может быть записан в виде
ifLdt
= / ехр [^ Eклас
О
О
= ехр (-J- 5класс.) / ехр fas' [у]) $y(t). A9)
О
Здесь мы видим, что интегрирование по траекториям
распространяется только на те траектории, которые
начинаются и кончаются в нуле. Таким образом, нам
удалось вытащить за знак интеграла множитель, в ко-
котором содержится вся зависимость амплитуды от кон-
концов траекторий а и Ь. Далее, легко показать, что если
лагранжиан явно не зависит от времени, то оставшийся
интеграл по траекториям может зависеть только от
промежутка времени гъ — 4, но не от самих абсолют-
абсолютных значений начального и конечного моментов вре-
времени.
Конечно, выражение A9) все еще содержит инте-
интеграл по траекториям, который нужно вычислять. Одна-
Однако для большого числа важных и интересных задач мно-
множитель, стоящий перед знаком интеграла, заключает
наиболее существенные физические сведения, а инте-
интеграл по траекториям играет роль немногим большую,
чем нормирующая константа. Действительно, во мно-
многих случаях абсолютная величина этого интеграла мо-
может быть фактически найдена как нормирующая кон-
константа для известного уже распределения вероятностей,
по крайней мере с точностью до неизвестного, но и не-
несущественного фазового множителя [т. е. ехр(/б), где
б — постоянная фаза]. В других случаях оставшийся
интеграл по траекториям можно иногда вычислить, рас-
рассматривая частный случай задачи, который может сов-
совпадать с предыдущим примером. Например, в случае
гармонического осциллятора вид этого интеграла мо-
может быть определен при помощи обращения к частному
случаю осциллятора с нулевой частотой, т. е. к случаю,
когда гармонический осциллятор совпадает со свобод-
свободной частицей. Если же никакие из этих трюков не по-
помогут, мы всегда можем вернуться к определению, за-
заданному формулой A1).
В заключение этой статьи я приведу краткое описа-
описание одного метода использования интеграла по траекто-
траекториям для определения наинизшего энергетического
уровня квантовомеханической системы. Существует уже
много технических приемов для такого вычисления. Ве-
Вероятно, самый известный из них — это вариационный
метод Рэлея — Ритца. Прежде всего допустим, что мы
определяем произвольное стационарное состояние си-
системы. Такие состояния, если они существуют, являются
собственными функциями <рп уравнения Шредингера
с собственными значениями Еп. Итак, мы можем напи-
написать
ЯлФл = Я<рл. B1)
Всякое решение уравнения Шредингера может быть
представлено в виде ряда из собственных функций
1> = S *лФл ехр (— /?Л*/Л). B2)
Допустим теперь, что мы всюду в нашей задаче делаем
замену +it = x. Мы получим те же самые собственные
функции и собственные значения, и всякое решение
уравнения Шредингера запишется по-прежнему в виде
ряда из собственных функций. Но теперь этот ряд при-
примет вид
Ф=2^Флехр(-?лт/А). B3)
Если мы выберем т достаточно большим (скажем, рав-
равным Г), то в выражение B3) все больший и больший
вклад будет давать первый член:
4>^<Woexp(-W)- B4)
Но мы уже знаем, что всякое решение уравнений
Шредингера выражается через интеграл по траекто-
траекториям. Таким образом, можно записать
т
<ф = J ехр (S/h) Зх (т), B5)
о
и если мы вычислим этот интеграл для достаточно боль-
больших значений Г, то результат будет пропорционален
ехр(-ВД:).
Вычисление интеграла может оказаться очень труд-
трудным, если S — достаточно сложная функция. Мы укажем
сейчас прием, позволяющий получить хорошую оценку
значений этого интеграла при помощи искусственно
построенной функции действия. Обозначим это новое
действие через 5i и постараемся подобрать его так,
чтобы оно было настолько близко к исходному дей-
действию 5, насколько это возможно, и в то же время при-
приводило к вычисляемому интегралу по траекториям.
Перепишем интеграл по траекториям в виде
т
•ф == J exp (S/h) 35х (т) =
о
т
= J ехр [E — SJ/Ь] exp (SJh) $x (т) B6)
о
и определим «среднее значение» функционала F следую-
следующим образом:
Г F exp (S/h) ®x (т)
• B7)
()
J
Обратимся теперь к одной важной и хорошо известной
лемме: для всякого среднего, определяемого с помощью
положительной весовой функции, выполняется неравен-
неравенство
(ехр/7)>ехр(/7>. B8)
Воспользовавшись определением среднего по фор-
формуле B7), определим энергию Е соотношением
т
{ ехр D- (S - S,)) ехр (^-) Ях (т) ~ exp (- ET/h)., B9)
О
Тогда из указанной леммы следует, что
Е>Е0. C0)
Таким образом, независимо от выбора 54 получающееся
значение Е всегда превосходит истинный нижний уро-
уровень энергии Ео. Чем меньшее значение мы найдем для
Е, тем лучшую оценку получим для Ео. Для того чтобы
вычислить ?, мы должны вычислить два интеграла по
траекториям
т
f exp (Sxfh) 3)х (т) = ехр (— ExT/h),
о
C1)
При искусном выборе Si эти интегралы можно вычис-
вычислить даже несмотря на то, что интеграл B5) не вычис-
вычисляется.
Мы можем несколько усовершенствовать этот прием,
выбирая Si так, чтобы оно зависело от нескольких не-
неопределенных параметров. Затем, вычислив Е как функ-
функцию этих параметров, мы можем, варьируя их, найти
минимум Е и тем самым улучшить оценку для Ео.
В этой статье я попытался, следуя профессору Кацу,
описать различного рода вероятностные меры и объяс-
объяснить те особенности, которыми обладает мера, исполь-
используемая в квантовой механике; я также слегка коснулся
новых вероятностных понятий, которые, по-видимому,
должны быть приспособлены для объяснения поведения
элементарных частиц, существующих в природе. Я по-
показал, каким образом эта мера и соответствующий ей
интеграл могут быть использованы не только для ре-
решения задач, возникающих в квантовой механике, но и
для более глубокого понимания основных физических
законов. Изложенный здесь метод интегралов по траек-
траекториям не привел пока ни к каким ошеломляющим от-
открытиям в области квантовой механики, однако во мно-
многих случаях (например, в последнем примере) эта тех-
техника может привести к лучшим результатам, чем преж-
прежние приемы, со значительно меньшей затратой сил. Но,
может быть, наиболее существенно в этом подходе то,
что он улучшает наше интуитивное представление о при-
природе.
По поводу изложенного в этой статье см.: F е у п-
m a n R., The concept of probability in quantum mecha-
mechanics, Proc. of the Second Berkeley Symposium on Mathe-
Mathematical Statistics and Probability, p. 533; The space-time
approach to non-relativistic quantum mechanics, Rev.
Modern Phys., 20 A948), 367; Slow electrons in a polar
crystal, Phys. Rev., 97 A955), 660.
ТЕОРИЯ ВАН-ДЕР-ВААЛЬСА О PABHOPFCHH
МЕЖДУ ГАЗОМ И ЖИДКОСТЬЮ*)
М. КАЦ, Г. Е. УЛЕНБЕК, П. К. ХЕММЕР
Часть I
ИЗУЧЕНИЕ ОДНОМЕРНОЙ МОДЕЛИ
!. Введение
В этой серии статей мы хотим вновь обсудить старую
теорию Ван-дер-Ваальса 1) **) о переходе вещества из
газообразного состояния в жидкое. Как известно, наи-
наибольшая заслуга этой теории состоит в том, что она
впервые, исходя из представлений кинетической теории,
дала качественную интерпретацию явления конденсации,
а также существования критической точки. С другой сто-
стороны, оказалось очень трудно сделать эту теорию более
строгой; поэтому в современной теории 2) уравнения со-
состояния неидеального газа следуют чаще всего идее Ка-
мерлинга Оннеса о представлении всех величин для
неидеального газа в виде ряда по степеням плотности —
так называемого вириального разложения. Этим спосо-
способом можно последовательно учитывать взаимодействие
двух, трех, четырех и т. д. частиц и вывести точные вы-
выражения для последовательных отклонений от законов
идеального газа в терминах межмолекулярного потен-
потенциала. Делалось много попыток3), однако до сих пор
совершенно безуспешных, построить строгую теорию фа-
фазовых переходов с помощью таких разложений. На са-
самом деле мы думаем, что такое построение выполнить
очень трудно, если вообще возможно4), поэтому нам
кажется целесообразной попытка переформулировать бо-
более строгим образом основные идеи Ван-дер-Ваальса.
*) К а с М., U h 1 е n b е с k G. Е., Н е m m е г Р. С, On the van
der Waals theory of the vapor-liquid equilibrium. I. Discussion of a
onedimensional model, II. Discussion of the distribution functions,
III Discussion of the critical region, Journal of Mathematical Physics,
4, 2 A963), 216—228, 229—247; 5, 1 A964), 60—74.
**) Примечания авторов см. в конце каждой части.— Прим. ред.
Мы старались это сделать, исходя раз и навсегда из
модели одномерного газа, предложенной М. Кацем5);
для этой модели все вычисления могут быть выполнены
точно. Вот описание этой модели: в отрезке длины L
движутся N частиц с парным взаимодействием, описы-
описываемым экспоненциальным притягивающим потенциалом
Рис. 1. Потенциал взаимодействия у(х).
ц)(х) с твердой сердцевиной размера б (рис. 1). Для этой
модели можно точно исследовать статистический инте-
интеграл в термодинамическом пределе L~>oo, N-+oo,
l = L/N — конечно. Как было показано ранее Кацем, за-
задача отыскания этого предела может быть сведена к ис-
исследованию линейного интегрального уравнения с поло-
положительно определенным ядром Гильберта—Шмидта.
Наибольшее собственное значение этого ядра определяет
термодинамический потенциал (гиббсовскую свободную
энергию) системы. Этот результат воспроизводится
в п. 2.
Для конечных y[y—показатель экспоненты потенциа-
потенциала ф(х), ф(х) = — уе~аУх, х>8], т. е. при конечном радиу-
радиусе действия сил притяжения, в системе не происходит
фазовых переходов, в соответствии со всеми известными
ранее результатами6) для одномерных систем. Однако,
если положить cc = ccoY и затем устремить у к нулю (т. е.
рассмотреть слабые, но очень дальнодействующие силы)
оо
гак, чтобы при этом интеграл J dxqnp(x)
оставался конечным (мы будем называть это ван-дер-
ваальсовским пределом), то возникнет фазовый пере-
переход, описываемый в точности уравнением Ван-дер-Ва-
Ван-дер-Ваальса
Р W
в сочетании с хорошо известным правилом Максвелла7).
Все это подробно показано в п. 3.
В п. 4 при указанном предельном переходе найдены
все собственные функции и собственные значения ин-
интегрального уравнения Каца. Это сделано с помощью
теории возмущений, причем за малый параметр вы-
выбрано у8. Фазовый переход соответствует двойному
вырождению наибольшего собственного значения; этот
эффект сохраняется в членах любой конечной степени
относительно у8. Следует заметить, что это разложе-
разложение справедливо только вдали от критической точки.
Область вблизи критической точки требует особого ис-
исследования; мы приведем его в третьей статье этой серии.
В последнем пункте обсуждается применимость на-
наших результатов к трехмерной задаче и их связь с обыч-
обычным выводом уравнения Ван-дер-Ваальса.
2. Интегральное уравнение Каца
Статистическая сумма для нашего одномерного газа
имеет вид
L L
Z(L, 7\ N) = ±~f ...
' о о
ХехрГ—^г
L
Г*
L i
где A2 = h2/2nmkT, v = a/kT и ступенчатая функция S(x)
определяется так:
О при \х\ < 6,
S(x =
1 при \х\ > 6.
Поскольку подинтегральное выражение симметрично
относительно переменных /ь /2, ..., tN, а твердая сердце-
сердцевина устанавливает линейный порядок частиц в L, мы
можем переписать формулу B) в виде
Z(L,
X
T, 1
V) е
г N
ехр
1
~TyVv ^,
••¦/
< ... <^<
ЛГ-1
П^A
л,
0+1-
. . . Ллг
-<yl).
X
C)
Притягивающая часть подинтегрального выражения так-
также может быть упорядочена, если воспользоваться ра-
равенством
ехр
N
ехр(— y\tt— tj\) \ =
/, ; = 1
оо
= Г... Г rfXi...
— оо
где
Р(х\у, /) = [{
Я (ху | xj+v t
j+v tJ+1
D)
X exp[-(y -
E)
Мотивировкой и доказательством тождества D) слу-
служит замечание, что ехр(—y\t{—^|) есть корреляционная
функция для' одномерного гауссовского марковского про-
цесса (так называемый О-У-процесс); разумеется, это
равенство может быть доказано и непосредственно. Под-
Подставляя D) в C) и применяя преобразование Лапласа
по L, мы увидим, что интеграл
7\ N)dL
можно переписать в виде
оо L L L I N-\
f (He-*1* f dtx fdt2fdt3... ( dtNJl Fj (tJ+1 - tj) =
о о /, /2 tN_x ;=i
oo oo oo oo N — 1
=/ dtx fdt2... fdtNf dLe-^ Ц FJ Cy+i - t})r F)
о tx tN_x tN i=l
где каждое переменное tj входит в разности только с со-
соседним переменным tj-\ или tj+\. Полагая
легко показать, что выражение F) принимает вид
N-1 оо
;=i о
Подставляя сюда соответствующее выражение для .Fj(z)f
мы получаем (опуская теперь переменную темпера-
температуры Т)
...dxNX
X exp [v1/. (x, + ... + ^)] W (xx) XT Л (^ I xj+i)* G)
о —°°
/V-l
где
оо
f)- (8)
То, что Хг упорядочены в последовательные пары, наво-
наводит на мысль рассмотреть ядро
и соответствующее интегральное уравнение, предложен-
предложенное впервые М. Кацем:
оо
fdyKs(x,
Легко видеть, что Ks (х, у) симметрично, и, кроме того,
можно показать (доказательство см. в работе Каца, ука-
указанной в примечании 5), что:
(а) ядро Ks (x, у) положительно определено, т. е.
квадратичная форма
J jK*(x>
всегда положительна для любой функции ty(x), отлич-
отличной от тождественного нуля;
(б) /Cs(*, у)—ядро Гильберта — Шмидта, т. е.
/ J
y)dxdy<oo.
Из этих двух свойств можно вывести, что уравнение A0)
имеет дискретное множество положительных собствен-
собственных значений Ki(s), начинающихся с наибольшего соб-
собственного значения Xo(s) и стремящихся к нулю при
f-voo; при этом соответствующие собственные функции
tyi(x, s) образуют полную ортонормированную систему и
ядро /Cs(x, у) может быть разложено в сходящийся ряд
Ks(х, у) = ^^1 (s)^ (х, 5)^ (у, s). A1)
Переписывая уравнение G) в виде
оо
fdLe~sLZ(L, N) =
— — Nv oo
2
J .. . fdx, ... dx^exp [^ (хг +xN)] X
N
X \W(xx) W(xN)ff
и используя разложение A1), проинтегрируем по #2, Хз,
..., Xjv-г, мы получим
A2)
О S ;=0
где
Л;- = fdx^j (х, s) W'k (x) eli*v™. A3)
Если теперь образовать большую статистическую
сумму
^(, N)(Azft A4)
N=1
то из уравнения A2) следует равенство
в предположении, что z<e1/2V/X0(s). Ясно поэтому, что
граница сходимости преобразования Лапласа функции
G(L, z) совпадает с тем значением 5, при котором
z = e4*v/X0{s). A6)
Поскольку, с другой стороны, эта граница равна также
пределу
HnwlnG(I, z), A7)
L-*oo L
который имеет термодинамический смысл величины p/kT,
то связь между z и давлением газа задается формулой
K(P/kT)=eli>Vz. A8)
Далее, поскольку z имеет термодинамический смысл ак-
активности, которая связана с химическим потенциалом -
(гиббсовской свободной энергией на одну частицу)
\х (р, Т) соотношением
A9)
то отсюда получается уравнение состояния:
ti B0)
где штрих означает дифференцирование по s.
Можно доказать следующие утверждения, касаю-
касающиеся наибольшего собственного значения A,o(s), а так-
также всего спектра собственных значений X{(s) (см. при-
приложение 1):
(а) все собственные значения являются монотонно
убывающими функциями 5 и стремятся к нулю при
5->оо;
(б) наибольшее собственное значение Xo(s) уходит в
бесконечность при s->0. Ни при каком значении 5 оно
не вырождено (однократно) и является аналитической
функцией от 5 для всех вещественных s>0. Наконец, вы-
выполняется неравенство
из которого следует, что производная h'o(s) всегда поло-
положительна;
(в) все другие собственные значения конечны при
5 = 0.
Кажется весьма правдоподобным, что кривые Ki(s),
/>0, также не пересекаются друг с другом, и в этом
случае спектр как функцию от s можно изобразить, как
показано на рис. 2.
Можно вывести, что для всякого z существует един-
единственное значение s, удовлетворяющее уравнению A6),
а из уравнений B0) и B1) тогда следует, что / — моно-
монотонно убывающая и аналитическая функция от s = p/kT
для всех положительных 5. Это означает отсутствие фа-
фазового перехода. Заметим, что в этой теории получается
Рис. 2. Спектр как функция от s.
явное выражение [см. A8) и A9)] для гиббсовской сво-
свободной энергии как функции давления, и поэтому удель-
удельный «объем» (точнее, удельная длина) / получается как
функция давления, а не давление выражается в виде
функции от /, как в теории Майера. Поэтому связь с ви-
риальным разложением для уравнения состояния доста-
достаточно сложна. Можно показать, что наибольшее соб-
собственное значение h(s) допускает разложение
Хо (s) = еЧ> v (s-i + а0 + axs + a2s2 +•••)• B2)
Коэффициенты аг- можно вычислять последовательно, и
они связаны с майеровскими групповыми интеграла-
интегралами Ъ{. Находим
ао = Ь2; ах = Ьъ — Ь\ B3)
и т. д. За доказательством мы снова отсылаем к при-
приложению 1. С помощью уравнений B2) и B3) можно
затем проверить, что уравнение состояния B0) для не-
небольших значений давления есть просто обращение
обычного вириального разложения
pl/kT = 1 + ВЦ + С//2 + ...,
где В = —Ь2, С=—2&3 + 4&2 и т. д. Мы не в состоянии
как-либо просто «графологически» охарактеризовать
коэффициенты аг.
3. Ван-дер-ваальсовский предел
Мы выясним теперь, что происходит с наибольшим
собственным значением A,0(s), если положить а = аоу и
перейти к пределу при y->Q. Чтобы сделать это, мы ис-
исследуем моменты 2^?E) распределения собственных
значений A,2(s). Имеем
CO
• • • К (*„, xt) = J .. . f dxx ... dxn X
Xexp[— 5(t!+ ... +тл
где vo = ao/kT и ^n+i=Xi. Можно выполнить интегриро-
интегрирование по хи а затем исследовать, что происходит в пре-
пределе при y->Q. Необходимые подробности содержатся
в приложении 2. Ответ дается следующей теоремой.
При у-+0 имеем
i —со
(оо n П
exp fo Bvo)'/2] J aft exp [- sx - i ft» + л») t] . B4)
Изложим теперь дальнейшие эвристические соображе-
соображения. Положим
оо
/ (?, л) = exp h Bv/2] J dx exp [- 5т -1 (|2 + т)*) т];
B5)
поскольку равенство B4) имеет место для всех я, мож-
можно ожидать, что для всякой «хорошей» функции g(x)
существует предел
^ ?(*-/) = •?• didT)g[f(h л)]- B6)
r г —оо
Возьмем теперь в качестве g(x) ступенчатую функцию
ори а < х < р,
для остальных х,
и пусть NT (a, P) — число собственных значений между
а и Р; из уравнения B6) вытекает, что
bec, P)~Sa8; B7)
Y->0 Y ZJl
—площадь области на плоскости (?, г]), где
f(, т])<р. Допустим, что f(g, т]) имеет абсолютный
максимум со E); тогда очевидно, что со E) при у-> 0 дол-
должна быть предельной точкой последовательности соб-
собственных значений, так как во всяком интервале между
со—е и со должно оказаться в пределе при y->0 беско-
бесконечно много собственных значений, поскольку площадь
области со—е</(?, г\) <со конечна. Поэтому кажется есте-
естественным ожидать, что со (s) при v^O является наи-
наибольшим собственным значением или, иначе, что
Hm l0 E, у) = со (s) = max / (?, r\) == max F (тО, B8)
где
exp [- б (s +1Л2) - In (^ +1 л2) + 4 Bvo)V2],
поскольку максимум функций f(g, ц) всегда достигается
при g = 0.
Заметим, что наше рассуждение на самом деле еще
не доказывает, что из уравнения B7) следует равенство
B8), поскольку B7) не исключает, что несколько ди-
дискретных собственных значений оказывается больше
со (s) при у->0. Однако уравнение B8) правильно, и рас-
рассуждение можно сделать вполне строгим. Мы здесь не
будем этого делать, потому что в следующем пункте мы
подробно исследуем предельный переход при -у-^О и
получим строгое доказательство уравнения B8).
Для дальнейшего рассмотрения формулы B8) заме-
заметим сначала, что значение v\(s), при котором дости-
достигается максимум ^(т]), удовлетворяет уравнению
. B9)
Уравнение dfs/dr) = O приводит к равенству
s + T^it1 ± A—8s6)V2]. C0)
Здесь мы должны различать два случая:
(a) 8s6>l. В этом случае f8(r\) —монотонно возра-
возрастающая функция г), и уравнение B9) имеет единствен-
единственное решение r](s); ему соответствует единственный мак-
максимум F(r\). Уравнение состояния принимает вид
[в последнем равенстве мы использовали уравнение B9)].
Подставляя s = p/kT и ц (s) = BvoI/2// в уравнение B9),
мы получим уравнение Ван-дер-Ваальса
kT а0
Р
(б) 85б<1. В этом случае функция fs(r[) имеет мак-
максимум и минимум (рис. 3), и легко проверить, что для
5=7вв МЫ Имеем fmin = fmax= (Z'h) C6I/г И ЧТО /mm И
f'max монотонно возрастают для убывающих 5; при этом
fmm остается конечным, в то время как /max стремится
к бесконечности при s -> 0.
Если теперь BvoI/2 < fmm, то снова существует толь-
только одно решение уравнения B9), соответствующее един-
Рис. 3. Функция fs(v\) в двухфазовой области,
ственному максимуму функции F(r\). To же самое будет
при Bvo)V2>/max. Однако еСЛИ fmin<Bvo)V2</max', TO
уравнение B9) имеет три корня; два крайних соответ-
Р и с. 4. Наибольшее собственное значение в ван-дер-ваальсовском
пределе для температуры ниже критической.
ствуют локальным максимумам функции F(v\), а вну-
внутренний— ее локальному минимуму. Мы должны теперь
выбрать тот из двух локальных максимумов, который
служит абсолютным максимумом F(r\). Очевидно, что
если менять vo при фиксированном 5 или менять 5 (не
царушая неравенства 8s6<l) при фиксированном vo, то
найдется такое значение s(vo), при котором оба макси-
максимума совпадут. При этом значении 5 нарушается анали-
аналитическое поведение со(s), поскольку r\(s) мгновенно пе-
перепрыгивает с ветви 1 кривой fs(r\) на ветвь 2 (рис. 3).
На самом деле можно показать, что при s = s производ-
производная co(s) имеет разрыв и, поскольку /=—a>'(s)/a)(s), на
соответствующей изотерме имеется горизонтальный уча-
участок (рис. 4 и 5). Далее, поскольку уравнение C1)
остается верным, как жидкая, так и газообразная часть
по-прежнему описывается уравнением Ван-дер-Ваальса.
Рис. 5. Изотерма, соответствующая рис. 4.
Наконец, равенство максимумов F(r\) при s=s или двух
значений со (s) означает равенство гиббсовских свобод-
свободных энергий обеих фаз при s = s, что в свою очередь
эквивалентно правилу Максвелла.
Критическая точка определяется из уравнений
8sKp6 - 1, BvKp.I/2 = /mIn (sKp.) = /max (V) = | C6)v\
Это приводит к хорошо известной формуле
C2)
4. Собственные функции
и собственные значения при малых y
Очевидно, что причина, по которой при малых у соб-
собственные значения Xn(s, у) уравнения Каца сгущаются
около точки to (s), должна быть связана с тем обстоя-
обстоятельством, что при у->0 функция Р(х\у, t) приближает-
ся к б-функции Дирака б(х— у). Однако если допустить,
что при y-^0 собственные функции tyn(x, s, у) сосредо-
сосредоточиваются в окрестности х = 0, как в обычной задаче
о собственных значениях, то из уравнения A0) следова-
следовало бы, что при у -> 0 собственные значения должны груп-
группироваться около e~s6/s — максимального собственного
значения для газа из твердых палочек. Этого противоре-
противоречия можно избежать, только если считать, что при
Y -> 0 собственные функции располагаются все дальше и
дальше от начала координат. В этом обстоятельстве
ключ к построению согласованных последовательных
приближений для собственных функций и собственных
значений при малых у.
В основном интегральном уравнении A0) сделаем
подстановку
I/ ч C3)
где t)=t)(s)— то значение tj, при котором функция
F(r],s), определенная формулой B8), достигает своего
абсолютного максимума. Рассмотрим сначала однофа-
зовую область, так что r\(s) единственно. Пусть
. C4)
Тогда уравнение A0) можно переписать в виде
оо оо
exp [r, Bv/>] / d? f dx [^-f P (x' | y', t) X
-1 (f Гth (тг)
Теперь ясно, что P(xf\y', т) ->б(х/—у') при y~~^0> если
h(x') сосредоточена около х' = 0. Собственные значения
стремятся к величине
оо
ехр [т) Bvo)Vs] J dx exp [— sx — -^]= со (s),
6
как и ожидалось. Мы можем сказать, что при помощи
подстановки C3) интегральное уравнение «приспосабли-
вается» к разложению вида
h (xf) = Л(о) (х') + V/sAA) (•*') + Ф2) (*') + .... C6)
Поскольку выкладки здесь довольно сложны, мы просто
укажем, как это делается. В левой части уравнения C5)
мы полагаем
и разлагаем все подинтегральное выражение в ряд по
степеням уЧ*. Интегрирование по ? сводится к гауссовым
квадратурам, а интегралы по т могут быть выражены с
помощью co(s) и ее производных. Если ограничиться раз-
разложением до порядка Y3/a и сократить на общий множи-
множитель соE), то левая часть уравнения C5) примет вид
h (х') + yl \tf (xf) + h (x) A -1 x'2 + ±. x'\ (I - 6J) ] +
— y x'h (xr) — h! (xr) - xrh!!
где мы воспользовались формулой C1), чтобы выразить
T)(s) через /. Если теперь подставить разложения C6)
в обе части уравнения C5) и приравнять одинаковые
степени у^, то мы получим в нулевом приближении
где использованы обозначения
В2 = Р — 2vo(l — 6J//, x' =
. C8)
Уравнение C7) есть уравнение для функций Вебера, и
отсюда можно заключить, что
(*«) = ¦§¦!/-Bл+1M],
z) = NnDn{z), C9)
где Nn — нормирующий множитель (B/2nl)i/4 (n!)~1/s. За-
Заметим, что величина В связана с сжимаемостью газа, по-
поскольку из уравнения Ван-дер-Ваальса получаем
В однофазовой области производная др/dl всегда отри-
отрицательна, и поэтому В можно выбрать положительным.
Наибольшее собственное значение соответствует поэто-
поэтому я = 0, и мы получаем в первом приближении
D1)
Это доказывает утверждение п. 3, что наибольшее соб-
собственное значение в ван-дер-ваальсовском пределе рав-
равняется 0E).
В первом приближении мы получаем
D2)
Можно без труда проверить, что правая часть здесь ор-
ортогональна Нп у так что уравнение D2) имеет единствен-
единственное решение. Явный вид этого решения, а также второго
приближения, которые нам понадобятся в следующей
статье этой серии, приведены в приложении 3.
Рассмотрим теперь двухфазовую область.
Ясно, что в этом случае наше рассуждение следует
уточнить, поскольку выбор r\(s) в подстановке C3) те-
теперь неединствен. Действительно, так как F(r\, s) имеет
теперь два равных максимума, существуют два значения
r\(s), соответствующие предельным объемам 1\ и /2 для
насыщенных газообразной и жидкой фаз (рис. 5). Для
каждого из этих двух значений можно произвести за-
замену C3) и повторить все наши рассуждения. Очевидно,
что в обоих случаях мы придем к одной и той же ве-
величине со (s) собственного значения нулевого порядка, но
получим разные собственные функции, поскольку
величина l/В различна для lx и 12. Мы можем сказать,
следовательно, что для 4</</ь т. е. в двухфазовой об-
области, наибольшее собственное значение в ван-дер-ва-
альсовском пределе дважды вырождено (двукратно) и в
наименьшем порядке собственная функция имеет вид
[поскольку D0(z)
где _
/1 и т,2 (s) = Bvo)vV/2-
Возникает вопрос, какая линейная комбинация соот-
соответствует удельной длине / —Ы1 + Ы2 (гДе h и Ъ— мо-
молярные доли жидкой и газообразной фаз), так что
?i + ?2=l- Мы увидим, что
g1 = a;. I2 = al D4)
Чтобы доказать это, заметим сначала, что при малых у
две гауссовы функции в D3) не перекрываются. Следо-
Следовательно, для нормированной собственной функции
г|)(х, 5) получаем aj -f- a| = 1. Далее, для всякого конеч-
конечного у из уравнения Каца следует, что
s, у),
= -X0(s, y)l= D5)
5, y)
[поскольку дифференцирование собственной-функции по
5 приводит к нулю, так как из условия нормировки
( , у) следует, что
(x, 5, У)-^%(х, 5, y)dx = 0].
Выберем теперь s = s, и пусть у->0. Поскольку для ка-
каждой из двух функций в формуле D3) выполняется
уравнение, подобное уравнению D5), с тем же самым s
и тем же самым Ko(s) =@E), но с /, соответственно
равным 1\ и U, и поскольку снова можно пренебречь
тем, что эти две функции перекрываются, из уравне-
уравнения D5) при y->0 получаем
Это и доказывает соотношение D4).
В заключение этого пункта сделаем следующие два
замечания:
Рис. 6. Обозначения: — go(s); — • —К(s, у) (точное значение);
X,(s, у) (значение с точностью до у6)\ Я (s, у)
(значение с точностью до ($J)
(а) Ясно, что наше разложение становится неверным
вблизи критической точки, так как в этой точке В->0 и
/i=/2. Поэтому нельзя уже пренебрегать перекрыванием
двух собственных функций в двухфазовой области.
В критической области следует уже иначе перестраивать
интегральное уравнение; как это делается, мы покажем
в третьей статье этой серии.
(б) Из уравнения D1) следует, что в первом порядке
по у функция Ko(s, у) по-прежнему имеет разрыв произ-
производной, и можно с уверенностью ожидать, что этот раз-
разрыв сохранится в любом члене ряда теории возмущений.
Для конечных у функция hois.,у) является аналитиче-
аналитической по 5 при 5>0. Это означает, что для малых у раз-
развитый нами метод последовательных приближений при-
приближает аналитическую функцию M(s,у) с помощью
ряда функций, имеющих разрыв первой производной
в области изменения s, где производная A,0(s, y) меняет-
меняется очень быстро (рис. 6). Отсюда следует, что фазовый
переход остается вплоть до любого конечного порядка
по у, хотя уравнение состояния в этом случае, конечно,
отличается от уравнения Ван-дер-Ваальса. В самом деле,
легко показать из уравнения D1), что уравнение состоя-
состояния в первом порядке по у в однофазовой области имеет
вид
D — JlL—ZL+V-lkT— l \kT
/3
Давление насыщенного газа и плотности насыщенного
газа и жидкости также соответственно изменятся. Нахо-
Находим
_«@) I у, kT
—Рн&с^гУ 2
kT ( Bj—B
[
2
(
2 [ li—l2
Л
где i'=l, 2.
5. Заключительные замечания
Чтобы оценить, насколько наш результат пригоден
для трехмерного случая, мы сначала напомним обычный
вывод уравнения Ван-дер-Ваальса из статистической
суммы8). Можно рассуждать так: если радиус действия
притягивающей силы очень велик, так что в сферу дей-
действия каждой молекулы попадает много других молекул,
то потенциальная энергия притягивающих сил должна
для почти всех конфигураций молекул равняться своему
среднему значению
Фпр. = — CN2/2 V, D6)
где
С = — J dx фпр. (г).
Уравнение D6) получается из того, что в среднем потен-
потенциальная энергия одной, молекулы пропорциональна
плотности N/V и фактически равна — CN/V. Множитель
У2 в уравнении D6) нужен потому, что каждая молеку-
молекула взаимодействует со всеми другими молекулами*).
Поэтому для дальнодействующих притягивающих сил
представляется разумным приблизить статистическую
сумму выражением
Z(V\ 7\ N) = ^j
... fdr1...drNJlS(\ri-rj\), D7)
V V i<j
где S(x) —та же самая ступенчатая функция, которую
мы уже использовали в п. 2.
Если теперь объем V очень велик по сравнению с об-
4
щим собственным объемом молекул М^о, % = -<$лг1, то
ясно, что интеграл приблизительно равен VN, в то время
как если V того же порядка, что и (Nv0, интеграл обра-
обращается в нуль приблизительно как (V — Nvo)N. Прибли-
Приближенное «интерполирование» интеграла с помощью фор-
формулы (V — b)N, где b~Nv0, немедленно приводит кура-*
внению Ван-дер-Ваальса
(p+-$r)(V-b) = RT, D8)
где a = \cN\
Этот вывод вызвал критику в основном по двум при-
причинам.
1. Истинный термодинамический предел статистиче-
статистического интеграла должен всегда давать устойчивую изо-
изотерму, для которой dp/dv < 0. Это было строго доказано
Ван Ховом 9) для межмолекулярных сил конечного ра-
радиуса действия с твердой сердцевиной. Поскольку ниже
критической температуры в уравнении Ван-дер-Ваальса
существует неустойчивая часть, это уравнение противо-
противоречит упомянутой теореме.
2. Приближение (V—6)^ для отталкивающей части
статистического интеграла должно быть очень грубым.
Даже если выбрать b так, чтобы получить правильный
*) То есть число пар молекул порядка №/2. — Прим. перев.
второй вириальный коэффициент (для этого нужно при-
принять b = 4Nvo), следующие вириальные коэффициенты,
которые могут быть вычислены точно, не согласуются
с ван-дер-ваальсовскими значениями.
Вернемся теперь к нашей одномерной системе. Заме-
Заметим, что те же самые рассуждения, что и выше, приво-
Рис. 7. Обозначения: —изотерма Ван-дер-Ваальса G = 0);
-; точная изотерма; изотерма с точностью до уб.
дят к следующему выражению для статистической
суммы:
, Г, *) =
, ^
X J... fdtx .•.dtNJTS(\ti~tj\). D9)
L L i<j
Здесь С=2ао (множитель 2 возникает ввиду того,
что мы рассматриваем притягивающий потенциал
—аоуехр[—yUI]). Огромное различие между уравнения-
уравнениями D7) и D9) состоит в том, что интеграл в уравнении
D9) может быть вычислен точно благодаря линейному
упорядочиванию в системе твердых палочек. В резуль-
результате получается (L — N6)N. Для газа из твердых пало-
палочек длины б уравнение состояния, как заметил Тонкс10),
имеет в точности ван-дер-ваальсовский вид
p = kT/(l-6). E0)
Второе возражение против уравнения Ван-дер-Ваальса
в одномерном случае исчезает, и поэтому не удивитель-
но, что для нашей модели в ван-дер-ваальсовском пре-
пределе уравнение D8) с b = N6 и a = a0N2 выполняется
точно. Остается только вопрос о противоречии между
уравнением D8) и теоремой Ван Хова. С точки зрения
изложенного в п. 2 и 3 ясно, откуда возникает это про-
противоречие. В приведенном выше выводе переход к тер-
термодинамическому и ван-дер-ваальсовскому пределам со-
совершается одновременно, в то время как это нужно де-
делать отдельно и в определенном порядке: сначала пе-
перейти к термодинамическому пределу для отталкиваю-
отталкивающих сил конечного радиуса действия, а затем устремить
этот радиус к бесконечности. Таким путем мы избежим
противоречия с теоремой Ван Хова и всегда получим
устойчивую изотерму и). Нам кажется поэтому, что пер-
первое возражение против уравнения Взн-дер-Ваальса не
так серьезно, как нам всегда внушали.
Чтобы подытожить наши рассмотрения, выскажем в
заключение несколько соображений.
(а) Представляется разумным, следуя примеру Ван-
дер-Ваальса, постараться в уравнении состояния отде-
отделить эффекты притяжения и отталкивания и расклады-
раскладывать всякую термодинамическую функцию по параметру:
Радиус действия отталкивающей силы ,ri\
" Радиус действия притягивающей силы * ^ '
Можно ожидать, что при р<С1 мы получим уравнение
состояния ван-дер-ваальсовского типа, из которого сле-
следует конденсация и существование критической точки.
Условия термодинамического равновесия будут автома-
автоматически вытекать из первоначального перехода к термо-
термодинамическому пределу.
(б) Только в одномерном случае мы получим в пре-
пределе при р->0 в точности ван-дер-ваальсовское уравне-
уравнение состояния для твердых отталкивающихся шариков.
Этот вывод не должен зависеть от точного вида притя-
притягивающей силы. Мы можем это подтвердить, обобщая
модель Каца для случая, когда притягивающие силы
имеют вид
m
Фпр. С*) = — 2 ct/Y exp (— yotx). E2)
Вычисление статистической суммы можно свести, как и
в п. 2, к интегральному уравнению для функции т пе-
переменных, а поведение наибольшего собственного значе-
значения в пределе при у-^-0 можно изучать тем же самым
способом, что и в п. 3. Получается снова уравнение B8),
с той только разницей, что 2vo заменяется величиной
E3)
Итак, снова получается уравнение Ван-дер-Ваальса, а
ван-дер-ваальсовская константа а по-прежнему пропор-
пропорциональна интегралу притягивающего потенциала.
(в) В трехмерном случае уравнение состояния для
газа из твердых шариков, конечно, не совпадает с урав-
уравнением p = kT/(v—b), хотя качественно его поведение
может быть похожим. Даже для очень дальнодействую-
щих притягивающих сил можно только надеяться прийти
к уравнению состояния, подобному уравнению Ван-дер-
Ваальса. В определенном смысле задача о газе из твер-
твердых шариков становится центральной. Верно ли, что та-
такой газ должен обнаруживать фазовый переход для
плотностей, близких к плотности плотной упаковки (так
называемый переход Кирквуда)? Это известный нере-
нерешенный вопрос. Нам кажется, что существуют веские
аргументы в пользу существования такого перехода и
что этот переход может быть идеализацией (или кари-
карикатурой!) перехода жидкости в твердое тело. Очевидно,
что в одномерном случае [см. E0)] такого перехода не
существует, и мы уверены поэтому, что даже при даль-
нодействующих силах, принуждающих молекулы к объе-
объединению, в одномерном случае существует не более од-
одного фазового перехода.
Наконец, следует упомянуть о двух вопросах, на ко-
которые мы пока не можем дать удовлетворительного от-
ответа.
1. Как связана наша теория с теорией конденсации
Ли и Янга? Ввиду существования твердой сердцевины
большая статистическая сумма G(L,z) является поли-
полиномом степени M = L/6 по г с положительными коэффи-
циентами. Полагая
мы можем написать
где Z{ — нули полинома G(L,z), которые не могут ле-
лежать на положительной части вещественной оси. Функ-
Функцию %(L,z) можно интерпретировать как комплексный
логарифмический потенциал М точечных зарядов вели-
величины 1/L, помещенных в точках Z{. В пределе при L->oo
величина зарядов становится все меньше и меньше, в то
время как их число М возрастает. Предположим теперь,
что в пределе ори L->oo заряды концентрируются около
некоторой дуги («простого слоя»), которая пересекает
положительную часть вещественной оси, скажем, в точке
г = г0. Предельная функция
%(z)= iim x(L, z\
?->oo
которая наверняка существует, будет тогда для поло-
положительных вещественных z состоять из двух аналитиче-
аналитических частей: одной — для z<zQ и другой — для z>z0.
В точке г0 эти две части имеют одно и то же значение,
но разные первые производные. Поскольку %(z)=p/kT,
получится такая кривая, как на рис. 4 (с переставлен-
переставленными абсциссой и ординатой), и произойдет конденсация.
Очевидно, что нечто подобное должно произойти и в на-
нашей модели в ван-дер-ваальсовском пределе. При конеч-
конечных у «простой слой» не должен пересекать положитель-
положительной части вещественной оси, и зазор между ними имеет
величину, скажем, порядка у. Для конечных у функция
i(z) будет тогда аналитической для всех вещественных
положительных г, но в ван-дер-ваальсовском пределе,
когда зазор исчезает, происходит конденсация. Однако
мы не в состоянии проверить эту картину, так как труд-
трудно изучить поведение собственных значений уравнения
Каца для комплексных значений s.
2. Как связана наша теория с теорией Урселла—
Майера? Мы уже упоминали о задаче «графологическо-
«графологического» истолкования коэффициентов щ в разложении Xo(s)
[см. уравнение B2)]. Существуют также и другие вопро-
вопросы. Например, можно было бы ввести майеровские функ-
функции f как для отталкивающей, так и для притягивающей
части межмолекулярного потенциала, которые привели
бы к графам с двумя типами линий. Тогда возникает
вопрос, какое появляется упрощение, если притягиваю-
притягивающие силы дальнодействующие, и можем ли мы, изу-
изучая одномерную модель, как-нибудь лучше характери-
характеризовать уравнение типа Ван-дер-Ваальса в трехмерном
случае.
Приложение 1
Доказательство утверждения (а) см. в работе Каца,
указанной в примечании 5. Там же доказывается, что
и поскольку при 5 = 0 интеграл расходится, Xo(s)-+oo
при 5-^0. Далее, так как можно показать, что правая
часть формулы (П. 1) соответствует приближению, когда
учитывается только взаимодействие между «ближайши-
«ближайшими соседями», следует ожидать, что для малых 5 (т. е.
малого давления) функция Xq(s) становится равной этой
правой части, откуда вытекает, что 'ko(s) ~elt2V/s при
s->0. Это подтвердится в дальнейшем, когда мы выведем
разложение B2).
Утверждение, что Kq(s) не может быть вырожденной
ни при каком значении s, следует из положительности
ядра Ks(x,y) для всех *, у при s>0. Поскольку
Г (dxdyv(x)Ks(x,y)v(y)
%о (s) > ^ ? (П. 2)
I dtf()
для любой функции ф(х) и поскольку максимум дости-
достигается при ф(х) =г|)о(л:), из неравенства Ks(x, У)>0 вы-
вытекает, что функция tyo(x) должна быть одного знака
для всех х, и мы можем считать поэтому г|H(*)>0. Да-
Далее tyo(x) не может обращаться в нуль ни при каком
значении х. Иначе для некоторого значения х, скажем х0,
Кя(хоУу) равнялось бы нулю тождественно по уу что про-
противоречит условию Ks>0. Теперь допустим, что при не-
некотором 5 значение Ko(s) вырождается и ему соответ-
соответствуют две собственные функции ^(х) и г|^2)(л;). Вы*
бирая ^}(х) > 0, можно построить линейную комбина-
комбинацию (р(х) из ^(х) и ^(х), которая ортогональна к
Щ}}(х) и удовлетворяет уравнению
Г fdxdyv(x)Kslx,y)v(y)
l0 (s) = ^ . (П. 3)
J
Поскольку ty{Q](x) не обращается в нуль, ф(х), будучи
ортогональной к я^Ч долл^на принимать как положитель-
положительные, так и отрицательные значения, что приводит к про-
противоречию. Из невырожденности Ko(s) вытекает, что
Xq(s) — аналитическая функция для всех вещественных
s>0. Это следует из того, что, как известно, Ki(s) яв-
являются нулями по X определителя Фредгольма 1)EД),
являющегося целой функцией К и аналитической функ-
функцией 5 для всех вещественных s>0. Следовательно,
Яг E) — аналитическая функция «, за исключением тех
значений 5, при которых два или большее число соб-
собственных значений совпадают.
Наконец, неравенство B1) доказывается так: из ра-
равенства
fjx, s)Ks(x, у)г|H(у, s),
где г|H(я, s)—нормированная собственная функция, по-
получаем, что квадратичная форма
равна
со
f fdxdy%(x,
(П. 4)
Из уравнения (9) для Ks(x,у) можно увидеть, что пере-
переменная 5 входит в Ks только через ps(x,y), а из уравне-
уравнения (8) следует, что первый член в равенстве (П. 4)
положителен для всех г. Второй член в (П. 4) также по-
положителен; действительно, воспользовавшись равен-
равенством
К* (х, у) = 2 К (s) % (х, s) % (у, s)
и тем обстоятельством, что для всякого 5 функции
i|)n(x, s) образуют ортонормированную систему, этот член
можно преобразовать к виду
-2 2 м*)
п=1
поскольку ^n(s)<Xo(s) при ai^-1, это выражение боль-
больше, чем
*) Здесь использовано то обстоятельство, что для нормирован-
нормированных фо (х, s))
оо
I dx^Q (л:, s) ——¦ =0. — Прим. перев.
Последнее же выражение равно нулю в силу равенства
Парсеваля, примененного к функции —г^-« Следователь-
Следовательно, Q(z)>0 для всех г, откуда и вытекает неравен-
неравенство B1).
Утверждение (в) из п. 2 следует из соотношения
оо
,= f dxKs(x,x) =
—оо
- Г **
которое показывает, что при s->0 сумма всех собствен-
собственных значений стремится к бесконечности, как eI/2V/s. По-
Поскольку это совпадает с поведением Xo(s) при s-й), все
остальные собственные значения должны оставаться ко-
конечными при s = 0.
Чтобы найти разложение B2) для Xo(s), следует
произвести вычисления по теории возмущений в окрест-
окрестности 5 = 0 для собственных значений уравнения
J dyKs (х, у) % (у, s) = ^ (s) % (х, s). (П. 5)
— оо
Сначала мы разложим Ks{x,y) в ряд по степеням s.
Чтобы сделать это, мы перепишем Ks(x, у) в виде
/С,(¦*. y) = exp[lv
(
п=0 6
(П. 6)
Теперь положим
h(s) = —z-(a-i + a0s + als2-+- ...),
(П. 7)
и пусть tyM(x) нормирована. Подставляя (П. 6) и (П. 7)
в (П. 5) и приравнивая члены, пропорциональные 1/s,.
мы получаем
оо
/ dy [W(x) W(y)]'h exp [i v1/. (x + y)]Vo) (y) =
— oo
= a_1^w(x)eli*v. (П. 8)
Легко проверить, что это уравнение имеет решение
—J + ^-Jf]- (П. 9)
Заметим, что если бы мы попытались определить таким
же путем величины других собственных значений Xn(s)
при 5 = 0, мы нашли бы, что в этом приближении a^J =
= 0, так что все Хп @) при п>0 вырождены, и чтобы
найти истинные значения, мы должны были бы найти
корни бесконечного «векового» детерминанта. Лишь
одно h(s) стремится к бесконечности при 5-^0, и только
для него можно продолжить вычисления с помощью тео-
теории возмущений.
Приравнивая в выражении (П. 5) члены, не завися-
зависящие от 5, найдем
Jdy exp [I v% (x + y)] {l-b[W(x) W(y)]'h +
Idx
^)]- (п. ю>
Умножим обе части этого равенства на tyW(x) и проин-
проинтегрируем по х. Используя уравнение (П. 9), ортогональ-
ортогональность г|?О)(х) к i|)(°)(x) и формулу
оо
[ J dx dy exp [v1/» (x + у) J W(x) P (x | у, т) =
которая является частным случаем уравнения D), по-
получаем
оо
.-Yt_l)}. (П. 11)
б
Правая часть может быть переписана так:
что совпадает с майеровским коэффициентом Ь2. С по-
помощью уравнения (П. 10) легко также проверить, что
оо
ф») (л) = — (по + 6) г|>@) (х) + е-1'*v ( dy я|/> (у) X
Мы можем продолжать таким же путем далее, но вы-
вычисления вскоре становятся очень длинными. Мы прове-
проверили, что в следующем приближении получается а1==
= b3 — #2>где майеровский коэффициент &з определяется-
формулой
Уш^
X [/12/13+/12/23 +/13/23 +/12/13/23]»
где
Общее выражение для п\ через майеровские коэффи-
коэффициенты Ъ\ отсутствует. Чтобы получить правильное урав-
уравнение состояния вплоть до четвертого вириального коэф"
фициента, а^ следует положить равным
но мы этого не проверяли.
Приложение 2
Чтобы понять, как выводится уравнение B4), доста-
достаточно рассмотреть случай я = 3. Имеем
оо
2 Л? = J / fdx, dx2 dxze-s^^ X
oo
X / / / dxx dx2 a0c3 exp f — (voy)Vj (*, + x2 + хг)] X
—сю
ХР(хг\х2, t^P^I^, T2)P(x3\xv t3),
где Р{х\у, т) задается уравнением E). Введем новые
переменные
Ъг = (х2 - ххе~ vti) A - е-ч
|2 = (х3 - х2е~ vt2) A - е-
1, = (хх - х,е~ vts) A _ ^-
Якобиан этого преобразования равен
dfl О - ехр [-
Интеграл по х% превращается в интеграл
{Bл)8/2[1 — 1
где
В таком виде удобно перейти к пределу при у
Поскольку Аг приближенно равняется 3BутгI/з, подин-
тегральное выражение в предыдущем интеграле не за-
зависит от у и мы получаем
оо
X [Bл//! (т, + т2 + тз)] f f fdh dl2 dU X
n
Чтобы отделить интегрирование по %i и ^, введем вспо-
вспомогательную переменную
и умножим обе части равенства (а) на
оо оо
-оо -оо
Здесь использовано представление б-функции в виде ин-
интеграла Фурье. Положим у = ш(т1+Т2 + тз) и проинте-
проинтегрируем сначала по !•*. Мы получим
оо оо
J rft exp [— Ti BvoI/2 4- /ttjw— у
X
Наконец, полагая ку = ?+ /rj, мы получаем уравнение B4)
для п = 3. Доказательство для произвольного п прово-
проводится таким же способом.
Приложение 3
Решение уравнения D2) можно переписать в виде
™ (z) = Nn [PnDn+3 (z) + QnDn+1 (z)
где
vQ2(/~6K(/~36)
P — n^
= — 9»2P — n? V+я W,
V = vf (I - 6O(
Чтобы получить уравнение для следующего приближе-
приближения, левую часть уравнения C5) следует разложить до
членов порядка у2. Используя разложения C6) и при-
приравнивая члены порядка у2, получаем
д2Н{2)
УЧ/_6)У/> /4v0 у уУч/-
4В^ \з/2~ / яН ?^
—вJ/ 1 „ , В
1 М „_
2 2В / ^
^ 2/3В
— ^g- A5/3 — 36/26 + 30/62 — 863)
l*B * dz f
откуда м42) и затем //(л2) можно определить обычным
путем.
Примечания к части I
1) Van der Waals J. D., Dissertation, Leiden, 1873. Это изло-
изложено в книге «Die Kontinuitat des gasformigen und fliissigen Zu-
standes» (Leipzig, 1899). См. также монографию: Kuenen J. P.,
Die Zustandsgleichung, Braunschweig, 1907.
2) Эта теория принадлежит в основном Дж. Майеру; она изло-
изложена в книге: М а й е р Дж., Гипперт-Майер М., Статистиче-
Статистическая механика, ИЛ, М., 1952, гл. 13, 14. Современное изложение
можно найти в монографии Уленбека и Форда в серии «Studies in
Statistical Mechanics» (Amsterdam, 1962, v. 1, part B).
3) Эти попытки также восходят к Майеру (см. книгу, цит. в
примечании 2, гл. 14). Более современное изложение можно найти
в статье Ike da К., Progr. of Theoret. Phys. (Kyoto), 19 A958),
653; 26 A961), 173. Многие исходили из аналогии с конденсацией
Бозе — Эйнштейна, на которую указали Кан и Уленбек (К a h n В.,
Uhlenbeck G. E., Physica, 5 A938) 399). Однако мы теперь ду-
думаем, что эта аналогия поверхностна и что на самом деле не суще-
существует никакой связи между конденсацией Бозе — Эйнштейна и
обычной конденсацией.
4) Эти трудности становятся особенно явными в той формули-
формулировке задачи о конденсации, которая принадлежит Янгу и Ли (см.
Yang С. N., Lee Т. D., Phys. Rev., 87 A952), 404; ср. также с
исследованием Уленбека и Форда, приведенным в гл. 3 книги
Lectures in Statistical Mechanics (Proceedings of the Summer Semi-
Seminar, Boulder, Colorado, 1960; published by the Amer. Math. Soc.
Providence, Rhode Island, 1963). [Перевод: Уленбек Г., Форд Г.,
Лекции по статистической механике, М., 1965.}
5) К а с М., Phys. Fluids, 2 A959), 8.
6) Отсутствие фазовых переходов в одномерных системах с
взаимодействием только между ближайшими частицами установле-
установлено впервые в работе: G u r s е у F., Proc. Cambridge Phil. Soc, 46
A950), 182. Обобщение для случая, когда каждая частица взаимо-
взаимодействует с конечным числом соседних частиц, получено Ван Ховом,
см. Van Hove L., Physica, 16 A950), 137; ср. также иссле-
исследование, приведенное А. Мюнстером в его книге «Statistische Ther-
modynamik» (Springer, Berlin, 1956), § 7.7, 8.8, где также можно
найти дальнейшие ссылки.
7) Так называемое правило равных площадей. См. Maxwell,
Collected Works, Dover reprint, V. II, p. 425.
8) Этот вывод восходит к Орнштейну (см. О г n s t e i n L. S.,
Dissertation, Leiden, 1908). Сам Ван-дер-Ваальс, а затем позднее
также Лоренц (Collected Papers, Martinus Nyhoff, The Hague, Ne-
Netherlands, 1935, v. 6, p. 40) исходили из вириальной теоремы Клау-
зиуса. Мы вернемся еще к этому во второй статье из этой серии.
9) Van Hove L., Physica, 15 A949), 951. Недавно Ван Кам-
пен указал на пробел в рассуждениях Ван Хова. Однако эту теоре-
теорему можно доказать даже при менее ограничительных условиях дру-
другим методом (см. недавнюю статью: R u е 11 е D., Helv. Phys. Ada,
36 A963), 183).
10) Tonks L., Phys. Rev., 50 A936), 955.
u) В нашей модели теорема Ван Хова выражается неравен-
неравенством B1) для наибольшего собственного значения X0(s,у), которое
справедливо для всякого значения у. Изотерма монотонно убывает
при всяком y» а поэтому и в пределе при у==0 и dp/dl^. 0.
Часть !1
ИЗУЧЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИИ
1. Введение
Первая попытка выйти за рамки вопросов, связанных
с уравнением состояния неидеального газа, и обратиться
к более глубокой проблеме корреляции положений мо-
молекул в газе или жидкости была сделана Орнштейном и
Цернике в их хорошо известной теории критической опа-
лесценции1). Позднее Цернике, Принс и др.2) использо-
использовали те же идеи, чтобы интерпретировать результаты по
рассеянию рентгеновских лучей в жидкости в терминах
так называемой двухточечной корреляционной функции.
Эта корреляционная функция совпадает, по существу,
с преобразованием Фурье углового распределения рассе-
рассеянных лучей, и поэтому непосредственно наблюдается.
Этого нельзя сказать о так называемых 5-точечных кор-
корреляционных функциях (s = 3, 4, ...); однако эти функ-
функции можно точно определить для системы, находящейся
в равновесии, и с возрастанием 5 они описывают струк-
структуру этой системы все более и более подробно.
Общая теория этих корреляционных функций или
функций распределения была развита в сороковых го-
годах, в основном Кирквудом, Ивоном, де Боером, Май-
ером и их сотрудниками3). Эти авторы получили общее
разложение функций распределения в ряды по степеням
активности или по степеням плотности 4). Найденные ими
разложения обобщают соответствующие вириальные
разложения для уравнения состояния. Они предложили
также различные схемы приближений, из которых наи-
наиболее известна кирквудовская схема суперпозиционного
приближения. Это привело к новым очень интересным
попыткам решить задачу о фазовом переходе5).
Насколько нам известно, никто не пытался систе-
систематическим образом связать эти общие разложения с
основными идеями Ван-дер-Ваальса. Поэтому нам
представляется интересным вывести выражения для
функций распределения в модели одномерного газа,
описанной в части I, и посмотреть, что произойдет с
этими функциями при переходе к ван-дер-ваальсовскому
пределу. В п. 2 выводится выражение для двухточечной
и трехточечной функций распределения. Этим путем мож-
можно построить также и общее выражение для 5-точечной
функции распределения. Оказывается, что в выражения
для функций распределения входят все собственные зна-
значения и собственные функции основного интегрального
уравнения Каца [часть I, A0)]. Можно сказать, что эти
выражения и дают физическое истолкование собствен-
собственным функциям и собственным значениям, хотя мы не
знаем еще, можно ли однозначно определить сами эти
собственные функции и собственные значения при по-
помощи всего набора функций распределения. В п. 2
выводится также другое общее выражение функций
распределения через резольвенту уравнения Каца и соб-
собственную функцию г|)о(#), соответствующую наиболь-
наибольшему собственному значению Xq(s). Это выражение
играет особенно важную роль при изучении функций
распределения в двухфазовой области.
В п. 3 выводятся хорошо известные вириальные и
флуктуационные теоремы. Общее доказательство этих
теорем, конечно, верно, но представляется ценным вы-
вывести их непосредственно из уравнения Каца. Поскольку
эти теоремы связывают двухточечные функции распре-
распределения с уравнением состояния, они служат важным
средством проверки для любого метода последователь-
последовательных приближений. Кроме того, они связаны с первона-
первоначальным выводом уравнения Ван-дер-Ваальса.
В п. 4 и 5 изучается ван-дер-ваальсовский предел и
последовательные приближения по степеням уб для двух-
двухточечной функции распределения в однофазовой обла-
области. Показано, что следует отличать случай, когда рас-
расстояние между двумя молекулами имеет порядок б, от
случая, когда это расстояние имеет порядок радиуса дей-
действия притягивающих сил \1у. Поскольку в ван-дер-
ваальсовском пределе притягивающие силы очень слабы,
двухточечная функция распределения при малых рас-
расстояниях в нулевом приближении, как и следовало ожи-
ожидать, совпадает с функцией распределения для газа из
твердых палочек.
В первом приближении притягивающие силы не-
несколько влияют на поведение двухточечной функции при
малых расстояниях, но гораздо более интересным обра-
образом этот эффект сказывается на поведении этой функ-
функции при больших расстояниях. Мы нашли, что в этом
приближении добавка к функции распределения экспо-
экспоненциально зависит от расстояния, причем показатель
экспоненты меняется в зависимости от сжимаемости
газа. Такое поведение связано с той формой, которая
предсказывается одномерным вариантом теории Орн-
штейна — Цернике, и при приближении к критической
области эта связь оказывается общей (т. е. не зависит
от вида дальнодействующей притягивающей силы). Од-
Однако в критической области наше разложение стано-
становится неверным, и следует ожидать отклонений от тео-
теории Орнштейна — Цернике. Мы вернемся к этому в
части III, где будем в деталях изучать поведение двух-
двухточечной функции распределения в критической области.
В п. 6 функции распределения в ван-дер-ваальсов-
ском пределе изучаются в двухфазовой области. Мы по-
показываем, что все функции распределения являются в
этой области линейными комбинациями двух функций
распределения, соответствующих насыщенной жидкости
и насыщенному газу, с коэффициентами, пропорцио-
пропорциональными молярным долям жидкой и газообразной фаз.
По нашему мнению, это показывает прежде всего, что
пространственное разделение жидкой и газообразной
фаз автоматически вытекает из теории. В самом деле,
это свойство функций распределения представляется
нам более глубокой формулировкой проблемы конденса-
конденсации, чем свойство постоянства давления газа (горизон-
(горизонтальная часть у изотермы), которое вытекает из преды-
предыдущего. Это указывалось уже в основной статье Май-
ера в 1947 г.6), и, возможно, наши результаты можно
рассматривать как строгое доказательство для частного
случая общих рассмотрений этой статьи, хотя точная
связь нам пока еще не ясна.
В п. 7 мы обсуждаем в деталях связь наших резуль-
результатов с теорией Орнштейна — Цернике, особенно в от-
отношении недавней очень интересной формулировки этой
теории, предложенной Лебовичем и Перкусом7). В за-
заключение мы делаем несколько замечаний о пригодно-
пригодности наших результатов в трехмерном случае.
2. Общее выражение для функции распределения
Сначала мы напомним общее определение функции
распределения. Для канонического ансамбля s-частич-
ная функция распределения определяется так:
ns(rv ..., r5, N, V) =
= <N-S)\ f '•• fdT* + l ••* dTNDN(Tv •••^N), A)
V V
где
Соответствующая формула для большого канонического
ансамбля имеет вид
p,(ri, .... г5, I/, z)=%ns(rv ...,г„ 1/, W)/V C)
где
PN = (Az)NZ(V, N)/G(V, z). D)
В дальнейшем мы всегда будем предполагать, что веще-
вещество находится в однофазовом состоянии. В этом случае
известно, что в термодинамическом пределе функции
распределения стремятся к определенным значениям
lim ns{rv ...yrs,N, V) = ns(rv ..., r,; v),
E)
и эти функции отличаются друг от друга только тем, что
зависят от разных переменных — соответственно v и г,
которые однозначно связаны друг с другом вторым соот-
соотношением Майера
\/v = zk'(z). F)
Кроме того, известно, что в этом случае ns и ps про-
пространственно однородны: если к переменным гь ..., г8до-
бавить один и тот же вектор, то функции ns и ps не изме-
изменятся. Следовательно, ft2(rbr2;t;) зависит только от
|i*i — г2|, Пз(гь r2, r3; v) зависит только от длин сторон
треугольника (гь г2, г3) и т. д. Наконец, известно, что
в этом случае функции ns и ps обладают свойством
мультипликативности. Это означает, что если 5 частиц
разбить на группы, содержащие с&ь сс2, ... частиц, то
для расположений, в которых эти группы отстоят далеко
одна от другой, с большой точностью выполняется ра-
равенство
7ls = 7iai -Па2... G)
и аналогично для ps. Заметим, что смысл слова «да-
«далеко» зависит от значений v или г. Из свойства мульти-
мультипликативности вытекает, что если все частицы находятся
далеко друг от друга, то ns->(l/v)s и ps^(pi)s. За-
Заметим, что это свойство мультипликативности является
лишь непосредственным соотношением между функ-
функциями ns или ps и более низкими функциями распреде-
распределения. Эти более низкие функции распределения нельзя
найти только с помощью интегрирования по положениям
некоторых частиц. Между этими функциями распреде-
распределения существуют интегральные соотношения — так на-
называемые флуктуационные теоремы, но эти соотношения
более сложны. Мы вернемся к ним в следующем пункте.
Для малых плотностей или малых z функция распре-
распределения приближается к больцмановскому множителю
ns(rl9 ..., IV v)->^exp — ¦^2ф(|г/ — гу|) , (8)
L J
и, как уже говорилось, можно получить полное вириаль-
ное разложение или разложение по степеням активности
(см. примечание 4).
После этих предварительных напоминаний вернемся
к нашей одномерной модели. Мы покажем, что все
функции распределения можно выразить через собствен-
собственные значения hn(s) и собственные функции грп(х, s)
интегрального уравнения Каца [часть I, A0)]. В ча-
частности, мы покажем, что
оо
/ j dx е-°гп2(х; /) =
о
= ]?@, s\n, s + o) ^o(^l_(^+(f, g) {n, s + a|0, s), (9а)
n = 0
oo oo
I J Jdxdye-°x-°rynz(x, y\ l) =
о о
/2=0
s + o>\0, s).
(96)
Здесь s = p/kT и символ {k, m\k\ m') = {k\ m!\k, m)
означает матричный элемент
{k, m\k\ m')= fdx^k(x, m)%, (x, mr). A0)
Функции распределения записаны в относительных коор-
координатах, так что
— h, h — t? I), t3^t2^tv A1)
где tu h, U — координаты частиц. Мы подробно не вы-
выводим преобразования Лапласа для s-частичной функ-
функции распределения, но структура выражений (9а) и (96)
настолько прозрачна, что их обобщение на случай выс-
высших функций распределения представляется очевидным.
Вывод уравнения (9а). Мы применим сле-
следующий искусственный прием: введем добавочное экспо-
экспоненциальное притяжение между всеми парами молекул
и будем исходить из новой статистической суммы
L L
^ fdt1...dtNJJ_S(\tl-rtJ\)x
0 ij
. A2)
где использованы те же обозначения, что и в части I, B).
Тогда легко показать, что
l
1 /• С dt
, JT).
Отсюда получается аналогичное выражение
L L
1 с С
Y J j dtldt2e-o\ti-t^p2(tv t2; Z,, z) A3)
d\x\G
8 = 0
о о
для статистической суммы в большом каноническом
ансамбле. Поскольку в термодинамическом пределе
In G-^L% (z, e), из формулы A3) получаем в пределе
при L -*• оо
с± оо
= Г'dxe-<*xp2(x, z),
•=о у
A4)
где х = t2 — t\.
Точно так же, как в части I, п. 2, мы можем связать
со статистической суммой A2) интегральное уравнение
оо оо
J fdydy'Ks(x, x'; у, у'
, х'), A5)
— оо —оо
где
У ) — [w(y)W{y')\ X
X ехр [-1. v1/. (* + у) + -j е1/2 (*' + f/')] X
(х | у, т) Ра (х' | у', т). A6)
Мы опускаем доказательство, так как оно должно быть
очевидно читателю. Обозначения здесь те же самые,
что и раньше, за исключением того, что индекс при
функций Р означает различные показатели экспоненты
притягивающего потенциала. Функция %(z, е) связана
с наибольшим собственным значением Ao(s, e) уравне-
уравнения A5) с помощью уравнения [подобного уравнению
A8), части I]
ЛоE, e) =
где 5 = p/kT = %{z,e). Чтобы вычислить левую часть
уравнения A4), следует по теории возмущений вычис-
вычислить Ло с точностью до членов первого порядка по е.
Легко показать, что при 8 = 0 в уравнении A5) пе-
переменные разделяются и собственные функции имеют
вид
4^V(*, х\ *) = яЫ*, s + n'o)Nn.Dn.{x'), A8)
а соответствующие собственные значения равны
А2)л'E) = ^E + лЧ A9)
где tyn(x,s), Kn(s)—собственные функции и собствен-
собственные значения уравнения Каца [часть I, A0)], Dn(x) —
функции Вебера и Nn — нормирующий множитель, рав-
лый Bл)~'/4(п!)~1/2. Полагая
ЛE, е) =
?(*, *', 5, e) = ^F@)(jc, x', )
мы найдем с помощью непосредственных вычислений по
теории возмущений наибольшее собственное значение
и соответствующую собственную функцию
X0(s)-kn
n=0
X<0, s\n,
X
Bo)
При выводе мы воспользовались полнотой системы
функций \f)nE + a):
2@, s\n, s + aJ = l. B1)
п
Возвращаясь теперь к уравнению A7), мы найдем
наибольшее собственное значение интегрального урав-
уравнения A5)
Введем здесь ^
где %(z) = p/kT, как следует из части I, A8). Тогда из
равенства A7), приравнивая члены, пропорциональные
е, получим ~
де
8e0" l L MX) J*
Здесь мы воспользовались уравнением B0) из части I.
Подставляя полученное выражение в формулу A4), мы
получим с помощью формулы B0) уравнение (9а), по-
поскольку в термодинамическом пределе р2(х, z) =
= п2(х, /), где 1// = 2х'(г).
Вывод уравнения (96). Чтобы обобщить
прием, использованный в предыдущем выводе, стоит
ввести три дополнительных потенциала, соответствую-
соответствующих трем расстояниям между тремя частицами. Однако,
чтобы обеспечить соотношения между этими расстояния-
расстояниями, которые существуют между сторонами треугольника,
необходимо приписать каждой молекуле «внутреннюю
координату» \iu принимающую два значения, \ц = ±1,
и усреднить затем по всем множествам значений {jj,*}. Мы
исходим, следовательно, из новой статистической суммы
L L
Z(L, N, elt е2, е3)= ^ ^ 2 / *'' f dti •¦'dtffX
M'Hyl . B3)
хШ(|*,-*,|)ехр
а=1
Дифференцируя по еа, полагая их равными нулю, сум-
суммируя по \ii и воспользовавшись еще тем обстоятель-
обстоятельством, что рз(^ь h> h\ L, z) симметрична по ^i, /2» ^з> мы
найдем, что
:• к, h\ L, z) X
дг2
pi
где сумма распространена на все шесть перестановок
индексов 1,2,3. Это выражение похоже на уравне-
уравнение A3). Переходя к термодинамическому пределу, по-
полагая In G = L%(z, 8ь 82, 83) и t2 — t\=x, U — t<i~y, полу-
получаем
~ оо оо
= Г Г dx dy"i>3 (х, у; г) X
= 0 J J
о о
X 21 ехР [~°р1х ~°Р2У —°рЛх + У)]- B4)
{дг2дь3 еа=0 о о
Это напоминает уравнение A4).
Теперь снова сопоставим статистической сумме B3)
соответствующее интегральное уравнение, а именно
JfIIdydyl
X fch ( 2 xaef J ch ( 2 у/A j V (у) - Л? (х), B5)
где х = (л:, хх, х2, х3), у = (у, yv y2, у3) и
К (х v)- pH*)^(*i)^(*»)^<*»)f' exn [I
Ao (x, y) — [ w (y) r (yi) r (yj) ^ (уз) J exp l 2
J
00 3
X / Л е- "PY (x I f/, t) JJ Paa (*в I г/а, т). B6)
б a=l
Эти формулы аналогичны формулам A5) и A6). Ги-
Гиперболический косинус вместо экспоненты возникает в
связи с суммированием по р,*. Наибольшее собственное
значение Ло($, ei, 82, 83) уравнения B5) снова связано
с функцией х(«г, 8ь 82, 8з) соотношением
Ло (s, е1э е2, е3) = ~ exp \~- (v + ех + Ч + е3)] » B7)
где s = plkT = %(z, 8Ь 82, ез). Чтобы определить левую
часть уравнения B4), надо вычислить Ло по теории воз-
возмущений до членов первого порядка по еь 82 и ез- Это
становится теперь значительно сложнее, чем раньше, и
мы отсылаем читателя к приложению А, где приводятся
детали, завершающие доказательство.
Если ввести резольвенту Я8(х, у\ р) интегрального
уравнения Каца [часть I, A0)], то выражения (9а) и
(96) для функций распределения можно преобразовать
к виду
оо оо
I fdx е-°хЪ2(х; 1) = ^^ f f dxdy%(x, s)X
О —сю
оо оо
I J fdxdy е-ы-о'УПг (х, у; I) = -^ J J J dxx dx2 dxz X
X % (Xi. s) Rs+a [xv x2; j^j) X
з» 5). B86)
Доказать это очень просто. Резольвента определяется
с помощью ряда из итерированных ядер
B9)
где +0О
K(sl)(x, y)= f dzKt'^x, z)K,(z, у)
— оо
и KsO)(x, y)==Ks(x, у). Так как итерированное ядро
выражается через собственные функции по формуле
) (х, у) = S Л?Н E) фя (л:, s) ^ (г/, 5), C0)
/г «0
то уравнения B8а) и B86) получаются из уравнений
(9а) и (96), если дроби в последних уравнениях разло-
разложить в ряды по степеням kn(s + o)/ko(s) и затем про-
просуммировать по п.
Мы закончим этот пункт проверкой общих формул
(9а) и (96) для некоторых простых случаев.
а) Для v = 0, т. е. для газа из твердых палочек, г|?п
не зависит от s, так что {0, sin, s + o) = 6no и X0(s) =
= e~s6/s. Поэтому уравнение (9а) дает
со
/ { йхе-°хЪ™'™л-(х\ /) = - т- . C1)
Здесь мы воспользовались соотношением s = p/kT =
= 1/A — б). Это эквивалентно хорошо известному ре-
результату, полученному впервые Цернике и Принсом8),
б) Для v = 0 получаем из уравнения (96) следующее
соотношение:
~ox~~o'y4*'n™'{x> у; /) =
оо
= / f dx е-охп™-™л-(х; I) -1 [ с1уе-°гУп1в-™л-(у\ /). C1а)
о с
Этого и следовало ожидать, поскольку известно, что для
одномерных систем с взаимодействием между ближай-
ближайшими соседями имеет место кирквудовский принцип
суперпозиции 9).
в) Для больших х имеем Пг(*; /)—*!?> поскольку
со
Iimn2(x; /) = lima f dxe-°xn2(x;./) = — lisifl = JL
x ->oo a->0 ^ / K0(s) I
и @, s | n, s) = 6n0.
Подобным же образом доказывается, что для больших у
со оо
lim f dxe-°xn3(x, у, l) = -j- f dx е~алп2{х; I).
Мы, таким образом, проверили свойство мультиплика-
мультипликативности для п2 и Пз- Можно также показать, что для
больших / величины п2 и я3 близки к соответствующему
больцмановскому множителю [см. уравнение (8)]; дока-
доказательство этого мы предоставляем читателю.
3. Флуктуационные и вириальные теоремы
Из ?войства мультипликативности функций распреде-
распределения ns и ps следует так называемое групповое свой-
свойство для соответствующих групповых функций, которые
определяются следующим образом:
Xifa; «) = p1(r1; z),
, г2; z) = p2(rv г2; ^) — pi (rx; ^)pi(r2; z\
г2, г3; г) = р3(г1э г2, г3; г) — р2(г1э r2; z)pi(r3; z) —
— Р2(г2, r3; zjpjfa; г)— р2(г3, ^; z)pi(r2; z) +
ri; г)р!(г2; ^)Р!(г3; г) C2)
и т. д.10) Групповое свойство означает, что для всякого
расположения, в котором s частиц разбиты на две или
большее число невзаимодействующих групп, функция
/s(ri, ..., rs; z) исчезает. Вследствие этого интегралы
lim -^ Г ... f\s(rv ..., iy, z)dr1 ... drs C3)
должны иметь термодинамический смысл, и соответ-
соответствующие результаты составляют так называемые флук-
флуктуационные теоремы. Из определений ps легко найти1),
что
К->оо у
lim -у j f j dr1dr2drsxs =
k2T2 д Г1 д /1\1 3kT д /1\ . 2 /QAfc\
— ^ _ \ — \-\ C46)
v dp \_v dp \v)\ v dp \v) ' v v ;
и Т. Д.
Эти результаты можно также вывести непосредствен-
непосредственно из выражений (9а) и (96) для функций распределе-
распределения. Например, из формулы (9а) получаем, что
оо
C5)
Здесь мы воспользовались соотношением полноты B1).
Теперь для а->0 имеем @, s|ai, s + o)-+0 при пФ 0 и
(О, s|0, s + a)->- 1 + О(а2), что вытекает из условия норми-
нормировки. Поэтому для а-^0 правая часть уравнения C5)
принимает вид
1 1 . Яр (s) [1 + 0 (о2)] =
012 l -oX'0(s)-±oX(s)- ...
1 1 X"(s) I kT dl
при этом мы воспользовались соотношением /
s = p/kT. Следовательно,
jirn -I
--L
откуда и следует уравнение C4а). Подобным же обра-
образом можно проверить уравнение C46).
Другая группа «термодинамических» соотношений
для функций распределения следует из того обстоятель-
обстоятельства, что гельмгольцевская свободная энергия \Р равна
—kTlnZ(V9 Г, N). Отсюда следует, что внутренняя
энергия задается уравнением
/7_ш т dw — 3NkT 1
Ч- \ f { dvx dv2 cp (| fl - r21) n2 (fl, r2; У, ^V), C7)
а давление — уравнением 12)
X«2(ri. г2: V, ЛО- C8)
Это уравнение в термодинамическом пределе дает
n2{n v). C9)
Это и называется вириальной теоремой, поскольку эту
формулу можно также непосредственно получить из ви-
вириальной теоремы Клаузиуса. Если межмолекулярный
потенциал ср(г) имеет твердую отталкивающую сердце-
сердцевину, то при r=d (d — диаметр этой сердцевины) произ-
производная dy/dr не определена и уравнение C9) следует
заменить уравнением
lf^2(r; v), D0)
где b = -7?ndz и n2(d+; v) = \\mti2{r\ v).
0 d
Заметим, что в одномерном случае уравнение D0)
имеет вид
оо
p = ^f + bkTn2 F+; l) — fdxx ^ п2 (х; /), D0а)
б
где б — по-прежнему длина твердой палочки.
Дифференцируя далее по Т и V, мы получим из фор-
формул C7) и C8) термодинамические соотношения, вклю-
включающие высшие функции распределения. Например, из
формулы C7) мы получаем для удельной теплоемкости
при постоянном объеме общее выражение
J
(г18)+ф (г23)] л3 (fi. r2, r3; v
ъ J f
Возникает вопрос, как проверить эти соотношения
непосредственно с помощью выражений (9) или B8)
для функций распределения, и здесь мы встречаемся
со следующей очевидной трудностью. Так как фпр.=
= —ае~чх, интегралы в C7) и D0а), включающие
пг(х\ /), похожи на преобразование Лапласа от т(х\1),
если а равно у. Однако в соответствии с формулой (9а)
преобразование Лапласа от пъ(х\ I) зависит от всех соб-
собственных значений и собственных функций уравнения
Каца, в то время как в соответствии с формулой C7)
[которая для нашей модели превращается в (& = E/N)]
мы имеем оо
kT г —
е = -2 a/J dxe-4xn2(x\ /); D1)
б
преобразование Лапласа имеет термодинамический
смысл и поэтому может зависеть только от наибольшего
собственного значения Хо. Причина такого очевидного
упрощения при о = у становится понятной, если возвра-
возвратиться снова к выводу уравнения (9а). Очевидно, что
при g=y добавка к притягивающему потенциалу ге~ох
сводится к увеличению константы взаимодействия v на е.
Уравнения A4) и A7) по-прежнему остаются верными,
но соответствующее интегральное уравнение теперь
почти в точности такое же, как уравнение Каца, за
исключением того, что v заменено на v + e. Ядро можно
разложить в ряд по степеням 8 и получить
Ks(x, у, e) = Ks(x
Применяя теорию возмущений, найдем
Ao(s, e) = 41)
где
— со
При помощи аналога уравнения B2) получаем вместо
уравнения (9а) уравнение
оо оо
/ /dxе-ч*щ{х\ I) = ±j- f dxx%{x)-±. D2)
Легко теперь проверить, что последнее уравнение экви-
эквивалентно уравнению D1). Действительно, поскольку
терминах химического потенциала можно написать
* = V-TTf-PT?
и [см. часть I, A8), A9)]
находим
При помощи этого равенства и уравнения
5, v) = yv — In г,
уравнение {41) сводится к D2).
Вириальную теорему C9а) можно проверить анало-
аналогичным способом. Мы опускаем детали, так как эта
проверка состоит в повторении обычных термодинамиче-
термодинамических рассуждений. Остается только вопрос, как вывести:
основные тождества вида уравнения D2), которое мож-
можно также записать в форме
со
= J J dx dy% (x, s) % (у, s) Rs+y (х, у; -j^j) *
— со
непосредственно из интегрального уравнения Каца. Та-
Такой вывод приведен в приложении Б.
4. Ван-дер-ваальсовский предел двухточечной
функции распределения. Поведение на близких
расстояниях
Для исследования того, как ведет себя функция
пъ(х\ I) на близких расстояниях порядка б после пере-
перехода к ван-дер-ваальсовскому пределу, т. е. при у-+0 и
одновременной замене v на voY, проще всего исходить
из уравнения B8а). Сначала мы перестроим ядро
Ks+a (*> У) так же> как в части I, п. 3, с помощью под-
подстановки
где v{{s) определяется уравнением B9) части I. Если
ограничиться первым членом ряда B9) для резольвен-
резольвенты, то левая часть уравнения B8а) примет вид
rT Idx e~(s+a)
б
б
X Ру (*' I у\ т) ехр {1 (voYI/2 (*' + у' + 2Ч B/Y)V2) -
- h2/Y + Л (х' + у'УРуL2] th (-I
где А(^) определяется уравнением C4) части I. Теперь
нужно подставить разложение C6) части I для h{xf)
и ho(s) и разложить все, что получится, в ряд по степе-
степеням у- Ввиду того что наше уравнение было пере-
перестроено, нулевое приближение будет очень простым; так
как при y-^0 мы имеем Ру(х'\у', %)->b(xf — у') и так
как №°)(х') нормировано, мы получим при y~>0
ft) (s) J (
б
ехр
Иначе можно сказать, что при y~^0 ядро Ks+o (x, у)
можно заменить на Ab(xf — у')=Ад(х — у), где А опре-
определяется уравнением D3). Следовательно, K(s+0(x, y)->
->А2Ь(х — у) и т. д. Мы получаем
воспользовавшись при этом равенством s + (у Л2) ^
= 1/A — б), которое следует из уравнений C0) и C1)
части I.
В нулевом приближении мы получаем, следователь-
следовательно, в точности тот же ответ, что и для газа из твердых
палочек [см. уравнение C1)]. Этого и следовало, ко-
конечно, ожидать, поскольку при малых у притягивающие
силы на расстояниях порядка 6 очень малы и в нулевом
приближении не влияют на расположение молекул. Эти
расположения будут определяться только отталкиваю-
отталкивающей твердой сердцевиной.
В первом приближении притягивающие силы уже
сказываются даже на расстояниях порядка б. Чтобы
вычислить этот эффект, мы должны собрать все члены
порядка у в ряде B9) для резольвенты. После этого мы
найдем
о
Г
J
+ D4)
1 +
^ IB {[i + a(/_6)K6-l}3^ •" '
В приложении В приведены эти длинные выкладки; при
этом надо воспользоваться еще результатами п. 3 ча-
части I.
Как мы уже упоминали в введении, интересно
сравнить эти результаты с вириальной теоремой_в фор-
форме D0а). Чтобы сделать это, мы должны найти п2{Ь'?\ I)
из уравнения D4). Умножив обе части уравнения D4)
на оеоЬ, перейдем затем к пределу при а~^оо. Левая
часть (где х' = х — 6) примет вид
оо
lim a f dx'e-ajc'n2(x'-\-b; /)«
оо
«л2(б+; i)ojdx'e-°x'=n2(l>+; l),
о
и, вычисляя предел правой части, мы получим
щ (б+; /) = Ml (I - 6) + Yv0 (/ - Ь)/РВ + . • • • D5)
Рассмотрим сначала нулевое приближение и подставим
в формулу D0а). Получим
Р
kT
= -^ — vof f dxxe-v*n2 (x; I).
Если мы сделаем замену в интеграле ух = х\ то, по-
поскольку в пределе при у-^0 имеем П2(х'/у; /) = 1//2, ин-
интеграл примет вид
Таким образом, снова получается уравнение Ван-дер-
Ваальса. Второй член в формуле D5) дает часть по-
поправки к ван-дер-ваальсовскому уравнению порядка уу
упоминавшемуся в конце части 1, в п. 4. Чтобы полу-
получить полную поправку, мы должны знать также поправ-
поправку порядка у к поведению функции fi2(x; l) при больших
расстояниях. Это требуется также для того, чтобы разо-
разобраться, почему первый член в формуле D4), подстав-
подставленный в флуктуационныи интеграл [уравнение C6)]„
не согласуется с уравнением Ван-дер-Ваальса. Действи-
Действительно, для первого члена уравнения D4) находим
что согласуется с уравнением C6), если p/kT=l/(t—6)-
Мы увидим, что выражение п2(х\ I) при больших рас-
расстояниях с точностью до порядка у дает вклад нулевого
порядка в флуктуационныи интеграл. Это приводит уже
уравнение C6) в соответствие с уравнением Ван-дер-
Ваальса.
5. Ван-дер-ваальсовский предел двухточечной
функции распределения. Поведение при больших
расстояниях
Чтобы определить поведение /г2(^;/) для х порядка
1/Y, мы воспользуемся уравнением (9а) для n2(x;t).
Заменим а на <ху, разложим затем правую часть по сте-
степеням у. Сначала рассмотрим матричный элемент
(О, s\n, s + oY>= fdx%(x, s, y)^n(x,s-i-oy,y). D7)
— оо
Мы знаем, что
где х=л:/ + г]E) B/yI/2 и ftW(*', s) определяются в п. 3
части I. Следовательно,
, y) =
Поскольку функция A^ ортогональна АоО) при /г>0, то
для таких д [если принять во внимание уравнения C8)
и C9) части I] найдем
(О, s\n, 5 + av> = -a(^-)/25-6nl + O(Y). D8)
При п = 0 получаем
(О, s 10, s + оу) = 1 - a^ (-§J + О (y%). D9)
Заметим, что уравнения D8) и D9) до членов поряд-
порядка у согласуются с условием полноты
оо
2@, s\n, s + oy>2 = 1.
п = 0
Затем рассмотрим собственные значения. Мы знаем, что
К (*. Y) = со E) [1 + У^ (s) + О (у% E0)
где м4!) задается уравнением C9) части I. Поэтому
Используя все эти формулы, получаем из уравнения (9а)
ifdxe-
00' L 2 0'
О2В I dr\ \2 Г^_ I 1 1 .
Теперь возникает следующая сложность: хотелось бы
заменить nV(s)/co(s) на (—/) в соответствии с уравне-
уравнением C1) части I, но это неправильно. Разложение соб-
собственных функций и собственных значений велось при
постоянном 5, в то время как преобразование Лапласа
функции п2(х;1) вычисляется при фиксированном значе-
значении / = — Xo(s)/lo(s). Поскольку X0(s) и о(s) отли-
отличаются на величину порядка у [см. уравнение E0)], мы
имеем
ds
и с точностью до членов порядка y
о
Эту поправку порядка у следует принять во внимание
в первом члене уравнения E2), но ею можно, конечно,
пренебречь в других членах. Поскольку в нулевом по-
порядке
" 1 dl _ , /(/ — бJ
/ ds ~ l В2 •
2_ 2vo(/-6L
формулу E2) можно упростить
Так как для газа из твердых палочек [см. уравнение
D6)] с точностью до членов нулевого порядка по у мы
нашли выражение
оо
/У v- p — G^XflTQ. пал. / у Л _ | ^ /
^ И„ I)— Y0/ 2/ -г 2/з '
и
ТО
Отсюда, обращая преобразование Лапласа, мы заклю-
заключаем, что
п2 (х; I) = Ъ?-пал- (х; l) + y Vo(//5~6L exp [- (S//) yx\. E4)
Это верно для х порядка 1/у, так что п\в-пал- (х\ I) сле-
следует заменить на I//2. Однако из выражения E4) для
функции распределения видно, что наш результат свя-
связан с выражением D4) для функции П2(х\1) при малых
расстояниях, выведенным в предыдущем пункте. Дей-
Действительно, из D4) следует, что при сг-Я)
О
так что при х—>оо мы получаем
и второй член является в точности амплитудой при убы-
убывающей экспоненте в выражении E4). Заметим также,
что если подставить выражение E4) в флуктуационный
интеграл C6) и воспользоваться формулой D6), то по-
получится
/<**[*(*; 1)-^] = -^
1 | (/-бJ
21 "•" 21В*
как и ожидалось, поскольку в соответствии с уравне-
уравнением Ван-дер-Ваальса
_kT_^i__ 1 dl _ (/ — бJ
2/3 dp ~ 2/3 ds — 21В2 ш
Легко также проверить, что уравнение E4) вместе с
уравнением D5) после подстановки в вириальный инте-
интеграл D0а) дает полную поправку порядка у к уравне-
уравнению Ван-дер-Ваальса.
Мы вычислим также члены порядка y2 B выражении
п2(х\ I) при больших расстояниях. Поскольку все вычис-
вычисления проводятся непосредственно, хотя и очень длинно,
мы лишь приведем окончательный результат, так как он
понадобится нам в части III. Обозначим обратное пре-
преобразование Лапласа от правой части уравнения D4)
через п2{х, /)близк.; оно состоит, следовательно, из
/г™*пал- (х\ I) и первой поправки, возникающей за счет
притягивающей силы. Тогда мы найдем, что
«,(*; I) = п,(х; ;),„,„, + та (/,~"' («-«м- -1) +
2v§(/ —бN Г v0 (/ — бJ D/2 + 18/6 — 27б2)
иш— L ^ ~ ' б/5
г-
В качестве проверки можно подставить это выражение
в флуктуационный интеграл и получить ожидаемый ре-
результат, причем дЦдр следует вычислять из уравнения
Ван-дер-Ваальса с поправкой порядка у. Наиболее ин-
интересная особенность формулы E5) состоит в том, что
в ней появляется экспонента с вдвое меньшим показа-
1елем, чем у экспоненты в первом приближении 13).
6. Функция распределения в двухфазовой области
Поскольку при том значении z активности г, при ко-
котором происходит конденсация, удельный объем v как
функция z имеет разрыв, все функции распределения
большого канонического ансамбля ps(rb ..., rs, z) изме-
изменяются в точке z от значения п8(ти ..., rs, v{) скачко-
скачкообразно к значению ns(ri, ..., rs, v2), где v\ и v2 — удель-
удельные объемы соответственно насыщенного газа и насы-
насыщенной жидкости. Таким образом, в области конденса-
конденсации функции ps(i*i, ..., rs, z) теряют смысл, но мы все
еще можем говорить о функциях распределения канони-
канонического ансамбля n8(ri9 ..., rs; v). Следуя Майеру, мы
утверждаем, что для каждого конечного s следует ожи-
ожидать, что
ns (г1э ..., r5; v) =
— v К^л (г1> • • •» г*; ^1)+h^s (ri r*; щ)Ь E6)
где gi и §2 — молярные доли жидкой и газообразной
фаз, v = liV\Jr7iJV2' Считается, что уравнение E6) вы-
выражает геометрическое разделение двух фаз. Это пред-
представление основано на следующем физическом рассу-
рассуждении: так как внешние силы отсутствуют, мы должны
ожидать, что в равновесном состоянии конденсированная
фаза образует большую сферу, окруженную газообраз-
газообразной фазой, причем положение этой сферы чисто случай-
случайное. Разумеется, этого нельзя детально обосновать, ибо
при переходе к термодинамическому пределу из рассмот-
рассмотрения выпадают все поверхностные эффекты; тем не ме-
менее можно ожидать, что все результаты будут находить-
находиться в согласии с такой картиной. Это относится, в част-
частности, и к уравнению E6). Первый множитель l/v з
формуле E6) равен плотности вероятности найти одну
частицу, скажем, в точке Гь Из-за случайного положения
жидкой сферы эта вероятность не зависит от того, к ка-
какой фазе принадлежит частица. Однако если первая ча-
частица принадлежит жидкой или, наоборот, газообразной
фазе, то все остальные (s — 1) частиц принадлежат той
же самой фазе: действительно, вероятность того, что
некоторые из них принадлежат другой фазе, пропорцио-
пропорциональна отношению поверхности жидкой сферы к ее
объему, и, следовательно, эта вероятность исчезает при
педеходе к термодинамическому пределу. Так как
Vins(ru ..., rs; v\) и v2ns(rli ..., rs, v2) равны условным
вероятностям найти E— 1) частиц в первой или во вто-
второй фазе, если первая частица находится в той же фазе,
и так как g4 и g2 равны безусловным вероятностям най-
найти первую частицу в первой или во второй фазе, то мы
и получаем второй множитель в формуле E6).
Следует отметить несколько обстоятельств.
__ а) Несмотря на существование двух фаз, функции
п8(ти ..., iy, v) по-прежнему пространственно однород-
однородны. Это происходит, очевидно, снова благодаря тому,
что положение жидкой сферы случайно.
б) Теперь уже ns(vu ..., rtS; v) не обладают свой-
свойством мультипликативности. Наличие двух фаз приводит
к корреляции даже тогда, когда частицы находятся да-
далеко друг от друга. В частности,
/L(r,, r2; <а)->-(-^- + —
при удалении двух частиц друг от друга, и поскольку
* v2
флуктуационный интеграл стремится к с», что согласует-
согласуется с постоянством давления в газе для двухфазовой об-
области.
в) Если выражение E6) подставить в левую часть
уравнения C9), выражающего вириальную теорему
для s = 2, и воспользоваться вириальной теоремой для
функций распределения каждой из фаз в отдельности»
то получится
^Л (г; v2)] = V- (— - л)+ Щ^ (^-Ps) = —~Ps*
Таким образом, мы видим, что давление действительно
постоянно и равно ps.
Все эти общие утверждения в действительности, ко-
конечно, до сих пор не доказаны. Поэтому чрезвычайно*
интересно, что для нашей одномерной модели соотно-
соотношение E6) в ван-дер-ваальсовском пределе получается
вполне строго. Это легко показать при помощи уравне-
уравнений B8а) и B86). Мы знаем из п. 4 части I, что в ван-
дер-ваальсовском пределе наибольшее собственное зна-
значение в двухфазовой области дважды вырождено и что
две собственные функции при малых y^ не перекры-
перекрываются. Так как мы уже показали, что соответствующая
удельной длине / = g^ + %2k собственная функция имеет вид
то отсюда с помощью уравнений B8а) и B86) полу-
получаем, что П2(X; I) и Пз(х, у; I) удовлетворяют одномер-
одномерному варианту общего уравнения E6) для s = 2 и s = 3.
Уравнения B8а) и B86) настолько очевидным образом
обобщаются на случай больших s, что нет никакого со-
сомнения в справедливости уравнения E6) для произ-
произвольных 5. * *"'
7. Связь с теорией Орнштейна — Цернике
Чтобы показать связь наших результатов с теориек
Орнштейна — Цернике, мы изложим сначала одномер-
одномерный вариант этой теории. Мы начнем с интегрального
уравнения, связывающего корреляционную функцик>
g(th /2)> которая определяется равенством
g (tv t2) = g(x) = l p, {x\ /)—?¦]. E7)
с так называемой прямой корреляционной функцией
c(ti, /2) =?(#)• Обе функции зависят только от абсо-
абсолютной величины расстояния x — t<i — t\ между двумя ча-
частицами в точках ti и t2 и в однофазовой области стре-
стремятся к нулю при я-*оо. Интегральное уравнение, о
котором идет речь, имеет вид
оо
g(tlt h) = c{tx, t2)+ fdt.gi^t^cit,, t2). E8)
— 00
Следующее рассуждение делает это уравнение правдо-
правдоподобным: корреляция положения двух частиц в первый
момент определяется их непосредственным взаимодей-
взаимодействием. Это и выражается первым членом c(t\, t2). Кро-
Кроме того, на них оказывает влияние третья частица, на-
находящаяся по соседству от этих двух; этот эффект
описывается вторым членом уравнения E8). Мы не пы-
пытаемся дать формальный вывод уравнения E8) и). При
использовании этого уравнения кажется очевидным, что
оно верно только в некотором асимптотическом смысле
и для дальнодействующих притягивающих сил. Заметим,
что его можно переписать в виде
оо
fdyg(x — y)c(y), E8a)
откуда вытекает, что для преобразований Фурье выпол-
выполняется простое соотношение
g(k) = c(k) + g(k)c(k). E9)
Заметим теперь, что вблизи критической точки функция
g{x) возрастает из-за малой сжимаемости газа. Это сле-
следует из флуктуационкой теоремы, которая дает
)r. F0)
Однако величина прямой корреляционной функции с(х)
не должна возрастать вблизи критической точки, по-
поскольку эта функция определяется притягивающей си-
силой. Это подтверждается соотношением
вытекающим из формул E9) и F0).
Поэтому в критической области Орнштейн и Цернике
разлагают g(x— у) в уравнении E8а) по степеням у
вплоть до у2. Поскольку мы рассматриваем область, где
g(x) ^>>c(x), можно пренебречь функцией с(х). Исполь-
Используя четность функции с(х), получаем дифференциальное
уравнение
¦S—*2* = 0, F2)
J dy c(y) _ /2i*\ /dp\
где
J dy уЧ (у) j dy уЧ (у)
— oo —oo
Уравнение F2) имеет решение
'-^L)e-™ F4)
{здесь использована формула F0)].
Это выражение можно теперь сравнить с видом функ-
функции п2(х; I) при больших х, который изучался в п. 6.
Очевидно, первое приближение E4) согласуется с фор-
формулой F4) как по форме, так и по зависимости от сжи-
сжимаемости dpjdl. Поскольку к зависит от неизвестной
функции с(х), мы ничего не можем больше сказать. Од-
Однако, как заметили Лебович и Перкус (см. примеча-
примечание 7), можно более подробно исследовать уравнение
Орнштейна — Цернике E8а), если воспользоваться ос-
основными идеями теории Ван-дер-Ваальса. Прежде всего
ясно, что для больших х функция с(х) должна быть про-
пропорциональна притягивающему потенциалу у(х) и что
только при х, близких к нулю, с(х) будет отклоняться от
ц)(х) из-за твердой сердцевины. Тогда, поскольку соот-
соответствующее уравнение Ван-дер-Ваальса имеет вид
„тв пал 0 /СЕЛ
р = pia' lld * j2~ » (DO)
где
oo
dx ф (x) = — 7T- ф @),
0
и так как с@) удовлетворяет уравнению F1), весьма
правдоподобно, что выражение для c(k) имеет вид*)
F6)
*) Далее в этом пункте постоянная Больцмана обозначается
&. — Прим. перев.
где
^ /2 ^ тв. пал.
сТв.пал.@) = 1+^_^^__. F7>
Б
Из уравнения F6) мы получаем g(k) с помощью фор-
формулы E9), и если мы теперь определим поведение g (k)
при больших расстояниях формулой
?дал. (k) = g(k)— ?TB- пал' @), F8)
где
^ СГтв. пал. /л\
о-тв. пал. @) = -L^ W_ f
5 V ; 1_ств.пал.@)»
то мы получим
g»-(*) = ~ 1к*Т - ^ • F9)
Ф @) +1* dpjdl ф (k) — ф @) — /3 dpjdl v
Этот результат принадлежит Лебовичу и Перкусу. Мож-
Можно проверить, что в нашей модели, где
из формулы_F9) получается в точности первое прибли-
приближение для /22 (х\ I) при больших расстояниях, которое
было выведено в п. 5.
Для малых плотностей /3-^- ~ — 1къТ очень велико,
и поэтому уравнение F9) принимает вид
?()
что согласуется с ожидаемым результатом
Вблизи критической точки производная др/dl очень ма-
мала, и уравнение F9) можно приблизить для малых k
уравнением
?»*• (k) »/АБГ/[1 ?' @) V - /з(<?/>/<?/)].
Отсюда получаем
где R определяется формулой
оо
•i f x^(x)dx
i
Функция в G1) имеет в точности тот же вид, что и у
Орнштейна — Цернике, с той только разницей, что те-
теперь радиус 1/х выражен через межмолекулярный по-
потенциал. Действительно, формула F4) превращается в
G1), если положить
«-*(-?*)*•
Мы уверены, что уравнение F9) представляет собой
точный результат в том смысле, что оно дает правиль-
правильный вид корреляционной функции в первом приближе-
приближении для всякого дальнодействующего потенциала и для
целого диапазона значений плотности, простирающегося
от малых значений, когда газ близок к идеальному, до
значений, лежащих на границе критической области.
Мы смогли подкрепить нашу уверенность тем, что обоб-
обобщили исследование, проведенное в п. 5, на случай, когда
притягивающий потенциал является суммой экспонент
[см. часть I, E2)], Мы снова нашли, что уравнение F9)
удовлетворяется точно. Поскольку вычисления прово-
проводятся так же, как и для одной экспоненты, мы наметим
только основной контур доказательства. Для потенциала
т
Фпр. V /
ТГГ = — yijviexP(-
/=1
где Vi = ai/kBTt интегральное уравнение Каца пишется
для функции m переменных и его ядро имеет вид
Ks (xv ..., xmJ yv ..., ym) =
= J dxе
exp [-i- (x.+yM Рв{1 (xt | у0 х).
Чтобы изучить, что происходит при y-^0, мы пере-
перестроим интегральное уравнение с помощью подстановки
где
^ _ л
1
Здесь г] определена так же, как и в части I, C3). В ну-
нулевом приближении тогда получаем вместо уравнения
C7) части I дифференциальное уравнение
~t~ 1 "Т fj
^, ..., *J = 0, G4)
где г/ = ^(а/)/* и матрица М задается формулой
Здесь
ct = 2vt (I — бJ/^/3. G6)
Поскольку матрицу М можно привести к диагональному
виду ортогональным преобразованием zt = 2 аи*Ук*
так что
2 М. z.z. = 2 Аку\, G7)
мы найдем в этом приближении
т "
ТпР„.М% G8)
где А//ь = (^!)~^2Bяа/)~1/4. Поскольку наибольшее соб-
собственное значение по-прежнему равно со (s), мы снова
получим ван-дер-ваальсовское уравнение состояния, как
уже отмечалось в части I. Ван-дер-ваальсовская кон-
константа ао дается формулой [см. часть I, E3)]
так что
2 (J (80>
где В снова определяется уравнением C8) части I.
С_^помощью этих результатов вычисление вида функ-
функции П2(х\ I) при больших х обобщается непосредствен-
непосредственно, и мы находим
я2 (х; I) = п™-пал- (х; /) + г ^ " 2i 5*Л* ехР 1~у
(81)
где
m
«л = 2а/*№а/> (82>
.При выводе мы должны использовать тождество
Л*5! = jr • (83)
которое немедленно следует из формулы G7), если по-
положить yk==c'tlEk' Для изучения уравнения (81) нам
понадобятся Ak. Теперь легко показать, что характери-
характеристический многочлен матрицы М можно записать в виде
т
-п«-
— А
Следовательно, Аи служат т вещественными корнями
уравнения
Подставляя выражение G6) для с\ и используя урав-
уравнение G9) и выражение для В, можно все это записать
так:
{t?— l \dl)T'
где r=A~4z. Из формулы (81) можно видеть, что т кор-
корней ri этого уравнения входят в показатели экспонент в
Рис. 1. Графическое решение уравнения (84).
выражении для п2(х\ I). График функции f(r) изобра-
изображен на рис. 1. При небольших плотностях —1гдр/д1^
^ikT, и, таким образом, значение f(r) очень велико. То-
Тогда ri-^l/ou и поскольку сг-->0, из уравнения G5) вид-
видно, 4^0 ортогональная матрица а^ стремится к 6ц9 а из
уравнения (82) следует, что амплитуды s\Xt экспо-
экспонент в формуле (81) становятся равными 2vk/Z, так что
п2(х; I) приближается к ожидаемому виду G0). Вблизи
критической точки величина —Pdp/dl очень мала, и из
рис. 1 видно, что гт становится очень большим, в то вре-
время как все остальные показатели остаются конечными.
Из формулы (84) можно найти, что в этом предельном
случае гт определяется из уравнения
1 у 2щ -3 др
т i I
которое можно переписать так:
где R определяется уравнением G2). Показатель т-й
экспоненты превращается, таким образом, в показатель
Орнштейна — Цернике G3). Чтобы показать, что ампли-
амплитуда также совпадает с той, которая получается в урав-
уравнении G1), заметим, что, поскольку в соответствии с
уравнением (80) вблизи критической точки Zi0*"*1*
собственный вектор щт должен быть близок к значению
B
потому что это дает и нулевое собственное значение, к
которому приближается Ат. Из формулы (82) тогда
следует, что
—2v°(/~6J ^
.2 — ,3 I ^ '
что и приводит к амплитуде из уравнения G1). Нако-
Наконец, мы можем показать, что не только показатели, но
и амплитуды остальных (т— 1) экспонент остаются ко-
конечными вблизи критической точки. Это следует из то-
тождества (83), поскольку оно позволяет нам заключить,
что
т-1
[ ^— — — — — А s2 —О(В4)
если при этом использовать формулы (85) и (86) и за-
заметить, что вблизи критической точки (—/3/2осо) (др/dl) ^
я*В2/12. Следовательно, так как все Аи положительны,
все si должны стремиться к нулю по крайней мере как
В4, и из формулы (81) следует, что все амплитуды, кро-
кроме m-й, остаются конечными в критической точке.
Таким образом, мы видим, что уравнение (81) ведет
себя так же, как формула Лебовича — Перкуса F9) и
в случае идеального газа, и в критической области. Что-
Чтобы показать, что преобразование Фурье выражения (81)
удовлетворяет уравнению F9) точно, требуется дока-
доказать тождество
v Aisi _Л у А ф(*)
где
*=1
Доказательство приводится в приложении Г.
8. Заключительные замечания
Хотя мы в основном ограничивались одномерным
случаем, ясно, что в некоторых аспектах наше исследо-
исследование обобщается и на трехмерный случай.
1. Связь между вириальной теоремой и уравнением
Ван-дер-Ваальса, изучавшаяся в п. 4, может быть та-
таким же образом изучена и в трехмерном случае. Для
слабого, но дальнодействующего притяжения вириаль-
ная теорема в форме уравнения D0) показывает, что
можно отделить в нулевом приближении действие твер-
твердой сердцевины от действия притягивающих сил. Функ-
Функция n2(d+; v) определяется отталкиванием твердых ша-
шариков, в то время как в последнем члене уравнения D0)
ti2(r; v) можно заменить асимптотическим значением
\/v2. Это приводит к уравнению
р=ртв. пал. —-iL, (88)
где
что согласуется с значением С/2, выведенным в п. 5 ча-
части I. Конечно, величина U2(d+; v) для газа из твердых
шариков неизвестна, так что, как и в п. 5 части I, мы
можем только заключить, что уравнение состояния есть
уравнение ван-дер-ваальсовского типа. Следует заметить
также, что этот вывод полностью эквивалентен ориги-
оригинальным рассмотрениям Ван-дер-Ваальса и Лоренца.
2. Теория Орнштейна — Цернике и, в частности,
уравнение F9), очевидно, остаются верными для лю-
любого числа измерений. Первое приближение поведения
П2{г\ v) при больших расстояниях, которое дает эта тео-
теория, согласуется с уравнением (88) ван-дер-ваальсов-
ван-дер-ваальсовского типа при помощи флуктуационнои теоремы и дает
поправку к давлению (—a/v2), которая получается с по-
помощью вириальной теоремы. Если бы удалось найти фи-
физические (а потому допускающие обобщения) основания
для (а) следующего приближения к П2(г; v) при малых
расстояниях, соответствующего последнему члену в урав-
уравнении D4), и (б) высших приближений поведения
га2(#; v) при больших х, соответствующих уравнению
E5), то можно было бы с помощью флуктуационных и
вириальных теорем развить метод последовательных
приближений для уравнения состояния, в котором урав-
уравнение (88) служило бы нулевым приближением.
3. Мы уверены, что линейное соотношение E6) для
функций распределения в двухфазовой области остается
верным при любом числе измерений. Мы показали в п. 6,
что с помощью вириальной теоремы эти соотношения
приводят к постоянству давления газа в двухфазовой об-
области. Конечно, это еще не доказывает, что существуют
две фазы. Линейное функциональное уравнение (подоб-
(подобное уравнению Каца), наибольшее собственное значение
которого было бы двукратным в области конденсации, а
собственные функции не перекрывались бы, в трехмер-
трехмерном случае отсутствует. Можно ли построить такое
функциональное уравнение с помощью всего набора
функций распределения, как это пытался сделать Майер,
и можно ли строго доказать вырожденность его наи-
наибольшего собственного значения и справедливость соот
ношения E6) — все это предстоит еще увидеть.
Приложение А Завершение доказательства
уравнения (96)
Мы должны решить интегральное уравнение B5) с
помощью теории возмущений по малому параметру г\
Полагая
Ыт (П1)
л Л @00) , V kl2 № т/2 A(klm) \lllJ
iV = l\. —f— ?j 81 82 83 iV »
немедленно находим, что в нулевом порядке собствен-
собственные функции и собственные значения имеют вид
з
W (п000) (х) = -фл (х; s + п1о1 + п2о2 + гг3а3) Д Nn. D^. (x/),
а (ооо) л / | -{-«а \ п а )
где n=(n, /ii, n2, п3). Нам нужно Лооо?) и, в частности,
Л(шоо- Поскольку вычисления очень длинные, мы будем
выписывать только те промежуточные результаты, кото-
которые потребуются для окончательного ответа. Легко ви-
видеть, что ¦y(ioo) = \j^oiO)=.v[/(ooi)_Q и ЧТо в Л дают вклад
только целые степени е/# Находим
л=0
где
и подобные выражения для "^оосю и ^оооо- Для члена
порядка 8i получаем
(П2)
0000 W== Zd
n=0
где
B00) _
и подобные формулы для членов порядка 82 и ез. Затем
для члена поряда 8182 находим
Аоооо =
J
(ПЗ)
Относительно функции "^оосюМ мы должны знать толь-
только, что интеграл
пропорционален 6Лз0.
В членах порядка 81(828зI/2 мы получим для коэффи-
коэффициентов а{п11) разложения ^от по ^Ж» т. е. для ин-
интегралов
следующее выражение
m=0
Другие коэффициенты разложения нам не нужны. Окон-
Окончательно это приводит в члене порядка 818283 к выра-
жению
лоооо
Ь. *-
оо оо
2S 2 [(°>5|/г'
{т,
+ два аналогичных члена, получающихся из преды-
предыдущего заменой (а2, а3), (а4, о2) на (а4, а3), (а4, о2) и
(alf а3), (а2, а3)]. (П4)
Чтобы вычислить левую часть уравнения B4), мы долж-
должны снова разложить уравнение B7) с помощью подста-
подстановки в разложение для Лоооо (s) выражения
S=p/kT = % (81? 82, ?3, Z) = % (z) ~\- 2 81 82 ?™' Л т«
Л, /, т
Приравнивая в формуле B7) члены с одинаковыми сте-
степенями 8г-, можно выразить у^Ыт) через функции
где теперь s = p/kT = %(z). Находим
-B00) _ --@20) _ -Х002) _ 0
и, наконец,
Н =4" +
Подставляя в это уравнение выражения (ПЗ) и (П4),
находим, что 1%{222) в точности равно удвоенной сумме в
уравнении (П4). Так как эта удвоенная сумма симмет-
симметрична по 0ь (i2, аз, все шесть членов правой части урав-
уравнения B4) равны друг другу, и мы можем записать это
уравнение в виде
6ljjdx dyps(jc, у; z) е-^-^у-
о
Поскольку преобразование Лапласа берется по двум от-
относительным расстояниям х и у, нам нужно только две
переменные а. Полагая
легко проверить, что все три члена удвоенной суммы в
(П4) становятся равными друг другу, и, следовательно,
формула (П6) приводит к уравнению (96).
Приложение Б. Доказательство тождества D2)
С помощью уравнений (8) и (9) из части I легко
проверить, что ядро Ks(x, у) интегрального уравнения
Каца удовлетворяет тождеству
dKs+y/ду + dKsfdx = \ v1/. (Ks+Y + К*) + у уК*+Y -
Умиожим это уравнение на ^п{у\ s) fn(^; s + y) и про-
проинтегрируем по х и у. В каждом члене можно выпол-
выполнить одно из этих интегрирований. После интегрирова-
интегрирования второго члена по частям ответ запишется в виде
/
— оо
оо
, s) —
— оо
оо
i f dxb(xi s + y-fc-^ix; s).
V'
— оо
Умножим это уравнение на
и просуммируем затем по всем п. В правой части, если
использовать соотношение полноты, получим
)
л=0
Член, содержащий д/дх, исчезает, и мы приходим к
формуле
оо
2 -Л
я=0
X
оо
fdx$k(x\
Это равенство выполняется для всех k. Полагая k = 0 и
используя равенство (9а), мы получаем уравнение D2).
Мы предоставляет читателю вывести аналогичным спосо-
способом тождество, вытекающее из вириальной теоремы D0а).
Приложение В. Доказательство уравнения D4)
После подстановки, перестраивающей уравнение Ка-
ца, и разложения ядра до членов О (у), вклад n-го члена
ряда резольвенты B9) в уравнение B8а) можно запи-
записать в виде
Y J
где
+ + |т12; а/ = 1 ц (I
и где ЯоE), h(xf) и А (у') по-прежнему определяются
разложением C6) из части I. Мы уже видели, что
в нулевом порядке получается (Л/ео)Л, где
Члены, пропорциональные у, возникают в шести местах*
1. В нулевом порядке s + у?}2 = 1/(^—6). Посколь-
Поскольку мы вели разложение при постоянном /, мы получаем
с точностью до первого порядка
где А/ = у d\i§yds, а ^(s) задается уравнением C9)
части I. Таким образом, вклад от нулевого приближения
равен
где
Р =
2. От Iq(s), очевидно, возникает вклад
3. От членов в квадратных скобках, содержащих у,
получаем
4. От членов с у1/* в квадратных скобках в сочетании
с поправкой О(у1/2) к собственным функциям h(x') и
h(y') получаем
5. От произведения двух членов с yi/2 в квадратных
скобках получаем
6. При нахождении всех этих вкладов мы заменили
функцию Ру(г\_х \z'v t^ ее нулевым приближением, а
именно 6B^. — zi_i)- Мы должны поэтому вычислить
еще вклад, возникающий из-за отклонения функции PY
от б-функции. Все другие множители можно при этом
заменить их значениями в нулевом приближении. При
помощи марковости функции Ру все интегралы по Zi
можно немедленно вычислить. Затем можно выполнить
интегрирование по у\ если использовать то, что с точ^
ностью до О (у) справедливо равенство
оо
/ dy'F (у') Ру (х' | у', t) = F (х') - yx'tF' (x') + ytF" (x').
— со
Интеграл по xf также можно вычислить, и мы оконча-
окончательно получаем
пРп Г (в 4 Ul - - + Vo(/-6J
nr jot Д1 f
1
J-
Объединяя все эти результаты и суммируя по п, мы
приходим к уравнению D4). Здесь, как и во многих дру-
других вычислениях, принцип максимальной простоты ока-
оказался очень действенным. До тех пор, пока окончатель-
окончательный ответ не получился простым, мы неизменно обнару-
обнаруживали, что совершили какую-нибудь алгебраическую
ошибку!
Приложение Г. Доказательство тождества (87)
Мы признательны за это доказательство д-ру Хал-
тону (J. Н. Н а 11 о n, Brookhaven National Laboratory).
Первый шаг состоит в разложении левой части уравне-
уравнения (87) по отрицательным степеням k2. Используя ра-
равенство
из которого, если положить zi =c1{ilop следует, что
мы получаем для левой части выражение
J
r=0
Теперь несколько более удобно ввести вместо матрицы
М [задаваемой уравнением G5)] матрицу
Таким образом, уравнение (П7) можно переписать в
виде
B 'r+f
Суммирование по i и / может быть сразу выполнено, и
мы получаем множитель
Введем обозначение рг= —o]/k2 и ради удобства записи
положим Сг= —rfi. Тогда легко видеть, что тождество
(87) можно переписать в виде
S ач1н
= -СТ. (П8)
где теперь
Подставляя L и подсчитывая это произведение, можно
проверить, что сумма по i\, 12, - - •> U может быть перепи-
переписана так:
где суммирование распространено на целые rh от 1 до
г— 1, связанные условием (оно обозначено штрихом)
Изменение порядка суммирования по г и 5 в формуле
(П8) приводит к тому, что левая часть этой формулы
превращается в
2.2 2 ПАр».
а,,.?.,.,,.?.,. ям*
где сумма по Ги берется от 1 до оо и не связывается ни-
никакими условиями. Итак, получаем
ОО с А СО
V V гг /feP/* -V/^1 d& V- ф
Za Za Jl Jl 1 — P/ Za[ Zd i — p/ ) l — ф *
5=1 /p ..., is k = l k 5=1 \ / /
что и доказывает формулу (Г18).
Примечания к части II
1) Or n stein L. S., Zernike R, Proc. Acad. Sci. Amsterdam,
17 A914), 793; Physik Z., 19 A918), 134; 27 A926), 761. См. также
Zernike F., Dissertation, Groningen, Netherlands 1916, reprinted in
Arch. Need. Zool., Ser. 13 A, 4 A917), 74. Более позднее изложение
см. в работах Ландау Л., Л и ф ш и ц Е., Статистическая физика,
М., 1951; Klein M., Tisza L., Phys. Rev., 76 A949), 1861; Fi-
erz M., Pauli Memorial Volume, New York, I960, p. 175, и в осо-
особенности Deb ye P., Non-Crystalline Solids, New York, I960, pp. 1—20;
/. Chem. Phys., 31 A959), 680.
2) Zernike F., Prins J. A., Z. Physik, 41 A927), 184; D e-
b у e P., M e n k e H., Physik. Z., 33 A932), 593.
3) Так как литература по этим вопросам весьма обширна, мы
отсылаем читателя к работам Yvon J., Fluctuations en densite,
Paris, 1937; Boer J. de, Rep. Progr. Phys., 12 A949), 305; Mun-
s t e r A., Statistische Thermodynamik, Berlin, 1956, Кар. 8; Mayer J.,
Handbuch der Physik, Berlin, 1958, B.XXII, S. 152.
4) Полное исследование этих разложений можно найти в ра-
работе Mayer J, E., Mont r oil E, W., Л Chem. Phys., 9 A941), 2.
См. также обзор, сделанный Уленбеком и Фордом в книге Studies
in Statistical Mechanics, Amsterdam, v. I, p. B.
5) Мы имели в виду, в частности, попытки Кирквуда и его со-
сотрудников получить фазовый переход жидкость — твердое тело и
показать, что такой переход существует уже в системе твердых ша-
шариков. См. Kir k wood J. G., Monroe E., У. Chem. Phys., 9
A941), 514; К i г к w о о d J. G., M a n n E. K., A 1 d e r B. J., У. Chem.
Phys., 18 A950), 1040.
6) Mayer J. E., У. Chem. Phys., 15 A947), 187. Ср. также с его
статьей в журнале J. Chem. Phys., 16 A948), 665, и с обзором
в книге Handbuch der Physik, Berlin, 1958, В. XII, S. 165.
7) L e b о w i t z J. L., Percus J. K., Asymptotic behavior of the
radial distribution function (preprint).
8) Результат Цернике и Принса, Z. Physik, 41 A927), 184, можно
записать в виде
Ятв.пал./ A — i-YS( Щ (x~kb)k~l
k — \
где S(y) —по-прежнему ступенчатая функция. Применив к этой
формуле преобразование Лапласа, получим выражение C1).
9) S а 1 s b u r g Z. W., Z w a n z i g R. W., К i r k w о о d J. G.,
У. Chem. Phys., 21 A953), 1098. Ср. также с исследованием одно-
одномерных систем: Munster A., Statistische Thermodynamik, 8.8.
10) Общее правило таково: разобьем s частиц на некоторое
число групп и перемножим функции распределения р*, каждая из
которых зависит только от положения частиц данной группы. Тогда
Xs составляется как сумма таких произведений по всевозможным
способам разбиения s частиц на группы, причем каждое слагаемое
входит с коэффициентом (—\)h~l(k—1)!, где k — число групп, соот-
соответствующих этому слагаемому^Аналогичные формулы справедливы
и для функций распределения ns. Мы получаем те же самые функ-
функции %s с той только разницей, что z должно быть выражено через v.
и) Здесь возникает следующая трудность. Уравнения C4а) и
C46) выводятся из нормирующего условия
i • • • *.Мг, г.; V, г)^(^щ)
V V
которое следует из определения ps.
Среднее величины N\/(N—s)\ no большому каноническому ан-
ансамблю можно выразить через N и его производные по хи-
химическому потенциалу jx, что и приводит к уравнениям C4а) и
C46). Если теперь использовать те же самые соображения для
функций распределения п8(ги ..., rs; Nt V) в каноническом ансам-
ансамбле, которые нормированы условием
f ... fdr, ...drtna(Tlt .... rs;N, V)= {N™s)l .
то получится другой ответ, так как усреднение по N выражается
через производные удельного объема по давлению. С другой сторо
ны, если вещество находится в однофазовом состоянии, предельные
функции п8{ти •.., rs; v) и ps(rb ..., rs, z) совпадают, а поэтому
и групповые функции, составленные из них, должны быть одинако-
одинаковыми, если v выразить через z или наоборот.
Этот парадокс часто обсуждался в литературе (см., например,
Mayer J. С, Handbuch der Physik, Springer, Berlin, 1958, В. XII,
S. 156). Математическая причина возникновения этой неувязки
должна заключаться в том, что при выводе уравнений C4а) и C46)
переставляется порядок двух предельных переходов. По-видимому,
такая перестановка запрещена в случае функций распределения ка-
канонического ансамбля, хотя точные причины этого нам еще не ясны.
12) Простейший вывод уравнения C8) получается для кубиче-
кубического сосуда объема V=L3 и принадлежит Грину [Green H. S.,
Proc. Roy. Soc. (London), 189 A947), 103]. Полагая r* = r//L, мы
добьемся того, что пределы интегрирования не будут зависеть от L,
и мы сможем дифференцировать по V или L под знаком интеграла.
13) Мы вычислили также с помощью уравнения B86) поведе-
поведение трехчастичной функции распределения при больших расстоя-
расстояниях. С точностью до членов порядка у находим
nz(x, «/;/) = л™-"»•(•*. у; /) +
+ ехр [— ^- ух] + ехр [— -J-
Следовательно, при больших расстояниях с точностью до О (у) вы-
выполняется принцип суперпозиции
Л3(*1, t2, ts; I) = l42(tv t2\ I)n2(tv tz; I)n2(t2, tz\ I).
Его следует сопоставить с той формой принципа суперпозиции для
твердых палочек, которая представлена уравнением C1а).
и) В статье L е b о w i t z J. L., P e г с u s J. K., Statistical ther-
thermodynamics of non-uniform fluids, дается формальный вывод урав-
уравнения Орнштейна — Цернике E8), которое они считают точным.
Однако в настоящее время еще не ясно, приводит ли это к такому
методу последовательных приближений, при котором можно было бы
исходить из уравнения F9) в качестве первого приближения.
Часть III
ИССЛЕДОВАНИЕ КРИТИЧЕСКОЙ ОБЛАСТИ
1. Введение
Как мы уже отмечали в части I и II, наше исследо-
исследование ван-дер-ваальсовского предела теряет силу вбли-
вблизи критической точки. Это становится ясным, если по-
посмотреть, каким образом величина В2, пропорциональная
dpldl, входит в разложения для собственных функций и
собственных значений уравнения Каца, а также в раз-
разложения для двухточечной функции распределения как
при малом, так и при большом расстоянии между точ-
точками. При В = 0 от всех этих разложений ничего не
остается. Поэтому для критической области необходимо
провести новое изучение асимптотики уравнения Каца
при у-^0. Это сделано в настоящей статье.
Оказывается, что критическую область для темпера-
температуры и удельного объема следует определить так:
(Т - Ткр.)/Ткр. «(уЬ)\ (I - /кр.)//кр. « (Y6I/3, A)
кр.)/Ткр. «(уЬ)\ (I - /кр.
где Гкр. и /кр. — ван-дер-ваальсовские критические значе-
значения и уд — по-прежнему отношение радиусов действия
отталкивающих и притягивающих сил. В п. 2 мы пока-
показываем, что в этой области можно снова так перестроить
уравнение Каца с помощью подходящей замены пере-
переменных, чтобы это привело к согласованному методу по-
последовательных приближений для собственных функций
и собственных значений. В отличие от однофазовой и
двухфазовой областей параметром разложения служит
уже не уд, а (убI/з, и собственными функциями нулево-
нулевого порядка являются уже не собственные функции гар-
гармонического осциллятора (функции Вебера), а соответ-
соответствующие собственные функции осциллятора, потенци-
потенциальная энергия которого задается полиномом четвертой
степени. В результате явно определить собственные
функции и собственные значения уже нельзя. Однако
можно проследить за качественным изменением соб-
ственных функций при удалении от критической области,
причем особенно интересно пронаблюдать различие ме-
между удалением в однофазовую и удалением в двухфазо-
двухфазовую область. В первом случае собственные функции
снова превращаются в функции Вебера, лишь слегка
искаженные, а во втором случае (двухфазовая область)
они приближаются к собственным функциям потенциала
с двумя равными или почти равными минимумами. Хо-
Хорошо известно, что у такого потенциала два наименьших
собственных значения очень близки, и это соответствует
началу вырождения, характерному для двухфазовой об-
области.
В п. 3 эти выводы обсуждаются в связи с видом изо-
изотермы в критической области. В первой статье мы уже
отмечали, что в любом порядке по уд метод последова-
последовательных приближений всегда дает фазовый переход и
получается уравнение состояния типа уравнения Ван-
дер-Ваальса. Мы обнаружим, что в критической области
(т. е. для конечных уд) семейство изотерм качественно
отличается от того, что предсказывает простая теория
Ван-дер-Ваальса (т. е. когда у6 = 0). Для конечных уд
переход из однофазового состояния в двухфазовое в кри-
критической области происходит непрерывно1). Строго го-
говоря, для Г<Гкр. изотермы не имеют горизонтальной ча-
части, и поэтому нельзя говорить отдельно о плотностях
двух совместно существующих фаз. Однако хотя трудно
делать точные утверждения из-за той неопределенности,
которая всегда возникает при попытках связать два раз-
различных асимптотических разложения одной и той же
функции, можно разумным образом продолжить геомет-
геометрическое место точек сосуществования фаз из двухфазо-
двухфазовой области в критическую область. Мы найдем тогда,
что для конечного уд критическая плотность по-прежне-
по-прежнему имеет ван-дер-ваальсовское значение, но критическая
температура уменьшается на ДГкр., причем АТкт>]Тт&
«0,702 (убJ/з. В этой новой критической точке кривая
сосуществования фаз снова является параболой, но бо-
более плоской, чем предсказывает теория Ван-дер-
Ваальса 2).
В п. 4 и 5 эти выводы обсуждаются в связи с двух-
двухточечной функцией распределения. Основной результат
состоит в том, что в критической области поведение этой
функции в случае больших расстояний между точками
представляется бесконечным рядом убывающих экспо-
экспонент. Показатели этих экспонент все имеют порядок
1/у(у6)Чз\ все их амплитуды также имеют один и тот же
порядок, а именно (уб)?/з. Следовательно, теория Орн-
штейна — Цернике неверна в критической области. Од-
Однако мы можем показать, что если удаляться из крити-
критической области в однофазовую область, го наши резуль-
результаты перейдут в разложение для двухточечной функции
распределения в случае большого расстояния между
точками, которое было выведено в части II и в котором
первый член совпал с экспонентой Орнштейна — Цер-
Цернике. Ситуация, по-видимому, такова, что при прибли-
приближении к критической точке все больше и больше экспо-
экспоненциальных членов вступает, так сказать, в игру. Вне
критической области эти члены убывают по величине, но
внутри критической области они дают заметный вклад.
Нам кажется, что эта картина, указывающая на воз^
никновение отклонений от теории Орнштейна — Цернике
при приближении к критической точке, вероятно, имеет
место и в трехмерном случае и не зависит от нашего
предположения об экспоненциальном убывании отталки-
отталкивающего потенциала. Действительно, как показано в
п. 6, все исследования п. 4 можно обобщить на случай,
когда отталкивающий потенциал состоит из суммы m
экспонент; при этом качественно картина не меняется.
В п. 7 мы делаем несколько замечаний о некоторых
недавних экспериментальных результатах по критиче-
критической опалесценции и так называемой аномалии удель-
удельной теплоемкости, для того чтобы увидеть, имеются ли
какие-нибудь экспериментальные указания на существо-
существование критической области.
2. Собственные функции и собственные значения
в критической области
Мы разложим все величины в окрестности критиче*
ской точки уравнения состояния нулевого порядка, т. е.
уравнения Ван-дер-Ваальса
s = !/(/_ 6) — vo/Z2
(в обозначениях, использованных в части I и II). Кри-
Критические величины имеют вид
V = 1/85, /кр. = 36, v0 кр. = -16. B)
Теперь основное интегральное уравнение Каца [см.
часть I, A0)] в окрестности критической точки следует
перестроить не так, как это делалось в части I при вы-
выводе формулы C3), а с помощью подстановки
г = (уЬI1«[х-чкр.B/УI/2Ъ C)
где г]кр.=г) (sKp.) = BvoKp.I/2/4<p.. Это объясняется тем,
что в однофазовой области перестроенные собственные
функции зависят от переменной [см. часть I, C8)]
z = (B/lf[x-nB/yf]. D)
Если мы теперь определим критическую область для
температуры и удельного объема с помощью уравнений,
соответствующих формулам A):
[H E)
F)
то найдем, что В/1 имеет порядок (^6L так что уравне-
уравнение D) переходит в уравнение C). Однако мы должны,
конечно, еще показать, что подстановка C) действи-
действительно работает! Мы поступим так же, как в части I.
Для переменной у в уравнении Каца мы сделаем ана-
аналогичную подстановку
4[f\
и положим
z' = ге-v* + (yb)'le I (I — e~*rfh,
f]~(yb)'lK H{z),
где множитель (уд)*112 вводится для нормировки H(z).
Наконец, напишем разложение для 5 3)
5 = 5кр.[1 -3v^6J/3+5^) + MY&L/3+ ...], G)
где числа sb s2, • • • зависят от данных чисел vi и k че-
через уравнение состояния, которое по-прежнему задается
формулой [см. часть I, B0)]
где ho(s) — наибольшее собственное значение уравнения
Каца.
Сделав все эти замены, введя разложения E) и G)
и разложив ядро по степеням (уб)/з до порядка (у6M/\
у р
мы придем после интегрирования по ? и т и использо-
использования формулы B) к следующему уравнению:
f - F)* z
.
+ Н{г) [ЗЛ +(§.)* z { (^-1) G6)'" + (-*-» v?)
=O. (9)
В этом уравнении новый собственный параметр Л свя-
связан с исходным собственным значением Я уравнением -
( 5 + v) (y6L/3 + ЗЛ. A0)
+ Т
Из формулы (9) видно, что можно получить сходящиеся
последовательные приближения, если положить
H{z) = Я@) (г) + (Y6I/3 ЯA) (z) + (Y6J/s ЯB) B) + ....
Л=в (ybf+Q (y6M's+a (y6J + •.. • (И)
В наименьшем порядке [т. е. (уд) /з ] мы получим
а в следующем порядке [т. е.
_ f/lV/2 ±z±-
Эти уравнения определяют в принципе собственные
функции Hf\z\ H(nl)(z) и соответствующие им собствен-
собственные значения 0n, Qn как функции постоянных vi, Si и s2.
Возвращаясь теперь к уравнению состояния, мы бу-
будем исходить из общего выражения
X
Xехр{Щ^- (x+y)}fdxхе-"Ру(х|у,х).
6
Разлагая vo и s в окрестности критических значений и
используя указанные подстановки для х и у, мы полу-
получаем
Г
_ Яо (s) = со EКр.) 36 — 6 FI/2 (Y6I/3 Jdzz (tff (z) f +
L —oo
f
+ (Y6J/3 - 26 F)V2 J dz zH^ (z) #oA) (z) +
I
(tff(*)J + f 6vx}+ ...|. A4)
J J
Из уравнения A0) и уравнения состояния (8) мы най-
найдем то, что нам требуется, сравнив полученное выраже-
выражение для / с определяющим его уравнением F);
Эти уравнения определяют в принципе зависимость S\ и
s2 от vi и 1\.
3. Семейство изотерм в критической области
Поскольку уравнение состояния выражается с по-
помощью наименьшего собственного значения и собствен-
собственной функции уравнения A2), которые нельзя найти в
замкнутом виде, для наших исследований удобно вос-
воспользоваться следующей физической аналогией. Пере-
Перепишем уравнение A2) в виде
^ A7)
где
±(±) . A8)
Ясно, что уравнение A2) можно рассматривать как
уравнение Шредингера для частицы, движущейся в по-
потенциальном поле V(z) под действием «квазиэлектриче-
«квазиэлектрического» поля напряженности F. Далее нетрудно показать,
что из уравнения A5) следует соотношение
A9)
Следовательно, 1\ пропорционально «электрическому мо-
моменту», создаваемому полем F, и исследование изотермы
становится эквивалентным исследованию эффекта Штар-
ка для наинизшего уровня частицы, движущейся в по-
потенциальном поле V(z).
Рассмотрим сначала случай, когда F мало. Поскольку
V(z) = V(—«г), наименьшая собственная функция //о(О)(z)
также симметрична по z, когда F = 0. Следовательно,
эффект Штарка квадратично зависит от F, так что /i = 0
при F = 0; это вытекает и непосредственно из A5). С по-
помощью обычной теории возмущений находим
I2
tfi0) +O(/*),B0)
Эя-е0
где вп и #i0) — собственные функции и собственные зна-
значения невозмущенного уравнения. Следовательно, для
^ = 0 имеем -я/72° < 0 и не только -37r = 0> но также ц
—А = 0. Отсюда вытекает, что при критической плот-
плотности, т. е. при /i = 0, все изотермы имеют точку перегиба
с отрицательным наклоном. Действительно, из A9) и
B0) мы получаем
Л=1
эта величина всегда отрицательна. Поэтому изотермы
не имеют горизонтальной части в критической области.
Однако поведение наклона B1) в зависимости от темпе-
температуры совершенно различно для положительного и от-
отрицательного vi, т. е. для Г<Гкр. и Г>Гкр.. Очевидно,
для отрицательного vi G">Гкр.) потенциал V(г) имеет
только минимум при г=0, а при vi<C—1 он превращает-
превращается в параболу, а собственные функции становятся функ-
функциями Вебера. Для vi<C—1 очень просто развить метод
теории возмущений для 6П и /Д0)(г) и, следовательно,
для наклона B1). Находим для vi<C — 1
[3)] <22>
Легко также показать, что это согласуется с уравнением
состояния в однофазовой области
где
которое было найдено в п. 4 части I. Используя E) и
F), мы получаем из B3) разложение G) для 5 со зна-
значением
Sl = 6vlll-^ll + 4 — 6ZiC/?— ^"Л B4)
откуда следует B2).
В случае vi>0, т. е. 5г<Гкр., используются совершен-
совершенно другие соображения. Потенциал V(z) имеет теперь
два минимума (рис. 1), и для vi^>l это приводит к хо-
хорошо известной почти вырожденности наименьшего
уровня энергии, соответствующей симметричной и анти-
антисимметричной комбинациям двух наименьших собствен-
Рис 1. Потенциал V(z) из уравнения A7) при температуре
значительно ниже критической.
ных функций гармонического осциллятора в окрестности
обоих минимумов. Используя метод ВКБ4), найдем
оо
ех - в0 * [Vvjb/n] ехр [- BV,L'], / dz zHW «FvxI/2.
— оо
В сумме B1) существен только первый член, так что для
Наклон изотермы, следовательно, быстро стремится к
нулю при возрастании vi.
Рассмотрим далее случай, когда F и, следовательно,
li не являются малыми. Снова, чтобы исследовать
МЛ, v0' мы Д°лжны различать два случая: vi<C—1 и
Vj^>1. Для температур выше rKp.(vi<C — 1) «потенциаль-
«потенциальная функция» V(z) —Fz по-прежнему имеет только один
минимум в точке z = Zo, определяемой из уравнения
-^ = О- B6)
«Энергия» 0о приблизительно равна
0о = V (го) - Fzo + 2/2 D - 2»г)\ B7)
где последний член представляет собой «нулевую энер-
энергию» -к^ы колебаний около Zq [при /? = 1, m=l/2 потен-
потенциальная энергия равна -?®2(г — гоJ=у("^г) (z—^оJ»
так что <o = 2*[
Из A9) и B7) с использованием B6) получаем
В нулевом приближении минимум z0 равен —(у) 2 /1#
Подставляя это значение в B6) и выражая F через s\
с помощью A8), мы получаем первые три члена урав-
уравнения состояния B4), которые также следуют из урав-
уравнения Ван-дер-Ваальса. Можно сказать, что эти ван-
дер-ваальсовские члены соответствуют «классическому»
приближению эффекта Штарка. В первом приближении
zo = - |У/2 h [1 - 2 Ff /x/C/? - 4*04
и это приводит к последнему члену уравнения состояния
B4), который, таким образом, представляет, так ска-
сказать, первую «квантовую» поправку к уравнению Ван-
дер-Ваальса. Заметим, что соответствующее выражение
для уровней энергии 0П имеет вид
а собственные функции в этом приближении являются
функциями Вебера Dn(y), где
{[^jh} B9)
Нетрудно также найти высшие приближения. Ответы
приведены в приложении 1, поскольку они понадобятся
нам в п. 4.
Для температур ниже TKVXv{^>\) потенциальная
функция V(z) —Fz может иметь два минимума разной
глубины, и какой из них глубже, определяет знак F [или
(si — 4)]. Если в нулевом приближении мы снова пред-
предположим, что энергия в0 равна значению потенциала в
наименьшем из минимумов, то найдем (в точности так
же, как и раньше), что уравнение состояния примет вид
/, = - 2v;a sign (s, - 4) - -fc^- + О (vrv.). C0)
Это следует также из уравнения Ван-дер-Ваальса [пер-
[первые три члена в уравнении B4)], дополненного прави-
правилом Максвелла (см. рис. 2). Опять можно сказать, что
Рис. 2. Форма изотермы ниже критической точки;—для уравнения
C0); — — для уравнения Ван-дер-Ваальса; для
уравнения C0а).
ван-дер-ваальсовское уравнение служит «классическим»
приближением для соответствующей задачи об эффекте
Штарка. В частности, горизонтальная часть изотермы
при 5i=4 возникает из-за того, что наименьший мини-
минимум переходит справа налево при изменении знака F.
Добавляя к наименьшей энергии нулевую энергию, мы
качественно не изменим картину: горизонтальная часть
изотермы сохранится. Конечный наклон изотермы, о ко-
котором мы говорили выше [см. уравнение B5)], возникает
из-за второго «квантовомеханического» эффекта, а имен-
но проникновения через барьер между двумя минимума-
минимумами, если их глубина становится почти одинаковой. Ис-
Используя метод В КБ, мсжно показать, что этот эффект
проникновения изменит уравнение C0), а именно
2^-4) ft-4)
Л—"[<*.--»)¦ + *]* 1*Г' C03)
где
Это согласуется с уравнением B5).
До сих пор мы изучали в основном семейство изо-
изотерм при v2<^—1 и vi^>l. Хотя качественной понятно,
каким образом изменяются изотермы, проходя через
критическую область, тем не менее трудно сделать точ-
точные утверждения, если vi имеет порядок единицы, и,
очевидно, нельзя сказать ничего определенного о форме
кривой сосуществования фаз в критической области. Од-
Однако представляется разумным считать, что в силу чет-
четности функции V(z) критическая плотность не изменяет-
изменяется для конечного yS, но критическая температура пони-
понижается, так как V(z) имеет два минимума при vi>0,
что некоторым образом указывает на разделение фаз.
Тогда можно определить новую критическую темпера-
температуру как такое значение vi, для которого нижний уро-
уровень энергии равен в точности нулю и совпадает тем
самым со значением V(z) в точке максимума. Чтобы
определить это значение, можно использовать один из
вариантов метода ВКБ, который был предложен Кра-
мерсом и Итманом5). С помощью этого метода мы най-
найдем, что соотношение между vi и во для /i = 0 и во,
близкого к нулю, имеет вид
?], C!)
где A, = 26ovf/2 и С — константа Эйлера. Следователь-
Следовательно, v1 = (-jg- Jtj 3 = 0,702, если 6с = 0. Таким образом,
критическая температура изменяется на ATKV^ причем
ДГкр./Гкр. = 0,702 (уб) \ Для более низких температур,
т. е. для vi>0,702, нижняя собственная функция имеет
два максимума. Представляется заманчивым отожде-
отождествить положение этих максимумов с тем значением
ЦТ; ' где заР0ЖДаются «газообразная» и «жидкая»
фазы. Проделав это, мы получим
l\ = Av^k\l\. C2)
Исключив |А,| из уравнений C1) и C2), мы придем к
экстраполированной кривой сосуществования фаз6)
vx = (^-J/з + ^ [in (Збя) + С + у] /? = 0,702 + ОД 43/?.
C3)
Это все еще парабола, но заметно более плоская, чем
парабола Ван-дер-Ваальса Vi=-^^ (см. рис. 3).
Рис. 3. Форма кривой сосуществования фаз вблизи критической
точки; для уравнения Ван-дер-Ваальса; — для уравнения
Ван-дер-Ваальса с поправкой порядка у [уравнение B3)];
—. для уравнения C3).
4. Двухточечная функция распределения
в критической области
Чтобы определить поведение в критической области
двухточечной функции распределения при больших рас-
расстояниях, мы применим тот же самый метод, что и в
п. 5 части II для однофазовой области. Однако, посколь-
поскольку в этой области Пг(х; /) стремится к I//2 по экспонен-
экспоненциальному закону Орнштейна — Цернике ехр(—Вух/1)
[часть II, E4)] и поскольку в критической области В/1
имеет порядок (у6I/з, следует ожидать, что в критиче-
критической области множитель при х в показателе экспоненты
имеет порядок 1/у(убI/з- Мы должны, следовательно, за-
заменить в основной формуле [часть II, (9а)] для преоб-
преобразования Лапласа функции П2(х\ I) переменную а пе-
переменной ау(уЬУ1ъ и исходить из представления
оо
/ Г dxn2 (х; I) exp [— oy (yoI/zx] =
где
оо
bn= f dxi|H(x; s)ф„(х; s + ay(yb)'1').
— оо
Сначала мы подсчитаем Ьп до членов порядка (\)
Введем переменную z по формуле C) и разложение
A1) для собственных функций. Заметим, что s + oy{yb)x^
получается из разложения G) для s добавлением 8а к
s2, так что уравнение A2) для #(°) не изменится при пе-
переходе от 5 к s + Gy(yb)l/K Используя ортонормирован-
ность, получаем
, s)X
X [M2) (z, s + oy (Y6)'/s) - M2) (z, sj\ +
' (z, s + oY (Y6I/s) - M4 (z, s)]}. C5)
Второй член можно вычислить так. Из уравнения A3)
для ЯA) и того обстоятельства, что переход от 5 к
s + oy(y6)^3 не затрагивает Я(л0) и 0Л, можно вывести, что
[йг* 48^ 4 ^
= [- (f )'A oz - Qn (a) + О„ @)] //„0) (z, s), C6)
где Qn (a) == Q,, (s + ay (уЬ)'1ъ). Умножая уравнение C6)
на //оО) (z, s) и интегрируя, получаем для пф О
оо
J
Чтобы вычислить следующие члены в уравнении C4),
содержащие собственные значения, нужно продолжить
разложение A0) до членов порядка (y^J. Это приводит
к выражению
К (s) -K(s + aY (Y6I/3) = со (sKp.) { 3 @„ - 0О + a) (ybf
+ 3[Q,(a)-Q0@)](Y6N/3 +
откуда находим
Hv, , 9v, Л , en-90
~4 ^T-l1
[QB(a) —Q@)]« S, (a) —8@))
[ + вв] Ъ )•
Заметим также, что из уравнения C6) для /г = 0 полу-
получается после умножения на ЯоО) (z, s) и интегрирования
следующее соотношение:
оо
Qo @) _ Qo@) = _ (||/га f dzz [М0) (г, s)f = ah C9)
— оо
[мы воспользовались уравнением состояния A5)].
Подставляя все эти результаты в формулу C4), мы
найдем после некоторых простых преобразований
со
.OY (Y6)'/3 / dx exp [- ay (y6)v» x] [n2(x;
ft D0)
Здесь буквой R обозначены все члены, которые приве-
приведены в приложении 2; там же мы покажем, что на са-
самом деле R = 0. Разумеется, формула D0) законна лишь
в критической области, так что / всегда задается урав-
уравнением F) и собственные значения 0П и собственные
функции #i0) следует определять из уравнения A2).
При R = 0 можно обратить преобразование Лапласа и
найти
со р оо
X
Xexp[-(en-e0)Yx(Y6)'/s]. D1)
Это окончательный результат. Он показывает, что в кри-
критической области П2{х] I) стремится на бесконечности к
I//2 [т. е. к тому значению П2(х; /), которое получается
без учета корреляции между молекулами] со скоростью,
определяемой бесконечной суммой экспонент, показа-
показатели которых имеют порядок 1/у(у6I/з-
Прежде чем подробно рассмотреть уравнение D1),
мы сделаем несколько замечаний.
(а) Флуктуационная теорема [см. часть II, C4а)]
может быть проверена следующим образом. Из уравне-
ния D1) получаем
оо
f
ОО г-
п=1 L—
Из уравнения B1) видно, что с точностью до порядка
(уб) ~ 3 правая часть равна (— -к l3)/(ds/dl), что также
получается и из флуктуационной теоремы.
(б) На расстояниях х~\/у уравнение D1) в наиниз-
наинизшем порядке дает
оо Г оо
Ч (х: D = } + ^ (Y6)% Ш& [*+ (})"/г /Л X
1
|2
1
D2)
Здесь используется уравнение состояния A5), чтобы
распространить суммирование от нуля до бесконечности,
после чего применяется, равенство Парсеваля. Можно
вывести уравнение D2) непосредственно из основной
формулы [часть II, (9а)], заменив а на оу и разложив
до порядка (у6J/з; мы предоставляем это читателю. Из
уравнения D2) ясно видно, что в критической области
расстояния порядка 1/у__не являются основными, по-
поскольку в этой области п2(х\ I) все еще отличается от
I//2 на величину порядка (у6J/з.
(в) Чтобы проверить вириальную теорему [см,
часть II, D0а)]
оо
—v0y2 J
в критической области, необходимо найти поправку по-
порядка (у&У1ъ к ti2(x; l) при малых расстояниях. В при-
ложении 3 мы докажем, что
D3)
Используя формулу D2) и разложения E), F) и G)
для vo, / и 5, легко проверить вириальную теорему с точ-
точностью до членов порядка (убJ'8.
5. Исследование уравнения D1)
Мы покажем, что уравнение D1) приводит к резуль-
результатам, полученным в части II, относительно поведения
П2(х; I) при больших расстояниях в однофазовой и двух-
двухфазовой областях.
Рассмотрим сначала двухфазовую область. Мы нашли
(см. часть II, п. 6), что здесь на расстояниях х~1/у и
до порядка у
п2(х\ /) = ^^Fj-- + Vo{lp'~6ry exp/—^
/2 ' /5 о w"f I T^ ЧХ I I ' D4)
Г. Г.
где |ж. и gr. — молярные доли жидкой и газообразной
фаз с удельными объемами /ж. и /г., так что
1г. Ч~ 1ж. == 1» ?гА. Ч~ ЕжУж. = '•
Воспользовавшись разложением E) для vo и разложе-
разложением F) для /ж. и /г., находим
^/// = (Y6I/3 (j l\i — Vi)V2. где / = ж. или г., D5)
* \ *ж. *г.
Далее, вблизи критической точки /1ж = — 2vl{* и /1г =
= 2v!/2, поскольку ван-дер-ваальсовская кривая сосуще-
сосуществования фаз определяется уравнением /^ = 4v1. Сле-
довательно, В/1= (y6)'/3Bvi)i/2 как для жидкой, так и для
газообразной фаз, так что две экспоненты в формуле
D4) становятся одинаковыми. Окончательно имеем
что дает
* 1 1 \zrJi
Подставляя все это в формулу D4), получаем
jJx}\. D6)
Это следует также из уравнения D1) при vi^>l. Да-
Давайте проверим это только в симметричном случае
(/i = 0). Мы видели в п. 3, что в этом случае уровни
энергии ®п образуют ряд близких дублетов, соответ-
соответствующих симметричным и антисимметричным комби-
комбинациям собственных функций гармонического осцилля-
осциллятора в окрестности двух минимумов. В сумму D1) дают
вклад только нечетные члены, и для первого приближе-
приближения следует рассматривать лишь п = 1 и /г = 3. Находим
3
так что уравнение D1) совпадает с уравнением D6)
при /i = 0.
Перейдем теперь в однофазовую область; это очень
интересно, поскольку здесь можно получить более по-
подробные результаты [см. часть II, п. 5, уравнения E4)
и E5)]. Для vi <С — 1 или лучше для C/? — 4vi)^>l мы
нашли в п. 3, что в первом приближении (см. уравне-
уравнение B8))
4 1/
л. собственные функции являются в точности функциями
Вебера Dn(y), где у задается уравнением B9), Тогда
легко проверить, что первый член суммы в формуле D1)
принимает вид
4
з/2
°'кр.
Это выражение совпадает с тем, что дает экспонента
Орнштейна — Цернике [см. часть II, E4)]
в критической области с точностью до порядка (убJ/з.
Надо только воспользоваться выражением D5) для В/1
и заменить vo и / их критическими значениями.
В следующем приближении, используя результаты,
выведенные в приложении 1, находим
2Cf
1 Г 2/2 1
r-U2 + « г-1—Eга2 —га)
?-4v,) L 31*-^ К >\
и с точностью до порядка е2
Здесь опущены члены, которые после возведения в квад-
квадрат не дают вклада в слагаемые нужного нам порядка.
В этом порядке нам, следовательно, в сумме D1) нуж-
нужны только первые два члена. Получаем
/кр. [з (з/2-
3 (З/2 - 4V,)'/' Y ^ } 9 (З/2 - 4VlK J Х
X ехр [-1 (Зй ~ 4v,)IA
32 l
\
УТ h^ 4vV
D7)
Можно проверить, что последние три члена в формуле
D7) соответствуют в точности трем поправкам поряд-
порядка у2 к выражению Орнштейна — Цернике в однофазо-
вой области [см. часть II, E5)], если эти поправки вы-
вычислять в критической области до порядка (у6J/з. Это
подтверждает общую картину, о которой упоминалось в
введении, и снова показывает, что экспонента Орнштей-
Орнштейна— Цернике является главным членом только вне кри-
критической области.
Так как в экспериментальных исследованиях по кри-
критической опалесценции наблюдается преобразование
Фурье двухточечной функции распределения, интересно
и для нашей модели изучить функцию
оо оо
= f dx eikxg (x) = l { dx eikx pj (x; /)-¦?-
— oo —oo
Для экспоненты Орнштейна — Цернике (при любом
числе измерений) g(k)—^2 , Ь2 , где б2 пропорциональ-
пропорционально сжимаемости. Следовательно, график l/g{k)=f(k)
как функции k2 должен быть прямой линией, пересекаю-
пересекающей ось f (k) в точке, которая стремится к нулю при при-
приближении к критической точке, если теория Орнштейна—
Цернике правильна. Так как уравнение D1) имеет вил
оо
л = 0
где ап и Ьп положительны, мы получаем для нашей мо-
модели в критической области
Для № больших по сравнению с Ь\ функция f(k) почти
линейна по k2. Действительно,
Чтобы исследовать кривизну при малых &2, заметим, что
можно написать
I2 /V п
J v n &
где штрихи означают дифференцирование по k2. Отсюда,
согласно неравенству Шварца, заключаем, что /"<С0;
т. е. кривая обращена выпуклостью к оси к2.
Для изучения зависимости графика Орнштейна —
Цернике от температуры мы ограничимся случаем /i = 0
(критическая плотность) и vi<C — 1. Тогда можно ис-
использовать уравнение D7); поскольку последний член
исчезает, мы можем написать g(x) в виде одной экспо-
экспоненты, помещая второй член снова в показатель экспо-
экспоненты. Мы получим
где
(убJ/
_
Так как наклон графика Орнштейна — Цернике равен
тг#А> то наклоны этих графиков при разных темпера-
температурах отличаются на величину порядка (—Vi)~3/a, т. е.
прямолинейные части графиков почти параллельны. Из
уравнения D8) видно далее, что пересечение графика с
осью f(k) находится в точке bJ2ai, или
Поскольку — (y6J/3vi= G1—Гкр.)/Гкр., то видно, что с
точностью до порядка (уб) в первом приближении
f(O)~T — Гкр.; это и есть результат Орнштейна — Цер-
Цернике. Однако ближе к критической точке /@) отклоняется
вверх и, как можно показать (используя точное уравне-
уравнение D1)), f@) остается конечным при Г=ГКр-§ Это откло-
нение от теории Орнштейна — Цернике, получающееся
в нашей модели, выглядит приблизительно так, как изо-
изображено на рис. 4.
Рис. 4. График Орнштейна—Цернике, соответствующий
уравнению D7).
Наконец, обсудим кратко так называемую аномалию
удельной теплоемкости7). Хорошо известно, что в соот-
соответствии с теорией Ван-дер-Ваальса удельная теплоем-
теплоемкость при постоянном объеме постоянна ( = -jAj в од-
нофазовой области и мгновенно возрастает, если мы
переходим в двухфазовую область при фиксированной
плотности. В частности, при критическом значении плот-
плотности находим
О для Г>Гкр.,
для Т < Гкр#.
D9)
Поскольку экспериментальные данные полностью расхо-
расходятся с этим результатом (в этом и состоит аномалия),
интересно посмотреть, что дает уравнение D1) для
удельной теплоемкости. Мы исходим из уравнения
kT а0
оо
— у у9- ( уФ fdz[z + lx (-|I/2]2 [ЯоО) (z) ]2. E0)
— со
которое вытекает из общего результата [см. часть II,
D1)], если выразить П2{х; I) с помощью формулы D2).
Поскольку в критической области
мы, дифференцируя равенство A2) для H^iz) no vi в
точке U и используя уравнение состояния A5), получаем
Это показывает, что наша модель дает в критической
области поправки к удельной теплоемкости порядка й,
так что в этом смысле в нашей модели обнаруживается
аномальное поведение cv. Для дальнейшего изучения
уравнения E1) рассмотрим сначала случай /i = 0. Легко
показать, что тогда
используя результаты п. 3, находим8) для vi<C—1
а для vx
В критической области скачок теплоемкости для нашей
модели несколько сглажен по сравнению с D9), т. е. с
тем, что следует из уравнения Ван-дер-Ваальса. Рас-
Рассмотрим далее зависимость Acv от U при фиксированном
vi. Из уравнения E1) следует, что
Здесь использовано соотношение
вытекающее из уравнения A9). Уравнение E2) в точ-
точности совпадает с переписанной в новых обозначениях
термодинамической формулой
Это показывает, что при критической плотности &cv
имеет всегда экстремум, потому что (si —4) — нечетная
функция /ь так что производная d2s1/dv2l равна нулю
при /i = 0. Далее, для малых 1\
bcv = kcv (lx = 0) + l\ rrzk (dzsjdv2 dl^t = 0 + ...,
что дает при vx <C! — 1
и при vx ^> 1
Acv = bcv (I, = 0) — ^- BV/2 exp [— B^K/а] /?+...,
так что экстремум, вероятно, всегда является максиму-
максимумом. Этот максимум становится все более острым, когда
мы приближаемся к критической точке из однофазовой
области, и затем быстро уплощается при удалении в
двухфазовую область. По-видимому, ширина максимума
наименьшая при vi порядка единицы.
6. Обобщение уравнения D1)
Чтобы показать, что качественное поведение двухто-
двухточечной функции распределения в критической области
нечувствительно к изменению вида притягивающего гки
тенциала (в предположении, что он остается дальнодей-
ствуюшим), мы обобщим исследование, проведенное в
п. 4, на случай, когда притягивающий потенциал состоит
из суммы т экспонент. Поскольку формулы здесь ока-
оказываются очень громоздкими, мы приведем только на-
набросок вычислений. Как и в п. 7 части II, мы запишем
притягивающий потенциал в виде
т
= — у 5v/ exP (— v°ix)>
где Vi = ai/kT. Мы будем исходить из интегрального
уравнения Каца, перестроенного тем же способом, что
в части II, за исключением того, что мы заменяем ц на
г)кр ==г) (sKp.). Разлагая ван-дер-ваальсовское значение
vo~ 2 (v//°/) [см. часть II, G9)] и 5 по формулам E) и
G) и вводя затем точно так же, как в части II, G5) t
новые переменные ут с помощью ортогонального преоб*
разования, которое приводит к диагональному виду
матрицу
где теперь
2v;Kp.(/Kp. —6J 8v/Kp.
C =
kP.
и viKV. = ai/kTKV>.. Отсюда следует, что S^/=l» в соот-
соответствии с уравнением (80) части II, поскольку fi = 0;
из исследования, приведенного в части II, вытекает, что
наименьшее собственное значение Ат равно 0, так что
m-l
Переменная ут играет особую роль; только в этой пере-
переменной мы должны сделать второе, приспособленное к
критической области изменение уравнения Каца
ym = z/(yb)\
после чего мы получим сходящуюся схему последова-
последовательных приближений по параметру (у6I/з. С точностью
до членов порядка (уб) получаем 9)
+(V*) -^ S А'Л + Л* = 0. E3)
Это уравнение заменяет уравнение (9) до указанного
порядка. В уравнении E3) h является функцией пере-
переменных у\, t/2, ..., f/rn-ь z, и новое собственное значение
Л определяется уравнением
(т \
заменяющим уравнение A0). Наконец, величина
определяется из уравнения
г=1
и — ортогональная матрица, приводящая матрицу
А1ц к диагональному виду. Введем вместо уъ новые пе-
переменные Wh с помощью формулы
Уравнение E3) можно переписать [всегда до порядка
(уд) */з ] в виде
Это уравнение допускает разделение переменных. Легко
проверить, что уравнение E5) удовлетворяется, если по-
положить
h(wx... wm_v z) = П NHfi4 {/itwu) #@) (*), E6)
где H@)(z) и © удовлетворяют уравнению
^2 48 4 "T" б1/*
Это уравнение имеет тот же самый вид, что и уравнение
A2). Действительно, если ввести новые переменные
Z = 2|J»2/8, Vx = VjjJ,"/3, 0 = 0|Л,~/8,
/ т т-\ \
и положить H{0)(z)=ixizH(z), то уравнение E7) пре-
превратится в уравнение
\j* ?4 ,
[ fifJ2 48 ""*"
48 * 4
1+1г2 Л^ +©п ЯпE) 0, E9)
очень напоминающее уравнение A2). Разница только в
том, что из-за крайнего члена, содержащего rih, соб-
собственные значения 6П и собственные функции Нп зави-
зависят от целого множества «квантовых» чисел п=я1э
^2, . •., пт. Заметим еще, что в обозначениях E8) при
Y = HY F0)
уравнение E) для критической температурной области
может быть переписано в виде
В то же время уравнение G) для давления превра-
превращается в уравнение
[/ т
1 _3^GбJ/'-И *! -4 + | 2с<-
\ 1=1
т-\
Г ПО О ¦ Г» II 'ч
1 АС «^2 ^ •
Наконец, уравнения E4) и E6) для собственных
значений Кп можно преобразовать к виду
Из уравнения E9) очевидно следует, что наибольшее
собственное значение и соответствующая собственная
функция, для которой все множество п обращается в
нуль, подчиняются относительно переменных с крышеч-
крышечкой точно такому же уравнению, что и раньше. Поэто-
Поэтому уравнение состояния по-прежнему определяется ра-
равенством
4). F1)
где Тх определяется из уравнения
/ = 4p.[i +
аналогичного уравнению F).
Обращаясь теперь к поведению двухточечной функции
распределения при расстояниях порядка 1/y(y^)'/3 с т04*
ностью до членов порядка (убJ/з, нетрудно показать, что
и в этом случае вычисления проводятся так же, как
выше. Исходной точкой является очевидное обобщение
уравнения C4). Покажем затем, что только члены
с П\ = п2= ... = nm-i = 0 дают вклад порядка (убJ/з. По-
Поскольку в этом случае уравнение для /?0.. onm(z) то же
самое, что и уравнение A2) для Hn(z), мы получаем в
полной аналогии с уравнением D1), что в общем случае
/sL F2)
где Нп есть та же самая функция от 2, что и М0) от z
в уравнении D1) и <ЭП равно ©п, входящему в уравне-
уравнение D1) 10). Следовательно, существенное изменение со-
состоит только в том, что у заменяется на y==Y!1- Теперь,
как мы видели в части II [см. уравнение, следующее за
уравнением (85)], в критической точке
Следовательно,
так как Ci~ (adoi) A/vakT). Поэтому мы можем напи-
написать
J ^фпр.(Н)
так что 1/y есть в точности расстояние /?, фигурирующее
в теории Орнштейна — Цернике [см. часть II, G2)].
Соображения, приведенные в п. 5 и показывающие, что
первый член ряда D1) превращается в однофазовой об-
области в экспоненту Орнштейна—Цернике, можно, сле-
следовательно, в точности повторить и в общем случае.
Мы не исследовали подробно, что происходит в выс-
фих приближениях, но кажется весьма правдоподобным,
что по крайней мере качественно ничего не меняется.
7. Заключительные замечания
Хорошо известно, что преобразование Фурье экспо-
экспоненты Орнштейна — Цернике [функция g(k) из п. 5]
не зависит от числа измерений, и можно поэтому на-
надеяться, что отклонения от теории Орнштейна — Цер-
Цернике, вытекающие из нашей модели для функции g(k),
по крайней мере качественно будут такими же и в трех-
трехмерном случае. Это подтверждается результатами Хем-
мера*), которому удалось обобщить на случай трех
измерений исследование поведения корреляционной
функции при больших расстояниях, проведенное нами
в части II. Поэтому интересно выяснить, существуют ли
какие-нибудь экспериментальные указания на отклонение
от теории Орнштейна — Цернике, обсуждавшиеся в п. 5
(см., в частности, рис. 411)). К сожалению, среди экспери-
экспериментов нет еще решающего. Недавние работы Томаса и
Шмидта 12) по критической опалесценции аргона не об-
обнаруживают никаких отклонений от теории Орнштейна —
Цернике. С другой стороны, такие отклонения описаны
для различных бинарных смесей, причем выглядят они
так же, как отклонения, показанные на рис. 413). Нам
представляется чрезвычайно интересным выяснить, пока-
покажут ли более тонкие эксперименты отклонения от тео-
теории Орнштейна — Цернике, поскольку такие отклонения
вблизи критической точки, возможно, послужат более
*) Эти результаты излагаются в части IV этой статьи [Нет-
тег Р. С, IV. The pair correlation function and equation of state
lor long-range forces, /. Math. Phys., 5, 1 A964), 75—84], перевод
которой здесь не приводится. — Прим. перев.
явным указанием на существование критической обла-
области.
Что касается аномалии удельной теплоемкости, то
эксперименты14) явно показывают, что величина cv не
постоянна в однофазовой области, а имеет как функция
плотности при постоянной температуре резко выражен-
выраженный максимум вблизи критической точки. Этот макси-
максимум расположен вблизи от критической плотности, и
в этом отношении аномалия качественно согласуется с
результатами для нашей модели. Однако cv зависит от
температуры совершенно иначе. Вместо сглаженного
ван-дер-ваальсовского скачка, предсказываемого нашей
моделью, в недавних экспериментах с аргоном получи-
получилось15), что при критической плотности cv как функция
температуры имеет асимметричную логарифмическую
особенность при критической температуре. Поэтому в
трехмерном случае, по-видимому, существует как крити-
критическая область, так и критическая точка! Будет ли это
явление общим, более или менее не зависящим от меж-
межмолекулярных сил, предстоит еще выяснить.
Приложение 1. Высшие приближения собственных
функций вблизи однофазовой области
Для систематического применения теории возмуще-
возмущений к основному уравнению A2), когда vi<C— 1, пере-
переменную z лучше заменить переменной у из уравнения
B9). Уравнение A2) примет тогда вид
\~Т'
где
— - + аУ+0| К{у) =
4 J
a = ^Crf-4vO"'''(i-l+}/?-{V,). (П.2)
В качестве малого параметра выберем
Заметим, что ^/{Щ — 4VjY/2 всегда порядка единицы.
Напишем формулу (П. 1) в виде
и введем разложения
а (е) = a0 + eax + е2а
2 + .....
В нулевом порядке получим
[d W -¦|У+<зд+е@)] к{0)=о. (п. 3)
Поскольку из уравнения состояния A5) вытекает, что
для основного состояния
(П. 4)
следовательно, и осо должно быть нулем. Отсюда
Kf{y)=NnDn{y)
и (П. 5)
е(°>=я+1/2.
В первом порядке получаем
]-' (П-6)
Так как [К{п](у)]2—четная функция от у, то умножая
формулу (П. 6) на К{п] и интегрируя по у, получаем
е(,Р = О. (П. 7)
Для я = 0 получаем из (П. 6)
Так как из формулы (П. 4) следует, что
то мы заключаем, что
-—('-HP <п-8>
Уравнение (П. 2) вместе с уравнениями (П. 5), (П. 7) и
(П. 8) приводит к результатам B4) и B8) для уравне-
уравнения состояния и энергии 6П. В первом порядке поправ-
поправки к собственным функциям получаются тогда из урав-
ния (П. 6)
Во втором порядке находим
). (П.9)
откуда получаем
(П. 10)
Из формулы (П. 4) заключаем, что
+ 0О
оо
Это приводит к а2 = 0; К{п\у) затем можно определить
обычным образом и т. д.
Приложение 2. Завершение вывода уравнения D1)
Неопределенная величина /?, стоящая в левой части
равенства D0), имеет вид
+ 2 J dz Hf W (z, s+ay (Y6)'A) — Hf
—oo
+OO
2
— GO
^--1. (ail)
где подразумевается, что явно не обозначенные аргу-
аргументы собственных функций всегда равны z и s. Это
выражение можно упростить, воспользовавшись тем
обстоятельством, что
оо
2 ьп = 1.
/г = 0
Подставляя выражение C5) и используя формулу C7),
мы видим, что второй и третий члены в (П. 11) равны
так что мы получаем
«—•Ь
р +ОО
So (а) — Ео @)
Теперь вычислим So (а)—Но(О). Для этого нам потре-
потребуется уравнение для Hn](z), которое получается про-
продолжением разложения (9) до членов порядка (убJ.
Мы не будем здесь приводить явное выражение, а лишь
заметим, что общий вид уравнений для определения по-
последовательных приближений собственной функции с
2)
о2)
точностью до члена #о2) (г) такой:
(П. 13а)
(П. 136)
(П. 13в)
где вид операторов Li и L2 усматривается из уравнений
A2) и A3). Заменив 5 на s + oy(ydL\ мы не изме-
изменим Li, но изменим L2 и Lz. Мы укажем на это, записав
новые операторы в видеL2(cr),L3(а).Собственное значе-
значение So входит в Lz, и для того чтобы вычислить So (а)—
— So(O), нужно найти L3(a)—L3. Продолжив разложе-
разложение (9) до членов порядка (удJ, найдем
\U (а) - Ц Я0@) (г) = -|- г2 Яо(О) (г) - [30 (а) - 30 @)] Я0@) (г).
Таким образом,
S0(o)-S0@) = f
Ч-оо
- /
Последний интеграл можно преобразовать с помощью
уравнения (П. 13в); мы получим
+ ОО
J
— оо
4-со
_ а (f уА J dz zhp w о*.
'u)-H^]. (П. 14)
— оо
Здесь мы использовали уравнение состояния A6), соот-
соотношение
L2 (а) = L2 - а (|I/г г + Йо @) - Qo (<*) (П. 15)
и то обстоятельство, что
оо
для s' = s и s' = s-\-oy(ybI'\
Подставляя формулу (П. 14) в равенство (П. 12),
получаем
оо г +оо -|2
— оо
+ OO
4)*
D)*
f
i / dzfU0)U[H!>l\z, s + vHybj'j-HP]. (ПЛ6)
— оо
foo
Выразим теперь Н™ (г, s + oy(y6)l/*) через весь набор
функций Нп. Из уравнения (п. 136), записанного для
5 + сгу(<у6I/з вместо s, получаем
Исключим таким образом все функции ЯA) из выраже-
выражения (П. 16) для R. Снова используя формулу (П. 15) и
то обстоятельство, что L2 — эрмитов оператор, мы при-
придем к ожидаемому результату
/? 0
Приложение 3. Доказательство уравнения D3)
Мы исходим из уравнения
п2 F+; /) == -^-f f dx dy % (x) % (у) [Щ-f X
— oo
X Py(xIy, 6) exp {|(voY)'/2 (x+y)}. (П. 17)
Это уравнение является точным следствием общей фор-
формулы [см. часть II, B8а)] для преобразования Лапласа
функции п2(х;1). Чтобы показать это, умножим уравне-
уравнение B8а) части II на аехр (об) и перейдем к пределу при
а->оо. Левая часть превратится тогда в 1п2F+;1). Вос-
Воспользовавшись в правой части рядом [см. часть II, B9)]
для резольвенты Rs+o и выражением [см. часть I, (9)]
для ядра Ks+a(x,y), легко показать, что первый член
этого ряда приводит к формуле (П. 17), так как
lim oe°6ps(x, y) = e-s6Py(x\y, 6),
а-»оо
а все остальные члены этого ряда исчезают в пределе
при сг->оо.
Перестроим теперь интеграл в (П. 17) с помощью той
же самой подстановки, что и в п. 2, заменяя переменные
х, у на z и ?. Разлагая подинтегральное выражение по
степеням (убI/з и используя разложения E), F), G)
и A1) для vo, /, 5 и собственной функции Я0(г), мы най-
дем, воспользовавшись также уравнениями A5) и A6),
что до членов порядка (у6J/з
+|(Y6J/'/ dzz2(ri0)(z)f\. (П. 18)
Легко проверить, что до членов порядка (у6J/з выраже-
выражение (П. 18) эквивалентно уравнению D3).
Примечания к части III
1) Понятие критической области в отличие от критической точки
часто обсуждалось, в особенности при объяснении различных ано-
аномальных критических явлений, явным образом противоречащих
уравнению Ван-дер-Ваальса. Для ознакомления с более ранней ли-
литературой см., например, Kuenen J. P., Die Zustandsgleichung,
Braunschweig, 1907, Кар. 5, особенно по поводу того, что касается
эффектов гравитации и неоднородностей в критических явлениях.
Нам известна лишь одна попытка ввести критическую область, сле-
следуя идеям Ван-дер-Ваальса. Эта попытка предпринята Баккером
[Bakker G., Z. Physik. Chern., 49 A904), 609]. Он указывал на то,
что может существовать область температур, где толщина капил-
капиллярного слоя того же порядка, что и г//3—vl2/s. В этой области не
должно быть мениска, хотя по-прежнему существуют две фазы. Это
было указано также Майером. Ознакомиться с его рассуждениями,
которые частично формальны, а частично носят физический харак-
характер и основаны на вириальных разложениях, можно по книге
Дж. Е. Майера и М. Гипперт-Майер «Статистическая механика»,
ИЛ, М, 1956, гл. 14. Авторы заключают, что может существовать
температура Гм. < ГКр., при которой мениск должен исчезнуть,
хотя изотерма по-прежнему имеет горизонтальную часть при тем-
температурах между Ти. и Гкр.. В этой области температур изотермы
входят в двухфазовую область с горизонтальной касательной. При
этом получается такая форма кривой сосуществования фаз вблизи
критической точки, что эту область часто называют «жокейской ша-
шапочкой» Майера.
С экспериментальной точки зрения существование такой крити-
критической области пока еще спорно. Обзор недавних эксперименталь-
экспериментальных результатов см. в книге: Гиршфельдер Дж., Кертис Ч.,
Берд Р., Молекулярная теория газов и жидкостей, ИЛ, М., 1961.
См. также работу Хабгуда и Шнейдера по ксенону [Н a b g о-
od H. W., Schneider W. G., Can. J. Chem., 32 A954), 98, 164].
2) Вопрос о форме кривой сосуществования фаз вблизи крити-
критической точки рассматривался многими авторами. Гуггенхейм [G u g-
g e n h e i m, /. Chem. Phys., 13 A945), 253] указывал, что экспери-
экспериментальным данным более соответствует закон v{—v2~ (Ткр.—T)lh,
чем ван-дер-ваальсовский результат vx—v2~(Tl<v.—7")V2, который
вытекает из параболической формы кривой сосуществования фаз
вблизи критической точки. См. также Weinberger M. А.,
Schneider W. GM Can. J. Chem., 30 A952), 442, и более позд-
позднее обсуждение в работе W i d о m В., Rice О. К., /. Chem. Phys.,
23 A955), 1250. Из результата Гуггенхейма следовало бы, что в
критической точке также и (d3p/dv3)T обращается в нуль, а Цимм
[Zimm В. Н„ J. Chem. Phys., 19 A951), 1019] привел правдоподоб-
правдоподобные аргументы в пользу исчезновения всех производных в критиче-
критической точке. Однако и в этом отношении не существует достоверных
результатов.
3) Как следует из уравнения Ван-дер-Ваальса и уравнений E)
и F), в разложении G) коэффициент при члене порядка (уЬJ1з
должен быть равен (—3vi). Нетрудно также показать, что только
в этом случае мы получим сходящиеся последовательные прибли-
приближения для уравнения Каца.
4) Ср. D e n n i s о n D. M., U h I e n b е с k G. E., Phys. Rev. 41
A932), 313.
5) Kramers H. A., Ittmann G. P., Z. Physik, 58 A929),
217. См. в особенности п. 6.
6) Заметим, что уравнение кривой сосуществования фаз, полу-
получаемое из уравнения Ван-дер-Ваальса с поправкой О (у) (см.
часть I, п. 4), имеет особенность в критической точке, так что не-
непосредственная экстраполяция невозможна.
7) Мы признательны д-ру Зенгерсу, указавшему нам, что было
бы интересно изучить эту аномалию в нашей модели.
8) Эти результаты можно вывести проще, не используя урав-
уравнение E1), а непосредственно обращаясь к общему результату (см.
часть II, D1)) и используя затем уравнение D6) для п2(х; /).
9) В этом уравнении vi не следует смешивать с vi = a\lkt.
Теперь у нас будут встречаться только критические значения
ViKP. и vi всегда будет означать число, определяемое уравне-
уравнением E).
10) Эти On не следует смешивать с О, входящим в уравнение
E7), коюрое связано с © уравнением E8).
п) Вопрос о законности теории Орнштейна — Цернике вблизи
критической точки изучался, в частности, Грином [Green M. S.,
/. Chem. Phys., 33 A960), 1403] Хотя мы и не согласны с его тео-
теоретическими положениями, мы очень признательны д-ру Грину за
то, что он рассказал нам о своей работе и сообщил об эксперимен-
экспериментальных результатах, указывающих на отклонение от теории Орн-
Орнштейна — Цернике. (См. также обзор Раиса в книге Thermodyna-
Thermodynamics and Physics of Matter (Princeton University Press, Princeton,
N J., 1955, sec. E), где приводится обширная библиография.)
12) Thomas J. E., Schmidt P. W., / Chem. Phys; (в пе-
печати).
13) См., в частности, М с I n t у г е D., W i m s A., Green M. S.,
J. Chem. Phys. 37 A962), 3019,
и) Наиболее полные данные имеются для аргона, но и другие
вещества обнаруживают такое же поведение (см. L e v е 11 J. М. Н.,
Dissertation, University of Amsterdam, 1958).
15) Б а га теки й М. И., Вор о не ль А. В., Гузак В. Г.,
Журн. экспер. теор. фаз., 43 A962), 728. Мы признательны д-ру
Фишеру, указавшему нам на эту работу.
Добавление переводчика
КРАТКИЕ СВЕДЕНИЯ
О ТЕОРИИ ФАЗОВЫХ ПЕРЕХОДОВ
В КЛАССИЧЕСКОЙ СТАТИСТИЧЕСКОЙ ФИЗИКЕ
Это добавление предназначено читателю, мало зна-
знакомому с теорией фазовых переходов в классической
статистической физике и ее нынешним состоянием. Хотя
почти все сообщаемые здесь сведения разбросаны в трех
статьях Каца, Уленбека и Хеммера об одномерной мо-
модели вещества, мы предпочли кратко изложить их в од-
одном месте, чтобы тем самым несколько подготовить чи-
читателя к чтению этих статей.
Для равновесной системы, состоящей из N одинако-
одинаковых частиц с парным взаимодействием, заключенных в
сосуде объема V, постулируется1), что плотность веро-
вероятности найти эти частицы в точках Xt, ..., xN равна
— р 2 UiXi — Xj)] A)
Kj J
(распределение Гиббса),
где р=1/?Г (k — постоянная Больцмана, Т — абсолют-
абсолютная температура), U(x) =U(\x\)—потенциал парного
взаимодействия между частицами, a Z—нормирующий
множитель, равный, очевидно,
Z(V,N, p) =
/
v v
Множитель -щ- возникает из-за того, что для нас несу-
несуществен порядок частиц и мы отождествляем все распо-
расположения (а их ЛП) частиц в точках л;ь..., xNi отличаю-
1) Считается, что этот постулат асимптотически (при больших
V и N) может быть выведен из общих принципов механики в пред-
предположении эргодичности системы. Однако строгого вывода, кроме
случая невзаимодействующих частиц, до сих пор нет, и поэтому
распределение A) удобнее просто постулировать.
щиеся порядком. Функция Z(V, N, (ЗI) называется ста-
статистической суммой (или конфигурационным интегра-
интегралом) и содержит, как мы сейчас увидим, почти всю не-
необходимую в термодинамике информацию о системе.
Следует сразу же заметить, что для реальных систем
значения V и N очень велики и сами по себе не имеют
физического смысла (по крайней мере в термодина-
термодинамике). Смысл имеет их отношение -^г = р (плотность)
или обратная величина v=~r (удельный объем). По-
Поэтому функцию Z(V, N, Р) следует изучать асимптоти-
асимптотически при У-^оо и W->oo, причем "дг—^^ (v — фиксиро-
фиксировано). Этот предельный переход обычно называют
термодинамическим пределом. Оказывается, что суще-
существует предел
lim lnZ<™ »=/(«,»). B)
Функция f(v, |3) называется обычно гельмгольцевской
свободной энергией и является одной из важнейших
функций, используемых в термодинамике. Существова-
Существование предела B) предполагалось физиками очень давно,
но строгое математическое доказательство было полу-
получено сравнительно недавно2). Кроме того, была дока-
доказана выпуклость функции f(v, |3) по переменной v.
Отметим, что предел B) существует лишь при опреде-
определенных ограничениях на потенциал, а именно достаточ-
0 Строго говоря, Z(V, N, |3) зависит не только от объема, но
также и от формы сосуда. Поэтому для определенности мы будем
считать сосуд кубическим. Однако приводимая ниже асимптотиче'
екая формула для Z(V, N, р), по-видимому, справедлива для сосу-
сосудов любой формы.
2) См. Van Hove L., Physica, 15 A949), 951. В этом дока-
доказательстве имеется некоторый пробел [см. Lee T. D., Yang С. N.,
Phys. Rev. 87 A952), 404, 410]. Наиболее полное доказательство
принадлежит Рюеллу [Rue lie D., Helv. Phys. Ada, 36 A963), 183].
Р. Л. Добрушин значительно обобщил работу Рюелла и нашел по-
почти исчерпывающие условия, которым должен удовлетворять по-
потенциал, для того чтобы существовал предел B), см. Теория ве-
вероятностей и ее применения, декабрь, 1964.
но быстрый рост в нуле и достаточно быстрое убывание
на бесконечности. Принимают, что реальные потенциалы
взаимодействия между молекулами газа имеют вид,
изображенный на рис. 1 или 2.
Область левее точки а называется отталкивающей,
а правее — притягивающей частью потенциала.
Для таких потенциалов предел B) существует.
Величина р = dv называется давлением, а
уравнение p=p(v, |3) —уравнением состояния вещества.
Если на плоскости (и, р) нарисовать семейство кривых
p = p(v, p) при разных значениях р, то полученные кри-
кривые называют изотермами. Из выпуклости функции
f(v, p) по переменному v следует, что каждая изотерма
не возрастает с ростом v. Однако не исключена воз-
возможность, что на некоторых участках она горизон-
горизонтальна. Такие участки называют участками фазового
перехода. Мы ясно сознаем, что такое определение по-
покажется формальным, но в этом кратком обзоре мы
затрудняемся привести хоть какое-нибудь физическое
истолкование этому чисто математическому определе-
определению, истолкование, которое взывало бы к нашему интуи-
интуитивному представлению о конденсации. В настоящее
время, по существу, ни для какой реальной модели газа
не доказано существование (или, наборот, отсутствие)
фазового перехода, хотя известно очень много хитро-
хитроумных догадок и предположений о том, как такое явле-
явление могло бы произойти. Мы находимся в положении
того бедняка, который прекрасно знал, как истратить
миллионы, будь они у него.
По-видимому, как говорит опыт, горизонтальный
участок существует не у всех изотерм. Картина прибли-
приблизительно такая, как изображено на рис. 3. Область, по-
покрываемая горизонтальными участками изотерм, за-
заштрихована. Значение Гкр., выше которого у изотермы
нет горизонтального участка, называется критическим.
Значения ркр. и иКр- в вершине заштрихованной области
также называют критическими значениями.
Наряду с описанием системы из большого числа
частиц с помощью распределения A) (называемого
обычно каноническим ансамблем) рассматривают так
Рис. 1. Здесь U{r) = oo при Рис. 2. Потенциал без твер-
г<г0. Эта область потении- дой сердцевины, но достаточ-
ала называется обычно твер- но быстро растущий в нуле,
дой сердцевиной.
Рис. 3.
называемый большой канонический ансамбль. Здесь
предполагается, что система может состоять из произ-
произвольного числа частиц, находящихся в области (кубе)
объема V, и плотность вероятности того, что в системе
находится ровно N частиц, расположенных в точках
Хи •••, Xn, задается формулой
J] C)
где z — параметр, называемый активностью, а S— нор-
нормирующий множитель, называемый большой статисти-
статистической суммой:
s(*f р, 10 =
со
N=0
Функцию S(z, p, V) следует снова рассматривать в тер-
термодинамическом пределе У->оо. Оказывается, что при
тех же условиях относительно потенциала U(X{ — Xj),
при которых существует предел B) в каноническом ан-
ансамбле, существует также предел
К-»со v
Функция хB»Р) называется гиббсовской свободной
энергией. Существует связь между термодинамическими
функциями канонического и большого канонического
ансамблей. В частности, функции %(z, P) и f(v, p) и их
аргументы v и z связаны соотношениями
Х(г, t) = f'(v). D)
Из этих формул видно, что на участках, где f(v) строго
выпукла, z и %(z, Р) монотонно убывают с ростом v.
Если же на участке [с^2, ^i] функция f(v, p) линейна
(участок фазового перехода), то z и %(z, C) остаются
постоянными, однако при этом значении г = 20 производ-
производная %'z(z, |3) терпит разрыв:
Таким образом, в терминах функции %(z, |3) фазовый
переход связан с изломом на графике этой функции.
Сверх того делают даже более сильное допущение
относительно функции %(г, р) (р постоянно): вне лю-
любой окрестности точек излома %(z, P) можно анали-
аналитически продолжить в некоторую окрестность положи-
положительной части вещественной оси1). Поскольку функция
%(z, Р) определяется с помощью 1пН, она аналитична,
как можно показать2), в окрестности вещественной оси,
не содержащей точек, предельных для нулей функций
S(z, V). Таким образом, если при У-^оо нули S(z, V)
не накапливаются к положительной части вещественной
оси, то фазовый переход отсутствует, и , наоборот, появ-
появлением фазового перехода мы обязаны тому, что нули
Н (z, V) при V -> оо достаточно густо подходят к ка-
какой-нибудь точке на положительной части вещественной
оси. Эти соображения привели Ли и Янга к более силь-
сильной гипотезе: нули семейства целых функций В (z, V)
[для потенциала, изображенного на рис. 1, S(z,V) —
многочлен степени ~V\ при У->оо концентрируются
вдоль некоторых кривых на комплексной плоскости с не-
некоторой предельной линейной плотностью. Фазовый пе-
переход имеет место тогда, когда какая-нибудь из этих
дуг пересекает положительную часть вещественной оси.
Хотя в общем случае гипотеза Ли и Янга не доказана,
она подтверждается для некоторых моделей.
Наиболее мощным и глубоким средством изучения си-
систем большого числа частиц служат так называемые
функции распределения (или, как их еще называют,
1) Аналитичность %(z, C) доказана пока только для малых зна-
значений г. См., например, Ruelle D., Ann. Phys., 25 A963), 109—120.
2) Доказательство принадлежит А. Я. Повзнеру (устное сообще-
сообщение на семинаре в МГУ).
корреляционные функции). Они определяются так:
9s (xi> • • • > xs> V, N)= (дг__^ ^
X / • • • / ехр
, N, р) ^
5 N-s
-р
— Р 2j U(У1—
— для канонического ансамбля;
p,(*i, ..., xs; z, V) =
N=0 V V
5 TV
— для большого канонического ансамбля.
Величины ps(агь ..., *8; V9 N) [ра(хи ..., xs; г, V)]
равны плотности вероятности обнаружить s частиц
в точках хи • • •, xs при произвольном расположении
остальных частиц. Эти функции также следует рассма-
рассматривать в термодинамическом пределе (F->oo, N->oo,
дт—>1>для канонического ансамбля, и просто 1/->оо для
большого канонического ансамбля). Предполагается,
что
Р3(хц ..., xs; I/, N)->ps(Xi> '..f xs; v)
при 1/->оо,
p5(xt, ..., x5; г, 10->РЛ-*1» •••> х3т* z) пРи ^~^oo,
E)
однако строгое доказательство в настоящее время по-
получено лишь для большого канонического ансамбля при
малых значениях zl). Как обстоит дело для больших г,
не известно. Считается, что в большом каноническом
ансамбле предел E) существует для всех значений z, от-
отличных от того, при котором происходит конденсация, а
в точке конденсации z = z0 все ps(#i, ..., xs\ z) меняются
скачком. Относительно функций канонического ан-
ансамбля предполагается существование термодинамиче-
термодинамического предела E) для всех значений плотности. При
этом считают, что на участке фазового перехода [t^,^]
справедливо следующее соотношение:
ps(хх, ...,xs; v) = |хр5(хг, ...,xs; v{) + %2ps(xv...,xs; v2)
где
Кроме того, считается, что в термодинамическом пре-
пределе функции распределения большого и малого кано-
канонических ансамблей вне области фазового перехода
совпадают, т. е.
ps(xlf ..., xs; v) =
причем v и z связаны соотношением D). Однако стро-
строгое доказательство почти всех этих фактов еще отсут-
отсутствует.
Самым эффективным средством изучения функций
распределения служат связывающие их системы беско-
бесконечного числа интегральных уравнений. Таких систем
существует довольно много2). При изучении каждой
такой системы обычно применяется какая-нибудь схема
аппроксимаций, состоящая, как правило, в том, что пред-
предполагается определенная зависимость высших функций
распределения от низших. Это дает возможность обо-
оборвать бесконечную цепочку уравнений, а оставшуюся
приближенную систему решать, например, численно.
Эти методы фактически применяются и часто дают ре-
результаты, хорошо согласующиеся с экспериментальными
данными. Иногда даже в этих схемах аппроксимаций
1) См. Ruelle D., Ann. Phys., 25 A963), 109—120.
2) См., например, книгу: Фишер 3. И., Статистическая теория
жидкостей, где даны ссылки на оригинальные работы.
возникают некоторые качественные указания на суще-
существование фазового перехода, но на самом деле мы еще
слишком мало знаем о качестве самих аппроксимаций,
чтобы доверять таким указаниям.
ФуНКЦИИ рв(*ь ,.., Xs\ V) ИЛИ pe(*i, .,•, Xs] z) CO-
держат гораздо больше информации о системе, чем
уравнение состояния. Более того, уравнение состояния
можно восстановить по самим функциям распределения
[достаточно второй функции распределения p2(xi, x2)] с
помощью различных интегральных соотношений, кото-
которые называются флуктуационными и вириальными тео-
теоремами.
В заключение хочется отметить, что излагаемая в
трех предшествующих статьях модель фазового пере-
перехода, хотя и далека от реальности и никак не вскрывает
математический механизм возникновения фазового пе-
перехода (в самой модели такой механизм является очень
специальным и, по-видимому, не может быть обобщен),
хороша, как и всякая модель, тем, что может служить
пробным камнем для разного рода гипотез и связей.
Сами авторы с завидной полнотой проследили все эти
связи и проверили все, что могли проверить. Исключе-
Исключение, правда, составила гипотеза Ли и Янга, а также
проверка каких-нибудь предположений о связи между
высшими и низшими функциями распределения, на ос-
основе которых строятся приближенные схемы.
УКАЗАТЕЛЬ
Авогадро число 170, 193
Адамар 40
Айринг 221
Боголюбов 162, 233, 240
Больцман 80, 152, 222, 227
Больших чисел закон слабый 39,
219
усиленный 39, 219
Большой канонический ансамбль
130
Боненблюет 74
Борель 219
Борн 233
Броуновское движение 163, 168,
172, 193, 215
Броут 154, 160, 224, 232
Ван Хов 244
Вейль 221
Вероятность последействия 169
— условная 93, 98
Винер 194, 196, 225
Винера интеграл 197, 198, 201
— мера 194, 196, 204
Возвращения время 120, 185,
191, 228
дисперсия 122
среднее 103, 120, 190,
222
— теорема Пуанкаре 83, 189,
228
Возмущений теория 48, 53
Время возвращения 120, 185, 191,
228
— — среднее 103, 120, 190, 191,
222
— устойчивости 183
Выборочное пространство 13, 27
Герб или решетка 34
Гесс 115
Гиббс 108, 223, 228
Град 224
Грин Г. 233
Грин М. 160, 224
Дисперсия времени возвращения
122
Диффузии коэффициент 170, 193
Дуб 93, 195, 197
Зигерт 115, 224
Ивон 233
Исключенный объем 55
Канонический ансамбль 130
Карамата 62
Кац 221, 222, 232, 251
Кирквуд 214, 233
Клаузиус 80
Клейн 122, 224
Кнудсена газ 191
Колмогоров 93, 173, 194, 219.
223
Кон 244
Кривая //-теоремы 129
Крупнозернистая плотность 134
Лаплас 26
Латтинджер 244
Леви 197, 220
Линдлей 225
Лиувилля оператор 131
— теорема 84, 104, 229
— уравнение 108, 132, 154,
232
Лошмидт 82
Максвелл 16, 80, 219, 227
Марков 221
Маркова процесс 179, 185, 230
— цепь 96
Марковский характер эренфе-
стовской модели 111, 120
Марковское свойство 111, 176
Метрическая транзитивность 89
Микроканонический ансамбль 130
Микроканоническое распределе-
распределение 229, 232
Молекулярный хаос 141
Моран 221
Навье — Стокса уравнение 239,
249
Неопределенности принцип 66,
221, 258
Объемный потенциал 218
Онзагер 222
Основное уравнение 131, 134,
136, 139, 232
Оффорд 25, 219
Плотность крупнозернистая 108,
229
Потенциала теория 214, 218
Произведение мер 164, 214
Пуанкаре 228
— теорема возвращения 83, 189,
228
— цикл 88, 228
Райе 220
Распределения функции 44
Рей 209
Реньи 220
Сведберг 162
Свободные от квадратов числа
33
Сегё 73, 222
Сильное перемешивание 95
Слабый закон больших чисел 17,
39, 213
Случайные блуждания 153, 220
— процессы 91, 163, 230
Смолуховского процесс 174
Спитцер 74, 222
Статистическое равновесие 167
Тауберова теорема 62, 208
Теплицева матрица 72
Тепловое равновесие 15
Термодинамики второй закон 82,
124
Уленбек 154, 161, 223
Усиленный закон больших чисел
219
Условная вероятность 169
Устойчивости время 183
Устойчивый процесс 179, 181
Фейнман 199, 200, 251
Фейнмана интеграл 200
Феллер 221
Фредгольма определитель 77
Халмош 223
Хант 68
Центральная предельная теоре-
теорема 78
Цермело 83, 222, 228
Чандрасекар 220, 224, 243
Частичное распределение 233,241
Числа, свободные от квадратов
33
Шредингера уравнение 201, 211,
263
Штейнгауз 219
Эйнштейн 193
Энтропия 82, 122, 227
Эратосфен 28
Эргодическая теорема 223
Эрдеш 25, 219, 222
Эренфест П. 96, 222
Эренфест Т. 96, 222
Эренфестовская модель 96
Эренфестовской модели марков-
марковский характер 111, 120
Яглом 226
ОГЛАВЛЕНИЕ
Предисловие переводчика 5
От американского редакционного комитета 7
Предисловие 9
Глава I. Теоретико-вероятностный способ рассуждений ... 13
Глава II. Некоторые аналитические средства и приемы теории
вероятностей 42
Глава III. Вероятность в некоторых задачах классической ста-
статистической механики 80
Глава IV. Интегрирование в функциональных пространствах и
некоторые приложения 193
Примечания и библиография 219
Приложение I. Уравнение Больцмана. Г. Е. Уленбек 227
Приложение II. Квантовая механика. А. Я. Гиббс 251
Приложение III. Теория Ван-дер-Ваальса о равновесии между
газом и жидкостью. М. Кац, Г. Е. Уленбек,
П. К. Хеммер 271
Часть I. Изучение одномерной модели 271
Часть II. Изучение функций распределения 307
Часть III. Исследование критической области 355
Добавление переводчика. Краткие сведения о теории фазо-
фазовых переходов в классической статистической физике. . . 396
Указатель 405
М. Кац
ВЕРОЯТНОСТЬ
И СМЕЖНЫЕ ВОПРОСЫ
В ФИЗИКЕ
Редактор Н. И. Плужников а
Художник Н. А. Усачёв
Художественный редактор В. И. Шаповалов
Технический редактор А. Г. Резоухова
Корректор И. С. Цветкова
Сдано в производство 8/1 1965 г.
Подписано к печати 18/V 1965 г.
Бумага 84х108Уд2 = 6,4 бум. л.
20,9 печ. л.
Уч.-изд. л. 18,06. Изд. № 1/2600.
Цена 1 р. 41 к. Зак. 1037
Темплан 1965 г. изд-ва «МИР». Пор. № 5.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2
имени Евгении Соколовой
Главполиграфпрома
Государственного комитета
Совета Министров СССР по печати
Измайловский проспект, 29