Author: Потапов А.А.
Tags: физика электромагнетизм электромагнитное поле электродинамика теория максвелла электротехника радиотехника радиофизика фракталы
ISBN: 5-98699-015-3
Year: 2005
А.А. Потапов
КТА Ы
В Р« ДИО»ИЗИК
РАД ОЛО
Топо оги* г. .орк
A.A. Потапов
ФРАКТАЛЫ
В РАДИОФИЗИКЕ
И РАДИОЛОКАЦИИ:
Топология выборки
и
Москва
«Университетская книга»
2005
Александр Алексеевич Потапов -
видный ученый в области
радиофизики и радиолокации, распознавания и
обработки изображения,
детерминированного хаоса, современной
топологии и фрактального анализа.
Уроженец Тамбовской области.
В 1979 г. окончил физический
факультет МГУ им. М.В. Ломоносова.
Доктор физико-математических наук,
главный научный сотрудник Института
радиоэлектроники РАН.
Автор более 220 научных трудов, в том числе семи монографий.
Главный редактор журнала «Нелинейный мир».
В 2003 году избран членом-корреспондентом Академии
инженерных наук им. A.M. Прохорова и Российской академии
естественных наук.
Книга А.А. Потапова «Фракталы в радиофизике и
радиолокации: Топология выборки» представляет собой итог многолетних
исследований автора и одновременно основу для дальнейшего
изучения проблем, перспективных для развития новых направлений
физики и математики.
УДК 530.1:537.86+621.396.96
ББК 22.311
П64
Федеральная целевая программа «Культура России»
(подпрограмма «Поддержка полиграфии и книгоиздания России»)
Потапов А. А.
П64 Фракталы в радиофизике и радиолокации: Топология
выборки. Изд. 2-е, перераб. и доп. - М: Университетская книга,
2005.-848 с: ил.
ISBN 5-98699-015-3
Освещается современное состояние нового бурно развивающегося направления в
теории детерминированного хаоса - теории фракталов в приложении к радиофизике и
радиолокации. Дано введение в теорию фракталов. Рассмотрены диффузионные процессы
во фрактальных пространствах, описания фрактальных поверхностей, методы решения
задач дифракции волн на фрактальной поверхности и во фрактальных средах,
самоподобие турбулентности* молний, дождей, облаков, атмосферных аэрозолей, сложных систем,
пространственных структур геосистем в дистанционном зондировании, современные
фрактальные антенны и их синтез, пути решения проблем нетрадиционной фрактальной
обработки изображений при различных отношениях сигнал/шум и обнаружения
малоконтрастных объектов, подходы к фрактальному моделированию в космической радиофизике и
космологии. В основу изложения положен общий подход, опирающийся на идеи
фрактальной геометрии, дробного интегродифференцирования и размерностей дробного
порядка. Представлены материалы о недифференцируемых функциях и множествах, о
разнообразных типах фрактальных антенн. Отдельная глава посвящена результатам
исследований по созданию новых информационных технологий с использованием текстурных
и фрактальных мер на основе синергетических принципов нелинейной динамики.
Обновлен и уточнен перечень перспективных направлений исследований.
Для физиков, математиков, интересующихся проблемой фракталов в радиофизике
и радиолокации. Может использоваться в учебном процессе высших учебных
заведений при подготовке специалистов и магистров по направлениям и специальностям 511600
«Прикладная математика и физика», 511500 «Радиофизика».
ББК 22.311
ISBN 5-98699-015-3 © Потапов А.А., 2002, 2004
© «Университетская книга», 2005
ОГЛАВЛЕНИЕ
Предисловие 9
Введение 10
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ 15
1.1. Меры фрактальной размерности и показатели Ляпунова 15
1.2. Стохастическое описание мультифракталов 32
1.3. Вычисление на ЭВМ значений фрактальных размерностей,
показателей Ляпунова и энтропии Колмогорова 37
1.4. Экспериментальное определение фрактальных размерностей.... 47
1.5. Эмпирический закон Херста для временных рядов 54
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ
И ДИФФУЗИОННЫЕ ПРОЦЕССЫ 57
2.1. Фрактальный анализ сигналов 57
2.2. Интегралы и производные дробного порядка
во фрактальной геометрии 73
2.3. Диффузия во фрактальных пространствах 83
2.4. Недифференцируемые, или фрактальные,
функции и множества 101
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ
ПОВЕРХНОСТЕЙ 131
3.1. Пространственные спектры мощности поверхностей 131
3.2. Фрактальные размерности параметров окружающей среды 136
3.3. Фрактальные размерности микроповерхностей 139
3.4. Морская поверхность как фрактальная структура 144
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН
ФРАКТАЛЬНОЙ ПОВЕРХНОСТЬЮ 154
4.1. Модель с фрактальными высотами неровностей 154
4.2. Радиолокационные рассеивающие характеристики в модели
с фрактальными высотами неровностей 166
4.3. Модель с фрактальными наклонами неровностей 172
4.4. Индекс мерцаний при рассеянии волн экраном
с фрактальными наклонами 186
4.5. Фрактоидная модель рассеяния волн 196
4.6. Обобщенное рэлеевское решение задачи рассеяния волн
фрактальной поверхностью 208
4.7. Индикатрисы рассеяния фрактальных поверхностей
в приближении Кирхгофа 220
4.8. Рассеяние импульсов фрактальной поверхностью 233
5
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ
ТУРБУЛЕНТНОСТИ, ГИДРОМЕТЕОРОВ, МОЛНИЙ
И АТМОСФЕРНЫХ АЭРОЗОЛЕЙ 244
5.1. Фрактальность турбулентности 244
5.2. Фрактальные модели дождей и облаков 260
5.3. Компьютерное моделирование фракталами молний
в атмосфере 272
5.4. Экспериментальное моделирование
фрактальных аэрозолей и аэрогелей 279
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН
ВО ФРАКТАЛЬНЫХ СРЕДАХ 294
6.1. Плоская волна в среде
с фрактальной диэлектрической проницаемостью 294
6.2. Диапазонно ограниченная фрактальная модель флуктуации
коэффициента преломления тропосферы 299
6.3. Волновые взаимодействия в многослойной канторовой
среде распространения 308
6.4. Дифракция плоской волны на диапазонно ограниченном
фрактальном фазовом экране 325
6.5. Распространение гауссова пучка излучения
в диапазонно ограниченной фрактальной среде 338
6.6. Рассеяние звука объемными неоднородностями
с фрактальным спектром в океане 352
6.7. Дифракция волн на фрактальных зазубренных апертурах 355
6.8. Рассеяние волн частицами неоднородной формы
на основе фрактального приближения 366
6.9. Рассеяние волн диэлектрическими фрактальными волокнами 379
6.10. Поглощение и рассеяние волн скоплениями
фрактальных частиц дыма 385
6.11. Многократное рассеяние волн фрактальными средами 405
6.12. Теории катастроф и фракталов в случайных волновых полях 416
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ
СЛОЖНЫХ СИСТЕМ И КОММУНИКАЦИЙ 423
7.1. Фрактальный анализ сложных компьютерных систем 423
7.2. Метод фрактальных графов в синтезе сложных систем 433
7.3. Фрактальный характер линий железнодорожной сети
большого города 435
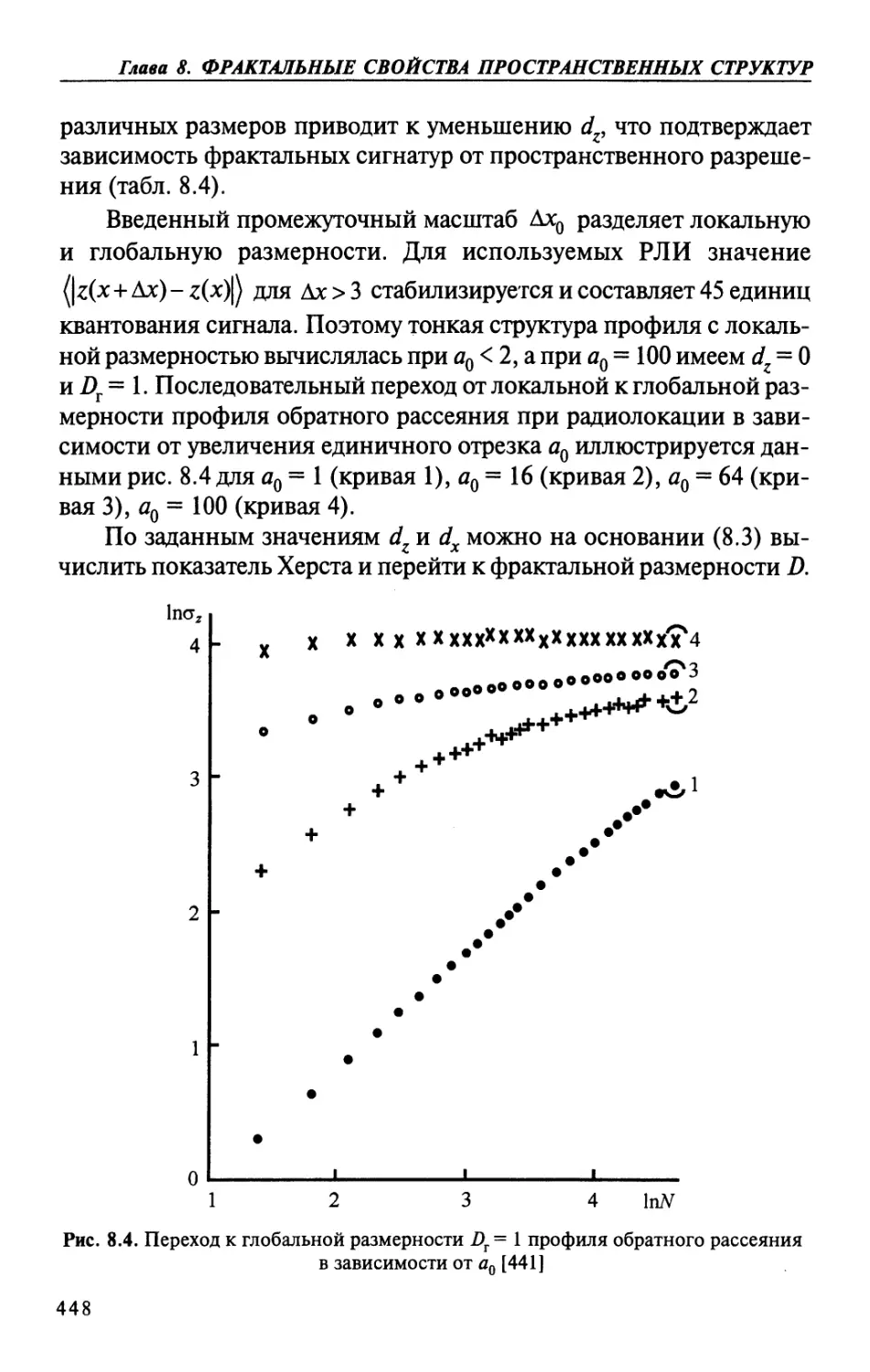
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ
СТРУКТУР ГЕОСИСТЕМ 440
8.1 Фрактальные размерности геосистем на основе
космических и самолетных снимков 440
6
8.2. Самоподобные свойства зеленых насаждений
в большом городе 452
8.3. Анализ самоподобного фрактального множества
морских льдов 455
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА
ИЗОБРАЖЕНИЙ 462
9.1. Фрактальные модели изображений земной поверхности 462
9.2. Анализ и синтез фрактальных карт местности 466
9.3. Сегментация текстур с помощью фрактального анализа 473
9.4. Фрактальная кластеризация данных
дистанционного зондирования 481
9.5. Многоуровневая фрактальная модель
для характеристики объектов 491
9.6. Различение человеком-оператором фрактальных текстур 501
9.7. Детерминированный хаос в сигнатурах
и радиолокационных изображениях земной поверхности 506
9.8. Стохастические сигналы и преобразование Радона в цифровом
радиолокаторе с фрактальной обработкой информации 521
9.9. Фрактальное обнаружение целей
на изображениях земной поверхности 541
9.10. Фрактальное распознавание целей 560
9.11. Фрактальное кодирование изображений 567
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ
В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ И КОСМОЛОГИИ 583
10.1. Кластеризация во Вселенной 583
10.2. Модель структурной функции пространственного
распределения галактик 587
10.3. Стохастический подход к кластеризации во Вселенной 591
10.4. Модификация тестов и алгоритма Мандельброта
моделирования распределений галактик фрактального типа 601
10.5. Скейлинговые свойства флуктуации космических лучей 606
10.6. Фрактальная модель солнечных пятен и роль кластеров
в их эволюции 609
10.7. Фрактальные свойства турбулентности
солнечного ветра и магнитных конфигураций 614
Глава И. ФРАКТАЛЬНЫЕ АНТЕННЫ
И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ 620
11.1. Фрактальные антенные решетки 620
11.2. Многодиапазонные фрактальные антенны Серпинского 626
11.3. Расчет фрактальных антенн на основе
7
итерационной модели линии передачи 637
11.4. Фрактальные кольцевые и эллиптические
несимметричные антенны 648
11.5. Древовидные фрактальные антенны 662
11.6. Микрополосковые фрактальные антенны
на основе снежинки Коха 665
11.7. Синтез фрактальных диаграмм направленности антенных
решеток на основе обобщенных функций Вейерштрасса 675
11.8. Синтез фрактальных диаграмм направленности линейных
антенн с использованием преобразования Фурье—Вейерштрасса... 683
11.9. Фрактальные решетки Фурье-Вейерштрасса 690
11.10. Синтез фрактальных диаграмм направленности
реконфигурируемых антенных решеток 695
11.11. Методы синтеза многодиапазонных фрактальных
антенных решеток на основе оконной фильтрации 703
11.12. Примеры синтеза многодиапазонной фрактальной
антенной решетки методами оконной фильтрации 710
11.13. Моделирование поверхностного импеданса
фрактальных структур 716
11.14. Фрактальные фотонные и магнонные кристаллы 718
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ НА ОСНОВЕ
ТЕКСТУРНЫХ И ФРАКТАЛЬНЫХ СИГНАТУР
С ИСПОЛЬЗОВАНИЕМ ПРИНЦИПОВ НЕЛИНЕЙНОЙ
ДИНАМИКИ: ЭТАПЫ СТАНОВЛЕНИЯ, РЕЗУЛЬТАТЫ 731
12.1. Некоторые актуальные задачи радиолокации и
статистической радиофизики: проблема малоконтрастных целей... 731
12.2. Текстурные меры и сигнатуры 734
12.3. Фрактальные меры и сигнатуры 740
12.4. Избранные результаты исследований по фрактальной
фильтрации малоконтрастных объектов 743
12.5. Топология выборки 755
12.6. Странный аттрактор в радиолокационном сигнале
от растительных покровов и паретианы 767
12.7. Фракталы и мультифракталы на нечетких множествах 777
12.8. Конструирование фрактальных антенн
и фрактальных частотно-селективных поверхностей и объемов .... 778
12.9. Фрактальные методы передачи информации 783
ЗАКЛЮЧЕНИЕ 785
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 788
8
ПРЕДИСЛОВИЕ
Первое издание монографии «Фракталы в радиофизике и
радиолокации» (2002 г.) быстро разошлось и получило положительную оценку среди
специалистов. Информация о монографии была размещена в рубрике
«Новые книги по физике и смежным наукам» журнала «Успехи
физических наук» (2002. Т. 172. № 4. С. 493). Результаты, полученные научным
коллективом под руководством автора в различных направлениях
фрактальной радиофизики и фрактальной радиолокации и вошедшие в
монографию, с интересом обсуждались в Институте прикладной математики
им. М.В. Келдыша РАН, Институте радиотехники и электроники РАН, на
семинаре «Информационные технологии в радиолокации» Отделения
информационных технологий и вычислительных систем РАН, Московском
электродинамическом семинаре и на НТС НИИ приборостроения им. В.В.
Тихомирова, на многочисленных международных и всероссийских
конференциях. Они были использованы в учебном процессе в Московском
государственном институте радиотехники, электроники и автоматики.
В настоящем издании, которое может, по-существу, считаться новой
книгой, исправлены неточности и замеченные опечатки. Глава 2 дополнена
материалом о недифференцируемых функциях и множествах.
Существенно переработана глава 7. Из нее выделена глава 11, которая значительно
расширена новыми материалами о разнообразных типах современных
фрактальных антенн. Включена дополнительно глава 12, в которой
приведены результаты исследований по созданию новых информационных
технологий с использованием текстурных и фрактальных мер на основе си-
нергетических принципов нелинейной динамики. В Заключении с учетом
последних идей обновлен и уточнен перечень перспективных направлений
исследований. Автор счел целесообразным расширить список литературы.
Обширная библиография даст читателям возможность ознакомиться с
различными подходами к теме, что может сыграть лишь положительную роль.
Автор надеется, что новое издание привлечет внимание широкого круга
читателей.
Автор благодарит своих коллег за научное сотрудничество и
дискуссии по обсуждаемым вопросам и хотел бы выразить особую благодарность
своему аспиранту, а теперь канд. физ.-мат. наук В.А. Герману - соавтору
большинства публикаций по фрактальной тематике. Автор искренне
признателен академику Ю.В. Гуляеву, а также членам-корреспондентам РАН
А.П. Реутову и С.А. Никитову за проявленный интерес к рассмотренным
в монографии научным направлениям, поддержку и содействие в
выполнении исследований.
Автор будет рад обсудить с заинтересованными читателями проблемы,
затронутые в книге. С этой целью можно обращаться по адресу:
125009, Москва, Моховая ул., 11, стр. 7, Институт радиотехники и
электроники РАН; электронная почта: potapov@mail.cplire.ru
А. Потапов
9
Посвящается светлой памяти
мамы — Любови Александровны,
папы — Алексея Николаевича и
тети — Зои Александровны
ВВЕДЕНИЕ
Новые знания часто изменяют наши представления о физике
привычных явлений природы. Как показывает опыт, серьезные
успехи в различных областях науки и техники являются результатом
применения новых математических идей и методов. Геометрия
природных объектов самых различных размеров - от атомов до
Вселенной - занимает центральное место в моделях, которыми мы
описываем природу. Если мы посмотрим на окружающий мир, то увидим,
что природа избегает равновесия. Для выживания система должна,
как утверждает И. Р. Пригожий, «находиться далеко от равновесия».
Большинство сложных естественных процессов моделируется
нелинейными дифференциальными или разностными уравнениями,
так как природа не упорядочена. Поэтому необходимы модели со
множеством возможных решений. Можно утверждать, что активно
развивающийся фрактальный анализ несомненно приведет к
расширению наших познаний об окружающем мире. Теория фракталов
давно уже вышла за рамки математических и физических
лабораторий. Фракталы изменяют наш взгляд на мир.
Развитие фрактальной геометрии — это одно из самых полезных
и прекрасных открытий в математике. Фракталы позволяют нам
создавать сложные природные формы путем простых итерационных
процедур. Сложность рождается из простоты. Фракталы придают
структуру и красоту хаосу. Большинство природных образований и
временных сигналов лучше всего описывается фракталами.
Поэтому нелинейность и фракталы являются геометрией хаоса. Под
хаосом понимается констатация сложности, непредсказуемости и
запутанности поведения фазовых траекторий динамической системы.
В неустойчивых системах «...совершенно ничтожная причина,
ускользающая от нас по своей малости, вызывает значительное
действие, которого мы не можем предусмотреть... Предсказание
становится невозможным, мы имеем перед собой явление случайное». Так
писал в 1908 г. А. Пуанкаре в книге «Наука и метод». Между
теорией фракталов, опирающейся на геометрию и теорию размерности, и
10
Введение
теорией хаоса, являющейся развитием теории динамических систем,
существует тесная связь.
Термин «фрактал» (от лат. frangere — ломать nfractus — дробный)
был введен в 1975 г. Бенуа Б. Мандельбротом, фундаментальные
междисциплинарные книги которого [1—3] лежат в основе
фрактального описания природы. Фрактальные модели объектов [1-4] обычно
строятся на основе различных математических алгоритмов с
использованием современной компьютерной графики [5-8].
Взгляд на мир под углом зрения фрактальной геометрии
значительно отличен от того, который трактуется евклидовой
геометрией. В евклидовой геометрии природа сведена к чисто симметричным
объектам: точке, линии, плоскости, телу. Среди тел имеется
известное число чисто симметричных форм: сферы, конусы, цилиндры с
правильной гладкой формой, без внешних неровностей. Для
евклидовой геометрии симметрия и сплошность были признаками
совершенства, которые предполагались только в природе.
В действительности природа отвергает симметрию так же, как
она не любит равновесия. Поэтому природные объекты огрубленных
форм не являются разновидностью чисто евклидовых форм.
Заслугой Бенуа Б. Мандельброта явилось обобщение кривых-монстров,
которые математики начали систематически находить со второй
половины XIX в. Данные кривые или математические тела назвали
монстрами из-за того, что они ни в одной точке не
дифференцируемы, не определяются на путях евклидовой геометрии и в свое
время рассматривались лишь как бесполезные причудливые курьезы.
Некоторые из них приведены далее в качестве иллюстраций
фрактальных кривых.
Неспособность евклидовой геометрии описывать природные
объекты можно представить следующим образом. В геометрии
Евклида с приближением своего взгляда к объекту последний
становится проще. Трехмерный параллелепипед становится двумерной
плоскостью, затем — одномерной линией и, наконец, точкой.
Природный объект дает нам все больше деталей по мере приближения
взгляда, вплоть до субатомного уровня. Таким же свойством
обладают фракталы. Чем с большей тщательностью мы их изучаем, тем
больше деталей мы сможем увидеть.
Так что же такое фрактал? Простым примером естественного
фрактала может служить дерево, ствол которого разделяется на две
ветви, которые в свою очередь разветвляются на две более мелкие
11
Введение
ветви и т.д. Можно сказать, что древесные ветви следуют
фрактальному скейлингу, или гипотезе самоподобия. В данном случае
каждое ответвление со своими собственными ветвями подобно всему
дереву целиком в качественном смысле. Поэтому вид фрактальной
структуры объекта существенно не меняется при масштабных
преобразованиях в определенном диапазоне.
Существует самоподобие пространственное и временное.
Возьмем ограниченную область евклидовой плоскости. Если ее
смять в комок, то получившаяся фигура не является двумерной, но
не будет и трехмерной. Из-за ее складок размерность будет больше
двух, но меньше трех. Поэтому говорят, и это математически
доказано, что полученное тело имеет дробную фрактальную размерность
и функция, описывающая его форму, не дифференцируема.
Фрактальная размерность описывает, как объект заполняет свое
пространство. Наш скомканный объект не заполняет полностью трехмерное
пространство, которое имеет топологическую размерность, или
размерность вложения. Следовательно, характеристикой
фрактального объекта является наличие своей собственной размерности, не
равной размерности вложения. Классические случайные распределения,
в частности белый шум, не обладают такой характеристикой.
В качестве фрактальных структур можно рассматривать,
например, линии берегов, рельеф местности, очертания облаков,
турбулентные потоки, организации живых систем, биение сердца,
кровеносную систему, молекулы веществ, странные аттракторы в фазовом
пространстве динамических систем с хаотическим поведением,
частоту слов в текстах, динамические процессы в экономике,
структуры месторождений, физические явления в решеточных
калибровочных теориях глюодинамики, дисперсные системы, объекты
голоморфной динамики, статистику ошибок при вызовах на
телефонных станциях и многое другое [9-33].
Принцип самоподобйя известен давно (тривиальный пример -
русская матрешка). Однако самоподобные структуры не
использовались вплоть до недавнего времени, когда они были как бы заново
открыты и вызвали взрыв теоретической и экспериментальной
активности. Математический формализм теории фракталов
стремительно переносится буквально на все области науки и наполняет
многие области исследований новым содержанием.
Фракталы можно разделить на детерминированные (созданные
с помощью детерминированных правил) и случайные (созданные с
12
Введение
помощью комбинации порождающих правил, выбранных наугад в
разных масштабах). Существуют фрактальные временные ряды,
обладающие трендами и являющиеся следствием
детерминированного хаоса. Во фрактальной статистике говорят о фрактальных
распределениях, к которым относятся распределения Парето, Леви и т.д.
В настоящее время тщательно изучаются мультифракталы с
показателем сингулярности Липшица-Гельдера.
Число монографий в мире о подобных исследованиях
непрерывно растет [1-3, 5-8, 18, 34—36]. В то же время в отечественной и
зарубежной литературе отсутствуют обобщающие работы по
использованию с единых позиций теории фракталов в важнейших
областях радиофизики, а именно в распространении волн и радиолокации.
Очевидно, что назрела необходимость в систематизации и
обобщении достигнутых научных результатов в этой области. В мировой
практике в связи с синтезом фрактальных антенн установился
термин «фрактальная электродинамика» [331]. В нашем более общем
случае следует говорить о фрактальной радиофизике и фрактальной
радиолокации [1011].
В предлагаемой читателю монографии сделана первая в
мировой литературе попытка последовательно и наглядно изложить
теорию фракталов, а также показать возможность решения конкретных
задач с использованием излучения и рассеяния волн фрактальными
структурами окружающей среды при их радиолокационном
зондировании.
Автор хотел показать красоту, глубину и новизну там, где ее не
ждали, - в теорий фракталов. Книга написана не о предмете,
«отлитом в бронзу». Наука о фракталах молода и бурно развивается. Не
все представления о фракталах сложились, имеются спорные
моменты. Но того, что уже надежно понято, достаточно для монографии,
а не просто для научного обзора.
Несомненно, что и после выхода книги будут появляться новые
результаты. Автор все же надеялся, что, рисуя достаточно полную
картину применения фракталов в радиофизике и радиолокации (в
принципе, во всей радиоэлектронике в широком смысле), он
облегчит читателю понимание новейших теоретических и
экспериментальных данных. Автор старался избегать, где это было возможно,
непривычных математических терминов и излишне строгих
математических формулировок. В случае необходимости их легко можно
13
Введение
восстановить по имеющимся ссылкам. При этом автор также
старался подчеркнуть междисциплинарный характер современной теории
фракталов и соблюсти баланс между математическими и
физическими методами.
При цитировании опубликованных работ не ставилась цель дать
исчерпывающий список. Тем не менее автор надеется, что
приведенный список литературы даст основу для более углубленного
изучения затронутых вопросов применения фракталов в радиофизике и
радиолокации. В ряде случаев, когда для встречающихся в теории
фракталов величин и их многочисленных приложений в
оригинальных работах используются различные символы, автор предпочитал
применять один из них, а не вводить новое обозначение. Это
привело к тому, что пришлось один и тот же символ использовать для
разных величин. Впрочем, смысл употребляемых символов всегда
ясен из контекста.
По существу, книга замкнута. Все необходимые факты
приведены в соответствующих главах. Конечной целью автора является
привнесение в классическую радиолокацию и некоторые области
радиофизики тех понятий и современных методов
функционального анализа, которые связаны с теорией множеств, общей
топологией, теорией размерности и геометрической теорией меры.
Глава 1
ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
1.1. Меры фрактальной размерности
и показатели Ляпунова
Топологическая размерность. Основным свойством фракталов
является нецелое значение их размерности, которая отличается от
топологической размерности фрактала.
Приведем два основных определения топологической
размерности множества А — индуктивную размерность ind А и
комбинаторную размерность dim A.
Индуктивная размерность ind А задается целым числом п > — 1.
При определении индуктивной размерности используется
индуктивная размерность множества Л в точке р, которая обозначается
символом ind А и принимает также целые неотрицательные значения.
Индуктивная размерность определяется тремя аксиомами:
1) равенство ind А = — 1 означает, что множество А пусто;
2) если множество А не пустое, то его индуктивная размерность
равна верхней грани значений ind А для всех точек/? из множества А;
3) неравенство indpA<(n+ I) означает, что в каждой
окрестности точки р содержится окрестность точки р, граница которой
имеет размерность меньше либо равную п.
Пустое множество имеет по определению размерность —1.
Множество нульмерно, если каждая его точка обладает произвольно
малыми окрестностями с пустой границей. Примерами нульмерных
множеств являются каждое непустое конечное или счетное
множество; множество действительных рациональных чисел; множество
действительных иррациональных чисел; любое множество
действительных чисел, не содержащих никакого интервала; множество
точек «-мерного векторного пространства, все координаты которых
рациональны [37, 660].
Комбинаторная размерность для множества А определяется
посредством кратности покрытий. Размерность dim А множества А есть
наименьшее число п, такое, что при любом малом числе е > 0
найдется замкнутое покрытие кратности < п + 1.
15
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Для любого множества справедливо неравенство
6im{A U В) < dim A + dimB +1,
и любое «-мерное множество может быть представлено как сумма
меньшего числа нульмерных множеств.
Основная теорема теории размерности гласит, что для
метрических пространств индуктивная и комбинаторная размерности
одного и того же множества совпадают:
dim A = ind A.
Любое метрическое со счетным базисом множество А
размерности dim А < п можно топологически включить в евклидово
пространство Е с dim (2л + 1). Число (2п + 1) невозможно понизить,
т.е. включить произвольное «-мерное пространство в евклидово
пространство Е2п.
Между топологическим понятием размерности и метрическим
понятием меры существует тесная связь, так как пространство
размером п должно иметь положительную «-мерную меру. Обратное,
однако, неверно.
Дробная размерность. Понятие дробной размерности опирается
на анализ понятия целой евклидовой 2? или топологической
размерности /)0. Фракталы можно рассматривать как множества точек,
вложенных в пространство. В частности, точка имеет
топологическую размерность DQ = 0. Гладкие кривые - окружности, прямые и
т.п. - имеют евклидову размерность D0 = 1. Размерность
поверхности D0 = 2, объемных тел D0 = 3, гипертел — более высокие
значения DQ.
Развитие теории размерности началось с работ Пуанкаре, Лебега,
Брауэра, Урысона и Менгера [37]. Для характеристики фрактальных
множеств были предложены различные определения типа
размерности [37-41]. Их можно подразделить на две группы:
характеристики меры, полученные из чисто геометрических соображений, и
характеристики, связанные с теорией информации [817].
Понятия фрактальной меры и фрактальной размерности
множеств, характеризующих их в целом, базируются на определениях,
введенных Хаусдорфом [42] и Безиковичем [43]. Первоначальное
пробное и формальное определение Мандельбротом фракталов [1—3]
относит к ним множества, размерность Хаусдорфа—Безиковича Dko-
16
7.7. Меры фрактальной размерности и показатели Ляпунова
торых строго больше их топологической размерности. Данному
определению можно придать конкретный физический смысл. Оно
характеризует усложнение множеств. Если это кривая, то ее можно
усложнять путем бесконечного числа изгибаний до такой степени, что
ее размерность достигнет двух, если она плотно покроет конечную
площадь.
В дальнейшем Мандельброт дал второе, менее общее
определение фракталов как структур, состоящих из частей, которые в каком-
то смысле подобны целому [3, 44, 45].
Строгого и полного определения фракталов пока не существует
[44]. Первое определение позволяет различать категории «гладкий»
и «хаотичный». Слабость этого определения в том, что не удается
различить категории «нерегулярный, но самоподобный» и
«геометрически хаотический». Это происходит вследствие того, что
понятие фрактальной размерности, по Хаусдорфу, является весьма
общим. Второе определение более физично и наглядно. Оно
подчеркивает существенный отличительный признак, наблюдаемый в
эксперименте, - фрактал одинаков в любых масштабах наблюдения.
Определение меры Хаусдорфа опирается на математическую
абстракцию практического способа измерения длин, площадей и
объемов, когда измеряемый объект покрывается эталонами с
определенными мерами. Для обычных объектов оценки мер сходятся при
предельном переходе к асимптотике, являющейся истинной мерой
объекта.
Для некоторых объектов (множеств) такие оценки не сходятся
либо дают нулевой результат. По Хаусдорфу, обобщение меры
заключается в том, что эталоны могут быть любыми множествами Ai из
некоторого класса, а приписываемая им мера определяется любой
неотрицательной функцией 1{А^ множеств из указанного класса. В
частности, пусть /(Л/) = (сИату1/)а,где diam^. - диаметр множества
Aj. В этом случае мера Хаусдорфа называется а-мерой (линейной при
а = 1 или плоской при а = 2).
Дадим точное определение размерности Хаусдорфа-Безикови-
ча. Пусть совокупность множеств Ai с диаметрами diamAi < г, где £ —
действительное число, образует счетное покрытие множества X.
Тогда для каждого £ > 0 определим mzd =inf ^(diam^.)^.
1 7
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Положим md{A) = supm%(A). Тогда, по определению размернос-
£>0
ти Хаусдорфа—Безиковича, D— это точная верхняя (sup) грань
множества таких действительных чисел d, для которых md(A) > 0.
Важно подчеркнуть, что D — не обязательно целое число и D не
является топологическим инвариантом, так как она зависит от метрики,
введенной на данном множестве. Однако нижняя грань (inf) для всех
Д соответствующих всем метрикам на данном множестве, есть его
топологическая размерность: inf D(A) = dim A.
Классические фрактальные множества. На практике фрактальную
размерность часто определяют через клеточное разбиение. Полностью
покроем данное множество А конечной системой замкнутых
множеств At с диаметрами diamyl/ < £. Определим минимальное число
_V(e) таких множеств для каждого е. Очевидно, что _V(e) > 0 для всех
£ > 0 и неограниченно возрастает при £ > 0, если только А не
состоит из конечного числа точек.
Предположим, что существует такое положительное число С, для
которого справедливо неравенство N(e) > С/гг для любого £ > 0, где
г— некоторое целое число. Тогда
D = liminf
е->0
Размерность Хаусдорфа, рассчитанная с использованием
формулы (1.1) для некоторых известных фрактальных множеств, приведена
в табл. 1.1.
Таблица 1.1
Хаусдорфова D и топологическая 2>0 размерности некоторых фрактальных
множеств [2, 3, 37, 45, 46]
1 Фрактальное множество
1 Канторово множество
(канторова пыль)
[Триадная кривая Коха
Кривая Мандельброта-Гивена
Салфетка Серпинского
Ковер Серпинского
Кривая Госпера
Универсальная кривая Менгера
D
1п2/1пЗ = 0,63
1п4/1пЗ«1,26
1п8/1пЗ-1,89
1пЗ/1п2-1,58
1п8/1пЗ«1,89
1пЗ/1п>/7«1,13
In 20/ In 3« 2,73
А
0
_________—1
logiV(e)
loge
(1.1)
18
1.1. Меры фрактальной размерности и показатели Ляпунова
Канторово множество, названное в честь Георга Кантора [37],
открывшего его в 1883 г., позволяет сформировать фрактальное
множество с размерностью 0 < D< 1. На рис. 1.1, а показана процедура
образования триадного множества, называемого канторовой пылью.
«Затравкой» служит единичный отрезок [0,1], разбиваемый на 3
одинаковые части. Образующий элемент удаляет среднюю треть. Затем
образующий элемент применяется к каждому из оставшихся
отрезков и т.д. Первые 5 поколений S отрезков приведены на рис. 1.1, а.
Сумма длин L удаленных отрезков в точности равна единице:
Т 1 2 4
Z=3 + 9 + 27 + -
1 °°
Г1\п
= 1.
\ J
(1.2)
II II
II II
II II
II Щ
II II
II II
а)
15 = 0
15 = 1
■ 5=2
■ И5=3
II 115=4
II 115=5
л=0
Рис. 1.1 (начало)
19
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Рис. 1.1. Этапы построения канторова множества (а), кривой Коха (б),
кривой Мандельброта-Гивена (в), салфетки (г) и ковра Серпинского (д)
Кривая на рис. 1.1, £ первоначально была описана Хельге фон
Кохом в 1904 г. [47]. «Затравкой» служит единичный отрезок,
являющийся нулевым поколением кривой Коха. Разделив отрезок на 3
части и выбрав среднюю часть, вместо нее строим две стороны
(длиной 1/3 каждая) равностороннего треугольника. Таким образом
получаем четыре звена длиной 1/3 каждое - первое поколение (п = 1).
Затем повторяем этот процесс на каждом звене ломаной еще и еще
раз. Кривая «-го поколения при конечном п называется предфрак-
талом с общей длиной (4/3)л и протяженностью каждого звена е = 3~л
при числе звеньев АГ(е) = 4я = z~D. В предельном случае нигде не
дифференцируемая непрерывная кривая Коха является линией бес-
20
1.1. Меры фрактальной размерности и показатели Ляпунова
конечной длины, ограничивающей конечную площадь на плоскости
(снежинка Коха).
Последовательные этапы построения кривой Мандельброта—
Гивена изображены на рис. 1.1, в. Образующий элемент делит
прямолинейный отрезок на части длиной по 1/3 и соединяет их в
петлю, к которой пристраивают две ветви. При каждом повторении
образующий элемент заменяет каждое прямолинейное звено в
предфрактале на Лг= 8 звеньев, уменьшенных на 1/3.
Построение треугольной салфетки и ковра Серпинского (1915 г.)
показано соответственно на рис. 1.1, г, д. В первом случае
«затравкой» служит треугольник со всеми внутренними точками, а во
втором - квадрат. На каждом следующем этапе треугольник в
салфетке Серпинского заменяется тремя треугольниками, уменьшенными
с коэффициентами 1/2.
Для ковра Серпинского образующий элемент состоит из N= 8
квадратов с коэффициентом сжатия 1/3. Справа на рис.
1Л,г,дпоказаны 4-е поколения предфракталов. Их бесконечное множество
поколений порождает фрактальную кривую. В этом случае черные
участки исчезают, а полный периметр дыр в ковре Серпинского
становится бесконечным. Ковер Серпинского является аналогом канторова
множества на квадрате. Универсальная кривая Менгера (см. табл. 1.1)
является аналогом канторова множества на кубе.
Разрывное канторово множество можно использовать для
построения непрерывной фрактальной функции, интегрируя какую-либо
функцию распределения. Пусть мы как-то распределили единичную
массу на интервале 0 < х < 1. При перераспределении массы на
оставшихся интервалах с каждым этапом плотность массы р (х)
возрастает на укорачивающихся канторовых отрезках, а полная масса
равна 1. Для л-го поколения число интервалов длиной (1/3)л равно 2п,
а плотность рп = (3/2)". Запишем массу на отрезке [0, х] при п -> ©о
X
в виде Af(x)= \p(x)dx, где плотность в промежутках р(х) = 0 и
о
р(х) -> оо на всех бесконечно многих точках канторова множества.
Масса М (х) = const на интервалах, соответствующих пустым
промежуткам, длина которых, согласно (1.2), равна 1. Отсюда можно
заметить, что М(х) = 0, и это было бы правильно для обычной,
гладкой кривой. Но масса возрастает скачками на точках канторова
множества, и эти скачки дают М(1) = 1. На рис. 1.2 показана одна из
21
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
О 0,2 0,4 0,6 0,8 1,0
Рис. 1.2. Масса триадного канторова множества Мп (х)
в зависимости от координаты х [48]
промежуточных функций Мп (х), называемая «чертова лестница»,
которая почти всюду горизонтальна. Выражение dM(x)/dx определяет
набор дельта-функций. Причины возникновения чертовой
лестницы во многих физических системах изложены в [48].
Отображения на плоскости. Другими примерами множеств с
фрактальной размерностью служат множества, возникающие при
отображениях, известных под названиями «преобразование пекаря» и
«подкова» [24,49, 50]. Первое отображение получило свое название
потому, что оно напоминает действия пекаря, раскатывающего кусок
теста, - раскатывание, растягивание и перекладывание (рис. 1.3, а, б).
«Преобразование пекаря» задается следующими формулами:
\К\ принес,
Хп+1~[2+Хьхп принес,
[уJ а принес, (1.3)
У -\ 1
U 0>л~а) принес.
11-сс
Здесь 0 < хп < 1, 0 < уп < 1, а < 1, Ха и Хь — числа, связанные с
показателями Ляпунова, служащими мерой экспоненциального разбега-
ния со временем двух соседних траекторий в фазовом пространстве.
22
L1, Меры фрактальной размерности и показатели Ляпунова
Для существования хаоса в динамической системе необходимо
условие X > О. Кроме того, показатель Ляпунова определяет среднюю
потерю информации за одну итерацию. Объект, получаемый путем
многократного воздействия этого отображения на единичный
квадрат, является странным аттрактором. Если обычное
«преобразование пекаря» (рис. 1.3, а) относится к классу обратимых отображс -
©
Ф
Q
Р
а)
У„
УпН
I—I /
хп+\
аши
Рис. 1.3. «Преобразование пекаря» (д), диссипативное «преобразование пекаря»
(б) и отображение «подкова» (в) [24]
ний, сохраняющих площадь (консервативные системы), то
диссипативное «преобразование пекаря» (рис. 1.3, б) не сохраняет площадь.
Под аттрактором понимают множество точек, или
подпространство в фазовом пространстве, к которому приближается траектория
после затухания переходных процессов [51]. Хаусдорфова размер-
23
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
ность множества, полученного посредством «преобразования
пекаря», при условии ка=Хь = Х на основании (1.1) равна
и не зависит от а.
При преобразовании типа «подкова» нижняя половина
прямоугольной области растягивается в одном направлении, сжимается в
поперечном направлении и отображается на вертикальную полоску
в некоторой части левой полуплоскости. Аналогичные операции
проводятся и с верхней половиной той же прямоугольной области,
которая отображается на правую полуплоскость. Процесс напоминает
преобразование исходной площадки в подковообразное множество,
отсюда и название (рис. 1.3, в).
Последовательные итерации порождают в фазовом пространстве
сложные орбиты, потерю информации о начальных условиях и
хаотическое поведение с фрактальными свойствами. Преобразование
типа «подкова» аналогично «преобразованию пекаря», и его
фрактальная размерность также определяется формулой (1.4).
Теория итераций рациональных отображений комплексной
плоскости в себя дает множество изображений семейств фракталов
[3,6,44]. В первую очередь сюда относятся множества Жюлиа и Ман-
дельброта, фрактальные границы которых совпадают с границами
областей притяжения аттракторов в фазовом пространстве [797].
Первые измерения фрактальной размерности. Определение
размерности Хаусдорфа требует предельного перехода к бесконечно
малым объемам. При физических измерениях такое определение
использовать невозможно, так как различные физические системы
обладают минимальными характерными размерами. Поэтому
предельный переход в формуле (1.1) заменяется измерением углового
коэффициента, или наклона графика In N(e) как функции от lne.
В одной из первых работ по фрактальной геометрии [52]
именно так и измерялись длины Цг) береговой линии (рис. 1.4). Здесь
же нанесены данные о береговой линии Норвегии [45]. Длина
границ измерялась как функция раствора циркуля. Граница N
аппроксимируется прямоугольными отрезками длиной £. При уменьшении
раствора циркуля £ число отрезков возрастает. Общая длина
аппроксимирующей ломаной L = N(z)£.
24
1.1. Меры фрактальной размерности и показатели Ляпунова
ЬДе) I 1 1 Г
Рис. 1.4. Длина береговой линии или сухопутной границы как функция
выбранного шага е [45, 52]: 1 - Португалия, D = 1,14; 2 - Великобритания, D = 1,25;
3 - Германия (1899 г.), D= 1,15; 4 - Южная Африка, D - 1,02;
5 - Австралия, D = 1,13; 6 - Норвегия, D = 1,52+0,01; 7 - окружность, D = 1
Длина обычной кривой N ~ е-1, или N = a/e, поэтому а - мера
длины границы. Но для фрактальных кривых N = ae~D.
Следовательно,
L(e) = ae1-D. (1.5)
Здесь D является внутренней фрактальной размерностью.
Полученные данные (см. рис. 1.4) хорошо описываются формулой (1.5).
Угловые коэффициенты всех прямых равны (1 — D). Для окружности,
как и следует ожидать, D=l.
Физическое определение фракталов должно включать свойство
самоподобия, что и отмечено Мандельбротом во втором
определении фракталов. Самоподобные фракталы обладают свойством
масштабной инвариантности, или скейлингом, и инвариантностью
относительно параллельного переноса. Есть ряд других множеств
точек, не обладающих такими симметриями. Например, окружность
не инвариантна ни относительно скейлинга, ни относительно
параллельного переноса, а инвариантна относительно поворота вокруг
собственного центра [45].
При случайном характере фракталов понятие самоподобия имеет
статистический смысл. Статистические характеристики структуры
фрактала будут сохраняться при преобразовании подобия.
25
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Отрезок прямой, прямоугольные плоскости и параллелепипед
можно покрыть их уменьшенными копиями с коэффициентами
подобия г, если выбрать соответственно
rx{N) = \/N9 r2(N) = (l/N)l/2, r3(N)=(l/N)l/3>
где N- любое целое число. В общем случае r(N) = (l/N)l/Dl.
Тогда размерность подобия D{ определяется выражением
Для самоподобных фракталов размерность Хаусдорфа равна
размерности подобия: D= Dv
Меры фрактальной размерности. Дополнительно к размерности
Хаусдорфа введем понятие поточенной размерности D2 [50, 53]. Для
этого на какой-нибудь траектории в фазовом пространстве сделаем
достаточно большую выборку точек. Опишем вокруг точки на
траектории сферу радиуса г и подсчитаем число выбранных точек N (г),
попавших внутрь сферы. Для полного набора выборочных точек N0
вероятность нахождения выборочной точки внутри сферы
P(r) = N(r)/N0.
При г^О и N0-*°° вероятность Р(г) линейна: P(r)~br или
квадратична: P(r)« br1 no r соответственно для одномерных орбит
или двумерной тороидальной поверхности. Тогда размерность
траектории в точке xi равна доле времени, проводимой траекторией
внутри малой сферы:
logffos,)
r"-i0 logr
Z)2=lim ьлу ' . (1.7)
При зависимости D2 от xi используется усредненная поточеч-
ная размерность D2 = — £l>2 (xt), где М< N0 - множество точек, в
каждой из которых вычисляется D2(xt).
Можно производить усреднение и вероятностей P(r,xf). Для
этого выбирается случайное подмножество из Af точек (M<cN0) и
предполагается, что
26
7.7. Меры фрактальной размерности и показатели Ляпунова
**±tnr«).*b или A = UmMZ£)IW
/■->о М £f г->о log r
Иногда операцию усреднения проводят по радиусам сфер или
размерам кубов в фазовом пространстве, содержащем одно и то же
количество точек N В различных точках {xj определяют rt(N) и
берут среднее по п точкам отсчета:
ni=l
При этом предполагается, что выполняется закон подобия
N = c(r)^.
Фрактальная размерность, называемая корреляционной,
успешно применяется экспериментаторами [24, 39, 50, 54-57]. Она
определяется корреляционным интегралом
который оценивается непосредственно для последовательности
точек. Здесь | xi - х • | — расстояние между парами точек xt и х ; 0 —
функция Хевисайда.
Для многих фракталов корреляционный интеграл зависит от г
при г -> 0 по степенному закону, т.е.
С(гЬА (1.9)
поэтому фрактальную корреляционную размерность D3 (или
корреляционный показатель v = D3) определяют по наклону прямой
графика lnC(r) = /(lnr).
Фрактальный кластер. Следующее определение размерности
фрактала связано с понятием фрактального кластера [18, 39,45, 54].
Под фрактальным кластером понимают систему взаимодействующих
частиц, которая обладает свойством масштабного самоподобия в
интервале размеров г, где 7^ «: г «: R. Здесь i^ - масштабная единица
измерения линейного размера R кластера.
27
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Суммирование в формуле (1.8) по двум индексам дает среднее
число частиц (п(г)), попадающих в r-окрестность: С(г)«(п(г)). Тогда
с учетом (1.9) можно записать:
(n(r))~rD*, (1.10)
а фрактальная размерность кластера определяется из (1.9) и (1.10) как
предел
Л ,. In С(г) -. Ып(г))
A=hm—-^ = lim ) ч. (1.11)
4 r->o In г г->о In r
Фрактальная размерность кластера является количественной
характеристикой заполнения им пространства. Масса М
фрактального кластера и число частиц N в нем определяются следующими
асимптотическими формулами:
M^m^R/R,)*; N^N^R/ltf4, (1.12)
где т0 — число составляющих фрактальный кластер частиц; NQ —
плотность числа частиц или мономеров в кластере. Плотность
фрактального кластера есть отношение числа частиц на радиусе R к
объему пространства, в котором фрактал находится:
p-iR/R^/iR/Mjb-iR/Bif*-*, (1.13)
где D0 — минимальная топологическая размерность пространства,
вмещающего кластер.
Как следует из формулы (1.13), плотность фрактального
кластера при увеличении его размеров убывает по степенному закону. При
D4 < D0 плотность фрактального кластера асимптотически (при
Ry>RQ) стремится к 0, т.е. частицы сосредоточиваются на все
меньшей части пространства. Поэтому фрактальная размерность
множества частиц (точек) служит мерой его прореженности.
Одновременно данное обстоятельство обусловливает значительную роль
флуктуации во фрактальном кластере. Из (1.13) также видно, что
плотность кластера в среднем постоянна, если только фрактальная
размерность D4 равна евклидовой размерности пространства, в
которое вложен кластер.
28
1.1. Меры фрактальной размерности и показатели Ляпунова
При исследовании свойств кинетики агрегации частиц,
газообразования и осаждения [45] обычно используют массовую
фрактальную размерность (см. формулу (1.9)). Для самоподобных фракталов
все рассмотренные размерности примерно совпадают.
Самоподобие и самоафинность. Анализ фрактальных структур
показывает, что необходимо различать фракталы самоподобные и
самоаффинные. Рассмотрим основные положения о самоподобных и
самоаффинных множествах [3, 45, 58, 59].
Ограниченное фрактальное множество точек А самоподобно с
отношением подобия г, если А является объединением N
неперекрывающихся подмножеств AVA2,A3,..., AN, каждое из которых
конгруэнтно множеству г (А), получаемому из А преобразованием
подобия с 0 < г < 1. Свойство конгруэнтности означает, что множество А(
совпадает с множеством г (А) после переноса и/или поворота. Тогда
гомотетическая размерность примет вид
Множество А статистически автомодельно, если оно является
объединением N отдельных подмножеств, каждое из которых
получено из А преобразованием подобия с коэффициентом г(0<г<1)и
обладает такими же статистическими свойствами, что и г (А).
Аффинное преобразование переводит точку х = (x{,...,xN) в
новую точку с координатами х' = (rlxl9...9rNxN), где не все
коэффициенты подобия r{,...,rN одинаковы. Ограниченное множество Асшо-
аффинно по отношению к вектору подобия г = (r{,...,rN), если А
является объединением #непересекающихся подмножеств Av ..., AN,
каждое из которых конгруэнтно множеству г (А), полученному из А
с помощью аффинного преобразования, которое определяется
вектором г.
Множество А статистически самоаффинно, если Л является
объединением ^непересекающихся подмножеств, каждое из которых
получено из исходного множества аффинным преобразованием с
помощью вектора подобия г и имеет в точности те же статистические
свойства, что и г (А). Примером самоаффинного фрактала является
траектория классического винеровского процесса броуновского
движения, так как координаты времени и смещения входят в соотно-
29
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
шение подобия с разными коэффициентами. Примером
самоаффинного фрактала служит также функция «чертова лестница» (см. рис. 1.2).
Информационные размерности и мультифрасталы. Более сложные
объекты — мулыпифракталы — являются объединением фракталов
различных размерностей и имеют более нетривиальные свойства, чем
непосредственно фракталы [3, 45, 59, 60]. Рассмотренные ранее
самоаффинные множества также принадлежит к мультифракталам. Для
характеристики таких структур вводятся в рассмотрение различные
информационные размерности, которые чувствительны к неодно-
родностям рассматриваемых множеств [39-41,53,54,61-63]. Одним
из наиболее содержательных описаний информационных
размерностей служат обобщенные размерности Реньи разных порядков [64, 65].
Предположим, что случайное множество точек разбито на ячейки
размером £ и пусть Pi (г) - вероятность попадания в /-ю ячейку.
Согласно [64, 65], обобщенные энтропии Kq (г) определяются
следующим образом:
Kq(z) = L^(z)\/(l-q), (1.14)
где q = 0, 1, 2, ..., п. При q -> 1, полагая #=1+г|иг|^0, получаем
Соответственно, размерности Реньи определяются как
fl*=-lm*(e)/lne. (1.15)
4 е-»0 н
При таком определении размерность Реньи D^ совпадает с
размерностью Хаусдорфа рассматриваемого множества. Размерность D*
называют информационной размерностью, a D*2 — показателем кор-
N
реляционного интеграла (1.8), так как С(г) = ^/)2(е).
/=о
Размерности Реньи удовлетворяют неравенству D* > D* при
р > q. Равенство достигается только для однородных множеств, в
которых вероятность Р. удовлетворяет закону подобия /?Де) ~ гв , где
D — любая размерность.
30
7.7. Меры фрактальной размерности и показатели Ляпунова
Поскольку прямое вычисление размерностей Реньи в общем
случае практически не осуществимо из-за недостаточного объема
памяти современных компьютеров и отсутствия статистической
сходимости, в [62, 63] был избран другой подход. Он основан на
континууме размерностей D{y) - функция размерностей),
определяемом через моменты (8у(л)) распределения Р (8, п) попарных
расстояний 8(h) между ближайшими соседями среди п точек фрактала:
оо
(Щп)) = Му(п) = j P(8, n) db = Kn~^D^\
о
Оказывается, что при y=D(y) значение функции размерности
совпадает со значением размерности самоподобия, по крайней мере
для автомодельных фракталов. Для этого же класса систем
доказано общее соотношение D[y = (l-q)D*}=D*. Поэтому вычисление
моментов (8у(я)) позволяет рекуррентно определить любые
размерности Реньи.
Как показано в [39, 54], информационная D[ и
корреляционная D3 размерности ограничивают хаусдорфову размерность D
снизу, т.е. D3<Di<D = D*0.
Показатели Ляпунова и фрактальная размерность. Значения D\\
показатели Ляпунова X динамических систем связаны между собой
обобщенной формулой Каплана-Йорка [40, 66] вида
ь,
^ = 7+1?Ч- (1Л6)
1*7+11
Здесь показатели Ляпунова упорядочены Х{ > Х2 >... > Хп, так что j
- наибольшее целое, для которого £х. > 0 . Для двумерного отобра-
/=о
жения [49] имеем D = \-Xx/Xr
Хотя формула (1.16) частично использовалась для некоторых
систем (табл. 1.2), определение границ ее применимости остается
актуальной задачей.
При оценке размерности аттрактора используют также
соответственно: формулы Мори и Янга:
3 1
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Таблица 1.2
Проверка гипотезы Каплана-Йорка [67]
Система
Отображение Хенона [68]
с внешними параметрами:
а= 1,2; Ъ = 0,3
а= 1,4; 6 = 0,3
Отображение Заславского
[69] (подталкиваемый
ротатор)
Значение Д полученное
численным расчетом
1,20210,003
1,26110,003
1,38010,007
по формуле (1.16) |
1,20010,001
1,26410,001
1,38710,001
т
ЪЧ
где А+ - положительные показатели Ляпунова, т - их число; Х\ -
отрицательные показатели Ляпунова, / - их число; к - число
неотрицательных показателей Ляпунова; \ > Х2 >... > Хп.
Очевидно, что М <Y <D. Показательно, что геометрия и
динамика странных аттракторов тесно связаны: по показателям
Ляпунова можно судить о геометрии аттракторов, а измеряя их
фрактальную размерность, можно получить сведения о значениях Ляпунове-
ких показателей системы.
1.2. Стохастическое описание мультифракталов
Стохастический анализ. Более общим подходом является
стохастическое описание мультифракталов. Рассмотрим основные
свойства мультифрактальных полей на основе процесса случайного
дробления больших структур на меньшие [60]. Данная модель
стохастического описания мультифракталов подходит для описания переноса
энергии от больших вихрей к малым в турбулентной жидкости, где
роль поля \\fx играет плотность потока энергии.
Многомасштабность поведения поля ^ при масштабном
соотношении Х = L/1 (Ln I - соответственно наибольший и наимень-
32
12. Стохастическое описание мультифракталов
шии рассматриваемые линейные масштабы в исследуемой среде)
может характеризоваться распределением вероятностей
Р(ух>ХУ)~Х~сМ (1.17)
или связанным с ним через преобразование Лапласа законом доя
моментов порядка q:
(\р*)«АЛ<*> «\X^X-C^dc(i). (1.18)
В соотношениях (1.17) и (1.18) показатель с (у) называется
коразмерностью, так как распределение вероятностей определяет долю
вероятностного пространства, занятого сингулярностями,
превышающими число у. При масштабном соотношении у данную
вероятность можно оценить как отношение числа Nx(y) соответствующих
структур к общему числу структур Nx :
PtoxbV)~Nx(y)/Nk. (1.19)
Геометрическая интерпретация коразмерности с (у) возможна при
D > с (у), где D— евклидова размерность пространства, в которое
вложено исходное множество А. В этом случае NX~XD и Nk(y) ~ XD^ с
положительной D(y), которая тогда является обычной фрактальной
размерностью.
Проинтегрируем поле ух по D-мерному пространству на
множестве А:
nk(A) = jvkd»x,
А
что определяет поток энергии (в турбулентности) или мультифрак-
тальную вероятность (для странных аттракторов). Из (1.17) и (1.19)
можно получить
^(п^) > гад) ~ xf^a^/xD
на шаре Вх размером L/X. Здесь показатель сингулярности сс^ и
размерность фракталов внутри мультифрактала/^ (ос^) связаны с у и с (у)
следующими соотношениями:
aD=D-y, fD(*D) = D-c(y).
фРакталы
33
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Далее запишем функцию разбиения (так называемый следовый
момент) для поля ух с использованием пространственного
усреднения по ансамблю реализаций:
Ъа< =(Х(%^)')-(1П,(\,)^ (1.20)
где суммирование по А дано при разрешении X, т.е. при (более или
менее оптимальном) покрытии NX(A)~\D шарами Ви\
Гг^~Гт^>, xD(q) = (q-l)D-K(q). (1.21)
Соотношение (1.21) устанавливает связь между функцией iD(q),
зависящей от Д и внутренней характеристикой поля K(q). В то время
как внутренние характеристики у, с (у), K(q) не зависят от
размерности множества А, величины сс^, fD (aD), %D (q) зависят от
размерности объемлющего пространства и расходятся при D -^ °°.
Как/(а) их(?), так и с (у) и K{q) связаны через
преобразование Лежандра:
K(q) = mzx[qy-c(y)], ? = с'(у);
у
c(y) = inax[qy-K(q)], y = K'(q).
я
Сингулярности. В работе [60] показано, что мультифрактальные
понятия включают более широкое разнообразие явлений, чем
предполагалось ранее. Поскольку функция коразмерности с (у) должна
иметь фиксированную точку у = Сх, одновременно соответствующую
среднему числу сингулярностей и их коразмерности, то в ней
Сх = с (Сх) соответствует q = с'(Сх) = 1 и также С{ = ^'(1). Случай Сх > D
соответствует в исследуемом пространстве почти везде нулевому
(вырождение) процессу, следовательно, Сх < D.
На рис. 1.5 приведена фазовая диаграмма достижимых
сингулярностей для мультифрактала, наблюдаемого в пространстве
размерностью D. Диаграмма показывает значение сингулярности Сх = с (Сх),
максимум сингулярностей при геометрическом подходе у^ = c~l(D)
и в микроканонических мультифракталах у^ = & . Сингулярности,
называемые в [59] «дикими» (wild) и рассмотренные далее, имеют
34
1.2. Стохастическое описание мультифракталов
Рис. 1.5. Фазовая диаграмма достижимых сингулярностей для мультифрактала,
наблюдаемого в пространстве размерностью D [60]
У> YmaL • Сингулярности «жесткие» (hard), когда Y> Y/> > Y^ ,
обусловливают расходимость статистических моментов высокой
степени. Соединяющиеся кривые показывают два экстремальных случая
с показателями сингулярности а = 0 и а = 2.
Рассмотрим основные положения классификации мультифрак-
тальных полей. Так как функция вида (Х/х/) является
убывающей по q, то TrA\\fqx <(nx(A)q}, q>\, и на основании (1.21) можно
определить критическую степень момента qD с помощью выражения
K(qD) = D(qD-l) вследствие (nx(A)q)^>oo для всех q^qD.
Коразмерность вида c(q) = K(q)/(q -1) соответствует наклону хорды,
связывающей точки (1,0) и (q, K(q).
Тогда qD соответствует критической хорде с наклоном c(qD) = D.
Моменты q-Vi степени расходятся в случае c(q) > D . Заметим, что
соотношение (1.21) не имеет силы при q^qD.
35
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Это «жесткое» поведение на первый взгляд удивительно
потому, что если рассматривать yXD = Поо(Вх)/06ъ&м(Вх) как оценку ух
на шаре Вх, то будем иметь совершенно разные статистические
свойства:
х)<00> при всех <7»
(¥Ь) = ^при^>^(>1). (L22)
Это несоответствие побудило авторов работы [59] различать две
величины поля: соответственно «обнаженную» (bare) и «одетую»
(dressed). Неудивительно, что «жесткие» сингулярности, отвечающие
за эти расхождения (1.22), также разрушают микроканоническое
сохранение потока П. Действительно, /)есть верхняя граница
«домашних» (calm) сингулярностей, соответствующих
микроканоническому описанию у ^ У^ = &• Эта граница должна удовлетворять
неравенству Ylx>\~D}J^Ylx, что достигается только в экстремальном
случае, когда вся плотность потока концентрируется в одиночном
подвихре объема X~D.
Значение у£^х меньше, чем критическая степень yD = K'(qD)
«жестких» сингулярностей, так как yD > c(qD) = D благодаря
выпуклости K(q) в точке (qD, K(qD)). Ширина интервала «мягких» (soft)
сингулярностей (у< yD), за исключением «жестких»,
yD-^=KbD)-D = (qD-l)c'(qD)>D,
так как qD>l, c'>0.
Наоборот: если по любой причине показатели сингулярности
ограничены сверху Утах(с(у) = °°, У> Ymax)> расходимость
подавляется (за исключением случая yD < ymax) и соответствующие мульти-
фракталы будут «мягкими». При утах < у^х = D они одновременно
«мягкие» и «домашние». Данное положение дополняет наиболее
распространенную классификацию множеств мультифракталов - на
микроканонические и геометрические. Для последних у^ = c~l(D) < у^
(см. рис. 1.5) и подтверждают тот факт, что микроканоническая
изменчивость более глубокая. «Жесткие» сингулярности, которые не
локализованы в пространстве, т.е. в окрестности некоторых точек не
36
1.3. Вычисление фрактальных размерностей, показателей Ляпунова ...
существует предела lim Ух(х), в принципе не охватываются геомет-
рической версией фрактального анализа.
1.3. Вычисление на ЭВМ значений фрактальных
размерностей, показателей Ляпунова и энтропии
Колмогорова
В настоящее время не существует приборов, дающих на выходе
сигнал, пропорциональный фрактальной размерности.
Электрооптические методы, однако, позволяют определить подход к решению
данной проблемы (см. разд. 1.4). На практике в численных и
физических экспериментах фрактальные размерности D находят
дискретизацией сигналов с последующей обработкой данных на
компьютере. В цифровых алгоритмах для вычисления D используется 103—106
точек, что требует огромных вычислительных затрат, хотя
существуют и более рациональные программы, содержащие примерно 500
отсчетов [70].
Цифровая обработка. При цифровой обработке используют один
из трех основных методов: временную дискретизацию переменных в
фазовом пространстве, вычисление отображений Пуанкаре или
одноразовые измерения временного ряда (метод вложения пространства).
В первом случае [57] берется выборка временных значений
физических переменных {x(t), y(t), z(t)}- В частности, переменные
могут иметь следующий вид: положение х; скорость х = V; фаза
периодической силы z = (ot. Каждому интервалу времени соответствует
точка х = {x(nt), y{nt), z(nt)} в фазовом пространстве. Для каждой из
случайно выбранных точек вычисляют расстояние rin до
ближайшего окружения. Подсчитывая количество точек в пробном
геометрическом теле размера £, находят вероятность
iV0 /=1
где 0 - функция Хевисайда; 0(г) = 1 при г > 0, 0(г) = 0 при г < 0.
Тогда усредненная поточечная размерность
2 М~х " " е->о 1пг
37
Глава L ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
На практике N0 «103 +106 точек, аМ* 0,27V0. Число точек
подбирают опытным путем, пока D2 не достигнет предела. Выбор
снизу ограничен уровнем реального шума или средней плотностью
точек р:
c>L/(2N^),
где L - средний глобальный масштаб аттрактора в трехмерном
пространстве.
Определение фрактальной размерности с помощью отображений
Пуанкаре применяется для нахождения, главным образом, D
странных аттракторов [57]. Если фрактальная размерность отображения
Пуанкаре (0 < D< 2) не зависит от фазы отображения Пуанкаре
(0 < otf < 2я), то размерность полного аттрактора есть DA = 1 + D.
При слабом затухании аттрактор будет заполнять все фазовое
пространство (D=2, DA=3), какгамильтонова система (с нулевым
затуханием) [50]. С возрастанием затухания отображение Пуанкаре
становится одномерным и DA = 2, как в уравнениях Лоренца [71].
Данный метод измерения применялся для нелинейной цепи [72].
Теорема Такенса. Измерение всех переменных состояния
одновременно не всегда возможно. В частности, для уравнения Маккея—
Гласса [73], описывающего регенерацию кровяных телец и
представляющего пример бесконечномерной системы, должны быть
известны величины х (t) на интервале {t, t-%) как начальные условия.
По теореме Такенса [74] можно вычислить корреляционный
интеграл (1.8) и фрактальную размерность по измерениям
временной последовательности лишь одной составляющей. Следуя Такен-
су, сконструируем пространство вложения (или псевдофазовое
пространство) с /w-мерным вектором по значениям одной физической
переменной:
Х/=^/) = {х(Г/),х(Г/+Г),...,х[Г/+(т~1)Г]},
взятым со сдвигом Т. Распределение векторов состояния
составляет реконструированное фазовое пространство размерностью т.
Считается, что зависимость (1.9) сохраняется для любого т > int[D], где
[D] - операция выделения целой части D, a D - истинная
размерность объекта.
38
1.3. Вычисление фрактальных размерностей, показателей Ляпунова ...
Величина N>int[D] + l определяет число дифференциальных
уравнений первого порядка, необходимых для описания физического
поведения исследуемого объекта. Именно Ф. Такенс вместе с Д. Рю-
эллем ввели в 1971 г. термин «странный аттрактор» [127].
При реконструкции динамического аттрактора по
упорядоченным измерениям одной переменной необходимо построить
пространство вложения размерности D' > 2N +1, чтобы описать все
возможные топологические особенности исходного аттрактора.
Для иллюстрации теоремы Такенса воспользуемся результатами
работы [39]. Графики на рис. 1.6 показывают зависимость
корреляционного интеграла log2C(r) от log2r для модели Лоренца.
Кривая 1 вычислялась по восстановленной последовательности одной
переменной вида [Щ), x{tt +т), x{tt +2т)}. Кривая 2 получена по
трехмерной последовательности {x(tf), y{tt), z{tt)\ Обе кривые имеют
одинаковый наклон D3 = 2,5.
Результаты измерения фрактальной размерности конвективной
ячейки в жидкости под действием градиента температуры [75]
показали, что величина D2 достигает насыщения при значении D2 = 2,8,
когда размерность вложения D' > 5 . Это согласуется с теоремой Та-
log2C(r)
О
-4
-8
-12
-16
-20
1 5 9 13
Рис. 1.6. Зависимости log2C(r) от log2rwM модели Лоренца:
1 - временная последовательность одной переменной;
2 - трехмерная последовательность [39]
" 1 1 1 1 \ Г
—1 1
I 1
//
\ У/ 1
уУ \
1 1 ! -1 1 -JL J 1
log,, г
39
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
кенса. В экспериментах использовалось 15 000 точек, и P(r,xf)
усреднялась по 100 случайным точкам.
Корреляционный интеграл (1.8) можно также использовать как
средство разделения динамического хаоса и внешнего белого шума.
Тщательное исследование этой проблемы проводилось в работе [76],
где моделировался странный аттрактор, контролирующий обратное
радиолокационное рассеяние от морской поверхности.
Исследовалась модель Лоренца, генерирующая 1500 отсчетов с интервалом 0,1
с при среднеквадратичном отклонении, равном 7,9. Аддитивные
шумы с нулевым средним имели гауссово распределение и
среднеквадратичное отклонение, равное 1,0.
На рис. 1.7 показаны результирующие функции
корреляционных интегралов для размерностей вложения D' = 4, 8, 12, 16 и 20.
Там же выделен интервал [- 2,0; - 4,0], соответствующий линейной
части С (г). Отличительной чертой кривых является наличие
колена, аппроксимирующего середину зависимостей. Выше отмеченной
точки А кривые отображают закономерности, типичные для
хаотического процесса. Ниже точки А поведение кривых характеризует
шумовой процесс с наклоном, увеличивающимся с возрастанием
размерности вложения. Объяснение этого явления и значительное
количество экспериментальных данных содержатся в работе автора,
кратко изложенной в [77].
logC(r)
/Г = 4
Рис. 1.7. Зависимость корреляционного интеграла от г
для размерностей вложения D' - 4, 8, 12, 16, 20 [76]
40
1.3. Вычисление фрактальных размерностей, показателей Ляпунова ...
Энтропия Колмогорова. По одной временной реализации также
можно определить нижнюю границу ^-энтропии Колмогорова [78],
показывающую меру хаоса [39, 54, 65, 79]. ^-энтропия,
определяемая как средняя скорость потери информации, равна 0 для
регулярного движения, бесконечна для случайных систем и постоянна для
систем с детерминированным хаосом.
Обобщим корреляционный интеграл (1.8) в виде
C(r)=lim~
число пар у, для которых
Л-1
т=0
2*(Xi+m Xj+m>
1/2
<r
- I е.л (L23)
и получим
K2 = lim lim In
Г->0 Л->оо
<K.
(1.24)
Значение K2 > О указывает достаточное условие существования
хаоса. На рис. 1.8 показаны результаты вычисления по формулам
(1.23) и (1.24) для последовательности точек отображения Хенона при
О log/
ОД
0,4
0,2
и
■
■ /=2
■ 1 ■
4 1 ЙГ
1 * ' 1
А
ifc—йгя
б)
Рис. 1.8. Влияние значений п на значение корреляционного интеграла (а)
и нижнюю границу колмогоровской энтропии (б) для отображения Хенона [39]
4 1
Глава h ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
N= 15000, а = 1,4, Ъ = 0,3. При п -> <*> и г -> 0 функция К2 (п, г)
стремится к значению К2 - 0,352 ± 0,2.
Требования к алгоритмам. Все рассмотренные ранее методы
вычисления D требуют использования мощных цифровых
компьютеров. Чаще всего при обработке данных рассчитывается
корреляционный показатель v = Z>3 (1.9), требуъощий N2m2 действий, где N-
число точек, т — размерность пространства [39, 54].
Расчеты в [54] проводились на ЭВМ типа IBM 370/165 с
быстродействием 107 оп./с. Вычисление v no N = 2104 точкам
занимало 15-30 мин. Для нахождения корреляционного показателя
существуют алгоритмы, позволяющие проводить расчет быстрее, чем для
большинства других фрактальных размерностей [80—84].
Как следует из теоремы Такенса, можно не рассматривать
множество m-мерных векторов, характеризующих координаты точки в
фазовом пространстве, а измерять одну координату х через
равноотстоящие интервалы времени xv х2,..., xNc шагом т, т.е. /, = (/ - 1)т,
где / = 1, 2,..., N. По этим данным строится набор m-мерных
векторов £, ={*,, xi+L, xi+2L,..., xi+{m_l)L}, k = N-(m-l)L. Здесь
элементы массива х берут с шагом At = Lx. Существует несколько
подходов к выбору параметров дискретизации т и At, а также к длине
числового ряда N[85-89]. Обычно выбирают т« (0,1-0,25)7, где Т-
характерный «период» системы [83]. Если At очень мало, то
проекция аттрактора на какую-либо плоскость в ^-пространстве будет
близка к диагонали. Часто используют первый нуль
автокорреляционной функции для х (t). Можно ввести более сложную функцию -
взаимную информацию и взять ее первый минимум [85—87].
Для обобщенных энтропии (1.14) на основе алгоритма [54]
позднее была разработана методика расчета для произвольных q [90,91].
Обобщенный корреляционный интеграл записывается в виде
Cq(e)=lim
1I
Nj*
(1.25)
Это дает наилучшие результаты, особенно для выборок
небольшой длины. Вычисление формулы (1.25) позволяет определять и
обобщенные энтропии К в виде
42
1.3. Вычисление фрактальных размерностей, показателей Ляпунова ...
Кп = - lim lim
^ е-»6 п->°° q — \
1
где If — вероятность того, что траектория последовательно прой-
дет кубики с номерами iv ..., in через промежутки времени АД
Можно записать [79, 90, 91], что
К =-lim lim J-HogC (e,m)l-L, (1.26)
* e->0 m->oo л _ L ч J тЛ/
где С (е, т) - корреляционный интеграл С (е), определенный ддя
пространства размерности т.
При анализе аттракторов с помощью коротких выборок и
небольших т максимальный вклад в С(е) дадут соседние точки по
траектории. К структуре аттрактора они не имеют никакого отношения,
и он будет восприниматься как одномерная кривая. Чтобы
достоверно определять корреляционный интеграл, в работе [92]
предлагается при анализе окрестности данной точки убирать соседние точки
по траектории. Тогда
^-ttWe0 £ eHc,-c2l). <L27>
\к~1Уо) 1=1 у=1+ЛГ0
Величину Л^ выбирают порядка L, т. е. оптимального шага
образования ^-векторов, но иногда необходимы NQ > Т.
Универсальных рекомендаций здесь нет, и оптимальное значение NQ
определяется экспериментально.
Алгоритмы вычисления корреляционного интеграла. Формула (1.27)
реализована в программах, разработанных в [80, 81, 83]. Опираясь на
их результаты, кратко опишем алгоритмы вычисления
корреляционного показателя, энтропии К2 и оценки v по массиву значений С(е).
Вычисление С(е) значительно убыстряется, если при определении
расстояния I Cl - С2 Р= (*/ ~ *j f + {Xi+L -Xj+L f + - + [XU{m-X)L ~XMm_l)Lf
суммирование проводить не вдоль строк и столбцов матрицы (/, j),
а вдоль диагоналей. В результате быстродействие алгоритма
практически не зависит от т, что при т »1 дает существенный выигрыш.
Суммирование необходимо проводить с двойной точностью.
Вычисления ведутся одновременно при нескольких т.
43
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
На практике линейная зависимость logC(e) от loge наблюдается
в некотором интервале масштабов [е1? е2]. Угловой коэффициент
находят обычно методом наименьших квадратов и принимают его
за оценку v. В работах [81,83] применялась следующая методика
определения линейного участка анализируемой кривой. Вначале
задавался некоторый минимальный интервал длины /^ по е (не менее 5
подряд лежащих точек), и для всех точек выборки, отстоящих от конца
не менее чем на 0,5/min, методом наименьших квадратов определялись
угловой коэффициент Ь5 прямой у = Ь5х + с и его погрешность 55.
Также рассчитывался коэффициент а5 параболы у = а5х2 +Ь5х + с,
характеризующей кривизну графика. По двум соседним точкам
определялся локальный наклон bv Затем вычислялись средние величины
а5, Ь5> 85.
При последующем анализе оставлялись только те точки,
которые удовлетворяли следующим критериям: | а5 \< \ а51; | S51< |551; Ь2
лежит в интервале (0,51 Ь2\, 21Ь21); 55 < 2| 551; оставлялись 75% точек с
минимальными значениями \а5\ и |55|. Затем для каждого критерия
выбирались интервалы / подряд идущих точек, и если / > lmhl, то для
/методом наименьших квадратов рассчитывалось значение Ъ ± 5,
которое и использовалось в качестве оценки v.
Предпринимался также поиск локальных минимумов в
массиве 85. Для каждого минимума проводилось расширение интервала в
обе стороны до тех пор, пока такое расширение приводило к
уменьшению 8. Окончательные значения Ъ ± 8 также предлагались в
качестве оценки v.
При экспериментальных исследованиях трудно считать
фракталом множество, для которого самоподобие наблюдается на
интервале изменения масштабов в 2—3 раза. Значительный интерес
вызывает вопрос о длине выборки, по которой можно получить разумный
результат. Согласно [93], для оценки фрактальной размерности с
точностью около 5% необходима выборка длиной N= 42a, где а -
целая часть размерности. Для а = 3 имеем около 70 000 отсчетов. Если
это так, то почему в ряде случаев хорошие результаты получаются
при гораздо меньших выборках? Простого и ясного ответа на этот
вопрос пока нет. В работе [94] приводится оценка lO01. Из этих
оценок следует, что линейный участок должен наблюдаться при
изменении масштаба в 42 или 10 раз. Оценка, полученная в работе [95],
44
1.3. Вычисление фрактальных размерностей, показателей Ляпунова ...
устанавливает жесткие ограничения: корреляционный показатель v
должен удовлетворять соотношению v < 21g 7V.
Алгоритмы вычисления энтропии. Рассмотрим по результатам [83]
алгоритмы оценки энтропии К2. При малых £ и достаточно больших
т (1.26) удовлетворяет соотношению [79, 90, 91]:
log С(г)« v log е - К2 Aim + const.
Исследование зависимости logC(£) от т при фиксированном и
достаточно малом £ дает значение К2 A t. Интерпретация результатов
в данном случае сложнее, чем при расчете v. Для систем малой
размерности оценки К2 хорошо согласуется с теорией и значениями ля-
пуновских показателей. Поэтому вместо вычисления Хх можно
рассчитывать К2. Интересно, что значение К2 оценивается по выборкам
в несколько тысяч точек, а увеличение длины выборки часто не
улучшает оценку.
В алгоритме оценки энтропии существенным является
произведение mAt. Обычно оно в 5—10 раз превышает значение,
используемое при расчете v. Оказалось [83], что хорошее приближение к К2
получается при значениях £ «е0, где £0 всего в 2-8 раз меньше
размеров аттрактора. При £ > £0 значение К2 близко к 0, а при £ « £0 оно
значительно завышено. Для каждого £ методом наименьших
квадратов определяется коэффициент к(г) зависимости log С(г, т)« -km + с
и погрешность Щг). Зависимость &к(г) весьма изрезана: на всем
интервале £ она может меняться в 10 раз и более. Однако в расчетах
может быть несколько локальных минимумов Щг) при
отличающихся К2. В тестах [83] получалось, что следует выбирать либо
минимум 8^ при наибольшем £, либо следующий. Неясно, впрочем,
насколько общим является это правило.
Недостатком алгоритма является также то, что значение К2 с
ростом т монотонно уменьшается. Точных критериев выбора
оптимального т пока нет. Для различных систем оптимальные тиг
могут значительно варьировать. По тестам [83] было отмечено, что
хорошие результаты дает использование значения К2, для которого &к
имеет локальный минимум как по £, так и по т. Для аттрактора
Лоренца при выборке длиной 5000 отсчетов т = 0,02, А7 = 0,12 и
полному интервалу т = 5+100 с шагом 5 оценка К2 = 1,40 ± 0,013 (для
т = 30+55 и £/£тах ^О'^), а значение ляпуновского показателя
^ =1,37.
45
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
Алгоритмы вычисления ляпуновских показателей. Алгоритмы
вычисления ляпуновских показателей по экспериментальным данным
обсуждаются в [53]. Вычисление максимального показателя
начинается с выбора опорной (реперной) траектории, точки на соседней
траектории и измерения расстояния между ними d0 в момент
времени tQ. Поскольку в системе есть положительный показатель X, то
расстояние между этими траекториями растет во времени и
становится равным dit^^l^'^d^. Когда расстояние d (t) становится
слишком большим, необходимо найти новую траекторию и
определить новое начальное значение d0(f), и т.д. до N-то шага.
Максимальный показатель Ляпунова определяется выражением
у 1 gw d{tk)
lN l0 JU1 V4-F
Критерий хаоса в терминах показателя Ляпунова принимает
следующий вид: X > О — хаотическое движение; X < О — регулярное
движение. В N-мерной динамической системе существует N
ляпуновских показателей, характеризующих данную траекторию на
аттракторе. Для странного аттрактора есть определенное число
положительных показателей Х{, ..., кк>0 (близкие траектории,
разбегающиеся отданной), один нулевой Хк+1 =0 и N-k-l отрицательных
(характеризуют сближающиеся траектории).
Если рассматривать объем начальных условий в фазовом
пространстве при хаотическом движении и моменте времени t0, то он
видоизменяется и при t > t0 отображается в эллипсоид с главными
осями ц^8, ц^8, ц^8. Поэтому для каждой динамической системы
есть спектр показателей Ляпунова {Xf}, A,,. =logfir С вычислительной
точки зрения данный спектр показателей находится на траектории
в фазовом пространстве при нашем знании об эволюции длины,
площади, объема и гиперобъема. В [53] разработан алгоритм
вычисления {XJ. Если X. упорядочены (Х{ >Х2 >...>XN), то длины
(расстояния между траекториями) изменяются по закону d(t)~2Xl'd0,
площади треугольников, одна из вершин которых находится на
опорной траектории, а две другие — в соседних с траекторией точках, по
закону i4(f)e2(A,i+A,2>'4), малые объемы - по закону К(0«2(Я,1+я,2+яз>'К0
и т.д. Поэтому
46
1.4. Экспериментальное определение фрактальных размерностей
7 ^ l Vino A{fk)
Аналитическое определение полного спектра ляпуновских
показателей и примеры вычисления.спектра {Xt} в явном виде
приведены в работе [49]. Можно также ввести понятие локальных
показателей Ляпунова [96], которые будут зависеть от участка траектории,
на котором они вычисляются. При усреднении локальных
показателей получаем осредненные локальные показатели, которые
являются функцией только длины участка траектории. В работе [97]
показано, что осредненные локальные показатели Ляпунова являются
оценкой сверху для глобальных показателей X..
Интервал предсказания. Возвращаясь к понятию ^-энтропии
Колмогорова, заметим, что для одномерных систем она равна
показателю Ляпунова. Для систем большей размерности она равна
усредненной сумме положительных показателей Ляпунова [98].
Величина #-энтропии обратно пропорциональна интервалу времени Г0, на
котором можно предсказать состояние хаотической системы [24]:
V-Linl.
Эти результаты показывают, что ^-энтропия -
фундаментальная величина, характеризующая хаотическое движение. Таким
образом, из сказанного следует, что анализ используемой выборки на
ЭВМ требует учета всей возможной дополнительной информации и
является элементом не только науки, но и искусства.
1.4. Экспериментальное определение
фрактальных размерностей
Радиооптическое измерение D. С точки зрения
экспериментатора естественен вопрос, нельзя ли измерять фрактальные
размерности непосредственно, используя аналоговые устройства. В общем
случае для динамической системы с многими степенями свободы ответ
неизвестен. В некоторых простых задачах фрактальная размерность
двумерного отображения Пуанкаре может быть измерена
экспериментально. Так, использование методов радиооптической параллель-
47
Глава L ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
ной обработки (см., например, [99, 100]) позволяет быстро
определить корреляционный интеграл (1.8).
Дальнейший материал основан на результатах работы [101], где
использована аппроксимация корреляционного интеграла из [39] для
больших Nb виде
c(>-)=^iieH*,-*7.|). (1.28)
1=1.7=1
Как видно из (1.28), ячейки в фазовом пространстве
описываются вокруг каждой точки xi и подсчитывается число таких точек в
каждой сфере. Это позволяет более эффективно, чем в формуле (1.8),
вычислять корреляционный интеграл.
Оптический метод, положенный в основу экспериментальной
установки (рис. 1.9), позволяет сразу находить число точек в
окрестности всех точек фрактального множества. Луч света, проходящий
через малое отверстие диаметра d при дифракции Фраунгофера,
образует в плоскости, расположенной на расстоянии L за отверстием,
пятно радиусом r = l,22XL/d, где X — длина волны. В данной
установке отверстием служит светлое пятнышко («точка») на негативе
плоского отображения Пуанкаре. Для некогерентного излучения
-~<"
I 10 I
—-рг-1
Рис. 1.9. Схема экспериментальной установки для радиооптического измерения
фрактальной размерности: 1- источник некогерентного света; 2 - диафрагма;
3 - прерыватель; 4 - светофильтр; 5 — диффузор; 6 — линзы; 7 и 8 - негативы;
9 — фотоэлемент; 10 - синхронизированный усилитель; 11 - эталонный сигнал;
12 - полезный сигнал; 13 - фиксированное расстояние; 14 - световой поток [101J
48
1.4. Экспериментальное определение фрактальных размерностей
количество света, испускаемого 2-м негативом (точной копией
первого), пропорционально числу светлых точек, оказавшихся внутри
кружка света. Полный световой поток будет пропорционален
корреляционному интегралу (1.28). Для изменения радиуса пятна г
необходимо изменять расстояние L между двумя негативами.
Пусть Ф(дс,г) - световой поток за 2-м негативом,
обусловленный потоком Ф/Л(*), проходящим через круглое отверстие в точке х
на первом негативе:
Ф(х,г) = п(х,г)АФ.>,(*)—у,
где п(х,г) = Xе(r~ Iх ~xj \) ~ число отверстий в круге света, созда-
J Л
ваемом потоком, проходящим через отверстие в точке х; А -
площадь светлой точки на первом негативе.
Видно, что Ф зависит от п и г. Однако необходимо измерить
только л. Используем линейное соотношение между L и г и определим
приведенный световой поток:
Ф*=(г/г0)2Ф,
где г0 - радиус освещенной площадки при Z = LQ (L0 - эталонное
расстояние). При суммировании по всем точкам на первом негативе
получаем
Хф>,х)=| -1 ХФи,г)=4-1ф^)«(^
В случае равномерного распределения интенсивности
падающего света на первом негативе имеем
( £ f Л Л
А>
J<<b0(xk,r) = J,n(r)~C(r). (1.29)
k=l k=\
Свет от источника проходит через светофильтр янтарно-оран-
жевого цвета, что позволяет оптимизировать отклик фотоэлемента
вблизи 6328А. Сечения Пуанкаре на негативах содержат по 4000
точек каждое. Размеры светлых точек не превышали 0,2 мм, поэтому
Z>/А,« 300. Для выделения сигнала на фоне шумов в установке пре-
49
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
дусмотрен механический прерыватель света и усилитель с
синхронизацией. Прерыватель работает на частоте около 100 Гц для
исключения шума в линиях спектра мощности.
Теоретически угловой коэффициент зависимости
приведенного светового потока Фх (1.29) от расстояния L в двойном
логарифмическом масштабе должен давать фрактальную размерность
С(г) ~ rD (г -^ 0, N -> °° )• Значения Фх измерялись примерно при
200 значениях L. При измерении углового коэффициента показано,
что существует оптимальный диапазон значений радиуса г. В случае
малых значений г возникает погрешность, обусловленная шумом,
которым сопровождается порождение отображения. Эта погрешность
приводит к увеличению углового коэффициента. При больших
значениях г достигаем размера самого аттрактора и С (г) выходит на
насыщение, что уменьшает наклон линии, или D.
График зависимости углового коэффициента (или D) от In L
приведен на рис. 1.10. Значение Д соответствующей плато, было
выбрано за истинную фрактальную размерность. Данные рис. 1.10
получены усреднением локальных угловых коэффициентов кривой
log С (г) по 30 точкам.
Тестовое изображение линейного отрезка дало значение D = 1,02.
Сравнение оптически измеренной фрактальной размерности с
теоретической размерностью проведено в табл. 1.3. Эти данные
хорошо согласуются.
D
2,2
2,0
1,8
1,6
1,4
1,2
1,0
0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 ^L
Рис. 1.10. Угловой коэффициент как функция расстояния L
между негативами [101]
50
1.4. Экспериментальное определение фрактальных размерностей
Таблица 1.3
Сравнение измеренных и вычисленных фрактальных размерностей
аттрактора Дуффинга-Холмса [57, 101]
Коэффициент затухания
0,075
0,105
0,135
Фрактальная размерность |
вычисленная
1,565
1,393
1,202
измеренная
1,558
1,417
1,162
Аналогичное сравнение оптических и численных методов для
отображений Пуанкаре, построенных по экспериментальным
данным для колебаний продольно изогнутой балки, приведено в табл. 1.4.
В данной серии экспериментов фаза сечения отображений
Пуанкаре изменялась. Видно, что фрактальная размерность не зависит от
фазы отображения Пуанкаре. Таким образом, фрактальная
размерность странного аттрактора равна 1 + Д где D — размерность
плоского изображения.
Таблица 1.4
Сравнение измеренных и вычисленных фрактальных размерностей
для отображений Пуанкаре [101]
Фазовый угол, град.
0
45
90
135
180
Фрактальная размерность
вычисленная
1,741*/1,628**
1,751/1,627
1,742/1,638
1,748/1,637
1,730/1,637
измеренная
1,678
1,671
1,631
1,676
1,635
* при 4 наименьших lnr
** при 7 наименьших lnr |
Оптическое преобразование Фурье. Мощным методом при
анализе пространственных частот фрактального процесса является
оптическое преобразование Фурье [102]. Данный метод также
позволяет непосредственно измерить размерность Хаусдорфа. Для
экспериментов были выбраны одномерные и двумерные автомодельные
объекты типа канторова множества и фрактала Вичека с
обобщением на случайные фракталы. Объекты вычислялись на компьютерах,
51
Глава L ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
вычерчивались графопостроителями, и изготовлялись слайды с
высоким разрешением. Конечная толщина линий ограничивала
построение фракталов примерно после 7 итераций.
Отношение наибольшего масштаба к наименьшему R/г «1000.
Существенное ограничение при анализе обусловлено конечными
размерами элементарного зерна в фотопленке £min « 2 мкм.
Распределение интенсивности In(q) на дифракционной картине
от канторова множества отрезков после п итераций при D = 1п2/1пЗ
одномерно и определяется соотношением
Ш = 22ле2
П-\
>о
Yd
Sin7tg£
щг
V
где ^ - координата в плоскости дифракционной картины; 22л е2 -
коэффициент, определяющий интенсивность в области нулевого
порядка дифракции при 9 = 0.
Распределение интенсивности изменяется как
[I(0W2~RDel-D.
(1.30)
Значение (1.30) определяет меру массы М, заключенной во
фрактале с линейным размером R При использовании диафрагм с
разными апертуарами для ограничения эффективно освещенной части
фрактальной решетки можно изменять R и, следовательно,
определить D.
Величина In(q) состоит из формфактора F(q) и структурного
фактора S(q). Формфактор F(q) соответствует интенсивности
света, дифрагировавшего на единичном элементе шириной г:
F(q) =
Г • Л2
nqz
Значение F(q) = 0 при qmax = e 1. В дальнейшем будем считать, что
Структурный фактор S(q) определяется распределением по
фракталу единичных элементов S(q) =
п-\
ncos(27i^-3/e)
./=о
52
1.4. Экспериментальное определение фрактальных размерностей
Автомодельность объекта в реальном пространстве отражается
в оптическом преобразовании Фурье существованием п — 1
частотных полос, масштабно-инвариантных относительно растяжений с
коэффициентом 3Bt, где 2>. - полоса частот. Средняя энергия (S(q)),
рассеянная в полосе частот В(, изменяется как
{S(q))~q-D.
(1.31)
На рис. 1.11 показано, как выглядят экспериментальный и
рассчитанный спектры канторова множества отрезков при п = 7 [102].
Так как первый нуль формфактора F(q) приходится на q = 1, то при
высоких пространственных частотах F(q) смазывает структуру
решетки. Масштаб г находится при измерении qmSK. При малых углах
(q < 0,25) формфактор F{q) ~ 1 и им можно пренебречь.
О 0,2 0,4 0,6 0,8 1,0
а)
0 0,2 0,4 0,6 0,8 1,0
6)
Рис. 1.11. Экспериментальный (а) и теоретический (б) пространственные спектры
канторова множества при п = 7 [102]
Частота осцилляции излучения (см. рис. 1.11) зависит от R~l9
что позволяет непосредственно измерять R. Далее нахождение (S(q))
по экспериментальному спектру приводит к степенному закону
изменения (1.31). Экспериментальное значение фрактальной
размерности совпадает с теоретическим в пределах 10%.
Изложенный метод допускает обобщение на любые двумерные
фракталы. Для полной записи I(q) необходимо сканирование по
двум координатам плоскости Фурье. При этом интенсивность
излучения, продифрагировавшего на одной оси (q), определяется
соотношением
I(p)= jexp(2niqy)
JT(x,y)dx
<fy,
53
Глава L ЭЛЕМЕНТЫ ТЕОРИИ ФРАКТАЛОВ
где Т(х, у) - коэффициент оптического пропускания исследуемого
фрактала.
Данную зависимость можно интерпретировать как оптическое
преобразование Фурье проекции фрактала на ось у. Однако эта
проекция может и не быть фракталом. Если же она является фракталом,
то ее фрактальная размерность, определяемая по измерениям I(q),
не обязательно совпадает с фрактальной размерностью исходного
объекта. В работе [103] показано, что в общем случае указанные две
величины совпадают при условии, что D< (D0 + 1), где D0 -
размерность евклидова пространства, в котором находится кластер.
Вейвлеты. Очень перспективным математическим аппаратом
представляется вейвлет-преобразование - аппарат, хорошо
приспособленный для исследования структуры неоднородных процессов
[104]. Термин «вейвлет» («маленькая волна») ввели в середине 1980-х
годов Гроссман и Морле. В отличие от традиционного
преобразования Фурье, вейвлет-преобразование имеет базис из солитонопо-
добных функций, локализованных и по времени, и по частоте.
Поэтому сигнал можно анализировать одновременно в физическом
(время, координата) и в частотном пространствах.
Вейвлет-преобразование представляет собой как бы непрерывный континуум
оконных преобразований Фурье с разными окнами для каждой частоты.
Характерным признаком базиса вейвлет-преобразования
является его самоподобие. Поэтому вейвлет-преобразование широко
применяется для анализа фрактальных и мультифрактальных
множеств, вычисления спектра их размерностей [104, 105]. Вопросы
теории вейвлет-преобразования остаются за рамками работы,
признаки вейвлета, свойства и возможности вейвлет-преобразования
при обработке физических данных представлены в работах [105,106,
803-808].
1.5. Эмпирический закон Херста для временных рядов
Многие наблюдения природных процессов приводят к
долговременным рядам измерений. Например, имеются длинные ряды
метеорологических измерений температуры воздуха и т.д. Оказалось,
что многие экспериментальные зависимости обладают фрактальной
статистикой, анализ которой может быть проведен с помощью
эмпирического анализа, предложенного Херстом [107, 108]. Всю свою
54
1.5. Эмпирический закон Херста для временных рядов
жизнь Херст занимался изучением Нила и решением задач,
связанных с накоплением водных ресурсов. Он также исследовал многие
природные процессы, такие как сток рек, отложение ила и рост
колец деревьев. Выводы Херста тесно связаны со статистикой
экстремальных значений [109].
Показатель Херста Н. Как показал Херст, при анализе
длительных наблюдений природных процессов, нормированный размах R/
S очень хорошо описывается эмпирическим соотношением
R/S = (x/2)H, (1.32)
где R(T) = maxX(t,T)-mmX(t,x) — максимальный размах амплитуд
1</<т 1<Г<т
случайного процесса; S — среднеквадратичное отклонение
процесса; t- дискретное время с целочисленными значениями; т -
длительность рассматриваемого промежутка времени.
Экспериментальные данные. Интересен для многих естественных
процессов (метеоданные, число солнечных пятен, водообмен,
слоистые отложения и т.п.) показатель Херста Н> 1/2 (табл. 1.5). На
практике [45] считают, что показатель Херста можно оценить,
анализируя временные ряды, состоящие примерно из 2500 измерений.
Значения Н> 1/2 вызывают интерес, потому что при отсутствии
долговременной статистической зависимости отношение R/Sдолжно
быть асимптотически пропорционально т1/2. Известно, что если
временные ряды связаны со случайными процессами с независимыми
значениями и конечной дисперсией, то
R/S = (kt/2)1/2.
Анализ одной из самых длинных выборок методом
нормированного размаха был проведен в работе [110] при исследовании древних
климатических изменений по толщине слоев в слоистых илистых
отложениях озера Тимискаминг (Канада). Обработанные данные
охватывают период в 1809 лет. Рассчитанное по ним значение
показателя Херста очень велико (Н= 0,96), и никаких отклонений от этой
зависимости нет. Почему же природные процессы подчиняются
статистике Херста? Это, несомненно, открытый вопрос. Ключ к
ответу заключается в учете эффекта памяти. Модель обобщенного
броуновского движения, рассматриваемая в разд. 2.1, учитывает
эффекты памяти.
55
Статистика оценки показателя Херста для различных естественных процессов [45, 108]
Таблица 1.5
Гидрометеорологическая
характеристика
Водообмен
Сток рек
Р. Рода
Уровень рек и осадков
Уровень осадков
Слоистые отложения озер
Саки
Моэн и Тимискаминг
Коринто и Хейлибери
Шетеоданные
Температура
Давление
Число солнечных пятен
Кольца деревьев
и индекс ветвления у ели
1 Суммарные и средние
шачения по разделам
Водообмен
Слоистые отложения
Метеоданные
1 Общие суммарные
\и средние значения
Период
годы
10-100
80-1080
44-176
24-211
50-2000
50-1200
50-650
29-60
29-%
38-190
50-900
—
10-2000
Число
объектов
39
1
4
39
1
2
2
18
8
1
5
83
5
32
120
Число наборов
измерений
94
66
13
173
114
90
54
120
28
15
105
346
258
268
872
Среднее Я
0,72
0,77
0,71
0,70
0,69
0,77
0,77
0,68
0,63
0,75
0,79
0,72
0,74
0,72
0,726
S
0,091
0,055
0,082
0,088
0,064
0,094
0,098
0,087
0,070
0,56
0,076
0,08
0,09
0,08
JL082
№)
0,50-0,94
0,58-0,86
0,59-0,85
0,46-0,91
0,56-0,87
0,50-0,95
0,51-0,91
0,46-0,92
0,51-0,76
0,65-0,85
0,56-0,94
0,46-0,94
0,50-0,95
0,46-0,94
0,46-0,95
**)*
0,025-0,26
0,07±0,08
0,07-0,11
-
—
—
' r(t) — коэффициент автокорреляции, включая сток рек.
IS
Глава 2
СЛУЧАЙНЫЕ ФРАКТАЛЫ
И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
2.1. Фрактальный анализ сигналов
В основе традиционного подхода к анализу случайных сигналов
лежит спектрально-корреляционная теория с фундаментальной
теоремой Винера-Хинчина. Однако, за исключением только класса
гауссовых процессов, полное статистическое описание случайных
сигналов требует оценки моментов высших порядков с учетом
многоточечных корреляций. Резкое возрастание сложности и объема
вычислений при ухудшении их точности ставит под сомнение само
описание случайных процессов такими характеристиками.
Альтернативой являются оценки фрактальных размерностей различных,
связанных с процессом геометрических объектов.
Бинеровский процесс. Фрактальное распределение во времени и
пространстве могут иметь плотности распределения различных
величин, графики сигналов, множества экстремумов случайных
процессов и т.д. Одним из примеров случайного процесса,
обладающего фрактальными свойствами, является классический винеровский
процесс броуновского движения В (t) - так называется
начинающийся в начале координат случайный процесс, приращения которого на
непересекающихся интервалах времени /независимы и имеют
гауссово распределение. Дисперсия данного процесса
{¥) = Кв*> (2-1)
где KD - коэффициент диффузии.
Траектория винеровского процесса обладает, как следует из (2.1),
свойством масштабной инвариантности, или скейлингом, -
процессы В (t) и b~l/2B(bt) инвариантны в смысле распределения р(£>) при
произвольном коэффициенте Ъ > 0:
р(% = $1% х = Ьт) = Ь-*/2р&т). (2.2)
Соотношение (2.2) показывает, что график броуновского
случайного процесса относится к классу самоаффинных фрактальных функ-
57
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
ций. Вероятностные свойства броуновского процесса не
изменяются при одновременном изменении масштаба времени в Ъ раз и
пространственного масштаба в bl/2 раз. Траектория и график винеровс-
кого процесса нигде не дифференцируемы и в то же время
непрерывны с вероятностью, равной 1. По сути дела, винеровский процесс
является первой недифференцируемой функцией, наблюдаемой в
физическом эксперименте,. Распределение вероятности координаты час-
п
тицы X(t = пх) = ££. имеет вид
Лад-Лад- ' ехр{-<^Ш
Оно удовлетворяет соотношению подобия P{bl/2\X(bt)- X(bt0)~\\=
= 6-1/2Р[ЛО-Л^0)]иимеетдиспеРсию ([X(t)-X(t0)¥) = KD\t-tQ\,
где X(t0) - координата частицы в начальный момент времени t0.
Винер [111] следующим образом вывел случайную функцию,
описывающую броуновское движение. Рассмотрим гауссов
случайный процесс с независимыми значениями шагов {£}. Приращение
координаты броуновской частицы определится выражением
X{t)-X{t,)~k\t-t,V\t>t, (2.3)
для любой пары моментов времени t и t0. Из (2.3) можно определить
координату X(t) по координате X(t0), выбирая случайное число % из
гауссова распределения, умножая его на степень приращения
времени \t —10\ и складывая результат с известной координатой X(t0).
Обобщенное броуновское движение. Понятие обобщенного
броуновского движения BH{t) было введено Мандельбротом [3,112]
заменой показателя в формуле (2.3) на любое действительное число из
интервала О <Н< 1. Случай Я= 1/2 соответствует независимым
приращениям и описывает классическое броуновское движение.
Показатель Я есть показатель Херста. Обобщенный броуновский процесс
имеет нулевое среднее приращение и дисперсию приращений Щ -10):
^-^о) = ([5я^-^^]2} = ^(1^^о1/^)2ЯН^^о12Я- (2-4)
58
2.1. Фрактальный анализ сигналов
Важно понять, что обобщенное броуновское движение имеет
бесконечно большое время корреляции. Положим Вн(0) = 0 и пусть
т = 1, a KDx = 1. Тогда из формулы (2.4) следует выражение для
коэффициента корреляции
r{t)A-^-t)BH(t))
() {вЩ L (2l5)
Заметим, что при #= 1/2 корреляция прошлых и будущих
приращений отсутствует при всех t. Из (2.5) следует, что r{t) *0 не
зависит от времени t. Случай Н> 1/2 соответствует положительной
корреляции; случай Н< 1/2 — отрицательной корреляции. Таким
образом, уникальное свойство обобщенного броуновского процесса
заключается в персистентности (сохранении тенденции) и антипер-
систентности. Для Н> 1/2 поддерживается имеющаяся тенденция.
Если приращения были положительными за некоторый период в
прошлом, то и впредь в среднем будет происходить увеличение.
Более того, это справедливо для произвольно больших t Для Н< 1/2
рост в прошлом означает уменьшение в будущем, и наоборот. Таким
образом, суть обобщения состоит в том, что обобщенный
броуновский процесс обладает памятью.
Примеры обобщенного броуновского движения. Иная полезная
формулировка свойства памяти для обобщенного броуновского
процесса приведена в работе [113]. Стимулом проведения исследований
[113] была необходимость понимания разнородности потоков
крови в сердце и легких. Для местных сердечных потоков крови
фрактальная размерность D~ 1/2 при коэффициенте корреляции 0,52.
Ранее было обнаружено, что местные потоки крови в органах
человека обладают свойством фрактальности. Здесь также статистика
Херста есть результат длинного потока взаимосвязанных событий.
Это не кратковременная память, которую часто называют
марковской. Фрактальная природа показателя Яопределяет меру смещения
событий. Тестом для проверки фрактальности потоков крови
являлись выражения для корреляций между искусственными сериями
моделирующих сигналов, разделенных интервалами.
Рассмотрение корреляции сумм значений сигнала на двух
интервалах, разнесенных на п смежных единичных отрезков, позволяет
получить следующие соотношения для значений коэффициента
корреляции гп:
59
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
r,=-23-2D-l=22w-1-l,
-Л.Н
У" 3 „
32й-2-Д
: (2-6)
rn=I(„+l)^-''f,(n-/+l)^-i(n+l) = I[(„-l)2«_2„^+(n + 1)2«j
Показатель Херста Ясвязан с фрактальной размерностью D
формулой Н= 2 - D для одномерных сигналов. В общем случае между
евклидовой, или топологической, размерностью Е и показателем
Херста Я имеет место следующее соотношение: #= ЕЛ-1 - D [114].
Значения коэффициента корреляции г (п) сигналов, разделенных
(п - 1) целыми интервалами для разных значений Я, приведены на
рис. 2.1. При увеличении числа интервалов п корреляция вначале
быстро спадает, но при больших п уменьшение г (п) происходит
медленнее. Для фрактальных сигналов с Ж 0,7 значения г (п) при п > 1
настолько низки, что мы имеем дело с фрактальным шумом. Из
формулы (2.6) следует, что ддя совершенно случайных фрактальных
потоков (г{ = 0) значение D= 1,5, а Н= 1/2.
На основании (2.6) получено асимптотическое соотношение
Гп _
Гп-1
\
2Н-2
/1-1
Рис. 2.1. Корреляционные зависимости г (л) для сигналов, разделенных (л - 1)
целыми интервалами, при разных значениях коэффициента Херста [113]
60
2.1. Фрактальный анализ сигналов
Используя аналогичные выводы, можно записать
КхЦ(|х-1|2Я-2|хр*+|* + 1|2я), (2.7)
где х> 0 — непрерывная переменная.
Корреляционные кривые (2.7) непрерывны без разрывов
производной, кроме крайнего случая #= 1/2, когда корреляция в
диапазоне 0 < х < 1 отображается прямой линией г = 1 — х и г = О для х > 1.
Вид зависимостей г (п) также интересен тем, что они
предсказывают спад в корреляции, однако более медленный, чем для
экспоненциальных или гауссовых кривых. Данное обс¥оятельство
иллюстрирует рис. 2.2, где изображена фрактальная корреляция г(п)
сегментов сигнала, разделенных интервалами из п элементов для
показателя Херста #= 0,8. Для сравнения там же показаны
экспоненциальные функции, выбранные так, что они имеют одинаковые
значения г при N= 2 и г = 1 при N=0. Корреляция является почти
степенной функцией п, тогда как экспоненциальная и гауссова
зависимости спадают более круто.
Для определения коэффициента Херста по формуле (2.6)
генерировался фрактальный сигнал из 32 768 равномерно
расположенных точек. Оценка проводилась выполнением обратного
преобразования Фурье в частотной области спектра вида 1//2>6 при Н = 0,8 и
г(п) г(п)
2 4 6 8 10 п 0,1 0,5 1 5 10 п
а) б)
Рис. 2.2. Фрактальная корреляция г (л) сегментов сигнала как функция числа
помещенных между ними п элементов для Н = 0,8 в линейном (а) и
логарифмическом (б) масштабах: 1 - г (л); 2 - ехр (- N/2); 3 - гауссова функция [113]
61
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
случайной фазе. Значение Я равнялось 0,8002 ± 0,0034. При
фрактальном сигнале из 512 точек показатель Херста Я был оценен
значением 0,743 ± 0,023. Двухточечные автокорреляционные функции
для сигнала с разными отсчетами приведены на рис. 2.3.
г
0,5
0,4
0,3
0,2
0,1
(п)
1
'I
» ' 1
г(
0,5
0,4
0,3
0,2
0,1
п)
т
С2
——1 ■ „]
о
10 20
10 20 п
Рис. 2.3. Проверка соответствия модели для фрактальной корреляции
синтезированного фрактального сигнала с Н= 0,8:
1 - массив из 32 768 точек; 2 - массив из 512 точек [113]
Из сказанного следует, что возможны ситуации, когда за
ограниченное время измерения вообще невозможно получить
достоверные данные о среднем процесса. Следовательно, нахождение
показателя Херста является необходимым элементом измерения
статистических свойств исследуемых процессов.
Численное моделирование обобщенного броуновского движения.
Для более глубокого понимания обобщенного броуновского
движения и его реализации численным моделированием в работе [112] была
введена случайная функция Bff(t) с нулевым средним вида
Bff(t) =
1
Г(# + 1/2)
l(t-f)H-l/2dB(n
(2.8)
Здесь Г(х) —гамма-функция. Согласно (2.8), значение случайной
функции в момент времени t зависит от всех предшествующих {? < t)
приращений dB{t') обычного гауссова случайного процесса B(t) = Bl/2(t)
с нулевым средним и единичной дисперсией. Обозначение dB{t*)
физически понятно при замене интеграла в формуле (2.8) суммой. Бу-
62
2.1. Фрактальный анализ сигналов
дем считать, что переменная t принимает целочисленные значения,
и запишем переменную интегрирования как t' = in, где / = -°о,...,-2/п,
-1/п, О, 1/л, ..., t/n . Тогда приращение dB{t') исходного гауссова
процесса с независимыми значениями можно записать в виде «"1/2^.,
где ^ — дискретная гауссова случайная переменная с нулевым
средним и единичной дисперсией. Множитель л~1/2 учитывает
перенормировку по соотношению (2.2). Тогда
1 nt f : \#-l/2
ПН+ 1/2)*
nJ
Данный ряд не сходится; следовательно, при t' -> -°° будет
расходиться интеграл (2.8). Поэтому более точно случайная функция
BH(t) в [112] при заданном значении Вн(0) определяется как
Вн^-внФ) = Г(Н\1/2) ) K(t-OdB(0 (2.9)
с модифицированным ядром
Г(Г-/')Я"1/2,0</'</,
K(t ° |[(/-Оя-1/2-Н,)я"1/2]^<0.
(2.10)
Соотношение (2.9) является общим уравнением линейного
отклика. Независимое гауссово приращение dB(t'), имеющее
значение 1 в момент t', в более поздний момент t вносит вклад в
смещение фрактальной броуновской частицы Bff(t), определяемый
функцией отклика Kit-t") [45]. Изменим масштаб времени, т. е.
BH(bt)-BH(0)=nHl+y2)bj K(bt-OdB(0,
и введем новую переменную интегрирования t' = bi. Используя (2.2)
в виде dB{t' = b) = bx/1dB{t) и замечая, что K(bt-bi) = bl^2K(t-i),
получаем выражение Вн(bt)-Вн(0) = bH\_BH{t)-BH(0)],
справедливое в статистическом смысле при всех значениях Ь. Считая t = 1 и
At = bt, приходим к тому, что приращение координаты фрактальной
броуновской частицы
63
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
BH(At)-Bff(0)=\At\*[Bff(l)-Bff(0)]~\At\H (2.11)
статистически пропорционально | At \H. Поэтому дисперсия
приращений будет определяться формулой (2.4) с t0 = 0 и At = t-t0.
В работах [115-117] получено следующее выражение для
дискретных приращений (фрактальный шум) при обобщенном
броуновском движении:
5я(/)-5я(/-1) = ^|^|х(0я-,/Ча+л(^н) +
n(M-i) 1
+ X [(»+»Н-1/2-(»Н-1/2%шм-1+»-»\> (2-12)
где М - конечный интервал целочисленных значений времени t;
{£,■} — набор гауссовых случайных чисел с единичной дисперсией и
нулевым средним; /= 1, 2,..., М.
По соотношению (2.12) с использованием последовательности
гауссовых случайных чисел можно получить последовательность
приращений Вн. Выражение (2.12) эквивалентно вычислению
скользящего среднего со степенной весовой функцией от гауссова
процесса. При /» М приращения становятся независимыми, и
^превращается в гауссов процесс с независимыми приращениями. Алгоритм
(2.12) неэкономичен, и поэтому в работах [118] был разработан
быстрый алгоритм моделирования фрактального шума, основанный на
весовом суммировании ряда марковских гауссовых переменных с
возрастающими временами корреляции и на учете высокочастотной
компоненты с марковскими свойствами. При расчете по (2.12) при
Я= 1/2 моделируется белый шум. По мере возрастания значения
коэффициента Херста [45] усиливается низкочастотный шум,
приводящий к большим отклонениям амплитуды.
Изменение во времени фрактальной броуновской функции Вн (t)
при Вн (0) = 0 описывает изменение положения частицы, начавшей
движение из начала координат. При возрастании Я увеличивается
амплитуда вариаций координаты положения частицы. При
фрактальном движении с Я> 1/2 отклонения от начала координат, по
сравнению с броуновским движением, аномально велики.
Действительно, используя выражение (2.4) совместно с соотношением Эйнштей-
64
2.1. Фрактальный анализ сигналов
на, можем определить коэффициент аномальной фрактальной
диффузии
KDH = KD\t\™-\
которая играет важную роль в анализе процессов фрактального
переноса. Подчеркнем [45], что в данном случае аномальный характер
диффузии связан с фрактальными свойствами блужданий в
евклидовом пространстве. Когда блуждание происходит на фрактальном
множестве в евклидовом пространстве, коэффициент диффузии
остается аномальным, но характеризуется другим показателем
степенной зависимости от времени [119]. Подробнее о современных
методах описания диффузии во фрактальных пространствах см. в разд. 2.3.
Соотношение подобия (2.11) показывает, что случайная
функция Bff(At) пропорциональна |Д* |я. Отсюда следует [3, 117], что
размах R (т) при запаздывании т также является,случайной функцией,
подчиняющейся закону подобия Л(т) ~ хн> Поскольку мы везде
полагали значение дисперсии S2 = 1, то окончательно можем записать:
R(z)/S~x* (2.13)
Показатель Херста можно оценить, аппроксимируя
экспериментальные результаты соотношением (2.13).
Алгоритмы построения не только обычной фрактальной
броуновской функции, но и фрактальных броуновских поверхностей и
объемов, на основе последовательного случайного сложения
предложены в работе [120]. Для построения обобщенной броуновской
кривой с вертикальной координатой, описываемой законом
обобщенного броуновского движения, необходимо, чтобы дисперсия
приращений координаты удовлетворяла условию V(t)=\t\2H о], где
о§ - начальная дисперсия случайных сложений.
В алгоритме отправной точкой служит последовательность
значений координаты Y(tx)9 Y(t2), ..., Y(tN)r заданных для моментов
времени tv tv ..., tN. Для примера рассмотрим простейший случай
N= 3 с моментами времени / = 0,1/2,1; исходные значения
координаты равны нулю. К значениям Y(t{), Y(t2), Y(t3) прибавляются
случайные числа с гауссовым распределением, нулевым средним и
единичной дисперсией о2 = а\ = 1. На каждом интервале вьщеляются
3 Фракталы
65
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
затем средние значения времени. Значения координаты в них
оцениваются интерполяцией. Следовательно, мы имеем временные
точки flv.., t5 = 0,1/4, 1/2, 3/4, 1. Снова ко всем координатам Y(tf)
прибавляются случайные числа с нулевым средним и уменьшенной
дисперсией с^ = (1/2)2Яа^. Затем между пятью новыми значениями
вновь проводится интерполяция к серединам временных интервалов,
что приводит к значениям координаты в девять моментов времени.
После л-кратного применения этого алгоритма получаем
значения координаты обобщенной броуновской частицы в (1 + 2п)
моментов времени. Дисперсия слагаемых л-го поколения
с2 =
п
т2Я , fi)2Hn 2
2 а°'
<*■! =
2
В [120] также показано, что заполненность синтезированных
фрактальных поверхностей контролируется выбором
коэффициента г ф 1/2, так что в л-м поколении суммирование проводится при
дисперсии <52п = r2Hcl. Достоинство рассмотренного алгоритма
состоит в том, что он может применяться до тех пор, пока не будет
достигнуто любое, наперед заданное разрешение. Синтезированные
сцены дают возможность очень просто алгоритмически описать
природные ландшафты при малом числе входных параметров. Данный
метод объединяет синтезирование ландшафтов с анализом
наблюдений, а это самый многообещающий подход.
Самоаффинность фрактальной броуновской функции. В
соотношение подобия (2.2) время и координата входят с разными
коэффициентами: когда время умножается на коэффициент Ь, координата
умножается на Ьн. Поэтому обобщенный броуновский процесс
относится к самоаффинным фракталам (см. разд. 1.1). Фрактальная
размерность самоаффинных фракталов не определяется однозначно.
При анализе самоаффинных фрактальных кривых следует различать
локальную и глобальную размерности [58].
Рассмотрим эту проблему на примере графика фрактальной
броуновской функции Вн (t) с длительностью рассматриваемого
периода Т. Тогда для покрытия оси времени необходимо Т /Ьх отрезков
длиной Ьх. В пределах каждого отрезка диапазон изменения
функции имеет величину порядка ABff(bx) = bHABff(x). Для покрытия
этого размаха необходимы bHABff(x)/(ba) рядов клеток высотой Ъа
каждая. Поэтому для покрытия всей кривой требуется
66
2.1. Фрактальный анализ сигналов
м='Чм.':.1.-м-».
N(b,a,x) = -M^L.±.^bM-2^b-vA (2И)
ba bx
клеток. В данном случае рассматриваются клетки, размер которых
мал по сравнению как с длительностью процесса Т, так и с
диапазоном изменения функции. Такие рассуждения неприменимы, если
для покрытия кривой используются клетки с немалым размером, по
сравнению с размахом кривой. Если выбрать значение а,
соответствующее характерной длине шага а = Jfe2) = 1, то на каждом временном
отрезке длительностью Ьх для покрытия кривой с размахом ABff(bx)
потребуется всего один ряд клеток и
N(b,a,x) = l .L„b-\„b~DT (2.15)
bx
Итак, при анализе самоаффинных фрактальных кривых
следует различать локальную фрактальную размерность Dn = 2 - Н и
глобальную фрактальную размерность DT = 1.
Рассмотрим внутреннюю размерность, которая получается, когда
для измерения кривой вдоль нее укладывается эталон, или
линейка, длиной 8. Для самоподобных фрактальных кривых (например,
береговых линий) получается длина порядка
Для самоаффинной кривой выбираем линейку длиной 8 и
считаем, что она покрывает временной шаг длительностью Ьх. Тогда
вклад в общую длину кривой составит [45]:
1/2
8 = {б2т2 + 62Я[ДЯя(т)/я]2} . (2.16)
При выборе достаточно большого увеличения по оси у
(достаточно малое а) второе слагаемое в (2.16) будет преобладать, и Ь~ЬН.
Число таких отрезков вдоль оси времени равно Т/(bx) ~ b~x ~ 8"1/я,
тогда общая длина L ~ 8М/Я ~ 81_/).
В локальном пределе, когда растягивается масштаб по оси у,
внутренняя размерность Dn = \/Н. При растяжении оси времени,
когда флуктуации X(t) становятся незаметными, преобладающим в
(2.16) станет первое слагаемое; тогда 8-6. Полная длина будет
61
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
I-8T/4-J, и поэтому D = 1. Иногда величину Dn = 1/Я
называют скрытой фрактальной размерностью [121]. Она связана с
фрактальной размерностью следа броуновской частицы. Показатель Хер-
ста Яносит название аффинного показателя [58]. Для ^-мерного
аффинного пространства при Е>2 имеется Е(Е-1)/2 аффинных
показателей. Сведения о различных видах фрактальной
размерности обобщенной броуновской функции приведены в табл. 2.1.
Таблица 2.1
Размерность фрактальной броуновской функции [45]
Размерность
Хаусдорфа
Клеточная
Внутренняя
Случайного блуждания
Подобия
Самоподобная кривая
1/Я
1/Я
1/Я
1/Я
Самоафинная кривая
локальная
2-Я
2-Я
1/Я
глобальная
1
1
Среди процессов с независимыми приращениями винеровский
процесс занимает, как отмечалось, особое положение. Его график
непрерывен, что имеет место только при гауссовом
распределении, Отказ от нормальности приращений ведет к разрывным
траекториям.
Устойчивые распределения и аномальная диффузия.
Предположение о «гауссовости» исследуемых процессов базируется на
центральной предельной теореме при конечной дисперсии случайных
слагаемых. В противном случае результирующий процесс может и не быть
гауссовым.
Общий класс распределений сумм большого числа независимых
случайных слагаемых при условии его самоподобия - это
устойчивые по Леви распределения [122]. Для взаимно независимых
случайных величин X, Xv Х2 с одним и тем же распределением при
любых положительных коэффициентах s и t доказано следующее
свойство подобия:
№ХХ +№Х2 i(s+t)V« X. (2.17)
d
Здесь знак = означает принадлежность распределений случайных
величин к одному классу. Характеристический показатель а лежит в
68
2.1. Фрактальный анализ сигналов
пределах 0 < а й 2. Для нормального распределения а = 2 и
формула (2.17) сводится к закону сложения дисперсий. Устойчивые
распределения с характеристическим показателем имеют моменты всех
порядков, меньших а. Для а < 2 имеем величину с бесконечной
дисперсией.
Диффузный процесс с независимыми приращениями,
распределения которых устойчивы по Леви с показателем а < 2, называют
«полетом Леви» [123-125]. При бесконечной дисперсии смещения
измерения ее за конечный интервал времени могут дать
определенный результат, но он может быть любым и не характеризует процесс.
Аналогом является сумма расходящегося ряда при перестановке его
членов [26].
В данных обстоятельствах очень важную роль играют измерения
фрактальной размерности. Траекторию «полета Леви» можно
представить набором точек поворота с прямолинейными скачками
между ними. В двумерном фазовом пространстве диффузионный
процесс, обладающий свойством (2.17), имеет фрактальную размерность
точек поворота с а < 2. При а = 2 возвращаемся к броуновскому
процессу.
Моделирование распределенных по Леви случайных величин
может приводить и к процессам аномальной диффузии с конечной
дисперсией приращений. Пусть процесс образован скачками с их
величиной, распределенной по Леви. Эти перемещения происходят за
время, пропорциональное величине скачка. Тогда дисперсия
приращений за известный интервал времени конечна, а фрактальным
объектом являются временные точки разрыва производной
процесса. Получаем в этом случае процесс с фрактальным временем [124—
125], называемый супердиффузионным процессом. Для данного
процесса Я может превышать единицу. Примером такого процесса
в природе являются, в частности, поперечные смещения волнового
пучка в неоднородной среде [126].
Функция Вейерштрасса-Мандельброта. В качестве примера
самоаффинной функции рассмотрим фрактальную функцию
Вейерштрасса-Мандельброта, определяемую соотношением [3]:
Wi,)- t ['-.Mffi*».). (2.18)
69
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Параметр D принимает значения 1 < D< 2, срл - произвольная
фаза. Функция Вейерштрасса-Мандельброта непрерывна, но не
дифференцируема ни в одной точке. Очень часто ее модификации
используют при моделировании рассеяния волн фрактальными
поверхностями. Косинусной фрактальной функцией
Вейерштрасса-Мандельброта называется действительная часть функции W{t)\
C(t) = ReW(t)= t (1:(ИГ)> <2Л9>
которая анализируется в [128]. Обычно считают, что эта функция
фрактальна с размерностью D. Если иметь в виду клеточную
размерность, то данная функция действительно имеет размерность D. Было
показано, что фрактальная размерность D (W) функции
Вейерштрасса-Мандельброта заключена в пределах [129]
D-(j)<D(W)<D.
Входящая в это неравенство постоянная В достаточно велика для
того, чтобы оно выполнялось и при больших значениях Ь. Значения
функции Вейерштрасса-Мандельброта вычислены в работе [45] при
дискретных параметрах в интервале 0 < t< 1. При значениях D~\
функция C(t) по существу гладкая. Если значение D= 2, функция
C(f) сильно флуктуирует и напоминает шум в электронных цепях.
Функция Вейерштрасса-Мандельброта является однородной и
удовлетворяет соотношению
C(bt) = b2-DC(t). (2.20)
Из этого соотношения следует, что если в исходной кривой
заменить / на ЬЧт C(t) на b4^2~D^C(t), то получится исходная функция.
В этом и проявляются скейлинговые свойства функции C(t).
Кривая С(0 является самоаффинной, так как в направлениях осей t и C(t)
используются разные масштабные множители.
Функцию Вейерштрасса-Мандельброта также используют для
получения случайных фрактальных кривых, выбирая случайным
образом фазу из интервала (0,2л). Данные функции
рассматриваются в [128].
70
2.1. Фрактальный анализ сигналов
Спектр обобщенного броуновского движения. Приведем
некоторые сведения о концепциях спектральных представлений
обобщенного броуновского движения BH(t), опираясь на результаты работы
[481]. Для этого определим обобщенный броуновский процесс [112]
из формулы (2.8) в виде
Bff(t) =
1
ЦН+ 1/2)
\{\t-s\H-^2-\s\H-^2)dB{s)+\\t-s\H-^2dB(s)
,(2.21)
учитывая свойства самоподобия и стационарности малых
приращений (инкрементов)
Bff(t + aT)-Bff(t)=aHBff(T).
Нахождение спектра обобщенного броуновского движения не
можем быть решено напрямую с использованием стандартной
спектральной плотности мощности. Поэтому необходимо ввести
зависимый от времени спектр с помощью частотно-временного анализа.
Для этого в [481] рассматривается спектр Винера—Билля
[ Wigner—Ville], который для нестационарного процесса x(t) с
функцией ковариации rx(t, s) задается выражением
Gx(t,со) = J rx(t + т/2, f -т/2)ехр(-/сот)dx. (2.22)
—оо
Эта (не обязательно положительная) величина обладает
многочисленными интересными свойствами. Она обобщает концепцию
спектра доя стационарного случая и сводится к ней, когда процесс
стационарен.
Имея в виду, что
и используя (2.22), можно получить
GB„ <fM = (1" 21-2* cos2erf) j-jJj^. (2.23)
71
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Аналогичным образом, похожим на нахождение белого
гауссова шума как производной от ординарного броуновского движения,
можно определить парциальный гауссов шум как производную от
обобщенного броуновского процесса. Можно показать [481], что
С/(/,©) = (о2<7;са,а)) + 7-1(?х(Г,со).
4Э/2'
Тогда
Ч(''ю) = |^м- (2-24)
Величина (2.24) не зависит от времени, что говорит о
стационарности рассматриваемого процесса, который является результатом
стационарности приращений обобщенного броуновского движения.
Стационарность приращений также подтверждается через спектр
Винера-Вилля: если положить Хн T(t) = Bff(t + T)- BH(t)9TOT№ из
формулы (2.22) следует
Gx (/,©) = 4
(. corf l
sin л
. 2 ,
|т|2Я+1-
(2.25)
Выражение (2.25) соответствует спектральной плотности
мощности стационарного процесса. Значение производной имеет вид
В'н(t) = Urn- • Хи,(/) и с учетом (2.24) приводится к выражению
которое точно повторяет выражение (2.24), соответствующее
парциальному гауссову шуму.
Усредненный спектр находится из (2.22) в виде
1 т
SxfaT)=±JGxMdt.
1 о
72
2,2, Интегралы и производные дробного порядка во фрактальной геометрии
Тогда из (2.23) имеем
Благодаря свойствам самоподобия, к обобщенному
броуновскому движению можно применить вейвлет-преобразование, которое
для процесса х (t) имеет вид
Tx(t9a) = j=]x(s)g(^y, (2.27)
где а > 0; g(t) - произвольный локализованный вейвлет.
При заданном базовом вейвлете g(t) уравнение (2.27)
позволяет провести анализ сигнала в большом диапазоне масштабов. Таким
образом, в [481] предлагаются два подхода к анализу обобщенного
броуновского движения.
2.2. Интегралы и производные дробного порядка
во фрактальной геометрии
Идеи фрактальной геометрии используются в современной
физике. Предпринимаются активные попытки объяснить степенные
зависимости с дробным показателем (т.е. фрактального вида)
решениями уравнений в дробных производных. Кроме того, разнообразные
релаксационные и диффузионные процессы во фрактальных
пространствах (см. далее) характеризуются уравнениями с дробными
производными по координатам и времени. Хотя математический
аппарат дробного исчисления хорошо разработан [130-132],
широкое применение дробных интегралов и производных ограничено из-
за отсутствия их ясной физической трактовки. Прежде чем показать
физическую интерпретацию дробного интеграла, данную в [133],
рассмотрим некоторые основополагающие вопросы дробного
исчисления, необходимые для дальнейшего использования. Изложение
ведется, следуя [131], являющейся своего рода энциклопедией по
дробному анализу.
Уравнение Абеля. Идея об обобщении понятия
дифференцирования dnf(x)/dxn на нецелые значения п возникла с самого зарож-
73
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
дения дифференциального исчисления. Дробные производные были
предметом некоторого внимания Лейбница (1695 г.). Эйлер (1738 г.)
интересовался дробными производными. Собственно историю
дробного исчисления следует вести с работ Абеля (1823 г.) и Лиувилля
(1832 г.) [130, 131,975].
Понятие дробного интегрирования тесно связано с
интегральным уравнением Абеля
7Гт1т-^Л = ^>' х>а> <2-28>
Г(а) Ja(x-t)1 a
где 0 < а < 1; г(а) - гамма-функция. Решение уравнения (2.28) имеет
вид
Цх) = —±—ЦЛ£-А. (2.29)
Для уравнения Абеля вида
Г(а){(х-0'-а
имеется формула обращения
^ ' T(\-ct\ drUr-m
J d\ fit)
Г(1-а) dx>(x-t)a
Методом математической индукции доказывается формула для
и-кратного интеграла вида
jdxjdx...j<p(x)dx = -—i— j(x-t)n-lq>(t)dt. (2.30)
п п п ^ ' п
Заметив, что (п-1)\ = Г(п), правой части (2.30) можно придать
смысл и при нецелых значениях п.
Дробные операторы Римана-Лиувилля. Дробными интегралами
Римана—Лиувилля дробного порядка (а > 0) являются
74
2.2. Интегралы и производные дробного порядка во фрактальной геометрии
1 1 Ч*)
(C'Xa-iwJu?^* »«■ (231>
Первый из них называют иногда левосторонним, а второй -
правосторонним. Чаще всего имеют дело с левосторонним дробным
интегрированием. Оператор 1"+ в англоязычной литературе
обозначается в виде aD* при замене в (2.31) знака а на противоположный,
т.е. при а < 0.
Формула дробного интегрирования по частям имеет вид
}ф(х)(1?+у)(х)& = J y(x)(I£q>)(x)&. (2.33)
Дробное интегрирование обладает полугрупповым свойством:
1?_1ф = 1Г%> ос>0, р>0.
Дробное дифференцирование вводится, естественно, как
операция, обратная дробному интегрированию. Поэтому дробные
производные Римана-Лиувилля порядка а при 0 < а < 1 имеют вид
1ъ'У»-яЬ&& <234)
(^Х*--^!^ (2.35)
Если дробные интегралы определены для любого порядка (а > 0),
то дробные производные пока только для порядка 0 < а < 1. Для
больших порядков (а>1) при их целой - [а] и дробной - {а}
(0 < {а} < 1) частях числа а = [а] + {а} имеем
75
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Da /" =
1
Г(л-сс)|
(А \пх.
f№
d)ni №
dx) J(x-/)a-"+1
л = [ос]+1,
(2.36)
jy. f- W (dV( №dt „-Ы+1
Db-f~ r(n-a)\dx ht-x)-^' ""lCtJ+1
(2.37)
Если a - целое число, то под дробной производной порядка a
понимается обычное дифференцирование
Da ш
— Da =
dx Г b~
( jTt
dx
, a = l, 2, 3,
Иногда пользуются также обозначениями D^f = I"«/ = (I^+)_1/,
a > 0, понимая под каждым из них производную (2.34) и (2.36).
Аналогично понимают и символы D%_f = Ij«/.
В качестве примера рассмотрим степенные функции ср(х) = (х - я)р_1
и ф(х) = (6-х)р"1, Rep>0. Для них дробные интегралы
Г(а + Р)
Г(а + Р)
Дробные интегралы (2.31) и (2.32) легко распространяются с
конечного отрезка [а, Ь] на полуоси (а, <») или (-«>, 6). Для общего
случая, когда -оо<х<оо, дробные интегралы по всей прямой
имеют вид
Подобно (2.34) и (2.35) вводятся лиувиллевы производные
(D*f\M- _J__df/m (2.38)
76
2.2. Интегралы и производные дробного порядка во фрактальной геометрии
где 0<ос<1 и -оо<х<оо, Для ос£1 при л = [ос] + 1 имеем
Дробные производные Лиувилля на оси можно привести к
более удобному виду, чем (2.38). Получаемые конструкции называются
дробными производными Маршо:
где 0<а<1 и -оо<х<оо.
В теории дробного интегродифференцирования функций
многих переменных, которое является дробной степенью (-Д)0*/2
оператора Лапласа, широко используется дробное риссово интегродиф-
ференцирование. В образах Фурье F данная операция
записывается в виде
(-д)°/2/ = ^Чх|-°//4 F/' Rect>0' n
1 } J ' ' J [D-*f9 Rea<0. <2
40)
Подробное изложение теории дифференцирования Рисса
приведено в [131]. Как следует из теоремы о свертке функций,
интеграл дробного порядка (lo+/)(*)> Rea>0 является сверткой
Лапласа вида
(ъ/)<*>-
х*-1
™т
, Rea>0,
следствием чего имеет место свойство совместного действия
преобразования Лапласа и оператора дробного интегрирования
{Ll%+f)(p) = p-«(Lf)(p).
11
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Обобщенное правило Лейбница. В заключение сформулируем
обобщенное правило Лейбница:
ос
к=0\
^+(f8)=lLmkf)g(k\oieRK
к=-о
+°° ( ос ^
vk+h
\{D^-kf){l%kg),
ГаЛ
где
Г(а+1) _ sin[(p - а)л] Г(а+1)Г(р - а)
Р Г(Р + 1)Г(а-р + 1)
V' /
ПР+1)
-
обобщенный биномиальный коэффициент; a, $eRl, Rl =(-°°, °°) и
аф-1,-2,... при нецелом (}.
Наряду с последними формулами имеет место формула
Лейбница с остаточным членом
k=o{KJ
r(-a)(n-l)\Ja \
которая не требует от функции v(x) бесконечной дифференцируемо-
сти.
Функция Фокса. При интегральных преобразованиях в
диффузионных процессах во фрактальном пространстве и использовании
дробных операторов широко применяется Я-функция Фокса Н™,
где 0<m<q , 0<n<p. Эта общая функция гипергеометрического
типа была введена и изучена в [134]. Теория данной функции
рассмотрена в [134-136].
Функция Фокса определяется как
PQ
(av a{), ..., (ар, ар)
\(bv ft), ..., (bq9 р,)
~jh(s)z'ds,
2л/
78
2,2, Интегралы и производные дробного порядка во фрактальной геометрии
h(s) = -^-
(=1
Йг(1-^+Р/)ЙгЦ-«,4
j-m+\
i=n+\
где r(s) - гамма-функция; параметры ос,.(/ = 0,1,...,/?) и Ру. (j = 0,
1, ...,#) - положительные числа; 0у. и ft. — комплексные числа,
удовлетворяющие условию az. (bh + 8) Ф рЛ Ц. -1 - X); 8 и X = 0, 1, ...;
Л = 1,..., т\ /= 1,.., я.
Контур интегрирования С в комплексной s-плоскости проходит
так, что полюсы Т{Ъ. — Э^)С/ = 0, 1, ..., m) находятся справа, а
полюсы (l-a. + ais)(i = l, ..., п) — слева от контура.
Преобразование Лапласа функции Фокса представляет собой
также функцию Фокса, но с другими индексами:
н(р)=-н^
Н(р) = ±.Н'»:Г}
P+lQ
(1,1), (l-q.a,)
j|(0, 1), (a,., a,)
P\ ty, P7)
, 0<ц<1,
Ц>1-
Для обратного преобразования Лапласа имеем
я(о=-я;
(\ (i-bj,Vj) )
%-а,,а,) (1,1)
0<ц<1,
Г
/>+!,?
Ц, ос,) (1, D1
(ЬР Р,)
, ^1-
Функция H(z) является аналитической функцией z при
выполнении условий: z*-0 при ц>0 и UKP"1 при ц = 0, где
и=£р,-1л. р=й«г'Йр^-
У=1 /=1
/=1 j=\
79
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Асимптотическое разложение функций Фокса дается выражением
справедливым для ц > О и п * О для | * |-> оо на каждом замкнутом
секторе | arg z I£ яА, / 2. При этом вычеты должны определяться в
точках $ = (£!,-l-vj/cc,; / = 1, ..., п\ v = 0, 1, ...
Различные аспекты применения математического аппарата
дробного исчисления в теории электромагнетизма обсуждаются в [137].
Физические интерпретации дробных операторов. Наличие прямой
связи между дробным интегралом и фрактальным множеством
Кантора (см. рис. 1.1) доказывается в [133]. Для наглядного понимания
физической интерпретации здесь рассмотрены два предельных
случая, широко используемых в физике. Пусть имеется некоторая
физическая система. Процесс ее эволюции описывается оператором
/(0-}*(/-х)/(х)Л.
о
В первом предельном случае функция памяти K(t) имеет
ступенчатый характер:
«,-„={'-'■ °<~''
[О, т>Л
Тогда в процессе эволюции система будет проходить через все
состояния непрерывным образом без потерь и
что соответствует полной памяти (эквивалент «прямой»). Здесь F(p) -
лапласов образ функции /(t).
Во втором предельном случае
/W = \Uf - х)/(х)Л = /(/) = ыр(-р№р),
о
система теряет все свои состояния, за исключением единственного
с бесконечно большой плотностью (эквивалент «точки»). Этот слу-
80
2,2, Интегралы и производные дробного порядка во фрактальной геометрии
чай соответствует марковскому процессу, или процессу без
последействия.
В [133] ставится вопрос: существуют ли физические системы,
которые в процессе развития занимают промежуточное положение
между прямой и точкой? Классическая геометрия не дает на него
утвердительного ответа, так как в ней не существует
промежуточного геометрического объекта между точкой и прямой. Фрактальная
геометрия отвечает на этот вопрос утвердительно, так как такой
объект существует и называется канторовым множеством.
При установлении связи между дробным интегралом и
фрактальным множеством Кантора используется ступенчатая функция
вида
Л(>!<т<>2) = Г
1, если т€ Up t2],
еслит ё [tv t2].
Алгоритм построения канторова множества описан в разд. 1.1.
Пусть временной интервал длины есть /. После удаления средней
части отрезка остаются два концевых отрезка длиной %t(%<\/2).
Затем процедура повторяется. Конечный вклад в интеграл от 2N
полосок на N-u этапе разбиения записывается в виде
1 '. iJL
о w=i
с преобразованием Лапласа
,w-pg^/rfxZ|i(<ifr)<x<<S3)/w <2-41>
Здесь
1-ехр (-/*$*)
Ф(Р) у ' 0,[/*(М)№)> (2.42)
G«W = 2-Jvff[l + exp(-^)]) (2.43)
л=0
где z = /tf(l-$).
Функция Qn(z), определяемая выражением (2.43),
удовлетворяет следующему функциональному уравнению:
81
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
которое при условиях
m-t>)<\pt\<KN (2.44)
и 0<т//< 1 принимает вид
Qn(z/Q~^QNA(z). (2.45)
В пределе при N -> оо уравнение (2.45) записывается как
Q(z/Q = ^Q(z) (2.46)
с решением
Q(z) = Avz-\ (2.47)
где v = D = 1п2/1п(1/£) - фрактальная размерность канторова
множества.
Таким образом, в [133] показано, что в промежуточной области
\pt\, удовлетворяющей (2.44), Ф(р) принимает форму
Ф(р)^А^1-^Г(р^Г(р). (2.48)
Соотношению (2.48) соответствует представление /(f) в форме
дробного интеграла
/(f) - 4,[f (1 - $)Г т^т Ь - тГ */(т)Л =
T(v)J
-<й|%))<1-«>,-,'<«<>* <2-49)
где 0<v<l; 0<i<f; коэффициент >4v=2"v/2.
Для £ = 1/2 значение v = D = l. При этом на основании (2.49)
величина /(f) связана с/(f) через полный интеграл и соответствует
первому случаю (полная память). Случай £ -»0 (v - D -»0)
соответствует линейной комбинации двух дельта-функций половинной
интенсивности, локализованных на концах выбранного интервала
[0, f], т.е. имеется система (процесс) с полным отсутствием памяти.
Таким образом, множество Кантора в пределе (N -> 0) сходится к
дробному интегралу. Показатель v дробного интеграла совпадает с
82
2.3. Диффузия во фрактальных пространствах
фрактальной размерностью множества, а также указывает на долю
сохраняющихся состояний в процессе эволюции физической
системы и охватывает случаи полностью замкнутой (v = 1) и марковской
(v = 0) систем.
Ряд физических систем, которые могут быть описаны
уравнениями в дробных производных, должны содержать каналы, входящие
в состав некоторой ветвящейся фрактальной структуры. В [133]
такие системы классифицируются как системы с остаточной памятью.
Поэтому процессы переноса в иерколяционных кластерах,
фрактальных деревьях, пористых системах должны тщательно
анализироваться, чтобы получать корректные уравнения переноса для таких
систем. Показатель дробного интеграла соответствует доли каналов или
ветвей, открытых для протекания.
Для процессов с потерями, обусловленными столкновениями,
также следует использовать уравнения в дробных производных. В
частности, для упругих сил в [133] получено обобщенное уравнение
переноса в дробных производных. Там же обсуждается применимость
таких уравнений для описания процессов релаксации наведенной
электрической поляризации в диэлектриках.
Изучению связей между операторами дробного интегродиффе-
ренцирования и фрактальной геометрией проводилось с точек
зрения математика и физика также в [631, 632, 789, 816, 828-834, 857,
860-863, 868-872, 875, 876, 899-904], где был получен ряд глубоких
результатов с учетом регуляризации и устойчивых распределений.
2.3. Диффузия во фрактальных пространствах
Аномальная диффузия. В настоящее время довольно широко
обсуждается возможность обобщения стандартного уравнения
диффузии [138-146]
^A = DAp(r,t),p(r,0) = b(r) (2.50)
и диффузии в самых разных системах в применении к аномальным
процессам. Моделирование таких систем и процессов часто
проводят с помощью фракталов. В результате скейлинга здесь начинают
проявляться эффекты памяти (см. разд. 2.2), и обычные операторы
дифференцирования заменяют соответствующими операторами
дробного порядка. Замена d/dt на (Э/Э/)р> Р<1 ассоциируется[138-141]
83
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
с влиянием распределенных в среде ловушек с бесконечным средним
значением времени пребывания частиц в них, а введение дробного
лапласиана Да/2 - с аномально широким распределением пробегов
частиц. В режиме аномальной диффузии, называемой
субдиффузией, диффузионный пакет At ~ f (т.е. ширина плотности
распределения p(r, t)) расплывается со временем медленнее (v < 1/2), чем при
обычной диффузии (v = 1/2), и быстрее, чем при супердиффузии
(v>l/2). Впервые уравнение с лапласианом дробного порядка
(v < 1 / 3) было рассмотрено А.С. Мониным [147,148] при описании
диффузии в турбулентной среде.
Рассмотрим подробно решение уравнения супердиффузии с
лапласианом Да/2 в ЛГ-мерном пространстве [149]. Определим дробную
производную Рисса через лапласиан [131] и, воспользовавшись
оператором (-Д)а/2 (2.40), запишем уравнение супердиффузии в виде
|£ = -Д-д)°/2р(г,,). (2.51)
Для ЛГ-мерного пространства с векторами х и к, со скалярным
произведением kx = klxl^... + kNxN и преобразованием Фурье
Ff*f(k) = jexp(ikx)f(x)dx
соотношение (2.40) остается в силе. Дробный лапласиан
записывается в виде гиперсингулярного интеграла
где (д£/)(х)= ^(-l)m[fyf(x-my) - нецентрированные разности;
п - любое число, превышающее a; dNi п (а) = J[l - exp(&j)]" | х \~N"a dx -
нормирующий множитель.
Процессы Леви и строго устойчивые распределения. В [149]
супердиффузию описывают в рамках обобщения винеровского
процесса. Для этого записывают уравнение Колмогорова-Чепмена для
стационарного марковского процесса с независимыми приращениями
p(x9t) = jp(x',t')p(x-xf, t-t')dx', 0<t'<t, p(x,0) = 8(x) (2.52)
84
2.3. Диффузия во фрактальных пространствах
и рассматривают класс автомодельных решений
р<а>(х,/) = {Dt)-N'*gM [х(Л)-1/а], (2.53)
где /)>0, а>0.
После применения преобразования Фурье к уравнениям (2.52)
и (2.53) и учета сферически-симметричных распределений g(a)(k)
[150] имеем
£<°<>(*) = ехр(-|*|а), 0<сс*2,
pM(k9t) = txp{-D\k\«t). (2,54)
Преобразование Фурье (2.54) удовлетворяет дифференциальному
уравнению
М^=-д|*|ар<а),
01
которое, согласно N-мерному аналогу (2.40), в результате обратного
преобразования приводит к уравнению для плотности вероятности
^. = -Д-Д)«/2р(«)(х, /), р(х, 0) = 8(х), (2.55)
ot
обобщающему (2.51) на ТУ-мерный случай. Для одномерного
пространства оператор (-Д)а/2 переходит в производную Маршо (2.39).
Данный процесс относится к процессам Леви, и при ос = 2 он
превращается в винеровский процесс.
Согласно (2.54), решения уравнения супердиффузии (2.55)
принадлежат к классу строго устойчивых N-мерных распределений [151,
152] и составляют подмножество сферически-симметрических
распределений этого класса, в число которых входит и многомерное
гауссово распределение (а = 2). Особенностью устойчивых
распределений, отличных от гауссова, является то, что абсолютные
моменты (I х Y) = JVa)(*) \xf dx бесконечны при ц £ ос. Поэтому для
характеристики ширины диффузионного пакета [149] удобно принять
радиус шара Rp(t), содержащего фиксированную вероятность/?:
J р<«>(х,/)А-р.
\x\<Rp(t)
85
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
После подстановки уравнения (2.53) имеем R (t)~tl/a, /->°°.
Кинетические уравнения. При ос = 2 получаем нормальную
скорость расширения диффузионного пакета; для а < 2 ширина пакета
растет быстрее, чем в нормальном режиме. При а < 1 ширина
диффузионного пакета растет быстрее, чем в баллистическом режиме.
Данный результат обусловлен автомодельностью процесса Леви, в
котором нет места понятию скорости свободного движения
частицы. Избавиться от этого можно переходом от винеровской модели
к модели случайного блуждания частицы с конечной скоростью
свободного движения v. Пусть в начальный момент времени t= О
частица находится в начале координат (х - 0) и пребывает там
случайное время т0, затем перемещается на случайный вектор \х со
скоростью v и вновь пребывает в состоянии покоя случайное время iv и
т. д. Считаем, что переменные т0, тр £р т2, £2,... взаимно
независимы, времена т. имеют одинаковую плотность вероятности вида
<7(0 = цехр(-ц,0> Ц>0> АГ-мерные векторы^, также распределены
одинаково. Вместо одной частицы здесь рассматривается множество
независимых траекторий, р(х, t) - плотность числа частиц.
Представляя плотность частиц р (х, t) как сумму двух
составляющих, относящихся к частицам в состоянии покоя (ловушки) р0(х, t)
и движения pv (xf t), получаем [149] следующие кинетические
уравнения:
pv(x, t) = ^\ck'jdtnx')b(f-^) щ>0(х-х\ t-t')= (2.56)
= ±jdx'P(x%p0(x-x\ t-f).
Здесь p(x)dx — вероятность того, что частица, вылетающая из
начала координат, испытает первое столкновение в элементе объема
dx = dSd | х |; P{x)dS — вероятность того, что частица пересечет
элементарную площадку dS сферы радиуса |х| без взаимодействия на пути
|х|. Система уравнений (2.56) при показательном распределении
пробега в трехмерном пространстве описывает нестационарный
перенос нейтронов с учетом запаздывания. При ц -> 0 она переходит в
86
2.3. Диффузия во фрактальных пространствах
нестационарное односкоростное кинетическое уравнение с
изотропным рассеянием, используемое в нейтронной физике [153, 154].
В предельном случае v = °°p(x, f) = Po(*> 0> что удовлетворяет
уравнению Колмогорова
|^ = -W) + 4^>(*')P(*-*', 0 (2.57)
для обобщенного пуассоновского процесса [122].
Из (2.57) следует уравнение для характеристической функции
p(k,t) распределения
& = Ml-P(k)]p(k,t),p(k,0) = l
ot
с решением
р(М) = ехр{-[1-Ш]И>
где р{к) -компонента Фурье плотности вероятности перехода р(х).
Асимптотика решения уравнения Колмогорова совпадает с точным
решением уравнения супердиффузии. Таким образом, уравнение
супердиффузии (2.55) описывает асимптотическое поведение
плотности распределения частицы, совершающей с бесконечной скоростью
блуждание в среде с ловушками, время пребывания в которых т
распределено по показательному закону, а плотность распределения
скачков частиц имеет степенной «хвост» вида г-"-1.
Конечная скорость частицы. Для учета влияния конечной
скорости свободного движения v блуждающей частицы на асимптотику
распределения р(х, t) в [149] полагают, что векторной сумме п
независимых случайных векторов ^
/=1
л
соответствует случайное время 0 = ^(т. +1 ^ |/v).
/=i
Если а > 1, то среднее ^ конечно и при п -> °о, в силу закона
больших чисел Q~t = n(l/ii + a/v), я=|?Д откуда л = (1+цд/у)_1|0/-
Считая t = - -—, имеем
l + \ia/v
Р«<*> t) = 0J)-N/«gM[x(Dvt)-V«l а>1. (2.58)
87
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Физически это означает, что наличие конечной скорости
свободного движения замедляет процесс расширения диффузионного
пакета по сравнению со случаем v = °o. Переписывая (2.58) с учетом
Dv = (l + \ia/v)-{D в виде
Р«<*.') = (fy)'N/*gM[*(А/)"1/а], а> 1,
можно для асимптотической плотности, диффундирующей с
конечной скоростью свободного движения частицы, записать уравнение
в дробных производных:
^ = -Dv(-A)^pJx9t).
В результате учет влияния конечной скорости при а > 1 сводится
лишь к уменьшению коэффициента диффузии в уравнении с
дробным лапласианом; форма распределения остается устойчивой. При
а < 1 ситуация совершенно иная. Как отмечено ранее, ширина, или
радиус, диффузионного пакета растет со временем
пропорционально t{/a. При конечной скорости v плотность распределения вне шара
радиуса Л = vf обращается в нуль. Если а > 1, влияние последнего
(кинематического) ограничения ослабевает с течением времени,
поскольку радиус пакета растет медленнее, чем R ж vt. Но при а < 1
распределение, даваемое диффузионным уравнением (2.55),
расплывается быстрее, чем R = vt9 и кинематическое ограничение
становится преобладающим фактором в формировании асимптотического
распределения. Это распределение, зажатое сферой R = v/, имеет
совершенно иной вид, чем устойчивое распределение.
Приведенные в [149] результаты моделирования методом
Монте-Карло одномерного блуждания частицы в сопоставлении с
решениями супердиффузионного уравнения подтверждают эти выводы:
при а < 1 решения супердиффузионного и кинетического уравнений
имеют совершенно разные асимптотики. По-видимому, это может
служить основанием для вывода о неприменимости
супердиффузионного уравнения (2.55) с лапласианом а/2 при а < 1 к описанию
реальных физических процессов.
Модель субдиффузии на основе интегральных уравнений.
Теоретическое исследование модели субдиффузии (v <l/2) для N-мерного
88
2.3. Диффузия во фрактальных пространствах
евклидова пространства с ловушками возвратного типа
рассмотрено в [ 155]. Развиваемый в указанной работе подход - от модели
блужданий, основанной на интегральных уравнениях, к
асимптотическим их решениям - позволяет не только выразить коэффициенты
аномальной диффузии через характеристики элементарных
распределений, но и установить соответствие между решениями,
полученными в рамках различных подходов. Идея искать решение
уравнений субдиффузии в терминах устойчивых законов базируется на двух
фактах. Во-первых, гауссово распределение - всего лишь одно из
бесконечного множества устойчивых законов, свойством которых
является то, что они описывают предельные распределения
нормированных специальным образом сумм независимых случайных
величин [150-152]. Гауссово распределение появляется в качестве
предельного только в случае слагаемых с конечной или логарифмически
расходящейся дисперсии. Во-вторых, в настоящее время установлена
связь между устойчивыми законами и функциями Фокса [134].
Далее на основе результатов [155] подробно приведено
математическое решение для модели субдиффузии.
Считаем, что частица может находиться в одном из двух
состояний: в состоянии обычной диффузии (1) и в состоянии покоя (0)
после попадания в ловушку. Процесс субдиффузии представляет
собой последовательную смену таких состояний со случайными
взаимно независимыми временами пребывания в них,
распределенными с плотностями соответственно qx(t) и q2(i). Предполагается, что
среднее время \ между выходом частицы из ловушки и
последующим попаданием в ловушку конечно (\ < «>) и определяется
плотностью ^(т). Среда считается пространственно однородной и
стационарной.
Пространственное распределение вероятности при непрерывной
диффузии р(х, t) для N-мерного пространства описывается
выражением
р(х9у) = (4nDtYN/2 exp(-x2 /(4/)/)).
Считаем, что р0(х, t) - распределение частицы в момент t9
начавшей свою историю с момента (t = 0) попадания в ловушку в
точке х = 0, а рх(х, t) - то же для частицы, история которой начинается
с выхода из ловушки в точке х = 0. Эти два распределения связаны
системой интегральных уравнений [155]:
89
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Р0(х, t) = Q0(t)5(x) + jdxq0(x)pl(x, t-x),
о
р{(х, t) = Q{(t)p(x, t) + jdxq{(x)p(x,x)*p0(x, t-x),
(2.59)
где Qi(t)=\qi(x)dx; символ * означает операцию свертки по про-
странственным переменным:
р(х, t)*p0(x, t-x) = jp(x\ x)p0(x-x', t-x)dNx'.
Введем обозначение st(t)= \\x\2 рДх, t)dNx, из (2.59) находим
s0(t) = jdxq0(x)s{(t-т), s{(t) = QY(t)s(t) + j dxq{(x)[s(x) + s0(t-x)],
о о
где s(t) = j\x\2 p(x, t)dNx = at, a = 2ND.
Применим к полученным уравнениям преобразование Лапласа
и получим алгебраическую систему уравнений для компонент
^о(^)= VoO^^O^)* ^iW = ^W + 9\0^)^оО^) с решением вида
l-q^q^X) 1-%(ЩО)
где
K(X) = jdtexp(-Xt)
Qx(t)s(t) + \dzqx(x)s(x)
— —a i и
dX X
+£'p.ftW].2Ml. (2.«>
XdX1
X2
Согласно тауберовой теореме [122], соотношение s.(t)~A,ta,
t->oo влечет за собой
s,(X) ~ Г(ос +1)4 Х~а~1, X -> 0,
(2.62)
90
2.3. Диффузия во фрактальных пространствах
и наоборот. Поскольку \<°°, можно записать:
1-?1(Х)~^, qjmJl^S^^ (2.бз)
и, следовательно, К(Х) ~ ах{ /X при X -> 0 . Подставив (2.62) в (2.60)
и определив выражение 1 - q0(X), находим необходимое и
достаточное условие субдиффузии:
l-q0(X)~bX«, Х->0, Ь=.а\А, ос<1, (2.64)
Да + 1)Л
где АХ=А2=А.
При переформулировке (2.63) для плотности распределения
#о(т) обращаемся внсшь к тауберовой теореме и применим ее к
функциям Q0(t) и Qq(X) = [1 -q0(X)]/X. Тогда
Оо«) = ]%Ш*~ВГ«, /->«, B = [nia_^)]2A (2.65)
или, для плотности,
q0(t)~aBt-«-1, Г->оо. (2.66)
Следовательно, субдиффузия возникает, если распределение
времени пребывания в ловушках имеет асимптотику степенного ввда
(2.65) с показателем а < 1. Это означает, что среднее время
пребывания частицы в ловушках должно быть бесконечным:
т0 = jxq0(x)dx = оо, ос<1.
о
При конечном т0 асимптотика q0(X) имеет вид
q0(X)~l-x0X, Х^О. (2.67)
Тогда после подстановки (2.63) и (2.67) в (2.60) следует, что
а
A.2(l+W
91
^)~
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
и влияние ловушек сводится лишь к уменьшению коэффициента
диффузии:
Я->
а асимптотический закон изменения среднего квадрата sx(t) со
временем остается линейным. Форма диффузионного пакета при этом
сохраняется гауссовой.
Модель субдиффузии на основе дифференциальных уравнений.
Применим к уравнениям (2.59) преобразования Фурье и Лапласа
соответственно по координатам и по времени и получим новую
систему уравнений с решением вида
,, ,4.„ft(X) + go(X)ft(x + ^fc2)
Ро( )= 1-д0(Щ(х+т '
(2.68)
Применяя в (2.68) условия (2.64)-(2.66), получим выражение для
главных асимптотических членов
р«(*,А,)я_-А - Я' = -Ь±-,
(2.69)
не зависящее от начального состояния. Найденное соотношение
можно представить в следующих трех эквивалентных формах [155]:
\*?"{к, X) = -D'k2pas(k, X) + X«-1,
Xp^ik, X)^-&k1Xx^pas{ki Х) + 1,
[рш(к9 X) = -D,k2X-apas(k9 JO + Ar1.
(2.70)
Известно [131], что на подходящем классе функций
преобразование Лапласа F(X) дробной производной Римана-Лиувилля (2.34)
F(t) = *„ связано с/(А,) дифференцируемой функции f(f) соот-
ношением F(X) = X^f(X). Применим обратное преобразование
Фурье-Лапласа к соотношениям (2.70) и получим уравнения в дробных
92
2.3. Диффузия во фрактальных пространствах
производных, описывающие асимптотическое поведение
субдиффузионного процесса:
\UL. = Dy2pas+_ -5(х),
Э*а Р 1X1-а)
p*=£'V2£_P_ + 5(x).
Эти уравнения имеют общее решение, компонента
Фурье-Лапласа которого представлена формулой (2.69). Отметим, что решение
3-го уравнения системы (2.71) было получено [142] с помощью
функций Фокса Н$. Другая форма решения [155] связывает его с
устойчивым распределением. Представим (2.69) в виде
оо
р"(*, Ь)»**-1/сч>{-[1>*2 +ЬаАу, сс<1, (2.72)
о
запишем обратное преобразование Лапласа p^Ofc, t) и, совершив
обратное преобразование Фурье, получаем следующий результат [155]:
р«(х, t) = {D'r«TN/\$(\x\/Ji№). (2.73)
Если gW(t) = (2ni)~{ Jexp(tf - sa)ds - односторонняя устойчивая плот-
Y
ность с характеристическим показателем a < 1, имеем
v|/£)(r) = (4n)-*/2JrfTexp(-rV/4)TAra/Va)(T), a<l (2.74)
о
- функция расстояния, зависящая от показателя субдиффузии а и
размерности пространства N. Односторонние устойчивые
плотности g(a)(0> ос<1 являются подмножеством семейства строго
устойчивых законов [155], определяемых следующим образом. Плотность g(t)
является строго устойчивой тогда и только тогда, когда для любых
положительных чисел Ъх и Ь2 найдется положительное Ъ такое, что
93
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
1 (t\(t\
¥i8
V*
s
ь2
ь2
т.е. форма строго устойчивых распределений является инвариантной
относительно операции свертки. Таблицы функций распределения
t
G^a\t)=\g{(x\x)dz и плотностей можно найти в [156].
о
Выражения (2.69) и (2.72) сохраняют смысл и при крайнем
значении а = 1, приводя к нормальной диффузии с тем же
коэффициентом Ъ', поэтому функцию (2.74) можно доопределить и для а = 1
соотношением \|/$}(г) = (4л;)-ЛГ/2 ехр(-г2 /4).
Субдиффузионное распределение (2.73) может быть выведено
также из простых вероятностных соображений, основанных на
использовании центральной предельной теоремы в ее обобщенном
варианте [151,152]. Устойчивые законы играют ту же роль в
суммировании независимых случайных величин с бесконечными
дисперсиями, что и обычный гауссов закон при конечных дисперсиях. В
частности, если независимые случайные величины Т{ < О
распределены с плотностью qQ(t), удовлетворяющей условию (2.65) при а < 1,
то нормированная сумма
п Т
при больших п распределена с плотностью g^(t). Другими
словами, плотность распределения q^\t) суммы ^Т. в асимптотике
больших п имеет вид
где Я*=ЯГ(1-ос).
Пренебрегая временем пребывания частицы в состоянии
диффузии при вычислении распределения числа попаданий частицы в
ловушки за время наблюдения t -> °о, можно получить
^=q$"+1)w-^',)(0=G(a)[(«JB*)-i/«r]-G(«){[(«+i)5*r,/a/}.
Представив аргумент вычитаемой функции в виде
[(Л + 1)^]1/аГ = [Л^Г1/аГ-Ы^Г1/аГ(Ла)-1
94
2.3. Диффузия во фрактальных пространствах
и разложив ее в ряд, получим асимптотическое выражение
рп ~[nB*rl/at(na)-igM{[пВ-Г1/%}, /->«,
При фиксированном п условное распределение координаты
частицы будет выражаться через обычную диффузионную плотность
соотношением р(х, t\ri)~p(x, n/\i). После усреднения по числу
актов непрерывной диффузии р(х, 0 = £р(х> Лп)Рп и перехода от
суммирования по л к интегрированию по переменной т = [пВ* ]~l/at
приходим к распределению (2.73).
Субдиффузионные распределения и моменты. Обсудим некоторые
свойства приведенных решений [155]. Пространственные моменты
выражаются формулой
V ' /" Г(ол + 1)Г(ЛГ/2) К '"
Второй момент
V*1' Г(ос + 1)
растет со временем пропорционально ta, О < а < 1, что является
признаком субдиффузного процесса. Отношение
ц(«) J*1'*) = 2»Г(п+1)т/2 + п)[Г(а+1)Г
Ц2л (|х|2) Nnr(an + l)r(N/2)
не зависит от времени, что указывает на постоянство формы
распределения. При а = 1 оно переходит в безразмерные моменты для
гауссова распределения
(l)J»nN/2+n)
В области, близкой к нулю, как и на больших расстояниях,
плотность у$(г) превышает нормальную, тогда как в средней области
расстояний ситуация обратная. Дифференцированием (2.74) по р
легко устанавливается следующее соотношение между
распределениями в N- и (N+ 2)-мерном пространствах:
У»+2(Г) 2nr dr ' Ц'1Ъ)
95
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Поведение проекции случайной точки, совершающей
субдиффузию в АГ-мерном пространстве на л-мерное подпространство,
описывается л-мерным уравнением субдиффузии с тем же показателем
а. В этом отношении ситуация подобна нормальной диффузии,
однако имеются и существенные отличия. В нормальной диффузии
разные координаты х{9 х2 диффундирующей частицы взаимно
независимы. При субдиффузии их совместное распределение не сводится
к произведению распределений. Поэтому случайные координаты хх
и х2 не являются более независимыми.
Как следует из (2.74), в одномерном случае (N= 1) плотность
распределения в начале координат существует:
оо
у[а)(0) = (An)-x'2\r*'2g(«\z)d^
о
поскольку плотность #(а)(т) имеет конечные моменты порядков,
меньших а. Тогда
1|/{а)(0) = [2Г(1-а/2)]-1.
В пространствах высших размерностей субдиффузионная
плотность имеет интегрируемую особенность. При N = 2 эта особенность
логарифмического типа. В пространстве трех и более измерений
особенность в нуле является гиперболической [155]. Полагая в формуле
(2.75) N- 1 и используя асимптотику, можно показать, что при г -> сю
flfv|/{a)(r) 2
dr -*"lXl-a)'
Отсюда следует, что в точке х = 0 производная функции \|^a)(jc)
имеет конечный разрыв, т.е. вершина распределения в одномерном
случае не гладкая, как при нормальной диффузии, а острая. При a -+1
производная обращается в нуль, и вершина становится гладкой.
Полученные в [155] аппроксимации у$(г) при ос>1/2
удовлетворительно описывают распределения субдиффузии во всей области, за
исключением малых расстояний, а при a -> 1 переходят в
нормальное распределение. Важнейшим отличием формы субдиффузионных
распределений от нормальной является более высокая концентрация
вероятности в области малых и больших расстояний. Для
одномерного случая при ос>1/2 субдиффузионные распределения действи-
96
2.3. Диффузия во фрактальных пространствах
тельно могут быть аппроксимированы гауссовой кривой с
субдиффузионной дисперсией, как это сделано в [157]. Для более высоких
размерностей нормальная аппроксимация не дает
удовлетворительных результатов.
Функции Фокса и процессы во фрактальных средах. Применение
аппарата функций Фокса [131, 134-136] при рассмотрении
процессов релаксации и диффузии в средах с фрактальной размерностью,
характеризуемых уравнением типа диффузии с дробными
производными по координатам и времени, продемонстрируем на основе
результатов, полученных в [158-160]. Из-за фрактальности - в
отличие от стандартного уравнения диффузии (2.50), когда поток
частиц j~dp/dt и у~Э2р/Эх2 - нарушается вследствие самоподобия
локальность таких связей. Величина потока начинает зависеть от
предыстории процесса - значений концентрации в более ранние
моменты времени:
jV)~l\p№(t,T)dx, (2.76)
т. е. процессы диффузии и релаксации становятся недебаевскими.
В формуле (2.76) ядро K(t, т) включает фрактальную размерность
D среды и в стационарном режиме зависит от разности аргументов.
Одновременно K(t,x) при замене фрактальной среды на обычную
должно удовлетворять стандартному уравнению диффузии.
Простейшим таким ядром является степенная функция K(t - т) = (/ - t)~v(jD)
с показателем степени, зависящим от фрактальной размерности
пространства диффузии D. В этом случае правая часть (2.76)
совпадает по структуре с определением дробной производной Римана-
Лиувилля (2.36) порядка 0< v< 1, т.е. j(x,t) ~3vp(x,0/dfv.
Одновременно вследствие сложности и запутанности траекторий движения
частиц производная по координате (градиент) становится
фрактальной и j ~ д2ур/дх2у. Уравнения недебаевской диффузии и
релаксации примут соответственно следующий вид:
av лэ2? av 1
aFp=jDa^p' э^р="7р'
где 0<v<l, 1<2у<2 [142-145, 158-160].
4 Фракталы " '
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Диффузионно-релаксационные процессы, исследуемые в [159,
160], описываются в одномерном случае уравнением
av Л э2? 1
(2.77)
и для их решения используется аппарат функций Фокса,
определяемых через обобщенный интеграл Меллина-Барнса [134, 135].
Действуя на правую и левую части уравнения (2.77) дробным
интегральным оператором (2.31) в виде
1 L- s(n
0^ = НГ>
mi" (t-ty-y!
получаем
p(x,t)-p0(x) = 0Df
Э2т./)-±
дх2У
р(х, t)\
(2.78)
при начальных условиях р(х, t)\j=0=p0(x). Дробное
дифференцирование (2.78) с помощью оператора 0DJ при условии 0D,V0Z)/"V=1 дает
0D?{p(x, t)-p0(x)}=
Э2т - 1
дх2У xv
р(х, t).
Далее необходимо использовать преобразование Фурье по
отношению к пространственной координате и преобразование Лапласа
оо
p(k,p) = jp(k, t)cxp(-pt)dt по времени. Для амплитуды Фурье
о
р(к, t) справедливо уравнение
0D?{p(k,t)-pQ(k)} =
Щк)2т-\
Р(*, 0
=-^содействие дробной производной по времени на не зависящую от
времени функцию р0(х) не равно нулю: 0D,vp0 = p0rv/r(l-v). Для
образа р(к, р) получим уравнение
р(к,р) = —^
1+Ш
гР0(*>-
98
2.3. Диффузия во фрактальных пространствах
Далее представим р(&, t) через функцию Фокса [159, 160]:
v
Пк)Р
l-1/v, 1/И
1-1/v, 1/v
и проведем обратное преобразование Лапласа
V '^
Решение уравнения (2.78) имеет вид
''' (ОД/v) ^
(0,1/v), (ОД)
1 °°
p(x,t) = — \ dkexp(ikx)pQ(k)Hl;l
-ty
{ikfW-\
(0,1)
(0,1), (0, v)
(2.79)
Представим функцию Н\\ в виде ряда и получим решение
уравнения (2.78) в виде
1 °° °° [D(ik№tv —tvx~v~\
р(х, t) = ± Г dkexp(ikx)p0(k)Zl =: г—J-. (2.80)
2kL Zq T(1 + VA2)
Интеграл (2.79) в ряде случаев вычисляется в явном виде. При
1/т = 0 формула (2.79) приводится к виду
1 °°
p(x,t) = — J йМ:р0(£)ехр(/&х,)#^
-№2"<
(0,1) 1
(0,1), (0, v)
(ДГ)-1/2уд2.81)
где x,=jc/CD/v)1/2y-
Для функций Фокса удобнее использовать синус (Fs) и косинус (Fc)
преобразования Фурье. Рассмотрим частный случай р0(А:) = р0 = const,
р0(дс) = р05(х), и пусть у = 1 — е, 0<е<0,5. После ряда преобразований
[159, 160] получим точное решение уравнения (2.78) с 1/t = 0 и
начальным условием p(x,t)\t=0=p08(x) при 0,5< у< 1:
99
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
p(x,t) =
Ро
(_1)е/2у
щ
7/2,1
(-l)-e/2Y+l/2
+ ~ нй
(-1)+е/2Т+1/2^2/
(-1)Е/2^!
(_l)-e/2YX]
(-1)£/2^
(_l)-e/2yXi
(1,1/2у), (l,v/2Y), (1,1/2)
'3,3
(1,1), (U/2Y), (1,1/2)
[(1,1/2Y), (l,v/2Y), (1,1/2)
(1,1), (1,1/2Y), (1,1/2)
(1,1/2Y), (l,v/2Y), (1/2,1/2)A
(1,1), (1,1/2Y), (1/2,1/2)
[(1,1/2Y), (l,v/2Y), (1/2.1/2Г
(1,1), (1,1/2Y), (1/2,1/2)
(2.82)
Для Y=v = l после ряда преобразований решение уравнения
(2.82) совпадает с хорошо известным решением обычного уравнения
диффузии.
Асимптотическое разложение для функции р(х, t) при 7-»<»
позволяет записать:
1 у (-*»■> 7 p0(t)exp(/fec)
^ ,)-55п1-К1.+1)]1[Л»Я'-1/^Г
Для конкретных р0(к) можно получить явные выражения (2.83).
Пусть р0(к) = р08(к), Z) = 0. Тогда
p(x,t) = p(t) = ±pQ%
-v(/i+l)
f-»°o,
2^ ,=oni-v(« + l)]^
что совпадает с результатами [145] и p(t)~l/tv.
Для р0(к) = р0 = const и 1 /xv = 0 имеем дело с чистой
диффузией. Решение дается выражением (2.82) и диффузионное смещение
частицы - со временем x~tv/2y. При v = y=l получаем известное
соотношение х2 ~ и Приближенное суммирование ряда по п в (2.80)
для больших t, которое осуществляется сохранением небольшого
числа слагаемых в ряде по п и замене функции Г(1 + vri) на функцию
(1 + п) при v -> 1, позволяет получить асимптотику по t и для у ф 1.
100
2.4. Недифференцируемые, или фрактальные, функции и множества
Волновое уравнение и фрактальные среды. Результаты
исследования нелинейного уравнения типа обобщенного волнового
уравнения во фрактальном пространстве, частным случаем которого
являются как волновое уравнение для нелинейной среды, так и
нелинейное уравнение диффузии, приведены в [161]. Это уравнение
учитывает процессы с сохранением временной и пространственной
памяти и записывается в виде
/>;,р(х, 0 = ад|Х[рв(*, t)Dy+xp(x, 0], v>0, у>0, (2.84)
где Dl t и Dl x - дробные производные Римана-Лиувилля
соответственно по времени и координате (см. разд. 2.2); х> 0; Д = const.
Данное уравнение отличается от уравнения нелинейной
диффузии [162] вида
—p(f, х) = —
dt дх
D0p°(t, x)^-p(t, x)
ох
(2.85)
с автоволновым решением
p = p0[v-1(vf-;C)]1/°, 0<x<vt (2.86)
заменой временных и пространственных производных на дробные
производные, рассматриваемые как обобщенные функции. При этом
граничные и начальные условия уравнения (2.85) сохраняются для
(2.84), а р(х, 0 рассматривается как обобщенная функция.
Уравнение (2.84) описывает распространение электромагнитных
волн в нелинейных фрактальных или слабофрактальных (v « 2, у «1)
средах при соответствующем выборе значений v, у, <j. При
добавлении нелинейных по р(х, f) слагаемых уравнение (2.84) будет
описывать как нелинейную диффузию, так и процессы
самоорганизации [162].
2.4. Недифференцируемые, или фрактальные,
функции и множества
В своем письме от 15 января 1898 г. (см, например, [633]) к
Ф. Клейну Л. Больцман специально отмечал, что «в Природе
существуют такие физические проблемы (статистическая механика), для
101
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
решения которых недифференцируемые функции абсолютно
необходимы, и если бы К. Вейерштрасс не придумал такие функции, то
физикам просто не осталось бы ничего другого, как самим их изобрести».
В настоящее время такие недифференцируемые кривые принято
называть фрактальными, или фракталами [1—4]. Примечательно
также то, что концепция самоподобия вошла в математику с двух
независимых направлений (через канторовы множества и функции Вей-
ерштрасса) примерно в одно и то же время для опорных понятий
математики: числа и функции. Напомним, что еще Г.В. Лейбниц в
своем трактате «Монадология», написанном в 1714 г. [634],
использовал понятие самоподобия («миры внутри миров»), а также
применял его в определении прямой.
Исторические аспекты. Непрерывные функции, не имеющие
производных, привлекали внимание многих математиков. Учитывая
необозримость данной проблемы, мы дадим ниже, следуя [635, 636],
только контуры этой ветви математики. Более подробно с
историческими и методологическими аспектами указанного направления
можно ознакомиться по [635-640].
После открытия дифференциального исчисления интуитивно
сложилось мнение, что каждую функцию можно дифференцировать
любое число раз. В 1806 г. Ампер сделал попытку теоретически
оправдать это убеждение на чисто аналитической основе в рамках
математических концепций Лагранжа. Позже одни математики
автоматически переносили утверждения Ампера на функции,
непрерывные в теперешнем смысле, другие, считая его фундаментом всего
дифференциального исчисления, приводили свои доказательства
этого утверждения и пользовались им при установлении других
результатов. Среди них Лакруа (1810), Галуа (1831), Раабе (1839), Дю-
амель (1847), Ламарле (1855), Фрейсине (1860), Бертран (1864), Серре
и Рубини (1868).
Однако время веры математиков о неразрывной связи
непрерывности функций и ее дифференцируемости истекало. В 1830 г. Б. Боль-
цано в рукописи «Учение о функции» строит первый пример
непрерывной, нигде недифференцируемой функции. Рукопись была
обнаружена лишь после Первой мировой войны около 1920 г. в Венской
государственной библиотеке [641]. Только через сто лет его работа
появилась в печати. В 1834-1835 гг. понятия дифференцируемости
и непрерывности четко разграничивает Н.И. Лобачевский. В 1854 г.
102
2.4. Недифференцируемые, или фрактальные, функции и множества
Дирихле отмечает, что в общем случае нельзя доказать
существование производной у произвольной непрерывной функции, и
высказывает убеждение в существовании непрерывной функции без
производной.
В 1861 г. Риман привел пример функции
/(х) = 1^. (2-87)
относительно которой Дюбуа-Реймон утверждал, что она недиффе-
ренцируема на всюду плотном множестве. Насколько трудным
оказался анализ примера (2.87) свидетельствует не только отказ Вейер-
штрасса провести его, но и то, что до 1916 г. не появилось ни
доказательства, ни опровержения примера Римана. Только в 1916 г.
Харди, опираясь на некоторые тонкие результаты диофантова
анализа, сумел показать, что (2.87) не имеет конечной производной ни
в какой точке fyi, где £, - иррациональное или рациональное число
вида 2т/(4п + 1) или (2т +1)/2(2л + 1), а т и п — целые. Затем он
несколько обобщил пример Римана [642]. В 1969 г. Гервер
расширил полученный результат [643], показав отсутствие конечной
производной у этой функции в точках £я, где £, - рациональное число
вида (2т + 1)/2я, am, п- целые и п > 1. Он установил наличие
производной, равной - 1/2, в точках £гс, где £ является рациональным
числом с нечетным знаменателем и числителем. Таким образом,
функция Римана дифференцируема на бесконечном множестве точек.
В следующей работе [644] Гервер показал, что других точек
дифференцируемое™, кроме указанных выше, у функции Римана нет.
До 1870 г., не считая указанной выше функции Римана, не было
опубликовано ни одного примера непрерывной функции, не
имеющей производной на бесконечном множестве точек. По словам Гю-
эля, который реферировал мемуар Ханкеля [645] о таких функциях,
«сегодня нет ни одного математика, который поверил бы в
существование непрерывных функций без производных» [646].
В 1870 г. Ханкель [645] предложил метод сгущения особенностей,
состоящий в построении функции при помощи абсолютно
сходящегося ряда, каждый член которого имеет особую точку. Именно так
он получил примеры непрерывных функций, у которых нет
производной на всюду плотном множестве рациональных точек. Одним из
таких примеров является функция вида
103
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
°° 1 ( 1 ^
/00 = Y—sin(rcwx)sin т-т г i П ЯЯ^
У ' Tin5 v ; sin(nwx) f V-**>
где n - натуральное число, s > 1.
В 1873 г. Шварц [647] построил другой пример монотонной
непрерывной функции, не имеющей производной на всюду плотном
множестве точек:
/<*>»£*1Г*. <2-89>
л=1 4
где ф(х) = [х] - yjx-[x], х > 0, [х] - целая часть х. Эту функцию Шварц
считал недифференцируемой, но, как оказалось позже, она почти
всюду имеет конечную производную.
Позже, как принято считать в 1861 г., Вейерштрасс построил,
свою знаменитую функцию [648]
/(*) = W(x) = f>" cos(^tcx). (2.90)
л=1
Здесь 0 < а < 1, b > 1 - нечетное целое число, аЬ > (1 + Зя/2).
Вейерштрасс доложил об этом Берлинской академии наук 18 июля 1872 г.,
сам пример был опубликован только в 1875 г. Дюбуа-Реймоном
[649]* Поэтому, как отмечено в [3], «год 1875 является не более чем
удобной символической датой для обозначения начала Великого
кризиса математики».
В предисловии к своей книге [650, с. 7] С. Сакс писал:
«Исследования, имеющие дело с неаналитическими функциями и
функциями, нарушающими те законы, которые предполагались всеобщими,
эти исследования рассматривались почти как распространение
хаоса и анархии там, где предшествующие поколения искали порядка
и гармонии». Ш. Эрмит писал Т. Стилтьесу в 1893 г.: «Я с ужасом и
отвращением отворачиваюсь от этой разрастающейся язвы функций,
не имеющих производной» [650, с. 7]. Даже в начале XX в. Дж. Бус-
сенеск был не одинок в мнении, что «весь интерес функции
заключается в обладании ею производной» [651, с. 15], имея в виду
обычную производную.
Независимо от Вейерштрасса к той же идее пришел Дарбу,
который обобщил примеры Ганкеля и Шварца и построил [652]
функцию
104
2.4. Не дифференцируемые, или фрактальные, функции и множества
- яп[(л + 1)!х]
/W = I—L-I] J» (2.91)
/1=1
не имеющую производной при любом х. Свои результаты Дарбу
доложил на заседании Французского математического общества 19
марта 1873 г. и 28 января 1874 г., т.е. до выхода в свет публикации
Дюбуа-Реймона [635]. Некоторые подробности приоритетной
пикировки между Вейерштрассом и Дарбу опубликованы в [648].
Классы недифференцируемых функций. Приведенные выше
исследования послужили основой для построения классов
недифференцируемых функций и поиска общих условий дифференцируемо-
сти непрерывных функций. Наибольший вклад в это направление
внес итальянский математик У. Дини, вплотную приблизившийся
к теореме Лебега о производной непрерывной монотонной функции.
В [653] он сформулировал, а в 1878 г. доказал [654, с. 148-153]
достаточно общую теорему существования непрерывных функций, не
имеющих производных (формулировка теоремы Дини нами дается
по [635]).
Теорема 2.1 [653, 654]. Пусть на 0<х<1 заданы функции fn{x),
удовлетворяющие следующим условиям:
1) все функции fn(x) непрерывны и имеют ограниченные
производные;
оо
2) ряд У/Л(х) сходится на [О, 1] к непрерывной функции f{x)\
3) каждая из/п(х) имеет конечное число экстремумов, причем число
их неограниченно возрастает вместе спи притом так, что для
всякого е > 0 можно найти такое п0, что при п >п0 расстояния между
точками экстремумов будут меньше е;
4) если Ъп — наибольшее расстояние между двумя
последовательными экстремумами, aDn — наибольшая по абсолютной величине
разность двух последовательных экстремальных значений, то
Нт(5л//)л) = 0;
5) если через hn обозначить для каждого х те два приращения (одно
из которых положительно, а другое отрицательно), для которых
х +hn дает первый правый (соответственно левый) экстремум, для
которого \fn(x + hn)-fn(x)\>-Dn, то можно задать такие
положительные числа гп, что для всех хе [0,1] и соответствующих каждому
105
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
х таких hn имеем |i^(x+/^)-i^(x) <2гл, где R^x) — остаток ряда
л=1
6) если сп - последовательность таких положительных чисел, что
\fn(x)\<cn для всех хе[0,1], то начиная с некоторого индекса
48 п Аг
-^lcv+^<B, 0<6<1;
ип v=l ип
7) знак разности fn(x + hn)-fn(x) начиная с некоторого п0 не
зависит от hn для всехх и п>п0.
оо
Тогда функция f(x), определенная рядом ]£/„(*) из п.2, ни в одной точ-
ке хе [0,1] не будет иметь конечной производной. Бесконечную производную она
может иметь на бесконечном множестве точек.
Затем Дини показал [654, с. 169-171], что при некоторых
дополнительных предположениях такая функция/(х) ни в одной точке не
будет иметь и бесконечной производной. Можно отметить, что класс
функций, удовлетворяющих теореме Дини, бесконечен [653], в
частности в нем содержится функция Вейерштрасса [654, с. 162].
В 1879 г. Дарбу предложил достаточно общий метод построения
недифференцируемых функций [655]. Он изучал функции ф(х),
определенные рядом
,(,).!№. ,2.92)
1 а
Л=1 Л
где апи Ьп — некоторые последовательности действительных чисел;
f(x) - непрерывная ограниченная функция с ограниченной второй
производной.
Если последовательности {ап} и {Ьп} выбраны так, что при
фиксированном к имеем
lim-^-0, MflA2+^+-+^=0,
"-*• ап+\ П~>~ ап
то ряд (2.92) сходится всюду к некоторой непрерывной функции ф(х).
При дальнейших ограничениях на выбор {ап}, {Ьп}, к и/(х) можно
106
2.4. Недифференцируемые, или фрактальные, функции и множества
получить непрерывные функции, не имеющие производной ни в
одной точке. Так, если Ъп = 1 ,к = 1, то на числа ап достаточно наложить
,. CU +CU +... + Я, Л
условие lim-i—* U-L = \), которому удовлетворяют, например,
числа ап = п !, чтобы можно было указать бесконечное множество
функций/(х), для которых функция (2.92) не дифференцируема ни
в одной точке. В частности, при всех/(х) = cos x функция ф(х)
нигде не дифференцируема. При выборе Ъп = п + 1, к = 3 и/(х) = sin x
получается функция ф(х) из [652]. В 1918 г. метод построения
непрерывных недифференцируемых функций был предложен К. Кноппом
[656]. Можно сказать, что после упомянутых работ была создана
целая индустрия по производству как отдельных функций, так и
целых их классов.
Отметим, что пример функции Вейерштрасса опирается на
свойства лакунарного ряда, т.е. такого ряда, в котором члены, отличные
от нуля, «очень редки и разбросаны» [657, 658]. Понятие
лакунарного тригонометрического ряда было введено Ж. Адамаром [659] в
1892 г. при изучении функций, не продолжаемых аналитически за
границу круга сходимости. Лакунарным (в смысле Адамара)
тригонометрическим рядом называют ряд вида
-Q- + ^akcosnkx + bksmnkx (2.93)
2 k=\
при nk+l/nk >q>\. Таким образом, номера пк лакунарного ряда (2.93)
при всех к растут не медленнее геометрической прогрессии со
знаменателем, большим единицы. В [642] было также доказано, что
функция Вейерштрасса W{x) не имеет конечной производной ни в
какой точке при условиях а< I, Ь> I и ab>\.
Множество недифференцируемых функций. Кратко рассмотрим
вопрос о месте, занимаемом дифференцируемыми функциями в
множестве всех непрерывных функций. Множество М называется
топологическим пространством [660—662], если всякому подмножеству
ХаМ можно поставить в соответствие множество ХаМ такое,
что выполняются следующие аксиомы:
1) JljY = X[jY, (2.94)
2) XczX,
107
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
3) 0 = 0, 0 - пустое множество,
4) ]? = Х.
Множество ^называется всюду плотным в топологическом про-
странстве.М, если Х-М. Множество ^называется граничным, если
его дополнение всюду плотно, т.е. М-Х = М. Множество Xнигде
не плотно, если его замыкание является граничным множеством, т.е.
М-Х = М. Множество Xтопологического пространства
Мявляется множеством первой категории на М, если оно является
объединением счетного семейства множеств, нигде не плотных на М.
Множества второй категории определяют как множества, не
являющиеся множествами первой категории. Эти определения были
сформулированы в 1899 г. Бэром. Иногда такие множества
называются резидуальными, или остаточными.
По теореме Бэра дополнение любого множества первой
категории на прямой является плотным. Никакой интервал на множестве
действительных чисел R не является множеством первой категории.
Каждое счетное множество на прямой будет множеством первой
категории и множеством меры нуль. В множестве действительных
чисел рациональные числа образуют множество первой категории.
Простейшим примером несчетного множества, принадлежащего к
множеству первой категории и множеству меры нуль, является канторово
множество, имеющее мощность континуума. Доказывается, что
прямую можно разбить на два дополняющих друг друга множества А и
В так, что А есть множество первой категории, а В имеет меру нуль.
Во многих проблемах топологии и теории функций множества
первой категории играют роль, аналогичную роли множеств меры нуль
в теории меры (множества, которыми можно пренебречь).
В настоящее время множества второй категории определяются
по Бэру, а дополнение к множеству первой категории называют
остаточным множеством [661, 662]. При доказательстве теорем
существования в теории множеств часто пользуются методом категорий,
который основан на теореме Бэра, по которой всякое полное
метрическое пространство является множеством второй категории на
самом себе [650]. На основе этого доказано следующее утверждение.
Теорема 2.2 [663, 664]. Пусть С — пространство непрерывных
функций х с периодом 1, наделенное нормой |х|| = тах|х(0|, 0</<1.
Пусть Т — множество функций из С, которые не имеют конечной
108
2.4. Недифференцируемые, или фрактальные, функции и множества
правой производной ни в какой точке te [0,1]. Тогда Т является
множеством второй категории Бэра на С, а его дополнение есть
множество первой категории.
Следовательно, множество функций, имеющих конечную
одностороннюю производную хотя бы в одной точке te [0,1], является
пренебрежимо малым в смысле категории Бэра по сравнению с
множеством всех непрерывных функций. Тем более это справедливо для
функций с конечной обычной производной. Доказательство этой
теоремы см., например, в [662], а в [665] показано, что множество
таких функций образует коаналитическое неборелевское подмножество
пространства [0, 1].
Как отмечено в [635], классы непрерывных функций без
производных, рассмотренные в XIX в. и в первые два десятилетия XX в.,
не давали примера такой сингулярной непрерывной функции, у
которой ни в одной точке не существовала конечная или
бесконечная односторонняя (левая или правая) производная. (У функции
Вейерштрасса (2.90), например, односторонняя производная имеется
на всюду плотном множестве). Первый пример такой в сильном
смысле недифференцируемой функции построил в 1922 г.
(опубликовал в 1924 г.) А.С. Безикович [666]. В связи с этим Банах и Штейн-
гауз поставили следующий вопрос о распространении с помощью
метода категорий результата С. Мазуркевича и Банаха на функции типа
Безиковича: можно ли показать, что дополнение множества всех
непрерывных функций, не имеющих ни в одной точке ни конечной,
ни бесконечной производной, является множеством первой
категории?
В 1932 г. Сакс дал отрицательный ответ на этот вопрос. Он
показал [667], что множество непрерывных на [0,1] функций, у
которых или существует конечная правая производная, или эта
производная равна +°о на множестве мощности континуум, есть
множество второй категории в пространстве всех непрерывных функций.
Таким образом, класс функций, односторонне дифференцируемых
хотя бы в одной точке, в смысле категорий существенно шире
класса функций, имеющих обычную производную хотя бы в одной
точке. Соответственно, класс функций, не имеющих ни конечной, ни
бесконечной односторонней производной в каждой точке области,
уже в том же смысле класса функций, нигде не имеющих
двусторонней производной. По словам Сакса, «это, быть может, объясняет
трудности с нахождением первого примера функции, не имеющей ко-
109
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
нечной или бесконечной односторонней производной в каждой точке»
[667, с. 212].
С целью расширения известных классов недифференцируемых
функций В. Орлич в 1947 г. нашел [668] достаточно общие условия,
при которых непрерывные функции, являющиеся суммами
равномерно сходящихся рядов, нигде не дифференцируемы. Однако
общность полученных результатов была достигнута за счет того, что
коэффициенты этих рядов задавались неэффективно, с
использованием метода категорий. Такой подход Орлич охарактеризовал как «в
некотором смысле промежуточный» [668, с. 46] между
«эффективными» способами задания недифференцируемых функций в виде
рядов и «неэффективным» методом С. Мазуркевича-Банаха.
Таким образом, класс непрерывных функций, не имеющих
производной ни в одной точке, неизмеримо богаче класса функций с
производными. Как метко замечено в [635, с. 222], «создалась любопытная
ситуация, когда оказалось, что те непрерывные функции, которые
изучались математиками на протяжении веков, те, которыми
пользовались для описания явлений внешнего мира, - эти функции
принадлежат лишь пренебрежимо малому классу всех непрерывных
функций». Постепенно математики привыкли к тому, что нигде не
дифференцируемые функции действительно существуют, но
физики долго не соглашались с этим и воспринимали такие функции в
виде уродливых порождений математической фантазии, не имеющих
отношения к реальному миру (исходили из принципа «в физике все
функции дифференцируемы») [669, с. 246].
С позиций современной науки функция без производной вовсе не
абстрактное понятие, а траектория броуновской частицы. В [670, с.
34] Н. Винер писал: «В рамках этой теории мне удалось подтвердить
замечание Перрена, показав, что за исключением множества
случаев, имеющих суммарную вероятность нуль, все траектории
броуновского движения являются непрерывными нигде не
дифференцируемыми кривыми». Существенно то, что в спектральной теории
стационарных случайных процессов недифференцируемые функции
возникают совершенно естественным образом и избежать их
возможно лишь при отказе от имеющего ясный физический смысл условия
стационарности, только и делающего данную теорию простой и
наглядной [669]. Кратко поясним этот факт.
При спектральном разложении стационарного процесса X(t)
использование интеграла Стилтьеса оказывается неизбежным, так
по
2.4. Не дифференцируемые, или фрактальные, функции и множества
как случайная функция Z(co) не является дифференцируемой ни в
каком смысле и поэтому никак нельзя перейти от интеграла Фурье-
Стилтьеса
X(t)= j ei(utdZ((o) (2.95)
к обычному интегралу Фурье. В случае существования спектральной
плотности /(ш) всегда
^Z((o)|2) = /(o>)flfca (2.96)
В силу (2.96) во всех реальных физических случаях, когда
процессу X(t) соответствует положительная спектральная плотность/(со),
средний квадрат приращения A Z(co) функции Z(w) на малом отрезке
Аш оси частот будет близок к/(ш)Аш, т.е. имеет тот же порядок
малости, что и Аш. В таком случае само значение A Z(co) имеет, как
правило, порядок (Аш)1/2, что несовместимо с допущением о
дифференцируемое™ функции A Z((o), т.е. о существовании предела
отношения AZ((o)/A(o при Аш->0. Как отмечено в [669, с. 113], «мы
сталкиваемся здесь с довольно редким случаем, когда в задаче,
имеющей реальный физический смысл, возникают нигде не
дифференцируемые функции, которые еще совсем недавно многим прикладникам
представлялись заумной математической абстракцией, которая не может
иметь никаких приложений».
В арсенале математики нашелся и аналитический аппарат для
описания таких объектов и процессов. Место обычной размерности
заняла размерность Хаусдорфа, а место производных — дробная
производная, или показатель Гельдера (см. разд. 2.2).
Построение недифференцируемых функций. Возвращаясь к
историческим примерам открытия функций без производных, заметим,
что конкретные примеры таких функций иногда приводят к
интересным выводам. В 1903 г. японский математик Такаги [671] открыл
простой пример нигде не дифференцируемой функции
T(x) = ^2-n№n-lx). (2.97)
п>\
Здесь ф(х) = 2|х-[х+(1/2)]|, где [х] - операция выделения целой
части х. Функция Т{х) - типичный пример «сгущения сингулярнос-
111
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
тей» [672, с. 401], поскольку это суперпозиция так называемых
пилообразных фунций. Функции Римана (2.87), Вейерштрасса (2.90) и
Такаги (2.97) имеют пики в счетном числе точек (рис. 2.4). Следует
сказать, что графики таких недифференцируемых функций
описываются бесконечным числом бесконечно малых извилин («волны с
рябью»), но почти невозможно дать о них наглядное представление,
не исказив их существенных черт [673].
Рис. 2.4. Графики недифференцируемых функций:
а - функция Вейерштрасса (1- W(x))/2 при значениях Ь - д_1=2;
б- функция Такаги; в - функция Римана [636]
Е. Гобсон [672, с. 410] также изучал ряд
5>Лф(6Лх), 0<я<1, (2.98)
п>\
и показал на основе метода Кноппа, что условия ab > 4 (когда b
целое четное число) или аЬ > 1 (когда b нечетное целое число)
запрещают существование конечной или бесконечной производной. Для
112
2.4. Недифференцируемые, или фрактальные, функции и множества
b = аг1 = 10 - это пример, который был дан Ван-дер-Варденом [674]
в 1930 г. (см. ниже). Де Рам [675] также указал, что если мы возьмем
b = я-1, считая b целым четным числом, то ряд (2.98) не будет иметь
конечной производной.
Функция Больцано. Теперь рассмотрим построение функции
Больцано В (х), опираясь на результаты [641, 676]. Определим
вспомогательную функцию Вп{х). Рассмотрим построение, приведенное
на рис. 2.5, а и заключающееся в том, что отрезок ^заменяется
ломаной ACDEB со следующими координатами точек: А[р, q],
ф + (8/4),*-(Д/2)], D[p+(2&/4),q], E[p+(38/4),q + (A/2)],
B[p + 5,q + A]. Пусть графиком функции В0(х) является отрезок
Ап(0, 0) и А25(1, 1); пусть АпР= а, А25Р = h (рис. 2.5, б). Заменим
АпА25 ломаной АпА22А23А24А25 по правилу, указанному выше.
Координаты характерных точек равны: ^=^(0,0), ^(1/4,-1/2),
^3(1/2,0), ^(3/4,1/2), ^25(1Д), что определяет функцию Вх(х) и
ее график, отмеченный точками Л1Л2Л3Л4Л5 • На рис.2.5,£
представлены графики функций В0(х) и В{(х), соответственно. По
функции Вх(х), как показано на рис. 2.5,в, строим функцию В2{х). На рис.
2.5,г указаны графики функций В2(х) и В3(х), соответственно.
Повторив эту операцию п раз, мы придем к функции Вп(х). Колебание
функции Вп{х) в каждом из промежутков
±а9^а\ * = 0,1,2,...,4"-1, « = 0,1,2,3,... (2.99)
( s s+l \ h
будет ю I — я, ——а = —. В промежутке (0, а) для колебания Вп(х)
можно получить юл(0,я) = й(2-2"л).
Определим теперь функцию Больцано В (х) в точках х=ка/4п
при коэффициентах 0<к <4п, к - целое, п = 0, 1, 2, 3,..., полагая
В (х) = Вп(х). Тогда колебание В (х) на множестве всех
рассматриваемых точек х = ка/4п, принадлежащих одному из промежутков
(2.97), будет ш[ -^а, ^-а
= h/2n~l. Для значений х, отличных от
х = ка/4п, функция Больцано определяется предельным переходом
B(x) = limB(t). Колебание В(х) в любом промежутке длины а /4п
из
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
< <
Я
Я
Я
в
i
VO
'о
Я
Я
О
Я Qq
О S
Я Qq
I Я
ii
3 *
Is
я s
Is-
I-
?!
&■*
Я
я
5
я
о
Я
Я
<<
I
О
Он
114
2.4. Недифференцируемые, или фрактальные, функции и множества
удовлетворяет неравенству со
х, х + —
4"
>h/2n. Таким образом,
функция Больцано В (х) определена на всем промежутке (0, а) и
непрерывна на нем.
В [641] рассмотрены еще два алгоритма синтеза функции
Больцано. Пусть каждому значению
-a=i+v+-+i+- (2100)
на интервале (0, а) соответствует
h "2 22 2*
Числа d. определяются по числам с.:
(2.101)
cJO|J_|2|J_L (2Л
^|0|т1|0|±1Г К }
Здесь необходимо брать нижние знаки, если среди чисел ck_v
ck_2, ..., <\ имеется нечетное число значений, равных нулю,
например:
5[(1/4 + 2/42 + 1/44)а] = (-1/2+1/24)А,
Я[(1/42+1/44)я] = (1/22+1/24)А.
Соотношениями (2.100)—(2.102) задается функция Больцано.
Рассмотрим третий алгоритм построения функции Больцано,
основанный на свойствах некоторого ряда [641]. Зададим на
отрезке А{ С длины а с координатами концов 0 (точка Ах) и а (точка С)
функции b0(x), bx(x), b2{x) отрезком А{А5 и ломаными линиями,
изображенными на рис. 2.6. Функции Ь{(х) соответствует ломаная со
звеньями, образованными боковыми сторонами треугольника с
основанием а и высотой ЗА/4, функции Ь2(х) —ломаная, образованная
боковыми сторонами четырех треугольников с основанием а/4 и
высотой ЗА/8. При продолжении этого процесса придем к функции
115
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Рис. 2.6. Третий алгоритм построения функции Больцано [641]
п
Bn(x) = y£bi(x). Полученный ряд при л->оо сходится равномерно,
а его сумма, равная В (х), дает нам функцию, непрерывную на (0, а)
и нигде не имеющую производной в данном промежутке.
Экстремумы функции Больцано В (х) наблюдаются в точках с абсциссами
ф+0,25)/4я"1 при s = 0,1,2,...,4я"1-1, п = 1,2,3,..., которые
(абсциссы) образуют всюду плотное множество на промежутке (0, а).
Функция Безиковича. Основываясь на [666], приведем все
этапы построения функции Безиковича. Для этого необходимо
построить ступенчатый треугольник. На рис. 2.7 показан отрезок АВ = 2аи
точки С (а, Ь)иО (а, 0). На отрезке AD строим отрезок 1{=а/4 = а/22,
помещая его центрально. Тогда отрезок AD разделится отрезком 1Х
на два равных отрезка; на каждом из них помещаем центрально
отрезки /2 = /3 = а 124. Отрезки 1{, /2, /3 разделяют отрезок AD на четыре
равных отрезка; на каждом из них помещаем центрально отрезки
(считая слева направо) l4=l5=l6=l7=ci/26 и т.д. Таким образом, на
отрезке AD будет построено бесконечное множество отрезков lv /2,
/3,..., объединение которых L является всюду плотным множеством
с суммарной длиной а/2. Подобную же систему отрезков строим и
на отрезке DB. Все отрезки вместе будем называть первой серией
отрезков. Обозначим через т{х) меру Лебега множества точек
интервала (0, х), не принадлежащих L, т.е. меру множества Zn(0,x). На
отрезке AD определим функцию ф(х), полагая
Ф(х) = — т(х). (2.103)
а
116
2.4. Недифференцируемые, или фрактальные, функции и множества
I I ►
A D В х
Рис. 2.7. Построение недифференцируемой функции Безиковича [666]
Из (2.103) следует, что функция ср(х) на любом отрезке /z имеет
постоянное значение. Таким образом, точки А и Сбудут соединены
некоторой ступенчатой кривой; точки Си В соединим такой же
ступенчатой кривой. Полученную после этого фигуру и называют
ступенчатым треугольником с основанием 2а и высотой Ъ.
На всех отрезках первой серии как на основаниях строим
ступенчатые треугольники, обращенные вершинами вниз, - равные на
равных основаниях. Высоту при этом выбираем так, чтобы
вершина самого нижнего из равных треугольников оказалась на стороне
АВ. Построение всех этих треугольников названо в [666] операцией
зазубривания треугольника ABC внутри. Проделав ту же операцию
внутреннего зазубривания над полученной бесконечной серией
треугольников (первой серией), получим вторую серию треугольников.
Их также подвергаем внутреннему зазубриванию и т.д.
Теперь определим на отрезке АВ функцию/(х): 1) в точках
отрезка АВ, не принадлежащих первой серии отрезков, - ординатами
сторон ступенчатого треугольника ABC; 2) в точках отрезков первой
серии, не принадлежащих отрезкам второй серии, - ординатами
сторон треугольников первой серии; 3) в точках отрезков второй серии,
не принадлежащих отрезкам третьей серии, — ординатами сторон
треугольников второй серии и т.д.; 4) в точках, принадлежащих
отрезкам всех серий (они составляют ансамбль меры нуль), — по
принципу непрерывности.
Определенная таким образом функция Безиковича является
сингулярной непрерывной функцией, которая ни в одной точке не
имеет ни правой, ни левой производной (доказательство см. [666]).
Функция Ван-дер-Вардена. Рассмотрим теперь функцию Ван-дер-
Вардена [674]. Идея данного примера основана на том, что после-
117
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
довательность, состоящая из целых чисел, сходится только тогда,
когда все ее члены, начиная с некоторого, совпадают. Пусть^ (х) -
функция, равная расстоянию от точки х до ближайшей
целочисленной точки:
г/ ч \х при0<х<1/2,
/oW = il-x щи 1/2***1, <2104>
где f0(x+l) = f0(x) для любого действительного х.
Функция^ (х) - непрерывная на всей числовой оси,
периодическая с периодом 1, линейная на каждом отрезке Г(^-1)/2; s/2], где
s - целое число, причем угловой коэффициент графика^ (х) на
каждом таком отрезке равен ± 1. Далее вводим последовательность
функций /я(я = 0,1,2,...):
fnM = ^- (2.105)
Для всякого натурального п функция^ (х) — непрерывная,
периодическая с периодом 4_л и максимальным значением 4~п /2, линей-
Г s-1 si
ная на каждом отрезке у-т^> ут^* ; угловой коэффициент ее
графика на каждом таком отрезке равен ± 1. Наконец, введем функцию
Лх) = £/я(х) = |;/0(4-х)/4-. (2.106)
л=0 и=0
Так как 0 < fQ(x) < 4~п, то по признаку Вейерштрасса ряд,
определяющий/^), равномерно сходится и из непрерывности всех/, (х)
следует непрерывность функции/(х). На рис. 2.8 представлены
графики функций /х(х), fx(x) + f2(x), /х{х) + /2{х)+/ъ{х). По мере
увеличения числа слагаемых число вершин, в которых функция/(х) не имеет
производной, неограниченно возрастает. Методы доказательства
недифференцируемости функции Ван-дер-Вардена описаны,
например, в [640, 673, 677].
Функциональные уравнения и недифференцируемые функции.
Кратко рассмотрим следующее функциональное уравнение:
f(x)-af(bx) = g(x). (2.107)
118
2.4. Недифференцируемые, или фрактальные, функции и множества
y=fjx)
У%(х)
Рис. 2.8. Первые три частные суммы в случае построения недифференцируемой
функции Ван-дер-Вардена
Именно де Рам заметил [675], что функция Вейерштрасса (2.90) и ряд
(2.98)удовлетворяют(2.107), если g(x) = acos(bwc) и g(x) = aty(bx)
соответственно. Функция ф(х) определена выше в выражении (2.97).
В [678, с. 82] показано, что если положить g(x) = acos(bnx), то
уравнение (2.107) будет иметь решение на интервале (-оо5+оо) j
зависящее от произвольной функции, и единственное непрерывное
решение — это функция Вейерштрасса.
Г. Фабер, рассматривая [679] функцию
ХЮ-Лф(2л!х),
Л>1
(2.108)
показал, что (2.108) не соответствует условию Липшица любого
порядка. Затем Ф. Катер [680] исследовал функцию
]T2-"!cos(2<2")!;c)
л>1
(2.109)
и показал, что она не имеет точек возврата и обладает интересными
экстремальными свойствами.
Рассмотрим теперь функциональное уравнение
7"
+ /
х+1
+•••+/
(х + р-1)
= №0.
(2.110)
119
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
Это уравнение исследовал Э. Артин [681], характеризуя гамма-
функцией Эйлера его единственное гладкое решение. В [682] на
основе (2.110) решена задача о нахождении собственного значения X
для некоторого оператора Пэррона-Фробениуса и исследованы
различные решения (2.110) относительно собственного значения. В [682]
также отмечено, что если Ъ > 2 - целое , то функция Вейерштрасса
Щ2х) + cos (2юс) удовлетворяет (2.110) при/? = b, |1 = 1 и X = а;
функция Такаги Цх) - 1/2 также удовлетворяет (2.110) при р = 2, |i = 1 и
X =1/2, а функция Римана удовлетворяет (2.110) при р = 2, |i = 2 и
А, =1/4.
Опираясь на понятие лакунарного ряда (см. выше), в [683]
изучен ряд
f(x) = ^anr(bnx), 0<я<1, (2.111)
где аЪ > 1 и г(х) - квазипериодическая функция. При определенных
ограничениях на г{х) ряд (2.111) либо непрерывно
дифференцируем, либо нигде не дифференцируем. В последнем случае размерность
графика функции (2.111) удовлетворяет равенству
D = 2 + [(lQgfl)/(lQgA)]. (2.112)
График функции убудет иметь фрактальную размерность D > 1,
когда g сингулярна. В [684] показано, что если g (x) принадлежит
классу Lip (5), 0 < 5 < 1, то функция имеет конечную fc-размерную
меру к = 2 - 5; также построена функция g, для которой fc-размер-
ная мера действительно положительна при 1 < к< 2 - 5. В [685]
более обобщенно показано, что если x(t) принадлежит классу Lip (5),a
у (0 классу Lip(5'), где 5 + 5' >1, 0 < 5' < 5 < 1, то кривая (x(t), y(t))
имеет конечную fc-размерную меру к = 2 - (5 + 5' - 1)/5. В [686]
построена такая кривая (x(f), y(f)), для которой размерность к = 2 -
-(5 + 8' — 1)/5 достигается. В [34] показано, что если
S(*) = XWM> (2-113)
при 0 < s < 1 и {Хп} - последовательность положительных чисел,
удовлетворяющих условиям Хп+1/Хп -><*>, log(A,w+1)/log(A,w) -> 1 при п -> оо,
то D = 2 - s.
120
2.4. Недифференцируемые, или фрактальные, функции и множества
Однако точно определить величину D для функции Вейерштрас-
са (2.90) и ряда (2.98) - задача трудная. Можно предположить, что в
обоих случаях
Z) = 2 + logtf/log£. (2.114)
Эта величина кажется довольно разумной, поскольку Харди
показал [642], что если £ = -(logtf)/(log£)<l, то JV(x + h)-W(x) = 0(\x\t)
и W{x+h) - W(x) ф о (| х |^) при любом значении х.
Хаотические отображения и недифференцируемые функции. В
заключение кратко приведем некоторые сведения о хаотических
отображениях. Рассмотрим одномерную динамическую систему,
описываемую логистическим одномерным отображением (отображение Фер-
хюльста):
у(х) = 4х(1-х) (2.115)
на единичном интервале /. Хорошо известно, что л-кратная
итерация у1 может быть выражена как
уп(х) = sin2 (2n arcsin 4x). (2.116)
Здесь у п(х) означает л-ую итерацию функции у (х), а не л-ую
степень у (х). В [687] было впервые предложено объединить у п с
функцией Вейерштрасса (2.90). В этом случае получается конечная
зависимость
Дя,х) = |>^4*) = ;^7^-:!^ (2Л17>
£[ 2(1 -а) 2£
и производящая функция F(a, x) нигде не дифференцируема при
1 / 2 < а < 1. Аналогично находим
F(a,x)=^antyn(x)=^antyn(2m-lx) для хе I. (2.118)
л=0 л=0
При рассмотрении (2.117) и (2.118) возникает вопрос
относительно того, какие типы функций со: / -> / вызывают
недифференцируемость своей производящей функции
121
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
F(a,x)=f^ancon(x) (2.119)
л=0
с учетом х. Ответ на этот вопрос дают теоремы, приведенные в [636].
Функция Вейерштрасса (2.90) при Ъ = 2 может быть также
представлена в виде
оо оо
]Гял cos(2"7ix) = ]Г я" С08(лфл(х)). (2.120)
л=0 л=0
Следовательно, функция Вейерштрасса и ряд (2.98) при
значении Ь = 2 есть частные случаи ряда
F(a,x) = f,a»gmx)), (2.121)
л=0
где F(0,x) = g(x) - гладкая функция на единичном интервале /.
Ряд (2.121) является единственным непрерывным решением
функционального уравнения
F(a9x)-aF(aMx)) = g(x). (2.122)
Для рядов типа (2.121) в [636] вводится замещающий оператор
5Ю в виде
SJf)(x) = №x)),xeI. (2.123)
В этом случае ряд (2.121) записывается как
F(a,x)=f,a*S;(g) = W-aSJ-l(gh (2.124)
л=0
где оператор (Id-aSJ~l известен как резольвента оператора £ф.
Поэтому оператор {Id-aS^)~l отображает g0(x) = cos(rac) на функцию
Вейерштрасса, a g{(x) = х - на ряд (2.98) при 6 = 2, т.е. он отображает
некоторую гладкую функцию на недифференцируемую нигде
функцию. Дальнейший математический формализм замещающего
оператора выходит за рамки нашего описания и подробно представлен в
[636].
122
2.4. Не дифференцируемые, или фрактальные, функции и множества
Функция Такаги (2.97) и ряд (2.118) являются частными
случаями функции вида
л=0
(2.125)
Исследованию свойств (2.125) посвящены работы [636,688,689].
Хотя не существует простых функциональных уравнений, которым
должен удовлетворять ряд (2.125) в целом, можно получить
семейство функциональных уравнений, единственными решениями
которых является данный ряд. Уместно обозначить множество узлов
решетки {{п,т)\ 0 < л <2т~1 -1, т> 1} как Q. Тогда искомые
уравнения суть
/
2л + 1
&
h}'
f/1 + lX
2«-i
= с„
(2.126)
при всех (п,т)е Q и граничных условиях/(0) = 0 и/(1) = с0.
Заметим, что левая часть (2.126) представляет, по-существу,
центральную разностную схему для функции/ В [636] рассмотрено
модифицированное уравнение (2.126) в виде
/
2л + 1
= (!-«)/
2«-i
+ ос/
Ли + П
2/л-1
(2.127)
с граничными условиями/(0) = 0и/(1) = 1,где0<ос<1-
константа. В [688] показано, что единственное непрерывное решение (2.127)
удовлетворяет функциональному уравнению
/(*) = ■
qf(2x), 0<х<1/2;
(1-а)/(2х-1) + а, 1/2<х<1.
(2.128)
Выражение (2.128) есть частный случай функционального
уравнения де Рама, которым доказана следующая теорема.
Теорема 2.3 [690]. Предположим, что F0 и F{ являются
сжимающими отображениями в R". Тогда функциональное уравнение
123
Глава 2, СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
/(*) = ■
F0(f(2x)), 0<х<1/2;
/<(/(2х-1)), 1/2<х<1
(2.129)
обладает единственным непрерывным решением тогда и только
тогда, когда F0(p{) = F{(p0), гдер0 ир{ - единственные неподвижные точки
для F0 и Fx соответственно.
Более того, де Рам показал, что решение Да, х) (2.128) строго
монотонно возрастающее и его производная обращается в нуль
почти всюду, если ос* 1/2 .
Такого рода функции известны как сингулярные функции Лебега
fa(x). Из (2.128) при значениях а = р = а и g(x) = cos(tlx:)
получается функция Вейерштрасса; при ос = р = 1/2 и g(x) = |x-[x + l/2]| -
функция Такаги; при р = 1-а, g(x) = aQ(x-l/2) - сингулярная
функция Лебега fa(x), когда 0 - ступенчатая функция. Для
сжимающих отображений характерно выполнение неравенства
||/7j - Ff21| < A|/j - /21 для некоторой постоянной 0 < X < 1, где
||/|| = suP[o,i] |/М| ~ супремум-норма. Решение Да, х) приведено
также в [691, 692]. В [688] получено следующее выражение:
Да,х) = х+|а--
п
2«_1
Х1ал-^)(1-аГ^л(х),
'/1=0 р=0
(2.130)
где т(р) = р-^[р/2п],
Л21
^W = 2"
2"
\х-
р + \
2"
2х-
2р + 1
2"
(2.131)
Из формулы (2.130) можно определить точную зависимость
между функцией Такаги (2.97) и решением уравнения (2.128) в виде [636]
Э Т(\ >*
:2Т(Х).
(2.132)
Выражение (2.130) применимо также для определения
комплексного параметра ае {z; \z\ < 1, |1 - z\ < 1} и дает непрерывное решение
для (2.128). В частности,
124
2.4. Недифференцируемые, или фрактальные, функции и множества
1 i
2 + ГХ
2"-1
= х+Х2-(л/2)-1Х^1Йи)ехр
л=0 р=0
т
(п + 2-2т(р))
(2.133)
определяет фрактальную кривую, которую исследовал П. Леви [693].
Уравнение, сопряженное (2.128), исследовалось в [636]:
/(*) =
|а/(2х), 0<х<1/2;
((1-а)/(2х-1) + а, 1/2<х<1.
(2.134)
Де Рам показал [690], что решением (2.134) является кривая
Коха, если ос = 1/2 + (>/3/б)/, и плотноупакованная кривая Пойа
(Polya), если а = 1 / 2 + / /2. Соответствующие разностные уравнения
для (2.134) являются частным случаем системы, записываемой в виде:
Hf^j^-^K^H*
R
4я + 3
2m+l
=»mR
•)т-\
Hl-nJR
n + l
2m-l
(n+Vi
2mA
(2.135)
для всех (п,т)е О, и граничных условий i?(0) = 0, R(l) = 1, i?(l/2) = a,
где 0 < Xm < \im < 1 и m > 1 - константы. Действительно, при условии
Хт =| а р и \im = 1-11 - a p непрерывное решение (2.135) также
удовлетворяет (2.134). Уравнения (2.135) имеют единственное
непрерывное решение, если 0 < inf Хп < supjj^ < 1.
п^ п>\
Понятно, что кривая R(I) лежит в треугольнике с вершинами
0,1 и а. В случае А,л < \in при п > 1 кривая R(I) становится кривой Жор-
дана, а при \ = [in и п > 1 - ьфивой Пеано. Двумерная размерность
Лебега кривой R(I) дается [636] выражением
|1та|П(1-Хл-^)
п>\
2.
Таким образом, при соответствующем выборе {Хп} и {цл} можно
считать положительную область кривой Жордана единственным
решением (2.135).
Построение фрактальных множеств. Для построения
самоподобных фрактальных множеств в пространстве № широко
применяются два метода. Первый, принятый Деккингом [694], использует эн-
125
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
доморфизмы символов в свободных группах, а второй - метод
Хатчинсона [695], основан на использовании системы итеративных
функций, т.е. на множестве сжимающих отображений. Следует иметь в
виду, что результат применения итеративных функций (аттрактор)
не всегда является фракталом. В общем случае это может быть
любой компакт. Как отмечено выше, отображение F: № -» W будет
сжимающим, если существует константа X е (О,1), для которой ||Дх) -
- F(y)\\ < \\х - )\\ для всех x,yeRp. Наименьшее X есть константа
Липшица Fa обозначается Lip(F). Единственная неподвижная точка F
обозначается здесь символом Fix(f). Тогда справедливо следующее
определение.
Определение 2.1 (Хатчинсон). Непустое подмножество Хиз RP
инвариантно относительно множества т сжимающих отображений
Fv F2, .--,Fm, если Xудовлетворяет равенству
X = Fl(X)vF2(X)v...vFm(X). (2.136)
Аналогичный метод описания самоподобия представлен также
в [696]. Некоторые результаты [695] приведены в [697].
Для множества сжимающих отображений Fv .,Fm, можно
определить отображение
Q>{X) = Fx{X)KjF2{X)Kj...KjFm{X), (2.137)
для произвольного подмножества ЛГиз RP. Очевидно,
последовательность (2.137) сходится к неподвижной точке Ф. Необходимо также
обратить внимание на следующий результат.
Теорема 2.4 (Вильяме [698], Хатчинсон [695]). Для множества
сжимающих изображений Fv ••-,Fm существует единственное
непустое компактное инвариантное множество К. Для произвольного
непустого компактного подмножества Хиз Rp система Фп(Х) сходится
в метрике Хаусдорфа к К при п-><*>.
В [699] было изучено модифицированное уравнение (2.136)
неоднородного вида
X = <b(X)vV = Fl(X)u...uFm(X)uV, (2.138)
где V — заданное компактное подмножество из Rp. При этом было
показано существование единственного непустого компактного ре-
126
2.4. Недифференцируемые, или фрактальные, функции и множества
шения X, удовлетворяющего (2.138). Там же приведен следующий
результат.
Теорема 2.5 [699]. Предположим, что Fv ...,Fm являются
непрерывными отображениями, такими, что множество Q Фп(Х) — пред-
л=0
компакт для любого компакта X. Тогда эквивалентны следующие
утверждения:
а) существует единственное решение (2.138) для любого
компакта V;
б) отображение Ф имеет единственную неподвижную точку.
Из определения хаусдорфовой размерности инвариантного
множества мы имеем следующую теорему.
Теорема 2.6 [700, 695]. Предположим, что каждое сжимающее
отображение Fj,l<j< m, является композицией операций
растяжения, поворота, сдвига и отражения. Предположим далее, что
существует открытое множество U, удовлетворяющее Ф(17)с17 и
Ft(U)nFj(U) = 0 , при i*j. Тогда s-размернаяхаусдорфовамера
инвариантного множества К конечна и положительна, т.е. dimH(K) = s,
где s определена с помощью Lip(/T1)^+...+ Lip(Fm)s=l.
Для связных инвариантных множеств имеем следующие теоремы.
Теорема 2.7 [698]. Пусть Lip(^) +...+ Lip(Fm) <1, и каждое Fj
инъективно. Тогда К полностью несвязно и совершенно.
Напомним, что инъективным отображением {инъекцией)
множества А в множество В называется взаимно однозначное
отображение/: Л-> В.
Для изучения связности инвариантных множеств в [696]
введена структурная матрица Мк = {т~) множества К:
Г1, если Fr(K)nFr(K) = 0,
тн =\ (2 139^
J [0 во всех остальных случаях. v * '
Теорема 2.8 [636]. Инвариантное множество К связно тогда и
только тогда, когда его структурная матрица Мк неприводима.
Более того, если К является связным, оно также является локально
связным континуумом и линейно связно.
Если два сжимающих отображения Fx и F2 удовлетворяют
равенству F{(F\x(F2)) = F2(¥ix(Fl)), то можно ввести параметризацию
инвариантного множества К, применяя теорему 2.3. Действительно,
пусть/(х) будет непрерывным решением (2.129). Тогда
127
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
/(/) = /([0Д/2])и/([1/2Д]) = ^(/(/))и^2(/(/)). (2.140)
Поэтому/(7) является компактным инвариантным множеством
для Fx и F2, так что K=f(I), как и требуется. С учетом этого
доказано следующее утверждение.
Теорема 2.9 [636]. Пусть fix) будет непрерывным решением
(2.129). Тогда,
а) если Lip(i71)Lip(/T2) < 1/4, то производная Фреше f обращается
в нуль почти везде;
б) если каждая Fj является гомеоморфизмом и Lip(/j_1) • LiptF2-1) <
<4, то f не является дифференцируемой по Фреше почти нигде; более
того, если Lip(Fj~l)<2,j= 1, 2, то/нигде не дифференцируема.
Заметим, что приведенные выше результаты обобщают теорему
Лэкса [701]. При такой параметризации легко получить хорошо
известную классическую кривую Пеано, построенную им в [702], а
также Гильбертом в [703] и Пойа в [704], использовавшими
определенные аффинные преобразования в пространстве R2. На рис. 2.9
с частичным использованием результатов [636] приведены
характерные примеры фрактальных множеств с параметрами, заданными
ниже:
1. Кривая Леви (рис. 2.9,а). Это единственное непрерывное
решение (2.128) при а = (1 + /)/2.
2. Кривая Коха (рис. 2.9,6). Это единственное непрерывное
решение (2.134) при а = 1 /2 + (V3 /6)/.
3. Единственное инвариантное множество для Fx(z) = (0,4614 +
+ 0,46140* и F2(z) = (0,622 -0,196/)U- 1) + 1, рис. 2.9,*.
4. Единственное инвариантное множество для F{ (z) = (0,3 + 0,3i)z
и ^2(z) = 0,82(?-l) + l, рис.2.9,г.
5. Единственное инвариантное множество для i*|(z) = (0,5+0,5/)z
и F2(z) = (-0,5+0,5i)(z-l)+l, рис. 2.9Д
6. Единственное инвариантное множество для F{(z) = (0,4614 +
+ 0,4614/)ги ВД = (0,2896-0,585/Ж-1) + 1, рис. 2.9,ж.
7. Единственное решение (2.138) для F{(z) = (0,5 + 0,6i)z,
F2(z) = (0,5 -0,6/)(z - 1) + 1, и Кявляется треугольником с
вершинами Р0, Рх(р0) и F2(p0), где/>0 = (1 - i)/2, рис. 2.9,з.
128
2.4. Недифференцируемые, или фрактальные, функции и множества
Рис. 2.9. Примеры фрактальных множеств
5 Фракталы
129
Глава 2. СЛУЧАЙНЫЕ ФРАКТАЛЫ И ДИФФУЗИОННЫЕ ПРОЦЕССЫ
8. Единственное решение (2.138) для FY(z) = (0,5 + 0,2i)z,
F2(z) = (0,5 -0,2i)(z-1) + 1, F3(z) = (0,6 + 0,l/)(z-0,5 -2/) + 0,5 + 2/
и Кявляется объединением трех сегментов, связывающих р0 с Fi (p0),
где/=1, 2, 3,/?0=0,5-0,2/ (рис. 2.9,к).
Целый ряд интересных классических и современных
результатов по недифференцируемым кривым и фрактальным множествам
представлен в [705-707]. В частности, некоторые теоремы о канто-
ровых проекторах приведены в [708]. Проектор, или проекционный
оператор, - это линейный оператор Р в векторном пространстве X
такой, что Р2 = Р. Оператор, обладающий таким свойством,
называется идемпотентным. Степень оператора к определяется, как
обычно, рекуррентной формулой Akx = A(Ak~lx), fc = 2,3,... .
Отметим в заключение, что, несмотря на значительное число
работ по недифференцируемым (фрактальным) функциям и
соответствующим множествам и отображениям говорить о создании их
современной целостной теории еще рано. Более того, интерес к ним
в настоящее время значительно возрастает.
130
Глава 3
ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ
ПОВЕРХНОСТЕЙ
3.1. Пространственные спектры мощности поверхности
В последние годы проведено множество исследований
фрактальных структур разнообразных поверхностей. Проанализированы
шероховатости естественных и искусственных поверхностей
разнообразных объектов - от лунного моря Познания до танкового
полигона в Форт-Ноксе, от поверхности тазобедренного сустава до
шлифованных деталей механизмов [163]. Подобие в структуре
поверхностей с такими различными масштабами приводит к мысли о
существовании общей природной закономерности, лежащей в основе
этого явления. Фрактальная природа поверхностей в приложении к
проблемам радиофизики и радиолокации должна иметь важные
выводы при решении задач дифракции электромагнитных волн на
поверхности (так называемые задачи фрактальной электродинамики).
Предположение [163] о том, что пространственный спектр
мощности G((d) для разных видов поверхностей обратно
пропорционален квадрату угловой пространственной частоты со=2я/, означает,
что образец конечной длины рассматриваемой поверхности
никогда не будет настолько длинным, чтобы в совершенстве представлять
ее свойства.
Пространственная частота связана с длиной волны неровностей
поверхности равенством / = 1/А,. Все физические системы с
конечной протяженностью /0 соответственно имеют минимальную
пространственную частоту /0 = (й^ /(2я) = 1//0. Дисперсия высоты
неровностей рельефа
оо
с2 = J G((o)d®. (3.1)
Предположим, что среднеквадратичная высота неровностей
является функцией длины образца, т. е. о = /(/). Чтобы исследовать
эффект увеличивающейся длины образца на с неровностей, рассмот-
131
Глава J. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
рим последовательно длины 1Х и /2. Полагая <52=<5\+<5\, можно
записать
/2(/1+/2) = /2(/1) + /2(/2). (3.2)
Единственная функция /(/), которая удовлетворяет условию
(3.2), является линейной:
а2-/. (3.3)
В данном случае исследуемый процесс соответствует
нестационарному процессу Винера-Леви, примером которого является
броуновское движение. Как известно, такой процесс непрерывен, но
нигде не имеет производных. В приложениях к рельефу это
означает, что наклоны, кривизна и распределение экстремумов не являются,
как считалось в большинстве случаев, существенными свойствами
поверхностей.
Соотношение (3.3) в спектральной форме связано через
константу L0 с высшей длиной волны отсечки Х0 следующей формулой:
а2 = 10^0 = 10//0=2я10/ш0. (3.4)
На рис. 3.1 приведены результаты экспериментального
исследования возрастания нормализованной среднеквадратичной высоты
неровностей о/Ц/2 при увеличении длины волны отсечки Х0 для
„1/2 1/2
CT/L0 , М
10
10
10
А
УХ
• i
J*l
А #2
i *-*
L
Д-1
• -2
А
И
10
-2
10
1 Км
Рис. 3.1. Теоретическая (сплошная линия) и экспериментальные зависимости
нормализованного среднеквадратичного отклонения от волны отсечки для ровной
(1) и шероховатой (2) песчаной поверхности [163]
132
3.1. Пространственные спектры мощности поверхности
ровной (L0 = 4,4 • Ю-12 м) и шероховатой (L0 = 1,7 • Ю-8 м) песчаной
поверхности. Там же прямой линией показана зависимость (3.4).
Рассматривая совместно соотношения (3.1) и (3.4) при условии
limG!(co) = 0, получаем
*~~ 2nL (L ^
3L
2%
v
I2
(О2
или
G(l/X) = L0X2. (3.5)
Экспериментальные нормированные спектры мощности L~lG(k~l)
возвышений для 23 типов поверхностей как функция длины волны
шероховатостей показаны на рис. 3.2. Там же прямой линией
представлена зависимость (3.5). При охватывании 8 декад по длине
волны получена удивительная сходимость результатов для всех
структур поверхностей.
Величину L0 в (3.4) и (3.5) называют топотезой поверхности, ее
значения для данных рис. 3.2 приведены в табл. 3.1. Топотеза
однозначно определяет статистические и геометрические свойства
случайных компонент изотропной поверхности для рассмотренного
диапазона длин пространственных волн X. Топотезы измеряются в
единицах длины.
В [164] отмечается, что статистически изотропные
поверхности, на которых выделен какой-либо масштаб и уровень которых
хорошо определен, но не дифференцируем, действительно могут иметь
пространственный спектр фрактального вида
o(f)=V/a =А)/~2Я_1=V"7+2Z)- (з.б)
Здесь спектральный параметр а определен формулой
а = 2#+1, (3.7)
где Н - показатель Херста.
Как показано в [3], показатель Яравен фрактальной
коразмерности и определяется через фрактальную размерность поверхности D:
D = 3-H. (3.8)
В общем случае евклидовой (топологической) размерности Е
имеет место соотношение [165]
H = E + \-D. (3.9)
133
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
105
104
103
W
10'
10°
ю-1
ю-2
10-3
10^
ю-5
ю-6
ю-7
10-8
ю-9
10-ю
ю-11
ю-12
1 1
Ь
h
h
h
h
h
h
V
V
V
Y
r
^
h
Г 1*
V l.:
i
Be
►
L
1
4
4*
jfjimfi
r-i
t
^fifc
&
L^
l 1
y?
r
!*
1
p-
♦ У
uT
«
►♦
l—.
1
p
♦-1
•-2
x-3
0-4
A-5
П-6
iO-7
*~8
в-1
B-i
©-1
+-1
■ -1
Д-1
•-1
!♦-!
jO-i
[ГЧ-1
C-2
▼-2
|Q-2
Lj
r-
ДДр»
0
1 -«гН
1 "*
2
з ,
4
5 _
6
7
8
9
0
1 ..
2
3
L
—T7"-|
H
.-]
•J
H
H
H
H
4
H
-^
1
•1
•j
4
1 1
ю-6 io-5 io^ io-3 ю-2 ю-1 о io1
102 IO3
X
Рис. З.2. Нормированный пространственный спектр мощности неровностей
поверхности как функция длины волны шероховатостей X [163]
134
3.1. Пространственные спектры мощности поверхности
Таблица 3.1
Топотезы поверхностей [163]
I Позиция на рис. 3.2
| 1
1 2
1 3
1 4
1 5
6
1 7
8
9
10
1 п
1 12
13
14
15
16
1 17
1 18
19
20
21
22
23
Тип поверхности
Автодорога
Обработанная почва
Лунная поверхность
Поток лавы
Лунное море Познания
Поверхность земли
Травяная дорожка
Бетонная взлетная полоса
Танковый полигон в Форт-Ноксе
Асфальтовая дорога
Поверхность из гравия
Поверхность тазобедренного сустава
Обшивка поверхности корабля
Обшивка супертанкера
Шлифованные детали механизмов
—
—
—
—
—
—
—
— j
( i«.M
3,6-10"7
2,0-Ю-2
3,7-Ю-4
2,3 Ю-2
1Д-Ю-3
ко. ю-3
3,9-Ю-6
15 Ю-7
3,0 Ю-4
2,4 10-7
1,7-Ю-8
2,4 Ю-10
7,5 ЛОГ9 1
1,0-10"" 1
1,0 1042 1
Ю10_12П
3,0 Ю-16
L0 10"13
7^ Ю-13
5,7 -Ю-14 1
7,0-Ю"13
3.0-Ю-11
2,0 Ю-13 1
Для броуновских поверхностей, когда статистика гауссова [163],
из (3.6) и (3.8) получается равенство (3.5), поскольку при этом Н= 1/2
и D= 2,5 [2]. Однако для параметра а необходимо найти значение,
обеспечивающее более точную аппроксимацию, и оно оказывается
135
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
л(а)|
Ю h
ш
Ли.
1,2 2,0 2,8
Рис. 3.3. Гистограмма значений
спектрального параметра а,
полученных из соответствия
степенному закону
видаю"а [166]
расстоянию L, на котором
сти близки к единичным:
а
в интервале 1,07 < а < 3,03 [164], что
соответствует по формулам (3.7) и
(3.8) фрактальной размерности
Л = (7-а)/2, (3.10)
равной от 2 до 3.
Проведение новой
аппроксимации данных рис. 3.2 позволило
построить гистограмму л (ос) оценок
спектрального параметра (рис. 3.3).
Полученные значения группируются
около гауссова значения а = 2, но
распределены в диапазоне от 1 до 3.
В общем случае топотезу лучше
определить [164] в виде длины
Г = Х1/(3-а))
(3.11)
пропорциональной горизонтальному
среднеквадратичные наклоны поверхно-
4-
< у2 > :
:Р0-1.
3.2. Фрактальные размерности параметров
окружающей среды
В [167] проведен анализ ряда измерений параметров
окружающей среды с целью получения оценки их фрактальной размерности
D (табл. 3.2). Эти данные можно рассматривать как ряды измерений
величины z, выполненные через регулярные интервалы значений
координаты х. Для случайной функции z (х) с множеством точек на
плоскости xz фрактальная размерность 1 < D < 2. Величина D = 1
соответствует абсолютно дифференцируемой функции. Значение D = 2
имеет место для функции, настолько неровной и иррегулярной, что
она полностью покрывает двумерное топологическое пространство.
Для поверхности соответствующие значения D лежат между D = 2
(абсолютно гладкая поверхность) и D = 3 (бесконечно «сморщенная»
поверхность).
136
3.2, Фрактальные размерности параметров окружающей среды
Дисперсия приращений V(Ax) = ([z(x+Ax)-z(x)] ) зависит от
разности координат: F(Ax)«|Ax| . Тогда фрактальную размерность
D = 2 - Н оценивают, пользуясь графиком дисперсии приращений,
построенным в двойном логарифмическом масштабе, или из
условия d\ogV{kx)ld\ogbx = A-2D при Дх-*0.
Данным методом получены значения фрактальной
размерности, обозначенные в табл. 3.2 буквой «а». Спектр мощности (3.6) также
позволяет оценить фрактальную размерность через оценку
коразмерности, результаты обозначены буквой «б». Результаты, полученные
из блочных дисперсий, помечены буквой «в», а оценки по ковари-
ациям - буквой «г». Все значения фрактальной размерности
составляют от 1,4 до 2,0. Интервал запаздывания х определяется типом
исследуемого образца и используется для оценки D при аппроксима-
Таблица3.2
Оценки D для различных параметров окружающей среды [167]
1 Параметр
1 Почвы:
• содержание натрия
• содержание камней
(оба — в четырех направлениях)
• толщина суглинка
• электропроводность
(4 направления)
Поверхность взлетной полосы
[Почвы:
• средний показатель конуса
• мелкозем и глина в слое 0-15 см
• средний диаметр камней
на поверхности
• крупнопесчаная фракция
в слое 0-15 см
Растительный покров
Золото
Почвы:
• уровень фосфора
• рН
• уровень калия
• объемная плотность
• вода, 0,1 бар
Запаздывание т
15,2 м
15,2 «
20,0 «
1,0 «
30 см
~ 1 км
~1 «
~1 «
~1 «
~ 1 км
Различное
5 м
5«
5«
5«
5«
Лн1
1,7-1,9
1,1-1,8
1,6
1,4-1,6
1,5
1,9
1,8
1,8
1,8
1,6
1,9
2,0
1,5
1,6
1,5
1,5
Метод]
а
а
а
а
б
в
в
в
в
в 1
а 1
в
в
в
в
в 1
137
Глава J. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
Продолжение табл. 3.2
1 Параметр
|Железная руда в породах:
• хлорит
• кварц
• кварц
• железо
• железо (В-3)
• железо (С-Ю)
• железо (В-3)
• железо (С-Ю)
Морские анемоны
Дождевые осадки
Железная руда
Уровень подземных вод
Пьезометр:
1
2
3
4
Марки нефти
Марки меди
Топографические возвышения
Почвы:
• содержание песка
• рН
Урожайность
Глубина грунтовых вод
Запаздывание т
15мкм
15 «
5 см
5 «
100 м
100«
500 «
500«
10 см
1км
Зм
1 день
1 «
1 «
1 «
60 см
2м
Юм
Юм
10 «
1-1000 м
250 м
*>+*
1,6
1,9
1,6
1,5
1,7
1,8
1,6
1,9
1,6
1,7
1,4
1,6
1,6
1,8
1,3
1,7
1,7
1,5
1,6-1,8
2,0
1,6-1,8
1,6
Метод
а
а
а
а
а
а
а
а
г
а
а
а
а
а
а
а
а |
а
а
а
в
а
ции временного/пространственного ряда фрактальной функцией
Вейерштрасса—Мандельброта W(t). При этом дисперсия
приращений V(x) = (\W(t)-W(t + T)f\ изменяется как x4~2D, а вариации
спектра мощности функции W{t) описываются приближенно как
со-(5-2/))<
Результаты исследований [167] вызывают интерес, но для оценки
их надежности необходимы анализ исходных данных и выявление
диапазона, в котором отсутствуют какие-либо пространственные
масштабы.
138
3.3. Фрактальные размерности микроповерхностей
Надежные оценки степенных показателей можно получить из
набора данных, охватывающего не менее трех декад. Оценка
значений D позволяет установить степени самоподобия в различных
пространственных масштабах природных образований и явлений, что
имеет огромное практическое значение. В свою очередь значения
фрактальной размерности D служат полезным индикатором
состояния окружающей среды для выявления определенных природных
процессов.
3.3. Фрактальные размерности микроповерхностей
Поверхности различных материалов могут быть шероховатыми
и даже фрактальными вплоть до масштабов молекулярного уровня.
Описание экспериментальных данных с помощью фракталов полезно
и позволяет рационально их представить. Измерение угловой
зависимости рассеяния волн — это практически единственный способ
измерения фрактальных размерностей различных материалов [9,45,
168-170].
Чаще всего измеряют корреляционную функцию плотности,
которая для фрактальных материалов пропорциональна выражению
(1.13). Для выяснения фрактальной структуры вещества, как
правило, применяют рентгеновское излучение, рассеяние нейтронов или
рассеяние света.
Интенсивность рассеянного излучения в единичный телесный
угол, как функция угла рассеяния 0, определяется выражением
Kq)~rD, (3-12)
где q = 4nX~l sin (0/2) - модуль вектора рассеяния; X - длина волны
выбранного излучения; D = lim——— фрактальная
размерно In г
ность кластера; < п(г) > — среднее число частиц; R^^r^R (Rq-
масштабная единица измерения линейного размера ^кластера).
Соотношение (3.12) верно в диапазоне R~l <: q «: R^1.
На рис. 3.4 приведены результаты измерения угловой
зависимости интенсивности рассеяния света и рентгеновского излучения
коллоидными агрегатами небольших частиц кварца радиусом
Rq -27 А. Весь диапазон волновых чисел (свет - 0,0001...0,001 А~ ,
рентгеновские лучи — 0,01 ...0,1 А~ ) перекрывается при рассеянии на
двух образцах, полученных в растворах с разным составом раство-
139
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
0,0001 05001 0,01 0,1
Рис. 3.4. Интенсивность малоуглового рассеяния света (1)
и рентгеновского излучения (2) на агрегатах из частиц кварца [168]
рителя. Измеренное значение D = 2,12 ±0,05 отличается высокой
точностью в диапазоне от Rq до R ~ 104 А. Кроссовер от рассеяния на
фрактальной структуре с размерностью D = 2,12 к рассеянию на
частицах с гладкой поверхностью, когда I ~q~*, происходит при
волновом числе q = Щ1, где Rq = 27 А.
Иная, чем в (3.12), связь показателя
угловой зависимости интенсивности с
фрактальной размерностью при рассеянии
на фрактальной структуре проявляется,
когда рассеиватель имеет фрактальную
поверхность с порами. В [169] для
интенсивности рассеяния рентгеновского
излучения фрактальной пористой поверхностью
получено выражение: I(q) ~ 0~(6_/)).
Измерения рассеяния на малые углы
образцами бурого угля показали, что
поверхность пор фрактальна с размерностью
Я = 2,56±0,03 (рис. 3.5).
Подборка фрактальных размерностей
различных поверхностей приведена в
табл. 3.3. Здесь встречаются поверхности
с фрактальными размерностями,
занимающими весь диапазон от D = 2 до D = 3.
Полученные результаты, несомненно,
"о
109
107
105
103
1
J 1
\
' \
\ 1
\
V 1
, , \ 1
ю-
ю-:
10°
6, рад
Рис. 3.5. Угловая
зависимость нормированной
интенсивности
рентгеновского излучения,
рассеянного образцами
бурого угля [169]
140
3.3. Фрактальные размерности микроповерхностей
Таблица 3.3
Фрактальные размерности D поверхностей по измерениям
молекулярной адсорбции [171]
1 Фрактальная
размерность
Происхождение образцов
Диапазон, А
1 Высокие значения
2,91±0,02
2,97±0,01
2,88±0,02
2,73±0,05
2,71±0,14
2,80±0,16
2,90±0,01
2,92±0,02
2,94±0,04
2,79±0,03
2,78±0,21
2,67±0,16
Доломитовая порода из Бельвью,
штат Огайо, США
Кальциевая порода из Идабель,
штат Оклахома
Гранитные породы с ядерного полигона в
штате Невада
Оплавленные породы с ядерного
полигона в штате Невада
Гранулы активированного угля из оболочек
кокосовых орехов (Цуруми НС-8)
Гранулы активированного угля из оболочек
кокосовых орехов (Фуджизава B-CG)
Карбонатная порода из артезианской
скважины, Юкка-Флэт, штат Невада
Почва (каолинит со следами галлуазита)
Пористый силикагель
Активированная окись алюминия марки
F-20 («Алькоа корп.»)
Животный уголь
Пористый древесный уголь из оболочек
кокосовых орехов («Стандарт
Кемикэл Ко.», Монреаль, Канада)
20-47 000
20-47 000
16-16 500
14-14 300
16-37
16-37
16-16 500
150-16 500
16-34
16-45 100
1400-180 000
16-47
Умеренные значения \
2,57±0,04
2,35±0,11
2,52±0,07
2,33±0,08
2,25±0,09
2,54±0,12
2,30±0,07
2,63±0,03
Пористый пигмент ос = FeOOH
для магнитных лент
Битое свинцовое стекло «Корнинг 0010»
Пыль из угольной шахты
в Западной Пенсильвании
Тоже
Газовая сажа
Слабопористый уголь из оболочек
кокосовых орехов («Стандарт
Кемикэл Ко.», Монреаль)
Тоже
Плавиковый шпат из Стефенс-Сити,
Виргиния
16-980 1
21-14 900
16-180
16-270
16-71
16-47
16-47
20-47 000
141
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
Окончание табл. 3.3
1 Фрактальная
размерность
2,58±0,01
2,46±0,11
2,29±0,06
Происхождение образцов
Доломит из Вудвилля, штат Огайо
Стекловидная оплавленная порода
с ядерного полигона в штате Невада
Почва (в основном полевошпатовый кварц
и лимонит)
Диапазон, А
20-47 000
14-14 300
150-21800
1 Низкие значения
2,02±0,06
2,15±0,06
2,14±0,06
1,95±0,04
2,02±0,05
2,07+0,01
2,04±0,16
2,13±0,16
2,04±0,04
1,97±0,02 1
2,16±0,04
Аэросиль — непористый кремнезем
(Degussa)
Сноувит — матовое кварцевое стекло
высокой чистоты
Мадагаскарский кварц («Термал
Синдикат»)
Периклаз — электрически плавленный и
дробленый магнезит
Синтетический фоязит
Na20 А1203 • 2,67Si02 mH20
(«Линде Эйр Продактс»)
Графит марки «Вулкан 3G» (2700)
(Национальная физическая лаборатория,
Тедцингтон, Великобритания)
Графой — частично графитизированная
газовая сажа, полученная нагреванием
до 3200 °С
Графой — графитизированная газовая сажа
(«Кейбот корп.»)
Непористый уголь из оболочек кокосовых
орехов («Стандарт Кемикэл Ко.»,
Монреаль)
Тоже
Исландский шпат, кальцит из Чиуауа,
Мексика
16-529
16-10 600
16-1850
16-720
16-68
16-178
15-41
1400-180 000
16-47
16-47
20-47 000
требуют проведения дальнейших исследований. В частности,
диапазон масштабов, в которых проводятся измерения, необходимо
распространить в области, достигающие нижнего и верхнего пределов
самоподобия. Вновь следует отметить, что оценки степенных
показателей ненадежны, если исходные данные не охватывают диапазон
по меньшей мере в три декады.
142
3,3. Фрактальные размерности микроповерхностей
Пористые песчаники изучались в [172] сканирующим
электронным микроскопом. Фрактальные свойства их поверхностей
исследовались по вторичной электронной эмиссии, индуцированной
сканирующим пучком электронов. Интенсивность вторичной
электронной эмиссии определяется свойствами пересечения линии
сканирования с пористой поверхностью.
Для объемного фрактала с поверхностной фрактальной
размерностью D пересечение с линией представляет собой множество
точек размерности D'=D-2. В результате экспериментов было
показано, что число N(L) геометрических особенностей на единицу
длины, разрешаемое при данном увеличении, зависит от масштаба
длины L по закону N(L) ~ L~^D~2\ Было получено значение D = 2,78.
Фрактальная структура пор песчаника прослеживается между
наименьшим масштабом 1Х ~ 20 А и наибольшим масштабом /2 (табл. 3.4).
Пористость определялась по формуле Ф = (l{ /l2)3~D.
Данное соотношение было использовано для оценки Ф по
измерениям величины /2. Однако серьезных доводов в пользу этого
соотношения не приводится, и оно не может иметь общий характер.
По этому поводу в [173, 174] ставятся дискуссионные вопросы и
даются ответы на них.
В материаловедении и металлургии использование, концепции
фракталов позволяет управлять структурообразованием в расплавах
и сплавах [175]. Это служит базой для получения материалов с
заданными свойствами (аморфные, с памятью формы,
функционально-градиентные и др.). Теория неравновесных фазовых переходов
опирается на самоорганизацию фрактальных структур. В настоящее
Таблица 3.4
Фрактальная размерность поверхности пор в песчанике [172]
Образец
Плотный газоносный
песок № 965
Плотный газоносный
песок № 466
Плато Коконино
г. Навахо
Сент-Питерс
Фрактальная
размерность
2,57
2,68
2,78
2,81
2,87
мкм
2,5
6
98
50
50
Пористость, %
рассчитанная
4,7
7,6
10
15
27
измеренная
5,3-5,6
6,9-7,6
11-12,5
16,4
24-28 1
143
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
время в материаловедении применяют самоорганизующиеся
технологии - инжекционную и ультразвуковую обработку расплавов,
комплексное легирование, сверхбыстрое охлаждение жидкого металла
(аморфные сплавы), электростимулированную прокатку,
механическое легирование (негидростатическое сжатие) и т. д. Для
проведения фрактального анализа широко применяют фрактографические
исследования профилей и поверхностей сплавов. Наиболее часто
используют метод островов среза, фурье-анализ профилей, метод
вертикальных сечений, метод преобразования подобия. При первом
методе исследования разломы образца стали сначала никелируются,
а затем их полируют. При этом выявляются «острова» стали,
окруженные «озерами» никеля. Затем картину изучают с помощью
анализатора изображения.
Фрактальные молекулярные поверхности исследуют путем
осаждения на них молекул разных размеров и «подсчета» их количества.
На практике площадь поверхности определяют, измеряя
адсорбционные изотермы. Количество грамм-молей п молекул, которые
адсорбируются на поверхности, является функцией давления при
заданной температуре. Метод определения п заключается в измерении
давления и объема до и после взаимодействия адсорбента с
поверхностью. Можно определять п и прямым взвешиванием до и после
адсорбции.
Более удобны методы определения фрактальной размерности по
скин-эффекту и импедансу шероховатой поверхности раздела.
3.4. Морская поверхность как фрактальная структура
Гравитационные и капиллярные волны. Морская поверхность
может служить одним, из примеров фрактальных структур,
наблюдаемых в природе. Фрактальное решение задачи о форме
взволнованной поверхности невязкой воды представлено в [176]. Однородная
случайная поверхность z = h(x) = h(x,y) определяется своим
пространственным спектром G(k) = G(k,k), который является фурье-
х у
преобразованием функции корреляции:
G(k) = -^\<h(x)h(x + r)>e-ikrdr.
(2я)2 \
При условии, что h - гауссов процесс, возможно восстановить
h из G посредством преобразования
144
3.4. Морская поверхность как фрактальная структура
h(x) = \a(k)cos[kx+x(k)UWic)dk,
k
где %(k) = z{k) - случайные фазы, имеющие равномерное
распределение в диапазоне (-я,я); а(к) - независимые случайные
амплитуды с единичным средним.
Для поверхности воды h есть функция времени, и через
дисперсионное отношение
uil = gk + sk3 (3.13)
фазы становятся зависящими от времени:
X(k) = E(k)-(0(k)t,
где k=\k\;g- ускорение свободного падения; s - отношение
коэффициента поверхностного натяжения к плотности жидкости.
Для собственно гравитационных (индекс «g») и капиллярных
(индекс «с») волн перепишем (3.13):
(о/ы*=(к/к*У,
где индексы «звездочка» использованы для масштабирования
переменных, а показатели
Т, = 1/2, ус = 3/2. (3.14)
Динамика волнового поля описывается спектральной
плотностью N{k, t), определяемой двумя компонентами - 1Ти IQ в виде
Ы
где
■ = /г + /о- (3.15)
h
1бте3 J/{f^^)^^ >- Л^С*)!^»!)+ЛГС^)!}- [к«-> (А:,^ ,^ )]2 х
-JV(ifc)Ar(ik1)}-[K<-)(ik2,ik1,ifc)]250fc+ik1 -^)5(ш+о^ - о^ ^d^i/i^;
145
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
IQ = 64n5jj\{N(k2)N(k3)[N(k) + Щк,)]- ЩкШЬ )х
хВД+М*з)1}[ПЦЛЛ)]28(*ЦЧ^)х
х5(со+ CDj - со2 - iu^dk^kjdk^.
Выражения для ядер К(_) и ^приведены в литературе (см.
ссылки в [176]). Для чисто гравитационных волн 1Т = 0, а для чисто
капиллярных волн часто можно пренебречь слагаемым IQ в
формуле (3.15).
Спектр G{k) определяется плотностью N(k) в виде
G(k) = [N(k)+N(-k)]k/2a>. (3.16)
Равенство dN/dt = IQ для гравитационных волн имеет два
стационарных решения:
N/N^(K/kf (3.17)
с р = р =23/6; 4. Для капиллярных волн dN/dt= 1Т имеем
решение как (3.17), но р = рс = 17/4. Из (3.16) и (3.17) получаем
G/G.=(kjkf, (3.18)
где pg = 10/3; 7/2 и рс = 19/4.
Тогда выражение для h(x,t) запишем в виде
h(x,t) = k\\ cos{fc(a>)[xcos9 + у sine]- шГ + е(ш,9)}(ох /cof1 /2 x
0-я
><7</(a>M)rfe, (319>
где
0^ = 11/3; 4 и а1с = 17/6. (3.20)
Для морской поверхности, заданной моделью (3.19) и (3.20),
локальные изменения h во времени в фиксированной точке есть
функция
/z(0 = 4b^K Jcos[arf + ф))](со* /со)а1/2^ (со/со,), (3.21)
о
146
3.4. Морская поверхность как фрактальная структура
а в пространстве
оо
т = A. Jcos[*C + t(k)\jF(g)d(k /*.), (3.22)
о
где f(?) = A; J — | cos р | ,. 7 в,)у <Ф, значения у и а,
определены соответственно в (3.14) и (3.20). Тогда
F(k) = 2y(k,/kf2 ]\cos$\«ai-l) d$ = 4y(k,/k)a2 B(l/2,a2/2). (3.23)
-К
Здесь В - бета-функция; ос2 = 1 + 7(04 -1). Подстановка (3.23) в (3.22)
дает
h(Q = 2h,[yB(l/2,a2/2)]l/2]cos[k^E(k^
о
Из (3.23) с учетом (3.14) и (3.20) можно найти a2g = 7/3; 5/2 и
a2c=15/4.
Стохастические процессы. Рассмотрим стохастический процесс
оо
вида V(t) = J cos(otf + e)7^(co)flfco при .?(©) = ara совместно с моделью
о
обобщенного броуновского движения (2.8), записав ее в виде
**(') = r(ff!l/2) I <t-tVA/2B<W, (3.24)
где J?(0 - гауссов белый шум.
Докажем, что процессы K(f) и 2?я(0 идентичны при условии
a = 2# +1. Функционально белый шум В (t) можно записать [176] в
оо
виде, аналогичном V(f), т.е. B(t) = Jcos(otf + e)V5a). Отметим, что
о
(3.24) на самом деле есть Яя(0=_/,я+1/2Ж0, где _/,я+1/2
-оператор Римана-Лиувилля (2.31) дробного порядка.
147
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
Изменив порядок интегрирования, применим результаты [177]:
оо оо
BH{t) = _/,я+1'2 Jcos(otf + E)yfdco = j^fd^Zl^2 cos(orf + e) =
= [yfchocos
Ш-
я+-
Л
n
2+£
(0
-(#+1/2) .
Jcos((or + e)((o-^+1^Q))1/2.
(3.25)
Сравнивая результирующее выражение в (3.25) с исходным
соотношением для V(t), находим, что эти процессы идентичны при
условии
ос = 2# + 1.
(3.26)
Фрактальные размерности морской поверхности. Так как
локальная фрактальная размерность обобщенной броуновской функции
D^-D'-l-E (см. табл. 2.1), то, исключая величину #с учетом
(3.26), можем записать выражение для фрактальной размерности
сечения поверхности:
Д' = (5-сс)/2, (3.27)
численное значение которой приведено в табл. 3.5.
Тогда фрактальная размерность непосредственно морской
поверхности будет:
Я = Я' + 1 = (7-сс)/2.
Рассчитанные значения фрактальной размерности 1У
сечений морской поверхности [176]
(3.28)
Таблица 3.5
1 Сечения
Временной ход возвышений в точке
Возвышения вдоль сечения
поверхности вертикальной плоскостью
Гравитационные
волны
2 1
3; 2
3 4
Капиллярные
волны
12
5
8
148
3.4. Морская поверхность как фрактальная структура
Таким образом, для гравитационных волн установлено, что
свободные поверхности могут обладать фрактальной размерностью
D = D' + l = 2\/;2\/. Для капиллярных волн существуют
субфрактальные поверхности с размерностью 2. Для временной
последовательности высот подъема воды в одной фиксированной точке
ситуация меняется на противоположную. В этом случае решение для
капиллярных волн генерирует последовательность с фрактальной
размерностью 1 V , а последовательность для гравитационных волн
— с размерностью 1.
Использование фрактального описания волн связано с шириной
диапазона, в котором применим степенной вид спектра (3.6).
Показано (см. ссылки в [176,178]), что для гравитационных волн
степенной вид спектра соблюдается в диапазоне пространственных длин
волн от 0,1 до 15 м (масштаб ~ 27), а для капиллярных волн в
диапазоне 2-16 мм (масштаб 23).
Хаотическая динамика морского волнения. Иной подход к
описанию фрактальных свойств волнения рассмотрен в [179]. С помощью
алгоритма Такенса была определена размерность аттрактора в
фазовом пространстве.
Фрактальные свойства зон обрушающихся волн на
поверхности моря рассмотрены в [180] на масштабах, превышающих интервал
корреляции волнения. Данный тип волн представляет собой особый
вид турбулентного движения, образующегося вследствие сложных
процессов взаимодействия ветровых и волновых движений.
Экспериментальный материал был получен дистанционным
оптическим зондированием акватории Каспийского моря.
Исследуемая площадь акватории составляла 39 1,5 км2. Наблюдалась
устойчивая температурная стратификация приводного слоя. Алгоритм
обработки данных заключался в следующем. Каждая из полученных
39 карт делилась на пк = 5 • 2к (к = 1,..., 8) равных ячеек. Ячейка
относилась к зоне обрушения, если в ней была хотя бы одна обруша-
ющаяся волна. В противном случае ячейки относились к зоне
молчания. При увеличении числа ячеек пк улучшается разрешение карты
и на ней появляются пустые зоны. Этому переходу соответствует к0 = 3
с площадью ячейки 0,037 км2 и характерным максимальным
размером зоны молчания 190 м. На рис. 3.6 показан один и тот же
фрагмент карт при разных масштабных разрешениях. Заштрихованные
ячейки содержат хотя бы одно обрушение (Nk > 1), для пустых Nk = 0.
149
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
Рис. 3.6. Структура карт поля обрушения морских волн
при разных масштабах разрешения [180]
. Согласно определению фрактальной размерности Щгк) = Nk,
т. е. числу зон обрушения на всех 39 картах, а гк = Slk/2 — это
линейный размер ячейки на карте при к-м шаге ее дробления. На рис. 3.7
приведены в двойном логарифмическом масштабе зависимости
количества заполненных^ и пустых Nk-Nk ячеек от линейного
размера пиксела гк , где Nk - число всех ячеек на к-м шаге. Первые
HNrNk)
2 3 4 5 6 1п(1/е*)
Рис. 3.7. Зависимость числа заполненных Nk и пустых N^-N^ ячеек
от линейного размера пиксела [ 180]
150
3.4. Морская поверхность как фрактальная структура
три квадрата соответствовали площадям пиксела в 1,5; 0,75 и 0,5 км2,
последующие 1,5/nk.
Участок кривой, имеющей фрактальную размерность D « 2,
соответствует очень крупной ячейке. Поэтому размерность D
совпадает здесь с размерностью плоскости. При к0 = 3 (/0 = 190 м)
полученная зависимость выходит на участок с фрактальной
размерностью D«0,5. Переходная область лежит в интервале &=3;4 с
линейным размером ячеек А/ = 100 -190 м.
Малая размерность зон обрушения указывает на особую роль зон
молчания в рассмотренном режиме турбулентности поверхностных
волн. Так как зона молчания всегда имеет положительную меру, то
ее относят к «жирным» фракталам [181]. Зависимость ]n(Nk-Nk)
от lnCl/e^), начиная с к = 4, описывается законом Nk-Nk~S%, где
/)-1,5.
Полученные результаты объясняются следующим образом [180].
При определенных условиях взаимодействие поверхностных волн
между собой и с ветром превышает некоторый порог и приводит к
возникновению хаотической динамики в форме обрушений. В этом
случае разгон волн заканчивается достижением их критической
скорости и их обрушением. Вычисленная фрактальная зависимость
фактически относится к зонам разгона волн, определяющим зону
молчания. По данным работы [182], средний размер зон молчания
лежит в пределах 110 м при их интервале в области 80-200 м и
характерной длине гравитационной волны примерно 40 м. Эти данные
хорошо совпадают с интервалом А/= 100-190 м.
Резкое изменение фрактальных свойств зон обрушения можно
соотнести с масштабами, характеризующими размер зон молчания.
Максимальной длине разгона волн соответствует расстояние около
5 длин волн. Эта величина является функцией скорости ветра и ряда
параметров приповерхностных процессов. По показателю фракталь-
ности D зон молчания возможна диагностика волнения на воде.
Фрактальная статистика высот волн. Статистика высот
характерной волны А0 рассматривалась в [45] по данным Норвежского
института метеорологии. Значение й0 определялось как среднее по 1/3
самых крупных волн за интервал 17 мин. Максимальный размер
волны примерно был равен 1,8А0 за этот же интервал наблюдений.
График hJt) рассматривался как фрактальная кривая.
151
Глава 3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ ПОВЕРХНОСТЕЙ
Применение закона Херста для данных, отфильтрованных от
сезонных вариаций, иллюстрирует рис. 3.8. Закон Херста
формулируется в виде (1.32).
Рис. 3.8. Графическое отображение закона Херста для статистики
нормированных высот морских волн при т < 10 и т > 20 дней [45]
На рис. 3.8 отчетливо видны две области с разными
свойствами: при т < 10 дней аппроксимация дает Н - 0,92 ± 0,02, а при т > 20
дней имеем Н = 0,52 ± 0,02 . Следовательно, для первого случая
характерна персистентная статистика, когда Н> 1/2, т.е. в процессе
поддерживается имеющаяся тенденция и он обладает памятью. При
т > 20 дней рассматриваемый процесс является статистически
независимым. Высокое значение показателя Херста указывает на
сильное отклонение статистики высоты волн от гауссовой. Проведенные
исследования говорят о том, что метод R/Sдействительно приводит
к робастной мере статистики временных рядов.
Результаты измерения локальной фрактальной размерности в
виде зависимости числа ячеек ЩЬ) размера abx от масштаба ячейки
Ъ приведены на рис. 3.9. Для оценки D были выбраны из 3-часовой
серии наблюдений по одному измерению. Данные рис. 3.9,а
описываются зависимостью N ~ b~D с фрактальной размерностью
D = 1,09± 0,02. Это соответствует формуле D=2- Япри найденном
показателе Херста #= 0,92. Увеличение размера клеток до т = 120 ч
приводит к фрактальной размерности D = 1,52 ± 0,03 (рис. 3.9,6), что
совпадает со значением Д ожидаемым для случайного процесса с
независимыми приращениями. При этом снова выполняется соотно-
152
3.4. Морская поверхность как фрактальная структура
Рис. 3.9. Число ячеек N(b) размера abx как функция масштаба ячейки Ь
для нормированных высот волн [45]
шение D = 2 - Н, где Н= 0,52 для т > 20 дней. Значение
коэффициента было равно 0,1 м. Важно отметить, что переход от D= 1,09 к
D — 1,52 объясняется не переходом от локальной к глобальной
фрактальной размерности самоаффинной кривой. Обе найденные
фрактальные размерности являются локальными. Наблюдаемое
изменение фрактальной размерности объясняется переходом от персистен-
тного к случайному поведению, которое обнаруживается при
локальных значениях D.
Приведенные в [45] результаты по фрактальной статистике
высот морских волн необходимо учитывать при предсказаниях самой
высокой волны, т.е. «девятого вала».
153
Глава 4
ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН
ФРАКТАЛЬНОЙ ПОВЕРХНОСТЬЮ
4.1. Модель с фрактальными высотами неровностей
Понятия «фрактал» и «фрактальная геометрия» нашли широкое
применение в современных областях физики при построении
моделей класса случайных масштабно-инвариантных структур. Их
практические приложения представляют интерес и для более
традиционных разделов радиофизики. Одним из таких примеров является
исследование рассеяния электромагнитных, или скалярных, волн
статистически неровной или неоднородной поверхностью. Теория
рассеяния волн статистически неровной поверхностью [183,184]
является синтезом теории дифракции волн на произвольной
поверхности и теории вероятностей. Ниже мы обсудим свойства волн,
претерпевших рассеяние на поверхностях с фрактальной структурой,
определим их модели рассеяния [185-187], отметим наиболее
существенные особенности и отличия от более знакомого специалистам
рассеяния на объектах с гладко изменяющейся поверхностью. В
частности, фрактальная поверхность предполагает наличие неровностей
всех масштабов относительно длины рассеиваемой волны. Это в
значительной степени меняет картину рассеяния волн на фракталах по
сравнению с классическими решениями задачи.
Постановка задачи. Рассмотрим модель с фрактальными
высотами неровностей. Особенности рассеяния волн такой фрактальной
поверхностью обусловлены ее недифференцируемостью. Наиболее
содержательное с точки зрения радиофизики решение данной
проблемы с привлечением теории дифракталов приведено в [188]. Дифрак-
талы — это волны, взаимодействующие с фрактальной
поверхностью. При рассмотрении данной модели рассеяния использовалось
приближение фазового экрана, т.е. вместо решения на случайной
поверхности h (x) оценим дифракцию волны, прошедшей одномерный
тонкий фазовый экран с распределением оптической толщины kh (x),
где к = 2к/Х — волновое число, соответствующее длине волны X.
Пусть плоская волна Ч*(х, z) = exp(ikz) (z < 0)
распространяющаяся вдоль оси z, падает на фазовый экран в точке z = 0. Волна под-
154
4.1. Модель с фрактальными высотами неровностей
вергается случайной фрактальной фазовой модуляции kh (x). Сразу
же за экраном
¥(х,0+) = ехр[Ш*(х)]. (4.1)
Геометрически это означает деформирование плоского
волнового фронта вблизи z = 0 в случайный фрактал z - - A (х), а
фактически - аппроксимацию волны, отраженную фрактальной
поверхностью. Для простоты и из-за отсутствия лучшей модели обычно
предполагается, что А (х) — гауссов фрактальный процесс, для
которого справедливо
(exp{i/[A(x)]}) = exp (i</»exp{-[</2> - (J)2 Щ (4.2)
где /— любой линейный функционал от А.
Для волновых задач важнейшей особенностью фрактальных
моделей является степенной вид пространственного спектра G (К)
неровностей Л (3.6):
G(K) = A/\K\a, 1<ос<3. (4.3)
Соответствующая структурная функция неровностей имеет вид
оо
([ h(x+X)-h(x)] 2) = JG(K)[<zxp(iKX)-l]dK=
= ^-sinf(2-a)r(2-a)|Jrr-1, (4.4)
a-1 2
где Г (...) - гамма-функция.
Из рассмотрения формулы (4.4) следует, что дисперсия <А2> и
среднеквадратичный наклон, заданный фурье-преобразованием
K2G(K), для заданной случайной поверхности являются
бесконечными при больших А", а А (х) — недифференцируемая функция,
подобно всем фракталам. Поэтому фрактальный фронт волны, являясь
недифференцируемым, не имеет нормали. Тем самым исключаются
понятия «лучевая траектория» и «эффекты геометрической оптики».
Однако хорды, соединяющие значения А, разделенные
расстоянием X, все-таки имеют конечный среднеквадратичный наклон (как
155
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
следует из формулы (4.4)) Ah/Ах. Это позволяет определить
коэффициент А в (4.3), ввести характерный масштаб L в виде
([h(x+L)-h(x)]2)/L2 = l (4.5)
и записать (4.4) следующим образом:
([Кх+Х) - h(x)f) = Z3"a \Х\а~1. (4.6)
Характерный масштаб длины L есть топотеза функции h (x). Она
равна длине, на которой наклоны поверхности близки к единичным.
Показатель степени а в (4.3) соотносится с фрактальной
размерностью D функции h (x) и показателем Херста Я как
/> = (5-<х)/2, # = (<х-1)/2. (4.7)
При изменении D от 1 до 2 спектральный параметр а лежит в
пределах соответственно от 3 до 1, а показатель Херста Н—ъ пределах
от 1 до 0. Из выражения (4.6) с учетом (4.7) следует, что при L < X
наклоны поверхности меньше единицы, а при L > X— больше
единицы. Согласно (4.6), функция h (x) подчиняется следующему закону
подобия: если график h (x) растянут вдоль оси х фактором/, а вдоль
h — фактором/2_/), то результирующая кривая статистически не
различима с оригиналом.
Функция когерентности. При достаточно малых значениях топо-
тезы L верно френелево приближение и амплитуда волны на
расстоянии z от фазового экрана имеет вид
¥(*,*) = ехр
4
^У }^ехр|^[2А(хО^(х-х02]}. (4.8)
Среднее значение <*Р> на основании формул (4.2) и (4.8) равно
<¥> = exp(fe)exp(-fc2<A2>/2) =0, (4.9)
так как (А2) велико.
Функция когерентности амплитуды с учетом формул (4.2) и (4.4)
записывается в виде
156
4.1. Модель с фрактальными высотами неровностей
{nx,z)V4xH,z)) = exp[-k4*D-^f2-D)/2] =
= ехр
-£■№-*>№
2#
(4.10)
Последнее равенство получается при использовании
показателя Херста Ни соотношения D = 2-H. Для ^ = 0 имеем (|*Р| ) = (/) = 1,
что следует из закона сохранения энергии.
Спектр мощности G^(K) функции ЧР определяется
преобразованием Фурье выражения (4.10) и определяет угловое распределение
интенсивности волны, приобретая островершинность при К= 0:
kGAK)~] duexp(iKu/k)exp\~(kL)4D-»\u\
2к J 2
,2(2-/))
г^Г
5-2D
4-2D
[m){DA)/{2-D)\
1*1-> о,
(^2(^-1)sin[7i(2-i))]r[(5-2i))/27u|^/^|5-2Z)], \К\^~. (4.11)
Для параксиального приближения, удовлетворяющего
требованию Gy(K)/Gy(Q) <z 1, когда угол рассеяния К / k » Q, где Q <к 1, из
(4.11) получим условие
(2=(Ш(/)-1)/(2"/)) =(Ш(1"Я)/Я, (4.12)
подтверждающее, что дифрагировавшие волны параксиальны, если
топотеза L достаточно мала.
Для маргинального дифрактала (D= 1), когда функция h{x)
почти гладкая, интеграл (4.4) расходится, при этом L исчезает из (4.6).
При введении среднеквадратичного значения наклона хорд любой
дайны р, т.е. /[ h(x + X)- h{x) ]2\ = р2Х2 при условии р «1, из (4.11)
следует соотношение вида G^K) = [l/(/:V2^)]exp[^2/(2A:2p2)],
предполагающего параксиальность для почти гладкого начального
волнового фронта.
Второй момент интенсивности. Флуктуации интенсивности
I2(z) = (I2(x>zy> ПРИ I(x,z) = \x¥(x,z)\2 на основании формул (4.6) и
(4.8) определяются интегральным выражением
157
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
хехр
^2 т^Л-П/л! |4-2Д ->| |4-2Д | |4-2Д | |4-2/>\
~YL (2\х\ +2\у\ -\х+у\ -\х-у\ )
(4.13)
с использованием оператора
([h(xl) + h(x2)-h(x3)-h(x4)]2) = L2(Z)-1)(|x1-x3|4"2D +
I \4-2D I |4-2D I i4-2D i \4-2D \ \4-2D\
+ |X2-X4| +\X2-X3\ +|X!-X4| "l^-^l -h-^l J'
Введем безразмерный параметр
C = fe(ikL^1)/(^)/2^4-2l,)=fae/21/(4-2fl), (4.14)
где угол рассеяния б определен соотношением (4.12). Перепишем
(4.13) в симметричном виде:
I2(Q=-zUu\dvcos^x
хехр{-[2«4-2/) +2v4"2Z) -(v+«)4-2^-(v-w)4-2Z)]}. (4.15)
Параметр £ (4.14) обладает масштабным самоподобием, т.е. скей-
лингом, и показывает, как изменяются флуктуации интенсивности
волны при переменной топотезе (4.5).
Спектр флуктуации интенсивности
Gf(K,z) = ± J ^([/(х + ^,^)-(/)][/(х^)-(/>]>ехр(/ЮГ)
определяется интегралом
71/(4-2/)) 7
kGI(K,z) = ^—— du
cos
21/(4-2/))
KQu
x(exp{-[2«4-2/) +2Щ A)4"2Z) -{u^K^/kf-2D-\u-K^/kf~w^-\\
(4.16)
158
4.1. Модель с фрактальными высотами неровностей
с асимптотикой
vriv \ J0' С-*0'
KUjKK,Z)->|2v(4-2Z»^^(2-V(4-2/»^)^ ^ _> ^ (4.17)
где G^ записывается согласно (4.11).
Уравнение (4.16) показывает, что спектр флуктуации
интенсивности подвержен скейлингу:
G^K/k, ft 0 = GT(K/kQ, 1, 50/G. (4.18)
Поэтому когда деформации волнового фронта (измеряемые
значением Q) велики, особенности спектра проявляются при больших
углах и близости к экрану.
В явном виде выражения для второго момента 12 и
пространственного спектра Gf могут быть получены при условии, что
начальный фронт волны описывается броуновским фракталом с
размерностью D = 1,5. Тогда из (4.15) имеем
/2(0=2|i-^-c((2c/ny/2)]2-^-^((2;/n)i/2)j
где С и S - интегралы Френеля, определенные как
C(t) + iS(t) = jckexp\i^x
о V 2
(4.19)
В предельном случае
wnfl + 2(2£/л)1/2, £->(),
W^{ 2-1/ою,С->- (4-20)
Спектр мощности на основании формулы (4.11)
G^K) = 2L/[n(k2I? +AK1 А2)], (4.21)
159
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
а спектр флуктуций интенсивности с учетом (4.16) имеет вид
Gl(K'Z)~iik2L2 + K2/k2Y
l-cxp(-LzkK)
Lk2 . zk2
zk2
K-smJT+cosK
(4.22)
с асимптотикой, удовлетворяющей (4.17).
Ближняя зона. Рассмотрим поведение флуктуации
интенсивности вблизи фазового экрана, когда % и z малы. Заменим в (4.15)
переменные и, v соответственно на ujt,, v-JC, и для всей плоскости
интегрирования, как в (4.13), получим
/2(0 =^ J ^" J ^exp(/«v)[l + С2-^ (-^M4_2Z> +2|«+v|4-2z>)]-
+0«*-2D),
(4.23)
где символ О (...) определяет отношение порядка. В окончательном
виде при малых % и z
I2(Q = 1 + 25~2D С2-» cos|(2 - D) Г
(5-2D\
)А/^ + 0(С4-2д). (4.24)
Для броуновской функции (D = 1,5) полученный результат
согласуется с (4.20). В предельном случае (D-» 2) значение 12 (х) очень
быстро растет до единицы, приближаясь к значениям, характерным
для дальней зоны /2 = 2. Для маргинального Дифрактала D = 1 + е,
где е -» 0, значение 12 имеет тенденцию к бесконечно медленному
линейному росту с увеличением £, а именно
/2(0 = 1 + 2те; + О(е2С2).
(4.25)
Интересно сопоставить выражение (4.25) с эволюцией почти
гладкого волнового фронта при функции корреляции вида
(h(x)h(x + X)) = Щ ехр(-Х2 /L2). В этом случае 12 растет квадратично:
160
4.1. Модель с фрактальными высотами неровностей
I2(z) = 1 + \212Щ IZ,4 + 0(z3). (4.26)
Дальняя зона. Рассмотрим поведение второго момента
интенсивности в дальней зоне. Интегрируя (4.15) по частям и выполняя
предельные переходы, можно записать:
(4.27)
xJ(u,Q + 0(^),
где
/(M)0 = 2(2-Z))Jrfwsiny[23-2/) +(v+M)3-2Z) -(v-u)3-w]x
(4.28)
xexp{-[2v4"2i) -(v + M)4-2Z) -(v-m)4"^]}.
При замене sin(wv/£) на mv/£ при больших £ результирующий
интеграл для /(и,!;) существует только при Z) > 1,5. В этом случае /< О
и второй момент
I2(Q^>2-A(D)Crl при /)>1,5и £->«. (4.29)
Аппроксимация для постоянной A (D) может быть получена,
когда D ~ 1,5. Тогда /определяется вкладом от больших значений v
в выражение (4.28) и равен
/(и,0«-4(2-/>)(/>-ly5"2^"1, 0<Д-1,5<1, С->°°-
Поэтому
„т 2Г[1/(2-Д)] 8(Д-1)Г[(3-Д)/(2-2))]
%(2-Z))(4-2^)1/(2-Z,) Л2(^)А2-^)
Рассмотренная процедура не годится для фракталов более
гладких, чем броуновские, и синусоидальная зависимость в выражении
(4.28) должна быть сохранена для того, чтобы обеспечить сходимость,
предполагая, что 12 приближается к 2 более медленно, чем £-1. Тогда
6 Фракталы
161
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Ди, 0 - 8(2 - D)(l,5 -D)(D- 1)и2 \dv sinyv3-^ x
*1
л=0
[^-^(l.S-D^V2^-1)]"
И!
1 + 0
V /J
(4.30)
При разделении диапазона интегрирования в (4.30) на две
области получаем:
/(и,0-2(2)-1) £ -Ь - =!— х
я=0
0 ' ^0
^)Г[ l-2(Z>-l)(« + l)]sin[ я(2>-1)(и + 1) ]
л=0
(л + 1)!
4(2-£)(1,5-Z>)m22>
1Л+1
л=0
^2(Z>-1)
4(2 - /))(1,5 - л)«+1и(4-2/>х«+1Ь2
«!С[1-2(/)-1)(Л + 1)]
+ ОК"1)- (4.31)
В последнем выражении предел суммирования
#(/)) = Int[(3-2£)/2(Z)- 1)],
где Int [...] - операция выделения целой части числа.
Первая группа элементов в выражении /(и, Q дает вклад,
спадающий медленнее, чем £-1. Согласно выражению для предела
суммирования, число таких элементов растет разрывно, когда
фрактальная размерность уменьшается от 1,5 до 1. Для 3/2 > D > 5/4 имеем
п = 0. При 5/4 > D > 7/6 наблюдаются только п = 0 и п = 1 вкладов,
и т.д. При значении D, заданном как Dn = (3 + 2п)/2(п +1), л-й
элемент начинает давать вклад в значение /(к, Q. Оставшиеся
элементы обозначены символом О (£-1) и не являются функциями D.
162
4.1. Модель с фрактальными высотами неровностей
Окончательно из (4.27), (4.28), (4.30) и (4.31) имеем
/2(С) = 2 + -
2 N4°)[42-D)Q95-D)Tl
*(2-2» Д
(й + 1)!
[Г[1-2(Д-1)(/|+1)]яп[я(Д-1)(/1 + 1)]Г[Д(/1 + 1)/(2-Д)]
х| 2/)(л+1)/(2-Д)£2(/ы)(/1+1)
2(Д-1)(/| + 1)Г[/| + 1+1/(2-Д)]|
2^i+i/(2-«^[1-2(2)-1)(л + 1)] J
2Г[1/(2-Д)] ,
K(2-D)(4-24-2D)W-D)C ( '
Главными элементами выражения (4.32) являются степени
£-2(д-1) ддя броуновского дифрактала (D = 1,5) элементы в
фигурных скобках не учитываются (п = 0) и оставшиеся элементы
согласуются с выражением (4.20). Результаты выражений (4.29) и (4.32)
показывают, что 12 приближается к 2 снизу для «неровных»
фракталов (2 > D > 1,5) и сверху для более гладких фракталов (1,5 > D > 1).
Поэтому 12 (0 имеет максимум при 1,5 > D > 1. Для
промежуточного случая D = 1,5 формула (4.19) показывает, что I2 (Q не имеет
максимума. Появляющийся максимум при D < 1,5 определяется
остаточными эффектами фокусировки волн, которая имеет место для
гладкого начального фронта. Для более «неровных» фракталов
эффект фокусировки не проявляется и флуктуации интенсивности
излучения сглаживаются.
Решение для маргинального дифрактала. Граничный случай (D =
1) интересен тем, что он отделяет дифракталы от физически очень
различных случайных волн. Просто полагая D = 1 в формуле (4.15),
получаем 12 = 1. Это говорит о том, что сшивка решений
происходит на бесконечно больших £. Более точной процедурой является
представление D в виде D = 1 + е при условии е -> 0, с
подстановкой в (4.15). Представив экспоненту в формуле (4.15) в виде
[2u*~2D + 2v4~2D -{v + u)A-2D -(v-w)4-2Z)] = 2w2exp(-2elnW) +
+2v2 exp(-2eln v) - (v + и)2 exp [-2eln(v + и)] - (v - u)2 exp [-2eln( v - u)]»
«-2ew2[2(v/w)2ln(v/w)-(l + v/w)2ln(l + v/W)-(v/w-l)2ln(v/w-l)]
163
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
при е^Ои полагая v/u = t, и2 =хС,, имеем
/2(0 = 1 + - f&f*cosxfexp[-2et#W]-
7Г'. * *
(4.33)
Здесь/(0 = (l + 02ln(l + 0 + (^-l)2ln|/-l|-2r2lnr^21n/ при/->оо,а
коэффициент 1 включен в решение (4.33) после тщательного
рассмотрения вклада от х = 0. При интегрировании (4.33) по
переменной х получаем
i2(Q=i + lj
2etjf(t)
я{/2 + 4е2С2/2М
Л.
(4.34)
Численные значения интеграла (4.34) представлены на рис. 4.1.
Функция имеет слабый максимум с координатами 12 = 2,211 и £ =
= 1, 58/(2) - 1). Спад от максимума до области сшивания (/= 2)
чрезвычайно медленный в функции от е£. При малых е£ слагаемым с
квадратичными членами в знаменателе (4.34) можно пренебречь,
тогда интеграл вычисляется аналитически. Отсюда можно снова
получить соотношение (4.25).
Асимптотика. Найдем асимптотические выражения для /2(Q при
условии е£ -»оо. Используем (4.34) с учетом того, что f(t) -> 2 In Г
при Моои найдем
ЗД-1 +
4(2eQ
dtlnt
к {f2 + (4e£lnf)2'
ef>l.
8
12 lg(2eC)
Рис. 4.1. Второй момент маргинального дифрактала (D * 1)
как функция расстояния от фазового экрана [188]
164
4.1. Модель с фрактальными высотами неровностей
Применяя разложение в ряд вида
2У «S (2" + 1)(2л+1>
и преобразование Меллина, получаем
г/,ч 1 1 YTn^)(-^exp[^ln(4eQ]^
2ig 2л/ J тс
IUY-i-o COS-К
где -1<у<0.
Найдя простые и кратные полюсы подынтегральной функции,
а также точки ветвления многозначной функции (- и)и при и = О,
после замыкания контура интегрирования получаем
2/7 Hv)!sh^ / к \
72(Q-1=— J ф _^_ехр --у ехрф1пу)ехр[-гу1п(4е0]+
к Jo У
+0
Когда е£ велико, то
* J
/2->2 + l/(ln2e£ + 0,69). (4.35)
Альтернативный способ нахождения /2(Q при е£ -> °о основан
на преобразовании более общего выражения (4.32). Когда D -> 1,
число элементов суммирования в (4.31) и (4.32) N(D) становится
бесконечным. Заменяя операцию суммирования по п
интегрированием по v = п + 1, запишем (4.32) в виде
тгп , 2lT, [4(l + e)(0,5-e)]vr(l-2ev)
/2(0-2->- J dv v!2(1+£)v/(1_£)c2£V х
xsin nzvT [(1 + e)v /(1 - e)],
при условии £ -»°°, e -> 0. Далее, используя формулу Стирлинга и
разложение по малым е, имеем
2 1 sin^xr(l-x)
/2-2->- J dc—* exp(xlnx)-exp[-xln(4e^/2)].
К 2е *
165
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Для больших е£ интеграл определяется его нижним пределом, т.е.
/2->2 + 1/(1п2е£ + 2,19), |£->~. (4-36)
Численная аппроксимация функции на рис. 4.1 позволяет
определить 12 как
/2->2 + 0,98/(1п2е£ + 4,13),
что хорошо согласуется с формулами (4.35) и (4.36).
Для экстремального фрактала (D= 2) предварительное изучение
показывает, что в случае точного знания границ корреляции
([А(х + X) - h(x)f) = 1?в(Х - 5),
где 0 обозначает единичную ступенчатую функцию, и при 5-» О
фрактал в пределе досягаем. Тогда второй момент скачкообразно
переходит от 12 = 1 к 12 = 2, в противоположность маргинальному диф-
ракталу, когда сшивка решений происходит бесконечно медленно.
4.2. Радиолокационные рассеивающие характеристики
в модели с фрактальными высотами неровностей
Характеристики морской поверхности. Для описания процесса
радиолокационного рассеяния радиоволн фрактальной морской
поверхностью результаты [188] были использованы в [178]. Для
фрактальной поверхности с топотезой L структурная функция (4.6),
обозначаемая как А (г), с учетом формулы (3.28), когда D- (7 - ос)/2, имеет
вид
A(r) = ([h(x + г) - h(x)f )-ТзГ* 1}^&W (4.37)
при фрактальной размерности 2 < D< 3 и изотропной поверхности.
Волновой пространственный спектр (3.18) волнения моря
G = S0K~P при Kq < К. Для гравитационных волн р < 4. Рассмотрим
связь между спектральной константой S0 и топотезой L.
Структурная функция (4.37) может быть определена следующим образом:
оо
Д(г) = 2 J dKG(K)(\-cosКг). (4.38)
166
4.2. Радиолокационные рассеивающие характеристики
Подставим выражение для пространственного спектра в (4.38),
проинтегрируем по частям и получим
4?
Д(г) = ^Г(3-р)яп
|(3-Р)
В
(I р-1
-м
2' 2
^ у
С учетом (4.37) топотеза морской поверхности
(4.39)
L =
4S,
р-2
^-r(3-p)sin
f(3-p)
„1.мГ*
-)]
где В (...) - бета-функция, р = 8 - 2D. В равновесном диапазоне р =
= 3,5; S0 - Ю-3 м1/2 и L = 1,3 • 1(И м.
Для гладкой поверхности с D = 2 имеем А(г)—^-»Ро а*2, где
Pg// J Х**КМ^(ф-ф)-%Ьф (4.40)
А'п -я
4-p
4-p
— среднеквадратичное значение наклона морской поверхности с
усеченным спектром в диапазоне волновых чисел К> Kd^> K0.
Характеристики рассеяния. При радиолокационном
зондировании поверхности океана в надир (без учета затенений и
многократного рассеяния) на основе приближения Кирхгофа удельную
эффективную площадь рассеяния можно представить в виде
a+=^j^exp[-2it2A(r)] = 4A:2jrexp[-2A:2A(r)]^, (4.41)
где к = 2п/Х - волновое число, соответствующее длине волны А,
радиолокатора.
Рисунок 4.2 иллюстрирует влияние малых волновых
пространственных чисел и изменения вида д(г) на эффективную площадь
рассеяния. На рис. 4.2, а приведены две структурные функции: для
фрактальной поверхности с2)=2,25и*У0 = 5- 10~3 м1/2 (кривая 1) и
для квадратичной поверхности (кривая 2). Соответствующие им
графики, построенные по значениям интегралов (4.41),
изображены на рис. 4.2, б. Площади под кривыми на рис. 4.2, Нравны
эффективным площадям рассеяния а для этих структурных функций. Вид-
167
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
дг. см2
ге-*«\ш
1,5
1
0,5
• Л\
- / v\
-/ \Vi
1 * X
1 1 1 V. ii
0 1 2 3 4 5 г, см 0 4 8 12 г, см
а) б)
Рис. 4.2. Структурные функции (а) и соответствующие им значения
интегралов (б) [178]
но, что для фрактальных структур, распространяющихся до
масштабов около 0,1 м, и топотез, малых относительно длины волны
зондирования (к = 6 см), оба интеграла сравнимы на малых масштабах.
Увеличение эффективной площади рассеяния от фрактальной
структуры начинает преобладать при средних и больших значениях г. На
практике при узких диаграммах направленности и коротком
импульсе радиолокатора этим увеличением можно пренебречь.
После подстановки в (4.41) выражения для А(г) (4.37) получаем
итоговое выражение для удельной эффективной площади рассеяния
а* =
1
2D-4
3-D
ШкЬ) з-Д Г
1
3-D
(4.42)
При £>-> 2 значение Z,2Z)_4 заменяется на (4.40), ио*-) с*0 = Pq2
соответствует модели зеркальных точек отражения [189].
Критерий отсечки. Рассмотрим вопрос о критерии при выборе
отсечки пространственного волнового числа при аппроксимации
фрактальной поверхности гладкой. Для простейшего случая, когда
используется отсечка, пропорциональная волновому числу волны
радиолокатора (Kd~ к), из (4.40) и (4.42)
c*0~V*"(4"P)>
2D-4
8-2р
(4.43)
[c^(kL)"^~=(kL) е-2 ~4у0-2/(р-2)л-(8-2Р)/<Р-2)э
168
4.2. Радиолокационные рассеивающие характеристики
за исключением (3 = 4 (D = 2). Это происходит из-за того, что
рассеивающая фрактальная поверхность скорее самоаффинная, чем
самоподобная, из-за различных факторов формирования в
горизонтальной и вертикальной плоскостях.
Для уточнения границы отсечки исследуем усредненное
значение k{h{rx)-h{r2)). Полагаем k' = ylk и с учетом скейлинга
Ah(yVHr) = yAh(r) (4.44)
при условии Н=(Ь — 2)/2 = 3 — 2). Это означает, что следует
восстанавливать г с помощью выражения у1/2г. Если отсечка для £есть
Kd, то отсечкой для к* будет K'd = y~x/HKd = у~21^~2)Кг
Для нахождения зависимости Kd от SQ зафиксируем к. Тогда,
восстанавливая 50 и А, имеем: Sq = ylS0 и h'(r{) = y~1/2A(Ji). Для
сохранения kAh'(r') = kAh(r) необходимо использовать
масштабирование г' = у1/2Нг. Следовательно, соответствующая отсечка
модифицируется до значения K'd = yr~l/(^~2^Kd, и объединенная зависимость Kd
от S0 и к есть
^ = с(Р)^/(р-2^2^-2) (4.45)
с безразмерным коэффициентом с(Р).
Аналогично (4.43) для гладкой поверхности находим
<**п
С-2/(М)£-(8-2Р)/(Р-2), (4.46)
что совпадает с выражением для о* из (4.43). Коэффициент с(р)
определяется путем сравнения эффективных площадей рассеяния о*0
из модели зеркальных точек с*0 = р^2, где ро определена равенством
(4.40), и о*, рассчитанной по формуле (4.42):
1 2Д-4 / 1 л __L 8-2P
«• = зГд(^) 3_jD г11Гог9(р)5оР"2/: Р"2' (4-48)
169
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
где
I -2/(р-2)
2 |2-(8-Р)/2
[|(3-Р)Ш, LlVo-P)! Г[2/ф-2].
Значение q (Р) = 3,5 • 10~2 для Р = 3,5. Пусть, например, длина
волны радиолокатора к = 3 см. Тогда о*0 = о* при 50 = 10~3 м1/2 (это
соответствует скорости ветра около 9 м/с на высоте 10 м над
уровнем моря) и значении с (3,5) = 4,99. В этом случает отсечка
наблюдается около 0,11м.
В работе [190] при изучении вопроса спектрального расщепления
между крупномасштабными и мелкомасштабными неровностями
использовался критерий 4к2 (Л|) = р0 = const, где (Л|) = J G{K)dK -
K>Kd
среднеквадратичное значение профиля поверхности с масштабами,
меньшими 2n/Kd, что соответствует пренебрежению малыми
неровностями.
о ОС
Для степенного спектра вида —~2" = (^я)= о о ^<t~^~ имеем
^=[8я/(р0(р-1))]^(Р~2)^(р"2)А:2/(р"2), что соответствует равенству
(4.45).
Оценки скорости ветра. В качестве приложения рассмотренных
теоретических вопросов уточним связь между характеристиками
рассеяния морской поверхности и скоростью ветра и над ней. Общеис-
пользуемая формула имеет вид
с, = №*,
где U и ц - константы; и - скорость ветра на определенной высоте.
Для спектральной постоянной S0 в [191] получено следующее
соотношение:
S0~uJgV2. (4.49)
Здесь к* - скорость трения, почти пропорциональная скорости
ветра и. Предполагаем с, ~ S§ и из (4.43) с учетом того, что
170
4,2. Радиолокационные рассеивающие характеристики
2> = 2>Ч1 = (7-а)/2 = (8-р)/2, а = р-1,
(4.50)
получаем ст+~50 '* =S0 ^ К
Равенство (4.49), которое характерно для р = 3,5, может быть
обобщено с помощью теории размерностей:
*о=<&Ф)
(ul **
g
(4.51)
Безразмерная функция qx (р) при р = 3,5 соответствует значению
1/(4я) в коэффициенте, обозначенном через а в [191]. Для р = 3,5
выражение (4.51) подобно (4.49). Объединим формулы (4.48) и (4.51)
и получим
ы
-V
а* = <72(Р)
где ?2(Р) = ?(Р)?1(Р)^№"2). В частности,
Р-2
(4.52)
а*~
Из выражения (4.52) скорость трения w* можно определить по
измеренной а*. При этом требуется знание Р; допустим, р = 3,5, тогда
^ = 0,01 и q2= 16 [191]. Применяя двухчастотный радиолокатор,
измеряющий значение а* в двух точках диапазона, можно оценить
величину р так же, как и*.
Таким образом, проведенный анализ показал, что некоторые
черты фрактальной модели могут быть воспроизведены
искусственным введением в модель зеркальных точек отсечки высоких
волновых чисел. Если фрактальная размерность поверхности
предположительно известна, то одночастотные измерения а* могут дать оценку
спектральной константы SQ и, следовательно, скорости ветра. В
противном случае нужно использовать двухчастотный режим работы
радиолокатора. В частности, эксперименты по дистанционному зон-
171
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
дированию морской поверхности показали [192], что с+ « и °'468. Из
(4.52) следует, что этот случай соответствует р = 3,79:
а+~и;°'4%-°'234.
Полученный результат хорошо согласуется с результатами,
известными из [178], когда р = 3,91 ± 0,09 и Р = 3,86. Значение^ = 3,79
соответствует, согласно (4.50), фрактальной размерности D = 2,1 в
диапазоне дециметровых гравитационных волн.
4.3. Модель с фрактальными наклонами неровностей
Постановка задачи. Наглядной иерархической моделью по
отношению к (4.6) является модель с фрактальными наклонами
неровностей. В данной модели рассматривается субфрактальная
поверхность рассеяния, структурная функция наклона которой
S(x) = (\m(0)-m(x)\\ фрактальна и определяется, согласно [193-
194], выражением
S(x) = \x\2{2-D)/L2V-D\ 1 < 2) < 2. (4.53)
Поверхность, обладающая свойством (4.53), однократно
дифференцируема, в отличие от (4.6), и имеет наклон, изменяющийся от
точки к точке непрерывно: т (х) = dh (x)/dx. Рассеиватели такого
рода были исследованы в связи с распространением радиоволн в
ионосфере [195]. В отличие от фрактальной модели высот
неровностей, фрактальная модель наклона неровностей приводит к
геометрической оптике, или к эффектам, описываемым с помощью
понятия «луча». Как и для моделей гладкой поверхности, угловое
распределение интенсивности определяется распределением наклона
поверхности, а статистика высокого порядка позволяет обнаружить
интересные особенности, характерные для иерархии масштабов,
присущей природе поверхности. Рассмотрение фрактальной
модели наклона проведем, опираясь на результаты работы [194].
Корреляторы. Для геометрии рассеяния, приведенной на рис. 4.3,
флуктуации интенсивности или плотности излучения могут быть
исследованы с применением функционала
(*j-y)"
R(y,z) = -l8
7 J
т(х{)--
dxv
111
4.3. Модель с фрактальными наклонами неровностей
Рис. 4.3. Геометрия рассеяния
записанного для одномерного решения задачи в точке (у, z) с
текущей координатой хх и локальным случайным наклоном т (х{).
Для гауссовых процессов нормированные корреляторы и-го
порядка в плоскости z имеют вид [193, 194, 196-199]:
(R(yi)R(y2)...R(yN)) _ 1
(R)N (2nz)
оо оо
хехр
N
ехр
-^ $ ... J dxv..dxNdXv..dXN x
—оо —оо
I N N
y=U=l
.* ОО оо оо
О ^ %_!
ЛГ
хехр ^2[*1(л) + *,--*}л)] х
ХеХР|2?Л'^
*=у+1 Ы2
(4.54)
173
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
где S(X) определена формулой (4.53); значение <R> = 1; знак
суммы перед интегралами получен за счет N\ перестановок {>>,},
обозначенных через {gjn)}. Если {yt} идентичны, то получаем N1 равных
элементов.
Подстановка формулы (4.53) в выражение (4.54) приводит для
произвольной фрактальной размерности к соотношениям:
(R2)/(R)2=(D-l)-\
/*3N//*N3 3! 7{4^4^ + 1-(^1)4-2^]2}1/2^
* 'А ; MD-l){ t*-2D+t2+t[t*-2D+l-(t + l)*-2D] '
В частном случае броуновского фрактала получен точный
результат (R?)/(R)3 = 3! для D = 1,5. Более того, при этом правая часть
равенства (4.54) с помощью преобразований типа
Xj->Xj+xk (у>£ + 1)
хк~>хк- X ху для А: = 2, 3,...,#-l
становится точно разрешимой:
для D= 1,5 и условий факторизации. Таким образом, для гауссовой
поверхности с броуновским фрактальным наклоном выражение
(4.54) ведет себя подобно интенсивности комплексного гауссово-
марковского процесса.
Низкостепенные корреляторы легко получаются из последнего
равенства для D = 1,5:
*—1 2 '=1+ехр'
(R)2
-^г\У1-У2\\ (4.55).
174
4.3. Модель с фрактальными наклонами неровностей
(R(y{)R(y2)R(y3)) (1L ,
+ехр
Также очевидно, что соотношение (RN(y))/(R)N =N\ дает
экспоненциальное распределение флуктуации лучевой плотности
p(R) = exp(-R),D = 1,5.
Флуктуации интенсивности поля. Начальной точкой для
дальнейших статистических расчетов является известная аппроксимация
интенсивности поля в точке (у, z) дифракционным интегралом
Гюйгенса—Френеля в виде
—оо —оо ^ '
xexpj/^АЦ)-/^)]}.
(4.56)
Из формулы (4.56) нетрудно показать, что для стационарного
процесса со структурной функцией D{y) = \[А(0) - h(y)f) и А (у),
обладающей свойствами (т(0)т(у)) = D\y) / 2, S(y) = D"(0) - D\y),
первые два момента интенсивности равны соответственно: (/) = 1 и
(Т2) 41с°°г 7
к2
~F{x,X)
COS-
кХх
(4.57)
где F(x, X) = 2D(X) + 2D(x) - D(X + x) - D(X - x), D'(y) = d2D/d2y.
Хорошо известно, что интеграл (4.57) для гладко
изменяющейся поверхности логарифмически расходится в коротковолновом
приближении [200]. Хотя D (х) является, строго говоря,
неопределенной для модели рассеяния с фрактальным наклоном (4.53), в [195]
показано, что конечные результаты могут быть получены для
второго момента в предположении
i)(x) = ^c2-UI2/(3-i))/[2(3-2))(5-22))Z2(2-^],
где А - постоянная величина.
175
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Для D =1,5 (броуновский процесс) равенство (4.57)
преобразуется к следующему виду:
(72)= 47ехр(-2хУЗ/»
(7)2- \ Ux2
х2 sin(x2 / р)
cos -—,-^-
dx,
(4.58)
где параметр р — kz3/4L2.
Численная оценка индекса мерцаний (рис. 4.4) показывает
монотонное увеличение (7)2 с насыщением, равным 4, если параметр
р - большой. Для данного случая коэффициент а, численное
значение которого приведено далее (4.68), равен значению а = <». Кривые
на рис. 4.4 рассчитаны по выражениям (4.58) и (4.67). Этот режим
соответствует пределу приближения геометрической оптики. Более
общий результат может быть получен на основании (4.57) при
условии малости значения X, когда
F(x,X) ~ X2 [DW - D"(x)} = X2S(x). (4.59)
Преобразование типа Х-^Х/к позволяет определить
коротковолновый предел в виде
lim<4 4
к^~ (I)2
= -I J dX j dxexp[-X2S(x)] cos—.
я"
о о
3
2
1
<I2>
i
<I>2
-
*—^. J. 1
I
4^5
J
a=oo
>ч%ччч-20
10 1 10 10 P
Рис. 4.4. Зависимость индекса мерцаний от нормализованного расстояния [194]
176
4.3. Модель с фрактальными наклонами неровностей
Сравнение с (4.54) показало, что предел
lim
</2> _ 2(R2
k->~{I)2 (R)2
для фрактальной модели наклона (4.53) преобразуется к виду
2
lim<4 —
, 1<Z)<2,
(4.60)
который, как видим, находится в соответствии с асимптотическим
поведением (см. рис. 4.4) для броуновского случая D = 1,5.
В приближении геометрической оптики определим N-й момент
распределения флуктуации интенсивности. Из (4.56) следует, что
aN)
а)
хехр
2я
Д
F = hd j\^Nidty..dtNtxp
ilr N
lF"''!)
{t|| i^i -h>*^i -и-щ -'»)-«'у-Ц-
В коротковолновом приближении основной вклад в интегралы
дают области, где вторая экспонента имеет стационарный характер.
Существуют М таких областей, которые имеют место при близости
s- к L Например, при N = 2 имеются только две такие области, а
именно: sx ~ tv s2 ~ t2 и s{ ~ tv s2 ~ tv По условиям симметрии
вклады от М областей равны, и достаточно рассмотреть случай s. ~ t.
Считая Sj - t = X. и (Sj + tj )/2 = x. и учитывая факт малости X. в
области (-Ej, Ej), имеем
Ит^=Вт(-^-1 NlldX. \ dX,...x
£i
N N
xj ^...^expf^XVyVp T^
"£2
f
( ь,-К
-Я
Xt+Xu
Xj-xk+-
D
-D
Xj-xk +
Xj Xk ■
Xj-Xb\
V**4
ill
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
В последней экспоненте элементы могут быть представлены для
малых X в форме
[...]- -XjXkD\Xj -xk) = 2XjXk(m{Xj)m{xk)),
которая при замене Ху. -> X.jk для больших к приводит к результату
aN)
с 1 \
lim ,, -. „
k*(I)N \2%z
1
N оо оо ( ' N
I N\ j ...jckv.xkNdXv..dXNexp\-^Xj(Xj-y^
'7=1
xexp
I N N
'y+lA:=l
Сравнение с равенством (4.54) позволяет записать:
что доказывает конечность флуктуации плотности излучения. Для
броуновского фрактала (D = 1,5) значения предела \im(IN)/(I)N =(N\)2,
что соответствует ^-распределению p(I) = 2KQ(2<JI).
Функция когерентности второго порядка в приближении
геометрической оптики с учетом (4.56) имеет вид
шш-^Н**
(D
XCOS-
кХх
к2
о
кХА кхА
cos +cos
Z Z
(4.61)
где А = \у{- у2\. Используя снова преобразование вида Х-*Х/к и
формулу (4.59), получаем
tafflffi».ifAJta,
к->- (I)2 nzi {
О О
X2S(x)
Хх
xcos—
Z
ХА кхА
COS + COS
z z
178
4.3. Модель с фрактальными наклонами неровностей
Для фрактальной модели (4.53) в броуновском случае при D = 1,5
,. </(0)/(Д)> - ( 21 А\
hmN v ' \ 7/ = 1+ехр
(I)2
*->•
V Z J
(2h+[l+(2kzA/L)2]
l + (2kZA/L)2
1/2]
V/2
(4.62)
что приводит при условии А = 0 к выражению (4.60), а при к -> оо и
фиксированном Д - к соотношению (4.55). График
асимптотической функции (4.62) представлен на рис. 4.5 в зависимости от
аргумента A(k2/2L)V3 при а = <*> и двух значениях параметра/? = kz3/4L2.
0 2 4 6 8 10 12 A(k2/2L)m
Рис. 4.5. Асимптотика функции (Д0)/(Д))/(/)2 [194]
Эффекты внешнего масштаба. Учет внешнего масштаба % в
модели достаточно легко произвести, полагая в (4.53)
ЗД =
\(УЬ)2^,\х\>^
(4.63)
при 1<Д<2и среднеквадратичном наклоне поверхности
г4={т2) = \
, t ^(2-D)
KLJ
(4.64)
179
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Второй момент плотности излучения с учетом (4.54) и (4.63)
выражается следующим образом:
(R2)
= erfc
*
^
2mnz
1
D-\
-erf
S
2m0z
(4.65)
(R)2
где интегралы вероятностей
erf(x) = -==\exp(-t2)dt, erfc(x)=-==\exp(-t2)dt, erf(x) + erfc(x) = l.
VitJ л/я;
Из (4.64) и (4.65) следует, что внешнемасштабные эффекты
незначительны при условии £/(2ffjQ.z)»1.
Для броуновской модели (D = 1,5) функция корреляции
лучевой плотности излучения может быть получена с учетом (4.54) и
(4.63) в виде
<Л(0)ЖЛ)> 1 1 ( 2LA
\ ww/ _i еХр'
(К)2 2
1 + erf
2/и0г
1
--ехр
Г21А\
lerfc
Г
1±А
2m0z
(4.66)
Здесь /я^ = \/{2L) из (4.64) при условии D = 1,5. Нетрудно
убедиться, что (4.66) переходит в (4.55) при £/(2/^)»1. Также видно, что
флуктуации уменьшаются из-за того, что некоррелированные
области поверхности начинают вносить вклад в рассеянное поле.
Второй момент распределения флуктуации интенсивности (4.57)
вычисляется для модели (4.63) более трудоемко. Чтобы учесть
внешний масштаб, структурную функцию Щх) нужно модифицировать:
т = К2*2 -Н2(3~7[2<3-Я)(5-2Я)№*>], х < §,
[В,
х>£»
где В - постоянная величина.
Формула (4.57) в этом случае может быть оценена численно, но
при условии сильного рассеяния (к2т^2»1 или к2£? /2L »1)
достаточно рассмотреть приведенные далее аналитические аппрокси-
180
4.3. Модель с фрактальными наклонами неровностей
мации. Вблизи рассеивателей при p<2L/(k2^3) или z<2L/(kQ и с
учетом D = 1,5 второй момент флуктуации интенсивности
записывается в виде
</2>_</2>
-2erfc
Ь-
U^/3J
(4.67)
(D2 </>2|
где уменьшаемое (I2 )/(I)2 L определено как функция параметра р
1£=оо
соотношением (4.58), а коэффициент
а/6
(4.68)
a = (k2tf/2L)
не зависит от координаты z- Результаты расчета по соотношению
(4.67) как функции р для различных а были приведены на рис. 4.4.
Для конечных значений а наблюдаемая область сшивания решений
лежит при привычной гауссовой статистике с уровнем (12)/(1)2 = 2.
При ос->°о следует режим насыщения с (12)/(1)2 =4 и в этой области
(Я)
</>2
-2
1 + erf
а
2Р1/3
,D = l,5.
(4.69)
Выражение (4.67) при a/(2pl/3) = E)/(2zm0) может быть
записано как
(I2) 2<Д2>
(4.70)
</>2 (Я)2 '
где второй момент плотности излучения дается уравнением (4.65) с
D = 1,5. Фактически для любого значения D в допустимой области
возможен режим, определяемый большим внешним масштабом, где
(4.70) будет оставаться в силе. Например, при использовании (4.59) и
модели (4.63) в выражении (4.61) при у=ос/(2У/3) = ^/(2^и0) имеем
1г_ (7(0)/(А)) _ (ЖО)ЖА)) , оРр f2erf№ + 2ikAz/L)^]
&-»<
+ exp(-)t2/n^A2)erf с [t(1 + ikAz / L)]\,
(4.71)
181
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
где (R(0)R(A)) дано равенством (4.66). Соотношение (4.71) при
^/(2m0z)»1 переходит в (4.62).
Модель случайных блужданий и масштабные эффекты.
Приведенные результаты можно более просто интерпретировать на языке
модели процесса случайного блуждания с шаговыми флуктуациями
[194,201,202]. В этой модели амплитуда рассеянной волны
представляется в виде двухразмерного случайного блуждания за N шагов со
статистически независимой длиной шага ап и фазой Фл,
распределенной равномерно в пределах 2п\
£=1ялехр(/Фл), 1 = \Е\2
Известно, что если N подчиняется отрицательному
биномиальному распределению
№)=
(N+v-l\ ((N)/v)N
N Ul + (N)/v)N+v'
(4.72)
_Q)/4l)(b4l
v
то Hm(^(/)) =
<ло-»~ r(v)
Ку_уЫ1), где 2/Ъ = ({1)/уУ'2;
KvA — функция Макдональда (v - 1)-го порядка или
модифицированная функция Бесселя третьего рода.
При больших N выражение (4.72) переходит в класс
гамма-переменных:
vN
{(Ю
y-l
exp
vN
'(Ю
WHv),
(4.73)
и если v = (N) = 1, то соотношения (4.72) и (4.73) совпадают с
распределением Р(1) = 2К0(2у/Т) . Следовательно, для модели (4.63) с
фрактальной размерностью 2)=1,5и/>»1 флуктуации плотности
излучения играют такую же роль, как и флуктуации в задаче
случайного блуждания.
Кроме того, выражение для функционала плотности излучения
(4.54) относится к классу комплексных гауссово-марковских
процессов, поэтому функция когерентности
182
4.3. Модель с фрактальными наклонами неровностей
</(0)/(Д)>
= 1 + ехр(-ГД)+2|я<2>(Д)|2
</>2
Здесь Г-1 - масштаб флуктуации; последнее слагаемое отражает
присутствие интерференционных эффектов, как в (4.62). Заметим, однако,
что в модели, приводящей к данному выражению для функции
когерентности, упомянутый эффект прямо соотнесен с коэффициентом
корреляции gM(A) = (E(0)E*(A))/(I), который для поверхностного
рассеяния задается в виде и не слишком
строго определен для модели со структурной функцией вида
D(x) = Ах2 -\x\2{3-D)/[2(3 - D)(5 -2£)Z2(2^)].
Следует отметить еще раз необычную зависимость
характеристик лучевой плотности излучения от расстояния, подразумеваемую
в (4.55). Нетрудно установить более общие масштабные
соотношения, следующие из выражений (4.53) и (4.54):
(R(yi)R(y2)„.R(yN)) = p^jp-DmD-i^mi-D)^ (4.74)
Фрактальная размерность 1 < D < 2; это означает, что все
эффекты лучевой модели возрастают как zl^D~!) с увеличением
расстояния от рассеивателей и находятся в резком контрасте с эффектами,
порожденными гладко изменяющейся одномасштабной
поверхностью и линейно зависящими от расстояния. Следовательно,
результат (4.74) может служить экспериментальным тестом для проверки
фрактальной модели наклона (4.53).
В геометро-оптическом или сильно рассеивающем приближении
(р »1) масштабные соотношения могут быть получены из (4.61) в
виде
Шп (ЛО)ДА)) = р (AL(2-D)/(D-1)ZW-D)) + Q(Akz(2-D)/(D-1)L(2-D)/(1-D)).
Второе слагаемое в этом равенстве отражает наличие спекл-кар-
тины с пятнами размером k-l(L/zY2~D)/(D~l), которые
уменьшаются с увеличением расстояния от рассеивающей поверхности. Это
снова находится в противоречии с моделью гладко изменяющейся
поверхности, для которой размер спекл-картины не зависит от z.
183
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Если модель содержит внешний масштаб, то при ослаблении
флуктуации плотности излучения статистики интенсивности
сходятся к гауссовым. Из данных рис. 4.4 следует, что при достаточно
больших значениях а характеристики интенсивности достигают (р »1)
асимптотических значений, имеющих место при отсутствии
внешнего масштаба, прежде чем процесс начал бы сходиться. При этом
может быть дана более простая интерпретация факта изменения
статистик интенсивности в режиме за пиком, изображенном на рис. 4.4.
Это основано на том, что
(R)2
1 (R2)
М M(R)2
(4.75)
1$==.
где М~l = erf
( рД-i "\
W— эффективный размер области рассея-
ния и W1 ~ 1Р^т/(о-\)г\/{\-т.
Соотношение (4.75) показывает, что ослабление флуктуации
лучевой плотности может быть представлено с помощью добавления
независимых лучевых плотностей M(z), флуктуирующих согласно
распределению при отсутствии в модели внешнего масштаба.
Равенство (4.66) может быть записано более ясно в терминах
эффективного размера рассеивающей области W= z 2/L и
параметра y=(Ji/2W)l/2 =a/(2y/3):
ЩО)Д(А)), 1 ( 2Д
- ±«*[%У1
1+erf
у+
/
Y-
2yW
2yW
(4.76)
Ha рис. 4.6 представлены функции, построенные по формулам
(4.66) и (4.76) в зависимости от аргумента 2L/z2 при различных
значениях у. Полученные данные показывают, что присутствие в модели
внешнего масштаба искажает простое экспоненциальное поведение
статистик (4.55).
Принципиально новым в функциональном описании функции
когерентности интенсивности (4.71) является присутствие
внешнего масштаба в последнем слагаемом. В приближении t,/W <к 1 этот
184
4.3. Модель с фрактальными наклонами неровностей
\<R(0)R(A)>
Рис. 4.6. Корреляционные функции лучевой плотности излучения
при отсутствии (у = °о) и наличии внешнего масштаба [194]
элемент продолжает существовать, в то время как другие
составляющие становятся малыми:
,т(Д0ЩА)) = 1 + ехр(_лЧ2д2)
£->
(4.77)
При достаточно больших к функция gM(A) = (E(Q)E*(A)) /(I) в
случае поверхностного рассеяния, когда второй элемент в модели
структурной функции D (х) с учетом внешнего масштаба мал,
записывается в виде
^)(А) = exp[-k2D(A)/2] = exp(-fc2/w02A2 /2),
а соотношение (4.77) будет выражено в форме
Функция (4.71), выраженная в элементах а, р и A(k2/2L)1/3, была
изображена на рис. 4.5. Эффект, вызванный присутствием конечного
внешнего масштаба в модели рассеяния, иллюстрируется сравнением
характеристик для случаев ос = °° и а = 2 при р = 103.
Рассеяние на двух экранах. Представляет интерес задача о
рассеянии на нескольких фазовых экранах. В этом случае [187] флук-
185
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
туации плотности излучения порождаются последовательно двумя
субфрактальными экранами и в приближении малого угла
рассеяния характеризуются вторым моментом
<Я2)_2г_[_
dx\d[
(v-2)/2
(R)2 к 4-vj[e[i+(i + r)x]2+|xr2(Ux)2'
Здесь v = 2(2 - D)\ r = l{/l2; l{ - расстояние между экранами; /2 -
расстояние между вторым экраном и приемником излучения.
Зависимость (R2) при различных значениях v приведена на рис.
4.7. При больших г (приемник находится у второго экрана) и при
малых г (экраны разделены небольшим промежутком) зависимость
(R2 )/(R )2 сводится к аналогичной для одного экрана, но при К г < 10
обнаруживаются значительно более сильные флуктуации.
(R2)
ч0,5
0
50
100
Рис. 4.7. Зависимость второго момента флуктуации плотности излучения от
относительного расстояния между экранами [187]
4.4. Индекс мерцаний при рассеянии волн экраном
с фрактальными наклонами
Индекс мерцаний характеризует относительные флуктуации
интенсивности. Анализ флуктуации в общем случае наталкивается на
значительные математические трудности. Рассмотрим данные
эффекты флуктуации более подробно.
Приближение Гюйгенса-Френеля. В зоне Фраунгофера
характеристики волны, рассеянной поверхностью с фрактальным наклоном,
при учете внешнего масштаба (4.63) определены в [203, 204]. Струк-
186
4.4. Индекс мерцаний при рассеянии волн экраном с фрактальными наклонами
турная функция поверхности D{r) = п й(0) - A(r)] \ записывается в
виде, обобщающем полученные ранее результаты:
плл = \mV - кГ2 /(v + 2)(v + \)D, \r\ < \,
[в, И>§.
где В - константа; £ - характерный масштаб в (4.63); v = 2(2 — D);
О < v < 2; т0 - среднеквадратичный наклон (4.64) поверхности.
Внутримасштабными эффектами можно пренебречь вблизи
зеркального направления (угол 0 мал) при условиях, что изменения
высоты ниже внутреннего масштаба / много меньше длины волны
X = 2п/к, т.е. щ «: X, и выполнения приближения Кирхгофа, если
Х2Г~2«1У.
Будем рассматривать негауссово рассеяние радиоволн
случайным фазовым экраном [205]. Формальное решение задачи в
приближении Гюйгенса-Френеля имеет вид
оо
xj d2r'exp[iKkr'2 -ikr'r/Я + /Ф(г',0-г'2 /W2],
(4.78)
где k = -~(R^1 +R iy, cos0 = z/R\ E(R9 t) — комплексная амплитуда
рассеянного поля в точке наблюдения R = (г, z) = (х, у, z) во время t\
Ф(г, t) - фазовые флуктуации в плоскости z = 0; W— ширина и R^ -
радиус кривизны профиля падающего гауссова пучка. Считаем, что
фазовые флуктуации Ф(г, t) распределены по нормальному закону
с автокорреляционной функцией
р(8) = <Ф(г)Ф(г + 6)>/<Ф2>.
Контраст С2 в терминах интенсивности рассеянного поля
I(R) H E(R, t) |2 определяется в виде С2 = (I2(R))/(I(R))2 -1 и может
быть выражен с помощью (4.78) для крайних случаев. Для френеле-,
ва предела kuW1»1
С2 + 1 = --Ц-|^2г^2/-'ехрГ-Ф2Дг, rO-i-r-Д (4.
79)
187
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
где F(r, r') = 2-2p(r')-2p(r) + p(r-r') + p(r + r'); (Ф2) = Ф^;
считается, что i^"1 = 0 без потери общности.
Для фраунгоферова предела h^2«l
оо
l6nW2 J d1r'd1r'd2r"vv[-<blG(r', r", /•") +
<? + ! = f= >
JrfVrfVexp{-<D2[l-p(/-')] +
-оо
+2/Ar'sin0-(r'2+r'2+r'2)/^2l (4'80)
""* ^2 >
+[flfc-r'sine]-(r^ +г'2)/2Ж2}]
где G(r', г', г*) = 2 - р(г'+О - р(г'- О - р('*+ О - р('' - О +
+ р(,'+0 + р(г'-0.
Будем считать функцию корреляции р(г) подчиняющейся
разложению Тейлора, тогда при rV = г —+г —- имеем:
х dx у dy
pW = l + ^(rV)2p(0) + i(r-V)4p(0) + O(r«); (4.81)
предполагаем, что рассеивающий экран изотропный, т.е. р(г) = р(г).
Дифракция Френеля. Для френелева приближения (4.79) с
учетом (4.81) получено выражение вида
С2 +1 = -i^. ~\rdr]r'dr' |^ехр{-Ф2г'2 [2)2р(г) -
00 ° (4.82)
- Z>2p(0) + г2 cos2 \|/D4p(r) ]]cos(/:/r^"1 cos \|/),
где D2 = , и соответственно
«•V)ft-r) = ?, (Z>V)F(r) = &.r)D2[F(r)l
Дальнейшее упрощение формулы (4.82) возможно при условии
г < а, где а = [-2D2p(0) / D4p(0)] . Используя разложение в ряд Тей-
4.4. Индекс мерцаний при рассеянии волн экраном с фрактальными наклонами
лора, т. е. D2p(r) - Z>2p(0) + (r2 / 2)Z>4p(0), и считая r2D4p(r) * r2D4p(0),
получаем аппроксимационную зависимость
тс °° ,
' X
Vz2{ r{ [а'
о о
А =-ТГТW^ln 4 exp[-O2^V(0)(H2cos2¥)/2]x
xcos(Ax1/2z_1 cosy) (4.83)
при условии t»1, где t = [Ф^2р(0)]2/[£4р(0)]. Формула (4.83)
определяет вклад негауссова рассеяния в значение контраста С. Контраст
уменьшается до 0 при больших значениях z, когда многие
корреляционные длины экрана дают вклад в характеристики
интенсивности рассеяния.
При г > а считаем, что D2p(r) = D4p(r) = 0, и, расширяя верхний
предел интегрирования по переменной г' в (4.82) до «>, получаем
h =Ц^^1^Мк2гУ[^2<^Ч (4-84)
Этот интеграл отражает присутствие спеклов из-за
интерференции пучков радиоволн. Выполнив интегрирование по частям,
имеем контраст
С2 +1 = 2ехр(-3у2) + yjby1 ехр(-у2) [1п(2тГ/ 3) + S(y)], (4.85)
где у2 = k2/[6z420D*p(0)]; S(y) = J^
о*
ехр(у2г)
-1
; у = ехр(с); с -
постоянная Эйлера.
На рис. 4.8 сплошными линиями показаны результаты расчетов по
формуле (4.82) для гауссовой одношкальной модели р(г) = ехр(-г2 / С2)
и нормализованного у. Значения контраста, вычисленные по
аналитической формуле (4.85), изображены на рис. 4.8 штриховыми
линиями. При Oq > Ю2 аналитические и численные результаты
соответствуют друг другу. Сопоставление результатов расчетов с
экспериментальными исследованиями рассеяния лазерного пучка на
фазовом экране, полученном турбулентным смешиванием горячего
и холодного воздуха, выявило их некоторое расхождение.
189
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
1+С2
8
6
4
2
О
-1 -0,5 0 0,5 1 1,5
-log(y)
Рис. 4.8. Контраст как функция нормализованного расстояния от экрана для
одномасштабной модели при цифровом и аналитическом расчетах [205]
Более точное описание экспериментальных данных было
получено при учете многомасштабности фазового экрана путем введения
в интеграл (4.82) корреляционной функции вида
р(г) = (1-6)ехр(-г2/С2)+*ехр(-г2/л2С2)
при а « 0,1 и Ъ « 0,01. Результат (кривая 2), который был получен при
а « 0,15 и Ъ « 0,01 с Oq = 120 (рис. 4.9, а) в области между
геометрическим фокусом и экраном, находится в лучшем соответствии с
первым набором экспериментальных значений, чем теоретическая од-
номасштабная кривая. При значениях а ~ 0,1 и Ъ = 0,01 с Ф^ = 10
(рис. 4.9, б) также видно, что соответствие теоретических кривых
второму экспериментальному набору много лучше в той же области.
Дифракция Фраунгофера. Для зоны Фраунгофера знаменатель в
правой части формулы (4.80) вьиисляется методом стационарной
фазы при условии Ф§»1 и равен
(4ii2^2//o)2exp(-A:2sin2 в//0), (4.86)
где/0=Ж-2-Ф2/)2р(0).
190
J I L
4.4. Индекс мерцаний при рассеянии волн экраном с фрактальными наклонами
3
2
1
ч\
Г 1
/ /
\& Л-1
\ff /
У *
У* *
'
\|./3
V*
^ч^
^>
-J
f
1
1+<г
10
100
Z,M
z, м
а)
б)
Рис. 4.9. Контраст как функция расстояния от фазового экрана при сравнении
одно- (1) и двухмасштабной (2) моделей с экспериментальными данными (3) [205]
Основной вклад в числитель формулы (4.80) вносит область с
малыми значениями г", поэтому его можно представить в виде ряда
G(r\ /•*, r~)**F(r\ n-[r"2D2+(r"-ryD*]p(n-
-[r4D2+(r^r02£4]p(r')
со значением ^из (4.79). После интегрирования по переменной г"
имеем
16k3W2 J rf)cJrcfrJrtfr7-1(r,x)exp[-A:2sine//(r,x)]x
0 0 0
хехр{-Ф1гЪ[о2р(г)-О2р(0) + г2со$2уО4р(г)]-(г2 + r'1)/W2} (4.87)
с функцией f(r,x) = W~2 -Ф2[о2р(0) + D2p(r) + r2 cos2yD4p(r)].
Далее полагаем, что интеграл по переменной г определен в двух
областях, разделенных границей ос/V2 , где ос определено ранее. Для
области [0, ос/л/2] с /(г, х)«/0 -Ф^/)2р(0) вклад в (4.87) равен
1б7С4Ж2 exp{[o2^4/)V(0)]~1-A:2sin2e[/0-O2/)2P(0)]-1
Ф^4р(0)
[/0-Ф2/)2Р(0)]
191
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
х^Ф2^^ (4.88)
где Ех{х) - эллиптический интеграл.
Для области [a/yfl, «>] установлено, что
/Яр(г)- Я2р(0) + г2cos2 уЯ4р(г) = -Я2р(0); /0 = /(г, х).
При условии Ф^ »1 получаем дополнительный вклад в (4.87),
равный
32тс4Ж4ехр
а2 к2 sin2 в
2^2 /о
'/о2-
(4.89)
Объединив формулы (4.88) и (4.89) и разделив на (4.86),
получим для дальней зоны
С2+1 = 2ехр(-5) + ^^^
t (5 + 2/)
хехр
'&_ k2W2Stsva2Q
t +(S + t)(S + 2t)
•IK
t
(4.90)
где S=a2 /2W2 = -D2p(0) /W2D4p(0), а значение tопределено в
формуле (4.83). Функции контраста С2+1, рассчитанные по формуле
(4.90), в зависимости от переменной S~l (освещенная область) при
различных значениях t («неровности») и 0 = 0 (вдоль оси)
приведены на рис. 4.10.
Результаты расчета. Возвращаясь к [203], отметим, что
формула (4.80) записывается в терминах структурной функции LHj)
рассеивающей поверхности
C2+l = l6nW2x
j d2r'd2r'd2r"<ixp[2ikr"smQ-k2G(r',r'',r")-(r/2 +r*2+r*2)W-2]
J d2r'd2r'exp\~D(r')+ikr'smQ-(r'2 +r'2)/2W2\
(4.91)
192
4А. Индекс мерцаний при рассеянии волн экраном с фрактальными наклонами
КС
О 0,5 1 (2у)ч/2
Рис. 4.10. Контраст в дальней зоне при угле зондирования 8 = 0 [205]
где 20{г'У,г") = D{r" +rm) + D{r" -r") + D{r* + r*) + D(r" -г*)-
-Дг'+О-Дг'-О.
Знаменатель уравнения (4.91), пропорциональный квадрату
средней интенсивности, при условии т^ » X, как и в [205], может
быть выражен в виде (4я2Ж2//0)2 exp(-fc2 sin2 в//0) при условии (ср.
с формулой (4.86)) /0 = W~2 + /и2/:2.
Аналогично формуле (4.87) числитель соотношения (4.91) равен
16я3Ж2 j ^\|/j/r/rjryr//-1(r,\|/)exp[-A:2sin2 6//(r,\|/)]x
0 0 0
хехр|уГ^[А2Дг)-А2Д0) + г^
/(г, v|/) = Ж"2 +^2[A2^0) + A2i)(r) + r2cos2\|/Дг)]; A2 =rl{d/dr).
где
7 Фракталы
193
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Разобьем полученный интеграл по переменной г на области с
г < § при /(г, у)« /0 + /я^2 и г > § с /(г, \|/)« /0 и запишем
окончательно:
т 1 о / сч 45(5 + О2 f W2#sin2e
С2+1 = 2ехр(-£) +—^ 7 expj ——__ _ >х
</
S + 2t r [ (5 + 0(^ + 20
r^{exp(-5r2)-exp[ -r\2S+trv) ] }
5+/rv
(4.92)
где S = Z?IW2; t = mfik2^2; W/2 - ширина коллимированного луча с
гауссовым профилем интенсивности; cos2\|/ = l. Полученное
уравнение (4.92) при условии v = 2 совпадает с (4.90). На рис. 4.11
показаны результаты численной оценки (4.92) для двух значений: v = 1,
</2>
</>2
ю Ь
| г
^ ^^^^
L /
р /
ГУ у
£/=105 /
г /
у /
г 1()4
1 l_i_L
1 Hill
V
'""'
т—1 1 1 inn 1
v=l 1
V Ч
**^v -1
J-L
^s. ^v J
>^. 1
ИтП
J III! III! 1
0,01
0,1
<I2>
<I>2
10
>io6 io5
0,001
Рис. 4.11. Значения нормализованных флуктуации интенсивности [203]
194
4.4. Индекс мерцаний при рассеянии волн экраном с фрактальными наклонами
D = 1,5 (рис. 4.11,а) и v = 0,5, D = 1,75 (рис. 4.11,6) как функции
S'l/2 при 0 = 0. Контраст возрастает от нуля при малых апертурах
(S »1), где определяющей является апертурная дифракция, до
максимума, зависящего от баланса между геометрическими и
дифракционными эффектами, а затем уменьшается до единицы (гауссов
случай) при S «: 1.
Однако наиболее интересной особенностью данных рис. 4.11 в
двойном логарифмическом масштабе является появление
линейного режима при больших значениях t, особенно когда v мало.
Исследование интеграла (4.92) показывает, что данный режим
наблюдается при условии 5»1 и (51+v/2/0(2"v)/v <cl. В этом случае
C2+USv/2exp(sin20/2m2). (4.93)
С другой стороны, при 5«1 и фиксированном большом t из
(4.92) получаем
C2+U2(l-5)+^exp(sin2e/2/?22)
а при дополнительном условии v -> 2 соответственно
C2+1^2(l-5) + |exp(sin20/2/n2)ln/.
Таким образом, в дальней зоне режим геометрической оптики
преобладает при условии, если освещенная область меньше
характерного внешнего масштаба, но больше размеров апертуры,
необходимой для того, чтобы дифракционная угловая ширина превышала
угловую ширину пучка лучей при заданном диапазоне наклонов
поверхности. В таком режиме падающий пучок преломляется на угол
Эр средний квадрат которого определяется значением структурной
функции наклона при аргументе, равном характерному внешнему
масштабу, т.е. \ =£1/2(£). Угловая ширина пучка 02 определяется
значением структурной функции при аргументе, равном значению
апертуры, т.е. 02 =S(W)l/2.
Максимальный контраст достигается при условии £1+v/2 ~ t, и
из соотношения (4.93) получаем С2 +1 ~ /v/<2+v>. Нетрудно показать,
что в первом приближении нормированные моменты
интенсивности имеют вид
1-Г
2+v
|ехр|^|ы
195
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
\~1Я
о J
и удовлетворяют соотношению (4.93) при п = 2. Степенная
зависимость от W отличается от зависимости, предсказываемой для
гладко изменяющихся поверхностей, которая порождает отклонение от
гауссовой статистики, обратно пропорциональное площади
освещенной поверхности, т.е. ~W~2. Это свойство может служить средством
распознавания фрактального рассеивания или методом измерения
фрактального индекса v.
4.5. Фрактоидная модель рассеяния волн
В работах [206, 207], исходя из принципов масштабной
инвариантности задач классической фотометрии (случай геометрической
оптики), предложен универсальный метод нахождения
фотометрических функций регулярных и случайных субфрактальных структур на
основе фрактоидной модели рассеяния. Данные структуры могут
служить неплохими моделями для описания как антропогенных, так и
природных объектов, например земных ландшафтов и небесных тел.
Фракталы и фрактоиды. Обычно предполагаемая стохастичность
структуры поверхности — важное обстоятельство, приближающее
модель к реальности, но и оно не в полной мере отражает сложность
задач рассеяния. Случайный рельеф соответствует скорее
иерархическому принципу и обладает определенным самоподобием при
различных масштабах его представления. Для моделирования этого
фактора в [206] вводятся в рассмотрение математические объекты,
называемые фрактоидами. Фрактоид - математический объект, тесно
связанный с фракталами. Обычно в физике используют, как
рассмотрено ранее, физические фракталы, или субфракталы. Для их
описания применяют параметр \i - количество генераций образующей
структуры. При ц->°о субфрактал переходит во фрактал.
Фрактоидами являются самоподобные структуры, имеющие
бесконечное число характерных масштабов, но при этом сохраняющие
равенство топологической D0 и фрактальной Dразмерностей, т.е. для
фрактоидов D = D0 даже при ц -> °°. Это свойство отличает
фрактоиды от фракталов. По аналогии субфрактоид определяется как струк-
</">
io
S{W)
{I)n Sn(W) ml
196
4.5. Фрактоидная модель рассеяния волн
тура, переходящая во фрактоид при \i -> «>. с точки зрения второго
определения фракталов, данного Мандельбротом, фрактоид является
частным случаем фрактала, но с точки зрения первого определения
фракталов, фрактоид - это математический объект другого рода.
Реализация фрактодов. Рассмотрим некоторые примеры фрак-
тоидов [206, 207]. Допустим, что фрагмент поверхности состоит из
N ступеней прямоугольного профиля (рис. 4.12,я) высотой А и
длиной L0 = 4/. Для выделенного фрагмента его размер L0N = 4N1.
Полагаем, что ступенчатая структура имеет ц поколений масштабов.
Найдем предел такой структуры LN при \i -> °° . Размер LN
складывается из длин L0Nn размеров всех боковых стенок Lh. Для первого
поколения Lh = 2Nh; для первого и второго - Lh = 2Nh + 4N2h ;
Aw
ддя первого, второго и третьего — Lh = 2Nh + 4N2hL~lNl + iN42L~^N. В
случае \i поколений с учетом того, что L0N/l = AN, длина кривой
LN=N[L, + Ah(\-2-»)]. Отсюда видно, что при |i -> оо длина
данной кривой остается конечной, т.е. мы имеем дело с фракгоидом.
Теперь рассмотрим поверхность, образованную #
углублениями 2/треугольного профиля с углом ската 0 и размером
горизонтального участка / (рис. 4.12,6). Построим субфрактал ц,-го поколения при
размере образующей структуры L0 = 2/ (1+2 cos 0). Длина искомого
субфрактала LN = (6Л0Ц/Ц. В то же время I^N =[2#(l + 2cos0)f /
Тогда LN = 1^(/ц /I^N)l'D9 где D = 1п6ЛУ[1п2Л^(1+2 cos 0)] -
фрактальная размерность [206]. Неравенство D> D0 выполняется только
при 0*0. Исключая значение / из выражений для LN и LQN,
получим
^«МУ(1+2сове))Г.
Отсюда следует, что при 0 Ф 0 и \l -> °° длина Z,^ расходится и суб-
фракгал переходит во фрактал. Переход от рассмотренного
субфрактала к субфрактоиду происходит в случае представления угла 0 в виде
02 = 5/|i, где 5 - параметр фрактоида. Тогда lim LN = L^N exp(5/3).
Рассмотрим теперь отрезок одномерногс^лучайного рельефа с
гауссовым распределением высот и среднеквадратичным наклоном
197
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
^7hJ77>777>7f7>7f7?7?77,
Ls7>7f77^777>7f7>7f7?7777/
а)
PL
Рис. 4.12. Построение фрактоидов с регулярными структурами ступенчатого (а) и
треугольного (б) профилей [207]
. Считаем, что длина отрезка значительно превышает размер
области корреляции высот неровностей. Пусть на этот случайный
рельеф наложена мелкомасштабная рябь с эквивалентными
статистическими характеристиками. В качестве меры отличия двух соседних
масштабов возьмем отношение r = /v//v+1 , где /v - размер области
корреляции высот для v-й генерации; v = 1, ..., \i— 1. Тогда
где Z) = lnr/ln[r(l-(Y2>/2)].
198
4.5. Фрактоидная модель рассеяния волн
Переход от субфрактала к субфрактоиду осуществляем с
помощью замены (у2) =8/ц,, где 8 — дисперсия наклонов на самом
мелком масштабе, который аккумулирует наклоны всех более крупных
масштабов. В этом случае значение \i может быть сколь угодно
большим, поскольку длина Lr субфрактала не зависит от |i: Lr=I^r exp(8 / 2).
Для двумерных случайных структур необходимо в полученных
формулах длину Lr заменить на площадь поверхности фрактоида Sr, a
L0r- на S0r, Здесь S0r - площадь проекции на плоскость отсчета
образующей структуры самого крупного масштаба. Такой фрактоид
может служить моделью рельефа реальных поверхностей.
Метод геометрической оптики. Пусть одномерная поверхность
регулярного ступенчатого профиля освещается и выглядит, как это
показано на рис. 4.12,а. Функция рассеяния дописывает зависимость
силы рассеянного света от углов а, % и параметра а =цЛ/(2/).
Далее используем принцип масштабной инвариантности задач
геометрической оптики. Изменим масштаб субфрактоида, убрав самую
мелкомасштабную генерацию, но одновременно достроим новую
генерацию в области крупных масштабов. Первый шаг означает, что
^Х%> а> ЗС) переходит в Дац_15 а, %). Второй шаг приводит к
образованию первоначальной структуры с масштабным коэффициентом
4JV, функция рассеяния которой ^(ац, ос, %) выражается через
функцию Лам, ос, х) '
4MF(a(l,o,x)="
= 2M^%_pa,x) + 2M^(aM,a,x){l-^[tgx + tg(a-x)]}, (4'94)
где к = А/2/-
Первое слагаемое в (4.94) описывает вклад незатененных
участков, а второе — затененных. Запишем (4.94) в виде
*-=? \ = xtg% + tg(a-x). (4.95)
При условии к < 1 и достаточно большом порядке
субфрактоида вместо функционального уравнения (4.95) можно использовать
дифференциальное уравнение первого порядка
199
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ...
dF _ sin a
do^ 2cos%cos(a-%)
с решением
F = g(a, ц)ехр
a sin a
2cos%cos(a-%)
(4.96)
Здесь g(a, ц,) - индикатриса рассеяния горизонтального элемента
субфрактоида на самом мелком масштабе - начальное условие. Для
ламбертовой индикатрисы, как известно, g(a, ц) = cos %cos(a - %). Из
(4.96) следует, что при a ~ 1 изучаемая структура должна обладать
выраженным обратным рассеянием за счет экспоненциального
множителя.
Для регулярного треугольного профиля (4.12,6) аналогично
получим
2M/,(8^,a,z)(l + 2cos6) =
= 2МЯ8ц_ра,х) + МЛ8м,а,Х + е) + М^(8м,а,х-е), (4.97)
где ац = ц,02 - параметр, характеризующий наклон поверхности.
В формуле (4.97) не учитываются эффекты затенения и
многократного рассеяния. Первое слагаемое учитывает рассеяние от
горизонтальных площадок, второе - от площадок, нормаль которых
отвернута от направления на наблюдателя, а третье — от площадок с
нормалями, повернутыми в сторону наблюдателя. Для малых 6 и
больших |i выражение (4.97) приводится к виду
ЭЛ5и,а,%) 1(дЩ&,а,х) J
Э8„
Э%2
+ F
(4.98)
с начальным F(0, a, %) = g(a, %) и граничным .Р(8Ц, ос, я/2) =
= F(8 , я/2 + Ъ X) = 0 условиями при выполнении принципа
взаимности Гельмгольца F(8 , a, %) = F(8 , a, a-%).
Общее решение уравнения (4.98) методом Фурье имеет вид
^,а)%)= Х^°)(а)ехр[-8Ц(С2 -l)/4]cos
т=\
а
Х-2
(4.99)
200
4.5. Фрактоидная модель рассеяния волн
где с
..S==2£, £<.,(a)=^*f,z^x).cos[cfx-f
OL-K/2 L V
Для ламбертовой индикатрисы имеем
/я
2(-1)
/я-1
Я-ОС
\
1 а ст . а
—cos--+ ™ , sin —
cw 2 ci-1 2
Коэффициенты ряда (4.99) убывают с ростом /я. Таким образом,
в выражении (4.99) при углах а > 40° доминирует фундаментальная
гармоника
Д5и, а,х)=£Ш<х)ехр
1 д oc(2jc - а)
"4 ^ (тс-а)2
cos
7С-0С
а
Х-2
где^°)=40)(«)/^0)(0) =
4тс
4 + тс
1а к .а
-C0S7T +—^ 7Sin7T
тс 2 а(2тс-а) 2
Теперь рассмотрим субфрактал со случайной структурой.
Уравнение, аналогичное уравнениям (4.94) и (4.97), имеет вид
Л V а, х) = (^[Vp а' Х(х)])[' (4Л0°)
где <...>|х означает пространственное усреднение на некотором
интервале Z, который должен быть достаточно велик, но в то же
время быть гораздо меньше области корреляции случайного профиля
соседнего крупного масштаба.
Параметр 8Ц в (4.100) определяется функцией распределения
углов наклона площадок случайного профиля W(Q) в виде 8Ц =|и(у2)
при<у2> = |Ж(е)е2</9 , где S- область интегрирования, соответству-
s
ющая таким 0, при которых не наступает затенения. Тогда вместо
(4.100) можно записать
Щ, а, %) = |Ж(в)Л8м,а, х + е)
£/8
COS6*
(4.101)
Интеграл (4.101) обобщает выражение (4.97). Для малых (у2)
левая часть интеграла (4.101) записывается в виде
201
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ...
dF(8.a,x) ,
F(511+1, a, j)-F(bu, a, Х) + ^-^<у2>,
Vi'
Э8.
а правая -
J(...)rf9^(8(1,a)X)+i
Я8и,а,%) + - И
Э%2
(Y2)-
В итоге получаем уравнение
2dF(^a'X)=[F;(8]l,a,x)+F(5ll,a,x)],
практически не отличающееся от уравнения для регулярного
субфрактала (см. (4.98)). Это означает, что для тех же граничных и
начальных условий, что и в задаче с регулярным профилем, решение
получается однотипным. Следовательно, рассеивающие свойства
некоторых субфракталов могут не зависеть от того, является
генерирующий профиль детерминированной или случайной функцией.
Задача Штурма-Лиувилля. Предложенный подход легко
распространяется на двумерные поверхности [206]. Пусть F(& , a, %, Р) —
функция рассеяния субфрактала, образованного \i генерациями
случайной поверхности. Каждая из генераций использует
предшествующую более крупномасштабную как поверхность отсчета (референс-
поверхность). Тройка углов: % — фотометрическая долгота,
отсчитываемая от центрального меридиана, р — фотометрическая широта,
отсчитываемая от экватора, и угол фазы a - связаны с углом
падения /, углом отражения е и азимутальным углом ср следующим
образом:
[cos i = cos P cos(% - a),
cos e = cos p cos x,
coscp = (cos a- cos /cos e)/(sin /sin e).
Углы / и е отсчитываются от нормали к референс-гоюскости
рельефа самого крупного масштаба.
Как и ранее, перемасштабируем субфрактал, убирая самую
мелкомасштабную генерацию и создавая новую со стороны крупного
масштаба. В итоге получаем уравнение
202
4,5. Фрактоидная модель рассеяния волн
F(S)1+va,x,V = yJJF[8il,a,x(x,y), fa, y)]-£&—, (4.102)
где х, у - пространственные координаты в плоскости отсчета; S0 -
площадь усреднения; 6 — угол локального отклонения нормали
случайной поверхности от нормали плоскости отсчета; % и р —
фотометрические координаты, возмущенные вариациями 0 и
изменяющиеся вблизи средних % и Р .
Функционально-интегральное уравнение (4.102), в отличие от
(4.94), является весьма сложным и может быть решено только при
упрощении задачи путем перехода от рассматриваемого
субфрактала к фрактоиду.
Предельный переход ц->«> при (у2) = 8/|и с учетом замены
пространственного усреднения в (4.102) на статистическое усреднение
2кк/2
j j
0 0
ZK 7C/Z
Л8ц+1, а, х, Р)= j j Ffa, а, %(Q, ф)Р(9, <р)]х
xW(a, x, p, -, 9, cp)sinfo/e</cp
и*
с разложением функции F(...) в ряд по степеням в позволяет
перейти от уравнения (4.102) к следующему дифференциальному
уравнению
^X>P)a|(Vi+2)mcbXtp) (4Л03)
с начальным /j5=0=g(0, %, p, а) и граничным F\^n/2 = /,|x=CMt/2 =
= ^1в=+я/2 = ^ Условиями ПРИ соблюдении условий взаимности Гельм-
гольца: F(89%,$, a) = F(6,x,-h a), 7^(8,%,р, a) = F(8, a-jc,p, a).
В формуле (4.103) V2 является дифференциальным оператором
э2 э э2
Лапласа: V2 = —т - tg р —-+cos-2 p —5-. Таким образом, мы приходим
эр2 эр Эх2 п п
к задаче Штурма-Лиувилля на сферическом секторе: a - - < % < -,
-— < р < —. Полное решение уравнения (4.103) методом Фурье
записывается в общем виде
203
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
XCOS
' оЛ
Х-2
/я=0 л=0
/J
cos** P2/<j
(4.104)
где см» =
fc (а) + -+2я
m 2
1 f , ч 7c(2/w +1)2 _, ч
"7' Ma) = \ „ > ^i(-) -гипер-
я-а
геометрическая функция Гаусса.
Коэффициенты Етп(а) находятся с помощью начальных условий
при использовании стандартной процедуры:
/я/Л ' ос-я/2 0
a
где
it/2 */2 r
^m»= J ^Xj ^COS2Vlp.C0S
a-n/2 0 I
л2и!(2/и+1)Г(А:т+и + 1)
*m|X-f
„( , 1 1 • ,„1 л2л!(2/и + 1)Щт+и + 1)
*Fi \n+km+-,-n,-,sm^U • " '_.
I 2 2 J (2km+4n+l)r^+njr\km+i + njcm
Для ламбертовой индикатрисы рассеяния g(0, %, р, a) =
= cos/cose-cos2Pcos%cos(x-oc)
коэффициентыЕтп(а)определяются формулой
е («м-р»»' 4cos?„ <V1+4">X
(2т + 1)л3/2л! к2т-А
2 + -*- | Г|
2
Г|| + Я|Г|1 + Я + *И
2-йТ Г2Ш 2
JL+O
Г(*и+1+")
204
4.5. Фрактоидная модель рассеяния волн
В случае зеркального рассеяния £(0,х,р,а)=7?(а)8(Р)8(%-ос/2),
где 8(х) — дельта-функция; R(a) - френелев коэффициент
отражения. Тогда
E(a) = R(a)
(2km+4n + l)kmr(km+l/2 + n)
к2п\(2т + 1)Г(к +/i + l)
Остановимся на границах применимости формулы (4.104). При
ее получении не учитывался теневой эффект, поэтому формула не
будет хорошо работать вблизи % « ос - я/2, % « я/2, р « ± л/2, а также
при больших а и больших значениях 8. Последнее означает, что
функция (4.104) описывает слабонеровные поверхности. Из-за
экспоненциальных множителей общего вида
Гш<а)««ф --
2т+ 1 . П
п + 2п-—
я-а 2 J
9
+ 4
двойной ряд в (4.104) быстро сходится даже при сравнительно
небольших значениях 8. Уже при углах наклона поверхности 30-40°
основной вклад дает первая гармоника
F00(8,xM = E00(a)exp
а(3гс-2а),
' 4(я-а)2 '
cos7t/(jc-a)pcos
к ( а
— х-х
я-а 2
Рассеяние на сферическом объеме. Рассмотрим также рассеяние
на двумерной частице, опираясь на результаты [207]. Пусть
сферический объем радиуса R$ состоит из большого количества частей,
которые в свою очередь представляют собой сферические объемы,
подобные исходному в статистическом смысле. Используя
масштабную инвариантность задачи, найдем фазовую функцию F(a) такой
частицы с д поколениями масштабов. Параметром задачи является
t =цт, где т = Rq/L; L — характерное расстояние между частицами
ближайшего мелкого масштаба. Считается, что т одинаково для
каждой из \i генераций.
Перемасштабируем субфрактал, убрав генерацию самого мелкого
масштаба и создав новую генерацию со стороны крупного
масштаба. При этом мы возвращаемся к исходной частице с новым
радиусом R » Rq . В приближении однократного рассеяния аналогично
формулам (4.94) и (4.97) получаем уравнение
205
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
/r(/|l+1,a) = z(x,a)/,(/(1,a).
Здесь
1
2я R
&><*) = —j J ^ф|Аг/гехр{-тЛ-1[/1(г,ф,а) + /2(г,ф,а)]}, (4.105)
пК о о
где /j и /2 - пути, которые волна проходит внутри вновь
образованной частицы соответственно до и после рассеяния в точке с
координатами г и ф (рис. 4.13). Из данных рис. 4.13 следует, что
/^(^-^Я^фУ^-ГСОВф, /2=[Д2-Г28Н12((Х-ф)] -ГС08((Х-ф).
Формула (4.105) в конечном виде не интегрируется. Разложим
подынтегральное выражение в ряд по т. При ограничении ряда
линейным членом получим тривиальный результат: F(t , а) = const g(a).
Здесь g(a) — индикатриса частиц самого мелкого масштаба. Данное
решение соответствует случаю сильно разреженного фрактального
кластера. При учете в разложении большего числа членов имеем
dF
— = Л)(т,а)-ф(/ a),
(4.106)
Рис. 4.13. Геометрия рассеяния волн на двумерной фрактальной частице [207]
206
4.5. Фрактоидная модель рассеяния волн
где 2)(T,a) = t-1[z(x,a)-l],
и ч ld2F ld3F
(4.107)
Решение неоднородного уравнения (4.106) имеет вид
'и
F = J ехр[/)(/ц -lf)](p(l/,a)rfl/ +*(a)exp(Z*|l). (4.108)
о
Интегральное уравнение, к которому сводится (4.108), при
учете разложения (4.107) решается методом итераций. В качестве
начального решения уравнения (4.106) берем F0 =g(a)exp(Dt ).
Тогда получаем:
F{ =gexp(-Dtll)(l+til{D+>rl[l-exp(-Dx)]})
и т.д. Главный вклад во всех приближениях зависимости F (ос) дает
множитель #(а)ехр£-2)(т, a)^J, который является и первым
приближением решения задачи. Если g(a) = const, индикатриса
рассеяния двумерного фрактального кластера определяется множителем
/ = ехрГ-/)(т, «)/^1. На рис. 4.14 приведены нормированные фазо-
Рис. 4.14. Нормированные фазовые зависимости яркости фрактальной частицы
при гц = 10 [207]
207
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
вые зависимости яркости двумерной частицы при / = 10. Из рис. 4.14
следует, что исследуемая частица при достаточно больших ти/й
характеризуется заметным обратным рассеянием.
4.6. Обобщенное рэлеевское решение задачи
рассеяния волн фрактальной поверхностью
В качестве традиционных математических моделей неровных
поверхностей ранее раздельно применялись детерминированные и
случайные функции [183, 184, 208]. Развитие фрактальной
геометрии дает новое средство для систематического исследования
неровных структур, так как фракталы учитывают различные
пространственные масштабы и могут быть непосредственно использованы при
описании и детерминированных, и случайных функций или их
комбинаций.
Постановка задачи. Физика волнового взаимодействия с
периодической средой или структурой хорошо описывается брэгговским
условием в виде закона сохранения момента между волновыми
векторами падающей и дифрагированной волны, с учетом
пространственного волнового вектора структурных гармоник. Метод Рэлея
использует эти условия при рассеянии волн периодическими
структурами. В работе [209] предпринято обобщение метода Рэлея для
исследования задачи рассеяния от почти периодических поверхностей,
включая фрактальные.
Рассеивающая поверхность моделировалась диапазонно
ограниченной непрерывной фрактальной функцией неровностей/(х),
являющейся модифицированной функцией Вейерштрасса JV(t),
свойства которой подробно исследованы в [128]. Данная функция имеет
конечный диапазон пространственных частот и проявляет свойство
самоподобия в пределах конечного диапазона разрешения:
f(x) = Cy£ansm(Kbnx+q>n), (4.109)
где С- коэффициент контроля амплитуды; N- число гармоник
(тонов); а — коэффициент масштаба неровностей (0 < а < 1); К—
основное пространственное волновое число; Ъ > 1 — параметр
пространственно-частотного масштабирования; сря — произвольная фаза.
208
4.6, Обобщенное рэлеевское решение задачи рассеяния волн фрактальной поверхностью
Коэффициент контроля амплитуды
С =
2(1 -й2)
1-й
2N
1/2
(4.110)
выбран так, что среднеквадратичное отклонение j{x) а = 1. В (4.109)
могут быть использованы и другие периодические функции.
Для функции (4.109) можно ввести несколько фрактальных
размерностей, потому что она самоаффинна (см. разд. 2.1). В общем
случае фрактальная размерность функции Вейерштрасса [128]
Z> = 2 + log5/log6.
Для точного описания формы неровностей в [209]
используется фрактальная размерность в виде
2) = 1 + д.
(4.111)
При D = 1 имеем гладкую периодическую кривую. С
увеличением D(D<2) получаем различные хаотические кривые.
Следовательно, D определяет в функции fix) меру поверхностных
неровностей.
Геометрия рассеяния падающей плоской волны Et = ехр(/Л • г) на
одномерной неровной, идеально проводящей фрактальной вдоль оси
х поверхности представлена на рис. 4.15. Индексы i и s относятся к
падающей и рассеянной волнам с волновыми векторами соответ-
Рис. 4.15. Геометрия рассеяния волн на фрактальной неровной поверхности
209
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
ственно kt и ks. Одномерная квазипериодическая поверхность
описывается уравнением
м
Z = %x) = h^aMmKMx + vM). (4.112)
Здесь параметр А контролирует среднеквадратическое значение
неровностей.
Поле рассеяния плоской волны. Поле рассеяния Es в плоскости
{х, z) может быть записано в форме рэлеевского обобщения
Es=- I 41)й2 „Mexp(/ftC."2-^).r), (4.113)
где суммирование проводится по всем комбинациям nv л2, ..., пм
[208]. Волновой вектор рассеяния имеет вид
k^nin2-nM) = k(smenn n ^+cos0ww n е7)
с углами дифракции вп п п , определяемыми из условия
^sinV-.^=^sin0'"^i"^2---%^M- (4.114)
Выражение (4.113) представляет операцию суммирования всех
возможных брэгговских взаимодействий между падающей и рассе-
яннной волнами от квазипериодической поверхности. Здесь каждое
взаимодействие характеризуется разными комбинациями
структурных гармоник. Отметим, что доминантными взаимодействиями
являются взаимодействия первого порядка, т.е. только одна из nv n2,
..., пм переменных имеет единичную величину (+1 или —1), тогда
как остальные зануляются.
Для сокращения записи обозначим все напряженности поля в
виде вектора
^ = | q\ Г*'^00-1...0'Л-10...0'^ЧШ..Ю'^ООО..Ю'^1(Ю...0'Л10...0'^001...0'••')'
где q использовано для обозначения перечня последовательности пх,
п2, ..., пм, -оо<д<оо. Тогда (4.113) будет иметь вид
210
4.6. Обобщенное рэлеевское решение задачи рассеяния волн фрактальной поверхностью
Es=-ZAqexp(i№r). (4.115)
Отметим, что при условии |sin 0/ - q К / к\ > 1, где
qK = qlKl+q2K2+... + qMKM9 (4.116)
возникает режим бесконечно малых по амплитуде волн, имеющих
значение в непосредственной близи к идеально проводящей
поверхности.
Пусть падающая волна Ех имеет горизонтальную поляризацию.
Применим граничные условия для идеально проводящей
поверхности (Е. +£5). ~ ) =0, тогда с учетом формулы (4.115) находим
оо
ехр [-iktyx) cos в,.] = £ Aq exp [-i(q • K)x + iktyx) cos 0^ ] (4.117)
Л=—оо
При использовании представления функций Бесселя первого
рода /и-го порядка в виде степенного ряда
оо
exp(//sincp)= ^ Jm(t)exp(jm<p) (4.118)
Ш--00
для левой части (4.117) с учетом (4.114) получаем
М оо
exp[-/^x)COSe,.] = n X Jpm('khamCOSQi)QXP['K(KmX^^m)] =
m=lpm=-oo
рт=-~т=\
= £ (-1)^>ехр(фф)ехр[/(1|ВДП^т(^ЧС08^)' (4119)
М
где к(р)=^Рт; рК имеет вид (4.116); /><р = р{% +Р2<Р2 + - + ЛАг
211
Глава 4, ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Правая часть формулы (4.117) определяется соотношениями
£ AqQxp[-i(q- K)x+ik^(x)cosQq^ = £ Aqexp[-i(qK)x]x
П——00 q=—oo
M ~
ХП I Jnm(khamC0SVeXP[.in^KmX + ^m)] =
m=lnm=-oo
m
oo oo M
= X ехр(шф) £ Aqtxp{i[(n-q)K]x][[Jnm(khamcosQq). (4.120)
я=-оо q=-co m=\
Полагая, что p = n-q, перепишем (4.120) в виде
oo oo M
£ ехр(|)хр)ехр[;0>фх] £ Aqexp(iq<f)]\Jp^qm(khamcosQq). (4.121)
р=~оо q=-oo /я=1
С учетом равенств (4.119) и (4.121) окончательно имеем
м
(_i)«o»j]/ №mcose,.)=
m=l m
= ZAqexp(.iqq>)f[JPm+qm(khamcosQq),
q /я=1
ГДе -оо<^<оо, -оо<?<оо,?ф = ?1ф1+^2ф2+... + ?мфм, /? = {р1? ^2, ...,
^РмЬ ?= tei» #2> • ^мЬ ^ краткой форме соотношение (4.122) имеет
вид ,Р = ЛГ, где F — вектор, содержащий элементы левой части
(4.122) для всех/?; А - вектор, включающий все взаимодействия; Т—
матрица согласования.
Таким образом, Г и /'можно легко рассчитать для заданных
величин к, 0,. и \{х). Коэффициенты А вьиисляются усечением/? и q
до конечной системы, чем определяется ее сходимость. Такая
конечная система дает быстро сходящееся решение для малых
неровностей при khai < 1. Условия сходимости будут рассмотрены далее.
Условия сходимости. Моделирование фрактальных
поверхностей проводилось в [209] специальной последовательностью
квазипериодических функций, обладающих свойствами самоподобия. По-
212
4.6. Обобщенное рэлеевское решение задачи рассеяния волн фрактальной поверхностью
ложим в выражении (4.112) ат=йт и Кт = Kif1. Тогда фрактальная
функция примет вид
м-\
$/(х) = оСУ£ ansm(Klfx+<pn) = of(x), (4.123)
где а - среднеквадратическая высота неровностей; fix) —
определяется формулой (4.109). Подставим (4.123) в (4.122) и получим
м-\
(_!)*(/>) Yl J (^xCcose,.) =
m=0 m
= I4g «ЧК* ■ Ф)П^+^ (fl«xCC0S вд), (4Л24)
^ /я=0
где х = fca.
Вследствие того, что pnq изменяются в диапазоне (-°°, °°),
выражение (4.124) является бесконечномерной линейной системой.
Можно решить конечномерную систему уравнений при усечении р
и q до значений (2N +1), т.е. каждая переменная должна лежать в
интервале от -Лдо N Для нулевого порядка существует только один
элемент, поэтому q = {0, 0,..., 0}. Подставляя это условие в
уравнение дифракционной решетки (4.114), находим 0^ = 6., что
определяет направление зеркального отражения. Если система усекается до
нулевого порядка (N= 0), ясно, что решением будет А = 1, т.е.
падающая волна полностью отражается в зеркальном направлении от
гладкой, бесконечно проводящей поверхности.
При взаимодействии первого порядка одна из переменных nv nv
..., пмпринимает единичное значение (1 или — 1), в то время как
остальные равны нулю. Тогда углы дифракции определяются по
формуле (4.114) в виде
sin9^=sine/±x*m, 0</и<М-1.
Здесь х = К/к = Х/А - отношение длины волны излучения к
пространственному периоду.
Существует всего 2Мтаких составляющих. Поэтому во
взаимодействии первого порядка при М— N появляется уже (2Af+ 1)
элемент. По аналогии: для взаимодействия 2-го порядка будет учиты-
213
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
ваться (2М)2 дополнительных членов и (2А/)3 для взаимодействия
3-го порядка. В общем случае усеченной системы /с-го порядка
,=о 2М-1
После усечения конечная линейная система решается путем
инверсии матрицы (27V + 1) х (2N + 1). В табл. 4.1 рассчитан
порядок системы для к взаимодействий с поверхностью, моделируемой
шестью гармониками (М= 6) фрактальной функции (4.123).
Оказывается, что расчет имеет смысл вести до взаимодействий первого или
второго приближения. Структура уравнений (4.122) и (4.124)
показывает, что относительные фазы гармоник срт не влияют на
амплитуды взаимодействующих напряженностей Ап. Они только
добавляют фазовый сдвиг пу ъАп. Это является характеристикой почти всех
периодических взаимодействий [210, 211]. Из данных табл. 4.1
видно, что число уравнений увеличивается экспоненциально по
отношению к порядку взаимодействия.
Таблица 4.1
Размеры матрицы (2JV+1), рассчитанной для усеченной системы
при взаимодействии *>го порядка [209]
Матрица
2ЛГ+1
Размер матрицы при к, равном ]
0
1
1
13
2
157
3
1885
4
22621
5
271453
Исследуем сходимость системы (4.122) или (4.124) на примере
простой синусоидальной поверхности [209]. Полагаем М = 1 и срй = О
во фрактальной функции (4.123). Напряженности рассеянного поля
для синусоидальной поверхности £ (x) = V2asinA3c с учетом (4.124)
находятся из соотношения
{-\yjp (W2 cos 67.) = X V™ (*^cos %)' <4' 125>
я
где 6 определяется дифракционным соотношением (4.114).
214
4.6. Обобщенное рэлеевское решение задачи рассеяния волн фрактальной поверхностью
Сходимость решения системы (4.125) изучалась для угла
падения 0/ = 30° и соотношения частот % = 0,1 при значениях х = ко = 0,2;
0,5; 1,0 и 2,0. Значения величин А при х = 0,2 рассчитаны с
помощью (4.125) для порядков взаимодействия к = 0-5 и
представлены в табл. 4.2.
Таблица 4.2
Значения коэффициентов Ап при рассеянии волн синусоидальной
поверхностью с jc = ко = 0,2 [209]
U,N
0
1
2
3
1 4
| 5
Аи
7,4 • Ю-5
7,4-Ю-5
Л-3
-0,0018
-0,0018
-0,0018
Л-1
0,0274
0,0273
0,0273
0,0273
^Li
-0,2410
-0,2383
-0,2383
-0,2383
-0,2383
А
1,0000
0,9410
0,9414
0,9414
0,9414
0,9414
А\
0,2415
0,2373
0,2373
0,2373
0,2373
4
0,0314
0,0311
0,0311
0,0311
4
0,0028
0,0028
0,0028
Л
1,9-10^
1,9-10^ |
При х = 0,2 система уравнений сходится очень быстро.
Результат точен до двух значащих цифр даже тогда, когда система усечена
до первого порядка N = 1.
На рис. 4.16 приведена зависимость порядка усечения /с,
необходимого для решения системы уравнений с точностью ±2% от
относительной среднеквадратичной высоты неровностей х = ко .
Видно, что высокие порядки в расчетах необходимы при больших не-
К
10
8
6
4
2
0 0,5 1,0 1,5 2,0 2,5 х
Рис. 4.16. Значения коэффициентов усечения /с, необходимых для решения
системы уравнений с точностью ±2% как функция х = ко [209]
215
J I I I L_J I I I L
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
ровностях поверхности. Отметим, что коэффициенты Ап почти
симметричны по амплитуде относительно п (см. табл. 4.2).
Другим условием, подтверждающим точность решения, является
критерий баланса энергии. Закон сохранения энергии требует,
чтобы параметр баланса энергии е = 1, т.е. поток падающей энергии,
должен равняться сумме рассеянных потоков по всем попарно
связанным направлениям. Данный параметр определяется в виде
^ . ,*cose„
-л*^- (4л2б>
Вычисленные по формуле (4.126) параметры баланса энергии для
синусоидальной (N = к) поверхности с x = fca=0,2; 0,5 и 1,0
представлены в табл. 4.3.
Таблица 4.3
Параметр баланса энергии е для синусоидальной поверхности
с х = ка= 0,2; 0,5; 1,0 и системы уравнений порядка (27V+ 1) и iV= к [209]
Параметр е
х=0,2
х=0,5
х=1,0
N=k ~ " ~|
1
1,0009
1,0296
1,3085
2
1,0000
1,0020
1,1030
3
1,0000
1,0001
1,0139
4
1,0000
1,0000
1,0011
5
1
1
1
Критерий баланса энергии выдерживается в пределах 1,5%,
кроме трех случаев. Можно отметить, что для фрактальной
квазипериодической поверхности имеет смысл проводить вычисления, когда
far< 0,5.
Численное моделирование. Рассмотрим результаты расчетов [209]
рассеянных взаимодействующих напряженностей для фрактальной
поверхности, описываемой уравнением (4.123). Для параметра
х = кс = 0,2 система уравнений решается точно при усечении до
первого порядка взаимодействия. Пусть в (4.123) имеем: Ъ = 1,3797,
X = 0,1, М= 6, х = 0,2. Так как фазы cpw не играют роли в
определении Ап, то полагаем ср^ = 0. Для отличных от нуля фаз полученный
результат необходимо умножить на (-ш<р). Результаты расчетов
13x13 конечномерной системы при угле падения 6. = 30°
приведены в табл. 4.4. Двенадцать взаимодействующих величин и одна
нулевого порядка с их углами рассеяния вычислены для фрактальных
216
Таблица 4.4
Значения взаимодействующих напряженностей и параметр баланса энергий для фрактальной поверхности
с Ь = 1,3797, М = б, ка = 0,2, х = од при 9,. = 30° [209]
к = 0,1
А-е
As
А^
А~3
А-г
А-1
А
А
Аг
Аг
А
А5
А
е
%
89,4°
59,6°
49,7°
43,7°
39,6°
36,9°
30,0°
23,6°
21,2°
18,0°
13,7°
7,9°
0,0°
Л-1,05
-7,5 • Ю-8
-1,5 • 10-*
-3,0 • Ю-5
-6,1 • 10^
-0,0122
-0,2408
0,9418
0,2413
0,0123
6,1 • 10"4
3,1 • Ю-5
1,5 • 10-*
7,7 • 10^
1,0026
D = 1,3
-6,6 • 10^
-0,0019
-0,0063
-0,0209
-0,0698
-0,2303
0,9418
0,2308
0,0702
0,0211
0,0063
0,0019
5,7 • 10^
1,0029
D-1,5
-0,0065
-0,0131
-0,0263
-0,0528
-0,1055
-0,2096
0,9417
0,2101
0,1060
0,0532
0,0266
0,0133
0,0067
1,0032
2>= 1,7
-0,0292
-0,0419
-0,0600
-0,0858
-0,1225
-0,1745
0,9421
0,1750
0,1231
i 0,0864
0,0606
0,0425
0,0297
1,0031
D = 1,95 1
-0,0859
-0,0908 1
-0,0958
-0,1011 1
-0,1065
-0,1121
0,9442
0,1125 |
0,1070 |
0,1018
0,0968 |
0,0920
0,0875
0,9996
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
размерностей Z>= 1,05; 1,30; 1,50; 1,70 и 1,95. Для ^характерно их
уменьшение при возрастании \т\. Скорость убывания Ат возрастает
при уменьшении значений D.
Результаты расчетов для D = 1 дают значения А$ = 0,9418, А_{ =
= -0,2411, А{ = 0,2416. Отличные от нуля А_х и Ах являются напря-
женностями первого порядка для синусоидальной поверхности (см.
табл. 4.2).
Для D= 2 получаем^) = 0,9444, А_т = -0,1, Ат = 0,1 при 1 < т < 6.
При свертке Aq (табл. 4.4) с простыми дифракционными
результатами мы получаем угловые зависимости характеристик рассеяния в
случае облучения конечной площадки фрактальной поверхности. С
использованием данных таблицы были построены зависимости
коэффициентов Ат от п - log К (1 < т < 6) для различных
поверхностей (рис. 4.17). Полученные графики приближаются к прямым
линиям с наклонами, характеризующими фрактальные значения
размерности поверхностей. Прямые на рис. 4.17 занимают положение
от вертикального до горизонтального, т.е. их наклон меняется от -°°
до 0 по мере роста D от 1 до 2.
Значение наклона S(D) для малых х определяется формулой
£(/)) = 101g(Z)-l). (4.127)
Из рис. 4.17 видно, что Ат линейно спадают при увеличении я,
что похоже на результаты расчета в приближении Кирхгофа [183,
184]. Наклон прямых определяется только фрактальной размерно-
-5
-15
-25
-35
0 12 3 4 5 6л
Рис. 4.17. Зависимость коэффициентов Ат от аргумента п - log К для разных
фрактальных значений размерности неровностей D [209]
218
АтлЪ
4.6. Обобщенное рэлеевское решение задачи рассеяния волн фрактальной поверхностью
стью неровностей поверхности. Это означает, что D можно
дистанционно восстановить по измерениям распределения рассеяния и
этим обосновать обратную задачу фрактальной геометрии. Расчеты
по формуле (4.127) совпадают с измеренными значениями с
точностью примерно до 0,2% при К D < 1,3; 0,7% при 1,5 < D < 1,7; 2%
при D = 1,95. В крайних точках D = 1 и D = 2 погрешность равна
нулю.
Сопоставление различных методов. Для известных и
экспериментально полученных данных по рассеянию покровами
электромагнитных волн значение D можно определить измерением наклона
логарифмической кривой удельной ЭПР а+. В работе [209] приведены
результаты измерений, представленные на рис. 4.18. Здесь угловое
распределение удельной ЭПР представлено в виде функции от
6 = sin95 -sin9;. для 0,- < Э5 < 90° в логарифмическом масштабе.
Измеренное таким методом значение наклона соотносится с
фрактальной размерностью как
S(D)J^^ = logb(D-l).
(4.128)
& дБ
Рис. 4.18. Зависимость коэффициента рассеяния волн ограниченной
фрактальной площадкой от аргумента Q = sin65 -sin6/ для 6. £ 05 <90°
(наклон прямой 1 равен -0,4; D= 1,7) [209]
219
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Таким образом, в [209] показано, что обобщенный рэлеевский
метод физически обоснован для решения задач рассеяния волн
квазипериодическими и фрактальными поверхностями. Решение
представлено в виде бесконечномерной линейной системы уравнений,
которая быстро сходится при малых ко. Фрактальная размерность
неровностей в логарифмическом масштабе линейно зависит от
наклона, связанного с пространственными частотами. Отношение
% = Х/А и угол падения 0, определяют направление рассеянного
луча. От параметра пространственно-частотного масштабирования
Ь зависит угловое распределение интенсивности рассеяния.
Относительные фазы Фт пространственных гармоник определяют фазы
полей рассеяния, но не влияют на амплитуды А.
Далее рассмотрим альтернативный подход на основе
приближения Кирхгофа. В методе Кирхгофа используется крупномасштаб-
1/2
ность р/Х »1, плавность а0 /X »1, пологость ((у2)) «: 1. Здесь р —
радиус корреляции неровностей; я0=[1 + (£/)2] Д" -локальный
радиус кривизны, ((у2)) — среднеквадратичное значение
тангенса угла наклона неровностей (штрихи означают порядок
производной) [184]. Обобщенное рэлеевское рассеяние обладает быстрой
сходимостью при малых высотах неровностей. Для него нет
ограничений на радиус корреляции неровностей. Результаты рассеяния
устойчивы в области перекрытия, где применимо как приближение
Рэлея, так и приближение Кирхгофа. Объединенные вместе, они
дают дополняющие друг друга методы решения задачи рассеяния
волн многомасштабными неровностями. В общем случае величина
D определяет угловое распределение энергии. Энергия рассеянного
поля концентрируется в зеркальном направлении при малых D и
диффузно распределена для больших значений фрактальной
размерности неровностей.
4.7. Индикатрисы рассеяния фрактальных поверхностей
в приближении Кирхгофа
Пространственные индикатрисы рассеяния, или угловые
распределения характеристик рассеянного поля от фрактальных
поверхностей, в настоящее время исследованы недостаточно. Исключением
220
4.7. Индикатрисы рассеяния фрактальных поверхностей в приближении Кирхгофа
являются оценки распределения энергии рассеянного поля на основе
обобщенного рэлеевского решения [209] и в приближении
Кирхгофа [212]. Первый метод был рассмотрен нами в разд. 4.6. Здесь
рассмотрим приближение Кирхгофа, пределы применимости которого
интенсивно изучаются [183, 184, 213-216]. Экспериментальные
исследования с использованием альтернативных фрактальных моделей
проводились ранее и опубликованы в [217].
Моделирование фрактальных поверхностей. При моделировании
использовалась диапазонно ограниченная фрактальная функция с
нулевым средним, записываемая на основе (4.109), (4.110) и (4.123)
в виде
^) = аСХ(^-1)л8ш(А^х+фл), 1<Я<2. (4.129)
Коэффициент контроля амплитуды С, определяемый с помощью
(4.110), выразим здесь через фрактальную размерность D следующим
образом:
\2\1-Ф-ЩГ f 2Ц2-Д) Г (4130)
° } 1-Ц>-1)!" J {l-fD-lFJ ' l '
Очевидно, что в (4.129) при необходимости могут быть
использованы и другие периодические функции. Примеры фрактальной
функции с различной фрактальной размерностью приведены на рис. 4.19 для
6 гармоник. Увеличение неровностей происходит с возрастанием
фрактальной размерности D. В левой части рис. 4.19 изображены
кривые с широким диапазоном пространственных частот с параметром
Ь = е~ 2,71828. В правой части рисунка показаны кривые с более
узким диапазоном при Ь = 2е/3 « 1,8122 и при тех же значениях D.
Кривые с узким диапазоном пространственных частот
используем при изучении рассеяния волн, так как они удовлетворяют
критерию приближения Кирхгофа.
Коэффициент контроля амплитуды (4.130) выбран так, чтобы
£(х) имела среднеквадратичное отклонение а. С увеличением
частоты периодические функции (4.129) описывают все более тонкую
структуру неровностей. Самоподобие функции £(х) демонстрируется
соотношением
221
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
6=2,71828
6=1,8122
D=lt50
-1 -0,5
D=l,95
Рис. 4.19. Фрагменты диапазонно-ограниченной фрактальной функции
неровностей с разной размерностью D и числом гармоник N= 6 при широком
(Ь=е = 2,71828) и узком (Ь = 1,8122) диапазонах пространственных частот [212]
которое означает, что кривая выглядит подобной оригиналу, когда
горизонтальная ось масштабируется коэффициентом Ь, а
вертикальная ось - коэффициентом (J9- I)"1.
Взаимосвязь статистических и фрактальных параметров. Из
формулы (4.129) следует, что профиль неровной поверхности
определяется параметрами a, D, Ъ, К, N. Традиционными параметрами при
моделировании случайной поверхности являются: а -
среднеквадратичное значение высоты неровностей; р — радиус их корреляции;
222
4.7. Индикатрисы рассеяния фрактальных поверхностей в приближении Кирхгофа
((Y )) "~ среднеквадратичное значение тангенса угла наклона
неровностей [183, 184]. Интересно найти связь между этими двумя
наборами параметров.
Для фрактальной модели среднеквадратичная высота
неровностей, как было отмечено ранее, принимается а. Тогда значение
1 /Л
((у2)) находится через среднеквадратичное значение первой
производной от функции (4.129). В результате имеем
«Y2»1/2=^o
l-(Z)-l)2 l-PN(D-l)2N
l-(D-l)2N l-W-l)2
1/2
(4.131)
1 /9
Из формулы следует, что ((у2)) = Kg при D = 1 или ЛГ= 1. Для
типового примера D = 1,5 при Ъ = е « 2,71828 и N = 6 имеем
(<Y2>)1/2 = 5,856Za.
1 /9
В табл. 4.5 даны результаты расчетов величины ((у2)) в
единицах Kg при разных значениях D и фиксированном N= 6.
Радиус корреляции р исследуемой модели находим с помощью
коэффициента автокорреляции р(т) фрактальной функции (4.129), который
имеет вид
р(т)=w(/f Sn1(d-!)2Л «яда*).
(4.132)
Таблица 4.5
Среднеквадратичные значения тангенса углов наклона
для фрактальной функции [212]
ь
е/2
2е/3
е
Зе/2
■ffi) при D, равном
1,05
1,001
1,003
1,008
1,020
1,3
1,045
1,136
1,575
4,329
1,5
1,175
1,705
5,856
35,00
1,7
1,567
3,727
21,08
145,4
1,95
2,551
8,551
57,37
415,7 |
223
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Из формулы (4.132) следует, что коэффициент автокорреляции
р(т) не зависит от высоты а неровностей. Радиус корреляции р
определяется как первый корень уравнения р(т) = е~1 при увеличении
т от нуля. Результаты расчета величины Ар при разных значениях Д
Ъ и N= 6 приведены в табл. 4.6.
Таблица 4.6
Радиус корреляции фрактальной функции [212]
ъ
е/2
2е/3
е
Зе/2
Кр при D, равном
1,05
1,20
1,20
1,20
1,20
1,3
1,17
1,15
1,13
1,18
1,5.
1,13
0,95
0,91
0,79
1,7
0,85
0,70
0,48
0,48
1,95
0,51
0,34
0,06
0,03
Данные таблицы свидетельствуют о том, что радиус корреляции
р уменьшается с ростом фрактальной размерности. Это
подтверждает тот факт, что фрактальная размерность является мерой
величины неровностей, как показано графически на рис. 4.19.
Таким образом, неровности фрактальной модели ЪЦх)
определяются фрактальной размерностью Д хотя среднеквадратичная
величина их есть а. Поэтому фрактальная поверхность может быть
точно определена и легко видоизменяться при варьировании
параметров К, Ъ, N, D. Способность быстрого контроля поверхности на
основе реализаций функции (4.129) с помощью ее параметров
делают такую фрактальную модель незаменимой при исследованиях
рассеяния волн земными покровами.
Индикатрисы рассеяния. Рассмотрим плоскую волну единичной
амплитуды с волновым вектором kt, падающую на одномерную
неровную поверхность, которая характеризуется фрактальной
функцией Цх), простирающейся от х = -Z до х = L (см. рис. 4.15).
Индексы i и s, как и прежде, относятся соответственно к падающей и
рассеянной волнам. Эффекты затенения не учитываются. В приближении
Кирхгофа поле рассеяния на расстоянии Rq от источника в
плоскости записывается в виде [183, 184, 208]
Ex = !^^](^-g)&W[ivxx + iv^x)]dx, (4.133)
224
4.7. Индикатрисы рассеяния фрактальных поверхностей в приближении Кирхгофа
где
/? = (1-F)sin0. + (1 + F)sin05,
?=(i+F)cose5-(i-F)cose/5
vx=/:(sin0/-sin05),
vz=-/:(cos0/+cos65).
(4.134)
(4.135)
(4.136)
(4.137)
Для упрощения расчетов в [212] рассматривается рассеяние от
идеально проводящей поверхности, когда френелевы
коэффициенты отражения Остановятся равными
к+=1,к-=ч
(4.138)
где индексы «+» и «—» означают поляризацию, соответственно
параллельную и перпендикулярную плоскости падения.
Для гладкой идеально проводящей поверхности поле рассеяния
при горизонтальной поляризации в направлении зеркального
отражения (9/ = 05) имеет вид £'0 = (/2/:Z2exp(//:J^))cose/)/(7Cj^). Вводя
индикатрису рассеяния g и интегрируя уравнение (4.133) по частям,
получаем
1
8 Е0 4Zcos0.
(( рухМ
J exp[ivxx+ivz^(x)jdx -
-|—езф[гухх+гу^(х)]
(4.139)
В формуле (4.139) второе слагаемое определяет краевой эффект,
пренебрежимо малый при L » X, где X - длина падающей волны.
Тогда с учетом формул (4.134), (4.135) и (4.138) имеем
/>+ = 2sin05, /r = 2sin0/, #+=2cos0^, q~ =20080,.;
далее на основе (4.136) и (4.137) и тригонометрических
преобразований записываем
8 Фракталы
225
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
fFvx + q±vz = 1 + cos(6/ + 6Д)
2v
cosG,+ cos6^
(4.140)
Для интеграла из (4.139) с учетом (4.129) получаем
1 х
/ = — J exp[fvxx + n^(x)]& =
= —J*exp(/vxx)exp
-L
L
N-l
пгоС^(В-1)пьт(КЬпх+<рп)
л=0
dx =
N-l
= -y J ехр(/ухх)Пехр[/С(/)-1)ЛУга8т(^Лх + фЛ)]^х. (4.141)
л=0
Применяя функции Бесселя Jm (и) и формулу (4.118), найдем
следующее выражение для интеграла (4.141):
1
2L
N-l
»п
л=0 т
-L J ехр(пус)П X ехр(шфл)/т[С(/)-1)лУго]ехр(ш6''Ах)^ =
у n=Q Jn=Q
( N-l
xexp
f ^-i ^
i^mnbnKx \dx= £ exp /Х^лФл
л=0
/я1,/Я2,...,/Ядг_1=
I «=0 у
X
xIl^[C(i)-irvza]^Jexp
1_
21
i
_
Г AM >
v, + I mnb»K
\ "=° J
X
_
dx =
f N-l yf-\
I exp i^mn% Wm.lW-W]*
m]im2i--->mN-\=~~00 V. n=® Jn=0
xsmc
( N~l )
{ n=Q )
l\
(4.142)
где sinc(x) = sinx/x.
226
4.7. Индикатрисы рассеяния фрактальных поверхностей в приближении Кирхгофа
С помощью комбинирования формул (4.139), (4.140) и (4.142)
окончательное выражение для индикатрисы рассеяния принимает
вид
l + cos(0/ + ef)
g±=±secOJ/ '"p"' ' ~s' £ ехр
cosG- +cos9 „ „ „
( N-l
5>яФя
Л
л=0
xUJmn[C(D-irvzc]smc
'(
N-\
л=0
\
L
j -j
(4.143)
Рассмотрим сначала специальный случай, когда L^>A0=2n/K ,
О, = 6^ и kc< l. Тогда из формулы (4.143) следует, что
N-\
S1 ~±n^[2C^-l№cos0j (4.144)
и g* не является функцией от Ъ и %. Учитывая аппроксимацию
при малых х (или, что эквивалентно, малых ко), находим
следующее приближение формулы (4.144):
^±«±[l-2(te)2cos2e/].
(4.145)
Индикатриса рассеяния не зависит от фрактальной
размерности D и числа гармоник N Из (4.145) также следует, что степень
затухания волны в направлении зеркального рассеяния
пропорциональна дисперсии неровностей поверхности и совпадает с
классической формулой [183, 208]. Этот результат показывает, что при
малых кс интенсивность рассеяния в зеркальном направлении
определяется только среднеквадратичной высотой неровностей,
независимо от того, фрактальная поверхность или нет.
Особенности рассеяния плоской волны. На рис. 4.20 в
логарифмическом масштабе изображены индикатрисы рассеяния,
рассчитанные по формулам (4.139) и (4.143) при Ъ = = 2е/3, N= 6 и разных
фрактальных размерностях. Плоская волна падает слева под углом
6, = 30°. Величина а = 0,05А,, размер площадки 2L = 40А,. Данные
227
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
рис. 4.20 получены при усреднении 10 реализаций с разными
значениями случайных фаз ср для £(х). Заметим, что индикатрисы
рассеяния рассчитывались в полярной системе координат и разметка на
рис. 4.20 дает шкалу g по радиальным направлениям в децибелах под
произвольным уровнем.
Рис. 4.20. Индикатрисы рассеяния неровных фрактальных поверхностей
при разных размерностях D [212]
Характеристики рассеяния при D= 1,05 (рис. 4.20,я), когда
неровности фрактальной поверхности пологие и поверхность почти
синусоидальная, показывают, что основная доля энергии
рассеивается в зеркальном направлении. Два боковых лепестка (по одному
на каждом направлении от зеркального) образуются из-за брэггов-
ского рассеяния синусоидой и представляют собой результат
первого порядка дифракции. С увеличением неровностей при D = 1,3
(рис. 4.20,6) и D = 1,5 (рис. 4.20,в) число боковых лепестков и их
интенсивность возрастают. Случай D = 1,95 (см. рис. 4.19) здесь не
рассматривается, так как он выходит за рамки применимости при-
228
4.7. Индикатрисы рассеяния фрактальных поверхностей в приближении Кирхгофа
ближения Кирхгофа. Нулевые значения g возникают из-за
присутствия функции sine в уравнении (4.143).
Ясно, что характеристики рассеяния имеют боковые лепестки
вблизи направления зеркального рассеяния при низких
фрактальных значениях размерности, когда высокие пространственные
частоты подавлены. Угловой диапазон боковых лепестков
расширяется с увеличением Д когда высокие пространственные частоты
играют существенную роль. Физически это объясняется условиями
рассеяния Брегга, как показано на рис. 4.21.
Рис. 4.21. Концепция сохранения момента на основе условий Брэгга,
использованная в механизме рассеяния [212]
Фрактальная функция (4.129) является результатом
суммирования Апериодических функций. Радиоволна действует как
измерительная линейка, выделяя пространственные частоты посредством
брэгговских условий. В общем случае для брэгговского рассеяния
i
где ksc - волновой вектор в направлении рассеяния; к — волновой
вектор в направлении зеркального рассеяния; Р,- -
пространственные волновые векторы структурных гармоник; mi - целые числа.
Для фрактальной функции (4.129) имеем ^1 = Kb?. Таким
образом, падающая волна будет взаимодействовать с различными гар-
229
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
мониками рассеивающей структуры. Направление рассеяния
каждого лепестка зависит от пространственной частоты гармоники р, а
интенсивность определяется фрактальной размерностью поверхности Д
которая регулирует амплитуду каждой гармоники. Высшие
пространственные частоты как бы связывают угловое распределение
рассеяния с большим отклонением от зеркального направления. Более
высокие фрактальные размерности стремятся к обеспечению
равномерных вкладов для различных пространственных частот, и
наоборот. Это означает, что фрактальная размерность неровной
поверхности может быть оценена из характеристик рассеяния.
Рассеяние волн ограниченной фрактальной площадью. Изменение
характеристик рассеяния при облучении поверхностей различных
размеров представляет интерес в задачах радиолокации и
дистанционного зондирования. На рис. 4.22 представлены индикатрисы
рассеяния при облучении площадок со сторонами 2,5Х, 10А,, 40А,, 160А,
и фрактальной размерностью D = 1,5. Остальные параметры
поверхности такие же, как для рис. 4.20.
Рис. 4.22. Индикатрисы рассеяния конечных фрактальных поверхностей
с D = 1,5 и разными линейными размерами сторон [212]
230
4.7. Индикатрисы рассеяния фрактальных поверхностей в приближении Кирхгофа
Размер площадки определяет ширину индикатрис рассеяния, что
очевидно из рис. 4.22. Для случая рассеяния фрактальной
поверхностью не существует качественного изменения, если размеры
площадки больше основного пространственного периода А0 = 2к/К = 10А,,
как на рис. 4.22. Чем меньше размер площадки, тем меньше
информации о неровностях будут давать характеристики рассеяния.
Заметим, что для малых площадок необходимо учитывать краевые
эффекты.
Необходимо отметить, что для рис. 4.20, в результаты получены
после усреднения 10 реализаций, а для рис. 4.22, в использовалась
только одна реализация. Эти рисунки мало чем отличаются друг от
друга, т. е. рассеяние в большей степени зависит от амплитуд
гармоник, чем от их фаз. Данный результат типичен для волнового
взаимодействия с почти периодическими структурами [211].
Для установления связи фрактальной размерности
поверхности с интенсивностью боковых лепестков обратимся снова к рис. 4.20
при 0j = 30—90°. На рис. 4.23 представлены зависимости
коэффициентов рассеяния от аргумента sin [(6^ - 30°)/2] при фрактальной раз-
Рис. 4.23. Зависимости коэффициентов рассеяния
от аргумента sin [(05 - 30°)/2] дБ при разных значениях
фрактальной размерности поверхности [212]
231
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
мерности D = 1,05 (a), D = 1,3 (б), D = 1,5 (в), D = 1,7 (г). Здесь же
нанесены две огибающие. Основная огибающая (прямая 1) с
наклоном (—1) обусловлена конечным размером площадок и связывает
основной лепесток с самым крайним боковым. Ее наклон всегда
почти постоянен при изменении фрактальной размерности.
Огибающая, связывающая боковые лепестки (прямая 2 на рис. 4.23),
определяется пространственными гармониками, и ее наклон
монотонно изменяется с изменением фрактальной размерности.
Наклоны дифрагированной огибающей на рис. 4.23 равны —2,5; -1,92;
-1,22; -0,72 соответственно для D= 1,05; 1,3; 1,5; 1,7. Это
означает, что для исследуемых непрерывных диапазонно-ограниченных
фрактальных поверхностей величина наклона изменяется
примерно как 2,7 (2 - В). Полученный результат подобен случаю
рассеяния волн на фрактальных агрегатах [218], для которого найдено, что
величина наклона равна (6 - D'), где D' = D + 1. Разница этих двух
выражений объясняется видом моделей: в работе [212] - это
непрерывная фрактальная модель, в [218] - модель дискретных рассеива-
телей. Очень важно, что наклоны дифракционных пиков позволяют
дистанционно измерить неровности или фрактальные размерности
поверхности.
Из полученных в [212] результатов можно сделать следующие
выводы.
Во-первых, интенсивность рассеяния в зеркальном направлении
зависит только от среднеквадратичной высоты неровностей. Это
соответствует результатам, полученным классическими методами.
Во-вторых, фрактальная размерность, определяющая
неровности поверхности, контролирует распределение энергии среди
лепестков диаграммы рассеяния.
В-третьих, от параметра пространственно-частотного
масштабирования b зависит угловое распределение лепестков в индикатрисе
рассеяния.
В-четвертых, на практике размер облучаемой площадки должен
быть по крайней мере в 2 раза больше основного периода
структуры поверхности, чтобы информация о ее фрактальных параметрах
содержалась в характеристиках рассеяния.
В-пятых, наклон дифракционных пиков через свою огибающую
дает количественную меру поверхностных неровностей и
фрактальной размерности.
232
4.8. Рассеяние импульсов фрактальной поверхностью
4.8. Рассеяние импульсов фрактальной поверхностью
Проблема взаимодействия зондирующего сигнала с земной
поверхностью является одной из центральных в радиолокации и
дистанционном зондировании. Специфической особенностью
отражения модулированных волн протяженной, статистически неровной
поверхностью является искажение закона их модуляции, что
довольно хорошо исследовано (см., например, [184]).
Постановка задачи. Исключительно интересным с точки зрения
обнаружения новых эффектов может быть рассмотрение вопросов
рассеяния модулированной волны фрактальной поверхностью.
Дальнейшее изложение проблемы базируется на результатах работы [219],
единственной по этому направлению. Фрактальная рассеивающая
поверхность моделировалась как фрактал размерностью в
диапазоне 2—3. Это означает, что неровности настолько экстремальны, что
конечная область поверхности имеет бесконечную площадь, но
нулевой объем. Далее будем обозначать размерность как D + 1. При
этом D — размерность фрактальной функции, полученной сечением
рассеивающей поверхности вдоль линии, т. е. 1 < D< 2. Пример
такой функции приведен в [128].
В [188] для волн, падающих на фрактальный экран,
рассматривался новый режим волновой теории, характеризующийся тем, что
приближение геометрической оптики никогда не выполняется (см.
разд. 4.1). Для фракталов коротковолновый предел характеризуется
D-зависимыми волновыми свойствами, т.е. скейлингом.
Далее будем рассматривать рассеивающую поверхность в виде
ансамбля гауссовых фрактальных функций h{R) с нулевым средним
<А> = 0, дисперсией <А2> = Н2 и структурной функцией
h(RQ+R)-h(RQ)]2yA(R).
При этом ограничимся исследованием рассеяния импульсов на
изотропных поверхностях, когда А зависит только от R = (X2 +У2)1/2,
и рифленых, для которых А — функция только X. В случае (D + 1)
фрактальной поверхности
\ L2D-2\X\4~2D
A(^o^|z22)_2i{4_2/ (4.146)
для рифленой и изотропной поверхностей соответственно (см. (4.6)).
233
[
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
В (4.146) значение фрактальной размерности лежит в пределах
1 < D< 2; L — топотеза, определяемая соотношением (4.5).
Доказательство того, что ансамбли гауссовых функций, подчиняющиеся
условию (4.146), действительно моделируют рассеивающие
поверхности с сечениями, имеющими фрактальную размерность Д
приведено в [188]. Крупномасштабные неровности поверхности
(«география») А влияют на поведение A(Jf) при R -> <*> , а именно
A(R) -> 2Н2 при R -^ оо или | X |-> оо . Простой моделью,
включающей эти ограничения, в изотропном случае является
Д(Л) = 2Я2 [1 - exp (-LW-2R*-2D / 2Н2)] (4.147)
с радиусом корреляции /, описывающим внешний масштаб
неровностей, равным
l = L(H/L)l/V-D\ (4.148)
Рассмотрим случай Н » L , так что /» L; масштабы влияния
фрактальности и «географии» четко разделяются. Специальный
случай D =1,5 относится к броуновскому фракталу. При этом (4.146)
предполагает линейность А при малых R или X, подобно
приращениям координаты h броуновской частицы. В предельном случае
D -> 1 (гладкая поверхность) топотеза L исчезает из (4.146), и для
изотропной поверхности имеем
где ((у2)) — среднеквадратичное значение тангенса угла наклона
неровностей. Тогда соотношения (4.147) и (4.148) преобразуются
следующим образом:
ЦК) = 2#2[1 -ехр(-<у2>Я2 /2Я2)], / = Н/Ш^
1 /9
при допущении ((у2)) »1 и /»/,.
Геометрия дифракционной задачи приведена на рис. 4.24.
Радиолокатор, расположенный в точке S на высоте Z относительно
средней плоскости R = (X, Y), излучает сферическую волну ф(г, t)
вида
234
4.8. Рассеяние импульсов фрактальной поверхностью
Z4-CX/2
Рис. 4.24. Геометрия рассеяния импульсного сигнала фрактальной
неровной поверхностью [219]
Kr,t) = F(t-r/c)/r.
(4.149)
Временная зависимость в формуле (4.149) определяется
квазимонохроматической функцией F(t) = ехр(/а>?)в(0, где со — несущая
угловая частота; a(t) — огибающая гауссова импульса
a(t) = a0exp(-c2t2/o2)
(4.150)
с двойной среднеквадратичной пространственной длительностью
импульса а, определяемой как [220]:
о = 2с
(
]dtt2a2(t) \dta\i)
Л1/2
Квазимонохроматичность обеспечивается малостью длины
волны Х«:а.
235
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Волновая функция. Рассмотрим статистику волновой функции
отраженного сигнала Ч^т) и зависимость интенсивности 7(т) = (|4/(т)|2)
как функцию временной задержки т относительного среднего
времени t = 2Z/c. Используем принцип Гюйгенса-Кирхгофа, при
котором \|/ выражается суперпозицией элементарных волн от
вторичных источников на поверхности; при этом пренебрежем
многократным рассеянием и затенениями. При рассмотрении фрактальной
поверхности, состоящей из крайне неровных обрывов с бесконечным
среднеквадратичным наклоном, необходимо учитывать, что
многократное рассеяние и затенения непременно присутствуют до тех пор,
пока мы не перейдем в область почти вертикального зондирования.
Поэтому рассмотрим параксиальное приближение для дифракции
Френеля, когда выражение для волновой функции [220] принимает
вид
*>-skM»^-£) (4Ш)
где дифференцирование функции F проводится по ее аргументу.
Формула (4.151) верна при допущении, что для временных
задержек т угол рассеяния 0 (см. рис. 4.24), определяемый как cos 6 =
= Z/(Z+ ст/2), достаточно мал, а именно
eL±(£L]Li. (4.152)
4! 24[2ZJ
Для плоской поверхности с А = 0 вычисление (4.151) дает
\|/(т) = -F(x)/2Z, что соответствует ожидаемому результату,
описывающему отражение с обратным знаком волны вида (4.149) от
изображения точки S на расстоянии 2Z В работе [188] также показано,
что если топотезы достаточно малы (это предполагает выполнение
условия (4.152)), то наибольшее количество энергии рассеивается
параксиально.
Интенсивность рассеяния. Вследствие условия
квазимонохроматичности F(t) ~ i(ueitiyia(t), интенсивность отраженного сигнала
выражается как
236
4.8. Рассеяние импульсов фрактальной поверхностью
X а
( 2h{Rx) Щ\ ( 2Щ) ЩЛ
т + -
cZ
т + -
ехр[-2/А;(А(Л1)-Л(Л2))]\х
cZ
Обозначим if = R{ - R2 и, используя (4.2), получим
г к *
(4.153)
/(*) =
2nZ2
К К
С CZ
xjdRtxp(-2k2A(R))txp(-2R^R\
(4.154)
Подробно обсудим условия, которые должны выполняться для
аппроксимации формулы (4.154). В (4.153) пренебрегаем
следующими элементами: в последней экспоненте Тх = kR2/Z, во втором
амплитудном сомножителе Т2 = R2/(cZ) и Тъ - 2RX • R/(cZ). Значение R
ограничено условием k2A(R)<l. Используя последнее неравенство,
с учетом (4.148) получаем R< L/ (kL){^{~D)\ Tx удовлетворяет
неравенству 7j < L/Z(kL)D^2'D), которое пренебрежимо мало для зоны
Франгоуфера при Z -> °о . Временные интервалы Т2 и Т3
необходимо брать относительно времени с/с, за которое амплитудный
фактор значительно изменяется.
Для Т2имеем cT2/c = R2/(Zc)<L2/(Zc(kL)2^2-^). Это
неравенство пренебрежимо мало для зоны Франгоуфера и для длинных
импульсов (o/L »1). Для Т3 должно выполняться условие
сТ3/о = 2R{R/(Zc) < 2LR{/(Zc(kL)^2-^).
Значение R{ ограничено условием параксиальности (4.152), так как
tg0 = Rx/Z, а также R{ < Z. Поэтому сТ^с пренебрежимо мало для
длинных импульсов.
237
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Для дальнейшего вычисления интеграла (4.154) перейдем к
полярным координатам и определим новую переменную т' = Щ /(cZ).
Тогда
I(x) = ncZ
Л*И*-*-т)"
(4.155)
2nZ2
xjdRtxp(-2k2A(R))J0{2kR^fciyz}9
где /0 - функция Бесселя нулевого порядка первого рода.
Примеры. Для гауссовой поверхности операция усреднения в
(4.155) определяется соотношением
т-т + —
V С
1
'л/ТкН
\dha7
, 2А
т-т +—
с
ехр(-А2/2#2),
и с учетом формы импульса (4.150) получаем
2А
-/i2
т-т +— \) = %—ехР
\Ш
( 2c2t2]
(4.156)
где ох = (а2 + 16Я2) - пространственная длина отраженного
импульса с учетом неровностей поверхности.
Формулы (4.154) и (4.155) дают правильную плоскозеркальную
трактовку для интенсивности отраженного сигнала при А = А = 0.
Более того, даже для неплоской поверхности эти формулы дают для
общей мощности отраженного сигнала такой результат:
]dxI(x) = -±T]dxa2(x)
4Z2_
Данное равенство характеризует факт, что для усредненной
неровной поверхности в параксиальном приближении обратное
отражение имеет такую же общую мощность, как и от плоской
поверхности. Конечно, распределение этой мощности будет зависеть от
природы поверхностных неровностей, что будет показано далее.
Для изотропных поверхностей А зависит только от R, и формула
(4.155) принимает вид
238
4.8. Рассеяние импульсов фрактальной поверхностью
I(x) = j£f\ м(аг ( х - %' + —1\ J dRR exp (-2k2A(R))J0 fekRjrfJz}
(4.157)
Для рифленой поверхности А зависит только от X, и тогда из
формулы (4.155) получаем
ад=Щ^И,-/+т))реч>(-2*гдт'><
xcos{2^V^72r}. (4Л58>
При нахождении этих интегралов важным упрощением
является замена A(J?) ее фрактально-ограниченной формой (4.146). В этом
случае получаем чисто фрактальное описание, независимое от
неровностей, соответствующих понятию «география», не считая
тривиальной зависимости сх от Я в (4.156). На основе модели (4.147)
нетрудно показать, что эта операция возможна при Нк> 1.
Форма отраженного сигнала. Результат (4.155) и частные случаи
(4.157) и (4.158) верны для гладкой и фрактальной поверхностей. Для
выделения дифрактальных характеристик (см. разд. 4.1) и
определения формы «хвоста» отраженного сигнала необходимо рассмотреть
положительные времена задержки т, которые превышают
ограниченную неровностями импульсную длительность ах/с (4.156). Тогда
переменная интегрирования т' будет изменяться до Gj/c с каждой
стороны т.
В этом диапазоне аргумент косинуса в формуле (4.158) для
рифленой поверхности варьирует в пределах
5(2kX4cz7z) = kX(2cl /с)фхуг «IkXfiJl.
Но Хъ свою очередь ограничена экспоненциальным
разложением в (4.158), как показано ранее, и это приводит к неравенству
8(2^V^7Z)<<2[(^(^1)/(2-^Z/a1)1/2]"1,
которое мало в коротковолновом приближении и в дальней зоне.
Усредняемая функция в (4.158) будет локализована около значения
т = т', и тогда для рифленой поверхности
239
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
оо
xj dX exp (-2k2 A(X))cos {ikXj^Tz).
(4.159)
Для изотропной поверхности (4.157) подобные рассуждения
приводят к соотношению
НА
к2с
ЩЛ]
\
Vai 2Z31
xjdRRexp(-2k^R))J0{2kRjcxlz].
(4.160)
Полученные интегралы необходимо вычислить для больших т.
Рассмотрим сначала рифленую поверхность. Второй интеграл в
(4.159) можно представить в виде
с параметром
Q(p) = jdu exp (-2u*-2D) cos(2up)
p = (cT/Zy/2/(kL)(D-»/V-Dl
(4.161)
После деформации контура интегрирования получаем решение в
виде ряда, сходящегося при D > 1,5 и асимптотического для D< 1,5:
1 ^ (-ir'sin[K/i(2-J))][/<4-2J))]!2^-3)
Q(P)=2Jh п^Щ • <4Л62>
Для больших значений параметра р ряд (4.162)
аппроксимируется первым членом, и форма «хвоста» отраженного сигнала
описывается выражением
/(*)->
2kZ3
/*И'*Т
2h\]
(Z\
усх;
?-D
240
4.8. Рассеяние импульсов фрактальной поверхностью
x(kL)2D-2 sin [п(2 - D)](4 - 2D)\ 22D~\ (4.163)
Из формулы (4.163) следует, что для рифленой поверхности
интенсивность в «хвосте» отраженного сигнала спадает, как
/(т)~1/т3-я.
(4.164)
При определении формы «хвоста» отраженного сигнала важно
избежать конфликта между условием р »1, от которого зависит
результат (4.163), и параксиальным приближением (4.152), согласно
которому сх не должно превышать Z Из формулы (4.161) следует, что
указанное расхождение удается преодолеть для слабофрактального
случая, когда
A;Z«1.
(4.165)
Данное условие, полученное здесь для параксиальных дифрак-
талов [219], было выведено ранее [188] для монохроматического
случая.
Чтобы оценить важность результатов (4.163) и (4.164), в работе
[219] их сравнивают со случаем формы «хвоста» сигнала,
отраженного гладкой рифленой поверхность (D - 1). Когда D->1, правые
части уравнений (4.162) и (4.163) стремятся к нулю. Однако
интеграл (4.159) с учетом А(Х),„ п -> (у2)Х2 вычисляется точно:
/(*)-*
4Z3«y2»1/2
j dtla
/ +
2h
V/2
2ncx
xexp
сх
{ 2Z(y2)
(4.166)
Интенсивность сигнала, отраженного сглаженной случайной
рифленой поверхностью, спадает по экспоненциальному закону.
Заметим, что этот результат не зависит от длины волны, что
иллюстрирует хорошо известный факт: коротковолновый предел при
отражении от гладких случайных поверхностей задается
геометрической оптикой. Наоборот, когда волновое число к увеличивается для
дифрактала, то происходит возрастание интенсивности (4.163) до тех
пор, пока не нарушится условие (4.165) и отражение импульса
больше не будет описываться параксиальным приближением.
241
Глава 4. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ ВОЛН ФРАКТАЛЬНОЙ ...
Теперь рассмотрим изотропную рассеивающую поверхность. Из
формулы (4.157) можно получить
S(p) = jduuexp(-2u*-2D)J0(2up) =
о
~ (-1)"*1 sin[wt(2-Z))]{[ n(2-D)\ f}2"
WZx
nlpn(4-2D)
(4.167)
что аналогично выражениям (4.161) и (4.162).
Замена ряда его первым членом при больших значениях р
позволяет определить форму «хвоста» отраженного сигнала:
№ =
2kZ3
14!(,+f
\zi~D
vcry
(Щ
2D-2,
xsin[7c(2-£)][(2-i))!]2
(4.168)
Полученное соотношение идентично уравнению (4.163), за
исключением отдельных коэффициентов, и также удовлетворяет
степенному закону (4.164).
Для сглаженной случайной поверхности интеграл (4.160) с
учетом A(i?)L 0->(у2)/?2 при Z>->1 вычисляется точно по формуле
/«=
S(f)Z3
jdt(ai\t + 2h
exp
ex
2{f)Z
(4.169)
Опять, как и в формуле (4.166), интенсивность отраженного
сигнала в «хвосте» спадает по экспоненциальному закону, но в (4.169)
нет добавочного сомножителя т~1/2.
Выводы. Таким образом, средняя мощность 1(х) сигнала,
рассеянного фрактальной случайной поверхностью, имеет форму,
значительно отличающуюся от формы сигнала, рассеянного
классической случайной поверхностью (см., например, [184, 221-229]). Более
того, в слабофрактальном случае (4.165) и параксиальном
приближении форма «хвоста» отраженного сигнала описывается степенным
242
4.8. Рассеяние импульсов фрактальной поверхностью
законом (4.164), зависящим от фрактальной размерности (D + 1)
поверхности, и инвариантна ее типу.
В сочетании с данными экспериментов по дистанционному
зондированию рассмотренная теория может быть использована для
нахождения фрактальных размерностей неровных поверхностей
естественного происхождения, которые (см. гл. 3) хорошо описываются
случайными фракталами. При этом следует также учитывать
эффекты поляризации, изменяющиеся удельные ЭПР ландшафтов [184,
230, 231] и расширенный угловой диапазон измерений.
Ранее задачи дифракции волн на статистически неровной
поверхности были преимущественно ориентированы на неровности одного
масштаба [208]. Затем было осознано, что многомасштабные
поверхности дают более адекватные модели [183]. Можно утверждать, что
физическое содержание дифракционной теории, включающей
многомасштабные поверхности, становится более четким при
фрактальном подходе и выделении значения параметра D как размерности.
Также необходимо отметить то, что учет фрактальности, по нашим
расчетам, значительно сближает теоретические и
экспериментальные угловые и частотные зависимости удельных ЭПР. Данный факт
часто интерпретировался (и продолжает интерпретироваться) как, в
основном, чисто инструментальная погрешность.
Глава 5
АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ
ТУРБУЛЕНТНОСТИ, ГИДРОМЕТЕОРОВ,
МОЛНИЙ И АТМОСФЕРНЫХ АЭРОЗОЛЕЙ
5.1. Фрактальность турбулентности
Сценарии перехода к хаосу. Проблема турбулентности с полным
основанием считается одной из главных в современной
классической физике. Условие перехода от регулярного ламинарного
движения к турбулентному по существу есть условие возникновения сто-
хастичности, или перемешивания, в фазовом пространстве.
Признаком перемешивания является быстрое затухание корреляционных
функций при больших временах, которое в физике известно как
условие расщепления временных корреляций. Признаком
перемешивания служит и непрерывность спектральных плотностей.
Следует иметь в виду, что возникновение хаотической
эволюции во времени еще не означает возникновения пространственного
хаоса. Описание стохастизации пространственной структуры более
сложно, так как требует расчета функций и от времени, и от
пространственных координат. При этом в пространственном хаосе
могут зарождаться упорядоченные структуры с относительно
большими временами жизни, так называемые когерентные структуры.
Пока не существует полного математического описания
турбулентных потоков. Подходы на основе появившихся
принципиально новых идей (автомодельность или скейлинг, странные
аттракторы, ренорм-групповые методы, сценарии стохастичности,
фракталы) вселяют оптимизм и оказались плодотворными при изучении
общей проблемы турбулентности [21, 23, 24, 29, 97, 127, 148, 232-
243].
Перечислим некоторые наиболее известные гипотезы о
последовательностях бифуркаций, называемых сценариями
самозарождения и развития хаоса. Для всех этих сценариев, или путей,
обнаружено их удивительное универсальное поведение, напоминающее
универсальность, найденную для равновесных фазовых переходов
244
5.1. Фронтальность турбулентности
второго рода. Здесь понятие универсальности означает
существование таких основных свойств системы (критические показатели
вблизи перехода к хаосу), которые зависят только от глобальных свойств
системы (например, размерности).
Еще в 1940-х годах Хопф [244] рассмотрел бифуркацию,
соответствующую рождению предельного цикла из неподвижной точки.
При этом в систему была введена новая основная частота. В 1944 г.
Ландау предложил путь перехода к турбулентности [245], по
которому хаотическое состояние достигается бесконечной
последовательностью неустойчивостей Хопфа, в результате которых появляется все
больше основных несоизмеримых частот. Спектр мощности здесь
всегда остается дискретным.
Переход к хаосу, значительно более короткий, чем у Ландау, был
предложен в 1971 г. Рюэлем и Такенсом [246]. Было показано, что
даже после двух бифуркаций Хопфа регулярное движение может
стать неустойчивым и перейти в хаотическое движение на странном
аттракторе. При этом считают, что хаотическое движение
возможно только после двух бифуркаций Хопфа, когда траектория может
выйти в дополнительные измерения, потому что двухпериодическое
движение соответствует траектории на торе (двумерной трубке), на
котором появление хаоса запрещается теоремой Пуанкаре-Бендик-
ссона [24]. Строгое доказательство этой теоремы дано в [247].
Однако после двух бифуркаций Хопфа появление странного
аттрактора не только возможно, но и практически неизбежно [248]. Данная
модель перехода к турбулентности носит название сценария Рюэля-
Такенса-Ньюхауза. По сценарию Фейгенбаума (1978 г.) [249]
переход к хаосу происходит в результате бесконечной
последовательности бифуркаций удвоения периода. Аналогия между фейнгенбаумов-
ским переходом к хаосу и равновесными фазовыми переходами
второго рода на основе ренорм-групповой теории предложена в [24].
Переход к хаосу через перемежаемость был впервые исследован
Помо и Манневилем [250, 251] в 1979 г. Перемежаемость означает,
что сигнал, развивающийся во времени регулярно (ламинарные
окна), прерывается статистически распределенными
нерегулярными всплесками. Среднее число этих всплесков нарастает при
увеличении внешнего управляющего параметра до тех пор, пока
движение не станет полностью хаотическим. Переход к хаосу через
перемежаемость обладает универсальными свойствами и представляет
собой один из редких примеров точного решения линеаризованных
245
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
ренорм-групповых уравнений. В [252] показана возможность
объяснения перемежаемости специальным видом отображения
Пуанкаре. Далее ограничимся лишь некоторыми наглядными результатами,
относящимися к непосредственному проявлению фрактальности в
турбулентности.
Методики измерений турбулентности. Отметим, что» при
турбулентных потоках фрактальными могут быть не только странные
аттракторы в фазовых пространствах, но также многие изоповерхнос-
ти, разделяющие турбулентные и нетурбулентные области, или же
изоповерхности значений физических характеристик
турбулентности. Асимптотически фрактальная структура будет наблюдаться [253,
254] в пределах от внутреннего Ц до внешнего /0 масштабов
турбулентности. Внутренний масштаб определяется формулой
Л = /0(Ке)-^, (5.1)
где Re = C/L/v — число Рейнольдса; Uh L — характерные масштабы
скорости и длины в рассматриваемом течении; v —кинематический
коэффициент вязкости жидкости.
При меньших масштабах (е < Ц) турбулентные неоднородности
поля скорости сглаживаются под действием молекулярной
вязкости. Непосредственно измерить фрактальные размерности D <3) изо-
поверхностей трудно. Чаще используют процедуры, основанные на
применении плоских сечений изоповерхностей с более низкими
значениями размерностей подпространств. Пусть Р является секущей
плоскостью турбулентного течения F в трехмерном пространстве.
Тогда для границы, определяемой операцией пересечения Pf)F,
фрактальная размерность
Д(2)=£(3)_1. (5.2)
Еще проще фиксировать сечения турбулентного объема прямой
линией А и определять фрактальную размерность /)(1) полученного
множествами^ точек, равную
2>0> =2)0)-2. (5.3)
Данные методы дают правильный результат в условиях
однородности и изотропности. При отсутствии таких свойств необходимо
246
5.1. Фракталъностъ турбулентности
ориентироваться на локальное определение фрактальности [41].
Заметим, что в общем случае можно ввести понятие коразмерности
H = D'-D«\ (5.4)
где D W - фрактальная размерность поверхности раздела объекта,
вложенного в пространство размерностью IY.
На практике плоские сечения поверхности между турбулентной
и нетурбулентной областями визуализируют, т.е. подкрашивают
турбулентную область краской (или дымом) или подсвечивают тонкий
плоский слой жидкости, вмещающий интересующее нас сечение.
Толщина слоя должна быть меньше, чем т\ из формулы (5.1). После
получения фотографии подкрашенного слоя ее оцифровывают с
шагом менее г) и квантуют по интенсивности. При выставлении
порога имеем итоговое цифровое изображение, где, например, каждая
темная точка принадлежит к турбулентной области, а каждая
светлая — к нетурбулентной.
Затем каждую из точек изображения покрываем окружностью
радиуса £. Всякий раз, когда окружность вокруг точки пересекает
границу, полученную интерполяцией между соседними светлыми и
темными точками, рассматриваемая точка считается граничной в
пределах £. Подсчитав число всех граничных точек N (г) при
изменении £, по наклону графика функции
Щг)~г2-°(2) (5.5)
в билогарифмических координатах можно определить значение
фрактальной размерности. Погрешность измерения D
пропорциональна величине гн, где Н- коразмерность (5.4).
На рис. 5.1 приведена логарифмическая зависимость (5.5) для
поперечного сечения подкрашенного дымом пограничного слоя
толщиной 10 см и с U„ =2,5 м/с. На врезке показаны значения
наклона, или Я, в соответствии с которыми фрактальная размерность
д(2) = 2_#= = 2- 0,63 = 1,37. Таким образом, D <3> = 2,37.
Нижний предел интервала постоянного наклона сравним с внутренним
масштабом Колмогорова. Верхняя точка отсечки постоянного
наклона лежит в области /q/6, где /0 - поперечный масштаб турбулентных
неоднородностей. Однако последний результат следует оценивать
247
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
logtf(e)0
-0,1
-0,21
-0,3
-0,4
-0,5
-0,6
л
и
г
/
•г-
10'
{ (
(
/о
>,7
i
>,6
0,j
Л Л
\
с
с
с
_|
>,2
U
0
L
н
t
о
-♦•
1С
Q
_£
WW™
£0,63
•
• 1
i
Vj
-J
й
0,2 0,4 0,6 0,4 1 1,2 1,4"]
мм
-0,7
-0,8
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 log б
Рис. 5.1. Логарифмическая зависимость N(e) = e3~d для поперечного сечения
пограничного слоя толщиной 10 см при UM = 2,5 м/с [255]
критически, так как для этой области необходима обработка
больших масштабов.
Влияние величины порога на значение наклона для
рассмотренного случая показано на рис. 5.2. Для пороговых значений в
относительных единицах 3000, 3500 и 4000 (см. соответствующие кривые)
погрешность определения фрактальной размерности турбулентного
слоя меняется незначительно. Относительная яркость цифрового
изображения составляла от 0 (черный фрагмент) до 12 000 (белый
фрагмент). Аналогичные данные для поперечного сечения
льющегося в затопленное пространство вертикального потока воды (Re =
= 2500, диаметр 5 мм), подкрашенного полистиреновыми
микросферами, дают значение коразмерности #= 3 - ZK3) = 0,67 + 15%. В
эксперименте часть потока в развитой области на расстоянии 15 см
рассекалась тонким лучом света и фотографировалась. Область
постоянного наклона лежала в пределах от т\ до /0/3. В [255] также
получены оценки 2)(3) = 2,4 ± 10% для фрактальной размерности
границы турбулентного пограничного слоя с 1/^ = 12 м/с на разных
248
5.1. Фрактальность турбулентности
\ '''
1 ^У
1 >*
U*
0
•
-3500
^У
3000
1
•
•
у
#х*—
о
о(
•
У
-4000
^У
logW(e) о
~0,2
-0,4
-0,6
-0,8
-1
-1,2
0 0,2 0,4 0,6 0,8 1 1,2 1,4
logs
Рис. 5.2. Влияние величины порога в относительных единицах
на значение наклона [255]
расстояниях от стенки z (0,75 < z < 1,0) и z = y/b .В опытах
применялся метод пересечения прямой линией (быстро движущимся
термоанемометром) и использовалась гапотеза «замороженной»
турбулентности.
Сценарий «порядок-фракталы-хаос». Суммарные данные о
фрактальной размерности поверхностей раздела турбулентных
течений представлены в табл. 5.1. Полученные оценки Z>(3>
практически одинаковы, что объясняется их сильной зависимостью от
турбулентных вихрей из интервала с универсальным самоподобием [237].
Отметим, что в [256] для поверхностей пузырьков воздуха, инъек-
Таблица 5.1
Фрактальная размерность поверхности, разделяющей турбулентную и
нетурбулентную области [255]
Тип турбулентных
течений
Пограничный слой
Осесимметричный слой
Плоский след
Слой перемешивания
Фрактальная размерность |
Сечение плоскостью
2,38
2,33
—
—
Сечение линией
2,40
2,32
2,37
2,40
249
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
тированных в вязкую жидкость, в ячейке Хеле-Шоу получено
значение/)<3>- 1 = 1,37.
Авторами [255] предлагается следующее объяснение полученных
значений D. Изоповерхность поля скорости с истинной площадью
S = S0(r\/l0)2~D рассматривается как слой толщиной r\ = X(Rex)~1/2 с
типичным поперечным градиентом скорости и / т\ или типичной
скоростью деформации и /X , где и - среднеквадратичное значение
Г 2Т1/2
пульсаций скорости; X = и (Эй / Эх) — тейлоровский
микромасштаб турбулентности; Rex =u'X/v = (л/^0)~2/3 = (Re)1/2 • Поэтому
вязкий поток импульса через изоповерхность записывается в виде
т/р -(v«7Tl)^ = P^2(Re)^"7/3)' (5'6)
где р ~ (u'/U)2; U- типичный перепад скоростей в потоке в целом.
Для турбулентного потока импульса надо произвести замену
vw'/Л на Uu , где иц =u'(Rea)~l/2 - скорость движения изоповерх-
ности, равная микромасштабу скорости. При этом получается
результат, аналогичный (5.6), но со значением $~и'/U. Для выполнения
условия инвариантности потока импульса через изоповерхности
относительно Re (т.е. подобие по числу Рейнольдса) необходимо
положить D = 7/3, что близко к эмпирическим оценкам. Для потока
пассивной примеси соответствующее выражение приведено в [237].
При измерении размерности изоповерхностей продольной
скорости u(t) используется также метод линейного сечения на уровне
и = и1с получением канторовой границы, который описан ранее. Для
изоповерхностей продольной скорости в пограничном слое
толщиной 8 = 4 см и U„ = 20 м/с результаты эксперимента представлены
на рис. 5.3. Размерность D =Д становится наибольшей при их -и,
где и — средняя скорость. Распределение и в пограничном слое
показано непрерывной линией. Значения D уменьшаются при
возрастании | их - и |, когда уменьшается вероятность события ^ « и.
Масштаб абсцисс для каждого из фрагментов D(3) тот же, что для
средней скорости. Значения Д(3) возрастают от 2,5 до 3 с ростом у /8 от
0 до 1,2 при соответствующем увеличении доли нетурбулентных
областей и уменьшении разброса и относительно и(у).
250
5.1. Фрактальность турбулентности
0,4 0,6 0,8 1,0
Рис. 5.3. Значения фрактальной размерности D изоповерхностей продольной
скорости в пограничном турбулентном слое от скорости и расстояния
от стенки [255]
При увеличении суммарной длины отрезка измерений Ах
области постоянного наклона становятся все более неопределенными
и исчезают при Ах « 500/0, когда D(1) -> 1. Рассматриваемый эффект
иллюстрируется в [255] для Дх = 50/0-430/0. На малых длинах Ах на
кривой N{z) всегда присутствуют области постоянного наклона в
пределах интересующих нас масштабов. Для больших сегментов Ах
области постоянного наклона существуют только вне пределов
интересующих нас масштабов. Тогда ZK3) = 3. При этом распределение
принимает форму, характерную для случайного процесса. Поэтому
изоповерхности скорости физически фрактальны на масштабах около
50 L Общий вывод: фракталы являются как бы промежуточным зве-
251
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
ном между совершенным порядком и полным хаосом. Иначе
говоря, короткопериодная статистическая упорядоченность
турбулентности через фрактальное самоподобие переходит в длиннопериод-
ныйхаос [237].
Фрактальное описание турбулентности применимо и к полю
скоростей диссипации турбулентной энергии, сосредоточенной, в
основном, в объемах минимального масштаба Л. Пусть D -
фрактальная размерность поля диссипации. После оценки
минимального масштаба Ц и определения числа Л^кубиков размера т|
фрактальная размерность D рассчитывается по определению как
Z) = log^/log(/0/Ti) (5.7)
или
N = (l0/i\)D. (5.8)
Так как области диссипации имеют объем (/0/л)3> то общий
объем области активной диссипации пропорционален (l0/r\)D~3-
Поэтому уровень диссипации в общем объеме превышает ее средний
уровень в (/0/т|)3-2) раз. Скорость диссипации турбулентной
энергии пропорциональна (Эй /Эх)2 [237] вследствие локальной
изотропности. Поэтому коэффициент уплощения, определяемый как
будет пропорционален произведению (/0/л)2(3-2)) на объем (10/t\)d~3,
и тогда имеем
K~(l0/4f-D~(Rex)W-»/2. (5.10)
Измерив значения А" и и Rex на основе гипотезы
«замороженной» турбулентности заменив ди/дх на Ьи/Ы , из соотношения
(5.10) можем определить коразмерность (3 - D) и фрактальную
размерность D. По измерениям Мандельброт [257] получил оценку
D= 2,6. На рис. 5.4 представлен сводный график, построенный по
многочисленным данным ряда иностранных источников. Для линии
252
5.1. Фрактальность турбулентности
100
К
10
1 Н
С"*■ив^""Т"^^"-!
f-
н
Г **
ка»°*
L
Г -Rc°'5
г-
1 III lii.l
~н—
** 3*
++А
• ■ 111 iiм
•
• •
****
*"'
| f^—у—у»
£><*& Л
K~RcX 4
-1
*п
' J
10 102 103 104 Re,
Рис. 5.4. Зависимость коэффициента уплощения от числа Rex [255, 258]
К ~ Re£'4 значение D = 2,73. Однако для К ~ Re^15 при малых
значениях Rex (Rex <150) получилось D= 2,9. Это означает, что при
малых числах Рейнольдса поле диссипации имеет меньшую
пятнистость.
Аналогичные доводы показывают, что для поля диссипации
температурных неоднородностей (dT/dt) существуют зависимости
/^(Re^) вида (5.10). На рис. 5.5 показаны сгруппированные
многочисленные экспериментальные данные, описываемые соотношением
^~(Rex)3^)/2. (5.11)
Среднее значение D = 2,6. Таким образом, область поля
диссипации температурных неоднородностей пространственно менее
заполнена, или более перемежающаяся. Подобные аргументы
позволяют сделать вывод, что так называемая гиперплоскость (т.е.
нормализованный шестой момент) величины (dT/dt) подчиняется
закономерности (Re^)^3-^. Экпериментальные данные,
представленные на рис. 5.6, хорошо согласуются с этим предположением при
Rex > 100.
Фрактальную размерность поля диссипации энергии в
турбулентности за решеткой можно оценить методом линейных пересечений.
Процедура измерений аналогична описанной ранее, за исключени-
253
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
* 1
102
10'
10°
г—1 *-Л » I
-, ~ 0-52
F0~Re,
l_l L_l l_l
—i—
—J
l
10 102 103 104 Re, Ю5
Рис. 5.5. Фрактальное поле диссипации температурных неоднородностей [255]
10'
ю h
ю г
Re, Ю
Рис. 5.6. Шестой момент #9 температурной производной в зависимости
от числа Rex [255]
254
5.1. Фрактальность турбулентности
ем того, что переменная и заменяется (du/dt)2. Была обнаружена
существенная зависимость Dot уровня диссипации и2/и2 [255].
Основной график на рис. 5.7 построен для порога, превышающего в 5
раз среднее значение й2, т.е. и2 /и2 = 5. На врезке показана
зависимость фрактальной размерности поля диссипации энергии от
уровней диссипации. Значение D уменьшается от 2,7 до 2,2 с ростом
и2 /и2 от 0 до 10. Области больших значений и2 /и2, как следует из
этих данных, имеют меньшие объемы, но и менее изрезанные
границы.
logtf
-0,5
0,5
1,5
2,5
loge
Рис. 5.7. Фрактальная размерность поля диссипации в турбулентности
за решеткой в зависимости от уровней диссипации [255]
Теория фракталов в описании турбулентности. Кратко
остановимся на некоторых идеях применения фрактальной топологии в
задачах теории турбулентности. В работе [259] разработаны основы
формализма, названного обобщенной масштабной инвариантностью
динамики атмосферы с сильной анизотропией и перемежаемостью, на
основе введения ряда метрик и спектра фрактальной размерности.
Данный формализм можно рассматривать как продолжение работ по
255
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
каскадным процессам. Простые примеры линейной обобщенной
масштабной инвариантности [260] возникают при использовании
кватернионов и применяются для построения в рамках модели
фрактальной суммы импульсов полей, обладающих такой
инвариантностью. Обобщенное понятие масштаба позволяет выделить
мультипликативную группу операторов, действующих на топологическом
пространстве. Можно также ввести анизотропные фрактальные
множества. Для мультипликативных операторов вводится множество
перемежающихся мер, инвариантных относительно таких операторов.
Данная мультипликативная процедура соответствует нелинейному
распаду вихрей на подвихри в турбулентности; при этом поток
энергии остается инвариантным. В данном случае возникает много
размерностей, что соответствует тензорным степеням меры потока
энергии. Существование многих размерностей приводит к
мультипликативному хаосу, описание которого является математической
проблемой.
В работе [259] подчеркивается, что многомерность для
мультипликативных процессов - это правило, а не исключение;
многомерность была подтверждена радиолокационными наблюдениями
дождевых полей. На основе выводов работ [259, 261], как следствий из
многомерности, изучены условия детектируемое™ размерности.
Разрешение масштабов часто недостаточно для оценки детектируемос-
ти явления. Например, самые интенсивные явления могут быть
утрачены, если множество наблюдений будет редким. В частности, сети
точек наблюдения должны иметь размерность меньше 2. Всемирная
сеть метеорологических станций, включающая свыше 9000 станций,
имеет D = 1,75, а закон подобия выполняется в диапазоне
масштабов примерно от 1 до 2000 км [261, 262].
В работе [263] рассмотрена фрактальная структура наземной озо-
нометрической сети, включающей свыше 100 станций. В расчете
учитывалась сферичность Земли. В диапазоне масштабов 60—400 км
выполняется закон подобия (1.9) с D = 1,67 ± 0,1. Следуя [261],
можно определить наибольший диапазон масштабов, в котором будет
выполняться закон подобия. Минимальное значение
корреляционного интеграла (1.8) C(r) ~ (n(r))min «137-1 = 7,3х10~3, а
максимальное (n(r))maK ~ 137/2 « 69 при 137 станциях. При выполнении закона
подобия Л1'67 имеем R^ « 50 км и RmsK « 10000 км. Для R > 1000 км
возможен другой закон подобия, но найти его пока нельзя из-за не-
256
5.1. Фрактальность турбулентности
достаточного количества станций и из-за насыщения функции (п(г))
при больших г.
Более полную информацию дает глобальная широтно-долготная
сеть на основе спутниковых измерений за много витков. Ее
фрактальные характеристики также рассчитаны в [263]. При этом
получается, что локальное значение фрактальной размерности
спутниковой сети - монотонная функция широты, которая изменяется от
1 на полюсах до 2 на экваторе. Для больших масштабов, вплоть до
15 000 км, D= 1,84. Согласно [261], наблюдательная сеть не может
регистрировать явления, пространственное распределение которых
характеризуется фрактальной размерностью D< Н, где Я-
коразмерность (5.4). Поэтому для наземной озонометрической сети
предел обнаружения ограничен значением D = 0,33, для широтно-дол-
готной сети - значением D = 0,16 на больших масштабах и D « 0,4-0,7
на малых масштабах. Таким образом, малая фрактальная размерность
наблюдательной сети приводит к искажению статистики (в данном
случае статистики озона) и к неправильному определению
пространственно-усредненных значений.
В предположении того, что области диссипации энергии не
описываются однородными фракталами, в [264] введены неоднородные
фрактальные объекты. Алгоритм их образования на каждом шаге по
иерархии масштабов выбирается случайным образом. Перенос
энергии при этом описывается с помощью модели случайной
фрагментации в предположении, что между разными этапами процесса нет
корреляции.
Для некоторых турбулентных движений характерна передача
энергии от мелкомасштабных движений к крупномасштабным [265].
В частности, общая циркуляция атмосферы может потреблять
энергию циклонов благодаря инверсному каскаду. Реальность процесса
дробления, а также обратного ему процесса соединения вихрей
подтверждается прямыми наблюдениями [266] в турбулентных потоках.
Направленность каскадного процесса (дробление или объединение
вихрей) влечет существенную нелинейность при статистическом
описании однородной турбулентности [267]. Развитая
турбулентность является системой с очень большим числом степеней
свободы N, зависящим от числа Рейнольдса [268], и в общем случае
трехмерного течения, имеющим порядок N~ (Re)9/4. Фактически здесь
можно говорить о числе вихрей [266]. Метод виртуально
сбалансированных каскадов, предложенный в [267], позволяет применить в
9 Фракталы
257
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
данной ситуации принцип максимума энтропии для виртуальной
системы, в которой, наряду с дроблением вихрей [237], существует
реверсный процесс. При этом для инерционного интервала
масштабов были получены спектральные плотности энергии вида &у,
кгЩкЬ), Ю In2(kL), ..., где к - модуль волнового вектора; L -
корреляционный (интегральный) масштаб турбулентности.
Физическим механизмом реверс-каскада может быть
объединение мелкомасштабных вихрей в более крупномасштабные
когерентные структуры, своеобразные вихревые кластеры [269]. Свойство
однородности в иерархии объединения малых вихрей в более
крупные может быть заменено скейлинговыми свойствами,
аналогичными тем, которые имеют место у фрактальных кластеров [16-18].
Фрактальность вихрей-кластеров — в общем случае явление,
существенно отличное от фрактального характера траекторий частиц и
вихрей в турбулентности [270, 271]. Фрактальный вихрь-кластер
создает перемежающееся движение. В работе [265] установлены связи
между фрактальной структурой турбулентных вихрей и
наблюдаемыми характеристиками турбулентности для различных физических
механизмов инверсного каскада, как реального, так и виртуального. Эти
данные приведены далее.
При движении элементарных вихрей в рамках броуновской
модели, и когда вихри-кластеры собираются поэлементно, в
образующихся кластерах Z> = 5/3 (двумерное пространство) и D«2,5
(трехмерное пространство). Тогда кластер со средним размером R
увеличивается во времени по закону i?~f1/(x, a = D -(£>'- 2), где
U - размерность пространства, в котором идет процесс ассоциации.
Для IX = 2 имеем R~t3/S. Для спектральной плотности энергии
Е(к) следует зависимость Е{к)-к~вл и Е~к~%1Ъ (двумерное
пространство).
Если траектория движения элементарных вихрей отлична от
броуновской и длина пробега их велика по сравнению с областью
кластеризации, то считается, что вихрь движется по прямолинейной
траектории. Тогда D = D', a R~t1/2 и Е ~ к~г. Отметим, что закон
«-3» для Е(к) в двумерной турбулентности широко известен. Для
вихрей-кластеров, образующихся из кластеров меньших размеров, и
траектории броуновского типа R~tl/D , а значение D = 10/7±2/5
(двумерный случай) [16]. Поэтому для диффузной
кластер-кластерной модели в двумерной турбулентности R ~ f7/10, Е ~ кР11.
258
5.1. Фрактальность турбулентности
Искусственные неоднородности в ионосфере. Применение
фрактального анализа при радиодиагностике естественных и
искусственных неоднородностей в ионосфере рассматривалось в [272]. Задача
радиодиагностики неоднородностей решается применением
резонансного рассеяния пробных коротковолновых радиосигналов с
дальнейшим спектральным и корреляционным анализом. С их
помощью удается восстановить средние характеристики
турбулентности на уровне первых моментов [273, 274].
Однако проблема рассмотрения мелкомасштабной ионосферной
турбулентности (масштабы / ~ 5.. .50 м) как динамической системы
остается открытой. Исследование эффектов рассеяния проводилось
измерительным комплексом на базе фазированной антенной
решетки радиотелескопа УТР-2 по схеме двухпозиционного зондирования.
В качестве зондирующих передатчиков использовались
широковещательные станции коротковолнового диапазона, расположенные на
расстоянии до 1000 км от приемного пункта
(Радиоастрономическая обсерватория РИ АН Украины, 49,66° с.ш., 36,83° в.д.).
Искусственная ионосферная турбулентность стимулировалась нагревным
стендом «Сура» (Нижний Новгород, 56,13° с.ш., 46,10° в.д.).
Оцифровка сигнала проводилась с шагом 50 мс при полосе
анализа 10 Гц и условии, что интервал корреляции исследуемых
процессов составлял 1-2 с. Длительность анализируемых реализаций
равнялась 100 с (2000 отсчетов). После цифрового детектирования
осуществлялась фильтрация огибающей прямоугольным фильтром
в полосе 2 Гц. Спектральный анализ показал, что в полосе ±2 Гц
относительно несущей сосредоточено 95-98% энергии сигнала.
Рассматривалось три случая: первый - сигналы, рассеянные на
естественных неоднородностях и принятые на слабонаправленную
антенну; второй - те же сигналы, принятые на остронаправленную
антенну; третий - сигналы, рассеянные ионосферной
искусственной турбулентностью, принятые на остронаправленную антенну.
Оказалось, что при 90%-ном доверительном интервале невозможно
четко различить исследуемые виды турбулентности.
При определении фрактальной размерности огибающей
производилась оценка корреляционного интеграла (1.8). Усредненные
зависимости Щ1У) для трех типов данных приведены на рис. 5.8 при
усреднении по четырем реализациям. Точка пересечения
экспериментальных прямых с линией D = D' соответствует фрактальной
размерности процесса.
259
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
Рис. 5.8. Фрактальные размерности огибающей коротковолновых радиосигналов,
рассеянных естественными De (1 - слабонаправленная антенна; 2 -
остронаправленная антенна) и искусственными Du (3 - остронаправленная антенна) неодно-
родностями ионосферы, в зависимости от размерности фазового пространства
вложения [272]
Максимальной фрактальной размерностью Du =2,85 обладает
огибающая сигналов, рассеянных искусственными неоднородностя-
ми ионосферы. Для естественной турбулентности значения De « 2,36
при двух типах антенн. Таким образом, фрактальный анализ
позволяет дифференцировать тип турбулентности даже при
неразличимых спектрах рассеяния. Оценка D дает основания предположить,
что ионосферная турбулентность порождается конечным числом
факторов и, следовательно, возможно построение модели в виде
конечной системы дифференциальных уравнений первого порядка.
Дополнительный ряд соображений о фрактальности
турбулентности, ее возникновении и свойствах содержится в [24, 60,61, 275-
278]. Как отмечено в [237], теоретический расчет D изоповерхнос-
тей в турбулентности есть вызов теоретикам.
5.2. Фрактальные модели дождей и облаков
Облака и осадки, представляющие собой скопления водных,
ледяных или сложных частиц, являются типичными
множественными целями, распределенными по объему [230]. Геометрические
характеристики дождевых зон и облаков чрезвычайно разнообразны.
Успешное применение методов радиолокации [127, 184, 279, 280] в
радиометеорологии и получение изображений гидрометеоров в раз-
260
5.2. Фрактальные модели дождей и облаков
личных участках электромагнитного спектра позволило использовать
понятие размерности Хаусдорфа для описания неупорядоченных
структур указанных атмосферных явлений.
Отношение «периметр-площадь». В работе [281] теория
фракталов была применена для исследований геометрии облаков и дождей,
площади которых составляют от 1 до 1,2 • 106 км2. Как показано Ман-
дельбротом в [1—3], отношение «периметр U- площадь S» для
фрактальных объектов подчиняется соотношению вида U ~ 4s^, в
отличие от объектов гладкой формы (окружности, квадрата и т. д.), для
которых U ~ y[S . Здесь D - фрактальная размерность граничной
линии наблюдаемого объекта.
На рис. 5.9 показано соотношение «S—U» для дождевых и
облачных зон Индийского океана. Зоны тропических дождей изучались с
помощью оцифрованных радиолокационных изображений при
разрешении 1x1 км2. Данные о системах облаков были получены в
инфракрасной области в узлах квадратной сетки 4,8 х 4,8 км2
геостационарным спутником GOES. Взятые раздельно радиолокационные
и спутниковые данные представляют собой две параллельные пря-
S, км2
106
104
102
10°
101 Ю3 105 С/, км
Рис. 5.9. Площади дождевых (1) и облачных (2) зон
как функции их периметров [281]
261
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
мые. Если спутниковые данные умножить на коэффициент
коррекции, эти линии будут совпадать, как показано на рис. 5.9; они дают
значение фрактальной размерности D = 1,35 ± 0,05 с
коэффициентом корреляции 0,994. Коэффициент коррекции необходимо
использовать из-за того, что радиолокационные данные имеют более
высокое разрешение и более чувствительны к детальной структуре
периметра.
В точной формулировке [1-3] соотношение
«периметр-площадь» имеет вид
U(S) = C5^D^[S(5)f/2. (5.12)
Здесь 8 - длина эталона измерения, С = NxXjf - коэффициент
пропорциональности, Nx - количество эталонов на измеряемой линии,
^0 - произвольный малый параметр.
Соотношение (5.12) лежит в основе практического определения
фрактальной размерности. Если периметр U имеет размерность Д
то длина периметра, измеренная с разрешением 52, больше длины
периметра, измеренного с разрешением 52, на значение фактора
коррекции (5j /52)1_i). Поэтому спутниковые данные (см. рис. 5.9) были
умножены на значение (1/4,8)~°>35 = 1,73. Данный множитель
соответствует множителю 81_/) в равенстве (5.12).
Радиолокатор принимает микроволновое излучение,
рассеиваемое преимущественно крупными каплями дождя. Зона дождя
определена как область, для которой интенсивность осадков превышает
0,2 мм/ч, что соответствует легкому моросящему дождю. Из-за
кривизны поверхности Земли радиолокационные измерения
ограничивались площадью до 40 000 км2.
Данные со спутника GOES во избежание эффектов увеличения
размера элемента изображения были ограничены областью между 20°
северной широты и 20° ю. ш. и внутри ±30° по долготе от точки
поверхности под спутником. Для облаков толщиной более 300 м
инфракрасное излучение несет информацию о температуре верхней
поверхности облака. Облачные и дождевые массивы физически тесно
связаны с тропиками, так как и те и другие появляются в областях
восходящих конвективных потоков, поднимающих от поверхности
262
5.2. Фрактальные модели дождей и облаков
влажный теплый воздух. При адиабатическом расширении этот
воздух охлаждается и образует в результате конденсации пара облака и
дождевые капли. Эти облака состоят в основном из
переохлажденной воды, а не льда. Элементы изображения, в которых
температура была ниже -10 °С, считались приходящимися на облака.
Следовательно, исследуемые облачные массивы включали как кучевые, так
и перистые облака.
Важным свойством данных, приведенных на рис. 5.9, является
отсутствие заметных изгибов характеристик в диапазоне,
охватывающем более чем 6 порядков по площади. Если выбрать другое
значение температуры, определяющее границу облака, то площади и
периметры меняются, но так, что соответствующие точки
смещаются, оставаясь на той же линии [281].
Площади и объемы дождевых фрактальных зон. Дальнейшим
развитием выводов работы [281] является установление
самоаффинности зон дождей и облаков, поскольку в стратифицированной
атмосфере вертикальное направление неравноправно с горизонтальным
[282]. Кроме того, сила Кориолиса приводит к закрутке облаков.
Результаты использования метода функционального расчета
фрактальной размерности по картам вертикального и
горизонтального распределения радиолокационной отражаемости Zдoждeй
приведены на рис. 5.10. Размер элементарных геометрических фигур 8
увеличивался с показателем степени 2. Девять порогов принятия
решения Г изменялись на 4 дБ и отмечены на рис. 5.10 разными
символами (7^ < Т9). Отметим, что наклон, или D(T), при
возрастании порога систематически снижается.
Для изотропной модели дождя фрактальные размерности Z) <2>( 7)
(рис. 5.10, а) и 7)<3)(7) (рис. 5.10, б) соотносятся как
DV\T) = l + DV\T). (5.13)
В экспериментах значения D (2)( 7) уменьшались от 1,24 до 0,40,
а БЩТ) - от 2,18 до 0,81. Из равенства (5.13) следует, что
коразмерности Ht (7), определяемые как (см. формулу (5.4))
Hi(T) = D/-D(i\T)
относительно размерности пространства вложения 7)' в ходе
проведения экспериментов сохраняются, т.е.
Н3(Т) = Н2(Т). (5.14)
263
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
N
10"
103
102
10'
2° 22 24 26 8
/V
104
103
ю2
10'
2° 2' 22 23 8
Рис. 5.10. Измеренное число эталонов N(b), покрывающих карты
радиолокационной отражаемости Zдoждeй элементарными площадками (а) и кубами (б) с
ребром 8, при различных значениях порога Т [282]
Соотношение (5.14) отражает тот факт, что при любом
масштабе 8 объемная или плоская часть пространства FT(S), охватываемая
фракталом, подчиняется закону
FT(5)5Dii)^/5D, = 5Hf(T\ (5.15)
Стратификация метеообразований. Однако атмосферные
области не изотропны, но стратифицированы. Это требует введения
целого спектра фрактальных размерностей. По-видимому, облака на
самом деле следует рассматривать как мультифракталы [60]. Следуя
результатам работы [282], введем понятие «эллиптическая
размерность» del областей, занятых дождями. На рис. 5.11 представлены
схематически модели средних атмосферных образований в виде эллипса
264
5.2. Фрактальные модели дождей и облаков
с размерностью del в трех различных
масштабах. Для покрытия исследуемых
образований использовались параллелепипеды,
показанные в плане прямоугольниками.
Асимптотически, путем подсчета числа
элементарных прямоугольников
определяется фрактальная размерность del. На рис.
5.11,а параллелепипеды слишком
наслоены, на рис. 5.11,#недостаточно наслоены,
и, наконец, данные на рис. 5.11,в дают
правильное наслоение Del = deV
Для облаков с горизонтальной длиной
8 толщина (мощность) их
пропорциональна 8А, где h - функция, характеризующая
степень стратификации [282].
Следовательно, объем, доступный для дождевых
структур, равен 5-5-Ън = 5^,
гдеdel<3-эллиптическая размерность, характеризующая
уровень стратификации. При совершенно
стратифицированных процессах h = О и
del= 2. Для изотропных полей h = 1 и del= 3,
как и ожидалось. Так как области дождя,
превосходящие фиксированный порог Т, не
заполняют все пространство, их «объем»
увеличивается, как bDel^T\ где Del{T) < deV
В случае правильных измерений из (5.14)
следует обобщающее равенство Hd (T) = H2(T). Если используется
не соответствующее пространство расчета с Del, то необходимо
проводить коррекцию вида Del /del, и тогда
Dei = dei
Рис. 5.11. Схематическая
модель определения
эллиптической размерности
усредненных вихрей,
представленных эллипсами
[282]
HD(T) = H2(T)^
"el
(5.16)
Формула (5.16) используется при нахождении оценки del
методом подбора эллиптической размерности. Для каждой степени
расслоения Del необходимо измерить HD (Tt) для всех значений
порога 7]. При этом Del = 1+1+Ар для параллелепипеда размером 5 5 ■ 5Ля .
265
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
В случае правильности выбора при Del = del имеем HD (7]) = #2(7])
для всех 7). Метод может быть улучшен статистически при
определении нуля функции
i=i L J
(5.17)
где эмпирические функции Нп и К определяют функциональным
"el L
расчетом по периметру. Для данных на рис. 5.10 сумма по / в (5.17)
есть общее число порогов, т.е. п = 9.
Из формул (5.16) и (5.17) следует, что
/«>«,)=
а.
ЕВД>
i=l
и функция f(Del) линейна.
На рйс. 5.12 показана функция f(Del), рассчитанная по
усредненным данным из 20 радиолокационных объемов зон дождя при 15
различных значениях Del и 9 порогах; в целом использовано
9x15x20 = 2700 измерений. Значение /^изменялось от 2,13 до 3.
Значение Del =2,13 есть наименьшее, доступное из набора данных. Это
соответствует покрытиям в виде элементарных параллелепипедов
1x1x1 пиксел и 190x190x2 пиксел, т.е. 2,13 = 2 + Iog2/logl90. Линей-
ADef)
0,051-
Рис. 5.12. Восстановление фрактальной размерности дождя Del
по линейной функции f(Dd) [282]
266
5.2. Фрактальные модели дождей и облаков
ная регрессия дает значение фрактальной размерности дождя
del= 2,22 ± 0,07. Очевидным применением полученных в работе [282]
результатов является количественная оценка степени стратификации.
Например, область дождя существенно более стратифицирована, чем
поле воздушного потока с фрактальной размерностью del = 23/9 «
«2,555..., измеренной по энергетическим спектрам и из
соображений размерности.
Фрактальная модель дождя. В работе [260] предложена
самоподобная фрактальная модель зон дождя. Дождевая зона здесь
рассматривается как суперпозиция отдельных элементов с
соответствующей интенсивностью. Распределение количества осадков по
площадям описывается гиперболическим распределением вида
P(S>s)~(S/s*), где 5* - максимальное значение S. Для процесса
временного масштабирования s* ~ (At)1*1, где Н{ - показатель Хер-
ста (см. формулу (1.28)). При использовании радиолокационных карт
осадков определялись вероятности Р(1> 10) превышения
интенсивности дождя /некоторого уровня 10 при различном
пространственном разносе Ах. В этом случае был определен показатель Херста Н2,
предсказывающий пределы пространственного масштабирования.
Последним параметром для моделирования зон дождей являлось
значение показателя В в распределении Р (S > s) ~ srB площадей s,
ограниченных фрактальными кривыми.
В табл. 5.2 приведены численные значения фрактальных
параметров, полученные экспериментально (верхняя строка) и при
моделировании зон дождей (нижняя строка), а также фрактальная
размерность границы зон дождей. Как показано в [3], D = 2-l/a.
На рис. 5.13 приведены изображения облаков, построенные с
помощью модели фрактальных сумм элементов на решетке 300 х 300
пиксел при изменении масштабирования. Области, в которых
интенсивность осадков меньше определенного значения, показаны
черным цветом. Интенсивность осадков откладывалась в логариф-
Таблица 5.2
Фрактальные параметры для модели зон дождей [260]
Параметр
Измерения
Модель
а
1,66 ±0,05
5/3
я,
0,64 ±0,05
0,72 ±0,05
Нг
0,50 ±0,02
3/5
В
0,75 ±0,05
0,50 + 0,05
D
1,35; 1,38;
1,345
7/5
267
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
Рис. 5.13. Синтезированные изображения облаков
при изменении масштабирования [260]
мическом масштабе, белый цвет соответствовал ее максимальному
значению. Полученные изображения выглядят вполне реалистично.
Подробности моделирования и большое количество
синтезированных зон осадков приведены в [260].
Фрактальная модель облаков. Фрактальная форма градовых
облаков изучалась в работах [283, 284]. Мощные конвективные облака
исследовались во время проведения научно-исследовательской
программы «Grossversuch IV» по предотвращению градообразования.
Радиолокационная информация поступала в виде спроектированных
на плоскость почти горизонтальных линий постоянного
коэффициента отражения радиосигнала. Радиолокационные изображения
получались при полном обороте антенны с постоянным углом места
5,5°. Время получения одного радиоизображения равнялось 1 мин.
Разрешение РЛС составляло Г по азимуту и 0,3 км по расстоянию
при 1 дБ по радиолокационной отражаемости на длине волны 10,1
см. Отражаемость определяется как
Z = JN(D0)D*dD0,
где N(DQ) - распределение диаметров гидрометеоров в единице
объема и в интервале диаметров от DQ до D0 + dDQ.
268
5,2, Фрактальные модели дождей и облаков
Обычно в практике радиолокационных метеонаблюдений
отражаемость выражается в виде 7=10 lg(Z/Z0), при этом /измеряется в
мм6/м3 или в дБг относительно Z0 = 1 мм6/м3. Для распределения
Пуассона N(DQ) ~ exp(-XD0), хорошо описывающего наблюдения,
можно получить /= const — 70 lg X, и значения /(дБ) монотонно
возрастают при увеличении размеров частиц при ^/?median = const.
Подробности обработки радиолокационных данных приведены в [285].
Типичная радиолокационная карта мгновенной формы
градового облака приведена на рис. 5.14. В частности, кривая с /= 45 дБг
обозначает область сильного дождя интенсивностью более 20 мм/ч.
Расстояние гх соответствует направлению к северу, г2 - к востоку.
Фрактальное поведение наблюдаемых градовых облаков проявляется во
фрактальных свойствах контуров с постоянными /(дБ). Площадь Sв
пределах контура фрактально зависит от периметра контура {/(5.12):
s=s0up,
где показатель Р связан с фрактальной размерностью D контура
соотношением Р= 2/D и соответственно с фрактальной размерностью
/К2) = D + 1 поверхности постоянных значений /, т. е. с
поверхностью градового облака.
На рис. 5.15 в билогарифмических координатах изображена
зависимость площади S, заключенной внутри контура, от периметра
Uконтура с /= 45 дБ. Каждая точка соответствует определенному
гъ км
•' 25
20
15
10
5
-15 -10 -5 0 5 10 15
Г\9 КМ
Рис. 5.14. Пример горизонтального сечения поверхностей постоянного
коэффициента отражения радиоволн для мгновенной формы градового облака [283]
269
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
5, км2
102
10'
1
10'
ю-2
КГ1 1 101 102 Цкм
Рис. 5.15. Соотношение «периметр U- площадь S»
при отражаемости 45 дБ [283]
моменту с интервалом времени 1 мин, в течение которого
происходит временное развитие бури. Аналогичные кривые были
построены для /= 55, 60 и 65 дБ. Точки меньших контуров располагались
на прямой, соответствующей степенному закону с угловым
коэффициентом Р = 2 и D = 1. Следовательно, эти контуры гладкие. При
обработке радиолокационных изображений 24 градовых облаков
были получены [283, 284] следующие результаты. При больших
значениях периметра Uфрактальная размерность D= 1,36 ± 0,1, Z*2* =
= 2,36 ±0,1, U> UQ. При малых С/фрактальная размерность D= 1,0 ±
± 0,1, #2> = 2,0 ± 0,1, U< UQ. Резкий переход в точке U= UQ,
отмеченной вертикальной линией, указывает на существование
характерной длины L0=U0/k = 3±1 km. Сильные ветры при фадовых бурях
приводят к смещению порога U0 в сторону больших значений,
вследствие чего большие контура кажутся гладкими.
Таким образом, для пространственных масштабов, меньших
примерно 3 км, границы облаков с крайне интенсивной
конвекцией оказываются нефрактальными. Полученные в [283, 284] данные
хорошо согласуются с результатами работы [281], в которой
определено D = 1,35 ± 0,05 (см. рис. 5.9).
Наблюдаемый переход при U= U0 свидетельствует о
существовании в проблеме градовых облаков характерной длины LQ. Ее
значение не зависит от уровня коэффициента отражения, т.е. от
размера частиц, но изменяется в зависимости от силы ветра. Более силь-
270
5.2. Фрактальные модели дождей и облаков
ные ветры сглаживают форму контура. Установлено, что особенно
мощные вертикальные выходящие и нисходящие потоки
существуют около центра грозовых и градовых облаков. Это позволяет
объяснить гладкость меньших контуров вблизи центра облака.
Сглаживание контуров больших облаков происходит при
значительном горизонтальном ветре из-за наличия конвективных токов
или дрейфа частиц. При больших скоростях дрейфа частицы
двигаются по гладким траекториям — вместо броуновских траекторий при
нулевом дрейфе, что является одним из возможных механизмов
сглаживания форм облаков.
Эти наблюдения иллюстрируются графиком, показанным на рис.
5.16, где изображена зависимость фрактальной размерности D
контура с отражаемостью 45 дБг от средней горизонтальной скорости
ветра V. Ясно видна тенденция уменьшения D при увеличении
скорости ветра. Полученные в [283, 284] результаты могут стать
основой метода определения полей облаков при сильных ветрах путем
измерения соответствующих фрактальных размерностей облаков.
D I
1,4 L
1,2 §
1 V
А/
I i i i
О 5 10 15 км/с
Рис. 5.16. Зависимость фрактальной размерности контура
с отражаемостью 45 дБг от средней горизонтальной скорости ветра [283]
Оценки коразмерности метеообразований. Интерпретация
фрактальной размерности формы облаков была предпринята в рамках
теории относительной турбулентной диффузии [286]. Решение этой
проблемы связано с тонким взаимодействием пространственных и
временных масштабов в развитой однородной турбулентности.
271
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
Ранее в работах [287, 288] было показано, что модель
фрактальной однородной турбулентности приводит к фрактальной
размерности турбулентного поля в пределах 2,5 < D< 2,75.
Как известно, состояние атмосферы определяется физическими
параметрами - температурой, давлением, содержанием водяного
пара, полем турбулентных скоростей, размером капель и т.д. В
работе [286] локальная температура f рассматривалась как переменная,
переносимая турбулентным полем скорости, и предполагалось, что
она не влияет на скорость. Состояние атмосферы тогда будет
определяться функцией t(x, у, z)- Таким образом, предложенная модель
пренебрегает физикой облаков, учитывая только пассивную
скалярную переменную t и турбулентное поле скоростей ветра,
переносящее ее.
Множество точек (t, x, у, z} в четырехмерном пространстве
является фрактальным с размерностью Dt = 4 — Д где коразмерность есть
величина К Поверхность облака определяется условием t (х, у, z) =
= /0 и представляет собой множество точек в обычном трехмерном
пространстве. Применяя операцию пересечения множеств [3],
получаем фрактальную размерность облака D = 3 - К Затем,
пересекая поверхность облака плоскостью, имеем множество точек с
границей размерностью D = 2 - К Поэтому, оценив коразмерность Н,
мы непосредственно получим оценку фрактальной размерности
облаков.
Результаты показывают, что Н= 0,65 ± 0,05 для облаков зон
дождей. Согласно [286], фрактальная размерность границ облаков
заключена в пределах 1,37 < D< 1,41, что прекрасно согласуется с
данными работ [260, 281, 283, 284]. Отсюда следует, что упрощенная
модель способна оценить фрактальную размерность облаков,
согласующуюся с наблюдениями.
5.3. Компьютерное моделирование фракталами молний
в атмосфере
Общая структура электромагнитного поля молний в атмосфере
вызывает большой интерес специалистов. Электромагнитное
излучение гроз обнаруживается в очень широком диапазоне частот - от
нескольких герц до сотен мегагерц. С точки зрения практики,
феноменологическая модель разряда, которая не учитывает микроско-
272
5.3. Компьютерное моделирование фракталами молний в атмосфере
пическое описание молнии, очень важна в технике связи и
управления. Фрактальное описание разряда молнии и канала ее
распространения приведено в работе [289]. Извилистый канал разряда
предполагается состоящим из АГсегментов. Общее электромагнитное поле
является суммой элементарных полей от импульсов тока в каждом
сегменте.
Модель канала разряда. Рассмотрим прямолинейный сегмент
длиной Ьп с центром, расположенным в гп и направлением s при токе
7(/,ш), где /е[-1,Л/2, £„/2]. Определим электромагнитное поле
Еп{г) в точке расположения наблюдателя г, считая гп=г-г'п.Ъ [289]
на основе результатов [290] при условии rn/ Ln >(Ln/4X)b~l
получено следующее выражение
£„(г,ш) = -(щЩ^^г + 5„(*вле + *9лФ)] х
х "{ 7(/,ш)ехр(ЯЦ/)Л, (518)
п п п п
Кт=ап=Г5п> Квп=* Sn> *ср„=ФЛ>
с - скорость света, 8 - коэффициент, определяющий фазовую ошибку.
Ток / (s, t) в канале длиной s считается импульсным со
скоростью распространения v:
i(s,t) = i0(t-s/v), I(s,ю) = /0(o))e-^/v.
Общее излученное поле
Er(r,(o) = 2Z0/0(co)X7£^^/(o(r''/c+^/v) <ХГп>®)(*т*'2 " e~im"/2)>
n=l4nr» (5.19)
x С
£a(r,®) = -Z0/0(©)£^e^
и-1 47СГ,
273
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
Здесь индекс а обозначает 9 или <р, Z0=^0/e0 - воЛновое
сопротивление среды распространения,
/1-1 Г
Сп=Кпп/(с/у-а)9 x=(l-av/c)L/v, * =У4,+-^,
m=l ^
~ ч с/г (с/г)2
/со О©)2
Полагая t(l) = rn/c + sn/v-xn/2, f<2) = f W + тя и применяя фурье-
преобразование к формулам (5.19), определим временные
компоненты результирующего поля EQ и Е ъ виде
С Г С f
с зависимостями /j (0 = - J *0 (f)dt\ il(t) = -)i2 (t')dt'.
г о ro
Компонента поля j?r получается из (5.20) заменой Са л на-2Сгл.
Численные результаты. Импульсная форма тока является
стандартной:
с параметрами ос = 2104 с"1, р = 2105 с"1, у = 2103 с"1,
5 = 2-104 с-1, /а = 30кА, 7^ = 2,5 кА.
Типичные результаты моделирования поля во фрактальном
канале приведены на рис. 5.17 и 5.18. Правильность моделирования
проверена сравнением с экспериментальными данными. Форма
канала rc(z) как функция высоты дописывается параметрическим
уравнением rc(z) = x(z)x+y(z)y + zz, где x(z) и y(z) - фрактальные
кривые. Алгоритмы генерации фрактальных кривых x(z) и y(z)
описаны в [289]. Моделирование проводилось для высоты z = 6 км и
средней длины сегментов L = 90 м. Скорость распространения
разряда была равна v = с/3. Проекции (х, z) и (у, z) канала выполнены
при числе сегментов N= 512. На рис. 5.17,в и 5.18,в изображены вер-
274
53, Компьютерное моделирование фракталами молний в атмосфере
£-, В/м
3
2
1
0
-1
- л
'■h
■
J
>_J
1
IN|
-1
1
К
V
l__
Ы\л
"Л,
L—.
V
1
1 1
v 1
1 1
1,2
0,8
0,4
0
-0,4
£г. В/м
■ ■ i
" 1
- к
- т
-
-
—|
i" i
UA
г ljy
I \f
—i—i—i—
i i 1
•ч
1,1 1
[U 1 ]
V4\* 1
4 Wy ]
i i 1
3,4
3,8
4,2
в)
xia4
', с
в)
Х10"
U с
4 6
Рис. 5.17. Проекции х, z (а) и у, z (б)
канала разряда молнии и вертикальная
компонента Ez излученного
электромагнитного поля на уровне земли (в) при
фрактальной размерности поля
D= 1,20 ±0,03 [289]
Рис. 5.18. Проекции х, z (а) и у, z (б)
канала разряда молнии и вертикальная
компонента Ez излученного
электромагнитного поля на уровне земли (в) при
фрактальной размерности поля
D= 1,50 ±0,03 [289]
тикальные компоненты Е излученного электромагнитного поля на
уровне земли (z = 0, 9 = 90°) при г = 100 км в сторону от основания
канала вдоль направления ф = 45°. Электромагнитное поле
положительно, когда оно направлено к поверхности земли.
В пределах структуры применяемой аппроксимации считается,
что временная форма излученного поля в зоне Фраунгофера имеет
примерно ту же фрактальную размерность, что и канал
распространения.
275
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
На рис. 5.19 изображена зависимость вертикальной
компоненты Ez излученного электромагнитного поля на уровне земли,
соответствующей данным рис. 5.18, но при скорости разряда v,
изменяющейся экспоненциально с высотой z при значении v(0) = с и v =
= с/3 при z " 6 км. Приведенные данные моделирования
соответствуют реальной эволюции развития молнии. В данном случае при
изменяющейся скорости v фрактальная размерность поля равнялась
D= 1,45 ±0,05.
£z, В/м
2,5
1,5
0,5
-0,5
3 4 5 6 /,с
х1(Г4
Рис. 5.19. Вертикальная компонента Ez излученного молнией электромагнитного
поля на уровне земли при экспоненциальной скорости разряда и фрактальной
размерности поля D = 1,45 ± 0,05 в зависимости от времени [289]
При анализе уравнений (5.19) и (5.20) можно заметить, что
временные события между последовательными прибытиями откликов
от сегментов со средним значением L пропорциональны
временным промежуткам т с мгновенными значениями тЛ. Очевидно, что
на промежутках хп < т волновой характер поля является гладким и
поэтому т устанавливает фрактальный порог излученного поля.
На рис. 5.20 показаны зависимости фрактальной размерности
канала распространения и временной зависимости поля,
соответствующие данным рис. 5.18. Расчет проводился при нормировке по
отношению кг = 6кми? = 300 мкс. При определении D
использовался алгоритм на основе покрытия кривой множеством N{k)
элементарных площадок со стороной 2~к (см. гл. 1). Рекурсивное
уменьшение размеров ячеек в виде последовательности 2~<к+1\ 2~<к+2) и т.д.
позволяет получить графическую зависимость N(k) = f(2k) в двой-
276
5.3. Компьютерное моделирование фракталами молний в атмосфере
\ogN(k)
10
8
6
4
2
h
у
l
[•
[
I
г *
i i i
\J?
j i i
1 1 i
2>^
Поле
1 1 L.
^ \
-1
\
\
\
\
\
6)
Iog2*
Рис. 5.20. Эволюция фрактальной размерности канала
распространения (а) и вертикальной компоненты
электромагнитного поля (б) разряда молнии [289]
ных логарифмических координатах, соответствующую прямой линии
на рис. 5.20. Наклон прямых на рис. 5.20,0 соответствует D = 1,50
(прямая 1) и 1 (прямая 2). Для данных на рис. 5.20,5 имеем наклон
1,49 (кривая 1) и 1 (прямая 2). Изменение наклона прямых
примерно соответствует 90 м (а) и 0,9 мке (б). Заметим также, что при z = 0
я = 0 и на основе (5.19) x«Z/v.
Энергетический спектр молний. Электромагнитное излучение
молний обнаруживается в весьма широком диапазоне частот.
Несмотря на то, что такое излучение регистрировалось на протяжении
десятков лет, до настоящего времени не получены достоверные
данные, характеризующие его спектральную плотность.
277
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
На рис. 5.21 изображен в двойном логарифмическом масштабе
энергетический спектр поля G(cg) = |1^(cg)| , рассчитанный по
формуле (5.19) для данных рис. 5.17,дс D- 1,2 и рис. 5.18,5с D = 1,5,
где D — фрактальная размерность канала распространения молнии.
201ogG(/),AB
-50
-150
-250
1 1 1 г"
^V 29,5 дБ/дек. £>=1,2
•^ц. 40 дБ/дек. Н
—1 i_i 1 1
W
201ogG(/), дБ
а)
107
/Гц
10?
-50
■150
-250
• 1
20,5 дБ/дек.
■ Лч,
1 ' »
-т 1 1
Я=1,5 I
40 дБ/дек. 1
-1 i
105 Ю7 109
б) /ГЦ
Рис. 5.21. Энергетический спектр электромагнитного поля разряда молнии
при D = 1,2 (a) vlD =1,5 (б) [289]
Энергетический спектр разряда имеет зависимость /~Р. Ранее
было найдено, что асимптотическая огибающая спектра спадает как
/~4 для вертикально направленного канала и как /~2 для
извилистого канала [291]. Предполагается, что показатель степени Р
является функцией фрактальной размерности канала, количественно
оценивающей его извилистость. При изменении D от 1 до 2 показатель
степени лежит в пределах 4-1. Это объясняется увеличением
высокочастотных компонент поля при возрастании нерегулярных
временных импульсных последовательностей.
278
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
Пороговое значение частоты в спектре, соответствующее
переходу к зависимости /~4, равняется/^ 1,6 МГц (рис. 5.21,а) и
/j ~ 0,6 МГц (рис. 5.21,6). Следовательно, если канал
распространения является фрактальным для пространственной шкалы, большей
L (L ~ 34 м для D = 1,2 и L « 90 м для D = 1,5) при
соответствующей временной шкале т (т = 0,34 мкс и т « 0,9 мкс), то можно
сделать вывод, что для частот / > /j = - х-1 (соответственно/j = 1,5 МГц
и/j « 0,6 МГц) канал будет прямолинейным с D = 1 при |3 -> 4.
Рассмотренная модель предполагает, что в среднем длина
ионизированного канала пропорциональна 2*(Z)~ *> с числом сегментов N= 2*.
5.4. Экспериментальное моделирование
фрактальных аэрозолей и аэрогелей
Роль фрактальных кластеров. Известно [16-18], что при
коагуляции движущихся по определенному закону частиц образуются
структуры, называемые фрактальными кластерами. Фрактальные
агрегаты характеризуются убывающей плотностью, развитой
структурой пор и высоким значением удельной поверхности. На размеры
элементов кластера накладывается единственное ограничение: они
должны быть много меньше размеров агломерата. При увеличении
размера кластера падает и его стабильность. Обычно фрактальный
кластер имеет размеры до нескольких десятков микрон и включает до 104
частиц. Физико-химические свойства кластеров существенно
отличаются от соответствующих свойств как эквивалентной однородной
частицы, так и системы независимых малых частиц. Компьютерные
модели составили основу представлений о таких объектах.
Интерес к фрактальным кластерам обусловлен несколькими
причинами. Они являются весьма распространенными природными
объектами и не могут быть макрочастицами. Установлено, что
некоторые типы атмосферных аэрозолей (частицы дыма,
вулканический пепел и пр.) являются фракталами. В связи с этим резко возрос
интерес к изучению их оптических [292-295] и транспортных [296,
297] свойств, определяющих степень участия аэрозолей в
атмосферных процессах.
Фрактальный кластер также является основной
структурообразующей частью аэрогелей. Начало получения аэрогелей и их иссле-
279
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
дования относятся к 1930-м годам. В то же время систематическое
изучение аэрогеля до настоящего времени носило ограниченный
характер, что связано с малой доступностью этого объекта.
Аэрогели с точки зрения состояния вещества не могут быть отнесены ни к
газовому, ни к твердому или жидкому состояниям и по сути
представляют собой новое физическое состояние вещества [298,299]. Их
специфические физико-химические свойства очень интересны для
прикладного использования в современных технологиях.
Однако развитие теоретических методов в исследованиях
фрактальных кластеров пока значительно опережает экспериментальное
исследование их свойств. Главная причина - сложность и
трудоемкость экспериментов. Синтез агрегатов с широким диапазоном
параметров возможен лишь на основе глубокого понимания
процессов формирования структуры. Компьютерные модели роста
кластеров [300-302] имеют довольно грубое приближение. Несоответствие
численных моделей реальному эксперименту заключается в том, что
в моделях заранее фиксируется механизм агрегации, характер
движения частиц или кластеров (прямолинейное или броуновское),
вероятность коагуляции и т.д. В реальности эти характеристики
непрерывно меняются.
Образование фрактальных кластеров и аэрогелей можно
осуществлять в газовой фазе (в том числе в атмосферном воздухе) при
разлете в пространство плазмы, образующейся при испарении
участков поверхности [299, 303]. Видимо, такой процесс может
происходить и в природе (разнообразные модели шаровой молнии) [16-
18, 298, 299]. Методы синтеза подразделяются на
низкотемпературные и высокотемпературные. Высокотемпературные методы
применяют при испарении тугоплавких металлов. В
низкотемпературных методах фрактальные агрегаты получают из материалов с
температурой плавления, не превышающей 1000 К.
В качестве высокотемпературного метода используют метод
электрического взрыва проволоки [304], дугового разряда [305],
лазерного испарения [306]. Данные методы возгонки
характеризуются испарением слабоионизированного пара с поверхности. Затем идет
цепь процессов, которые представлены в табл. 5.3 при плотности
потока излучения 107 Вт/см2 и размере облучаемой поверхности
~ 1 мм. Процесс испарения сопровождается появлением плотной
плазмы вблизи поверхности с температурой з несколько тысяч
градусов и давлением до сотни атмосфер. Затем фрактальные кластеры
280
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
Таблица 5.3
Процессы в лазерной плазме [299]
Процесс
Формирование пучка
Остывание до начала конденсации
Конденсация атомов на ионах и коагуляция
Образование фрактальных кластеров
Образование аэрогелеподобных структур
Время, с
ю-*
ю-7
ю-5
ю-2
ю2
могут объединяться в аэрогелеподобные структуры. Внешнее
электрическое поле для структур, образуемых в газе, вызывает
анизотропию их роста. В результате возникают фрактальные нити с
размерами, значительно превышающими размер кластеров, из которых
они формируются.
В качестве примера приведем некоторые характеристики
фрактальных нитей. При энергии импульса лазерного излучения 100 Дж,
ширине пятна 1 мм и напряженности внешнего электрического поля
300 В/см диаметр нити равен 30 мкм при длине около 1 см, размер
первоначального фрактального кластера (и размер пор в структуре)
около 1 мкм, диаметр частиц, из которых состоит кластер, 20 нм. В
естественных условиях такие нити перепутываются и образуют
клубок. В [299] отмечается, что такие аэрогелеподобные структуры
могут быть использованы в детекторах инфракрасного излучения с
высокой чувствительностью и малым временем релаксации ^10~5 с.
Теоретические вопросы роста фрактальных кластеров в плазме
обсуждаются в [303].
Генерация фрактальных кластеров. Рассмотрим некоторые
экспериментальные методы получения фрактальных кластеров.
Конструкция генератора фрактальных кластеров приведена на
рис. 5.22. В генераторе имеется пассивный испаритель с
охлаждаемыми стенками. Исходное вещество нагревается излучением от
трубчатого нагревателя. Охлаждение осуществлялось прокачкой газа
(расход W3) через полость испарителя. В качестве исходных веществ в
генераторе используются соединения иодида свинца (РЫ2) и
диоксида висмута (Bi203). Данные вещества сравнительно легко
переводятся в парообразное состояние и обладают высокой контрастное -
281
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
Рис. 5.22. Схема генератора фрактальных кластеров [303, 307]: 1 - пассивный
испаритель; 2 - трубчатый нагреватель; 3 - конденсационная камера; 4 — коагуля-
ционная камера; 5 - многослойный фильтр; 6 — подложка; 7 — термоосадитель
тью изображения на электронном микроскопе. В других
экспериментах можно использовать сажу, которая образуется от дугового
разряда.
Поток азота {Wx) при поступлении в генератор смешивается с
парами вещества. Затем газовая смесь, нагретая до 1000 К,
поступает в конденсационную камеру, в которой происходит
перемешивание с холодным газом (JV2) и резкое охлаждение пара до 400 К с
его конденсацией. Расходы Wx и W2 поддерживаются на уровне
0,82 л/мин, поэтому концентрация частиц на выходе зависит лишь
от давления пара РЫ2, которое определяется температурой расплава.
При этих параметрах генератора спектр размеров частиц составляет
20-40 нм.
Агрегация частиц происходит в коагуляционной камере, где
совершается дальнейший рост первичных образований, главным
образом, по механизму кластер-кластерной агрегации. В качестве
камеры используется медная сфера объемом 20 л, соединяемая с
атмосферой через многослойный фильтр. Время коагуляции отсчи-
тывается с момента окончания заполнения объема до необходимой
концентрации. Отбор частиц на подложку осуществляется термооса-
дителем. Скорость прокачки через него поддерживается на уровне
0,45 л/мин. Перепад температур между горячей и холодной
пластинами составляет 25 °С при расстоянии между пластинами 0,5 мм.
Пробы из коагуляционной камеры отбираются с интервалом 10 мин
в течение 1,5 ч. Для анализа фрактальной структуры кластеров
используется метод электронной микроскопии.
282
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
В работах [303,307,308] приведены зависимости фрактальной
размерности D от начальной концентрации частиц (0,4-1,8) • 106 см-3 и
времени коагуляции. В первые 40 мин характерно уменьшение D.
Существенно то, что на данном этапе роста образующиеся агрегаты
(на основе механизма «кластер—частица») состоят из небольшого
числа мономеров и пока не могут считаться фракталами. Дальнейший
рост приводит к формированию разветвленных цепочечных
структур [309]. Затем по мере связывания мономеров в кластеры механизм
«кластер—частица» замещается агрегацией «кластер—кластер», что
приводит к формированию симметричных фрактальных структур с
более высоким значением D. В работе [303] было также показано, что
внешняя активная зона (глубина проникновения), собирающая все
присоединяющиеся к кластеру новые мономеры, почти линейно
увеличивается с ростом размера кластера R. Эта особенность
характерна для ранней стадии коагуляции, когда кластеры представляют
собой сильно разреженные структуры.
Затем на определенной стадии коагуляции все мономеры будут
связаны и дальнейший рост активной зоны прекратится. Для
кластеров с ярко выраженной фрактальной структурой при радиусе ги-
рации R = R/ V2 ~ 1,2 мкм и числе частиц « 2800 среднее значение
D = 1,47 ± 0,05. Радиус гирации — это среднеквадратичный радиус
кластера, измеряемый от его центра тяжести [45]. Для области
кластер-кластерной агрегации (> 50 мин) значение D близко к
теоретической оценке 1,42 [309].
Процесс кластер-кластерной агрегации формирует скейлинго-
вое распределение кластеров по их размерам. Функция
распределения агрегатов по их размерам записывается в виде [310]
Cs(t)~r<»s-V{s/tz). (5.21)
Здесь Cs - плотность числа кластеров; s - число независимых
частиц в них; t - время коагуляции; со и z - динамические скейлинго-
вые показатели; т - статистический показатель;/(х) - некоторая
функция, не зависящая от начального распределения и
удовлетворяющая условиям: f(x) -»1 (х «: 1) и /(х)-»0(х»1).
Показатель со описывает степенной спад плотности числа
кластеров всех размеров со временем в процессе агрегации. Показатель
z определяет рост среднего размера кластеров S(t) ~ Рв системе. Эти
показатели связаны соотношением подобия
283
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
©=(2-t)z. (5.22)
Экспериментальные скейлинг-распределения по размерам для
кластеров иодида свинца с размерами исходных частиц 20—40 нм при
начальной плотности аэрозолей (0,4-1,8) • 106 см~3 в моменты
времени t= 0, 5, 15, 30, 45, 60, 90 мин приведены в [303].
Для экспоненциальной функции/(х) с учетом (5.21) получаем
СЛ)~Гш5-техр
( s
S(t)
(5.23)
Из формулы (5.23) по экспериментальным значениям Cs (t) и S(t)
определяются скейлинговые показатели со = 0,44 ± 0,08 , z = 1,1 ± 0,3,
т = 1,62 ± 0,18 . Эти показатели в пределах погрешности
удовлетворяют соотношению (5.22), но существенно отличаются от результатов
компьютерного моделирования [302]. Данное обстоятельство
указывает на более сложный характер физического механизма реального
процесса агрегации.
Так как по данным [309] при кластер-кластерной агрегации
броуновских частиц фрактальные размерности кластеров зависят от
степени анизотропии исходных частиц, установка (см. рис. 5.22)
была дополнена электродиффузионным сепаратором частиц [303].
Электродиффузионный сепаратор представляет собой вариант
диффузионной батареи сетчатого типа. В каждый каскад батареи
установлен сетчатый электрод. Между ним и пакетом сеток с размером
ячеек 1 мм прикладывалось напряжение до 8 кВ.
При прохождении аэродисперсной смеси через сепаратор
возникает эффект преимущественной коагуляции частиц вдоль
вектора напряженности электрического поля Е. За время нахождения
частиц внутри сепаратора образуются цепочечные агрегаты из
мономерных частиц с ярко выраженной анизотропией формы. При росте
Е от 0 до 6 кВ/см коэффициент анизотропии увеличивается от 1,40
до 2,17. Одиночные ядра, не успевшие проагрегировать из-за
высокой диффузионной подвижности, оседают на сетках сепаратора.
Поэтому выходящий поток был обогащен большим числом малых
кластеров. Дальнейший рост первичных кластеров происходит в коагу-
ляционной камере.
Обсудим результаты проведенных экспериментов [303, 308]. На
начальной стадии коагуляции скорость роста модифицированных
284
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
частиц выше, чем немодифицированных. После того как
мономерные частицы связаны в кластеры, механизмы коагуляции
становятся идентичными и скорости роста выравниваются. Отметим, что в
области малых размеров частиц во всех случаях D уменьшается из-
за формирования на ранней стадии роста структур с ярко
выраженной анизотропией формы. На второй стадии, при ассоциации
модифицированных частиц, вырастают сильно разреженные структуры с
низкими значениями Д а частицы без модификации образуют
относительно компактные образования с более высокой фрактальной
размерностью.
Диапазон изученных времен коагуляции для
модифицированных частиц позволяет обнаружить переход от масштабной
инвариантности внутренней структуры отдельных кластеров к самоподобию
всего ансамбля агрегирующих частиц. Следовательно, можно
контролировать процесс роста кластеров и их фрактальную структуру
изменением напряженности Е и времени нахождения кластеров в
коагуляционной камере.
На рис. 5.23 представлена схема установки для исследования
поведения частиц сажи в температурном поле и в среде
конденсирующегося водяного пара. В установку входят генераторы частиц,
сорбционная камера с системой подачи активных примесей,
трубчатая печь, термостатирующая камера, холодильник, два устройства
отбора проб - термопреципитатор и электроосадитель. На первой
стадии экспериментов исследовалось поведение частиц сажи,
полученных при сжигании на воздухе (генератор 1) нефти, древесины
(сосна) и природного газа.
Для эксперимента с модельными объектами используется
генератор чисто углеродной сажи. Генератор представляет собой
металлический цилиндр диаметром 40 мм с двумя графитовыми
электродами. Их испарение происходит в плазме дугового разряда в потоке
гелия при температуре ~104 К. Процесс формирования происходит
в сорбционной камере, где на поверхность углеродных кластеров
осаждаются активные примеси: двуокись кремния из баллона, пары
органического вещества и частицы хлористого натрия из
генератора. Для образования смол в результате пиролиза используется поли-
этиленгликоль (ПЭГ) со средней молекулярной массой 300. Смесь
ПЭГ с гелием образуется в испарителе продувкой газа над
поверхностью жидкости при температуре 100 °С. Образцы для измерений
отбираются с помощью электроосадителя.
285
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
Рис. 5.23. Схема экспериментальной установки [311]: 1 и 2 - генераторы частиц
сажи; 3 — сорбционная камера; 4 — трубчатая печь; 5 — термостатирующая камера;
6 - холодильник; 7 - термопреципитатор; 8 - электроосадитель; 9 - баллон с
двуокисью серы; 10 - генератор хлористого натрия; 11 - испаритель
При исследовании воздействия на частицы паров воды
дисперсная система увлажняется в камере, затем поступает в холодильник,
где пар конденсируется на частицах сажи. Жидкость в камере
поддерживается при температуре 90 °С, холодильник охлаждается
проточной водой с температурой 15 °С. В трубчатой печи температура
изменяется в пределах 100-700 °С.
Структурная изменчивость частиц сажи связана с факторами их
старения, крайней неоднородностью химического состава и сильным
их взаимодействием с атмосферной влагой. Частицы сажи имеют
чрезвычайно разреженную структуру (плотность 0,01-0,04 г/см3) и
слабую энергию связи межчастичного контакта. В физике
фрактальных систем парадигма «размерность—свойства» приобретает очень
большое значение, так как она выступает в роли основного методо-
286
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
логического инструмента. Оказалось, что размерность таких систем
не является топологической константой. Это дало возможность
перейти от чисто эмпирического описания геометрии таких частиц к
количественному определению их структурных характеристик,
фрактальная размерность стала ключевым параметром моделей.
Кратко рассмотрим результаты экспериментов, приведенные в
[311]. Для двухсекундного времени прохождения частиц сажи через
зону конденсации были получены следующие изменения значений
фрактальных размерностей D сажевых агрегатов: древесина - от 1,76
до 1,88; нефть - от 1,72 до 1,85; углерод - от 1,74 до 1,76. Средний
размер агрегатов изменялся при этом от 0,59 до 0,47 мкм
(древесина), от 0,53 до 0,40 мкм (нефть). Для частиц сажи от сжигания
углерода (средний размер частиц 0,45 мкм) и газа (0,19 мкм) изменений
зафиксировано не было. Следовательно, эффект старения [294]
агрегата сажи, т.е. уплотнение структуры в среде конденсирующегося
водяного пара, выражается в виде перехода относительно
разреженной структуры в более компактное образование с соответствующим
увеличением D. Конденсация пара на поверхности первоначально
разреженных сажевых агрегатов приводит к образованию глобул.
Процесс трансформации в более плотные структуры
сопровождается (кроме углерода) существенным уменьшением анизотропии
формы частиц: A = Rf /Щ, где Rx и Щ - главные размеры гирации;
R,<R2.
Количество пара, поглощаемого природными сажами, почти на
порядок выше, чем пара, поглощаемого частицами чисто
углеродной сажи. При температурных исследованиях изучались три вида
объектов: чисто углеродная сажа, модельная система «углерод +
ПЭГ» и сажа от сжигания нефти. Для нефтяных кластеров и
модельных частиц характерно уменьшение площади проекции кластеров
в диапазонах температур 20-100 °С и 300-500 °С. Всегда
уменьшение площади сопровождается уменьшением анизотропии формы
агрегатов. Свыше 700 °С кластеры сажи из нефти необратимо
разрушаются, а углеродные кластеры не претерпевают изменений вплоть
до 1000 °С.
Модель влияния капиллярных сил на процессы реструктуринга
сажевых кластеров была предложена в [311]. Рассмотрим
фрактальный кластер размерности D с числом частиц N ~rD. Число частиц
ДАТ на поверхности капли радиусом R, т.е. число ветвей, пересекаю-
287
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
щих поверхность жидкости, на которые действуют капиллярные
силы, определяется в виде
AN~DRD-1. (5.24)
На каждую частицу, находящуюся на поверхности капли,
действует сила поверхностного натяжения^. Давление Рза счет
капиллярных сил пропорционально числу частиц (5.24) и обратно
пропорционально площади поверхности капли:
P~fnDRD-\ (5.25)
Из формулы (5.25) видно, что при D< 3 давление Рна кластер
растет по мере уменьшения радиуса капли, как ВР~Ъ. Данные из [312,
313] показывают, что кластер претерпевает как упругие, так и
вязко-пластические деформации, и граница между ними зависит от
приложенной нагрузки, материала частиц и структуры кластера.
Следовательно, для каждого кластера существует некоторый порог
давления Рс — предел упругой деформации, начиная с которого
деформации становятся вязкопластическими и структура кластера
меняется необратимо. Тогда из (5.25) для смачиваемого
фрактального кластера следует существование критического радиуса
сконденсировавшейся на нем капли Rc.
Детальное описание деформации фрактального кластера
является громоздкой задачей и проводится с помощью численного
моделирования [312]. Качественная оценка исходит из предположения,
что по мере высыхания капли возрастает капиллярное давление на
кластер, и окончательно сформировавшаяся глобула радиуса Rgl
состоит по крайней мере из частиц, находящихся ранее внутри капли
критического радиуса Rc. Поэтому
RC~R3JD, (5.26)
а оценка значения предела упругости для фрактального кластера с
учетом (5.25) и (5.26) имеет вид
Rc~fnDRf-D)ID. (5.27)
Из (5.27) видно, что чем прочнее кластер, тем меньше размер
образующейся глобулы. С другой стороны, размер глобулы и Rc за-
288
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
висят от значения капиллярных сил fn. Чем лучше смачиваемость, тем
больше радиус капли, при котором начинается уплотнение кластера,
а значит, больше размер образующейся глобулы. Итогом процесса
трансформации частиц является уменьшение анизотропии,
увеличение Р агрегатов и смещение спектра в область малых размеров.
Свойства фрактальных кластеров. Рассмотрим
аэродинамические свойства фрактальных кластеров, полученных на установке (см.
рис. 5.22). Характеристики рассчитывались по данным
экспериментальных исследований скорости гравитационного оседания
агрегатов. Для этого в коагуляционной камере устанавливались две
подложки для отбора осевших частиц. Подложка в верхней части
камеры необходима для учета искажений спектров размеров и
концентрации кластеров из-за броуновской диффузии на стенки
камеры. По данным электронно-микроскопического анализа
определялась функция осевших частиц по размерам ns (R),
аппроксимируемая затем Г-распределением с 10%-й погрешностью.
Скорость оседания v(R) кластеров (рис. 5.24,а) размером R =
V(R) = ns(R)/[n(R)Ax]. (5.28)
Здесь п (R) - функция распределения частиц по размерам в
коагуляционной камере, усредненная за время оседания Ат = 60 мин. На
рис. 5.24 кривые 1-3 соответствуют фрактальным размерностям
соответственно D = 1,60 ± 0,05; 1,56 ± 0,05; 1,50 ± 0,05. Видно, что
фрактальные кластеры обладают высокой седиментационной
устойчивостью. В области больших размеров наблюдается аномальная, по
сравнению со стоксовской (кривая 4), зависимость скорости
оседания. Данный результат показывает, что по мере роста кластера
увеличивается размер пустот в нем и падает его средняя плотность.
Этот эффект иллюстрируется данными на рис. 5.24,5 для
относительной плотности кластера и тех же значений фрактальной
размерности
P*=p(r)/p0=(r0/RgfN, (5.29)
где р0 и г0 - плотность и размер первичных ядер; N— число частиц.
Малый по отношению к эквивалентному радиусу Re = 7V1/3r0
аэродинамический, или стоксовского, радиус Ra (рис. 5.24,в) явля-
10 Фракталы 2 89
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
л
10 12
Чпах» МКМ
а)
р*
0,05
0,04
0,03
0,02
0,01
0
\\. L
0,5 1,0 1,5 2,0 2,5
/?с, МКМ
б)
1,0 1,5 2,0 2,5
Ra, МКМ
«)
Рис. 5.24. Аэродинамические свойства фрактальных кластеров в виде скорости
оседания (а), относительной их плотности (б) и приведенного аэродинамического
радиуса (в) [314]
ется следствием низкой плотности кластеров. Приведенные данные
подтверждают, что в гравитационном поле фрактальные кластеры
оседают значительно медленнее, чем компактные частицы той же
массы. Это различие в большей степени проявляется для агрегатов,
образованных при кластер-кластерном механизме агрегации
модифицированных частиц.
Часто метод определения D основан на анализе
аэродинамического поведения фрактальных кластеров в гравитационном и
электрическом полях [315]. Эквивалентный и седиментационный
радиусы кластера связаны следующим образом [316]:
R R2D/3(D-l) (530)
290
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
При этом значении Re определяется счетно-весовым анализом,
a Rs - по данным седиментационных размеров. Однако выражение
(5.30) справедливо для стоксовского режима кластера в газовой среде,
которое нельзя считать в данном случае достаточно корректным.
Хотя размеры самого агрегата значительно превышают длину
свободного пробега молекул в газе, диаметр исходных дисперсных
частиц сравним, а часто и гораздо меньше этого значения [303].
Длина свободного пробега молекул X, при средней плотности числа ча-
(R/r0)D
стиц в кластере п = . ".. определяется из соотношения
Xf=l/(nnr02) = R(r0/R)D-2. (5.31)
Согласно (5.31) для фрактальных кластеров с D< 2
выполняется условие Xf > R. В свою очередь условие применимости формулы
Стокса имеет вид X «: R и Xf «: R, где X - длина свободного
пробега молекул относительно столкновения друг с другом. Видно, что
для фрактальных агрегатов, синтезируемых газофазным способом,
эти условия не выполняются, в силу чего соотношение (5.30) с
формулой Стокса для таких систем неприменимо (см. рис. 5.24,д).
Адсорбционные свойства фракталов исследованы в [303, 314] на
некоторых разновидностях аэрогеля РЫ2, получаемых
непосредственно в электродиффузном сепараторе (см. рис. 5.23). Для этого в
качестве электрода во всех каскадах используется сетка с шагом 70
мкм. При прохождении аэродисперсной системы сквозь сетчатый
фильтр из-за поляризационного взаимодействия и вследствие
инерционных сил значительная часть частиц оседает на его
поверхности, образуя гигантский макрокластер. Полученный аэрозоль
представляет собой высокопористое вещество с насыпной плотностью
0,01-0,03 г/см3, в зависимости от напряженности J?электрического
поля.
Влияние Е на процессы роста аэрогеля выражается в
формировании более разреженных структур, фрактальная размерность
которых почти линейно убывает с D « 1,55 до D « 1,2 при увеличении Е
от 0 до 7 кВ/см. Такие агрегаты обладают также более развитой
удельной поверхностью S, которая возрастает с 20 м2/г до 30 м2/г при
уменьшении Dot 1,6 до 1,1. Изменение 5аэрогеля происходит
главным образом за счет изменения среднего координационного числа v
291
Глава 5. АНАЛИЗ САМОПОДОБИЯ ПРИ ОПИСАНИИ ТУРБУЛЕНТНОСТИ ...
в агрегате. Удельная поверхность для системы неконтактирующих
частиц определяется по их суммарной поверхности, и для гладких
монодисперсных сфер радиуса г0 с плотностью р0 она равна [317]:
^о=3/(>ЬРо)-
(5.32)
Для удельной поверхности S аэрогеля, образованного в
процессе агрегации, поглощающая поверхность уменьшается на значение,
равное суммарной площади контактов между частицами. Тогда
S = Sn
Sv
(5.33)
где S - средняя площадь поверхности отдельной частицы; Sc -
средняя площадь единичного контакта между частицами.
Величина v связана с фрактальной размерностью и радиусом ги-
рации соотношением v-R^1*'1^ [293]. Оценки показали [303, 314],
что для кластеров со структурой типа «связанные петли» в первом
приближении v = x\D при ц -> 2 , когда R -> оо . Для исследуемых
аэрогелей г| = 1,8 + 0,5. В результате из (5.33) получим
S = Sn
(5.34)
что хорошо согласуется с практикой. Наилучшее сглаживание
экспериментальных данных по формуле (5.34) получается при Sc /S =
= 0,21. Близкое значение для доли поверхностного контакта, равное
0,20 ± 0,08, получалось при обработке микрофотографий с
использованием соотношения Sc/S = h/2r0, в котором предполагается, что
зона контакта имеет форму сферического сегмента с высотой А. Для
v = 0 (неконтактирующие частицы) в [303] было получено S0 = 53 м2/г,
а расчет по формуле (5.33) для г0 = 18 нм дает S'0 = 27 м2/г.
Отношение SQ/S'0 характеризует меру шероховатости первичных ядер,
является константой поверхности и определяется условиями
генерации первичных частиц.
Исследование особенностей капиллярной конденсации
проводилось на аэрогелях Bi203 методом равновесного элюирования с
292
5.4. Экспериментальное моделирование фрактальных аэрозолей и аэрогелей
использованием бензола в качестве адсорбата. С помощью изотерм
адсорбции восстанавливались функции распределения объема пор по
значениям эффективных радиусов. С уменьшением значения D
исходный спектр объема пор переходит в систему с многомодовым
распределением, причем расстояние между модами увеличивается.
Эти закономерности связаны с изменениями фрактальной
структуры аэрогеля.
Действительно, в зависимости от напряженности поля в
электростатическом коагуляторе первичные кластеры формируются из
структурных элементов разной длины. При увеличении J? доля
первичных нитевидных структур в спектре размеров увеличивается.
Вследствие этого спектр пор в макроагрегате, состоящем из этих
элементов, смещается в область больших размеров, а число мод
постепенно сокращается,
Попытка осуществить контролируемое смещение спектра пор в
область малых размеров предпринималась в эксперименте по
деформации структуры аэрогеля. Возможные механизмы, приводящие к
уплотнению структуры фрактального агрегата, рассмотрены в [318].
Процесс реструктуринга является длительным (от часа до
нескольких суток). Для ускорения этого процесса образец в течение 5 мин
выдерживался в центрифуге под нагрузкой от 0,015 кПа до 122,6 кПа.
Из экспериментальных данных [303] видно, что влияние нагрузки
на поры разных размеров не одинаково. Наиболее заметна она для
пор в области 8 нм и выше. При этом вначале с ростом давления
относительное содержание таких пор увеличивается, что обусловлено
разрушением более крупных и менее устойчивых пор. Дальнейшее
увеличение нагрузки приводит к обратной зависимости.
Перераспределение при этом происходит за счет деформации первичных ядер.
Рассмотренные здесь способы воздействия на структуру создают
предпосылки для целенаправленного изменения адсорбционных
характеристик аэрогелей с целью решения важных прикладных задач.
Глава 6
РАСПРОСТРАНЕНИЕ ВОЛН
ВО ФРАКТАЛЬНЫХ СРЕДАХ
6.1. Плоская волна в среде с фрактальной
диэлектрической проницаемостью
При распространении волны через турбулентную среду
амплитуда и фаза этой волны претерпевают флуктуации, обусловленные
флуктуациями показателя преломления среды. Классическая
статистическая теория распространения волн в оптике, радиофизике и
акустике подробно разработана (см., например, [274, 319-326]).
Однако вопросы распространения волн во фрактальных средах,
являющиеся важным современным самостоятельным научным
направлением, не систематизированы и не представлены широко в
литературе.
Постановка задачи. Проблема распространения волн через
фрактальные среды (далее - фракталы), в основном, решается с помощью
различных аппроксимаций [209—211, 327-331]. Справедливость
таких приближений трудна для проверки различных решений
вследствие пренебрежения некоторыми внешними эффектами. Вполне
естественно выглядит поиск такой задачи в распространении волн,
которая давала бы точные результаты, используемые в виде теста для
стандартных аппроксимаций. Это важно и для решения ряда
технических проблем, например, синтеза поглощающих фрактальных
материалов и т.п.
В [332] была рассмотрена среда распространения длиной L с
диэлектрический проницаемостью е(х), описываемой канторовским
множеством (см. рис. 1.1,я). На л-й стадии (п — 1,2,...) из образующей
величины е(х) = е0 удаляют среднюю треть из интервала гп(х) = гп, а
гп в оставшихся интервалах увеличивают в 3/2 раза.
Непосредственно г(х) получается в результате бесконечного числа таких итераций
с конечной мерой е0 (так называемые жирные фракталы).
Пусть на данный слой нормально справа падает гармоническая
плоская волна exp (—ikx). Волновая функция Т(х) на интервале [0, LQ]
удовлетворяет уравнению Гельмгольца
294
6.1. Плоская волна в среде с фрактальной диэлектрической проницаемостью
dhyjx)
dx2
+ k2(l + z(x))y = 0.
(6.1)
За пределами среды y(x) = ^(-ikx) + V0exp(ikx) при х > L0 и
\|/(х) = Т0 ехр(-/Ах) при х < О, где К0иГ0- соответственно
комплексные коэффициенты отражения и пропускания слоя.
Решение задачи. Найдем величину |Г0|2 = 1 - \V0\2,
характеризующую часть энергии, прошедшую через фрактальную среду. Для этой
цели используется формализм матрицы рассеяния [333]. Пусть S -
матрица рассеяния, связывающая правые и левые амплитуды волны,
падающей на фрактальную среду протяженностью Ln = LQ /3я. Так как
канторовский фрактал состоит из двух самоподобных слоев,
разделенных пустым промежутком (длина всех слоев (£л+1 = Ln/3), то
можно записать
^п ~**л+Гя+А+1»
(6.2)
где Fn = diag{exp(-/fcZn), Qxp(ikLn)} - диагональная матрица
передачи свободного пространства.
Выражая Sn и Sn+l в терминах соответствующих комплексных
коэффициентов Тт и Vm (т = п, п + 1), из (6.2) в [332] получена
система разностных уравнений
1
-1=-
4со82(фл+1+/:1л+1)
л+1
1
-1
L/i+l|
Ъ% =
sm(2%+l+kLn+l)-(l-\Tn+l\ )sin(£Z„+1)
cos(29/|+1 + kLn+l) + (1 -\TnJ)cos(kLn+l)"
(6.3)
Для решения уравнений (6.3) их дополняют условиями, которые
следуют из рассмотрения асимптотики Тп при п -> <». Нужно иметь
в виду, что большие п соответствуют прохождению через фрактал
гп(х) с толщиной £->«>. при таком предположении из (6.1) для
волны уп(х), распространяющейся внутри фрактала, получаем
уравнение непрерывности
295
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
V||(x) = Тп exp(-ifoc) + kjdx'sin [{х'-х^ф^хГ (6.4)
о
Коэффициент пропускания Тп определяется при условии х = Ln.
В пределе Ln -> 0 величина Vn(Ln) аппроксимируется выражением
При комбинировании (6.5) с соответствующим выражением для
у'п при п -> оо можно получить для х- Ln
Т ~
л
Г, ^ЛТ1
1 2Л+1 '
(6.6)
У
Система уравнений (6.3) вместе с (6.6) дает необходимое
решение задачи.
Представляет интерес зависимость коэффициента пропускания
Т0 от толщины слоя. В общем случае нелинейная система (6.3)
решается только численными методами. Однако в специальном
случае \Тп\ »1, т.е. при слабом взаимодействии волны с фрактальной
средой и линеаризации уравнений (6.3) в окрестности точки \Тп\«1,
можно получить
<P„ = 2<P„+i+*I„+1. (6.8)
Уравнение (6.8), асимптотически удовлетворяющее условию
(6.6), имеет решение
%=kLn+kz0L0/2»+K (6.9)
Подставим (6.9) в (6.7) и, принимая в расчет, что для больших
п и реальных £0 значение |КЛ| ~ kL^ /2n+l, получим
296
6.1. Плоская волна в среде с фрактальной диэлектрической проницаемостью
N-^nH2*^+*W2"+1)|- (6-ю)
Подчеркнем, что это выражение выведено при допущении
незначительности отражений при произвольно малых
пространственных масштабах. Если ^е0 < 2, коэффициент отражения (6.10) мал,
и все модули | Vn\ определяются с помощью линеаризованной
системы (6.7), (6.8). Условия (6.10) подобны борновскому приближению
[320—322]. Максимальное число шагов Л^при численном решении
(6.3) определяется точностью решения. В [332] значение
^выбиралось в пределах 24—35.
Анализ результатов. Зависимости модуля коэффициента
пропускания |Г0р от нормализованной толщины слоя kL0 для е0 = 0,1; 1,2
и 30,75 показаны на рис. 6.1. Сплошным кривым соответствуют
численные решения уравнений (6.3), пунктирным — борновское
приближение в соответствии с (6.10). Кривая из точек соответствует
однородной среде распространения с постоянным значением е(х) = е0.
Отметим, что для значений kLQ < (1 + е0)-1 зависимость
коэффициента пропускания во фрактальной среде почти идентична
аналогичной зависимости для однородной среды с е(лс) = е0. Для
kL0 > (1 + е0)-1 дифрактальный коэффициент пропускания | Г0р
имеет немонотонное и нерегулярное поведение с конечным числом
пиков. Значение пиков достигает единицы. Подобные пики
наблюдаются и при комплексных е0.
Первый факт свидетельствует о том, что фрактальные
масштабы, меньшие длины волны излучения, слабо влияют на
распространяющуюся волну.
Второе свойство коэффициента пропускания объясняется
самоподобием фрактальной среды. В самом деле, пусть для некоторых
частных значений Ц и £q величина |7J[| ~1. Рассмотрим слой с
e|!J = (2/3)£q толщиной L^. Если Ц = 3Z^, то новый фрактал
образуется из двух с параметрами £q и Ц . Из условия [7^ ~ 1 следует, что
|Г0'| также близок к единице. Это верно и в том случае, когда
аргумент косинуса в (6.3) принимает значения тс/2 + /ял, т = 0,1, 2... Это
позволяет интерпретировать появление пиков как самоподобное по-
297
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
вторение начального пика при kL0 < (1 + е0)-1 для фрактала с
образующим параметром (2/3)т. Частота появления пиков
увеличивается с возрастанием е0. Это хорошо видно при сравнении числа
пиков на рис. 6.1, б я в. Борновское приближение выполняется при
условии к1^г0 < 2, как следует из формулы (6.10) и рис. 6.1.
Рис. 6.1. Зависимость коэффициента пропускания |Г0р
от нормализованной толщины слоя kL0 при разных значениях е0 [332]
298
6.2. Диапазонно ограниченная фрактальная модель флуктуации...
6.2. Диапазонно ограниченная фрактальная модель
флуктуации коэффициента преломления тропосферы
Моделирование показателя преломления функцией Вейерштрас-
са. Феноменологическое моделирование локально однородного
показателя преломления тропосферы на основе фрактальной
концепции рассматривалось в [334]. В работе использовалась широко
применяемая во фрактальных исследованиях диапазонно ограниченная
функция Вейерштрасса [45,128]. Часто удобно представлять спектр
турбулентности несколькими интервалами и рассматривать их
базисные функции. В [335] фурье-пространство спектра турбулентности
моделировалось в логарифмическом масштабе в терминах
локализованных последовательностей самоподобных импульсов.
Соответственно спектр турбулентности можно представить
ансамблем произвольно локализованных косинусоидальных функций
для каждого логарифмически разбитого диапазона
пространственных шкал. Функция Вейерштрасса многомасштабна, самоподобна и
может иметь внутренний и внешний масштабы, что согласуется с
теорией Колмогорова. Следовательно, диапазонно ограниченная
функция Вейерштрасса может описывать общие характеристики
атмосферной турбулентности в явном виде. Справедливость
модели, предложенной в [334], проверялась сравнением с колмогоровс-
ким спектром в пределах инерционного интервала. Применимость
феноменологической модели в различных случаях может быть
оправдана, если требуется выяснить качественные особенности
радиофизических эффектов при распространении волн во фрактальных
средах.
Одномерный показатель преломления п (х) тропосферы запишем
как функцию координаты х в виде
п(х) = (п(х)) + п[(х). (6.11)
Здесь (п(х)) — среднее значение показателя преломления; п{(х) — его
пространственные вариации; угловые скобки — процедура
усреднения по статистике среды.
Введем в рассмотрение внутренний и внешний масштабы
турбулентности. Так как флуктуации рассматриваются только в
инерционном интервале, то предполагаем, что шкалы масштабов много
больше внешнего масштаба. Моделирование флуктуационной час-
299
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
ти показателя преломления пх{х) в [334] производится функцией
Вейерштрасса. Удивительно, что еще в 1926 г. Ричардсон [336]
предложил использовать функцию Вейерштрасса для моделирования
частиц воздуха.
В явном виде
*<*>= PiХ [1 ■ feU)^!)] 1/2 lb2(D-2)n «*W*/L + %)> (6-12)
ГДе {2(^}[1-62^-2)]} !/2 [l-62(/>-2)(AT+l)-J-1/2 _ коэффициент норма_
лизации; Р{ определяет соотношение между совокупными флуктуа-
циями (nj\ и флуктуациями (п^ в инерционном диапазоне; Ъ>1 —
параметр пространственно-частотного масштабирования; D-
фрактальная размерность, принимающая значение 5/3 при одномерных
флуктуациях; 7V+ 1 — число масштабов, или интервалов в
логарифмическом разбиении; срл - произвольная фаза, связанная с
соответствующим масштабом и равномерно распределенная как (2к)А на
отрезке [0, 2к].
Так как масштабы существуют в интервале от внутренней
шкалы /до внешней L, то фундаментальная пространственная частота,
или параметр пространственно-частотного масштабирования Ь,
должна удовлетворять соотношению bN - L/l.
Непрерывность масштабов. Рассмотрим сначала случай, когда
характеристики перемежаемости функции Вейерштрасса игнорируются
[334]. Это означает, что 4-^1 и все масштабы пространственно
заполнены благодаря отсутствию функции локализации. Тогда
корреляционная функция R(x"), полученная усреднением по ср , равна
р2/л2\П__й2(/)-2)1 N
Д(*)= 1У£в-Ш+1) lbW-»»cos(2nb»x'/L). (6.13)
л=0
Одномерный энергетический спектр G (К), соответствующий
(6.13), определяется как
G(K) = -!- 1 RWexpQKxW. (6.14)
300
6.2. Диапазонно ограниченная фрактальная модель флуктуации...
Подставив (6.13) в (6.14) и рассматривая только положительные
пространственные частоты, получим
G{K) = 2Г1 -%-W+Vl ^******"2nlf /L)- (6Л5)
Так как Ь -> 1, то дискретные волновые числа в (6.15) становятся
почти непрерывными. Положим # = 1 + х,где%->1и M^+1) ~bN = L/l.
Тогда формулу (6.15) можно переписать в виде
R2(n2f)(4-2D)% n
™--{1'1»«Аъ *K-™/Ly <б1б)
При D = 5/3 и £»/ из (6.16) имеем
P?lnl\y N
G{K) = AA^2b-2n/V-2Kbn/L). (6.17)
По методу [128] непрерывная аппроксимация (6.17) дается
усреднением по интервалу АК в виде
__ 1 К+АК/2
W = TF J WW- (6.18)
Полагаем, что аргументы дельта-функции в (6.17) постоянны в
интервале [ К - АК, К + АК ], и при малом AJ5Tна основе (6.18)
получим
г рНп1)х(кт\2П г^
g{k)~Ik з [%} AKdn(K)/dK> ^ <бЛ9>
где n(K) = ln(KL/2n)/lnb.
При dn(K) /dK = l I{К In b) соотношение (6.19) переходит в
уравнение
301
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
G(K) = l9l35Pl2(nj)L-2^K-5/\ (6.20)
которое по форме соответствует колмогоровскому спектру
G(K) = 092A(rff)lr2'*K-5/\ (6.21)
Если положить Рх = 0,46, то уравнения (6.20) и (6.21)
становятся идентичными. Одномерный колмогоровский спектр
пропорционален K~D, где D = 5/3. Для одномерных фрактальных функций было
найдено [188], что их спектры пропорциональны K~^5~2DK Если
D= 5/3, спектр, полученный в [188], пропорционален К~5/3 = K~D,
что соответствует результатам [334].
Перемежаемость. Рассмотрим характеристики перемежаемости
флуктуации коэффициента преломления тропосферы с помощью
подходящим образом определенных функций локализации, которые
определяют волновые пакеты каждой косинусоидальной функции в
(6.12). Функция флуктуации с предложенной в [334] локализацион-
ной зависимостью записывается как
т=0 Г1_й2(Д-2)(ЛГ+1)у л=0
^^~UC/dm]}cos(2nb"mx/Lm +Фш). (6-22)
Здесь Fn(x)={(b™/dJl/hea[(x-bmJb™/dm]}-$yHKUwiJiOKimK3a-
ции; J F2(x)dx = l; ос - фактор локализации; dm — характеристика
внешнего масштаба; £ — случайная переменная, центрирующая
/1, И<1/2,
волновой пакет каждого масштаба; rect х = <
[0, |х| > 1/2.
Из-за различных местоположений пространственно-частотных
компонент составляющая пх{х) становится неоднородной
фрактальной функцией. Поэтому вместо D необходимо использовать
усредненную фрактальную размерность D . Следует заметить, что D = D = 5/3
302
6,2, Диапазонно ограниченная фрактальная модель флуктуации,,.
для одномерного случая, так как при проведении усреднения по
различным реализациям перемежающихся флуктуации характер их
поведения подчиняется уравнению (6.22). Хотя уравнение (6.22)
имеет математически сложный вид, оно наглядно представимо с
помощью фурье-разложения (рис. 6.2), в котором характеристическая
длина dm и фактор локализации а определяют размер сгустка и
ширину волнового пакета, меньшую, чем внешний масштаб.
-Зууё—w—м-
r-dX*
1 ■ 1
Рис. 6.2. Диаграмма фурье-разложения перемежающейся модели показателя
преломления на основе функции Вейерштрасса [334]
Из уравнения (6.22) следует, что ширина волнового пакета,
соответствующего л-му масштабу в /и-м сгустке, становится равной
(^пРтт • Следовательно, малые масштабы более локализованы по мере
возрастания а. На рис. 6.3 приведены флуктуации коэффициента
преломления п{(х) на основе модели диапазонно ограниченной
функции Вейерштрасса и их спектры для Fn(x) = 1 (рис. 6.3,а) и с
различными факторами локализации (рис. 6.3,5—г). Если допустить, что
разные сгустки статистически независимы для заданных dm, то
соответствующие значения dm можно трактовать как интервал
корреляции.
Одномерная модель. Определим одномерный спектр для
перемежающихся флуктуации [334]Уйз-за перемежаемости значения п{(х)
будут локализованы. Следовательно, переменные, входящие в эту
функцию, - последовательность случайных фаз, интервал
корреляции, размер внешнего масштаба - будут статистически
независимыми от сгустка к сгустку. Для удобства положим Ьт = b, dm = d, Lm = L.
Усреднение по этим переменным можно произвести при известных
распределениях вероятностей.
303
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рис. 6.3. Флуктуации коэффициента преломления п{(х) на основе модели диапа-
зонно ограниченной функции Вейерштрасса (слева) и их спектры (справа) [334]
Спектр мощности, усредненный по ФЛ, выражается формулой
(ОД)ф = ^ ] (R(x\ ap(l&)&. (6.23)
—оо
Функция корреляции, усредненная по (рл с значением ,0 = 5/3
при условии L »/, определяется в виде
<Л(дО>,-((и,(х + *>,(х)),> -((«.(х+х^Сх)^^-
304
6.2. Диапазонно ограниченная фрактальная модель флуктуации...
= Р? (nj)(l - b-W)%{Fn(x + x-)Fn{x))x b-W cos(2nb"x'/L) =
= P? (л2 )(1 - 6-2/3)£л(6™х7^~2л/3 cos(2nb»x'/L), (6.24)
fl-Ы, Ы<1,
гдел(х)= ' '
[О, |х|>1.
Следовательно, соответствующий одномерный спектр равен
С(Л = ^2(^>(1-^2/3)Х*-(2/3+а)лх
л=0
d sin2[db-™{K-2%b»/L)/2]
(6.25)
Отметим, что (6.25) аппроксимирует (6.15) при а -> 0 и tf -> оо.
Из (6.22) получается, что 0 < ос < 2/3. Величина b определяется
условием Ъ -1 «с LI d, так как в спектре по мере возрастания d
начинают проявляться более мелкие детали. Как следует из рис. 6.3,
спектры G с разными а графически неотличимы от кривой К~5/3. Это
означает, что модель [334] нечувствительна к значениям а и Ъ в
интервале b-l<KL/d. Поэтому в совокупности с выражением (6.20)
данное обстоятельство подтверждает гипотезу о том, что спектры
диапазонно ограниченной функции Вейерштрасса хорошо
аппроксимируют колмогоровский спектр.
Трехмерная модель. Рассмотрим два варианта трехмерного
обобщения одномерных функций коэффициента преломления. Первый
вариант — это применение квазиизотропной функции флуктуации,
а второй — анизотропной функции.
Рассмотрим сначала квазиизотропную трехмерную функцию
флуктуации пх (х, у, z) [334]
{(8/3)(^2)[1-й2^-4)]}1/2
nl(x,y,Z)-P2 n_b2(D-4)(N+l)ll/2 X
305
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
xcoKV+<)+coK^x+<)coKV<)coK^+<)+
+cos (hqrx + q>]r )cos [fqrsy +.98, )cos (j^z + cp9„)], (6.26)
где /«* = (2ti^ /Z)sin[(7c/2)sin(7cr/2i?0)]cos(7w/2i?0);
gqrs =(2nb« /Z)sin[(7c/2)sin(7cr/2i{0)]sin(7w/2i?0);
hqr=(2n№ / L)cos[(n/2)sm(nr/2R0)],
а девять фазовых аргументов косинуса являются независимыми
переменными в интервале [0,2тс]. Фрактальная размерность D в
трехмерном случае принимает значение 11/3. Данная функция
флуктуации коэффициента преломления симметрична для компонент по х,
у, z, что позволяет избежать превалирующего направления.
Функция корреляции
R(x' V rl- * //L -х
*Ч* > У ><. ) - 2 j __ £2(/)-4)(ЛГ+1) А
•"О 9=0 r=\ s=l
+cos(gq„x')cos(hqryycos(fg„z) + cos(hgrx)cos(f^y)cos(ggrsz')], (6.27)
а соответствующий спектр имеет вид
_ i Р^ (nj)[1- ^-4>]
^^'^'^) = 3 8n_62(/)-4)(JV+l)] X
>4 i £ i *2(*-4* {[«*,+/?j+«*, - /•.>>
Л) ?=0 r=l s=l
306
6.2. Диапазонно ограниченная фрактальная модель флуктуации...
х[ЦКу +gqJ + b(Ky -gqj][b(Kz +hgr) + 5(Kz -hgr)] +
+[*** + V> + 8<^ "ЪЛ*КУ + V> + 6<^ "V>]x
x[8(^ + /,J + 8(^-/era)][S(^+^) + 8(^-^)]}. (6.28)
Если рассматривать локализации дельта-функций в (6.28), то
оказывается, что существует 24 Щ таких функций на поверхности
сферы радиуса К, где
К = (К1 + Ц+К1)У2={f}n+g2qn+hlf2= 2kV/L. (6.29)
Поэтому, когда 6 -> 1 и R^ -> °°, дельта-функции в (6.28) почти
непрерывны на АГ-пространстве. Непрерывная аппроксимация,
определенная в (6.30), подобна одномерному случаю (6.18) и
записывается в виде
ё(Л = -^ J G(Kx,Ky,Kz)dV, (6.30)
АК AV
где AV - оболочка, офаниченная внутренним К-АК/2 и внешним
К + АК/2 радиусами. Подстановкой (6.28) в (6.30) с D= 11/3
получаем непрерывно аппроксимируемый спектр (6.31) с помощью
такой же процедуры, что и в одномерном случае:
G(K) = 0,W}(n2f)L-2^K-n/\ (6.31)
Трехмерный колмогоровский спектр для локально однородной
и изотропной турбулентности равен
G(K) = 0,063(^)1-2/3^-11/3. (632)
Если Р2 = 0,59, то (6.31) и (6.32) будут идентичными.
307
Глава 6, РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рассмотрим теперь возможную анизотропную модель.
Ненормализованная анизотропная функция флуктуации показателя
преломления запишется как
ny{x9y9z) ~ i 2X(# + Ь2/ +b2z^D-4)/2cos(2n%x/L + <p*)x
gr=0r=0*=0
xcos(2nbryy/ L + q>y)cos(2nbszz/ L + q>zs). (6.33)
Спектр с фрактальной размерностью D= 11/3 имеет вид
WKx,Ky,Kz)~L-2'4K2x+K2y+^^ (6.34)
Так как часто атмосферная турбулентность анизотропна,
приведенная функция флуктуации показателя преломления дает
полезную модель для таких случаев. Косинус-фурье-разложение
флуктуации показателя преломления с помощью метода фазовых экранов
рассмотрено в [337]. Фрактальный подход, представленный в [334]
для традиционной задачи радиолокации и радиосвязи, может дать
новый полезный взгляд на распространение волн в атмосфере.
6.3. Волновые взаимодействия в многослойной
канторовои среде распространения
Обобщенная канторова решетка. Проблема отражения и
пропускания электромагнитных волн семейством фрактально
распределенных дискретных слоев важна для практики радиолокации, геофизики
и медицины. Данная задача формулируется в терминах обобщенной
модели канторовои решетки. При этом можно наблюдать влияние
роста фрактала и его размерности на режим распространения волн
в такой среде.
Рассмотрим модель на основе простой канторовои решетки с
фрактальной размерностью D = log2/log3 = 0,631 [338,339]. Первые
пять поколений ее были показаны на рис. 1.1,я(см.гл. 1),откуда
следует, что общая длина канторовои решетки с увеличением порядка
поколения s уменьшается на 1/3, а число сегментов удваивается. По
мере роста стадий образования общая длина решетки стремится к
нулю (см. (1.2)), а число решеток становится неограниченным.
308
6.3. Волновые взаимодействия в многослойной канторовой среде распространения
Разобьем каждую из существующих решеток на N сегментов.
Затем удалим Nm сегментов. В этом случае фрактальная размерность
такого множества имеет вид
DJS^M. (6.35)
Такое построение позволяет конструировать дискретные
фрактальные структуры с фрактальной размерностью, изменяющейся от
О до 1. На рис. 6.4,а показаны три различные обобщенные канторовы
решетки на их третьей стадии развития с разными значениями D.
Вверху приведена регулярная канторова решетка с D = 0,631, когда
отбрасывается треть сегмента. В середине изображена структура,
порождаемая повторяющимся удалением средней половины каждого
сегмента с D = 0,5. Внизу показана обобщенная канторова решетка,
образованная отбрасыванием средней 3/5 сегмента с D= 0,431.
Геометрия задачи приведена на рис. 6.4 Д Здесь образована
двухуровневая канторова решетка с коэффициентом преломления
среды, изменяющимся между двумя фиксированными значениями.
Белые области на рис. 6.4,5имеют коэффициент преломления
основной среды п0, а заштрихованные участки представляют внедренные
слои с коэффициентом преломления nv Электромагнитная волна
падает перпендикулярно слою фрактала и распространяется слева
направо. Общая толщина дискретных фрактальных слоев равна А.
Коэффициенты отражения и пропускания. Формулы (6.36) и (6.37)
дают значения коэффициентов отражения и пропускания плоской
волны:
it и и и
/)=0,631 Падающая волна __ __ „ __
II II II II т ■■ И И И Прошедшая волна
0=0,500 *
ц ц ц .. Отраженная волна
/>=0,431
а)
Рис. 6.4. Примеры обобщенных канторовых решеток
с разными значениями D (а) и геометрия задачи распространения волн
через дискретные фрактальные слои (б) [339]
309
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
v =-V=-!hz±} у у .ИШЬ., (б.зб)
^01 = ^ = -^?-' TXQ = T'=-^-, (6.37)
где порядковые индексы обозначают порядок слоев и поверхности,
которые исследуются.
Эффективные коэффициенты отражения и пропускания
одиночного слоя толщиной d, в котором принимаются в расчет
множественные эффекты отражения и пропускания внутри слоя, имеют вид
т=-у+Т^^^ы)' (6-38)
т=йгЧ^Ш)' (639)
где к = 2п/Х — волновое число падающей волны.
Метод расчета по самоподобию. Для задач отражения и
распространения (см. рис. 6.4,6) необходимо учитывать множественные
отражения между слоями. Прямое сложение каждой составляющей или
подход на основе матричного метода [332] становится очень
громоздким и включает экспоненциально возрастающее число операций для
фрактального слоя на высоких стадиях поколений. В [339]
разработан новый метод решения таких задач, основанный на эффекте
самоподобия. Он значительно сокращает машинное время счета по
сравнению с матричным.
Сначала рассмотрим отражение и распространение в слоях кан-
торовой решетки на первой стадии, где два идентичных слоя
толщиной ^разделены расстоянием d. Представим этот элементарный слой
как эквивалентный одиночный блок толщиной d с
коэффициентами отражения и пропускания (6.38) и (6.39). Принимая во
внимание множественные отражения внутри данного эквивалентного
блока, запишем эквивалентные коэффициенты отражения К7и
пропускания Tj в виде
310
6.3. Волновые взаимодействия в многослойной канторовой среде распространения
r2(rf)exp(/p^)
7 l-VHcDtxpiUr^kd)' ( }
Эти формулы показывают, что эффективные коэффициенты
отражения и пропускания последовательности канторовых решеток
на первой стадии могут быть рассчитаны из аналогичных
коэффициентов канторовых решеток нулевой генерации для одиночного
слоя по известным коэффициентам поверхности раздела. Данный
алгоритм распространяется на любое число поколений фракталов, т.е.
можно будет рассчитать стадию s из стадии s— 1.
Расширение уравнений (6.40) и (6.41) до более высоких стадий
роста начинается с определения функций gv {x, y,d)ngt (x, y,d)B виде
[338,339]:
/ л\ , Vexp(/2«fa/)
Ф^^^^2,т^ыу (6.42)
у2 exp(iprukd)
8*Х>у4)=1-хЧщ>{Пщк<1У (6-43)
Допустим, что V(s, А) и T(s, А) представляют эффективные
коэффициенты отражения и пропускания набора слоев фрактальных
канторовых решеток на стадии s с общей толщиной А. Данные
коэффициенты находят рекурсивным методом с помощью соотношений
V(s,A) = gv[V(s-l, Зг1д), Г(*-1, З^А), З^Д], (6.44)
T(s,A) = gt[V(s-1, З-1 A), T(s-1, З-1 А), З"1 д], (6.45)
с начальными условиями
К(0,3-*Д) = К(3-*Д), (6.46)
Г(0,3-5А) = Г(3-5Д), (6.47)
где V(d) и Т(d) определены формулами соответственно (6.38) и (6.39).
311
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Концепция, используемая при выводе формул (6.42)-(6.47),
носит название метода расчета по самоподобию. Данный метод может
быть использован в различных расчетах фрактальных структур.
Например, сокращенная форма данного метода была применена для
расчета эквивалентного сопротивления фрактальных сетей с
заполнением по Паскалю-Серпинскому [340]. Метод отражает формализм
решения, благодаря чему геометрическая рекурсия напрямую
связана с рекурсией решения. Это позволяет объединить физику
рассеяния и распространения с геометрией задачи. В качестве примера
отметим, что для слоев N канторовой решетки требуется только N
итераций. Между тем при использовании матричного подхода
необходимо произвести (2^+1 - 1) операций [338].
Коэффициенты отражения и пропускания обобщенной
канторовой решетки (6.35) порядка Nn степени Nm на стадии s
рассчитывают рекурсивно [339] по соотношениям
V(s,A) = gv
s-l
tn
2N
5-1,
N-Nm Л
22./
2N
N
N
, (6.48)
T(s,A) = gt
V\s-l,
2N
,T\s-l,
N-N_ Л N.
IN
■i?A
(6.49)
с начальными условиями
V(0,d) = V(d),T(0,d) = T(d).
(6.50)
Уравнения (6.38)—(6.41), а также (6.44)—(6.50) удовлетворяют
закону сохранения энергии в виде VV*+TT* = 1, где звездочкой
обозначена операция комплексного сопряжения.
Результаты расчета. Рассчитаем коэффициенты отражения
фрактальных слоев канторовой решетки с использованием итерационного
алгоритма, описанного ранее [339]. В основном, рассмотрим Кпри
вариации частоты падающей волны. Полагаем, что п0=1ипх = 1,5.
В дальнейшем проведем аналитическую аппроксимацию для
восстановления фрактальной размерности D и стадии роста (поколения) s.
На рис. 6.5 отображена зависимость амплитуды V и фазы ф
коэффициентов отражения Кдля фракталов из канторовой решетки на
разных стадиях роста (s = 0,..., 3) от нормализованной толщины слоя
312
6,3, Волновые взаимодействия в многослойной канторовой среде распространения
0,1 0,2 0,3 0,4 0.5 0,6 0,7 0,8 0,9 1
5
/
/
/
/
/
и
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
5
Рис. 6.5. Зависимость амплитуды V и фазы Ф коэффициентов отражения
для фрактальных слоев канторовой решетки на разных стадиях роста
от нормализованной толщины слоя 5 [339]
313
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
8 = А/Х. Ясно, что амплитуды коэффициентов отражения являются
периодической функцией от 8. Их периоды составляют
соответственно 1, 3, 9, 27 в относительных единицах. Из уравнения (6.38)
следует, что амплитуда коэффициента отражения простого
одиночного диэлектрического слоя (рис. 6.5,а) периодически изменяется
между 0 и 0,385. Поэтому асимптотическая аппроксимация имеет вид
K0(8)«0,385|sin(6ic5)|, (6.51)
где нижний индекс обозначает стадию роста слоев канторовои
решетки.
Для амплитуды коэффициентов отражения многослойной
канторовои решетки на первой стадии роста с относительным периодом 3
(рис. 6.5,6) было получено
^(6)-1,742
cos
10тс5Л
3 J
о,3
К | М,67
sin(27c8)cos
10тс8
(6.52)
Аналогично для второй стадии роста (рис. 6.5,в) амплитуда имеет
относительный период 9, и аппроксимация дается выражением
К2(8)« 1,38|cos(28tc5/9)|K1 (8/3) =
= 0,925 |sin (2tc5/3)cos (10tc5/9) cos (28tc5/9)| .
(6.53)
Спектр отражения канторовои решетки на данной стадии роста
всегда является модификацией спектра предыдущей стадии и са-
моподобен. Аппроксимации (6.51)—(6.53) будут точнее при условии
n0~nv Стадии роста фракталов определяются числом
гармонических факторов при получении V. Фазы коэффициентов отражения
Ф почти линейно изменяются с ростом 8, а фазовые скачки на 180°
происходят каждый раз, когда амплитуда V = 0.
Период А коэффициента отражения для канторовых слоев на
стадии роста s задается формулой
Ар=У (6.54)
для случая п0 = 1 и пх = 1,5. Эффективный коэффициент
преломления пе среды со слоями канторовои решетки может быть найден при
низкочастотном спектре или длинноволновом пределе. Первый пик,
появляющийся в низкочастотном спектре, характеризует среднюю,
314
6.3. Волновые взаимодействия в многослойной канторовой среде распространения
или эффективную, диэлектрическую проницаемость фрактальной
среды
^=«0 + (2/ЗУЦ-«0). (6.55)
Для расчета коэффициентов отражения и пропускания среды с
обобщенной канторовой решеткой необходимо использовать
итерационные формулы (6.48) и (6.49). На рис. 6.6 представлены зависи-
V £М),631 ср° £=0,631
1 200 I
150
100
50
0
-50
-100
-150
-200
Рис. 6.6. Зависимость амплитуды V и фазы ф коэффициентов отражения для
слоев с обобщенными канторовыми решетками на второй стадии роста (s = 2)
от нормализованной толщины 6 [339)
315
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
мости амплитуды V и фазы ф коэффициентов отражения
обобщенных канторовых решеток на второй ступени роста в зависимости от
нормализованной толщины 8. По мере роста D пики отражения
расширяются, а фазовые вариации возрастают. В общем случае период
А коэффициента отражения многослойной канторовой решетки
порядка Nh на стадии роста 5* определяется по формуле
Ap=Ns (6.56)
для коэффициентов преломления п0 = 1 и пх = 1,5. Для рис. 6.6
значения А равны соответственно 9, 16 и 25. Стадия роста
определяется фундаментальными гармониками амплитуды коэффициента
отражения V и может быть найдена фурье-преобразованием.
Эффективный коэффициент преломления для многослойной обобщенной
канторовой решетки записывается [339] в виде
(N-N Y
Пе = п«+ \~1Г* г"1'"**' (6'57)
Из рис. 6.6 следует, что амплитуда первых пиков подавляется по
мере уменьшения D. Это означает, что эффективный коэффициент
преломления уменьшается по мере того, как структура слоев
становится реже, что согласуется с геометрической интерпретацией.
Более того, если известна стадия развития s, то из (6.57) можно
определить значения Nn Nm, которые по (6.35) дают значение
фрактальной размерности.
В высокочастотном пределе рассмотренные структуры ведут себя
как цепочки связанных резонаторов Фабри-Перо, в которых все
системные отклики являются суперпозицией индивидуальных резонан-
сов. Все это дает хаотично изменяющийся отклик отражения,
типичный для высокой стадии роста. По мере роста числа стадий
формирования s, частоты и общей толщины слоев, пики коэффициента
отражения распределяются по частотам, подобно распределению
канторовой пыли (см. разд. 1.1). Это происходит из-за
распределения плотности диапазонных пустот, связанных с электромагнитными
свойствами структуры.
Обобщенный метод расчета. Более общий случай рассеяния волн
фрактальными сверхрешетками с изменяющимся заполнением рас-
316
6.3. Волновые взаимодействия в многослойной канторовой среде распространения
смотрен в [418]. Здесь исследуется влияние изменения фрактальной
размерности, степени роста, количества интервалов и угла падения
на коэффициенты отражения для перпендикулярной и параллельной
поляризаций. При этом интерес проявляется, главным образом, к
тому способу, которым вся совокупность сверхрешеток Кантора
передает свою фрактальную информацию рассеянным волнам. Здесь
усматривается четкая связь между характеристиками рассеянных волн
и фрактальными дескрипторами канторовой группы, которая
определяет сверхрешетку.
Лакунарность. Хотя в большинстве случаев фракталы
характеризуются своей размерностью, это не обеспечивает их полного
описания. На рис. 6.7 представлены слева направо трех-, четырех- и пя-
тиинтервальные канторовы группы, каждая из которых имеет
размерность D = 3/4 и D = 1/2. В данном случае видна разница между
группами с одинаковой фрактальной размерностью.
Дополнительной характеристикой фракталов является их заполнение или
лакунарность (lacunarity) А . Этот термин был введен Б. Мандельбротом [3]
для описания степени однородности фракталов.
I п'
1
III!
= 3 D = 1/2
S'= 0
1 1
Illl - Illl
S'^ 2
1
Illl
п' =
■
1111
= 3 D = 3/4
Sis 0
S ■= 1
Illl Illl
S = 2
■
Illl
1 n'=* P = ifl
1 S = 0
Illl
S = 1
Illl
S«2
1
1
*
! n'=5 P*l/2
S'sO
1 1 II 1
1 1 II 1
Ss2
f
^Hi 1
1
.1
rV~= 4 D = 3/4
S * 0
inn inn snni' inn inn
S's 2
Vs"5" D=3/4
S - 0
iiiiii и iTii mi» iiiiii
Ss 2
Рис. 6.7. Канторовы группы с фрактальными размерностями D = 1/2 и D = 3/4
при числе интервалов п'= 3, 4, 5 на стадиях роста s = 0, 1, 2 [418]
В [418] рассмотрено взаимодействие волн с распределением
коэффициента преломления, описываемого канторовыми группами на
конечных стадиях роста. Для симметричных канторовых групп (см.
рис. 6.7) мы определим заполнение через величину е, зависящую от
фрактальной размерности (1.6). Сначала свяжем е с традиционными
мерами заполнения, одной из которых является величина
317
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
A(R) = Z%\R)/[ZM(R)]\ (6.58)
где
zgHiO^M'QiMji) (659)
- момент ^-го порядка функции Q (M, R), которая является
вероятностью того, что поверхность, облегающая фрактал, обладает массой
М. Обозначим через MR массу поверхности радиусом R и запишем:
A(R) = ^~b- (6.60)
Для обобщенной канторовой группы Е(г) с нормализованной
шириной интервала е можно ввести характеристическую функцию
[1, хеЕ(е),
Хш(х) = \о>Х*Е(е). <661>
Тогда масса, содержащаяся в сглаженной поверхности радиуса
R и сосредоточенная в точке т, есть
*W = J %E(£)(x)dx = J X*(e)(*)V* " №> (6-62)
i-R -~
где введена функция окна
f 1, хе [-R,R],
h'(X)'\o,»[-R,R], <««)
чтобы иметь возможность вести вычисления с использованием
взаимной корреляции. Если проинтегрировать К*[(К*)2~^ по всем
возможным т, получится искомая величина Mt(R)\M*(R)\. Тогда
заполнение (параметр лакунарности) принимает вид
/г i2
ттах / Ттах
Л,(Л)= J K*&dx/\ J K*(x)dx\ , (6.64)
Tmin / LTmin J
где т^, ттах будут определяться далее.
318
6.3. Волновые взаимодействия в многослойной канторовой среде распространения
При определении способов измерения меры лакунарности нет
единства относительно подхода к рассмотрению влияния кромок
фрактальных групп. Для начальной группы [О, L] в [418]
выбирается [ Tmin> Tmaxl так> чт°бы они попадали в интервал [Л, L - R]. Затем
вычисляют \(R) для е в диапазоне от 0 до BmSK=(l-Nr)/n\ где
п = N -1, т. е. число интервалов в канторовой группе. При этом
заполнение является функцией от R и е. Однако для проведения
качественных сравнений функция от е может быть более полезной.
Чтобы достигнуть этого, необходимо положить R = R , где 27? = г+еп
и определить
max '
Л(е) = Л(Л)
(6.65)
для заданной конечной стадии роста. Выражение (6.65) и е
полностью определяют заполнение, которое рассмотрено в [418].
На рис. 6.8 изображена зависимость Л(е) при первой и второй
стадиях роста s для полос с тремя, четырьмя и пятью интервалами
при D = 3/4. Для каждого значения л' значение Л(е) обычно
меньше во второй стадии, чем в первой; значения етах =0,1233 (л'=3),
етах «0,1038 (я' = 4), етах -0,0899 (я' = 5).
При наибольшей однородности группа имеет период 2R , а Л(е)
стремится, как и ожидалось, к единице.
Рис. 6.8. Заполнение Л канторовых групп для первой и второй стадий роста s
при числе интервалов и'=3, 4, 5 [418]: для кривых 1,2 п' = 3;
для кривых 3, 4 п' = 4; для кривых 5, 6 п'= 5
319
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Отражательные формулы. В эксперименте электромагнитная
волна падает под углом к поверхности фрактальной сверхрешетки
общей длиной L, состоящей из слоев переменной толщины с
показателями преломления пх и п0 (основная среда) (рис. 6.9). Для
сверхрешетки, описываемой канторовой группой Е, показатель
преломления по оси z равен nv если ze Е ,ип0-в противном случае. Угол
падения в областях с п0 равен 60, а угол, под которым
распространяется волна в слоях с коэффициентом nv равен в{. Преломляющие
слои имеют длину rL, а внешние интервалы — длину гЬ.
Рис. 6.9. Схема падения электромагнитной волны на канторову сверхрешетку
с тремя интервалами п'= 3 при первой стадии роста [418]
Расчет коэффициентов отражения и пропускания ведется по
методике, предложенной в [338, 339]. Сначала записывается общая
форма для коэффициентов отражения и пропускания многослойной
оптической структуры с числом поверхностей раздела N,
разделенных областями с показателем преломления п0. Полученная общая
форма выражается через коэффициенты отражения и пропускания
отдельных поверхностей раздела. Данные поверхности раздела
временно замещают все N копий, из которых состоит фрактал. Такая
конструкция создается с помощью рекурсии по числу интервалов.
Вторая рекурсия получается по стадии роста s канторовой полосы.
На этой стадии коэффициент отражения (пропускания) в общей
форме, рассмотренной ранее, заменяется коэффициентом отражения
(пропускания) канторовой полосы длиной rL при стадии роста s—l.
Данная процедура повторяется до тех пор, пока s не достигнет нуля;
на этой стадии коэффициенты простой диэлектрической пластины
используются при подстановке.
320
6.3. Волновые взаимодействия в многослойной канторовой среде распространения
Функции генерирования имеют вид:
х + (у2 -x2)Fv(ri -Х^ху^щка^со^)
у(П) l-xFyin'-l^xpilir^k^Lcos^) ' <666)
= у^г(^- l)exp(pi^q.£cos90)
rV ' их^Ся'-ОехрСг/^а^созео)' (Ь0/)
где ri > 1 удовлетворяет начальным условиям Fv (0) = х и FT (0) = у;
к — волновое число опорной волны в свободном пространстве; а,. -
размеры интервалов, приведенные к длине L, i = 1, 2, ..., ri.
Уравнения (6.66) и (6.67) используются в операциях первой
рекурсии для вывода обобщенных функций отражения и пропускания:
gv(x,y9L) = Fv(fO, (6.68)
gt(x,y,L) = FT(n'). (6.69)
Коэффициенты отражения и пропускания для канторового слоя
стадии s общей длиной L вьиисляются с помощью второй рекурсии
по формулам
V(s,L) = gv[V(s-l rL), T(s-l, rL), L], (6.70)
T(s,L) = gt[V(s-l,rL), T(s-lrL),L]. (6.71)
Начальные условия для этих выражений задаются
коэффициентами отражения и пропускания единичной пластины произвольной
длины dc показателем преломления nv расположенной в
бесконечной области с показателем преломления п0:
v(0 * >oi +(^о^>1 -^ol^o)^oexP(2^fa/cose,)
W,a)- [i-K^exp^iWcoee!)] ' (bU)
'^"[l-^exp^Mcos^)]' (673)
где Vy=-(hi-hJ)/(hi + hJ), Ty = 2hieijmi + hJ).
Для параллельной поляризации 0 = cos 9; / cos 9 , ht = n( / cos 9;,
для перпендикулярной поляризации @у = 1, я, = -и, cos Qr
11 Фракталы 321
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Все полученные выражения справедливы для любых значений
фрактальной размерности Д стадии роста s, показателей
преломления л0 и /ip числа интервалов п', типов поляризации, углов падения
90 и заполнения Л или е. В частном случае получаются
выражения, выведенные ранее в [338, 339].
Интерференция волн на канторовых решетках. Результаты
расчетов показаны на спиральных диаграммах (рис. 6.10). Амплитуда от-
0 50 100150 200 250 300 0 20 40 60 80 100
kL kL
0 100 200 300 400 0 20 40 60 80 100120
kL kL
Рис. 6.10. Спиральные диаграммы коэффициентов отражения как функции kL и
е для канторовых сверхрешеток на первой стадии роста при D = 1/2 (слева)
и D = 3/4 (справа) для л'= 3, 4, 5 (сверху вниз) [418]
322
6.3. Волновые взаимодействия в многослойной канторовой среде распространения
раженной волны изображена линиями с градациями серого цвета от
нуля (черный цвет) до максимального значения (белый цвет).
Нулевая структура (черные линии) является наиболее
устойчивой и характерной чертой этих спиральных диаграмм. В [418] все
нули разделяют на три семейства. Первое и наиболее четко
выраженное - это семейство вертикальных линий. Оно образуется в
результате интерференции волн от передней и задней поверхностей
раздела каждого слоя с коэффициентом преломления пх и является,
таким образом, независимым от заполнения, потому что ширина
каждого слоя задана масштабным коэффициентом и стадией роста.
Нули второго семейства, или семейства дуговых нулей,
изгибаются вверх и образуют изогнутую кривую, идущую от верхнего
левого края диаграмм к нижнему правому. Эти нули возникают в
результате общих отражений от передней (или задней) поверхности
преломляющих слоев с коэффициентом преломления nv целиком
находящихся на левой или правой стороне сверхрешетки. Эти общие
отражения зависят от расстояния между отдельными слоями с
коэффициентом преломления пх и, таким образом, являются
функциями заполнения.
Третье семейство нулей называется семейством полосовых
нулей. Оно образует самую тонкую структуру спиральной диаграммы,
прочерчивая спиральные линии в направлении сверху вниз от левого
нижнего края диаграммы к правому верхнему. Эти линии
появляются в результате интерференции между группами преломляющих
слоев с коэффициентом пу Данный вид интерференции возникает
между группой слоев слева и справа от центра. При этом
интерференция меняется при изменении положения слоев или заполнения.
Вертикальные нули соответствуют формуле
kL = ^-9 m = l 2, ..., (6.74)
где r = N~l/D — фактор масштабирования для заданной
размерности Д г\=1\/щ.
Дуговые нули определяются из выражения
ашо**т»1Щ*шЯш1Л ,.,,2 |ВДЫ, (6.75)
in^r + 2e
где [N/2] — самое большое целое число, меньшее или равное N/2.
323
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Полосовые нули определяются по формуле
kL =
(2т + 1)д
(N -[N /Ity^r + l-Nr-dN /2]-1)е
, т = 1, 2,... (6.76)
Структура нулей канторовых сверхрешеток описываемых
уравнениями (6.74)-(6.76), приведена на рис. 6.11 для D = 3/4.
Сравнение структуры нулей с правой колонкой рис. 6.10 показывает
полезность приложения простого вида интерференции для объяснения
нулей на спиральной диаграмме.
1
щш
Щ
20 40 60 80 kL
п'=4
0 20 40 60 80 100 120 kL
п'~5
Рис. 6.11. Теоретическая структура нулей для канторовых сверхрешеток
с л'= 3,4, 5 при/) =3/4 [418]
324
6.4. Дифракция плоской волны...
Результаты, полученные в [339, 418], применимы в синтезе и
анализе фрактальных решеток, поглощающих фрактальных
материалов, резонансных систем миллиметрового, субмиллиметрового,
оптического диапазонов волн и в ряде других приложений.
6.4. Дифракция плоской волны на диапазонно
ограниченном фрактальном фазовом экране
Физические фракталы и функция Вейерштрасса. При изучении
дифракции волны на фазовых экранах полезно ввести понятие
физических фракталов, которые самоподобны в определенном
масштабе и в какой-то степени имеют производные. При более высоком
разрешении физические фракталы не дифференцируемы, что
согласуется с естественными явлениями. Полезным эффектом при этом
является то, что физические фракталы дают не только адекватные
физические модели, но и предполагают возможность аналитических
и численных решений для гладких или нерегулярных функций. Для
представленной задачи дифракции плоской волны на диапазонно
ограниченном экране здесь, как и ранее, использовалась диапазонная
функция Вейерштрасса, записываемая в виде [341]
Ф« = _ ^ т X Ъ^-Ъ* cos(2nsb»x + cp„), (6.77)
где Л - амплитуда возмущений; Ь - параметр
пространственно-частотного масштабирования; s - фактор масштабирования; ср - фаза,
распределенная равномерно на интервале [0, 2я]. Число гармоник
в функции (6.77) N= N2 - N{ + 1. Параметр
пространственно-частного масштабирования й определяет соотношение пространственных
гармоник.
Ясно, что Ф(х) - периодическая функция при рациональном
числе Ь и квазипериодическая функция, когда Ъ — иррациональное
число. В дальнейшем полагаем Ь иррациональным числом. Фактор
масштабирования определяет размещение гармоник по спектру.
Отметим, что Ф(х) описывает математические фракталы при N -> оо.
Физические фракталы также можно определить с помощью
функции Ф (х), так как она самоподобна на масштабах от (sbNl)~l до
(sbN2)~l. При D-+2 и возрастании N кривые Вейерштрасса стано-
325
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
вятся все более хаотическими, стремятся заполнить всю плоскость
и в них начинают преобладать высокочастотные компоненты.
Для уравнения (6.77) автокорреляционная функция Д^(х + т,х)
равна
^(ХИ,Х)=2[1-У(М)1 %bW-»»cos(2nsb4), (6.78)
т.е. опять получаем функцию Вейерштрасса, но с другой
эффективной фрактальной размерностью Z>.
Энергетический спектр D(v) определяется соотношением
&(У)=4Г1-^-2)1 Ё^^^-^ + ^ + Л")]- (6-79>
Амплитуду возмущений Ц находим при фиксированной
дисперсии сг£ = Лф(0) функции Вейерштрасса. Комбинируя (6.77) и (6.78),
запишем в окончательном виде нормализованную, диапазонно
ограниченную функцию Вейерштрасса
72a,Jl-ft2(i)-2)l n *1
Ф(х) = ^ J ш У #м>лсо8(2я^х + ф_). (6.80)
Двумерная форма диапазонно ограниченной функции
Вейерштрасса может быть образована подходящей комбинацией двух
функций Вейерштрасса, каждая из которых имеет форму (6.80).
Определим непрерывное приближение диапазонно
ограниченного спектра функции Вейерштрасса для Ь > 1 в виде
^V) = T" J G(V)rfv', (6.81)
AVv-iv/2
которое с использованием (6.79) равно
1 Ц2(^^(ап ^^^
G(y) Av4[l- б2^-2) ]{dv
326
6.4. Дифракция плоской волны...
Так как dn/dv = [vlnft] , выражение (6.82) перепишем в виде
G(v) = ^ v(2D-5)
UW 4[l-^-2)]in6V •
(6.83)
Фрактальный фазовый экран. Геометрия задачи дифракции на
фрактальном фазовом экране показана на рис. 6.12. Квадратный
фазовый фрактальный экран размером Lx Lb плоскости {х\ О, У}
К*у)
fx
Рис. 6.12. Геометрия задачи дифракции на квадратном фрактальном фазовом
экране при падении на него плоской волны у¥(х\у') [341]
при z = 0 освещается падающей плоской волной единичной
амплитуды. Дифрагированное поле Ч*(х,у), или интенсивность
I(x,y) = lP(jc,<y)xF*(jc,)>), наблюдается на расстоянии z в плоскости {х,
О, у}. Фазовый экран имеет передаточную функцию
Кх') = «х'У) = ехр[1Ф(х')]
и апертурную функцию
Р(х*) = Р(х',)0 = rect(x'/Z)rect(//Z),
где х=(х\ у\ 0), а Ф(х') определена формулой (6.80).
(6.84)
(6.85)
327
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Дифракционное поле. Поле в плоскости фрактального фазового
экрана записывается в виде ¥(*') = /(*'). Используя уравнения (6.80)
и (6.84), можно получить
\|/(дО = ехр
'X Cncos(2nsbnx'+q>n)
ИЛИ
ЛГо
л=м
где
1/2
ИЛИ
(6.86)
у(дО = П ехр[/Слсо8(2^6лхЧФл)], (6.87)
(6.88)
п rb2(D-2)N{ __ b2(D-2)(N2+l) 11/2 '
Применим разложение (4.118) и выразим (6.87) как
N2 Г ос 1
¥(д0= П I ехр(^д/2)//Сл)ехр[^(2^яхЧФл)] (6.89)
ЛГ2 Г ос ]
У(х') = П I /,(Ся)ехр(/2тс^лх')ехр[^(фл + тс/2)] • (6.90)
Непосредственно из (6.90) получаем
w= X X - I [y^VV-VMx
^=-оо^2=-оо qN=-oo
хехр
хехр[/(^ф^ + q2<pNi+l +... + qN<?Ni)],
где Ся определяется формулой (6.88); <рл = Ф„ +тс/2-
328
(6.91)
6.4. Дифракция плоской волны...
На расстоянии z от экрана в плоскости {х, 0, v}, заданной
координатами х = (х, у, z), дифракционное поле записывается в виде
оо
ВД = {-ilk) \ J44*W)#(*, * W (6.92)
—оо
в элементах функции Грина свободного пространства
ехр(/£|х-*1)
Я(*'*> 4к\Х-х] (6-93)
и волнового числа к падающего излучения.
Дифракция Фраунгофера. Рассмотрим вначале случай фраунго-
феровой дифракции [341], когда функция Грина аппроксимируется
параксиальным приближением
Щх,х') =
={exp(/fe)exp[/A:(jc2 +y2)/2z]exp[-ik(xx'+yyr)/z]}/(4nz). (6-94)
Дальнейшее интегрирование (6.92) с использованием уравнений
(6.85), (6.91) и (6.94) дает
'!'(*)- [( ^)exp(fe)exp[ *(х2 + У2)/^] 1
х 2 2 ••• 2 [VcWc*.*i>-Vc*>] x
x{exp[/(^ + q2<?Ni+l +... + ^ф^)]} x
xfsinc
х{ишс[Ьу/(Щ, (695)
где sinc(x) = sin nx/(nx) ,X = 2n/k.
Мгновенная интенсивность 1(х) может быть найдена из (6.88)
и (6.95). Однако более интересна средняя интенсивность (1(х)),
которая для равномерного распределения переменной фЛ равна
329
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
x(sinc2{l[x/(^)-^1*-^26(^1+1)-"--JV^2]}) х
x[sinc2(I^/(U))]. (6,96)
Средняя интенсивность показывает, что есть некоторое число
выбросов вдоль оси х, каждый из которых соответствует дифракции
на различных комбинациях гармоник фазового экрана. Их
амплитуды взвешены с помощью подходящего набора бесселевых
функций. Для малой дисперсии набор бесселевых функций в (6.96)
может быть аппроксимирован несколькими первыми элементами
низкого порядка. Исключение элементов с порядком, высшим, чем С2
(6.88), приводит к тому, что формула (6.96) представляется в виде
+
п-
</(x)) = ^U(l-<u) *ак*{Ьх/{Щ +
£ | S |sinc2[z:( x/(Xz)-sb")]Unc2(Ly/(Xz)).
(6.97)
Максимальный элемент для малой дисперсии является
когерентной составляющей поля, задаваемой условием qx = q2 = ... = qN= О
в выражении (6.96) или первым членом в уравнении (6.97).
Когерентная компонента поля соответствует той составляющей поля,
которая не подвержена влиянию фазового экрана и, следовательно,
распространяется вдоль оси z в плоскости наблюдения. Некогерентная
интенсивность определяется вторым элементом в (6.97) и
пропорциональна дисперсии фазового экрана. Пики некогерентной
интенсивности удовлетворяют условию Брэгга для каждой гармоники
(тона) фазового экрана. Для малой дисперсии распределение
средней некогерентной интенсивности в дальней зоне становится таким
же, как энергетический спектр функции Вейерштрасса, а дельта-
функции замещаются sinc-функциями из-за эффектов дифракции на
фазовом экране конечных размеров.
Дифракция Френеля. Для дифракции Френеля результаты
получают аналогичной, но более трудоемкой процедурой. При этом в
уравнении (6.92) функция Грина записывается в виде
330
6.4. Дифракция плоской волны...
Щх', х)-(exp(fe)exp{/A:[(x-x')2 + (у-yf]/2z})/(4nz). (6.98)
Дифракционное поле находится подстановкой (6.85), (6.91) и
(6.98) в формулу (6.92):
/ Uxp(ikz)txp\ik(x2+y2)/2z~}}
*(*)=! ^ jjx
x{exp[i(^ +q2%l+i +... + ^Ф^2)]}х
exp({-ik/2z){x-zb[qibNi +q2b<N^ + ...+qNbNi]f
х{[С(л2) - C(V] + i[S(i\2) - S(4l)]}x
xlC&)-C&)]+i[S&)-S&)Ti, (6.99)
где %х =-[k/(nz)f2{L/2 + x-zls[qlbN^ +q2b^+l) + ... + qNbN2]},
$2=-[k/(nz)] V2 {L/2-x + zXs[qlbNi+q2blN^+... + qNbN2]},
Л, =-[k/(nz)]l/2(L/2 + y), Лз =-[k/(nz)]l/2(L/2-y),
Си S— интегралы Френеля.
Мгновенная интенсивность 1(х) определяется непосредственно
подстановкой (6.99) в выражение 1(х) = Ч*(лсУР(,х), а средняя
интенсивность записывается в виде
('(*» 4 I I ••• I \J4CN)J4C )...Р (С )1х
/7»=—ооОлг—оо «»г =—оо ■— -*
ql=-°oq2=-°° qN
331
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
х{[С(^)-С^)]2 + [^2)-5(^)]2}х
х^ать)-^)]^^)-^^)]2}. (6.Ю0)
При малой дисперсии фазового экрана серия бесселевых
функций аппроксимируется первыми членами, и тогда формула (6.100)
при условии учета членов, не превышающих С2п, имеет вид
(/(х))Л((1-а|){[С(^4)-С(^)]2+[^4)-^з)]2}+
+1 f {[^6)-c(^)]2+№6)-^5)]2f
x{[C(ti2)-C(V]24^2)-^1,)]2}> (6.101)
где $з = "Windf2 (L/2 + x)> Ъ = W(nz)]l/2 (L/2- x),
Ъ =-[k/(nz)]l/2(L/2 + x-zXsb»), Z,6 = [k/(nz)]i/2(L/2-x + zXsb").
Элемент, соответствующий, как и прежде, условию ql = q2 = ...
= qN — 0, в (6.100) дает когерентную интенсивность. Отношение
когерентной составляющей мощности к общей мощности
находится непосредственно из уравнений (6.97) и (6.101):
Я(/(,,У,г» ^д1
Левое равенство справедливо при дисперсии, много меньшей
единицы. Отсюда следует вывод, что дисперсия о| контролирует
распределение средней мощности между когерентными и
некогерентными полями, в то время как Д Nn L определяют структуру
некогерентного поля. Некогерентное поле является частью общего поля,
332
6.4. Дифракция плоской волны...
которое взаимодействует с экраном и рассеивается им. В частности,
средняя некогерентная интенсивность в дальней зоне имеет
энергетический спектр функции фазовой модуляции при малой
дисперсии экрана и его больших размерах. Для фракталов со свободным
масштабом и очень большой дисперсией [188] показано, что
когерентное поле исчезающе мало. Соотношение (6.102) отражает этот
факт в пределе бесконечной дисперсии, но в более общем виде.
Эволюция интенсивности дифракционного поля. Вариации
нормализованной дифракционной средней (1(х)/1(0)) и мгновенной
1(х)/1(0) интенсивностей для фрактальных фазовых экранов как
функция нормализованных координат x/L при различных
расстояниях до точки наблюдения z/L приведены на рис. 6.13-6.15.
Апертура и ее размеры задаются условием X/L = 10~5. Для каждого из рис.
6.13-6.15 s= 103, Ь = (2п)1/\ оф = 1, N{ = 0 и N= N2 + 1 = 10.
Значения фрактальной размерности равны D= 1,01 (относительно
гладкий экран - рис. 6.13), Z>= 5/3 (колмогоровский спектр - рис. 6.14)
и D = 1,99 (заполнена почти вся плоскость - рис. 6.15). Нижние
рисунки подходят для области Фраунгофера, где расстояние от экрана
равно 1,16 108Х . Нормализованная средняя интенсивность
показана в левой стороне рис. 6.13-6.15 и рассчитана по формуле (6.100).
В ближней зоне (зона индукции) средняя интенсивность имитирует
распределение прямоугольной апертуры фрактального экрана. По
мере увеличения расстояния энергия вблизи геометрической тени
слегка спадает от границ дифракционных характеристик с
образованием дополнительных пиков и характеризует дифракцию Френеля.
Часть энергии дифрагирует на относительно большие углы и не
учтена на рис. 6.13-6.15. По мере роста D высокие пространственные
частоты становятся более выраженными (рис. 6.15).
Проанализируем результаты эволюции мгновенной
интенсивности для одиночной реализации фазового экрана, когда порядок
возникает из хаоса. Это явление демонстрируется на правой
стороне рис. 6.13-6.15. Расчеты в [341] проводились по соотношению
I(z) = 4,(x)4'*(x) с использованием (6.99) с учетом равномерного
распределения фаз на интервале [0, 2 к]. В ближней зоне
мгновенная интенсивность зависит от хаотического характера экрана. Однако
по мере дальнейшего распространения поля от плоскости экрана
интенсивность растет и становится подобна усредненной из-за
присутствия дискретных пространственно-частотных компонент. По мере
333
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
///max 1
0,6 [
0,2 [
п
2/1=10
1
0,6
0,2
; ill
II'
Ш
Ч 1
к._! i L.L.
2/1-10
£N1,01
N=10 °М
Рис. 6.13. Вариации относительной средней интенсивности (/(*)/7(0)) (слева) и
мгновенной интенсивности 1(х)/1(0) (справа) за фрактальным фазовым экраном
размером X/L = 10~5 для D= 1,01 при разных расстояниях z/L от экрана [341]
334
6.4. Дифракция плоской волны...
///max 1
2/1=10
D=5/3
№=10
Рис. 6.14. Вариации относительной средней интенсивности (1(х)/1(0)) (слева) и
мгновенной интенсивности /(*)/ДО) (справа) за фрактальным фазовым экраном
размером X/L = 10~5 для D = 5/3 при разных расстояниях z/L от экрана [341]
335
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рис. 6.15. Вариации относительной средней интенсивности (1(х)/1(0)) (слева) и
мгновенной интенсивности 1(х)/1(0) (справа) за фрактальным фазовым экраном
размером X/L = Ю-5 для D = 1,99 при различных расстояниях z/L от экрана [341]
336
6.4. Дифракция плоской волны...
роста D поля приобретают все более сложную форму вблизи экрана
и мгновенная интенсивность изменяется быстрее, чем средняя
интенсивность.
Полученные результаты легко понять, рассматривая простую
брэггову модель дифракции дая каждой пространственно-частотной
гармоники экрана. Брэггово условие дает значение угла дифракции
Q = arctg(2psbn/k) по отношению к оси Zm* каждой гармоники с
частотой sbn. Используя этот результат, можно подтвердить
расположение дифракционного пика и уточнить условия для селекции
дифрагировавших полей. В зоне Френеля расстояние разделения
дифракционных полей от двух соседних пространственно-частотных
компонент должно быть больше размера экрана, т.е.
Z>L/[XsbNi(b-l)]. (6.103)
В данном случае при длине волны -Ю-6 м выражение (6.103) дает
значение соотношения zf\ ~ 700. Это говорит о том, что все
диаграммы с zj\ ~ 700 показывают разделение дифракционного поля,
невзирая на фрактальную размерность. Данные рис. 6.13-6.15
демонстрируют это явление. Если значение z из (6.103) находится в зоне
Фраунгофера, то величина L в (6.103) должна быть заменена
шириной дифракционного пучка. Также должно удовлетворяться условие
sbNi(b-l)>2/L. (6.104)
Из неравенства (6.103) ясно, что для бесконечного экрана (L > °о)
или непрерывного спектра мощности (Ь > 1) условие разделения
полей не может выполняться.
Работа [341] является базисной для дальнейшего исследования
распространения пучка во фрактальной среде. Полученные
результаты потенциально полезны для задач распространения волн в
случайной среде, их рассеяния и определения характеристик
окружающей среды в дистанционном зондировании и радиолокации, так как
применение фракталов при решении этих задач встречается пока
редко, хотя интерес к ним чрезвычайно высок [330, 331].
337
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
6.5. Распространение гауссова пучка излучения
в диапазонно ограниченной фрактальной среде
Методы решения. При распространении пучка оптического
излучения флуктуации коэффициента преломления непрерывной
среды аппроксимируются серией фрактальных экранов, обладающих
степенным спектром [342]. Обычно в моделировании применяется
диапазонно ограниченная функция Вейерштрасса [128, 339]. Она
подходит, как отмечено ранее, для описания раздельных
флуктуации коэффициента преломления. Спектр данной функции
является степенным с самоподобным масштабом. Данный спектр полезен
для изучения волнового распространения в атмосфере, так как спектр
Колмогорова также степенной [334].
При высокочастотной аппроксимации непрерывное изменение
коэффициента преломления заменяется действием серии фазовых
экранов. Метод множественных фазовых экранов был использован
ранее в [337] при условии слабого рассеяния, которое оказывается
существенным лишь при большой длине пути оптического или
акустического сигнала. При этом на длину волны не накладывалось
каких-либо других ограничений. По существу данный метод
основан на физических или геометрических соображениях, а не на
математических выкладках. Требуемые условия для распространения
луча были получены количественно в [343].
При распространении оптического излучения через
многочисленные фазовые экраны можно использовать двухшаговый подход
[342]. Первый шаг - найти геометрическое место точек центров
преломления луча, которое возникает из-за фазовых фрактальных
экранов, с помощью законов сохранения энергии и моментов на
примере брэгговской дифракции. На втором шаге следует описать
распространение в свободном пространстве с помощью френелева
приближения. При слабом рассеянии среднее распределение
интенсивности получается накоплением когерентных лучей при
дифракции первого порядка. Когда путь распределения становится больше,
чем длина когерентности, следует рассматривать и
дифрагированные лучи более высоких порядков.
Волновое уравнение. В физической модели распространения [342]
допускается, что среда распространения удовлетворяет следующим
условиям: флуктуации коэффициента преломления среды
испытывают слабое возмущение, минимальный масштаб среды значителъ-
338
6.5. Распространение гауссова пучка излучения,,.
но превышает длину падающей волны. На основе таких
предположений можно игнорировать эффект деполяризации. Второе
допущение позволяет использовать параксиальное приближение. Волновое
уравнение для компоненты волны 4?(x9y,z), распространяющейся
вдоль оси z во флуктуирующей среде, записывается в виде
{v2 + kl [1 + ^улЩч^ул) = 0, (6.105)
где к0 - волновое число в свободном пространстве; п{(х, у, z) -
флуктуации коэффициента преломления.
В высокочастотном приближении уравнение (6.105) может быть
преобразовано в параболическое [322]. При игнорировании
эффекта дифракции в свободном пространстве можно показать, что поле
*Р при z + Az записывается как
4>(x,y,z + Az) = 4(x,y,z)exp[ip(x,y,z)], (6.106)
где модулирующая фаза р (х, у, z) определена флуктуациями
коэффициента преломления от z до z + Az в виде [343]
z?
P(x,y,zm) = k0 J nfotytfdz', m = l, 2,... (6.107)
Здесь zm - дискретная переменная вдоль направления
распространения. Уравнения (6.106) и (6.107) предполагают, что непрерывность
флуктуации коэффициента преломления среды может быть дискре-
тизирована рядом тонких фазовых экранов с передаточной функцией
exp[ip(x,y,zm)l
Следовательно, геометрия задачи становится такой, что
множественные фазовые экраны (1,2,...) разделены промежутком Az, как
показано на рис. 6.16. Первый фазовый экран освещается в
плоскости {хр у{} коллимированным гауссовым пучком ¥0 . Распределение
средней интенсивности <1(х, у)> наблюдается в плоскости {х, у}.
Так как эффекты фазовой модуляции и дифракции в свободном
пространстве рассматриваются раздельно, то расчеты справедливы,
пока Az мало [343]. При этом необходимо соблюдать два условия.
Первое: Az должно выбираться так, чтобы в формуле (6.107)
p(x,y,zm)<£ 1. Второе условие основано на параксиальном прибли-
339
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рис. 6.16. Геометрия множества фрактальных фазовых экранов, освещаемых
коллимированным пучком 4^ [342]
жении и получено из того, что разность между длинами траекторий
когерентных и преломленных лучей должна быть меньше Х/2 в
пределах Az. Эти условия записываются в виде
/>(*>)>> О <<1 д<£2Д>
(6.108)
где £ - размер шкалы, определенной так, что основная энергия в
среде распространения содержится на масштабах, больших, чем % .
В работе [342] рассмотрены экраны со степенным спектром, хотя
процедура расчета может быть применена и дая многомасштабных
структур.
Для удобства положим, что р (х, у, zm) = pm (х, у), что означает
фазовую модуляцию на т-м экране. Тогда
Pm(^y) = k0Um(x)Vm(y),
(6.109)
где Um (х) и Vm (у) - диапазонно ограниченные функции Вейершт-
расса, связанные с флуктуациями коэффициента преломления
уравнением (6.107).
Диапазонно ограниченная функция Вейерштрасса в данном
случае записывается в виде
1/2
UJx) =
{2(Ul)[X-b^Y ^
[l_fc2(Z)-2)(tf+l)-p „to
£^-2>"
COS
2пЪпх
- + Ф*
(6.110)
340
6.5. Распространение гауссова пучка излучения...
Здесь (iffy - дисперсия флуктуации функции Um(x); b - параметр
пространственно-частотного масштабирования; 1 < D < 2 —
фрактальная размерность для одномерных флуктуации; N + 1 — общее
число масштабов; L — максимальный масштаб флуктуации; ср^ —
случайная фаза, связанная с п-и масштабом и равномерно
распределенная по закону (2л)"1 на интервале [0,2 тс]. Функция Vm{y) имеет
отличные от Um(x) параметры.
Аналитическое решение для коллимированного пучка. Рассмотрим,
следуя [342], аналитическое решение для усредненного
распределения интенсивности в случае коллимированного пучка. Так как
пучок модулирован с помощью фазового экрана и распространяется в
свободном пространстве между соседними экранами, то поле
дифракции перед (т + 1)-м фазовым экраном *Р~+1(х,у) получается из
поля от т-то фазового экрана *Р~ (х,)>) через интеграл вида
оо
ЧГ^Ъу^-Щ J J4*-m(x\yyjx\ymx,y,x\yykty\ (6.111)
где Н(х,у,х',у') - функция Грина свободного пространства, а
передаточная функция т-то фазового экрана fm (*'>/) определяется как
^(х',Я = ехр[/^т(хОКт(Я]. (6.112)
Из закона сохранения энергии следует, что
>>'./) - [1 - Ч (WSOO)]"* + ikJJJ&VJf). (6.113)
Аппроксимация (6.113) справедлива для переменной части
коэффициента преломления. Функция Грина в (6.111) во френелевом
приближении равна соотношению (6.98). Используя для (6.111)
сокращенную запись FRD\4^ , подстановкой (6.113) в (6.111)
получаем Ч*2(х,у) в терминах ^\{х,у)
4>-2(х,у) = (1 - kffif FRD[4>;(x,y)]2{ +
+ik,FW[Ux{x)Vx{y)^-{x^x, (6ЛИ)
где g\ =(U?(x)Vf(y)} — дисперсия первого фазового экрана.
341
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Гауссов пучок. Как следует из (6.114), падающий луч
ослабляется (первый член) и модулируется (второй член) с помощью
первого фазового экрана. Ослабленная часть распространяется в
направлении падающего луча, а модулированная часть изменяет
направление своего распространения. Процедуры расчета по х- и
у-компонентам одинаковы. В (6.114) рассмотрим коллимированный
пучок с гауссовым распределением амплитуды по осям х и у :
V0(x,y) = Aexp[-(x2+y2)/W02], (6.115)
где W0 - ширина пучка.
При распространении коллимированного пучка в направлении
оси z профиль луча из-за дифракции в свободном пространстве
становится равным [344]
Т/х,у,г) = Жг)ехр[/^]ехр{-[(хЧу2)/Ж02(г)]}, (6.116)
где A(z) = A/(l + iaz); W2(z) = 2(1+ iaz)/(kQa), а = Х/(к}¥2).
Уравнение (6.116) справедливо для z<^n3W^ /X3 [322].
Ослабленная часть волнового пучка выражается с помощью (6.116), а
перенаправленная составляющая требует решения дифракционного
интеграла Френеля. Дифракционное поле перед вторым экраном при
передаточной функции в виде диапазонно ограниченной функции
Вейерштрасса дается выражением
™[^(х)ТГ(х,у)]; =еХу} [jU^x^ix'^x
~ (6.117)
xexpjtf^ -x? +(y2-yr)2]/2Az}dx'dy'-
Здесь *Р;-(х',/) = Л(Дг)ехр{-(х'2 +y'2)/Wf (Az)}. Из выражения (6.110)
соотношение для U^x") можно переписать в виде
N
I
п=0
U^^a^cos^x'+yJ, (6.118)
342
6.5. Распространение гауссова пучка излучения...
где
1/2
1Л~ П_^2(^-2)(ЛГ+1)-|1/2
0i =
№№-ь*™Т .„-,,
^"2)Л, (6.119)
K]ri=2nbn/L.
Подстановка (6.118) в (6.117) дает линейную комбинацию
интегралов, которые вьиисляются методом стационарной фазы [345],
и в итоге
JJ*;4x^exp(/^
-(HAz^ix^K^Az/k^yJ. (6.120)
Соотношение (6.117) с учетом аппроксимации (6.120) тогда
становится равным
FWlUiWjfayjfi = Х^ехр(/*0Дг)х
х[ехр(/Х1лх)ехр(/ф1л)Ч/;-(х-А'1лАг//:05у) +
+ехр(-/Х1лх)ехр(-/ф1л)Ч'1-(х+^1лАг//:0,у)]. (6.121)
Когерентные и некогерентные составляющие поля. После того как
пучок дифрагировал на первом экране, поле перед вторым экраном
будет
^-(х2,};2) = (1-ед)1/2ехр(^0Аг)^(х2,};2) +
N си
+^ехр(^Дг)£^[ехр(^^
+ехр(-/ЛГ1лх2)ехр(-/ф1л)^(х2+Л:1лАг//:0^2)]. (6.122)
Первый элемент в (6.122) — когерентное поле, второй - его
некогерентная составляющая. Из (6.122) ясно, что когерентное поле
вблизи оси z просто ослабляется. Центральные области
некогерентных полей сдвинуты на ±KlnAz/k0, их направления
распространения определяются углами 6 = ±arctg(^Tlw / k0) относительно оси z.
343
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Этот сдвиг может быть объяснен с помощью сохранения моментов,
которые присутствуют на каждом масштабе фазового экрана из-за
дифракции Брэгга (рис. 6.17,я). Извилистые линии соединяют
центры дифракции пучка с плоскостью наблюдения (рис. 6.17,6).
а)
Рис. 6.17. Диаграмма сохранения моментов, соответствующих одиночному
фрактальному фазовому экрану (а) и множеству таких экранов (б) [342]
На следующем шаге значение ¥" в (6.122) замещается на Ч-
из (6.116) и т.д. В общем случае для Мфрактальных фазовых
экранов поле в плоскости наблюдения записывается [342] в виде
11 1 <!£ъ!* qM*
?1=0?2=0 ?я=0л,=0я2=0 пм=0\
М
\(l/2)6fli
П( 1-*оЧГ^°
,т=\
Qxp(ik0zt)x
цЫ*/2)9*
_т=\
хехр[/(±^1л1 tq^ ±...±qMKMnM)xy
X¥f[x±qlKllliMAz/k0±qJK2Hi(M-l)Az/kQ±...±
±ЯмкмПм^/ко' У' фхрЦЩУщ ±«2% +-±<*м<?мпм)} (6.123)
Здесь 5 — символ Кронекера; zt - общее расстояние
распространения пучка; qm = О или 1. Если qm = 1, то пучок перенаправляется с
344
6.5. Распространение гауссова пучка излучения,,.
помощью т-то фрактального экрана. При qm = О пучок просто
ослабляется /и-м экраном.
Дифракционное поле в свободном пространстве ч?. в (6.123)
получается с помощью (6.116). Ясно, что x¥f может быть записано в
виде
Ч//(х5};5г/) = Жг/)ехр(/^/)ехр{-(хЧу2)/Ж02(г/)}. (6.124)
В параксиальном приближении расстояние zt равно (m + l)Az, так
как волновое число свободного пространства к0 больше
пространственного волнового числа Ктп. Отметим, что когерентное поле
соответствует элементу, для которого все qm = 0 (т = 1, 2,..., М) в
уравнении (6.123), как отмечено в разд. 6.4. Некогерентная
составляющая соответствует элементам с qm = 1. Дифракционное поле первого
порядка получается при наличии только одного qm = \{т = 1, 2,..., М).
Дифракционное поле у-го порядка есть поле, которое
перенаправляется фазовыми экранами у раз во время распространения. Общее
число элементов в уравнении (6.123) есть (2N+ \)м. Число
элементов, соответствующих дифракции Q-io порядка есть С^ (2N) , где
С^ означает число сочетаний из М по Q. В приближении слабого
рассеяния поле может быть найдено с помощью суммирования
когерентного поля и дифракционного поля первого порядка.
Эволюция средней интенсивности первого порядка дифракции.
Средняя интенсивность (1(х,у)) = (х¥(х,у)х¥*(х,у)} получается из
формулы (6.123) в виде [342]
1 qfl qjN qMN
1 1 1 Ч\" 47" ЧА£Г
01=О$2=О $М=(Ц=0Л2=0 пм=0\
М
П
П(1-ВД)8?-°
ftfe/4 У""' \y\¥f[x±qxKXnMbz/k,±
±q2K2n2(M-l)Az/k0±...±qMKMnMAz/k0,y,zt] f, (6.125)
345
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
где
' м ,
П(1-*оЧ)""°
т=1
*и-1 V т '
т=\
коэффициент,
полученный из условия сохранения энергии.
Рассмотрим на основе (6.125) изменение профиля средней
интенсивности при распространении пучка в среде распространения
[342]. Предполагается, что все фрактальные экраны одинаковы, за
исключением случайных фаз. Считаем, что средняя интенсивность
меняется только вдоль оси х. Из формулы (6.125) следует, что
когерентный пучок ослабляется на величину (1 - Цо2) при
прохождении серии фрактальных экранов. Данное значение ослабления
получено при условии малости дисперсии на фазовом экране
kfo2«: 1. Однако с использованием техники перенормировки
коэффициент пропорциональности для когерентной интенсивности
может быть выражен в виде
(l-kfo2f ~ехр(-Ж2а2), (6.126)
где Mkfo2 -общая дисперсия ддя Af фрактальных фазовых экранов.
Когерентная интенсивность уменьшается из-за ослабления по
мере распространения пучка. С другой стороны, рассеянная
мощность — это некогерентная мощность, и она дает вклад в полную
интенсивность. Для дифрагирующего пучка первого порядка
среднее распределение интенсивности находится суммированием
только по индексу qm = 1 из формулы (6.125) и может быть записано в
виде свертки
(1(х,у)\ =^12(1 + а2г2)"1ехр[-А:0а (х2+/)/(1 + а2г2)]*
*Х1№±«а (6127)
/^=1^=0
где
_ (1 -к2с2)^-^2а2[1-^-2)]^-2)^
С"- 2[l-b2(D-2(N+V] ' (6Л28)
gn = 2nbnAz/(k0L), звездочка - оператор свертки.
346
6.5. Распространение гауссова пучка излучения...
Начальный профиль луча задан уравнением (6.115). Уравнение
(6.127) есть свертка двух функций, которые представляют
фундаментально различные физические процессы. Первая функция
определяется дифракцией в свободном пространстве коллиминированно-
го гауссова пучка, а вторая (геометрический фактор первого
порядка) зависит от геометрии и параметров множества фрактальных
фазовых экранов. Непрерывная аппроксимация [128] может быть
применена к геометрическому фактору первого порядка, когда b -> 1.
Для этого необходимо аппроксимировать сумму по л в виде
N 1 х+Ах/2 #
%bW-24(x-mgn)~ J ^b2^H(x'-mgnW =
/i=0 A*jc-Ac/2 "=0
= —[k0Lx/(2nmAz)]2(D~2) [dn(x)/dx]Ax, (6.129)
где bn =k0Lx/(2nmAz).
Так как dn(x) / dx = (l/lnb)(l/ x), последнее равенство в (6.129)
становится равным
Xb*D-2H(x-mgn) = ^[kbL/{2nmbzfD-2)x2D~5, x0 < x <xr(6.130)
Здесь Xq = 2nmAz/(kQL), xt = 2nmAz/(k0l); Lnl- соответственно
внешний и внутренний масштабы. При использовании соотношения
bN = L/l и допущении 6 = 1 + % имеем
X СпЬ(х - mgn) « Cg [k0L /(27cmA^)]2(Z)"2)x^-5rect[xH,(x-xc)],(6.131)
л=0
где C^ = (2-i))(l-^V)^-^0V/[l-a//)2^-2)]; хж = 1/(х7.-х0),
xc=(x0+x7.)/2.
Уравнение (6.131) с коэффициентами Cg, x0 и х7 будет
непрерывной аппроксимацией для суммы по л в формуле (6.127).
Аналогичная аппроксимация, соответствующая 5(x+mgw), находится таким
347
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
же способом. Отметим, что геометрический фактор первого
порядка обусловлен одиночным фазовым экраном с зависимостью x2D~5,
которая следует из степенного спектра фрактальной функции [128,
188]. По мере распространения пучка геометрический фактор
первого порядка выражается с помощью добавления вкладов от всех
фазовых экранов, через которые проходит пучок. Как показано
ранее, направление распространения дифракционного пучка первого
порядка обусловлено размером фазового экрана и составляет углы
Q = ±arctg(Xbn /L) относительно оси z- Следовательно, луч первого
порядка дифрагирует в более широком угле по мере уменьшения L.
На рис. 6.18 показана пространственная эволюция средней
интенсивности первого порядка ддя трех значений D = 1,01; 5/3 и 1,99.
Длина волны излучения равна 1(Н м, L = 0,1 м = 105Х, / = 10~3 м =
= 103Х. Гауссов пучок шириной W0 = 0,1 м (Ю5Х) распространяется
через множество экранов М = 10, 20, 30, 40, 50 с дисперсией Ща\ =
= 0,05, разделенных Аг = 50 м (5 • Ю7Х). С возрастанием
фрактальной размерности функция средней интенсивности <1(х, у)>{
расширяется из-за более выраженных высокочастотных компонент.
Данные рис. 6.18 показывают, что трудно выделить значение D из
средней интенсивности первого порядка, так как она зависит от всех
экранов и свертки с пучком, дифрагировавшим в свободном
пространстве. Интенсивность дифракции первого порядка возрастает до
20 фазовых экранов (общая дисперсия стремится к 1), а затем
начинает уменьшаться независимо от значения D. Этот факт обозначает
рост интенсивности более высоких порядков дифракции.
Пространственные изменения суммы когерентной
интенсивности и интенсивности первого порядка дифракции приведены на рис.
6.19 для значений параметров рис. 6.18. В противоположность
данным рис. 6.18, суммарная интенсивность монотонно уменьшается по
мере прохождения пучка через множество фрактальных фазовых
экранов из-за того, что когерентная интенсивность ослабляется в
большей степени.
Средняя интенсивность при дифракции высоких порядков. Тот
факт, что когерентная и составляющая первого порядка дифракции
уменьшаются по мере распространения пучка в среде, означает, что
необходимо рассматривать дифрагирующие интенсивности более
высоких порядков. Общая интенсивность IQ (m) за /и-м фазовым
экраном для Q-to дифракционного порядка записывается в виде [342]
348
6.5. Распространение гауссова пучка излучения...
-0,5 0 0,5 -0,5 0 0,5 -0,5 О
0,5
Рис. 6.18. Изменение средней интенсивности первого порядка <1(х, у)>{
для трех значений фрактальных размерностей [342]
IQ(m)= J \(I(x,y))Qd*fy~Cj>(l-k*6^ (6.132)
где С^ - число сочетаний из т по Q.
На рис. 6.20 приведены зависимости IQ (т) для Q = 0, 1, ..., 5
при дисперсии фазового фрактального экрана kfol — 0,05. Как по-
349
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
D=\,99
М=10
20
30
JL
40
j^
50
■ У\
0 0,5 -0,5
0,5 -0,5
О
0,5
Рис. 6.19. Вариация суммы когерентной интенсивности <1(х, у)> и средней
<1(х,у)>{ интенсивности первого порядка при значениях параметров,
идентичных рис. 6.18 [342]
казано ранее, общая когерентная составляющая поля монотонно
уменьшается. С другой стороны, /^(/и) имеет максимум при Q > 0.
С ростом Q этот максимум удаляется, а пик становится более
острым при малых Q.
350
6.5. Распространение гауссова пучка излучения,,.
Ш)\
0,75
0,5
0,25
\ Q=o
1/ТЧ
50 100 150 т
Рис. 6.20. Значения интенсивности IQ{m) при дисперсии фазового экрана
kfol для разных значений Q [342]
Процедура расчета распределения средней интенсивности для
дифракции более высоких порядков чрезвычайно усложняется с
возрастанием Q. При этом в уравнении (6.125) число элементов
суммирования становится большим. Для дифракции второго порядка
можно получить [342]
(I(x,y))2 =^2(l + aV)-1exp[-A:0a(x2+};2)/(l + aV)]*/T25 (6.133)
где геометрический фактор второго порядка F2 записывается в виде
2 2
М N М N
АИ1=1^=0 /7*2=1/12=0
М N
/и3=1 Лз=0
(6.134)
Значения Сп и gn задаются уравнением (6.128). Отметим, что F2 -
это аппроксимация свертки двух геометрических факторов первого
порядка, если отбросить константу 1/2 и скорректировать
некоторые элементы.
Геометрический фактор Q-ro порядка есть аппроксимирующая
свертка Q геометрических факторов первого порядка с необходимым
числом коррекций. При доминировании более высоких порядков
(см. рис. 6.20) распределение средней интенсивности меньше
обусловлено влиянием начального профиля пучка потому, что геомет-
351
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
рический фактор преобладает из-за увеличения числа сверток, и
становится примерно гауссовым по мере увеличения расстояния.
Методика изложенного расчета может быть применена к
распространению лазерного и миллиметрового пучков в атмосфере или
акустического пучка в воде с подходящим подбором фрактальных
фазовых экранов.
6.6. Рассеяние звука объемными неоднородностями
с фрактальным спектром в океане
Рассмотрим рассеяние звука случайными объемными
неоднородностями или флуктуациями коэффициента преломления с
фрактальным спектром в океане в приближении метода малых
возмущений [346]. Степенной спектр флуктуации записывается в виде
G(q)~q«, (6.135)
где q - волновое число неоднородностей; ос = Z> - 2D'; D' -
размерность пространства вложения [45].
Коэффициент рассеяния звука флуктуациями показателя
преломления в первом приближении метода малых возмущений
описывается выражением [346, 347]
mv(eres) = 2nk4G{q). (6.136)
оо
Здесь G(q) = (2n)~3 f R(p)exp(iqp)dp - пространственный
энергетический спектр флуктуации показателя преломления; R(p) — их
корреляционная функция; q = k(es -ef) - волновой вектор резонансной
гармоники в спектре флуктуации; к — волновое число звука; et ие5 —
единичные векторы, определяющие направления распространения
соответственно падающей и рассеянной волн.
Функция корреляции R(p), соответствующая фрактальному
энергетическому спектру, должна быть физически обоснована для
резко анизотропных неоднородностей, когда отношение
горизонтального масштаба к вертикальному составляет 102—103 [348]. Фун-
352
6.6. Рассеяние звука объемными неоднородностями с фрактальным спектром...
кция корреляции флуктуации показателя преломления в океане
может быть записана в виде [349]
Л(р) = (ц2)Л1(^2(л), <p) = ft,ii}, (6.137)
где (у2} - средний квадрат флуктуации; Щ%) и ^(ti)
-коэффициенты корреляции соответственно в горизонтальной плоскости и
по глубине.
В [346] коэффициент корреляции крупномасштабных
составляющих выбран в виде
Щ) = [2^Ш]~1 {Ш *v Ш~Ш*. (6-138)
где Kv(x) - функция Макдональда порядка v; r(v)
-гамма-функция; £0 — горизонтальный радиус корреляции.
Функция такого типа была предложена Карманом для
аппроксимации корреляционных функций в теории турбулентности [320,
322]. Тогда пространственный энергетический спектр
крупномасштабных флуктуации
Gx(qi) = (2nr2 J ^©expfe^^v^^a + e^ij^ (6Л39)
1/9
где q± = k[cos2 x7 + cos2 %s -2cosx7 cos%s cos(cp5 - cp7.)] -
горизонтальное волновое число резонансной гармоники в спектре
флуктуации; (х,-, ф7) и (х5, Ф5) - углы направления распространения
соответственно падающей и рассеянной волн.
Коэффициент корреляции мелкомасштабных флуктуации, как
утверждается в работе [346], при qr\0 «: 1 не существен, так как для
них
G2(qz) = (2n)'1 J R2(r\)exp(iqzT])dT\^r\Q/n = const, (6.140)
где q — вертикальная компонента волнового числа резонансной
гармоники; Ло — вертикальный радиус корреляции. При учете
12 Фракталы 3 3 3
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
G(q) = (\i2)Gl(.q1)G2(qz) на основе формул (6.136), (6.139) и (6.140) в
[346] получено
mv(ei,es)^2{^)vk\^(qi^r^)/n (6.141)
для условия (qj^) »1.
Свободный параметр v задачи выбирается так, чтобы обеспечить
требуемую экспериментальную частотную зависимость
коэффициента затухания р , равного [349]
P = J/iV(e/,eJ)£/a, (6.142)
где Q. - телесный угол, соответствующий рассеянным волнам.
После подстановки (6.141) в (6.142) и последующего
интегрирования по угловым переменным с v = 0,25 получаем р ~ /3/2 с
учетом qL~k . Такая частотная зависимость коэффициента затухания
звука следует из эмпирической формулы Шихи-Хэлли [350].
Из формулы (6.139) следует, что при значениях [qj^) »1hv =
= 0,25 энергетический спектр крупномасштабных флуктуации
G{(Qi) ~ 0±5/2- Дробный показатель степени свидетельствует о
фрактальной природе случайных неоднородностей; так как размерность
пространства вложения равна D = 2, из (6.135) получаем D = 1,5.
Отметим, что фрактальная размерность крупномасштабных
неоднородностей совпадает с показателем степени в частотной
зависимости затухания звука, что характеризует неупорядоченные
фрактальные среды. Ранее (см. разд. 5.2) были представлены фрактальные
размерности границ облаков в атмосфере, которые заключены в
интервале 1,37 < D< 1,41 [286]. Сопоставляя эти значения, можно
видеть, что фрактальная размерность неоднородностей в океане
близка к фрактальной размерности облаков.
Авторы работы [351] отмечают, что для стратифицированной
атмосферы облака в общем случае не самоподобны, а самоаффин-
ны. Поэтому облака относятся к мультифрактальным структурам
[282]. Подтверждение этого описания содержится в работе [352]. Эти
доводы можно, как утверждается в работе [346], отнести и к
объемным неоднородностям в стратифицированном океане. Поэтому
354
6.7. Дифракция волн на фрактальных зазубренных апертурах
флуктуации показателя преломления (объемные неоднородности)
должны описываться мультифрактальным спектром фрактальных
размерностей, или спектром сингулярностей.
Анализ усредненных экспериментальных данных для различных
районов океана показал, что частотная зависимость коэффициента
затухания в диапазоне частот 0,1—5,0 кГц подчиняется закону/1'45
[353]. Если считать, что в (6.141) v = 0,275, то частотная зависимость
коэффициента затухания и, следовательно, фрактальная
размерность будут следовать закону/1'45. Положив в (6.135) D' = 2,
получаем D= 1,45. Как отмечается в [346], абсолютные значения
коэффициента затухания, рассчитанные на основе предложенной
модели, согласуются с экспериментальными данными. Согласно расчету,
по данным работы [349], при (ц2) = 8,4-10~8, т]0 = 1 м, 70 < ^0 < 140 м
и im=7 значения коэффициента затухания лежат в диапазоне
(2,74ч-1,94) • 10~2/3/2 дБ/км, что достаточно близко к данным,
приведенным в [353]. Таким образом, в работе [346] установлена
фрактальная природа затухания звука в подводном канале.
6.7. Дифракция волн
на фрактальных зазубренных апертурах
Общее решение в квадратурах. Исследование взаимодействия
оптических когерентных волн с зазубренными фрактальными
апертурами проводилось в [354] на основе физической оптики для
скалярных волн. Периметр таких апертур описывается фрактальными
кривыми. Задача была решена для произвольной, однозначно заданной
апертурной границы в представлении бесконечных рядов.
Рассмотрим дифракцию нормально падающей гармонической
плоской волны единичной амплитуды на зазубренной апертуре
(рис. 6.21), находящейся в плоскости {х\ у'}. Характеристики
дифракционного поля наблюдаются в фурье-плоскости {/#/}.
Скалярное поле в дальней зоне в параксиальном приближении *Р (х, у, z)
запишем в терминах поля *¥.(х?,у',0) с помощью выражений [355]
фурье-оптики
^(х,^г) = С|^Дх>;0)ехр[^27с(/Х + /3//)]л,^,5 (6.143)
А
355
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рис. 6.21. Геометрия задачи дифракции волн на фрактальной зазубренной
апертуре [354]
где C = exp[ikz + i)k/2z)(x2 +y2)]/(ikz),fx=x/(kz),fyy/(te)
-пространственные частоты в декартовых координатах; интегрирование
проводится по апертуре А при z = 0.
Для (6.143) удобно использовать цилиндрическую систему
координат:
тс Д(8)
x¥(p,q>,z) = CJ J 4//(r,e,0)exp[-/prcos(e-9)]rt/rt/e. (6.144)
-тс 0
Здесь г и в - цилиндрические координаты на апертуре; р = (f2 + f2 )1/2;
cp = arctg/ //Y в плоскости наблюдения. Предел интегрирования
R(Q) математически определяет неровности апертуры. Для
раздельного исследования эффектов дифракции на круговой апертуре со
средним радиусом а и неровностях, описываемых функцией/(0) с
нулевым средним, перепишем R (в) как
Д(в) = в + /(в). (6.145)
Тогда формула (6.144) с использованием (6.145) записывается в
виде
I Л U
4f(p,(?,z) = C(Il +I2) = C\ J JxF/(r,e,0)exp[-/prcos(e-9)]rflf/t/e +
-тс 0
356
6.7. Дифракция волн на фрактальных зазубренных апертурах
п д+/(в) 1
+ J J 4//(r,e,0)exp[-/prcos(e-9)]rJn/eL (6.146)
-к a J
Первый интеграл 1Х в решении (6.146)
1х=г%аЩар)1(щ>), (6.147)
где J{(ap) - функция Бесселя первого порядка.
Второй интеграл в (6.146) разделяется на две составляющие с
новой переменной г\ = г-а9 и тогда
я /(9)
/2=0jexp[-/p0cos(9-(p)] J exp[-/pr|COs(e-9)]Jr|Je +
-71 О
ТС /О)
+ Jexp[-/p0cos(9-(p)] J r|exp[-/pr|Cos(e-9)]Jr|Je. (6.148)
-тс О
Интеграл 12 раскрывается с помощью разложений в рады
подынтегральных функций exp[-/pflCos(G-(p)] и exp[-/pr|cos(e-(p)] в виде
оо
exp[-ipecos(6-q>)]= £ (-0%(ря)ехр[/?(в-ср)].
д=-оа
Для функции Бесселя Jp(pr\) используем представление
',№ = 1{(-У№(Р+5)Щ№2)Г2'- (6-149)
Ы)
Тогда с учетом всех введенных рядов получим оценку 12.
Окончательно сумма 7, + 12 дает дифракционное поле
ч>(р,ср,г) = С{2%а2 Jx (ар)/(ор) +
+аХ X f,(-i)*+4-iy/[sKp+s)}(p+2s + l)]x
p=-00q=-oas=-°°
х/9(ар)(р/2К^ехр[-/(^ + 9)Ф]J [f(Q)]p+2s+l&xp[i(p + q)Q]dQ +
-К
357
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
+ 11 I (-/)*+А(-1Г/ [mKg + m)\(g + 2m + 2)]x
х/А(ар)(р/2)«+2'»ехр[-/(5 + Л)ф] } [Дв)Г2т+2exp[i(g + h)Q]d&. (6.150)
-К
Уравнение (6.150) является одним из фундаментальных
результатов работы [354]. Оно показывает простое решение в квадратурах
при дифракции в дальней зоне для апертуры произвольного вида,
определяемой непрерывной функцией/(G).
Далее рассмотрим косинусоидальную и фрактальную
зазубренную апертуры на основе диапазонно ограниченной функции Вейер-
штрасса
(2а2Г1-^-2)1}1/2 й п
Д(6) = д+ г J^ ^ Л 1ч V2 X b4D-2>cos(b»Q + ^n). (6.151)
ШП-2Щ _b2(D-2)(N2+l)l^ „^
Здесь о2 —дисперсия, 6 > 1 — параметр
пространственно-частотного масштабирования, D — фрактальная размерность, £>п — случайная
фаза. Существует (N2 — iVj + 1) фурье-компонентов для формулы
(6.151). Параметр масштабирования Ъ является целым числом, так
как R(Q) должна быть периодической функцией с периодом 2 п для
непрерывной функции.
Косинусоидальная апертура. Перед расчетом дифракции на
фрактальной апертуре рассмотрим пример косинусоидальной апертуры
[354], так как эта функция определяет базис действительной части
функции Вейерштрасса-Мандельброта. Для косинусоидальной
апертуры N{ = N2 и R(Q) = а + r\cos(nQ), где г|«: а - амплитуда
возмущений, п - целое число. Тогда /(0) = r|cos(«G). Характеристики
дифракции получим подстановкой/(в) в формулу (6.150). Затем выделяются
элементы, пропорциональные степеням Т|. Для выполнения этого
условия найдем подходящие индексы (р, q, s, g, h, m) для частных
случаев г\. В [354] данный процесс выполнен графически. Так как п\
очень велико при п - целом отрицательном, то p+s>0, s>0,
g + m>0, /w > 0 . На рис. 6.22 показана диаграмма для суммирующих
индексов {р, s} (а) и {g, т) (б). Порядок ц задан в виде цр+2^ и
358
6.7. Дифракция волн на фрактальных зазубренных апертурах
II 1 1 1 ||
■*}
\р
к
т л ■ ■ ■ ■ ь
Кх^2
Т X"3
■ I i i i I
б)
1g
Ка-3 т
Рис. 6.22. Диаграммы суммирующих индексов {р, s} и {g, m) [354]
ц8+2т+2. Целые числа в верхней правой стороне графиков являются
действительными точками суммирования. Для первого порядка
возмущений Ц имеем р + 2,y+l=:l,g + 2/« + 2 = l (точка 1 на рис. 6.22).
Для второго порядка ц2 необходимо р + 2s + 1 = 2, g + 2т + 2 = 2
(точки 2 на рис. 6.22). Для третьего порядка г|3 имеем р + 2s + 1 = 3,
g + 2т + 2 = 3 (точки 3 на рис. 6.22).
Результирующее дифракционное поле для круговой апертуры с
порядком г|° есть x¥^(p,(f,z) = 2Cna2Jl(ap)/(ap). Характеристики
359
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
дифракции, соответствующие ri1, получаются при р = О и s = О
(рис. 6.22). Данное дифракционное поле обозначим через ¥(1), и оно
равно
У(1)(р,Ф,£)= X Са(-0^д(ра)схр(-1д^Щ/2)х
q=-oo
xj{exp[i(n+q)Q]+exp[-i(n-q)e]}dQ . (6.152)
Интеграл в (6.152) стремится к нулю, за исключением q = ±п
(брэгговские условия сохранения углового момента). Тогда (6.152)
становится пропорциональным Л:
^(1)(р,Ф,г) = 2Cnar\(-i)nJn(ap)cos(nq>), (6.153)
где J_n(pa) = (-l)nJn(pa).
Угловую зависимость в (6.153) можно понять при рассмотрении
условий сохранения углового момента, когда изменения на
апертуре с угловым моментом от -п до п делят падающую волну на две
соответствующие цилиндрические гармоники в полях дифракции.
Поэтому из-за брэгговских условий дифракционные поля с угловыми
моментами пи—п более выражены, чем поля с другими угловыми
моментами, как показано в (6.152) и на рис. 6.23. Угловые моменты
для косинусоидальной апертуры и дифракционного поля
обозначены соответственно внутренней и внешней окружностями.
Рис. 6.23. Диаграмма сохранения углового момента: внутренняя окружность -
угловой момент для косинусоидальной апертуры, внешняя окружность - момент
для дифракционного поля [354]
360
б. 7. Дифракция волн на фрактальных зазубренных апертурах
Дифракционные характеристики, соответствующие второму
порядку у\2, получаются из условий (s = О, р = 1), (s = 1, р = -1) и
(g = 0, /л = 0). При 5 = 0 и р = 1 индекс q принимает значения (-2л - 1),
(2л - 1) и —1. При s = 1 и/; = -1 значения нравны (-2л + 1), (2п + 1)
и 1. Если g = 0 и т = 0, индекс h принимает значения -2л, 2л, 0.
Осуществляя процедуру, аналогичную процедуре при нахождении
V(1)(p,9,^)j можно определить *F(2)(p,q>,z) для второго порядка г\2
в виде
¥<2)(р,ф,г) =
= СУ {(-1)2(я/8)ехр(/2лф)[2/2л(др) -ф/2л+1(др) -ф/_2л+1(ф)] +
+(-1)2(тс/8)ехр(~/1лф)[2/2Дф)-др/2л+1(др)--др/_2л+1(др)] +
+(тс/4)[2/0(ф)-Лр/1(ф) + ф/_1(ф)]}. (6.154)
Все другие комбинации индексов s, p, g, h, m дают компоненты
поля, пропорциональные третьему порядку г|3 или выше.
Фрактальная апертура. Для фрактальной апертуры (6.151)
характеристики дифракции первого порядка могут быть получены
игнорированием полей, пропорциональных г|2 и выше. Это приводит к
тому, что остаются поля нулевого и первого порядков возмущений
хр(0)+(1) ^ КОТОрЫе определены в [354] в виде соотношения
= С
4f^(p,9,*) =
2паЩар)/(ар)+ £ 2naan(-i)nJt(n)(ap)cos(bn(p^n)
n=Nx
(6.155)
"I1/2 ,/л_о\и Г iWn-WN^Ul-l/l
Здесь оя = {2о2[1-А2Д-4]}1/'£Мд-2)«[А2(/,-2)(^)]-,/% ,(„) = £«. Для
фрактальных апертур дифракционные поля нулевого и первого
порядка являются суммой соответствующих взвешенных
дифракционных полей от косинусоидальных апертур. Весовые функции
напрямую связаны с фрактальной размерностью D.
361
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Далее будут приведены численные решения уравнений (6.153)
и (6.155) и дан анализ результатов экспериментов, полученных в [354]
и дополнительно автором в [99, 100, 184, 230, 356, 357].
Экспериментальные результаты. Рассмотрим сначала
дифракционные характеристики для косинусоидальных апертур. В
экспериментальных установках использовался гелий-неоновый лазер (X =
= 0,63 мкм). Луч лазера через точечную диафрагму и коллиматор
направлялся на транспарант и затем распространялся на расстояние 4
м (~107А,). Средний диаметр апертуры равнялся 2 мм. На границе
дальней зоны (z ^ па2 /Х = 4,98 м) записывалась интенсивность поля.
Для косинусоидальной апертуры при п = 6 и 11= 0,1 я
дифракционное поле вычислялось до первого порядка по уравнению (6.153).
Соответствующая интенсивность записывалась в виде [354]
^)б+(1)(р,Ф,г) = |^(р5ф,г)|2 =
= 4я2|^2д4[/1(ф)/(ф)-0,1/6(ф)со8(6ф)]2. (6.156)
Первый элементе (6.156) обусловлен круговой апертурой, имеет
пик при Л = 0 и исчезает при р-3/2 для больших р .
Дифракционная интенсивность (рис. 6.24,а) исследовалась в трех различных
направлениях, когда cos(6cp) = 1 (сплошная кривая), 0 (пунктирная
кривая), -1 (штрихпунктирная кривая). При cos(6cp) = l пик
дифракционной интенсивности /тах наступает при яр « 5 , в то время как /^
для ар ~ 8 соответствует cos(6cp) = -1. Следовательно, в направлении
cos(6cp) = 1 расположены 6 пятен вокруг области ар ~ 5 . Кроме того,
существует 6 пятен в направлении cos(6cp) = -1, и они
располагаются вблизи ар«8. На рис. 6.25,а, как и ожидалось, имеются 12
пятен. Однако можно наблюдать и незначительное смещение
соседних пятен, которые меньше предсказанных из аналитических
расчетов (рис. 6.24,я). Это обусловлено пренебрежением высоких
порядков в расчетах [354]. В среднем интенсивность высоких
порядков меньше 0,01/тах. На полученные данные также влияют
погрешности измерения и их поведение вблизи границы зоны Фра-
унгофера.
Рассмотрим другой пример, когда п = 12. В данном случае
интенсивность
362
6.7. Дифракция волн на фрактальных зазубренных апертурах
0Г0075
0(006 Ч
0,0045 Ч
0(003 Ч
0,0015
0,005
0,004
0,003 Ч
0,002
0Т001 Ч
12 пятен
\ л
>*ч\ /гУ^З^Т^/] ар
15 20 25 30
Рис. 6.24. Дифракционные интенсивности для косинусоидальных апертур [354]
При этом центр распределения дифракционной интенсивности
занят дифракционными кольцами Эйри из-за круговой апертуры.
Снова рассматриваем три случая (см. рис. 6.24,6): cos(12cp) = l
363
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рис. 6.25. Экспериментальные
результаты для косинусоидальной апертуры
(я), фрактальной апертуры (б) [354] и
результаты измерения фурье-спектров
калибровочных объектов (в) [100, 184,
230, 357]
в)
(сплошная кривая), 0 (пунктирная кривая), -1(штрихпунктирная
кривая). Когда cos(12cp) = 1, значение /тах наблюдается при ар ~ 12 ,
для cos(12cp) = -1 центр 12 пятен находится в области ар «14 . На фу-
рье-плоскости при этом должно наблюдаться 24 пятна. Погрешно-
364
6.7. Дифракция волн на фрактальных зазубренных апертурах
сти имеют такую же природу, как и для п = 6. Радиальное
расстояние этих 24 пятен (л = 12) превышает соответствующее радиальное
расстояние 12 пятен (п = 6), так как пики /12 находятся на большем
расстоянии, чем у /6.
Для зубчатых фрактальных апертур дифракционная
интенсивность первого порядка вычисляется с помощью (6.155) в виде
соотношения
= \С?
/Г(1)(р>ф>*)=
2тшЩщ>)/(щ>) + X 2яшл(-/)л//(л)(ф)со8(АлФ + ^)
2
.(6.158)
Отметим, что фурье-компоненты фрактальных выступов
связаны как с радиальными изменениями (функции Бесселя), так и с
круговыми вариациями (косинусоидальные функции) в
дифракционной картине. Для малых значений D фурье-компоненты низких
пространственных частот более выражены, чем соответствующие
компоненты более высоких пространственных частот. Для высоких
фрактальных размерностей D все фурье-компоненты почти равны
[341]. Поэтому для D = 1,01 амплитуда ос„, соответствующая л = JVj,
более высока, чем другие. Таким образом, дифракционная картина
при D = 1,01 показывает более сильную угловую зависимость от
cos2(6^cp). Однако угловые вариации уменьшаются при D = 1,99,
когда все пространственные частотные компоненты почти
одинаковы. Экспериментальные результаты для D=1,01hD=1,50
показаны на рис. 6.25,5. В этом случае JVj = О, N2 = 9, Ъ = 2. Значение а
выбиралось так, что отношение максимальной зубчатости к среднему
радиусу а примерно равнялось 0,1. Таким образом, для фрактальных
апертур угловое распределение дифракционного поля связано с5и
периметром апертуры. На рис. 6.25,в представлены фотографии
нескольких калибровочных объектов, соответствующие в какой-то
степени физическим фракталам, и их двумерные фурье-спектры.
Полученные результаты могут быть использованы при
рассеянии луча на апертурах, при распознавании образов, при разработке
фрактальных антенн оптического и микроволнового диапазонов,
изучении дифракции на световодах с неровной границей и т.д.
365
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
6.8. Рассеяние волн частицами неоднородной формы
на основе фрактального приближения
Теория рассеяния волн несферическими частицами находится
в стадии развития. В последние годы, особенно с развитием теории
фракталов, интерес к изучению несферических частиц заметно
возрос, так как в природе однородные сферические частицы являются
скорее исключением, чем правилом. На сегодняшний день
существует множество точных и приближенных методов определения
поглощения и рассеяния на несферических частицах регулярной (гладкие
кривые) и нерегулярной форм (см., например, [358, 360]). Наиболее
часто применяются метод разделения переменных, метод
поточечной сшивки, методы возмущений, метод Парселла-Пеннипакера,
метод Г-матриц, метод статистического подхода.
Амплитуда рассеяния. Далее будем рассматривать только
фрактальные частицы. Отметим, что несферические частицы вблизи
направления вперед рассеивают аналогично шарам равного сечения
(рассеяние Ми), но различия наблюдаются с увеличением угла
рассеяния [359].
В работе [361] было получено выражение для амплитуды
рассеяния частицы при описании ее поверхности фрактальной
функцией и принимающее в расчет форму частицы. Угловая зависимость
интенсивности дифракции от неровной поверхности характеризуется
значительным обратным рассеянием и мощными флуктуациями. Для
точной проверки и установки модельных представлений изучалось
(в [361]) рассеяние электромагнитных волн с X = 8,56 мм на трех
разных объектах (рис. 6.26). Точные измерения выполнялись во всей
угловой области с разрешением менее Г. Теория данного типа
рассеяния основана на формализме эйконала и будет приведена далее.
Все три объекта имеют одинаковые средний диаметр 16 см и
коэффициент преломления п = 1,89 + / 0,01 при цилиндрической
симметрии вдоль оси z- Объект первого типа (линия 1 на рис. 6.26)
состоит из 8 выпуклых четвертей окружностей радиусом 2 см. Для
объекта второго типа (кривая 2) существует 16 выпуклостей
размером в четверть окружности радиусом 1 см. Объект третьего типа
(линия 3) имеет 8 четвертьвыпуклых окружностей радиусом 2 см с
противоположными выпуклостями. Симметрия по оси z выбрана для
удобства расчетов и технологии изготовления объектов. Однако фор-
366
6.8. Рассеяние волн частицами неоднородной формы,,.
Рис. 6.26. Формы поверхности рассеяния Ь - S(z) [361]
мализм эйконала может быть распространен и на несимметричные
поверхности.
Эйконалом называется фазовый путь Ф волны в приближении
геометрической оптики, когда любая компонента электромагнитного
поля может быть представлена в виде / = Лехр(/£ф), где А -
медленно изменяющаяся во времени и в пространстве амплитуда; к -
волновое число в вакууме [274].
Амплитуда рассеяния миллиметровых волн на объекте со
средним радиусом а » d и размером наименьшей неоднородности d » X
равна
ik2
f(Q) = l-!^jbdbJQ(kbsmQ)
\-n2(b)
ехр(/^2)ехр
r.ik^-n4b))^
q-[l-nHb)]k/2
(z2-zl)-t*Wqzx)
I
7=2
exp
• £ fj-l
-i-{\-n\b)) X(*2/-32/-l)-*2y-l
1 \Ы\
( (
exp
A\-n\b))
]~K 2
Z2J
-exp
q-k
(l-n2(b)))
•2y-l
(6.159)
367
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
где п - комплексный коэффициент преломления объекта; q =
= 2£sin2( 0/2 ) - волновой вектор рассеяния; Ъ - параметр влияния.
Пусть S (z) - выражение для границы рассеяния объекта.
Примем для Ь произвольное значение Ь0 и получим для 0 < z ^ 2а
решение zt(b0), где /€ l9...,Nb для уравнения S(z) = 60. Для
рассматриваемых трех объектов (см. рис. 6.26) уравнение S(z) = bQ
характеризуется точками пересечения zx и z2, и поэтому член в (6.159) с суммой
по у отсутствует.
Сечение рассеяния. Сечение рассеяния задается выражением
/(e) = fc2|/(6)|2. (6.160)
Далее в [361] было рассчитано рассеяние миллиметровых
радиоволн указанными объектами. Это исследование дает границы
формулы (6.159) для /(G) от d/X, так как объект второго типа
находится на допустимом пределе эйконала (d/X~l).
На рис. 6.27 приведены интенсивности рассеяния для объектов
первого, второго и третьего типов при п = 1,89 + /0,01. Там же
пунктиром нанесена интенсивность рассеяния для идеальной сферы. Во
всех случаях наблюдается увеличение обратного рассеяния и
сильные осцилляции. На рис. 6.27 можно наблюдать корреляцию между
числом четвертей окружностей и числом пиков интенсивности в
угловой области 85° ^ 0 ^ 180°. Для 8 окружностей получается 5 пиков
на углах 88°, 110°, 129°, 146°, 165° (рис. 6.27,я), хотя для 16
окружностей пики на углах 110° и 146° исчезают (рис. 6.27,6). Эти углы
находятся посередине между указанными максимумами. Поэтому
можно провести аналогию с дифракционной решеткой [333], где
частота осцилляции пропорциональна расстоянию между двумя
последовательными элементарными структурами, которые в нашем
случае соответствуют радиусу четверти элемента поверхности.
Интенсивность рассеяния для объекта третьего типа подобна
предыдущим двум для в < 60°. На больших углах 0 осцилляции возрастают,
а интенсивность пиков падает (рис. 6.27,в).
Поскольку интерференция волн наблюдается от разных
участков объекта, то естественно изучить, как окружности разного
радиуса (или наличие асимметрии поверхности с разным числом
вкраплений слева Nx или справа N2) влияют на полученные результаты. На
368
6.8. Рассеяние волн частицами неоднородной формы...
О 20 40 60 80 100 120140 160
а)
О 20 40 60 80 100 120140 160
б)
Рис. 6.27. Сечения рассеяния /(8)
в зависимости от угла рассеяния 0
для объектов первого (я), второго (б),
третьего (в) типов на длине волны
8,56 мм [361]
рис. 6.28 показана
интенсивность рассеяния от 16 частей
поверхности, не соизмеримых по
радиусам неровностей 1 ± ОД см.
Здесь наблюдается возрастание
обратного рассеяния и
снижение амплитуды пиков.
Сечение рассеяния для асимметричного объекта с JVj = 6 и N2 = 4
окружностями несоизмеримых радиусов как функция угла
рассеяния дано на рис. 6.29. Осцилляции сильно уменьшаются по
амплитуде из-за разрушения интерференции. Хотя пики интенсивности
исчезли, увеличение интенсивности обратного рассеяния остается.
Этот эффект показывает некоторое подобие со слабым эффектом
локализации [362], возникающим в физике твердого тела, когда
локализация приводит к конструктивной интерференции.
0 20 40 60 80 100 120 140 160
в)
369
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
0 20 40 60 80 100 120 140 160 9°
Рис. 6.28. Сечение рассеяния для
объектов второго типа при не
соизмеримых по радиусу неровностях
1 ± ОД см как функция 0 [361]
0 20 40 60 80 100 120 140 160 в°
Рис. 6.29. Сечение рассеяния для
асимметричного объекта с N{ = 4
окружностями слева и N2 = 6 справа
как функция угла рассеяния 0 [361]
У объекта второго типа при Х= 0,2 мм интенсивность первого
порядка увеличивается в диапазоне 20° < 6 < 150° при сильном
возрастании прямых и обратных пиков. Таким образом, значение пиков
обратного рассеяния зависит от соотношений d/X и а/ X. Поэтому
исследование интенсивности рассеяния, особенно в угловых
областях 150° ^ Э < 180°, дает возможность оценить средний радиус и
степень неровностей объекта - как, например, в акустике [363].
Общая теория эйконала. Представим теперь теорию эйконала,
следуя работе [364]. Рассмотрим рассеяние плоской
монохроматической волны с волновым вектором к на частице с комплексным
коэффициентом преломления п (г). При описании
электромагнитного поля как совокупности фотонов уравнение Шредингера часто
оказывается имеющим вид уравнения Гельмгольца. Поэтому для фотона
потенциал рассеяния
V(r) = l-n2(r).
(6.161)
Значения V(r) и импульса р определяют оператор Гамильтона.
Решение уравнения Гельмгольца или приведенного волнового
уравнения имеет вид xF(r) = exp(/A: г) ф(г). Изложенные далее условия
называются предположениями Глаубера [365]. Для объема
Vv=(4/3)na3 выполняется условие кая>1. Произведение У{г)фг)
для любой точки г внутри объема Vv изменяется медленно на рас-
370
6.8. Рассеяние волн частицами неоднородной формы,,.
стояниях, меньших X. Это означает, что коэффициент преломления
не может существенно меняться на длинах X, поэтому флуктуации
в масштабах X во внимание не принимаются. Одновременно для
точки г внутри Vv произведение V(r)y(r) заметно изменяется на
расстояниях, значительно больших X. Потенциал рассеяния имеет ось
симметрии Oz \\ к.
В цилиндрических координатах г = Ь + ez z, где Ь - параметр
влияния, амплитуда рассеяния записывается в виде [364] соотношения
ik
хехрUk\b + ezz)--f J dz'll-nHkz')]\dbdz, (6.162)
где ks = kr0/r0 — волновой вектор рассеяния; г0 - вектор точки
наблюдения. Форма поверхности описывается кривой S(z) в
плоскости {b, z}, как показано на рис. 6.30. Принимая в расчет
азимутальную симметрию, выражение (6.162) перепишем в виде
к2
f(Q) = ~jbdbJ0(kbsinQ)g(b),
где
с q, определенным в формуле (6.159).
Рис. 6.30. Геометрия рассеяния [364]
(6.163)
g(b)= ]dz[l-n2(b,z)]exp(ikz)exp -| J[l-^,0]*j, (6.164)
371
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Вначале рассмотрим интегрирование по оси z- Если bQ -
произвольное значение переменной Ь, то зависимость [1 — п2 (bQ, z)] от z
выражается графиком, показанным на рис. 6.31. Точки Zj(b0) -
точки пересечения прямой линии bQ = b и кривой b0 = S(z) для 0 < z ^ 2а.
Максимальное число точек поперечного сечения обозначим через
Nb (например, для данных рис. 6.30, где | Ь \ = bQ , имеем 4 точки
пересечения). Поэтому, согласно рис. 6.31, коэффициент преломления
есть последовательность прямоугольных функций. Для удобства
запишем
N-t
l-n4b0,z) = V(b0,z)= I K/°(z),
ы
(6.165)
где Vlu°(z) = V0(b0) = l-nHb0) wlz21_x<z<z21, V{ °(z) = V0(b0)/2 для
z= z2l_ i или z = z2!, Vj °(z) = 0 для z < z2l_ x или z > z2r
V(b0iz)\
0 z}(b0) z2(b0) z3(b0)z4(bo) z^b0) z6(b0)*** Zvb-i(k) zNbft0) z
Рис. 6.31. Форма V(b0,z) = l-n2(b0,z) для фиксированного параметра
влияния b [364]
После подстановки (6.165) в (6.164) имеем
^) = |11*ехр(/^)К^)ехр -|}[l-^f^]^l
Рассмотрим сначала элемент, соответствующий у = 1 в этом
уравнении. Тогда получим
372
6.8. Рассеяние волн частицами неоднородной формы...
Ч
g(b)\j=l = \ dzV0(b)exp(iqz)exp
-4ко(*)К
W
я-
kVQ(b)
-bxp(/gz2)exp
-^V,{b){z2-zx)
-exp(iqZl) .(6.166)
Другие элементы из выражения (6.165) дают вклад
Nk
ь1г к
у-1
Z,\Z2l~Z2l-\)~Z2j-l
ехри
i<
i-^4b)
4i -exp и
Q-\v,(b)
!-
9~V0(b)
Z2j-l
(6.167)
Тогда амплитуда рассеяния (6.159) запишется в терминах
потенциала рассеяния следующим образом [364]:
/(9) = i—°jbdbJQ(kbsinQ) V^ x
■*1
2
Я~У0(Ь)
x-jexp(i'gz2)exp
"ьг. г
-^0<*)<*2-*1>
У=1
ехр -/-К0(6)
-ехр(е^) +
Aj(Z21 ~ Z2l-\) ~ Z2j-\
(
QXpU
{-!"•
(*)
ы
«2/ "eXPi'
2
Я~У0(Ь)
Z2j-\
М
(6.168)
Выражение (6.168) справедливо для всей угловой области. Для
сферических частиц уравнение b = S(z) характеризуется точками
za{b) и zb{b). Для этого случая решение получено в [365]. Выражение
(6.168) справедливо только при обеспечении непрерывности по Ъ для
коэффициента преломления.
373
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Вариации формы частиц. Далее обсудим различные
аналитические выражения для кривых, описывающих разные формы частицы
[364]. Для сферической частицы радиуса а уравнение поверхности
должно быть
e(z) = [a2-(z-a)2f2. (6.169)
При исследовании эффектов, связанных с нерегулярной
поверхностью, рассмотрим сферу с вкраплением в виде эллипсоида с
полуосями осг (вертикальная) и г (горизонтальная), расположенным
относительно Zq для ze \_Zq - г, Zq + г]:
d(z) = [a2Hz-a)2]l/\a[r2-(z-z0)2f2. (6.170)
В качестве иллюстрации на рис. 6.32,а приведена кривая,
заданная уравнением (6.170) с ос = 3, г = 0,1 я, Zq = 0,2а, где а = 50 мкм.
Введем далее некоторую девиацию от идеальной сферы с помощью
добавления все более мелких окружностей Sj (z) радиусом aj = a/MJ,
где М- число поддиапазонов диаметра. Эти окружности
описываются уравнением вида
Sj<z) = [al-(Zj-aj)2]l/2 (6.171)
при Zj = z- 2ajmi{zJ2aj), где int(x) - целая часть числах.
Уравнение поверхности тогда равно
S(z)= £ Sj(z). (6.172)
7=0
Предел Nmax = int [log(a /X)/ log M] вводится для уменьшения
влияния флуктуации, меньших X. Соотношение (6.171) легко
обобщается на случай неровных поверхностей умножением каждой
гармоники S (z) на Af(Z)~ 1)/Z), где D - фрактальная размерность. Величина D
рассчитывается следующим образом. Значение Sj может быть
получено из S _ j следующим алгоритмом: малая полуось делится на М
частей, большая полуось умножается на M(Z)~1)/Z). Тогда —-M(ZM)/Z) =
М
= M~l/D, а фрактальная размерность равна D = —г—= -=г.
logLGtf-1^)"1]
374
6.8. Рассеяние волн частицами неоднородной формы...
в)
Рис. 6.32. Формы поверхностей частиц, описываемые
уравнениями (6.170) и (6.172) [364]
375
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Для моделирования очень малых флуктуации введем случайную
фазу Фу. Тогда из (6.172) имеем
Nn
lV2
S(z)= £ Гв?-(г,-в,)21 МЛ^-1)/^со8ф.. (6.173)
у=0 L J
Данный случай не соответствует картине эйконала, потому что
неоднородности, вводимые случайной фазой, имеют выбросы,
меньшие, чем X. На рис. 6.32,6 представлены частицы с формой,
описываемой (6.172) при U = 5, D = 1, Ф7: = 0, а на рис. 6.32,в - частицы с
U = 5 и D = 1,3 без случайных фаз (Фу = 0, Vy). При очень
больших Мимеем NTogx = 1, что соответствует идеальной сфере. Для
моделирования фрактальных частиц также широко используется
функция Вейерштрасса-Мандельброта [128], записываемая для
данного случая в виде
W(z) = Re
~ [1-ехр(/у"г)]ехр(/Ф/1)
L M-D)n
И=-оо I
(6.174)
с параметром у и случайной фазой ф„. Для удовлетворения условий
Глаубера необходимо ограничить диапазон у:
у*™* 2а = 2я -* итах = int [log(rc /a) / logy],
y^nX = 2% -> nmin = int[log(2rc A)/logy].
(6.175)
Тогда
п=птгх COSф„-COS
W{z)= I —
"=*min
a
y(2-Z))(/i-%ax)
(6.176)
Для получения вклада от субгармоник при z = 2а на значение у
необходимо наложить условие у = т~1, где те N*. Разные формы
функции Вейерштрасса-Мандельборта представлены в [128].
376
6.8. Рассеяние волн частицами неоднородной формы...
Характеристики рассеяния. Теперь перейдем к расчету сечения
рассеяния /, задаваемого уравнением (6.160), для разных типов
частиц.
В [364] рассматривается рассеяние света с X = 0,6328 мкм
однородными частицами различных форм со средним радиусом 50 мкм.
Коэффициент преломления п{Ь) = 1,1 + /5-10~3 (внутри частицы) и
п{Ь) = 1 (вне частицы). Для идеальной сферы с дефектом формы (см.
рис. 6.32,я) характеристики рассеяния приведены на рис. 6.33, а. Там
же пунктиром показано /(G) для идеальной сферы. Эффекты
флуктуации особенно выражены в окрестности угла 6 < 90°, где сечение
рассеяния уменьшается на два порядка, а в обратном направлении
(180°) заметно возрастает.
Для рис. 6.32,6 с параметрами М = 5 и D = 1 сечение рассеяния
сравнивается с сечением рассеяния от идеальной сферы (рис. 6.33,6).
Видно, что частота флуктуации возросла, а уровень пиков снизился
по сравнению с первым случаем (рис. 6.33,а). На рис. 6.33,в
изображено сечение рассеяния от частицы с формой, заданной рис. 6.32,в,
отличающейся от данных рис. 6.32,бтолько значением D= 1,3. Здесь
также ярко выражены неоднородные области, и среднее сечение
рассеяния увеличивается из-за роста D, т.е. неровностей частицы.
Для рис. 6.33, г поверхность частицы такая же, как на рис. 6.32,<?
(D = 1,3), но коэффициент преломления увеличен до значения п{Ь) =
= 1,5 + /0,01. Здесь интенсивность рассеяния имеет те же самые
черты, как и прежде. Однако осцилляции вокруг кривой рассеяния от
гладкой сферы значительно возросли. Почти вся кривая /(G) для
фрактальной частицы имеет абсолютные значения, лежащие выше
кривой на рис. 6.3,в с той же фрактальной размерностью. Данные
расчетов в [364] подтверждаются экспериментальными результатами из
[366], полученными для одиночных частиц размером до 100 мкм при
длине волны 0,633 мкм.
Можно отметить, что угловая область от 160 до 180° является
наиболее чувствительной для степени неровностей поверхности
частицы. Данный подход может быть распространен на частицы с
соотношением а/Х<к 1, когда амплитуда рассеяния не может быть
описана в терминах геометрической оптики. Развитый в работе [364]
метод дает большую область применения: это изучение рассеяния
света межпланетной пылью, исследование неровных поверхностей
377
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
60 100 140 180
0°
а)
20 60 100 140 180
0°
б)
20 60 100 140 180
0°
е)
20 60 100 140 180
0°
г)
Рис. 6.33. Сечения рассеяния /(0) для частиц, форма поверхности которых
описывается уравнениями (6.170) и (6.172), см. рис. 6.32 [364]
378
6.9. Рассеяние волн диэлектрическими фрактальными волокнами
и микроволнового рассеяния неоднородными макроскопическими
объектами.
6.9. Рассеяние волн диэлектрическими
фрактальными волокнами
Длина волны как средство измерения. В [367] на примере
рассеяния от фрактальных волокон рассмотрена роль длины волны,
зондирующей фрактальную структуру. Показано, что X действует как
измерительная линейка. Для низких частот отражение происходит от
крупных масштабов неровностей. Высокие частоты выявляют
рассеяние от мелких неровностей. Как обычно, в исследованиях
использовалась диапазонно ограниченная функция Вейерштрасса [128, 341,
342].
Вначале рассмотрим, следуя [367], более подробно соотношения
между измеряемой критериальной фрактальной размерностью Д
введенной Мандельбротом [1-3], и действительной фрактальной
размерностью D диапазонно ограниченной функции Вейерштрасса. В
классическом варианте фрактальную размерность D определяет число
эталонов N{z), покрывающих кривую. При этом длина линии Цг)
Де) = Се1-^, N(e) = Ce-V, (6.177)
где С- const.
Тогда при постоянной величине D можно записать: D = [log С -
- log N(t) ]/log e или в виде соответствующей производной
D = -d[\ogN(e)]/d[\oge]. (6.178)
Соотношение (6.178) дает классический способ измерения D для
случая, когда D есть функция е. Это согласуется с концепцией
ограниченных фракталов, характеристики которых могут изменяться с
изменением масштаба. По этой причине в [367] введено обобщение
7V(e) = Cexp
]ш№
(6.179)
которое при D(e) = D совпадает с приведенным.
379
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Нормализованная, диапазонно ограниченная функция
Вейерштрасса здесь записывается в виде
nyf2[l-b2^D-2^2 *i
W{z) = - !—J- -L—- £ ^-«cospiHfr^ + eJ, (6.180)
где b > 1 - параметр пространственно-частотного масштабирования;
1 < D< 2 - фрактальная размерность; s - фактор масштабирования;
0т - случайная фаза; N= N2 — N{ + 1 — число гармоник; г|2 —
дисперсия.
Как было отмечено, длина кривой L(e) является функцией
длины эталона е. Фрактальная размерность D функции Вейерштрасса
есть число, зависящее от D и от Ь. Полная длина кривой
L = \(l + JV'2f2dZ. (6.181)
о
Длина (6.181) определяется при измерениях эталоном, который
короче самого малого масштаба (sbNl) , в то время как верхняя
оценка длины L получается при эталоне, который длиннее
крайнего масштаба (sbNl) . Оценки L и L будут ниже или выше предела
1(e). Из (6.178) имеем
D = -d[\ogN(e)]/d(logE) = 1 -d[logL(e)]/d(loge). (6.182)
Предположим линейную связь между log L(e) и log 8 и получим
log(L/L)
где
Z/I = lj [1 + ^2]1/2* = ((1 + ^'2)1/2). (6.184)
380
6.9. Рассеяние волн диэлектрическими фрактальными волокнами
Результат сравнения измеренной фрактальной размерности D
для диапазонно ограниченной функции Вейерштрасса с заданным
значением D = 1,75 при различных значениях коэффициента Ь
показан на рис. 6.34. Выявленные различия между DnD вызывают
вопрос: какое из значений — D или D — «увидит» зондирующая
волна? При сильном взаимодействии с пространственной структурой в
[367] предполагается, что зондирующая волна более чувствительна
к А чем к D.
£2,0
Рис. 6.34. Сравнение измеренной фрактальной размерности й с заданным
значением D= 1,75 диапазонно ограниченной функции Вейерштрасса
при разных значениях Ь [367]
Четвертый момент функции W (z)
^=(Ж4) = Т14
3-^
3 \-t \ + tN\
2 1 + / 1-/*
где t = 62(Z)" 2\ Для N -*оо и Ь > 1 получено
(6.185)
^=(*H)=V
з-- —
2 \ + t
(6.186)
Из (6.185) и (6.186) видно, что четвертый момент имеет слабую
зависимость от фрактальной размерности D и зависит только от N,
а не от N{ и N2 в отдельности.
Приближение Рэлея-Ганса. Геометрия рассеяния
электромагнитных волн тонкими диэлектрическими волокнами с фрактальной
381
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
поверхностью приведена на рис. 6.35. Волокно имеет средний радиус
а и длину /.
Рис. 6.35. Геометрия рассеяния волн фрактальными волокнами [367]
Там же показаны плоскости падения и рассеяния волн.
Электрическое поле E(p,q>,z) в цилиндрических координатах
удовлетворяет уравнению Гельмгольца
{v2 + k2[U(n2-l)f(p,z)]}E(p^z) = 0 (6.187)
с дискретной функцией
f(p,z) =
\lp<a[l + W(z)l
\0,p>a[l + mz)].
В приближении Рэлея—Ганса [358, 359] и при выполнении
условий («-1)«1и(«- \)ка «: 1 сечения рассеяния на
перпендикулярной do/dQ,1^1 и параллельной dc/d£l^ поляризациях являются
функцией азимутального угла Ф и равны соответственно
da
da
'i->i
= j(n2-l) к*\ J dz j jhkbsm^\bdb\ ,
4 [-//2 О V 2J J
382
6.9. Рассеяние волн диэлектрическими фрактальными волокнами
dc
da
м
Г1/2 a[l+W(z)] ( . ]2
-Lcos2(p(>j2-l) кЧ \ dz \ /0 2Ш1п| \bdb\ . (6.188)
4 [-//2 О V 2) J
С учетом тождества |/0(х)хЛ = х/1(х) и нормализованного
параметра 0 = 2&0sin((p/2) уравнения (6.188) записываются в виде
*±->±
_^_ = 1(„2-1)2(Ь)4/2 j[l + W(x)]^Jl^ + W(x)]Q}dx\ ,
da
da -> do
= COSz ф-
(6.189)
И
</Q
'!->!
В низкочастотном приближении при ка <к 1 и Q «: 1
соотношение (6.189) переходит в соотношение
dQ.
da =1^-1)2(ка)ЧЦ1+ц2)2
(6.190)
±->±
При W(z) - 0 формула (6.189) описывает сечение рассеяния
однородного цилиндра
dQ
^2_ = I(„2_1)2(M4/2
л А\ ) v 7
±->±
■ДО
(6.191)
Сравнивая (6.189) и (6.191), можно заметить, что функция
фрактальной поверхности W(z) является переменной частью весовой
функции [1 + W{z)]. Уравнение (6.190) показывает, что
эффективный объем волокна растет вместе с параметром (1 + г)2).
Анализ результатов. Расчеты в [367] по (6.189) проводились для
коэффициента преломления п = 1,015. Значение Ь = п1/2 =1,77245
при N=9 гармониках. Результаты численных расчетов
нормализованных сечений рассеяния (da/dQ.)H =4(n2-l)~l(ka)~4r2(da/d£l1^1)
в зависимости от значений нормализованного параметра Q в
двойном логарифмическом масштабе приведены на рис. 6.36 и 6.37.
Отметим, что режим промежуточных частот имеет фрактальный харак-
383
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
тер, а в области низких и высоких частот наблюдаются
нефрактальные режимы. На низких частотах (Q > 1) происходит рэлеевское
рассеяние. При фиксированной фрактальной размерности D = 1,5
наклон огибающих s{ принимает значения sx = -3 (гладкое волокно -
рис. 6.36, я)> sx = -3,38 (легкая волнистость - рис. 6.36, 6), sx = -4
(промежуточная волнистость - рис. 6.36, в), sx = -4,4 (крупная
волнистость - рис. 6.36, г).
Данные на рис. 6.37 демонстрируют монотонную зависимость
нормализованного сечения рассеяния фрактального волокна
(dc/dQ1_J>1)H от фрактальной размерности D при фиксированном
значении Л = ОД. Для D= 1,05 (относительно гладкая поверхность
-рис. 6.37, a), D= 1,5 (рис. 6.37, б), D= 1,75 (рис. 6.37, в), D= 1,95
(высокая волнистость - рис. 6.37, г) наклоны огибающих s2 равны
соответственно s2 = —3,88, s2 = —4, s2 = —4,54, s2 = —4,82.
Отметим, что результаты моделирования зависят в значительной
степени от фрактальной размерности функции Вейерштрасса, а не
от обычной D.
0
-20
-40
-60
-80
: л=о
■—-ч
^=-3,00
\ aV4
[/rvH
1
-10 -5
а)
10 15
б.дБ
0
-20
-40
-60
-ЯП
71=0,15
"^\ч S=-4340
1 V \пУ
-10 -5
г)
10 15
а дБ
Рис. 6.36. Зависимость нормализованного сечения рассеяния фрактального
волокна (da/dQlr^1) от параметра (?для £>= 1,5 [367]
384
6.10. Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
0
-20
-40
-60
-8Л
| <; :
' £>=1,05
—-^ ij=-j,00
Пк J
Щ
10 15
а дБ
0
-20
-40
-60
-ЯП
Г|=0,05
~^u, S =-3,38 |
\/г
У yW \
щ
-10 -5
10 15
е.дв
(»
-20
-40
-60
ЯП
11=0,15
б)
^"Чч £=-3,40
| !к\
Щ
-10 -5
г;
10 15
& ДБ
Рис. 6.37. Зависимость нормализованного сечения рассеяния фрактального
волокна (do/dQ±_^±) от параметра (?для л =0,1 [367]
Расчеты, проведенные в [367], аналогичны вычислениям в [368]
для оптического диапазона. Изменения в сечениях рассеяния
могут быть описаны в терминах импеданса. Поверхностная
волнистость создает слой, состоящий из волокон и окружающего воздуха
с эквивалентным промежуточным коэффициентом преломления
1 < л < 1,015. Данная аналогия более эффективна на высоких
частотах.
6.10. Поглощение и рассеяние волн скоплениями
фрактальных частиц дыма
Морфология частиц дыма. Частицы дыма являются наиболее
распространенными из атмосферных аэрозолей, представляющих
сложные агломераты из множества мелких однородных частиц. От
масштабных лесных пожаров частицы дыма попадают на высоту до
нескольких километров. Дымы промышленного происхождения
выводятся на высоту сотен метров. Пожары от ядерных взрывов выб-
13 Фракталы
385
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
расывают частицы на еще большие высоты. Время жизни дымовых
частиц измеряется часами и сутками, а их перемещение достигает
десятков и сотен километров. Частицы дыма состоят в основном из
сажи, т.е. сложной смеси продуктов неполного сгорания.
В настоящее время для исследования разнообразных свойств
таких образований успешно применяют методы теории фракталов.
В качестве фракталов рассматривают агрегаты из множества (N «
« 102-103) частиц, обладающих одинаковыми физико-химическими
свойствами с размерами, много меньше размеров системы [369]. Это
определение показывает, что атмосферные аэрозоли как
фрактальные системы можно рассматривать только в первом приближении,
потому что всегда есть определенная полидисперсность. Однако
исследования подтверждают, что такое приближение позволяет
вполне удовлетворительно описывать структуру и многие свойства
дымов. Частицы дымов можно рассматривать как фракталы, имеющие
средний радиус частицы а « 0,005-0,05 мкм, N~ 102 - 104 и D « 1,78
[294, 370].
Парнокорреляционная вероятность. Наиболее полно теория
оптических свойств фрактальных агрегатов разработана в [371].
Центральным предположением этой теории является то, что длина
волны X » а . Однако размер кластера R (внешний масштаб фрактала)
возрастает при агрегации от a (N= 1) до i?» X (N ~ 104).
Рассмотрим сначала кластерные статистики с А/частицами.
Размер этих кластеров определяется радиусом гирации R = R /V2 . Для
кластера с фрактальной размерностью 1 < D < 3 имеем
R = aNVD, (6.192)
а плотность убывает по закону
'-]F-SisW (6Л93>
Важное значение имеет парнокорреляционная вероятность Р(г)
того, что расстояние между двумя случайно выбранными
частицами в составе агрегата равно r = r.-rr Самоподобие вместе с
изотропией означает, что
386
6.10. Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
Р(г) =
4яД3
P(r/R),
(6.194)
где Jrfjcjc2/>(jc) = l.
При строгой кластеризации число частиц в центрированной
сфере радиуса 5« R пропорционально 8° так, что
р(х) -» -jtjj- при х->0.
(6.195)
Для подробного расчета запишем выражение (6.195) в более
удобной форме [371]:
р(х) = -Т^ехр(-Ьх),
(6.196)
где A=[(D+ l)D)]D/2/T(D), b = [(D + \)В\Х'2.
Когда D - 1,78, то А = 4,48, Ь = 2,22. Для сравнения парно
корреляционная вероятность при случайном блуждании (D = 2) равна
Р(х) =
8
(2Л)!/2
(l + x2)Jrfvexp --xV
Предельные значения р (х) будут
Р(х)
1-ехр
^ 1 "v
--Х2
v 2 ,
(6.197)
[4/х, х->0,
1бехр(-х2/2)
(2*)VV
(6.198)
Конкретный вид парнокорреляционной функции
принципиального значения не имеет, необходимо лишь, чтобы р(х) убывало при
х-> оо быстрее, чем дг1. Масштабирование заканчивается на
внутреннем фрактальном масштабе, ир(х) = 0 при х < 2а/R. Однако для
всех усреднений по парам частиц интегралы отр(х) сходятся при
предельной форме выражения (6.195). Поэтому малая отсечка по хпри-
ведет к незначительной погрешности, которая в дальнейшем
игнорируется.
387
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Уравнения рассеяния для скалярных волн. Рассмотрим скалярный
случай для частиц с коэффициентом преломления л = пх + in2.
Характерные значения п = 1,75 + /0,3 (видимый диапазон) и п = 3 + /
(инфракрасный диапазон) [371, 372]. Скалярные волны
удовлетворяют уравнению
V2¥(r) + k2n2{r)4{r) = 0, (6.199)
где п{г) = п внутри частиц и п(г) = 0 снаружи. Падающая волна
Ч?. ехр(/^. - г) взаимодействует с N-м кластером и порождает
рассеянную волну с асимптотикой
у,=3*ИМЛ), (6.200)
где k=kr/r,f- амплитуда рассеяния, \f(k. к.)\ = s-—1—. Тог-
s ' s l ' dQ
да сечение рассеяния
сечение ослабления
схе(*,) = уIm/(*,., к,) (6.202)
и сечение поглощения
аа(*,.) = ае(Л,.)-аД.). (6.203)
Амплитуда рассеяния для одиночной частицы fx=t/k с
T = sinr|exp(/r|), где фазовый сдвиг г| равен
т\ = \(ка)\п2 -1). (6.204)
Для действительных п значение г\ также действительно, и
тождество |т| =Imx гарантирует выполнение условий оптической
теоремы [333]. Для комплексного п сечения одиночной частицы
388
6.10. Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
о?) =-na2(ka)4\n2 -if,
<#) «aW « ^7ca20fca)Im«2. <6-205>
3
Для дыма из сажи все три сечения много меньше
геометрического размера частиц, и поглощение значительно превышает
рассеяние.
Для кластера, где центры сфер помещены в точках #}, ..., rN,
общая рассеянная волна записывается как сумма парциальных волн
от каждой частицы:
У
№
где Ч*. — суммарная волна, падающая нау-ю частицу, состоящая из
падающей волны и рассеянной волны ку-й частице от всех других
частиц:
_ ехр(/£г,)
yy=exp(ftrry) + TXy/ ь, > (6.207)
/*у ^
Запишем теперь: *р . = с. ехр(/^ г). Тогда точное соотношение
для амплитуды рассеяния
где с. определяется как
cj = l + *lci I ' ' ■ (6.209)
Уравнение (6.208) является основным для расчета оптических
свойств малых индивидуальных кластеров.
389
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Многократное рассеяние в случае скалярных волн. Найдем,
следуя [371], условие, при котором можно пренебречь многократным
рассеянием, т.е. условие пренебрежения (N- 1) элементами в
сумме (6.209), когда с. «1. Считая все /^равными наименьшему
возможному значению г{. = 2д, получаем из итерационных соотношений
cr[\-Nx/{2ka)Y\ (6.210)
т.е. многократным рассеянием можно пренебречь, когда
Л^<2/|т|~1/(^)2. (6.211)
В терминах кластерной размерности (6.192) условие (6.211)
принимает вид
kR«\/{ka)^D-K (6.212)
Из (6.212) следует, что многократным рассеянием можно
пренебречь при D< 2. Более точную оценку можно найти при
последовательном учете многократного рассеяния, получаемого
итерациями (6.209), и усреднении каждого элемента по отдельности. Это
является трудоемкой процедурой, так как последующие переотражения
от частиц приводят к существенным усложнениям в топологии
рассеяния. Более того, всякий конечный порядок аппроксимации
многократного рассеяния нарушает оптическую теорему. Другой
возможностью является численная инверсия матрицы NxN из
коэффициентов (6.209), и здесь интерес представляет случай N-*°<> при
переменных ка и D.
Можно аппроксимировать среднее поле, получаемое
усреднением N(N— l)/2 элементов матрицы в (6.209), считая все су. = с, так
что
c = [l-(N-l)xQ]-\ (6.213)
где
390
6.10* Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
а скобки означают усреднение по всем расстояниям Гц в ансамбле из
N кластеров. При этом в точности выполняется оптическая теорема.
Из (6.208) с учетом (6.202) выражение для сечения ослабления
равно
4nN 4nN[lmx + \xf(N-l)lmQ]
(а ) = —-г—1тсс = - ^ =* =
N e/ k2 k2\l-(N-l)x$2
4nN (im t + |t|2 (N -1) ((sin krg / fop cos(*, ■ гц)))
= P|l_(JV-l)xQ|2 ' (6'215)
сечение рассеяния имеет вид
4nN\xf (l + (N- l)([smkre /(fy)]cos(fc. ■ rtj)))
#\l-(N-l>tQf ' (6'216)
а сечение поглощения
. x_ 4кЩ1тх-\х\2)
{С°)=к2\1-(М-1)х$2 (6'217)
исчезает, как того и требует оптическая теорема при непоглощаю-
щих частицах (п и Ц - действительные числа).
В пределах этой аппроксимации многократным рассеянием
можно пренебречь, если
(#-1)|т<2|«1. (6.218)
Использование (6.194) дает
(?,^]Лх2/<х)«Ф^*о.^ад> (6219)
391
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Для распределения (6.196) выражение (6.219) можно точно
проинтегрировать и при (6.192), когда N »1, оно равно
V (2ka)D(2-D)(D-l)
( b2
•d-D/2
4k2R2
+ 1
exp
-/(2-Z))arctgf— 1
Л-D]
2kR
(6.220)
При kR<cl данное соотношение с учетом условия fx=i/k и
формулы (6.204) приводится к виду
|лгте|«
2l-D\n2-l\[(D + l)D]
D/2
3(Z>-1)
-(ка)
3-D
(2kR\
D-\
«1 (6.221)
и подтверждает тот факт, что многократное рассеяние незначительно
для небольших кластеров из малых частиц. Результат для больших
кластеров очевиден. При kR »1 соотношение (6.220) дает
\NxQi
Jl~D [(D + l)D]D/2\n2-l\(ka)
чЗ-Z)
3(2-2))(Л-1)
-, D<2,
\n>zq\=
D(D + l)\n2-l\(ka)Nl-2'D
6(D-2)(D-l)
(6.222)
D>2.
Предел при D< 2 не зависит от TV и говорит о том, что при
достаточно малых ка многократным рассеянием можно пренебречь на
всех стадиях агрегации. Предел при D > 2 показывает, что
многократное рассеяние необходимо учитывать при N~ {ka)~D^D~2\ т.е.
когда kR ~ (ka)~Q ~ D^D~2\ Ддя D = 3 имеем (п2 -\)kR~\, что
является корректным условием при рассеянии от однородного
кластера. Зависимость \NiQ\ от ка и N в (6.222) остается одной и той же
при любой р{х), удовлетворяющей (6.194) и (6.195), т.е. имеем
инвариантность относительно частного вида (6.196).
392
6.10. Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
Интуитивно аргументы подтверждают различие между D < 2 и
D > 2: при D < 2 кластер «просвечивающий» (площадь проекции
скорее Nna2, чем nR2; при D > 2 кластер геометрически
непрозрачен. Если оценить объемный коэффициент преломления пс для
кластера согласно элементарному правилу
п„ ~1 + 4я
V" J
с
Д3
т , 4тс(и2-1)
р>~1+ дгз/д-1 ' (6-223)
то фазовое приращение для лучей при прохождении кластера есть
Щпе -1) ~ |ф2 -1| kaN1-2?». (6.224)
Оно исчезающе мало при N -> ©о и Z> < 2 и увеличивается для
D> 2. Тем не менее нельзя исключить возможность того, что при
D< 2 флуктуации матричных элементов (6.209), которые не
учитывались в аппроксимации среднего поля, могут скрывать причину, по
которой следует принимать в расчет многократное рассеяние,
когда N превышает некоторую критическую величину,
пропорциональную (ka)~D.
Первое приближение многократного рассеяния фрактальным
кластером: скалярный случай. Рассмотрим [371] случай единичного
рассеяния 7V-M кластером скалярной волны, когда амплитуда
определяется (6.208) при с = 1. Простое усреднение по направлениям между
частицами дает следующее выражение дифференциального поперечного
сечения для угла в :
\da I da { I 2kBxsm(Q/2) J v '
где da^/dQ, = |т|2 /k2 - изотропное сечение рассеяния одной
частицы. Для фрактальной парнокорреляционной функции р(х) вида
(6.196) усреднение в (6.225) выполняется в точности:
*>m)/{H<gyw.
dQ.
393
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
= 1 +
(N -1) sin ((D - l)arctg {2 kR/ 6sin( 6/ 2)})
{D-\){\ + 4k2R2 sin2(e/2)/^-i)/22^in( в/2)/ Ь (6,226)
В (6.226) величина Fd(Q) - фактор усиления, показывающий, во
сколько раз возрастает рассеяние от частиц из-за эффекта
когерентности, обусловленного фрактальностью. В прямом направлении,
как для любой структуры, существует полная когерентность и
фактически
F,(Q)~N при Q<&(kR)~l.
(6.227)
Для большого углового рассеяния при коагуляции (росте N)
наступает насыщение и
F*(Q) = (D-l)[2kasm(e/2)/b)° при 6»(Щ-. (6.228)
Насыщение возникает из-за фрактальной структуры и не
проявляется при однородном распределении частиц системы. Если D = 3,
предел (6.228) равен нулю, хотя (6.226) при большом угловом
рассеянии уменьшается по закону N~l/3. Основные характеристики
фактора усиления Fd(Q) приведены на рис. 6.38. При малых Ncy-
Ig^H
N/"'
—i—i i—i—i i
.10'
1 t
J 1 L—
/102
-1 1 1 1
—1 1—
0 ■—«—»—i—i—i 1—i—»—i—»—i « i i i i i ffl°
90 180
Рис. 6.38. Фактор усиления Fd(Q) для кластерного рассеяния (6.226)
при D = 1,78, ка = 0,111 и разных значениях N [371]
394
6.10. Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
ществует режим изотропного рассеяния, т. е. кластер меньше
длины волны. При больших N появляется пик при рассеянии вперед и
наступает насыщение, когда 6 велико. Асимптотика угловой
зависимости рассеяния (6.228) подтверждена экспериментально при
рассеянии рентгеновского излучения для систем с разными D [ 168, 373].
Поперечное сечение рассеяния является интегралом от (6.226)
по всем направлениям, и фактор усиления Fs для рассеяния легко
рассчитывается из (6.226) или (6.216) как [1 + (N - 1)1т(Д, где Q
задано (6.220):
(cs) 2(iV-l){(l+X2)^cos[(2-i))arctgJ]-l}
S = {JW\ (D-1)(2-DVP ' (6'229)
где Х= 2kR/b. Для малых кластеров получаем тривиальный предел
FS~N (6.230)
при kR <к 1, т.е. N «: (ka)~D . Для больших кластеров предельное
поведение зависит от значения фрактальной размерности:
2сов[(2-Д)и/2]
*~(D-l)(2-D)(2ka/b)D'
ln(4k2a2N/b)
(2ka/b)2
Л~—Т^ГТШ—' D-Z> (6.231)
F 2Nl~2/D D>2
s~{D-\){2-D){2kalb)2'
где £Я»1 и N^>{kaYD .
Непрерывные кривые на рис. 6.39 иллюстрируют зависимость
фактора когерентного усилия Fs от Nn D (1 < D< 3). Расчет в [371]
проводился по формулам (6.229) и (6.192). При D< 2 рассеяние на
одной частице увеличивается на коэффициент, который достигает
значения (ka)'D и не зависит от N Если D > 2, то при коагуляции
продолжается возрастание Fs до тех пор, пока N ~ (ka)~D/(D ~2) (см.
(6.222)). При D= 2 кривая отражает логарифмическую зависимость.
395
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рис. 6.39. Когерентный фактор усиления Fs для поперечного сечения рассеяния
на кластере для скалярных (сплошные кривые) и векторных (штриховые кривые)
волн при ка = 0,111 [371]
Поперечное сечение поглощения, согласно формулам (6.217) при
Q = 0 и (6.205), есть результат суммирования по всем частицам, а
именно
(оа) = ЛГо») = (4nN/k2)(Imx-\x\2)NTUi2 ^kalmn2. (6.232)
Если действительная и мнимая части коэффициента
преломления сравнимы, то поглощение значительно превышает рассеяние
даже для больших кластеров на значение, которое можно найти
из (6.231), (6.232) и (6.205), и имеет порядок l/(ka)*-D для D< 2
и IAN1 " 2/Dka) для D > 2. Поэтому для дыма ослабление от
фрактальных кластеров определяется поглощением.
Сравним рассеяние и поглощение для больших (kR »1)
фрактальных кластеров при D< 2 на основе заведомо ошибочного
предположения, что коагуляция порождает большое поглощение
твердыми частицами (D = 3). По этому предположению поперечное
сечение ослабления TV-го кластера, согласно геометрической оптике,
равно
cTe=nR2=na2N2/\ (6.233)
В этом случае
(оа)/сте =^lmn2NV4a = llmn2kR. (6.234)
396
6.10. Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
Отношение (6.234) превышает единицу для больших твердых
сфер, поэтому в предположении «твердой» коагуляции
недооценивается ослабление. Подобная оценка для рассеяния показывает, что
данное обстоятельство особенно велико для больших кластеров
[N> (ka)~3(*~~D)]9 когда доминирует фрактальное рассеяние.
Уравнения рассеяния для векторных волн. Рассмотрим теперь
случай векторных волн. Считаем, что электромагнитные поля
удовлетворяют уравнениям Максвелла. Тогда вместо падающей волны в
(6.199) будем рассматривать поляризованную волну с единичным
вектором поляризации е7 вида Et =е7ехр(Л7-г). Рассеянная волна
записывается в следующем виде
^ = ехррО/(^Л) (6235)
Поперечные сечения рассеяния и ослабления равны
соответственно
da (6.236)
ce = (4n/k)Imf(krk^er
Условие ka «с 1 предполагает, что каждый шаровидный рассеи-
ватель представляет собой диполь излучения. На этой стадии в [371]
не используется приближение Рэлея или Борна, так как в данном
случае не удовлетворяется оптическая теорема для действительного
коэффициента преломления л. В [371] применена точная теория Ми
[358, 359], согласно которой одиночная сфера порождает рассеянную
волну
*,=»{<» ^^e,>-e,](^-i
(6.237)
2/f ^n2-\
где n = rlr\ p = sin5exp(/5); 5~-^(£я)3-о—~ - фазовый сдвиг.
3 п1 +2
Для одиночной рассеивающей частицы шаровой формы
амплитуда рассеяния
Зр„, ,,.., 3pf„ (*,-е,)х*,
fl(ksA)=2^(ksei)xks=^
«'" &
(6.238)
397
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Вместо (6.205) поперечные сечения для комплексных п
записываются с помощью (6.201) и (6.236) в виде
dQ.
Ц,*,)«*4а«
и2-1
и2+2
[i-(V«,)V*2],
оУ=?;каНка)4
s 3
л2-1
и2+ 2
(6.239)
оУ~оМ~4каНка)1т
л2+2
Для неполяризованного излучения фактором направленности в
dc^/dQ. становится величина (l+cos0)/2.
Рассеянная кластером волна, по аналогии с (6.206), из
формулы (6.237) записывается в виде
Е =
где Е- — суммарное поле, падающее нау'-ю частицу, которое равно
^.=е,.ехр(^.г,)+-^Х
i*j
-[З*^, •*,)-*,]
( 1 i"
exp(ikrM)
(krnf krn
Д
кг
(6.241)
Л
Затем в [371] вводится коэффициент многократного рассеяния dy
EJ=djexp(ikrrj). (6.242)
В итоге записывается векторное волновое уравнение, точное при
малых ка:
ПК k^^tiksXdj^exMki-kJFj], (6.243)
398
6,10, Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
где
1 1*1
(пм xdjxtij, +[3Hj,(Hjrd,) -d,]
xexpOkrj-ikf-rj,) .
<*Гд)2 кгл
(6.244)
Многократное рассеяние в случае векторных волн. По аналогии
со скалярным случаем оценим действие многократного рассеяния с
использованием аппроксимации среднего поля, в которой все dj
одинаковы и параллельны поляризации падающей волны
d."de..
j j
Тогда матричные элементы в (6.244) заменяют их средними
значениями, и их компоненты вдоль et дают (ср. с формулами (6.213) и
(6.214)):
d =
l-±(N-l)pP
(6.245)
где
Р =
( kr. cos(Vry/)x
1_(й.е.)2+|-3(„.е.)2-1]
(krj,)2 (krj,y
(6.246)
п = гя/ги.
Снова данное приближение удовлетворяет оптической теореме.
Это более удивительно, чем в скалярном случае, потому что Р в
(6.246) включает элементы ближней зоны диполя, а рассеяние
включает только поле дальней зоны. Чтобы показать это, в [371]
записано выражение для поперечного сечения ослабления на основе (6.243):
/ \ 6nN ¥ ,
(ae) = ^rlmPd =
6nN
Imp + ||p|2(iV-l)ImP
k2
1-±(ЛГ_1)рР|
(6.247)
399
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Поперечное сечение рассеяния
|2ц|2
9|Pf|</f " "
M=-^m^dQM^-ksH]
1+щ^(1№*^-**гА1-
1-(*L*
6тсЛГ|р|2
8л
АЧ
cos(*rry7)
к2
l-±(N-l)pP\
(6.248)
Вычисления показьшают, что интеграл в точности равен 4я1т Р,
а поперечное сечение поглощения
i \ 67tiV(Imp-|p|2)
[°а) Л:2|1-1,5(ЛГ-1)рР|2
(6.249)
исчезает для непоглощающих частиц.
В пределах описываемого подхода можно пренебречь
многократным рассеянием, если
1,5(#-1)|PJP|«1.
Использование (6.198) дает
(6.250)
Р =
1
k2R2
\dxx2p(x)
exp(zX)
1 х2 + х4 + х
l-^
*nX+W-j^+!l
bosJirk (6.251)
где X= kRx.
Величина Р здесь имеет сходство с Q для скалярного случая
(6.219), а коэффициент в фигурных скобках формулы (6.251)
замещает величину sinX Когда Х->0, интеграл (6.251) сходится при
фрактальном распределении р(х) кластера. Это означает, что вектор-
но-волновое условие (6.250) зависит от N, D и ка также, как в ска-
лярно-волновом случае (6.218), не говоря уже о численных коэффи-
400
6.10. Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
циентах. Таким образом, основные выводы, полученные при
исследовании (6.220)—(6.222), справедливы и для векторного случая:
многократным рассеянием можно пренебречь при D< 2 и ка «: 1.
Первое приближение многократного рассеяния фрактальным
кластером: векторный случай. При однократном рассеянии от N-to
кластера амплитуду рассеяния находят из (6.243) при </ = ег При этом
по аналогии с (6.225) используют усреднение (6.239). Расчет
поперечного сечения рассеяния из (6.248) с учетом распределения (6.196)
приводит к тому, что
{os)/(NoV) = Fs,
(6.252)
где фактор усиления Fs для рассеяния от кластера имеет вид [371]:
F=l+J(NzlL
s (D-l)X2
+sin[(2-Z>)arctgJ]
(1+X2y-Dl2 cos[(2 - i))arctgZ]
( ТТЛ
T T Л
XX*
Ъ+J + J
(6.253)
где Х= 2kR/b и
1
2 2 4
T° 2-D 4-D'6-D
T =
8 8
■ + -
3-D 4-D 5-D 6-D
10 24 12
- +
2-D 3-D 4-D 5-D 6-D'
7>
24 24
- + -
3-D 4-D 5-D 6-D'
L =
8 12
■ +
8 2
+ -
2-D 3-D 4-D 5-D 6-D'
(6.254)
1 2
иЛ =
0 2-D'
2
4 2
■ + -
2-D 3-D 4-2D'
12 8 2
4 2-D 3-D 4-D 5-D 6-2D'
401
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Полученное векторное соотношение эквивалентно (6.229) и
имеет похожий режим в предельном случае. Для малых кластеров
небольшие сокращения приводят к тому, что
Г.-N,
(6.255)
если kR<K\ и N <s:(ka) D. Для больших кластеров пределы зависят
от фрактальной размерности ГУ.
3cos[(2-Z))V2]
f:-
(D-l)(2-D)(2ka/b)D
3ln(4k2a2 N/b)
(2ka/b)2 '
3Nl-2/D
5" (Z)-l)(2-Z»)(2A:a/A)2'
1-
4(2-/)) 1
(4-D)(6-D)\
, D<2,
D = 2,
D>2,
(6.256)
где kR?>l и Ny>(ka)-D.
Пунктирная линия на рис. 6.39 рассчитана по формулам (6.253)
и (6.192) для ка = 0,111. Очевидно, что векторное и скалярное
решения количественно и качественно почти одинаковы. Поперечное
сечение поглощения есть сумма всех поглощений:
(ca) = N($) =^(lmo-\p2\) = Nna^
л2+2
(6.257)
Выводы. Таким образом, для скалярных и векторных волн
поперечные сечения рассеяния фрактального кластера размерности D,
состоящие из N малых частиц, различны для D > 2 и D< 2. При D > 2
рассеяние на частицах больших кластеров растет при агрегации по
закону N1 ~2/Z). Для D< 2 (дым) рассеяние растет до насыщения,
которое превышает значение рассеяния на уединенной частице на
значение порядка (ka)~^~D\ Поперечное сечение поглощения не
зависит от D и равно сумме поглощений всех частиц.
Любой реальный дым включает ансамбль кластеров разного
размера со случайной переменной N Когда дым имеет п частиц на
единицу объема и коагулирует в редкое распределение из n/N
кластеров с N частицами в среднем, тогда длина поглощения или рассея-
402
6.10, Поглощение и рассеяние волн скоплениями фрактальных частиц дыма
ния (при экспоненциальном ослаблении) падающей волны имеет
значение
L = [(n/N)c]-\
где а — соответствующее поперечное сечение.
Для рассеяния в дыме (D < 2) значение L уменьшается с
падением Nro постоянного значения. Полученные результаты [371]
основаны на пренебрежении многократным рассеянием. Это
подтверждено (для всех N, когда D< 2, и для N < (ka)~D^D~2), когда D > 2)
оценкой результатов многократного рассеяния с помощью теории
среднего поля.
Расчет фактора усиления. Теория, изложенная в [371], была
проверена в ряде работ [314, 369]. На основе предпосылок [371] можно
получать вполне реальные оценки оптических характеристик частиц
дымов, которые резко отличаются от свойств системы отдельных
малых частиц. Так, для малых частиц сажи вероятность
выживания фотона (альбедо однократного рассеяния Wa=as/ar где cs —
сечение рассеяния; Gt=Gs+Ga - полное сечение, равное сумме
сечений рассеяния и поглощения) WQ «0,01-5-0,03. Для кластера из
N- 500 частиц И^«0,01 и при JV —104 н-105 достигает значений
0,4-0,6 [314].
На рис. 6.40 приведены графические результаты расчета
фактора усиления Fs рассеяния фрактала относительно аналогичной по
числу частиц системы независимых частиц. Там же показано, что
оптические характеристики фрактальных кластеров значительно
зависят от р0 =2ка/Х для D = 1,1^-2,8 и от значений комплексных
коэффициентов преломления частиц п.
Расчет оптических характеристик. В [369] проведены расчеты
оптических характеристик частиц дымов. Использовалось модельное
значение коэффициента преломления п = 1,75 — /0,65 для видимой
области спектра. На рис. 6.41 представлены кривые коэффициентов
ослабления ае, поглощения ocfl, рассеяния ос5 и обратного
рассеяния ос^ агрегата с фрактальной структурой D - 1,78 (кривые 1 и 2) в
сравнении с соответствующими характеристиками системы мелких
невзаимодействующих частиц сажи (кривые 3 и 4). Число частиц
варьировало от N= 200, N = 500 ло N= 2000. Ясно видно резкое от-
403
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
4 5
а)
7\gN
0,01 0,020,03 0,05 0,10 0,20 0,30 Р0
б)
Рис. 6.40. Зависимость фактора усиления от логарифма числа частиц сажи
в кластере (а) и от значения р0 =2па/Х<к1 (б)
для фрактальной размерности D = 1,1-5-2,9 [314]
0,3 0,5 0,7 1
А,, мкм
0,3 0,5 0,7 1 0,3 0,5 0,7 1 0,3 0,5 0,7 1
а) б) в) г)
Рис. 6.41. Зависимости коэффициентов ослабления (я), поглощения (б),
рассеяния (в) и обратного рассеяния (г) от длины волны для модели частиц дыма
при N- 200 (штрихпунктирная линия), N= 500 (штриховая линия), N= 2000
(сплошная линия) для агрегатов с фрактальной структурой cD= 1,78
(кривые 1 и 2) и системы невзаимодействующих частиц (кривые 3 и 4) [369]
404
6.11. Многократное рассеяние волн фрактальными средами
личие кривых для фрактальных и обычных систем частиц. Для
кривых 1,3 а = 0,02 мкм, для кривых 2, 4 а = 0,01 мкм. Полученные в
[314, 369] результаты убедительно свидетельствуют о вполне
реалистичном описании результатов экспериментов с помощью теории
фракталов.
Теория [371] неявно предполагает сферическую симметрию
фрактальных кластеров, что часто не соответствует
действительности. Для учета пространственной анизотропии делаются попытки
описания в рамках теории мультифракталов [374]. В теории [371]
также не учтено взаимодействие частиц в кластере. Отметим, что при
D< 1,5 учет взаимного влияния частиц не приводит к
сколько-нибудь существенным поправкам, вплоть до N ~ 104 ч-105.
6.11. Многократное рассеяние волн
фрактальными средами
Фрактальная концепция. Теория многократного рассеяния волн
является интенсивно развивающейся областью радиофизики (см.,
например, [183, 274, 322]). Однако наряду с раскрытием
основополагающих физических принципов многие проблемы многократного
рассеяния волн во фрактальных средах все еще остаются и могут дать
нетрадиционные результаты [376-381]. Основы общей теории
многократного рассеяния электромагнитных волн во фрактальных
средах на основе модификации теории Фолди-Тверского в первом
приближении разработаны в [379]. Идея фрактальности, как известно,
основана на отсутствии характеристической длины. Фрактальная
размерность есть число, показывающее, насколько плотно данная
конфигурация занимает метрическое пространство, в котором
находится.
Рассмотрим фрактальную концепцию многократного рассеяния
[379]. Пусть фрактальный объект имеет размер /0. Из определения
фрактальной размерности следует, что при изменении масштаба от
/0 до /, где / < /0, получим N объектов, содержащих часть фрактала:
N = (l0/l)D, (6.258)
где D - фрактальная размерность.
405
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Из равенства (6.258) следует, что для топологической
размерности пространства D0
NlDo=(l0/l)DlDo. (6.259)
Тогда вероятность занятия фракталом пространства есть его
объем, отнесенный к общему объему /^°:
P(l) = {l/lo)D°~D, (6.260)
что совпадает с плотностью фрактального кластера (см. формулу
(1.13)).
Интегральные уравнения. Полагаем частоту волны высокой,
поэтому эффект поляризации будет пренебрежимо мал. Также
считаем, что корреляция фрактальных объектов может быть
проигнорирована. Примером такой среды является слой снега. Исследуем поле
Ча в точке а пространства. Обозначим через ср? падающую волну в
точке га в отсутствии частиц. Здесь верхний индекс обозначает
точку, в которой рассматривается поле, а нижний — происхождение
этого поля. Тогда поле Ч"7 в га представляет собой сумму падающей
волны ср? и вкладов от каждой из JV->w частиц, расположенных в
точках rs, s = 1,2,.... Когерентное поле < Ч!а >, на основе теории
Тверского [322] с учетом (6.260), записывается в виде
W = Ф? + J^№*i +\\PsPt<uHdrtdrs +
Л Л Л Л
где ^^/(0, i)exp(ikr)/r - оператор рассеяния; /(0, i)
-амплитуда рассеяния; r = \ra-rs\; 0 = (ra-rs)/\ra -rs\ - единичный вектор в
направлении ra -rs; k = ki; ps- функция плотности вероятности в
точке пространства s.
Интегральное уравнение Тверского для второго момента
многократно рассеянной волны имеет вид
(¥*¥*•) = (¥*)(¥*) +J (6.262)
406
6Л1. Многократное рассеяние волн фрактальными средами
где
vas=u°+ju?vlptdrr (6.263)
Когерентное поле. Рассмотрим проблему обратного рассеяния
волн. Для плоской волны единичной амплитуды ФДг) = ехр(/^),
падающей на фрактальный слой толщины d, из предыдущего анализа
(6.261) можно получить
(ВД) = exp(fe) +J*, J dxs) dysPsm ^^[^Г7Г^(У(г,))-(6.264)
О -ос -ос V rS\
Используя известную процедуру [322], можно показать, что среднее
поле {^(z)) соответствует волновому уравнению (у2 +К2)(}¥(г)) = 09
v . 2nf(i, i)
где К = k+— ps - постоянная распространения в слое,
/с
Заметим, что амплитуда /(/, /) —комплексная величина даже для
непоглощающих рассеивателей, поэтому в процессе
распространения когерентное поле (^(z)) ослабляется. Такое ослабление
обусловлено рассеянием и связано с сечением рассеяния. Для плоской
падающей волны во фрактальной среде когерентная интенсивность
Иг))|2=ехр -
4nps
zV (6.265)
Im/(i,i)
4тс л л
Согласно оптической теореме —Im/(i, i) = cs + afl, где os -ce-
AC
чение рассеяния; оа — сечение поглощения. Тогда равенство (6.265)
принимает вид
\(4>(z))\2 = ехр[-/>>5 + aa)z], 0<z<d.
Рассматривая область вне слоя z > d, имеем
(4(z)) = exp[iKd + ik(z-d)],
|(*fe)>f=exp[-^a, + afl)<],z>£/.
407
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Радиолокационный случай. Применим полученные результаты
для радиолокационного случая. На рис. 6.42 показана геометрия
задачи. Луч радиолокатора РЛС шириной ва направлен к зениту под
углом 6 от вертикали. Плоский рассеиватель находится в
вертикальной плоскости, проходящей через зенит и ось луча. Штриховыми
линиями показана область взаимодействия плоской фрактальной цели
с радиолокационным объемом в нормальной плоскости г. Только
точечные цели на расстоянии г в заштрихованной области дают вклад
в отраженный сигнал.
т Зенит
РЛС
Рис. 6.42. Геометрия задачи рассеяния для радиолокационного случая при
ширине диаграммы направленности антенны 6fl [379]
Введем эффективные сечения рассеяния Tls и поглощения Ъа,
поддающиеся измерению на практике:
*,=№*> *а=Р,°а- (6-266)
Мощность принимаемого сигнала определяется из уравнения
радиолокации
Р = ff * С 1 -ЯЩ-г2) ф. d
где Pt — мощность излучения. С использованием (6.266) имеем
408
6.11* Многократное рассеяние волн фрактальными средами
*,'i$l\-?Fzirm'i~* **г (6-267)
'1 '2 *s
Подставим в формулу (6.267) выражение (6.260) и получим
5 4тс2 »jr*
( , \D-Do
v°v
e-2ik(rrr2)d^df.^ =
•^kwi'Wi-ps
(i \D-D°
v'o,
e-2ik(rx-r2) ^
Здесь А — коэффициент пропорциональности. Величину /0 можно
рассматривать как размер фрактального объекта, а / - длину,
сравнимую с длиной волны. Для плоской цели D0 = 2 и /j « r2 « г, что дает
чл г, г2 ^<0 j
I1/2
где |р| = [г2 + ^ - 2г,г2 008(9, - 02)] « V^l-cos^-G^.
Следовательно, мощность принятого сигнала
е01 е02
r+Ar/2 r+Ar/2~{D-2)/2rD-2 „.,, ч ЛР Y 2(В~2^2
х [ dr [ c-llk{r'-r^dr - tZ*s // (6 268)
Х J аГ\ J -2/D-2 ^ ai2 An2[D-2r4r-D Vr> VO.^DO;
г-Дг/2 r-Ar/2 Г l0 ЧП f0 Г
0П1 6fi
где
01 02
/e= J dQx J [l-cos(01-e2)](/)"2)/2t/e2,
e01 e02
r+Ar/2 r+Ar/2
r-Ar/2 r-Ar/2
r+Ar/2 r+Ar/2 „:~2/bA-\
409
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Из (6.268) следует, что принимаемая мощность
Ps~l/r4-D. (6.269)
Данный результат хорошо согласуется с результатом
моделирования, графически показанном прямой линией на рис. 6.43, где
Ps = r"P. Там же приведены экстремальные случаи, соответствующие
точечной (D = 0) и объемной (D = 3) целям. Аналогично из
выражения (6.268) для объемно-распределенной цели сД0 = 3 можно
получить
Ps~l/r5~D. (6.270)
О 1 2 3D
Рис. 6.43. Рассчитанные зависимости спектрального параметра р от фрактальной
размерности в соотношении Ps = г~р: объемная и точечная цели (соответственно
точки 1 и 2); численный эксперимент по 20 реализациям (точки 3-7);
аппроксимация для малых квадратных целей (пунктирная линия), кубический сплайн,
построенный по семи точкам (сплошная линия) [377]
Полученный результат совпадает с криволинейной частью
графика на рис. 6.43 (сплайн из семи точек). Следовательно, исследуя
мощность принятого сигнала, можно определить фрактальную
размерность D изучаемой среды (слой снега и т.п.).
Эксперименты. В работе [380] экспериментально исследовалось
прохождение оптического излучения сквозь фрактальные гели,
являющиеся дисперсными системами с жидкой или газообразной сре-
410
б.//. Многократное рассеяние волн фрактальными средами
дой. Кинетика образования частиц геля может быть описана с
помощью механизма агрегации кластеров (см. разд. 5.4). Зарождение
кластеров происходит при склейке мономеров. Во фрактальной
среде плотность кластера в диапазоне масштабов Rq- R описывается
выражением (1.13) и убывает с ростом его размеров: рк =(R/RQ)D~3.
Среднее число мономеров в кластере N = (R/R^)3.
При монодисперсном распределении размеров кластера
отношение между средним размером кластера R в конечном геле и
начальной плотностью р0 мономеров в конгломерате
Л/До=рГ~3)- (6-271)
К сожалению, адекватного описания распределения размеров
кластера не существует. Однако доказано, что наиболее
реалистичное распределение размеров кластера n(R)~ R~zexp(-R/Rmsx) (где т-
константа, зависящая от состояния конгломерата) приводит к
аналогичной зависимости для монодисперсного случая.
Гель выгладит однородным в масштабах, больших R или
меньших Rq. В промежуточном интервале R$- R фрактальная структура
геля может быть исследована экспериментально. В [380] показано,
что для фрактальных гелей с большими частицами (а/Х>1)
фрактальное поведение все еще проявляется в характеристиках
распространения когерентной волны. Интуитивно ясно, что при D < 2
кластеры частично прозрачны и к ним применимо приближение
однократного рассеяния. При фрактальной размерности D > 2 необходимо
принимать во внимание эффекты многократного рассеяния.
В итоге выражение для коэффициента рассеяния фрактального
геля [380] с учетом соотношения (6.271) имеет вид
(6.272)
Экспериментальная проверка соотношения (6.272) проводилась
в различных гелях, полученных окислением раствора молока. В
лабораторном стенде использовался гелий-неоновый лазер с длиной
волны X = 0,63 мкм. Коэффициент пропускания Тъ геле определялся
нормировкой интенсивности прошедшего света на значение,
полученное при прохождении кюветы, заполненной водой. На рис. 6.44
411
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Рис. 6.44. Логарифмическая зависимость коэффициента пропускания Г лазерного
пучка с длиной волны X = 0,63 мкм от толщины ячейки U с гелем (1) и
раствором снятого молока (2) [380]
показана зависимость log Гкак функция толщины ячейки V с
фрактальным гелем и раствором снятого молока в воде при
концентрации с = 16 г/л.
Типичная зависимость рассеянной интенсивности I{q) от вектора
рассеяния q = (2n/X)sin(Q/2) для геля с концентрацией с = 32 г/л
приведена на рис. 6.45. На вставке показаны экспериментальные
значения фрактальной размерности D при разных концентрациях с гелей.
Значение D не имеет систематической зависимости от значения кон-
ад и
т—I—I I I I I \
Е 1,5
<D>=2,18±0,12 |
■ I i i * i i
10
20 30 40 с, г/л
i i i i i i i I
10z
10'
q, мм
Рис. 6.45. Зависимость интенсивности рассеяния I(q) от вектора рассеяния q для
геля с концентрацией 32 г/л при X = 0,63 мкм и экспериментальные значения D
при разных концентрациях гелей [380]
412
6.11. Многократное рассеяние волн фрактальными средами
центрации. Среднее значение D = 2,18 ±0,12. Данные измерений
показали возможность определения размеров эквивалентных частиц
не менее 0,8 мкм с коэффициентом преломления 1,45 с учетом того,
что физические рассеиватели в молочных растворах имеют
характерные размеры 0,05—0,3 мкм.
Длина рассеяния ls = (рс^)-1 как функция концентрации для геля
и раствора молока показана на рис. 6.46. Здесь р - плотность
частиц, os - сечение рассеяния частиц. На рис. 6.46 также указаны
соответствующие значения коэффициентов А = (D - З)"1 для
соотношений (6.272). Изложенная методика измерений дает хорошие
результаты, вплоть до значений с « 30 г/л. Если считать плотность массы
равной 0,3 г/см3, то значение ограничения, соответствующего объему
фракции, составляет около 10%. Эта относительно высокая плотность
рассеивателей получена в предположении, что эквивалентный
размер рассеивателей, как отмечено ранее, действительно больше
длины волны излучения.
Г^
г
h
1 1 1 11
1
1 1 1 1
\
А=-1
III!
ттгс—
■ч
\
Y
\
jlU
1
V-
ч
2^
i
Т III»
-1,34
ь ■
■V1
\ N
1 1 Ni I
1 ■ 1
•j
\
j
\
\ Л
-LkJ
10 102
Рис. 6.46. Длина рассеяния ls=(pGs)~l для Х= 0,63 мкм как функция
концентрации для геля (1) и раствора молока (2) при соответствующих коэффициентах
A = (i)-3)-1 [380J
Экспериментальные данные рис. 6.46 согласуются с
зависимостью ls ~ с-1»34, из которой получено значение D = 2,25.
Следовательно, эксперименты по рассеянию (см. рис. 6.45) и прохождению
света через гели (см. рис. 6.44) имеют хорошее соответствие. Многие ис-
413
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
следователи используют молочные растворы для моделирования
биологических тканей [381]. В этом отношении результаты [380]
многообещающи ддя проникновения в суть феномена, происходящего
в таких средах.
Многократное рассеяние субфрактальной поверхностью. Метод
нахождения функций рассеяния субфрактальных поверхностей,
предложенный в [206, 207], также допускает учет многократного
рассеяния. Рассмотрим кратко результаты [207] по многократному
рассеянию света субфрактальной структурой, изображенной на рис. 4.12,6
(см. разд. 4.5).
Пусть функция рассеяния F зависит от величины альбедо
однократного рассеяния со, т.е. F = Fm; тогда уравнение (4.97)
перепишем в виде
2М^-(5ц+1,а,х)(1 + 2со8в) = 2М^(ац,а,Х) +
+МФ(оц,а,х + в) + МФ(ац,а,х - в).
(6.273)
Здесь функция Ф учитывает многократное рассеяние внутри
отраженной поверхности. В [207] показано, что члены высоких
порядков рассеяния функционального уравнения для Ф быстро убывают
с ростом коэффициента (сов2 /2)Л, где п - порядок итерации.
Нелинейное интегральное уравнение для Fm с учетом условий
формулы (4.98) примет вид
exp
( с1-к ^
*»+f Jexp
ci-\
х<р_(т)Л
KOS
a
X-j
(6.274)
я/2
где <pm(t, a) = —— J (p(T,ocz)cos
a-7c/2
a
X-2
<*X-
Коэффициенты Ст и уравнения, определяющие Е^(а),
приведены в гл. 4. Полученное уравнение (6.274) решается методом
итераций, если значения альбедо со достаточно мало.
414
6.11. Многократное рассеяние волн фрактальными средами
На рис. 6.47 приведены результаты расчета вклада
многократного рассеяния в фотометрическую функцию субфрактала (см.
рис. 4.12, б) при использовании в качестве начальных условий
закона Ламберта и зеркального рассеяния (% = ос/2). Зависимости
нормированы на единицу при а = 0.
F
1
0,8
0,6
0,4
0,2
30 60 90 120 150 ав
Рис. 6.47. Вклад многократного рассеяния в фотометрическую функцию пред-
фрактала при альбедо ю= 0,2 и ю= 0 [207]
Как следует из полученных данных, влияние многократного
рассеяния сводится к уменьшению крутизны функции обратного
рассеяния из-за увеличения вклада многократного рассеяния на
больших углах а.
Краткий обзор. В работе [382] представлены результаты расчета
эффективных сечений поглощения электромагнитных волн
кластерами сфер, к которым относятся и капли облаков с малыми
углеродными гранулами. Рассмотрены и оценены взаимосвязи ориентации
сложных частиц с типом поляризации облучающего
электромагнитного поля.
Масштабно-инвариантная Теория оптических спектров
фрактальных кластеров вблизи центра полосы поглощения развита в [383].
Показано, что частотная зависимость отклика частицы в кластере
резко отличается от резонансной кривой отдельной частицы.
Поглощение падающей волны имеет большое значение и вдали от
резонанса, где оно медленно спадает по степенному закону с ростом рас-
415
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
стройки частоты. Установлено повышение локальных флуктуации
поля, приводящее к существенному увеличению нелинейных
эффектов.
В работе [375] с применением диаграммной техники [384]
рассмотрено многократное рассеяние света фрактальным кластером из
металлических частиц с дипольным поверхностным резонансом.
Показано, что фрактальная размерность D = 3/2 является
критической. При D > 3/2 мономеры кластера рассеивают свет
некогерентно. При D < 3/2 наблюдалось значительное увеличение сечения
рассеяния, связанное с появлением дальнодействующих корреляций в
расположении частиц фрактального кластера.
6.12. Теории катастроф и фракталов
в случайных волновых полях
Активно развивающиеся прикладные математические теории —
теория катастроф [23,385-391] и теория фракталов - становятся
полезным и эффективным средством аналитического рассмотрения
различных процессов. Предмет теории катастроф - изучение
зависимости качественной природы решений интегро-дифференциаль-
ных уравнений от значений параметров, присутствующих в
заданных уравнениях. Теория фракталов, как следует из данной
монографии, основана на свойствах масштабной инвариантности
(склейлинга) и дробной размерности.
Лучи и каустики. В самом общем случае распространяющиеся
волны случайны и описываются волновыми функциями *р и интен-
сивностями /. Стохастичность волновой функции *р не связана
простым образом со случайной средой распространения или экраном S.
Наиболее содержательными являются моменты интенсивности
In = (ln) = (l^l2"), где угловыми скобками обозначено усреднение по
ансамблю S. Рассмотрим, основываясь на результатах работы [388],
два случайных волновых режима, где взаимодействие Ч* и £не
может быть описано теорией возмущений. Эти режимы различаются
отсутствием или наличием в функции ^характерного масштаба,
близкого к длине волны X. При отсутствии такой характеристики, т.е.
при гладкой функции S на масштабе длины волны, применимо
решение, основанное на методе геометрической оптики [392]. При этом
возникают каустики (огибающие семейства лучей). Непосредственно
416
6.12. Теории катастроф и фракталов в случайных волновых полях
на каустиках (в рамках лучевой теории) поля сингулярны из-за
обращения в нуль сечений лучевых трубок; в этом случае говорят о
каустических фокусировках. На каустиках интенсивность /
возрастает до больших значений. В общем случае роль теории катастроф
состоит в том, что она дает полезную классификацию всех каустик,
принадлежащих к классу топологических структурно-устойчивых
особенностей.
На масштабах длины волны каустики как бы украшаются
характеристиками дифракционных катастроф, т.е. их топологическими
особенностями. Если среда распространения £ обладает
характеристиками в широком диапазоне масштабов, включая длину волны X,
то метод геометрической оптики неприменим. Вместо этого £
можно смоделировать с помощью фракталов, т.е. с помощью
иерархической структуры при дробной фрактальной размерности. В этом
режиме возникают «дифракталы» [188]. Математически это может
оказаться полезным для понимания разницы между двумя режимами в
коротковолновом пределе X -> 0. Если S - гладкая функция на
конечных масштабах, то геометрическая оптика применима для X -> 0.
Но если S- фрактал, то по мере уменьшения X предел
геометрической оптики не будет достигнут.
На языке теории катастроф лучи и каустики существуют в
контрольном пространстве С. Его величина многоразмерна, и ей
соответствует не только пространственно-временное положение точки
наблюдения (г, f), но и случайная переменная v, определяющая
элемент ансамбля S. Поэтому для волны 4{r,t, v) усреднение дает
In=j^dvP(vp(r,t,v)\2n, (6.275)
где Р(у) - плотность реализаций в ансамбле S; г и t -
фиксированные значения.
Пусть X = 0. Тогда /л -> °° на каустиках, что следует из закона
сохранения энергии. Первый момент 1{ = </> при этом существует,
но более высокие степени 1п будут расходиться. При конечной X
вводятся критические показатели, определяемые в виде
*-=й|Щ' '•-*"• (6276>
и показывающие, как расходятся 1п при X > 0.
14 Фракталы
417
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Для малых длин волн интеграл (6.275) определяется теми
значениями v, которые находятся на каустиках. При этом интеграл
можно разбить на составляющие 1п (/) для различных катастроф,
определяемых/ Тогда
/ЛС/)~Ь"Ч (6.277)
где v — показатель, устанавливающий вклад у-й катастрофы в л-й
момент. Значение Улу определяется некоторым коэффициентом
сингулярности р. в виде
Щ~Х~*', (6.278)
где р . — мера мощности дифракционной катастрофы.
Также существует мера у., показывающая, как волновая
функция |*Р| расходится при X -> 0:
VT~XyJ. (6.279)
Здесь VT — гиперобъем максимума дифракционной катастрофы в
контролируемом пространстве.
Коэффициенты у. и р. определяются из дифракционного
интеграла для *Р приу-й катастрофе. В [388] общая процедура расчета
иллюстрируется на примере.складки, когда *Р — функция Эйри:
XF(V) = 1_ J dSexp[2Ki(S3/3 + vS)/X]. (6.280)
Выражение в скобках есть стандартная функция потенциала для
этой складки. Величина S- переменная форма, которая обычно
характеризует расположение некоторого начального фронта, от
которого волна дифрагирует в направлении {г, t}. При замене
переменной из (6.280) получаем
^)=ш i dS'expY
уз
3
• + v
г2то2/зс;
vb
(6.281)
а в терминах интегрального представления функции Эйри
V(v') = ^-]dS'exp
2я
( «Г'З ^"
вЛОО.
418
6Л2. Теории катастроф и фракталов в случайных волновых полях
Значение модуля |*Р| растет как 0(Аг1/6) на самой каустике
(v = 0), и ширина первой полосы есть 0(Х2/3). Поэтому р = 1/6 и
Y = 2/3 для складки дифракционной катастрофы.
Зная р. и у., можно определить соответствующий вклад /^ в
интеграл (6.275) в виде
jW~X-2n*JXyJ, (6.283)
где yj=2n$j-vnj.
Каждая катастрофа вносит свой вклад в каждый момент
интенсивности. Суммирование вкладов для л-го момента дает 1п -> ^СпХ~*4
J
при X -> 0. Критический показатель
уя=тах(уяу). (6.284)
В работе [388] показано, что суммарный набор v . зависит
только от размерности D0 топологического пространства, в котором
распространяется *Р . Число существенных для задачи внешних
параметров называется коразмерностью каустик. Коразмерность не
может превышать DQ — 1. В табл. 6.1 приведены типичные элементарные
катастрофы по классификации Тома—Арнольда.
Таблица 6.1
Элементарные катастрофы
Классификация по Тому
Складка
Сборка
Ласточкин хвост
Бабочка
Вигвам
Гребень волны (гиперболический омбилик)
Волосок (эллиптический омбилик)
Гриб (параболический омбилик)
Второй гиперболический омбилик
Второй эллиптический омбилик
Символический омбилик
Классификация
по Арнольду
А
4
А
4
А
Щ
Ъ
А
Щ
щ
*6
Коразмерность!
1
2
3
4
5
3
3
4
5
5
5
419
Глава б. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
Критические показатели и вклады, вносимые катастрофами
(2 < п < 5), приведены в табл. 6.2 для DQ = 2 и D0 = 3. Значение v2 = О
означает, что второй момент 12 не имеет особенностей при X -> 0.
Реально In~log(X-{).
Таблица 6.2
Критические показатели v„ [388]
Показатель
1 v2 (два пространственных размера)
Доминантная катастрофа
v3 (три пространственных размера)
Доминантная катастрофа
л
2
0
0
3
1/3
А
1/3
4 й Л
4
3/4
4
1
Д4
5
5/4
4
5/3
Новые режимы в волновой физике. Если структура S является
фракталом, то *Р есть дифрактал [188,388]. В [188] решается
простейшая дифрактальная задача (см. разд. 4.1), устанавливающая новые
режимы в волновой физике. Начальный волновой фронт задан
фрактальной кривой z = h(x) с граничным условием ^(х, 0) = exp [-2nih(x) / X].
Нахождение флуктуации интенсивности возможно при точном
определении А(х), которая описывается гауссовой кривой со
среднеквадратичным приращением h относительно X:
{{[h(x+X)-h(x)f )}1/2 = lP-t\X\2-D. (6.285)
Расстояние L - топотеза волнового фронта (см. разд. 3.1),
определяющая меру его деформации. Моменты интенсивности 1п
зависят от фрактальной размерности D и параметра £ (см. формулу
(4.14)), объединяющего z, L, X в виде
С = [TZ )[TL) /21/(4-2Z)). (6.286)
Даже для простых задач очень трудно рассчитать высокие
моменты интенсивности. Двойной интеграл для 12 изучался ранее [393]
420
6.12. Теории катастроф и фракталов в случайных волновых полях
1+0(0
2-0(0
1,5</К2
а)
'2|
2
1
• /^
1 1+0(0
2+0(С"2(У>,))
1</К1,5
б)
2+0(l/lnQ
е)
г)
Рис. 6.48. Развитие флуктуации интенсивности 12 как функции расстояния
для трех дифракталов (а-в) и одной волны при развитии
от гладкого начального фронта (г) [388]
421
Глава 6. РАСПРОСТРАНЕНИЕ ВОЛН ВО ФРАКТАЛЬНЫХ СРЕДАХ
в связи с распространением лазерного излучения в атмосфере.
Развитие флуктуации интенсивности 12 как функции расстояния для
трех дифракталов и для одной волны, развивающейся от
начального гладкого волнового фронта, показано на рис. 6.48. Для всех
кривых 12 (0) = 1 и 12 (оо) = 2. Для промежуточных £ максимум 12> 2
может быть или не быть. Для 12 при D > 1,5 максимума не существует.
При 1 < D< 1,5 есть слабый максимум в 1п (£). Это служит
предвестником очень сильного пика I2 -logХ-1, проявляющегося, когда
первоначальный волновой фронт развивается от дифракционных
катастроф. Кривая на рис. 6.48, г иллюстрирует негауссовский второй
момент интенсивности. Фрактальный и обычный режимы
разделяет маргинальный случай, когда D -> 1 (рис. 6.48, в).
Рассмотренные асимптотики получены из разложения
степенных функций, не имеющих аналогов в волновой теории [188].
Таким образом, топологические концепции катастроф и фракталов
можно плодотворно применять в волновой физике. Это особенно
важно в статистических задачах, где усреднение по ансамблю
различных реализаций динамических систем означает, что их свойства
будут преобладать над теми гомеоморфизмами [395], которые
структурно стабильны.
В обоих случаях теорий катастроф и фракталов форма
интенсивности распределения вероятности является неизвестной и заведомо
негауссовой. Имеется лишь некоторая информация о моментах 1п. Для
катастроф, когда волны падают на гладкие случайные формы S,
флуктуации интенсивности 1п подчиняются универсальному закону
масштабирования (6.276) при X -> 0. Для дифрактальной ситуации
все рассмотренные случаи пока не дают никакой информации о
моментах I v Также известно не очень много о волнах в пределах
фрактала, хотя некоторые выводы о распределении мод во
фрактальных резонаторах представлены в [394].
Глава 7
ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ
СИСТЕМ И КОММУНИКАЦИЙ
7.1. Фрактальный анализ сложных компьютерных систем
Пространственная организация. При конструировании реальных
компьютерных и радиотехнических сложных систем, пока сложность
соединений в них невелика, используют три пространственных
измерения. В сложных компьютерных системах, как отмечено в [396—
398], начинают доминировать более универсальные процессы
конструирования с другими значениями размерности. При росте
количества соединений, параметры, характеризующие их сложность,
становятся основными для конструирования систем.
Первая попытка охарактеризовать крупномасштабные схемные
свойства компьютеров, была предпринята в [399]. Используемое
приближение базировалось на понятии произведения Лагранжа. Эта
работа была позднее продолжена с использованием принципа
максимума энтропии для получения распределений, которые близки к
наблюдаемым в физике электронов в полупроводниках (см. ссылку
[4] в [398]). Концепция компьютерной схемы, как некоторого «газа
соединений», основана на алгоритме, предложенном в [400]. Данный
алгоритм может широко использовать метод Монте-Карло для
максимизации энтропии соединений.
В дальнейшем были опубликованы наблюдения масштабного
поведения широкого множества коммерческих процессорных
систем. Эти данные показывают наличие степенной зависимости [402,
403] вида
Т = АКР. (7.1)
Здесь Т— число контактов или выводов микросхем; К— число
процессорных элементов; р — степенной показатель 0 < р < 1; А —
среднее число контактов в несложном процессорном элементе,
состоящем из 2-5 логических устройств [404]. Типичные зависимости числа
контактов от числа процессорных элементов для различных компь-
423
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
ютеров и микропроцессоров даны на рис. 7.1; расшифровка
символических обозначений рис. 7.1 приведена в табл. 7.1. Характерные
значения степенного показателя р и фрактальной размерности
соединений D для некоторых систем приведены в табл. 7.2.
Рис. 7.1. Типичные зависимости числа контактов Гот числа ^процессорных
элементов для различных цифровых систем [398]
Простая декомпозиционная модель [404, 405] предложена для
исследования внутренней структуры большой системы, состоящей
из С процессорных элементов. В данном случае допускаем, что
процессорный элемент выполняет примитивные функции. Соединения
между крупными процессорными блоками системы считаем
расположенными на нулевом уровне т = 0. Рекурсивное деление
системы на все меньшие и меньшие процессорные элементы создает
самоподобную иерархическую структуру. Данный процесс продолжим
до тех пор, пока не будет достигнут мельчайший уровень т = п.
Примером мельчайшего уровня могут служить проводящие
дорожки между отдельными транзисторами в микросхеме. Точная форма,
по которой проводится деление, не критична для расчета
фрактальной размерности.
Будем считать, что система рекурсивно подразделяется на четыре
уровня, как показано на рис. 7.2. Следовательно, она состоит из
С = 4Л элементов. На т-м иерархическом уровне, появляющемся
424
7.1. Фрактальный анализ сложных компьютерных систем
Расшифровка позиций на рис. 7.1 [398]
Таблица 7.1
[Позиция
ф
1-0-1
|-Ф-|
<8>
А
•
*
0
0
1 9
•
о
Наименование |
Компьютер с
высокими
эксплуатационными
данными:
IBM ECL date array
IBM 3081 TCM
IBM 3081 board
NEC SX
Логические элементы:
LSI Logic CMOS
Toshiba CMOS
Fujitsu CMOS
Hitachi CMOS
NTT ECL
Siemens ECL
Интегральные схемы
запоминающих
устройств:
Static RAM
Dynamic RAM J
Позиция
*
0
V
•
•
<l
*
О
V
X
о
0
<=>
><
1 V
Наименование |
Микропроцессоры:
Intel 8008 1
Intel 8080, 8085, 8086
Intel iAPX-43xxx
Intel 80286
Intel 80386
Motorola 6800
Motorola 68000
Motorola 68020
Zilog Z8000
Fairchild Clipper
цУАХ 32720
Bellmac - 32A
HP 32bit CPU
Stanford MIPS
Berkley RISCI
Таблица 7.2
Значения степенного показателя и фрактальной размерности соединений
для некоторых систем [398]
Тип системы
Статистическое ЗУ
Микропроцессор
Логические элементы
Быстродействующий компьютер
Р
0,12
0,45
0,50
0,63
■ А .
2,76
2,10
2,00
1,74 J
425
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
после т делений начальной системы, будем иметь подсистему с
g _ ^п-т процессорными элементами. Полное число контактов на
этом уровне
Тт=±(АКР) = АСК-«-Р\
К
(7.2)
где С/К- число блоков в системе размером К.
■1в|а|а|а|а|в|
□□□□□□
DDDDDD
пппппп
□□DQDD
ODDODD
ODDODD
Рис. 7.2. Квадратичная сегментная модель системы [398]
В общем случае число соединений в полученной системе
меньше числа контактов, так как любое соединение предполагает два или
более контактов. Тогда число соединений
Г=аТ=аАСК-«-Р\
m ш
(7.3)
Далее полагаем а«1/2. Это хорошее приближение для
большинства традиционных компьютерных схем. Для более высокого
уровня архитектуры (нейронные сети) ос* 1/2, но все равно ос не
зависит от р. Некоторые из / соединений будут проходить между С/К
блоками и будут находиться только на гп-и уровне. Другие
соединения будут проходить в более высокие уровни и должны быть изъяты
из общего числа. Общее число соединений, приходящихся на m-й
уровень, равно [398]:
М(т) = 1т-1т_1=М04т«-Р\ 1<т<п,
(7.4)
426
7.1. Фрактальный анализ сложных компьютерных систем
где М0 = аАСр[\-4-^-^ - среднее число соединений,
используемых для связи вне системы.
Ясно, что внутренняя структура, генерируемая таким процессом,
будет очень разветвленной. Различные уровни иерархии будут
содержать различное число соединений, каждое со своими диапазонами
длин, толщин и т.д. Однако проблема может возникнуть при
подсчете соединений на подложке, размерность которой не
обязательно соответствует двумерной поверхности.
Фрактальность подложки. При измерении размерности
покрытием «кубиков» размером е их число для евклидовой размерности
равно N(t) ~ lim г~Е, где е = 2~п /L; L - линейный размер системы.
Если Nm(e) — число кубиков со стороной е, необходимое для
покрытия одного соединения на т-м уровне, то общее их число для
всей системы
N(E) = %M(m)Nm(e), (7.5)
т=\
где сумма берется по всем иерархическим уровням.
Данное соотношение (7.5) предполагает, что большинство
соединений имеют длины, близкие к известному значению /. Формула (7.5)
также может быть развита применением понятия самоподобия [406].
Число кубиков, необходимых для покрытия соединений на m-м
уровне должно быть равно числу кубиков, покрывающих внутреннюю
подсистему, если более крупные кубики масштабированы с
фактором гт = 2~т . Следовательно, Nm{z) = N(e/rm), и при суммировании
из (7.5) получаем
Щг)=^М04>»«-Р)Щг/гт). (7.6)
Далее полагаем [398]:
e-A^^4-(^)(e/rm)-A. (7.7)
т=1
427
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
Соотношение (7.7) можно записать в эквивалентном виде как
1~12-(2-ад^, (7.8)
/и=1
а так как гт = 2~т , уравнение для Dt будет иметь вид
1~Х2"т(Л+2/"2)- (7.9)
Полученное уравнение (7.9) имеет решение, так как из условия
п
п->оо следует, что ^2_/и=1. Тогда
/и=1
D7. + 2/?-2 = l (7.10)
и окончательно
Ц=3-2р. (7.11)
Интепретация фрактальных размерностей. Размерность Dt
подложки соединений варьируется от D/min = 1 (р = 1) до Dinm = 3 (р = 0).
Характерные данные для Dt приведены в табл. 7.2. Проанализируем
распределения длин соединений. Природа фрактального анализа
диктует справедливость полученных соотношений для больших
систем п -> оо. Поэтому необходим переход к индексу т так, чтобы не
было зависимости от размеров системы. Определим глубину
иерархии, как
х = т/п. (7.12)
В пределе и -> °°, поэтому глубину иерархии х можно считать
конечной величиной 0< х< 1. Тогда с учетом (7.4) число соединений
на иерархическом уровне от х до х + dx равно
M(x)dx^M04nx^-P^dx, 0<х<1. (7.13)
Так как выполняется (7.11), то имеем
M{x)dx~2^Dr^dx. (7.14)
428
7.1. Фрактальный анализ сложных компьютерных систем
Длину соединений обозначим через / (х). Величина / (х) зависит
от глубины иерархии х, так как уменьшается длина соединений при
движении в иерархической структуре к уровню, где расположены
транзисторы. В большой системе пределом / (х) можно считать
наиболее вероятную длину в иерархической структуре, а так как
используется квадратная модель соединения, то средняя длина соединений
будет уменьшаться в 2 раза при каждом делении. Следовательно, / (х)
можно записать как
/(хЬг-1*, (7.15)
где / (х) измеряется в единицах наименьшей дистанции между
соседними элементами на/п = « иерархическом уровне.
На основе соотношения (7.14) с учетом dx~-dl//, получаем
число связей с длиной между / и / + dl в виде
M(l)dl~rDidl, 1<1<L, (7.16)
где L — линейные размеры системы.
Уравнение (7.16) дает строгие ограничения на диапазон
размерностей. Следуя аргументам, приведенным в [407], можно положить,
что каждый проводник имеет толщину d0, независимую от его
длины. По определению каждый процессорный элемент занимает
площадь^, пропорциональную схемной матрице. Обозначим через р (/)
вероятность того, что проводник длиной от /до /+ dl связан с
определенным процессорным элементом. Тогда
AQ=]d0lp(l)dl. (7.17)
1
Таккак Q~/ и М(1)~1~2:
M(l)dl = Qp(l)dl, (7.18)
можно отметить, что общее число проводников увеличивается как
логарифм длины. Для любых функций, которые не убывают со
скоростью / ~2 система оказывается быстро заполненной проводниками.
Поэтому размерность соединений должна быть выше евклидовой
429
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
размерности, иначе говоря, любая система, сконструированная до
более высокого уровня сложности (увеличение п), должна
характеризоваться степенным показателем р > 1/2. Эти наблюдения
сообразуются с исследованиями связи между сложностью системы и
исполнением ее, так как высокое исполнение характеризуется более
высоким значением р (см. табл. 7.2).
На рис. 7.3 показаны измеренные распределения длины
соединений для двух коммерческих процессорных систем А и В со
статистическими параметрами, приведенными в табл. 7.3; N - общее
число соединений в системе; L - «ширина» системы в единицах
измерения через число схемных матриц (Ср); /0 - общая длина
проводников в единицах (С_). Множество А было получено при анализе
схем компьютеров, множество В — при анализе схем
микрокалькуляторов. Экспериментальные данные обозначены на рис. 7.3
точками. Коэффициент пропорциональности, который подразумевается
в (7.16), здесь определен в предположении, что площадь кривой
пропорциональна общей длине всех соединений /0, присущих данной
системе.
10"
105
102
10'
10°
Щ1)
к.
"
:
**
Л»^
1*4^
l^N»
^ж4^
\v
V |
•
о •
В ;о
о* о
А
11
I
1 *
1
1 I
о ', Iя1"
1 1 1 1 1 f I I 1| « 1« 1 t , ,^ми 1 L.
н
—гттттт
-j
•1
-^
J
q
J
1
•1
3
J
J
J
1 A„ I,. 1
101
102
/, с
Рис. 7.3. Зависимость общего числа соединений М от длины проводников /для
систем А (компьютер) и В (микрокалькулятор) [398]
430
7.1. Фрактальный анализ сложных компьютерных систем
Таблица 7.3
Суммарные статистические параметры для систем А и В [408]
Система
А
' в
N
7301
1046
L
48
24
/о
25 699
2309
D
1,5
1,82
Спектр размерности. Рассчитаем собственную фрактальную
размерность D{x) соединений в каждом иерархическом слое [398]. На
уровне х число соединений подсчитывается из уравнения (7.14):
Щх)-**-1»" (7.19)
с длиной каждого соединения
/(х)-2-« (7.20)
Если число кубиков е - 2~п /L, то для покрытия одного
соединения в слое необходимо
N^d-Kx)/*-!-**-» (7.21)
кубиков. В общем случае для покрытия всех соединений слоя
необходимо Щг) кубиков:
Щг) ~ M(x)Nx(e) ~ г-*2-2**-1!. (7.22)
С учетом £~2_л уравнение (7.22) имеет вид
N(e)~e-[H2-Di)x]. (7.23)
Сравнив (7.23) с соотношением N(E)~lime~E, можно записать
выражение для фрактальной размерности на иерархическом уровне
х в следующем виде:
Дх) = 1-(2-/)/)х (7.24)
Из уравнения (7.24) следует, что размерность подложки Di
(1 < Dt < 3) порождает конечный спектр размерности Дх) с уровнем
431
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
иерархии х. Функция (7.24) для нескольких значений Di показана на
рис. 7.4. Так как 0<х<1, то размерность D{x) лежит в пределах
О < D{x) < 2. Хотя каждый из слоев должен иметь размерность ниже,
чем 2, суперпозиция данных слоев может привести к размерности 3
при п -> оо. Поэтому процесс разделения двухмерной поверхности
(см. рис. 7.2) приводит к тому, что результирующая структура
соединений может иметь Df<E = 3. В данном случае следует говорить о
мультифрактальных мерах.
О 0,1 0,2 0,3 0,4 0.5 0,6 0,7 0,8 0,9 1
х
Рис. 7.4. Спектр размерности Дх) на иерархическом уровне х
для нескольких значений Df [398]
Таким образом, в [398] показано существование фрактальной
размерности, которая характеризует подложку соединений как
последовательный самоподобный процесс. Полученные результаты
можно интерпретировать в терминах термодинамической
температуры Т [406], которая характеризует распределение соединений
среди разных уровней, т.е. Т =l/Dn и следует из сравнения методов
фрактальной теории и ренормализационных групп [409, 410]. На
основе таких обобщений можно показать [398], что сложные
системы, у которых размерность соединений стремится к евклидовой
размерности, имеют минимальную общую длину соединений.
432
7.2. Метод фрактальных графов в синтезе сложных систем
1.1. Метод фрактальных графов
в синтезе сложных систем
Фрактально-графовые сети. Существующие тенденции развития
современных связных и распределенных вычислительных систем
говорят о необходимости разработки эффективных методов
моделирования и оптимизации сетей больших размеров. Та же тенденция
отмечается и в таких областях, как проектирование СБИС,
биологические нейронные сети, транспортные системы. Большими
считаются такие сети, которые содержат не менее 105 или 106
стягивающих деревьев.
Для разработки систематизированной основы синтеза больших
сетей формируется набор канонических фрактально-графовых
систем [411]. Функцию плотности узлов р(г) можно рассматривать как
число узлов на единицу объема в соответствующей топологической
размерности и представить в виде p(r) ~ rD~DQ, где D0 - обычная
топологическая размерность.
Такой подход позволяет говорить о фрактальном кластере, так
как число узлов монотонно спадает в направлении от некоторой
центральной точки (см. разд. 1.1). Этот подход соответствует
эмпирическому закону Зипфа о распределении населения вокруг
городских центров. Канонические 200-узловые фрактальные структуры,
пригодные для больших сетей, показаны на рис. 7.5. В данном
случае они соответствуют 10455 стягивающим деревьям в полном
помеченном графе. Ради удобства на верхних рисунках взят масштаб 6:1,
что отмечено радиальными расстояниями г. Узлы планарных (D0 = 2)
графов распределены случайным образом по соответствующей
функции плотности. Ветви соединяются по правилу ближайшего
соседа, исходя из начальной точки, и дают структуры, представляющие
собой минимальные стягивающие деревья.
Фрактально-графовые сети выявляют несколько значительных
фрактальных характеристик. Во-первых, каждый граф в верхней
части рис. 7.5 имеет монотонно убывающую по мере удаления от
начальной точки плотность узлов, так как топологическая
размерность D0 = 2 больше фрактальной размерности 1,1< D< 1,9.
Во-вторых, по мере приближения фрактальной размерности к D0 = 2 узлы
сети будут равномерно покрывать круг заданного радиуса, а за
пределами этого радиуса не окажется ни одного узла.
433
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
0=u
-150
-75
0 75
D-1.9
150 -25 -15
15 25
Рис. 7.5. Канонические 200-узловые фрактальные структуры с/)=1,1и/)=1,9и
добавочные реализации таких структур при D = 1,5 [411]
Каждая из изображенных в верхней части рис. 7.5 сетей
является выборочной реализацией множества возможных фрактальных
графов заданной фрактальной размерности. В нижней части рис. 7.5
показаны две добавочные реализации этих канонических структур
с фрактальной размерностью D= 1,5.
Характеристики фрактальных графов. Фрактальная размерность
D не единственный параметр, пригодный для описания
фрактальных графов. Значительную роль для оценки характеристик и стоимо-
434
7.3, Фрактальный характер линий железнодорожной сети большого города
200
сти сети играют средняя длина
между парами узлов и среднее
число узлов между парами узлов. Для
многократно связанных деревьев
эти две величины дают меру роба-
стности. Кроме того, существуют
понятия полной длины сети и
моментов масс узлов, которые
связывают топологию сети с рабочими
характеристиками и стоимостью.
Для 200-фрактальных графов,
построенных при условии
минимальности стягивающего дерева на
рис. 7.6 показаны характеристики
средней длины между парами узлов R в зависимости от расстояния
гот начальной точки (усреднение по нескольким репрезентативным
выборкам). Из рисунка следует, что с увеличением фрактальной
размерности растет и наклон каждой линии, т. е.
Рис. 7.6. Зависимость средней длины
между парами узлов R от
радиального расстояния г от центра для сетей с
Z>= 1,1; 1,5; 1,9 [411]
dr
: const DD\
где U « 0,768 - фрактальная размерность наклона средней линии.
Это соотношение изменяется в зависимости от связности, но оно
показывает, что при заданном числе узлов средняя длина пути и
скорость его увеличения с расстоянием характеризуются двумя
фрактальными размерностями -D и D'. Фрактально-графовый подход
позволяет изучать рост сложных сетей и дает метод манипулирования
такими сетями на глобальном уровне, не прибегая к детальному
описанию. Другие применения данного подаода рассмотрены в [412].
7.3. Фрактальный характер линий
железнодорожной сети большого города
В качестве примера приведем сведения о фрактальности
городских коммуникаций, имеющих структуру графов. Стереотипы
антропогенного поведения на основе функций коллективной
полезности и порядка коллективного благосостояния [413] показывают, что
435
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
антропогенная деятельность может иметь фрактальный характер.
Это, в частности, относится к транспортной сети метро в Париже
[414] и развитию некоторых английских городов [415]. Дальнейшее
изложение основано на результатах работы [414].
Численность совокупного населения I\R) Парижа в
окружности радиуса R как функция расстояния R от центра города показана
на рис. 7.7,а. Производная dP/dR (рис. 7.7,6) характеризуется
относительно плоским максимумом при R ~ 5,5 км, который
приблизительно является радиусом административной части Парижа.
Согласно данной структуры железнодорожная транспортная система
Парижа состоит из линий двух видов: сети метро (Regie Autonome des
Transports Parisiens - R.A.T.P.) и железнодорожной пассажирской
сети, соединяющей центр города с периферией. Железнодорожная
сеть в свою очередь состоит из двух взаимосвязанных систем - the
Societe National des Chemins de Fer (S.N.C.F) и - the Resean Express
Regional (R.E.R.).
dPIdR
A 600 h
J 200
30 /?,км
20 Л,км
Рис. 7.7. Численность совокупного населения P(R) Парижа (а) и ее производная
dP(R)/dR (б) как функция радиуса R окружности [414]
В [414] использовалась карта S.N.C.F. масштабом 1:100 000
издания 1989 г. Подсчитывалось число N(R) станций, расположенных
внутри окружностей радиусом R с центром на станции Chatelet около
Не de la Cite, являющейся «геометрическим центром» города (рис.
7.8). При равномерном распределении вдоль прямых линий
значение N(R) пропорционально дистанции R.
Если пространственное распределение станций компактно, т. е.
если их плотность (число станций на единицу площади) постоянна,
значение N(R) пропорционально R2. При фрактальном распределе-
436
7.3. Фрактальный характер линий железнодорожной сети большого города
Рис. 7.8. Эскиз железнодорожной сети большей части Парижа
на основе транспортных систем R.E.R и S.N.C.F [414]
нии значение N(R) пропорционально RD, где D - фрактальная
размерность ансамбля. Это означает, что плотность числа станций
уменьшается с возрастанием R.
Следовательно, для окружности радиуса Rn площади,
пропорциональной R2, плотность p(R) есть
p(R)~N(R)/R2~RD-2y
что соответствует формуле (1.13). Так как D< 2, то плотность p(R)
уменьшается с увеличением R. Полученные результаты показаны в
двойном логарифмическом масштабе на рис. 7.9. Вблизи центра
437
Глава 7. ФРАКТАЛЫ В МОДЕЛИРОВАНИИ СЛОЖНЫХ СИСТЕМ
XogN
7 I 1 1 ■ 1 1 1 г
l_i I ' I ■ ■ ■
-10 12 3 4
log*
Рис. 7.9. Число станций N(R) в двойных логарифмических координатах [414]
плотность станций пропорциональна значению R2. При удалении
большем, чем R$ « 5,5 км, наблюдается резкий переход к
закономерности вида N(R) ~ /J0'47.
Значение R$ примерно соответствует радиусу административного
центра Парижа. Следовательно, при ЖВ^ъ городе преобладает сеть
метро R.A.T.P., а число станций изменяется как квадрат расстояния
от центра. Для R > Rq сеть станций S.N.C.F.-R.E.R образует
фрактал с размерностью около 0,5. Плотность станций определяется
уравнением
Тщательное исследование сетей S.N.C.F.-R.E.R позволило
рассчитать общую длину пути L внутри окружности радиуса R
относительно центра (рис. 7.10). Средний наклон кривой оказался равным
1,47, что и дает оценку фрактальной размерности D = 1,47 для
системы путей.
Рассмотренные данные из [414] укладываются в концепцию
модели диффузионно ограниченной агрегации [415], описывающую
образование кластеров из коллоидальных образований [45]. В этой
модели мономеры поступают из удаленного источника и
диффундируют, совершая случайные блуждания. Достигнув кластера,
блуждающие мономеры прилипают к нему. Процесс агрегации такого рода
порождает кластеры с фрактальной размерностью D = 1,71 в случае
диффузии йа плоскости.
438
7.3. Фрактальный характер линий железнодорожной сети большого города
\ogL(N)
6
4
2
0 12 3 4
log/?
Рис. 7.10. Общая длина пути как функция удаленности
в логарифмическом масштабе [414]
Разницу между полученным в [414] значением Z>« 1,5 и
вышеприведенным значением D ~ 1,7 можно объяснить следующим
образом. Во-первых, сеть железных дорог обладает рядом бифуркаций.
Во-вторых, существующие петли дорог соединяют различные
выходящие ветви и дают возможность обратных поездок. Поэтому,
представляет интерес дальнейшее сравнение модели диффузионно
ограниченной агрегации с результатами исследования всей сети
железных дорог, которая должна быть самоподобной.
Известно, что транспортные системы обусловливают развитие
и рост городов, причем с сильной обратной связью. Следовательно,
не лишено смысла представление транспортных магистралей как
своеобразной картины города. Также очень интересно обсуждение
кривой заселенности как функции расстояния с этой же точки
зрения. Следовательно, можно предположить в дальнейшем
построение моделей роста городов с использованием исторических,
географических и экономических аспектов. Также актуален вопрос о
существовании постоянной фрактальной размерности во времени
развивающейся системы дорог и других коммуникаций с целью
предсказания их эволюции и повышения эффективности использования.
439
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
Глава 8
ФРАКТАЛЬНЫЕ СВОЙСТВА
ПРОСТРАНСТВЕННЫХ СТРУКТУР
ГЕОСИСТЕМ
8.1. Фрактальные размерности геосистем
на основе космических и самолетных снимков
Пространственная структура геосистемы — это распределение
компонентов структуры и их сочетаний. Важной задачей при этом
становится сравнение различных структур и определение
взаимного расположения компонентов системы. Изучение региональных и
глобальных процессов, происходящих на земле и в атмосфере,
производится на основе самолетных и космических снимков, сделанных
при различном пространственном разрешении. При дистанционном
зондировании создается множество многомерных физических
полей - спектрального альбедо, радиояркостной температуры,
рассеяния радиоволн и т.д.
Фрактальность агротехнических геосистем. Из анализа
космических снимков следует, что пространственная структура геосистем
обладает фрактальными свойствами [438,439]. Для оценки степени
неоднородности структур по формулам (1.6) и (1.15) определяют два вида
пространственной размерности D и D . Фрактальная размерность D
связана с усредненной локальной или глобальной характеристикой,
a D чувствительна к неоднородностям.
Фрактальные размерности сельскохозяйственных геосистем Dn
D приведены в табл. 8.1. В Курской области по космическим
снимкам интервал самоподобия 36-103-720-103 м2 был охвачен полностью.
Для территории Польши самоподобие определялось в
ограниченном интервале 0,8103-900103 м2. Полученные результаты
показывают, что агротехнические геосистемы обладают фрактальностью,
характеристики которой можно использовать при дифференциации
систем землепользования.
Структуры сельскохозяйственных геосистем выделялись из
снимков, полученных камерой МКФ-6 со станции «Салют-7» (1985 г.),
440
8.1. Фрактальные размерности геосистем...
Таблица 8.1
Фрактальные размерности сельскохозяйственных геосистем
Курская область
Класс
Пшеница
Ячмень
(Пар
Пропашные + травы
D
1,41
1,18
0,97
1,79
Л,
1,39
1,16
0,96
1,67
Польша
Класс
Пшеница
Пропашные
Травы
Рапс
Лес
D
1,75
1,69
1,49
1,35
1.47
°<
1,59
1,54
1,33
1,35
1,45 |
многоканальной сканирующей системой МСУ-Э с ИСЗ «Космос-
1939» (1989 г.) и «Landsat-TM» (1988 г.).
Фрактальность рек. Несколько другой тип пространственной
структуры образует речная и эрозионная сеть, имеющая
ветвящийся характер. На рис. 8.1 приведена схема эрозионной сети верховья
реки Сейм центра Среднерусской возвышенности,
дешифрированная с пространственным
разрешением 30 м.
Фрактальную размерность
ветвящейся структуры вычисляют по
распределению радиальной
плотности различных ее элементов. Для
этого из узла структуры проводят
концентрические окружности,
которые пересекаются с ветвями.
Число точек пересечения
обозначим через р0(г). В кольцах между
двумя смежными окружностями
подсчитываются свободные концы
р* и число узлов ветвления р+.
Тогда для фрактальных объектов
p0(r)~rD-1 и р-'+~гЯ"2.
Рис. 8.1. Схема эрозионной сети верховья
реки Сейм при пространственном
разрешении 30 м [439]
441
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
На рис. 8.2 показано число пересечений (кривая 1), узлов
(кривая 2) и свободных концов (кривая 3) в зависимости от радиуса зоны
ветвления, а в табл. 8.2 приведены фрактальные размерности
структур эрозионной сети. Для модели роста ветвящихся структур
необходимо знание среднего расстояния (L(r)) между парами ближайших
ветвей вдоль окружностей с радиусами гп, гЛ+1. Размер растущей зоны
будет гп+1 — гп. Модель роста основана на описании процесса в виде
ветвящейся структуры лапласовским фракталом, для которого
Dq-D
(L(r)) = rDo-x, (8.1)
где D0 - топологическая размерность пространства.
Следовательно, параметры модели роста (L(r)) ~ rN можно
определить или по распределению средних расстояний или из
уравнения (8.1). В последнем случае значение D в (8.1) вычисляют по рас-
\r\N
6
5
4
3
2
1
0
-
-
о +
\
1\Л#
2Ч/М
о •
+
о + •
+
!ж 1
.IjSJff
D°'**2,22
£>**2,86
Z)#*2,86
i i_
Рис. 8.2. Зависимость числа
пересечений о, узлов + и
свободных концов • от
радиуса растущей зоны ветв-
" Г "У 7 Z ~7~ ления в двойном логариф-
lnr мическом масштабе [439]
442
8.1. Фрактальные размерности геосистем...
Таблица 8.2
Фрактальная размерность структур эрозионной сети [439]
Бассейны
[река Сейм (Курская область)
Река Богучар (приток Дона)
[Часть бассейна реки Канзас (штат Канзас)
LP
2,22
1,82
2,66
Z>+
2,86
2,22
2,86
D'
2,86
2,22
2,86
пределению радиальной плотности различных элементов — типа
р°, р*, р+. Наилучшее согласование достигается для фрактальной
размерности, определяемой по плотности пересечений ветвей по
окружностям р0(г). Для реки Сейм было получено (Дг)) = г'0'2, и при
D = 2,22 имеем (Цг)) = г~°>22. Соответственно для эрозийной
системы полигона Канзас (Дг)) = г'0'83 и при D = 2,66 получаем
(L(r)) = г"066. Различие фрактальных размерностей D°, D+ и D9
вынуждает признать, что структуры эрозионной и речной сетей, как и
других ветвящихся процессов, возможно, не определяются одним
масштабом.
Самоаффинность земных покровов. В действительности
геофизические структуры самоаффинны и мультифрактальны. При
многоуровневых измерениях с различных носителей характеристики
земной поверхности измеряют с различным пространственным
разрешением. В [440,441] рассмотрена задача о возможности сохранения
адекватной характеристики структуры исследуемого поля при
различном пространственном разрешении. В более общей постановке
данная задача соответствует установлению взаимосвязей
фрактальных размерностей пространственных структур на микро-, мезо- и
макроуровнях.
Скейлинговые свойства геофизических полей различны по осям
координат, так как единицы измерений независимы. В
самоаффинном случае необходимо рассматривать несколько различных
фрактальных размерностей. Для исследования самоаффинных
фрактальных поверхностей и кривых [442] предложен метод с использованием
масштабно-инвариантных соотношений ширины полосы и
эффективной высоты.
Рассмотрим заданные по профилю измерения z =/(*).
Откладывая последовательно на кривой единичный отрезок а0 с фиксацией
443
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
координат, получим множество точек Pt (xi9 z{). Далее, разделив всю
кривую на секции длиной Na0, вычислим в каждой из них
дисперсии о2х и о2у :
I N j N
I N i N
1У 1=1 1У 1=1
Для некоторого стационарного состояния существуют
масштабно-инвариантные соотношения
ox~Ndz, oz~Ndz. (8.2)
В общем случае показатели степени dx и d связаны между
собой показателем Херста Я в виде
°z~a?> (8.3)
d
где Н = -г, 0<Ж1. Для самоаффинных фракталов rf=l и
d
0<dz< 1. В частном случае для самоподобных фрактальных кривых
dx=zdz=l D~l, где D - фрактальная размерность, а #= 1 теряет смысл.
Из соотношений (8.2) следует, что вычисление фрактальных
размерностей основано на выборе длины отрезка а0. Для
самоаффинных фрактальных кривых z = f(x) вычисления размерностей
неявно зависят от отношения а0 /(\Az\). В [58] введена единица
измерения Ах0, названная промежуточным масштабом:
\z(x+Ax)-z(x)\~\Ax0\. (8.4)
Данное условие при экстраполяции соотношений cz ~ Nd*-,
о г ~ о f к наибольшим длинам секций Na0 приводит к появлению
локальной Dn и глобальной DT размерностей (см. гл. 1). Когда
aQ « Ах0, показатель степени dz определяет Dn до достижения
предельной длины секции NaQ. При %>Ах0 значение DT=l. Для
444
8.1. Фрактальные размерности геосистем...
Oq < Ах^ получаемая размерность равна Н~х. При построении
графика oz ~ N * в логарифмическом масштабе переходные области
отображаются гладкими кривыми между двумя отрезками прямых,
определяющих локальную и глобальную размерности.
В экспериментах [440, 441] были использованы космические
снимки МСУ-СК и МСУ-Э с ИСЗ «Космос-1939», «Landsat-TM» и
радиолокатора с синтезированной апертурой со станции «Алмаз»
(длина волны 9,6 см). Трассовые измерения с высоким
разрешением получены с самолета синхронно четырьмя приборами: четырех-
лучевым СВЧ-радиометром на длине волны X = 8 мм,
радиовысотомером, лидаром и оптическим яркомером.
Сравнение профилей спектральных яркостей в ближней ИК-
зоне, измеренных на европейской территории России в Курской
области устройствами МСУ-Э и МСУ-СК с пространственным
разрешением 30 и 200 м для сельскохозяйственных территорий,
проведено на рис. 8.3,а. Здесь общий массив данных L = 2500 пиксел,
а0 = 4. При измерении устройством МСУ-Э: точки 1 определяют аг,
точки 2 - о • d =0,94; d7 =0,65; d7 =0,29. При измерении уст-
ройством МСУ-СК: точки 3 определяют cz, точки 4 - gx; dx = 0,94;
d7 =0,58; d7 =0,09.
1пах, lnoz
1
*-++:г
,88
#ч
+ i
•2
• 3
о4
3
4 lruV
а)
lncx,\noz
4
3
2
1
0 1
*
•
л
*
•
о
о
о
о
о
о
о
о°
о
о
** ?:••"
•
•
•
•
•
1 1 L
+1
• ?,
• 3
о4 1
4 InN
б)
Рис. 8.3. Зависимость среднеквадратичного отклонения сх и аг от координат х и
z поверхности при космических (а) и самолетных (б) измерениях [440]
445
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
Оба профиля характеризуются как самоаффинные фрактальные
кривые с отчетливо выделенными значениями d и d_ . Эти раз-
мерности не только не равны, но и принадлежат существенно
разным интервалам самоаффинного подобия. При пространственном
разрешении 30 м оно сохраняется до 2,4 км, а при 200 м достигает
11,2 км.
Для профиля рельефа длиной 30 км, измеренного в Московской
области с самолета при высоте полета около 200 м и скорости 100 м/с,
радиовысотомером (ширина диаграммы направленности 3,5°) и ли-
даром (ширина диаграммы направленности 0,5°) с точностью
измерения высоты 1,0 и 0,3 м получены аналогичные зависимости
(рис. 8.3, б). Трасса проходила через сельскохозяйственные угодья, лес
и населенные пункты. Длина всего профиля равнялась 17 900 пиксел.
Данные рис. 8.3 соответствуют а0 = 4; лидар: cz — (кривая 1), ох -
(кривая 2), d = 1,02; d7 =0,63; rf =0,11; радиовысотомер: а7 -
(кривая 3), ох - (кривая 4), dx= 1,02; dz=0,52.
Видно, что профиль поверхности имеет самоаффинную
фрактальную размерность, а ее величина зависит от элемента
пространственного разрешения. При измерении лидаром выделяются две
размерности: локальная и глобальная с границей перехода около 90 м.
Радиовысотомером определяется лишь одно значение.
Из (8.2) следует соотношение среднеквадратичных отклонений
по оси z для самоаффинных фрактальных кривых, полученных с
разным пространственным разрешением oz/dl = о\/е*2- Данные рис.
8.3 подтверждают, что дисперсия значений падает при снижении
пространственного разрешения. Поэтому, если о_ < о_, то неравен-
ство d2 < dx ведет к уменьшению фрактальной размерности и
изменению показателя Херста в скейлинговом уравнении LHf(x) = f(Lx).
Это означает, что преобразование статистических свойств
вероятности распределения значений геофизического поля из одного
масштаба в другой зависит от пространственного разрешения [441].
Поэтому результаты дистанционного зондирования с разным
пространственным разрешением приводят к различным фрактальным
сигнатурам, а локальные значения размерности будут относиться к
различным площадям поверхности. Полученные на этой же трассе
профили радиояркостной температуры и оптической яркости также
446
8.1. Фрактальные размерности геосистем,,.
обладают самоаффинными свойствами: для радиояркостной
температуры dz = 0,36 при чувствительности ~3 К, а для оптической
яркости в видимой зоне dz = 0,68.
С помощью радиолокационных изображений (РЛИ) от РЛС СА
«Алмаз» с пространственным разрешением 10—15 м на
горизонтальной поляризации проанализированы зависимости показателей dz и
dx от выбора единичного отрезка а0, коэффициента усиления и
пространственного разрешения (табл. 8.3 и 8.4). Длина строки
составляет 5120 элементов разрешения, что соответствует примерно 26 км.
Таблица 8.3
Влияние изменения коэффициента усиления РЛС СА «Алмаз»
на определение dz [441]
Коэффициент усиления сигнала Aq
1
0,5
0,25
яо
1
0,88
0,82
QJ1
2
0,81
QJ5
0,60
4
0Г72
0,63
0,51
8
0,67
0,47
0,25
16
0,49
0,26
0,15
Таблица 8.4
Влияние изменения пространственного разрешения снимков РЛС СА
«Алмаз» на определение dz [441]
Размер окна усреднения
2x2
4x4
8x8
«0
1
0,84
0,80
0,78
2
0,77
0,72
0,69
4
0,72
0,59
0,57
8
0,57
0,49
0,46
16
0,35
0,38
0,43
Видно, что только значения d очень чувствительны к
перечисленным характеристикам, a dx « 0,9 остается без изменения. При
определении dzndxB пределах интервала самоаффинного подобия с
локальной размерностью вплоть до переходной зоны ослабление
сигнала компенсируется соответствующим увеличением А^я0, что дает
примерно одинаковые значения dz. Например, при К0 = 0,5 и а0 = 1
значение d = 0,82, чему соответствует К$ = 1, а0 = 2 и dz = 0,71
(подчеркнуто в табл. 8.3). Сглаживание сигнала путем усреднения в окне
447
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
различных размеров приводит к уменьшению dv что подтверждает
зависимость фрактальных сигнатур от пространственного
разрешения (табл. 8.4).
Введенный промежуточный масштаб Лх0 разделяет локальную
и глобальную размерности. Для используемых РЛИ значение
(\z(x+Ах) - z(x)\) ддя Ах > 3 стабилизируется и составляет 45 единиц
квантования сигнала. Поэтому тонкая структура профиля с
локальной размерностью вычислялась при а0 < 2, а при а0 = 100 имеем dz = 0
и DT = 1. Последовательный переход от локальной к глобальной
размерности профиля обратного рассеяния при радиолокации в
зависимости от увеличения единичного отрезка а0 иллюстрируется
данными рис. 8.4 ддя а0 = 1 (кривая 1), а0 = 16 (кривая 2), а0 = 64
(кривая 3), а0 = 100 (кривая 4).
По заданным значениям dz и dx можно на основании (8.3)
вычислить показатель Херста и перейти к фрактальной размерности D.
\пс2
4
2h
1Г
х х х х xxxxxxxxxxxxxxxxxxx74
°zz$i
♦♦♦**
lntf
Рис. 8.4. Переход к глобальной размерности DT= 1 профиля обратного рассеяния
в зависимости от а0 [441]
448
8.1. Фрактальные размерности геосистем...
Для модели обобщенного броуновского движения справедлива
зависимость (2.14), откуда следует ВЛ=2-Н, DT=l. Однако, как
показано в [440, 441], все измеренные профили скоррелированы и не
удовлетворяют условию (2.14). Для самоаффинной изотропной
поверхности фрактальная размерность, определяемая по сечениям,
равна D = 2 + К Для профилей анизотропных геофизических полей
D = 1 + Н и может интерпретироваться как степень изрезанности
профиля потенциального рельефа или физической поверхности
(табл. 8.5).
Таблица 8.5
Фрактальные размерности профилей геофизических полей [440, 441]
Регион
Тип прибора
4,
А ]
Космические измерения
Курская область
Канзас (США)
Южное Приаралье
Польша
МСУ-СК
МСУ-Э
МСУ-Э
РЛССА «Алмаз»
«Landsat-TM»
1,58
1,65
1,56
1,72
1,56
1,09
1,29
1,18 |
1,00
1,19
Самолетные измерения \
Московская область
Радиовысотомер
Лидар
Радиометр (X = 8 мм)
Яркомер
1,52
1,63
1,36
1,68
1,11
Фрактальные сигнатуры геофизических полей зависят от
размеров элемента пространственного разрешения измерительной
аппаратуры. Скейлинговые соотношения для данных полей или профилей
при разном пространственном разрешении определяются
показателем Я, зависящим от соотношения горизонтального и вертикального
масштабов. Уменьшая или увеличивая разрешение, можно получить
адекватные оценки для геосистем различного уровня.
Геология и фракталы. Анализ линеаментной сети территории
Кольского полуострова, выявленной по космическим снимкам
разных масштабов, доказывает мультифрактальность плотностей лине-
is Фракталы
449
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
аментов и возможность геологической интерпретации спектра
фрактальных размерностей [443]. Сети линеаментов на снимках
являются объективными отображениями некоторых характеристик
геологической среды, искаженных неоднородностями условий
обнаженности и антропогенными модификациями ландшафта. Они
адекватны системам разломно-трещинных структур, образующихся
вследствие тектонических напряжений. В настоящее время
доказана фрактальность линеаментных сетей и показано соответствие
различных перколяционных кластеров определенным тектоническим
блокам или структурным комплексам [444, 445]. Эффективность
мультифрактального подхода в физико-химических науках
продемонстрирована на отдельных примерах [446—448].
Длина линеаментов M(L) в квадрате со стороной L
определяется зависимостью
M(L)~LD. (8.5)
Плотность линеаментов d в квадрате со стороной L равна M(L)/L =
= LP~X. Для квадратов с размерами L2 и L{ при условии L2 > Lx
получаем d2/dx = (L2/Ll)D~x. При D < 2 выполняется неравенство
d2/d{ < L2/Lv т. е. с увеличением размера клетки приращение
плотности dl-J>d2 происходит медленнее.
При растровом изображении линеаментной сети с
разрешением Ш определении плотности d в квадратах Lt х Lt форма
гистограммы плотностей фрактальных структур зависит от размера клетки L.
При этом меняются и значения самих плотностей, и
соответствующий интервал [dmhl, dmax]. В [443] исследуется распределение
плотностей фрактального перколяционного кластера восточной части
Балтийского щита [445] с подразделением на девять уровней
яркости при пространственном разрешении 3820 м. Каждая клетка LxL
содержит свободный конец линеамента или проходное звено,
пересекающее клетку, либо пересечение самих линеаментов, или
остается пустой. Поэтому значения плотностей в клетке LxL=9x9
создают гистограмму, разделенную натри области [1,8], [9,16], [17,40].
Пространственное распределение плотностей исследовалось с
помощью матрицы смежностей или матрицы распределения градиентов
[184,230]. Наибольшая частота сочетаний отмечена для однотипных
моделей структур, представленных проходными звеньями,
наименьшая - для свободных концов с пересечениями.
450
8.1. Фрактальные размерности геосистем...
Элементы матрицы, определяющие вероятность соседства в
сочетаниях Pidjdj), удовлетворяют соотношению P(did.) = P(di)P(dj),
где P(dt) и P(dj) - вероятности появления плотностей dt и dJ9
определяемые из гистограммы.
Уравнение (8.5) описывает масштабное самоподобие перколяци-
онного кластера в среднем. Однако разброс значений M(L)
относительно среднего значения <M(L)> становится одним из показателей
структуры сети. При этом плотность рассматривается как мера,
распределенная на фрактальном или нефрактальном носителе. Когда
флуктуации меры относительно среднего значения малы, то
фрактал считается однородным. При большом разбросе d(L) полная
информация о природе распределения плотностей будет содержаться
в моментах М(к) порядка к :
M(k) = ^n(d)dk,
а вместо (8.5) можно записать
где D{k) - размерность, зависящая от к; т(к) - переменный
показатель степени.
Для нефрактальных структур показатели степени имеют
линейную зависимость от к. Для фракталов моменты не подчиняются
простому линейному закону. На практике для конечных L интервал к
ограничен предельными значениями плотностей dmkl, dmxi на
гистограмме распределения. Поэтому для характеристики подобного
распределения требуется не одна размерность, а бесконечное
количество показателей степени, определяющих мультифрактальную
структуру.
С помощью преобразования Л ежандра задаются параметрические
представления кривой /(ос) и показателя Липшица-Гельдера а [45]:
a = dx(k)/dk, f(a) = ka-x(k). (8.6)
Независимые переменные х и к определяют функциональные
соотношения между L и значениями d* и n(d*) в виде
<T~L«»\L^, n(d*)~L-f«*\ (8.7)
где /(ос) — фрактальная размерность.
451
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
Уравнения (8.7) связывают плотность линеаментов d в клетке
размером L через показатель Липшица—Гельдера и определяют
фрактальную размерность множества клеток массой d* ~ La(^k\ Отметим,
что при возрастании порядка момента к показатель степени а(к)
уменьшается.
Спектр фрактальных размерностей для плотности линеаментов
Кольского полуострова приведен в [443] в виде функции /(ос). При
к = 0 фрактальная размерность всего домена линеаментной сети
/(ос) =1,81, что согласуется с фрактальной размерностью перколя-
ционного кластера, являющегося геометрическим носителем
домена D= 1,74. Максимум кривой /(ос) = 1,81 и определяет
фрактальную размерность домена. Спектры фрактальных размерностей в виде
функции /(ос) совпадают при различных пространственных
разрешениях. Отметим, что распределение плотности линеаментов не
только отображает известные геологические структуры, но и
показывает некоторые неоднородности строения, неизвестные или
недооценивавшиеся ранее.
8.2. Самоподобные свойства зеленых насаждений
в большом городе
Эксперименты. В техногенной городской геосистеме
растительность существенно влияет на климат. В [449] на основе
космических снимков МСУ-Э с ИСЗ «Космос-1939» и системы SPOT
показано, что зеленые насаждения в Москве образуют самоподобную
структуру. Пространственное разрешение снимков составило 40 м в
диапазоне X = 0,5—0,6 мкм. Ареалы зеленых насаждений в Москве
имеют D= 1,86. Раздельное определение фрактальной размерности
для северной и южной частей города относительно центра не
приводит к различиям в D более 0,03. Интервал самоподобия заключен
между г — 4—40 линейных размеров элементов разрешения.
Фрактальные самоподобные структуры наиболее близко
связаны с гиперболическим распределением вероятности
P(s) = P(S>s) = Fs-D (8.8)
и показателем степени, равным фрактальной размерности Д где
случайная переменная s есть площадь «острова» зеленых насаждений.
452
8.2. Самоподобные свойства зеленых насаждений в большом городе
Интеграл от P(s) при тщательных измерениях определяет площадь
зеленых насаждений. _
Выборочная оценка коэффициента F в (8.8) на основе метода
наименьших квадратов равна
F = ±sf°Nt(s)/±(sf°f,
1=1 / 1=1
где si - площадь ареала в пикселах; Nt(s) - число ареалов.
Для полученных данных F = 15000. На рис. 8.5 приведены
теоретические (кривая 1) и экспериментальные (кривая 2)
зависимости гиперболического распределения ареалов зеленых насаждений в
Москве. Удовлетворительное согласование кривых позволило
определить площадь зеленых насаждений на основе интегрирования
уравнения (8.8).
Ф)
800
600
400
200
20 40 60 s, пиксел
Рис. 8.5. Гиперболическое распределение ареалов зеленых насаждений
в Москве вида n(s) = Fs~D (F= 15 000, D= 1,86) [449]
Анализ. Для известных параметров гиперболического
распределения можно расчет п (s) экстраполировать до установленного
предела s^, составляющего доли элемента разрешения. В [449]
считалось 5,min = 1/16 пиксела, что составляло 2,5 х 2,5 м2 и
соответствовало в физической интерпретации кроне отдельного дерева. Тогда из
уравнения п (s) = 15 000s _1'86 были получены следующие оценки:
общая площадь — 45,5%; число ареалов — 2829170; площадь лесопар-
453
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
ков - 11,2%; внутриквартальные насаждения, скверы, аллеи - 34,3%.
Примечательно, что среди внутриквартальных насаждений ареалы
площадью до 40 х 40 м2 составляют 91%.
Следовательно, размещение зеленых насаждений в Москве
характеризуется фрактальными свойствами со скейлинговым
соотношением M(Xr) = X~DM(r). Зеленые насаждения Москвы,
занимающие около половины ее территории, существенно влияют на
структуру полей альбедо и температуры поверхности.
Для понимания взаимосвязи конвективных потоков на микро-
и макроскопическом уровнях необходимо определить свойства
трехмерного радиационного поля, рассматривая его как потенциальный
рельеф. Так как поле альбедо Москвы определяется мелкой
структурой зданий, дорог и зеленых насаждений, то для измерения длин
фрактальных кривых следует использовать единичный отрезок д0,
меньший, чем значение кроссовера Ах7(а0 <Ах;). Тогда тонкая
структура профиля альбедо будет определяться фрактальной
размерностью D = 1/#.
Графики зависимостей на основе (8.2) приведены на рис. 8.6.
Прямолинейные отрезки, характеризующие зависимость az ~ Nd*,
lna , Ina
1 с
i
1 4
1 ... £
/
у
1 А
>1
•3
4 —
У
А
S%
А
••99У\
и
\nN
Рис. 8.6. Зависимость
среднеквадратичного
отклонения <ух и аг поля
альбедо поверхности при
a* = Nd* и аг = N*z для
двух каналов яркости
[449]
454
8.3. Анализ самоподобного фрактального множества морских льдов
определяют локальное значение фрактальной размерности.
Локальное и глобальное значения (d = 0) разделяются кроссовером на
криволинейном участке. Для канала 2 с X = 0,6—0,7 мкм d = 0,775 (точки
1), dx = 0,883 (точки 2). Для канала 3 с Х= 0,8-0,9 мкм значение
d = 0,666 (точки 3) и d = 0,892 (точки 4).
С помощью уравнений (8.2) и (8.3) можно вычислить
фрактальные размерности профилей в спектральной зоне 0,6-0,7 мкм
(Z> = 1,13) и в зоне 0,8-0,9 мкм (D = 1,36). По графикам
зависимостей на спрямленных участках (рис. 8.6) определяют интервал
масштабной инвариантности, который составляет 40—50 элементов
разрешения, что соответствует 1600—2000 м.
При увеличении пространственного разрешения или единичного
отрезка а0 до 160 м фрактальные размерности D = 1 + Я будут
характеризовать более крупные структуры. Тогда D на каналах 2 и 3
будут равны 1,54 и 1,36 соответственно, а интервал масштабной
инвариантности составит 480—6400 м.
Учитывая связь теплового поля с концентрацией газовых
примесей в приземном слое, можно предполагать, что трехмерная
структура поля загрязнения также будет фрактальной, и установить
интервалы интерполяции и экстраполяции опорных наземных
измерений для интерпретации космических экспериментов.
8.3. Анализ самоподобного фрактального множества
морских льдов
При построении моделей климата часто используют данные о
поле температур поверхности океана [450]. Взаимодействие льдов и
атмосферы, а также расчет прогнозов ледяных полей определяются
характеристиками пространственного распределения покрова по
толщине, сплоченности, раздробленности и т.д. В [451] на основе
принципа масштабной инвариантности доказана фрактальность
однолетних ледяных полей в Охотском море, а также гиперболичность
распределения размеров льдин для участков акваторий с
фрактальной однородностью.
Гиперболическое распределение лагун. Рассмотрим, следуя [451],
некоторое фрактальное множество, состоящее из N0 частей,
полученных преобразованием подобия. Введем понятие генератора
образования множества лагун или островов [1—3]. Для исходного острова
455
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
с площадью 5 его диаметр /0 пропорционален (S )1/2. Затем
добавляем N0 островов диаметром г/0. В рекуррентной процедуре на т-м шаге
генерируется уже Nff островов диаметром / = г%. Данное
множество будет подчиняться гиперболическому распределению
N(L>l) = F'l-D
(8.9)
или
N(S>s) = F"s-D'2,
(8.10)
где N(L > I) и N{S> s) - число островов с диаметром L > /или
площадью S > s; F'hF"— масштабные коэффициенты.
Предположим, что полученное множество изображено на
снимках с разрешением пх и п2 элементов {пх > п2) по строке
сканирования. Тогда число островов с размерами сторон 1/пх и 1/п2 будет
Nl(l) = Fl(l/nl)-I>,
(8.11)
N2{l) = F2{lln2YD.
(8.12)
Площади, занимаемые элементами данных множеств на обоих
снимках:
кщ
I
/=1
\~Dr 1 Л2
/
V 2 J
На интервалах самоподобия [/, кп{] и [/, £л2] при 0 < к < 1
выполни ^2
няется условие ^Su = Х*У2/- Тогда
/=i
/=i
F ^2 /Г Ц
А»
/=1
(8.13)
Полученное соотношение (8.13) определяет связь между
коэффициентами Fx и F2 в уравнениях гиперболического распределения
456
(У. J. Анализ самоподобного фрактального множества морских льдов
(8.11) и (8.12). На основе (8.13) находим соотношение числа
островов Nl(s)/N2(s) разных размеров. Здесь Nx(s) и N2(s) соответствуют
числу островов, площади которых изображаются равным
количеством пикселов s при разных разрешениях:
n = Nx(s)/N2(s) = -^
/2
ч
кпл
(8.14)
/2
/=1
где s = /2; п выполняет роль коэффициента экстраполяции.
Из (8.14) следует, что при изображении самоподобной
фрактальной структуры отношение Nx{s)/N2{s) зависит от значений
пространственного разрешения и фрактальной размерности D. Значение
коэффициента экстраполяции п при различных D приведено на рис. 8.7
для соотношения размеров пикселов Nx /N2 = 2, 4, 8 и 16.
Экспериментальные результаты. Исследования ледяного поля
[451] были проведены на основе синхронных снимков, полученных
весной с ИСЗ «Космос-1939» аппаратурой МСУ-Е и МСУ-СК в
спектральных диапазонах 0,8-0,9 и 0,8-1,0 мкм соответственно с
пространственным разрешением 40 и 160 м. Сплоченность морских
льдов составляла 7—8 баллов. Ледяное поле было представлено
полным набором сочетаний размеров льдин: обширным, большим,
обломками и крупнобитым льдом.
Задача эксперимента [451]
состояла в том, чтобы определить
свойства пространственной
структуры и распределения
элементов ледяного поля, а также
показать возможность оценки
распределения морских льдов
Рис. 8.7. Зависимость коэффициента
экстраполяции п = Nx(s)/N2(s) для
изображений фрактальных множеств
с различным пространственным
разрешением от разных фрактальных
размерностей D [451]
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
\пЩЬ)
по снимкам малого разрешения на уровне снимков высокого
разрешения путем экстраполяции гиперболического распределения
самоподобной фрактальной структуры.
После предварительной обработки оба снимка были приведены
в бинарную форму, отображающую ледяное поле в двух масштабах
с минимальными размерами,
ограниченными пространственным
разрешением 40 и 160 м.
На основе уравнения (8.5),
записанного в виде М(L) ~ LP (где M(L) -
масса, содержащаяся в пересечении
множества с квадратом со стороной L;
D — массовая размерность),
установлено, что морские льды образуют
фрактальное множество (рис. 8.8).
Для изображений МСУ-Э (точки 1)
значение D = 1,972 ± 0,01 с
интервалом самоподобия [L^, LmJ = [5;
171] пиксел или [200; 6840 м]. Для
изображений МСУ-СК (точки 2)
значение D = 1,985 ± 0,01 при интервале
самоподобия [3; 85] пиксел или [480; 13
600 м].
Свойство морских льдов
представлять собой фрактальное множество
связано с гиперболическим
распределением размеров льдин в соответствии
с (8.10), что иллюстрируется данными
на рис. 8.9. Экспериментальные
данные для сканеров МСУ-Е (кривая 1) и
МСУ-СК (кривая 2)
удовлетворительно согласуются с соответствующими расчетными зависимостями
N(s) = 55h-°'987 (кривая 3) и N(s) = 17&\у°>987 (кривая 4). Результаты
экстраполяции значений, полученных по МСУ-СК до разрешения,
соответствующего изображению МСУ-Е, рассчитывались из
уравнения N(sE) = nN(sCK) (кривая 5) при п = 3,841, полученном из (8.14).
Здесь sE и sCK - значения площади льдин в пикселах на
изображениях сканеров МСУ-Е и МСУ-СК соответственно.
9
7
5
1
1
1
V
/
/
Щг
j
/
к
ПЛ
J
/
г
о-1
А-2
Г J
1 3 5 InL
Рис. 8.8. К определению
фрактальной размерности ледяных
полей Охотского моря по
космическим снимкам [451]
458
8.3. Анализ самоподобного фрактального множества морских льдов
800
600
400
200
■1
.||
"и
" V
в
А 2
-3;4
• 5
12
18
.у, пиксел
Рис. 8.9. Гиперболическое распределение
размеров льдин на изображениях,
полученных сканерами МСУ-Е (кривая 1),
МСУ-СК (кривая 2), расчет по формулам
#(5) = 55Lr°>987 (кривая 3) и
N(s) = 178s-0'987 (кривая 4) при
соответствующей экстраполяции вида
N(sE) = nN(sCK) (точки 5) [451]
Определим потери детальности
разрешения, возникающие при
изображении их на снимке с
ограниченным пространственным
разрешением. Для этого необходимо сгруппировать значения N(sE) на
гистограмме МСУ-Е в интервалы [1, 16], [17, 32], [33, 48], ..., (кривая 1),
соответствующие sCK= 1, 2, 3,... из гистограммы МСУ-СК (кривая 2),
и сравнить их между собой (рис. 8.10).
Из рисунка следует, что, начиная с sE = [256, 271] и sCK = 16,
вплоть до максимальных размеров 2^ N(sE) = ^ N(sCK). Вин-
sE=256 SCK=16
тервале sE = [1, 256] и sCK = [1, 15] имеются две области потерь на
снимках МСУ-СК. Отдельные
льдины размером sE из интервала
[1,8] не покрывают половины
площади пиксела МСУ-СК и
поэтому не будут отображаться.
Так как параметры
гиперболического распределения льдов на
снимках МСУ-Е известны,
можно вычислить соотношение
8/16 8/16
у N(s) = F V s~D/2
Z^ iVw * ^ ь иопреде-
5=1/16 5=1/16
Рис. 8.10. Распределения размеров
льдин на изображениях с разрешением
40 м (МСУ-Е) - кривая 1
и 160 м (МСУ-СК) - кривая 2 [451]
0 7
П.8][9,24]
14 21
[249,264]
459
Глава 8. ФРАКТАЛЬНЫЕ СВОЙСТВА ПРОСТРАНСТВЕННЫХ СТРУКТУР
лить потери информативности снимка. Для этого случая отношение
8/16 /16/16
]Г N{s) jT N(s) = 0,8, т.е. только 20% льдин из интервала
5=1/16 / 5=1/16
sE = [1, 16] может изобразиться на снимке с разрешением в 4 раза
мельче.
Кроме этого могут появиться потери из-за объединения льдин
малого размера или слияния их с большими. По экспериментальным
данным 2^ N(sE) = 2900, поэтому только 730 льдин из их общего
sE=\
числа отображается на снимках МСУ-СК. Из них потеря 1360 льдин
(50%) приходится на интервал ^=[1,8] пиксел, а остальные 790 —
на интервал sE = [9, 255] пиксел.
Масштабно-инвариантные свойства самоподобных фрактальных
структур позволяют экстраполировать и интерполировать детали
изображения к размерам, меньшим величины разрешения.
Поэтому можно анализировать структуры сколь угодно малых размеров в
пределах самоподобия.
Если считать, что для морских льдов Охотского моря интервал
самоподобия [102, 15 0002 м2], то за счет экстраполяции
гиперболического распределения МСУ-Е на основе соотношения N{sE) =
= nN{sCK) можно добавить еще 6700 единиц крупнобитого льда в
интервале [102, 402 м2]. Для всего интервала [102, 15 0002 м2] на участке
Охотского моря можно заключить, что льды покрывают 75%
поверхности данной акватории.
Модель развития полей льда. Экспериментально установленное
свойство скейлинга морских льдов можно обосновать вероятностной
моделью их растрескивания [451]. Предположим, что р- вероятность
разделения льдин на две части. На первом этапе из N0 льдин
максимального размера s0 образуется 27^ льдин размера sQ /2 и NQq льдин
сохраняется, где q= 1 — р. На втором этапе возникает 22N0p льдин
размером s0/4 и сохранится IN^pq льдин с размером sQ/2.
Для гиперболического распределения при тех же вероятностях
выполняется условие
NSn+l=Ns2°/>. (8.15)
460
8.3. Анализ самоподобного фрактального множества морских льдов
Число льдин размером s определяется выражением Ns = N^jfq.
При выполнении (8.15) вероятность^ = 2(Z)/2)_1. Тогда вероятность
возникновения льдин PiNm) размером s0 • 2~т после т растрескиваний
равна
P[Nm(sm)] = 2(m+D№-1 Г^п+В1^-Х.
Для морских льдов Охотского моря при D = 1,98 ир = 0,993
значения P[Nm(sm)] согласуются с гиперболическим распределением
P(S > 0) = Fs~D/2. Например, чтобы льдина размером на изображении
в 3000 пиксел раздробилась до частей размеров в 1 пиксел,
потребуется около 12 растрескиваний. Конечно, полученная фрактальная
размерность ледяных полей будет характеризовать мгновенную
ледовую обстановку и изменяется в процессе таяния.
На рассмотренном примере доказано, что скейлинг
самоподобных структур позволяет однозначно оценить информационные
потери при снижении пространственного разрешения
аэрофотоснимков и радиолокационных изображений. При этом можно
производить экстраполяцию к малым размерам, превосходящим
пространственное разрешение используемых систем.
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Глава 9
ЦИФРОВАЯ ФРАКТАЛЬНАЯ
ОБРАБОТКА ИЗОБРАЖЕНИЙ
9.1. Фрактальные модели изображений
земной поверхности
Текстуры и фракталы. При решении задач тематической
обработки данных часто приходится анализировать пространственную
структуру поля интенсивности изображений. При статистическом
описании изображений с учетом их информативности различают два
типа изображений: детальные и текстурные [184, 230, 452]. Для
детальных изображений характерно наличие целей и стохастического
фона. Для текстурных изображений с точки зрения
информативности необходимо учитывать параметры всего изображения.
Практически в любых изображениях земных покровов можно выделить
области, относящиеся к текстурным изображениям.
Анализ текстур проводится обычно статистическими и
структурными методами [453-462]. Статистические методы состоят из
вычисления автокорреляционных функций, оптических и цифровых
преобразований, использования структурных элементов, статистик
первого и второго порядков (матрицы смежности или распределения
градиентов). Структурные подходы основываются на представлении
текстуры множеством непроизводных элементов, размещенных по
заданным правилам. Наиболее универсален метод анализа
текстурных изображений с помощью ансамбля из 28 признаков,
определяемых по матрице распределения градиентов в пространственной
области [463]. Предложена также система из 28 текстурных признаков
в области пространственных частот [464].
В последние годы для анализа природных объектов все чаще
используются методы фрактальной геометрии. Так в [465]
измерение локальной фрактальной размерности изображений D
проводилось с помощью радиолокатора с синтезированной апертурой (РСА).
Радиальное разрешение составляло 30 см на расстоянии 7 км.
Система обеспечивала разделение поляризаций не хуже, чем на 30 дБ.
462
9.1. Фрактальные модели изображений земной поверхности
Отношение сигнал/шум q\ =-10 дБ при ЭПР цели а* = -30дБ/м2.
Цифровое изображение состояло из512х512 пиксел.
В [466-469] фрактальная размерность оценивалась при простой
текстурной сегментации природных сцен и сегментации
медицинских изображений. Алгоритмы сегментации используются для
создания алгоритмов с фиксированным значением вероятности ложной
тревоги (CFAR), для обнаружения границ рассеивателей, для
обнаружения протяженных искусственных целей на фоне природных
образований. Адаптивные алгоритмы CFAR для РСА определяют
локальную область — домен, по которому оценивается некоторый
функционал кластера.
Броуновские процессы. Статистическая модель броуновского
фрактального процесса играет важную роль в компьютерном
моделировании [112, 115, 128, 470]. Она также представляет основу для
анализа и описания масштабно инвариантных текстур. Фрактальный
броуновский процесс описывается случайной функцией вида (2.4);
в данном случае [465]
(\V(x,y)-V(x + Ax,y + Ay)\2\ = \Ax2+Ay2\H, (9.1)
где 0 <Н< 1 - показатель Херста (см. п. 1.5).
При #= 1 поверхность рассеяния гладкая, а при #= 0 она
соответствует очень неровной текстуре. Энергетический спектр
такого процесса
<<?(/)) ~/"р. (9-2)
Аналитическое выражение для спектра обобщенного
броуновского процесса получено в [470, 471]. При этом величины D, Ни р
связаны между собой соотношениями
P = 2# + D0, D = 3-H, (9.3)
где DQ - топологическая размерность.
Алгоритмы измерения фрактальной размерности. При знании
параметров Ни р можно вычислить фрактальную размерность
случайного процесса. Для измерения фрактальной размерности
используются обычно три алгоритма: во-первых, это метод покрытия
поверхности эталонами; во-вторых, дисперсионное масштабирование,
463
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
основанное на оценке закона функции распределения средних
квадратов (9.1); в-третьих, оценка Dno степени аппроксимирующего
полинома для спектра мощности процесса. В настоящее время
первый способ наиболее распространен.
В [466] обстоятельно исследован локальный спектр мощности
для оценки D. В экспериментах использовалось окно 8x8 пиксел,
для которого вычислялся двумерный пространственный спектр.
Затем определялся показатель (9.2). В предположении изотропности
броуновской функции была получена линейная аппроксимация
log G(f) от log/по двум ортогональным направлениям в
дискретной фурье-плоскости, а затем производилось усреднение.
В ранее проводимых экспериментах [472] осуществлялась
проверка указанных трех методов. Локальная фрактальная размерность
вычислялась с помощью окна 9x9 пиксел, выборка составляла 61 504
измерения. Среднее из таких измерений рассматривалось как
значение D. Первый метод был самым быстродействующим. Метод
использования спектра мощности — наиболее точен, к нему
приближается по точности второй метод. Метод покрытия отличается
большими ошибками. Для диапазона D = 2 - 3 имеем [472] следующие
значения среднеквадратичного отклонения: первый метод — 0,364;
второй метод — 0,234; третий метод — 0,233.
Моделирование реальных изображений. В [465] рассмотрены
синтезированные изображения деревьев, травы и т.д. при различных
типах поляризации на длине волны 8,6 мм. Для когерентного
изображения РСА и высоком разрешении использована
мультипликативная модель, когда
X = S(I + iQ), (9.4)
где S— текстурная компонента; (/+ iQ) — спекл-компонента,
представляющая собой комплексную случайную переменную.
Текстурная компонента традиционно моделируется как
квадратный корень из логнормальной величины, но также можно
применять распределение Вейбулла. Спектры рассчитаны для окон 64 х 64
пиксела. Реальные изображения были схожи с модельными на
основе (9.4). Гистограммы показателей пространственных спектров
приведены на рис. 9.1 для изображений травы и деревьев. Затем были
определены локальные D растительности. Результатом исследований
явилось доказательство четкого сегментирования по значениям
фрактальной размерности изображений травы, деревьев и шума.
464
9.1. Фрактальные модели изображений земной поверхности
Рис. 9.1. Гистограммы показателей пространственных спектров
двух растительных покровов [465]
В общем случае изображения земной поверхности с
расположенными на ней антропогенными и природными объектами обладают
значительной неоднородностью и разнообразием. Поэтому
достаточно трудно сопоставить фрактальную модель броуновского движения
таким изображениям, так как гауссово распределение не учитывает
действительную статистику. В качестве адекватной модели
предлагается в ряде случаев использовать фрактальную модель движения
Леви [473]. В ее основе лежит симметричное стационарное
а-распределение приращений яркости. Характеристическая функция а
-распределения имеет вид [474]:
Ф(со) =
ехр
ехр
/8о>-|осо|а
f. 0 со . ясО
со 2
/5а>-1 асо | 1 — р7—г-!11!03!
|со|гс
(9.5)
Здесь а - экспоненциальная характеристика стационарности,
0<ос <2; Р - коэффициент симметрии, -1 < р < 1; а - параметр
протяженности, а > 0; 8 — параметр положения. Если а = 2 и Р = 0 име-
465
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
ем гауссов закон распределения, при ос = 1 и Р = О получаем
распределение Коши.
Во фрактальной модели движения Леви используется упрощенная
запись выражения (9.5) с учетом симметрии Ф(со) = ехр(/8о>-|асо|а).
Применимость фрактальной модели Леви к космическим
изображениям проверена экспериментально [473] на выборке из 17
изображений размером 512 х 512 пиксел с 256 градациями яркости.
Изображения выбирались в соответствии с требованиями устранения
влияния неоднородностей из-за различий ландшафта, освещенности и
альбедо зондируемой поверхности [466]. Для последующего
использования снимки подразделялись на две группы с отличным и
средним качеством. Для первой группы были получены значения
ос= 1,73; Н= 0,58, а для второй - сс= 1,51 и Н= 0,60. Значение о
для всех снимков оказалось равным 127. Фрактальная размерность
определялась как D = E + l-H, где £ - число независимых
измерений, Н- параметр Херста. Полученные распределения приращений
яркости хорошо аппроксимировались а -распределением.
9.2. Анализ и синтез фрактальных карт местности
Краткий обзор. Процесс синтеза оптических и
радиолокационных изображений относится к области обратных задач. При этом
решается вопрос, как по заданным значениям признаков
синтезировать изображение земного покрова, соответствующие статистики
которого будут близки к характеристикам аналогичного изображения
естественной поверхности. Интерес к созданию и
совершенствованию алгоритмов синтеза изображений постоянно растет. Это
связано с решением актуальных задач радиолокации, радионавигации,
дистанционного зондирования, картографии, распознавания образов.
Существует несколько подходов к решению задач синтеза
текстурных полей - на основе моделей Юлеша, линейного
программирования, авторегрессионных рядов и условных математических
ожиданий [184, 475, 476].
Фрактальный синтез карт местности. Методы фрактального
анализа и синтеза цифровых топографических карт описаны в [477].
Методы фрактального анализа учитывают различия между
самоподобными и самоаффинными природными фракталами. Линейный
профиль топографического рельефа является примером самоаффинного
466
9.2. Анализ и синтез фрактальных карт местности
фрактала. Рассмотрим вначале одномерный спектральный подход.
Как известно, пространственный спектр мощности имеет степенную
зависимость вида (3.6) от волнового числа
G{K)~K~*. (9.6)
Для одномерного топографического профиля h{x) дисперсия
определяется в виде
1 L
oHL) = jj[h(x)-h0]2dx,
Lo
где L - длина профиля со средней высотой неровностей /^ = {И).
Необходимым условием фрактальности профиля является степенная
зависимость o2(L) от длины
o2(L)~L2H (9.7)
при среднеквадратичном отклонении
o(L) = [o2(L)]V2~LH. (9.8)
При определении фрактальной размерности вводится эталон
покрытия. Для самоподобных фракталов эталоном является куб, для
самоаффинных фракталов - параллелепипед со сторонами L и
высотой а. Рассмотрим набор эталонов со сторонами Ln = L/n и
высотой hn =с/п (п — целое). Тогда число Nn эталонов л-го порядка,
требуемых для покрытия области L с высотой оп =o(L/n), равно
п п
что позволяет с использованием (9.8) записать
2±=«УА=\. (9.10)
При сопоставлении (9.9) и (9.10) получаем
Nn=n2-H=(L/Lny-H. (9.11)
467
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Сравнивая (9.11) с определением фрактальной размерности (1.1),
имеем для одномерного случая
D' = 2-H. (9.12)
Пространственный спектр мощности связан с переменной o(L)
соотношениями вида (9.9) и (9.10). Тогда
G(L) = Lo(L)~L«~Ll+2H, (9.13)
откуда с учетом (9.12) получаем
Д' = (5-сс)/2, (9.14)
что совпадает с формулой (4.7). Для одномерного профиля 1 < D' < 2,
тогда 3 > а > 1. Для модели броуновского движения а = 2, Н = 0,5 и
D=l,5.
Рядом авторов использовано одномерное фурье-преобразование
для измерения глубины океана (см., например, [478]). Исследования
показывают хорошее соответствие с соотношением (9.6) при ос = 2 и
длинах пространственных волн от 0,1 до 103 км. Броуновский процесс
в ряде случаев хорошо моделирует топографию местности.
Спектральный метод фрактального фурье-преобразования для
одномерных профилей может быть распространен на двумерные
изображения. Рассмотрим решетку Nx Nравномерно расположенных
точек в квадрате с линейным размером L. Данные N2 точек
обозначим через hnm, причем пит определяют их расположение по
направлениям х и у соответственно. Сначала [477] выполним двумерное
дискретное фурье-преобразование массива hnm от N2 точек данных.
Решетка Nx ^комплексных коэффициентов Hst определяется в виде
N-\ N-\
(9.15)
Hst = l lhnntQXP
л=0 /и=0
■—(sn + tm)
где s— преобразование в направлении х (s = 0,1, 2,..., N- 1); / —
преобразование в направлении у (t= 0, 1, 2, ..., N- 1).
Каждый коэффициент преобразования Hst определяется
эквивалентным радиальным числом г = (s2 + /2)1/2. Для каждого радиального
волнового числа Kj средний пространственный спектр мощности
468
9.2. Анализ и синтез фрактальных карт местности
С2,=^Ж,|2, (9.16)
"j 1
где N. — число коэффициентов, удовлетворяющих условиюу < г <j + 1,
и суммирование выполняется для коэффициентов Hst в этой
области. Двумерный эквивалент выражения (9.6) выглядит, как
G2j~Kjl*. (9.17)
Тогда пространственный спектр мощности
G2(L) ~ I?o(L) ~ I1+a ~ L2+2H, (9.18)
откуда для двумерного случая
D = 3-H = (7-a)/2. (9.19)
Экспериментальные результаты. Анализ цифровых
топографических данных проводился в [477] для рельефа штата Орегон (США) при
разрешении 7 точек/км. Для проверки фрактального поведения
данных сначала выполнялся одномерный спектральный анализ на трех
участках с различными геометрическими и тектоническими
характеристиками. К примеру, долина Уилламетта (Willamette)
сформирована под влиянием осадочных процессов. Горы Уоллова (Wallowa)
образованы, главным образом, тектоническим поднятием. Область
Кламат-Фолс (Klamath-Falls) принадлежит бассейну и области
тектонического режима.
Для каждой из трех местностей анализировалось 20 одномерных
профилей длиной 512 точек, ориентированных в разных
направлениях. На рис. 9.2,а,б,в приведено по восемь спектральных
зависимостей соответственно для долины Уилламетта, гор Уоллова и
области Кламат-Фолс. Все графики достаточно хорошо подчиняются
степенной зависимости, что говорит о их фрактальности. Средние
одномерные фрактальные размерности (табл. 9.1) близки к значению
D' = 1,5. Их небольшие изменения во взаимно перпендикулярных
направлениях дают основание считать, что топография штата
Орегон относительно изотропна. В табл. 9.1 помещены также данные о
высотах неровностей в относительных единицах.
469
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Iog(G, м )
-3,0-2,0-1,0 0,0 1,0 -3,0-2,0-1,0 0,0 1,0 -3,0-2,0-1,0 0,0 1,0
log(£, км"1)
Рис. 9.2. Пространственные спектры мощности G(K)
для различных местностей [477]
Таблица 9.1
Фрактальность одномерных профилей штата Орегон [477]
| Область
1 Долина Уилламетта:
широта
долгота
Горы Уоллова:
широта
долгота
Кламат-Фолс:
широта
долгота
D'
1,436
1,507
1,499
1,485
1,492
1,500
А, отн. ед.
5,948
6,354
6,549
6,830
5,825
5,963 |
Синтез карт местности. На следующем этапе экспериментов была
поставлена задача синтеза фрактальной карты местности. Для этого
использовались области размером 32 х 32 пиксел. В данном случае
фрактальные размерности и амплитуды неровностей получены для уча-
470
9.2. Анализ и синтез фрактальных карт местности
стков 4,5 х 4,5 км. Для меньших областей ошибки в определении D
и h становятся большими. Для больших областей пространственное
разрешение топокарты падает.
Основные этапы синтеза карт значений фрактальной
размерности и амплитуды неровностей следующие. Выбирается набор из 32 х 32
оцифрованных участков местности, т.е. N- 32. Устраняются
средние значения и линейные тренды. Выполняется двумерное фурье-
преобразование, и с помощью (9.15) создается решетка из Nx
^комплексных коэффициентов Hst. Для каждого значения Hst
определяется радиальное волновое число г = (s2 + /2)1/2. На основе (9.16) для
каждого волнового числа К. рассчитывается среднее значение
пространственного спектра мощности s2j. С использованием формул
(9.17) и (9.19) по среднему наклону графика S2j(Kj) в двойных
логарифмических координатах определяется фрактальная размерность D.
Выделение значений при К},= 1 км-1 дает амплитуду неровностей.
Полученные спектральные зависимости для четырех типовых
областей штата Орегон (США) приведены на рис. 9.3. Линейный
наклон графиков говорит о фрактальности процессов. Итоговые
значения средних D приведены в табл. 9.2. Среднее значение для
всего штата Орегон близко к среднему значению D штата Аризона,
log(G2, м4)
-0,8 -0,6 -0,4
0,2 0,4 0,6
logtK, км"1)
Рис. 9.3. Теоретические (линии) и экспериментальные (точки) значения
пространственного спектра мощности в логарифмических координатах [477]
471
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Таблица 9.2
Средние фрактальные размерности топографических карт местности [477]
Объект
Штат Орегон (США)
Синтезированная
карта местности
Одномерный анализ
D'
1,487
1,58
1,65
1,91
с„-
0,149
0,167
0,192
0,205
Двумерный анализ
D
2,586
2,60
2,70
3,00
oD
0,123
—
полученному ранее. Видно, что результаты хорошо согласуются с
выражением D = D'+1. В [477] приведены изображения карт
фрактальной размерности и высот неровностей. Как и ожидалось,
значение D мало изменяется относительно среднего значения и
находится в интервале 2,4 < D < 2,9. Изменения амплитуды
неровностей более чувствительны к текстуре изображения.
Синтез изображений местности. Значительный интерес в
практических приложениях, как отмечено выше, представляет синтез
изображений местности и их фрактальный анализ. В [477] синтез
изображений происходил по следующему алгоритму.
Каждой точке изображения сопоставляется значение,
основанное на гауссовской статистике
P(y)dy = l/2exv(-y2/2)dy.
Используя (9.15), получаем набор двумерных коэффициентов
Фурье Hst из данного набора N2 случайных значений. Находим
значения D и а из формулы (9.19). Новый набор комплексных
коэффициентов H*t =Н^/К^/2. С помощью обратного фурье-преобра-
зования получаем новое изображение.
Примеры синтезированных изображений для модели белого
шума без фрактальной фильтрации (ос = 0), при фильтрации <х= 1
и D = 3, а также при а = 1,8; D = 2,6 приведены на рис. 9.4.
Синтезированное изображение при D - 2,6 выглядит очень реально для
типовой топографической карты. Данный результат хорошо
согласуется с результатами картографирования штата Орегон, для
которого D = 2,586.
Таким образом, на основе двумерного фрактального анализа
цифровых топографических данных можно утверждать, что тексту-
472
9.3. Сегментация текстур с помощью фрактального анализа
ра подстилающей поверхности количественно анализируется в
элементах фрактальной размерности и амплитуды неровностей. Данный
метод может быть применен и к другим цифровым изображениям,
если они удовлетворяют фрактальным статистикам.
9.3. Сегментация текстур
с помощью фрактального анализа
Определение. Сегментация текстур представляет собой
разделение или разбиение текстур на области по сходству свойств их точек.
При сегментации не учитывается информация, характеризующая
объекты в целом. Кроме того, в процессе сегментации не делается
попытки распознать отдельные сегменты, установить их взаимные
соотношения и пометить их соответствующими символами.
В [466] представлены доказательства того, что большинство
естественных поверхностей являются пространственно изотропными
фракталами и что двумерные поля интенсивностей от таких
поверхностей также являются фракталами. Однако только сама по себе
фрактальная размерность не достаточна для описания и характери-
зации текстуры.
т
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Двумерные статистики. В [467] вводятся новые признаки,
основанные на концепции заполнения, которые используют статистику
второго порядка для фрактальных поверхностей. Представим
связную область А в топологическом «-пространстве. Говорят, что
область А самоподобна, когда А является объединением N отдельных
неперекрывающихся самоподобных копий, каждая из которых
уменьшена на коэффициент г по всем осям координат. Фрактальная
размерность области А задается соотношением
D= l0gN . (9.20)
log(l/r)
Естественные фрактальные поверхности обычно не обладают
такой характерной самоподобностью. Фрактальные поверхности
проявляют статистическое самоподобие, т. е. они состоят из N
отдельных подобластей, каждая из которых является уменьшенной
копией с коэффициентом г и идентична по всем статистическим
характеристикам оригинальной поверхности. Фрактальная размерность
таких поверхностей также задается выражением (9.20).
Хотя определение размерности фрактала с помощью
самоподобия является прямым, часто бывает, что это определение трудно
произвести с помощью данных изображения. Однако, связанная с
фрактальной размерностью величина меры может быть гораздо легче
вычислена из области А на множестве Rn. Предположим, что
можно покрыть область А л-мерным кубом размером Z,^. Если область А
получена уменьшением через коэффициент г, то существует N= r~D
подобластей. Поэтому число кубов размером L = rLmSK, необходимых
для покрытия всей области, дается выражением
NiD-W^L^ILf. (9.21)
Самый простой способ определить D из соотношения (9.21) - это
покрыть пространство, обладающее размерностью п, сеткой из
кубов с длиной боковой стороны L и подсчитать число непустых
кубов [482]. Если N(L) вычислено для нескольких значений L, то D
определяется по наклону линии, проходящей через
последовательность заполненных ячеек наименьшего размера, расположенных
вдоль этой линии {In L; — In N(L)}.
474
9.3. Сегментация текстур с помощью фрактального анализа
В [165] предложено другое определение фрактальной
размерности поверхности изображения А. Пусть Р(т, L) — вероятность того,
что т точек внутри куба размером L сосредоточено вокруг
произвольной точки поверхности изображения А. Для каждого значения L
имеем
X №£) = !,
/и=1
где N— число возможных точек внутри куба.
Пусть общее число точек в изображении равно М. Если
нанести на изображение сетку из кубов с длиной стороны L, то число
кубов, содержащих т точек внутри куба, равно (М/т)Р(т, L).
Следовательно, ожидаемое число кубов, необходимых для покрытия
всего изображения, равно
w)=xw*i)^i(i//«№i).
/и=1 т=\
Поэтому, если положить
N(L)=f^(l/m)P(m,L), (9.22)
то это значение также будет пропорционально L~D и его можно
использовать для определения D.
Синтез поверхностей. Чтобы протестировать способы
определения D в [467] методом спектральной плотности было
сформировано десять фрактальных поверхностей с размерностями от 2,0 до 2,9
[466]. На рис. 9.5 графически показаны три из этих поверхностей. Для
каждого участка на изображении размером Мх #(при условии, что
самым большим из используемых размеров куба будет £тах) число
точек т внутри каждого куба размером L, сосредоточенных в
пикселе {х, y,f(x,y)}, может быть записано как m(L, x, у). При этом не
учитывается ряд шириной (Lmax — l)/2 на границе. Уменьшенное
изображение размером [M-(Lmax- l)/2] на [N-(Lmax-1)/2] затем
делится на перекрывающиеся или граничащие окна. Для
оцифрованных поверхностей изображений значения т составляют от 1 до L3 для
куба со стороной L. Значением D является наклон линии, получен-
475
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
в)
Рис. 9.5. Поверхности, синтезированные с помощью фурье-преобразования,
имеющие фрактальную размерность D = 2,6 (a), D = 2,4 (б), D = 2,2 (в) [467]
ной при обработке последовательности заполненных ячеек
наименьшего размера и принадлежащих набору данных {In L; — In N(L)} при
N(L), задаваемым уравнением (9.22). Подпрограмма данного
алгоритма приведена в приложении к [467].
476
9.3. Сегментация текстур с помощью фрактального анализа
В табл. 9.3 содержатся значения вычисленных фрактальных
размерностей для десяти синтезированных текстур. Отсюда можно
сделать два вывода. Прямой подход к определению D приближает
значения найденных размерностей к середине истинного интервала. Это
особенно заметно, когда реально существующая фрактальная
размерность приближается к значению 3. Одной из основных причин
этого эффекта является процесс квантования. Настоящий фрактал
должен быть самоподобным при всех масштабах разрешения. В
действительности, популярная модель синтеза фрактальных поверхностей на
основе броуновского движения является бесконечномерной
функцией [466]. При приближении фрактальной размерности
поверхности к 3 поверхность становится высоко нерегулярной и после
квантования точки на поверхности с градациями серого имеют широкие
промежутки между собой. Данное обстоятельство приводит к
большому количеству кубических пространственных поверхностей при
малом L, содержащих только центральную точку, и уменьшает
определяемую размерность поверхности.
Таблица 9.3
Значения фрактальных размерностей синтезированных текстур [467]
Исходные значения D
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
Значения D, полученные методом
подсчета кубов
2,07
2,12
2,18
2,25
2,34
2,42
2,48
2,52
2,53
2,53
интерполяции
2,09
2,16
2,26
2,38
2,49
2,59
2,67
2,73
2,77
2,81
Чтобы исключить частично эти явления, возможен новый
подход [467]. При этом фрактальная поверхность, находящаяся между
центральной точкой куба и соседней с ней, аппроксимируется с
помощью линейной интерполяции. Образовавшаяся в результате
интерполяции поверхность пересекается с кубом, при этом
записывается количество точек в кубе со стороной L. В [467] каждая точка
с координатами {х, y,f(x, у)} на поверхности соединяется с точками
{х— 1, y,f(x— 1,у)}и{х+ l,y,f(x+ l,y)} с помощью линий. После
477
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
того как для каждого у проведены линии процесс повторяется для
фиксированных координат х. Это новая группа точек поверхности
используется для алгоритма подсчета кубов. Полученные с помощью
указанного алгоритма значения D также приведены в табл. 9.3. Они
не только лучше аппроксимируют размерности исследуемых
поверхностей, но также имеют лучшую разделяемость.
Лакунарность. Разные фрактальные образования могут иметь
одинаковую размерность, но при этом резко различающуюся текстуру.
Это подтверждает то, что сама по себе фрактальная размерность не
дает достаточно информации для описания и сегментации
естественных текстур. В [467] исследовалось восемь типов текстур (табл. 9.4).
Изображения были оцифрованы с разрешением 256 х 256 и имели
256 градаций серого цвета. Хотя существует некоторая разница между
найденными значениями фрактальных размерностей, но она
недостаточна для полного и надежного различения текстур.
Следовательно, сегментация, использующая только численные размерности
фракталов, будет бесполезна в практическом применении к этим
естественным текстурам.
Таблица 9.4
Значения фрактальных размерностей для изображения текстур [467, 483]
Текстура
Трава
Свиная кожа
Песок
Рафия
Значения D
2,39
2,40
2,22
2,29
Текстура
Шерсть
Кора дерева
Дерево
Вода
Значения D
2,28
2,33
2,34
2,32 |
В [3] был специально введен термин «заполнение» или
«лакунарность» (lacunarity) для описания тех характеристик фракталов,
которые имеют одинаковые размерности, но разный внешний вид или
текстуру. Было предложено несколько альтернативных определений
для этого признака, но самый полезный имеет вид
А{щ-'])- (9-23)
где М- масса фрактального образования; <М> - ожидаемая масса.
Заполнение Л определяет разницу между фактической массой и
478
9.3. Сегментация текстур с помощью фрактального анализа
ожидаемой. Заполнение относится к статистическим
характеристикам второго порядка и изменяется следующим образом: заполнение
мало для плотной текстуры и велико, когда текстура
крупнозернистая. В [3] показано, что
M(L) = KLD,
т.е. заполнение является функцией L. На практике [467] заполнение
предлагается вычислять из того же самого распределения
вероятности Р(т, L), которое используется для определения фрактальной
размерности
M4L)-[M(L)?
АЩ~ [M(L)f ' (У24)
где M(L)=^mP(m,L), M2(L)=^m2P(m,L).
т=\ т=\
На рис. 9.6 показаны функции заполнения в зависимости от L
для восьми рассмотренных текстур. Сравнивая данные табл. 9.4 и
рис. 9.6, можно отметить, что хотя D указанных текстур схожи,
функции заполнения имеют разное поведение, особенно при малых L.
Это дает основание говорить о том, что характеристики фракталов
можно использовать для описания естественных текстур.
Распознавание текстур можно повысить использованием комбинации
фрактальных характеристик и других статистических признаков по
градациям серого тона.
Вероятность Р (т, L) содержит усредненную информацию
распределения массы по фрактальному образованию. Как показано в [3],
заполнение тесно связано с распределением массы. Определение
заполнения, соответствующее формуле (9.23), хорошо работает для
больших по площади текстур, но оно не обеспечивает адекватного
различения для меньших кусочков, встречающихся в процессе
сегментации. В [467] введена другая величина для измерения
заполнения, также использующая функцию Р(т, L). Для каждого значения
L можно записать
M(L)-N(L)
C{L)-M(L) + N(Ly {*-25)
479
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
0,75
0,65 А
0,55-|
0,45
0,35 ^
0,25
0,15
-+• -2
-* -3
-^ -4
♦ -5
<у -6
-+- -7
t ■
10
1 1 ■
20
1 i '
30
' 1
40
j
50
L, отн. ед.
0,05
Рис. 9.6. Функции заполнения Л для восьми естественных текстур:
1 - кора дерева; 2 - свиная кожа; 3 - трава; 4 - песок; 5 - вода; 6 - дерево;
7 - шерсть; 8 - рафия [467]
где М(L) — усредненная плотность массы внутри куба со стороной
L; N(L) - число, пропорциональное числу кубов со стороной L,
необходимых для полного покрытия фрактального образования.
Фактически, N(L) есть число покрывающих образование кубов,
деленное на число точек в данном фрактальном образовании, т. е.
N(L) - это часть куба, содержащая одну точку. Для текстуры, когда
ее мельчайший элемент меньше размера куба, масса фрактального
образования будет равномерно распределена в каждом кубе.
Следовательно, M(L) и N(L) приблизительно равны, a C(L) будет
близка к нулю.
Если мельчайший элемент текстуры велик по сравнению с
кубом, то плотность массы будет большая, и число кубов,
необходимых для покрытия, мало. Тогда C(L) -»1. Естественно, с ростом L
значение С (L) -»1 для всех фрактальных образований. Поэтому
значения С (L) для малых размеров кубов будут содержать информацию
о текстуре. Однако значение, при котором C(L) приближается к
единице, также отражает размер мельчайшего элемента текстуры.
480
9.4. Фрактальная кластеризация данных дистанционного зондирования
9.4. Фрактальная кластеризация данных
дистанционного зондирования
Исходные положения. Анализ современного состояния
проблемы классификации данных дистанционного зондирования
показывает [479], что ее наиболее эффективное решение возможно лишь в
автоматическом режиме с использованием адекватных алгоритмов
для компьютеров. Ввиду большого разнообразия методов,
используемых на практике, предварительно кратко рассмотрим методы
кластеризации изображений. Практически все методы распознавания
изображений можно разделить на две группы [99, 100, 184, 452].
Первая основана на понятии пространства признаков и обработки в
этом пространстве, вторая - на исследования структуры
рассматриваемых образов (синтаксическое распознавание).
Для изображений характерны признаки, основанные на
выделении пространственных частот и измерении статистических
характеристик уровней интенсивности. К последним относятся
текстурные признаки [184, 463, 464].
Вариограмма. Рассмотрим фрактальные подходы к
распознаванию изображений. В [46] использована концепция вариограмм и
понятие фрактальной размерности для классификации природных
текстур. Вариограмма V(h) для текстур вводится следующим способом.
Пусть множество случайных функций G^coe Q) описывает
определенный класс текстур, а (7 - реализацию конкретной тексту-
ры. Тогда для рассматриваемого класса изображений при векторе
пространственных координат х имеем
E[G(u(x)-G(0(x + h)]=m(h), (9.26)
Е^(х)-0„(х + /1)]2}-т2(/1) = 2У(/1). (9.27)
При условии стационарности, как известно, выполняется равенство
V(h) = o2[l-p(h)l (9.28)
где с2 — дисперсия процесса с коэффициентом автокорреляции р(Л).
В общем случае условия стационарности для земных покровов
и окружающей среды не выполняются, что иллюстрируется
данными рис. 9.7 для облачного покрова. Реальная функция V(h) (кривая
1) не совпадает с функцией (9.28), показанной кривой 2.
16 Фракталы
481
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Щ)
261
24 J
22 J
20-
18-
16-
14-
12-
10-
8-
б-
4-
2-
л_
0-
с
1
2
■ 1
4
1
6
1 V
"Т"
10 12
У^>2
i f'
14 16
18 20
h
Рис. 9.7. Влияние нестационарности на изображение облачного покрова
в зависимости от шага квантования [46]
Рассмотрим различные модели для V(h), описывающие
достаточно разнообразное число природных текстур. Значение V(h),
определенное равенством (9.27), может быть записано в виде
К(А) = К(А1, A2) = -i- X [G(xv x2)-G(xx+hl9 х2 + Л2)]2, (9.29)
х=(х±, X2)eU
где h = (Aj, A2) мало по сравнению с размером области г/образа; TV-
число элементов в равенстве (9.29).
Значение V(h) априори зависит от ориентации вектора А. Если
образ не анизотропен, то можно считать h = (hf + h%)1/2 и
исследовать однопараметрическую вариограмму V(h). Точной
аппроксимацией (9.29) является выражение
— X (°(Х1 + h>X2> ~ G(*l>*2))2 +
2N
дс=(х1,х2)е£/'
+ (G(xl,x2+h)-G(xl,x2))
(9.30)
482
9.4. Фрактальная кластеризация данных дистанционного зондирования
которое легко вычисляется при обработке данных. Значение V(h)
также зависит от выбора окна. С увеличением окна значение (9.29)
приближается к пределу. Но если {/очень большое, то
предположение об однородности текстуры может не выполняться.
Экспериментально наблюдалось [46], что для достоверного описания
статистического значения V(h) при he [Amin, Amax] размер окна должен
составлять около 3/*тах.
Текстурные модели. Наиболее часто используется
математическая модель кривой V(h) в экспоненциальном виде [46]:
V(h) = C[l-exp(-h/a)], (9.31)
где Си а — положительные константы.
Модель (9.31) хорошо описывает текстуры городских застроек,
холмистой местности и растительности. На рис. 9.8 представлен
I i \ i г i i i » > 1
0 2 4 б 8 10 12 14 16 18 20
Рис. 9.8. Спутниковый снимок лесного холма с измеренной (кружки)
и смоделированной (линия) вариаграммой [46]
483
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
снимок лесной местности, полученной с помощью ИСЗ «Landsat» на
третьем канале зондирования. Там же нанесены экспериментальные
(точки) и теоретические (сплошная линия) значения V(h).
Горизонтальная асимптотика V(h) отражает тот факт, что на расстоянии Л0
соответствующее влияние хих+А0 незначительно.
Следующая модель определяется формулой
V(h) = Ch + b (9.32)
с константой Ъ. Результаты моделирования по (9.32) показаны на
рис. 9.9 для изображения облачного покрова, полученного с
помощью платформы NOAA-7 (второй канал), и соответствующего
данным рис. 9.7.
Рис. 9.9. Спутниковый снимок облачного покрова с измеренной (кружки) и
смоделированной (линия) вариаграммой [46]
484
9.4. Фрактальная кластеризация данных дистанционного зондирования
Степенная модель вида [46]:
V(h) = Cha
(9.33)
хорошо описывает лесную местность. В качестве примера на рис. 9.10
приведено инфракрасное (ИК) изображение пихтового леса с
пикселем около 3 см2 на местности.
Щ)
3500-
3200-
2800-
2400-
2000-
1600-
1200-
800-
40-j
п J
с
1
1 2
• J^
I t 1 1 i
4 6 8 10 12
ii мШ^^'^ВгаШ'*? жДЯ
^^НШ^н^^&Я^^Шш л Щл
1 1 1 1
14 16 18 20
Рис. 9.10. Спутниковый снимок пихтового леса в ИК-диапазоне с измеренной
(кружки) и смоделированной (линия) вариаграммой [46]
Комбинированные модели описывают разнообразные текстуры
с различным масштабом. Для примера на рис. 9.11 показано ИК
изображение елового леса, которое промоделировано функциями
V{h) = Cxh + bv 0<h<hd,
V(h) = C2h«, h>\.
(9.34)
Здесь Cv C2, a — соответствующие константы. Заметим, что hQ
соответствует 20 см на местности.
485
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Щ)
2700-1
2400-1
2100-1
1800-1
1600Н
1200Н
900-1
600-1
300-1
о4
т
ТЧ 1
1 ii il 2I
h
Рис. 9.11. Спутниковый снимок елового леса в ИК-диапазоне с измеренной
(кружки) вариаграммой и комбинированная модель вариаграммы (линия) [46]
Пример специального случая, не описываемого
рассмотренными моделями (9.31)-(9.34), приведен в ссылках [46, 479]. Данный
случай соответствует полевой местности и получен системой Landsat
(третий канал). Наблюдаемая псевдопериодичность V(h) при h > h0
обусловлена изменением текстуры поля. Поэтому здесь возможно
применение корреляционного анализа и фурье-преобразований.
Фрактальные модели. Применение к описанию различных текстур
фрактального анализа, как показано в [46], позволяет считать, что
K(A)-qA**, he[Q,hmSK].
(9.35)
Теоретически нижняя граница для h равна нулю. Фактически,
AelAiin' Anax]> ^min>^- Фрактальная размерность из (9.35)
задается выражением
D = 3-C,
(9.36)
486
9.4. Фрактальная кластеризация данных дистанционного зондирования
Поверхность фрактальна, если D > 2. Следовательно^ G(x)
будет фракталом, если обе постоянные Сх и С2 удовлетворяют
формуле (9.35). Тогда фрактальная размерность будет равна (9.36).
Достойно внимания то, что модели (9.32) при Ъ = 0 и (9.33) имеют форму
соотношения (9.35).
Для данных рис. 9.9 и модели (9.32) было получено D = 5/2. Для
модели (9.33) фрактальная размерность D = 3-oc/2. Например,
данные рис. 9.10 показывают, что фрактальная размерность
изображения лесного массива D = 2,67. Для елового леса при h < h0 имеем
D~ 5/2 и при h > h0 D~ 2,88 [46].
Из выражения (9.35) следует, что если V(h) ограничена, то она
не может описывать фрактал, так как С2 = 3 - D > 0. Для примера,
данные рис. 9.8 не описывают фрактальный объект. Кроме того, фрак-
талъностъ объекта не предполагает возможность определения
корреляционной функции, а только существование вариограммы V(h).
Для функции V(h) необходимо выполнение условия
1ипГК(Л)/й2] = 0, что приводит к неравенству ос< 2 в соотношении
(9.33) и означает D = 3-oc/2>2.
Распознавание текстур. Знание констант в моделях позволяет
распознавать различные классы текстур. Рассмотрим модель вида (9.31).
Тестовая выборка из 22 групп спутниковых данных (Landsat, третий
канал) для коэффициентов а и С приведена на рис. 9.12 для текстур
городских застроек (точки), полей (крестики) и лесов
(треугольники). Заслуживает внимания то, что коэффициент а, в отличие от С,
является хорошим индикатором типа текстур. Значения а для
городских застроек находятся в пределах 1,0-1,7 со средним 1,6, для
полей — 1,8—3,1 со средним 2,3, для лесных массивов — 3,1—4,0 со
средним 3,2.
Практически коэффициенты Спав модели (9.31)
определяются следующими выражениями
C=]imV(h) = (G2(x)),
« = -Г/1оЕ[1-К(1)/С^], (9'37)
где U- размер сканируемого окна по изображению.
В [46] рассмотрено также применение модели (9.31) для
синтеза текстур земных покровов в качестве этапа формирования темати-
487
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
а
▼
▼
+
+
.л
• • •
J I I I I I I
20 40 60 80 100 120 140 160 180
С
Рис. 9.12. Разделение классов текстур в параметрическом пространстве: городские
застройки (точки), поля (крестики), леса (треугольники) [46]
ческих карт местности. Полученные результаты и выводы
находятся в хорошем согласии с данными автора [184, 230, 459, 484], хотя и
отличаются подходами.
Влияние пространственного разрешения на функцию V(h)
исследовалось для синтезированных изображений при различном
коэффициенте масштабирования г (изображение с разрешением грхгр
получалось из оригинала с разрешениемрхр). На рис. 9.13
показано семейство функций V(h) с десятью различными
пространственными разрешениями. В качестве оригинала использовалось
изображение холмистого лесного массива, полученное системой Landsat на
третьем канале. Видно, что рост г уменьшает спад кривых, а также
асимптотическое значение коэффициента С, в результате чего
ослабляется общий контраст изображения. Из рисунка следует также, что
это значение Сдостигается более быстро при уменьшении разреше-
j,u г
4,0 к
з,о F
2,0 к
i,o U
488
9.4. Фрактальная кластеризация данных дистанционного зондирования
1 i I I I I 1 I \ I I
О 2 4 6 8 10 12 14 16 18 20 h
Рис. 9.13. Семейство кривых V{h) для разных г = 1-10 [46]
ния (т.е. при увеличении значения г), что вызывает дополнительную
потерю информации.
Кривые зависимости а от коэффициента масштабирования г для
текстур изображений города, поля и леса показаны на рис. 9.14, я и
от длины волны X при дистанционном зондировании лесных
массивов на холмистой местности и равнине - на рис. 9.14,5. С точки
зрения классификации данные рис. 9.14,я подтверждают увеличение
трудностей различения текстур при уменьшении
пространственного разрешения. Так, при г > 5, что соответствует пикселу 150 х 150 м2,
невозможно различить текстуры городской застройки. Лесные
массивы с большей пространственной корреляцией хорошо различаются
от других типов местности. Поэтому разрешение в 30 м (г = 1)
более соответствует разделению текстур городских зон и полей, а
коэффициенты масштабирования г = 3—10 подходят для
классификации лесов и полей.
Влияние длины волны на значение коэффициента а в (9.31)
иллюстрируется данными рис. 9.14,б для каналов 1-7 (кроме шес-
489
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
т 1 1 1 1 1 1 I 1 л т 1 ■ ■ i 1 1 1
123456789 10 v 1 2 3 4 5 7
г Канал X
а) б)
Рис. 9.14. Зависимость параметра а от коэффициента масштабирования г
для текстур изображений города (1), поля — (2), леса — (3) и от длины волны X
при дистанционном зондировании лесных массивов на холмистой
местности (кривые 1) и равнине (кривые 2) [46]
того), работающих в диапазоне волн 0,45; 0,52-0,6; 0,63-0,69; 0,76-
0,9; 1,55-1,75; 2,08-2,35 мкм соответственно. Пространственное
разрешение каналов составляло 30 х 30 м2. Канал 6 имел
разрешение 120 х 120 м2 и не был использован в эксперименте. Графики на
рис. 9. Появляются спектральными сигнатурами для текстур леса.
Эволюция кривых а(Х) для городской территории (кривые 1),
поля (кривые 2), равнинного леса (кривая 3 на рис. 9.15,я) и
холмистого леса (кривая 3 на рис. 9.15,6) представлена на рис. 9.15.
Коэффициент а стабилен для изображений городов. Для
культивированных полей значение а изменяется с длиной волны излучения, но все
же видно явное его отличие от значения а для городских
территорий. Третий канал оптимален, к примеру, для различения
городских застроек от полей (рис. 9.15,д), четвертый канал - для
классификации равнинных и холмистых лесов (рис. 9.15,6) и т.д.
Высокая изменчивость параметров в природных ландшафтах
приводит к специфике методов исследования, например к методу
вариаграмм. Данный метод обобщает метод автокорреляционной
функции, который пригоден только для строгих гипотез. Более того,
если автокорреляционная функция не может быть определена, то
существование фрактальной размерности очевидно в методе
вариаграмм.
490
9.5. Многоуровневая фрактальная модель для характеристики объектов
Канал X Канал А,
а) б)
Рис. 9.15. Эволюция кривых а в зависимости от номера канала (длины волны)
t для городской территории (кривая 1), поля (кривая 2), равнинного
леса (кривая 3 на рис. а) и холмистого леса (кривая 3 на рис. б) [46]
9.5. Многоуровневая фрактальная модель
для характеристики объектов
Универсальное описание естественных и антропогенных
объектов в оптическом диапазоне представлено в [485]. Здесь
фрактальная размерность рассчитывается как фрактальная сигнатура для
различения поверхностных неровностей. Фрактальные сигнатуры,
полученные с помощью морфологического фильтра, использованы для
идентификации ландшафтов и объектов военной техники на фоне
земных покровов. Оценка фрактальной размерности проводилась
модифицированным методом покрытий, разработанным для анализа
текстурных изображений [486].
Метод покрытий в анализе текстур. Суть данного метода
состоит в том, что квантованные значения интенсивности двумерного
сигнала должны располагаться между двумя функциями,
называемыми верхней и нижней поверхностями. Верхняя поверхность
г/содержит множество точек, значения которых всегда, по крайней мере,
на один квант превышают интенсивность входного сигнала.
Нижняя поверхность L имеет значения точек, которые всегда ниже, по
крайней мере, на один квант интенсивности входного изображения.
491
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Верхняя и нижняя поверхности при нулевой шкале масштабов
определяются как
U(iJ,0) = L(iJ,0) = g(iJ), (9.38)
где g(i,j) — входное изображение. В общем случае
U(iJ,z +1) = max\U(iJ,t) +1,max[U(k,m,t)] ,
L к,тет\ J
L(ij\z + l) = min\L(ij\z)-l,min[L(k,m,z)]
l к,теч\
где г| = {(к,т) | расстояние [(к,m),(i, j)] < 1}.
Сконструированное покрытие, образованное двумя указанными
функциями, имеет толщину 2е. Для двумерного сигнала площадь
«поверхности» есть объем, занятый покрытием и деленный на
величину 2е. Площадь «поверхности» интенсивности А(г) в пределах
окна наблюдения R рассчитывают вычитанием точки за точкой
нижней «поверхности» из верхней с дальнейшим суммированием по
всему окну:
X U(iJ,t)-L(ij\t)
Де) = -^ = ^. (9.40)
2е 2е
Фрактальную размерность определяют по наклону log А(г) как
функцию log е. В [486] измеряемая «поверхность» А^г) определяется
разностью объемов при последовательных масштабах:
Al(t) = {V(z)-V(z-l))/2. (9.41)
На основе (9.40) получаем
У(г) = 2гА(г). (9.42)
Тогда из [3] имеем
У(г) = 2Кг3-в, (9.43)
где К- постоянная величина.
492
9.5. Многоуровневая фрактальная модель для характеристики объектов
Рассчитанное значение Ax(z) является аппроксимацией
производной V(e) по 8 и определяется по формуле
A(e)~0,5<^ = (3-D)Kz2-d. (9.44)
1 дг
Реальные изображения всегда имеют шумовую составляющую,
поэтому расчет А{(г) по (9.44) может дать оценку шума. В качестве
примера на рис. 9.16,а приведено изображение размером 32 х 32
пиксел дерева, а на рис. 9.16,5— соответствующие фрактальные
сигнатуры, рассчитанные по формулам (9.40) и (9.41). Значения Д
соответствующие (9.40), находятся в ожидаемом диапазоне от 2 до 3 при
котором D — 2 соответствует плоской поверхности. Фрактальная
сигнатура, рассчитанная по (9.41), превышает допустимую верхнюю
границу, равную 3. Следовательно, расчет по производной дает
сильную шумовую составляющую.
Рис. 9.16. Изображение дерева (а) и фрактальные сигнатуры (б),
определенные по формуле (9.40) - кривая 1 и (9.41) - кривая 2 [485]
Фрактальная размерность D (/, j) при нахождении пиксела (/, j)
на всех масштабах оценивается в [487] как взвешенная сумма
локальных фрактальных размерностей Fz(iJ) в виде
WJ) = lC£Ft(iJ)^C£ (9.45)
е / е
493
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
при
с ^ loge-log(e-l) р =logA(iJ,t)-logA(iJ,t-l) g
log2 ' e loge-log(e-l)
Вследствие свойства масштабирования фракталов величина
F(i,j) является результатом деления A(i, j, е) на A(i, j, е-1):
А(Ш-1) К(г-1Я^
Логарифмируя (9.47), имеем
logA(iJ,z)-logA(i,j,E-l)
( с \2'D
г
е-1
(9.47)
loge-log(e-l)
= 2-D = F0J). (9.48)
Локальные фрактальные размерности FE(i,j) рассчитывают
только на промежуточных этапах. Затем последовательные значения
Fe(i,j) накапливаются с определенными весами по всему
диапазону шкал для получения оценки фрактальной размерности D (/, j).
Соотношение (9.45) является функцией только первой и последней
шкал масштабов.
Элемент суммы числителя в (9.45)
C/£(/,y) = {logH(e)]-logU(e-D]}/log2.
Тогда
Хс/е(/,7,е)={ад^
е
-logM(/)7,e-2)]+logH(/)7,e-2)]-...-logM(/)7)l)]}/log2 =
= {\og[A(i,JM-\o%[A{i,j,\)]}l\og2, (9.49)
а ХСе = fl08 £ " 10ё(£ - *) +108(£ - *) " l08(£ ~ 2) +
е
+ log(e-2)-...-log(l)]/log2 = [loge-log(l)]/log2.
Уравнение (9.49) показывает, что оценка фрактальной
размерности определяется наклоном, порождаемым первым и последним
494
9.5. Многоуровневая фрактальная модель для характеристики объектов
масштабами, в то время как промежуточные масштабы не дают
вклада в расчеты.
Морфологическое осуществление метода. Рассматриваемый
метод покрытий для нахождения D прост и одновременно эффективен
в реализации. Он определен в рекурсивной форме, позволяющей
вести расчеты при больших массивах данных. К тому же метод имеет
морфологическое осуществление, что дает возможность
использовать расчетные преимущества морфологической обработки.
Расчеты верхней и нижней поверхностей по (9.39) эквивалентны
морфологическому расширению и разрушению [488]. Данные операции
определяются как:
разрушение: (g © к) (х, у) = min{g(x + п, у + т) - к(п, т)}, п,те Ros(k),
расширение: (g®k)(x,y) = max{g(x + n,y + m) + k(n,m)}, n,meRos(k).
Здесь (к) - двумерные фигуры, размер, форма и пространственная
ориентация которых определяют фильтрующие свойства; Ros(£) -
область содержания к. Данные о выходной точке получаются
расположением ядра к на определенной доле входного образа и
действием min-оператором (при разрушении) или max-оператором (при
расширении) на значения, объемлемые ядром. Такая операция
повторяется при перемещении ядра по всему образу g.
Разнообразие функциональных морфологических операций
может быть достигнуто использованием этих простейших действий.
На рис. 9.17 показано создание верхней Un нижней L
«поверхностей» при различных масштабах. Можно считать, что изображения
являются комбинацией различных сероуровневых «поверхностей»,
которые самоподобны в определенном диапазоне масштабов и
поэтому их соответствующие фрактальные размерности стабильны на
малом числе шкал. Схема расчета фрактальной сигнатуры по
формуле (9.40) морфологическим фильтром приведена на рис. 5 в [485]
и на рис. 53 в [479].
Каждая точка изображения (к, I) определяется оценкой
площади при масштабе 8. Для начальной нулевой шкалы верхние и
нижние «поверхности» идентичны и равны истинному изображению (см.
(9.38)). Для конечного числа масштабов оценка А (к, /, 8) следует из
соотношения
495
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
k/Y\J
I
ffl
а) в)
б) г)
Рис. 9.17. Конструирование верхней Un нижней L «поверхностей»
при различных масштабах:
а — истинный одномерный сигнал; б - масштаб е = 1; в - е = 2;г- е=3 [485]
k+w l+w
£ £ U(i,j,e)-L(i,j,t)
A(k,l,e) = '+" »* , ,
2е
где окно размером (2w + l)x(2w + 1) имеет переменные размеры,
устанавливаемые нижней и верхней шкалами масштабов.
Фрактальное распознавание природных объектов. Неровности
природных объектов могут меняться в различных масштабах. В [485]
рассматривается четыре ИК-изображения (размером 256 х 190) двух
классов облаков - 1 (типа а, б) и 2 (типа а, б). Соответствующие
фрактальные сигнатуры приведены на рис. 9.18. Можно отметить, что
текстуры одной и той же категории дают в результате подобные
сигнатуры.
При использовании фрактальных сигнатур для определения
объекта или природных текстур важно установить условия их
независимости от размеров окна. В исследованиях применялись три
природные сцены в ИК и оптическом диапазонах: два класса
облаков и лесной массив размером 64 х 64 [485]. Класс изображений
облаков 1 (тип б) был разделен на две вертикальные равные части.
Соответствующие сигнатуры целого изображения и половинок
(заштрихованные квадраты) показаны на рис. 9.19,а. Все три сигнатуры
достаточно точно совпадают друг с другом.
496
9.5. Многоуровневая фрактальная модель для характеристики объектов
Рис. 9.18. Фрактальные сигнатуры
четырех изображений двух классов
облаков [485]
Далее класс изображений
облаков 2 (тип б) был разделен
на две горизонтальные и две
вертикальные половины.
Рассчитанные сигнатуры показаны
на рис. 9.19,5 и в. Фрактальные
сигнатуры половинок изображе-
30^
2,6-
2»5:
2»4:
2,3-
2,2-
2»V
2,0-
■— — 2(<)
» — 2(»)
—О 1(1)
• — 1(a)
- - - 1
S*5^^*»*^^
^^^ппЩПЩ
■ i ■ i'
10
20
ний расположены вокруг сигнатуры полного изображения. Однако,
сигнатуры левой и правой половинок изображения гораздо ближе к
сигнатуре целого изображения, чем сигнатуры вертикальных
половинок. Следовательно, левая и правая половинки изображения имеют
Рис. 9.19. Последовательность фрактальных сигнатур:
а - класс Цтип б) изображений облака; б— класс 2 (тип б) изображений облака с
их правыми и левыми половинами; в - класс 2 (тип б) изображений с их верхними
и нижними половинами; г — изображение лесного массива [485]
497
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
более схожие текстуры, чем другие половинки. Сигнатуры полного
изображения леса и верхней левой четверти изображения
приведены на рис. 9.19,г. Во всех примерах фрактальные сигнатуры
относительно постоянны и слабо меняются при изменении масштаба.
Фрактальное распознавание искусственных объектов. В
предшествующих исследованиях считалось, что в окне имеется только
интересующая нас единственная текстура, и нет кромок и
антропогенных объектов. В [489] предложен адаптивный алгоритм, основанный
на концепции кромкосохраняющего сглаживания для правильной
оценки фрактальной размерности в
окрестности краев. Для двух
однородных областей в [466]
экспериментально показано, что
измеренная фрактальная размерность при
всех масштабах меньше
топологической размерности.
В то же время в [485] показано
с использованием метода покрытий,
что кромки проявляют себя как
неровные поверхности при больших
масштабах и имеют фрактальную
размерность, превышающую
топологическую. Для иллюстрации
этого факта приведены результаты
экспериментов с синтезированными и
реальными изображениями.
На рис. 9.20,а приведено
изображение квадрата с геометрическим
размером 32 х 32 пиксел на черном
фоне с соответствующей
фрактальной сигнатурой (рис. 9.20,в).
Изображение ступенчатой кромки и ее
фрактальной сигнатуры дано на рис.
9.20,5и рис. 9.20,в соответственно.
Для обоих случаев неровности уве-
е)
Рис. 9.20. Изображение квадрата на
черном фоне (а), ступенчатой кромки (б)
и их фрактальные сигнатуры (в) [485]
498
9.5. Многоуровневая фрактальная модель для характеристики объектов
личиваются с возрастанием масштаба, и всегда значения D больше
топологической размерности DQ. Аналогичные результаты получены
для реальных изображений горной местности.
В приведенных экспериментах условие D < DQ может иметь
место для аномально малых образований. Иллюстрацией данного
положения являются результаты исследования фрактальных сигнатур
узких перепадов яркости на изображениях 32 х 32 пиксел,
приведенные на рис. 9.21. Вся сигнатура для узкого перепада яркости (рис.
9.21,а) состоит из D< 2, а для более широкого перепада яркости (рис.
9.21,6) это происходит только на некоторых масштабах. Для
изображения дерева (рис. 9.21,г) значение D< 2 наблюдается только при
е> 6 (рис. 9.21,д).
Рис. 9.21. Изображения узкого (а) и широкого (б) перепадов яркости, а также
дерева (г), с их фрактальными сигнатурами {в, д) [485]
Искусственные объекты состоят из относительно гладких
частей, поэтому их фрактальные сигнатуры будут отражать гладкость на
малых масштабах и неровность при больших е. С учетом того, что
фрактальные сигнатуры земных покровов относительно постоянны,
возможно создание эффективных алгоритмов идентификации целей
на фоне земной поверхности. Эксперименты в [485] проводились с
499
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
тремя классами изображений (32 х 32 пиксел): растительный покров,
деревья и средства передвижения - машина и два танка.
Соответствующие фрактальные сигнатуры приведены на рис. 9.22.
Рис. 9.22. Фрактальные сигнатуры для движущихся (машина и танки)
объектов (я), деревьев (б) и фона (в) [485]
Образцы изображений фона имели почти постоянные
неровности в большинстве масштабов. Два из трех образцов обладали
относительно большими значениями D. Для изображений деревьев
фрактальная сигнатура имела слегка увеличивающийся наклон. Для
изображений танков было отмечено резкое возрастание значений D при
увеличении е. Сигнатура джипа более похожа на сигнатуру
деревьев, чем на сигнатуру танков. Поэтому танки на фоне растительных
покровов эффективнее обнаруживать по изменениям наклона
фрактальных сигнатур.
Распознавание, основанное на использовании единственного
масштаба, иллюстрируется в [485] на изображении зданий на
склоне горы. Объекты типа зданий на изображении имеют более
высокую яркость. Из-за «гладкой» структуры яркостного поля они обла-
500
9.6. Различение человеком-оператором фрактальных текстур
дают низким значением фрактальной размерности. При пороге
разделения, равном 2,2 на шкале е= 2, результаты фрактальной
обработки позволяют выделить здания, ранее замаскированные фоном.
Одношкальное обнаружение танков между деревьями также
было проведено в [485]. Результаты фрактальной обработки
показали, что большинство образов танков сохранено на изображении при
значительном снижении влияния земных помех. Фон частично
сохранился, вследствие многомасштабности его характерных
неровностей и размеров. Таким образом, использование фрактальных
сигнатур для задач обнаружения и идентификации различных целей
является основой многообещающих методов.
В [490, 800, 815] рассмотрен метод распознавания
искусственных объектов на фоне природного пейзажа, основанный на модели
фрактальности, т.е. системы характерных геометрических
признаков. Представлено описание модели в форме набора уравнений
плоскостных кривых и показано, что такие признаки целей, как прямые
линии, образующие силуэты, могут быть использованы для
обнаружения объектов. Приведены результаты экспериментальных
исследований по выделению танков и морских судов на естественном фоне
с помощью ИК датчика изображений и алгоритма фрактального
оценивания.
Применение теории хаотических и мультифрактальных
колебаний для обработки радиолокационных сигналов при определении
параметров цели и ее идентификации исследовано в [491]. Методом
корреляционных интегралов получены оценки размерности
эхо-сигналов от множественных целей. Рассчитаны показатели Ляпунова
для пяти различных сечений, характеризующих сходимость
результатов. Экспериментальное сравнение результатов распознавания
радиолокационных целей показало, что применение теории
хаотических колебаний и фракталов весьма перспективно при обработке
радиолокационных сигналов и идентификации радиолокационных
целей.
9.6. Различение человеком-оператором
фрактальных текстур
Ряд экспериментов по различению человеком фрактальных
текстур был выполнен в [492]. В исследованиях применялись
изображения, синтезированные на основе модели обобщенного броуновс-
501
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
кого движения (2.4). Пространственный спектр мощности
двумерного изотропного процесса записывается в виде
G(f) = K/f\
(9.50)
где К— постоянная; / = (/2 +2 )Ш; а = 8 - 2D — спектральный пара-
х у
метр; fx — пространственные частоты.
На рис. 9.23 в логарифмических координатах показаны
пространственные спектры мощности (вернее, их проекции) двух
фрактальных процессов с D = 2,5 (а = 3) и D = 3 (а = 2). Видно, что
спектры спадают линейно с наклоном, задаваемым спектральным
параметром. Реализации отдельных хаотических синтезированных
изображений из выборок представлены в [492]. Наблюдаемое
различие в текстурах дает также дополнительное свидетельство о связи
текстурных характеристик с фрактальной размерностью.
Изображения размером 64 х 64 пиксел и диапазоном
пространственных частот в пять октав отображались на экране дисплея с раз-
6*]logG(/)
4
2
ОН
•21
А'
-в
-в
.10
-124
•и4-
5
log/*
Рис. 9.23. Проекция пространственного спектра мощности обобщенного
броуновского процесса при а = 2 и а = 3 [492]
502
9.6. Различение человеком-оператором фрактальных текстур
решением 1152x900 точек. Среднеквадратичная величина
контраста ансамбля текстур
С =
nw*>f>w*#y-m2)/m2
V2
(9.51)
где т — среднее по ансамблю.
Для пространственно-изотропных текстур (9.51) преобразуется
к виду
С = \2к
]fG(f)df
•г
(9.52)
где/определено в (9.50).
Синтезированные изображения масштабировались так, чтобы
значение среднеквадратичного контраста равнялось 35%.
Эксперименты ставили задачу, в которой три оператора должны были
ответить на вопрос, какой из двух образов относится к ансамблю с более
высокой размерностью. Для оценки порога различимости
спектрального параметра использовалась усовершенствованная процедура
лестничного типа QUEST. Пороги были определены для десяти
значений: ос = 0,8; 1,2; 1,6; 2,0; 2,4; 2,8; 3,2; 3,6; 4,0; 4,4. Пороги
различимости выбирались для трех ситуаций: 1 — высококонтрастная
близкая (ВБ), 2 - низкоконтрастная близкая (НБ), 3 -
высококонтрастная далекая (ВД). Высоко контрастному близкому условию
соответствовало расстояние 1 м до экрана и среднеквадратичный
контраст 35%. Для низкоконтрастных близких среднеквадратичный
контраст был уменьшен до 17,5%. Высококонтрастные далекие
условия соответствовали среднеквадратичному контрасту 35% и
дистанции 1,5 м.
Эксперимент был организован из 12 серий, включающих десять
блоков по 50 испытаний. Результирующие данные состояли из
первоначальных откликов и 12 оценок порога для каждого значения а.
Приращения между эталоном и тестовым изображением изменялись
от -10 до 19 дБ, причем 1 дБ соответствовал 12% возрастанию в
спектральной расходимости. Изображения отображались в течение
250 ± 50 мс с интервалом 500 ± 50 мс. Подробности применения
критерия идеального наблюдателя для автоматизированной оценки а
приведены в [492].
503
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
На рис. 9.24 показаны оценки порога различимости как
функции спектрального параметра для первого (а), второго (б) и
третьего (в) операторов соответственно в трех ситуациях: 1 - ВБ, 2 - НБ,
3 — ВД. Значения среднеквадратичного отклонения оценок
показаны на правой стороне каждого рисунка. Горизонтальные линии над
кривыми характеризуют границы диапазона спектрального
параметра, определяющего фрактальные ансамбли. Кривые порогов имеют
общие черты, а именно: спад во фрактальной области и, при
некоторых условиях, второй спад для наименьшего спектрального
параметра.
Указанная задача различения может быть выполнена и несколько
иначе. Как видно из рис. 9.23 спектры мощности ансамблей с
различными значениями спектрального параметра, но равными
среднеквадратичными контрастами, имеют точку пересечения на опре-
ю
8
6^
4
21
01
-2
-4
-И
Да, дБ
(^8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8
О)
10 1
8-
6 ■
4 -
2 -
0 ■
-2 •
-4 -
-6 <
-8 .
Да, дБ
X,
»*>
t
t
*
'A
f /
* \
/ /ч.
^^£f
к^^У \
\y^^ I
ТТГ.—2
—• -3
—— \4
" '1 ■ I1 ■ 1 ■ 1 ■ 1 ■ >
0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8
в)
10
8
6-j
4-1
2
0
-2
-41
-6 4
Да, дБ
1 I ■ I » I ' ' I ' 1"^ T " I » 1 ' T ' I » I
0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8
v а
*)
Рис. 9.24. Кривые порогов
различения для первого (а), второго (б)
и третьего (в) операторов [492]
504
9.6. Различение человеком-оператором фрактальных текстур
деленной частоте/0. Этот факт предполагает стратегию для решения
задачи различения в низкочастотном (НЧ) или высокочастнотном
(ВЧ) диапазонах.
При моделировании заранее имелась информация о частоте
пересечения/о для каждого значения спектрального параметра.
Первая группа НЧ моделей использовала переменное решение,
даваемое соотношением
лЛ-
] fGx{f)df-тА \]
fG2(f)df-т22
1/2
(9-53)
Модель выбирает первое изображение, если А < 1, и второе, если
А > 1. Вторая группа ВЧ моделей основана на выражении
А-Л->
Щ
Щ
\fGx{f)df-m\
/о
]fG2(f)df-ml
/о
1/2
(9.54)
В данном случае модель выбирает первое изображение, когда
А > 1, и второе - в обратной ситуации. Пороги различения обеих
моделей резко снижаются, когда спектральные параметры
изображений уменьшаются. Кривые порогов различения для НЧ модели
показаны на рис. 9.24 под индексом 4.
Усредненные значения порогов различения для трех операторов
(кривые 1, 2, 3 соответственно) при условии обнаружения текстур
со значением ос>2 приведены на рис. 9.25. Видно, что самое
лучшее различение текстур операторами выполняется для а = 2,8-3,6.
Моделирование показало, что абсолютный порог при
использовании критерия идеального наблюдателя обратно пропорционален
корню квадратному из размеров изображения (табл. 9.5). Поэтому
можно определить приемлемую меру эффективности как
возведенное в квадрат отношение порога идеального наблюдателя Лос0 к по-
рогу наблюдения оператора, т.е. Е = (Досо/Дос,.) .
Следовательно, первый оператор имел эффективность Ех - 10%,
второй Е2 = 7%, третий Е3 = 13%.
505
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
да, дБ
А
■ i » i ■ i • i ■—i » i * 1 » i ' 1 » 1 » i
0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8
а
Рис. 9.25. Усредненные кривые порогов различения для трех операторов [492]
Таблица 9.5
Пороги для критерия идеального наблюдателя при а = 3,2 [492]
Размер изображения, пикселы
16* 16 (ЛГ=256)
32x32 (ЛГ=1024)
64x64 (JV =4096)
128 х 128 (N=16384)
Порог, дБ
0,17 (Да = 0,204)
-5,6 (Да = 0,106)
-12,2 (Да = 0,50)
-18,7 (Да = 0,024)
9.7. Детерминированный хаос в сигнатурах и
радиолокационных изображениях земной поверхности
Синергетические модели для радиолокационного отклика. С
классической точки зрения нерегулярность поведения в природе
физического явления обусловлена наличием большого числа степеней
свободы процесса. Радиолокационный сигнал, рассеянный
земными покровами, моделируется как случайный шумовой процесс.
Модели шума весьма успешно подтверждаются в описании процес-
6 J
5 ■]
4 J
3 J
2 J
l j
0 J
-lj
"21
-3 j
-4H
506
9.7. Детерминированный хаос в сигнатурах и радиолокационных изображениях...
са рассеяния электромагнитных волн. Однако прогресс в теории
нелинейных динамических систем позволяет рассмотреть более
детально эту проблему с других позиций.
Теория случайных процессов опирается на эмпирический метод,
помогающий справиться с недостаточной информацией о
физических источниках, ответственных за создание изучаемого явления, но
она (теория) ничего не говорит о причинах случайностей. В
соответствии с теорией нелинейных динамических систем очень низкое
число степеней свободы достаточно для создания
детерминированного хаоса, который сильно нерегулярен. В дальнейшем под
детерминированным хаосом подразумевается хаотическое движение,
порожденное нелинейными системами, для которых динамические
законы будут однозначно определять эволюцию во времени состояния
системы при известной предыстории.
Поведение динамической системы может быть описано в
терминах вариации определенного числа независимых параметров в
многомерном фазовом пространстве. Тогда временное развитие
системы определяется многомерной фазовой траекторией. Область
внутри фазового пространства, в которой сходятся все фазовые
траектории (притягивающие траектории), называется аттрактором.
Размерность аттрактора измеряется числом степеней свободы,
присущих процессу. Эта размерность может иметь и дробное, т.е.
фрактальное, значение, тогда говорят о странном аттракторе.
Хаотические модели успешно используют для описания
гидродинамических процессов. Идея применения таких моделей для
описания радиолокационного отклика весьма привлекательна.
Результаты экспериментов указывают на существование малоразмерного
странного аттрактора, контролирующего обратное
радиолокационное рассеяние от морской поверхности [493, 494].
Эти данные находятся в резком контрасте с традиционным
стохастическим моделированием. Модель шума подразумевает
бесконечное число степеней свободы. Хаотическая модель при конечном числе
степеней свободы способствует более глубокому пониманию
природы рассматриваемого явления. Исследования характеристик
странного аттрактора, контролирующего радиолокационное рассеяние в
диапазоне миллиметровых волн, проведенные автором, кратко
представлены в гл. 12.
Эксперименты. Результаты [493, 494] были получены при
работе на радиолокационной станции (РЛС) с горизонтальной поляри-
507
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Рис. 9.26. Временная выборка
отраженного сигнала [493]
зацией излучения со следующими
параметрами: дальность действия —
4725 м, частота повторения
импульсов — 2 кГц, длительность импульса
- 200 не. Радиолокатор работал в
обзорном режиме, зондируя
поверхность океана вдоль радиальной
линии. Временные выборки
отраженного сигнала в относительных
координатах для фиксированной
дальности приведены на рис. 9.26.
Выборка состояла из 2000 отсчетов.
Экспериментальные данные обрабатывались на основе
корреляционного интеграла с использованием алгоритма временных
реализаций. Этот метод восстанавливает фазовую траекторию при условии,
что размерность вложения превосходит значение (2D +1), где D —
фрактальная размерность аттрактора.
Оценка D находится по наклону графика log C{r) от log r. Если
последовательность оценок сходится к пределу, то в результате
получается истинное значение фрактальной размерности аттрактора.
Если последовательность оценок не ограничена даже при
значительных размерностях вложения 1У, то процесс случаен или определен
большим числом степеней свободы, что обычно для классических
статистических методов.
На рис. 9.27 показаны логарифмические кривые
корреляционного интеграла С(г) при различных значениях размерности
вложения U. С использованием данных рис. 9.27 получены зависимости
корреляционной размерности (кривая 2) странного аттрактора D от
размерностей вложения D' (рис. 9.28). Величина D= 6,4-6,7
определяет размерность странного аттрактора, управляющего
механизмом обратного радиолокационного рассеяния от морской
поверхности. На рис. 9.28 также показана прямая 1, соответствующая гауссо-
вому шуму, для которой нет тенденции к насыщению. Поэтому
гауссовому шуму соответствует аттрактор бесконечной
размерности. Это различие широко используется при обработке временных
реализаций неизвестной природы.
Существование аттрактора морских отражений низкой
размерности показывает, что существенные черты их долговременных
эволюции можно рассматривать как проявление определенного дина-
508
9.7. Детерминированный хаос в сигнатурах и радиолокационных изображениях...
logC(r)
20
10
D
^
/х
/ /2
■ » 1
10
20
Рис. 9.27. Логарифмическая кривая
корреляционного интеграла С(г) при
различных значениях размерности
вложения D' [493]
Рис. 9.28. Анализ размерностей
аттракторов [493]
мического режима с конечным числом переменных. Размерность
D~ 6,5 объясняет причину случайного характера процесса
отражения и позволяет предположить, что не более семи независимых
переменных необходимо иметь для описания процесса,
представленного на рис. 9.26. Динамический режим длился от нескольких
миллисекунд до одной секунды.
Подробное исследование модели детерминированного хаоса для
флуктуации удельной ЭПР морской поверхности при наличии
аддитивных и мультипликтивных шумов (спеклов) проведено в [76].
Изучение спеклов особенно актуально при широком использовании
на практике когерентных РЛС и радиолокаторов с синтезируемой
апертурой высокого разрешения.
Вычисление корреляционного интеграла. Проверка алгоритма
вычисления корреляционной фрактальной размерности была проведена
на примерах аттрактора Лоренца и гауссова белого шума [76].
Графики корреляционного интеграла для модели Лоренца показаны на
рис. 9.29 для размерностей вложения D' = 4, 8, 12, 16и20.
Реализация фазовой переменной модели Лоренца содержала 512 отсчетов на
временном отрезке 50 с. Из рис. 9.29 видно, что для больших
значений г корреляционный интеграл нелинеен. Основываясь на
наблюдениях за динамикой кривых, было решено представить линейную
зависимость только на интервале [-4; -2] значений log C(r).
Зависимости фрактальной размерности аттрактора D от
размерности вложения П изображены на рис. 9.30 (сплошная кривая). До-
509
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
полнительно на рис. 9.30 нанесена линия cD= 2,06, являющейся
фрактальной размерностью аттрактора Лоренца. Можно отметить,
что для значений D' < 10 оценка 2) не соответствует истинной
фрактальной размерности.
D
2,4
Рис. 9.29. Логарифмическая кривая
корреляционного интеграла С(г) для
аттрактора Лоренца при различной
размерности вложения D' [76]
1,6
0
10
15
В
Рис. 9.30. Зависимость фрактальных
размерностей странного аттрактора
(сплошная линия) и аттрактора
Лоренца (штриховая линия) от
размерности вложения D' [76]
Аналогичные результаты для гауссова белого шума приведены
на рис. 9.31 и 9.32. Последовательность из 512 некоррелированных
случайных чисел была получена из выборки гауссова процесса с
нулевым средним и среднеквадратичным отклонением, подобным
временной реализации модели Лоренца. Корреляционный интеграл
для шума изображен на рис. 9.31 для размерностей вложения D' =
4, 8, 12, 16 и 20. Тщательное исследование показало, что ни одна из
зависимостей не является полностью линейной.
Результаты наблюдений объясняют изменения фрактальной
размерности D для гауссова белого шума от размерностей вложения D'
(рис. 9.32 — сплошная линия). Теоретически фазовые траектории для
белого шума насыщаются любым пространством вложения с
размерностью U, а фрактальная размерность будет определяться
штриховой линией. Однако наклон функции корреляционного интеграла
равен размерности вложения лишь при малых значениях D' из-за
неидеальности моделирования выборки шума.
Из сравнения данных на рис. 9.30 и 9.32 следует метод
различения шумовых и хаотических процессов. Для шума наклон корреляци-
510
9.7. Детерминированный хаос в сигнатурах и радиолокационных изображениях...
logC(r)
• • * Г
• 2 •
2,5
3,5
4,5 logr
Рис. 9.31. Логарифмическая кривая
корреляционного интеграла С(г)
белого гауссова шума при различных
значениях размерности вложения D'
[76]
D
20
15
10
5
0
5 10 15 D'
Рис. 9.32. Изменения фрактальных
размерностей 1>для гауссовского
белого шума (теория — штриховая
линия) и экспериментальных
реализаций (сплошная линия)
от размерностей вложения D' [76]
онного интеграла возрастает с увеличением размерности вложения,
для хаотического процесса значение наклона стремится к
постоянному значению, определяющему фрактальную размерность
аттрактора.
Реальные и синтезированные изображения. В [76] описаны
эксперименты, которые проводились для определения фрактальной
размерности реальных и синтезированных радиолокационных
изображений морской поверхности. Реальные изображения были
получены некогерентным радиолокатором сантиметрового диапазона волн
с пространственным разрешением 4,2 х 20 м2 при двух видах
линейной поляризации. Измеренные значения фрактальной размерности
D приведены на рис. 9.33 для трех реальных и трех синтезированных
изображений морской поверхности при вертикальной поляризации
излучения. Отметим, что на реальном изображении присутствует
хаотический процесс со значением D = 3—4. Синтезированное
изображение с шумом показывает эквивалентное поведение кривых.
Радиолокационные образы при горизонтальной поляризации
излучения имеют несколько иной характер зависимости
фрактальной размерности D для реальных (рис. 9.34,я) и синтезированных
(рис. 9.34,6) изображений. Для реальных изображений неочевидно
стремление наклона функции корреляционного интеграла к конеч-
511
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
D
4
3
2
1
0
"
5
■
10
а)
•
15
D'
D
5
4
3
2
1
0
- /
/.
<t
Г
5
~ ^ -L-—
— -*1 ~^^^«U«.
i i
10 15
б)
г!
Рис. 9.33. Измеренные значения фрактальной размерности D для трех
реальных (а) и трех синтезированных (б) изображений морской поверхности
при вертикальной поляризации излучения [76]
J_
-L
10 15
б)
D
Рис. 9.34. Экспериментальные значения фрактальной размерности D для трех
реальных (а) и трех синтезированных (б) изображений морской поверхности при
горизонтальной поляризации излучения [76]
ному пределу. Одновременно синтезированное изображение
показывает наличие малоразмерного хаотического процесса. Различие в
характеристиках реальных и синтезированных образов может быть
объяснено неоднородностью в экспериментальных данных, которая
не учитывалась при синтезе. Неоднородность морской поверхности
из-за внешних условий, а следовательно, и природа странного
аттрактора, изменяется со временем. Поэтому любые измерения
корреляционного интеграла должны быть выполнены во временном
масштабе, когда аттрактор фактически структурно устойчив и типи-
512
9.7. Детерминированный хаос в сигнатурах и радиолокационных изображениях.,.
чен. Однако стремление к точной оценке корреляционного
интеграла приводит к тому, что на практике требуемый компромисс
иногда не обеспечивается.
Влияние аддитивных шумов на корреляционный интеграл. Метод
оценки фрактальной размерности корреляционным интегралом
достаточно широко обсуждается в [495]. Некоторые из недостатков
метода будут освещены далее и использованы для объяснения ряда
противоречивых результатов, полученных в [76]. Так, при недостатке
данных невозможно получить статистически точную оценку в
масштабе малых наклонов и, следовательно, невозможно проверить
степенной закон (1.9) в этом диапазоне. Короткие временные
реализации гауссова белого шума (см. рис. 9.32) приводят к недооценке
корреляционной фрактальной размерности. Кроме того, наличие корреляции
во временных реализациях уменьшает количество независимых
отсчетов. При условии, что данных достаточно, присутствие корреляции
будет фактором, препятствующим сходимости корреляционного
интеграла к постоянному значению при увеличении размерности
вложения. Это ввдно на примере аттрактора Лоренца, когда сходимость
достигается при /У > 10 (см. рис. 9.30).
В [496] показано, что стохастические временные ряды со
спектром мощности типа 1//а могут иметь ограниченную
корреляционную размерность для произвольно больших наборов данных. Если
этот вид аномального поведения встречается в большом классе
спектров, то использование оценки корреляционной размерности для
различения шума и малоразмерного хаоса может быть
малоэффективно. Исследование влияния аддитивных шумов на оценку
фрактальной размерности проводилось в [76] для временных реализаций
из 1500 отсчетов с интервалом в 0,1 с, которые генерировались
системой Лоренца при среднеквадратичном отклонении, равном 7,9.
Шумы моделировались добавлением к каждому отсчету
независимого случайного числа с гауссовым распределением при нулевом
среднем и среднеквадратичным отклонением, равным 1,0.
На рис. 1.7 (см. гл. 1) приведены результирующие функции
корреляционных интегралов для размерностей вложения 4, 8, 12, 16 и
20. Там же выделен параллельными линиями интервал [—2; —4],
соответствующий линейной части корреляционного интеграла.
Отличительной чертой этих кривых является наличие «колена»,
аппроксимирующего середину зависимостей. Выше отмеченной
точки А кривые отображают закономерности, типичные для хаотичес-
17 Фракталы ^13
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
кого процесса. Ниже отмеченной точки А поведение кривых
характеризует шумовой процесс с наклоном, увеличивающимся по мере
возрастания размерности вложения.
Для объяснения этого явления предположим, что все точки на
фазовой траектории разбросаны в л-мерном пространстве.
Аддитивные шумы являются причиной возмущений в положениях этих
точек. Корреляционный интеграл измеряет совокупное распределение
длин между всеми возможными парами точек. Для точек,
взаимосвязанных с шумовой амплитудой, распределения длин будут
определяться аддитивными шумами. Однако на точки, удаленные от
шумов, последние будут иметь малое влияние, и распределение длин
не слишком сильно изменится.
Из рис. 9.35 видно, что величина
наклона (сплошная линия) стремится
к постоянному значению, показывая
наличие малоразмерного аттрактора.
Но оценка корреляционной
размерности завышена по сравнению с
фрактальной размерностью аттрактора
Лоренца /)=2,06 (штриховая прямая).
Причина этого явления — влияние
аддитивных шумов.
Основным ограничением при
идентификации хаотического
процесса на фоне аддитивного шума
является отношение сигнал-шум. В
рассматриваемом примере отношение сигнал-
шум составляло 18 дБ. При более
низком отношении величины сигнал-
шум «колено» сдвигается вверх,
скрывая хаотическое поведение, и наоборот.
Влияние мультипликативных шумов на корреляционный интеграл.
При изучении влияния мультипликативного шума на оценку
корреляционной фрактальной размерности интенсивность временных
реализаций модели Лоренца была выбрана в качестве сигнала,
искаженного дополнительным шумом. Влияние спеклов учитывалось
воздействием на сигнал набором случайных чисел, выбранных из
ансамбля с отрицательным экспоненциальным распределением со
средним значением, равным реальной интенсивности.
514
D\
2,4 L
2 V
1,6 L
I i i i
О 5 10 15 D'
Рис. 9.35. Зависимость
фрактальной размерности D
странного аттрактора модели Лоренца в
присутствии аддитивных шумов
(сплошная линия) и
непосредственно аттрактора Лоренца
(штриховая линия) от
размерности вложения D' [76]
9.7. Детерминированный хаос в сигнатурах и радиолокационных изображениях...
При усреднении нескольких радиолокационных изображений
интенсивность парциальных сигналов умножалась на выборку
случайных чисел с гамма-распределением и средним значением,
равным единице. При усреднении 64 изображений отношение сигнал-
шум составило около 18 дБ, что совпадает с примером воздействия
аддитивного шума, обсужденного ранее.
Влияние мультипликативного шума на оценку корреляционной
размерности для одного радиолокационного изображения при
размерностях вложения 8, 16, 24, 32 и 40 показано на рис. 9.36. Там же
отмечен линейный интервал [-7; -3]. Из рисунка ввдно, что наклоны
линейной части кривых увеличиваются с возрастанием
размерности вложения.
log C(r)\
-20246 logr
Рис. 9.36. Логарифмическая кривая корреляционного интеграла С(г)
для аттрактора Лоренца при воздействии мультипликативного шума
и при различных значениях размерности вложения U [76]
Данные рис. 9.37 иллюстрируют влияние усреднения 64
изображений на значение корреляционного интеграла при размерностях
вложения 8, 16, 24, 32 и 40. Видно, что кривые имеют «колена»,
подобные «коленам» на рис. 1.7. В этом случае поведение
корреляционных размерностей для аддитивных и мультипликативных
шумов фактически идентично. Здесь линейный интервал лежит в
пределах [-4; -2].
На рис. 9.38 показаны зависимости фрактальной размерности D
от размерности вложения D' для интенсивности временной серии
515
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
log ОМ
0
-2
-4
-6
-8
Z
/М
'z*=8
16-
//// 40
//Я-32
-ПГ24
о
logr
Рис. 9.37. Влияние усреднения 64 изображений на значение корреляционного
интеграла С(г) для аттрактора Лоренца при различных значениях размерности
вложения D' [76]
D
10
8
6
4
2
1 1—L
Х^З
Л -
~~^7
1 1 1 \ 1
10 20
30
40 D
Рис. 9.38. Зависимость фрактальной
размерности D от размерности
вложения D' для временной серии Лоренца
в отсутствие шума (1), при усреднении
64 радиолокационных изображений (2)
и для интенсивности одного
изображения (3) [76]
Лоренца в отсутствии шума,
интенсивности 64 усредненных
радиолокационных изображений и
интенсивности одного
изображения. При отсутствии шумов
(кривая 1) фрактальная размерность стремится к постоянному значению
D~ 2. При усреднении (кривая 2) фрактальная размерность также
стремится к приемлемому постоянному значению. Такое поведение
идентично тому, что наблюдалось при аддитивном шуме (см. рис.
9.35). Для одного изображения (кривая 3) фрактальная размерность
увеличивается с ростом размерности вложения и не отражает
присутствия хаотического процесса. Это поведение аналогично случаю
аддитивных шумов при низком отношении сигнал-шум, когда
корреляционный интеграл определяется шумом на всей шкале длин г.
516
9.7. Детерминированный хаос в сигнатурах и радиолокационных изображениях...
Из рассмотренных примеров следует, что воздействие
мультипликативного шума (спеклы) на метод оценки корреляционной
фрактальной размерности будет, по существу, таким же, как
воздействие аддитивных шумов. При высоком отношении сигнал-шум
хаотический процесс определяется выбором линейного интервала.
Странный аттрактор и скорость поверхностного ветра. В [497]
рассматривается вопрос контроля радиолокационных отражений от
морской поверхности и поверхностных ветров одной и той же
низкоразмерной динамической системой со странным аттрактором. Если это
так, то становится возможным в течение ограниченного времени
более точно предсказывать характеристики поверхностного ветра на
основе принятых радиолокационных сигналов с использованием
детерминированной, а не статистической модели. В настоящее время
на практике применяются только статистические модели, например,
в спутниковой системе SEASAT, когда сигнал обратного рассеяния
обрабатывается как случайный гауссов процесс [498].
Эксперименты по зондированию поверхности океана
сантиметровым когерентным радиолокатором проводились в сентябре 1993 г.,
РЛС располагалась на высоте 573 м. Данные о поле ветра были
получены системой атмосферного зондирования приповерхностного
слоя, размещенной на борту платформы FLIP и находившейся на
расстоянии 31 км от РЛС. Измерительный полигон имел ширину
150 х 100 м2 и располагался на расстоянии 1 км от платформы FLIP.
Ежедневные 8-часовые сеансы зондирования при линейных видах
поляризации позволили получить репрезентативные данные о
значениях удельной эффективной площади рассеяния (ЭПР) морской
поверхности и доплеровских спектров. Горизонтальные и
вертикальные составляющие ветрового потока регистрировались на
платформе FLIP в течение 8-часовых интервалов трехкоординатным
звуковым анемометром.
На рис. 9.39 приведены коэффициенты автокорреляции допле-
ровского сигнала при вертикальной поляризации (1), сигналов
обратного рассеяния при вертикальной (2) и горизонтальной (3)
поляризациях, горизонтальных (4) и вертикальных (5) составляющих
ветрового потока.
В экспериментах динамический диапазон сигнала всегда
оставался большим по сравнению с аддитивным шумом. Поэтому на
зависимостях логарифма функции корреляционного интеграла от
логарифма евклидовой метрики при размерностях вложения /У =3,
517
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Рис. 9.39. Коэффициент
автокорреляции доплеровского
сигнала при вертикальной
поляризации (1), сигналов
обратного рассеяния при
вертикальной (2) и
горизонтальной (3) поляризациях,
горизонтальных (4) и вертикальных (5)
составляющих ветрового потока
[497]
4, 5, 6, 7, 8, 9, 10, 11, 12 (рис. 9.40) нет специфических искажений
типа «колен», как на рис. 1.7. Полученные кривые типичны для всех
экспериментальных данных. Они показывают определенные
области линейного масштабирования без учета влияния шумов.
Следуя алгоритму [54], были рассчитаны зависимости
корреляционной фрактальной размерности странного аттрактора D от
размерностей вложения/)' (рис. 9.41). Обозначения на рис. 9.41
соответствуют данным рис. 9.39. Здесь же дополнительно приведена
зависимость (6) для шумового процесса. Тот факт, что насыщение
кривых для сигнала обратного рассеяния при вертикальной
поляризации (2) и горизонтальной составляющей ветрового потока (4)
происходит синхронно, наводит на мысль о существовании
низкоразмерного странного аттрактора, одновременно управляющего этими
двумя временными характеристиками. Остальные
радиолокационные и геофизические характеристики (даже такие, как доплеровский
сигнал с гораздо большим интервалом автокорреляции) не
проявляют такой тенденции.
Наиболее привычным методом исследования океанских
поверхностных ветров по радиолокационному сигналу обратного
рассеяния является алгоритм SEASAT [498]. Скорость горизонтальной
составляющей поверхностного ветра v находится из формулы
а, = 10[<?(е,ф) + Же,ф)1оёу].
(9.55)
518
9.7. Детерминированный хаос в сигнатурах и радиолокационных изображениях...
Рис. 9.40. Экспериментальные логарифмические кривые корреляционного
интеграла С(г) при отражении от морской поверхности [497]
Рис. 9.41. Фрактальная
размерность D странного аттрактора в
зависимости от размерности
вложения D' для доплеровского
сигнала (1), сигналов обратного
рассеяния при вертикальной (2) и
горизонтальной (3) поляризациях,
горизонтальной (4) и вертикальной
(5) составляющих ветрового потока
и шумового процесса (6) [497]
D
15
10
5 V
л-
-L.
10
15 20 25 D
Здесь а* — удельная ЭПР морской поверхности; 9 — угол падения;
Ф - угол между направлением зондирования и вектором скорости
ветра. Параметры Си Я были определены эмпирически и
приведены в [498].
519
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Алгоритм (9.55) предназначен для предсказания поверхностных
ветров по измеренным удельным ЭПР. Однако его характеристики
могут быть использованы как стандартные для сравнения с
«детерминированным» методом предсказания. С этой целью расчет по
(9.55) проводился с использованием нескольких данных,
полученных экспериментально. Соответствующие значения Си Я затем
использовались в (9.55) для предсказания значений v из измеренных
значений а*. Считалось, что углы 9 и ф для периода предсказания
не изменяются слишком сильно. Успех предсказания
количественно определялся расчетом взаимосвязей между предсказанными и
действительными значениями скорости ветра через коэффициент
корреляции предсказания [499].
Обработка производилась с помощью обучающихся
классификаторов на нейронных структурах с обратной связью [496]. Для
классификатора использовался принцип обучения с учителем на основе
первой половины временных серий сигнала обратного рассеяния при
вертикальной поляризации и горизонтальной составляющей
ветрового потока. Затем характеристики предсказания оценивались с
использованием второй половины временных рядов.
Коэффициенты корреляции между предсказанными и
измеренными значениями были рассчитаны для серий данных:
горизонтальная скорость ветра — сигнал при вертикальной поляризации (рис.
9.42,а); вертикальная скорость ветра - сигнал при вертикальной
поляризации (рис. 9.42,6) по предложенной методике (кривая 1) и
методике SEASAT (кривая 2).
Для серии горизонтальная скорость ветра — сигнал на
вертикальной поляризации (см. 9.42,а) предсказания детерминированной
модели на основе нейронной структуры достигают более высокого
коэффициента корреляции для некоторой временной задержки (-3—4
мин.), после которой детерминированная модель предсказывает не
лучше, чем статистическая модель SEASAT. Для данных рис. 9.42,6,
как и ожидалось, характеристики предсказания ниже, чем в первом
случае.
Рассмотренный метод был также использован при обнаружении
небольших айсбергов [494]. Дальнейшие исследования
предполагают получение данных о низкоразмерных динамических системах,
контролирующих температуру, течения и моменты приливов при
радиолокационном зондировании поверхности океана.
520
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
1
0,8
0,6
0,4
0,2
^2
-LZ 1
^\
^_J 1 1
Л(т)
0,8
0,4 Ь
100 200
а)
300 т,с
-I L.
JL
100 200
б)
300 т,с
Рис. 9.42. Коэффициенты корреляции между предсказанными и измеренными
значениями ветрового потока для горизонтальной (а) и для вертикальной (б)
составляющих ветрового потока при вертикальной поляризации [497]
9.8. Стохастические сигналы и преобразование Радона
в цифровом радиолокаторе с фрактальной обработкой
информации
Широкополосные сигналы. Освоение диапазона миллиметровых
волн для перспективных радиотехнических систем требует поиска
новых подходов при решении задач радиолокации, формирования
радиолокационных изображений и радиолокационных образов
районов навигационной коррекции (корреляционно-экстремальные
системы). Специфика радиолокационных задач обусловила и форму
зондирующего сигнала. Применение широкополосных зондирующих
сигналов в обстановке активного радиопротиводействия позволяет
увеличить дальность действия при ограниченной пиковой
мощности передатчика, повысить точность определения координат при
решении навигационных задач, увеличить обнаруживаемость
малоразмерных целей на фоне земной поверхности, улучшить их
распознаваемость, разнообразить структуру алгоритмов обработки.
Таким сигналом, в большей степени удовлетворяющим
требования широкого класса задач по уровням боковых лепестков тела
неопределенности %(%, £2) в плоскости координат «задержка - т » и
«доплеровская частота — О.», является импульсный сигнал с гладкой
521
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
огибающей и линейной частотной модуляцией (ЛЧМ) [500].
Гладкая огибающая обеспечивает низкий уровень боковых лепестков по
оси О. при любом законе внутриимпульсной модуляции с целью
пространственно-скоростной селекции.
Обработка радиолокационного сигнала с помощью окна или
весовых функций [501] позволяет изменить уровень боковых
лепестков 5j. Для сигналов с ЛЧМ большие базы сигнала т = FT трудно
получить из-за аппаратной реализуемости формирующего и
свертывающего фильтров с заданным коэффициентом широкополосности
или коэффициентом сжатия, диапазона однозначного измерения
дальности (период повторения зондирующих импульсов), допустимой
«мертвой» зоны (длительность зондирующих импульсов). Здесь F—
ширина спектра сигнала, Т- длительность зондирующего сигнала.
Невозможность удовлетворения всем требованиям заставила
вести поиск в классе известных дискретных сигналов.
Недостаточное внимание, уделяемое ранее этим дискретным сигналам, было
обусловлено, с одной стороны, сравнительно небольшими
значениями баз (я2<104), когда сигналы с фазовой кодовой модуляцией
(ФКМ) уступают по уровням боковых лепестков сигналам с ЛЧМ,
а с другой стороны — ^просматривавшейся возможностью
перехода к квазинепрерывному режиму работы (подобно связным системам
[502]), так как обеспечение требуемой глубины развязки между
приемным и передающим каналами при однопозиционной
радиолокации казалось невозможным.
Параметрон и квазинепрерывный режим РЛС. Только с
реализацией казинепрерывного режима работы на параметронах
открывается перспектива применения сверхширокополосных ФКМ
зондирующих сигналов. Параметрические квантователи фазы (ПКФ)
формируют на несущей частоте зондирующий сигнал и дают оцифровку
на несущей принимаемого эхо-сигнала вплоть до диапазона
миллиметровых волн [503, 504]. Параметроны основаны на использовании
нелинейных явлений в полупроводниковых р-л-переходах.
Основной частью параметрона является резонансный контур с
нелинейным элементом, настроенным на частоту^, близкую к половине
частоты накачки/н /2. Вопросы схемной и конструктивной реализаций
параметронов в современных устройствах с учетом ряда реальных
факторов рассмотрены в [503, 505].
Следует отметить, что применение квазинепрерывного ФКМ
зондирующего сигнала может легко сочетаться с обработкой, при-
522
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
меняемой для ЛЧМ сигналов. В частности, парциальная свертка
ФКМ сигнала возможна на конвольверах, использующих
поверхностно акустические волны. Однако будем рассматривать только
цифровую обработку. Отметим, что детектирование оцифрованного на
несущей частоте сигнала приводит непосредственно к естественной
цифровой форме его представления в стохастической системе
счисления.
Рассмотрим особенности применения в радиолокации
квазинепрерывных зондирующих сигналов с ФКМ по псевдослучайному
закону. Вместе с тем использование преобразования Радона
позволяет по-новому подойти к проблеме создания систем радиолокации и
радионавигации. Ограничимся наиболее интересным подшумовым
случаем. При таком предположении базу сложного ФКМ сигнала
можно идентифицировать с базой стохастического кода [506].
В отличие от позиционных кодов, в которых разряды имеют
различный вес {yk = 2k, где к — номер разряда), в стохастическом
коде все разряды равнозначны. Поэтому из-за псевдослучайного
характера как принятого, так и опорного сигналов вероятность
совпадения формы эхо-сигнала с опорным оценивается отношением
числа совпадающих позиций сигналов к общему числу позиций (базе
сложного ФКМ сигнала) и пропорциональна интенсивности
отраженного сигнала.
Если обозначить через Р(0) и Р(п) вероятности устойчивых
состояний выходного сигнала ПКФ, то разность этих вероятностей ДР
при бинарном квантовании фазы будет зависеть от входного
отношения сигнал-шум #о и от фазы сигнала ср5 относительно сигнала
накачки параметрона [507]:
AP = P(0)-P(K) = -J2=cosys.
При отсутствии регулярного сигнала вероятности выходных
состояний ПКФ совпадают: Р(0) = Р(п) = 1/2. Присутствие во
входной смеси регулярного сигнала нарушает равновесие системы
(ДР*0), что свидетельствует о наличии сигнала. Отсюда следует,
что ПКФ обладает фазовой избирательностью. Причем амплитуда
сигнала, фаза которого находится на сепаратрисе, разделяющей
устойчивые состояния ПКФ, не влияет на выходное состояние
параметрона.
523
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Физика выделения слабого сигнала на фоне шума и мощной
помехи обусловлена тем, что мешающие сигналы всегда
несинхронны относительно сигнала накачки. Поэтому стохастический код на
выходе ПКФ будет коррелирован со слабым полезным сигналом на
тех позициях стохастического кода, на которых суммарная фаза
помехи находится на сепаратрисе или в ее окрестности. Эти зоны
расширяются или сужаются в зависимости от интенсивности помехи.
Нормализация сигнала интенсивной помехой автоматически
поддерживает его в динамическом диапазоне входных воздействий, если
база стохастического кода достаточна для воспроизведения
динамического диапазона входных сигналов. База сигнала т (число
позиций стохастического кода) определяет динамический диапазон D
стохастической системы D = 20logm, подобно разрядности г в
позиционных системах счисления Д = 201og2r. Так, если т = 2г, где г—
разрядность аналого-цифрового преобразователя, то Ь = Ьу
При стохастическом кодировании информации с помощью ПКФ
осуществляется автоматическое нормирование выходного сигнала
более мощным компонентом, подобно тому, как это происходит в
системах с жестким ограничением и последующей фильтрацией.
Поэтому при анализе рассматриваемых систем под воздействием
помех и шумов могут быть использованы результаты, полученные в
[508].
Побочным положительным эффектом применения
квазинепрерывного ФКМ сигнала в сочетании с использованием ПКФ для
преобразования принимаемого сигнала в стохастический код
является простота аппаратной реализации арифметических устройств.
Этот факт основан на глубокой аналогии и связи, существующей
между событийной теорией вероятностей и математической логикой
[509]. Так, сложению двух чисел в стохастическом коде соответствует
операции дизъюнкции, умножению — операция конъюнкции, а
изменению знака — операция инверсии «0» -»«1» и «1» -> «0» [506, 510].
Достаточно просто в этой системе счисления может быть
реализован квадратичный детектор. Так как задержанная хотя бы на один
такт стохастическая последовательность некоррелирована с
исходной, то квадратор представляет конъюнкцию задержанной и
исходной последовательностей.
Результат оцифровки с помощью ПКФ входного процесса,
представляющего собой комбинацию сигнала обратного рассеяния и
524
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
доминирующего шума, представляет собой бюффоновский процесс
[511], в котором решетка - это семейство сепаратрис ПКФ,
выборка — состояние фазы ПКФ в установившемся режиме, а механизм
случайного бросания на решетку обусловлен шумом, на фоне
которого наблюдается полезный сигнал.
Наличие обнаруживаемого или распознаваемого объекта
проявляется в статистике выходного процесса ПКФ. При отсутствии
полезного сигнала (регулярного компонента входной смеси)
случайное многократное «бросание» входного процесса на решетку полос,
разделяемых сепаратрисами на четные и нечетные, приведет к тому,
что в среднем в половине случаев «бросания» входной процесс
попадает в четные полосы (состояние относительной фазы «О») столько
же раз, сколько и в нечетные полосы (состояние «тс»). Если во
входной смеси присутствует полезный сигнал, то равновесие между
попаданиями в четные и нечетные полосы нарушается в ту или иную
сторону. Превалирующее состояние определяет знак, а
количественное различие — амплитуду полезного сигнала на выходе в
стохастической системе счисления.
Преобразование Радона в радиолокации. Рассмотрим теперь
некоторую двумерную область Д имеющую площадь S и периметр
внешней границы L. Предположим, что данная область
характеризуется некоторой плотностью dG хорд с, физический смысл
которых может быть интерпретирован как текстурные границы
подстилающей поверхности (участки рек, дорог, мостов и т.д.). Прямая
линия G на плоскости может быть определена углом <р между
направлением, перпендикулярным к(?,и фиксированным
направлением (0 < ф < 2к) и значением р (расстоянием прямой от начала
координат). Уравнение соответствующей прямой G имеет вид
xcoscp + }>sin(p-/? = 0.
Мера всякого множества Упрямых может быть определена
интегралом [511]
m(X) = jf(p,y)dpAdy.
х
Здесь фл^ф - внешняя дифференциальная форма [511—513], а
функция / зависит от природы задачи. Основным свойством внешней
525
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
дифференциальной формы или внешнего произведения dxY и dx2
является кососимметрия, т.е. dx{ асЬс2 =-dx2 *dx{, dx лек. = 0. Если
(xvx2) — прямоугольные координаты, то внешнее произведение
dxy лск2 означает элемент ориентированной площади на плоскости.
В радиолокации функция/определяется шириной диаграммы
направленности антенны, углом наклона оси антенны к поверхности
и радиальной дискретизацией, которая совместно с множеством X
задает импульсный объем, интеграл от которого есть принимаемый
эхо-сигнал. Мера т (X) должна быть инвариантной относительно
группы движений плоскости.
Тогда плотность dG хорд будет определяться дифференциальной
формой dG = dp л d<$. Среднее значение хорды может быть записано
в виде
а= J cdG/ j dG,
Gf)D*0 I G(V)*0
в котором числитель пропорционален площади £ области Д так как
cdp есть элемент площади:
J adG= J афл</ф = тс J Gdp = nS,
GT\D*0 G(W*0 Gf)D*0
а знаменатель равен периметру L:
J dG- J фл*/ф = тс J pdy = L.
GPlD*0 Gf]D*0 GnD*0
Таким образом, <j можно интерпретировать как некоторую
информативность области D:
o = nS/L.
Так как максимум определенной таким образом
информативности достигается при такой конфигурации области Д которая
характеризуется максимальной площадью £при минимально возможном
периметре L, то, очевидно, что такой границей является окружность.
Всякая замкнутая область Д площадью Sx и длиной периметра
L{ может быть покрыта числом ц фундаментальных областей
площади ос0 и длиной периметра LQ [511], причем
526
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе..,
2я(а0+^1) + 1011
2яа0
где is(v) — среднее значение числа кусков, на которые замкнутая
область Dx разделяется, когда она случайно бросается на решетку
фундаментальных областей. Решеткой фундаментальных областей на
плоскости называют последовательность конгруэнтных регионов
(областей, объединенных с некоторыми из своих граничных точек)
области (Xj, oc2,..., которая удовлетворяет следующим условиям.
Каждая точка Р в плоскости принадлежит одному и только одному
региону осг Каждое ос. может быть совмещено с ос0 движением ti так,
что при этом каждое ah совмещается с некоторым as, т.е. это
движение переводит всю решетку в себя ос0 = /.о^. [511].
Заметим, что задача получения растрового радиолокационного
изображения зондируемой области может быть интерпретирована в
терминах решеток фигур, а порогом обнаружения объектов класса
{Dv Sl9 L{) может служить определенный ранее параметр м~ Если же
такая кластеризация слишком груба (например, когда требуется
идентифицировать в обзорном растре радиолокатора конкретный
объект, поддающийся формализации), то следует перейти к более
тонкой структуре области (объекта).
Рассмотрим модель энергетического обмена [923, 931, 935]. На
подвижной платформе расположен радиолокатор, обладающий
антенной с ножевидным лучом. Луч направлен к земной поверхности
под углом у и вращается относительно местной вертикали. Если луч,
повернутый относительно оси на некоторый угол ср, на каком-то
рубеже г встречает рассеивающий или излучающий объект, то в
приемнике будет зарегистрирован интегральный эффект, зависящий от
угла ф и некоторого параметра р = п|/, в совокупности
определяющих положение следа луча на поверхности [514]
/?(/?, ф) = jjf(x,y)8(xcosy + ysmy-p)dxdy.
Перейдем к другой системе координат {х, у'}, повернутой
относительно {х, у} на угол ф, т.е. х = x'cos ф - /sin ф, у = x'sin ф + /cos ф.
Проинтегрировав по х , получим
527
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
-К(Аф)= J /0?cos9-/sin9,/?sin9+/cos<p)afy'.
W)1/2
Здесь а - радиус окружности, являющейся границей засвеченной
лучом области. Эти выражения являются преобразованием Радона
функции/ Используя символику 8 -функции, можно записать
интеграл функции Дх) по гиперплоскости (£,х) = р в следующей
удобной форме [515]: R(^,p)= \f(x)8[p-(^,x)]dxy где dx = dxl...dxn.
В рассматриваемой модели энергетического обмена в
стохастическом представлении задается дискретизированное по р и ер
преобразование Радона рассеивающего (для радиолокации) или
излучающего (для радиометрии) объекта. Для восстановления функции
обратного рассеяния J{x, у) достаточно вычислить обратное
преобразование Радона.
Алгоритм восстановления этой функции следующий:
а) осуществляем преобразование Фурье радоновского образа:
б) результат умножаем на гс|со|;
в) осуществляем обратное преобразование Фурье произведения
/т-1{тс|со|^(а>,ф)} = /(5»;
г) аргументу s' присваиваем значение xcoscp+}>sin<p;
д) производим интегрирование функции по углу
xcos<p + ysinq>)t/<p = f(x,y).
"о
Если R(p,<?) представлена в стохастической системе счисления,
то целесообразно все указанные преобразования осуществлять в этой
же системе счисления, для чего весовые функции преобразования
Фурье и кусочно-линейную функцию |со| (образ операции
дифференцирования) следует представлять стохастическими кодами.
528
у«
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе.,.
В общем случае [515] в пространстве нечетной размерности п
функцияДдс) выражается через свое преобразование Радона R(^,p):
где со(£) = ]Г(-1)* 1^^1л...л^_1л^+1л...л^л - дифференци-
альная форма, а интеграл по поверхности Г охватывает точку £ = О,
(£*) = $Л+■■■ + $,,*,,■
Для пространства четной размерности п формула обращения
преобразования Радона приобретает вид
т={ l)]%l) l\jm,p) [P-^x)]-"dp\ <ф,
где интеграл по р следует понимать в смысле регуляризованного
значения:
j p-ny(p)dp =
= ]р-"Ш) + <((-Р)-2
ф(0)+^-ф'(0) + ...+^у[Ф<"-2>(0)
Следует заметить, что в нечетномерном случае для
восстановления функции/в точке х достаточно знать только интегралы по
гиперплоскостям, проходящим через точку х и по бесконечно близким
к ним, так как dp - оператор параллельного переноса
гиперплоскости. Следовательно, в нечетномерном пространстве формула
обращения локальна. Для четномерного пространства, чтобы определить
значение функции/в точке пространства, необходимо знать ее
интегралы по всем плоскостям.
Томография в навигации и радиолокации. Практическая
целесообразность описанной томографической модели
радиолокационного обзора может быть оправдана в корреляционно-экстремальных
навигационных системах [516], использующих опорные карты в виде
529
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
радиолокационных образов районов навигационной коррекции.
Однако в подобных случаях не требуется восстановление самой
функции/, а представляет интерес обнаружение (идентификация)
известного образа. В этих случаях целесообразно синтезировать
эталоны в виде радоновских образов. Это избавляет от необходимости
обращения фрагментов растра и позволяет сразу приступить к
идентификации в стохастической системе счисления. В этой связи
представляется неслучайным тот факт, что в
корреляционно-экстремальной системе РАДАГ обзор района цели осуществляется коническим
сканированием относительно местной вертикали ножевидным лучом.
Рассмотрим в качестве примера радиолокационную
корреляционно-экстремальную систему на базе радоновских карт, помня, что
преобразование Радона для фиксированного угла Ф представляет
собой плоскую волну [517]. На рис. 9.43 показан эталонный объект в
виде круга радиусом гь энергетически доминирующий над фоном /.
Внутри большого круга имеется другой круг меньшего радиуса г2 с
более высокой интенсивностью /0 обратного рассеяния
(эффективной площадью рассеяния). Радиолокационный датчик расположен
над картинной плоскостью объекта на расстоянии г.
[о
След луча антенны
Граница преобразования Радона
Рис. 9.43. Эталонный образ в виде кругов с радиусами г{ и г2
на фоне однородной поверхности [534]
530
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
Синтез эталона осуществляется сканированием по двум
аргументам: по Ф - коническим сканированием с углом полураскрыва
конуса У, так что р = п|/; по р - изменением значения полураскрыва
конуса у конического сканирования или радиальным
перемещением, например приближением к картинной плоскости объекта, либо
горизонтальным перемещением. В последнем случае образуется
сечение радоновского образа плоскостью Ф = Ф0> а для получения
всего образа необходимо повторить пролет над объектом для всего
набора ракурсов {ф7}. Этот способ синтеза эталона запатентован [954].
Синтезированный таким способом эталонный радоновский
образ является решетчатой функцией двух переменных: {/?,} и {ф,-}. На
рис. 9.44,а изображен интерполированный радоновский образ
объекта, представленного на рис. 9.43. Объект с радиусами гх и г2
располагался на однородном фоне, а его преобразование ограничено по
параметру р кругом радиуса R. При перемещении объекта внутри
круга радиусом R конфигурация радоновского образа
трансформируется. Если фрагмент радиуса г2 характеризуется пониженной
интенсивностью 7j обратного рассеяния (водная поверхность при
слабом ветре и наклонном угле зондирования [231]), то радоновский
образ объекта будет соответствовать образу на рис. 9.44 Д Видно, что
в этом случае существует выемка на выпуском множестве, в
отличие от данных рис. 9.44,я, где область г2 с повышенной
интенсивностью обратного рассеяния более выпукла.
Для корреляционно-экстремальной системы эталон может быть
задан в виде полного радоновского образа. Однако текущее радонов-
ское сечение может быть получено частично, например для одного
значения Ф = Ф,, если информативность такого сечения достаточна
для идентификации с требуемой достоверностью. На рис. 9.44
показаны сечения: Ф = Ф0
(фиксированныйракурс)ир=р0(фиксированный радиус конического сканирования, так что р0 = rtg\|/0,
причем для малых значений углов pQ = ryQ.
Задача выбора числа ракурсов Af решается индивидуально для
каждого конкретного случая с привлечением дополнительной
информации об объекте. В частности, в медицинской диагностике
применяют методы реконструкции, основанные на решении
интегральных уравнений первого рода типа свертки. Результаты
вычислительного эксперимента [518] показывают, что при N< 64
погрешность восстановления тонкой структуры объекта становится
достаточно большой и составляет около 10%. Для радиолокационных задач
531
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Рис. 9.44. Радоновские образы исследуемых объектов
при/0 >/(e) и/^/о (б) [534]
при пониженной разрешающей способности результат
реконструкции может оказаться приемлемым даже при N= 10. В итоге
сравнение по той или иной мере сходства эталонного и текущего образов
позволяет сопоставить координатам экстремума ошибку
собственного местоположения.
532
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
Новый тип радиолокатора. Для решения поставленных задач был
разработан и изготовлен на основе теоретических и
экспериментальных результатов, полученных в НПО «Алмаз» и ИРЭ РАН, макет
нового поколения малогабаритных радиолокаторов, характеристики
которого удовлетворяют самым высоким современным требованиям к
устройствам такого рода [184, 504, 519-529]. Не имея аналогов в
мире, созданный с использованием особенностей сантиметрового и
миллиметрового диапазонов волн и новых способов обработки
широкополосных сигналов, базовый радиолокатор может
способствовать решению широкого круга задач, в том числе и разработкам
малогабаритных труднообнаруживаемых и надежных средств
радиолокации двойного назначения.
Преимущественными особенностями нового цифрового
твердотельного радиолокатора (ЦТР) являются [923, 951, 998]:
• обработка входного подшумового сигнала на несущей частоте
в микроволновом диапазоне непосредственно на выходе при-
емно-передающей антенны без предварительного усиления и
преобразования частоты;
• применение квазинепрерывного сложного ФКМ-сигнала с
уникальной базой (>106);
• 100-процентная глубина цифровой обработки информации;
• исключение из приемного тракта ЦТР преобразователей и
усилителей промежуточной частоты;
• простота модификации при адаптации радиолокатора к
решению задач различных классов;
• малые массогабаритные характеристики при высокой
технологичности изготовления, обусловленные твердотельным
исполнением и модульностью конструкции.
Выполнение аппаратуры на современной элементной базе
позволяет уменьшить массу ЦТР до 10 кг и менее. Применение в
качестве сигнального процессора и выходного устройства
малогабаритного современного компьютера обеспечивает хорошую
эргономическую конструкцию и повышает наглядность представления
радиолокационного изображения местности в широкой гамме псев-
доцветов, а также решает задачу программного селективного
увеличения фрагментов наблюдаемого объекта. С помощью модемного
интерфейса, совместимого с компьютером, возможна передача
радиолокационной информации на базовую станцию. Наличие
компьютера в составе ЦТР позволяет повысить функциональную гибкость
533
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
системы и стандартизованную совместимость с внешними
абонентами.
Схемотехника ЦТР. В разработанном ЦТР с одной антенной и
длительностью зондирующего сигнала (или периода модуляции),
значительно превышающей время распространения радиоволны до
цели и обратно, использован квазинепрерывный режим работы. В
качестве зондирующего сигнала выбран широкополосный сигнал со
скважностью 2 и поимпульсной однократной фазовой модуляцией
{О, тс} по псевдослучайному закону кодовой последовательностью
максимальной длины (М-последовательность) с относительной
кратковременной нестабильностью несущей частоты Ю-8 за 150 мкс. М-
последовательность соответствует порождающему полиному с
периодом М= 220 - 1, что определяет базу сложного сигнала т = 1 048 576.
При оптимальной обработке такого сигнала энергетический
потенциал комплекса возрастает на 60 дБ. Таким образом, по энергетике
выбранный сложный зондирующий сигнал при пиковой мощности
1 Вт эквивалентен классическому импульсному сигналу мощностью
106 Вт. Используемый закон модуляции обеспечивает гибкое
программное изменение радиальной разрешающей способности при
постоянном режиме излучения. Такой режим работы оказывается
полезным как при обзоре воздушного пространства, так и при
кластеризации объектов в зоне обзора.
Электромагнитная совместимость ЦТР, работающих в одном
частотном диапазоне, определяется ортогональным набором
модулирующих М-последовательностей, обеспечивающих высокую крип-
тостойкость. При степени порождающего полинома к = 20 число
используемых ортогональных последовательностей превышает 105.
Особенности и преимущества сложных сигналов с большой
базой известны давно, но отсутствие практического способа
реализации при электромагнитной развязке между приемными и
передающими каналами на 180—200 дБ не позволяло использовать их для
задач радиолокации. В предлагаемом варианте ЦТР эта проблема решена
применением параметронов для формирования зондирующего сигнала и
параметрических квантователей фазы для оцифровки принимаемого
сигнала на несущей частоте.
Схема основного варианта ЦТР приведена на рис. 9.45,а. Здесь
для упрощения изложенного принципа действия ЦТР показан один
из двух идентичных фазированных приемных каналов. В блоке
опорных частот 5 твердотельным ЛПД-генератором вырабатывается не-
534
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
м
4
4 |
:
и
♦
/ \»
Л 2
*| '1
5 к
И /1
7 |-
L8
3
р-
[_4 1
-ГТ
"1 Л
М-последо- 1
Пвательность 1
1 [ м
п б F
|—
«;
-послсдо-
гельность
/о
П Г
9 Щ
И
ю |ц
L
2 [
/i~ IM-послс
'• 1 | ватсльнс
1 * НЧ
1 гтп.л
1 / 1-
, I I М-лосле
**% (вательно
я 1
1
до-1
сгь|
■'Н
«0-1
сть 1
12
л
б)
Рис. 9.45. Структурные схемы одночастотного (а) и двухчастотного (б) ЦТР
со сложным ФКМ-сигналом [184, 504, 526, 534, 923, 951]
прерывный сигнал частотой/в сантиметровом или миллиметровом
диапазоне. Отфильтрованная вторая гармоника 2/используется в
качестве сигнала накачки для импульсного параметрического
генератора 1 и параметрического квантователя фазы 7.
Для повышения надежности срабатывания параметронов
генератор накачки должен быть стабилизирован по частоте и иметь
минимальные фазовые шумы. Тактирование параметрического
генератора осуществляется импульсом гашения U синхронизатора 6. В
синхронизаторе генерируется М-последовательность с тактовой
частотой^ = 30 МГц и периодом М = 220 - 1. Длительность
парциальных импульсов равна 15 не.
Элементарная зондирующая посылка формируется при подаче
в резонатор генератора от фазового модулятора 2 сигнала
мощностью 10~10 Вт и смещении сигналом U параметрического диода
генератора в рабочую точку. Через 15 не после начала генерации импульс
535
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
гашения U открывает параметрический диод генератора и срывает
его колебания. Сформированный короткий высокочастотный
импульс через циркулятор 4 излучается антенной 3 в свободное
пространство. Выбранный метод формирования позволяет
непосредственно на выходе генератора получить ФКМ-сигнал, состоящий из
большого числа парциальных импульсов.
Через 5 не после срыва колебаний в генераторе сигналом
управления начинает плавно выводиться в рабочую точку
параметрический диод в параметрическом квантователе фазы 7. Таким образом,
параметрический квантователь фазы сначала работает в предосцил-
ляционном режиме интегрирования, где устанавливается его фаза,
а затем он переходит в режим устойчивой генерации. Отраженный
от цели сигнал через антенну и циркулятор поступает на вход
параметрического квантователя фазы. Минимальный входной сигнал для
запуска параметрического квантователя фазы сравним с уровнем
теплового шума, т.е. при полосе пропускания 60 МГц он должен быть
примерно равен -126 дБ. Однако, с учетом потерь в передающих
линиях, а также собственных шумов минимальный входной сигнал не
может быть меньше —(120—122) дБ. На выходе параметрического
квантователя фазы формируется последовательность
высокочастотных импульсов, несущая фазовую информацию об отраженном
сигнале.
По прошествии еще 10 не колебания параметрического
квантователя фазы срываются. К этому времени сгенерированный импульс
с квантованной фазой оказывается уже продетектированным в
фазовом детекторе 8. Видеосигнал с фазового детектора приемного
канала с помощью блока логики 9 преобразуется к необходимым
уровням ±1 и далее подвергается преобразованиям в блоке
цифровой обработки 10. Здесь используется фильтрация в 20 дальностных
каналах. Затем выходной сигнал поступает на магнитный
регистратор 11 и компьютер 12. Для уменьшения времени обзора
проводится параллельный анализ 20 элементов дистанции с помощью
многоканальной цифровой обработки. Это позволяет наблюдать
одновременно несколько целей в селектируемом окне, которое может
перемешаться по дальности.
Предельная чувствительность, полученная в экспериментах, при
когерентном накоплении составляла около —174 дБВ или Р~ 10~17 Вт
в полосе частот 140 Гц. Характерные формы огибающей ФКМ-сиг-
нала, отраженного бетонной взлетно-посадочной полосой, лугом,
536
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
лиственным лесом, берегом реки и населенным пунктом, при
противоположных азимутах приведены в [184, 521]. Измерения
проводились с борта вертолета при высоте полета 50-70 м. Ширина
диаграммы направленности антенны составляла 8°. Использовалось
излучение с вертикальной поляризацией на длине волны 8,6 мм.
Полученные изображения служили исходным материалом для
оценки эффективности фрактального обнаружения целей*
При когерентном зондирующем ФКМ-сигнале движущиеся
объекты (человек, автомобиль, самолет) наблюдались на экране
индикатора с непосредственной оценкой их скорости перемещения.
В частности, у неподвижно стоящего человека даже небольшие
колебания складок-одежды приводят к резкому (до десятка децибел)
изменению амплитуды отраженного сигнала [184].
Во второй модификации ЦТР используется метод двухчастотно-
го излучения (рис. 9.45,6). Здесь имеется общий синхронизатор 5 и
цифровые твердотельные радиолокаторы 2 и 8, собранные по схеме,
приведенной на рис. 9,45,а. Через фильтры 1 и 7, препятствующие
взаимному влиянию рабочих каналов, и коммутирующее устройство
4 сформированные импульсы на частотах/J и/2 поступают
поочередно на антенну 3, выполненную в виде плоской щелевой решетки с
диаграммой направленности 3,2°х7,5° на волне 8,6 мм. Система
управления антенной обеспечивает заданное положение диаграммы
направленности в зависимости от режима работы и обзора.
Радиолокационная информация отображается на дисплее компьютера 9
через блок цифровой обработки 6. Были получены следующие
уникальные характеристики двухчастотного ЦТР:
Длина волны, мм 8,6 .20
Пиковая мощность, мВт 10 500
База сигнала >106
Дальность действия, км < 5 < 100
Потребляемая мощность, Вт < 150
Наработка на отказ, ч 104
Масса (без антенны), кг < 20
Объем (без антенны), дм3 < 20
Внешний вид приемопередающего модуля радиолокатора с вол-
новодно-щелевым вариантом антенного устройства приведен в [184,
526, 923, 951]. Там же помещены характерные радиолокационные
537
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
изображения местности, полученные в натурных экспериментах.
Степень разрешения радиолокационных изображений на длине
волны 8,6 мм достаточна для отображения линии электропередачи на
местности. Нетрадиционное применение рассмотренных
радиолокаторов для решения задач обнаружения человека приведено в [184].
Так, эффективная площадь рассеяния человека массой 80 кг и
ростом 175 см составила 0,6-1,0 м2 на длине волны 2 см и 0,8-1,4 м2 на
длине волны 8,6 мм.
Фрактальная обработка информации подразумевает
использование методов фрактального анализа для определения природных
текстур или классов объектов и их кластеризации [77, 479, 530, 531].
Алгоритмы обнаружения могут использовать как полную
фрактальную сигнатуру, так и ее часть или наклон. Двухчастотный режим
радиолокатора позволяет выявлять структуру исследуемых
поверхностей в различных пространственных масштабах. При одночастот-
ном режиме необходимо проводить операцию логарифмирования
выходного сигнала для различных частот дискретизации и
определять фрактальную сигнатуру.
Новый тип радиоизмерительных систем. Обсудим аппаратно-ме-
тодический базис фрактально-кластерной топологизации
контролируемых признаков многофункциональной радиотехнической
измерительной системы нового поколения. Система обладает высокой
чувствительностью и помехоустойчивостью, использует полное
поляризационное зондирование контролируемой среды
широкополосным (коэффициент компрессии 105-1010) сигналом. Ее отличают ма-
логабаритность и экологическая безопасность. Широкие
возможности системы, реализующей топологические методы
фрактально-кластерной предварительной идентификации и обнаружения при
одновременном измерении расхода и контроля качества
транспортируемого материала, обеспечиваются программно, тактически и аппа-
ратно конфигурированием элементарно простых, идентичных
модулей и сменой программно-алгоритмического обеспечения с
использованием нетрадиционных методов фрактального анализа [531-534].
Основными областями использования фрактально-кластерной
измерительной системы являются:
• контроль электрофизических характеристик потоков
неконтактными методами (внутренняя электродинамика);
• контроль электрофизических характеристик потоков методами
дистанционного зондирования (внешняя электродинамика);
538
9.8. Стохастические сигналы и преобразование Радона в цифровом радиолокаторе...
• обзор летного поля аэродрома для информационной
поддержки в обеспечении безопасности воздушного движения в
системе управления воздушным движением (наземное и
мобильное базирования);
• обзор необорудованных площадок для информационной
поддержки посадки летательных аппаратов по классу ШС
(мобильное базирование);
• визуально-информационная поддержка экипажа в условиях
нулевой видимости при решении оперативных задач слепой
посадки, в том числе и на необорудованные площадки (бортовое
базирование);
• обзор необорудованных площадок с целью контроля
несанкционированных перемещений объектов наблюдения
(мобильное, бортовое базирование);
• картографирование местности (бортовое и лопастное,
мобильное, корабельное или космическое базирование);
• обнаружение малоразмерных и малоконтрастных объектов на
поверхности земли, в снегу или на водной поверхности при
проведении поисковых, поисково-спасательных или иных
мероприятий (бортовое, мобильное или корабельное
базирование);
• обнаружение и контроль мелкоочаговых лесных пожаров
(бортовое базирование);
• контроль воздушной среды и обнаружение вредных выбросов
в атмосферу в процессе экологического мониторинга
природной среды (наземное, бортовое или мобильное базирование);
• исследование электрофизических свойств естественных и
антропогенных объектов;
• фрактально-кластерная идентификация подшумовых
обнаруженных неоднородностей с учетом поляризационного
структурирования полной матрицы рассеяния для всех
перечисленных применений.
Непрерывная интенсификация производства и расширение
сортамента, химического состава и структуры материалов,
канализируемых в замкнутых и открытых потоках, обусловливает и в то же время
усложняет проблему обеспечения многоплановости применения
измерительных систем. Решение проблемы сочетания методической
и потребительской многофункциональности лежит в максимальной
комплексной автоматизации процесса принятия решений с исполь-
539
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
зованием новых методов фрактально-кластерной идентификации в
обстановке неполной и искаженной помехами и шумами
информации на основе скейлинговых фрактальных характеристик.
Сложность проблемы состоит в том, что она не решается
локальным применением каких-то новых или готовых к внедрению
известных методов. Решение проблемы лежит в системной завязке
основных достижений современной прикладной радиоизмерительной
науки и техники, таких как: разработка новых методов комплекси-
рования неконтактных и дистанционных измерительных систем,
позволяющих деформировать назначение системы программно либо
тактикой применения или конфигурированием простых,
идентичных модулей; разработка новых методов измерения с применением
сложных широкополосных шумовых зондирующих сигналов с базой
105-1010 и тонкой структурой, управляемой программно;
разработка новых методов фрактальной кластеризации и распознавания
образов с учетом поляризационной селекции для повышения
информативности базы данных, извлекаемых из зондирующего эхо-сигнала
и повышения достоверности измерений; разработка новых методов
и аппаратных средств, обеспечивающих максимальную глубину
цифровой обработки радиоизмерительной информации (гомодинный
прием сигнала, обеспечивающий оцифровку эхо-сигнала на несущей
частоте и устранение зеркального канала); разработка новых
методов повышения системной помехоустойчивости] разработка новых
методов повышения сигнальной чувствительности системы без
ухудшения помехоустойчивости; разработка новых методов и
эффективных алгоритмов цифровой некогерентной обработки ракурсной
информации, обеспечивающих получение тангенциальной
разрешающей способности, равной радиальной, независимо от дальности;
ориентация всех программно-алгоритмических средств на работу в
реальном масштабе времени.
В результате исследований применения фрактальных методов
ведется разработка действующего макета многофункциональной
измерительной системы. Он должен обеспечивать большой объем
информации повышенного качества и обладать близкой к
потенциальной помехоустойчивостью, электромагнитной совместимостью с
существующими и перспективными радиоэлектронными
измерительными средствами. Целевое конфигурирование системы как
дистанционного радиолокационного измерителя позволит реализовать
разрешающую способность в плане не хуже « 2,5 м в широком диа-
540
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
пазоне дальностей при воздействии индустриальных и иных помех.
Из-за малой подшумовой мощности зондируемого сигнала
измерительная система экологически безопасна и создает плотность
мощности в окружающей среде на один-два порядка ниже, чем
бытовая микроволновая печь. Макет [521] может быть
ориентирован на натурные испытания как в неконтактном, так и
дистанционном варианте (см. также [184, 231, 953, 998]).
Теоретическая часть проекта в значительной степени
базируется на работах авторов проекта, в том числе в области
микроволнового зондирования термоядерной плазмы и плазмы промышленных
магнитогидродинамических генераторов, а также на результатах
исследований рассеивающих свойств естественных и антропогенных
объектов на фоне подстилающей поверхности в интересах
корреляционно-экстремальной навигации, включающих разработку новых
методов фрактально-кластерной идентификации с учетом
поляризационных свойств объектов и потоков и отработку новых
принципов комплексирования систем (более подробно - [923, 951]).
9.9. Фрактальное обнаружение целей
на изображениях земной поверхности
Текстурные и фрактальные методы. Существует множество
фундаментальных и прикладных задач, которые могут быть
сформулированы как проблемы обнаружения малоконтрастных протяженных
целей на фоне местности. Такие задачи возникают в радиофизике и
радиолокации, при обработке изображений и дистанционном
зондировании окружающей среды. Применяемые алгоритмы обычно
используют корреляционный и контурный подходы. Они
реализуются методами согласованной фильтрации и дифференциальными
методами. При согласованной фильтрации возникают трудности при
обработке протяженных перепадов яркости. Дифференциальные
методы характеризуются низкой помехоустойчивостью.
В большинстве локационных приложений типичным является
случай формирования малоконтрастных изображений местности, для
которых отношение полезного сигнала к шумовому, в общем случае
негауссовому, фону (сигнал-фон) #о<1- Вопросы обнаружения
малоконтрастных целей еще не достаточно полно освещены в
литературе. Исследованы лишь некоторые алгоритмы обнаружения при ма-
541
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
лых q\ : дисперсионный метод на основе /-статистики [535, 536],
метод обнаружения с помощью линейно моделированных эталонов
[537] и метод на основе ансамбля текстурных признаков [462].
Поиск нетрадиционных путей решения привел к идее
использования фрактальных подходов [184]. Если в методах [462, 535-537]
формально использовалось условие превышения обобщенным
функционалом некоторого заданного порога (в том числе и
адаптивного), то рассматриваемый фрактальный метод основан на
принципиально ином подходе, а именно на парадигме дробной фрактальной
размерности природных процессов.
Применение для анализа изображений спектральных и
корреляционных характеристик целей оказывается часто
малоэффективным при малоконтрастных изображениях. В радиолокации малая
контрастность целей чаще всего проявляется при сканировании
антенны в диапазоне скользящих углов. В этом случае спектральные
характеристики помеховых сигналов от подстилающей
поверхности перекрывают спектры полезных сигналов, отраженных целями.
При выборе информативных и устойчивых признаков для
распознавания целей на изображениях, помимо радиолокационных
сигнатур, чрезвычайно перспективно использование фрактальных
сигнатур, что показывает опыт их разработки [538]. Обнаружение
целей может быть основано на таких признаках, как полная
фрактальная сигнатура, ее часть или наклон. В экспериментах использовались
синтезированные, оптические (аэрофотосъемка (АФС)) и
радиолокационные (РЛИ) изображения земных покровов [184].
Модель реальных изображений. При радиолокационном и
оптическом зондировании полезный двумерный сигнал от цели (ее
образа) S (х, у) является частью общего изображения, создаваемого
всеми отражающими элементами наблюдаемых фрагментов фона,
окружающего цель. Поэтому на практике сигналы от этих элементов
образуют помеховую составляющую. Для реальных неоднородных
изображений ландшафтов целесообразна концепция текстуры.
Согласно [184] текстура описывает пространственные свойства
участков изображений земной поверхности с локально-однородными
статистическими характеристиками. Искомая цель затеняет участок
фона, поэтому предположение об аддитивности полезного сигнала
S (х, у) и фона оправдано тогда, когда цель занимает
незначительную часть изображения [539, 540].
542
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
На анализируемые изображения оказывают влияние случайные
шумы приемника п (х, у). Случайный шум обычно считается
стационарным гауссовым шумом с нулевым средним и спектральной
плотностью мощности NQ. Кроме того, изображение должно
описываться неотрицательной функцией, в отличие от входного
знакопеременного сигнала. Поэтому модель реальных изображений должна быть
сложнее [540] простой радиотехнической модели аддитивного
сложения сигнала и шума вида f(x,y) = S(x,y) + п(х,у).
Будем считать [539], что в области анализа А заданы: f(x, у) -
функция анализируемого изображения (х,уе A); S(x, у) — функция
цели (х,уе As, As с Л); g(x, у) - текстурная функция вокруг цели
(х,уе А-А ); п (х, у) - функция случайного шума (х,уе А).
Реальная нестационарная помеха р (х, у) имеет вид:
(>0, прих,уе А-А ,
р(*, У) = g(x, У)п(х, у) при g(x, у) -> \
= 0, при x,yeAs,
где g(x,y) = £&(*>У); / - число текстур; g. (x, у) - реализация
случайного поля, описывающего /-ую текстуру. Тогда модель
анализируемого изображения с учетом среды распространения формально
сводится к виду
f(x,y) = e[gQ+S(x,y)] + g(x,y)n(x,y), (9.57)
где е - уровень атмосферных (из-за вариаций коэффициента
преломления среды) мультипликативных помех; gQ — постоянная
составляющая, определяемая средним уровнем контраста и
обеспечивающая условие /(х, у) > 0.
В этом случае задачу фильтрации можно сформулировать
следующим образом: приемное устройство анализирует функцию f(x, у)
и производит выбор одной из двух гипотез. Примем в качестве
нулевой гипотезы Н0 наличие лишь помехи, а в качестве
альтернативы Н{ — помехи и сигнала. С точки зрения теории статистических
решений выбор той или иной гипотезы основан на вычислении
интегральных функционалов, зависящих от выбранных условий
оптимизации.
543
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Как правило, практическая реализация непрерывной по
пространству А обработки функции f(x, у) затруднительна. Цифровая
обработка требует перевода непрерывных функций в дискретный
массив чисел. Процесс дискретизации описывается произведением
исходной функции f(x, у) на пространственно-дискретизирующую
функцию [452]. В идеальном случае пространственно-дискретизи-
рующая функция является пространственной решеткой с
расположенными в узлах дельта-функциями
Щх,у)= JT f^5(x-kAx,y-lAy)y
к=-оо /=-оо
где Ахи Ау — шаг решетки по координатам хиу соответственно.
Тогда дискретизованное изображение fH(x,y) = f(x,y)H(x,y)
можно рассматривать как проекцию непрерывной реализации f(x, у)
на линейную оболочку системы функций пространственных
координат:
/н(х>У)=Ъ tf(kAxMy)S(x-kAx,y-lAy).
£=-оо/=-оо
В реальных системах дискретизирующая решетка имеет
конечные размеры. В итоге получаем растровое изображение в виде
массива точек яркости^. ., где / = 0, 1, ..., Nx и у = 0, 1, ..., N . В
приводимых далее результатах компьютерного моделирования / = 0-600,
у = 0-400.
В экспериментах обрабатывались АФС и РЛИ реальных
природных ландшафтов с лиственным лесом, рекой, лугом и т.д. [184],
полученные синхронно в видимом и миллиметровом (длина волны
X = 8,6 мм) диапазонах волн с борта вертолета МИ-8 в маршрутном
режиме при средней скорости полета 60 км/ч и высоте полета от
нескольких десятков до тысяч метров.
В видимом диапазоне аэрофотосъемку производили
фотоаппаратом АФА-41/7,5 с объективом «Ортогон-4» на пленку «Изопанх-
ром-17» со светофильтром ОС-14. Разрешение по центру кадра
составляло примерно 47 лин/мм. Время экспозиции 350-1 с. При
формировании РЛИ использовался радиолокатор с косекансной
544
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
диаграммой направленности антенны шириной 0,4x10°.
Длительность зондирующего импульса была 100 не, частота сканирования
антенны 0,5 Гц, поляризация излучения — вертикальная при
импульсной мощности излучения 40 кВт. Угол обзора земной поверхности
равнялся 80°. Наклонная дальность изменялась до 10 км при угле
падения 80°. Съемку РЛИ производили с экрана электронно-лучевого
индикатора на пленку типа КН-4. Из-за малых высот учет
мультипликативной составляющей г в модели сигнала не проводился, т.е.
полагаем 8 = 1.
Под сложными изображениями в дальнейшем будем понимать
изображения местности с расположенными на ней целями.
Предлагаемые методы обработки сложных изображений базируются на
понятиях фрактальной размерности [3,479]. Многочисленными
исследователями в течение десятков лет было установлено, что
большинство природных ландшафтов, а также участки поверхности Луны и
Венеры [1011] могут рассматриваться как фрактальные в различных
диапазонах пространственных масштабов. Обширные исследования
фрактальной структуры разнообразных поверхностей и дискуссии о
них обобщены в [479]. Для изображений планеты Венера на длине
волны Х= 8 см (рис. 9.46) были получены значения фрактальных
размерностей в диапазоне D = 2,24893-2,38222 [479, 541].
Рис. 9.46. Примеры радиолокационных изображений поверхности Венеры
с фрактальными размерностями 2,26343 (а), 2,24932 (б),
2,24893 (в), 2,27376 (г) [479]
18 Фракталы
545
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Методы вычисления. Фрактальную размерность D естественных
и искусственных объектов удобно измерять по изменениям
некоторого параметра при различных масштабах. На практике
фрактальную размерность D измеряют косвенно — по наклону зависимости
S = S(S), где S - измеряемое значение, например длина линий или
площадь образований и т.д.; 8 — шаг измерения или размер
сканирующего окна. Для фрактального объекта величина D описывается
формулой
S(8) = k8-D, (9.58)
где к - коэффициент пропорциональности.
Установление инвариантности фрактальной размерности D
изображений природных образований от их яркости [538] явилось
основной предпосылкой для перехода к фрактальной обработке сложных
изображений. Один из возможных подходов к формализации
данной задачи состоит в следующем. Любая детерминированная цель в
пределах физически охватываемых масштабов наблюдения
остается неизменной, и оценка ее характерных размеров или площади
всегда стремится к определенному пределу, а в идеальном случае
является постоянной величиной. Одновременно при изменении
масштаба изображения местности площадь фрактальных образований
также изменяется. Поэтому появление на любом изображении
некоторой искусственной цели изменит значение фрактальной
размерности D изображения в целом.
Варьирование масштаба производится рамочной фильтрацией
исходного изображения А в изображении А. Пусть, как и ранее, f~ —
элементы изображения fff(x, у) размером Nx и N, которое
подвергается рамочной фильтрации, а /^ - элементы получающегося при
этом изображения Гн{х,у) размером NxxNy. Тогда для фильтрации
с рамкой или окном из (2М + 1)(2N + 1) элементов получаем
1 т+М n+N
A^A'-fLn ^г(2М + 1)(2М + 1)1_м1/г (9-59)
Разумеется, описываемая модель является лишь пояснением
принципов фрактальных методов обработки сложных изображений.
Обнаружение целей, как отмечено выше, может быть основано на
таких признаках, как полная фрактальная сигнатура, ее часть или
546
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
наклон. Как следует из экспериментальных данных, фрактальные
признаки изображений в пределах классов компактны, а
пространство признаков разделяется на сепарабельные множества.
Для компьютерного моделирования фрактальных сцен (далее
фракталы) и сложных изображений, расчета их сигнатур, были
созданы программы [538, 542], написанные на языке C++. Различные
алгоритмы синтезирования двумерных фрактальных изображений,
в том числе и цветных, были разработаны в [538]. Результаты
обширных компьютерных экспериментов по моделированию фракталов, а
также по измерениям фрактальных характеристик множеств Ман-
дельброта и Жюлиа представлены в [538, 543]. Основные
результаты, полученные на первом этапе исследований сложных
фрактальных оптических, радиолокационных и синтезированных
изображений, были изложены в [479, 543-545].
Изображения природных ландшафтов, как правило, получают с
помощью оцифровки фотографий, и они представляют собой
растровые картины. Для измерения фрактальных сигнатур желательно
иметь изображение местности в различных масштабах. Однако это
не всегда возможно не только из-за очень большого объема
информации, но и из-за его отсутствия. Поэтому для анализа чаще всего
используется одна фотография. Для получения других изображений
необходимо генерировать их из данного.
Наиболее просто эта операция осуществляется при загрублении
масштаба исходного изображения. Каждой точке нового
изображения присваивается некоторое значение, представляющее собой
сравненную с определенным порогом линейную комбинацию значений
соседних точек исходного изображения. Для получения более
детального изображения следует применять известные методы деконволю-
ции [546]. Такой подход более трудоемок и не всегда применим из-
за отсутствия необходимой информации. Таким образом, при
измерении фрактальной размерности природных образований
используются черно-белые изображения, полученные с помощью
аэрофотосъемки или радиолокатора. Далее проводится загрубление
масштаба и строятся зависимости £(8), по которым определяется
размерность изображения. Для загрубления применяется метод кон-
волюции исходного изображения с помощью сканирующего окна.
Отклик окна сравнивается с некоторым порогом и затем
принимается решение о видимости точки с координатами,
соответствующими центру окна.
547
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Фрактальные стохастические сцены синтезировались по
методу, предложенному в [538]. В первом варианте (рис. 9.47,а) на
нулевом шаге от точки 0 под равномерно распределенными углами
проводились пять лучей со средней длиной 1. На следующих шагах из
конца каждого луча строились пять отрезков длиной 1/3, затем 1/9
и т.д. Размерность данного фрактала составляет D = 1п5/1пЗ.
Минимальный размер «ветки» был равен двум точкам на экране. Второй
фрактал (рис. 9.47,6) строился аналогично первому, за
исключением того, что вместо лучей использовались круги.
а) б)
Рис. 9.47. Фракталы, полученные с помощью алгоритмов,
использующих лучи (а) и окружности (б) [538]
Несмотря на то, что фракталы, приведенные на рис 9.47,
имеют стохастический характер, вид их зависимостей IgS = /(lg 8)
практически одинаков. Это свидетельствует о важной особенности
стохастических фрактальных изображений, а именно, слабой
зависимости размерности от вида конкретной реализации. Для рис. 9.47 было
получено D = 2,2545 и D = 2,2601. Следовательно, можно надеяться
на стабильность значений размерности реальных изображений
земных покровов в предположении, что процессы формирования
изображения близких классов поверхностей идентичны.
Новые методы обнаружения или фильтрации целей. По данным
[184] были измерены дробные размерности предположительно
фрактальных РЛИ и АФС реальных природных ландшафтов (рис. 9.48).
На РЛИ приведены лиственный лес и река, на АФС — лес, луг и до-
548
9. 9. Фрактальное обнаружение целей на изображениях земной поверхности
Рис. 9.48. Типовые примеры АФС с высоты 50 м (а)
и РЛИ с высоты 250 м на длине волны 8,6 мм (б) [184]
рога. Фрактальные размерности изображений оказались равными
D = 2,0974 и D = 2,1299 для РЛИ и АФС соответственно.
Сигнатуры дробной меры приведены на рис. 9.49.
Большое различие в размерностях фрактальных и
нефрактальных объектов может быть использовано в задачах обнаружения.
Проводились эксперименты, когда часть изображений (АФС, РЛИ) была
закрыта прямоугольной областью. Площадь прямоугольного объекта
равнялась 1/32 общей площади изображений. Полученные
результаты для АФС и РЛИ представлены на рис. 9.50. Как и следовало
ожидать, вариации фрактальной размерности изображения тем
значительней, чем большая часть поверхности покрыта искусственным
lg(S)
0,5
0,4
0,3
0,2
0,1
0 0,143 0,286 0,431 lg(5)
Рис. 9.49. Пример фрактальных сигнатур [545]
549
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Рис. 9.50. Зависимость фрактальной размерности АФС (а) и РЛИ (б)
от числа искусственных детерминированных объектов [545]:
- нижняя кривая — при отсутствии объекта; верхняя — для пяти объектов;
б — кривая 1 — для двух объектов; кривая 2 — без объектов
объектом, иначе говоря, чем больше точек, составляющих
фрактальное изображение, покрыто нефрактальным объектом. Для
повышения чувствительности алгоритма целесообразно разбивать
первоначальное изображение на части, что приведет к резкому изменению
значений размерности D при появлении нефрактального объекта.
Результаты обнаружения искусственных объектов на фоне
синтезированной фрактальной поверхности (рис. 9.51,д,б)
представлены на рис. 9.51,в. Видно, что в данном случае размерность выше, чем
у реальных изображений. Это связано с размытостью изображений
(АФС, РЛИ) земных покровов. Для уменьшения размытости таких
изображений следует использовать различные методы деконволюции
[546].
В задачах обнаружения полезный объект (цель) всегда имеет
некоторую случайную составляющую в любом из его параметров. В
данном случае таким меняющимся параметром считалась площадь,
покрываемая нефрактальным объектом. Была проведена серия
экспериментов, при которых площадь, покрытая нефрактальным
объектом, имела гауссово распределение со средним Ю-1 от общей
площади изображения и среднеквадратическим отклонением около 30%.
Примеры таких изображений представлены на рис. 9.52, а—г, а
изменения их фрактальной размерности показаны на рис. 9.52, д.
Фрактальные размерности для данных рис. 9.52, б-г равны D= 2,5476,
D= 2,5502 и D= 2,5502 соответственно.
550
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
а) б)
—I 1 1 1
3
2
1
i i 1 ■ ■ ■
О 0,143 0,286 0,431 lg(8)
в)
Рис. 9.51. Изменение размерности синтензированной фрактальной сцены (а, б)
при размещении на ней детерминированных объектов (в) [545]:
кривая 1 - без объектов, D - 2,4663; кривая 2 - для одного объекта, D - 2,3625;
кривая 3 - для двух объектов, D - 2,2627
Для получения статистических данных о значениях фрактальных
размерностей изображений поверхности были проведены измерения
размерностей участков изображения. По полученным значениям
строились эмпирические распределения размерности. В ходе
экспериментов фрактальное изображение, синтезированное методом,
описанным в [538], и имеющее размер 1600x1200 точек, разбивалось
на ряд элементарных изображений размером 200x100 точек. Затем в
центр каждого элемента помещался объект — прямоугольник от 20x20
до 60x60 точек (рис. 9.53,а).
По ансамблям значений размерностей (рис. 9.53,6),
полученных таким способом, были построены эмпирические
распределения (рис. 9.53,в), которые могут быть использованы для синтеза
обнаружителей. Гистограмма, максимум которой находится вблизи
0,6
0,4
0,2
1 г—
~^х
■
1 '—
551
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Igtf).
0,8
i i i i i i i
i i 1
i i ■ i
0
0,431 lg(8)
0,143 0,286
д)
Рис. 9.52. Примеры изображений при обнаружении объекта в шумах (а-г)
и вариации их фрактальных сигнатур (д):
а - исходный фон; б-г - различные флуктуации изображения объекта;
кривые 1-4 соответствуют позициям (а-г) [545]
значения 2,5, соответствует серии, полученной для чисто
фрактального изображения. Другая серия со средним, равным -2,2,
получена для изображения с объектом. Строя такие гистограммы для
различных классов изображений реальных поверхностей, можно
синтезировать фрактальные непараметрические обнаружители.
При определении размерностей можно использовать не только
описанный алгоритм, но и алгоритм, основанный на связи
спектральных и фрактальных характеристик изображений. Так как
фрактальные характеристики не содержат информации о конкретном виде
552
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
*■
—
и*
[т ;
if
ж.
"•■v<T¥ ^
-. ф.'тк^
к.. **->, it.^2
' 4F
£•
'
а;
0,1
т—г
j i i i i i i_
0,143 0,286 0,431
W(D)
б)
lg(S)
1,0
0,6
0,2
—1 1 1 г-
<
1 1 1
—1—I—1—1—\—I
Л н
Л' 1
V-^ J
.1. 1^"-.. 1.1 1
2,0
2.2
2,4
в)
2,5 2,8 D
Рис. 9.53. Флуктуирующий фрактальный фон с объектами (я), вариации
фрактальной размерности (б) и эмпирические распределения размерностей (в):
кривая 1 - фрактальное изображение + объект; кривая 2 - фрактальный фон [545]
объекта, а являются показателем его топологической сложности, то
данный алгоритм может быть наиболее эффективен в задачах,
связанных с обнаружением «подозрительных областей» при радиолока-
553
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
ционном зондировании. Это важно при обнаружении
малоконтрастных целей, так как позволяет резко снизить число зондируемых
объектов.
В итоговой серии экспериментов рассматривалось влияние
контрастности изображения полезного объекта на значение
фрактальной размерности изображения. В экспериментах использовались
фракталы, смоделированные согласно [538] и представленные на рис.
9.51. Яркость объекта определялась по его цвету, т.е. по 256
градациям яркости. Относительная яркость 1/10 прямоугольников
изменялась от белой (1/10 = 0) до черной (1/10 = 100%).
Площадь прямоугольника в первом эксперименте равнялась 1/20
общей площади изображения S, а во втором площадь объекта
составляла 1/5 общей площади S (рис. 9.54). Поведение кривых
подтверждает слабую зависимость фрактальной размерности изображения от
яркости объекта. Это свойство очень полезно при обнаружении
малоконтрастных целей. Наибольшее влияние на значение
фрактальной размерности оказывает доля площади цели на АФС и РЛИ.
D
3
2
0 20 40 60 80 //4%
Рис. 9.54. Зависимость D изображения от яркости объекта
при S0 = S/20 и S/5 [545]
Избранные результаты первого этапа исследований. В
компьютерных экспериментах, описываемых далее, использовались
синтезированные и реальные оптические и радиолокационные сложные
изображения. Для синтезированных изображений была измерена их
фрактальная размерность D почти по 100 реализациям. В результате
были построены экспериментальные распределения значений
фрактальной размерности. Полученные распределения имеют максимум
554
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
в точке D= 2,79384 со среднеквадратичным отклонением
примерно равным 0,02. При этом черному цвету соответствовала яркость
/= 0, а белому - 1 в отн. ед.
Измерение фрактальной размерности проводилось с помощью
загрубления исходного изображения. Масштаб менялся от 1:1 до 1:20.
Фрактальная сигнатура строилась в виде вертикальных отрезков для
каждого окна. Данная зависимость, как обычно, строилась в
логарифмическом масштабе. Фрактальная сигнатура в данном случае, как
впервые показано в [543], характеризует пространственный
фрактальный кепстр изображения. На рис. 9.55 в левой части показан вид
экрана компьютера до проведения экспериментов. В правой части
рис. 9.55 представлен вид экрана компьютера после окончания
эксперимента, а также фрактальная сигнатура, дающая оценку
D= 2,794.
Затем на фрактальный фон помещалась протяженная цель в виде
прямоугольника. При проведении экспериментов изменялись
размеры и яркость цели. Относительные вариации яркости составляли
0-1, а размеры цели составляли 1/3-1/64 общей площади
изображений. Соответствующие результаты компьютерных экспериментов
приведены на рис. 9.55,5 (D= 2,4983) при отношении Sn/S = 1/25,
а на рис. 9.55,в (Z> = 2,5543) при Sn/S = 1/64. Здесь Sn и S -
площади цели и изображения соответственно.
По результатам проведенных исследований были построены
зависимости фрактальных размерностей от контраста цели
относительно фона по интенсивности А" и от отношения площади
протяженной цели Sn к площади всего изображения £(рис. 9.56). Кривая
на рис. 9.56,# была построена для одной реализации фрактала,
когда цель черная, т.е. интенсивность сигнала стремится к нулю.
Данные на рис. 9.56,а позволяют говорить об уверенном обнаружении
цели при отношении сигнал-фон, меньшем -10 дБ. В дальнейших
экспериментах наблюдалось устойчивое обнаружение цели и при
более низких отношениях сигнал-фон. Наибольшее влияние на
вероятность обнаружения цели оказывают ее размеры. Поэтому при
обработке изображений вместо отношения сигнал-фон целесообразно
использовать отношение площади цели к площади всего
изображения [538, 541-545].
Аналогичные данные для РЛИ местности с изгибами реки, лугом
и лесом приведены на рис. 9.57. При отсутствии цели (рис. 9.57,а)
фрактальная размерность D = 2,8379. Когда на РЛИ находится цель,
555
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
а)
Рис. 9.55. Вид экрана компьютера до эксперимента (слева) и после окончания
эксперимента (справа) с синтезированными изображениями:
а - при отсутствии цели, D - 2,7940;
б— для цели размером S /S= 25_1, D = 2,4983;
в - для цели размером £ЦА?= 64"1, D = 2,5543 [77, 479, 916, 919]
при отношении £ц /S= 1/25 значение фрактальной размерности
падает до D = 2,5533, а при £ц /S= 1/64 - до D = 2,6809. Для каждого
изображения на рис. 9.57 были получены разрезы пространственной
яркости (интенсивности), по которым можно судить об отношении
сигнал-шум.
556
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
Без объектов
У ^
л*
251>
-10 -6 0/СдЬ*
а)
I | : 1 зц/5
0 0,5 1,0
б)
Рис. 9.56. Зависимости фрактальной размерности D синтезированных сложных
изображений от контраста цели К (а) и отношения Su/S (б) [545]
Зависимости фрактальной размерности РЛИ от контраста цели
и отношения Sn/Sимеют вид, аналогичный кривым рис. 9.56.
Однако, в отличие от данных рис. 9.56, для РЛИ наблюдается переход
от более крутого участка кривой D = D (£ц /S) к более пологому при
значении параметра S /S= 0,5. Данное значение £ц /S аналогично
полученному в [535] для РЛИ.
Соответственно, экспериментальные данные для АФС
местности с дорогой, лиственным лесом и травой представлены на рис. 9.58.
В отсутствие цели (рис. 9.58,а) фрактальная размерность D = 2,8235.
При наличии цели с относительными размерами Sn/S= 1/25
имеем D= 2,5502 (рис. 9.58,6), при отношении Sn/S= 1/64 значение D
увеличивается до 2,5809 (рис. 9.58,в).
Следует отметить почти одинаковые значения фрактальной
размерности для РЛИ и АФС с типовыми подстилающими покровами.
Таким образом, исследованы фрактальные характеристики как
синтезированных, так и реальных изображений местности. С помо-
557
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
а)
Рис. 9.57. Фрактальные сигнатуры при обнаружении цели на РЛИ:
а — при отсутствии цели, D = 2,8379;
б- для цели размером SJS = 25~1, D = 2,5533 [77, 479, 916, 919]
558
9.9. Фрактальное обнаружение целей на изображениях земной поверхности
if *V^ Л^% V** '*'*
Рис. 9.58. Фрактальные сигнатуры при обнаружении цели на АФС:
а - при отсутствии цели, D - 2,8235; б— для цели размером 5Ц/S -25-1,
D = 2,5502; в - для цели размером 5Ц /S = 64"1, Д = 2,5809 [77, 479, 916, 919]
559
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
щью компьютерного моделирования построены эмпирические
распределения D. Подтверждено влияние наличия объектов на
значение фрактальной размерности всего изображения.
Установлено, что плотность изображения нефрактального
объекта влияет на изменение размерности слабее, чем отношение
площадей, покрываемых объектом и фрактальным изображением. Данное
свойство особенно ценно в задачах обнаружения малоконтрастных
целей и выявления подозрительных областей. Предложенный метод
измерения фрактальной размерности имеет простую реализацию. В
общем случае он не требует какой-либо дополнительной обработки,
легко может быть распараллелен. Однако применение
прямоугольного окна приводит к естественным ошибкам при измерении.
Эксперименты, проведенные с изображениями реальных земных
поверхностей, полученных с помощью аэрофотосъемки и
радиолокационного зондирования миллиметровым цифровым
радиолокатором (см. разд. 9.8), доказывают возможность применения
фрактальных размерностей или функций от них при реализации устройств
вторичной обработки сигналов. По измеренным фрактальным
размерностям реальных изображений можно построить базу данных,
содержащую информацию о разнообразных классах природных покровов.
Впервые разработанные алгоритмы обнаружения цели [538],
использующие фрактальные признаки, стабильно функционируют
при низких значениях сигнал-фон. Данное обстоятельство трудно
переоценить при обнаружении малоконтрастных целей. Время
принятия решения о наличии цели на изображении любой природы
(оптика, инфракрасное излучение, радиоволны) позволяет говорить о
высокой оперативности измерений в режиме реального времени при
наличии спецпроцессора.
9.10. Фрактальное распознавание целей
Методы распознавания. Распознавание образов представляет
собой задачу преобразования входной информации в выходную,
которая дает вывод о том, к какому классу относится распознаваемый
образ [547-549]. Распознавание любых объектов или явлений требует
создания специальных систем распознавания. Не существует
универсальных систем распознавания для всех объектов.
Все методы распознавания можно разделить на две большие
группы. Первая использует понятие пространства признаков и об-
560
9.10. Фрактальное распознавание целей
работку в данном пространстве, вторая основана на исследовании
конструкции рассматриваемых образов.
Понятие фрактального распознавания образов вводится впервые.
Алгоритмы фрактального распознавания образов основаны на
использовании парадигмы «топология цели - ее фрактальная
размерность» [77, 550]. Методической основой алгоритмов является отказ
от топологических констан!4^ описание классов целей на языке
признаков в виде размерностей по Хаусдорфу D или их сигнатур.
Априорное пространство детерминированных или вероятностных
признаков определяется с помощью динамического теста.
Динамический тест. Как отмечено в [539], выбор и подготовка
тестового материала для экспериментального исследования процесса
распознавания существенно влияют на достоверность результатов
исследования. Наилучшим тестовым материалом для изучения
конкретной задачи распознавания является набор изображений, реально
соответствующих данным объектам. В качестве универсального
тестового материала для исследования вопросов распознавания
образов на изображениях любой природы удобно использовать набор
древнейшей китайской игры «Танграм», известной в Китае под
названием чи-чао-тю («хитроумный узор из семи частей») [552]. В
течение вот уже нескольких тысячелетий эта игра служит любимым
развлечением в странах Востока, а в начала XIX века она начала
распространяться и на Западе.
Игра «Танграм» состоит из семи элементов («танов») особым
образом разрезанного квадрата, окрашенного с двух сторон в черный
цвет. В каждой фигуре должны быть использованы все семь
элементов «Танграма». В проведенных компьютерных экспериментах были
исследованы 16 фигур «Танграма», включающие в себя
многоугольники, силуэты человека, животных, искусственных сооружений,
самолета, корабля и т.д. (рис. 9.59). Выбор такого универсального
динамического теста определялся тем, что все фигуры при разных
конфигурациях имеют одинаковую площадь. Поэтому нет
необходимости в центрировании и нормировке различных функционалов
сравнения. Кроме того, возможность составления фигур с
различным числом граней (от 3 до 23) и различной степенью сложности
создает удобства в подборе тестовых изображений, близких к
реальным.
Создание тестовой выборки с аддитивным шумом различного
вида возможно впечатыванием хаотических синтезированных или
561
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
11-Щ .11 fM
* * л
Рис. 9.59. Китайский «Танграм» (вверху слева) и 16 фигур,
составленные из семи «танов» [919]
природных изображений в транспаранты с набором
рассматриваемых фигур. Первые «грубые» результаты измерения фрактальных
размерностей D и кластеризации на пять кластеров (рис. 9.60) тестовых
изображений приведены в табл. 9.6, где указано также число граней
Ми уголков Л^для каждого «тана».
Углубленное изучение фрактального метода распознавания
образов позволило построить усредненные регрессионные
зависимости D=f(N,M) для силуэтов искусственных сооружений («таны»
№ 2,4,7—11) в виде D = 0,037V+ 2,0 и силуэтов биологических объек-
562
9.10. Фрактальное распознавание целей
D
2,8 |-
2,7
2,6
О
2,5
2,4
2,3
2,2
2,1
2
■С
•
,
У/
Ci--^jM-5-14""-5)lll
ПО ^-"
! кластер
1 l 1 l
10
15
20
25
N,M
Рис. 9.60. Результаты кластеризации в зависимости
от фрактальной размерности D и числа уголков N или граней М
тов («таны» человека и животных № 1, 3, 6, 14—16) в виде
D = 0,047V+ 1,6, где N - число уголков, 2 < D< 3. Силуэты
самолета (12) и корабля (13) образуют отдельный кластер (рис. 9.61).
Увеличение размерности пространства признаков. В дальнейшем
усилия были направлены на увеличение информативности
пространства признаков с применением методов фрактальной топологии.
Использование понятия текстуры изображений, фрактальных
характеристик (фрактальная размерность Д фрактальная сигнатура, ее
наклон, пространственный фрактальный кепстр, дробные показатели
пространственного спектра) и понятий интегральной геометрии
позволяет повысить размерность вектора измерений и более четко
выделить классы естественных и антропогенных объектов.
563
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Таблица 9.6
Распределение фигур по кластерам и фрактальным размерностям
в зависимости от числа уголков или от числа граней
Фигуры
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Значение
D
2,34567
2,32546
2,54983
2,12143
2,34028
2,28672
2,11721
2,42878
2,43682
2,24856
2,09813
2,74953
2,72222
2,33933
2,35132
2,29562
Число уголков
N
18
12
23
3
23
16
4
17
16
8.
4
10 (4 внутри)
17 (3 внутри)
20
19
16
Число граней
М
18
12
23
3
23
16
4
17
16
8
4
10 (4 внутри)
17 (3 внутри)
20
19
16
Кластер 1-5
3
3
4
1
3
2
1
4
4
2
1
5
5
3
3
2
При компьютерном экспериментировании применялись
радиолокационные изображения на вертикальной поляризации для
дельты р. Волга. Рассматривались карты подтопления района с
определением уровня фунтовых вод с точностью 0,5 м до глубины 2,5 м в
диапазонах длин волн: 4 см, 68 см и 2,5 м. Была создана
специальная программа. Она предназначена для выделения характерных
кластеров на изображениях местности, полученных радиолокаторами в
различных диапазонах.
Программа производит вычисление локальных фрактальных
размерностей для каждого пиксела изображения. Для этого
необходимо иметь, по крайней мере, два изображения одного и того же
участка земной поверхности, полученных на разных частотах радио-
564
9.10. Фрактальное распознавание целей
D
2,8
2,6
2,4
2,2
2,0
5 15 25 N,M
Рис. 9.61. Регрессионные зависимости D=f(N,M)
для 16 фигур динамического теста [673]
локаторов. При этом изображения, полученные на больших длинах
волн, окажутся более «грубыми» (крупный масштаб), а изображения,
соответствующие малым длинам будут детальными (мелкий
масштаб). Предполагая, что большинство природных образований могут
описываться фракталами, можно ожидать, что на изображениях
появятся области с близкими по значениям фрактальными
размерностями.
Программа вычисляет так называемую дисперсионную
фрактальную размерность. При этом в каждом пикселе изображения
оценивается дисперсия величины сигнала (цвета). Если изображение
нефрактально — дисперсия инвариантна масштабу.
При измерении дисперсии используются окна различных
размеров: 21x21, 11x11, 5x5. Естественно, чем больше окно, тем
монотонней значение дисперсии для любого изображения, что приводит к
уменьшению количества кластеров.
Распределение размерностей для типичного изображения
представлено на рис. 9.62. Данное эмпирическое распределение получе-
12
13
565
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Рис. 9.62. Распределение фрактальных размерностей
для типового изображения дельты р. Волга
но при размере окна 21x21. Отчетливо выделяются три группы
точек с близкими фрактальными размерностями, соответствующими
участкам с определенными текстурами. После анализа первичной
информации и установления типов поверхностей была произведена
обработка изображения с размером окна 11 точек. Обработка
позволила выделить около 10 кластеров. Результаты обработки
представлены на рис. 9.63.
На рис. 9.63 показано поле полученных фрактальных
размерностей, соответствующее трем приведенным изображениям одного
участка местности. Интересно отметить, что на обработанных
изображениях, кроме устойчивого разделения по типам, отмечаются не
видимые до фрактальной обработки особенности (участок отмели).
Это позволяет говорить о возможности применения фрактального
распознавания для идентификации участков изображения,
«невидимых» при классических методах кластеризации по яркостному полю.
В итоге можно отметить, что данные исследования являются
частью более общих исследований по применению фрактальной
геометрии в задачах радиолокационного и оптического обнаружения и
распознавания целей в интенсивных шумах и помехах (см. гл. 12).
Кардинальную важность в этих работах приобретает синтез
эталонного словаря фрактальных признаков классов целей [997].
566
9.11. Фрактальное кодирование изображений
Рис. 9.63. Поле фрактальных размерностей с выявленными кластерами
9.11. Фрактальное кодирование изображений
Фрактальные подходы. За последние годы много усилий было
направлено на разработку цифровых систем кодирования изображений.
Экономное кодирование позволяет ускорить передачу изображений,
увеличить их передаваемое число по каналу связи, снизить
требования к энергетическим характеристикам передатчика, уменьшить
объем оборудования для запоминания и хранения изображений. Все
существующие методы можно условно разделить на несколько
классов: аналоговые методы кодирования, цифровое кодирование с
поэлементной обработкой; цифровое кодирование изображений с
пространственной обработкой. Исчерпывающая информация об этих
методах содержится в [452].
В настоящее время успешно развиваются фрактальные методы
сжатия или кодирования изображений, которые основаны на
фрактальных итерационных преобразованиях. Детерминированные
фракталы при чрезвычайно высокой визуальной сложности обладают
очень низким информационным содержанием, так как порождают-
567
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
ся простыми рекурсивными алгоритмами [243]. Поэтому этот класс
фракталов можно отнести к математическим объектам с высокой
степенью избыточности в том смысле, что они получены путем
преобразования либо их копий, либо их частей. Под фрактальным
сжатием изображений понимается тот факт, что объекты реального мира
и их изображения могут быть смоделированы
детерминированными фрактальными объектами - аттракторами и набором двумерных
аффинных преобразований [240, 553, 554, 805].
Математические принципы фрактального кодирования
изображений основаны на теории их итерационного сжатия [555, 556].
Обозначим через (М, d) метрическое пространство цифровых
изображений, где d — метрика искажений. Пусть \i{ — исходный вектор
данных, соответствующий начальному изображению, которое
необходимо закодировать. Обратная задача в теории итерационных
преобразований состоит в построении сжатого преобразованного
изображения т в пространстве (М, d), для которого [i{ —
аппроксимируемая фиксированная точка. Обозначим через /"некоторый набор всех
допустимых преобразований в пространстве (М, d). Требования к т
формулируются следующим образом:
3s<\ для Vji,veAf, ф(ц),т(у)]<я/(ц,у); (9.60)
4h>^i)]->°- (9.61)
Здесь V — квантор общности, 3 — квантор существования, s —
контрактивность или коэффициент сжатия для е. При этих условиях и
допущении, что т имеет более низкую сложность, чем начальное
изображение, можно считать, что т характеризует потери
цифрового кодирования для \iv С помощью триангулярного неравенства [557]
легко показать, что для любого произвольного начального
изображения ц,0 и положительного целого п выполняется неравенство.
rf^pX-^jJ^^rffjipTOi^J + jVOipjio). (9.62)
При s< 1 из (9.61) и (9.62) видно, что после некоторого числа
начальных итераций элементы последовательности {р.л = тй(и-о)} >Q
характеризуют оригинальное изображение как кластер. В простран-
568
9.11. Фрактальное кодирование изображений
стве квантованных дискретных изображений данная
последовательность точно сходится к стабильному изображению, которое
является результатом этого итерационного построения, и оно должно быть
фракталом. Следует отметить, что близость in(\i0) к \i{ обусловлена
искажением rfQipT^)]. Из (9.62) ясно, что сходимость зависит от
s < 1. При т = (j-j имеем нулевое сжатие, и, хотя это равенство
удовлетворяет условиям (9.60) и (9.61), оно не принадлежит набору F.
Такие преобразования т по F, удовлетворяющие условиям (9.60) и
(9.61), называются фрактальным кодом для \iv При этом \i{
аппроксимируется самопреобразованием по т. Система фрактального
кодирования — декодирования изображений, основанная на изложенных
принципах, в общем виде представлена на рис. 9.64.
Фрактальные коды. Рассмотрим структуру и построение
фрактальных кодов для изображений. Тот факт, что избыточность
цифровых изображений описывается блочным самопреобразованием,
приводит к необходимости концентрации внимания на классе
преобразований изображений общей формы
0<i<N
0<i<N
где Р = {Ц] — неперекрывающиеся части изображения в N
диапазонных квадратных ячейках или блоках. Символом а »
обозначено ограничение изображения [i до ячейки Rf. Тогда \i = ^ |Хд,
0<i<N
ш
Кодер
*(Hi)*Hi
Канал
связи
ЯДекодер
Ц2
ц2 = Шпт^Сио)
tf-w»
Х(Ц)
Рис. 9.64. Обобщенная схема системы фрактального
кодирования — декодирования и последовательность необходимых операций [556]
569
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
т.е. изображение в целом определяется просто суммой частных
ячеек. Символом xz обозначен элементарный блок преобразований от
доминирующей ячейки Dt к диапазонной ячейке R.. Значение xz
записывается как некоторая композиция геометрических £. и
массовых 7) подмножеств элементарного блока преобразований,
определяемых далее,
т, = 7;.о5.. (9.63)
Применение преобразования изображений т, определенного
блочно, к изображению \i иллюстрируется рис. 9.64. Фрактальное
блочное кодирование \х{ для каждого индекса / от доминирующей
ячейки Dt к диапазонной R. предполагает, что преобразованный блок
т. ([i{ ) является близкой аппроксимацией оригинального диапазон-
ного блока jllx . Под /-м шагом понимается кодирование /-го блока
изображения \х{ на множестве Р.
При построении системы фрактального блочного кодирования
необходимо провести разбиение изображения, выбрать меру
искажений между двумя изображениями и определить конечный класс
преобразований изображений, определяемый последовательностью
разбиений и схемой квантования параметров. Начальное
изображение jlLj разбивается на неперекрывающиеся квадратные ячейки Sдвух
различных размеров, т. е. имеем двухуровневое квадратное
разбиение. Данный вид разбиения близок к квадратно-древовидному [558,
559]. Ячейки большего размера ВхВ называются родительскими, а
меньшего — детскими В/2 х В/2. Родительские могут быть
разделены на четыре неперекрывающиеся детские. Такое разбиение
независимо от вида изображения позволяет в кодере использовать
большие ячейки для гладко изменяющихся областей изображения, а
малые — для описания деталей сложных частей, таких как неровные
границы и мелкие текстуры.
Выбор размеров и форм ячеек на изображении зависит от ряда
факторов. Малые блоки (4 х 4 и менее) предусмотрены для того,
чтобы легче проводить анализ и классификацию, быстро определять
межблочное расстояние, проводить точное шифрование. Они
приводят к робастной системе кодирования, т. е. ее характеристики
устойчивы к различным воздействиям. Большие блоки (5 х 5 и более)
570
9.11. Фрактальное кодирование изображений
позволяют избежать избыточности для гладких областей
изображения и приводят к более высокой степени сжатия.
Измерение искажения между изображениями основано на
измерении таких искажений между блоками. Пусть S(i0J0, В) —
квадратный блок ВхВс индексами в нижнем левом углу /0 иу0.
Изображение [i имеет размеры гх г и Д — аппроксимация \i. Обозначим через
\l и Д. величину ограничений изображения до ячейки S(i0J0, В), а
через \ifJ - уровень серого в пикселе (i,j). Среднеквадратичное
отклонение искажений между блоками ц. и й определяется в виде
^Ч'М =
|1/2
0<iJ<B
Определим расстояние d между двумя изображениями, как
сумму всех блочных искажений. Тогда максимальное отношение сигнал/
шум #q определяется формулой
«g-lOlg- ^)2
d{\L&)/r2
где dr ([i) — динамический диапазон \i.
Аффинные преобразования. Далее опишем класс ^дискретных
аффинных преобразований сжатия изображений, определяемых
кодером на основе (9.63). Рассмотрим сначала геометрическое
подмножество S преобразований. Для дискретной формы Dn В
применяется специальный оператор сжатия 5, сопоставляющий блоки из
доминирующей ячейки Di = S(id, jd, D) с блоками из диапазонной
ячейки Rt = S(ir, jr, В). В простом случае (D= 2B) имеем
(SV-\+iJr+j =[^I(i),J(J) +^/(/>1,/(7) +^/(/),/(7>1 +^/(/>1/0>1_|/4
для всех i,je {0,...,B-1}, где индексные функции /и
/определяются как ДО = id+ 2/ и Ду) = jd + 2у.
В массовом подмножестве 7) используют массовые
преобразования, которые применяют при обработке блоков изображения в ячейке
Rt. Рассмотрим некоторые такие преобразования [556] в блоке
размером ВхВ. К ним относятся:
571
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
1) поглощение уровня серого g0 € ivkU<k<G :
ти=Ео> (9.64)
2) смещение яркости на постоянное значение Age {±vk}0uk<G :
(ЧО^^ + ДК (9.65)
3) контрастное масштабирование осе [0,1]:
(<^)и = щ1и. (9.66)
Следующие преобразования, называемые изометрией,
перемещают пикселы в пределах диапазонного блока. Существуют восемь
изометрий квадратного блока, а именно:
1) идентичность:
My^/j; (9.67)
2) ортогональное отражение по средней вертикальной оси (/ =
= 0В-1)/2) в блоке:
т,1=Нв-л-г (9-68)
3) ортогональное отражение по средней горизонтальной оси (/ =
= СВ-1)/2) в блоке:
(¥)/,; =^-1-/,У; (9.69)
4) ортогональное отражение относительно первой диагонали
(/=/) в блоке:
М/,,^ (9.70)
5) ортогональное отражение относительно второй диагонали
(/ +J = В - 1) в блоке:
WjJ^B-i-jj-i-i' (9.71)
6) поворот вокруг центра блока на 90°:
(^и=Нв-1-г (9-72)
572
9.11. Фрактальное кодирование изображений
7) поворот вокруг центра блока на 180°:
^)ij^B-i-i,B-i-r (9.73)
8) поворот вокруг центра блока на - 90°:
ти^в+и- <9-74>
Другие преобразования могут быть построены с помощью этих,
более простых преобразований. Массовые преобразования позволяют
получить из простого блока целое семейство геометрически
связанных преобразованных блоков, которые дают согласованную область
просмотра в процессе кодирования.
Технология фрактального кодирования. На основе описанных
процедур рассмотрим пошаговое построение фрактального блока для
любого начального изображения. Пусть для кодирования дано
цифровое изображение размером гхг, квантованное на 256 уровней
серого. Обозначим через {^}0</<ЛГ разбиение изображений на ячейки двух
различных размеров. Напомним, что т= ^ тр где xz. определено
формулой (9.63). ~1<N
Ячейка Rf размером ВхВ для xz создается через два этапа
преобразования Stn ^соответственно. Конструирование
пространственного сжатия Sf происходит на основе блока изображения \ld
размером DxD, который суживается до блока ^(Ир.) размером ВхВ.
Важно отметить, что определение доминирующей ячейки Di (ее
положение и размеры) эквивалентно описанию пространственного
сжатия St (трансляция вектора и фактор сжатия). Второй этап в
создании xz. состоит в выборе соответствующего преобразования
сжатого доминирующего блока Si(\LJ)), т.е. в нахождении
преобразования 7), которое минимизирует искажения между Т. °Si(iLD.) и щ„ .
Таким образом, можно формально определить некоторую
область доминирующих блоков Д которые в целом должны составить
изображение. Также можно ввести совокупность массовых
преобразований Т, созданную из всего набора 7}. Кодирование диапазонного
блока (in состоит в нахождении наилучших пар (D^T^eDxT, для
которых искажения di^^oS^^)] минимальны. Совокупность
573
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
DxT называется глобальной областью или виртуальным кодовым
словарем [556]. Кодирование диапазонного блока символически
иллюстрируется рис. 9.65.
Рис. 9.65. Кодирование диапазонного блока R- [556]
Рассмотрим вопросы обнаружения наилучшей пары (Dt, Tt) с
помощью анализа диапазонного блока и кодирования по всему
ансамблю доминирующих блоков. Под максимальной доминирующей
областью, соответствующей диапазонному блоку В х В, понимается
совокупность всех блоков изображения размером DxD(D> В),
размещенных по всему кодируемому изображению. При
соответствующей процедуре поиска можно найти оптимальный основной блок.
Начальный основной блок D задается сканированием окна
DxD(D= 2B) по всему оригинальному изображению. Сначала окно
помещается в нижний левый угол с координатами (0, 0). Затем оно
перемещается на 5Л пиксел горизонтально вправо и на 5V пиксел
вертикально вверх, оставаясь все время внутри изображения. Обычно
шаги выбираются равными В или В/2. Затем доминирующие блоки
области D классифицируют по их геометрическим чертам.
Используемая здесь классификация блоков изображения описана в [560].
574
9.11. Фрактальное кодирование изображений
Необходимо определить три вида блоков и создать их классы D , D
и Ьт для теневых, краевых и среднедиапазонных блоков
соответственно.
Теневые блоки являются гладкими с отсутствием градиента.
Краевые блоки имеют значительное изменение интенсивности, что
характерно для границ объекта, проходящих через данный блок.
Среднедиапазонные блоки обладают умеренным градиентом. Они
допускают изотропность, что характерно для текстуры [184,197-199,
484, 560, 561]. В общем случае доминирующая область Ь
определяется совокупностью D = Ds\JDe\JDm, где De можно подразделить на
простые Dse и смешанные Ьте краевые блоки: De = Dse\JDme.
Теневые блоки не используют в качестве доминирующих, так как они
инварианты к любым преобразованиям, а поглощение порождает их
единообразное множество.
Рассмотрим далее процедуру построения преобразований в
области Ти исследуем результирующую область D х Т. Для каждого
диапазонного блока |i| n оригинального изображения схема
кодирования состоит в следующем. Пусть ^ - теневой блок. В этом случае
необходимо аппроксимировать ^„ с помощью однообразного серого
блока с уровнем серого, равным среднему уровню серого Д,-.
Преобразование т., которое порождает однородный блок, является
просто поглощением, и g. = квант (Д.»), где квантовая функция
определяется равномерными уровнями с 6 битами в диапазоне [0,255].
Перейдем теперь к случаю, когда ^ является среднедиапазон-
ным или краевым блоком. При этом каждый элемент ц^
доминирующей области относится к тому же типу, что и сканируемый блок
[1,„ . Анализ этой пары (|LX|» , Му>.) определяет выбор преобразования
т/5 используемого для кодирования щ» . Далее считаем, что щ„ -
среднедиапазонный блок. Тогда ограничимся массовыми
преобразованиями, являющимися композицией контрастного масштабирования
и смещения яркости: Ti(SJ^D) = ai(SJ^D) + Agi. Здесь а.
-коэффициент контрастного масштабирования. Значение Ag. рассчитываем
так, чтобы средние уровни серого в диапазонном и доминирующем
блоках были примерно одинаковы: Agt = квантЩ„ -оу!^ ), где
функция «квант» представляет равномерное квантование с
байтами в диапазоне [-128, 127].
575
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Если |i| n - краевой блок, то анализ пары (ц,п, \i,D), состоящей
из грубо сегментированных блоков Ц|» и Su,D , основывается на
расчете гистограмм уровней серого [90, 184, 484].
Допустим, что блоки изображений достаточно малы и могут быть
сегментированы на две однородные области: темную и светлую,
разделенные границей. Сегментированные блоки обозначим через ц,5п
и SuL соответственно. Затем по их разнице в уровне серого
рассчитаем динамический диапазон сегментированных блоков. После
применим массовые преобразования, которые запишем в виде
композиции контрастного масштабирования, смещения яркости и
изометрии:
wv=sb(5>4)+A4
Значение а. рассчитаем так, чтобы цЛ и Sj[iL имели
одинаковый динамический диапазон a^drfa^/driSjii^). Затем af
квантуем к ближайшим значениям. Значение Agt также
определяется и квантуется так, что уровни серого для светлых и темных
областей были одинаковы. В итоге выбираем одну из восьми
изометрии (С)0</<7 п0 формулам (9.67)—(9.74), которая минимизирует
искажения.
Анализ пар (ш», ^уМр.) и соответствующее этому построение
претендующих массовых преобразований 7], проводятся для каждого
домена ц^ в доминирующей области. Затем выбираются такой
доминирующий блок щВт и связанное с ним массовое преобразование
7), которое минимизирует искажения ^Г|% >Tt oSi(\iy) )1.
Оптимально преобразованный доминирующий блок ^(ц^.) называется
блоком согласования для Ц|« .
Технология фрактального декодирования. Восстановление
изображения из фрактального закодированного иллюстрируется в [556]
на одноцветном изображении размером 512x512. Там же
приведены спецификация фрактального кодирования и численные значения
576
9.11. Фрактальное кодирование изображений
статистик массовых преобразований для родительских и детских
трансформаций. Одна из схем декодирования включает в себя
итерации фрактального кода т на начальном изображении ц0 до тех пор,
пока не будет получена наилучшая стабильная сходимость.
Последовательность изображений {\in =^n(^}n=0 называется
последовательностью реконструкции для кода т с начальным изображением
[i0 . Преобразование изображения при фрактальном кодировании
проводится последовательно. Для каждой ячейки с индексом /
преобразование Tf применяется к текущему блоку изображения в
пределах доминирующей ячейки Dt и сравнивается с диапазонной
ячейкой R..
В [556] обсуждается также и другая схема декодирования.
Отметим, что преобразования в .Раффинны [557] в нормализованном
векторном пространстве (N, ||||), связанном с метрическим, т.е. код
т имеет вид V|ie N,x(\i) = L(\i) + v0, где L - линейное
преобразование сжатия; v0 - изображение, которое неоднородно в блочном
смысле.
Значение N-й итерации в восстановленной последовательности
есть
/=о
Это выражение для \iN представляет собой ряд порядка N- 1.
Элемент Z/(v0) является элементом /-го порядка в данной
последовательности, a LN([i0) - остаток в разложении. Отметим, что остаток -
единственный член в разложении \iN, зависящий от начального
изображения ц0.
Качество фрактального кодирования. Важной характеристикой
фрактального кодирования является соотношение бит q, равное
числу бит, необходимых для описания фрактального кода, деленному
на общее число пиксел в изображении. Для изображения,
обрабатываемого в [556], значение q = 0,06 бит/пиксел. Для получения
формулы для величины q, обозначим через Ns, Nm и Ne - общее число
детских (размер В/2 х В/2) и взрослых (размер ВхВ) ячеек теневых,
среднедиапазонных и краевых блоков в изображении. Для примера,
19 Фракталы
577
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
исследуемого в [556], размеры доминирующих блоков были 16x16
(взрослые) и 8 х 8 (детские), а размеры диапазонных блоков
уменьшались в 2 раза соответственно. Горизонтальные и вертикальные
сдвиги доменных блоков равнялись bh=bv = 4. Количество
информации в битах для величин Ns, Nm и Ne обозначим через Is, Im и 1е
соответственно. Для приведенных параметров и значений ocz. =2
бита, Д^.= 6 бит, /Л =3 бита рассчитаны значение 1т = 16 бит и
1е = 19 бит (взрослые блоки), а также 1т = 18 бит и 1е = 21 бит
(детские блоки).
Кодирование диапазонного родительского блока выполняется
следующим образом. Сначала область родительских преобразований
исследуется на наилучшее преобразование (см. ранее). Затем
изображение родительского доминирующего блока при найденном
преобразовании (родительский блок согласования) расщепляется на
четыре блока. После этого измеряют искажения между
полученными и детскими блоками в начальном изображении. В зависимости
от значения искажений при кодировании родительского блока
выполняется или не выполняется переход на следующий уровень.
Для каждого детского блока с большими искажениями
применяют также преобразования, и они совмещаются с родительским
преобразованием. При необходимости выполнения трех или
четырех детских преобразований вместе с ними выполняется
родительское преобразование, и блок кодируется как четыре детских блока.
Следовательно, имеется 12 возможных конфигураций в
родительском блоке, символически изображенных на рис. 9.66. Поэтому
определенная конфигурация может быть закодирована с помощью
1С = 4 бит.
а) б) в) г)
Рис. 9.66. Кодовые конфигурации в родительском блоке [556]:
а - блоки: 1 родительский, нет детских (одна конфигурация); б— блоки: 1
родительский, 1 детский (4 конфигурации); в - блоки: 1 родительский, 2 детских (6
конфигураций); г - блоки: нет родительских, 4 детских (1 конфигурация)
578
9.11. Фрактальное кодирование изображений
Среднее соотношение бит рассчитывается по формуле, бит/пиксел
п NpIc+NsIs+NJm+NeIe
q~ NpB>
где N = (г/В)2 — общее число родительских блоков в изображении.
Фрактальный код состоит из описания разбиения изображения
и упорядоченного списка преобразований диапазонных блоков
{(т,.,т^т}2, x2\xf2),0<i<N}.
Здесь т),1,т!,2,т/2,1,т?'2 — четыре детских преобразования, которые,
возможно, присоединяются к родительскому преобразованию т..
Структура фрактального кода показана на рис. 9.67.
Сравнение фрактального и векторного кодирования. Фрактальное
блочное кодирование в определенном смысле связано с методом
блочного кодирования, известным как векторное квантование [560—
563]. В табл. 9.7 приведен сравнительный перечень характеристик,
которыми описываются эти два метода. Необходимо подчеркнуть
следующее. Доминирующие блоки не представлены и не нужны для
декодера, отсюда возник термин «виртуальный кодовый словарь».
Этот словарь используются лишь в течение фазы кодирования при
построении фрактального кода. Кодирование не связано с существо-
Рис. 9.67. Структура фрактального блочного кода для изображения [556]
579
/
Ц\
1 х' ( Г
т?
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Таблица 9.7
Сравнение методов векторного квантования
и фрактального блочного кодирования [556]
Векторное кодирование
Разбиение изображения:
Квадратные блоки
Возможны различные размеры
блоков
Кодовый словарь:
Обучение по набору изображений
Кодовый словарь построения
Используется автономная
передача кодового словаря
Сопоставление блоков
декодирование:
Код изображений - перечень
адресов блоков в кодовом словаре
Прямое восстановление
Фрактальное блочное кодирование
Разбиение изображения:
Квадратные блоки
Возможны различные размеры блоков
Виртуальный кодовый словарь:
Сжатие и обработка доминирующих
блоков, выделенных из начального
изображения
Упорядочивание доминирующих
областей
Не используется передача
доминирующих блоков 1
Кодирование диапазонных блоков |
Декодирование:
Фрактальный код - перечень
блочных преобразований
Итерационное восстановление
ванием какого бы то ни было «внешнего кодового словаря», но
основывается на избыточности в самом начальном изображении.
Поэтому «виртуальный кодовый словарь» может называться и
«адаптивной картиной» в том смысле, что он определяется начальным
изображением.
Эти черты делают фрактальное блочное кодирование отличным
от векторного квантования. Ухудшение качества изображения
одинаково для обоих методов, хотя резкие границы очень хорошо
сохраняются при фрактальном кодировании. Интересно отметить, что
размер блоков, при которых начинает ухудшаться качество
изображения, примерно одинаков для обоих методов.
Улучшение качества фрактального кодирования. Различные
способы усовершенствования фрактального метода кодирования пред-
580
9.11. Фрактальное кодирование изображений
ставлены в [555, 556, 564—572]. Они рассматривают: влияние типа
разбиения изображения, блочных преобразований и их
оптимизацию; уменьшение сложности процесса кодирования; возможность
объединения методов фрактального блочного кодирования с
традиционными блочными; развитие теории для трехмерного случая.
Как было показано выше, блочные преобразования являются
аффинными и записываются в общем виде как
Т0 о S(iilD) = a0J(S^D) + Ag, (9.75)
где индексы, соответствующие диапазонным и доминирующим
блокам, опущены для простоты.
Оператор (сс0/ о S) представляет собой линейную часть
преобразования, которая соответствует адаптивной картине в процессе
сравнения. Трансляционный элемент Ag может быть априорно
ограничен до светового сдвига по диапазонному блоку R [556].
В [564] исследуется оптимальное число бит для равномерного
квантования величин сс0, Ag, наилучшего выбора сстах и верхней
границы сс0 при всех блочных преобразованиях, составляющих
фрактальный код. Там же проведен оптимальный выбор параметров
равномерного квантования сс0 и Ag с 5 и 7 битами соответственно при
атах=1>5.
Выбор трансляционного элемента Ag в трехмерном пространстве
ХВхв рассмотрен в [570], при
где {(XpOc^o^} — реальные коэффициенты; {^^А^}
—фиксированные базисные векторы, описываемые тремя матрицами:
4(/,у) = 1, A2(i,j)=i, A3(iJ) = j доя 0<i,j<B.
Постоянный элемент Ag может быть геометрически
визуализирован как наклонная плоскость в трехмерном пространстве,
образуемом плоскостью изображения и третьей осью для уровня серого.
Значение Ag рассматривается как элемент двумерного полинома,
определяемого коэффициентами а{, ос2 и ос3.
Если базисные векторы ортогональны, то оптимальные
коэффициенты легко рассчитываются без использования обратных матриц.
581
Глава 9. ЦИФРОВАЯ ФРАКТАЛЬНАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
После ортогонализации необходимо пересчитать только
коэффициент а0 для каждого нового доминирующего блока и оптимизировать
скалярные коэффициенты в (9.75) и (9.76). Иногда вводят гладкие
блоки, к которым относятся блоки изображения, хорошо
аппроксимируемые оптимальными квадратичными полиномами от / и у в виде
P(i, j) = a2i2 + Oj/ + b2j2 + Zy + cQij +t0
для Q<i,j<B.
Уменьшение времени кодирования и числа доминирующих
блоков возможно [567-569] при использовании более содержательных,
чем в (9.75), аффинных блочных преобразований:
3 3
к=\ к=\
При этом существенно повышается качество изображения.
Использование семи изометрий для квадратного блока i{-i7 (9.68)-(9.74)
проводилось в [569]. Применением блочно-ориентированной
стратегии в [564] достигнуто уменьшение сложности кодирования.
Ранее была описана процедура для кодирования при
двухуровневом квадратном разбиении изображения на 8x8 и 4x4
(родительские и детские). Иногда допускают более чем один уровень рекурсии
в разбиении изображения. Древовидное разбиение для порождения
блоков размерами 32x32,16x16, 8x8 и 4x4 использовалось в [564]. Там
же исследованы доминирующие блоки со сторонами, повернутыми
на 45° по отношению к стороне квадрата. При этом увеличивается
время кодирования, но улучшается качество изображения.
При сравнении различных методов показано, что для блоков с
резкими границами фрактальное кодирование предпочтительнее,
чем векторное квантование [573], но они примерно одинаковы в
случае текстурных областей. Рассматриваемое блочное кодирование
также сравнивалось с адаптивным [564]. Интересно отметить
применение фрактального блочного кодирования изображений для
трехмерного случая и доминирующих блоков размером 12x12x12 [555].
Таким образом, фрактальное кодирование изображений, основанное
на избыточности информации и итерационных преобразованиях,
является новым, быстро развивающимся направлением в цифровой
обработке многомерных сигналов.
582
Глава 10
ФРАКТАЛЬНЫЕ СТРУКТУРЫ В
КОСМИЧЕСКОЙ РАДИОФИЗИКЕ И
КОСМОЛОГИИ
10.1. Кластеризация во Вселенной
Распределение вещества во Вселенной. В космологии одно из
первых мест занимает проблема образования и эволюции
крупномасштабной структуры Вселенной. Этому способствовало создание в
конце 60-х годов прошлого столетия каталогов положений галактик
Цвикки, Ликский, Ягеллонский и др. [574]. Накопленный
материал позволил существенно продвинуть изучение реальной структуры
Вселенной и дал новый импульс обсуждению космологического
принципа однородности и изотропности Вселенной [574-578].
В масштабах звезд, галактик и скоплений вещество
распределено очень неоднородно. Галактики представляют собой системы с
массой 107-1012 М0 размером 10-Ю2 кпс и превышениями до 105 раз
по сравнению со средней плотностью. Здесь MQ - масса Солнца
(1 парсек, пс = 3,0857 • 1016м = 3,2 св. года). Распределение
галактик на небесной сфере наилучшим образом представлено в Ликском
каталоге. В нем приведены подсчеты до предельной звездной
величины т = 19, выполненные на площадках размером Ю'х 10'. Эти
площадки покрывают две трети небесной сферы. Эффективная
глубина каталога примерно равна 200/г1 Мпс. Безразмерный параметр h
лежит в пределах 0,5 < h < 1.
Приведем некоторые определения из области астрономии.
Движение и распределение вещества с высокой точностью изотропны на
масштабах ~ сН^1 = 300/г1 Мпс. Здесь rff = сН^1 - расстояние Хаббла.
Оно приближенно равно расстоянию, которое излучение прошло с
начала расширения Вселенной. Величина Я0 = 100/* (км/с) • Мпс-1
называется постоянной Хаббла; Н^1 = 1х1010 лет. Известный закон
Хаббла v = Н0г устанавливает связь между скоростями далеких
галактик v и расстоянием до них г. Красное смещение объекта, соб-
583
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
ственное расстояние г до которого меньше с#-1, z = H0r / с. Это
выражение служит хорошим приближением при z<^ 1. Современная
средняя плотность вещества записывается в виде р0 = 1,88 • 10-29£20А2
г/см3, где £20 - параметр плотности и 0,03 <£20< 1.
Группы галактик состоят из нескольких десятков галактик и
имеют массу 1012-1014 М0, размеры их Ю-1—10 Мпс, а превышение
над средней плотностью составляет 103 раз. Местная группа
состоит примерно из 20 членов, из которых наиболее крупными
являются наша Галактика и Туманность Андромеды. Скопления
представляют агломераты из нескольких тысяч галактик с массой порядка
1015 MQ, размерами порядка 10 Мпс и превышением плотности над
средней в 102 раз и более. Примером служат нерегулярные
скопления в Деве и регулярные скопления типа Волос Вероники.
Сверхскопления содержат несколько скоплений и имеют
неправильную форму. Они обладают массой порядка 1017 М0 и
размерами около 102 Мпс при плотности, превышающей среднюю
примерно в 2-3 раза. Типичным примером сверхскопления является
местное сверхскопление с центром в Деве. Преобладающая часть объема
Вселенной практически лишена галактик. Кроме сверхскоплений
существуют и полости, такие, как, например, огромная полость в
Волопасе. Таким образом, распределение вещества во Вселенной,
весьма неоднородное на малых масштабах (скучивание вещества),
приобретает все более однородный характер по мере приближения
к масштабам порядка 102 Мпс.
Многоточечные корреляционные функции. При статистическом
подходе для измерения скучивания галактик предпочтение
отдается различным модификациям автокорреляционной функции.
Основной принцип общепринятой космологической теории состоит в том,
что доступная наблюдениям часть Вселенной является
представительной выборкой Вселенной в целом. При этом пренебрегается тем,
что галактики наблюдаются в световом конусе, обращенном в
прошлое, а не в фиксированный момент космологического времени
[574]. Это хорошее приближение, так как большая часть
имеющихся данных относится к малой части расстояния Хаббла сН^1.
Пространственная двухточечная корреляционная функция ^п)
определяется совместной вероятностью найти одновременно
галактики в объемах 8V{ и 5V2, разделенных расстоянием гп при
средней плотности галактик п:
584
10.1. Кластеризация во Вселенной
bP = it[l + Z£rl2)]bVl5V2. (10.1)
Поэтому если в ансамбле выбрана галактика, то вероятность
того, что у нее есть сосед в объеме 5 К на расстоянии г,
8Р = п[1 + %г)]8У. (10.2)
Для случайно выбранного объекта среднее число соседей,
расстояние до которых меньше г, равно интегралу от (10.2):
n0=Urh + n]^(r)dV (10.3)
5 о
По аналогии с (10.1) можно определить трехточечную ^ш
корреляционную функцию через вероятность найти галактики
одновременно в каждом из трех элементов объема 8V{, 5V2, 5 V3:
6Р = /!П1 + ад + «Ъ) + $^ (Ю.4)
где ra b c — стороны треугольника с вершинами в трех
рассматриваемых точках; Ъ(га,гь,гс) = $173.
Предположение об однородности и изотропности означает, что
£ является симметричной функцией длины трех сторон. Для
значительного диапазона расстояний г двухточечная корреляционная
функция галактик хорошо аппроксимируется степенным законом
§(г)~(г/г0)т, у. ij8 (10.5)
в диапазоне 0,1 А-1 Мпс < г < ЮЛ-1 Мпс и радиусом корреляции
галактик г0 = (4—5)А-1 Мпс.
Очень часто распределение галактик описывают непрерывной
функцией плотности р(г) со средним значением <р(г)> = п и
автокорреляционной функцией JL(r) = (p(r + Ar)p(A)). Эта функция
связана с двухточечной корреляционной функцией (10.1) соотношением
«г) = [5р(г)/(Л2)]-1. (10.6)
585
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
Кластеры или скопления с большим числом галактик
коррелируют по тому же закону (10.5), но с другими параметрами [578]:
у« 1,8, 7/г1 Мпс < г < 150/г1 Мпс, г0 ~ 25/г1 Мпс. По этому поводу
ведутся дискуссии, так как получается, что галактики и кластеры не
могут быть хорошими метками распределения масс. Постоянный
наклон ^(г12) из формулы (10.5) для галактик и кластеров,
по-видимому, указывает на их возникновение в ходе единого
масштабно-инвариантного процесса, в то время как различные амплитуды
корреляций обусловлены неодинаковостью последующих процессов.
Данные по трех-четырехточечным функциям корреляции очень
хорошо аппроксимируются симметричной суммой произведений
двухточечных функций в иерархической форме. Критический
анализ следствий из иерархической формы приводится в [574].
Модели распределений галактик. Так как для фрактала £р (г) ~ rD~D°
(см. формулу (1.13)), то соотношение (10.5) можно
интерпретировать как подтверждение фрактальных распределений с фрактальной
размерностью /)« 1,2, где D0 = 3 — евклидова размерность
пространства. Для получения фрактальной размерности были предложены
степенная кластерная модель [574], модель непрерывной
масштабно-инвариантной иерархии [579] и нитевидная модель [575]. Как
указывается в [21], однотипные крупномасштабные фрактальные
структуры с фрактальной размерностью D « 4/3 могут возникать в
лабораторной турбулентности (пространственный масштаб Ю-1 м),
в океане и во Вселенной.
Изящный метод построения непрерывной иерархии скучивания
был предложен Б.Мандельбротом [3, 579]. На каждой ступени
галактики располагаются в соответствии с процессом случайного
блуждания Рэлея—Леви. Пусть имеется одна первичная галактика.
Поместим следующую галактику на расстоянии г в случайно заданном
направлении от первой. Значение г выбирается из распределения
а распределение для одного шага, получаемое из уравнения (10.7),
записывается в виде
Ua/4n)r«/ra+\ г>г0,
586
10.2. Модель структурной функции пространственного распределения галактик
Данная процедура повторяется неограниченное число раз, при
этом всегда значение и направление г выбираются независимо. Там
же [3, 579] показано, что средняя плотность числа галактик на
расстоянии г от первичной (затравочной) галактики при а < 2 имеет
асимптотический вид
п{г)~Сг«-\ /■->«>, (10.9)
согласующийся с гипотезой о фрактальной структуре Вселенной, так
как а = D > 0 — фрактальная размерность.
Необходимо отметить, что спорные статистические данные о
том, насколько характерны для кластерной морфологии нити,
пустоты и полосы, и острые дискуссии о различных сценариях
возникновения галактик лишний раз подтверждают настоятельную
необходимость альтернативной и дополнительной статистики, более
чувствительной к топологии галактик. В современной космологии это
представляет пока открытую проблему.
10.2. Модель структурной функции
пространственного распределения галактик
Модель Б.Мандельброта не может быть распространена на
случай однородного распределения многих различных процессов
случайного блуждания Рэлея—Леви с различными начальными
точками, поскольку при этом расходилась бы пространственная средняя
плотность. Конечное значение п может быть лишь в случае, когда
каждая цепь определяется конечным числом шагов [574].
Согласно анализу CfA-каталога (Center for Astrophysics),
проведенному в [577], плотность распределения п{г) относительно
галактики, находящейся в центре координат, при малых г имеет вид (10.9),
а при больших гскучивание исчезает и переходит в однородный фон:
На рис. 10.1 показано нормированное распределение или
структурная функции g(r) = n(r)/n = 1 + Z,(r) для выборки S65 каталога CfA
[577]сг0 = (5,83±0,11)Мпс, У= 1,88 ± 0,03и D= 3 - У = 1,16 + 0,11.
587
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
Кружки и точки показывают результаты различных методов
обработки одной и той же выборки. Точками 3 изображена скейлинговая
часть распределения (10.10), полученная для фрактала с ос = D = 1,16.
igfeM]
1,5
1,0
0,5
0
-0,5
0 5 10 15 20
г, Мпс
Рис. 10.1. Структурная функция g(r) = l + Zs(r) в зависимости
от расстояния г для выборки S65:
1 и 2 - результаты обработки; 3 - скейлинговое представление;
4 - аппроксимация по формуле (10.14) при D = 1,16 и b = 17,6 [577]
Из данных рис. 10.1 видно, что скейлинг нарушается в области
г > 5/г1 Мпс, и при г > 5/г1 Мпс структурная функция g(r) -> 1 для
пуассоновского процесса g(r) = 1. Для десяти выборок (535, 540,...,
580) в [577] приведен диапазон разброса Y = 1,67-1,88 и D = 1,15-
1,39. На рис. 10.2 представлены типичные билогарифмические
зависимости двухточечной корреляционной функции Ь>{г) для
выборок 535, 545, 565 и 575. Там же прямой линией нанесена
асимптотика с У= 1,77.
Рассмотрим на основе результатов [580] переход от схемы
случайных блужданий к формуле (10.10). Для траекторий с
фиксированным числом шагов N структурная функция имеет вид
588
10.2. Модель структурной функции пространственного распределения галактик
ю2
ю к
1 \-
п 1—i i i 11
Т I I ММ
10
1
10
г, Мпс
Рис. 10.2. Билогарифмические зависимости двухточечной корреляционной
функции £(/*) для разных выборок [577]
О п
4=1 L
1 —
N + 1
ftW»
(10.11)
где р(г) - (к- 1)-кратная свертка распределений р(г) =р{(г).
Действительно, если в точке г = 0 имеется галактика, то с
вероятностью (7V+ I)-1 она является галактикой к-то поколения, где к =
= 0,1,..., N (значение к = 0 относится к затравочной галактике).
Усредненное распределение остальных галактик данной траектории
имеет вид
i=l i=l /=l
(10.12)
При умножении (10.12) на вероятности (7V+ I)-1, суммировании
по к от 0 до N и добавлении усредненного вклада в плотность для
точки г от других траекторий
К
N
b{r-r') + Y.PM-r')
/=i
dV
приходим к выражению (10.11), в котором п - n0(N+ 1).
589
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
В качестве р(г) [580] было применено не степенное
распределение (10.8), а трехмерное симметричное устойчивое распределение
[151] с асимптотикой, как у (10.8),
Р(г) =
1
п(«)
ГГ\
Vм J
аПа + 2К.7тсоЛ
2тс2
-sin
V /
-а-3
Г->оо5
P{a)(x)^7—f\txp(iqx-\q\-)dq
(2л)
и сверткой, выражающейся через исходные распределения, с
помощью масштабного преобразования
p{ka)(x) = k-V(XpM(xk-V<x).
(10.13)
Подставляя (10.13) в (10.12) и используя предельный переход
вида N->°o, л^->0 для фиксированного значения n = n0(N+ 1),
получаем
g(r) = l + ^^k-y«pia\rk-V«a-i).
па
к=\
Для оценки асимптотики этого выражения необходимо
проинтегрировать его по переменной у = гк~{/аа~1 в пределах от 0 до °о и
учесть соотношения между плотностями трехмерного р(а\г) и
одномерного f{a)(x) симметричных устойчивых распределений.
Применив выражение для абсолютных моментов одномерных
распределений
J|x|v/(«)(x)^= ^"У v<a;
J r(l-v)cos(7iv/2)
/*«>(/•) =
2nr\
dx
590
10.3. Стохастический подход к кластеризации во Вселенной
можно записать [580], что
g{r)~\ + A{r/br-\ (10.14)
где Л = а(1-а)/[2лГ(1 + а)со8(ла/2)], b = (naa)l^a~^ -единственный
материальный параметр в (10.14).
Для определения структурной функции (10.14) необходимо знать
а = D и материальный параметр Ь. При D = 1,16, получаем Л = 0,11.
Выбрав опорную точку г = 5,5 на рис. 10.1, определяем значение
Ъ = 17,6. Результаты расчета [580] по формуле (10.14), показанные
сплошной кривой на рис. 10.1, вполне удовлетворительно
описывают скейлинг на малых расстояниях и его нарушение на больших в
согласии с данными CfA-каталога.
10.3. Стохастический подход
к кластеризации во Вселенной
Обзор стохастических моделей. Степенные законы (10.5) и (10.9),
охватывающие все более широкий диапазон масштабов, стали в
последние годы предметом интенсивных исследований. Однако пока
удовлетворительного теоретического объяснения этих законов не
существует. Часто допущение о существовании такого закона
принимается для того, чтобы исходя из других свойств, вычислить его
характеристики [574]. Наиболее распространенная точка зрения на
происхождение степенного закона опирается на результаты
численных экспериментов задачи ТУтел, согласно которым большие
флуктуации плотности возникают от усиления первичных флуктуации,
инвариантных к масштабам. В свою очередь усиление связывается
с конкуренцией между расширением и гравитационным
притяжением.
В численных экспериментах существует серьезная проблема
масштабов, так как отдельная галактика содержит примерно 1010
звезд, а в моделировании задачи N тел используется несколько
тысяч частиц и конечный средний объект содержит около 30
начальных частиц [581]. Поэтому не исключено, что некоторые
флуктуации не могут развиваться плотностью.
В [576] сформулирована стохастическая модель, в которой
гравитация учитывается через вероятность необратимой агрегации (сли-
591
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
яния) двух объектов (галактик), сблизившихся на достаточно малое
расстояние. Такой подход позволяет исследовать достаточно
подробно асимптоматическое развитие флуктуации и управлять им. Пусть
в начальный момент N~ 1000 частиц равной массы случайно
распределены на решетке. Каждая частица имеет свое собственное
направление и передвигается дискретно. Две частицы при
столкновении с вероятностью ра соединяются и с вероятностью 1 - ра
претерпевают рассеяние. После столкновения вылетающая частица с
удвоенной массой или две исходные частицы движутся по новым
случайным направлениям. Данная модель напоминает модели
кластер-кластерной агрегации, но отличается от них по двум важным
моментам. Во-первых, частицы между двумя последовательными
столкновениями не совершают случайных блужданий, а движутся по
прямолинейным траекториям. Изменение направления происходит
только после столкновения с другой частицей. Это обстоятельство
устанавливает определенную связь между пространственным
распределением и динамическими свойствами, которой нет в моделях
кластер-кластерной агрегации. Во-вторых, здесь пренебрегают
внутренней структурой отдельных кластеров, рассматривая их как точки и
принимая во внимание только их глобальное распределение в
пространстве.
Моделирование эффекта гравитации проводилось с помощью
вероятности агрегации ра, зависящей от масс частиц в виде
ра ~ (MfM )а, где а = 0 — 2. Для приближения к закону сохранения
импульса все частицы с тройной начальной массой просто
останавливались. Показано, что такой класс моделей порождает
распределения с агрегацией начальных частиц в более крупные, но без
настоящей кластеризации. В итоге получаются равномерные
распределения по всем крупным масштабам. Полученная система
однородна и не является фракталом. Такая однородность
обусловлена тем, что большая масса возникает в определенной точке
независимо от ее окружения.
Как известно, термализация орбит звезд в галактике обусловлена
не столько двухтельными столкновениями, сколько флуктуациями
гравитационного поля [576]. Это приводит к тому, что
столкновение, происходящее в окрестности других масс, приводит к
агрегации с большей вероятностью, чем столкновение в изолированной
области. В следующей серии экспериментов было показано, как
592
10.3. Стохастический подход к кластеризации во Вселенной
эффект динамического трения из-за наличия других масс влияет на
вероятность возникновения связанного состояния. Этот случай
соответствует приписыванию большей вероятности слиянию частиц, когда
оно происходит в населенной области. Учет локального характера
таких эффектов производится введением для каждой массы Mt в
точке rt резко спадающей функции вида f. {n ,M.) = exp(- \r-r.\/ Mf).
Суммарное влияние конкретного распределения масс задается
функцией F{r) = ^fjifyMf). В свою очередь функция F{r) связыва-
ется с вероятностью агрегации степенным законом, записываемым
как pa(r) ~ [F(r)f. Данная модель приводит к кластеризации во всех
масштабах и к развитию больших пустот. Такое распределение
действительно фрактально. Фрактальная размерность D на различных
временах в модели с динамическим трением показана на рис. 10.3.
В экспериментах использовались значения Р = 1/2 и 1; 5 = 1, 2 и 3.
Значения D рассчитывались из корреляционной функции
плотности £ (г), изменяющейся по степенному закону £Лг)~г~у- Анализ
полученных конечных распределений в терминах корреляционной
функции плотности показывает спонтанное развитие фрактального
распределения из однородного начального. Асимптотическое
значение D зависит от конкретных предположений, заложенных в модель.
Итак, в [576] установлен динамический процесс, спонтанно порож-
2,5
2,0
1,5
1 П
р
ill 1
А
А А А А A J
1 1 1 1 1 1 L J 1 1
Время
Рис. 10.3. Фрактальная размерность D на различных временах в модели
с динамическим трением, приводящая к фрактальной кластеризации [576]
593
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
дающий фрактальное распределение из однородного без расширения
системы. Это показывает, что расширение отнюдь не обязательно
является существенным признаком развития фрактального
распределения.
Отметим, что использование теории фракталов [1—3] позволяет
объяснить и знаменитый парадокс Олберса [582] о светимости
ночного неба.
Стохастический подход для формализации математических
моделей системы Л^тел и создания методов исследования таких
моделей представлен в [583]. При этом математические модели
динамических систем N тел принимают стохастическую форму, а
поведение тел описывается системой булевых вероятностных пространств
(Xt, Ft, Pt). Здесь Xi — выборочные пространства (траектории
динамической системы), Ft — алгебры событий на X., Pt — вероятностные
меры на классах событий Ft. Решения задачи Л^тел строятся в этих
пространствах методом вероятностных карт. Методы вероятностных
карт, построение которых осуществляется по схеме Бернулли, для
компьютерного моделирования нелинейных корректно
поставленных задач применимы всегда. Они не имеют ограничений и не
требуют выполнения условий эргодичности и марковости для
исследуемых объектов.
Стохастический образ эволюции динамической системы
описывается другой системой булевых вероятностных пространств (Yi9 Gz,
Rf). Выборочные пространства Yt для системы ТУтел строятся в
области изменения элементов кеплеровского движения. Тогда
эволюция системы А^тел будет описываться не вероятностно-временной
структурой положений и скоростей тел в выбранной системе
координат, а стохастической трансформацией целых траекторий всех тел
системы во времени. При этом можно упростить и оптимизировать
процедуру классификации классов траектории ТУтел и определения
топологических свойств множеств, определяющих условия и время
нахождения объектов в том или ином классе.
В [584] предложена модель образования галактик и их
скоплений в результате самопроизвольного рождения флуктуации
магнитного поля на фрактальной геометрии. Такие флуктуации могли
существовать в ранней Вселенной в эпоху излучения (t~ 1-1013 с,
красное смещение z ~ 1010-103) и в определенных условиях способствуют
существенным возмущениям плотности плазмы [585, 586].
Несмотря на то, что возможная роль первичного поля в зарождении галак-
594
10.3. Стохастический подход к кластеризации во Вселенной
тик обсуждалась в [574, 587], применение фрактального анализа
вместе с теорией групп Ли [588, 589] дает новые результаты [590—592].
Согласно температурной истории ранней Вселенной [593]
после Большого взрыва на малых временах t существовала эпоха
высоких температур, выше 1012 К. Вселенная содержала большое
разнообразие частиц и античастиц, находящихся в тепловом равновесии.
По мере расширения Вселенной температура Т снижалась и при
Г« 1010 К (f = 1 с) электронные нейтрино перестали эффективно
взаимодействовать с частицами. Этот момент времени знаменует конец
лептонной эры и начало эры излучения (плазменной эры) [585, 593]
при t ~ 1-Ю13 с, z = 1010-103. В этой эре из четырех
фундаментальных взаимодействий (сильное, слабое, электромагнитное,
гравитационное) доминирует электромагнитное. Плазменная эра
простиралась до эпохи рекомбинации (Т~ 4 х 103 К) или эры преобладания
вещества, когда протоны присоединяют электроны и
превращаются в нейтральный водород HI.
Механизм спонтанной генерации флуктуации магнитного поля
в первичной плазме обсуждается в [585, 587], где показано, что
время жизни т флуктуации с линейным размером X будет т ~ А,2. Это
означает [574], что наиболее стабильными являются
крупномасштабные фрактальные кластеры из магнитных флуктуации - магнитные
полимеры [585, 587, 594-596] с фрактальной размерностью 0 < D< 3.
С учетом минимального размера флуктуации магнитного поля
1 = 2кс/(йе плотность флуктуации как функция пространственного
масштаба х = г /I»1 согласно [3, 317] есть п(х) ~ xD~3, где юв -
электронная плазменная частота.
Рождение, а также аннигиляция флуктуации магнитного поля
подчиняется кинетике химических реакций 0 +± \i+\i~ с
противоположными направлениями магнитных моментов Ц [584]. При
нарушении внешним магнитным полем динамического равновесия
какие-то магнитные диполи изменяют свою ориентацию на
противоположную (допустим 2|а+) и т.д., что приводит к спонтанной
полимеризации магнитных флуктуации и, следовательно, к
зарождению фрактальных агрегатов из диполей.
Полимеризация магнитных флуктуации происходит во
фрактальном множестве, т.е. в эффективной среде с аномальными
свойствами. Данные свойства определяются фрактальной размерностью
среды 0 < D< 3 и индексом аномальной диффузии а (а = 0 в евк-
595
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
лидовом пространстве), определяющим связность фрактального
множества [597]. Аномальная скорость реакции вида 0«=>ц+|и~ на
фрактальном множестве связана с порядком реакции в = 4/D,,
отличающимся от своего нормального значения 0 = 2. Универсальное
соотношение, известное как анзац Александера-Орбаха [598], вводит
в рассмотрение фрактонную размерность
Df = 2D/(2 + o). (10.15)
Фрактонная (спектральная) размерность /^играет роль
размерности пространства в асимптотике плотности колебательных
состояний и определяет эффективное число степеней свободы.
Для случая полимеризации магнитных флуктуации
эффективное число степеней свободы составляет Df=Df-1, где -1 учитывает
локальное направление внешнего поля, т.е. это поле уменьшает
эффективное число степеней свободы на единицу. Тогда аномальная
скорость реакции полимеризации равна 0 = 4/1),.
В [584] получено нелинейное кинетическое уравнение для
полимеризации магнитных диполей на фрактальном множестве вида
^- = Ap + Q(x)p». (10.16)
at
Диффузионный член Ар правой части (10.16) описывает
диффузию магнитных диполей на фрактальном множестве
размерности D и записывается в виде [599, 600]:
Ар = -
1 Э
xD~x дх
K{x)xD~x^-
дх
(10.17)
Выражение (10.17) является обобщением трехмерного евклидова
оператора диффузии AFp = x~2 —
L дх
г
Эх
на множество с
размерностью D. Коэффициент аномальной диффузии К{х) в (10.17)
выражается через индекс аномальной диффузии а соотношением
К(х) = Кх-°. (10.18)
596
10.3. Стохастический подход к кластеризации во Вселенной
Здесь К= const, х =| х |. Второй член в правой части (10.16)
определяет скорость полимеризации магнитных флуктуации. Функция
р = р(х, f) есть плотность вероятности найти магнитный диполь |i+
в точке х в момент времени t. Значение Q(x) ~ n(x) ~ xD~3
показывает среднюю вероятность нарушения закона симметрии в реакции
O^iiV-
Группы симметрии дифференциальных уравнений. Применение
теории групп Ли эффективно при исследовании аномального
поведения систем на фрактальной геометрии [590-592, 595, 596].
Рассмотрим инвариантное решение pinv уравнения (10.16) относительно
допускаемой группы Ли точечных преобразований [584]. Это позволяет
точно определить значение D магнитных полимеров. При введении
новой функции u(x,t) = x~V/2p(x,t) и использовании (10.16)—(10.18)
получим
Р(Р + 2) и
4 х
где
^=^^ + *4-*v"e> (Ю.19)
P = 1 + g-Z> = const, (10.20)
v = a + Z>-3-P(l-e)/2; ё>1; а>-2; К= 1. Индексы х и /в (10.19)
обозначают частные производные по хи /соответственно. Как
подробно показано в [584], уравнение (10.19) будет инвариантно
относительно непрерывной группы точечных преобразований
t' = te\ х' = хехр[я/(2 + а)], u' = uem, (10.21)
где со= (v + 2)/[(a+ 2)(1 - 9)]; а - любое действительное число.
С помощью инфинитезимального оператора X,
соответствующего группе преобразований (10.21),
1 = Д + ^|- + со*Д (10.22)
dt 2 + аЭх du v '
получим характеристическое уравнение [588, 589] вида
dt ,~ ,dx 1 du
— = (2 + a)—= , 10.23)
t X (О U
597
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
откуда находим два инварианта
/ = х2+аД, / = ыГш. (10.24)
Так как инвариант / = ср(7) [589], то инвариантное решение
уравнения (10.19) записывается в виде «/яу = ф(/)/ш. Функция
Ф(/) = С^Я/Ш находится подстановкой uinvB (10.19), где Cinv
удовлетворяет соотношению
4Св;1=р2+2р + 4(о(2 + а)[((о-1)(а+2) + (а+1)]. (10.25)
Окончательно из (10.24) получим решение уравнения (10.16) в
виде
Pim = ^\m = Cinvx-^D-m-l)> (Ю.26)
не содержащее в явном виде параметр (J. Так как pinv ~ n(x) ~ xD~3, то
а+Д-1 = (ё-1)(3-/)). (10.27)
Второе соотношение между аиЛв виде
c = D-3 (10.28)
находим из (10.20) при подстановке Р = fiE = -2 для трехмерного
евклидова пространства.
Численные оценки характеристик полимеризации магнитных
флуктуации. С учетом того, что, как было показано, 9 = 4 / Df, Df=Df-\
и (10.15), из уравнений (10.27) и (10.28) в [584] получено
квадратное уравнение
5Z>2-16Z> + 11 = 0 (10.29)
с корнем D = 11/5. Поэтому с учетом (10.15)Zt= 11/3, Df =8/3,
0 = 3/2, Cinv= 16/625, a = D-3 = -4/5.
Из решения (10.26) легко определяется среднеквадратичное
смещение магнитных диполей, диффундирующих в объеме
магнитного полимера, которое с учетом (10.24) и (10.26) принимает вид
598
10.3. Стохастический подход к кластеризации во Вселенной
(х2(0)1/2~/1/(2+а)~/5/6. (10.30)
Формула (10.30) обобщает результаты, полученные в [599, 600]
для линейного диффузионного уравнения dp/dt = Ap с помощью
оператора Лапласа в форме (10.17). Из уравнения (10.30) следует, что
диффузия магнитных флуктуации в первичной космологической
плазме есть супердиффузионный процесс (см. разд. 2.3, а также [599—
601]), протекающий намного интенсивнее, чем нормальная
диффузия в евклидовом пространстве: (x2(t)\ ~V7.
Можно предположить, что сами магнитные полимеры в первом
приближении также являются диполями с магнитным моментом М,
подчиняющимися реакции вида 0 <=> М+М~ *=> 2M+, т.е. происходит
суперполимеризация с размерностью D = 11/5. Обсудим далее
влияние суперполимеров на образование галактик и их скоплений
после завершения процесса рекомбинации (/ > 1013 с) [584].
Магнитное поле суперполимеров вызывает флуктуации
плотности космологической плазмы порядка [574]:
5p/p~(VL)2, (10.31)
где Хв - магнитная длина Джинса; L - корреляционный интервал
магнитного поля (совпадает с характерным размером магнитного
полимера). Теория гравитационной неустойчивости требует к
моменту рекомбинации существования флуктуации плотности порядка
8р /р ~ Ю-2 - Ю-3 для образования галактик и их скоплений.
Согласно [585], характерное время полимеризации много меньше «хабблов-
ского» времени tn ~ H^l{t). Значение L из (10.24) и (10.27)
пропорционально времени полимеризации L~t5/6 [584]. Окончательно в
размерных переменных из (10.16) получаем
2кс
ДО«-^т(*о+1)
(t \5/6
(10.32)
Здесь t0 — время начала процесса полимеризации; Zq — красное
смещение в момент /0. Если предположить, что начало полимеризации
совпадает с эрой излучения, то t0 =1 с, z0 « Ю10 [593]. Для t0 = 1 с
599
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
плотность числа электронов во Вселенной порядка n(tQ) ~ 4 х 1031 см-3,
тогда (ue=2(%nn(t0)/me]l/2 ~3,5xl020 с"1 [585]. Окончательно, из
(10.32) Д/Г)^4х10псм. Магнитное поле полимеров В при
минимальном пространственном масштабе флуктуации /« 2кс/ со
оценивается из объемной энергии поля (В2 /8я)(4я/3 /3)~Г. Так как в
эпоху рекомбинации (/~/г ~1013 с) плотность числа электронов
л(/г)~103, а температура Г-Г ~4х103 К, то /(/г)~105 см, а
(x)e(tr)« 2х106 с-1. Тогда значение магнитного поля В в конце
плазменной эры (эры излучения) порядка B~[6Tl~3(tr)]l/2 ~6xl0-14 Гс,
что не противоречит экспериментальным данным [587]. Магнитная
длина Джинса в конце плазменной эры hB(tr) ~ ЗхЮ10 см. Тогда из
(10.31) 5р/р~5х10~3 является, как было отмечено, необходимым
условием для образования галактик и их скоплений в эпоху
вещества (t>tr). Для характерного размера суперполимеров L{(tr) в
момент рекомбинации из (10.32) следует, что L{(tr)« 2,5хЮ22 см.
Размер космологического горизонта к моменту рекомбинации порядка
Lh(tr)~3x\№zu»Lx(tr).
После рекомбинации главенствующую роль начинает играть
гравитационное взаимодействие. Гравитационная неустойчивость
[574] из-за магнитных полей суперполимеров приводит к
нарастанию первичных неоднородностей плотности плазмы, и в итоге - к
формированию наблюдаемой крупномасштабной структуры
Вселенной. Действительно, масса вещества в объеме суперполимера
М{ ~(4п/3)рЦ(1г)~1047 г~5х1013 М0, что соответствует массе
небольшого скопления галактик. Характерный корреляционный
интервал для гравитационного взаимодействия при t>tr порядка
размера магнитного суперполимера: rQ(tr) ~ ^г)« 2,5хЮ22 см. Тогда
современное значение корреляционного интервала для скопления
галактик го с «(zr + 1)/q(^) = 12,5 Мпс, где zr «1,5 х 103 - красное
смещение рекомбинации [574].
Первичные возмущения плотности плазмы концентрируются
вдоль фрактальных броуновских траекторий магнитных полимеров,
диффундирующих на фрактальном множестве размерности D = 11/5
[584]. Эти персистентные броуновские траектории можно рассмат-
600
10.4. Модификация тестов и алгоритма Мандельброта...
ривать как фрактальные кривые с фрактальной размерностью D
траекторий, равной из (10.30): Z> = 2 + g = 6/5 = 1,2 и соответствующей
наклону двухточечной функции корреляции y=3-D = 9/5 = l,8.
Полученные оценки у hDb [584] хорошо согласуются с
данными наблюдений [574]. Важно отметить, что магнитные полимеры
вызывают изотермические, а не адиабатические возмущения
плотности плазмы [585, 586], что не противоречит наблюдаемым
ограничениям на флуктуации космического микроволнового
излучения ЭТ/ТкЮ'4. Все сказанное относится к масштабам порядка
rOs=(zr + l)r0(tr)~l0h-1 Мпс
Сверхбольшие масштабы. В настоящее время значительное
внимание уделяется проблеме происхождения структуры Вселенной на
сверхбольших масштабах (> 50/г1 Мпс). Открытие Великого
аттрактора, Великой пустоты и Великой стены [602] стимулировало
бурный прогресс в данной области. Ранее неизвестная особенность,
называемая Великой стеной [626], ограничена лишь размерами
поля наблюдения. Ее двумерная проекция покрывает область
60А_1х170А-1 Мпс и содержит около половины всех имеющихся в
этих областях галактик. Для примера, наблюдаемый сегодня объем,
или сфера Хаббла, имеет радиус порядка 3000/г1 Мпс. Оценки
массы этой части Великой стены составляют примерно 2 • 1016 М0, что
в десять раз превышает массу Местного суперскопления. Можно
также предположить [584], что структура Вселенной на сверхбольших
масштабах связана с корреляциями между магнитными
суперполимерами в конце эпохи излучения (/ < 1013 с). Адекватный учет таких
корреляций определил бы изменения фрактальной размерности D и
наклона у . В работах [603, 604] получены данные, что такие
изменения действительно происходят при г ~ ЗОЛ-1 Мпс, причем Д
описывающая пространственное распределение вещества, становится
равной D « 2,2, а наклон у = 3 - D ~ 0,8.
10.4. Модификация тестов и алгоритма Мандельброта
моделирования распределений галактик фрактального
типа
Математические особенности монополя и диполя. Как показано
в [574], на основе существования далеких корреляций степенного
601
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
типа среднее число галактик внутри сферы радиуса R с центром в
одной из галактик зависит от R по степенному закону
(N(R))=BRD, (10.33)
где фрактальная размерность D лежит в диапазоне 1—1,5. Это
обстоятельство, как было отмечено, послужило основанием для
гипотезы о фрактальном строении Вселенной.
Главным свойством фракталов является их самоподобие в
различных масштабах и, как следствие, неаналитичность.
Действительно, в предположении справедливости (10.33) при любых Re (0,oo)
нельзя ввести понятие средней плотности числа галактик во
Вселенной
«-^-^
которая не зависела бы от радиуса обзора: при R -> 0 значение
n(R) -> оо , а при R -> ©о имеем n(R) -> 0. Следовательно, возникает
проблема формулировки космологического принципа и разработки
соответствующих статистических тестов. В качестве пробных тестов
(см., например, [605-607]) используются характеристики
^(') = Хпгр (Ю.35)
Д') = 1(^> (Ю.36)
называемые монополем и диполем соответственно. Суммирование
здесь ведется по всем галактикам в рассматриваемом объеме.
Среднее значение монополя (10.35) выражается через
структурную функцию
1 d(N(r))
MS?* <1037>
602
10.4. Модификация тестов и алгоритма Мандельброта...
в виде
R
{M(R)) = 4n{m)\g(r)dr. (10.38)
о
Для распределения Пуассона плотность числа галактик в точке
г не зависит от наличия или отсутствия галактики в начале
координат и совпадает со средней плотностью п, т.е. g(r) = n, и тогда из
(10.38) получаем (M(R)) = 4n(m)nR.
Таким образом, ожидаемая зависимость M{R) является
линейной от радиуса сферы. Для фрактального распределения
/ \ с/ \-l dN(r) BD D-Ъ (\ п о
g(r) = S(r) l—— = -т-И* \ 0<D<2.
dr 4я
Здесь S(r) - площадь сферической оболочки радиуса г. Видно, что
интеграл (10.38) в этом случае расходится. В [578] рассмотрено
поведение монополя и диполя с возрастанием радиуса обзора для
однородного пуассоновского распределения галактик и фрактальных
распределений двух типов: детерминированного фрактала и
фрактала, полученного в рамках (J-модели [608]. Результаты расчетов
монополя и диполя в относительных единицах для фрактала с D = 1,4
приведены на рис. 10.4. Из результатов численного моделирования
M(R), D(R)>
отн. ед. 4
3
2
1
0
0,2 0,3 0,4 0,5
Л, отн. ед.
Рис. 10.4. Результаты расчетов монополя и диполя в относительных единицах
для фрактала с D = 1,4 [578]
603
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
следует, что дипольный момент фрактального распределения
насыщается с ростом г подобно диполю для однородного пуассоновско-
го распределения. Этот факт в [578] рассматривается как признак
изотропности в стохастическом смысле фрактальной структуры,
являющейся неоднородной во всех масштабах по определению.
Монопольный момент растет, хотя и не столь быстро, как для
однородной среды.
В [609] более строго, чем в [578], доказано, что расходимость
интеграла (10.38) во фрактальной модели не является
принципиальной, так как связана с малыми масштабами. Исходя из этого
получено, что при минимальном расстоянии е между галактиками в
исходной (наблюдаемой) системе среднее значение монополя
(M(R)) = 4n{m)]g(r) dr = f^- (г°-2 - RD~2)
e
с асимптотикой
при соответствующей структурной функции ge(r) в виде
[0, Г<£,
ge(r) =
g(r), Г>£.
Поэтому для фрактала с размерностью D< 2 монополь
насыщается при увеличении R. Отсюда следует и аналогичное поведение
модуля диполя:
D(r) =
Wi
к-13
<-1^-м,у
Этому результату противоречит вывод [578] о неограниченном
росте <M(R)> с увеличением радиуса сферы.
Ветвящиеся процессы. Моделирование фрактального
распределения галактик в [609] проведено модифицированным методом
Б.Мандельброта [3, 579]. В [3] была рассмотрена бесконечная мар-
604
10.4. Модификация тестов и алгоритма Мандельброта...
ковская цепь {х, ^, ^2,...}, x,^eR3 с фиксированной начальной
точкой х и переходной вероятностью
p(x^>x')dx' = Ar-3-adx', r=\x-x'\>0, ос>0. (10.39)
При этом среднее число узлов данной цепи в сфере радиусом R
с центром в точке х при ос < 2 имеет асимптотический вид
(N(R))~BRa, R^oo. (10.40)
Получаемое таким образом распределение случайных точек имеет
асимптотически фрактальный характер с размерностью D = ос [3].
Однако, как отмечено в [609], различные точки этой цепи
стохастически не эквивалентны. Самая первая точка х имеет только
одного ближайшего соседа в цепи, точка ^ имеет уже двух
ближайших соседей первого порядка и одного соседа второго порядка
и т.д. Чтобы удовлетворить требованию стохастической
однородности, необходимо начальную траекторию {х, £г £2,...} дополнить
до целой вида {..., £_2, £_1? х, ^, £2,...}. Из-за изотропности
переходной вероятности р(х - х') = р(х'- х) построение такой траектории
сводится к объединению двух независимых траекторий {х, b,v ^2,...}
Следует отметить, что асимптотика (10.40) для траектории
{jc, ^,...,^}, N<°°, имеет вид (N(R))-> С< оо? что показывает
исчезновение фрактальных свойств на больших масштабах. На
практике моделируются лишь конечные траектории. Поэтому были
введены ветвящиеся траектории за предельным радиусом Rq,
аналогичные траекториям нейтронов в размножающейся среде [154, 610], но
с распределением пробегов не экспоненциальным, а степенным вида
(10.39).
Среднее число всех точек на траектории (А/Х°°)) = °°, но теперь
индивидуальное значение N(oo) не есть °°, как ранее, а является
случайной величиной с распределением wN, так что (N(°°)) = ^,NwN = «>.
В теории ветвящихся процессов случай qk = 1 (q — вероятность
возникновения частицы при столкновении) называется
критическим, для которого с вероятностью 1 число узлов конечно. Это не
противоречит условию равенства бесконечности среднего числа всех
605
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
точек на траектории, а означает лишь, что wN -^ О, N -^ «>. В
частности, при q = 1/2 и А: = 2 имеем 7V= 2л - 1, п = 1, 2, ..., а
распределение записывается в виде w0„ , =^—-^-. Через к обозначено
2/2-1 2Лл!
число частиц, образующихся после столкновения и
распространяющихся независимо друг от друга.
Алгоритм моделирования из [609] в окончательном виде
выглядит следующим образом. Начало координат помещается в точку х.
За условный пространственный масштаб принимается радиус
сферы Rq = 1 при минимальном шаге в цепи г = 10~3 и менее. Для
траектории внутри сферы нет ни поглощения, ни ветвления. При
выходе траектории из сферы она прекращается с вероятностью 1/2 и с
такой же вероятностью делится на две. Каждая из траекторий снова
может поглощаться или делиться на две и т.д. Если траектория
снова попадает в сферу, ее моделирование продолжается опять без
поглощений и ветвлений. По окончании этого процесса моделируется
парная ей траектория, и их объединение рассматривается как одна
реализация случайного распределения в сфере Rq=1. Как и в [578],
здесь также считаем массы галактик одинаковыми и равными
единице.
Проведенное моделирование [609] показало насыщение моно-
поля (10.35) и модуля диполя (10.36) при увеличении R.
Полученные результаты согласуются с приведенными ранее
аналитическими оценками. Таким образом, поведение монополя также может
служить признаком однородности распределения галактик: для
однородного распределения M(R) линейно растет, а при
фрактальном распределении насыщается.
10.5. Скейлинговые свойства флуктуации
космических лучей
Скейлинговый характер динамики флуктуации космических
лучей на различных фазах 11-летнего цикла солнечной активности
рассмотрен в [611]. Основываясь на традиционных корреляционных
и спектральных методах анализа случайных процессов, трудно что-
либо сказать о породивших их источнике, т.е. являются ли они
порождением динамической системы, либо это типичный «белый» шум.
С помощью фрактального анализа удается решить эту проблему.
606
10.5. Скейлинговые свойства флуктуации космических лучей
Конечная фрактальная размерность D означает, что данный сигнал
можно синтезировать динамической системой порядка D + 1 и не
более высокого, чем 2D + 1. Поэтому значение D дает оценку числа
степеней свободы системы или среды. При этом, как известно,
размерность «белого» шума стремится к бесконечности.
В последнее время активно обсуждается проблема описания
солнечной активности низкоразмерным аттрактором. Так, в [612]
утвердительного ответа не получено. Возможно, это связано с малой
информативностью чисел Вольфа W{t). В [613] отмечается, что
числа Вольфа из-за их специфического подсчета вряд ли могут быть
гладкой функцией истинной динамической переменной. Вариации
D достигали по результатам разных авторов 2-4,7. По данным [613],
состояние крупномасштабного магнитного поля Солнца,
определяемого интегральной энергией этого поля, является корректным
индикатором числа активности, а сама энергия магнитного поля
Солнца может быть истинной динамической переменной.
При разложении магнитного поля Солнца на совокупность
составляющих с учетом типа симметрии поля (дипольный или квад-
рупольный) получены следующие значения фрактальной
размерности: D дипольного типа составляет 1,1—2,8 (энтропия Колмогорова
0,06-0,08 бит/пол-оборота Солнца); D квадрупольного типа - 1,1-
1,5 (энтропия Колмогорова 0,05-0,07 бит/пол-оборота Солнца).
Расчеты в [613] проводились с помощью корреляционного интеграла
(1.8) при размерности пространства вложения D' = 4 - 8.
Типичные виды аттракторов в модели долговременной
солнечной активности приведены в [614] для дифференциальных
уравнений вектора с N= 7 компонентами при учете 11-летних вариаций
числа пятен по Вольфу и 22-летней повторяемости магнитного поля.
Наиболее известное ослабление активности носит название
минимума Маундера. Первые четыре уравнения характеризуют
магнитное поле Солнца, остальные три — его гидродинамическое
движение. При этом учитывалась и 57-летняя модуляция. Эта модель
качественно согласуется с результатами наблюдений и предсказывает
эффекты типа минимума Маундера. Однако здесь можно
рассчитывать только на прогноз нескольких долговременных колебаний
солнечной активности.
В [611] значения индекса мерцаний сначала усреднялись за одни
сутки, а затем за 27 суток. Было установлено, что на обеих ветвях
спада 11-летнего солнечного цикла 1980-1983 и 1989-1992 гг. гипо-
607
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
теза о гауссовом характере распределения индекса мерцания не
может быть принята. Только для выборки 1984-1987 гг. в годы
минимума солнечной активности на уровне значимости 90% может быть
принята гипотеза о нормальности распределения индекса мерцаний.
Для ветвей спада солнечной активности корреляционная
размерность составляла D « 2,5. Вблизи минимума (1984-1987 гг.)
зависимость D от размерности вложения скорее характерна для
случайного процесса.
В [615] было показано, что количество коронарных выбросов
массы увеличивается при распаде крупномасштабных магнитных
полей на ветви спада солнечной активности. Отмечалось также [616]
необычное поведение процентного содержания ударных волн из-за
выброса массы. Этот процентный максимум приходится на ветвь
спада 11-летнего цикла. Поэтому значение D « 2,5 является
корреляционной размерностью нестационарных возмущений,
доминирующих на фазе распада крупномасштабного поля Солнца [611].
По мере удаления от Солнца магнитные облака продолжают
расширяться и вступают в нелинейное взаимодействие. В
результате из магнитных облаков формируются суперкластеры
(монофрактальные объекты). В [617] утверждается, что наиболее мощные
понижения интенсивности космических лучей 1991 г. представляли
собой, скорее всего, детерминированные процессы. Как показано в
[611], исходя из обратной зависимости фрактальной размерности и
показателя наклона спектра флуктуации [618], повышение
размерности (падение показателя спектра флуктуации) указывает на
восстановление мелкомасштабных неоднородностей магнитных полей
ближе к минимуму и непосредственно на фазе минимума солнечной
активности. Поэтому поведение солнечной активности (вариации
индекса мерцаний космических лучей в 11-летнем цикле)
описывается низкоразмерным аттрактором на геоэффективной фазе
11-летнего цикла. Конечное значение корреляционной размерности
процесса в хаотической динамике солнечной активности указывает на
возможность прогноза геоэффективной фазы цикла при оценке
катастрофических проявлений геофизической активности.
608
10.6. Фрактальная модель солнечных пятен и роль кластеров в их эволюции
10.6. Фрактальная модель солнечных пятен
и роль кластеров в их эволюции
Фрактально-кластерная структура. Солнечные пятна
формируются следующим образом [619,620]. Вначале в центре ячейки
всплывает магнитный поток. Затем за период времени 4-5 часов
основания магнитных силовых трубок, из которых формируются
магнитные облака, двигаются к границам ячеек. В месте стыка ячеек
примерно через 45 мин образуется пора, которая темнее
окружающей полусферы. Большинство солнечных пятен начинает свою жизнь
в виде пор. Продолжительность их жизни составляет несколько
часов или суток, а напряженность поля в них превышает 1500 Гс.
В фазе роста солнечного пятна (примерно, 3-10 суток) его
магнитный поток непрерывно возрастает. Такие объекты имеют
центральную темную область, окруженную «щупальцами» из темных
волокон. В [594] предложена фрактальная модель солнечных пятен.
Солнечные пятна по этой модели представлены в виде
фрактального кластера из магнитных силовых трубок. По степени изрезаннос-
ти солнечного пятна можно определять свойства отдельных силовых
трубок и найти функции распределения плазмы, формирующей сами
трубки. Темные и светлые радиальный волокна имеют обычно в
длину 5000-7000 км и в ширину 300-400 км. Отдельные солнечные
пятна входят в состав скоплений пятен.
Центральная темная часть солнечного пятна состоит из сильно
сжатых, плотно упакованных силовых магнитных трубок. В [594]
вводится функция N (г) — отношение радиуса а силовой трубки,
находящейся на расстоянии г»а от центра пятна, к радиусу а0 неде-
формированной силовой трубки. Считаем, что N(p) - число силовых
трубок внутри круга радиуса р, p = r/aQ. Значение 7V(p)~[p/N(p)]2,
если функция к (г) изменяется мало на расстояниях aQ. При
возрастании р степень сжатия силовых трубок уменьшается, и при р = X
(граница тени и полутени) становится около единицы. Режим
агрегации меняется при р> X , когда силовые трубки уже не сжаты. Если
Л - полный радиус пятна (в единицах а0), то число силовых трубок
dN( р) в кольце с внутренним р и внешним d + dp радиусами
(^<р<Л, dp>\) записывается в виде dN(p) = DpD~ldp [317], где!>-
фрактальная размерность, 1 < D< 2.
20 Фракталы
609
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
В [594] получены выражения для распределения магнитного
поля в тени и полутени пятна. Когда фрактальная размерность
полутени пятна D = 2 - Я, фрактальная размерность границы
полутени и фотосферы 1 + Н = 3 — D. Для фрактальных структур
поверхностные или граничные эффекты бывают порядка объемных.
Поэтому наряду с объемной энергией токов необходимо учитывать
поверхностную энергию кластера. Мера поверхности Sn оценивается
как объем (3 - D)-мерного шара
3Vt =а.
те(3-/»/2
п ~"о /
3-D
+ 1
Л3"Я.
Фрактальная размерность солнечных пятен находится из
условия минимума объемной и поверхностной энергии кластера и при
Л»1 равна:
4 11п(3/8тсА21п2)
3 + 3 In Л
(10.41)
где A = jpv(p)dp; v(p) = ns(p)/nj, n^— плотность электронной или
о
ионной компоненты плазмы вдали от пятна. Значение А можно
определить через параметр неравновесности плазмы р > 0:
Д = -
3/7 + 2
/> + 1|0> + 2)
2(/> +!)(/; +2)
тР+\
(10.42)
Случай р -»оо соответствует максвелловской функции
распределения частиц. Из (10.41) следует также, что
Д =
3
1/2
8тг1п2
д(4-3/))/2
(10.43)
Численное решение (10.42) и (10.43) при наблюдаемой
фрактальной размерности солнечных пятен D « 1,24 и Л ~ 100 позволяет
определить/? я 6,9. Фрактальные свойства солнечных пятен зависят от
610
10.6. Фрактальная модель солнечных пятен и роль кластеров в их эволюции
функции распределения частиц плазмы. Конечность/?
свидетельствует о существенно неравновесном характере физических процессов,
которые приводят к образованию солнечных пятен.
Нелинейная динамика солнечных пятен. Рассмотрим модель
эволюции солнечных пятен как фрактальных кластеров [595]. Диаметр
развитого солнечного пятна по порядку величины совпадает с
характерным размером супергранул L0« 20 000—54 000 км со средним
значением 32000 [620]. Из-за турбулентных вихрей происходит
сближение магнитных трубок. Характерный масштаб Этаких вихрей
составляет d ~ 1000 км с характерной скоростью К« 1 км/с. Коэффициент
турбулентной магнитной диффузии \\~Vd, а характерное время
образования кластера т0 ~Ц/г\; тогда т| ~ 103 км2/с, т0 ~9 • 105с «10 сут.
Время жизни кластера будет определяться характерным
временем затухания магнитного поля в трубках. Время жизни силовых
трубок, составляющих пятно, ^~a\hm, где а0 = 100 км —
характерный радиус трубок; vm =107см2/с — магнитная вязкость. Поэтому
т «107 с « 3,9 мес. Учет диссипации приводит к зависимости
показателя/7 от времени [595]:
*А-\*
1-
^2^-3^)ЛП_1
2А-1
(10.44)
где т«107 с — характерное время затухания магнитного поля в
трубках.
Следует отметить, что p(t) -> оо при t -> т.. Поэтому параметр %
будет определять не только время диссипации магнитного поля в
трубках, но и время максвеллизации функции распределения плазмы. При
увеличении р распределение магнитного поля становится более
пологим, а энергия связи трубок между собой уменьшается. В
результате радиус тени солнечного пятна уменьшается, а исчезающие из
тени трубки уносят с собой магнитный поток. В этом случае полный
размер фрактального кластера Л растет с увеличением р.
Пусть для определенности «испарение» пятна происходит по
модельному закону А(р) = А0(р/p0f. Подставив это соотношение
в (10.41) и используя асимптотику Д(/?) = 6/р при больших/?,
получаем
611
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
4 lln[^/96icln2)]
3 3 \n[A0(p/p0f\
С ростом р величина D увеличивается и при р -> «> стремится к
топологической размерности Z>0 = 2 при (3 = 1. Рост D связан с тем,
что уходящие силовые трубки заполняют пустые пространства во
фрактальной «бахроме» вокруг тени пятна. Как только вся тень пятна
исчезнет и число трубок в кластере перестанет увеличиваться, дис-
сипативные процессы «разрыхляют» остатки пятна и D начинает
уменьшатся. Таким образом, D солнечных пятен максимально в
момент исчезновения их теней и составляет Z>max « 1,37.
Рассчитаем скорость «испарения» тени. Число N магнитных
силовых трубок, образующих фрактальный кластер радиуса Л,
определяется простым соотношением N = AD.
С учетом (10.45) имеем N = ap2, где а = [А$/(96пр*]п2)]1/3 = 6.
Значение dN /dt дает число трубок, поступающих из тени в
полутень в единицу времени, и с учетом (10.44) оно равно
dN_2ay4n(l/y)
IT'TT^F9 (10-46)
где Q = (x-t)/x - безразмерное время; у=(2р0-3)/(2р0-1) = 0,84.
Площадь тени солнечного пятна ST = na^N уменьшается со
скоростью
dt т (1-у0)3
После интегрирования (10.47) получаем
ST(t)-ST(0) = -a^-^, (10.48)
где ST(0) = n(X0a0)2; X0 - начальный радиус тени в единицах а0.
Полное исчезновение тени соответствует моменту времени 0О:
90 = ^/[Х01п(1/у)]. (10.49)
612
10.6. Фрактальная модель солнечных пятен и роль кластеров в их эволюции
Для типичных значений Х0 « 50 из (10.49) следует 90 =0,3.
Поэтому время разрушения солнечного пятна составляет rQ « 0,7т « 2,7
месяца.
Оценим скорость потери пятном магнитного потока O = B0ST.
С помощью (10.47) можно записать:
ЭФ 0 и /ВД/у)
(10.50)
Тогда среднее значение
ЭФ\
Эг/
_ лау,А
ео
1
(1_уво)2
1
d-Y)2J
(10.51)
Из формулы (10.51) получаем (ЭФ/д*) = 2-1010 Вб/ч, а с
помощью (10.50) при 0 = 90 имеем ЭФ/Э/ = 4 1010 Вб/ч. Эмпирические
значения ЭФ/Э/ составляют 6 ■ 109 — 8 ■ 1011 Вб/ч [620].
Характерная скорость оттока магнитных силовых трубок из тени
в полутень
К-
ST(0)dN
2кХ0 dt
откуда К(90)« 3,8 км/с; (К) = 2,1 км/с. Соответствующее
эмпирическое значение F-2 км/с [620].
В заключение в [595] рассматривается зависимость радиуса тени
от времени. Безразмерный радиус тени X(t) определяется (10.47).
Зависимость X(t) при t -> т0 имеет вид
Мв) =
2X0Voc
1/2'е-е0*'2
еЛ
у
Такая зависимость соответствует фазовым переходам второго
рода, причем радиус тени Х(д) имеет смысл параметра порядка.
Поэтому распад тени солнечного пятна можно интерпретировать как
613
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
переход через своеобразную «точку Кюри». Магнитные силовые
трубки как бы играют роль доменов в ферромагнетике, а сам
фазовый переход объясняется диссипативными процессами в плазме.
Эффективный размер пятна, т.е. радиус полутени RT = а0Ат
меняется более плавно. Для оценки зависимости Лг от времени в [595]
предполагается, что поток магнитных силовых трубок из тени в
полутень компенсируется потоком силовых трубок, «испаряющихся»
из полутени через границу с фотосферой. Тогда можно положить
Л£=Л^°, откуда AT/A0 = A{0D«-D)/D, и с учетом (10.44) и (10.45)
получаем /?(в0)~ 20,5; D(90)«l,37 и Лг(90)/Л0 =0,65.
Следовательно, к моменту разрушения тени пятна его эффективный размер
уменьшается более чем в полтора раза.
10.7. Фрактальные свойства турбулентности
солнечного ветра и магнитных конфигураций
Фрактальные и мультифрактальные свойства турбулентности
солнечного ветра рассмотрены в [621, 622]. Межпланетная и
околосолнечная плазма обязана своим существованием постоянным
потокам ионизированного газа из фотосферы Солнца. Потоки плазмы
движутся примерно по радиальным направлениям от Солнца.
Данное явление получило название «солнечного ветра». Спектральный
анализ экспериментальных данных по магнитному полю,
полученных прямыми измерениями с помощью космических аппаратов,
показал, что спектры мощности описываются степенной функцией
вида /-« [623, 624]. Анализ крупномасштабных флуктуации
скорости солнечного ветра для шести различных временных интервалов
проведен в [625].
В основу фрактальной модели солнечного ветра положен тот
факт, что турбулентные потоки плазмы в конвективной зоне и
фотосфере Солнца переносят магнитное поле в виде магнитных
силовых трубок и распределяет их по поверхности Солнца в сильно
перемежаемом структурированном виде [622]. Магнитограммы
высокого разрешения показывают, что структура магнитного поля на
пространственных масштабах от Imin = 400 км до 1пшх = 40 000 км
имеет фрактальное строение с размерностью D = 1,4-1,7 [626] и
наиболее вероятным значением D— 1,56 ± 0,08 [627]. Пространствен-
614
10.7. Фрактальные свойства турбулентности солнечного ветра...
ная фрактальная размерность D определяет количество магнитных
силовых трубок внутри круга радиуса г в виде
N~rD, \<D<2. (10.52)
Фрактальное распределение магнитных силовых трубок
обусловлено фрактальным строением и топологией турбулентных потоков
или ячеек в фотосфере Солнца. Эволюция таких ячеек
представляет собой процесс, при котором энергия передается от ячейки —
супергранулы (/тах ~ 3 ■ 104 км) к ячейкам-мезогранулам (/ ~ 6 • 103 км)
и, наконец, к ячейкам-гранулам (^min~103 км). Видно, что
^min-Ui-103 KM'^max^max-3'104 KM, ЧТО Дает Оценку/)- 1,54.
Фрактальные образования на поверхности Солнца,
соответствующие Imin -103 км, могут рассматриваться как агрегаты трубок с
размерностью Д зависящей от параметров функции распределения
плазмы [592, 594], и определяемой формулой (10.41). Значение Л при
радиусе интенсивных трубок г ~ 100 км равно A«Zmin/2r~5.
Подстановка Z>= 1,54 в (10.41) дает значение А ~ 0,25. При этом
предполагается, что функция распределения плазмы солнечного ветра
формируется в нижней атмосфере Солнца. Поднимаясь к верхним
слоям атмосферы фрактальные агрегаты подхватываются потоками
солнечного ветра и радиально расширяются со скоростью Vr ~ G V/ 2,
где 0 ~ 4 • 10~2 — типичный угол расширения трубок; V ~ 400 км/с —
средняя скорость солнечного ветра. На некотором
гелиоцентрическом расстоянии Rx соседние трубки начинают перекрываться. Это
расстояние определяется формулой [621, 622]:
^=(377/6. (10.53)
Здесь р - Imin / R - угол, разделяющий фрактальные агрегаты на
поверхности Солнца; Rs~ 700 000 км - радиус Солнца; Ts - период
вращения Солнца. Подставив в (10.53) значения (J ~ 1/700, 0~41О~2,
Ts ~ 26 суток, V- 400 км/с, получим Rx ~ 0,2 а.е. Следовательно, на
расстояниях R> R{b солнечном ветре начинают зарождаться
мелкомасштабные фрактальные кластеры с размером A(i^)>A0=5.
Полагая A(i?j)« ЗА0 = 15, из (10.52) получаем размерность
мелкомасштабных кластеров из силовых трубок D(j^)«l,46. С другой сторо-
615
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
ны, пространственное распределение таких кластеров в солнечном
ветре будет определяться иерархией конвективных ячеек в
фотосфере, имеющих D~ 1,54. Поэтому для описания структуры
межпланетного магнитного поля на R > 0,2 а.е. требуется не менее двух
фрактальных размерностей, что определяет мультифрактальность
исследуемой структуры [624, 628].
В свою очередь перекрытие рассмотренных фрактальных
кластеров начинается на расстояниях Щ ~ (Lrmx / Lr^n)Rl ~ 40R{ « 8 а.е. В
результате такого перекрытия образуются суперкластеры из
магнитных силовых трубок [621]. Мультифрактальные свойства
солнечного ветра на интервале R{< R< R2 изучены в [622].
Изменение пространственной фрактальной размерности
означает изменение спектра флуктуации межпланетного магнитного
поля. Для вычисления спектра флуктуации необходимо определить
связь D с фрактальной размерностью временных рядов. Прямые
измерения на космических аппаратах напряженности магнитного
поля и скорости ионного компонента солнечного ветра представляют
собой временные ряды. Для них можно определить временную
фрактальную размерность U, но не пространственную размерность.
Однако нетрудно получить соотношение, связывающее Dn U [621, 622].
Для этого введем временной масштаб т, определяющий
интервал усреднения измеряемой величины B{t). Данная функция может
быть представлена в виде гистограммы с шириной каждого
элемента т и высотой, равной среднему значению измеряемой величины
B(t) при tk<t<tk+T, которое обозначим через B(tk). Тогда длина
кривой определяется соотношением
L(x) = ^\B(tk+x)-B(tk)[ (10.54)
являющимся функцией т, и для статистически самоаффинных
кривых [623] L(i) = LQx~s, где 0<tk<TQ; T0 = Nx;N- целое; L0n S-
некоторые постоянные. Фрактальная размерность временных рядов
U связана с показателем S простым соотношением [3, 623]:
IT = S + l. (10.55)
616
10.7. Фрактальные свойства турбулентности солнечного ветра...
Переходя в (10.54) к пространственным координатам через
xk =Vtk и учитывая, что среднее магнитное поле пропорционально
xD~2, получаем Дт) = L0td~2 , откуда
/)' = 3-Д D = 3-D'. (10.56)
Величина U связана с показателем энергетического спектра а
соотношением [188]:
Д' = (5-а)/2, (10.57)
тогда
Д = (сс + 1)/2, (10.58)
т.е. пространственная фрактальная размерность D связана с
показателем спектра флуктуации и динамическими характеристиками
турбулентности.
Для анализа модели в [622] использовались временные ряды
скорости протонов солнечного ветра, измеренные с временным
разрешением около 300 с в эксперименте на космическом аппарате
ISEE-3, находившемся в точке либрации L1. По формулам (10.54) и
(10.55) вычислялись значения фрактальных длин от начального
значения т~ 3 • 104 с до масштабов -2 • 105 с. Спектр фрактальных
линий L временного ряда скорости протонов в двойном
логарифмическом масштабе показан на рис. 10.5. В табл. 10.1 приведены
значения наклонов S, временных фрактальных размерностей D' и
показателей спектров мощности а на трех временных масштабах т.
Фрактальная размерность в высокочастотной области /_1 < 2 • 104 с
зависит от внутренней структуры мелкомасштабных кластеров из
силовых трубок. В области 2 • 104 < /_1 < 105 с величина D связана с
пространственным распределением мелкомасштабных кластеров в
солнечном ветре. Разделение временных фрактальных размерностей
D' происходит на частоте /12 (/^ «2-Ю4 с). Частота/12 изменяется
как 1/7? с увеличением гелиоцентрического расстояния, так как
кластеры радиально расширяются с некоторой постоянной скоростью
кг~ек/2.
Значение частоты./^, разделяющей следующие фрактальные
размерности, может быть связано с конечным размером крупномасш-
617
Глава 10. ФРАКТАЛЬНЫЕ СТРУКТУРЫ В КОСМИЧЕСКОЙ РАДИОФИЗИКЕ
L
104
103
К
1111 1 1 1 1
» 1
Я
1 1 1 |1И
103
V г0'55
L 1 1 IIIM 1
104
Г0,36
""""-"V г0.77
1 *^С#
1 i щи 1 .1 1 1 1IUI
105 106
х,с
Рис. 10.5. Спектр фрактальных длин временного ряда скорости протонов в
зависимости от временного масштаба т с границами трех характерных временных
масштабов [622]
Таблица 10.1
Значения S, 1У, а на трех временных масштабах т [622]
т
<~2-104
2 • 104-105
>105
S
0,55±0,01
0,36±0,05
0,77±0,02
1У
1,55±0,01
1,36±0,05
1,77±0,02
а
1,99+0,02
2,28±0,01
1,46±0,04
табных фрактальных структур LmaK « 40 000 км. Можно отметить, что
/2^ sa(LmBK/Rs)Ts^l93-lOs с неплохо согласуется с данными рис.
10.5, где /2^ «105 с. На очень низких частотах/</^3> когда/-1 > 105 с,
временная фрактальная размерность, вероятно, связана с флуктуа-
циями крупномасштабных образований на поверхности Солнца.
Топология магнитных конфигураций относится к важнейшей
проблеме современной космической физики [620]. Характеристики
крупномасштабных космических полей зависят от тонкой
структуры токовых слоев и магнитных силовых трубок. Примером
является формирование солнечных пятен в фотосфере Солнца. В [629, 630]
с использованием методов дробного дифференциального
исчисления (см. разд. 2.2) получен явный вид дифференциальных уравне-
618
10.7. Фрактальные свойства турбулентности солнечного ветра.,.
ний, описывающих крупномасштабное магнитное поле. Там же
рассмотрено решение дробного волнового уравнения на фрактальном
множестве.
В [630] показано, что возбуждение магнитозвуковых колебаний
на фрактальных кластерах солнечного ветра приводит к перестройке
их внутренней тонкой структуры и к формированию степенного
спектра флуктуации межпланетного магнитного поля вида G{f) ~/_5/з в
широком диапазоне частот. Магнитозвуковые колебания на
фрактальных кластерах необходимо рассматривать как фрактоны —
особый вид акустических волн на множестве дробной размерности.
Анализ волновых процессов на множествах дробной размерности
имеет свои особенности, связанные с модификацией дисперсионного
соотношения для волн на фракталах, и является одним из
стремительно развивающихся направлений фрактальной радиофизики (см.
например, гл. 2, а также [631, 632]).
Глава 11
ФРАКТАЛЬНЫЕ АНТЕННЫ
И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
11.1. Фрактальные антенные решетки
Возникновение фрактальных антенных решеток. Понятие
фракталов является мощным средством для анализа и формирования
геометрических структур в самых различных областях математики и
физики. В [416] понятие фракталов применяется для инженерного
синтеза случайных антенных решеток и позволяет объединить
достоинства равноамплитудных и случайных решеток.
Первый тип антенных решеток обладает относительно
небольшими боковыми лепестками, но чувствителен к ошибкам
размещения элементов и значениям токов возбуждения. Второй тип
решеток робастен к ошибкам размещения элементов и их отказам, но
характеризуется относительно большим уровнем боковых лепестков.
Применение свойства самоподобия к теории случайных решеток
позволяет управлять диаграммой направленности в области боковых
лепестков.
Для иллюстрации этих идей вводим понятия инициирующего
(возбудитель) и порождающего (генератор) элементов (рис. 11.1).
Рассмотрим левую часть рисунка. При создании фрактального
дерева для синтеза решетки наращиваются ветви возбудителя
соответствующим образом уменьшенным по размеру генератором.
Результат трех этапов применения данного алгоритма показан на рис. 11.1
вверху слева. Но в нашем случае фрактальное дерево является
детерминированным. Для устранения детерминированности в синтез
вводится некоторый элемент случайности.
На первом этапе применяются один возбудитель и два
генератора. На каждом этапе роста дерева хаотически выбирается один из
двух генераторов, и он используется на следующем этапе роста.
Результирующая структура показана справа в верхней части рисунка.
Самоподобие случайного дерева очевидно при операции усреднения
на каждом этапе.
620
11. 1. Фрактальные антенные решетки
Детерминированная Случайная
V
генератор
v
возбудитель
V У
генераторы
v
возбудители
Рис. 11.1. Фрактальные деревья для синтеза антенных решеток [416]
Случайные фрактальные антенные решетки синтезируются
посредством введения эквидистантных подрешеток (генераторов) в
случайные решетки (возбудители), что позволяет управлять энергией
боковых лепестков диаграмм излучения.
На рис. 11.2 представлена структура множителя различных
типов антенных решеток gN, где индекс 7Vозначает число
элементарных излучателей. Здесь 180 элементов распределены на интервале,
равном 360 длинам волн. Графики слева показывают увеличенные
области правых графиков вблизи главного лепестка. Средняя
фрактальная размерность обозначена D, а угол между точкой
наблюдения и осью решетки - G. Как следует из данных рис. 11.2,а,
максимальный уровень боковых лепестков у случайной решетки оказался
относительно большим, а их расположение заранее не известным.
Фрактальная решетка образована при размещении
трехэлементных эквидистантных подрешеток в 60 выбираемых случайным
образом местах на интервале в 360 длин волн. При этом диаграмма
излучения подрешетки (рис. 11.2,6) является огибающей общей
диаграммы, вследствие чего диаграмма излучения по боковым
лепесткам (вне главного лепестка подрешетки) становится хорошо
управляемой. В то же время, вариации энергии в главном лепестке конт-
621
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
&г,ДБ
Случайная D
-5,7
случайная и= \ •+
11
0.1 0
of—
1 Детерминированная фрактальная
J D= 0,545 |
0,25
0,5
Случайная фрактальная
Z)=0,8
Рис. 11.2. Диаграмма направленности множителя gN
различных типов антенных решеток:
а - случайная решетка, D = 1; б - детерминированная фрактальная случайная
решетка, D = 0,545; в - случайно-фрактальная случайная решетка D = 0,8 [416]
ролировать довольно сложно. В [416] этот тип решеток назван
детерминированными фрактальными случайными решетками.
Для случайно-фрактальной случайной решетки используются
шесть различных эквидистантных решеток (рис. 11.2,в). Расстояния
между элементами различных подрешеток равны 0,8; V2x0,8;
>/Зх0,8; V5x0,8; V7x0,8 hVTTx0,8 длинам волн. В результате
диаграмма излучения по боковым лепесткам выравнивается за счет
усреднения шести независимых диаграмм.
Для количественного описания процесса синтеза введем
модифицированную фрактальную размерность
622
11.1. Фрактальные антенные решетки
D = loeN/logrl,
где N- число элементов в одной подрешетке; r= rx/r^ гх — среднее
расстояние между элементами подрешетки (генератора); г2 —
среднее расстояние между элементами случайного возбудителя.
Значения модифицированной фрактальной размерности для
рассмотренных фрактальных решеток указаны на рис. 11.2. Из
вышеизложенного следует, что большие значения D свидетельствуют
о меньшей концентрации излучаемой энергии вблизи главного
лепестка и меньшей степени управляемости уровнем боковых
лепестков. Рассеяние волн фрактальными решетками с изменяющимся
заполнением рассмотрено в [417, 418].
Фрактальные концентрические решетки. В [419] представлена
техника синтеза определенных классов фрактальных характеристик
излучения для специальных симметрично расположенных антенных
решеток [420]. Синтез фрактальных диаграмм направленности
проводится с помощью функции Вейерштрасса.
Класс функций, известный как обобщенные функции
Вейерштрасса, представляется в виде
f{x) = t.rtD-2)n&Wx), (ИЛ)
где 1 < Z> < 2; г| > 1; g— ограниченная периодическая функция.
Рассмотрим решетку в виде одного кольца излучателей радиуса
а (рис. 11.3). Кольцо излучателей лежит в плоскости {х, у}. На
границе кольца расположены М изотропных излучающих элементов.
Пусть / - ток, возбуждаемый элементом /и, расположенным под
углом ф = Ф0, набег фаз ат = -kasin 0O cos(90 - q>m). Расчетные
положения максимума луча (0О, <р0) и фт=2я/я/М, /и = 1, 2, ..., М.
Следовательно, диаграмма направленности кольца излучателей имеет
вид
м
F(Q,(p)=^ImQxp[ikasmQcos((p-yJ + iaJ. (11.2)
т=\
Для больших Мпри рассмотрении максимума луча в
направлении z (в = 0 или 180°) и при условии малости значений функций
Бесселя высокого порядка имеем
623
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
х —-Ф
Рис. 11.3. Кольцевая решетка в выбранной системе координат [419]
F(Q) = ItJ0(kasinQ)9
(11.3)
где It = MI — общий ток в кольце.
Множитель решетки концентрических окружностей
получается суммированием вкладов от каждого кольца:
N
gN(u) = ^InJQ(kanu\
(П.4)
где w = sin0, N— число концентрических окружностей, а — радиус
п-й окружности.
Сравнивая (11.1) и (11.4), с учетом g(x) = J0(x) получаем
г =Vi{D-2)n
кап = ц\
(П-5)
(П.6)
624
11.1. Фрактальные антенные решетки
Поэтому множитель решетки может быть записан в виде
формулы
N
п=1
(И.7)
Таким образом, синтезирована фрактальная диаграмма
направленности антенны. Фрактальная концентрическая решетка
рассчитывается на основе уравнений (11.5)—(11.7). Рисунок 11.4,а
иллюстрирует скейлинговые свойства диаграммы направленности
решетки F(u) при л= 2,34; D = 1,9; N = 10. На рис. 11.4,5 показана
увеличенная область левого графика, когда |sin0|<O,l. Эти кривые
подобны. Из-за усечения F(u) теряются лишь некоторые тонкие
детали в поведении характеристик излучения.
-1,0 -0,5 0 0,5 1,0 -0,Ю -0,05 0 0,05 0,10
sin 6 sin 6
а) б)
Рис. 11.4. Скейлинговые свойства диаграммы направленности
фрактальной концентрической решетки [419]
Коэффициент направленного действия антенны Z>(0, ф) в
зависимости от фрактальной размерности D для нескольких
концентрических решеток показан на рис. 11.5. Как видно, при уменьшении
D главный лепесток диаграммы направленности расширяется и
значение коэффициента направленного действия уменьшается.
Продолжением исследований [419, 421] являются работы [422,
423, 480], в которых рассмотрены канторовы концентрические ре-
625
Глава П. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Д(е,ср)
25
20:
15
10
1,1 1,3 1,5 1,7 1,9
D
Рис. 11.5. Зависимость коэффициента направленного действия D(Q, ф)
концентрической решетки от фрактальной размерности D при различных N [419]
шетки с числом элементов до 754. Картина излучения исследовалась
в широкой области пространственных частот.
11.2. Многодиапазонные фрактальные
антенны Серпинского
Фрактальная электродинамика. Теория взаимодействия
электромагнитных волн с фракталами создана недавно и интенсивно
развивается [330, 331]. Подтверждением этого являются основные
тенденции развития многодиапазонных или сверхширокополосных антенн.
Свойства таких антенн и их характеристики - входное
сопротивление, диаграмма направленности и коэффициент направленного
действия — изменяются в заданных пределах в очень широкой полосе
частот, не меньшей нескольких октав.
Широкий диапазон частотно-независимых антенн был
исследован и тщательно проанализирован в начале 1960-х годов [424].
Наиболее наглядными примерами таких антенн являются спиральные и
логопериодические антенны. Форма структур частотно-независимых
антенн инвариантна относительно некоторых масштабных преобра-
626
11.2. Многодиапазонные фрактальные антенны Серпинского
зований, т. е. наблюдается электродинамическое подобие.
Фрактальные антенны — это следующий шаг в построении новых
сверхширокополосных антенн.
Фрактальные структуры, как известно, самоподобны при
различных масштабах и не обладают характеристическим размером,
поскольку в одном объекте наблюдается бесконечное число масштабов
и размеров. Благодаря такому свойству фрактальные структуры мно-
годиапазонны в электромагнитном смысле.
Описываемый далее класс антенн основан на салфетке
Серпинского, предложенной в 1915 г. [425]. Первые работы по
исследованию таких антенн появились в 1996 г. [426,427]. Ниже на основе
результатов [428] проведен анализ характеристик фрактальных антенн
Серпинского, являющихся масштабной версией антенны,
представленной в [426]. Салфетка Серпинского образуется с помощью
вычитания центральных треугольников на каждом шаге итерации из
главной треугольной формы. В такой структуре каждая часть состоит из
трех оставшихся долей, точно равных всему периметру целого
объекта (см. рис. 1.1,г).
Конструкция фрактального монополя и его электродинамические
параметры. Антенна Серпинского, выполненная на тонкой
диэлектрической подложке Culcad 250 (ег = 2,5; толщина 1,588 мм),
помещена углом вниз на проводящей квадратной плоской основе
размером 800x800 мм, как показано на рис. 11.6. Такая конфигурация
антенны выбрана из-за простоты запитывающего устройства
(коаксиального кабеля с волновым сопротивлением 50 Ом).
Антенна синтезирована посредством пяти итераций, которые обозначены
окружностями (см. рис. 11.6). Если пренебречь вкладом от
центральной области на характеристики и допустить, что ток от фидера
концентрируется в той области антенны, которая сравнима с длиной
волны, то можно ожидать, что поведение такой структуры будет
подобно пяти симметричным вибраторам с треугольными плечами,
работающим каждый на своей резонансной частоте. Коэффициент
масштаба 8 = 2 означает, что высоты салфетки Серпинского будут
равны 89; 44,5; 22,3; 11,1; 5,5 мм [428] или 109; 54,5; 27,2; 13,6; 6,8
мм [426].
Входной коэффициент отражения Г связан с входным
сопротивлением антенны ^х и волновым сопротивлением Рф фидерной
линии соотношением
627
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
800 мм
Рис. 11.6. Фрактальная антенна Серпинского, синтезированная
пятью итерациями с коэффициентом масштаба 5 = 2 [428]
Г = (^вх-Рф)/(^х+Рф)- (П.8)
На рис. 11.7 показаны частотные зависимости входного
коэффициента отражения монополя Серпинского и пяти симметричных
вибраторов с треугольными плечами того же размера, что и все пять
эквивалентных салфеток Серпинского. Кривые построены
относительно сопротивления фидера 50 Ом. В табл. 11.1 приведены
основные параметры монополя Серпинского, полученные при
проведении лабораторных исследований.
Пять диапазонов в табл. 11.1 соответствуют значениям
коэффициента стоячей волны КСВ по напряжению, не превышающих 2. Ча-
628
11.2. Многодиапазонные фрактальные антенны Серпинского
Г, дБ
О
-4
-8
б) "«
Ив
-20
О
•4
-в
в) -12
-16
-20
О
■4
-8
г) -12
-16
-20
О
-4
-8
-12
-16
-20
ftvT
г\
.4
1
Г\ _г
[Л/.
1
Я^Я
Гсм
"1
•• -1
s^^^j
J
-J
д)
е)
о
-4
-6
-12
-16
-20
10 12
10 12
10 12
14
14
16
Г\~
V
Г V
"Ч
.. \
... . V
V
д^ттг
_уГ>ц.
/
I
ICM
v/
X/
. -|
J
"*ч**|
J
-I
ЕТ
\
[■"
[
Tt=7Z.
Гсм
__j
J
^ J
н
\
10 12 14 16
к
к
Y
^n"
_S.
Л=1,1
см
.
J
J
^^И
\
10 12 14 16
f
к
[
h
lv_
^ч
jr^nj?.
v__
CM
]
—н
J
J
J
Л ГГц
Рис. 11.7. Частотные зависимости входного коэффициента отражения монополя
Серпинского (а) и пяти симметричных вибраторов с треугольными плечами
(б—ё), соответствующих пяти высотам фрактальной антенны [428]
629
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Таблица 111
Основные измеренные параметры монополя Серпинского [428]
(Диапазон
я
1
2
3
4
5
/,. ГГц
Хи, мм
0,52
578
1,74
172
3,51
85,5
6,95
43,2
13,89
21,6
Ширина
диапазона, %
7,15
9,04
20,5
22
25
1,дБ
10
14
24
19
20
4Ч (5)
3,50
2,02
1,98
2,00
А« 1
К
0,153
0,258
0,261
0,257
0,255
стоты и длины волн, соответствующие минимумам КСВ,
обозначены^ и Хп соответственно, а входные потери - L.
Монополь Серпинского имеет логопериодические свойства в
пяти диапазонах. Антенна сохраняет значительную степень подобия
с большой шириной полосы частот. Для лучшего понимания лого-
периодических свойств монополя Серпинского на рис. 11.8
изображены действительная и мнимая части полного входного
сопротивления ^ Измеренные параметры показаны непрерывной линией,
а расчетные - штриховой.
Частотная зависимость антенны имеет вид [428]:
/„ = 0,26^5", (11.9)
где с — скорость света в вакууме; h — высота максимальной
салфетки Серпинского; 8 = 2- логарифмический коэффициент масштаба;
п — целое число.
Диапазоны (см. табл. 11.1) слегка отличаются от диапазонов
фрактальной антенны из [426], где h/X « 0,29. Это связано с
толщиной подложки (она стала равной 1,588 мм вместо 1,27 мм), и ее
более высокой диэлектрической проницаемостью (гг = 2,5 по сравне-
630
11.2. Многодиапазонные фрактальные антенны Серпинского
I М ММ ~ Hi I 1 I 1 1 N1 |
I 2 4 S 16
/,ГГц
Рис. 11.8. Действительная (а) и мнимая (б) части входного сопротивления
монополя Серпинского [428]
нию с гг = 2,17). Такие параметры делают всю структуру
электрически слегка длиннее.
Наблюдаемый небольшой сдвиг теоретических частот
относительно измеренных объясняется влиянием в высокочастотном
диапазоне нагрузки от других салфеток Серпинского. Отсутствие
периодичности и скейлинга в нижних диапазонах связано с усечением
антенны из-за конечного числа итераций. В реальных случаях всегда
имеется только физический фрактал с конечным числом итераций,
что ограничивает число рабочих диапазонов. Такой эффект
усечения обнаруживается наиболее четко при рассмотрении
распределения тока по плоскости антенны.
Характеристики излучения. Основные сечения диаграммы
направленности (ф = О, Ф = 90°, 0 = 90°) фрактального монополя
Серпинского измерены в безэховой камере размером 10x7,5x7,5 м для
верхних четырех диапазонов (рис. 11.9). Как показано в [426-428],
у всех нормированных диаграмм направленности степень
самоподобия достаточно определенная. При Ф = 0 характеристики для ком-
631
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Ф=0° ф=90° 6=90°
Рис. 11.9. Нормализованные диаграммы направленности фрактальной антенны
Серпинского для/2 = 1,74 ГГц (я),/3 = 3,51 ГГц (<5),/4 = 6,95 ГГц (в),
/5 = 13,89 ГГц (г) [428]
поненты Е имеют двухдолевую структуру, разнесенную примерно
на 30е. При Ф = 90° вид диаграммы примерно такой же.
Азимутальные сечения характеризуются эллиптической формой с более
сильной компонентой излучения по оси х.
Эти результаты сильно отличаются от типичных для однодиа-
пазонных антенн. Следует отметить, что при анализе диаграмм
направленности (рис. 11.9) необходимо принимать во внимание эффект
конечного размера в основной плоскости. Например, диаграмма
направленности верхних диапазонов имеет флуктуации из-за
эффекта дифракции на краях излучающей плоскости. Частота флуктуации
возрастает с увеличением рабочего диапазона, так как эта плоскость
не самоподобна.
Фрактальный диполь. В [428] также изучен фрактальный диполь
Серпинского. Антенна запитывалась с помощью коаксиального сим-
632
11.2. Многодиапазонные фрактальные антенны Серпинского
метрирующего устройства [429], работающего в диапазоне 1-16 ГГц.
Оба плеча антенны изготовлены на той же подложке, что и в
предыдущем случае. Измерения выполнялись во всей азимутальной
плоскости, ф= 0. Полученные результаты (рис. 11.10,а)
сравнивались с результатами для симметричных вибраторов с треугольными
плечами (рис. 11.10, б). В [428] приведены данные и для <р = 90°.
Интересно отметить значительное сходство характеристик во
всех четырех диапазонах для антенн Серпинского. Сходство
особенно заметно при 2, 4, 8 и 16 ГГц, и сильно отличается от результатов
для симметричных вибраторов с треугольными плечами. Последний
тип антенны не относится к многодиапазонным. Но антенна
Серпинского - многодиапазонна, так как полное входное
сопротивление и диаграмма направленности сохраняют подобие в различных
частотных диапазонах. Однако антенна Серпинского не является
частотно-независимой из-за существования сильных изменений как
диаграммы направленности, так и входного сопротивления в
каждом логарифмическом периоде (см. рис. 11.8).
При сравнении характеристик диполя и монополя можно
выявить неидентичность диаграмм направленности в основной
плоскости. Симметрирующее устройство не дает идеального баланса
между обоими плечами диполя. Следовательно, сечения в
ортогональных плоскостях по отношению к плоскости ху показывают слабую
асимметрию. Вследствие этого увеличивается излучение по
направлению оси z (см. данные для частот 3,6 и 7,2 ГГц на рис. 11.10,а),
что скрывает некоторые нули диаграммы направленности. Другая
интересная черта антенн Серпинского - это характеристики трех-
лепестковой структуры в сечении ср = 0.
Физика работы фрактальных антенн. В [428] был разработан
алгоритм расчета распределения плотности тока на фрактальной
поверхности. Антенна возбуждалась синусоидальным сигналом в
четырех верхних диапазонах. В каждом диапазоне поверхностный ток
концентрируется сообразно масштабу субструктуры антенны.
Активная область - наименьшая для частот верхнего диапазона (п = 5);
тогда значительная часть структуры антенны Серпинского
становится как бы отключенной.
Причина этого заключается в следующем. Когда
электромагнитная волна X запитывает вершину антенны, она начинает
распространяться по структуре в направлении плоского торца салфетки
Серпинского. При встрече с кластером, сравнимым по размерам с дли-
633
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
got-4-AT( *g)—18 5он-
1
v:
ев
а
ю
К
и
X
д
К
» •-. IX.
« гч
sh
Д \о
К -<
К I
D- оо
IS
2 м
К К
tt ев
2 s
2 §
S ь
н о
if
д |
ё ^
а§
д s
Л Д
II
Р< >»
b w
|&
4 о
Ч *
£ О
Д а
я о
ев Н
И
О
со
S
&
'- • S
634
11.2. Многодиапазонные фрактальные антенны Серпинского
ной волны, волна излучается. Поэтому мощность
распространяющейся волны теряется, и в итоге ток не достигает торца антенны.
Структура имеет много разрывов, которые усиливают излучение
и придают некоторые особенности этому процессу. При больших X
малые треугольники антенны вносят небольшой вклад в общее
излучение, и ток распространяется по всей структуре. При более
высоких частотах антенна теряет свойства самоподобия.
Модификации фрактальных антенн. В описываемых здесь
антеннах Серпинского логопериодический коэффициент масштаба 8 = 2.
В [427] представлены две современные излучающие структуры,
основанные на салфетке Серпинского с 8, равной 1,66 и 1,5. С
помощью этого возмущающего фактора можно сдвигать частотные
диапазоны в таких фрактальных антеннах. При построении антенн
размеры треугольников в каждой итерации уменьшаются в (3/5)" раз
(рис. 11.11,а)и (2/3)лраз(рис. 11.11,6). В данном случае следует
говорить о самоаффинных антеннах (см. п. 1.1), так как копии
треугольников искажены.
80 см 80 см
Рис. 11.11. Две современные разработки фрактальных антенн Серпинского [427]
Антенны были изготовлены на диэлектрической подложке
Cuclad 250 (ег =2,5; толщина 1,588 мм) с использованием
стандартной техники печатного монтажа. Они монтировались в монолитную
конфигурацию с помощью квадратной проводящей плоскости
размером 800x800 мм. Входной коэффициент отражения измерялся в
диапазоне 0,2-12 ГГц. В табл. 11.2 приведены резонансные частоты
635
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
двух фрактальных антенн с различными 8 . Данные таблицы
свидетельствуют о почти логопериодическом распределении верхних
диапазонов. Более низкие диапазоны сдвинуты к оригиналам (см.
табл. 11.1) из-за эффекта усечения.
Таблица 11.2
Резонансные частоты двух фрактальных антенн [427]
6 = 1,66 (5/3)
fn
0,45
1,61
2,76
4,54
7,52
/// ,
J п' J п-\
3,57
1,71
1,65
1,66
6 = 1,50 (3/2)
fn
0,44
1,54
2,43
3,69
5,43
/// ,
J п ' J п-\
3,46
1,57
1,51
1,47
Характеристики излучения таких антенн подобны
характеристикам рассмотренной выше антенны Серпинского.
Многодиапазонное поведение фрактальных антенн позволяет применять их в
движущихся средствах, работающих от одной базовой станции, для
управления несколькими телекоммуникационными системами с одной
антенной [430] и в некоторых радиолокаторах.
Переходные процессы. В [431] рассчитаны переходные
процессы резонансной антенны и фрактальной антенны Серпинского.
Поверхности были смоделированы плоскими треугольниками. Их
изучение выполнено с помощью численного решения интегрального
уравнения для электрического поля во временной области.
Прямой метод расчета переходного процесса в таких антеннах
требует больших временных затрат. Этот недостаток можно
преодолеть, применяя метод параметрического моделирования при
выделении комплексных резонансных частот антенн. По значениям этих
частот можно восстановить полный переходный процесс в виде
суммы комплексных показательных функций.
Расчет комплексных резонансных частот проводился в [432]
расширенным методом Прони в сочетании с декомпозицией
сингулярных значений. Вычислительная схема включала 1696 треугольников.
Антенна запитывалась гауссовым импульсом. Отметим, что
переходный процесс во фрактальной антенне заканчивается быстрее, чем в
резонансной.
636
11.3. Расчет фрактальных антенн на основе итерационной модели линии передачи
11.3. Расчет фрактальных антенн на основе
итерационной модели линии передачи
Итерационная матричная модель. Многополосный режим
работы фрактального диполя Серпинского был представлен и обсужден
выше. Распределение тока в салфетке Серпинского показывает, что
большая часть плотности тока сконцентрирована в узлах и кромках
различных треугольных кластеров, составляющих общую
фрактальную структуру. В [709] предложена простая модель для расчета
антенны Серпинского. Эта модель основана на итерационной линии
передач, и ранее была успешно применена для описания микропо-
лосковых схем [710]. Модель показала, что многополосный режим
работы фрактальной антенны Серпинского есть следствие ее
фрактальной природы. Обоснованность метода оценивается с помощью
применения итерационной модели линии передачи к трем
фрактальным антеннам с углами раствора <х= 30°, 60°, 90°. В то же время
можно изменять входное сопротивление антенны изменением угла
ее раствора [711]. Похожий результат достигнут и для фрактальной
антенны Серпинского.
На рис. \1Л2,а,б,в изображены три салфетки Серпинского с
углами раствора <х= 90°, 60°, 30°. Антенны изготавливались на
диэлектрической подложке 8Г= 2,5, толщина = 1,588 мм. Высота всех
трех антенн составляла 8,9 см. Монопольные антенны
устанавливались на заземленных пластинах размерами 80 х 80 см.
Коэффициент входного отражения был измерен относительно величины 50 Ом.
Способ, которым создается салфетка Серпинского, можно
представить как итерационный процесс с обратной связью, где ряд
самоподобных преобразований многократно применяется к
основополагающему элементу. Для салфетки Серпинского требуются три
подобных преобразования, каждое из которых заключается в
уменьшении масштабного коэффициента в 2 раза и повороте
относительно оригинала. Именно такой процесс на основе введения матрицы
[S\ и использовался в [709, 710] при определении итерационной
модели линии передачи. Для салфетки Серпинского в виде трехпор-
товой сети основополагающим элементом был принят
равнобедренный треугольник. В связи с симметрией и соотношением
взаимности матрица [S\ имеет следующую структуру (см. рис. П.2,г,д,е):
637
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
г)
д)
Рис. 11.12. Салфетки Серпинского с различными углами раствора и схема
итеративной сети из S матриц:
а — а = 90°, б— а = 60°, в — а = 30°, г — одна ^матрица,
д — сеть из трех S матриц, е - сеть из девяти S матриц [709]
[S]-
а
Р
LP
Р
Y
8
Р1
S
У.
(11.10)
Как следует из (11.10), необходимы четыре элемента, чтобы
полностью описать сеть. Задав одну итеррацию, мы строим
следующую итерацию. После простого, но довольного длинного анализа
638
11.3. Расчет фрактальных антенн на основе итерационной модели линии передачи
можно показать [709, 710], что соответствующие элементы итерации
[Sn+l] записываются в виде
<Vi = «„ + 2P«
Р2 ^
" 1-Х
1
1-(ул + бп)[ал + Р2(1-Уя)-1]' <11Л2>
Кх =
5 л
!-У,
Р2
Ул+1 = У« +
\-ВЕ
п п
S„+r
Ь(ЕСn + F) + 8(BF+C)
1-В_Е_
где параметры В, С, Е, F, G, Я определяются как
В =
У+
8а + тР
1-ау
2\
Р
1-у2-р2(5+у2)(1-осу)-1'
С =
Е =
l-y^p^S+y^a-ay)"1'
Р[у+8(а8 + у)]
l-ay-SCa^ + p^Xl-ay)-1'
F =
Р5(1-у)
(7 =
l-ay-SCa^ + p^a-ay)-1'
pty+S^l + aXl-ay)-']
l-ay-SCa^ + p^a-ay)"1'
H =
Sfy+p^l + yKl-ay)-1]
l-y2-p2(8 + y2)(l-ay)-
-l-
(11.13)
(11.14)
(11.15)
(11.16)
(11.17)
(11.18)
(11.19)
(11.20)
(11.21)
639
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Входной коэффициент отражения Гвх трехпортовой сети, когда
ее входы 2 и 3 при нагрузках характеризуются величинами Г2 и Г3,
равен
р2
гвх = «+^-г2
1+-
5Г\
1-7Г,
4^
(
1+-
8Г,
1-уГ,
где параметры Z>, и D2 определяются в виде
62Г\Г\
/),=1-уГ2-
2'3
1-уГ3'
(11.22)
(11.23)
2 3 1-уг2
(11.24)
Для равностороннего треугольника Серпинского при угле
раствора а = 60° имеется дополнительное условие симметрии и
матрицу (11.10) можно записать в виде
[S] =
а
Р
Lp
р
а
р
р]
р
а
(11.25)
Тогда рекурсивные зависимости (11.12)—(11.15) упрощаются до
соотношений
««+!=«„ +
2Р2К+Р2(1-«Л>
-И
i-(«,+Wl".+№-<rlY
(11.26)
Рл+1 =
pfl+p,q -«.)-']
i-K+PJK+P^-s)"1]'
(11.27)
Описанная в [709] рекурсивная модель позволяет предсказать
изменения входных параметров антенны Серпинского на любой
итерационной стадии. Любая симметричная взаимная трехпортовая
сеть, способная запасать электрическую и магнитную энергию, мо-
640
11.3. Расчет фрактальных антенн на основе итерационной модели линии передачи
жет быть использована в качестве основополагающего элемента или
инициатора в данной модели. Были получены результаты для
симметрических Y узлов с потерями. Длину эквивалентной линии
передачи можно определить, зная высоту салфетки Серпинского, число
итераций и угол раствора. Для объяснения излучательных
способностей был рассмотрен конечный фактор Q, зависящий от
коэффициента ослабления в линии передачи.
Теория и эксперимент. Отметим, что рассматриваемая модель
дает большую погрешность на низких частотах, т.е. ниже первого
резонанса. Частотная зависимость сопротивления нагрузки
определяется в виде
h
(h Л
С
(11.28)
где h - высота фрактальной антенны. На высоких частотах
эффектом нагрузки можно пренебречь, так как из-за потерь на излучение
в антенне ток не достигает вершин антенны.
На рис. 11.13 представлены результаты численных расчетов
основных характеристик фрактальных антенн при использовании
итерационной модели линии передачи, а на рис. 11.14 — результаты
экспериментов. Коэффициент входного отражения Г измерялся
относительно волнового сопротивления фидера 50 Ом. За исключением
первой зоны резонансные частоты для монопольной антенны
Серпинского можно вычислить по формуле, обобщающей соотношение
(П.9):
/r = 0,152^cos^. (11.29)
Как видно из рис. 11.13 и 11.14 в первом диапазоне монополь
Серпинского подобен антенне в виде симметричного вибратора с
треугольными плечами (антенна типа «галстук — бабочка»). На
первом резонансе эффект усечения явно доминирует в антенне
Серпинского, а влияние вытравленных отверстий, как указано в [428],
незначительно из-за малости их размеров по сравнению с длиной
волны. Из соотношения (11.29) вытекают два важных факта о работе
монополя Серпинского: логопериодическое поведение, и связь
резонансных частот, определяемых размерами и формами салфеток, с
максимальной высотой h антенны.
21 Фракталы
641
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Г, дБ --в-90Г — л=6<Г — ct=WT
1 10 /,ГГц
Рис. 11.13. Теоретические частотные зависимости входного коэффициента
отражения Г и составляющих входного сопротивления zm = Re^x + Ят^
монополя Серпинского при различных углах раствора а [709]
Итерационная модель линии передачи верно предсказывает
число резонансов, а также тот факт, что с увеличением угла
раствора а все резонансы сдвигаются в область нижних частот. При одной
642
11,3, Расчет фрактальных антенн на основе итерационной модели линии передачи
Рис. 11.14. Экспериментальные частотные зависимости входного коэффициента
отражения Г и составляющих входного сопротивления zm монополя Серпинского
при различных углах раствора а [709]
643
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
и той же высоте антенны для трех рассматриваемых случаев
увеличение угла раствора подразумевает удлинение граней треугольников.
Данный факт подтверждает, что распределение тока в антенне в
основном определяется гранями. Хотя итерационная модель линии
передачи не предполагает каких-либо взаимодействий между
различными фрактальными антенными кластерами, она достаточно точно
описывает общее поведение свойств антенны. Эта модель позволяет
предсказать даже двойные резонансы, которые появляются при
а = 30° на трех высокочастотных диапазонах.
Характеристики излучения. Измеренные диаграммы
направленности фрактальных монополей Серпинского при а = 90° и а = 30°
представлены на рис 11.15 и 11.16 соответственно. Диаграммы
направленности для а = 60° приведены в разд. 11.2. Некоторые детали
картины излучения при а = 90° еще проявляют свойства
соответствующих картин излучения при а = 60°. У фрактального монополя с
углом раствора а = 30° при увеличении рабочего диапазона частот
возрастает число лепестков.
Данный электромагнитный режим более близок к режиму
линейного монополя, чем к многодиапазонному режиму фрактальных
антенн.
Распределение тока по апертуре. Лучше понять режим работы
антенны позволяет знание распределения тока. Общая картина
распределения тока по апертуре для всех трех антенн была получена с
помощью метода конечных элементов FDTD и показана на рис. 11.17.
В случаях а = 60° и а = 90° распределение тока имеет схожую
картину в каждом диапазоне. Активная область антенны уменьшается
с коэффициентом 2 каждый раз, когда частота увеличивается в 2 раза.
И наоборот, при а = 30° распределение тока не замкнуто в
активной области, а распределено по всей геометрии фрактальной
антенны.
В [709] дано следующее объяснение режиму работы
фрактального монополя с учетом укорочения длины граней треугольных
кластеров при а = 30°: антенна становится плохим излучателем и
распределение тока не ограничивается активной областью и достигает
краев антенны. Ранее это было определено на основе рассчитанных
входных параметров антенны. То, что для а = 30° двойной резонанс
был предсказан итерационной моделью линии передачи и
действительно измерен, наводит на мысль о двойном режиме работы такой
фрактальной антенны. Один из них - тот, который в [709] назван «ре-
644
<p=0°
ф=90°
6=90°
т~ »
3-й
диапазон
л £&
4-й
диапазон
ъ*-+\*
/-2.8^ГГц /±3.00 ГГц
, [ кхЩЖ 3. (\1уЩГ\/\ ,
/±2.80 ГГц М-ООГГц /=2.80ГГц f-ХООГГц
да -*
W
ш^
Л-.У/\
-Ю г
5-й
диапазон
.« «V./ /:::^:.^ L/l» \ ч ихйкЬ У...Л »
мАгГц М-ООГГц
>*ж^
/»б.ооГГц
Swi ££&£ \2x „ L.^OS^l 13?... J
/^11.20ГГц f-П.ООГГц
/=5.60ГГц /=6.00ГГц
о о
* 3W ..-'■'-file \"
/~5.ЮГГц
-ЭО г.?..^ 90
/*11.20ГГц /-12.001Гц /ЧиоГГц /^12.00 ГГц
Рис. 11.15. Экспериментальные диаграммы направленности монополя Серпинского с углом раствора а = 90° [709]
ф=0°
ф=90°
0=9О()
2-й
диапазон
>>.
■; 'vaiz;v \
•/WW
/-2.00ТГЦ
V
/=1.8оГГц
■*» г* ^*
3"Й -Л<^4
диапазон /^)^>£Л £3£чЭД%_
/- 3.20 ГГц f-4.00 ГГц
/-1.80ГГЦ
У±2.ооГГц /=1.80ГГц ^2.ооГГц
9 о о о
>•' \ • -10 / ,'М^ i/r )Ч\ / s'SxV'* /''" !-»".v\ Ч
u...^4u^f*£-..rTT.._; _.t « t....V^..—.•..„rsJUs.^a X./..J м as •■ i • os as -^я*^" us
jo r~-
4-И «.
диапазон
5-й
диапазон
/"3.20 ГГц
9 -j-Л... JO
/-4.00ГГц
-» r~5-.. »
/^з.2оГГц /~4.ооГГц
._.l.v- яо as
/-6.4£ГГц
40 .^-... • 30
f-8.qflITif
/~6.40ГГц /-8МГГЦ
/=22.80ГГц
/-ниюггц
/~12.80ГГц
/-16.00ГГЦ
та '"■—i....--''' u* as ''• L -' us
/=12.80ГГц /=/а00ГГц
Рис. 11.16. Экспериментальные диаграммы направленности монополя Серпинского с углом раствора а = 30° [709]
11.3. Расчет фрактальных антенн на основе итерационной модели линии передачи
-40 дБ 0 дБ
Рис. 11.17. Картина распределений тока во фрактальных
монополях Серпинского [709]
жимом Серпинского», связан с резонансом на соответствующем
масштабе фрактала. Другой режим соответствует гармоническим резо-
нансам на больших масштабах фрактала. Суперпозиция обоих
режимов вызывает распределение тока по всей фрактальной апертуре
антенны. Конечный результат виден на диаграммах направленности
антенны, представленных на рис. 11.15 и 11.16. Физически этот
результат показывает, что фрактальная антенна Серпинского может
быть интерпретирована как последовательность резонаторов, вне-
647
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
дренных друг в друга. В этом случае размеры каждого из
резонаторов уменьшены соответственно масштабу в 2 раза, а собственная
резонансная частота удваивается для каждого резонатора. При
больших углах раствора возбуждается только основная мода одного
резонатора. Для меньших углов раствора и снижения потерь на
излучение создаются условия для возбуждения гармонических мод
следующих резонаторов. Таким образом, конечная самоподобная
структура обладает логопериодичностью, которая в определенных
случаях может быть искажена гармоническими резонансами в
структуре.
11.4. Фрактальные кольцевые и эллиптические
несимметричные антенны
Фракталы и телекоммуникации. Процесс развития современных
телекоммуникаций неразрывно связан с расширением спектра
используемых частот и увеличением скорости передачи и обработки
информации. Ясно, что запросы потребителя на системы
высокоскоростной передачи данных обусловлены развиваемыми
технологиями. Развитие рынка радиосистем массового потребления в будущем,
как отмечено в [712—714], связано с широким внедрением
многополосных или широкополосных терминалов. Радиотерминалы не
полностью удовлетворяют существующей инфраструктуре, а также
обеспечению необходимых рабочих характеристик для тех радиосистем,
которые пока еще не стандартизованы в пределах одного
терминальной единицы. Радиооптическая пикоячейка, описанная в [715]
является примером такой инфраструктуры в терминале. В этом случае
оптически доставленный сигнал преобразуется в микроволновый, а
сама антенна работает как оконечный селектор сигналов.
Характеристики и диаграмма направленности фрактального вибратора (мо-
нополя), установленного на заземленном экране, хорошо
приспособлены к работе в таких пикоячейках.
Конструкция фрактальной кольцевой антенны.
Многодиапазонные и широкополосные фрактальные монополи, как показано выше,
составляют современную сферу технологических интересов (см.
также [716-719]). Фрактальные системы с плоскими, круговыми,
эллиптическими и квадратными излучателями исследовались в [720—725].
При соответствующей оптимизации координат точки запитывания
648
11.4. Фрактальные кольцевые и эллиптические несимметричные антенны
реализовывалось до восьми рабочих диапазонов [721,722]. Ниже
рассмотрим свойства фрактальных кольцевых и эллиптических антенн,
разработанных в Великобритании [726-728].
Первый тип антенн, как показано на рис. 11.18,а, представляет
ряд замкнутых масштабированных круговых колец. Черный цвет
указывает на металлические элементы антенны. Кольца помечены
номерами от 1 до 4. Каждый диаметр последующего круга
составляет половину диаметра предыдущего кольца. Таким образом, диаметр
диска под номером 5 составляет половину диаметра 4-го кольца.
Элементы скомпонованы так, что составляют единый блок антенны, как
показано на рис. 11.18,5. Отметим, что только часть антенны по
структуре схожа с салфеткой Серпинского или монопольной
антенной Парени (Рагапу) [719]. Антенна, приведенная на рис. 11.18,5,
является пятой итерацией составных колец несимметричного
вибратора, где первая итерация есть круговой диск. Заметим, что в
рассматриваемой конструкции под процессом итерации понимается
добавление колец внутрь большого диска. Другой пример итерации
в таком приложении к фрактальным антеннам можно найти также
в [719].
Можно указать ряд причин для синтеза такой конфигурации
антенных устройств. Во-первых, круговые кольца обеспечивают дис-
а)
^^^^ h=%6 мм
® »у и 15 см
б)
Рис. 11.18. Конструкция фрактального кольцевого несимметричного вибратора
при пяти итерациях [728]
649
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
кретный токтздоль кромки колец. Этим подразумевается, что при
работе на высоких частотах линия тока полностью определена, что
подобно работе круглой дисковой антенне, работающей на своей
самой низкой частоте или частоте основной "моды. Данное свойство
дает хорошее управление формой диаграммы направленности
антенны. Во-вторых, рабочие диапазоны частот и полосы пропускания
могут регулироваться размерами колец и их шириной,
соответственно. В третьих, поскольку путь тока элементов круговой, антенна в
высоту будет короче, чем соответствующий несимметричный
вибратор.
Изготовленная антенна имеет полную высоту 86 мм и
дискретные высоты 43; 21,5; 10,75 и 5,5 мм. Это отвечает второму—пятому
рабочим диапазонам частот. Центральные частоты этих диапазонов
равны, ГГц: 0,69 ifx), 1,565 (£), 3,5 (f3), 6,925 (/4) и 12,5 (fs). Полосы
пропускания второго, третьего и четвертого диапазонов по уровню
Sn < —10 дБ равны 44, 40 и 48% сооответственно. Антенна
изготовлена по традиционной печатной технологии на подложке толщиной
0,5 мм из материала FR4 (гг = 4,4), а затем установлена
перпендикулярно на металлической пластине размером 15x15 см. Для запи-
тывания антенны в центре пластины был установлен 50-омный
разъем поверхностного монтажа, через который возбуждался пятый
элемент в виде диска.
Электродинамические параметры фрактального кольцевого моно-
поля. Обратные потери (*УИ = Г) фрактальной антенны в
зависимости от частоты были измерены с помощью анализатора типа
НР8720С. Для экспериментов было изготовлено несколько антенн
с различным числом колец, подобных варианту, приведенному на
рис. 11.18,5. Входные коэффициенты отражения исследованных
фрактальных кольцевых несимметричных вибраторов с различным
порядком итераций приведены на рис. 11.19. Кривые на рис. 11.19,а
соответствуют фрактальным антеннам со вторым и третьим
порядками итераций, в то время как на рис. 11.19,6показаны кривые для
этих же антенн с четвертым и пятым порядками итераций.
Фрактальный несимметричный вибратор со вторым порядком итераций (одно
кольцо и один диск) имеет единственную резонансную полосу вблизи
0,69 ГГц, повторяющуюся при широкополосном режиме и условии
потерь по уровню Sn < -10 дБ вблизи 2 ГГц. Фрактальная антенна
с третьим порядком итераций (два кольца и один диск) дает улуч-
650
11.4. Фрактальные кольцевые и эллиптические несимметричнее антенны
О 2 4 6 8 10 12 14 16 18 20
/ГГц
а)
О 2 4 6 8 10 12 14 16 18 20
/ГГц
б) J
Рис. 11.19. Измеренный входной коэффициент отражения фрактального
кольцевого несимметричного вибратора [728]: а - второй и третий порядок итераций,
б— четвертый и пятый порядок итераций
шенное согласование во втором диапазоне и при широкополосном
режиме вблизи частоты 6,1 ГГц. Похожие результаты с
дополнительным ярко выраженным резонансом в третьем диапазоне были
получены для вибратора с четвертой итерацией. Фрактальный
несимметричный вибратор с пятым порядком итераций имеет периодические
резонансы на частотах, ГГц: 0,69 (/j); 1,565 (f2); 3,5 (f3) и 6,925 (f4).
651
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
За пределами 12,5 ГГц (f5) в широкополосном режиме антенна
фактически может рассматриваться как круговой дисковый
несимметричный вибратор. Частотное разнесение между диапазонами,
обозначаемое как/Л /fn+l (n - номер диапазона), равно 0,44; 0,45; 0,5 и
0,55 соответственно. Это достаточно тесно связано с относительной
высотой колец антенны. В такой антенне плохое согласование
характеристик в первом диапазоне является неустранимым и не зависит
от числа итераций. Характеристики согласования схожи с
соответствующими характеристиками антенны, выполненной в виде
симметричного вибратора с треугольными плечами, и фрактальной
антенны на основе салфетки Серпинского, где согласование в первом
диапазоне также недостаточное [428].
Резонансные частоты рассматриваемого фрактального
кольцевого несимметричного вибратора могут быть оценены по уровню
5п = -10дБ [722,728]:
- _ 0,24ф
где р = 0,875; с — скорость света в вакууме; h — высота антенны; г —
радиус кольца; Ъп = (hn/hn+l)-1.
Как показано в [728], были достигнуты разумные оценки для
резонансных полос, создаваемых каждым круговым кольцом. Однако
расчеты для кругового диска внутри составных кольцевых
элементов не так точны. Например, диск четвертой итерации антенны и
четвертое кольцо пятой итерации другой антенны имеют одну и ту же
высоту, равную 10,75 мм. Однако при уровне отражения Sn = -10 дБ
ширина полосы частот в первом случае составляет 6,1 ГГц, в то время
как во втором случае - 5,2 ГГц. Разница почти в 1 ГГц может быть
объяснена тем фактом, что дыры внутри площади поверхности диска
были удалены. За счет собственной индуктивности резонансная
частота антенны смещается вниз.
Характеристики фрактальных антенн на основе третьей и
четвертой итераций, показанные на нижнем графике рис. 11.19, были
рассчитаны методом конечных элементов при помощи пакета
программ HP HFSS. Сравнение между численным моделированием и
экспериментальными результатами показано на рис. 11.20. Для
простоты моделирование было выполнено в диапазоне от 0 до 10 ГГц.
h/r
1 + (А/г)
(11.30)
652
11.4. Фрактальные кольцевые и эллиптические несимметричные антенны
012 3 4 56789 10
/ГГц
Рис. 11.20. Частотная зависимость входного коэффициента отражения
фрактальных кольцевых антенн с четвертым и пятым порядком итераций [728]:
моделирование (4-я итерация); - • - • измерения (4-я итерация);
моделирование (5-я итерация); -+-+ измерения (5-я итерация)
Также были точно рассчитаны пересечения графика обратных
потерь по уровню —10 дБ для каждого частотного диапазона. В [728]
отмечено, что соответствие между расчетными и
экспериментальными данными для первого и четвертого диапазонов не очень хорошее.
Это связано с изменением условий электрического согласования
[429, 723]. В конечном итоге численные результаты действительно
позволили определять диапазон резонансных частот антенны.
Распределение суммарного поля is фрактального монополя,
полученное численным моделированием, показано на рис. 11.21.
Можно видеть, что при удвоении рабочей частоты, следующее соседнее
кольцо меньшего диаметра создает более высокую интенсивность
поля. Этим фактом подтверждается то, что резонанс антенны
главным образом определяется его основным резонирующим кольцом.
Однако из-за почти непрерывного состава колец на круговом
дисковом элементе возможен многорезонаторный составной путь тока.
Это дает соответствующий вклад в структуру суммарного излучения,
из-за сложного источника излучения.
Характеристики излучения. Диаграммы направленности
фрактального кольцевого несимметричного вибратора (см. рис. 11.18) на
вертикальной поляризации для рабочих диапазонов выше четвер-
653
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
0,68 ГГц 1,65 ГГц 3,15 ГГц 7 ГГц
Мин Макс
Рис. 11.21. Смоделированное распределение поля Е фрактального монополя с
итерацией четвертого порядка круговых колец [728]
того приведены на рис. 11.22 (плоскость Z-X) и рис. 11.23
(плоскость X—Y). Для упрощения картина в плоскости Z—Yhq показана.
Везде 9 иф - обычные полярные координаты. В первом рабочем
диапазоне создается устойчивая монопольная диаграмма
направленности, поэтому она здесь не показана. Диаграммы направленности
антенны характеризуются двумя лепестковыми структурами
относительно обеих плоскостей Z-Хи Z-Y Глубокий провал,
перпендикулярный проводящей плоскости, типичен для конфигурации монопо-
лей. Диаграммы направленности фрактальной антенны, конечно,
искажаются на высших резонансах каждой рабочей полосы. Однако в
отличие от традиционной монопольной антенны ее диаграмма
излучения все еще достаточно хорошо формируется, за исключением
пятого диапазона, по всем направлениям (вдоль X—Y, Z—X, Z—Y).
Вклад из-за утечки тока на больших кольцевых элементах
может быть значительным на высоких частотах, вызывая возмущение
лепестков. Два лепестка относительно плоскостей Z—Хи Z— 7оче-
видны, но неизбежно искажение диаграмм направленности в
плоскости X— Y. Данный эффект от вклада множества источников более
выражен в пятой рабочей полосе. Коэффициенты усиления всех
исследованных фрактальных антенн приведены в табл. 11.3. Для
кольцевых антенн измеренное значение коэффициента усиления в
первом диапазоне мало, что объясняется плохим согласованием
антенны. Средний выигрыш на более высоких диапазонах составляет
величину около 4,7 дБ, что типично для монополя.
Фрактальный эллиптический монополь и его характеристики.
Рассмотрим теперь монополь на основе множества эллиптических ко-
654
2-й
диапазон
диапазон
5-й :*й
диапазон
Mmmatcrm круг0п Мншжто wwtmtim Кру ншдо диск
#*ШЯ1*-: f—14 ГГц
Щрени
Рис. 11.22. Сравнение в плоскости Z-X($ = 0) измеренных диаграмм направленности фрактальных антенн [728]:
параллельная поляризация, EQ; кроссполяризация, ^ф
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Мндадоэдо&дед JHbo^^ Крупишднск Паре»»
-Г-НПЪ Г=14ГГц f=14m* f~l4*T*
Рис. 11.23. Сравнение в плоскости ЛГ-7 (6 = 90е) измеренных диаграмм
направленности фрактальных антенн [728]:
параллельная поляризация, EQ; кроссполяризация, £ф
лец. Если первый тип фрактальных антенн (см. рис. 11.18) состоял
из ряда замкнутых масштабированных круговых колец, то для
второго типа антенн характерно множество самоподобных
эллиптических структур. Отношение Ад; к Az определяет эллиптическую фор-
656
11.4. Фрактальные кольцевые и эллиптические несимметричные антенны
Таблица 11.3
Результаты измерения центральной частоты (ЦЧ), ГГц, полосы
пропускания (ПП), % и коэффициента усиления (КУ), дБ рабочих диапазонов
фрактальных антенн [728]
Частота
л
h
/з
Л
h
Частота
л
&
/з
Л
h
Круговые
кольца
ЦЧ
0,69
1,565
3,5
6,925
12,5->
ПП
-
44,09
40
48,37
-
КУ
0,41
4,73
4,73
4,83
3,70
Салфетка Серпинского
ЦЧ
0,57
1,8
3,685
7,525
15,25
ПП
-
22,22
19,26
15,28
15,08
КУ
0,59
2,93
6,81
4,23
6,75
Эллиптические
кольца
ЦЧ
0,74
1,725
3,745
7,575
14->
ПП
-
49,27
55,81
62,71
-
КУ
-0,37
2,76
4,73
3,37
5,29
Антенна Парени |
ЦЧ
0,57
1,9
3,79
7,475
14,15
ПП
-
28,94
10,03
8,695
4,95
КУ
0,563
3,13 1
4,99 |
5,63 1
4,55 1
му антенны, показанную на рис. 11.24. В рассматриваемом случае
была выбрана величина отношения Ay/Az = 0,75. Изготовленный
фрактальный несимметричный вибратор на основе множества
эллиптических колец имел, как и в первом рассмотренном случае,
полную высоту 86 мм и дискретные высоты 43; 21,5; 10,75 и 5,5 мм.
Это соответствует второму—пятому рабочим диапазонам частот.
Частотные зависимости входного коэффициента отражения
фрактальной эллиптической антенны показаны на рис. 11.25
сплошной линией, а фрактального кольцевого несимметричного
вибратора — штриховой линией. Заметим, что в каждом диапазоне уровень
Sn = —10 дБ соответствует почти одинаковым точкам пересечения
657
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Ау=Ь
£©1
Земля
Рис. 11.24. Конструкция фрактального несимметричного вибратора на основе
множества эллиптических колец при Ay/Az = 0,75 [728]
0 2 4 6 8 10 12 14 16 18 20
/ГГц
Рис. 11.25. Сравнение измеренного входного коэффициента отражения
фрактальных кольцевых и эллиптических антенн пятой итерации:
эллиптический монополь, кольцевой монополь [728]
для обеих (эллиптической и круговой) антенн, что говорит о
возможности применения формулы (11.30) для расчета эллиптической
системы. Кроме того, ширина полосы пропускания фрактальной
эллиптической антенны во втором, третьем и четвертом диапазонах
увеличивается примерно на 5—15 % относительно кругового
эквивалента. В [728] предполагают, что это увеличение связано с
взаимосвязью множества проводящих дорожек.
Сравнительный анализ фрактальных антенн. На рис. 11.22 и 11.23
дано сравнение измеренных диаграмм направленности фрактальных
658
11.4. Фрактальные кольцевые и эллиптические несимметричные антенны
кольцевых и эллиптических антенн в плоскостях Z-Хи X—Y.
Минимальное расстояние между проводниками, определяющее самую
короткую резонансную длину волны, значительно увеличивает эффект
расщепления диаграммы направленности на более высоких рабочих
частотах пятой полосы. Дальнейшее оптимизирование антенн может
улучшить их характеристики. Численное сравнение рассматриваемых
фрактальных антенн проведено в табл. 11.3. По сравнению с
круговым диском коэффициент усиления фрактальных кольцевых и
эллиптических антенн в некоторых диапазонах несколько ниже из-за
увеличения взаимосвязи между частями структур.
Характеристики излучения кругового диска и фрактальной
антенны Парени [719] были также измерены и сравнены с
рассматриваемыми фрактальными монополями. Все типы исследованных антенн
показаны на рис. 11.26. Хотя антенна Парени похожа на салфетку
Серпинского, ее характеристики несколько хуже. Антенна Парени
Рис. 11.26. Сравнительные виды монополей [728]: а - фрактальная кольцевая
антенна, б — круговой диск, в — фрактальная антенна на основе
салфетки Серпинского, г — фрактальная антенна Парени
масштабируема с коэффициентом скейлинга hn/hn+l= 0,5, где h -
высота, п - номер итерации. Для общности исследований, все
фрактальные антенны были напечатаны на одинаковых подложках
толщиной 0,5 мм из материала FR4 (ег = 4,4) и имели равную высоту
86 мм. Отдельные высоты каждого масштабируемого элемента в
салфетке Серпинского и антенне Парени определялись относительно
минимального размера кругового дискового монополя.
Непосредственно круговой дисковый монополь запитывался по периферии.
Измеренные входные коэффициенты отражения всех
фрактальных антенн показаны на рис. 11.27. Ширина полосы пропускания,
определяемая по частотной характеристике входного сопротивления
фрактальной кольцевой антенны (см. рис. 11.26,я), фрактальной
антенны на основе салфетки Серпинского (см. рис. 11.26,#) и фракталь-
659
Глава П. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Рис. 11.27. Измеренные входные коэффициенты отражения для [728]:
1 фрактальной кольцевой антенны;
2 — • — • — кругового дискового монополя;
3 - •• - •• — фрактальной антенны на основе салфетки Серпинского;
4 - - — фрактальной антенны Парени
ной антенны Парени (см. рис. 11.26,г), носит логарифмический
характер. Как показано в [426, 428, 719] (за исключением первой
полосы), частотное разнесение между каждой парой смежных
диапазонов определяется коэффициентом 0,5. Полосы пропускания
фрактальных кольцевого и эллиптического несимметричных вибраторов
для резонансных частот/2, f3 nf4 более, чем на 40% превышают
соответствующие значения для монополя Серпинского и монопольной
антенны Парени. В табл. 11.3 суммированы все полученные
результаты.
Все диаграммы излучения фрактальной кольцевой антенны,
фрактальной эллиптической антенны, кругового дискового
монополя, фрактальной антенны Серпинского и фрактальной антенны
Парени вблизи центральных рабочих частот показаны на рис. 11.22
и 11.23 соответственно. Следует заметить, что в сравнении с моно-
полем Парени, лучшая диаграмма излучения получена с монополем
на основе салфетки Серпинского.
В заключение кратко проведем сравнительный анализ
фрактальных кольцевых монополей с круговым дисковым монополем,
монопольной антенной на фрактале Серпинского и монопольной
антенной Парени [728].
660
11.4. Фрактальные кольцевые и эллиптические несимметричные антенны
Сравнение с круговым дисковым монополем. В низкочастотных
диапазонах/j nf2 диаграммы направленности по азимуту и углу
места сложных кольцевых и круговых дисковых монополей носят
идентичный характер. В диапазоне/^ все антенны имеют довольно
хорошие диаграммы направленности. В высокочастотном диапазоне f4
фрактальные кольцевые монополи еще формируют две диаграммы
излучения, в то время, как для кругового диска относительно
плоскости Z—Хвсе четыре диаграммы начинают сливаться в одну. При
этом наблюдается максимальный уровень кросс-поляризации. Для
диапазона/5 фрактальный кольцевой монополь все еще формирует
два лепестка относительно плоскости Z— X. Однако характер
излучения эллиптического и дискового монополей уже не может
хорошо контролироваться. При увеличении частоты от третьего до
пятого рабочего диапазона, диаграммы направленности кругового
диска, как показано на рис. 11.23, перестают быть всенаправленными
в азимутальной плоскости X—Y. Фрактальные кольцевые и
эллиптические антенны сохраняют всенаправленность даже в четвертом
диапазоне.
Минимумы диаграммы направленности наблюдались у
фрактальной кольцевой антенны при Ф = 90° и Ф = 270°, а максимумы
были направлены вперед и назад относительно антенной плоскости.
Это отчетливо заметно, например, в третьем диапазоне (см.
рис. 11.23). В пятом диапазоне диаграммы направленности
фрактальной кольцевой антенны и кругового дискового монополя схожи
между собой. Более глубокие и частые минимумы в диаграмме
направленности фрактального кольцевого монополя связаны с
местоположением множества источников, формирующих дискретные
линии тока. В эллиптических кольцах такие источники возбуждения
расположены более плотно. Следовательно, такая фрактальная
антенна способна создавать лучшие всенаправленные (изотропные)
диаграммы направленности, даже в пятом диапазоне.
Сравнение с фрактальным монополем на основе салфетки Серпин-
ского и фрактальным монополем Парени. В первых двух рабочих
диапазонах такие фрактальные антенны демонстрируют хорошие
диаграммы направленности в плоскостях X— Y(азимут), Z— 7 и Z—X
(угол места). В более высокочастотных диапазонах наблюдаются
осцилляции диаграммы направленности (плоскость Z—X). Эти
осцилляции могут быть связаны с резкими искажениями и изломами
соединительных проводящих линий (из-за конечного масштаба и ог-
661
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
раниченного порядка итераций) при формировании апертуры
антенн. Это менее заметно во фрактальных кольцевых и
эллиптических антеннах. Фрактальные монополи Серпинского и Парени
имеют всенаправленные диаграммы направленности в плоскости X-Y.
Однако во втором диапазоне их диаграммы направленности
похожи на диаграммы направленности кругового дискового монополя.
Отметим, что сравнение мощности принятых такими антеннами
сигналов по азимуту и углу места проведено в [726, 727].
Таким образом, в [728] численными и экспериментальными
исследованиями установлено, что фрактальные кольцевые и
эллиптические несимметричные вибраторы позволяют улучшить
управление диаграммой направленности при значительных полосах
пропускания. Это объясняется дискретной структурой множества колец.
Изменение отношения Ax/Az в эллиптическом фрактальном
монополе дает возможность дополнительной оптимизации полосы
пропускания и диаграммы направленности. Сферой применения таких
фрактальных антенн, как специально отмечено в [728], могут быть
радиосистемы типа TETRA, GSM, DCS1800, DECT, PHS, UMTS,
WLAN, Bluetooth и HIPERLAN. Для удобства читателей отметим,
что аббревиатуры расшифровываются следующим образом: TETRA
— Terrestrial Trunked Radio, GSM - Global System for Mobile
communications, DCS 1800 - Digital Communications System, DECT -
Digital Enhanced Communication Technology, PHS - Personal Handy
— phone System, UMTS - Universal Mobile Telecommunications System,
WLAN - Wireless Local Area Network, HIPERLAN - High PErformance
Radio Local Area Networks [747].
11.5. Древовидные фрактальные антенны
Древовидная фрактальная антенна в виде монополя приведена
на рис. 11.28. Она была разработана с целью получения более
компактного по сравнению с антенной Серпинского (рис. 11.6)
распределения частотных диапазонов. Монополь собран на проводящей
подложке размером 800 х 800 мм. Фрактальная структура антенны
получена электрохимическим осаждением. Осадок был выделен из
тонкого слоя электролита с ионами металла, которые слоями
осаждались между двумя стеклянными пластинами. Природа и
морфология такого рода осадков образует хорошо организованные денд-
662
11.5. Древовидные фрактальные антенны
80 см
а) б)
Рис. 11.28. Фрактальная древовидная антенна (а) и два увеличенных
фрагмента антенны относительно точки питания (б) [433]
риты, изменяющиеся в зависимости от условий эксперимента [434].
В рассматриваемом случае электрохимическая ячейка формировалась
в пространстве ПО х ПО х 5 мм между стеклянными пластинами.
Электролитический раствор содержал сульфат меди. Электроосадок
нарастал при напряжении 12 В между электродами.
После окончания процесса агрегации изображение осадка
фотографировалось цифровой видеокамерой. Затем изображение
наносилось на диэлектрическую подложку марки Cuclad 250 (ег =2,5;
толщина 1,588 мм) с помощью стандартной технологии печатного
монтажа. Фрактальная размерность древовидной антенны D = 1,71.
Коэффициент подобия в экспериментах равнялся семи.
Частотная характеристика входного коэффициента отражения
антенны измерена в диапазоне 0,9-8 ГГц (рис. 11.29,а).
Действительная и мнимая части полного входного сопротивления антенны
показаны на рис. 11.29 Д в соответственно. Аналогичные параметры мо-
нополя Серпинского того же размера (7,8 см) изображены на рисунке
штриховыми линиями.
Фрактальное дерево ясно отражает богатую спектральную
структуру со многими резонансными частотами, которые наблюдаются как
минимум в 15-ти диапазонах внутри исследованного частотного
интервала (рис. 11.29,г). Гистограмма построена в предположении,
что каждый элемент фрактальной структуры резонирует на длине
волны, в несколько раз превышающей его длину. В общем случае
древовидная структура лучше, чем монополь Серпинского,
согласована со всем частотным диапазоном, так как действительная и
мнимая части ее входного сопротивления имеют меньшие вариации.
663
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Г, дБ
1тг„х. Ом
а)
300
200
100
0
Re£BX, Ом
• 1 '•
'лк/\л/*
/
i
\
—1 1
* 1 *
14' -J^-l
"1
•' \\
\ б)
е)
мгшр[
ILFI |UUU|
■рпсюои
г)
Рис. 11.29. Частотная зависимость входного коэффициента отражения (а),
действительной (б) и мнимой (в) части полного входного сопротивления
древовидной антенны в соответствии с гистограммой частотных резонансов (г) [433]
Главные сечения диаграммы направленности при <р = 0 и <р = 90°
для компоненты поля Е исследовались в безэховой камере и
приведены в [433]. Диаграмма направленности при Ф = 0 обладает
значительным самоподобием вплоть до 5 ГГц. При Ф = 90° в
диаграмме направленности существует случайный наклон слева направо
через один диапазон. Такое поведение может быть связано с несим-
меричностью древовидной структуры относительно плоскости X—Z,
когда активная зона простирается до различных ветвей
конфигураций.
664
11.6. Микрополосковые фрактальные антенны на основе снежинки Коха
11.6. Микрополосковые фрактальные антенны
на основе снежинки Коха
Фрактальные антенны и резонаторы. Фрактальные антенны, как
отмечалось ранее, имеют ряд особенностей, обусловленных их
геометрией. Сложность фрактальных структур можно распространить
также на весь объем резонатора [720, 730]. Скейлинговые свойства
полезны при проектировании многодиапазонных фрактальных
антенн — они позволяют уменьшить линейные размеры некоторых
антенных систем. Характеристики фрактальных резонаторов
неоднократно были предметом теоретических и экспериментальных
исследований [731- 734]. При этом наибольший интерес
представляют поведение фундаментальной моды и существование мод
высшего порядка, а также их локализация во фрактальных объемах.
Микрополосковые антенны в первом приближении могут быть
смоделированы как резонатор. В [735-737] исследовано влияние
сложной границы фрактальной поверхности микрополосковых
антенн на возбуждаемую основную моду и колебания высших
порядков. Ниже рассмотрим, следуя [737], наиболее существенные
результаты в этой области. Исследования [737] выполнены на
микрополосковых фрактальных антеннах, созданных итерациями снежинки Коха
(см. рис. 1.1,6).
Конструкция антенны. Последовательные этапы построения
снежинки Коха изображены на рис. 11.30. Из-за недостаточного
разрешения (см. рис. 1.1,6) итерации на рис. 11.30 практически не
различаются. Видно, что с каждой новой итерацией к площадь снежинки
Коха увеличивается.
Если через Ак обозначить площадь, образующуюся на к-м шаге,
то итерации вычисляются как
V3
(А \к~1
Ak+i-A+-]2
J,
а2, (11.31)
где а — сторона первоначального треугольника площадью
\ = (-Л /4)а2. Ряд (11.31) сходится к пределу
Л = |ТЗо2. (11.32)
665
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Кох1
Кох 2
Рис. 11.30. Различные итерации построения снежинки Коха [737]
Все итерации располагаются в окружности конечного радиуса
г = у/За/3. Периметр фигуры для к-й итерации имеет величину
'rW
(11.33)
Для снежинки Коха периметр бесконечной длины ограничивает
конечную площадь. Сама снежинка Коха была изготовлена методом
фототравления. Количество
итераций ограничивалось конечным
разрешением применяемого
метода. Генерация снежинки Коха
производилась треугольником со
стороной 118,2 мм. Использовалась
подложка с относительной
диэлектрической постоянной ег = 4,17 и
толщиной 1,6 мм.
На рис. 11.31 показана
конфигурация фрактальной антенны с
тремя итерациями кривой Коха.
Плоскость антенны расположена
на высоте h = 3,4 мм от
заземленной квадратной плоскости. Все
сконструированные фрактальные
Подложка iiiiiriiniiiiiin
Воздух
Основание жттттжтящ
;
и
Коаксиальный зонд
I
Рис. 11.31. Конфигурация
фрактальной антенны с тремя
итерациями кривой Коха [737]
666
//. 6. Микрополосковые фрактальные антенны на основе снежинки Коха
антенны запитываются зондами через коаксиальный кабель, точка
питания размещена на расстояниии 16,5 мм от центра снежинок
Коха. Координаты точки питания определялись экспериментально
с целью оптимизации условий согласования антенны.
Электродинамические параметры фрактальных антенн Коха. Для
фундаментальной моды в [737] исследовались значения резонансных
частот и добротности. Полученные результаты сравнивались с
данными, полученными для эквивалентных антенн, имеющих простую
евклидову форму. Численные результаты были проведены на
основе метода моментов. Теоретические частотные характеристики
действительной и мнимой частей входного сопротивления фрактальных
антенн с числом итераций к =1...5 приведены на рис. 11. 32.
Видно, что резонансная частота уменьшается с увеличением итераций.
Разброс резонансных частот между антеннами, обозначенными Кох
5 и Кох 4, составляет всего А5 4 « 0,27%, тогда как для антенн Кох 2
и Кох 1 эта величина достигает уже А21 s 9%. Экспериментальные
частотные характеристики составляющих входного сопротивления
изготовленных фрактальных антенн приведены на рис. 11.33.
Поведение кривых соответствует теоретическим расчетам, однако антенна
Кох 4 имеет меньшее значение резонансной частоты, чем антенна
Кох 5. Соответственно Д54 = 0,96%. Зависимость коэффициента
уменьшения резонансных частот фрактальных антенн Not числа
итераций приведена на рис. 11.34. Значение ^нормировано
относительно соответствующей величины для антенны Кох 1.
Заслуживает внимания тот факт, что резонансная частота
евклидовой круговой апертуры, Офаничивающей снежинки Коха, равна
1,19 ГГц. Следовательно, для данного объема, занимаемого
излучающим элементом, по сравнению с круговой областью более низкой
резонансной частотой обладает фрактальная снежинка Коха. Кроме
того, площадь снежинки Коха составляет всего 0,66 от площади
кругового раскрыва, обрамляющего фрактал. Эти соображения
необходимо принимать во внимание с целью уменьшения экономических
затрат при массовом производстве разнообразных антенн.
Представляет интерес величина добротности Q антенны Коха,
а также ее зависимость от числа итераций и сравнение с
соответствующей величиной для евклидовой микрополосковой антенны. В
случае равномерного распределения поля по апертуре добротность
антенны Q определяется выражением
667
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
1,1 1,15 1,2 1,25 1,3 1,35 /,ГТц
100Г
Я 50
О
-50
1 1
Кох 4
Кох S :^ j
i
Кох 3:
1
Кох 2
i г " "7" "
Кох 1:
i i 1 1
б)
1,1
1,15
1,2 1,25 1,3 1,35 у; ГГц
Рис. 11.32. Теоретические частотные характеристики действительной (а)
и мнимой (5) частей входного сопротивления фрактальных антенн,
изготовленных на основе итераций кривой Коха [737]
* hG/l
(11.34)
Здесь h — высота расположения антенны; G/1 — удельная
проводимость; /— длина апертуры; Е— распределение амплитуды поля по
апертуре антенны S; К— коэффициент редукции резонансной
частоты:
668
11.6. Микрополосковые фрактальные антенны на основе снежинки Коха
2 50
О
о Ь
-50
| 1 1 ; i
Кох KVL Кох 3 : _ ;
К^^\|\\_^^: \Kox2: .
\ гР 5 ^&*\^*^\*^~~
\ \ \
Кох
1 i
i
-1
1
1,1
1,15
1,2
1,25
1,3
б)
1,35 /,ГТц
Рис. 11.33. Экспериментальные частотные характеристики значения
действительной (о) и мнимой (б) части входного сопротивления фрактальных
антенн, изготовленных на основе снежинок Коха [737]
\\\E\2ds
j)\E\2dl'
(11.35)
В табл. 11.4 приведены результаты сравнения фрактальных
антенн на основе снежинки Коха с антеннами (евклидовых, как их
обозначили в [737]), имеющими круговую и гексагональную структу-
669
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Рис. 11.34. Зависимость
нормированного коэффициенга N
изменения резонансных частот
фрактальных антенн, изготовленных на
основе снежинок Коха, от числа
итераций к: измерения (кривая 1),
моделирование (кривая 2) [737]
12 3 4 5 6 7 8
Таблица 11.4
Значения резонансных частот и добротностей фрактальных и евклидовых
антенн при их одинаковой площади [737]
Параметр
/ГГц
0(738]
С [739]
Антенна
Кох\
1,78
24,3
21,7
Кох!
1,71
27,8
21,2
КохЪ
1,69
27,2
26,4
Кох А
1,66
25,4
25,7
Круговая
2
12,3
12,6
Гексагональная
2,03
17,3
17,9
ру. Для всех антенн значение А = 5 мм, а их площадь составляла
величину примерно 44,8 см2. Расчеты Q проводились методами,
изложенными в [738, 739].
Добротность фрактальных антенн выше добротности антенн с
целой размерностью. Однако последние имеют более высокие
резонансные частоты. В табл. 11.5 приведены результаты сравнения
фрактальных апертур Кох 3 и Кох 5 с круговыми апертурами для случая
примерно одинаковых резонансных частот. Расстояние от
подложки составляло 3,4 мм. Видно, что фрактальная антенна в данном
случае имеет меньшие размеры, чем эквивалентные ей структуры
гексагональной и круговой форм. Это вызывает определенный
интерес при использовании в антеннах дорогих материалов типа
сверхпроводников.
Локализация мод. Далее проведем анализ некоторых результатов
исследований мод высшего порядка и их локализации в
рассматриваемых фрактальных структурах [735,737]. Эффекты локализации за-
670
1,2
1,15
1,1
1,05!
1
0.951
N
! 1 J.--!"""
У^А—12
/ \ \
\ \ \
11.6. Микрополосковые фрактальные антенны на основе снежинки Коха
Таблица 11.5
Сравнение характеристик фрактальных и евклидовых антенн
в случае одинаковых резонансных частот [737]
Параметр
/ГГц
S, см2
Q, [738]
0, [739]
Антенна
КохЗ
1,19/1,2
93,6/93,6
60,36/56,54
56,97/57,22
Кох 5
1,17/1,17
96,23/96,23
54,12/58,57
54,22/59
Круговая
1,19/1,17
146,3/146,3
46,1/40,7
46,25/39,72
Примечание. В числителе дано измеренное значение, в знаменателе — расчетное.
нимают видное место в физике конденсированных сред.
Локализация в данном случае — следствие деструктивной интерференции
волн, отраженных нерегулярной границей. Токи, по существу,
сконцентрированы в области, примыкающей к границе фрактальной
структуры. Экспериментальные результаты пространственного
эффекта локализации моды шестого порядка на структуре снежинки
Коха третьего порядка приведены в [737]. Вследствие того, что в
области максимума плотности тока
сфазированы, а электрические
эквивалентные размеры
конструкции на исследуемых модах
выше, можно получать более
высокую направленность
излучения, чем на фундаментальной
моде. Геометрия фрактальной
конструкции, с помощью
которой исследовались моды
высшего порядка, приведена на
рис. 11.35. Фрактал был создан на
подложке толщиной 0,8 мм с гг =
= 3,38. Дополнительный
воздушный зазор между подложкой и
основанием был равен 7 мм.
Для устранения паразитной
индуктивности запитывающего
Подножка
j Возд. зазор'j •! Основание |^ |
I Коаксиальный зонд
Рис. 11.35. Геометрия фрактального
элемента на основе снежинки Коха
для исследования мод высшего
порядка [737]
671
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
зонда на плате был создан
емкостной элемент круговой формы.
Точка подключения зонда
находится на расстоянии 19,2 мм от
центра. Измеренная частотная
характеристика входного
коэффициента отражения рассматриваемой
конструкции приведена на рис.
11.36. Значение полосы
пропускания при ослаблении -14 дБ
составляет 12% несущей частоты.
Нормализованные компоненты Ев и Е
фрактальной конструкции на
основе третьей итерации снежинки
Коха, а также результирующая
диаграмма направленности на центральной частоте 3,52 ГГц
показаны на рис. 11.37. Ширина диаграммы направленности составляла в
Я-плоскости 36,9°, а в ^-плоскости - 27,4°. При этом
фундаментальный резонанс наблюдался на частоте 1,11 ГГц.
Рис. 11.36. Измеренный входной
коэффициент отражения для
фрактальной антенны, изготовленной на
основе третьей итерации снежинки
Коха [737]
ш
Рис. 11.37. Нормализованные компоненты EQ и 2Гф излучения фрактальной
антенны на основе третьей итерации снежинки Коха в ^-плоскости и Я-плоско-
сти, а также результирующая диаграмма направленности на частоте 3,52 ГГц [737]
672
11.6. Микрополосковые фрактальные антенны на основе снежинки Коха
Фрактальный диполь Коха и
его параметры. Генерация
локализованных мод в таких структурах
— это результат высоко
нерегулярной фрактальной границы. В [737]
описана также конструкция
фрактального диполя на основе
снежинки Коха третьей итерации (см.
рис. 11.38). Экспериментальные
характеристики данной
конструкции были измерены на частоте
5-й моды 2,81 ГГц. Измеренный
входной коэффициент отражения
при входном сопротивлении
снежинки Коха 50 Ом показан на
рис. 11.39. Нормализованные
компоненты Ее и Е фракталь-
Воэд, ядер Г Оснежите $ ;
КФЖСИЮЫЫЙ 90НЯ
Рис. 11.38. Конструкция
фрактального диполя на основе
снежинки Коха третьей
итерации [737]
ного диполя на основе снежинки
Коха, а также результирующая
диаграмма направленности на частотах 0,81 ГГц (основная мода) и
2,84 ГГц (локализованная мода) приведены на рис. 11.40 и 11.41 со-
Г,дБ
о
-2
-4
-6
-8
-10
-12
-14
-16
-18
-20
2,7 2,75 2,8 2,85 2,9 2,95 3
/,ГТц
Рис. 11.39. Измеренный входной коэффициент отражения фрактального
диполя на основе снежинки Коха [737]
Ш| / i » I
■ щ а а ■ Jm-m9 »«»т«>» ««.«■■■(■■■■•«•«■I
-4 -..-5"—-«—i -<|
22 Фракталы
673
Глава П. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
44
ДНА
ISO
ISO
216- I....--1S0
Рис. 11.40. Нормализованные компоненты EQ и Е фрактального диполя на
основе снежинки Коха, а также результирующая диаграмма направленности на
частоте 0,81 ГГц (основная мода) [737]
«S^-^i -"ЙО
Рис. 11.41. Нормализованные компоненты EQ и Е фрактального диполя на
основе снежинки Коха, а также результирующая диаграмма направленности на
частоте 2,84 ГГц (локализованная мода) [15]
674
11.7. Синтез фрактальных диаграмм направленности антенн
ответственно. Максимальный коэффициент направленного действия
фрактального диполя на фундаментальной моде равен 9 дБ, а на
локализованной моде - 13,4 дБ. Это объясняется правильной фазиров-
кой токов локализованных мод во фрактальной апертуре.
Экспериментальные результаты показывают, что фрактальный
диполь на основе снежинок Коха имеет более узкую диаграмму
направленности, чем диаграмма направленности классических
евклидовых антенн. Подобный результат может быть получен с решеткой
из 2x2 прямоугольных или круговых элементов. Однако
рассматриваемая фрактальная антенна имеет менее сложную цепь запитки, так
как необходима только одна точка подключения.
11.7. Синтез фрактальных диаграмм направленности
антенных решеток на основе обобщенных
функций Вейерштрасса
Новые режимы во фрактальной электродинамике. Рассмотрим
теоретические основы синтеза и процедуры конструирования
фрактальных диаграмм направленности антенн [435]. Данные вопросы
относится к фрактальной электродинамике, которая оформилась как
научная дисциплина в 1990 г. и соединила теорию фракталов с
теорией электромагнетизма. В отличие от традиционных методов, когда
синтезируются гладкие диаграммы направленности антенны, в
основе теории фрактального синтеза изначально заложена идея
реализации характеристик излучения с повторяющейся структурой на
произвольных масштабах. Это дает возможность создавать новые
режимы во фрактальной электродинамике.
Существует ряд прикладных направлений, в которых
возможность синтеза фрактальных характеристик изучения может быть
очень желательна. Это особенно важно для изучения
распространения и рассеяния электромагнитных волн фрактальными природными
средами (атмосфера, земные покровы и т.д.), при обработке
радиолокационных сигналов, при создании искусственных неоднородно-
стей в плазме и ионосфере с помощью мощных передатчиков и т.д.
Недифференцируемые функции как множитель решетки.
Семейство функций, известное как обобщенные функции Вейерштрасса
[128], играет определяющую роль в синтезе фрактальных характери-
675
Глава П. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
стик излучения. Эти функции везде непрерывны, нигде не
дифференцируемы и фрактальны на всех масштабах, они могут быть
представлены в виде
/w=i^-2)w*), (H.36)
где 1 < D< 2; g — подходящая ограниченная и периодическая
функций; л> 1.
В настоящее время особенно актуальны задачи конструирования
антенных решеток. Распределение излучателей по пространству дает
третью переменную, вдобавок к амплитуде и фазе тока возбуждения
решетки, с помощью которых удается управлять диаграммой
направленности антенны. Множитель неоднородной или неэквидистантной,
но симметрично распределенной решетки из 2Nизлучателей,
показанной на рис. 11.42, записывается в виде
N
f(Q) = 2y£lncos(kdncosQ + an).
(11.37)
л=1
Здесь к = 2п/\\ I и ап — амплитуда и фаза тока возбуждения; dn —
расстояние между соседними излучателями. Предположим, что
множитель решетки с бесконечным числом излучателей
выражается через обобщенную функцию Вейерштрасса (11.36) с косинусои-
дальной функцией g и случайной фазой а:
f(u) = 2]Г т1(/)-2>л cos(ar\nu + ап),
/2=1
(11.38)
где а — некоторая постоянная.
К точке наблюдения
Рис. 11.42. Симметричная решетка из 2N элементов с распределением тока
возбуждения [435]
676
11.7. Синтез фрактальных диаграмм направленности антенн
Сравнивая (11.37) и (11.38), можно найти, что амплитуда тока
и расположение элементов удовлетворяют следующим условиям:
In=4(D-2)n, kdn=axf (11.39)
при и = cos 0. Фрактальная диаграмма направленности (11.38)
обладает свойством самоподобия в бесконечном диапазоне масштабов.
Однако физически реализуемые решетки состоят из конечного
числа элементов, т.е. при этом получается усеченный ряд
N
fN{u) = 2£л(/)"2)л cos(mf и + ап). (11.40)
Выражение (11.40) представляет коэффициент решетки из 2Nm-
лучателей с амплитудами и фазами, распределенными согласно
(11.39). Таким образом, в данном случае частичная сумма (11.40) есть
диапазонно ограниченная функция Вейерштрасса, а результирующая
диаграмма направленности является фракталом в конечном
диапазоне масштабов с нижней границей 2n/(ar\N). Поэтому диапазон
масштабов контролируется с помощью числа излучателей решетки
N. Фактически, диаграмма направленности ставится более
детализированной при увеличении N.
Максимальное значение (11.40) для угла наблюдения G равно
/*Ц>) = 22>1(Д-2)Л (11.41)
/2=1
и определяется выбором фазы тока возбуждения ап = -cn\nuQ при
и0 =cos90. Ряд (11.41) есть геометрическая профессия, поэтому
fN(u0) = 2r(°-V
а нормализованный коэффициент решетки Вейерштрасса получается
делением (11.40) на (11.42), что дает
N
^incos(ar\"u + an), (11.43)
л=1
677
l_T,(£-2)iV
1-Л№-2)
(11.42)
**(«) =
1-п(Д-2)
Глава J J. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
где нормализованная амплитуда возбуждающего тока
^
(D-2)(n-\)
(11.44)
Сравнивая (11.39) и (11.44), получаем, что фрактальная
размерность диаграммы направленности может контролироваться
распределением тока по решетке.
Условия реализуемости. Расстояние между любыми двумя
соседними излучателями решетки оценивается соотношением
*п+\
ч=
Я(Г|-1)Г|Л
2тс
X, /2 = 1,2,...,7V-1.
(11.45)
Так как 11 > 1, то цп >т\ при п > 1. Следовательно,
dn+\-dn>di-dv n = l2,...,N-l.
(11.46)
Пусть х будет ограничивающим фактором, налагаемым на
минимальное расстояние между двумя последовательными
излучателями решетки. Тогда существуют два возможных случая,
удовлетворяющих данному условию:
\)d2-dx=x и dx>x/2;
2) dx = т/2 и d2-dx>%.
(11.47)
Из неравенства (11.46) следует, что при выполнении (11.47)
всегда пространственный разнос между всеми другими парами
последовательных излучателей решетки будет удовлетворять критерию
минимального расстояния т. Выражение для коэффициента а как
функции т и т| получается при совместном решении (11.39) и (11.47).
Тогда
а = -
кх
л(л-1)
кх_
V
, 1<л<3,
л>з.
(11.48)
Следует отметить, что параметр ц управляет сходимостью
выражения для коэффициента решетки Вейерштрасса. Чем ближе л к
678
И. 7. Синтез фрактальных диаграмм направленности антенн
единице, тем больше излучателей требуется для данной решетки. В
то же время пространственный разнос между последовательными
элементами решетки уменьшается при стремлении Л к единице. С
другой стороны, можно отметить, что амплитуды 1п и фазы ап тока
возбуждения, а также пространственные размещения dn излучателей
могут быть определены итерационным алгоритмом:
/ -AD-Dj J _л(/>-2)
ln-n 1n-v l\-n
осл = л«л_Р ах=-сщи0, (11.49)
dH=i\dnA9 dx=ar\/k,
где п = 2, 3, ..., N
Примеры синтеза фрактальных антенных решеток. Предположим,
что рассматривается решетка Вейерштрасса с х = Х/2, тогда из (11.48)
при а = 1 следует, что Л = 2,34. Эти значения используются в (11.49)
для определения пространственного разноса излучателей решетки.
На рис. 11.43 показаны синтезированные множители решеток с 16-
ю излучателями при фрактальном распределении тока возбуждения
с D= 1,1 (a), D= 1,5 (б), D= 1,9 (в), D= 1,5 для максимума
излучения при угле наблюдения 0 = 60° (г). В данном случае множители
решеток отождествляют с диаграммами направленности антенных
решеток Вейерштрасса. Можно сделать вывод, что фрактальная
размерность D управляется распределением тока по решетке. С
повышением D характеристики излучения усложняются и все в большей
степени заполняют пространство сканирования.
На рис. 11.44,а показаны нормализованные распределения тока,
приводящие к диапазонно ограниченным фрактальным диаграммам
направленности, представленным на рис. 11.43 для симметричной
16-элементной решетки Вейерштрасса. Высокая степень спада
амплитуды тока возбуждения необходима для синтеза диаграмм
направленности с более низкой фрактальной размерностью. В табл. 11.6
содержится перечень координат расположения излучателей для
указанной решетки Вейерштрасса, геометрия которой описывается с
помощью параметров л = 2,34 и а = 1.
Направленность фрактальной антенной решетки. Коэффициент
направленного действия решетки Вейерштрасса определяется
формулами (11.40) и (11.42) в виде
679
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
8р)
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
г
г
Ь J
Г !■
I Ы
VI
-1 -
«ДО
11
0,9
0,8
0,7
0,6
0,51
0,4
0,3
0,2
0,1
ol
-0,5
\ 1
: [
if ' 1J
1 | II
' ■:
:
0
б)
i
ц >
1 'li I
' 1
0,5 1
и
1Л li
1 1
-1 -0,5
Рис. 11.43. Нормализованные множители для 16-элементной
решетки Вейерштрасса при и0= 0, т = 0,5Х, л = 2,34, N= 8
для разных фрактальных размерностей D [435]
Таблица 11.6
Координаты излучателей для 16-элементной решетки Вейерштрасса [435]
Номер
излучателя»
1
2
3
4
Расположение
излучателя, dJX
0,372
0,872
2,039
4,772
Номер
излучателя л
5
6
7
8
Расположение
излучателя, djk
11,166
26,129
61,141
143,069
680
77.7. Синтез фрактальных диаграмм направленности антенн
G(uQ), дБ
14 г
5 Pi 111111 м 11 и 111111111 и 111111111111 it 1111м 11111
1 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2
Рис. 11.44. Нормализованные распределения тока /^для получения диаграмм
направленности с различными D (а) и коэффициент направленного действия
G(u0) в зависимости от значения D (б) при различных N [435]
681
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
G(u0) = 2f2(u0)I ]fi(u)du, (11.50)
где
N N
/^(w) = 4^^V/)"2)(m+',)cos(^,"« + aOT)cos(^« + aw). (11.51)
т=\п=\
Интегрирование (11.51) дает
}/^(«№ = 4ХХ^"2)(т+л)л^^ * "о)> (П.52)
_1 т=\ л=1
что позволяет записать
л-1
G(uQ) =
1-л(/)-2)
££^2)MAje^) 5 (ц.53)
от=1л=1
где
1
Лотл(а,л5"0)= Jcos[OTiw(i/-i^)]cos[OTf(i/-i^)] du =
-i
= cos[a(rjOT +r|,,)«0]sinc[a(r|/" +Tf)] +
H-cos^ri7" -Ti,l)^]sinc[fl(Tiw -ту1)]- (11.54)
Частный случай D = 2 соответствует решетке с однородным
распределением тока возбуждения
О(и0) = 2^/^Атп(а,ц,и0), (11,55)
/ т=\п=\
что дает G(0) = 2N, когда г|л заменяется на значение пп/а и w0 = 0.
Значения коэффициента направленного действия как функции D
приведены на рис. 11.44,5 для нескольких размеров решетки. Видно,
что по мере уменьшения D главный лепесток диаграммы
направленности расширяется, а соответствующее значение G{u) уменьшается.
682
11.8. Синтез фрактальных диаграмм направленности линейных антенн ...
11.8. Синтез фрактальных диаграмм направленности
линейных антенн с использованием преобразования
Фурье-Вейерштрасса
Преобразование Фурье—Вейерштрасса. Исследуем длинную
линейную излучающую систему L с непрерывным изменением тока
I(z), геометрия которой приведена на рис. 11.45. Такие антенны
К точке наблюдения
/
-L/2 1/2 z
Рис. 11.45. Геометрия непрерывной линейной излучающей системы длиной X,
расположенной вдоль оси г [435]
называются линейными. Для линейного источника бесконечной
дайны характеристики излучения F(u) и распределение тока I(z)
связаны парой преобразований Фурье
F(u)= \ I(s)rxp(i2nus)ds, I(s)= J F(u)exp(-i2nsu)du, (11.56)
где s = z/K w = cos0.
Любая фрактальная функция строится с применением
рекурсивных алгоритмов с подходящей генераторной функцией.
Предположим, что диаграмма направленности линейного источника
бесконечной длины может быть представлена диапазонно ограниченной
обобщенной функцией Вейерштрасса в виде
W=XV"2)W") О1-57)
/1=0
с генераторной функцией g(u). Считаем, что g(u) периодическая и
четная: g (и + 2) = g (и), g (-и) = g (и). Следовательно, функцию g (и)
можно представить косинусоидальным рядом Фурье
683
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
g(") = ^+IflOTcos(m™), (П58)
а фурье-коэффициенты ряда определяются выражением
1
ат =2Jg(u)cos(mnu)du. (11.59)
о
Тогда, подставив (11.58) в (11.57), получим выражение для
диаграммы направленности в виде
а ~AD-7)N 1 - N-\
т = ^ ,D_2) _} + II aJD~V» сов(иясп^). (11.60)
Без потерь общности в (11.60) можно заменить и на (и + 1). В
результате имеем
а n(D-2)N 1 ~ ftf-1 1
^> = f (D-2) 1 + I am I ^"^ <X*[™*T(U + В] » (H.61)
^ Л А ю=1 U=0 J
1
am=2Jg(u-l)cos(mnu)du, (11.62)
о
где т|> 1 и К 2)< 2.
Выражение (11.61) представляет разложение Фурье фрактальной
диаграммы направленности F(u) в базисе диапазонно ограниченных
косинусоидальных функций Вейерштрасса. В [435] данное
представление получило название преобразование Фурье-Вейерштрасса.
Распределение тока возбуждения линейного источника, требуемое для
получения заданной диаграммы направленности, записывается в виде
1
I(s) = J F(u)exp(-i2nsu)du. (11.63)
-i
Здесь F(u) находится с помощью (11.61), и тогда
n(D-2)N _ 1 - N-l
1(<s>> = ао (в 2) , sinc(2re) +11 ^-2)"{exp(//mnf) x
TV ~ L m=\ /i=0
xsinc(2^ - ттщп) + exp(-//w^r|/I)sinc(2^ + ттщп)}. (11.64)
684
11.8. Синтез фрактальных диаграмм направленности линейных антенн ...
Фрактальный линейный источник конечной длины. Выражение
(11.64) представляет требуемое распределение тока для линейного
источника бесконечной длины. Для источника конечной длины
Щ = Щ, \s\<L/2X,)
/(*) = 0, \s\>L/2X.\
(11.65)
Соответствующее выражение для синтезированных фрактальных
диаграмм направленности линейной излучающей системы L
находится с помощью (11.56) и (11.65). Откуда
а «(Я-2)лг_1
F(U) = £ 0-2> -1 {Si[<L/l)(Uu)]+Si[n(L/X)(l-u)]}+
1
N-l
+Т" 11 W(D-1)n {^[тщ"{и + l)]Smn(u) +
Zn m=\ л=0
+sin[/mctf(" + l)]C'm>)},
(11.66)
где
Smn(u) = Si[it(L/X-rm\")(i+u)] +Si[iiL/X+mr\")(l+u)] +
+Si[n(L/X-rm\n)(\-u)] + Si[n(L/X + rm\n)(l-u)], -1<и<1,
Cmn(u) = Ci[n\L/X-rm\n\(l + u)]-Ci[n(L/X + rm\n)(} + u)]-
-Ci[ii\L/X-rm)"\(l-u)] + Ci[n(L/X+mJ\n)(l-u)],
CmM = ln
l + u
-1<м<1, rmf*L/X,
-Ci[2-n(L/X)(l + u)] + Ci[2TtL/X)(l-u)],
1<м<1, rm\n=L/X,
Cmn(±\) = ± \Ci[2%\L/X-rm\n |]-Ci[2jc(IA + /mf)]-ln
L/X-гщ"
L/X + rm\n\\
rm\n*L/X,
685
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Cmn(±l) = ±{y + ln[4iiL/X)]-Ci[4it(L/X)]}, /mf=ZA,
Я(*) = рЕ1*,
C0S/-1
~ч ч f COST . , fCOSr-l .
Ci(jc) = —J df = y+lnx + J dt,
у = 0,57721... - постоянная Эйлера.
Легко показать, что lim F(u) = F(u) и Si(°o) = rc/2, Ci(oo) =0,
SmnH=2n,CmnH=0.
Примеры синтеза. Для иллюстрации процедуры синтеза
линейного источника излучения рассмотрим следующий пример.
Предположим, что нам надо синтезировать фрактальную диаграмму
направленности, которая основана на генераторной функции вида
g(G) = l-|cos6|, 0<9<71,
которая преобразуется в треугольную функцию
g(u) = l-\u\, \и\<1.
(11.67)
(11.68)
Коэффициенты Фурье ат с использованием (11.62) записываются
в виде системы уравнений
1
ат = 2Jucos(mnu)du = 1, т = 0,
ат = 2 f ucos(mnu)du = -
( 2 Л
кт%;
, /я = 1Д5,...,
am=2Ju cos(mnu)du = 0, т = 2,4,6,...
(11.69)
После подстановки полученных выражений в (11.61) при Ц = 2
получаем диаграмму направленности линейной фрактальной излу-
686
11.8. Синтез фрактальных диаграмм направленности линейных антенн ...
чающей системы с размерностью Д которая создана рекурсивным
алгоритмом:
т-\
2(D-2)N+2(D-2) _2
а \
2(в-2)-1
2 о= N-1 2(Л-2)л
1"|-
КП;
т=\ /1=1 УШ " V
(11.70)
с условиями F(±l) = 0 и F(0) = 1. Из уравнения (11.70) следует, что
при N= 1 диаграмма редуцируется до g(u) = 1 - \и\. Для диаграммы
направленности вида (11.70) необходимо нормализованное
распределение тока возбуждения
i(s) = ^ =
w ДО)
2(D-2)N _2(D-2)
2(D-2)N _ I
suic(2tw) +
2<д-2>-1
2(D-2)N _ J
-I
Л J
2(д-2)-1
2(D-2)N _l
-.ЛМ 2(D-2)n
sinc2(7w)-
:{8тс[2тс5-(2т-1)2л7с] + 8тс[2тс5+(2т--1)2л7с]}, (П-71)
где Д0) = [2^-2)^]/[2^-2)^-1].
Интересно отметить, что за исключением краевого эффекта,
функция sine самопободна с коэффициентом подобия, равным двум.
Распределение тока линейного источника (11.71) используется для
синтеза диаграмм направленности с желаемой фрактальной
размерностью, базирующейся на треугольной генераторной функции
(11.68). Примеры нормализованных диаграмм направленности
линейных источников F(u) с заданными значениями D = 1,3; 11= 2;
N= 14 и D= 1,7; Ц = 2; N= 26 приведены на рис. II.46,а,б, а их
нормализованные распределения токов / (s) показаны на рис. 11.46,в,г.
Снова можно отметить увеличение неоднородности диаграмм
направленности при возрастании D.
Для линейного источника конечной длины L распределение тока
будет усечено согласно (11.65), и в результате этого диаграмма
направленности имеет вид
687
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
-20-15-10 -5 0 5 10 15 20
\ s
-20-15-10 -5 0 5 10 15 20
г)
Рис. 11.46. Синтезированные диаграммы направленности с заданными
значениями D(a, б) и их нормированные распределения тока (в, г) [435]
F(u) =
J_
2л
2(D-2)N _2(D-2)
2(^-2)-1
{Si[jc(LA)(l+«)]+Si[jc(LA)(l-«)]}+
+-{(l + u)Si[iiL/X)(l+u)]+(l-u)Si[TiL/X)(l-u)]-
n
- 2«Si [it(L I X)u] - 2sinc [4L/2X)]sin [n(L/ 2X)]cos [it(I/ X)u]} -
i / j \2 ~ N-l %D-2)n r
2я
vn;
m=\ n=\
+sin[(2m-l)2"n«]C2m_ln(«)}.
(11.72)
688
U.S. Синтез фрактальных диаграмм направленности линейных антенн ...
Здесь
S2m_ln(u) = Si[liL/X-(2m-l)2")(l+U)] +
+Si[n(L/X + (2m-l)2")(l + u)] + Si[riL/X-(2m-l)2")(l-u)] +
+Si[n(L/X+(2m-l)2n)(l-u)~], -1<и<1,
Clm_ln(u) = Ci[n\L/X-(2m-l)2»\(l+U)]-
-Ci[iiL/\ + (2m-l)2")(l + u)]-Ci[%\L/X-(2m-l)2n\(l-u)] +
+Ci[%(L/X+(2m-l)2»)(l-u)], -1<и<1, (2m-l)2n*L/X,
О + гЛ
C2ffl_,„(«) = ln
K\-Uj
-а[2я<1/Я.)(1 + и)] + а[2я(1/А,)(1-и)],
-1<и<1, (2m-l)2n=L/X,
C2m_u(±\) = ±{y+ln[4ii(L/X)}-Ci[4it(L/X)]}, (2m-l)2« = L/X,
C2m_in(±l) = ±\ci[2Ti\L/X-(2m-l)2»\]-Ci[2iz(L/X + (2m-l)2n)]-
\L/X-{2m-\)2n[
-In
>, (2m-l)2"*L/X.
\L/X + (.2m-l)2n\
Отметим, что в (11.72) элемент, содержащий sin[n(L/2X)],
исчезает, если L/2 равна целому числу длин волн X.
В качестве следующего примера рассмотрим форму
£(0 = sin29, 0<8<тс, (11.73)
или в эквивалентном виде
g(u) = l-u2, -1<и<1. (11.74)
С использованием (11.62) и (11.74) можно получить требуемые
коэффициенты для преобразования Фурье-Вейерштрасса:
am=4/3, m = 0,j
am=-[2/(nm)f, m*0.J
(11.75)
689
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
На рис. 11.47 показаны первые восемь стадий (N= 1-8) синтеза
фрактальных диаграмм направленности на основе преобразования
Фурье-Вейерштрасса для формы (11.74).
-1 -0,5 0 0,5 1 «
Рис. 11.47. Первые восемь стадий iV=l-8 в синтезе фрактальных диаграмм
направленности при D = 1,1 и Л = 2 [435]
11.9. Фрактальные решетки Фурье-Вейерштрасса
Метод, кратко представленный ниже, является обобщением
метода синтеза фрактальных диаграмм направленности антенных
решеток на основе обощенных функций Вейерштрасса (см. разд.
11.7). Это обобщение включает преобразование
Фурье—Вейерштрасса, которое обеспечивает добавочную гибкость в выборе подходящей
генераторной функции [435]. Иначе говоря, хотя оба метода
синтеза обеспечивают необходимое значение фрактальной
размерности Z>, изучаемый здесь метод позволяет ввести дополнительную
степень свободы выбором геометрической структуры самой
антенной решетки.
Переходя к диапозонно ограниченным решеткам
Фурье-Вейерштрасса, запишем (11.61) в виде
F(u) = I0 + 2±Nflmncos(kdmnu + amn), (11.76)
690
11.9. Фрактальные решетки Фурье—Вейерштрасса
где
W i-V2> ' 7-=fл(/>_2)"' w« = w"n"' »« = ««n"-
Коэффициенты разложения ат, соответствующие особенностям
порождающих генераторных функций, могут быть получены из
(11.62). Уравнение (11.76) представляет множитель дискретной
решетки Фурье-Вейерштрасса с бесконечным числом элементов.
Полезное представление множителя решетки с конечным
числом излучателей получим простым усечением внешней суммы в
(11.76) с переменной порядка суммирования. Тогда
N-l M
m = I0+2^ I/m„cos(Mmn« + amn). (11.77)
Поэтому двойное суммирование в (11.77) можно
интерпретировать как суперпозицию парциальных диаграмм направленности N
подрешеток, состоящих из Мизлучателей. Непосредственно из
равенства kdmn = ктх\п следует, что расположение каждого из Мизлу-
чателей подчиняется уравнению
25
\=dm+ln-dmn=4n^ л = 0,1,2,...,#-1, (11.78)
которое удовлетворяет рекуррентному соотношению
\+i=4\, A0=V2. (11.79)
Таким образом, итерационная процедура определяет
пространственное размещение элементов в последовательности линейных
подрешеток.
Соответствующие рекуррентные процедуры для амплитуд токов
возбуждения и их фаз имеют вид
4л+1=П(0-2)/тл, «mn+1=11am„, 1т,=%П, «т0=™. (11-80)
Делением 1тп на /0 получаем амплитуды нормализованного
возбуждения тока:
691
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
1(\ — *' 1тп ~~
(аЛ( 1-л(/)-2) "1
V ° Л
1_Л(2)-2)ЛГ
JD-2)n
(11.81)
Пусть необходимо синтезировать фрактальную решетку Фурье -
Вейерштрасса с диаграммой направленности, основанной на
треугольной генераторной функции (11.68) с Ц = 2. Легко показать [435],
что
2(D-2)n
(2w-l)2'
а = (2m-l)2"ic, rf = (2ет -1)2""^.
°"2 1-2^-2) ' ш" 2he
(11.82)
Различные стадии конструирования решетки Фурье-Вейершт-
расса показаны на рис. 11.48 при Л= 2, N= 4, М= 5, Дй+1 =2Дл и
А0 = А,. Таким образом, расположение элементов для каждой
последовательности подрешеток получается удвоением пространства
предыдущей подрешетки. Самоподобие подрешеток ясно видно на
♦ 1 I I I I I I I I 1 II
II II II II II
ввввв
1'1'Н'И 1111)11
"Г <N Ъ
т
а а а а а
И1ИЯИНИ
Т V «i?
а а а
MIHItlllHI
г-н (N
II II
а а
I 1 1 И 111 1 11 П
1-1ЧПМ-1 М 1 Н И
++
■и-
Начальный
элемент
Стадия О
<л = 0)
Стадия 1
Стадия 2
(п = 2)
Стадия 3
(" = 3)
Геометрия
фрактальной
решетки
Рис. 11.48. Алгоритм построения фрактальной решетки при г| = 2, N= 4, М = 5,
\+1=2\и Д0=* [435]
"а
+
++
++
1
4
692
11.9. Фрактальные решетки Фурье—Вейерштрасса
рис. 11.48. На рис. 11.49 показана синтезированная диаграмма
направленности с D= 1,1; Л=2;М=4;Лг=8и треугольной
генераторной функцией. В табл. 11.7 перечислены пространственные
элементы решетки Фурье-Вейерштрасса и соответствующие им токи
возбуждения. Чем больше элементов мы используем в антенной
решетке, тем все более тонкая структура проявляется в диаграмме
направленности.
Рис. 11.49. Нормализованная синтезированная диаграмма направленности
решетки Фурье-Вейерштрасса с D = 1,1, ц = 2, JV= 8, М= 4и треугольной
генераторной функцией [435]
Вопросы синтеза фрактальных решеток и их реализация также
рассмотрены в [436]. Там представлены различные конфигурации
фрактальных лакунарных канторовых антенн. В их состав входят
спиральные, круговые, радиальные и нерегулярные канторовы
решетки, имеющие весьма сложный вид характеристик излучения.
e
о
CD OO CD
о
oo о
о о
OO О OO О О О О
ооооооооооооооооооооо
о 0
° I
+ ш
ё ~
8 °-
-* I
о о
I I
W W
оо со
оо *о
г«- оо
fN
о
fN
со
н (N (N
о о о
I
fN
о
ОО^ fN^ t-^ Ол ^ Г^ ~нл ОО^
fN~ т}-" t-^ ~н* ~н* Г$ *rt *гГ
I I I I I I I I
со fN
О О
I I
Ш Ш
ON ON
~н С)
^ °1
ОО" ~н"
I I
fN
О
СО СП
о о
Ш Ш
о tj-
fN fN
fN ~н
щ щ ш ш ш ш
и |s о Tt (N н
1П tv (?\ 1^ СП Г^
СП tJ- ^н ЧО СП Tj-
Т*-" ЧО" ~н" ^н" of ГО
I I I I I I
ГЛ ГЛ Tt Tt t
О CD О О CD
I I I I I
Ш Ш Ш Ш W
ON CD ON ЧО t^
" ЧО ~н ON ЧО
О
I
OO
ON fN^
OO" ^ ~н
I I I
OO Tj-
On oo
en \D On ^h
I I I I
OO
iO OO
ГО ОО ^н
Ю lO Ю
•» fN ~ CH
~н fN CO
Tj- Ю ЧО t^.
CD Tj" OO fN
fN fN fN CO
OO ЧО Tj-
tj- in чо
^-s vo fN CD fN Tj-
° >£ -и ЧО ON fN
OOON^^S
О oo
fN CO Tt
O^HfNCOTj-lOVOt^OOON
CD^HfNCOTj-юЧОГ-ОО
ONCD^HfNCOTj-ir)40r^OOONO^HfN
^HfNfNfNfNfNCNfNfNfNfNCOCOCO
ON
11.10. Синтез фрактальных диаграмм направленности ре конфигурируемых ...
11.10. Синтез фрактальных диаграмм направленности
реконфигурируемых антенных решеток
Линейная антенная решетка. Методология синтеза фрактальных
характеристик излучения антенных решеток с использованием
функций Вейерштрасса и Коха была изложена выше, а также
представлена в [420,435, 740]. Планарные антенные решетки, изготовленные
на основе ковра Серпинского, описывались в [741-744]. Широкий
обзор современных разработок фрактальных решеток дан в [745,
1011]. Ниже рассмотрим более общую методику синтеза
фрактальных диаграмм направленности антенных решеток, которая в
частных случаях позволяет получить результаты для функций
Вейерштрасса и Коха [746].
Множитель линейной решетки изображенной на рис. 11.50,
записывается в виде
N
/(0)= £ IneJnkdcosQm
(11.83)
d d
*—►h—н
d d
<—►Ц—И
i*
I., Л, /_, I. ', ', h
Рис. 11.50. Геометрия линейной решетки
Обозначая w = cos9, получаем
n=-N
При п -> оо переходим к разложению в ряд Фурье:
(11.84)
695
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
/л=(х)2^/(м;)е"У (1L85)
Id
на интервале -X/2d<w<X/2d.
Данный факт хорошо известен и лежит в основе методики
синтеза диаграмм излучения антенных решеток с однородным
расположением элементов. Другими словами, для некоторой
определенной диаграммы излучения распределение токов возбуждения,
приводящее к этой диаграмме, непосредственно может быть получено
из (11.85). Одним из недостатков этой методики синтеза является
применение ее только для синтеза узкополосных антенн вследствие
периодичности расположения элементов. Боковые лепестки
диаграммы направленности начинают расти, как только рабочая
частота антенной решетки выйдет за расчетный (достаточно узкий)
диапазон.
В [746] разработана методика синтеза, пригодная для
конструирования многодиапазонных антенн. Это достигается обобщением
техники синтеза фрактальных антенных решеток, разработанной в
[435] и описанной выше. Основой развития такой техники синтеза
многодиапазонных решеток является то, что самоподобная
рекурсивная диаграмма направленности излучения может быть
сформирована путем суперпозиции излучения последовательности
линейных антенных решеток, в которых относительные положения
элементов и распределения токов возбуждения соответственно
масштабированы.
Метод эквидистантных подрешеток. Первый шаг в разработке
технологии синтеза фрактальной диаграммы направленности антенной
решетки схематично показан на рис. 11.48. В рассматриваемом
методе (рис. 11.51,а—г) на каждой стадии р = п + 1 масштабированию
подвергается подпространство предыдущей подрешетки (в данном
случае происходит увеличение расстояния между излучателями в 2
раза) и распределение тока возбуждения (на каждой стадии
амплитуда уменьшается в 2 раза). Здесь п — номер стадии
конструирования решетки (см. рис. 11.48). Суперпозиция четырех эквидистантных
подрешеток с учетом того, что затравкой служат 5 излучателей,
представляет собой неоднородную фрактальную решетку (рис. 11.51,д).
696
НЛО, Синтез фрактальных диаграмм направленности реконфигурируемых ...
а)
р=\
* т •
h h h
-> п
б)
р=2
«)
р=Ъ
к
4
г)
р=4
д)
2
L
4
L
-*■ п
-+ п
-> п
■> п
Рис. 11.51. Алгоритм построения фрактальной антенной решетки
из четырех эквидистантных подрешеток (Р= 4) с пятью элементами:
четыре подрешетки (а-г), их суперпозиция (д) [746]
Из-за симметрии на рис. 11.51 приведена только половина антенной
решетки.
Обобщение этой концепции приводит к фрактальной антенной
решетке с самоподобной диаграммой направленности:
/рИ = 1 I
р=\ п-
j2nn\-\p-lw
рп '
(11.86)
где
р-\
1рп = ШР h
(11.87)
697
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
1 =
Ж
-jlnri — lv
f(w)e l^Jdw,
(11.88)
2d
f(w) - заданная генерирующая функция; Р - максимальное число
итераций в синтезируемой структуре антенной решетки; s —
коэффициент скейлинга; у - дополнительный амплитудный
коэффициент масштаба.
При Р= 1 выражение (11.86) редуцируется до
/.w=IV
jlnn\ — \v
(11.89)
которое описывает линейную эквидистантную антенную решетку с
излучателями, расположенными на расстоянии flf друг от друга. При
четной функции/(w) =/(— w) получаем
/л=|т- If/(w)cos
V К )о
(2d ,
dw.
(11.90)
Из (11.90) следует, что 1_п =/я и соотношение (11.86)
приобретает вид:
fP(w) = I,
\-(l/ys)P г
1-ОМ)
2Ц/
рп
COS
ПК
(2d Л
\sp~xw
(11.91)
Уравнения (11.90) и (11.91) описывают антенную решетку с
симметричным амплитудным распределением тока возбуждения.
Метод неэквидистантных подрешеток. Стандартные технологии
для фазированных линейных антенн могут легко обобщены на
рассматриваемый здесь неоднородный вариант построения антенных
решеток. Это является прямым следствием того факта, что класс
неоднородных антенных решеток может быть представлен, как следует
из рис.11.51, рядом последовательно масштабируемых однородных
антенных решеток. Следовательно, требуемые фазовые соотношения
между излучателями решетки могут быть получены из формулы
698
11.10. Синтез фрактальных диаграмм направленности реконфигурируемых ...
apn=-nkdsP~lw0, (11.92)
где wQ =cos0o, 0o — угол наблюдения максимума лепестка
диаграммы направленности.
Принимая во внимание текущее фазовое распределение,
запишем на основе (11.91) выражение для множителя решетки:
l-(l/ys)P р °°
/f(w)=/°Hi^+2^V^C0S[#"1(w"Wfl)} (1L93)
Теперь предположим, что антенная решетка состоит из
конечного числа излучателей. Тогда из формулы (11.93) получаем
следующее выражение для множителя решетки:
где
Wf(w) = X (Vysf' cos[nkdsP~l(w- w0)]. (11.95)
p=\.
Выражение (11.94) можно интерпретировать как суперпозицию
диаграмм направленности раздельно масштабированных антенных
решеток. На рис. 11.52 показано такое разложение для двух (N= 2)
масштабированных восьмиэлементных линейных антенных решеток
с Р = 4. При этом исходный элемент при п = О рассматривается
отдельно.
Сравнение рис. 11.51 ,д с рис. 11.52,г показывает полное сходство
синтезированных самоподобных фрактальных антенных решеток.
Интересно отметить [435, 745, 746], что рассматриваемые здесь
масштабированные фрактальные антенные решетки очень близки к
фрактальным антенным решеткам Вейерштрасса (см. разд. 11.7).
Фактически ряд Wf(w) представляет диапазонно ограниченную
функцию Вейерштрасса при условии \/s< у< 1. Фрактальная
размерность D функции Вейерштрасса, определенной при условии
Р->ооу равна
D = l-ln(y)/ln(s). (11.96)
699
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
а)
72=0
ISA
-+ Р
б)
в)
п=2
г)
• • •
4
i
+ Р
-+Р
8
->/>
Рис. 11.52. Алгоритм построения фрактальной антенной решетки из двух
самоподобных подрешеток (N=2): один элемент в начале построения (а),
первая подрешетка (б), вторая подрешетка (в), их суперпозиция (г) [746]
Обратим внимание на то, что в теоретическом плане
рассмотренные здесь самоподобные фрактальные антенные решетки
адекватны многодиапазонным антеннам с бесконечным набором
рабочих частот. Для доказательства устремим число итераций к
бесконечности Р -> оо ;
f(w)=limfp(w).
(11.97)
Здесь нормализованный множитель решетки на основе [746]
имеет вид
/»=
1-
ys
1 т(Р+1) (1У
ys
ys
р=-Рп=0
(11.98)
V2X/„
/1=1
700
11.10. Синтез фрактальных диаграмм направленности ре конфигурируемых ...
где
1, л = 0,
» = \2,п>0, (И-99)
k{=2n/Xv (11.100)
</ = оЛ15 (11.101)
а - безразмерный параметр.
Если мы предполагаем, что антенная решетка работает с
дискретным набором частот, то необходимо считать, что
* = \IK = fmlfi = WM~l> V*>1> « = 1,2,..„ (H-102)
где/j — частотная полоса отдельного диапазона.
Тогда из (11.97) и (11.98) следует:
/(aw) = op/(w), (11.103)
Р = (1/тГ\ y>Vs. (11.104)
Следовательно, скейлинг, описываемый соотношением (11.103),
обеспечивает получение многодиапазонных режимов. Необходимо,
однако, учесть, что многодиапазонность возможна для антенных
решеток с бесконечным числом излучателей. Как только, антенные
решетки усекаются, свойство многодиапазонности быстро ухудшается.
Планарные антенные решетки. Представленная выше
методология синтеза линейных антенных решеток была обобщена в [746] на
случай планарных антенных решеток (рис. 11.53). Множитель
решетки в этом случае записывается в виде
/(«,V)= X X J^jmkdiu-^jnkdiv-vo)^ (Ц.105)
m=-N n=-N
где
w = sin8cos(p; v=sin0sin(p; (11.106); (11.107)
M0=sineocoscp0; v0 =sine0sincp0. (11.108); (11.109)
701
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Р(гАч>)
Рис. 11.53. Геометрия планарной антенной решетки
Если мы считаем, что
тп т л'
то (11.105) факторизуется:
где
f(u,v) = fx(u)fy(v),
N
n=-N
N
т= 1 vMd(v-vo).
n=-N
702
(11.110)
(11.111)
/»= I /„е***"-^; (П.112)
(11.113)
//.//. Методы синтеза многодиапазонных фрактальных антенных решеток ...
При условии 1_т = 1т и Ln = 1п формулы (11.112) и (11.113)
записываются в виде
/»= IeAcos[w^("-"o)L (П.114)
/я=0
Полученные соотношения позволяют образовать
последовательность самоподобных планарных решеток. Результирующая
фрактальная диаграмма направленности таких решеток рассчитывается по
формуле [746]:
//>(«, v) =
Р N N
= IIIv^cos[m^^1("-wo)]cos[^^"Kv-v0)]^ (11.116)
р=1т=0п=0
где
п
h-
\—\j f(w)cos[qkdw]dw (11.118)
V П Jo
для q=m или п.
Рассмотренная процедура синтеза неоднородных планарных
антенных решеток с двумерным самоподобным фрактальным
размещением излучателей базируется на операциях масштабирования и
трансляции заданной генерирующей функции/(и).
11.11. Методы синтеза многодиапазонных фрактальных
антенных решеток на основе оконной фильтрации
Антенные решетки и окна. В [746] также рассмотрена методика
синтеза фрактальных антенных решеток с использованием оконных
весовых функций, правильный выбор которых приводит к конструк-
703
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
циям многодиапазонных решеток с минимальными физическими
размерами. Оконные функции, рассмотренные в [746], дают низкий
уровень боковых лепестков и быстрый спектральный спад. Оконные
функции с такими свойствами целесообразно использовать в
задачах синтеза антенн, так как результирующие токи элементов
быстро уменьшаются и имеют незначительную величину при увеличении
расстояния. Это обстоятельство позволяет разработать эффективную
технику «прореживания», позволяющую значительно уменьшить
число элементов и физические размеры антенных решеток.
Классические окна. Широкий набор современных оконных
функций с описанием их характеристик представлен в [501, 748]. В [746]
были рассмотрены три окна: Блэкмана, Блэкмана-Хэрриса и
Кайзера-Бесселя. Окно Блэкмана определяется выражением
f(w) = 0,42 -0,5 cos
'2n[w+(A/2)]]
Г41сГ* + (Д/2)1] д д (11.119)
где А - ширина главного лепестка.
Максимальный уровень боковых лепестков у окна Блэкмана
составляет -56 дБ. Окно Блэкмана и его первая производная
непрерывны на границах, поэтому уровень боковых лепестков спадает
как1/мР со скоростью -18 дБ на октаву.
Подставляя (11.119) в (11.118), получаем следующее выражение
для коэффициентов Фурье [746]:
/9 = 0,42
Ы_
\1%J
(qkdA
Asinc
I 2
+ 0,5
fkd}
\2%j
( \\
v2y
sine
qkdA
+0,5
{2nj
— sine
2J
(qkdA л
+ 0,08 — II — |smc
+ 0,08
l2n)
fAV
— sine
2
[2n
(qkdA
[ 2
qkdA
-In
+ 2n
(11.120)
704
//.//. Методы синтеза многодиапазонных фрактальных антенных решеток ...
Таким образом, токи возбуждения I для линейной решетки или
I для планарной решетки могут быть рассчитаны подстановкой
выражения (11.120) в формулы (11.87) или (11.117) соответственно.
Окно Блэкмана-Хэрриса определено в [746] как
[2тсГи> + (А/2)]1 [41сГ* + (Д/2)1]
/(w) = flb-g|cos] L ; ;J Ufl2cos L ^ >4-
A
-a3 cos
[fa(w + (A/2))|
, -A/2<w<A/2.
(11.121)
В формуле (11.121) коэффициенты а0 = 0,35875, ax = 0,48829,
a2 = 0,14128, a3 = 0,01168. Максимальный уровень боковых
лепестков у окна Блэкмана-Хэрриса равен —92 дБ, а скорость их спада
составляет -6 дБ на октаву. Коэффициенты ряда Фурье при
использовании (11.121) имеют вид [746]:
7, = flb
гы\
. 2тг ,
A sine
qkdA
v
сы\
+ 01
kd_
\2п/
sine
qkdA
+а*
fkd_^
\2nJ
v2,
sine
qkdA
— + n\+a2
fkdYA')
. In ,
v2y
sine
qkdA
-In +
+ Я0
^Л Л
V27
sine
#ЫД
+ 2я
+ a.
{2nj
(qkdA ~
Isinc ^— Ъп
2
+a.
'Arf
v2rcy
л
sine
J
qkdA
+ 3n
(11.122)
Окно Кайзера-Бесселя определяется выражением [746]:
/(>v) = /0(7caVl-(2>v/A)2)//o(7ca), -|^<|. (11.123)
где 10(х) - модифицированная функция Бесселя первого рода
нулевого порядка.
Окно Кайзера-Бесселя, в отличие от первых двух окон (11.119)
и (11.121), позволяет ввести дополнительную степень свободы через
параметр а, контролирующий форму окна. При a = 0 имеем пря-
23 Фракталы
705
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
моугольное окно шириной А, а при а->оо приближение
8-функции. Это позволяет варьировать ширину луча по уровню -3 дБ
независимо от первого нуля, что невозможно с окнами Блэкмана или
Блэкмана-Хэрриса.
В случае окна Кайзера-Бесселя замкнутые формы для
соответствующих интегралов (11.118) получить невозможно. Однако
полезная аппроксимация для фурье-преобразования окна
Кайзера-Бесселя приведена в [501]:
~ д sinh(V(7ca)2-(^/2)2)
Тогда формула (11.118) с учетом обозначения и = qkd
принимает вид:
ы a sinh(V(7ca)2~(2^/A)2)
/ я^_а v. . '-. (11.125)
п 2я/0(ш) J(na)2-(2qkd/A)2
я
Характерное поведение рассмотренных окон и их фурье-преоб-
разований показано на рис. 11.54. Видно, что данные окна
эффективны и в случае их применения в теории антенн.
Метод усечения подрешеток. Одним из основных препятствий
конструирования многодиапазонных антенных решеток по методу,
предложенному в [740], является уменьшение эквивалентного
электрического расстояния между элементами антенной решетки по мере
перехода от высокочастотного диапазона к низкочастотному.
Предположим, что необходимо синтезировать четырехдиапазонную
антенную решетку с коэффициентом масштабирования (скейлинга)
s = 3. Пусть минимальное расстояние между элементами решетки
d0=X0/2 при самой высокой рабочей частоте f=f0. Переходя к
следующему диапазону с центральной частотой/^ =/0/39 мы видим,
что минимальное расстояние между элементами решетки становится
равным dx =X{ /6. Для третьего диапазона с /=/2 =Уо/9 и
четвертого диапазона с /=/3 =f0/27 находим, что d2 =X2/IS и d3=Xz/54,
соответственно. На практике в таких антеннах возникают
существенные взаимосвязи вследствие близости элементов решетки,
особенно в низкочастотном диапазоне.
706
11.11. Методы синтеза многодиапазонных фрактальных антенных решеток ...
№
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
л
""Ч
'•■X
V-2
\ \\
\ч
1 1 '"'•■•
1
2
3
^i-rifah.
Блэкман-Харрис
Блэкман ;
Кайзер-Бессель j
0.1
0.2
0.3
0.4
0.5
W
I/u), ДБ
-20 Ь
-40
-60
-80
-100
-120
V
1 Блэкман-Харрис
2 Блэкман
3 Кайзер-Бессель
\И
,л*
• •.л
Ял
ш
л
50
100
150
200
и
Рис. 11.54. Сравнение оконных функций и их фурье-преобразований [746]
707
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Для того чтобы обойти эту проблему, в [746] предлагается
ввести схему переключения диапазонов, которая коммутирует
подрешетки при изменении частоты. В этом случае используют свойство
самоподобия решеток, позволяющее включать и выключать
минимальное число элементов при переходе от одного рабочего диапазона к
другому.
Тогда процесс проектирования многодиапазонной антенной
решетки, разработанный в [746], начинают с выбора
соответствующего коэффициента скейлинга s и необходимого числа частотных
диапазонов Р. Индивидуальные диапазоны центрируются на частотах
f0,f0/s,f0/s2,...,f0/sp~l. Для высокочастотного диапазона 1 cf=f0
все подрешетки возбуждены. Однако когда антенная решетка
переключается на диапазон 2 с частотой f=f0/s, первая подрешетка,
соответствующая/? = 1, выключается. Когда антенная решетка работает
в диапазоне 3, где/=^ А2, первая и вторая подрешетки (р = 1 ир = 2)
соответственно выключаются. Этот процесс повторяется до самого
низкочастотного диапазона с номером Р, для которого /0 = /0 /sp~l,
и все подрешетки (или субрешетки), за исключением последней,
отключены.
Как отмечено выше, выбор подходящей оконной функции, на
основе которой будет синтезирована фрактальная самоподобная
антенная решетка, является важной частью процесса
конструирования таких антенн. На основе рассмотренных оконных функций
(11.119), (11.121) и (11.123) в [746] разработаны алгоритмы усечения,
обеспечивающие заданный вид диаграммы направленности при
определенных физических размерах и числе элементов синтезируемых
антенных решеток.
Порог возбуждения. Множители многодиапазонных решеток
(11.93) и (11.116) показывают, что такие типы решеток можно
представить в виде суперпозиции однородных подрешеток,
распределение токов в которых масштабировано относительно друг друга.
Учитывая этот факт, алгоритм усечения может быть применен к каждой
подрешетке. Более определенно, если ток возбуждения каждой из Р
подрешеток нормализован относительно максимального значения,
то часть токов, меньших порога возбуждения г, можно положить
равными нулю. Как только эта процедура применена,
распределение токов на каждой из подрешеток будет уже не нормализованным.
Иначе говоря, нормализованные распределения токов подрешеток
708
11.11. Методы синтеза многодиапазонных фрактальных антенных решеток ...
заново перемасштабируются на фактор (l/ys)p~l для/? = 1, 2,..., Р. В
итоге, число Р индивидуальных подрешеток образуют сложную
линейную или планарную многодиапазонную решетку.
Представленный в [746] подход полностью отличается от алгоритмов,
предложенных ранее в [740, 749, 750], где схему усечения применяют ко всей
фрактальной решетке вместо индивидуальных подрешеток. Другим
важным преимуществом подхода [746], является сохранение
рассмотренной выше реконфигурируемой схемы с переключением
диапазонов.
Выбор порога возбуждения г представляет собой компромисс
между точностью синтезирования диаграммы направленности
антенны, ее размерами и числом элементов решетки. Для
многодиапазонных решеток, синтезируемых с помощью окон Блэкмана, Блэкма-
на-Хэрриса и Кайзера-Бесселя, в [746] было найдено, что
практически допустимые ошибки округления находятся в пределах
0 < 8 < 0,1. Значения е, близкие к величине 0,1, приводят к меньшим
размерам антенн с малым числом элементов. Однако при этом
возрастает расхождение между расчетной и синтезированной
диаграммами направленности антенны.
Успешное применение на практике представленной в [746]
техники синтеза многодиапазонных антенных решеток требует
надлежащего выбора антенных элементов. Одна из возможностей
заключается в том, чтобы использовать один и тот же коэффициент скей-
линга s как для всей антенной решетки, так и для ее отдельных
многодиапазонных элементов. Реконфигурируемая апертура может
быть сконструирована в виде физически отдельных зон с
переключателями, выполненными, например, по технологии MEMS (Micro-
Electro-Mechanical Switching), или с другими типами СВЧ
переключателей. Технология MEMS реализует электромеханическую
коммутацию на микроуровне (например, в оптических коммутирующих
подсистемах) [747]. Эти переключатели расположены между
некоторыми (или всеми) зонами. Выбор, с помощью переключения
различных комбинаций зон позволяет сформировать необходимые
фрактальные (и нефрактальные) излучающие элементы.
709
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
11.12. Примеры синтеза многодиапазонной фрактальной
антенной решетки методами оконной фильтрации
Применение весовой функции Блэкмана. Для иллюстрации
описанных в разд. 11.10 и 11.11 методов, рассмотрим пример синтеза
многодиапазонной фрактальной диаграммы излучения [746]. Пусть
необходимо синтезировать многодиапазонную планарную антенную
решетку с четырьмя диапазонами на центральных частотах^, f0/3,
fo/9, Уо/27. В этом случае Р = 4 и s = 3. Применим окно Блэкмана
(11.119) с шириной главного лепестка 39° между пересечениями нуля
и А =2/3. Тогда ширина окна по уровню 3 дБ или половинной
мощности, определяемая из соотношения
/(>v0) = l/V2, (11.126)
примерно равна 1Г. Строго говоря, соотношение (11.126) применимо
только при значении Р — 1, но если ys> 10, то вкладом
последовательных стадий масштабирования на характеристики главного
лепестка можно пренебречь [746]. Выбором параметра у= 4 можно
установить уровень первых боковых лепестков на 20 дБ ниже пика
главного лепестка. Наконец, межэлементное расстояние d0
выбирается равным половине длины волны на самом высоком рабочем
диапазоне решетки, т. е на частоте f=f0. Следовательно, идеальная
диаграмма направленности будет образована суперпозицией
масштабированных и смещенных вариантов окна Блэкмана (подробности
представлены в [745]).
Картина излучения синтезированной планарной решетки с
использованием окна Блэкмана представлена на рис. 11.55 и 11.56, при
е = 0. На рис. 11.55 приведены горизонтальные сечения
пространственных диаграмм излучения для каждого из четырех диапазонов,
а на рис. 11.56 - сечения диаграмм направленности плоскостью X—Z
(ф = 0). Заметим, что полуволновая периодичность между
активными антенными элементами соблюдается для каждого из четырех
диапазонов. Это достигнуто применением одного из вариантов
переключающей схемы, обсуждаемой в разд. 11.11 [745, 746].
Синтезированная планарная решетка состоит из четырех подре-
шеток с числом элементов 91x91 в каждой. Таким образом,
коэффициенты ряда Фурье в соотношении (11.116) учитываются вплоть до
N= 45. В результате синтеза [746] получена сложная многодиапазон-
710
11.12. Примеры синтеза многодиапазонной фрактальной антенной решетки ...
V Диапазон 1 у Диапазон 2
Рис. 11.55. Горизонтальные сечения (0 = 90°) пространственных диаграмм
излучения фрактальной антенной решетки на основе окна Блэкмана
приР=4, 5 = 3, #=45, е=0[746]
ная планарная антенная решетка с числом элементов 30421 для
перекрытия всех четырех диапазонов.
Рассмотрим влияние порога возбуждения е на характеристики
излучения фрактальных антенн. Трехмерный вид синтезированных
диаграмм излучения фрактальной антенной решетки представлен на
рис. 11.57, а их сечения плоскостью X-Z(9 = 0) приведены на рис.
11.58. Как и следует ожидать, увеличение е приводит к возрастанию,
в среднем, уровня боковых лепестков. Более важным является тот
факт, что характеристики главного лепестка и максимальный
уровень боковых лепестков сохраняются при использовании алгоритма
прореживания. Наконец, на рис. 11.59 показаны сечения диаграмм
711
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
ЯлрДБ
Диапазон 1
J
III!
\\
\
ii
III
л
а
т
Й»ДБ
Диапазон 3
-0,5
0-5 U
. А '
-
(\
/ \
:. I
I I
А
0,5
£^ДБ
Диапазон 2
4
I
. I
А
/I -
I I fl
I
^ДБ
и -0,5
Диапазон 4
0,5
0.5 U
I ' ■
I
I
Рис. 11.56. Сечения плоскостью X-Z (ф = 0) диаграмм направленности
фрактальной антенной решетки, изготовленной на основе окна Блэкмана,
приР = 4, 5 = 3, N=45, £=0[746]
излучения в плоскости X-Z (<р = 0) при отклонении главного
лепестка на угол Э0 = 45° в каждом диапазоне.
Применение весовой функции Кайзера-Бесселя. Рассмотренные
выше примеры синтеза многодиапазонных фрактальных антенных
решеток основывались на оконной функции Блэкмана. Однако
большая гибкость может быть достигнута при конструировании таких
антенн с использованием окна Кайзера-Бесселя. Это следует из
выражения (11.123), в котором присутствует параметр а, позволяющий
варьировать шириной луча и уровнем боковых лепестков в области
преобразования. В рассмотренном случае данное обстоятельство
позволяет более свободно выбирать общие размеры антенной
решетки и полное число ее лепестков при использовании техники
прореживания. Примеры этого представлены на рис. 11.60.
712
11.12. Примеры синтеза многодиапазонной фрактальной антенной решетки ...
Диапазон 1 Диапазон 2
Рис. 11.57. Трехмерный вид синтезированных диаграмм излучения фрактальной
антенной решетки, изготовленной на основе окна Блэкмана,
при Р= 4, s = 3, #=45 для случая £=0,1 [746]
При изменении параметра а от 2,5 до 1,1 число требуемых
элементов для соответствующей фрактальной антенной решетки (s = 3,
у = 4, Р= 4) можно уменьшить, хотя и за счет некоторого
изменения ширины главного лепестка. Например, из рис. 11.60,#видно, что
окно Кайзера-Бесселя с параметрами А =2/3 и а = 1,8 приводит к
антенной решетке с числом элементов 281 вместо прежнего числа
409. При использовании значений А =2/3 и а = 1,5 получаем 249
элементов антенной решетки (рис. 11.60,#), а при А =2/3 и ос = 1,1 -
всего 165 элементов (рис. 11.60, г).
Антенная решетка Вейерштрасса. На рис. 11.61 показано сечение
пространственной диаграммы излучения планарной фрактальной
антенной решетки Вейерштрасса при s = 3, У = 0,5, Р= 5. Из рис. 11.61
видна богатая самоподобная структура диаграммы направленности
на основе классической функции Вейерштрасса. Данная антенная
решетка синтезировалась в [746] на основе окна Блэкмана с
параметром А =2/3. Основной ее недостаток - это ограниченный диапазон
713
Глава П. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
&»ДБ
2*>ДБ
-0,5 0 0,5 U -0,5 0 0,5 U
Рис. 11.58. Сечения плоскостью X—Z (ср = 0) диаграмм направленности
фрактальной антенной решетки, изготовленной на основе окна Блэкмана,
при Р= 4, s = 3, N = 45 для случая £=0,1 [746]
ftp ДБ
7Т
Л
Л/ WW М
п/
-20»
-401
•60)
Диапазон 2
А%А
■ 1 1
А-
««.ДБ
0
««.ДБ
Диапазон 4
Л
\
\ -
-о.в о o,e U -о.в о 0,6 и
Рис. 11.59. Сечения плоскостью X-Z (ср = 0) диаграмм направленности
фрактальной антенной решетки, изготовленной на основе окна Блэкмана, при Р= 4, s = 3,
N=45, £ =0,1 и отклонении главного лепестка на угол Э0 = 45° [746]
714
11.12. Примеры синтеза многодиапазонной фрактальной антенной решетки ...
£№ДБ
Диапазон 1, а=2,5, 409 элементов оhP Д Диапазон 1, си=1,8, 281 элемент
V
-20
-40
-60
Г
1
и А л'
' /
Vv
1 j
0,5
&№ д Диапазон 1, а=1,5, 249 элементов 6^ м^ Диапазон 1, а=1,1, 165 элементов
Ал
т
-0,5
Ai yj
0,5
ft». ДБ
0
Рис. 11.60. Диаграммы направленности фрактальной антенной решетки на
основе окна Кайзера-Бесселя в первом диапазоне при г =0,1 в зависимости от
значения параметра а [746]
изменения параметров, определяемый условием l/s<y<l, что
приводит к достаточно значительному уровню боковых лепестков.
Например, для диаграммы излучения
планарной фрактальной антенной
решетки Вейерштрасса (рис. 11.61)
уровень боковых лепестков
приближенно равен 201g(ys), что дает
величину около 8 дБ относительно пика
главного лепестка.
Рис. 11.61. Сечение пространственной
диаграммы излучения планарной
фрактальной антенной решетки Вейерштрасса
при 5 = 3, Y = 0,5, Р= 5 с использованием
окна Блэкмана и параметром А =2/3 [746]
715
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
11.13. Моделирование поверхностного импеданса
фрактальных структур
В работе [437] исследуется полное поверхностное
сопротивление zs двух тонких проводящих медных пленок с фрактальной
структурой. Сопротивление измеряется в свободном пространстве в
частотном диапазоне 10-20 ГГц для двумерной кривой Коха (рис. 11.62,а)
и ковра Серпинского (рис. 11.62,5) с фрактальной размерностью
D= 1,5 и D = 1,89 соответственно при четырех итерациях.
шли
w
шз
щ
ФШЦ
HHS
ш
ЁШ
а) б)
Рис. 11.62. Фрактальные поверхности в виде кривой Коха (а)
и ковра Серпинского (б) [437]
Образцы помещают между двумя антеннами. Передающая
антенна закрепляется неподвижно, а приемная устанавливается на
поворотном стенде. Для уменьшения влияния окружающей среды
применяется пространственная фильтрация и фокусированные антенны.
При численном моделировании рассматривается задача
прохождения радиоволн частотой 1-80 ГГц через два слоя воздуха,
отверстия в медном покрытии толщиной 35 мкм и диэлектрическую
подложку толщиной 1600 мкм. Поверхностное сопротивление
рассчитывают по формуле
Е,
Кг=
:=0)/Я:
Кг=0)'
(11.127)
где E^z=y и HL,~ - суммы тангенциальных компонент полей Е
и Яна поверхности пленки при z = 0.
В процессе моделирования получены системы из 22 уравнений
для ковра Серпинского и 30 уравнений для кривой Коха.
Теоретические (кривая 1) и экспериментальные (кривая 2) результаты для
716
11.13. Моделирование поверхностного импеданса фрактальных структур
активной Rs и мнимой Xs составляющих поверхностного
сопротивления zs представлены на рис. 11.63,а (ковер Серпинского), на
рис. 11.63,5 (кривая Коха) и в детальном виде изображены на
рис. 11.63,#,г. Значение Rs для ковра Серпинского колеблется около
50 Ом и около 90 Ом для пространственной кривой Коха.
По составляющим Rs и Xs можно определить фрактальную
размерность поверхности
D =
in(A4/M+i)2
\n(AFt/AFM)
1/2 '
(11.128)
где АА. и Щ - амплитудные и частотные диапазоны парциальных
колебаний (рис. 11.63), Д4+1 < Д4> Щ+\ < ^/- Для обоих образцов
среднее значение принятого сигнала непосредственно связано с
числом отверстий.
/^,Омюо
*,Ом»1
"1
-и
■я
lit II II»HU«I1 I*
Лс,Ом
/;ггц
в)
Л ГГц
Rs,Ou
а;, Ом
1».
ioo-
jo-
0-
100-
Нч
ч>
^^г
-!??*
V ■■ 1 "Г
fe*
-?<
<
1^>»»
<s>^
<2JS«NK
l""l > 1
10 tl 12 13 14 15 1« 17 It
f,TTu
6)
Rs,Om
X.Om
!»•
100-
•0-
«■
40-
S f
^tn^-^cL^ г
^--^r4^
2^^^- Л
1 1
^^w7^
_2 [
13.2 13,4 1X<
ил
/;ггц
Рис. 11.63. Теоретические (кривая 1) и экспериментальные (кривая 2) результаты
исследования активной Rs и мнимой Xs составляющих поверхностного
сопротивления zs для ковра Серпинского (а, в) и кривой Коха (б, г)
в частотном диапазоне/[437]
717
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
11.14. Фрактальные фотонные и магнонные кристаллы
Новые искусственные среды для передачи информации.
Неослабевающий интерес к композиционным «наборным» периодическим
средам связан с конструктивными возможностями получения
желаемых электродинамических характеристик таких сред. В частности,
микроскопическая трехмерная структура или фотонная решетка
создается на основе кремния и позволяет передавать когерентный свет
в оптическом диапазоне длин волн с минимальными потерями.
Эффективность передачи приближается при этом до 95%, что
значительно превосходит показатель стандартных светопередающих сред
(около 30%), используемых в настоящее время [713, 714]. При этом
можно направлять лучи по сложной траектории, содержащей
«изгибы», практически под прямым углом в заданную точку. Такая
решетка представляет собой пачку тонких кремниевых двумерных
решеток, каждый слой которой повернут на 90° относительно соседнего.
Для создания работающей фотонной решетки достаточно
примерно десяти таких слоев.
Исследования в области физики фотонных кристаллов
стимулировали создание таких кристаллов, работающих в диапазоне
частот видимого света, на основе синтетических опалов, коллоидных
частиц, пленок с наноструктурами и др. Фотонные кристаллы —
искусственно созданные периодические структуры с соответствующим
изменением показателя преломления. Свойства электромагнитных
волн, распространяющихся в таких структурах, подобны свойствам
электронов в кристаллах. Аналогично эффекту возникновения
зонной структуры в полупроводниках, в данном случае в спектре волн
возникает запрещенная зона. Свойства фотонных кристаллов, в
частности, существование фотонной запрещенной зоны (ФЗЗ),
зависят от длины волны распространяющегося света. Миниатюрные
устройства на основе фотонных кристаллов могут быть созданы
только для кристаллов с длиной волны видимого, либо инфракрасного
диапазона. Фотонные кристаллы с запрещенной зоной в области
радиочастот имеют достаточно большие размеры из-за большой
длины электромагнитных волн.
Наряду с созданием фотонных кристаллов появилась идея
создания кристаллов, в которых подобными свойствами обладают волны
иной природы, а именно, фононы или акустические волны, а также
магноны или спиновые волны. В частности, магнонные кристаллы (см.,
718
11.14. Фрактальные фотонные и магнонные кристаллы
например, [713, 714]) на основе магнитных материалов имеют ряд
преимуществ по сравнению с фотонными. Во-первых, длина
спиновой волны, а соответственно, и свойства таких кристаллов зависят
от внешнего магнитного поля и могут управляться этим полем. Во-
вторых, для широкого класса ферромагнитных материалов длина
волны распространяющихся спиновых волн в микроволновом
диапазоне порядка десятков или сотен микрон. Следовательно, можно
создать кристаллы с фотонной (или магнонной) запрещенной зоной
размерами порядка нескольких миллиметров. Такие кристаллы
могут быть изготовлены с использованием технологий планарной
геометрии, что чрезвычайно важно при создании интегральных
устройств, в частности, избирательных оптических или СВЧ-фильтров
и высокоскоростных переключателей.
Простейший магнонный кристалл - это строго периодическая
многослойная структура, состоящая из магнитных слоев с разной
намагниченностью, либо такая же структура, но состоящая из
магнитных и немагнитных слоев.
Реализовать желаемую структуру для магнонного кристалла
довольно сложно, поскольку при росте слоев легко нарушается
периодичность их магнитных свойств и, в конечном итоге, структура
магнонного кристалла разрушается. В [713, 714] описана технология
изготовления образцов двумерного магнонного кристалла на
основе ферромагнитных пленок. При этом кристалл представляет собой
ферромагнитный волновод с двумерными неоднородностями
намагниченности в нем. В качестве неоднородностей могут быть либо
имплантированные элементы другого ферромагнетика, либо
отверстия. При создании магнонного кристалла выбиралась
ферромагнитная пленка железоиттриевого граната (ЖИГ), выращенная эпитак-
сиально на немагнитной подложке из галлий-гадолиниевого
граната. Магнитостатические спиновые волны (МСВ) в таких пленках
легко возбуждаются с помощью микрополосковых преобразователей.
При высоком качестве пленок и небольших потерях на
распространение, МСВ в них могут распространяться на расстояния,
составляющие много длин волн.
Конструирование фотонных запрещенных зон с помощью
фрактальных структур. Традиционные материалы с ФЗЗ используют брэггов-
ское рассеяние для создания запрещенных зон. Естественным
следствием брэгговского механизма рассеяния является то, что
толщина и поперечные размеры фотонных кристаллов должны составлять
719
Глава 11. ФРАКТАЛЬНЫЕ^АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
несколько длин волн. Значительный научный и практический
интерес представляет использование уникальных свойств фрактальных
структур в создании таких рассматриваемых кристаллов. Как
подробно показано в данной главе, на основе свойств скейлинга
(масштабной инвариантности) функционируют все фрактальные
антенны. Классические частотно — избирательные поверхности (ЧИП)
селективно отражают электромагнитную волну заданной частоты.
Они функционируют по принципу собственного резонанса ряда
взаимодействующих металлических элементов, расположенных
периодически. Системы ФЗЗ и ЧИП работают обычно в одном
частотном диапазоне с определенной длиной волны, затухающей в объеме
периодически расположенных базовых функциональный блоков.
В основе синтеза фрактальных антенн заложена идея
реализации характеристик излучения с повторяющейся структурой на
произвольных масштабах. Это дает возможность создавать новые
режимы во фрактальной электродинамике (например, моделировать
частотно-независимые импедансы с помощью фрактальных структур -
см. разд. 11.13 и [437]).
Особый вид плоских проводящих фракталов дает возможность
создавать сложные отражающие и пропускающие зоны в широком
диапазоне частот. Фрактальная структура может быть
сверхволновой и моделировать трехмерные кристаллы. Многополосный режим
функционирования, перекрытие обширного спектрального
диапазона, а также значения полосы пропускания, соответствующие длинам
волн, которые значительно больше размеров образца, делают
фрактальные пластины интересной и потенциально очень полезной
частотно - избирательной средой. Такие уникальные свойства,
повторим еще раз, есть результат проявления ряда самоподобных
собственных резонансов во фрактальных структурах.
Ряд электродинамических свойств стохастических фрактальных
структур рассмотрен в [979—981, 1011], а также в гл. 6 монографии.
При конструировании фрактальных фотонных и магнонных
кристаллов удобны детерминированные геометрические фракталы,
которые имеют легко прогнозируемые характеристики и могут быть
достаточно просто сгенерированы [1011]. Именно они и
применяются чаще всего во фрактальных антеннах и фрактальных селективных
радиоволновых системах.
Эксперимент. В частности, в [859] была использована
фрактальная структура на основе дерева Кейли, приведенная на рис. 11.64,я.
720
11.14. Фрактальные фотонные и магнонные кристаллы
0,25 0,5 1
Рис. 11.64. Фрагмент части фрактальной структуры (а), измеренный (кружки) и
рассчитанный (непрерывные линии) коэффициент пропускания (б) и
коэффициент отражения (в) поляризованных волн [859]
Фрактальная сигнатура определялась затравкой длиной а = 144,78 мм.
Этот исходный отрезок считался первым порядком фрактальной
721
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
структуры, размещенной параллельно оси у в плоскости ху.
Поколение порядка (к + 1) будет содержать 2к линий, средние точки
каждой из которых под прямым углом соединены с концами линий к-то
порядка. Число поколений или уровней N, начальная длина линии
я, их толщина и длина (все вместе) определяют требуемую
фрактальную структуру.
Фрактал основан на Н-генераторе без самопересечений с
коэффициентом геометрического масштабирования 2. При N -> «>
структура приобретает вид плитки с площадью 2а х 2а, плотно
заполненной фрактальной кривой. На рис. 11.64,я изображена часть
фрактала 15-го порядка, сгенерированного компьютером. Исследуемый
образец был выполнен технологией травления с помощью
теневой маски на диэлектрической пластине размером 30 см х 30 см х
1 мм. Ширина и толщина медных проводников, изображенных на
рис. 11.64,а светлыми линиями, равнялась 0,1 мм.
Измеренные нормальные коэффициенты пропускания Ти
отражения V от фрактальной пластины в диапазоне частот от 1 до
16 ГГц показаны на рис. 11.64,£и 11.64,* соответственно. Генератор
типа НР83711В, был связан через волновод с рупорной антенной,
облучающей фрактальную структуру. Другая такая же антенна
приемника была расположена на расстоянии 100 см от источника и
соединялась с ваттметром типа Agilent E4418B.
Фрактальная пластина размещалась на платформе,
находящейся в 15 см от антенны приемника, и могла вращаться вокруг оси z
на угол 8 (вектор Еперпендикулярен плоскости падения) и
наклоняться на угол ф (вектор £ параллелен плоскости падения).
Измерения коэффициента отражения были выполнены при условии, что
антенны генератора и приемника находятся с одной стороны и
разведены на малый угол, равный примерно 8°. Светлые кружки
на рис. 11.64, б и 11.64, в обозначают измеренные коэффициенты
пропускания и отражения соответственно, при поляризованном вдоль
оси};падающем нормально поле Е(для перпендикулярно падающего
поля ^результаты приведены ниже). Измерения коэффициента
пропускания (рис. 11.64,6) показали три полосы ослабления в
диапазоне 1—18 ГГц, в которых передаваемая волна сильно затухала, а
данные рис. 11.64,в показывают сильное отражение в тех же трех
диапазонах частот.
Между любыми участками затухания есть полосы пропускания,
в которых максимальное пропускание близко к 100%. Это очень
722
11.14. Фрактальные фотонные и магнонные кристаллы
интересно, поскольку металлические линии связаны и покрывают
все пластину. Рассматриваемый рабочий диапазон частот включает
длины электромагнитных волн, намного превышающих расстояния
между металлическими проводниками.
Теория. Расчеты, подтвердившие наблюдаемые эффекты, были
проведены с использованием алгоритма FDTD (Finite Difference Time
Domain) при учете точных граничных условий на границе раздела
металл-воздух. При расчетах рассматривалась бесконечная
фрактальная плоскость с диэлектрической проницаемостью подложки гг = 5,3.
Результаты численного моделирования воспроизводят все заметные
особенности экспериментов и приведены также на рис. 11.64.
В частности, оба спектра (вычисленный и измеренный)
логарифмически периодичны, что является неотъемлемым следствием
самоподобия фрактальной картины. Кроме проявления особой
математической красоты самоподобия, логарифмическая периодичность
означает, что резонансы (а, следовательно, и полосы затухания)
фрактальных структур охватывают чрезвычайно широкий диапазон
частот. Это уникальное свойство нельзя даже сопоставить с
периодичностью традиционных структур ФЗЗ или ЧИП, которые
обычно имеют единственный доминирующий отклик.
На рис. 11.65 приведены более подробные данные по
измеренным (кружки) и вычисленным (линии) коэффициентам
пропускания и отражения электромагнитной волны с горизонтальной (а, б)
и вертикальной {в, г) поляризациями для рассмотренной выше
фрактальной линейной структуры с 15-ю итерациями.
Анализ результатов моделирования показал, что
электромагнитная волна возбуждает токи в металлических проводниках планарного
фрактала, амплитуда которых достигает максимума в диапазоне
сильно отражающих частот. Фаза тока по отношению к фазе падающей
волны всякий раз испытывает прыжок на величину к, когда
рабочая частота переходит через точки, определяемые максимальными
коэффициентами отражения, указывая на резонансное поведение.
Численное моделирование на основе алгоритма FDTD показало, что
фрактал N-to порядка имеет ^резонансов. Каждый резонанс
определяется током возбуждения в проводящих линиях определенного
порядка, который (ток) течет по направлению к структурам более
высокого порядка. Например, для резонанса на частоте 13,1 ГГц
характерен поверхностный ток, текущий с обеих сторон к линиям
более высокого порядка. Фрактал, взаимодействующий с электро-
723
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Рис. 11.65. Подробные экспериментальные и теоретические данные
магнитной волной при нормальном падении, достаточно точно
моделируется [859] тонкой однородной пластиной (такой же толщины)
с эффективной диэлектрической проницаемостью:
%//(/)= 4 + lj^tf2> (11 129)
где/- частота в ГГц, индекс / определяет номер резонанса, е0, ft и
Р, — параметры, получаемые из вычисленного с помощью
алгоритма FDTD спектра.
Из уравнения (11.129) следует, что при изменении от одной
резонансной частоты^ к следующей f.+{, обязательно найдется точка,
в которой e^ = 1, а, следовательно, существуют определенные
полосы пропускания. Для данных рис. 11.64 в [859] получены
следующие значения параметров (при размерностях [ Р, ] - ГГц2, [ft] — ГГц):
^=11; fy= 10; р2=23; Р3=6°; Р4= 190; р5 = 500;/; = 0,274;
/2 = 0,623;/3 = 1,529;/0 = 4,19;/5 = 13,056.
Модуляция параметров падающей электромагнитной волны.
Всегда желательно, чтобы коэффициент отражения / прохождения
можно было регулировать с помощью внешней «ручки управления». Как
724
11.14. Фрактальные фотонные и магнонные кристаллы
мы видим, каждый сегмент линий во фрактале соединен друг с
другом. Это свойство дает возможность использовать внешний
источник для управления поверхностным током на фрактальной структуре
так, чтобы в результате интерференции с током, возбужденным
основной падающей волной, изменялась диаграмма излучения в зоне
Фраунгофера. При этом, вторичным источником может быть
внешний электрический ток, который подводится к центру линии
первого уровня с определенной фазой.
Данные рис. 11.66 показывают эффекты модуляции,
достигнутые подачей тока во фрактал [859]. Фрактальная пластина с
итерациями до 15-го порядка включительно помещалась перед антенной
приемника. В качестве последнего использовался спектральный
анализатор типа HP 8563. Фрактальная пластина имела точно такую
же структуру, как и на рис. 11.64, за исключением того, что самая
длинная металлическая линия (первый порядок итерации)
нарушалась в середине, чтобы через внешний кабель подать управляющий
высокочастотный сигнал. На другую сторону пластины нормально
падала поляризованная вдоль оси х электромагнитная волна
частотой 2,13 ГГц (см. левую вставку на рис. 11.66).
Рис. 11.66. Схема эксперимента, осциллограммы сигналов и рассчитанный
эффект модулирования коэффициента пропускания фрактальной пластины [859]
725
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ Л МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Осциллограмма (А) на рис. 11.66 показывает измеренный
коэффициент пропускания электромагнитной волны в случае работы
основного генератора, когда управляющий источник тока был
выключен. Осциллограммы (В) и (С) показывают тот же коэффициент
пропускания, когда управляющий источник тока был включен (на
той же частоте 2,13 ГГц). Фаза источника тока менялась, усиливая
(рис. 11.66, осциллограмма В) или ослабляя (рис. 11.66,
осциллограмма С) прямое прохождение электромагнитной волны.
Эффект модуляции был подтвержден в [859] с помощью
численного моделирования на основе алгоритма FDTD. Чтобы не
усложнять расчеты, моделирование проводилось с использованием
фрактала 7-го порядка. На правой вставке рис. 11.66 показан
вычисленный коэффициент пропускания для фрактальной пластины 7-го
порядка при модулирующем токе с разной фазой. В процессе
моделирования основная (падающая на пластину) волна имела частоту 6,8
ГГц, а модулирующий ток той же частоты подпитывал фрактальную
структуру от источника, помещенного в середину линии первого
порядка. Таким образом, фрактал теперь исполняет роль активного
элемента с мощностью излучения основного пучка. Модулирование
коэффициента пропускания фрактальной пластины определялось
разностью фаз (или временной задержкой принимаемого сигнала
относительно основного падающего пучка) между падающей волной
и подпитывающим током.
При наложении двух идентичных фрактальных пластин, когда
одна повернута на 90° относительно другой, можно синтезировать
инвариантную структуру относительно операции вращения.
Полученная фрактальная структура может моделировать эффекты полного
отражения, не зависящие от угла падения и поляризации
электромагнитной волны, что обычно является характерной особенностью
3D фотонных кристаллов.
На рис. 11.67 показан коэффициент пропускания такой двойной
фрактальной структуры, с учетом ее поворота и наклона, чтобы
изменять угол падения волны [859]. Здесь ромбики и квадратики
обозначают измеренный нормальный коэффициент прохождения через
двойную фрактальную среду волны с вектором Д поляризованным
вдоль осей Хи Y, соответственно, и показывают интервалы частот,
в которых этот коэффициент не зависит от вида поляризации.
Круги и треугольники — это коэффициент пропускания в плоскостях, по-
726
11.14. Фрактальные фотонные и магнонные кристаллы
Рис. 11.67. Коэффициент пропускания двух фрактальных пластин,
поворачиваемых друг относительно друга [859]
вернутых (угол 0) и наклоненных (угол <р ) на угол 30°
относительно нормали, соответственно.
Было обнаружено, что коэффициент пропускания
приблизительно одинаков для разных углов падения, следовательно,
спектральные зоны частот постоянны с учетом большого диапазона углов
падения. Кроме того, коэффициент пропускания не зависит от
поляризации электромагнитной волны, поскольку двойная структура
обладает вращательной инвариантностью.
Следует отметить, что размеры традиционного 3D фотонного
кристалла должны составлять, по крайней мере, несколько длин
волн, прежде чем он сможет полностью проявлять свои ФЗЗ
свойства; таким образом, для волны с частотой 1 ГГц толщина
кристалла должна быть порядка 1 метра.
С другой стороны, плоские фрактальные структуры таковы, что
их относительная полоса пропускания Л///0, определяемая
законом подобия (А///0 выражается через отношение полосы
запрещенной зоны к середине запрещенной зоны, в частности, А///0 ~ 5%
для одной фрактальной пластины), может быть значительно
увеличена с помощью наложения друг на друга одинаковых фрактальных
пластин. Увеличение толщины фрактальных пластин приводит к
возрастанию крутизны границ полос пропускания.
Эффекты, проявляющиеся при сложении до пяти фрактальных
пластин, хорошо видны на рис. 11.68 для трех резонансных частот
727
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
Рис. 11.68. Вычисленное отношение
полосы запрещенной зоны к середине
запрещенной зоны, как функция числа
наложенных друг на друга слоев п
для частоты 1,6 ГГц (квадраты),
4,4 ГГц (кружки)
и 13 ГГц (треугольники) [859]
~"~1 2 3 4 5
П
1,6; 4,4 и 13 ГГц. Диэлектрические фрактальные пластины
толщиной 1 мм разделялись в экспериментах воздушными зазорами в 1 мм.
Толщина сборки до семи фрактальных пластин (с соответствующим
их поворотом на 90°), все еще пренебрежимо мала по толщине
относительно рабочих длин волн. Полосы ослабления также могут быть
увеличены с помощью более широких металлических проводников
на фрактальных пластинах.
Эмпирическая формула для резонансных частот фрактальной
структуры N-то порядка имеет вид [859]:
N+\-i
h = >fc S <*J)W+J-i). О1'130)
В выражении (11.130) множество {А,,.} определено для линейных
поляризаций вида Y(X), если / нечетное (четное) число; {а(1) =
= а(2) = 2,1; а(3)= а(4) = 3,5; а(2/+1)= а(2/+2) = 2а(2/-1) =
= 2 а (2/) при / > 2} — множество эмпирических параметров; b(i) -
максимальная длина линии /-й итерации, гг = (гг +1)/2. Уравнение
(11.130) можно экстраполировать на низкие и высокие частоты, когда
прямое моделирование слишком дорого. Из анализа (11.130)
следует Xf /Xi+l -> 2 при N -»сю (помня при этом, что b(i) = 2b(i + 2)), т. е.
получаем точное самоподобие в пределе больших значений N.
Сверхволновые отражатели. Прямым следствие уравнения
(11.130) является то, что резонансные длины волн могут быть
намного больше, чем размеры образца. Это происходит потому, что
низкочастотный резонанс определяется самой длинной металлической
линией во фрактале, а такая линия, естественно, намного длиннее,
чем линейные размеры фрактала. Это придает фракталу его
«сверхволновые» свойства, т. е. фрактальная пластина может эффективно
728
11.14. Фрактальные фотонные и магнонные кристаллы
отражать электромагнитные волны с длинами, намного большими,
чем ее поперечные размеры.
Например, в [859] экспериментально и численно показано, что
пластина размерами 28 мм х 29 мм, содержащая фрактал 6-го
порядка, почти полностью отражает электромагнитные волны частотой
3,85 ГГц (совпадающие с одной из резонансных линий
фрактального образца), в то время, как медной пластинке такого же размера не
удастся преградить путь этой волне, поскольку она (пластина)
гораздо меньше длины волны, приблизительно равной ^=78 мм.
На рис. 11.69 слева приведена схема эксперимента, а справа -
измеренная картина излучения. Приемная антенна (не показана)
размещалась на расстоянии 10 см от фрактальных пластин. В
правой части рис. 11.69 приведены картины вторичного
электромагнитного поля для фрактальной и медной пластины. Фрактальная или
медная пластины размером 28 мм х 29 мм помещались вблизи
несимметричного вибратора на расстоянии 24 мм от него.
Сплошными линиями представлены результаты расчета. Видно, что
«сверхволновая» фрактальная структура задерживает направленное
излучение, в то время, как металлическая пластина не выполняет такой
операции.
Такие «сверхволновые» свойства означают, что фрактальная
пластина может действовать как компактный отражатель. Заметим,
Медная пластинка
Рис. 11.69. Схема эксперимента
729
Глава 11. ФРАКТАЛЬНЫЕ АНТЕННЫ И МЕТОДЫ ИХ ПРОЕКТИРОВАНИЯ
что единственный резонанс низкой частоты может быть также
достигнут в периодически резонирующей системе, такой, как «высоко
импедансная поверхность» [437], в то время, как фрактал имеет
многочисленные низкочастотные резонансы.
Таким образом, фрактальные картины всегда имеют самодобный
ряд резонансов, приводящих к логарифмической периодичности
рабочих зон. Связанная топологическая фрактальная структура
делает возможным модулирование коэффициента пропускания
электромагнитных волн. Самая нижняя частота ослабления соответствует
длинам волн, которые значительно превышают внешние размеры
фрактальной пластины, делая такие фрактальные структуры
сверхволновыми отражателями.
Выводы. В связи с этим, работы в области создания новой
элементной базы на основе фрактальных фотонных и магнонных
кристаллов и их модификаций, являются чрезвычайно важными,
поскольку именно такая элементная база позволит создать новейшие
устройства обработки и передачи информации. Проведенный анализ
показывает, что физические фракталы допускают ряд
самоподобных резонансов, которые приводят к сложным запрещенным зонам
и серии полос пропускания электромагнитных волн в чрезвычайно
широком частотном диапазоне. Многополосный режим
функционирования, перекрытие обширного спектрального диапазона и
полосы пропускания, соответствующие длинам волн, которые
значительно больше размеров образцов, делают фрактальные пластины
чрезвычайно интересной и полезной частотно избирательной средой. В
частности [713, 714], перспективы создания оптического компьютера
с использованием фотонно-кристаллической элементной базы
также весьма повышаются.
Глава 12
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ НА
ОСНОВЕ ТЕКСТУРНЫХ И ФРАКТАЛЬНЫХ
СИГНАТУР С ИСПОЛЬЗОВАНИЕМ
ПРИНЦИПОВ НЕЛИНЕЙНОЙ ДИНАМИКИ:
ЭТАПЫ СТАНОВЛЕНИЯ, РЕЗУЛЬТАТЫ
12.1. Некоторые актуальные задачи радиолокации и
статистической радиофизики: проблема
малоконтрастных целей
Радиофизика исторически сформировалась как область физики
электромагнитного излучения, имеющая дело с колебаниями и
волнами в очень широком диапазоне частот. На базе радиофизики
развивались и радиотехнические науки, в частности радиолокация. В
любых технических приложениях радиофизики радиосигнал
является носителем информации. Прием сигнала в реальных условиях
становится принципиально статистической задачей. Формирование
статистической теории обнаружения сигналов связано с
фундаментальными работами академика В. А. Котельникова по теории
потенциальной помехоустойчивости, т.е.теоретически предельно
достижимой помехоустойчивостью [751, 752].
К современным радиолокационным системам предъявляются
жесткие требования по обеспечению таких показателей, как
способность функционирования в условиях сильных помех, высокое
пространственное разрешение и т. д. [753-755]. В последние годы
ведущие страны мира ведут интенсивные работы по уменьшению
радиолокационной заметности объектов с помощью перспективных
стелс-технологий [756] (рис. 12.1). По данным зарубежной
литературы, уменьшение эффективной площади рассеяния (ЭПР) с 10-15
до 0,3 м2 значительно снижает боевые потери (рис. 12.2).
Для успешного решения таких радиолокационных задач
требуется поиск и разработка нетрадиционных алгоритмов и новых
адаптивных прикладных решений обработки информации об интересу-
731
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Торнадо РЗ
F-16A»
F-15C
Мираж F-1С, Е
модернизация
,F-117A^F.22AyF.2Q00^
1970 1975 1980 1985 1990 1995 2000
Год принятия на вооружение
2005
Рис. 12.1. Тенденции изменения радиолокационной заметности самолетов [756]
Относительные потери
0,10,5 1
Рис. 12.2. Потери самолетов при преодолении ПВО в зависимости
от их ЭПР [756]
ющем объекте на фоне мешающих сигналов. Можно выделить
несколько перспективных направлений обработки сигналов, такие как
цифровая адаптивная пространственно-временная обработка
радиолокационных сигналов, методы с использованием текстур и
фрактальная обработка, основанная на теории детерминированного
хаоса и теории дробной меры.
Адаптивная пространственно-временная обработка, имеющая
в своей основе структуру, которая изменяется под воздействием
окружающей радиообстановки, широко применяется в фазированных
антенных решетках, цифровых следящих фильтрах, компенсаторах
помех, а также при многопозиционной радиолокации.
732
12.1. Некоторые актуальные задачи радиолокации и статистической радиофизики...
Классические методы фильтрации позволяют вести
оптимальную обработку радиолокационных сигналов от объектов лишь при
гауссовых помехах. В реальных условиях помехи почти всегда
негауссовы и имеют значительную интенсивность в различных
спектральных диапазонах. В подобных ситуациях использование
классических алгоритмов фильтрации не всегда возможно по причине
больших интервалов времени накопления сигнала при малых отношениях
сигнал-фон q\ и резком усложнении аппаратуры.
Указанные причины требуют принципиально новых подходов к
решению традиционных задач радиолокации. Назрела насущная
необходимость рассматривать современные радиолокационные
системы в совокупности с каналом зондирования и множеством целей
с синергетическои точки зрения эволюции сложных неравновесных
систем, открытых для потоков энергии, энтропии и информации.
Все это и определило развитие новых информационных технологий
в радиолокации и радиофизике с использованием текстурных
(середина 1980-х годов [99, 100, 184, 197-199, 223-231, 280, 357, 458,
459, 462, 484, 521, 527, 535-537, 912-914,1011]) и фрактальных
(середина 1990-х годов [77, 184-186, 236, 390, 479, 528-534, 538, 541-545,
550, 551, 561, 915—1013]) мер на основе принципов нелинейной динамики.
По результатам этих исследований автором в монографии [1011]
были введены понятия текстурных и фрактальных сигнатур, а
данное научное направление было кратко обозначено как фрактальная
радиолокация и фрактальная радиофизика. По сути дела,
развивается новое научное направление в радиофизике - применение теории
динамических систем и фрактальной топологии в задачах
повышения информативности радиосистем, функционирующих в
диапазонах оптических и миллиметровых волн.
В основу новых прорывных (критических) информационных
технологий обнаружения и распознавания (в общем случае -
фильтрации) протяженных мало контрастных целей в сложной помеховой
обстановке были заложены нетрадиционные методы на основе
теории текстур, фракталов и детерминированного хаоса. При этом
необходимо исследовать потенциальные возможности указанных
методов для широкого класса изображений фона и целей при
отношении сигнал-фон q\ < 1. Ниже будут конспективно рассмотрены
этапы становления и некоторые физические результаты прорывных
(критических) информационных технологий, предложенных и раз-
733
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
виваемых в ИРЭ РАН. В [184] было особо отмечено, что «В качестве
наиболее существенных и перспективных путей дальнейшего
развития данного направления следует указать детализацию и
углубление наших знаний о текстуре изображений земных покровов, а
также моделирование пространственно-временных картин
геосистем с помощью теории фракталов и их связь с характеристиками
поля рассеяния радиоволн» (С. 24) и там же «...необходимо
использование дополнительного ряда других классов признаков, в том
числе и основанных на тонкой структуре отраженных модулированных
миллиметровых волн... В этом смысле большое будущее
принадлежит новому направлению — фрактальной геометрии природы, т.е.
фрактальной размерности пространственных структур геосистем»
(С. 368-369).
В 1997 г. автором были сделаны первые доклады по вопросу
применения теории фракталов к перспективным задачам радиофизики
и радиолокации [77,186]. Следует отметить, что в работах ИРЭ РАН,
в отличие от зарубежных, с самого начала была заложена идея
фрактальной обработки малоконтрастных изображений, в том числе и
фрактальных целей на фрактальном фоне. В последующем
изложении всегда подразумеваются радиофизические исследования в
оптическом и миллиметровом диапазонах длин волн.
При написании данной главы автор существенно использовал
свои и совместные с коллегами научные публикации, в которых
отражено его видение рассматриваемых проблем.
12.2. Текстурные меры и сигнатуры
Вокруг цели всегда присутствуют участки фоновых отражений,
объединенные общим понятием текстуры. Это предоставляет
возможность предложить новые подходы к обнаружению
малоконтрастных протяженных целей на фоне земных покровов в полученных
РЛИ. В отличие от тона и цвета, которые относятся к отдельным
фрагментам изображения, текстура связана более чем с одним
фрагментом (см. разд. 9.1). Общий метод описания текстур изображения
земных покровов предполагает ее связи с пространственными
распределениями и взаимозависимостью значений яркости локальной
области изображения или блока. Поэтому текстурные признаки
основаны на статистических характеристиках уровней интенсивности
734
12.2. Текстурные меры и сигнатуры
элементов изображения и относятся к вероятностным признакам,
случайные значения которых распределены по всем классам
природных объектов. Решение о принадлежности текстуры к тому или
иному классу может приниматься только на основании конкретных
значений признаков данной текстуры.
В таком случае принято говорить о сигнатуре текстуры. С
нашей точки зрения, сигнатура — это распределение генеральной
совокупности измерений для текстуры в сценах такого же типа, как
данная. Как хорошо известно, радиолокационные сигнатуры включают
в себя временные, спектральные и поляризационные особенности
отраженного сигнала. Применение оптических и радиолокационных
изображений земной поверхности позволяет дополнить
традиционные признаки новыми, весьма существенными, позволяющими
уменьшить перекрытие сигнатур [184, 229, 230, 459, 1011].
Пространственная организация текстуры может быть
структурной, функциональной и вероятностной [452, 463, 842]. Признаки
текстуры описывают характерные свойства, общие для
рассматриваемого класса текстур. При статистическом анализе текстур
используют статистики первого или второго порядка. Во втором случае
непосредственно текстурные признаки извлекаются с помощью
матриц распределения вероятности пространственной зависимости
градации яркости Р, называемой такие матрицей распределения
градиентов. Данный метод был предложен в [463]. Экспериментально
показано [452, 463], что признаки, основанные на параметрах
корреляционных функций, не так хорошо оценивают текстуру, как
признаки, определенные по матрице градиентов Р.
Кратко рассмотрим классический подход к получению
текстурных признаков. Пусть анализируемое изображение является
прямоугольным и имеет Nx элементов разрешения по горизонтали и N
элементов по вертикали. При этом G— {1,2,...,7V} - множество N
квантованных значений яркости. Тогда изображение /описывается
функцией значений яркости из множества G, т. е. I: L xZ, ->G,
где Lx= { 1, 2,..., Nx}nLy={l, 2,..., Ny} - горизонтальные и
вертикальные пространственные области соответственно. Набор Nxn N
есть набор элементов разрешения в растровом изображении.
Матрица распределения градиентов содержит относительные частоты;?.,
наличия на изображении соседних элементов, расположенных на
расстоянии d друг от друга, с яркостями i,je G. Обычно различают
735
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
горизонтальные (а = 0°), вертикальные (а = 90°) и поперечно -
диагональные (а = 45° и а =135°) пары элементов. Соотношения,
определяющие исходный набор текстурных признаков, представлены
в табл. 12.1, где введены следующие обозначения:
p(i,j) = P(ij)/M; X и £ SI и £ ; Pxti) = tp(iJ);
i j /=1 У=1 j=\
N N N
Руи) = Лр(иУ, Л.(л) = ХХ^"'./) ПРИ i+J=n и n = 2,3,...,2N;
hi i=lj=l
N N
^_(л) = ХХ^'Л ПРИ \i-J\ = n и n = 0,\,...,N-l'9 (12.1)
i=ij=\
Ж*) = -X^(0iog^(0; ЩУ) = -f,pyU)\ogPyU)\
/=i j=\
Q=tp№)pUM/[px(»PyU)]',
/=i
т. тл> и a.av — средние значения и среднеквадратичные отклоне-
х у х у
ния для px(i) и р (j), соответственно.
Большой объем вычислений при нахождении текстурных
признаков затрудняет определение их полного ансамбля (см. табл. 12.1).
Впервые расчет всего ансамбля текстурных признаков и детальный
синхронный анализ признаков fx—fn для реальных (оптических и
радиолокационных текстур в диапазоне миллиметровых волн), а
также синтезированных текстур проведен в 1985 г. в ИРЭ РАН
автором совместно с Воронежским государственным университетом и
представлен полностью в [184]. При этом была поставлена и
решена задача расчета текстурных признаков с учетом дрейфа сигнатур
при изменении времени года. Частично статистические
характеристики текстур-прототипов и их внешний вид были приведены в [230,
459], и полностью, как отмечалось выше, с базой данных из 84
значений для каждого текстурного признака — в [184]. Отметим также, что
в [463] не были рассмотрены вопросы информативности всех 28
текстурных признаков и нет оценки влияния размера окон на точность
736
12.2. Текстурные меры и сигнатуры
Таблица 12.1
Пространственные текстурные признаки ft [463]
1 Наименования
Второй угловой
момент
Контраст
Коэффициент
корреляции
Дисперсия
Момент обратной
разности
Суммарное
среднее
Суммарная
дисперсия
Суммарная
энтропия
Энтропия
Дифференциальная
дисперсия
Дифференциальная
энтропия
Информационная
мера корреляции
Информационная
мера
Максимальный
коэффициент
корреляции
! Дисперсии/!-/14
Формулы
ЛМ
п=0
XXp(/.j)
1 / - j 1 = /2
i J
/4=XXa-"02/>(U)
i j
f5=ll[l + (i-J)2]lp(U)
i J
IN
/1=2
IN
/7=Х(«-/б)2р+(»)
/1=2
IN
fs=^P+W°ZP+(n)
/1=2
/9=-X X pfo лlos pO"» л
1 j 1
/10=2:
/1=0
n-Y*p-(m>>
m=0
2 I
PM,\i-J\=m
/ii=-X^-^10^-^
/71=0
/12 = |/9 + II^7l[log^(0^(7)] /тах{Я(х),Я(у)}
/n =
l-expj-2
-ZZ^w^o'jipg^co^y) -/9
и
1/2
/14 = (второе наибольшее собственное значение Q)l/2
J15 ~h% 1
24 Фракталы
737
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
определения текстурных признаков. Выбор размеров окна обусловлен
тем, что текстура определяется окрестностью точки изображения.
В работе [184] проведено исследование влияния размера окна на
правильную интерпретацию численных значений текстурных
признаков. Показано, что в окнах размером 3x3 или 5x5 пс
статистические текстурные меры больше действуют как обнаружители
перепадов яркости, а не как измерители текстуры, хотя при этом
сокращается время вычислений. Слишком большие размеры окон могут
исказить результаты из-за влияния краев структур и границ
изображений. Однако большое окно позволяет достигнуть высокой
статистической достоверности. Как оказалось, окна 20x20 пс наиболее
эффективны ддя текстурной обработки аэрокосмических
фотографий сельскохозяйственных угодий, пастбищ, лесных массивов и
других сходных объектов. В [184] показано, что при изменении
размеров окна от 80x80 до 20x20 пс численные значения текстурных
признаков изменялись на 5... 10%. Дальнейшее изменение размера
окон приводило к значительному искажению текстурных признаков.
В качестве исходных текстур использовались оптические (в виде
аэрофотоснимков - АФС) и радиолокационные изображения (РЛИ)
на длине волны 8,6 мм и линейной поляризации излучения.
Эксперименты по формированию изображений проводили совместно с
НПО «Алмаз» в летнее и зимнее время года с борта вертолета МИ-8
при средней скорости полета 60 км/ч и высоте от нескольких
десятков до сотен метров (см. подробнее в [184, 231, 521]). Анализ
полученных данных позволил отметить очень важную особенность
[184]: одномерные области существования текстурных признаков
РЛИ в диапазоне миллиметровых волн (множество R) почти
полностью вкладываются в соответствующие области признаков АФС
(множество A): Re А. Таким образом, области признаков РЛИ как
бы сжимаются по сравнению с областями признаков АФС. Это
происходит из-за сглаживания в РЛИ тонкой структуры исследуемых
покровов, характерной для АФС. Следовательно, со значительной
степенью достоверности множество R можно прогнозировать по
множеству А. Экспериментальное исследование тонкой структуры
отраженных земными покровами радиолокационных сигналов в
диапазоне миллиметровых радиоволн было проведено в [184, 227].
При возможности осуществления декомпозиции текстуры
выявляются два основных фактора: первый соотносит текстуру с
непроизводными элементами, из которых составлено изображение в це-
738
12.2. Текстурные меры и сигнатуры
лом, а второй служит для описания пространственной зависимости
между ними. Тоновые непроизводные элементы представляют собой
области изображения, характеризуемые определенными
значениями яркости, пропорциональной интенсивности отраженного
сигнала, зависящей в свою очередь от значений ЭПР а+ земной
поверхности. Так как понятие удельной ЭПР значимо только для
пространственно однородного объекта, то текстура изображения реального
земного покрова определяется пространственными изменениями а+.
Все указанное выше позволяет установить взаимосвязь между
удельной ЭПР подстилающего покрова и его текстурой. Когда не-
. большой участок изображения характеризуется малым изменением
типовых непроизводных элементов, то преобладающим свойством
этого участка является значение удельной ЭПР. При заметном
изменении яркости этих элементов преобладающий признак заложен
в текстуре. Иначе говоря, при уменьшении числа различимых
типовых непроизводных элементов в изображении роль энергетических
признаков (в частности, а*) возрастает. Фактически для одного
элемента разрешения единственными признаками являются
энергетические. Если число различимых типовых непроизводных элементов
растет, то начинают доминировать текстурные признаки.
Ранее автором были впервые предложены и реализованы с
коллегами следующие нетрадиционные эффективные методы обнаружения
сигналов при малых q\: дисперсионный на основе / статистик [184,
230, 459, 535, 536, 913], обнаружения при помощи линейно
моделированных эталонов [184, 230, 537] и прямого использованием
ансамбля текстурных признаков [184, 230,462]. Наиболее полно
потенциальные возможности текстурных методов обработки оптических и
радиолокационных изображений были изложены в [184], где
впервые была доказана перспективность использования текстурных
признаков при обнаружении слабых радиолокационных сигналов, когда
отношение сигнал-фон q% < 1. В результате теоретических и
экспериментальных исследований было также показано, что
использование текстурных признаков ослабляет действие пассивных помех от
земной поверхности и улучшает выделение и обнаружение слабых
полезных сигналов. Кроме того, важным достоинством текстурных
методов обработки, является возможность нейтрализации спеклов на
когерентных изображениях земной поверхности, полученных с
помощью РСА.
739
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
12.3. Фрактальные меры и сигнатуры
Методы фрактального анализа находят все большее применение
в различных сферах науки. Основные понятия теории фракталов,
носящей междисциплинарный характер, пока еще находятся в
процессе становления, но поле их приложений непрерывно
расширяется. Теория фракталов рассматривает вместо целочисленных мер
дробные и базируется на новых количественных показателях в виде
дробных размерностей Dm соответствующих фрактальных сигнатур.
Фрактальные дробные размерности D характеризуют не только
топологию объектов, но и отражают процессы эволюции
динамических систем и связаны с их свойствами. Теория фракталов и
нелинейность составляют геометрию хаоса. По-видимому, фракталы - это
не только язык хаоса, но и язык природы. По своему содержанию
контуры всех природных объектов суть динамические процессы,
внезапно застывшие в физических формах и объединяющие в себе
устойчивость и хаос. Фракталы относятся к множествам с крайне
нерегулярной разветвленной или изрезанной структурой. Можно
отметить, что одним из важнейших вопросов фрактальной геометрии
является связь фракталов и текстур.
Понятие фрактала, введенное в научный обиход Б. Мандельб-
ротом [1-4], пока не имеет строгого определения. Разработанная
автором на основе результатов [1011] классификация фракталов
опубликована в [971] и приведена на рис. 12.3. Здесь кратко описаны их
свойства при условии, что DQ — топологическая размерность
пространства, в котором рассматривается фрактал с дробной
размерностью D. Существующие в реальном мире фракталы называются
физическими и имеют конечный интервал масштабов. Исходя из
структуры данных рис. 12.3 и базируясь на [1011], можно дать следующее
формализованное математическое определение фрактала: «Фрактал
— это функциональное отображение или множество, получаемое
бесконечным рекурсивным процессом и имеющее следующие свойства:
1) самоподобие или масштабную инвариантность (бесконечный
скейлинг), т.е. фракталы на малых масштабах выглядят в среднем так
же, как и на больших; 2) их размерность (называемую размерностью
Хаусдорфа), дробную и строго больше топологической
размерности; 3) недифференцируемость и оперирование дробными
производными и интегралами».
740
12 J. Фрактальные меры и сигнатуры
ФРАКТАЛЫ
Математические
Число итераций
л-»°°
Дробная размерность
Хаусдорфа D> D0
Бесконечное число
масштабов, самоподобие
(скейлинг)
Дробные производные и
интегралы
Физические
Число итераций п
конечное
Дробная размерность
Хаусдорфа D>D0
Конечный интервал
масштабов,
самоподобие (скейлинг)
Кусочно-дифференцируемая функция
Рис. 12.3. Классификация и морфология фрактальных множеств (сигнатур)
Физическое определение фрактала следующее: «Фракталы- это
геометрические о&ьекты (линии, поверхности, тела), имеющие
сильно изрезанную структуру и обладающие свойством самоподобия в
ограниченном масштабе». Подобно всем геометрическим понятиям,
фрактал - это прежде всего абстракция, теоретическая модель,
результат предельного перехода, недостижимый в действительности.
Как отмечено в [838], «любой портрет фрактала - не более чем
условное, выполненное с конечной разрешающей способностью и
потому огрубленное изображение основной тенденции - тренда,
своего рода карикатура, обладающая портретным сходством с
оригиналом, но отличающееся от портрета, выполненного в реалистической
манере».
Поясним понятие «фрактал» применительно к радиофизическим
задачам. В общем случае РЛИ можно представить как множество
элементов Xk, значения которых пропорциональны ЭПР к-то
элемента разрешения РЛС. На рис.12.4,я показано РЛИ местности,
полученное на длине волны 8,6 мм с вертолета [184, 231]. На рис.12.4,5
показано РЛИ того же участка местности, полученное РЛС на
длине волны примерно 30 см. Оба изображения являются двумерными
с уровнем серого, пропорциональным ЭПР. Предположим, что для
741
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
а)
б)
в)
LaS
г)
0=2.440393
ИЩИ
1
Ln5
д)
Рис. 12.4. Примеры, объясняющие сущность фрактальной обработки (а-г) и
фрактальный пространственный кепстр РЛИ (д) [1005]
каждого РЛИ построена поверхность (рис. 12А,в) с высотами h,
пропорциональными уровням серого. Пусть требуется измерить
площадь получившейся поверхности. На РЛИ, соответствующем
длине волны 30 см, площадь получится меньше, чем для РЛИ на
длине волны 8,6 мм из-за того, что с уменьшением ее длины
различается больше деталей местности. Зондирующая электромагнитная
волна выступает в этом случае как некоторая «измерительная»
линейка. При этом начинает сказываться все более тонкая структура
пространственно-временных сигналов или волновых полей [184,227,
229].
Если в нашем распоряжении имеется РЛИ, полученное в еще
более коротковолновом диапазоне, то его площадь будет больше, и
т. д. Уменьшая длину волны, будем получать возрастающие
значения площадей. Возникает вопрос: а какова в действительности
площадь поверхности, с которой получены РЛИ? Если поверхность
покрыта простыми объектами, например прямоугольным
возвышением (рис 12.4,г) и размеры этого возвышения гораздо больше
длины волны, то площади РЛИ объектов на коротких и длинных
волнах будут примерно одинаковыми. Тогда на поставленный вопрос
742
12.4. Избранные результаты исследований по фрактальной фильтрации ...
можно было бы ответить, подсчитав число элементов разрешения,
покрывающих объект. В этом случае площадь поверхности была бы
равна:
S = S(X) = N(X)b(k), (12.2)
где Ь(Х) -площадь элемента разрешения РЛС; N(X) - число
элементов разрешения, необходимых для покрытия объекта; X — длина
волны РЛС. Как уже было сказано для простого объекта (рис. 12.4,г)
S(X) = const.
Для РЛИ, приведенных на ржА2А,а,б, можно построить
зависимость S(X) = f(X), а, предположив, что Ь(Х) = К(Х), где К-
известная функция, зависимость S(k) = f(S). Оказывается, что
измеренная площадь S поверхности прекрасно описывается формулой
S(X) = kX-D. (12.3)
Тогда log(S(k)) = logk-DlogА, (где knD- константы), и мы можем
вычислить параметр D. Зависимость log 5(A) =/(log 5),
определяющая собой фрактальную сигнатуру РЛИ (см. рис.12.4,я,б) показана
на рис. 12.4,5. Она характеризует пространственный фрактальный
кепстр изображения (данное понятие введено автором в 1997 г. [77,
186]). Для РЛИ объектов, имеющих простой геометрический вид
(прямоугольники, круги, гладкие кривые), фрактальная размерность
совпадает с топологической, т. е. равна значению 2 для двумерных
РЛИ, и определяется угловым коэффициентом прямых (12.2) в
логарифмических координатах. Однако значение D для большинства
изображений реальных покровов и метеорологических образований
(см. гл. 3 и 5) оказывается большим, чем топологическая размерность
2, что подчеркивает их сложность и хаотичность.
12.4. Избранные результаты исследований
по фрактальной фильтрации малоконтрастных объектов
В настоящее время в ИРЭ РАН ведутся работы по созданию и
развитию информационных технологий для решения современных
задач радиолокации и радиофизики. На рис. 12.5 схематически
показаны основные направления этих фрактальных исследований и
приведены краткие сведения о начале соответствующих работ и
первых публикациях. Условно здесь можно проследить два этапа. На
743
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
ФРАКТАЛЫ В РАДИОЛОКАЦИИ И РАДИОФИЗИКЕ
Фрактальные и текстурные
сигнатуры изображений
Рассеяние волн фрактальной
поверхностью
Обнаружение малоконтрастных
целей (текстуры + фракталы)
Распознавание контуров целей
(текстуры + фракталы)
Синтез изображений местности
Кластеризация изображений
Динамические модели рассеяния
радиоволн на основе теории
детерминированного хаоса
Фрактальное кодирование
радиолокационной информации
Фрактальные селективные
и радиоволновые системы
Фрактальные антенны
и их конструирование
ИРЭ РАН,
1987 г.
ИРЭ РАН,
1997 г.
ИРЭ РАН,
1987 г.; 1997 г.
ИРЭ РАН,
19?7гт;1997г.
ИРЭ РАН,
1996 г.
ИРЭ РАН,
1997 г.
ИРЭ РАН,
1997 г.
ИРЭ РАН,
ЦКБ «Алмаз»,
1988 г.
ИРЭ РАН,
МИРЭА,
2001 г.
Рис. 12.5. Эскиз развития новых информационных технологий на основе текстур,
фракталов и детерминированного хаоса
744
12.4. Избранные результаты исследований по фрактальной фильтрации ...
первом этапе акцент был сделан на экспериментальной проверке
фрактальности различных природных и искусственных образований,
что позволило применить к ним понятия дробной размерности и
масштабной инвариантности и начать разработки методов фрактальной
фильтрации объектов в различных помехах. Второй этап целиком
посвящен усовершенствованию созданных алгоритмов фрактальной
цифровой обработки сигналов и изображений, фрактальным
методам обнаружения, распознавания, повышения контрастности, т. е.
фрактальной обобщенной фильтрации.
Как подробно показано в разд. 9.9 и 9.10, поиск
нетрадиционных путей для решения задач фильтрации малоконтрастных
объектов привел к идее использования фрактальных подходов. Если в
текстурных методах [99, 100, 184, 197-199, 223-231, 280, 357, 458, 459,
462, 484, 521, 527, 535-537, 912-914, 1011] формально
использовалось условие превышения обобщенным функционалом некоторого
заданного порога (в том числе и адаптивного), то фрактальные
методы, как отмечено выше, основаны на принципиально ином
подходе. Они базируются на дробной фрактальной размерности Dn
соответствующих фрактальных сигнатурах физических процессов.
Установление определенной инвариантности фрактальной размерности
D сцен в зависимости от их яркости, как отмечено выше, и явилось
основной предпосылкой для перехода к фрактальной цифровой
обработке малоконтрастных изображений.
Один из возможных подходов к формализации данной задачи
состоит в следующем. Любой детерминированный объект в ряде
физически охватываемых масштабов наблюдения остается
неизменным, и оценка его характерных размеров или площади всегда
стремится к определенному пределу, а в идеальном случае является
величиной постоянной. В то же время при изменении масштаба
изображения местности площадь фрактальных образований также
изменяется. Следовательно, появление на любом изображении
некоторого искусственного объекта (или другого фрактала) изменит
величину фрактальной размерности D сложного изображения в
целом. Повторим, что обнаружение объектов может быть основано на
таких признаках, как полная фрактальная сигнатура, ее часть или
наклон. Основные результаты, полученные по данному
фундаментальному направлению на первом этапе исследований,
представлены в известных работах [77, 184 - 186, 236, 390, 479, 528-534, 538,
541-545, 550, 551, 561, 915-1013] и кратко суммированы ниже.
745
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Автором впервые показано, что такие понятия, как «фрактал» и
«фрактальный анализ» вместе со своим нетрадиционным
математическим аппаратом дает возможность значительно продвинуться в
изучении многих физических явлений, включая прикладные
задачи радиолокации. Объективное наличие у фракталов дробной
размерности и масштабной инвариантности — скейлинга - позволяет
рассмотреть вопросы радиолокационного обнаружения и
распознавания целей с новой точки зрения, особенно при малых
отношениях сигнал-фон q\ . Отметим, что во всех наших «фрактальных»
работах под величиной q\ понимаем отношение средней яркости
сложного изображения (фон + цель) к среднеквадратичному значению
гауссова шума.
Разработаны алгоритмы построения детерминированных и
стохастических фракталов. Показана эффективность моделирования для
прикладных задач фракталов с помощью Z-функций, итерационных
процедур и фрактального морфинга. Описание программного
обеспечения алгоритмов фрактальной обработки одномерных и
многомерных сигналов (полей) дается в работах [542, 543, 916, 987-990,
1005]. Предложена и исследована модель анализируемых
радиосигналов и изображений с учетом аддитивных и мультипликативных
фоновых помех при обработке сложных (наличие объектов и целей)
двумерных сцен. Применение стандартной фрактальной обработки
обычно требует большого числа изображений местности в
различных масштабах и значительных массивов данных. Созданные
алгоритмы используют операции конволюции, позволяют обходиться
только единичными изображениями и работают в режиме
реального времени. Следует отметить, что разработанный пакет программ с
самого начала был ориентирован на общие задачи распознавания
фрактала на фрактале по значениям дробной размерности D и
соответствующего ансамбля фрактальных сигнатур [1005].
Исследованы фрактальные характеристики как
синтезированных, так и реальных изображений местности. Подтверждена
эффективность разработанных методов фрактальной обработки
синтезированных, оптических и радиолокационных изображений. Впервые
показано, что плотность изображения не фрактальной цели влияет
на изменение размерности слабее, чем отношение площадей,
занимаемых объектами и фрактальным изображением. Данное свойство
особенно ценно в задачах обнаружения малоконтрастных объектов
746
12.4. Избранные результаты исследований по фрактальной фильтрации ...
и выявления «подозрительных» областей. Зависимости фрактальной
размерности синтезированных и реальных радиолокационных
изображений от относительной площади объектов имеют схожий
характер.
Оказалось, что разработанные алгоритмы, использующие
фрактальные признаки, стабильно функционируют при низких значениях
сигнал-фон. Результаты начальных компьютерных экспериментов
показывают, что фрактальные методы эффективны для фильтрации
модельных объектов на изображениях в оптическом и
радиодиапазоне при отрицательном {в децибелах) отношении сигнал-фон.
Гауссовы флуктуации площадей прямоугольных объектов со
среднеквадратичным отклонением порядка 30% практически не влияют на
качество их обнаружения.
Анализ влияния количества объектов с различной топологией на
характеристики всего изображения в целом проведен с помощью двух
методов: классического (скользящее окно) и
локально-дисперсионного [1005]. Была доказана инвариантность фрактальной
размерности сложных изображений относительно ориентации объектов.
Выявлена функциональная зависимость величины фрактальной
размерности сложного изображения от количества искусственных объектов.
Проведенные компьютерные эксперименты показали связь
наиболее эффективного размера окна с интервалом корреляции
исходного изображения. Острые кромки объектов всегда увеличивают
фрактальную размерность, а сглаживание их форм способствует ее
уменьшению. С увеличение общего периметра объектов фрактальная
размерность растет пропорционально их количеству. По
периодичности амплитуд пространственного фрактального кепстра можно
оценить размеры объектов. Кроме того, построенные в ходе
компьютерного моделирования эмпирические распределения
вероятностей фрактальной размерности реализаций «изображение + фон» и
«изображение» часто имеют одномодовый характер с резко
различающимися средними значениями.
Сводная таблица некоторых видов различных поверхностей, для
которых были измерены их фрактальные сигнатуры и определены
характерные диапазоны изменения фрактальной размерности D,
оформлена в виде рис. 12.6 [986, 989, 990, 995,996, 1005-1007, 1010].
Исследованы синтезированные фрактальные сцены; фотографии,
полученные на сканирующем электронном микроскопе; результаты
аэрофотосъемки; РЛИ.
747
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
1 Тип изображения
Ьгакг Щ
Оптические (АФС) ШШШ$-
РЛИ земной поверхности j^MBr
Ь=8,6 мм,1996 г.) ^Щв
1 РЛИ поверхности ЫКйййад ,
планеты Венера ШШш!ш№
\(Х= 8,0 см, КА"Венера- 15,16й, Ш^^^Я
поляризация - ГГ) ЮШШшШ—
Оптические изображения 1
планеты Марс шдрш?ш
(КА - "Opportunity", jjpjp
январь 2004 г.) И^^
Нанокерамические ЩЖ Ш- %
материалы шШ^Ш
(март 2003 г.) &ЮП£
Образцы металлических поверхностей ^^И^В
для РКТ при различных видах обработки ИИйВ
(сканирующий зондовый микроскоп (SPM) НиИЗ
компании NT - MDT, г. Зеленоград, ИШВМ
апрель 2003 г.) ИИ^И
D
2,5-2,9
2,55-2,75
2,55-2,65
2,2-2,5
2,4-2,55
2,35-2,55
2,1-2,4
Рис. 12.6. Характерные диапазоны значений фрактальной размерности D
для природных и искусственных поверхностей: КА - космический аппарат,
РКТ - ракетно-космическая техника
С 2003 г. проводится качественное улучшение алгоритмов и
методов фрактальной обобщенной фильтрации малоконтрастных
объектов. В связи с этим решается задача исследования
потенциальных возможностей разрабатываемых фрактальных методов для
широкого класса изображений фона и объектов на нем. Основные
результаты заключаются в следующем.
Компьютерные эксперименты показали громадный диапазон
возможного применения фрактальных методов в научных и
технических приложениях (в частности, при исследовании наноструктур
748
12.4. Избранные результаты исследований по фрактальной фильтрации ...
Рис. 12.7. Фрактальная сигнатура оптического изображения планеты Марс
(КА "Opportunity", январь 2004 г.) [1005]
вала значений D на практике наиболее эффективно использовать всю
фрактальную сигнатуру, ее часть или наклон. Созданные в ИРЭ РАН
алгоритмы и методы измерения фрактальных сигнатур
работоспособны в очень широком диапазоне физических размеров
характерных деталей изображений и позволяют легко находить и
детектировать эффекты скейлинга, даже замаскированные шумами. В
частности, разработанные методы успешно применены для оценки качества
микрорельефа поверхности сложных изделий тяжелой
промышленности [969, 1004-1007, 1010]. Оказалось, что при современных
методах обработки поверхности очень часто результирующая
шероховатость имеет вид фрактальных кластеров (рис. 12.10и 12.11).
Определение одномерных фрактальных сигнатур по площади
исследуемых изображений в различных направлениях дает новый
749
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
а)
6)
Ф9&# tifam-f* t*m*& &аф- Р$№Ш&<
#Шз&
! 11.3096602202107 *]
108628473447023 ~
10.5621971217539
10.3075339295198
10.1156051355338 ,
9.85268318225618
[9.6266071023906 "*
|9 50474027570299
[9.42352883011205
[9.29878050767156 j*j
в)
12 п
11 -
со о
8 -
7
i
2
i
3
4
i
5
6
7
Орион
i i i i i i i i
8 9 10 11 12 13 14 15
Орион
Рис. 12.8. Цифровая фрактальная обработка изображения туманности Ориона (а)
в диапазоне 2 мкм, измерение фрактальной сигнатуры (б): слева — изображение,
справа — фрактальный кепстр и фрактальная сигнатура (в) [1005]
750
12.4. Избранные результаты исследований по фрактальной фильтрации ...
а)
Щ:;т/^:^:::.Ж::ЩФШш
б)
ШЫ\
М*1
2.16192673476341
0&K>F~
8.23125994671117
7.95451664889746
7 81037129803547
17,71671952738717
7.64879592981771
7.59047347242236
7 54169361905093
7 50598815844657
7.47117208750998
7 43781969050281
zi
в)
Плеяды
■ Плеяды
7 8 9 10 11 12 13 14 15
Рис. 12.9. Цифровая фрактальная обработка изображения звездного скопления
Плеяды (а), измерение фрактальной сигнатуры (б): слева — изображение,
справа - фрактальный кепстр и фрактальная сигнатура (в) [1005]
751
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
а)
«Зайя Шихт Фяаш $ш
Ик-jfiijL
б)
0»юР
Ф»йи ОЬркти' Снашъ фк*«? «ВД^Ив** ;йювн
'i # J0.498168498168498 [
1;d|2. 13612668804284 ~ .
■G ]0,0590704207943774
ii!
W
'"£
JIj.\.,?}•■■ а5ия»т>* I p»<p»?wwmw1 m ] х |
Рис. 12.10. Цифровая фрактальная обработка изображения поверхности образца
(а), обработанного алмазным точением: фрактальный кепстр образца (б), поле и
экспериментальное распределение локальных фрактальных распределений (в)
752
12.4. Избранные результаты исследований по фрактальной фильтрации ...
2 28776269991203
б)
в)
Рис.12.11. Цифровая фрактальная обработка изображения поверхности образца
(а), обработанного микродуговым оксидированием (режим № 7): фрактальный
кепстр образца (б), поле и экспериментальное распределение локальных
фрактальных распределений (в)
753
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
#J2.13656368383048
$ J0,0725306574915007
[•'CTJKp—if i ^.;
s t) j j •$? _ y$**rj» Ф»,- [ \й>мяю;Ций£Цу* | *Jjt 4[ 1V Г , ч' I ,*Д„
<9
KHfW.iK
- 'V э--#* '- . •: Г. X'V -'*У
Рис. 12.12. Фрактальная кластеризация изображения (а) звездного скопления
Плеяды: фрактальное выделение крупномасштабного кластера (б), фрактальное
выделение мелкомасштабных кластеров, звезд (в) [ 1005]
754
12.5. Топология выборки
метод измерения анизотропии изображений поверхности. Параметры
измеряющего фрактальные сигнатуры D алгоритма достаточно
сильно влияют на ошибки измерений. В разработанных алгоритмах
применяют два характерных окна: масштабное и измерительное.
Объективные измерения получаются при масштабных окнах,
превышающих размеры измерительного окна. С помощью масштабного окна
выбирается необходимый масштаб измерений. Это окно
определяет минимальное и максимальное значения масштабов, в которых
наблюдается скейлинг. Поэтому масштабное окно служит для
селекции распознаваемого объекта и последующего описания его в
рамках фрактальной теории. С помощью измерительного окна по
обычным методам статистики определяется локальная дисперсия яркости
или интенсивности изображения. Результаты цифровой фрактальной
классификации, кластеризации и распознавания объектов
представлены выше (см. разд. 9.10). В качестве примера на рис. 12.12
приведены результаты фрактальной кластеризации для звездного скопления
Плеяды [1005]. Подбирая параметры измерительного алгоритма
(размеры масштабного и измерительного окон), можно проводить
селекцию крупно- и мелкомасштабных кластеров (см. рис. 12.12).
12.5. Топология выборки
Решение задач обнаружения и распознавания происходит
всегда в условиях некоторой неопределенности. Методы преодоления
априорной неопределенности принято классифицировать
следующим образом: методы непараметрической статистики;
асимптотические методы; методы адаптации по обучающей выборке; методы
параметрической статистики, основанные на принципах
инвариантности, подобия или минимакса.
Дальнейшее развитие фрактальной обобщенной фильтрации
малоконтрастных объектов автор связывает с понятием топологии
выборки, введенным им в [976, 1008]. Точнее, фрактальные методы,
развиваемые в ИРЭ РАН, позволяют частично преодолевать
априорную неопределенность с помощью информации о виде (топологии)
выборки — одномерной или многомерной, т.е. в случае сигналов,
изображений и волновых полей. Особо отметим, что
разрабатываемые фрактальные (топологические) методы составляют
самостоятельную область исследований и не связаны напрямую ни с
классическими вероятностными распределениями математической стати-
755
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
стики, ни с классической теорией выбросов, ни с вопросами
статистической топографии случайных процессов и полей. При этом
большое значение приобретают топологические особенности каждой
конкретной индивидуальной выборки, а не усредненные реализации,
которые могут иметь совершенно другой характер.
Для того чтобы акцентировать внимание на учете именно этих
особенностей, автор специально ввел в [976, 1008] термин «размер-
ностный склероз» физических сигналов и сигнатур. Заметим, что при
описании немарковских процессов для раскрытия физического
смысла дробных производных используется термин
«асимптотический склероз» [869, с. 862]. В общем случае всегда можно говорить о
фильтрации сигналов одномерных, двумерных, ..., многомерных.
Следовательно, мы должны принять гипотезу о том, что все
характерные сигнатуры (признаки) необходимо рассматривать как
составляющие некоторого обобщенного спектра. В этом случае мы сможем
вполне свободно ввести новый термин «словарь фрактальных
признаков» и приступать к его созданию (что фактически и делается в
настоящее время [976, 989, 990, 997, 1000-1002, 1008]).
Если при синтаксическом или структурном распознавании
исследуют структуру объектов, ее иерархию и связи между ними, то
при фрактальном распознавании исследуют топологию объекта и
фона, отображенных в одно- и многомерных принятых
радиолокационных сигналах. При фрактальном подходе необходимо искать,
реализовывать и использовать правила, которым подчиняется
дробная (сложная) топология рассматриваемых образов. Тогда
процедура фрактального распознавания - это сопоставление с фрактальным
словарем признаков, состоящим из фрактальных символов.
В этом случае мы будем выделять фрактальные «примитивы» —
элементы фрактального языка. Неизбежно возникает вопрос о
составе фрактальных примитивов - фрактальных символах, являющихся
наименьшими элементами фрактального языка. Множество
используемых фрактальных символов мы назовем фрактальным алфавитом
или фрактальным словарем, обозначаемым символом Ф. На основе
последнего можно составлять фрактальные строки — конечные
последовательности символов, входящих в алфавит. Длина строки
может быть любой. Все возможные строки фрактального алфавита
образуют универсальное множество строк или замыкание . Если
ввести множество пустых строк, то конечное или счетное
бесконечное подмножество замыкания фрактального алфавита и есть более
756
12.5. Топология выборки
точное определение понятия «фрактальный язык». Отдельные
фрактальные строки, составленные из его фрактальных символов, мы
назовем фрактальными словами.
Правила создания, преобразования и взаимодействия
фрактальных слов будут определяться фрактальной грамматикой [1008].
Для ее построения возможно использование идей и методов
формальной грамматики, разрабатываемой в математической
лингвистике. Для формальных грамматик характерны две особенности [547,
548]. Во-первых, они описывают только совокупность возможных
результатов и не дают прямых указаний, как получить результат для
определенной задачи. Во-вторых, в них все утверждения
формулируются исключительно в терминах небольшого числа четко
определенных и элементарных символов и операций. Поэтому формальные
грамматики просты с точки зрения их логического построения.
Формальная грамматика может быть определена порождающей
грамматикой - системой G = (Ct, Cn, Р, А), состоящей из четырех
частей: терминального (основного) словаря Ct, нетерминального
(вспомогательного) словаря Сп, множестве правил подстановки Р,
начального символа или начальной аксиомы А (As Cn).
Терминальный (основной) словарь С, - набор непроизводных
терминальных элементов или признаков, из которых строят
цепочки, порождаемые грамматикой. Выбор непроизводных элементов
относится к проблеме определения информативных и устойчивых
признаков для распознавания. Нетерминальный (вспомогательный)
словарь Сп - набор символов, которыми обозначаются классы
исходных элементов или цепочек исходных элементов, а также некоторые
специальные нетерминальные или вспомогательные элементы.
Начальный символ А — выделенный нетерминальный символ,
обозначающий совокупность или класс все тех же языковых объектов, для
описания которых предназначена данная грамматика (например, в
грамматике, порождающей предложения, начальный символ - это
символ, означающий предложение, и т.п.). Множество правил
подстановки Р — конечное множество правил вида <р -»у , где <р и \|/ —
слова в словаре (алфавите) Cn\jCt и «->» - символ, не
принадлежащий Сп uCt. Порождающая грамматика не является алгоритмом,
потому что правила подстановки представляют собой совокупность
решений, а не последовательность предписаний.
757
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Для формальной грамматики характерны следующие соотношения:
C = C„uC„ CnnCt=09 (12A)
где С-словарь.
Процесс создания языка начинается с аксиомы А, к которой
применяются одно за другим правила подстановок. В качестве
операций над высказываниями, чтобы получать новые, используют
конъюнкцию, дизъюнкцию, отрицание. В реальных задачах
естественен аппарат нечеткой логики и нечетких множеств, который ввел
Л.А. Заде в 1965 г. Теория нечетких множеств повышает гибкость и
возможности математических операторов, отражающих характерные
особенности конкретных приложений, в частности в радиолокации.
Основные теоретические положения формализма нечетких множеств
и нечетких интегралов изложены, например, в [940, 949, 955].
Гибкость аппарата нечетких множеств позволяет значительно расширить
описание классов объектов за счет признаков, которые трудно
формализовать.
Рассмотрим пример формирования некоторых фрактальных
примитивов. На практике для получения фрактальной грамматики
необходим ее вывод по заданному ансамблю обучающих объектов.
Для определения класса цели производилось ее сравнение с
несколькими танами из динамического теста «Танграм» (см. рис. 9.59).
Для примера приведем результаты обнаружения реальной цели
с использованием парадигмы «топология цели — ее фрактальная
сигнатура». В частности, производилось сравнение реального
изображения с шестым таном «Танграма». Избранные результаты
экспериментов приведены на рис. 12.13 и 12.14, где показаны и часть
других экспериментальных данных. Компьютерные эксперименты
специально проводились при достаточно малом отношении площади
объекта к площади фона всего анализируемого изображения
(S0/S~ 1/5, площадь S= 300x200 пикселей) и различной
контрастности, чтобы в очередной раз продемонстрировать
работоспособность фрактальных алгоритмов в неблагоприятных условиях. Из
полученных данных видно, что фрактальные сигнатуры реальной
цели (кривые 1 и 2) на определенных масштабах идентичны
фрактальной сигнатуре динамического теста (кривая 5).
Таким образом, мы можем распространить понятия топологии
выборки на любые типы сигналов и полей, связав их с идентифици-
758
12.5. Топология выборки
Рис. 12.13. Изображение реальной цели на фоне (а)
и соответствующий ей шестой тан (б) [989, 990, 1005]
Р**&^
^ч
\ \v
Vv \
^■ч^Ч ■
^****~***>
масштаб
—♦— снимок с помехами
-■-1-й тан
-а-2-й тан
■*■ 6- й тан
НН чистый снимок
Рис. 12.14. Фрактальные сигнатуры цели
и танов динамического теста [989, 990, 1005]
руемыми объектами. Данная концепция может найти широкое
практическое применение в современных задачах искусственного
интеллекта, радиолокации, радионавигации и динамических систем (ДС)
при зашумленных потоках данных. Рассмотрим примеры
фрактальной фильтрации характерных малоконтрастных объектов [995, 996,
999-1001,1005,1008].
Изображение самолета (рис. 12.15) маскировалось аддитивным
гауссовым шумом. На рис. 12.16 представлено одно из полученных
759
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Рис. 12.15. Самолет на поворотной платформе наземного
измерительного комплекса [756]
^'.3 Вариант 3
Х(о,3956043Э5604396 j^
•- ■ ■
Рис. 12.16. Изображение самолета в гауссовых шумах q\ = — 3 дБ
сложных изображений при отношении сигнал-шум q\ = —3 дБ.
Видно, что вся полезная информация скрыта шумовым фоном.
Результаты фрактальной непараметрической фильтрации
такого изображения приведены на рис. 12.17—12.19. Выбор оптимального
режима фильтрации контуров или объектов производится
оператором по автоматически построенному пространственному
распределению фрактальных размерностей сцены, которое отображается на
экране компьютера справа (рис. 12.17—12.19).
760
12,5, Топология выборки
'*&* &***' «м *п&а «xSptprf <***: Jafo»«k "W й****&, " - »-*»• «->ч
fenNPtst
,/*..&«■
■ Jtw^^uJU
MUurt.n,trt'v.,,„^.JL.
JSfc
Рис. 12.17. Пример фрактальной непараметрической фильтрации
изображения самолета при текущем значении D(1) ~ X
{ iyty 5ч' S^'8***'"»-
Mlj№**^iitfs^^
Рис. 12.18. Пример фрактальной непараметрической фильтрации
изображения самолета при текущем значении IK2) > ZK1)
Результаты соответствующей непараметрической фрактальной
фильтрации изображения самолетов В-2 и F117 приведены на рис. 12.20-12.23
и 12.24 соответственно и не требуют пояснений. В случае
адаптивного порога или цепей обратных связей можно производить
автоматическое выделение контуров и распознавание (в том числе и
адаптивное) протяженных малоконтрастных объектов.
761
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
шшшшшшшшшшшшшшштшюшштшшшт^
■■ фа* ЗДмсз &Ч- «tt-S?** Феди Ормк .й&иа» фа» iww*»?-
, Ислравлетя 8 юпененнои докунвн * ajjwiKV "*&■ %> ^ ♦ £^ ♦ ii ^ **? $R »
■в
•*•*» «»жвд&5«йьад№ю»Я^*щ^мсн
УйШ
ПР
!**Ш»^
§и
JB
Рис. 12.19. Пример фрактальной непараметрической фильтрации
изображения самолета при значении ZK3) >ZK2) > ZK1)
Рис. 12.20. Изображение самолета В-2 «Стеле»
Во всех без исключения экспериментах подтверждена
устойчивая работа впервые предложенных фрактальных алгоритмов и
методов при малых отношениях сигнал-шум (сигнал/фон), даже при
наблюдении полезных фрактальных объектов на фоне мешающих
фрактальных образований с другими значениями D. Все это позволяет
говорить о реальных возможностях проектирования и макетирова-
762
12.5. Топология выборки
Рис. 12.21. Изображение самолета В-2 «Стеле» в гауссовых шумах q\ = -3 дБ
Рис. 12.22. Пример фрактальной непараметрической фильтрации изображения
самолета В-2 «Стеле» при текущем значении Z>(1) °c X
ния фрактального непараметрического обнаружителя
радиолокационных сигналов (ФНОРС) [989, 990, 997, 1005].
При фрактальной обработке реализаций сигналов в шумах
показано, что при отношении сигнал-шум q\ = +10 дБ мы точно
измеряем статистику сигнала. С уменьшением значения q\ в сторону
отрицательных значений (например, q\ = -3 дБ) происходит сме-
763
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Рис. 12.23. Пример фрактальной непараметрической фильтрации изображения
самолета В-2 «Стеле» при текущем значении ZK2) > ZK1)
щение максимума (моды) итогового фрактального распределения в
сторону значений фрактальной размерности шума или помехи. При
этом всегда в окрестности значения фрактальной размерности
полезной составляющей присутствует «тяжелый хвост» фрактального
распределения (паретиана), достигающий стабильной величины
а)
Рис. 12.24 (начало)
764
12.5. Топология выборки
Рис. 12.24 (продолжение)
765
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
д)
й^Шж^^^и^л^Ж^Жлй^Ш
V - - -: Ch
*.,£;!■■
,£|Т
г
12.51783664708263
^ |0.105855186394142^ -,,
*&*&: , яхт**»' т 33
L * \<Z ',' > ' »f"\'t''' '4 '//*"
Рис. 12.24. Цифровая фрактальная обработка изображения самолета (a) F 117:
(б) - изображение самолета F 117 в интенсивных импульсных помехах, пример
фрактальной непараметрической фильтрации изображения самолета при текущем
значении D(1) ос X (в), пример фрактальной непараметрической фильтрации
изображения самолета при текущем значении 1№ > &1) (г), пример фрактальной
непараметрической фильтрации изображения самолета
при значении #3> > jp) > #i) (^) [Ю05]
порядка 20%. Данная тенденция сохраняется и при гораздо меньших
значениях q\, равных -10 и -20 дБ, как показано на рис. 12.25, где
приведены результаты фрактальной фильтрации двух синтезирован-
2,204
2,324
2,444
2,564
2,684 D
-А)-10дБ.
-В)-10дБ-
-А)-20дБ-
- В) -20дБ
Рис. 12.25. Эмпирические фрактальные распределения с тяжелыми хвостами
для изображений в сильных гауссовских помехах
766
12.6. Странный аттрактор в радиолокационном сигнале от растительности
ных фрактальных сцен (А и В) в гауссовых помехах [984, 985, 989,
990, 995-997, 999-1002, 1005, 1008, 1011].
Необходимо отметить, что роль фрактальных распределений
(имеющих «тяжелые хвосты») в задачах радиолокации ранее
вообще не принималась во внимание. В лучшем случае говорилось о
логнормальных распределениях удельных ЭПР, что помогало в
какой-то степени сблизить результаты теории рассеяния
электромагнитных волн земными покровами с экспериментальными
значениями удельных ЭПР а+. Роль фрактальных распределений (паретиа-
нов) и их громадное значение рассмотрим ниже.
Крайне важная роль паретианов будет сначала нами
продемонстрирована на двух примерах цифровой фрактальной обработки двух
типовых объектов иностранной техники. На рис. 12.26,а рассмотрен
старт баллистической ракеты в плохих метеорологических
условиях. Вид полученного экспериментального паретиана с выделенными
участками приведен на рис. 12.26,5. По этим участкам также
можно выделить информационные составляющие. На рис. 12.26,в—г
представлены результаты цифровой фрактальной фильтрации при
различных значениях текущего поля фрактальной размерности D.
Аналогичные результаты, но более эффектные, демонстрируются
данными рис. 12.27,я-е, где приведены результаты цифровой
фрактальной обработки изображения атакующего вертолета в сложно-
пересеченной местности. В данном случае оператор может разделить
гораздо более тонкие детали, в том числе отделить газовое облако от
подстилающей поверхности.
12.6. Странный аттрактор в радиолокационном сигнале
от растительности и паретианы
Экспериментальное доказательство наличия режима
детерминированного хаоса и странного аттрактора, управляющего
радиолокационным рассеянием миллиметровых волн (ММВ) от растительных
покровов, было впервые получено в [941, 944, 945]. Данная
гипотеза была высказана автором еще в 1997 г. [77, 186]. В качестве
экспериментальных данных были использованы авторские результаты из
[184, 912], полученные на длине волны Х= 2,2 мм при круговой
поляризации излучения. Для обнаружения странного аттрактора были
767
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
рассчитаны оценки фрактальной размерности D, размерности
вложения т, максимального показателя Ляпунова Хг и времени
предсказания хтах. Расчет корреляционного интеграла С (г) проводился
по выборке из 50 000 отсчетов, соответствующей углу падения
электромагнитной волны 0 = 50°. Экспериментальные зависимости С (г)
для гауссова шума показаны на рис. 12.26, а для радиолокационных
отражений в диапазоне ММВ - на рис. 12.27.
факел-ракета
б)
Рис. 12.26 (начало)
768
12.6. Странный аттрактор в радиолокационном сигнале от растительности
Рис. 12.26. Результаты цифровой фрактальной обработки изображения
старта баллистической ракеты: а — исходное изображение; б— вид полученного
эмпирического распределения D; в—д — результаты фрактальной фильтрации
при различных значениях текущей фрактальной размерности D
Были получены следующие значения: 2) «2,8; т — 1\ \ >0,6
бит/с; хтах «1,7 с при времени корреляции интенсивности
отраженного сигнала х « 210 мс (скорость ветра 3 м/с). Следовательно, если
текущие условия измеряются с точностью до 1 бита, то вся
предсказательная мощность во времени потеряется примерно за 1,7 с.
Тогда интервал предсказания интенсивности радиолокационного
сигнала превышает время корреляции примерно в 8 раз. Полученные
результаты показывают, что для корректного описания данного
процесса рассеяния радиоволн требуется не более пяти независимых
переменных. Корреляционный интеграл С (г) можно также применять
как средство разделения режимов детерминированного хаоса и
белого шума, так как для гауссова процесса нет тенденции к
насыщению (см. рис. 12.2) (более подробно см. разд. 1.3 и 9.7).
25 Фракталы
769
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
W(D)/W(D)at
r^^\J
1,7
/
2,0
Л
\
D
вертолет
^ подстилающая
поверхность
б)
д)
е)
Рис. 12.27. Результаты цифровой фрактальной обработки изображения
атакующего вертолета: а - исходное изображение; б— вид полученного
эмпирического распределения Z>; в-е - результаты фрактальной фильтрации
при различных значениях текущей фрактальной размерности D
110
12.6. Странный аттрактор в радиолокационном сигнале от растительности
В следующей серии экспериментов с использованием
алгоритма повторного дифференцирования проводилось исследование
сечений (сигнатур) странных аттракторов, контролирующих процесс
рассеяния. Серия полученных результатов показана на рис. 12.28
[964]. Моделирование классического аттрактора Хенона показало
правильность работы созданных компьютерных программ расчета
характеристик динамических процессов по коротким выборкам.
Полученные данные совместно с семейством фрактальных
распределений лежат в основе новой динамической модели сигналов,
рассеянных растительными покровами [941, 944, 945, 947, 964, 974].
Оказалось, что в радиолокационных экспериментах [912] ни одно
значение удельной ЭПР не описывается экспоненциальным
распределением. Это наглядно иллюстрируется соответствующей
диаграммой Пирсона в [912]. Полученные экспериментальные точки очень
хорошо располагались вблизи некоторых распределений Пирсона.
В то же время в теоретических оценках законов распределения
флуктуации отраженных сигналов наиболее распространены две
электродинамические модели поверхности. В первой, релеевской,
отраженный сигнал формируется ансамблем случайных рассеивате-
лей, имеющих случайные амплитуды и фазы. Во второй модели
предполагается наличие преобладающего нефлуктуирующего
отражателя на фоне менее интенсивных флуктуирующих отражателей. При
отсутствии стабильно отражающего элемента эти модели
равноценны. В реальности экспериментальные результаты заметно отличаются
от теоретических общепринятых моделей. Число примеров,
указывающих на это отличие, может быть увеличено, но в этом нет
необходимости.
На основе теории ДС можно предложить более содержательную
модель радиолокационного рассеяния, о чем сказано выше.
Известно, что некоторые распределения Пирсона (типа 6 и 11) в частном
случае переходят в распределение Парето:
р(х) = (а/х0)(х0/хГ+К (12.5)
В выражении (12.5)Xq >0и oc>0- параметры. Математическое
ожидание распределения Парето конечно и равно осх0/(ос -1),
дисперсия конечна при а > 2 и равна осх^/[(ос - 1)(ос - 2)], медиана
равна 21/осх0. Функция распределения Парето имеет вид
F(x) = l-(x0/xr. (12.6)
771
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
...А
It in ф А
г 2
i
f
1 ф о
■ Ч>
о
■г
1 5-
Г Ь-
L
1' ■
(D 1
[1 Г
i С
- CD
■ сч
> (
- «9
i Ц]
В ч>
I
-1
■
_■
S
00
<£
■
5-
■ ■
5-
■
ш - -
UO
{
N
г "*
- О
1
^^
^
_ о
■
1 О
-■
■
ш
772
12.6. Странный аттрактор в радиолокационном сигнале от растительности
ш
1 >-
р 1
>-
■ _
— 1 —
и
ч
**
1*
! 4 «
* 3
.*
:*
< J
« *
"'I
1
1
4
4 4
1 1 1 1 1
) Tlv 1Л <С0 1Л (N
4
„ «
\
1
4
4 4
■4
t
4
«
4
4
-.- ■
«
Ifl т
т-
1
- Ц) С
О
1
о
о
Г "^
"r" I
о 1
Г °-
т—
о
L о
Г ^
сГ
о J
г о ч
* °
о
о
- ID
О
о
- о
т—
1
о
- 1Л
1
■
773
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Распределение Парето получило распространение в
экономической статистике и было предложено в 1897 г. для учета
распределения доходов. Наблюдения Парето показали, что доход хорошо
описывается логнормальным распределением, за исключением
приблизительно 3% наивысших индивидуальных доходов. На этом участке
доход начинает следовать обратному степенному закону, что дает
утолщение «хвоста». Похожий обратно-степенной закон был найден
Ципфом в 1948 г. для частот используемых слов. В 1926 г. Лотка
привел примеры обратно-степенных законов из области социологии.
Во всех перечисленных случаях «утолщенные хвосты» или «тяжелые
хвосты» (Heavy Tails или Fat Tails) являются следствием обратной
связи, усиливающей события.
Моменты распределений высокого порядка q при
р(х)осХ-^ (12.7)
расходятся, если q > ос. Для распределения Парето с ос < 1
бесконечно уже среднее значение. При этом расходимость моментов
обусловлена «тяжелым хвостом» распределения. В общем случае
рассматривают только «хвост», отвлекаясь от поведения распределения при
малых х. Можно показать [122], что для распределений
неотрицательных величин с «тяжелыми хвостами» величины Sn =x^ +х2 +... + хи
при нормировке на л1/" и тп =тах{х1,х2,...,хл} имеют одинаковый
порядок, а математическое ожидание их отношения
Ит(*>„) = 1/(1-<х). (12.8)
П—>о°
Соотношение (12.8), на первый взгляд, парадоксально, а
именно: сумма положительных эффектов с точностью до множителя
1/(1-а) определяется лишь одним, максимальным значением тп, и
этот эффект справедлив для сколь угодно больших выборок. В
обычной ситуации для случайной величины с конечными моментами
отношение Sn/mn, естественно, стремится к бесконечности с ростом
п. При этом вклад любого слагаемого, в том числе и
максимального, в сумму Sn стремится к нулю. Для распределений с «тяжелыми
хвостами» выборочные средние неустойчивы и мало информативны
из-за неприменимости закона больших чисел.
Степенные законы распределения представляют собой одну из
отличительных черт сложности. Для простых систем типичны
экспоненциальное и гауссово распределения. Типичный вид плотнос-
774
12.6. Странный аттрактор в радиолокационном сигнале от растительности
ти вероятности величин, распределенных в соответствии с
гауссовым, экспоненциальным и степенным законами с различным
представлением данных по осям приведен на рис. 12.29. На среднем
графике гауссово и экспоненциальное распределения изображаются в
виде параболы и прямой. Внизу в случае двойного
логарифмического масштаба только степенной закон распределения имеет вид
прямой, что говорит о скейлинговом (отсутствие выделенных масштабов
при таком законе) фрактальном поведении.
Разница между гауссовым и степенным распределениями
имеет не формальный, а принципиальный характер. Природа степенных
законов распределения связана с сильной взаимозависимостью
событий (эффект не «домино», а «цепной реакции» [827]). Вследствие
статистического самоподобия (рис. 12.29) степенные распределения
называются фрактальными. Свойства таких распределений
первоначально были изучены Леви и опубликованы еще в 1925 г. Иногда
«тяжелые хвосты» и высокий пик распределений называют также лепто-
эксцессом, а само семейство фрактальных распределений —
устойчивым паретианом. Фрактальные распределения являются следствием
детерминированного хаоса. Распределения с «тяжелыми хвостами»
также входят в класс устойчивых распределений, представляющих
собой предельные законы для сумм независимых одинаково
распределенных слагаемых [122, 151]. Распределения с «тяжелыми
хвостами» являются не альтернативой гауссовского распределения, а его
естественным дополнением. Методика статистической обработки
таких распределений не тривиальна и имеет свои особенности.
Необходимо сказать, что устойчивый паретиан является
отличительной чертой многих сложных открытых систем, обменивающихся
с окружающими телами веществом, энергией и информацией с
перераспределением энтропии. Кроме того, представленные здесь
данные непосредственно входят в круг общих синергетических
вопросов эволюции (самоорганизация и деградация) открытых
распределенных радиосистем при изменении внешних параметров (появление
точек бифуркаций) [973]. При этом бифуркации ассоциируются с
катастрофическими изменениями или конфликтами. Между
точками бифуркаций открытая диссипативная система подчиняется
детерминистическим законам, а в окрестности таких точек только
флуктуации определяют поведение системы.
Поэтому столь велика роль флуктуации в окрестностях точек
бифуркации. Хаотические процессы на микроуровне могут «взлететь»
775
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Рис. 12.29. Типичный вид плотностей вероятности
на макроуровень и влиять на всю систему. При этом способность
открытой системы находиться в режиме детерминированного хаоса
стимулирует информационные процессы вне зависимости от
начальных условий. Это относится в общем случае к любым техническим,
776
12.7. Фракталы и мулыпифракталы на нечетких множествах
экологическим, биологическим, экономическим и социальным
сложным открытым системам (см, например, [24, 157, 162, 175,196,
232, 234, 235, 239-241, 757-767, 770, 771, 778-780, 782, 801, 811, 819,
822-827, 837, 840, 845-847, 849, 852, 855-857, 893, 990, 992, 994-
1011]). Для конкретных задач радиолокации лишь отметим, что учет
фрактальности земных покровов, как показано ранее, позволяет
значительно точнее описывать индикатрисы рассеяния земных покровов,
чем используемые в настоящее время классические модели.
12.7. Фракталы и мультифракталы
на нечетких множествах
В процессе исследования многих радиофизических процессов
приходится сталкиваться с явлениями, требующими расширения
понятия фрактала на сложные популяции с более, чем одним
показателем скейлинга. В этом случае говорят о мультифракталах.
Многие странные аттракторы нелинейных динамических систем (ДС)
также обладают ярко выраженной мультифрактальной структурой.
Мультифрактал определяется множеством точек со спектром
обобщенных фрактальных размерностей Dq для дробной меры [1011].
Следовательно, фрактальная мера может быть распространена на
фрактальные подмножества. Для синтеза таких подмножеств и
новых фрактальных функций в [936, 940, 949, 955] было предложено
использовать формализм нечетких множеств. При этом синтез
аффинных фракталов и мультифракталов с различными
коэффициентами подобия Гр ..., гп будет определяться функциями
принадлежности и нечеткими мерами. По сути дела, мы получаем метод
преобразования детерминированных фракталов в случайные с
различными порождающими правилами. В частности, при размытии
сигнатур (текстурных, фрактальных, амплитудных,
поляризационных и т.п.) можно применить нечеткие метки посредством
отображения на интервал [0, 1]. Исключительной особенностью
мультифракталов является то, что большинство природных объектов на
самом деле принадлежат к мультифракталам.
Для нахождения спектра сингулярностей мультифрактала /(ос)
используем условие Липшица-Гельдера, которое гласит, что для
любых двух точек Хр х2е[а, Ь] приращение функции/(х)
удовлетворяет неравенству
777
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
\f{xx)-f{x2)\<L,\x{-x2^ (12.9)
где L0 — постоянная Гельдера; а — показатель Липшица-Гельдера.
Величина сс^ соответствует наименее, а остах - наиболее
вероятной части мультифрактала. Из соотношения (12.8) можно
получить параметрическое представление кривой /(ос), т. е.
фрактальной размерности /(ос) носителя сингулярностей меры с показателем
Липшица-Гельдера. Кривая /(ос) характеризует меры используемых
множеств. В общем случае можно сформировать сложную
хаотичную мультифрактальную среду, что крайне необходимо в задачах
диффузии во фрактальных средах, моделировании структур микро-
и макросистем, а также при создании фрактальных поглощающих
материалов, фрактальных антенн, фрактальных частотно-селективных
поверхностей и объемов, фрактальных фотонных и магнонных
кристаллов [921, 979-981, 1011].
На основе такого подхода можно синтезировать новые классы
фрактальных и мультифрактальных подмножеств на нечетких
подмножествах. Пробными функциями в нечетких операторах могут
быть любые фрактальные функции, например классические
функции Больцано, Ван-дер-Вардена, Безиковича, Вейерштрасса,
Кантора, Фабера, Такаги, решения уравнения де Рама на основе
сжимающих отображений и т.д. (см. разд. 2.4 и [915, 921, 981, 1011]).
12.8. Конструирование фрактальных антенн
и фрактальных частотно-селективных
поверхностей и объемов
В настоящее время, как отмечено во введении и гл. 11 данной
монографии, в мировой практике прочно утвердился термин
«Фрактальная электродинамика», введенный в научный обиход в 1990 г.
В настоящее время теория взаимодействия электромагнитных волн
с фракталами интенсивно развивается. Одна из первых работ по
методологии проектирования фрактальных антенных решеток была
опубликована в ТИИЭР (1986) [416]. При этом всегда имеется в виду
реализация характеристик излучения и поглощения с повторяющейся
структурой на произвольных масштабах.
Спиральные и логопериодические антенны, как известно,
являются наиболее наглядными примерами частотно-независимых ан-
778
12.8. Конструирование фрактальных антенн, поверхностей и объемов
тенн. Форма структур таких антенн инвариантна относительно
некоторых масштабных преобразований, т.е. наблюдается
электродинамическое подобие. Фрактальные антенны явились следующим
шагом в построении новых сверхширокополосных и
многодиапазонных антенн. Скейлинг фрактальных структур придает им свойства
определенной многодиапазонности в электромагнитном смысле.
Первая фрактальная антенна была испытана в 1989 г. [519]*
В [77, 921, 930, 963, 978] описаны методы конструирования и
результаты лабораторных исследований отечественной фрактальной
антенны на основе салфетки Серпинского. Там же приведены
различные конфигурации заготовок фрактальных антенн и
фрактальных решеток на основе множества Кантора и дерева Кейли, хорошо
представляющем метрику фрактального множеств.
Антенна на основе салфетки Серпинского выполнена на
диэлектрической подложке, а ее апертура состояла из 8 поколений
треугольной затравки (рис. 12.30,я) с коэффициентом масштаба 5 = 2 и
начальным размером 230 мм. В идеальных условиях поведение такой
структуры будет подобно 8 симметричным вибраторам с
треугольными плечами, работающим каждый на своей резонансной частоте.
На рис. 12.30,6представлена частотная зависимость коэффициента
отражения изготовленной фрактальной антенны.
Измерительная аппаратура не позволила наблюдать все полосы
пропускания фрактальной антенны, поэтому на рис. 12.30,#показаны
о
-5-
-10-
-15-
VV %-У -20-
ъ2у "25_
■ -30-
2 4 6 8 10 12 14 16
/ГГц
а) б)
Рис. 12.30. Шаблон антенны «Монополь Серпинского» (а) и зависимость (б) ее
коэффициента отражения от частоты
1,ДЬ
779
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
только три рабочие полосы. Данная антенна хорошо принимает
дециметровые каналы московского телецентра в городской черте.
В [963, 978] также представлены результаты разработки новых
лакунарных фрактальных антенн для задач приема и передачи
телевизионных, радио- и телекоммуникационных сигналов.
Достоинством таких антенн является малогабаритность, простота технологии
изготовления, возможность изготовления на гибком материале,
достаточно высокая чувствительность и частотная селективность.
Примеры таких фрактальных антенн на основе элементарных
преобразований канторова множества приведены на рис. 12.31 и рис. 12.32.
Рис. 12.31. Различные варианты фрактальных антенн на основе классических
множеств: «Канторов монополь» (а), «Канторов диполь» (б),
«Канторов двойной диполь» (в)
Рис. 12*32. Всенаправленная фрактальная антенна «Канторов квадрат монополей»
780
12.8. Конструирование фрактальных антенн, поверхностей и объемов
Еще один вид разработанных лакунарных фрактальных антенн —
это конфигурации на основе фрактального дерева Кэйли. Одна из
таких антенн представлена на рис. 12.33. На основе этой антенны
разработаны «Монополь Кэйли учетверенный», а также
«Спиральный монополь Кэйли» (рис. 12.34) и «Спиральный монополь Кэй-
ли-4» (учетверенный монополь). Особенностью последних двух ан-
Рис. 12.33. Фрактальная антенна на основе дерева Кэйли «Монополь удвоенный»
Рис. 12.34. Фрактальная антенна на основе дерева Кэйли
«Спиральный монополь»
781
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
тенн является расположение точек ветвления каждой секции на
логарифмической спирали. Все рассмотренные здесь конфигурации
найдут применение во фрактальных антенных решетках.
Применение фрактальных структур позволяет создавать среды,
которые проявляют сложные отражающие и пропускающие свойства
в обширном диапазоне частот, и способны моделировать
трехмерные фотонные и магнонные кристаллы, являющиеся новыми
средами передачи информации (см. подробнее разд. 11.14 и [979-981]).
Можно соответствующим образом подобрать конфигурацию и
размеры фрактальных структур и проверить такие необычные свойства
для диапазона частот по схеме на рис. 11.69.
Видно, что «дырявая сверхволновая» фрактальная структура
задерживает направленное излучение, в то время как металлическая
пластина не выполняет такой функции.
Данные «сверхволновые» свойства означают, что фрактальная
пластина может действовать как компактный отражатель. Для таких
технологий разработаны алгоритмы и программмы, позволяющие
рассчитывать различные конфигурации фрактальных структур
рассматриваемых моделей кристаллов. В качестве примера на рис. 12.35
и 12.36 представлены фрактальные образцы некоторых заготовок для
таких структур на основе ковра Серпинского с шестым порядком
итерации и деревьев Кейли соответственно [980, 981, 1011].
Отметим, что фрактальные структуры всегда имеют
самоподобный ряд резонансов, приводящих к логарифмической
периодичности рабочих зон. Связанная топологическая фрактальная структура
делает возможным модулирование коэффициента пропускания
электромагнитных волн. Самая нижняя частота ослабления соответствует
длинам волн, которые могут значительно превышать внешние раз-
Рис. 12.35. Образец первой фрактальной заготовки
782
12.9. Фрактальные методы передачи информации
Рис. 12.36. Образец второй фрактальной заготовки
меры фрактальной пластины, делая такие фрактальные структуры
сверхволновыми отражателями, обладающими интересными
свойствами. Более подробно данный материал представлен в [981].
12.9. Фрактальные методы передачи информации
В данном разделе конспективно рассмотрены общие вопросы
применения теории фракталов для разработки новых методов
модуляции и демодуляции сигналов, а также методов кодирования и
декодирования информации. Разрабатываемые автором фрактальные
методы объединены под общим названием фрактальных методов
передани информации [1009]. Декларируемый здесь подход позволяет
перейти к конкретным структурным схемам фрактальных
модуляторов и фрактальных демодуляторов сигналов.
Как известно, фракталы характеризуются масштабной
инвариантностью (скейлингом), дробной размерностью, рекурсивным
процессом^ также использованием дробных операторов интегродиффе-
ренцирования. При этом, как отмечено в разд. 12.5, большое
значение приобретают топологические особенности индивидуальной
выборки, а не усредненные реализации, имеющие зачастую
совершенно другой характер [1008]. Эти положения можно применить и
в системах передачи информации, что и было начато автором в
1997 г. [77, 186].
783
Глава 12. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ
Следует выделить непосредственно фрактальную модуляцию,
когда модулируемые параметры высокочастотного сигнала
формируют по фрактальному закону с заданным скейлингом. В этом
случае возможно использование классических фрактальных функций и
множеств (например, канторово и т.п.) на основе /-го и А:-го
порядков рекурсии. Применяя фрактальные законы изменения
параметров гармонического колебания и электромагнитной волны, получаем
фрактальные: амплитудную (ФАМ), частотную (ФЧМ), фазовую
(ФФМ) и поляризационную (ФПМ) виды модуляции. Также
осуществляется двойная модуляция с поднесущей. Для дискретных
систем передачи информации можно реализовать фрактальные:
амплитудно-импульсную (ФАИМ), широтно-импульсную (ФШИМ),
частотно-импульсную (ФЧИМ), фазоимпульсную (ФФИМ),
импульсно-кодовую (ФИКМ) виды модуляции. Вторая ступень
модуляции для радиоканалов может быть и традиционной (AM, ЧМ,
ФМ, поляризационная).
Особого внимания заслуживает новый класс фрактальных
шумоподобных сигналов, когда в качестве переносчика информации
используется случайный процесс с распределением мгновенных
амплитуд по закону «устойчивого паретиана», т.е. когда применяется
фрактальное распределение с тяжелыми хвостами (см. рис. 12.25 и
12.29). Некоторые результаты модельных компьютерных
экспериментов приведены в [1009]. Предлагаются алгоритмы заполнения
частотно-временной плоскости реализациями случайных фракталов
с исключением артефактов. В данном случае мы получаем
возможность синтеза фрактальных шумоподобных составных сигналов. Так
же можно использовать известное стохастическое кодирование
информации, в котором выделяются необходимые участки скейлинга.
784
Заключение
ЗАКЛЮЧЕНИЕ
Заканчивая рассмотрение вопросов применения фрактальной
геометрии и фрактального анализа в радиофизике и радиолокации,
отметим, что фрактальные понятия находят все большее
применение в различных сферах указанных наук. Наука о фракталах
относительно молода. Основные понятия теории фракталов, носящей
междисциплинарный характер, пока еще находятся в процессе
становления, но поле их приложений непрерывно расширяется.
Теория фракталов позволила ввести принципиально новые
количественные показатели в виде дробных размерностей и фрактальных
сигнатур. Они характеризуют не только топологию объектов и целей, но
и отражают процессы эволюции систем и определяют их
динамические свойства.
Следует сказать, что фрактальные методы являются
эффективным математическим аппаратом анализа достаточно широкого класса
процессов. Как было отмечено, фрактальная концепция заняла
прочное место во многих областях естествознания, но только в последнее
время она стала очевидной для задач радиофизики в приложении к
радиолокации, распространению радиоволн, дистанционному
зондированию и другим актуальным научным и техническим
направлениям радиоэлектроники. В настоящее время поток научных
публикаций, связанных с фракталами, растет лавинообразно.
Множество результатов интересных примеров, касающихся фракталов,
рассмотрено в [757-1017]. Автор считает, что для ученых книга
явится стимулом обратиться к многочисленным проблемам, связанным
с фракталами, а также послужит целям научного обмена мнениями
для тех, кто уже работает в этой области.
Впервые предложенные и развиваемые в ИРЭ РАН новые
информационные технологии для современных задач радиофизики,
радиолокации и других отраслей современной радиоэлектроники с
использованием текстурных (середина 80-х годов XX в.) и
фрактальных (середина 90-х годов XX в.) мер на основе принципов нелинейной
динамики показали их перспективность и дали обнадеживающие
результаты. На основе [77, 99,100,184-186, 223-231, 236, 280, 357, 390,
458,459,462,479,484, 504, 519-538, 541-545, 550, 551, 561,912-1015]
можно указать следующие перспективные направления исследований:
26 Фракталы
785
Заключение
1. Исследование возможностей текстурных (пространственных
и спектральных), фрактальных и энтропийных признаков для
радиолокационных задач обнаружения.
2. Синтез новых моделей рассеяния радиолокационных
сигналов земными покровами на основе теории детерминированного
хаоса, странных аттракторов и фрактальных вероятностных
распределений - устойчивых паретианов.
3. Исследование волновых явлений (распространение и
рассеяние волн, процессы диффузии) во фрактальных неоднородных
средах на основе операторов дробного интегродифференцирования.
4. Синтез моделей каналов радиолокационных и
телекоммуникационных систем на основе пространственных фрактальных
обобщенных корреляторов и фрактальных частотных функций
когерентности.
5. Исследование возможностей распознавания формы или
контуров целей с помощью фрактальных, текстурных и энтропийных
признаков.
6. Исследование потенциальных возможностей и ограничений
фрактального метода обработки радиолокационных и связных
сигналов, в том числе фрактальной модуляции и демодуляции,
фрактального кодирования и сжатия информации, фрактального
синтеза изображений, фрактальных фильтров.
7. Исследование адаптивной пространственно-временной
обработки сигналов на основе дробной топологической размерности.
8. Поиск и исследование новых комбинированных методов
обнаружения и распознавания классов малоконтрастных целей.
9. Исследование возможностей создания новых сред для
передачи информации, многодиапазонных фрактальных поглощающих
материалов, конструирование фрактальных антенн и фрактальных
частотно - селективных поверхностей и объемов.
10. Синтез новых классов фракталов и мультифракталов с
обобщением понятия меры множеств.
11. Изучение вида или топологии выборки одномерного
(многомерного) сигнала для задач искусственного интеллекта с целью
создания словаря фрактальных признаков на основе фрактальных
примитивов, являющихся элементами фрактального языка с
фрактальной грамматикой, т.е. исследование проблемы «размерностного
склероза» физических сигналов и сигнатур [976, 1008]. Эти понятия,
введенные автором, предполагают исследование топологических осо-
786
Заключение
бенностей каждой конкретной индивидуальной выборки, а не
усредненных реализаций, имеющих зачастую совершенно другой
характер.
12. Развитие фрактальной неинерциальной релятивистской
радиолокации в искривленном пространстве-времени связанных
структур, т.е. фрактальной геометрии пространства - времени
детерминированных структур [962, 968, 1012].
13. Прогноз механизмов формирования и характеристик
шероховатости с целью управления геометрическими параметрами
микрорельефа для получения заданных физико - химических и
эксплуатационных свойств изделий при современных неравновесных
технологиях обработки их поверхностного слоя [969, 1004-1007,1010].
Многое здесь определено стремлением автора подчеркнуть ряд
нерешенных задач, представляющихся основными. Решение
большинства из них, как нам кажется, потребует оригинальных идей и
методов. Концепция автора сводится к тому, что новые
геометрические и топологические представления фрактального анализа в будущем
станут такой же непременной частью анализа сигналов, полей и волн
в радиофизике и радиоэлектронике, какой стал фурье-анализ.
В заключение отметим, что развитие и внедрение новых
информационных технологий на основе принципов фрактальной
радиофизики и фрактальной радиолокации необратимо связано с
подготовкой высококвалифицированных специалистов по данным научным
направлениям. В первую очередь необходима (см. рис. 12.3)
систематическая постановка в ряде институтов и университетов
Российской Федерации курсов лекций по одновременному изучению основ
теории фракталов, теории детерминированного хаоса, теории
дробных операторов и их физико-технических приложений.
Методологическая база (см., например, данную монографию и [1011], а
также учебное пособие [932] и статью [958] с библиографическими
ссылками в них) для этих целей уже достаточно хорошо проработана.
В связи с этим необходимо также отметить рождение нового
научно-технического и теоретического журнала «Нелинейный мир»,
выходящего в свет с 2003 г. Этот журнал будет стремиться отражать
фундаментальные направления физики, математики, других
естественных и гуманитарных наук с междисциплинарных позиций
синергетики и нелинейной динамики. При журнале «Нелинейный
мир» создана библиотека, включающая в себя серию книг,
объединенных общим названием «Фракталы. Хаос. Вероятность».
787
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Mandelbrot В. В. Les Objects Fractals: Forme, Hasard et Dimension. -
Paris: Flammarion, 1975.-187 p.
2. Mandelbrot В. В. Fractals: Forme, Chance and Dimension. - San-
Francisco: Freeman, 1977. - 365 p.
3. Mandelbrot В. В. The Fractal Geometry of Nature. - N. Y.: Freeman,
1982. - 468 p.
4. Mandelbrot В. В. Fractals//Encyclopedia of Physical Science and
Technology. - N. Y.: Academic Press, 1987. V. 5. P. 579-593.
5. Le Mehaut. A. Fractal Geometries. - Boca Raton, FL: CRC Press, 1990.
6. Пайтген Х. -О., Рихтер П. X. Красота фракталов/Пер. с англ.; Под
ред. А. Н. Шарковского. - М.: Мир, 1993. - 176 с.
7. BundeA, Halvin S. Fractals in Science. - Berlin: Springer-Verlag, 1995.
- 298 p.
8. BundeA, Halvin S. Fractals and Disordered Systems. - Berlin: Springer-
Verlag, 1995. - 408 p.
9. Proceedings Int. Conf. Honouring B. B. Mandelbrot on his 65-th birthday.
- Vence, France//Physica D. 1989. V. 38, № 1-3. - 395 p.
10. Жен П.-Ж. де. Идеи скейлинга в физике полимеров/ Пер с англ.;
Под ред. И. М. Лифшица. - М.: Мир, 1982. - 368 с.
11. Зельдович Я. Б., Соколов Д. Д. Фракталы, подобие, промежуточная
асимптотика//УФН. 1985. Т. 146, № 3. С. 493-506.
12. StaufferD. Introduction to Percolation Theory. - L.: Taylor & Francis,
1985. - 382 p.
13. Абдуллаев С С, Заславский Г. М. Классическая нелинейная
динамика и хаос лучей в задачах распространения волн в неоднородных средах//
УФН. 1991. Т. 161, № 8. С. 1-43.
14. Смирнов Б. М. Фрактальный клубок - новое состояние вещества//
УФН. 1991. Т. 161, № 8. С. 141-153.
15. Батунин А. В. Фрактальный анализ и универсальность Фейнген-
баума в физике адронов//УФН. 1995. Т. 165, № 6. С. 645-660.
16. Смирнов Б. М. Фрактальные кластеры//УФН. 1986. Т. 149, № 2.
С. 177-219.
17. Lauwerier H. Fractals. - Amsterdam: Aramith Uitgevers, 1987.
18. Смирнов Б. М. Физика фрактальных кластеров. - М.: Наука, 1991.
-134 с.
19. Mandelbrot В. В. Multifractals and Lacunarity. - N. Y.: Springer-Verlag,
1998.
20. Niemeyer L. Pietronero L., Wiesmann H. J. Fractal Dimension of
Dielectric Breakdown//Phys. Rev. Lett. 1984. V. 52, № 12. P. 1033-1036.
788
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
21. Бершадский А. Г. Крупномасштабные фрактальные структуры в
лабораторной турбулентности, океане и астрофизике//УФН. 1990. Т. 160,
№ 12. С. 189-194.
22. Поликарпов М. И. Фракталы, топологические дефекты и
невылетание в решеточных калибровочных теориях//УФН. 1995. Т. 165, № 6.
С. 627-644.
23. Гилмор Р. Прикладная теория катастроф: В 2 т. / Пер с англ.; Под
ред. Ю. П. Гупало и А. А. Пионтковского. - М.: Мир, 1984. Т. 1. - 350с. -
Т. 2. - 285 с.
24. Шустер Г. Детерминированный хаос: Пер. с англ.; Под ред. А. В.
Гапонова-Грехова и М. И. Рабиновича. - М.: Мир, 1988. - 240 с.
25. Зосимов В. В., Лямшев Л. М. Фракталы и скейлинг в акустике//Акуст.
журн. 1994. Т. 40, № 5. С. 709-737.
26. Зосимов В. В., Лямшев Л. М. Фракталы в волновых процессах//УФН.
1995. Т. 165, №4. С. 361-402.
27. Соколов И. М. Размерности и другие геометрические критические
показатели в теории протекания//УФН. 1986. Т. 150, № 2. С. 221-255.
28. Смирнов Б. М. Излучательные процессы с участием фрактальных
структур//УФН. 1993. Т. 163, № 7. С. 51-63.
29. Рабинович И. М., Сущик М. М. Регулярная и хаотическая динамика
структур в течениях жидкости//УФН. 1990. Т. 160, № 1. С. 3-64.
30. Konotop V. V., Bulgakov S. A. Two-Scale Method in the Theory of
Scattering by Fractal Structures: One-Dimensional Regular Problems//Phys. Rev.
A. 1992. V. 45, № 8. P. 5994-6007.
31. Vicsek T. Fractal Growth Phenomena. - L.: World Scientific, 1989.
32. Fleischmann M., Tildesley D. J., Ball R. C. Fractals in the Natural
Sciences. -Princeton: Princeton Univ. Press, 1989.
33. Гарднер М. От мозаик Пенроуза к надежным шифрам: Пер. с англ. -
М.: Мир, 1993. - 416 с.
34. Falconer К. J. The Geometry of Fractal Sets. - Cambridge: Cambridge
Univ. Press, 1985.
35. Davaney R. L. Chaos, Fractals and Dynamics. - N. Y.: Addison-Wesley,
1990.
36. Barnsley M. Fractals Everywhere. - Boston: Academic Press, 1988.
37. Гуревич В., Волмэн Г Теория размерности: Пер. с англ. - М.: ИЛ,
1948. - 232 с; 2-е изд., испр. - М.: Едиториал УРСС, 2004. - 304 с.
38. Хаусдорф Ф. Теория множеств/Пер. с нем.; Под ред. и с доп. П.С.
Александрова и А.Н. Колмогорова. - М.-Л.: ОНТИ, 1937. - 304 с; 2-е изд., испр. -
М.: Едиториал УРСС, 2004. - 304 с.
39. GrassbergerP., Procaccia L Characterization of Strange Attractors//Phys.
Rev. Lett. 1983. V. 50, № 5. P. 346-349.
40. Termonia Y., Alexandrowicz Z. Fractal Dimension of Strange Attractors
from Radius Versus Size of Arbitrary Cluster//Phys. Rev. Lett. 1983. V. 51, № 14.
P. 1265-1268.
789
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
41. Монин А. С, Якобсон М. В. О локальной фрактальности//ДАН
СССР. 1986. Т. 287, № 4. С. 795-798.
42. HausdorffF. Dimension und Ausseres Mass//Math. Annal. 1919. B. 79.
S. 157-179.
43. Besicovitch A. S. On the Sum of Digits of Real Numbers Represented in
the Dyadic System (On Set of Fractional Dimension H)//Math. Annal. 1934.
B. 110, №3. S. 321-330.
44. Мандельброт Б. Б. Фракталы и возрождение теории итераций//Рих-
тер П. X., Пайтген X. -О. Красота фракталов. - М.: Мир, 1993. - С. 131-140.
45. Федер Е. Фракталы: Пер. с англ. - М.: Мир, 1991. - 262 с.
46. Ramstein G., Raffy M. Algorithms d'analise Fractal de Contours en
Teledetectionet Applications//Int. J. Remote Sens. 1990. V. 11, № 2. P. 191-208.
47. Koch H. von. Sur une Courbe Continue sans Tangente Obtenue par une
Construction Geometrique Elementaire//Arkiv for Matematik, Astronomi och
Fysik. 1904. V. 1. P. 681-704.
48. BakP. The Devil's Staircase//Phys. Today. 1986. V. 39, № 1. P. 38-45.
49. Farmer J. D., Ott E., Yorke J. A. The Dimension of Chaotic Attractors//
Physica D. 1983. V. 7, № 1-3. P. 153-170.
50. Мун Ф. Хаотические колебания: Пер. с англ. - М.: Мир, 1990. -
312 с.
51. Дмитриев А. С, Кислое В. Я. Стохастические колебания в
радиофизике и электронике. - М.: Наука, 1989. - 280 с.
52. Mandelbrot В. В. How Long Is the Coast of Britain? Statistical Self-
Similarity and Fractional Dimension//Science. 1967. V. 156, № 3775. P. 636-638.
53. Wolf A., Swift J. В., Swinney H. L., Vastano J. A. Determining Lyapunov
Exponents from a Time Series//Physica D. 1985. V. 16, № 3. P. 285-317.
54. Grassberger P., Procaccia I. Measuring the Strangeness of Strange
Attractors//Physica D. 1983. V. 9, № 1-2. P. 189-208.
55. Malraison G., Atten P., Berge P., Dubois M. Dimension of Strange
Attractors: An Experimental Determination of the Chaotic Regime of Two
Convective Systems//! Phys. Lett. 1983. V. 44, № 22. P. L897-L902.
56. Ciliberto S., Gollub J. P. Chaotic Mode Competition in Parametrical by
Forced Surface Waves//! Fluid Mech. 1985. V. 158. P. 381-398.
57. Moon F. C, Li G. -X. The Fractal Dimension of the Two-Well Potential
Strange Attractors//Physica D. 1985. V. 17, № 1. P. 99-108.
58. Мандельброт Б. Б. Самоаффинные фрактальные множества//Фрак-
талы в физике/Пер. с англ.; Под ред. Я. Г. Синая и И. М. Халатникова. -
М.: Мир, 1988. С. 9-47.
59. Paladin G, VulpianiA. Anomalous Scaling Laws in Multifractal Objects//
Phys. Rep. 1987. V. 156, № 4. P. 147-225.
60. Schertzer D., Lovejoy S. Hard and Soft Multifractal Processes//Physica
A. 1992. V. 185, № 1-4. P. 187-194.
61. GuckenheimerJ., Buzyna G. Dimension Measurements for Geostrophic
Turbulence//Phys. Rev. Lett. 1983. V. 51, № 16. P. 1438-1441.
790
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
62. Badii Я, PolitiA. Hausdorff Dimension and Uniformity Factor of Strange
Attractors//Phys. Rev. Lett. 1984. V. 52, № 19. P. 1661-1664.
63. Бадии Р., Политы А. Численное исследование неоднородных фрак-
талов//Фракталы в физике/Пер. с англ.; Под ред. Я. Г. Синая и И. М. Ха-
латникова. - М.: Мир, 1988. С. 632-637.
64. RenyiA. Probability Theory. - Amsterdam: North-Holland, 1970. - 238 p.
65. Grassberger P., Procaccia I. Dimensions and Entropies of Strange
Attractors from a Fluctuating Dinamics Approach//Physica D. 1984. V. 13, № 1.
P. 34-54.
66. Kaplan J. L., Yorke J. A, Chaotic Behaviour in Multidimensional
Difference Equations. - Lecture Notes in Mathematics. - Berlin: Springer-
Verlag, 1978. V. 730. P. 228.
67. RysselD. A., Hansen J. D., OttE. Dimension of Strange Attractors//Phys.
Rev. Lett. 1980. V. 45, № 14. P. 1175-1178.
68. Xenon M. A. A Two-Dimensional Map with a Strange Attractor//
Commun. Math. Phys. 1976. V. 50, № 1. P. 69-77.
69. Zaslavsky G. M. The Simplest Case of a Strange Attractor//Phys. Lett.
A. 1978. V. 69, № 3. P. 145-147.
70. Abraham N., Albano A. M., Das В., DeGuzman G. et al. Calculating the
Dimension of Attractors from Small Data Sets//Phys. Lett. A. 1986. V. 114, № 5.
P. 217-221.
71. LorenzE. N. Deterministic Non-Periodic Flow//J. Atmos. Sci. 1963.
V. 20, № 1. P. 130-141.
72. Linsay P. A. Period Doubling and Chaotic Behavior in a Driven,
Anharmonic Oscillator//Phys. Rev. Lett. 1981. V. 47, № 19. P. 1349-1352.
73. Maskey M. C, Glass L. Oscillation and Chaos in Physiological Control
Systems//Science. 1977. V. 197, № 4300. P. 287-289.
74. Takens F. Detecting Strange Attractors in Turbulence//Dynamical
Systems and Turbulence. - Lecture Notes in Mathematics. - Berlin: Springer-
Verlag, 1981. V. 898. P. 366-381.
75. Malraison G., Atten P., Berge P., Dubois M. Dimension of Strange
Attractors: An Experimental Determination of the Chaotic Regime of Two
Convective Systems//! Phys. Lett. 1983. V. 44, № 8. P. 897-902.
76. Blacknell D., Oliver C. J. Recognizing Chaos in Radar Images//! Phys.
D. 1994. V. 27, № 8. P. 1608-1618.
77. Потапов А. А. Детерминированный хаос в радиолокационных
изображениях земной поверхности и фрактальные сигнатуры распознавания//
Тез. докл. LII Научной сессии, поев. Дню радио. - М.: Изд. РНТО РЭС
им. А. С. Попова, 1997. Т. 1. С. 169-170.
78. Колмогоров А. Н. О сохранении условно периодических движений
при малом изменении функции Гамильтона//ДАН СССР. 1954. Т. 98, № 4.
С. 527-530.
79. Grassberger P., Procaccia I. Estimation of the Kolmogorov Entropy from
a Chaotic Signal//Phys. Rev. A. 1983. V. 29, № 4. P. 2591-2593.
791
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
80. Малинецкий Г. Г., Потапов А. Б. О вычислении размерностей
странных аттракторов. - М.: Изд. ИПМатем. АН СССР, 1987. - Препринт № 101.
81. Малинецкий Г. Г., Потапов А. Б. О вычислении размерностей
странных аттракторов//Журн. вычисл. матем. и матем. физ. 1988. Т. 28, № 7.
С. 1021-1037.
82. Franaszek M. Optimized Algorithm for the Calculation of Correlation
Integrals//Phys. Rev. A. 1989. V. 39, № 10. P. 5440-5443.
83. Потапов А. Б. Программы вычисления корреляционного
показателя и оценки обобщенной энтропии по временному ряду. - М.: Изд.
ИПМатем. АН СССР, 1991. - Препринт № 27.-31 с.
84. Малинецкий Г. Г. Синергетика, предсказуемость и
детерминированный хаос//Пределы предсказуемости / Под ред. Ю. А. Кравцова. - М.:
ЦентрКом, 1997. С. 78-139.
85. Fraser A. M.y Swinney H. L. Independent Coordinates for Strange
Attractors from Mutual Information//Phys. Rev. A. 1986. V. 33, № 2. P. 1131-
1140.
86. Fraser A. M. Information and Entropy in Strange Attractors//IEEE
Trans. 1989. V. IT-35, N2. P. 245-262.
87. Fraser A. M. Reconstructing Attractors from Scalar Time Series: a
Comparison of Singular System and Redundancy Criteria//Physica D. 1989.
V. 34, № 3. P. 391-404.
88. Liebert W.y Schuster H. G. Proper Choice of the Time Delay for the
Analysis of Chaotic Time Series//Phys. Lett. A. 1989. V. 142, № 2-3. P. 107-
111.
89. AlbanoA. M., Muench J., Schwartz C. et al. Singular-Value Decomposition
and the Grassberger-Procaccia Algorithm//Phys. Rev. A. 1988. V. 38, № 6.
P. 3017-3026.
90. PawelzikK., Schuster H. G. Generalised Dimensions and Entropies from
a Measured Time Series//Phys. Rev. A. 1987. V. 35, № 1. P. 481-484.
91. Schuster H. G. Information Content of Chaotic Signals//Physica Scripta.
1989. V. 40, № 3. P. 367-372.
92. Theiler J. Spurious Dimensions from Correlation Algorithm Applied to
Limited Time-Series Data//Phys. Rev. A. 1986. V. 34, № 3. p. 2427-2432.
93. Smith L. A. Intrinsic Limits on Dimension Calculations//Phys. Lett. A.
1988. V. 133, №6. P. 283-288.
94. Mayer-Kress C. Application of Dimension Algorithms to Experimental
Chaos//Directions in Chaos. - Singapoure: World Scientific, 1987. P. 122-147.
95. Ruelle D. Deterministic Chaos: the Science and the Fiction//Proc. Roy.
Soc. (London). 1990. V. A427, № 1873. P. 241-248.
96. Abarbanel H. D. L, Brown R., Sidorovich J. J., Tsimring L. Sh. Analysis
of Observed Chaotic Data in Physical Systems//Rev. Mod. Phys. 1993. V. 65,
№4. P. 1331-1390.
97. Дымников В. П., Филатов А. Н. Основы математической теории
климата. - М.: ВИНИТИ, 1994. - 256 с.
792
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
98. Лесин Я. Б. Характеристические показатели Ляпунова и гладкая эр-
годическая теория//УМН. 1977. Т. 32, № 4 (196). С. 55-112.
99. Потапов А. А., Колесников А. И. Корреляционные характеристики
изображений земной поверхности//Радиотехника и электроника. 1993.
Т. 38, № 7. С. 1270-1279.
100. Потапов А. А., Колесников А. И. Спектральные характеристики
изображений земной поверхности//Радиотехника и электроника. 1993.
Т. 38, № 10. С. 1851-1862.
101. Lee С. -К, Moon F. С. An Optical Technique for Measuring Fractal
Dimensions of Planar Poincare Maps//Phys. Lett. A 1986. V. 114, № 5. P. 222-226.
102. Аллен Ky Клуатр М. Оптические преобразования Фурье фракта-
лов//Фракталы в физике: Пер. с англ.; Под ред. Я. Г. Синая и И. М. Ха-
латникова. - М.: Мир, 1988. С. 91-97.
103. Weitz D. A.f Oliveha М. Fractal Structures Formed by Kinetic
Aggregation of Aqueous Gold Golloids//Phys. Rev. Lett. 1984. V. 52, № 16.
P. 1433-1436.
104. Wavelet Analysis and Its Applications. - San Diego: Academ. Press Inc.,
1992. V. 1,2.
105. Muzy /. F., Bacry E., Arneodo A. Wavelets and Multifractal Formalism
for Singular Signals: Application to Turbulent Data//Phys. Rev. Lett. 1991. V. 67,
№ 25. P. 3515-3518.
106. Добеши Я. Десять лекций по вейвлетам: Пер. с англ.; Под ред. А.П.
Петухова. - М.: Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001.
- 464 с.
107. Mandelbrot В. B.f Wallis J. R. Noah, Joseph, and Operational
Hydrology//Water Resour. Res. 1968. V. 4, № 5. P. 909-918.
108. Hurst H. E., Black R. P., Simaika Y. M. Long-Term Storage: An
Experimental Study. - L.: Constable, 1965.
109. Гумбель Э. Статистика экстремальных значений: Пер с англ.; Под
ред. Д. М. Чибисова. - М.: Мир, 1965. - 452 с.
110. Mandelbrot В. В., Wallis J. R. Some Long-Run Properties of Geophysical
Records//Water Resours. Res. 1969. V. 5, № 2. P. 321-340.
111. Wiener N. Differential-Space//! Math. Phys. Mass. Inst. Technol. 1923.
V. 2. P. 131-174.
112. Mandelbrot В. В., Van Ness J. W. Fractional Brownian Motions,
Fractional Noises and Applications//SIAM Rev. 1968. V. 10, № 4. P. 422-437;
см. также Манделъброт Б. Фракталы, случай и финансы: Пер. с франц.; Под
ред. А.Р. Логунова. - М.: Ижевск: НИЦ «Регулярная и хаотическая
динамика», 2004. - 256 с.
113. Bassingthwaighte J. В., Beyer R. P. Fractal Correlation in Heterogeneous
Systems//Physica D. 1991. V. 53, № 1. P. 71-84.
114. Voss R. F. Fractals in Nature: from Characterization to Simulation//
The Science of Fractal Images / Ed. by H. O. Peitgen, D. Saupe. - N. Y.:
Springer, 1988. P. 21-70.
793
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
115. Mandelbrot В. В., Wallis J. R. Computer Experiments with Fractional
Gaussian Noises. Part 1. Averages and Variances//Water Resour. Res. 1969. V. 5,
№ 1. P. 228-241.
116. Item. Part 2. P. 242-259.
117. Item. Part 3. P. 260-267.
118. Mandelbrot В. В. A Fast Fractional Gaussian Noise Generator//Water
Resour. Res. 1971. V. 7, № 3. P. 543-553.
119. Gefen Y, AharonyA., Alexanders. Anomalous Diffusion on Percolating
Clusters//Phys. Rev. Lett. 1983. V. 50, № 1. P. 77-80.
120. Voss R. F. Random Fractal Forgeries//Fundamental Algorithms in
Computer Graphics/ Ed. by R. A. Earnshaw. - Berlin: Springer-Verlag. 1985.
P. 805-835.
121. Mandelbrot В. В. Fractals in Physics: Squig Clusters, Diffusions, Fractal
Measures, and the Unicity of Fractal Dimensionality//!. Stat. Phys. 1984. V. 34,
№ 5/6. P. 895-930.
122. Феллер В. Введение в теорию вероятностей и ее приложения: Пер.
с англ. - М.: Мир, 1967. Т. 1. - 500 с. - Т. 2. - 752 с.
123. Shlesinger M. F, West В. J., KlafterJ. Levy Dynamics to turbulence//
Phys. Rev. Lett. 1987. V. 58, № 11. P. 1100-1103.
124. Zaslavsky G. M., Tippet M. K. Connection between Recurrence-Time
Statistics and Anomalous Transport//Phys. Rev. Lett. 1991. V. 67, № 23. P. 3251-
3254.
125. Shlesinger M. R, Zaslavsky G. M., KlafterJ. Strange Kinetics//Monthly
Nature. 1993. V. 1, № 5. P. 45-51.
126. Feng S., Golubovie L., Zhang Y. -C. Directed Wave Propagation in
Random Media: Superdiffusion and Phase Transition//Phys. Rev. Lett. 1990.
V.65, №8. P. 1028-1031.
127. Странные аттракторы: Сб. статей. Пер. с англ.; Под ред Я. Г.
Синая, Л. П. Шильникова. - М.: Мир, 1981. - 256 с.
128. Berry М. V., Lewis Z. V. On The Weierstrass - Mandelbrot Fractal
Function//Proc. R. Soc. (London). 1980. V. A370, № 1743. P. 459-484.
129. Mauldin R. D. On the Hausdorff Dimension of Graphs and Random
Recursive Objects//Dimensions and Entropies in Chaotic Systems/ Ed. by
G. Mayer-Kress. - Berlin: Springer-Verlage, 1986. P. 28-33.
130. Oldham K. B.y SpanierJ. The Fractional Calculus. - N. Y.: Academic
Press, 1974. -234 p.
131. Самко С. Г., Килбас А. А.у Маричев О. И. Интегралы и
производные дробного порядка и некоторые их применения. - Минск: Наука и
техника, 1987. - 688 с.
132. Брычков Ю. А., Прудников А. П. Интегральные преобразования
обобщенных функций. - М.: Наука, 1977. - 288 с.
133. Нигматуллин Р. Р. Дробный интеграл и его физическая интерпре-
тация//Теор. и мат. физика. 1992. Т. 90, № 3. С. 354-368.
794
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
134. Fox С. The G and H Functions as Symmetrical Fourier Kernels//Trans.
Amer. Math. Soc. 1961. V. 98, № 3. P. 395-429.
135. Mathai A. M., Saxena R. K. The H-function with Applications in
Statistics and Other Disciplines. - New Delhi: Wiley Eastern Limited, 1978. -
192 p.
136. Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды.
Допонительные главы. - М.: Наука, 1986. - 800 с.
137. Engheta N. On the Role of Fractional Calculus in Electromagnetic
Theory//IEEE Antennas and Propagation Magazine. 1997. V. 39, № 4. P. 35-46.
138. BouchaudJ. -P., Georges A. Anomalous Diffusion in Disordored Media:
Statistical Mechanisms, Models and Physical Applications//Phys. Rep. 1990.
V. 195, № 4&5. P. 127-293.
139. Isichenko M. B. Percolation, Statistical Topography, and Transport in
Random Media//Rev. Mod. Phys. 1992. V. 64, № 4. P. 961-1043.
140. FogedbyH. C. Levy Flights in Random Environments//Phys. Rev. Lett.
1994. V. 73, № 19. P. 2517-2520.
141. Чукбар К. В. Стохастический перенос и дробные производные//
ЖЭТФ. 1995. Т. 108, № 5(11). С. 1875-1884.
142. Schneider W. R., Wyss W. Fractional Diffusion and Wave Equations//
J. Math. Phys. 1989. V. 30, № 1. P. 134-144.
143. Friedrich C. Relaxation and Retardation Functions of the Maxwell
Model with Fractional Derivates//Rheologica Acta. 1991. V. 30, № 2. P. 151-
158.
144. Glockle W. G., Nonnenmacher T. F. Fractional Integral Operators and
Fox Functions in the Theory of Viscoelasticity//Macromolecules. 1991. V24,
№ 24. P. 6426-6434.
145. Glockle W. G} Nonnenmacher T. F. Fox Function Representation of
Non- Debye Relaxation Processes//! Stat. Phys. 1993. V. 71. № 3/4. P. 741-
757.
146. Metzler R.} Glockle W. G., Nonnenmacher T. F. Fractional Model
Equation for Anomalous Diffusion//Physica A. 1994. V. 211, № 1. P. 13-24.
147. МонинА. С. Уравнение турбулентной диффузии//ДАН СССР. 1955.
Т. 105, № 2. С. 256-259.
148. Монин А. С.у Яглом А. М. Статистическая гидромеханика. Ч. 2. -
М.: Наука, 1967. - 720 с.
149. Золотарев В. М., Учайкин В. В., Саенко В. В. Супердиффузия и
устойчивые законы//ЖЭТФ. 1999. Т. 115, № 4. С. 1411-1425.
150. Леей П. Стохастические процессы и броуновское движение: Пер.
с франц.; Под ред. Н. Н. Ченцова. - М.: Наука, 1972. - 375 с.
151. Золотарев В. М. Одномерные устойчивые распределения. - М.:
Мир, 1983. - 304с.
152. Гнеденко Б. В., Колмогоров А. Н. Предельные распределения для
сумм независимых случайных величин. - М. -Л.: ГИТТЛ, 1949. - 264 с.
795
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
153. Крянев А. В., Шихов С. Б. Вопросы математической теории
реакторов. - М.: Энергоатомиздат, 1973. - 280 с.
154. Кейз К, Цвайфелъ П. Линейная теория переноса: Пер. с англ.; Под
ред. М. В. Масленникова. - М.: Мир, 1972. - 384 с.
155. Учайкин В. В. Субдиффузия и устойчивые законы//ЖЭТФ. 1999.
Т. 115, № 6. С. 2113-2132.
156. Большее Л. Н., Золотарев В. М., Кедрова Е. С, Рыбинская М. А.
Таблицы устойчивых односторонних распределений//Теория
вероятностей и ее применения. 1970. Т. XV, № 2. С. 309-319.
157. Климонтович Ю. Л. Статистическая теория открытых систем. - М.:
Янус. 1995. - Т. 1. - 624 с; 1999. - Т. 2. - 440 с; 2001. - Т. 3. -508 с.
158. Кобелев В. Л, Кобелева О. Л., Кобелев Я. Л., Кобелев Л. Я. О
диффузии через фрактальную поверхность//ДАН. 1997. Т. 355, № 3. С. 326-327.
159. Кобелев В. Л., Романов Е. П., Кобелев Я. Л., Кобелев Л. Я. Недеба-
евская релаксация и диффузия во фрактальном пространстве//ДАН. 1998.
Т. 361, № 6. С. 755-758.
160. Кобелев В. Л., Романов Е. П., Кобелев Л. Я.у Кобелев Я. Л.
Релаксационные и диффузионные процессы во фрактальных пространствах//Из-
вестия РАН. Серия физическая. 1998. Т. 62, № 12. С. 2401-2408.
161. Кобелев Я. Л., Кобелев Л. Я., Романов Е. П. Автоволновые
процессы при нелинейной фрактальной диффузии//ДАН. 1999. Т. 369, № 3.
С. 332-333.
162. Васильев В. А., Романовский Ю. М.у Яхно В. Г. Автоволновые
процессы. - М.: Наука, 1987. - 240 с.
163. Sayles R. S., Thomas Т R. Surface Topography as a Nonstationary
Random Process//Nature. 1978. V. 271, № 5644. P. 431-434.
164. Berry M. V., Hannay J. H. Topography of Random Surfaces//Nature.
1978. V. 273, № 5663. P. 573.
165. Woss R. F. Random Fractals: Characterization and Measurement//
Scaling Phenomena in Disordered Systems/ Ed. by R. Pynn & A. Skjeltorp. N. Y.:
Plenum Press. 1985. P. 1-11.
166. Sayles R. S., Thomas T. R. Reply to «Topography of Random Surfaces»
by M. V. Berry and J. H. Hannay//Nature. 1978. V. 273, № 5663. P. 573.
167. Burrough P. A. Fractal Dimensions of Landscapes and Other
Environmental Data//Nature. 1981. V. 294, № 5838. P. 240-242.
168. SchaeferD. W., Martin J. E., JViltziusR, CannellD. S. Fractal Geometry
of Colloidal Aggregates//Phys. Rev. Lett. 1984. V. 52, № 26. P. 2371-2374.
169. BaleH. D., Schmidt P. Ж Small-Angle X-Ray-Scattering Investigation
of Submicroscopic Porosity with Fractal Properties//Phys. Rev. Lett. 1984. V. 53,
№ 6. P. 596-599.
170. Sinha S. К Scattering from Fractal Structures//Physica D. 1989. V. 38,
№ 1-3. P. 310-314.
171. AvnirD., Farin D., PfeiferP. Molecular Fractal Surfaces//Nature. 1984.
V. 308, № 5956. P. 261-263.
796
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
172. KatzA. J.} Thompson A. Y. Fractal Sandstone Pores: Implications for
Conductivity and Pore Formation//Phys. Rev. Lett. 1985. V. 54, № 12. P. 1325-
1328.
173. Roberts J. N. Comment about Fractal Sandstone Pores//Phys. Rev. Lett.
1986. V. 56, № 19. P. 2111.
174. KatzA. J., Thompson A. Y Katz and Thompson Respond//Phys. Rev.
Lett. 1986. V. 56, № 19. P. 2112.
175. Иванова В. С, БаланкинА. С, Бунин И. Ж., Оксогоев А. А.
Синергетика и фракталы в материаловедении. - М.: Наука, 1994. - 383 с.
176. Stiassnie M., Agnon Y} ShemerL. Fractal Dimensions of Random Water
Surfaces//Physica D. 1991. V. 47, № 3. P. 341-352.
177. Mikolas M. On The Recent Trends in the Development, Theory and
Applications of Fractional Culculus//Fractional Calculus and its Applications /
Ed. by B. Ross//Lecture Notes in Mathematics. - Berlin: Springer-Verlag, 1975.
V. 457. P. 357-375.
178. Angon Y, Stiassnie M. Remote Sensing of the Roughness of Fractal Sea
Surfaces//! Geoph. Res. 1991. V. 96, № C7. P. 12773-12779.
179. Elgar S., Mager-Kress G. Observation of Fractal Dimension of Deep
and Shallow Water Ocean Surface Gravity Waves//Physica D. 1989. V. 37, № 1.
P. 104-108.
180. Заславский Г. М., Жаркое Е. А. Фрактальные свойства зон
обрушения волн на поверхности моря//ДАН СССР. 1987. Т. 294. С. 1362-1366.
181. Umberger D. К., Farmer J. D. Fat Fractals on Energy Surface//Phys.
Rev. Lett. 1985. V. 55, № 7. P. 661-664.
182. Покровская И. В., Шарков Е. А. Пенная активность на морской
поверхности как марковский случайный процесс//ДАН СССР. 1987. Т. 293,
№5. С. 1108-1111.
183. Басе Ф. Г., Фукс И. М. Рассеяние волн на статистически
неровной поверхности. - М.: Наука, 1972. - 424 с.
184. Потапов А. А. Синтез изображений земных покровов в
оптическом и миллиметровом диапазонах волн: Дис. ... доктора физ. -мат. наук. -
М.: ИРЭ РАН, 1994. - 436 с.
185. Потапов А. А.у Чеканов Р. Н. Рассеяние волн фрактальными по-
верхностями//Тез. докл. LII Научной сессии, поев. Дню радио. - М.: Изд.
РНТО РЭС им. А. С. Попова, 1997. - Т. 1. С. 171-172.
186. Потапов А. А. Фракталы в радиофизике и радиолокации//Тез. докл.
Региональной XXIII конф. по распространению радиоволн. - СПб.: Изд.
СПГУ, 1997. С. 25.
187. Джейкмен Э. Рассеяние на фракталах//Фракталы в физике/Пер.
с англ.; Под ред. Я. Г. Синая и И. М. Халатникова. - М.: Мир, 1988.
С. 82-90.
188. Berry М. К Diffractals//J. Phys. A. 1979. V. 12, № 6. Р. 781-797.
189. Barrick D. E. Wind Dependence of Quasy-Specular Microwave Sea
Scatter//IEEE Trans. 1974. V. AP-22, № 1. P. 135-136.
797
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
190. BaharE., Barrick D. E., FitzwaterM. A. Computations of Scattering Cross
Section for Composite Surfaces and the Specifications of the Wavenumber Where
Spectral Splitting Occurs//IEEE Trans. 1983. V. AP-31, № 5. P. 698-709.
191. Philips 0. M. Spectral and Statistical Properties of the Equilibrium Range
in Wind-Generated Gravity Waves//J. Fluid. Mech. 1985. V. 156. P. 505-531.
192. Chelton D. B.f McCabe P. J A Review of Satellite Altimeter
Measurement of Sea Surface Wind Speed//J. Geoph. Res. 1985. V. 90, № C3.
p. 4707-4720.
193. Jakeman E. Scattering by a Corrugated Random Surface with Fractal
Slope//J. Phys. A. 1982. V. 15, № 2. P. L55-L59.
194. Jakeman E. Fresnel Scattering by a Corrugated Random Surface with
Fractal Slope//J. Opt. Soc. Am. 1982. V. 72, № 8. P. 1034-1041.
195. Rino C. L. A Power Low Phase Screen Model for Ionosphere
Scintillation//Radio Sci. 1979. V. 14, № 6. P. 1135-1155.
196. Гардинер К. В. Стохастические методы в естественных науках. -
М.: Мир, 1986. - 528 с.
197. Потапов А. А. Функциональный подход к корреляции радиоволн,
рассеянных анизотропной шероховатой поверхностью//Электромагнитные
волны и электронные системы. 1996. Т. 1, № 1. С. 32-37.
198. Потапов А. А. Обобщенный коррелятор полей, рассеянных
шероховатыми поверхностями//Радиотехника и электроника. 1996. Т. 41, № 7.
С. 816-823.
199. Потапов А. А. Рассеяние миллиметровых радиоволн
изотропными и анизотропными хаотически неровными поверхностями и
пространственно-частотные функции корреляции//Электромагнитные волны и
электронные системы. 1997. Т. 2, № 5. С. 68-75.
200. Taylor L. S., Infosino С. I. Diffraction Theory of Optical Scintillatoin
due to Turbulent Layers//! Opt. Soc. Am. 1975. V. 65, № 1. P. 78-84.
201. Jakeman E., Rusey P. N. Significance of k Distributions in Scattering
Experiments//Phys. Rev. Lett. 1978. V. 40, № 9. P. 546-550.
202. Jakeman E. On the Statistics of K-Distributed Noise//J. Phys. A. 1980.
V. 13, № 1. P. 31-48.
203. Jakeman E. Fraunhofer Scattering by a Sub-Fractal Diffuser//Optica
Acta. 1983. V. 30, № 9. P. 1207-1212.
204. Walker J. G., Jakeman E. Observation of Sub-Fractal Behaviour in a
Light Scattering System//Optica Acta. 1984. V. 31, № 10. P. 1185-1196.
205. Jakeman E., Mc WhirterJ. G. Non-Gaussian Scattering by a Random
Phase Screen//Appl. Phys. B. 1981. V. 26, № 2. P. 125-131.
206. Шкуратов Ю. Г. Фрактоиды и фотометрия твердых поверхностей
небесных тел//Астрономический вестник. 1995. Т. 29, № 6. С. 483-496.
207. Шкуратов Ю. Г. Фотометрические свойства физических фракта-
лов//Оптика и спектроскопия. 1995. Т. 79, № 1. С. 110-117.
208. Beckman P., Spizzichino A. The Scattering of Electromagnetic Waves
from Rought Surfaces. - N. Y.: Pergamon Press, 1963. - 503 p.
798
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
209. JaggardD. L., Sun X. Fractal Surface Scattering: A Generalized Rayleigh
Solution//! Appl. Phys. 1990. V. 68, № 11. P. 5456-5462.
210. JaggardD. L., MickelsonA. R. The Reflection of Electromagnetic Waves
from Almost Periodic Structures//Appl. Phys. 1979. V. 19, № 4. P. 405-412.
.211. Mickelson A. R., Jaggard D. L. Electromagnetic Wave Propagation in
Almost Periodic Media//IEEE Trans. 1979. V. AP-27, № 1. P. 34-40.
212. Jaggard D. L., Sun X. Scattering from Fractally Corrugated Surfaces//
J. Opt. Soc. Am. A. 1990. V. 7, № 6. P. 1131-1139.
213. Chen M. R, Fung A. K. A Numerical Study of the Regions of Validity
of the Kirchhoff and Small-Perturbation Rough Surface Scattering Models//
Radio Sci. 1988. V. 23, № 2. P. 163-170.
214. Ivanova K, Yordanov O. I. Bistatic Properties of KirchofF Difractals/^
Radio Sci. 1996. V. 31, № 6. P. 1901-1906.
215. Soto-GrespoJ. M., Nieto-Vesperinas M. Electromagnetic Scattering from
Very Rough Random Surfaces and Deep Reflection Gratings//J. Opt. Soc. Am.
A. 1989. V. 6, № 3. P. 367-384.
216. Бъерно Л., Сан Ш. Применение приближения Кирхгофа к задачам
рассеяния на упругих неровных поверхностях//Акуст. журн. 1995. Т. 41,
№ 5. С. 725-736.
217. Jordan D. L., Rollins R. С, Jakeman E. Experimental Measurement of
Non-Gaussian Scattering by a Fractal Diffuser//Appl. Phys. B. 1983. V. 31, № 1.
P. 179-186.
218. Teixeira J. Experimental Methods for Studying Fractal Aggregates//On
Growth and Form / Ed. by H. E. Stanley and N. Ostrovsky. - Boston: NijhofF,
1986. P. 145-162.
219. Berry M. V., Blackwell Т. М. Difractal Echoes/A Phys. A. 1981. V. 14,
№ 11. P. 3101-3110.
220. Berry M. V. The Statistical Properties of Echoes Diffracted from Rough
Surfaces//Philosophical Transactions of the Royal Society of London A. 1973.
V. 273, № 1237. P. 611-654.
221. Андреев Г. А., Потапов А. А. Влияние хаотических неровностей
поверхности на отраженный импульсный сигнал миллиметровых волн //
Радиотехника и электроника. 1986. Т. 31, № 7. С. 1405-1414.
222. Andreyev G. A., PotapovA. A. The Effect of Chaotic Surface Roughness
on Radio Impulce Scattering//Proc. URSI Int. Symp. on Electromagnetic
Theory. - Budapest: Akademiai Kiado. 1986. Pt. A. P. 235-237.
223. Потапов А. А. Применение модулированных ММВ для
формирования и идентификации изображений//Радиотехника. 1989. № 12. С. 61-64.
224. Потапов А. А. О дистанционном измерении высоты и
характеристик хаотических покровов по частотной функции когерентности//Тез.
докл. Всесоюзн. конф. «Применение дистанционных радиофизических
методов в исследованиях природной среды». - Ереван: АН Арм. ССР, 1990.
С. 122-123.
799
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
225. Потапов А. А. Дифракция модулированных волн на хаотической
поверхности с крупномасштабными неровностями//Тез. докл. X Всесо-
юзн. симп. по дифракции и распространению волн «СДВ-10». - М: Изд.
физич. общ-ва СССР. 1990. Т. 2. С. 183-186.
226. Потапов А. А. К применению методов теории систем и
преобразований для исследования задач рассеяния//Тез. докл Межд. науч. -техн.
конф. «Статистические методы в теории передачи и преобразования
информационных сигналов». - Киев: КНИГА. 1992. С. 85-86.
227. Павелъев В. А., Потапов А. А. Влияние земной поверхности на
структуру импульсного сигнала в диапазоне миллиметровых волн//Радио-
техника и электроника. 1994. Т. 39, № 4. С. 573-582.
228. Потапов А. А., Соколов А. 2?. Частотная функция когерентности
волнового поля, рассеянного шероховатой поверхностью с большим
параметром Рэлея//Радиотехника и электроника. 1996. Т. 41, № 9. С. 1071-1076.
229. Потапов А. А. Дис. ... канд. техн. наук. - М.: ИРЭ РАН, 1989. -
254 с.
230. Потапов А. А. Радиофизические эффекты при взаимодействии
электромагнитного излучения миллиметрового диапазона волн с
окружающей средой//Зарубежная радиоэлектроника. 1992. № 8. С. 36-76; № 9.
С. 4-28; № 11. С. 23-48; 1993. № 3. С. 36-48; № 7-9. С. 32-49; 1994. № 7/8.
С. 11-30; 1995. № 1. С. 27-36 (журнальный вариант монографии).
231. Потапов А. А., Опаленов Ю. В. Многолетние измерения в
диапазоне миллиметровых волн характеристик рассеяния земных покровов с
вертолета//Электромагнитные волны и электронные системы. 1997. Т. 2,
№ 3. С. 71-74.
232. Баренблатт Г. И. Подобие, автомодельность, промежуточная
асимптотика. - Л.: Гидрометеоиздат, 1982. - 256 с.
233. Обухов А. М. Турбулентность и динамика атмосферы. - Л.:
Гидрометеоиздат, 1988. - 414 с.
234. Неймарк Ю. И., Ланда П. С. Стохастические и хаотические
колебания. - М.: Наука, 1987. - 424 с.
235. Анищенко В. С. Сложные колебания в простых системах. - М.:
Наука, 1990.-312 с.
236. Потапов А. А., Соколов А. В., Чеканов Р. И. Применение теории
фракталов к изучению флуктуации на ММВ//Тез. докл. Научной сессии,
посвященной Дню радио. - М: Изд. РНТО РЭС им. А. С. Попова, 1997. -
Т. 1. С. 167-168.
237. Монин А. С.у ЯгломА. М. Статистическая гидромеханика: Теория
турбулентности. - СПб.: Гидрометеоиздат, 1992. - Т. 1. - 696 с.
238. Shivamoggi S. К. Multi-Fractal Aspects of the Fine-Scale Structure of
Temperature Fluctuation in Isotropic Turbulence//Phys. A. 1995. V. 221, № 4.
P. 460-477.
800
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
239. Васильев А, Н. Квантовополевая ренормгруппа в теории
критического поведения и стохастической динамике. - СПб.: Изд-во ПИЯФ, 1998.
- 774 с.
240. Анищенко В. С, Вадивасова Т. Е., Астахов В. В. Нелинейная
динамика хаотических и стохастических систем. - Саратов: Изд. СГУ, 1999. -
368 с.
241. Заславский Г. М. Стохастичность динамических систем. - М.:
Наука, 1984. - 272 с.
242. Рабинович М. И. Стохастические автоколебания и турбулентность//
УФН. 1978. Т. 125, № 1. С. 123-168.
243. Морозов А. Д., Драгунов Т. Н., Войкова С. А., Малышева О. В.
Инвариантные множества динамических систем в Windows. - М.: Эдиториал
УРСС, 1998. -240 с.
244. Hop/ E. Alzweigungen Einer Pereodisehen Lozung von Einer
Stationaren Lozung Eines Differentialgleichungssystems//Ber. Math. Phys.
Sachsishe Akademic der Wissenshaften, Leipzig. 1942. B. 94, P. 1-22.
245. Ландау Л, Д. К проблеме турбулентности//ДАН СССР. 1944. Т. 44,
№ 8. С. 339-342.
246. Ruelle D., Tokens F. On the Nature of Turbulence//Commun. Math.
Phys. 1971. V. 20, № 2. P. 167-192.
247. Hirsh H. W., Smale S. Differential Equations, Dynamic Systems and
Linear Algebra. - N. Y.: Academic Press, 1965.
248. Newhouse S., Ruelle D., Takens F. Occurence of Strange Axiom a
Attractors Near Quasi Periodic Flows on Tm, m > 3//Commun. Math. Phys. 1978.
V. 64, № 1. P. 35-40.
249. Feigenbaum M. J. Quantitative Universality for a Class of Nonlinear
Transformations//J. Stat. Phys. 1978. V. 19, № 1. P. 25-32.
250. Manneville P., Pomeau Y. Intermittency and the Lorenz Model//Phys.
Lett. 1979.V. 75A, № LP. 1-2.
251. Manneville P., Pomeau Y. Different Ways to Turbulence in Dissipative
Dynamical Systems//Physica D. 1980. V. 1, № 2. P. 219-226.
252. Рабинович М. И., Трубецков Д. И. Введение в теорию колебаний и
волн. - М.: Наука, 1984. - 432 с.
253. Mandelbrot В. В. Intermittent Turbulence in Self-Similar Cascades:
Divergence of High Moments and Dimension of the Carrier//J. Fluid Mech.
1974. V. 62, №2. P. 331-358.
254. Mandelbrot В. В. On the Geometry of Homogeneous Turbulence, with
Stress on the Fractal Dimension of the Iso-Surfaces of Scalars//J. Fluid Mech.
1975. V. 72, № 3. P. 401-416.
255. Sreenivasan K. R., Meneveau C. The Fractal Facets of Turbulence//!
Fluid Mech. 1986. V. 173. P. 357-386.
256. Maxworthy T. Buble Formation, Motion and Interaction in Hale-Shaw
Cell//! Fluid Mech. 1986. V. 173. P. 95-114.
801
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
257. КиоА. -Y., Corrsin S. Experiments on Internal Intermittency and Fine-
Structure Distribution Functions in Fully Turbulent Fluid//! Fluid Mech. 1971.
V. 50. P. 285-319.
258. Van Atta C. W., Antonia R. A. Reynolds Number Dependence of
Skewness and Flatness Factor of Turbulent Velocity Derivatives//Phys. Fluids.
1980. V. 23, № 2. P. 252-257.
259. Шертцер Д., Лавджой Ш. Обобщенная масштабная
инвариантность и анизотропные неоднородные фракталы в турбулентности//Фрак-
талы в физике: Пер. с англ.; Под ред. Я. Г. Синая и И. М. Халатникова. -
М.: Мир, 1988. С. 638-643.
260. Lovejoy S., Mandelbrot В. В. Fractal Properties of Rain, and a Fractal
Model//Tellus. 1985. V. 37 A, № 3. P. 209-232.
261. Lovejoy S., Scherzer D., Ladoy P. Fractal Characterization of
Inhomogeneuos Geophysical Measuring Networks//Nature. 1986. V. 319,
№ 60482. P. 43-44.
262. Lovejoy S., Scherzer D. Our Multifractal Atmosphere: a Unique
Laboratory for Non-Linear Dynamics//Phys. Can. 1990. V. 46, № 4. P. 62-71.
263. Груздев А. Н. Фрактальная структура озонометрической сети//Изв.
РАН. Физика атмосферы и океана. 1993. Т. 29, № 1. С. 140-142.
264. Паладин Дж., Вулъпиани А. Фрактальные модели двух- и
трехмерной турбулентности//Фракталы в физике: Пер. с англ.; Под ред. Я. Г.
Синая и И. М. Халатникова. - М.: Мир, 1988. С. 624-631.
265. Бершадский А. Г. Фрактальная структура турбулентных вихрей//
ЖЭТФ. 1989. Т. 96, № 2(8). С. 625-631.
266. Offen J. R., Kline S. J. A Proposed Model of the Bursting Process in
Turbulent Boundary Layer//J. Fluid Mech. 1975. V. 70, № 2. P. 209-228.
267. Бершадский А. Г. Виртуальное статистическое равновесие и
квазистационарные спектры однородной турбулентности//ЖЭТФ. 1988. Т. 94,
№9. С. 117-122.
268. Ландау Л. Д., Лившиц Е. М. Гидродинамика. - М.: Наука, 1988. -
736 с.
269. Липманн Г У. Взлет и падение идей в турбулентности//УФН. 1984.
Т. 143, № 4. С. 641-656.
270. HentselH. G. Е., Procaccia I. Fractal Nature of Turbulence as Manifested
in Turbulent Diffiision//Phis. Rev. A. 1983. V. 27, № 2. P. 1266-1269.
271. Зельдович Я. Б.} Молчанов С. А.у Рузмайкин А. А., Соколов Д. Д.
Перемежаемость в случайной среде//УФН. 1987. Т. 152, № 1. С. 3-32.
272. Булгаков С. А., Пономаренко П. В., Ямполъский Ю. М.
Фрактальный анализ KB сигналов, рассеянных мелкомасштабными ионосферными
неоднородностями//Изв. вузов. Радиофизика. 1995. Т. 38, № 6. С. 557-565.
273. Гинзбург В. Л. Распространение электромагнитных волн в плазме. -
М.: Наука, 1967.-684 с.
274. Рытое С. М., Кравцов Ю. А., Татарский В. И. Введение в
статистическую радиофизику. - М.: Наука, 1978. - Ч. II. - 464 с.
802
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
275. Ruelle D., Takens F. On the Nature of Turbulence//Commun. Math.
Phys. 1971. V. 20. P. 167.
276. Shlesinger M. F., West B. J., KlafterJ. Levy Dinamics to Turbulence//
Phys. Rev. Lett. 1987. V. 58, № 11. P. 1100-1103.
277. Goldburg W. L., Tong P.f Рак H К. A Light Scattering Study of
Turbulence//Physica D. 1989. V. 38, № 1-3. P. 134-140.
278. Meneveau C.} Sreenivasan K. R. Simple Multifractal Cascade Model for
Fully Developed Turbulence//Phys. Rev. Lett. 1987. V. 59, № 13. P. 1424-1427.
279. Кадыгров Е. Н., Потапов А. А. Некоторые результаты
использования радиоволн миллиметрового диапазона при наличии осадков//Труды
ЦАО. - М.: Гидрометеоиздат,1990. Вып. 168. С. 76-82.
280. Потапов А. А. О метеорологическом дешифрировании мезострук-
тур микроволновых изображений//Тез. докл. Межд. науч. -техн. конф.
«Статистические методы в теории передачи и преобразования
информационных сигналов». - Киев: Изд. КНИГА, 1992. С. 106-107.
281. Lovejoy S. Area-Perimeter Relation for Rain or Cloud Areas//Science.
1982. V. 216, № 4542. P. 185-187.
282. Lovejoy S., Schertzer D., Tsonis A. A. Functional Box-Counting and
Multiple Elliptical Dimensions in Rain//Science. 1987. V. 235, № 4792. P. 1036-
1038.
283. RysF. S., WaldvogelA. Fractal Shape of Hail Clouds//Phys. Rev. Lett.
1986. V. 56, №7. P. 784-787.
284. Рис Ф., Вальдфогель А. Анализ фрактальной размерности облаков
с мощными конвективными токами//Фракталы в физике /Пер. с англ.; Под
ред. Я. Г. Синая и И. М. Халатникова. - М.: Мир, 1988. С. 644-649.
285. WaldvogelA., Schmid W. The Kinetic Energy of Hailfalls. Part III:
Sampling Errors Inferred from Radar Data//J. of Applied Meteorology. 1982.
V. 21, №9. p. 1228-1238.
286. Hentschel H., Procaccia I. Relative Diffusion in Turbulent Media: The
Fractal Dimension of Clouds//Phys. Rev. A. 1984. V. 29, № 3. P. 1461-1470.
287. Hentschel H. G. E., Procaccia I. Intermittency Exponent in Fractally
Homogeneous Turbulence//Phys. Rev. Lett. 1982. V. 49, № 16. P. 1158-1161.
288. Hentschel H. G. E., Procaccia I. Fractal Nature of Turbulence an
Manifested in Turbulent Diffusion//Phys. Rev. A. 1983. № 3. P. 1266-1269.
289. Vecchi G., Labate D., Canavero F. Fractal Approach to Lightning
Radiation on a Tortuous Channel//Radio Sci. 1994. V. 29, № 4. P. 691-704.
290. Фелсен Л., Маркувиц Н. Излучение и рассеяние волн / Пер. с англ.;
Под ред. М. Л. Левина. - М.: Мир, 1978. - Т. 1. -547 с; Т. 2. - 555 с.
291. Le Vine D. M., MeneghiniR. Simulation of Radiation from Lighting Return
Strokes: The Effect of Tortuosity//Radio Sci. 1978. V. 13, № 5. P. 801-809.
292. Berry M. V., Percival I. C. Optics of Fractal Cluster Such as Smoke//
Optica Acta. 1986. V. 33, № 5. P. 577-591.
293. Meakin P. Fractal Aggregates in Geophysics//Rev. Geoph. 1991. V. 29,
№ 3. P. 317-354.
803
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
294. Colbeck J., Appleby L., Hardman E. J., Harrison R. M. The Optical
Properties and Morphology of Cloud-Processed Carbonaceous Smoke//J. Aerosol.
Sci. 1990. V. 21, № 4. P. 527-538.
295. Pearson A., Anderson R. W. Long-Range Pair Correlation and Its Role
in Small-Angle Scattering from Fractal Clusters//Phys. Rev. B. 1993. V. 48, № 9.
P. 5865-5885.
296. Wiltzius P. Hydrodinamic Behavior of Fractal Aggregates//Phys. Rev.
Lett. 1987. V. 58, № 7. P. 710-713.
297. Chen Z. -Y, Meakin P., Deutch J. M. Comment on «Hydrodinamic
Behavior of Fractal Aggregates»//Phys. Rev. Lett. 1987. V. 59, № 18. P. 2121.
298. Смирнов Б. М. Аэрогели//УФН. 1987. Т. 152, № 1. С. 133-157.
299. Лушников А. А., Негин А. Е., Пахомов А. В., Смирнов Б. М. Аэро-
гельные структуры в газе//УФН. 1991. Т. 161, № 2. С. 113-123.
300. Witten Т. A., Sander L. M. Diffusion-Limited Aggregation, a Kinetic
Critical Phenomenon//Phys. Rev. Lett. 1981. V. 47, № 20. P. 1400.
301. Meakin P. Formation of Fractal Clusters and Networks by Irreversible
Diffusion-Limited Aggregation//Phys. Rev. Lett. 1983. V. 51, № 13. P. 1119—
1122.
302. Kolb M.} Botet R., Jullien R. Scaling of Kinetically Growing Clusters//
Phys. Rev. Lett. 1983. V. 51, № 13. P. 1123-1126.
303. Михайлов Е. Ф., Власенко С. С. Образование фрактальных
структур в газовой фазе//УФН. 1995. Т. 165, № 3. С. 263-283.
304. Forrest S. R., Witten Г. A. Long-Range Correlatons in Smoke-Particle
Aggregates//! Phys. A. 1979. V. 12, № 5. P. L109-L118.
305. Ugarte D. Morphology and Structure of Graphitic Soot Particles
Generated in Arc-Discharge C60 Production//Chem. Phys. Lett. 1992. V. 198,
№ 6. P. 596-602.
306. Лушников А. А., Пахомов А. В., Черняева Г. А. Фрактальная
размерность агрегатов, образующихся при лазерном испарении металлов//ДАН
СССР. 1987. Т. 292, № 1. С. 86-88.
307. Михайлов Е. Ф., Власенко С. С. Экспериментальные исследования
фрактальных свойств растущих кластеров на примере иодида свинца//Хим.
физика. 1990. Т. 9, № 11. С. 1569-1573.
308. Михайлов Е. Ф., Власенко С. С Влияние анизотропии частиц на
рост фрактальных кластеров РЫ2 в газовой фазе//Хим. физика. 1991. Т. 10,
№ 7. С. 1017-1022.
309. Jullien R. A New Model of Cluster Aggregation//! Phys. A. 1986. V. 19,
№ 11. P. 2129-2136.
310. Vicsek Т., Family F. Dynamic Scaling for Aggregation of Clusters//Phys.
Rev. Lett. 1984. V. 52, № 19. P. 1669-1672.
311. Михайлов Е. Ф., Власенко С. С, Киселев А. А., Рышкевич Т. И.
Факторы структурной изменчивости частиц сажи//Изв. АН. Физика атмосферы
и океана. 1998. Т. 34, № 3. С. 345-356.
804
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
312. Potanin A. A. On the Model of Colloid Aggregates and Aggregating
Colloids/A Chem. Phys. 1992. V. 96, № 12. P. 9191-9200.
313. Де Рой Р., Потанин А. А., Ван дер ЭндеД., Меллема Й.
Реологические свойства слабоагрегированных коллоидов, вязкость структуры,
создаваемой установившимся потоком//Коллоидный журнал. 1994. Т. 56, № 4.
С. 549-559.
314. Андреев С. Д., Михайлов Е. Ф. Фрактальные системы и
исследования атмосферных аэрозолей//Изв. АН. Физика атмосферы и океана. 1996.
Т. 32, № 6. С. 808-817.
315. Емец Е. П., Новоселова А. Э., Полуэктов П. П. In situ-определение
фрактальной размерности аэрозольных частиц//УФН. 1994. Т. 164, № 9,
С. 959-966.
316. On Growth and Form. Fractal and Non-Fractal Pattern in Physics /
Ed. by H. E. Stanley, N. Ostrovsky. - Dordrecht: Martinus NijhofF Publishers,
1986. - 308 p.
317. Жульен Р. Фрактальные агрегаты//УФН. 1989. Т. 157, № 2. С. 339—
357.
318. Jullien R., Meakin P. Simple Models for the Restructuring of Three-
Dimensional Ballistic Aggregates//! Colloid Interface Sci. 1989. V. 127, № 1.
P. 265-272.
319. Чернов Л. А. Волны в случайно-неоднородных средах. М.: Наука,
1975. - 172 с.
320. Татарский В. А. Распространение волн в турбулентной
атмосфере. - М.: Наука, 1967. - 548 с.
321. Каток А. Б., Хасселблат Б. Введение в современную теорию
динамических систем: Пер. с англ. - М.: Факториал, 1999. - 768 с.
322. ИсимаруА. Распространение и рассеяние волн в
случайно-неоднородных средах: Пер. с англ. - М.: Мир, 1981. - Т. 1. - 280 с; Т. 2. - 320 с.
323. Ахманов С. А, Дьяков Ю. Е.у ЧиркинА. С. Введение в
статистическую радиофизику и оптику. - М.: Наука, 1981. - 640 с.
324. Кравцов Ю. А., Фейзулин 3. И.} Виноградов А. Г. Прохождение
радиоволн через атмосферу Земли. - М.: Радио и связь, 1983. - 224 с.
325. Апресян Л. А., Кравцов Ю. А. Теория переноса излучения:
Статистические и волновые аспекты. - М.: Наука, 1983. - 216 с.
326. Осташев В. Е. Распространение звука в движущихся средах. - М.:
Наука, 1992. - 208 с.
327. Jaggard D. L. Prolog to Special Section on Fractal in Electrical
Engineering//Proc. IEEE. 1993. V. 81, № 10. P. 1423-1427.
328. Chandra K, Thompson C. Ultrasonic Characterization of Fractal Media//
Proc. IEEE. 1993. V. 81, № 10. P. 1523-1533.
329. Savaidis S., Frangos P., Jaggard D. L., Hizanidis К Scattering from
Fractally Corrugated Surfaces with use of the Extended Boundary Condition
Method//! Opt. Soc. Am. A. 1997. V. 14, № 2. P. 475-485.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
330. Jaggard D. L. Fractal Electrodynamics: Wave Interaction with
Discretely Self-Similar Structures//Symmetry in Electrodynamics / Ed. by С
Baum, H. N. Kritikos. - L.: Taylor & Francis, 1995.
331. Jaggard D. L. On Fractal Electrodynamics//Recent Advances in
Electromagnetic Theory / Ed. by H. N. Kritikos, D. L. Jaggard. - N. Y.: Springer-
Verlag, 1990. P. 183-223.
332. Konotop V. U., Yordanov 0. L, Yurkevich I. V Wave Transmission
through a One-Dimensional Cantor-Like Fractal Medium//Europhys. Lett. 1990.
V. 12, № 6. P. 481-485.
333. Бори М., Вольф Э. Основы оптики: Пер. с англ.; Под ред. Г. П. Мо-
тулевич. - М.: Наука, 1973. - 720 с.
334. Kim Y., Jaggard D. L. Band-Limited Fractal Model of Atmospheric
Refractivity Fluctuation / J. Opt. Soc. Am. 1988. V. 5, № 4. P. 475-480.
335. Siggia E. D. Model of Intermittency in Three-Dimensional Turbulence//
Phys. Rev. A. 1978. V. 17, № 3. P. 1166-1176.
336. Richardson L. F. Atmospheric Diffusion Shown on a Distance-
Neighbour Graph//Proc. R. Soc. (London). 1926. V. 110, № A756. P. 709-737.
337. Ли P., ХарпДж. Слабое рассеяние в случайной среде в
применении к дистанционному зондированию/уТИИЭР. 1969. Т. 57, № 4. С. 7-40.
338. Jaggard D. L., Sun X. Reflection from Fractal Multilayers//Optics Lett.
1990. V. 15, № 24. P. 1428-1430.
339. Sun X., Jaggard D. L. Wave Interactions with Generalised Cantor Bar
Fractal Multilayers//! Appl. Phys. 1991. V. 70, № 5. P. 2500-2507.
340. Bedrosian S D., Sun X. //J. Franclin Inst. 1989. V. 326. P. 503.
341. Jaggard D. L., Kim Y Diffraction by Band-Limited Fractal Screens//
J. Opt. Soc. Am. A. 1987. V. 4, № 6. P. 1055-1062.
342. Kim Y.y Jaggard D. L. Optical Beam Propagation in a Band-Limited
Fractal Media//! Opt. Soc. Am. A. 1988. V. 5, № 9. P. 1419-1426.
343. Van RoeyJ., Van derDonkJ, LagasseP. E. Beam-Propagation Method:
Analysis and Assesment//J. Opt. Soc. Am. 1981. V. 71, № 7. P. 803-810.
344. ИсимаруА. Использование флуктуации сфокусированного
волнового пучка для зондирования атмосферной турбулентности//ТИИЭР. 1969.
Т. 57, № 4. С. 40-48.
345. Олвер Ф. Введение в асимптотические методы и специальные
функции: Пер. с англ.; Под ред. А. П. Прудникова. - М.: Наука, 1978. -
376 с; см. также: Олвер Ф. Асимптотика и специальные функции: Пер. с
англ.; Под ред. А.П. Прудникова. - М.: Наука, 1990. - 528 с.
346. Лысанов Ю. П., ЛямшевЛ. М. Рассеяние звука случайными
объемными неоднородностями с фрактальным спектром//Акуст. журн. 1998.
Т. 44, № 4. С. 506-509.
347. Бреховских Л. М., Лысанов Ю. П. Теоретические основы акустики
океана. - Л.: Гидрометеоиздат, 1982. - 264 с.
806
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
348. Сабинин К. Д., Деев М. Г Локальный радиус Россби и параметры
внутритермоклинных вихрей (линз) в океане//Океанология. 1991. Т. 31,
№5. С. 714-719.
349. Лысанов Ю. П., Сазонов И. А. О частотной зависимости
коэффициента затухания звука в океане//Акуст. журн. 1993. Т. 39, № 4. С. 697-702.
350. Sheehy M. Т., Halley R. Measurement of the Attenuation of Low-
Frequency Sound//J. Acoust. Soc. Am. 1957. V. 29, № 4. P. 464-469.
351. Lovejoy S., SchertzerD. Generalized Scale Invariance in the Atmosphere
and Fractal Models of Rain//Water Resour. Res. 1985. V. 21. № 8. P. 1233-1250.
352. Mellen R. M., Silling G. Sound Propagation through Atmospheric
Turbulence: Multifractal Mass Fluctuations//J. Acoust. Soc. Am. 1995. V. 97,
№ 1. P. 141-146.
353. Вадов P. А. Затухание низкочастотного звука в океане//Пробле-
мы акустики океана / Под. ред. Л. М. Бреховских, И. Б. Андреевой. - М.:
Наука, 1984. С. 31-42.
354. Kim Y., Grebel H., Jaggard D. L. Diffraction by Fractally Serrated
Apertures//J. Opt. Soc. Am. 1991. V. 8, № 1. P. 20-26.
355. Гудмен Дж. Введение в фурье-анализ: Пер. с англ.; Под ред.
Г. И. Косоурова. - М.: Мир, 1970. - 364 с.
356. Андреев Г. А., Потапов А. А., Галкина Т. В. и др.
Аналого-цифровой метод анализа анизотропии текстурных изображений//Тез. докл. III
Всесоюзн. конф. «Методы и средства обработки сложной графической
информации». - Горький: Изд. ГГУ, 1988. Ч. 1. С. 57-58.
357. Потапов А. А.} Колесников А. И. Анализ изображений текстур
земных покровов на оптических и миллиметровых волнах в области
пространственных частот//Тез. докл. IV Всесоюзн. школы по распростр.
миллиметровых и субмиллиметровых волн в атмосфере. - Н. Новгород: НИРФИ, 1991.
С. 255-256.
358. Ван де Хюлст Г Рассеяние света малыми частицами: Пер. с англ.;
Под ред. В. В. Соболева. - М.: ИЛ, 1961. - 536 с.
359. Борен К, Хафмен Д Поглощение и рассеяние света малыми
частицами/ Пер. с англ. - М.: Мир, 1986. - 664 с.
360. Yeh С, Mei К К. On the Scattering from Arbitrary by Shaped
Inhomogeneous Particles-Exact Solution//Light Scattering by Irregularly Shaped
Particles / Ed. by D. Schurerman. - N. Y.: Plenum, 1980. P. 201-206.
361. Bourrely C, TorresaniB., ChiappettaP. Scattering of an Electromagnetic
Wave by a Irregularly Shaped Object//Opt. Commun. 1986. V. 58, № 6. P. 365-
368.
362. PannetierB., ChaussyJ., RommalA, GanditP. //Phys. Rev. Lett. 1984.
V. 53, №7. P. 718-721.
363. Maze G., Ripoche J. Methode d' isolement et d' identification des
Resonances (M. 1.1. R.) de Cylindres et de Tubes Soumis aune Onde Acoustique
Plane dans Г eau//Rev. Phys. Appl. 1983. V. 18, № 6. P. 319-326.
807
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
364. Bourrely С, Chiappetta P., Torresani B. Light Scattering by Particles of
Arbitrary Shape: a Fractal Approach//J. Opt. Soc. Am. A. 1986. V. 3, № 2. P. 250-
255.
365. Perrin J. M., Chiappetta P. Light Scattering by Large Particles. I. A New
Theoretical Description in the Eikonal Picture//Optica Acta. 1985. V. 32, № 8.
P. 907-921.
366. Weiss- Wrana K. Optical Properties of Interplanetary Dust: Comparison
with Light Scattering by Larger Meteoretic and Terrestrial Grains//Astronom.
Astrophys. 1983. V. 126, № 2. P. 240-250.
367. JaggardD. L., Sun X. Scattering from Bandlimited Fractal Fibers//IEEE
Trans. 1989. V. AP-37, № 12. P. 1591-1597.
368. Chen Z., Sheng P., Weitz D. A. et al. Optical Properties of Aggregate
Clusters//Phys. Rev. 1988. V. B37, № 10. P. 5232-5235.
369. Андреев С. Д., Ивлев Л. С, Михайлов Е. Ф., Киселев А. А.
Оптические характеристики частиц дымов//Оптика атмосферы и океана. 1995. Т. 8,
№ 5. С. 687-692.
370. Colbeck L, Hardman Е. J., Harrison R. M. Optical and Dinamical
Properties of Fractal Clusters of Carbonaceous Smoke//J. Aerosol. Sci. 1989.
V. 20, № 5. P. 765-774.
371. Berry M. V., Persival I. С Optics of Fractal Clusters Such as Smoke//
Optica Acta. 1986. V. 33, № 5. P. 577-591.
372. Chylek P., Ramaswamy V., Cheng R., Pinnick R. G, Optical Properties
and Mass Concentration of Carbonaceous Smokes//Appl. Optics. 1981. V. 20,
№ 17. P. 2980-2985.
373. Weitz D. A., HyangJ. S., Lin M. Y, Sung J. Limits of Fractal Dimension
for Irrevesible Kinetic Aggregation og Gold Colloids//Phys. Rev. Lett. 1985. V. 54,
№ 13. P. 1416-1419.
374. Chen Z - Y, Weakliene P., Gelbart W M., Meakin P. Second-Order Light
Scattering and Local Anizatropy of Diffusion - Limited Aggregates and Bond-
Percolated Clusters//Phys. Rev. Lett. 1987. V. 58, № 19. P. 1996-1999.
375. Максименко В. В., Душников А. А. Фазовый переход видимость-
невидимость в фрактальном кластере//Письма в ЖЭТФ. 1993. Т. 57, № 4.
С. 204-209.
376. Jullien R., Botet R. Geometrical Optics in Fractals//Physica D. 1989.
V. 38, № 1-3. P. 208-212.
377. RastogiP. K., ScheucherK. F. Range Dependence of Volume Scattering
from a Fractal Medium: Simulation Results//Radio Sci. 1990. V. 26, № 5.
P. 1057-1063.
378. WestB. J. Sensing Scaled Scintillations//J. Opt. Soc. Am. A. 1990. V. 7,
№6. P. 1074-1100.
379. Wang Z -S., Lu B. -W. The Scattering of Electromagnetic Waves in
Fractal Media//Waves in Random Media. 1994. V. 4, № 1. P. 97-103.
380. DogariuA, UozumiJ., Asakura T. Ballistic Propagation of Light Through
Fractal Gels//Waves in Random Media. 1994. V. 4, № 1. P. 1-6.
808
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
381. Schmitt J. M., KnuttelA., Knutson J. R. Interference of Diffusive Light
Waves//J. Opt. Soc. Am. A. 1992. V. 9, № 10. P. 1832-1843.
382. Fuller K. A. Scattering and Absorption Cross Sections of Compounded
Sphere. II. Calculations for External Aggregation//!. Opt. Soc. Am. A. 1995. V. 12,
№ 5. P. 881-892.
383. Маркель В. А, Муратов Л. С, Штокман М. И. Теория и
численное моделирование оптических свойств фракталов//ЖЭТФ. 1990. Т. 98,
№3(9). С. 819-837.
384. Максименко В. В., Крикунов В. А., ЛушниковА. А. Сильная
локализация света в плотноупакованной гранулированной среде//ЖЭТФ. 1992.
Т. 102, №5(11). С. 1571-1586.
385. Постом Т., Стюарт И. Теория катастроф и ее приложения: Пер.
с англ. - М.: Мир, 1980. - 607 с.
386. Арнольд В. И., ВарченкоА. Н, Гусейн-Заде С. М. Особенности
дифференцируемых отображений: Классификация критических точек, каустик
и волновых фронтов. - М.: Наука, 1982. - 304 с.
387. Арнольд В. И., ВарченкоА. Н., Гусейн-Заде С. М. Особенности
дифференцируемых отображений: Монодромия и асимптотики интегралов. -
М.: Наука, 1984. - 336 с; см. также: Арнольд В. И.} ВарченкоА. Н.} Гусейн-
Заде С. М. Особенности дифференцируемых отображений. - М.: МЦНМО,
2004. - 672 с.
388. Berry M. V. Catastrophe and Fractal Regimes in Random Waves//
Structural Stability in Physics / Ed. by W. Guttinger, H. Eikemeier. - N. Y.:
Springer, 1979. P. 43-50.
389. Крюковский А. С, Лукин Д. С.} Палкин Е. А. Краевые и угловые
катастрофы в задачах дифракции и распространения волн. - Казань: Изд.
КАИ, 1988. - 200 с.
390. Потапов А. А.} Герман В. А., Чеканов Р. Н. Теории катастроф и
фракталов в волновой физике/уТруды VII Всерос. школы-семинара «Волновые
явления в неоднородных средах». - М.: Изд. МГУ, 2000. Т. 2. С. 62-66.
391. Арнольд В.И. Теория катастроф. - М.: Наука, 1990. - 128 с; см.
также: Арнольд В.И. Особенности каустик и волновых фронтов. - М.:
ФАЗИС, 1996.-334 с.
392. Кравцов Ю. А., Орлов Ю. И. Геометрическая оптика неоднородных
сред. - М.: Наука, 1980. - 304 с.
393. Гочелашвили К. С, Шишов В. И. Волны в случайно-неоднородных
средах (Итоги науки и техники. Серия: Радиофизика. Т. 1.). - М.: Изд.
ВИНИТИ, 1981.- 144 с.
394. Berry M. V. Distribution of Modes in Fractal Resonators//Structural
Stability in Physics/ Ed. by W. Guttinger, H. Eikemeier. - N. Y.: Springer, 1979.
P. 51-53.
395. Фоменко А. Т. Наглядная геометрия и топология: Математические
образы в реальном мире. - М.: Изд. МГУ, 1998. - 416 с.
809
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
396. Keyes R W. The Power of Interconnections//IEEE Circuits and Devises
Mag. 1991. V. 7, № 3. P. 32-35.
397. Keyes R. W. The Wire-Limited Logic Chip//IEEE J. Solid-State
Circuits//1982. V. SC-17, № 6. P. 1232-1233.
398. Christie P. A Fractal Analysis of Interconnection Complexity//Proc.
IEEE. 1993. V. 81, № 10. P. 1492-1499.
399. Donath W. E. Statistical Properties of the Placement of a Graph//SIAM
J. Appl. Math. 1968. V. 16, № 2. P. 439-457.
400. Kirkpatrick S., Gellat C. D., Vecchi M. P. Optimization by Simulated
Annealing//Science. 1983. V. 220, № 4598. P. 671-680.
401. Биндер К, ХеерманД. В. Моделирование методом Монте-Карло в
статистической физике: Пер. с англ. - М.: Наука, 1995. - 144 с.
402. Landman В. S., Russo R. L. On a Pin Versus Relationship for Partitions
of Logic Graphs//IEEE Trans. 1971. V. C-20, № 12. P. 1469-1479.
403. Russo R. L. On the Tradeoff Between Logic Performance and Circuit
to Pin Ratio for LSI//IEEE Trans. 1972. V. C-21, № 2. P. 147-155.
404. Donath W. P. Placement and Average Interconnection Lengths of
Computer Logic//IEEE Trans. 1979. V. CAS-26, № 4. P. 272-277.
405. Cotter J. E., Christie P. The Analytical Form of the Lenght Distribution
Function for Computer Interconnections//IEEE Trans. Circuits Syst. 1991.
V. 38, №3. P. 317-320.
406. Tel T. Fractals, Multifractals and Thermodynamics: An Introductory
Review//Z. Naturforsch. 1988. V. 43a, № 12. P. 1154 -1174.
407. Mead С Neuromorphic Electronic Systems//Proc. IEEE. 1990. V. 78,
№ 10. P. 1629-1636.
408. Donath W. E. Wire Lenght Distribution for Placements of Computer
Logic//IBM J. Res. Develop. 1981. V. 25, № 3. P. 152-155.
409. Ma С. -К. Renormalization Group by Monte Carlo Methods//Phys.
Rev. Lett. 1976. V37, № 8. P. 461-464.
410. Kohmoto M. Entropy Function for Multifractals//Phys. Rev. A. 1988.
V. 37, № 4. P. 1345-1350.
411. Бедросян С. Д., Джаггард Д. Л. Применение метода фрактальных
графов к большим сетям//ТИИЭР. 1987. Т. 75, № 7. С. 112-115.
412. Jaggard D. L., Bedrosian S. D., Dayanim J. F. Large Fractal - Graph
Networks//Proc. IEEE Intern. Symp. on Circuits and Systems (Philadephia, PA,
May 7, 1987). - N. Y., 1987. V. 3. P. 948-951.
413. Мулен Э. Кооперативное принятие решений: Аксиомы и модели:
Пер. с англ.; Под ред. И. С. Меньшикова. - М.: Мир, 1991. — 464 с.
414. Benguigui L., Daoud M. Is the Suburban Railway System a Fractal?//
Geographical Analysis. 1991. V. 23, № 4. P. 362-368.
415. Batty M. Cities as Fractals: Simulating Growth and Form//Fractal and
Chaos / Ed. by A. Grilly, R. Earnashaw, H. Jones. - N. Y.: Springer, 1991.
P. 43-69.
810
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
416. Ким Й., Джаггард Д. Л. Фрагментарно-самоподобные
(фрактальные) случайные решетки//ТИИЭР. 1986. Т. 74, № 9. С. 124-126.
417. JaggardD. L., JaggardA. D. Polyadic Cantor Superlattices with Variable
Lacunarity//Optics Lett. 1997. V. 22, № 3. P. 145-147.
418. JaggardA. D., Jaggard D. L. Scattering from Fractal Superlattices with
Variable Lacunarity//J. Opt. Soc. Am. A. 1998. V. 15, № 6. P. 1626-1635.
419. Liang X., Zhensen W., Wenbung W. Synthesis of Fractal Pattern from
Concentric-Ring Arrays//Electron. Lett. 1996. V. 32, № 21. P. 1940-1941.
420. Werner D. H., Werner P. L. Frequency-Independent Features of Self-
Similar Fractal Antennas//Radio Sci. 1996. V. 31, № 6. P. 1331-1343.
421. JaggardD. L, Spielman T. Triadic Cantor Target Diffraction//Microw.
Opt. Technol. Lett. 1992. V. 5, № 9. P. 460-466.
422. JaggardA. D., JaggardD. L. CantorDifractalsand Lacunarity//Proc. IEEE
Antennas and Propagation Society Int. Symp. - Atlanta: 1998. V 2. P. 862-865.
423. JaggardD. L., JaggardA. D. Cantor Ring Arrays//Proc. IEEE Antennas
and Propagation Society Int. Symp. - Atlanta: 1998. V. 2. P. 866-868.
424. Рамзей В. Частотно-независимые антенны: Пер. с англ.; Под ред.
А. Ф. Чаплина. - М.: Мир, 1968. - 176 с.
425. Sierpinski M. W. Sur une Courbe dont tour Point est in Point de
Ramification//Compt. Rend. Hebdomadaires des Seances de L' Academie des
Sciences (Paris). 1915. V. 160. P. 302-305.
426. Puente C, Romeu J., Pous R. et al. Fractal Multiband Antenna Based
on the Sierpinski Gasket//Electron. Lett. 1996. V 32, № 1. P. 1-2.
427. Puente C, Romeu J, Bartoleme R., Pous R. Perturbation on the Sierpinski
Antenna to Allocate Operating Bands//Electron. Lett. 1996. V. 32, № 24.
P. 2186-2188.
428. Puente-Baliarda C, Romeu J., Pous R., CardamaA. On the Behavior of
the Serpinski Multiband Fractal Antenna//IEEE Trans. 1998. V. AP-46, № 4.
P. 517-524.
429. Duncan J. W.} Minerva V. P. 100:1 Bandwidth Balun Transformer//Proc.
IRE. 1960. V. 48, № 2. P. 156-164.
430. New Fractal Antennas for Compact and Versatile Telecommunication
Services//Microwave J. 2000. V. 43, № 1. P. 196, 198, 200, 202, 204.
431. Callejon J. F., Bretones A. R., Martin R. G. On the Application of
Parametric Models to the Transient Analysis of Resonant ant Multiband
Antennas//IEEE Trans. V. AP-46, № 3. P. 312-317.
432. Марпл С. Л. Цифровой спектральный анализ и его приложения:
Пер. с англ.; Под ред. И. С. Рыжака. - М.: Мир, 1990. - 584 с.
433. Puente С, Claret J.y Sagues F. et al. Multiband Properties of a Fractal
Tree Antenna Generated by Electrochemical Deposition//Electron. Lett. 1996.
V. 32, № 25. P. 2298-2299.
434. Trigueros P. P., Claret J., Mas F, Sagues F. Pattern Morfologies in Zinc
Electrodeposition//J. Electroanal. Chem. 1991. V. 312, № i_2. P. 219-235.
811
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
435. Werner D. H., Werner P. L. On the Synthesis of Fractal Radiation
Patterns//Radio Sci. 1995. V. 30, № 1. P. 29-45.
436. Goutelard С Fractal Theory for Large Lacunar Antenna Arrays//
Electromagnetic Wave Propagation Panel Symp. (AGARD-CP-528). - 1992.
P. 35/1-35/15.
437. Troncet E., Abbart G., Allam L. Microwave Characterization and
Modeling of the Surface Impedance of Fractal Structure Copper Films//IEEE
Trans. 1998. V. AP-46. № 3. P. 434-441.
438. Васильев Л. Н., Тюфлин А. С. Фрактальность пространственных
структур геосистем//ДАН СССР. 1990. Т. 314, № 6. С. 1488-1490.
439. Васильев Л. Н., Тюфлин А. С. Фрактальность пространственных
структур геосистем//Исслед. Земли из космоса. 1991. № 4. С. 59-67.
440. Васильев Л. Н.} Тюфлин А. С. Фрактальность геофизических полей,
определяемых аэрокосмическими методами//ДАН РАН. 1992. Т. 325, № 1.
C. 154-158.
441. Васильев Л. Н., Тюфлин А. С. Фрактальность геофизических полей,
определяемых аэрокосмическими методами//Исслед. Земли из космоса.
1992. № 6. С. 44-52.
442. Matsushita M., Ouchi S. On the Self-Affinity of Various Curves//Physica
D. 1989. V. 38, № 1-3. P. 246-251.
443. Васильев Л. Н., Качалин А. Б., Моралев В. М. и др. Мультифрак-
тальность плотности линеаментов (на примере Кольского полуострова)//
Исслед. Земли из космоса. 1996. № 2. С. 25-32.
444. Nirata T. Fractal Dimension of Fault System in Japan: Fractal Structure
in Rock Fracture Geometry at Various Scales//Pageophys. 1989. V. 131, № 1/2.
P. 157-170.
445. Васильев Л. Н., Качалин А. Б., Моралев В. М., Терехов Е. Н.
Фрактальные перколяционные кластеры в сети линеаментов, выявленных по
космическим снимкам, и тектоническое районирование восточной части
Балтийского щита//Исслед. Земли из космоса. 1994. № 5. С. 39-50.
446. De Arcangelis L., Redner S., Coniglio A. Multifractaling Approach in
Random Resistor and Random Superconducting Networks//Phys. Rev. B. 1986.
V. 34, № 7. P. 4656-4673.
447. Meakin P., Coniglio A., Stanley H. Scaling Properties for the Surfaces
of Fractal and Nonfractal Objects: An Infinite Hierarchy of Critical Exponents//
Phys. Rev. A. 1986. V. 34, № 4. P. 3325-3340.
448. Stanley H., Meakin P. Multifractal Phenomena in Physics and
Chemistry//Nature. 1988. V. 335, № 29. P. 405-409.
449. Васильев Л. Н., Качалин А. Б., Тюфлин А. С. Пространственная
структура зеленых насаждений в Москве и ее определение по космическим
снимкам//Исслед. Земли из космоса. 1994. № 1. С. 86-92.
450. Barry R. G., Serreze M. С, Maslanik J. The Arctic Sea Ice-Climate System:
Observations and Modeling//Rev. Geophys. 1993. V. 31, № 4. P. 397-422.
812
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
451. Васильев Л. Н.} Качалин А. Б., Тюфлин А. С. Фрактальность
морских льдов и свойство их разномасштабных изображений//Исслед. Земли
из космоса. 1995. № 2. С. 88-97.
452. Прэтт У. К. Цифровая обработка изображений: В 2 т. / Пер. с
англ.; Под ред. Д. С. Лебедева. - М.: Мир, 1982. Т. 1. - 312 с; Т. 2. - 480 с.
453. Андреев Г. А., Потапов А. А., Галкина Т. В. и др. Машинная
классификация текстурных изображений земных покровов//Тез. докл.
Региональной конф. «Обработка изображений и дистанционное зондирование -
ОИДИ-87». - Новосибирск: Изд. ВЦ СО АН СССР, 1987. С. 32.
454. Андреев Г А} Потапов А. А., Галкина Т. В. и др. Синтез
стохастических полей, имитирующих земные покровы, и их текстурные признаки//
Тез. докл. X Всесоюзн. науч. -техн. конф. «Статистические методы в
теории передачи и преобразования информационных сигналов». - Киев: Изд.
КНИГА, 1988. С. 23-24.
455. Андреев Г. А., Потапов А. А. Анализ и синтез двухзональных
текстурных изображений//Тез. докл. I Всесоюзн. конф. по искусственному
интеллекту. - М.: Изд. ВИНИТИ, 1988. Т. 2. С. 104-108.
456. Андреев Г А., Потапов А. А. Стохастический авторегрессионный
синтез изображений текстур земных покровов. - М.: ИРЭ АН СССР.
Препринт № 23 (498). 1988.-31с.
457. Андреев Г. А., Потапов А. А, Галкина Т. В. и др. Машинный
синтез текстур, имитирующих земную поверхность//Исслед. Земли из
космоса. 1989. № 1.С. 115-121.
458. Потапов А. А., Галкина Т. В., Орлова Т. И. Цифровой
статистический анализ радиоизображений природных сред//Тез. докл. II Республ.
семинара «Проблемы создания систем обработки, анализа и распознавания
изображений». - Ташкент: Изд. ИК с ВЦ НПО «Кибернетика» АН УзССР,
1989. Ч. 1. С. 3-4.
459. Потапов А. А. Статистический подход к описанию изображений
текстур земной поверхности в оптическом и радиодиапазоне//Тез. докл. IV
Всесоюзн. конф. «Математические методы распознавания образов»
(MMPO-IV). - Рига: Изд. МИПКРРиС при СМ Латв. ССР, 1989. Ч. 4.
С. 150-151.
460. Андреев Г А} Потапов А. А., Горбунов А. В. и др. Сравнительный
анализ статистических признаков оптических и радиоизображений почвенно-
растительных объектов//Исслед. Земли из космоса. 1990. № 1. С. 112-121.
461. Андреев Г А, Потапов А. А, Галкина Т. В. и др. О классификации
изображений по их текстурным признакам//Исслед. Земли из космоса.
1990. №2. С. 91-96.
462. Галкина Т. В., Орлова Т. И., Потапов А. А, Хлявич Я. Л.
Машинный метод обнаружения искажений текстурных картин//Тез. докл.
Всесоюзн. конф. «Физика и конверсия». - М.: Изд. Физ. Общ-ва СССР, 1991.
С. 97.
813
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
463. Haralick R. M., Shanmugam К., Dinstein I. Textural Features for Image
Classification//IEEE Trans. 1973. V. SMC-3, № 6. P. 610-621.
464. Song-Sheng L., Jernigan M. E. Texture Analysis and Discrimination in
Additive Noise//Comput. Vision, Graph., Image Process. 1990. V. 49, № 1.
P. 52-67.
465. Stewart С V., Moghaddam В., Hintz K. J., Novak L. M. Fractional
Brownian Motion Models for Synthetic Aperture Radar Imagery Scene
Segmentation//Proc. IEEE. 1993. V. 81, № 10. P. 1511-1522.
466. Pentland A. P. Fractal-Based Description of Natural Scenes//IEEE
Trans. 1984. V. PAMI-6, № 6. P. 661-674.
467. Keller J. M., Chen S., Grownover R. M. Texture Description and
Segmentation through Fractal Geometry//Comput. Vision, Graph., Image
Process. 1989. V. 45, № 2. P. 150-166.
468. Peleg S., Naor J., Hartley R, Avnir D. Multiple Resolution Texture
Analysis and Classification//IEEE Trans. 1984. V. PAMI-6, № 4. P. 518-523.
469. Chen С -С, Daponte J. S., Fox M. D. Fractal Feature Analysis and
Classification in Medical Imaging//IEEE Trans. 1989. V. MI-8, № 2. P. 133-142.
470. WornellG. W., OppenheimA. К Estimation of Fractal Signals from Noisy
Measurements Using Wavelets//IEEE Trans. 1992. V. SP-40, № 3. P. 611-623.
471. Flandrin P. On the Spectrum of Fractional Brownian Motions//IEEE
Trans. 1989. V. IT-35, № 1. P. 197-199.
472. Moghaddam В., Hintz К. J., Stewart С К A Comparison of Local Fractal
Dimension Estimation Methods//Pattern Recogn. Image Anal. 1992. V. 2, № 1.
P. 93-96.
473. Марков Е. П. Фрактальная модель космических
оптико-электронных изображений//Исслед. Земли из космоса. 1996. № 1. С. 56-61.
474. Kogon S. M. Fractal-Based Modeling and Interpolation of non Gaussian
Images//SPIE. 1994. V. 2308. P. 467-477.
475. Харалик Р. М. Статистический и структурный подходы к
описанию текстур//ТИИЭР. 1979. Т. 67, № 5. С. 98-120.
476. Прэтт У. К., Фожра О. Д., ГагаловичА. Применение моделей
стохастических текстур для обработки изображений//ТИИЭР. 1981. Т. 69, № 5.
С. 54-64.
477. Huand J., Turcotte D. L. Fractal Image Analysis: Application to the
Topography of Oregon and Synthetic Images//J. Opt. Soc. Am. A. 1990. V. 7,
№6. P. 1124-1130.
478. Barenblatt G. L, Zhivago A. V., Neprochov Y. P., Ostrovskiy A. A. The
Fractal Dimension: A Quantative Characteristic of Ocean-Bottom Relief//
Oceanology. 1984. V. 24. P. 695-697.
479. Потапов А. А. Фракталы в дистанционном
зондирование/Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 2000.
№ 6. С. 3-65.
480. Yang Xf Chiochetti J., Papadopoulos, Susman L. Fractal Antenna
Elements and Arrays//Applied Microwave & Wireless. 1999. № 5. P. 34-46..
814
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
481. Flandrin P. On the Spectrum of Fractal Brownian Motions//IEEE
Trans. 1989. V. IT-35. № 1. P. 197-199.
482. Pickover C, KhorasaniA. Fractal Characterization of Speech Waveform
Graphs//Comput. Graphics. 1986. V. 10, № 1. P. 51-61.
483. Brodatz P. Texture: A Photographic Album. - N. Y.: Dover, 1956.
484. Потапов А. А. Радиофизическая модель формирования эталонных
радиолокационных карт неоднородной местности в диапазоне
миллиметровых волн//Электромагнитные волны и электронные системы. 1997. Т. 2,
№4. С. 31-34.
485. Peli Т. Multiscale Fractal Theory and Object Characterization//J. Opt.
Soc. Am. A. 1990. V. 7, № 6. P. 1101-1112.
486. Peleg S., Naor J., Hartely R., Avnir D. Multiple Resolution Texture
Analysis and Classification//IEEE Trans. 1984. V. PAMI-6, № 5. P. 518-523.
487. Carlotto M. J., Stein M. С Detecting Man-Made Change in Imagery//
Proc. Soc. Photo-Optical Instruments Engineering. 1985. V. 1002, № 1. P. 6-11.
488. Serra J. Image Analysis and Mathematical Morphology. - L.: Academic
Press, 1982.
489. Arduini F., Dambra C, Dellepiane S. et al. Fractal Dimension by Adaptive
Mask Selection//Proc. IEEE Intern. Conf. on Acoustics, Speech and Signal
Processing. - N. Y.: 1988. P. 1116-1119.
490. Zhao Y., Zhu H. A New Feature Based on Fractal Models and its
Applications in Automatic Target Recognition//! Infrared and Millimeter Waves
(China). 1997. V. 16, № 3. P. 215-220.
491. Xion M., Zhuang Z., Xiao S., Guo G. The Analyse and Recognition of
Radar Targets Scattering Signal with Chaos Multifractal Theory//J. National
University of Defense Technology (China). 1998. V. 20, № 2. P. 60-64.
492. Knill D. C, Field D., Kersten D. Human Discrimination of Fractal
Images//! Opt. Soc. Am. A. 1990. V. 7, № 6. P. 1113-1123.
493. Leung H., Haykin S. Is there a Radar Clutter Attractor?//Appl. Phys.
Lett. 1990. V. 56, № 6. P. 593-595.
494. Leung H., Lo T. Chaotic Radar Signal Processing over the Sea//IEEE
J. Oceanic. Eng. 1993. V. OE-18, № 2. P. 287-295.
495. TheilerJ. Estimating Fractal Dimension//! Opt. Soc. Am. A. 1990. V. 7,
№ 6. P. 1055-1073.
496. Osborne A. R.} ProvenzaleA. Finite Correlation Dimension for Stochastic
Systems with Power-Law Spectra//Physica D. 1983. V. 35, № 3. P. 357-381.
497. Palmer A. J., Kropfli R. A., Fairall C. W. Signatures of Deterministic
Chaos in Radar Sea Clutter and Ocean Surface Winds//Chaos. 1995. V. 5, № 3.
P. 613-616.
498. SchroederL. C.} Boggs D. H., Dome G. et al. The Relationship Between
Wind Vector and Normalized Radar Cross Section Used to Derive SEAS AT - A
Satellite Scatterometer Winds//! Geophys. Res. 1982. V. 87, № 2. P. 3318-3336.
499. Eisner J., TsonisA. Nonlinear Prediction, Chaos and Noise//Bulletyne
of Am. Meteorol. Soc. 1992. V. 73, № 1. P. 49-60.
815
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
500. Кук Ч, БернфельдМ. Радиолокационные сигналы: Пер. с англ.; Под
ред В. С. Кельзона. - М.: Сов. радио, 1971. - 568 с.
501. Хэррис Ф. Дж. Использование окон при гармоническом анализе
методом дискретного преобразования Фурье//ТИИЭР. 1978. Т. 66, № 1.
С. 60-96.
502. Алексеев А. И., Шереметьев А. Г., Тузов Г. И., Глазов Б. И. Теория
и применение псевдослучайных сигналов. - М.: Сов. радио, 1969. - 367 с.
503. Кнорре К. Г, Тузов В. М., Шур Г. И. Фазовые и частотные
информационные СВЧ элементы. - М.: Сов. радио, 1975. - 352 с.
504. Опаленов Ю. В., Потапов А. А., Федюнин С. Ю. Формирование
сложных фазоманипулированных сигналов в задачах дистанционного
зондирования/Дез. докл. науч. -техн. конф. «Формирование сложных
сигналов». - М.: Изд. Союза НИО СССР, 1988. С. 49.
505. Новые физические принципы оптической обработки
информации/ Под ред. С. А. Ахманова и М. А. Воронцова. - М.: Наука, 1990. - 400с.
506. Яковлев В. В., Федоров Р. Ф. Стохастические вычислительные
машины. - Л.: Машиностроение, 1974. - 343 с.
507. Комолое В. П., Трофименко И. Т. Квантование фазы при
обнаружении радиосигналов. - М.: Сов. радио, 1976. - 224 с.
508. ДжоунсДж. Идеальное ограничение процесса, состоящего из двух
синусоидальных сигналов и случайного шума//Некоторые проблемы
обнаружения сигнала, маскируемого флуктуационной помехой: Пер. с англ.;
Под ред. И. И. Шнер. - М.: Сов. Радио, 1965. - С. 237-263.
509. Нейман Д. Автоматы/ Под ред. К. Шеннона и Дж. Маккарти: Пер.
с англ.; Под ред. А. А. Ляпунова. - М.: ИЛ, 1956. - С. 68.
510. Поспелов Д. А. Логические методы анализа и синтеза схем. - М.:
Энергия, 1974. - 368 с.
511. Сантало М. Интегральная геометрия и геометрические
вероятности: Пер с англ.; Под ред. Р. В. Амбарцумяна. - М.: Наука, 1983. - 358с.
512. Хелгасон С. Дифференциальная геометрия и симметрические
пространства: Пер. с англ. - М.: Мир, 1964. - 534 с.
513. Стернберг С. Лекции по дифференциальной геометрии: Пер. с
англ.; Под ред. А. Л. Онищика. - М.: Мир, 1970. - 412 с.
514. Троицкий И. Н. Статистическая теория томографии. - М.: Радио
и связь, 1989. - 239 с.
515. Гельфанд И. М., Граев М. К, Виленкин Н. Я. Интегральная
геометрия и связанные с ней вопросы теории представлений. - М.: Физматгиз,
1962. - 656 с.
516. Белоглазое И. Н., Джанджгава Г И., Чигин Г. П. Основы
навигации по геофизическим полям. - М.: Наука, 1985. - 328 с.
517. Хелгасон С. Преобразование Радона: Пер. с англ.; Под ред. Б.И.
Завьялова. - М.: Мир, 1983. - 150 с.
518. Тихонов А. Н., Арсенин В. Я., Тимонов А. А. Математические задачи
компьютерной томографии. - М.: Наука, 1987. - 158 с.
816
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
519. Опаленов Ю. В., Потапов А. А., Федюнин С. Ю. Радиофизический
измерительный комплекс со сложным фазоманипулированным сигналом
для исследования природных ресурсов: принципы построения и анализ
экспериментальных результатов//Тез. докл. II Всесоюзн. науч.-техн. конф.
«Теория и техника пространственно-временной обработки сигналов». —
Свердловск: Изд. УПИ, 1989. С. 110-111.
520. Дмитриев С. В., Опаленов Ю. В., Потапов А. А.} Федюнин С. Ю. О
дистанционном зондировании земных покровов совмещенными
радиофизическими системами с квазинепрерывным шумоподобным
фазоманипулированным сигналом//Тез. докл. Всесоюзн. конф. «Дистанционное
зондирование агропочвенных и водных ресурсов». - Барнаул: Изд. АлГу, 1990.
С. 17-18.
521. Опаленов Ю. В., Потапов А. А., Федюнин С. Ю. Радиофизический
измерительный комплекс со сложным ФМ сигналом в диапазоне
миллиметровых волн//Радиотехника. 1991. № 11. С. 67-70.
522. Потапов А. А. Рассеивающие свойства биологических объектов в
микроволновом диапазоне//Тез. докл. науч.-техн. конф. «Биологическое
и экологическое приборостроение: наука, промышленность, рынок». —
Рязань: Изд. РРТИ, 1992. С. 34.
523. Опаленов Ю. В., Потапов А. А, Федюнин С. Ю. Радиофизические
цифровые системы зондирования со сложным ФМ сигналом на ММВ//
Тез. докл. науч. -техн. семинара «Распространение и дифракция
электромагнитных волн в неоднородных средах». - М.: Изд. РНТО РЭС им.
А. С. Попова, 1992. С. 166-168.
524. Опаленов Ю. В., Потапов А. А., Федюнин С. Ю. Экологические
цифровые радиолокаторы со сложным сигналом для дистанционных
исследований/Дез. докл. II науч. конф. «Применение дистанционных
радиофизических методов в исследованиях природной среды». - М.: Изд. ИРЭ
РАН, 1992. С. 119-120.
525. Опаленов Ю. В., Потапов А. А. Исследование возможностей
экологических цифровых радиолокаторов со сложным ФМ сигналом//Тез.
докл. XVII конф. по распространению радиоволн. - Ульяновск: Изд. УлПИ,
1993. С. 115.
526. Опаленов Ю. В., Потапов А. А., Соколов А. В. Цифровые
когерентные радиолокационные станции со сложным сигналом в диапазонах
сантиметровых и миллиметровых волн//Электромагнитные волны и
электронные системы. 1996. Т. 1, № 1. С. 103-107.
527. Opalenov U. V.f Potapov A. A.f Sokolov A. V. Solid Digital Millimeter
Wave Radar with Phasemanipulated Signal//Final Programme PIERS Workshop
on Advances in Radar Methods, European Commision, Baveno (Italy): Joint
Research Centre, 1998. P. 96.
528. Опаленов Ю. В., Потапов А. А. Радиолокационные стохастические
сигналы и преобразование Радона//Труды VII Всерос. школы-семинара
«Физика и применение микроволн». - М.: Изд. МГУ, 1999. Т. 2. С. 186.
27 Фракталы о 1 7
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
529. Опаленов Ю. В., Потапов А. А. Цифровые радиолокаторы со
сложным сигналом и фрактальной обработкой информации//Труды VII Всерос.
школы-семинара «Физика и применение микроволн». - М.: Изд. МГУ,
1999. Т. 2. С. 199.
530. Потапов А. А. Фракталы в радиофизике, радиолокации и
дистанционном зондировании. - Там же. С. 140.
531. Опаленов Ю. В., Потапов А. А., Реутов В. Ф. Аппаратно-методи-
ческий базис фрактальной радиолокационной многофункциональной
измерительной системы характеристик потоков и материалов//Труды VII
Всерос. школы-семинара «Волновые явления в неоднородных средах». -
М.: Изд. МГУ, 2000. Т. 2. С. 69-72.
532. Opalenov Yu. V., PotapovAA., Reutov V. F. Hardware-Methodical Base
of a Fractal Multifunction Meter of the Characteristics of Flows and Materials//
Book of Abstracts Second Intern. Conf. «Modern Trends in Computational
Physics». - Dubna (Russia): JINR, 2000. P. 124.
533. Опаленов Ю. В., Потапов А. А.} Реутов В. Ф.
Аппаратно-методический базис многофункционального фрактального измерителя
характеристик потоков и материалов//Доклады 3-й Международной конференции-
выставки «Цифровая обработка сигналов и ее применение». - М.: Изд.
РНТО РЭС им. А. С. Попова, 2000. Т. 3. С. 99-101.
534. Опаленов Ю. В., Потапов А. А. Стохастические сигналы и
преобразование Радона при получении растровых радиолокационных изображений
микроволновым цифровым радиолокатором с фрактальной обработкой
информации/Радиотехника и электроника. 2000. Т. 45, № 12. С. 1447-1458.
535. Потапов А. А.} Галкина Т. В., Орлова Т. И.} Хлявич Я. Л.
Дисперсионный метод обнаружения детерминированных объектов в стохастических
полях//Радиотехника и электроника. 1990. Т. 35, № 11. С. 2295-2301.
536. Потапов А. А.} Галкина Т. В., Орлова Т. И.} Хлявич Я. Л. Метод
выделения контуров протяженных детерминированных объектов в
стохастических полях//Радиотехника и электроника. 1991. Т. 36, № 11. С. 2240-2242.
537. Потапов А. А., Галкина Т. В., Колесников А. И. и др. Линейно
моделированные эталоны в корреляционном опознавании статистических
текстурных полей//Тез. докл. X Всес. науч. -техн. конф. «Статистические
методы в теории передачи и преобразования информационных сигналов». -
Киев: Изд. КНИГА, 1988. С. 143-144.
538. Потапов А. А., Герман В. А. Обнаружение искусственных
объектов с помощью фрактальных сигнатур//Тез. докл. 3-й Всерос. с участием
стран СНГ конф. «Распознавание образов и анализ изображений: новые
информационные технологии». - Н. Новгород: Изд. НИИ ПМК при
ННГУ, 1997. Ч. 1. С. 213-217.
539. Василенко Г И. Голографическое опознавание образов. - М.: Сов.
радио, 1977. - 328 с.
540. Trabca E. A.} Roelting P. G. Shape Detection Using Incoherent
llumination//J. Opt. Soc. Am. 1967. V. 57, № 1. P. 108-110.
818
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
541. Потапов А. А., Герман В. А. Детерминированный хаос в
изображениях природных сред//Труды VII Всерос. школы-семинара «Физика и
применение микроволн». - М.: Изд. МГУ, 1999. Т. 2. С. 196-197.
542. Герман В. А., Потапов А. А. Об измерении фрактальных
характеристик радиолокационных и оптических изображений. - Там же. С. 185.
543. Потапов А. А., Герман В. А. Фрактальные сигнатуры в методах
обнаружения малоконтрастных объектов на радиолокационных и
оптических изображениях земной поверхности. - Там же. С. 200.
544. Герман В. А., Потапов А. А. Фрактальные размерности
изображений природных ландшафтов//Тез. докл. I Междисциплинарного
семинара «Фракталы и прикладная синергетика». - М.: Классика, 1999. С. 51-53.
545. Потапов А. А., Герман В. А. Применение фрактальных методов для
обработки оптических и радиолокационных изображений земной поверх-
ности//Радиотехника и электроника. 2000. Т. 45, № 8. С. 946-953.
546. Реконструкция изображений /Под ред. Г. Старка: Пер. с англ.; Под
ред. Б. С. Кругликова. - М.: Мир, 1992. - 636 с.
547. Горелик А. Л., Скрипкин В. А. Методы распознавания. - М.:
Высшая школа, 1989. - 232 с.
548. Фор А. Восприятие и распознавание образов: Пер. с франц.; Под
ред. Г. П. Катыса. - М.: Машиностроение, 1989. - 272 с.
549. Селекция и распознавание на основе локационной информации/
Под ред. А. Л. Горелика. - М.: Радио и связь, 1990. - 240 с.
550. PotapovA. A.f German V. A. Chines «Tangram» in Problems of Fractal
Resolution//Book of Abstracts Second Intern. Conf. «Modern Trends in
Computational Physics». - Dubna (Russia): JINR, 2000. P. 133.
551. PotapovA. A., German V. A. Conceptual Aspects of a Fractal Detection
and Descernments of the Targets//Proc. 3rd Inter. Conf. and Exhibition on
«Digital Signal Processing and Its Applications». - Moscow (Russia): 2000. V. 2.
P. 46-47.
552. Гарднер М. Математические головоломки и развлечения: Пер. с
англ.; Под ред. А. Я. Смородинского. - М.: Мир, 1971. - 511 с.
553. Barnsley M. F. Iterated Function Systems and Global Construction of
Fractals//Proc. R. Soc. (London). 1985. V. A399, № 1817. P. 243-275.
554. Barnsley M. R, Ervin V., Hardin D., Lancaster J. Solution of an Inverse
Problem for Fractals and Other Sets//Proc. Nat. Acad. Sci. USA. 1986. V. 83,
№ 7. P. 1975-1977.
555. Beaumont J. M. Image Data Compression Using Fractal Techniques//
ВТ Technol. J. 1991. V. 9, № 4. P. 93-109.
556. JacquinA. E. Fractal Image Coding: A Review//Proc. IEEE. 1993. V. 81,
№ 10. P. 1451-1465.
557. Данфорд К, Шварц Дж. Линейные операторы: Пер. с англ. - М.:
Мир, 1962. - Т. 1 - 895 с; 1996. - Т. 2. - 1063 с; 1974. - Т. 3. - 661 с.
558. Samet H. The Quand-Three and Related Hierarchical Data Structures//
ACM Comput. Surv. 1984. V. 16, № 2. P. 188-260.
819
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
559. Vaisey J, GershoA. Image Compression with Block Size Segmentation//
IEEE Trans. 1992. V. SP-40, № 8. P. 2040-2060.
560. Ramamurthi В., Gersho A. Classified Vector Quantization of Images//
IEEE Trans. 1986. V. COM-34, № 11. P. 1105-1115.
561. Потапов А. А. Фрактальное кодирование изображений//Труды VII
Всерос. школы-семинара «Волновые явления в неоднородных средах». -
М: Изд. МГУ, 2000. Т. 2. С. 67-69.
562. GershoA., Gray R. М. Vector Quantization and Signal Compression. -
Dordrecht, The Netherlands: Kluwer, 1992.
563. Vector Quantization//Ed. by H. Abut. - N. Y.: IEEE Press, 1990.
564. Jacobs E. W.f Fisher Y.f Boss R. D. Image Compression: A Study of the
Iterated Transform Method//Signal Process. 1992. V. 29, № 3. P. 251-263.
565. Jacquin A. E. Image Coding Based on a Fractal Theory of Iterated
Contractive Image Transformations//IEEE Trans. 1992. V. IP-1, № 1. P. 18-30.
566. Lepsoy S.f Oien G. E., Ramstad T. A. Attractor Image Compression with
a Fast Non-Iterative Decoding Algorithm//Proc. ICASSP-93.1993. P. 337-340.
567. Monro D. M., Dudbridge F. Fractal Approximation of Image Blocks//
Proc. ICASSP-92. 1992. V. HI. P. 485-488.
568. Monro D. M., Dudbridge F. Fractal Block Coding of Images//Electron.
Lett. 1992. V. 28, № 11. P. 1053-1055.
569. Monro D. M. Generalised Fractal Transforms: Complexity Issues//Proc.
Data Compression Conf. 1993. P. 254-261.
570. Oien G. E., Lepsoy S., Ramstad T. A. An Inner Product Space Approach
to Image Coding by Contractive Transforms//Proc. ICASSP-91. 1991. P. 2773-
2776.
571. Rinaldo R, Zakhor A. Fractal Approximation of Images//Proc. Data
Compression Conf. 1993. P. 451.
572. Vaisey J., GershoA. Variable Block-Size Image Coding//Proc. ICASSP-
87. 1987. P. 1051-1054.
573. Linde Y., Buzo A., Gray R. M. An Algorithm for Vector Quantizer
Design//IEEE Trans. 1980. V. COM-28, № 1. P. 84-95.
574. Пиблс Ф. Дж. Э. Структура Вселенной в больших масштабах: Пер.
с англ.; Под ред. А. Г. Дорошкевича. - М.: Наука, 1983. - 408 с.
575. Луккин Ф. Кластеризация во Вселенной//Фракталы в физике: Пер. с
англ.; Под ред. Я. Г. Синая и И. М. Халатникова. - М.: Мир, 1988. С. 446-453.
576. Пъетронеро Л., Купере Р. Стохастический подход к
крупномасштабной кластеризации материи во Вселенной. - Там же. С. 454-462.
577. Martinez V. J., Jones В. J. T. Why the Universe is not a Fractal//Mon.
Not. R. Astr. Soc. 1990. V. 242, № 3. P. 517-521.
578. LabiniF. S. Isotropy, Homogeneity, and Dipole Saturation//Astrophys.
J. 1994. V. 433, № 2. Pt. 1. P. 464-467.
579. MandelbrotB. B. Sur un Modele Decomposable d' Universe Hierarchise:
Deduction des Correlations Galactiques sur la Sphere Celestre//Compt. Rend.
Acad. Sc. (Paris). 1975. V. 280A, № 22. P. 1551-1554.
820
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
580. Учайкин В. В., Гусаров Г Г Анализ структурной функции
пространственного распределения галактик в модели случайных блужданий//Изв.
вузов. Физика. 1997. № 8. С. 3-7.
581. Efstathiou G., Eastwood J. W. On the Clustering of Particles in an
Expanding Universe//Mon. Not. R. Astr. Soc. 1981. V. 194, № 2. P. 503-525.
582. Секей Г Парадоксы в теории вероятностей и математической
статистике: Пер. с англ.; Под ред. В. В. Сазонова. - М.: Мир, 1990. - 240 с.
583. Мышее А. В. Порядок, хаос и фракталы в небесно-механических
системах//Изв. РАН. Сер. Физическая. 1998. Т. 62, № 9. С. 1907-1913.
584. Милованов А. В. Крупномасштабная структура скоплений
галактик и спонтанная полимеризация на фрактальной геометрии//Астроном.
журн. 1994. Т. 71, № 3. С. 360-367.
585. Tajima Т., Cable S., Shibata К., Kulsrud R. M. On the Origin of
Cosmological Magnetic Fields//Astrophys. J. 1992. V. 390, № 2. P. 309-321.
586. Tajima Т., Cable S., Kulsrud R. M. On Zero-Frequency Magnetic
Fluctuations in Plasmas//Phys. Fluids B. 1992. V. 4, № 7. P. 2338-2345.
587. Рузмайкин А. А., Соколов Д. Д., Шукуров А. М. Магнитные поля
галактик. - М.: Наука, 1988. - 280 с.
588. Олвер П. Применения групп Ли к дифференциальным
уравнениям: Пер. с англ.; Под ред. А. Б. Шабата. - М.: Мир, 1989. - 639 с.
589. Ибрагимов Н. X. Группы преобразований в математической
физике. - М.: Наука, 1983. - 280 с.
590. Зеленый Л. М., Милованов А. В. Приложения групп Ли к теории
равновесия цилиндрически-симметричных силовых трубок магнитного
поля//Астроном. журн. 1992. Т. 69, № 1. С. 147-158.
591. Милованов А. В. Ренормализационные симметрии и аномальная
диффузия в шаровых звездных скоплениях//Астроном. журн. 1993. Т. 70,
№ 4. С. 680-690.
592. Milovanov А. V., Zelenyi L. M. Applications of Fractal Geometry to
Dynamical Evolution of Sunspot//Phys. Fluids B. 1993. V. 5, № 7. P. 2609-2615.
593. Вейнберг С. Гравитация и космология: Пер. с англ.; Под ред.
Я. А. Смородинского. - М.: Мир, 1975. - 696 с.
594. Зеленый Л. М.у Милованов А. В. Фрактальные свойства солнечных
пятен//Письма в «Астроном, журн.» 1991. Т. 17, № 11. С. 1013-1019.
595. Зеленый Л. М.у Милованов А. В. Эволюция солнечных пятен:
кластерная модель//Письма в «Астроном, журн. «. 1992. Т. 18, № 7. С. 622-629.
596. Milovanov А. V.. Zelenyi L. M. Fractal Model for Sunspot Evolution//
Geophys. Res. Lett. 1992. V. 19, № 14. P. 1419-1422.
597. Gefen Y., AharonyA., Alexanders. Anomalous Diffusion on Percolating
Clusters//Phys. Rev. Lett. 1983. V. 50, № 1. P. 77-80.
598. Alexander S., Orbach R. Density of States on Fractal: «Fractons»//J.
de Phys. Lett. (Paris). 1982. V. 43, № 17. P. L-625-L-631.
599. O'Shaughnessy В., Procaccia I. Analytical Solutions for Diffusion on
Fractal Objects//Phys. Rev. Lett. 1985. V. 54, № 5. P. 455-458.
821
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
600. O'Shaughnessy В., Procaccia J. Diffusion on Fractals// Phys. Rev. A.
1985. V. 32, № 5. P. 3073-3083.
601. Halvin S., Ben -Avraham D. Diffusion in Disordered Media//Advanc.
in Phys. 1987. V. 36, № 6. P. 695-798.
602. Tully R. В., Scaramella R., Vettolani G., Zamorani G. Possible Geometric
Pattern in 0. 1 с Scale Structure//Astrophys. J. 1992. V. 388, № 1. P. 9-16.
603. Calzetti D., Giavalisco M., Meiksin A. The Shape of the Two-Point
Correlation Function: Evidence for a Double Power Law//Astrophys. J. 1992.
V. 398, № 2. P. 429-440.
604. Guzzo G., IovinoA., Chincarini G. et al. Scale-Invariant Clustering in
the Large-Scale Distribution of Galaxies//Astrophys. J. 1991. V. 382, № 1.
P. L5-L9.
605. Lahav O., Kaiser N., Hoffman S. Y. Local Gravity and Peculiar Velocity:
Probes of Cosmological Models//Astrophys. J. 1990. V. 352, № 2. P. 448-456.
606. Rowan-Robinson M., et al. A Spars Sampled Redshift Survey of IRAS
Galaxies. - 1. The Convergence of the IRAS Dipole and the Origin of our Motion
with Respect to the Microwave Background//Mon. Not. R. Astr. Soc. 1990.
V. 247, № 1. P. 1-18.
607. Plionis M., Coles P., Catelan P. The QDOT and Cluster Dipoles:
Evidence for a low-?0 Universe?//Mon. Not. R. Astr. Soc. 1993. V. 262, № 2.
P. 465-474.
608. Paladin G., VulpianiA. Anomalous Scaling Laws in Multifractal Objects//
Phys. Rep. 1987. V. 156, № 4. P. 147-225.
609. Учайкин В. В., КоробкоД. А., Гисмятов И. Ф. Модифицированный
алгоритм Мандельброта стохастического моделирования распределения
галактик фрактального типа//Изв. вузов. Физика. 1997. № 8. С. 7-13.
610. Дэвисон Б. Теория переноса нейтронов: Пер. с англ.; Под ред.
Г. И. Марчука. - М.: Атомиздат, 1960. - 519 с.
611. Козлов В. И. Оценка скейлинговых свойств динамики флуктуации
космических лучей в цикле солнечной активности//Геомагнетизм и
аэрономия. 1999. Т. 39, № 1. С. 100-104.
612. Carbonell М., Oliver R, BallesterJ. L. A Search for Chaotic Behaviour
in Solar Activity//Astronomy and Astrophysics. 1994. V. 290, № 3. P. 983-994.
613. Михайлуца В. П., Фатьянов М. П. Размерность и структура
солнечного аттрактора по значениям энергии магнитного поля Солнца в 21-м
цикле//Солнечные данные. 1989. № 11. С. 109-116.
614. Малинецкий Г. Г., РузмайкинА. А., Самарский А. А. Модель
долговременных вариаций солнечной активности. - М.: Изд. ИП матем. АН
СССР, 1986. Препринт № 170. - 28 с.
615. Lindsay G. M., Russell С. Т., Luhman J. G., Gazis P. On the Sources
of Interplanetary Shocks at 0,72AU//J. Geophys. Res. 1994. V. 99, № Al.
P. 11-17.
822
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
616. Luhman J. G., Zhang Т. -L., Petrinec S. M. et al. Solar Cycle 21 Effects on
the Interplanetary Magnetic Field and Related Parameters at 0,7 and 1,0 AU//J.
Geophys. Res. 1993. V. 98, № A4. P. 5559-5572.
617. Burlaga L. F, Ness N F. Merged Interaction Regions and Large-Scale
Magnetic Field Fluctuations During 1991: Voyager 2 Observations//!. Geophys.
Res. 1994. V. 99, № A10. P. 19341-19350.
618. Kudela K., Venkatesan D. Fractal Structure of Cosmic Ray Intensity
Variations//Nuclear Phys. B. (Proc. Suppl. ). 1995. V. 39A. P. 127-135.
619. Брей Р., Лоухед Р. Солнечные пятна: Пер с англ.; Под ред. В. Е.
Степанова. - М.: Мир, 1967. - 384 с.
620. Прист Э. Р. Солнечная магнитогидродинамика: Пер. с англ.; Под
ред. В. Н. Обридко. - М.: Мир, 1985. - 592 с.
621. Зеленый Л. М., Милованов А. В. Фрактальные и мультифракталь-
ные структуры в солнечном ветре//Геомагнетизм и аэрономия. 1993. Т. 33,
№ 4. С. 18-28.
622. Милованов А. В., АвановЛ. А., Застенкер Г. Н., Зеленый Л. М. Муль-
тифрактальные свойства турбулентности солнечного ветра: теория и наблю-
дения//Космич. исследования. 1996. Т. 34, № 5. С. 451-456.
623. Burlaga L. F., Klein L. W. Fractal Structure of the Interplanetary
Magnetic Field//J. Geophys. Res. 1986. V. 91, № Al. P. 347-350.
624. Burlaga L. F. Multifractal Structure of Speed Fluctuations in Reccurent
Streams at 1AU and Near 6 AU//Geophys. Res. Lett. 1991. V. 18, № 8. P. 1651-
1654.
625. Burlaga L. F. Intermittent Turbulence in Large-Scale Velocity
Fluctuations at 1AU Near Solar Maximum//J. Geophys. Res. 1993. V. 98, № A10.
P. 17467-17473.
626. Клапдор — Клайнгротхаус Г. В., Цюбер К. Астрофизика
элементарных частиц: Пер. с нем.; Под ред. В. А. Беднякова. - М.: Изд. редакции
журнала «УФН», 2000. - 496 с.
627. Lawrence J. К. Diffusion of Magnetic Flux Elements on a Fractal
Geometry//Solar Phys. 1991. V. 135, № 2. P. 249-259.
628. Burlaga L. F, Mish W. H., Roberts D. A. Large-Scale Fluctuations in
the Solar Wind at 1 AU: 1978-1982//J. Geophys. Res. 1989. V. 94, № Al.
P. 177-184.
629. Зеленый Л. М., Милованов А. В. Фрактальные свойства
крупномасштабных магнитных конфигураций: приближение бессилового поля//Ас-
троном. журн. 1996. Т. 73, № 5. С. 805-811.
630. Зеленый Л. М., Милованов А. В. Динамическая модель флуктуации
межпланетного магнитного поля: фрактонные возбуждения и степенные
спектры//Геомагнетизм и аэрономия. 1997. Т. 37, № 1. С. 1-13.
631. Lawrence /. К, Schrijver С. J. Anomalous Diffusion of Magnetic Elements
Across the Solar Surface//Astrophys. J. 1993. V. 411, № 1. P. 402-405.
823
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
632. Nakayama Т., YakuboK., OrbachR. L. Dynamical Properties of Fractal
Networks: Scaling, Numerical Simulations, and Physical Realizations//Rew.
Mod. Phys. 1994. V. 66, № 2. P. 381-443.
633. Шредер М. Фракталы, хаос, степенные законы. Миниатюры из
бесконечного рая.: Пер. с англ.; Под ред. А.В. Борисова.- М.; Ижевск: НИЦ
«Регулярная и хаотическая динамика». 2001. - 528 с.
634. Лейбниц Т.Е. Сочинения в четырех томах. - М.: Мысль, 1982. Т. 1.
С. 413-429.
635. Медведев Ф.А. Очерки истории теории функций действительного
переменного. - М.: Наука, 1975. - 248 с.
636. Hata M. Fractals in Mathematics // Pattern and Waves: Qualitative
Analysis of Nonlinear Differential Equations (Studies in Mathematics and its
Applications, v. 18) / Ed. by T. Nishida, M. Mimura, H. Fujii. - Tokyo:
Kinokuniya Сотр. Ltd., 1986. P. 259-278.
637. Pascal E. Esercizi e Note Critiche di Calcolo Infinitesimale. - Milano,
1895.
638. Brunschvicg L. Les Etapes de la Philosophic Mathematique. - Paris,
1912.
639. Hawkins Th. Lebesgue's Theory of Integration. Its Origins and
Development. — London, 1970.
640. Гелбаум Б., Олмстед Дж. Контрпримеры в анализе: Пер. с англ.;
Под. ред. П.Л. Ульянова. - М.: Мир, 1967. - 252 с.
641. Бржечка В.Ф. О функции Больцано //УМН. 1949. Т. IV. № 2(30).
С. 15-21.
642. Hardy G.H Weierstrass's Non - Differentiable Function/yTrans. Amer.
Math. Soc. 1916. V. 17, N 3. P. 301-325.
643. Gerver J. The Differentiability of the Riemann Function at Certain
Rational Multiples of n // Proc. Nat. Acad. Sci. U.S.A. 1969. V. 62, № 3.
P. 668-670.
644. Gerver J. More on the Differentiability of the Riemann Function//
Amer. J. Math. 1971. V. 93, № 1. P. 33-41.
645. Hankel H. Untersuchungen uber die unendlich oft oszillierenden und
unstetigen Funktionen (1870) //Ostwalds Klassiker der exacten Wissenschaften
(Leipzig). 1905. N 153. P.44-45.
646. Houel J., Hankel H. Untersuchungen uber die unendlich oft
oszillierenden und unstetigen Funktionen. Ein Beitrag zur Feststellung des
Begriffs der Function uberhaupt. Universitats - programm zum 6 Marz
1870.Tubingen. - Bull. Sci. Math, et Astron. 1870. V. 1. P. 117-124.
647. Schwarz H.A. Beispiel einer stetigen nicht differentiirbaren Function
(1873) //Ges. Math. Abhandlungen (Berlin). 1890. B. 2. P. 269-274.
648. Dugac P. Elements d' analyse de Karl Weierstrass // Archive for Hist.
Exact. Sci. 1973. V. 10. P. 41-176.
649. Du Bois — Reymond P. Verch einer Classification der Willkurlichen
Functionen reeler Argumente nach ihren Aenderungen in den kieinsten
824
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Intervallen//J. fur die reine und angewandte Mathematiques (Crelle). 1875. V. 79.
P. 21-37.
650. Сакс С. Теория интеграла: Пер. с англ. - М.: ИЛ, 1949. - 496 с;
М.: Факториал-Пресс, 2004. - 496 с.
651. DenjoyA, Felix L., Montel P. Henri Lebesgue, le savant, le professeur,
Г homme // L' Enseign. Math. 1957. Ser. 2. V. 3. P. 1-18.
652. Darboux G. Memoire sur les fonctions discontinues //Ann. Sci. Ecole
Norm. Super. 1875. Ser.2. V. 4. P. 57-112.
653. DM U. Sopra una classe di funzioni finite e cjntinue che non hanno
mai una derivata (1877) // Opere Matem. (Roma). 1954. V. II. P. 5-7.
654. DM U. Fondamenti per la teorica delle funzioni de variabili reali. -
Pisa, 1878.
655. Darboux G. Addition au memoire sur les fonctions discontinues//Ann.
Sci. Ecole Norm. Super. 1879. Ser.2. V. 8. P. 195-202.
656. Knopp K. Ein einfaches Verfahren zur Bildung stetiger, nirgends
differenzierbarer Funktionen // Math. Zeitschrift. 1918. V. 2. P. 1-26.
657. Зигмунд А. Тригонометрические ряды: Пер. с англ.; Под ред. Н.К.
Бари. - М.: Мир, 1965. Т.1. - 616 с.
658. Гапошкин В. Ф. Лакунарные ряды и независимые функции // УМН.
1966. Т. XXI, № 6 (132). С. 3-82.
659. Hadamard J. Essai sur Г etude des fonctions donnees par leur
developpement de Taylor//Journ. Math. 1892. V. 8. P. 101-186.
660. Куратовский К. Топология: Пер. с англ. - М.: Мир, 1966. Т. 1. -
596 с; 1969. Т. 2. - 624 с.
661. Бэр Р. Теория разрывных функций: Пер. с франц.; Под ред. АЯ. Хин-
чина. - М.-Л.: ГТТИ, 1932. - 136 с.
662. ОкстобиДж. Мера и категория: Пер. с англ. - М.: Мир, 1974. -
160 с.
663. Banach S. Uber die Baire'sche Kategorie gewisser Funktionenmengen//
Stud. Math. 1931. V. 3. P. 174-179.
664. Mazurkiewicz S. Sur les fonctions non derivables // Stud. Math. 1931.
V. 3. P. 92-94.
665. Mauldin R.D. The Sets of Continuous Nowhere Differentiable Fuctions//
Pacif. J. Math. 1979. V. 83, № 1. P. 199-205.
666. Безикович А.С. Исследование непрерывных функций в связи с
вопросом об их дифференцируемости //Матем. сб. 1924. Т. 31. № 3-4.
С. 529-556.
667. Saks S. On the functions of Besicovitch in the space of continuous
functions // Fund. Math. 1932. V. 19. P. 211-219.
668. Orlicz W. Sur les fonctions continues non derivables // Fund. Math.
1947. V. 34. P. 45-60.
669. Яглом A.M. Корреляционная теория стационарных случайных
функций. - Л.: Гидрометеоиздат, 1981. - 280 с.
670. Винер Н. Я - математик: Пер. с англ. - М.: Наука, 1964. - 356 с.
825
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
671. Takagi T. A Simple Example of the Continuous Function Without
Derivative // Proc. Phys. Math. Soc. Japan. 1903. V. 1. P. 176-177; The CoUected
Papers of Teiji Takagi. - Tokyo: Iwanami Shoten PubL, 1973. P. 5-6.
672. Hobson E. W. The Theory of Functions of a Real Variable and the Theory
of Fourier's Series. - Cambridge: Cambridge at the University Press, 1926.
673. Титчмарш Е. Теория функций: Пер. с англ. - М.-Л.: ГИТТЛ, 1951.
- 508 с.
674. van der Waerden B.L. Ein einfaches Beispieleiner nicht-differenzierbaren
stetigen Funktion//Math. Z. 1930. V. 32. P. 474-475.
675. Rham G. de. Sur un exemple de fonction continue sans derivee//
Enseign. Math. 1957. V. 3. P. 71-72.
676. Дринфельд Г.И. Дополнения к общему курсу математического
анализа. - Харьков: Изд. ХГУ, 1958.
677. Рисе Ф., Секефалъви-Надъ Б. Лекции по функциональному
анализу: Пер. с франц.; Под ред. СВ. Фомина. - М.: ИЛ, 1954. - 500 с.
678. Kuczma M. Functional Equations in a Single Variable//PWN-Polish
Sci. Publ. - Warszawa, 1968.
679. Faber G. Einfaches Beispiel einer stetigen nirgends difFerentiierbaren
Funktion // Jahresber. Deutsch. Math. Verein. 1907. V. 16. P. 538-540.
680. KaterF. S. A Tupical Nowhere differentiable Function // Canad. Math.
Bull. 1983. V. 26. P. 149-151.
681. Artin E. The Gamma Function. -Austin: Holt, Rinehart and Winston, 1964.
682. Rata M. On the functional equation // J. Math. Kyoto. Univ. 1985.
V. 25, № 2. P. 357-364.
683. Kaplan J. L.} Mallet-Paret J., Yorke J. A. The Lyapunov Dimension of
a Nowhere Differentiable Attracting Torus // Ergodic Theory Dynamical Systems.
1984. V. 4. P. 261-281.
684. Besicovitch A. S, Ursell H. D. Sets of Fractional Dimension, V: On
Dimensional Numbers of Some Continuous Curves //J. London Math. Soc. 1937.
V. 12. P. 18-25.
685. Love E. R.} YoungL. C. Sur une classe de fonctionelles lineaires // Fund
Math. 1937. V. 28. P. 243-257.
686. Kline S. A. On Curves of Fractional Dimensions // J. London Math.
Soc. 1945. V. 20. P. 79-86.
687. Yamaguti M.,Hata M. Weierstrass's function and chaos // Hokkaido
Math. J. 1983. V. 12. P. 333-342.
688. Hata M., Yamaguti M. The Takagi function and its generalization //
Japan J. Appl. Math. 1984. V. 1. P. 183-199.
689. Faber G. Uberstetige Funktionen//Math. Ann. 1910. V. 69. P. 372-443.
690. Rham G. de. Sur quelques courbes definites par des equations
fonctionnelles // Rend. Sem. Mat. Torino 1957. V. 16. P. 101-113.
691. Lomnicki Z., Ulam S. Sur la theorie de la mesure dans les espaces
combinatoires et son application au calcul des probabilites I: Variables
independantes // Fund. Math. 1934. V. 23. P. 237-278.
826
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
692. Salem R. On some singular monotonic functions which are strictly
increasing // Trans. Amer. Math. Soc. 1943. V. 53. P. 427-439.
693. Levi P. Les courbes planes ou gauches et les surfaces composees de
parties semblables au tout // J. Ecole Poly. Serie III. 1938. V. 7-8. P. 227-292,
694. DekkingF.M. Recurrent Sets//Adv. in Math. 1982. V. 44. P. 78-104.
695. Hutchinson J.E. Fractals and Self- Similarity //Indiana Univ. Math.
J. 1981. V. 30. №5. P. 713-747.
696. Hata M. On the structure of self - similar sets // Japan J. Appl. Math.
1985. V. 2. P. 381-414.
697. Mattila P. On the structure of self- similar fractals //Ann. Acad. Sci.
Fenn. Ser. A. 1982. V. 7. P. 189-195.
698. Williams R.F. Composition of contractions // Bol. Soc. Brasil. Mat.
1971. V. 2. P. 55-59.
699. Hata M. On some properties of set - dynamical systems // Proc. Japan
Acad. Ser. A. 1985. V. 61. P. 99-102.
700. Marion J. Le calcul de la mesure Hausdorff des sous - ensembles parfaits
isotypiques de //C. R. Acad. Sci. Paris. Ser. A. 1979. V. 289. P. 65-68.
701. Lax P.D. The differentiability of Polia's function // Adv. in Math. 1973.
V. 10. P. 456-464.
702. Peano G. Sur une courbe, qui remplit toute une aire plane // Math.
Ann. 1890. V. 36. P. 157 - 160.
703. Hilbert D. Uber die stetige Abbildung einer Linie auf ein Flachenstuck
// Math. ann. 1891. V. 38. P. 459-460.
704. Polya G. Uber eine Peanosche Kurve // Bull. Acad. Sci. Cracovie. 1913.
Ser. A. P. 305-313.
705. Fractals: Non - Integral Dimensions and Applications/Ed. by
G. Cherbit. - N.Y.: Wiley & Sons, 1991.-249 p.
706. Tricot C. Curves and Fractal Dimension. - N.Y.: Springer-Verlag. 1993.
- 323 p.
707. Classics on Fractals /Ed. by G.A. Edgar. - N.Y.: Addison-Wesley, 1993.
- 366 p.
708. Турбин А. Ф., Працевитый Н.В. Фрактальные множества, функции,
распределения. - Киев: Наукова думка, 1992. - 208 с.
709. Puente С, Borja С, Navarro M., Romeu J. An Iterative Model for Fractal
Antennas: Application to the Sierpinski Gasket Antenna // IEEE Trans. 2000.
V.AP-48, №5. P. 713-719.
710. Borja C, Puente C, Medina A. Iterative Network Model to Predict the
Behavior of a Sierpinski Fractal Network // Electron. Lett. 1998. V. 34, № 15.
P. 1443-1445.
711. Brown G.H., Woodward O.M. Experimentally Determined Radiation
Characteristics of Conical and Trangular Antennas // RCA Rev. 1952. P. 425-452.
712. Samukic A. UMTS Universal Mobile Telecommunications System:
Development of Standards for the Third Generation // IEEE Trans. Veh.
Technol. 1998. V. 47. P. 1099-1104.
827
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
713. Гуляев Ю.В., Никитов С.А. Фотонные и магнитофотонные
кристаллы - новая среда для передачи информации // Радиотехника. 2003. № 8.
С. 26-30.
714. Гуляев Ю.В., Никитов С.А. Перспективы развития
телекоммуникаций // Нелинейный мир. 2003. Т. 1, № 1-2. С. 3-11.
715. Wake D., Moodie D. Passive Picocell - a Future Integrated Wireless
Communications Network // B.T. Eng. 1997. V. 16 P. 106-112.
716. Puente C, Navarro M., Romeu J., Pous R. Variation on the Fractal
Sierpinski Antenna Flare Angle // Proc. IEEE Antennas and Propagation Society
Int. Symp. -Atlanta: 1998. P. 2340-2343.
717. Puente C, Romeu J., Bartolome R., Pous R. Perturbation of the Sierpinski
Antenna to Allocate Perating Bands // Inst. Elect. Eng. Electron. Lett. 1996.
V. 32. P. 2186-2188.
718. Song С. Т. P., Hall P. S., Ghafouri-Shiraz H, Wake D. Sierpinski
Monopole Antenna with Controlled Band Spacing and Input Impedance // Inst.
Elect. Eng. Electron. Lett. 1999. V. 35, № 13. P. 1036-1037.
719. Puente С Fractal Antennas: Ph.D. dissertation.- Univ. Politecnica de
Catalunya., Dept. Signal Theory and Commun., 1997.
720. Hatamoto Y, Abe M. Constant Impedance Characteristics with Planar
Antenna// Proc. General Conf. Inst. Elect. Commun. Eng. 1982. P. 3-68.
721. Honda S., Ito M., Seki H, Jinbo Y A Disk Monopole Antenna with 1:8
Impedance Bandwidth and Omnidirectional Pattern // Proc. ISAP' 92 (Japan).
-Sapporo, 1992. P. 1145-1148.
722. Agrawall N P., Kumar G., Ray K. P. Wide-Band Planar Monopole
Antennas // IEEE Trans. 1998. V. AP-46. № 2. P. 294-295.
723. Hammond M., Poey P., Colombel F. Matching the Input Impedance of
a Broadband Disc Monopole // Inst. Elec. Eng. Electron. Lett. 1993. V. 29, № 4.
P. 406-407.
724. Ammann M. J. Square Planar Monopole Antenna // Proc. National
Conf. Antennas Propagation Inst. Elect. Eng. 1999. P. 37-40.
725. Wheeler HA. Small Antennas//IEEE Trans. 1975. V. AP-23. P. 462-469.
726. Song С. Т.Р., Hall P. S., Ghafouri-Shiraz H, Wake D. Quasilog Periodic
Circular Ring Monopole Antenna// AP 2000 Conf. (Switzerland). - Davos, 2000.
727. Song С. Т. P., Hall P. S., Ghafouri-Shiraz H, Wake D. Multi-Circular
Loop Monopole Antenna//Inst. Elect. Eng. Electron. Lett. 2000. V. 36, № 5.
P. 391-393.
728. Song C.T.P.f Peter S.H, Ghafouri-Shiraz H Multiband Multiple Ring
Monopole Antennas//IEEE Trans. 2003. V. 51, № AP-51. № 4. P. 722-729.
729. Parker E., El Sheikh A.N.A. Convoluted Array Elements and Reduced
Size Unit Cells for Frequency -Selective Surfaces // Proc. IEE. 1991. V. H 138,
№ 1. P. 19-22.
730. Puente C, Romeu J., CardamaA. The Koch Monopole: A Small Fractal
Antenna//IEEE Trans. 2000. V. AP-48. № 11. P. 1773-1781.
828
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
731. Sapoval B.f Gobron Th. Vibrations of Strongly Irregular or Fractal
Resonators // Phys. Rev. E. 1993. V. 47, № 5. P. 3013-3024.
732. Russ S., Sapoval В., Haeberle 0. Irregular and Fractal Resonators with
Neumann Boundary Conditions: Density of States and Localization//Phys. Rev.
E. 1997. V. 55, №2. P. 1413-1421.
733. Even G, Russ S., Repain V., Pieranski P., Sapoval В. Localizations in
Fractal Drums: An Experimental Study//Phys. Rev. Lett. 1999. V. 83, № 4.
P. 726-729.
734. Lapidus M.L., Neuberger J.W., Renka R.J., Griffith C.A. Snowflake
Harmonics and Computer Graphics: Numerical Computation of Spectra on
Fractal Drums // Int. J. Bifurcation and Chaos. 1996. V. 6, № 7. P. 1185-1210.
735. Borja G, Font G, Blanch S., Romeu J. High Directivity Fractal Boundary
Microstrip Patch Antenna // Electron. Lett. 2000. V. 36, № 9. P. 778-779.
736. Borja G, Romeu J. Fracton Vibration Modes in the Sierpinski Microstrip
Patch Antenna // Proc. IEEE Antennas and Propagation Society Int. Symp. -
Boston: 2001. P. 612-615.
737. Borja G, Romeu J. On the Behavior of Koch Island Fractal Boundary
Microstrip Patch Antenna // IEEE Trans. 2003. V. AP-51, № 6. P. 1281-1291.
738. Aitken J.A. Swept - Frequency Microwave Q - Factor Measurement //
Proc. IEE. 1976. V. H-123, № 9. P. 855-861.
739. Kajfez D., Hwan E.J. Q - Factor Measurement with Network Analyzer
// IEEE Trans. 1984. V. MTT - 32. P. 666-670.
740. Puente-Baliarda G, PousR. Fractal Design of Multiband and Low Side-
Lobe Arrays // IEEE Trans. 1996. V. AP-44, № 5. P. 730-739.
741. Haupt R.L., Werner D.H. Fast Array Factor Calculations for Fractal
Arrays// Proc. 13th Annu. Review Progress in Applied Computational
Electromagnetics. - Monterey, 1997. P. 291-296.
742. Werner D.H., Haypt R.L. Fractal Constructions of Linear and Planar
Arrays // Proc. IEEE Antennas and Propagation Society Int. Symp. -Montreal:
1997. V. 3. P. 1968-1971.
743. Werner D.H., Haupt R.L., Werner P.L. Fractal Antenna Engineering:
the Theory and Design of Fractal Antenna Arrays // IEEE Antennas Propagat.
Mag. 1999. V. 41, №5. P. 37-59.
744. Werner D.H, Anushko К. С, Werner P.L. The Generation of Sum and
Difference Patterns Using Fractal Subarrays // Microwave Opt. Technol. Lett.
1999. V. 22, № 1. P. 54-57.
745. Frontiers in Electromagnetics //Ed. by D.H. Werner and R. Mittra.
- Piscataway: IEEE Press, 2000.
746. Werner D.H, Gingrich M.A., Werner P.L. A Self-Similar Fractal
Radiation Pattern Synthesis Technique for Reconfigurable Multiband Arrays //
IEEE Trans. 2003. V. AP-51, № 7. P. 1486-1498.
747. Климов Д.А. Англо-русский словарь-справочник сокращений,
аббревиатур и специальных обозначений, принятых в современных
компьютерных технологиях. - М.: ТЕИС, 2003. - 781 с.
829
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
748. Хемминг Р.В. Цифровые фильтры: Пер. с англ.; Под ред. О.А.
Потапова. - М.: Недра, 1987. - 221 с.
749. El-Khamy S.E.,Aboul-Dahab M.A., Elkashlan M.L Simplifying and Size
Reduction of Kaiser - Koch Multiband Fractal Arrays Using Windowing and
QuantizationTechniques // Proc. 17th Nat. Radio Science Conf. - Egypt: 2000.
P. B13-1-B13-9.
750. El-Khamy S.E.,Aboul-Dahab M.A., Elkashlan M.L A Simplified Koch
Multiband Fractal Arrays Using Windowing and QuantizationTechniques // Proc.
IEEE Antennas and Propagation Soc. Int. Symp. - Salt Lake City: 2000. V.3.
P. 1716-1719.
751. Котельников В.А. Теория потенциальной помехоустойчивости. -
М.-Л.: Госэнергоиздат, 1956. - 152 с.
752. Котельников В.А. Сигналы с максимальной и минимальной
вероятностями обнаружения // Радиотехника и электроника. 1959. Т. 4. № 3.
С. 354-358.
753. Ширман Я.Д., Лосев Ю.И., Минервин Н.Ни др. Радиоэлектронные
системы: основы построения и теория / Под ред. Я.Д. Ширмана. - М.:
МАКВИС, 1998. - 825 с.
754. Бункин Б.В., Реутов А.П., Потапов А.А. и др. Вопросы
перспективной радиолокации (Коллективная монография): Под ред. А.В. Соколова.
- М.: Радиотехника, 2003. - 512 с.
755. Информационные технологии в радиотехнических системах: Под
ред. И.Б. Федорова. - М.: Изд. МГТУ им. Н.Э. Баумана, 2003. - 671 с.
756. Лагаръков А.Н., Погосян М.А. Фундаментальные и прикладные
проблемы стелс-технологий // Вестник РАН. 2003. Т. 73, № 9. С. 779-787.
757. Николис Г., Пригожим И. Самоорганизация в неравновесных
системах: Пер. с англ.; Под ред. Ю.А. Чизмаджева. - М.: Мир, 1979. - 512 с.
758. Хакен Г. Синергетика: Пер. с англ.; Под ред. Ю.Л. Климонтови-
ча.-М.: Мир,1985. -419 с.
759. Хакен Г. Информация и самоорганизация: Пер. с англ. - М.: Мир,
1991.-240 с.
760. Пригожий И. Введение в термодинамику необратимых процессов:
Пер. с англ.; Под ред. Н.С. Акулова. - М.: Ижевск: НИЦ «Регулярная и
хаотическая динамика», 2001. - 160 с.
761. Пригожий И. Конец определенности. Время, хаос и новые
законы природы: Пер. с англ. - М.: Ижевск: НИЦ «Регулярная и хаотическая
динамика», 2001. - 208 с.
762. Пригожий И, Стенгерс И. Время, хаос, квант: Пер. с англ.; Под
ред. В.И. Аршинова. - М.: Эдиториал УРСС, 2001. - 240 с.
763. Пригожий И, Стенгерс И. Порядок из хаоса: Пер. с англ. - М.:
Эдиториал УРСС, 2001. - 312 с.
764. Пригожий И От существующего к возникающему: Пер с англ.; Под
ред. Ю.Л. Климонтовича. - М.: Эдиториал УРСС, 2002. - 288 с.
830
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
765. Пригожим И., Кондепуди Д. Современная термодинамика. От
тепловых двигателей до диссипативных структур: Пер. с англ.; Под ред.
Е.П. Агеева. - М.: Мир, 2002. - 461 с.
766. Chaos, Fractals, and Dynamic / Ed. P. Fischer, W.R. Smith. - N.-Y.:
Dekker, 1985. - 261 p.
767. Chaos, Noise and Fractals / Ed. E.R. Pike, L.A. Lugiato. - Bristol:
Hilger, 1987. - 249 p.
768. Takayasu H. Fractals in Physical Sciences . - N. Y.: Wiley & Sons,
1990.-170 p.
769. Peitgen H.-O., JurgensH., Saupe D. Fractals for the Classroom. - N.Y.:
Springer-Verlag, 1991. - 500 p.
770. Ахромеева Т.С, Курдюмов СИ, Малинецкий Г.Г., Самарский АЛ.
Нестационарные структуры и диффузионный хаос. - М.: Наука, 1992. -
544 с.
771. Капица СП., Курдюмов СП., Малинецкий Г.Г. Синергетика и
прогнозы будущего. - М.: Наука, 1977. - 285 с.
772. Franceschetti G., IodiceA., Riccio D. Scattering from Dielectric Random
Fractal Surface via Method of Moments // IEEE Trans. 2000.V. GRS-38, № 4.
P. 1644-1655.
773. Brown S. R., Scholz С Н. Broad Bandwidth Study of the Topography
of Natural Rock Surfaces//J. Geoph. Res. 1985. V.90, № B14. P. 12575-12582.
774. Фракталы в прикладной физике / Под ред. А.Е. Дубинова. - Ар-
замас-16: Изд. ВНИИЭФ, 1995. - 218 с.
775. Franceschetti G., Migliaccio M., Riccio D. An Electromagnetic Fractal-Based
Model for the Study of Fading // Radio Sci. 1996. V. 31, № 6. P. 1749-1759.
776. Mandelbrot B.B. Multifractals and 1/f Noise. - N. Y.: Springer-Verlag,
1998.-442 p.
777. Chaos and Fractals: A Computer Graphical Journey / Ed. С A. Pickover.
- Amsterdam: Elsevier, 1998. - 452 p.
778. Зам В. Б. Синергетическая экономика. Время и перемены в
нелинейной экономической теории: Пер. с англ.; Под ред. В.В. Лебедева и
В.Н. Разжевайкина. - М.: Мир, 1999. - 355 с.
779. Петере Э. Хаос и порядок на рынках капитала. Новый
аналитический взгляд на циклы, цены и изменчивость рынка: Пер. с англ.; Под ред.
А.Н. Романова. - М.: Мир, 2000. - 333 с.
780. Труды семинара «Время, Хаос и математические проблемы».
Вып. 1. - М.: Книжный дом «Университет», 1999. - 250 с.
781. Franceschetti G, IodiceA. Fractals and the Smal perturbation Scattering
Model // Radio Sci. 1999. V. 34, № 5. P.1043-1054.
782. Малинецкий Г.Г., Потапов А.Б. Современные проблемы
нелинейной динамики. - М.: Эдиториал УРСС, 2000. - 336 с.
783. Кроновер P.M. Фракталы и хаос в динамических системах: Пер. с
англ.; Под ред. Т.Э. Кренкеля. - М.: Постмаркет, 2000. - 350 с.
831
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
784. Proios G. The Haysdorff Dimension of a Class of Fractals, which are
Determined by the Distribution of Dyadic Digits // Chaos, Solitons & Fractals.
2000. V. 11, № 1-3. P. 269 - 274.
785. Karanikas C. The Haysdorff Dimension of Very Weak Self- Similar
Fractals Described by the Haar Wavelet System // Chaos, Solitons & Fractals.
2000. V. 11, № 1-3. P. 275-280.
786. Weron A, Weron R. Fractal Market Hypothesis and Two Power-Laws //
Chaos,Solitons & Fractals. 2000. V. 11, № 1-3. P. 289-296.
787. Нао В., Lee H.C., ZhangS. Fractals Related to Long DNA Sequences and
Complete Genomes//Chaos, Solitons & Fractals. 2000. Vll, № 6. P. 825-836.
788. О 'Neil T.C. The Myltifractal Spectra of Projected Measuring in
Euclidean paces // Chaos, Solitons & Fractals. 2000. V. 11, № 6. P. 901-922.
789. Saied E.A. Anomalous Diffusion on Fractal Objects: Additional Analytic
Solutions // Chaos, Solitons & Fractals. 2000. V. 11, № 9. P. 1369-1376.
790. ArgyrisJ., Giubotariu C.I., Weingaertner W.E. Fractal Space Signatures
in Quantum Physics and Cosmology. - I. Space, Time, Matter, Fields and
Gravitation // Chaos, Solitons & Fractals. 2000. V. 11, № 12. P. 1671-1720.
791. Bigerelle M., lost A. Fractal Dimension and Classification of Music//
Chaos, Solitons & Fractals. 2000. V. 11, № 14. P. 2179-2192.
792. Chen J., Lo Т., Livtva J. Scattering of Electromagnetic Waves from a Time
Varying Fractal Surface//Microw. Opt. Tech. Lett. 1993. V. 6, № 1. P. 87-91.
793. Lixin G., Zhensen W. Fractal Model and Electromagnetic Scattering from
Time - Varying Sea Surface // Electron. Lett. 2000. V. 36, № 2LP. 1810-1812.
794. Romeu J, Rahmat-Samii Y. Fractal FSS: A Novel Dual - Band
Frequency Selective Surface//IEEE Trans. 2000. V. AP-48, № 7. P. 1097-1105.
795. McMulenn C.T. Hausdorff Dimensions and Conformal Dynamics I;
Strong Convergence of Kleinian Groups // J. Differential Geometry. 1999. V.51,
№ 3. P. 471-515.
796. ИудинД.И, Трахтенгерц В.Ю. Фрактальная динамика
электрического заряда в грозовом облаке // Известия РАН. Физика атмосферы и
океана. 2000. Т. 36, № 5. С. 650-662; Фрактальная структура нелинейной
динамики электрического заряда в грозовом облаке//Изв. вузов. Радиофизика.
2001. Т. 44, №5-6. С. 419-437.
797. МилнорДж. Голоморфная динамика: Пер. с англ. - Ижевск: НИЦ
«Регулярная и хаотическая динамика». 2000. - 320 с.
798. Илъяшенко Ю. С, Ли Вейгу. Нелокальные бифуркации: Пер. с англ.
- М.: МЦНМО-ЧеРо, 1999. - 416 с.
799. Мс CauleyJ.L. Chaos, Dynamics and Fractals an Algorithmic Approach
to Deterministic Chaos. - N. Y.: Cambridge Univ. Press., 1993. - 323 p.
800. Du Can, Zhang Qun, Zhang Shou-Hong. Радиолокационное
обнаружение надводных кораблей, основанное на анализе фрактальных
параметров высокого порядка // J. Xidian Univ. 1999. V.26, № 6. P. 724 - 727.
801. Табор М. Хаос и интегрируемость в нелинейной динамике: Пер. с
англ.; Под ред. В.А. Журавлева. - М.: Эдиториал УРСС, 2001. - 320 с.
832
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
802. Бланк МЛ. Устойчивость и локализация в хаотической
динамике. - М.: МЦНМО, 2001. - 351 с.
803. Новиков И.Я., Стечкин СБ. Основные конструкции всплесков //
Фундам. и прикл. матем. 1997. Т.З, № 4. С. 999-1028.
804. Новиков И.Я., Стечкин СБ. Основы теории всплесков // УМН.
1998. Т. 53. № 6 (324). С. 53 - 128.
805. Уэлстэд С Фракталы и вейвлеты для сжатия изображений в
действии: Пер. с англ. - М.: Триумф, 2003. - 320 с.
806. Дремин И.М., Иванов О.В., Нечитайло В.А. Вейвлеты и их
использование // УФН. 2001. Т.171, № 5. С. 465-501.
807. Чуй К. Введение в вэйвлеты: Пер. с англ. - М.: Мир, 2001. -
412 с.
808. Столниц Э., ДеРоуз Т., СалезинД. Вейвлеты в компьютерной
графике: Пер. с англ. -М.; Ижевск: НИЦ «Регулярная и хаотическая
динамика», 2002. - 272 с.
809. СолодухаАМ., НестеренкоЛ.П. Фрактальная размерность странного
аттрактора для хаотических колебаний в контуре с сегнетоэлектриком //
Физика твердого тела. 1996. Т. 38, № 6. С. 1896-1898.
810. Марсден Дж, Мак-Кракен М. Бифуркация рождения цикла и ее
приложения: Пер. с англ. Под ред. Н.Н. Баутина и Е.А. Леонтовича. - М.:
Мир, 1980. -368 с.
811. Рабинович М.И., Езерский А.Б. Динамическая теория
формообразования. - М.: Янус-К, 1998. - 192 с.
812. Штиллер В. Уравнение Аррениуса и неравновесная кинетика: Пер.
с англ. - М.: Мир, 2000. - 176 с.
813. Биллингслей П. Эргодическая теория и информация: Пер. с англ.;
Под ред. Б.М.Гуревича. - М.: Мир, 1969. - 240 с.
814. Mane R. On the Dimension of the Compact Invariant Sets of Certain
Non - Linear Maps // Dynamical Systems and Turbulence.- Lecture Notes in
Mathematics. - N.Y.: Springer-Verlag, 1981. V. 898. P. 230-242.
815. Xue D., Zhu Y.,Zhu G. Recognition of Low - Contrast FLIR Tank
Object Based on Multiscale Fractal Character Vector // Proc. of SPIE. 1996.
V. 2756. Automatic Object Recognition VI. P. 38-45.
816. ЗахарченкоВД., БрыжинАА. Использование дробного
дифференцирования в задачах цифровой обработки доплеровских сигналов при
оценке центра тяжести спектра // Доклады 3-й Междунар. конф. и выставки
«Цифровая обработка сигналов и ее применение».- М.: Изд. РНТО РЭС им.
А.С.Попова, 2000. Т. 1. С. 311-313.
817. Rogers CA. Hausdorff Measures. - Cambridge: Univ. Press, 1970. -
180 p.
818. Teman R. Infinite-Dimensional Dynamical Systems in Mechanics and
Physics.-Berlin: Springer-Verlag, 1988. - 500 p.
819. Бабин А.В., Вишик М.И. Аттракторы эволюционных уравнений:
Под ред. П.Я. Кочина. - М.: Наука, 1989. - 294 с.
833
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
820. Gerald А.Е. Measure, Topology, and Eractal Geometry. - N.Y.:
Springer-Veriag, 1990. -232 p.
821. Pattern and Waves / Ed. by T. Nishida, M. Mimura, H. Fujii. - Tokyo:
Kinokuriya Сотр. Ltd., 1991.-692 p.
822. Beck C, SchloglF. Thermodynamics of Chaotic Systems. - Cambridge:
Univ. Press, 1993. - 286 p.
823. ГлейкД. Хаос. Создание новой науки: Пер. с англ. - СПб.:
Амфора, 2001. - 398 с.
824. Abarbanel H.D.I. Analysis of Observed Chaotic Data. - Berlin: Springer
-Veriag, 1995.-272p.
825. Морозов А.Д. Введение в теорию фракталов. - М.: Ижевск:
Институт компьютерных исследований, 2002. - 160 с.
826. Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент.
- М.: Эдиториал УРСС, 2000. - 256 с.
827. Владимиров В.А., Воробьев Ю.Л., Малинецкий Г.Г. и др. Управление
риском. Риск. Устойчивое развитие. Синергетика. - М.: Наука, 2000. -
431 с.
828. Fractional Calculus and Its Applications. - Lecture Notes in
Mathematics / Ed. by A. Dold and B. Eckmann.- Berlin: Springer - Veriag, 1975.
V. 457. - 382 p.
829. Fractional Calculus. - Research Notes in Mathematics / Ed. by AC.
McBride & G.F. Roach. - London: Pitman Advanced Publishing Program, 1985.
V. 138.-214 p.
830. Rutman R.S. On the paper by R.R. Nigmatullin «Fractional integral and
its physical interpretation» // Теоретическая и математическая физика. 1994.
Т. 100, № 3. С.476-478.
831. Rutman R.S. On physical interpretations of fractional integration and
differentiation // Теоретическая и математическая физика. 1995. Т. 105, № 3.
С.393-404.
832. Applications of Fractional Calculus in Physics //Ed. by R.Hilfer.-
Singapore: World Scientific Publishing Co. Pte. Ltd, 2000. - 463 p.
833. Нахушев A.M. Дробное исчисление и его применение. - М.: Физ-
матлит, 2003. - 272 с.
834. Рехвиашвили С.Ш. Формализм Лагранжа с дробной производной
в задачах механики // Письма в ЖТФ. 2004. Т. 30, № 2. С. 33-37.
835. Лахно В.Д. Кластеры в физике, химии, биологии. - М.; Ижевск:
НИЦ «Регулярная и хаотическая динамика», 2001. - 256 с.
836. Божокин С.В.} Паршин Д.А. Фракталы и мультифракталы. - М.;
Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. - 128 с.
837. Кадомцев Б.Б. Динамика и информация. - М.: Изд. редакции
журнала «УФН», 1999. - 400 с.
838. Данилов Ю.А. Лекции по нелинейной динамике. - М.: Постмар-
кет, 2001.- 184 с.
834
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
839. Встовский Г.В., КолмаковА.Г., Бунин И.Ж. Введение в мультифрак-
тальную параметризацию структур материалов. - М.; Ижевск: НИЦ
«Регулярная и хаотическая динамика», 2001. - 116 с.
840. РюэльД. Случайность и хаос: Пер. с франц.; Под ред. А.В. Борисова.
- М.; Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. - 192 с.
841. Embrechts P., Kluppelberg С, Mikosch T. Modeling Extremal Events,
- Berlin: Springer, 1997. - 645 p.
842. Винклер Г. Анализ изображений, случайные поля и динамические
методы Монте - Карло. Математические основы: Пер. с англ. -
Новосибирск: Изд. СО РАН, филиал «Гео», 2002. - 343 с.
843. Евдокимов Н.В., Комолое В.П., Комолое ИВ. Интерференция
динамического хаоса гамильтоновых систем: эксперимент и возможности
радиофизических приложений// УФН. 200L Т. 171, №7. С. 775-795.
844. Пономарев Д.Ю. Вероятностно—временные характеристики
асинхронных информационных сетей с учетом самоподобия. - Красноярск:
НИИ СУВПТ, 2002, - 194 с.
845. Зубарев Д.Н., Морозов В.Г., Репке Г. Статистическая механика
неравновесных процессов: В 2 т.: Пер. с англ.; Под ред. В.Г. Морозова. - М.:
Физматлит, 2002. Т. 1. - 432 с; Т. 2. - 296 с.
846. РюэлъД. Термодинамический формализм. Математические
структуры классической равновесной статистической механики: Пер. с англ.;
Под ред. Б.М. Гуревича. — М.: Институт компьютерных исследований, 2002.
- 288 с.
847. Шильников Л.П., Шильников А.П., Тураев Д.В., Чу а Л. Методы
качественной теории в нелинейной динамике. Ч. 1.: Пер. с англ. - М.;
Ижевск: Институт компьютерных исследований, 2004. — 416 с.
848. Тарасенко В. В. Фрактальная логика.- М.: Прогресс - Традиция,
2002.- 160 с.
849. Дмитриев А. С, Панас А.И. Динамический хаос: новые носители
информации для систем связи. - М.: Физматлит, 2002. - 252 с.
850. Чистяков Д.В. Фрактальная геометрия образов непрерывных
вложений адических чисел и соленоидов в евклидовы пространства //
Теоретическая и математическая физика. 1996. Т. 109, № 3. С.323 - 337.
851. Терстон У. Трехмерная геометрия и топология: Пер. с англ.; Под
ред. О.В. Шварцмана. - М.: МЦНМО, 2001. - 312 с.
852. Кузнецов СП. Динамический хаос. - М.: Физматлит, 2001. - 296 с.
853. Могилевский Э.И. Фракталы на Солнце. - М.: Физматлит, 2001. -
152 с.
854. Карпенко В.И., Даник Ю.Г., Маляров М.В. Обнаружение объектов
во фрактальных структурах // Радиотехника. 2002. № 1. С. 9-12.
855. Симо К, Смет С, Шенгине А. и др. Современные проблемы
хаоса и нелинейности: Пер. с англ.; Под ред. А.В. Борисова и А.А. Килина. -
М.; Ижевск: Институт компьютерных исследований, 2002. - 304 с.
835
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
856. Лесин Я.Б. Теория размерности и динамические системы:
современный взгляд и приложения: Пер. с англ.; Под ред. Б.М. Гуревича. - М.;
Ижевск: Институт компьютерных исследований, 2002. - 404 с.
857. Климонтович Ю.Л. Введение в физику открытых систем. - М.:
Янус-К, 2002. - 284 с.
858. Мешаное Р.П., Янполов М.С. Особенности фазовой траектории
«фрактального» осциллятора//Письма в ЖТФ. 2002. Т. 28, № 1. С. 67-73.
859. Weijia Wen, Lei Zhou, Jensen Li, Weikun Ge, Chan СТ., Ping Sheng.
Subwavelength Photonic Band Gaps from Planar Fractals // Phys. Rev. Lett.
2002. V. 89, № 22. P. 223901-1 - 223901-4.
860. Забурдаев В.Ю., Чукбар КВ. Ускоренная супердиффузия и
конечная скорость полетов Леви // ЖЭТФ. 2002. Т. 121, № 2. С. 299-307.
861. Кобелев Я.Л., Кобелев ЛЯ., Климонтович Ю.Л. Аномальная
диффузия с памятью, зависящей от времени и координат // ДАН. 2003. Т. 390,
№ 5. С. 605-609.
862. Кобелев Л.Я., Кобелев ЯЛ., Климонтович Ю.Л. Равновесная
статистическая физика в фрактальных средах с постоянной и переменной
памятью// ДАН. 2003. Т. 391, № 1. С. 35-39.
863. Кобелев Я.Л., Кобелев Л.Я. Уравнения Ландау - Лившица для
магнитных систем с постоянной и переменной памятью //ДАН. 2003. Т. 391,
№ 5. С. 614-618.
864. Espinal R, Huntsberger Т., Jawerth B.D., Kubota T. Wavelet - Based
Fractal Signature Analysis for Automatic Target Recognition // Opt. Eng. 1998.
V. 37, № LP. 166-174.
865. Гамба ИМ., Панферов В., Виллами С. О неупругом уравнении Боль-
цмана с диффузионным форсированием // Нелинейные задачи
математической физики и смежные вопросы П. В честь академика О.А
Ладыженской: Сб. статей / Под ред. М.Ш. Бирмана, С. Гильдебрандта, В.А. Солон-
никова, Н.Н. Уральцевой. - Междунар. матем. сер. - Новосибирск: Изд-во
«Тамара Рожковская», 2002. Т. 2. С. 165-177.
866. Малек Й., Празак Д. О размерности глобального аттрактора для
модифицированной системы Навье - Стокса//Там же. С. 243-258.
867. Моско У Неравенства Гарнака на масштабных нерегулярных
коврах Серпинского // Там же. С. 277-298.
868. Uchaikin V.V. Anomalous Transport Equations and their Application
to Fractal Walking // Physica A. 1998. V. 255, № 1-2. P. 65-92.
869. Учайкын В.В. Автомодельная аномальная диффузия и устойчивые
законы // УФН. 2003. Т. 173, № 8. С. 847-876.
870. Учайкин В.В. Аномальная диффузия и дробно - устойчивые
распределения // ЖЭТФ. 2003. Т. 124, № 4 (10). С. 903-920.
871. СаичевА.И, Уткин С. Г. Асимптотические законы супердиффузии
// ЖТФ. 2003. Т. 73, № 7. С. 1-6.
872. Бакунин О.Г. Корреляционные и перколяционные свойства
турбулентной диффузии // УФН. 2003. Т. 173, № 7. С. 757-768.
836
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
873. Рапис Е. Г. Свойства и виды симметрии твердотельной
кластерной фазы белка // ЖТФ. 2001. Т. 71, № 10. С. 104-111.
874. Рапис Е.Г. «Твист» растущих бактериальных колоний // ЖТФ.
2003. Т. 73, № 12. С. 76-80.
875. Станиславский А.А. Вероятностная интерпретация интеграла
дробного порядка//Теоретическая и математическая физика. 2004. Т. 138, № 3.
С. 491-507; English transl.: Stanislavsky A.A. Probability Interpretation of the
Integral of Fractional Order // Theoretical and Mathematical Physics. 2004.
V. 138, № 3. P. 418-431.
876. Станиславский A.A. Распространение лучей в случайно -
неоднородной среде // ЖЭТФ. 2004. Т. 125, № 4. С. 805-807.
877. Серов И.Н., Вельская Т.Е., Марголин В.И., Потсар Н.А. Влияние
фрактально - матричных резонаторов на свойства получаемых тонких
пленок меди // Письма в ЖТФ. 2002. Т. 28, № 24. С. 67-74.
878. ЧмельА, ПетровскийГ.Т., СеменовА.Д., СмирновА.Н., ШашкинB.C.
Влияние связанной воды на фрактальную геометрию наноразмерных
трещин в стекле, полученном вакуумно - компрессионным спеканием //
Физика и химия стекла. 2001. Т. 27, № 5. С. 673-678.
879. Нащекин А.В., Колмаков А.Г., Сошников И.П., Шмидт Н.М.,
Лоскутов А. В. Применение концепции мультифракталов для характеризации
структурных свойств композитных пленок фуллерена, легированных CdTe//
Письма в ЖТФ. 2003. Т. 29, № 14. С. 8-14.
880. Соколов Ю.В., Железный B.C. Фрактальная структура углеродного
депозита, получаемого при распылении графита в электрической дуге//
Письма в ЖТФ. 2003. Т. 29, № 8. С. 91-94.
881. Соколов Ю.В., Железный B.C. Получение, структура и некоторые
физические свойства углеродного депозита и хрома, имеющих
фрактальное строение // Письма в ЖТФ. 2003. Т. 29, № 15. С. 24-28.
882. Шевченко И.И., Мельников А.В. Показатели Ляпунова в задаче
Хенона-Хейлеса // Письма в ЖЭТФ. 2003. Т. 77, № 12. С. 772-777.
883. Карпов СВ., Басько А.Л., Попов А.К., Слабко В.В. Влияние
электродинамического взаимодействия частиц на спектры поглощения золей
серебра в процессе их агрегации // Оптика и спектроскопия. 2003. Т. 95,
№ 2. С. 248-258.
884. Карпов СВ., Басько А.Л., Попов А.К, Слабко В.В. Особенности
спектров поглощения фрактально - структурированных золей серебра //
Там же. С. 259-265.
885. Новоселов О.К, Морозов М.С., Смирнов СМ., Шкардун А.П.
Синтез многомерных нелинейных феноменологических уравнений и
фрактальный анализ электрокардиограмм // Радиотехника и электроника. 2003.
Т. 48, №6. С. 707-714.
886. Иванова B.C., Новиков В.У. Фракталы и прикладная синергетика.
(Итоги Международного симпозиума «ФиПС-03)//Нелинейный мир. Т. 2,
№ 3. С. 197-202.
837
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
887. Чуприков Н.Л., Жабин Д.Н. Матрица переноса фрактального
потенциала в форме канторовой лестницы // Изв. вузов. Физика. 2003. № 9.
С. 64 - 70.
888. Иванова B.C., Фалманис Г.Э. Самоуправляемый синтез наночас-
тиц в неравновесных физико-химических процессах//Нелинейный мир.
2004. Т. 2, №2. С. 81-85.
889. ЛямшевЛ.М., Урусовский И.А. Дифракция звука на ковре Серпин-
ского //Акустический журнал. 2003. Т. 49, № 6. С. 820-823.
890. Коверда В.П., Скоков В.П. Функции распределения при
масштабных преобразованиях 1//- флуктуации //ДАН. 2003. Т. 393, № 2. С. 184-
187.
891. Короновский А.А., Стародубов А.В., Храмов А. Е. Время покрытия
аттрактора, временная размерность и ее связь с емкостной размерностью
// Письма в ЖТФ. 2003. Т. 29, № 24. С. 54-60.
892. Шелухын О.И., ТенякшевА.М., ОсинА.В. Фрактальные процессы в
телекоммуникациях. - М.: Радиотехника, 2003. - 480 с.
893. Нелинейные волны 2002 / Под ред. А.В. Гапонова-Грехова и
В.И. Некоркина. - Н.Новгород: ИПФ РАН, 2003. - 448 с.
894. Перминов СВ., Раутиан С.Г., Сафонов В.П. К теории оптических
свойств фрактальных кластеров // ЖЭТФ. 2004. Т. 125, № 4. С. 789-804.
895. Калошин ДА., Магницкий НА., Сидоров СВ. О некоторых
особенностях перехода к хаосу в системе уравнений Лоренца// Нелинейная
динамика и управление. Вып.З: Сб. статей / Под ред. СВ. Емельянова и
С.К. Коровина. - М.: Физматлит, 2003. С 99-106.
896. Головинский П.А., Назаров В.М., Рясной П.В. Влияние
распределения плотности частиц на оптический резонанс внутри фрактального
кластера // Изв. вузов. Физика. 2004. № 4. С 84-86.
897. Титов В.В., РезниченкоЛА., Титов СВ., Комаров В.Д., Ахназарова
В.А. Мультифрактальные свойства зеренных структур в бинарной системе
на основе ниобата натрия с неизоструктурными компонентами // Письма
в ЖТФ. 2004. Т. 30, № 7. С. 42-47.
898. Каплий С.А., Проказников А.В., Рудь И.А. Формирование
кластеров в детерминированных и стохастических полях // ЖТФ. 2004. Т. 74, № 5.
С. 6-11.
899. Учайкин В.В., Сибатов Р.Т. Одномерное фрактальное блуждание
с конечной скоростью свободного движения // Письма в ЖТФ. 2004. Т. 30,
№ 8. С. 27-33.
900. Учайкин В.В., Коробко Д.А. Фрактальная модель переноса:
малоугловое приближение // ЖТФ. 2004. Т. 74, № 5. С. 12-19.
901. СаичевА.И., Уткин С. Г. Случайные блуждания с промежуточной
аномально - диффузионной асимптотикой // ЖЭТФ. 2004. Т. 126, № 2.
С 502-508.
902. Учайкин В.В. Фрактальные блуждания и блуждания на фракталах
// ЖТФ. 2004. Т. 74, № 7. С. 123-126.
838
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
903. Драников И.Л., Кондратенко П. С, Матвеев Л. В. Режимы
аномального переноса в модели стохастической адвекции - диффузии // ЖЭТФ.
2004. Т. 125, № 5. С. 1082-1091.
904. Ben-Avraham D., Havlin S. Diffusions and Reactions in Fractal and
Disordered Systems. - Cambridge: Cambridge University Press, 2000.
905. Майоров С.А. Динамика малых колебаний частицы в поле двух волн
// Краткие сообщения по физике ФИАН. 2004. № 2. С. 11-21.
906. Лоскутов А.Ю., Джаноев А. Р. Подавление хаоса в окрестности
сепаратрисы // ЖЭТФ. 2004. Т. 125, № 5. С. 1194 - 1203.
907. Кузьмин Ю.И. Депиннинг на начальной стадии резистивного
перехода в сверхпроводниках с фрактальной кластерной структурой // Письма
в ЖТФ. 2004. Т. 30, № 11. С. 29-37.
908. Балханов В. К., Башку ев Ю.Б. Электрические свойства
подстилающей среды с учетом фрактального распределения проводимости //
Электромагнитные волны и электронные системы. 2004. Т.9, № 7. С. 34—38.
909. Привезенцев А.П., Черепенин В.А. Фрактальные свойства
колебаний виртуального катода // Радиотехника и электроника. 1998. Т. 43, № 6.
С. 738-742.
910. Будянский М.В., Улейский М.Ю., Пранц СВ. Хаотическое
рассеяние, транспорт и фракталы в простом гидродинамическом потоке//ЖЭТФ.
2004. Т. 126, № 5 (11). С. 1167-1179.
911. Гостинцев ЮЛ, Фортов В.Е., Шацких Ю.В. Автомодельный закон
распространения и фрактальная структура поверхности свободного
расширяющегося турбулентного сферического пламени //ДАН. 2004. Т. 397, № 1.
С. 68-71.
912. Потапов А.А. Исследование влияния растительного покрова на
обратно рассеянное поле миллиметровых волн // Радиотехника и
электроника. 1991. Т. 36, № 2. С. 239-246.
913. Галкина Т.В., Орлова Т.Н., Потапов А.А., Хлявич Я.Л. Выделение
детерминированных объектов на текстурном фоне дисперсионным
методом // Тез. докл. II Всес. конф. «Искусственный интелект-90». - Минск:
Изд. ИТК АН БССР, 1990. С. 116-119.
914. Потапов АЛ. Статистика пространственно - временных
характеристик рассеяния земной поверхности на миллиметровых волнах //
Электромагнитные волны и электронные системы. 1997. Т. 2, № 1. С. 77-80.
915. Потапов А.А. К вопросу о перспективных приложениях теории
фракталов в радиофизике и радиолокации // Труды VII Всероссийской
школы-семинара «Волновые явления в неоднородных средах». - М.: Изд.
МГУ, 2000. Т.2. С. 57-58.
916. Потапов АЛ.у Герман В.А. Концептуальные аспекты
фрактального обнаружения целей на радиолокационных, оптических и
синтезированных изображениях земной поверхности // Там же. С. 58-62.
917. Потапов АЛ. Фракталы в радиофизике и радиолокации.
Элементы теории фракталов // Радиотехника и электроника. 2000. Т. 45, № 11.
С. 1285-1292.
839
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
918. Потапов А.А., Герман В.А., Соколов А.В. Радиолокационное
обнаружение цели на фоне земной поверхности фрактальным методом //
Радиотехника. 2000. № 8. С. 57-63.
919. Потапов А.А., Герман ВА. Концептуальные аспекты
фрактального обнаружения и распознавания целей // Докл. 3-й Междунар. конф.
«Цифровая обработка сигналов и ее применение». - М.: Изд. РНТО РЭС
им. А.С. Попова, 2000. Т. 2. С. 44-46.
920. PotapovAA., German V.A. Fractal Method of Detection of Weak Signals
from Complex Images // Book of Abstracts Second Int. Conf. «Modern Trends
in Computational Physics».- Dubna (Russia): JINR, 2000. P. 132.
921. PotapovAA., German VA. Fractals, Fractal Target Selection and Fractal
Antennas // Proc.Ist Int. Workshop on Mathematical Modeling of Physical
Processes in Inhomogeneous Media.- Guanajuato (Mexico): 2001. P. 44-46.
922. Bistrov R.P., Zasovin EA., PotapovAA., SokolovA. V. Millimeter Radar
of a High Resolution with the Use of a Fractal Method for Detection // Proc.
1st Int. Workshop on Mathematical Modeling of Physical Processes in
Inhomogeneous Media. - Guanajuato (Mexico): 2001. P. 99-101.
923. Опаленов Ю.В., Потапов АА. Фракталы, преобразование Радона
в радиолокаторах с обработкой на несущей частоте и перспективы их
применения // Зарубежная радиоэлектроника. Успехи современной
радиоэлектроники. 2001. № 4. С. 3-15.
924. Потапов АА. Фракталы в радиофизике и радиолокации.
Фрактальный анализ сигналов // Радиотехника и электроника. 2001. Т. 46, № 3.
С. 261-270.
925. PotapovAA., German VA. Fractal Selection of Artificial Objects from
Radar Images on Inhomogeneous Baskground // Proc. the Fourth Symp. «Physics
and Engineering of Millimeter and Sub-Millimeter Waves».- Kharkov (Ukraine):
Kharkov State University, 2001. V. 1. P. 268-270.
926. Bistrov R.P., PotapovAA., SokolovA. V., SokolovSA. Fractal Methods
of Selection of Objects and Millimeter Wave Radar Imaging of the High
Resolution // Ibid. P. 286.
927'. Kravchenco V.F., PotapovAA. Nev Class of Atomic - Fractal Functions
and Their Applications // Ibid. P. 102-107.
928. Kravchenco V.F., PotapovAA. Atomic - Fractal Antenna Arrays // Proc.
URSI Int. Symp. on Electromagnetic Theory. - Victoria (Canada): University
of Victoria, 2001. P. 660-662.
929. Кравченко В.Ф., Потапов АА, Масюк В.М. Атомарно -
фрактальные функции в задачах синтеза антенн // Зарубежная радиоэлектроника.
Успехи современной радиоэлектроники. 2001. № 6. С. 4-40.
930. Засовин ЗА., Бармотин В.Я., Потапов А.А, Соколов А. В.
Фрактальные антенны на основе салфетки Серпинского // Труды X Междунар. конф.
по спиновой электронике. - М.: Изд. УНЦ-1, МЭИ (ТУ), 2001. С. 208-214.
931. Опаленов Ю.В., Потапов АА. Радиолокационная радонометрия и
фрактальная топология // Там же. С. 226-258.
840
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
932. Засовин Э.А., Борзое А.Б., Быстрое Р.П., Илясов Е.П., Потапов А.А.,
Соколов А.В., Титов А.Н. Радиотехнические и радиооптические системы. -
М.: Круглый год, 2001. - 752 с.
933. Потапов А.А., Герман В.А. Фракталы в кластеризации
радиолокационных изображений поверхностных и подповерхностных объектов //
Доклады 4-й Междунар. конф. и выставки «Цифровая обработка сигналов и ее
применение». - М.: РНТО РЭС им. А.С. Попова, 2002. Т.1. С. 217-219.
934. Потапов А.А., Чеканов Р.Н. Обобщенный фрактальный
коррелятор полей обратного рассеяния // Труды VIII Всерос. школы - семинара
«Волновые явления в неоднородных средах». - М.: Изд. МГУ, 2002. Т.2.
С. 69-70.
935. Опаленов Ю.В., Потапов А.А. Статистическая структура
фрактальной радиолокационной радонометрии // Тез. докл. Второго Междунар.
конгресса «Нелинейный динамический анализ (НДА-2)». - М.: Изд. МАИ
(ТУ), 2002. С. 230.
936. Потапов А.А. Фракталы и нечеткие множества // Тез. докл.
Второго Междунар. конгресса «Нелинейный динамический анализ (НДА-2)».
- М.: Изд. МАИ (ТУ), 2002. С. 234.
937. Потапов А.А., Герман В.А. Классификация и распознавание
объектов фрактальными методами// Тез. докл. Второго Междунар. конгресса
«Нелинейный динамический анализ (НДА-2)». - М.: Изд. МАИ (ТУ), 2002.
С. 235.
938. Потапов А.А., Герман В.А. Возможность применения теории
детерминированного хаоса в моделях каналов радиолокационных и
телекоммуникационных систем // Тез. докл. IV Междунар. науч.-техн. конф.
«Электроника и информатика-2002». - М.: Изд. МИЭТ (ТУ), 2002. Т.2.
С. 219-220.
939. Потапов А.А., Чеканов Р.Н. Частотная функция когерентности
фрактального радиоканала // Там же. С. 221-222.
940. Потапов А.А. Топология фрактальных множеств, индуцированная
на нечеткие подмножества // Труды XI Междунар. конф. по спиновой
электронике. - М.: Изд. УНЦ-1, МЭИ (ТУ), 2002. С. 281-297.
941. Потапов А.А., Герман В.А. Странные аттракторы,
детерминированный хаос и устойчивые паретианы как элементы новой модели
отраженного радиолокационного сигнала // Там же. С. 263-280.
942. Реутов В.Ф., Озерецковский КВ., Потапов А.А. Операторный метод
селекции отраженных сигналов в поляриметрической радиолокации // Там
же. С. 247-262.
943. Потапов А.А. Фракталы в радиофизике и радиолокации. Основы
теории рассеяния волн фрактальной поверхностью // Радиотехника и
электроника. 2002. Т. 47, № 5. С. 517-544.
944. Потапов А.А., Герман В.А. Эффекты детерминированного хаоса и
странный аттрактор при радиолокации динамической системы типа
растительного покрова // Письма в ЖТФ. 2002. Т. 28. № 14. С. 19-25.
841
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
945. Potapov A.A., German V.A. Effects of Deterministic Chaos and Strange
Attractor in the Radar of Dynamic Systems of the Vegetative Cover Type// Techn.
Phys. Lett. 2002. V. 28, № 7. P. 586-588.
946. Быстрое Р.П., Дмитриев В.Г., Потапов А.А., Соколов А.В.
Проблемы радиолокационного обнаружения малоконтрастных объектов// Вопросы
перспективной радиолокации; Под ред. А.В. Соколова. - М.: Радиотехника,
2003. С. 20-48.
947. Потапов А.А., Герман В.А. Реконструкция странного аттрактора в
отраженных радиолокационных сигналах // Там же. С. 83-102.
948. Потапов А.А., Герман В.А., Соколов А.В. Фрактальная
классификация и кластеризация оптических и радиолокационных изображений
поверхностных и подповерхностных объектов // Там же. С. 103-118.
949. Потапов А.А. Формализм нечетких множеств и нечетких
интегралов в синтезе новых классов фракталов и мультифракталов для задач
радиолокации // Там же. С. 64-82.
950. Опаленов Ю.В., Потапов АЛ. Эффективность нового метода
радиолокации на основе радоновского преобразования // Там же. С. 132-147.
951. Опаленов Ю.В., Потапов А.А. Фрактальные и радоновские
преобразования в радиолокаторах нового поколения с обработкой на несущей
частоте // Там же. С. 148-177.
952. Реутов В.Ф., Озерецковский Н.В., Потапов АЛ. Операторный
метод обработки информации в двухканальных поляриметрических
радиолокаторах// Там же. С. 319-332.
953. Опаленов Ю.В., Потапов АЛ., Соколов СЛ. Современные
информационные технологии в радиолокационном комплексе нового поколения
для исследования природных ресурсов // Радиоэлектроники, 2003. № 1. -
http://jre.cplire.rU/jre/jan03/2/text.html (электронный журнал ИРЭ РАН).
954. Опаленов Ю.В., Потапов АЛ. Способ синтеза радиолокационного
изображения и устройство для его осуществления. Пат. № 2211461 на
изобретение по заявке № 2001116248/09(017637), приоритет от 18 июня 2001//
Бюл. изобретений. 2003. № 24. Ч. 3. С. 791.
955. Потапов АЛ. Фракталы на нечетких множествах //
Электромагнитные волны и электронные системы. 2003. Т.8, № 1. С. 26-35.
956. Потапов АЛ., Соколов А.В. Перспективные методы обработки
радиолокационных сигналов // Труды IX Всерос. школы-семинара «Физика
и применение микроволн». - М.: Изд. МГУ, 2003. T.l. C.71-72.
957. Потапов АЛ., Потапов АЛ. (мл.), Потапов ВЛ., Соколов СЛ.
Радиолокационное обнаружение малоконтрастных целей с помощью
топологических признаков // Там же. С.73-74.
958. Потапов АЛ. Фракталы, хаос, рекурсия // Высшее образование
сегодня. 2003. № 4. С. 18 - 26.
959. Потапов АЛ. Фракталы, текстурные меры и динамические
системы как основа перспективных информационных технологий бортовых и
наземных радиосистем // Труды V Междунар. науч.-техн. конф. «Перспек-
842
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
тивные технологии в средствах передачи информации - ПТСПИ 2003». -
Владимир: ВлГУ, 2003. С. 230-231.
960. Потапов А.А. Фракталы, текстуры и динамический хаос как
основа новых информационных технологий в радиолокации: Ч. I.
Полученные результаты // Тез. докл. I науч.-техн. конф. «Радиооптические
технологии в приборостроении». - М.: Изд. МГТУ им. Н.Э. Баумана, 2003.
С. 58-59.
961. Потапов А.А. Фракталы, текстуры и динамический хаос как основа
новых информационных технологий в радиолокации: Ч. П.
Перспективные направления // Там же. С. 60-61.
962. Подосенов С.А., Потапов А.А. О фрактальной геометрии
пространства - времени детерминированных структур // Там же. С. 62-63.
963. Засовин Э.А., Потапов А.А. Анализ и синтез лакунарных
фрактальных антенн на основе классических множеств // Там же. С. 64-65.
964. Потапов А.А., Герман В.А. Экспериментальные исследования
странных аттракторов в реальных радиолокационных процессах отражения
миллиметровых волн // Там же. С. 66-67.
965. Потапов А.А. Методы обработки сигналов и полей на основе
теории фракталов // Труды Первой Всероссийской науч. конф. «Методы и
средства обработки информации». - М.: Изд. МГУ, 2003. С. 559-565.
966. Потапов А.А. Фракталы, текстурные меры и динамические
системы как основа новых информационных технологий в современных
задачах радиофизики и радиолокации // Труды Междунар.
междисциплинарного симпозиума «Фракталы и прикладная синергетика - ФИПС-03». -
М.: Изд. МГОУ, 2003. С. 165-168.
967. Потапов А.А., Герман В.А. Влияние топологии, размеров и
количества объектов на фрактальные характеристики сложных изображений //
Там же. С. 218-221.
968. Подосенов С.А., Потапов А.А. Фрактальная геометрия
пространства-времени детерминированных структур // Там же. С. 227-229.
969. Булавкин В.В., Потапов А.А., Вячеславова О.Ф., Герман В.А.
Перспективы применения теории фракталов для решения задач формирования
и оценки качества поверхности изделий // Там же. С. 250-253.
970. Потапов А.А. Фрактальный анализ в современных задачах
радиолокации и радиофизики //Радиотехника. 2003. № 8. С. 55-66.
971. Потапов А.А. Новые информационные технологии на основе
вероятностных текстурных и фрактальных признаков в радиолокационном
обнаружении малоконтрастных целей // Радиотехника и электроника. 2003.
Т. 48, №9. С. 1101-1119.
972. Потапов А.А., Соколов А.В. Перспективные методы обработки
радиолокационных сигналов на основе фрактальных и текстурных мер //Изв.
РАН. Сер. Физика. 2003. Т. 67, № 12. С. 1775-1778.
973. Потапов А.А. От редактора// Нелинейный мир. 2003. Т. 1. № 1-2.
С. 3; 2004. Т.2. № 1. с. 3.
843
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
974. Реутов А.П., Потапов А.А., Герман В.А. Странные аттракторы и
фракталы как основа новой динамической модели радиолокационных
сигналов, рассеянных растительным покровом // Нелинейный мир. 2003. Т. 1.
№ 1-2. С. 12-27.
975. Потапов А.А. Краткое историческое эссе о зарождении и
становлении теории дробного интегродифференцирования // Там же. С. 69 - 81.
976. Потапов АЛ. Фракталы в задачах искусственного интеллекта:
подходы, модели, некоторые результаты // Сборник трудов третьего
расширенного семинара «Использование методов искусственного
интеллекта и высокопроизводительных вычислений в аэрокосмических
исследованиях - АКИИ 03». - М.: Физматлит, 2003. С. 76-90.
977. Потапов А.А. Перспективные информационные технологии
бортовых и наземных радиосистем на основе фракталов, текстурных мер и
динамических систем // Тез. докл. третьей науч.-техн. конф.
«Перспективы использования новых технологий и научно-технических решений в
изделиях ракетно-космической техники разработки ГКНПЦ им. М.В.
Хруничева». - М.: Изд. ИПУ РАН, 2003. С. 272-275.
978. Засовин Э.А., Потапов А.А. Исследования лакунарных
фрактальных антенн на основе классических множеств // Труды 12-й Междунар.
конф. по спиновой электронике. - М.: Изд. УНЦ - 1, МЭИ (ТУ), 2003.
С. 523-527.
979. Гуляев Ю.В., Никитов С.А., Матвеев Е.Н., Потапов А.А.
Математика и физика фракталов: теоремы, модели, некоторые результаты //
Труды XLVI науч. конф. МФТИ «Современные проблемы фундаментальных
и прикладных наук». Ч. V «Квантовая и физическая электроника». -
М.Долгопрудный: Изд. МФТИ (ГУ), 2003. Ч. V. С. 103-104.
980. Гуляев Ю.В., Никитов С.А., Матвеев Е.Н., Потапов А.А.
Фракталы в новых средах передачи информации // Там же. С. 105-107.
981. Гуляев Ю.В., Никитов С.А., Потапов А.А., Матвеев Е.Н.
Фракталы в фотонных и магнонных кристаллах // Труды 12-й Междунар. конф.
по спиновой электронике. - М.: Изд. УНЦ-1, МЭИ (ТУ), 2003. С. 7-42.
982. Потапов А.А., Матвеев Е.Н. Фрактальная аномальная диффузия
и операторы дробного интегродифференцирования // Труды IX Всерос.
школы-семинара «Волновые явления в неоднородных средах».- М.: Изд.
МГУ, 2004. С. 23-24.
983. Потапов А.А.у Матвеев Е.Н. Диффузионные уравнения дробных
порядков для описания волновых процессов во фрактальных средах // Там
же. С. 25-26.
984. Потапов А.А., Герман В.А. Распределения фрактальных
размерностей синтезированных и реальных изображений // Там же. С. 45-46.
985. Потапов А.А., Герман В.А. Параметрический анализ
распределений фрактальной размерности изображений с помощью диаграммы
Пирсона // Там же. С. 47-48.
844
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
986. Потапов А.А., Герман В.А. О применимости фрактальной
концепции к структурам во Вселенной // Труды Гос. астрономического института
им. П.К. Штернберга (Тез. докл. Всерос. Астрономической конф. ВАК-2004
«Горизонты Вселенной»). - М.: Изд. ГАИШ МГУ, 2004. Т. 75. С. 176-177.
987. Герман В.А., Потапов А.А. Программное обеспечение алгоритмов
фрактального выделения контуров // Тез. докл. Междунар. науч. конф.
«Интеллектуализация обработки информации (ИОИ 2004)». -
Симферополь: Крымский научный центр НАН Украины, 2004. С. 47.
988. Потапов А.А., Герман В.А. Фрактальное распознавание образов //
Тез. докл. Междунар. науч. конф. «Интеллектуализация обработки
информации (ИОИ 2004)».- Симферополь: Крымский научный центр НАН
Украины, 2004. С. 130.
989. Potapov A.A., German V.A. Fractal Radiolocation and Fractal
Radiophysics: Stage in the Making, Results, Perspectives // Proc. X Int. Scientific
- Research Conf. «Radiolocation, Navigation, Communication». - Voronezh
(Russia): NPF «Sakvoee», 2004. P. 318-341.
990. Потапов А.А., Герман В.А. Фрактальная радиолокация и
фрактальная радиофизика: Этапы становления, результаты, перспективы // Труды
X Междунар. науч.-техн. конф.»Радиолокация, навигация, связь». -
Воронеж: Изд. НПФ «Саквоее», 2004. Т. III. С. 1869-1896.
991. Potapov A.A. Fractals, Texture and Deterministic Chaos in New
Information Technologies: Synergetic Approaches, Models and Results // Proc.
2nd IEEE Int. Conf. Circuits and Systems for Communications (ICCSC-2004).
- M.: MTUCI (Russia), 2004. - 4 p.
992. Потапов А.А. Фракталы, текстуры и детерминированный хаос в
новых информационных технологиях: синергетические подходы, модели
и результаты // Сб. материалов Междунар. науч. конф.»Перспективы
синергетики в XXI веке». - Белгород: Изд. БГТУ им. В. Г. Шухова, 2004.
Т. III. С. 52-58.
993. Потапов А.А. Фракталы и динамический хаос в современных
проблемах дистанционного зондирования // Сб. докл. Второй Всерос. науч.
конф. «Дистанционное зондирование земных покровов и атмосферы
аэрокосмическими средствами». - СПб.: РГГМУ, 2004. Т. 3. С. 51-56.
994. Потапов А.А. Синергетика и радиофизические процессы в
радиолокации // Материалы Первой Международной научно-практической
конф. «Стратегии динамического развития России: единство
самоорганизации и управления». - М.: «Проспект» Российской академии
государственной службы при Президенте РФ, 2004. Т. III. Ч. 3. С. 129-135.
995. Потапов А.А. Идеи синергетики, фрактальной геометрии и
детерминированного хаоса в радиолокационных технологиях: фрактальная
радиолокация и фрактальная радиофизика // Материалы Междунар. науч. -
практ. конф. «Фундаментальные проблемы радиоэлектронного
приборостроения (INTERMATIC-2004)». - М.: МИРЭА-ЦНИИ «Электроника»,
2004. Ч. 2. С. 20-25.
845
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
996. Потапов А.Л, Герман В.А.Фрактальные сигнатуры: от нанометров
до парсеков // Там же. С. 77-82.
997. Потапов А.А., Герман В.А. Опыт разработки первого эталонного
словаря фрактальных признаков классов целей // Тез. докл. II науч.-техн.
конф. «Радиооптические технологии в приборостроении». - М.: Изд. МГТУ
им. Н.Э. Баумана, 2004.
998. Опаленов Ю.В., Потапов А.А., Струков А.З. Экспериментальные
исследования РЛС с полным цифровым поляризационным
зондированием и фрактально - радоновской фильтрацией // Там же.
999. Потапов А.А. Идеи синергетики, фрактальной геометрии и
детерминированного хаоса в современных технологиях радиотехнических
систем// Сб. докл. 2-й Всерос. науч. конф. «Управление и информационные
технологии (УИТ-2004)». - Пятигорск: Изд. «Спецпечать», 2004. Т. 1.
С. 235-242.
1000. Потапов АЛ. О теории и методах цифровой фрактальной
обработки слабых радиолокационных сигналов // Тез. докл. 10-й юбилейной
междунар. науч. конф. «Теория и техника передачи, приема и обработки
информации». - Харьков: ХНУРЭ, 2004. Ч. 1. С. 155-156.
1001. Потапов АЛ. Геометрия хаоса и фрактальная топология
выборки как основа технологий современных радиосистем // Труды Междунар.
науч.-техн. конф. «Прикладная синергетика-Н», поев, памяти Ильи При-
гожина. - Уфа: УГНТУ, 2004.
1002. Потапов АЛ. О стохастичности и фрактальности в современных
радиолокационных задачах // Труды Междунар. конф. «Трансформация
волн, когерентные структуры и турбулентность» - (МСС-04), посвящ.
памяти С.С. Моисеева. - М.: ИКИ РАН, 2004. С. 508-513.
1003. Potapov A.A. Fractal Radiolocation and Fractal Radiophysics: New
Information Technologies // Proc. 13 th Int. Conf. Computational
Electromagnetics and Its Applications (ICCEA-2004) (China, November 1-4). -
Beijing: Beijing Institute of Technology, 2004.
1004. Потапов АЛ., Вячеславова О.Ф. Качественная и количественная
оценка поверхности деталей машин на основе фрактальной размерности
и фрактальных сигнатур // Обозрение прикладной и промышленной
математики. 2004. Т. 11, № 4. С. 902-905.
1005. Потапов АЛ., Герман В.А. О методах измерения фрактальной
размерности и фрактальных сигнатур многомерных стохастических
сигналов // Радиотехника и электроника. 2004. Т. 49, № 12. С. 1468-1491.
1006. Потапов АЛ.у Булавкин В.В., Герман В.А., Вячеславова О.Ф.
Исследование микрорельефа обработанных поверхностей с помощью
методов фрактальных сигнатур // ЖТФ. 2005. Т. 75.
1007. Булавкин В.В., Потапов А.А., Герман В.А., Вячеславова О.Ф.
Теория фракталов в проблеме формирования и оценки качества поверхности
изделий // Тяжелое машиностроение. 2005.
846
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1008. Потапов АЛ. Топология выборки// Нелинейный мир. 2004. Т. 2.
№ 1.С. 4-13.
1009. Потапов АЛ. Фрактальные методы передачи информации // Тез.
докл. III Всерос. конф. «Необратимые процессы в природе и технике». -
М.: Изд. МГТУ им. Н.Э. Баумана, 2005. С. 252-253.
1010. Булавкин В.В., ПотаповА.А., Вячеславова О.Ф. Синергетический
подход на основе фрактальных сигнатур в задачах качественной и
количественной оценки микрорельефа обработанных поверхностей изделий //
Нелинейный мир. 2005. Т. 3. № 1-2. С. 128-145.
1011. Потапов А.А. Фракталы в радиофизике, и радиолокации. - М.:
Логос, 2002. - 664 с. - (1-е изд.).
1012. Подосенов С.А., Потапов А.А., Соколов А.А. Импульсная
электродинамика широкополосных радиосистем и поля связанных структур/ Под
ред. А.А. Потапова. - М.: Радиотехника, 2003. - 720 с.
1013. Быстрое Р.П., Потапов А.А., Соколов А.В. Миллиметровая
радиолокация с фрактальной обработкой. - М.: Радиотехника, 2005.
1014. Горбачев А.А., Потапов А.А., Тараканков СП. Дистанционная
диагностика динамических систем на основе нелинейного рассеяния
электромагнитных волн//Нелинейный мир. 2004. Т. 2. № 5-6. С. 310-314.
1015. Нелинейная радиолокация: Сб. статей; Под ред. А.А. Горбачева,
А.П. Колданова, А.А. Потапова, Е.П. Чагина (Библиотека журнала
«Нелинейный мир». Научная серия «Фракталы. Хаос. Вероятность»). - М:
Радиотехника, 2005. Ч. 1. - 96 с.
1016. Манделъброт Б. Фрактальная геометрия природы: Пер. с англ. -
М.: Институт компьютерных исследований, 2002. - 656 с.
1017. Пенроуз Р. Новый ум короля: О компьютерах, мышлении и
законах физики: Пер. с англ.; Под ред. В.О. Малышенко. - М.: Едиториал
УРСС, 2003. - 384 с.
847
Научное издание
Потапов Александр Алексеевич
ФРАКТАЛЫ
в радиофизике и радиолокации: Топология выборки
Монография
Редактор Е.В. Комарова
Корректор Л. Я. Трифонова
Оформление Т.Ю. Хрычевой
Компьютерная верстка О.Г. Лавровой
Подписано в печать 07.02.2005. № 3(п). Формат 60x90/16
Печать офсетная. Бумага офсетная. Печ. л. 53,0
Тираж 2 000 экз. Заказ № 816
Отпечатано с готовых диапозитивов во ФГУП ИПК
«Ульяновский Дом печати». 432980, г. Ульяновск, ул. Гончарова, 14
По вопросам приобретения литературы
обращаться по адресу: 105318, Москва, Измайловское ш., 4
Тел./факс: (095) 369-5819, 369-5668, 369-7727
Электронная почта: universitas@mail.ru
Дополнительная информация на сайте http://logosbook.ru
ISBN 5-98699-015-3