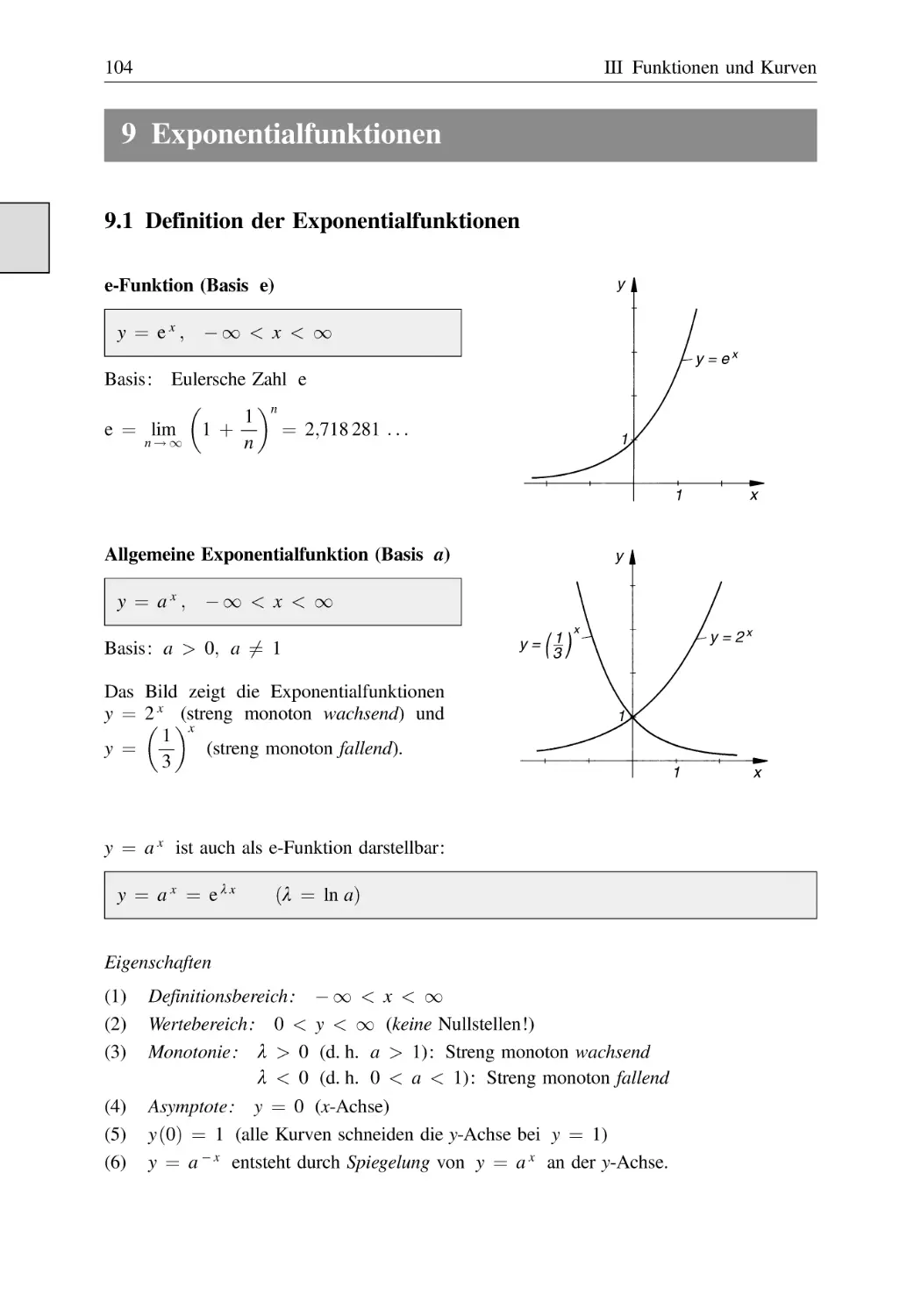
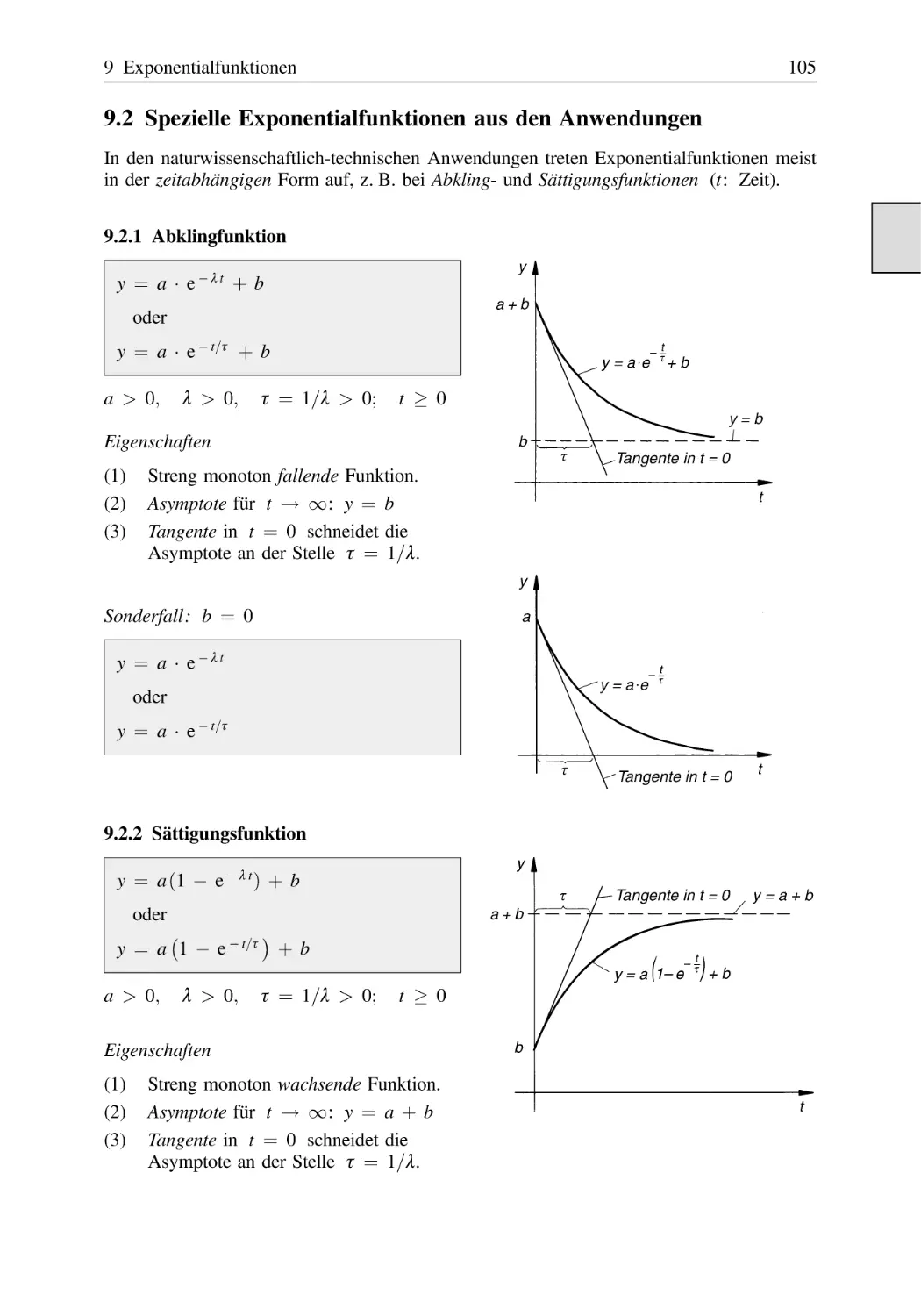
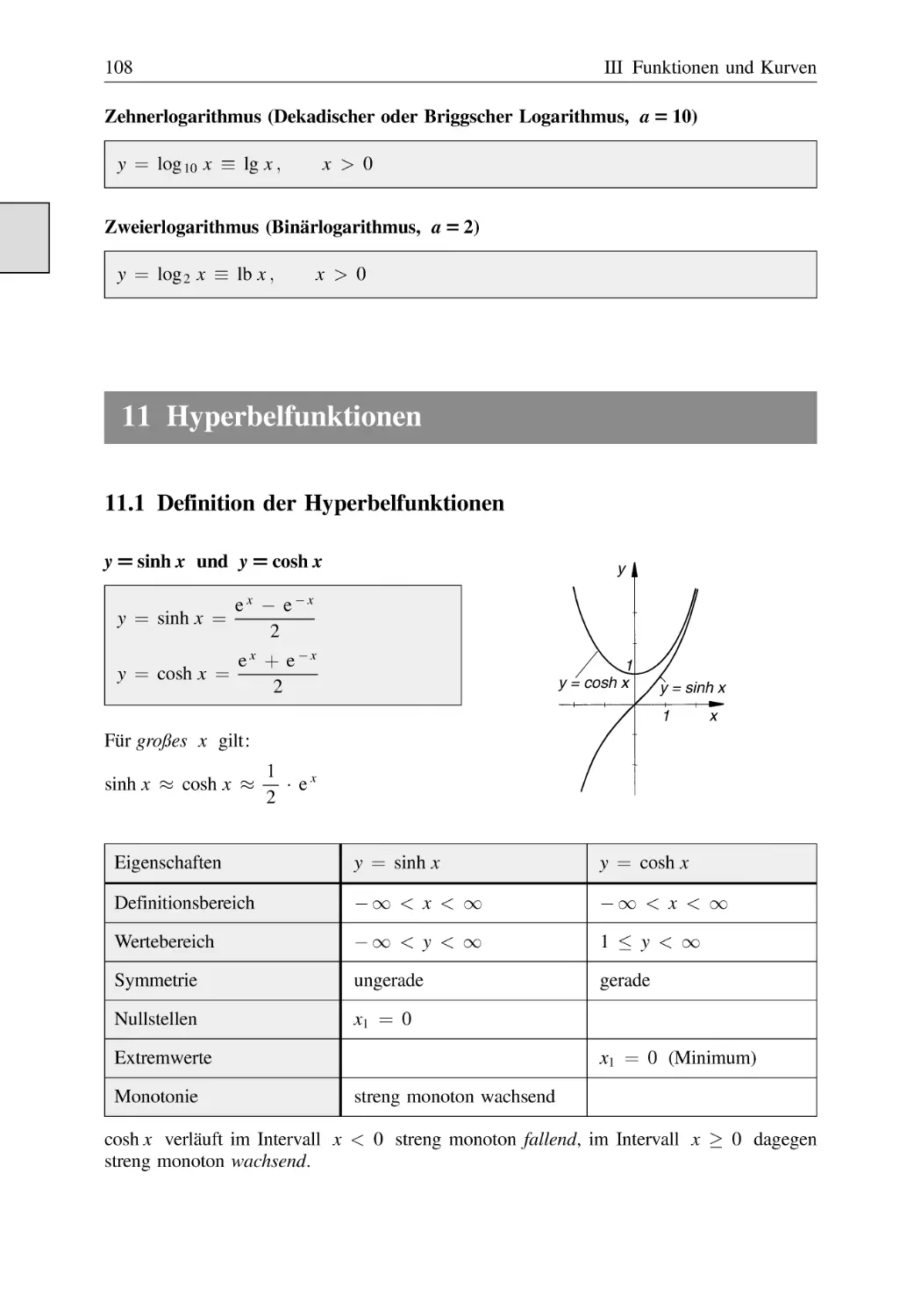
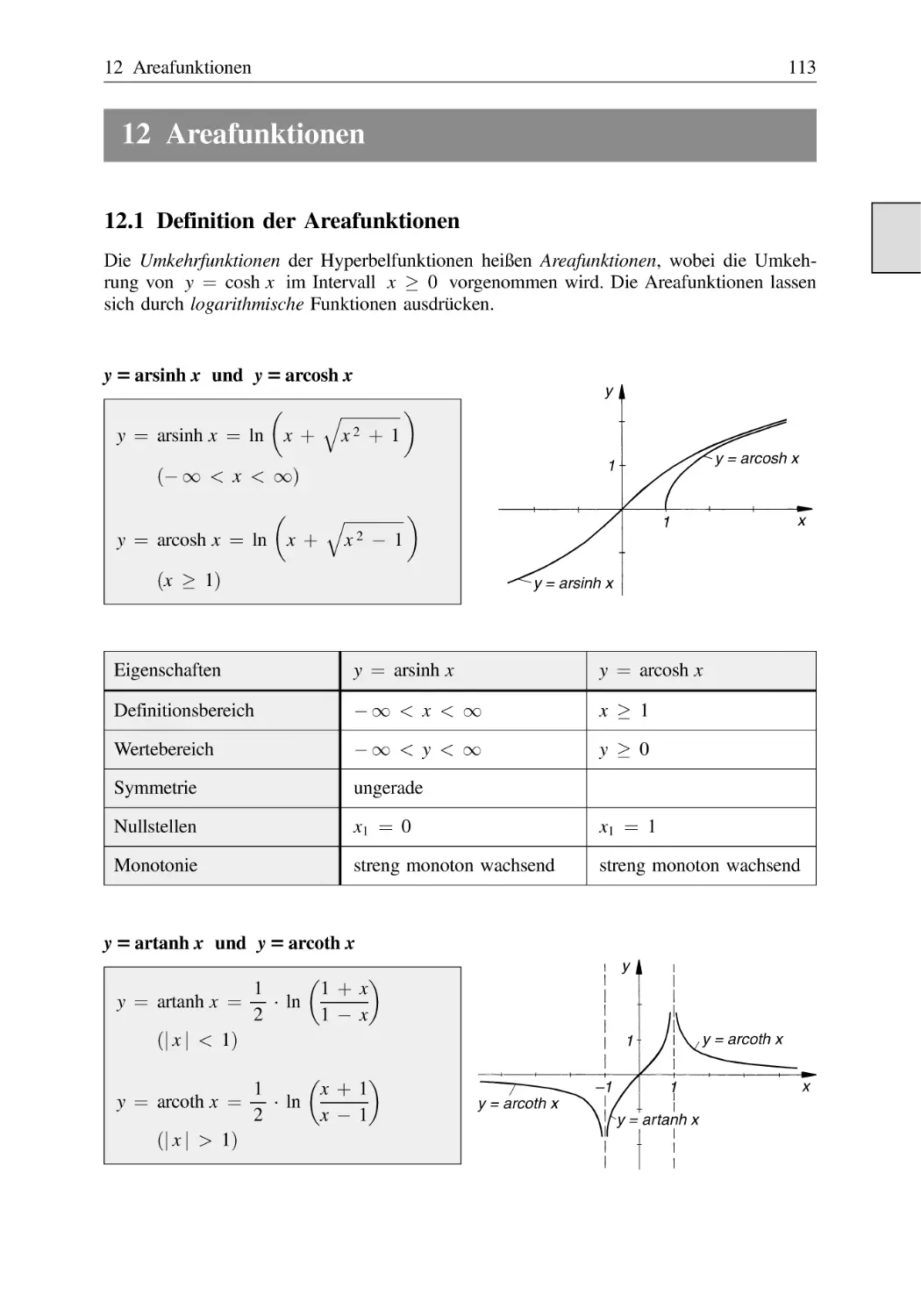
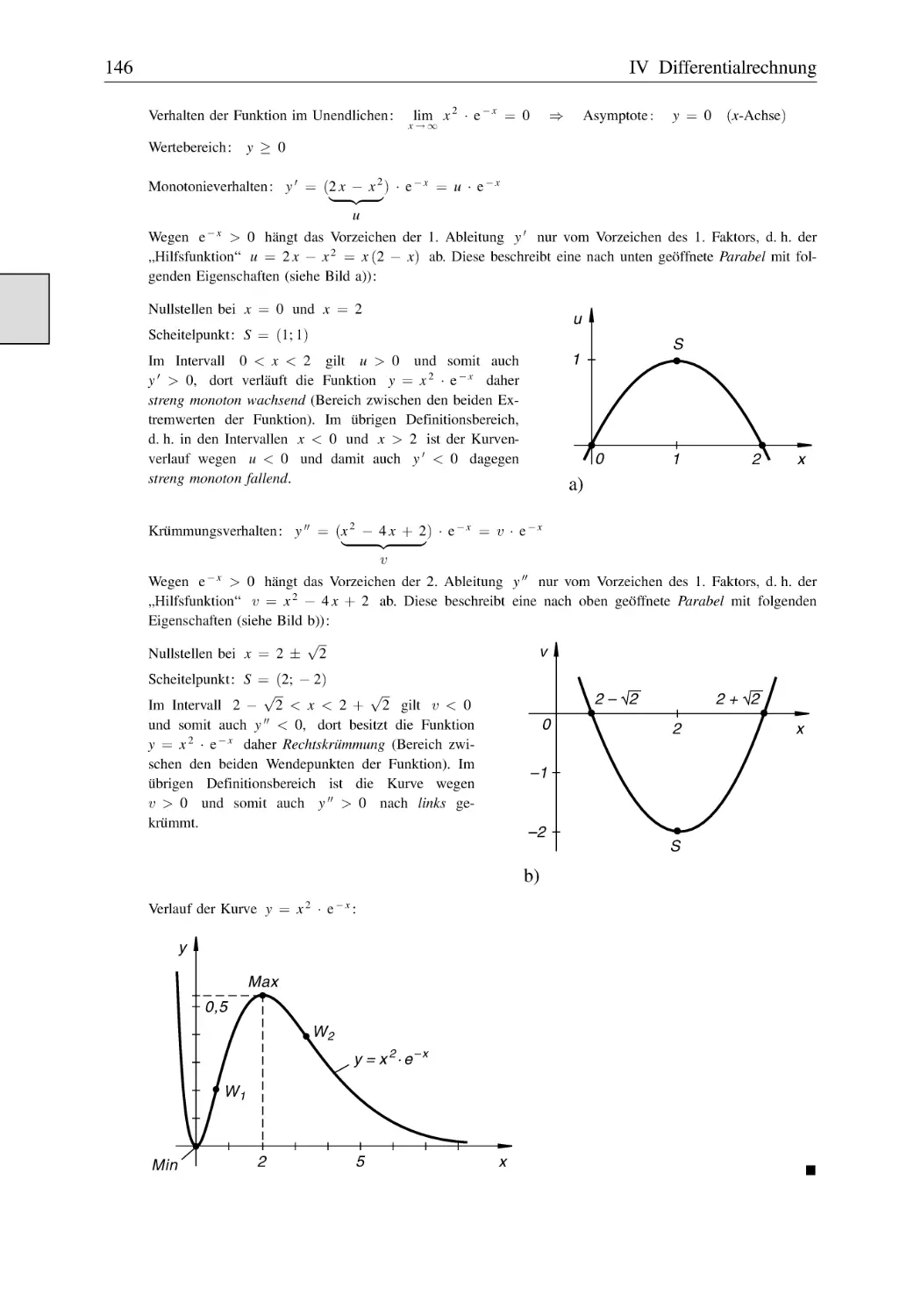
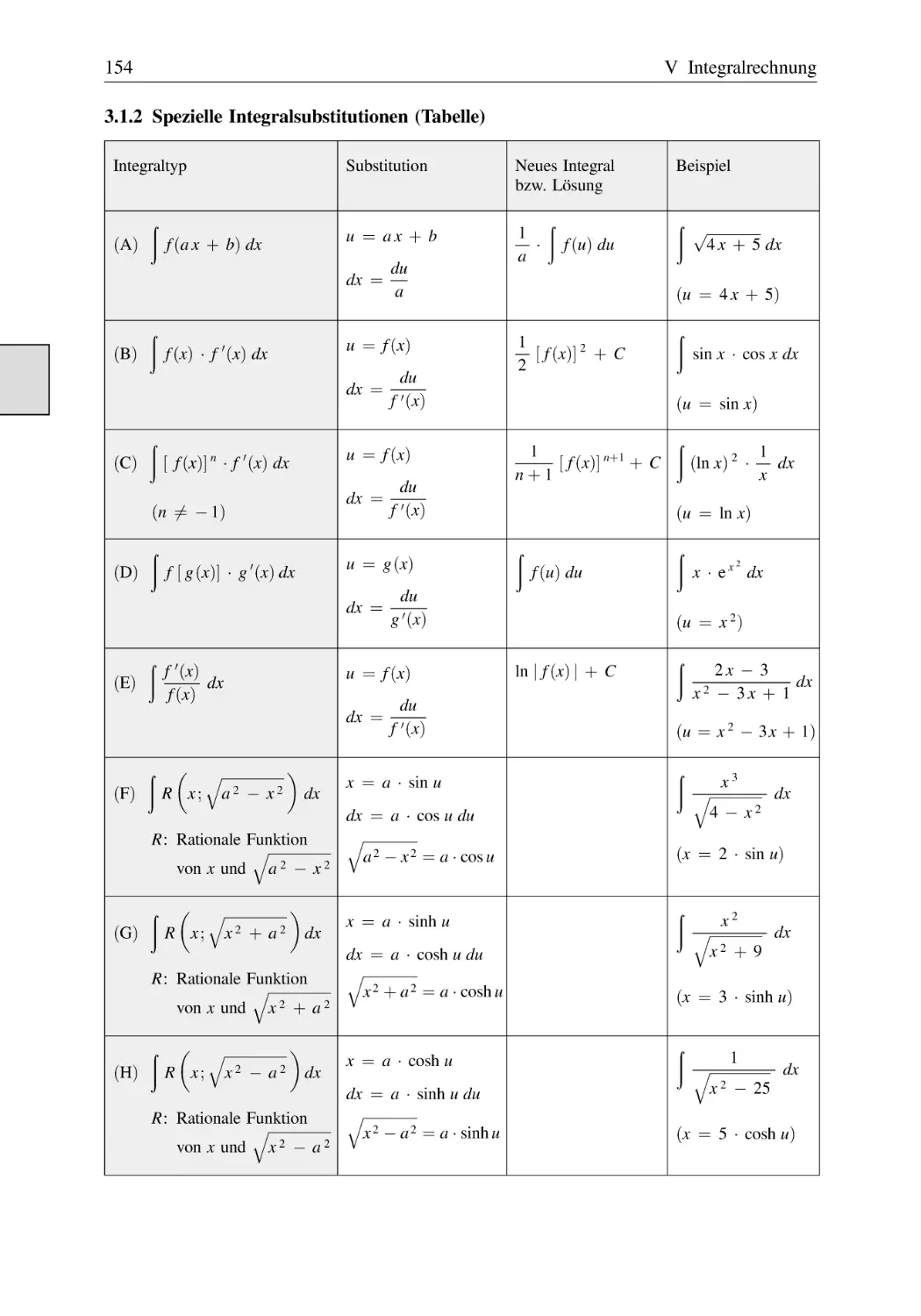
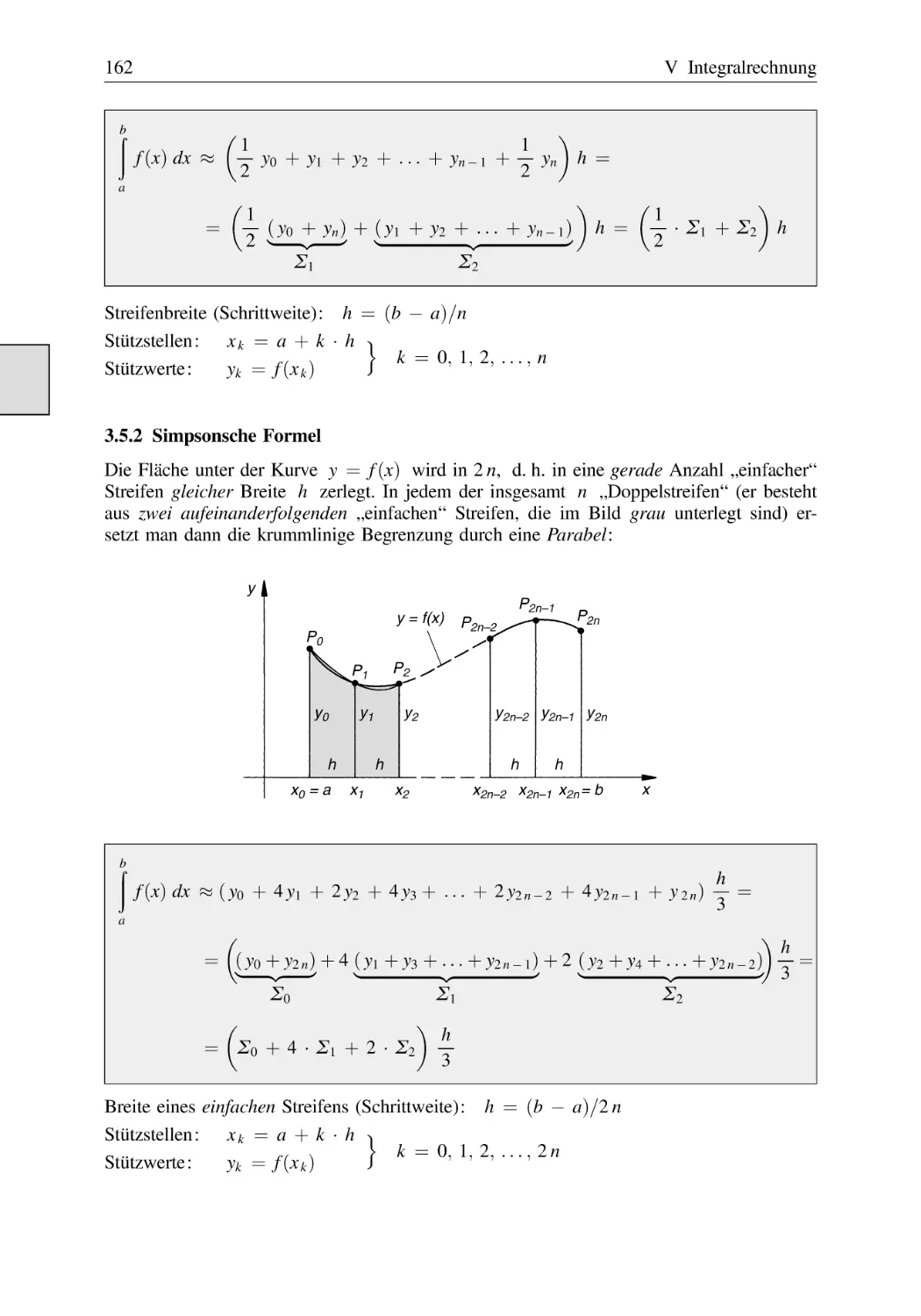
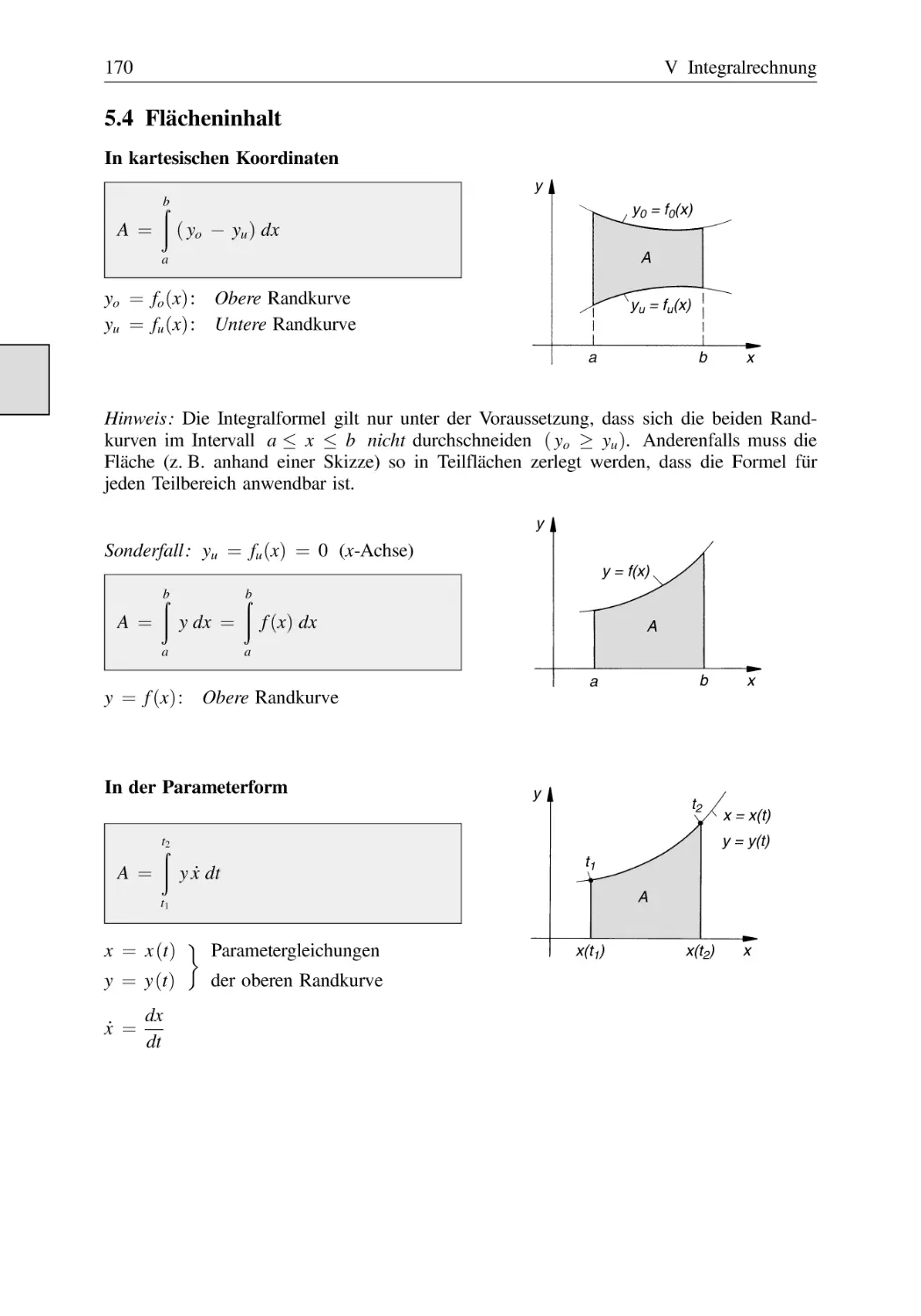
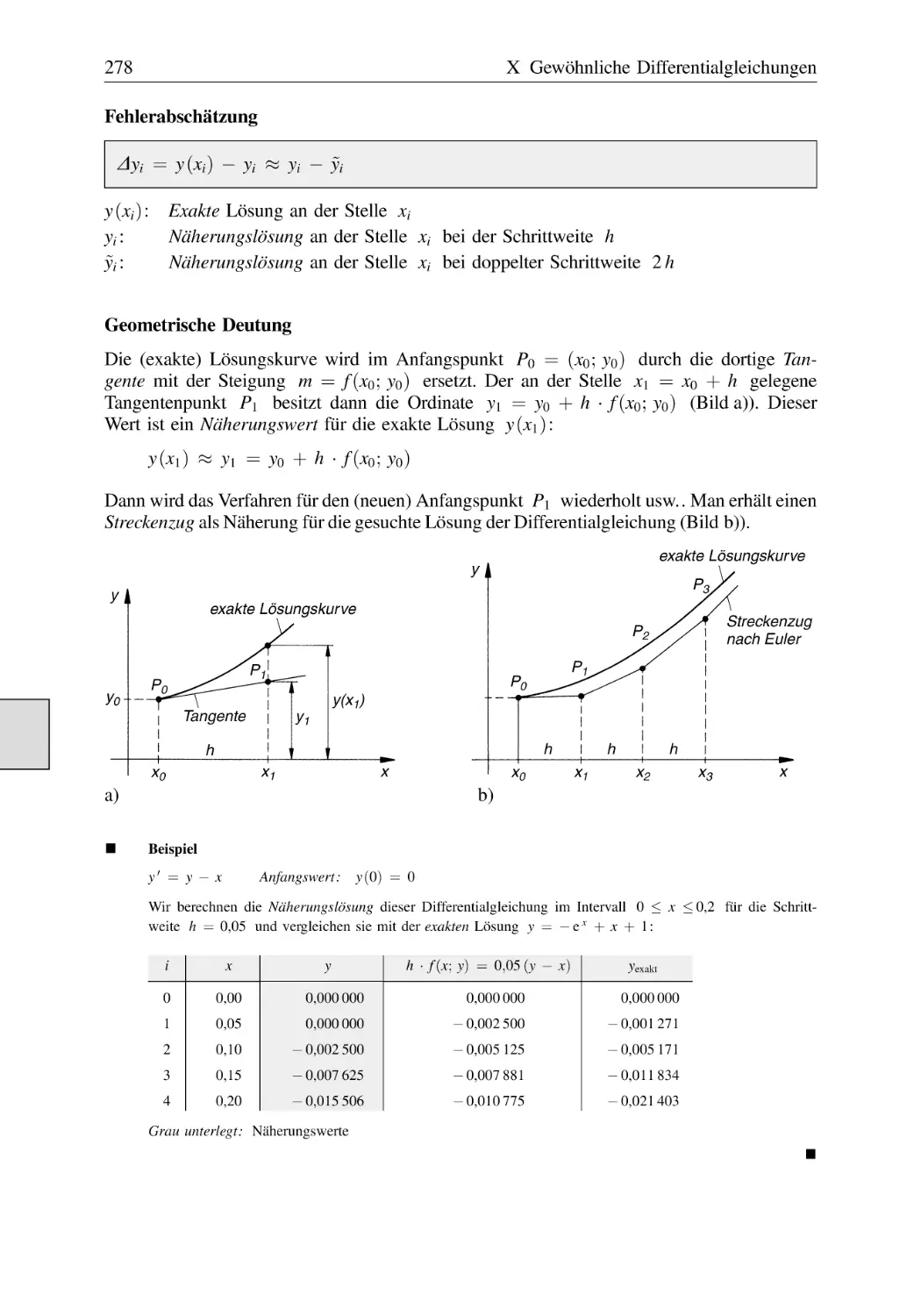
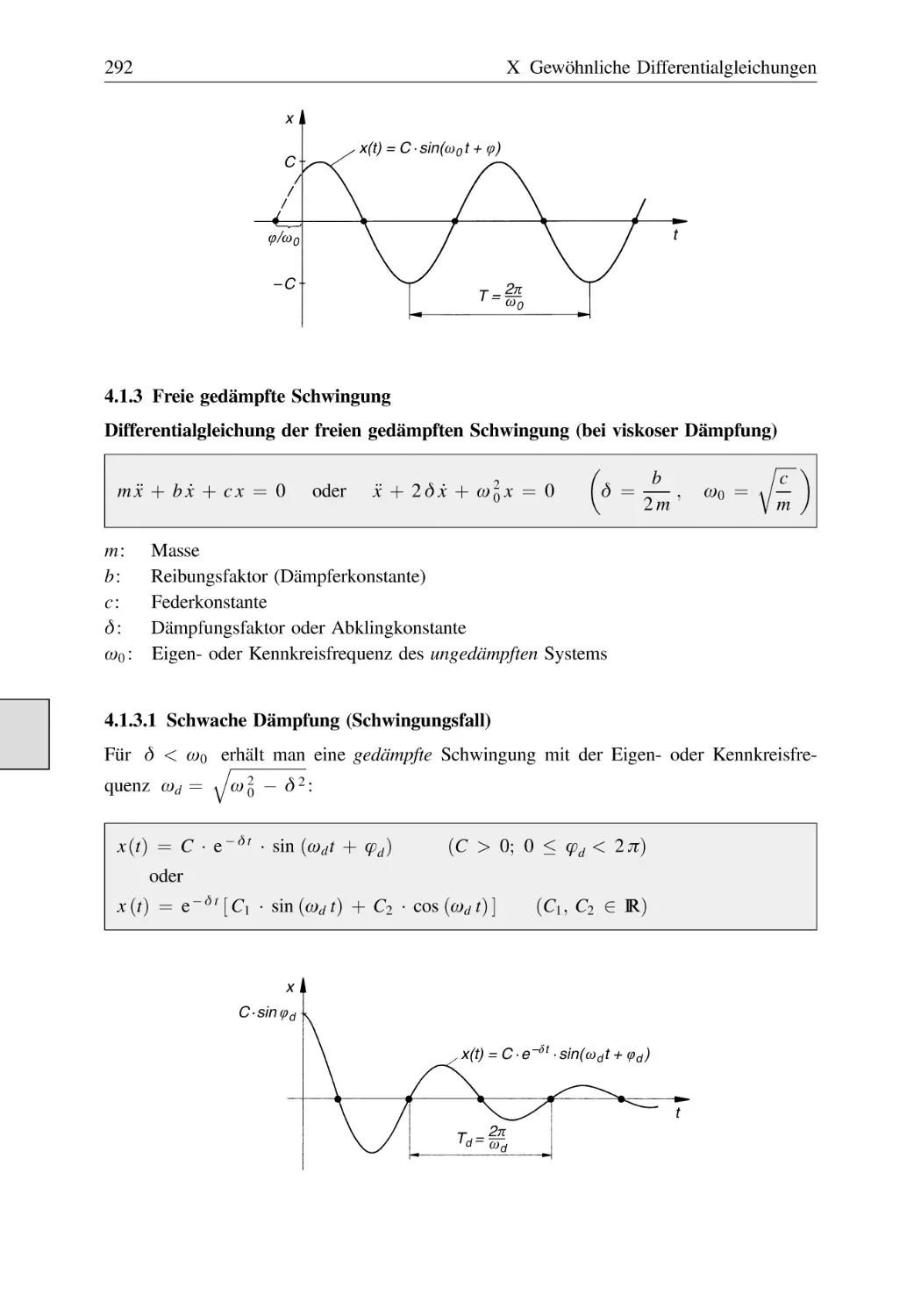
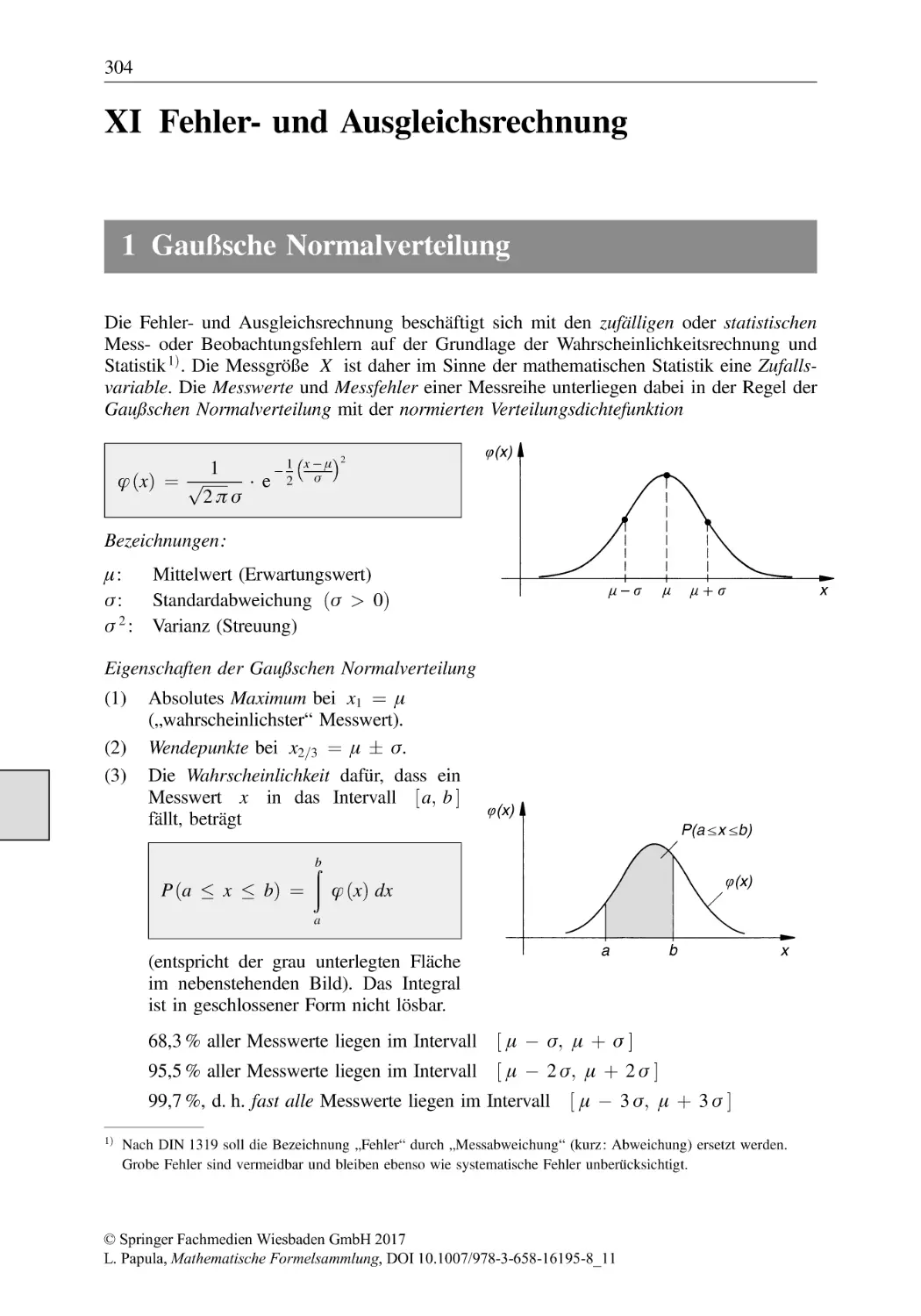
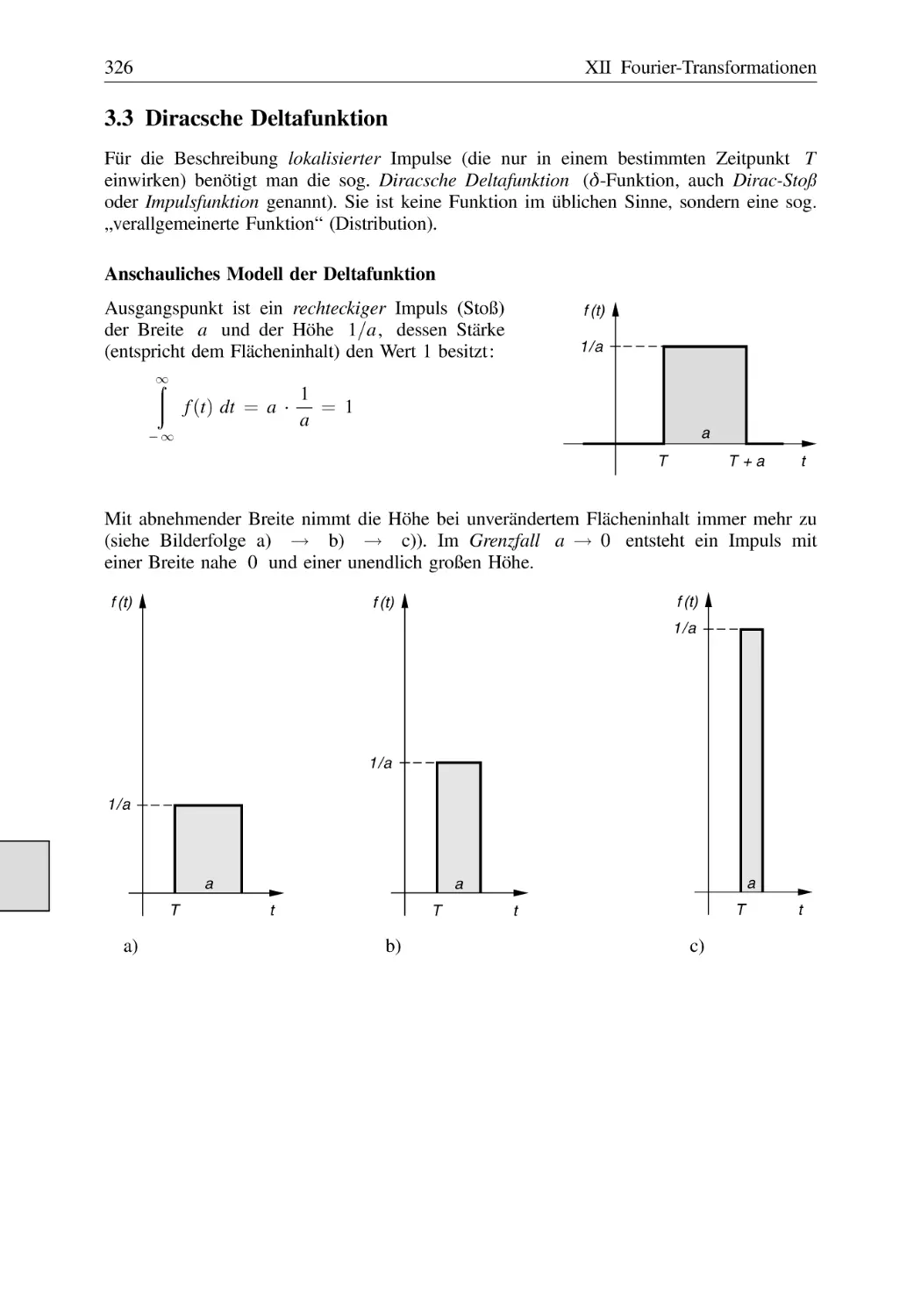
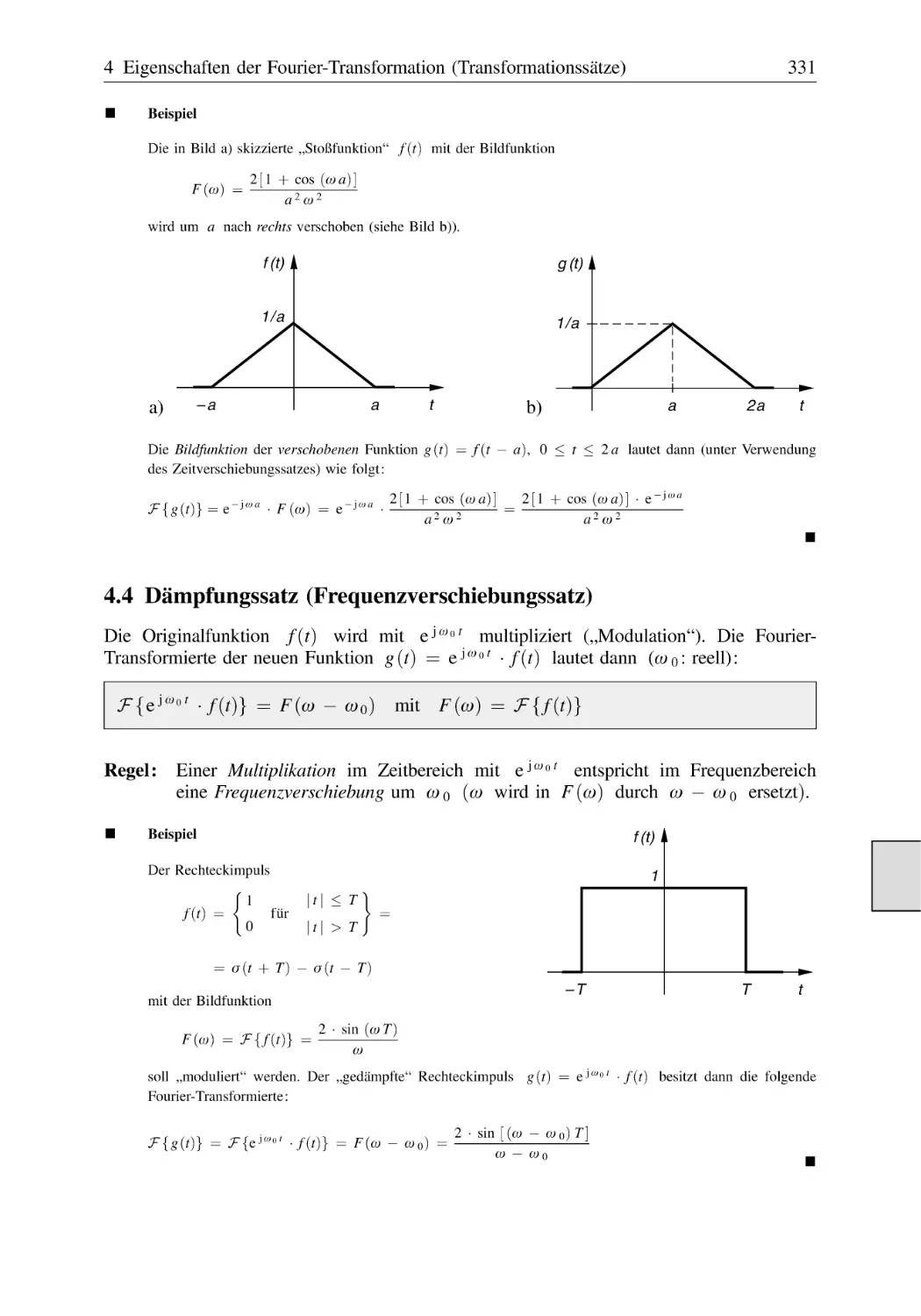
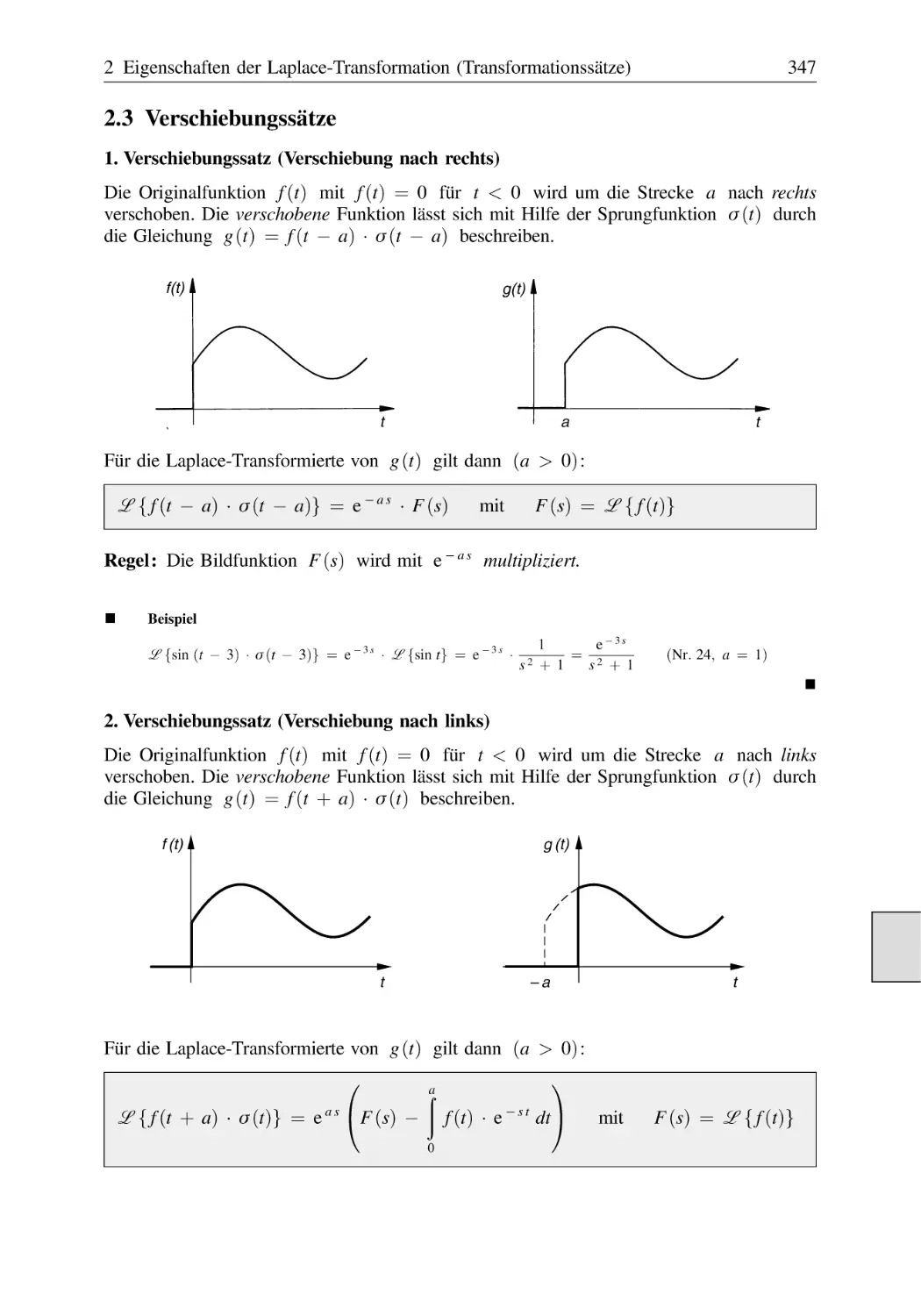
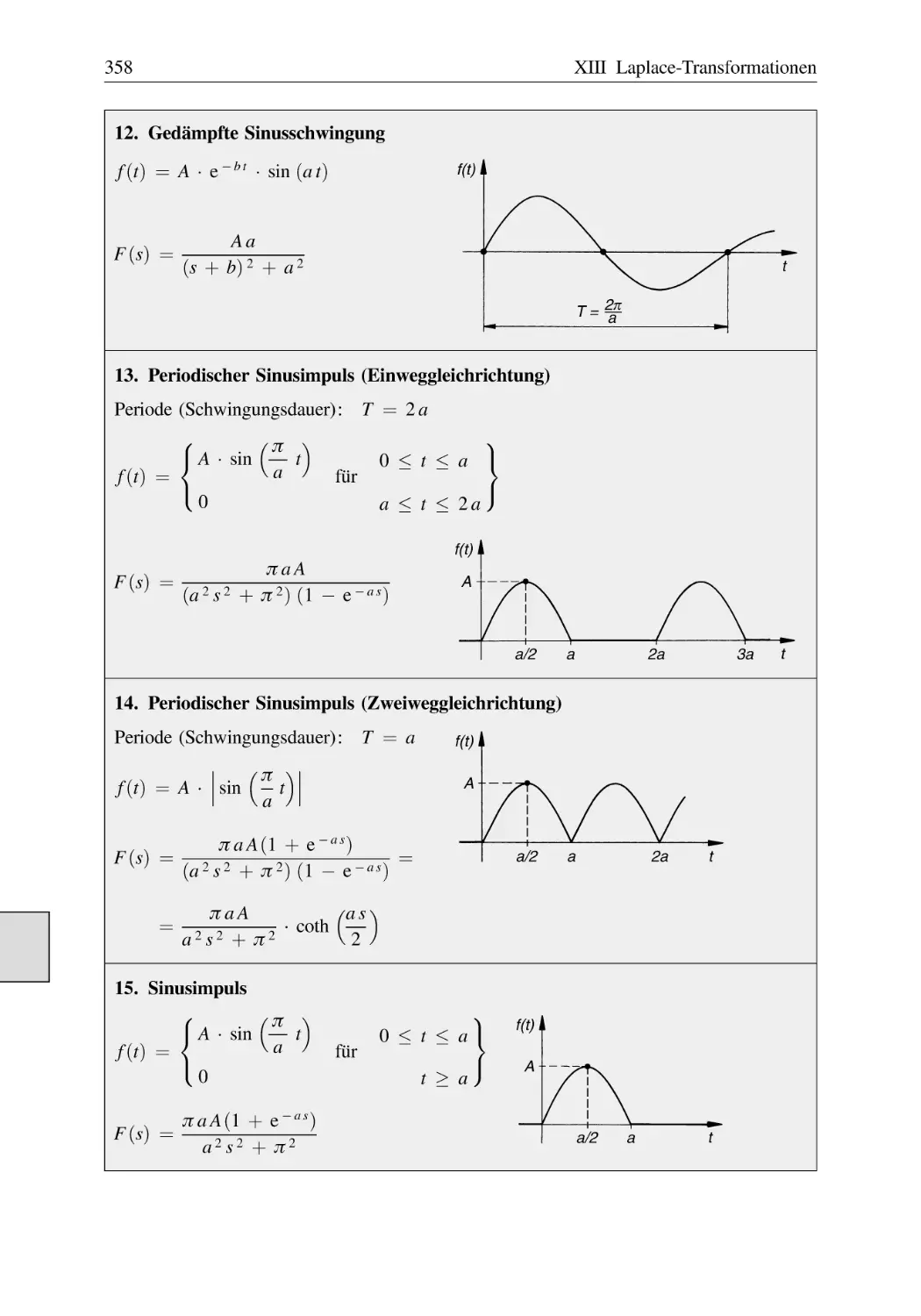
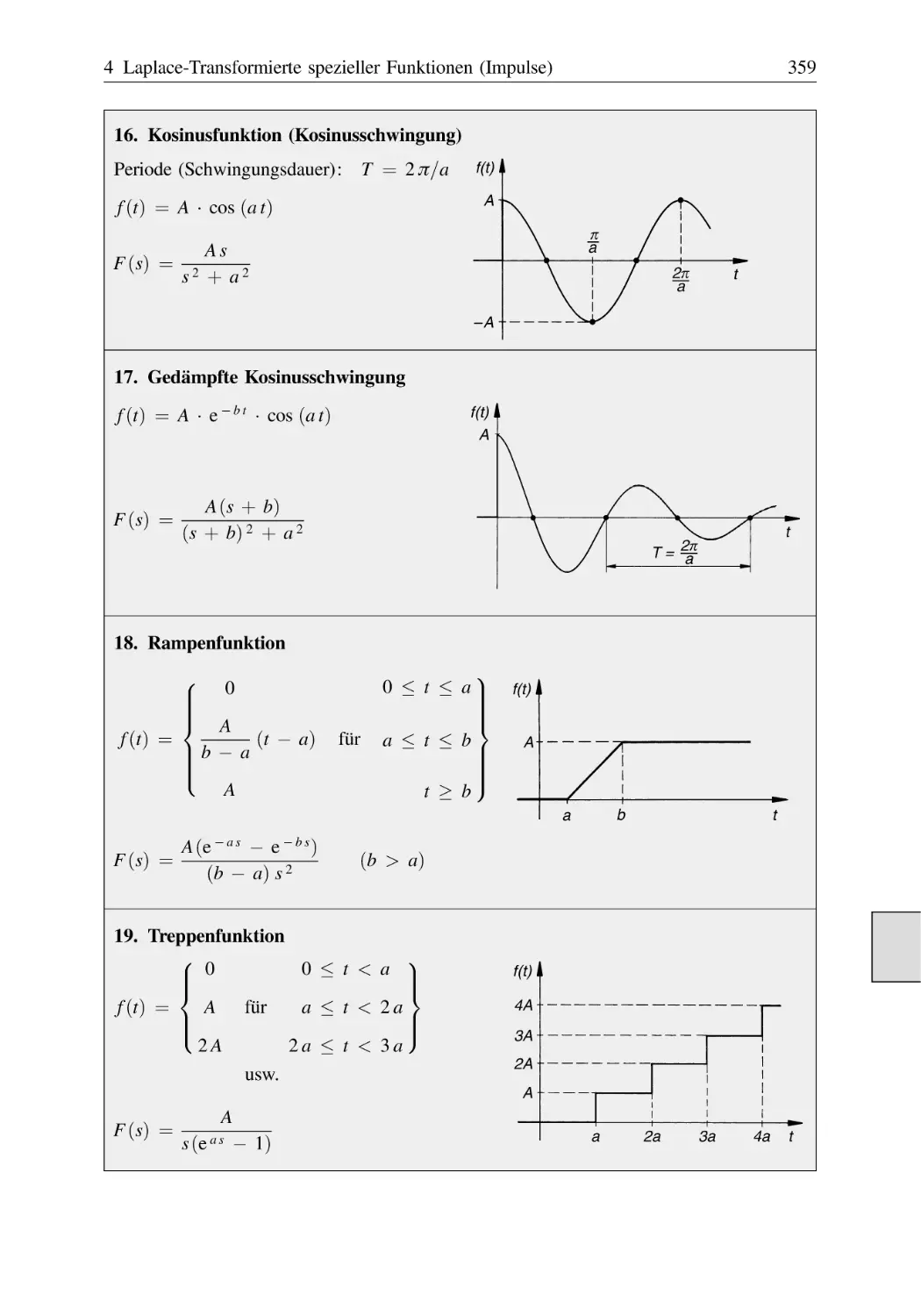
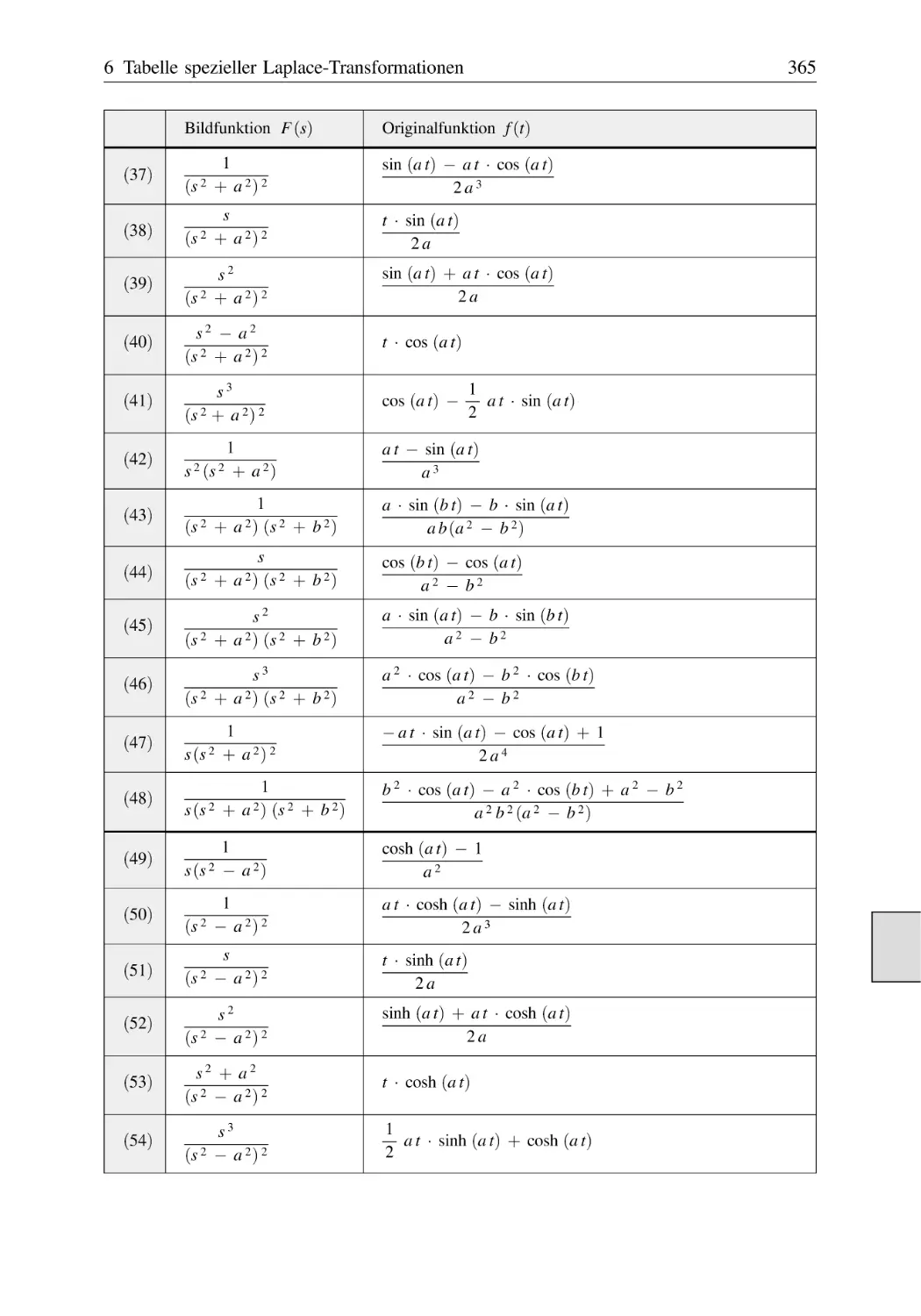
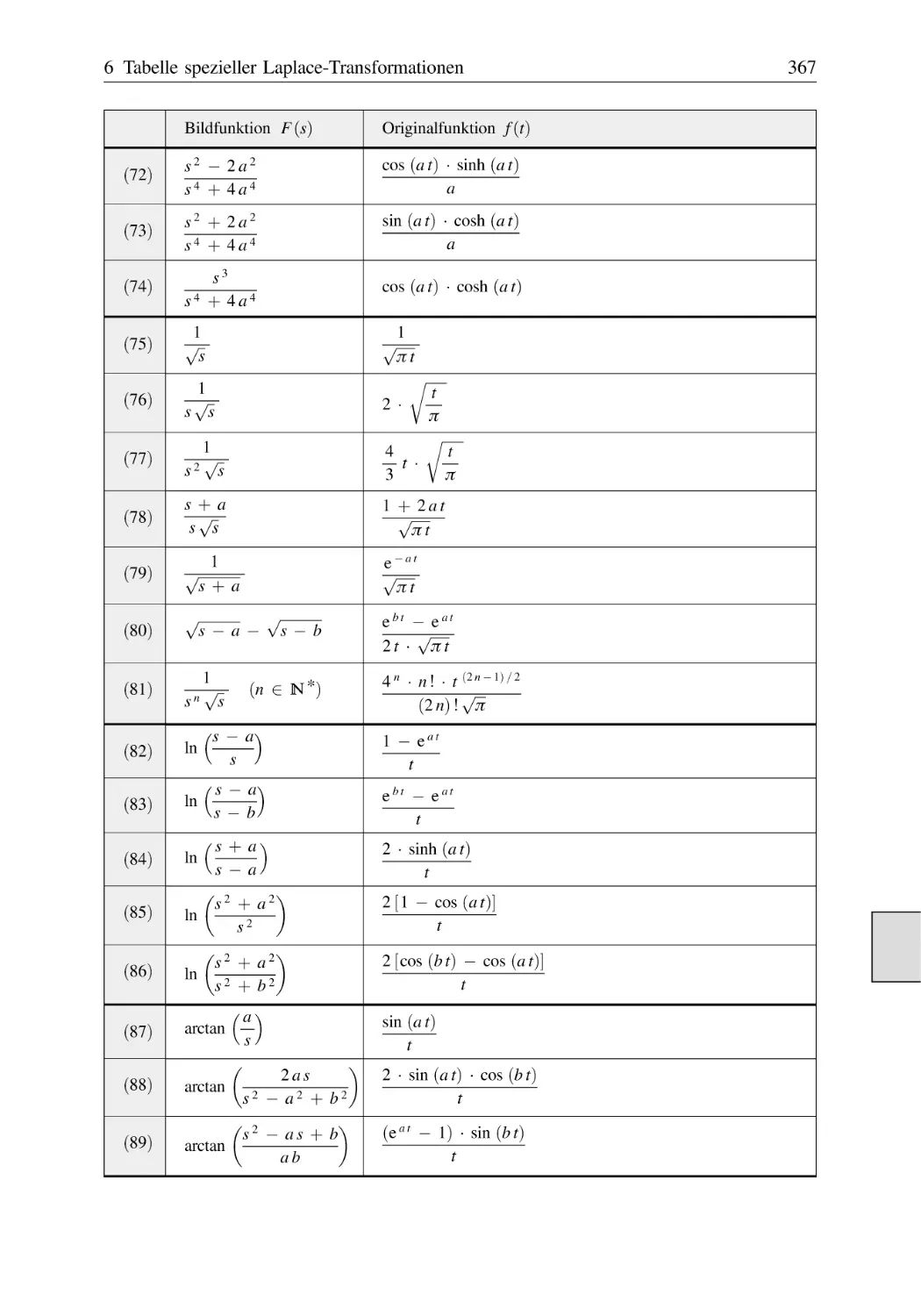
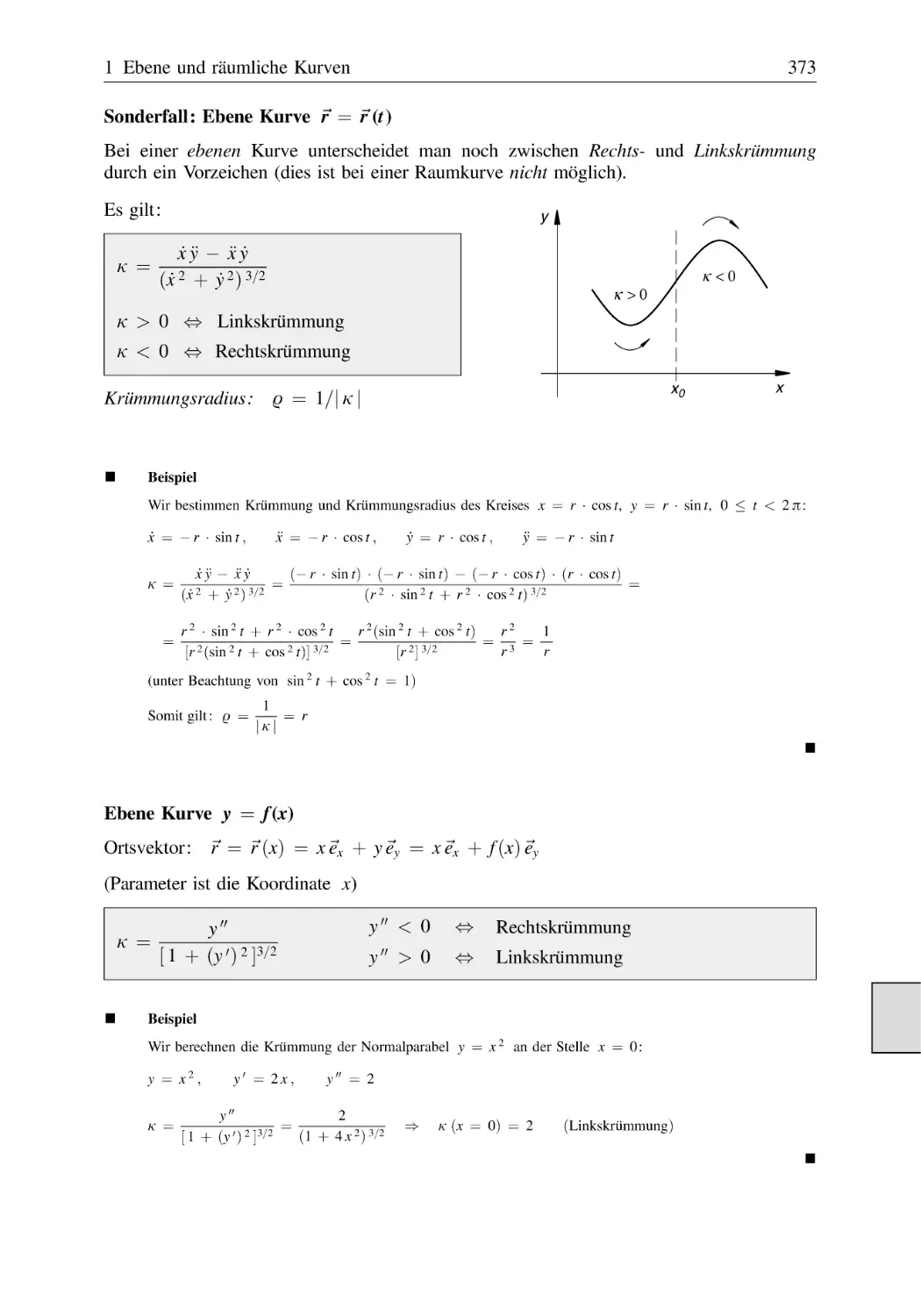
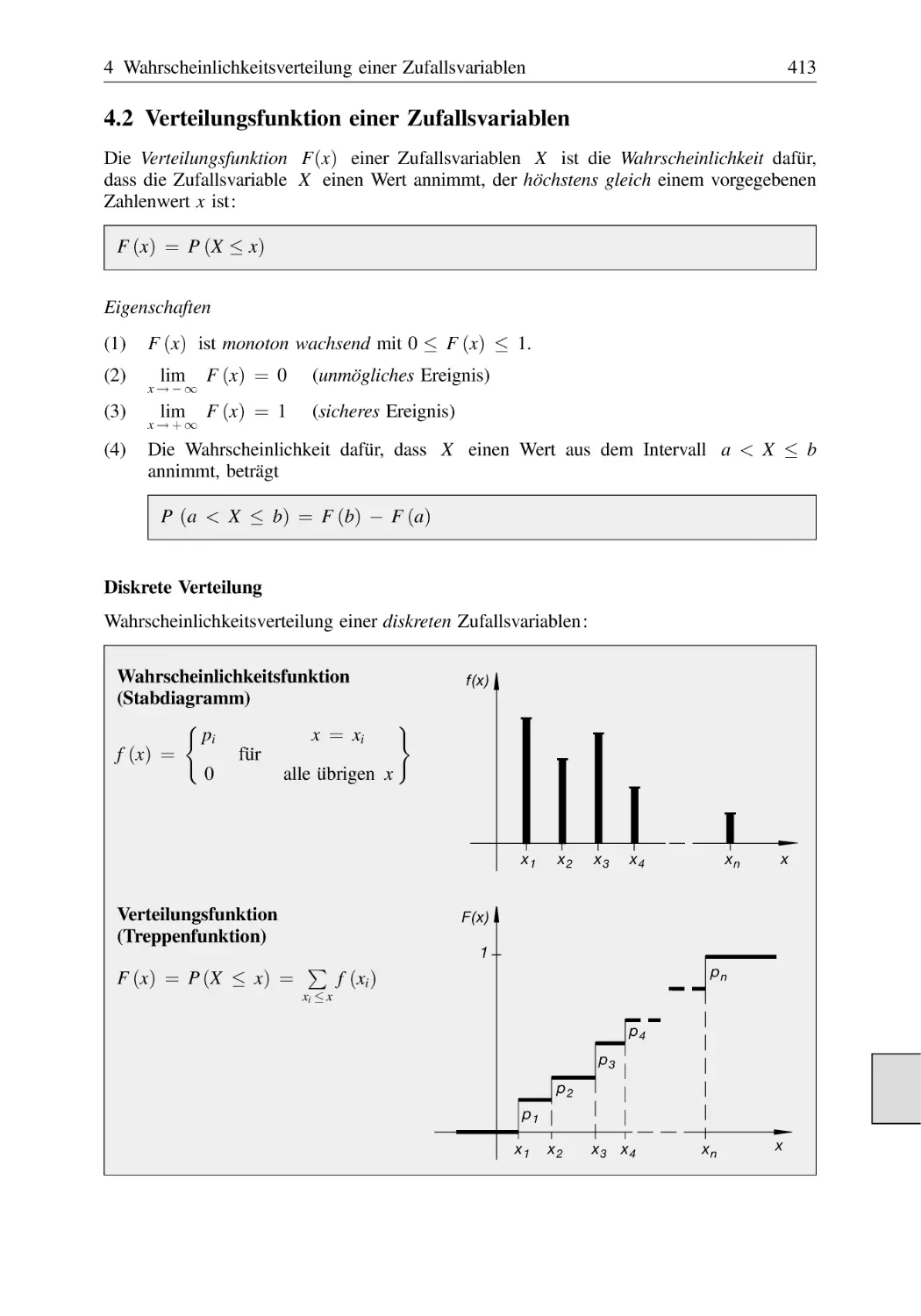
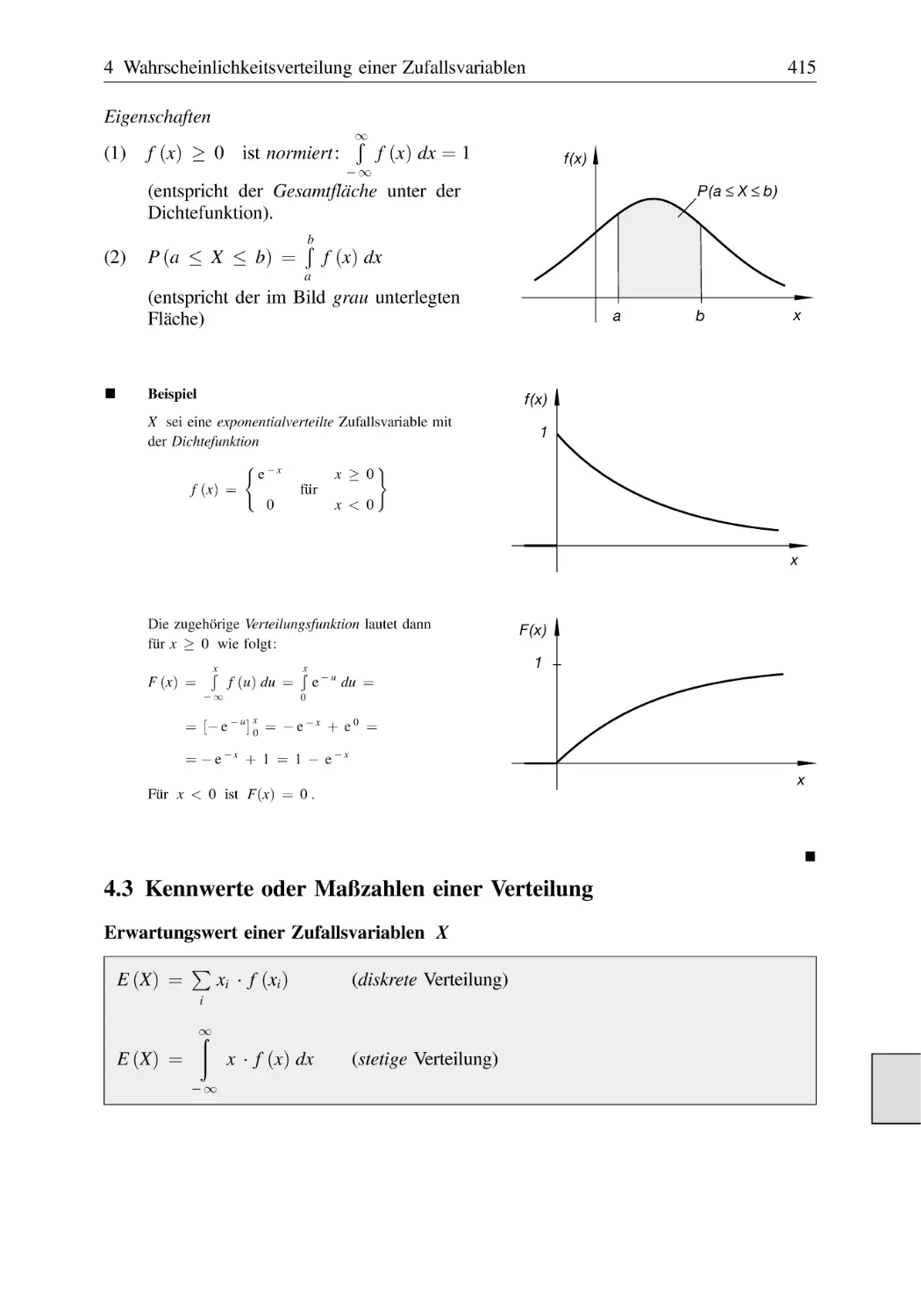
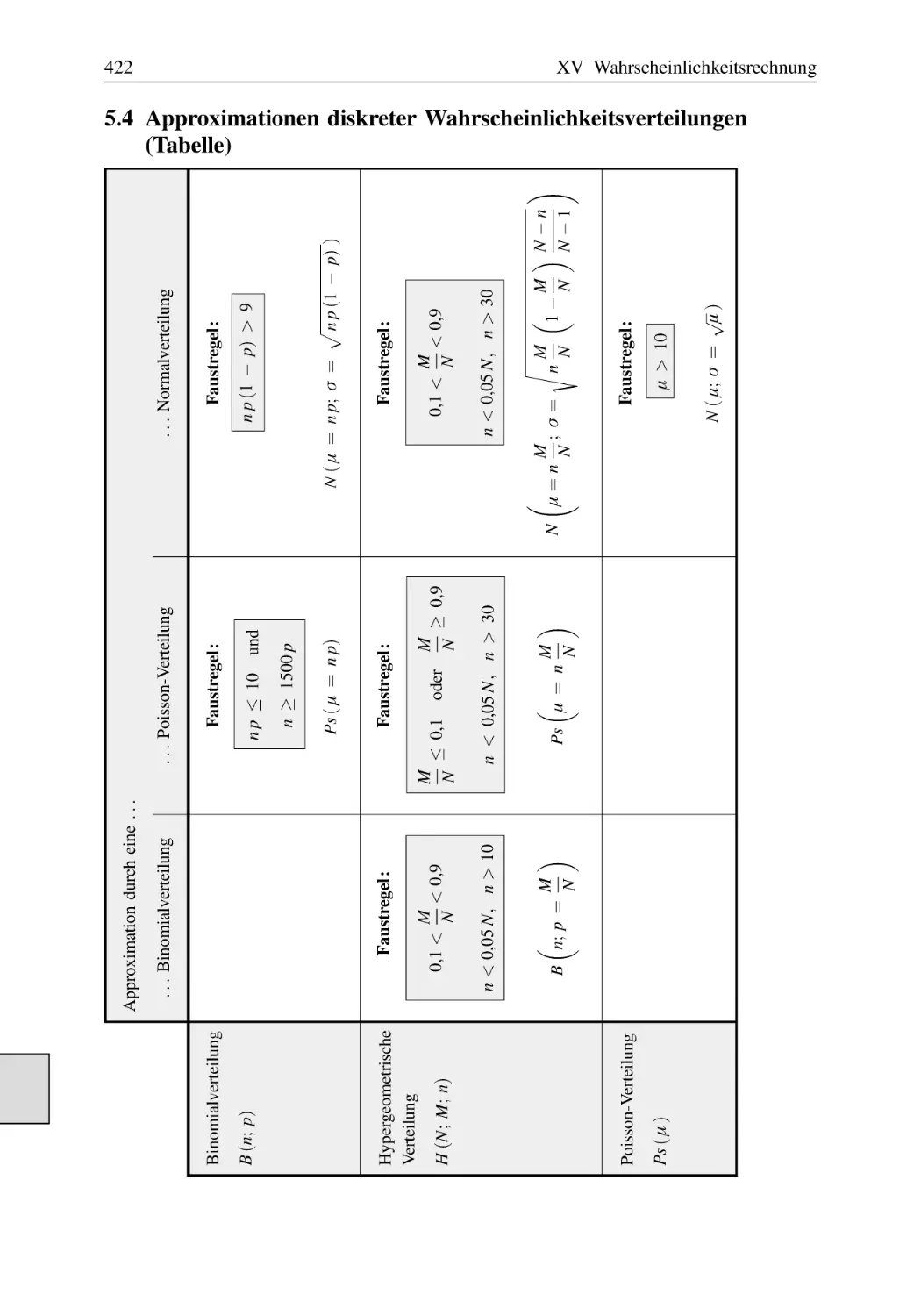
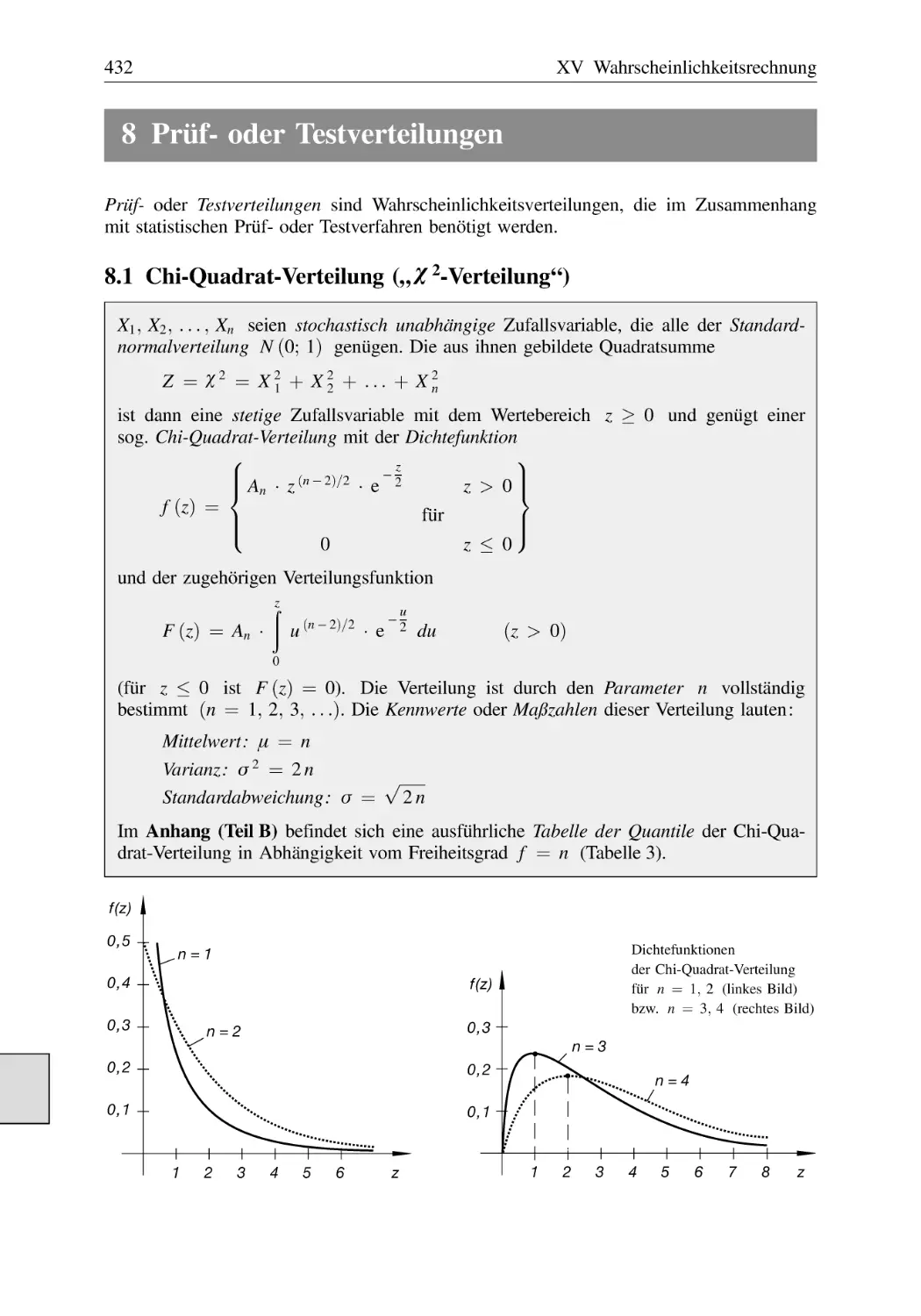
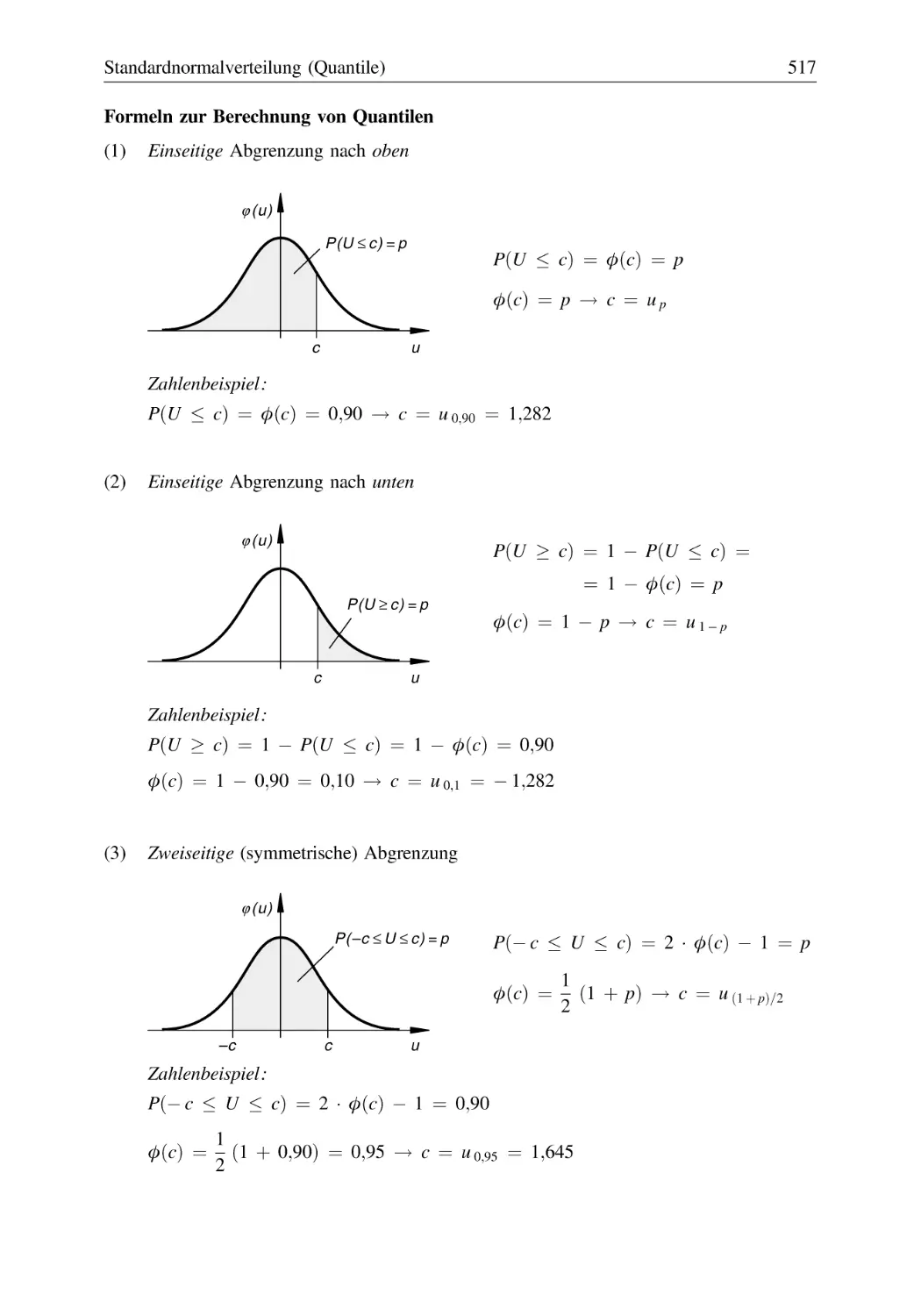
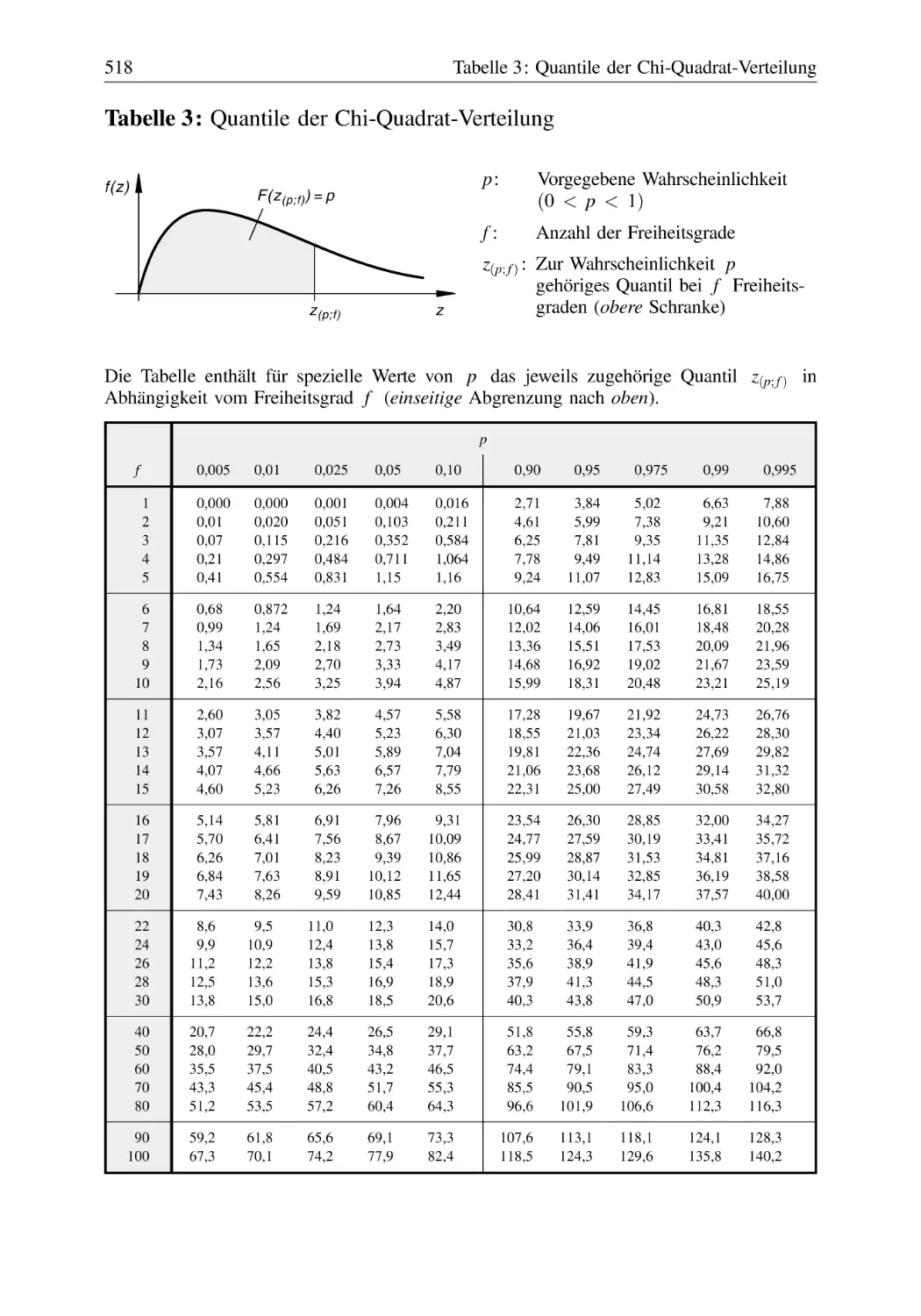
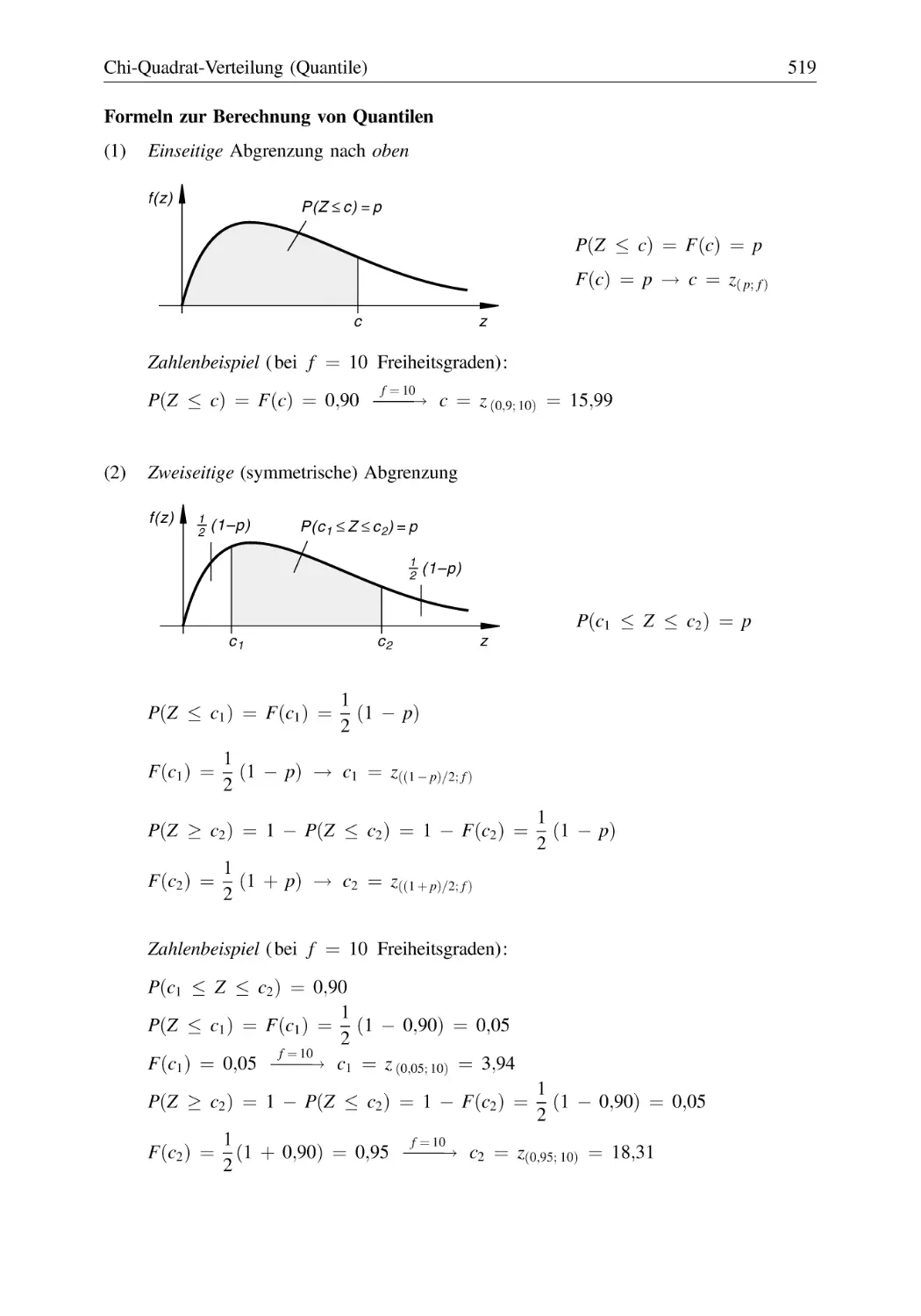
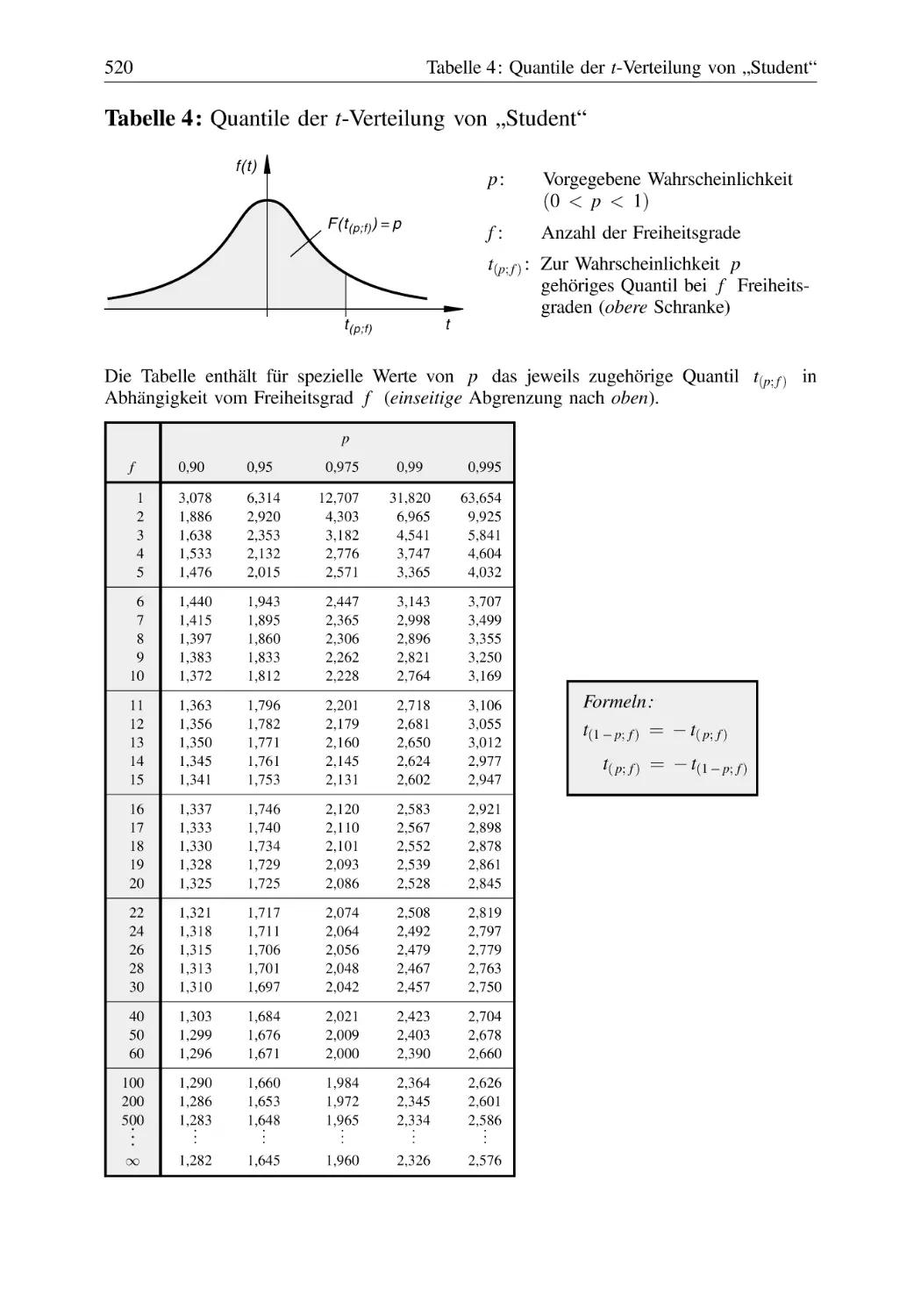
Text
Lothar Papula
Mathematische
Formelsammlung
Für Ingenieure und Naturwissenschaftler
12., überarbeitete Auflage
Mit über 400 Abbildungen, zahlreichen
Rechenbeispielen und einer ausführlichen
Integraltafel
Lothar Papula
Wiesbaden, Deutschland
ISBN 978-3-658-16194-1
DOI 10.1007/978-3-658-16195-8
ISBN 978-3-658-16195-8 (eBook)
Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliografie; detaillierte bibliografische Daten sind im Internet über http://dnb.d-nb.de abrufbar.
Springer Vieweg
© Springer Fachmedien Wiesbaden GmbH 1986, 1988, 1990, 1994, 1998, 2000, 2001, 2003, 2006, 2009, 2014,
2017
Springer Vieweg ist Teil von Springer Nature
Die eingetragene Gesellschaft ist Springer Fachmedien Wiesbaden GmbH
Die Anschrift der Gesellschaft ist: Abraham-Lincoln-Strasse 46, 65189 Wiesbaden, Germany
Vorwort
Das Studium der Ingenieur- und Naturwissenschaften verlangt nach rasch zugänglichen
Informationen. Die vorliegende Mathematische Formelsammlung für Ingenieure und
Naturwissenschaftler wurde dementsprechend gestaltet.
Zur Auswahl des Stoffes
Ausgehend von der elementaren Schulmathematik (z. B. Bruchrechnung, Gleichungen mit
einer Unbekannten, Lehrsätze aus der Geometrie) werden alle für den Ingenieur und Naturwissenschaftler wesentlichen mathematischen Stoffgebiete behandelt. Dabei wurde der bewährte Aufbau des dreibändigen Lehrbuches Mathematik für Ingenieure und Naturwissenschaftler konsequent beibehalten. Der Benutzer wird dies sicherlich als hilfreich
empfinden.
Im Anhang dieser Formelsammlung befinden sich eine ausführliche Integraltafel mit über
400 in den naturwissenschaftlich-technischen Anwendungen besonders häufig auftretenden
Integralen (Teil A) sowie wichtige Tabellen zur Wahrscheinlichkeitsrechnung und Statistik
(Teil B). Der Druck erfolgte hier auf eingefärbtem Papier, um einen raschen Zugriff zu
ermöglichen.
Behandelt werden folgende Stoffgebiete:
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
Vektorrechnung
Funktionen und Kurven
Differentialrechnung
Integralrechnung
Unendliche Reihen, Taylor- und Fourier-Reihen
Lineare Algebra
Komplexe Zahlen und Funktionen
Differential- und Integralrechnung für Funktionen von mehreren Variablen
Gewöhnliche Differentialgleichungen
Fehler- und Ausgleichsrechnung
Fourier-Transformationen
Laplace-Transformationen
Vektoranalysis
Wahrscheinlichkeitsrechnung
Grundlagen der mathematischen Statistik
Zur Darstellung des Stoffes
Die Darstellung der mathematischen Begriffe, Formeln und Sätze erfolgt in anschaulicher
und allgemeinverständlicher Form. Wichtige Formeln wurden gerahmt und grau unterlegt
und zusätzlich durch Bilder verdeutlicht. Zahlreiche Beispiele helfen, die Formeln treffsicher auf eigene Problemstellungen anzuwenden. Die in einigen Beispielen benötigten
Integrale wurden der Integraltafel im Anhang (ab Seite 476) entnommen (Angabe der
laufenden Nummer und der Parameterwerte). Ein ausführliches Inhalts- und Sachwortverzeichnis ermöglicht ein rasches Auffinden der gewünschten Informationen.
Eine Bitte des Autors
Für sachliche und konstruktive Hinweise und Anregungen bin ich stets dankbar. Sie sind
eine unverzichtbare Voraussetzung und Hilfe für die stetige Verbesserung dieser Formelsammlung.
Ein Wort des Dankes . . .
. . . an alle Fachkollegen und Studierende, die durch Anregungen und Hinweise zur Verbesserung dieses Werkes beigetragen haben,
. . . an den Cheflektor des Verlages, Herrn Thomas Zipsner, für die hervorragende Zusammenarbeit,
. . . an Frau Diane Schulz vom Druck- und Satzhaus Beltz (Bad Langensalza) für den ausgezeichneten mathematischen Satz,
. . . an Herrn Dr. Wolfgang Zettlmeier für die hervorragende Qualität der Abbildungen.
Wiesbaden, Frühjahr 2017
Lothar Papula
Inhalt
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie . . . . . .
1
1 Grundlegende Begriffe über Mengen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.1
1.2
Definition und Darstellung einer Menge . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Mengenoperationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
2
2 Rechnen mit reellen Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2.1
2.2
2.3
2.4
2.5
2.6
2.7
Reelle Zahlen und ihre Eigenschaften . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.1.1
Natürliche und ganze Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
2.1.2
Rationale, irrationale und reelle Zahlen . . . . . . . . . . . . . . . . . . . . . 4
2.1.3
Rundungsregeln für reelle Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.1.4
Darstellung der reellen Zahlen auf der Zahlengerade . . . . . . . . . . . 5
2.1.5
Grundrechenarten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Zahlensysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Intervalle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Bruchrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Potenzen und Wurzeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Logarithmen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Binomischer Lehrsatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3 Elementare (endliche) Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
3.1
3.2
3.3
3.4
Definition einer (endlichen) Reihe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Arithmetische Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Geometrische Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spezielle Zahlenreihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
16
16
16
4 Gleichungen mit einer Unbekannten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
4.1
4.2
4.3
4.4
4.5
Algebraische Gleichungen n-ten Grades . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.1
Allgemeine Vorbetrachtungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.2
Lineare Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.3
Quadratische Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.4
Kubische Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.5
Biquadratische Gleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Allgemeine Lösungshinweise für Gleichungen . . . . . . . . . . . . . . . . . . . . . . . .
Graphisches Lösungsverfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Regula falsi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Tangentenverfahren von Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
17
18
18
18
20
21
22
23
24
5 Ungleichungen mit einer Unbekannten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
X
Inhaltsverzeichnis
6 Lehrsätze aus der elementaren Geometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
6.1
6.2
6.3
6.4
6.5
6.6
6.7
Satz des Pythagoras . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Höhensatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kathetensatz (Euklid) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Satz des Thales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Strahlensätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Sinussatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kosinussatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
26
27
27
27
28
28
7 Ebene geometrische Körper (Planimetrie) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
7.1
7.2
7.3
7.4
7.5
7.6
7.7
7.8
7.9
7.10
7.11
7.12
Dreiecke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.1.1
Allgemeine Beziehungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.1.2
Spezielle Dreiecke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.1.2.1 Rechtwinkliges Dreieck . . . . . . . . . . . . . . . . . . . . . . . . . .
7.1.2.2 Gleichschenkliges Dreieck . . . . . . . . . . . . . . . . . . . . . . . .
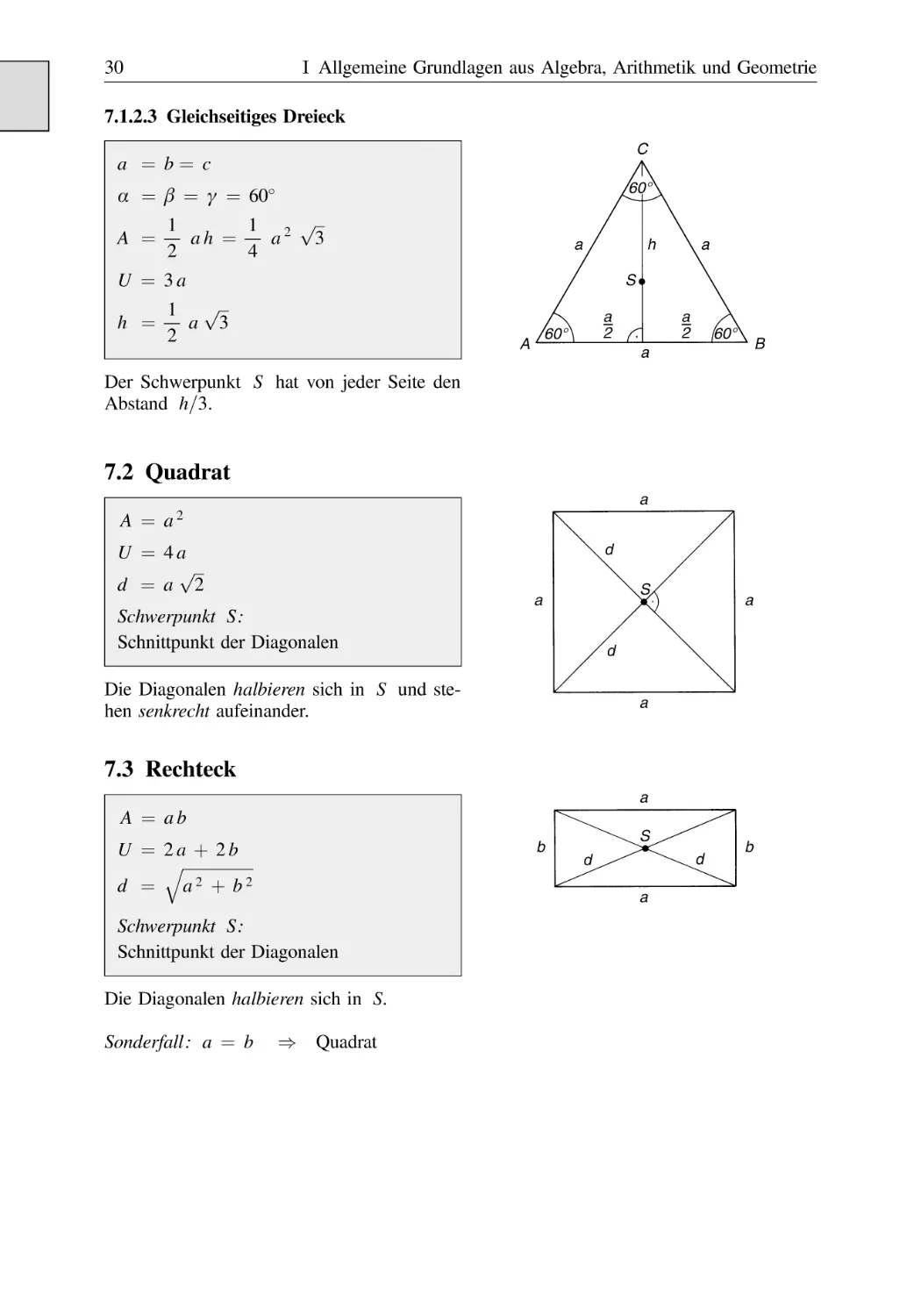
7.1.2.3 Gleichseitiges Dreieck . . . . . . . . . . . . . . . . . . . . . . . . . . .
Quadrat . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rechteck . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Parallelogramm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rhombus oder Raute . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Trapez . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
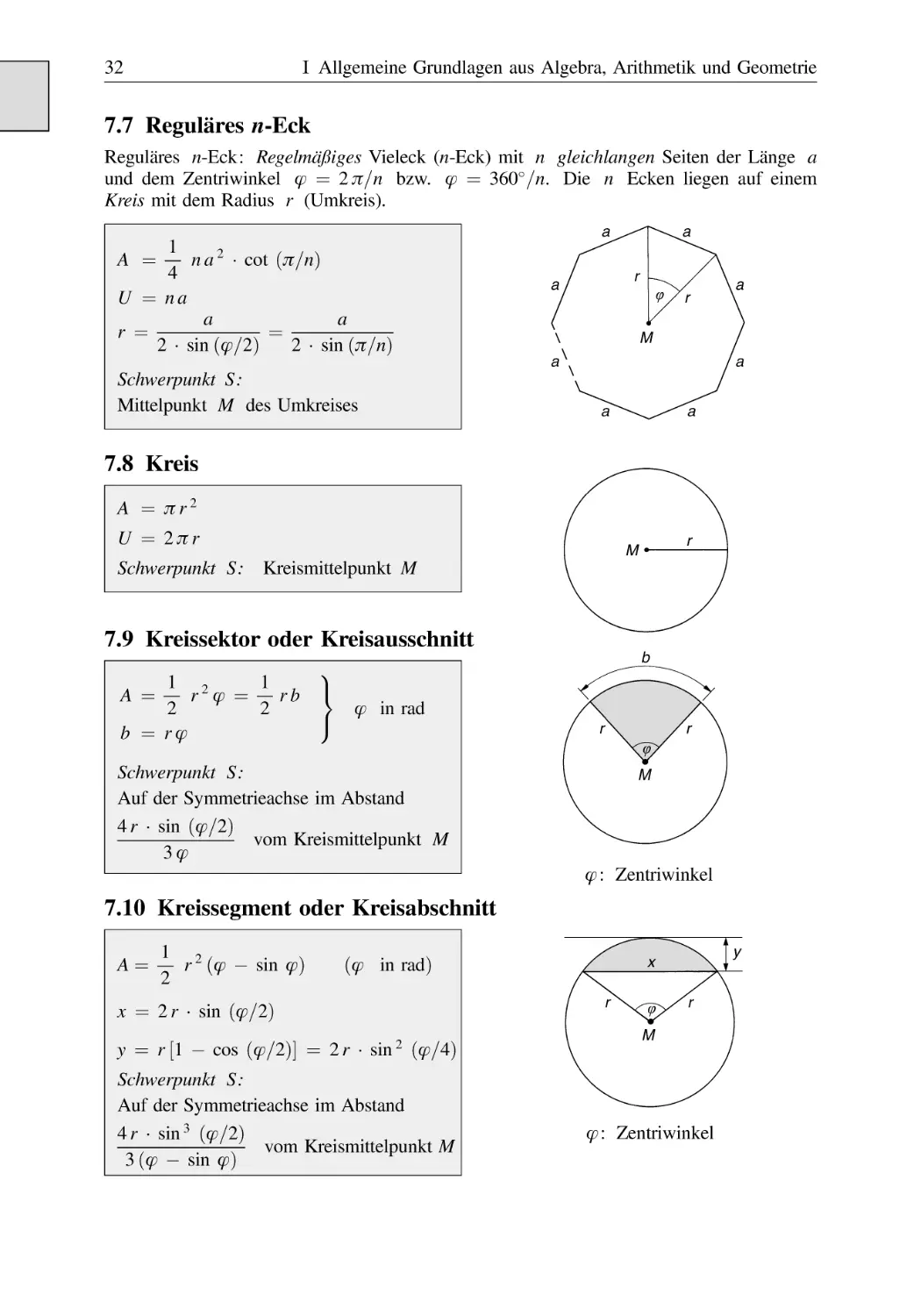
Reguläres n-Eck . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kreis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kreissektor oder Kreisausschnitt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kreissegment oder Kreisabschnitt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kreisring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ellipse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
28
29
29
29
30
30
30
31
31
31
32
32
32
32
33
33
8 Räumliche geometrische Körper (Stereometrie) . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
8.1
8.2
8.3
8.4
8.5
8.6
8.7
8.8
8.9
8.10
8.11
8.12
8.13
8.14
8.15
8.16
8.17
8.18
8.19
Prisma . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Würfel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Quader . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Pyramide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Pyramidenstumpf . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Tetraeder oder dreiseitige Pyramide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Keil . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Gerader Kreiszylinder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Gerader Kreiskegel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Gerader Kreiskegelstumpf . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kugel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kugelausschnitt oder Kugelsektor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kugelschicht oder Kugelzone . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kugelabschnitt, Kugelsegment, Kugelkappe oder Kalotte . . . . . . . . . . . . . . .
Ellipsoid . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rotationsparaboloid . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Tonne oder Fass . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Torus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Guldinsche Regeln für Rotationskörper . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
34
34
34
35
35
36
36
36
37
37
37
38
38
38
39
39
40
40
Inhaltsverzeichnis
XI
9 Koordinatensysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
9.1
9.2
Ebene Koordinatensysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.1.1
Rechtwinklige oder kartesische Koordinaten . . . . . . . . . . . . . . . . .
9.1.2
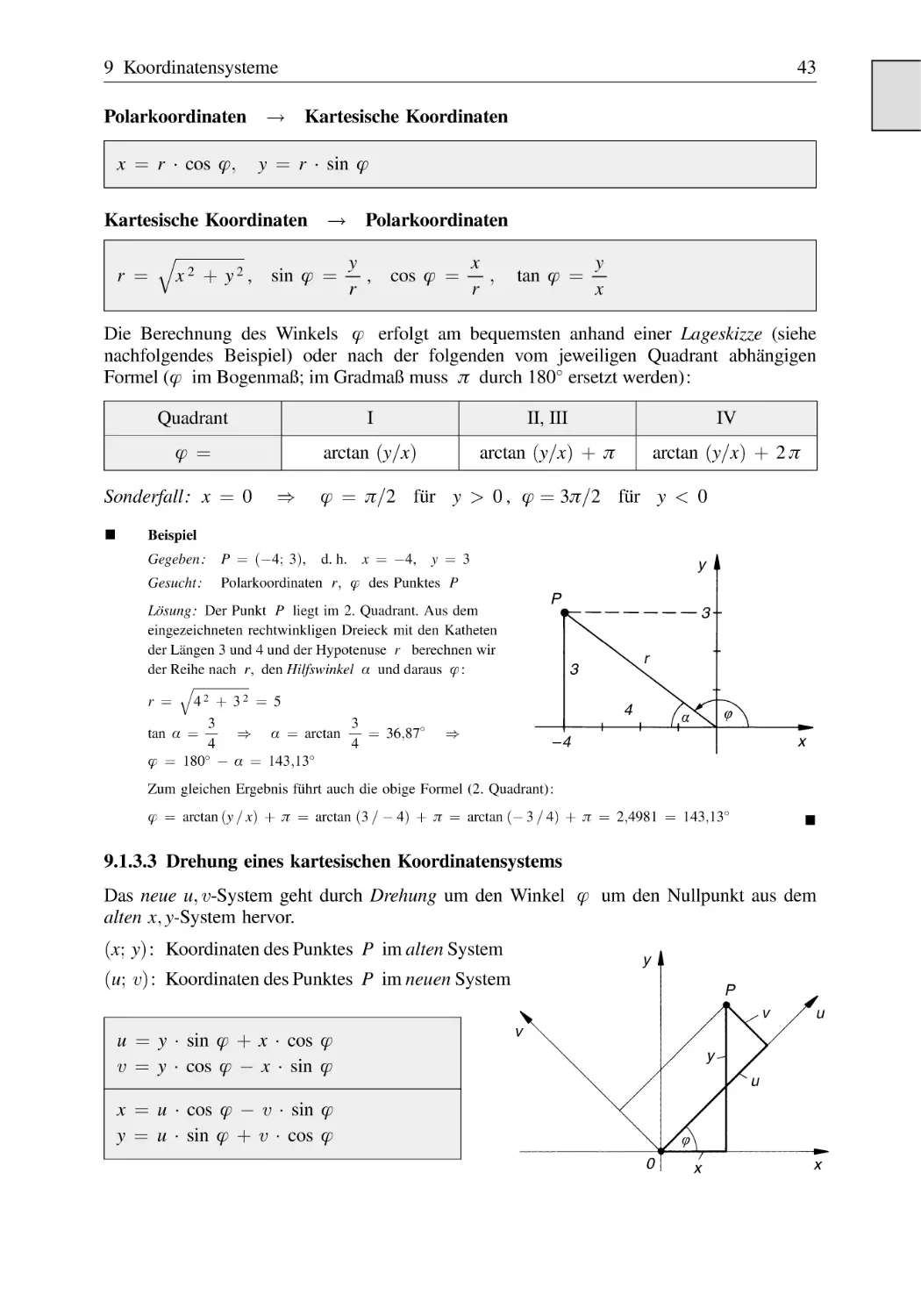
Polarkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.1.3
Koordinatentransformationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.1.3.1 Parallelverschiebung eines kartesischen
Koordinatensystems . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.1.3.2 Zusammenhang zwischen den kartesischen und
den Polarkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.1.3.3 Drehung eines kartesischen Koordinatensystems . . . . . . .
Räumliche Koordinatensysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2.1
Rechtwinklige oder kartesische Koordinaten . . . . . . . . . . . . . . . . . .
9.2.2
Zylinderkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2.3
Zusammenhang zwischen den kartesischen und
den Zylinderkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2.4
Kugelkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2.5
Zusammenhang zwischen den kartesischen und
den Kugelkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
41
42
42
42
42
43
44
44
44
44
45
45
II Vektorrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
1.1
1.2
1.3
1.4
Vektoren und Skalare . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spezielle Vektoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Gleichheit von Vektoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kollineare, parallele und antiparallele Vektoren, inverser Vektor . . . . . . . . . .
46
46
47
47
2 Komponentendarstellung eines Vektors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
2.1
2.2
2.3
Komponentendarstellung in einem kartesischen Koordinatensystem . . . . . . . 48
Komponentendarstellung spezieller Vektoren . . . . . . . . . . . . . . . . . . . . . . . . . 48
Betrag und Richtungswinkel eines Vektors . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
3 Vektoroperationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
3.1
3.2
3.3
3.4
3.5
3.6
Addition und Subtraktion von Vektoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Multiplikation eines Vektors mit einem Skalar . . . . . . . . . . . . . . . . . . . . . . . .
Skalarprodukt (inneres Produkt) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vektorprodukt (äußeres Produkt, Kreuzprodukt) . . . . . . . . . . . . . . . . . . . . . .
Spatprodukt (gemischtes Produkt) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Formeln für Mehrfachprodukte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
51
51
53
55
56
4 Anwendungen. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.1
4.2
Arbeit einer konstanten Kraft . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vektorielle Darstellung einer Geraden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.1
Punkt-Richtungs-Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.2
Zwei-Punkte-Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.3
Abstand eines Punktes von einer Geraden . . . . . . . . . . . . . . . . . . .
56
57
57
57
58
XII
4.3
Inhaltsverzeichnis
4.2.4
Abstand zweier paralleler Geraden . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.5
Abstand zweier windschiefer Geraden . . . . . . . . . . . . . . . . . . . . . .
4.2.6
Schnittpunkt und Schnittwinkel zweier Geraden . . . . . . . . . . . . . .
Vektorielle Darstellung einer Ebene . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.1
Punkt-Richtungs-Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.2
Drei-Punkte-Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.3
Ebene senkrecht zu einem Vektor . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.4
Abstand eines Punktes von einer Ebene . . . . . . . . . . . . . . . . . . . . .
4.3.5
Abstand einer Geraden von einer Ebene . . . . . . . . . . . . . . . . . . . . .
4.3.6
Abstand zweier paralleler Ebenen . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.7
Schnittpunkt und Schnittwinkel einer Geraden mit einer Ebene . .
4.3.8
Schnittwinkel zweier Ebenen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.9
Schnittgerade zweier Ebenen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
59
60
60
60
61
62
62
63
64
65
66
66
III Funktionen und Kurven . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
1.1
1.2
Definition einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Darstellungsformen einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1
Analytische Darstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2
Parameterdarstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.3
Kurvengleichung in Polarkoordinaten . . . . . . . . . . . . . . . . . . . . . . .
1.2.4
Graphische Darstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
67
67
67
68
68
2 Allgemeine Funktionseigenschaften . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
2.1
2.2
2.3
2.4
2.5
Nullstellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
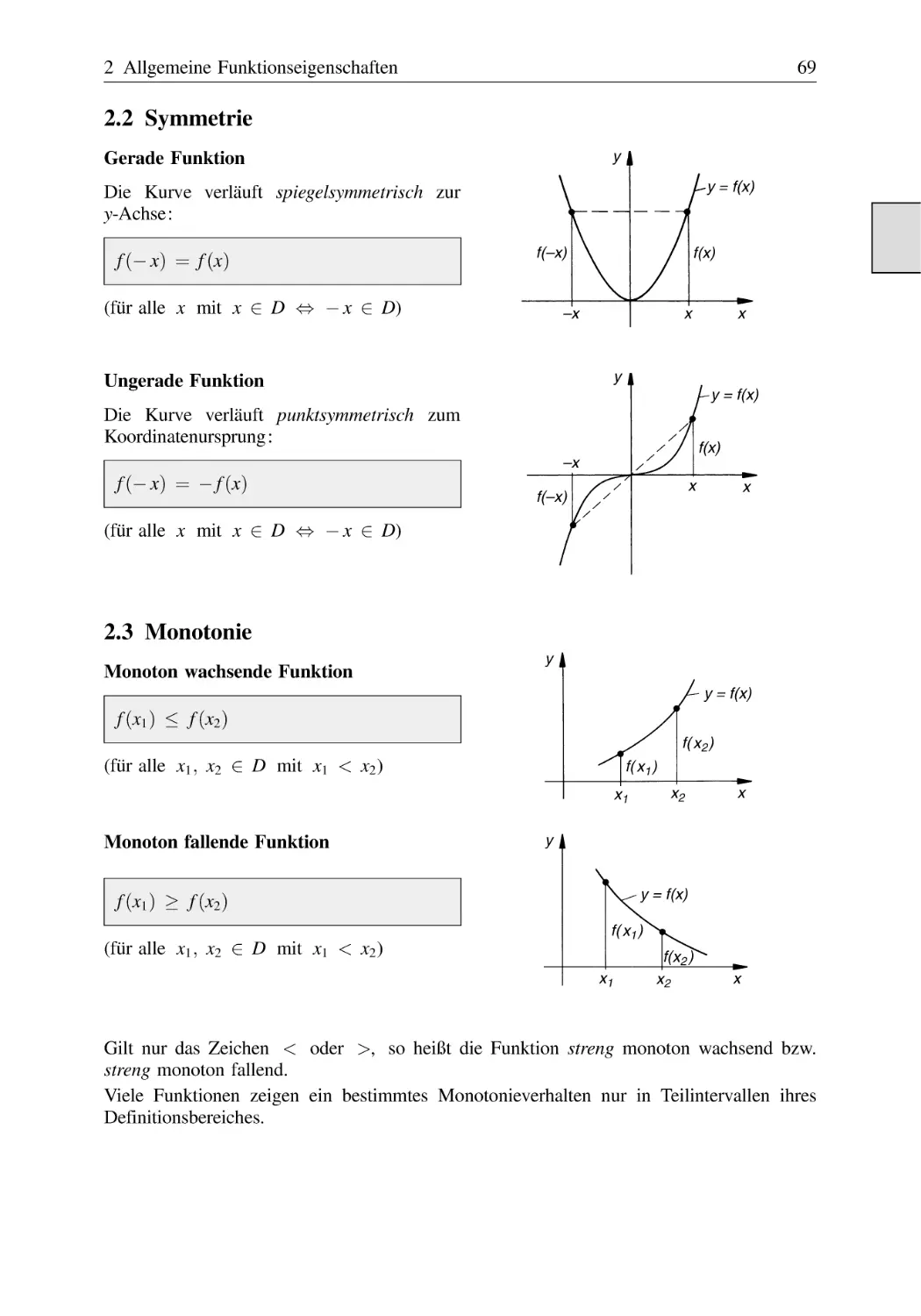
Symmetrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Monotonie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Periodizität . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Umkehrfunktion (inverse Funktion) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
69
69
70
70
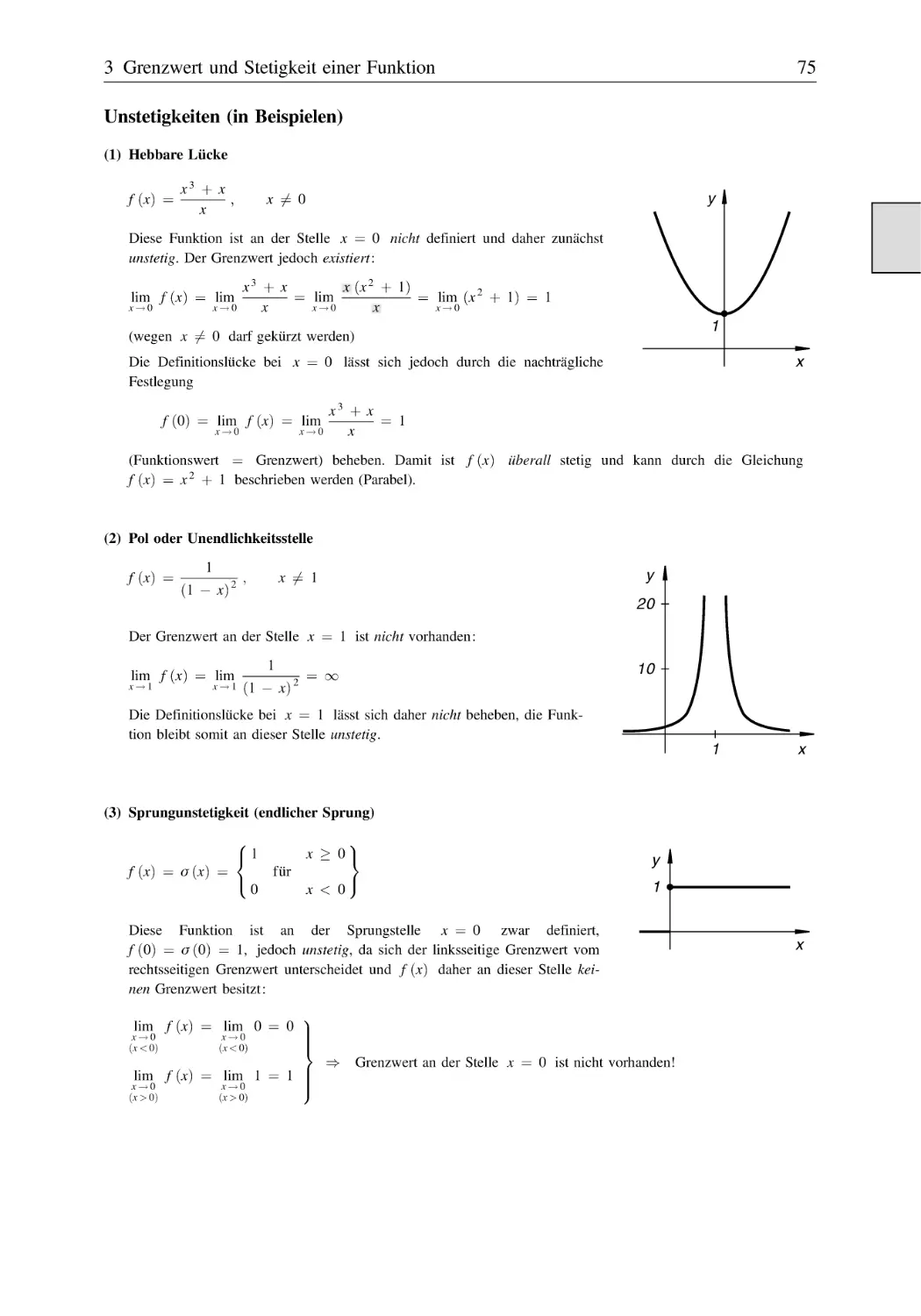
3 Grenzwert und Stetigkeit einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
3.1
3.2
3.3
3.4
3.5
Grenzwert einer Folge . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Grenzwert einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1
Grenzwert für x ! x0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2
Grenzwert für x ! + 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rechenregeln für Grenzwerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Grenzwertregel von Bernoulli und de l’Hospital . . . . . . . . . . . . . . . . . . . . . .
Stetigkeit einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
71
72
72
72
72
73
74
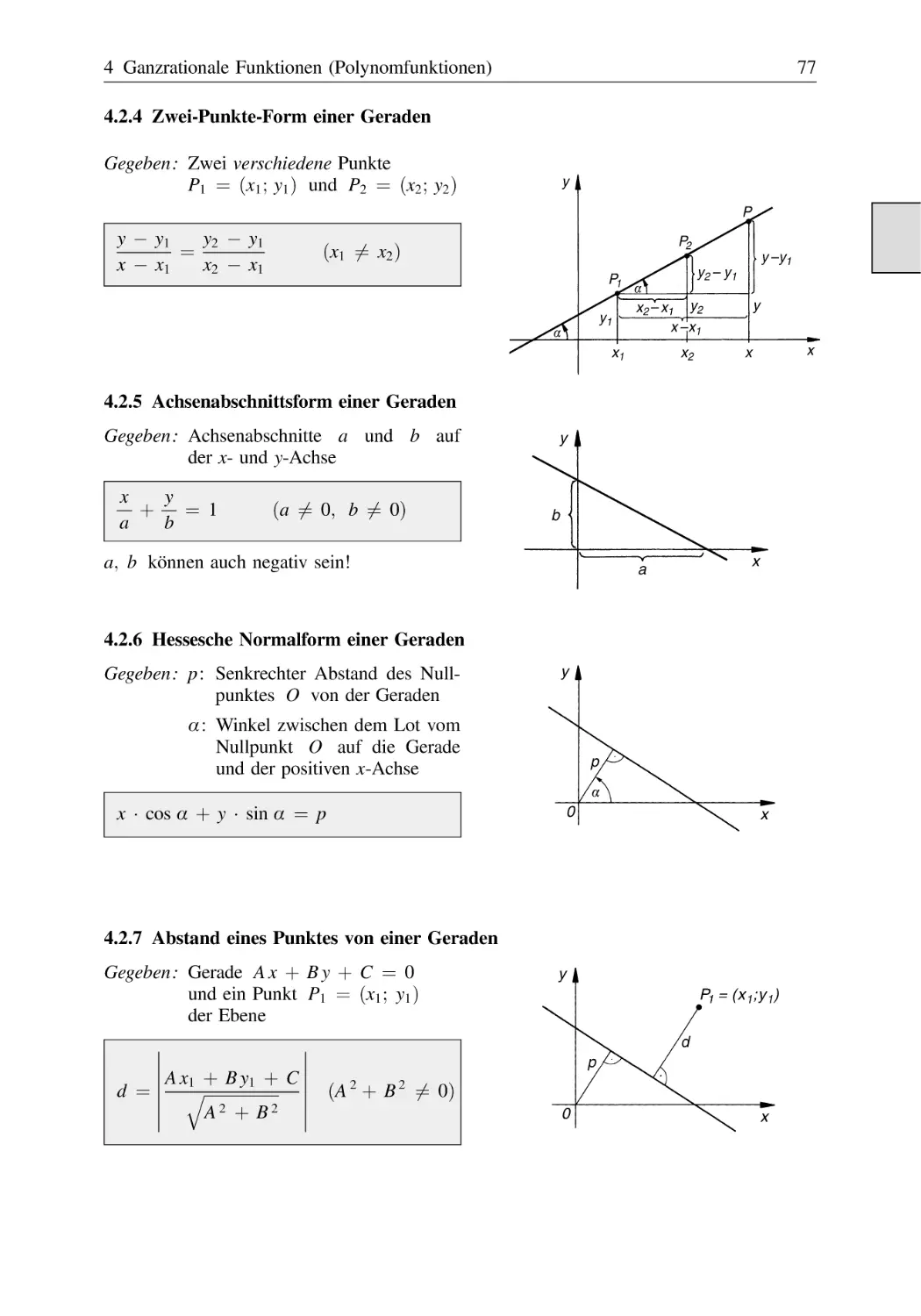
4 Ganzrationale Funktionen (Polynomfunktionen) . . . . . . . . . . . . . . . . . . . . . . . . . . 76
4.1
4.2
Definition der ganzrationalen Funktionen (Polynomfunktionen) . . . . . . . . . .
Lineare Funktionen (Geraden) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.1
Allgemeine Geradengleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.2
Hauptform einer Geraden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.3
Punkt-Steigungs-Form einer Geraden . . . . . . . . . . . . . . . . . . . . . . .
4.2.4
Zwei-Punkte-Form einer Geraden . . . . . . . . . . . . . . . . . . . . . . . . . .
76
76
76
76
76
77
Inhaltsverzeichnis
4.3
4.4
4.5
4.6
4.7
4.2.5
Achsenabschnittsform einer Geraden . . . . . . . . . . . . . . . . . . . . . . . .
4.2.6
Hessesche Normalform einer Geraden . . . . . . . . . . . . . . . . . . . . . . .
4.2.7
Abstand eine Punktes von einer Geraden . . . . . . . . . . . . . . . . . . . .
4.2.8
Schnittwinkel zweier Geraden . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
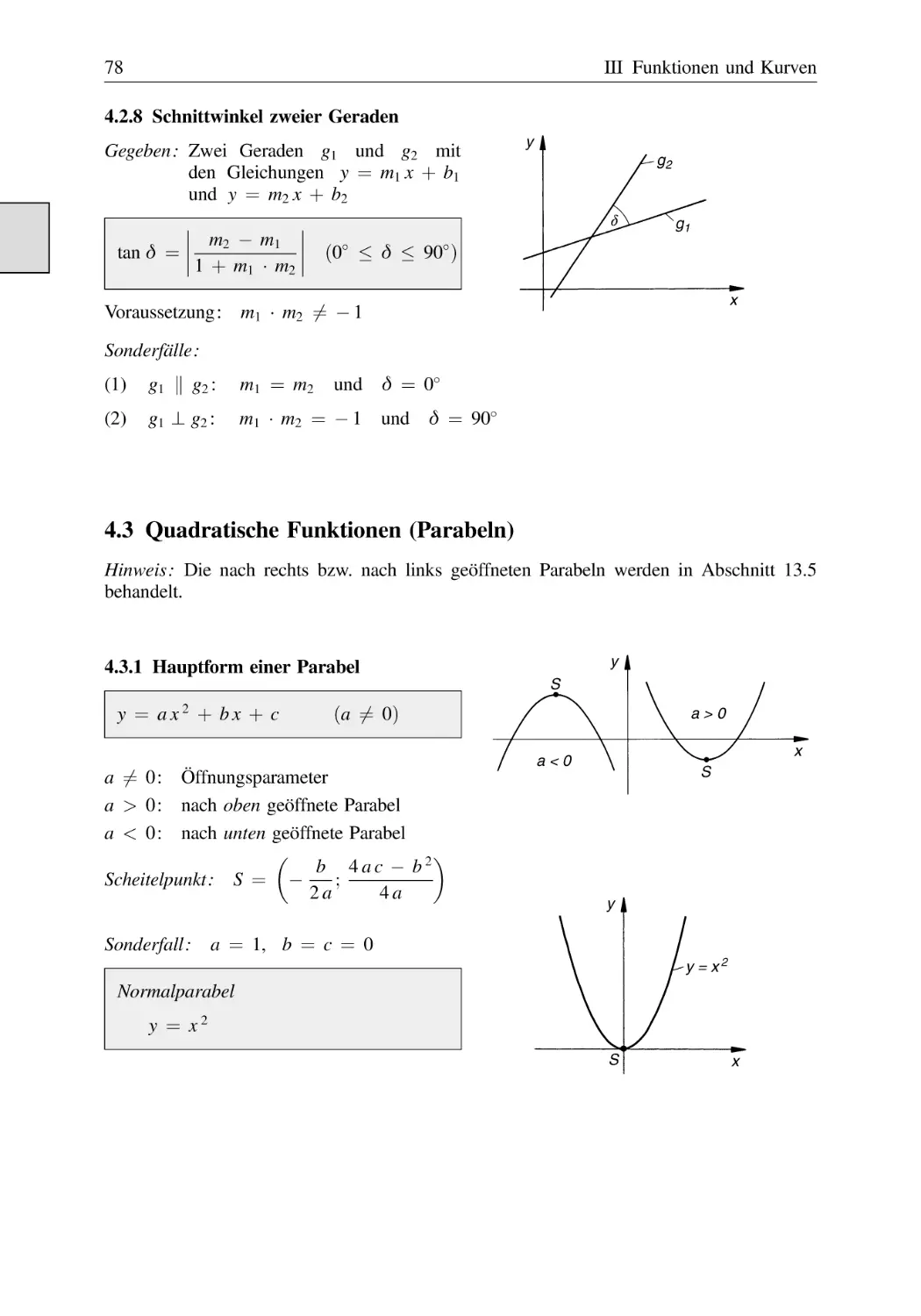
Quadratische Funktionen (Parabeln) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.1
Hauptform einer Parabel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.2
Produktform einer Parabel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.3
Scheitelpunktsform einer Parabel . . . . . . . . . . . . . . . . . . . . . . . . . . .
Polynomfunktionen höheren Grades (n-ten Grades) . . . . . . . . . . . . . . . . . . . .
4.4.1
Abspaltung eines Linearfaktors . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.2
Nullstellen einer Polynomfunktion . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.3
Produktdarstellung einer Polynomfunktion . . . . . . . . . . . . . . . . . . .
Horner-Schema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Reduzierung einer Polynomfunktion (Nullstellenberechnung) . . . . . . . . . . . .
Interpolationspolynome . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7.1
Allgemeine Vorbetrachtungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7.2
Interpolationsformel von Lagrange . . . . . . . . . . . . . . . . . . . . . . . . .
4.7.3
Interpolationsformel von Newton . . . . . . . . . . . . . . . . . . . . . . . . . .
XIII
77
77
77
78
78
78
79
79
79
79
79
79
80
81
82
82
82
84
5 Gebrochenrationale Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
5.1
5.2
5.3
Definition der gebrochenrationalen Funktionen . . . . . . . . . . . . . . . . . . . . . . . 86
Nullstellen, Definitionslücken, Pole . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Asymptotisches Verhalten im Unendlichen . . . . . . . . . . . . . . . . . . . . . . . . . . 88
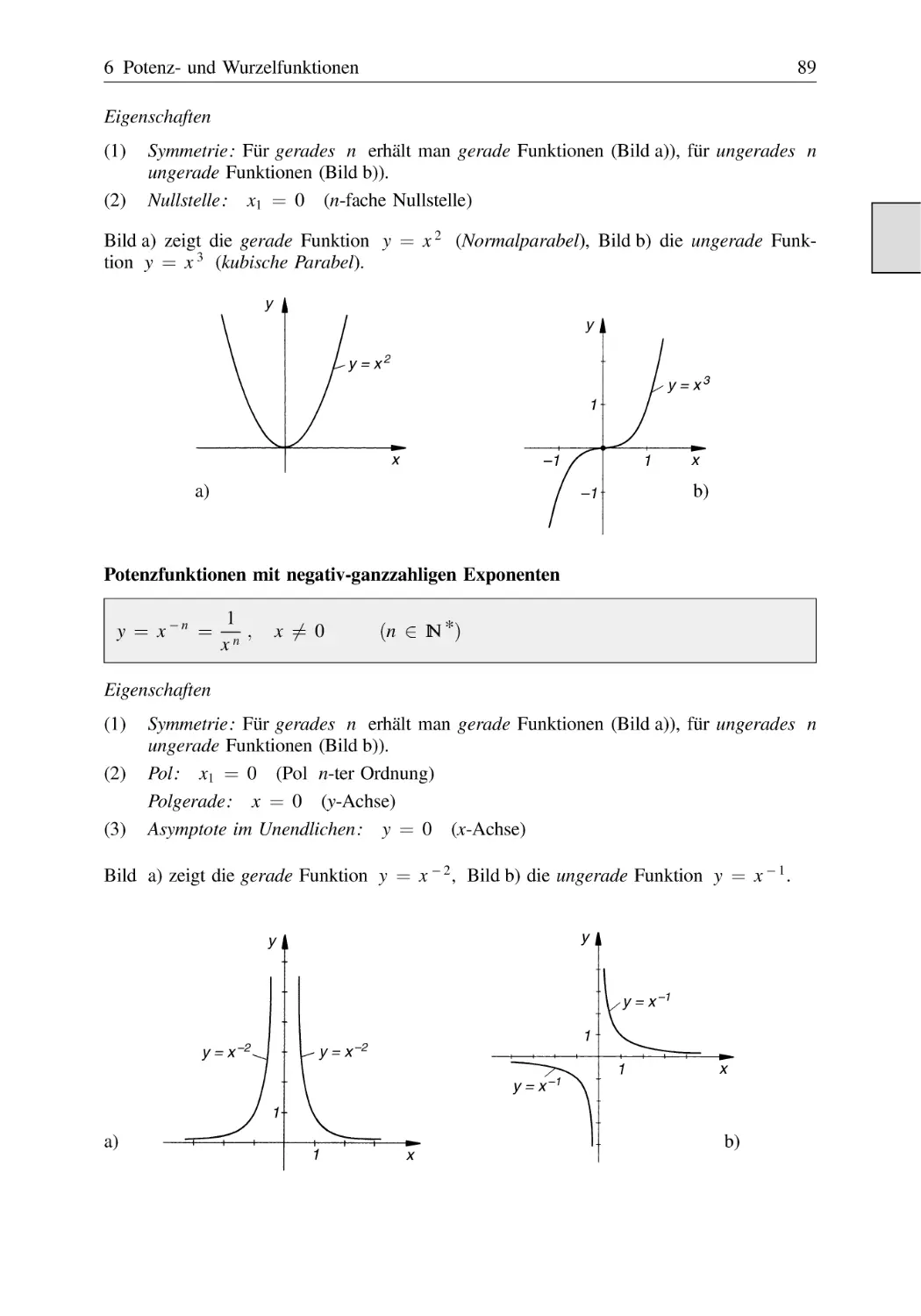
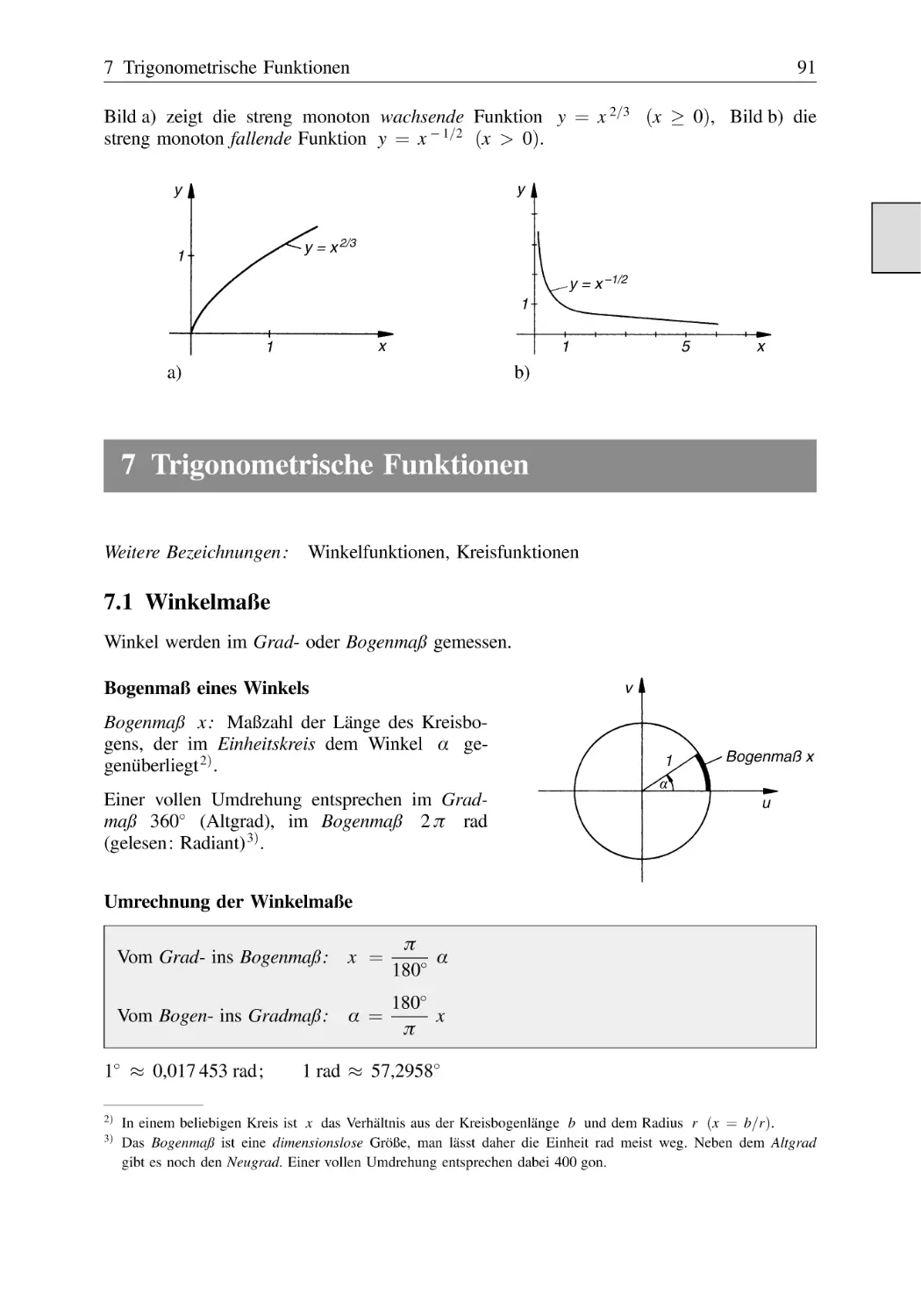
6 Potenz- und Wurzelfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
6.1
6.2
6.3
Potenzfunktionen mit ganzzahligen Exponenten . . . . . . . . . . . . . . . . . . . . . . 88
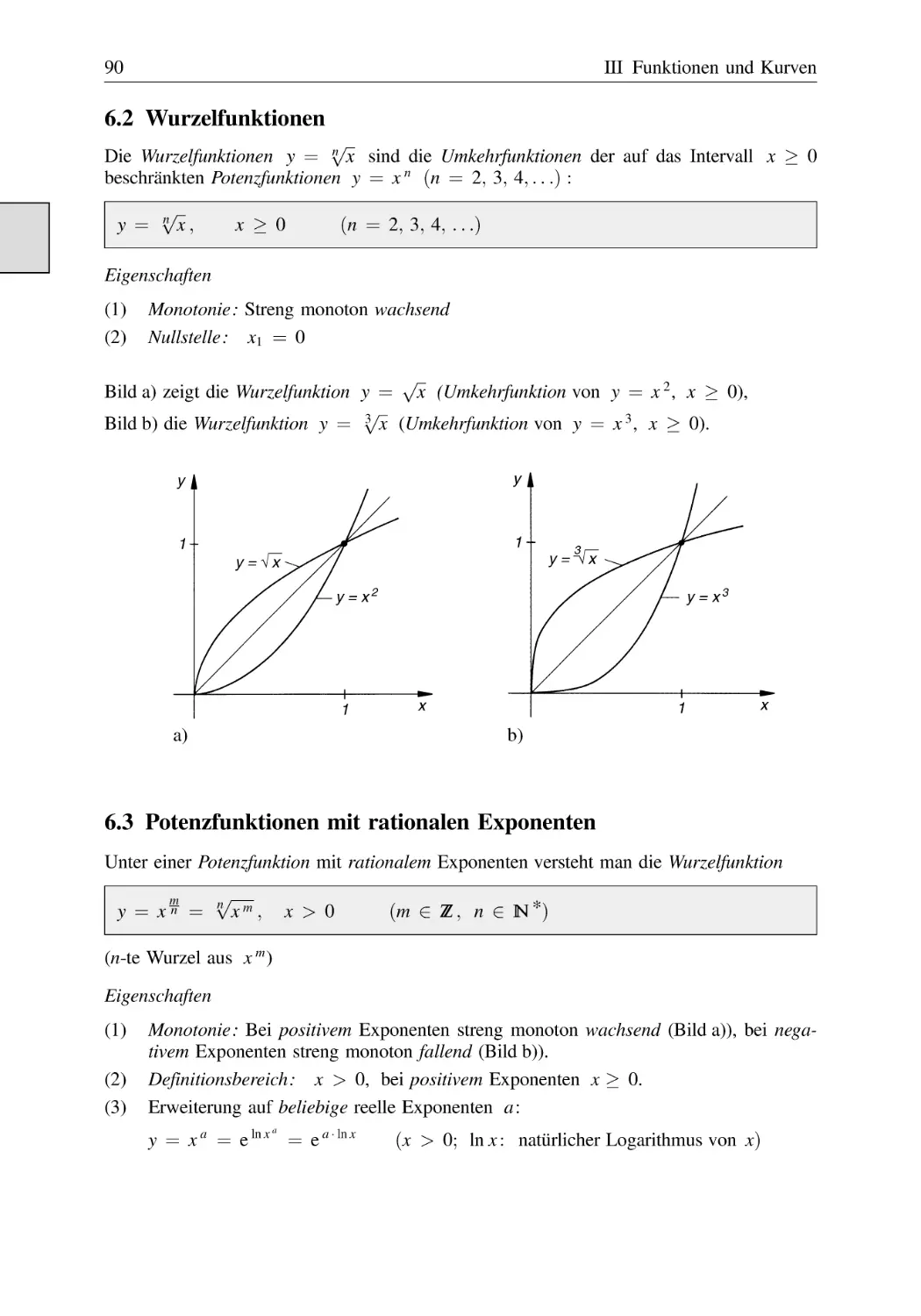
Wurzelfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
Potenzfunktionen mit rationalen Exponenten . . . . . . . . . . . . . . . . . . . . . . . . . 90
7 Trigonometrische Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
7.1
7.2
7.3
7.4
7.5
7.6
7.7
Winkelmaße . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Definition der trigonometrischen Funktionen . . . . . . . . . . . . . . . . . . . . . . . . .
Sinus- und Kosinusfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
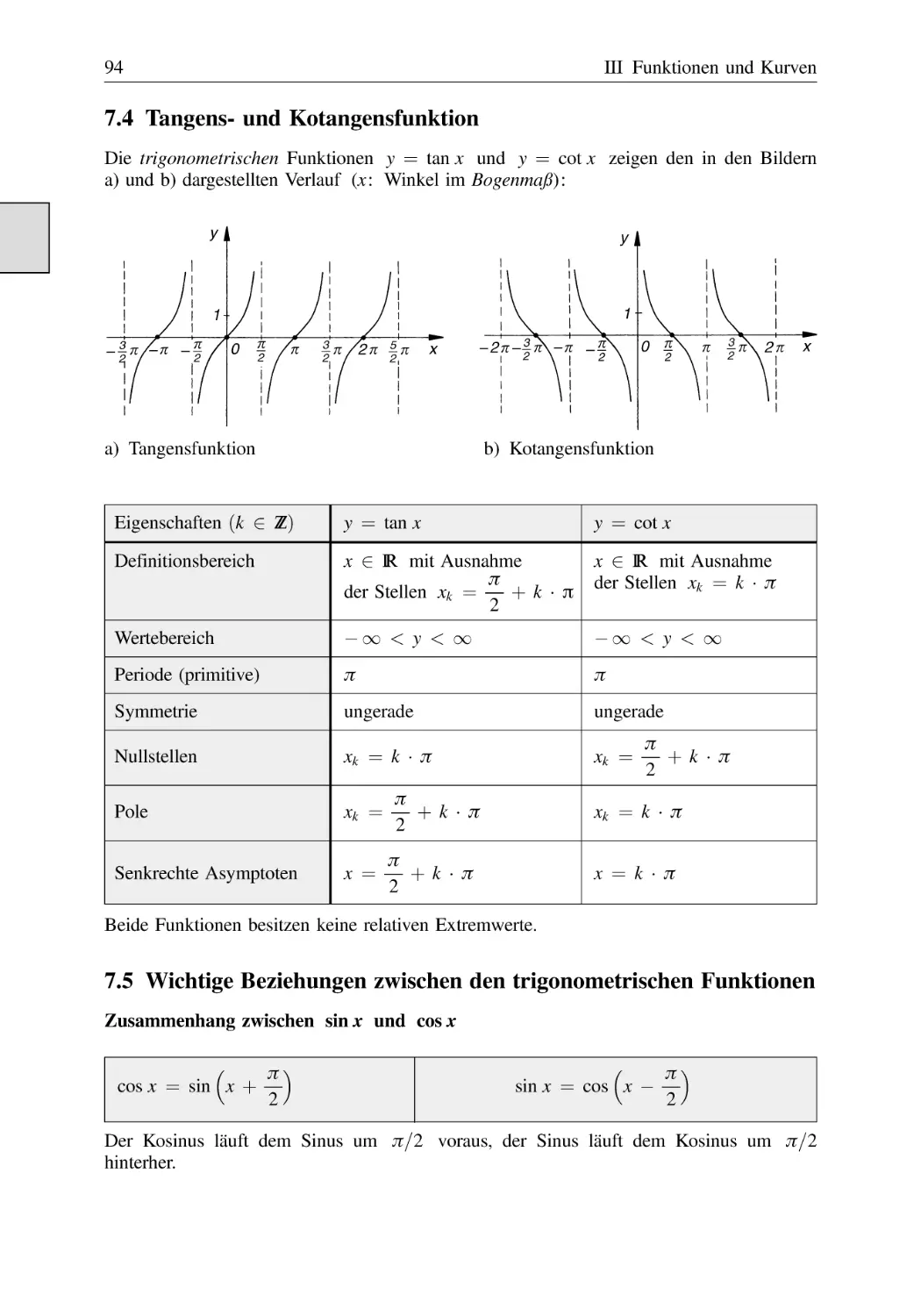
Tangens- und Kotangensfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wichtige Beziehungen zwischen den trigonometrischen Funktionen . . . . . .
Trigonometrische Formeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.6.1
Additionstheoreme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.6.2
Formeln für halbe Winkel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.6.3
Formeln für Winkelvielfache . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.6.4
Formeln für Potenzen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.6.5
Formeln für Summen und Differenzen . . . . . . . . . . . . . . . . . . . . . .
7.6.6
Formeln für Produkte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Anwendungen in der Schwingungslehre . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.7.1
Allgemeine Sinus- und Kosinusfunktion . . . . . . . . . . . . . . . . . . . . .
7.7.2
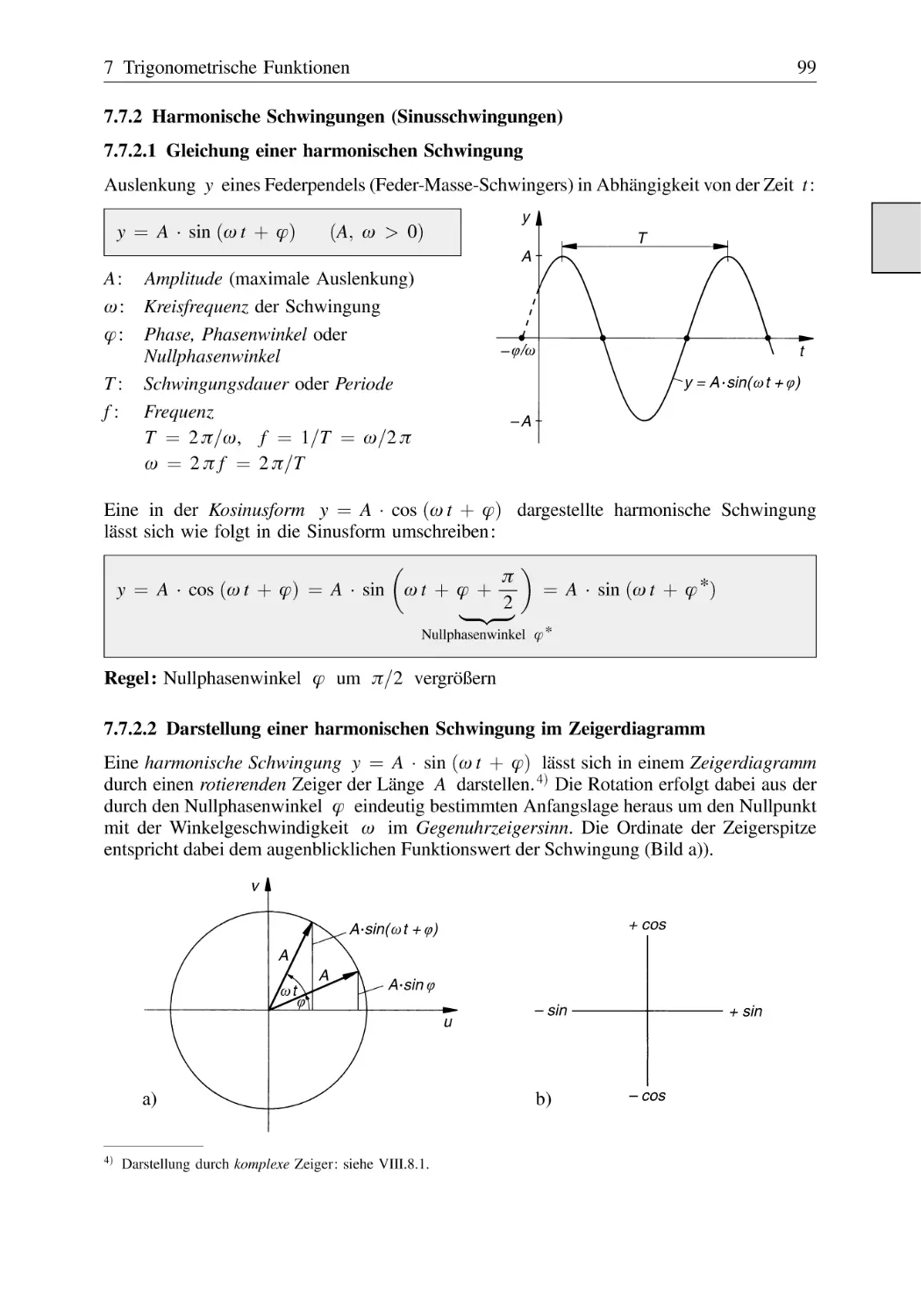
Harmonische Schwingungen (Sinusschwingungen) . . . . . . . . . . . .
7.7.2.1 Gleichung einer harmonischen Schwingung . . . . . . . . . .
7.7.2.2 Darstellung einer harmonischen Schwingung
im Zeigerdiagramm . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
92
93
94
94
95
95
96
96
97
97
98
98
98
99
99
99
XIV
Inhaltsverzeichnis
7.7.3
Superposition (!berlagerung) gleichfrequenter
harmonischer Schwingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
8 Arkusfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
8.1
8.2
8.3
Arkussinus- und Arkuskosinusfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
Arkusstangens- und Arkuskotangensfunktion . . . . . . . . . . . . . . . . . . . . . . . . . 102
Wichtige Beziehungen zwischen den Arkusfunktionen . . . . . . . . . . . . . . . . . 103
9 Exponentialfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
9.1
9.2
Definition der Exponentialfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spezielle Exponentialfunktionen aus den Anwendungen . . . . . . . . . . . . . . . .
9.2.1
Abklingfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2.2
Sättigungsfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2.3
Wachstumsfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2.4
Gauß-Funktion (Gaußsche Glockenkurve) . . . . . . . . . . . . . . . . . . .
9.2.5
Kettenlinie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
104
105
105
105
106
106
106
10 Logarithmusfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
10.1
10.2
Definition der Logarithmusfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
Spezielle Logarithmusfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
11 Hyperbelfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
11.1
11.2
11.3
Definition der Hyperbelfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wichtige Beziehungen zwischen den Hyperbelfunktionen . . . . . . . . . . . . . . .
Formeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11.3.1 Additionstheoreme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11.3.2 Formeln für halbe Argumente . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11.3.3 Formeln für Vielfache des Arguments . . . . . . . . . . . . . . . . . . . . . . .
11.3.4 Formeln für Potenzen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11.3.5 Formeln für Summen und Differenzen . . . . . . . . . . . . . . . . . . . . . .
11.3.6 Formeln für Produkte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11.3.7 Formel von Moivre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
108
109
110
110
110
111
111
112
112
112
12 Areafunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
12.1
12.2
Definition der Areafunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
Wichtige Beziehungen zwischen den Areafunktionen . . . . . . . . . . . . . . . . . . 114
13 Kegelschnitte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
13.1
13.2
Allgemeine Gleichung eines Kegelschnittes . . . . . . . . . . . . . . . . . . . . . . . . . .
Kreis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.2.1 Geometrische Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.2.2 Mittelpunktsgleichung eines Kreises (Ursprungsgleichung) . . . . . .
13.2.3 Kreis in allgemeiner Lage (Hauptform, verschobener Kreis) . . . . .
13.2.4 Gleichung eines Kreises in Polarkoordinaten . . . . . . . . . . . . . . . . .
13.2.5 Parameterdarstellung eines Kreises . . . . . . . . . . . . . . . . . . . . . . . . .
115
115
115
116
116
116
116
Inhaltsverzeichnis
13.3
13.4
13.5
Ellipse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.3.1 Geometrische Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.3.2 Mittelpunktsgleichung einer Ellipse (Ursprungsgleichung) . . . . . .
13.3.3 Ellipse in allgemeiner Lage (Hauptform, verschobene Ellipse) . . .
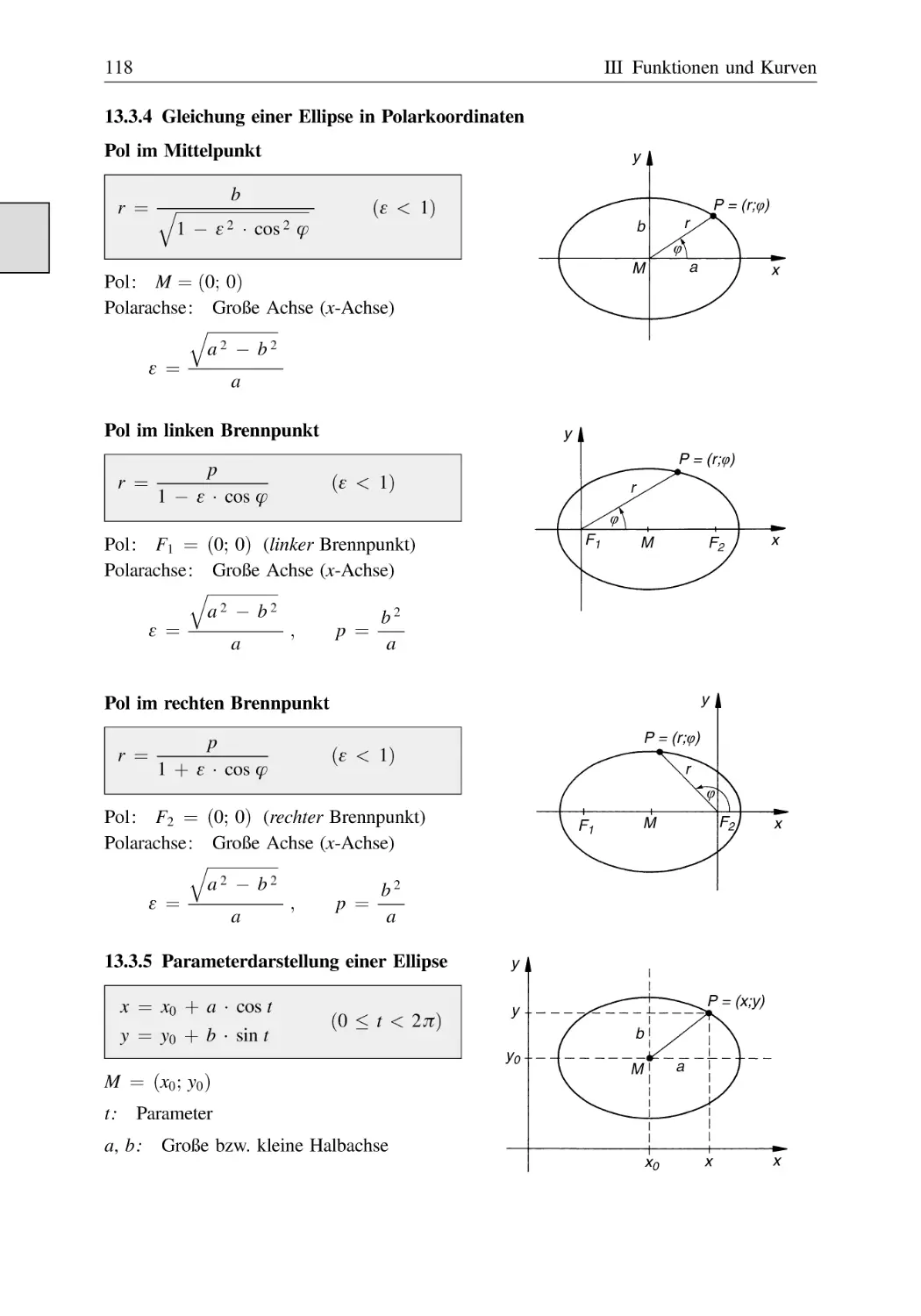
13.3.4 Gleichung einer Ellipse in Polarkoordinaten . . . . . . . . . . . . . . . . . .
13.3.5 Parameterdarstellung einer Ellipse . . . . . . . . . . . . . . . . . . . . . . . . . .
Hyperbel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.4.1 Geometrische Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.4.2 Mittelpunktsgleichung einer Hyperbel (Ursprungsgleichung) . . . . .
13.4.3 Hyperbel in allgemeiner Lage (Hauptform, verschobene Hyperbel)
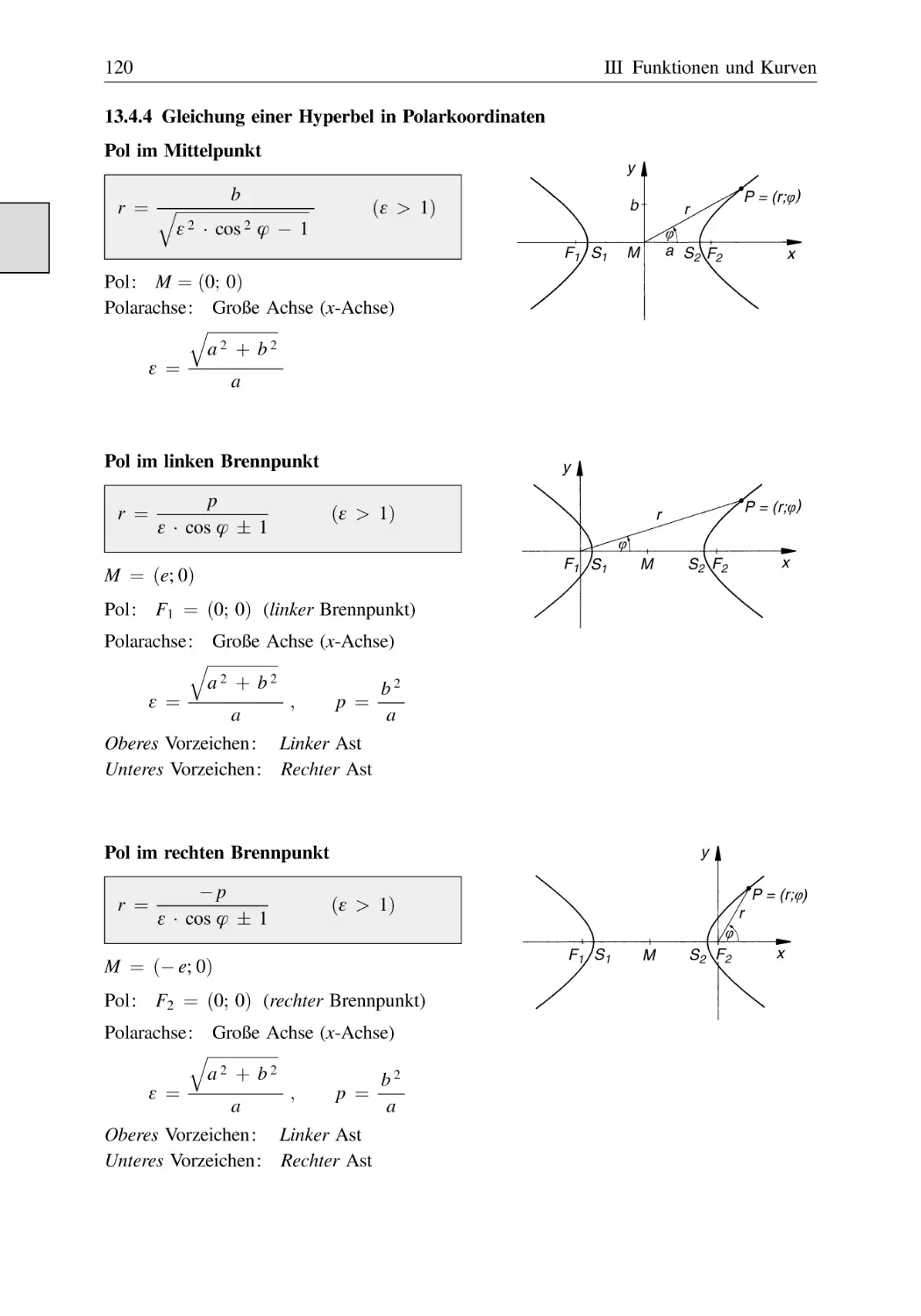
13.4.4 Gleichung einer Hyperbel in Polarkoordinaten . . . . . . . . . . . . . . . .
13.4.5 Parameterdarstellung einer Hyperbel . . . . . . . . . . . . . . . . . . . . . . . .
13.4.6 Gleichung einer um 90" gedrehten Hyperbel . . . . . . . . . . . . . . . . .
13.4.7 Gleichung einer gleichseitigen oder rechtwinkligen Hyperbel
ða ¼ bÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Parabel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.5.1 Geometrische Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.5.2 Scheitelgleichung einer Parabel . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13.5.3 Parabel in allgemeiner Lage (Hauptform, verschobene Parabel) . . .
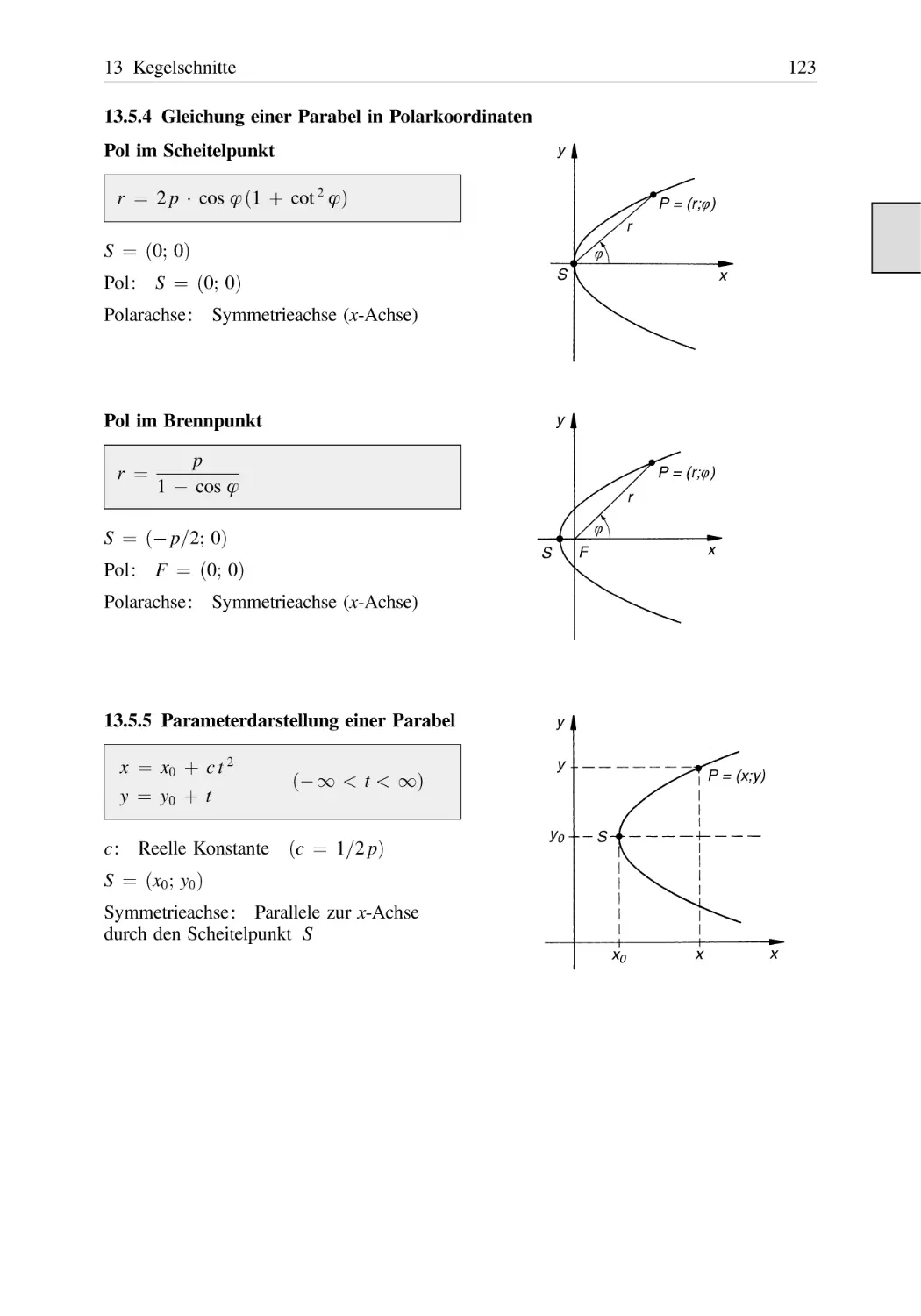
13.5.4 Gleichung einer Parabel in Polarkoordinaten . . . . . . . . . . . . . . . . .
13.5.5 Parameterdarstellung einer Parabel . . . . . . . . . . . . . . . . . . . . . . . . .
XV
117
117
117
117
118
118
119
119
119
119
120
121
121
121
122
122
122
122
123
123
14 Spezielle Kurven . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
14.1
14.2
14.3
14.4
14.5
14.6
14.7
14.8
14.9
14.10
Gewöhnliche Zykloide (Rollkurve) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Epizykloide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Hypozykloide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
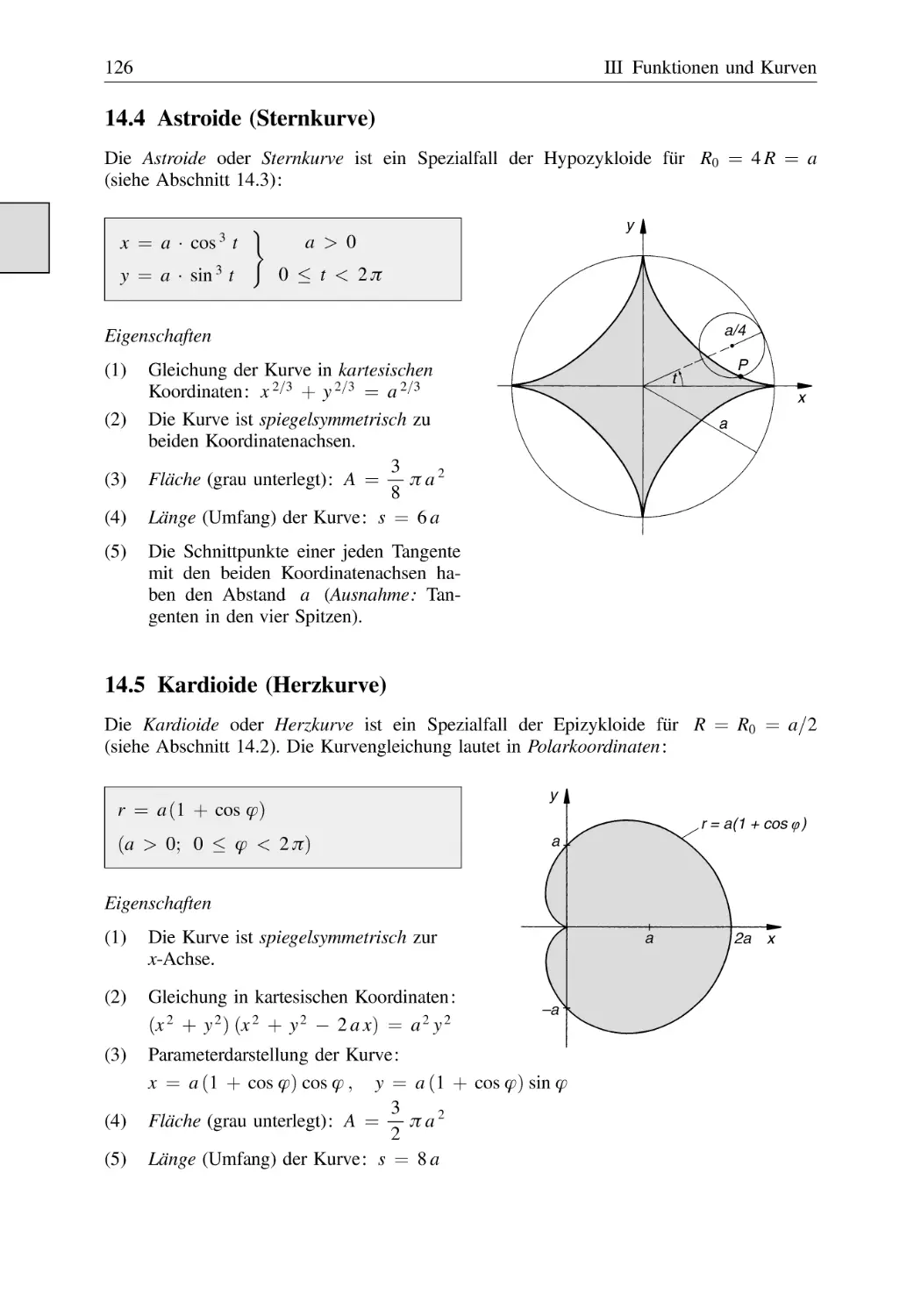
Astroide (Sternkurve) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kardioide (Herzkurve) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
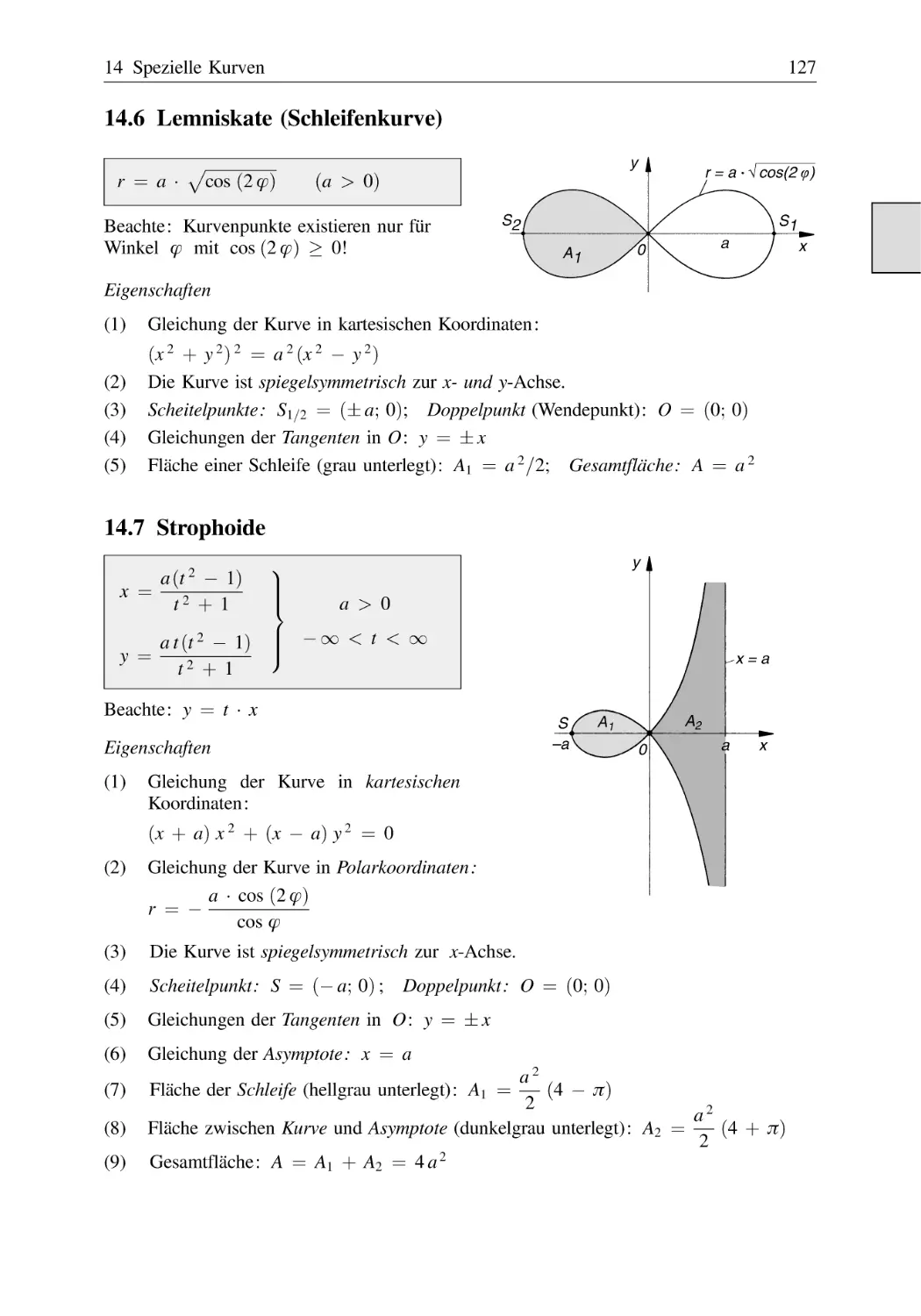
Lemniskate (Schleifenkurve) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
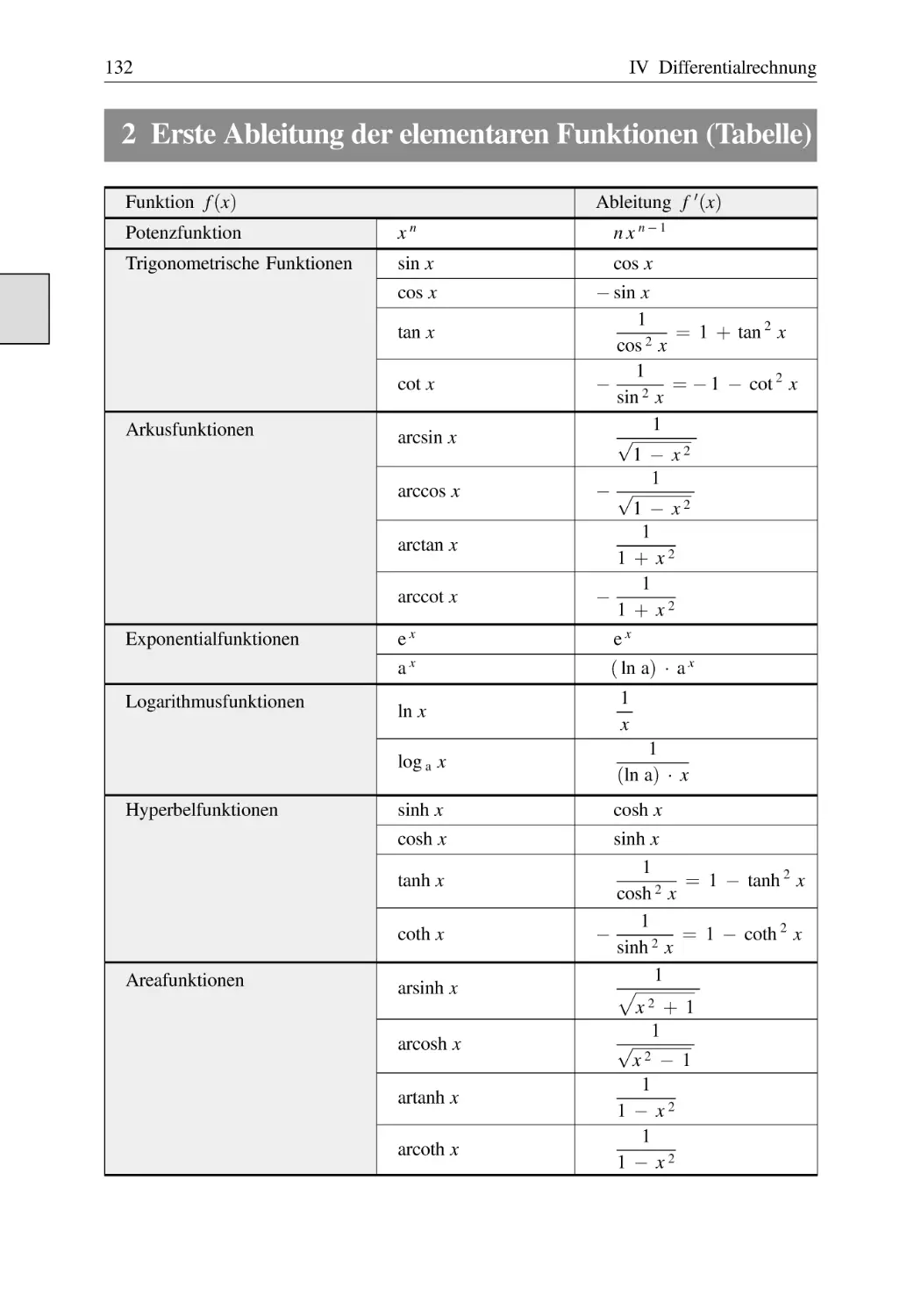
Strophoide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Cartesisches Blatt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
„Kleeblatt‘‘ mit n bzw. 2n Blättern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spiralen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14.10.1 Archimedische Spirale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14.10.2 Logarithmische Spirale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
124
124
125
126
126
127
127
128
128
129
129
129
IV Differentialrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
1 Differenzierbarkeit einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
1.1
1.2
1.3
1.4
1.5
Differenzenquotient . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Differentialquotient oder 1. Ableitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ableitungsfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Höhere Ableitungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Differential einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
130
130
130
131
131
2 Erste Ableitung der elementaren Funktionen (Tabelle) . . . . . . . . . . . . . . . . . . . . . 132
XVI
Inhaltsverzeichnis
3 Ableitungsregeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
Faktorregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Summenregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Produktregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Quotientenregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kettenregel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Logarithmische Differentiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ableitung der Umkehrfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Implizite Differentiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ableitungen einer in der Parameterform dargestellten Funktion (Kurve) . . .
Ableitungen einer in Polarkoordination dargestellten Kurve . . . . . . . . . . . . .
133
133
133
134
134
136
136
137
137
138
4 Anwendungen der Differentialrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
4.1
4.2
4.3
4.4
4.5
4.6
4.7
Geschwindigkeit und Beschleunigung einer geradlinigen Bewegung . . . . . .
Tangente und Normale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Linearisierung einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
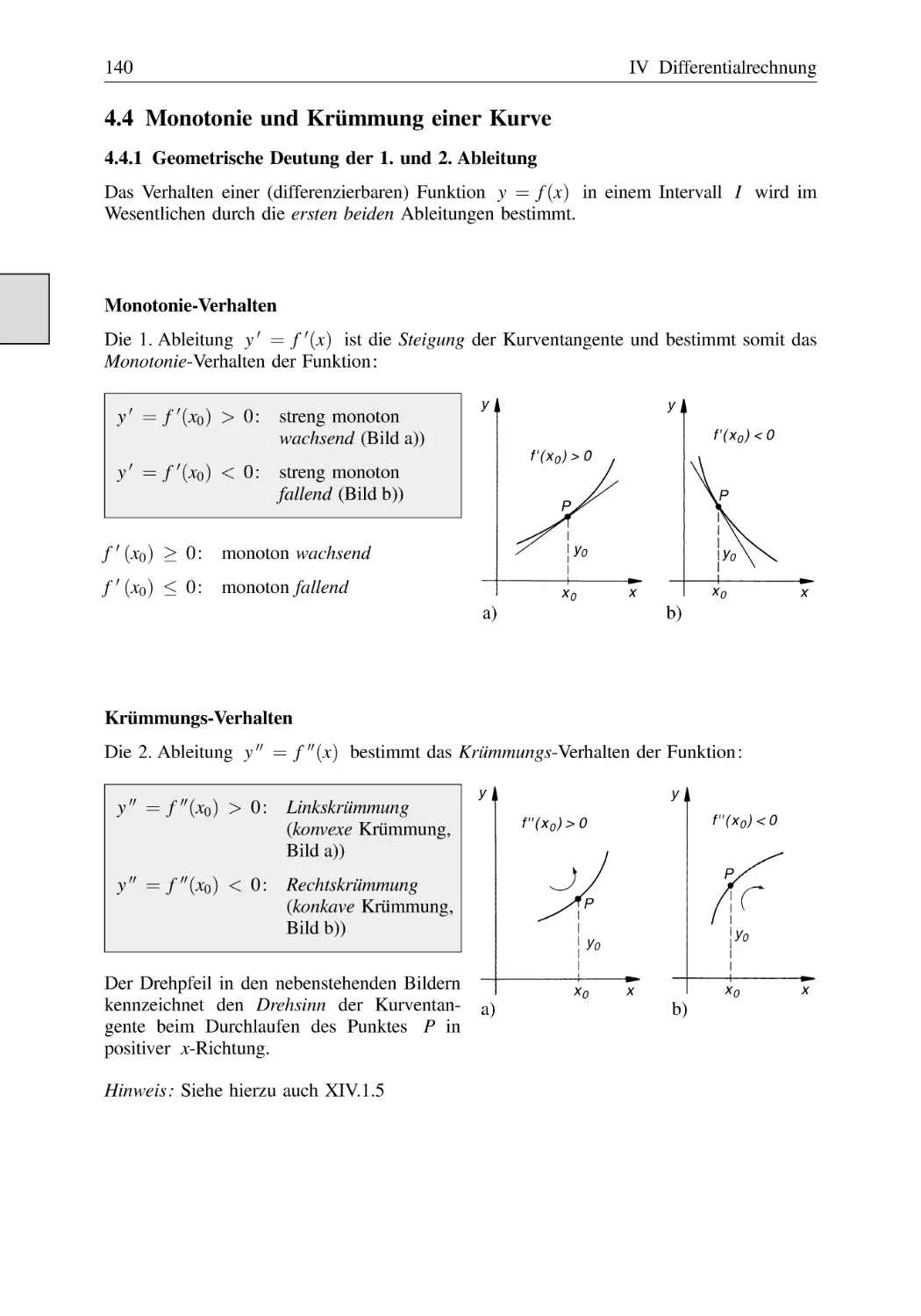
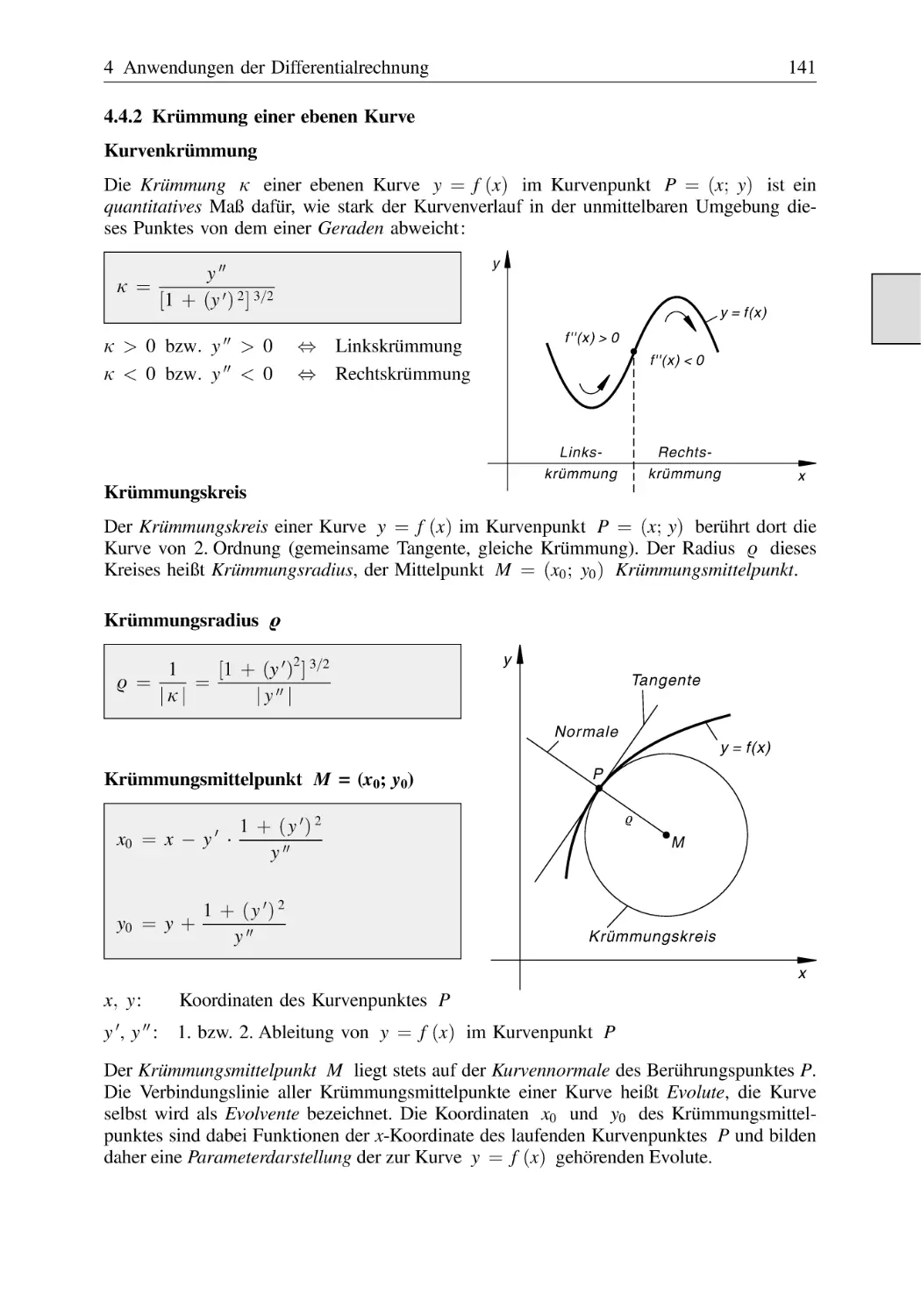
Monotonie und Krümmung einer Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.1
Geometrische Deutung der 1. und 2. Ableitung . . . . . . . . . . . . . . .
4.4.2
Krümmung einer ebenen Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . .
Relative Extremwerte (relative Maxima, relative Minima) . . . . . . . . . . . . . . .
Wendepunkte, Sattelpunkte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Kurvendiskussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
138
139
139
140
140
141
142
144
145
V Integralrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
1 Bestimmtes Integral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
1.1
1.2
1.3
Definition eines bestimmten Integrals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
Berechnung eines bestimmten Integrals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
Elementare Integrationsregeln für bestimmte Integrale . . . . . . . . . . . . . . . . . 149
2 Unbestimmtes Integral . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150
2.1
2.2
2.3
Definition eines unbestimmten Integrals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150
Allgemeine Eigenschaften der unbestimmten Integrale . . . . . . . . . . . . . . . . . 150
Tabelle der Grund- oder Stammintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152
3 Integrationsmethoden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
3.1
3.2
3.3
3.4
3.5
Integration durch Substitution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1.
Allgemeines Verfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2
Spezielle Integralsubstitutionen (Tabelle) . . . . . . . . . . . . . . . . . . . .
Partielle Integration (Produktintegration) . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Integration einer gebrochenrationalen Funktion durch Partialbruchzerlegung
des Integranden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.1
Partialbruchzerlegung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.2
Integration der Partialbrüche . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Integration durch Potenzreihenentwicklung des Integranden . . . . . . . . . . . . .
Numerische Integration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.1
Trapezformel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.2
Simpsonsche Formel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.3
Romberg-Verfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
153
153
154
156
157
157
160
161
161
161
162
164
Inhaltsverzeichnis
XVII
4 Uneigentliche Integrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
4.1
4.2
Unendliches Integrationsintervall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167
Integrand mit einer Unendlichkeitsstelle (Pol). . . . . . . . . . . . . . . . . . . . . . . . . 167
5 Anwendungen der Integralrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
Integration der Bewegungsgleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Arbeit einer ortsabhängigen Kraft (Arbeitsintegral) . . . . . . . . . . . . . . . . . . . .
Lineare und quadratische Mittelwerte einer Funktion . . . . . . . . . . . . . . . . . .
5.3.1
Linearer Mittelwert . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3.2
Quadratischer Mittelwert . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3.3
Zeitliche Mittelwerte einer periodischen Funktion . . . . . . . . . . . . .
Flächeninhalt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Schwerpunkt einer homogenen ebenen Fläche . . . . . . . . . . . . . . . . . . . . . . . .
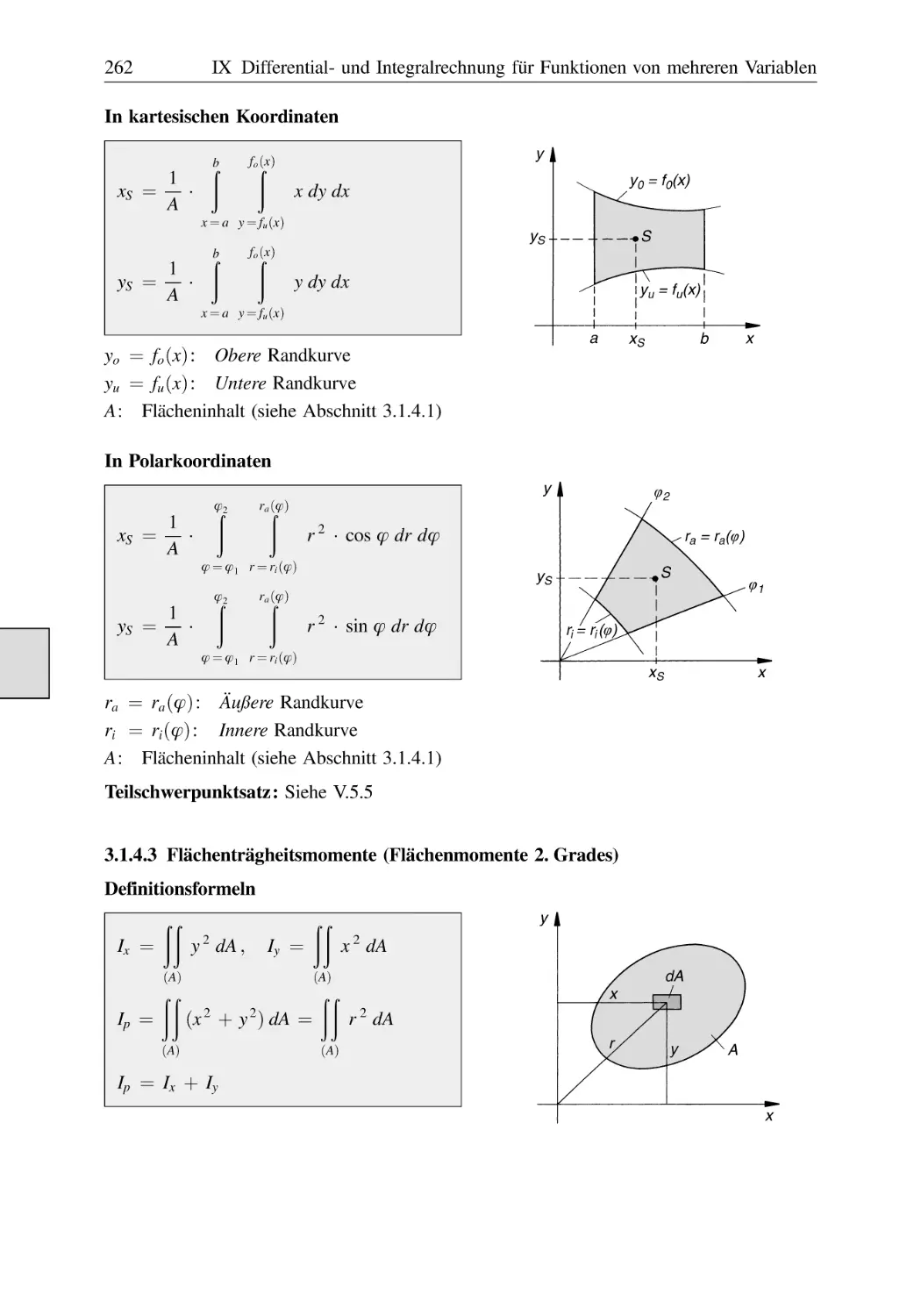
Flächenträgheitsmomente (Flächenmomente 2. Grades) . . . . . . . . . . . . . . . .
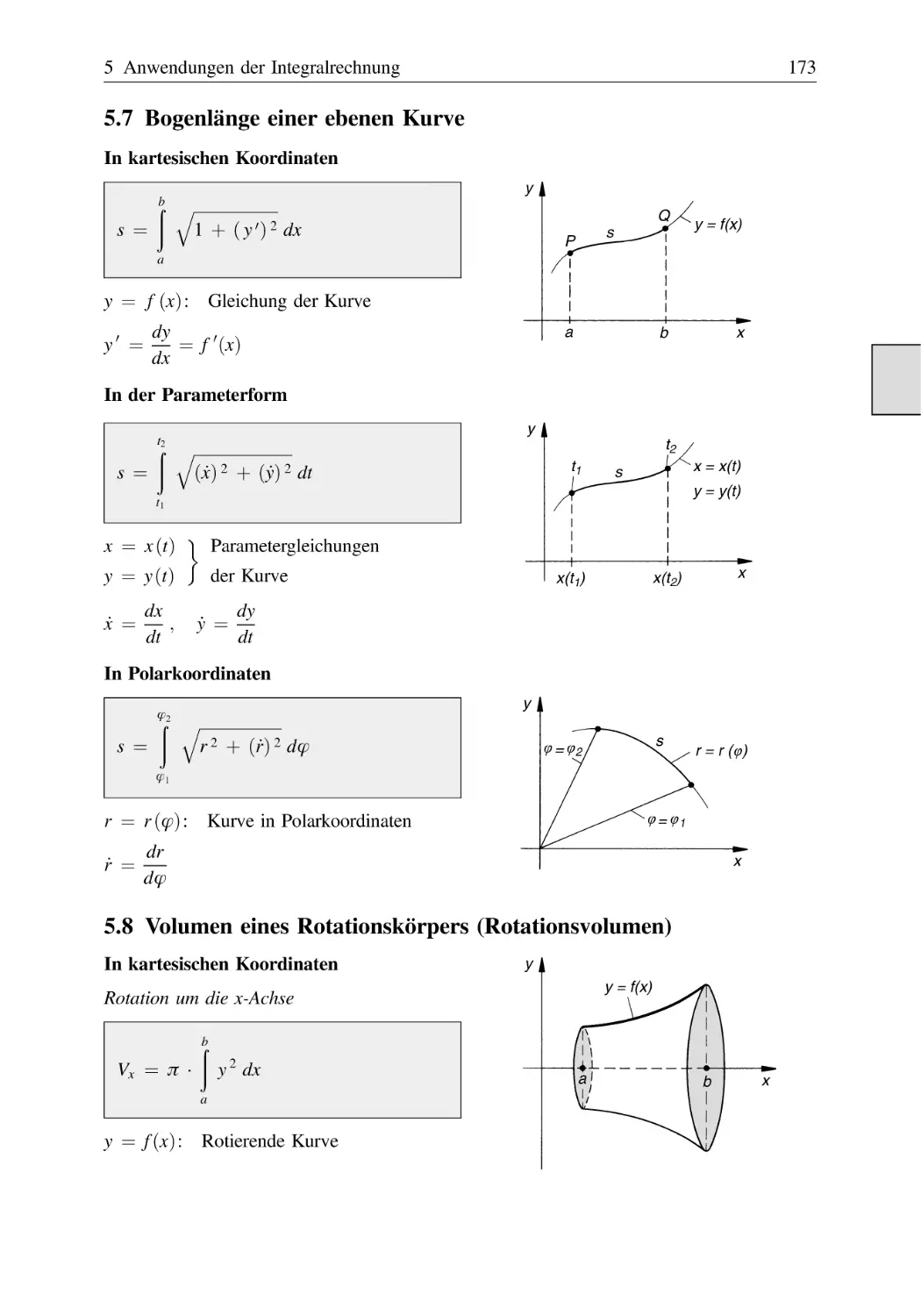
Bogenlänge einer ebenen Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Volumen eines Rotationskörpers (Rotationsvolumen) . . . . . . . . . . . . . . . . . . .
Mantelfläche eines Rotationskörpers (Rotationsfläche) . . . . . . . . . . . . . . . . .
Schwerpunkt eines homogenen Rotationskörpers . . . . . . . . . . . . . . . . . . . . . .
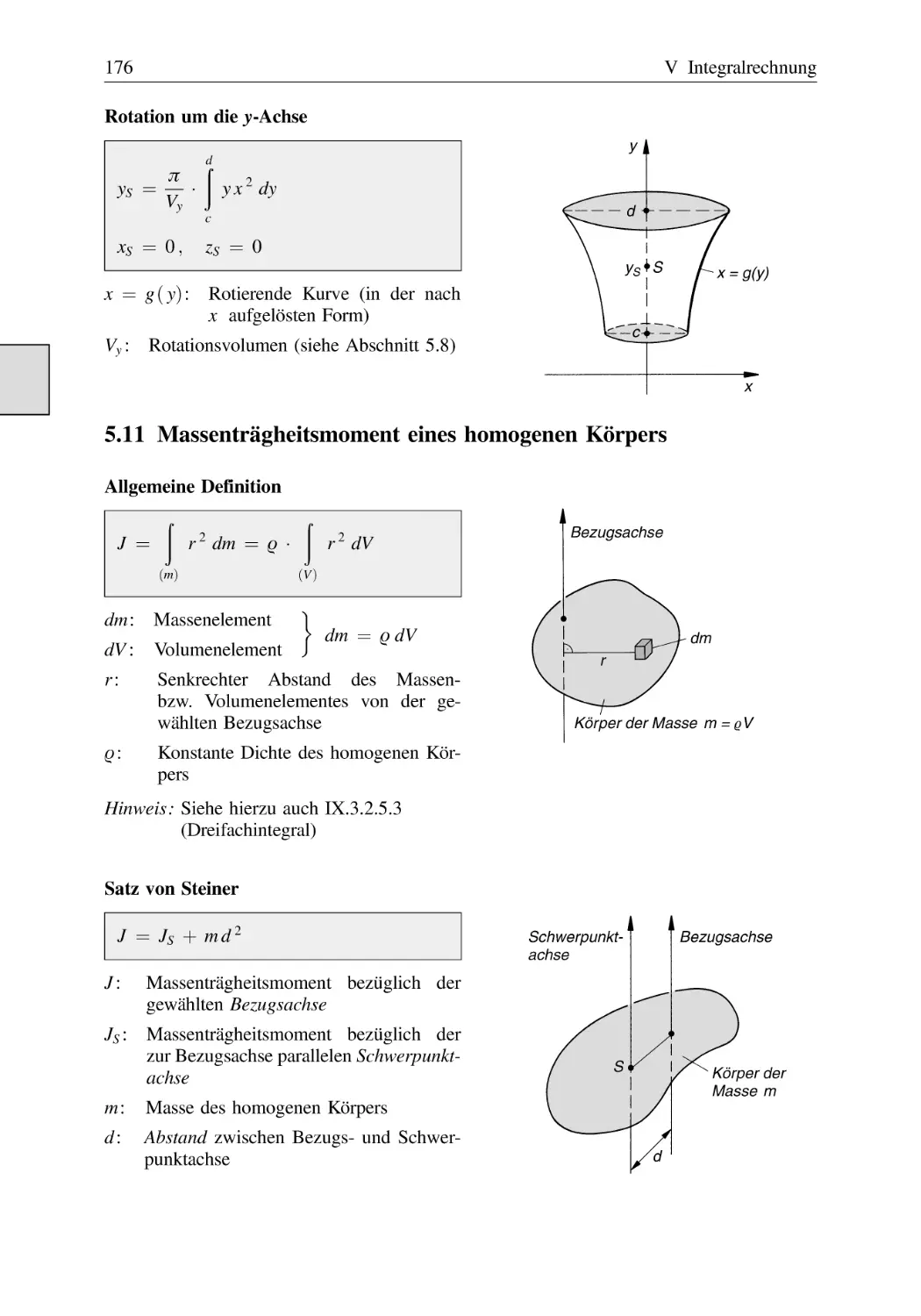
Massenträgheitsmoment eines homogenen Körpers . . . . . . . . . . . . . . . . . . . .
168
169
169
169
169
169
170
171
172
173
173
175
175
176
VI Unendliche Reihen, Taylor- und Fourier-Reihen . . . . . . . . . . . . . . . . . . . . . 178
1 Unendliche Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
1.1
1.2
1.3
Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.1
Definition einer unendlichen Reihe . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.2
Konvergenz und Divergenz einer unendlichen Reihe . . . . . . . . . . .
Konvergenzkriterien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1
Quotientenkriterium . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2
Wurzelkriterium . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.3
Vergleichskriterien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.4
Leibnizsches Konvergenzkriterium für alternierende Reihen . . . . .
1.2.5
Eigenschaften konvergenter bzw. absolut konvergenter Reihen . . .
Spezielle konvergente Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
178
178
178
179
179
180
180
181
181
181
2 Potenzreihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182
2.1
2.2
2.3
Definition einer Potenzreihe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182
Konvergenzradius und Konvergenzbereich einer Potenzreihe . . . . . . . . . . . . 183
Wichtige Eigenschaften der Potenzreihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183
3 Taylor-Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
3.1
3.2
3.3
3.4
3.5
Taylorsche und Mac Laurinsche Formel . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1
Taylorsche Formel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2
Mac Laurinsche Formel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Taylorsche Reihe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Mac Laurinsche Reihe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
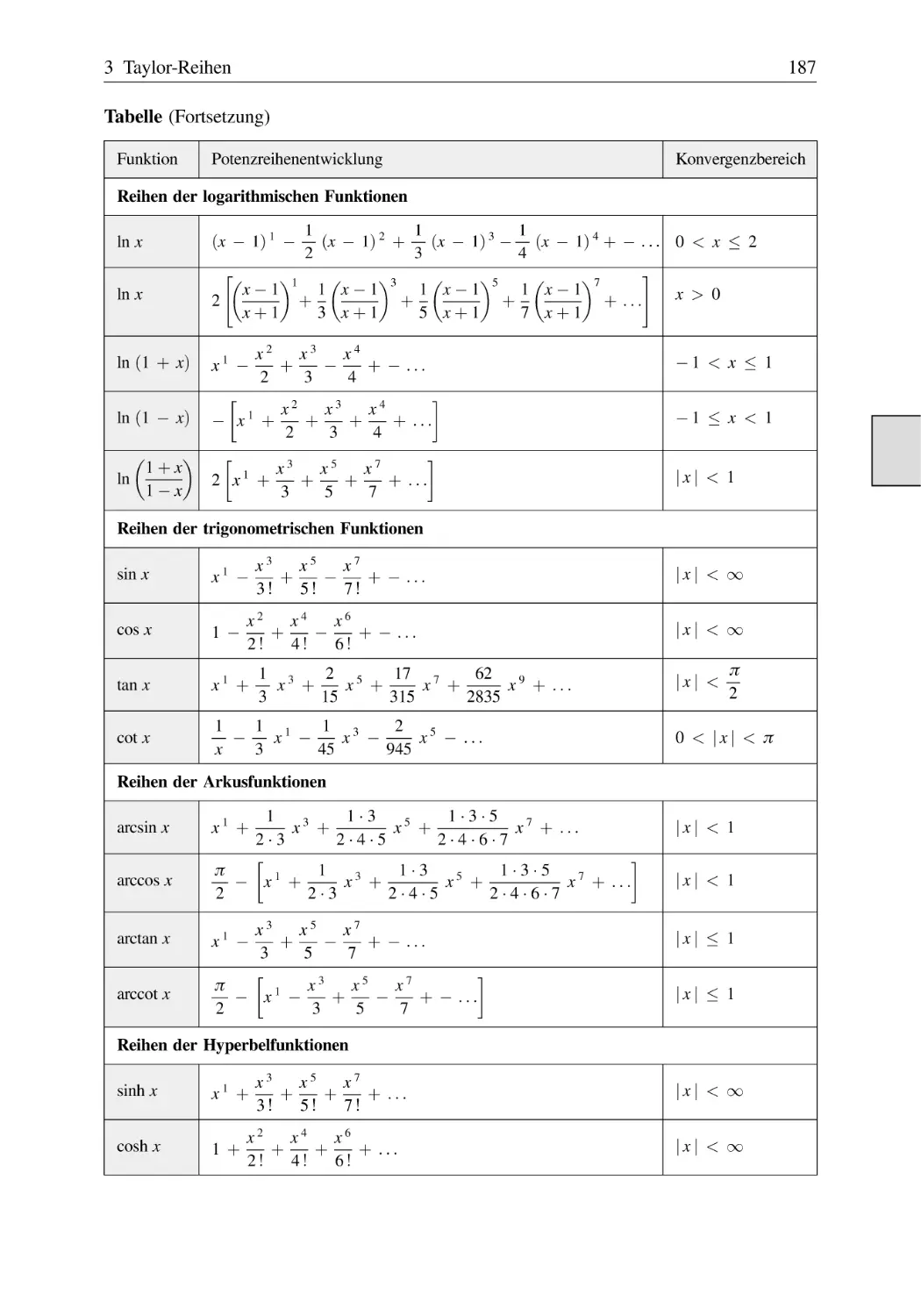
Spezielle Potenzreihenentwicklungen (Tabelle) . . . . . . . . . . . . . . . . . . . . . . .
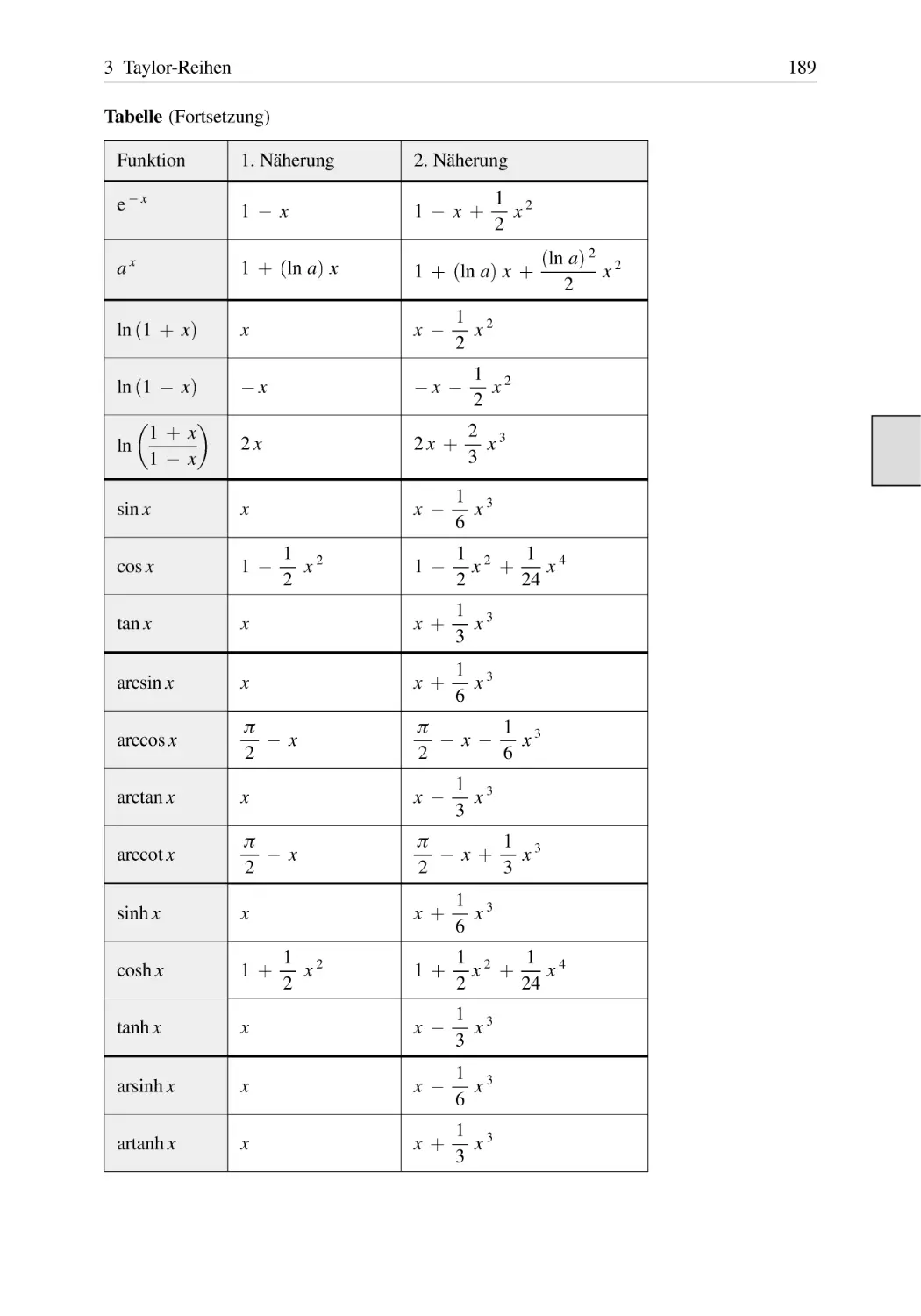
Näherungspolynome einer Funktion (mit Tabelle) . . . . . . . . . . . . . . . . . . . . .
184
184
184
185
185
186
188
XVIII
Inhaltsverzeichnis
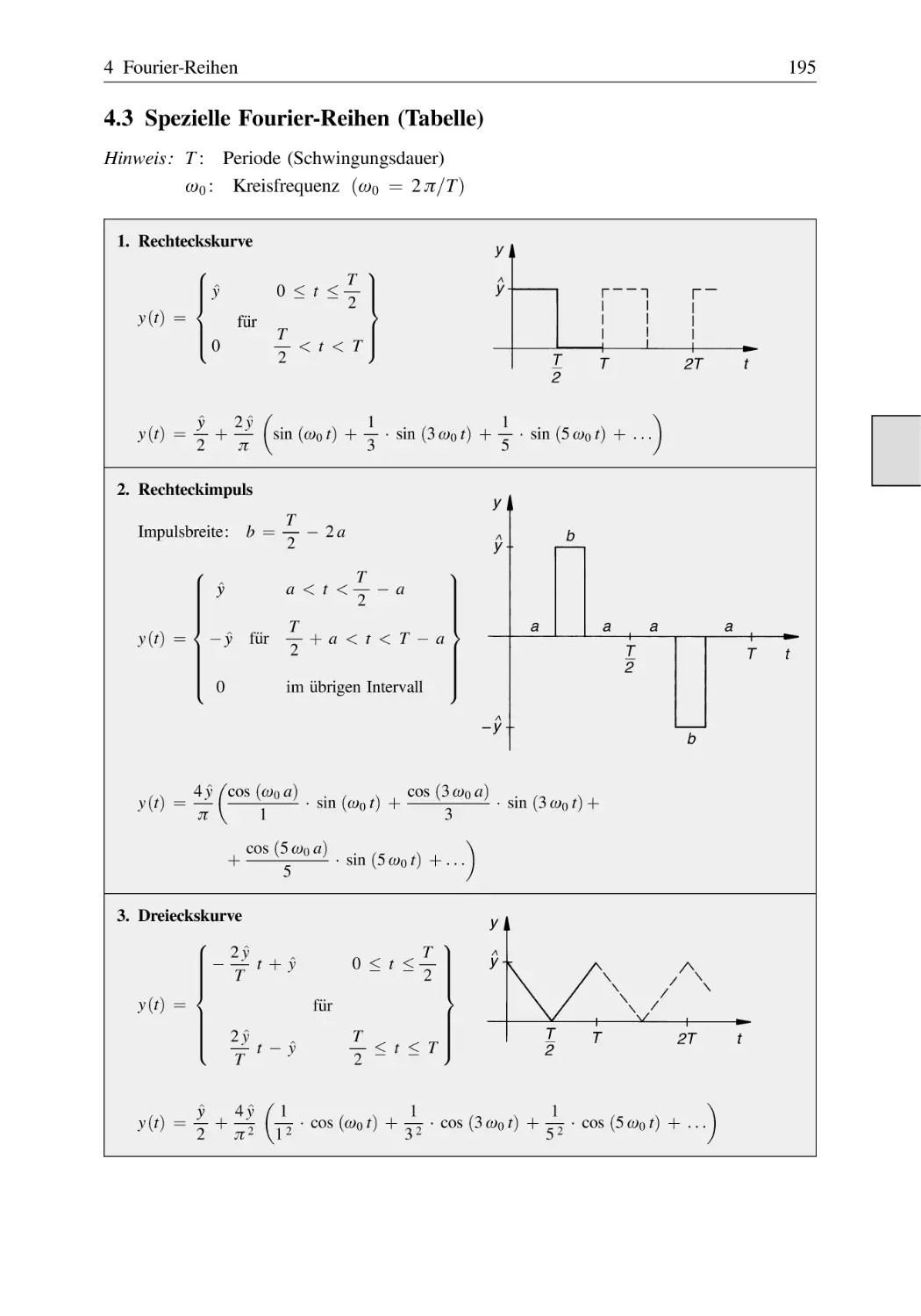
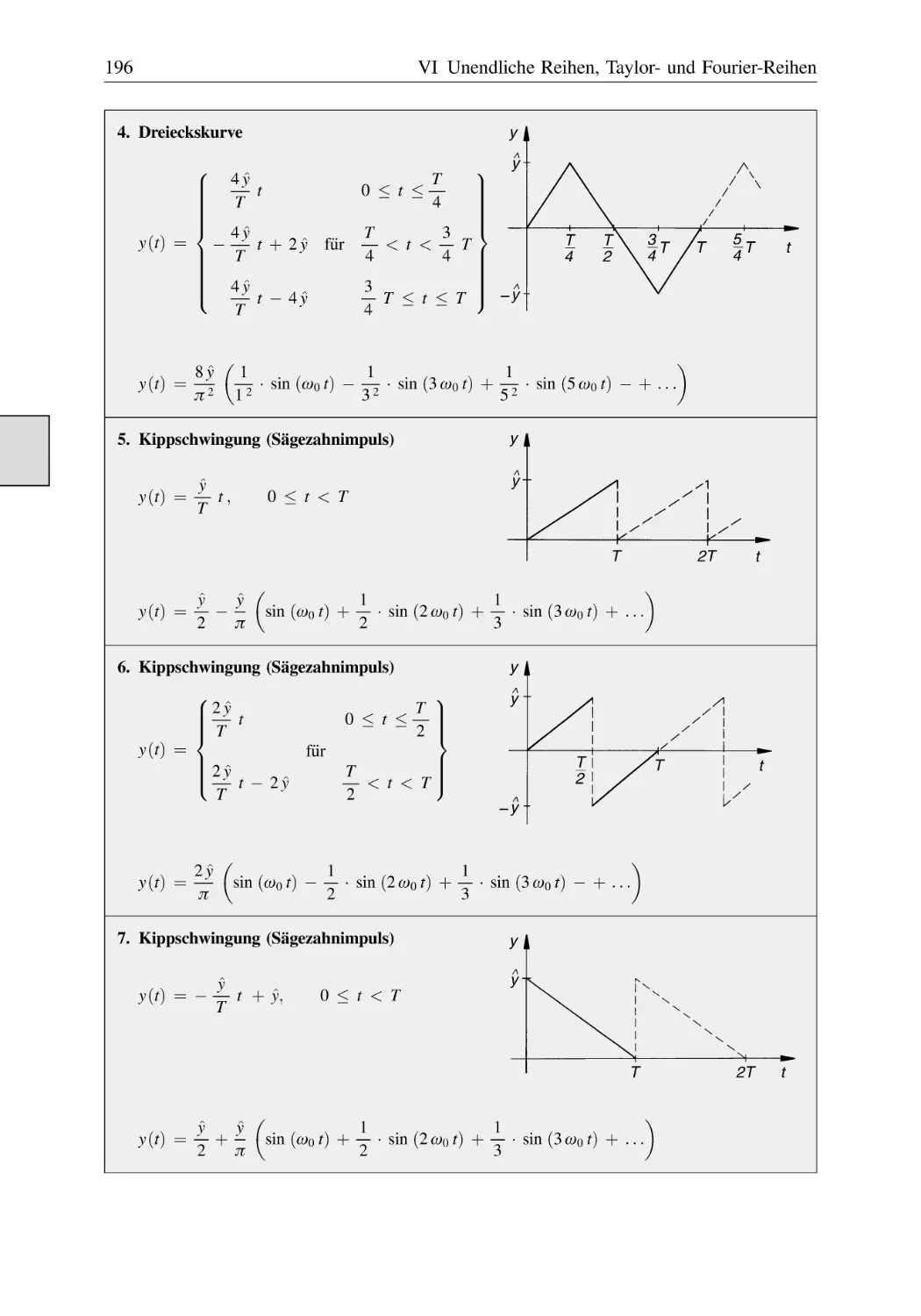
4 Fourier-Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1
Fourier-Reihe einer periodischen Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2
Fourier-Zerlegung einer nichtsinusförmigen Schwingung . . . . . . . . . . . . . . .
4.3
Spezielle Fourier-Reihen (Tabelle) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
190
190
193
195
VII Lineare Algebra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 198
1 Reelle Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1
Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.1
n-dimensionale Vektoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.2
Definition einer reellen Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.3
Spezielle Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.1.4
Gleichheit von Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2
Spezielle quadratische Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1
Diagonalmatrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2
Einheitsmatrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.3
Dreiecksmatrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.4
Symmetrische Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.5
Schiefsymmetrische Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.6
Orthogonale Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3
Rechenoperationen für Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.1
Addition und Subtraktion von Matrizen . . . . . . . . . . . . . . . . . . . . .
1.3.2
Multiplikation einer Matrix mit einem Skalar . . . . . . . . . . . . . . . . .
1.3.3
Multiplikation von Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.4
Reguläre Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5
Inverse Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5.1
Definition einer inversen Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5.2
Berechnung einer inversen Matrix . . . . . . . . . . . . . . . . . . . . . . . . . .
1.5.2.1 Berechnung der inversen Matrix A/1
unter Verwendung von Unterdeterminanten . . . . . . . . . . .
1.5.2.2 Berechnung der inversen Matrix A/1 nach dem
Gaußschen Algorithmus (Gauß-Jordan-Verfahren) . . . . .
1.6
Rang einer Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.6.1
Definitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.6.1.1 Unterdeterminanten einer Matrix . . . . . . . . . . . . . . . . . . .
1.6.1.2 Rang einer Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.6.1.3 Elementare Umformungen einer Matrix . . . . . . . . . . . . . .
1.6.2
Rangbestimmung einer Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.6.2.1 Rangbestimmung einer (m; n)-Matrix A
unter Verwendung von Unterdeterminanten . . . . . . . . . . .
1.6.2.2 Rangbestimmung einer (m; n)-Matrix A
mit Hilfe elementarer Umformungen . . . . . . . . . . . . . . . .
2 Determinanten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1
Zweireihige Determinanten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2
Dreireihige Determinanten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3
Determinanten höherer Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.1
Unterdeterminate Dik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.2
Algebraisches Komplement (Adjunkte) Aik . . . . . . . . . . . . . . . . . .
2.3.3
Definition einer n-reihigen Determinante . . . . . . . . . . . . . . . . . . . .
198
198
198
200
201
201
201
202
202
202
202
202
203
203
203
203
204
205
205
205
206
206
206
207
207
207
207
207
208
208
208
209
209
210
211
211
211
211
Inhaltsverzeichnis
2.4
2.5
2.6
Laplacescher Entwicklungssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rechenregeln für n-reihige Determinanten . . . . . . . . . . . . . . . . . . . . . . . . . . .
Regeln zur praktischen Berechnung einer n-reihigen Determinante . . . . . . .
2.6.1
Elementare Umformungen einer n-reihigen Determinante . . . . . . .
2.6.2
Reduzierung und Berechnung einer n-reihigen Determinante . . . .
XIX
212
212
214
214
214
3 Lineare Gleichungssysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215
3.1
3.2
3.3
3.4
3.5
3.6
Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1
Definition eines linearen Gleichungssystems . . . . . . . . . . . . . . . . .
3.1.2
Spezielle lineare Gleichungssysteme . . . . . . . . . . . . . . . . . . . . . . . .
Lösungsverhalten eines linearen (m; n)-Gleichungssystems . . . . . . . . . . . . . .
3.2.1
Kriterium für die Lösbarkeit eines linearen (m; n)-Systems
Ax ¼ c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2
Lösungsmenge eines linearen (m; n)-Systems Ax ¼ c . . . . . . . . .
Lösungsverhalten eines quadratischen linearen Gleichungssystems . . . . . . .
Lösungsverfahren für ein lineares Gleichungssystem nach Gauß
(Gaußscher Algorithmus) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.1
#quivalente Umformungen eines linearen (m; n)-Systems . . . . . . .
3.4.2
Gaußscher Algorithmus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Cramersche Regel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lineare Unabhängigkeit von Vektoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
215
215
215
216
216
216
217
218
218
218
221
221
4 Komplexe Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 222
4.1
4.2
4.3
4.4
4.5
Definition einer komplexen Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rechenoperationen und Rechenregeln für komplexe Matrizen . . . . . . . . . . .
Konjugiert komplexe Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Konjugiert transponierte Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Spezielle komplexe Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.1
Hermitesche Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.2
Schiefthermitesche Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.3
Unitäre Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
222
223
223
224
224
224
224
225
5 Eigenwertprobleme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225
5.1
5.2
Eigenwerte und Eigenvektoren einer quadratischen Matrix . . . . . . . . . . . . . . 225
Eigenwerte und Eigenvektoren spezieller n-reihiger Matrizen . . . . . . . . . . . . 227
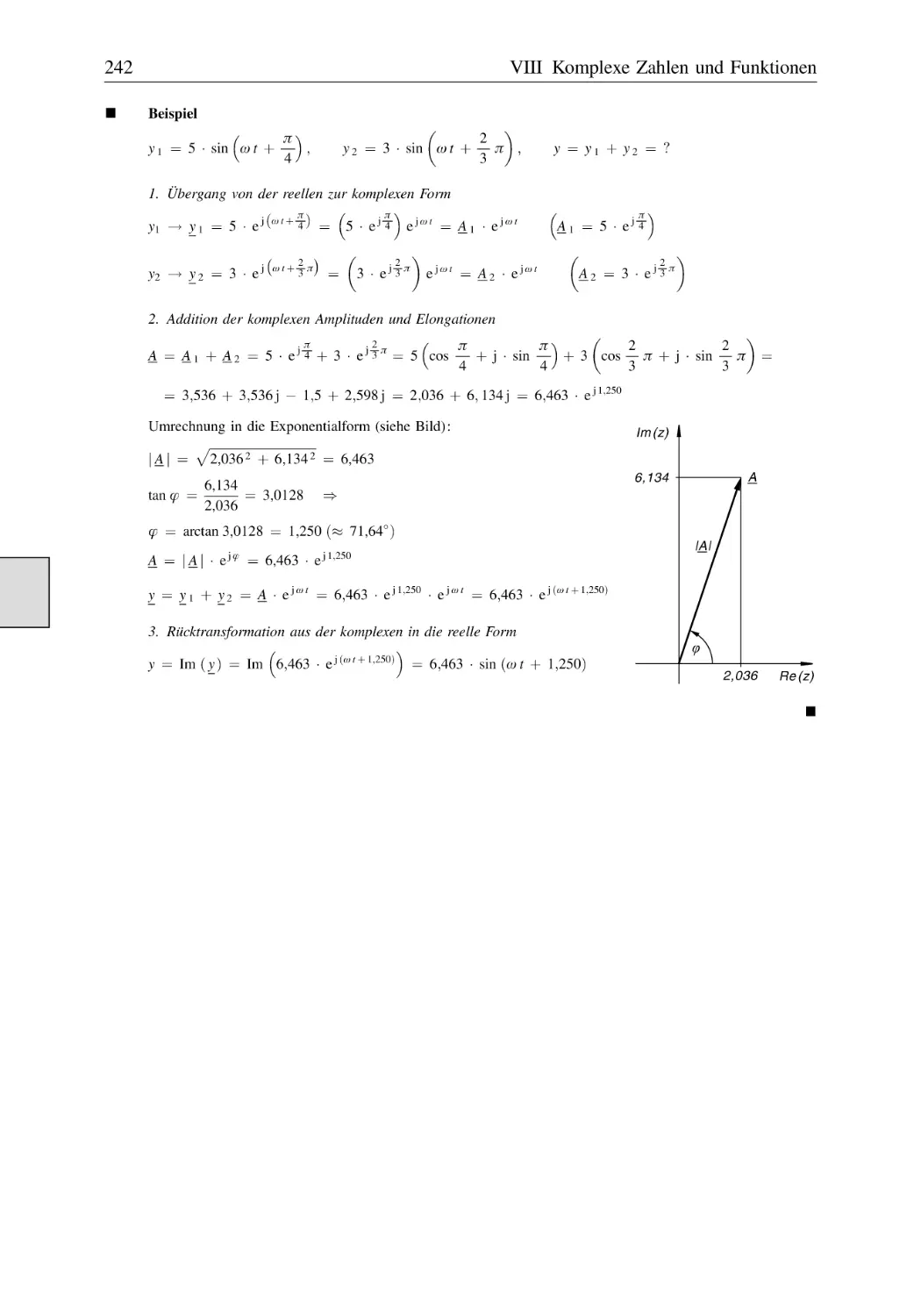
VIII Komplexe Zahlen und Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228
1 Darstellungsformen einer komplexen Zahl . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228
1.1
1.2
1.3
Algebraische oder kartesische Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Polarformen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.1
Trigonometrische Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2
Exponentialform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Umrechnungen zwischen den Darstellungsformen . . . . . . . . . . . . . . . . . . . . .
1.3.1
Polarform ! Kartesische Form . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.2
Kartesische Form ! Polarform . . . . . . . . . . . . . . . . . . . . . . . . . . .
228
229
229
229
230
230
230
XX
Inhaltsverzeichnis
2 Grundrechenarten für komplexe Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
2.1
2.2
2.3
Addition und Subtraktion komplexer Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . 231
Multiplikation komplexer Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
Division komplexer Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232
3 Potenzieren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233
4 Radizieren (Wurzelziehen) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 234
5 Natürlicher Logarithmus einer komplexen Zahl . . . . . . . . . . . . . . . . . . . . . . . . . . 235
6 Ortskurven . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 236
6.1
6.2
6.3
Komplexwertige Funktion einer reellen Variablen . . . . . . . . . . . . . . . . . . . . . 236
Ortskurve einer parameterabhängigen komplexen Zahl . . . . . . . . . . . . . . . . . 236
Inversion einer Ortskurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 237
7 Komplexe Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 238
7.1
7.2
7.3
Definition einer komplexen Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Definitionsgleichungen einiger elementarer Funktionen . . . . . . . . . . . . . . . . .
7.2.1
Trigonometrische Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2.2
Hyperbelfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2.3
Exponentialfunktion (e-Funktion) . . . . . . . . . . . . . . . . . . . . . . . . . .
Wichtige Beziehungen und Formeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.1
Eulersche Formeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.2
Zusammenhang zwischen den trigonometrischen Funktionen
und der komplexen e-Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.3
Trigonometrische und Hyperbelfunktionen mit imaginärem
Argument . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.4
Additionstheoreme der trigonometrischen und Hyperbelfunktionen
für komplexes Argument . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.3.5
Arkus- und Areafunktionen mit imaginärem Argument . . . . . . . . .
238
238
238
238
239
239
239
239
239
239
240
8 Anwendungen in der Schwingungslehre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 240
8.1
8.2
Darstellung einer harmonischen Schwingung durch einen rotierenden
komplexen Zeiger . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 240
Ungestörte !berlagerung gleichfrequenter harmonischer Schwingungen
(„Superpositionsprinzip‘‘) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 241
IX Differential- und Integralrechnung für Funktionen
von mehreren Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243
1 Funktionen von mehreren Variablen und ihre Darstellung . . . . . . . . . . . . . . . . . . 243
1.1
1.2
Definition einer Funktion von mehreren Variablen . . . . . . . . . . . . . . . . . . . . .
Darstellungsformen einer Funktion von zwei Variablen . . . . . . . . . . . . . . . . .
1.2.1
Analytische Darstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2
Graphische Darstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2.1 Darstellung einer Funktion als Fläche im Raum . . . . . . .
1.2.2.2 Schnittkurvendiagramme . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2.3 Höhenliniendiagramm . . . . . . . . . . . . . . . . . . . . . . . . . . . .
243
243
243
244
244
244
244
Inhaltsverzeichnis
1.3
Spezielle Flächen (Funktionen) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.1
Ebenen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.2
Rotationsflächen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.2.1 Gleichung einer Rotationsfläche . . . . . . . . . . . . . . . . . . .
1.3.2.2 Spezielle Rotationsflächen . . . . . . . . . . . . . . . . . . . . . . . .
XXI
245
245
245
245
246
2 Partielle Differentiation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247
2.1
2.2
2.3
2.4
2.5
Partielle Ableitungen 1. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.1
Partielle Ableitungen 1. Ordnung von z ¼ f ðx; yÞ . . . . . . . . . . . .
2.1.2
Partielle Ableitungen 1. Ordnung von y ¼ f ðx1 ; x2 ; . . . ; xn Þ . . . .
Partielle Ableitungen höherer Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Verallgemeinerte Kettenregel (Differentiation nach einem Parameter) . . . . . .
Totales oder vollständiges Differential einer Funktion . . . . . . . . . . . . . . . . . .
Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.1
Linearisierung einer Funktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.2
Relative Extremwerte (relative Maxima, relative Minima) . . . . . . .
2.5.3
Extremwertaufgaben mit Nebenbedingungen
(Lagrangesches Multiplikatorverfahren) . . . . . . . . . . . . . . . . . . . . . .
247
247
248
249
250
251
253
253
254
255
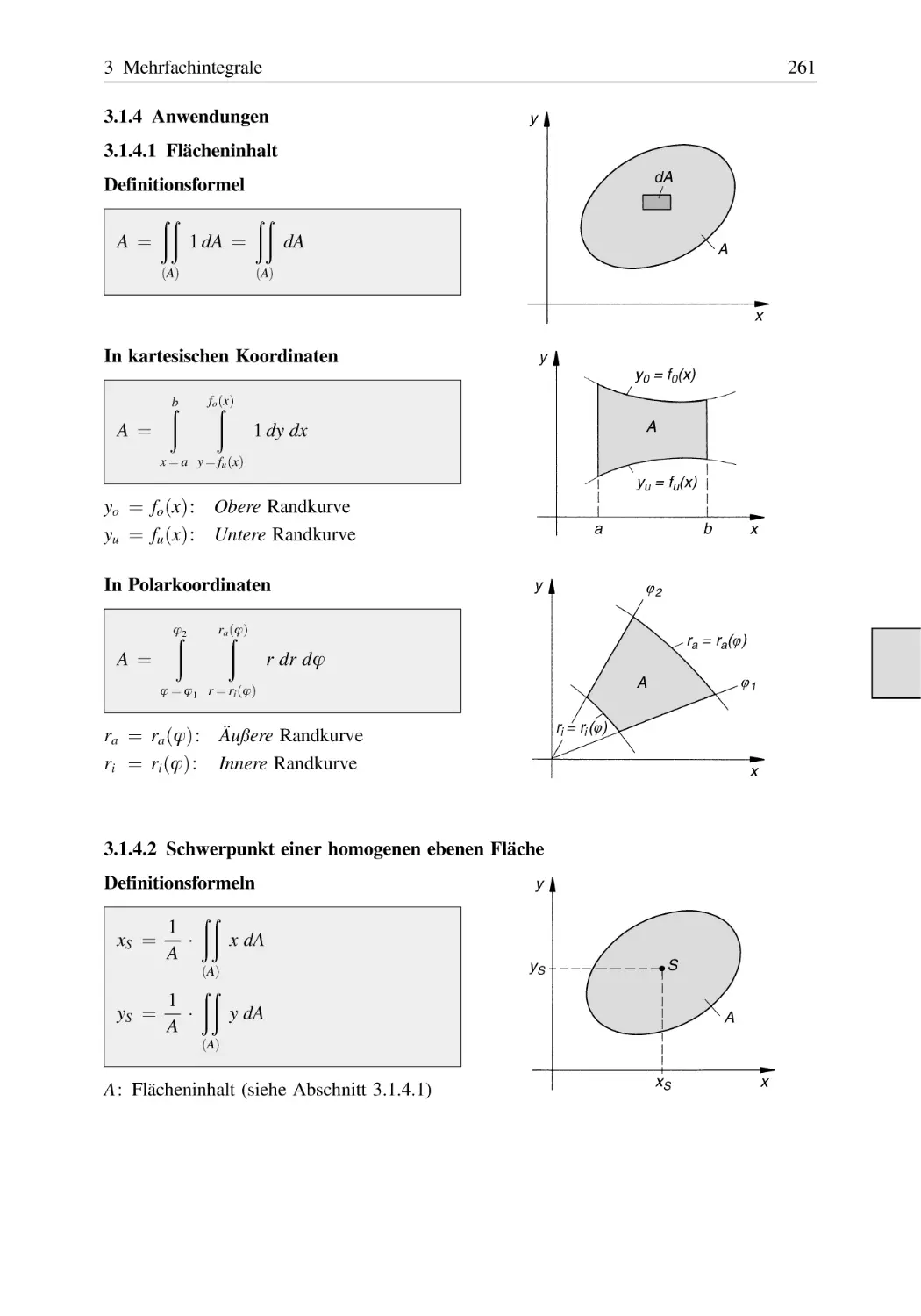
3 Mehrfachintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257
3.1
3.2
Doppelintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1
Definition eines Doppelintegrals . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2
Berechnung eines Doppelintegrals in kartesischen Koordinaten . .
3.1.3
Berechnung eines Doppelintegrals in Polarkoordinaten . . . . . . . . .
3.1.4
Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.4.1 Flächeninhalt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.4.2 Schwerpunkt einer homogenen ebenen Fläche . . . . . . . .
3.1.4.3 Flächenträgheitsmomente (Flächenmomente 2. Grades)
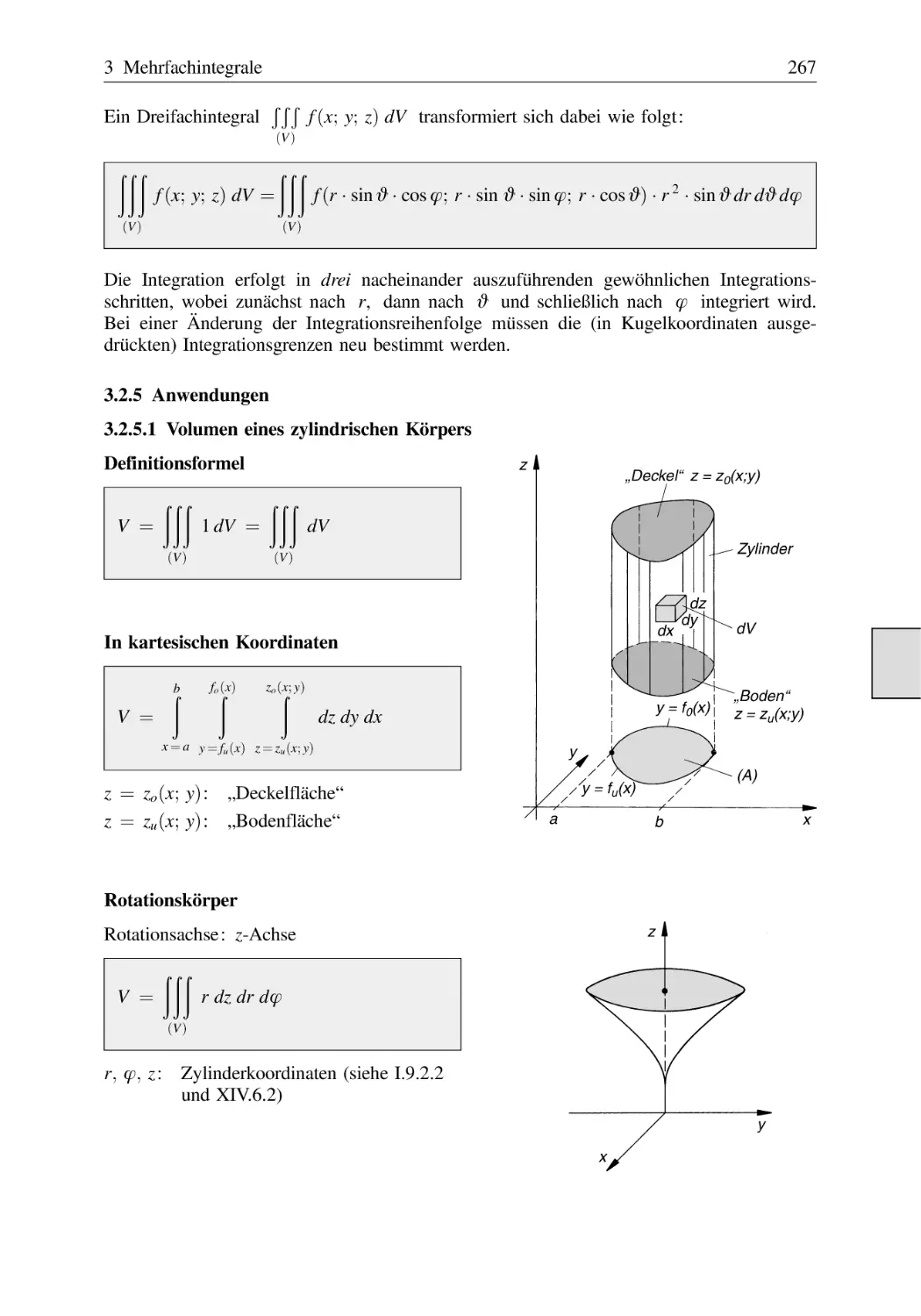
Dreifachintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1
Definition eines Dreichfachintegrals . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2
Berechnung eines Dreichfachintegrals in kartesischen
Koordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.3
Berechnung eines Dreifachintegrals in Zylinderkoordinaten . . . . .
3.2.4
Berechnung eines Dreifachintegrals in Kugelkoordinaten . . . . . . .
3.2.5
Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.5.1 Volumen eines zylindrischen Körpers . . . . . . . . . . . . . . .
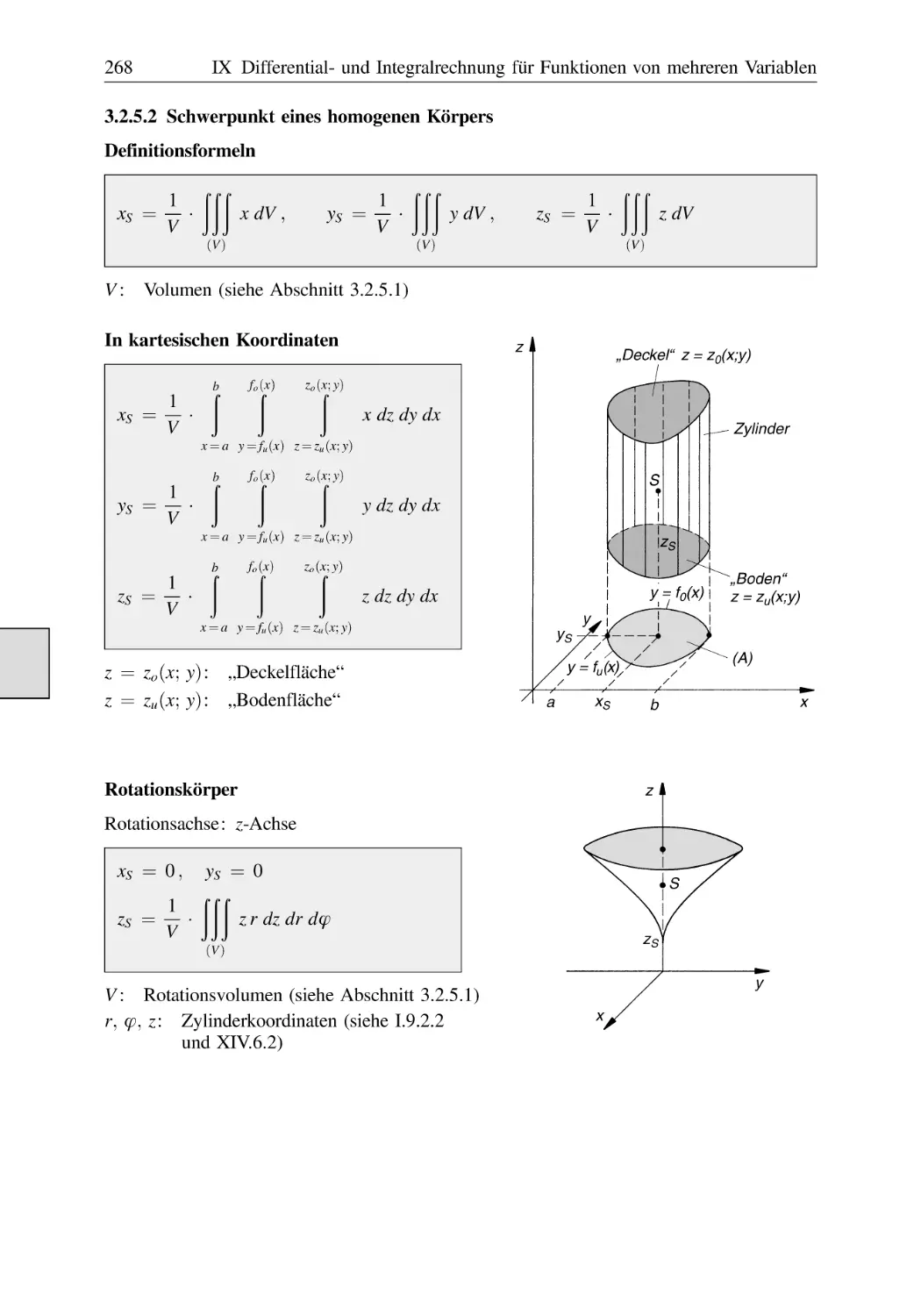
3.2.5.2 Schwerpunkt eines homogenen Körpers . . . . . . . . . . . . .
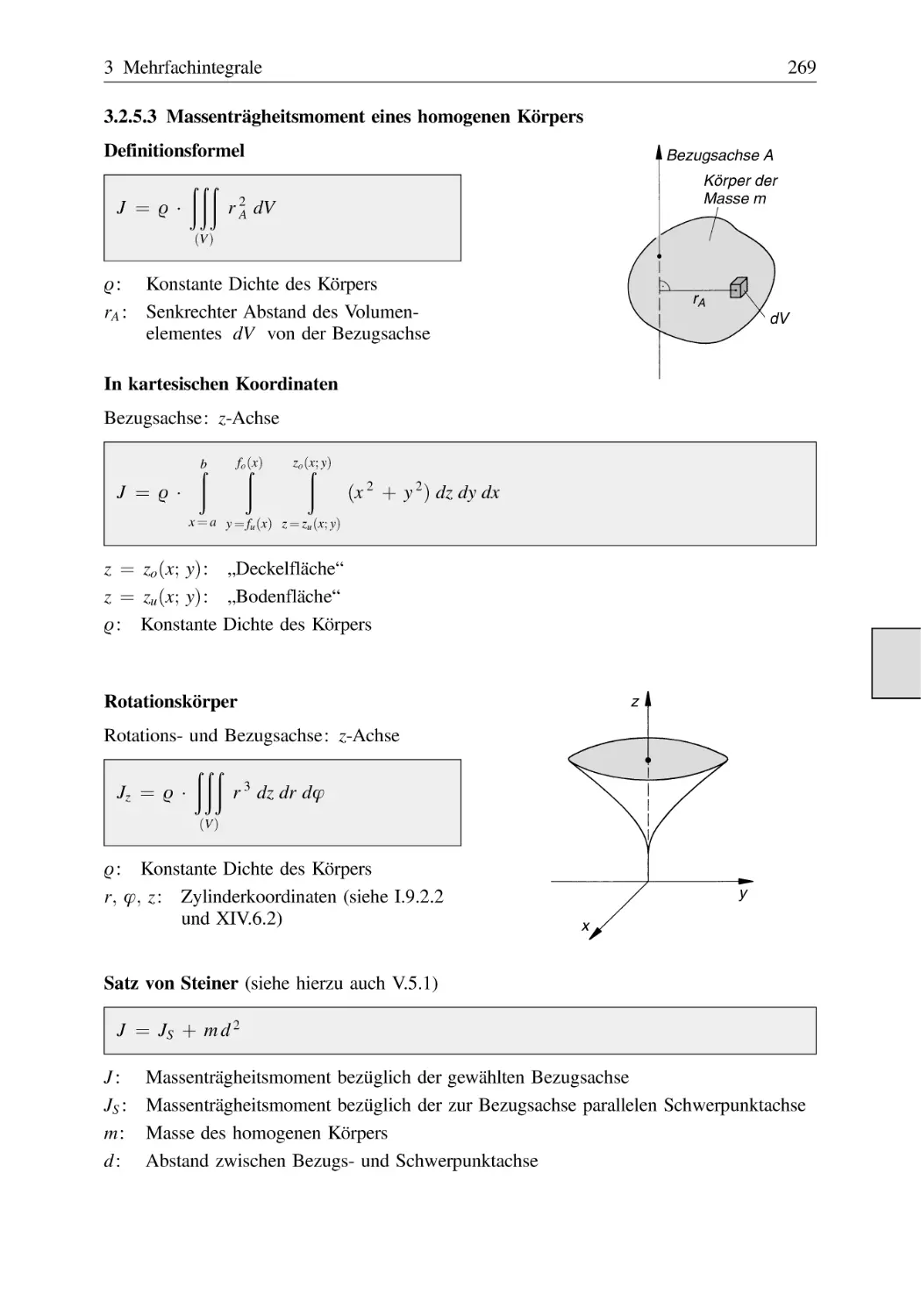
3.2.5.3 Massenträgheitsmoment eines homogenen Körpers . . . .
257
257
258
260
261
261
261
262
263
263
264
266
266
267
267
268
269
X Gewöhnliche Differentialgleichungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
1.1
1.2
1.3
1.4
Definition einer gewöhnlichen Differentialgleichung n-ter Ordnung . . . . . . .
Lösungen einer Differentialgleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Anfangswertprobleme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Randwertprobleme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
270
270
270
271
XXII
Inhaltsverzeichnis
2 Differentialgleichungen 1. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271
2.1
2.2
2.3
2.4
2.5
Differentialgleichungen 1. Ordnung mit trennbaren Variablen . . . . . . . . . . . .
Spezielle Differentialgleichungen 1. Ordnung, die durch Substitutionen
lösbar sind (Tabelle) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Exakte Differentialgleichungen 1. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . .
Lineare Differentialgleichungen 1. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1
Definition einer linearen Differentialgleichung 1. Ordnung . . . . . .
2.4.2
Integration der homogenen linearen Differentialgleichung . . . . . . .
2.4.3
Integration der inhomogenen linearen Differentialgleichung . . . . .
2.4.3.1 Integration durch Variation der Konstanten . . . . . . . . . . .
2.4.3.2 Integration durch Aufsuchen einer partikulären Lösung
2.4.4
Lineare Differentialgleichungen 1. Ordnung
mit konstanten Koeffizienten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Numerische Integration einer Differentialgleichung 1. Ordnung . . . . . . . . . .
2.5.1
Streckenzugverfahren von Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.2
Runge-Kutta-Verfahren 2. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.3
Runge-Kutta-Verfahren 4. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . .
271
272
273
274
274
274
274
274
275
275
277
277
279
280
3 Differentialgleichungen 2. Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 283
3.1
3.2
3.3
Spezielle Differentialgleichungen 2. Ordnung, die sich auf
Differentialgleichungen 1. Ordnung zurückführen lassen . . . . . . . . . . . . . . .
Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten . .
3.2.1
Definition einer linearen Differentialgleichung 2. Ordnung
mit konstanten Koeffizienten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2
Integration der homogenen linearen Differentialgleichung . . . . . . .
3.2.2.1 Wronski-Determinante . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2.2 Allgemeine Lösung der homogenen linearen
Differentialgleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.3
Integration der inhomogenen linearen Differentialgleichung . . . . .
Numerische Integration einer Differentialgleichung 2. Ordnung . . . . . . . . . .
283
284
284
284
284
284
285
288
4 Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
4.1
4.2
Mechanische Schwingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.1
Allgemeine Schwingungsgleichung der Mechanik . . . . . . . . . . . . .
4.1.2
Freie ungedämpfte Schwingung . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.3
Freie gedämpfte Schwingung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.3.1 Schwache Dämpfung (Schwingungsfall) . . . . . . . . . . . . .
4.1.3.2 Aperiodischer Grenzfall . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.3.3 Aperiodisches Verhalten bei starker Dämpfung (Kriechfall)
4.1.4
Erzwungene Schwingung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.4.1 Differentialgleichung der erzwungenen Schwingung . . .
4.1.4.2 Stationäre Lösung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Elektrische Schwingungen in einem Reihenschwingkreis . . . . . . . . . . . . . . .
291
291
291
292
292
293
293
294
294
294
295
5 Lineare Differentialgleichungen n-ter Ordnung mit konstanten Koeffizienten . . 296
5.1
Definition einer linearen Differentialgleichung n-ter Ordnung
mit konstanten Koeffizienten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 296
Inhaltsverzeichnis
5.2
5.3
XXIII
Integration der homogenen linearen Differentialgleichung . . . . . . . . . . . . . . .
5.2.1
Wronski-Determinante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.2
Allgemeine Lösung der homogenen linearen Differentialgleichung
Integration der inhomogenen linearen Differentialgleichung . . . . . . . . . . . . .
296
296
297
298
6 Systeme linearer Differentialgleichungen 1. Ordnung mit konstanten
Koeffizienten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 300
6.1
6.2
6.3
Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Integration des homogenen linearen Systems . . . . . . . . . . . . . . . . . . . . . . . . .
Integration des inhomogenen linearen Systems . . . . . . . . . . . . . . . . . . . . . . .
6.3.1
Integration durch Aufsuchen einer partikulären Lösung . . . . . . . . .
6.3.2
Einsetzungs- oder Eliminationsverfahren . . . . . . . . . . . . . . . . . . . .
300
300
301
301
302
XI Fehler- und Ausgleichsrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304
1 Gaußsche Normalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304
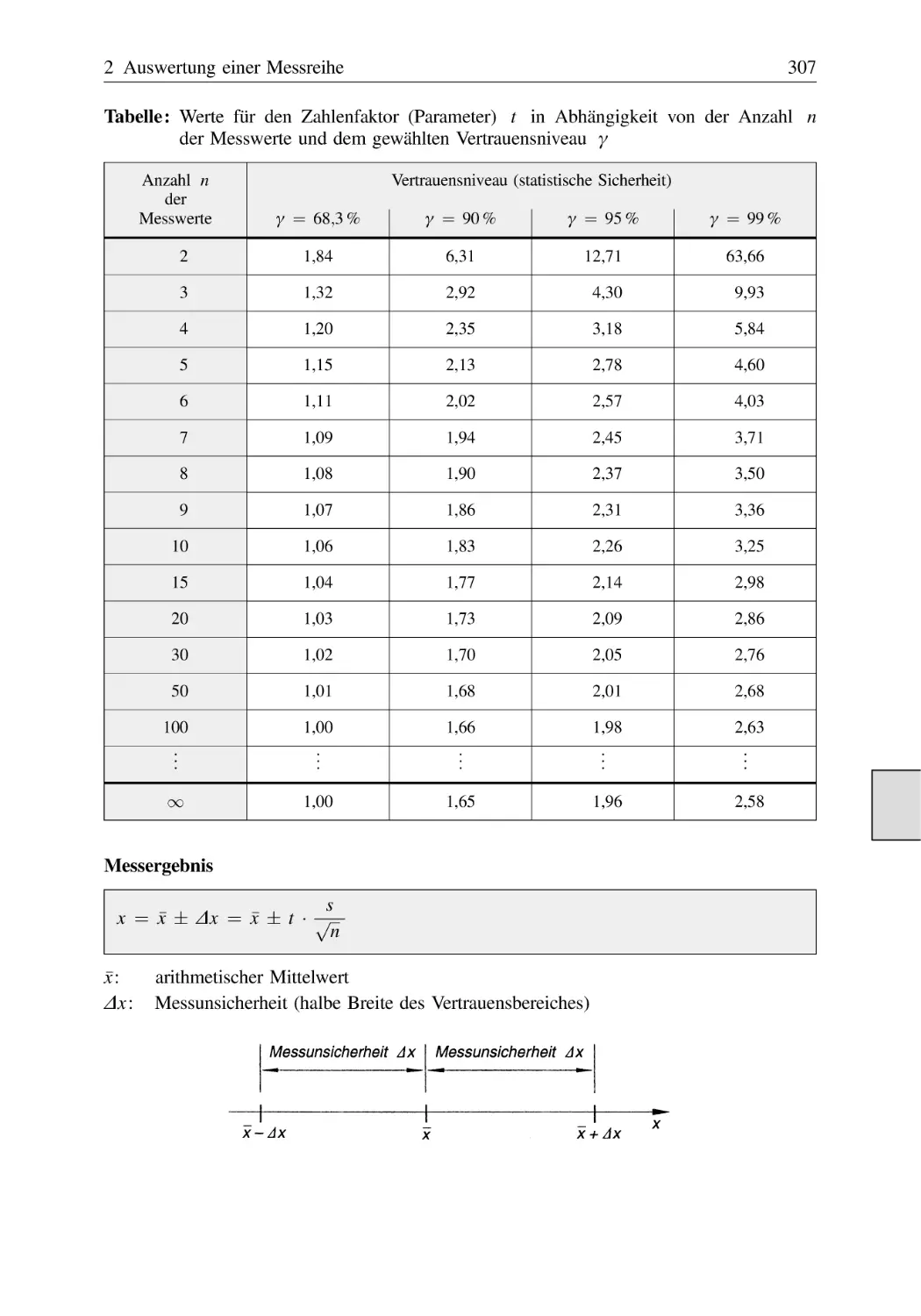
2 Auswertung einer Messreihe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305
3 Gaußsches Fehlerfortpflanzungsgesetz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 308
3.1
3.2
Gaußsches Fehlerfortpflanzungsgesetz für eine Funktion
von zwei unabhängigen Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 308
Gaußsches Fehlerfortpflanzungsgesetz für eine Funktion
von n unabhängigen Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310
4 Lineares Fehlerfortpflanzungsgesetz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310
5 Ausgleichskurven . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 312
5.1
5.2
5.3
Ausgleichung nach dem Gaußschen Prinzip der kleinsten Quadrate . . . . . . . 312
Ausgleichs- oder Regressionsgerade . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 313
Ausgleichs- oder Regressionsparabel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315
XII Fourier-Transformationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 316
1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 316
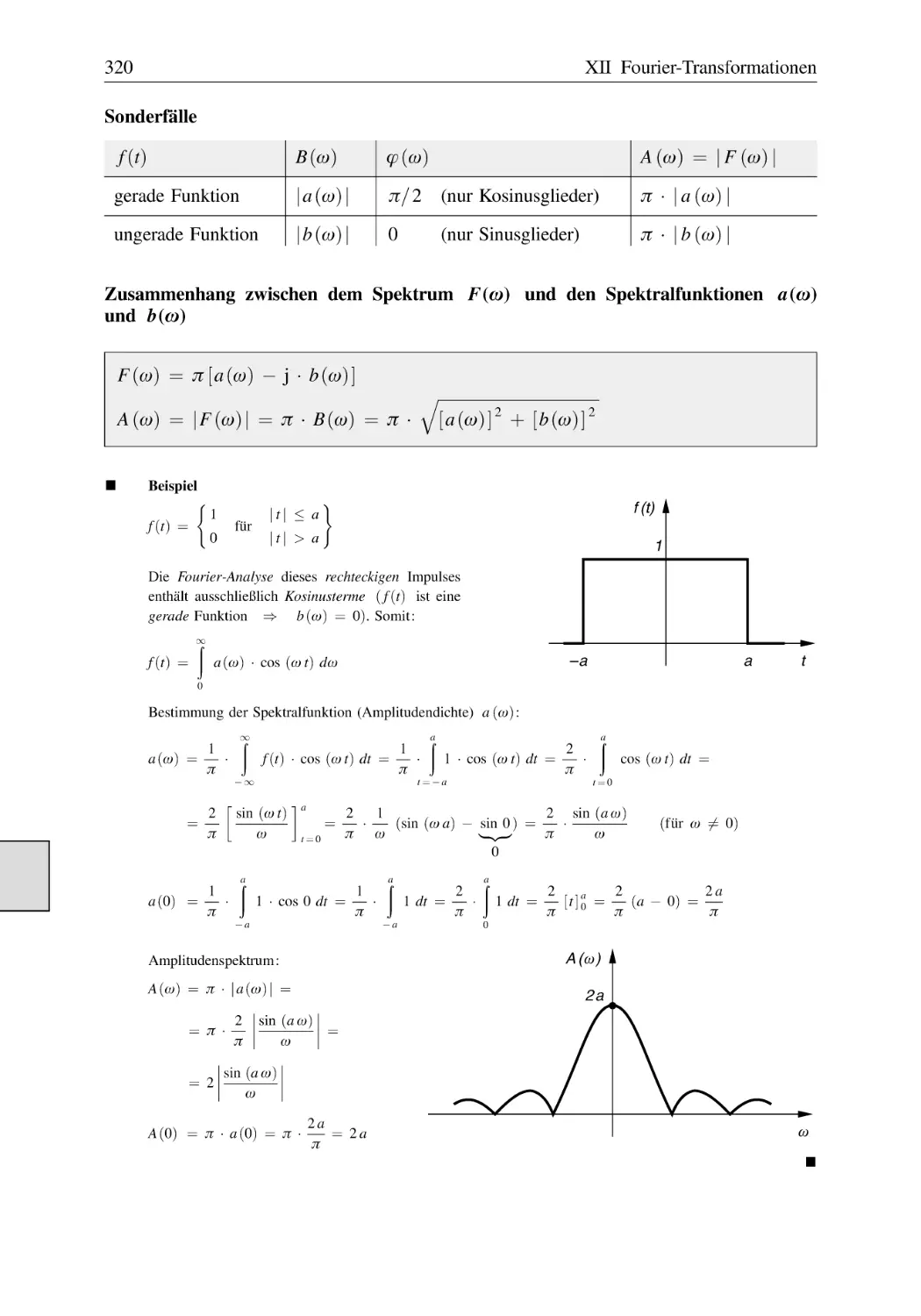
2 Spezielle Fourier-Transformationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321
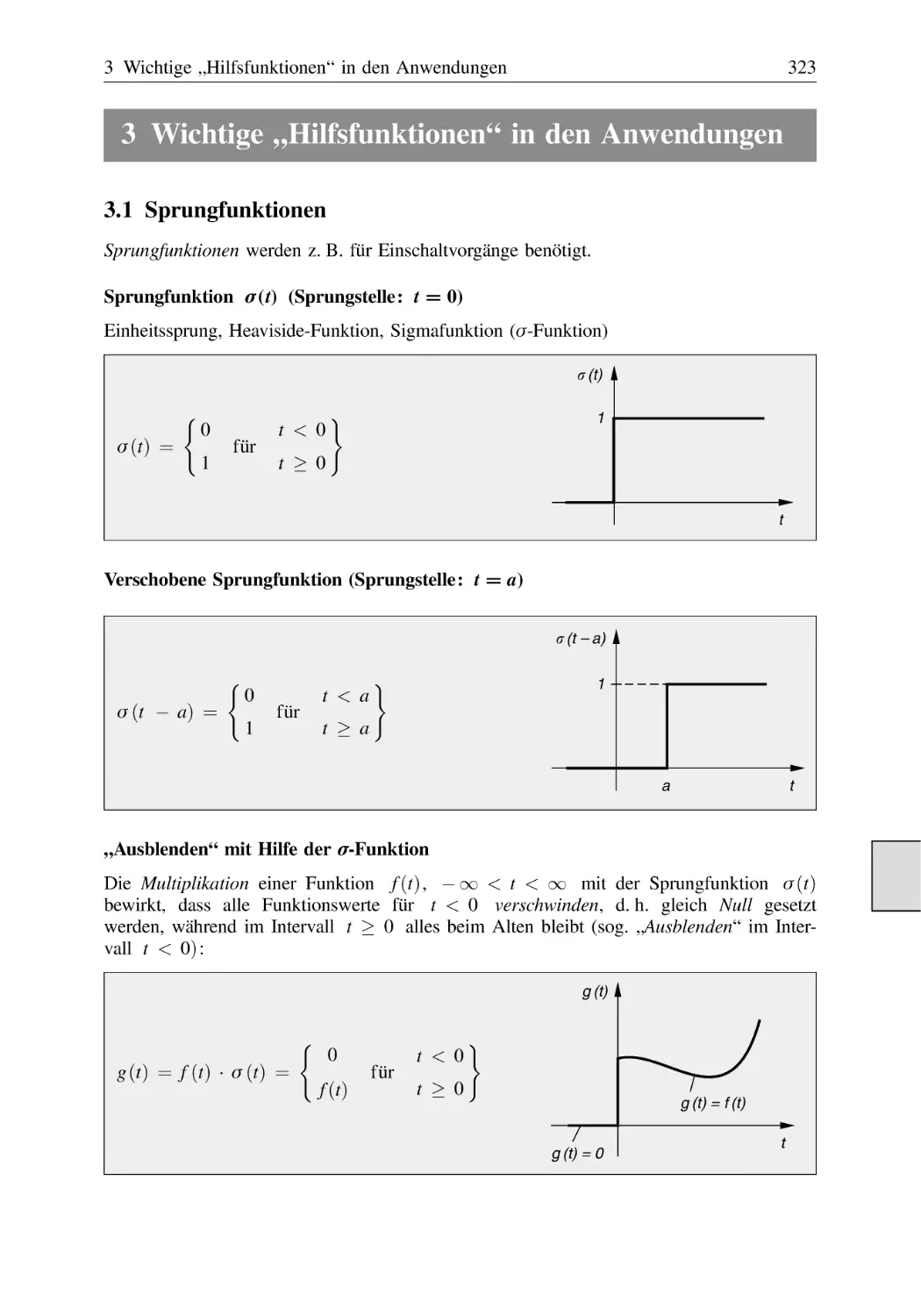
3 Wichtige „Hilfsfunktionen“ in den Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . 323
3.1
3.2
3.3
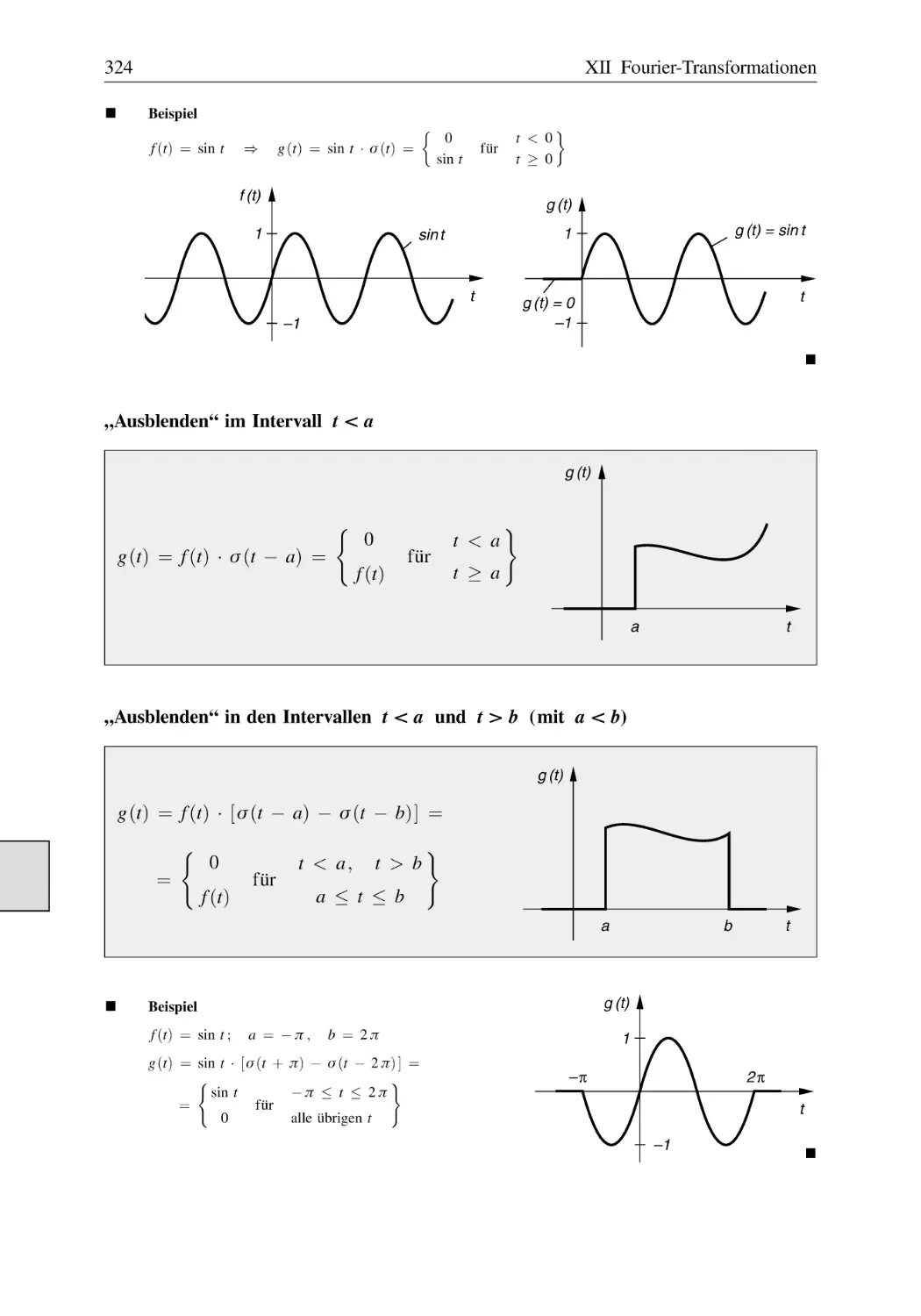
Sprungfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323
Rechteckige Impulse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 325
Diracsche Deltafunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 326
4 Eigenschaften der Fourier-Transformation (Transformationssätze) . . . . . . . . . . . 329
4.1
4.2
4.3
4.4
Linearitätssatz (Satz über Linearkombinationen) . . . . . . . . . . . . . . . . . . . . . .
#hnlichkeitssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Verschiebungssatz (Zeitverschiebungssatz) . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dämpfungssatz (Frequenzverschiebungssatz) . . . . . . . . . . . . . . . . . . . . . . . . .
329
329
330
331
XXIV
4.5
4.6
4.7
4.8
Inhaltsverzeichnis
Ableitungssätze (Differentiationssätze) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.1
Ableitungssatz (Differentiationssatz) für die Originalfunktion . . . .
4.5.2
Ableitungssatz (Differentiationssatz) für die Bildfunktion . . . . . . .
Integrationssätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Faltungssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vertauschungssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
332
332
333
334
334
335
5 Anwendung: Lösung linearer Differentialgleichungen mit konstanten
Koeffizienten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336
5.1
5.2
5.3
Allgemeines Lösungsverfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336
Lineare Differentialgleichungen 1. Ordnung mit konstanten Koeffizienten . . 336
Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten . . 337
6 Tabellen spezieller Fourier-Transformationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 338
XIII Laplace-Transformationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344
1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344
2 Eigenschaften der Laplace-Transformation (Transformationssätze) . . . . . . . . . . 345
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
Linearitätssatz (Satz über Linearkombinationen) . . . . . . . . . . . . . . . . . . . . . .
#hnlichkeitssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Verschiebungssätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dämpfungssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Ableitungssätze (Differentiationssätze) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.1
Ableitungssatz (Differentiationssatz) für die Originalfunktion . . . .
2.5.2
Ableitungssatz (Differentiationssatz) für die Bildfunktion. . . . . . . .
Integrationssätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.1
Integrationssatz für die Originalfunktion . . . . . . . . . . . . . . . . . . . . .
2.6.2
Integrationssatz für die Bildfunktion . . . . . . . . . . . . . . . . . . . . . . . .
Faltungssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Grenzwertsätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
345
346
347
348
348
348
350
350
350
351
352
353
3 Laplace-Transformierte einer periodischen Funktion . . . . . . . . . . . . . . . . . . . . . . 354
4 Laplace-Transformierte spezieller Funktionen (Impulse) . . . . . . . . . . . . . . . . . . . 355
5 Anwendung: Lösung linearer Anfangswertprobleme . . . . . . . . . . . . . . . . . . . . . . . 360
5.1
5.2
5.3
Allgemeines Lösungsverfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 360
Lineare Differentialgleichungen 1. Ordnung mit konstanten Koeffizienten . . 361
Lineare Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten . . 362
6 Tabelle spezieller Laplace-Transformationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363
Inhaltsverzeichnis
XXV
XIV Vektoranalysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 368
1 Ebene und räumliche Kurven . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 368
1.1
1.2
1.3
1.4
1.5
Vektorielle Darstellung einer Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Differentiation eines Vektors nach einem Parameter . . . . . . . . . . . . . . . . . . .
1.2.1
Ableitung einer Vektorfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.2
Tangentenvektor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2.3
Ableitungsregeln für Summen und Produkte . . . . . . . . . . . . . . . . .
1.2.4
Geschwindigkeits- und Beschleunigungsvektor
eines Massenpunktes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bogenlänge einer Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Tangenten- und Hauptnormaleneinheitsvektor einer Kurve . . . . . . . . . . . . . .
Krümmung einer Kurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
368
369
369
369
369
370
371
371
372
2 Flächen im Raum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 374
2.1
2.2
2.3
2.4
Vektorielle Darstellung einer Fläche . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Flächenkurven . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Flächennormale und Flächenelement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Tangentialebene . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1
Tangentialebene einer Fläche vom Typ ~
r ¼~
r ðu; vÞ . . . . . . . . . . .
2.4.2
Tangentialebene einer Fläche vom Typ z ¼ f ðx; yÞ. . . . . . . . . . . .
2.4.3
Tangentialebene einer Fläche vom Typ Fðx; y; zÞ ¼ 0 . . . . . . . . .
374
375
375
376
376
377
377
3 Skalar- und Vektorfelder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 378
3.1
3.2
Skalarfelder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 378
Vektorfelder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 378
4 Gradient eines Skalarfeldes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 380
5 Divergenz und Rotation eines Vektorfeldes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 382
5.1
5.2
5.3
Divergenz eines Vektorfeldes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 382
Rotation eines Vektorfeldes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 383
Spezielle Vektorfelder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 384
6 Darstellung von Gradient, Divergenz, Rotation und Laplace-Operator
in speziellen Koordinatensystemen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 385
6.1
6.2
6.3
Darstellung in Polarkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 385
Darstellung in Zylinderkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 387
Darstellung in Kugelkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 390
7 Linien- oder Kurvenintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 392
7.1
7.2
7.3
7.4
7.5
Linienintegral in der Ebene . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Linienintegral im Raum . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wegunabhängigkeit eines Linien- oder Kurvenintegrals . . . . . . . . . . . . . . . .
Konservative Vektorfelder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Arbeitsintegral (Arbeit eines Kraftfeldes) . . . . . . . . . . . . . . . . . . . . . . . . . . . .
392
394
394
395
396
XXVI
Inhaltsverzeichnis
8 Oberflächenintegrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 397
8.1
8.2
Definition eines Oberflächenintegrals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Berechnung eines Oberflächenintegrals . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8.2.1
Berechnung eines Oberflächenintegrals in symmetriegerechten
Koordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8.2.2
Berechnung eines Oberflächenintegrals unter Verwendung
von Flächenparametern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
397
398
398
399
9 Integralsätze von Gauß und Stokes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 400
9.1
9.2
Gaußscher Integralsatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 400
Stokesscher Integralsatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 401
XV Wahrscheinlichkeitsrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403
1 Hilfsmittel aus der Kombinatorik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403
1.1
1.2
1.3
Permutationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403
Kombinationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 404
Variationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 404
2 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 405
3 Wahrscheinlichkeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 407
3.1
3.2
3.3
3.4
3.5
3.6
3.7
Absolute und relative Häufigkeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wahrscheinlichkeitsaxiome von Kolmogoroff . . . . . . . . . . . . . . . . . . . . . . . . .
Laplace-Experimente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bedingte Wahrscheinlichkeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Multiplikationssatz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Stochastisch unabhängige Ereignisse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Mehrstufige Zufallsexperimente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
407
408
408
409
409
410
410
4 Wahrscheinlichkeitsverteilung einer Zufallsvariablen . . . . . . . . . . . . . . . . . . . . . . 412
4.1
4.2
4.3
Zufallsvariable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 412
Verteilungsfunktion einer Zufallsvariablen . . . . . . . . . . . . . . . . . . . . . . . . . . . 413
Kennwerte oder Maßzahlen einer Verteilung . . . . . . . . . . . . . . . . . . . . . . . . . 415
5 Spezielle diskrete Wahrscheinlichkeitsverteilungen . . . . . . . . . . . . . . . . . . . . . . . . 417
5.1
5.2
5.3
5.4
Binomialverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Hypergeometrische Verteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Poisson-Verteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Approximationen diskreter Wahrscheinlichkeitsverteilungen (Tabelle) . . . . .
417
419
421
422
6 Spezielle stetige Wahrscheinlichkeitsverteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . 423
6.1
Gaußsche Normalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 423
6.1.1
Allgemeine Normalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 423
6.1.2
Standardnormalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 424
Inhaltsverzeichnis
XXVII
6.1.3
6.2
Berechnung von Wahrscheinlichkeiten mit Hilfe der tabellierten
Verteilungsfunktion der Standardnormalverteilung . . . . . . . . . . . . . 425
6.1.4
Quantile der Standardnormalverteilung . . . . . . . . . . . . . . . . . . . . . . 426
Exponentialverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 427
7 Wahrscheinlichkeitsverteilungen von mehreren Zufallsvariablen . . . . . . . . . . . . . 428
7.1
7.2
Mehrdimensionale Zufallsvariable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Summen, Linearkombinationen und Produkte von Zufallsvariablen . . . . . . .
7.2.1
Additionssätze für Mittelwerte und Varianzen . . . . . . . . . . . . . . . .
7.2.2
Multiplikationssatz für Mittelwerte . . . . . . . . . . . . . . . . . . . . . . . . .
7.2.3
Wahrscheinlichkeitsverteilung einer Summe . . . . . . . . . . . . . . . . . .
428
430
430
431
431
8 Prüf- oder Testverteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 432
8.1
8.2
Chi-Quadrat-Verteilung („ c 2-Verteilung“) . . . . . . . . . . . . . . . . . . . . . . . . . . . 432
t-Verteilung von Student . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 434
XVI Grundlagen der mathematischen Statistik . . . . . . . . . . . . . . . . . . . . . . . . . 436
1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 436
1.1
1.2
1.3
Zufallsstichproben aus einer Grundgesamtheit . . . . . . . . . . . . . . . . . . . . . . . . 436
Häufigkeitsverteilung einer Stichprobe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 437
Gruppierung der Stichprobenwerte bei umfangreichen Stichproben . . . . . . . 439
2 Kennwerte oder Maßzahlen einer Stichprobe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 442
2.1
2.2
2.3
Mittelwert, Varianz und Standardabweichung einer Stichprobe . . . . . . . . . . . 442
Berechnung der Kennwerte unter Verwendung der Häufigkeitsfunktion . . . . 444
Berechnung der Kennwerte einer gruppierten Stichprobe . . . . . . . . . . . . . . . 445
3 Statistische Schätzmethoden für unbekannte Parameter
(„Parameterschätzungen“) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 446
3.1
3.2
3.3
Aufgaben der Parameterschätzung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Schätzfunktionen und Schätzwerte für unbekannte Parameter
(„Punktschätzungen“) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1
Schätz- und Stichprobenfunktionen . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.2
Schätzungen für den Mittelwert m und die Varianz s 2 . . . . . . . .
3.2.3
Schätzungen für einen Anteilswert p
(Parameter p einer Binomialverteilung) . . . . . . . . . . . . . . . . . . . . .
3.2.4
Schätzwerte für die Parameter spezieller Wahrscheinlichkeitsverteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vertrauens- oder Konfidenzintervalle für unbekannte Parameter
(„Intervallschätzungen“) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.1
Vertrauens- oder Konfidenzintervalle . . . . . . . . . . . . . . . . . . . . . . . .
3.3.2
Vertrauensintervalle für den unbekannten Mittelwert m
einer Normalverteilung bei bekannter Varianz s 2 . . . . . . . . . . . . .
3.3.3
Vertrauensintervalle für den unbekannten Mittelwert m
einer Normalverteilung bei unbekannter Varianz s 2 . . . . . . . . . . .
446
446
446
447
448
448
449
449
450
451
XXVIII
Inhaltsverzeichnis
3.3.4
3.3.5
3.3.6
3.3.7
Vertrauensintervalle für den unbekannten Mittelwert m
bei einer beliebigen Verteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vertrauensintervalle für die unbekannte Varianz s 2
einer Normalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vertrauensintervalle für einen unbekannten Anteilswert p
(Parameter p einer Binomialverteilung) . . . . . . . . . . . . . . . . . . . . .
Musterbeispiel für die Bestimmung eines Vertrauensintervalls . . . .
452
453
454
455
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“) . . . . . 456
4.1
4.2
Statistische Hypothesen und Parametertests . . . . . . . . . . . . . . . . . . . . . . . . . .
Spezielle Parametertests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.1
Test für den unbekannten Mittelwert m einer Normalverteilung
bei bekannter Varianz s 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.2
Test für den unbekannten Mittelwert m einer Normalverteilung
bei unbekannter Varianz s 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.3
Tests für die Gleichheit der unbekannten Mittelwerte m1 und m2
zweier Normalverteilungen („Differenzentests“) . . . . . . . . . . . . . . .
4.2.3.1 Differenzentests für Mittelwerte bei abhängigen
Stichproben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.3.2 Differenzentests für Mittelwerte bei unabhängigen
Stichproben . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.4
Tests für die unbekannte Varianz s 2 einer Normalverteilung . . .
4.2.5
Tests für den unbekannten Anteilswert p
(Parameter p einer Binomialverteilung) . . . . . . . . . . . . . . . . . . . . .
4.2.6
Musterbeispiel für einen Parametertest . . . . . . . . . . . . . . . . . . . . . .
456
457
457
459
460
461
462
466
468
470
5 Chi-Quadrat-Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 471
XXIX
Anhang
Teil A
Integraltafel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 476
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
ax þ b . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ax þ b und px þ q . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a2 þ x2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a2 / x2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ax2 þ bx þ c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a3 + x3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a4 þ x4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a4 / x4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b und px þ q . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b und
px þ q . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 / x 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 / a2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax2 þ bx þ c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sin ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cos ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sin ðaxÞ und cos ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
tan ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cot ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
einer Arkusfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
eax . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ln x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sinh ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cosh ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sinh ðaxÞ und cosh ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
tanh ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
coth ðaxÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
einer Areafunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
477
478
479
480
482
484
484
484
485
486
487
488
490
492
494
496
498
500
503
503
504
505
506
508
509
510
511
511
512
XXX
Anhang
Teil B
Tabellen zur Wahrscheinlichkeitsrechnung und Statistik . . . . . . . . . . . 513
Tabelle 1:
Verteilungsfunktion fðuÞ der Standardnormalverteilung . . . . . . . . . . . . . . 514
Tabelle 2:
Quantile der Standardnormalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 516
Tabelle 3:
Quantile der Chi-Quadrat-Verteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 518
Tabelle 4:
Quantile der t-Verteilung von „Student“ . . . . . . . . . . . . . . . . . . . . . . . . . . . 520
Sachwortverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 522
1
I Allgemeine Grundlagen aus Algebra,
Arithmetik und Geometrie
1 Grundlegende Begriffe über Mengen
1.1 Definition und Darstellung einer Menge
Menge
Unter einer Menge M versteht man die Zusammenfassung gewisser wohlunterschiedener
Objekte, Elemente genannt, zu einer Einheit.
a 2 M : a ist ein Element von M ða gehört zur Menge MÞ
a 62 M : a ist kein Element von M ða gehört nicht zur Menge MÞ
Beschreibende Darstellungsform:
M ¼ fx j x besitzt die Eigenschaften E1 ; E2 ; E3 ; . . .g
Aufzählende Darstellungsform:
M ¼ fa1 ; a2 ; . . . ; an g: Endliche Menge mit n Elementen
M ¼ fa1 ; a2 ; a3 ; . . .g: Unendliche Menge
Leere Menge
Eine Menge heißt leer, wenn sie kein Element enthält. Symbolische Schreibweise: f g; ˘
Teilmenge
Eine Menge A heißt Teilmenge einer Menge B,
wenn jedes Element von A auch zur Menge B
gehört. Symbolische Schreibweise: A & B. A heißt
Untermenge, B Obermenge.
B
A
Gleichheit von Mengen
Zwei Mengen A und B heißen gleich, wenn jedes Element von A auch Element von B
ist und umgekehrt. Symbolische Schreibweise: A ¼ B
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_1
2
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
1.2 Mengenoperationen
Durchschnitt zweier Mengen (Schnittmenge)
Die Schnittmenge A \ B zweier Mengen A
und B ist die Menge aller Elemente, die sowohl zu A als auch zu B gehören:
A \ B ¼ fx j x 2 A
A
B
A
B
A
B
und x 2 Bg
Vereinigung zweier Mengen (Vereinigungsmenge)
Die Vereinigungsmenge A [ B zweier Mengen A und B ist die Menge aller Elemente,
die zu A oder zu B oder zu beiden Mengen gehören:
A [ B ¼ fx j x 2 A oder
x 2 Bg
Differenz zweier Mengen (Differenzmenge, Restmenge)
Die Differenz- oder Restmenge A n B zweier Mengen A und B ist die Menge aller
Elemente, die zu A, nicht aber zu B gehören:
A n B ¼ fx j x 2 A und
x 62 Bg
2 Rechnen mit reellen Zahlen
2.1 Reelle Zahlen und ihre Eigenschaften
2.1.1 Natürliche und ganze Zahlen
N ¼ f0; 1; 2; . . .g
Menge der natürlichen Zahlen
N* ¼ f1; 2; 3; . . .g
Menge der positiven ganzen Zahlen
Hinweis: Die Zahl 0 gehört nach DIN 5473 zu den natürlichen Zahlen. N* ist die Menge der natürlichen Zahlen ohne 0, d. h. N* ¼ N n f0g.
Eigenschaften: Addition und Multiplikation sind in der Menge N unbeschränkt durchführbar.
2 Rechnen mit reellen Zahlen
3
Primzahl p
Natürliche Zahl größer als 1, die nur durch 1 und sich selbst teilbar ist.
&
Beispiele
Die ersten Primzahlen lauten: 2, 3, 5, 7, 11, 13, . . .
&
Zerlegung in Primfaktoren
Jede natürliche Zahl n ( 2 lässt sich eindeutig in ein Produkt aus Primzahlen zerlegen.
&
Beispiel
140 ¼ 2 . 70 ¼ 2 . 2 . 35 ¼ 2 . 2 . 5 . 7 ¼ 2 2 . 5 . 7
&
Größter gemeinsamer Teiler (ggT)
ggT mehrerer Zahlen: größte Zahl, die gemeinsamer Teiler der gegebenen Zahlen ist.
Regel: Man zerlegt die Zahlen in Primfaktoren und bildet das Produkt der höchsten Potenzen von Primfaktoren, die allen gegebenen Zahlen gemeinsam sind.
&
Beispiel
60 ¼ 2 2 . 3 1 . 5 1
72 ¼ 2 3 . 3 2
2
ggT ¼ 2 . 3
1
¼ 12
9
>
=
>
;
)
12 ist die größte Zahl, durch die 60 und 72 gemeinsam teilbar sind.
&
Kleinstes gemeinsames Vielfaches (kgV)
kgV mehrerer Zahlen: kleinste Zahl, die alle gegebenen Zahlen als Teiler enthält.
Regel: Man zerlegt die Zahlen in Primfaktoren und bildet das Produkt der jeweils höchsten Potenzen von Primfaktoren, die in mindestens einer der gegebenen Zahlen auftreten.
&
Beispiel
60 ¼ 2 2 . 3 1 . 5 1
72 ¼ 2 3 . 3 2
kgV ¼ 2 3 . 3 2 . 5 1 ¼ 360
9
>
=
>
;
)
360 ist die kleinste Zahl, die durch 60 und 72 teilbar ist.
&
4
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
Einige Teilbarkeitsregeln
Eine natürliche Zahl
ist teilbar durch . . .
wenn . . .
2
die letzte Ziffer durch 2 teilbar ist,
3
die Quersumme durch 3 teilbar ist,
4
die aus den beiden letzten Ziffern
gebildete Zahl durch 4 teilbar ist,
5
die letzte Ziffer eine 5 oder 0 ist.
Ganze Zahlen
Z ¼ f0; + 1; + 2; + 3; . . .g
Menge der ganzen Zahlen
Eine weitere übliche Schreibweise: Z ¼ f. . . , / 3, / 2, / 1, 0, 1, 2, 3, . . .g
Addition, Subtraktion und Multiplikation sind in der Menge Z unbeschränkt durchführbar.
2.1.2 Rationale, irrationale und reelle Zahlen
Die Menge Q der rationalen Zahlen enthält alle endlichen und unendlichen periodischen
Dezimalbrüche (Dezimalzahlen):
Q ¼
n
x j x ¼
a
b
mit
a 2 Z
o
und b 2 N *
Menge der rationalen Zahlen
Die irrationalen Zahlen bestehen aus allen unendlichen nichtperiodischen Dezimalbrüchen
(Dezimalzahlen).
Die Menge R der reellen Zahlen enthält die rationalen und irrationalen Zahlen und somit sämtliche (endlichen und unendlichen) Dezimalbrüche (Dezimalzahlen).
&
Beispiele
(1)
(2)
(3)
33
¼ 4;125
8
1
¼ 0;333333 . . .
3
pffiffiffi
2 ¼ 1;414213 . . .
endliche Dezimalzahl (rational)
unendliche periodische Dezimalzahl (rational)
unendliche nichtperiodische Dezimalzahl (irrational)
&
2 Rechnen mit reellen Zahlen
5
2.1.3 Rundungsregeln für reelle Zahlen
In der Praxis wird mit endlich vielen Dezimalstellen nach dem Komma gerechnet. Bei
Rundung auf n Dezimalstellen nach dem Komma gelten dann folgende Regeln:
(1)
(3)
Es wird abgerundet, wenn in der ðn þ 1Þ-ten Dezimalstelle nach dem Komma eine
0, 1, 2, 3 oder 4 steht.
Es wird aufgerundet, wenn in der ðn þ 1Þ-ten Dezimalstelle nach dem Komma eine
5, 6, 7, 8 oder 9 steht.
Rundungsfehler: ) 0;5 . 10 /n
&
Beispiele
(2)
Wir runden die nachfolgenden Zahlen auf 3 Dezimalstellen nach dem Komma (die in der 4. Dezimalstelle
nach dem Komma stehende Ziffer (Pfeil) entscheidet dabei über Ab- oder Aufrundung):
4;517863 . . . ' 4;518
#
Aufrundung
Fehler: ) 0;5 . 10 /3 ¼ 0;0005
0;417346 . . . ' 0;417
#
Abrundung
Fehler: ) 0;5 . 10 /3 ¼ 0;0005
&
2.1.4 Darstellung der reellen Zahlen auf der Zahlengerade
Zahlengerade
Die bildliche Darstellung einer reellen Zahl erfolgt durch einen Punkt auf einer Zahlengerade, wobei positive Zahlen nach rechts und negative Zahlen nach links, jeweils vom Nullpunkt aus, abgetragen werden:
–2,5 –2
–1
0
1
2
2,5
Anordnung der reellen Zahlen auf der Zahlengerade
a < b (a kleiner b)
a
a ¼ b (a gleich b)
a > b
(a größer b)
Weitere Ungleichungen:
a ) b (a kleiner oder gleich b)
a ( b
(a größer oder gleich b)
b
a=b
b
a
6
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
Betrag einer reellen Zahl
Der Betrag j a j einer reellen Zahl a ist der Abstand des Bildpunktes vom Nullpunkt:
8
< a
jaj ¼
0
:
/a
fur
€
9
a > 0=
a
ðj a j ( 0Þ
a ¼ 0
;
a < 0
0
a
Rechenregeln für Beträge
(1)
ja + bj ) jaj þ jbj
(2)
jaj / jbj ) jaj þ jbj
(3)
j a1 þ a2 þ a3 þ . . . þ an j ) j a1 j þ j a2 j þ j a3 j þ . . . þ j an j
(4)
jabj ¼ jaj . jbj
"a"
jaj
" "
ðb 6¼ 0Þ
" " ¼
b
jbj
(5)
Beachte:
jxj ¼ a
,
(Dreiecksungleichung)
x1= 2 ¼ + a
ða > 0Þ
Signum (Vorzeichen) einer reellen Zahl
8
< 1
sgn ðaÞ ¼
0
:
/1
fur
€
9
a > 0=
a ¼ 0
;
a < 0
2.1.5 Grundrechenarten
Es sind vier Grundrechenarten erklärt:
1. Addition
! Summe a þ b
(a, b: Summanden)
2. Subtraktion
! Differenz a / b
(a, b: Minuend bzw. Subtrahend)
3. Multiplikation
! Produkt a . b
a
! Quotient
b
(a, b: Faktoren)
4. Division
(a, b: Dividend bzw. Divisor; b 6¼ 0Þ
Summen, Differenzen, Produkte und Quotienten zweier reeller Zahlen ergeben wieder
reelle Zahlen. Ausnahme: Die Division durch die Zahl 0 ist verboten!
a
Andere Schreibweisen für Produkte bzw. Quotienten: a . b oder a b bzw.
oder
b
a = b oder a : b.
2 Rechnen mit reellen Zahlen
7
Rechenregeln
Kommutativgesetze
Assoziativgesetze
aþb ¼ bþa
ab ¼ ba
a þ ðb þ cÞ ¼ ða þ bÞ þ c
a ðb cÞ ¼ ða bÞ c
a ðb þ cÞ ¼ a b þ a c
Distributivgesetz
2.2 Zahlensysteme
Dezimalsystem (dekadisches oder Zehnersystem)
Basis: a ¼ 10
Zehn Ziffern: 0; 1; 2; . . . ; 9
Die Darstellung einer (reellen) Zahl erfolgt durch Entwicklung nach fallenden Potenzen der
Basis a ¼ 10. Es handelt sich dabei um ein Stellenwert- oder Positionssystem, d. h. der
Wert einer Ziffer hängt von der Position (Stelle) ab.
&
Beispiel
1998 ¼ 1000 þ 900 þ 90 þ 8 ¼ 1 . 10 3 þ 9 . 10 2 þ 9 . 10 1 þ 8 . 10 0
#
#
#
#
1
9
9
8
Schreibweise: (1998)10 , wobei der Index 10 die Basis des Systems kennzeichnet. Sind Mißverständnisse
ausgeschlossen, darf der Index weggelassen werden.
&
Dualsystem (binäres oder Zweiersystem)
Basis: a ¼ 2
Zwei Ziffern:
0, 1
Die Entwicklung einer (reellen) Zahl erfolgt hier nach fallenden Potenzen der Basis
a ¼ 2 (Rechenbasis der Computersysteme).
&
Beispiele
(1)
(2)
ð1001:1Þ2 ¼ 1 . 2 3 þ 0 . 2 2 þ 0 . 2 1 þ 1 . 2 0 þ 1 . 2 /1 ¼
1
¼ 8þ0þ0þ1þ
¼ ð9;5Þ10
2
Wir stellen die Zahl ð11Þ10 aus dem Dezimalsystem im Dualsystem dar:
ð11Þ10 ¼ 11 ¼ 8 þ 2 þ 1 ¼ 1 . 2 3 þ 0 . 2 2 þ 1 . 2 1 þ 1 . 2 0
#
#
#
#
1
0
1
1
Ergebnis: ð11Þ10 ¼ ð1011Þ2
&
8
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
2.3 Intervalle
Intervalle sind spezielle Teilmengen von R, die auf der Zahlengerade durch zwei Randpunkte a und b begrenzt werden ða < bÞ.
Endliche Intervalle
½ a; b % ¼ fx j a ) x ) bg
oder
a ) x ) b
½ a; b Þ ¼ fx j a ) x < bg oder
a ) x < b
ða; b % ¼ fx j a < x ) bg oder
a < x ) b
ða; b Þ ¼ fx j a < x < bg
a < x < b
oder
)
abgeschlossenes Intervall
halboffene Intervalle
offenes Intervall
Unendliche Intervalle
½ a; 1Þ
¼ fx j a ) x < 1Þ
oder
a ) x < 1
oder
x ( a
ða; 1Þ
¼ fx j a < x < 1Þ
oder
a < x < 1
oder
x > a
ð/1; b %
¼ fx j /1 < x ) bg
oder
/1 < x ) b
oder
x ) b
ð/1; b Þ ¼ fx j /1 < x < bg
oder
/1 < x < b oder
x < b
ð/1; 0Þ 0 R /
oder
0 Rþ
oder
ð0; 1Þ
ð/1; 1Þ 0 R
oder
/1 < x < 0
oder
x < 0
0 < x < 1 oder
x > 0
/1 < x < 1
oder
jxj < 1
2.4 Bruchrechnung
Hinweis: Die nachfolgenden Begriffe und Regeln lassen sich sinngemäß auch auf mathematische Ausdrücke übertragen.
Ein Bruch a = b heißt echt, wenn j a j < j b j ist, sonst unecht.
Kehrwert einer Zahl
Der Kehrwert von
8
< a
:
a=b
ist
9
1=a =
b=a
;
ðmit a 6¼ 0
und
b 6¼ 0Þ
Regel: Bei der Kehrwertbildung werden Zähler und Nenner miteinander vertauscht.
&
Beispiel
Der Kehrwert von 2 ist
1
3
4
¼ 0,5, der Kehrwert von
ist
.
2
4
3
&
2 Rechnen mit reellen Zahlen
9
Erweitern eines Bruches mit einer Zahl k 6¼ 0
a
a.k
¼
b
b.k
Regel: Zähler und Nenner werden mit derselben Zahl k 6¼ 0 multipliziert.
&
Beispiel
Wir erweitern den Bruch
2
mit der Zahl 3:
5
2
2 .3
6
¼
¼
5
5.3
15
&
Kürzen eines Bruches durch eine Zahl k 6¼ 0
a
a=k
c
¼
¼
b
b=k
d
bzw.
a
k .c
c
¼
¼
b
k .d
d
(Kurzen
€
des gemeinsamen Faktors kÞ
Regel: Zähler und Nenner werden durch dieselbe Zahl k 6¼ 0 dividiert.
&
Beispiel
Wir kürzen den Bruch
15
15=5
3
¼
¼
25
25=5
5
15
durch 5:
25
bzw:
15
5.3
3
¼
¼
25
5.5
5
&
Addition und Subtraktion zweier Brüche
a
c
a.d +b.c
+
¼
b
d
b.d
Regel: Die Brüche werden gleichnamig gemacht, d. h. auf einen gemeinsamen Nenner,
den sog. Hauptnenner, gebracht. Der Hauptnenner ist das kleinste gemeinsame
Vielfache der Einzelnenner.
&
Beispiel
3
2
3.5þ2.4
15 þ 8
23
þ
¼
¼
¼
4
5
4.5
20
20
ðHauptnenner : 4 . 5 ¼ 20Þ
&
10
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
Multiplikation zweier Brüche
a c
a.c
.
¼
b d
b.d
Regel: Zwei Brüche werden multipliziert, indem man ihre Zähler und ihre Nenner miteinander multipliziert.
&
Beispiel
3 5
3.5
15
.
¼
¼
4 7
4.7
28
&
Division zweier Brüche (Doppelbruch)
a c
a d
a.d
:
¼
.
¼
b d
b c
b.c
Regel: Zwei Brüche werden dividiert, indem man mit dem Kehrwert des Divisors (Kehrwert des Nennerbruches) multipliziert.
&
Beispiel
4 5
4 7
4.7
28
:
¼
.
¼
¼
3 7
3 5
3.5
15
3
Divisor :
5
7
2
&
2.5 Potenzen und Wurzeln
Potenz a n
Unter einer Potenz a n versteht man ein Produkt mit n gleichen Faktoren a:
an ¼ a . a . a ... a
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
n gleiche Faktoren
a: Basis oder Grundzahl
ða 2 RÞ
n: Exponent oder Hochzahl ðn 2 N *Þ
Ferner (für a 6¼ 0Þ: a 0 ¼ 1; a /n ¼
&
1
an
Beispiele
(1)
5 4 ¼ 5 . 5 . 5 . 5 ¼ 625
(2)
2 /3 ¼
1
1
1
¼
¼
23
2.2.2
8
&
2 Rechnen mit reellen Zahlen
11
Rechenregeln für Potenzen
a m . a n ¼ a mþn
(2)
am
¼ a m/n
an
(3)
ða m Þ n ¼ ða n Þ m ¼ a m . n
(4)
a n . b n ¼ ða . bÞn
! a 4n
an
¼
ðb 6¼ 0Þ
n
b
b
(5)
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
(1)
ða 6¼ 0Þ
m; n 2 N *; a; b 2 R
Im Falle a > 0; b > 0 gelten die Potenzregeln sogar für beliebige reelle Exponenten.
Ferner (für a > 0Þ: a b ¼ e b . ln a ( ln a: natürlicher Logarithmus von a)
Beispiele
&
(1)
3 2 . 3 3 ¼ 3 2 þ 3 ¼ 3 5 ¼ 243
(2)
ð2 3 Þ 2 ¼ 2 3 . 2 ¼ 2 6 ¼ 64
(3)
5 2 . 3 2 ¼ ð5 . 3Þ 2 ¼ 15 2 ¼ 225
(4)
(5)
64
¼ 6 4 / 2 ¼ 6 2 ¼ 36
62
(6)
ð5 4 Þ 2 ¼ 5 4 . 2 ¼ 5 2 ¼ 25
3 23
20 3
20
¼ 4 3 ¼ 64
¼
53
5
Wurzel
1
1
&
p
ffiffiffi
n a
Die eindeutig bestimmte nichtnegative Lösung x der Gleichung x n ¼ a mit a ( 0
heißt n-te Wurzel aus a ðn ¼ 2; 3; 4; . . .Þ. Symbolische Schreibweise:
x ¼
p
ffiffiffi
n a
oder
1
x ¼ an
a: Radikand ða ( 0Þ
n: Wurzelexponent ðn ¼ 2; 3; 4; . . .Þ
Anmerkungen
pffiffiffi
(1) n a ist diejenige nichtnegative Zahl, deren n-te Potenz gleich a ist.
pffiffiffi
(2) n a lässt sich
pffiffiffi auch als Potenz der Basis a mit dem rationalem Exponenten 1=n
darstellen: n a ¼ a 1=n . Es gelten die Potenzregeln (1) bis (5).
pffiffiffi
pffiffiffi
(3) 2 a ¼ a : Quadratwurzel aus a (der Wurzelexponent wird meist weggelassen)
p
ffiffiffi
3 a : Kubikwurzel aus a
pffiffiffiffiffiffi
(4) Man beachte: a 2 ¼ j a j
(5)
Das Wurzelziehen oder Radizieren ist die zum Potenzieren inverse Operation:
pffiffiffi
b ¼ a n , a ¼ n b (nur für a ( 0, b ( 0)
12
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
p
ffiffiffiffiffiffi
pffiffiffi
1
1
m
n
a m ¼ ða m Þ n ¼ ða n Þ m ¼ a n ¼ ð n aÞ m
pffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
1 1
1
m p
n a ¼ m a1
n ¼ ða n Þ m ¼ a m . n ¼ m . n a
pffiffiffiffiffiffi
p
ffiffiffi pffiffiffi
1
1
n a . n b ¼ ða 1
n Þ . ðb n Þ ¼ ða bÞ n ¼ n a b
rffiffiffiffiffi
p
ffiffiffi
1
! a 41n
n a
an
n a
p
ffiffiffi ¼ 1 ¼
¼
ðb > 0Þ
n
b
b
b
bn
(1)
(2)
(3)
(4)
Merke:
(2)
(3)
m; n 2 N *; a ( 0; b ( 0
pffiffiffi
p
ffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
n
a + b 6¼ n a + n b
Beispiele
ffiffiffi
p
pffiffiffi
2
(1)
9 ¼ 9 ¼ 3;
&
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Rechenregeln für Wurzeln
p
ffiffiffiffiffi
3
21 ¼ 2;7589 ;
qffiffiffiffiffiffi
ffiffiffiffiffiffiffiffi
p
1
1
4
256 ¼ 4 2 8 ¼ ð2 8 Þ 4 ¼ 2 8 . 4 ¼ 2 2 ¼ 4
qffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
2
1
6
2;5 2 ¼ 2;5 6 ¼ 2;5 3 ¼ 3 2;5 ¼ 1;3572
qffiffiffiffiffiffi
ffiffiffiffiffiffiffiffi
p
ffiffiffi
pffiffiffi
4
1
1 1
1 1
1
4 p
3
6 ¼
6 3 ¼ ð6 3 Þ 4 ¼ 6 3 . 4 ¼ 6 12 ¼ 12 6 ¼ 1;1610
&
2.6 Logarithmen
Logarithmus log a r
Jede positive Zahl r > 0 ist als Potenz einer beliebigen positiven Basis a > 0, a 6¼ 1
in der Form r ¼ a x darstellbar. Die eindeutig bestimmte Lösung x der Gleichung
r ¼ a x heißt Logarithmus von r zur Basis a. Symbolische Schreibweise:
r: Numerus ðr > 0Þ
x ¼ log a r
a: Basis ða > 0; a 6¼ 1Þ
Anmerkungen
(1)
(2)
(3)
Logarithmen können nur von positiven Zahlen gebildet werden und sind noch von
der Basis abhängig!
Für jede (zulässige) Basis a gilt: log a a ¼ 1; log a 1 ¼ 0
log a ða x Þ ¼ x (für a > 0; a 6¼ 1 und x 2 R)
(4)
a log a x ¼ x
&
Beispiele
(für a > 0; a 6¼ 1 und x > 0)
(1)
5 x ¼ 125
(2)
log 4 64 ¼ log 4 4 3 ¼ 3
(3)
log 10
)
x ¼ log 5 125 ¼ 3
1
¼ log 10 10 / 2
100
ðwegen 125 ¼ 5 3 Þ
ðwegen 64 ¼ 4 3 Þ
3
2
1
1
¼ /2
wegen
¼
¼ 10 / 2
2
100
10
&
2 Rechnen mit reellen Zahlen
13
(1)
(2)
(3)
(4)
log a ðu . vÞ ¼ log a u þ log a v
!u4
¼ log a u / log a v
log a
v
log a ðu k Þ ¼ k . log a u
3 2
p
ffiffiffi
1
n
. log a u
log a u ¼
n
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Rechenregeln für Logarithmen
a > 0; u > 0; v > 0; k 2 R
n ¼ 2; 3; 4; . . .
Spezielle Logarithmen
1. Zehnerlogarithmus (Briggscher oder dekadischer Logarithmus): log 10 r 0 lg r
2. Zweierlogarithmus (binärer Logarithmus): log 2 r 0 lb r
3. Natürlicher Logarithmus (Logarithmus naturalis): log e r 0 ln r
ðe ¼ 2;718281 . . . ¼ Eulersche ZahlÞ
Beispiele
&
(1)
(2)
(3)
1
¼ log 2 1 / log 2 8 ¼ 0 / 3 ¼ / 3
ðwegen 1 ¼ 2 0 und 8 ¼ 2 3 Þ
8
ln 104 ¼ 4;6444
pffiffiffiffiffi
1
1
1
lg 3 24 ¼ lg ð24 3 Þ ¼
. lg 24 ¼
. 1;3802 ¼ 0;4601
3
3
log 2
&
Umrechnung von der Basis a in die Basis b (mit a > 0, b > 0, a 6¼ 1, b 6¼ 1)
log b r ¼
log a r
1
¼
. log a r ¼ K . log a r
log a b
log a b
ðr > 0Þ
Regel: Beim Basiswechsel a ! b werden die Logarithmen mit einer Konstanten K
(dem Kehrwert von log a b) multipliziert.
Sonderfälle
(1)
Basiswechsel 10 ! e:
lg r
lg r
ln r ¼
¼
¼ 2;3026 . lg r
lg e
0;4343
(2)
Basiswechsel e ! 10:
ln r
ln r
lg r ¼
¼
¼ 0;4343 . ln r
ln 10
2;3026
14
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
2.7 Binomischer Lehrsatz
n-Fakultät
n! (gelesen: „ n Fakultät“) ist definitionsgemäß das Produkt der ersten n positiven ganzen Zahlen:
n ! ¼ 1 . 2 . 3 . . . ðn / 1Þ n ¼
n
Q
k¼1
ðn 2 N *Þ
k
Ergänzend definiert man: 0 ! ¼ 1
Zerlegung: ðn þ 1Þ ! ¼ 1 . 2 . 3 . . . n . ðn þ 1Þ ¼ n ! ðn þ 1Þ
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
n!
Der Binomische Lehrsatz
Die Potenzen eines Binoms a þ b lassen sich nach dem Binomischen Lehrsatz wie folgt
entwickeln ðn 2 N *Þ:
ða þ bÞ n ¼ a n þ
þ
¼
Die Koeffizienten
dungsgesetz lautet:
k
¼
1
!n4
4
n ! 4
X
n
k¼0
!n4
!n4
k
!n4
k
a n/1 . b 1 þ
!n4
2
a n/2 . b 2 þ
a n/4 . b 4 þ . . . þ
a n/k . b k ¼
!
n ! 4
X
n
k¼0
k
!n4
3
a n/3 . b 3 þ
n 4 1
a . b n/1 þ b n ¼
n/1
a k . b n/k
(gelesen: „ n über k “) heißen Binomialkoeffizienten, ihr Bil-
n ðn / 1Þ ðn / 2Þ . . . ½n / ðk / 1Þ%
n!
¼
k!
k ! ðn / kÞ !
ðk ) nÞ
Entwicklung für ða / bÞ n : Im Binomischen Lehrsatz wird b formal durch / b ersetzt
(Vorzeichenwechsel bei den ungeraden Potenzen von b).
Anmerkung
Lässt man für den Exponenten n auch reelle Werte zu, so erhält man die allgemeine
(unendliche) Binomische Reihe (siehe Tabelle in VI.3.4). Das Bildungsgesetz der Binomialkoeffizienten bleibt dabei erhalten.
2 Rechnen mit reellen Zahlen
15
Einige Eigenschaften der Binomialkoeffizienten
!n4
0
!n4
k
¼
¼
!n4
n
!
!n4
¼ 1
n
n/k
¼ 0
k
4
fur
€
3
!n4
n
k þ1
þ
k
k > n
2
3
¼
nþ1
k þ1
2
!n4
1
¼
!
n 4
¼ n
n/1
Pascalsches Dreieck zur Bestimmung der Binomialkoeffizienten
!n4
Der Binomialkoeffizient
steht in der ðn þ 1Þ-ten Zeile an ðk þ 1Þ-ter Stelle.
k
Zeile
1
1
1
2
1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
1
2
3
1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
1
3
3
4
1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
1
4
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
1
5
6
4
5
1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
10
10
5
6
1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
1
:
&
6
:
:
15
:
20
" :
3 2
6
3
15
:
6
:
1
7
:
Beispiel
3 2
6
¼ 20 (7. Zeile, 4. Stelle von links; eingekreiste Zahl im obigen Pascalschen Dreieck)
3
Die ersten binomischen Formeln
ða þ bÞ 2 ¼ a 2 þ 2 a b þ b 2
(1. Binom)
ða þ bÞ 3 ¼ a 3 þ 3 a 2 b þ 3 a b 2 þ b 3
ða þ bÞ 4 ¼ a 4 þ 4 a 3 b þ 6 a 2 b 2 þ 4 a b 3 þ b 4
ða / bÞ 2 ¼ a 2 / 2 a b þ b 2
ða / bÞ
3
3
2
(2. Binom)
2
¼ a / 3a b þ 3a b / b3
ða / bÞ 4 ¼ a 4 / 4 a 3 b þ 6 a 2 b 2 / 4 a b 3 þ b 4
ða þ bÞ ða / bÞ ¼ a 2 / b 2
(3. Binom)
&
16
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
3 Elementare (endliche) Reihen
3.1 Definition einer (endlichen) Reihe
Unter einer endlichen Reihe versteht man die Summe
a1 þ a2 þ a3 þ . . . þ an ¼
a1 : Anfangsglied
n
P
k¼1
ak
an : Endglied
ak : allgemeines Reihenglied (k ¼ 1, 2, . . . , nÞ
3.2 Arithmetische Reihen
Die Differenz zweier aufeinanderfolgender Glieder ist konstant: ak þ 1 / ak ¼ const: ¼ d.
Die Reihe besitzt den Summenwert
a þ ða þ dÞ þ ða þ 2 dÞ þ . . . þ ½ a þ ðn / 1Þ d % ¼
3
2
n
¼
2 a þ ðn / 1Þ d
2
a: Anfangsglied
n
P
k¼1
½ a þ ðk / 1Þ d % ¼
an ¼ a þ ðn / 1Þ d : Endglied
Bildungsgesetz der arithmetischen Reihe: ak ¼ a þ ðk / 1Þ d
3.3 Geometrische Reihen
Der Quotient zweier aufeinanderfolgender Glieder ist konstant:
Reihe besitzt den Summenwert
a þ a q þ a q 2 þ . . . þ a q n/1 ¼
a: Anfangsglied
n
P
k¼1
a q k/1 ¼
a ðq n / 1Þ
q/1
ðq 6¼ 1Þ
ðk ¼ 1; 2; . . . ; nÞ
Für q ¼ 1 hat die geometrische Reihe den Summenwert n a
3.4 Spezielle Zahlenreihen
(2)
ak þ 1
¼ const: ¼ q. Die
ak
an ¼ a q n / 1 : Endglied
Bildungsgesetz der geometrischen Reihe: ak ¼ a q k / 1
(1)
ðk ¼ 1; 2; . . . ; nÞ
n
P
n ðn þ 1Þ
2
k¼1
n
P
1 þ 3 þ 5 þ . . . þ ð2 n / 1Þ ¼
ð2 k / 1Þ ¼ n 2
1 þ 2 þ 3 þ ... þ n ¼
k ¼
k¼1
4 Gleichungen mit einer Unbekannten
n
P
17
(3)
2 þ 4 þ 6 þ ... þ 2n ¼
(4)
12 þ 22 þ 32 þ ... þ n2 ¼
(5)
1 2 þ 3 2 þ 5 2 þ . . . þ ð2 n / 1Þ 2 ¼
(6)
13 þ 23 þ 33 þ ... þ n3 ¼
k¼1
2 k ¼ n ðn þ 1Þ
n
P
k¼1
n
P
k¼1
k2 ¼
n ðn þ 1Þ ð2 n þ 1Þ
6
n
P
k¼1
k3 ¼
ð2 k / 1Þ 2 ¼
n ð2 n / 1Þ ð2 n þ 1Þ
3
n 2 ðn þ 1Þ 2
4
4 Gleichungen mit einer Unbekannten
4.1 Algebraische Gleichungen n-ten Grades
4.1.1 Allgemeine Vorbetrachtungen
Eine algebraische Gleichung n-ten Grades besitzt die allgemeine Form
an x n þ an / 1 x n / 1 þ . . . þ a1 x þ a0 ¼ 0
ðan 6¼ 0; ak 2 RÞ
Eigenschaften
(1)
(2)
(3)
Die Gleichung besitzt höchstens n reelle Wurzeln oder Lösungen. Lässt man auch
komplexe Lösungen zu, so gibt es genau n Lösungen, wobei grundsätzlich mehrfache Werte entsprechend oft gezählt werden (Fundamentalsatz der Algebra, siehe
auch VIII.4).
Für ungerades n hat die Gleichung mindestens eine reelle Lösung, für gerades n
dagegen braucht die Gleichung keine reelle Lösung zu haben.
Komplexe Lösungen treten (wenn überhaupt) stets paarweise auf, nämlich in konjugiert komplexer Form (siehe auch VIII.1.1).
Allgemeine Lösungsformeln existieren nur für n ) 4. Für n > 4 ist man auf Näherungsverfahren angewiesen (z. B. auf das Tangentenverfahren von Newton, siehe Abschnitt 4.5).
Ist eine reelle Lösung x1 der algebraischen Gleichung n-ten Grades bekannt (eine solche
Lösung lässt sich häufig durch Erraten oder Probieren finden), so kann der Grad der Gleichung durch Abspalten des zugehörigen Linearfaktors x / x1 um 1 erniedrigt werden
(siehe Horner-Schema, III.4.5).
18
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
4.1.2 Lineare Gleichungen
Allgemeine Form einer linearen Gleichung (mit Lösung):
a1 x þ a0 ¼ 0
)
x1 ¼ /
a0
a1
ða1 6¼ 0Þ
4.1.3 Quadratische Gleichungen
Allgemeine Form
a2 x 2 þ a1 x þ a0 ¼ 0
ða2 6¼ 0Þ
Normalform mit Lösungen (sog. „ p, q-Formel“)
2
x þ px þ q ¼ 0
)
Die Diskriminante D ¼
D > 0:
D ¼ 0:
D < 0:
x1=2
p
¼ /
+
2
s3
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
pffiffiffiffi
p 2
p
/q ¼ /
+ D
2
2
3 22
p
/ q entscheidet dabei über die Art der Lösungen:
2
Zwei verschiedene reelle Lösungen
Eine doppelte reelle Lösung
Zwei zueinander konjugiert komplexe Lösungen (siehe auch VIII.1.1)
Vietascher Wurzelsatz
x1 þ x2 ¼ / p ;
x1 ; x2 :
&
x1 x2 ¼ q
Wurzeln (Lösungen) der quadratischen Gleichung x 2 þ p x þ q ¼ 0
Beispiel
x2 / 4x / 5 ¼ 0
ð p ¼ / 4; q ¼ / 5Þ
3 22
3 22
p
/4
/q ¼
þ 5 ¼ ð/ 2Þ 2 þ 5 ¼ 4 þ 5 ¼ 9 > 0
D ¼
2
2
Zwei verschiedene reelle Lösungen:
pffiffiffi
x1=2 ¼ 2 + 9 ¼ 2 + 3; d. h. x1 ¼ 5;
)
x2 ¼ / 1
x1 þ x2 ¼ 5 / 1 ¼ 4 ¼ / p
x1 x2 ¼ 5 . ð/ 1Þ ¼ / 5 ¼ q
&
4.1.4 Kubische Gleichungen
Allgemeine Form
a3 x 3 þ a2 x 2 þ a1 x þ a0 ¼ 0
ða3 6¼ 0Þ
4 Gleichungen mit einer Unbekannten
19
Normalform mit Lösungen
x3 þ ax2 þ bx þ c ¼ 0
3 23 3 22
p
q
3b / a2
2a3
ab
þ
mit p ¼
und q ¼
/
þc
3
2
3
27
3
entscheidet dabei über die Art der Lösungen:
Die Diskriminante D ¼
D > 0:
D ¼ 0:
D < 0:
Eine reelle und zwei zueinander konjugiert komplexe Lösungen
Drei reelle Lösungen, darunter eine doppelte Lösung 1Þ
Drei reelle Lösungen
Cardanische Lösungsformel
x1 ¼ u þ v /
a
3
uþv
a
u / v pffiffiffi
/
þ
3j
2
3
2
uþv
a
u / v pffiffiffi
x3 ¼ /
/
/
3j
2
3
2
x2 ¼ /
9
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
;
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffi
q
3
/
þ D
2
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffi
q
v ¼ 3 /
/ D
2
u ¼
j : Imaginare
€ Einheit
mit
j2 ¼ / 1
Hinweis: Numerische Lösungsmethoden führen meist schneller zum Ziel.
Sonderfall D < 0
Für D < 0 erhält man die drei reellen Lösungen meist bequemer mit Hilfe des folgenden
trigonometrischen Lösungsansatzes:
rffiffiffiffiffiffiffi
! j4
jpj
a
x1 ¼ 2 .
/
. cos
3
3
3
rffiffiffiffiffiffiffi
!
4
jpj
j
a
x2 ¼ 2 .
. cos
þ 120" /
3
3
3
rffiffiffiffiffiffiffi
!
4
jpj
j
a
x3 ¼ 2 .
. cos
þ 240" /
3
3
3
9
>
>
>
>
>
>
>
>
=
>
>
>
>
>
>
>
>
;
cos j ¼ /
q
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 23
jpj
2.
3
Der Hilfswinkel j wird aus der angegebenen Gleichung berechnet.
Vietascher Wurzelsatz
x1 þ x2 þ x3 ¼ / a ;
x1 ; x2 ; x3 :
1Þ
x1 x2 þ x2 x3 þ x3 x1 ¼ b ;
x1 x2 x3 ¼ / c
Wurzeln (Lösungen) der kubischen Gleichung x 3 þ a x 2 þ b x þ c ¼ 0
Für den Spezialfall p ¼ q ¼ 0 erhält man eine dreifache Lösung: x1=2=3 ¼ / a=3:
20
&
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
Beispiel
x 3 þ x 2 / 8 x / 12 ¼ 0
p ¼
ða ¼ 1; b ¼ / 8; c ¼ / 12Þ
3 b / a2
3 ð/ 8Þ / 1 2
25
¼
¼ /
3
3
3
2 a3
ab
2. 13
1 ð/ 8Þ
2
8
2 þ 8 . 9 / 12 . 27
250
þc ¼
/ 12 ¼
þ
/ 12 ¼
¼ /
/
/
3
3
27
3
27
27
27
27
3 2 23
3 3 22
! p 43 ! q 42 3 2523 3 12522
6
5
5
/ 5 þ 56
þ
¼
þ
¼ /
þ /
¼ /
¼0
Diskriminante: D ¼
2
3
3
2
9
27
3
3
36
q ¼
Es gibt also drei reelle Lösungen, darunter eine Doppellösung. Wegen D ¼ 0 ist ferner u ¼ v:
sffiffiffiffiffiffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffi
rffiffiffiffiffiffiffiffiffiffi
3 23
q
5
5
3
3 125
u ¼ v ¼ 3 /
¼
¼
¼
2
27
3
3
Lösungen nach der Cardanischen Lösungsformel unter Beachtung von u þ v ¼ 2 u und u / v ¼ 0:
x1 ¼ 2 u /
x 2=3 ¼ /
a
10
1
9
¼
/
¼
¼ 3
3
3
3
3
2u
a
a
5
1
6
/
¼ /u /
¼ /
/
¼ /
¼ /2
2
3
3
3
3
3
Sonderfall: x 3 + a x 2 + b x = 0
&
(Absolutglied c = 0)
Die Gleichung zerfällt in eine lineare Gleichung mit der Lösung x1 ¼ 0 und in eine
quadratische Gleichung mit möglicherweise zwei weiteren Lösungen:
x ¼ 0
x 3 þ a x 2 þ b x ¼ x ðx 2 þ a x þ bÞ ¼ 0
&
)
x1 ¼ 0
x2 þ ax þ b ¼ 0
Beispiel
x 3 / 2 x 2 / 15 x ¼ 0
x ðx 2 / 2 x / 15Þ ¼ 0
Lösungen:
x ¼ 0
)
x1 ¼ 0
x 2 / 2 x / 15 ¼ 0
)
x2=3 ¼ 1 + 4
x1 ¼ 0; x2 ¼ 5; x3 ¼ / 3
&
4.1.5 Biquadratische Gleichungen
Eine algebraische Gleichung 4. Grades mit ausschließlich geraden Exponenten heißt biquadratisch:
a4 x 4 þ a2 x 2 þ a0 ¼ 0
oder
x4 þ ax2 þ b ¼ 0
ða4 6¼ 0Þ
Sie lässt sich mit Hilfe der Substitution u ¼ x 2 in eine quadratische Gleichung überführen. Aus den beiden Wurzeln dieser Gleichung erhält man durch Rücksubstitution die
(reellen) Lösungen der biquadratischen Gleichung 2Þ .
2Þ
Allgemeines Lösungsverfahren für eine beliebige Gleichung 4. Grades: siehe Bronstein-Semendjajew
4 Gleichungen mit einer Unbekannten
&
21
Beispiel
x 4 / 10 x 2 þ 9 ¼ 0
Substitution u ¼ x 2 :
u 2 / 10 u þ 9 ¼ 0
)
u1=2 ¼ 5 + 4;
u1 ¼ 9 ;
u2 ¼ 1
Rücksubstitution mittels x 2 ¼ u:
x 2 ¼ u1 ¼ 9
)
x1=2 ¼ + 3
x 2 ¼ u2 ¼ 1
)
x3=4 ¼ + 1
Lösungen:
x1 ¼ 3 ;
x2 ¼ / 3 ;
x3 ¼ 1;
x4 ¼ / 1
&
4.2 Allgemeine Lösungshinweise für Gleichungen
Für viele Gleichungen wie beispielsweise Wurzelgleichungen, trigonometrische oder goniometrische Gleichungen, Exponential- und logarithmische Gleichungen gibt es kein allgemeines Lösungsverfahren. Sie lassen sich daher meist nur mit Näherungsmethoden behandeln (siehe graphische und numerische Lösungsverfahren). In Sonderfällen gelingt es, die
Gleichung mit Hilfe elementarer Umformungen oder einer geeigneten Substitution in eine
algebraische Gleichung n-ten Grades zu überführen, die dann mit den in Abschnitt 4.1
dargelegten Methoden gelöst werden kann.
Wichtiger Hinweis: Der !bergang von der gegebenen Gleichung zu einer algebraischen
Gleichung n-ten Grades ist oft nur mit Hilfe nichtäquivalenter Umformungen 3Þ möglich
(Beispiel: Quadrieren von Wurzelausdrücken, siehe nachfolgendes Beispiel (1)). Dabei
kann sich die Lösungsmenge der Gleichung verändern, d. h. es können sog. „Scheinlösungen“ auftreten. Es ist daher stets durch Einsetzen der gefundenen Werte in die Ausgangsgleichung zu prüfen, ob auch eine Lösung dieser Gleichung vorliegt oder nicht.
&
Beispiele
(1)
Wurzelgleichung
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4x þ1 þ1 ¼ 2x
Die Wurzel wird zunächst isoliert und anschließend durch Quadrieren (also eine nichtäquivalente Umformung) beseitigt:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 x þ 1 ¼ 2 x / 1 j quadrieren
4 x þ 1 ¼ ð2 x / 1Þ 2 ¼ 4 x 2 / 4 x þ 1
4x2 / 8x ¼ 0 j : 4
)
x 2 / 2 x ¼ x ðx / 2Þ ¼ 0
)
x1 ¼ 0 ;
x2 ¼ 2
Wir prüfen durch Einsetzen in die Ausgangsgleichung (Wurzelgleichung), ob diese Werte auch die
Wurzelgleichung lösen:
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4.0þ1þ1 ¼ 2.0 )
1þ1 ¼ 1þ1 ¼ 2 ¼ 0
x1 ¼ 0
x1 ¼ 2
Widerspruch: x1 ¼ 0 ist somit keine Lösung der Wurzelgleichung
pffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 .2 þ 1 þ 1 ¼ 2 . 2 )
9þ1 ¼ 3þ1 ¼ 4 ¼ 4
x2 ¼ 2 ist eine (und zwar die einzige) Lösung der Wurzelgleichung
Lösung der Wurzelgleichung:
3Þ
x ¼ 2
Bei einer äquivalenten Umformung bleibt die Lösungsmenge einer Gleichung erhalten. Umformungen, die zu
einer Veränderung der Lösungsmenge führen können (aber nicht müssen), heißen nichtäquivalente Umformungen.
22
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
(2)
Trigonometrische Gleichung cos 2 x ¼ sin x þ 0;25
Unter Verwendung der Beziehung cos 2 x ¼ 1 / sin 2 x („trigonometrischer Pythagoras“) und der
sich anschließenden Substitution u ¼ sin x erhalten wir zunächst eine quadratische Gleichung mit
zwei verschiedenen reellen Lösungen:
sin 2 x þ sin x / 0;75 ¼ 0
1 / sin 2 x ¼ sin x þ 0;25
oder
u 2 þ u / 0;75 ¼ 0
u1 ¼ 0;5 ;
)
u2 ¼ / 1;5
Rücksubstitution mittels sin x ¼ u:
sin x ¼ u1 ¼ 0;5
)
p
þ k . 2p
6
5
¼
p þ k . 2p
6
x1 k ¼
x2 k
9
>
>
=
>
>
;
y
y = sin x
1
ðk 2 ZÞ
(Schnittstellen von y ¼ sin x mit der Geraden
y ¼ 0;5)
sin x ¼ u2 ¼ / 1;5 ) Keine Lösungen
p
Lösungen: x1 k ¼
þ k . 2p;
6
5
x2 k ¼
p þ k . 2p
6
y = 0,5
0,5
p
2p
x
p
5 p
6
6
–1
&
4.3 Graphisches Lösungsverfahren
Die Lösungen der Gleichung f ðxÞ ¼ 0 sind die Nullstellen der Funktion y ¼ f ðxÞ. Um
diese zu bestimmen, erstellt man eine Wertetabelle, zeichnet die Funktion und liest die
Nullstellen aus der Zeichnung ab. Meist ist es jedoch günstiger, die Gleichung f ðxÞ ¼ 0
zunächst durch Termumstellungen auf die Form f1 ðxÞ ¼ f2 ðxÞ zu bringen. Die gesuchten
Lösungen sind dann die Abszissen der Schnittpunkte der beiden (meist wesentlich einfacheren) Kurven y ¼ f1 ðxÞ und y ¼ f2 ðxÞ.
Nachteil der graphischen Methode: Geringe Ablesegenauigkeit
Beispiel
y
e /x þ x 2 / 4 ¼ 0
4
Aufspalten durch Termumstellungen:
y = 4 – x2
f1 ðxÞ
f
e /x ¼ 4 / x 2
f
&
f2 ðxÞ
Lösungen nach nebenstehendem Bild
(Schnittstellen der Parabel y ¼ 4 / x 2
mit der Exponentialfunktion y ¼ e / x ):
x1 ' / 1;05;
1
x2 ' 1;95
y = e –x
1
≈ –1,05
x
≈1,95
&
4 Gleichungen mit einer Unbekannten
23
4.4 Regula falsi
Es werden zunächst zwei Näherungswerte (Startwerte) x1 und x2 für die gesuchte Lösung x der Gleichung f ðxÞ ¼ 0 so bestimmt, dass sie auf verschiedenen Seiten der
Lösung x liegen. Dies ist bei einer stetigen Funktion der Fall, wenn f ðx1 Þ . f ðx2 Þ < 0
ist, d. h. die Funktion muss in den beiden Startpunkten ein unterschiedliches Vorzeichen
haben. Die gesuchte Lösung x liegt somit im Intervall ½ x1 ; x2 %. Einen besseren Näherungswert erhält man dann aus der Gleichung
x3 ¼ x2 /
x2 / x1
y2
y2 / y1
mit
y1 ¼ f ðx1 Þ ;
y2 ¼ f ðx2 Þ
Dann wiederholt man das beschriebene Verfahren mit den Startwerten x1 ; x3 oder x2 ; x3,
je nachdem, ob f ðx1 Þ . f ðx3 Þ < 0 oder f ðx2 Þ . f ðx3 Þ < 0 ist usw.
Geometrische Deutung
y
Die Kurve y ¼ f ðxÞ wird zwischen x1 und
x2 durch die dortige Sekante ersetzt. Der
Schnittpunkt dieser Sekante mit der x-Achse
liefert einen verbesserten Näherungswert für
die gesuchte Lösung (Nullstelle x). Dann
wird das Verfahren mit den Startwerten
x1 ; x3 oder x2 ; x3 wiederholt (siehe weiter
oben).
P2
Sekante
y2
y = f(x)
x1
x3
y1
x
x
x2
P1
&
Beispiel
Nullstellenberechnung der Funktion f ðxÞ ¼ x 3 / 0;1 x / 1: x 3 / 0;1 x / 1 ¼ 0 oder x 3 ¼ 0;1 x þ 1
Startwerte: x1 ¼ 0;95 und x2 ¼ 1;05
(aus der Skizze entnommen, die gesuchte Lösung
liegt in der Nähe von x ¼ 1):
y
y = 0,1x + 1
f ðx1 Þ . f ðx2 Þ ¼ f ð0;95Þ . f ð1;05Þ ¼
¼ ð/ 0;2376Þ . ð0;0526Þ < 0
Verbesserter Wert nach der Regula Falsi:
x2 / x1
x3 ¼ x2 /
. y2 ¼
y2 / y1
¼ 1;05 /
1;05 / 0;95
. 0;0526 ¼
0;0526 / ð/ 0;2376Þ
¼ 1;0319 ' 1;032
Kontrolle:
f ð1;0319Þ ¼ / 0;0044 ' 0
y = x3
1,5
1
0,5
1,5
0,5
x
≈1
&
24
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
4.5 Tangentenverfahren von Newton
Ausgehend von einem geeigneten Startwert x0 (auch Roh-, Näherungs- oder Anfangswert
genannt) erhält man nach der Iterationsvorschrift
xn ¼ xn / 1 /
f ðxn / 1 Þ
f 0 ðxn / 1 Þ
ðn ¼ 1; 2; 3; . . .Þ
eine Folge von Näherungswerten x0 ; x1 ; x2 ; . . . für die gesuchte Lösung x der Gleichung f ðxÞ ¼ 0. Im Falle der Konvergenz verdoppelt sich mit jedem Iterationsschritt die
Anzahl der gültigen Dezimalstellen.
Konvergenzbedingung
Die Folge der Näherungswerte x0 ; x1 ; x2 ; . . . konvergiert gegen die gesuchte Lösung x
der Gleichung f ðxÞ ¼ 0, wenn im Intervall ½ a; b %, in dem alle Näherungswerte liegen,
die folgende Bedingung erfüllt ist:
"
"
" f ðxÞ . f 00 ðxÞ "
"
"
" ½ f 0 ðxÞ% 2 " < 1
y
y = f(x)
Tangente
in P0
P0
Geometrische Deutung
Die Kurve y ¼ f ðxÞ wird an der Stelle x0
durch die dortige Tangente ersetzt. Der
Schnittpunkt der Tangente mit der x-Achse
liefert dann einen verbesserten Näherungswert x1 für die gesuchte Lösung (Nullstelle
x). Dann wird das beschriebene Verfahren
mit x1 als Startwert wiederholt usw..
&
Beispiel
P1
y0
y1
x
x2
x1
x
x0
y
ln x þ x / 2;8 ¼ 0
oder
ln x ¼ / x þ 2;8
Startwert nach nebenstehendem Bild: x0 ¼ 2
y = –x + 2,8
f ðxÞ ¼ ln x þ x / 2;8
f 0 ðxÞ ¼
Tangente
in P1
1
þ 1;
x
f 00 ðxÞ ¼ /
1
x2
Konvergenzbedingung für den Startwert
f ð2Þ ¼ / 0;10685 ;
"
"
" f ð2Þ . f 00 ð2Þ "
"
"
" ½ f 0 ð2Þ% 2 " ¼
y = ln x
x0 ¼ 2:
f 0 ð2Þ ¼ 1;5 ;
f 00 ð2Þ ¼ / 0;25
"
"
" ð/ 0;10685Þ . ð/ 0;25Þ "
"
" ¼
"
"
2
1;5
¼ 0;01187 < 1
Die Konvergenzbedingung ist somit erfüllt.
1
1
x
≈2
5 Ungleichungen mit einer Unbekannten
25
Newton-Iteration (zwei Schritte):
n
xn / 1
f 0 ðxn / 1 Þ
f ðxn / 1 Þ
xn
1
2
/0,106 85
1,5
2,071 23
2
2,071 23
/0,000 63
1,482 80
2,071 65
Lösung:
x ¼ 2;071 65
ðKontrolle :
f ð2;071 65Þ ¼ / 0;000 005 ' 0Þ
&
5 Ungleichungen mit einer Unbekannten
Ungleichungen mit einer Unbekannten x entstehen, wenn man zwei Terme T1 ðxÞ und
T2 ðxÞ durch eines der Relationszeichen „< “, „> “, „) “, „( “, miteinander verbindet.
Sie lassen sich in vielen Fällen (ähnlich wie Gleichungen) durch sog. „äquivalente Umformungen“ lösen. Zu diesen gehören:
1. Die Seiten einer Ungleichung dürfen miteinander vertauscht werden, wenn gleichzeitig
das Relationszeichen umgedreht wird.
2. Auf beiden Seiten einer Ungleichung darf ein beliebiger Term TðxÞ addiert oder subtrahiert werden.
3. Eine Ungleichung darf mit einem beliebigen positiven Term TðxÞ > 0 multipliziert
oder durch einen solchen Term dividiert werden.
4. Eine Ungleichung darf mit einem beliebigen negativen Term TðxÞ < 0 multipliziert
oder durch einen solchen Term dividiert werden, wenn gleichzeitig das Relationszeichen
umgedreht wird.
Anmerkungen
(1)
(2)
&
Bei der Multiplikation bzw. Division mit einem Term TðxÞ muss TðxÞ ¼
6 0 vorausgesetzt werden. Kann TðxÞ sowohl positiv als auch negativ werden, so ist eine Fallunterscheidung durchzuführen.
Die Lösungsmengen von Ungleichungen sind in der Regel Intervalle bzw. Vereinigungen von Intervallen.
Beispiel
x2 < x
oder
x 2 / x ¼ x ðx / 1Þ < 0
Wir lösen diese Ungleichung wie folgt durch Fallunterscheidung (das Produkt kann nur negativ sein, wenn
die Faktoren x und x / 1 ein unterschiedliches Vorzeichen haben).
'
1. Fall: x > 0
) x > 0 und x < 1 ) 0 < x < 1
x /1 < 0
2. Fall:
x < 0
x /1 > 0
Lösungsintervall:
'
)
0 < x < 1
x < 0
und
x > 1
)
Widerspruch
&
26
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
Häufig lassen sich Ungleichungen mit Hilfe einer Skizze anschaulich lösen, wie wir am
soeben behandelten Beispiel zeigen wollen.
Beispiel
&
Die Lösungen der Ungleichung x 2 < x liegen dort, wo die Parabel y ¼ x 2 unterhalb der Geraden
y ¼ x verläuft. Lösungsweg: Kurvenschnittpunkte berechnen, Skizze anfertigen und das Lösungsintervall
„ablesen“.
Kurvenschnittpunkte:
x2 ¼ x
x1 ¼ 0 ;
oder
y
x ðx / 1Þ ¼ 0
)
Aus der Skizze folgt:
y=x
1
x2 ¼ 1
L ¼ ð0;1Þ
0,5
y = x2
0,5
1
x
0<x<1
&
6 Lehrsätze aus der elementaren Geometrie
6.1 Satz des Pythagoras
In einem rechtwinkligen Dreieck gilt:
C
c2 ¼ a2 þ b2
a; b:
c:
Katheten
Hypotenuse
a
b
A
B
c
6.2 Höhensatz
In einem rechtwinkligen Dreieck gilt:
C
h2 ¼ p . q
a; b: Katheten
h:
Höhe
c:
Hypotenuse ðc ¼ p þ qÞ
p; q: Hypotenusenabschnitte
b
A
h
q
a
p
c=p+q
B
6 Lehrsätze aus der elementaren Geometrie
27
6.3 Kathetensatz (Euklid)
In einem rechtwinkligen Dreieck gilt:
a2 ¼ c . p
a; b:
c:
p; q:
und
C
b2 ¼ c . q
Katheten
Hypotenuse ðc ¼ p þ qÞ
Hypotenusenabschnitte
b
q
A
a
h
p
c=p+q
6.4 Satz des Thales
B
C2
Jeder Peripheriewinkel über einem Kreisdurchmesser AB ist ein rechter Winkel. Die
Winkel bei C1 ; C2 und C3 sind jeweils
rechte Winkel.
C1
C3
A
B
M
6.5 Strahlensätze
1. Strahlensatz
Werden zwei von einem gemeinsamen Punkt
S ausgehende Strahlen von Parallelen geschnitten, so verhalten sich die Abschnitte
auf dem einen Strahl wie die entsprechenden
Abschnitte auf dem anderen Strahl:
S A1
S B1
¼
S A2
S B2
bzw:
S A1
S B1
¼
B1 B2
A1 A2
B2
B1
S
A1
A2
2. Strahlensatz
Werden zwei von einem gemeinsamen Punkt
S ausgehende Strahlen von Parallelen geschnitten, so verhalten sich die Abschnitte
auf den beiden Parallelen wie die entsprechenden Abschnitte auf einem Strahl, vom
Schnittpunkt S aus gemessen:
A1 B1
S A1
S B1
¼
¼
A2 B2
S A2
S B2
B2
B1
S
A1
A2
28
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
6.6 Sinussatz
In einem beliebigen Dreieck gilt:
C
g
a
b
c
¼
¼
sin a
sin b
sin g
a
b
A
6.7 Kosinussatz
a
b
c
In einem beliebigen Dreieck gilt:
B
C
g
a 2 ¼ b 2 þ c 2 / 2 b c . cos a
a
b
b 2 ¼ a 2 þ c 2 / 2 a c . cos b
c 2 ¼ a 2 þ b 2 / 2 a b . cos g
A
a
b
c
B
7 Ebene geometrische Körper (Planimetrie)
Bezeichnungen
A: Fläche
d : Diagonale
h: Höhe
r; R: Radius
U : Umfang
7.1 Dreiecke
7.1.1 Allgemeine Beziehungen
C
a þ b þ g ¼ 180"
1
1
ch ¼
b c . sin a ¼
2
2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ s ðs / aÞ ðs / bÞ ðs / cÞ ðs ¼ U=2Þ
g
b
A ¼
U¼ aþbþc
Schwerpunkt S:
Schnittpunkt der Seitenhalbierenden
a
b
c
Sinussatz:
¼
¼
sin a
sin b
sin g
Kosinussatz: a 2 ¼ b 2 þ c 2 / 2 b c . cos a
b 2 ¼ a 2 þ c 2 / 2 a c . cos b
c 2 ¼ a 2 þ b 2 / 2 a b . cos g
A
a
S
c
h
a
b
B
Der Schwerpunkt S teilt die Seitenhalbierenden jeweils im Verhältnis
2 : 1 (von der jeweiligen Ecke aus betrachtet).
7 Ebene geometrische Körper (Planimetrie)
29
Inkreis eines Dreiecks
C
Mittelpunkt M des Inkreises:
Schnittpunkt der Winkelhalbierenden
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðs / aÞ ðs / bÞ ðs / cÞ
r ¼
s
ðs ¼ U=2Þ
a
r
b
M
A
B
c
Umkreis eines Dreiecks
C
Mittelpunkt M des Umkreises:
Schnittpunkt der Mittelsenkrechten
b
abc
R ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 s ðs / aÞ ðs / bÞ ðs / cÞ
M
A
ðs ¼ U=2Þ
a
R
B
c
7.1.2 Spezielle Dreiecke
7.1.2.1 Rechtwinkliges Dreieck
g ¼ 90"
A ¼
und
1
1
hc ¼
ab
2
2
b
Pythagoras:
c2 ¼ a2 þ b2
Höhensatz:
h2 ¼ p . q
Kathetensatz:
a 2 ¼ c . p;
p, q:
C
a þ b ¼ 90"
A
a
h
p
a q
b
B
c=p+q
b2 ¼ c . q
Hypotenusenabschnitte
7.1.2.2 Gleichschenkliges Dreieck
C
g ¼ 180" / 2 a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
1
A ¼
hc ¼
c 4a2 / c2
2
4
a ¼ b,
a ¼ b,
U ¼ 2a þ c
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
h ¼
4a2 / c2
2
g
a
A
a
a
h
c
2
c
c
2
a
B
30
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
7.1.2.3 Gleichseitiges Dreieck
C
a ¼ b¼ c
60°
a ¼ b ¼ g ¼ 60"
A ¼
1
1 2 pffiffiffi
ah ¼
a
3
2
4
a
U ¼ 3a
h ¼
a
h
S
1 pffiffiffi
a 3
2
a
2
60°
A
a
a
2
60°
B
Der Schwerpunkt S hat von jeder Seite den
Abstand h=3.
7.2 Quadrat
a
A ¼ a2
d
U ¼ 4a
pffiffiffi
d ¼ a 2
Schwerpunkt S:
Schnittpunkt der Diagonalen
S
a
a
d
Die Diagonalen halbieren sich in S und stehen senkrecht aufeinander.
a
7.3 Rechteck
a
A ¼ ab
b
U ¼ 2a þ 2b
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
d ¼ a2 þ b2
d
a
Schwerpunkt S:
Schnittpunkt der Diagonalen
Die Diagonalen halbieren sich in S.
Sonderfall: a ¼ b
S
d
) Quadrat
b
7 Ebene geometrische Körper (Planimetrie)
31
7.4 Parallelogramm
Parallelogramm: Viereck, dessen gegenüberliegende Seiten parallel und gleichlang sind.
a
A ¼ a h ¼ a b . sin a
U ¼ 2a þ 2b
h ¼ b . sin a
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
d1=2 ¼ a þ b + 2 a b 2 / h 2
Schwerpunkt S:
Schnittpunkt der Diagonalen
b
h
a
d1
S
b
d2
a
a
a: Grundlinie
b: Seitenlinie
Die Diagonalen halbieren sich in S.
Sonderfall: a ¼ 90" ) Rechteck
7.5 Rhombus oder Raute
Rhombus oder Raute: Parallelogramm mit vier gleichlangen Seiten ða ¼ bÞ.
a
1
d1 d2
A ¼ a h ¼ a . sin a ¼
2
U ¼ 4a
a
2
h ¼ a . sin a
d1 ¼ 2 a . cos ða=2Þ
d1
a
S
h
d2
d2 ¼ 2 a . sin ða=2Þ
Schwerpunkt S:
Schnittpunkt der Diagonalen
a
a
a
Die Diagonalen halbieren sich in S und stehen senkrecht aufeinander.
Sonderfall: a ¼ 90" ) Quadrat
7.6 Trapez
Trapez: Viereck mit zwei gegenüberliegenden parallelen Seiten (Seitenlängen: a; b).
b
1
ða þ bÞ
2
1
A ¼ mh ¼
ða þ bÞ h
2
m ¼
Schwerpunkt S:
Auf der Verbindungslinie der Mitten der
beiden parallelen Grundlinien im Abstand
h ða þ 2 bÞ
von der Grundlinie a
3 ða þ b Þ
h
a
m
a
b
h
2
a, b:
Grundlinien ða k bÞ
m:
Mittellinie
32
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
7.7 Reguläres n-Eck
Reguläres n-Eck: Regelmäßiges Vieleck (n-Eck) mit n gleichlangen Seiten der Länge a
und dem Zentriwinkel j ¼ 2 p=n bzw. j ¼ 360" =n. Die n Ecken liegen auf einem
Kreis mit dem Radius r (Umkreis).
1
A ¼
n a 2 . cot ðp=nÞ
4
U ¼ na
a
a
r ¼
¼
2 . sin ðj=2Þ
2 . sin ðp=nÞ
Schwerpunkt S:
Mittelpunkt M des Umkreises
a
a
r
a
f
r
a
M
a
a
a
a
7.8 Kreis
A ¼ pr2
U ¼ 2pr
Schwerpunkt S:
Kreismittelpunkt M
7.9 Kreissektor oder Kreisausschnitt
9
1 2
1
r j ¼
rb =
A ¼
j in rad
2
2
;
b ¼ rj
Schwerpunkt S:
Auf der Symmetrieachse im Abstand
4 r . sin ðj=2Þ
vom Kreismittelpunkt M
3j
r
M
b
r
f
r
M
j: Zentriwinkel
7.10 Kreissegment oder Kreisabschnitt
A¼
1 2
r ðj / sin jÞ
2
x ¼ 2 r . sin ðj=2Þ
y ¼ r ½1 / cos ðj=2Þ% ¼ 2 r . sin 2 ðj=4Þ
Schwerpunkt S:
Auf der Symmetrieachse im Abstand
4 r . sin 3 ðj=2Þ
vom Kreismittelpunkt M
3 ðj / sin jÞ
y
x
ðj in radÞ
r
f
r
M
j: Zentriwinkel
8 Räumliche geometrische Körper (Stereometrie)
33
7.11 Kreisring
R
A ¼ p ðR 2 / r 2 Þ
U ¼ 2 p ðr þ RÞ
Schwerpunkt S:
Mittelpunkt M der beiden
konzentrischen Kreise
r, R:
r
M
Innen- bzw. Außenradius
7.12 Ellipse
A ¼ pab
/
pffiffiffiffiffiffi .
U ' p 1;5 ða þ bÞ / a b
b
a
M
Schwerpunkt S:
Mittelpunkt M der Ellipse
a, b: Große bzw. kleine Halbachse
8 Räumliche geometrische Körper (Stereometrie)
Bezeichnungen
A: Grundfläche
d:
Raumdiagonale
O: Oberfläche
r, R: Radius
h: Höhe
M: Mantelfläche
s: Mantellinie
V: Volumen
8.1 Prisma
Die beiden Grundflächen eines schiefen Prismas liegen in parallelen Ebenen und sind
kongruente n-Ecke (grau unterlegt), die n Seitenflächen sind Parallelogramme.
A0
Ao ¼ Au
V ¼ Ao h ¼ Au h
Schwerpunkt S:
Liegt auf der Verbindungslinie der Schwerpunkte der beiden Grundflächen und halbiert diese Linie
h
Au
·
34
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
Spat oder Parallelepiped: Die Grundflächen sind Parallelogramme, der Schwerpunkt S
liegt im Schnittpunkt der Raumdiagonalen (diese halbieren sich in S).
Gerades Prisma: Die Kanten stehen senkrecht auf den beiden Grundflächen
(Sonderfälle: Quader und Würfel).
Reguläres Prisma: Ein gerades Prisma, dessen Grundflächen reguläre n-Ecke sind.
8.2 Würfel
V ¼ a3
O ¼ 6a2
pffiffiffi
d ¼ a 3
d
S
Schwerpunkt S:
Schnittpunkt der Raumdiagonalen
a:
a
a
Kantenlänge
a
8.3 Quader
V ¼ abc
d
O ¼ 2 ða b þ a c þ b cÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
d ¼ a2 þ b2 þ c2
S
Schwerpunkt S:
Schnittpunkt der Raumdiagonalen
a, b, c:
c
b
a
Kantenlängen
Sonderfall: a ¼ b ¼ c
)
Würfel
8.4 Pyramide
Die Grundfläche ist ein Vieleck (Dreieck, Viereck usw.), die Seitenflächen sind Dreiecke,
die in der Spitze zusammenlaufen.
1
Ah
3
Schwerpunkt S:
Auf der Verbindungslinie der Spitze mit
dem Schwerpunkt der Grundfläche im
Abstand h=4 von der Grundfläche
V ¼
Reguläre oder gleichseitige Pyramide:
Die Grundfläche ist ein regelmäßiges Vieleck, die Pyramidenspitze liegt senkrecht über
dem Schwerpunkt der Grundfläche.
h
A
8 Räumliche geometrische Körper (Stereometrie)
35
8.5 Pyramidenstumpf
Die Schnittflächen Au und Ao sind parallel, die Seitenflächen sind Trapeze.
4
pffiffiffiffiffiffiffiffiffiffiffi
h !
Au þ Au Ao þ Ao
3
Schwerpunkt S:
Auf der Verbindungslinie der Schwerpunkte der beiden Schnittflächen Au
und Ao im Abstand
1
0
pffiffiffiffiffiffiffiffiffiffiffi
h Au þ 2 Au Ao þ 3 Ao
1
0
pffiffiffiffiffiffiffiffiffiffiffi
4 Au þ Au Ao þ Ao
A0
V ¼
h
Au
von der Schnittfläche Au (Grundfläche)
A u : Grundfläche
A o : Deckfläche
h: Höhe
8.6 Tetraeder oder dreiseitige Pyramide
Das Tetraeder ist ein Spezialfall der Pyramide, die Grundfläche ist ein Dreieck.
V ¼
1
Ah
3
Schwerpunkt S:
Auf der Verbindungslinie der Spitze mit
dem Schwerpunkt der Grundfläche im
Abstand h=4 von der Grundfläche
h
A
A: Grundfläche
h: Höhe
Reguläres Tetraeder: Die vier Flächen sind gleichseitige Dreiecke mit der Seitenlänge a.
Volumen und Oberfläche berechnen sich wie folgt:
1 3 pffiffiffi
a
2
12
pffiffiffi
O ¼ a2 3
V ¼
36
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
8.7 Keil
Die Grundfläche ist ein Rechteck, die vier Seitenflächen gleichschenklige Dreiecke bzw.
gleichschenklige Trapeze.
c
1
V ¼
b h ð2 a þ cÞ
6
a; b: Grundseiten
c:
Obere Kantenlinie
h
·
·
b
a
8.8 Gerader Kreiszylinder
r
V ¼ pr2h
M ¼ 2prh
O ¼ 2 p r ðr þ hÞ
h
S
Schwerpunkt S:
Auf der Symmetrieachse im Abstand h=2
von der Grundfläche
r
8.9 Gerader Kreiskegel
1
pr2h
3
M ¼ prs
V ¼
O ¼ p r ðr þ sÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s ¼ r2 þ h2
Schwerpunkt S:
Auf der Symmetrieachse im Abstand h=4
von der Grundfläche
s
h
S
r
8 Räumliche geometrische Körper (Stereometrie)
37
8.10 Gerader Kreiskegelstumpf
Die beiden kreisförmigen Schnittflächen mit den Radien r und R sind parallel.
1
V ¼
p h ðR 2 þ R r þ r 2 Þ
3
M ¼ p ðR þ rÞ s
r
s
h
S
O ¼ p ½ R 2 þ r 2 þ ðR þ rÞ s%
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s ¼ h 2 þ ðR / r Þ 2
Schwerpunkt S:
Auf der Symmetrieachse im Abstand
2
2
h ðR þ 2 R r þ 3 r Þ
4 ðR 2 þ R r þ r 2 Þ
R
h: Höhe des Kegelstumpfes
s: Seitenlinie (Mantellinie)
von der Grundfläche (Radius R)
Sonderfall: r ¼ 0
)
Kreiskegel
8.11 Kugel
4
pR3
3
O ¼ 4pR2
V¼
R
Schwerpunkt S:
Kugelmittelpunkt M
M
8.12 Kugelausschnitt oder Kugelsektor
V ¼
2
pR2h
3
O ¼ p R ð2 h þ rÞ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ h ð2 R / hÞ
r
h
R
R
M
Schwerpunkt S:
Auf der Symmetrieachse im Abstand
3
ð2 R / hÞ vom Kugelmittelpunkt M
8
Sonderfälle: h ¼ R ) Halbkugel
h ¼ 2 R ) Kugel
h: Höhe des Kugelausschnitts
38
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
8.13 Kugelschicht oder Kugelzone
1
p h ð3 r 21 þ 3 r 22 þ h 2 Þ
6
M ¼ 2pRh
O ¼ p ð2 R h þ r 21 þ r 22 Þ
r1
V ¼
Schwerpunkt S:
Auf der Symmetrieachse im Abstand
3 ðr 42 / r 41 Þ
2 h ð3 r 21 þ 3 r 22 þ h 2 Þ
vom Kugelmittelpunkt M
Sonderfälle: h ¼ 2 R ) Kugel
r1 ¼ 0 ) Kugelabschnitt
r2
h
M
R
r1 ; r2 : Radien der kreisförmigen
Grundflächen
h: Höhe der Kugelschicht
(Schichtdicke)
8.14 Kugelabschnitt, Kugelsegment, Kugelkappe oder Kalotte
1
p h 2 ð3 R / hÞ ¼
3
1
¼
p h ð3 r 2 þ h 2 Þ
6
M ¼ 2pRh
V ¼
O ¼ p ð2 R h þ r 2 Þ ¼ p h ð4 R / hÞ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ h ð2 R / hÞ
Schwerpunkt S:
Auf der Symmetrieachse im Abstand
3 ð2 R / hÞ 2
4 ð3 R / hÞ
r
RR
M
r:
h:
Radius der kreisförmigen
Grundfläche
Höhe der Kugelkappe
vom Kugelmittelpunkt M
Sonderfälle: h ¼ r ¼ R ) Halbkugel
h ¼ 2 R ) Kugel
8.15 Ellipsoid
4
pabc
3
Schwerpunkt S:
Mittelpunkt M des Ellipsoids
c
V ¼
Sonderfall: a ¼ b ¼ c ) Kugel mit
dem Radius R ¼ a
h
M
a
a, b, c:
b
Halbachsen des
Ellipsoids
8 Räumliche geometrische Körper (Stereometrie)
Rotationsellipsoid
Rotationsachse:
V ¼
39
(a = b)
Achse 2 c
4
pa2 c
3
8.16 Rotationsparaboloid
1
pr2 h
2
Schwerpunkt S:
Auf der Symmetrieachse im Abstand
r
V¼
S
h
2
h vom Scheitelpunkt
3
r:
h:
Scheitelpunkt
Radius der kreisförmigen Deckfläche
Höhe des Rotationsparaboloids
8.17 Tonne oder Fass
Der Rotationskörper wird erzeugt durch Drehung einer Kurve mit sphärischer, elliptischer oder parabolischer Krümmung. Die beiden parallelen Grundflächen sind Kreise
vom Radius r.
Sphärische oder elliptische Krümmung
V¼
1
p h ð2 R 2 þ r 2 Þ
3
Parabolische Krümmung
V ¼
2r
1
p h ð8 R 2 þ 4 R r þ 3 r 2 Þ
15
2R
h
40
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
8.18 Torus
Die in Bild a) skizzierte Kreisfläche erzeugt bei Drehung um die eingezeichnete Achse den
in Bild b) dargestellten Torus ðRing mit einem kreisförmigen Querschnitt; r < RÞ.
V ¼ 2p2r2R
2r
O ¼ 4p2rR
R
r
a)
R
b)
8.19 Guldinsche Regeln für Rotationskörper
Mantelfläche eines Rotationskörpers (1. Guldinsche Regel)
Die Mantelfläche eines Rotationskörpers ist gleich dem Produkt aus der Länge der rotierenden Kurve, die diesen Körper erzeugt, und dem Umfang des Kreises, den der Schwerpunkt
der Kurve bei der Rotation beschreibt:
M ¼ s ð2 p x0 Þ ¼ 2 p x0 s
s:
x0 :
Länge der rotierenden Kurve
Abstand des Schwerpunktes S
der rotierenden Kurve von der
Rotationsachse
y
x0
S
s
x
&
Beispiel
Für den Torus gilt (siehe Abschnitt 8.18):
s ¼ 2pr
x0 ¼ R
(Umfang des rotierenden Kreises)
(Abstand Kreislinienschwerpunkt –– Rotationsachse)
Somit ist
M ¼ 2 p x0 s ¼ 2 p . R . 2 p r ¼ 4 p 2 r R
die Mantelfläche (Oberfläche) des Torus.
&
9 Koordinatensysteme
41
Volumen eines Rotationskörpers (2. Guldinsche Regel)
Das Volumen eines Rotationskörpers ist gleich dem Produkt aus dem Flächeninhalt des
rotierenden Flächenstücks, das diesen Körper erzeugt, und dem Umfang des Kreises, den
der Schwerpunkt des Flächenstücks bei der Rotation beschreibt:
y
V ¼ A ð2 p x0 Þ ¼ 2 p x0 A
A:
Flächeninhalt des rotierenden
Flächenstücks
x0 : Abstand des Schwerpunktes S des
rotierenden Flächenstücks von der
Rotationsachse
x0
S
A
x
Beispiel
&
Für den Torus gilt (siehe Abschnitt 8.18):
A ¼ pr2
x0 ¼ R
(Fläche des rotierenden Kreises)
(Abstand Kreisflächenschwerpunkt –– Rotationsachse)
Somit ist
V ¼ 2 p x0 A ¼ 2 p . R . p r 2 ¼ 2 p 2 r 2 R
das Volumen des Torus.
&
9 Koordinatensysteme
9.1 Ebene Koordinatensysteme
9.1.1 Rechtwinklige oder kartesische Koordinaten
Die beiden Koordinatenachsen stehen senkrecht aufeinander, die Lage des Punktes P wird
durch zwei mit einem Vorzeichen versehene Abstandskoordinaten x und y, die sog.
rechtwinkligen oder kartesischen Koordinaten, beschrieben:
O:
x:
y:
Ursprung, Nullpunkt
Abszisse o
des Punktes P
Ordinate
j x j; j y j: Abstand des Punktes P
von der y- bzw. x-Achse
y
P = (x;y)
y
0
x
x
42
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
9.1.2 Polarkoordinaten
Die Lage des Punktes P wird durch eine Abstandskoordinate r ( 0 und eine Winkelkoordinate j, die sog. Polarkoordinaten, beschrieben (siehe hierzu auch XIV.6.1):
O: Pol
r : Abstand des Punktes P vom Pol O
j: Winkel zwischen dem Strahl OP
und der Polarachse
P = (r;f)
r
0
f
Polarachse
Der Winkel j wird positiv gemessen bei Drehung im Gegenuhrzeigersinn, negativ bei
Drehung im Uhrzeigersinn. Er ist nur bis auf ganzzahlige Vielfache von 2 p bzw. 360"
bestimmt. Man beschränkt sich daher bei der Winkelangabe meist auf den im Intervall
0 ) j < 2 p gelegenen Hauptwert (im Gradmaß: 0" ) j < 360" ) 4Þ . Für den Pol
selbst ist r ¼ 0, der Winkel j dagegen ist unbestimmt.
9.1.3 Koordinatentransformationen
9.1.3.1 Parallelverschiebung eines kartesischen Koordinatensystems
Das neue u; v-System geht durch Parallelverschiebung aus dem alten x, y-System hervor:
ðx; yÞ: Koordinaten des Punktes P im alten System (x, y-System)
ðu; vÞ: Koordinaten des Punktes P im neuen System (u, v-System)
ða; bÞ: Koordinaten des Nullpunktes O 0 des neuen u, v-Systems, bezogen auf das alte
x,y-System
a:
Verschiebung der y-Achse (a > 0: nach rechts; a < 0: nach links)
b:
Verschiebung der x-Achse (b > 0: nach oben; b < 0: nach unten)
x ¼ uþa
bzw.
y ¼ vþb
u ¼ x /a
v ¼ y/b
y
v
P
v
y
a
u
0'
0
b
x
x
9.1.3.2 Zusammenhang zwischen den kartesischen und den Polarkoordinaten
Bezeichnungen:
Pol:
y
P
Koordinatenursprung O
Polarachse:
x-Achse
r
y
f
0
4Þ
u
x
Unter dem Hauptwert wird häufig auch der im Intervall / p < j ) p gelegene Wert verstanden.
x
9 Koordinatensysteme
Polarkoordinaten
x ¼ r . cos j;
!
43
Kartesische Koordinaten
y ¼ r . sin j
Kartesische Koordinaten
r ¼
!
Polarkoordinaten
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y
x
, cos j ¼
;
x 2 þ y 2 , sin j ¼
r
r
tan j ¼
y
x
Die Berechnung des Winkels j erfolgt am bequemsten anhand einer Lageskizze (siehe
nachfolgendes Beispiel) oder nach der folgenden vom jeweiligen Quadrant abhängigen
Formel (j im Bogenmaß; im Gradmaß muss p durch 180" ersetzt werden):
Quadrant
I
II, III
IV
j ¼
arctan ðy=xÞ
arctan ðy=xÞ þ p
arctan ðy=xÞ þ 2 p
Sonderfall: x ¼ 0
&
)
j ¼ p=2 für y > 0 , j ¼ 3p=2 für y < 0
Beispiel
Gegeben:
P ¼ ð/4; 3Þ,
Gesucht:
Polarkoordinaten r; j des Punktes P
d. h.
x ¼ /4,
y ¼ 3
y
P
Lösung: Der Punkt P liegt im 2. Quadrant. Aus dem
eingezeichneten rechtwinkligen Dreieck mit den Katheten
der Längen 3 und 4 und der Hypotenuse r berechnen wir
der Reihe nach r, den Hilfswinkel a und daraus j:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ 42 þ 32 ¼ 5
3
3
tan a ¼
) a ¼ arctan
¼ 36;87" )
4
4
j ¼ 180" / a ¼ 143;13"
3
r
3
4
f
a
x
–4
Zum gleichen Ergebnis führt auch die obige Formel (2. Quadrant):
j ¼ arctan ðy = xÞ þ p ¼ arctan ð3 = / 4Þ þ p ¼ arctan ð/ 3 = 4Þ þ p ¼ 2;4981 ¼ 143;13"
&
9.1.3.3 Drehung eines kartesischen Koordinatensystems
Das neue u; v-System geht durch Drehung um den Winkel j um den Nullpunkt aus dem
alten x; y-System hervor.
ðx; yÞ: Koordinaten des Punktes P im alten System
y
ðu; vÞ: Koordinaten des Punktes P im neuen System
u ¼ y . sin j þ x . cos j
v ¼ y . cos j / x . sin j
P
v
v
u
y
u
x ¼ u . cos j / v . sin j
y ¼ u . sin j þ v . cos j
f
0
x
x
44
I Allgemeine Grundlagen aus Algebra, Arithmetik und Geometrie
9.2 Räumliche Koordinatensysteme
9.2.1 Rechtwinklige oder kartesische Koordinaten
Die drei Koordinatenachsen (x; y- und z-Achse) stehen paarweise senkrecht aufeinander
und besitzen die gleiche Orientierung wie Daumen, Zeige- und Mittelfinger der rechten
Hand (rechtshändiges System). Die Lage des Raumpunktes P wird durch drei Abstandskoordinaten x, y und z, die sog. rechtwinkligen oder kartesischen Koordinaten, beschrieben:
O:
z
Ursprung, Nullpunkt
z
x; y; z: Senkrechte (mit einem Vorzeichen
versehene) Abstände des Raumpunktes P von den drei
Koordinatenebenen
P = (x;y;z)
z
x; y; z 2 R
z:
y
0
Höhenkoordinate
y
x
x
y
x
9.2.2 Zylinderkoordinaten
Die Lage des Raumpunktes P wird durch zwei Abstandskoordinaten r, z und eine Winkelkoordinate j, die sog. Zylinderkoordinaten, beschrieben (siehe hierzu auch XIV.6.2) 5) :
O:
z
Ursprung, Nullpunkt
z
r; j: Polarkoordinaten des Projektionspunktes P 0 in der x; y-Ebene
ðr ( 0; 0 ) j < 2 pÞ
z:
r:
r
P
Höhenkoordinate
(entspricht der kartesischen
Koordinate z mit z 2 R)
z
0
Senkrechter Abstand des Punktes P von
der z-Achse
x
x
f
r
y
y
x
y
P'
9.2.3 Zusammenhang zwischen den kartesischen und den Zylinderkoordinaten
Zylinderkoordinaten ( r; j; z)
x ¼ r . cos j;
5Þ
! Kartesische Koordinaten (x; y; z)
y ¼ r . sin j;
z ¼ z
Statt r verwendet man häufig auch r (wenn Verwechslungen mit der Kugelkoordinate r auszuschließen sind).
9 Koordinatensysteme
45
Kartesische Koordinaten (x; y; z)
r ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 þ y2;
Sonderfall: x ¼ 0
sin j ¼
)
y
;
r
!
Zylinderkoordinaten ( r; j; z)
cos j ¼
x
;
r
tan j ¼
y
;
x
z ¼ z
j ¼ p=2 für y > 0 , j ¼ 3p=2 für y < 0
9.2.4 Kugelkoordinaten
z
Die Lage des Raumpunktes P wird durch
eine Abstandskoordinate r und zwei Winkelkoordinaten J und j, die sog. Kugelkoordinaten, beschrieben (siehe hierzu auch
XIV.6.3):
z
r
P
r
u
0
z
y
y
f
x
x
x
O:
r:
y
Ursprung, Nullpunkt
*!
Abstand des Punktes P vom Nullpunkt (Länge des Ortsvektors ~
r ¼ OP ; r ( 0)
J:
Winkel zwischen dem Ortsvektor ~
r und der positiven z-Achse (Breitenkoordinate
mit 0 ) J ) p)
j:
Winkel zwischen der Projektion des Ortsvektors ~
r auf die x; y-Ebene und der
positiven x-Achse (Längenkoordinate mit 0 ) j < 2 p)
9.2.5 Zusammenhang zwischen den kartesischen und den Kugelkoordinaten
Kugelkoordinaten (r; J; j)
x ¼ r . sin J . cos j;
! Kartesische Koordinaten (x; y; z)
y ¼ r . sin J . sin j;
Kartesische Koordinaten (x; y; z)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ x 2 þ y 2 þ z 2;
!
J ¼ arccos
z ¼ r . cos J
Kugelkoordinaten (r; J; j)
!
z
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ;
x2 þ y2 þ z2
tan j ¼
y
x
Hinweis: Berechnung der Längenkoordinate j unter Verwendung der in Abschnitt 9.1.3.2
angegebenen Formeln.
46
II Vektorrechnung
1 Grundbegriffe
1.1 Vektoren und Skalare
Vektoren sind gerichtete Größen, die durch
eine Maßzahl und eine Richtung vollständig
beschrieben und in symbolischer Form durch
einen Pfeil dargestellt werden (Bild a)). Die
Länge des Pfeils heißt Betrag j ~
a j ¼ a des
Vektors ~
a, die Pfeilspitze legt die Richtung
(Orientierung) des Vektors fest.
Q
a
a = PQ
a =a
a)
P
b)
Ein Vektor ~
a lässt sich auch eindeutig durch einen Anfangs- und Endpunkt festlegen:
*!
~
a ¼ PQ (Bild b)). Bei einer physikalisch-technischen Vektorgröße gehört zur vollständigen Beschreibung noch die Angabe der Maßeinheit.
Skalare dagegen sind Größen ohne Richtungseigenschaft. Sie sind durch Angabe einer
Maßzahl (bzw. einer Maßzahl und einer Maßeinheit) eindeutig beschrieben.
In
1.
2.
3.
den Anwendungen unterscheidet man:
Freie Vektoren: Sie dürfen parallel zu sich selbst verschoben werden.
Linienflüchtige Vektoren: Sie sind längs ihrer Wirkungslinie verschiebbar.
Gebundene Vektoren: Sie werden von einem festen Punkt aus abgetragen.
1.2 Spezielle Vektoren
Nullvektor ~
0 : Vektor der Länge 0 (seine Richtung ist unbestimmt)
Einheitsvektor ~
e : Vektor der Länge 1
*!
Ortsvektor ~
r ðPÞ ¼ OP : Vom Nullpunkt O zum Punkt P gerichteter Vektor
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_2
1 Grundbegriffe
47
1.3 Gleichheit von Vektoren
Zwei Vektoren heißen gleich, wenn sie sich durch Parallelverschiebung zur Deckung bringen lassen. Sie stimmen in Betrag und Richtung und somit auch in ihren Komponenten
überein (siehe II.2.1).
a
~
a ¼ b~ , ax ¼ bx ; ay ¼ by ; az ¼ bz
b
ax ; ay ; az : Skalare Komponenten von ~
a
bx ; by ; bz : Skalare Komponenten von b~
1.4 Kollineare, parallele und antiparallele Vektoren, inverser Vektor
Kollineare Vektoren lassen sich stets durch Parallelverschiebung in eine gemeinsame Linie
bringen (Bild a)).
Parallele Vektoren haben gleiche Richtung (Bild b)). Symbolische Schreibweise: ~
a " " b~:
Antiparallele Vektoren haben entgegengesetzte Richtung (Bild c)). Symbolische Schreibweise: ~
a " # b~.
b
a
b
a
a
b
a
–a
b
a)
b)
c)
d)
Parallele bzw. anti-parallele Vektoren sind demnach kollinear.
Zu jedem Vektor ~
a gibt es einen inversen oder Gegenvektor / ~
a (Bild d)). Er entsteht
aus dem Vektor ~
a durch Richtungsumkehr. Die Vektoren ~
a und / ~
a sind somit gleichlang, ihre Komponenten unterscheiden sich lediglich im Vorzeichen.
48
II Vektorrechnung
2 Komponentendarstellung eines Vektors
2.1 Komponentendarstellung in einem kartesischen Koordinatensystem
Die Einheitsvektoren ~
ex ; ~
ey und ~
ez , auch Basisvektoren genannt, stehen paarweise senkrecht aufeinander und bilden in dieser Reihenfolge ein Rechtssystem (rechtshändiges System), d. h. sie haben dieselbe Orientierung wie Daumen, Zeige- und Mittelfinger der rechten
Hand (Bild a)). Statt ~
ex ; ~
ey ; ~
ez verwendet man auch die Symbole ~
e1 ; ~
e2 ; ~
e3 oder ~
i; ~
j; k~.
z
z
az
P
ez
ex
x
a
ey
ay
y
a)
ax
x
y
b)
In diesem System besitzt ein Vektor ~
a die folgende Komponentendarstellung (Bild b)) 1Þ :
0
1
ax
~
a ¼~
ax þ ~
ay þ ~
az ¼ ax ~
ex þ ay ~
ey þ az ~
ez ¼ @ ay A
az
~
ax ; ~
ay ; ~
az : Vektorkomponenten von ~
a
ax ; ay ; az : Vektorkoordinaten oder skalare Vektorkomponenten von ~
a
0 1
ax
@ ay A : Schreibweise in Form eines sog. Spaltenvektors
az
Schreibweise als Zeilenvektor: ~
a ¼ ðax ay az Þ
2.2 Komponentendarstellung spezieller Vektoren
0
1
x2 / x1
**!
P1 P2 ¼ ðx2 / x1 Þ~
ex þ ðy2 / y1 Þ~
ey þ ðz2 / z1 Þ~
ez ¼ @ y2 / y1 A
z2 / z1
0 1
x
*!
Ortsvektor von P: ~
r ðPÞ ¼ OP ¼ x ~
ex þ y~
ey þ z~
ez ¼ @ y A
z
**!
Vektor P1 P2 :
1Þ
Bei ebenen Vektoren verschwindet die dritte Komponente.
2 Komponentendarstellung eines Vektors
49
0 1
0
Nullvektor: ~
0 ¼ 0~
ex þ 0~
ey þ 0~
ez ¼ @ 0 A
0
0 1
0 1
0 1
1
0
0
Basisvektoren: ~
ex ¼ 1~
ex þ 0~
ey þ 0~
ez ¼ @ 0 A ; analog: ~
ey ¼ @ 1 A ; ~
ez ¼ @ 0 A
0
0
1
2.3 Betrag und Richtungswinkel eines Vektors
Betrag (Länge) eines Vektors
j~
aj ¼ a ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffi
a 2x þ a 2y þ a 2z ¼ ~
a.~
a
ðj ~
a j ( 0Þ
Richtungswinkel eines Vektors (Richtungskosinus)
Für die Richtungswinkel a; b und g, die
der Vektor ~
a 6¼ ~
0 mit den drei Koordinatenachsen (Basisvektoren) bildet, gelten folgende Beziehungen:
cos a ¼
z
a
g
ax
ay
az
; cos b ¼
; cos g ¼
j~
aj
j~
aj
j~
aj
cos 2 a þ cos 2 b þ cos 2 g ¼ 1
a
b
y
x
Hinweis: Für den Nullvektor ~
0 lassen sich keine Richtungswinkel angeben.
Umgekehrt lassen sich die Vektorkoordinaten aus dem Betrag und den drei Richtungswinkeln (Richtungskosinus) des Vektors berechnen:
ax ¼ j ~
a j . cos a ;
&
ay ¼ j ~
a j . cos b ;
az ¼ j ~
a j . cos g
Beispiel
Wir berechnen den Betrag und die drei Richtungswinkel des Vektors ~
a ¼ 4~
ex / 2~
ey þ 5~
ez :
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
4
j~
a j ¼ 4 2 þ ð/ 2Þ 2 þ 5 2 ¼ 45 ¼ 6;71 ;
cos a ¼ pffiffiffiffiffi ¼ 0;5963 ) a ¼ 53;4"
45
/2
cos b ¼ pffiffiffiffiffi ¼ / 0;2981
45
)
b ¼ 107;3" ;
5
cos g ¼ pffiffiffiffiffi ¼ 0;7454
45
)
g ¼ 41;8"
Kontrolle: cos 2 a þ cos 2 b þ cos 2 g ¼ 0;5963 2 þ ð/ 0;2981Þ 2 þ 0;7454 2 ¼ 1
&
50
II Vektorrechnung
3 Vektoroperationen
3.1 Addition und Subtraktion von Vektoren
Geometrische Darstellung
Addition und Subtraktion zweier Vektoren erfolgen nach der Parallelogrammregel.
Summenvektor
Differenzvektor
~
s ¼ ~
aþ
~
d ¼~
a/
b
b~
b~
s
d
Differenzvektor: Zu ~
a wird der inverse
1 Vektor
0
von b~ addiert: d~ ¼ ~
a / b~ ¼ ~
a þ / b~ .
Die Addition mehrerer Vektoren erfolgt nach
der Polygonregel (Vektorpolygon).
a
an
a3
~
s ¼~
a1 þ ~
a2 þ ~
a3 þ . . . þ ~
an
Summenvektor s
Hinweis: Das Vektorpolygon liegt i. Allg.
nicht in einer Ebene.
a2
a1
Komponentendarstellung
Addition und Subtraktion zweier Vektoren erfolgen komponentenweise:
0
1
0 1
0
1
ax
bx
ax + bx
~
a + b~ ¼ @ ay A + @ by A ¼ @ ay + by A
az
bz
az + bz
Rechenregeln
Kommutativgesetz
Assoziativgesetz
~
a þ b~ ¼
0
~
a þ b~ þ ~
c ¼
1
b~ þ ~
a
1
0
~
a þ b~ þ ~
c
3 Vektoroperationen
51
3.2 Multiplikation eines Vektors mit einem Skalar
Geometrische Darstellung
la
l~
a : Vektor mit der Länge j l j . j ~
a j und
der Richtung oder Gegenrichtung des
Vektors ~
a:
a
l > 0 : l~
a "" ~
a
für
la = l a
l < 0 : l~
a "# ~
a
~
l ¼ 0 : l~
a ¼ 0
(Skizze: l > 0)
Komponentendarstellung
Die Multiplikation eines Vektors mit einem reellen Skalar erfolgt komponentenweise:
0
1
0
1
ax
l ax
l~
a ¼ l @ ay A ¼ @ l ay A
az
l az
Rechenregeln
Assoziativgesetz
Distributivgesetze
ðl 2 RÞ
9
lðm ~
a Þ ¼ mðl ~
a Þ ¼ ðl mÞ ~
a >
=
1
0
l; m 2 R
l ~
a þ b~ ¼ l ~
a þ l b~
>
;
ðl þ mÞ ~
a ¼ l~
a þ m~
a
Normierung eines Vektors
a
Für den in Richtung des Vektors ~
a 6¼ ~
0 weisenden Einheitsvektor ~
ea gilt:
0
~
ea ¼
ax =j ~
aj
1
~
a
B
C
¼ @ ay =j ~
ajA;
j~
aj
az =j ~
aj
ea
j~
ea j ¼ 1
a =a
1
(Skizze: j ~
a j > 1)
3.3 Skalarprodukt (inneres Produkt)
Definition eines Skalarproduktes
Das Skalarprodukt ~
a . b~ zweier Vektoren ~
a
~
und b ist der wie folgt definierte Skalar:
" "
~
a . b~ ¼ j ~
a j . " b~" . cos j
j: Winkel zwischen den beiden Vektoren mit
0" ) j ) 180"
b
f
a
52
II Vektorrechnung
Skalarprodukt in der Komponentendarstellung
0
1 0 1
ax
bx
~
a . b~ ¼ @ ay A . @ by A ¼ ax bx þ ay by þ az bz
az
bz
Regel: Komponentenweise multiplizieren, die Produkte aufaddieren.
Sonderfälle
(1)
(2)
(3)
~
a.~
a ¼ a 2x þ a 2y þ a 2z ¼ j ~
aj2
" "
(
)
~
a " " b~
j~
a j . " b~"
~
a . b~ ¼
" " für
~
a " # b~
/ j~
a j . " b~"
Die Einheitsvektoren ~
ex ; ~
ey ; ~
ez bilden eine orthonormierte Basis 2Þ :
~
ex . ~
ex ¼ ~
ey . ~
ey ¼ ~
ez . ~
ez ¼ 1 ;
~
ex . ~
ey ¼ ~
ey . ~
ez ¼ ~
ez . ~
ex ¼ 0
Rechenregeln
Kommutativgesetz
Distributivgesetz
Assoziativgesetz
~
a . b~ ¼
1
0
~
a . b~ þ ~
c ¼
1
0
l ~
a . b~ ¼
b~ . ~
a
~
a . b~ þ ~
a.~
c
1 0
ðl ~
a Þ . b~ ¼ ~
a . l b~
ðl 2 RÞ
Schnittwinkel zweier Vektoren
Den Schnittwinkel j zweier vom Nullvektor verschiedener Vektoren ~
a und b~ berechnet
man aus der folgenden Gleichung ð0" ) j ) 180" Þ:
cos j ¼
~
a . b~
ax bx þ ay by þ az bz
" " ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"
j~
a j . b~
a 2x þ a 2y þ a 2z . b 2x þ b 2y þ b 2z
cos j ¼ 0
cos j > 0
&
)
)
rechter Winkel
spitzer Winkel ðstrumpfer Winkel bei cos j < 0Þ
Beispiel
1
0 1
1
5
Wir bestimmen den Schnittwinkel j der Vektoren ~
a ¼ @ 2 A und b~ ¼ @/1 A :
/3
/5
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
" "
pffiffiffiffiffi
" b~" ¼ 5 2 þ ð/ 1Þ 2 þ ð/ 5Þ 2 ¼ pffiffiffiffiffi
j~
a j ¼ 12 þ 2 2 þ ð/ 3Þ 2 ¼ 14 ;
51
0 1 0 1
5
1
~
a . b~ ¼ @ 2 A . @/1 A ¼ 5 / 2 þ 15 ¼ 18 ;
/3
/5
0
cos j ¼
~
a . b~
18
¼ pffiffiffiffiffi pffiffiffiffiffi ¼ 0;6736
14 . 51
j~
a j . j b~j
j ¼ arccos 0;6736 ¼ 47;7"
2Þ
Orthonormierte Vektoren sind Einheitsvektoren, die paarweise aufeinander senkrecht stehen.
)
&
3 Vektoroperationen
53
Orthogonalität zweier Vektoren
a und b~ stehen genau dann senkrecht aufZwei vom Nullvektor verschiedene Vektoren ~
einander, wenn ihr Skalarprodukt verschwindet:
~
a . b~ ¼ 0 , ~
a ? b~
(orthogonale Vektoren)
Projektion eines Vektors auf einen zweiten Vektor
Durch Projektion des Vektors b~ auf den Vektor ~
a 6¼ ~
0 entsteht der folgende Vektor
~
(Komponente von b in Richtung von ~
a Þ:
b~a ¼
~
a . b~
j~
aj2
!
b
1
0
~
a ¼ b~ . ~
ea ~
ea
f
a
ba
~
a mit
ea : Einheitsvektor in Richtung von ~
~
a
~
ea ¼
j~
aj
3.4 Vektorprodukt (äußeres Produkt, Kreuzprodukt)
Definition eines Vektorproduktes
Das Vektorprodukt ~
c ¼ ~
a - b~ zweier Vektoren ~
a und b~ ist der eindeutig bestimmte
Vektor ~
c mit den folgenden Eigenschaften:
(1)
" "
j~
c j ¼ j~
a j . " b~" . sin j
c =a ×b
(2) ~
c ?~
a und ~
c ? b~
ð~
c.~
a ¼~
c . b~ ¼ 0Þ
(3) ~
a; b~; ~
c:
Rechtssystem
b
f
j: Winkel zwischen den Vektoren ~
a und b~ mit 0" ) j ) 180"
a
Geometrische Deutung: Der Betrag des Vektorproduktes ~
c ¼~
a - b~ ist gleich dem Flächeninhalt des von den Vektoren ~
a und b~ aufgespannten Parallelogramms:
"
"
" "
AParallelogramm ¼ j~
c j ¼ "~
a - b~" ¼ j ~
a j . " b~" . sin j
ð0" ) j ) 180" Þ
Das Vektorprodukt ~
c ¼~
a - b~ steht senkrecht auf der Parallelogrammfläche.
54
II Vektorrechnung
Vektorprodukt in der Komponentendarstellung
0
1
0 1
0
1
ay bz / az by
ax
bx
~
a - b~ ¼ @ ay A - @ by A ¼ @ az bx / ax bz A
ax by / ay bx
az
bz
Anmerkung
xi
Durch zyklisches Vertauschen der Indizes erhält man
aus der ersten Komponente die zweite und aus dieser
schließlich die dritte Komponente.
&
?
y
z
7
Beispiel
0 1
1
Wir berechnen mit Hilfe des Vektorproduktes den Flächeninhalt A des von den Vektoren ~
a ¼ @ 4 A und
0
1
0
/2
~
@
b ¼
5 A aufgespannten Parallelogramms:
3
0 1 0
1
0
1
0
1 0
1
1
/2
4.3/0.5
12 / 0
12
~
a - b~ ¼ @ 4 A - @ 5 A ¼ @ 0 . ð/ 2Þ / 1 . 3 A ¼ @ 0 / 3 A ¼ @ / 3 A
0
3
1 . 5 / 4 . ð/ 2Þ
5þ8
13
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"
A ¼ "~
a - b~" ¼ 12 2 þ ð/ 3Þ 2 þ 13 2 ¼ 17;94
)
&
Vektorprodukt in der Determinantenschreibweise
"
"~
" ex
"
~
~
a - b ¼ " ax
"
" bx
~
ey
ay
by
"
~
ez ""
"
az "
"
bz "
Die dreireihige Determinante lässt sich formal nach der Regel von Sarrus berechnen (siehe
VII.2.2).
Sonderfälle
(1)
(2)
(3)
Für kollineare Vektoren ist ~
a - b~ ¼ ~
0 und umgekehrt (entartetes Parallelogramm).
~
~
a-~
a¼0
ey ; ~
ez gilt (sie bilden
Für die Einheitsvektoren ~
ex ; ~
in dieser Reihenfolge ein Rechtssystem):
~
ex - ~
ex ¼ ~
ey - ~
ey ¼ ~
ez - ~
ez ¼ ~
0
~
ex - ~
ey ¼ ~
ez ;
~
ey - ~
ez ¼ ~
ex ;
~
ez - ~
ex ¼ ~
ey
ez
ex
ey
3 Vektoroperationen
55
Rechenregeln
Antikommutativgesetz
Distributivgesetze
Assoziativgesetz
~
a - b~ ¼
1
0
~
a - b~ þ ~
c ¼
1
0
~
a þ b~ - ~
c¼
1
0
l ~
a - b~ ¼
1
0
/ b~ - ~
a
~
a - b~ þ ~
a -~
c
~
a -~
c þ b~ - ~
c
1 0
ðl ~
a Þ - b~ ¼ ~
a - l b~
ðl 2 RÞ
Kollineare Vektoren
Zwei vom Nullvektor verschiedene Vektoren ~
a und b~ sind genau dann kollinear, wenn
ihr Vektorprodukt verschwindet:
~
a - b~ ¼ ~
0 , ~
a " " b~
oder
~
a " # b~
(kollineare Vektoren)
3.5 Spatprodukt (gemischtes Produkt)
Definition eines Spatproduktes
/
.
Das Spatprodukt ~
a b~~
c dreier Vektoren ~
a;
b~ und ~
c ist das skalare Produkt aus den
Vektoren ~
a und b~ - ~
c :
/
.
1
~
a b~~
c ¼~
a . b~ - ~
c
0
a
c
b
/
.
Das Spatprodukt ~
a b~~
c ist positiv, wenn die Vektoren ~
a; b~ und ~
c in dieser Reihenfolge ein Rechtssystem bilden, sonst negativ.
/
.
Geometrische Deutung: Der Betrag des Spatproduktes ~
a b~~
c ist das Volumen des von
den Vektoren ~
a; b~ und ~
c aufgespannten Spats (auch Parallelepiped genannt):
"/
."
VSpat ¼ " ~
a b~~
c "
Spatprodukt in der Komponentendarstellung
/
.
~
a b~~
c ¼ ax ðby cz / bz cy Þ þ ay ðbz cx / bx cz Þ þ az ðbx cy / by cx )
Spatprodukt in der Determinantenschreibweise
/
"
" ax
"
"
~
a b~~
c ¼ " bx
"
" cx
.
ay
by
cy
"
az ""
"
bz "
"
cz "
56
II Vektorrechnung
Rechenregeln
/
.
/
.
/
.
~
a b~~
c ¼ b~~
c~
a ¼ ~
c~
a b~
(1)
~
a; b~ und ~
c dürfen zyklisch vertauscht werden:
(2)
Vertauschen zweier Vektoren bewirkt einen Vorzeichenwechsel des Spatproduktes:
/
.
/
.
z. B. ~
a b~~
c ¼/ ~
a~
c b~ (die Vektoren b~ und ~
c wurden vertauscht)
Komplanare Vektoren
Drei Vektoren sind genau dann komplanar, wenn ihr Spatprodukt verschwindet:
/
.
~
a b~~
c ¼0 , ~
a; b~; ~
c sind komplanar (d. h. sie liegen in einer Ebene)
Beispiel
&
Das Spatprodukt
"
" 1
"
/
.
"
~
a b~~
c ¼" 4
"
" /2
0
1
0 1
0
1
1
4
/2
der Vektoren ~
a ¼ @ / 2 A; b~ ¼ @ 1 A und ~
c ¼ @/ 5 A verschwindet:
4
2
6
"
"
/2 4 "
"
a; b~; ~
c sind komplanar
1 2 " ¼ 6 þ 8 / 80 þ 8 þ 10 þ 48 ¼ 0 ) ~
"
/5 6 "
&
3.6 Formeln für Mehrfachprodukte
(1)
(2)
Entwicklungssätze:
1
0
1
0
~
a - b~ - ~
c ¼ ð~
a .~
c Þ b~ / ~
a . b~ ~
c
1
0
1
0
~
~
~
~
a - b -~
c ¼ ð~
a.~
cÞb / b . ~
c ~
a
1
0 1
0
1
0
~
a - b~ . ~
c - d~ ¼ ð~
a.~
c Þ b~ . d~ /
Spezialfall ~
c¼~
a; d~ ¼ b~:
1
0 1
0
1
0
~
a - b~ . ~
a - b~ ¼ ð~
a.~
a Þ b~ . b~ /
1
01
0
~
a . d~ b~ . ~
c
1
02
~
a . b~
4 Anwendungen
4.1 Arbeit einer konstanten Kraft
~ verrichtet beim Verschieben eines Massenpunktes m um den
Eine konstante Kraft F
Vektor ~
s die folgende Arbeit (Skalarprodukt aus Kraft- und Verschiebungsvektor):
F
~.~
~j . j~
W ¼F
s ¼ jF
s j . cos j ¼ Fs s
Fs : Kraftkomponente in Wegrichtung
s ¼ j~
s j: Verschiebung
m
f
Fs
s
4 Anwendungen
57
4.2 Vektorielle Darstellung einer Geraden
4.2.1 Punkt-Richtungs-Form
In der Parameterdarstellung
Gegeben: Ein Punkt P1 auf der Geraden g
mit dem Ortsvektor ~
r1 und ein
Richtungsvektor ~
a der Geraden
r1
P1
a
la
P
~
r ðlÞ ¼ ~
r1 þ l ~
a
l: Parameter; l 2 R; ~
a 6¼ ~
0
&
g
r ( l)
0
Beispiel
Die Vektorgleichung der durch den Punkt P1 ¼ ð1; / 2; 5Þ verlaufenden Geraden mit dem Richtungsvektor
0
1
2
~
a ¼ @/4 A lautet:
2
0
1
0
1
0
1
1
2
1 þ 2l
~
r ðlÞ ¼ ~
r1 þ l~
a ¼ @/ 2 A þ l @ / 4 A ¼ @ / 2 / 4 l A
ðl 2 RÞ
5
2
5 þ 2l
&
In der Determinantenschreibweise
"
" ~
" ex
" ax
"
" x / x1
~
ex ; ~
ey ; ~
ez :
ax ; ay ; az :
x1 ; y1 ; z1 :
x; y; z:
~
ey
ay
y / y1
~
ez
az
z / z1
"
"
"
" ¼ 0
"
"
Einheitsvektoren (Basisvektoren)
Skalare Vektorkomponenten des Richtungsvektors ~
a
Koordinaten des festen Punktes P1 der Geraden
Koordinaten des laufenden Punktes P der Geraden
4.2.2 Zwei-Punkte-Form
Gegeben: Zwei verschiedene Punkte P1 und
P2 auf der Geraden g mit den
Ortsvektoren ~
r1 und ~
r2
r1
r2 – r1
P2
r2
**!
~
r ðlÞ ¼ ~
r1 þ l P1 P2 ¼ ~
r1 þ l ð~
r2 / ~
r1 Þ
l: Parameter; l 2 R
~
r2 / ~
r1 : Richtungsvektor der Geraden
P1
l ( r2 – r1)
P
r ( l)
0
g
58
II Vektorrechnung
Beispiel
&
Die Vektorgleichung der Geraden durch die beiden Punkte P1 ¼ ð/1; 5; 0Þ und P2 ¼ ð1; /3; 2Þ lautet:
0
1
0
1
0
1
/1
1þ1
/1 þ 2 l
@
A
@
A
@
~
r ðlÞ ¼ ~
r1 þ l ð~
r2 / ~
r1 Þ ¼
5 þ l /3 / 5 ¼
5 / 8lA
ðl 2 RÞ
0
2/0
2l
&
4.2.3 Abstand eines Punktes von einer Geraden
Gegeben: Eine Gerade g mit der Gleichung
~
r ðlÞ ¼ ~
r1 þ l ~
a und ein Punkt Q
mit dem Ortsvektor ~
rQ
d ¼
~
a:
P1
a
rQ
g
Richtungsvektor der Geraden
)
Q
d
j~
a - ð~
rQ / ~
r1 Þ j
j~
aj
d ¼ 0
&
r1
0
Q liegt auf der Geraden.
Beispiel
Wir berechnen den Abstand d des Punktes Q ¼ ð1; 5; 3Þ von der Geraden mit der Vektorgleichung
0 1
0
1
1
2
~
r ðlÞ ¼ ~
r1 þ l ~
a ¼ @ 1 A þ l@ /3 A:
4
5
0
1 0
1
0
1 0
1
0
1
0
1
2
1/1
2
0
3 / 20
/ 17
@
A
@
A
@
A
@
A
@
@
A
~
a - ð~
rQ / ~
r1 Þ ¼ / 3 - 5 / 1 ¼ / 3 4 ¼ 0þ 2 ¼
2A
5
3/4
5
/1
8/ 0
8
j~
a - ð~
rQ / ~
r1 Þ j ¼
d ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
ð/17Þ 2 þ 2 2 þ 8 2 ¼ 357 ;
j~
aj ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
2 2 þ ð/ 3Þ 2 þ 5 2 ¼ 38
pffiffiffiffiffiffiffiffi
j~
a - ð~
rQ / ~
r1 Þ j
357
¼ pffiffiffiffiffi ¼ 3;065
j~
aj
38
&
4.2.4 Abstand zweier paralleler Geraden
Gegeben: Zwei parallele Geraden g1 und
g2 mit den Gleichungen
r2
~
r ðl1 Þ ¼ ~
r1 þ l1 ~
a1 und
P1 a
1
~
r ðl2 Þ ¼ ~
r2 þ l2 ~
a2
d ¼
j~
a1 - ð~
r2 / ~
r1 Þ j
j~
a1 j
P2
a2
d
g2
r1
0
g1
Die Geraden g1 und g2 mit den Richtungsvektoren ~
a1 und ~
a2 sind genau dann
parallel, wenn die beiden Richtungsvektoren kollinear sind, d. h. ~
a1 - ~
a2 ¼ ~
0 ist. In der
Abstandsformel darf der Vektor ~
a1 durch den Vektor ~
a2 ersetzt werden.
d ¼ 0
)
Die Geraden g1 und g2 fallen zusammen.
4 Anwendungen
&
59
Beispiel
P1 ¼ ð1; 0; 5Þ ist ein Punkt der Geraden g1 ; P2 ¼ ð0; 2; 1Þ ein solcher der Geraden g2 . Der gemein0 1
2
same Richtungsvektor ist ~
a1 ¼ ~
a2 ¼ @ 1 A . Wir bestimmen den Abstand d dieser parallelen Geraden:
1
0 1 0
1
0 1 0
1
0
2
0/1
2
/1
/4 /
~
a1 - ð~
r2 / ~
r1 Þ ¼ @ 1 A - @ 2 / 0 A ¼ @ 1 A - @ 2 A ¼ @ / 1 þ
1
1/5
1
/4
4þ
j~
a1 - ð~
r2 / ~
r1 Þ j ¼
d ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
ð/6Þ 2 þ 7 2 þ 5 2 ¼ 110 ;
j~
a1 - ð~
r2 / ~
r1 Þ j
¼
j~
a1 j
j~
a1 j ¼
1
0
1
2
/6
8A ¼ @ 7A
1
5
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
22 þ 12 þ 12 ¼ 6
pffiffiffiffiffiffiffiffi
110
pffiffiffi ¼ 4;282
6
&
4.2.5 Abstand zweier windschiefer Geraden
Gegeben: Zwei windschiefe Geraden g1 und
g2 mit den Gleichungen
P2
a2
~
r ðl1 Þ ¼ ~
r1 þ l1 ~
a1 und
~
r ðl2 Þ ¼ ~
r2 þ l2 ~
a2
d ¼
d
j ½~
a1 ~
a2 ð~
r2 / ~
r1 Þ% j
j~
a1 - ~
a2 j
P1
Die Geraden g1 und g2 sind genau dann
windschief (d. h. nicht parallel und kommen
nicht zum Schnitt), wenn die Bedingungen
~
a1 - ~
a2 6¼ ~
0 und ½~
a1 ~
a2 ð~
r2 / ~
r1 Þ% 6¼ 0 erfüllt sind.
&
g2
r2
g1
a1
r1
0
Beispiel
0 1
0 1
0
1
0 1
5
1
2
3
~
r ðl1 Þ ¼ ~
r1 þ l1 ~
a1 ¼ @ 2 A þ l1 @ 1 A und ~
r ðl2 Þ ¼ ~
r2 þ l2 ~
a2 ¼ @/1 A þ l2 @ 2 A sind die Glei1
3
0
1
chungen zweier windschiefer Geraden g1 und g2 , deren Abstand d wir berechnen wollen:
"
"
1
1
"
~
~
½~
a1 a2 ð~
r2 / r1 Þ% ¼ ""
3
2
" ð2 / 5Þ ð/ 1 / 2Þ
3
1
ð0 / 1Þ
"
"
"
" 1
"
"
" ¼" 3
"
"
"
" /3
1
2
/3
3
1
/1
"
"
"
" ¼
"
"
¼ / 2 / 3 / 27 þ 18 þ 3 þ 3 ¼ / 8
0 1 0 1 0
1 0
1
1
3
1/6
/5
@
A
@
A
@
A
@
~
a1 - ~
a2 ¼ 1 - 2 ¼ 9 / 1 ¼
8A;
3
1
2/3
/1
d ¼
j½~
a1 ~
a2 ð~
r2 / ~
r1 Þ% j
j / 8j
¼ pffiffiffiffiffi ¼ 0;843
j~
a1 - ~
a2 j
90
j~
a1 - ~
a2 j ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
ð/ 5Þ 2 þ 8 2 þ ð/ 1Þ 2 ¼ 90
&
60
II Vektorrechnung
4.2.6 Schnittpunkt und Schnittwinkel zweier Geraden
Unter dem Schnittwinkel j zweier Geraden
versteht man den Winkel zwischen den zugehörigen Richtungsvektoren (auch dann, wenn
sich die Geraden nicht schneiden).
g2
a2
a2
a1
Gegeben: Zwei Geraden g1 und g2 mit
den Richtungsvektoren ~
a1 und ~
a2
3
j ¼ arccos
~
a1 . ~
a2
j~
a1 j . j~
a2 j
g1
f
a1
2
Die Geraden g1: ~
r ¼~
r1 þ l1 ~
a1 und g2: ~
r ¼~
r2 þ l2 ~
a2 schneiden sich genau dann in
einem Punkt, wenn die Bedingungen
~
a1 - ~
a2 6¼ ~
0 und
[~
a1 ~
a2 ð~
r2 / ~
r1 Þ% ¼ 0
erfüllt sind. Ihren Schnittpunkt S erhält man durch Gleichsetzen der beiden Ortsvektoren:
~
r1 þ l1 ~
a1 ¼ ~
r2 þ l2 ~
a2
Diese Vektorgleichung führt (komponentenweise geschrieben) zu einem linearen Gleichungssystem mit drei Gleichungen und den beiden Unbekannten l1 und l2 . Die (eindeutige)
Lösung liefert die zum Schnittpunkt S gehörigen Parameterwerte. Den Ortsvektor ~
rS des
gesuchten Schnittpunktes S erhält man dann durch Einsetzen des Parameterwertes l1 in die
Gleichung der Geraden g1 (alternativ: l2 in die Gleichung der Geraden g2 einsetzen).
&
Beispiel
0
1
0 1
3
2
Die beiden Geraden g1 und g2 mit den Richtungsvektoren ~
a1 ¼ @ 1 A und ~
a2 ¼ @ 5 A schneiden
/2
3
sich unter dem folgenden Winkel:
0
1
3
2
~
a1 . ~
a2
3 . 2 þ 1 . 5 þ ð/ 2Þ . 3
B
C
¼ arccos @qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi A ¼ arccos 0;2168 ¼ 77;5"
j ¼ arccos
j~
a1 j . j~
a2 j
2
2
2
2
2
2
3 þ 1 þ ð/ 2Þ . 2 þ 5 þ 3
&
4.3 Vektorielle Darstellung einer Ebene
4.3.1 Punkt-Richtungs-Form
In der Parameterdarstellung
Gegeben: Ein Punkt P1 der Ebene E mit
dem Ortsvektor ~
r1 und zwei
nichtkollineare Richtungsvektoren
~
a 6¼ ~
0 und b~ 6¼ ~
0 der Ebene
~
r ðl; mÞ ¼ ~
r1 þ l ~
a þ m b~
l; m:
Parameter; l; m 2 R
~
a - b~: Normalenvektor der Ebene
P
mb
r (l; m)
b
E
P1
a
r1
0
la
4 Anwendungen
&
61
0 1
8
a ¼ @1A
Eine Ebene E enthalte den Punkt P1 ¼ ð1; 3; 5Þ und besitze die beiden Richtungsvektoren ~
0
1
3
1
~
@
und b ¼ /2 A. Ihre Vektorgleichung lautet dann:
4
0 1
0 1
0
1
0
1
1
8
1
1 þ 8l þ m
~
@
A
@
A
@
A
@
~
r ðl; mÞ ¼ ~
r1 þ l ~
a þ m b ¼ 3 þ l 1 þ m /2 ¼ 3 þ l / 2 m A
ðl; m 2 RÞ
5
3
4
5 þ 3l þ 4m
Beispiel
&
In der Determinantenschreibweise
"
" ax
"
"
" bx
"
" x / x1
ay
by
y / y1
ax ; ay ; az :
"
"
"
"
bz " ¼ 0
"
z / z1 "
az
)
bx ; by ; bz :
x1 ; y1 ; z1 :
x; y; z:
Skalare Vektorkomponenten der Richtungsvektoren ~
a und b~
Koordinaten des festen Punktes P1 der Ebene
Koordinaten des laufenden Punktes P der Ebene
4.3.2 Drei-Punkte-Form
In der Parameterdarstellung
**
*!
**
*!
~
r ðl; mÞ ¼ ~
r1 þ l P1 P2 þ m P1 P3 ¼
¼~
r1 þ l ð~
r2 / ~
r1 Þ þ m ð~
r3 / ~
r1 Þ
l; m: Parameter;
l; m 2 R
Die Ebene ist eindeutig bestimmt, wenn die drei
Punkte nicht in einer Geraden liegen. Dies ist
der Fall, wenn ð~
r2 / ~
r1 Þ - ð~
r3 / ~
r1 Þ ¼
6 ~
0 ist.
Die Vektoren ~
r2 / ~
r1 und ~
r3 / ~
r1 sind
Richtungsvektoren, ihr Vektorprodukt somit
ein Normalenvektor der Ebene.
&
P3
r3 –
r1
Gegeben: Drei verschiedene Punkte P1 ; P2
und P3 der Ebene E mit den
Ortsvektoren ~
r1 ; ~
r2 und ~
r3
r3
P1
P
r (l; m)
r2 – r1
r1
E
P2
r2
0
Beispiel
Die Gleichung der Ebene durch die drei Punkte P1 ¼ ð1; 1; 2Þ; P2 ¼ ð0; 4; /5Þ und P3 ¼ ð/ 3; 4; 9Þ
lautet wie folgt:
0 1
0
1
0
1
1
0/1
/3 / 1
~
r ðl; mÞ ¼ ~
r1 þ l ð~
r2 / ~
r1 Þ þ m ð~
r3 / ~
r1 Þ ¼ @ 1 A þ l @ 4 / 1 A þ m @ 4 / 1 A ¼
2
/5 / 2
9/2
0 1
0
1
0
1
0
1
1
/1
/4
1 / l / 4m
¼ @1A þ l@ 3A þ m@ 3A ¼ @1 þ 3l þ 3mA
ðl; m 2 RÞ
2
/7
7
2 / 7l þ 7m
&
62
II Vektorrechnung
In der Determinantenschreibweise
"
"
"
"
"
"
"
"
"
1
1
1
1
x
x1
x2
x3
y
y1
y2
y3
z
z1
z2
z3
"
"
"
"
"
"¼0
"
"
"
xi ; yi ; zi : Koordinaten des festen Punktes Pi der Ebene ði ¼ 1; 2; 3Þ
x; y; z:
Koordinaten des laufenden Punktes der Ebene
4.3.3 Ebene senkrecht zu einem Vektor
Gegeben: Ein Punkt P1 der Ebene E mit
dem Ortsvektor ~
r1 und ein Normalenvektor ~
n der Ebene (steht
senkrecht auf der Ebene)
~
n . ð~
r /~
r1 Þ ¼ 0
oder
n
P1
~
n .~
r ¼~
n .~
r1
r – r1
r1
P
E
r
Koordinatendarstellung der Ebene:
ax þ by þ cz þ d ¼ 0
0
Beispiel
&
0 1
2
Die Gleichung einer Ebene durch den Punkt P1 ¼ ð10; / 3; 2Þ und senkrecht zum Vektor ~
n ¼ @1A
5
(Normalenvektor) lautet wie folgt:
0 1 0
1
2
x / 10
~
n . ð~
r /~
r1 Þ ¼ @ 1 A . @ y þ 3 A ¼ 2 ðx / 10Þ þ 1 ðy þ 3Þ þ 5 ðz / 2Þ ¼ 0 )
5
z/ 2
2 x þ y þ 5z ¼ 27
&
4.3.4 Abstand eines Punktes von einer Ebene
Gegeben: Eine Ebene E mit der Gleichung
~
n . ð~
r /~
r1 Þ ¼ 0 und ein Punkt
Q mit dem Ortsvektor ~
rQ
d ¼
Q
rQ
j~
n . ð~
rQ / ~
r1 Þj
j~
nj
d
n
P1
Q0 :
Fußpunkt des Lotes von Q auf die
Ebene E
d ¼ 0 ) Q liegt in der Ebene.
0
E
r1
Q'
4 Anwendungen
&
63
Beispiel
0
Eine Ebene verläuft durch den Punkt P1 ¼ ð3; 1;
berechnen den Abstand d des Punktes Q ¼ ð1; 2;
0
1 0
1
0
1
/1
1/3
/1
@
A
@
A
@
~
n . ð~
rQ / ~
r1 Þ ¼
5 . 2/1 ¼
5A .
3
0/8
3
j~
nj ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
ð/1Þ 2 þ 5 2 þ 3 2 ¼ 35 ;
d ¼
8Þ und steht senkrecht zum Vektor ~
n ¼@
0Þ von dieser Ebene:
0
1
/2
@ 1 A ¼ 2 þ 5 / 24 ¼ / 17
/8
1
/1
5 A : Wir
3
j~
n . ð~
rQ / ~
r1 Þ j
j / 17 j
¼ pffiffiffiffiffi ¼ 2;874
j~
nj
35
&
4.3.5 Abstand einer Geraden von einer Ebene
Gegeben: Eine Ebene E mit der Gleichung
~
n . ð~
r /~
r0 Þ ¼ 0 und eine zu dieser Ebene parallele Gerade g mit
der Gleichung ~
r ðlÞ ¼ ~
r1 þ l ~
a
d ¼
&
P1
d
r1
j~
n . ð~
r1 / ~
r0 Þ j
j~
nj
n
P0
Eine Gerade mit dem Richtungsvektor ~
a
verläuft genau dann parallel zu einer Ebene
mit dem Normalenvektor ~
n, wenn das Skalarprodukt ~
a.~
n verschwindet. Die Gerade
g * liegt in der Ebene E und verläuft parallel zur Geraden g.
d ¼ 0
g
a
Parallele
zu g
g*
E
r0
0
) Gerade g liegt in der Ebene E.
Beispiel
0
1
2
Die Ebene E verlaufe durch den Punkt P0 ¼ ð1; 3; 2Þ und senkrecht zum Vektor ~
n ¼ @/1 A ; die
5
0
1
2
Gerade g gehe durch den Punkt P1 ¼ ð0; 7; /3Þ und besitze den Richtungsvektor ~
a ¼ @/1 A : Wegen
0
1 0
1
/1
2
2
~
a.~
n ¼ @/ 1 A . @/1 A ¼ 4 þ 1 / 5 ¼ 0
/1
5
gilt g k E. Wir berechnen den Abstand d zwischen Gerade und Ebene:
0
1 0
1
0
1 0
1
2
0/1
2
/1
~
n . ð~
r1 / ~
r0 Þ ¼ @ / 1 A . @ 7 / 3 A ¼ @ / 1 A . @ 4 A ¼ / 2 / 4 / 25 ¼ / 31
5
/3 / 2
5
/5
j~
nj ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
2 2 þ ð/1Þ 2 þ 5 2 ¼ 30 ;
d ¼
j~
n . ð~
r1 / ~
r0 Þ j
j / 31 j
¼ pffiffiffiffiffi ¼ 5;660
j~
nj
30
&
64
II Vektorrechnung
4.3.6 Abstand zweier paralleler Ebenen
Gegeben: Zwei parallele Ebenen E1 und
E2 mit den Gleichungen
n2
P2
~
n1 . ð~
r /~
r1 Þ ¼ 0 und
E2
r2
~
n2 . ð~
r /~
r2 Þ ¼ 0
d
j~
n1 . ð~
r1 / ~
r2 Þ j
j~
n2 . ð~
r1 / ~
r2 Þ j
¼
j~
n1 j
j~
n2 j
d ¼
Q
Q :
Beliebiger Punkt der Ebene E2
Q0 :
Fußpunkt des Lotes von Q auf die
zweite Ebene E1
n1
P1
r1
Q'
E1
0
Zwei Ebenen sind genau dann parallel, wenn ihre Normalenvektoren ~
n1 und ~
n2 kollinear
sind, d. h. ~
n1 - ~
n2 ¼ ~
0 ist.
d ¼ 0
&
) Die beiden Ebenen fallen zusammen.
Beispiel
Gegeben sind zwei Ebenen E 1 und E 2 mit den folgenden Eigenschaften:
0
1
2
B
C
Ebene E1 : P1 ¼ ð3; 1; / 2Þ, Normalenvektor ~
n1 ¼ @ /1 A
4
0
Ebene E2 :
P2 ¼ ð/ 4; 3; 0Þ,
B
Normalenvektor ~
n2 ¼ @
/4
1
C
2A
/8
Die Ebenen sind parallel, da ~
n2 ¼ / 2 ~
n1 und somit ~
n1 - ~
n2 ¼ ~
0 ist:
0
1
0
1
/4
2
B
C
B
C
~
n2 ¼ @ 2 A ¼ / 2 @ / 1 A ¼ / 2 ~
n1 ) ~
n1 - ~
n2 ¼ ~
n 1 - ð/ 2 ~
n 1 Þ ¼ / 2 ð~
n1 - ~
n 2Þ ¼ ~
0
|fflfflfflfflffl{zfflfflfflfflffl}
/8
4
~
0
|{z}
~
n1
Wir berechnen den Abstand d der Ebenen:
0
1 0
1
0
1 0
1
2
3þ4
2
7
B
C B
C
B
C B
C
~
n1 . ð~
r1 / ~
r2 Þ ¼ @ / 1 A . @ 1 / 3 A ¼ @ /1 A . @ /2 A ¼ 14 þ 2 / 8 ¼ 8
4
/2
4
/2 / 0
j~
n1 j ¼
d ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
2 2 þ ð/1Þ 2 þ 4 2 ¼ 21
j~
n1 . ð~
r1 / ~
r2 Þ j
8
¼ pffiffiffiffiffi ¼ 1;746
j~
n1 j
21
&
4 Anwendungen
65
4.3.7 Schnittpunkt und Schnittwinkel einer Geraden mit einer Ebene
Gegeben: Eine Gerade g mit der Gleichung ~
r ðlÞ ¼ ~
r1 þ l ~
a und eine
Ebene E mit der Gleichung
~
n . ð~
r /~
r0 Þ ¼ 0
g
n
Ortsvektor des Schnittpunktes S:
S
n
~
n . ð~
r0 / ~
r1 Þ
~
~
a
rS ¼ ~
r1 þ
~
n.~
a
Schnittwinkel j:
3
2
j~
n.~
aj
j ¼ arcsin
j~
n j . j~
aj
P0
r1
rs
r0
P1
0
f
a
E
a
g
a und eine Ebene mit dem Normalenvektor ~
n
Eine Gerade mit dem Richtungsvektor ~
kommen genau dann zum Schnitt, wenn ~
n.~
a 6¼ 0 ist.
&
Beispiel
Gegeben sind eine Gerade g und eine Ebene E :
0
1
0 1
3
2
E:
g: ~
r ðlÞ ¼ ~
r1 þ l ~
a ¼ @ 0 A þ l @ /4 A ;
5
/1
1
0 1 0
x/1
2
~
n . ð~
r /~
r0 Þ ¼ @ 1 A . @ y / 1 A ¼ 0
1
z/2
Wir berechnen den Schnittpunkt S sowie den Schnittwinkel j.
Schnittpunkt S:
0 1 0
1
0 1 0
1
2
1/2
2
/1
@
A
@
A
@
A
@
~
n . ð~
r0 / ~
r1 Þ ¼ 1 . 1 / 0 ¼ 1 .
1A ¼ / 2 þ 1 / 3 ¼ / 4
1
2/5
1
/3
0 1 0
1
2
3
@
A
@
~
n.~
a ¼ 1 . / 4 A ¼ 6 / 4 / 1 ¼ 1 6¼ 0
1
/1
)
Gerade und Ebene schneiden sich
0
1
0 1
0
1
0 1
0
1 0 1
2
/ 12
2
3
2
3
~
n . ð~
r0 / ~
r1 Þ
/
4
@ /4 A ¼ @ 0 A / 4 @ / 4 A ¼ @ 0 A þ @ 16 A ¼
~
~
rS ¼ ~
r1 þ
a ¼ @0A þ
~
1
n.~
a
5
/1
5
/1
5
4
0
1 0
1
2 / 12
/ 10
¼ @ 0 þ 16 A ¼ @ 16 A ) S ¼ ð/10; 16; 9Þ
5þ 4
9
Schnittwinkel j:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
j~
n j ¼ 22 þ 12 þ 12 ¼ 6 ;
3
j ¼ arcsin
j~
aj ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
3 2 þ ð/ 4Þ 2 þ ð/ 1Þ 2 ¼ 26
2
3
2
j~
n.~
aj
1
¼ arcsin pffiffiffi pffiffiffiffiffi ¼ arcsin 0;0801 ¼ 4;6"
j~
n j . j~
aj
6 . 26
&
66
II Vektorrechnung
4.3.8 Schnittwinkel zweier Ebenen
Unter dem Schnittwinkel j zweier Ebenen
versteht man den Winkel zwischen den zugehörigen Normalenvektoren der beiden Ebenen.
E2
Gegeben: Zwei Ebenen E1 und E2 mit
den Normalenvektoren ~
n1 und ~
n2
3
j ¼ arccos
n1
f
2
n2
~
n1 . ~
n2
j~
n1 j . j~
n2 j
E1
Voraussetzung: ~
n1 - ~
n 2 6¼ ~
0
&
Beispiel
Wir bestimmen den Schnittwinkel j zweier Ebenen E1 und E2 mit den Normalenvektoren
0
1
0
1
3
2
@
A
@
~
n1 ¼ / 2
und ~
n2 ¼
1 A:
3
/1
0
1 0
1
3
2
@
A
@
~
n1 . ~
n2 ¼ / 2 .
1A ¼ 6 / 2 / 3 ¼ 1
3
/1
j~
n1 j ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffi
3 2 þ ð/ 2Þ 2 þ 3 2 ¼ 22 ;
3
j ¼ arccos
~
n1 . ~
n2
j~
n1 j . j~
n2 j
3
2
¼ arccos
j~
n2 j ¼
1
pffiffiffiffiffi pffiffiffi
22 . 6
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
2 2 þ 1 2 þ ð/ 1Þ 2 ¼ 6
2
¼ arccos 0;0870 ¼ 85;0"
&
4.3.9 Schnittgerade zweier Ebenen
Gegeben: Zwei Ebenen E1 und E2 mit den Vektorgleichungen ~
n1 . ð~
r /~
r1 Þ ¼ 0 und
~
n2 . ð~
r /~
r2 Þ ¼ 0
Gleichung der Schnittgeraden g:
r ðlÞ ¼ ~
r0 þ l ~
a
ðl 2 RÞ
Richtungsvektor der Schnittgeraden: ~
a ¼~
n1 - ~
n2
Der Ortsvektor ~
r0 eines (noch unbekannten) Punktes P0 ¼ ðx0 ; y0 ; z0 Þ der Schnittgeraden g wird aus dem linearen Gleichungssystem
~
n1 . ð~
r0 / ~
r1 Þ ¼ 0 ;
~
n2 . ð~
r0 / ~
r2 Þ ¼ 0
bestimmt, wobei eine der drei Unbekannten x0 , y0 , z0 frei wählbar ist (z. B. x0 ¼ 0
setzen).
Voraussetzung: ~
n1 - ~
n 2 6¼ ~
0
67
III Funktionen und Kurven
1 Grundbegriffe
1.1 Definition einer Funktion
Unter einer Funktion von einer Variablen versteht man eine Vorschrift, die jedem Element
x 2 D genau ein Element y 2 W zuordnet. Symbolische Schreibweise: y ¼ f ðxÞ:
Bezeichnungen:
x:
y:
D:
W:
Unabhängige Veränderliche (Variable) oder Argument
Abhängige Veränderliche (Variable) oder Funktionswert
Definitionsbereich der Funktion
Wertebereich oder Wertevorrat der Funktion
In den naturwissenschaftlich-technischen Anwendungen sind x und y in der Regel reelle
Variable, y ¼ f ðxÞ ist dann eine reellwertige Funktion der reellen Variablen x.
1.2 Darstellungsformen einer Funktion
1.2.1 Analytische Darstellung
Die Funktion wird durch eine Funktionsgleichung dargestellt:
Explizite Form:
y ¼ f ðxÞ
Implizite Form:
Fðx; yÞ ¼ 0
1.2.2 Parameterdarstellung
y
Die Variablen (Koordinaten) x und y
hängen von einem (reellen) Parameter t ab,
sind somit (stetige) Funktionen von t :
x ¼ x ðtÞ
y ¼ y ðtÞ
t2
t
t1
)
y(t)
t1 ) t ) t2
x(t)
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_3
x
68
III Funktionen und Kurven
1.2.3 Kurvengleichung in Polarkoordinaten
r ¼ r ðjÞ
y
f2
ðj1 ) j ) j2 Þ
Pol: Koordinatenursprung
Polarachse: x-Achse
j: Polarwinkel
r : Abstand vom Pol ðr ( 0Þ
r( f2 )
f
r(f)
f1
r( f1 )
Pol
x
Polarachse
1.2.4 Graphische Darstellung
Die Funktion y ¼ f ðxÞ wird in einem rechtwinkligen Koordinatensystem durch eine
Punktmenge dargestellt (Funktionskurve, Schaubild oder Funktionsgraph genannt). Dem
Wertepaar ðx0 ; y0 Þ mit y0 ¼ f ðx0 Þ entspricht dabei der Kurvenpunkt P ¼ ðx0 ; y0 Þ.
x0 ; y0 :
x0 :
y0 :
Kartesische Koordinaten von P
'
Abszisse
von P
Ordinate
y
y0
Jede Parallele zur y-Achse schneidet die Kurve
höchstens einmal.
P
y = f(x)
x0
x
2 Allgemeine Funktionseigenschaften
2.1 Nullstellen
Schnitt- bzw. Berührungspunkte der Funktionskurve mit der x-Achse:
y
y = f(x)
f ðx0 Þ ¼ 0
Doppelte Nullstelle:
Berührungspunkt mit der x-Achse
x0
x
2 Allgemeine Funktionseigenschaften
69
2.2 Symmetrie
Gerade Funktion
y
y = f(x)
Die Kurve verläuft spiegelsymmetrisch zur
y-Achse:
f ð/ xÞ ¼ f ðxÞ
f(–x)
(für alle x mit x 2 D , / x 2 D)
f(x)
x
–x
y
Ungerade Funktion
y = f(x)
Die Kurve verläuft punktsymmetrisch zum
Koordinatenursprung:
f ð/ xÞ ¼ / f ðxÞ
x
f(x)
–x
x
f(–x)
x
(für alle x mit x 2 D , / x 2 D)
2.3 Monotonie
Monoton wachsende Funktion
y
y = f(x)
f ðx1 Þ ) f ðx2 Þ
f( x2 )
(für alle x1 ; x2 2 D mit x1 < x2 )
f( x1 )
x2
x1
Monoton fallende Funktion
y
y = f(x)
f ðx1 Þ ( f ðx2 Þ
(für alle x1 ; x2 2 D mit x1 < x2 )
x
f( x1 )
x1
f(x2 )
x2
x
Gilt nur das Zeichen < oder >, so heißt die Funktion streng monoton wachsend bzw.
streng monoton fallend.
Viele Funktionen zeigen ein bestimmtes Monotonieverhalten nur in Teilintervallen ihres
Definitionsbereiches.
70
2.4 Periodizität
Die Funktionswerte wiederholen sich, wenn
man in der x-Richtung um eine Periode p
fortschreitet:
f ðx + pÞ ¼ f ðxÞ
(für alle x 2 D)
III Funktionen und Kurven
y
Periode p
f(x)
x
f(x + p)
y = f(x)
x+p
x
Mit p ist auch + k . p eine Periode der Funktion ðk 2 N *Þ. Die kleinste (positive)
Periode heißt primitive Periode.
2.5 Umkehrfunktion (inverse Funktion)
Definition
Eine Funktion y ¼ f ðxÞ heißt umkehrbar, wenn aus x1 6¼ x2 stets f ðx1 Þ 6¼ f ðx2 Þ folgt
(zu verschiedenen Abszissen gehören verschiedene Ordinaten).
Die Umkehrfunktion von y ¼ f ðxÞ wird durch das Symbol y ¼ f /1 ðxÞ oder besser
y ¼ g ðxÞ gekennzeichnet.
Bestimmung der Funktionsgleichung der Umkehrfunktion
Jede streng monoton fallende oder wachsende Funktion ist umkehrbar. Bei der Umkehrung
werden Definitions- und Wertebereich miteinander vertauscht. In vielen Fällen lässt sich die
Funktionsgleichung der Umkehrfunktion schrittweise wie folgt ermitteln:
1. Die Funktionsgleichung y ¼ f ðxÞ wird zunächst nach der Variablen x aufgelöst:
x ¼ g ðyÞ 1Þ .
2. Durch formales Vertauschen der beiden Variablen erhält man hieraus die Umkehrfunktion y ¼ g ðxÞ von y ¼ f ðxÞ.
Die Rechenschritte dürfen auch in der umgekehrten Reihenfolge ausgeführt werden.
Zeichnerische Konstruktion der Umkehrfunktion
Die Kurve y ¼ f ðxÞ wird Punkt für Punkt an
der Winkelhalbierenden des 1. Quadranten,
d. h. an der Geraden y ¼ x gespiegelt.
y
y = f(x)
y=x
y = g(x)
x
1Þ
Die Auflösung muss möglich und eindeutig sein. x ¼ g ðyÞ heißt auch „die nach x aufgelöste Form von
y ¼ f ðxÞ“.
3 Grenzwert und Stetigkeit einer Funktion
&
71
Beispiel
y ¼ f ðxÞ ¼
x þ2
,
x
x 6¼ 0
Auflösen der Gleichung nach x :
xy ¼ x þ 2
)
x y / x ¼ x ðy / 1Þ ¼ 2
Vertauschen der beiden Variablen führt zur Umkehrfunktion:
y ¼ g ðxÞ ¼
2
;
x /1
) x ¼ g ðyÞ ¼
2
y/1
x 6¼ 1
&
3 Grenzwert und Stetigkeit einer Funktion
3.1 Grenzwert einer Folge
Definition einer Zahlenfolge
Unter einer (reellen) Zahlenfolge ( kurz als Folge bezeichnet) versteht man eine geordnete
Menge reeller Zahlen. Jeder positiven ganzen Zahl n wird dabei in eindeutiger Weise eine
reelle Zahl an zugeordnet.
Symbolische Schreibweise:
han i ¼ a1 ; a2 ; a3 ; . . . ; an ; . . .
a1 ; a2 ; a3 ; . . .:
Glieder der Folge
ðn 2 N *Þ
an : allgemeines Glied der Folge (n-tes Glied)
Grenzwert einer Zahlenfolge
Die reelle Zahl g heißt Grenzwert oder Limes der Zahlenfolge han i, wenn es zu jedem
e > 0 eine positive ganze Zahl n0 gibt, so dass für alle n ( n0 stets j an / g j < e ist.
Eine Folge han i heißt konvergent, wenn sie einen Grenzwert g besitzt. Symbolische
Schreibweise:
lim an ¼ g
n!1
Eine Folge han i, die keinen Grenzwert besitzt, heißt divergent. Eine Folge hat höchstens
einen Grenzwert.
&
Beispiel
Die Folge han i ¼
& %
1
1 1
1
1
¼ 1; ; ; . . . ; ; . . . ist konvergent mit dem Grenzwert g ¼ lim
¼ 0
n!1 n
n
2 3
n
(sog. Nullfolge).
&
72
III Funktionen und Kurven
3.2 Grenzwert einer Funktion
3.2.1 Grenzwert für x ! x0
Eine Funktion y ¼ f ðxÞ sei in einer Umgebung von x0 definiert. Gilt dann für jede im
Definitionsbereich der Funktion liegende und gegen die Stelle x0 konvergierende Zahlenfolge hxn i mit xn 6¼ x0 stets lim f ðxn Þ ¼ g, so heißt g der Grenzwert von y ¼ f ðxÞ
n!1
für x ! x0 (Grenzwert an der Stelle x0 ). Symbolische Schreibweise:
lim f ðxÞ ¼ g
x ! x0
Man beachte, dass die Funktion an der Stelle x0 nicht definiert sein muss. Der Grenzwert
an dieser Stelle (Definitionslücke) kann trotzdem vorhanden sein.
Beispiel
&
lim
x!1
ðx þ 1Þ ðx / 1Þ
x2 / 1
¼ lim ðx þ 1Þ ¼ 2
¼ lim
x!1
x!1
x /1
x /1
Kürzen des gemeinsamen Faktors x / 1 ist erlaubt, da dieser wegen x 6¼ 1 von 0 verschieden ist!
&
3.2.2 Grenzwert für x ! + 1
Besitzt eine Funktion y ¼ f ðxÞ die Eigenschaft, dass die Folge ihrer Funktionswerte für
jede über alle Grenzen hinaus wachsende Zahlenfolge hxn i ðxn 2 DÞ gegen eine Zahl g
strebt, so heißt g der Grenzwert von y ¼ f ðxÞ für x ! 1 (Grenzwert im „Unendlichen“). Symbolische Schreibweise:
lim f ðxÞ ¼ g
x!1
Analog wird der Grenzwert
lim
x ! /1
f ðxÞ erklärt.
Beispiel
&
lim
x!1
0
1
x
1
¼
lim
A ¼ 0
x!1 @ 1
1 þ x2
þx
x
ðZähler ¼ 1 ;
Nenner ! 1Þ
&
3.3 Rechenregeln für Grenzwerte
Voraussetzung: Alle auftretenden Grenzwerte sind vorhanden.
(1)
(2)
(3)
lim C . f ðxÞ ¼ C .
!
lim f ðxÞ
x ! x0
4
ðC 2 RÞ
x ! x0
lim ½ f ðxÞ + gðxÞ% ¼ lim f ðxÞ + lim g ðxÞ
x ! x0
lim ½ f ðxÞ . g ðxÞ% ¼
x ! x0
x ! x0
!
x ! x0
4 !
4
lim f ðxÞ . lim g ðxÞ
x ! x0
x ! x0
3 Grenzwert und Stetigkeit einer Funktion
3
(4)
lim
x ! x0
lim
(5)
x ! x0
f ðxÞ
g ðxÞ
2
¼
lim
x ! x0
!
x ! x0
(8)
lim g ðxÞ ¼
6 0Þ
x ! x0
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
ffiffiffiffiffiffiffiffi
n
f ðxÞ ¼ n lim f ðxÞ
h
x ! x0
(7)
ðVoraussetzung :
lim g ðxÞ
x ! x0
lim ½ f ðxÞ % n ¼
(6)
lim f ðxÞ
x ! x0
73
a f ðxÞ
4
¼ a
lim f ðxÞ
in
x ! x0
1
0
lim f ðxÞ
x ! x0
lim ½ log a f ðxÞ % ¼ log a
!
x ! x0
lim f ðxÞ
x ! x0
4
ð f ðxÞ > 0Þ
Diese Regeln gelten sinngemäß auch für Grenzübergänge vom Typ x ! þ 1 bzw.
x ! / 1.
3.4 Grenzwertregel von Bernoulli und de l’Hospital
0“
1“
Für Grenzwerte, die auf einen unbestimmten Ausdruck der Form
oder
führen,
„0
„1
gilt die sog. Bernoulli-de l’Hospitalsche Regel:
lim
x ! x0
f ðxÞ
f 0 ðxÞ
¼ lim 0
x ! x0 g ðxÞ
g ðxÞ
Voraussetzung: f ðxÞ und g ðxÞ sind in einer Umgebung von x 0 stetig differenzierbar
und der Grenzwert auf der rechten Seite existiert.
Anmerkungen
(1)
(2)
In einigen Fällen ist die Regel mehrmals anzuwenden, ehe man zu einem Ergebnis
kommt; es gibt jedoch auch Fälle, in denen die Regel versagt.
Die Regel gilt auch für Grenzübergänge vom Typ x ! + 1.
&
Beispiel
lim
x!0
sin 2 x
0
!
1 / cos x
0
(Zähler und Nenner streben jeweils gegen 0)
Regel von Bernoulli-de l’Hospital:
lim
x!0
sin 2 x
ðsin 2 xÞ 0
2 . sin x . cos x
¼ lim
¼ lim
¼ lim ð2 . cos xÞ ¼ 2 . cos 0 ¼ 2 . 1 ¼ 2
x ! 0 ð1 / cos xÞ 0
x!0
x!0
1 / cos x
sin x
&
74
III Funktionen und Kurven
Unbestimmte Ausdrücke der Form 0 . 1, 1 / 1, 0 0 , 1 1 oder 1 0 lassen sich in vielen
0
1
oder
zurückführen:
Fällen wie folgt durch elementare Umformungen auf den Typ
0
1
Funktion j ðxÞ
(A)
lim j ðxÞ
Elementare Umformung
x ! x0
u ðxÞ
1
0.1
u ðxÞ . vðxÞ
1.0
vðxÞ
1
vðxÞ
(B)
u ðxÞ / vðxÞ
1/1
(C)
u ðxÞ v ðxÞ
0 0, 1 0, 1 1
&
ðu ðxÞ > 0Þ
oder
vðxÞ
1
u ðxÞ
/
1
u ðxÞ
1
u ðxÞ . vðxÞ
e v ðxÞ . ln u ðxÞ
Beispiel
lim ðx . ln xÞ ! 0 . 1
x!0
(vom Vorzeichen abgesehen; x > 0Þ
Elementare Umformung ( Typ (A) mit u ðxÞ ¼ x und v ðxÞ ¼ ln x; 2. Version):
0
1
ln x
1
lim ðx . ln xÞ ¼ lim @
!
x!0
x!0
1
1 A
x
Regel von Bernoulli-de L’Hospital:
1
1
B x C
ln x
ðln xÞ
C ¼ lim ð/ xÞ ¼ 0
¼ lim 3 20 ¼ lim B
lim ðx . ln xÞ ¼ lim @
1 A
x!0
x!0
x!0
x!0 @
x!0
1A
1
/ 2
x
x
x
0
1
0
0
&
3.5 Stetigkeit einer Funktion
Eine in x0 und einer gewissen Umgebung von x0 definierte Funktion y ¼ f ðxÞ heißt an
der Stelle x0 stetig, wenn der Grenzwert der Funktion für x ! x0 vorhanden ist und mit
dem dortigen Funktionswert übereinstimmt:
lim f ðxÞ ¼ f ðx0 Þ
x ! x0
Eine Funktion, die an jeder Stelle ihres Definitionsbereiches stetig ist, heißt eine stetige
Funktion.
Eine Funktion y ¼ f ðxÞ heißt an der Stelle x0 unstetig, wenn f ðx 0 Þ nicht vorhanden ist
oder f ðx 0 Þ vom Grenzwert verschieden ist oder dieser nicht existiert. Es gibt dabei verschiedene Arten von Unstetigkeitsstellen (z. B. Lücken, Pole oder Unendlichkeitsstellen, Sprünge;
siehe hierzu auch Abschnitt 5.2).
3 Grenzwert und Stetigkeit einer Funktion
75
Unstetigkeiten (in Beispielen)
(1) Hebbare Lücke
f ðxÞ ¼
x3 þ x
;
x
y
x 6¼ 0
Diese Funktion ist an der Stelle x ¼ 0 nicht definiert und daher zunächst
unstetig. Der Grenzwert jedoch existiert:
lim f ðxÞ ¼ lim
x!0
x!0
x3 þ x
x ðx 2 þ 1Þ
¼ lim
¼ lim ðx 2 þ 1Þ ¼ 1
x!0
x!0
x
x
1
(wegen x 6¼ 0 darf gekürzt werden)
x
Die Definitionslücke bei x ¼ 0 lässt sich jedoch durch die nachträgliche
Festlegung
f ð0Þ ¼ lim f ðxÞ ¼ lim
x!0
x!0
x3 þ x
¼ 1
x
(Funktionswert ¼ Grenzwert) beheben. Damit ist f ðxÞ überall stetig und kann durch die Gleichung
f ðxÞ ¼ x 2 þ 1 beschrieben werden (Parabel).
(2) Pol oder Unendlichkeitsstelle
f ðxÞ ¼
1
ð1 / xÞ 2
;
y
x 6¼ 1
20
Der Grenzwert an der Stelle x ¼ 1 ist nicht vorhanden:
lim f ðxÞ ¼ lim
x!1
1
x!1
ð1 / xÞ 2
10
¼ 1
Die Definitionslücke bei x ¼ 1 lässt sich daher nicht beheben, die Funktion bleibt somit an dieser Stelle unstetig.
1
x
(3) Sprungunstetigkeit (endlicher Sprung)
f ðxÞ ¼ s ðxÞ ¼
8
<1
:
0
f ür
9
x ( 0=
y
;
1
x < 0
lim f ðxÞ ¼ lim 0 ¼ 0
x!0
ðx < 0Þ
x!0
ðx < 0Þ
lim f ðxÞ ¼ lim 1 ¼ 1
x!0
ðx > 0Þ
x!0
ðx > 0Þ
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Diese Funktion ist an der Sprungstelle x ¼ 0 zwar definiert,
f ð0Þ ¼ s ð0Þ ¼ 1, jedoch unstetig, da sich der linksseitige Grenzwert vom
rechtsseitigen Grenzwert unterscheidet und f ðxÞ daher an dieser Stelle keinen Grenzwert besitzt:
)
Grenzwert an der Stelle x ¼ 0 ist nicht vorhanden!
x
76
III Funktionen und Kurven
4 Ganzrationale Funktionen (Polynomfunktionen)
4.1 Definition der ganzrationalen Funktionen (Polynomfunktionen)
f ðxÞ ¼ an x n þ an / 1 x n / 1 þ . . . þ a1 x þ a0
ðan 6¼ 0Þ
n: Polynomgrad ðn 2 N Þ
a0 ; a1 ; . . . an : Reelle Polynomkoeffizienten
Ganzrationale Funktionen oder Polynomfunktionen sind überall definiert und stetig. Sie werden in der Regel nach fallenden Potenzen geordnet (siehe hierzu III.4.5, Horner-Schema).
Sonderfall: n ¼ 0
) Konstante Funktion f ðxÞ ¼ a 0 ¼ const:
4.2 Lineare Funktionen (Geraden)
4.2.1 Allgemeine Geradengleichung
Ax þ By þ C ¼ 0
ðA 2 þ B 2 6¼ 0Þ
4.2.2 Hauptform einer Geraden
Gegeben: Steigung m und Achsenabschnitt b
(Schnittpunkt mit der y-Achse)
y
y = mx + b
y ¼ mx þ b
m ¼ tan a
b
a
x
(a: Steigungswinkel)
4.2.3 Punkt-Steigungsform einer Geraden
Gegeben: Ein Punkt P1 ¼ ðx1 ; y1 Þ und die
Steigung m oder der Steigungswinkel a ðm ¼ tan aÞ
y / y1
¼ m
x / x1
y
P
P1
a
y1
x1
y – y1
a
x – x1
y
x
x
4 Ganzrationale Funktionen (Polynomfunktionen)
77
4.2.4 Zwei-Punkte-Form einer Geraden
Gegeben: Zwei verschiedene Punkte
P1 ¼ ðx1 ; y1 Þ und P2 ¼ ðx2 ; y2 Þ
y
P
y / y1
y2 / y1
¼
x / x1
x2 / x1
P2
ðx1 6¼ x2 Þ
P1
y1
a
y – y1
y2 – y 1
a
x 2 – x1 y2
x – x1
x1
x2
y
x
x
4.2.5 Achsenabschnittsform einer Geraden
Gegeben: Achsenabschnitte a und b auf
der x- und y-Achse
x
y
þ
¼ 1
a
b
ða 6¼ 0; b 6¼ 0Þ
y
b
a; b können auch negativ sein!
x
a
4.2.6 Hessesche Normalform einer Geraden
Gegeben: p: Senkrechter Abstand des Nullpunktes O von der Geraden
y
a: Winkel zwischen dem Lot vom
Nullpunkt O auf die Gerade
und der positiven x-Achse
p
x . cos a þ y . sin a ¼ p
0
a
x
4.2.7 Abstand eines Punktes von einer Geraden
Gegeben: Gerade A x þ B y þ C ¼ 0
und ein Punkt P1 ¼ ðx1 ; y1 Þ
der Ebene
"
"
"
"
"Ax þ By þ C"
" 1
"
1
d ¼ " qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
"
"
2
2
A þB
"
"
y
P1 = (x 1 ;y 1 )
d
p
ðA 2 þ B 2 6¼ 0Þ
0
x
78
III Funktionen und Kurven
4.2.8 Schnittwinkel zweier Geraden
Gegeben: Zwei Geraden g1 und g2 mit
den Gleichungen y ¼ m1 x þ b1
und y ¼ m2 x þ b2
"
"
" m2 / m1 "
"
"
tan d ¼ "
1 þ m1 . m2 "
Voraussetzung:
y
g2
d
"
g1
"
ð0 ) d ) 90 Þ
x
m1 . m2 6¼ / 1
Sonderfälle:
(1)
g1 k g2 :
m1 ¼ m 2
und
(2)
g1 ? g2 :
m1 . m2 ¼ / 1
d ¼ 0"
und d ¼ 90"
4.3 Quadratische Funktionen (Parabeln)
Hinweis: Die nach rechts bzw. nach links geöffneten Parabeln werden in Abschnitt 13.5
behandelt.
4.3.1 Hauptform einer Parabel
y ¼ ax2 þ bx þ c
y
S
ða 6¼ 0Þ
a ¼
6 0:
a > 0:
a < 0:
"ffnungsparameter
nach oben geöffnete Parabel
nach unten geöffnete Parabel
3
2
b 4ac / b2
Scheitelpunkt: S ¼ /
;
2a
4a
a>0
x
a<0
S
y
Sonderfall: a ¼ 1, b ¼ c ¼ 0
y = x2
Normalparabel
y ¼ x2
S
x
4 Ganzrationale Funktionen (Polynomfunktionen)
79
4.3.2 Produktform einer Parabel
y
y ¼ a ðx / x1 Þ ðx / x2 Þ
a 6¼ 0: "ffnungsparameter
x1 ; x2 :
Nullstellen der Parabel
'
x / x1
Linearfaktoren
x / x2
Sonderfall:
x1
x2
x
S
x1 ¼ x2 ) y ¼ aðx / x1 Þ 2 )
Die Parabel berührt die x-Achse im
Scheitelpunkt S ¼ ðx1 ; 0Þ („doppelte Nullstelle“).
4.3.3 Scheitelpunktsform einer Parabel
y
y / y0 ¼ a ðx / x0 Þ 2
a 6¼ 0:
"ffnungsparameter
x0 ; y0 :
Koordinaten des Scheitelpunktes S
x0
x
y0
S
4.4 Polynomfunktionen höheren Grades (n-ten Grades)
4.4.1 Abspaltung eines Linearfaktors
Ist x1 eine Nullstelle der Polynomfunktion f ðxÞ vom Grade n, d. h. f ðx1 Þ ¼ 0, so ist
f ðxÞ in der Produktform
f ðxÞ ¼ ðx / x1 Þ . f1 ðxÞ
darstellbar. Der Faktor ðx / x1 Þ heißt Linearfaktor, f1 ðxÞ ist das sog. 1. reduzierte Polynom vom Grade n / 1.
4.4.2 Nullstellen einer Polynomfunktion
Eine Polynomfunktion n-ten Grades besitzt höchstens n reelle Nullstellen (Fundamentalsatz der Algebra, siehe hierzu auch VIII.4).
4.4.3 Produktdarstellung einer Polynomfunktion
f ðxÞ ¼ an ðx / x1 Þ ðx / x2 Þ . . . ðx / xn Þ
x1 ; x2 ; . . . ; xn : Nullstellen von f ðxÞ
ðan 6¼ 0Þ
80
III Funktionen und Kurven
Die Faktoren ðx / x1 Þ; ðx / x2 Þ; . . . ; ðx / xn Þ heißen Linearfaktoren, die Produktdarstellung daher auch Zerlegung der Polynomfunktion in Linearfaktoren. Ist zum Beispiel x1
eine k-fache Nullstelle von f ðxÞ, so tritt der Linearfaktor ðx / x1 Þ k-mal auf.
Ist die Anzahl k der (reellen) Nullstellen kleiner als der Polynomgrad n, so lautet die
Zerlegung wie folgt:
f ðxÞ ¼ an ðx / x1 Þ ðx / x2 Þ . . . ðx / xk Þ . f *ðxÞ
f *ðxÞ:
&
ðan 6¼ 0Þ
Polynomfunktion vom Grade n / k ohne (reelle) Nullstellen
Beispiel
y ¼ 3 x 3 þ 18 x 2 þ 9 x / 30
Nullstellen:
x1 ¼ / 5 ;
Produktdarstellung:
x2 ¼ / 2 ;
x3 ¼ 1
y ¼ 3 ðx þ 5Þ ðx þ 2Þ ðx / 1Þ
&
4.5 Horner-Schema
Für eine Polynomfunktion 3. Grades vom Typ
f ðxÞ ¼ a3 x 3 þ a2 x 2 þ a1 x þ a0
ða3 6¼ 0Þ
erfolgt die Berechnung des Funktionswertes an der Stelle x0 nach dem folgenden Schema
(Horner-Schema):
a3
x0
%:
#:
a1
#
ða2 þ a3 x0 Þ x0
a0
#
ða1 þ a2 x0 þ a3 x 20 Þ x0
%
%
a1 þ a2 x0 þ a3 x 20 a0 þ a1 x0 þ a2 x 20 þ a3 x 30
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
f ðx0 Þ
Multiplikation mit x0
a3
%
a2
#
a3 x0
a2 þ a3 x0
Addition der in der 1. und 2. Zeile untereinander stehenden Werte
Anmerkungen
(1)
(2)
&
Das Horner-Schema gilt sinngemäß auch für Polynomfunktionen höheren Grades
ðn > 3Þ. Das Polynom muss dabei nach fallenden Potenzen geordnet sein.
Fehlt in der Funktionsgleichung eine Potenz, so ist im Horner-Schema der entsprechende Koeffizient gleich null zu setzen!
Beispiel
f ðxÞ ¼ 3;2 x 3 / 2 x 2 þ 5;1 x þ 10;
3,2
x0 ¼ 2
3,2
f ð2Þ ¼ ?
/2
5,1
10
6,4
8,8
27,8
4,4
13,9
37,8
Ergebnis:
f ð2Þ ¼ 37;8
&
4 Ganzrationale Funktionen (Polynomfunktionen)
81
4.6 Reduzierung einer Polynomfunktion (Nullstellenberechnung)
Ist x1 eine Nullstelle von f ðxÞ ¼ a3 x 3 þ a2 x 2 þ a1 x þ a0 , so gilt (Abschnitt 4.4.1):
f ðxÞ ¼ ðx / x1 Þ . f1 ðxÞ ¼ ðx / x1 Þ ðb2 x 2 þ b1 x þ b0 Þ
Dabei ist f1 ðxÞ ¼ b2 x 2 þ b1 x þ b0 das 1. reduzierte Polynom von f ðxÞ vom Grade 2,
dessen Koeffizienten man wie folgt aus dem Horner-Schema erhält:
a3
x1
a2
a1
a0
a3 x1
ða2 þ a3 x1 Þ x1
ða1 þ a2 x1 þ a3 x 21 Þ x1
a3
a2 þ a3 x1 a1 þ a2 x1 þ a3 x 21 a0 þ a1 x1 þ a2 x 21 þ a3 x 31
|ffl{zffl} |fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
b2
b1
b0
f ðx1 Þ ¼ 0
Die restlichen (reellen) Nullstellen von f ðxÞ sind dann (falls überhaupt vorhanden) die
Lösungen der quadratischen Gleichung f1 ðxÞ ¼ 0.
Anmerkungen
(1)
(2)
(3)
&
Die Reduzierung einer Polynomfunktion 3. Grades setzt die Kenntnis einer Nullstelle
x1 voraus. Diese lässt sich oft durch Probieren, Erraten oder durch graphische oder
numerische Rechenverfahren ermitteln (siehe hierzu I.4.3, I.4.4 und I.4.5).
Bei Polynomfunktionen 4. und höheren Grades erfolgt die Nullstellenberechnung analog durch mehrmalige Reduzierung, bis man auf eine quadratische Gleichung stößt.
Bei der Reduzierung spielt die Reihenfolge, in der die Nullstellen bestimmt werden,
keine Rolle. Die Produktdarstellung der Polynomfunktion ist davon unabhängig.
Beispiel
f ðxÞ ¼ / x 3 þ 5 x 2 / 3 x / 9
Durch Probieren findet man eine Nullstelle bei x1 ¼ 3. Abspaltung des zugehörigen Linearfaktors ðx / 3Þ
mit Hilfe des Horner-Schemas führt zu:
/1
x1 ¼ 3
5
/3
/9
/3
6
9
/1
2
3
0
|fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflffl{zfflfflfflfflffl}
b2
b1
b0
f ð3Þ
1. reduziertes Polynom :
Weitere Nullstellen:
Produktdarstellung:
f1 ðxÞ ¼ / x 2 þ 2 x þ 3
/x2 þ 2x þ 3 ¼ 0
oder
x2 / 2x / 3 ¼ 0
)
x2 ¼ / 1 ;
x3 ¼ 3
2
f ðxÞ ¼ / ðx / 3Þ ðx þ 1Þ ðx / 3Þ ¼ / ðx / 3Þ ðx þ 1Þ
&
82
III Funktionen und Kurven
4.7 Interpolationspolynome
4.7.1 Allgemeine Vorbetrachtungen
Von einer unbekannten Funktion y ¼ f ðxÞ sind n þ 1 verschiedene Kurvenpunkte (sog.
Stützpunkte) bekannt:
P0 ¼ ðx0 ; y0 Þ;
P1 ¼ ðx1 ; y1 Þ;
P2 ¼ ðx2 ; y2 Þ; . . . ;
Pn ¼ ðxn ; yn Þ
Die Abszissen x0 ; x1 ; x2 ; . . . ; xn heißen Stützstellen, die zugehörigen Ordinaten
y0 ; y1 ; y2 ; . . . ; yn Stützwerte. Wir setzen dabei voraus, dass die Stützstellen xi paarweise
voneinander verschieden sind. Es gibt dann genau eine Polynomfunktion n-ten (oder auch
niedrigeren) Grades, die durch diese Punkte verläuft.
y
Pn–1
P0
Nährungspolynom
P1
y0
x0
y1
x1
Pn
P2
y2
x2
yn–1
xn–1
yn
xn
x
Diese Näherungsfunktion wird als Interpolationspolynom bezeichnet, da man mit ihr z. B.
beliebige Zwischenwerte der (unbekannten) Funktion im Intervall x0 ) x ) xn näherungsweise berechnen kann.
In der Praxis erweist sich der direkte Lösungsansatz
y ¼ a0 þ a1 x þ a2 x 2 þ . . . þ an x n
als wenig geeignet. Setzt man nämlich der Reihe nach die Koordinaten der n þ 1 Stützpunkte P0 ; P1 ; P2 ; . . . ; Pn in diesen Ansatz ein, so erhält man ein lineares Gleichungssystem mit n þ 1 Gleichungen und ebenso vielen unbekannten Koeffizienten
a0 ; a1 ; a2 ; . . . ; an , das sich jedoch nur mit erheblichem Rechenaufwand (Gaußscher Algorithmus!) lösen lässt.
4.7.2 Interpolationsformel von Lagrange
Das Lagrangesche Interpolationspolynom durch n þ 1 verschiedene Punkte besitzt die
Form
y ¼ y0 . L0 ðxÞ þ y1 . L1 ðxÞ þ y2 . L2 ðxÞ þ . . . þ yn . Ln ðxÞ
x0 ; x1 ; x2 ; . . . ; xn :
y0 ; y1 ; y2 ; . . . ; yn :
Stützstellen
Stützwerte
L0 ðxÞ; L1 ðxÞ; L2 ðxÞ; . . . ; Ln ðxÞ:
Lagrangesche Koeffizientenfunktionen
4 Ganzrationale Funktionen (Polynomfunktionen)
83
Die Lagrangeschen Koeffizientenfunktionen Lk ðxÞ sind Polynome n-ten Grades und wie
folgt definiert:
L0 ðxÞ ¼
ðx / x1 Þ ðx / x2 Þ ðx / x3 Þ . . . ðx / xn Þ
ðx0 / x1 Þ ðx0 / x2 Þ ðx0 / x3 Þ . . . ðx0 / xn Þ
L1 ðxÞ ¼
ðx / x0 Þ ðx / x2 Þ ðx / x3 Þ . . . ðx / xn Þ
ðx1 / x0 Þ ðx1 / x2 Þ ðx1 / x3 Þ . . . ðx1 / xn Þ
ðx / x0 Þ ðx
L2 ðxÞ ¼
ðx2 / x0 Þ ðx2
..
.
ðx / x0 Þ ðx
Ln ðxÞ ¼
ðxn / x0 Þ ðxn
/ x1 Þ ðx / x3 Þ . . . ðx / xn Þ
/ x1 Þ ðx2 / x3 Þ . . . ðx2 / xn Þ
/ x1 Þ ðx / x2 Þ . . . ðx / xn / 1 Þ
/ x1 Þ ðxn / x2 Þ . . . ðxn / xn / 1 Þ
Anmerkungen
(1)
(2)
&
In der Koeffizientenfunktion Lk ðxÞ fehlt genau der Faktor ðx / xk Þ. Der Nenner ist
dabei stets der Wert des Zählers an der Stelle xk ðk ¼ 0; 1; . . . ; nÞ.
Nachteil der Interpolationsformel von Lagrange (z. B. gegenüber der Newton-Interpolation, siehe Abschnitt 4.7.3): Soll ein weiterer Stützpunkt hinzugenommen werden,
um den Grad des Näherungspolynoms um 1 zu erhöhen, so müssen sämtliche Koeffizientenfunktionen neu berechnet werden.
Beispiel
k
0
1
2
3
xk
0
2
5
7
yk
12
/ 16
/ 28
54
Das Lagrangesche Näherungspolynom durch diese vier Stützpunkte ist von höchstens 3. Grade.
Lösungsansatz: y ¼ y0 . L0 ðxÞ þ y1 . L1 ðxÞ þ y2 . L2 ðxÞ þ y3 . L3 ðxÞ
Bestimmung der Koeffizientenfunktionen:
L0 ðxÞ ¼
ðx / x1 Þ ðx / x2 Þ ðx / x3 Þ
ðx / 2Þ ðx / 5Þ ðx / 7Þ
1
¼
¼/
ðx 3 / 14 x 2 þ 59 x / 70Þ
ðx0 / x1 Þ ðx0 / x2 Þ ðx0 / x3 Þ
ð0 / 2Þ ð0 / 5Þ ð0 / 7Þ
70
L1 ðxÞ ¼
ðx / x0 Þ ðx / x2 Þ ðx / x3 Þ
ðx / 0Þ ðx / 5Þ ðx / 7Þ
1
¼
¼
ðx 3 / 12 x 2 þ 35 xÞ
ðx1 / x0 Þ ðx1 / x2 Þ ðx1 / x3 Þ
ð2 / 0Þ ð2 / 5Þ ð2 / 7Þ
30
L2 ðxÞ ¼
ðx / x0 Þ ðx / x1 Þ ðx / x3 Þ
ðx / 0Þ ðx / 2Þ ðx / 7Þ
1
¼
¼ /
ðx 3 / 9 x 2 þ 14 xÞ
ðx2 / x0 Þ ðx2 / x1 Þ ðx2 / x3 Þ
ð5 / 0Þ ð5 / 2Þ ð5 / 7Þ
30
L3 ðxÞ ¼
ðx / x0 Þ ðx / x1 Þ ðx / x2 Þ
ðx / 0Þ ðx / 2Þ ðx / 5Þ
1
¼
¼
ðx 3 / 7 x 2 þ 10 xÞ
ðx3 / x0 Þ ðx3 / x1 Þ ðx3 / x2 Þ
ð7 / 0Þ ð7 / 2Þ ð7 / 5Þ
70
84
III Funktionen und Kurven
Näherungspolynom nach Lagrange:
y ¼ y 0 . L 0 ðxÞ þ y 1 . L 1 ðxÞ þ y 2 . L 2 ðxÞ þ y 3 . L 3 ðxÞ ¼
3
2
3 2
1
1
¼ 12 . /
ðx 3 / 14 x 2 þ 59 x / 70Þ / 16 .
ðx 3 / 12 x 2 þ 35 xÞ /
70
30
3
2
3 2
1
1
/ 28 . /
ðx 3 / 9 x 2 þ 14 xÞ þ 54 .
ðx 3 / 7 x 2 þ 10 xÞ ¼
30
70
¼ x 3 / 5 x 2 / 8 x þ 12
&
4.7.3 Interpolationsformel von Newton
Das Newtonsche Interpolationspolynom durch n þ 1 verschiedene Punkte besitzt die
Form
y ¼ a0 þ a1 ðx / x0 Þ þ a2 ðx / x0 Þ ðx / x1 Þ þ a3 ðx / x0 Þ ðx / x1 Þ ðx / x2 Þ þ . . .
. . . þ an ðx / x0 Þ ðx / x1 Þ ðx / x2 Þ . . . ðx / xn / 1 Þ
x0 ; x1 ; x2 ; . . . ; xn :
y0 ; y1 ; y2 ; . . . ; yn :
Stützstellen
Stützwerte
Pk ¼ ðxk ; yk Þ: k-ter Stützpunkt ðk ¼ 0, 1, 2, . . . , nÞ
Die Berechnung der Koeffizienten a0 ; a1 ; a2 ; . . . ; an erfolgt zweckmäßigerweise nach
dem sog. Steigungs- oder Differenzenschema:
k
xk
yk
I
a0
0
x0
y0
1
x1
y1
2
x2
y2
3
x3
y3
.
.
.
.
.
.
n
.
.
.
.
.
.
xn
.
.
.
.
.
.
yn
II
a1
½ x0 ; x1 %
½ x1 ; x2 %
½ x2 ; x3 %
......
III
a2
½ x0 ; x1 ; x2 %
½ x1 ; x2 ; x3 %
......
a3
½ x0 ; x1 ; x2 ; x3 %
......
......
4 Ganzrationale Funktionen (Polynomfunktionen)
85
Die Größen ½ x0 ; x1 %; ½ x0 ; x1 ; x2 %; ½ x0 ; x1 ; x2 ; x3 %; . . . heißen dividierte Differenzen 1., 2.,
3., . . . Ordnung und sind wie folgt definiert:
Dividierte Differenzen 1. Ordnung (Spalte I)
Sie werden aus zwei aufeinanderfolgenden Stützpunkten gebildet:
y0
x0
y1
½ x1 ; x2 % ¼
x1
..
.
½ x0 ; x1 % ¼
/
/
/
/
y1
x1
y2
x2
Dividierte Differenzen 2. Ordnung (Spalte II)
Sie werden aus drei aufeinanderfolgenden Stützpunkten gebildet:
½ x0 ; x1 ; x2 % ¼
½ x0 ; x1 % / ½ x1 ; x2 %
x0 / x2
½ x1 ; x2 ; x3 % ¼
½ x1 ; x2 % / ½ x2 ; x3 %
x1 / x3
..
.
Dividierte Differenzen 3. Ordnung (Spalte III)
Sie werden aus vier aufeinanderfolgenden Stützpunkten gebildet:
½ x0 ; x1 ; x2 ; x3 % ¼
½ x0 ; x1 ; x2 % / ½ x1 ; x2 ; x3 %
x0 / x3
½ x1 ; x2 ; x3 ; x4 % ¼
½ x1 ; x2 ; x3 % / ½ x2 ; x3 ; x4 %
x1 / x4
..
.
Entsprechend sind die dividierten Differenzen höherer Ordnung definiert.
Anmerkung
Vorteil der Interpolationsformel von Newton (z. B. gegenüber der Lagrange-Interpolation,
siehe Abschnitt 4.7.2): Die Anzahl der Stützpunkte kann beliebig vergrößert (oder auch
verkleinert) werden, ohne dass die Koeffizienten neu berechnet werden müssen (das Rechenschema ist nur entsprechend zu ergänzen).
86
&
III Funktionen und Kurven
Beispiel
k
0
1
2
3
xk
0
2
5
7
yk
12
/ 16
/ 28
54
Das Newtonsche Näherungspolynom durch diese vier Stützpunkte ist von höchstens 3. Grade.
Lösungsansatz:
y ¼ a0 þ a1 ðx / x0 Þ þ a2 ðx / x0 Þ ðx / x1 Þ þ a3 ðx / x0 Þ ðx / x1 Þ ðx / x2 Þ
Berechnung der Koeffizienten nach dem Steigungs- oder Differenzenschema:
k
xk
yk
I
II
III
a0
a1
0
12
0
1
2
/ 16
2
5
/ 28
3
7
54
a2
/ 14
/4
2
9
a3
1
41
a0 ¼ 12;
a1 ¼ / 14;
a2 ¼ 2;
a3 ¼ 1
Näherungspolynom nach Newton:
y ¼ a0 þ a1 ðx / x0 Þ þ a2 ðx / x0 Þ ðx / x1 Þ þ a 3 ðx / x0 Þ ðx / x1 Þ ðx / x2 Þ ¼
¼ 12 / 14ðx / 0Þ þ 2 ðx / 0Þ ðx / 2Þ þ 1 ðx / 0Þ ðx / 2Þ ðx / 5Þ ¼
¼ 12 / 14 x þ 2 x ðx / 2Þ þ x ðx / 2Þ ðx / 5Þ ¼
¼ 12 / 14 x þ 2 x 2 / 4 x þ x ðx 2 / 7 x þ 10Þ ¼
¼ 12 / 14 x þ 2 x 2 / 4 x þ x 3 / 7 x 2 þ 10 x ¼
¼ x 3 / 5 x 2 / 8 x þ 12
&
5 Gebrochenrationale Funktionen
5.1 Definition der gebrochenrationalen Funktionen
f ðxÞ ¼
gðxÞ
am x m þ am / 1 x m / 1 þ . . . þ a1 x þ a0
¼
hðxÞ
bn x n þ bn / 1 x n / 1 þ . . . þ b1 x þ b0
ðam 6¼ 0; bn 6¼ 0Þ
g ðxÞ:
Zählerpolynom vom Grade m
h ðxÞ:
Nennerpolynom vom Grade n
n > m: Echt gebrochenrationale Funktion (sonst unecht gebrochen)
Definitionsbereich:
x 2 R mit Ausnahme der Nullstellen des Nennerpolynoms h ðxÞ
5 Gebrochenrationale Funktionen
87
5.2 Nullstellen, Definitionslücken, Pole
Nullstelle x0
Es gilt f ðx0 Þ ¼ 0, d. h. g ðx0 Þ ¼ 0 und hðx0 Þ ¼
6 0.
Definitionslücke x0
Der Nenner der gebrochenrationalen Funktion verschwindet an der Stelle x0 , also gilt
h ðx0 Þ ¼ 0. Die Definitionslücken fallen daher mit den (reellen) Nullstellen des Nenners
zusammen. Es gibt somit höchstens n (reelle) Definitionslücken, ermittelt aus der Gleichung h ðxÞ ¼ 0.
Pol oder Unendlichkeitsstelle x0
Ein Pol x0 ist eine Definitionslücke besonderer Art: Nähert man sich der Stelle x0 , so strebt
der Funktionswert gegen þ 1 oder / 1. In einer Polstelle gilt somit h ðx0 Þ ¼ 0 und
g ðx0 Þ ¼
6 0, falls Zähler und Nenner keine gemeinsamen Nullstellen haben (siehe auch weiter
unten). Die in einem Pol errichtete Parallele zur y-Achse heißt Polgerade (senkrechte Asymptote). Verhält sich die Funktion bei Annäherung an den Pol von beiden Seiten her gleichartig,
so liegt ein Pol ohne Vorzeichenwechsel, anderenfalls ein Pol mit Vorzeichenwechsel vor.
Ist x0 eine k-fache Nullstelle des Nennerpolynoms h ðxÞ, so liegt ein Pol k-ter Ordnung vor:
k ¼ gerade
) Pol ohne Vorzeichenwechsel
k ¼ ungerade ) Pol mit Vorzeichenwechsel
Berechnung der Nullstellen und Pole
Falls Zähler und Nenner gemeinsame Nullstellen und somit auch gemeinsame Linearfaktoren haben, geht man wie folgt vor:
1. Man zerlegt zunächst das Zähler- und Nennerpolynom jeweils in Linearfaktoren und
kürzt gemeinsame Faktoren heraus.
2. Die im Zähler verbliebenen Linearfaktoren liefern dann die Nullstellen, die im Nenner
verbliebenen Linearfaktoren die Pole der gebrochenrationalen Funktion.
Durch das Herauskürzen gemeinsamer Linearfaktoren können u. U. Definitionslücken behoben und somit der Definitionsbereich der Funktion erweitert werden.
&
Beispiel
y ¼
3 x 4 / 12 x 3 / 9 x 2 þ 42 x / 24
3ðx þ 2Þ ðx / 1Þ 2 ðx / 4Þ
¼
x3 þ x2 / x / 1
ðx / 1Þ ðx þ 1Þ 2
ðx 6¼ 1; /1Þ
Zähler und Nenner wurden in Linearfaktoren zerlegt, gemeinsame Linearfaktoren herausgekürzt:
y ¼
3 ðx þ 2Þ ðx / 1Þ ðx / 4Þ
ðx þ 1Þ 2
Nullstellen:
x1 ¼ / 2 ;
x2 ¼ 1 ;
x3 ¼ 4
Pole:
x4 ¼ / 1
(Pol ohne Vorzeichenwechsel)
Polgerade:
x
(Parallele zur y-Achse)
¼ /1
Die ursprünglich vorhandene Definitionslücke bei x ¼ 1 wurde somit behoben.
&
88
III Funktionen und Kurven
5.3 Asymptotisches Verhalten im Unendlichen
Echt gebrochenrationale Funktion
Eine echt gebrochenrationale Funktion nähert sich im Unendlichen (d. h. für x ! + 1Þ
stets der x-Achse:
Asymptote im Unendlichen:
y ¼ 0
Unecht gebrochenrationale Funktion
Eine unecht gebrochenrationale Funktion f ðxÞ wird zunächst durch Polynomdivision in
eine ganzrationale Funktion (Polynomfunktion) pðxÞ und eine echt gebrochenrationale
Funktion r ðxÞ zerlegt: f ðxÞ ¼ p ðxÞ þ r ðxÞ. Im Unendlichen verschwindet r ðxÞ und
die Funktion f ðxÞ nähert sich daher asymptotisch der Polynomfunktion p ðxÞ:
Asymptote im Unendlichen:
&
y ¼ p ðxÞ
(Polynom vom Grade m / n)
Beispiel
y ¼
3 x 4 / 12 x 3 / 9 x 2 þ 42 x / 24
x3 þ x2 / x / 1
ðunecht gebrochenrationale Funktion; m ¼ 4; n ¼ 3Þ
Polynomdivision:
9 x 2 þ 30 x / 39
ð3 x 4 / 12 x 3 / 9 x 2 þ 42 x / 24Þ : ðx 3 þ x 2 / x / 1Þ ¼ 3 x / 15 þ 3
x þ x2 / x / 1
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
/ ð3 x 4 þ 3 x 3 / 3 x 2 / 3 xÞ
p ðxÞ
r ðxÞ
/ 15 x 3 / 6 x 2 þ 45 x / 24
/ ð/ 15 x 3 / 15 x 2 þ 15 x þ 15Þ
9 x 2 þ 30 x / 39
Asymptote im Unendlichen:
y ¼ 3 x / 15
(Polynom vom Grade 1 ! Gerade)
&
6 Potenz- und Wurzelfunktionen
6.1 Potenzfunktionen mit ganzzahligen Exponenten
Potenzfunktionen mit positiv-ganzzahligen Exponenten
y ¼ xn;
/1 < x < 1
(sog. Parabel n-ter Ordnung)
ðn 2 N *Þ
6 Potenz- und Wurzelfunktionen
89
Eigenschaften
(1)
(2)
Symmetrie: Für gerades n erhält man gerade Funktionen (Bild a)), für ungerades n
ungerade Funktionen (Bild b)).
Nullstelle: x1 ¼ 0 (n-fache Nullstelle)
Bild a) zeigt die gerade Funktion y ¼ x 2 (Normalparabel), Bild b) die ungerade Funktion y ¼ x 3 (kubische Parabel).
y
y
y = x2
y = x3
1
x
–1
a)
1
x
b)
–1
Potenzfunktionen mit negativ-ganzzahligen Exponenten
y ¼ x /n ¼
1
;
xn
x 6¼ 0
ðn 2 N *Þ
Eigenschaften
(1)
(2)
(3)
Symmetrie: Für gerades n erhält man gerade Funktionen (Bild a)), für ungerades n
ungerade Funktionen (Bild b)).
Pol: x1 ¼ 0 (Pol n-ter Ordnung)
Polgerade: x ¼ 0 (y-Achse)
Asymptote im Unendlichen: y ¼ 0 (x-Achse)
Bild a) zeigt die gerade Funktion y ¼ x / 2 , Bild b) die ungerade Funktion y ¼ x / 1 .
y
y
y = x –1
1
y = x –2
y = x –2
y = x –1
1
x
1
a)
1
x
b)
90
III Funktionen und Kurven
6.2 Wurzelfunktionen
pffiffiffi
Die Wurzelfunktionen y ¼ n x sind die Umkehrfunktionen der auf das Intervall x ( 0
beschränkten Potenzfunktionen y ¼ x n ðn ¼ 2; 3; 4; . . .Þ :
y ¼
ffiffiffi
p
n
x;
x ( 0
ðn ¼ 2; 3; 4; . . .Þ
Eigenschaften
(1)
(2)
Monotonie: Streng monoton wachsend
Nullstelle: x1 ¼ 0
pffiffiffi
Bild a) zeigt die Wurzelfunktion y ¼ x (Umkehrfunktion von y ¼ x 2 , x ( 0),
pffiffiffi
Bild b) die Wurzelfunktion y ¼ 3 x (Umkehrfunktion von y ¼ x 3 , x ( 0).
y
y
1
1
y = √x
3
y = √x
y = x2
1
a)
y = x3
x
1
x
b)
6.3 Potenzfunktionen mit rationalen Exponenten
Unter einer Potenzfunktion mit rationalem Exponenten versteht man die Wurzelfunktion
m
y ¼ xn ¼
ffiffiffiffiffiffi
p
n m
x ;
x > 0
ðm 2 Z ; n 2 N *Þ
(n-te Wurzel aus x m )
Eigenschaften
(1)
(2)
(3)
Monotonie: Bei positivem Exponenten streng monoton wachsend (Bild a)), bei negativem Exponenten streng monoton fallend (Bild b)).
Definitionsbereich: x > 0, bei positivem Exponenten x ( 0.
Erweiterung auf beliebige reelle Exponenten a:
a
y ¼ x a ¼ e ln x ¼ e a . ln x
ðx > 0; ln x : natürlicher Logarithmus von xÞ
7 Trigonometrische Funktionen
91
Bild a) zeigt die streng monoton wachsende Funktion y ¼ x 2=3 ðx ( 0Þ, Bild b) die
streng monoton fallende Funktion y ¼ x / 1=2 ðx > 0Þ.
y
y
y = x 2/3
1
y = x –1/2
1
x
1
5
1
a)
x
b)
7 Trigonometrische Funktionen
Weitere Bezeichnungen:
Winkelfunktionen, Kreisfunktionen
7.1 Winkelmaße
Winkel werden im Grad- oder Bogenmaß gemessen.
Bogenmaß eines Winkels
v
Bogenmaß x : Maßzahl der Länge des Kreisbogens, der im Einheitskreis dem Winkel a gegenüberliegt 2Þ .
Einer vollen Umdrehung entsprechen im Gradmaß 360" (Altgrad), im Bogenmaß 2 p rad
(gelesen: Radiant) 3Þ .
1
a
Bogenmaß x
u
Umrechnung der Winkelmaße
Vom Grad- ins Bogenmaß:
x ¼
p
a
180"
Vom Bogen- ins Gradmaß:
a ¼
180"
x
p
1" ' 0,017 453 rad;
2Þ
3Þ
1 rad ' 57,2958"
In einem beliebigen Kreis ist x das Verhältnis aus der Kreisbogenlänge b und dem Radius r ðx ¼ b=rÞ.
Das Bogenmaß ist eine dimensionslose Größe, man lässt daher die Einheit rad meist weg. Neben dem Altgrad
gibt es noch den Neugrad. Einer vollen Umdrehung entsprechen dabei 400 gon.
92
III Funktionen und Kurven
Drehsinn eines Winkels
v
Die Winkel erhalten wie folgt ein Vorzeichen: Im Gegenuhrzeigersinn überstrichene
Winkel werden positiv, im Uhrzeigersinn
überstrichene Winkel negativ gezählt.
P
x
a
–a
u
–x
P'
7.2 Definition der trigonometrischen Funktionen
Darstellung im rechtwinkeligen Dreieck
a ist ein spitzer Winkel in einem rechtwinkeligen Dreieck ð0" ) a ) 90" Þ. Definitionsgemäß gilt dann:
sin a ¼
Gegenkathete
a
¼
Hypotenuse
c
cos a ¼
Ankathete
Hypotenuse
tan a ¼
Gegenkathete
a
¼
Ankathete
b
cot a ¼
Ankathete
b
¼
Gegenkathete
a
¼
b
c
c
a
a
b
a, b: Katheten
c: Hypotenuse
Darstellung im Einheitskreis
Für einen beliebigen (positiven oder negativen) Winkel a gilt definitionsgemäß (P ist
dabei der zum Winkel a gehörende Kreispunkt):
„Obere Tangente“
cot a
P
sin a ¼ Ordinate von P
1
cos a ¼ Abszisse von P
sin a
tan a ¼ Abschnitt auf der
„rechten Kreistangente“
cot a ¼ Abschnitt auf der
„oberen Kreistangente“
v
a
cos a
u
tan a
„Rechte
Tangente“
7 Trigonometrische Funktionen
93
Quadrantenregel (Vorzeichenregel)
Quadrant
I
II
III
IV
Sinus
þ
þ
/
/
Kosinus
þ
/
/
þ
Tangens
þ
/
þ
/
Kotangens
þ
/
þ
/
v
II
I
a
u
III
IV
7.3 Sinus- und Kosinusfunktion
Die trigonometrischen Funktionen y ¼ sin x und y ¼ cos x zeigen den folgenden Verlauf (x : Winkel im Bogenmaß):
y
y = cos x
y = sin x
1
–p
–p
2
0
p
2
p
3
2
p
2p
5
2
p
3p
x
–1
Eigenschaften ðk 2 ZÞ
y ¼ sin x
y ¼ cos x
Definitionsbereich
/1 < x < 1
/1 < x < 1
Wertebereich
/1 ) y ) 1
/1 ) y ) 1
Periode (primitive)
2p
2p
Symmetrie
ungerade
gerade
Nullstellen
xk ¼ k . p
xk ¼
Relative Maxima
xk ¼
p
þ k . 2p
2
xk ¼ k . 2 p
Relative Minima
xk ¼
3
p þ k . 2p
2
xk ¼ p þ k . 2 p
p
þk .p
2
94
III Funktionen und Kurven
7.4 Tangens- und Kotangensfunktion
Die trigonometrischen Funktionen y ¼ tan x und y ¼ cot x zeigen den in den Bildern
a) und b) dargestellten Verlauf (x : Winkel im Bogenmaß):
y
y
1
1
p
– 23 p – p – 2
0
p
2
p
3
2
p 2p
5
2
p
x
– 2 p – 23
a) Tangensfunktion
p –p – p
2
0 p
2
p
3
2
p
2p
x
b) Kotangensfunktion
Eigenschaften ðk 2 ZÞ
y ¼ tan x
y ¼ cot x
Definitionsbereich
x 2 R mit Ausnahme
p
der Stellen xk ¼
þk .p
2
x 2 R mit Ausnahme
der Stellen xk ¼ k . p
Wertebereich
/1 < y < 1
/1 < y < 1
Periode (primitive)
p
p
Symmetrie
ungerade
ungerade
Nullstellen
xk ¼ k . p
xk ¼
Pole
xk ¼
Senkrechte Asymptoten
x ¼
p
þk .p
2
p
þk .p
2
xk ¼ k . p
p
þk .p
2
x ¼ k .p
Beide Funktionen besitzen keine relativen Extremwerte.
7.5 Wichtige Beziehungen zwischen den trigonometrischen Funktionen
Zusammenhang zwischen sin x und cos x
!
p4
cos x ¼ sin x þ
2
!
p4
sin x ¼ cos x /
2
Der Kosinus läuft dem Sinus um p=2 voraus, der Sinus läuft dem Kosinus um p=2
hinterher.
7 Trigonometrische Funktionen
95
Trigonometrischer Pythagoras
sin 2 x þ cos 2 x ¼ 1
Weitere elementare Beziehungen
tan x ¼
sin x
1
¼
cos x
cot x
cot x ¼
cos x
1
¼
sin x
tan x
Umrechnungen zwischen den trigonometrischen Funktionen
sin x
cos x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
+ 1 / cos 2 x
sin x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / sin 2 x
cos x
+
tan x
sin x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / sin 2 x
cot x
+
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / sin 2 x
sin x
+
tan x
cot x
tan x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ tan 2 x
1
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ cot 2 x
1
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ tan 2 x
cot x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ cot 2 x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / cos 2 x
1
cot x
cos x
cos x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / cos 2 x
1
tan x
Das Vorzeichen wird nach der Quadrantenregel bestimmt (siehe Abschnitt 7.2).
7.6 Trigonometrische Formeln
7.6.1 Additionstheoreme
sin ðx1 + x2 Þ ¼ sin x1 . cos x2 + cos x1 . sin x2
cos ðx1 + x2 Þ ¼ cos x1 . cos x2 * sin x1 . sin x2
tan ðx1 + x2 Þ ¼
tan x1 + tan x2
1 * tan x1 . tan x2
cot ðx1 + x2 Þ ¼
cot x1 . cot x2 * 1
cot x2 + cot x1
96
III Funktionen und Kurven
7.6.2 Formeln für halbe Winkel
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / cos x
2
2
r
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!x4
1 þ cos x
cos
¼ +
2
2
r
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!x4
1 / cos x
sin x
1 / cos x
tan
¼ +
¼
¼
2
1 þ cos x
1 þ cos x
sin x
sin
!x4
¼ +
Das Vorzeichen wird nach der Quadrantenregel bestimmt (siehe Abschnitt 7.2).
7.6.3 Formeln für Winkelvielfache
Formeln für doppelte Winkel
sin ð2 xÞ ¼ 2 . sin x . cos x
cos ð2 xÞ ¼ cos 2 x / sin 2 x ¼ 1 / 2 . sin 2 x ¼ 2 . cos 2 x / 1
tan ð2 xÞ ¼
2 . tan x
1 / tan 2 x
Formeln für dreifache Winkel
sin ð3 xÞ ¼ 3 . sin x / 4 . sin3 x
cos ð3 xÞ ¼ 4 . cos 3 x / 3 . cos x
tan ð3 xÞ ¼
3 . tan x / tan 3 x
1 / 3 . tan 2 x
Formeln für n-fache Winkel (n = 2, 3, 4, . . .)
sin ðn xÞ ¼
!n4
1
þ
. sin x . cos n / 1 x /
!n4
5
k
:
3
. sin 3 x . cos n / 3 x þ
. sin 5 x . cos n / 5 x / þ . . .
cos ðn xÞ ¼ cos n x /
!n4
!n4
!n4
2
. sin 2 x . cos n / 2 x þ
Binomialkoeffizient (siehe I.2.7)
!n4
4
. sin 4 x . cos n / 4 x / þ . . .
7 Trigonometrische Funktionen
7.6.4 Formeln für Potenzen
sin 2 x ¼
1
½1 / cos ð2 xÞ%
2
sin 3 x ¼
1
½3 . sin x / sin ð3 xÞ%
4
sin 4 x ¼
1
½ cos ð4 xÞ / 4 . cos ð2 xÞ þ 3%
8
cos 2 x ¼
1
½1 þ cos ð2 xÞ%
2
cos 3 x ¼
1
½3 . cos x þ cos ð3 xÞ%
4
cos 4 x ¼
1
½ cos ð4 xÞ þ 4 . cos ð2 xÞ þ 3%
8
7.6.5 Formeln für Summen und Differenzen
!x þ x 4
!x / x 4
1
2
1
2
. cos
2
2
!x þ x 4
!x / x 4
1
2
1
2
. sin
sin x1 / sin x2 ¼ 2 . cos
2
2
!x þ x 4
!x / x 4
1
2
1
2
cos x1 þ cos x2 ¼ 2 . cos
. cos
2
2
!x þ x 4
!x / x 4
1
2
1
2
cos x1 / cos x2 ¼ / 2 . sin
. sin
2
2
sin x1 þ sin x2 ¼ 2 . sin
tan x1 + tan x2 ¼
sin ðx1 + x2 Þ
cos x1 . cos x2
sin ðx1 þ x2 Þ þ sin ðx1 / x2 Þ ¼ 2 . sin x1 . cos x2
sin ðx1 þ x2 Þ / sin ðx1 / x2 Þ ¼ 2 . cos x1 . sin x2
cos ðx1 þ x2 Þ þ cos ðx1 / x2 Þ ¼ 2 . cos x1 . cos x2
cos ðx1 þ x2 Þ / cos ðx1 / x2 Þ ¼ / 2 . sin x1 . sin x2
97
98
III Funktionen und Kurven
7.6.6 Formeln für Produkte
sin x1 . sin x2 ¼
1
½ cos ðx1 / x2 Þ / cos ðx1 þ x2 Þ%
2
cos x1 . cos x2 ¼
1
½cos ðx1 / x2 Þ þ cos ðx1 þ x2 Þ%
2
sin x1 . cos x2 ¼
1
½ sin ðx1 / x2 Þ þ sin ðx1 þ x2 Þ%
2
tan x1 . tan x2 ¼
tan x1 þ tan x2
cot x1 þ cot x2
7.7 Anwendungen in der Schwingungslehre
7.7.1 Allgemeine Sinus- und Kosinusfunktion
y
Allgemeine Sinusfunktion
y ¼ a . sin ðb x þ cÞ
a
ða > 0; b > 0Þ
x0
Eigenschaften
(1)
(2)
(3)
x
y = a sin(bx + c)
–a
Periode: p ¼ 2 p=b
Wertebereich: / a ) y ) a
Verschiebung auf der x-Achse, bezogen auf die elementare Sinusfunktion y ¼ sin x
(„Startpunkt“): x0 ¼ / c=b (für c > 0 ist die Kurve nach links, für c < 0 nach
rechts verschoben)
Allgemeine Kosinusfunktion
y ¼ a . cos ðb x þ cÞ
Eigenschaften
(1)
(2)
(3)
p = 2 p/b
y
a
y = a cos(bx + c)
ða > 0; b > 0Þ
x0
–a
x
p = 2 p/b
Periode: p ¼ 2 p=b
Wertebereich: / a ) y ) a
Verschiebung auf der x-Achse, bezogen auf die elementare Kosinusfunktion y ¼ cos x
(„Startpunkt“): x0 ¼ / c=b (für c > 0 ist die Kurve nach links, für c < 0 nach
rechts verschoben)
7 Trigonometrische Funktionen
99
7.7.2 Harmonische Schwingungen (Sinusschwingungen)
7.7.2.1 Gleichung einer harmonischen Schwingung
Auslenkung y eines Federpendels (Feder-Masse-Schwingers) in Abhängigkeit von der Zeit t :
y ¼ A . sin ðw t þ jÞ
A:
w:
j:
T:
f:
y
ðA; w > 0Þ
T
A
Amplitude (maximale Auslenkung)
Kreisfrequenz der Schwingung
Phase, Phasenwinkel oder
Nullphasenwinkel
Schwingungsdauer oder Periode
Frequenz
T ¼ 2 p=w, f ¼ 1=T ¼ w=2 p
w ¼ 2 p f ¼ 2 p=T
– f/v
t
y = A sin( vt + f)
–A
Eine in der Kosinusform y ¼ A . cos ðw t þ jÞ dargestellte harmonische Schwingung
lässt sich wie folgt in die Sinusform umschreiben:
y ¼ A . cos ðw t þ jÞ ¼ A . sin
3
2
p
¼ A . sin ðw t þ j *Þ
wt þ j þ
2
|fflfflffl{zfflfflffl}
Nullphasenwinkel j *
Regel: Nullphasenwinkel j um p=2 vergrößern
7.7.2.2 Darstellung einer harmonischen Schwingung im Zeigerdiagramm
Eine harmonische Schwingung y ¼ A . sin ðw t þ jÞ lässt sich in einem Zeigerdiagramm
durch einen rotierenden Zeiger der Länge A darstellen. 4Þ Die Rotation erfolgt dabei aus der
durch den Nullphasenwinkel j eindeutig bestimmten Anfangslage heraus um den Nullpunkt
mit der Winkelgeschwindigkeit w im Gegenuhrzeigersinn. Die Ordinate der Zeigerspitze
entspricht dabei dem augenblicklichen Funktionswert der Schwingung (Bild a)).
v
+ cos
A sin( v t + f)
A
vt
A
f
A sin f
u
a)
4Þ
Darstellung durch komplexe Zeiger: siehe VIII.8.1.
– sin
b)
+ sin
– cos
100
III Funktionen und Kurven
Bei der bildlichen Darstellung einer Schwingung im Zeigerdiagramm zeichnet man verabredungsgemäß nur die Anfangslage (Zeiger der Länge A unter dem Winkel j gegen die
Horizontale). Lässt man auch einen negativen „Amplitudenfaktor“ A zu, so gelten für das
Abtragen der unverschobenen Schwingungen ðj ¼ 0Þ die folgenden Regeln (A < 0
bedeutet eine Vergrößerung des Phasenwinkels um p, d. h. eine zusätzliche Drehung des
Zeigers um 180" (Bild b)):
Schwingungstyp
A > 0
A < 0
y ¼ A . sin ðw tÞ
Zeiger nach rechts abtragen
Zeiger nach links abtragen
y ¼ A . cos ðw tÞ
Zeiger nach oben abtragen
Zeiger nach unten abtragen
Liegen die Schwingungen in der „phasenverschobenen“ Form y ¼ A . sin ðw t þ jÞ
bzw. y ¼ A . cos ðw t þ j) vor, so erfolgt eine zusätzliche Drehung um den Nullphasenwinkel j (für j > 0 im Gegenuhrzeigersinn, für j < 0 im Uhrzeigersinn).
+ cos
Beispiel
&
Das nebenstehende Bild zeigt die Anfangslage
der folgenden Zeiger:
!
p4
y1 ¼ 4 . sin w t þ
4
!
p4
y2 ¼ / 3 . sin w t /
3
3
2
3
y3 ¼ 3 . cos w t /
p
4
y2
3
60°
4
45°
135°
y1
+ sin
3
y3
&
7.7.3 Superposition (!berlagerung) gleichfrequenter harmonischer Schwingungen
Die ungestörte !berlagerung zweier gleichfrequenter harmonischer Schwingungen
y1 ¼ A1 . sin ðw t þ j1 Þ und y2 ¼ A2 . sin ðw t þ j2 Þ führt zu einer resultierenden
Schwingung der gleichen Frequenz (Superpositionsprinzip der Physik). Im Zeigerdiagramm
werden die Zeiger von y1 und y2 nach der aus der Vektorrechnung bekannten Parallelogrammregel zu einem resultierenden Zeiger y ¼ A . sin ðw t þ jÞ zusammengesetzt.
Amplitude A und Nullphasenwinkel j können direkt abgelesen oder nach den folgenden
Formeln berechnet werden ðA1 > 0; A2 > 0Þ:
y = y1 + y2
y ¼ y1 þ y2 ¼ A . sin ðw t þ jÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
A ¼ A 21 þ A 22 þ 2 A1 A2 . cos ðj2 / j1 Þ
tan j ¼
A1 . sin j1 þ A2 . sin j2
A1 . cos j1 þ A2 . cos j2
Anmerkungen
(1)
y2
A
A2
f2 f
A1
y1
f1
Bei der Berechnung des Nullphasenwinkels j aus der angegebenen Gleichung ist
die Lage des resultierenden Zeigers zu berücksichtigen (Skizze anfertigen und den
Quadranten des Winkels bestimmen).
8 Arkusfunktionen
101
(2)
Die Formeln für Amplitude A und Phasenwinkel j gelten auch dann, wenn beide Einzelschwingungen in der Kosinusform vorliegen. Die resultierende Schwingung ist dann
ebenfalls eine (gleichfrequente) Kosinusschwingung vom Typ y ¼ A . cos ðw t þ jÞ.
&
Beispiel
y = y1 + y2
Ungestörte !berlagerung zweier Sinusschwingungen:
3
2
!
p4
2
y1 ¼ 4 . sin w t þ
;
y2 ¼ 3 . sin w t þ
p
8
3
A
y2
p
2
;
j2 ¼
p
8
3
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
2ffi
2
p
A ¼ 4 2 þ 3 2 þ 2 . 4 . 3 . cos
¼
p /
3
8
A1 ¼ 4 ;
¼
A2 ¼ 3 ;
j1 ¼
f
4,7
62°
y1
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
2ffi
13
16 þ 9 þ 24 . cos
p ¼ 4;68
24
2
2
p
8
3
3
2 ¼ 1;8806
tan j ¼
!p4
2
þ 3 . cos
p
4 . cos
8
3
4 . sin
!p4
3
þ 3 . sin
)
j ¼ arctan 1;8806 ¼ 1;082 ¼ 62"
Resultierende Schwingung: y ¼ y1 þ y2 ¼ 4;68 . sin ðw t þ 1;082Þ
&
8 Arkusfunktionen
Die Umkehrfunktionen der auf bestimmte Intervalle beschränkten trigonometrischen Funktionen heißen Arkus- oder zyklometrische Funktionen. Die Intervalle müssen dabei so gewählt werden, dass die trigonometrischen Funktionen dort in streng monotoner Weise sämtliche Funktionswerte durchlaufen und somit umkehrbar sind. Der Funktionswert einer
Arkusfunktion ist ein im Bogen- oder Gradmaß dargestellter Winkel.
8.1 Arkussinus- und Arkuskosinusfunktion
y
p
Arkussinusfunktion
y ¼ arcsin x mit / 1 ) x ) 1 ist die
Umkehrfunktion der auf das Intervall
/ p=2 ) x ) p=2 beschränkten Sinusfunktion.
Der Arkussinus liefert nur Winkel aus dem
1. und 4. Quadrant.
2
y = arcsin x
1
–1
–p
2
x
102
III Funktionen und Kurven
y
Arkuskosinusfunktion
p
y ¼ arccos x mit / 1 ) x ) 1 ist die
Umkehrfunktion der auf das Intervall
0 ) x ) p beschränkten Kosinusfunktion.
p
2
y = arccos x
Der Arkuskosinus liefert nur Winkel aus dem
1. und 2. Quadrant.
1
–1
x
Eigenschaften
y ¼ arcsin x
y ¼ arccos x
Definitionsbereich
/1 ) x ) 1
p
p
/
) y )
2
2
/1 ) x ) 1
Wertebereich
0 ) y ) p
Symmetrie 5Þ
ungerade
Nullstellen
x1 ¼ 0
x1 ¼ 1
Monotonie
streng monoton wachsend
streng monoton fallend
8.2 Arkustangens- und Arkuskotangensfunktion
Arkustangensfunktion
y
p
y ¼ arctan x mit / 1 < x < 1 ist
die Umkehrfunktion der auf das Intervall
/ p=2 < x < p=2 beschränkten Tangensfunktion.
Der Arkustangens liefert nur Winkel aus dem
1. und 4. Quadrant.
Arkuskotangensfunktion
y ¼ arccot x mit / 1 < x < 1 ist
die Umkehrfunktion der auf das Intervall
0 < x < p beschränkten Kotangensfunktion.
Der Arkuskotangens liefert nur Winkel aus dem
1. und 2. Quadrant.
5Þ
y ¼ arccos x verläuft punktsymmetrisch zum Symmetriezentrum
2
y = arctan x
x
1
–
p
2
y
p
p
y = arccot x
2
1
P ¼ ð0; p=2Þ auf der y-Achse.
x
8 Arkusfunktionen
103
Eigenschaften
y ¼ arctan x
y ¼ arccot x
Definitionsbereich
/1 < x < 1
/1 < x < 1
Wertebereich
/
Symmetrie 6Þ
ungerade
Nullstellen
x1 ¼ 0
Monotonie
streng monoton wachsend
streng monoton fallend
Asymptoten
p
y ¼ +
2
y ¼ 0;
p
p
< y <
2
2
0 < y < p
y ¼ p
Die Berechnung der Funktionswerte von y ¼ arccot x erfolgt nach der Formel
arccot x ¼
p
/ arctan x
2
Bei Verwendung des Gradmaßes muss p=2 durch 90" ersetzt werden.
8.3 Wichtige Beziehungen zwischen den Arkusfunktionen
arcsin x þ arccos x ¼ p=2
arctan x þ arccot x ¼ p=2
arcsin x ¼ arctan
!
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / x2
arctan x ¼ arcsin
!
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ x2
arccos x ¼ arccot
!
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / x2
arccot x ¼ arccos
!
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ x2
arccot x ¼
8
<
:
arctan ð1=xÞ
arctan ð1=xÞ þ p
fur
€
9
x > 0=
x < 0
;
Formeln für negative Argumente
6Þ
arcsin ð/ xÞ ¼ / arcsin x
arccos ð/ xÞ ¼ p / arccos x
arctan ð/ xÞ ¼ / arctan x
arccot ð/ xÞ ¼ p / arccot x
y ¼ arccot x verläuft punktsymmetrisch zum Symmetriezentrum P ¼ ð0; p=2Þ auf der y-Achse.
104
III Funktionen und Kurven
9 Exponentialfunktionen
9.1 Definition der Exponentialfunktionen
e-Funktion (Basis e)
y ¼ ex ;
y
/1 < x < 1
y = ex
Basis:
Eulersche Zahl e
3
2
1 n
e ¼ lim 1 þ
¼ 2;718 281 . . .
n!1
n
1
1
Allgemeine Exponentialfunktion (Basis a)
y ¼ ax ;
x
y
/1 < x < 1
( )
y= 1
3
Basis: a > 0; a 6¼ 1
Das Bild zeigt die Exponentialfunktionen
y ¼ 3
2 x 2(streng monoton wachsend) und
1 x
y ¼
(streng monoton fallend).
3
x
y = 2x
1
y ¼ a x ist auch als e-Funktion darstellbar:
y ¼ a x ¼ e lx
ðl ¼ ln aÞ
Eigenschaften
(1)
(2)
(3)
Definitionsbereich:
Wertebereich: 0 <
Monotonie: l > 0
l < 0
/1 < x < 1
y < 1 (keine Nullstellen!)
(d. h. a > 1): Streng monoton wachsend
(d. h. 0 < a < 1): Streng monoton fallend
(4)
(5)
(6)
Asymptote: y ¼ 0 (x-Achse)
y ð0Þ ¼ 1 (alle Kurven schneiden die y-Achse bei y ¼ 1)
y ¼ a / x entsteht durch Spiegelung von y ¼ a x an der y-Achse.
1
x
9 Exponentialfunktionen
105
9.2 Spezielle Exponentialfunktionen aus den Anwendungen
In den naturwissenschaftlich-technischen Anwendungen treten Exponentialfunktionen meist
in der zeitabhängigen Form auf, z. B. bei Abkling- und Sättigungsfunktionen (t: Zeit).
9.2.1 Abklingfunktion
y
y ¼ a . e /lt þ b
a+b
oder
y ¼ a . e / t=t þ b
a > 0;
l > 0;
t ¼ 1=l > 0;
– tt
y=a e
t ( 0
Eigenschaften
(1)
(2)
(3)
+b
y=b
b
Streng monoton fallende Funktion.
Asymptote für t ! 1: y ¼ b
Tangente in t ¼ 0 schneidet die
Asymptote an der Stelle t ¼ 1=l.
t
Tangente in t = 0
t
y
Sonderfall: b ¼ 0
a
y ¼ a . e /lt
– tt
y=a e
oder
y ¼ a . e / t=t
t
Tangente in t = 0
t
t
Tangente in t = 0
y=a+b
9.2.2 Sättigungsfunktion
y
y ¼ a ð1 / e / l t Þ þ b
oder
a+b
1
0
y ¼ a 1 / e / t=t þ b
a > 0;
l > 0;
t ¼ 1=l > 0;
t ( 0
Eigenschaften
(1)
(2)
(3)
(
Streng monoton wachsende Funktion.
Asymptote für t ! 1: y ¼ a þ b
Tangente in t ¼ 0 schneidet die
Asymptote an der Stelle t ¼ 1=l.
– tt
y = a 1– e
)+b
b
t
106
III Funktionen und Kurven
Sonderfall: b ¼ 0
y
1
0
y ¼ a 1 / e /lt
a
t
Tangente in t = 0
y=a
oder
1
0
y ¼ a 1 / e / t=t
(
– tt
y = a 1– e
)
t
9.2.3 Wachstumsfunktion
y ¼ y0 . e a t ,
y
t ( 0
y0 > 0:
Anfangsbestand (zur Zeit t ¼ 0)
a > 0:
Wachstumsrate
y = y0 · e at
y0
t
9.2.4 Gauß-Funktion (Gaußsche Glockenkurve)
2
y ¼ a . e / b ðx / x0 Þ ,
/1 < x < 1
y
a
a > 0, b > 0
y = a e – b ( x – x0 )
Eigenschaften
(1)
(2)
(3)
Maximum bei x0 : y ðx0 Þ ¼ a
Symmetrieachse: x ¼ x0 (Parallele
zur y-Achse durch das Maximum)
Asymptote im Unendlichen: y ¼ 0
(x-Achse)
y
9.2.5 Kettenlinie
Eine an zwei Punkten P1 und P2 in gleicher
Höhe befestigte, freihängende Kette nimmt unter dem Einfluss der Schwerkraft die geometrische Form einer Kettenlinie an ða > 0Þ:
y ¼ a . cosh
x
x0
!x4
a
4
a ! x=a
¼
e
þ e / x=a
2
P2
P1
a
x
y = a cosh a
( )
x
2
10 Logarithmusfunktionen
107
10 Logarithmusfunktionen
10.1 Definition der Logarithmusfunktionen
Die Logarithmusfunktionen sind die Umkehrfunktionen der Exponentialfunktionen.
Allgemeine Logarithmusfunktion
y ¼ log a x mit x > 0 ist die Umkehrfunktion der Exponentialfunktion y ¼ a x
ða > 0, a 6¼ 1Þ.
Das nebenstehende Bild zeigt die Funktionen
y ¼ log e x 0 ln x (streng monoton wachsend) und y ¼ log 0;5 x (streng monoton fallend).
y
y = ln x
1
1
5
–1
x
y = log0,5 x
Eigenschaften
(1)
(2)
(3)
(4)
Definitionsbereich: x > 0
Wertebereich: / 1 < y < 1
Nullstellen: x1 ¼ 1
Monotonie: 0 < a < 1: Streng monoton fallend
a > 1: Streng monoton wachsend
(5)
(6)
(7)
Asymptote: x ¼ 0 (y-Achse)
Für jede (zulässige) Basis a gilt: log a 1 ¼ 0; log a a ¼ 1
Die Funktionskurve von y ¼ log a x erhält man durch Spiegelung von y ¼ a x an
der Winkelhalbierenden des 1. Quadranten.
10.2 Spezielle Logarithmusfunktionen
Natürlicher Logarithmus (a = e)
y ¼ log e x 0 ln x ;
y
y = ex
y=x
x > 0
(Umkehrfunktion von y ¼ e x )
Das nebenstehende Bild zeigt, wie man
y ¼ ln x durch Spiegelung von y ¼ e x an
der Winkelhalbierenden y ¼ x erhält.
1
y = ln x
1
x
108
III Funktionen und Kurven
Zehnerlogarithmus (Dekadischer oder Briggscher Logarithmus, a = 10)
y ¼ log 10 x 0 lg x ;
x > 0
Zweierlogarithmus (Binärlogarithmus, a = 2)
y ¼ log 2 x 0 lb x ;
x > 0
11 Hyperbelfunktionen
11.1 Definition der Hyperbelfunktionen
y=
= sinh x und y == cosh x
y ¼ sinh x ¼
e x / e /x
2
y ¼ cosh x ¼
e x þ e /x
2
y
1
y = cosh x
y = sinh x
1
x
Für großes x gilt:
sinh x ' cosh x '
1
. ex
2
Eigenschaften
y ¼ sinh x
y ¼ cosh x
Definitionsbereich
/1 < x < 1
/1 < x < 1
Wertebereich
/1 < y < 1
1 ) y < 1
Symmetrie
ungerade
gerade
Nullstellen
x1 ¼ 0
Extremwerte
Monotonie
x1 ¼ 0 (Minimum)
streng monoton wachsend
cosh x verläuft im Intervall x < 0 streng monoton fallend, im Intervall x ( 0 dagegen
streng monoton wachsend.
11 Hyperbelfunktionen
109
y = tanh x und y = coth x
y ¼ tanh x ¼
e x / e /x
e x þ e /x
y ¼ coth x ¼
e x þ e /x
e x / e /x
y
y = coth x
Asymptote
1
Für großes x gilt:
y = tanh x
1
–1
tanh x ' coth x ' 1
y = coth x
Eigenschaften
y ¼ tanh x
y ¼ coth x
Definitionsbereich
/1 < x < 1
jxj > 0
Wertebereich
/1 < y < 1
jyj > 1
Symmetrie
ungerade
ungerade
Nullstellen
x1 ¼ 0
Pole
Asymptote
x1 ¼ 0
Monotonie
streng monoton wachsend
Asymptoten
y ¼ +1
x ¼ 0 (y-Achse)
y ¼ +1
coth x verläuft in den Intervallen x < 0 und x > 0 jeweils streng monoton fallend.
11.2 Wichtige Beziehungen zwischen den Hyperbelfunktionen
Hyperbolischer Pythagoras
cosh 2 x / sinh 2 x ¼ 1
Weitere elementare Beziehungen
tanh x ¼
sinh x
cosh x
coth x ¼
cosh x
1
¼
sinh x
tanh x
x
110
III Funktionen und Kurven
Umrechnungen zwischen den Hyperbelfunktionen
sinh x
cosh x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
+ cosh 2 x / 1
sinh x
cosh x
tanh x
coth x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sinh 2 x þ 1
sinh x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sinh 2 x þ 1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
sinh 2 x þ 1
sinh x
+
tanh x
coth x
tanh x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / tanh 2 x
1
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
coth x / 1
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / tanh 2 x
coth x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
coth 2 x / 1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cosh 2 x / 1
1
coth x
cosh x
cosh x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cosh 2 x / 1
1
tanh x
Oberes Vorzeichen für x ( 0, unteres Vorzeichen für x < 0.
11.3 Formeln
11.3.1 Additionstheoreme
sinh ðx1 + x2 Þ ¼ sinh x1 . cosh x2 + cosh x1 . sinh x2
cosh ðx1 + x2 Þ ¼ cosh x1 . cosh x2 + sinh x1 . sinh x2
tanh ðx1 + x2 Þ ¼
tanh x1 + tanh x2
1 + tanh x1 . tanh x2
coth ðx1 + x2 Þ ¼
1 + coth x1 . coth x2
coth x1 + coth x2
11.3.2 Formeln für halbe Argumente
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cosh x / 1
sinh
¼ +
(Oberes Vorzeichen für x ( 0, unteres für x < 0Þ
2
2
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!x4
cosh x þ 1
cosh
¼
2
2
!x4
sinh x
cosh x / 1
¼
¼
tanh
2
cosh x þ 1
sinh x
!x4
11 Hyperbelfunktionen
111
11.3.3 Formeln für Vielfache des Arguments
Formeln für doppelte Argumente
sinh ð2 xÞ ¼ 2 . sinh x . cosh x
cosh ð2 xÞ ¼ cosh 2 x þ sinh 2 x ¼ 2 . cosh 2 x / 1
tanh ð2 xÞ ¼
2 . tanh x
1 þ tanh 2 x
Formeln für dreifache Argumente
sinh ð3 xÞ ¼ 3 . sinh x þ 4 . sinh 3 x
cosh ð3 xÞ ¼ 4 . cosh 3 x / 3 . cosh x
tanh ð3 xÞ ¼
3 . tanh x þ tanh 3 x
1 þ 3 . tanh 2 x
Formeln für n-fache Argumente (n = 2, 3, 4, . . .)
!n4
!n4
sinh ðn xÞ ¼
. cosh n / 1 x . sinh x þ
. cosh n / 3 x . sinh 3 x þ
1
3
!n4
þ
. cosh n / 5 x . sinh 5 x þ . . .
5
!n4
!n4
cosh ðn xÞ ¼ cosh n x þ
. cosh n / 2 x . sinh 2 x þ
. cosh n / 4 x . sinh 4 x þ . . .
2
4
!n4
: Binomialkoeffizient (siehe I.2.7)
k
11.3.4 Formeln für Potenzen
1
½ cosh ð2 xÞ / 1 %
2
1
½ sinh ð3 xÞ / 3 . sinh x %
sinh 3 x ¼
4
1
sinh 4 x ¼
½ cosh ð4 xÞ / 4 . cosh ð2 xÞ þ 3 %
8
sinh 2 x ¼
1
½cosh ð2 xÞ þ 1 %
2
1
cosh 3 x ¼
½cosh ð3 xÞ þ 3 . cosh x %
4
1
cosh 4 x ¼
½cosh ð4 xÞ þ 4 . cosh ð2 xÞ þ 3 %
8
cosh 2 x ¼
112
III Funktionen und Kurven
11.3.5 Formeln für Summen und Differenzen
!x þ
1
2
!x þ
1
sinh x1 / sinh x2 ¼ 2 . cosh
2
!x þ
1
cosh x1 þ cosh x2 ¼ 2 . cosh
2
!x þ
1
cosh x1 / cosh x2 ¼ 2 . sinh
2
sinh x1 þ sinh x2 ¼ 2 . sinh
tanh x1 + tanh x2 ¼
x2 4
!x /
1
2
4
!
x2
x1 /
. sinh
2
4
!
x1 /
x2
. cosh
2
4
!
x2
x1 /
. sinh
2
. cosh
x2 4
x2 4
x2 4
x2 4
sinh ðx1 + x2 Þ
cosh x1 . cosh x2
11.3.6 Formeln für Produkte
sinh x1 . sinh x2 ¼
1
½ cosh ðx1 þ x2 Þ / cosh ðx1 / x2 Þ%
2
cosh x1 . cosh x2 ¼
1
½ cosh ðx1 þ x2 Þ þ cosh ðx1 / x2 Þ%
2
sinh x1 . cosh x2 ¼
1
½ sinh ðx1 þ x2 Þ þ sinh ðx1 / x2 Þ%
2
tanh x1 . tanh x2 ¼
tanh x1 þ tanh x2
coth x1 þ coth x2
11.3.7 Formel von Moivre
ðcosh x + sinh xÞ n ¼ cosh ðn xÞ + sinh ðn xÞ ¼ e + n x
Sonderfall:
ex
n ¼ 1
¼ cosh x þ sinh x
e / x ¼ cosh x / sinh x
ðn 2 N*Þ
12 Areafunktionen
113
12 Areafunktionen
12.1 Definition der Areafunktionen
Die Umkehrfunktionen der Hyperbelfunktionen heißen Areafunktionen, wobei die Umkehrung von y ¼ cosh x im Intervall x ( 0 vorgenommen wird. Die Areafunktionen lassen
sich durch logarithmische Funktionen ausdrücken.
y = arsinh x und y = arcosh x
3
y ¼ arsinh x ¼ ln
y
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2
x þ x2 þ 1
3
y ¼ arcosh x ¼ ln
y = arcosh x
1
ð/ 1 < x < 1Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2
x þ x2 / 1
x
1
ðx ( 1Þ
y = arsinh x
Eigenschaften
y ¼ arsinh x
y ¼ arcosh x
Definitionsbereich
/1 < x < 1
x ( 1
Wertebereich
/1 < y < 1
y ( 0
Symmetrie
ungerade
Nullstellen
x1 ¼ 0
x1 ¼ 1
Monotonie
streng monoton wachsend
streng monoton wachsend
y = artanh x und y = arcoth x
1
y ¼ artanh x ¼
. ln
2
ðj x j < 1Þ
1
y ¼ arcoth x ¼
. ln
2
ðj x j > 1Þ
3
1þx
1/x
y
2
y = arcoth x
1
3
2
x þ1
x /1
y = arcoth x
–1
1
y = artanh x
x
114
III Funktionen und Kurven
Eigenschaften
y ¼ artanh x
y ¼ arcoth x
Definitionsbereich
/1 < x < 1
jxj > 1
Wertebereich
/1 < y < 1
jyj > 0
Symmetrie
ungerade
ungerade
Nullstellen
x1 ¼ 0
Pole
x1=2 ¼ + 1
Monotonie
streng monoton wachsend
Asymptoten
x ¼ +1
x1=2 ¼ + 1
x ¼ +1
y ¼ 0 (x-Achse)
arcoth x verläuft in den Intervallen x < / 1 und x > 1 jeweils streng monoton fallend.
12.2 Wichtige Beziehungen zwischen den Areafunktionen
Umrechnungen zwischen den Areafunktionen
arsinh x
arsinh x
arcosh x
artanh x
qffiffiffiffiffiffiffiffiffiffiffiffiffi
+ arcosh x 2 þ 1
x !
artanh qffiffiffiffiffiffiffiffiffiffiffiffiffi arcoth
x2 þ 1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
arcosh x arsinh x 2 / 1
artanh
arcoth x
qffiffiffiffiffiffiffiffiffiffiffiffiffi!
x2 / 1
x
0
1
!
x
1
artanh x arsinh qffiffiffiffiffiffiffiffiffiffiffiffiffi +arcosh @qffiffiffiffiffiffiffiffiffiffiffiffiffiA
1 / x2
1 / x2
0
1
!
1
x
q
ffiffiffiffiffiffiffiffiffiffiffiffiffi
arcoth x arsinh @
A +arcosh qffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 / 1
x2 / 1
qffiffiffiffiffiffiffiffiffiffiffiffiffi!
x2 þ 1
!
x
arcoth qffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 / 1
arcoth
3 2
1
artanh
x
Oberes Vorzeichen für x > 0, unteres Vorzeichen für x < 0.
x
3 2
1
x
13 Kegelschnitte
115
Additionstheoreme
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
! qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
arsinh x1 + arsinh x2 ¼ arsinh x1 1 þ x 22 + x2 1 þ x 21
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
!
arcosh x1 + arcosh x2 ¼ arcosh x1 x2 + ðx 21 / 1Þ ðx 22 / 1Þ
3
2
x1 + x2
1 + x1 x2
3
2
1 + x1 x2
arcoth x1 + arcoth x2 ¼ arcoth
x1 + x2
artanh x1 + artanh x2 ¼ artanh
13 Kegelschnitte
13.1 Allgemeine Gleichung eines Kegelschnittes
Kegelschnitte sind ebene Kurven, die beim Schnitt eines geraden Kreiskegels mit Ebenen
entstehen. Zu ihnen gehören Kreis, Ellipse, Hyperbel und Parabel.
Gleichung eines Kegelschnittes in achsenparalleler Lage
Ax2 þ By2 þ Cx þ Dy þ E ¼ 0
ðA 2 þ B 2 6¼ 0Þ
Verlaufen die Symmetrieachsen der Kegelschnitte nicht parallel zu den Koordinatenachsen, so
enthält die Kegelschnittgleichung noch ein gemischtes Glied (x; y-Glied). Durch eine Drehung
des x; y-Systems lässt sich dann stets die achsenparallele Lage erzeugen (siehe I.9.1.3.3).
Art des Kegelschnittes
Kreis:
A ¼ B
Ellipse:
A.B > 0
Hyperbel:
A.B < 0
Parabel:
A ¼ 0; B 6¼ 0
13.2 Kreis
und
A 6¼ B
oder
y
13.2.1 Geometrische Definition
M P ¼ const: ¼ r
B ¼ 0; A 6¼ 0
r
M
P
x
M : Mittelpunkt des Kreises
r : Radius des Kreises ðr > 0Þ
Symmetrieachsen: Durchmesser, d. h. jede Gerade durch den Kreismittelpunkt M
116
III Funktionen und Kurven
13.2.2 Mittelpunktsgleichung eines Kreises (Ursprungsgleichung)
y
x2 þ y2 ¼ r2
P = (x;y)
y
M ¼ ð0; 0Þ
Symmetrieachsen: Jeder Durchmesser
Tangente in P1 ¼ ðx1 ; y1 Þ:
x x1 þ y y1 ¼ r
r
x
M
x
2
13.2.3 Kreis in allgemeiner Lage (Hauptform, verschobener Kreis)
ðx / x0 Þ 2 þ ðy / y0 Þ 2 ¼ r 2
y
P = (x;y)
y
M ¼ ðx0 ; y0 Þ
r
y0
Tangente in P1 ¼ ðx1 ; y1 Þ:
M
ðx / x0 Þ ðx1 / x0 Þ þ ðy / y0 Þ ðy1 / y0 Þ ¼ r 2
Der verschobene Kreis kann durch eine Parallelverschiebung des Koordinatensystems auf den
Mittelpunktskreis (Ursprungskreis) zurückgeführt
werden ðM ¼ ðx0 ; y0 Þ als Nullpunkt wählen).
x
x0
x
13.2.4 Gleichung eines Kreises in Polarkoordinaten
r 2 / 2 r0 r . cos ðj / j0 Þ þ r 20 ¼ R 2
y
P = (r;f)
M ¼ ðr0 ; j0 Þ (in Polarkoordinaten)
R:
r
Radius des Kreises
x-Achse
0
13.2.5 Parameterdarstellung eines Kreises
x ¼ x0 þ r . cos t
y ¼ y0 þ r . sin t
M ¼ ðx0 ; y0 Þ
t:
M
r0
Pol: O ¼ ð0; 0Þ
Polarachse:
R
ð0 ) t < 2 pÞ
f0
f
x
y
P = (x;y)
y
y0
M
r
t
Winkelparameter
r : Radius des Kreises
x0
x
x
13 Kegelschnitte
117
13.3 Ellipse
13.3.1 Geometrische Definition
y
F1 P þ F2 P ¼ const: ¼ 2 a
P
M:
F1 ; F2 :
2 a:
2 b:
e > 0:
Mittelpunkt
Brennpunkte
Große Achse (Hauptachse)
Kleine Achse1 (Nebenachse)
0
Brennweite F1 M ¼ F2 M ¼ e
e2 ¼ a2 / b2
ða > b > 0Þ
e ¼ e=a: Numerische Exzentrizität ðe < 1Þ
Symmetrieachsen:
b
F1
e
M
x
F2
a
Koordinatenachsen
Sonderfall b > a: Die Brennpunkte liegen jetzt auf der y-Achse (um 90" gedrehte
Ellipse mit der Hauptachse 2 b, der Nebenachse 2 a und e 2 ¼ b 2 / a 2 Þ:
Sonderfall a ¼ b:
Kreis mit dem Radius r ¼ a
13.3.2 Mittelpunktsgleichung einer Ellipse (Ursprungsgleichung)
y
x2
y2
þ
¼ 1
a2
b2
P = (x;y)
y
M ¼ ð0; 0Þ
b
Symmetrieachsen:
M
Koordinatenachsen
x x1
y y1
þ 2 ¼ 1
Tangente in P1 ¼ ðx1 ; y1 Þ:
a2
b
a
x
x
13.3.3 Ellipse in allgemeiner Lage (Hauptform, verschobene Ellipse)
ðx / x0 Þ 2
ðy / y0 Þ 2
þ
¼ 1
a2
b2
M ¼ ðx0 ; y0 Þ
Symmetrieachsen: Parallelen zu den Koordinatenachsen durch den Mittelpunkt M
y
P = (x;y)
y
b
y0
a
M
Tangente in P1 ¼ ðx1 ; y1 Þ:
ðx / x0 Þ ðx1 / x0 Þ
ðy / y0 Þ ðy1 / y0 Þ
þ
¼1
a2
b2
x0
x
x
Die verschobene Ellipse kann durch eine Parallelverschiebung des Koordinatensystems auf
die Ursprungsellipse zurückgeführt werden ðM ¼ ðx0 ; y0 Þ als Nullpunkt wählenÞ.
118
III Funktionen und Kurven
13.3.4 Gleichung einer Ellipse in Polarkoordinaten
Pol im Mittelpunkt
b
r ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / e 2 . cos 2 j
y
ðe < 1Þ
f
M
Pol: M ¼ ð0; 0Þ
Polarachse: Große Achse (x-Achse)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 / b2
e ¼
a
Pol im linken Brennpunkt
r ¼
p
1 / e . cos j
P = (r;f)
r
b
a
y
P = (r;f)
ðe < 1Þ
r
f
F1
Pol: F1 ¼ ð0; 0Þ (linker Brennpunkt)
Polarachse: Große Achse (x-Achse)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 / b2
b2
;
p ¼
e ¼
a
a
M
F2
p
1 þ e . cos j
x
y
Pol im rechten Brennpunkt
r ¼
x
P = (r;f)
ðe < 1Þ
r
f
Pol: F2 ¼ ð0; 0Þ (rechter Brennpunkt)
Polarachse: Große Achse (x-Achse)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 / b2
b2
e ¼
;
p ¼
a
a
13.3.5 Parameterdarstellung einer Ellipse
x ¼ x0 þ a . cos t
y ¼ y0 þ b . sin t
ð0 ) t < 2 pÞ
M ¼ ðx0 ; y0 Þ
t:
F1
F2
M
x
y
P = (x;y)
y
b
y0
a
M
Parameter
a, b:
Große bzw. kleine Halbachse
x0
x
x
13 Kegelschnitte
119
13.4 Hyperbel
13.4.1 Geometrische Definition
"
"
" F P / F P " ¼ const: ¼ 2 a
1
2
M:
F1 ; F2 :
S1 ; S2 :
2 a:
2 b:
e > 0:
e ¼ e=a:
Mittelpunkt
Brennpunkte
Scheitelpunkte
Große oder reelle Achse
Kleine oder imaginäre
Achse
1
0
Brennweite F1 M ¼ F2 M ¼ e ;
Numerische Exzentrizität ðe > 1Þ
y
P
b
F 1 S1
e
a S2 F 2
M
e2 ¼ a2 þ b2
x
ða > 0; b > 0Þ
Symmetrieachsen: Koordinatenachsen
13.4.2 Mittelpunktsgleichung einer Hyperbel (Ursprungsgleichung)
x2
y2
/
¼ 1
a2
b2
y
b
Asymptote y = – a
x
y
M ¼ ð0; 0Þ
P = (x;y)
b
Symmetrieachsen: Koordinatenachsen
b
x
Asymptoten: y ¼ +
a
x x1
y y1
Tangente in P1 ¼ ðx1 ; y1 Þ:
/ 2 ¼ 1
a2
b
F 1 S1
M
a S2 F 2 x
x
Asymptote y = b x
a
13.4.3 Hyperbel in allgemeiner Lage (Hauptform, verschobene Hyperbel)
ðx / x0 Þ 2
ðy / y0 Þ 2
/
¼ 1
a2
b2
M ¼ ðx0 ; y0 Þ
Symmetrieachsen: Parallelen zu den Koordinatenachsen durch den Mittelpunkt M
b
Asymptoten: y ¼ y0 +
ðx / x0 Þ
a
Tangente in P1 ¼ ðx1 ; y1 Þ:
y
y
Asymptote
P = (x;y)
b
y0
F 1 S1
M
a S2 F 2
Asymptote
x0
x
x
ðx / x0 Þ ðx1 / x0 Þ
ðy / y0 Þ ðy1 / y0 Þ
/
¼1
a2
b2
Die verschobene Hyperbel kann durch eine Parallelverschiebung des Koordinatensystems
auf die Ursprungshyperbel zurückgeführt werden ðM ¼ ðx0 ; y0 Þ als Nullpunkt wählenÞ.
120
III Funktionen und Kurven
13.4.4 Gleichung einer Hyperbel in Polarkoordinaten
Pol im Mittelpunkt
b
r ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
e 2 . cos 2 j / 1
y
ðe > 1Þ
b
F1 S1
P = (r;f)
r
f
a S2 F 2
M
x
Pol: M ¼ ð0; 0Þ
Polarachse: Große Achse (x-Achse)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ b2
e ¼
a
Pol im linken Brennpunkt
r ¼
p
e . cos j + 1
y
ðe > 1Þ
P = (r;f)
r
f
F 1 S1
M ¼ ðe; 0Þ
M
x
S2 F 2
Pol: F1 ¼ ð0; 0Þ (linker Brennpunkt)
Polarachse: Große Achse (x-Achse)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ b2
b2
;
p ¼
e ¼
a
a
Oberes Vorzeichen: Linker Ast
Unteres Vorzeichen: Rechter Ast
Pol im rechten Brennpunkt
r ¼
/p
e . cos j + 1
y
ðe > 1Þ
M ¼ ð/ e; 0Þ
Pol: F2 ¼ ð0; 0Þ (rechter Brennpunkt)
Polarachse: Große Achse (x-Achse)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ b2
b2
e ¼
;
p ¼
a
a
Oberes Vorzeichen: Linker Ast
Unteres Vorzeichen: Rechter Ast
F 1 S1
M
f
S2 F 2
r
P = (r;f)
x
13 Kegelschnitte
121
13.4.5 Parameterdarstellung einer Hyperbel
x ¼ x0 + a . cosh t
y ¼ y0 þ b . sinh t
y
ð/ 1 < t < 1Þ
Asymptote
y
P = (x;y)
b
M ¼ ðx0 ; y0 Þ
y0
F 1 S1
t: Parameter
Oberes Vorzeichen: Rechter Ast
Unteres Vorzeichen: Linker Ast
a S2 F2
M
Asymptote
x
x0
x
13.4.6 Gleichung einer um 90" gedrehten Hyperbel
y2
x2
/
¼ 1
a2
b2
y
M ¼ ð0; 0Þ
y
P = (x;y)
F2
Große Achse: y-Achse (Länge 2a)
Kleine Achse: x-Achse (Länge 2b)
a
S2
b
M
Symmetrieachsen: Koordinatenachsen
a
Asymptoten: y ¼ +
x
b
Asymptote
S1
F1
x
x
Asymptote
Verschobene Hyperbel
ðy / y0 Þ 2
ðx / x0 Þ2
/
¼ 1
a2
b2
M ¼ ðx0 ; y0 Þ
13.4.7 Gleichung einer gleichseitigen oder rechtwinkeligen Hyperbel (a = b)
x2
y2
/
¼ 1
a2
a2
oder
x2 / y2 ¼ a2
M ¼ ð0; 0Þ
Asymptoten: y ¼ + x (stehen aufeinander senkrecht)
Legt man die Koordinatenachsen in Richtung der Asymptoten, so lautet die Gleichung der
gleichseitigen Hyperbel x y ¼ a 2 =2.
Verschobene Hyperbel
ðx / x0 Þ 2
ðy / y0 Þ 2
/
¼ 1
a2
a2
Asymptoten:
oder
ðx / x0 Þ 2 / ðy / y0 Þ 2 ¼ a 2
y ¼ y0 + ðx / x0 Þ ðstehen aufeinander senkrechtÞ
M ¼ ðx0 ; y0 Þ
122
III Funktionen und Kurven
13.5 Parabel
Hinweis: Gleichungen der nach oben bzw. unten geöffneten Parabel siehe Abschnitt 4.3.
13.5.1 Geometrische Definition
AP ¼ F P
S: Scheitelpunkt
F : Brennpunkt
L: Leitlinie
p: Parameter (Abstand des Brennpunktes
von der Leitlinie:
j p j ¼ 2 e) 2
3
j pj
SF ¼ e ¼
e: Brennweite
2
p > 0: Nach rechts geöffnete Parabel
p < 0: Nach links geöffnete Parabel
Symmetrieachse: x-Achse
13.5.2 Scheitelgleichung einer Parabel
y2 ¼ 2px
S ¼ ð0; 0Þ
Symmetrieachse: x-Achse
Tangente in P1 ¼ ðx1 ; y1 Þ: y y1 ¼ p ðx þ x1 Þ
y
L
P
A
S F
x
p
y
y
P = (x;y)
x
x
S
13.5.3 Parabel in allgemeiner Lage (Hauptform, verschobene Parabel)
ðy / y0 Þ 2 ¼ 2 p ðx / x0 Þ
S ¼ ðx0 ; y0 Þ
Symmetrieachse: Parallele zur x-Achse durch
den Scheitelpunkt S
Tangente in P1 ¼ ðx1 ; y1 Þ:
y
y
y0
P = (x;y)
S
ðy / y0 Þ ðy1 / y0 Þ ¼ p ðx þ x1 / 2 x0 Þ
Die verschobene Parabel kann durch eine
Parallelverschiebung des Koordinatensystems
auf die Scheitelgleichung zurückgeführt werden ðS ¼ ðx0 ; y0 Þ als Nullpunkt wählenÞ.
x0
x
x
13 Kegelschnitte
123
13.5.4 Gleichung einer Parabel in Polarkoordinaten
Pol im Scheitelpunkt
y
r ¼ 2 p . cos j ð1 þ cot 2 jÞ
P = (r;f)
r
S ¼ ð0; 0Þ
f
S
Pol: S ¼ ð0; 0Þ
Polarachse:
Symmetrieachse (x-Achse)
Pol im Brennpunkt
r ¼
y
p
1 / cos j
P = (r;f)
r
f
S ¼ ð/ p=2; 0Þ
Polarachse:
x
F
S
Pol: F ¼ ð0; 0Þ
Symmetrieachse (x-Achse)
13.5.5 Parameterdarstellung einer Parabel
x ¼ x0 þ c t 2
y ¼ y0 þ t
c:
x
Reelle Konstante
ð/1 < t < 1Þ
ðc ¼ 1=2 pÞ
y
y
y0
P = (x;y)
S
S ¼ ðx0 ; y0 Þ
Symmetrieachse: Parallele zur x-Achse
durch den Scheitelpunkt S
x0
x
x
124
III Funktionen und Kurven
14 Spezielle Kurven
Hinweis: Die Kurvengleichungen liegen in der Parameterform x ¼ x ðtÞ, y ¼ y ðtÞ oder
in der Polarkoordinatenform r ¼ r ðjÞ vor.
14.1 Gewöhnliche Zykloide (Rollkurve)
Ein Punkt P ¼ ðx; yÞ auf dem Umfang eines Kreises, der auf einer Geraden (x-Achse)
abrollt (ohne zu gleiten), beschreibt eine als Rollkurve oder gewöhnliche Zykloide bezeichnete periodische Bahnkurve:
x ¼ R ðt / sin tÞ
y ¼ R ð1 / cos tÞ
y
ð/1 < t < 1Þ
R:
Radius des Kreises
t:
Parameter („Wälzwinkel“) im Bogenmaß
2R
P
R
t
A
pR
2 pR
x
Eigenschaften
(1)
(2)
(3)
Periode der Bahnkurve: p ¼ 2 p R (Kreisumfang!)
Fläche unter einem Bogen (grau unterlegt): A ¼ 3 p R 2
Länge (Umfang) eines Bogens: s ¼ 8 R
14.2 Epizykloide
Ein Punkt P ¼ ðx; yÞ auf dem Umfang eines Kreises, der auf der Außenseite eines zweiten
(festen) Kreises abrollt (ohne zu gleiten), beschreibt eine als Epizykloide bezeichnete Bahnkurve:
3
2
R0 þ R
x ¼ ðR0 þ RÞ cos t / R . cos
.t
R
3
2
R0 þ R
y ¼ ðR0 þ RÞ sin t / R . sin
.t
R
y
s
A
R
ð/ 1 < t < 1Þ
R0
R0 :
Radius des festen Kreises
R:
Radius des abrollenden Kreises
t:
Winkelparameter (Polarwinkel des
Punktes, in dem sich die beiden Kreise
berühren)
j:
Wälzwinkel ðj ¼ R0 t=RÞ
t
f
P
x
14 Spezielle Kurven
125
Eigenschaften
(1)
Die Gestalt der Kurve hängt vom Verhältnis m ¼ R0 =R der beiden Radien ab. Die
Epizykloide ist in sich geschlossen, wenn m rational ist. Ist m ganzzahlig, so besteht die Epizykloide aus genau m Bögen. Für den Spezialfall R ¼ R0 erhält man
eine Kardioide (siehe Abschnitt 14.5).
(2)
Länge eines Bogens: s ¼
(3)
Fläche zwischen einem Bogen und dem festen Kreis (grau unterlegt):
A ¼
8 R ðR0 þ RÞ
8 ðR0 þ RÞ
¼
R0
m
p R 2 ð3 R0 þ 2 RÞ
p R ð3 R0 þ 2 RÞ
¼
R0
m
14.3 Hypozykloide
Ein Punkt P ¼ ðx; yÞ auf dem Umfang eines Kreises, der auf der Innenseite eines zweiten
(festen) Kreises abrollt (ohne zu gleiten), beschreibt eine als Hypozykloide bezeichnete
Bahnkurve:
3
2
R0 / R
x ¼ ðR0 / RÞ cos t þ R . cos
.t
R
3
2
R0 / R
.t
y ¼ ðR0 / RÞ sin t / R . sin
R
ð/ 1 < t < 1; R0 > RÞ
R0 :
Radius des festen Kreises
R:
Radius des abrollenden Kreises
t:
Winkelparameter
y
s
A
t
R
P
R0
x
Eigenschaften
(1)
Die Gestalt der Kurve hängt vom Verhältnis m ¼ R0 =R der beiden Radien ab. Die
Hypozykloide ist in sich geschlossen, wenn m rational ist. Ist m ganzzahlig, so
besteht die Hypozykloide aus genau m Bögen. Für den Spezialfall R0 ¼ 4 R erhält
man eine Astroide (siehe Abschnitt 14.4).
(2)
Länge eines Bogens: s ¼
(3)
Fläche zwischen einem Bogen und dem festen Kreis (grau unterlegt):
A ¼
8 R ðR0 / RÞ
8 ðR0 / RÞ
¼
R0
m
p R 2 ð3 R0 / 2 RÞ
p R ð3 R0 / 2 RÞ
¼
R0
m
126
III Funktionen und Kurven
14.4 Astroide (Sternkurve)
Die Astroide oder Sternkurve ist ein Spezialfall der Hypozykloide für R0 ¼ 4 R ¼ a
(siehe Abschnitt 14.3):
x ¼ a . cos 3 t
)
y ¼ a . sin 3 t
y
a > 0
0 ) t < 2p
a/4
Eigenschaften
(1)
(2)
(3)
(4)
(5)
Gleichung der Kurve in kartesischen
Koordinaten: x 2=3 þ y 2=3 ¼ a 2=3
Die Kurve ist spiegelsymmetrisch zu
beiden Koordinatenachsen.
3
Fläche (grau unterlegt): A ¼
pa2
8
Länge (Umfang) der Kurve: s ¼ 6 a
P
t
x
a
Die Schnittpunkte einer jeden Tangente
mit den beiden Koordinatenachsen haben den Abstand a (Ausnahme: Tangenten in den vier Spitzen).
14.5 Kardioide (Herzkurve)
Die Kardioide oder Herzkurve ist ein Spezialfall der Epizykloide für R ¼ R0 ¼ a=2
(siehe Abschnitt 14.2). Die Kurvengleichung lautet in Polarkoordinaten:
r ¼ a ð1 þ cos jÞ
ða > 0; 0 ) j < 2 pÞ
y
r = a(1 + cos f)
a
Eigenschaften
(1)
Die Kurve ist spiegelsymmetrisch zur
x-Achse.
(2)
Gleichung in kartesischen Koordinaten:
ðx 2 þ y 2 Þ ðx 2 þ y 2 / 2 a xÞ ¼ a 2 y 2
(3)
Parameterdarstellung der Kurve:
x ¼ a ð1 þ cos jÞ cos j ; y ¼ a ð1 þ cos jÞ sin j
3
Fläche (grau unterlegt): A ¼
pa2
2
Länge (Umfang) der Kurve: s ¼ 8 a
(4)
(5)
a
–a
2a
x
14 Spezielle Kurven
127
14.6 Lemniskate (Schleifenkurve)
r ¼ a.
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
cos ð2 jÞ
y
ða > 0Þ
Beachte: Kurvenpunkte existieren nur für
Winkel j mit cos ð2 jÞ ( 0!
r = a √ cos(2 f)
S2
A1
S1
a
0
x
Eigenschaften
(1)
Gleichung der Kurve in kartesischen Koordinaten:
(2)
(3)
(4)
(5)
ðx 2 þ y 2 Þ 2 ¼ a 2 ðx 2 / y 2 Þ
Die Kurve ist spiegelsymmetrisch zur x- und y-Achse.
Scheitelpunkte: S1=2 ¼ ð+ a; 0Þ; Doppelpunkt (Wendepunkt): O ¼ ð0; 0Þ
Gleichungen der Tangenten in O: y ¼ + x
Fläche einer Schleife (grau unterlegt): A1 ¼ a 2 =2; Gesamtfläche: A ¼ a 2
14.7 Strophoide
aðt 2 / 1Þ
x ¼
t2 þ 1
y ¼
9
>
>
>
=
y
a > 0
/1 < t < 1
>
a t ðt 2 / 1Þ >
>
;
2
t þ1
Beachte: y ¼ t . x
S
–a
Eigenschaften
(1)
x=a
A2
A1
0
a
x
Gleichung der Kurve in kartesischen
Koordinaten:
ðx þ aÞ x 2 þ ðx / aÞ y 2 ¼ 0
(2)
Gleichung der Kurve in Polarkoordinaten:
a . cos ð2 jÞ
r ¼ /
cos j
(3)
Die Kurve ist spiegelsymmetrisch zur x-Achse.
(4)
Scheitelpunkt: S ¼ ð/ a; 0Þ ;
(5)
Gleichungen der Tangenten in O: y ¼ + x
(6)
Gleichung der Asymptote: x ¼ a
(7)
Fläche der Schleife (hellgrau unterlegt): A1 ¼
(8)
(9)
Doppelpunkt: O ¼ ð0; 0Þ
a2
ð4 / pÞ
2
a2
Fläche zwischen Kurve und Asymptote (dunkelgrau unterlegt): A2 ¼
ð4 þ pÞ
2
Gesamtfläche: A ¼ A1 þ A2 ¼ 4 a 2
128
III Funktionen und Kurven
14.8 Cartesisches Blatt
9
3at
>
>
x ¼
=
1 þ t3 >
>
3at2 >
>
;
y ¼
1 þ t3
y
a > 0 ; t 6¼ / 1
–a
A2 0
x
Asymptote
(1)
Gleichung der Kurve in kartesischen
Koordinaten: x 3 þ y 3 ¼ 3 a x y
(2)
Kurvengleichung in Polarkoordinaten:
3 a . sin j . cos j
r ¼
sin 3 j þ cos 3 j
Symmetrieachse: y ¼ x (Winkelhalbierende des 1. und 3. Quadranten)
3
2
3
3
Scheitelpunkt: S ¼
a;
a ; Doppelpunkt: O ¼ ð0; 0Þ
2
2
(3)
(4)
–a
(5)
Gleichungen der Tangenten in O: y ¼ 0 (x-Achse) und x ¼ 0 (y-Achse)
(6)
Gleichung der Asymptote: y ¼ / x / a
(7)
Fläche der Schleife (hellgrau unterlegt): A1 ¼
(8)
(9)
45°
A1
Beachte: y ¼ t . x
Eigenschaften
S
3 2
a
2
3 2
Fläche zwischen Kurve und Asymptote (dunkelgrau unterlegt): A2 ¼
a
2
2
Gesamtfläche: A ¼ A1 þ A2 ¼ 3 a
14.9 „Kleeblatt“ mit n bzw. 2 n Blättern
r ¼ a . cos ðn jÞ
ða > 0; n 2 N *Þ
y
120°
Eigenschaften
(1)
Symmetrieachse: x-Achse
(2)
Die Kurve umschließt n Blätter. Das
nebenstehende Bild zeigt ein „3-blättriges Kleeblatt“.
(3)
A
a
Fläche eines Blattes (grau unterlegt):
A ¼
pa2
4n
240°
x
14 Spezielle Kurven
129
(4)
Die Gleichung r ¼ j a . cos ðn jÞ j beschreibt ein „Kleeblatt“ mit 2 n Blättern
(Verdoppelung der Blattzahl).
(5)
Parameterdarstellung: x ¼ a . cos j . cos ðn jÞ,
y ¼ a . sin j . cos ðn jÞ
14.10 Spiralen
14.10.1 Archimedische Spirale
Archimedische Spirale: Bahnkurve eines Massenpunktes, der sich mit der konstanten Geschwindigkeit v auf einem Strahl radial nach außen bewegt, wobei sich dieser zugleich
mit der konstanten Winkelgeschwindigkeit w im Gegenuhrzeigersinn um den Nullpunkt
dreht. Der Bahnradius r wächst dabei proportional zum Drehwinkel j.
r ¼ aj
y
ða > 0; 0 ) j < 1Þ
Polarwinkel j im Bogenmaß
j1 , j2 : Polarwinkel der Punkte P1 und P2
Fläche des Sektors P1 O P2
(grau unterlegt):
A ¼
(2)
1 2 3
a ðj 2 / j 31 Þ
6
_
Länge des Bogens P1 P2 : s ¼
P1
r1
A
r = af
Eigenschaften
(1)
s
P2
r2
–a p
a
2
ap
2
0
x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2)j2
j j 2 þ 1 þ ln j þ j 2 þ 1
j1
14.10.2 Logarithmische Spirale
r ¼ a . e bj
y
ða > 0, b > 0; 0 ) j < 1Þ
Polarwinkel j im Bogenmaß
P1
s
P2
A
j1 , j2 : Polarwinkel der Punkte P1 und P2
0
Fläche des Sektors P1 O P2
(grau unterlegt):
A ¼
r 22 / r 21
a 2 h 2 b j ij 2
¼
e
j1
4b
4b
_
r1
r2
Eigenschaften
(1)
r = a e bf
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ b2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ b2 h
e bj
ij2
(2)
Länge des Bogens P1 P2 : s ¼
(3)
Alle vom Nullpunkt ausgehenden Strahlen schneiden die Kurve unter dem gleichen
Tangentenwinkel a ¼ cot b.
b
ðr2 / r1 Þ ¼
a
a
b
j1
x
130
IV Differentialrechnung
1 Differenzierbarkeit einer Funktion
1.1 Differenzenquotient
y
Dy
f ðx0 þ DxÞ / f ðx0 Þ
¼
Dx
Dx
Sekante
Q
Dy
y = f(x)
Geometrische Deutung
Steigung der Sekante durch P und Q:
Dy
ms ¼ tan e ¼
Dx
P
e
Dx
y0
x0 + Dx
x0
x
1.2 Differentialquotient oder 1. Ableitung
"
dy ""
Dy
f ðx0 þ DxÞ / f ðx0 Þ
¼ lim
¼ lim
Dx ! 0
dx " x ¼ x0 Dx ! 0 Dx
Dx
Geometrische Deutung
Steigung der Kurventangente im Punkt P:
"
dy ""
mt ¼ tan a ¼
dx " x ¼ x0
Dy
vorhanden, so heißt
Dx
die Funktion y ¼ f ðxÞ an der Stelle x0 differenzierbar. Der Grenzwert selbst wird als 1. Ableitung
von f ðxÞ an der Stelle x0 bezeichnet. "
dy ""
Schreibweisen: y 0 ðx0 Þ ; f 0 ðx0 Þ ;
dx "
Ist der Grenzwert
lim
Dx ! 0
y
y = f(x)
P
a
y0
x0
Tangente
x
x ¼ x0
1.3 Ableitungsfunktion
Die Ableitungsfunktion y 0 ¼ f 0 ðxÞ ordnet jeder Stelle x aus einem Intervall I den Steigungswert der dortigen Kurventangente als Funktionswert zu. Man spricht dann kurz von
der (ersten) Ableitung oder dem Differentialquotienten von y ¼ f ðxÞ.
Schreibweisen:
y0 ;
f 0 ðxÞ ;
dy
dx
Eine differenzierbare Funktion ist immer stetig (die Umkehrung gilt nicht). Eine Funktion
mit einer stetigen (ersten) Ableitung wird als stetig differenzierbar bezeichnet.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_4
1 Differenzierbarkeit einer Funktion
Differentialoperator
Der Differentialoperator
1. Ableitung y 0 ¼ f 0 ðxÞ:
131
d
erzeugt durch „Einwirken“ auf die Funktion y ¼ f ðxÞ die
dx
d
dy
½ f ðxÞ% ¼ f 0 ðxÞ ¼
¼ y0
dx
dx
&
Beispiel
y ¼ 5 x 3 / 2 . sin x / 7
)
y0 ¼
d
½ 5 x 3 / 2 . sin x / 7 % ¼ 15 x 2 / 2 . cos x
dx
&
1.4 Höhere Ableitungen
Die höheren Ableitungen sind wie folgt definiert:
2. Ableitung:
3. Ableitung:
..
.
d 2y
d
¼
½ f 0 ðxÞ%
dx 2
dx
d 3y
d
y 000 ¼ f 000 ðxÞ ¼
¼
½ f 00 ðxÞ%
3
dx
dx
..
.
d ny
d
y ðnÞ ¼ f ðnÞ ðxÞ ¼
¼
½ f ðn / 1Þ ðxÞ%
dx n
dx
!
n-te Ableitung:
y 00 ¼ f 00 ðxÞ ¼
Differentialquotient n-ter Ordnung
1.5 Differential einer Funktion
Zuwachs des Funktionswertes bzw. der
Ordinate auf der Kurve:
y
y = f(x)
Q
Dy ¼ f ðx0 þ DxÞ / f ðx0 Þ
Zuwachs des Funktionswertes bzw. der
Ordinate auf der Kurventangente:
dy ¼ f 0 ðx0 Þ dx
ðdx ¼ DxÞ
Dy Tangente
Q'
dy
P
y0
x0
dx = Dx
x0 + Dx
x
Dx und Dy sind die Koordinatenänderungen auf der Kurve, dx und dy die entsprechenden Koordinatenänderungen auf der in P errichteten Kurventangente, jeweils bezogen auf
den Berührungspunkt P. Die Größe dy ¼ f 0 ðx0 Þ dx heißt Differential von f ðxÞ und
beschreibt die "nderung der Ordinate auf der Kurventangente, wenn man in der xRichtung um dx ¼ Dx fortschreitet. Für kleine #nderungen dx ¼ Dx gilt dann:
Dy ' dy ¼ f 0 ðx0 Þ dx ¼ f 0 ðx0 Þ Dx
132
IV Differentialrechnung
2 Erste Ableitung der elementaren Funktionen (Tabelle)
Ableitung f 0 ðxÞ
Funktion f ðxÞ
Potenzfunktion
xn
n x n/1
Trigonometrische Funktionen
sin x
cos x
cos x
tan x
cot x
Arkusfunktionen
arcsin x
arccos x
arctan x
arccot x
Exponentialfunktionen
Logarithmusfunktionen
Hyperbelfunktionen
ex
ex
ax
ð ln aÞ . a x
ln x
1
x
log a x
1
ðln aÞ . x
sinh x
cosh x
cosh x
tanh x
coth x
Areafunktionen
/ sin x
1
¼ 1 þ tan 2 x
cos 2 x
1
/
¼ / 1 / cot 2 x
sin 2 x
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / x2
1
/ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 / x2
1
1 þ x2
1
/
1 þ x2
arsinh x
arcosh x
artanh x
arcoth x
sinh x
1
¼ 1 / tanh 2 x
cosh 2 x
1
/
¼ 1 / coth 2 x
sinh 2 x
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 þ 1
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 / 1
1
1 / x2
1
1 / x2
3 Ableitungsregeln
133
3 Ableitungsregeln
3.1 Faktorregel
Ein konstanter Faktor C bleibt beim Differenzieren erhalten:
y ¼ C . f ðxÞ
y 0 ¼ C . f 0 ðxÞ
)
3.2 Summenregel
Eine endliche Summe von Funktionen darf gliedweise differenziert werden:
y ¼ f1 ðxÞ þ f2 ðxÞ þ . . . þ fn ðxÞ
)
y 0 ¼ f 01 ðxÞ þ f 02 ðxÞ þ . . . þ f 0n ðxÞ
Linearkombinationen von Funktionen, z. B. ganzrationale Funktionen (Polynomfunktionen)
werden mit Hilfe der Faktor- und Summenregel differenziert.
3.3 Produktregel
Bei zwei Faktorfunktionen:
y ¼ u ðxÞ . v ðxÞ
)
y 0 ¼ u 0 ðxÞ . vðxÞ þ v 0 ðxÞ . u ðxÞ
Beispiel
&
y ¼ ðx 2 / 3 xÞ . sin x
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl} |ffl{zffl}
u
v
ðu 0 ¼ 2 x / 3 ;
v 0 ¼ cos xÞ
y 0 ¼ u 0 v þ v 0 u ¼ ð2 x / 3Þ . sin x þ cos x . ðx 2 / 3 xÞ
&
Bei drei Faktorfunktionen:
y ¼ u ðxÞ . v ðxÞ . w ðxÞ
)
y ¼ u ðxÞ . vðxÞ . wðxÞ þ u ðxÞ . v 0 ðxÞ . w ðxÞ þ u ðxÞ . v ðxÞ . w 0 ðxÞ
0
&
0
Beispiel
y ¼ x 3 . e x . arctan x
|{z} |{z} |fflfflfflffl{zfflfflfflffl}
u
v
w
3
u0 ¼ 3x2 ;
v0 ¼ ex ;
w0 ¼
1
1 þ x2
2
1
y 0 ¼ u 0 v w þ u v 0 w þ u v w 0 ¼ 3 x 2 . e x . arctan x þ x 3 . e x . arctan x þ x 3 . e x .
¼
1
þ
x2
3
2
x
¼ x 2 . e x ð3 þ xÞ . arctan x þ
1 þ x2
&
134
IV Differentialrechnung
3.4 Quotientenregel
y ¼
u ðxÞ
vðxÞ
y0 ¼
)
u 0 ðxÞ . v ðxÞ / v 0 ðxÞ . u ðxÞ
½ vðxÞ% 2
ðv ðxÞ ¼
6 0Þ
Gebrochenrationale Funktionen werden nach dieser Regel differenziert.
&
Beispiel
y ¼
3x2 / x
sin x
y0 ¼
u0 v / v0 u
ð6 x / 1Þ . sin x / cos x . ð3 x 2 / xÞ
¼
v2
sin 2 x
ðu ¼ 3 x 2 / x ;
v ¼ sin x ;
u0 ¼ 6x / 1;
v 0 ¼ cos xÞ
&
3.5 Kettenregel
Die Ableitung einer aus den beiden (elementaren) Funktionen y ¼ F ðuÞ und u ¼ uðxÞ
zusammengesetzten (verketteten) Funktion y ¼ F ðu ðxÞÞ ¼ f ðxÞ ist das Produkt aus der
äußeren und der inneren Ableitung (sog. Kettenregel):
dy
dy du
¼
.
dx
du dx
oder
f 0 ðxÞ ¼ F 0 ðuÞ . u 0 ðxÞ
Bezeichnungen:
y ¼ F ðuÞ:
u ¼ u ðxÞ:
"ußere Funktion
Innere Funktion
'
y ¼ F ðu ðxÞÞ ¼ f ðxÞ
dy
¼ F 0 ðuÞ: "ußere Ableitung (Ableitung der äußeren Funktion)
du
du
¼ u 0 ðxÞ: Innere Ableitung (Ableitung der inneren Funktion)
dx
Zur Anwendung der Kettenregel
Die vorgegebene (nicht elementar differenzierbare) Funktion y ¼ f ðxÞ wird zunächst mit
Hilfe einer möglichst einfachen Substitution u ¼ u ðxÞ in eine von der „Hilfsvariablen“ u
abhängige (elementare) Funktion y ¼ F ðuÞ übergeführt:
Substitution
y ¼ f ðxÞ /////////! y ¼ F ðuÞ
u ¼ u ðxÞ
Die Substitution u ¼ u ðxÞ ist dabei die innere Funktion, y ¼ F ðuÞ die äußere Funktion. Beide Funktionen müssen elementar nach der jeweiligen unabhängigen Variablen
(d. h. nach x bzw. nach u) differenzierbar sein. Die beiden Ableitungen (innere und äußere Ableitung) werden dann miteinander multipliziert, anschließend wird die Hilfsvariable u
durch „Rücksubstitution“ beseitigt.
3 Ableitungsregeln
&
135
Beispiel
Gegeben:
y ¼ f ðxÞ ¼ ln ð1 þ x 2 Þ
Gesucht:
y 0 ¼ f 0 ðxÞ
„Grundform“:
Substitution:
Logarithmusfunktion ln u
u ¼ u ðxÞ ¼ 1 þ x 2
#ußere und innere Funktion:
y ¼ F ðuÞ ¼ ln u
mit
u ¼ u ðxÞ ¼ 1 þ x 2
Kettenregel (mit nachträglicher Rücksubstitution):
y0 ¼
dy
dy du
d
d
1
2x
2x
¼
.
¼
ðln uÞ .
ð1 þ x 2 Þ ¼
. 2x ¼
¼
dx
du dx
du
dx
u
u
1 þ x2
&
Kettenregel für zweifach verschachtelte Funktionen
Gegeben ist die Funktion
y ¼ F ðvÞ
mit v ¼ v ðuÞ
und
u ¼ uðxÞ :
Die Ableitung der mittelbar von der Variablen x abhängigen (verketteten) Funktion
y ¼ F ðv ðu ðxÞÞÞ ¼ f ðxÞ nach der Variablen x wird wie folgt gebildet:
y0 ¼
dy
dy dv du
¼
.
.
dx
dv du dx
oder
f 0 ðxÞ ¼ F 0 ðvÞ . v 0 ðuÞ . u 0 ðxÞ
Die vorgegebene Funktion y ¼ f ðxÞ wird mit Hilfe zweier Substitutionen in eine elementar differenzierbare Funktion der „Hilfsvariablen“ v übergeführt (die Substitutionen werden von innen nach außen ausgeführt). Dabei müssen die äußere Funktion y ¼ F ðvÞ und
die beiden inneren Funktionen v ¼ v ðuÞ und u ¼ u ðxÞ nach der jeweiligen unabhängigen Variablen elementar differenzierbar sein.
Regel: y zunächst nach v, dann v nach u und schließlich u nach x differenzieren
und die drei Ableitungen dann miteinander multiplizieren.
&
Beispiel
y ¼ f ðxÞ ¼ sin 3 ðx 2 þ xÞ ;
y 0 ¼ f 0 ðxÞ ¼ ?
Schrittweise Zerlegung der nicht elementaren Funktion von innen nach außen mit Hilfe zweier Substitutionen.
1. Substitution:
u ¼ x2 þ x
2. Substitution:
v ¼ sin u
Somit gilt:
y ¼ v
3
mit
y ¼ sin 3 u ¼ ðsin uÞ 3
)
)
y ¼ v3
v ¼ sin u
und
u ¼ x2 þ x
Kettenregel (erst y nach v differenzieren, dann v nach u und schließlich u nach x):
y0 ¼
dy
dy dv du
¼
.
.
¼ 3 v 2 . cos u . ð2 x þ 1Þ ¼ 3 ð2 x þ 1Þ v 2 . cos u
dx
dv du dx
Rücksubstitution (in der Reihenfolge v ! u ! xÞ:
y 0 ¼ 3 ð2 x þ 1Þ . ðsin uÞ 2 . cos u ¼ 3 ð2 x þ 1Þ ½sin ðx 2 þ xÞ % 2 . cos ðx 2 þ xÞ
&
136
IV Differentialrechnung
3.6 Logarithmische Differentiation
Bei der logarithmischen Differentiation wird die Funktion y ¼ f ðxÞ zunächst beiderseits
logarithmiert und anschließend unter Verwendung der Kettenregel differenziert. Die Ableitung der logarithmierten Funktion ln y ¼ ln f ðxÞ heißt logarithmische Ableitung von
y ¼ f ðxÞ. Es gilt:
d
1
f 0 ðxÞ
ðln yÞ ¼
. y0 ¼
dx
y
f ðxÞ
Anwendung findet die logarithmische Differentiation z. B. bei Funktionen vom Typ
y ¼ ½ u ðxÞ% v ðxÞ mit u ðxÞ > 0.
&
Beispiel
y ¼ f ðxÞ ¼ x cos x ,
ln y ¼ ln x cos x ¼ cos x . ln x
Logarithmieren:
Differenzieren:
x > 0
d
d
ðln yÞ ¼
ðcos x . ln xÞ
dx
dx
Die linke Seite wird nach der Kettenregel, die rechte Seite nach der Produktregel differenziert:
1
1
/ x . sin x . ln x þ cos x
. y 0 ¼ / sin x . ln x þ cos x .
¼
)
y
x
x
3
2
3
2
/ x . sin x . ln x þ cos x
/ x . sin x . ln x þ cos x
¼ x cos x
y0 ¼ y
x
x
&
3.7 Ableitung der Umkehrfunktion
y ¼ f ðxÞ sei eine umkehrbare Funktion, x ¼ g ðyÞ die nach der Variablen x aufgelöste
Form von y ¼ f ðxÞ ðy ¼ f ðxÞ , x ¼ g ðyÞÞ. Zwischen den Ableitungen f 0 ðxÞ
und g 0 ðyÞ besteht dann die Beziehung
f 0 ðxÞ . g 0 ðyÞ ¼ 1
oder
g 0 ðyÞ ¼
1
f
ð f 0 ðxÞ ¼
6 0Þ
0 ðxÞ
aus der sich die Ableitung g 0 ðxÞ der Umkehrfunktion y ¼ g ðxÞ bestimmen lässt, indem
man zunächst in der Ableitung f 0 ðxÞ die Variable x durch gðyÞ ersetzt und anschließend auf beiden Seiten die Variablen x und y miteinander vertauscht.
&
Beispiel
f 0 ðxÞ ¼
1
¼ 1 þ tan 2 x
cos 2 x
Gegeben:
y ¼ f ðxÞ ¼ tan x ;
Gesucht:
Ableitung der Umkehrfunktion gðxÞ ¼ arctan x
)
g 0 ðyÞ ¼
Nach Vertauschen der beiden Variablen folgt hieraus:
g 0 ðxÞ ¼
y ¼ f ðxÞ ¼ tan x
,
x ¼ g ðyÞ ¼ arctan y
1
1
1
¼
¼
f 0 ðxÞ
1 þ tan 2 x
1 þ y2
d
1
ðarctan xÞ ¼
dx
1 þ x2
&
3 Ableitungsregeln
137
3.8 Implizite Differentiation
Die Gleichung der Funktion (Kurve) liege in der impliziten Form F ðx; yÞ ¼ 0 vor. Die
Ableitung lässt sich dann nach einer der beiden folgenden Methoden bestimmen.
1. Methode: Implizite Differentiation unter Verwendung der Kettenregel
Die Funktionsgleichung F ðx; yÞ ¼ 0 wird gliedweise nach der Variablen x differenziert,
wobei y als eine von x abhängige Funktion zu betrachten ist. Daher ist jeder die Variable y enthaltende Term unter Verwendung der Kettenregel zu differenzieren. Anschließend
wird die Gleichung nach y 0 aufgelöst (falls überhaupt möglich).
&
Beispiel
x 2 þ y 2 ¼ 16
Kreis:
oder
F ðx; yÞ ¼ x 2 þ y 2 / 16 ¼ 0
d
ðx 2 þ y 2 / 16Þ ¼ 2 x þ 2 y . y 0 ¼ 0
dx
)
y0 ¼ /
x
y
Der Term y 2 wurde dabei nach der Kettenregel differenziert (Ergebnis: 2 y . y 0 ).
&
2. Methode: Implizite Differentiation unter Verwendung partieller Ableitungen
Die linke Seite der impliziten Funktionsgleichung F ðx; yÞ ¼ 0 wird als eine von den
beiden Variablen x und y abhängige Funktion z ¼ F ðx; yÞ betrachtet.
y0 ¼ /
Fx ðx; yÞ
Fy ðx; yÞ
Fx ðx; yÞ; Fy ðx; yÞ:
ðFy ðx; yÞ ¼
6 0Þ
Partielle Ableitungen 1. Ordnung von z ¼ F ðx; yÞ (siehe IX.2.1)
Die Ableitung y 0 wird i. Allg. von beiden Variablen, d. h. von x und y abhängen.
&
Beispiel
Kreis:
x 2 þ y 2 ¼ 16
Fx ðx; yÞ ¼ 2 x ;
oder
F ðx; yÞ ¼ x 2 þ y 2 / 16 ¼ 0
Fy ðx; yÞ ¼ 2 y
)
y0 ¼ /
Fx ðx; yÞ
2x
x
¼ /
¼ /
Fy ðx; yÞ
2y
y
&
3.9 Ableitungen einer in der Parameterform dargestellten Funktion
(Kurve)
Erste Ableitung (Kurvenanstieg) und zweite Ableitung einer in der Parameterform
x ¼ x ðtÞ, y ¼ y ðtÞ dargestellten Funktion (Kurve) lassen sich wie folgt bilden:
y0 ¼
dy
y_
¼
dx
x_
y 00 ¼
d 2y
x_ y€ / y_ x€
¼
dx 2
x_ 3
ðx_ 6¼ 0Þ
Die Punkte kennzeichnen dabei die Ableitungen nach dem Parameter t.
138
&
IV Differentialrechnung
Beispiel
Mittelpunktsellipse:
x ¼ a . cos t,
x_ ¼ / a . sin t ;
y_ ¼ b . cos t
y ¼ b . sin t,
)
y0 ¼
0 ) t < 2p
y_
b . cos t
b
¼
¼ /
. cot t
x_
/ a . sin t
a
&
3.10 Ableitungen einer in Polarkoordinaten dargestellten Kurve
Eine in Polarkoordinaten dargestellte Kurve mit der Gleichung r ¼ r ðjÞ lautet in der
Parameterform wie folgt:
x ðjÞ ¼ r ðjÞ . cos j ;
yðjÞ ¼ r ðjÞ . sin j
Für die erste Ableitung (Kurvenanstieg) und die zweite Ableitung gelten dann:
y0 ¼
r_ . sin j þ r . cos j
dy
¼
dx
r_ . cos j / r . sin j
y 00 ¼
d2y
r 2 þ 2 r_ 2 / r r€
¼
dx 2
ðr_ . cos j / r . sin jÞ 3
Die Punkte kennzeichnen dabei die Ableitungen nach dem Winkelparameter j.
&
Beispiel
Wir bestimmen den Anstieg (die Steigung) der Kardioide r ¼ 1 þ cos j (mit 0 ) j < 2 pÞ in dem zum
Polarwinkel j ¼ p=4 gehörenden Kurvenpunkt:
r ¼ 1 þ cos j ;
y0 ¼
¼
r_ ¼
dr
¼ / sin j
dj
r_ . sin j þ r . cos j
/ sin j . sin j þ ð1 þ cos jÞ . cos j
/ sin 2 j þ cos j þ cos 2 j
¼
¼
¼
r_ . cos j / r . sin j
/ sin j . cos j / ð1 þ cos jÞ . sin j
/ 2 . sin j . cos j / sin j
/ ð1 / cos 2 jÞ þ cos j þ cos 2 j
2 . cos 2 j þ cos j / 1
¼
/ sin j ð1 þ 2 . cos jÞ
/ sin j ð1 þ 2 . cos jÞ
)
y 0 ðj ¼ p=4Þ ¼ / 0;414
&
4 Anwendungen der Differentialrechnung
4.1 Geschwindigkeit und Beschleunigung einer geradlinigen Bewegung
Geschwindigkeit v und Beschleunigung a einer geradlinigen Bewegung erhält man als
1. bzw. 2. Ableitung des Weg-Zeit-Gesetzes s ¼ s ðtÞ nach der Zeit t :
Geschwindigkeit-Zeit-Gesetz:
vðtÞ ¼ s_ ðtÞ
Beschleunigung-Zeit-Gesetz:
a ðtÞ ¼ v_ ðtÞ ¼ s€ðtÞ
4 Anwendungen der Differentialrechnung
139
4.2 Tangente und Normale
Tangente und Normale im Kurvenpunkt P ¼ ðx0 ; y0 Þ einer Kurve y ¼ f ðxÞ stehen senkrecht aufeinander. Ihre Gleichungen lauten (in der Punkt-Steigungs-Form):
y
Tangente:
y / y0
¼ f 0 ðx0 Þ
x / x0
Normale:
y / y0
1
¼ / 0
x / x0
f ðx0 Þ
y = f(x)
y0
f 0 ðx0 Þ ¼
6 0
&
Tangente
P
Normale
x0
x
Beispiel
y ¼ f ðxÞ ¼ x 3 / 3 x 2 þ 4 ;
x0 ¼ 1 ;
y 0 ¼ f 0 ðxÞ ¼ 3 x 2 / 6 x
f 0 ð1Þ ¼ / 3
Tangente:
Normale:
)
y0 ¼ f ð1Þ ¼ 2 ;
P ¼ ð1; 2Þ
y/2
¼ / 3 ) y / 2 ¼ / 3 ðx / 1Þ ¼ / 3 x þ 3 ) y ¼ / 3 x þ 5
x /1
y/2
1
1
1
1
1
1
5
¼ /
¼
) y/2 ¼
ðx / 1Þ ¼
x /
) y ¼
x þ
x /1
/3
3
3
3
3
3
3
&
4.3 Linearisierung einer Funktion
Eine nichtlineare Funktion y ¼ f ðxÞ lässt sich in der unmittelbaren Umgebung des Kurvenpunktes P ¼ ðx0 ; y0 Þ (in den Anwendungen meist als Arbeitspunkt bezeichnet) durch
die dortige Kurventangente, d. h. durch eine lineare Funktion approximieren. Die Gleichung der linearisierten Funktion lautet:
y
y / y0 ¼ f 0 ðx0 Þ . ðx / x0 Þ
y = f(x)
oder
P
Dy ¼ f 0 ðx0 Þ . Dx
Dx; Dy:
&
y0
Relativkoordinaten bezüglich des
Arbeitspunktes P ¼ ðx0 ; y0 Þ
ðDx ¼ x / x0 ; Dy ¼ y / y0 Þ
Linearisierte Funktion
(Tangente)
x0
x
Beispiel
Wir linearisieren die Funktion y ¼ ðx þ 1Þ . e x in der Umgebung der Stelle x0 ¼ 0:
y0 ¼ y ð0Þ ¼ 1
0
x
)
x
Arbeitspunkt:
P ¼ ð0; 1Þ
y ¼ 1 . e þ e . ðx þ 1Þ ¼ ðx þ 2Þ . e x
Linearisierte Funktion:
)
y / 1 ¼ 2 ðx / 0Þ ¼ 2 x
y 0 ð0Þ ¼ 2
oder
y ¼ 2x þ 1
Bei Verwendung von Relativkoordinaten bezüglich des Arbeitspunktes P:
Dy ¼ 2 Dx
&
140
IV Differentialrechnung
4.4 Monotonie und Krümmung einer Kurve
4.4.1 Geometrische Deutung der 1. und 2. Ableitung
Das Verhalten einer (differenzierbaren) Funktion y ¼ f ðxÞ in einem Intervall I wird im
Wesentlichen durch die ersten beiden Ableitungen bestimmt.
Monotonie-Verhalten
Die 1. Ableitung y 0 ¼ f 0 ðxÞ ist die Steigung der Kurventangente und bestimmt somit das
Monotonie-Verhalten der Funktion:
y 0 ¼ f 0 ðx0 Þ > 0:
y 0 ¼ f 0 ðx0 Þ < 0:
f 0 ðx0 Þ ( 0:
0
f ðx0 Þ ) 0:
streng monoton
wachsend (Bild a))
y
y
f' ( x 0 ) < 0
f' ( x 0 ) > 0
streng monoton
fallend (Bild b))
P
P
y0
monoton wachsend
monoton fallend
a)
y0
x
x0
b)
x0
x
Krümmungs-Verhalten
Die 2. Ableitung y 00 ¼ f 00 ðxÞ bestimmt das Krümmungs-Verhalten der Funktion:
y 00 ¼ f 00 ðx0 Þ > 0:
Linkskrümmung
(konvexe Krümmung,
Bild a))
y 00 ¼ f 00 ðx0 Þ < 0:
Rechtskrümmung
(konkave Krümmung,
Bild b))
Der Drehpfeil in den nebenstehenden Bildern
kennzeichnet den Drehsinn der Kurventangente beim Durchlaufen des Punktes P in
positiver x-Richtung.
Hinweis: Siehe hierzu auch XIV.1.5
y
y
f'' ( x 0 ) < 0
f'' ( x 0 ) > 0
P
P
y0
y0
a)
x0
x
b)
x0
x
4 Anwendungen der Differentialrechnung
141
4.4.2 Krümmung einer ebenen Kurve
Kurvenkrümmung
Die Krümmung j einer ebenen Kurve y ¼ f ðxÞ im Kurvenpunkt P ¼ ðx; yÞ ist ein
quantitatives Maß dafür, wie stark der Kurvenverlauf in der unmittelbaren Umgebung dieses Punktes von dem einer Geraden abweicht:
j ¼
y
y 00
½1 þ ðy 0 Þ 2 % 3=2
j > 0 bzw: y 00 > 0
j < 0 bzw: y 00 < 0
y = f(x)
f''(x) > 0
, Linkskrümmung
, Rechtskrümmung
f''(x) < 0
Linkskrümmung
Krümmungskreis
Rechtskrümmung
x
Der Krümmungskreis einer Kurve y ¼ f ðxÞ im Kurvenpunkt P ¼ ðx; yÞ berührt dort die
Kurve von 2. Ordnung (gemeinsame Tangente, gleiche Krümmung). Der Radius r dieses
Kreises heißt Krümmungsradius, der Mittelpunkt M ¼ ðx0 ; y0 Þ Krümmungsmittelpunkt.
Krümmungsradius r
r ¼
1
½1 þ ðy 0 Þ2 % 3=2
¼
jjj
j y 00 j
y
Tangente
Normale
Krümmungsmittelpunkt M = (x0; y0)
x0 ¼ x / y 0 .
y0 ¼ y þ
r
1 þ ð y 0Þ 2
y 00
1 þ ð y 0Þ 2
y 00
y = f(x)
P
M
Krümmungskreis
x
x; y:
0
Koordinaten des Kurvenpunktes P
00
y ,y :
1. bzw. 2. Ableitung von y ¼ f ðxÞ im Kurvenpunkt P
Der Krümmungsmittelpunkt M liegt stets auf der Kurvennormale des Berührungspunktes P.
Die Verbindungslinie aller Krümmungsmittelpunkte einer Kurve heißt Evolute, die Kurve
selbst wird als Evolvente bezeichnet. Die Koordinaten x0 und y0 des Krümmungsmittelpunktes sind dabei Funktionen der x-Koordinate des laufenden Kurvenpunktes P und bilden
daher eine Parameterdarstellung der zur Kurve y ¼ f ðxÞ gehörenden Evolute.
142
IV Differentialrechnung
Sonderfälle
Gerade:
&
j ¼ 0,
r ¼ 1;
j j j ¼ 1=r, r ¼ r
Kreis:
(r : Kreisradius)
Beispiel
Wir bestimmen die Krümmung und den Krümmungskreis der Sinusfunktion an der Stelle x ¼ p=2, d. h. im
Punkt P ¼ ðp=2; 1Þ:
y 0 ¼ cos x ;
y ¼ sin x ;
j ¼
y 00
½ 1 þ ðy 0 Þ 2 % 3=2
¼
y 00 ¼ / sin x
/ sin x
½1 þ cos 2 x% 3=2
)
j ðp=2Þ ¼
Krümmungsradius:
y
1
1
r ðp=2Þ ¼
¼
¼ 1
j jðp=2Þ j
j / 1j
Krümmungsmittelpunkt:
/ sin ðp=2Þ
/1
¼
¼ /1
½1 þ cos 2 ðp=2Þ% 3=2
ð1 þ 0 2 Þ 3=2
P
1
M ¼ ðp=2; 0Þ
y = sin x
Begründung: Im Punkt P verläuft die Tangente
waagerecht, die Normale somit parallel zur y-Achse.
Der Krümmungsmittelpunkt M liegt im Abstand
r ¼ 1 unterhalb von P und somit auf der x-Achse.
M
p /2
x0 ¼ x / y 0 .
1 þ ðy 0 Þ 2
p
1 þ 02
p
¼
/0.
¼
y 00
2
/1
2
y0 ¼ y þ
1 þ ðy 0 Þ 2
1 þ 02
¼ 1þ
¼ 0
y 00
/1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
y 0 ¼ cos ðp=2Þ ¼ 0 ;
y ¼ sin ðp=2Þ ¼ 1 ;
x
–1
Die Gleichungen für die Koordinaten x0 und y0
des Krümmungsmittelpunktes M (siehe Seite 141)
führen natürlich zum gleichen Ergebnis:
x ¼ p=2 ;
p
)
y 00 ¼ /sin ðp=2Þ ¼ / 1
M ¼ ðx0 ; y0 Þ ¼ ðp=2; 0Þ
&
4.5 Relative Extremwerte (relative Maxima, relative Minima)
Eine Funktion y ¼ f ðxÞ besitzt an der Stelle x0 ein relatives Maximum bzw. ein relatives
Minimum, wenn in einer gewissen Umgebung von x0 stets
f ðx0 Þ > f ðxÞ
bzw.
f ðx0 Þ < f ðxÞ
ist ðx 6¼ x0 Þ. Die folgenden Bedingungen sind hinreichend (Voraussetzung: f ðxÞ ist
mindestens zweimal differenzierbar):
Relatives Maximum (Hochpunkt)
Die Kurve besitzt an der Stelle x0 eine
waagerechte Tangente und Rechtskrümmung:
f 0 ðx0 Þ ¼ 0
und
f 00 ðx0 Þ < 0
y
Maximum
y = f(x)
f(x0)
x0
x
4 Anwendungen der Differentialrechnung
143
Relatives Minimum (Tiefpunkt)
y
Die Kurve besitzt an der Stelle x0 eine
waagerechte Tangente und Linkskrümmung:
f 0 ðx0 Þ ¼ 0
y = f(x)
Minimum
f 00 ðx0 Þ > 0
und
f(x0)
x
x0
Beispiel
&
Wir bestimmen die relativen Extremwerte der Funktion y ¼ x 2 . e / x . Die dabei benötigten Ableitungen y 0
und y 00 erhalten wir jeweils mit Hilfe der Produkt- und Kettenregel:
u
y 0 ¼ u 0 v þ v 0 u ¼ 2 x . e / x þ e / x . ð/ 1Þ . x 2 ¼ ð2 x / x 2 Þ . e / x
)
f
f
y ¼ x 2 . e /x
v
y ¼ ð2 x / x 2 Þ . e / x
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
u
)
f
0
v
y 00 ¼ u 0 v þ v 0 u ¼ ð2 / 2 xÞ . e / x þ e / x . ð/ 1Þ . ð2 x / x 2 Þ ¼ ð2 / 4 x þ x 2 Þ . e / x
)
ð2 x / x 2 Þ . e / x ¼ 0
f
y0 ¼ 0
)
2 x / x 2 ¼ xð2 / xÞ ¼ 0
)
y2 ¼ 0;541
)
x1 ¼ 0 ;
x2 ¼ 2
6¼ 0
x1 ¼ 0
)
y1 ¼ 0 ;
00
y ðx1 ¼ 0Þ ¼ 2 > 0
00
y ðx2 ¼ 2Þ ¼ / 2 . e
x2 ¼ 2
)
/2
< 0
Min ¼ ð0; 0Þ
)
Max ¼ ð2; 0;541Þ
&
Allgemeines Kriterium für einen relativen Extremwert
In einigen Fällen versagen die oben genannten Kriterien, wenn nämlich neben f 0 ðx0 Þ
auch f 00 ðx0 Þ verschwindet. Dann entscheidet die nächstfolgende, nichtverschwindende Ableitung f ðnÞ ðx0 Þ wie folgt über Existenz und Art eines Extremwertes:
f 0 ðx0 Þ ¼ 0
(waagerechte Tangente)
Die nächstfolgende, nichtverschwindende Ableitung sei f
n ¼ gerade
f
ðnÞ
)
Extremwert
ðx0 Þ ¼
6 0
n ¼ ungerade )
Sattelpunkt
ðnÞ
ðx0 Þ
ðn ( 2Þ:
f
ðnÞ
ðx0 Þ < 0:
Maximum
f
ðnÞ
ðx0 Þ > 0:
Minimum
(siehe Abschnitt 4.6)
144
&
IV Differentialrechnung
Beispiel
Wir untersuchen die Funktion y ¼ x 4 auf relative Extremwerte:
y ¼ x4;
0
y ¼ 4x
y0 ¼ 4x3 ;
3
¼ 0
y 00 ¼ 12 x 2
)
x0 ¼ 0
y ð0Þ ¼ 0
)
Kriterium versagt
y 000 ¼ 24 x
)
y 000 ð0Þ ¼ 0
00
y
ð4Þ
¼ 24
)
y
ð4Þ
y
y = x4
ð0Þ ¼ 24 6¼ 0
1
Es ist n ¼ 4, d. h. gerade und y ð4Þ ð0Þ > 0. Die
Funktion y ¼ x 4 besitzt somit an der Stelle
x0 ¼ 0 ein (sogar absolutes) Minimum.
x
–1 Minimum 1
&
4.6 Wendepunkte, Sattelpunkte
y
Wendepunkt
In einem Wendepunkt ändert sich die Art der
Kurvenkrümmung, d. h. die Kurve geht dort
von einer Links- in eine Rechtskurve über
oder umgekehrt. In einem Wendepunkt ändert
sich somit der Drehsinn der Kurventangente.
Die folgende Bedingung ist hinreichend:
f 00 ðx0 Þ ¼ 0
und
Wendetangente:
f''(x) > 0
f''(x) < 0
y = f(x)
W
Wendetangente
f 000 ðx0 Þ ¼
6 0
x
x0
Tangente im Wendepunkt
Sattelpunkt
Ein Sattelpunkt (auch Terrassenpunkt genannt) ist ein Wendepunkt mit waagerechter Tangente. Die hinreichende Bedingung lautet daher:
f 0 ðx0 Þ ¼ 0 ;
&
f 00 ðx0 Þ ¼ 0
und
f 000 ðx0 Þ ¼
6 0
y
Beispiel
y'' > 0
Die kubische Parabel y ¼ x 3 besitzt an der Stelle
x0 ¼ 0 einen Sattelpunkt:
y0 ¼ 3x2 ;
0
y 00 ¼ 6 x ;
00
y ð0Þ ¼ y ð0Þ ¼ 0 ;
Sattelpunkt:
y ð0Þ ¼ 6 6¼ 0
ð0; 0Þ
Wendetangente:
1
y 000 ¼ 6
000
y ¼ 0 (x-Achse)
y=x3
Sattelpunkt
–1
1
x
–1
y'' < 0
&
4 Anwendungen der Differentialrechnung
145
4.7 Kurvendiskussion
Feststellung der Eigenschaften einer Funktion nach dem folgenden Schema (Funktionsanalyse):
•
•
•
•
•
•
•
•
•
•
Definitionsbereich/Definitionslücken
Symmetrie (gerade, ungerade Funktion)
Nullstellen, Schnittpunkte mit der y-Achse
Pole, Polgeraden (bei gebrochenrationalen Funktionen)
Ableitungen (in der Regel bis zur 3. Ordnung)
Relative Extremwerte (Maxima, Minima)
Wendepunkte, Sattelpunkte
Verhalten der Funktion im Unendlichen (Asymptote im Unendlichen)
Wertebereich
Zeichnung der Funktion (Kurve) in einem geeigneten Maßstab
Eventuell: Monotonie- und Krümmungsverhalten
&
Beispiel
y ¼ x2 . e/x
Definitionsbereich:
/1 < x < 1
oder
x 2 R
Symmetrie:
keine
Nullstellen:
y ¼ 0 ) x 2 . e / x ¼ 0 ) x 2 ¼ 0 (wegen e / x > 0 und somit e / x 6¼ 0Þ
x1=2 ¼ 0 (doppelte Nullstelle und somit Berührungspunkt)
)
Ableitungen (unter Verwendung der Produkt- und Kettenregel):
y 0 ¼ 2 x . e / x þ e / x . ð/ 1Þ . x 2 ¼ ð2 x / x 2 Þ . e / x
y 00 ¼ ð2 / 2 xÞ . e / x þ e / x . ð/ 1Þ . ð2 x / x 2 Þ . e / x ¼ ðx 2 / 4 x þ 2Þ . e / x
y 000 ¼ ð2 x / 4Þ . e / x þ e / x . ð/ 1Þ . ðx 2 / 4 x þ 2Þ ¼ ð/ x 2 þ 6 x / 6Þ . e / x
Relative Extremwerte:
0
y ¼ 0
y0 ¼ 0;
2
)
ð2 x / x Þ . e
00
y ð0Þ ¼ 2 > 0
)
/x
y 00 6¼ 0
¼ 0
)
2 x / x 2 ¼ x ð2 / xÞ ¼ 0
00
Min ;
y ð2Þ ¼ / 2 . e
/2
< 0
Ordinaten an den Stellen x3 ¼ 0 und x4 ¼ 2: y3 ¼ 0,
Minimum:
ð0; 0Þ ;
Wendepunkte:
y
00
¼ 0
)
x5 ¼ 3;414 ;
y
00
Maximum :
¼ 0;
y
000
x3 ¼ 0 ;
x4 ¼ 2
Max
y4 ¼ 0,541
ð2; 0;541Þ
6¼ 0
2
ðx / 4 x þ 2Þ . e / x ¼ 0
)
x2 / 4x þ 2 ¼ 0
)
x5=6 ¼ 2 +
pffiffiffi
2
)
x6 ¼ 0;586
000
y ð3;414Þ ¼ 0;093 6¼ 0
y 000 ¼ ð0;586Þ ¼ / 1;574 6¼ 0
)
)
Ordinaten an den Stellen x5=6 ¼ 2 +
Wendepunkte:
)
)
Wendepunkte
pffiffiffi
2 : y5 ¼ 0,384,
W1 ¼ ð0;586; 0;191Þ;
y6 ¼ 0,191
W2 ¼ ð3;414; 0;384Þ (keine Sattelpunkte, da jeweils y 0 6¼ 0)
146
IV Differentialrechnung
Verhalten der Funktion im Unendlichen:
Wertebereich:
lim x 2 . e / x ¼ 0
)
x!1
Asymptote :
y ¼ 0
ðx-AchseÞ
y ( 0
Monotonieverhalten: y 0 ¼ ð2 x / x 2 Þ . e / x ¼ u . e / x
|fflfflfflfflffl{zfflfflfflfflffl}
u
Wegen e / x > 0 hängt das Vorzeichen der 1. Ableitung y 0 nur vom Vorzeichen des 1. Faktors, d. h. der
„Hilfsfunktion“ u ¼ 2 x / x 2 ¼ x ð2 / xÞ ab. Diese beschreibt eine nach unten geöffnete Parabel mit folgenden Eigenschaften (siehe Bild a)):
Nullstellen bei x ¼ 0 und x ¼ 2
u
Scheitelpunkt: S ¼ ð1; 1Þ
S
1
Im Intervall 0 < x < 2 gilt u > 0 und somit auch
y 0 > 0, dort verläuft die Funktion y ¼ x 2 . e / x daher
streng monoton wachsend (Bereich zwischen den beiden Extremwerten der Funktion). Im übrigen Definitionsbereich,
d. h. in den Intervallen x < 0 und x > 2 ist der Kurvenverlauf wegen u < 0 und damit auch y 0 < 0 dagegen
streng monoton fallend.
0
1
2
x
a)
Krümmungsverhalten: y 00 ¼ ðx 2 / 4 x þ 2Þ . e / x ¼ v . e / x
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
v
Wegen e / x > 0 hängt das Vorzeichen der 2. Ableitung y 00 nur vom Vorzeichen des 1. Faktors, d. h. der
„Hilfsfunktion“ v ¼ x 2 / 4 x þ 2 ab. Diese beschreibt eine nach oben geöffnete Parabel mit folgenden
Eigenschaften (siehe Bild b)):
pffiffiffi
v
Nullstellen bei x ¼ 2 + 2
Scheitelpunkt: S ¼ ð2; / 2Þ
pffiffiffi
pffiffiffi
Im Intervall 2 / 2 < x < 2 þ 2 gilt v < 0
00
und somit auch y < 0, dort besitzt die Funktion
y ¼ x 2 . e / x daher Rechtskrümmung (Bereich zwischen den beiden Wendepunkten der Funktion). Im
übrigen Definitionsbereich ist die Kurve wegen
v > 0 und somit auch y 00 > 0 nach links gekrümmt.
2– 2
0
2+ 2
2
x
–1
–2
S
b)
Verlauf der Kurve y ¼ x 2 . e / x :
y
Max
0,5
W2
y = x 2· e – x
W1
Min
2
5
x
&
147
V Integralrechnung
1 Bestimmtes Integral
1.1 Definition eines bestimmten Integrals
Das bestimmte Integral
Ðb
a
f ðxÞ dx lässt sich in anschaulicher Weise als Flächeninhalt A
zwischen der stetigen Funktion y ¼ f ðxÞ, der x-Achse und den beiden zur y-Achse parallelen Geraden x ¼ a und x ¼ b deuten, sofern die Kurve im gesamten Intervall
a ) x ) b oberhalb der x-Achse verläuft.
y
y = f(x)
f(x0)
f(x1)
Dx
Dx
x0 = a
x1
f(x2)
f(x3)
Dx
Dx
x2
f(xn–1) f(xn)
x3
xn–1 xn = b
x
b/a
, ersetzen
n
jeden Streifen in der aus der Abbildung ersichtlichen Weise durch ein Rechteck (im Bild
grau unterlegt) und summieren dann über alle Rechtecksflächen. Dies führt (bei einer
monoton wachsenden Funktion) zu der sog. Untersumme
Wir zerlegen zunächst die Fläche in n Streifen gleicher Breite Dx ¼
Un ¼ f ðx0 Þ Dx þ f ðx1 Þ Dx þ f ðx2 Þ Dx þ . . . þ f ðxn / 1 Þ Dx ¼
die einen Näherungswert für den gesuchten Flächeninhalt darstellt.
n ! 1 (und somit Dx ! 0Þ strebt die Untersumme Un gegen
als bestimmtes Integral von f ðxÞ in den Grenzen von x ¼ a bis x
und geometrisch als Flächeninhalt A unter der Kurve y ¼ f ðxÞ im
interpretiert werden darf.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_5
n
P
k¼1
f ðxk / 1 Þ Dx
Beim Grenzübergang
einen Grenzwert, der
¼ b bezeichnet wird
Intervall a ) x ) b
148
V Integralrechnung
Symbolische Schreibweise:
ðb
n
P
f ðxÞ dx ¼ lim Un ¼ lim
n!1
a
n!1 k¼1
f ðxk / 1 Þ Dx
Bezeichnungen:
x:
Integrationsvariable
f ðxÞ: Integrandfunktion (kurz: Integrand)
a; b: Untere bzw. obere Integrationsgrenze
Das Integral existiert, wenn f ðxÞ stetig ist oder aber beschränkt ist und nur endlich viele
Unstetigkeiten im Integrationsintervall enthält.
1.2 Berechnung eines bestimmten Integrals
ðb
f ðxÞ dx ¼ ½ F ðxÞ% ba ¼ F ðbÞ / F ðaÞ
ðHauptsatz der IntegralrechnungÞ
a
F ðxÞ ist dabei irgendeine Stammfunktion von f ðxÞ
&
ðF 0 ðxÞ ¼ f ðxÞ, siehe Abschnitt 2.2).
Beispiele
(1)
p=2
Ð
0
p=2
cos x dx ¼ ½sin x% 0
¼ sin ðp=2Þ / sin 0 ¼ 1 / 0 ¼ 1
Denn F ðxÞ ¼ sin x ist wegen F 0 ðxÞ ¼
(2)
Ð3
/3
d
ðsin xÞ ¼ cos x eine Stammfunktion von f ðxÞ ¼ cos x.
dx
ðx 2 / 4 x þ 1Þ dx ¼ ?
1 3
x / 2 x 2 þ x ist eine Stammfunktion des Integranden f ðxÞ ¼ x 2 / 4 x þ 1 , da
3
3
2
d
1 3
F 0 ðxÞ ¼
x / 2 x 2 þ x ¼ x 2 / 4 x þ 1 ¼ f ðxÞ
dx 3
FðxÞ ¼
gilt. Somit:
ð3
/3
ðx 2 / 4 x þ 1Þ dx ¼
+
1 3
x / 2x2 þ x
3
)3
/3
¼ ð9 / 18 þ 3Þ / ð/ 9 / 18 / 3Þ ¼ 24
&
1 Bestimmtes Integral
149
1.3 Elementare Integrationsregeln für bestimmte Integrale
Regel 1: Faktorregel
Ein konstanter Faktor C darf vor das Integral gezogen werden:
ðb
ðb
C . f ðxÞ dx ¼ C .
a
f ðxÞ dx
ðC 2 RÞ
a
Regel 2: Summenregel
Eine endliche Summe von Funktionen darf gliedweise integriert werden:
ðb
ðb
½ f1 ðxÞ þ . . . þ fn ðxÞ% dx ¼
a
ðb
f1 ðxÞ dx þ . . . þ
a
fn ðxÞ dx
a
Regel 3: Vertauschungsregel
Vertauschen der Integrationsgrenzen bewirkt einen Vorzeichenwechsel des Integrals:
ða
ðb
f ðxÞ dx
f ðxÞ dx ¼ /
a
b
Regel 4: Fallen die Integrationsgrenzen zusammen ða ¼ bÞ; so ist der Integralwert
gleich null:
ða
f ðxÞ dx ¼ 0
a
Geometrische Deutung:
Flächeninhalt unter der Kurve ¼ 0
Regel 5: Für jede Stelle c aus dem Integrationsintervall gilt:
ðb
ðc
f ðxÞ dx ¼
a
ðb
f ðxÞ dx þ
a
Geometrische Deutung:
f ðxÞ dx
ða ) c ) bÞ
c
Zerlegung der Fläche in zwei Teilflächen
150
V Integralrechnung
2 Unbestimmtes Integral
2.1 Definition eines unbestimmten Integrals
Das unbestimmte Integral I ðxÞ ¼
Ðx
a
f ðtÞ dt beschreibt den Flächeninhalt A zwischen der
stetigen Kurve y ¼ f ðtÞ und der t-Achse im Intervall a ) t ) x in Abhängigkeit von
der oberen (variabel gehaltenen) Grenze x und wird daher auch als Flächenfunktion
bezeichnet (Voraussetzung für diese geometrische Interpretation: f ðtÞ ( 0 und x ( a).
y
ðx
I ðxÞ ¼
f ðtÞ dt
y = f(t)
a
variabel
A
Man beachte: Ein bestimmtes Integral ist eine
Zahl (Flächeninhalt A), ein unbestimmtes
Integral dagegen eine Funktion der oberen
Grenze x ðFlächenfunktion I ðxÞÞ!
a
x
t
2.2 Allgemeine Eigenschaften der unbestimmten Integrale
1. Zu jeder stetigen Funktion f ðxÞ gibt es unendlich viele unbestimmte Integrale, die sich
in ihrer unteren Integrationsgrenze voneinander unterscheiden.
2. Die Differenz zweier unbestimmter Integrale von f ðxÞ ist eine Konstante.
Ðx
3. Differenziert man ein unbestimmtes Integral I ðxÞ ¼ f ðtÞ dt nach der oberen Grenze
a
x, so erhält man die Integrandfunktion f ðxÞ (sog. Fundamentalsatz der Differentialund Integralrechnung):
ðx
I ðxÞ ¼
f ðtÞ dt
a
)
dI
¼ I 0 ðxÞ ¼ f ðxÞ
dx
Allgemein wird eine differenzierbare Funktion F ðxÞ mit der Eigenschaft F 0 ðxÞ ¼ f ðxÞ
als eine Stammfunktion von f ðxÞ bezeichnet. In diesem Sinne lässt sich der FundamentalÐx
satz auch wie folgt formulieren: Jedes unbestimmte Integral IðxÞ ¼ f ðtÞ dt von f ðxÞ
a
ist eine Stammfunktion von f ðxÞ.
2 Unbestimmtes Integral
151
4. Ist F ðxÞ irgendeine Stammfunktion von f ðxÞ und C1 eine geeignete reelle Konstante,
so gilt
ðx
I ðxÞ ¼
f ðtÞ dt ¼ F ðxÞ þ C1
a
Die Konstante C1 lässt sich aus der Bedingung I ðaÞ ¼ F ðaÞ þ C1 ¼ 0 berechnen:
C1 ¼ / F ðaÞ.
Ðx
5. Die Menge aller Funktionen vom Typ I ðxÞ þ K ¼ f ðtÞ dt þ K wird als unbea
Ð
stimmtes Integral von f ðxÞ bezeichnet und durch das Symbol
f ðxÞ dx gekennzeichnet (die Integrationsgrenzen werden weggelassen):
ð
ðx
f ðxÞ dx 0
f ðtÞ dt þ K
ðK 2 RÞ
a
Die Begriffe „Stammfunktion von f ðxÞ“ und „unbestimmtes
Integral von f ðxÞ“ sind
Ð
somit gleichwertig. Das unbestimmte Integral
f ðxÞ dx von f ðxÞ ist daher in der
Form
ð
f ðxÞ dx ¼ F ðxÞ þ C
ðF 0 ðxÞ ¼ f ðxÞÞ
darstellbar, wobei F ðxÞ irgendeine Stammfunktion zu f ðxÞ bedeutet und die Integrationskonstante C alle reellen Werte durchläuft. Das Aufsuchen sämtlicher Stammfunktionen F ðxÞ zu einer vorgegebenen Funktion f ðxÞ heißt unbestimmte Integration:
f ðxÞ
unbestimmte
!
Integration
F ðxÞ
mit
F 0 ðxÞ ¼ f ðxÞ
Geometrische Deutung der Stammfunktionen: Die Stammfunktionen (oder Integralkurven) zu einer stetigen Funktion f ðxÞ bilden eine einparametrige Kurvenschar. Jede
Integralkurve entsteht dabei aus jeder anderen durch Parallelverschiebung in der y-Richtung.
6. Faktor- und Summenregel für bestimmte Integrale gelten sinngemäß auch für unbestimmte Integrale (siehe Abschnitt 1.3).
&
Beispiel
Ð
ð2 x / sin xÞ dx ¼ ?
Stammfunktion zu f ðxÞ ¼ 2 x / sin x: FðxÞ ¼ x 2 þ cos x, da F 0 ðxÞ ¼ 2 x / sin x ¼ f ðxÞ
Ð
Lösung:
ð2 x / sin xÞ dx ¼ F ðxÞ þ C ¼ x 2 þ cos x þ C
ðC 2 RÞ
ist.
&
152
V Integralrechnung
2.3 Tabelle der Grund- oder Stammintegrale
C, C1 , C2 : Reelle Integrationskonstanten
ð
0 dx ¼ C
ð
ð
x n dx ¼
ð
ð
x nþ1
þC
nþ1
ðn 6¼ / 1Þ
ð
e x dx ¼ e x þ C
ð
ð
ð
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx ¼
1 / x2
(
arcsin x þ C1
)
ð
/ arccos x þ C2
Z
a x dx ¼
ax
þC
ln a
1
dx ¼ / cot x þ C
sin 2 x
1
dx ¼
1 þ x2
(
arctan x þ C1
)
/ arccot x þ C2
ð
cosh x dx ¼ sinh x þ C
sinh x dx ¼ cosh x þ C
Z
1
dx ¼ ln j x j þ C
x
cos x dx ¼ sin x þ C
1
dx ¼ tan x þ C
cos 2 x
ð
ð
dx ¼ x þ C
ð
sin x dx ¼ / cos x þ C
ð
ð
1 dx ¼
1
dx ¼ tanh x þ C
cosh 2 x
ð
1
dx ¼ / coth x þ C
sinh 2 x
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
1
"
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx ¼ arsinh x þ C ¼ ln " x þ x 2 þ 1 " þ C
x2 þ 1
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
1
"
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx ¼ sgn ðxÞ . arcosh j x j þ C ¼ ln " x þ x 2 / 1 " þ C
x2 / 1
8
3
2
1
1þx
>
>
>
artanh x þ C1 ¼
. ln
þ C1
>
>
ð
2
1/x
<
1
fur
€
dx ¼
3
2
>
1 / x2
>
>
1
x þ1
>
>
þ C2
. ln
: arcoth x þ C2 ¼
2
x /1
ðj x j > 1Þ
9
>
>
jxj < 1>
>
>
=
>
>
>
>
jxj > 1>
;
Hinweis: Im Anhang, Teil A befindet sich eine ausführliche Integraltafel mit über 400
weiteren Integralen (gedruckt auf gelbem Papier).
3 Integrationsmethoden
153
3 Integrationsmethoden
3.1 Integration durch Substitution
3.1.1 Allgemeines Verfahren
Ð
Das vorgegebene Integral
f ðxÞ dx wird mit Hilfe einer geeigneten Substitution wie folgt
in ein Grund- oder Stammintegral übergeführt 1Þ :
1. Aufstellung der Substitutionsgleichungen:
u ¼ g ðxÞ ;
du
¼ g 0 ðxÞ ;
dx
dx ¼
du
g 0 ðxÞ
2. Durchführung der Integralsubstitution:
ð
ð
f ðxÞ dx ¼ j ðuÞ du
Das neue Integral enthält nur die „Hilfsvariable“ u und deren Differential du.
3. Integration (Berechnung des neuen Integrals):
ð
j ðuÞ du ¼ F ðuÞ
ðmit F 0 ðuÞ ¼ j ðuÞÞ
4. Rücksubstitution:
ð
ð
f ðxÞ dx ¼ j ðuÞ du ¼ F ðuÞ ¼ F ðg ðxÞÞ ¼ F ðxÞ
Anmerkungen
(1)
In bestimmten Fällen ist es günstiger, die „Hilfsvariable“ u durch eine Substitution
vom Typ x ¼ h ðuÞ einzuführen. Die Substitutionsgleichungen lauten dann:
x ¼ h ðuÞ ,
dx
¼ h 0 ðuÞ ,
du
dx ¼ h 0 ðuÞ du
(2)
Die Substitutionen u ¼ g ðxÞ und x ¼ h ðuÞ müssen monotone und stetig differenzierbare Funktionen sein.
(3)
Bei einem bestimmten Integral kann auf die Rücksubstitution verzichtet werden, wenn
man die Integrationsgrenzen mit Hilfe der Substitutionsgleichung u ¼ g ðxÞ bzw.
x ¼ hðuÞ mitsubstituiert.
1Þ
Dies gelingt nicht immer im 1. Schritt. Gegebenenfalls muss das neue Integral nach einer anderen Integrationstechnik weiterbehandelt werden.
154
V Integralrechnung
3.1.2 Spezielle Integralsubstitutionen (Tabelle)
Integraltyp
ð
ðAÞ
f ða x þ bÞ dx
Substitution
Neues Integral
bzw. Lösung
u ¼ ax þ b
1
.
a
dx ¼
ð
ðBÞ
f ðxÞ . f 0 ðxÞ dx
du
a
u ¼ f ðxÞ
du
dx ¼ 0
f ðxÞ
ð
ðCÞ
½ f ðxÞ% n . f 0 ðxÞ dx
ðn 6¼ / 1Þ
ð
ðDÞ
f ½ gðxÞ% . g 0 ðxÞ dx
u ¼ f ðxÞ
dx ¼
u ¼ gðxÞ
dx ¼
ð
ðEÞ
f 0 ðxÞ
dx
f ðxÞ
ðFÞ
x ¼ a . sin u
3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2
R x ; x 2 þ a 2 dx
x ¼ a . sinh u
dx ¼ a . cosh u du
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R: Rationale Funktion
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 2 þ a 2 ¼ a . cosh u
von x und x 2 þ a 2
ð
ðHÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2
R x ; a 2 / x 2 dx
du
f 0 ðxÞ
dx ¼ a . cos u du
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R: Rationale Funktion
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 / x 2 ¼ a . cos u
von x und a 2 / x 2
ð
ðGÞ
3
3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2
R x ; x 2 / a 2 dx
f ðuÞ du
x ¼ a . cosh u
dx ¼ a . sinh u du
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R: Rationale Funktion
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 2 / a 2 ¼ a . sinh u
von x und x 2 / a 2
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4 x þ 5 dx
ðu ¼ 4 x þ 5Þ
1
½ f ðxÞ% 2 þ C
2
ð
sin x . cos x dx
ðu ¼ sin xÞ
1
½ f ðxÞ% nþ1 þ C
nþ1
ð
ðln xÞ 2 .
1
dx
x
ðu ¼ ln xÞ
ð
ð
f ðuÞ du
du
g 0 ðxÞ
u ¼ f ðxÞ
dx ¼
ð
du
f 0 ðxÞ
ð
Beispiel
2
x . e x dx
ðu ¼ x 2 Þ
ln j f ðxÞ j þ C
ð
2x / 3
dx
x2 / 3x þ 1
ðu ¼ x 2 / 3x þ 1Þ
ð
x3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx
4 / x2
ðx ¼ 2 . sin uÞ
ð
x2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx
x2 þ 9
ðx ¼ 3 . sinh uÞ
ð
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx
2
x / 25
ðx ¼ 5 . cosh uÞ
3 Integrationsmethoden
155
Tabelle (Fortsetzung)
Integraltyp
Substitution
ð
ðIÞ
R: Rationale Funktion
von sin x und cos x
ð
R ðsinh x ; cosh xÞ dx
R: Rationale Funktion
von sinh x und cosh x
&
Beispiel
ð
u ¼ tan ðx=2Þ
R ðsin x; cos xÞ dx
ðJÞ
Neues Integral
bzw. Lösung
2
du
1 þ u2
dx ¼
sin x ¼
2u
1 þ u2
cos x ¼
1 / u2
1 þ u2
u ¼ e x ; dx ¼
ð
du
u
sinh x ¼
u2 / 1
2u
cosh x ¼
u2 þ 1
2u
1 þ cos x
dx
sin x
sinh x þ 1
dx
cosh x
Beispiel
p=2
Ð
0
sin 4 x . cos x dx ¼ ?
Integraltyp (C):
Substitution:
Ð
½ f ðxÞ% n . f 0 ðxÞ dx
u ¼ sin x ;
mit
du
¼ cos x ;
dx
dx ¼
x ¼ 0
)
u ¼ sin 0 ¼ 0
Obere Grenze:
x ¼ p=2
)
u ¼ sin ðp=2Þ ¼ 1
p=2
ð
sin 4 x . cos x dx ¼
0
ð1
0
u 4 . cos x
und
n ¼ 4
du
cos x
Untere Grenze:
Integration:
f 0 ðxÞ ¼ cos x
f ðxÞ ¼ sin x ,
du
¼
cos x
ð1
u 4 du ¼
0
+
1 5
u
5
)1
0
¼
1
1
/0 ¼
5
5
Alternative: Die Integrationsgrenzen werden nicht mitsubstituiert, die Integration zunächst unbestimmt vorgenommen (Substitution u ¼ sin x wie oben). Dann wird rücksubstituiert und mit der gewonnenen Stammfunktion das bestimmte Integral berechnet (die Integrationskonstante darf weggelassen werden).
ð
ð
ð
du
1 5
1
sin 4 x . cos x dx ¼ u 4 . cos x
¼ u 4 du ¼
u þC ¼
ðsin xÞ 5 þ C
cos x
5
5
p=2
ð
0
sin 4 x . cos x dx ¼
i p=2
i
1 h
1 h
1
1
ðsin xÞ 5
ðsin p=2Þ 5 / ðsin 0 Þ 5 ¼
ð1 / 0Þ ¼
¼
0
5
5
5
5
|fflfflfflffl{zfflfflfflffl}
|ffl{zffl}
1
0
&
156
V Integralrechnung
3.2 Partielle Integration (Produktintegration)
Die Formel der partiellen Integration lautet:
ð
u ðxÞ . v 0 ðxÞ dx ¼ u ðxÞ . v ðxÞ /
ð
u 0 ðxÞ . vðxÞ dx
Ð
In vielen Fällen lässt sich ein (unbestimmtes) Integral f ðxÞ dx mit Hilfe dieser Formel
wie folgt lösen. Der Integrand f ðxÞ wird in „geeigneter“ Weise in ein Produkt aus zwei
Funktionen uðxÞ und v 0 ðxÞ zerlegt: f ðxÞ ¼ u ðxÞ . v 0 ðxÞ. Dabei ist v 0 ðxÞ die erste Ableitung einer zunächst noch unbekannten Funktion vðxÞ. Dann gilt nach obiger Formel:
ð
ð
uðxÞ . v 0 ðxÞ dx ¼ u ðxÞ . vðxÞ /
|fflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflffl}
ð
u 0 ðxÞ . vðxÞ dx
!
f ðxÞ dx ¼
|{z}
Zerlegung in ein Produkt
Die Integration gelingt, wenn sich eine Stammfunktion zum „kritischen“ Faktor v 0 ðxÞ angeben lässt und das neue „Hilfsintegral“ der rechten Seite elementar lösbar ist.
Anmerkungen
(1)
(2)
In einigen Fällen muss man mehrmals hintereinander partiell integrieren, ehe man auf
ein Grundintegral stößt.
Die Formel der partiellen Integration gilt sinngemäß auch für bestimmte Integrale:
ðb
0
vðxÞ% ba
u ðxÞ . v ðxÞ dx ¼ ½ u ðxÞ .
ðb
a
&
u 0 ðxÞ . vðxÞ dx
/
a
Beispiel
p=2
Ð
0
x . cos x dx ¼ ?
Zerlegung des Integranden f ðxÞ ¼ x . cos x in zwei Faktoren u ðxÞ und v 0 ðxÞ:
u ðxÞ ¼ x ;
v 0 ðxÞ ¼ cos x
)
u 0 ðxÞ ¼ 1 ;
v ðxÞ ¼ sin x
Partielle Integration (zunächst unbestimmt):
Ð
Ð
Ð
x . cos x dx ¼ x . sin x /
1 . sin x dx ¼ x . sin x / sin x dx ¼
|{z} |fflffl{zfflffl}
|{z} |fflffl{zfflffl}
|{z} |fflffl{zfflffl}
|fflfflfflfflffl{zfflfflfflfflffl}
u
v0
u
v
u0
v
Grundintegral
¼ x . sin x / ð/ cos xÞ þ C ¼ x . sin x þ cos x þ C
Berechnung des bestimmten Integrals ðC ¼ 0 gesetzt):
p=2
ð
p=2
x . cos x dx ¼ ½ x . sin x þ cos x % 0
0
¼
p
p
. sin ðp=2Þ þ cos ðp=2Þ / 0 / cos 0 ¼
/1
2 |fflfflfflfflffl{zfflfflfflfflffl} |fflfflfflfflfflffl{zfflfflfflfflfflffl}
2
|ffl{zffl}
1
0
1
&
3 Integrationsmethoden
157
3.3 Integration einer gebrochenrationalen Funktion
durch Partialbruchzerlegung des Integranden
Die Integration einer gebrochenrationalen Funktion f ðxÞ geschieht nach dem folgenden
Schema:
1. Ist die Funktion f ðxÞ unecht gebrochenrational, so wird sie zunächst durch Polynomdivision in eine ganzrationale Funktion p ðxÞ und eine echt gebrochenrationale Funktion
rðxÞ zerlegt (siehe III.5.3):
f ðxÞ ¼ pðxÞ þ r ðxÞ
Diese Zerlegung entfällt natürlich bei einer echt gebrochenrationalen Funktion f ðxÞ.
2. Der echt gebrochenrationale Anteil r ðxÞ wird in Partialbrüche zerlegt (siehe Partialbruchzerlegung, Abschnitt 3.3.1).
3. Anschließend erfolgt die Integration des ganzrationalen Anteils p ðxÞ sowie sämtlicher
Partialbrüche (siehe Abschnitt 3.3.2).
Die echt gebrochenrationale Funktion r ðxÞ ist dann als Summe sämtlicher Partialbrüche
darstellbar. Besitzt der Nenner N ðxÞ z. B. ausschließlich n verschiedene einfache Nullstellen x1 ; x2 ; . . . ; xn , so lautet die Partialbruchzerlegung wie folgt:
r ðxÞ ¼
Z ðxÞ
A1
A2
An
¼
þ
þ ... þ
N ðxÞ
x / x1
x / x2
x / xn
N ðxÞ, Z ðxÞ:
Nenner- bzw. Zählerpolynom der echt gebrochenrationalen Funktion r ðxÞ
A1 ; A2 ; . . . ; An : Reelle Konstanten (noch unbekannt)
3.3.1 Partialbruchzerlegung
Z ðxÞ
hängt
Die Partialbruchzerlegung einer echt gebrochenrationalen Funktion r ðxÞ ¼
N
ðxÞ
noch von der Art der Nennernullstellen ab. Wir unterscheiden zwei Fälle:
1. Fall: Der Nenner N (x) besitzt ausschließlich reelle Nullstellen
Jeder Nullstelle x1 des Nenners N ðxÞ wird nach dem folgenden Schema in eindeutiger
Weise ein Partialbruch zugeordnet:
x1 :
Einfache Nullstelle
!
A
x / x1
x1 :
..
.
Zweifache Nullstelle
!
A1
A2
þ
x / x1
ðx / x1 Þ 2
x1 :
r-fache Nullstelle
!
A1
A2
Ar
þ
þ ... þ
2
x / x1
ðx / x1 Þ
ðx / x1 Þ r
158
V Integralrechnung
Berechnung der in den Partialbrüchen auftretenden Konstanten:
Alle Brüche werden zunächst auf einen gemeinsamen Nenner gebracht (Hauptnenner) und
dann mit diesem Hauptnenner multipliziert. Durch Einsetzen bestimmter x-Werte (z. B. der
Nullstellen des Nenners) erhält man ein lineares Gleichungssystem, aus dem sich die noch
unbekannten Konstanten berechnen lassen. Eine weitere Methode zur Bestimmung der
Konstanten ist der Koeffizientenvergleich.
&
Beispiel
r ðxÞ ¼
Z ðxÞ
/ x 2 þ 2 x / 17
¼ 3
N ðxÞ
x / 7 x 2 þ 11 x / 5
Nullstellen des Nenners:
ðecht gebrochenrationale FunktionÞ
x 3 / 7 x 2 þ 11 x / 5 ¼ 0
)
x1=2 ¼ 1 ;
x3 ¼ 5
Zuordnung der Partialbrüche:
x1=2 ¼ 1 ðzweifache NullstelleÞ :
A1
A2
þ
x /1
ðx / 1Þ 2
x3 ¼ 5
B
x /5
ðeinfache NullstelleÞ :
Ansatz für die Partialbruchzerlegung:
x3
/ x 2 þ 2 x / 17
/ x 2 þ 2 x / 17
A1
A2
B
¼
¼
þ
þ
2
/ 7 x þ 11 x / 5
ðx / 1Þ 2 ðx / 5Þ
x /1
ðx / 1Þ 2
x /5
Berechnung der Konstanten A1 ; A2 und B (Hauptnenner bilden):
/ x 2 þ 2 x / 17
A1 ðx / 1Þ ðx / 5Þ þ A2 ðx / 5Þ þ B ðx / 1Þ 2
¼
2
ðx / 1Þ ðx / 5Þ
ðx / 1Þ 2 ðx / 5Þ
Zähler gleichsetzen:
/ x 2 þ 2 x / 17 ¼ A1 ðx / 1Þ ðx / 5Þ þ A2 ðx / 5Þ þ B ðx / 1Þ 2
Wir setzen für x zweckmäßigerweise der Reihe nach die Werte 1, 5 und 0 ein:
x ¼ 1
)
/ 16 ¼ / 4 A2
)
A2 ¼
x ¼ 5
)
/ 32 ¼ 16 B
)
B ¼ /2
x ¼ 0
)
/ 17 ¼ 5 A1 / 5 A2 þ B
)
/ 17 ¼ 5 A1 / 5 . 4 / 2
/ 17 ¼ 5 A1 / 22
)
4
5 A1 ¼ 5
)
)
A1 ¼ 1
Partialbruchzerlegung:
x3
/ x 2 þ 2 x / 17
A1
A2
B
1
4
2
¼
þ
þ
¼
þ
/
/ 7 x 2 þ 11 x / 5
x /1
x /5
x /1
ðx / 1Þ 2
x /5
ðx / 1Þ 2
&
2. Fall: Der Nenner N (x) besitzt neben reellen auch komplexe Nullstellen
Die komplexen Lösungen der Gleichung N ðxÞ ¼ 0 treten immer paarweise, d. h. in konjugiert komplexer Form auf. Für zwei einfache konjugiert komplexe Nennernullstellen x1
und x2 lautet der Partialbruchansatz wie folgt:
Bx þ C
Bx þ C
¼ 2
ðx / x1 Þ ðx / x2 Þ
x þ px þ q
3 Integrationsmethoden
159
Dabei sind x1 und x2 die konjugiert komplexen Lösungen der quadratischen Gleichung
x 2 þ p x þ q ¼ 0: Entsprechend lautet der Ansatz für mehrfache konjugiert komplexe
Nullstellen:
B1 x þ C1
B2 x þ C2
Br x þ Cr
þ 2
þ ... þ 2
x2 þ px þ q
ðx þ p x þ qÞ 2
ðx þ p x þ qÞ r
(der Nenner N ðxÞ besitzt die jeweils r-fach auftretenden konjugiert komplexen Nullstellen
x1 und x2 ; Sie sind die Lösungen der quadratischen Gleichung x 2 þ p x þ q ¼ 0Þ:
Die Berechnung der Konstanten erfolgt wie im 1. Fall.
&
Beispiel
r ðxÞ ¼
Z ðxÞ
3 x 2 / 11 x þ 15
¼ 3
N ðxÞ
x / 4 x 2 þ 9 x / 10
Nullstellen des Nenners:
ðecht gebrochenrationale FunktionÞ
N ðxÞ ¼ x 3 / 4 x 2 þ 9 x / 10 ¼ 0
)
x1 ¼ 2 ;
x2=3 ¼ 1 + 2 j
Zuordnung der Partialbrüche:
x1 ¼ 2 ðreell; einfachÞ :
A
x /2
x2=3 ¼ 1 + 2 j ðkonjugiert komplex; einfachÞ :
Bx þ C
x2 / 2x þ 5
Hinweis: x2=3 ¼ 1 + 2 j sind die konjugiert komplexen Lösungen der quadratischen Gleichung
x 2 / 2 x þ 5 ¼ 0, die man durch Reduzieren der kubischen Gleichung erhält:
N ðxÞ ¼ x 3 / 4 x 2 þ 9 x / 10 ¼ ðx / 2Þ ðx 2 / 2 x þ 5Þ ¼ 0
Ansatz für die Partialbruchzerlegung:
x3
3 x 2 / 11 x þ 15
3 x 2 / 11 x þ 15
A
Bx þ C
¼
¼
þ 2
2
/ 4 x þ 9 x / 10
ðx / 2Þ ðx 2 / 2 x þ 5Þ
x /2
x / 2x þ 5
Berechnung der Konstanten A; B und C (Brüche auf den Hauptnenner bringen):
3 x 2 / 11 x þ 15
A ðx 2 / 2 x þ 5Þ þ ðB x þ CÞ ðx / 2Þ
¼
ðx / 2Þ ðx 2 / 2 x þ 5Þ
ðx / 2Þ ðx 2 / 2 x þ 5Þ
Zähler gleichsetzen:
3 x 2 / 11 x þ 15 ¼ A ðx 2 / 2 x þ 5Þ þ ðB x þ CÞ ðx / 2Þ
Wir setzen für x zweckmäßigerweise der Reihe nach die Werte 2, 1 und 0 ein:
x ¼ 2
)
x ¼ 1
)
x ¼ 0
)
5 ¼ 5A
7 ¼ 4A / B / C
15 ¼ 5 A / 2 C
)
A ¼ 1
)
B ¼ 2;
)
C ¼ /5
Partialbruchzerlegung:
r ðxÞ ¼
x3
3 x 2 / 11 x þ 15
A
Bx þ C
1
2x / 5
¼
þ 2
¼
þ 2
/ 4 x 2 þ 9 x / 10
x /2
x / 2x þ 5
x /2
x / 2x þ 5
&
160
V Integralrechnung
3.3.2 Integration der Partialbrüche
Bei der Integration der Partialbrüche treten insgesamt vier verschiedene Integraltypen auf.
Bei reellen Nullstellen des Nenners N (x)
ð
ð
>
>
>
ðr ( 2Þ >
;
dx
1
¼
þ C2
r
ðx / x1 Þ
ð1 / rÞ ðx / x1 Þ r / 1
Beispiel
ð
/ x 2 þ 2 x / 17
dx ¼ ?
3
x / 7 x 2 þ 11 x / 5
&
9
>
>
>
>
=
dx
¼ ln j x / x1 j þ C1
x / x1
jeweils gelost
€ durch
die Substitution
u ¼ x / x1 ;
du ¼ dx
ðder Integrand ist eine echt gebrochenrationale FunktionÞ
Partialbruchzerlegung des Integranden (siehe 1. Beispiel aus Abschnitt 3.3.1):
/ x 2 þ 2 x / 17
1
4
2
¼
þ
/
x 3 / 7 x 2 þ 11 x / 5
x /1
ðx / 1Þ 2
x /5
Integration der Partialbrüche:
ð
ð
ð
ð
/ x 2 þ 2 x / 17
dx
dx
dx
dx ¼
þ4.
/2.
¼
3
2
2
x / 7 x þ 11 x / 5
x /1
ðx / 1Þ
x /5
ð
ð
ð
du
du
dv
4
þ4.
¼ ln j u j /
/ 2 . ln j v j þ C ¼
¼
/2.
2
u
u
v
u
¼ ln j x / 1 j /
(die Substitutionen u ¼ x / 1,
du ¼ dx
4
/ 2 . ln j x / 5 j þ C
x /1
bzw.
v ¼ x / 5,
dv ¼ dx wurden grau unterlegt)
&
Bei konjugiert komplexen Nullstellen des Nenners N (x)
Im Falle einfacher konjugiert komplexer Nullstellen:
ð
Bx þ C
B
dx ¼
. ln j x 2 þ p x þ q j þ
x2 þ px þ q
2
0
1
0
1
B 2C / Bp C
B 2x þ p C
þ @qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi A . arctan @qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi A þ C3
4q / p2
4q / p2
Die bei mehrfachen konjugiert komplexen Nullstellen des Nenners auftretenden Integrale vom
ð
ð
dx
x dx
Typ
bzw.
mit r ( 2 entnimmt man der
2
r
2
ðx þ p x þ qÞ
ðx þ p x þ qÞ r
Integraltafel im Anhang, Teil A (falls p ¼
6 0 ! Integrale 63 bis 70; falls p ¼ 0 !
Integrale 29 bis 34).
3 Integrationsmethoden
161
3.4 Integration durch Potenzreihenentwicklung des Integranden
Der Integrand f ðxÞ des bestimmten oder unbestimmten Integrals wird in eine Potenzreihe
entwickelt und anschließend gliedweise integriert ( Voraussetzung: Der Integrationsbereich
liegt innerhalb des Konvergenzbereiches der Reihe).
&
Beispiel
Ð1
0
cos
1pffiffiffi 0
x dx ¼ ?
Potenzreihe (Mac Laurinsche Reihe) für cos z (siehe VI.3.4):
cos z ¼ 1 /
z2
z4
z6
þ
/
þ / ...
2!
4!
6!
Substitution z ¼
cos
ðj z j < 1Þ
pffiffiffi
x:
1pffiffiffi 0
x
x2
x3
x ¼ 1/
þ
/
þ / ...
2!
4!
6!
ðx ( 0Þ
Gliedweise Integration:
ð1
cos
0
2
+
)1
ð1 3
1pffiffiffi 0
x
x2
x3
x2
x3
x4
x dx ¼
þ
/
þ / . . . dx ¼ x /
þ
/
þ / ... ¼
1/
2!
4!
6!
2 . 2!
3 . 4!
4 . 6!
0
0
¼ 1/
1
1
1
þ
/
þ / . . . ' 0;763
2 . 2!
3 . 4!
4 . 6!
ðauf drei Nachkommastellen genauÞ
&
3.5 Numerische Integration
3.5.1 Trapezformel
Die Fläche unter der Kurve y ¼ f ðxÞ wird zunächst in n Streifen gleicher Breite h
zerlegt, dann wird in jedem Streifen die krummlinige Begrenzung durch die Sekante ersetzt
(der „Ersatzstreifen“ besitzt die Form eines Trapezes, im Bild grau unterlegt):
y
y = f(x)
P0
P1
y0
y1
Pn–1
Pn–2
Pn
P2
y2
h
h
x0 = a x1
x2
yn–2
h
xn–2
yn–1
yn
h
xn–1 xn= b
x
Die nachfolgende Trapezformel gilt unabhängig von dieser geometrischen Deutung (sofern
das Integral existiert).
162
V Integralrechnung
3
ðb
f ðxÞ dx '
a
1
1
y0 þ y1 þ y2 þ . . . þ yn / 1 þ
yn
2
2
3
¼
2
1
ð y0 þ yn Þ þ ð y1 þ y2 þ . . . þ yn / 1 Þ
2 |fflfflfflfflfflffl{zfflfflfflfflfflffl} |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
S1
S2
h ¼
2
3
h ¼
1
. S1 þ S2
2
2
h
Streifenbreite (Schrittweite): h ¼ ðb / aÞ=n
Stützstellen: x k ¼ a þ k . h o
k ¼ 0; 1; 2; . . . ; n
Stützwerte:
yk ¼ f ðx k Þ
3.5.2 Simpsonsche Formel
Die Fläche unter der Kurve y ¼ f ðxÞ wird in 2 n, d. h. in eine gerade Anzahl „einfacher“
Streifen gleicher Breite h zerlegt. In jedem der insgesamt n „Doppelstreifen“ (er besteht
aus zwei aufeinanderfolgenden „einfachen“ Streifen, die im Bild grau unterlegt sind) ersetzt man dann die krummlinige Begrenzung durch eine Parabel:
y
y = f(x)
P0
y1
h
x0 = a
y2
h
x1
P2n–1
P2n
P2
P1
y0
P2n–2
y2n–2 y2n–1 y2n
h
x2
h
x2n–2 x2n–1 x2n = b
x
ðb
f ðxÞ dx ' ð y0 þ 4 y1 þ 2 y2 þ 4 y3 þ . . . þ 2 y2 n / 2 þ 4 y2 n / 1 þ y 2 n Þ
a
h
¼
3
3
2
h
¼ ð y0 þ y2 n Þ þ 4 ð y1 þ y3 þ . . . þ y2 n / 1 Þ þ 2 ð y2 þ y4 þ . . . þ y2 n / 2 Þ
¼
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} 3
S0
S1
S2
3
2
h
¼ S0 þ 4 . S1 þ 2 . S2
3
Breite eines einfachen Streifens (Schrittweite): h ¼ ðb / aÞ=2 n
Stützstellen: x k ¼ a þ k . h o
k ¼ 0; 1; 2; . . . ; 2 n
Stützwerte:
yk ¼ f ðx k Þ
3 Integrationsmethoden
163
Beim Simpsonverfahren muss die Anzahl der Stützpunkte Pk ¼ ðxk ; yk Þ ungerade sein
(2 n þ 1 Stützpunkte; 2 n einfache und somit n Doppelstreifen). Die Simpsonsche Formel gilt unabhängig von der geometrischen Deutung (sofern das Integral existiert).
Fehlerabschätzung
Voraussetzung: 2 n ist durch 4 teilbar (und n damit gerade)
1
ðIh / I2 h Þ
15
DI '
Ih :
Näherungswert bei der Streifenbreite h
I2 h : Näherungswert bei doppelter Streifenbreite 2 h
Gegenüber Ih verbesserter Wert:
Iv ¼ Ih þ DI
&
Beispiel
Ð1
0
2
e / x dx ¼ ?
(Fläche unter der Gaußkurve im Intervall 0 ) x ) 1)
Wir wählen 2 n ¼ 4 und somit h ¼ 0;25.
k
xk
Zweitrechnung ðh* ¼ 2 h ¼ 0;5Þ
Erstrechnung ðh ¼ 0;25Þ
2
2
yk ¼ e / x k
0
1
2
3
4
0
0,25
0,5
0,75
1
yk ¼ e / x k
1
1
0,939 413
0,778 801
0,778 801
0,569 783
0,367 879
0,367 879
1,367 879
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
S0
Ih ¼ ðS0 þ 4 . S1 þ 2 . S2 Þ
1,509 196
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
S1
0,778 801
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
S2
1,367 879
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
S *0
0,778 801
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
S *1
0
|fflfflfflfflffl{zfflfflfflfflffl}
S *2
h
0;25
¼ ð1;367 879 þ 4 . 1;509 196 þ 2 . 0;778 801Þ
¼ 0;746 855
3
3
h*
0;5
I 2 h ¼ I * ¼ ðS *0 þ 4 . S *1 þ 2 . S *2 Þ
¼ ð1;367 879 þ 4 . 0;778 801 þ 2 . 0Þ
¼ 0;747 181
h
3
3
Fehlerabschätzung:
DI ¼
Verbesserter Integralwert:
1
1
ðIh / I2 h Þ ¼
ð0,746 855 / 0,747 181Þ ¼ / 0,000 022
15
15
Ð1
0
2
e / x dx ' Iv ¼ Ih þ DI ¼ 0,746 855 / 0,000 022 ¼ 0;746 833
&
164
V Integralrechnung
3.5.3 Romberg-Verfahren
Romberg-Schema
Nach bestimmten (weiter unten beschriebenen) Rechenvorschriften werden für das gesuchte
Ðb
bestimmte Integral f ðxÞ dx zunächst Folgen von Näherungswerten Ti; k berechnet und
a
wie folgt im sog. Romberg-Schema angeordnet:
T0; 1 /
/!
T1; 2/
T1; 1
/!
T2; 2
T2; 3/
T2; 1
/!
T3; 4/
T3; 2
T3; 3
T3; 1
..
..
.. ///
..
.
.
.
.
!
TN; 1
TN; 2
TN; 3
1. Index:
Zeilenindex
2. Index:
Spaltenindex
TN; N þ 1
TN; 4
Dann gilt näherungsweise:
ða
f ðxÞ dx ¼ TN; N þ 1
b
Anmerkungen
(1)
(2)
Jede der Spalten konvergiert für N ! 1 gegen den gesuchten Integralwert, ebenso
die durch Pfeile gekennzeichnete Diagonalfolge.
Die Rechnung ist abzubrechen, wenn sich zwei benachbarte Elemente einer Spalte
innerhalb der gewünschten Stellenzahl nicht mehr voneinander unterscheiden.
Berechnung der Elemente T i, 1 aus Spalte 1 (i = 0, 1, . . . , N)
Das Integrationsintervall a ) x ) b wird der Reihe nach in 1; 2; 4; 8; . . . ; 2 N Teilintervalle gleicher Länge zerlegt (Prinzip der fortlaufenden Halbierung der Schrittweite).
Mit der Trapezformel aus Abschnitt 3.5.1 werden dann für diese Zerlegungen NäheÐb
rungswerte Ti; 1 für das Integral f ðxÞ dx berechnet, die die Elemente der 1. Spalte bila
den (grau unterlegt). Der Zeilenindex i kennzeichnet dabei die Anzahl der Teilintervalle
(2 i Teilintervalle).
3 Integrationsmethoden
165
Die Berechnungsformeln lauten:
b/a
½ f ðaÞ þ f ðbÞ%
2
+
3
2)
1
b/a
¼
T0; 1 þ ðb / aÞ . f a þ
2
2
+
( 3
2
3
2')
1
b/a
b/a
3 ðb / aÞ
¼
T1; 1 þ
f aþ
þf aþ
2
2
4
4
T0; 1 ¼
T1; 1
T2; 1
..
.
Ti; 1
2
1 4
b/a
Ti / 1; 1 þ ði / 1Þ .
¼
2
2
P
2 ð i / 1Þ
j¼1
3
2
ð2 j / 1Þ ðb / aÞ 5
f aþ
2i
3
ði ¼ 1; 2; . . . ; NÞ
Aus diesen Elementen lassen sich alle übrigen Elemente berechnen.
Berechnung der Elemente T i, 2 aus Spalte 2 (i = 1, 2, . . . , N)
Die Berechnung dieser Elemente erfolgt aus den Elementen der 1. Spalte nach der Formel
Ti; 2 ¼
4 . Ti; 1 / Ti / 1; 1
3
ði ¼ 1; 2; . . . ; NÞ
Berechnung der Elemente T i, 3 aus Spalte 3 (i = 2, 3, . . . , N)
Die Berechnung dieser Elemente erfolgt aus den Elementen der 2. Spalte nach der Formel
Ti; 3 ¼
16 . Ti; 2 / Ti / 1; 2
15
ði ¼ 2; 3; . . . ; NÞ
Berechnung der Elemente T i, k aus Spalte k (k = 2, 3, . . . , N + 1; i = k – 1, k, . . . , N)
Die Berechnung dieser Elemente erfolgt aus den Elementen der ðk / 1Þ-ten Spalte nach
der Formel
Ti; k ¼
4 ðk / 1Þ . Ti; k / 1 / Ti / 1; k / 1
4 ð k / 1Þ / 1
ðk ¼ 2; 3; . . . ; N þ 1; i ¼ k / 1; k; . . . ; NÞ
(allgemeine Romberg-Formel).
&
Beispiel
Wir berechnen das Integral
Ð1
0
2
e / x dx für N ¼ 3, d. h. für Zerlegungen in 1, 2, 4 und 8 Teilintervalle.
166
V Integralrechnung
Mit a ¼ 0, b ¼ 1 und f ðxÞ ¼ e / x
2
erhalten wir:
Berechnung der Elemente Ti; 1 ði ¼ 0; 1; 2; 3Þ
T0; 1 ¼
1
1
½ f ð0Þ þ f ð1Þ% ¼
ðe 0 þ e / 1 Þ ¼ 0;683 940
2
2
1
1
½ T0; 1 þ f ð0;5Þ% ¼
ð0;683 940 þ e / 0;25 Þ ¼ 0;731 370
2
2
+
)
+
)
1
1
1
1
T1; 1 þ f f ð0;25Þ þ f ð0;75Þg ¼
0;731 370 þ ðe / 0;0625 þ e / 0;5625 Þ ¼ 0;742 984
¼
2
2
2
2
+
)
1
1
¼
T2; 1 þ
f f ð0;125Þ þ f ð0;375Þ þ f ð0;625Þ þ f ð0;875Þg ¼
2
4
+
)
1
1
¼
0;742 984 þ ðe / 0;015 625 þ e / 0;140 625 þ e / 0;390 625 þ e / 0;765 625 Þ ¼ 0;745 866
2
4
T1; 1 ¼
T2; 1
T3; 1
Berechnung der Elemente Ti; 2 ði ¼ 1; 2; 3Þ
T1; 2 ¼
4 . T1; 1 / T0; 1
4 . 0;731 370 / 0;683 940
¼
¼ 0;747 180
3
3
T2; 2 ¼
4 . T2; 1 / T1; 1
4 . 0;742 984 / 0;731 370
¼
¼ 0;746 855
3
3
T3; 2 ¼
4 . T3; 1 / T2; 1
4 . 0;745 866 / 0;742 984
¼
¼ 0;746 827
3
3
Berechnung der Elemente Ti; 3 ði ¼ 2; 3Þ
T2; 3 ¼
16 . T2; 2 / T1; 2
16 . 0;746 855 / 0;747 180
¼
¼ 0;746 833
15
15
T3; 3 ¼
16 . T3; 2 / T2; 2
16 . 0;746 827 / 0;746 855
¼
¼ 0;746 825
15
15
Berechnung des Elementes T3; 4
T3; 4 ¼
64 . T3; 3 / T2; 3
64 . 0;746 825 / 0;746 833
¼
¼ 0;746 825
63
63
Romberg-Schema
k
i
Ð1
0
1
2
3
4
///
/!
0
0,683 940
1
0,731 370
2
0,742 984
0,746 855
3
0,745 866
0,746 827
0,747 180/
///
!
0,746 833
///
/!
0,746 825
0,746 825
2
e / x dx ' T3;4 ¼ 0;746 825
Exakter Wert (auf 6 Dezimalstellen nach dem Komma genau):
0,746 824
&
4 Uneigentliche Integrale
167
4 Uneigentliche Integrale
Uneigentliche Integrale werden durch Grenzwerte erklärt. Ist der jeweilige Grenzwert vorhanden, so heißt das uneigentliche Integral konvergent, sonst divergent.
4.1 Unendliches Integrationsintervall
Die Integration erfolgt über ein unendliches
Intervall. Man setzt (falls der Grenzwert vorhanden ist; l > a):
1
ð
y
y = f(x)
ðl
f ðxÞ dx ¼ lim
l!1
a
f ðxÞ dx
a
ða
x
l
a
ða
f ðxÞ dx ¼
/1
lim
l!/1
1
ð
f ðxÞ dx ¼
/1
f ðxÞ dx
lim
l!/1
ðl < aÞ
l
ðc
ðm
f ðxÞ dx
f ðxÞ dx þ lim
m!1
l
c
(Integral aufspalten; beide Grenzwerte müssen existieren; c: beliebige Stelle)
Beispiel
1
Ð /x
e dx ¼ ?
&
0
Integration von 0 bis l ðl > 0Þ:
Grenzübergang l ! 1:
I ðlÞ ¼
Ðl
0
lim I ðlÞ ¼ lim
l!1
e / x dx ¼ ½ / e / x % l0 ¼ / e / l þ e 0 ¼ 1 / e / l
Ðl
l!1 0
e / x dx ¼ lim ð1 / e / l Þ ¼ 1 / 0 ¼ 1
l!1
Das uneigentliche Integral ist somit konvergent und besitzt den Wert 1.
&
4.2 Integrand mit einer Unendlichkeitsstelle (Pol)
Der Integrand f ðxÞ besitzt an der oberen Integrationsgrenze x ¼ b einen Pol. Man setzt
(falls der Grenzwert vorhanden ist; l > 0):
ðb
y = f(x)
bð
/l
f ðxÞ dx ¼ lim
a
y
l!0
f ðxÞ dx
a
a
b–l
b
x
168
V Integralrechnung
Pol an der unteren Integrationsgrenze x ¼ a:
Ðb
Ðb
f ðxÞ dx ¼ lim
f ðxÞ dx
ðmit l > 0Þ
l!0 aþl
a
Pol im Innern des Integrationsintervalls (Stelle x ¼ c mit a < c < b):
Ðb
a
f ðxÞ dx ¼ lim
l!0
c Ð/ l
a
f ðxÞ dx þ lim
Ðb
m!0 cþm
f ðxÞ dx
(Integral aufspalten; beide Grenzwerte müssen existieren; x ¼ c:
m > 0)
&
Polstelle; l > 0,
Beispiel
ð1
0
dx
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ ?
1 / x2
ðPol an der oberen Grenze x ¼ 1, der Nenner des Integranden verschwindet
an dieser StelleÞ
Integration von x ¼ 0 bis x ¼ 1 / l ðl > 0Þ:
1ð
/l
I ðlÞ ¼
0
dx
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ ½ arcsin x% 10 / l ¼ arcsin ð1 / lÞ / arcsin 0 ¼ arcsin ð1 / lÞ
|fflfflfflffl{zfflfflfflffl}
1 / x2
0
1ð
/l
Grenzübergang l ! 0:
lim I ðlÞ ¼ lim
l!0
l!0
0
dx
p
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ lim ð arcsin ð1 / lÞÞ ¼ arcsin 1 ¼
l!0
2
2
1/x
Das uneigentliche Integral ist somit konvergent und hat den Wert p=2.
&
5 Anwendungen der Integralrechnung
5.1 Integration der Bewegungsgleichung
Aus der Beschleunigungs-Zeit-Funktion a ¼ a ðtÞ einer geradlinigen Bewegung erhält
man durch ein- bzw. zweimalige Integration bezüglich der Zeitvariablen t den zeitlichen
Verlauf von Geschwindigkeit v und Weg s:
v ¼ vðtÞ ¼
Ð
a ðtÞ dt
s ¼ sðtÞ ¼
Ð
vðtÞ dt
Die Integrationskonstanten werden i. Allg. durch Anfangswerte festgelegt:
s ð0Þ ¼ s0 :
Anfangsweg (Wegmarke zur Zeit t ¼ 0)
vð0Þ ¼ v0 :
Anfangsgeschwindigkeit (Geschwindigkeit zur Zeit t ¼ 0Þ
5 Anwendungen der Integralrechnung
169
5.2 Arbeit einer ortsabhängigen Kraft (Arbeitsintegral)
~¼ F
~ðsÞ geradlinig von s1
Ein Massenpunkt m wird durch eine ortsabhängige Kraft F
nach s2 verschoben. Die dabei verrichtete Arbeit beträgt:
ðs2
W ¼
~ . d~
F
s ¼
s1
F
ðs2
Fs ðsÞ ds
s1
m
FS(s)
s1
s
s2
ds
Fs ðsÞ: Skalare ortsabhängige Kraftkomponente in Richtung des Weges
s: Ortskoordinate (Wegmarke);
ds: Wegelement
5.3 Lineare und quadratische Mittelwerte einer Funktion
5.3.1 Linearer Mittelwert
y!linear
1
¼
.
b/a
ðb
f ðxÞ dx
a
Geometrische Deutung: Die Fläche unter der
Kurve y ¼ f ðxÞ im Intervall a ) x ) b
entspricht dem Flächeninhalt eines Rechtecks
mit den Seitenlängen b / a und y!linear
(Voraussetzung: Die Kurve verläuft oberhalb
der x-Achse). Allgemein ist der lineare
Mittelwert eine Art mittlere Ordinate der
Kurve y ¼ f ðxÞ im Intervall a ) x ) b.
y
y = f(x)
ylinear
b
a
x
5.3.2 Quadratischer Mittelwert
y!quadratisch
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u
ðb
u
u 1
. ½ f ðxÞ% 2 dx
¼ t
b/a
a
5.3.3 Zeitliche Mittelwerte einer periodischen Funktion
y ¼ f ðtÞ ist eine zeitabhängige periodische Funktion mit der Periode T.
y!linear
ðTÞ:
1
¼
.
T
ð
f ðtÞ dt
ðTÞ
y!quadratisch
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
u1 ð
u
2
¼ t .
½ f ðtÞ% dt
T
ðTÞ
Integration über eine Periode T
Hinweis: Bei Wechselströmen und Wechselspannungen werden die quadratischen Mittelwerte als Effektivwerte (von Strom bzw. Spannung) bezeichnet.
170
V Integralrechnung
5.4 Flächeninhalt
In kartesischen Koordinaten
y
ðb
A ¼
y0 = f0(x)
ð yo / yu Þ dx
A
a
yo ¼ fo ðxÞ:
yu ¼ fu ðxÞ:
Obere Randkurve
Untere Randkurve
yu = fu(x)
a
b
x
Hinweis: Die Integralformel gilt nur unter der Voraussetzung, dass sich die beiden Randkurven im Intervall a ) x ) b nicht durchschneiden ð yo ( yu Þ. Anderenfalls muss die
Fläche (z. B. anhand einer Skizze) so in Teilflächen zerlegt werden, dass die Formel für
jeden Teilbereich anwendbar ist.
y
Sonderfall: yu ¼ fu ðxÞ ¼ 0 (x-Achse)
ðb
A ¼
y = f(x)
ðb
y dx ¼
a
f ðxÞ dx
A
a
y ¼ f ðxÞ:
In der Parameterform
b
a
Obere Randkurve
y
t2
ð
y x_ dt
t1
A
t1
x ¼ x ðtÞ
y ¼ y ðtÞ
x_ ¼
dx
dt
x = x(t)
y = y(t)
t2
A ¼
x
'
Parametergleichungen
der oberen Randkurve
x(t1)
x(t2)
x
5 Anwendungen der Integralrechnung
Leibnizsche Sektorformel
171
y
t1
" t2
"
"ð
"
"
"
1 "
. " ðx y_ / y x_ Þ dt ""
A ¼
2 "
"
x = x(t), y = y(t)
t2
A
t1
x ¼ x ðtÞ
'
y ¼ y ðtÞ
x_ ¼
dx
;
dt
x
Parametergleichungen
der oberen Randkurve
y_ ¼
dy
dt
In Polarkoordinaten
A ¼
1
.
2
y
j2
ð
r 2 dj
r = r( f)
f = f2
j1
r ¼ r ðjÞ:
A
Randkurve in Polarkoordinaten
f = f1
x
5.5 Schwerpunkt einer homogenen ebenen Fläche
1
xS ¼
.
A
ðb
x ð yo / yu Þ dx
a
yo ¼ fo ðxÞ:
Obere Randkurve
yu ¼ fu ðxÞ:
Untere Randkurve
A:
a
ð yo2
/
a
y0 = f0(x)
Multipliziert man die Formeln mit der Fläche
A, so erhält man die statischen Momente
Mx und My der Fläche bezogen auf die xbzw. y-Achse:
ðb
ð y 2o / y 2u Þ dx
y
Flächeninhalt (siehe Abschnitt 5.4)
1
Mx ¼ A . ys ¼
.
2
ðb
1
yS ¼
.
2A
yu2
S
yS
yu = fu(x)
a
xS
b
x
ðb
Þ dx
My ¼ A . xs ¼
x ð yo / yu Þ dx
a
172
V Integralrechnung
Teilschwerpunktsatz
Der Schwerpunkt S der Fläche A liegt auf der Verbindungslinie der beiden Teilflächenschwerpunkte S1 und S2 :
A xS ¼ A1 xS1 þ A2 xS2
y
A yS ¼ A1 yS1 þ A2 yS2
A ¼ A1 þ A2 :
A1 ; A2 :
S ¼ ðxS ; yS Þ:
S1 ¼ ðxS1 ; yS1 Þ:
S2 ¼ ðxS2 ; yS2 Þ:
S
Fläche
Teilflächen von A
Schwerpunkt der Fläche A
Schwerpunkt der Teilfläche A1
Schwerpunkt der Teilfläche A2
S2
A2
S1
A1
x
5.6 Flächenträgheitsmomente (Flächenmomente 2. Grades)
Ix ; Iy :
Axiale oder äquatoriale Flächenmomente 2. Grades bezüglich der x- bzw. y-Achse
Ip :
Polares Flächenmoment 2. Grades bezüglich des Nullpunktes
Ix ¼
1
.
3
ðb
Iy ¼
ðb
ð yo3 / yu3 Þ dx
y
y0 = f0(x)
a
x 2 ð yo / yu Þ dx
a
yu = fu(x)
Ip ¼ Ix þ Iy
yo ¼ fo ðxÞ:
Obere Randkurve
yu ¼ fu ðxÞ:
Untere Randkurve
a
b
Satz von Steiner
Schwerpunktachse
I ¼ IS þ A d 2
I:
Flächenmoment bezüglich der gewählten
Bezugsachse
IS :
Flächenmoment bezüglich der zur Bezugsachse parallelen Schwerpunktachse
A:
Fläche
d:
Abstand zwischen Bezugs- und Schwerpunktachse
x
A
S
Bezugsachse
d
5 Anwendungen der Integralrechnung
173
5.7 Bogenlänge einer ebenen Kurve
In kartesischen Koordinaten
ðb qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 þ ð y 0 Þ 2 dx
s ¼
y
a
y ¼ f ðxÞ:
y0 ¼
Q
s
P
y = f(x)
Gleichung der Kurve
dy
¼ f 0 ðxÞ
dx
a
x
b
In der Parameterform
ðt2 qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx_ Þ 2 þ ðy_Þ 2 dt
s ¼
y
t1
t2
s
y = y(t)
t1
x ¼ x ðtÞ
'
Parametergleichungen
y ¼ y ðtÞ
x_ ¼
dx
;
dt
x = x(t)
der Kurve
y_ ¼
x
x(t2)
x(t1)
dy
dt
In Polarkoordinaten
j2
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s ¼
r 2 þ ðr_Þ 2 dj
y
s
f = f2
r = r ( f)
j1
r ¼ r ðjÞ:
r_ ¼
Kurve in Polarkoordinaten
f = f1
dr
dj
x
5.8 Volumen eines Rotationskörpers (Rotationsvolumen)
In kartesischen Koordinaten
y
y = f(x)
Rotation um die x-Achse
ðb
Vx ¼ p .
y 2 dx
a
y ¼ f ðxÞ:
Rotierende Kurve
a
b
x
174
V Integralrechnung
Rotation um die y-Achse
y
ðd
x 2 dy
Vy ¼ p .
d
c
x ¼ gð yÞ:
Rotierende Kurve (in der nach
x aufgelösten Form)
x = g(y)
c
x
In der Parameterform
Rotation um die x-Achse
ðt2
Vx ¼ p .
y
y 2 x_ dt
t1
t2
x = x(t)
y = y(t)
t1
x ¼ x ðtÞ
'
y ¼ y ðtÞ
x_ ¼
x
Parametergleichungen
der rotierenden Kurve
dx
dt
Rotation um die y-Achse
ðt2
Vy ¼ p .
y
x 2 y_ dt
t2
t1
x ¼ x ðtÞ
y ¼ y ðtÞ
y_ ¼
dy
dt
'
Parametergleichungen
x = x(t)
y = y(t)
der rotierenden Kurve
t1
x
5 Anwendungen der Integralrechnung
175
5.9 Mantelfläche eines Rotationskörpers (Rotationsfläche)
Rotation um die x-Achse
ðb
Mx ¼ 2 p .
y
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y 1 þ ð y 0 Þ 2 dx
y = f(x)
a
y ¼ f ðxÞ:
y0 ¼
a
Rotierende Kurve
x
b
dy
¼ f 0 ðxÞ
dx
Rotation um die y-Achse
ðd
My ¼ 2 p .
y
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 þ ðx 0 Þ 2 dy
d
c
x ¼ gð yÞ:
x0 ¼
Rotierende Kurve (in der nach
x aufgelösten Form)
x = g(y)
dx
¼ g 0 ð yÞ
dy
c
x
5.10 Schwerpunkt eines homogenen Rotationskörpers
Rotation um die x-Achse
p
xS ¼
.
Vx
yS ¼ 0 ;
y ¼ f ðxÞ:
Vx :
ðb
y
y = f(x)
x y 2 dx
a
zS ¼ 0
Rotierende Kurve
Rotationsvolumen (siehe Abschnitt 5.8)
a
S
xS
b
x
176
V Integralrechnung
Rotation um die y-Achse
yS ¼
p
.
Vy
xS ¼ 0 ;
y
y x 2 dy
d
c
zS ¼ 0
x ¼ gð yÞ:
Vy :
ðd
yS S
Rotierende Kurve (in der nach
x aufgelösten Form)
x = g(y)
c
Rotationsvolumen (siehe Abschnitt 5.8)
x
5.11 Massenträgheitsmoment eines homogenen Körpers
Allgemeine Definition
ð
J ¼
r 2 dm ¼ r .
ðmÞ
ð
r 2 dV
ðVÞ
'
dm:
Massenelement
dV :
Volumenelement
r:
Senkrechter Abstand des Massenbzw. Volumenelementes von der gewählten Bezugsachse
r:
Bezugsachse
dm ¼ r dV
dm
r
Körper der Masse m = rV
Konstante Dichte des homogenen Körpers
Hinweis: Siehe hierzu auch IX.3.2.5.3
(Dreifachintegral)
Satz von Steiner
J ¼ JS þ m d 2
J:
Massenträgheitsmoment bezüglich der
gewählten Bezugsachse
JS :
Massenträgheitsmoment bezüglich der
zur Bezugsachse parallelen Schwerpunktachse
m:
Masse des homogenen Körpers
d:
Abstand zwischen Bezugs- und Schwerpunktachse
Schwerpunktachse
Bezugsachse
S
Körper der
Masse m
d
5 Anwendungen der Integralrechnung
177
Massenträgheitsmoment eines Rotationskörpers
Rotation um die x-Achse ð¼ BezugsachseÞ
1
Jx ¼ p r .
2
ðb
y
y = f(x)
y 4 dx
a
y ¼ f ðxÞ: Rotierende Kurve
r: Konstante Dichte des homogenen
Rotationskörpers
a
b
Rotation um die y-Achse ð¼ BezugsachseÞ
Jy ¼
1
pr .
2
ðd
y
x 4 dy
c
x ¼ gð yÞ:
r:
Rotierende Kurve (in der nach
x aufgelösten Form)
Konstante Dichte des homogenen
Rotationskörpers
d
x = g(y)
c
x
x
178
VI Unendliche Reihen, Taylorund Fourier-Reihen
1 Unendliche Reihen
1.1 Grundbegriffe
1.1.1 Definition einer unendlichen Reihe
Aus den Gliedern einer unendlichen Zahlenfolge han i ¼ a1 ; a2 ; a3 ; . . . ; an ; . . . werden
wie folgt Partial- oder Teilsummen sn gebildet:
sn ¼ a1 þ a2 þ a3 þ . . . þ an ¼
n
P
k¼1
ak
(n-te Partialsumme)
Die Folge hsn i dieser Partialsummen heißt „Unendliche Reihe“. Symbolische Schreibweise:
1
P
n¼1
an ¼ a1 þ a2 þ a3 þ . . . þ an þ . . .
Bildungsgesetz einer unendlichen Reihe: an ¼ f ðnÞ
mit
n 2 N*
1.1.2 Konvergenz und Divergenz einer unendlichen Reihe
Besitzt die Folge der Partialsummen sn einen Grenzwert s, lim sn ¼ s, so heißt die
n!1
1
P
unendliche Reihe
an konvergent mit dem Summenwert s. Symbolische Schreibweise:
n¼1
1
P
n¼1
an ¼ a1 þ a2 þ a3 þ . . . þ an þ . . . ¼ s
Besitzt die Partialsummenfolge keinen Grenzwert, so heißt die unendliche Reihe divergent.
1
P
Eine unendliche Reihe
an heißt absolut konvergent, wenn die aus den Beträgen ihrer
Glieder gebildete Reihe
n¼1
1
P
n¼1
j an j konvergiert. Eine absolut konvergente Reihe ist immer
konvergent. Eine Reihe mit dem „Summenwert“ s ¼ þ 1 oder s ¼ / 1 heißt bestimmt divergent.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_6
1 Unendliche Reihen
179
1.2 Konvergenzkriterien
Die Bedingung lim an ¼ 0 ist zwar notwendig, nicht aber hinreichend für die Konvern!1
1
P
genz der Reihe
an . Die Reihenglieder einer konvergenten Reihe müssen also (notn¼ 1
wendigerweise) eine Nullfolge bilden.
&
Beispiel
1
P
Die unendliche Reihe
n¼1
ð1 þ 0;1 n ) divergiert, da die Reihenglieder wegen
lim ð1 þ 0;1 n Þ ¼ 1 6¼ 0
n!1
keine Nullfolge bilden.
&
Die nachfolgenden Kriterien stellen hinreichende (aber nicht notwendige) Konvergenzbedingungen dar. Sie ermöglichen in vielen Fällen eine Entscheidung darüber, ob eine vorgegebene Reihe konvergiert oder divergiert. Der Summenwert einer konvergenten Reihe lässt
sich jedoch nur in einfachen Fällen exakt bestimmen. Näherungswerte erhält man (wenn
auch meist sehr mühsam) durch gliedweises Aufaddieren der Reihenglieder bis zum Erreichen der gewünschten Genauigkeit.
1.2.1 Quotientenkriterium
"
"
" an þ 1 "
" ¼ q < 1
lim ""
n!1
a "
n
ðKonvergenz; an 6¼ 0Þ
Für q > 1 divergiert die Reihe, für q ¼ 1 versagt das Kriterium, d. h. eine Entscheidung über Konvergenz oder Divergenz ist anhand dieses Kriteriums nicht möglich.
&
Beispiel
Wir zeigen mit Hilfe des Quotientenkriteriums, dass die folgende Reihe konvergiert:
1þ
1
1
1
1
1
þ
þ
þ ... þ
þ
þ ...
1!
2!
3!
n!
ðn þ 1Þ !
Mit an ¼
1
n!
und
an þ 1 ¼
1
ðn þ 1Þ !
folgt unter Beachtung von ðn þ 1Þ ! ¼ n ! ðn þ 1Þ:
1
"
"
" an þ 1 "
n!
n!
1
ðn þ 1Þ !
"
"
lim
¼ lim
¼ lim
¼ lim
¼ lim
¼ 0
1
n ! 1 " an "
n!1
n ! 1 ðn þ 1Þ !
n ! 1 n ! ðn þ 1Þ
n!1 n þ 1
n!
Wegen q ¼ 0 < 1 konvergiert die Reihe.
&
180
VI Unendliche Reihen, Taylor- und Fourier-Reihen
1.2.2 Wurzelkriterium
lim
n!1
p
ffiffiffiffiffiffiffiffiffi
n
j an j ¼ q < 1
ðKonvergenzÞ
Für q > 1 divergiert die Reihe, für q ¼ 1 versagt das Kriterium, d. h. eine Entscheidung über Konvergenz oder Divergenz ist anhand dieses Kriteriums nicht möglich.
&
Beispiel
Wir untersuchen die unendliche Reihe
lim
n!1
ffiffiffiffiffiffiffiffiffi
p
n
j an j ¼ lim
n!1
1 3 2n
P
2
n¼1
n
mit Hilfe des Wurzelkriteriums auf Konvergenz:
s3
ffiffiffiffiffiffiffiffiffiffiffiffiffi
2
3 2
2 n
2
n
¼ lim
¼ 0
n!1
n
n
Die Reihe ist somit wegen q ¼ 0 < 1 konvergent.
&
1.2.3 Vergleichskriterien
1
P
an mit positiven Gliedern kann oft
1
P
bn (mit
mit Hilfe einer geeigneten (konvergenten bzw. divergenten) Vergleichsreihe
Das Konvergenzverhalten einer unendlichen Reihe
n¼1
n¼1
ebenfalls positiven Gliedern) bestimmt werden. Mit dem Majorantenkriterium kann die
Konvergenz, mit dem Minorantenkriterium die Divergenz einer Reihe festgestellt werden.
Majorantenkriterium
Die vorliegende Reihe konvergiert, wenn die Vergleichsreihe konvergiert und zwischen
den Gliedern beider Reihen die Beziehung (Ungleichung)
an ) bn
ðf ür alle n 2 N *Þ
besteht.
Die konvergente Vergleichsreihe wird als Majorante (Oberreihe) bezeichnet. Es genügt,
wenn die angegebene Bedingung an ) bn von einem gewissen n0 an, d. h. für alle Reihenglieder mit n ( n0 erfüllt wird.
Minorantenkriterium
Die vorliegende Reihe divergiert, wenn die Vergleichsreihe divergiert und zwischen den
Gliedern beider Reihen die Beziehung (Ungleichung)
an ( bn
ðf ür alle n 2 N *Þ
besteht.
Die divergente Vergleichsreihe wird als Minorante (Unterreihe) bezeichnet. Es genügt,
wenn die angegebene Bedingung an ( bn von einem gewissen n0 an, d. h. für alle Reihenglieder mit n ( n0 erfüllt wird.
1 Unendliche Reihen
181
1.2.4 Leibnizsches Konvergenzkriterium für alternierende Reihen
Eine alternierende Reihe
1
P
ð/ 1Þ n þ 1 . an ¼ a1 / a2 þ a3 / a4 þ / . . .
n¼1
ðalle
ai > 0Þ
konvergiert, wenn sie die folgenden (hinreichenden) Bedingungen erfüllt:
a1 > a2 > a3 > . . . > an > an þ 1 > . . .
und
lim an ¼ 0
n!1
Die Glieder einer konvergenten alternierenden Reihe bilden dem Betrage nach eine monoton fallende Nullfolge. Die Reihe konvergiert auch dann, wenn die erste der beiden Bedingungen erst von einem bestimmten Glied an erfüllt ist.
Beispiel
&
Die sog. alternierende harmonische Reihe (auch Leibnizsche Reihe genannt) 1 /
1
1
1
þ
/
þ / ...
2
3
4
1
mit dem Bildungsgesetz an ¼ ð/ 1Þ n þ 1 .
konvergiert, da ihre Glieder dem Betrage nach eine monoton
n
fallende Nullfolge bilden:
3 2
1
1
1
1
1
1 >
lim
¼ 0
>
> ... >
>
> ...
und
n!1
2
3
n
nþ1
n
&
1.2.5 Eigenschaften konvergenter bzw. absolut konvergenter Reihen
(1)
(2)
(3)
(4)
(5)
Eine konvergente Reihe bleibt konvergent, wenn man endlich viele Glieder weglässt
oder hinzufügt oder abändert. Dabei kann sich jedoch der Summenwert ändern.
Klammern dürfen i. Allg. nicht weggelassen werden, ebenso wenig darf die Reihenfolge der Glieder verändert werden.
Aufeinander folgende Glieder einer konvergenten Reihe dürfen durch eine Klammer
zusammengefasst werden; der Summenwert der Reihe bleibt dabei erhalten.
Eine konvergente Reihe darf gliedweise mit einer Konstanten multipliziert werden,
wobei sich auch der Summenwert der Reihe mit dieser Konstanten multipliziert.
Konvergente Reihen dürfen gliedweise addiert und subtrahiert werden, wobei sich
ihre Summenwerte addieren bzw. subtrahieren.
Eine absolut konvergente Reihe ist stets konvergent. Für solche Reihen gelten sinngemäß die gleichen Rechenregeln wie für (endliche) Summen (gliedweise Addition,
Subtraktion und Multiplikation, beliebige Anordnung der Reihenglieder usw.).
1.3 Spezielle konvergente Reihen
Geometrische Reihe
1
P
n¼1
a q n/1 ¼ a þ a q 1 þ a q 2 þ . . . þ a q n/1 þ . . . ¼
q ¼ const::
Quotient zweier aufeinanderfolgender Glieder
Für j q j ( 1 divergiert die geometrische Reihe.
a
1/q
ðj q j < 1Þ
182
VI Unendliche Reihen, Taylor- und Fourier-Reihen
Wichtige konvergente Reihen
(1)
1þ
1
1
1
1
þ
þ
þ ... þ
þ ... ¼ e
1!
2!
3!
n!
(2)
1/
1
1
1
1
þ / þ / . . . þ ð/ 1Þ n þ 1 .
þ . . . ¼ ln 2
2
3
4
n
(Eulersche Zahl)
(alternierende harmonische Reihe)
1
1
1
1
p
þ / þ / . . . þ ð/ 1Þ n þ 1 .
þ ... ¼
3
5
7
2n / 1
4
(3)
1/
(4)
1
1
1
1
1
p2
þ 2 þ 2 þ 2 þ ... þ 2 þ ... ¼
2
1
2
3
4
n
6
(5)
1
1
1
1
1
p2
nþ1
/
þ
/
þ
/
.
.
.
þ
ð/
1Þ
.
¼
12
22
32
42
n2
12
(6)
1
1
1
1
1
þ
þ
þ
þ ... þ
þ ... ¼ 1
1.2
2.3
3.4
4.5
n ðn þ 1Þ
2 Potenzreihen
2.1 Definition einer Potenzreihe
Entwicklung um die Stelle x0
PðxÞ ¼
1
P
n¼0
an ðx / x0 Þ n ¼ a0 þ a1 ðx / x0 Þ 1 þ a2 ðx / x0 Þ 2 þ . . . þ an ðx / x0 Þ n þ . . .
a0 , a1 , a2 , . . ., an , . . .: Reelle Koeffizienten der Potenzreihe
Entwicklung um den Nullpunkt
Sonderfall der allgemeinen Entwicklung für x0 ¼ 0:
P ðxÞ ¼
&
1
P
n¼0
an x n ¼ a0 þ a1 x 1 þ a2 x 2 þ . . . þ an x n þ . . .
Beispiele
(1)
PðxÞ ¼
(2)
PðxÞ ¼
1 xn
P
x1
x2
xn
¼ 1þ
þ
þ ... þ
þ ...
1!
2!
n!
n¼0 n !
1
P
n¼1
ð/ 1Þ n þ 1 .
ðEntwicklungszentrum: x0 ¼ 0Þ
ðx / 1Þ n
ðx / 1Þ 1
ðx / 1Þ 2
ðx / 1Þ 3
¼
/
þ
/ þ ...
n
1
2
3
(Entwicklungszentrum: x 0 ¼ 1Þ
&
2 Potenzreihen
183
2.2 Konvergenzradius und Konvergenzbereich einer Potenzreihe
Der Konvergenzbereich einer Potenzreihe
1
P
n¼0
an x n besteht aus dem offenen Intervall
j x j < r, zu dem gegebenenfalls noch ein oder gar beide Randpunkte hinzukommen. Die
positive Zahl r heißt Konvergenzradius. Für j x j > r divergiert die Potenzreihe.
Divergenz
?
Konvergenz
?
x1 = – r
0
x2 = r
Divergenz
x
Berechnung des Konvergenzradius r ( bei lückenloser Potenzfolge)
"
"
" an "
1
" oder r ¼
"
p
ffiffiffiffiffiffiffiffiffi
r ¼ lim "
n ! 1 an þ 1 "
lim n j an j
n!1
Diese Formeln gelten auch für eine um die Stelle x0 entwickelte Potenzreihe. Die Reihe
konvergiert dann im Intervall j x / x0 j < r, zu dem gegebenenfalls noch ein oder gar
beide Randpunkte hinzukommen.
Sonderfälle:
r ¼ 0:
Potenzreihe konvergiert nur für x ¼ x0
r ¼ 1:
&
Potenzreihe konvergiert beständig (d. h. für jedes x 2 RÞ
Beispiel
P ðxÞ ¼ 1 þ x þ x 2 þ x 3 þ . . . þ x n þ x n þ 1 þ . . .
ðan ¼ an þ 1 ¼ 1Þ
"
"
3 2
" an "
1
" ¼ lim
Konvergenzradius: r ¼ lim ""
¼ lim 1 ¼ 1
n ! 1 an þ 1 "
n!1
n!1
1
Verhalten in den beiden Randpunkten:
x1 ¼ /1
1 / 1 þ 1 / 1 þ /...
x2 ¼ 1
1 þ 1 þ 1 þ 1 þ ...
divergent (divergente alternierende Reihe)
divergent („Summenwert“ ¼ 1)
Konvergenzbereich der Potenzreihe: / 1 < x < 1
oder
jxj < 1
&
2.3 Wichtige Eigenschaften der Potenzreihen
(1)
(2)
(3)
Eine Potenzreihe konvergiert innerhalb ihres Konvergenzbereiches absolut.
Eine Potenzreihe darf innerhalb ihres Konvergenzbereiches gliedweise differenziert
und integriert werden. Die neuen Potenzreihen haben dabei denselben Konvergenzradius r wie die ursprüngliche Reihe.
Zwei Potenzreihen dürfen im gemeinsamen Konvergenzbereich der Reihen gliedweise
addiert, subtrahiert und multipliziert werden. Die neuen Potenzreihen konvergieren
dann mindestens im gemeinsamen Konvergenzbereich der beiden Ausgangsreihen.
184
VI Unendliche Reihen, Taylor- und Fourier-Reihen
3 Taylor-Reihen
3.1 Taylorsche und Mac Laurinsche Formel
3.1.1 Taylorsche Formel
Eine ðn þ 1Þ-mal differenzierbare Funktion f ðxÞ lässt sich um das „Entwicklungszentrum“ x0 wie folgt entwickeln (sog. Taylorsche Formel ):
f 0 ðx0 Þ
f 00 ðx0 Þ
f ðnÞ ðx0 Þ
f ðxÞ ¼ f ðx0 Þ þ
ðx / x0 Þ 1 þ
ðx / x0 Þ 2 þ . . . þ
ðx / x0 Þ n þ Rn ðxÞ
1
!
2
!
n
!
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|ffl{zffl}
Taylorsches Polynom fn ðxÞ vom Grade n
Somit:
Restglied
f ðxÞ ¼ fn ðxÞ þ Rn ðxÞ
Restglied nach Lagrange
Rn ðxÞ ¼
f ðn þ 1Þ ðxÞ
ðx / x0 Þ n þ 1
ðn þ 1Þ !
ðx liegt zwischen x und x0 Þ
3.1.2 Mac Laurinsche Formel
Die Mac Laurinsche Formel ist ein Spezialfall der allgemeinen Taylorschen Formel für das
Entwicklungszentrum x0 ¼ 0 (Nullpunkt):
f 0 ð0Þ 1
f 00 ð0Þ 2
f ðnÞ ð0Þ n
f ðxÞ ¼ f ð0Þ þ
x þ
x þ ... þ
x þ Rn ðxÞ
1!
2 ffl!{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl
n!
ffl} |ffl{zffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl
Mac Laurinsches Polynom fn ðxÞ vom Grade n
Somit:
f ðxÞ ¼ fn ðxÞ þ Rn ðxÞ
Restglied nach Lagrange
Rn ðxÞ ¼
f
ðn þ 1Þ
ðJ xÞ n þ 1
x
ðn þ 1Þ !
ð0 < J < 1Þ
Restglied
3 Taylor-Reihen
185
3.2 Taylorsche Reihe
f 0 ðx0 Þ
f 00 ðx0 Þ
ðx / x0 Þ 1 þ
ðx / x0 Þ 2 þ . . . ¼
1!
2!
f ðxÞ ¼ f ðx0 Þ þ
x0 :
1
P
n¼0
f ðnÞ ðx0 Þ
ðx / x0 Þ n
n!
Entwicklungszentrum oder Entwicklungspunkt
Voraussetzung: f ðxÞ ist in der Umgebung von x0 beliebig oft differenzierbar und das
Restglied Rn ðxÞ in der Taylorschen Formel verschwindet für n ! 1.
&
Beispiel
Wir entwickeln die Sinusfunktion um die Stelle x0 ¼ p=2:
f ðxÞ ¼ sin x
)
f ðp=2Þ ¼ sin ðp=2Þ ¼ 1
f 0 ðxÞ ¼ cos x
)
f 0 ðp=2Þ ¼ cos ðp=2Þ ¼ 0
00
)
f 00 ðp=2Þ ¼ / sin ðp=2Þ ¼ / 1
000
)
f 000 ðp=2Þ ¼ / cos ðp=2Þ ¼ 0
)
f
f ðxÞ ¼ / sin x
f ðxÞ ¼ / cos x
f
ð4Þ
..
.
ðxÞ ¼ sin x
ð4Þ
ðp=2Þ ¼ sin ðp=2Þ ¼ 1
Die Taylorreihe lautet damit wie folgt (die Sinusfunktion verläuft spiegelsymmetrisch zur Geraden x ¼ p=2,
daher verschwinden die Koeffizienten der ungeraden Potenzen):
sin x ¼ 1 /
¼
1
P
n¼0
1
1
ðx / p=2Þ 2
ðx / p=2Þ 4
ðx / p=2Þ 2 þ
ðx / p=2Þ 4 / þ . . . ¼ 1 /
þ
/ þ ... ¼
2!
4!
2!
4!
ð/ 1Þ n .
ðx / p=2Þ 2 n
ð2 nÞ !
&
3.3 Mac Laurinsche Reihe
Die Mac Laurinsche Reihe ist eine spezielle Form der Taylorschen Reihe für das Entwicklungszentrum x0 ¼ 0 (Nullpunkt):
f ðxÞ ¼ f ð0Þ þ
f 0 ð0Þ 1
f 00 ð0Þ 2
x þ
x þ ... ¼
1!
2!
1
P
n¼0
f
ðnÞ
ð0Þ n
x
n!
Bei einer geraden Funktion treten nur gerade Potenzen auf, bei einer ungeraden Funktion
nur ungerade Potenzen.
&
Beispiel
Wir bestimmen die Mac Laurinsche Reihe von f ðxÞ ¼ e x :
f ðxÞ ¼ f 0 ðxÞ ¼ f 00 ðxÞ ¼ . . . ¼ f
0
00
f ð0Þ ¼ f ð0Þ ¼ f ð0Þ ¼ . . . ¼ f
ex ¼ 1 þ
ðnÞ
ðxÞ ¼ . . . ¼ e x
ðnÞ
ð0Þ ¼ . . . ¼ e 0 ¼ 1
x1
x2
xn
þ
þ ... þ
þ ... ¼
1!
2!
n!
1
P
xn
n¼0
n!
Die Reihe konvergiert beständig, d. h. für jedes reelle x.
&
186
VI Unendliche Reihen, Taylor- und Fourier-Reihen
3.4 Spezielle Potenzreihenentwicklungen (Tabelle)
Funktion
Potenzreihenentwicklung
Konvergenzbereich
1Þ
Allgemeine Binomische Reihe
!n4
!n4
!n4
!n4
ð1 + xÞ n
1+
x1 þ
x2 +
x3 þ
x4 + ...
1
2
3
4
ða + xÞ n
an +
!n4
1
an/1 . x 1 þ
!n4
2
an/2 . x 2 +
!n4
3
n > 0 : jxj ) 1
n < 0 : jxj < 1
a n / 3 . x 3 þ . . . n > 0 : j x j ) jaj
n < 0 : j x j < jaj
Spezielle Binomische Reihen
ð1 + xÞ 4
1
1+
1 1
1.3 2
1.3.7 3
1 . 3 . 7 . 11 4
x /
x +
x /
x + . . . jxj ) 1
4
4.8
4 . 8 . 12
4 . 8 . 12 . 16
ð1 + xÞ 3
1
1+
1 1
1.2 2
1.2.5 3
1.2.5.8 4
x /
x +
x /
x + ...
3
3.6
3.6.9
3 . 6 . 9 . 12
jxj ) 1
ð1 + xÞ 2
1
1+
1 1
1.1 2
1.1.3 3
1.1.3.5 4
x /
x +
x /
x + ...
2
2.4
2.4.6
2.4.6.8
jxj ) 1
3
1+
3 1
3.1 2
3.1.1 3
3.1.1.3 4
x þ
x *
x þ
x * ...
2
2.4
2.4.6
2.4.6.8
jxj ) 1
ð1 + xÞ / 4
1
1*
1 1
1.5 2
1.5.9 3
1 . 5 . 9 . 13 4
x þ
x *
x þ
x * . . . jxj < 1
4
4.8
4 . 8 . 12
4 . 8 . 12 . 16
ð1 + xÞ / 3
1
1*
1 1
1.4 2
1.4.7 3
1 . 4 . 7 . 10 4
x þ
x *
x þ
x * ...
3
3.6
3.6.9
3 . 6 . 9 . 12
jxj < 1
ð1 + xÞ / 2
1
1*
1 1
1.3 2
1.3.5 3
1.3.5.7 4
x þ
x *
x þ
x * ...
2
2.4
2.4.6
2.4.6.8
jxj < 1
ð1 + xÞ / 1
1 * x1 þ x2 * x3 þ x4 * ...
ð1 + xÞ 2
3
3 1
3.5 2
3.5.7 3
3.5.7.9 4
x þ
x *
x þ
x * ...
2
2.4
2.4.6
2.4.6.8
ð1 + xÞ / 2
1*
ð1 + xÞ / 2
1 * 2x1 þ 3x2 * 4x3 þ 5x4 * ...
ð1 + xÞ / 3
1*
1
ð2 . 3 x 1 * 3 . 4 x 2 þ 4 . 5 x 3 * 5 . 6 x 4 þ . . .Þ
2
jxj < 1
jxj < 1
jxj < 1
j xj < 1
Reihen der Exponentialfunktionen
ex
e /x
ax
1Þ
1þ
x1
x2
x3
x4
þ
þ
þ
þ ...
1!
2!
3!
4!
j xj < 1
1/
x1
x2
x3
x4
þ
/
þ
/ þ ...
1!
2!
3!
4!
j xj < 1
1þ
ðln aÞ 1 1
ðln aÞ 2 2
ðln aÞ 3 3
ðln aÞ 4 4
x þ
x þ
x þ
x þ . . . j xj < 1
1!
2!
3!
4!
Für den Spezialfall n 2 N * erhält man ein Polynom n-ten Grades. Die Entwicklungskoeffizienten
die Binomialkoeffizienten (siehe I.2.7).
!n4
k
sind
3 Taylor-Reihen
187
Tabelle (Fortsetzung)
Funktion
Potenzreihenentwicklung
Konvergenzbereich
Reihen der logarithmischen Funktionen
1
1
1
ðx / 1Þ 2 þ
ðx / 1Þ 3 / ðx / 1Þ 4 þ / . . . 0 < x ) 2
2
3
4
"3
#
21
3
23
3
25
3
2
x/1
1 x/1
1 x/1
1 x/1 7
x > 0
2
þ
þ
þ
þ ...
xþ1
3 xþ1
5 xþ1
7 xþ1
ðx / 1Þ 1 /
ln x
ln x
ln ð1 þ xÞ
ln ð1 / xÞ
3
ln
1þx
1/x
2
x1 /
+
x2
x3
x4
þ
/
þ / ...
2
3
4
)
x2
x3
x4
/ x þ
þ
þ
þ ...
2
3
4
+
)
x3
x5
x7
2 x1 þ
þ
þ
þ ...
3
5
7
1
/1 < x ) 1
/1 ) x < 1
jxj < 1
Reihen der trigonometrischen Funktionen
x3
x5
x7
þ
/
þ / ...
3!
5!
7!
sin x
x1 /
cos x
1/
tan x
x1 þ
cot x
1
1 1
1 3
2
/
x /
x /
x5 / ...
x
3
45
945
x2
x4
x6
þ
/
þ / ...
2!
4!
6!
1 3
2 5
17 7
62
x þ
x þ
x þ
x9 þ ...
3
15
315
2835
jxj < 1
jxj < 1
jxj <
p
2
0 < jxj < p
Reihen der Arkusfunktionen
arcsin x
arccos x
arctan x
arccot x
1
1.3
1.3.5
x3 þ
x5 þ
x7 þ ...
2.3
2.4.5
2.4.6.7
+
)
p
1
1.3
1.3.5
/ x1 þ
x3 þ
x5 þ
x7 þ ...
2
2.3
2.4.5
2.4.6.7
x1 þ
x3
x5
x7
þ
/
þ / ...
3
5
7
+
)
p
x3
x5
x7
/ x1 /
þ
/
þ / ...
2
3
5
7
x1 /
jxj < 1
jxj < 1
jxj ) 1
jxj ) 1
Reihen der Hyperbelfunktionen
sinh x
x1 þ
cosh x
1þ
x3
x5
x7
þ
þ
þ ...
3!
5!
7!
x2
x4
x6
þ
þ
þ ...
2!
4!
6!
jxj < 1
jxj < 1
188
VI Unendliche Reihen, Taylor- und Fourier-Reihen
Tabelle (Fortsetzung)
Funktion
Potenzreihenentwicklung
Konvergenzbereich
tanh x
x1 /
coth x
1
1 1
1 3
2
þ
x /
x þ
x5 / þ ...
x
3
45
945
1 3
2 5
17 7
62
x þ
x /
x þ
x9 / þ ...
3
15
315
2835
jxj <
p
2
0 < jxj < p
Reihen der Areafunktionen
1
1.3
1.3.5
x3 þ
x5 /
x7 þ / ...
2.3
2.4.5
2.4.6.7
arsinh x
x1 /
arcosh x
ln ð2 xÞ /
artanh x
x1 þ
arcoth x
1
1
1
1
þ
þ
þ
þ ...
x
3x3
5x5
7x7
1
1.3
1.3.5
/
/
/ ...
2 . 2 x2
2 . 4 . 4 x4
2 . 4 . 6 . 6 x6
x3
x5
x7
þ
þ
þ ...
3
5
7
jxj < 1
x > 1
jxj < 1
jxj > 1
3.5 Näherungspolynome einer Funktion (mit Tabelle)
Bricht man die Potenzreihenentwicklung einer Funktion f ðxÞ nach der n-ten Potenz ab, so
erhält man ein Näherungspolynom fn ðxÞ vom Grade n für f ðxÞ (sog. Mac Laurinsches
bzw. Taylorsches Polynom). Funktion f ðxÞ und Näherungspolynom fn ðxÞ stimmen an der
Entwicklungsstelle x0 in ihrem Funktionswert und in ihren ersten n Ableitungen miteinander überein.
Fehlerabschätzung
Der durch den Abbruch der Potenzreihe entstandene Fehler lässt sich i. Allg. anhand der
Lagrangeschen Restgliedformel abschätzen (siehe Abschnitt 3.1). Er liegt in der Größenordnung des größten Reihengliedes, das in der Näherung nicht mehr berücksichtigt wurde.
Näherungspolynome spezieller Funktionen (Tabelle)
1. Näherung: Abbruch nach dem ersten nichtkonstanten Glied
2. Näherung: Abbruch nach dem zweiten nichtkonstanten Glied
Diese Näherungen liefern in der Umgebung des Nullpunktes sehr brauchbare und nützliche
Ergebnisse.
Funktion
1. Näherung
2. Näherung
ð1 + xÞ n
1 + nx
1 + nx þ
ex
1þx
1þx þ
n ðn / 1Þ 2
x
2
1 2
x
2
3 Taylor-Reihen
189
Tabelle (Fortsetzung)
Funktion
1. Näherung
2. Näherung
e /x
1/x
1/x þ
ax
1 þ ðln aÞ x
1 þ ðln aÞ x þ
ln ð1 þ xÞ
x
x /
ln ð1 / xÞ
/x
/x /
3
2
1þx
ln
1/x
1 2
x
2
2x
2x þ
2 3
x
3
sin x
x
x /
1 3
x
6
cos x
1/
1/
1 2
1 4
x þ
x
2
24
tan x
x
x þ
1 3
x
3
arcsin x
x
x þ
1 3
x
6
arccos x
p
/x
2
p
1 3
/x /
x
2
6
arctan x
x
x /
arccot x
p
/x
2
p
1 3
/x þ
x
2
3
sinh x
x
x þ
1 3
x
6
cosh x
1þ
1þ
1 2
1 4
x þ
x
2
24
tanh x
x
x /
1 3
x
3
arsinh x
x
x /
1 3
x
6
artanh x
x
x þ
1 3
x
3
1 2
x
2
1 2
x
2
1 2
x
2
ðln aÞ 2 2
x
2
1 2
x
2
1 3
x
3
190
VI Unendliche Reihen, Taylor- und Fourier-Reihen
4 Fourier-Reihen
4.1 Fourier-Reihe einer periodischen Funktion
Eine periodische Funktion f ðxÞ mit der Periode p ¼ 2 p lässt sich unter bestimmten
Voraussetzungen (siehe weiter unten) in eine unendliche trigonometrische Reihe der Form
f ðxÞ ¼
1
P
a0
½ an . cos ðn xÞ þ bn . sin ðn xÞ%
þ
2
n¼1
entwickeln ðsog. Fourier-Reihe von f ðxÞ in reeller FormÞ.
y
y = f(x)
p = 2p
2p
6p
4p
x
Berechnung der Fourier-Koeffizienten an und bn
1
a0 ¼
.
p
1
an ¼
.
p
2ðp
f ðxÞ dx
0
2ðp
f ðxÞ . cos ðn xÞ dx ;
0
1
bn ¼
.
p
2ðp
f ðxÞ . sin ðn xÞ dx
ðn 2 N *Þ
0
Anmerkungen
(1)
(2)
Voraussetzung ist, dass die folgenden Dirichletschen Bedingungen erfüllt sind:
1. Das Periodenintervall lässt sich in endlich viele Teilintervalle zerlegen, in denen
f ðxÞ stetig und monoton ist.
2. Besitzt die Funktion f ðxÞ im Periodenintervall Unstetigkeitsstellen (es kommen
nur Sprungunstetigkeiten mit endlichen Sprüngen infrage), so existiert in ihnen
sowohl der links- als auch der rechtsseitige Grenzwert.
In den Sprungstellen der Funktion f ðxÞ liefert die Fourier-Reihe von f ðxÞ das arithmetische Mittel aus dem links- und rechtsseitigen Grenzwert der Funktion.
4 Fourier-Reihen
191
Symmetriebetrachtungen
f ðxÞ ist eine gerade Funktion:
f ðxÞ ¼
1
P
a0
þ
an . cos ðn xÞ
2
n¼1
ðbn ¼ 0
n 2 N *Þ
f ür
f ðxÞ ist eine ungerade Funktion:
f ðxÞ ¼
&
1
P
bn . sin ðn xÞ
n¼1
ðan ¼ 0
f ür
n 2 NÞ
Beispiel
y
Wir bestimmen die Fourier-Reihe der im Bild dargestellten
periodischen Funktion mit der Periodendauer p ¼ 2 p :
1
f ðxÞ ¼
1
x;
2p
0 ) x < 2p
Berechnung der Fourier-Koeffizienten ðn 2 N *Þ:
a0 ¼
an ¼
2ðp
1
.
p
f ðxÞ dx ¼
0
1
1
.
.
p 2p
2ðp
1
.
p
f ðxÞ . cos ðn xÞ dx ¼
0
2ðp
1
2p2
x dx ¼
0
1
1
.
.
p 2p
2p
+
1 2
x
2
)2p
1
. 2p2 ¼ 1
2p2
¼
0
x
4p
2ðp
1
2p2
x . cos ðn xÞ dx ¼
0
+
cos ðn xÞ
x . sin ðn xÞ
þ
n2
n
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
)2 p
0
¼
Integral 232 mit a ¼ n
¼
bn ¼
1
2p2
1
.
p
+
cos ðn 2 pÞ
2 p . sin ðn 2 pÞ
cos 0
0 . sin 0
/
þ
/
n2
n
n2
n
2ðp
f ðxÞ . sin ðn xÞ dx ¼
0
1
1
.
.
p 2p
)
¼
2ðp
x . sin ðn xÞ dx ¼
0
3
1
2p2
1
2p2
+
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
1
1
þ0/ 2 /0
n2
n
2
¼ 0
)
sin ðnxÞ
x . cos ðnxÞ 2 p
/
¼
2
n
n
0
Integral 208 mit a ¼ n
+
¼
1
2p2
sin ðn 2 pÞ 2 p . cos ðn 2 pÞ sin 0 0 . cos 0
/
/ 2 þ
n2
n
n
n
¼
1
/2p
1 1
.
¼/
.
2p2
n
p n
Hinweis: cos ðn 2 pÞ ¼ cos 0 ¼ 1,
)
¼
1
2p 2
3
0/
2p
/0þ0
n
2
¼
sin ðn 2 pÞ ¼ sin 0 ¼ 0
Die Fourier-Reihe beginnt daher wie folgt:
f ðxÞ ¼
1 1
1
1 P
1
1
/
.
. sin ðn xÞ ¼
/
2
p n¼1 n
2
p
3
sin x þ
1
1
. sin ð2 xÞ þ
. sin ð3 xÞ þ . . .
2
3
2
&
192
VI Unendliche Reihen, Taylor- und Fourier-Reihen
Komplexe Darstellung der Fourier-Reihe
f ðxÞ ¼
1
P
n ¼ /1
cn . e j n x
mit
cn ¼
1
.
2p
2ðp
f ðxÞ . e/ j n x dx
ðn 2 ZÞ
0
Die komplexe Fourier-Reihe lässt sich auch wie folgt aufspalten:
f ðxÞ ¼
1
P
n¼/1
cn . e j n x ¼ c0 þ
1
P
n¼1
c/n . e/jnx þ
1
P
n¼1
cn . e j n x
Der Koeffizient c / n ist dabei konjugiert komplex zu cn , d. h. c / n ¼ c*n .
Zusammenhang zwischen den Koeffizienten an , bn und cn
1. !bergang von der reellen zur komplexen Form
c0 ¼
1
a0 ;
2
cn ¼
1
ðan / j bn Þ ;
2
1
c / n ¼ c*n ¼
ðan þ j bn Þ
2
ðn 2 N*Þ
2. !bergang von der komplexen zur reellen Form
a0 ¼ 2 c0 ;
&
an ¼ cn þ c/ n ;
bn ¼ j ðcn / c/ n Þ
ðn 2 N*Þ
Beispiel
Die reelle Form der Fourier-Reihe von f ðxÞ ¼
f ðxÞ ¼
1 1
1
1 P
/
.
. sin ðn xÞ
2
p n¼1 n
1
x, 0 ) x ) 2 p lautet (siehe vorheriges Beispiel):
2p
Aus den reellen Fourier-Koeffizienten
a0 ¼ 1,
an ¼ 0,
bn ¼ /
1 1
.
p n
ðn 2 N*Þ
berechnen wir mit Hilfe der Transformationsgleichungen die Koeffizienten der komplexen Darstellungsform:
3
2
1
1
1
1
1
1 1
1
1
c0 ¼
a0 ¼
.1 ¼
,
cn ¼
ðan / j bn Þ ¼
0þj
.
¼ j
.
,
2
2
2
2
2
p n
2p n
3
2
*
1
1
c/ n ¼ c*n ¼ j 1 . 1
¼ /j
.
2p n
2p n
Die komplexe Form der Fourier-Reihe lautet damit wie folgt:
f ðxÞ ¼ c0 þ
¼
1
P
n¼1
1
P
1
þ
2
n¼1
cn . e j n x þ
1
P
n¼1
c/ n . e / j n x ¼ c0 þ
1
P
n¼1
ðcn . e j n x þ c/ n . e / j n x Þ ¼
3
2
1
P
1
1
1
1
1
1
1
j
.
. ejnx / j
.
. e/jnx ¼
þj
.
ðe j n x / e / j n x Þ
2p n
2p n
2
2 p n¼1 n
4 Fourier-Reihen
193
Alternative Lösung: Direkte Berechnung der komplexen Fourier-Koeffizienten mit der angegebenen Integralformel:
1
.
2p
c0 ¼
¼
f ðxÞ . e/ j 0 x dx ¼
0
+
1
ð2 pÞ 2
1
.
2p
cn ¼
2ðp
2ðp
1
ð2 pÞ 2 / 0
2
)
¼
f ðxÞ . e/ j n x dx ¼
0
2ðp
1
.
2p
0
1
.
ð2 pÞ 2
1
.
2p
2ðp
0
1
1
x . 1 dx ¼
.
2p
ð2 pÞ 2
2ðp
x dx ¼
0
1
+
ð2 pÞ 2
1 2
x
2
)2p
0
¼
1
1
ð2 pÞ 2 ¼
2
2
2ðp
1
1
x . e / j n x dx ¼
.
2p
ð2 pÞ 2
x . e / j n x dx ¼
0
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
Integral Nr: 313 mit a ¼ / j n
¼
¼
¼
1
+
ð2 pÞ 2
jnx þ 1
. e/jnx
n2
)2p
0
¼
ð j n 2 p þ 1Þ . e / j n 2 p / 1 . e / 0
ð2 p nÞ 2
j ð2 p nÞ
ð2 p nÞ
Somit: c0 ¼
2
¼
1
,
2
j
1
1
¼ j
.
2pn
2p n
cn ¼ j
1
1
. ,
2p n
h
1
ð2 p nÞ 2
¼
ðj n x þ 1Þ . e / j n x
i2p
0
ð j n 2 p þ 1Þ . 1 / 1 . 1
ð2 p nÞ 2
¼
¼
j ð2 p nÞ þ 1 / 1
ð2 p nÞ 2
¼
ðn 6¼ 0Þ
1
1
c/ n ¼ c*n ¼ / j
.
2p n
ðn 2 N*Þ
&
4.2 Fourier-Zerlegung einer nichtsinusförmigen Schwingung
y
T
2T
3T
t
T
Eine nichtsinusförmig verlaufende Schwingung y ¼ y ðtÞ wie im obigen Bild mit der
Kreisfrequenz w0 und der Schwingungsdauer (Periode) T ¼ 2 p=w0 lässt sich nach
Fourier wie folgt in ihre harmonischen Bestandteile (Grundschwingung und Oberschwingungen) zerlegen (Fourier-Zerlegung in reeller Form):
y ðtÞ ¼
1
P
a0
þ
½ an . cos ðn w0 tÞ þ bn . sin ðn w0 tÞ%
2
n¼1
w0 :
Kreisfrequenz der Grundschwingung ðw0 ¼ 2 p=T Þ
n w0 :
Kreisfrequenzen der harmonischen Oberschwingungen ðn ¼ 2; 3; 4; . . .Þ
194
VI Unendliche Reihen, Taylor- und Fourier-Reihen
Berechnung der Fourier-Koeffizienten an und bn
a0 ¼
2
.
T
2
.
an ¼
T
ðT Þ:
ð
y ðtÞ dt
ðTÞ
ð
y ðtÞ . cos ðn w0 tÞ dt ;
ðTÞ
2
bn ¼
.
T
ð
y ðtÞ . sin ðn w0 tÞ dt
ðn 2 N *Þ
ðTÞ
Integration über ein beliebiges Periodenintervall der Länge T
Fourier-Zerlegung in phasenverschobene Sinusschwingungen
y ðtÞ ¼
1
P
a0
½ an . cos ðn w0 tÞ þ bn . sin ðn w0 tÞ% ¼
þ
2
n¼1
1
P
¼ A0 þ
n¼1
An . sin ðn w0 t þ jn Þ
Berechnung von Amplitude An und Nullphasenwinkel jn aus den Fourier-Koeffizienten
an und bn :
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a0
an
A0 ¼
,
An ¼ a 2n þ b 2n ,
ðn 2 N *Þ
tan jn ¼
2
bn
An , jn : Amplituden- bzw. Phasenspektrum (sog. Linienspektren)
Fourier-Zerlegung in komplexer Form
y ðtÞ ¼
1
P
n¼/1
c n . e j n w0 t
Berechnung der komplexen Fourier-Koeffizienten cn :
1
cn ¼
.
T
ðT
T ¼ 2 p=w0 :
j cn j:
y ðtÞ . e / j n w0 t dt
ðn 2 ZÞ
0
Schwingungsdauer
Amplitudenspektrum (Linienspektrum)
4 Fourier-Reihen
195
4.3 Spezielle Fourier-Reihen (Tabelle)
Hinweis: T : Periode (Schwingungsdauer)
w0 : Kreisfrequenz ðw0 ¼ 2 p=TÞ
1. Rechteckskurve
yðtÞ ¼
yðtÞ ¼
8
>
>
>
< y^
fur
€
>
>
>
:0
y^
2 y^
þ
p
2
y
9
T >
>
0 ) t )
>
2 =
y^
>
>
T
;
< t < T>
2
T
2
t
2T
3
2
1
1
sin ðw0 tÞ þ
. sin ð3 w0 tÞ þ
. sin ð5 w0 tÞ þ . . .
3
5
2. Rechteckimpuls
Impulsbreite:
T
y
T
/ 2a
b ¼
2
8
>
y^
>
>
>
>
>
>
<
yðtÞ ¼ / y^ fur
€
>
>
>
>
>
>
>
: 0
a < t <
b
y^
T
/a
2
9
>
>
>
>
>
>
>
=
T
þa < t < T /a
>
2
>
>
>
>
>
;
im €ubrigen Intervall >
a
a
a
a
T
2
T
^
–y
yðtÞ ¼
3
4 y^ cos ðw0 aÞ
cos ð3 w0 aÞ
. sin ðw0 tÞ þ
. sin ð3 w0 tÞ þ
p
1
3
2
cos ð5 w0 aÞ
þ
. sin ð5 w0 tÞ þ . . .
5
3. Dreieckskurve
8
2 y^
>
>
/
t þ y^
>
>
>
T
>
<
yðtÞ ¼
fur
€
>
>
>
>
>
2 y^
>
:
t / y^
T
yðtÞ ¼
b
y^
4 y^
þ 2
2
p
3
9
T >
>
0 ) t )
>
>
2 >
>
=
>
>
>
>
>
T
;
) t ) T>
2
y
y^
T
2
T
t
2T
1
1
1
. cos ðw0 tÞ þ 2 . cos ð3 w0 tÞ þ 2 . cos ð5 w0 tÞ þ . . .
12
3
5
2
t
196
VI Unendliche Reihen, Taylor- und Fourier-Reihen
4. Dreieckskurve
yðtÞ ¼
yðtÞ ¼
8
>
>
>
>
>
>
>
>
<
>
>
>
>
>
>
>
>
:
/
8 y^
p2
y
y^
T
0 ) t )
4
4 y^
t þ 2 y^ fur
€
T
T
3
< t <
T
4
4 >
>
>
>
>
>
>
3
> ^
T ) t ) T ; –y
4
4 y^
t / 4 y^
T
T
4
3
T
4
T
2
5
T
4
t
2
1
1
1
.
sin
ðw
tÞ
/
.
sin
ð3
w
tÞ
þ
.
sin
ð5
w
tÞ
/
þ
.
.
.
0
0
0
12
32
52
y
y^
t;
T
y^
0 ) t < T
T
yðtÞ ¼
T
3
5. Kippschwingung (Sägezahnimpuls)
yðtÞ ¼
9
>
>
>
>
>
>
>
>
=
4 y^
t
T
y^
y^
/
2
p
2T
t
3
2
1
1
sin ðw0 tÞ þ
. sin ð2 w0 tÞ þ
. sin ð3 w0 tÞ þ . . .
2
3
6. Kippschwingung (Sägezahnimpuls)
yðtÞ ¼
yðtÞ ¼
8
2 y^
>
>
t
>
>
< T
0 ) t )
>
>
>
2 y^
>
:
t / 2 y^
T
2 y^
p
fur
€
9
>
>
>
>
=
>
>
>
T
;
< t < T>
2
3
2
1
1
sin ðw0 tÞ /
. sin ð2 w0 tÞ þ
. sin ð3 w0 tÞ / þ . . .
2
3
7. Kippschwingung (Sägezahnimpuls)
yðtÞ ¼ /
T
2
y^
t þ y^;
T
0 ) t < T
y
y^
T
yðtÞ ¼
y^
y^
þ
2
p
3
2
1
1
sin ðw0 tÞ þ
. sin ð2 w0 tÞ þ
. sin ð3 w0 tÞ þ . . .
2
3
2T
t
4 Fourier-Reihen
197
8. Sinusimpuls (Einweggleichrichtung)
yðtÞ ¼
yðtÞ ¼
8
>
y^ . sin ðw0 tÞ
>
>
<
>
>
>
:
0
0 ) t )
fur
€
y
T
2
9
>
>
>
=
y^
>
>
>
T
) t ) T;
2
T
2
T
3
y^
y^
2 y^
1
1
þ
. sin ðw0 tÞ /
. cos ð2 w0 tÞ þ
. cos ð4 w0 tÞ þ
p
2
p 1.3
3.5
2
1
þ
. cos ð6 w0 tÞ þ . . .
5.7
9. Sinusimpuls (Zweiweggleichrichtung)
yðtÞ ¼ y^ j sin ðw0 tÞ j ;
0 ) t ) T
y
y^
T
T/2
yðtÞ ¼
2 y^
4 y^
/
p
p
4 y^
T2
1
1
. cos ð2 w0 tÞ þ
. cos ð4 w0 tÞ þ
1.3
3.5
2
1
þ
. cos ð6 w0 tÞ þ . . .
5.7
y
3
2
T 2
;
t /
2
0 ) t ) T
y^
T
2
y ðtÞ ¼
y^
4 y^
þ 2
3
p
t
3
10. Parabelbögen
yðtÞ ¼
t
3
T
3
T
2
1
1
1
. cos ðw0 tÞ þ 2 . cos ð2 w0 tÞ þ 2 . cos ð3 w0 tÞ þ . . .
2
1
2
3
t
2
198
VII Lineare Algebra
1 Reelle Matrizen
1.1 Grundbegriffe
1.1.1 n-dimensionale Vektoren
n-dimensionaler Vektor
n reelle Zahlen in einer bestimmten Reihenfolge bilden einen n-dimensionalen Vektor. Sie
werden in der linearen Algebra üblicherweise durch kleine lateinische Buchstaben in Fettdruck (aber ohne Pfeil) gekennzeichnet: a, b, c, . . .
Schreibweisen:
0
a1
1
Ba C
B 2C
C
a ¼ B
B .. C
@ . A
an
a ¼ ða1
a2
n-dimensionaler Spaltenvektor mit den n Vektorkoordinaten
(skalaren Vektorkomponenten) a1 , a2 , . . . , an
...
an Þ
n-dimensionaler Zeilenvektor
Rechenoperationen und Rechenregeln
Die n-dimensionalen Vektoren bilden in ihrer Gesamtheit den n-dimensionalen Raum Rn .
Rechenoperationen und Rechenregeln sind die gleichen wie bei ebenen und räumlichen
Vektoren, d. h. Vektoren des R 2 bzw. R 3 , siehe hierzu Kap. II. Ausnahmen: Vektor- und
Spatprodukte sind nur im 3-dimensionalen Anschauungsraum definiert.
1. Addition und Subtraktion erfolgen komponentenweise:
0 1
0 1
0
1
a1
b1
a1 + b1
Ba C
Bb C
Ba + b C
2C
B 2C
B 2C
B 2
B
B
C
C
C
a+b ¼ B . C+B . C ¼ B
..
B
C
.
.
@ . A
@ . A
@
A
.
an
bn
an + bn
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_7
1 Reelle Matrizen
199
2. Die Multiplikation eines Vektors mit einem Skalar erfolgt komponentenweise:
0 1
0
1
l a1
a1
Ba C
Bla C
B 2C
B 2C
B
C
C
ðl 2 RÞ
la ¼ l B . C ¼ B
B .. C
.
@ . A
@ . A
an
l an
3. Das Skalarprodukt zweier Vektoren wird gebildet, indem man zunächst die einander
entsprechenden (d. h. gleichstelligen) Vektorkoordinaten miteinander multipliziert
und dann die insgesamt n Produkte aufaddiert:
0
1 0 1
a1
b1
Ba C Bb C
n
X
2
B C B 2C
C B C
a.b ¼ B
ai bi
B .. C . B .. C ¼ a1 b1 þ a2 b2 þ . . . þ an bn ¼
@ . A @ . A
i¼1
an
bn
4. Betrag eines Vektors:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffi
j a j ¼ a ¼ a 21 þ a 22 þ . . . þ a 2n ¼ a . a
Spezielle Vektoren
Nullvektor 0: Vektor der Länge 0, alle Vektorkoordinaten haben den Wert 0.
Einheitsvektor e: Vektor der Länge 1 (normierter Vektor).
Orthogonale Vektoren a, b: Vektoren, deren Skalarprodukt verschwindet ða . b ¼ 0Þ.
Komponentendarstellung eines Vektors
a ¼ a1 e1 þ a2 e2 þ . . . þ an en
ei : Einheitsvektor (Basisvektor), dessen i-te Vektorkoordinate den Wert 1 besitzt, während
alle übrigen Vektorkoordinaten verschwinden ði ¼ 1, 2, . . . , nÞ.
8
9
i ¼ j=
<1
ei . ej ¼ di j ¼
f ür
(di j : Kronecker-Symbol)
:
;
0
i 6¼ j
Die Einheitsvektoren ei bilden eine Basis des n-dimensionalen Raumes R n , d. h. jeder
n-dimensionale Vektor a lässt sich in eindeutiger Weise als Linearkombination dieser
(linear unabhängigen) Bassisvektoren darstellen 1Þ . Multipliziert man einen Vektor a mit
dem Kehrwert seines Betrages j a j, so erhält man einen Einheitsvektor gleicher Richtung
(sog. Normierung des Vektors a).
1Þ
Zum Begriff der linearen Unabhängigkeit von Vektoren siehe Abschnitt 3.6.
200
&
VII Lineare Algebra
0
Beispiel
1
1
0
/2
B 0C
B
B
C
B
Gegeben sind die Vektoren a ¼ B
C und b ¼ B
@ 2A
@
/1
men den Vektor a þ 3 b, das Skalarprodukt a . b sowie
0
1
1
0
/2
1
0
1
1
0
/6
1
1C
C
C des 4-dimensionalen Raumes R 4 . Wir bestim5A
3
den Betrag von a:
1
0
1/6
1
0
/5
1
B 0C
B 1C
B 0C
B 3C
B 0þ3 C
B 3C
B
C
B
C
B
C
B
C
B
C
B
C
a þ 3b ¼ B
C þ 3B
C ¼ B
C
CþB
C ¼ B
C ¼ B
@ 2A
@ 5A
@ 2A
@ 15 A
@ 2 þ 15 A
@ 17 A
/1
3
/1
9
/1 þ 9
8
1
1 0
/2
1
B 0C B 1C
C
C B
B
a.b ¼ B
C ¼ 1 . ð/ 2Þ þ 0 . 1 þ 2 . 5 þ ð/ 1Þ . 3 ¼ / 2 þ 0 þ 10 / 3 ¼ 5
C.B
@ 2A @ 5A
3
/1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1 2 þ 0 2 þ 2 2 þ ð/ 1Þ 2 ¼ 1 þ 0 þ 4 þ 1 ¼ 6
jaj ¼
0
&
1.1.2 Definition einer reellen Matrix
Unter einer reellen Matrix A vom Typ
len bestehendes rechteckiges Schema mit
recht angeordneten Spalten:
0
a11 a12 . . . a1 k . . .
B
B a21 a22 . . . a2 k . . .
B
B
..
..
B ..
B .
.
.
B
A ¼ B
B ai 1 ai 2 . . . a
...
ik
B
B
B ..
..
..
B .
.
.
@
a m 1 am 2
"
1. Spalte
...
am k . . .
"
k-te Spalte
ðm; nÞ versteht man ein aus m . n reellen Zahm waagerecht angeordneten Zeilen und n senka1 n
1
C
a2 n C
C
C
.. C
. C
C
C
ai n C
C
C
.. C
. C
A
1. Zeile
i-te Zeile
am n
Bezeichnungen:
ai k :
Matrixelemente ði ¼ 1; 2; . . . ; m; k ¼ 1; 2; . . . ; nÞ
i:
Zeilenindex ði ¼ 1; 2; . . . ; mÞ
m: Zeilenzahl
k:
Spaltenindex ðk ¼ 1; 2; . . . ; nÞ
n:
Spaltenzahl
Schreibweisen:
A;
Aðm; nÞ ;
ðai k Þ;
ðai k Þðm; nÞ
Die m Zeilen werden auch als Zeilenvektoren (mit hochgestelltem Index), die n Spalten
auch als Spaltenvektoren (mit tiefgestelltem Index) bezeichnet.
1 Reelle Matrizen
201
0
Schreibweisen:
a1 k
1
B
C
B a2 k C
B
C
ak ¼ B . C
B .. C
@
A
am k
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
i
a ¼ ðai 1 ai 2 . . . ai n Þ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
i-ter Zeilenvektor
k-ter Spaltenvektor
Die ðm; nÞ-Matrix A ist dann wie folgt darstellbar:
0 11
a
B a2 C
B
C
C
A ¼ ða1 a2 . . . an Þ ¼ B
B .. C
@ . A
am
(Zeile aus n Spaltenvektoren bzw. Spalte aus m Zeilenvektoren)
1.1.3 Spezielle Matrizen
Nullmatrix 0:
Spaltenmatrix:
Zeilenmatrix:
Quadratische Matrix:
Transponierte Matrix A T :
Alle Elemente sind gleich null.
Matrix mit nur einer Spalte, auch Spaltenvektor genannt.
Matrix mit nur einer Zeile, auch Zeilenvektor genannt.
Matrix mit gleichvielen Zeilen und Spalten ðm ¼ n; sog.
n-reihige Matrix oder Matrix n-ter Ordnung).
Sie entsteht aus der ðm; nÞ-Matrix A, indem man Zeilen
und Spalten miteinander vertauscht („Stürzen“ einer Matrix).
A T ist daher vom Typ ðn; mÞ. Es gilt stets ðA T Þ T ¼ A.
Beim Transponieren wird aus einem Zeilenvektor ein Spaltenvektor und umgekehrt.
1.1.4 Gleichheit von Matrizen
Zwei Matrizen A ¼ ðai k Þ und B ¼ ðbi k Þ vom gleichen Typ heißen gleich, A ¼ B, wenn
sie in ihren entsprechenden (d. h. gleichstelligen) Elementen übereinstimmen: ai k ¼ bi k für
alle i; k.
1.2 Spezielle quadratische Matrizen
Allgemeine Gestalt einer n-reihigen Matrix:
Hauptdiagonale
Nebendiagonale
Hauptdiagonalelemente:
ai i
mit
i ¼ 1, 2, . . . , n
Nebendiagonalelemente:
ai; n þ 1 / i
mit
i ¼ 1, 2, . . . , n
202
VII Lineare Algebra
Spur einer quadratischen Matrix
Die Summe aller Hauptdiagonalelemente heißt Spur der Matrix A:
Sp ðAÞ ¼ a11 þ a22 þ . . . þ ann
1.2.1 Diagonalmatrix
Alle außerhalb der Hauptdiagonalen liegenden Elemente verschwinden:
ai k ¼ 0 für alle
i 6¼ k
Schreibweise: diag ða11 ; a22 ; . . . ; an n Þ
1.2.2 Einheitsmatrix
Diagonalmatrix mit
ai i ¼ 1 für alle
i
Schreibweisen: E, I, ðdi k Þ
1.2.3 Dreiecksmatrix
Alle Elemente oberhalb bzw. unterhalb der Hauptdiagonalen verschwinden:
Untere Dreiecksmatrix:
ai k ¼ 0 für alle
Obere Dreiecksmatrix:
i < k
ai k ¼ 0
für alle
i > k
1.2.4 Symmetrische Matrix
Alle spiegelbildlich zur Hauptdiagonalen stehenden Elemente sind paarweise gleich:
A ¼ AT
oder
ai k ¼ ak i
für alle
i; k
1.2.5 Schiefsymmetrische Matrix
A ¼ /AT
oder
ai k ¼ / ak i
für alle
i; k
Die Hauptdiagonalelemente verschwinden: ai i ¼ 0 für alle i. Bei der Spiegelung an der
Hauptdiagonalen ändern die Elemente ihr Vorzeichen.
1 Reelle Matrizen
203
1.2.6 Orthogonale Matrix
A . AT ¼ E
Die Zeilen- bzw. Spaltenvektoren sind zueinander orthogonal und normiert, sie bilden ein
sog. orthonormiertes Vektorsystem. Dabei gilt stets det A ¼ 1 oder det A ¼ / 1. Eine
orthogonale Matrix ist immer regulär, die inverse Matrix A /1 existiert somit und ist
ebenfalls orthogonal und es gilt A T ¼ A /1 . Das Produkt orthogonaler Matrizen ist wiederum orthogonal.
1.3 Rechenoperationen für Matrizen
1.3.1 Addition und Subtraktion von Matrizen
Zwei Matrizen vom gleichen Typ werden addiert bzw. subtrahiert, indem man ihre entsprechenden (d. h. gleichstelligen) Elemente addiert bzw. subtrahiert:
A + B ¼ ðai k Þ + ðbi k Þ ¼ ðai k + bi k Þ
ði ¼ 1; 2; . . . ; m; k ¼ 1; 2; . . . ; nÞ
Rechenregeln
A; B; C sind Matrizen vom gleichen Typ:
Kommutativgesetz
Assoziativgesetz
Transponieren
AþB ¼ BþA
A þ ðB þ CÞ ¼ ðA þ BÞ þ C
ðA þ BÞ T ¼ A T þ B T
1.3.2 Multiplikation einer Matrix mit einem Skalar
Die Multiplikation einer Matrix mit einem reellen Skalar erfolgt, indem man jedes Matrixelement mit dem Skalar multipliziert:
l . A ¼ l . ðai k Þ ¼ ðl . ai k Þ
ðl 2 R; i ¼ 1; 2; . . . ; m; k ¼ 1; 2; . . . ; nÞ
Folgerung: Ein allen Matrixelementen gemeinsamer Faktor darf vor die Matrix gezogen
werden.
Rechenregeln
A und B sind Matrizen vom gleichen Typ, l und m reelle Skalare:
Assoziativgesetz
Distributivgesetze
l ðm AÞ ¼ mðl AÞ ¼ ðl mÞ A
ðl þ mÞ A ¼ l A þ m A
lðA þ BÞ ¼ l A þ l B
Transponieren
ðl AÞ T ¼ l A T
204
VII Lineare Algebra
1.3.3 Multiplikation von Matrizen
A ¼ ðai k Þ sei eine Matrix vom Typ ðm; nÞ; B ¼ ðbi k Þ eine Matrix vom Typ ðn; pÞ.
Dann heißt die ðm; pÞ-Matrix C ¼ A . B ¼ ðci k Þ mit
ci k ¼ ai 1 b1 k þ ai 2 b2 k þ . . . þ ai n bn k ¼
n
P
j¼1
ai j bj k
das Produkt der Matrizen A und B ði ¼ 1; 2; . . . ; m; k ¼ 1; 2; . . . ; pÞ.
Anmerkungen
(1)
(2)
Die Produktbildung ist nur möglich, wenn die Spaltenzahl von A mit der Zeilenzahl
von B übereinstimmt. Der Multiplikationspunkt darf auch weggelassen werden.
Das Matrixelement ci k des Matrizenproduktes A . B ist das Skalarprodukt aus dem
i-ten Zeilenvektor von A und dem k-ten Spaltenvektor von B (siehe Falk-Schema
weiter unten).
Falk-Schema zur Berechnung eines Matrizenproduktes C = A . B
Matrix A: Typ ðm; nÞ
Matrix B: Typ ðn; pÞ
k-te Spalte
;
B
A.B
ci k
:
i-te Zeile
A
:
Skalarprodukt aus dem i-ten Zeilenvektor von A
und dem k-ten Spaltenvektor von B
Rechenregeln
Voraussetzung: Alle Rechenoperationen der linken Seiten müssen durchführbar sein.
Assoziativgesetz
Distributivgesetze
A ðB CÞ ¼ ðA BÞ C
A ðB þ CÞ ¼ A B þ A C
ðA þ BÞ C ¼ A C þ B C
Transponieren
ðA BÞ T ¼ B T A T
Man beachte, dass die Matrizenmultiplikation nicht kommutativ ist, d. h. im Allgemeinen
gilt A . B 6¼ B . A (die Faktoren eines Produktes dürfen nicht vertauscht werden).
1 Reelle Matrizen
&
205
0
1
2
1
4
3 0
1 0
3
@
Wir berechnen das Matrizenprodukt C ¼ A . B mit A ¼
und B ¼ 1
1 /1 3 A:
2 1 /4
0 /2 /3 2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
(2,3)-Matrix
(3,4)-Matrix
Beispiel
A
1
2
3
0
1
B
1
1
0
4
1
/2
3
/1
/3
0
3
2
3
/4
1
3
/2
17
/6
17
6
/5
c11 ¼ 1 . 1 þ 0 . 1 þ 3 . 0 ¼ 1
)
c12 ¼ 1 . 4 þ 0 . 1 þ 3 . ð/ 2Þ: ¼ / 2
3
2
1 /2 /6
6
C ¼ A.B ¼
3 17 17 /5
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
(2,4)-Matrix
usw.
C ¼ A.B
B . A dagegen existiert nicht, da B vier Spalten, A aber nur zwei Zeilen hat.
&
1.4 Reguläre Matrix
Eine n-reihige Matrix A heißt regulär, wenn ihre Determinante einen von Null verschiedenen Wert besitzt: det A 6¼ 0. Ihr Rang ist dann Rg ðAÞ ¼ n.
Ist det A ¼ 0, so heißt A singulär. Es ist dann Rg ðAÞ < n.
&
Beispiele
0
1 2
A ¼ @ /1 3
0 1
A ist regulär
3
B ¼
1
/3
/5
15
1
5
2A
8
)
"
" 1
"
det A ¼ "" /1
" 0
2
3
1
)
"
" 1
det B ¼ ""
/3
"
/5 ""
¼ 15 / 15 ¼ 0
15 "
2
5
2
8
"
"
"
" ¼ 24 þ 0 / 5 / 0 / 2 þ 16 ¼ 33 6¼ 0
"
"
)
)
B ist singulär
&
1.5 Inverse Matrix
1.5.1 Definition einer inversen Matrix
Die regulären Matrizen (und nur diese) lassen sich umkehren, d. h. zu jeder regulären
Matrix A gibt es genau eine inverse Matrix A / 1 mit
A . A /1 ¼ A /1 . A ¼ E
Eine quadratische Matrix A ist demnach genau dann invertierbar, wenn det A 6¼ 0 und
somit Rg ðAÞ ¼ n ist. Man beachte: A und A /1 sind kommutative Matrizen.
Weitere Bezeichnungen für A / 1 : Kehrmatrix, Umkehrmatrix oder Inverse von A.
Rechenregeln für reguläre Matrizen
ðA /1 Þ /1 ¼ A ;
ðA /1 Þ T ¼ ðA T Þ /1 ;
ðA . BÞ /1 ¼ B /1 . A /1
206
VII Lineare Algebra
1.5.2 Berechnung einer inversen Matrix
1.5.2.1 Berechnung der inversen Matrix A–1 unter Verwendung
von Unterdeterminanten
0
A /1
Ai k :
Di k :
A11
1 B
B A12
¼
B .
det A @ ..
A1 n
A21
A22
..
.
A2 n
...
...
...
1
An 1
An 2 C
C
.. C
. A
ðdet A 6¼ 0Þ
An n
Algebraisches Komplement (Adjunkte) von ai k in det A ðAi k ¼ ð/ 1Þ i þ k . Di k Þ
ðn / 1Þ-reihige Unterdeterminante von det A (in det A wird die i-te Zeile und
k-te Spalte gestrichen)
Hinweis: Zunächst die Matrix ðA i k Þ bilden (sie enthält in der i-ten Zeile die algebraischen
Komplemente A i 1 , A i 2 , A i 3 , . . ., A i n ), diese dann transponieren („stürzen“) und die so
erhaltene adjungierte Matrix Aadj ¼ ðA i k Þ T mit dem Kehrwert der Determinante det A
multiplizieren:
A /1 ¼
1
1
. ðA i k Þ T ¼
. Aadj
det A
det A
1.5.2.2 Berechnung der inversen Matrix A–1 nach dem Gaußschen Algorithmus
(Gauß-Jordan-Verfahren)
Man bildet zunächst aus den n-reihigen Matrizen A und E (Einheitsmatrix) die Matrix
0
a11
B a21
B
ðA j EÞ ¼ B ..
@ .
a12
a22
..
.
...
...
a1 n
a2 n
..
.
an 1 an 2 . . . an n
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
A
"
"
"
"
"
"
"
"
1
1 0 ... 0
0 1 ... 0C
C
.. ..
.. C
. .
.A
0 0 ... 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
E
vom Typ ðn; 2 nÞ und bringt diese dann durch elementare Zeilenumformungen (siehe hierzu Abschnitt 1.6.1.3 und Abschnitt 3.4.1) auf die spezielle Form
0
1 0 ... 0
B0 1 ... 0
B
..
B .. ..
@. .
.
0 0 ... 1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
E
1
"
" b11 b12 . . . b1 n
"
" b21 b22 . . . b2 n C
C
" .
..
.. C ¼ ðE j A / 1 Þ
" .
.
. A
" .
"
bn 1 bn 2 . . . bn n
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
B ¼ A /1
Dies ist bei einer regulären und daher umkehrbaren Matrix A stets möglich. Die Einheitsmatrix E hat jetzt den Platz der Matrix A eingenommen, die Matrix B ist die gesuchte
inverse Matrix A / 1 .
1 Reelle Matrizen
&
207
Beispiel
1
1 0
2
@
1 A ist regulär und somit invertierbar ðdet A ¼ 1 6¼ 0Þ. Für ihre
Die 3-reihige Matrix A ¼ 4 1
3 2 /7
Inverse A / 1 erhalten wir (die jeweils durchgeführte Operation wird rechts angeschrieben; Zi : i-te Zeile):
"
"
0
1
0
1
1 0
2 "" 1 0 0
1 0
2 "" 1 0 0
ðA j EÞ ¼ @ 4 1
1 "" 0 1 0 A / 4 Z1 ) @ 0 1 / 7 "" /4 1 0 A
)
3 2 /7 " 0 0 1 / 3 Z1
0 2 /13 " /3 0 1 / 2 Z2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
|fflfflfflffl{zfflfflfflffl}
A
E
"
"
0
1
0
1
1 0
2 "" 1
0 0 / 2 Z3
1 0 0 "" /9
4 /2
@ 0 1 /7 " /4
A þ 7 Z3 ) @ 0 1 0 " 31 /13
A ¼ ðE j A / 1 Þ
1
0
7
"
"
0 0
1
1 " 5 /2 1
0 0 1 " 5 / 2
|fflfflfflffl{zfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
E
A /1
0
1
/9
4 /2
7A
Somit gilt: A / 1 ¼ @ 31 /13
5 /2
1
Kontrollmöglichkeit:
0
A . A /1 ¼ A /1 . A ¼ E
(Produkte mit dem Falk-Schema berechnen)
&
1.6 Rang einer Matrix
1.6.1 Definitionen
1.6.1.1 Unterdeterminanten einer Matrix
Werden in einer Matrix A vom Typ ðm; nÞ m / p Zeilen und n / p Spalten gestrichen, so heißt die Determinante der p-reihigen Restmatrix eine Unterdeterminante p-ter
Ordnung oder p-reihige Unterdeterminante von A.
1.6.1.2 Rang einer Matrix
Unter dem Rang einer Matrix A vom Typ ðm; nÞ wird die höchste Ordnung r aller
von null verschiedenen Unterdeterminanten von A verstanden. Symbolische Schreibweise: Rg ðAÞ ¼ r.
1.6.1.3 Elementare Umformungen einer Matrix
Der Rang r einer Matrix A ändert sich nicht, wenn sie den folgenden elementaren Umformungen unterworfen wird:
1. Zwei Zeilen (oder Spalten) werden miteinander vertauscht.
2. Die Elemente einer Zeile (oder Spalte) werden mit einer beliebigen von null verschiedenen Zahl multipliziert oder durch eine solche Zahl dividiert.
3. Zu einer Zeile (oder Spalte) wird ein beliebiges Vielfaches einer anderen Zeile (bzw.
anderen Spalte) addiert.
208
VII Lineare Algebra
1.6.2 Rangbestimmung einer Matrix
1.6.2.1 Rangbestimmung einer (m, n)-Matrix A unter Verwendung
von Unterdeterminanten
Wir beschreiben das Verfahren für den Fall m ) n. Ist jedoch m > n, so ist im folgenden die Zahl m durch die Zahl n zu ersetzen.
1. Der Rang r der Matrix A ist höchstens gleich m, d. h. r ) m. Man berechnet
daher zunächst die m-reihigen Unterdeterminanten von A. Gibt es unter ihnen wenigstens eine von null verschiedene Determinante, so ist r ¼ m.
2. Verschwinden aber sämtliche m-reihigen Unterdeterminanten von A, so ist r höchstens gleich m / 1. Es ist dann zu prüfen, ob es wenigstens eine von null verschiedene
ðm / 1Þ-reihige Unterdeterminante gibt. Ist dies der Fall, so ist r ¼ m / 1. Anderenfalls ist r höchstens gleich m / 2. Das beschriebene Verfahren wird dann solange
fortgesetzt, bis man auf eine von null verschiedene Unterdeterminante von A stößt. Die
Ordnung dieser Determinante ist der gesuchte Rang der Matrix A.
&
Beispiel
3
2
A ¼
0
3
4
1
2
2
)
m ¼ 2;
n ¼ 3
und somit
r ) 2.
"
"2
Es gibt eine von null verschiedene 2-reihige Unterdeterminante, z. B. ""
0
"
3 ""
¼ 8 (in der Matrix A wurde
4"
die 3. Spalte gestrichen). Die Matrix A besitzt damit den Rang r ¼ 2.
&
1.6.2.2 Rangbestimmung einer (m, n)-Matrix A mit Hilfe elementarer Umformungen
Die ðm; nÞ-Matrix A wird zunächst mit Hilfe elementarer Umformungen in die folgende
Trapezform gebracht ðbi i 6¼ 0 für i ¼ 1; 2; . . . ; rÞ:
0
bb11111 bb1212
B 0 b
B 0 b2222
B .
...
B ...
...
B ..
B
B 00 00
B
B
B
B 00 00
B
B 00 00
B ..
...
@ ...
...
.
00 00
...... bb11rr
...... bb22rr
...
...
...... bbrrrr
......
......
......
00
00
...
...
00
bb1;1,rrþ+11 bb1;1,rrþ+22 ...... bb11nn
bb2;2,rrþ+11 bb2;2,rrþ+22 ...... bb22nn
...
...
...
...
bbr;r,rrþ+11 bbr;r,rrþ+22 ...... bbrrnn
00
00
...
...
00
00
00
...
...
00
......
......
......
00
00
...
...
00j
1 9
>
>
>
C >
C =
C
C >
C >
>
C >
C ;
C
C
C 9
C >
C >
C =
C
A >
>
;
r Zeilen
ðm / rÞ Nullzeilen
Der Rang von A ist dann gleich der Anzahl r der nicht-verschwindenden Zeilen:
Rg ðAÞ ¼ r.
2 Determinanten
209
Beispiel
&
0
1
Wir bringen die (3,4)-Matrix A ¼ @ 2
/1
die gewünschte
0
1 3
A ¼@ 2 7
/1 0
Somit gilt:
3
7
0
/5
/8
11
1
0
7 A mit Hilfe elementarer Umformungen zunächst in
21
Trapezform und lesen aus dieser den Rang ab:
0
1
0
1
/5
0
1 3 /5
0
1
A
@
A
/8
7 / 2 Z1 ) 0 1
2
7
) @0
0
11 21 þ Z1
0 3
6 21 / 3 Z2
3
1
0
/5
2
0
1
0
7A
0
Nullzeile
Rg ðAÞ ¼ 2
&
2 Determinanten
Determinanten n-ter Ordnung (auch n-reihige Determinanten genannt) sind reelle Zahlen,
die man den n-reihigen quadratischen Matrizen aufgrund einer bestimmten Rechenvorschrift zuordnet.
Schreibweisen:
D;
det A;
j A j;
j ai k j;
"
"
"
"
"
"
"
"
"
a11
a21
..
.
an 1
a12
a22
..
.
an 2
...
...
...
a1 n
a2 n
..
.
an n
"
"
"
"
"
"
"
"
"
ai k :
Elemente der Determinante
ði; k ¼ 1; 2; . . . ; nÞ
2.1 Zweireihige Determinanten
Definition einer zweireihigen Determinante
Unter der Determinante einer 2-reihigen Matrix A ¼ ðaik Þ versteht man die reelle Zahl
"
" a11
"
" a21
"
a12 ""
¼ a11 a22 / a12 a21
a22 "
Berechnung einer 2-reihigen Determinante
"
" a11
"
"
"a
21
"
a12 ""
" ¼ a11 a22 / a12 a21
a22 "
///// Hauptdiagonale
/ / / Nebendiagonale
Regel: Der Wert einer 2-reihigen Determinante ist gleich dem Produkt der beiden Hauptdiagonalelemente minus dem Produkt der beiden Nebendiagonalelemente.
&
Beispiel
"
" 4
det A ¼ ""
/3
"
7 ""
¼ 4 . 8 / ð/3Þ . 7 ¼ 32 þ 21 ¼ 53
8"
&
210
VII Lineare Algebra
2.2 Dreireihige Determinanten
Definition einer dreireihigen Determinante
Unter der Determinante einer 3-reihigen Matrix A ¼ ðai k Þ versteht man die reelle Zahl
"
" a11
"
" a21
"
" a31
a12
a22
a32
a13
a23
a33
"
"
"
" ¼
"
"
¼ a11 a22 a33 þ a12 a23 a31 þ a13 a21 a32 / a13 a22 a31 / a11 a23 a32 / a12 a21 a33
Berechnung einer 3-reihigen Determinante nach der Regel von Sarrus
///// Hauptdiagonalprodukte
/ / / Nebendiagonalprodukte
:
D ¼ a11 a22 a33 þ a12 a23 a31 þ a13 a21 a32 / a13 a22 a31 / a11 a23 a32 / a12 a21 a33
Regel: Die Spalten 1 und 2 der Determinante werden nochmals rechts an die Determinante gesetzt. Den Determinantenwert erhält man dann, indem man die drei Hauptdiagonalprodukte (////Þ addiert und von dieser Summe die drei Nebendiagonalprodukte (/ / /) subtrahiert.
&
Beispiel
""
"1
"
det A ¼ "" 2
"
"6
/2
0
5
"
3 ""
"
1 "" ¼ ?
"
1"
det A ¼ 1 . 0 . 1 þ ð/ 2Þ . 1 . 6 þ 3 . 2 . 5 / 6 . 0 . 3 / 5 . 1 . 1 / 1 . 2 . ð/ 2Þ ¼
¼ 0 / 12 þ 30 / 0 / 5 þ 4 ¼ 17
&
2 Determinanten
211
2.3 Determinanten höherer Ordnung
2.3.1 Unterdeterminante Di k
Die aus einer n-reihigen Determinante D durch Streichen der i-ten Zeile und k-ten Spalte
hervorgehende ðn / 1Þ-reihige Determinante heißt Unterdeterminante Di k :
Di k
""
"
"
"
"
"
¼ ""
"
"
"
"
"
a11
a21
..
.
a12
a22
..
.
...
...
an 1
an 2
...
ai 1
..
.
ai 2
..
.
...
a1 k
a2 k
..
.
...
...
an k
...
ai k
..
.
...
""
"
"
"
"
"
"
ai n ""
"
... "
"
an n "
a1 n
a2 n
..
.
i-te Zeile
"
k-te Spalte
2.3.2 Algebraisches Komplement (Adjunkte) Ai k
Die Größe Ai k ¼ ð/ 1Þ i þ k . Di k heißt algebraisches Komplement oder Adjunkte des Elementes ai k in der Determinante D. Der Vorzeichenfaktor ð/ 1Þ i þ k kann nach der
Schachbrettregel bestimmt werden:
þ
/
þ
...
/
þ
/
...
þ
..
.
/
..
.
þ
..
.
...
Schachbrettregel: Der Vorzeichenfaktor von Ai k steht
im Schnittpunkt der i-ten Zeile mit
der k-ten Spalte.
2.3.3 Definition einer n-reihigen Determinante 2Þ
Der Wert einer n-reihigen Determinante D ¼ det A wird rekursiv nach der folgenden
„Entwicklungsformel“ berechnet („Entwicklung nach den Elementen der 1. Zeile“):
D ¼ det A ¼
A1 k :
n
P
k¼1
a1 k A1 k ¼ a11 A11 þ a12 A12 þ . . . þ a1 n A1 n
Algebraisches Komplement (Adjunkte) von a1 k in D
Prinzipiell lässt sich damit eine n-reihige Determinante durch wiederholte Anwendung der
Entwicklungsformel auf 3-reihige Determinanten zurückführen, die nach der Regel von
Sarrus berechnet werden können. Dieses Verfahren erweist sich jedoch in der Praxis als
ungeeignet, da die Anzahl der dabei anfallenden 3-reihigen Determinanten mit zunehmender Ordnung n der Determinante rasch ansteigt. Beispiel: Für n ¼ 5 sind 20, für
n ¼ 6 bereits 120 3-reihige Determinanten zu berechnen! Ein praktikables Rechenverfahren wird in Abschnitt 2.6 angegeben.
2Þ
Für eine 1-reihige Matrix A ¼ ðaÞ wird det A ¼ a festgesetzt.
212
VII Lineare Algebra
2.4 Laplacescher Entwicklungssatz
Eine n-reihige Determinante lässt sich nach den Elementen einer beliebigen Zeile oder
Spalte entwickeln (Laplacescher Entwicklungssatz):
Entwicklung nach den Elementen der i-ten Zeile
n
P
D ¼
ai k Ai k
ði ¼ 1; 2; . . . ; nÞ
k¼1
Entwicklung nach den Elementen der k-ten Spalte
n
P
ai k Ai k
ðk ¼ 1; 2; . . . ; nÞ
D ¼
i¼1
Ai k :
Algebraisches Komplement (Adjunkte) von ai k in D ðAi k ¼ ð/ 1Þ i þ k . Di k )
Di k :
ðn / 1Þ-reihige Unterdeterminante von D (siehe Abschnitt 2.3.1)
&
Beispiel
""
"
"
Wir entwickeln die 4-reihige Determinante D ¼ ""
"
"
1
4
9
8
2
0
0
1
0
/3
0
3
/1
2
4
1
""
"
"
" nach den Elementen der 3. Zeile:
"
"
"
D ¼ a31 A31 þ a32 A32 þ a33 A33 þ a34 A34 ¼ 9 A31 þ 4 A34
|{z}
|{z}
|{z}
|{z}
9
0
0
4
""
""
2
0
/1
"
"
A31 ¼ þ "" 0 /3
2 "" ¼ / 6 þ 0 þ 0 / 3 / 12 / 0 ¼ / 21
"1
3
1"
A34
""
"1
¼ / "" 4
"8
2
0
1
0
/3
3
""
"
" ¼ / ð0 / 48 þ 0 / 0 þ 3 / 24Þ ¼ 69
"
"
D ¼ 9 A31 þ 4 A34 ¼ 9 . ð/ 21Þ þ 4 . ð69Þ ¼ / 189 þ 276 ¼ 87
&
2.5 Rechenregeln für n-reihige Determinanten
Regel 1: Der Wert einer Determinante ändert sich nicht, wenn Zeilen und Spalten miteinander vertauscht werden („Stürzen“ einer Determinante):
det A ¼ det A T
Regel 2: Beim Vertauschen zweier Zeilen (oder Spalten) ändert eine Determinante ihr
Vorzeichen.
Regel 3: Werden die Elemente einer beliebigen Zeile (oder Spalte) mit einem Skalar l
multipliziert, so multipliziert sich die Determinante mit l.
Regel 4: Eine Determinante wird mit einem Skalar l multipliziert, indem man die Elemente einer beliebigen Zeile (oder Spalte) mit l multipliziert.
2 Determinanten
213
Regel 5: Besitzen die Elemente einer Zeile (oder Spalte) einen gemeinsamen Faktor l,
so darf dieser vor die Determinante gezogen werden:
Regel 6: Eine Determinante besitzt den Wert null, wenn sie eine der folgenden Bedingungen erfüllt:
1. Alle Elemente einer Zeile (oder Spalte) sind Nullen.
2. Zwei Zeilen (oder Spalten) sind gleich.
3. Zwei Zeilen (oder Spalten) sind zueinander proportional.
4. Eine Zeile (oder Spalte) ist als Linearkombination der übrigen Zeilen (bzw.
Spalten) darstellbar.
Regel 7: Der Wert einer Determinante ändert sich nicht, wenn man zu einer Zeile (oder
Spalte) ein beliebiges Vielfaches einer anderen Zeile (bzw. anderen Spalte)
addiert.
Regel 8: Für zwei n-reihige Matrizen A und B gilt das Multiplikationstheorem:
det ðA . BÞ ¼ ðdet AÞ . ðdet BÞ
Das heißt die Determinante eines Matrizenproduktes A . B ist gleich dem
Produkt der Determinanten der beiden Faktoren A und B.
Regel 9: Die Determinante einer n-reihigen Dreiecksmatrix A besitzt den Wert
det A ¼ a11 a22 . . . an n
Das heißt die Determinante einer Dreiecksmatrix ist gleich dem Produkt der
Hauptdiagonalelemente (gilt somit auch für eine Diagonalmatrix).
Regel 10: Für die Determinante der inversen Matrix von A gilt:
det ðA / 1 Þ ¼
Regel 11:
&
1
det A
ðdet A 6¼ 0Þ
det ðl AÞ ¼ l n . det A
Beispiel
ðl 2 RÞ
0
Mit den dreireihigen Matrizen
4
A ¼ @1
0
/2
3
1
1
5
7A
2
0
und
1
B ¼ @1
4
0
2
/1
1
3
5A
8
berechnen wir die
Determinante des Matrizenprodukt A . B unter Verwendung des Multiplikationstheorems (Regel 8):
"
" "
"
" 4 /2 5 " " 1
0 3 ""
"
" "
"
"
"
det ðA . BÞ ¼ ðdet AÞ . ðdet BÞ ¼ " 1
3 7"."1
2 5 "" ¼
"0
1 2 " " 4 /1 8 "
¼ ð24 þ 0 þ 5 / 0 / 28 þ 4Þ . ð16 þ 0 / 3 / 24 þ 5 / 0Þ ¼ 5 . ð/ 6Þ ¼ / 30
(Berechnung der beiden Determinanten nach der Regel von Sarrus)
&
214
VII Lineare Algebra
2.6 Regeln zur praktischen Berechnung einer n-reihigen Determinante
2.6.1 Elementare Umformungen einer n-reihigen Determinante
Der Wert einer n-reihigen Determinante ändert sich nicht, wenn man eine der folgenden
elementaren Umformungen vornimmt:
1. Ein den Elementen einer Zeile (oder Spalte) gemeinsamer Faktor l darf vor die Determinante gezogen werden (Regel 5).
2. Zu einer Zeile (oder Spalte) darf ein beliebiges Vielfaches einer anderen Zeile (bzw.
anderen Spalte) addiert werden (Regel 7).
3. Zwei Zeilen (oder Spalten) dürfen miteinander vertauscht werden, wenn man zugleich
das Vorzeichen der Determinante ändert (Folgerung aus Regel 2).
2.6.2 Reduzierung und Berechnung einer n-reihigen Determinante
Die Berechnung einer n-reihigen Determinante kann für n > 3 nach dem folgenden Schema erfolgen:
1. Mit Hilfe elementarer Umformungen werden zunächst die Elemente einer Zeile (oder
Spalte) bis auf ein Element zu Null gemacht.
2. Dann wird die n-reihige Determinante nach den Elementen dieser Zeile (oder Spalte)
entwickelt. Man erhält genau eine ðn / 1Þ-reihige Unterdeterminante.
3. Das unter 1. und 2. beschriebene Verfahren wird nun auf die ðn / 1Þ-reihige Unterdeterminante angewandt und führt zu einer ðn / 2Þ-reihigen Unterdeterminante. Durch
wiederholte Reduzierung gelangt man schließlich zu einer einzigen 3-reihigen Determinante, deren Wert dann nach der Regel von Sarrus berechnet wird.
Hinweis: Um in einer Zeile (bzw. Spalte) Nullen zu erzeugen, sind Spalten (bzw. Zeilen)
zu addieren.
&
Beispiel
"
" 1
"
" 2
Die 4-reihige Determinante det A ¼ ""
" /3
" /1
4
1
2
/5
3
/1
2
/4
2
/1
/2
1
"
"
"
"
"
"
"
"
lässt sich wie folgt mit Hilfe elementarer Um-
formungen auf eine 3-reihige Determinante zurückführen: Wir addieren zur zweiten, dritten und vierten Zeile
der Reihe nach das ð/ 2Þ-fache, 3-fache bzw. 1-fache der 1. Zeile und entwickeln die Determinante anschließend nach den Elementen der 1. Spalte (diese enthält 3 Nullen):
"
"
"
"
det A ¼ ""
"
"
1
0
0
0
4
/7
14
/1
3
/7
11
/1
2
/5
4
3
"
"
"
"
" /7
"
"
" ¼ 1 . " 14
"
"
"
" /1
"
/7
11
/1
/5
4
3
"
"
"
" ¼ / 231 þ 28 þ 70 / 55 / 28 þ 294 ¼ 78
"
"
(Berechnung der Determinante nach der Regel von Sarrus)
&
3 Lineare Gleichungssysteme
215
3 Lineare Gleichungssysteme
3.1 Grundbegriffe
3.1.1 Definition eines linearen Gleichungssystems
Ein aus m linearen Gleichungen mit n Unbekannten x1 ; x2 ; . . . ; xn bestehendes System
a11 x1 þ a12 x2 þ . . . þ a1 n xn ¼ c1
a21 x1 þ a22 x2 þ . . . þ a2 n xn ¼ c2
..
..
..
..
.
.
.
.
am 1 x1 þ am 2 x2 þ . . . þ am n xn ¼ cm
oder
Ax ¼ c
heißt lineares Gleichungssystem oder lineares ðm; nÞ-System.
Bezeichnungen:
aik :
A:
x:
c:
Koeffizienten des linearen Gleichungssystems ði ¼ 1; 2; . . . ; m; k ¼ 1; 2; . . . ; nÞ
Koeffizientenmatrix des Systems
Lösungsvektor
Spaltenvektor aus den absoluten Gliedern des Systems
0
a11
B a21
B
A ¼ B ..
@ .
am 1
a12
a22
..
.
am 2
...
...
...
1
a1 n
a2 n C
C
.. C ;
. A
am n
1
x1
B x2 C
B C
x ¼ B .. C ;
@ . A
0
xn
1
c1
B c2 C
B C
c ¼ B .. C
@ . A
0
cm
Erweiterte Koeffizientenmatrix (A j c)
0
"
1
a11 a12 . . . a1 n "" c1
"
B a21 a22 . . . a2 n " c2 C
C
B
ðA j cÞ ¼ B ..
..
.. "" .. C
@ .
.
. " . A
am 1 am 2 . . . am n " cm
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl} |{z}
A
c
Die erweiterte Koeffizientenmatrix ðA j cÞ spielt eine entscheidende Rolle bei der Untersuchung des Lösungsverhaltens eines linearen ðm; n)-Systems (siehe Abschnitt 3.2).
3.1.2 Spezielle lineare Gleichungssysteme
Homogenes System:
A x ¼ 0 (alle ci ¼ 0, d. h. c ¼ 0)
Inhomogenes System: A x ¼ c (nicht alle ci ¼ 0, d. h. c 6¼ 0)
Quadratisches System: m ¼ n
(auch ðn; nÞ-System genannt)
216
VII Lineare Algebra
3.2 Lösungsverhalten eines linearen (m, n)-Gleichungssystems
3.2.1 Kriterium für die Lösbarkeit eines linearen (m, n)-Systems A x = c
Rg ðAÞ ¼ Rg ðA j cÞ ¼ r
Ein lineares Gleichungssystem ist stets lösbar, wenn der Rang der Koeffizientenmatrix A
mit dem Rang der erweiterten Koeffizientenmatrix ðA j cÞ übereinstimmt.
Bei einem homogenen System A x ¼ 0 ist die Lösbarkeitsbedingung immer erfüllt. Ein
homogenes System ist daher stets lösbar.
3.2.2 Lösungsmenge eines linearen (m, n)-Systems A x = c
Lineares ðm; nÞ-System
Ax¼c
?
Rg ðAÞ ¼ Rg ðA j cÞ ¼ r
?
r ¼ n
Genau eine
Lösung
?
?
r < n
Unendlich viele
Lösungen mit
n / r Parametern
?
Rg ðAÞ ¼
6 Rg ðA j cÞ
?
Keine Lösung
Der im Schema durch den gestrichelten Weg angedeutete Fall kann nur für ein inhomogenes System eintreten (ein homogenes System ist stets lösbar). Im einzelnen gilt somit:
Homogenes lineares (m, n)-Gleichungssystem A x = 0
Das homogene System besitzt entweder genau eine Lösung, nämlich die triviale Lösung
x ¼ 0, oder unendlich viele Lösungen (darunter die triviale Lösung).
Inhomogenes lineares (m, n)-Gleichungssystem A x = c (c =/ 0)
Das inhomogene System besitzt entweder genau eine Lösung oder unendlich viele Lösungen oder keine Lösung.
&
Beispiele
(1)
Wir prüfen, ob das inhomogene lineare (2,3)-System
0 1
3
2 x
3 2
x1 / 2 x2 þ x3 ¼ 1
1 /2
1 @ 1A
1
oder
x2
¼
8
1
1 /4
x1 þ x2 / 4 x3 ¼ 8
x3
lösbar ist.
3 Lineare Gleichungssysteme
217
Dazu bestimmen wir den Rang der Matrizen A und ðA j cÞ mit Hilfe elementarer Umformungen:
3
ðA j cÞ ¼
3
)
1
0
/2
3
" 2
1 "" 1
/5 " 7
}
" 2
1 /2
1 "" 1
1
1 /4 " 8 / Z1
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
A
c
Die Matrizen ðA j cÞ und A besitzen jetzt Trapezform. Es ist Rg ðAÞ ¼ Rg ðA j cÞ ¼ 2. Das Gleichungssystem ist somit lösbar. Wegen n / r ¼ 3 / 2 ¼ 1 erhalten wir unendlich viele Lösungen
mit einem Parameter.
(2)
Wir zeigen, dass das inhomogene lineare (3,2)-System
0
1
0
1
1
2 3 2
4
x
@5
9A
¼ @ 9A
y
2 /3
/10
nicht lösbar ist:
"
1
0
4
1
2 ""
9 A / 5 Z1
ðA j cÞ ¼ @ 5
9 ""
2 /3 " /10 / 2 Z1
|fflfflfflffl{zfflfflfflffl} |{z}
A
c
0
1
) @0
0
2
/1
/7
"
1
"
4
"
" /11 A
"
" /18 / 7 Z2
0
1
) @0
0
2
/1
0
"
1
"
4
"
" /11 A
"
" 59
Die Matrizen ðA j cÞ und A besitzen jetzt Trapezform. Es ist Rg ðAÞ ¼ 2 (A enthält eine Nullzeile, grau unterlegt), aber Rg ðA j cÞ ¼ 3 und somit Rg ðAÞ 6¼ Rg ðA j cÞ: Das lineare Gleichungssystem ist daher nicht lösbar.
&
3.3 Lösungsverhalten eines quadratischen linearen Gleichungssystems
Für den Spezialfall eines quadratischen ðn; nÞ-Systems gilt das folgende Kriterium für die
Lösbarkeit und Lösungsmenge:
Lineares ðn; nÞ-System
Ax¼c
?
det A 6¼ 0
(A ist regulär)
?
Genau eine
Lösung
?
det A ¼ 0
(A ist singulär)
?
Rg ðAÞ ¼ Rg ðA j cÞ ¼ r < n
Unendlich viele Lösungen
mit n / r Parametern
?
Rg ðAÞ ¼
6 Rg ðA j cÞ
Keine Lösung
Ein homogenes lineares ðn; nÞ-System A x ¼ 0 ist stets lösbar. Für det A 6¼ 0 erhält
man als einzige Lösung die triviale Lösung x ¼ 0, im Falle det A ¼ 0 besitzt das
homogene System unendlich viele Lösungen mit n / r Parametern. Der durch den gestrichelten Weg angedeutete Fall kann nur für ein inhomogenes System eintreten.
218
&
VII Lineare Algebra
Beispiel
0
10 1
0
1
x1 / 2 x2 þ x3 ¼ 6
1 /2
1
x1
6
2 x1 þ x2 / x3 ¼ /3 oder @ 2
1 / 1 A @ x2 A ¼ @ / 3 A
/ x1 / 4 x2 þ 3 x3 ¼ 14
/1 /4
3
x3
14
"
"
" 1 /2
1 ""
"
det A ¼ "" 2
1 /1 "" ¼ 3 / 2 / 8 þ 1 / 4 þ 12 ¼ 2
" /1 /4
3"
Das vorliegende quadratische lineare Gleichungssystem besitzt wegen det A ¼ 2 6¼ 0 eine reguläre Koeffizientenmatrix A und somit genau eine Lösung.
&
3.4 Lösungsverfahren für ein lineares Gleichungssystem nach Gauß
(Gaußscher Algorithmus)
3.4.1 "quivalente Umformungen eines linearen (m, n)-Systems
Umformungen, die die Lösungsmenge eines linearen ðm; nÞ-Systems nicht verändern,
heißen äquivalente Umformungen. Zu ihnen gehören:
1. Zwei Gleichungen dürfen miteinander vertauscht werden.
2. Jede Gleichung darf mit einer beliebigen von Null verschiedenen Zahl multipliziert oder
durch eine solche Zahl dividiert werden.
3. Zu jeder Gleichung darf ein beliebiges Vielfaches einer anderen Gleichung addiert
werden.
3.4.2 Gaußscher Algorithmus
Ein lineares ðm; nÞ-Gleichungssystem A x ¼ c lässt sich stets mit Hilfe äquivalenter
Umformungen in ein äquivalentes gestaffeltes Gleichungssystem A * x ¼ c * vom Typ
*
*
*
*
*
a*
11 x1 þ a 12 x2 þ . . . þ a 1 r xr þ a 1; r þ 1 xr þ 1 þ . . . þ a 1 n xn ¼ c 1
*
*
*
*
a*
22 x2 þ . . . þ a 2 r xr þ a 2; r þ 1 xr þ 1 þ . . . þ a 2 n xn ¼ c 2
.
.
.
.
.
.
.
.
.
.
.
.
a *r r xr þ a *r; r þ 1 xr þ 1 þ . . . þ a *r n xn ¼ c *r
0
¼ c r*þ 1
0
¼ c r*þ 2
.
.
.
.
.
.
*
¼ cm
0
überführen ða *i i 6¼ 0 für i ¼ 1; 2; . . . ; rÞ, wobei gegebenenfalls auch Spaltenvertauschungen, d. h. Umnumerierungen der Unbekannten notwendig sind.
3 Lineare Gleichungssysteme
219
Es ist dann und nur dann lösbar, wenn c *r þ 1 ¼ c *r þ 2 ¼ . . . ¼ c *m ¼ 0 ist. Im Falle der
Lösbarkeit erhält man somit ein gestaffeltes Gleichungssystem mit r Gleichungen und n
Unbekannten, das sukzessiv von unten nach oben gelöst werden kann. Dabei sind noch
zwei Fälle zu unterscheiden:
1. Fall: r = n
Das gestaffelte System besteht aus n Gleichungen mit n Unbekannten und besitzt genau
eine Lösung.
2. Fall: r < n
Das gestaffelte System enthält weniger Gleichungen ðrÞ als Unbekannte ðnÞ. Daher sind
n / r der Unbekannten, z. B. xr þ 1 ; xr þ 2 ; . . . ; xn , frei wählbare Größen (Parameter).
Man erhält dann unendlich viele Lösungen mit n / r Parametern.
Beschreibung des Eliminationsverfahrens von Gauß
1. Im 1. Rechenschritt wird z. B. die Unbekannte x1 eliminiert, indem man zur i-ten Gleichung das / ðai 1 =a11 Þ-fache der 1. Gleichung addiert ða11 6¼ 0; i ¼ 2; 3; . . . ; mÞ.
Bei der Addition verschwindet dann jeweils x1 .
2. Das unter 1. beschriebene Verfahren wird jetzt auf das reduzierte Gleichungssystem,
bestehend aus m / 1 Gleichungen mit den n / 1 Unbekannten x2 ; x3 ; . . . ; xn , angewandt. Dadurch wird die nächste Unbekannte (z. B. x2 ) eliminiert (Voraussetzung:
a22 6¼ 0Þ. Nach insgesamt m / 1 Schritten bleibt eine Gleichung mit einer oder mehreren Unbekannten übrig.
3. Die Eliminationsgleichungen bilden dann zusammen mit der letzten Gleichung ein gestaffeltes lineares Gleichungssystem, aus dem sich die Unbekannten sukzessiv von unten
nach oben berechnen lassen.
4. Sollte bei einem Schritt die weiter oben genannte Voraussetzung (Diagonalelement
6¼ 0) nicht erfüllt sein, so muss eine Zeilenvertauschung vorgenommen werden, um zu
einem von Null verschiedenen Pivotelement zu gelangen. Der Prozeß endet, wenn eine
solche Vertauschung nicht mehr möglich ist.
Anmerkungen
(1)
(2)
Es spielt keine Rolle, in welcher Reihenfolge die Unbekannten eliminiert werden.
Den äquivalenten Umformungen eines linearen Gleichungssystems A x ¼ c entsprechen in der Matrizendarstellung elementare Zeilenumformungen in der erweiterten
Koeffizientenmatrix ðA j cÞ. Damit ergibt sich der folgende Lösungsweg:
1. Zunächst wird die erweiterte Koeffizientenmatrix ðA j cÞ mit Hilfe elementarer
Zeilenumformungen in die Trapezform ðA * j c *Þ gebracht (dies ist im Falle der
Lösbarkeit stets möglich).
2. Anschließend wird das äquivalente gestaffelte System A * x ¼ c * sukzessiv von
unten nach oben gelöst.
220
&
VII Lineare Algebra
Beispiele
(1)
Wir lösen das lineare (3,3)-Gleichungssystem
x1 / 2 x2 þ
2 x1 þ
6
0
x3 ¼ /3
@
x3 ¼
x2 /
oder
/ x1 / 4 x2 þ 3 x3 ¼ 14
1
2
/1
10 1
0
1
1
x1
6
A
@
A
@
/1
x2
¼ /3A
3
x3
14
/2
1
/4
mit Hilfe des Gaußschen Algorithmus. Das System besitzt wegen det A ¼ 2 6¼ 0 genau eine Lösung. Wir verwenden hier das „elementare“ Rechenschema mit Zeilensummenprobe (E : eliminierte
Gleichung; ci : Absolutglied; si : Zeilensumme):
x1
x2
E1
/ 2 . E1
x3
ci
si
1
/2
1
6
6
2
1
/1
/ 3
/ 1
/2
4
/2
/12
/12
/1
/4
3
14
12
1
/2
1
6
6
5
/3
/15
/13
/6
4
20
18
E1
E2
1;2 . E2
6
/3;6
/18
/15;6
0;4
2
2;4
Die grau unterlegten Zeilen
bilden das gesuchte gestaffelte
System.
Gestaffeltes System:
x1 / 2 x2 þ
6
)
x1 ¼ 1
5 x2 / 3 x3 ¼ /15
)
x2 ¼ 0
0;4 x3 ¼
)
x3 ¼ 5
Lösung:
(2)
x3 ¼
x1 ¼ 1 ;
2
x2 ¼ 0 ;
ðx1 ¼ 6 þ 2 x2 / x3 ¼ 6 þ 0 / 5 ¼ 1Þ
"
ð5 x2 ¼ / 15 þ 3 x3 ¼ / 15 þ 15 ¼ 0Þ
"
x3 ¼ 5
Ist das homogene lineare (4,3)-Gleichungssystem
x1 þ
0
x2 þ 2 x3 ¼ 0
x2 /
x3 ¼ 0
3 x1 þ 4 x2 þ 5 x3 ¼ 0
3 x1 þ 5 x2 þ 4 x3 ¼ 0
oder
1
B0
B
@3
3
1
1
4
5
1
0 1
0
2 0 1
x
1
B C
/1C
C @ x2 A ¼ B 0 C
@0A
5A
x3
4
0
nichttrivial lösbar?
Zunächst bringen wir die Koeffizientenmatrix A auf Trapezform:
0
0
1
0
1
1 1
2
1 1
2
1
B0
B 0 1 /1 C
B 0 1 /1 C
B
B
C
B
C
A ¼@
) @
) @
3 4
5 A / 3 Z1
0 1 /1 A / Z2
0
0
3 5
4 / 3 Z1
0 2 /2 / 2 Z2
1
1
0
0
1
2
/1 C
Co
0A
Nullzeilen
0
Es ist r ¼ Rg ðAÞ ¼ 2 (A enthält 2 Nullzeilen, grau unterlegt), aber n ¼ 3, d. h. r < n. Das
homogene System ist somit nichttrivial lösbar. Das gestaffelte Gleichungssystem
x1 þ x2 þ 2 x3 ¼ 0
x2 /
wird gelöst durch
x3 ¼ 0
x1 ¼ / 3 l;
x2 ¼ l;
x3 ¼ l
ðx3 wurde als Parameter gewählt; l 2 RÞ.
&
3 Lineare Gleichungssysteme
221
3.5 Cramersche Regel
Ein quadratisches lineares ðn; nÞ-Gleichungssystem A x ¼ c mit regulärer Koeffizientenmatrix A besitzt die eindeutig bestimmte Lösung
xi ¼
Di
D
ði ¼ 1; 2; . . . ; nÞ
(Cramersche Regel; nur für kleines n praktikabel).
D:
Di :
Koeffizientendeterminante (D ¼ det A 6¼ 0Þ
Hilfsdeterminante, die aus D hervorgeht, indem man die i-te Spalte durch die Absolutglieder c1 ; c2 ; . . . ; cn des Gleichungsystems ersetzt.
&
Beispiel
Das quadratische lineare Gleichungssystem
2 x1 þ
x1 /
x2 þ
x3 ¼
5 x1 þ 2 x2 þ 4 x3 ¼
0
2
x2 þ 3 x3 ¼ /7
1
oder
2
@1
5
1
/1
2
10 1
0
1
1
x1
2
3 A @ x2 A ¼ @ / 7 A
4
x3
1
besitzt eine reguläre Koeffizientenmatrix A und ist somit eindeutig lösbar:
"
"
"2
1 1 ""
"
"
D ¼ det A ¼ " 1 /1 3 "" ¼ / 8 þ 15 þ 2 þ 5 / 12 / 4 ¼ / 2 6¼ 0
"5
2 4"
Berechnung der benötigten Hilfsdeterminanten (nach der Regel von Sarrus):
"
"
"
"
"
"2
"2
" 2
2 1 ""
1 1 ""
"
"
"
"
"
"
"
D1 ¼ " /7 /1 3 " ¼ / 2 ;
D3 ¼ "" 1
D2 ¼ " 1 /7 3 " ¼ / 4 ;
"
"5
"
"
" 1
5
1 4
2 4
Lösung:
x1 ¼
D1
/2
¼
¼ 1;
D
/2
x2 ¼
D2
/4
¼
¼ 2;
D
/2
x3 ¼
1
/1
2
2
/7
1
D3
4
¼
¼ /2
D
/2
"
"
"
" ¼ 4
"
"
&
3.6 Lineare Unabhängigkeit von Vektoren
n Vektoren a1 ; a2 ; . . . ; an aus dem m-dimensionalen Raum R m heißen linear unabhängig, wenn die lineare Vektorgleichung
l1 a1 þ l2 a2 þ . . . þ ln an ¼ 0
nur für l1 ¼ l2 ¼ . . . ¼ ln ¼ 0 erfüllt werden kann. Verschwinden jedoch nicht alle
Koeffizienten in dieser Gleichung, so heißen die Vektoren linear abhängig. Im Falle der
linearen Abhängigkeit gibt es also mindestens einen von null verschiedenen Koeffizienten.
Enthält das Vektorsystem a1 ; a2 ; . . . ; an den Nullvektor oder zwei gleiche (oder kollineare)
Vektoren oder ist mindestens einer der Vektoren als Linearkombination der übrigen darstellbar, so sind die Vektoren linear abhängig.
222
VII Lineare Algebra
Kriterium für linear unabhängige Vektoren
Die n Vektoren a1 ; a2 ; . . . ; an des Raumes R m werden zu einer Matrix A vom Typ
ðm; nÞ zusammengefaßt. Der Rang r dieser Matrix entscheidet dann darüber, ob die Vektoren linear unabhängig sind oder nicht. Es gilt:
r ¼ n
, linear unabhängig
r < n
, linear abhängig
Ist A quadratisch, d. h. liegen n Vektoren des R n vor, so gelten folgende Aussagen:
1. A ist regulär, d. h. det A 6¼ 0
,
linear unabhängig
2. A ist singulär, d. h. det A ¼ 0
, linear abhängig
3. Im R n gibt es maximal n linear unabhängige Vektoren. Mehr als n Vektoren
sind immer linear abhängig.
&
Beispiel
0 1
1
a1 ¼ @ 0 A ;
1
"
"1
"
det A ¼ "" 0
"1
0 1
2
a2 ¼ @ 1 A ;
3
2
1
3
4
1
1
0 1
4
a3 ¼ @ 1 A
1
0
)
A ¼ ða1
"
"
"
" ¼ 1 þ 2 þ 0 / 4 / 3 / 0 ¼ / 4 6¼ 0
"
"
)
1
a3 Þ ¼ @ 0
1
a2
A
2
1
3
1
4
1A
1
ist regulär
Die drei Vektoren des 3-dimensionalen Raumes sind daher linear unabhängig.
&
4 Komplexe Matrizen
4.1 Definition einer komplexen Matrix
Eine ðm; nÞ-Matrix A mit komplexen Elementen ai k ¼ bi k þ j . ci k heißt komplexe
Matrix ðbi k ; ci k 2 R; j: imaginäre EinheitÞ:
A ¼ ðai k Þ ¼ ðbi k þ j . ci k Þ ¼ ðbi k Þ þ j . ðci k Þ ¼ B þ j . C
'
B ¼ ðbi k Þ: Realteil von A ðbi k 2 RÞ
i ¼ 1; 2; . . . ; m; k ¼ 1; 2; . . . ; n
C ¼ ðci k Þ: Imaginärteil von A ðci k 2 RÞ
B und C sind reelle Matrizen vom gleichen Typ wie A.
&
Beispiel
3
1 þ 2j
A ¼
4 / 3j
2 þ 2j
5/j
2
3
¼
1
4
2
5
2
3
þ
2j
/3 j
2j
/j
2
3
¼
2
3
2
1 2
2
2
þj
¼ Bþj.C
4 5
/3 /1
|fflffl{zfflffl}
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
B
C
&
4 Komplexe Matrizen
223
4.2 Rechenoperationen und Rechenregeln für komplexe Matrizen
Die für reelle Matrizen geltenden Rechenoperationen, Rechenregeln und Aussagen lassen
sich sinngemäß auch auf komplexe Matrizen übertragen (siehe hierzu Abschnitt 1):
1. Komplexe Matrizen vom gleichen Typ werden elementweise addiert und subtrahiert.
2. Die Multiplikation einer komplexen Matrix mit einem (reellen oder komplexen) Skalar
erfolgt elementweise.
3. Zwei komplexe Matrizen werden wie im Reellen multipliziert, indem man die Zeilenvektoren des linken Faktors der Reihe nach skalar mit den Spaltenvektoren des rechten
Faktors multipliziert (unter den in Abschnitt 1.3.3 genannten Voraussetzungen).
4. Spiegelt man die Elemente einer komplexen Matrix A an der Hauptdiagonalen, so erhält man ihre Transponierte A T .
5. Für eine quadratische komplexe Matrix lässt sich wie im Reellen eine Determinante
bilden, die i. Allg. jedoch einen komplexen Wert besitzen wird.
&
Beispiel
Matrizenprodukt C ¼ A . B (Falk-Schema, siehe Abschnitt 1.3.3):
B
A
j
5/j
c11 ¼ ð1 þ 2 jÞ j þ ð3 / jÞ 2 ¼
2
1/j
¼ j þ 2 j2 þ 6 / 2 j ¼
¼ j / 2 þ 6 / 2j ¼ 4 / j
1 þ 2j
3/j
4/
j
9 þ 5j
2 / 2j
1þj
4 þ 4j
10 / 12 j
C ¼ A.B
analog: c12 , c21 , c22
&
4.3 Konjugiert komplexe Matrix
Die Matrixelemente ai k ¼ bi k þ j . ci k werden durch die konjugiert komplexen Elemente
a *i k ¼ bi k / j . ci k ersetzt:
A * ¼ ða *i k Þ ¼ ðbi k þ j . ci k Þ * ¼ ðbi k / j . ci k Þ ¼ ðbi k Þ / j . ðci k Þ
bzw.
A * ¼ ðB þ j . CÞ * ¼ B / j . C
Der !bergang A ! A * wird als Konjugation bezeichnet (formal: j ! / jÞ.
Rechenregeln
ðA *Þ * ¼ A ;
&
ðA1 þ A2 Þ * ¼ A *1 þ A *2 ;
ðA1 . A2 Þ * ¼ A *1 . A *2
Beispiel
3
2
3
2
j!/j
1þj
5
1/j
5
A ¼
/////! A * ¼
2 / j 3 / 2j
2 þ j 3 þ 2j
&
224
VII Lineare Algebra
4.4 Konjugiert transponierte Matrix
Die komplexe Matrix A ¼ ðai k Þ wird zunächst konjugiert, dann transponiert:
A
Konjugieren
! A*
ai k ! a *i k ! a *k i
)
Transponieren
! ðA *Þ T ¼ A
ai k ¼ a *k i
Die Operationen „Konjugieren“ und „Transponieren“ sind vertauschbar: ðA *Þ
T
¼ ðA T Þ *
Rechenregeln
A ¼ A;
ð A1 þ A2 Þ ¼ A1 þ A2 ;
ð A1 . A2 Þ ¼ A2 . A1
Beispiel
3
2
3
3
2
j!/j
1 / j 2 / 3j
1/ j
1 þ j 2 þ 3j
! ðA *Þ T ¼ A ¼
A ¼
/////! A * ¼
4þj
5
2 / 3j
4/j
5
&
4þj
2
5
&
4.5 Spezielle komplexe Matrizen
4.5.1 Hermitesche Matrix
Eine n-reihige komplexe Matrix A ¼ ðai k Þ heißt hermitesch, wenn
A ¼ A
oder
ai k ¼ a *k i
für alle i; k gilt.
Eigenschaften
(1)
Alle Hauptdiagonalelemente ai i sind reell.
(2)
Die komplexe Matrix A ¼ B þ j . C ist dann und nur dann hermitesch, wenn der
Realteil B symmetrisch und der Imaginärteil C schiefsymmetrisch ist.
(3)
Die Determinante einer hermiteschen Matrix ist reell.
(4)
Im Reellen fallen die Begriffe „hermitesch“ und „symmetrisch“ zusammen.
4.5.2 Schiefhermitesche Matrix
Eine n-reihige komplexe Matrix A ¼ ðai k Þ heißt schiefhermitesch, wenn
A ¼ /A
oder
für alle i; k gilt.
ai k ¼ / a *k i
5 Eigenwertprobleme
225
Eigenschaften
(1)
Alle Hauptdiagonalelemente ai i sind imaginär.
(2)
Eine komplexe Matrix A ¼ B þ j . C ist dann und nur dann schiefhermitesch,
wenn der Realteil B schiefsymmetrisch und der Imaginärteil C symmetrisch ist.
(3)
Im Reellen fallen die Begriffe „schiefhermitesch“ und „schiefsymmetrisch“ zusammen.
4.5.3 Unitäre Matrix
Eine n-reihige komplexe Matrix A ¼ ðai k Þ heißt unitär, wenn
A.A ¼ E
gilt (E ist die n-reihige Einheitsmatrix).
Eigenschaften
(1)
A ist regulär, die Inverse A / 1 existiert somit und es gilt A / 1 ¼ A. Die Inverse A / 1 ist ebenfalls unitär. Die Matrizen A und A sind kommutativ:
A . A ¼ A . A ¼ E.
(2)
Es ist stets j det A j ¼ 1.
(3)
Im Reellen fallen die Begriffe „unitär“ und „orthogonal“ zusammen.
(4)
Das Produkt unitärer Matrizen ist immer unitär.
5 Eigenwertprobleme
5.1 Eigenwerte und Eigenvektoren einer quadratischen Matrix
Ist A eine n-reihige (reelle oder komplexe) Matrix und E die n-reihige Einheitsmatrix,
so wird durch die Matrizengleichung
Ax ¼ lx
oder
ðA / l EÞ x ¼ 0
ein sog. n-dimensionales Eigenwertproblem beschrieben. Diese auch als Eigenwertgleichung bezeichnete Gleichung repräsentiert ein homogenes lineares Gleichungssystem mit
dem noch unbekannten Parameter l.
Bezeichnungen:
l:
x 6¼ 0:
A / l E:
Eigenwert der Matrix A
Eigenvektor der Matrix A zum Eigenwert l
Charakteristische Matrix von A
226
VII Lineare Algebra
Die Eigenwerte und Eigenvektoren lassen sich schrittweise wie folgt berechnen:
1. Die Eigenwerte sind die Lösungen der sog. charakteristischen Gleichung
det ðA / l EÞ ¼ 0
(algebraische Gleichung n-ten Grades mit n Lösungen l 1 ; l 2 ; . . . ; l n ).
2. Einen zum Eigenwert l i gehörenden Eigenvektor x i erhält man als Lösungsvektor
des homogenen linearen Gleichungssystems
ðA / l i EÞ x i ¼ 0
ði ¼ 1; 2; . . . ; nÞ
Er wird üblicherweise in der normierten Form angegeben. Bei einem mehrfachen
Eigenwert können auch mehrere Eigenvektoren auftreten, siehe weiter unten.
Die Eigenwerte der Matrix A sind also die Nullstellen des charakteristischen Polynoms
p ðlÞ ¼ det ðA / l EÞ.
Die Eigenwerte und Eigenvektoren besitzen die folgenden Eigenschaften:
1. Die Spur der Matrix A ist gleich der Summe aller Eigenwerte:
Sp ðAÞ ¼ l 1 þ l 2 þ . . . þ l n
2. Die Determinante von A ist gleich dem Produkt aller Eigenwerte:
det A ¼ l 1 l 2 . . . l n
3. Sind alle Eigenwerte voneinander verschieden, so gehört zu jedem Eigenwert ein
Eigenvektor, der bis auf einen beliebigen von Null verschiedenen konstanten Faktor eindeutig bestimmt ist. Die n Eigenvektoren werden üblicherweise normiert
und sind linear unabhängig.
4. Tritt ein Eigenwert dagegen k-fach auf, so gehören zu diesem Eigenwert mindestens
ein, höchstens aber k linear unabhängige Eigenvektoren.
5. Die zu verschiedenen Eigenwerten gehörenden Eigenvektoren sind immer linear unabhängig.
Ist A eine reguläre Matrix, so sind alle Eigenwerte von null verschieden (und umgekehrt).
Die Kehrwerte der Eigenwerte einer regulären Matrix A sind die Eigenwerte der zugehörigen inversen Matrix A /1 .
&
Beispiel
3
Wie lauten die Eigenwerte und Eigenvektoren dieser Matrix A ¼
3
Charakteristische Matrix: A / l E ¼
/2
/5
1
4
2
3
/l
1
0
0
1
/2
/5
1
4
2
3
¼
2
?
/2 / l
/5
1
4/l
2
5 Eigenwertprobleme
227
Charakteristische Gleichung mit Lösungen:
"
"
" /2 / l
/5 "
" ¼ ð/2 / lÞ ð4 / lÞ þ 5 ¼ l 2 / 2 l / 3 ¼ 0
det ðA / l EÞ ¼ ""
1
4/l"
l1 ¼ /1 ;
)
l2 ¼ 3
Eigenwerte der Matrix A:
l1 ¼ /1 ;
l2 ¼ 3
Berechnung des Eigenvektors zum Eigenwert l1 ¼ /1: ðA / l1 EÞ x ¼ ðA þ EÞ x ¼ 0
3
23 2
3 2
'
/1 /5
x1
0
/ x1 / 5 x2 ¼ 0
¼
oder
) x1 ¼ / 5 x2
1
5
x2
0
x1 þ 5 x2 ¼ 0
Lösung (x2 ¼ a gesetzt mit a 2 R):
Normierter Eigenvektor:
1
~x1 ¼ pffiffiffiffiffi
26
3
x1 ¼ /5 a ;
2
/5
x2 ¼ a
1
Analog wird der (normierte) Eigenvektor zum Eigenwert l2 ¼ 3 bestimmt:
1
~
x2 ¼ pffiffiffi
2
3
/1
1
2
.
Ergebnis: Das 2-dimensionale Eigenwertproblem führt zu zwei verschiedenen Eigenwerten l1 ¼ /1 und
l2 ¼ 3, die zugehörigen Eigenvektoren ~x1 und ~
x2 sind daher linear unabhängig.
&
5.2 Eigenwerte und Eigenvektoren spezieller n-reihiger Matrizen
Bei einer Diagonal- bzw. Dreiecksmatrix
Die Eigenwerte sind identisch mit den Hauptdiagonalelementen: li ¼ ai i ði ¼ 1; 2; . . . ; nÞ
Bei einer symmetrischen Matrix
Die Eigenwerte und Eigenvektoren einer n-reihigen symmetrischen Matrix A besitzen die
folgenden Eigenschaften:
1. Alle n Eigenwerte sind reell.
2. Es gibt insgesamt genau n linear unabhängige Eigenvektoren.
3. Zu jedem einfachen Eigenwert gehört genau ein linear unabhängiger Eigenvektor, zu
jedem k-fachen Eigenwert dagegen genau k linear unabhängige Eigenvektoren.
4. Eigenvektoren, die zu verschiedenen Eigenwerten gehören, sind orthogonal.
Bei einer hermiteschen Matrix
Die Eigenwerte und Eigenvektoren einer n-reihigen hermiteschen Matrix A besitzen die
folgenden Eigenschaften:
1. Alle n Eigenwerte sind reell.
2. Es gibt insgesamt genau n linear unabhängige Eigenvektoren.
3. Zu jedem einfachen Eigenwert gehört genau ein linear unabhängiger Eigenvektor, zu
jedem k-fachen Eigenwert dagegen stets k linear unabhängige Eigenvektoren.
228
VIII Komplexe Zahlen und Funktionen
1 Darstellungsformen einer komplexen Zahl
1.1 Algebraische oder kartesische Form
Im(z)
z ¼ x þ jy
oder
z ¼ x þ yj
P(z) = (x;y)
y
j: Imaginäre Einheit 1Þ mit j 2 ¼ / 1
x : Realteil von z ðRe ðzÞ ¼ xÞ
y: Imaginärteil von z ðIm ðzÞ ¼ yÞ
a)
Eine komplexe Zahl z ¼ x þ j y lässt sich
in der Gaußschen Zahlenebene durch einen
Bildpunkt P ðzÞ ¼ ðx; yÞ (Bild a)) oder
durch einen vom Koordinatenursprung 0
zum Bildpunkt P ðzÞ gerichteten Zeiger
z ¼ x þ j y (unterstrichene komplexe Zahl,
Bild b)) bildlich darstellen. Die Länge des
Zeigers heißt der Betrag j z j der komplexen
Zahl z ¼ x þ j y:
x
Im(z)
z = x + jy
y
z
b)
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
jzj ¼ x2 þ y2
Sonderfälle
Re(z)
Re(z)
Im(z)
Reelle Zahl: Im ðzÞ ¼ 0
z = jy (Imaginäre Zahl)
z ¼ x þ j0 0 x
Imaginäre Zahl: Re ðzÞ ¼ 0
z=x
(Reelle Zahl)
z ¼ 0 þ jy 0 jy
Re(z)
Menge der komplexen Zahlen
C ¼
1Þ
-
z j z ¼ x þ jy
mit
x; y 2 R
,
Das in der reinen Mathematik übliche Symbol i für die imaginäre Einheit wird in der Technik nicht verwendet,
um Verwechslungen mit der Stromstärke i zu vermeiden.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_8
1 Darstellungsformen einer komplexen Zahl
229
Gleichheit zweier komplexer Zahlen
Zwei komplexe Zahlen z1 und z2 heißen genau dann gleich, z1 ¼ z2 , wenn ihre Bildpunkte zusammenfallen, d. h. x1 ¼ x2 und y1 ¼ y2 ist ( !bereinstimmung im Realteil
und im Imaginärteil).
Konjugiert komplexe Zahl
Im(z)
Die zu z ¼ x þ j y konjugiert komplexe
Zahl z * liegt spiegelsymmetrisch zur reellen
Achse. z und z * unterscheiden sich also in
ihrem Imaginärteil durch das Vorzeichen:
z = x + jy
y
x
z * ¼ ðx þ j yÞ * ¼ x / j y
Realteil und Betrag bleiben also erhalten:
Re ðz *Þ ¼ Re ðzÞ ¼ x ;
jz*j ¼ jzj
–y
Re(z)
z = x – jy
Ferner gilt:
ðz *Þ * ¼ z ;
z ¼ z*
,
z ist reell
In der reinen Mathematik verwendet man das Symbol !z statt z *.
1.2 Polarformen
In der Polarform erfolgt die Darstellung einer komplexen Zahl durch die Polarkoordinaten
r und j, wobei die Winkelkoordinate j unendlich vieldeutig ist. Man beschränkt sich
bei der Winkelangabe daher meist auf den im Intervall ½0; 2 pÞ gelegenen Hauptwert
(siehe I.9.1.2). Im technischen Bereich wird als Winkel j oft der kleinstmögliche Drehwinkel angegeben (1. und 2. Quadrant: Drehung im Gegenuhrzeigersinn; 3. und 4. Quadrant: Drehung im Uhrzeigersinn). Die Winkel liegen dann im Intervall / p < j ) p.
1.2.1 Trigonometrische Form
Im(z)
z ¼ r ðcos j þ j . sin jÞ
r:
j:
z = r(cos f + j · sin f)
r
Betrag von z ðr ¼ j z jÞ
Argument ( Winkel, Phasenwinkel) von z
f
Konjugiert komplexe Zahl:
z * ¼ r ðcos j / j . sin jÞ
Re(z)
1.2.2 Exponentialform
Im(z)
z ¼ r . e jj
r:
j:
z = r·e jf
Betrag von z ðr ¼ j z jÞ
Argument ( Winkel, Phasenwinkel) von z
Konjugiert komplexe Zahl:
z * ¼ r . e /jj
r
f
Re(z)
230
VIII Komplexe Zahlen und Funktionen
Eulersche Formeln
e j j ¼ cos j þ j . sin j
Spezielle Werte:
e / j j ¼ cos j / j . sin j
1 ¼ 1 . e j0 ;
/ 1 ¼ 1 . e jp ;
j ¼ 1.e
j
p
2
;
/j ¼ 1 . e
3
j p
2
1.3 Umrechnungen zwischen den Darstellungsformen
1.3.1 Polarform ! Kartesische Form
Die Umrechnung aus der Polarform z ¼ r . e j j ¼ r ðcos j þ j . sin jÞ in die kartesische Form z ¼ x þ j y geschieht wie folgt („ausmultiplizieren“):
z ¼ r . e j j ¼ r ðcos j þ j . sin jÞ ¼ r . cos j þ j . r . sin j ¼ x þ j y
|fflfflfflfflffl{zfflfflfflfflffl}
|fflfflfflfflffl{zfflfflfflfflffl}
x
y
&
Beispiel
Wir bringen die komplexe Zahl z ¼ 3 . e j 30
z ¼ 3.e
j 30 "
"
"
auf die kartesische Form:
"
¼ 3 ðcos 30 þ j . sin 30 Þ ¼ 3 . cos 30 " þ j . 3 . sin 30 " ¼ 2;598 þ 1;5 j
&
1.3.2 Kartesische Form ! Polarform
Die Umrechnung aus der kartesischen Form z ¼ x þ j y in eine der Polarformen
z ¼ r ðcos j þ j . sin jÞ oder z ¼ r . e j j erfolgt mit Hilfe der Transformationsgleichungen
r ¼ jzj ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 þ y2,
tan j ¼
y
,
x
sin j ¼
y
,
r
cos j ¼
x
r
Winkelbestimmung (Hauptwert): Anhand einer Lageskizze oder nach den folgenden vom
Quadranten abhängigen Formeln (siehe hierzu auch I.9.1.3):
Quadrant
I
II, III
IV
j ¼
arctan ðy=xÞ
arctan ðy=xÞ þ p
arctan ðy=xÞ þ 2 p
Beim Gradmaß muss p durch 180 " ersetzt werden.
&
Beispiel
Wir bringen die im zweiten Quadrant liegende
komplexe Zahl z ¼ / 4 þ 3 j in die Polarform:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ j z j ¼ ð/ 4Þ 2 þ 3 2 ¼ 5
Im(z)
z = –4 + 3 j
3
tan j ¼
¼ / 0;75 )
/4
j ¼ arctan ð/ 0;75Þ þ p ¼ 2;498 ' 143;1"
z ¼ / 4 þ 3 j ¼ 5 ðcos 2;498 þ j . sin 2;498Þ ¼
¼ 5 . e j 2;498
3
r
f
–4
Re(z)
&
2 Grundrechenarten für komplexe Zahlen
231
2 Grundrechenarten für komplexe Zahlen
2.1 Addition und Subtraktion komplexer Zahlen
z1 + z2 ¼ ðx1 þ j y1 Þ + ðx2 þ j y2 Þ ¼ ðx1 + x2 Þ þ j ðy1 + y2 Þ
Regel: Zwei komplexe Zahlen werden addiert bzw. subtrahiert, indem man ihre Real- und
Imaginärteile (jeweils für sich getrennt) addiert bzw. subtrahiert.
Hinweis: Addition und Subtraktion sind nur in der kartesischen Form durchführbar.
Geometrische Deutung:
Im(z)
Die Zeiger z 1 und z 2 werden nach der aus
der Vektorrechnung bekannten Parallelogrammregel geometrisch addiert bzw. subtrahiert.
z1 + z 2
z2
Rechenregeln
Kommutativgesetz
z1 þ z2 ¼ z2 þ z1
Assoziativgesetz
z1 þ ðz2 þ z3 Þ ¼ ðz1 þ z2 Þ þ z3
z1 – z 2
z1
Re(z)
2.2 Multiplikation komplexer Zahlen
In kartesischer Form
z1 . z2 ¼ ðx1 þ j y1 Þ . ðx2 þ j y2 Þ ¼ ðx1 x2 / y1 y2 Þ þ j ðx1 y2 þ x2 y1 Þ
Regel: Wie im Reellen wird jeder Summand der ersten Klammer mit jedem Summand der
zweiten Klammer unter Beachtung von j 2 ¼ / 1 multipliziert.
&
Beispiel
ð3 / 4 jÞ . ð2 þ 5 jÞ ¼ 6 þ 15 j / 8 j / 20 j 2 ¼ 6 þ 15 j / 8 j þ 20 ¼ 26 þ 7 j
|ffl{zffl}
/ 20
&
In der Polarform
z1 . z2 ¼ ½ r1 ðcos j1 þ j . sin j1 Þ% . ½ r2 ðcos j2 þ j . sin j2 Þ% ¼
¼ ðr1 r2 Þ . ½ cos ðj1 þ j2 Þ þ j . sin ðj1 þ j2 Þ%
z1 . z2 ¼ ðr1 . e j j1 Þ . ðr2 . e j j2 Þ ¼ ðr1 r2 Þ . e j ðj1 þ j2 Þ
Regel: Zwei komplexe Zahlen werden multipliziert, indem man ihre Beträge multipliziert
und ihre Argumente (Winkel, Phasenwinkel) addiert.
232
VIII Komplexe Zahlen und Funktionen
Geometrische Deutung:
Im(z)
Der Zeiger z 1 ¼ r1 . e
streckung unterworfen:
j j1
z 2 · z1
wird einer Dreh-
1. Drehung des Zeigers um den Winkel j2
im positiven Drehsinn (Gegenuhrzeigersinn) falls j2 > 0. Für j2 < 0 erfolgt
die Drehung im negativen Drehsinn (Uhrzeigersinn).
r2 · r1
r1
f2
2. Streckung des Zeigers auf das r2 -fache.
&
r1
z1
f1
Re(z)
Beispiel
"
"
ð3 . e j 30 Þ . ð5 . e j 80 Þ ¼ ð3 . 5Þ . e j ð30
"
þ 80 " Þ
"
¼ 15 . e j 110 ¼ 15 ðcos 110 " þ j . sin 110 " Þ ¼
¼ 15 . cos 110 " þ ð15 . sin 110 " Þ j ¼ / 5;130 þ 14;095 j
&
Rechenregeln
Kommutativgesetz
Assoziativgesetz
Distributivgesetz
z1 z2 ¼ z2 z1
z1 ðz2 z3 Þ ¼ ðz1 z2 Þ z3
z1 ðz2 þ z3 Þ ¼ z1 z2 þ z1 z3
Formeln
(1)
z . z* ¼ x2 þ y2 ¼ jzj2
(2)
Potenzen von j:
j 4 n ¼ 1;
j 2 ¼ / 1;
j 4 n þ 1 ¼ j;
)
jzj ¼
j 3 ¼ / j;
j 4 n þ 2 ¼ / 1;
qffiffiffiffiffiffiffiffiffiffiffiffi
z . z*
j 4 ¼ 1;
j 5 ¼ j;
j 4nþ3 ¼ / j
usw.
ðn 2 Z)
2.3 Division komplexer Zahlen
In kartesischer Form
z1
x1 þ j y1
ðx1 þ j y1 Þ . ðx2 / j y2 Þ
x1 x2 þ y1 y2
x2 y1 / x1 y2
¼
¼
¼
þj
2
2
z2
x2 þ j y2
ðx2 þ j y2 Þ . ðx2 / j y2 Þ
x2 þ y2
x 22 þ y 22
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
Regel: Zähler und Nenner des Quotienten werden zunächst mit dem konjugiert komplexen
Nenner, d. h. der Zahl z *2 ¼ x2 / j y2 multipliziert (dadurch wird der Nenner reell ).
Ausnahme: Die Division durch die Zahl 0 ist (wie im Reellen) verboten!
&
Beispiel
4 / 2j
ð4 / 2 jÞ ð6 / 8 jÞ
24 / 32 j / 12 j þ 16 j 2
24 / 32 j / 12 j / 16
¼
¼
¼
¼
6 þ 8j
ð6 þ 8 jÞ ð6 / 8 jÞ
36 / 64 j 2
36 þ 64
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
3. Binom
¼
8 / 44 j
8
44
¼
/
j ¼ 0;08 / 0;44 j
100
100
100
&
3 Potenzieren
233
In der Polarform
3 2
z1
r1 ðcos j1 þ j . sin j1 Þ
r1
¼
¼
½ cos ðj1 / j2 Þ þ j . sin ðj1 / j2 Þ%
r2 ðcos j2 þ j . sin j2 Þ
z2
r2
3 2
z1
r1 . e j j1
r1
¼
¼
. e j ðj1 / j2 Þ
r2 . e j j2
z2
r2
Regel: Zwei komplexe Zahlen werden dividiert, indem man ihre Beträge dividiert und
ihre Argumente (Winkel, Phasenwinkel) subtrahiert.
Geometrische Deutung:
z1
Im(z)
Der Zeiger z 1 ¼ r1 . e j j1 wird wie folgt
einer Drehstreckung unterworfen:
r1
1. Zurückdrehung des Zeigers um den Winkel j2 für j2 > 0 (Drehung im Uhrzeigersinn). Vorwärtsdrehung für j2 < 0
(Drehung im Gegenuhrzeigersinn).
2. Streckung des Zeigers auf das 1=r2 -fache.
f1
r1
r2
z1
z2
Re(z)
Beispiel
&
r1
f2
"
8 ðcos 240 " þ j . sin 240 " Þ
8 . e j 240
¼
¼
2 ðcos 75 " þ j . sin 75 " Þ
2 . e j 75 "
3 2
8
"
"
"
. e j ð240 / 75 Þ ¼ 4 . e j 165 ¼
2
¼ 4 ðcos 165 " þ j . sin 165 " Þ ¼ / 3;864 þ 1;035 j
&
Formeln
3 2
1
. e /jj
r
(1)
1
1
¼
¼
z
r . e jj
(2)
1
1
x
y
¼
¼ 2
/j 2
;
z
x þ jy
x þ y2
x þ y2
1
¼ /j
j
3 Potenzieren
In kartesischer Form (n 2 N * )
z n ¼ ðx þ j yÞ n ¼ x n þ j
!n4
1
x n/1 . y þ j 2
!n4
2
x n/2 . y 2 þ . . . þ j n y n
Regel: Entwicklung nach dem binomischen Lehrsatz (siehe I.2.7).
234
VIII Komplexe Zahlen und Funktionen
In der Polarform (Formel von Moivre, n 2 Z)
z n ¼ ½ r ðcos j þ j . sin jÞ % n ¼ r n ½cos ðn jÞ þ j . sin ðn jÞ %
z n ¼ ½ r . e jj % n ¼ r n . e jnj
Regel: Eine in der Polarform vorliegende komplexe Zahl wird in die n-te Potenz erhoben,
indem man ihren Betrag r in die n-te Potenz erhebt und ihr Argument (ihren
Winkel) j mit dem Exponenten n multipliziert.
&
Beispiel
Wir erheben die komplexe Zahl z ¼ 3 ðcos 20 " þ j . sin 20 " Þ in die vierte Potenz:
z 4 ¼ ½ 3 ðcos 20 " þ j . sin 20 " Þ % 4 ¼ 3 4 ½cos ð4 . 20 " Þ þ j . sin ð4 . 20 " Þ % ¼
¼ 81 ðcos 80 " þ j . sin 80 " Þ ¼ 14;066 þ 79;769 j
&
4 Radizieren (Wurzelziehen)
Definition
Eine komplexe Zahl z heißt eine n-te Wurzel aus a, wenn sie der algebraischen
Gleipffiffiffi
chung z n ¼ a genügt ða 2 C; n 2 N *Þ. Symbolische Schreibweise: n a
Fundamentalsatz der Algebra
Eine algebraische Gleichung n-ten Grades vom Typ
an z n þ an / 1 z n / 1 þ . . . þ a1 z þ a0 ¼ 0
(ai : reell oder komplex; an 6¼ 0)
besitzt in der Menge C der komplexen Zahlen stets genau n Lösungen (auch Wurzeln
genannt). Bei ausschließlich reellen Koeffizienten ai treten komplexe Lösungen (falls es
solche überhaupt gibt) immer paarweise in Form konjugiert komplexer Zahlen auf.
Wurzeln der Gleichung z n = a ðmit a 2 CÞ
Die n Wurzeln der Gleichung
z n ¼ a ¼ a0 . e j a
mit a0 > 0 und n 2 N * lauten:
zk ¼
+
3
2
3
2)
p
ffiffiffiffiffi
a þ k . 2p
a þ k . 2p
n
þ j . sin
a0 cos
n
n
Hauptwert ðk ¼ 0Þ:
ðk ¼ 0; 1; . . . ; n / 1Þ
+
!a4
! a 4)
p
ffiffiffiffiffi
n
z0 ¼ a0 cos
þ j . sin
n
n
Für k ¼ 1; 2; . . . ; n / 1 erhält man die Nebenwerte. Die Winkel können auch im Gradmaß angegeben werden (2 p ist dann durch 360 " zu ersetzen).
5 Natürlicher Logarithmus einer komplexen Zahl
235
Geometrische Deutung:
Im(z)
Die zugehörigen Bildpunkte liegen auf
dem Mittelpunktskreis
mit dem Radius
pffiffiffiffiffi
R ¼ n a0 und bilden die Ecken eines
regelmäßigen n-Ecks. Das nebenstehende Bild zeigt die drei Lösungen der
Gleichung z 3 ¼ a0 . e j a . Die Zeiger
(Lösungen) z1 und z2 gehen dabei
aus dem Zeiger (der Lösung) z0 durch
Drehung um 120 " bzw. 240 " im Gegenuhrzeigersinn hervor.
a = a0·e ja
z0
a0
3
√ a0
z1
a
120°
120°
a
3
Re(z)
z2
&
Beispiel
"
Wir bestimmen die drei Wurzeln der Gleichung z 3 ¼ 8 ðcos 150 " þ j . sin 150 " Þ ¼ 8 . e j 150 :
a0 ¼ 8 ;
a ¼ 150 "
3
2
3
2#
pffiffiffi
150 " þ k . 360 "
150 " þ k . 360 "
z k ¼ 3 8 cos
þ j . sin
¼
3
3
n ¼ 3;
"
¼ 2 ½cos ð50 " þ k . 120 " Þ þ j . sin ð50 " þ k . 120 " Þ%
"
"
z0 ¼ 2 ðcos 50 þ j . sin 50 Þ ¼ 1;286 þ 1;532 j
"
ðk ¼ 0; 1; 2Þ
(Hauptwert)
"
z1 ¼ 2 ðcos 170 þ j . sin 170 Þ ¼ / 1;970 þ 0;347 j
z2 ¼ 2 ðcos 290 " þ j . sin 290 " Þ ¼ 0;684 / 1;879 j
)
Nebenwerte
&
Einheitswurzeln
Die n Lösungen der Gleichung z n ¼ 1 heißen n-te Einheitswurzeln. Sie lauten:
z n ¼ 1 ) z k ¼ cos
3
2
3
2
k . 2p
k . 2p
k.2p
þ j . sin
¼ ej n
n
n
ðk ¼ 0; 1; . . . ; n / 1Þ
5 Natürlicher Logarithmus einer komplexen Zahl
Der natürliche Logarithmus einer komplexen Zahl
z ¼ r . e j j ¼ r . e j ðj þ k . 2 pÞ
ð0 ) j < 2 p; k 2 ZÞ
2Þ
ist unendlich vieldeutig :
ln z ¼ ln r þ j ðj þ k . 2 pÞ
2Þ
ðk 2 ZÞ
Der Hauptwert des Winkels wird häufig auch im Intervall / p < j ) p angegeben (siehe hierzu Abschnitt
9.1.2 in Kapitel I ).
236
VIII Komplexe Zahlen und Funktionen
Man beachte den folgenden wesentlichen Unterschied: Im Komplexen ist der Logarithmus
für jede komplexe Zahl z 6¼ 0 (also auch für negative reelle Zahlen) definiert, im Reellen
dagegen nur für positive reelle Zahlen x.
Hauptwert ðk ¼ 0Þ:
Ln z ¼ ln r þ j j
(Schreibweise: Ln z statt ln z)
Für k ¼ + 1; + 2; + 3; . . . erhält man die sog. Nebenwerte.
Spezielle Werte:
ln 1 ¼ k . 2 p j
!p
4
þ k . 2p j
ln j ¼
2
&
ln ð/ 1Þ ¼ ðp þ k . 2 pÞ j
3
2
3
ln ð/ jÞ ¼
p þ k . 2p j
2
Beispiel
z ¼ 3 þ 4 j ¼ 5 . e j 0;9273 ¼ 5 . e j ð0;9273 þ k . 2 pÞ
ln ð3 þ 4 jÞ ¼ ln 5 þ j ð0;9273 þ k . 2 pÞ ¼ 1;6094 þ j ð0;9273 þ k . 2 pÞ
Hauptwert ðk ¼ 0Þ:
ðk 2 ZÞ
Ln ð3 þ 4 jÞ ¼ 1;6094 þ 0;9273 j
&
6 Ortskurven
6.1 Komplexwertige Funktion einer reellen Variablen
Die von einem reellen Parameter t abhängige komplexe Zahl
z ¼ z ðtÞ ¼ x ðtÞ þ j . y ðtÞ
ða ) t ) bÞ
heißt komplexwertige Funktion z ðtÞ der reellen Variablen t. Realteil x ðtÞ und Imaginärteil y ðtÞ sind reelle Funktionen von t.
6.2 Ortskurve einer parameterabhängigen komplexen Zahl
Die von einem parameterabhängigen komplexen Zeiger z ¼ z ðtÞ in der Gaußschen
Zahlenebene beschriebene Bahn heißt Ortskurve:
z ðtÞ ¼ x ðtÞ þ j . y ðtÞ
ða ) t ) bÞ
x ðtÞ; y ðtÞ: Reelle Funktionen des reellen
Parameters t
Im(z)
t=a
t
z = z(t)
z(t)
t=b
Re(z)
6 Ortskurven
&
237
Beispiel
Im(z)
Die Ortskurve des komplexen Zeigers
z ðtÞ ¼ 2 þ j t
ð0 ) t < 1Þ
beschreibt die im nebenstehenden Bild dargestellte
Halbgerade.
t
z
z = 2 + jt
1
1
2
Re(z)
&
6.3 Inversion einer Ortskurve
Inversion einer komplexen Zahl
Der !bergang von einer komplexen Zahl
z 6¼ 0 zu ihrem Kehrwert w ¼ 1=z heißt
Inversion:
z ¼ r . e jj ! w ¼
1
¼
z
Im(z)
Im(w)
z
z
3 2
1
. e /jj
r
=
r
Re(w)
f
–f
Re(z)
w
=
r
1/
Regel: Vorzeichenwechsel im Argument,
Kehrwertbildung des Betrages von z.
w=1
z
Geometrische Deutung:
Der Zeiger wird zunächst an der reellen Achse gespiegelt und dann auf das 1=r 2 -fache
gestreckt.
Inversionsregeln für Ortskurven
Invertiert man eine Ortskurve Punkt für Punkt, so erhält man wiederum eine Ortskurve, die
sog. invertierte Ortskurve. Für die in den Anwendungen besonders häufig auftretenden
Geraden und Kreise gelten dabei die folgenden Inversionsregeln:
z-Ebene
1. Gerade durch den Nullpunkt
2. Gerade, die nicht durch den
Nullpunkt verläuft
3. Mittelpunktskreis
4. Kreis durch den Nullpunkt
5. Kreis, der nicht durch den
Nullpunkt verläuft
w-Ebene
! Gerade durch den Nullpunkt
! Kreis durch den Nullpunkt
! Mittelpunktskreis
! Gerade, die nicht durch den Nullpunkt verläuft
! Kreis, der nicht durch den Nullpunkt verläuft
238
VIII Komplexe Zahlen und Funktionen
Bei der Inversion einer Ortskurve erweisen sich auch folgende Regeln als nützlich:
1. Der Punkt mit dem kleinsten Abstand (Betrag) vom Nullpunkt führt zu dem Bildpunkt
mit dem größten Abstand (Betrag) und umgekehrt.
2. Ein Punkt oberhalb der reellen Achse führt zu einem Bildpunkt unterhalb der reellen
Achse und umgekehrt.
7 Komplexe Funktionen
7.1 Definition einer komplexen Funktion
Unter einer komplexen Funktion versteht man eine Vorschrift, die jeder komplexen Zahl
z 2 D genau eine komplexe Zahl w 2 W zuordnet. Symbolische Schreibweise:
w ¼ f ðzÞ: D und W sind Teilmengen von C.
7.2 Definitionsgleichungen einiger elementarer Funktionen
7.2.1 Trigonometrische Funktionen
9
z3
z5
>
>
þ
/ þ ... >
sin z ¼ z /
=
3!
5!
Periode: p ¼ 2 p
>
>
z2
z4
>
cos z ¼ 1 /
þ
/ þ ... ;
2!
4!
9
sin z
>
tan z ¼
>
=
cos z
Periode: p ¼ p
>
cos z
1
>
;
¼
cot z ¼
sin z
tan z
7.2.2 Hyperbelfunktionen
sinh z ¼ z þ
z3
z5
þ
þ ...
3!
5!
z2
z4
cosh z ¼ 1 þ
þ
þ ...
2!
4!
9
>
>
>
=
>
>
>
;
sinh z
cosh z
9
>
>
=
cosh z
1
coth z ¼
¼
sinh z
tanh z
>
>
;
tanh z ¼
Periode:
p ¼ j2p
Periode:
p ¼ jp
7 Komplexe Funktionen
239
7.2.3 Exponentialfunktion (e-Funktion)
ez ¼ 1 þ
z
z2
z3
þ
þ
þ ...
1!
2!
3!
ðPeriode:
p ¼ j 2 pÞ
7.3 Wichtige Beziehungen und Formeln
7.3.1 Eulersche Formeln
e j x ¼ cos x þ j . sin x
e / j x ¼ cos x / j . sin x
7.3.2 Zusammenhang zwischen den trigonometrischen Funktionen
und der komplexen e-Funktion
sin x ¼
1
ðe j x / e / j x Þ
2j
tan x ¼ / j
e jx / e /jx
e jx þ e /jx
cos x ¼
1
ðe j x þ e / j x Þ
2
cot x ¼ j
e jx þ e /jx
e jx / e /jx
7.3.3 Trigonometrische und Hyperbelfunktionen mit imaginärem Argument
sin ðj xÞ ¼ j . sinh x
sinh ðj xÞ ¼ j . sin x
cos ðj xÞ ¼ cosh x
cosh ðj xÞ ¼ cos x
tan ðj xÞ ¼ j . tanh x
tanh ðj xÞ ¼ j . tan x
7.3.4 Additionstheoreme der trigonometrischen und Hyperbelfunktionen
für komplexes Argument
sin ðx + j yÞ ¼ sin x . cosh y + j . cos x . sinh y
cos ðx + j yÞ ¼ cos x . cosh y * j . sin x . sinh y
tan ðx + j yÞ ¼
sin ð2 xÞ + j . sinh ð2 yÞ
cos ð2 xÞ þ cosh ð2 yÞ
sinh ðx + j yÞ ¼ sinh x . cos y + j . cosh x . sin y
cosh ðx + j yÞ ¼ cosh x . cos y + j . sinh x . sin y
tanh ðx + j yÞ ¼
sinh ð2 xÞ + j . sin ð2 yÞ
cosh ð2 xÞ þ cos ð2 yÞ
240
VIII Komplexe Zahlen und Funktionen
7.3.5 Arkus- und Areafunktionen mit imaginärem Argument
arcsin ðj xÞ ¼ j . arsinh x
arsinh ðj xÞ ¼ j . arcsin x
arccos ðj xÞ ¼ j . arcosh x
arcosh ðj xÞ ¼ j . arccos x
arctan ðj xÞ ¼ j . artanh x
artanh ðj xÞ ¼ j . arctan x
8 Anwendungen in der Schwingungslehre
8.1 Darstellung einer harmonischen Schwingung
durch einen rotierenden komplexen Zeiger
Eine harmonische Schwingung vom Typ
y ¼ A . sin ðw t þ jÞ mit A > 0 und
w > 0 lässt sich in der Gaußschen Zahlenebene durch einen mit der Winkelgeschwindigkeit w um den Nullpunkt rotierenden
(und damit zeitabhängigen) komplexen Zeiger
der Länge A darstellen (sog. Zeigerdiagramm):
Im(y)
v
y(t) = A·e jvt
A
vt
f
A
y ðtÞ ¼ A . e j ðw t þ jÞ ¼ A . e j w t
A ¼ A . e jj:
e jwt :
y(0) = A
Re(y)
Komplexe Amplitude
Zeitfunktion
Die Drehung erfolgt im Gegenuhrzeigersinn. Die komplexe Schwingungsamplitude A beschreibt dabei die Anfangslage des Zeigers y ðtÞ zur Zeit t ¼ 0, d. h. es ist y ð0Þ ¼ A.
Eine in der Kosinusform vorliegende Schwingung lässt sich wie folgt in die Sinusform umschreiben:
y ¼ A . cos ðw t þ jÞ ¼ A . sin ðw t þ j þ p=2Þ ¼ A . sin ðw t þ j *Þ
Der Nullphasenwinkel beträgt somit j * ¼ j þ p=2, d. h. der Zeiger ist (gegenüber
einer Sinusschwingung) um 90" vorzudrehen.
8 Anwendungen in der Schwingungslehre
241
8.2 Ungestörte !berlagerung gleichfrequenter harmonischer
Schwingungen („Superpositionsprinzip“)
Durch ungestörte !berlagerung der gleichfrequenten harmonischen Sinusschwingungen
y 1 ¼ A 1 . sin ðw t þ j 1 Þ
und y 2 ¼ A 2 . sin ðw t þ j 2 Þ
entsteht nach dem Superpositionsprinzip der Physik eine resultierende Schwingung mit
derselben Frequenz:
y ¼ y 1 þ y 2 ¼ A 1 . sin ðw t þ j 1 Þ þ A 2 . sin ðw t þ j 2 Þ ¼ A . sin ðw t þ jÞ
ðA 1 > 0, A 2 > 0, A > 0, w > 0Þ
Berechnung der Schwingungsamplitude A und des Phasenwinkels j
1. !bergang von der reellen zur komplexen Form
y 1 ¼ A 1 . sin ðw t þ j 1 Þ
!
y 1 ¼ A 1 . e jwt
ð A 1 ¼ A 1 . e jj1Þ
y 2 ¼ A 2 . sin ðw t þ j 2 Þ
!
y 2 ¼ A 2 . e jwt
ð A 2 ¼ A 2 . e jj2Þ
2. Addition der komplexen Amplituden und Elongationen
Im(z)
A ¼ A 1 þ A 2 ¼ A . e jj
y ¼ y1 þ y2 ¼ A . e
jwt
¼ A.e
j ðw t þ jÞ
A = A1 + A2
A2
A
Zeichnerische Lösung: Parallelogrammregel
f
A1
Re(z)
3. Rücktransformation aus der komplexen in die reelle Form
y ¼ y1 þ y2 ¼ Im ð y Þ ¼ Im ð A . e j w t Þ ¼ Im ðA . e j ðw t þ jÞ Þ ¼ A . sin ðw t þ jÞ
Sonderfälle
(1)
!berlagerung einer Sinusschwingung mit einer Kosinusschwingung: Letztere erst
auf die Sinusform bringen (siehe Abschnitt 8.1).
(2)
!berlagerung zweier Kosinusschwingungen: Beide erst auf die Sinusform bringen
oder die resultierende Schwingung ebenfalls als Kosinusschwingung darstellen, wobei
bei der Rücktransformation der Realteil von y ¼ A . e j ðw t þ jÞ zu nehmen ist.
242
&
VIII Komplexe Zahlen und Funktionen
Beispiel
3
2
2
y 2 ¼ 3 . sin w t þ
p ;
3
!
p4
;
y 1 ¼ 5 . sin w t þ
4
1. !bergang von der reellen zur komplexen Form
!
p
p4
y1 ! y 1 ¼ 5 . e j ðw t þ 4 Þ ¼ 5 . e j 4 e j w t ¼ A 1 . e j w t
y2 ! y 2 ¼ 3 . e j
1
wtþ
2
p
3
0
3
¼
2
3 . ej 3 p
2
e jwt ¼ A 2 . e jwt
y ¼ y1 þ y2 ¼ ?
!
p4
A1 ¼ 5 . ej 4
3
2
2
A2 ¼ 3 . ej 3 p
2. Addition der komplexen Amplituden und Elongationen
3
2
!
2
p
p
p4
2
2
A ¼ A 1 þ A 2 ¼ 5 . e j 4 þ 3 . e j 3 p ¼ 5 cos
þ j . sin
þ 3 cos
p þ j . sin
p ¼
4
4
3
3
¼ 3;536 þ 3;536 j / 1;5 þ 2;598 j ¼ 2;036 þ 6; 134 j ¼ 6;463 . e j 1;250
Umrechnung in die Exponentialform (siehe Bild):
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
j A j ¼ 2,036 2 þ 6,134 2 ¼ 6,463
tan j ¼
6,134
¼ 3,0128
2,036
)
j ¼ arctan 3,0128 ¼ 1,250 ð' 71,64" Þ
A ¼ j A j . e j j ¼ 6,463 . e j 1;250
Im (z)
A
6,134
|A|
y ¼ y 1 þ y 2 ¼ A . e j w t ¼ 6;463 . e j 1;250 . e j w t ¼ 6;463 . e j ðw t þ 1;250Þ
3. Rücktransformation aus der komplexen in die reelle Form
!
4
y ¼ Im ð y Þ ¼ Im 6;463 . e j ðw t þ 1;250Þ ¼ 6;463 . sin ðw t þ 1;250Þ
f
2,036
Re (z)
&
243
IX Differential- und Integralrechnung
für Funktionen von mehreren Variablen
1 Funktionen von mehreren Variablen
und ihre Darstellung
1.1 Definition einer Funktion von mehreren Variablen
Unter einer Funktion von zwei unabhängigen Variablen versteht man eine Vorschrift, die
jedem geordneten Zahlenpaar ðx; yÞ aus einer Menge D genau ein Element z aus einer
Menge W zuordnet. Symbolische Schreibweise: z ¼ f ðx; yÞ.
Bezeichnungen:
x; y:
z:
D:
W:
Unabhängige Variable (Veränderliche)
Abhängige Variable (Veränderliche) oder Funktionswert
Definitionsbereich der Funktion
Wertebereich oder Wertevorrat der Funktion
Bezeichnungen bei drei und mehr Variablen:
u ¼ f ðx; y; zÞ:
Funktion von drei unabhängigen Variablen x; y und z
y ¼ f ðx1 ; x2 ; . . . ; xn Þ: Funktion von n unabhängigen Variablen x1 ; x2 ; . . . ; xn
Die Variablen sind im Regelfall reell.
1.2 Darstellungsformen einer Funktion von zwei Variablen
1.2.1 Analytische Darstellung
Die Funktion wird durch eine Funktionsgleichung dargestellt:
Explizite Form:
z ¼ f ðx; yÞ
Implizite Form:
F ðx; y; zÞ ¼ 0
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_9
244
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
1.2.2 Graphische Darstellung
1.2.2.1 Darstellung einer Funktion als Fläche im Raum
z
Die Variablen x; y und z einer Funktion
z ¼ f ðx; yÞ werden als rechtwinklige oder
kartesische Koordinaten eines Raumpunktes
P gedeutet: P ¼ ðx; y; zÞ. Der Funktionswert z ¼ f ðx; yÞ ist dabei die Höhenkoordinate des zugeordneten Bildpunktes. Man erhält als Bild der Funktion eine über dem
Definitionsbereich liegende Fläche.
Fläche z = f(x;y)
P
y
y
z
x
x
y
x
Definitionsbereich D
1.2.2.2 Schnittkurvendiagramme
Die Schnittkurvendiagramme einer Funktion z ¼ f ðx; yÞ erhält man durch Schnitte der
zugehörigen Bildfläche mit Ebenen, die parallel zu einer der drei Koordinatenebenen
verlaufen. Die Schnittkurven werden noch in die jeweilige Koordinatenebene projiziert und
repräsentieren einparametrige Kurvenscharen. Ihre Gleichungen erhält man aus der
Funktionsgleichung z ¼ f ðx; yÞ, indem man der Reihe nach jeweils eine der drei
Variablen (Koordinaten) als Parameter betrachtet. In den naturwissenschaftlich-technischen
Anwendungen werden die Schnittkurvendiagramme als Kennlinienfelder bezeichnet.
1.2.2.3 Höhenliniendiagramm
Das Höhenliniendiagramm ist ein spezielles Schnittkurvendiagramm
Höhenkoordinate z als Kurvenparameter („Linien gleicher Höhe“):
mit
der
f ðx; yÞ ¼ const: ¼ c
c: Zulässiger Wert der Höhenkoordinate z
&
Beispiel
Die Höhenlinien der in Bild a) dargestellten Fläche z ¼ x 2 þ y 2 (Mantel eines Rotationsparaboloids) sind
pffiffiffi
konzentrische Mittelpunktskreise mit der Kurvengleichung x 2 þ y 2 ¼ c und dem Radius R ¼ c mit
c > 0 (Bild b)).
y
z
z=
3
z=
2
z=
z= 1
0,5
z = x2+ y2
a)
y
x
x
b)
&
1 Funktionen von mehreren Variablen und ihre Darstellung
245
1.3 Spezielle Flächen (Funktionen)
1.3.1 Ebenen
Die Bildfläche einer linearen Funktion ist eine Ebene.
Gleichung einer Ebene
ax þ by þ cz þ d ¼ 0
z
a, b, c, d : Reelle Konstanten
x=0
y=0
Koordinatenebenen
y
x; y-Ebene: z ¼ 0
x; z-Ebene: y ¼ 0
y; z-Ebene: x ¼ 0
z=0
x
Parallelebenen
z
Ebene parallel zur x; y-Ebene: z ¼ a
(siehe nebenstehendes Bild für a > 0)
Ebene parallel zur x; z-Ebene: y ¼ a
Ebene parallel zur y; z-Ebene: x ¼ a
z=a
a
y
x
j a j: Abstand Ebene –– Parallelebene
1.3.2 Rotationsflächen
1.3.2.1 Gleichung einer Rotationsfläche
Eine Rotationsfläche entsteht durch Drehung einer ebenen Kurve z ¼ f ðxÞ um die z-Achse:
z
z
x
r
z = f(x)
z = f(r)
z
z
a
a)
b
x
b)
x
y
246
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Ihre Funktionsgleichung lautet:
In Zylinderkoordinaten 1Þ ( formale Substitution x ! r):
z ¼ f ðrÞ
In kartesischen Koordinaten
z ¼ f
!
formale Substitution x !
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
x2 þ y2 :
3qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2
x2 þ y2
1.3.2.2 Spezielle Rotationsflächen
Kugel (Oberfläche)
z
x2+ y 2+ z2= R 2
x2 þ y2 þ z2 ¼ R2
oder
2
r þz
2
R
¼ R
2
M
Obere bzw. untere Halbkugel (in kartesischen
Koordinaten bzw. Zylinderkoordinaten):
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
z ¼ + R2 / x2 / y2
bzw:
z ¼ +
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
R2 / r2
Kreiskegel (Mantelfläche)
x2 þ y2 ¼
R2 2
z
H2
oder
z
jzj ¼
H
r
R
Die Gleichungen beschreiben einen Doppelkegel (Kegelspitze: Nullpunkt). Für z ( 0
erhält man den Mantel des gezeichneten
Kegels mit der Funktionsgleichung
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
H
H
z ¼
x2 þ y2 ¼
r
R
R
1Þ
y
R
H
2
x2+ y2= R2 z2
H
y
x
Zylinderkoordinaten: siehe I.9.2.2 und XIV.6.2. Den senkrechten Abstand von der z-Achse bezeichnen wir hier mit
r (statt r).
2 Partielle Differentiation
247
Kreiszylinder (Mantelfläche)
x2 þ y2 ¼ R2
oder
z
R
r ¼ R
Höhenkoordinate: z 2 R
x2+ y2= R2
Zylinder der Höhe H
(Boden in der x, y-Ebene):
x 2 þ y 2 ¼ R 2, 0 ) z ) H
y
x
Ellipsoid (Oberfläche)
x2
y2
z2
þ
þ
¼ 1
a2
b2
c2
Durch Auflösen nach z erhält man zwei
Funktionen (oberer bzw. unterer Mantel des
Ellipsoids).
Für a ¼ b erhält man ein Rotationsellipsoid
(Rotationsachse: z-Achse).
c
b
a
x
2 Partielle Differentiation
2.1 Partielle Ableitungen 1. Ordnung
2.1.1 Partielle Ableitungen 1. Ordnung von z = f (x; y)
Partielle Ableitung 1. Ordnung nach x
fx ðx; yÞ ¼ lim
Dx ! 0
f ðx þ Dx; yÞ / f ðx; yÞ
Dx
Regel: y festhalten, nach x differenzieren.
Partielle Ableitung 1. Ordnung nach y
fy ðx; yÞ ¼ lim
Dy ! 0
f ðx; y þ DyÞ / f ðx; yÞ
Dy
Regel: x festhalten, nach y differenzieren.
2
x2 + y + z2 = 1
2
a
b2 c2
z
y
248
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Geometrische Deutung:
z
Tangente in P
fx ðx0 ; y0 Þ ¼ tan a und fy ðx0 ; y0 Þ ¼ tan b
sind die Steigungen der Flächentangenten im
Bildpunkt P ¼ ¼ ðx0 ; y0 ; z0 Þ in der x- bzw.
y-Richtung:
k2
k1
P
z0
k1 : Schnittkurve der Fläche z ¼ f ðx; yÞ mit
der Ebene y ¼ y0
x0
k2 : Schnittkurve der Fläche z ¼ f ðx; yÞ mit
der Ebene x ¼ x0
x
k1
Tangente in P
z = f(x;y)
y0
k2
y
b
a
Schreibweisen:
fx ðx; yÞ ;
zx ðx; yÞ ;
@f
ðx; yÞ ;
@x
@z
ðx; yÞ
@x
fy ðx; yÞ ;
zy ðx; yÞ ;
@f
ðx; yÞ ;
@y
@z
ðx; yÞ
@y
@f
;
@x
@f
@y
bzw:
@z
;
@x
@z
:
@y
Partielle Differentialquotienten 1. Ordnung
Partielle Differentialoperatoren
Die partiellen Differentialoperatoren @=@x und @=@y erzeugen durch „Einwirken“ auf
die Funktion z ¼ f ðx; yÞ die partiellen Ableitungen 1. Ordnung:
@
½ f ðx; yÞ% ¼ fx ðx; yÞ ;
@x
@
½ f ðx; yÞ% ¼ fy ðx; yÞ
@y
2.1.2 Partielle Ableitungen 1. Ordnung von y = f (x1 ; x2; . . .; xn )
Für eine Funktion y ¼ f ðx1 ; x2 ; . . . ; xn Þ von n unabhängigen Variablen lassen sich
insgesamt n verschiedene partielle Ableitungen 1. Ordnung bilden:
fx k ¼
@f
@xk
ðk ¼ 1; 2; . . . ; nÞ
Die partielle Ableitung fx k nach der Variablen xk erhält man, indem man in der
Funktionsgleichung alle Variablen bis auf xk festhält, d. h. als Parameter behandelt und
anschließend die Funktion mit Hilfe der bekannten Ableitungsregeln (siehe IV.3) nach xk
differenziert.
2 Partielle Differentiation
249
Schreibweisen:
@f
;
@xk
@y
;
@xk
@
½ f % ¼ fx k
@xk
fx k ;
yx k ;
@
:
@xk
Partieller Differentialoperator 1. Ordnung
Beispiel
&
Wir differenzieren die Funktion f ðx; y; zÞ ¼ x 2 y . e 3 z þ z . sin ðx yÞ partiell nach der Variablen x :
@f
@
¼
½ x 2 y . e 3 z þ z . sin ðx yÞ% ¼ 2 x y . e 3 z þ y z . cos ðx yÞ
@x
@x
&
2.2 Partielle Ableitungen höherer Ordnung
Partielle Ableitungen höherer Ordnung erhält man, indem man die gegebene Funktion
mehrmals nacheinander partiell differenziert.
Für eine Funktion z ¼ f ðx; yÞ lassen sich die höheren Ableitungen nach dem folgenden
Schema bilden:
Schreibweisen:
3 2
@ @f
@ 2f
fx x ¼
¼
;
@x @x
@x 2
fy x
@
¼
@x
fx y x ¼
@
@x
3 2
@f
@ 2f
¼
;
@y
@y @x
3
fx y
@
¼
@y
3 2
@f
@ 2f
¼
@x
@x @y
fy y
@
¼
@y
3 2
@f
@ 2f
¼
@y
@y 2
2
@2f
@ 3f
¼
@x @y
@x @y @x
usw:
Vereinbarung: Die einzelnen Differentiationsschritte sind grundsätzlich in der Reihenfolge
der Indizes durchzuführen. Beispiel fx y : Erst nach x, dann nach y differenzieren.
Abweichungen sind nur zulässig, wenn der folgende Satz von Schwarz erfüllt ist.
Satz von Schwarz
Sind alle partiellen Ableitungen k-ter Ordnung stetig, so ist die Reihenfolge der
Differentiationen beliebig vertauschbar.
250
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Unter diesen Voraussetzungen gilt für eine Funktion z ¼ f ðx; yÞ:
fx y ¼ fy x
fx x y ¼ fy x x ¼ fx y x ;
&
fy y x ¼ fx y y ¼ fy x y
Beispiel
Wir bilden die partiellen Ableitungen 1. und 2. Ordnung von z ¼ f ðx; yÞ ¼ x 3 y 2 þ e x y :
Partielle Ableitungen 1. Ordnung:
zx ¼
@
½ x 3 y 2 þ e x y% ¼ 3 x 2 y 2 þ y . e x y ;
@x
zy ¼
@
½ x 3 y 2 þ e x y% ¼ 2 x 3 y þ x . e x y
@y
Partielle Ableitungen 2. Ordnung:
zx x ¼
@
@
ðzx Þ ¼
½ 3 x 2 y 2 þ y . e x y % ¼ 6 x y 2 þ y 2 . e x y ¼ y 2 ð6 x þ e x y Þ
@x
@x
zx y ¼
@
@
ðzx Þ ¼
½ 3 x 2 y 2 þ y . e x y % ¼ 6 x 2 y þ e x y þ x y . e x y ¼ 6 x 2 y þ ðx y þ 1Þ . e x y ¼ zy x
@y
@y
zy y ¼
@
@
ðzy Þ ¼
½ 2 x 3 y þ x . e x y % ¼ 2 x 3 þ x 2 . e x y ¼ x 2 ð2 x þ e x y Þ
@y
@y
&
2.3 Verallgemeinerte Kettenregel
(Differentiation nach einem Parameter)
Die unabhängigen Variablen x und y der Funktion z ¼ f ðx; yÞ hängen noch von einem
(reellen) Parameter t ab, sind also Funktionen dieses Parameters:
x ¼ x ðtÞ ;
y ¼ y ðtÞ
ðt1 ) t ) t2 Þ
Dann ist auch z eine sog. zusammengesetzte, verkettete oder mittelbare Funktion des
Parameters t :
z ¼ f ðx ðtÞ ; y ðtÞÞ ¼ F ðtÞ
ðt1 ) t ) t2 Þ
Ihre Ableitung nach dem Parameter t erhält man nach der folgenden verallgemeinerten
Kettenregel:
dz
@z dx
@z dy
¼
.
þ
.
dt
@x dt
@y dt
oder
z_ ¼ zx . x_ þ zy . y_
x_; y_; z_:
Ableitungen nach dem Parameter t
zx ; zy :
Partielle Ableitungen 1. Ordnung von z ¼ f ðx; yÞ
Nach erfolgter Rücksubstitution (x und y werden durch die Parametergleichungen ersetzt)
hängt die Ableitung z_ nur noch vom Parameter t ab.
2 Partielle Differentiation
251
Alternative: In der Funktion z ¼ f ðx; yÞ zunächst die Variablen x und y durch ihre
Parametergleichungen x ðtÞ und y ðtÞ ersetzen, dann die jetzt nur noch von t abhängige
Funktion nach diesem Parameter differenzieren (gewöhnliche Differentiation).
&
Beispiel
z ¼ f ðx; yÞ ¼ x 2 y / 2 x 3
2
zx ¼ 2 x y / 6 x ;
mit
x ¼ x ðtÞ ¼ t 2
und
2
x_ ¼ 2 t ;
y_ ¼ 2
zy ¼ x ;
y ¼ y ðtÞ ¼ 2 t þ 1
Die verallgemeinerte Kettenregel liefert zunächst:
z_ ¼ zx . x_ þ zy . y_ ¼ ð2 x y / 6 x 2 Þ . 2 t þ x 2 . 2 ¼ 4 x y t / 12 x 2 t þ 2 x 2
Rücksubstitution ðx ¼ t 2 ; y ¼ 2 t þ 1Þ:
z_ ¼ 4 t 2 . ð2 t þ 1Þ . t / 12 t 4 . t þ 2 t 4 ¼ 4 t 3 ð2 t þ 1Þ / 12 t 5 þ 2 t 4 ¼
¼ 8 t 4 þ 4 t 3 / 12 t 5 þ 2 t 4 ¼ /12 t 5 þ 10 t 4 þ 4 t 3
Alternativer Lösungsweg:
z ¼ x 2 y / 2 x 3 ¼ ðt 2 Þ 2 ð2 t þ 1Þ / 2 ðt 2 Þ 3 ¼ t 4 ð2 t þ 1Þ / 2 t 6 ¼ / 2 t 6 þ 2 t 5 þ t 4
z_ ¼ / 12 t 5 þ 10 t 4 þ 4 t 3
)
&
2.4 Totales oder vollständiges Differential einer Funktion
Tangentialebene
Alle im Flächenpunkt P ¼ ðx0 ; y0 ; z0 Þ an die Bildfläche von z ¼ f ðx; yÞ angelegten
Tangenten liegen in der Regel in einer Ebene, der sog. Tangentialebene. Die Gleichung der
Tangentialebene lautet wie folgt (in symmetrischer Schreibweise):
z / z0 ¼ fx ðx0 ; y0 Þ . ðx / x0 Þ þ fy ðx0 ; y0 Þ . ðy / y0 Þ
z
Q
Fläche z = f(x;y)
Dz
Q'
dz
y0
=D
x
dy = Dy
dx
x
0
P
z0
x
y
Tangentialebene in P
252
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Totales Differential von z = f (x; y)
dz ¼ fx dx þ fy dy ¼
@f
@f
dx þ
dy
@x
@y
dx; dy: unabhängige Differentiale;
dz: abhängiges Differential
Geometrische Deutung:
Das totale Differential dz ¼ fx ðx0 ; y0 Þ dx þ fy ðx0 ; y0 Þ dy beschreibt die "nderung der
Höhenkoordinate bzw. des Funktionswertes z auf der im Flächenpunkt P ¼ ðx0 ; y0 ; z0 Þ
errichteten Tangentialebene, wenn sich die beiden unabhängigen Koordinaten (Variablen)
x und y um dx ¼ Dx bzw. dy ¼ Dy ändern (Verschiebung des Punktes P in den
Punkt Q 0 ). Die exakte #nderung der Höhenkoordinate z dagegen beträgt
Dz ¼ f ðx0 þ Dx; y0 þ DyÞ / f ðx0 ; y0 Þ
( Höhenzuwachs auf der Fläche, Verschiebung des Punktes P in den Punkt Q)
Für kleine Koordinatenänderungen dx ¼ Dx und dy ¼ Dy gilt näherungsweise:
Dz ' dz ¼ fx dx þ fy dy ¼ fx Dx þ fy Dy
&
Beispiel
z ¼ f ðx; yÞ ¼ x 2 y / x y 3
x ¼ 1;
y ¼ 3;
z ¼ f ð1; 3Þ ¼ 1 2 . 3 / 1 . 3 3 ¼ / 24 ;
dx ¼ Dx ¼ 0;2 ;
dy ¼ Dy ¼ / 0;1
Zuwachs Dz auf der Fläche (exakte #nderung des Funktionswertes):
x ¼ 1;
y ¼ 3
!
x ¼ 1 þ Dx ¼ 1 þ 0;2 ¼ 1;2 ;
y ¼ 3 þ Dy ¼ 3 / 0;1 ¼ 2;9
Dz ¼ f ð1;2; 2;9Þ / f ð1; 3Þ ¼ ð1,2 2 . 2,9 / 1,2 . 2,9 3 Þ / ð/ 24Þ ¼ / 25;0908 þ 24 ¼ / 1;0908
Zuwachs dz auf der Tangentialebene (näherungsweise #nderung des Funktionswertes):
fx ðx; yÞ ¼ 2 x y / y 3
fy ðx; yÞ ¼
x2 / 3xy2
)
fx ð1; 3Þ ¼ 2 . 1 . 3 / 3 3 ¼ 6 / 27 ¼ / 21
)
fy ð1; 3Þ ¼ 1 2 / 3 . 1 . 3 2 ¼ 1 / 27 ¼ / 26
dz ¼ fx ð1; 3Þ dx þ fy ð1; 3Þ dy ¼ / 21 . 0;2 / 26 . ð/ 0;1Þ ¼ / 4; 2 þ 2; 6 ¼ / 1;6
&
Totales Differential von y = f (x1 ; x2; . . .; xn )
dy ¼ fx1 dx1 þ fx2 dx2 þ . . . þ fxn dxn ¼
@f
@f
@f
dx1 þ
dx2 þ . . . þ
dxn
@x1
@x2
@xn
Für kleine #nderungen der unabhängigen Variablen liefert das totale Differential dy einen
brauchbaren Näherungswert für die #nderung des Funktionswertes y.
2 Partielle Differentiation
253
2.5 Anwendungen
2.5.1 Linearisierung einer Funktion
Linearisierung von z = f (x; y)
Die nichtlineare Funktion z ¼ f ðx; yÞ wird in der unmittelbaren Umgebung des
Flächenpunktes P ¼ ðx0 ; y0 ; z0 Þ (in den Anwendungen meist als Arbeitspunkt
bezeichnet) durch eine lineare Funktion, nämlich das totale oder vollständige Differential
der Funktion, ersetzt:
z / z0 ¼ fx ðx0 ; y0 Þ . ðx / x0 Þ þ fy ðx0 ; y0 Þ . ðy / y0 Þ
oder
3
Dz ¼ fx ðx0 ; y0 Þ Dx þ fy ðx0 ; y0 Þ Dy ¼
Dx; Dy; Dz:
@f
@x
2
0
3
Dx þ
@f
@y
2
0
Dy
Abweichungen (Relativkoordinaten) gegenüber dem Arbeitspunkt P
Dx ¼ x / x0 ; Dy ¼ y / y0 ; Dz ¼ z / z0
3 2 3 2
@f
@f
;
: Partielle Ableitungen 1. Ordnung im Arbeitspunkt P
@x 0
@y 0
Geometrische Deutung:
Die im Allgemeinen gekrümmte Bildfläche von z ¼ f ðx; yÞ wird in der unmittelbaren
Umgebung des Arbeitspunktes P durch die dortige Tangentialebene ersetzt.
&
Beispiel
Wir linearisieren die Funktion z ¼ f ðx; yÞ ¼ x 2 y þ 2 x . e y in der unmittelbaren Umgebung des Punktes
P ¼ ð1; 0; 2Þ:
Partielle Ableitungen in P:
fx ðx; yÞ ¼ 2 x y þ 2 . e y
)
fx ð1; 0Þ ¼ 2 . 1 . 0 þ 2 . e 0 ¼ 0 þ 2 . 1 ¼ 2
fy ðx; yÞ ¼ x 2 þ 2 x . e y
)
fy ð1; 0Þ ¼ 1 2 þ 2 . 1 . e 0 ¼ 1 þ 2 . 1 ¼ 3
Linearisierte Funktion (in der Umgebung des Punktes P):
Dz ¼ fx ð1; 0Þ Dx þ fy ð1; 0Þ Dy ¼ 2 Dx þ 3 Dy
oder (mit Dx ¼ x / 1;
Dy ¼ y / 0 ¼ y;
z / 2 ¼ 2 ðx / 1Þ þ 3 y ;
d. h.
Dz ¼ z / 2Þ
z ¼ 2x þ 3y
&
254
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Linearisierung von y = f (x1 ; x2; . . .; xn )
3
@f
@x1
Dy ¼
2
3
@f
@x2
Dx1 þ
0
2
3
0
Dx2 þ . . . þ
Dx1 ; Dx2 ; . . . ; Dxn ; Dy:
3
@f
@x1
2
3
0
;
@f
@x2
2
0
3
; ...;
@f
@xn
2
0
Dxn
Abweichungen gegenüber dem Arbeitspunkt P
(Relativkoordinaten)
2
0
@f
@xn
:
Partielle Ableitungen 1. Ordnung im Arbeitspunkt P
2.5.2 Relative Extremwerte (relative Maxima, relative Minima)
Eine Funktion z ¼ f ðx; yÞ besitzt an der Stelle ðx0 ; y0 Þ ein relatives Maximum bzw. ein
relatives Minimum, wenn in einer gewissen Umgebung von ðx0 ; y0 Þ stets
f ðx0 ; y0 Þ > f ðx; yÞ
bzw:
f ðx0 ; y0 Þ < f ðx; yÞ
ist ððx; yÞ ¼
6 ðx0 ; y0 ÞÞ. Die entsprechenden Punkte auf der Bildfläche werden als Hochbzw. Tiefpunkte bezeichnet.
In einem relativen Extremum besitzt die Bildfläche von z ¼ f ðx; yÞ eine zur x; y-Ebene
parallele Tangentialebene. Somit ist notwendigerweise
fx ðx0 ; y0 Þ ¼ 0
und
z
fy ðx0 ; y0 Þ ¼ 0
Fläche z = f(x;y)
Im nebenstehenden Bild ist P ¼ ðx0 ; y0 ; z0 Þ
ein Tiefpunkt (relatives Minimum)
Tangentialebene in P
z0
x
x
P
0
y
y0
Hinreichende Bedingungen für einen relativen Extremwert
Eine Funktion z ¼ f ðx; yÞ besitzt an der Stelle ðx0 ; y0 Þ mit Sicherheit einen relativen
Extremwert, wenn die folgenden Bedingungen erfüllt sind:
1. fx ðx0 ; y0 Þ ¼ 0
und
fy ðx0 ; y0 Þ ¼ 0
2. D ¼ fx x ðx0 ; y0 Þ . fy y ðx0 ; y0 Þ / fx 2y ðx0 ; y0 Þ > 0
fx x ðx0 ; y0 Þ < 0
) Relatives Maximum
fx x ðx0 ; y0 Þ > 0
) Relatives Minimum
2 Partielle Differentiation
D < 0:
D ¼ 0:
255
Es liegt ein Sattelpunkt vor.
Das Kriterium ermöglicht in diesem Fall keine Entscheidung darüber, ob an der
Stelle ðx0 ; y0 Þ ein relativer Extremwert vorliegt oder nicht.
Notwendige Bedingungen für einen relativen Extremwert bei einer Funktion von n
unabhängigen Variablen:
@f
¼ 0;
@x1
@f
¼ 0;
@x2
@f
¼ 0
@xn
...;
Alle partiellen Ableitungen 1. Ordnung müssen also verschwinden.
&
Beispiel
3
Wir berechnen die relativen Extremwerte der Funktion z ¼ f ðx; yÞ ¼ x y / 27
y 6¼ 0:
1
1
/
x
y
2
mit x 6¼ 0,
Partielle Ableitungen 1. und 2. Ordnung:
fx ðx; yÞ ¼ y þ
fx x ðx; yÞ ¼ /
27
;
x2
fy ðx; yÞ ¼ x /
54
;
x3
27
y2
fx y ðx; yÞ ¼ fy x ðx; yÞ ¼ 1 ;
fy y ðx; yÞ ¼
Notwendige Bedingungen:
fx ðx; yÞ ¼ 0
fy ðx; yÞ ¼ 0
27 x 4 ¼ 27 2 x
)
)
)
yþ
x /
27
¼ 0
x2
27
¼ 0
y2
x 3 ¼ 27
)
)
)
y ¼ /
27
x2
)
y2 ¼
54
y3
3
/
27
x2
22
¼
>
>
>
>
;
27
x
y2 ¼
x ¼ 3;
9
27 2 >
>
>
=
x4 >
)
27 2
27
¼
x4
x
)
y ¼ /3
Hinreichende Bedingungen:
fx x ð3; / 3Þ ¼ / 2 ;
fx y ð3; / 3Þ ¼ 1 ;
fy y ð3; / 3Þ ¼ / 2
D ¼ fx x ð3; / 3Þ . fy y ð3; / 3Þ / fx2y ð3; / 3Þ ¼ ð/ 2Þ ð/ 2Þ / 1 2 ¼ 3 > 0
fx x ð3; / 3Þ ¼ / 2 < 0
)
Relatives Maximum
Relative Extremwerte: Die Funktion besitzt an der Stelle ð3; / 3Þ ein relatives Maximum, der Flächenpunkt
P ¼ ð3; / 3; / 27Þ ist somit ein Hochpunkt.
&
2.5.3 Extremwertaufgaben mit Nebenbedingungen
(Lagrangesches Multiplikatorverfahren)
Die Extremwerte einer Funktion z ¼ f ðx; yÞ mit der Neben- oder Kopplungsbedingung
j ðx; yÞ ¼ 0 lassen sich nach Lagrange schrittweise wie folgt bestimmen:
1. „Hilfsfunktion“ bilden:
F ðx; y; lÞ ¼ f ðx; yÞ þ l . j ðx; yÞ
(l: sog. Lagrangescher Multiplikator)
256
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
2. Die partiellen Ableitungen 1. Ordnung der von den drei Variablen x; y und l
abhängigen Hilfsfunktion F ðx; y; lÞ werden gleich null gesetzt:
Fx ¼ fx ðx; yÞ þ l . jx ðx; yÞ ¼ 0
Fy ¼ fy ðx; yÞ þ l . jy ðx; yÞ ¼ 0
Fl ¼ j ðx; yÞ ¼ 0
Aus diesem Gleichungssystem mit drei Gleichungen und drei Unbekannten werden die gesuchten Extremwerte bestimmt.
Die angegebenen Bedingungen sind notwendig, nicht aber hinreichend. Der Lagrangesche
Multiplikator ist eine Hilfsgröße ohne Bedeutung und sollte daher möglichst früh aus den
Rechnungen eliminiert werden.
Alternativer Lösungsweg:
Die Nebenbedingung j ðx; yÞ ¼ 0 nach x oder y auflösen, den gefundenen Ausdruck
dann in z ¼ f ðx; yÞ einsetzen. Man erhält eine Funktion von einer Variablen, deren
Extremwerte dann mit der in Kap. IV (Abschnitt 4.5) beschriebenen Methode bestimmt
werden können.
&
Beispiel
Welches Rechteck mit den noch unbekannten Seitenlängen x und y hat bei einem vorgegebenen Umfang
von U ¼ 20 m den größten Flächeninhalt?
Flächeninhalt: A ¼ f ðx; yÞ ¼ x y
ðx; y in m; A in m2 Þ
Nebenbedingung: U ¼ 2 x þ 2 y ¼ 20
)
j ðx; yÞ ¼ x þ y / 10 ¼ 0
Hilfsfunktion bilden: F ðx; y; lÞ ¼ f ðx; yÞ þ l . j ðx; yÞ ¼ x y þ l ðx þ y / 10Þ
Gleichungssystem für die Unbekannten x; y und l mit Lösung:
)
Fx ¼ y þ l ¼ 0
) l ¼ /y ¼ /x ) x ¼ y
Fy ¼ x þ l ¼ 0
Fl ¼ x þ y / 10 ¼ 0
)
x þ x / 10 ¼ 2 x / 10 ¼ 0
Lösung der Aufgabe: x ¼ y ¼ 5 m ;
Amax ¼ 25 m
2
)
x ¼ 5
ðQuadratÞ
&
Verallgemeinerung für eine Funktion von
Nebenbedingungen:
n
unabhängigen Variablen mit
F ðx1 ; x2 ; . . . ; xn ; l1 ; l2 ; . . . ; lm Þ ¼ f ðx1 ; x2 ; . . . ; xn Þ þ
m
P
i¼1
m < n
li . ji ðx1 ; x2 ; . . . ; xn Þ
l1 ; l2 ; . . . ; lm : Lagrangesche Multiplikatoren
Alle n þ m partiellen Ableitungen 1. Ordnung werden dann gleich null gesetzt (notwendige
Bedingungen).
3 Mehrfachintegrale
257
3 Mehrfachintegrale
3.1 Doppelintegrale
3.1.1 Definition eines Doppelintegrals
ÐÐ
Das Doppelintegral
f ðx; yÞ dA lässt sich in anschaulicher Weise als das Volumen des in
ðAÞ
Bild a) skizzierten zylindrischen Körpers einführen, sofern f ðx; yÞ ( 0 ist. Der „Boden“
des Zylinders besteht aus dem Bereich ðAÞ der x; y-Ebene, sein „Deckel“ ist die
Bildfläche der Funktion z ¼ f ðx; yÞ:
z
Fläche z = f(x;y)
z
Fläche z = f(x;y)
Pk
Säule
Mantellinien
Zylinder
y
y
Bereich (A)
a)
zk
x
b)
Zylinder
Bereich (A)
DAk
x
Wir zerlegen zunächst den Zylinder in n zylindrische Röhren, deren Mantellinien parallel
zur z-Achse verlaufen, und ersetzen dann jede Röhre in der aus Bild b) ersichtlichen Weise
durch eine quaderförmige Säule vom Volumen DVk ¼ z k . DAk ¼ f ðxk ; yk Þ DAk mit
k ¼ 1; 2; . . . ; n. Dabei ist ðxk ; yk Þ eine beliebige Stelle aus dem Teilbereich („Boden‘‘)
DAk und zk ¼ f ðxk ; yk Þ die Höhenkoordinate des Punktes Pk auf der Fläche ðdieser
Punkt liegt senkrecht über der Stelle ðxk ; yk ÞÞ. Durch Summierung über alle Röhren
(Säulen) erhält man schließlich den folgenden Näherungswert für das Zylindervolumen V :
V '
n
P
k¼1
DVk ¼
n
P
k¼1
f ðxk ; yk Þ DAk
Beim Grenzübergang n ! 1 (und somit DAk ! 0Þ strebt diese Summe gegen einen
Grenzwert, der als 2-dimensionales Bereichsintegral von f ðx; yÞ über ðAÞ oder kurz als
Doppelintegral bezeichnet wird und geometrisch als Zylindervolumen interpretiert werden
darf (unter der Voraussetzung, dass die Bildfläche der Funktion z ¼ f ðx; yÞ im Bereich
ðAÞ oberhalb der x; y-Ebene liegt). Symbolische Schreibweise:
ðð
f ðx; yÞ dA ¼ lim
ðAÞ
n
P
n!1 k¼1
f ðxk ; yk Þ DAk
258
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Bezeichnungen:
x; y:
f ðx; yÞ:
dA:
ðAÞ:
Integrationsvariable
Integrandfunktion (kurz: Integrand)
Flächendifferential oder Flächenelement
Flächenhafter Integrationsbereich
3.1.2 Berechnung eines Doppelintegrals in kartesischen Koordinaten
Wir legen den folgenden kartesischen Normalbereich ðAÞ zugrunde (seitliche Begrenzung
durch zwei zur y-Achse parallele Geraden):
yu ¼ fu ðxÞ:
Untere Randkurve
yo ¼ fo ðxÞ:
Obere Randkurve
y
y0 = f0(x)
dA
dA ¼ dy dx
(
)
fu ðxÞ ) y ) fo ðxÞ
ðAÞ :
a ) x ) b
dx
yu = fu(x)
a
Das Doppelintegral
ÐÐ
ðAÞ
dy
b
x
f ðx; yÞ dA lässt sich dann schrittweise durch zwei nacheinander
auszuführende gewöhnliche Integrationen berechnen:
ðð
ðb
foð
ðxÞ
f ðx; yÞ dy dx
f ðx; yÞ dA ¼
ðAÞ
x ¼ a y ¼ fu ðxÞ
Inneres Integral
#ußeres Integral
1. Innere Integration (nach der Variablen y)
Die Variable x wird zunächst als Parameter festgehalten und die Funktion f ðx; yÞ
unter Verwendung der für gewöhnliche Integrale gültigen Regeln nach der Variablen y
integriert. In die ermittelte Stammfunktion setzt man dann für y die variablen, von x
abhängigen Integrationsgrenzen fo ðxÞ und fu ðxÞ ein und bildet die entsprechende Differenz.
2. "ußere Integration (nach der Variablen x)
Die jetzt nur noch von der Variablen x abhängige Funktion wird in den Grenzen von
x ¼ a bis x ¼ b integriert (gewöhnliche Integration nach x).
3 Mehrfachintegrale
259
Bei einer Integration über den speziellen kartesischen Normalbereich
x ¼ g1 ðyÞ:
y
Linke Randkurve
b
x ¼ g2 ðyÞ: Rechte Randkurve
(
)
g1 ðyÞ ) x ) g2 ðyÞ
ðAÞ :
a ) y ) b
x=g1(y)
dA
dx
dy
x = g2(y)
a
dA ¼ dx dy
x
gilt (Begrenzung unten und oben durch Parallelen zur x-Achse):
ðb
ðð
g2ððyÞ
f ðx; yÞ dx dy
f ðx; yÞ dA ¼
y ¼ a x ¼ g1 ðyÞ
ðAÞ
Hier wird zuerst nach x und dann nach y integriert, wobei die Integrationsgrenzen des
inneren Integrals im Allgemeinen noch von der Variablen y abhängen.
&
Beispiel
Ð1
x 2Ðþ 1
x¼0 y¼x
y
2
2
x y dy dx ¼ ?
y0 = x 2 + 1
Innere Integration nach der Variablen y:
x 2Ðþ 1
y¼x
¼
x 2 y dy ¼ x 2 .
1
x
2
/
2
x 2Ðþ 1
y¼x
ðx 2 þ 1Þ 2 / x
y dy ¼
.
2
¼
1 2 / 2. x 2 þ 1
x y y¼x ¼
2
1
1
ðx 6 þ x 4 þ x 2 Þ
2
yu = x
1
x
"ußere Integration nach der Variablen x:
+
)
3
2
Ð1
1
1 1 7
1 5
1 3 1
1 1
1
1
71
.
ðx 6 þ x 4 þ x 2 Þ dx ¼
x þ
x þ
x
þ
þ
¼
¼
2 x¼0
2 7
5
3
2
7
5
3
210
0
Ergebnis:
Ð1
x 2Ðþ 1
x¼0 y¼x
x 2 y dy dx ¼
71
210
&
Allgemeine Regel für die Berechnung eines Doppelintegrales
Die Reihenfolge der durchzuführenden Integrationen ist eindeutig durch die Anordnung
(Reihenfolge) der Differentiale im Doppelintegral festgelegt. Sie ist nur dann vertauschbar,
wenn sämtliche Integrationsgrenzen konstant sind (der Integrationsbereich ist in diesem
Fall ein achsenparalleles Rechteck).
260
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Sonderfall: f ðx; yÞ ¼ f1 ðxÞ . f2 ðyÞ und konstante Integrationsgrenzen x1 ) x ) x2 ,
y1 ) y ) y2 . Das Doppelintegral ist dann als Produkt zweier gewöhnlicher
Integrale darstellbar:
xð2
yð2
xð2
yð2
y1
x1
x ¼ x1 y ¼ y1
f2 ðyÞ dy
f1 ðxÞ dx .
f ðx; yÞ dy dx ¼
3.1.3 Berechnung eines Doppelintegrals in Polarkoordinaten
Wir legen den folgenden Normalbereich (A) in Polarkoordinaten zugrunde:
r ¼ ri ðjÞ:
Innere Randkurve
r ¼ ra ðjÞ:
"ußere Randkurve
y
f2
f + df
dA ¼ r dr dj
(
)
ri ðjÞ ) r ) ra ðjÞ
ðAÞ :
j1 ) j ) j2
df
Das Doppelintegral
ðAÞ
j
ð2
r+dr
f ðx; yÞ dA lässt sich dann schrittweise durch zwei nacheinander
berechnen
(man
setzt
x ¼ r . cos j;
rað
ðjÞ
f ðr . cos j; r . sin jÞ . r dr dj
f ðx; yÞ dA ¼
ðAÞ
r
x
auszuführende gewöhnliche Integrationen
y ¼ r . sin j und dA ¼ r dr djÞ:
ðð
r
(f)
= ri
f1
dr
f
y ¼ r . sin j
ÐÐ
f
dA
rd
x ¼ r . cos j ;
r = ra(f)
j ¼ j1 r ¼ ri ðjÞ
Inneres Integral
#ußeres Integral
Zunächst wird dabei nach der Variablen r, d. h. in radialer Richtung integriert, wobei die
Winkelkoordinate j als Parameter festgehalten wird (innere Integration). Dann folgt die
äußere Integration nach der Variablen j.
3 Mehrfachintegrale
261
3.1.4 Anwendungen
y
3.1.4.1 Flächeninhalt
dA
Definitionsformel
ðð
A ¼
ðð
1 dA ¼
dA
ðAÞ
A
ðAÞ
x
In kartesischen Koordinaten
ðb
y
y0 = f0(x)
foð
ðxÞ
A ¼
A
1 dy dx
x ¼ a y ¼ fu ðxÞ
yo ¼ fo ðxÞ:
yu ¼ fu ðxÞ:
Obere Randkurve
Untere Randkurve
In Polarkoordinaten
j
ð2
yu = fu(x)
a
y
b
f2
rað
ðjÞ
A ¼
x
ra = ra(f)
r dr dj
f1
A
j ¼ j1 r ¼ ri ðjÞ
ri = ri (f)
ra ¼ ra ðjÞ: "ußere Randkurve
ri ¼ ri ðjÞ: Innere Randkurve
x
3.1.4.2 Schwerpunkt einer homogenen ebenen Fläche
Definitionsformeln
1
xS ¼
.
A
yS ¼
1
.
A
y
ðð
x dA
yS
ðAÞ
ðð
S
y dA
A
ðAÞ
A: Flächeninhalt (siehe Abschnitt 3.1.4.1)
xS
x
262
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
In kartesischen Koordinaten
1
.
xS ¼
A
yS ¼
1
.
A
ðb
y
foð
ðxÞ
y0 = f0(x)
x dy dx
x ¼ a y ¼ fu ðxÞ
ðb
yS
foð
ðxÞ
S
y dy dx
yu = fu(x)
x ¼ a y ¼ fu ðxÞ
a
yo ¼ fo ðxÞ: Obere Randkurve
yu ¼ fu ðxÞ: Untere Randkurve
A: Flächeninhalt (siehe Abschnitt 3.1.4.1)
xS
x
b
In Polarkoordinaten
xS ¼
1
.
A
1
yS ¼
.
A
j
ð2
rað
ðjÞ
y
r 2 . cos j dr dj
j ¼ j1 r ¼ ri ðjÞ
j
ð2
rað
ðjÞ
f2
ra = ra(f)
S
yS
r 2 . sin j dr dj
f1
ri = ri (f)
j ¼ j1 r ¼ ri ðjÞ
xS
x
ra ¼ ra ðjÞ: "ußere Randkurve
ri ¼ ri ðjÞ: Innere Randkurve
A: Flächeninhalt (siehe Abschnitt 3.1.4.1)
Teilschwerpunktsatz: Siehe V.5.5
3.1.4.3 Flächenträgheitsmomente (Flächenmomente 2. Grades)
Definitionsformeln
ðð
Ix ¼
y 2 dA ;
ðð
Iy ¼
ðAÞ
ðð
Ip ¼
y
x 2 dA
ðAÞ
ðx 2 þ y 2 Þ dA ¼
ðAÞ
ðð
ðAÞ
r 2 dA
x
r
dA
y
A
Ip ¼ Ix þ Iy
x
3 Mehrfachintegrale
263
In kartesischen Koordinaten
y
foð
ðxÞ
ðb
y0 = f0(x)
2
y dy dx
Ix ¼
x ¼ a y ¼ fu ðxÞ
foð
ðxÞ
ðb
Iy ¼
yu = fu(x)
x 2 dy dx
x ¼ a y ¼ fu ðxÞ
foð
ðxÞ
ðb
Ip ¼
a
ðx 2 þ y 2 Þ dy dx
x ¼ a y ¼ fu ðxÞ
x
b
yo ¼ fo ðxÞ:
Obere Randkurve
yu ¼ fu ðxÞ:
Untere Randkurve
y
f2
In Polarkoordinaten
j
ð2
rað
ðjÞ
Ix ¼
r 3 . sin 2 j dr dj
ra = ra(f)
j ¼ j1 r ¼ ri ðjÞ
j
ð2
rað
ðjÞ
Iy ¼
f1
r 3 . cos 2 j dr dj
ri = ri (f)
j ¼ j1 r ¼ ri ðjÞ
j
ð2
rað
ðjÞ
Ip ¼
x
r 3 dr dj
j ¼ j1 r ¼ ri ðjÞ
ra ¼ ra ðjÞ:
"ußere Randkurve
ri ¼ ri ðjÞ:
Innere Randkurve
Satz von Steiner: Siehe V.5.6
3.2 Dreifachintegrale
3.2.1 Definition eines Dreifachintegrals
u ¼ f ðx; y; zÞ sei eine im Zylinderbereich ðVÞ definierte und dort stetige Funktion. Wir
zerlegen den Zylinder zunächst in n räumliche Teilbereiche DVk , wählen in jedem
Teilbereich einen beliebigen Punkt Pk ¼ ðxk ; yk ; zk Þ, bilden das Produkt f ðxk ; yk ; zk Þ DVk
und summieren schließlich über alle Teilbereiche ðk ¼ 1; 2; . . . ; n; siehe hierzu das obere
Bild auf der nächsten Seite):
n
P
k¼1
f ðxk ; yk ; zk Þ DVk
264
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Beim Grenzübergang n ! 1 (und zugleich DVk ! 0Þ strebt diese Summe gegen
einen Grenzwert, der als 3-dimensionales Bereichsintegral von f ðx; y; zÞ über ðVÞ oder
kurz als Dreifachintegral bezeichnet wird. Symbolische Schreibweise:
ððð
f ðx; y; zÞ dV ¼ lim
ðVÞ
n
P
n!1 k¼1
f ðxk ; yk ; zk Þ DVk
Bezeichnungen:
z
x; y; z:
f ðx; y; zÞ:
Integrationsvariable
Integrandfunktion
(kurz: Integrand)
dV : Volumendifferential oder
Volumenelement
ðVÞ: Räumlicher Integrationsbereich
Bereich (V)
(Körper)
Pk
Teilbereich DVk
zk
y
yk
xk
x
3.2.2 Berechnung eines Dreifachintegrals in kartesischen Koordinaten
Wir legen den folgenden kartesischen Normalbereich ðVÞ zugrunde:
z ¼ zu ðx; yÞ:
„Bodenfläche“
z ¼ zo ðx; yÞ:
„Deckelfläche“
z
„Deckel“ z = z0(x;y)
Zylinder
dV ¼ dx dy dz ¼ dz dy dx
8
9
zu ðx; yÞ ) z ) zo ðx; yÞ >
>
>
>
<
=
ðVÞ :
fu ðxÞ ) y ) fo ðxÞ
>
>
>
>
:
;
a ) x ) b
dx
dz
dy
y = f0(x)
dV
„Boden“
z = zu(x;y)
y
(A)
y = fu(x)
a
b
x
3 Mehrfachintegrale
265
ÐÐÐ
Ein Dreifachintegral
ðVÞ
f ðx; y; zÞ dV
lässt sich dann
schrittweise
durch drei
nacheinander auszuführende gewöhnliche Integrationen berechnen:
ððð
ðb
foð
ðxÞ
zo ðx;
ð yÞ
f ðx; y; zÞ dV ¼
f ðx; y; zÞ dz dy dx
x ¼ a y ¼ fu ðxÞ z ¼ zu ðx; yÞ
ðVÞ
1. Integration
2. Integration
3. Integration
Es wird in der Reihenfolge z; y; x integriert. Bei einer Abänderung dieser Integrationsreihenfolge müssen die Integrationsgrenzen jeweils neu bestimmt werden. Zuletzt
wird dabei stets über die Variable mit festen Genzen integriert. Die Reihenfolge der
Integrationen ist jedoch beliebig vertauschbar, wenn sämtliche Integrationsgrenzen
konstant sind (quaderförmiger Integrationsbereich mit achsenparallelen Seiten).
&
Beispiel
Ð2
Ðx
x Ðþ y
x¼1 y¼0 z¼0
ðx / yÞ z dz dy dx ¼ ?
1. Integrationsschritt (Integration nach der Variablen z):
x Ðþ y
z¼0
ðx / yÞ z dz ¼ ðx / yÞ .
x Ðþ y
z¼0
z dz ¼
1
1
xþy
ðx / yÞ ½ z 2 % z ¼ 0 ¼
ðx / yÞ ðx þ yÞ 2 ¼
2
2
1
1
ðx / yÞ ðx 2 þ 2 x y þ y 2 Þ ¼
ðx 3 þ 2 x 2 y þ x y 2 / x 2 y / 2 x y 2 / y 3 Þ ¼
2
2
1
¼
ðx 3 þ x 2 y / x y 2 / y 3 Þ
2
¼
2. Integrationsschritt (Integration nach der Variablen y):
+
)
Ðx 1
1
1 2 2
1
1 4 x
ðx 3 þ x 2 y / x y 2 / y 3 Þ dy ¼
x3y þ
x y /
xy3 /
y
¼
2
2
3
4
y¼0 2
y¼0
¼
1
2
3
x4 þ
1 4
1 4
1 4
x /
x /
x
2
3
4
2
¼
1
2
3
1
1
1
1þ
/
/
2
3
4
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
11=12
2
x4 ¼
1 11 4
11 4
.
x ¼
x
2 12
24
3. Integrationsschritt (Integration nach der Variablen x):
Ð2 11 4
11 1 h 5 i 2
11
341
x dx ¼
.
x
¼
ð32 / 1Þ ¼
1
24 5
120
120
x ¼ 1 24
Ergebnis:
Ð2
Ðx
x Ðþ y
x¼1 y¼0 z¼0
ðx / yÞ z dz dy dx ¼
341
120
&
266
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
Sonderfall:
xð2
yð2
f ðx; y; zÞ ¼ f1 ðxÞ . f2 ðyÞ . f3 ðzÞ
und konstante Integrationsgrenzen
x1 ) x ) x2 , y1 ) y ) y2 , z1 ) z ) z2 . Das Dreifachintegral ist dann
als Produkt dreier gewöhnlicher Integrale darstellbar:
ðz2
xð2
f ðx; y; zÞ dz dy dx ¼
x ¼ x1 y ¼ y1 z ¼ z1
yð2
f1 ðxÞ dx .
x1
ðz2
f2 ðyÞ dy .
y1
f3 ðzÞ dz
z1
3.2.3 Berechnung eines Dreifachintegrals in Zylinderkoordinaten
Hinweis: Die Zylinderkoordinate r (senkrechter Abstand von der z-Achse) wird hier
mit r bezeichnet, um Verwechslungen mit der Dichte r zu vermeiden
(Zylinderkoordinaten: siehe I.9.2.2 und XIV.6.2).
Beim !bergang von den kartesischen Raumkoordinaten ðx; y; zÞ zu den Zylinderkoordinaten ðr; j; zÞ gelten die Transformationsgleichungen
x ¼ r . cos j ;
y ¼ r . sin j ;
Ein Dreifachintegral
ÐÐÐ
ðVÞ
ððð
dV ¼ r dz dr dj
f ðx; y; zÞ dV transformiert sich dabei wie folgt:
ððð
f ðx; y; zÞ dV ¼
ðVÞ
z ¼ z;
f ðr . cos j; r . sin j; zÞ . r dz dr dj
ðVÞ
Die Integration erfolgt dabei in drei nacheinander auszuführenden gewöhnlichen Integrationsschritten, wobei zunächst nach z , dann nach r und schließlich nach j integriert
wird. Bei einer Abänderung der Integrationsreihenfolge müssen die (in Zylinderkoordinaten
ausgedrückten) Integrationsgrenzen neu bestimmt werden.
3.2.4 Berechnung eines Dreifachintegrals in Kugelkoordinaten
Beim !bergang von den kartesischen Raumkoordinaten ðx; y; zÞ zu den Kugelkoordinaten ðr; J; jÞ gelten die folgenden Transformationsgleichungen:
x ¼ r . sin J . cos j ;
y ¼ r . sin J . sin j ;
dV ¼ r 2 . sin J . dr dJ dj
(Kugelkoordinaten: siehe I.9.2.4 und XIV.6.3).
z ¼ r . cos J
3 Mehrfachintegrale
267
ÐÐÐ
Ein Dreifachintegral
ðVÞ
ððð
ððð
f ðx; y; zÞ dV ¼
ðVÞ
f ðx; y; zÞ dV transformiert sich dabei wie folgt:
f ðr . sin J . cos j; r . sin J . sin j; r . cos JÞ . r 2 . sin J dr dJ dj
ðVÞ
Die Integration erfolgt in drei nacheinander auszuführenden gewöhnlichen Integrationsschritten, wobei zunächst nach r, dann nach J und schließlich nach j integriert wird.
Bei einer #nderung der Integrationsreihenfolge müssen die (in Kugelkoordinaten ausgedrückten) Integrationsgrenzen neu bestimmt werden.
3.2.5 Anwendungen
3.2.5.1 Volumen eines zylindrischen Körpers
Definitionsformel
ððð
V ¼
z
„Deckel“ z = z0(x;y)
ððð
1 dV ¼
ðVÞ
dV
Zylinder
ðVÞ
dx
In kartesischen Koordinaten
foð
ðxÞ
ðb
zo ðx;
ð yÞ
y = f0(x)
dz dy dx
V ¼
x ¼ a y ¼ fu ðxÞ z ¼ zu ðx; yÞ
z ¼ zo ðx; yÞ:
z ¼ zu ðx; yÞ:
„Deckelfläche“
„Bodenfläche“
dz
dy
dV
„Boden“
z = zu(x;y)
y
(A)
y = fu(x)
a
x
b
Rotationskörper
z
Rotationsachse: z-Achse
ððð
V ¼
r dz dr dj
ðVÞ
r; j; z:
Zylinderkoordinaten (siehe I.9.2.2
und XIV.6.2)
y
x
268
IX Differential- und Integralrechnung für Funktionen von mehreren Variablen
3.2.5.2 Schwerpunkt eines homogenen Körpers
Definitionsformeln
1
.
xS ¼
V
V:
ððð
x dV ;
ðVÞ
1
yS ¼
.
V
ððð
ððð
1
zS ¼
.
V
y dV ;
ðVÞ
z dV
ðVÞ
Volumen (siehe Abschnitt 3.2.5.1)
In kartesischen Koordinaten
1
xS ¼
.
V
1
yS ¼
.
V
zS ¼
1
.
V
foð
ðxÞ
ðb
z
„Deckel“ z = z0(x;y)
zo ðx;
ð yÞ
x dz dy dx
Zylinder
x ¼ a y ¼ fu ðxÞ z ¼ zu ðx; yÞ
foð
ðxÞ
ðb
zo ðx;
ð yÞ
S
y dz dy dx
x ¼ a y ¼ fu ðxÞ z ¼ zu ðx; yÞ
foð
ðxÞ
ðb
zS
zo ðx;
ð yÞ
y = f0(x)
z dz dy dx
x ¼ a y ¼ fu ðxÞ z ¼ zu ðx; yÞ
z ¼ zo ðx; yÞ:
z ¼ zu ðx; yÞ:
„Deckelfläche“
„Bodenfläche“
yS
y
(A)
y = fu (x)
a
„Boden“
z = zu(x;y)
xS
Rotationskörper
x
b
z
Rotationsachse: z-Achse
xS ¼ 0 ;
yS ¼ 0
ððð
1
.
z r dz dr dj
zS ¼
V
S
zS
ðVÞ
V : Rotationsvolumen (siehe Abschnitt 3.2.5.1)
r; j; z: Zylinderkoordinaten (siehe I.9.2.2
und XIV.6.2)
y
x
3 Mehrfachintegrale
269
3.2.5.3 Massenträgheitsmoment eines homogenen Körpers
Definitionsformel
ððð
J ¼ r.
Bezugsachse A
Körper der
Masse m
r 2A dV
ðVÞ
r: Konstante Dichte des Körpers
rA : Senkrechter Abstand des Volumenelementes dV von der Bezugsachse
rA
dV
In kartesischen Koordinaten
Bezugsachse: z-Achse
ðb
foð
ðxÞ
zo ðx;
ð yÞ
J ¼ r.
ðx 2 þ y 2 Þ dz dy dx
x ¼ a y ¼ fu ðxÞ z ¼ zu ðx; yÞ
z ¼ zo ðx; yÞ: „Deckelfläche“
z ¼ zu ðx; yÞ: „Bodenfläche“
r: Konstante Dichte des Körpers
Rotationskörper
z
Rotations- und Bezugsachse: z-Achse
ððð
Jz ¼ r .
r 3 dz dr dj
ðVÞ
r: Konstante Dichte des Körpers
r; j; z: Zylinderkoordinaten (siehe I.9.2.2
und XIV.6.2)
y
x
Satz von Steiner (siehe hierzu auch V.5.1)
J ¼ JS þ m d 2
J : Massenträgheitsmoment bezüglich der gewählten Bezugsachse
JS : Massenträgheitsmoment bezüglich der zur Bezugsachse parallelen Schwerpunktachse
m: Masse des homogenen Körpers
d : Abstand zwischen Bezugs- und Schwerpunktachse
270
X Gewöhnliche Differentialgleichungen
1 Grundbegriffe
1.1 Definition einer gewöhnlichen Differentialgleichung n-ter Ordnung
Eine Gleichung, in der Ableitungen einer unbekannten Funktion y ¼ y ðxÞ bis zur n-ten
Ordnung auftreten, heißt eine gewöhnliche Differentialgleichung n-ter Ordnung.
Fðx; y; y 0 ; . . . ; y ðnÞ Þ ¼ 0
Explizite Form:
y ðnÞ ¼ f ðx; y; y 0 ; . . . ; y ðn / 1Þ Þ
|fflfflffl{zfflfflffl}
Implizite Form:
n 2 N*
1.2 Lösungen einer Differentialgleichung
Eine Funktion y ¼ y ðxÞ heißt eine Lösung der Differentialgleichung, wenn sie mit ihren
Ableitungen die Differentialgleichung identisch erfüllt.
Allgemeine Lösung
Die allgemeine Lösung einer Differentialgleichung n-ter Ordnung enthält n voneinander
unabhängige Parameter oder Integrationskonstanten.
Spezielle oder partikuläre Lösung
Man erhält aus der allgemeinen Lösung eine spezielle oder partikuläre Lösung, indem man
den n Parametern feste Werte zuweist (z. B. durch zusätzliche Bedingungen wie Anfangsoder Randbedingungen).
Singuläre Lösung
Eine Lösung der Differentialgleichung, die sich nicht aus der allgemeinen Lösung gewinnen lässt, heißt singulär.
1.3 Anfangswertprobleme
Von der gesuchten Lösung y ¼ yðxÞ einer Differentialgleichung n-ter Ordnung sind genau n Werte, nämlich der Funktionswert sowie die Werte der ersten n / 1 Ableitungen
an einer Stelle x0 vorgegeben: y ðx0 Þ; y 0 ðx0 Þ; y 00 ðx0 Þ; . . . ; y ðn / 1Þ ðx0 Þ (sog. Anfangswerte).
Aus diesen Anfangsbedingungen lassen sich die n Integrationskonstanten C1 ; C2 ; . . . ; Cn
der allgemeinen Lösung bestimmen.
Dies bedeutet für eine
Dgl. 1. Ordnung: Gesucht ist die Lösungskurve y ¼ y ðxÞ durch den Punkt P ¼ ðx0 ; y0 Þ.
Dgl. 2. Ordnung: Gesucht ist die Lösungskurve y ¼ y ðxÞ durch den Punkt P ¼ ðx0 ; y0 Þ,
die in diesem Punkt die Steigung y 0 ðx0 Þ ¼ m besitzt.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_10
2 Differentialgleichungen 1. Ordnung
271
1.4 Randwertprobleme
Von der gesuchten Lösung y ¼ y ðxÞ einer Differentialgleichung n-ter Ordnung sind oft die
Funktionswerte an n verschiedenen Stellen x1 ; x2 ; . . . ; xn vorgegeben: y ðx1 Þ; yðx2 Þ; . . .
. . . ; y ðxn Þ (sog. Randwerte; n ( 2). Aus diesen Randbedingungen lassen sich dann die n
Integrationskonstanten C1 ; C2 ; . . . ; Cn der allgemeinen Lösung bestimmen 1Þ .
Allgemeiner formuliert: Ein Randwertproblem (auch Randwertaufgabe genannt) liegt vor,
wenn die gesuchte Lösung einer Differentialgleichung n-ter Ordnung und gewisse ihrer
Ableitungen an mindestens zwei verschiedenen Stellen des Definitionsbereiches vorgeschriebene Werte annehmen sollen (insgesamt n Randbedingungen).
2 Differentialgleichungen 1. Ordnung
2.1 Differentialgleichungen 1. Ordnung mit trennbaren Variablen
Eine Differentialgleichung 1. Ordnung vom Typ
y0 ¼
dy
¼ f ðxÞ . g ðyÞ
dx
wird durch „Trennung der Variablen“ wie folgt gelöst:
1. Zunächst werden die beiden Variablen und ihre zugehörigen Differentiale voneinander
getrennt, d. h. auf verschiedene Seiten der Gleichung gebracht.
2. Dann erfolgt die Integration auf beiden Seiten der Gleichung. Die Lösung lautet (in
impliziter Form):
ð
dy
¼
g ðyÞ
ð
1
dy ¼
g ðyÞ
ð
f ðxÞ dx
ðgðyÞ ¼
6 0Þ
Weitere Lösungen: Jede Lösung der Gleichung g ðyÞ ¼ 0 (sie sind vom Typ y ¼ const:).
&
Beispiel
y 0 ¼ ðcos xÞ . y
oder
dy
¼ ðcos xÞ . y
dx
Trennen der beiden Variablen:
dy
¼ cos x dx
y
ð f ür y 6¼ 0Þ
Integration auf beiden Seiten:
ð
ð
dy
¼ cos x dx ) ln j y j ¼ sin x þ ln j C j
y
1Þ
)
"y"
" "
ln j y j / ln j C j ¼ ln " " ¼ sin x
C
Nicht jedes Randwertproblem ist lösbar, in bestimmten Fällen können auch mehrere Lösungen auftreten.
272
X Gewöhnliche Differentialgleichungen
Allgemeiner Hinweis: Beim Auftreten logarithmischer Terme wird die Integrationskonstante zweckmäßigerweise in der Form ln j C j angesetzt. Man beachte ferner, das in diesem Beispiel auch y ¼ 0 eine Lösung ist.
Lösung (nach Entlogarithmierung der Gleichung):
y ¼ C . e sin x
ðC 2 RÞ
&
2.2 Spezielle Differentialgleichungen 1. Ordnung,
die durch Substitutionen lösbar sind (Tabelle)
Differentialgleichung
ðAÞ
ðBÞ
Substitution
y 0 ¼ f ða x þ b y þ cÞ
y0 ¼ f
!y4
x
u ¼ ax þ by þ c
1. Trennung der Variablen
2. Rücksubstitution
y
x
f ðuÞ / u
x
1. Trennung der Variablen
2. Rücksubstitution
u0 ¼
y 0 þ g ðxÞ . y ¼ h ðxÞ . y n
u 0 ¼ a þ b . f ðuÞ
u0 ¼ a þ by0
u ¼
ðx 6¼ 0Þ
(homogene Dgl)
ðCÞ
Neue Dgl/Lösungsweg
u0 ¼
xy0 / y
x2
u ¼ y 1/n
u 0 þ ð1 / nÞ g ðxÞ . u ¼
u 0 ¼ ð1 / nÞ y / n y 0 ¼ ð1 / nÞ hðxÞ
(Bernoullische Dgl; n 6¼ 1Þ
1. Lineare Dgl (siehe X.2.4)
2. Rücksubstitution
Man beachte: y ist eine Funktion von x, dies gilt daher auch für die „Hilfsvariable“ u.
&
Beispiel
!y4
2y / x
¼ 2
/ 1; x ¼
6 0;
x
x
y
Substitution: u ¼
; y ¼ xu )
x
y0 ¼
Neue Dgl:
u þ xu0 ¼ 2u / 1
Trennung der Variablen:
ð
Integration:
du
¼
u/1
Entlogarithmierung:
x
ð
homogene Dgl vom Typ ðBÞ
y0 ¼ 1 . u þ x . u0 ¼ u þ xu0
xu0 ¼ u / 1
)
du
¼ u/1
dx
dx
x
)
u / 1 ¼ Cx
)
du
dx
¼
u/1
x
ðx 6¼ 0; u 6¼ 1Þ
ln j u / 1 j ¼ ln j x j þ ln j C j ¼ ln j C x j
)
Allgemeine Lösung (nach Rücksubstitution):
u ¼ Cx þ 1
y ¼ x u ¼ x ðC x þ 1Þ ¼ C x 2 þ x
ðC 2 RÞ
Hinweis: Aus u ¼ 1 erhält man die spezielle Lösung y ¼ x, die in der allgemeinen Lösung bereits enthalten
ist (für C ¼ 0).
&
2 Differentialgleichungen 1. Ordnung
273
2.3 Exakte Differentialgleichungen 1. Ordnung
Eine Differentialgleichung 1. Ordnung vom Typ
g ðx; yÞ dx þ h ðx; yÞ dy ¼ 0
mit
@g
@h
¼
@y
@x
heißt exakt oder vollständig. Die lineare Differentialform g ðx; yÞ dx þ h ðx; yÞ dy ist dann
das totale oder vollständige Differential du einer Funktion u ¼ u ðx; yÞ. Somit gilt:
@u
¼ g ðx; yÞ
@x
und
@u
¼ h ðx; yÞ
@y
Die Lösung der exakten Differentialgleichung lautet dann in geschlossener Form:
)
ð
ð+
ð
@g
g ðx; yÞ dx þ
h ðx; yÞ /
dx dy ¼ const: ¼ C
@y
&
Beispiel
Die Dgl ð1 / xÞ y 0 þ x / y ¼ 0 oder ðx / y Þ dx þ ð1 / x Þ dy ¼ 0 ist exakt:
|fflffl{zfflffl}
|fflffl{zfflffl}
9
g
h
@g
@
>
¼
ðx / yÞ ¼ / 1 >
>
=
@y
@y
@g
@h
)
¼
¼ /1
>
@y
@x
>
@h
@
>
¼
ð1 / xÞ ¼ / 1 ;
@x
@x
Integration (nach obiger Lösungsformel):
)
)
ð
ð+
ð
ð +
ð
@
1 2
ðx / yÞ d x þ
1/x /
ðx / yÞ dx d y ¼
x / xy þ
1 / x þ 1 dx dy ¼
@y
2
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
|fflffl{zfflffl}
x
ð /1
1 2
1 2
¼
x / x y þ 1 dy ¼
x / xy þ y ¼ C
2
2
Lösung:
1 2
x / xy þ y ¼ C
2
oder
y ¼
x2 / 2C
2 ðx / 1Þ
ðx 6¼ 1; C 2 RÞ
&
Integrierender Faktor
Häufig lässt sich eine nichtexakte Differentialgleichung 1. Ordnung durch Multiplikation
mit einer geeigneten Funktion l ¼ l ðx; yÞ in eine exakte Differentialgleichung überführen. Der „integrierende Faktor“ l ðx; yÞ muss dabei die Integrabilitätsbedingung
.
.
@ /
@ /
l ðx; yÞ . g ðx; yÞ ¼
lðx; yÞ . h ðx; yÞ
@y
@x
erfüllen. In vielen Fällen hängt der integrierende Faktor nur von x oder y ab, d. h.
l ¼ l ðxÞ bzw. l ¼ l ðyÞ.
&
Beispiel
@
@
ð1 þ x yÞ ¼ x 6¼
ðx y þ x 2 Þ ¼ y þ 2 x
@y
@x
Diese Dgl ist also nichtexakt, sie lässt sich jedoch mit Hilfe des „integrierenden Faktors‘‘ l ¼ 1=x in eine
exakte Dgl überführen:
ð1 þ x yÞ dx þ ðx y þ x 2 Þ dy ¼ 0 ;
274
X Gewöhnliche Differentialgleichungen
1
1
ð1 þ x yÞ dx þ
ðx y þ x 2 Þ dy ¼
x
x
Neue (exakte) Dgl:
@g
@
¼
@y
@y
3
1
þy
x
2
¼
@h
@
¼
ðy þ xÞ ¼ 1
@x
@x
)
3
2
1
þ y dx þ ð y þ xÞ dy ¼ 0
x
|fflffl{zfflffl}
|fflfflffl{zfflfflffl}
h
g
exakte Dgl
ð3
2
)
ð+
ð
1
1 2
þ y dx þ
y þ x / 1 dx dy ¼ ln j x j þ x y þ
y ¼ C
x
2
|fflfflffl{zfflfflffl}
x
1 2
y ¼ C
ðC 2 RÞ
ln j x j þ x y þ
2
Integration:
Lösung:
Hinweis: Den „integrierenden Faktor‘‘ l ¼ 1=x erhält man aus der Integrabilitätsbedingung unter der
Annahme, dass der gesuchte Faktor nur von der Variablen x abhängt ðAnsatz: l ¼ l ðxÞÞ.
&
2.4 Lineare Differentialgleichungen 1. Ordnung
2.4.1 Definition einer linearen Differentialgleichung 1. Ordnung
y 0 þ f ðxÞ . y ¼ g ðxÞ
Die Funktion g ðxÞ wird als Störfunktion oder Störglied bezeichnet. Fehlt das Störglied,
d. h. ist g ðxÞ 0 0, so heißt die lineare Differentialgleichung homogen, sonst inhomogen.
2.4.2 Integration der homogenen linearen Differentialgleichung
y 0 þ f ðxÞ . y ¼ 0
Lösung durch „Trennung der Variablen“:
y ¼ C . e/
&
Ð
f ðxÞ dx
ðC 2 RÞ
Beispiel
y0 / 2xy ¼ 0
)
y ¼ C .e
Ð
2 x dx
¼ C . ex
2
ðC 2 RÞ
&
2.4.3 Integration der inhomogenen linearen Differentialgleichung
2.4.3.1 Integration durch Variation der Konstanten
Eine inhomogene lineare Differentialgleichung 1. Ordnung vom Typ y 0 þ f ðxÞ . y ¼ g ðxÞ
lässt sich durch „Variation der Konstanten“ wie folgt lösen:
1. Integration der zugehörigen homogenen Differentialgleichung
durch „Trennung der Variablen“. Allgemeine Lösung:
Ð
y ¼ K . e / f ðxÞ dx
ðK 2 RÞ
y 0 þ f ðxÞ . y ¼ 0
2 Differentialgleichungen 1. Ordnung
275
2. „Variation der Konstanten“: Die Integrationskonstante K wird durch eine (noch unbekannte) Funktion K ðxÞ ersetzt: K ! K ðxÞ. Mit dem Lösungsansatz
y ¼ K ðxÞ . e /
Ð
f ðxÞ dx
geht man in die inhomogene lineare Differentialgleichung ein und erhält eine einfache
Differentialgleichung 1. Ordnung für die Faktorfunktion K ðxÞ, die durch unbestimmte
Integration direkt gelöst werden kann.
&
Beispiel
y0 /
y
¼ x2
x
oder
y0 /
1
y ¼ x2
x
ðx 6¼ 0Þ
y
1. Homogene Differentialgleichung: y 0 /
¼ 0
x
Integration durch „Trennung der Variablen“:
ð
ð
dy
dx
dy
dx
¼
;
¼
;
ln j y j ¼ ln j x j þ ln j K j ¼ ln j K . x j
y
x
y
x
Lösung der homogenen Differentialgleichung:
y ¼ K .x
y
2. Inhomogene Differentialgleichung: y /
¼ x2
x
Integration durch „Variation der Konstanten“: K ! K ðxÞ
ðK 2 RÞ
0
Lösungsansatz:
y 0 ¼ K 0 ðxÞ . x þ K ðxÞ
y ¼ K ðxÞ . x ;
(Produktregel)
K ðxÞ . x
1 2
¼ x2;
K 0 ðxÞ . x ¼ x 2 ;
K 0 ðxÞ ¼ x ) K ðxÞ ¼
K 0 ðxÞ . x þ K ðxÞ /
x þC
x
2
3
2
1 2
1 3
Lösung: y ¼ K ðxÞ . x ¼
x þC . x ¼
x þ Cx
ðC 2 RÞ
2
2
&
2.4.3.2 Integration durch Aufsuchen einer partikulären Lösung
Man löst zunächst die zugehörige homogene Differentialgleichung yÐ 0 þ f ðxÞ . y ¼ 0
durch „Trennung der Variablen“ (allgemeine Lösung: y0 ¼ C . e / f ðxÞ dx ) und versucht dann mit Hilfe eines geeigneten Lösungsansatzes, der im Wesentlichen vom Typ
des Störgliedes g ðxÞ abhängt und einen oder mehrere Parameter enthält, eine partikuläre Lösung yp der inhomogenen Differentialgleichung y 0 þ f ðxÞ . y ¼ g ðxÞ zu bestimmen. Die allgemeine Lösung y der inhomogenen Differentialgleichung ist dann die Summe aus y0 und yp :
y ¼ y0 þ yp ¼ C . e /
Ð
f ðxÞ dx
þ yp
ðC 2 RÞ
2.4.4 Lineare Differentialgleichungen 1. Ordnung mit konstanten Koeffizienten
y 0 þ a y ¼ g ðxÞ
ða 2 RÞ
ðSpezialfall der allgemeinen linearen Differentialgleichung 1. Ordnung für f ðxÞ ¼ aÞ
276
X Gewöhnliche Differentialgleichungen
Die Integration dieser Differentialgleichung erfolgt entweder durch „Variation der Konstanten“ (siehe Abschnitt 2.4.3.1) oder durch „Aufsuchen einer partikulären Lösung“ (siehe
Abschnitt 2.4.3.2), wobei sich die letztere Lösungsmethode in den meisten Fällen als die
zweckmäßigere erweist, da der Lösungsansatz für eine partikuläre Lösung yp im Wesentlichen dem Funktionstyp des Störgliedes g ðxÞ entspricht.
Die zugehörige homogene Gleichung y 0 þ a y ¼ 0 wird durch die Exponentialfunktion
y0 ¼ C . e / a x gelöst. Für die allgemeine Lösung der inhomogenen Differentialgleichung
gilt somit:
y ¼ y0 þ yp ¼ C . e / a x þ yp
ðC 2 RÞ
Den Lösungsansatz für eine partikuläre Lösung yp entnimmt man der folgenden Tabelle.
Tabelle: Lösungsansatz yp für spezielle Störfunktionen (Störglieder)
Störfunktion g ðxÞ
Lösungsansatz yp ðxÞ
1. Konstante Funktion
Konstante Funktion yp ¼ c0
2. Lineare Funktion
Lineare Funktion yp ¼ c1 x þ c0
3. Quadratische Funktion
Quadratische Funktion
yp ¼ c2 x 2 þ c1 x þ c0
4. Polynomfunktion vom Grade n
Polynomfunktion vom Grade n
yp ¼ cn x n þ . . . þ c1 x þ c0
5. g ðxÞ ¼ A . sin ðw xÞ
6. g ðxÞ ¼ B . cos ðw xÞ
7. g ðxÞ ¼ A . sin ðw xÞ þ B . cos ðw xÞ
8. g ðxÞ ¼ A . e b x
„Stellparameter“: c0 ; c1 ; . . . ; cn ;
9
yp ¼ C1 . sin ðw xÞ þ C2 . cos ðw xÞ
>
>
=
oder
>
>
;
yp ¼ C . sin ðw x þ jÞ
(
)
b 6¼ / a
C . e bx
für
yp ¼
b ¼ /a
C x . e bx
C; C1 ; C2 ;
j
Anmerkungen zur Tabelle
(1)
(2)
(3)
Die im jeweiligen Lösungsansatz enthaltenen Parameter („Stellparameter‘‘) sind so
zu bestimmen, dass der Ansatz die vorgegebene Differentialgleichung löst.
Ist die Störfunktion g ðxÞ eine Summe aus mehreren Störgliedern, so erhält man den
Lösungsansatz für yp als Summe der Lösungsansätze für die einzelnen Störglieder.
Ist die Störfunktion gðxÞ ein Produkt aus mehreren Faktoren, so werden die Ansätze
für die einzelnen Faktoren miteinander multipliziert.
2 Differentialgleichungen 1. Ordnung
277
Beispiel
&
y0 / 2y ¼ 4x / 2
y0 / 2y ¼ 0
1. Homogene Differentialgleichung:
Lösung:
y0 ¼ C . e 2 x
ðC 2 RÞ
y0 / 2y ¼ 4x / 2
2. Inhomogene Differentialgleichung:
Lösungsansatz für yp (aus der Tabelle entnommen):
ðStörglied: g ðxÞ ¼ 4 x / 2Þ
yp ¼ a x þ b ;
y 0p ¼ a
Bestimmung der Konstanten a und b:
a / 2 ða x þ bÞ ¼ 4 x / 2 ;
Koeffizientenvergleich:
'
/2a
¼ 4
)
a / 2b ¼ /2
Partikuläre Lösung:
/2ax þ a / 2b ¼ 4x / 2
a ¼ /2;
b ¼ 0
yp ¼ / 2 x
Lösung der inhomogenen Differentialgleichung:
y ¼ y0 þ yp ¼ C . e 2 x / 2 x
ðC 2 RÞ
&
2.5 Numerische Integration einer Differentialgleichung 1. Ordnung
2.5.1 Streckenzugverfahren von Euler
Die Lösungskurve y ðxÞ der Differentialgleichung y 0 ¼ f ðx; yÞ für den Anfangswert
y ðx0 Þ ¼ y0 lässt sich an den Stellen x1 ¼ x0 þ h, x2 ¼ x0 þ 2 h, x3 ¼ x0 þ 3 h; . . .
näherungsweise wie folgt berechnen (h: gewählte Schrittweite):
y ðx0 Þ ¼ y0
(vorgegebener Anfangswert)
y ðx1 Þ ' y1 ¼ y0 þ h . f ðx0 ; y0 Þ
y ðx2 Þ ' y2 ¼ y1 þ h . f ðx1 ; y1 Þ
y ðx3 Þ ' y3 ¼ y2 þ h . f ðx2 ; y2 Þ
..
.
Rechenschema
i
x
y
h . f ðx; yÞ
0
x0
y0 (Anfangswert)
h . f ðx0 ; y0 Þ
1
x1 ¼ x0 þ h
y1 ¼ y0 þ h . f ðx0 ; y0 Þ
h . f ðx1 ; y1 Þ
2
x2 ¼ x0 þ 2 h
y2 ¼ y1 þ h . f ðx1 ; y1 Þ
h . f ðx2 ; y2 Þ
3
..
.
x3 ¼ x0 þ 3 h
..
.
y3 ¼ y2 þ h . f ðx2 ; y2 Þ
..
.
h . f ðx3 ; y3 Þ
..
.
278
X Gewöhnliche Differentialgleichungen
Fehlerabschätzung
Dyi ¼ y ðxi Þ / yi ' yi / y~i
Exakte Lösung an der Stelle xi
Näherungslösung an der Stelle xi bei der Schrittweite h
Näherungslösung an der Stelle xi bei doppelter Schrittweite 2 h
y ðxi Þ:
yi :
y~i :
Geometrische Deutung
Die (exakte) Lösungskurve wird im Anfangspunkt P0 ¼ ðx0 ; y0 Þ durch die dortige Tangente mit der Steigung m ¼ f ðx0 ; y0 Þ ersetzt. Der an der Stelle x1 ¼ x0 þ h gelegene
Tangentenpunkt P1 besitzt dann die Ordinate y1 ¼ y0 þ h . f ðx0 ; y0 Þ (Bild a)). Dieser
Wert ist ein Näherungswert für die exakte Lösung yðx1 Þ:
y ðx1 Þ ' y1 ¼ y0 þ h . f ðx0 ; y0 Þ
Dann wird das Verfahren für den (neuen) Anfangspunkt P1 wiederholt usw.. Man erhält einen
Streckenzug als Näherung für die gesuchte Lösung der Differentialgleichung (Bild b)).
exakte Lösungskurve
y
y
P3
exakte Lösungskurve
Streckenzug
nach Euler
P2
y0
P1
P0
Tangente
y(x1)
y1
h
h
a)
&
P1
P0
x1
x0
x
b)
x0
h
x1
h
x2
x3
x
Beispiel
y0 ¼ y / x
Anfangswert:
y ð0Þ ¼ 0
Wir berechnen die Näherungslösung dieser Differentialgleichung im Intervall 0 ) x ) 0,2 für die Schrittweite h ¼ 0,05 und vergleichen sie mit der exakten Lösung y ¼ / e x þ x þ 1:
i
x
y
h . f ðx; yÞ ¼ 0;05 ðy / xÞ
yexakt
0
0,00
0,000 000
0,000 000
0,000 000
1
0,05
0,000 000
/ 0,002 500
/ 0,001 271
2
0,10
/ 0,002 500
/ 0,005 125
/ 0,005 171
3
0,15
/ 0,007 625
/ 0,007 881
/ 0,011 834
4
0,20
/ 0,015 506
/ 0,010 775
/ 0,021 403
Grau unterlegt: Näherungswerte
&
2 Differentialgleichungen 1. Ordnung
279
2.5.2 Runge-Kutta-Verfahren 2. Ordnung
Die Lösungskurve y ðxÞ der Differentialgleichung y 0 ¼ f ðx; yÞ für den Anfangswert
y ðx0 Þ ¼ y0 lässt sich an den Stellen x1 ¼ x0 þ h; x2 ¼ x0 þ 2 h, x3 ¼ x0 þ 3 h; . . .
näherungsweise wie folgt berechnen (h: gewählte Schrittweite):
y ðx0 Þ ¼ y0
(vorgegebener Anfangswert)
1
ðk1 þ k2 Þ
2
k1 ¼ h . f ðx0 ; y0 Þ
y ðx1 Þ ' y1 ¼ y0 þ
k2 ¼ h . f ðx0 þ h; y0 þ k1 Þ
1
ðk1 þ k2 Þ
2
k1 ¼ h . f ðx1 ; y1 Þ
y ðx2 Þ ' y2 ¼ y1 þ
k2 ¼ h . f ðx1 þ h; y1 þ k1 Þ
1
ðk1 þ k2 Þ
2
k1 ¼ h . f ðx2 ; y2 Þ
y ðx3 Þ ' y3 ¼ y2 þ
k2 ¼ h . f ðx2 þ h; y2 þ k1 Þ
..
.
Rechenschema
Abkürzung: K ¼
i
0
1
ðk1 þ k2 Þ
2
x
y
f ðx; yÞ
k ¼ h . f ðx; yÞ
x0
y0
f ðx0 ; y0 Þ
k1 ¼ h . f ðx0 ; y0 Þ
x0 þ h
y0 þ k1
f ðx0 þ h; y0 þ k1 Þ
k2 ¼ h . f ðx0 þ h; y0 þ k1 Þ
K ¼
1
x1 ¼ x0 þ h
..
.
y1 ¼ y0 þ K
......
Grau unterlegt: Näherungswert für y ðx1 Þ
1
ðk1 þ k2 Þ
2
280
X Gewöhnliche Differentialgleichungen
Fehlerabschätzung
Dyi ¼ y ðxi Þ / yi '
y ðxi Þ:
yi :
y~i :
&
1
ðyi / y~i Þ
3
Exakte Lösung an der Stelle xi
Näherungslösung an der Stelle xi bei der Schrittweite h
Näherungslösung an der Stelle xi bei doppelter Schrittweite 2 h
Beispiel
y0 ¼ y / x;
Anfangswert:
y ð0Þ ¼ 0
Wir berechnen die Näherungslösung dieser Differentialgleichung im Intervall 0 ) x ) 0,3 für die Schrittweite h ¼ 0,1 und vergleichen sie mit der exakten Lösung y ¼ / e x þ x þ 1:
i
x
y
f ðx; yÞ ¼ y / x
k ¼ 0;1 ðy / xÞ
0
0,0
0,000 000
0,000 000
0,000 000
0,1
0,000 000
/ 0,100 000
/ 0,010 000
yexakt
0,000 000
K ¼ / 0,005 000
1
0,1
/ 0,005 000
/ 0,105 000
/ 0,010 500
0,2
/ 0,015 500
/ 0,215 500
/ 0,021 550
/ 0,005 171
K ¼ / 0,016 025
2
0,2
/ 0,021 025
/ 0,221 025
/ 0,022 103
0,3
/ 0,043 128
/ 0,343 128
/ 0,034 313
/ 0,021 403
K ¼ / 0,028 208
3
0,3
/ 0,049 859
/ 0,049 233
Näherungslösung
im Vergleich zur exakten Lösung
(gute !bereinstimmung):
x
y (Näherung)
yexakt
0,0
0,000 000
0,000 000
0,1
/ 0,005 000
/ 0,005 171
0,2
/ 0,021 025
/ 0,021 403
0,3
/ 0,049 233
/ 0,049 859
&
2.5.3 Runge-Kutta-Verfahren 4. Ordnung
Die Lösungskurve y ðxÞ der Differentialgleichung y 0 ¼ f ðx; yÞ für den Anfangswert
y ðx0 Þ ¼ y0 lässt sich an den Stellen x1 ¼ x0 þ h; x2 ¼ x0 þ 2 h, x3 ¼ x0 þ 3 h; . . .
näherungsweise nach dem folgenden Schema berechnen (h: gewählte Schrittweite).
2 Differentialgleichungen 1. Ordnung
y ðx0 Þ ¼ y0
281
(vorgegebener Anfangswert)
y ðx1 Þ ' y1 ¼ y0 þ
1
ðk1 þ 2 k2 þ 2 k3 þ k4 Þ
6
k1 ¼ h . f ðx0 ; y0 Þ
3
2
h
k1
k2 ¼ h . f x0 þ ; y0 þ
2
2
3
2
h
k2
k3 ¼ h . f x0 þ ; y0 þ
2
2
k4 ¼ h . f ðx0 þ h; y0 þ k3 Þ
1
ðk1 þ 2 k2 þ 2 k3 þ k4 Þ
6
k1 ¼ h . f ðx1 ; y1 Þ
3
2
h
k1
k2 ¼ h . f x1 þ ; y1 þ
2
2
3
2
h
k2
k3 ¼ h . f x1 þ ; y1 þ
2
2
y ðx2 Þ ' y2 ¼ y1 þ
k4 ¼ h . f ðx1 þ h; y1 þ k3 Þ
..
.
Rechenschema
Abkürzung: K ¼
i
0
1
ðk1 þ 2 k2 þ 2 k3 þ k4 Þ
6
x
y
x0
f ðx; yÞ
y0
x0 þ
h
2
y0 þ
k1
2
x0 þ
h
2
y0 þ
k2
2
x0 þ h
y0 þ k3
k ¼ h . f ðx; yÞ
f ðx0 ; y0 Þ
3
2
h
k1
f x0 þ ; y0 þ
2
2
3
2
h
k2
f x0 þ ; y0 þ
2
2
k1
f ðx0 þ h; y0 þ k3 Þ
k4
k2
k3
K¼
1
x1 ¼ x0 þ h
..
.
y1 ¼ y0 þ K
......
Grau unterlegt: Näherungswert für y ðx1 Þ
1
ðk1 þ 2 k2 þ 2k3 þ k4 Þ
6
282
X Gewöhnliche Differentialgleichungen
Fehlerabschätzung
Dyi ¼ y ðxi Þ / yi '
y ðxi Þ:
yi :
y~i :
&
1
ðyi / y~i Þ
15
Exakte Lösung an der Stelle xi
Näherungslösung an der Stelle xi bei der Schrittweite h
Näherungslösung an der Stelle xi bei doppelter Schrittweite 2 h
Beispiel
y0 ¼ y / x;
Anfangswert:
y ð0Þ ¼ 0
Wir berechnen die Näherungslösung dieser Differentialgleichung im Intervall 0 ) x ) 0,3 für die Schrittweite h ¼ 0,1 und vergleichen sie mit der exakten Lösung y ¼ / e x þ x þ 1:
i
x
y
f ðx; yÞ ¼ y / x
k ¼ 0;1 ðy / xÞ
0
0,00
0,000 000
0,000 000
0,000 000
0,05
0,000 000
/ 0,050 000
/ 0,005 000
0,05
/ 0,002 500
/ 0,052 500
/ 0,005 250
0,10
/ 0,005 250
/ 0,105 250
/ 0,010 525
yexakt
0,000 000
K ¼ / 0,005 171
1
0,10
/ 0,005 171
/ 0,105 171
/ 0,010 517
0,15
/ 0,010 430
/ 0,160 430
/ 0,016 043
0,15
/ 0,013 193
/ 0,163 193
/ 0,016 320
0,20
/ 0,021 491
/ 0,221 491
/ 0,022 149
/ 0,005 171
K ¼ / 0,016 232
2
0,20
/ 0,021 403
/ 0,221 403
/ 0,022 140
0,25
/ 0,032 473
/ 0,282 473
/ 0,028 247
0,25
/ 0,035 527
/ 0,285 527
/ 0,028 553
0,30
/ 0,049 956
/ 0,349 956
/ 0,034 996
/ 0,021 403
K ¼ / 0,028 456
3
0,30
/ 0,049 859
/ 0,049 859
Näherungslösung
im Vergleich zur exakten Lösung
(sehr gute !bereinstimmung):
x
y (Näherung)
yexakt
0,0
0,000 000
0,000 000
0,1
/ 0,005 171
/ 0,005 171
0,2
/ 0,021 403
/ 0,021 403
0,3
/ 0,049 859
/ 0,049 859
&
3 Differentialgleichungen 2. Ordnung
283
3 Differentialgleichungen 2. Ordnung
3.1 Spezielle Differentialgleichungen 2. Ordnung, die sich auf
Differentialgleichungen 1. Ordnung zurückführen lassen
Die in der nachfolgenden Tabelle zusammengestellten Differentialgleichungen 2. Ordnung
lassen sich mit Hilfe geeigneter Substitutionen auf Differentialgleichungen 1. Ordnung
zurückführen.
Differentialgleichung
ðAÞ
y 00 ¼ f ðyÞ
Substitution
y0 ¼
dy
¼ u
dx
du
du dy
¼
.
¼
dx
dy dx
du
¼
.u
dy
y 00 ¼
Neue Dgl/Lösungsweg
u
du
¼ f ðyÞ
dy
1. Integration durch Trennung
der Variablen:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Ð
u ¼ + 2 . f ðyÞ dy
2. Rücksubstitution ðu ¼ y 0 Þ:
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Ð
y 0 ¼ + 2 . f ðyÞ dy
3. Integration durch Trennung
der Variablen
ðBÞ
y 00 ¼ f ðy 0 Þ
y0 ¼ u
u 0 ¼ f ðuÞ
y 00 ¼ u 0
1. Integration durch Trennung
der Variablen:
ð
du
¼ x þC
f ðuÞ
(nach u auflösen: u ¼ u ðxÞÞ
2. Rücksubstitution ðu ¼ y 0 Þ:
y 0 ¼ uðxÞ
3. Direkte Integration:
Ð
y ¼ u ðxÞ dx
ðCÞ
ðDÞ
y 00 ¼ f ðx; y 0 Þ
y 00 ¼ f ðy; y 0 Þ
y0 ¼ u
u 0 ¼ f ðx; uÞ
y 00 ¼ u 0
Weiterer Lösungsweg hängt vom
Typ der Funktion f ðx; uÞ ab
y0 ¼
dy
¼ u
dx
u
du
¼ f ðy; uÞ
dy
y 00 ¼
du dy
du
.
¼
.u
dy dx
dy
Weiterer Lösungsweg hängt vom
Typ der Funktion f ðy; uÞ ab
284
&
X Gewöhnliche Differentialgleichungen
Beispiel
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y 00 ¼ 1 þ ðy 0 Þ 2
y 00 ¼ u 0
ðmit u ¼ u ðxÞÞ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
0
Neue Differentialgleichung 1. Ordnung: u ¼ 1 þ u 2
Substitution vom Typ (B):
y0 ¼ u;
Integration nach „Trennung der Variablen“:
ð
Z
du
du
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ dx ;
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ dx
1 þ u2
1 þ u2
)
arsinh u ¼ x þ C1
)
u ¼ sinh ðx þ C1 Þ
Rücksubstitution mit anschließender Integration:
Ð
y 0 ¼ u ¼ sinh ðx þ C1 Þ ) y ¼ sinh ðx þ C1 Þ dx ¼ cosh ðx þ C1 Þ þ C2
Lösung:
y ¼ cosh ðx þ C1 Þ þ C2
ðC1 ; C2 2 RÞ
&
3.2 Lineare Differentialgleichungen 2. Ordnung
mit konstanten Koeffizienten
3.2.1 Definition einer linearen Differentialgleichung 2. Ordnung
mit konstanten Koeffizienten
y 00 þ a y 0 þ b y ¼ gðxÞ
ða; b 2 RÞ
Die Funktion g ðxÞ wird als Störfunktion oder Störglied bezeichnet. Fehlt das Störglied,
d. h. ist g ðxÞ 0 0, so heißt die lineare Differentialgleichung homogen, sonst inhomogen.
3.2.2 Integration der homogenen linearen Differentialgleichung
3.2.2.1 Wronski-Determinante
Zwei Lösungsfunktionen y1 und y2 der homogenen linearen Differentialgleichung
y 00 þ a y 0 þ b y ¼ 0 heißen Basisfunktionen oder Basislösungen der Differentialgleichung, wenn die aus ihnen gebildete Wronski-Determinante
"
" y1
W ðy1 ; y2 Þ ¼ "" 0
y1
"
y2 ""
¼ y1 y 02 / y2 y 01
y 02 "
von null verschieden ist. Die Basislösungen bilden eine sog. Fundamentalbasis der Differentialgleichung, sie werden auch als linear unabhängige Lösungen bezeichnet.
3.2.2.2 Allgemeine Lösung der homogenen linearen Differentialgleichung
Die allgemeine Lösung y der homogenen linearen Differentialgleichung y 00 þ a y 0 þ by ¼ 0
ist als Linearkombination zweier linear unabhängiger Lösungen (Basisfunktionen) y1 und
y2 darstellbar:
y ¼ C1 y1 þ C2 y2
ðC1 ; C2 2 RÞ
3 Differentialgleichungen 2. Ordnung
285
Eine solche Fundamentalbasis y1 ; y2 lässt sich durch den Lösungsansatz y ¼ e l x gewinnen (Exponentialansatz). Die Basisfunktionen hängen dabei noch von der Art der Lösungen l1 und l2 der zugehörigen charakteristischen Gleichung
l2 þ al þ b ¼ 0
ða; b: Koeffizienten der DglÞ
ab, wobei drei Fälle zu unterscheiden sind ðC1 ; C2 2 RÞ:
1. Fall: l1 =/ l2 (reell)
Fundamentalbasis:
Allgemeine Lösung:
y1 ¼ e l1 x ;
y2 ¼ e l2 x
y ¼ C1 . e l1 x þ C2 . e l2 x
2. Fall: l1 = l2 = c (reell)
Fundamentalbasis: y1 ¼ e c x ;
y2 ¼ x . e c x
Allgemeine Lösung: y ¼ ðC1 þ C2 xÞ . e c x
3. Fall: l1/2 = a + j w (konjugiert komplex)
Fundamentalbasis: y1 ¼ e a x . sin ðw xÞ ;
y2 ¼ e a x . cos ðw xÞ
Allgemeine Lösung: y ¼ e a x ½ C1 . sin ðw xÞ þ C2 . cos ðw xÞ%
&
Beispiel
y 00 þ 2 y 0 þ 10 y ¼ 0
Charakteristische Gleichung mit Lösungen:
l 2 þ 2 l þ 10 ¼ 0
Fundamentalbasis:
Lösung:
y ¼ e
/x
)
y1 ¼ e
l1=2 ¼ / 1 + 3 j ð3. Fall:
/x
. sin ð3 xÞ ;
y2 ¼ e
½ C1 . sin ð3 xÞ þ C2 . cos ð3 xÞ%
a ¼ / 1; w ¼ 3Þ
/x
. cos ð3 xÞ
ðC1 ; C2 2 RÞ
&
3.2.3 Integration der inhomogenen linearen Differentialgleichung
Eine inhomogene lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten
vom Typ y 00 þ a y 0 þ b y ¼ g ðxÞ wird schrittweise wie folgt gelöst:
1. Zunächst wird die allgemeine Lösung y0 der zugehörigen homogenen linearen Differentialgleichung y 00 þ a y 0 þ b y ¼ 0 bestimmt (siehe Abschnitt 3.2.2).
2. Dann ermittelt man mit Hilfe eines speziellen, aus der nachfolgenden Tabelle entnommenen Lösungsansatzes eine partikuläre Lösung yp der inhomogenen linearen Differentialgleichung.
3. Die allgemeine Lösung y der inhomogenen linearen Differentialgleichung ist dann die
Summe aus y0 und yp :
y ¼ y0 þ yp
286
X Gewöhnliche Differentialgleichungen
Tabelle: Lösungsansatz yp für spezielle Störfunktionen (Störglieder)
Störfunktion g ðxÞ
1. Polynomfunktion vom Grade n
gðxÞ ¼ Pn ðxÞ
Lösungsansatz yp ðxÞ
8
< Qn ðxÞ
yp ¼ x . Qn ðxÞ
: 2
x . Qn ðxÞ
Qn ðxÞ:
gðxÞ ¼ e
cx
fur
€
Polynom vom Grade n
Parameter:
2. Exponentialfunktion
9
b 6¼ 0
=
a 6¼ 0 ; b ¼ 0
;
a ¼ b ¼ 0
Koeffizienten des Polynoms Qn ðxÞ
(1) c ist keine Lösung der charakteristischen Gleichung:
yp ¼ A . e c x
(Parameter: A)
(2) c ist eine r-fache Lösung der charakteristischen
Gleichung ðr ¼ 1; 2Þ:
yp ¼ A . x r . e c x
3. g ðxÞ ¼ Pn ðxÞ . e c x
ðPn ðxÞ ist dabei eine
Polynomfunktion vom Grade nÞ
(Parameter: A)
(1) c ist keine Lösung der charakteristischen Gleichung:
yp ¼ Qn ðxÞ . e c x
Qn ðxÞ: Polynom vom Grade n
Parameter: Koeffizienten des Polynoms Qn ðxÞ
(2) c ist eine r-fache Lösung der charakteristischen
Gleichung ðr ¼ 1; 2Þ:
yp ¼ x r . Qn ðxÞ . e c x
Qn ðxÞ: Polynom vom Grade n
Parameter: Koeffizienten des Polynoms Qn ðxÞ
4. Sinusfunktion
gðxÞ ¼ sin ð b xÞ
(1) j b ist keine Lösung der charakteristischen Gleichung:
yp ¼ A . sin ð b xÞ þ B . cos ð b xÞ
oder
oder
Kosinusfunktion
yp ¼ C . sin ð b x þ jÞ
gðxÞ ¼ cos ð b xÞ
Parameter: A, B
oder
eine Linearkombination
aus beiden Funktionen
bzw.
C; j
(2) j b ist eine Lösung der charakteristischen Gleichung:
yp ¼ x ½A . sin ð b xÞ þ B . cos ð b xÞ%
oder
yp ¼ C . x . sin ð b x þ jÞ
Parameter: A, B
bzw.
C; j
3 Differentialgleichungen 2. Ordnung
Störfunktion g ðxÞ
5. gðxÞ ¼ Pn ðxÞ . e
287
Lösungsansatz yp ðxÞ
cx
. sin ð b xÞ
(1) c þ j b ist keine Lösung der charakteristischen
Gleichung:
oder
gðxÞ ¼ Pn ðxÞ . e c x . cos ð b xÞ
yp ¼ e c x ½Qn ðxÞ . sin ð b xÞ þ Rn ðxÞ . cos ð b xÞ%
ðPn ðxÞ ist dabei eine
Polynomfunktion vom Grade nÞ
Qn ðxÞ; Rn ðxÞ: Polynome vom Grade n
Parameter: Koeffizienten der beiden Polynome
(2) c þ j b ist eine Lösung der charakteristischen
Gleichung:
yp ¼ x . e c x ½ Qn ðxÞ . sin ð b xÞ þ Rn ðxÞ . cos ð b xÞ%
Qn ðxÞ; Rn ðxÞ: Polynome vom Grade n
Parameter: Koeffizienten der beiden Polynome
Anmerkungen zur Tabelle
(1)
(2)
(3)
(4)
(5)
Der jeweilige Lösungsansatz gilt auch dann, wenn die Störfunktion zusätzlich noch
einen konstanten Faktor enthält.
Die im jeweiligen Lösungsansatz enthaltenen Parameter („Stellparameter‘‘) sind so
zu bestimmen, dass der Ansatz die vorgegebene Differentialgleichung löst.
Ist die Störfunktion g ðxÞ eine Summe aus mehreren Störgliedern, so erhält man den
Lösungsansatz für yp als Summe der Lösungsansätze für die einzelnen Störglieder.
Ist g ðxÞ ein Produkt aus mehreren „Störfaktoren“, so erhält man in vielen (aber
nicht allen) Fällen einen Lösungsansatz für yp, indem man die Lösungsansätze der
„Störfaktoren“ miteinander multipliziert.
Bei periodischen Störfunktionen vom Typ g ðxÞ ¼ sin ð b xÞ oder g ðxÞ ¼ cos ð b xÞ
verwendet man häufig auch komplexe Lösungsansätze der allgemeinen Form
yp ðxÞ ¼ C . e j ð b x þ jÞ
ðC; j:
ParameterÞ
Die gesuchte (reelle) Lösung ist dann der Real- bzw. Imaginärteil der komplexen Lösung.
&
Beispiel
y 00 / 2 y 0 / 8 y ¼ 6 . e 4 x
1. Homogene Differentialgleichung:
Charakteristische Gleichung:
y 00 / 2 y 0 / 8 y ¼ 0
2
l / 2l / 8 ¼ 0
Lösung der homogenen Differentialgleichung:
2. Inhomogene Differentialgleichung:
)
l1 ¼ 4 ;
l2 ¼ / 2
y0 ¼ C1 . e 4 x þ C2 . e / 2 x
y 00 / 2 y 0 / 8 y ¼ 6 . e 4 x
Lösungsansatz für yp (aus der Tabelle entnommen):
yp ¼ A x . e 4 x
4x
(Störglied: g ðxÞ ¼ 6 . e ; c ¼ 4 ist eine einfache Lösung der charakteristischen Gleichung)
Bestimmung der Konstanten A:
yp ¼ A x . e 4 x ;
ð8 A þ 16 A xÞ . e
y 0p ¼ ðA þ 4 A xÞ . e 4 x ;
4x
/ 2 ðA þ 4 A xÞ . e
4x
y 00p ¼ ð8 A þ 16 A xÞ . e 4 x
/ 8 A x . e 4x ¼ 6 . e 4x j : e 4x
8 A þ 16 A x / 2 ðA þ 4 A xÞ / 8 A x ¼ 6
8 A þ 16 A x / 2 A / 8 A x / 8 A x ¼ 6
)
6A ¼ 6
)
A ¼ 1
288
X Gewöhnliche Differentialgleichungen
Partikuläre Lösung:
yp ¼ x . e 4 x
Lösung der inhomogenen Differentialgleichung:
y ¼ y0 þ yp ¼ C1 . e 4 x þ C2 . e / 2 x þ x . e 4 x ¼ ðC1 þ xÞ . e 4 x þ C2 . e / 2 x
ðC1 ; C2 2 RÞ
&
3.3 Numerische Integration einer Differentialgleichung 2. Ordnung
Runge-Kutta-Verfahren 4. Ordnung
Die Lösungskurve y ðxÞ der Differentialgleichung y 00 ¼ f ðx; y; y 0 Þ für die Anfangswerte
y ðx0 Þ ¼ y0 , y 0 ðx0 Þ ¼ y 00 lässt sich an den Stellen x1 ¼ x0 þ h, x2 ¼ x0 þ 2 h,
x3 ¼ x0 þ 3 h . . . näherungsweise wie folgt bestimmen (h: gewählte Schrittweite):
y ðx0 Þ ¼ y0
)
(vorgegebene Anfangswerte)
y 0 ðx0 Þ ¼ y 00
1
ðk1 þ 2 k2 þ 2 k3 þ k4 Þ
6
1
ðm1 þ 2 m2 þ 2 m3 þ m4 Þ
¼ y 00 þ
6
y ðx1 Þ ' y1 ¼ y0 þ
y 0 ðx1 Þ ' y 01
k1 ¼ h . y 00
!
m1 4
k2 ¼ h y 00 þ
2
!
m2 4
k3 ¼ h y 00 þ
2
m1 ¼ h . f ðx0 ; y0 ; y 00 Þ
3
2
h
k1 0
m1
m2 ¼ h . f x0 þ ; y0 þ ; y 0 þ
2
2
2
3
2
h
k2 0
m2
m3 ¼ h . f x0 þ ; y0 þ ; y 0 þ
2
2
2
k4 ¼ h ðy 00 þ m3 Þ
m4 ¼ h . f ðx0 þ h; y0 þ k3 ; y 00 þ m3 Þ
1
ðk1 þ 2 k2 þ 2 k3 þ k4 Þ
6
1
y 01 þ
ðm1 þ 2 m2 þ 2 m3 þ m4 Þ
6
h . y 01
m1 ¼ h . f ðx1 ; y1 ;
3
!
m1 4
h y 01 þ
m2 ¼ h . f x1 þ
2
3
!
m2 4
h y 01 þ
m3 ¼ h . f x1 þ
2
y ðx2 Þ ' y2 ¼ y1 þ
y 0 ðx2 Þ ' y 02 ¼
k1 ¼
k2 ¼
k3 ¼
k4 ¼ h ðy 01 þ m3 Þ
..
.
y 01 Þ
h
k1
m1
; y1 þ ; y 01 þ
2
2
2
h
k2
m2
; y1 þ ; y 01 þ
2
2
2
m4 ¼ h . f ðx1 þ h; y1 þ k3 ; y 01 þ m3 Þ
2
2
3 Differentialgleichungen 2. Ordnung
289
Rechenschema
Abkürzungen:
i
0
K ¼
x
x0
h
2
h
x0 þ
2
x0 þ h
x0 þ
1
ðk1 þ 2 k2 þ 2 k3 þ k4 Þ ;
6
y0
y
y0
k1
2
k2
y0 þ
2
y0 þ k3
y0 þ
M ¼
1
ðm1 þ 2 m2 þ 2 m3 þ m4 Þ
6
k ¼ h . y0
y 00
m1
y 00 þ
2
m
2
y 00 þ
2
y 00 þ m3
m ¼ h . f ðx; y; y 0 Þ
k1
m1
k2
m2
k3
m3
k4
m4
1
ðk1 þ 2 k2 þ 2 k3 þ k4 Þ
6
1
M ¼
ðm1 þ 2 m2 þ 2m3 þ m4 Þ
6
K ¼
1
x1 ¼ x0 þ h
..
.
y1 ¼ y0 þ K
y 01 ¼ y 00 þ M
......
Grau unterlegt: Näherungswerte für y ðx1 Þ und y 0 ðx1 Þ
&
Anfangswerte:
y ð0Þ ¼ 0 ;
y 0 ð0Þ ¼ 4
3,327 683
0,180 000
0,367 000
0,364 333
0,05
0,10
0,10
2,867 923
0,672 562
0,20
2,862 260
0,674 566
0,20
0,000 000
0,364 333
0,672 562
0,0
0,1
0,2
0,672 591
0,364 353
0,000 000
yexakt
2,867 923
3,327 683
4,000 000
y 0 (Nährung)
2,867 838
3,327 626
4,000 000
y 0exakt
M ¼ / 0,459 760
K ¼ 0,308 229
y (Näherung)
/ 0,370 082
/ 0,465 423
/ 0,450 698
0,286 226
0,310 233
0,304 957
/ 0,556 237
M ¼ / 0,672 317
K ¼ 0,364 333
0,332 768
/ 0,553 900
/ 0,680 000
/ 0,660 000
/ 0,800 000
m ¼ h . f ðx; y; y 0 Þ ¼ 0;1ð3 y / 2 y 0 Þ
0,332 000
0,367 000
0,360 000
0,400 000
k ¼ h . y 0 ¼ 0;1 y 0
x
3,102 334
3,049 565
0,530 717
0,516 812
0,15
3,670 000
3,600 000
0,15
Näherungslösung
im Vergleich zur exakten Lösung
(gute !bereinstimmung):
2
1
3,320 000
0,200 000
0,05
4,000 000
0,000 000
0,00
0
y0
x
i
y
0,672 591
0,364 353
0,000 000
yexakt
2,867 838
3,327 626
4,000 000
y 0exakt
&
Wir berechnen die Näherungslösung dieser Differentialgleichung im Intervall 0 ) x ) 0;2 für die Schrittweite h ¼ 0;1 und vergleichen sie mit der exakten Lösung
y ¼ e x / e / 3 x, y 0 ¼ e x þ 3 . e / 3 x :
y 00 ¼ 3 y / 2 y 0 ;
Beispiel
290
X Gewöhnliche Differentialgleichungen
4 Anwendungen
291
4 Anwendungen
4.1 Mechanische Schwingungen
4.1.1 Allgemeine Schwingungsgleichung der Mechanik
Das Federpendel (Feder-Masse-Schwinger)
dient als Modell für ein schwingungsfähiges
mechanisches System. Bei viskoser Dämpfung gilt dann:
Elastische Feder
m x€ þ b x_ þ c x ¼ F ðtÞ
Gleichgewichtslage
m:
Masse
b:
Reibungsfaktor (Dämpferkonstante)
c:
Federkonstante
x ðtÞ: Auslenkung zur Zeit t
F ðtÞ: Von außen auf das System einwirkende
(zeitabhängige) Kraft
Pendelmasse
x(t)
Dämpfung
4.1.2 Freie ungedämpfte Schwingung
Differentialgleichung der freien ungedämpften Schwingung
m x€ þ c x ¼ 0
oder
x€ þ w 20 x ¼ 0
m: Masse
c:
Federkonstante
!
pffiffiffiffiffiffiffiffiffiffi 4
w0 : Eigen- oder Kennkreisfrequenz des Systems w0 ¼ c=m
T:
Schwingungsdauer (Periode); w0 ¼ 2 p=T
Allgemeine Lösung (Bild: siehe nächste Seite oben)
x ðtÞ ¼ C . sin ðw0 t þ jÞ
ðC > 0; 0 ) j < 2 pÞ
oder
x ðtÞ ¼ C1 . sin ðw0 tÞ þ C2 . cos ðw0 tÞ
ðC1 ; C2 2 RÞ
Die Integrationskonstanten werden meist aus den Anfangswerten bestimmt:
x ð0Þ ¼ x0 :
Anfangslage;
x_ ð0Þ ¼ vð0Þ ¼ v0 :
Anfangsgeschwindigkeit
292
X Gewöhnliche Differentialgleichungen
x
x(t) = C · sin(v0 t + f)
C
t
f/v0
–C
T = 2p
v0
4.1.3 Freie gedämpfte Schwingung
Differentialgleichung der freien gedämpften Schwingung (bei viskoser Dämpfung)
m x€ þ b x_ þ c x ¼ 0
m:
b:
c:
d:
w0 :
oder
x€ þ 2 d x_ þ
w 20
3
x ¼ 0
b
d ¼
;
2m
rffiffiffiffiffiffi 2
c
w0 ¼
m
Masse
Reibungsfaktor (Dämpferkonstante)
Federkonstante
Dämpfungsfaktor oder Abklingkonstante
Eigen- oder Kennkreisfrequenz des ungedämpften Systems
4.1.3.1 Schwache Dämpfung (Schwingungsfall)
Für d < w0 qerhält
man eine gedämpfte Schwingung mit der Eigen- oder Kennkreisfreffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
quenz wd ¼ w 0 / d 2 :
x ðtÞ ¼ C . e / d t . sin ðwd t þ jd Þ
ðC > 0; 0 ) jd < 2 pÞ
oder
x ðtÞ ¼ e / d t ½ C1 . sin ðwd tÞ þ C2 . cos ðwd tÞ %
ðC1 ; C2 2 RÞ
x
C · sin fd
x(t) = C · e –dt · sin( vd t + fd )
p
Td = 2
vd
t
4 Anwendungen
293
4.1.3.2 Aperiodischer Grenzfall
Für d ¼ w0 tritt der aperiodische Grenzfall ein. Das System ist zu keiner echten Schwingung mehr fähig und bewegt sich aperiodisch, d. h. asymptotisch auf die Gleichgewichtslage zu:
x ðtÞ ¼ ðC1 t þ C2 Þ . e / d t
ðC1 ; C2 2 RÞ
Das nebenstehende Bild zeigt die Abhängigkeit der Lösung von den physikalischen Anfangsbedingungen:
x
A
a) x ð0Þ ¼ A > 0 ;
vð0Þ ¼ x_ ð0Þ ¼ 0
b) x ð0Þ ¼ A > 0 ;
v ð0Þ ¼ x_ ð0Þ ¼ v 0 > 0
c) x ð0Þ ¼ A > 0 ;
vð0Þ ¼ x_ ð0Þ ¼ v 0 < / d A
Umkehrpunkt der
Bewegung
a)
b)
c)
t
Umkehrpunkt der
Bewegung
4.1.3.3 Aperiodisches Verhalten bei starker Dämpfung (Kriechfall)
Für d > w0 wird die Dämpfung so stark, dass das System zu keiner echten Schwingung
mehr fähig ist. Es bewegt sich asymptotisch auf die Gleichgewichtslage zu:
x ðtÞ ¼ C1 . e / k1 t þ C2 . e / k2 t
ðC1 ; C2 2 RÞ
l1 ¼ / k1 und l2 ¼ / k2 sind dabei die Lösungen der charakteristischen Gleichung
l2 þ 2 d l þ w 20 ¼ 0 ðk1 ; k2 > 0Þ.
Das nebenstehende Bild zeigt den zeitlichen
Verlauf der Kriechbewegung in Abhängigkeit
von den physikalischen Anfangsbedingungen:
a) x ð0Þ ¼ A > 0 ;
vð0Þ ¼ x_ ð0Þ ¼ 0
b) x ð0Þ ¼ A > 0 ;
v ð0Þ ¼ x_ ð0Þ ¼ v 0 > 0
c) x ð0Þ ¼ A > 0 ;
vð0Þ ¼ x_ ð0Þ ¼ v 0 < / k2 A
x
A
Umkehrpunkt der
Bewegung
a)
b)
c)
Umkehrpunkt der
Bewegung
t
294
X Gewöhnliche Differentialgleichungen
4.1.4 Erzwungene Schwingung
4.1.4.1 Differentialgleichung der erzwungenen Schwingung
Das System wird durch die periodische Kraft F ðtÞ ¼ F0 . sin ðw tÞ zu Schwingungen
erregt. Bei viskoser Dämpfung gilt dann:
m x€ þ b x_ þ c x ¼ F0 . sin ðw tÞ oder
rffiffiffiffiffiffi
b
c
F0
;
w0 ¼
;
K0 ¼
d ¼
2m
m
m
F0 : Amplitude der Erregerkraft
w: Kreisfrequenz des Erregersystems
d:
Dämpfungsfaktor oder Abklingkonstante
w0 : Eigenkreisfrequenz des ungedämpften Systems
m: Masse
b: Reibungsfaktor
(Dämpferkonstante)
c:
x€ þ 2 d x_ þ w 20 x ¼ K0 . sin ðw tÞ
Federkonstante
4.1.4.2 Stationäre Lösung
Nach einer gewissen Einschwingphase schwingt das System harmonisch mit der Kreisfrequenz w des Erregers:
x ðtÞ ' xp ðtÞ ¼ A . sin ðw t / jÞ
x
xp(t) = A · sin(vt – f)
A
f/v
t
–A
T = 2p
v
Schwingungsamplitude A und Phasenverschiebung j (gegenüber dem Erreger-System)
sind dabei frequenzabhängige Größen (sog. Frequenzgang, siehe hierzu Bild a) und b)).
f
p
A
F0
c
a)
Frequenzgang A = A(v)
der Amplitude
(Resonanzkurve)
v0
Resonanzstelle vr
Frequenzgang f = f(v)
der Phasenverschiebung
p
2
v
v0
b)
v
4 Anwendungen
295
Ihre Berechnung erfolgt nach den folgenden Formeln:
A ðwÞ ¼
F0
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
m ðw 20 / w 2 Þ 2 þ 4 d 2 w 2
3
2
8
2dw
>
>
arctan
>
>
w 20 / w 2
>
>
<
j ðwÞ ¼ p=2
>
>
3
2
>
>
2dw
>
>
þp
: arctan
w 20 / w 2
ðBild aÞ; siehe vorherige Seite untenÞ
9
>
w < w0 >
>
>
>
>
=
w ¼ w0
>
>
>
>
>
w > w0 >
;
fur
€
ðBild bÞ; siehe vorherige
Seite untenÞ
Resonanzfall
Das System schwingt bei der Resonanzkreisfrequenz
wr ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
w 20 / 2 d 2
mit größtmöglicher Amplitude (Resonanzfall, siehe Bild a) auf der vorherigen Seite unten):
4.2 Elektrische Schwingungen in einem Reihenschwingkreis
Die Differentialgleichung einer elektrischen Schwingung in einem Reihenschwingkreis
lautet wie folgt:
d 2i
di
1 dua ðtÞ
þ 2d
þ w 20 i ¼
.
dt 2
dt
L
dt
i(t)
3
R
d ¼
;
2L
R
L
uR(t)
uL(t)
1
w0 ¼ pffiffiffiffiffiffiffi
LC
2
C
uC(t)
ua(t)
R: Ohmscher Widerstand
d:
Dämpfungsfaktor (Abklingkonstante)
L:
w0 :
Eigen- oder Kennkreisfrequenz
Induktivität
C : Kapazität
ua ðtÞ:
iðtÞ: Stromstärke
Von außen angelegte Spannung (Erregerspannung)
uR ðtÞ; uL ðtÞ; uC ðtÞ:
Spannungsabfall an R; L bzw. C
296
X Gewöhnliche Differentialgleichungen
Der elektromagnetische Reihenschwingkreis ist das elektrische Analogon des mechanischen
Schwingkreises (siehe Abschnitt 4.1). In beiden Fällen wird die Schwingung durch eine
lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten vom allgemeinen Typ
y€ þ 2 d y_ þ w 20 y ¼ f ðtÞ
beschrieben, wobei folgende Zuordnung gilt:
Schwingkreis
y ðtÞ
d
Mechanischer
Schwingkreis
Auslenkung
x ¼ x ðtÞ
Elektrischer
Reihenschwingkreis
Stromstärke
i ¼ i ðtÞ
b
2m
R
2L
w0
rffiffiffiffiffi
c
m
1
pffiffiffiffiffiffi
LC
Störglied f ðtÞ
F ðtÞ
m
1 dua ðtÞ
.
L
dt
Alle Aussagen über den mechanischen Schwingkreis gelten daher auch sinngemäß für den
elektromagnetischen Reihenschwingkreis.
5 Lineare Differentialgleichungen n-ter Ordnung
mit konstanten Koeffizienten
5.1 Definition einer linearen Differentialgleichung n-ter Ordnung
mit konstanten Koeffizienten
y ðnÞ þ an / 1 . y ðn / 1Þ þ an / 2 . y ðn / 2Þ þ . . . þ a1 . y 0 þ a0 . y ¼ gðxÞ
a0 ; a1 ; . . . ; an / 1 : Reelle Koeffizienten
Fehlt das Störglied gðxÞ, so heißt die Differentialgleichung homogen, sonst inhomogen.
5.2 Integration der homogenen linearen Differentialgleichung
5.2.1 Wronski-Determinante
n Lösungen y1 ; y2 ; . . . ; yn der homogenen linearen Differentialgleichung heißen Basisfunktionen oder Basislösungen, wenn die aus ihnen gebildete sog. Wronski-Determinante
"
" y1
"
"
" y 01
W ðy1 ; y2 ; . . . ; yn Þ ¼ ""
..
"
" ðn./ 1Þ
"y
1
y2
...
yn
y 02
...
y 0n
...
/ 1Þ
y ðn
n
ðn / 1Þ
y2
"
"
"
"
"
"
"
"
"
"
von null verschieden ist. Die Basislösungen bilden eine sog. Fundamentalbasis der Differentialgleichung, sie werden auch als linear unabhängige Lösungen bezeichnet.
5 Lineare Differentialgleichungen n-ter Ordnung mit konstanten Koeffizienten
297
5.2.2 Allgemeine Lösung der homogenen linearen Differentialgleichung
Die allgemeine Lösung der homogenen linearen Differentialgleichung ist als Linearkombination von n linear unabhängigen Lösungen (Basisfunktionen) y1 ; y2 ; . . . ; yn wie folgt
darstellbar:
y ¼ C1 y1 þ C2 y2 þ . . . þ Cn yn
ðCi 2 R; i ¼ 1; 2; . . . ; nÞ
Eine solche Fundamentalbasis y1 ; y2 ; . . . ; yn lässt sich durch den Lösungsansatz
y ¼ e l x gewinnen (Exponentialansatz). Die Basisfunktionen hängen dabei noch von der
Art der Lösungen der zugehörigen charakteristischen Gleichung
l n þ an / 1 l n / 1 þ an / 2 l n / 2 þ . . . þ a1 l þ a0 ¼ 0
ab, wobei die folgenden drei Fälle zu unterscheiden sind:
1. Fall: Es treten nur einfache reelle Lösungen auf
Jede einfache reelle Lösung li liefert den (additiven) Beitrag Ci . e li x zur
Gesamtlösung ðCi 2 R; i ¼ 1; 2; . . . ; nÞ.
2. Fall: Es treten auch mehrfache reelle Lösungen auf
Eine r-fache reelle Lösung l1 ¼ l2 ¼ . . . ¼ lr ¼ a liefert den Beitrag
C ðxÞ . e a x , wobei C ðxÞ eine Polynomfunktion vom Grade r / 1 ist.
3. Fall: Es treten konjugiert komplexe Lösungen auf
Eine einfache konjugiert komplexe Lösung l1=2 ¼ a + j w liefert den Beitrag
e a x ½C1 . sin ðw xÞ þ C2 . cos ðw xÞ%
ðC1 ; C2 2 RÞ
Tritt das konjugiert komplexe Paar jedoch r-fach auf, so müssen die beiden
Konstanten C1 und C2 durch Polynome vom Grade r / 1 ersetzt werden.
Gesamtlösung (allgemeine Lösung der homogenen Differentialgleichung)
Die allgemeine Lösung der homogenen Differentialgleichung ist dann die Summe der
in den Fällen 1 bis 3 beschriebenen Einzelbeiträge.
&
Beispiel
y ð4Þ þ 3 y 00 / 4 y ¼ 0
(homogene Differentialgleichung 4. Ordnung)
Charakteristische Gleichung mit Lösungen:
l4 þ 3l2 / 4 ¼ 0
)
l1=2 ¼ + 1
(1. Fall), l3=4 ¼ 0 + 2 j ¼ + 2 j
(3. Fall)
Sie liefern folgende Beiträge zur Gesamtlösung:
C1 . e x ;
C2 . e / x
und
C3 . sin ð2 xÞ þ C4 . cos ð2 xÞ
Allgemeine Lösung:
y ¼ C1 . e x þ C2 . e / x þ C3 . sin ð2 xÞ þ C4 . cos ð2 xÞ
ðC1 ; . . . ; C4 2 RÞ
&
298
X Gewöhnliche Differentialgleichungen
5.3 Integration der inhomogenen linearen Differentialgleichung
Wie bei den inhomogenen linearen Differentialgleichungen 1. und 2. Ordnung gilt auch
hier für die gesuchte allgemeine Lösung:
y ¼ y0 þ yp
y0 :
yp :
Allgemeine Lösung der zugehörigen homogenen linearen Differentialgleichung (siehe
X.5.2)
Irgendeine partikuläre Lösung der inhomogenen linearen Differentialgleichung
Einen Lösungsansatz für eine partikuläre Lösung yp , der im Wesentlichen vom Störglied
g ðxÞ der Differentialgleichung abhängt, entnimmt man der folgenden Tabelle (Fallunterscheidungen beachten).
Tabelle: Lösungsansatz yp für spezielle Störfunktionen (Störglieder)
Störfunktion g ðxÞ
1. Polynomfunktion
vom Grade n
g ðxÞ ¼ Pn ðxÞ
Lösungsansatz yp ðxÞ
8
< Qn ðxÞ
yp ¼
fur
€
: k
x . Qn ðxÞ
Qn ðxÞ:
9
=
a0 6¼ 0
a0 ¼ a1 ¼ . . . ¼ ak / 1 ¼ 0
Polynom vom Grade n
Parameter: Koeffizienten des Polynoms Qn ðxÞ
2. Exponentialfunktion
g ðxÞ ¼ e
cx
(1) c ist keine Lösung der charakteristischen Gleichung:
yp ¼ A . e c x
(Parameter:
A)
(2) c ist eine r-fache Lösung der charakteristischen
Gleichung:
yp ¼ A . x r . e c x
3. g ðxÞ ¼ Pn ðxÞ . e c x
ðPn ðxÞ ist dabei eine
Polynomfunktion vom
Grade nÞ
(Parameter:
A)
(1) c ist keine Lösung der charakteristischen Gleichung:
yp ¼ Qn ðxÞ . e c x
Qn ðxÞ: Polynom vom Grade n
Parameter: Koeffizienten des Polynoms Qn ðxÞ
(2) c ist eine r-fache Lösung der charakteristischen
Gleichung:
yp ¼ x r . Qn ðxÞ . e c x
Q n ðxÞ: Polynom vom Grade n
Parameter: Koeffizienten des Polynoms Qn ðxÞ
;
5 Lineare Differentialgleichungen n-ter Ordnung mit konstanten Koeffizienten
299
Störfunktion g ðxÞ
Lösungsansatz yp ðxÞ
4. Sinusfunktion
(1) j b ist keine Lösung der charakteristischen Gleichung:
g ðxÞ ¼ sin ð b xÞ
oder
Kosinusfunktion
yp ¼ A . sin ð b xÞ þ B . cos ð b xÞ
g ðxÞ ¼ cos ð b xÞ
Parameter: A, B
oder
yp ¼ C . sin ð b x þ jÞ
oder
eine Linearkombination
aus beiden Funktionen
bzw. C, j
(2) j b ist eine r-fache Lösung der charakteristischen
Gleichung:
yp ¼ x r ½ A . sin ð b xÞ þ B . cos ð b xÞ%
oder
yp ¼ C . x r . sin ð b x þ jÞ
Parameter: A, B
bzw. C, j
Anmerkungen zur Tabelle
(1)
(2)
(3)
(4)
(5)
&
Der jeweilige Lösungsansatz gilt auch dann, wenn die Störfunktion zusätzlich noch
einen konstanten Faktor enthält.
Die im jeweiligen Lösungsansatz enthaltenen Parameter („Stellparameter“) sind so zu
bestimmen, dass der Ansatz die vorgegebene Differentialgleichung löst.
Ist die Störfunktion g ðxÞ eine Summe aus mehreren Störgliedern, so erhält man den
Lösungsansatz für yp als Summe der Lösungsansätze für die einzelnen Störglieder.
Ist die Störfunktion g ðxÞ ein Produkt aus mehreren „Störfaktoren“, so erhält man in
vielen (aber leider nicht allen) Fällen einen geeigneten Lösungsansatz für yp in Form
eines Produktes, dessen Faktoren die Lösungsansätze der einzelnen „Störfaktoren“ sind.
Bei periodischen Störgliedern wie z. B. sin ð b xÞ oder cos ð b xÞ lassen sich ähnlich
wie bei Differentialgleichungen 2. Ordnung auch komplexe Lösungsansätze verwenden (siehe Abschnitt 3.2.3).
Beispiel
y 000 þ y 0 ¼ 4 . e x
(inhomogene Differentialgleichung 3. Ordnung)
y 000 þ y 0 ¼ 0
1. Homogene Differentialgleichung:
Charakteristische Gleichung:
3
l þ l ¼ l ðl 2 þ 1Þ ¼ 0
Lösung der homogenen Differentialgleichung:
2. Inhomogene Differentialgleichung:
)
l1 ¼ 0 ;
l2=3 ¼ + j
y0 ¼ C1 þ C2 . sin x þ C3 . cos x
y 000 þ y 0 ¼ 4 . e x
Lösungsansatz (aus der Tabelle entnommen): yp ¼ A . e x ;
x
y 0p ¼ y 00p ¼ y 000
p ¼ A . e
(Störglied: g ðxÞ ¼ 4 . e x ; c ¼ 1 ist keine Lösung der charakteristischen Gleichung)
Einsetzen in die Differentialgleichung:
A . ex þ A . ex ¼ 4 . ex j : ex
Partikuläre Lösung:
yp ¼ 2 . e
)
A þ A ¼ 2A ¼ 4
)
A ¼ 2
x
3. Allgemeine Lösung der inhomogenen Differentialgleichung:
y ¼ y0 þ yp ¼ C1 þ C2 . sin x þ C3 . cos x þ 2 . e x
ðC1 ; C2 ; C3 2 RÞ
&
300
X Gewöhnliche Differentialgleichungen
6 Systeme linearer Differentialgleichungen
1. Ordnung mit konstanten Koeffizienten
6.1 Grundbegriffe
Wir beschränken uns auf Systeme aus zwei inhomogenen linearen Differentialgleichungen
1. Ordnung mit konstanten Koeffizienten (gekoppelte Differentialgleichungen):
y 01 ¼ a11 y1 þ a12 y2 þ g1 ðxÞ
Bezeichnungen:
3
2
a11 a12
A ¼
;
a21 a22
3
y ¼
y1
y2
2
;
y 0 ¼ A y þ g ðxÞ
oder
y 02 ¼ a21 y1 þ a22 y2 þ g2 ðxÞ
y0 ¼
3
y 01
y 02
3
2
;
g ðxÞ ¼
g1 ðxÞ
g2 ðxÞ
2
A: Koeffizientenmatrix (reell)
y: Lösungsvektor (mit den beiden „Komponenten“ y1 und y2 )
y 0 : Ableitung des Lösungsvektors
g ðxÞ: „Störvektor“ (aus den beiden „Störgliedern“ g1 ðxÞ und g2 ðxÞ gebildet)
Homogenes System:
y 0 ¼ A y (keine Störglieder)
Inhomogenes System: y 0 ¼ A y þ g ðxÞ
mit
g ðxÞ ¼
6 0
Das Differentialgleichungssystem hat die Ordnung 2 (¼ Summe der Ordnungen der beiden
zum System gehörenden Differentialgleichungen 1. Ordnung).
6.2 Integration des homogenen linearen Systems
Das homogene lineare System y 0 ¼ A y lässt sich mit den Exponentialansätzen
y1 ¼ K1 . e l x und y2 ¼ K2 . e l x lösen. Die Werte des noch unbekannten Parameters l
sind die Eigenwerte der Koeffizientenmatrix A und damit die Lösungen der charakteristischen Gleichung
"
" a11 / l
det ðA / l EÞ ¼ ""
a21
"
a12 ""
¼ 0
a22 / l "
Der Lösungsvektor y hängt dabei von der Art der Lösungen l1 und l2 dieser quadratischen Gleichung ab. Es sind folgende drei Fälle zu unterscheiden:
1. Fall: l1 =/ l2 (reell)
y1 ¼ C1 . e l1 x þ C2 . e l2 x
y2 ¼
1
ð y 01 / a11 y1 Þ
a12
ðC1 ; C2 2 RÞ
6 Systeme linearer Differentialgleichungen 1. Ordnung mit konstanten Koeffizienten
301
2. Fall: l1 = l2 = a (reell)
y1 ¼ ðC1 þ C2 xÞ . e a x
y2 ¼
ðC1 ; C2 2 RÞ
1
ð y 01 / a11 y1 Þ
a12
3. Fall: l1/2 = a + j w (konjugiert komplex)
y1 ¼ e a x ½C1 . sin ðw xÞ þ C2 . cos ðw xÞ%
y2 ¼
&
ðC1 ; C2 2 RÞ
1
ð y 01 / a11 y1 Þ
a12
Beispiel
y 01 ¼ 4 y1 / 3 y2
y 02 ¼ 3 y1 / 2 y2
oder
y 01
!
y 02
¼
4
/3
3 /2
|fflfflffl{zfflfflffl}
A
!
y1
!
y2
Charakteristische Gleichung mit Lösungen:
"
"
" ð4 / lÞ
"
/3
" ¼ ð4 / lÞ ð/ 2 / lÞ þ 9 ¼ 0
det ðA / l EÞ ¼ ""
3
ð/2 / lÞ "
l2 / 2l þ 1 ¼ 0
)
l1=2 ¼ 1
)
(2. Fall)
Allgemeine Lösung des linearen Systems ðC1 ; C2 2 RÞ:
y1 ¼ ðC1 þ C2 xÞ . e x ;
y 01 ¼ C2 . e x þ ðC1 þ C2 xÞ . e x
3
2
1
1
y2 ¼
ð y 01 / a11 y1 Þ ¼
C2 . e x þ ðC1 þ C2 xÞ . e x / 4 ðC1 þ C2 xÞ . e x ¼
a12
/3
1
1
¼ /
ðC2 þ C1 þ C2 x / 4 C1 / 4 C2 xÞ . e x ¼ /
ð/ 3 C1 þ C2 / 3 C2 xÞ . e x ¼
3
3
3
2
1
C2 þ C2 x . e x
¼ C1 /
3
&
6.3 Integration des inhomogenen linearen Systems
6.3.1 Integration durch Aufsuchen einer partikulären Lösung
Das inhomogene lineare System y 0 ¼ A y þ gðxÞ lässt sich schrittweise wie folgt lösen:
1. Integration des zugehörigen homogenen Systems y 0 ¼ A y (siehe X.6.2). Man erhält
die Lösung y1 ð0Þ , y2 ð0Þ .
2. Bestimmung einer partikulären Lösung y1 ðpÞ , y2 ðpÞ des inhomogenen Systems. Dies
geschieht mit Hilfe der Tabelle aus Abschnitt 3.2.3, wobei im Lösungsansatz für y1 ðpÞ
und y2 ðpÞ jeweils beide Störglieder entsprechend zu berücksichtigen sind.
3. Die gesuchte allgemeine Lösung y1 ; y2 ist dann die Summe der Teillösungen aus den
ersten beiden Schritten:
y1 ¼ y1 ð0Þ þ y1 ðpÞ ;
y2 ¼ y2 ð0Þ þ y2 ðpÞ
302
&
X Gewöhnliche Differentialgleichungen
Beispiel
y 01 ¼ 4 y1 / 3 y2 þ x
'
y 02 ¼ 3 y1 / 2 y2
inhomogenes System
Störglieder : g1 ðxÞ ¼ x ;
g2 ðxÞ ¼ 0
Die Lösung des zugehörigen homogenen Systems ist bereits aus dem Beispiel in Abschnitt 6.2 bekannt:
3
2
1
C2 þ C2 x . e x
y1 ð0Þ ¼ ðC1 þ C2 xÞ . e x ;
y2 ð0Þ ¼ C1 /
3
Bestimmung einer partikulären Lösung des inhomogenen Systems aus der Tabelle im Abschnitt 3.2.3 für die
Störglieder g1 ðxÞ ¼ x und g2 ðxÞ ¼ 0:
y1 p ¼ a x þ b ;
y2 p ¼ A x þ B ;
y 01 p ¼ a ;
y 02 p ¼ A
Einsetzen in die beiden inhomogenen Dgln:
a ¼ 4 ða x þ bÞ / 3 ðA x þ BÞ þ x ¼ ð4 b / 3 BÞ þ ð4 a / 3 A þ 1Þ x
A ¼ 3 ða x þ bÞ / 2 ðA x þ BÞ ¼ ð3 b / 2 BÞ þ ð3 a / 2 AÞ x
Koeffizientenvergleich führt zu 4 Gleichungen mit 4 Unbekannten:
(I)
a ¼ 4b / 3B
(II)
0 ¼ 4a / 3A þ 1
(III)
A ¼ 3b / 2B
(IV)
0 ¼ 3a / 2A
Aus den Gleichungen (II) und (IV) folgt a ¼ 2, A ¼ 3, aus den Gleichungen (I) und (III) nach Einsetzen
dieser Werte b ¼ 5, B ¼ 6.
Somit:
y1 p ¼ 2 x þ 5 ,
y2 p ¼ 3 x þ 6
Lösung des inhomogenen Systems:
y1 ¼ y1 ð0Þ þ y1 p ¼ ðC1 þ C2 xÞ . e x þ 2 x þ 5
3
2
1
y2 ¼ y2 ð0Þ þ y2 p ¼ C1 /
C2 þ C2 x . e x þ 3 x þ 6
3
&
6.3.2 Einsetzungs- oder Eliminationsverfahren
Das Lösungsverfahren für ein inhomogenes lineares System y 0 ¼ A y þ g ðxÞ lässt sich
wie folgt auf die Integration einer inhomogenen linearen Differentialgleichung 2. Ordnung
mit konstanten Koeffizienten zurückführen:
1. y1 genügt der folgenden inhomogenen linearen Differentialgleichung 2. Ordnung mit
konstanten Koeffizienten:
y 001 þ a y 01 þ b y1 ¼ g~ ðxÞ
Lösungsverfahren: siehe Abschnitt 3.2
Dabei bedeuten:
a ¼ / Sp ðAÞ ¼ / ða11 þ a22 Þ
(mit / 1 multiplizierte Spur von AÞ
b ¼ det A ¼ a11 a22 / a12 a21
(Determinante von AÞ
g~ ðxÞ ¼
g 01 ðxÞ
/ det B
B: Hilfsmatrix (in der Koeffizientenmatrix A wird die 1. Spalte durch die beiden Störglieder g1 ðxÞ und g2 ðxÞ ersetzt)
6 Systeme linearer Differentialgleichungen 1. Ordnung mit konstanten Koeffizienten
303
2. Aus der 1. Komponente y1 lässt sich dann die 2. Komponente y2 folgendermaßen
berechnen:
0
1 1 0
y2 ¼
y 1 / a11 y1 / g1 ðxÞ
a12
Beispiel
y 01 ¼ / y1 þ 3 y2 þ x
y 02 ¼ 2 y1 / 2 y2
y 01
oder
y 02
a ¼ / Sp ðAÞ ¼ / ð/ 1 / 2Þ ¼ 3 ;
"
"x
3
g~ ðxÞ ¼ g 01 ðxÞ / det B ¼ 1 / ""
0 /2
!
/1
¼
3
2 /2
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
A
"
" /1
b ¼ det A ¼ ""
2
"
"
" ¼ 1 þ 2x
"
Differentialgleichung 2. Ordnung für y1 :
!
y1
y2
!
þ
x
!
0
f
&
g ðxÞ
"
3"
" ¼ 2 / 6 ¼ /4
/2 "
ðg1 ðxÞ ¼ x; g2 ðxÞ ¼ 0 ; g 01 ðxÞ ¼ 1Þ
y 001 þ 3 y 01 / 4 y1 ¼ 1 þ 2 x
Lösen der zugehörigen homogenen Differentialgleichung:
Charakteristische Gleichung mit Lösungen:
y 001 þ 3 y 01 / 4 y1 ¼ 0
l2 þ 3l / 4 ¼ 0
)
l1 ¼ / 4 ;
l2 ¼ 1
Allgemeine Lösung der homogenen Differentialgleichung:
y1 ð0Þ ¼ C1 . e / 4 x þ C2 . e x
ðC1 ; C2 2 RÞ
Partikuläre Lösung der inhomogenen Differentialgleichung (Störglied: g ðxÞ ¼ 1 þ 2 xÞ:
y 01 ðpÞ ¼ A ;
y1 ðpÞ ¼ A x þ B ;
y 001 ðpÞ ¼ 0
3 A / 4 ðA x þ BÞ ¼ 3 A / 4 A x / 4 B ¼ 1 þ 2 x
)
/ 4 A x þ ð3 A / 4 BÞ ¼ 2 x þ 1
Koeffizientenvergleich:
/4A ¼ 2
)
A ¼ / 1=2
3A / 4B ¼ 1
)
/4B ¼ 1 / 3A ¼ 1 / 3 .
Partikuläre Lösung:
y1 ðpÞ ¼ /
1
5
x/
2
8
3
2
1
3
5
/
¼1þ
¼
2
2
2
)
B¼/
5
8
Lösung des Systems:
y1 ¼ y1 ð0Þ þ y1 ðpÞ ¼ C1 . e / 4 x þ C2 . e x /
1
5
x /
2
8
0
1 1 0
y 1 / a11 y1 / g1 ðxÞ ¼
a12
3
2
1
1
1
5
/ 4 C1 . e / 4 x þ C2 . e x /
þ C1 . e / 4 x þ C2 . e x /
x /
/x ¼
¼
3
2
2
8
3
2
1
3
9
/ 3 C1 . e / 4 x þ 2 C2 . e x /
x /
¼
3
2
8
y2 ¼
&
304
XI Fehler- und Ausgleichsrechnung
1 Gaußsche Normalverteilung
Die Fehler- und Ausgleichsrechnung beschäftigt sich mit den zufälligen oder statistischen
Mess- oder Beobachtungsfehlern auf der Grundlage der Wahrscheinlichkeitsrechnung und
Statistik 1Þ . Die Messgröße X ist daher im Sinne der mathematischen Statistik eine Zufallsvariable. Die Messwerte und Messfehler einer Messreihe unterliegen dabei in der Regel der
Gaußschen Normalverteilung mit der normierten Verteilungsdichtefunktion
1
1
/
j ðxÞ ¼ pffiffiffiffiffiffiffi . e 2
2ps
1x / m02
f(x)
s
Bezeichnungen:
m:
s:
s 2:
Mittelwert (Erwartungswert)
Standardabweichung ðs > 0Þ
Varianz (Streuung)
m– s
m
x
m+s
Eigenschaften der Gaußschen Normalverteilung
(1)
(2)
(3)
Absolutes Maximum bei x1 ¼ m
(„wahrscheinlichster“ Messwert).
Wendepunkte bei x2=3 ¼ m + s.
Die Wahrscheinlichkeit dafür, dass ein
Messwert x in das Intervall ½a; b %
fällt, beträgt
f(x)
P(a „x „b)
ðb
P ða ) x ) bÞ ¼
f(x)
jðxÞ dx
a
(entspricht der grau unterlegten Fläche
im nebenstehenden Bild). Das Integral
ist in geschlossener Form nicht lösbar.
a
68,3 % aller Messwerte liegen im Intervall
½ m / s; m þ s %
95,5 % aller Messwerte liegen im Intervall
½ m / 2 s; m þ 2 s %
b
x
99,7 %, d. h. fast alle Messwerte liegen im Intervall ½ m / 3 s; m þ 3 s %
1Þ
Nach DIN 1319 soll die Bezeichnung „Fehler“ durch „Messabweichung“ (kurz: Abweichung) ersetzt werden.
Grobe Fehler sind vermeidbar und bleiben ebenso wie systematische Fehler unberücksichtigt.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_11
2 Auswertung einer Messreihe
(4)
305
(5)
Bei einer „unendlichen“ Messreihe würde der Messwert x ¼ m mit der größten
Häufigkeit auftreten. Wären Messungen ohne Messfehler möglich, so würde man
stets den Messwert x ¼ m erhalten. Daher wird der Mittelwert m häufig auch als
„wahrer“ Wert der Messgröße X bezeichnet. Die Standardabweichung s ist ein
geeignetes Maß für die Streuung der einzelnen Messwerte um ihren Mittelwert m
(s bestimmt im Wesentlichen die Breite der Glockenkurve).
1
Ð
j ðxÞ ist normiert:
j ðxÞ dx ¼ 1 (alle Messwerte liegen im Intervall ð/ 1; 1ÞÞ
(6)
Standardisierte Normalverteilung
/1
f(x)
ðm ¼ 0; s ¼ 1Þ:
0,4
f(x) =
1
1
/ x2
j ðxÞ ¼ pffiffiffiffiffiffiffi . e 2
2p
–2
Absolutes Maximum bei x ¼ 0,
–1
1
x2
1 · e– 2
√2p
2
x
Wendepunkte bei x ¼ + 1.
2 Auswertung einer Messreihe
Die normalverteilte Messreihe x1 ; x2 ; . . . ; xn bestehe aus n unabhängigen Messwerten
gleicher Genauigkeit (gleiche Messmethode, gleiches Messinstrument, gleicher Beobachter).
Mittelwert einer Messreihe
Der „günstigste“ Schätzwert für den „wahren“ Wert der Messgröße X ist der arithmetische Mittelwert (auch arithmetisches Mittel genannt):
n
P
x1 þ x2 þ . . . þ xn
¼
x! ¼
n
i¼1
xi
n
Standardabweichung der Einzelmessung
s ¼
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
uP
u n
u
v2
ti ¼ 1 i
n/1
¼
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
uP
u n
u
ðx / x!Þ 2
ti ¼ 1 i
n/1
ðn ( 2Þ
vi ¼ xi / x!: Abweichung des Messwertes xi vom Mittelwert x! ði ¼ 1; 2; . . . ; nÞ
306
XI Fehler- und Ausgleichsrechnung
Die Standardabweichung s ist ein Schätzwert für den Parameter s (gleichen Namens)
der normalverteilten Messgröße. Alte (aber weiterhin übliche) Bezeichnung für s: mittlerer Fehler der Einzelmessung ðmx Þ.
n
P
Kontrolle:
vi ¼ 0
i¼1
Standardabweichung des Mittelwertes
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u P
u n
v2
u
t i¼1 i
s
¼
s x! ¼ pffiffiffi ¼
n ðn / 1Þ
n
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
uP
u n
ðxi / x!Þ 2
u
ti ¼ 1
nðn / 1Þ
ðn ( 2Þ
Alte (weiterhin übliche) Bezeichnung für sx! : mittlerer Fehler des Mittelwertes.
Vertrauensintervall (Vertrauensbereich)
Es lässt sich ein zum arithmetischen Mittelwert x! symmetrisches Intervall angeben, in dem
der unbekannte Mittel- oder Erwartungswert m der normalverteilten Messgröße X mit
einer vorgegebenen Wahrscheinlichkeit g (auch Vertrauensniveau oder statistische Sicherheit genannt) vermutet wird (sog. Vertrauensintervall oder Vertrauensbereich).
s
Vertrauensgrenzen: x! + t . pffiffiffi
n
(obere bzw. untere Grenze)
+
Vertrauensbereich (Vertrauensintervall):
s
x! / t . pffiffiffi ;
n
s
x! þ t . pffiffiffi
n
)
Vertrauensgrenzen
x–t s
√n
x
x+t s
√n
x
2t s
√n
Der Faktor t hängt dabei noch vom gewählten Vertrauensniveau g (z. B. g ¼ 95 %)
und der Anzahl n der Einzelmessungen ab und kann der nachfolgenden Tabelle auf
Seite 302 entnommen werden (sie enthält die t-Werte für die in der Praxis üblichen statistischen Sicherheiten).
Regel: Je größer die statistische Sicherheit, umso breiter das Vertrauensintervall! In Naturwissenschaft und Technik wird meist g ¼ 95 % gewählt.
2 Auswertung einer Messreihe
307
Tabelle: Werte für den Zahlenfaktor (Parameter) t in Abhängigkeit von der Anzahl n
der Messwerte und dem gewählten Vertrauensniveau g
Anzahl n
der
Messwerte
Vertrauensniveau (statistische Sicherheit)
g ¼ 68;3 %
g ¼ 90 %
g ¼ 95 %
g ¼ 99 %
2
1,84
6,31
12,71
63,66
3
1,32
2,92
4,30
9,93
4
1,20
2,35
3,18
5,84
5
1,15
2,13
2,78
4,60
6
1,11
2,02
2,57
4,03
7
1,09
1,94
2,45
3,71
8
1,08
1,90
2,37
3,50
9
1,07
1,86
2,31
3,36
10
1,06
1,83
2,26
3,25
15
1,04
1,77
2,14
2,98
20
1,03
1,73
2,09
2,86
30
1,02
1,70
2,05
2,76
50
1,01
1,68
2,01
2,68
100
..
.
1,00
..
.
1,66
..
.
1,98
..
.
2,63
..
.
1
1,00
1,65
1,96
2,58
Messergebnis
s
x ¼ x! + Dx ¼ x! + t . pffiffiffi
n
x!:
Dx :
arithmetischer Mittelwert
Messunsicherheit (halbe Breite des Vertrauensbereiches)
308
&
XI Fehler- und Ausgleichsrechnung
Beispiel
Widerstandsmessung ðn ¼ 6 EinzelmessungenÞ
i
Ri
W
Ri / R!
W
0,2
ðRi / R!Þ 2
W2
1
60,3
0,04
2
60,2
0,1
0,01
3
59,9
/ 0,2
0,04
4
59,9
/ 0,2
0,04
5
60,2
0,1
0,01
6
P
60,1
0,0
0,00
360,6
0
0,14
6
P
Ri
360;6 W
¼ 60;1 W
¼
6
6
vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
u 6
u P
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! 2
u
t i ¼ 1 ðRi / R Þ
0;14 W 2
s ¼
¼
¼
5
6/1
R! ¼
i¼1
¼ 0;167 W
Bei einer statistischen Sicherheit von g ¼ 95 % entnehmen wir der Tabelle der t-Faktoren den Wert
t ¼ 2;57 für n ¼ 6.
Messunsicherheit:
s
0;167 W
DR ¼ t . pffiffiffi ¼ 2;57 . pffiffiffi
¼ 0;175 W ' 0;2 W
n
6
Messergebnis: R ¼ R! + DR ¼ ð60;1 + 0;2Þ W
&
3 Gaußsches Fehlerfortpflanzungsgesetz
Hinweis: Bei der Fehlerfortpflanzung werden für die Messunsicherheiten meist die Standardabweichungen der Mittelwerte verwendet.
3.1 Gaußsches Fehlerfortpflanzungsgesetz für eine Funktion
von zwei unabhängigen Variablen
Das Messergebnis für zwei direkt gemessene Größen x und y laute:
x ¼ x! + Dx ;
y ¼ y! + Dy
ðDx ¼ sx!; Dy ¼ sy!Þ
Für die von x und y abhängige Größe z ¼ f ðx; yÞ gilt dann:
Mittelwert z!
!z ¼ f ð x!; y!Þ
Regel: In z ¼ f ðx; yÞ werden für x und y deren Mittelwerte eingesetzt.
3 Gaußsches Fehlerfortpflanzungsgesetz
309
Standardabweichung des Mittelwertes (mittlerer Fehler des Mittelwertes)
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Dz ¼ sz! ¼
ð fx ð x!; y!Þ DxÞ 2 þ ð fy ð x!; y!Þ DyÞ 2
(Gaußsches Fehlerfortpflanzungsgesetz für die Standardabweichung des Mittelwertes)
)
fx ð x!; y! Þ
Partielle Ableitungen 1. Ordnung von z ¼ f ðx; yÞ
an
der Stelle x ¼ x!; y ¼ y!
fy ð x!; y!Þ
Messergebnis
z ¼ !
z + Dz
&
Beispiel
Wir berechnen die Turmhöhe h sowie den mittleren Fehler des Mittelwertes von h aus der Entfernung e
und dem Erhebungswinkel a:
e ¼ ð75;2 + 2;5 mÞ;
a ¼ ð30 + 1Þ "
Aus dem rechtwinkligen Dreieck folgt:
h
tan a ¼
) h ¼ h ðe; aÞ ¼ e . tan a
e
! Þ ¼ e! . tan a
! ¼
h! ¼ h ð e!; a
¼ 75;2 m . tan 30 " ¼ 43;417 m ' 43;4 m
Partielle Ableitungen 1. Ordnung an der Stelle e! ¼ 75;2 m, a ¼ 30 " :
@h
¼ tan a
@e
)
@h
! Þ ¼ tan 30 " ¼ 0;5774
ð e!; a
@e
@h
e
¼
@a
cos 2 a
)
@h
75;2 m
!Þ ¼
ð e!; a
¼ 100;2667 m
@e
cos 2 30 "
Mittlerer Fehler des Mittelwertes (Standardabweichung des Mittelwertes):
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
s3
22 3
22ffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
@h
@h
Dh ¼
De þ
Da
¼ ð0;5774 . 2;5 mÞ 2 þ ð100;2667 m . 0;01745Þ 2 ¼
@e
@a
¼ 2;2683 m ' 2;3 m
ðDa muss aus Dimensionsgründen im Bogenmaß angegeben werden: Da ¼ 1" ' 0;017 45 rad:Þ
Messergebnis:
h ¼ h + Dh ¼ ð43;4 + 2;3Þ m
Die Turmhöhe beträgt h! ¼ 43,4 m bei einer Messunsicherheit von Dh ¼ 2,3 m (prozentual ' 5,3 %).
&
310
XI Fehler- und Ausgleichsrechnung
Gaußsches Fehlerfortpflanzungsgesetz für spezielle Funktionen (C 2 R)
Funktion
z ¼ x þy
z ¼ x /y
z ¼ Cxy
z ¼ C
x
y
z ¼ Cxayb
Standardabweichung des Mittelwertes (mittlerer Fehler des Mittelwertes)
Dz ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðDxÞ 2 þ ðDyÞ 2
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
" "
"
"2 " "2
" Dz "
"
"
" "
" " ¼ " Dx " þ " Dy "
" !z "
" x! "
" y! "
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"2 "
"2
" "
"
"
"
" Dz "
"
"
" " ¼ " a Dx " þ " b Dy "
" !z "
" x! "
" y! "
(absoluter Fehler)
ðrelativer FehlerÞ
ðrelativer FehlerÞ
Prozentualer Fehler ¼ (relativer Fehler) . 100 %
3.2 Gaußsches Fehlerfortpflanzungsgesetz für eine Funktion
von n unabhängigen Variablen
Das Messergebnis von n direkt gemessenen Größen x1 ; x2 ; . . . ; xn laute wie folgt:
xi ¼ x!i + Dxi
ðDxi ¼ sx!i ; i ¼ 1; 2; . . . ; nÞ
Für die von x1 ; x2 ; . . . ; xn abhängige indirekte Messgröße y ¼ f ðx1 ; x2 ; . . . ; xn Þ gelten
dann folgende Formeln für den Mittelwert y! und die Standardabweichung Dy:
y! ¼ f ð x!1 ; x!2 ; . . . ; x!n Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Dy ¼ ð fx1 Dx1 Þ 2 þ ð fx2 Dx2 Þ 2 þ . . . þ ð fxn Dxn Þ 2
Messergebnis:
fx1 ; fx2 ; . . . ; fxn :
y ¼ y! + Dy
Partielle Ableitungen 1. Ordnung von y ¼ f ðx1 ; x2 ; . . . ; xn Þ an der
Stelle x1 ¼ x!1 ; x2 ¼ x!2 ; . . . ; xn ¼ x!n
Hinweis: Für Summen und Produkte aus mehr als zwei unabhängigen Messgrößen gelten
ähnliche Formeln wie bei zwei unabhängigen Messgrößen (siehe Tabelle in Abschnitt 3.1).
4 Lineares Fehlerfortpflanzungsgesetz
Das lineare Fehlerfortpflanzungsgesetz liefert eine obere Fehlerschranke für den absoluten
Fehler einer von mehreren Messgrößen abhängigen „indirekten“ Messgröße (Fehlerabschätzung mit Hilfe des totalen Differentials). Diese Fehlerschranke wird als maximaler
oder größtmöglicher Fehler oder maximale Messunsicherheit des Mittelwertes bezeichnet.
4 Lineares Fehlerfortpflanzungsgesetz
311
Bei zwei unabhängigen Messgrößen gilt ðz ¼ f ðx; yÞÞ:
Dz max ¼ j fx ð x!; y!Þ Dx j þ j fy ð x!; y!Þ Dy j
Messergebnis: z ¼ !z + Dz max
(mit !z ¼ f ð!
x; y!ÞÞ
fx ; fy :
Partielle Ableitungen 1. Ordnung von z ¼ f ðx; yÞ für x ¼ x!; y ¼ y!
Dx; Dy:
Messunsicherheiten der unabhängigen Messgrößen (Standardabweichungen der
beiden Mittelwerte)
Das lineare Fehlerfortpflanzungsgesetz wird häufig für !berschlagsrechnungen verwendet,
insbesondere auch dann, wenn die Messunsicherheiten der unabhängigen Größen unbekannt sind und man daher auf Schätzwerte angewiesen ist.
Lineares Fehlerfortpflanzungsgesetz für spezielle Funktionen (C 2 R)
Funktion
Maximale Messunsicherheit des Mittelwertes
z ¼ x þy
z ¼ x /y
z ¼ Cxy
z ¼ C
x
y
z ¼ Cxayb
Dz max ¼ Dx þ Dy
(absoluter Fehler)
"
"
"
"
" "
"
" Dz max "
"
" "
" ¼ " Dx " þ " Dy "
"
" !z "
" x! "
" y! "
ðrelativer FehlerÞ
"
"
"
"
"
"
"
"
" Dz max "
"
"
" ¼ " a Dx " þ " b Dy "
"
" !z "
" x! "
" y! "
ðrelativer FehlerÞ
Entsprechende „lineare Fehlerfortpflanzungsgesetze“ gelten auch für Summen mit mehr als
zwei Summanden und Potenzprodukte mit mehr als zwei Faktoren.
Bei n unabhängigen Messgrößen gilt analog ðy ¼ f ðx1 ; x2 ; . . . ; xn ÞÞ:
Dy max ¼ j fx1 Dx1 j þ j fx2 Dx2 j þ . . . þ j fxn Dxn j
Messergebnis: y ¼ y! + Dy max
(mit y! ¼ f ð!
x1 ; x!2 ; . . . ; x!n ÞÞ
In die partiellen Ableitungen 1. Ordnung der Funktion y ¼ f ðx1 ; x2 ; . . . ; xn Þ sind die
Mittelwerte der unabhängigen Messgrößen einzusetzen, Dx1 ; Dx2 ; . . . ; Dxn sind die Messunsicherheiten (Standardabweichungen der Mittelwerte) oder deren Schätzwerte.
&
Beispiel
Maximaler Fehler der Turmhöhe (Beispiel aus Abschnitt 3.1):
"
"
"
"
" @h
"
" @h
"
Dh max ¼ ""
De "" þ ""
Da "" ¼ j 0;5774 . 2;5 m j þ j 100;2667 m . 0;017 45 j ¼
@e
@a
¼ 1;4435 m þ 1;7497 m ¼ 3;1932 m ' 3;2 m
&
312
XI Fehler- und Ausgleichsrechnung
5 Ausgleichskurven
5.1 Ausgleichung nach dem Gaußschen Prinzip der kleinsten Quadrate
Unter einer Ausgleichskurve versteht man eine Kurve, die sich n vorgegebenen Messpunkten Pi ¼ ðxi ; yi Þ mit i ¼ 1; 2; . . . ; n „optimal“ anpasst:
y
Pi = (xi ; yi )
vi
yi
Ausgleichskurve
y = f(x)
f(xi )
xi
x
Man bestimmt sie nach Gauß wie folgt:
1. Zunächst muss man anhand des konkreten Falles eine Entscheidung über den speziellen
Funktionstyp, der der Ausgleichsrechnung zugrunde gelegt werden soll, treffen (z. B.
Gerade, Parabel, Potenz- oder Exponentialfunktion). Der Lösungsansatz y ¼ f ðxÞ enthält dabei noch gewisse Parameter a; b; c; . . . :
2. Dann wird für jeden Messpunkt Pi ¼ ðxi ; yi Þ die vertikale Abweichung vi ¼ yi / f ðxi Þ
von der Ausgleichskurve y ¼ f ðxÞ bestimmt und daraus die Summe der Abweichungsquadrate:
S ða; b; c; . . .Þ ¼
n
P
i¼1
v 2i ¼
n
P
i¼1
½ yi / f ðxi Þ% 2
Sie hängt noch von den Kurvenparametern a; b; c; . . . ab.
3. Nach Gauß passt sich diejenige Kurve den vorgegebenen Messpunkten „am besten“ an,
für die diese Summe minimal wird (Methode der kleinsten Quadrate). Die Parameter
a; b; c; . . . lassen sich dann aus den sog. Normalgleichungen (Extremalbedingungen)
@S
¼ 0;
@a
berechnen.
@S
¼ 0;
@b
@S
¼ 0; . . .
@c
5 Ausgleichskurven
313
Einfache Lösungsansätze für spezielle Ausgleichskurven
Lösungsansatz
Parameter
Lineare Funktion (Gerade):
y ¼ ax þ b
a; b
Quadratische Funktion (Parabel):
y ¼ ax2 þ bx þ c
a; b; c
Polynomfunktion vom Grade n:
y ¼ an x n þ an / 1 x n / 1 þ . . . þ a1 x þ a0
an ; an / 1 ; . . . ; a1 ; a0
Potenzfunktion:
y ¼ a . xb
a; b
Exponentialfunktion:
y ¼ a . e bx
a; b
Logarithmusfunktion:
y ¼ a . ln ðb xÞ
a; b
Gebrochenrationale Funktionen:
y ¼
a
;
x þb
y ¼
ax þ b
b
¼ aþ
x
x
y ¼
ax
;
x þb
a; b
Exponential- und Potenzfunktion lassen sich im halb- bzw. doppellogarithmischen Maßstab
durch lineare Funktionen, d. h. durch Geraden darstellen:
Exponentialfunktion
y ¼ a . e bx :
ln y ¼ ln ða . e b x Þ ¼ ln a þ ln e b x ¼ ln a þ b x . ln e ¼ b x þ ln a
|{z}
1
Mit z ¼ ln y und c ¼ ln a erhalten wir die Gerade z ¼ b x þ c :
Potenzfunktion y ¼ a . x b :
ln y ¼ ln ða . x b Þ ¼ ln a þ ln x b ¼ ln a þ b . ln x ¼ b . ln x þ ln a
Mit u ¼ ln x; v ¼ ln y und c ¼ ln a erhalten wir die Gerade v ¼ b u þ c .
Hinweis: Für die linearisierte Exponential- bzw. Potenzfunktion ist die Summe der Abweichungsquadrate nur für die transformierten Wertepaare minimal, nicht aber für die Wertepaare selbst. Die mit dem vereinfachten Verfahren berechneten Werte sind daher nur (für
die Praxis jedoch meist völlig ausreichende) Näherungen der Kurvenparameter.
5.2 Ausgleichs- oder Regressionsgerade
Diejenige Gerade y ¼ a x þ b, die sich n vorgegebenen Messpunkten Pi ¼ ðxi ; yi Þ
„optimal“ anpasst, heißt Ausgleichs- oder Regressionsgerade ði ¼ 1; 2; . . . ; n; n ( 3Þ.
Steigung a (auch Regressionskoeffizient genannt) und Achsenabschnitt b werden wie
folgt berechnet:
314
XI Fehler- und Ausgleichsrechnung
n.
a ¼
3
n
P
i¼1
n
P
i¼1
b ¼
D¼ n .
3
xi yi /
x 2i
i¼1
i¼1
23
xi
2
n
P
i¼1
x 2i /
3
yi
3
/
i¼1
xi
n
P
i¼1
D
n
P
2
n
P
i¼1
D
23
n
P
n
P
22
yi
23
xi
n
P
i¼1
2
xi yi
ð,,Hilfsgröße‘‘)
Die Ausgleichsgerade kann auch in der symmetrischen Form
y / y! ¼ a ðx / x!Þ
dargestellt werden. Sie verläuft durch den sog. „Schwerpunkt“ S ¼ ð x!; y!Þ der aus den n
Messpunkten gebildeten Punktwolke ð x!; y!: Mittelwerte der x- bzw. y-Koordinaten der n
Messpunkte; a: Regressionskoeffizient).
Korrelationskoeffizient
n
P
xi yi / n x! y!
i¼1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
r ¼ s3
2ffi ;
23 n
n
P 2
P
2
2
2
y i / n y!
x i / n x!
/1 ) r ) 1
i¼1
i¼1
Die n Messpunkte liegen immer dann nahezu auf einer Geraden, wenn r sich nur wenig
von / 1 oder þ 1 unterscheidet. Im Falle j r j ¼ 1 liegen die Messpunkte exakt auf
einer Geraden.
&
Beispiel
Wir zeigen zunächst, dass die 5 Messpunkte P1 ¼ ð0; 0;6Þ; P2 ¼ ð2; 3;9Þ; P3 ¼ ð3; 5;8Þ; P4 ¼ ð5; 9;7Þ
und P5 ¼ ð8; 14;6Þ nahezu auf einer Geraden liegen und bestimmen dann die Ausgleichsgerade mit Hilfe
der folgenden Tabelle:
x 2i
y 2i
i
xi
yi
xi yi
1
0
0,6
0
0,36
2
2
3,9
4
15,21
7,8
17,4
0
3
3
5,8
9
33,64
4
5
9,7
25
94,09
48,5
5
P
8
14,6
64
213,16
116,8
18
34,6
102
356,46
190,5
5 Ausgleichskurven
315
Berechnung des Korrelationskoeffizienten r
n
P
x! ¼
i¼1
xi
n
n
P
18
¼ 3;6 ;
¼
5
y! ¼
i¼1
yi
¼
n
34;6
¼ 6;92
5
n
P
xi yi / n x! y!
190;5 / 5 . 3;6 . 6;92
i¼1
r ¼ vffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!
!ffi ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ 0;9994
u
n
n
u P
P
ð102
/
5 . 3;6 2 Þ ð356;46 / 5 . 6;92 2 Þ
t
x 2i / n x! 2
y 2i / n y! 2
i¼1
i¼1
r ¼ 0;9994 ' 1
)
Die Punkte liegen nahezu auf einer Geraden.
Bestimmung der Ausgleichsgeraden y = a x + b
3 n 22
n
P
P
D ¼ n.
x 2i /
xi ¼ 5 . 102 / 18 2 ¼ 186
i¼1
n.
n
P
i¼1
3
x i yi /
n
P
23
xi
n
P
2
yi
5 . 190;5 / 18 . 34;6
¼ 1;773
186
3 n
23 n 2
3 n 23 n
2
P 2
P
P
P
xi
yi /
xi
xi yi
102 . 34;6 / 18 . 190;5
i¼1
i¼1
i¼1
b ¼ i¼1
¼ 0;539
¼
186
D
a ¼
i¼1
i¼1
i¼1
D
Ausgleichsgerade:
¼
y ¼ 1;773 x þ 0;539
&
5.3 Ausgleichs- oder Regressionsparabel
Diejenige Parabel y ¼ a x 2 þ b x þ c, die sich den n Messpunkten Pi ¼ ðxi ; yi Þ
„optimal“ anpasst, heißt Ausgleichs- oder Regressionsparabel ði ¼ 1; 2; . . . ; n; n ( 4Þ.
Die Kurvenparameter a; b und c lassen sich aus den folgenden Normalgleichungen eindeutig bestimmen ( lineares Gleichungssystem mit drei Gleichungen und drei Unbekannten
a; b und c):
3
n
P
i¼1
3
n
P
i¼1
3
n
P
i¼1
x 4i
x 3i
x 2i
2
3
.aþ
2
i¼1
3
.aþ
2
n
P
i¼1
3
.aþ
n
P
n
P
i¼1
x 3i
x 2i
2
3
.bþ
2
i¼1
3
.bþ
n
P
n
P
i¼1
x 2i
.c ¼
2
xi
2
xi
2
.bþn.c ¼
.c ¼
n
P
i¼1
yi
n
P
i¼1
n
P
i¼1
x 2i yi
x i yi
316
XII Fourier-Transformationen
Hinweis: Die in den Beispielen benötigten Fourier-Transformationen wurden der Tabelle 1
in Abschnitt 6 entnommen (Angabe der laufenden Nummer und der Parameterwerte).
1 Grundbegriffe
Fourier-Transformation
Die Fourier-Transformation ist eine Integraltransformation. Sie ordnet einer nichtperiodischen (in den Anwendungen meist zeitabhängigen) Funktion f ðtÞ, / 1 < t < 1 wie
folgt eine Funktion F ðwÞ der reellen Variablen w zu 1Þ :
1
ð
F ðwÞ ¼
f ðtÞ . e / j w t dt
/1
Das uneigentliche Integral der rechten Seite heißt Fourier-Integral. Es existiert, wenn f ðtÞ
absolut integrierbar ist, d. h.
1
Ð
/1
j f ðtÞj dt < 1
gilt. Geometrische Deutung: Die Fläche unter der Kurve y ¼ j f ðtÞj besitzt einen endlichen Wert.
Bezeichnungen:
f ðtÞ:
F ðwÞ:
Originalfunktion (Zeitfunktion)
Bildfunktion (Fourier-Transformierte von f ðtÞ, Spektraldichte)
Weitere symbolische Schreibweisen:
F ðwÞ ¼ F f f ðtÞg
F:
ðFourier-Transformierte von f ðtÞÞ
Fourier-Transformationsoperator
f ðtÞ "///! F ðwÞ
(Korrespondenz)
Originalfunktion f ðtÞ und Bildfunktion F ðwÞ ¼ F f f ðtÞg bilden ein zusammengehöriges Funktionenpaar.
1Þ
Die Variable w ist bei zeitabhängigen Funktionen die Kreisfrequenz.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_12
1 Grundbegriffe
317
Anmerkungen
(1)
Wegen der im Fourier-Integral enthaltenen (komplexen) Exponentialfunktion spricht
man häufig auch von der exponentiellen Fourier-Transformation.
(2)
Die Fourier-Transformierte F ðwÞ ist eine im Allgemeinen komplexwertige und stetige
Funktion der reellen Variablen w, die im Unendlichen verschwindet:
lim F ðwÞ ¼ 0
(3)
Eine Funktion f ðtÞ heißt Fourier-transformierbar, wenn das Fourier-Integral F ðwÞ
existiert. Die Menge aller (transformierbaren) Originalfunktionen wird als Originalbereich, die Menge der zugeordneten Bildfunktionen als Bildbereich bezeichnet.
&
Beispiel
(
jwj ! 1
f ðtÞ ¼
f (t)
1
für
0
jtj ) a
)
1
jtj > a
Die Fourier-Transformierte dieses Rechteckimpulses
existiert (Fläche unter der Kurve ¼ 2 a):
1
ð
F ðwÞ ¼
f ðtÞ . e / j w t dt ¼
/1
ða
1 . e / j w t dt ¼
t¼/a
–a
+
1
. e /jwt
/jw
a
)a
t¼/a
¼ /
1
1
2 . sin ða wÞ
¼
ðe j a w / e / j a w Þ ¼
. 2 j . sin ða wÞ ¼
j w |fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
jw
w
2 j . sin ða wÞ
Hinweis:
F ð0Þ ¼
e j x / e / i x ¼ 2 j . sin x
1
Ð
/1
f ðtÞ . e 0 dt ¼
Ða
/a
mit
t
1
ðe / j w a / e j w a Þ ¼
jw
ðf ür w 6¼ 0Þ
x ¼ a w, siehe VIII.7.3.2
1 dt ¼
F ( v)
¼ ½ t % a/ a ¼ a þ a ¼ 2 a
2a
Somit gilt (für w 6¼ 0):
F f f ðtÞ g ¼ F ðwÞ ¼
f ðtÞ
"///!
2 . sin ða wÞ
w
v
2 . sin ða wÞ
w
&
Inverse Fourier-Transformation
Für die Rücktransformation aus dem Bild- in den Originalbereich schreibt man symbolisch
F / 1 fFðwÞg ¼ f ðtÞ
ðinverse Fourier-Transformierte)
oder
FðwÞ !///" f ðtÞ
(Korrespondenz)
318
XII Fourier-Transformationen
Die Rücktransformation ist durchführbar, wenn f ðtÞ stückweise monoton, stetig und absolut integrierbar ist und in den eventuell vorhandenen Sprungstellen die beiderseitigen Grenzwerte existieren. Es gilt dann die folgende Integraldarstellung für die Originalfunktion:
1
f ðtÞ ¼
.
2p
1
ð
F ðwÞ . e j w t dw
/1
In den Sprungstellen liefert das uneigentliche Integral der rechten Seite das arithmetische
Mittel der beiderseitigen Grenzwerte.
&
Beispiel
(
F ðwÞ ¼
1
0
für
jwj ) w0
F ( v)
)
1
jwj > w0
Aus der (rechteckigen) Bildfunktion F ðwÞ lässt sich
wie folgt die zugehörige Originalfunktion gewinnen:
– v0
f ðtÞ ¼
1
.
2p
1
ð
F ðwÞ . e j w t dw ¼
/1
1
.
2p
wð0
1 . e j t w dw ¼
w¼/w0
v0
v
1
1
0
. ½ e j t w% w
w ¼ / w0 ¼
2p jt
1
1
1
1
1
1 sin ðw 0 tÞ
.
ðe j w 0 t / e / j w 0 t Þ ¼
.
. 2 j . sin ðw 0 tÞ ¼
. sin ðw 0 tÞ ¼
.
¼
p t 2 j |fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
pt 2j
pt
p
t
2 j . sin ðw 0 tÞ
ðf ür t 6¼ 0Þ
Hinweis: e j x / e / j x ¼ 2 j . sin x
f ð0Þ ¼
1
.
2p
wð0
1 . e 0 dw ¼
/w0
1
.
2p
mit
x ¼ w 0 t, siehe VIII.7.3.2
wð0
1 dw ¼
/w0
1
1
w0
0
½w % w
ðw 0 þ w 0 Þ ¼
/w0 ¼
2p
2p
p
&
Physikalische Deutung der Fourier-Transformation
Die nichtperiodische zeitabhängige Funktion f ðtÞ kann als Grenzfall einer periodischen
Funktion mit der Periode T ¼ 1 aufgefasst werden. Sie wird in ihre harmonischen
Bestandteile zerlegt, die durch harmonische Schwingungen in der komplexen Exponentialform e j w t beschrieben werden (sog. Fourier-Analyse). Anders wie bei der Zerlegung
periodischer Funktionen treten hier sämtliche Kreisfrequenzen aus dem Intervall
/ 1 < w < 1 auf. An die Stelle der komplexen Fourier-Koeffizienten c n tritt die Fourier-Transformierte F ðwÞ, aus dem Linienspektrum wird ein kontinuierliches Spektrum:
periodische Zeitfunktion
! Linienspektrum
nichtperiodische Zeitfunktion
! kontinuierliches Spektrum
1 Grundbegriffe
319
Im naturwissenschaftlich-technischen Bereich sind folgende Bezeichnungen üblich:
F ðwÞ:
Spektrum von f ðtÞ (Frequenzspektrum, Spektraldichte, Spektralfunktion)
A ðwÞ ¼ j F ðwÞ j:
Amplitudenspektrum (spektrale Amplitudendichte)
j ðwÞ ¼ arg ðF ðwÞÞ:
Phasenspektrum (spektrale Phasendichte)
Polardarstellung der Fourier-Transformierten
F ðwÞ ¼ j F ðwÞj . e j j ðwÞ ¼ A ðwÞ . e j j ðwÞ
"quivalente Fourier-Darstellungen (in reeller Form)
f ðtÞ:
reelle Zeitfunktion (absolut integrierbar)
Entwicklung nach Kosinus- und Sinusschwingungen
1
ð
f ðtÞ ¼
½ a ðwÞ . cos ðw tÞ þ b ðwÞ . sin ðw tÞ% dw
0
1
a ðwÞ ¼
.
p
1
b ðwÞ ¼
.
p
a ðwÞ, b ðwÞ:
1
ð
f ðtÞ . cos ðw tÞ dt
/1
1
ð
f ðtÞ . sin ðw tÞ dt
/1
Spektralfunktionen (Amplitudendichten)
Sonderfälle
f ðtÞ:
gerade Funktion
)
b ðwÞ ¼ 0 (nur Kosinusschwingungen)
f ðtÞ:
ungerade Funktion
)
a ðwÞ ¼ 0
(nur Sinusschwingungen)
Entwicklung nach phasenverschobenen Sinusschwingungen
1
ð
f ðtÞ ¼
B ðwÞ . sin ½w t þ j ðwÞ % dw
0
B ðwÞ ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
½ a ðwÞ % 2 þ ½ b ðwÞ % 2 ;
p . B ðwÞ:
Amplitudenspektrum
j ðwÞ:
Phasenspektrum
tan j ðwÞ ¼
a ðwÞ
b ðwÞ
320
XII Fourier-Transformationen
Sonderfälle
f ðtÞ
B ðwÞ
j ðwÞ
A ðwÞ ¼ j F ðwÞ j
gerade Funktion
j aðwÞ j
p= 2
(nur Kosinusglieder)
p . j a ðwÞ j
ungerade Funktion
j bðwÞ j
0
(nur Sinusglieder)
p . j b ðwÞ j
Zusammenhang zwischen dem Spektrum F(w) und den Spektralfunktionen a(w)
und b(w)
F ðwÞ ¼ p ½a ðwÞ / j . b ðwÞ%
A ðwÞ ¼ j F ðwÞ j ¼ p . B ðwÞ ¼ p .
&
Beispiel
(
f ðtÞ ¼
1
für
0
jtj ) a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
½ a ðwÞ% 2 þ ½ b ðwÞ% 2
)
f (t)
jtj > a
1
Die Fourier-Analyse dieses rechteckigen Impulses
enthält ausschließlich Kosinusterme ð f ðtÞ ist eine
gerade Funktion ) b ðwÞ ¼ 0Þ. Somit:
1
ð
f ðtÞ ¼
–a
aðwÞ . cos ðw tÞ dw
a
t
0
Bestimmung der Spektralfunktion (Amplitudendichte) a ðwÞ:
a ðwÞ ¼
¼
a ð0Þ ¼
1
.
p
2
p
+
1
.
p
1
ð
f ðtÞ . cos ðw tÞ dt ¼
/1
1
.
p
ða
1 . cos ðw tÞ dt ¼
t¼/a
sin ðw tÞ
w
)a
t¼0
¼
1 . cos 0 dt ¼
1
.
p
cos ðw tÞ dt ¼
t¼0
ða
1 dt ¼
/a
2
.
p
ða
1 dt ¼
0
ðf ür w 6¼ 0Þ
2
2
2a
½ t % a0 ¼
ða / 0Þ ¼
p
p
p
A (v)
Amplitudenspektrum:
A ðwÞ ¼ p . j aðwÞ j ¼
"
"
2 "" sin ða wÞ ""
¼ p .
"
" ¼
p
w
"
"
" sin ða wÞ "
"
¼ 2 ""
"
w
A ð0Þ ¼ p . a ð0Þ ¼ p .
ða
2
1
2 sin ða wÞ
.
ðsin ðw aÞ / sin 0 Þ ¼
.
p w
p
w
|ffl{zffl}
0
ða
/a
2
.
p
2a
¼ 2a
p
2a
v
&
2 Spezielle Fourier-Transformationen
321
2 Spezielle Fourier-Transformationen
Neben der exponentiellen Fourier-Transformation gibt es noch zwei weitere spezielle
Fourier-Transformationen.
Fourier-Kosinus-Transformation
1
ð
Fc ðwÞ ¼ F c f f ðtÞg ¼
f ðtÞ . cos ðw tÞ dt
0
Fc ðwÞ:
Fourier-Kosinus-Transformierte von f ðtÞ
Für eine gerade Funktion gilt:
F ðwÞ ¼ 2 . Fc ðwÞ
Fourier-Sinus-Transformation
1
ð
Fs ðwÞ ¼ F s f f ðtÞg ¼
f ðtÞ . sin ðw tÞ dt
0
Fs ðwÞ: Fourier-Sinus-Transformierte von f ðtÞ
Für eine ungerade Funktion gilt:
F ðwÞ ¼ / 2 j . Fs ðwÞ
&
Beispiel
8
t þa
>
>
<
f ðtÞ ¼
/t þ a
>
>
:
0
für
f (t)
9
/a ) t ) 0>
>
=
0 ) t ) a
>
>
;
jtj ( a
Für diese gerade Dreiecksfunktion erhalten wir mit
Hilfe der Fourier-Kosinus-Transformation die folgende Bildfunktion:
a
–a
a
t
322
XII Fourier-Transformationen
1
ð
ða
F ðwÞ ¼ 2 . Fc ðwÞ ¼ 2 .
f ðtÞ . cos ðw tÞ dt ¼ 2 .
0
ða
¼ 2.
t¼0
ð/ t þ aÞ . cos ðw tÞ dt ¼
0
+
½ / t . cos ðw tÞ þ a . cos ðw tÞ % dt ¼ 2
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral 232
mit a ¼ w
/
cos ðw tÞ
t . sin ðw tÞ
a
/
þ
. sin ðw tÞ
w2
w
w
)a
t¼0
¼
+
)
cos ðw aÞ
a . sin ðw aÞ
a
cos 0
0 . sin 0
a
¼ 2 /
/
þ
.
sin
ðw
aÞ
þ
þ
/
.
sin
0
¼
w2
w
w
w2
w
w
3
2
3
2
cos ða wÞ
a . sin ða wÞ
a . sin ða wÞ
1
cos ða wÞ
1
¼ 2 /
/
þ
þ
þ
0
/
0
¼
2
/
þ
¼
w2
w
w
w2
w2
w2
3
2
/ cos ða wÞ þ 1
2 ½ 1 / cos ða wÞ %
¼ 2
¼
ð f ür w 6¼ 0Þ
2
w
w2
1
ð
ða
F ð0Þ ¼ 2 . Fc ð0Þ ¼ 2 .
0
+
¼ 2
f ðtÞ . cos 0 dt ¼ 2 .
/
1 2
t þ at
2
)a
ða
ð/ t þ aÞ . 1 dt ¼ 2 .
0
3
2
1 2
1 2
¼ 2 /
a þ a2 ¼ 2 .
a ¼ a2
2
2
0
ð/ t þ aÞ dt ¼
0
&
Zusammenhang zwischen den Fourier-Transformationen F(w), Fc (w) und Fs (w)
Jede Funktion f ðtÞ lässt sich wie folgt in eine Summe aus einer geraden Funktion gðtÞ
und einer ungeraden Funktion h ðtÞ zerlegen:
f ðtÞ ¼
1
1
1
1
½ f ðtÞ þ f ð/ tÞ % þ
½ f ðtÞ / f ð/ tÞ % ¼
gðtÞ þ
h ðtÞ
2 |fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
2 |fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
2
2
gðtÞ
h ðtÞ
Dann gilt:
F ðwÞ ¼
1
1
G ðwÞ þ
H ðwÞ ¼ G c ðwÞ / j . H s ðwÞ
2
2
G ðwÞ, H ðwÞ:
Fourier-Transformierte von g ðtÞ bzw. h ðtÞ
G c ðwÞ:
Fourier-Kosinus-Transformierte von g ðtÞ
H s ðwÞ:
Fourier-Sinus-Transformierte von h ðtÞ
Berechnung der Fourier-Transformation mit Hilfe von Korrespondenztabellen
! Tabelle 1 (Seite 338 bis 339): Exponentielle Fourier-Transformationen
! Tabelle 2 (Seite 340 bis 341): Fourier-Sinus-Transformationen
! Tabelle 3 (Seite 342 bis 343): Fourier-Kosinus-Transformationen
3 Wichtige „Hilfsfunktionen“ in den Anwendungen
323
3 Wichtige „Hilfsfunktionen“ in den Anwendungen
3.1 Sprungfunktionen
Sprungfunktionen werden z. B. für Einschaltvorgänge benötigt.
Sprungfunktion s (t) (Sprungstelle: t == 0)
Einheitssprung, Heaviside-Funktion, Sigmafunktion (s-Funktion)
s(t)
(
s ðtÞ ¼
0
1
f ür
t < 0
)
1
t ( 0
t
Verschobene Sprungfunktion (Sprungstelle: t == a)
s(t – a)
(
s ðt / aÞ ¼
0
1
f ür
t < a
)
1
t ( a
a
t
„Ausblenden“ mit Hilfe der s-Funktion
Die Multiplikation einer Funktion f ðtÞ, / 1 < t < 1 mit der Sprungfunktion s ðtÞ
bewirkt, dass alle Funktionswerte für t < 0 verschwinden, d. h. gleich Null gesetzt
werden, während im Intervall t ( 0 alles beim Alten bleibt (sog. „Ausblenden“ im Intervall t < 0Þ:
g (t)
(
g ðtÞ ¼ f ðtÞ . s ðtÞ ¼
0
f ðtÞ
f ür
t < 0
)
t ( 0
g (t) = f (t)
g (t) = 0
t
324
&
XII Fourier-Transformationen
Beispiel
(
f ðtÞ ¼ sin t
)
g ðtÞ ¼ sin t . s ðtÞ ¼
0
sin t
f ür
t < 0
t ( 0
f (t)
'
g (t)
1
1
g (t) = sin t
g (t) = 0
–1
t
sin t
t
–1
&
„Ausblenden“ im Intervall t < a
g (t)
(
g ðtÞ ¼ f ðtÞ . s ðt / aÞ ¼
0
f ðtÞ
f ür
t < a
)
t ( a
a
t
„Ausblenden“ in den Intervallen t < a und t > b (mit a < b)
g (t)
g ðtÞ ¼ f ðtÞ . ½ s ðt / aÞ / s ðt / bÞ% ¼
(
¼
0
f ðtÞ
f ür
t < a;
t > b
)
a ) t ) b
a
&
t
g (t)
Beispiel
f ðtÞ ¼ sin t ;
b
a ¼ /p;
b ¼ 2p
g ðtÞ ¼ sin t . ½ s ðt þ pÞ / s ðt / 2 pÞ % ¼
(
)
/p ) t ) 2p
sin t
¼
f ür
0
alle übrigen t
1
–π
2π
t
–1
&
3 Wichtige „Hilfsfunktionen“ in den Anwendungen
325
„Ausblenden“ einer verschobenen Funktion
Die Funktion f ðtÞ wird zunächst um a verschoben und dann im Intervall t < a „ausgeblendet“:
(
g ðtÞ ¼ f ðt / aÞ . s ðt / aÞ ¼
0
f ðt / aÞ
f ür
t < a
)
t ( a
3.2 Rechteckige Impulse
Intervall:
a ) t ) b
f (t)
ða < bÞ
1
f ðtÞ ¼ s ðt / aÞ / s ðt / bÞ ¼
(
)
a ) t ) b
1
¼
f ür
0
alle übrigen t
Symmetrisches Intervall: / a ) t ) a
f ðtÞ ¼ s ðt þ aÞ / s ðt / aÞ ¼
(
)
jtj ) a
1
¼
f ür
0
jtj > a
a
b
t
f (t)
ða > 0Þ
1
–a
a
t
f (t)
Intervall:
0 ) t ) a
f ðtÞ ¼ s ðtÞ / s ðt / aÞ ¼
(
)
0 ) t ) a
1
f ür
¼
0
alle übrigen t
Intervall:
1
a
f (t)
/a ) t ) 0
f ðtÞ ¼ s ðt þ aÞ / s ðtÞ ¼
(
)
/a ) t ) 0
1
¼
f ür
0
alle übrigen t
t
1
–a
t
326
XII Fourier-Transformationen
3.3 Diracsche Deltafunktion
Für die Beschreibung lokalisierter Impulse (die nur in einem bestimmten Zeitpunkt T
einwirken) benötigt man die sog. Diracsche Deltafunktion (d-Funktion, auch Dirac-Stoß
oder Impulsfunktion genannt). Sie ist keine Funktion im üblichen Sinne, sondern eine sog.
„verallgemeinerte Funktion“ (Distribution).
Anschauliches Modell der Deltafunktion
Ausgangspunkt ist ein rechteckiger Impuls (Stoß)
der Breite a und der Höhe 1=a, dessen Stärke
(entspricht dem Flächeninhalt) den Wert 1 besitzt:
1
ð
f ðtÞ dt ¼ a .
/1
f (t)
1/a
1
¼ 1
a
a
T
T +a
t
Mit abnehmender Breite nimmt die Höhe bei unverändertem Flächeninhalt immer mehr zu
(siehe Bilderfolge a) ! b) ! c)). Im Grenzfall a ! 0 entsteht ein Impuls mit
einer Breite nahe 0 und einer unendlich großen Höhe.
f (t)
f (t)
f (t)
1/a
1/a
1/a
a
T
a)
a
a
t
T
b)
T
t
c)
t
3 Wichtige „Hilfsfunktionen“ in den Anwendungen
327
Symbolische Schreibweise und Darstellung der Deltafunktion
d(t – T)
(
d ðt / TÞ ¼
0
1
f ür
t 6¼ T
)
∞
t ¼ T
T
t
Eigenschaften der Deltafunktion
Normierung
1
ð
d ðt / TÞ dt ¼ 1
ð,,Flächeninhalt‘‘ ¼ 1Þ
/1
„Ausblendeigenschaft“
Für bestimmte Zeitfunktionen f ðtÞ , / 1 < t < 1 gilt:
)
(
ðb
a ) T ) b
f ðTÞ
d ðt / TÞ . f ðtÞ dt ¼
f ür
0
alle übrigen T
a
Anmerkungen
(1)
Die Integrale sind nur symbolisch zu verstehen, sie können nicht im üblichen Sinne
„berechnet“ werden (es handelt sich um sog. „verallgemeinerte Integrale“).
(2)
Das „Ausblendintegral“ ist nur dann von null verschieden, wenn T zwischen a und b
liegt.
&
Beispiele
2ðp
ð1Þ
0
d ðt / pÞ . e / t . cos t dt ¼ f ðpÞ ¼ e / p . cos p ¼ e / p . ð/ 1Þ ¼ / e / p
|fflfflfflfflfflffl{zfflfflfflfflfflffl}
f ðtÞ
Begründung: p liegt im Integrationsintervall.
1
ð
ð2Þ
/1
d ðt / T Þ . cos t dt ¼ f ðTÞ ¼ cos T
|{z}
f ðtÞ
Begründung: Die reelle Zahl T liegt stets im Integrationsbereich ð/ 1 < T < 1Þ.
&
328
XII Fourier-Transformationen
„Verallgemeinerte Fourier-Transformierte“ der Deltafunktion
1
ð
F fd ðt / TÞg ¼ F ðwÞ ¼
d ðt / TÞ . e / j w t dt ¼ e / j w T
/1
Sonderfall T == 0 :
F fd ðtÞg ¼ F ðwÞ ¼ 1
Das Frequenzspektrum enthält dann alle Frequenzen mit gleichem Gewicht (alle „Amplituden“ haben den Wert 1 ! sog. „weißes“ Spektrum).
Zusammenhang zwischen der Delta- und der Sigmafunktion
ðt
ðt
d ðt / TÞ dt ¼ s ðt / TÞ
/1
d ðtÞ dt ¼ s ðtÞ
/1
D
s ðt / TÞ ¼ d ðt / TÞ
Dt
D
s ðtÞ ¼ d ðtÞ
Dt
Die Deltafunktion ist somit die sog. „verallgemeinerte Ableitung“ der Sigmafunktion
(Sprungfunktion).
„Verallgemeinerte Ableitung“ einer Funktion f (t)
Die sog. „verallgemeinerte Ableitung“ einer Funktion f ðtÞ, die an der Stelle t ¼ t 0 eine
Sprungunstetigkeit aufweist und sonst für jedes t 6¼ t 0 stetig differenzierbar ist, wird wie
folgt gebildet:
D f ðtÞ
d f ðtÞ
¼
þ a . d ðt / t 0 Þ ¼ f 0 ðtÞ þ a . d ðt / t 0 Þ
Dt
dt
D f ðtÞ D
¼
f ðtÞ:
Dt
Dt
„Verallgemeinerte Ableitung“ von f ðtÞ
d f ðtÞ
d
¼
f ðtÞ ¼ f 0 ðtÞ:
dt
dt
„Gewöhnliche Ableitung“ von f ðtÞ
a ¼ f ðt 0 þ 0Þ / f ðt 0 / 0Þ:
Höhe des Sprunges an der Stelle t ¼ t 0 (Differenz der
beiderseitigen Funktionsgrenzwerte an der Stelle t ¼ t 0 )
Die „verallgemeinerte Ableitung“ unterscheidet sich nur an der Sprungstelle t ¼ t 0 von
der „gewöhnlichen Ableitung“ f 0 ðtÞ. An der Sprungstelle kommt noch ein Dirac-Stoß
hinzu.
4 Eigenschaften der Fourier-Transformation (Transformationssätze)
329
4 Eigenschaften der Fourier-Transformation
(Transformationssätze)
4.1 Linearitätssatz (Satz über Linearkombinationen)
Für die Fourier-Transformierte einer Linearkombination von Originalfunktionen gilt:
F fc 1 . f 1 ðtÞ þ c 2 . f 2 ðtÞ þ . . . þ c n . f n ðtÞg ¼
¼ c 1 . F f f 1 ðtÞg þ c 2 . F f f 2 ðtÞg þ . . . þ c n . F f f n ðtÞg ¼
¼ c 1 . F 1 ðwÞ þ c 2 . F 2 ðwÞ þ . . . þ c n . F n ðwÞ
c 1 ; c 2 ; . . . ; c n : Reelle oder komplexe Konstanten
F i ðwÞ ¼ F f f i ðtÞg : Fourier-Transformierte von f i ðtÞ
Regel:
ði ¼ 1; 2; . . . ; nÞ
Es darf gliedweise transformiert werden, konstante Faktoren bleiben erhalten.
Beispiel
&
g ðtÞ ¼ 2 . e / t . s ðtÞ þ 3 . e / 6 t . s ðtÞ ;
F f gðtÞg ¼ ?
Unter Verwendung der Korrespondenzen
F fe / t . s ðtÞg ¼
1
1 þ jw
und
F fe / 6 t . s ðtÞg ¼
1
6 þ jw
(Nr. 9 mit a ¼ 1 bzw. a ¼ 6) erhält man mit Hilfe des Linearitätssatzes:
F f gðtÞg ¼ F f2 . e / t . s ðtÞ þ 3 . e / 6 t . s ðtÞg ¼ 2 . F f e / t . s ðtÞg þ 3 . F f e / 6 t . s ðtÞg ¼
¼ 2.
¼
1
1
2 ð6 þ j wÞ þ 3 ð1 þ j wÞ
12 þ 2 j w þ 3 þ 3 j w
¼
þ3.
¼
¼
1 þ jw
6 þ jw
ð1 þ j wÞ ð6 þ j wÞ
6 þ jw þ 6 jw þ j 2 w2
15 þ 5 j w
15 þ j 5 w
¼
6 þ 7 jw / w2
ð6 / w 2 Þ þ j 7 w
&
4.2 "hnlichkeitssatz
Die Originalfunktion f ðtÞ wird der "hnlichkeitstransformation t ! a t mit a 6¼ 0
unterworfen. Die neue Funktion g ðtÞ ¼ f ða tÞ zeigt dabei einen ähnlichen Kurvenverlauf
wie f ðtÞ (gezeichnet: Bild a) f ðtÞ ¼ e / j t j , Bild b) g ðtÞ ¼ f ð2 tÞ ¼ e / 2 j t j Þ:
f (t)
g (t)
g (t) = f (at)
a)
t
b)
t
330
XII Fourier-Transformationen
Für die Fourier-Transformierte von g ðtÞ ¼ f ða tÞ gilt dann ( a 6¼ 0 : reell):
F f f ða tÞg ¼
Regel:
!w4
1
.F
jaj
a
mit F ðwÞ ¼ F f f ðtÞg
In der Bildfunktion F ðwÞ wird zunächst w durch w=a ersetzt, dann wird die
neue Funktion F ðw=aÞ mit dem Kehrwert von j a j multipliziert.
j a j < 1:
Dehnung der Zeitachse
j a j > 1:
Stauchung der Zeitachse ! Dehnung der Frequenzachse
a ¼ / 1:
Richtungsumkehr der Zeitachse
&
! Stauchung der Frequenzachse
!
gðtÞ ¼ f ð/ tÞ
Beispiel
Unter Verwendung der Korrespondenz
F ðwÞ ¼ F fe / j t j g ¼
2
1 þ w2
ðNr: 8 mit a ¼ 1Þ
erhalten wir für die Originalfunktion g ðtÞ ¼ e / j 2 t j ¼ e / 2 j t j die folgende Fourier-Transformierte ða ¼ 2Þ:
!w4
1
1
2
1
1
4
F fe / 2 j t j g ¼
¼
.F
¼
.
¼
¼
2
2
2 1 þ ðw=2Þ 2
1 þ w 2 =4
ð4 þ w 2 Þ=4
4 þ w2
&
4.3 Verschiebungssatz (Zeitverschiebungssatz)
Die Originalfunktion f ðtÞ wird um die Strecke j a j auf der Zeitachse verschoben
( a > 0: nach rechts; a < 0: nach links). Man erhält die neue Funktion g ðtÞ ¼ f ðt / aÞ:
f (t)
g (t)
t
g (t) = f (t – a)
a
t
Für die Fourier-Transformierte von g ðtÞ ¼ f ðt / aÞ gilt dann ð a 6¼ 0Þ:
F f f ðt / aÞg ¼ e / j w a . F ðwÞ
Regel:
mit
F ðwÞ ¼ F f f ðtÞg
Die Bildfunktion F ðwÞ wird mit dem „Phasenfaktor“ e / j w a multipliziert.
Bei einer Verschiebung im Zeitbereich bleibt das Amplitudenspektrum A ðwÞ ¼ j F ðwÞj
erhalten.
4 Eigenschaften der Fourier-Transformation (Transformationssätze)
&
331
Beispiel
Die in Bild a) skizzierte „Stoßfunktion“ f ðtÞ mit der Bildfunktion
F ðwÞ ¼
2½ 1 þ cos ðw aÞ %
a2 w2
wird um a nach rechts verschoben (siehe Bild b)).
a)
f (t)
g (t)
1/a
1/a
–a
a
t
b)
a
2a
t
Die Bildfunktion der verschobenen Funktion g ðtÞ ¼ f ðt / aÞ, 0 ) t ) 2 a lautet dann (unter Verwendung
des Zeitverschiebungssatzes) wie folgt:
F f gðtÞg ¼ e / j w a . F ðwÞ ¼ e / j w a .
2½ 1 þ cos ðw aÞ %
2½ 1 þ cos ðw aÞ % . e / j w a
¼
a2 w2
a2 w2
&
4.4 Dämpfungssatz (Frequenzverschiebungssatz)
Die Originalfunktion f ðtÞ wird mit e j w 0 t multipliziert („Modulation“). Die FourierTransformierte der neuen Funktion g ðtÞ ¼ e j w 0 t . f ðtÞ lautet dann (w 0 : reell):
F fe j w 0 t . f ðtÞg ¼ F ðw / w 0 Þ
Regel:
&
mit F ðwÞ ¼ F f f ðtÞg
Einer Multiplikation im Zeitbereich mit e j w 0 t entspricht im Frequenzbereich
eine Frequenzverschiebung um w 0 ðw wird in F ðwÞ durch w / w 0 ersetztÞ.
Beispiel
f (t)
Der Rechteckimpuls
(
1
f ðtÞ ¼
f ür
0
jtj ) T
1
)
jtj > T
¼
¼ s ðt þ TÞ / s ðt / TÞ
–T
mit der Bildfunktion
F ðwÞ ¼ F f f ðtÞg ¼
T
t
2 . sin ðw TÞ
w
soll „moduliert“ werden. Der „gedämpfte“ Rechteckimpuls gðtÞ ¼ e j w 0 t . f ðtÞ besitzt dann die folgende
Fourier-Transformierte:
F f gðtÞg ¼ F fe j w 0 t . f ðtÞg ¼ F ðw / w 0 Þ ¼
2 . sin ½ ðw / w 0 Þ T %
w / w0
&
332
XII Fourier-Transformationen
4.5 Ableitungssätze (Differentiationssätze)
4.5.1 Ableitungssatz (Differentiationssatz) für die Originalfunktion
Die Fourier-Transformierten der Ableitungen der Originalfunktion f ðtÞ nach der Variablen t lauten wie folgt:
1. Ableitung
F f f 0 ðtÞg ¼ j w . F ðwÞ
mit
F ðwÞ ¼ F f f ðtÞg
f 0 ðtÞ ist Fourier-transformierbar und der Grenzwert von
Voraussetzung:
f ðtÞ für
j t j ! 1 verschwindet.
2. Ableitung
F f f 00 ðtÞg ¼ ð j wÞ 2 . F ðwÞ ¼ / w 2 . F ðwÞ
mit F ðwÞ ¼ F f f ðtÞg
f 00 ðtÞ ist Fourier-transformierbar und die Grenzwerte von f ðtÞ und
Voraussetzung:
f 0 ðtÞ für j t j ! 1 verschwinden.
n-te Ableitung
F ff
ðnÞ
ðtÞg ¼ ð j wÞ n . F ðwÞ
f ðnÞ ðtÞ
ist Fourier-transformierbar und die Grenzwerte
f ðtÞ; f 0 ðtÞ; . . . ; f ðn / 1Þ ðtÞ für j t j ! 1 verschwinden.
Voraussetzung:
Regel:
&
mit F ðwÞ ¼ F f f ðtÞg
von
Jeder Differentiationsschritt im Originalbereich bewirkt eine Multiplikation mit
dem Faktor j w im Bildbereich.
Beispiel
Ausgehend von der (als bekannt vorausgesetzten) Korrespondenz
pffiffiffiffiffiffiffiffi
2
2
f ðtÞ ¼ e / 0;5 t
"///! F ðwÞ ¼ 2 p . e / 0;5 w
2
lässt sich die Bildfunktion von gðtÞ ¼ t . e / 0;5 t wie folgt aus dem Ableitungssatz bestimmen
ðgðtÞ ist –– vom Vorzeichen abgesehen –– genau die 1. Ableitung von f ðtÞÞ:
f ðtÞ ¼ e / 0;5 t
2
)
2
2
f 0 ðtÞ ¼ e / 0;5 t . ð/ tÞ ¼ / t . e / 0;5 t ¼ / g ðtÞ
F f f 0 ðtÞg ¼ F f/ gðtÞg ¼ / F f gðtÞg ¼ j w . F ðwÞ ¼ j w .
2
F f gðtÞg ¼ F ft . e / 0;5 t g ¼ / j w .
pffiffiffiffiffiffiffiffi
2
2 p . e / 0;5 w
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffi
2
2
2 p . e / 0;5 w ¼ / j . 2 p . w . e / 0;5 w
&
4 Eigenschaften der Fourier-Transformation (Transformationssätze)
333
4.5.2 Ableitungssatz (Differentiationssatz) für die Bildfunktion
Die Ableitungen der Fourier-Transformierten F ðwÞ ¼ F f f ðtÞg nach der Variablen w
lauten wie folgt:
1. Ableitung
F 0 ðwÞ ¼ ð/ j Þ 1 . F ft 1 . f ðtÞg ¼ / j . F ft . f ðtÞg
Voraussetzung: Die Funktion t . f ðtÞ ist Fourier-transformierbar.
2. Ableitung
F 00 ðwÞ ¼ ð/ j Þ 2 . F ft 2 . f ðtÞg ¼ / F ft 2 . f ðtÞg
Voraussetzung: Die Funktion t 2 . f ðtÞ ist Fourier-transformierbar.
n-te Ableitung
F ðnÞ ðwÞ ¼ ð/ j Þ n . F ft n . f ðtÞg
Voraussetzung: Die Funktion t n . f ðtÞ ist Fourier-transformierbar.
Regel:
&
Die n-te Ableitung der Bildfunktion F ðwÞ ¼ F f f ðtÞg erhält man als FourierTransformierte der mit der Potenz t n multiplizierten Originalfunktion f ðtÞ,
multipliziert mit ð/ jÞ n . Dieser Satz wird daher auch als Multiplikationssatz
bezeichnet.
Beispiel
2
Die Fourier-Transformierte von g ðtÞ ¼ t . e / 0;5 t lässt sich auch mit Hilfe des Ableitungssatzes für die
Bildfunktion aus der als bekannt vorausgesetzten Korrespondenz
f ðtÞ ¼ e / 0;5 t
2
"///!
F ðwÞ ¼
pffiffiffiffiffiffiffiffi
2
2 p . e / 0;5 w
ðNr: 13 mit a ¼ 0,5Þ
gewinnen, da g ðtÞ ¼ t . f ðtÞ ist:
2
F 0 ðwÞ ¼ / j . F f t . f ðtÞg ¼ / j . F f g ðtÞg ¼ / j . F ft . e / 0;5 t g
Nach Multiplikation mit j folgt aus dieser Gleichung unter Beachtung von j 2 ¼ / 1:
2
4
d !pffiffiffiffiffiffiffi
2
2 p . e / 0;5 w ¼
dw
pffiffiffiffiffiffiffiffi
2
. ð/ wÞ ¼ / j . 2 p . w . e / 0;5 w
F f gðtÞg ¼ F ft . e / 0;5 t g ¼ j . F 0 ðwÞ ¼ j .
¼ j.
pffiffiffiffiffiffiffiffi
2
2 p . e / 0;5 w
&
334
XII Fourier-Transformationen
4.6 Integrationssätze
Integrationssatz für die Originalfunktion
F
8 t
< ð
:
/1
9
=
1
f ðuÞ du ¼
. F ðwÞ
;
jw
mit
F ðwÞ ¼ F f f ðtÞg
1
ð
f ðtÞ dt ¼ 0
Voraussetzung:
/1
Regel:
Die Bildfunktion F ðwÞ von f ðtÞ wird mit dem Kehrwert von j w multipliziert.
Parsevalsche Gleichung
1
ð
j f ðtÞj 2 dt ¼
/1
1
.
2p
1
ð
j F ðwÞj 2 dw
mit
F ðwÞ ¼ F f f ðtÞg
/1
Voraussetzung: Die Originalfunktion f ðtÞ ist quadratisch integrierbar.
4.7 Faltungssatz
Faltungsprodukt
Unter dem Faltungsprodukt f 1 ðtÞ , f 2 ðtÞ zweier Originalfunktionen f 1 ðtÞ und f 2 ðtÞ
versteht man das uneigentliche Integral
1
ð
f 1 ðtÞ , f 2 ðtÞ ¼
f 1 ðuÞ . f 2 ðt / uÞ du
/1
(Faltungsintegral, 2-seitige Faltung der Funktionen f 1 ðtÞ und f 2 ðtÞÞ
Voraussetzung: Beide Funktionen sind absolut integrierbar.
Rechenregeln
Kommutativgesetz
f 1 ðtÞ , f 2 ðtÞ ¼ f 2 ðtÞ , f 1 ðtÞ
Assoziativgesetz
½ f 1 ðtÞ , f 2 ðtÞ% , f 3 ðtÞ ¼ f 1 ðtÞ , ½ f 2 ðtÞ , f 3 ðtÞ %
Distributivgesetz
f 1 ðtÞ , ½ f 2 ðtÞ þ f 3 ðtÞ% ¼ f 1 ðtÞ , f 2 ðtÞ þ f 1 ðtÞ , f 3 ðtÞ
4 Eigenschaften der Fourier-Transformation (Transformationssätze)
335
Faltungssatz
Die Fourier-Transformierte des Faltungsproduktes f 1 ðtÞ , f 2 ðtÞ ist gleich dem Produkt
der Fourier-Transformierten von f 1 ðtÞ und f 2 ðtÞ:
F f f 1 ðtÞ , f 2 ðtÞg ¼ F f f 1 ðtÞg . F f f 2 ðtÞg ¼ F 1 ðwÞ . F 2 ðwÞ
F 1 ðwÞ ¼ F f f 1 ðtÞg;
F 2 ðwÞ ¼ F f f 2 ðtÞg
Spezielle Form des Faltungssatzes (Rücktransformation):
f 1 ðtÞ , f 2 ðtÞ ¼ F / 1 f F 1 ðwÞ . F 2 ðwÞg
&
Beispiel
Für die Fourier-Transformation einer Gauß-Funktion mit dem „Breitenparameter“ s gilt die folgende Zuordnung (Korrespondenz):
3
2
t2
s2 w2
1
1
/
/
2
Nr: 13 mit a ¼
f ðtÞ ¼ pffiffiffiffiffiffiffi
. e 2 s 2 "///! F ðwÞ ¼ F f f ðtÞg ¼ e
2
2s
2p . s
Wir interessieren uns für die Faltung zweier Gauß-Funktionen mit den Breitenparametern s 1 und s 2 . Aus
dem Faltungssatz folgt dann:
3 2 2 2 22
F f f 1 ðtÞ , f 2 ðtÞg ¼ F 1 ðwÞ . F 2 ðwÞ ¼ e
¼ e
/
ðs 21
þ s 22 Þ
2
w
2
¼ e
/
/
s 21 w 2
2
s w
2
.e
/
s 22 w 2
2
¼ e
/
s1w
2
/
s2 w
2
¼
2
2
(mit s 2 ¼ s 21 þ s 22 Þ. Durch Rücktransformation erhalten wir das Faltungsprodukt:
(
)
s2 w2
t2
1
/
/
2
¼ pffiffiffiffiffiffiffi
f 1 ðtÞ , f 2 ðtÞ ¼ F / 1 f F 1 ðwÞ . F 2 ðwÞg ¼ F / 1 e
. e 2s2
2p . s
Folgerung: Die Faltung zweier Gauß-Funktionen mit den Breitenparametern s 1 und s 2 führt wieder auf
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
eine (breitere!) Gauß-Funktion mit dem Breitenparameter s ¼ s 21 þ s 22 .
&
4.8 Vertauschungssatz
Aus einer vorgegebenen Korrespondenz
f ðtÞ
"///!
F ðwÞ
erhält man durch Vertauschen von Originalfunktion und Bildfunktion wie folgt eine neue
Korrespondenz (sog. Vertauschungssatz, auch als t-w-Dualitätsprinzip bezeichnet):
F ðtÞ
"///!
2 p . f ð/ wÞ
F ðtÞ ist die neue Originalfunktion, 2 p . f ð/ wÞ die neue zugehörige Bildfunktion.
336
XII Fourier-Transformationen
Beispiel
&
Aus der (als bekannt vorausgesetzten) Korrespondenz
f ðtÞ ¼ e / j t j
"///!
F ðwÞ ¼
2
1 þ w2
ðNr: 8 mit a ¼ 1Þ
erhält man mit Hilfe des Vertauschungssatzes die folgende neue Korrespondenz:
F ðtÞ ¼
2
1 þ t2
Somit gilt:
"///!
1
1 þ t2
2 p . f ð/ wÞ ¼ 2 p . e / j / w j ¼ 2 p . e / j w j
"///!
p . e /jwj
ðsiehe auch Nr: 6 mit a ¼ 1Þ
&
5 Anwendung:
Lösung linearer Differentialgleichungen
mit konstanten Koeffizienten
5.1 Allgemeines Lösungsverfahren
Eine (gewöhnliche) lineare Differentialgleichung mit konstanten Koeffizienten lässt sich
mit Hilfe der Fourier-Transformation schrittweise wie folgt lösen:
(1)
Die lineare Differentialgleichung wird mit Hilfe der Fourier-Transformation in eine
algebraische Gleichung übergeführt (Transformation vom Originalbereich in den
Bildbereich).
(2)
Die Lösung dieser Gleichung ist die Bildfunktion Y ðwÞ der gesuchten Originalfunktion yðtÞ.
(3)
Durch Rücktransformation (inverse Fourier-Transformation), in der Regel unter Verwendung einer Transformationstabelle, erhält man aus der Bildfunktion Y ðwÞ die
gesuchte Lösung y ðtÞ. Als sehr nützlich erweist sich auch der Faltungssatz, sofern
die Bildfunktion Y ðwÞ faktorisiert werden kann ðY ðwÞ ¼ Y 1 ðwÞ . Y 2 ðwÞÞ. Bei
einer gebrochenrationalen Bildfunktion zerlegt man diese zunächst in Teilbrüche
(Partialbrüche), die dann gliedweise rücktransformiert werden.
Vorteil dieser Lösungsmethode: Die Rechenoperationen sind im Bildbereich meist einfacherer Art.
5.2 Lineare Differentialgleichungen 1. Ordnung
mit konstanten Koeffizienten
Differentialgleichung im Originalbereich
y 0 þ a y ¼ g ðtÞ
ða : Konstante ;
g ðtÞ : StörfunktionÞ
5 Anwendung: Lösung linearer Differentialgleichungen mit konstanten Koeffizienten
337
Transformierte Differentialgleichung im Bildbereich (mit Lösung)
j w . Y ðwÞ þ a . Y ðwÞ ¼ F ðwÞ
Lösung:
)
y ðtÞ ¼ F / 1 fY ðwÞg ¼ F / 1
Y ðwÞ ¼
(
F ðwÞ
a þ jw
F ðwÞ
a þ jw
'
Y ðwÞ:
Fourier-Transformierte der (gesuchten) Lösung y ðtÞ
F ðwÞ:
Fourier-Transformierte der Störfunktion g ðtÞ
&
Beispiel
y 0 / y ¼ e / t . s ðtÞ
Transformation der Dgl in den Bildbereich ða ¼ / 1 ; g ðtÞ ¼ e / t . s ðtÞÞ:
1
j w . Y ðwÞ / Y ðwÞ ¼ F fe / t . s ðtÞ ¼
1 þ jw
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Nr: 9 mit a ¼ 1
)
Y ðwÞ . ð j w / 1Þ ¼
1
1 þ jw
Lösung im Bildbereich:
Y ðwÞ ¼
1
1
1
1
1
¼
¼
¼
¼ /
ð j w / 1Þ ð1 þ j wÞ
ð j w / 1Þ ð j w þ 1Þ
/ w2 / 1
1 þ w2
ð j wÞ 2 / 1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
3: Binom
Rücktransformation in den Originalbereich (Nr. 8 mit a ¼ 1):
(
'
(
'
1
1
1
y ðtÞ ¼ F / 1 f Y ðwÞg ¼ F / 1 /
¼ / F /1
¼ /
. e/jtj
2
2
1þw
1þw
2
5.3 Lineare Differentialgleichungen 2. Ordnung
mit konstanten Koeffizienten
Differentialgleichung im Originalbereich
y 00 þ a y 0 þ b y ¼ gðtÞ
ða; b : Konstanten ;
g ðtÞ : StörfunktionÞ
Transformierte Differentialgleichung im Bildbereich (mit Lösung)
/ w 2 . Y ðwÞ þ a j w . Y ðwÞ þ b . Y ðwÞ ¼ F ðwÞ
Lösung:
y ðtÞ ¼ F / 1 fY ðwÞg ¼ F / 1
)
(
Y ðwÞ ¼
'
F ðwÞ
ðb / w 2 Þ þ j a w
Y ðwÞ:
Fourier-Transformierte der (gesuchten) Lösung y ðtÞ
F ðwÞ:
Fourier-Transformierte der Störfunktion g ðtÞ
F ðwÞ
ðb / w 2 Þ þ j a w
&
338
XII Fourier-Transformationen
6 Tabellen spezieller Fourier-Transformationen
Tabelle 1: Exponentielle Fourier-Transformationen
Hinweis: a > 0 ; b > 0
Bei den Korrespondenzen Nr. 18 bis Nr. 26 handelt es sich um die FourierTransformierten sog. „verallgemeinerter“ Funktionen (Distributionen).
Originalfunktion f ðtÞ
Bildfunktion F ðwÞ
s ðt / aÞ / s ðt / bÞ ¼
(1)
(
¼
1
0
f ür
a ) t ) b
'
j.
alle übrigen t
e/jbw / e/jaw
w
ðmit a < bÞ
s ðt þ aÞ / s ðt / aÞ ¼
(2)
(
¼
1
0
f ür
jtj ) a
2 . sin ða wÞ
w
'
alle übrigen t
s ðt þ aÞ / s ðtÞ ¼
(3)
(
¼
1
0
f ür
/a ) t ) 0
'
j.
1 / e jaw
w
j.
e/jaw / 1
w
alle übrigen t
s ðtÞ / s ðt / aÞ ¼
(4)
(
¼
(
(5)
1
0
f ür
a / jtj
0
(6)
1
a2 þ t2
(7)
t
a2 þ t2
(8)
e/a jtj
0 ) t ) a
'
alle übrigen t
f ür
jtj ) a
alle übrigen t
'
2 ½1 / cos ða wÞ%
w2
p
. e/a jwj
a
8
/a jwj
>
< jp . e
0
>
:
/ j p . e/a jwj
2a
a2 þ w2
f ür
9
w < 0=
>
w ¼ 0
>
;
w > 0
6 Tabellen spezieller Fourier-Transformationen
(9)
339
Originalfunktion f ðtÞ
Bildfunktion F ðwÞ
e / a t . s ðtÞ
1
a þ jw
(10)
t . e / a t . s ðtÞ
(11)
t 2 . e / a t . s ðtÞ
(12)
t n . e / a t . s ðtÞ
1
ða þ j wÞ 2
2
ða þ j wÞ 3
n!
ða þ j wÞ n þ 1
rffiffiffiffiffiffiffi
w2
p
/
. e 4a
a
/at2
(13)
e
(14)
t . e/at
2
/
j
.
2a
rffiffiffiffiffi
w2
p
/
. w . e 4a
a
8
>
< p
p=2
>
:
0
9
jwj < a>
=
jwj ¼ a
>
;
jwj > a
(15)
sin ða tÞ
t
(16)
e / a t . sin ðb tÞ . s ðtÞ
(17)
e / a t . cos ðb tÞ . s ðtÞ
(18)
dðtÞ
(19)
d ðt þ aÞ
e jaw
(20)
d ðt / aÞ
e/jaw
(21)
e jat
2 p . d ðw / aÞ
(22)
e/ jat
2 p . d ðw þ aÞ
(23)
1
2 p . d ðwÞ
(24)
cos ða tÞ
p ½d ðw þ aÞ þ d ðw / aÞ%
(25)
sin ða tÞ
j p ½d ðw þ aÞ / d ðw / aÞ %
(26)
dðt þ aÞ þ dðt / aÞ
2 . cos ða wÞ
(27)
dðt þ aÞ / dðt / aÞ
2 j . sin ða wÞ
ðDirac-StoßÞ
f ür
b
ða þ j wÞ 2 þ b 2
a þ jw
ða þ j wÞ 2 þ b 2
1
340
XII Fourier-Transformationen
Tabelle 2: Fourier-Sinus-Transformationen
Hinweis: a > 0 ; b > 0
Originalfunktion f ðtÞ
Bildfunktion FS ðwÞ
s ðtÞ / s ðt / aÞ ¼
(1)
(2)
(
¼
8
>
<
>
:
2/t
(4)
1
pffiffiffi
t
(7)
(8)
(9)
(10)
f ür
0
9
0 ) t ) 1>
=
1 ) t ) 2
>
;
t ( 2
1 / cos ða wÞ
w
4 . sin w . sin 2 ðw = 2Þ
w2
p
2
rffiffiffiffiffiffiffiffiffi
p
2w
b
b 2 þ ða / tÞ 2
aþt
b2
'
alle übrigen t
t
1
t
(6)
0 ) t ) a
f ür
0
(3)
(5)
1
þ ða þ tÞ
t
a2 þ t2
t ða 2
1
þ t 2Þ
t
a2 / t2
t ða 2
1
/ t 2Þ
(11)
e/at
(12)
t . e/at
(13)
e/at
t
2
/
/
b
b 2 þ ða þ tÞ 2
a/t
b2
þ ða / tÞ 2
p . e / b w . sin ða wÞ
p . e / b w . cos ða wÞ
p
. e/aw
2
p
2a2
/
3
2
1 / e/aw
p
. cos ða wÞ
2
p
2a2
3
2
1 / cos ða wÞ
w
a2 þ w2
2aw
ða 2
þ w 2Þ 2
arctan
!w4
a
6 Tabellen spezieller Fourier-Transformationen
Originalfunktion f ðtÞ
(14)
(15)
(16)
t . e/at
(17)
sin ða tÞ
t
(18)
sin ða tÞ
t2
(19)
"
t ""
t"
2
sin ða tÞ
t
sin 2 ða tÞ
t2
(21)
sin ða tÞ . sin ðb tÞ
t
cos ða tÞ
t
/bt
rffiffiffiffiffiffiffi
w2
p
/
. w . e 4a
a
! p w4
p
1
. coth
/
4
2
2w
(20)
(22)
Bildfunktion FS ðwÞ
1
.
4a
2
1
e2t / 1
"
"a þ
ln ""
a/
341
(23)
e
(24)
e / b t . sin ða tÞ
t
. sin ða tÞ
sin ða wÞ
w
"
"
"a þ w"
1
"
. ln ""
2
a / w"
p .
(
p w= 2
p a= 2
8
>
< p= 4
p= 8
>
:
0
1
4
f ür
f ür
w ) a
w ( a
)
9
0 < w < 2a>
=
w ¼ 2a
>
;
w > 2a
+
ðw þ 2 aÞ . ln ðw þ 2 aÞ þ
1
þ ðw / 2 aÞ . ln j w / 2 a j /
w . ln w
2
(
p= 4
0
8
>
< 0
p= 4
>
:
p= 2
b
2
"
f ür
a/b < w < aþb
t
f ür
9
0 < w < a>
=
w ¼ a
>
;
w > a
1
b 2 þ ða / wÞ 2
1
. ln
4
/
'
1
b 2 þ ða þ wÞ 2
b 2 þ ðw þ aÞ 2
b 2 þ ðw / aÞ 2
!
#
)
342
XII Fourier-Transformationen
Tabelle 3: Fourier-Kosinus-Transformationen
Hinweis: a > 0 ; b > 0
(1)
(2)
Originalfunktion f ðtÞ
Bildfunktion FC ðwÞ
s ðtÞ / s ðt / aÞ ¼
(
'
0 ) t ) a
1
¼
f ür
0
alle übrigen t
sin ða wÞ
w
8
>
<
>
:
t
2/t
f ür
0
9
0 ) t ) 1=
>
1 ) t ) 2
>
;
t > 2
4 . cos w . sin 2 ðw = 2Þ
w2
(3)
1
pffiffiffi
t
rffiffiffiffiffiffiffiffiffi
p
2w
(4)
1
a2 þ t2
p
. e/aw
2a
(5)
b
b2
þ ða / tÞ
2
aþt
(6)
b 2 þ ða þ tÞ 2
(7)
e/at
(8)
t . e/at
(9)
pffiffiffi
t . e/at
þ
þ
b
b2
þ ða þ tÞ 2
a/t
b 2 þ ða / tÞ 2
p . e / b w . cos ða wÞ
p . e / b w . sin ða wÞ
a
a2 þ w2
a2 / w2
ða 2 þ w 2 Þ 2
+
1 pffiffiffiffiffi
p .
2
cos
! w 4)
3
. arctan
2
a
ða 2 þ w 2 Þ 3=4
(10)
e/at
pffiffiffi
t
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p a þ a2 þ w2
.
2
a2 þ w2
(11)
e/at / e/bt
t
1
. ln
2
(12)
e
/at2
1
2
3
b2 þ w2
a2 þ w2
rffiffiffiffiffiffiffi
w2
p
/
. e 4a
a
2
6 Tabellen spezieller Fourier-Transformationen
Originalfunktion f ðtÞ
3
a2 þ t2
b2 þ t2
(13)
ln
(14)
" 2
" a þ t2
ln "" 2
b / t2
343
Bildfunktion FC ðwÞ
2
"
"
"
"
p .
e /bw / e /aw
w
p .
cos ðb wÞ / e / a w
w
8
>
< p= 2
p= 4
>
:
0
9
w < a>
=
w ¼ a
>
;
w > a
(15)
sin ða tÞ
t
(16)
sin 2 ða tÞ
t
" 2
" w / 4a2
1
. ln ""
4
w2
(17)
sin ða tÞ . sin ðb tÞ
t
"
" ða þ bÞ 2 / w 2
1
. ln ""
2
ða / bÞ 2 / w 2
"
"
"
"
2
8 3
< p 2a / w
4
:
0
9
w ) 2a=
w > 2a;
2
f ür
(18)
sin ða tÞ
t2
(19)
1 / cos ða tÞ
t
" 2
" w / a2
1
. ln ""
2
w2
(20)
1 / cos ða tÞ
t2
8p
< ða / wÞ
2
:
0
(21)
e
/bt
/bt
1
2
. sin ða tÞ
b
2
"
"
"
"
"
f ür
"
"
"
"
9
w ) a=
w > a;
f ür
aþw
b 2 þ ða þ wÞ 2
"
1
þ
þ
b 2 þ ða / wÞ 2
1
(22)
e
(23)
e / t . sin t
t
1
. arctan
2
(24)
sin ða t 2 Þ
1
2
rffiffiffiffiffiffiffiffi +
3 22
3 22 )
p
w
w
cos
/ sin
2a
4a
4a
(25)
cos ða t 2 Þ
1
2
rffiffiffiffiffiffiffi +
3 22
3 22 )
p
w
w
cos
þ sin
2a
4a
4a
. cos ða tÞ
b 2 þ ða / wÞ 2
3
2
w2
#
a/w
b 2 þ ða þ wÞ 2
2
#
344
XIII Laplace-Transformationen
Hinweis: Die in den Beispielen benötigten Laplace-Transformationen werden der Tabelle
in Abschnitt 6 entnommen (Angabe der laufenden Nummer und der Parameterwerte).
1 Grundbegriffe
Laplace-Transformation
Die Laplace-Transformation ist eine Integraltransformation. Sie ordnet einer (in den Anwendungen meist zeitabhängigen) Funktion f ðtÞ mit f ðtÞ ¼ 0 für t < 0 wie folgt eine
Funktion F ðsÞ der (komplexen) Variablen s zu:
1
ð
F ðsÞ ¼
f ðtÞ . e / s t dt
0
Bezeichnungen:
f ðtÞ: Original- oder Oberfunktion, auch Zeitfunktion genannt
F ðsÞ: Bild- oder Unterfunktion, Laplace-Transformierte von f ðtÞ
Das uneigentliche Integral der rechten Seite heißt Laplace-Integral. Es existiert, wenn f ðtÞ
stückweise stetig ist (in jedem endlichen Intervall nur endlich viele Sprungstellen liegen)
und für hinreichend große t-Werte die Bedingung
j f ðtÞj ) K . e a t
ða > 0; K > 0 : reelle KonstantenÞ
erfüllt (hinreichende Bedingung). Das Laplace-Integral konvergiert dann für Re ðsÞ > a.
Weitere symbolische Schreibweisen:
F ðsÞ ¼ lf f ðtÞg
l:
ðLaplace-Transformierte von f ðtÞÞ
Laplace-Transformationsoperator
f ðtÞ "///! F ðsÞ
(Korrespondenz)
Originalfunktion f ðtÞ und Bildfunktion F ðsÞ ¼ lf f ðtÞg bilden ein zusammengehöriges Funktionenpaar.
Anmerkungen
(1)
Die Laplace-Transformierte F ðsÞ verschwindet im Unendlichen: lim F ðsÞ ¼ 0
(2)
Eine Funktion f ðtÞ mit f ðtÞ ¼ 0 für t < 0 lässt sich mit Hilfe der s-Funktion
auch in der Form f ðtÞ . s ðtÞ darstellen. Sie heißt Laplace-transformierbar, wenn
das Laplace-Integral F ðsÞ existiert. Die Menge aller (transformierbaren) Originalfunktionen wird als Originalbereich, die Menge der zugeordneten Bildfunktionen als
Bildbereich bezeichnet.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_13
s!1
2 Eigenschaften der Laplace-Transformation (Transformationssätze)
Beispiel
(
&
f ðtÞ ¼
0
t < 0
für
t
345
f(t)
)
t ( 0
1
Die Laplace-Transformierte dieser Funktion lautet:
1
ð
F ðsÞ ¼
t . e / s t dt ¼
0
+
ð/ s t / 1Þ . e / s t
s2
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Integral 313 mit a ¼ / s
)1
t¼0
¼
1
s2
1
t
(das uneigentliche Integral existiert nur für Re ðsÞ > 0). Somit gilt:
l ftg ¼
1
s2
oder
t "///!
1
s2
&
Inverse Laplace-Transformation
Für die Rücktransformation aus dem Bild- in den Originalbereich schreibt man symbolisch
l / 1 fFðsÞg ¼ f ðtÞ
ðinverse Laplace-Transformierte)
oder
FðsÞ !///" f ðtÞ
&
(Korrespondenz)
Beispiel
Aus l fsin tg ¼
(
'
1
1
/1
folgt
durch
Umkehrung
l
¼ sin t .
s2 þ 1
s2 þ 1
&
2 Eigenschaften der Laplace-Transformation
(Transformationssätze)
2.1 Linearitätssatz (Satz über Linearkombinationen)
Für die Laplace-Transformierte einer Linearkombination von Originalfunktionen gilt:
l fc 1 . f 1 ðtÞ þ c 2 . f 2 ðtÞ þ . . . þ c n . f n ðtÞg ¼
¼ c 1 . l f f 1 ðtÞg þ c 2 . l f f 2 ðtÞg þ . . . þ c n . l ff n ðtÞg ¼
¼ c 1 . F 1 ðsÞ þ c 2 . F 2 ðsÞ þ . . . þ c n . F n ðsÞ
c 1; c 2; . . . ; c n :
Reelle oder komplexe Konstanten
F i ðsÞ ¼ l f f i ðtÞg: Laplace-Transformierte von f i ðtÞ
ði ¼ 1; 2; . . . ; nÞ
Regel: Es darf gliedweise transformiert werden, konstante Faktoren bleiben dabei erhalten.
346
&
XIII Laplace-Transformationen
Beispiel
Die Laplace-Transformierten von f1 ðtÞ ¼ t und f2 ðtÞ ¼ sin t lauten:
l ftg ¼
1
s2
und
l fsin tg ¼
1
s2 þ 1
(Nr. 4 und Nr. 24 mit a ¼ 1Þ
Für die Laplace-Transformierte der Linearkombination f ðtÞ ¼ 4 t þ 5 . sin t erhält man dann:
l f4 t þ 5 . sin tg ¼ 4 . l ftg þ 5 . l fsin tg ¼ 4 .
¼
1
1
4
5
þ5. 2
¼ 2 þ 2
¼
s2
s þ1
s
s þ1
4 ðs 2 þ 1Þ þ 5 s 2
4s2 þ 4 þ 5s2
9s2 þ 4
¼
¼ 2 2
s ðs þ 1Þ
s 2 ðs 2 þ 1Þ
s 2 ðs 2 þ 1Þ
&
2.2 "hnlichkeitssatz
Die Originalfunktion
t ! a t mit a > 0
t < 0 zeigt dabei
f ðtÞ ¼ sin t, Bild b)
f ðtÞ mit f ðtÞ ¼ 0 für t < 0 wird der "hnlichkeitstransformation
unterworfen. Die neue Funktion g ðtÞ ¼ f ða tÞ mit g ðtÞ ¼ 0 für
einen ähnlichen Kurvenverlauf wie f ðtÞ ðgezeichnet: Bild a)
g ðtÞ ¼ f ð2 tÞ ¼ sin ð2 tÞÞ:
f(t)
g(t)
1
1
0
p
2p
–1
a)
0
t
p
2p t
–1
b)
Für die Laplace-Transformierte von g ðtÞ ¼ f ða tÞ gilt dann ðmit a > 0Þ:
lf f ða tÞg ¼
!s4
1
.F
a
a
mit
F ðsÞ ¼ l f f ðtÞg
Regel: Der Parameter s in der Bildfunktion F ðsÞ wird durch s=a ersetzt und die neue
Funktion F ðs=aÞ anschließend mit dem Kehrwert von a multipliziert.
a < 1: Dehnung der Funktion f ðtÞ längs der t-Achse
a > 1: Stauchung der Funktion f ðtÞ längs der t-Achse
&
Beispiel
Wir bestimmen die Laplace-Transformierte von sin ða tÞ unter Verwendung der Korrespondenz
1
(Nr. 24 mit a ¼ 1):
F ðsÞ ¼ l fsin tg ¼ 2
s þ1
!s4
1
1
1
1
1
1
1
.F
¼
. ! 42
¼
.
¼
.
¼
s
a
a
a
a s2
a s2 þ a2
þ1
þ1
2
2
a
a
a
1
a2
a
¼
.
¼ 2
a s2 þ a2
s þ a2
l fsin ða tÞg ¼
&
2 Eigenschaften der Laplace-Transformation (Transformationssätze)
347
2.3 Verschiebungssätze
1. Verschiebungssatz (Verschiebung nach rechts)
Die Originalfunktion f ðtÞ mit f ðtÞ ¼ 0 für t < 0 wird um die Strecke a nach rechts
verschoben. Die verschobene Funktion lässt sich mit Hilfe der Sprungfunktion s ðtÞ durch
die Gleichung g ðtÞ ¼ f ðt / aÞ . s ðt / aÞ beschreiben.
f(t)
g(t)
a
t
)
t
Für die Laplace-Transformierte von g ðtÞ gilt dann ða > 0Þ:
lf f ðt / aÞ . s ðt / aÞg ¼ e / a s . F ðsÞ
mit
F ðsÞ ¼ l f f ðtÞg
Regel: Die Bildfunktion F ðsÞ wird mit e / a s multipliziert.
&
Beispiel
l fsin ðt / 3Þ . s ðt / 3Þg ¼ e / 3 s . l fsin tg ¼ e / 3 s .
1
e /3s
¼ 2
s2 þ 1
s þ1
ðNr: 24; a ¼ 1Þ
&
2. Verschiebungssatz (Verschiebung nach links)
Die Originalfunktion f ðtÞ mit f ðtÞ ¼ 0 für t < 0 wird um die Strecke a nach links
verschoben. Die verschobene Funktion lässt sich mit Hilfe der Sprungfunktion s ðtÞ durch
die Gleichung g ðtÞ ¼ f ðt þ aÞ . s ðtÞ beschreiben.
f (t)
g (t)
t
–a
t
Für die Laplace-Transformierte von g ðtÞ gilt dann ða > 0Þ:
0
lf f ðt þ aÞ . s ðtÞg ¼ e a s @F ðsÞ /
ða
0
1
f ðtÞ . e / s t dt A
mit
F ðsÞ ¼ l f f ðtÞg
348
XIII Laplace-Transformationen
Regel: Von der Bildfunktion F ðsÞ wird zunächst das Integral
Ða
0
f ðtÞ . e / s t dt subtrahiert,
anschließend wird die neue Funktion mit e a s multipliziert.
Beispiel
&
2
3
Ðp
l fsin ðt þ pÞ . s ðtÞg ¼ e p s l fsin tg / sin t . e / s t dt ¼
0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral 322 mit a ¼ 1; b ¼ / s
¼ eps
¼ /
3
+ /st
) 2
3
2
1
e
ð/ s . sin t / cos tÞ p
1
e /ps
1
ps
¼
e
¼
/
/
/
s2 þ 1
s2 þ 1
s2 þ 1
s2 þ 1
s2 þ 1
0
1
s2 þ 1
ðNr: 24 mit a ¼ 1Þ
&
2.4 Dämpfungssatz
Die Originalfunktion f ðtÞ mit f ðtÞ ¼ 0 für t < 0 wird exponentiell gedämpft, d. h. mit
dem Faktor e / a t multipliziert. Die Laplace-Transformierte der gedämpften Funktion
g ðtÞ ¼ e / a t . f ðtÞ mit gðtÞ ¼ 0 für t < 0 lautet dann 1Þ :
lf e / a t . f ðtÞg ¼ F ðs þ aÞ
mit
F ðsÞ ¼ lf f ðtÞg
Regel: In der Bildfunktion F ðsÞ wird der Parameter s durch s þ a ersetzt.
Beispiel
&
Die Laplace-Transformierte der gedämpften Schwingung g ðtÞ ¼ e / 2 t . cos t lautet unter Verwendung der
s
Transformation F ðsÞ ¼ l fcos tg ¼ 2
(Nr. 25 mit a ¼ 1) wie folgt:
s þ1
l fe / 2 t . cos tÞ ¼ F ðs þ 2Þ ¼
ðs þ 2Þ
sþ2
¼ 2
ðs þ 2Þ 2 þ 1
s þ 4s þ 5
&
2.5 Ableitungssätze (Differentiationssätze)
2.5.1 Ableitungssatz (Differentiationssatz) für die Originalfunktion
Die Laplace-Transformierten der gewöhnlichen Ableitungen einer Originalfunktion f ðtÞ
nach der Variablen t lauten wie folgt:
1. Ableitung
lf f 0 ðtÞg ¼ s . F ðsÞ / f ð0Þ
f ð0Þ:
1Þ
mit
F ðsÞ ¼ lf f ðtÞg
Anfangswert von f ðtÞ zur Zeit t ¼ 0
Die Konstante a kann reell oder komplex sein. Eine Dämpfung im physikalischen Sinne erhält man nur für
a > 0. Für a < 0 bewirkt der Faktor e / a t eine Verstärkung.
2 Eigenschaften der Laplace-Transformation (Transformationssätze)
349
2. Ableitung
lf f 00 ðtÞg ¼ s 2 . F ðsÞ / s . f ð0Þ / f 0 ð0Þ
f ð0Þ; f 0 ð0Þ:
mit
F ðsÞ ¼ lf f ðtÞg
Anfangswerte von f ðtÞ; f 0 ðtÞ zur Zeit t ¼ 0
n-te Ableitung
lf f
ðnÞ
ðtÞg ¼ s n . F ðsÞ / s n / 1 . f ð0Þ / s n / 2 . f 0 ð0Þ / . . . / f
f ð0Þ; f 0 ð0Þ; . . . ; f
ðn / 1Þ
ð0Þ: Anfangswerte von f ðtÞ; f 0 ðtÞ; . . . ; f
ðn / 1Þ
ðn / 1Þ
ð0Þ
ðtÞ zur Zeit t ¼ 0
Voraussetzung: Die n-te Ableitung von f ðtÞ ist Laplace-transformierbar.
Regel: Die Bildfunktion F ðsÞ ¼ l f f ðtÞg wird zunächst mit s n multipliziert, dann
wird ein Polynom ðn / 1Þ-ten Grades in der Variablen s subtrahiert ðdie
Polynomkoeffizienten sind die Anfangswerte der Originalfunktion f ðtÞ und ihrer
Ableitungen f 0 ðtÞ; f 00 ðtÞ; . . . ; f ðn / 1Þ ðtÞÞ.
Anmerkungen
(1)
Bei Sprungfunktionen mit einer Sprungstelle bei t ¼ 0 sind für die Anfangswerte
f ð0Þ; f 0 ð0Þ; . . . ; f
ðn / 1Þ
ð0Þ jeweils die rechtsseitigen Grenzwerte einzusetzen.
(2)
Sollte die Anfangsstelle bei t 6¼ 0 liegen, so muss f ðtÞ vorher entsprechend verschoben werden.
&
Beispiel
1
(Nr. 24 mit a ¼ 1). Nach dem
s2 þ 1
Ableitungssatz (1. Ableitung) erhält man dann für die Laplace-Transformierte der 1. Ableitung f 0 ðtÞ, d. h. für die
Laplace-Transformierte der Kosinusfunktion unter Berücksichtigung des Anfangswertes f ð0Þ ¼ sin 0 ¼ 0:
Zur Originalfunktion f ðtÞ ¼ sin t gehört die Bildfunktion F ðsÞ ¼
l fðsin tÞ 0 g ¼ l fcos tg ¼ s . F ðsÞ / f ð0Þ ¼ s .
1
s
/0 ¼ 2
s2 þ 1
s þ1
&
Ableitungssatz für eine verallgemeinerte Originalfunktion
Der Ableitungssatz gilt sinngemäß auch für die verallgemeinerte Differentiation einer
verallgemeinerten Funktion, wenn man die Anfangswerte (bzw. rechtsseitigen Grenzwerte) durch die linksseitigen Grenzwerte ersetzt. Für die 1. verallgemeinerte Ableitung gilt
dann:
(
l
D f ðtÞ
Dt
'
¼ s . F ðsÞ / f ð/ 0Þ
f ð/ 0Þ ist dabei der linksseitige Grenzwert von f ðtÞ an der Stelle t ¼ 0.
350
XIII Laplace-Transformationen
2.5.2 Ableitungssatz (Differentiationssatz) für die Bildfunktion
Die Ableitungen der Laplace-Transformierten F ðsÞ ¼ lf f ðtÞg nach der Variablen s lauten:
1. Ableitung
F 0 ðsÞ ¼ lfð/ tÞ 1 . f ðtÞg ¼ / lft . f ðtÞg
2. Ableitung
F 00 ðsÞ ¼ lfð/ tÞ 2 . f ðtÞg ¼ l ft 2 . f ðtÞg
n-te Ableitung
F ðnÞ ðsÞ ¼ lfð/ tÞ n . f ðtÞg ¼ ð/ 1Þ n . l ft n . f ðtÞg
Voraussetzung: Die Funktion ð/ tÞ n . f ðtÞ ist Laplace-transformierbar.
Regel: Die n-te Ableitung der Bildfunktion F ðsÞ ist die Laplace-Transformierte der mit
ð/ tÞ n multiplizierten Originalfunktion f ðtÞ:
Beispiel
&
Die Laplace-Transformierte von g ðtÞ ¼ t . sin t lässt sich wie folgt durch Anwendung des Ableitungssatzes
(1. Ableitung) auf das Funktionenpaar
f ðtÞ ¼ sin t "///! F ðsÞ ¼
1
s2 þ 1
gewinnen:
l ft . f ðtÞg ¼ l ft . sin tg ¼ / F 0 ðsÞ ¼ /
d
ds
3
1
s2 þ 1
2
¼ /
d 2
2s
ðs þ 1Þ / 1 ¼ 2
ds
ðs þ 1Þ 2
&
2.6 Integrationssätze
2.6.1 Integrationssatz für die Originalfunktion
Es wird zunächst über die Originalfunktion f ðtÞ integriert. Für die Laplace-Transformierte
des Integrals gilt dann:
Integration über das Intervall 0 ) u ) t
l
8t
<ð
:
0
f ðuÞ du
9
=
;
¼
1
. F ðsÞ
s
mit
F ðsÞ ¼ l f f ðtÞg
Regel: Die Bildfunktion F ðsÞ wird mit dem Kehrwert von s multipliziert.
2 Eigenschaften der Laplace-Transformation (Transformationssätze)
351
Integration über das Intervall a ) u ) t (mit a > 0)
l
8t
<ð
:
f ðuÞ du
a
9
=
;
0
1 @
F ðsÞ /
s
¼
ða
1
f ðuÞ duA
mit
F ðsÞ ¼ lf f ðtÞg
0
Regel: Von der Bildfunktion F ðsÞ wird zunächst das Integral
Ða
0
f ðuÞ du subtrahiert,
anschließend wird die neue Funktion mit dem Kehrwert von s multipliziert.
Beispiel
&
Die Laplace-Transformierte von f ðtÞ ¼ t lautet F ðsÞ ¼ 1=s 2 (Nr. 4). Aus dem Integrationssatz lässt sich
dann die Laplace-Transformierte von gðtÞ ¼ t 2 wie folgt bestimmen ðmit f ðuÞ ¼ uÞ:
l
8t
<ð
:
u du
0
9
=
;
(+
¼ l
Somit ist l ft 2 g ¼
1 2
u
2
)t '
(
¼ l
0
1 2
t
2
'
¼
1
1
1 1
1
. l ft 2 g ¼
. F ðsÞ ¼
.
¼ 3
2
s
s s2
s
2
die Laplace-Transformierte von g ðtÞ ¼ t 2 .
s3
&
2.6.2 Integrationssatz für die Bildfunktion
Es wird über die Bildfunktion F ðsÞ ¼ lf f ðtÞg integriert. Dann gilt:
(
1
ð
F ðuÞ du ¼ l
s
'
1
. f ðtÞ
t
Voraussetzung: Die Funktion
1
. f ðtÞ ist Laplace-transformierbar.
t
Regel: Die Originalfunktion f ðtÞ von F ðsÞ wird zunächst mit dem Kehrwert von t
multipliziert, dann wird die Laplace-Transformierte der neuen Funktion
g ðtÞ ¼ ð1=tÞ . f ðtÞ bestimmt.
&
Beispiel
Aus der bekannten Korrespondenz
f ðtÞ ¼ t 2 "///! F ðsÞ ¼
2
s3
ðNr: 10Þ
lässt sich mit Hilfe des Integrationssatzes die Laplace-Transformierte von g ðtÞ ¼ t wie folgt bestimmen
ðmit F ðuÞ ¼ 2=u 3 Þ:
(
l
1
. f ðtÞ
t
'
(
¼ l
1
. t2
t
'
1
ð
¼ l ftg ¼
s
Somit gilt die folgende Korrespondenz: t "///!
+
)
2
1 1
1
1
du
¼
/
¼ 0þ 2 ¼ 2
u3
u2 s
s
s
1
s2
&
352
XIII Laplace-Transformationen
2.7 Faltungssatz
Faltungsprodukt
Unter dem Faltungsprodukt f1 ðtÞ , f2 ðtÞ zweier Originalfunktionen f1 ðtÞ und f2 ðtÞ versteht man das Integral
ðt
f1 ðtÞ , f2 ðtÞ ¼
f1 ðuÞ . f2 ðt / uÞ du
0
ðFaltungsintegral, einseitige Faltung der Funktionen f1 ðtÞ und f2 ðtÞÞ
Rechenregeln
Kommutativgesetz
f1 ðtÞ , f2 ðtÞ ¼ f2 ðtÞ , f1 ðtÞ
Assoziativgesetz
½ f1 ðtÞ , f2 ðtÞ % , f3 ðtÞ ¼ f1 ðtÞ , ½ f2 ðtÞ , f3 ðtÞ %
Distributivgesetz
f1 ðtÞ , ½ f2 ðtÞ þ f3 ðtÞ % ¼ f1 ðtÞ , f2 ðtÞ þ f1 ðtÞ , f3 ðtÞ
Faltungssatz
Die Laplace-Transformierte des Faltungsproduktes f1 ðtÞ , f2 ðtÞ ist gleich dem Produkt der
Laplace-Transformierten von f1 ðtÞ und f2 ðtÞ:
lf f1 ðtÞ , f2 ðtÞg ¼ l f f1 ðtÞg . lf f2 ðtÞg ¼ F1 ðsÞ . F2 ðsÞ
F1 ðsÞ ¼ lf f1 ðtÞg;
F2 ðsÞ ¼ l f f2 ðtÞg
Spezielle Form des Faltungssatzes (Rücktransformation):
f1 ðtÞ , f2 ðtÞ ¼ F / 1 fF1 ðsÞ . F2 ðsÞg
&
Beispiel
1
Wir bestimmen mit Hilfe des Faltungssatzes die zur Bildfunktion F ðsÞ ¼ 2
gehörende Originalðs þ 1Þ s 2
funktion f ðtÞ. Es ist:
1
1
1
¼ 2
.
¼ F1 ðsÞ . F2 ðsÞ
ðs 2 þ 1Þ s 2
s þ 1 s2
|fflfflfflffl{zfflfflfflffl} |{z}
F1 ðsÞ F2 ðsÞ
Nach dem Faltungssatz gilt dann:
l f f ðtÞg ¼ F ðsÞ ¼
l f f ðtÞg ¼ l f f1 ðtÞ , f2 ðtÞg ¼ F1 ðsÞ . F2 ðsÞ
D. h., die gesuchte Originalfunktion f ðtÞ ist das Faltungsprodukt der Originalfunktionen f1 ðtÞ und f2 ðtÞ zu
den bekannten Bildfunktionen F1 ðsÞ und F2 ðsÞ:
2 Eigenschaften der Laplace-Transformation (Transformationssätze)
353
ðt
f ðtÞ ¼ f1 ðtÞ , f2 ðtÞ ¼
f1 ðuÞ . f2 ðt / uÞ du
0
Die Originalfunktionen zu
f1 ðtÞ ¼ l / 1
(
s2
1
þ1
F1 ðsÞ ¼
1
s2 þ 1
'
F2 ðsÞ ¼
f2 ðtÞ ¼ l / 1
¼ sin t ;
Dann aber ist:
und
ðt
t . sin u du /
u¼0
ðNr: 24 und Nr: 4Þ
ðt
f1 ðuÞ . f2 ðt / uÞ du ¼
u¼0
ðt
entnehmen wir aus der Tabelle:
( '
1
¼ t
s2
ðt
f ðtÞ ¼ f1 ðtÞ , f2 ðtÞ ¼ ðsin tÞ , t ¼
¼
1
s2
ðsin uÞ . ðt / uÞ du ¼
u¼0
u . sin u du ¼ ½ / t . cos u% tu ¼ 0 / ½sin u / u . cos u% tu ¼ 0 ¼
u¼0
|fflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflffl}
Integral Nr: 208 mit a ¼ 1
¼ ð/ t . cos t þ t . cos 0Þ / ðsin t / t . cos t / sin 0 / 0 . cos 0Þ ¼
¼ ð/ t . cos t þ t . 1Þ / ðsin t / t . cos t / 0 þ 0Þ ¼
¼ / t . cos t þ t / sin t þ t . cos t ¼ t / sin t
&
2.8 Grenzwertsätze
Das Verhalten der Originalfunktion f ðtÞ für t ! 0 ðAnfangswert f ð0ÞÞ bzw. für
t ! 1 ðEndwert f ð1ÞÞ lässt sich aus der zugehörigen Bildfunktion FðsÞ ¼ l f f ðtÞg
auch ohne Rücktransformation bestimmen (unter der Voraussetzung, dass f ð0Þ bzw.
f ð1Þ, d. h. die aufgeführten Grenzwerte auf der jeweils linken Seite existieren):
Anfangswert f (0) (rechttsseitiger Grenzwert für t ! 0)
f ð0Þ ¼ lim f ðtÞ ¼ lim ðs . F ðsÞÞ
s !1
t!0
&
mit
F ðsÞ ¼ lf f ðtÞg
Beispiel
Die Bildfunktion einer (nicht näher bekannten) Originalfunktion f ðtÞ lautet:
F ðsÞ ¼ l f f ðtÞg ¼
1
s2 þ 1
Dann besitzt die Originalfunktion f ðtÞ den folgenden Anfangswert:
3
f ð0Þ ¼ lim f ðtÞ ¼ lim ðs . F ðsÞÞ ¼ lim
t!0
s !1
s!1
2
3
2
s
1
¼
lim
¼ 0
s ! 1 s þ 1=s
s2 þ 1
&
1) (Grenzwert für t ! 1)
Endwert f (1
f ð1Þ ¼ lim f ðtÞ ¼ lim ðs . F ðsÞÞ
t!1
s!0
mit
F ðsÞ ¼ l f f ðtÞg
354
XIII Laplace-Transformationen
Beispiel
&
2s þ 1
s ðs þ 3Þ
F ðsÞ ¼ l f f ðtÞg ¼
Die zugehörige Originalfunktion f ðtÞ besitzt den folgenden Endwert:
3
f ð1Þ ¼ lim f ðtÞ ¼ lim ðs . F ðsÞÞ ¼ lim
t!1
s!0
s!0
2
3
2
s ð2 s þ 1Þ
2s þ 1
1
¼ lim
¼
s!0
s ðs þ 3Þ
sþ3
3
&
3 Laplace-Transformierte einer periodischen Funktion
Die Laplace-Transformierte F ðsÞ einer
periodischen Funktion f ðtÞ lautet 2Þ :
1
F ðsÞ ¼
.
1 / e /sT
T:
&
ðT
f(t)
f ðuÞ . e / s u du
T
0
2T
t
T
Periode (Schwingungsdauer) von f ðtÞ
Beispiel
f(t)
Die Laplace-Transformierte der Rechteckskurve
(
)
1
0 < t < a
f ðtÞ ¼
für
0
a < t < 2a
1
mit der Periode T ¼ 2 a lautet wie folgt:
a
2 a
ð
1
4
F ðsÞ ¼
/
2
a
s
1/e
1.e
/su
¼
1
1 / e /2as
/
1
. e /su
s
0.e
u¼a
u¼0
+
3
2ða
du þ
)a
u¼0
¼
2a
/su
du5 ¼
1
.
1 / e /2as
ða
3a
4a
t
e / s u du ¼
u¼0
h
ia
1
/ e /su
¼
u¼0
ð1 / e / 2 a s Þ s
1
1
1 / e /as
ð/ e / a s þ e 0 Þ ¼
ð/ e / a s þ 1Þ ¼
¼
/
2
a
s
/
2
a
s
ð1 / e
Þs
ð1 / e
Þs
ð1 / e / 2 a s Þ s
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
3: Binom
1 / e /as
1
1
¼
¼
¼
/
a
s
/
a
s
Þs
s ðe
þ 1Þ
ð1 / e / a s Þ ð1 þ e / a s Þ s ð1 þ e
¼
Hinweis zum 3. Binom: ð1 þ e / a s Þ ð1 / e / a s Þ ¼ 1 2 / ðe / a s Þ 2 ¼ 1 / e / 2 a s
&
2Þ
Die Periodizität bleibt auf den positiven Zeitbereich beschränkt ð f ðtÞ ¼ 0 für t < 0Þ.
4 Laplace-Transformierte spezieller Funktionen (Impulse)
355
4 Laplace-Transformierte spezieller Funktionen
(Impulse)
Hinweis: Es ist stets f ðtÞ ¼ 0 für t < 0.
1. Sprungfunktion s ( t ) (Sigmafunktion)
(
)
f (t)
0
t < 0
f ðtÞ ¼ s ðtÞ ¼
für
1
t ( 0
1
1
F ðsÞ ¼
s
t
/
2. Verschobene Sprungfunktion s ( t a)
(
)
f (t)
0
t < a
für
f ðtÞ ¼ s ðt / aÞ ¼
t ( a
1
1
e /as
F ðsÞ ¼
s
a
t
3. Periodische Rechteckskurve
Periode (Schwingungsdauer): T ¼ 2 a
8
9
0 ) t < a =
< A
f ðtÞ ¼
für
;
:
/A
a ) t < 2a
!a s 4
A ð1 / e / a s Þ
A
¼
.
tanh
F ðsÞ ¼
s ð1 þ e / a s Þ
s
2
f(t)
A
a
2a
3a
4a
t
–A
4. Periodische Rechteckskurve
Periode (Schwingungsdauer): T ¼ 2 a
8
9
0 ) t < a =
<A
f ðtÞ ¼
für
:
;
0
a ) t < 2a
F ðsÞ ¼
A
s ð1 þ e / a s Þ
f(t)
A
a
2a
3a
4a
t
356
XIII Laplace-Transformationen
5. Rechteckimpuls
8
9
0
0 ) t < a>
>
>
>
<
=
f ðtÞ ¼ A für a ) t ) b
>
>
>
>
;
:
0
t > b
F ðsÞ ¼
A
A ðe / a s / e / b s Þ
s
6. Rechteckimpuls
8
A
>
>
<
f ðtÞ ¼ / A für
>
>
:
0
F ðsÞ ¼
f(t)
9
0 ) t < a >
>
=
a ) t ) 2a
>
>
;
t > 2a
A ð1 / e / a s Þ 2
s
a
t
b
f(t)
A
a
2a
t
–A
7. Periodische Dreieckskurve
Periode (Schwingungsdauer): T ¼ 2 a
9
8
A
>
>
>
>
t
0
)
t
)
a
>
>
< a
=
f ðtÞ ¼
für
>
>
>
>
>
>
: / A ðt / 2 aÞ
a ) t ) 2a;
a
f(t)
F ðsÞ ¼
A ð1 / e / a s Þ
a s 2 ð1 þ e / a s Þ
A
a
2a
3a
4a
t
4 Laplace-Transformierte spezieller Funktionen (Impulse)
357
8. Dreieckimpuls
f ðtÞ ¼
8
>
>
>
>
>
>
>
>
>
<
9
>
>
>
>
>
>
>
2a ) t ) a þ b>
>
=
0
0 ) t ) 2a
A
ðt / 2 aÞ
b/a
>
>
A
>
>
/
ðt / 2 bÞ
>
>
b
/
a
>
>
>
:
0
für
ðb > aÞ
>
>
>
>
>
>
>
>
>
;
a þ b ) t ) 2b
t ( 2b
f(t)
F ðsÞ ¼
A ðe / a s / e / b s Þ 2
ðb / aÞ s 2
A
a
2a
a+b
t
2b
9. Sägezahnfunktion (Kippschwingung)
Periode (Schwingungsdauer):
f ðtÞ ¼
A
t
a
F ðsÞ ¼
A ð1 þ a s / e a s Þ
a s 2 ð1 / e a s Þ
für
T ¼ a
0 ) t < a
f(t)
A
a
2a
3a
a
2a
3a
t
10. Sägezahnfunktion (Kippschwingung)
Periode (Schwingungsdauer):
f ðtÞ ¼ /
F ðsÞ ¼
A
ðt / aÞ
a
für
T ¼ a
0 ) t < a
f(t)
A
A ðe / a s þ a s / 1Þ
a s 2 ð1 / e / a s Þ
t
11. Sinusfunktion (Sinusschwingung)
Periode (Schwingungsdauer):
f ðtÞ ¼ A . sin ða tÞ
T ¼
2p
a
f(t)
A
3p
2a
Aa
F ðsÞ ¼ 2
s þ a2
p
2a
–A
2p
a
t
358
XIII Laplace-Transformationen
12. Gedämpfte Sinusschwingung
f ðtÞ ¼ A . e / b t . sin ða tÞ
F ðsÞ ¼
f(t)
Aa
ðs þ bÞ 2 þ a 2
t
T = 2p
a
13. Periodischer Sinusimpuls (Einweggleichrichtung)
Periode (Schwingungsdauer): T ¼ 2 a
8
9
!
4
< A . sin p t
0 ) t ) a =
a
f ðtÞ ¼
für
:
;
0
a ) t ) 2a
paA
F ðsÞ ¼ 2 2
ða s þ p 2 Þ ð1 / e / a s Þ
f(t)
A
a/2
a
2a
a
2a
3a
14. Periodischer Sinusimpuls (Zweiweggleichrichtung)
Periode (Schwingungsdauer):
"
! p 4"
"
"
f ðtÞ ¼ A . " sin
t "
a
F ðsÞ ¼
¼
ða 2
f(t)
A
p a A ð1 þ e / a s Þ
¼
s 2 þ p 2 Þ ð1 / e / a s Þ
a/2
t
!a s 4
paA
.
coth
a2 s2 þ p2
2
15. Sinusimpuls
8
!
4
< A . sin p t
a
f ðtÞ ¼
:
0
F ðsÞ ¼
T ¼ a
p a A ð1 þ e / a s Þ
a2 s2 þ p2
für
9
0 ) t ) a=
;
t ( a
f(t)
A
a/2
a
t
t
4 Laplace-Transformierte spezieller Funktionen (Impulse)
359
16. Kosinusfunktion (Kosinusschwingung)
Periode (Schwingungsdauer):
T ¼ 2 p=a
f(t)
A
f ðtÞ ¼ A . cos ða tÞ
p
a
As
F ðsÞ ¼ 2
s þ a2
2p
a
t
–A
17. Gedämpfte Kosinusschwingung
f ðtÞ ¼ A . e / b t . cos ða tÞ
F ðsÞ ¼
f(t)
A
A ðs þ bÞ
ðs þ bÞ 2 þ a 2
t
T = 2p
a
18. Rampenfunktion
f ðtÞ ¼
8
>
>
>
>
<
0
A
ðt / aÞ
>
b
/
a
>
>
>
:
A
für
9
0 ) t ) a>
>
>
>
>
=
a ) t ) b
>
>
>
>
>
;
t ( b
f(t)
A
b
a
F ðsÞ ¼
A ðe / a s / e / b s Þ
ðb / aÞ s 2
ðb > aÞ
19. Treppenfunktion
8
9
0
0 ) t < a >
>
>
>
<
=
a ) t < 2a
f ðtÞ ¼
A für
>
>
>
>
:
;
2A
2a ) t < 3a
usw.
F ðsÞ ¼
A
s ðe a s / 1Þ
t
f(t)
4A
3A
2A
A
a
2a
3a
4a
t
360
XIII Laplace-Transformationen
5 Anwendung: Lösung linearer Anfangswertprobleme
5.1 Allgemeines Lösungsverfahren
Eine (gewöhnliche) lineare Differentialgleichung (Dgl) mit konstanten Koeffizienten und
vorgegebenen Anfangswerten (Anfangswertproblem) lässt sich mit Hilfe der Laplace-Transformation wie folgt lösen:
Originalbereich
Lineare Dgl mit
direkter
konstanten Koeffizienten
Lösungsweg
- Spezielle Lösung
der Dgl
6
(1) Laplace-Transformation
(3) Rücktransformation
?
Algebraische Gleichung
(2) Lösen der
Gleichung
- Lösung der algebraischen Gleichung
Bildbereich
Lösungsschritte
1. Die lineare Differentialgleichung wird mit Hilfe der Laplace-Transformation in eine algebraische Gleichung übergeführt.
2. Als Lösung dieser Gleichung erhält man die Bildfunktion Y ðsÞ der gesuchten Originalfunktion y ðtÞ.
3. Durch Rücktransformation (inverse Laplace-Transformation) gewinnt man aus der Bildfunktion Y ðsÞ mit Hilfe einer Transformationstabelle (z. B. der Tabelle in Abschnitt 6)
und / oder spezieller Methoden (wie z. B. der Partialbruchzerlegung bei gebrochenrationalen Funktionen) die gesuchte Lösung y ðtÞ der vorgegebenen Anfangswertaufgabe.
Vorteil dieser Lösungsmethode: Die Rechenoperationen sind im Bildbereich meist einfacher ausführbar.
5 Anwendung: Lösung linearer Anfangswertprobleme
361
5.2 Lineare Differentialgleichungen 1. Ordnung
mit konstanten Koeffizienten
Differentialgleichung im Originalbereich (Anfangswertproblem)
y 0 þ a y ¼ g ðtÞ
a:
Anfangswert:
Reelle Konstante;
g ðtÞ:
y ð0Þ
Störfunktion
Transformierte Differentialgleichung im Bildbereich (mit Lösung)
½ s . Y ðsÞ / y ð0Þ% þ a . Y ðsÞ ¼ F ðsÞ
Lösung:
Y ðsÞ ¼
F ðsÞ þ y ð0Þ
sþa
Y ðsÞ ¼ lf y ðtÞg:
Laplace-Transformierte der (gesuchten) Lösung y ðtÞ
F ðsÞ ¼ lf g ðtÞg:
Laplace-Transformierte der Störfunktion g ðtÞ
Durch Rücktransformation (z. B. unter Verwendung der Tabelle in Abschnitt 6) erhält man
aus Y ðsÞ die zugehörige Originalfunktion y ðtÞ, d. h. die gesuchte Lösung der Differentialgleichung für den Anfangswert y ð0Þ. Die Lösungsfunktion y ðtÞ lässt sich auch in
geschlossener Form angeben:
y ðtÞ ¼ g ðtÞ , e / a t þ yð0Þ . e / a t
g ðtÞ , e / a t :
&
Faltungsprodukt der Funktionen gðtÞ und e / a t
Beispiel
y 0 þ 2 y ¼ 10 ;
Anfangswert:
y ð0Þ ¼ 0
Transformation der Dgl in den Bildraum ða ¼ 2; g ðtÞ ¼ 10Þ:
10
½ s . Y ðsÞ / 0 % þ 2 . Y ðsÞ ¼ l f10g ¼ 10 . l f1g ¼
s
|fflfflffl{zfflfflffl}
Nr: 2
Lösung im Bildraum:
Y ðsÞ ¼
10
5
5
¼
/
¼ l f y ðtÞg
s ðs þ 2Þ
s
sþ2
oder
s . Y ðsÞ þ 2 . Y ðsÞ ¼
10
s
ðnach PartialbruchzerlegungÞ
Rücktransformation in den Originalraum:
(
'
( '
(
'
5
5
1
1
y ðtÞ ¼ l / 1 f Y ðsÞg ¼ l / 1
/
¼ 5 . l /1
/ 5 . l /1
¼
s
sþ2
s
sþ2
¼ 5 . 1 / 5 . e / 2 t ¼ 5ð1 / e / 2 t Þ
(Nr. 2 und Nr. 3 mit a ¼ / 2)
Lösung der Anfangswertaufgabe:
y ðtÞ ¼ 5 ð1 / e / 2 t Þ
ðf ür t ( 0Þ
oder
y ðtÞ ¼ 5 ð1 / e / 2 t Þ . s ðtÞ
&
362
XIII Laplace-Transformationen
5.3 Lineare Differentialgleichungen 2. Ordnung
mit konstanten Koeffizienten
Differentialgleichung im Originalbereich (Anfangswertproblem)
y 00 þ a y 0 þ b y ¼ gðtÞ
a; b:
Reelle Konstanten;
Anfangswerte:
g ðtÞ:
y ð0Þ;
y 0 ð0Þ
Störfunktion
Transformierte Differentialgleichung im Bildbereich (mit Lösung)
½ s 2 . Y ðsÞ / s . y ð0Þ / y 0 ð0Þ% þ a ½ s . Y ðsÞ / y ð0Þ% þ b . Y ðsÞ ¼ F ðsÞ
Lösung:
Y ðsÞ ¼
F ðsÞ þ y ð0Þ . ðs þ aÞ þ y 0 ð0Þ
s2 þ as þ b
Y ðsÞ ¼ lf y ðtÞg:
Laplace-Transformierte der (gesuchten) Lösung y ðtÞ
F ðsÞ ¼ l f g ðtÞg:
Laplace-Transformierte der Störfunktion g ðtÞ
Durch Rücktransformation (z. B. unter Verwendung der Tabelle in Abschnitt 6) erhält man
aus Y ðsÞ die zugehörige Originalfunktion y ðtÞ, d. h. die gesuchte Lösung der Differentialgleichung für die Anfangswerte y ð0Þ und y 0 ð0Þ. Die Lösungsfunktion y ðtÞ lässt sich
auch in geschlossener Form angeben:
y ðtÞ ¼ g ðtÞ , f1 ðtÞ þ y ð0Þ . f2 ðtÞ þ y 0 ð0Þ . f1 ðtÞ
f1 ðtÞ:
f2 ðtÞ:
1
s2 þ as þ b
sþa
Originalfunktion zu F2 ðsÞ ¼ lf f2 ðtÞg ¼ 2
s þ as þ b
Originalfunktion zu F1 ðsÞ ¼ lf f1 ðtÞg ¼
g ðtÞ , f1 ðtÞ:
&
Faltungsprodukt der Funktionen g ðtÞ und f1 ðtÞ
Beispiel
y 00 þ 2 y 0 þ y ¼ 0 ;
Anfangswerte:
y ð0Þ ¼ 0 ;
y 0 ð0Þ ¼ 1
Transformation der Dgl in den Bildraum ða ¼ 2; b ¼ 1; g ðtÞ ¼ 0Þ:
½ s 2 . Y ðsÞ / s . 0 / 1 % þ 2 ½ s . Y ðsÞ / 0 % þ 1 . Y ðsÞ ¼ l f0g ¼ 0
s 2 . Y ðsÞ þ 2 s . Y ðsÞ þ Y ðsÞ ¼ ðs 2 þ 2 s þ 1Þ . Y ðsÞ ¼ 1
Lösung im Bildraum:
1
1
Y ðsÞ ¼ 2
¼
s þ 2s þ 1
ðs þ 1Þ 2
Rücktransformation in den Originalraum (Nr. 6 mit a ¼ / 1):
(
'
1
y ðtÞ ¼ l / 1 f Y ðsÞg ¼ l / 1
¼ t . e /t
2
ðs þ 1Þ
Lösung der Anfangswertaufgabe:
y ðtÞ ¼ t . e / t
ðf ür t ( 0Þ
oder
y ðtÞ ¼ t . e / t . s ðtÞ
&
6 Tabelle spezieller Laplace-Transformationen
6 Tabelle spezieller Laplace-Transformationen
Bildfunktion F ðsÞ
Originalfunktion f ðtÞ
ð1Þ
1
d ðtÞ
ð2Þ
1
s
1 ðSprungfunktion s ðtÞÞ
ð3Þ
1
s/a
e at
ð4Þ
1
s2
t
ð5Þ
1
s ðs / aÞ
e at / 1
a
ð6Þ
1
ðs / aÞ 2
t . e at
ð7Þ
1
ðs / aÞ ðs / bÞ
e at / e bt
a/b
ð8Þ
s
ðs / aÞ 2
ð1 þ a tÞ . e a t
ð9Þ
s
ðs / aÞ ðs / bÞ
a . e at / b . e bt
a/b
ð10Þ
1
s3
1 2
t
2
ð11Þ
1
s 2 ðs / aÞ
e at / a t / 1
a2
ð12Þ
1
s ðs / aÞ 2
ða t / 1Þ . e a t þ 1
a2
ð13Þ
1
ðs / aÞ 3
1 2
t . e at
2
ð14Þ
1
s ðs / aÞ ðs / bÞ
b . e at / a . e bt þ a / b
a bða / bÞ
ð15Þ
1
ðs / aÞ ðs / bÞ ðs / cÞ
ð16Þ
s
ðs / aÞ 3
ðb / cÞ . e a t þ ðc / aÞ . e b t þ ða / bÞ . e c t
ða / bÞ ða / cÞ ðb / cÞ
3
2
1
a t 2 þ t . e at
2
ð17Þ
s
ðs / aÞ ðs / bÞ 2
a . e a t / ½ a þ bða / bÞ t % . e b t
ða / bÞ 2
ð18Þ
s
ðs / aÞ ðs / bÞ ðs / cÞ
aðb / cÞ . e a t þ bðc / aÞ . e b t þ cða / bÞ . e c t
ða / bÞ ða / cÞ ðb / cÞ
(Diracsche Deltafunktion)
363
364
XIII Laplace-Transformationen
Bildfunktion F ðsÞ
ð19Þ
s2
ðs / aÞ 3
Originalfunktion f ðtÞ
3
2
1 2 2
a t þ 2 a t þ 1 . e at
2
ð20Þ
s2
ðs / aÞ ðs / bÞ 2
a 2 . e a t / ½ b 2 ða / bÞ t þ 2 a b / b 2 % . e b t
ða / bÞ 2
ð21Þ
s2
ðs / aÞ ðs / bÞ ðs / cÞ
a 2 ðb / cÞ . e a t þ b 2 ðc / aÞ . e b t þ c 2 ða / bÞ . e c t
ða / bÞ ða / cÞ ðb / cÞ
ð22Þ
1
sn
t n/1
ðn / 1Þ !
ð23Þ
1
ðs / aÞ n
ð24Þ
1
s2 þ a2
sin ða tÞ
a
ð25Þ
s
s2 þ a2
cos ða tÞ
ð26Þ
ðsin bÞ . s þ a . cos b
s2 þ a2
sin ða t þ bÞ
ð27Þ
ðcos bÞ . s / a . sin b
s2 þ a2
cos ða t þ bÞ
ð28Þ
1
ðs / bÞ 2 þ a 2
e b t . sin ða tÞ
a
ð29Þ
s/b
ðs / bÞ 2 þ a 2
e b t . cos ða tÞ
ð30Þ
1
s2 / a2
sinh ða tÞ
a
ð31Þ
s
s2 / a2
cosh ða tÞ
ð32Þ
1
ðs / bÞ 2 / a 2
e b t . sinh ða tÞ
a
ð33Þ
s/b
ðs / bÞ 2 / a 2
e b t . cosh ða tÞ
ð34Þ
1
s ðs 2 þ 4 a 2 Þ
sin 2 ða tÞ
2a2
ð35Þ
s2 þ 2a2
s ðs 2 þ 4 a 2 Þ
cos 2 ða tÞ
ð36Þ
1
s ðs 2 þ a 2 Þ
1 / cos ða tÞ
a2
ðn 2 N *Þ
ðn 2 N *Þ
t n/1 . e at
ðn / 1Þ !
6 Tabelle spezieller Laplace-Transformationen
365
Bildfunktion F ðsÞ
Originalfunktion f ðtÞ
ð37Þ
1
ðs 2 þ a 2 Þ 2
sin ða tÞ / a t . cos ða tÞ
2a3
ð38Þ
s
ðs 2 þ a 2 Þ 2
t . sin ða tÞ
2a
ð39Þ
ð40Þ
ð41Þ
ðs 2
sin ða tÞ þ a t . cos ða tÞ
2a
s2
þ a 2Þ 2
s2 / a2
ðs 2 þ a 2 Þ 2
t . cos ða tÞ
s3
þ a 2Þ 2
cos ða tÞ /
ðs 2
1
a t . sin ða tÞ
2
ð42Þ
1
s 2 ðs 2 þ a 2 Þ
a t / sin ða tÞ
a3
ð43Þ
1
ðs 2 þ a 2 Þ ðs 2 þ b 2 Þ
a . sin ðb tÞ / b . sin ða tÞ
a bða 2 / b 2 Þ
ð44Þ
s
ðs 2 þ a 2 Þ ðs 2 þ b 2 Þ
cos ðb tÞ / cos ða tÞ
a2 / b2
ð45Þ
ðs 2
þ
s2
ðs 2 þ b 2 Þ
a 2Þ
a . sin ða tÞ / b . sin ðb tÞ
a2 / b2
ð46Þ
s3
ðs 2 þ a 2 Þ ðs 2 þ b 2 Þ
a 2 . cos ða tÞ / b 2 . cos ðb tÞ
a2 / b2
ð47Þ
1
s ðs 2 þ a 2 Þ 2
/ a t . sin ða tÞ / cos ða tÞ þ 1
2a4
ð48Þ
1
s ðs 2
þ
a 2Þ
ðs 2
þ
b 2Þ
b 2 . cos ða tÞ / a 2 . cos ðb tÞ þ a 2 / b 2
a 2 b 2 ða 2 / b 2 Þ
ð49Þ
1
s ðs 2 / a 2 Þ
cosh ða tÞ / 1
a2
ð50Þ
1
ðs 2 / a 2 Þ 2
a t . cosh ða tÞ / sinh ða tÞ
2a3
ð51Þ
s
ðs 2 / a 2 Þ 2
t . sinh ða tÞ
2a
ð52Þ
s2
ðs 2 / a 2 Þ 2
sinh ða tÞ þ a t . cosh ða tÞ
2a
ð53Þ
s2 þ a2
ðs 2 / a 2 Þ 2
t . cosh ða tÞ
ð54Þ
s3
ðs 2 / a 2 Þ 2
1
a t . sinh ða tÞ þ cosh ða tÞ
2
366
XIII Laplace-Transformationen
Bildfunktion F ðsÞ
Originalfunktion f ðtÞ
ð55Þ
1
s 2 ðs 2 / a 2 Þ
sinh ða tÞ / a t
a3
ð56Þ
1
s ðs 2 / a 2 Þ 2
ð57Þ
1
s3 þ a3
ð58Þ
s
s3 þ a3
a t . sinh ða tÞ / 2 . cosh ða tÞ þ 2
a4
+
3pffiffiffi 2
3pffiffiffi 2
)
1 pffiffiffi
3at
3at
/ 3 a t=2
/
cos
þ
e
. e a t=2
3
.
sin
3a2
2
2
+
3pffiffiffi 2
3pffiffiffi 2
)
1 pffiffiffi
3at
3at
3 . sin
þ cos
/ e / 3 a t=2 . e a t=2
3a
2
2
+
3pffiffiffi 2)
1
3at
e / a t þ 2 . e a t=2 . cos
3
2
ð59Þ
s3
s2
þ a3
ð60Þ
1
s3 / a3
ð61Þ
s
s3 / a3
ð62Þ
s3
s2
/ a3
ð63Þ
1
s4 þ a4
ð64Þ
s
s4 þ a4
ð65Þ
ð66Þ
s4
s2
þ a4
s4
s3
þ a4
+
3pffiffiffi 2
3pffiffiffi 2)
pffiffiffi
1
3at
3at
3 a t=2
e
/ 3 . sin
/ cos
. e / a t=2
3a2
2
2
+
3pffiffiffi 2
3pffiffiffi 2)
pffiffiffi
1
3at
3at
3 a t=2
e
þ 3 . sin
/ cos
. e / a t=2
3a
2
2
+
3pffiffiffi 2)
1
3at
at
/ a t=2
e /2.e
. cos
3
2
+ 3
2
3
2
3
2
3
2)
1
at
at
at
at
pffiffiffi sin pffiffiffi . cosh pffiffiffi / cos pffiffiffi . sinh pffiffiffi
2
2
2
2
a3 2
3
2
3
2
at
at
sin pffiffiffi . sinh pffiffiffi
2
2
a2
+ 3
2
3
2
3
2
3
2)
1
at
at
at
at
pffiffiffi cos pffiffiffi . sinh pffiffiffi þ sin pffiffiffi . cosh pffiffiffi
2
2
2
2
a 2
3
2
3
2
at
at
cos pffiffiffi . cosh pffiffiffi
2
2
ð67Þ
1
s4 / a4
sinh ða tÞ / sin ða tÞ
2a3
ð68Þ
s
s4 / a4
cosh ða tÞ / cos ða tÞ
2a2
ð69Þ
s2
s4 / a4
sinh ða tÞ þ sin ða tÞ
2a
ð70Þ
ð71Þ
s4
s3
/ a4
s
s4 þ 4a4
cosh ða tÞ þ cos ða tÞ
2
sin ða tÞ . sinh ða tÞ
2a2
6 Tabelle spezieller Laplace-Transformationen
Bildfunktion F ðsÞ
Originalfunktion f ðtÞ
ð72Þ
s2 / 2a2
s4 þ 4a4
cos ða tÞ . sinh ða tÞ
a
ð73Þ
s2 þ 2a2
s4 þ 4a4
sin ða tÞ . cosh ða tÞ
a
s3
þ 4a4
cos ða tÞ . cosh ða tÞ
ð74Þ
s4
ð75Þ
1
pffiffi
s
ð76Þ
1
pffiffi
s s
ð77Þ
s2
1
pffiffiffiffiffiffi
pt
rffiffiffiffiffiffi
t
2.
p
rffiffiffiffiffiffi
4
t
t .
3
p
1
pffiffi
s
ð78Þ
sþa
pffiffi
s s
1 þ 2at
pffiffiffiffiffiffi
pt
ð79Þ
1
pffiffiffiffiffiffiffiffiffiffiffiffi
sþa
e /at
pffiffiffiffiffiffi
pt
ð80Þ
pffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffi
s/a/ s/b
e bt / e at
pffiffiffiffiffiffi
2t . pt
ð81Þ
sn
ð82Þ
ln
ð83Þ
ln
ð84Þ
ð85Þ
ð86Þ
ð87Þ
ð88Þ
ð89Þ
1
pffiffi
s
ðn 2 N *Þ
!s / a 4
s
! s / a4
s/b
!s þ a4
s/a
3 2
2
s þ a2
ln
s2
3 2
2
s þ a2
ln
s2 þ b2
!a4
arctan
s
3
2
2as
arctan
2
2
2
s /a þb
3 2
2
s / as þ b
arctan
ab
ln
4 n . n ! . t ð2 n / 1Þ = 2
pffiffiffi
ð2 nÞ ! p
1 / e at
t
e bt / e at
t
2 . sinh ða tÞ
t
2 ½1 / cos ða tÞ%
t
2 ½cos ðb tÞ / cos ða tÞ%
t
sin ða tÞ
t
2 . sin ða tÞ . cos ðb tÞ
t
ðe a t / 1Þ . sin ðb tÞ
t
367
368
XIV Vektoranalysis
1 Ebene und räumliche Kurven
1.1 Vektorielle Darstellung einer Kurve
Eine ebene oder räumliche Kurve wird durch einen parameterabhängigen Ortsvektor
~
r ¼~
r ðtÞ beschrieben (t: reeller Kurvenparameter mit t1 ) t ) t2 Þ. Die Vektorkoordinaten sind dabei stetige Funktionen von t.
Ortsvektor einer ebenen Kurve
~
r ðtÞ ¼ xðtÞ ~
ex þ yðtÞ ~
ey ¼
xðtÞ; yðtÞ:
xðtÞ
!
y
P1
yðtÞ
Kurve
r(t1)
Vektorkoordinaten von ~
r ðtÞ
~
ex ; ~
ey : Basisvektoren der Ebene
)=
ey
Beispiel
3
Normalparabel: ~
r ðtÞ ¼ t ~
ex þ t 2 ~
ey ¼
t
t
r = r(t)
)
r(t
r(P
ex
&
P = (x(t); y(t))
y(t)
r(t2)
x(t)
P2
x
2
2
;
/1 < t < 1
&
Ortsvektor einer Raumkurve
0
1
xðtÞ
~
r ðtÞ ¼ xðtÞ ~
ex þ yðtÞ ~
ey þ zðtÞ ~
ez ¼ @ yðtÞ A
zðtÞ
xðtÞ; yðtÞ; zðtÞ:
~
ex ; ~
ey ; ~
ez :
Vektorkoordinaten von ~
r ðtÞ
Basisvektoren des Raumes
Vektorfunktion ~
a ¼~
a ðtÞ: Allgemeine Bezeichnung für einen von einem reellen Parameter t abhängigen Vektor ~
a mit den Vektorkoordinaten ax ðtÞ; ay ðtÞ und az ðtÞ.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_14
1 Ebene und räumliche Kurven
369
1.2 Differentiation eines Vektors nach einem Parameter
1.2.1 Ableitung einer Vektorfunktion
Die Differentiation einer Vektorfunktion ~
a ¼ ~
a ðtÞ nach dem Parameter t erfolgt komponentenweise (die Vektorkoordinaten ax ðtÞ; ay ðtÞ und az ðtÞ müssen dabei differenzierbare
Funktionen des Parameters t sein, die Ableitungen werden üblicherweise durch Punkte
gekennzeichnet):
0
a_ x ðtÞ
1
d
B
C
~
a ðtÞ ¼ ~
a_ðtÞ ¼ a_ x ðtÞ ~
ex þ a_ y ðtÞ ~
ey þ a_ z ðtÞ ~
ez ¼ @ a_ y ðtÞ A
dt
a_ z ðtÞ
:::
Analog werden höhere Ableitungen ~
a€; ~
a; . . . gebildet. Alle Ableitungen sind wieder
(parameterabhängige) Vektoren!
1.2.2 Tangentenvektor
Die 1. Ableitung eines Ortsvektors ~
r ¼~
r ðtÞ nach dem Parameter t ergibt den in der
Tangentenrichtung liegenden Tangentenvektor ~
r_ ¼ ~
r_ ðtÞ.
Tangentenvektor einer ebenen Kurve ~
r ¼~
r (t )
~
r_ ðtÞ ¼ x_ ðtÞ ~
ex þ y_ðtÞ ~
ey ¼
x_ ðtÞ
y
!
P
y_ðtÞ
r(t)
x_ ðtÞ; y_ðtÞ: Ableitungen der Vektorkoordinaten
von ~
r ðtÞ
&
Kurve
r(t)
x
Beispiel
2
~
r ðtÞ ¼ t ~
ex þ 3t ~
ey
) ~
r_ ðtÞ ¼ 2 t ~
ex þ 3~
ey
&
Tangentenvektor einer Raumkurve ~
r ¼~
r (t )
0
x_ ðtÞ
1
B
C
~
r_ ðtÞ ¼ x_ ðtÞ ~
ex þ y_ðtÞ ~
ey þ z_ðtÞ ~
ez ¼ @ y_ðtÞ A
z_ðtÞ
x_ ðtÞ; y_ðtÞ; z_ðtÞ:
r ðtÞ
Ableitungen der Vektorkoordinaten von ~
1.2.3 Ableitungsregeln für Summen und Produkte
Summen werden gliedweise, Produkte nach der Produktregel differenziert (ähnlich wie bei
Funktionen).
370
XIV Vektoranalysis
Summenregel
0
d 1
_
~
a þ b~ ¼ ~
a_ þ b~
dt
Produktregel
d
dt
d
dt
a) Skalarprodukt:
b) Vektorprodukt:
c) Produkt aus dem Skalar j
und dem Vektor ~
a:
1
0
_
~
a_ . b~ þ ~
a . b~
a . b~ ¼ ~
1
0
_
~
a - b~ ¼ ~
a_ - b~ þ ~
a - b~
d
ðj ~
a Þ ¼ j_ ~
a þ j~
a_
dt
Voraussetzung: ~
a ¼~
a ðtÞ, b~ ¼ b~ðtÞ und j ¼ jðtÞ sind differenzierbare Funktionen.
1.2.4 Geschwindigkeits- und Beschleunigungsvektor eines Massenpunktes
~
r ¼~
r ðtÞ:
Zeitabhängiger Ortsvektor der Bahnkurve eines Massenpunktes
Geschwindigkeitsvektor ~
v ¼ ~
v (t )
0
x_ ðtÞ
1
B
C
~
v ðtÞ ¼ ~
r_ ðtÞ ¼ x_ ðtÞ ~
ex þ y_ðtÞ ~
ey þ z_ðtÞ ~
ez ¼ @ y_ðtÞ A
z_ðtÞ
Beschleunigungsvektor ~
a ¼ ~
a (t )
0
x€ðtÞ
1
B
C
~
a ðtÞ ¼ ~
v_ ðtÞ ¼ ~
r€ðtÞ ¼ x€ðtÞ ~
ex þ y€ðtÞ ~
ey þ €z ðtÞ ~
ez ¼ @ y€ðtÞ A
€zðtÞ
&
Beispiel
0
1
cos t
~
r ðtÞ ¼ @ sin t A ;
t
t ( 0
ist der Ortsvektor der schraubenlinienförmigen Bahnkurve eines Elektrons um
die z-Achse. Wir bestimmen ~
v ðtÞ und ~
a ðtÞ:
0
1
0
1
/ sin t
/ cos t
~
v ðtÞ ¼ ~
r_ ðtÞ ¼ @ cos t A ;
~
a ðtÞ ¼ ~
v_ ðtÞ ¼ ~
r€ðtÞ ¼ @ / sin t A
1
0
Folgerung:
Der Beschleunigungsvektor ~
a ðtÞ ist ein ebener Vektor senkrecht zur z-Achse.
&
1 Ebene und räumliche Kurven
371
1.3 Bogenlänge einer Kurve
Bogenlänge einer ebenen Kurve ~
r ¼~
r (t )
P1
ðt2 " "
ðt2 qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"
_
s ¼ ~
r dt ¼
x_ 2 þ y_ 2 dt
t1
y
s
t1
P
x_ ðtÞ; y_ðtÞ: Ableitungen der Vektorkoordinaten
von ~
r ðtÞ
P2
r(t)
y(t)
x(t)
x(t1) = a
&
Beispiel
3
Kreis (Radius r): ~
r ðtÞ ¼ r
cos t
sin t
2
;
0 ) t < 2p
) ~
r_ ¼ r
3
/ sin t
cos t
2
;
x(t2) = b x
" "
"~
r_ " ¼ r
Kreisumfang (Bogenlänge des Vollkreises):
s ¼
2Ðp "
0
2Ðp
2Ðp
"
"~
r_ " dt ¼
r dt ¼ r .
dt ¼ r ½ t %2p
0 ¼ r ð2 p / 0Þ ¼ 2 p r
0
0
&
r ¼~
r (t )
Bogenlänge einer Raumkurve ~
ðt2 " "
ðt2 qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"
_
s ¼ ~
r dt ¼
x_ 2 þ y_ 2 þ z_ 2 dt
t1
x_ ðtÞ; y_ðtÞ; z_ðtÞ:
t1
Ableitungen der Vektorkoordinaten von ~
r ðtÞ
1.4 Tangenten- und Hauptnormaleneinheitsvektor einer Kurve
Jedem Punkt P einer ebenen oder räumlichen Kurve mit dem Ortsvektor ~
r ¼~
r ðtÞ lassen sich zwei aufeinander senkrecht stehende Einheitsvektoren zuordnen: Tangentenein~¼ N
~ ðtÞ.
heitsvektor ~
T ¼ ~
T ðtÞ und Hauptnormaleneinheitsvektor N
~
Tangenteneinheitsvektor T
~
r_
1 _
~
r;
T ¼ "" "" ¼ "" "" ~
~
~
r_
r_
j T~j ¼ 1
~
T liegt in der Kurventangente.
T
P
N
Kurve
372
XIV Vektoranalysis
~
Hauptnormaleneinheitsvektor N
~_
~ ¼ " T" ¼ " 1 " ~
N
T_ ;
_
_
"
"
"~
"
~
T
T
~j ¼ 1
jN
~ steht senkrecht auf der Kurventangente und zeigt in Richtung der Kurvenkrümmung
N
(siehe Abschnitt 1.5).
&
Beispiel
3
Kreis (Radius r): ~
r ¼ r
cos t
sin t
2
Tangenteneinheitsvektor ~
T:
3
2
" "
/ sin t
"~
~
r_ ¼ r
;
r_ " ¼ r
cos t
;
0 ) t < 2p
1 _
1
~
r ¼
T ¼ "" "" ~
.r
r
~
r_
)
~:
Hauptnormaleneinheitsvektor N
3
2
3
2
/ cos t
cos t
~
T_ ¼
¼ /
;
/ sin t
sin t
" "
"~
T_ " ¼ 1
)
3
/ sin t
cos t
2
3
¼
/ sin t
cos t
2
1 ~_
~ ¼ "1" ~
T_ ¼
T ¼ ~
T_ ¼ /
N
_
"~
"
1
T
3
cos t
sin t
2
~ ist stets auf den Mittelpunkt des Kreises gerichtet.
N
&
1.5 Krümmung einer Kurve
Die Krümmung j einer Raumkurve ist ein Maß für die Abweichung der Kurve von einer
Geraden und somit für die Richtungsänderung der Kurventangente pro Bogenlängenänderung ðj ( 0Þ.
Krümmung einer Raumkurve ~
r ¼~
r (s) (s: Bogenlänge)
"
"
"
"
" d T~" """ _ """
"~
€ðsÞ"
"
" ¼ ~
j ¼ "
T
ðsÞ
¼
r
ds "
T(s) = κ N
Kurve
~
r ¼~
r ðsÞ: „Natürliche“ Darstellung der Kurve
(Parameter: Bogenlänge s)
P
Krümmung einer Raumkurve ~
r ¼~
r (t ) (t : beliebiger Parameter)
"
"
"~
r_ - ~
r€"
j ¼ " "3
"~
r_ "
Krümmungsradius:
ð~
r_ 6¼ ~
0Þ
r ¼ 1=j (Kehrwert der Krümmung)
T
1 Ebene und räumliche Kurven
373
Sonderfall: Ebene Kurve ~
r ¼~
r (t )
Bei einer ebenen Kurve unterscheidet man noch zwischen Rechts- und Linkskrümmung
durch ein Vorzeichen (dies ist bei einer Raumkurve nicht möglich).
Es gilt:
j ¼
y
x_ y€ / x€ y_
ðx_ 2 þ y_ 2 Þ 3=2
κ <0
κ >0
j > 0 , Linkskrümmung
j < 0 , Rechtskrümmung
Krümmungsradius:
&
x0
r ¼ 1=j j j
x
Beispiel
Wir bestimmen Krümmung und Krümmungsradius des Kreises x ¼ r . cos t, y ¼ r . sin t, 0 ) t < 2 p:
x_ ¼ / r . sin t ;
j ¼
¼
x€ ¼ / r . cos t ;
y_ ¼ r . cos t ;
y€ ¼ / r . sin t
x_ y€ / x€ y_
ð/ r . sin tÞ . ð/ r . sin tÞ / ð/ r . cos tÞ . ðr . cos tÞ
¼
¼
ðx_ 2 þ y_ 2 Þ 3=2
ðr 2 . sin 2 t þ r 2 . cos 2 tÞ 3=2
r 2 . sin 2 t þ r 2 . cos 2 t
r 2 ðsin 2 t þ cos 2 tÞ
r2
1
¼
¼ 3 ¼
r
r
½r 2 ðsin 2 t þ cos 2 tÞ% 3=2
½r 2 % 3=2
(unter Beachtung von sin 2 t þ cos 2 t ¼ 1Þ
Somit gilt : r ¼
1
¼ r
jjj
&
Ebene Kurve y ¼ f (x)
Ortsvektor: ~
r ¼~
r ðxÞ ¼ x ~
ex þ y~
ey ¼ x ~
ex þ f ðxÞ~
ey
(Parameter ist die Koordinate x)
j ¼
&
y 00
½ 1 þ ðy 0 Þ 2 %3=2
y 00 < 0
y
00
> 0
,
Rechtskrümmung
,
Linkskrümmung
Beispiel
Wir berechnen die Krümmung der Normalparabel y ¼ x 2 an der Stelle x ¼ 0:
y ¼ x2;
j ¼
y0 ¼ 2x;
y 00 ¼ 2
y 00
2
¼
ð1 þ 4 x 2 Þ 3=2
½ 1 þ ðy 0 Þ 2 %3=2
)
j ðx ¼ 0Þ ¼ 2
ðLinkskr ümmungÞ
&
374
XIV Vektoranalysis
2 Flächen im Raum
2.1 Vektorielle Darstellung einer Fläche
Ortsvektor einer Fläche im Raum (Bild a))
0
1
xðu; vÞ
~
r ¼~
r ðu; vÞ ¼ xðu; vÞ ~
ex þ yðu; vÞ ~
ey þ zðu; vÞ ~
ez ¼ @ yðu; vÞ A
zðu; vÞ
u; v:
Voneinander unabhängige (reelle) Parameter (sog. Flächenparameter)
z
en
ini
L
u-
Fläche
u = const. = a1
u = const. = a2
P
y
&
v = const. = b2
ien
x
Lin
y
x
v = const. = b3
v-
z
a)
u = const. = a3
P(a2;b2)
r
v = const. = b1
b)
Beispiel
Ortsvektor der Mantelfläche eines Rotationsparaboloids (Rotationsachse: z-Achse):
0
1
u
2
2
@
A
~
r ðu; vÞ ¼ u~
ex þ v~
ey þ ðu þ v Þ~
ez ¼
v
ðu; v 2 RÞ
u2 þ v2
&
Parameter- oder Koordinatenlinien einer Fläche (Bild b))
u-Linien (u: variabel, v: fest): ~
r ¼~
r ðu; v ¼ const:Þ ¼ ~
r ðuÞ
v-Linien (u: fest, v: variabel): ~
r ¼~
r ðu ¼ const:; vÞ ¼ ~
r ðvÞ
Tangentenvektoren an die Koordinatenlinien
~
tu ¼
@~
r
;
@u
~
tv ¼
@~
r
@v
~
tu und ~
tv sind die partiellen Ableitungen
1. Ordnung des Ortsvektors ~
r ¼~
r ðu; vÞ
v-Linie
tv
P
tu
u-Linie
2 Flächen im Raum
375
2.2 Flächenkurven
Sind die Parameter u und v einer Fläche
~
r ¼~
r ðu; vÞ selbst Funktionen einer (reellen)
Variablen t, so beschreibt der Ortsvektor
Flächenkurve r(t)
~
r ¼~
r ðtÞ ¼ ~
r ðuðtÞ; vðtÞÞ
eine Flächenkurve (d. h. eine auf der Fläche
gelegene Kurve).
r
P
r(t)
Fläche r(u; v)
0
Tangentenvektor an eine Flächenkurve
~
r_ ¼ ~
r_ ðtÞ ¼ u_ ðtÞ ~
tu þ v_ ðtÞ ~
tv
u_ ðtÞ; v_ ðtÞ:
~
tu ; ~
tv :
Ableitungen der Flächenparameter u und v nach t
Tangentenvektoren an die Koordinatenlinien der Fläche
2.3 Flächennormale und Flächenelement
Jedem Punkt P einer Fläche mit dem Ortsvektor ~
r ¼~
r ðu; vÞ lassen sich eine Flächen~ und ein Flächenelement dA zuordnen.
normale N
~
Flächennormale N
~ steht senkrecht auf der Tangentialebene
N
bzw. dem Flächenelement dA.
~
~
~ ¼ " tu - tv " ;
N
"~
~
tu - tv "
~
tu ; ~
tv :
" "
"N
~" ¼ 1
Tangentenvektoren an die Koordinatenlinien der Fläche
N
P
tv
tu
Fläche r(u; v)
&
Beispiel
0
1
x
A : Ebene durch den Nullpunkt ðz ¼ / x / yÞ
y
/x / y
0
1
0
1
0
1
0 1
0 1
1
0
0þ1
1
1
~
~
t
t
1
x
y
~¼
~
ty ¼ @ 0 A - @ 1 A ¼ @ 0 þ 1 A ¼ @ 1 A ;
N
¼ pffiffiffi @ 1 A
tx - ~
~
j
t
j
t
j
3
x
y
/1
/1
1/0
1
1
~
r ¼ @
Folgerung:
~ ist ein konstanter Vektor.
N
&
376
XIV Vektoranalysis
Flächenelement dA
u + du
Das Flächenelement dA wird durch je zwei
benachbarte u- und v-Linien begrenzt.
R
dv
Flächenelement dA
u = const.
dA ¼ j~
tu - ~
tv j du dv
~
tu ; ~
tv :
v+
S
tv dv
Tangentenvektoren an die Koordinatenlinien der Fläche
v = const.
Q
tu du
P
2.4 Tangentialebene
Die Tangentialebene in einem Flächenpunkt P enthält alle Tangenten, die man in diesem
Punkt an die Fläche anlegen kann.
2.4.1 Tangentialebene einer Fläche vom Typ ~
r ¼~
r (u; v )
~0 . ð~
N
r /~
r0 Þ ¼ 0
oder
ð~
r /~
r0 Þ ¼ 0
tu - ~
tv Þ0 . ð~
~0 :
N
Flächennormale in P
~
r0 :
Ortsvektor von P
~
r:
Ortsvektor eines beliebigen
Punktes Q der Tangentialebene
Tangentialebene in P
N
~
tu ; ~
tv : Tangentenvektoren in P (spannen
die Tangentialebene in P auf)
&
Q
tv
P
~
r ðu; vÞ ¼ u~
ex þ v~
ey þ ðu 2 þ v 2 Þ ~
ez ¼
0
1
u
A
¼ @
v
ðu; v 2 RÞ
u2 þ v2
r
tu
r0
Beispiel
PQ
0
Wir bestimmen die Tangentialebene für die Flächenparameter u ¼ 1 und v ¼ 1, d. h. im Flächenpunkt
P ¼ ð1; 1; 2Þ:
0 1
0 1
0 1
0 1
1
0
1
0
@~
r
@~
r
@
A
@
A
@
A
~
~
~
¼
0
¼
1
tu ¼
;
tv ¼
) ~
tu ð1; 1Þ ¼ 0 ;
tv ð1; 1Þ ¼ @ 1 A
@u
@v
2u
2v
2
2
0 1 0 1
0
1
1
0
/2
~
tu ð1; 1Þ - ~
tv ð1; 1Þ ¼ @ 0 A - @ 1 A ¼ @ /2 A ;
2
2
1
0 1 0 1
0
1
x
1
x /1
~
r /~
r0 ¼ @ y A / @ 1 A ¼ @ y / 1 A
z
2
z/2
0
1 0
1
/2
x /1
1
0
@
A
@
Tangentialebene : ~
tu ð1; 1Þ - ~
tv ð1; 1Þ . ð~
r /~
r0 Þ ¼ /2 . y / 1 A ¼ 0
1
z/2
/2 ðx / 1Þ / 2ðy / 1Þ þ 1ðz / 2Þ ¼ 0
)
z ¼ 2x þ 2y / 2
)
&
2 Flächen im Raum
377
2.4.2 Tangentialebene einer Fläche vom Typ z ¼ f (x; y)
Vektordarstellung der Fläche (die unabhängigen Variablen x und y dienen dabei als Flächenparameter):
0
1
x
~
r ¼~
r ðx; yÞ ¼ x ~
ex þ y~
ey þ f ðx; yÞ ~
ez ¼ @ y A
f ðx; yÞ
Tangentialebene im Flächenpunkt P = (x0 ; y0 ; z0 = f (x0 ; y0))
1
0
~
tx - ~
ty 0 . ð~
r /~
r0 Þ ¼ 0 oder
0 1
1
@~
r
~
¼ @ 0 A;
tx ¼
@x
fx
fx ; fy :
~0 . ð~
N
r /~
r0 Þ ¼ 0
0 1
0
@~
r
~
ty ¼
¼ @ 1 A;
@y
fy
0
1
/ fx
1
~ ¼ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi @ /fy A
N
fx2 þ fy2 þ 1
1
Partielle Ableitungen 1. Ordnung von z ¼ f ðx; yÞ
Tangentialebene im Flächenpunkt P in expliziter Form
z ¼ fx ðx0 ; y0 Þ . ðx / x0 Þ þ fy ðx0 ; y0 Þ . ðy / y0 Þ þ z0
(Siehe hierzu auch IX.2.4)
fx ðx0 ; y0 Þ, fy ðx0 ; y0 Þ:
Partielle Ableitungen 1. Ordnung von z ¼ f ðx; yÞ im Flächenpunkt P ¼ ðx0 ; y0 ; z0 Þ mit z0 ¼ f ðx0 ; y0 Þ
2.4.3 Tangentialebene einer Fläche vom Typ F(x; y; z) = 0
ðgrad Fðx; y; zÞÞ0 . ð~
r /~
r0 Þ ¼ 0
~
r0 : Ortsvektor des Flächenpunktes P ¼ ðx0 ; y0 ; z0 Þ
Der Gradient von F ðx; y; zÞ wird im Flächenpunkt P gebildet (siehe Abschnitt 4).
Bezeichnungen wie oben; der Gradient von Fðx; y; zÞ wird im Flächenpunkt P gebildet
(siehe hierzu Abschnitt 4).
&
Beispiel
Gleichung der Tangentialebene an die Kugeloberfläche
P ¼ ð2; 2; 1Þ:
0 1
2x
2
2
2
grad F ¼ grad ðx þ y þ z / 9Þ ¼ @ 2 y A )
2z
0 1
4
r /~
r0 Þ ¼ @ 4 A .
Tangentialebene in P : ðgrad FÞ0 . ð~
2
4 ðx / 2Þ þ 4 ðy / 2Þ þ 2 ðz / 1Þ ¼ 0
)
Fðx; y; zÞ ¼ x 2 þ y 2 þ z 2 / 9 ¼ 0 im Punkt
0 1
4
Gradient in P : ðgrad FÞ0 ¼ @ 4 A
2
0
1
x /2
@y / 2A ¼ 0 )
z/1
z ¼ /2x / 2y þ 9
&
378
XIV Vektoranalysis
3 Skalar- und Vektorfelder
3.1 Skalarfelder
Ein Skalarfeld ordnet jedem Punkt P eines ebenen oder räumlichen Bereiches in eindeutiger Weise einen Skalar zu.
Ebenes bzw. räumliches Skalarfeld
f ðPÞ ¼ f ðx; yÞ
bzw.
f ðPÞ ¼ f ðx; y; zÞ
Stationäres Feld: Das skalare Feld verändert sich nicht im Laufe der Zeit, ist also zeitunabhängig.
Niveau- oder "quipotentialflächen: Flächen im Raum, auf denen das Skalarfeld einen konstanten Wert annimmt: f ðx; y; zÞ ¼ const:
Niveaulinien eines ebenen Skalarfeldes: Kurven, auf denen das Skalarfeld einen konstanten
Wert annimmt: f ðx; yÞ ¼ const:
&
Beispiel
Elektrostatisches Potential in der Umgebung einer geladenen Kugel. Niveau- oder #quipotentialflächen: konzentrische Kugelschalen.
&
3.2 Vektorfelder
Ein Vektorfeld ordnet jedem Punkt P eines ebenen oder räumlichen Bereiches in eindeutiger Weise einen Vektor zu.
Ebenes Vektorfeld
~ðx; yÞ ¼ Fx ðx; yÞ~
F
ex þ Fy ðx; yÞ~
ey ¼
3
2
Fx ðx; yÞ
¼
Fy ðx; yÞ
Fx ; Fy :
Skalare Komponenten des ebenen
~ðx; yÞ ðvon x und
Vektorfeldes F
y abhängige FunktionenÞ
y
)
F(P
P
y
x
=F
(x;
y)
Fy (x; y)
Fx (x; y)
x
3 Skalar- und Vektorfelder
379
Räumliches Vektorfeld
0
1
Fx ðx; y; zÞ
~ðx; y; zÞ ¼ Fx ðx; y; zÞ~
F
ex þ Fy ðx; y; zÞ~
ey þ Fz ðx; y; zÞ~
ez ¼ @ Fy ðx; y; zÞ A
Fz ðx; y; zÞ
Fx ; Fy ; Fz :
&
~ðx; y; zÞ
Skalare Komponenten des räumlichen Vektorfeldes F
(von x; y und z abhängige Funktionen)
Beispiel
Geschwindigkeitsfeld einer strömenden Flüssigkeit: Zu jedem Flüssigkeitsteilchen (Massenpunkt) gehört ein
Geschwindigkeitsvektor.
&
Feldlinien
Kurven, die in jedem Punkt P eines Vektorfel~¼ F
~ðPÞ durch den dortigen Feldvektor
des F
tangiert werden. Gleichung der Feldlinien:
~- ~
F
r_ ¼ ~
0
oder
F(P)
P
Feldlinie
~ - d~
F
r ¼~
0
~
r : Ortsvektor von P
Feldlinien schneiden sich nicht!
&
Beispiel
Elektrisches Feld in der Umgebung einer positiven Punktladung: Die elektrischen Feldlinien verlaufen radial
nach außen.
&
Spezielle Vektorfelder
***!
~ (P) = const:
1. Homogenes Vektorfeld: F
Der Feldvektor hat überall die gleiche Richtung und den gleichen Betrag.
Beispiel: Elektrisches Feld (elektrische Feldstärke) in einem geladenen Plattenkondensator.
~(P) = f (r) ~
2. Kugel- oder radialsymmetrisches Vektorfeld (Zentralfeld): F
er
Der Feldvektor hat radiale Richtung (Einheitsvektor ~
er ), sein Betrag hängt nur vom
"
"
"
"
~ðPÞ ¼ j f ðrÞ j.
Abstand r vom Nullpunkt ab: F
Beispiel: Gravitationsfeld der Erde.
~ (P) = f (r) ~
3. Zylinder- oder axialsymmetrisches Vektorfeld: F
er
Der Feldvektor hat axiale Richtung ðEinheitsvektor ~
er Þ, sein Betrag hängt nur vom
"
"
"
"
~ðPÞ ¼ j f ðrÞ j.
Abstand r von der Zylinderachse ab: F
Beispiel: Elektrisches Feld in der Umgebung eines homogen geladenen Zylinders.
380
XIV Vektoranalysis
4 Gradient eines Skalarfeldes
Definition des Gradienten (in kartesischen Koordinaten)
0
1
@f=@x
@f
@f
@f
~
~
~
grad f ¼
ex þ
ey þ
ez ¼ @ @f=@y A
@x
@y
@z
@f=@z
f ¼ f ðx; y; zÞ: Räumliches Skalarfeld
Darstellung des Gradienten in Polar-, Zylinder- und Kugelkoordinaten: siehe Abschnitt 6
Bei einem ebenen Feld verschwindet die dritte Vektorkomponente (z-Komponente).
Beispiel
&
Gradient des räumlichen Skalarfeldes f ¼ x 2 þ y 2 þ z im Punkt P ¼ ð1; 0; 2Þ:
0 1
0 1
2x
2
@f
@f
@f
grad f ¼
~
ex þ
~
ey þ
~
ez ¼ 2 x ~
ex þ 2 y ~
ey þ 1~
ez ¼ @ 2 y A ) ðgrad fÞ0 ¼ @ 0 A
@x
@y
@z
1
1
&
Nabla-Operator
0
1
@=@x
r ¼ @ @=@y A
@=@z
!
Die skalaren Komponenten sind die
partiellen Differentialoperatoren
@=@x, @=@y und @=@z (siehe IX.2.1)
!
Der Vektor grad f ist formal auch als Produkt des Nabla-Operator r mit dem Skalar f
darstellbar:
0
1
0
1
@=@x
@f=@x
grad f ¼ r f ¼ @ @=@y A f ¼ @ @f=@y A
@=@z
@f=@z
!
Anmerkungen
(1)
Der Operator „grad“ (Nabla-Operator) ist ein Differentialoperator 1. Ordnung.
(2)
Der Gradient eines räumlichen Skalarfeldes fðx; y; zÞ steht immer senkrecht auf
den Niveauflächen fðx; y; zÞ ¼ const: und zeigt in die Richtung des größten Zuwachses von f.
(3)
Bei einem ebenen Skalarfeld fðx; yÞ ist grad f ein ebener Vektor, der senkrecht
zu den Niveaulinien fðx; yÞ ¼ const: verläuft.
4 Gradient eines Skalarfeldes
381
Rechenregeln
f und y sind skalare Felder, c eine reelle Konstante:
(1)
grad c ¼ 0
(2)
grad ðc fÞ ¼ cðgrad fÞ
(3)
grad ðf þ yÞ ¼ grad f þ grad y
(4)
grad ðf þ cÞ ¼ grad f
(5)
grad ðf . yÞ ¼ fðgrad yÞ þ yðgrad fÞ
(Summenregel)
(Produktregel)
Richtungsableitung
@f
a ist ein Maß
eines Skalarfeldes f in Richtung des Vektors ~
@~
a
für die "nderung des Funktionswertes von f, wenn man von einem Punkt P aus in
Richtung von ~
a um eine Längeneinheit fortschreitet:
Die Richtungsableitung
@f
1
¼ ðgrad fÞ . ~
ea ¼
ðgrad fÞ . ~
a
@~
a
j~
aj
@f
ist die Projektion des Gradienten von f auf den normierten Rich@~
a
~
a
tungsvektor ~
ea ¼
. Der Maximalwert wird in Richtung des Gradienten erreicht.
j~
aj
Der Vektor
&
Beispiel
2
f ¼ xy þ z ;
0 1
1
~
a ¼ @1A;
1
P ¼ ð1; 1; 2Þ
Wir berechnen die Richtungsableitung des skalaren Feldes f im Punkt P in Richtung des Vektors ~
a:
0 1
0 1
y
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
grad f ¼ @ x A ) ðgrad fÞ0 ¼ @ 1 A ;
j~
aj ¼
12 þ 12 þ 12 ¼ 3
2z
4
3
0 1 0 1
pffiffiffi
2
1
1
pffiffiffi
@f
1
1 @ A @ A
1
6
6 3
ðgrad fÞ0 . ~
a ¼ pffiffiffi
1 . 1 ¼ pffiffiffi ð1 þ 1 þ 4Þ ¼ pffiffiffi ¼
¼ 2 3
¼
3
@~
a 0 j~
aj
3
3
3
4
1
&
382
XIV Vektoranalysis
5 Divergenz und Rotation eines Vektorfeldes
5.1 Divergenz eines Vektorfeldes
Definition der Divergenz (in kartesischen Koordinaten)
~¼
div F
@Fx
@Fy
@Fz
þ
þ
@x
@y
@z
~ðx; y; zÞ
Fx , Fy , Fz : Skalare Komponenten des Vektorfeldes F
Bei einem ebenen Feld verschwindet der dritte Summand.
Darstellung der Divergenz in Polar-, Zylinder- und Kugelkoordinaten: siehe Abschnitt 6
Beispiel
0
&
1
x2y
~ ¼ @x þ yA
F
yz
)
~¼
div F
@
@
@
ðx 2 yÞ þ
ðx þ yÞ þ
ðy zÞ ¼ 2x y þ 1 þ y
@x
@y
@z
Divergenz im Punkt P ¼ ð1; 2; 0Þ:
1
~
div F
0
0
¼ 4þ1þ2 ¼ 7
&
!
~ ist formal auch als Skalarprodukt des Nabla-Operators r mit dem
Der Skalar div F
~ darstellbar:
Vektor F
!
~¼ r. F
~
div F
Anmerkungen
(1)
Der Operator „div“ ist ein Differentialoperator 1. Ordnung.
(2)
Die Bezeichnung „Divergenz“ stammt aus der Hydrodynamik und bedeutet „Auseinanderströmen einer Flüssigkeit“ („Divergieren“).
~ heißt auch „Quelldichte“ oder „Quellstärke pro Volumeneinheit“. Ein Vektordiv F
~, dessen Divergenz verschwindet, heißt quellenfrei. Gilt in einem Punkt
feld F
~ > 0, so hat das Vektorfeld dort eine „Quelle“, für div F
~ < 0 eine „Senke“.
div F
(3)
Rechenregeln
~ und B
~ sind Vektorfelder, ~
A
a ein konstanter Vektor, f ein skalares Feld und c eine
reelle Konstante:
(1)
(2)
(3)
(4)
(5)
div ~
a ¼ 0
1 0
1
0
~ ¼ c div A
~
div c A
1
0
~þB
~ þ div B
~ ¼ div A
~
div A
(Summenregel)
1
0
~þ~
~
div A
a ¼ div A
1
0
1
0
~ ¼ ðgrad fÞ . A
~ þ f div A
~
div f A
(Produktregel)
5 Divergenz und Rotation eines Vektorfeldes
383
5.2 Rotation eines Vektorfeldes
Definition der Rotation (in kartesischen Koordinaten)
0
1
@Fz
@Fy
/
B
B @y
C
@z C
B
C
B @F
@Fz C
x
B
C
~
rot F ¼ B
/
C
@x C
B @z
B
C
@ @Fy
@Fx A
/
@x
@y
~ðx; y; zÞ
Skalare Komponenten des Vektorfeldes F
Fx , Fy , Fz :
Beispiel
&
Regel : Durch zyklisches Vertauschen
der Variablen ðx ! y ! z ! xÞ
erhält man aus der 1: Komponente die
2: und aus dieser die 3: Komponente:
0
1
xy z
@
~
F ¼ x þ yA
z2
1
@
@
2
ðz
Þ
/
ðx
þ
yÞ
C
B @y
@z
C
B
0
1 0
1
C
B
0/0
0
C
B @
@
2
@
A
@
C
B
~
¼
xy A
rot F ¼ B
ðx y zÞ /
ðz Þ C ¼ x y / 0
@x
C
B @z
1
/
x
z
1
/
xz
C
B
A
@@
@
ðx þ yÞ /
ðx y zÞ
@x
@y
0
)
&
!
~ ist formal auch als Vektorprodukt des Nabla-Operators r mit dem
Der Vektor rot F
~
Vektor F darstellbar:
!
~ ¼ r -F
~
rot F
Determinantenschreibweise
"
" ~
" ex
"
~
rot F ¼ " @=@x
"
" F
x
~
ey
@=@y
Fy
"
"
"
"
@=@z "
"
Fz "
~
ez
~
ex ; ~
ey ; ~
ez : Basisvektoren des Raumes
@=@x; @=@y; @=@z: Partielle Differentialoperatoren 1. Ordnung (siehe IX.2.1)
Durch Entwicklung der Determinante nach den Elementen der 1. Zeile erhält man die weiter oben stehende Definitionsformel der Rotation.
Anmerkungen
(1)
(2)
(3)
(4)
Der Operator „rot“ ist ein Differentialoperator 1. Ordnung.
Die Bezeichnung „Rotation“ stammt aus der Hydrodynamik und beschreibt dort die
Bildung von „Wirbeln“ (geschlossene Feldlinien in den Geschwindigkeitsfeldern strömender Flüssigkeiten).
~ heißt auch „Wirbeldichte“ oder „Wirbelfeld“ zu F
~.
Der Vektor rot F
~, dessen Rotation verschwindet, heißt wirbelfrei.
Ein Vektorfeld F
384
XIV Vektoranalysis
Rotation eines ebenen Vektorfeldes (Fz = 0)
~¼
rot F
3
@Fy
@Fx
/
@x
@y
2
~
ez
Die Komponenten in x- und y-Richtung verschwinden!
Rechenregeln
~ und B
~ sind Vektorfelder, ~
A
a ein konstanter Vektor, f ein skalares Feld und c eine
reelle Konstante:
(1) rot ~
a ¼~
0
1 0
1
0
~ ¼ c rot A
~
(2) rot c A
1
0
~þB
~ þ rot B
~ ¼ rot A
~
(3) rot A
(Summenregel)
1
0
~þ~
~
(4) rot A
a ¼ rot A
1
0
1
0
~ ¼ ðgrad fÞ - A
~ þ f rot A
~
(5) rot f A
(Produktregel)
5.3 Spezielle Vektorfelder
~= 0
Quellenfreies Vektorfeld: div F
~ lässt sich stets als Rotation eines Vektorfeldes E
~, VektorEin quellenfreies Vektorfeld F
potential genannt, darstellen:
~¼ 0
div F
)
~ ¼ rot E
~
F
~ ¼ rot E
~ ist quellenfrei:
Auch die Umkehrung gilt: Ein Wirbelfeld F
~ ¼ rot E
~
F
)
~ ¼ div ðrot E
~Þ ¼ 0
div F
Quellenfreie Felder: Elektrisches Feld einer Punktladung, Gravitationsfeld der Erde.
~= 0
Wirbelfreies Vektorfeld: rot F
~ lässt sich stets als Gradient eines skalaren Feldes f darEin wirbelfreies Vektorfeld F
stellen:
~¼ 0
rot F
)
~ ¼ grad f
F
~ ¼ grad f ist wirbelfrei:
Auch die Umkehrung gilt: Ein Gradientenfeld F
~ ¼ grad f
F
)
~ ¼ rot ðgrad fÞ ¼ ~
rot F
0
Wirbelfreie Felder: Homogenes elektrisches Feld in einem Plattenkondensator, Zentralfelder
wie z. B. das Gravitationsfeld der Erde, zylindersymmetrische Felder.
6 Darstellung von Gradient, Divergenz, Rotation und Laplace-Operator
385
~ = 0 und rot F
~=~
Quellen- und wirbelfreies Vektorfeld: div F
0
~ ist als Gradient eines skalaren Feldes f
Ein quellen- und wirbelfreies Vektorfeld F
~
darstellbar, d. h. F ¼ grad f, wobei f der Laplaceschen Differentialgleichung
Df ¼
@ 2f
@ 2f
@ 2f
þ
þ
¼ 0
2
2
@x
@y
@z 2
genügt. Dabei ist D der sog. Laplace-Operator
!
!
D ¼ r . r ¼ div ðgradÞ ¼
@2
@2
@2
þ
þ
@x 2
@y 2
@z 2
!
(Differentialoperator 2. Ordnung, Skalarprodukt des Nabla-Operators r mit sich selbst)
Df ¼ f ðx; y; zÞ: Poisson- oder Potentialgleichung, deren Lösungen als Potentialfunktionen bezeichnet werden.
6 Darstellung von Gradient, Divergenz, Rotation und
Laplace-Operator in speziellen Koordinatensystemen
6.1 Darstellung in Polarkoordinaten
Polarkoordinaten
Die Polarkoordinaten r; j eines Punktes P der Ebene bestehen aus einer Abstandskoordinate r und einer Winkelkoordinate j (Bild a)):
r:
j:
Abstand des Punktes P vom Koordinatenursprung O ðr ( 0Þ
*!
Winkel zwischen dem Ortsvektor ~
r ¼ OP des Punktes P und der positiven
x-Achse (Hauptwert: 0 ) j < 2p bzw. 0" ) j < 360" Þ.
Siehe hierzu auch I.9.1.2.
y
y
f = const.
(r-Linie)
P
r
y
x
r = const.
(f-Linie)
f
0
a)
x
x
b)
386
XIV Vektoranalysis
Koordinatenlinien (Bild b), siehe vorherige Seite unten)
Das Polarkoordinatensystem ist ein sog. krummliniges Koordinatensystem mit den folgenden Koordinatenlinien:
r = const.:
Konzentrische Kreise um den Koordinatenursprung ðj-LinienÞ
j = const.:
Radial vom Koordinatenursprung nach außen laufende Strahlen ðr-LinienÞ
Die r- und j-Linien schneiden sich in jedem Punkt senkrecht, d. h. die Polarkoordinaten
sind (wie die kartesischen Koordinaten) orthogonale ebene Koordinaten.
Zusammenhang zwischen den Polarkoordinaten und den kartesischen Koordinaten
Polarkoordinaten ! Kartesische Koordinaten
x ¼ r . cos j ,
y ¼ r . sin j
Kartesische Koordinaten ! Polarkoordinaten
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y
x
;
cos j ¼
;
r ¼ x2 þ y2;
sin j ¼
r
r
Vektordarstellung in Polarkoordinaten
tan j ¼
y
a
~
a ¼ ar ~
er þ aj ~
ej
~
er , ~
ej :
ar , aj :
Tangenteneinheitsvektoren an die
r- bzw. j-Koordinatenlinie
(Basisvektoren)
af
Vektorkoordinaten
Orthogonale Transformationsmatrix
3
2
cos j sin j
A ¼
/ sin j cos j
y
x
r
ef
er
ar
P
f
x
Matrix A regelt die Transformation der Basisvektoren und Vektorkoordinaten (kartesische
Koordinaten ! Polarkoordinaten).
Gradient, Divergenz, Rotation und Laplace-Operator in Polarkoordinaten
Skalarfeld in Polarkoordinaten
f ¼ f ðr; jÞ
Vektorfeld in Polarkoordinaten
~¼ F
~ðr; jÞ ¼ Fr ðr; jÞ~
F
er þ Fj ðr; jÞ~
ej
6 Darstellung von Gradient, Divergenz, Rotation und Laplace-Operator
387
Gradient des Skalarfeldes f (r; j)
grad f ¼
@f
1 @f
~
~
er þ
ej
.
@r
r @j
Divergenz des Vektorfeldes F~(r; j)
~ ¼ 1 . @ ðr . Fr Þ þ 1 . @Fj ¼ 1
div F
r @r
r
r
@j
3
@Fj
@
ðr . Fr Þ þ
@r
@j
2
Rotation des Vektorfeldes F~ (r; j)
Es existiert nur eine Komponente senkrecht zur x; y-Ebene (z-Richtung):
3
2
1 @
1 @Fr
1 @
@Fr
~
½ rot F %z ¼
.
ðr . Fj Þ /
.
¼
ðr . Fj Þ /
r @r
r @j
r @r
@j
Laplace-Operator
Df ¼
@ 2f
1 @f
1 @ 2f
þ
.
þ 2 .
2
@r
r @r
r
@j 2
6.2 Darstellung in Zylinderkoordinaten
Zylinderkoordinaten
Die Zylinderkoordinaten r, j und z eines Raumpunktes P bestehen aus den Polarkoordinaten r und j des Projektionspunktes P 0 in der x; y-Ebene und der (kartesischen)
Höhenkoordinate z 1Þ :
r ( 0;
z
0 ) j < 2p ;
/1 < z < 1
z
·
r
Siehe hierzu auch I.9.2.2
P = (x; y; z)
z
0
f
r
x
x
1Þ
y
·
y
x
y
P' = (x; y)
Die Zylinderkoordinate r gibt den senkrechten Abstand des Raumpunktes P von der z-Achse an und ist daher
nicht zu verwechseln mit dem Abstand r desselben Punktes vom Koordinatenursprung 0, d. h. mit der Länge
*!
des Ortsvektors ~
r ¼ OP . Sie wird häufig auch (wenn Verwechslungen auszuschließen sind) mit r bezeichnet.
388
XIV Vektoranalysis
Koordinatenflächen
Koordinatenflächen entstehen, wenn jeweils eine der drei Zylinderkoordinaten festgehalten
wird:
r = const.:
j = const.:
Zylindermantel
Halbebene durch die z-Achse
z = const.:
Parallelebene zur x; y-Ebene in der „Höhe“ z
Die Koordinatenflächen stehen paarweise senkrecht aufeinander.
Koordinatenlinien
Koordinatenlinien entstehen, wenn jeweils zwei der drei Zylinderkoordinaten festgehalten
werden. Sie sind somit Schnittkurven zweier Koordinatenflächen:
j, z = const.:
r, z = const.:
Halbgerade senkrecht zur z-Achse (r-Linie; r ( 0)
Kreis um die z-Achse parallel zur x; y-Ebene (j-Linie)
r, j = const.:
Mantellinie des Zylinder (z-Linie)
Die Koordinatenlinien stehen in jedem Punkt paarweise senkrecht aufeinander (Ausnahme:
Koordinatenursprung). Die Zylinderkoordinaten sind daher (wie die kartesischen Koordinaten) orthogonale räumliche Koordinaten.
Zusammenhang zwischen den Zylinderkoordinaten und den kartesischen Koordinaten
Zylinderkoordinaten ! Kartesische Koordinaten
x ¼ r . cos j ,
y ¼ r . sin j ,
z ¼ z
Kartesische Koordinaten ! Zylinderkoordinaten
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
y
x
r ¼ x2 þ y2 ;
sin j ¼
;
cos j ¼
;
r
r
tan j ¼
y
;
x
z ¼ z
Die Zylinderkoordinaten stimmen mit den kartesischen Koordinaten in der „Höhenkoordinate“ z überein.
Linienelement ds
Das Linienelement ist der Verbindungsbogen zweier differentiell benachbarter Punkte, die
sich in ihren Zylinderkoordinaten um dr, dj, dz voneinander unterscheiden. Es besitzt
die Länge
ds ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðdrÞ 2 þ r 2 ðdjÞ 2 þ ðdzÞ 2
Flächenelement dA auf dem Zylindermantel ( r = const.)
Flächenstück auf dem Zylindermantel, begrenzt durch je zwei benachbarte j- und z-Koordinatenlinien, mit dem Flächeninhalt
dA ¼ r dj dz
6 Darstellung von Gradient, Divergenz, Rotation und Laplace-Operator
389
Volumenelement dV
dV ¼ r dr dj dz
Vektordarstellung in Zylinderkoordinaten
z
ez
~
a ¼ ar ~
er þ aj ~
ej þ az ~
ez
r
~
er , ~
ej , ~
ez :
Tangenteneinheitsvektoren an
die r-, j- bzw. z-Koordinatenlinie (Basisvektoren)
ar , aj , az : Vektorkoordinaten
Orthogonale Transformationsmatrix
0
1
cos j sin j 0
A ¼ @ / sin j cos j 0 A
0
0
1
ef
z
f
r
ep
y
x
Matrix A regelt die Transformation der Basisvektoren und Vektorkoordinaten (kartesische
Koordinaten ! Zylinderkoordinaten).
Gradient, Divergenz, Rotation und Laplace-Operator in Zylinderkoordinaten
Skalarfeld in Zylinderkoordinaten
f ¼ f ðr; j; zÞ
Vektorfeld in Zylinderkoordinaten
~¼ F
~ðr; j; zÞ ¼ Fr ðr; j; zÞ ~
F
er þ Fj ðr; j; zÞ ~
ej þ Fz ðr; j; zÞ ~
ez
Gradient des Skalarfeldes f ( r; j; z)
grad f ¼
@f
1 @f
@f
~
~
~
er þ
.
ej þ
ez
@r
r @j
@z
~ ( r; j; z)
Divergenz des Vektorfeldes F
~¼
div F
1 @
1 @Fj
@Fz
.
ðr . Fr Þ þ
.
þ
@z
r @r
r @j
~ ( r; j; z)
Rotation des Vektorfeldes F
3
2
3
2
3
2
@Fr
@Fr
@Fz
1
@
~ ¼ 1 . @Fz / @Fj ~
~
~
rot F
/
ðr . Fj Þ /
ez
er þ
ej þ
r @j
@z
@z
@r
r @r
@j
Laplace-Operator
3
2
1 @
@f
1 @ 2f
@ 2f
Df ¼
.
r.
þ 2 .
þ
r @r
@r
r
@j 2
@z 2
390
XIV Vektoranalysis
6.3 Darstellung in Kugelkoordinaten
Kugelkoordinaten
Die Kugelkoordinaten r, J und j eines Raumpunktes P bestehen aus einer Abstandskoordinate r und zwei Winkelkoordinaten J und j:
r:
*!
Länge des Ortsvektors ~
r ¼ OP
J:
Winkel zwischen dem Ortsvektor ~
r und der positiven z-Achse ð0 ) J ) pÞ
j:
Winkel zwischen der Projektion des Ortsvektors ~
r auf die x; y-Ebene und der
positiven x-Achse ð0 ) j < 2 pÞ
ðr ( 0Þ
Siehe hierzu auch I.9.2.4
J:
Breitenkoordinate;
j:
z
Längenkoordinate
·
Koordinatenflächen
r = const.:
J = const.:
Kugeloberfläche (Kugelschale)
Mantelfläche eines Kegels (Kegelspitze im Koordinatenursprung)
j = const.:
Halbebene durch die z-Achse
Die Koordinatenflächen stehen in jedem Punkt paarweise senkrecht aufeinander.
P
r
Koordinatenflächen entstehen, wenn jeweils eine
der drei Kugelkoordinaten festgehalten wird:
r
z
u
0
y
f
x
·
x
y
Koordinatenlinien
Koordinatenlinien entstehen, wenn jeweils zwei der drei Zylinderkoordinaten festgehalten
werden. Sie sind somit Schnittkurven zweier Koordinatenflächen:
J, j = const.:
r, J = const.:
Radialer Strahl vom Koordinatenursprung nach außen (r-Linie)
Breitenkreis mit dem Radius r . sin J (j-Linie)
r, j = const.:
Längenkreis (J-Linie)
Die Koordinatenlinien stehen in jedem Punkt paarweise senkrecht aufeinander. Die Kugelkoordinaten sind daher (wie die kartesischen Koordinaten und die Zylinderkoordinaten)
orthogonale räumliche Koordinaten.
Zusammenhang zwischen den Kugelkoordinaten und den kartesischen Koordinaten
Kugelkoordinaten ! Kartesische Koordinaten
x ¼ r . sin J . cos j ,
y ¼ r . sin J . sin j ,
z ¼ r . cos J
6 Darstellung von Gradient, Divergenz, Rotation und Laplace-Operator
Kartesische Koordinaten ! Kugelkoordinaten
0
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
z
B
C
J ¼ arccos @qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi A ;
r ¼ x2 þ y2 þ z2;
2
2
2
x þy þz
391
tan j ¼
y
x
Linienelement ds
Das Linienelement ist der Verbindungsbogen zweier differentiell benachbarter Punkte, die
sich in ihren Kugelkoordinaten um dr, dJ, dj voneinander unterscheiden. Es besitzt die
Länge
ds ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðdrÞ 2 þ r 2 ðdJÞ 2 þ r 2 . sin 2 J ðdjÞ 2
Flächenelement dA auf der Kugeloberfläche (r = const.)
Flächenstück auf der Kugeloberfläche, begrenzt durch je zwei benachbarte J- und jKoordinatenlinien, mit dem Flächeninhalt
dA ¼ r 2 . sin J dJ dj
Volumenelement dV
dV ¼ dA dr ¼ r 2 . sin J dr dJ dj
Vektordarstellung in Kugelkoordinaten
z
~
a ¼ ar ~
er þ aJ ~
eJ þ aj ~
ej
~
er , ~
eJ , ~
ej :
Tangenteneinheitsvektoren an
die r-, J- bzw. j-Koordinatenlinie (Basisvektoren)
ar , aJ , aj :
Vektorkoordinaten
Orthogonale Transformationsmatrix
0
1
sin J . cos j sin J . sin j cos J
A ¼ @ cos J . cos j cos J . sin j / sin J A
/ sin j
cos j
0
er
P
ef
r
u
f
y
eu
x
Matrix A regelt die Transformation der Basisvektoren und Vektorkoordinaten (kartesische
Koordinaten ! Kugelkoordinaten).
392
XIV Vektoranalysis
Gradient, Divergenz, Rotation und Laplace-Operator in Kugelkoordinaten
Skalarfeld in Kugelkoordinaten
f ¼ f ðr; J; jÞ
Vektorfeld in Kugelkoordinaten
~¼ F
~ðr; J; jÞ ¼ Fr ðr; J; jÞ~
F
er þ FJ ðr; J; jÞ~
eJ þ Fj ðr; J; jÞ~
ej
Gradient des Skalarfeldes f (r; J; j)
grad f ¼
@f
1 @f
1
@f
~
~
~
er þ
.
eJ þ
.
ej
@r
r @J
r . sin J @j
Divergenz des Vektorfeldes F~(r; J; j)
3
2
@Fj
1
@
~ ¼ 1 . @ ðr 2 . Fr Þ þ
ðsin
J
.
F
Þ
þ
div F
J
r 2 @r
r . sin J @J
@j
~(r; J; j)
Rotation des Vektorfeldes F
3
2
1
@
@FJ
~
~
rot F ¼
ðsin J . Fj Þ /
er þ
r . sin J @J
@j
3
2
3
2
1
1
@Fr
@
1 @
@Fr
~
þ
.
/
ðr . Fj Þ ~
eJ þ
ðr . FJ Þ /
ej
r sin J @j
@r
r @r
@J
Laplace-Operator
2
3
2
( 3
'
1
@
@f
1
@
@f
1
@ 2f
Df ¼ 2
r2 .
þ
.
sin J .
þ
.
r
@r
@r
sin J @J
@J
sin 2 J @j 2
7 Linien- oder Kurvenintegrale
7.1 Linienintegral in der Ebene
~¼ F
~ðx; yÞ sei ein ebenes Vektorfeld, ~
F
r ¼~
r ðtÞ der Ortsvektor einer von P1 nach P2
verlaufenden ebenen Kurve C mit t1 ) t ) t2 und ~
r_ ¼ ~
r_ ðtÞ der zugehörige Tangentenvektor der Kurve.
Dann heißt das Integral
ð
C
~ . d~
F
r ¼
ðt2 1
0
~.~
F
r_ dt
t1
das Linien- oder Kurvenintegral des Vektor~ längs der Kurve C.
feldes F
y
P1
P
r(t1)
F
r(t)
C
P2
r(t2)
x
7 Linien- oder Kurvenintegrale
393
In ausführlicher Schreibweise:
ðt2
ð
ðFx x_ þ Fy y_Þ dt
ðFx ðx; yÞ dx þ Fy ðx; yÞ dyÞ ¼
t1
C
~ðx; yÞ
Fx ; Fy : Skalare Komponenten des ebenen Vektorfeldes F
_
x_ ; y_ : Koordinaten des Tangentenvektors ~
r
Berechnung eines Linienintegrals
Für die Variablen x und y werden die parameterabhängigen Koordinaten xðtÞ und yðtÞ
der Integrationskurve C eingesetzt, für x_ und y_ deren Ableitungen. Anschließend wird
der nur noch vom Parameter t abhängende Integrand in den Grenzen von t1 bis t2
integriert.
Sonderfall: Falls die Kurve C in der expliziten Form y ¼ f ðxÞ vorliegt, ersetzt man im
Linienintegral die Koordinate y durch f ðxÞ und das Differential dy durch f 0 ðxÞ dx und
erhält so ein gewöhnliches Integral mit der Variablen x :
ð
~ . d~
F
r ¼
xð2
½Fx ðx; f ðxÞÞ þ Fy ðx; f ðxÞÞ . f 0 ðxÞ% dx
x1
C
x1 ; x2 :
Abszissen der beiden Kurvenrandpunkte
Anmerkungen
(1)
Man beachte, dass der Wert eines Linien- oder Kurvenintegrals i. Allg. nicht nur vom
Anfangs- und Endpunkt des Integrationsweges, sondern auch noch vom eingeschlagenen Verbindungsweg abhängt.
(2)
Wird der Integrationsweg C in der umgekehrten Richtung durchlaufen (symbolische
Schreibweise: / C), so tritt im Integral ein Vorzeichenwechsel ein:
ð
ð
~ . d~
~ . d~
F
r ¼ / F
r
/C
(3)
C
Für ein Kurvenintegral längs einer geschlossenen Linie C verwenden wir das SymÞ
Þ
~ . d~
~ . d~
bol F
r oder auch F
r . Ein solches Kurvenintegral wird in den physikaC
~ längs der
lisch-technischen Anwendungen auch als Zirkulation des Vektorfeldes F
geschlossenen Kurve C bezeichnet.
394
XIV Vektoranalysis
Beispiel
&
Wir berechnen das Linien- oder Kurvenintegral
yðtÞ ¼ t, 0 ) t ) 1:
x ¼ 2t;
Ð
C
dx ¼ x_ dt ¼ 2 dt ;
ðx 2 y dx þ x y 2 dyÞ ¼
Ð1
0
y ¼ t;
Ð
C
ðx 2 y dx þ x y 2 dyÞ längs des Weges C : xðtÞ ¼ 2 t,
dy ¼ y_ dt ¼ 1 dt ¼ dt
ð4 t 2 . t . 2 dt þ 2 t . t 2 dtÞ ¼
Ð1
0
10 t 3 dt ¼
5 / 4. 1
5
5
t 0 ¼
ð1 / 0Þ ¼
2
2
2
&
7.2 Linienintegral im Raum
~¼ F
~ðx; y; zÞ längs
Das Linien- oder Kurvenintegral eines räumlichen Vektorfeldes F
einer Raumkurve C mit dem Ortsvektor ~
r ¼~
r ðtÞ, t1 ) t ) t2 lautet:
ð
ðt2 1
0
~.~
~ . d~
F
F
r ¼
r_ dt
C
t1
~
r_ :
Tangentenvektor von C
In ausführlicher Schreibweise:
ðt2
ð
ðFx x_ þ Fy y_ þ Fz z_Þ dt
ðFx ðx; y; zÞ dx þ Fy ðx; y; zÞ dy þ Fz ðx; y; zÞ dzÞ ¼
t1
C
~ðx; y; zÞ
Fx ; Fy ; Fz : Skalare Komponenten des räumlichen Vektorfeldes F
_
x_ ; y_; z_ : Koordinaten des Tangentenvektors ~
r
Berechnung eines Linienintegrals
Die Berechnung erfolgt wie beim Linienintegral in der Ebene. Alle dort gemachten Bemerkungen gelten sinngemäß auch für Linienintegrale im Raum.
7.3 Wegunabhängigkeit eines Linien- oder Kurvenintegrals
Ein Linien- oder Kurvenintegral
Ð
C
~ . d~
F
r ist genau dann wegunabhängig, wenn das Vek-
~ in einem einfachzusammenhängenden Bereich, der den Integrationsweg C enttorfeld F
hält, die folgende Integrabilitätsbedingung erfüllt:
Integrabilitätsbedingung für ein ebenes Vektorfeld
@Fx
@Fy
¼
@y
@x
oder
1
0
~ z¼ 0
rot F
7 Linien- oder Kurvenintegrale
395
Integrabilitätsbedingung für ein räumliches Vektorfeld
@Fx
@Fy
¼
;
@y
@x
@Fy
@Fz
¼
;
@z
@y
@Fz
@Fx
¼
@x
@z
~¼~
rot F
0
oder
Die Bedingungen sind notwendig und hinreichend.
Anmerkungen
(1)
Ein Bereich heißt einfachzusammenhängend, wenn sich jede im Bereich gelegene
geschlossene Kurve auf einen Punkt „zusammenziehen“ lässt. Ein ebener einfachzusammenhängender Bereich wird von einer einzigen geschlossenen Kurve begrenzt.
Beispiele: rechteckiger Bereich (siehe Bild a)) bzw. kreisförmiger Bereich (siehe Bild b)).
y
y
a)
b)
x
x
(2)
Im Falle der Wegunabhängigkeit verschwindet das Linienintegral längs einer
geschlossenen Kurve.
&
Beispiel
~ðx; yÞ mit den skalaren Komponenten Fx ¼ 3 x 2 y 2 und Fy ¼ 2 x 3 y erfüllt die
Das ebene Vektorfeld F
Integrabilitätsbedingung:
@Fx
@
¼
ð3x 2 y 2 Þ ¼ 6x 2 y ;
@y
@y
@Fy
@
@Fx
@Fy
¼
ð2 x 3 yÞ ¼ 6 x 2 y )
¼
¼ 6x2 y
@x
@x
@y
@x
Þ
Þ
Daher verschwindet das Linienintegral
ðFx dx þ Fy dyÞ ¼ ð3 x 2 y 2 dx þ 2 x 3 y dyÞ für jede geschlosC
C
sene Kurve C.
&
7.4 Konservative Vektorfelder
~ heißt konservativ oder Potentialfeld, wenn das
Ein (ebenes oder räumliches) Vektorfeld
F
Ð
~
Linien- oder Kurvenintegral
F . d~
r nur vom Anfangs- und Endpunkt, nicht aber vom
C
eingeschlagenen Verbindungsweg C der beiden Punkte abhängt.
Eigenschaften eines konservativen Vektorfeldes
~ besitzt in einem einfachzusammenhängenden Bereich die
Ein konservatives Vektorfeld F
folgenden gleichwertigen Eigenschaften:
Ð
~ . d~
1. Das Linien- oder Kurvenintegral
F
r längs einer Kurve C, die zwei (beliebige)
C
Punkte P1 und P2 verbindet, ist unabhängig vom eingeschlagenen Verbindungsweg,
solange dieser vollständig im Bereich liegt.
396
XIV Vektoranalysis
2. Das Linienintegral längs einer im Bereich liegenden geschlossenen Kurve C hat stets
den Wert null:
þ
~ . d~
F
r ¼ 0
C
~ ist überall im Bereich als Gradient einer Potentialfunktion f dar3. Der Feldvektor F
stellbar:
~ ¼ grad f
F
~ ist im Bereich wirbelfrei:
4. Das Vektorfeld F
~¼~
rot F
0
~ . d~
5. Das Skalarprodukt F
r ist das totale oder vollständige Differential einer Potentialfunktion f:
~ . d~
df ¼ F
r
Beispiel
&
Ein Zentralfeld ist stets konservativ. Das Linienintegral eines solchen Feldes verschwindet daher längs einer
jeden geschlossenen Kurve (diese darf nicht durch den Nullpunkt verlaufen). Beispiele für Zentralfelder sind
das Gravitationsfeld der Erde und das elektrische Feld einer Punktladung.
&
7.5 Arbeitsintegral (Arbeit eines Kraftfeldes)
~¼ F
~ðx; y; zÞ verrichtet an einem Massenpunkt beim Verschieben längs
Ein Kraftfeld F
einer Kurve C vom Punkt P1 in den Punkt P2 die folgende Arbeit (sog. Arbeitsintegral):
ð
W ¼
~ . d~
F
r ¼
C
~
r ¼~
r ðtÞ:
~
r_ ¼ ~
r_ ðtÞ:
d~
r:
ðt2
z
ðF
~.~
r_ Þ dt
P1
t1
r(t1)
r(t)
Ortsvektor der Kurve C
F
C
P2
r(t2)
Tangentenvektor der Kurve C
Differentielles Wegelement
P
x
y
8 Oberflächenintegrale
397
8 Oberflächenintegrale
8.1 Definition eines Oberflächenintegrals
~¼ F
~ðx; y; zÞ durch eine orientierte Fläche A wird
Der „Fluss“ eines Vektorfeldes F
durch das als Oberflächenintegral bezeichnete Integral
ðð
~¼
~ . dA
F
ðAÞ
ðð
z
~. N
~ Þ dA
ðF
N
Fläche A
ðAÞ
F(x;y;z)
P
beschrieben.
Flächenelement dA
Bezeichnungen:
~:
N
~:
dA
z
Flächennormale
Orientiertes Flächenelement
vom Betrag dA
~. N
~:
F
x
x
y
y
~
Normalkomponente von F
1
0
~. N
~ dA ist der Fluss des Vektorfeldes F
~ durch das Flächenelement dA, anschlieF
ßend werden die Beiträge aller Flächenelemente aufsummiert.
Anmerkungen
(1)
~ eindeutig festgelegt.
Die Orientierung der Fläche ist durch die Flächennormale N
Bei einer geschlossenen Fläche, z. B. der Oberfläche einer Kugel, eines Zylinders
~ vereinbarungsgemäß nach außen. Bei einer offenen
oder eines Quaders, zeigt N
Fläche wird die Randkurve der Fläche so durchlaufen, dass mit der Flächennormale
Rechtsschraubung entsteht.
(2)
Auch die folgenden Bezeichnungen für das Oberflächenintegral sind gebräuchlich:
~ oder kurz „Fluss“ des Feldvektors F
~ durch die
„Flussintegral“ des Vektorfeldes F
~
Fläche A oder auch Flächenintegral des Vektorfeldes F über die orientierte Fläche A.
(3)
Das Oberflächenintegral über eine geschlossene Fläche A wird durch das Symbol
ÐÐ
ÐÐ
~ oder # ðF
~ . dA
~. N
~ Þ dA gekennzeichnet. Folgende Bezeichnungen für ein
# F
ðAÞ
ðAÞ
solches Integral sind in den Anwendungen üblich: „Hüllenintegral“ oder „Fluss“ des
~ durch die geschlossene Fläche A oder auch „Ergiebigkeit“ des FeldFeldvektors F
~.
vektors F
398
XIV Vektoranalysis
8.2 Berechnung eines Oberflächenintegrals
Ein Oberflächenintegral lässt sich stets auf ein Doppelintegral zurückführen (siehe IX.3.1).
8.2.1 Berechnung eines Oberflächenintegrals in symmetriegerechten Koordinaten
ÐÐ
ÐÐ
~¼
~. N
~ Þ dA erfolgt in vier
~ . dA
ðF
F
Die Berechnung eines Oberflächenintegrals
ðAÞ
ðAÞ
Schritten:
1. Zunächst werden geeignete Koordinaten ausgewählt, die sich der Symmetrie des Problems in optimaler Weise anpassen. Zur Auswahl stehen dabei:
–– Kartesische Koordinaten x; y; z
–– Zylinderkoordinaten r; j; z (Abschnitt 6.2)
–– Kugelkoordinaten r; J; j (Abschnitt 6.3)
~, berechnet anschließend das Skalarpro2. Man bestimmt dann die Flächennormale N
~. N
~ und drückt dieses sowie das Flächenelement dA durch die gewählten
dukt F
Koordinaten aus.
3. Festlegung der Integrationsgrenzen im erhaltenen Doppelintegral.
4. Berechnung des Doppelintegrals in der bekannten Weise (siehe IX.3.1).
&
Beispiel
~ ¼ ð1=r 2 Þ ~
Wir berechnen den Fluss des Zentralfeldes F
er durch die (geschlossene) Oberfläche A der
~¼~
konzentrischen Einheitskugel. Auf der Kugeloberfläche gilt r ¼ 1 und daher F
er , die Flächennormale
~ ist der radiale Einheitsvektor ~
N
er . Somit gilt:
ÐÐ
#
ðAÞ
~. N
~ Þ dA ¼
ðF
ÐÐ
#
ðAÞ
ð~
e .~
e Þ dA ¼
|fflfflfflfflr ffl{zfflfflfflfflrffl}
1
ÐÐ
#
ðAÞ
1 dA ¼
ÐÐ
#
ðAÞ
dA ¼ A ¼ 4 p
(Oberfläche der Einheitskugel: A ¼ 4 p)
&
Sonderfälle
(1)
Der Fluss eines homogenen Vektorfeldes durch eine beliebige geschlossene Oberfläche
ist stets null.
(2)
~ ¼ f ðrÞ~
Der Fluss eines zylindersymmetrischen Vektorfeldes F
er durch die geschlossene Oberfläche eines (zur z-Achse) koaxialen Zylinders beträgt:
ÐÐ
~. N
~ Þ dA ¼ f ðRÞ . 2 p R H
# ðF
ðAÞ
(R: Zylinderradius; H : Zylinderhöhe; Symmetrieachse ¼ z-Achse)
(3)
~ ¼ f ðrÞ~
Der Fluss eines Zentralfeldes F
er durch die geschlossene Oberfläche A
einer (konzentrischen) Kugel beträgt:
ÐÐ
~. N
~ Þ dA ¼ f ðRÞ . 4 p R 2
# ðF
ðAÞ
(R: Kugelradius; Kugelmittelpunkt ¼ Koordinatenursprung)
8 Oberflächenintegrale
399
8.2.2 Berechnung eines Oberflächenintegrals unter Verwendung
von Flächenparametern
~¼ F
~ðx; y; zÞ „durchflutete“ Fläche A sei durch einen von
Die von einem Vektorfeld F
den beiden Parametern u und v abhängigen Ortsvektor ~
r ¼~
r ðu; vÞ gegeben. Für den
„Fluss“ durch diese Fläche gilt dann:
ðð 1
ðð /
ðð
.
0
~~
~ . ð~
~. N
~ dA ¼
F
tu ~
F
tu - ~
tv Þ du dv ¼
tv du dv
F
ðAÞ
ðAÞ
ðAÞ
Die Integralberechnung erfolgt in vier Schritten:
~ wird zunächst durch die Flächenparameter u und v ausgedrückt,
1. Das Vektorfeld F
indem man die Koordinaten x; y und z durch die parameterabhängigen Koordinaten
xðu; vÞ, yðu; v) und zðu; vÞ des Ortsvektors ~
r ðu; vÞ der Fläche ersetzt.
~
2. Man bestimmt dann die Tangentenvektoren tu und ~
tv der Fläche und mit ihnen das
~ . ð~
~~
gemischte Produkt (Spatprodukt) F
tu - ~
tv Þ ¼ ½ F
tu ~
tv %.
3. Festlegung der Integationsgrenzen im erhaltenen Doppelintegral.
4. Berechnung des Doppelintegrals in der bekannten Weise (siehe IX.3.1).
&
Beispiel
0
1
0
1
cos u
y
~¼ F
~ðx; y; zÞ ¼ @ x A; Fläche A: ~
Vektorfeld: F
r ¼~
r ðu; vÞ ¼ @ sin u A mit 0 ) u ) p, 0 ) v ) 1
z2
v
~ durch die Fläche A (halber Mantel eines Zylinders mit dem Radius
Wir berechnen den Fluss des Feldes F
0
1
sin u
~ über in F
~ ¼ @ cos u A :
R ¼ 1 und der Höhe H ¼ 1). Mit x ¼ cos u, y ¼ sin u und z ¼ v geht F
v2
Tangentenvektoren der Fläche:
0
1
0 1
/ sin u
0
@~
r
@~
r
~
~
tu ¼
¼ @ cos u A ;
tv ¼
¼ @0A
@u
@v
0
1
Integrand des Flussintegrals:
0
1
0 1
0
1
0
1
/ sin u
0
cos u / 0
cos u
~
tu - ~
tv ¼ @ cos u A - @ 0 A ¼ @ 0 þ sin u A ¼ @ sin u A
0
1
0 / 0
0
0
1 0
1
sin u
cos u
~ . ð~
F
tu - ~
tv Þ ¼ @ cos u A . @ sin u A ¼ sin u . cos u þ cos u . sin u þ 0 ¼
v2
0
¼ 2 . sin u . cos u ¼ sin ð2 uÞ
~ durch die Fläche A):
Flussintegral (Fluss des Vektorfeldes F
ÐÐ 1
ðAÞ
0
ÐÐ
Ð1
~. N
~ dA ¼
~ . ð~
F
F
tu - ~
tv Þ du dv ¼
ðAÞ
Ðp
v¼0 u¼0
sin ð2 uÞ du dv
400
XIV Vektoranalysis
Berechnung des Doppelintegrals (hier als Produkt zweier gewöhnlicher Integrale darstellbar, siehe IX.3.1):
+
)p
/ .1
Ð1
Ðp
Ð1
Ðp
1
¼
sin ð2 uÞ du dv ¼
dv .
sin ð2 uÞ du ¼ v v ¼ 0 . /
. cos ð2 uÞ
2
v¼0 u¼0
v¼0
u¼0
u¼0
+
)
3
2
/
.
1
1
1
1
¼ 1 / 0 . / . cos ð2 pÞ þ
. cos 0 ¼ 1 /
.1þ
.1 ¼ 0
2
2
2
2
0
ÐÐ 1
~. N
~ dA ¼ 0
Ergebnis:
F
ðAÞ
&
9 Integralsätze von Gauß und Stokes
9.1 Gaußscher Integralsatz
Gaußscher Integralsatz im Raum
Der Gaußsche Integralsatz im Raum stellt eine Verbindung her zwischen einem Oberflächenintegral und einem Volumenintegral. Er lautet wie folgt:
~¼ F
~ðx; y; zÞ über eine ge„Das Oberflächenintegral eines räumlichen Vektorfeldes F
~, erstreckt über
schlossene Fläche A ist gleich dem Volumenintegral der Divergenz von F
das von der Fläche A eingeschlossene Volumen V “:
ðð
#
~. N
~ Þ dA ¼
ðF
ðAÞ
ðð
#
~¼
~ . dA
F
ðAÞ
ððð
~ dV
div F
ðVÞ
~:
N
Nach außen gerichtete Flächennormale
~ ist stetig differenzierbar.
Voraussetzung: F
Anmerkung
~ ¼ 0Þ ist der Gesamtfluss durch eine geschlossene
Bei einem quellenfreien Feld ðdiv F
Oberfläche gleich null.
&
Beispiel
~¼~
Wir berechnen den Fluss des Zentralfeldes F
r ¼ r~
er durch die Oberfläche A einer konzentrischen
Kugel vom Radius R mit Hilfe eines Volumenintegrals. Unter Verwendung von Kugelkoordinaten erhalten
wir für die Divergenz des Zentralfeldes mit Fr ¼ r :
~ ¼ div ~
div F
r ¼ div ðr ~
er Þ ¼
1 @
1 @
1
@
1
.
ðr 2 . Fr Þ ¼ 2 .
ðr 2 . rÞ ¼ 2 .
ðr 3 Þ ¼ 2 . 3 r 2 ¼ 3
r 2 @r
r
@r
r
@r
r
Aus dem Gaußschen Integralsatz folgt dann:
ÐÐ
ÐÐÐ
ÐÐÐ
ÐÐÐ
4
~. N
~ Þ dA ¼
~ dV ¼
# ðF
div F
3 dV ¼ 3 .
dV ¼ 3 V ¼ 3 .
pR3 ¼ 4p R3
3
ðAÞ
ðV Þ
ðV Þ
ðVÞ
(Kugelvolumen: V ¼ 4 p R 3 =3Þ
&
9 Integralsätze von Gauß und Stokes
401
Gaußscher Integralsatz in der Ebene
Der Gaußsche Integralsatz gilt sinngemäß auch in der Ebene, wobei „Volumen“ durch
„Fläche“ und „Oberfläche“ durch „geschlossene Kurve“ (Randkurve der Fläche) zu ersetzen sind. Er verbindet ein Kurven- oder Linienintegral mit einem zweidimensionalen Bereichsintegral (Doppelintegral) und lautet wie folgt:
~¼ F
~ðx; yÞ
„Das Kurvenintegral der Normalkomponente eines ebenen Vektorfeldes F
längs einer geschlossenen Kurve C ist gleich dem Bereichsintegral (Doppelintegral) über
~, erstreckt über die von der Kurve C eingeschlossene Fläche A“:
die Divergenz von F
þ1
ðð
0
~. N
~ ds ¼
~ dA
F
div F
C
A
ðAÞ
N
~ : Nach außen gerichtete Kurvennormale
N
ds: Linienelement der Randkurve C
Randkurve C
~ ist stetig differenzierbar
Voraussetzung: F
und die Randkurve C wird so durchlaufen,
dass die Fläche A linker Hand liegen bleibt.
9.2 Stokesscher Integralsatz
Der Integralsatz von Stokes ermöglicht die Umwandlung eines Oberflächenintegrals in ein
Kurven- oder Linienintegral und umgekehrt. Er lautet wie folgt:
~¼ F
~ðx; y; zÞ längs
„Das Kurven- oder Linienintegral eines räumlichen Vektorfeldes F
~
einer geschlossenen Kurve C ist gleich dem Oberflächenintegral der Rotation von F
über eine beliebige Fläche A, die durch die Kurve C berandet wird‘‘:
þ
C
~:
N
~ . d~
F
r ¼
ðð 1
ðð 1
0
0
~¼
~ . dA
~ . N
~ dA
rot F
rot F
ðAÞ
ðAÞ
Flächennormale
räumliche Fläche
~ ist stetig differenzierbar
Voraussetzung: F
und die Randkurve C der Fläche A ist
orientiert (d. h. ein Beobachter, der in die
~ blickt,
Richtung der Flächennormale N
durchläuft die Randkurve C so, dass die
Fläche linker Hand liegen bleibt).
N
Flächenelement dA
Randkurve C
402
XIV Vektoranalysis
Anmerkungen
ÐÐ 1
0
~ . N
~ dA wird auch als „Wirbelfluss“ bezeichnet.
rot F
(1)
Das Oberflächenintegral
(2)
Der Wirbelfluss durch eine geschlossene Fläche ist gleich null und für alle Flächen,
die von der gleichen Kurve C berandet werden, gleich groß.
Der Stokessche Satz gilt auch für Flächen, die von mehreren geschlossenen Kurven
berandet werden.
(3)
&
ðAÞ
Beispiel
0
~¼B
Wir berechnen den Wirbelfluss des Vektorfeldes F
@
x2 þ y2
0
1
C
A durch den Mantel A der Halbkugel
z2
2
2
x þy þz
2
¼ 1, z ( 0 mit Hilfe eines Linienintegrals.
Nach Stokes gilt:
ÐÐ 1
ðAÞ
0
Þ
~¼ F
~ . dA
~ . d~
rot F
r
z
C
1
A
Parameterdarstellung der Randkurve C (Einheitskreis):
x ¼ cos t ;
y ¼ sin t ;
dx
¼ / sin t ;
dt
z ¼ 0
dy
¼ cos t ;
dt
dx ¼ / sin t dt ;
)
dz
¼ 0
dt
dy ¼ cos t dt ;
)
dz ¼ 0
~ . d~
Skalarprodukt F
r des Linienintegrals:
0
B
~ . d~
F
r ¼@
x2 þ y2
0
z2
1
0
x
1
y
C: x 2 + y 2 = 1
1
0 1
dx
C B C
A . @ dy A ¼ ðx 2 þ y 2 Þ dx þ 0 dy þ z 2 dz ¼ ðx 2 þ y 2 Þ dx þ z 2 dz ¼
dz
¼ ðcos 2 t þ sin 2 t Þ . ð/ sin t dtÞ þ 0 2 . 0 ¼ / sin t dt
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
1
Berechnung des Wirbelflusses:
ÐÐ 1
ðAÞ
2Ðp
0
/
.2p
Þ
~¼ F
~ . dA
~ . d~
rot F
r ¼ / sin t dt ¼ cos t 0 ¼ cos ð2 pÞ / cos 0 ¼ 1 / 1 ¼ 0
C
0
&
403
XV Wahrscheinlichkeitsrechnung
1 Hilfsmittel aus der Kombinatorik
1.1 Permutationen
Eine Anordnung von n Kugeln (allgemein: Elementen) in einer bestimmten Reihenfolge
heißt Permutation. Für die Anzahl der möglichen Permutationen gilt dann:
1. Alle n Kugeln sind voneinander verschieden:
P ðnÞ ¼ n !
2. Unter den n Kugeln befinden sich jeweils n1 ; n2 ; . . . ; nk einander gleiche:
P ðn; n1 ; n2 ; . . . ; nk Þ ¼
ðn1 þ n2 þ . . . þ nk ¼ n
k:
&
n!
n1 ! n2 ! . . . nk !
und
k ) nÞ
Anzahl der verschiedenen Kugeln
Beispiele
(1)
Es gibt P ð3Þ ¼ 3 ! ¼ 6 verschiedene Möglichkeiten, 3 verschiedenfarbige Kugeln anzuordnen:
(2)
In einer Urne befinden sich 5 Kugeln, 3 weiße und 2 rote. Sie lassen sich auf
P ð5; 3, 2Þ ¼
5!
3! . 4 . 5
4.5
¼
¼
¼ 2 . 5 ¼ 10
3! 2!
2
3! . 2
verschiedene Arten anordnen.
&
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_15
404
XV Wahrscheinlichkeitsrechnung
1.2 Kombinationen
Aus einer Urne mit n verschiedenen Kugeln werden nacheinander k Kugeln entnommen
und in beliebiger Weise angeordnet (Urnenmodell). Eine solche Anordnung heißt Kombination k-ter Ordnung. Für die Anzahl der möglichen Kombinationen k-ter Ordnung gilt dann:
1. Die Ziehung der k Kugeln erfolgt ohne Zurücklegen (sog. Kombinationen k-ter
Ordnung ohne Wiederholung):
!n4
n!
C ðn; kÞ ¼
¼
ðk ) nÞ
k
k ! ðn / kÞ !
2. Die Ziehung der k Kugeln erfolgt mit Zurücklegen (sog. Kombinationen k-ter Ordnung mit Wiederholung):
3
2
nþk /1
Cw ðn; kÞ ¼
ðk ¼ 1; 2; 3; . . .Þ
k
Bei einer Ziehung mit Zurücklegen kann k auch größer als n sein!
&
Beispiel
Einer Warenlieferung von 10 Glühbirnen von jeweils 100 Watt soll zu Kontrollzwecken eine Stichprobe von
3 Glühbirnen entnommen werden (die gezogenen Glühbirnen werden nicht zurückgelegt, die Reihenfolge der
Ziehung ist ohne Bedeutung). Es gibt dann
3 2
10 . 9 . 8
10
C ð10; 3Þ ¼
¼
¼ 5 . 3 . 8 ¼ 120
1.2.3
3
verschiedene Möglichkeiten, aus den 10 Glühbirnen 3 auszuwählen.
&
1.3 Variationen
Einer Urne mit n verschiedenen Kugeln werden nacheinander k Kugeln entnommen und
in der Reihenfolge ihrer Ziehung angeordnet. Eine solche Anordnung heißt Variation k-ter
Ordnung. Für die Anzahl der möglichen Variationen k-ter Ordnung gilt dann:
1. Die Ziehung der k Kugeln erfolgt ohne Zurücklegen (sog. Variationen k-ter Ordnung ohne Wiederholung):
n!
V ðn; kÞ ¼
ðk ) nÞ
ðn / kÞ !
2. Die Ziehung der k Kugeln erfolgt mit Zurücklegen (sog. Variationen k-ter Ordnung mit Wiederholung):
Vw ðn; kÞ ¼ n k
ðk ¼ 1; 2; 3; . . .Þ
&
Beispiel
Bei einem 100-Meter-Lauf starten 8 Läufer. Für die ersten 3 Plätze gibt es Medaillen (Gold, Silber, Bronze).
Wieviel verschiedene Zieleinläufe für die ersten 3 Plätze sind möglich?
Lösung: Von n ¼ 8 Läufern werden k ¼ 3 Läufer die Plätze 1, 2 und 3 belegen. Da die Reihenfolge des
Einlaufs eine wesentliche Rolle spielt, handelt es sich somit um Variationen 3. Ordnung und zwar ohne Wiederholung, da jeder Läufer nur einen Platz belegen kann. Die Anzahl der möglichen Zieleinläufe ist somit
V ð8; 3Þ ¼
8!
8!
5! . 6 . 7 . 8
¼
¼
¼ 6 . 7 . 8 ¼ 336
ð8 / 3Þ !
5!
5!
&
2 Grundbegriffe
405
2 Grundbegriffe
Zufallsexperiment
Lässt sich ein Experiment unter den gleichen äußeren Bedingungen beliebig oft wiederholen, wobei mehrere sich gegenseitig ausschließende Ergebnisse möglich sind und ist das
Ergebnis bei einer konkreten Durchführung des Experiments ungewiss, d. h. zufallsbedingt,
so spricht man von einem Zufallsexperiment.
&
Beispiele
Wurf einer Münze oder eines Würfels, zufällige Entnahme von Kugeln aus einer Urne, Stichprobenentnahme
aus der laufenden Produktion eines Massenartikels zwecks Qualitätskontrolle.
&
Elementarereignisse, Ergebnismenge eines Zufallsexperiments
Elementarereignisse heißen die möglichen sich gegenseitig ausschließenden Ergebnisse eines
Zufallsexperiments. Symbolische Schreibweise: w1 ; w2 ; w3 ; . . .
Die Menge aller Elementarereignisse heißt Ergebnismenge des Zufallsexperiments. Symbolische Schreibweise: W ¼ fw1 ; w2 ; w3 ; . . .g
&
Beispiel
Beim „Wurf einer homogenen Münze“ gibt es die beiden Elementarereignisse Z ¼ Zahl und W ¼ Wappen.
Ergebnismenge: W ¼ fZ; Wg
&
Ereignisse, Ereignisraum oder Ereignisfeld
Alle möglichen Ergebnisse (Versuchsausgänge) eines Zufallsexperiments werden als Ereignisse bezeichnet. Ein Ereignis A ist daher immer eine Teilmenge der Ergebnismenge W,
die bekanntlich sämtliche Elementarereignisse enthält.
Die Menge aller Ereignisse heißt Ereignisraum oder Ereignisfeld. Der Ereignisraum enthält
also alle Teilmengen der Ergebnismenge W und somit definitionsgemäß auch die leere
Menge ; und die Ergebnismenge W selbst. ; beschreibt das sog. unmögliche Ereignis
(d. h. ein Ereignis, das nie eintreten kann), W dagegen das sog. sichere Ereignis (d. h. ein
Ereignis, das immer eintreten wird).
&
Beispiel
Beim „Wurf eines homogenen Würfels“ gibt es 6 Elementarereignisse, nämlich das Auftreten einer der 6 Zahlen („Augen“) 1; 2; . . . ; 6.
Ergebnismenge: W ¼ f1; 2; 3; 4; 5; 6g
Ereignisse sind z. B. die folgenden Teilmengen von W:
f2; 4; 6g: Würfeln einer geraden Zahl
f1; 6g: Würfeln einer „1“ oder einer „6“
W ist das sichere Ereignis, da bei jedem Wurf eine der Zahlen 1; 2; . . . ; 6 oben liegt!
&
406
XV Wahrscheinlichkeitsrechnung
Verknüpfungen von Ereignissen
Ereignisse werden durch Teilmengen der Ergebnismenge W beschrieben und lassen sich
daher wie Mengen verknüpfen. Dies führt zu den folgenden zusammengesetzten Ereignissen (A und B sind dabei beliebige Ereignisse):
Verknüpfungssymbol
mit Euler-Venn-Diagramm
Bedeutung des zusammengesetzten Ereignisses
Vereinigung der Ereignisse A und B:
A U B
A
U
A
B
Entweder tritt A ein oder B oder A und B
gleichzeitig
Ω
Symbolische Schreibweise: A [ B
B
Durchschnitt der Ereignisse A und B:
A und B treten gleichzeitig ein
A
Ω
Symbolische Schreibweise: A \ B
B
Zu A komplementäres Ereignis:
Ω
A
A tritt nicht ein
A
Symbolische Schreibweise: A
Anmerkungen
(1) Das Ereignis A [ B wird auch als Summe aus A und B bezeichnet (symbolische
Schreibweise: A þ B).
(2)
Das Ereignis A \ B heißt auch Produkt aus A und B (symbolische Schreibweise:
A . B oder kurz A B).
(3)
A ist die Restmenge (Differenzmenge) von W und A: A ¼ W n A
(4)
Für sich gegenseitig ausschließende Ereignisse gilt A \ B ¼ ; (sog. „disjunkte“
Mengen).
&
Beispiel
Zufallsexperiment: „Wurf einer homogenen Münze“
A ¼ fZg: „Zahl“ liegt oben
)
A ¼ fWg: „Wappen“ liegt oben
&
3 Wahrscheinlichkeit
407
De Morgansche Regeln
A [ B ¼ A \ B;
A \ B ¼ A[B
A; B: Beliebige Ereignisse
3 Wahrscheinlichkeit
3.1 Absolute und relative Häufigkeit
Ein Zufallsexperiment wird n-mal durchgeführt, dabei tritt das Ereignis A genau n ðAÞmal ein. Dann heißt n ðAÞ die absolute und hn ðAÞ ¼ n ðAÞ=n die relative Häufigkeit des
Ereignisses A.
Eigenschaften und Regeln für relative Häufigkeiten
(1)
0 ) hn ðAÞ ) 1
(2)
Für das sichere Ereignis W gilt hn ðWÞ ¼ 1.
(3)
Für sich gegenseitig ausschließende Ereignisse A und B gilt der Additionssatz
hn ðA [ BÞ ¼ hn ðAÞ þ hn ðBÞ
(4)
&
ðA \ B ¼ ;Þ
Erfahrungsgemäß gilt: Wird die Anzahl n der Versuche laufend vergrößert, so
„stabilisiert“ sich i. Allg. die relative Häufigkeit hn ðAÞ eines Ereignisses A und
schwankt somit immer weniger um einen bestimmten (konstanten) Wert h ðAÞ.
Beispiel
Das Zufallsexperiment „Wurf eines homogenen Würfels“ wurde n ¼ 100 Mal durchgeführt und führte zu
der folgenden Verteilungstabelle mit dem nebenstehenden Stabdiagramm:
i
1
2
3
4
5
6
ni
15
18
14
17
19
17
hi
0,15
0,18
0,14
0,17
0,19
0,17
ni :
Anzahl der Würfe mit der Augenzahl i
ði ¼ 1; 2; . . . ; 6Þ
hi ¼ ni =100
hi
0,20
0,15
0,10
0,05
1
2
3
4
5
6
i
&
408
XV Wahrscheinlichkeitsrechnung
3.2 Wahrscheinlichkeitsaxiome von Kolmogoroff
Jedem Ereignis A eines Zufallsexperiments mit der Ergebnismenge W wird eine reelle
Zahl P ðAÞ, Wahrscheinlichkeit des Ereignisses A genannt, so zugeordnet, dass die folgenden Axiome erfüllt sind:
Axiom 1:
0 ) P ðAÞ ) 1
Axiom 2:
P ðWÞ ¼ 1
Axiom 3:
Für paarweise sich gegenseitig ausschließende Ereignisse A1 ; A2 ; A3 ; . . .
gilt der Additionssatz
( Wahrscheinlichkeit für das sichere Ereignis)
P ðA1 [ A2 [ A3 [ . . .Þ ¼ P ðA1 Þ þ P ðA2 Þ þ P ðA3 Þ þ . . .
In der Praxis gilt: Die meist unbekannte Wahrscheinlichkeit P ðAÞ eines Ereignisses A
wird näherungsweise durch die in umfangreichen Versuchsreihen beobachtete relative Häufigkeit hn ðAÞ ersetzt: P ðAÞ ' hn ðAÞ (sog. „statistischer“ oder „empirischer“ Wahrscheinlichkeitswert).
Rechenregeln für Wahrscheinlichkeiten
(1)
(2)
Für das unmögliche Ereignis ; gilt P ð;Þ ¼ 0.
Für das zum Ereignis A komplementäre Ereignis A gilt
P ðAÞ ¼ 1 / P ðAÞ
(3)
Additionssatz für zwei beliebige Ereignisse A und B:
(4)
Additionssatz für zwei sich gegenseitig ausschließende Ereignisse A und B:
P ðA [ BÞ ¼ P ðAÞ þ P ðBÞ / P ðA \ BÞ
P ðA [ BÞ ¼ P ðAÞ þ P ðBÞ
&
ðA \ B ¼ ;Þ
Beispiel
Zufallsexperiment: „Wurf einer homogenen Münze“
Ergebnismenge: W ¼ fZ; Wg
Z ¼ Zahl, W ¼ Wappen
Festlegung der Wahrscheinlichkeiten: P ðZÞ ¼ P ðWÞ ¼ 0,5 (die Elementarereignisse Z und W sind
gleichwahrscheinlich, d. h. bei einer großen Anzahl von Würfen können wir davon ausgehen, dass je zur
Hälfte Zahl und Wappen auftreten).
&
3.3 Laplace-Experimente
Ein Laplace-Experiment liegt vor, wenn alle m Elementarereignisse w1 ; w2 ; . . . ; wm die
gleiche Wahrscheinlichkeit p ¼ 1=m besitzen. Für ein beliebiges Ereignis A gilt dann:
P ðAÞ ¼
g ðAÞ:
g ðAÞ
m
Anzahl der für das Ereignis A günstigen Fälle (d. h. derjenigen Fälle, in denen A
eintritt)
3 Wahrscheinlichkeit
&
409
Beispiel
Zufallsexperiment: „Wurf eines homogenen Würfels“
Die Wahrscheinlichkeit p ðiÞ für das Würfeln der Augenzahl „i“ ist für alle 6 möglichen Augenzahlen
gleich (Laplace-Experiment): p ðiÞ ¼ 1=6 für i ¼ 1; 2; . . . ; 6. Für das Ereignis A: „Würfeln einer geraden Zahl“ gilt dann:
1
1
1
3
1
þ
þ
¼
¼
6
6
6
6
2
Denn es gibt unter den m ¼ 6 Elementarereignissen genau 3 für das Ereignis A günstige Fälle (A tritt ein
P ðAÞ ¼ p ð2Þ þ p ð4Þ þ p ð6Þ ¼
bei der Augenzahl „2“, „4“ oder „6“). Daher ist g ðAÞ ¼ 3 und somit P ðAÞ ¼
g ðAÞ
3
1
¼
¼ .
m
6
2
&
3.4 Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit P ðB j AÞ für das Eintreten des Ereignisses B unter der Bedingung oder Voraussetzung, dass das Ereignis A bereits eingetreten ist, beträgt
P ðB j AÞ ¼
P ðA \ BÞ
P ðAÞ
ðP ðAÞ ¼
6 0Þ
(sog. bedingte Wahrscheinlichkeit von B unter der Bedingung AÞ
&
Beispiel
Zufallsexperiment: „Wurf eines homogenen Würfels“
A: gerade Augenzahl
)
A ¼ f2; 4; 6g
B: Augenzahl „6“
)
B ¼ f6g
A \ B ¼ f6g: Augenzahl „6“
P ðB j AÞ ¼
mit
mit
P ðAÞ ¼ 1=2
P ðA \ BÞ ¼ 1=6
P ðA \ BÞ
1=6
1 2
2
1
¼
¼
.
¼
¼
P ðAÞ
1=2
6 1
6
3
P ðB j AÞ ist dabei die Wahrscheinlichkeit dafür, die Augenzahl „6“ zu erhalten, wenn bereits bekannt ist,
dass die gewürfelte Augenzahl gerade ist.
&
3.5 Multiplikationssatz
Die Wahrscheinlichkeit für das gleichzeitige Eintreten der Ereignisse A und B beträgt
P ðA \ BÞ ¼ P ðAÞ . P ðB j AÞ ¼ P ðBÞ . P ðA j BÞ
Entsprechend bei drei gleichzeitig eintretenden Ereignissen A, B und C :
P ðA \ B \ CÞ ¼ P ðAÞ . P ðB j AÞ . P ðC j A \ BÞ
410
XV Wahrscheinlichkeitsrechnung
3.6 Stochastisch unabhängige Ereignisse
Ist das Eintreten des Ereignisses B unabhängig davon, ob das Ereignis A bereits eingetreten ist oder nicht und umgekehrt, so heißen die Ereignisse A und B stochastisch unabhängig. Es gilt dann:
P ðA \ BÞ ¼ P ðAÞ . P ðBÞ
Entsprechend bei drei stochastisch unabhängigen Ereignissen A; B und C :
P ðA \ B \ CÞ ¼ P ðAÞ . P ðBÞ . P ðCÞ
&
Beispiel
Eine homogene Münze wird zweimal geworfen. Mit welcher Wahrscheinlichkeit erhalten wir zunächst „Zahl“
und dann „Wappen“?
Lösung:
A: „Zahl“ beim 1. Wurf
)
P ðAÞ ¼ 1=2
B: „Wappen“ beim 2. Wurf
)
P ðBÞ ¼ 1=2
Die beiden Ereignisse sind unabhängig voneinander. Die Wahrscheinlichkeit für das Ereignis
A \ B: Zunächst „Zahl“, dann „Wappen“
beträgt dann:
P ðA \ BÞ ¼ P ðAÞ . P ðBÞ ¼
1 1
1
.
¼
2 2
4
&
3.7 Mehrstufige Zufallsexperimente
Ereignisbaum (Baumdiagramm)
Ein mehrstufiges Zufallsexperiment besteht aus mehreren nacheinander ablaufenden Zufallsexperimenten. Es lässt sich anschaulich durch einen Ereignisbaum, auch Baumdiagramm genannt, darstellen:
Pfad mit 2 Zweigen
B5
A1 ; A2 :
Verzweigungspunkte
(mögliche Ergebnisse
der 1. Stufe, d. h.
Zwischenergebnisse)
A2
B4
Wurzel
Zweig
B3
B1 ; . . . ; B5 :
Mögliche Endergebnisse
P(A 1 )
A1
Verzweigungspunkt
(mögliches Zwischenergebnis)
B2
B1
mögliches
Endergebnis
3 Wahrscheinlichkeit
411
Pfadregeln
Die Berechnung von Wahrscheinlichkeiten längs bestimmter Pfade (die aus mehreren Zweigen bestehen) geschieht mit Hilfe der folgenden Pfadregeln:
(1)
Die Wahrscheinlichkeiten längs eines Pfades werden miteinander multipliziert.
(2)
Führen mehrere Pfade zum gleichen Endergebnis, so addieren sich ihre Wahrscheinlichkeiten.
Totale Wahrscheinlichkeit
Ein Ereignis B trete stets in Verbindung
mit genau einem der sich paarweise gegenseitig
ausschließenden Ereignisse A1 ; A2 ; . . . ; An
auf, d. h. die Ereignisse Ai sind die möglichen
„Zwischenstationen“ auf dem Wege zum
Ereignis B (siehe Bild).
An
Aj
0
P(A j )
P(B/A j )
B
A2
A1
Die sog. totale Wahrscheinlichkeit für das Eintreten des Ereignisses B beträgt dann
P ðBÞ ¼
P
i
P ðAi Þ . P ðB j Ai Þ
P ðAi Þ . P ðB j Ai ): Wahrscheinlichkeit dafür, das Ereignis B über die „Zwischenstation“
Ai zu erreichen (Wahrscheinlichkeit längs des Pfades O Ai BÞ
Regel: Die Wahrscheinlichkeiten aller nach B führenden Pfade werden addiert.
Bayessche Formel
Die Wahrscheinlichkeit dafür, dass das bereits eingetretene Ereignis B über die „Zwischenstation“ Aj , d. h. längs des Pfades O Aj B erreicht wurde, beträgt
P ðAj j BÞ ¼
P ðO Aj BÞ
P ðAj Þ . P ðB j Aj Þ
¼ P
P ðBÞ
P ðAi Þ P ðB j Ai Þ
ðBayessche FormelÞ
i
Regel: Die Wahrscheinlichkeit längs des einzigen „günstigen“ Pfades O Aj B wird durch
die totale Wahrscheinlichkeit P ðBÞ dividiert.
412
&
XV Wahrscheinlichkeitsrechnung
Beispiel
Auf zwei Maschinen M1 und M2 werden Glühbirnen vom gleichen Typ hergestellt und zwar mit einem
Anteil von 80 % bzw. 20 % an der Gesamtproduktion. Die Ausschussanteile betragen jeweils 2 %. Aus der
Gesamtproduktion wird zufällig eine Glühbirne entnommen und auf ihre Funktionstüchtigkeit hin überprüft.
a) Mit welcher Wahrscheinlichkeit zieht man dabei eine defekte Glühbirne?
b) Wie groß ist dann die Wahrscheinlichkeit dafür, dass diese auf der Maschine M1 produziert wurde?
Lösung:
Ai : Die entnommene Glühbirne wurde auf der Maschine Mi produziert ði ¼ 1; 2Þ
B: Die entnommene Glühbirne ist defekt
Zwei Pfade führen nach B („Zwischenstationen“ sind A1 bzw. A2 ). Aus dem Ereignisbaum lassen sich
dann die gesuchten Wahrscheinlichkeiten mit Hilfe der Pfadregeln leicht berechnen:
P ðO A1 BÞ ¼ P ðA1 Þ . P ðB j A1 Þ ¼
¼ 0,8 . 0,02 ¼ 0,016
P ðO A2 BÞ ¼ P ðA2 Þ . P ðB j A2 Þ ¼
¼ 0,2 . 0,02 ¼ 0,004
0,2
A2
0,02
B
O
0,8
A1
0,02
a) Die gesuchte Wahrscheinlichkeit ist die totale Wahrscheinlichkeit des Ereignisses B:
P ðBÞ ¼ P ðO A1 BÞ þ P ðO A2 BÞ ¼ 0,016 þ 0,004 ¼ 0,020 ¼ 2 %
b) Die gesuchte Wahrscheinlichkeit P ðA1 j BÞ berechnen wir mit Hilfe der Bayesschen Formel:
P ðA1 j BÞ ¼
P ðO A1 BÞ
P ðBÞ
¼
0,016
¼ 0,8 ¼ 80 %
0,020
&
4 Wahrscheinlichkeitsverteilung einer Zufallsvariablen
4.1 Zufallsvariable
Eine Zufallsvariable oder Zufallsgröße X ist eine Funktion, die jedem Elementarereignis
w aus der Ergebnismenge W genau eine reelle Zahl X ðw) zuordnet. Sie heißt diskret,
wenn sie endlich viele oder abzählbar unendlich viele Werte annehmen kann, stetig dagegen, wenn sie jeden Wert aus einem bestimmten Intervall annehmen kann.
4 Wahrscheinlichkeitsverteilung einer Zufallsvariablen
413
4.2 Verteilungsfunktion einer Zufallsvariablen
Die Verteilungsfunktion FðxÞ einer Zufallsvariablen X ist die Wahrscheinlichkeit dafür,
dass die Zufallsvariable X einen Wert annimmt, der höchstens gleich einem vorgegebenen
Zahlenwert x ist:
F ðxÞ ¼ P ðX ) xÞ
Eigenschaften
(1)
(2)
(3)
(4)
F ðxÞ ist monoton wachsend mit 0 ) F ðxÞ ) 1.
lim
F ðxÞ ¼ 0
(unmögliches Ereignis)
lim
F ðxÞ ¼ 1
(sicheres Ereignis)
x!/1
x!þ1
Die Wahrscheinlichkeit dafür, dass X einen Wert aus dem Intervall a < X ) b
annimmt, beträgt
P ða < X ) bÞ ¼ F ðbÞ / F ðaÞ
Diskrete Verteilung
Wahrscheinlichkeitsverteilung einer diskreten Zufallsvariablen:
Wahrscheinlichkeitsfunktion
(Stabdiagramm)
(
)
x ¼ xi
pi
..
f ðxÞ ¼
fur
..
alle ubrigen x
0
f(x)
x1
Verteilungsfunktion
(Treppenfunktion)
F ðxÞ ¼ P ðX ) xÞ ¼
x2
x3
x4
xn
x
F(x)
P
xi ) x
1
pn
f ðxi Þ
p4
p3
p2
p1
x1
x2
x3 x4
xn
x
414
XV Wahrscheinlichkeitsrechnung
Eigenschaften
(1)
(2)
pi ist die Wahrscheinlichkeit dafür, dass die Zufallsvariable X den Wert xi annimmt ð pi > 0Þ.
P
P
f ðxÞ ( 0 ist normiert, d. h.
f ðxi Þ ¼
pi ¼ 1 :
&
Beispiel
i
i
Zufallsexperiment: „Wurf einer homogenen Münze“ (Laplace-Experiment)
Zufallsvariable: X ¼ Anzahl „Wappen“
X ist diskret, mögliche Werte sind 0 (Zahl) und 1 (Wappen).
Verteilungstabelle:
xi
0
1
f ðxi Þ
0,5
0,5
Stabdiagramm und Treppenkurve:
F(x)
f(x)
1
0,5
0,5
0
1
0
x
1
x
&
Stetige Verteilung
Wahrscheinlichkeitsverteilung einer stetigen Zufallsvariablen:
Wahrscheinlichkeitsdichtefunktion
f(x)
(kurz: Dichtefunktion)
f ðxÞ ¼ F 0 ðxÞ
x
Verteilungsfunktion
F(x)
ðx
F ðxÞ ¼ P ðX ) xÞ ¼
f ðuÞ du
1
/1
x
4 Wahrscheinlichkeitsverteilung einer Zufallsvariablen
Eigenschaften
(1)
f ðxÞ ( 0 ist normiert:
1
Ð
/1
415
f ðxÞ dx ¼ 1
f(x)
(entspricht der Gesamtfläche unter der
Dichtefunktion).
(2)
P ða ) X ) bÞ ¼
Ðb
a
P(a ≤ X ≤ b)
f ðxÞ dx
(entspricht der im Bild grau unterlegten
Fläche)
&
Beispiel
a
b
x
f(x)
X sei eine exponentialverteilte Zufallsvariable mit
der Dichtefunktion
(
f ðxÞ ¼
e /x
0
..
fur
x ( 0
1
)
x < 0
x
Die zugehörige Verteilungsfunktion lautet dann
für x ( 0 wie folgt:
F ðxÞ ¼
¼
Ðx
/1
f ðuÞ du ¼
x
½/ e / u % 0
Ðx
0
e / u du ¼
F(x)
1
¼ / e /x þ e 0 ¼
¼ / e /x þ 1 ¼ 1 / e /x
x
Für x < 0 ist FðxÞ ¼ 0 .
&
4.3 Kennwerte oder Maßzahlen einer Verteilung
Erwartungswert einer Zufallsvariablen X
E ðXÞ ¼
P
i
xi . f ðxi Þ
(diskrete Verteilung)
1
ð
E ðXÞ ¼
x . f ðxÞ dx
/1
(stetige Verteilung)
416
XV Wahrscheinlichkeitsrechnung
Beispiele
&
(1)
Wir berechnen den Erwartungswert einer
diskreten Zufallsvariablen X mit der
nebenstehenden Verteilungstabelle:
E ðXÞ ¼
(2)
P
i
xi . f ðxi Þ ¼ 0 .
xi
0
1
2
3
f ðxi Þ
1/8
3/8
3/8
1/8
1
3
3
1
3
6
3
12
3
þ1.
þ2.
þ3.
¼
þ
þ
¼
¼
8
8
8
8
8
8
8
8
2
Die stetige Zufallsvariable X mit der Dichtefunktion f ðxÞ ¼ e / x für x ( 0 (sonst f ðxÞ ¼ 0Þ
besitzt den folgenden Erwartungswert:
E ðXÞ ¼
1
Ð
/1
1
Ð
1
x . e / x dx ¼ ½ð/ x / 1Þ . e / x % 0 ¼ 0 þ e 0 ¼ 0 þ 1 ¼ 1
0
|fflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflffl}
Integral 313 mit a ¼ / 1
x . f ðxÞ dx ¼
&
Erwartungswert einer Funktion Z ¼ g (X)
E ðZÞ ¼ E ½ g ðxÞ % ¼
P
i
gðxi Þ . f ðxi Þ
(diskrete Verteilung)
1
ð
E ðZÞ ¼ E ½ g ðxÞ % ¼
g ðxÞ . f ðxÞ dx
(stetige Verteilung)
/1
f ðxÞ: Wahrscheinlichkeits- bzw. Dichtefunktion der Zufallsvariablen X
Rechenregeln für Erwartungswerte
a, b und c sind Konstanten.
(1)
E ðcÞ ¼ c
(2)
E ða . g1 ðxÞ þ b . g2 ðxÞÞ ¼ a . E ðg1 ðxÞÞ þ b . E ðg2 ðxÞÞ
Mittelwert, Varianz und Standardabweichung einer Zufallsvariablen
Mittelwert m, Varianz s 2 und Standardabweichung s sind die drei Maßzahlen oder
Kennwerte einer Zufallsvariablen X. Sie sind wie folgt definiert:
Kennwerte (Maßzahlen)
Mittelwert m ¼ E ðXÞ
Varianz s 2 ¼ Var ðXÞ
Standardabweichung s
diskret
P
i
P
i
xi . f ðxi Þ
ðxi / mÞ 2 . f ðxi Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Var ðXÞ
stetig
1
Ð
/1
1
Ð
/1
x . f ðxÞ dx
ðx / mÞ 2 . f ðxÞ dx
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Var ðXÞ
5 Spezielle diskrete Wahrscheinlichkeitsverteilungen
417
Anmerkungen
(1)
Der Mittelwert m ist der Erwartungswert von X.
(2)
Die Varianz s 2 ist ein Maß für die mittlere quadratische Abweichung der Einzelwerte vom Mittelwert m („Streuung“ der Einzelwerte um den Mittelwert). s 2 ist
der Erwartungswert der Funktion (Zufallsvariablen) Z ¼ ðX / mÞ 2 .
(3)
s 2 ¼ E ðX 2 Þ / m 2 („bequemere“ Rechenformel für die Varianz)
(4)
m, s 2 und s werden auch als Kennwerte (Maßzahlen) der Verteilung bezeichnet.
(5)
Bei einer symmetrischen Verteilung mit dem Symmetriezentrum x0 gilt:
m ¼ E ðXÞ ¼ x0 .
Rechenregeln für lineare Funktionen
(1)
E ða . X þ bÞ ¼ a . E ðXÞ þ b
(2)
Var ða . X þ bÞ ¼ a 2 . Var ðXÞ
)
a, b: Konstanten
5 Spezielle diskrete Wahrscheinlichkeitsverteilungen
5.1 Binomialverteilung
Bernoulli-Experiment
Ein Zufallsexperiment mit nur zwei sich gegenseitig ausschließenden Ergebnissen (Ereignissen) heißt Bernoulli-Experiment.
&
Beispiel
Beim Zufallsexperiment „Wurf einer homogenen Münze“ gibt es nur die beiden sich gegenseitig ausschließenden Ergebnisse „Zahl“ oder „Wappen“. Es handelt sich also um ein Bernoulli-Experiment.
&
Urnenmodell
Eine Urne enthalte weiße und schwarze Kugeln. Die zufällige Entnahme einer Kugel ist
dann ein Bernoulli-Experiment. Wird dieses Experiment n-mal nacheinander durchgeführt,
wobei die jeweils gezogene Kugel vor der nächsten Ziehung in die Urne zurückgelegt wird
(„Ziehung mit Zurücklegen“), so ist die diskrete Zufallsvariable
X ¼ Anzahl der insgesamt gezogenen weißen Kugeln
binomialverteilt (mögliche Werte für X : 0; 1; 2; . . . ; nÞ.
418
XV Wahrscheinlichkeitsrechnung
Binomialverteilung
Die Verteilung einer diskreten Zufallsvariablen X mit der Wahrscheinlichkeitsfunktion
3 2
n
f ðxÞ ¼ P ðX ¼ xÞ ¼
p x . q n/x
ðx ¼ 0; 1; 2; . . . ; nÞ
x
und der zugehörigen Verteilungsfunktion
3 2
n
F ðxÞ ¼ P ðX ) xÞ ¼
p k . q n/k
k
P
k)x
heißt Binomialverteilung mit den Parametern n und p ðn ¼ 1; 2; 3; . . . ;
0 < p < 1; q ¼ 1 / p). Die Kennwerte oder Maßzahlen dieser Verteilung lauten:
Mittelwert: m ¼ n p
Varianz: s 2 ¼ n p q ¼ n p ð1 / pÞ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffi
Standardabweichung: s ¼
npq ¼
n p ð1 / pÞ
f(x)
0,6
0,5
0,4
0,3
0,2
0,1
n = 6 , p = 0,1
Wahrscheinlichkeitsfunktion f ðxÞ
einer Binomialverteilung mit den
Parametern n ¼ 6 und p ¼ 0,1
0
1
2
3
4
5
6
x
Anmerkungen
(1)
(2)
(3)
Symbolische Schreibweise für die Binomialverteilung: B ðn; pÞ
Anwendung findet die Binomialverteilung überall dort, wo alternative Entscheidungen zu treffen sind. Beispiele: Münzwurf (Zahl oder Wappen), Qualitätskontrollen
(einwandfrei oder Ausschuß).
Wird ein Bernoulli-Experiment mit den beiden sich gegenseitig ausschließenden Ereignissen A und A n-mal nacheinander ausgeführt (sog. mehrstufiges Bernoulli-Experiment vom Umfang n), so ist die diskrete Zufallsvariable
X ¼ Anzahl der Versuche, in denen das Ereignis A eintritt
binomialverteilt mit den Parametern n und p. Dabei bedeuten:
p : Konstante Wahrscheinlichkeit für das Eintreten des Ereignisses A beim Einzelversuch ð0 < p < 1Þ
q: Konstante Wahrscheinlichkeit für das Eintreten des zu A komplementären Ereignisses A beim Einzelversuch ðq ¼ 1 / pÞ
n: Anzahl der Ausführungen des Bernoulli-Experiments (Umfang des mehrstufigen
Bernoulli-Experiments)
5 Spezielle diskrete Wahrscheinlichkeitsverteilungen
(4)
!blich sind auch folgende Bezeichnungen:
A ¼ Erfolg,
(5)
(7)
A ¼ Mißerfolg,
p ¼ Erfolgswahrscheinlichkeit
Nützliche Rekursionsformel für die Praxis:
f ðx þ 1Þ ¼
(6)
419
ðn / xÞ p
. f ðxÞ
ðx þ 1Þ ð1 / pÞ
ðx ¼ 0; 1; 2; . . . ; n / 1Þ
Sonderfall n ¼ 1: Die Zufallsvariable X kann nur die Werte 0 und 1 annehmen
(sog. „Null-Eins-Verteilung“):
X ¼ 0
)
A
ist eingetreten
X ¼ 1
)
A
ist eingetreten
Die Binomialverteilung B ðn; pÞ darf für großes n und kleines p näherungsweise
durch die (rechnerisch bequemere) Poisson-Verteilung mit dem Parameter m ¼ n p
ersetzt werden (Faustregel: n p < 10 und n > 1500 p).
5.2 Hypergeometrische Verteilung
Urnenmodell
In einer Urne befinden sich N Kugeln, darunter M weiße und N / M schwarze Kugeln. Entnimmt man der Urne ganz zufällig n Kugeln, wobei die jeweils gezogene Kugel
vor der nächsten Ziehung nicht in die Urne zurückgelegt wird („Ziehung ohne Zurücklegen“), so genügt die diskrete Zufallsvariable
X ¼ Anzahl der insgesamt gezogenen weißen Kugeln
einer hypergeometrischen Verteilung (mögliche Werte für X : 0; 1; 2; . . . ; n).
Hypergeometrische Verteilung
Die Verteilung einer diskreten Zufallsvariablen X mit der Wahrscheinlichkeitsfunktion
3 2 3
2
M
N /M
.
x
n/x
ðx ¼ 0; 1; 2; . . . ; nÞ
f ðxÞ ¼ P ðX ¼ xÞ ¼
3 2
N
n
und der zugehörigen Verteilungsfunktion
3 2 3
2
M
N /M
.
k
n/k
F ðxÞ ¼
3 2
N
k)x
n
P
heißt hypergeometrische Verteilung mit den Parametern
ðN ¼ 1; 2; 3; . . . ; M ¼ 1; 2; 3; . . . ; N; M ) N; n ) N).
N,
M
und
n
420
XV Wahrscheinlichkeitsrechnung
Die Kennwerte oder Maßzahlen dieser Verteilung lauten:
Mittelwert: m ¼ n
Varianz: s 2 ¼
M
N
n M ðN / MÞ ðN / nÞ
N 2 ðN / 1Þ
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n M ðN / MÞ ðN / nÞ
Standardabweichung: s ¼
N 2 ðN / 1Þ
f(x)
0,5
N=50,M=10,n=5
0,4
0,3
0,2
Wahrscheinlichkeitsfunktion f ðxÞ
einer hypergeometrischen Verteilung
mit den Parametern N ¼ 50,
M ¼ 10 und n ¼ 5
0,1
0
1
2
3
4
5
x
Anmerkungen
(1)
(2)
(3)
Symbolische Schreibweise für die hypergeometrische Verteilung: H ðN; M; nÞ.
Anwendungen: Qualitäts- und Endkontrollen eines Herstellers von Massenartikeln,
Abnahmekontrollen des Kunden bei der Warenanlieferung.
Zum Urnenmodell: Die Urne repräsentiert eine Grundgesamtheit mit N Elementen
(Kugeln), die entweder die Eigenschaft A (weiß) oder A (schwarz) besitzen.
M : Anzahl der Elemente mit der Eigenschaft A
n: Umfang der Stichprobe
x : Anzahl der in der Stichprobe enthaltenen Elemente mit der Eigenschaft A
(4)
Nützliche Rekursionsformel für die Praxis:
f ðx þ 1Þ ¼
ðn / xÞ ðM / xÞ
ðx þ 1Þ ðN / M / n þ x þ 1Þ
. f ðxÞ
ðx ¼ 0; 1; 2; . . . ; n / 1Þ
(5)
Für N $ n lässt sich die hypergeometrische Verteilung näherungsweise durch eine
Binomialverteilung mit den Parametern n und p ¼ M = N ersetzen (Faustregel: n < 0,05 NÞ.
(6)
Merke: Ziehung mit Zurücklegen ! Binomialverteilung
Ziehung ohne Zurücklegen ! hypergeometrische Verteilung
5 Spezielle diskrete Wahrscheinlichkeitsverteilungen
421
5.3 Poisson-Verteilung
Die Verteilung einer diskreten Zufallsvariablen X mit der Wahrscheinlichkeitsfunktion
mx
. e /m
x!
und der zugehörigen Verteilungsfunktion
ðx ¼ 0; 1; 2; . . .Þ
f ðxÞ ¼ P ðX ¼ xÞ ¼
F ðxÞ ¼ P ðX ) xÞ ¼ e / m .
P
k)x
mk
k!
heißt Poisson-Verteilung mit dem Parameter m > 0. Die Kennwerte oder Maßzahlen
dieser Verteilung lauten:
Mittelwert: m
Varianz: s 2 ¼ m
pffiffiffiffi
Standardabweichung: s ¼ m
f(x)
0,4
µ=1
0,3
0,2
Wahrscheinlichkeitsfunktion f ðxÞ
einer Poisson-Verteilung
mit dem Parameter m ¼ 1
0,1
0
1
2
3
4
x
Anmerkungen
(1)
(2)
(3)
Symbolische Schreibweise für die Poisson-Verteilung: Ps ð mÞ
Anwendung findet die Poisson-Verteilung bei mehrstufigen Bernoulli-Experimenten,
in denen das Ereignis A mit geringer Wahrscheinlichkeit p, d. h. sehr selten eintritt
(z. B. radioaktiver Zerfall).
Nützliche Rekursionsformel für die Praxis:
m
f ðx þ 1Þ ¼
. f ðxÞ
ðx ¼ 0; 1; 2; . . .Þ
x þ1
Ps ð m Þ
Poisson-Verteilung
H ðN; M; nÞ
Hypergeometrische
Verteilung
B ðn; pÞ
Binomialverteilung
M
< 0,9
N
M
B n; p ¼
N
3
2
n < 0,05 N; n > 10
0,1 <
Faustregel:
. . . Binomialverteilung
Approximation durch eine . . .
und
oder
M
( 0,9
N
M
Ps m ¼ n
N
3
2
n < 0,05 N; n > 30
M
) 0,1
N
Faustregel:
Ps ð m ¼ n pÞ
n ( 1500 p
n p ) 10
Faustregel:
. . . Poisson-Verteilung
N
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n p ð1 / pÞ Þ
M
< 0,9
N
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!
3
2
M
M
N/n
n
1/
N
N
N/1
N ð m; s ¼
pffiffiffi
mÞ
m > 10
Faustregel:
M
m¼n ; s¼
N
n < 0,05 N; n > 30
0,1 <
Faustregel:
N ð m ¼ n p; s ¼
n p ð1 / pÞ > 9
Faustregel:
. . . Normalverteilung
422
XV Wahrscheinlichkeitsrechnung
5.4 Approximationen diskreter Wahrscheinlichkeitsverteilungen
(Tabelle)
6 Spezielle stetige Wahrscheinlichkeitsverteilungen
423
6 Spezielle stetige Wahrscheinlichkeitsverteilungen
6.1 Gaußsche Normalverteilung
6.1.1 Allgemeine Normalverteilung
Die Verteilung einer stetigen Zufallsvariablen X mit der Dichtefunktion
! 4
1 x/m 2
/
1
f ðxÞ ¼ pffiffiffiffiffiffiffi . e 2 s
ð/ 1 < x < 1Þ
2p s
und der zugehörigen Verteilungsfunktion
ðx
1
F ðxÞ ¼ P ðX ) xÞ ¼ pffiffiffiffiffiffiffi .
2p s
e
/
1
2
!
t/m
s
42
dt
/1
heißt Gaußsche Normalverteilung mit den Parametern m und s > 0. Die Kennwerte
oder Maßzahlen dieser Verteilung lauten:
Mittelwert: m
Varianz: s 2
Standardabweichung: s
f(x)
f(x) =
1
2π σ
e
–
1
2
(
x–µ 2
σ )
Dichtefunktion f ðxÞ der Gaußschen Normalverteilung („Gaußsche Glockenkurve“)
µ−σ
µ
µ+σ
x
Anmerkungen
(1)
(2)
Symbolische Schreibweise für die Gaußsche Normalverteilung: N ð m; sÞ
Eigenschaften der Dichtefunktion f ðxÞ:
a) f ðxÞ ist spiegelsymmetrisch zur Geraden x ¼ m.
b) Das absolute Maximum liegt bei x1 ¼ m und ist zugleich Symmetriezentrum, die
beiden Wendepunkte liegen symmetrisch zum Maximum an den Stellen
x2=3 ¼ m + s.
c) f ðxÞ ist normiert (die Fläche unter der Dichtefunktion hat den Wert 1):
1
1
1
0
ð
ð
1 x/m 2
/
1
s
2
f ðxÞ dx ¼ pffiffiffiffiffiffiffi .
e
dx
2p s
/1
/1
424
(3)
(4)
(5)
XV Wahrscheinlichkeitsrechnung
Die Dichtefunktion wird ihrer Form wegen auch als Gaußsche Glockenkurve bezeichnet.
Der Parameter s (Standardabweichung) bestimmt im Wesentlichen Breite und Höhe
der Glockenkurve: je kleiner s, umso höher und steiler die Kurve.
Anwendung findet die Normalverteilung in der Fehlerrechnung und Statistik.
6.1.2 Standardnormalverteilung
Die allgemeine Gaußsche Normalverteilung mit den Parametern m und s lässt sich stets
auf die sog. Standardnormalverteilung mit den speziellen Parameterwerten m ¼ 0 und
s ¼ 1 zurückführen. Dies entspricht einem !bergang von der normalverteilten Zufallsvariablen X zur sog. standardnormalverteilten Zufallsvariablen U mit Hilfe der linearen
Transformation (Substitution)
X /m
s
(sog. Standardisierung oder Umrechnung in Standardeinheiten).
U ¼
Standardnormalverteilung einer stetigen Zufallsvariablen U
Eine Normalverteilung mi den Parametern m ¼ 0 und s ¼ 1 heißt Standardnormalverteilung oder auch standardisierte Normalverteilung. Ihre Dichtefunktion ist
1
/ u2
1
j ðuÞ ¼ pffiffiffiffiffiffiffi . e 2
2p
ð/ 1 < u < 1Þ
und besitzt den im Bild dargestellten typischen Verlauf („Glockenkurve“). Die zugehörige Verteilungsfunktion lautet:
1
f ðuÞ ¼ P ðU ) uÞ ¼ pffiffiffiffiffiffiffi .
2p
ðu
e
1
/ t2
2
dt
/1
Eine ausführliche Tabelle der Verteilungsfunktion f ðuÞ befindet sich im Anhang,
Teil B (Tabelle 1).
ϕ(u)
0,4
Fläche = 1
Dichtefunktion j ðuÞ
der Standardnormalverteilung
–2
–1
1
2
u
6 Spezielle stetige Wahrscheinlichkeitsverteilungen
425
Anmerkungen
(1)
Symbolische Schreibweise für die Standardnormalverteilung: N ð0; 1Þ
(2)
Eigenschaften der Dichtefunktion j ðuÞ:
a) j ðuÞ ist achsensymmetrisch, d. h. eine gerade Funktion.
b) Das Maximum liegt bei u1 ¼ 0 und ist zugleich Symmetriezentrum, die beiden
Wendepunkte befinden sich an den Stellen u2=3 ¼ + 1:
c) j ðuÞ ist normiert, d. h. die Fläche unter der Dichtefunktion hat den Wert 1:
1
ð
/1
(3)
1
j ðuÞ du ¼ pffiffiffiffiffiffiffi .
2p
1
ð
e
/ 1 u2
2
du ¼ 1
/1
Die Verteilungsfunktion f ðuÞ wird auch als Gaußsches Fehlerintegral bezeichnet.
6.1.3 Berechnung von Wahrscheinlichkeiten mit Hilfe der tabellierten Verteilungsfunktion der Standardnormalverteilung
1. Fall: Die Zufallsvariable ist standardnormalverteilt
Die wichtigsten Formeln zur Berechnung von Wahrscheinlichkeiten bei ein- bzw. zweiseitiger Abgrenzung befinden sich aus Gründen der Zweckmäßigkeit im Anhang (Teil B) gegenüber der Tabelle 1 (Seite 514 / 515).
2. Fall: Die Zufallsvariable ist normalverteilt mit den Parametern m und s
Die normalverteilte Zufallsvariable X wird zunächst durch die Transformation (Substitution) U ¼ ðX / mÞ=s in die standardnormalverteilte Zufallsvariable U übergeführt
(Umrechnung in Standardeinheiten). Bei ein- bzw. zweiseitiger Abgrenzung gelten dann
folgende Formeln:
Einseitige Abgrenzung
Abgrenzung nach oben
f(t)
Abgrenzung nach unten
f(t)
P(X ≤ x)
P(X ≤ x)
P(X ≥ x)
x
x
t
t
P ðX ) xÞ ¼ f ðuÞ
P ðX ( xÞ ¼ 1 / P ðX ) xÞ ¼ 1 / f ðuÞ
mit u ¼ ðx / mÞ=s
mit u ¼ ðx / mÞ=s
426
XV Wahrscheinlichkeitsrechnung
Zweiseitige Abgrenzung
unsymmetrisches Intervall
f(x)
symmetrisches Intervall
f(x)
P(a ≤ X≤ b)
a
b
P ða ) X ) bÞ ¼ f ðb *Þ / f ða *Þ
mit a * ¼ ða / mÞ=s und b * ¼ ðb / mÞ=s
&
µ – kσ
x
µ
µ + kσ
x
P ðj X / m j ) k sÞ ¼ 2 . f ðkÞ / 1
Beispiel
Die Zufallsvariable X ist normalverteilt mit dem Mittelwert m ¼ 10 und der Standardabweichung s ¼ 2.
Wir berechnen die Wahrscheinlichkeit P ð5 ) X ) 12Þ:
Umrechnung der Grenzen in Standardeinheiten:
83,5%
a/m
5 / 10
¼
¼ / 2,5
a ¼ 5 ) a* ¼
s
2
b ¼ 12 ) b * ¼
b/m
12 / 10
¼
¼ 1
s
2
5
10
12
x
Berechnung der Wahrscheinlichkeit mit Hilfe der Tabelle 1 im Anhang, Teil B:
P ð5 ) X ) 12Þ ¼ P ð/ 2,5 ) U ) 1Þ ¼ f ð1Þ / f ð/ 2,5Þ ¼ f ð1Þ / ½1 / f ð2,5Þ% ¼
¼ f ð1Þ þ f ð2,5Þ / 1 ¼ 0,8413 þ 0,9938 / 1 ¼ 0,8351
&
6.1.4 Quantile der Standardnormalverteilung
Bei einer einseitigen Abgrenzung nach oben beschreibt die Verteilungsfunktion f ðuÞ der
Standardnormalverteilung die Wahrscheinlichkeit dafür, dass die standardnormalverteilte
Zufallsvariable U einen Wert zwischen / 1 und u annimmt ( Fläche unter der Dichtefunktion bis hin zur oberen Grenze u): P ðU ) uÞ ¼ f ðuÞ. Zu jedem Wert u gehört
somit genau ein Wahrscheinlichkeitswert f ðuÞ.
6 Spezielle stetige Wahrscheinlichkeitsverteilungen
427
Umgekehrt gehört zu einem vorgegebenen Wahrscheinlichkeitswert p genau eine obere
Grenze oder Schranke, die als Quantil up zum Wahrscheinlichkeitswert p bezeichnet
wird. Das Quantil up genügt der Gleichung
P ðU ) up Þ ¼ f ðup Þ ¼ p
ϕ (u)
und lässt sich für die in der Praxis gängigen
Wahrscheinlichkeitswerte aus der Tabelle 2
im Anhang, Teil B bestimmen. Formeln für
die Berechnung der Intervallgrenzen bei einbzw. zweiseitiger Abgrenzung findet der Leser im Anhang, Teil B gegenüber der Tabelle 2 (Seite 516 / 517).
&
P(U ≤ u p ) = p
up
u
ϕ (u)
Beispiel
p = 0,9
P ðU ) cÞ ¼ 0,9
c ¼ ?
P ðU ) cÞ ¼ f ðcÞ ¼ 0,9
c = up
u
Aus der Tabelle 2 im Anhang, Teil B entnehmen wir: Zum Wahrscheinlichkeitswert p ¼ 0,9 gehört das
Quantil u 0;9 ¼ 1,282. Somit ist c ¼ u 0;9 ¼ 1,282.
&
6.2 Exponentialverteilung
Die Verteilung einer stetigen Zufallsvariablen X mit der Wahrscheinlichkeitsdichtefunktion
(
)
0
x < 0
..
f ðxÞ ¼
fur
l . e /lx
x ( 0
und der zugehörigen Verteilungsfunktion
(
0
F ðxÞ ¼ P ðX ) xÞ ¼
1 / e /lx
..
fur
x < 0
)
x ( 0
heißt Exponentialverteilung mit dem Parameter l > 0. Die Kennwerte oder Maßzahlen dieser Verteilung lauten:
Mittelwert: m ¼ 1=l
Varianz: s 2 ¼ 1=l 2
Standardabweichung: s ¼ 1=l
428
XV Wahrscheinlichkeitsrechnung
f(x)
λ
x
Dichtefunktion einer exponentialverteilten
Zufallsvariablen X
Anmerkungen
(1)
(2)
Mittelwert und Standardabweichung stimmen überein: m ¼ s ¼ 1=l
Anwendungen: Lebensdauer von Bauelementen und Lebewesen.
7 Wahrscheinlichkeitsverteilungen
von mehreren Zufallsvariablen
7.1 Mehrdimensionale Zufallsvariable
2-dimensionale Zufallsvariable
Zufallsexperimente, in denen gleichzeitig zwei Merkmale beobachtet werden, lassen sich
durch eine 2-dimensionale Zufallsvariable ðX; YÞ , auch 2-dimensionaler Zufallsvektor
genannt, darstellen. Die Verteilung wird dabei vollständig durch die Verteilungsfunktion
F ðx; yÞ ¼ P ðX ) x; Y ) yÞ
beschrieben ( Wahrscheinlichkeit dafür, dass die Zufallsvariablen X und Y gleichzeitig
Werte annehmen, die kleiner oder gleich x bzw. y sind). F ðx; yÞ wird auch als gemeinsame Verteilung der Zufallsvariablen X und Y bezeichnet.
Bei einer diskreten Verteilung sind X und Y beide diskret. Die normierte Wahrscheinlichkeitsfunktion f ðx; yÞ ordnet dann jedem möglichen Wertepaar ðxi ; yk Þ einen Wahrscheinlichkeitswert pik > 0 zu.
Eine stetige Verteilung (X und Y sind beide stetig) lässt sich durch die normierte Wahrscheinlichkeitsdichtefunktion f ðx; yÞ ( 0 mit der Verteilungsfunktion
ðx
ðy
F ðx; yÞ ¼
f ðu; vÞ dv du
u¼/1 v¼/1
vollständig beschreiben.
7 Wahrscheinlichkeitsverteilungen von mehreren Zufallsvariablen
&
429
Beispiel
Das Zufallsexperiment „Wurf mit zwei unterscheidbaren homogenen Würfeln“ beschreiben wir durch die 2dimensionale Zufallsvariable ðX; YÞ mit den beiden stochastisch unabhängigen Komponenten
X ¼ Augenzahl des 1. Würfels
Y ¼ Augenzahl des 2. Würfels
die unabhängig voneinander die Werte 1, 2, 3, 4, 5 und 6 annehmen können. Insgesamt gibt es 36 gleichwahrscheinliche Elementarereignisse (Laplace-Experiment):
ð1; 1Þ, ð1; 2Þ, ð1; 3Þ, ð1; 4Þ, ð1; 5Þ, ð1; 6Þ, ð2; 1Þ, . . . ; ð6; 6Þ
Sie treten jeweils mit der Wahrscheinlichkeit p ¼ 1=36 auf. Die Wahrscheinlichkeitsfunktion lautet daher:
(
)
1=36
x; y ¼ 1; 2; . . . ; 6
..
f ðx; yÞ ¼
fur
..
alle ubrigen ðx; yÞ
0
&
n-dimensionale Zufallsvariable
Zufallsexperimente mit n gleichzeitig beobachteten Merkmalen werden durch eine
n-dimensionale Zufallsvariable ðX1 ; X2 ; . . . ; Xn Þ; auch n-dimensionaler Zufallsvektor
genannt, beschrieben. Alle bisherigen Begriffe lassen sich sinngemäß übertragen.
Stochastisch unabhängige Zufallsvariable
Zwei Zufallsvariable X und Y heißen stochastisch unabhängig, wenn stets gilt
F ðx; yÞ ¼ F1 ðxÞ . F2 ðyÞ
F1 ðxÞ, F2 ðyÞ:
Verteilungsfunktionen von X bzw. Y
Anderenfalls die sind die beiden Zufallsvariablen stochastisch abhängig. Für die zugehörigen Wahrscheinlichkeits- bzw. Dichtefunktionen gilt (im Falle der Unabhängigkeit)
f ðx; yÞ ¼ f1 ðxÞ . f2 ðyÞ
f1 ðxÞ; f2 ðyÞ:
Wahrscheinlichkeits- bzw. Dichtefunktionen von X bzw. Y (auch Randverteilungen der 2-dimensionalen Verteilung genannt)
Diese Bedingung ist notwendig und hinreichend für die Unabhängigkeit. Analoge Beziehungen gelten für n stochastisch unabhängige Zufallsvariable.
430
XV Wahrscheinlichkeitsrechnung
7.2 Summen, Linearkombinationen und Produkte von Zufallsvariablen
Summen, Linearkombinationen und Produkte von n Zufallsvariablen X1 ; X2 ; . . . ; Xn sind
wiederum Zufallsvariable (alle Xi sind dabei entweder diskret oder stetig).
7.2.1 Additionssätze für Mittelwerte und Varianzen
Für Summen vom Typ Z ¼ X1 þ X2 þ . . . þ Xn
gelten folgende Sätze:
Additionssatz für Mittelwerte
E ðZÞ ¼ E ðX1 Þ þ E ðX2 Þ þ . . . þ E ðXn Þ
oder (in anderer Schreibweise)
mz ¼ m1 þ m2 þ . . . þ mn
E ðXi Þ ¼ mi :
Regel:
Mittelwert von Xi
ði ¼ 1; 2; 3; . . . ; nÞ
Die Mittelwerte werden addiert.
Additionssatz für Varianzen
Voraussetzung: X1 ; X2 ; . . . ; Xn sind stochastisch unabhängig
Var ðZÞ ¼ Var ðX1 Þ þ Var ðX2 Þ þ . . . þ Var ðXn Þ
oder (in anderer Schreibweise)
s 2z ¼ s 21 þ s 22 þ . . . þ s 2n
Var ðXi Þ ¼ s 2i :
Regel:
Varianz von Xi
ði ¼ 1; 2; 3; . . . ; nÞ
Die Varianzen werden addiert.
Additionssätze für Linearkombinationen
Die Additionssätze für Mittelwerte und Varianzen gelten unter den genannten Voraussetzungen auch für Linearkombinationen vom Typ
Z ¼ a1 . X1 þ a2 . X2 þ . . . þ an . Xn
(ai : Reelle Konstanten)
E ðZÞ ¼ a1 . E ðX1 Þ þ a2 . E ðX2 Þ þ . . . þ an . E ðXn Þ
Var ðZÞ ¼ a 21 . Var ðX1 Þ þ a 22 . Var ðX2 Þ þ . . . þ a 2n . Var ðXn Þ
oder (in anderer Schreibweise)
mz ¼ a1 . m1 þ a2 . m2 þ . . . þ an . mn
s 2z ¼ a 21 . s 21 þ a 22 . s 22 þ . . . þ a 2n . s 2n
7 Wahrscheinlichkeitsverteilungen von mehreren Zufallsvariablen
&
431
Beispiel
Zufallsexperiment: „Wurf mit zwei unterscheidbaren homogenen Würfeln“
Zufallsvariable: Xi ¼ Augenzahl des i-ten Würfels ði ¼ 1; 2Þ
X1 und X2 sind stochastisch unabhängige Zufallsvariable mit den Mittelwerten m1 ¼ m2 ¼ 3,5 und den
Varianzen s 21 ¼ s 22 ¼ 35=12. Dann gilt für die Summe Z ¼ X1 þ X2 :
mz ¼ E ðZÞ ¼ m1 þ m2 ¼ 3,5 þ 3,5 ¼ 7
s 2z ¼ Var ðZÞ ¼ s 21 þ s 22 ¼
35
35
70
35
þ
¼
¼
12
12
12
6
&
7.2.2 Multiplikationssatz für Mittelwerte
Für ein Produkt Z ¼ X1 . X2 . . . Xn aus n stochastisch unabhängigen Faktoren gilt der
folgende Multiplikationssatz für Mittelwerte:
E ðZÞ ¼ E ðX1 Þ . E ðX2 Þ . . . E ðXn Þ
oder (in anderer Schreibweise)
mz ¼ m1 . m2 . . . mn
E ðXi Þ ¼ mi :
Regel:
Mittelwert von Xi
ði ¼ 1; 2; 3; . . . ; nÞ
Die Mittelwerte werden multipliziert.
7.2.3 Wahrscheinlichkeitsverteilung einer Summe
Eine Summe Z ¼ X1 þ X2 þ . . . þ Xn von n normalverteilten und stochastisch unabhängigen Zufallsvariablen X1 ; X2 ; . . . ; Xn besitzt folgende Eigenschaften:
Z ist normalverteilt mit dem Mittelwert
mz ¼ m1 þ m2 þ . . . þ mn
und der Varianz
s 2z ¼ s 21 þ s 22 þ . . . þ s 2n
Regel:
Mittelwerte und Varianzen werden jeweils addiert.
Sonderfall: mi ¼ m,
s 2i ¼ s 2
)
mz ¼ n m,
s 2z ¼ n s 2
Für die Praxis wichtiger Hinweis:
Sind die Summanden Xi zwar stochastisch unabhängig, jedoch beliebig verteilt, so ist die
Summe näherungsweise normalverteilt, falls die Anzahl n der Summanden hinreichend
groß ist ( Faustregel: n > 30Þ und keiner der Summanden dominiert.
432
XV Wahrscheinlichkeitsrechnung
8 Prüf- oder Testverteilungen
Prüf- oder Testverteilungen sind Wahrscheinlichkeitsverteilungen, die im Zusammenhang
mit statistischen Prüf- oder Testverfahren benötigt werden.
8.1 Chi-Quadrat-Verteilung („ c 2-Verteilung“)
X1 ; X2 ; . . . ; Xn seien stochastisch unabhängige Zufallsvariable, die alle der Standardnormalverteilung N ð0; 1Þ genügen. Die aus ihnen gebildete Quadratsumme
Z ¼ c 2 ¼ X 21 þ X 22 þ . . . þ X 2n
ist dann eine stetige Zufallsvariable mit dem Wertebereich z ( 0 und genügt einer
sog. Chi-Quadrat-Verteilung mit der Dichtefunktion
9
8
z
/
>
>
ðn
/
2Þ=2
>
2
=
< An . z
z > 0>
.e
..
f ðzÞ ¼
fur
>
>
>
>
;
:
0
z ) 0
und der zugehörigen Verteilungsfunktion
ðz
u
/
F ðzÞ ¼ An . u ðn / 2Þ=2 . e 2 du
ðz > 0Þ
0
(für z ) 0 ist F ðzÞ ¼ 0). Die Verteilung ist durch den Parameter n vollständig
bestimmt ðn ¼ 1; 2; 3; . . .Þ. Die Kennwerte oder Maßzahlen dieser Verteilung lauten:
Mittelwert: m ¼ n
Varianz: s 2 ¼ 2 n
pffiffiffiffiffiffiffi
Standardabweichung: s ¼ 2 n
Im Anhang (Teil B) befindet sich eine ausführliche Tabelle der Quantile der Chi-Quadrat-Verteilung in Abhängigkeit vom Freiheitsgrad f ¼ n (Tabelle 3).
f(z)
0,5
Dichtefunktionen
der Chi-Quadrat-Verteilung
für n ¼ 1; 2 (linkes Bild)
bzw. n ¼ 3; 4 (rechtes Bild)
n=1
0,4
f(z)
0,3
0,3
n=2
0,2
0,2
0,1
0,1
1
2
3
4
5
6
z
n=3
n=4
1
2
3
4
5
6
7
8
z
8 Prüf- oder Testverteilungen
433
Anmerkungen
(1)
(2)
(3)
(4)
Der Parameter n bestimmt die Anzahl f der Freiheitsgrade der Verteilung: f ¼ n
ðn ¼ 1; 2; 3; . . .Þ.
An ist eine noch vom Freiheitsgrad f ¼ n abhängige Normierungskonstante, die
mit Hilfe der Gamma-Funktion berechnet werden kann (siehe weiter unten).
Eigenschaften der Dichtefunktion f ðzÞ:
f ðzÞ ist normiert (Fläche mit der z-Achse ¼ 1), verläuft für n ) 2 streng monoton fallend und besitzt für n > 2 ein absolutes Maximum an der Stelle z ¼ n / 2.
Die Chi-Quadrat-Verteilung lässt sich für hinreichend großes n durch eine Normalverteilung mit dem Mittelwert m ¼ n und der Varianz s 2 ¼ 2 n annähern
( Faustregel: n > 100).
Berechnung der Normierungskonstante An
Die Berechnung der Normierungskonstante
!4
An ¼
2
n
2
1
ðn ¼ 1; 2; 3; . . .Þ
3 2
n
.G
2
erfolgt über die Gamma-Funktion
1
ð
G ðaÞ ¼
t a / 1 . e / t dt
ðmit a > 0Þ
0
mit Hilfe der folgenden speziellen Werte und Rekursionsformeln:
(1)
3 2
pffiffiffi
1
¼ p;
G
2
(2)
G ða þ 1Þ ¼ a . G ðaÞ
(3)
G ðn þ 1Þ ¼ n !
ðn ¼ 1; 2; 3; . . .Þ
3
2
1
1 . 3 . 5 . . . ð2 n / 1Þ pffiffiffi
G nþ
¼
. p
n
2
2
(4)
G ð1Þ ¼ 1
ða > 0Þ
ðn ¼ 1; 2; 3; . . .Þ
434
XV Wahrscheinlichkeitsrechnung
8.2 t-Verteilung von Student
X und Y seien zwei stochastisch unabhängige Zufallsvariable mit den Eigenschaften
X:
standardnormalverteilt
Y:
Chi-Quadrat-verteilt mit f ¼ n Freiheitsgraden
Die aus ihnen gebildete Größe
X
T ¼ pffiffiffiffiffiffiffiffiffi
Y=n
ist dann eine stetige Zufallsvariable, die einer sog. t-Verteilung von Student mit der
Dichtefunktion
1
f ðtÞ ¼ An . 3
2 ðn þ 1Þ=2
t2
1þ
n
ð/ 1 < t < 1Þ
und der zugehörigen Verteilungsfunktion
ðt
F ðtÞ ¼ An .
/1
du
3
2 ðn þ 1Þ=2
u2
1þ
n
genügt. Die Verteilung ist dabei durch den Parameter n vollständig bestimmt
ðn ¼ 1; 2; 3; . . .Þ. Die Kennwerte oder Maßzahlen dieser Verteilung lauten:
Mittelwert 1Þ : m ¼ 0
Varianz 1Þ : s 2 ¼
für
n ( 2
n
n/2
für n ( 3
rffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
Standardabweichung 1Þ : s ¼
für n ( 3
n/2
Im Anhang (Teil B) befindet sich eine ausführliche Tabelle der Quantile der t-Verteilung in Abhängigkeit vom Freiheitsgrad f ¼ n (Tabelle 4).
f(t)
0,4
0,2
Dichtefunktion f ðtÞ
einer t-Verteilung
mit dem Parameter
n ¼ 2
0,1
–2
1Þ
–1
1
2
t
Für n ¼ 1 existiert kein Mittelwert, für n ¼ 1; 2 keine Varianz.
8 Prüf- oder Testverteilungen
435
Anmerkungen
(1)
(2)
(3)
(4)
Der Parameter n bestimmt die Anzahl der Freiheitsgrade der Verteilung: f ¼ n
ðn ¼ 1; 2; 3; . . .Þ.
An ist eine noch vom Freiheitsgrad f ¼ n abhängige Normierungskonstante, die
mit Hilfe der Gamma-Funktion berechnet werden kann (siehe weiter unten).
Eigenschaften der Dichtefunktion f ðtÞ:
f ðtÞ ist normiert (Fläche mit der t-Achse ¼ 1), verläuft achsensymmetrisch (gerade
Funktion), besitzt bei t ¼ 0 ein absolutes Maximum und an den Stellen
rffiffiffiffiffiffiffiffiffiffiffiffiffi
n
t ¼ +
Wendepunkte und nähert sich im Unendlichen asymptotisch der
nþ2
t-Achse. Der Kurvenverlauf ähnelt daher stark der Gaußschen Glockenkurve (Normalverteilung)!
Die t-Verteilung lässt sich für hinreichend großes n durch die Standardnormalverteilung näherungsweise ersetzen ( Faustregel: n > 30).
Berechnung der Normierungskonstante An
Die Berechnung der Normierungskonstante
3
2
nþ1
G
2
An ¼
!n4
pffiffiffiffiffiffiffi
np . G
2
ðn ¼ 1; 2; 3; . . .Þ
erfolgt über die Gamma-Funktion (siehe Tabelle spezieller Werte und Rekursionsformeln
auf Seite 433).
436
XVI Grundlagen der mathematischen Statistik
1 Grundbegriffe
1.1 Zufallsstichproben aus einer Grundgesamtheit
Eine grundlegende Aufgabe der Statistik besteht darin, Kenntnisse und Informationen über
die Eigenschaften oder Merkmale einer bestimmten Menge von Objekten (Elementen) zu
gewinnen, ohne dass dabei alle Objekte in die Untersuchung miteinbezogen werden müssen. Dies ist aus den folgenden Gründen meist auch nicht möglich:
–– Zu hoher Zeit- und Kostenaufwand
–– Die Anzahl der Elemente, die untersucht werden müssten, ist zu groß
–– Die Untersuchungsobjekte könnten unter Umständen zerstört werden (Beispiel: Zerstörung einer Glühbirne beim Testen der Lebensdauer)
Grundgesamtheit
Unter einer Grundgesamtheit versteht man die Gesamtheit gleichartiger Objekte oder Elemente, die hinsichtlich eines bestimmten Merkmals untersucht werden sollen. Das dabei
interessierende Merkmal wird durch eine Zufallsvariable X beschrieben. Die Grundgesamtheit kann aus endlich vielen oder unendlich vielen Elementen bestehen.
Zufallsstichprobe (kurz: Stichprobe)
Eine aus der Grundgesamtheit nach dem „Zufallsprinzip“ herausgegriffene Teilmenge mit
n Elementen wird als Zufallsstichprobe vom Umfang n bezeichnet. Die Auswahl der
Elemente muss also wahllos und unabhängig voneinander geschehen; alle Elemente der
Grundgesamtheit müssen dabei grundsätzlich die gleiche Chance haben, ausgewählt (d. h.
gezogen) zu werden. Die beobachteten Merkmalswerte x1 ; x2 ; . . . ; xn der n Elemente
sind Realisierungen der Zufallsvariablen X und heißen Stichprobenwerte.
Da es in der Praxis aus den weiter oben genannten Gründen nicht möglich ist, alle Elemente einer Grundgesamtheit auf ein bestimmtes Merkmal X hin zu untersuchen, beschränkt
man sich auf die Untersuchung einer Stichprobe vom Umfang n, die der Grundgesamtheit
nach dem Zufallsprinzip entnommen wurde.
Die Aufgabe der mathematischen Statistik besteht dann u. a. darin, aus einer solchen Zufallsstichprobe mit Hilfe der Wahrscheinlichkeitsrechnung gewisse Rückschlüsse auf die
Grundgesamtheit zu ermöglichen.
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8_16
1 Grundbegriffe
437
1.2 Häufigkeitsverteilung einer Stichprobe
Urliste: Sie enthält die n Stichprobenwerte in der Reihenfolge ihres Auftretens
Spannweite der Stichprobe: Abstand zwischen dem kleinsten und dem größten Wert
Die Stichprobenwerte werden ihrer Größe nach geordnet, dann wird festgestellt, wie oft
jeder Wert vorkommt. Ist der Stichprobenwert xi genau ni -mal in der Stichprobe enthalten, so heißt diese Zahl absolute Häufigkeit des Stichprobenwertes xi ði ¼ 1; 2; . . . ; k
und k < nÞ. Dividiert man die absolute Häufigkeit ni durch die Anzahl n der Stichprobenwerte, so erhält man die relative Häufigkeit hi ¼ ni =n, wobei gilt
0 < hi ) 1
und
k
P
i¼1
hi ¼ h1 þ h2 þ . . . þ hk ¼ 1
Verteilungstabelle
Absolute und relative Häufigkeit werden in einer Verteilungstabelle dargestellt:
Stichprobenwert xi
x1
x2
x3
x4
...
xk
absolute Häufigkeit ni
n1
n2
n3
n4
...
nk
relative Häufigkeit hi
h1
h2
h3
h4
...
hk
Häufigkeitsfunktion f (x) einer Stichprobe
Die Verteilung der einzelnen Stichprobenwerte in einer geordneten Stichprobe vom Umfang n mit k verschiedenen Werten x1 ; x2 ; . . . ; xk lässt sich durch die folgende Häufigkeitsfunktion beschreiben:
(
f ðxÞ ¼
hi
0
..
fur
Graphische Darstellung:
Stabdiagramm
x ¼ xi
ði ¼ 1; 2; 3; . . . ; kÞ
..
alle ubrigen x
)
f (x)
h1
x1
h2
x2
h3
h4
x3
x4
hk
xk
x
438
XVI Grundlagen der mathematischen Statistik
Verteilungsfunktion F(x) einer Stichprobe
Die Summe der relativen Häufigkeiten aller Stichprobenwerte, die kleiner oder gleich x
sind, heißt Summenhäufigkeits- oder Verteilungsfunktion FðxÞ der Stichprobe:
FðxÞ ¼
P
xi ) x
f ðxi Þ
Graphische Darstellung:
Treppenfunktion (stückweise konstante
Funktion, an der Stelle xi erfolgt ein
Sprung um f ðxi Þ ¼ hi , Endwert ¼ 1)
F(x)
1
f(x k )
f(x 4 )
f(x 3 )
f(x 2 )
f(x 1 )
x1
&
x2
x3
x4
xk
x
Beispiel
Der Tagesproduktion von Gewindeschrauben mit dem Solldurchmesser 5,0 mm wurde eine Stichprobe vom
Umfang n ¼ 25 mit der folgenden Verteilungstabelle entnommen:
xi
mm
4,7
4,8
4,9
5,0
5,1
5,2
ni
1
3
6
9
4
2
hi
0,04
0,12
0,24
0,36
0,16
0,08
Häufigkeitsfunktion f ðxÞ und Verteilungsfunktion FðxÞ haben damit das folgende Aussehen:
xi
mm
4,7
4,8
4,9
5,0
5,1
5,2
f ðxi Þ
0,04
0,12
0,24
0,36
0,16
0,08
Fðxi Þ
0,04
0,16
0,40
0,76
0,92
1
&
1 Grundbegriffe
439
1.3 Gruppierung der Stichprobenwerte bei umfangreichen Stichproben
Bei umfangreichen Stichproben mit vielen verschiedenen Werten gruppiert man die Stichprobenwerte zweckmäßigerweise in sog. Klassen. Zunächst wird die Stichprobe geordnet
und der kleinste und größte Wert bestimmt ðxmin bzw. xmax ). Dann wird das Intervall I
festgelegt, in dem sämtliche Stichprobenwerte liegen und dieses schließlich in k Teilintervalle DIi gleicher Breite Dx zerlegt. Die Mitte eines jeden Klassenintervalls DIi heißt
Klassenmitte x~i .
linker Randpunkt
Δx
rechter Randpunkt
x min
Klassen-Nr.
1
x max
2
3
x
k
Allgemeine Regeln für die Gruppierung einer umfangreichen Stichprobe
(Einteilung der Stichprobenwerte in Klassen)
(1)
Man wähle möglichst Klassen gleicher Breite Dx.
(2)
Die Klasseneinteilung sollte so gewählt werden, dass die Klassenmitten durch
möglichst einfache Zahlen (z. B. ganze Zahlen) charakterisiert werden.
(3)
Fällt ein Stichprobenwert in einen der beiden Randpunkte einer Klasse, so zählt
man ihn je zur Hälfte den beiden angrenzenden Klassen zu.
(4)
Bei der Festlegung der Anzahl k der Klassen bei n Stichprobenwerten verwende
man die folgende Faustregel:
pffiffiffi
k ' n
f ür
50 < n < 500
Bei Stichproben mit einem Umfang n > 500 wähle man höchstens k ¼ 30
Klassen.
Anmerkung
Eine weitere häufig empfohlene Faustregel für die Klassenanzahl k lautet: k ) 5 . lg n
Durch Auszählen wird festgestellt, welche Stichprobenwerte in welche Klassen fallen. Die
Anzahl ni der Stichprobenwerte, die in der i-ten Klasse liegen, heißt absolute Klassenhäufigkeit. Dividiert man diese durch die Anzahl n aller Stichprobenwerte, so erhält man
die relative Klassenhäufigkeit hi ¼ ni =n ði ¼ 1; 2; . . . ; kÞ. Für die Weiterverarbeitung
der Stichprobenwerte wird vereinbart, dass allen Elementen einer Klasse genau die Klassenmitte als Wert zugeordnet wird.
440
XVI Grundlagen der mathematischen Statistik
Verteilungstabelle einer gruppierten Stichprobe
Klassenmitte x~i
x~1
x~2
x~3
x~4
...
x~k
relative Klassenhäufigkeit hi
h1
h2
h3
h4
...
hk
Häufigkeitsfunktion einer gruppierten Stichprobe
Die Häufigkeitsfunktion f ðxÞ einer gruppierten Stichprobe beschreibt die relative Klassenhäufigkeit hi in Abhängigkeit von der Klassenmitte x~i :
(
f ðxÞ ¼
hi
0
f ür
x ¼ x~i
ði ¼ 1; 2; 3; . . . ; kÞ
)
alle übrigen x
Der Verlauf dieser Funktion lässt sich graphisch durch ein Stabdiagramm oder durch ein
sog. Histogramm verdeutlichen. Beim Stabdiagramm trägt man dabei über der Klassenmitte x~i die relative Klassenhäufigkeit hi ab (d. h. einen Stab der Länge hi ).
f (x)
h3
h1
~
x
~
x
1
h4
h2
hk
~
~
x
x3
2
~
x
4
x
k
Ein Histogramm oder Staffelbild entsteht, wenn man über den Klassen gleicher Breite Dx
Rechtecke errichtet, deren Höhen den relativen Klassenhäufigkeiten entsprechen. Die Flächeninhalte der Rechtecke sind dabei den relativen Klassenhäufigkeiten proportional.
f (x)
h3
h1
h2
h4
hk
~
x
1
~
x
2
x~3
~
x
~
x
Δx
Δx
Δx
Δx
Δx
4
k
x
1 Grundbegriffe
441
Verteilungsfunktion einer gruppierten Stichprobe
FðxÞ ¼
P
x~i ) x
F(x)
f ð~
xi Þ
1
f( ~
xk )
FðxÞ heißt auch Summenhäufigkeits- oder
empirische Verteilungsfunktion.
f( ~
x4 )
Graphische Darstellung:
Treppenfunktion
f( ~
x3 )
f( ~
x1)
~
x
1
&
f( ~
x2 )
~
x
2
~
x
3
~
x
~
x
4
k
x
Beispiel
Mit einer automatischen Abfüllanlage wird Wein in Literflaschen gefüllt. Eine nachträgliche Stichprobenuntersuchung an n ¼ 20 gefüllten Flaschen ergab die folgenden Fehlmengen, beschrieben durch die Zufallsvariable X (in cm3 ):
Klasse i
Fehlmenge (in cm3 )
Anzahl der Flaschen
1
0 ) x ) 10
9
2
10 < x ) 20
6
3
20 < x ) 30
4
4
30 < x ) 40
1
Man erhält die folgende Verteilung (Klassenmitte, Häufigkeits- und Verteilungsfunktion, Histogramm):
i
1
2
3
4
x~i
5
15
25
35
f ð~
xi Þ
0,45
0,30
0,20
0,05
Fð~
xi Þ
0,45
0,75
0,95
1
f(x)
0,45
0,40
0,35
0,30
0,25
0,20
0,15
0,10
0,05
5
15
25
35
x/cm 3
&
442
XVI Grundlagen der mathematischen Statistik
2 Kennwerte oder Maßzahlen einer Stichprobe
2.1 Mittelwert, Varianz und Standardabweichung einer Stichprobe
Mittelwert x! einer Stichprobe
Der Mittelwert x! einer (geordneten) Stichprobe x1 ; x2 ; . . . ; xn vom Umfang n ist das
arithmetische Mittel der Stichprobenwerte:
x! ¼
n
x1 þ x2 þ . . . þ xn
1 P
xi
¼
.
n
n i¼1
kleinster Wert
x1
größter Wert
x2 x3
xn
x
Mittelwert x
Kontrolle:
n
P
i¼1
ðxi / x!Þ ¼ 0
Weitere übliche Bezeichnungen für x!:
Stichprobenmittelwert, empirischer Mittelwert
Varianz s 2 und Standardabweichung s einer Stichprobe
Ein geeignetes Maß für die Streuung der Einzelwerte xi um den Mittelwert x! ist die
Varianz
s2 ¼
n
P
ðx1 / x!Þ 2 þ ðx2 / x!Þ 2 þ . . . þ ðxn / x!Þ 2
1
¼
.
ðxi / x!Þ 2
n/1
n / 1 i¼1
Die Quadratwurzel aus der Varianz s 2 heißt Standardabweichung s der Stichprobe.
Merke: Die Summe der n Abweichungsquadrate wird durch n / 1 und nicht (wie naheliegend) durch n dividiert.
2 Kennwerte oder Maßzahlen einer Stichprobe
443
Anmerkungen
(1)
(2)
(3)
(4)
Weitere übliche Bezeichnungen für die Varianz s 2 einer Stichprobe sind Stichprobenvarianz oder auch empirische Varianz.
Beide Kennwerte, sowohl die Varianz s 2 als auch die Standardabweichung s, sind
ein Maß für die Streuung der Stichprobenwerte x1 ; x2 ; . . . ; xn um ihren Mittelwert
x!. Die Standardabweichung s hat dabei den Vorteil, dass sie dieselbe Dimension
und Einheit besitzt wie die einzelnen Stichprobenwerte und deren Mittelwert x!.
Die Varianz s 2 ist eine Art mittleres Abweichungsquadrat. Es gilt stets s 2 > 0
und somit auch s > 0.
Rechnerisch bequemere Rechenformel für die Varianz:
s2 ¼
&
1
n/1
+
n
P
i¼1
x 2i / n . x! 2
)
Beispiel
Aus der Tagesproduktion von Widerständen mit dem Sollwert 10 W wurde eine Stichprobe vom Umfang
n ¼ 8 entnommen:
9,8;
10,1;
10,3;
10,2;
10,2;
10,0;
9,9;
10,3
(jeweils in W)
Die Auswertung führt zu dem folgenden Ergebnis:
i
xi
W
x 2i
W2
1
9,8
96,04
2
10,1
102,01
3
10,3
106,09
4
10,2
104,04
5
10,2
104,04
6
10,0
100,00
7
9,9
98,01
8
10,3
106,09
S
80,8
816,32
x! ¼
s2 ¼
8
1 P
1
.
. 80;8 W ¼ 10;1 W
xi ¼
8 i¼1
8
1
8/1
"
8
P
i¼1
#
x 2i / 8 . x! 2
¼
1
ð816;32 W 2 / 8 . ð10;1 WÞ 2 Þ ¼
7
1
ð816;32 / 816;08Þ W 2 ¼
¼
7
1
¼
. 0;24 W 2 ¼ 0;034 W 2
7
¼
s ¼ 0;19 W
&
444
XVI Grundlagen der mathematischen Statistik
2.2 Berechnung der Kennwerte unter Verwendung
der Häufigkeitsfunktion
Voraussetzung: Es liegt eine geordnete Stichprobe vom Umfang n mit k verschiedenen
Werten x1 ; x2 ; . . . ; xk und der Häufigkeitsfunktion f ðxÞ vor.
Mittelwert x!
x! ¼
k
P
i¼1
xi . f ðxi Þ
Varianz s 2
s2 ¼
&
k
P
n
n
ðxi / x!Þ 2 . f ðxi Þ ¼
.
n / 1 i¼1
n/1
+
k
P
i¼1
x 2i . f ðxi Þ / x! 2
)
Beispiel
Bei 10 Würfen eines homogenen Würfels erhielt man die folgenden „Augenzahlen“:
2, 1, 6, 4, 3, 4, 4, 6, 3, 5
Die Auswertung dieser Stichprobe führt zu dem folgenden Ergebnis (xi ¼ Augenzahl):
i
xi
ni
f ðxi Þ
xi . f ðxi Þ
x 2i
x 2i . f ðxi Þ
1
1
1
0,1
0,1
1
0,1
2
2
1
0,1
0,2
4
0,4
3
3
2
0,2
0,6
9
1,8
4
4
3
0,3
1,2
16
4,8
5
5
1
0,1
0,5
25
2,5
6
6
2
0,2
1,2
36
7,2
10
1,0
3,8
S
x! ¼
6
P
i¼1
s2 ¼
16,8
xi . f ðxi Þ ¼ 3;8
10
10 / 1
+
6
P
i¼1
x 2i . f ðxi Þ / x! 2
)
¼
10
10
10
ð16;8 / 3;8 2 Þ ¼
ð16;8 / 14;44Þ ¼
. 2;36 ¼ 2;62
9
9
9
s ¼ 1;62
&
2 Kennwerte oder Maßzahlen einer Stichprobe
445
2.3 Berechnung der Kennwerte einer gruppierten Stichprobe
Voraussetzung: Es liegt eine in k Klassen aufgeteilte Stichprobe vom Umfang n mit den
Klassenmitten x~1 ; x~2 ; . . . ; x~k und der Klassenhäufigkeitsfunktion f ðxÞ vor.
Mittelwert x!
x! ¼
k
P
i¼1
x~i . f ð~
xi Þ
Varianz s 2
s
&
2
k
P
n
n
¼
ð~
xi / x!Þ 2 . f ð~
xi Þ ¼
.
n / 1 i¼1
n/1
+
k
P
i¼1
x~ 2i
. f ð~
xi Þ / x!
2
)
Beispiel
Wir werten die in Abschnitt 1.3 beschriebene Stichprobe (Fehlmengen bei der automatischen Abfüllung von
Wein in Literflaschen) aus:
x~ 2i
x~ 2i . f ð~
xi Þ
i
x~i
ni
f ð~
xi Þ
x~i . f ð~
xi Þ
1
5
9
0,45
2,25
25
11,25
2
15
6
0,30
4,50
225
67,50
3
25
4
0,20
5,00
625
125,00
4
35
1
0,05
1,75
1225
61,25
20
1,00
13,50
S
x! ¼
4
P
i¼1
s2 ¼
¼
x~i . f ð~
xi Þ ¼ 13;5
20
20 / 1
+
4
P
i¼1
x~i in cm 3
x~ 2i in cm 6
265,00
(in cm 3 Þ
x~ 2i . f ð~
xi Þ / x! 2
)
¼
20
ð265 / 13;5 2 Þ ¼
19
20
20
ð265 / 182;25Þ ¼
. 82;75 ¼ 87;11
19
19
s ¼ 9;33
n ¼ 20
(in cm 6 Þ
(in cm 3 Þ
&
446
XVI Grundlagen der mathematischen Statistik
3 Statistische Schätzmethoden für unbekannte
Parameter („Parameterschätzungen“)
3.1 Aufgaben der Parameterschätzung
Die Zufallsvariable X genüge einer Wahrscheinlichkeitsverteilung mit der vom Typ her
bekannten Verteilungsfunktion FðxÞ, deren Parameter jedoch unbekannt sind.
&
Beispiel
X ist normalverteilt, die Parameter m und s bzw. s 2 jedoch sind unbekannt.
&
Die Parameterschätzung hat dann auf der Basis einer konkreten Stichprobe die folgenden
Aufgaben zu lösen:
1. Bestimmung von Schätz- oder Näherungswerten für die unbekannten Parameter (sog.
„Punktschätzung“).
2. Konstruktion von Konfidenz- oder Vertrauensintervallen, in denen die unbekannten
Parameter mit einer vorgegebenen (großen) Wahrscheinlichkeit vermutet werden (sog.
„Intervallschätzung“). Diese Intervalle ermöglichen Aussagen über die Genauigkeit
und Zuverlässigkeit der Schätzwerte.
3.2 Schätzfunktionen und Schätzwerte für unbekannte Parameter
(„Punktschätzungen“)
3.2.1 Schätz- und Stichprobenfunktionen
Stichprobenfunktionen
Eine Funktion (Zufallsvariable) Z ¼ gðX1 ; X2 ; . . . ; Xn Þ, die von n stochastisch unabhängigen Zufallsvariablen X1 ; X2 ; . . . ; Xn abhängt, die alle der gleichen Verteilungsfunktion FðxÞ genügen, heißt Stichprobenfunktion. Die Zufallsvariablen X1 ; X2 ; . . . ; Xn
können dabei auch als Komponenten einer n-dimensionalen Zufallsvariablen
ðX1 ; X2 ; . . . ; Xn Þ, auch n-dimensionaler Zufallsvektor genannt, aufgefasst werden. Eine
konkrete Stichprobe mit den Stichprobenwerten x1 ; x2 ; . . . ; xn ist dann eine Realisierung
des Zufallsvektors. Einsetzen dieser Werte in die Stichprobenfunktion Z liefert einen
Schätz- oder Näherungswert für diese Zufallsvariable.
Schätzfunktionen
Schätzfunktionen sind Stichprobenfunktionen für bestimmte unbekannte Parameter einer
Wahrscheinlichkeitsverteilung. Eine Schätzfunktion Q ¼ gðX1 ; X2 ; . . . ; Xn Þ für den unbekannten Parameter J wird als „optimal“ angesehen, wenn sie die folgenden Eigenschaften
besitzt:
1. Die Schätzfunktion Q ist erwartungstreu, d. h. ihr Erwartungswert ist gleich dem zu
schätzenden Parameter: EðQÞ ¼ J
3 Statistische Schätzmethoden für unbekannte Parameter („Parameterschätzungen“)
447
2. Die Schätzfunktion Q ist konsistent (passend), d. h. Q konvergiert mit zunehmendem
Stichprobenumfang n gegen den Parameter J.
3. Die Schätzfunktion Q ist effizient (wirksam), d. h. es gibt bei gleichem Stichprobenumfang n keine andere erwartungstreue Schätzfunktion mit einer kleineren Varianz.
3.2.2 Schätzungen für den Mittelwert m und die Varianz s 2
Voraussetzung: Die Zufallsvariablen X1 ; X2 ; . . . ; Xn genügen alle der gleichen Verteilung
mit dem Mitttelwert m und der Varianz s 2
Unbekannter
Parameter
Schätzfunktion für den
unbekannten Parameter
Erwartungsoder Mittelwert
X ¼
EðXÞ ¼ m
Schätzwert für den
unbekannten Parameter
Mittelwert der konkreten
Stichprobe x1 ; x2 ; . . . ; xn :
n
1 P
Xi
.
n i¼1
n
1 P
xi
.
n i¼1
m^ ¼ x! ¼
Varianz
S2 ¼
Var ðXÞ ¼ s 2
n
Varianz der konkreten
P
1
ðXi / X Þ 2 Stichprobe x1 ; x2 ; . . . ; xn :
.
n / 1 i¼1
n
P
1
^s 2 ¼ s 2 ¼
ðxi / x!Þ 2
.
n / 1 i¼1
Anmerkungen
(1)
(2)
(3)
(4)
&
Die Schätzfunktionen X und S 2 sind erwartungstreu und konsistent, X außerdem
noch effizient.
Sind alle Zufallsvariablen Xi außerdem noch normalverteilt, so ist auch die Schätzfunktion X eine normalverteilte Zufallsgröße mit dem Erwartungs- oder Mittelwert
EðXÞ ¼ m und der Varianz Var ðXÞ ¼ s 2 =n.
Bei beliebig verteilten Zufallsvariablen Xi mit EðXi Þ ¼ m und Var ðXi Þ ¼ s 2 ist
die Schätzfunktion X näherungsweise normalverteilt mit dem Mittelwert EðXÞ ¼ m
und der Varianz Var ðXÞ ¼ s 2 =n.
pffiffiffiffiffiffi
Die Stichprobenfunktion S ¼ S 2 ist eine Schätzfunktion für die Standardabweichung s der Grundgesamtheit. Sie ist jedoch nicht erwartungstreu.
Beispiel
Mittlere Lebensdauer eines bestimmten elektronischen Bauelements (in Stunden)
Stichprobe vom Umfang n ¼ 8:
i
1
2
3
4
5
6
7
8
ti =h
950
980
1150
770
1230
1210
990
1120
Mittlere Lebensdauer:
!t ¼
8
1 P
1
.
ð950 þ 980 þ 1150 þ . . . þ 1120 Þ h ¼ 1050 h
ti ¼
8 i¼1
8 |fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
8400
&
448
XVI Grundlagen der mathematischen Statistik
3.2.3 Schätzungen für einen Anteilswert p ( Parameter p einer Binomialverteilung)
Schätzfunktion für den Anteilswert p
X
P^ ¼
n
X ¼ Anzahl der „Erfolge“ ( Eintreten des Ereignisses AÞ bei n-maliger Durchführung des
Bernoulli-Experiments
Die binomialverteilte Zufallsvariable P^ ist bei umfangreichen Stichproben näherungsweise
normalverteilt mit dem Mittelwert EðP^Þ ¼ p und der Varianz Var ðP^Þ ¼ pð1 / pÞ=n.
Schätzwert für den Anteilswert p
p^ ¼ hðAÞ ¼
k
n
k : Anzahl der „Erfolge“ ( Eintreten des Ereignisses A) bei n-maliger Durchführung des
Bernoulli-Experiments ( Ergebnis einer konkreten Stichprobe vom Umfang n)
&
Beispiel
Ausschussanteil p einer Serienproduktion von Glühbirnen
Eine Stichprobe vom Umfang n ¼ 300 enthielt k ¼ 6 defekte Glühbirnen. Schätzwert für den Ausschussanteil p:
p^ ¼
k
6
2
¼
¼
¼ 0;02 ¼ 2 %
n
300
100
&
3.2.4 Schätzwerte für die Parameter spezieller Wahrscheinlichkeitsverteilungen
Verteilung
Schätzwert für . . .
Bemerkungen
Binomialverteilung
!n4
f ðxÞ ¼
p x ð1 / pÞ n/ x
x
Parameter p:
k
p^ ¼
n
k : Anzahl der „Erfolge“
bei einer n-fachen Ausführung des BernoulliExperiments
Poisson-Verteilung
mx
f ðxÞ ¼
. e /m
x!
Mittelwert m:
x!: Mittelwert der Stichprobe
Exponentialverteilung
Parameter l:
f ðxÞ ¼ l . e / l x
1
l^ ¼
x!
m^ ¼ x!
Gaußsche Normalverteilung
x/m
1
/1 ð
Þ
f ðxÞ ¼ pffiffiffiffiffiffiffi
.e 2 s
2p s
2
a) Mittelwert m:
m^ ¼ x!
b) Varianz s 2 :
s^ 2 ¼ s 2
x!: Mittelwert der Stichprobe
x!: Mittelwert der Stichprobe
s 2 : Varianz der Stichprobe
3 Statistische Schätzmethoden für unbekannte Parameter („Parameterschätzungen“)
449
3.3 Vertrauens- oder Konfidenzintervalle für unbekannte Parameter
(„Intervallschätzungen“)
3.3.1 Vertrauens- oder Konfidenzintervalle
Vertrauens- oder Konfidenzintervalle ermöglichen Aussagen über die Genauigkeit und Zuverlässigkeit von Parameterschätzungen auf der Grundlage der Wahrscheinlichkeitsrechnung. Mit einer vorgegebenen (großen) Wahrscheinlichkeit g lässt sich aus einer konkreten Stichprobe stets ein sog. Vertrauens- oder Konfidenzintervall bestimmen, in dem der
wahre (aber unbekannte) Wert des Parameters vermutet wird. Die Grenzen dieses Intervalls
heißen Vertrauens- oder Konfidenzgrenzen, die vorgegebene Wahrscheinlichkeit g wird als
statistische Sicherheit oder als Vertrauens- oder Konfidenzniveau bezeichnet. Die Größe
a ¼ 1 / g heißt Irrtumswahrscheinlichkeit.
Vertrauensgrenzen
cu : untere Grenze
cu
co
Zahlengerade
co : obere Grenze
Vertrauensintervall
Verschiedene Stichproben führen zu verschiedenen Vertrauensintervallen. Vor der Durchführung der Stichprobe besteht die Wahrscheinlichkeit g ¼ 1 / a, ein Intervall zu erhalten, das den unbekannten Parameter „ überdeckt “. Nach der Durchführung der Stichprobe
darf man darauf vertrauen, dass bei einer Vielzahl von durchgeführten Stichproben der
wahre Parameterwert in g . 100 % aller Fälle innerhalb und nur in a . 100 % aller Fälle
außerhalb des Vertrauensintervalls liegt. Der wahre Wert des Parameters muss also nicht
unbedingt im berechneten Vertrauensintervall liegen, sondern er kann auch (mit der Irrtumswahrscheinlichkeit a ¼ 1 / g) außerhalb des Intervalls liegen. In diesem Fall trifft
man eine Falschaussage (sog. Fehler 1. Art).
In der Praxis übliche Werte für g sind 0;95 ¼ 95 % oder 0;99 ¼ 99 %. Dabei gilt: Je
größer g, umso breiter ist das Vertrauensintervall und damit umso unschärfer die Aussage.
Vertrauensintervall für γ = 0,99
Zahlengerade
Vertrauensintervall
für γ = 0,95
Die Vertrauensgrenzen sind Zufallsvariable und somit abhängig von der zugrunde gelegten
Stichprobe. Sie lassen sich anhand einer konkreten Stichprobe bei vorgegebener (hoher)
Wahrscheinlichkeit g aus der Bedingung
P ðcu ) Z ) co Þ ¼ g
mit Hilfe der Tabellen im Anhang (Teil B) bestimmen, sofern die Verteilung der Zufallsvariablen (Stichprobenfunktion) Z bekannt ist (Z genügt in vielen Fällen der Standardnormalverteilung, in anderen Fällen auch der t-Verteilung oder der Chi-Quadratverteilung,
siehe nachfolgende Abschnitte).
450
XVI Grundlagen der mathematischen Statistik
3.3.2 Vertrauensintervalle für den unbekannten Mittelwert m einer Normalverteilung
bei bekannter Varianz s 2
X sei eine normalverteilte Zufallsvariable mit dem unbekannten Mittelwert m und der als
bekannt vorausgesetzten Varianz s 2 . Für den Mittelwert m lässt sich dann unter Verwendung einer konkreten Stichprobe x1 ; x2 ; . . . ; xn schrittweise wie folgt ein Vertrauens- oder
Konfidenzintervall bestimmen:
1. Man wähle zunächst ein bestimmtes Vertrauensniveau g (in der Praxis meist
g ¼ 0;95 ¼ 95 % oder g ¼ 0;99 ¼ 99 %Þ.
2. Berechnung der Konstanten c aus der Bedingung
Pð/ c ) U ) cÞ ¼ g
für die standardnormalverteile Zufallsvariable
X /m
pffiffiffi
U ¼
s= n
unter Verwendung von Tabelle 2 im Anhang, Teil B. Dabei bedeuten:
X : Schätzfunktion für den unbekannten Mittelwert m der normalverteilen
Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
s : Standardabweichung der normalverteilten Grundgesamtheit (als bekannt
vorausgesetzt)
n: Umfang der verwendeten Stichprobe
3. Berechnung des Mittelwertes x! der konkreten Stichprobe x1 ; x2 ; . . . ; xn .
4. Das Vertrauensintervall für den unbekannten Mittelwert m der normalverteilten
Grundgesamtheit lautet dann:
s
s
x! / c pffiffiffi ) m ) x! þ c pffiffiffi
n
n
Der wahre Wert des Mittelwertes m liegt dabei mit einem Vertrauen von
g . 100 % in diesem Intervall (siehe Bild).
γ = 1–α
α/2
α/2
cu
x
co
x
Vertrauensintervall
Anmerkungen
(1)
(2)
Häufig wird die Irrtumswahrscheinlichkeit a vorgegeben (meist a ¼ 0;05 ¼ 5 %
oder a ¼ 0;01 ¼ 1 %). Das Vertrauensniveau ist dann g ¼ 1 / a.
pffiffiffi
Das Vertrauensintervall besitzt die Länge l ¼ 2 c s= n und lässt sich stets durch eine
Vergrößerung des Stichprobenumfangs n verkürzen (für feste Werte von s und g).
Hinweis: Musterbeispiel für die Berechnung eines Vertrauensintervalls ! Abschnitt 3.3.7
3 Statistische Schätzmethoden für unbekannte Parameter („Parameterschätzungen“)
451
3.3.3 Vertrauensintervalle für den unbekannten Mittelwert m einer Normalverteilung
bei unbekannter Varianz s 2
X sei eine normalverteilte Zufallsvariable mit dem unbekannten Mittelwert m und der
ebenfalls unbekannten Varianz s 2 . Für den Mittelwert m lässt sich dann unter Verwendung einer konkreten Stichprobe x1 ; x2 ; . . . ; xn schrittweise wie folgt ein Vertrauens- oder
Konfidenzintervall bestimmen:
1. Man wähle zunächst ein bestimmtes Vertrauensniveau g (in der Praxis meist
g ¼ 0;95 ¼ 95 % oder g ¼ 0;99 ¼ 99 %Þ.
2. Berechnung der Konstanten c aus der Bedingung
Pð/ c ) T ) cÞ ¼ g
für die einer t-Verteilung mit f ¼ n / 1 Freiheitsgraden genügenden Zufallsvariablen
T ¼
X /m
pffiffiffi
S= n
unter Verwendung von Tabelle 4 im Anhang, Teil B. Dabei bedeuten:
X : Schätzfunktion für den unbekannten Mittelwert m der normalverteilen
Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
S: Schätzfunktion für die unbekannte Standardabweichung s der normalverteilten Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
n: Umfang der verwendeten Stichprobe
3. Berechnung des Mittelwertes x! und der Varianz s 2 bzw. der Standardabweichung s der konkreten Stichprobe x1 ; x2 ; . . . ; xn .
4. Das Vertrauensintervall für den unbekannten Mittelwert m der normalverteilten
Grundgesamtheit lautet dann:
s
s
x! / c pffiffiffi ) m ) x! þ c pffiffiffi
n
n
Der wahre Wert des Mittelwertes m liegt dabei mit einem Vertrauen von g . 100 %
in diesem Intervall (siehe Bild).
γ = 1–α
α/2
α/2
cu
x
Vertrauensintervall
co
x
452
XVI Grundlagen der mathematischen Statistik
Anmerkungen
(1)
(2)
(3)
(4)
Häufig wird die Irrtumswahrscheinlichkeit a vorgegeben (meist a ¼ 0;05 ¼ 5 %
oder a ¼ 0;01 ¼ 1 %). Das Vertrauensniveau ist dann g ¼ 1 / a.
pffiffiffi
Das Vertrauensintervall besitzt die Länge l ¼ 2 c s= n. Eine Verkürzung des Vertrauensintervalls lässt sich stets durch eine entsprechende Vergrößerung des Stichprobenumfangs n erreichen.
Bei unbekannter Varianz s 2 sind die Vertrauensintervalle für den Mittelwert m
stets breiter als bei bekannter Varianz (bei gleichem Vertrauensniveau g und gleichem Stichprobenumfang n).
Bei umfangreichen Stichproben ( Faustregel: n > 30) kann die unbekannte Standardabweichung s der Grundgesamtheit durch die Standardabweichung s der Stichprobe
geschätzt werden: s ' s. In diesem Sonderfall darf man daher von einer normalverteilten Grundgesamtheit mit der bekannten Varianz s 2 ' s 2 ausgehen und das bereits
im vorangegangenen Abschnitt 3.3.2 besprochene Verfahren anwenden.
Hinweis: Musterbeispiel für die Berechnung eines Vertrauensintervalls ! Abschnitt 3.3.7
3.3.4 Vertrauensintervalle für den unbekannten Mittelwert m bei einer beliebigen
Verteilung
X sei eine beliebig verteilte Zufallsvariable mit dem unbekannten Mittelwert m und der
(bekannten oder unbekannten) Varianz s 2 . Für die Konstruktion von Vertrauensintervallen
für den Mittelwert m gelten dann bei Verwendung hinreichend großer Stichproben ( Faustregel: n > 30) die bereits in den Abschnitten 3.3.2 und 3.3.3 beschriebenen Methoden.
Sie liefern in guter Näherung brauchbare Vertrauensintervalle, wobei noch zwei Fälle zu
unterscheiden sind:
1. Ist die Varianz s 2 der Grundgesamtheit bekannt, so ist das in Abschnitt 3.3.2 beschriebene Verfahren anzuwenden (Standardnormalverteilung).
2. Bei unbekannter Varianz s 2 ist dagegen die in Abschnitt 3.3.3 dargestellte Methode
anzuwenden (t-Verteilung mit f ¼ n / 1 Freiheitsgraden).
Die Näherung ist umso besser, je größer der Umfang n der verwendeten Stichprobe ist.
Für großes n besteht dann kein wesentlicher Unterschied mehr zwischen den beiden Vertrauensintervallen, die man durch die Fallunterscheidung erhält.
3 Statistische Schätzmethoden für unbekannte Parameter („Parameterschätzungen“)
453
3.3.5 Vertrauensintervalle für die unbekannte Varianz s 2 einer Normalverteilung
X sei eine normalverteilte Zufallsvariable mit dem ( bekannten oder unbekannten) Mittelwert m und der unbekannten Varianz s 2 . Für die Varianz s 2 lässt sich dann unter
Verwendung einer konkreten Zufallsstichprobe x1 ; x2 ; . . . ; xn wie folgt schrittweise
ein Vertrauens- oder Konfidenzintervall bestimmen:
1. Man wähle zunächst ein bestimmtes Vertrauensniveau g (in der Praxis meist
g ¼ 0;95 ¼ 95 % oder g ¼ 0;99 ¼ 99 %Þ.
2. Berechnung der beiden Konstanten c1 und c2 aus der Bedingung
Pðc1 ) Z ) c2 Þ ¼ g
für die einer Chi-Quadrat-Verteilung mit f ¼ n / 1 Freiheitsgraden genügenden
Zufallsvariablen
S2
Z ¼ ðn / 1Þ 2
s
oder aus den beiden gleichwertigen Bestimmungsgleichungen
1
1
Fðc1 Þ ¼
ð1 / gÞ und Fðc2 Þ ¼
ð1 þ gÞ
2
2
unter Verwendung von Tabelle 3 im Anhang, Teil B. Dabei bedeuten:
S2:
Schätzfunktion für die unbekannte Varianz s 2 der normalverteilen
Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
n:
Umfang der verwendeten Stichprobe
FðzÞ: Verteilungsfunktion der Chi-Quadrat-Verteilung mit f ¼ n / 1
Freiheitsgraden (Tabelle 3 im Anhang, Teil B)
3. Berechnung des Varianz s 2 der konkreten Stichprobe x1 ; x2 ; . . . ; xn .
4. Das Vertrauensintervall für die unbekannte Varianz s 2
Grundgesamtheit lautet dann:
der normalverteilten
ðn / 1Þ s 2
ðn / 1Þ s 2
) s2 )
c2
c1
Der wahre Wert der Varianz s 2 liegt dabei mit einem Vertrauen von g . 100 % in
diesem Intervall.
Anmerkungen
(1)
Häufig wird die Irrtumswahrscheinlichkeit a vorgegeben (meist a ¼ 0;05 ¼ 5 %
oder a ¼ 0;01 ¼ 1 %). Das Vertrauensniveau ist dann g ¼ 1 / a.
(2)
Das Vertrauensintervall besitzt die Länge l ¼
(3)
Aus dem Vertrauensintervall für die Varianz s 2 erhält man durch Wurzelziehen ein
entsprechendes Vertrauensintervall für die Standardabweichung s.
ðn / 1Þ ðc2 / c1 Þ s 2
.
c1 c2
Hinweis: Musterbeispiel für die Berechnung eines Vertrauensintervalls ! Abschnitt 3.3.7
454
XVI Grundlagen der mathematischen Statistik
3.3.6 Vertrauensintervalle für einen unbekannten Anteilswert p
( Parameter p einer Binomialverteilung)
Der Parameter p einer Binomialverteilung sei unbekannt. Der binomialverteilten Grundgesamtheit wird daher eine umfangreiche Stichprobe entnommen, in dem das dieser Verteilung zugrunde liegende Bernoulli-Experiment n-mal nacheinander ausgeführt und dabei die
Anzahl k der erzielten „Erfolge“ festgestellt wird. Als „Erfolg“ wird das Eintreten des
Ereignisses A, als „Mißerfolg“ demnach das Eintreten des zu A komplementären Ereignisses A! gewertet. Die beobachtete relative Häufigkeit für das Ereignis A („Erfolg“)
beträgt somit hðAÞ ¼ k=n und ist ein Schätzwert für den unbekannten Parameter p der
Binomialverteilung (Anteilswert p).
Unter Verwendung dieser Stichprobe lässt sich dann für den unbekannten Parameter p
schrittweise wie folgt ein Vertrauens- oder Konfidenzintervall konstruieren:
1. Man wähle zunächst ein bestimmtes Vertrauensniveau g (in der Praxis meist
g ¼ 0;95 ¼ 95 % oder g ¼ 0;99 ¼ 99 %Þ.
2. Berechnung der Konstanten c aus der Bedingung
Pð/ c ) U ) cÞ ¼ g
für die (näherungsweise) standardnormalverteilte Zufallsvariable
n P^ / n p
U ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n pð1 / pÞ
unter Verwendung von Tabelle 2 im Anhang, Teil B. Dabei bedeuten:
P^: Schätzfunktion für den Parameter p einer binomialverteilen Grundgesamtheit (siehe hierzu Abschnitt 3.2.3)
n: Umfang der verwendeten Stichprobe
3. Berechnung des Schätzwertes p^ ¼ k=n für den Parameter p aus der konkreten
Stichprobe („ k Erfolge bei insgesamt n Ausführungen des Bernoulli-Experiments“).
4. Unter der Voraussetzung, dass die Bedingung
D ¼ n p^ð1 / p^Þ > 9
für eine umfangreiche Stichprobe erfüllt ist, lautet das Vertrauensintervall für den
unbekannten Parameter p der binomialverteilten Grundgesamtheit wie folgt:
c pffiffiffiffi
c pffiffiffiffi
D ) p ) p^ þ
D
p^ /
n
n
Der wahre Wert des Parameters p liegt dabei mit einem Vertrauen von g . 100 %
in diesem Intervall (siehe Bild auf der nächsten Seite).
3 Statistische Schätzmethoden für unbekannte Parameter („Parameterschätzungen“)
455
γ = 1–α
α/2
α/2
c
p– n
Δ
p
c
p+ n
Δ
p
Vertrauensintervall
Anmerkungen
(1)
Häufig wird die Irrtumswahrscheinlichkeit a vorgegeben (meist a ¼ 0;05 ¼ 5 %
oder a ¼ 0;01 ¼ 1 %). Das Vertrauensniveau ist dann g ¼ 1 / a.
pffiffiffiffi
(2) Eine Verkürzung des Vertrauensintervalls der Länge l ¼ 2 ðc=nÞ D lässt sich stets
durch eine entsprechende Vergrößerung des Stichprobenumfangs n erreichen.
Hinweis: Musterbeispiel für die Berechnung eines Vertrauensintervalls ! Abschnitt 3.3.7
3.3.7 Musterbeispiel für die Bestimmung eines Vertrauensintervalls
Qualitätskontrolle bei der Serienproduktion eines bestimmten elektronischen Bauteils
Eine Stichprobe vom Umfang n ¼ 500 enthält k ¼ 27 defekte Teile. Für den unbekannten Ausschussanteil p der binomialverteilten Grundgesamtheit soll ein Vertrauensintervall
bestimmt werden. Das Verfahren ist in Abschnitt 3.3.6 ausführlich beschrieben.
Wahl des Vertrauensniveaus:
g ¼ 0;95 ¼ 95 %
Berechnung der Konstanten c aus der Bedingung P ð/ c ) U ) cÞ ¼ g ¼ 0;95:
P ð/ c ) U ) cÞ ¼ 2 . fðcÞ / 1 ¼ 0;95
fðcÞ ¼ 0;975
)
c ¼ u 0;975 ¼ 1;960
)
(aus Tabelle 2 im Anhang, Teil B)
Schätzwert für den unbekannten Ausschussanteil p:
k
27
54
¼
¼
¼ 0;054 ¼ 5;4 %
n
500
1000
Die Bedingung für eine umfangreiche Stichprobe ist erfüllt:
p^ ¼
D ¼ n p^ ð1 / p^Þ ¼ 500 . 0;054 ð1 / 0;054Þ ¼ 500 . 0;054 . 0;946 ¼ 25;542 > 9
Vertrauensintervall für den unbekannten Ausschussanteil p:
c pffiffiffiffi
1;960 pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a ¼
. 25;542 ¼ 0;020
D ¼
n
500
p^ / a ) p ) p^ þ a
0;034 ) p ) 0;074
)
0;054 / 0;020 ) p ) 0;054 þ 0;020
,
3;4 % ) p ) 7;4 %
Mit einem Vertrauen von 95 % können wir davon ausgehen, dass der Ausschussanteil p
zwischen 3,4 % und 7,4 % liegt.
456
XVI Grundlagen der mathematischen Statistik
4 Statistische Prüfverfahren
für unbekannte Parameter („Parametertests“)
4.1 Statistische Hypothesen und Parametertests
Statistische Hypothese
Unter einer statistischen Hypothese ( kurz: Hypothese) versteht man irgendwelche Annahmen, Vermutungen oder Behauptungen über die Wahrscheinlichkeitsverteilung einer Zufallsvariablen oder einer Grundgesamtheit und deren Parameter.
Parametertest
Ein Parametertest ist ein statistisches Prüfverfahren für einen unbekannten Parameter in
der Wahrscheinlichkeitsverteilung einer Zufallsvariablen oder Grundgesamtheit, wobei die
Art der Verteilung (d. h. der Verteilungstyp wie z. B. Binomialverteilung oder Gaußsche
Normalverteilung) als bekannt vorausgesetzt wird. Ein solcher Test dient der !berprüfung
einer Hypothese über einen bestimmten Parameter der Verteilung mit Hilfe einer Stichprobenuntersuchung der betreffenden Grundgesamtheit. Die zu überprüfende Hypothese wird
meist als Nullhypothese H0 bezeichnet. Ihr wird oft eine Alternativhypothese H1 gegenübergestellt. Es ist dann das erklärte Ziel eines Parametertests, eine Entscheidung darüber
zu ermöglichen, ob man die Nullhypothese H0 beibehalten (d. h. nicht ablehnen) kann, da
die Auswertung des verwendeten Stichprobenmaterials in keinem Widerspruch zur Nullhypothese steht oder ob man sie zugunsten der Alternativhypothese H1 ablehnen oder
verwerfen muss. Mit einem Parametertest kann also über Ablehnung oder Beibehaltung
( Nichtablehnung) einer aufgestellten Hypothese („Nullhypothese“) entschieden werden. Allerdings: Wie auch immer die Entscheidung ausfallen sollte, sie kann richtig aber auch
falsch sein.
&
Beispiel
Ein Großhändler bestellt direkt beim Hersteller einen größeren Posten eines bestimmten elektronischen Bauelements und vereinbart dabei, dass die Ware einen maximalen Ausschussanteil von p0 ¼ 1 % enthalten
darf. Bei der Anlieferung der Ware wird er daher mit einem speziellen statistischen Test prüfen, ob die
vereinbarte maximale Ausschussquote auch nicht überschritten wurde. Der Großhändler wird daher mit Hilfe
einer Stichprobenuntersuchung die Nullhypothese
H0 : p ) p0 ¼ 1 %
gegen die Alternativhypothese
H1 : p > p0 ¼ 1 %
testen (sog. einseitiger Parametertest, da hier die Alternativhypothese nur Werte p > p0 zulässt). Sollte
dabei die Testentscheidung zugunsten der Alternativhypothese H1 ausfallen, so darf er davon ausgehen, dass
der Ausschussanteil p größer ist als vereinbart, d. h. größer als 1 %. Der Großhändler wird in diesem Fall
die Annahme der gelieferten Bauelemente verweigern. Trotzdem kann die getroffene Entscheidung falsch
sein! Denn sie beruht ausschließlich auf der verwendeten Stichprobe. Eine weitere Stichprobe könnte durchaus zu einer anderen Entscheidung führen.
&
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“)
457
4.2 Spezielle Parametertests
4.2.1 Test für den unbekannten Mittelwert m einer Normalverteilung
bei bekannter Varianz s 2
Zweiseitiger Test
X sei eine normalverteilte Zufallsvariable mit der bekannten Varianz s 2 . Es soll geprüft
werden, ob der unbekannte Mittelwert m (wie vermutet) den speziellen Wert m0 besitzt.
Auf der Basis einer Zufallsstichprobe x1 ; x2 ; . . . ; xn vom Umfang n wird daher die
Nullhypothese H0 : m ¼ m0
gegen die
Alternativhypothese H1 : m 6¼ m0
getestet. Die Durchführung des Tests erfolgt dabei schrittweise wie folgt:
1. Man wähle zunächst eine bestimmte Signifikanzzahl (Irrtumswahrscheinlichkeit) a
(in der Praxis meist a ¼ 0;05 ¼ 5 % oder a ¼ 0;01 ¼ 1 %Þ.
2. Test- oder Prüfvariable ist die standardnormalverteile Zufallsvariable
U ¼
X / m0
pffiffiffi
s= n
Dabei bedeuten:
X : Schätzfunktion für den unbekannten Mittelwert m der normalverteilen
Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
m0 : Vermuteter Wert des unbekannten Mittelwertes m
s : Standardabweichung der normalverteilten Grundgesamtheit (wird hier als
bekannt vorausgesetzt)
n: Umfang der verwendeten Stichprobe
/c
Die Berechnung des kritischen Wertes c und damit der kritischen Grenzen þ
erfolgt aus der Bedingung
P ð/ c ) U ) cÞH0 ¼ 1 / a
unter Verwendung von Tabelle 2 im Anhang, Teil B. Der nichtkritische Bereich
(Annahmebereich) lautet dann:
/c ) u ) c
3. Berechnung des Mittelwertes x! der konkreten Stichprobe x1 ; x2 ; . . . ; xn sowie des
Test- oder Prüfwertes
x! / m0
pffiffiffi
u^ ¼
s= n
der Testvariablen U.
458
XVI Grundlagen der mathematischen Statistik
4. Testentscheidung: Fällt der Test- oder Prüfwert u^ in den nichtkritischen Bereich
(Annahmebereich), d. h. gilt
/ c ) u^ ) c
so wird die Nullhypothese H0 : m ¼ m0 beibehalten, anderenfalls zugunsten der
Alternativhypothese H1 : m 6¼ m0 verworfen (siehe Bild). „Beibehalten“ bedeutet
dabei lediglich, dass die Nullhypothese H0 aufgrund der verwendeten Stichprobe
nicht abgelehnt werden kann.
H 0 beibehalten
1– a
a/ 2
–c
Ablehnung
(kritischer
Bereich)
H 0 ablehnen
a/ 2
0
u^
c
Annahmebereich
(nichtkritischer
Bereich)
u^
u
Ablehnung
(kritischer
Bereich)
Hinweis: Musterbeispiel für einen Parametertest ! Abschnitt 4.2.6
Einseitige Tests
Analog verlaufen die einseitigen Tests (Abgrenzung nach oben bzw. nach unten), bei denen es nur eine kritische Grenze gibt.
1–α
Abgrenzung nach oben
H0 : m ) m0
α
H1 : m > m0
P ðU ) cÞH0 ¼ 1 / a
0
Annahmebereich: u ) c
c
Annahmebereich
u
Ablehnung
kritische Grenze
Abgrenzung nach unten
1–α
H0 : m ( m0
H1 : m < m0
α
P ðU < cÞH0 ¼ a
c
Annahmebereich: u ( c
Ablehnung
kritische Grenze
0
Annahmebereich
u
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“)
459
4.2.2 Test für den unbekannten Mittelwert m einer Normalverteilung
bei unbekannter Varianz s 2
Zweiseitiger Test
X sei eine normalverteilte Zufallsvariable mit der unbekannten Varianz s 2 . Es soll geprüft werden, ob der ebenfalls unbekannte Mittelwert m (wie vermutet) den speziellen
Wert m0 besitzt. Auf der Basis einer Zufallsstichprobe x1 ; x2 ; . . . ; xn vom Umfang n
wird daher die
Nullhypothese H0 : m ¼ m0
gegen die
Alternativhypothese H1 : m 6¼ m0
getestet. Die Durchführung des Tests erfolgt dabei schrittweise wie folgt:
1. Man wähle zunächst eine bestimmte Signifikanzzahl (Irrtumswahrscheinlichkeit) a
(in der Praxis meist a ¼ 0;05 ¼ 5 % oder a ¼ 0;01 ¼ 1 %Þ.
2. Test- oder Prüfvariable ist die Zufallsvariable
T ¼
X / m0
pffiffiffi
S= n
die der t-Verteilung mit f ¼ n / 1 Freiheitsgraden genügt. Dabei bedeuten:
X : Schätzfunktion für den unbekannten Mittelwert m der normalverteilen
Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
m0 : Vermuteter Wert des unbekannten Mittelwertes m
S: Schätzfunktion für die unbekannte Standardabweichung s der normalverteilten Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
n: Umfang der verwendeten Stichprobe
/c
Die Berechnung des kritischen Wertes c und damit der kritischen Grenzen þ
erfolgt aus der Bedingung
P ð/ c ) T ) cÞH0 ¼ 1 / a
unter Verwendung von Tabelle 4 im Anhang, Teil B. Der nichtkritische Bereich
(Annahmebereich) lautet dann:
/c ) t ) c
3. Berechnung des Mittelwertes x! und der Standardabweichung s der vorgegebenen
konkreten Stichprobe x1 ; x2 ; . . . ; xn sowie des Test- oder Prüfwertes
x! / m0
^t ¼
pffiffiffi
s= n
der Testvariablen T.
460
XVI Grundlagen der mathematischen Statistik
4. Testentscheidung: Fällt der Test- oder Prüfwert ^t in den nichtkritischen Bereich
(Annahmebereich), d. h. gilt
/ c ) ^t ) c
so wird die Nullhypothese H0 : m ¼ m0 beibehalten, anderenfalls zugunsten der
Alternativhypothese H1 : m 6¼ m0 verworfen (siehe Bild). „Beibehalten“ bedeutet
dabei lediglich, dass die Nullhypothese H0 aufgrund der verwendeten Stichprobe
nicht abgelehnt werden kann.
1– a
H 0 beibehalten
H 0 ablehnen
a/ 2
^t
Ablehnung
(kritischer
Bereich)
a/ 2
–c
0
^t
Annahmebereich
(nichtkritischer Bereich)
c
t
Ablehnung
(kritischer
Bereich)
Anmerkung
Bei einer umfangreichen Stichprobe ( Faustregel: n > 30Þ ist die Testvariable T näherungsweise standardnormalverteilt und man darf daher das in Abschnitt 4.2.1 besprochene
Testverfahren anwenden ðs 2 ' s 2 Þ.
Hinweis: Musterbeispiel für einen Parametertest ! Abschnitt 4.2.6
Einseitige Tests
Die einseitigen Tests (Abgrenzung nach oben bzw. nach unten) verlaufen ähnlich wie im
Fall bekannter Varianz (siehe Abschnitt 4.2.1). Bei der Berechnung der kritischen Grenze
ist dabei die t-Verteilung mit f ¼ n / 1 Freiheitsgraden anstelle der Standardnormalverteilung zu verwenden ( Testvariable ist die weiter oben beschriebene Zufallsvariable T).
4.2.3 Tests für die Gleichheit der unbekannten Mittelwerte m1 und m2
zweier Normalverteilungen („Differenzentests“)
Abhängige und unabhängige Stichproben
Zwei Stichproben heißen voneinander abhängig, wenn sie den gleichen Umfang haben und
zu jedem Wert der einen Stichprobe genau ein Wert der anderen Stichprobe gehört und
umgekehrt. Zwischen abhängigen Stichproben besteht somit eine Kopplung. Man spricht
daher in diesem Zusammenhang auch von verbundenen oder korrelierten Stichproben.
Zwei Stichproben, die diese beiden Bedingungen nicht zugleich erfüllen, heißen dagegen
voneinander unabhängig (unabhängige Stichproben). So sind beispielsweise zwei Stichproben von unterschiedlichem Umfang stets voneinander unabhängig.
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“)
461
4.2.3.1 Differenzentests für Mittelwerte bei abhängigen Stichproben
Bei abhängigen oder verbundenen Stichproben lässt sich der Differenzentest auf die in den
Abschnitten 4.2.1 und 4.2.2 beschriebenen Parametertests für den Mittelwert m einer normalverteilten Grundgesamtheit zurückführen.
X und Y seien zwei normalverteilte Zufallsvariable mit den unbekannten Mittelwerten m1
und m2 . Es soll geprüft werden, ob die beiden Mittelwerte (wie vermutet) übereinstimmen.
Auf der Basis zweier abhängiger Stichproben
x1 ; x2 ; . . . ; xn
und
y1 ; y2 ; . . . ; yn
vom (gleichen) Umfang n wird daher die
Nullhypothese H0 : m1 ¼ m2
gegen die
Alternativhypothese H1 : m1 6¼ m2
getestet. Diesen zweiseitigen Parametertest führen wir zweckmäßigerweise auf einen entsprechenden Test des Hilfsparameters
m ¼ m1 / m2
(Differenz der beiden Mittelwerte m1 und m2 ) zurück. Getestet wird dann die
Nullhypothese H0 : m ¼ 0
gegen die
Alternativhypothese H1 : m 6¼ 0
wie folgt:
Zunächst bildet man aus den beiden abhängigen Stichproben die entsprechenden Differenzen
zi ¼ xi / yi
ði ¼ 1; 2; 3; . . . ; nÞ
und betrachtet diese Werte als Stichprobenwerte einer neuen (normalverteilten) Stichprobe vom Umfang n:
z1 ; z2 ; . . . ; zn
Es lässt sich dann mit den in den Abschnitten 4.2.1 und 4.2.2 beschriebenen Verfahren
prüfen, ob der Mittelwert !z ¼ x! / y! dieser Stichprobe in den Annahmebereich fällt
oder nicht. Fällt der Mittelwert !z in den Annahmebereich, so wird die Nullhypothese
H0 : m ¼ 0 bzw. H0 : m1 ¼ m2 beibehalten, d. h. nicht abgelehnt und man kann
davon ausgehen, dass die Mittelwerte m1 und m2 der beiden normalverteilten Grundgesamtheiten übereinstimmen. Anderenfalls wird die Nullhypothese H0 zugunsten der
Alternativhypothese H1 : m 6¼ 0 bzw. H1 : m1 6¼ m2 verworfen. Die Mittelwerte m1
und m2 der beiden normalverteilten Grundgesamtheiten können in diesem Fall als
verschieden betrachtet werden.
Es wird also getestet, ob die durch Differenzbildung erhaltene Stichprobe z1 ; z2 ; . . . ; zn
einer normalverteilten Grundgesamtheit mit dem Mittelwert m ¼ 0 entstammt. Dabei sind
noch zwei Fälle zu unterscheiden.
462
XVI Grundlagen der mathematischen Statistik
1. Fall: Die Varianzen s 21 und s 22 der Zufallsvariablen X und Y sind bekannt
Dann gilt
s 21
s2
s 2 þ s 22
þ 2 ¼ 1
n
n
n
und man darf das in Abschnitt 4.2.1 besprochene Prüfverfahren anwenden (die verwendete
Testvariable ist in diesem Fall standardnormalverteilt mit der bekannten Varianz s 2 ).
Diese Aussage gilt näherungsweise auch bei unbekannten Varianzen, sofern die verwendeten abhängigen Stichproben hinreichend umfangreich sind ( Faustregel: n > 30). In diesem Fall verwendet man als Schätzwert für die unbekannte Varianz s 2 die Stichprobenvarianz s 2 (d. h. die Varianz der Stichprobe z1 ; z2 ; . . . ; zn Þ.
s2 ¼
2. Fall: Die Varianzen s 21 und s 22 der Zufallsvariablen X und Y sind unbekannt
Dann bleibt auch die Varianz s 2 unbekannt und man muss das in Abschnitt 4.2.2 dargestellte Testverfahren verwenden (die Testvariable genügt jetzt einer t-Verteilung mit
f ¼ n / 1 Freiheitsgraden). Dieser Fall tritt ein bei kleinen abhängigen Stichproben mit
n ) 30.
Anmerkung
#hnlich verläuft der Differenzentest bei einseitigen Fragestellungen.
Hinweis: Musterbeispiel für einen Parametertest ! Abschnitt 4.2.6
4.2.3.2 Differenzentests für Mittelwerte bei unabhängigen Stichproben
Zweiseitiger Differenzentest bei bekannten Varianzen
X und Y seien zwei unabhängige und normalverteilte Zufallsvariable mit den unbekannten Mittelwerten m1 und m2 , aber bekannten Varianzen s 21 und s 22 . Es soll geprüft
werden, ob die beiden Mittelwerte (wie vermutet) übereinstimmen. Auf der Basis zweier
unabhängiger Zufallsstichproben
x1 ; x2 ; . . . ; xn1
und
y1 ; y2 ; . . . ; yn2
mit den Stichprobenumfängen n1 und n2 wird daher die
Nullhypothese H0 : m1 ¼ m2
gegen die
Alternativhypothese H1 : m1 6¼ m2
getestet.
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“)
463
Die Durchführung des Tests erfolgt dabei schrittweise wie folgt:
1. Man wähle zunächst eine bestimmte Signifikanzzahl (Irrtumswahrscheinlichkeit) a
(in der Praxis meist a ¼ 0;05 ¼ 5 % oder a ¼ 0;01 ¼ 1 %Þ.
2. Test- oder Prüfvariable ist die standardnormalverteilte Zufallsvariable
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
X /Y
s 21
s2
U ¼
mit
s ¼
þ 2
s
n1
n2
Dabei bedeuten:
X; Y : Schätzfunktionen für die unbekannten Mittelwerte m1 und m2 der
beiden normalverteilen Grundgesamtheiten (siehe hierzu Abschnitt 3.2.2)
s 1 ; s 2 : Standardabweichungen der beiden normalverteilten Grundgesamtheiten
(hier als bekannt vorausgesetzt)
n1 ; n2 : Umfänge der verwendeten unabhängigen Stichproben
s:
Standardabweichung der Zufallsvariablen X / Y
/c
Die Berechnung des kritischen Wertes c und damit der kritischen Grenzen þ
erfolgt aus der Bedingung
P ð/ c ) U ) cÞH0 ¼ 1 / a
unter Verwendung von Tabelle 2 im Anhang, Teil B. Der nichtkritische Bereich
(Annahmebereich) lautet dann:
/c ) u ) c
3. Berechnung der Mittelwerte x! und y! der beiden vorgegebenen unabhängigen
Stichproben sowie des Test- oder Prüfwertes
x! / y!
u^ ¼
s
der Testvariablen U.
4. Testentscheidung: Fällt der Test- oder Prüfwert u^ in den nichtkritischen Bereich
(Annahmebereich), d. h. gilt
/ c ) u^ ) c
so wird die Nullhypothese H0 : m1 ¼ m2 beibehalten, anderenfalls zugunsten der
Alternativhypothese H1 : m1 6¼ m2 verworfen (siehe Bild). „Beibehalten“ bedeutet
dabei lediglich, dass man die Nullhypothese H0 aufgrund der verwendeten Stichprobe nicht ablehnen kann.
H 0 beibehalten
1– a
a/ 2
–c
Ablehnung
(kritischer
Bereich)
H 0 ablehnen
a/ 2
0
u^
Annahmebereich
(nichtkritischer
Bereich)
c
u^
Ablehnung
(kritischer
Bereich)
u
464
XVI Grundlagen der mathematischen Statistik
Anmerkungen
(1)
(2)
Dieser Differenzentest lässt sich in ähnlicher Weise auch für einseitige Fragestellungen durchführen. In diesem Fall gibt es nur eine kritische Grenze.
Bei umfangreichen Stichproben ( Faustregel: n1 ; n2 > 30Þ dürfen die Varianzen
s 21 und s 22 näherungsweise durch ihre Schätzwerte s 21 und s 22 , d. h. durch die
Stichprobenvarianzen ersetzt werden, falls sie unbekannt sein sollten.
Hinweis: Musterbeispiel für einen Parametertest ! Abschnitt 4.2.6
Zweiseitiger Differenzentest bei gleicher (aber unbekannter) Varianz
X und Y seien zwei unabhängige und normalverteilte Zufallsvariable mit den unbekannten Mittelwerten m1 und m2 und zwar gleicher, aber unbekannter Varianz ðs 21 ¼ s 22 Þ.
Es soll geprüft werden, ob die beiden Mittelwerte (wie vermutet) übereinstimmen. Auf der
Basis zweier unabhängiger Zufallsstichproben
x1 ; x2 ; . . . ; xn1
und
y1 ; y2 ; . . . ; yn2
mit den Stichprobenumfängen n1 und n2 wird daher die
Nullhypothese H0 : m1 ¼ m2
gegen die
Alternativhypothese H1 : m1 6¼ m2
getestet. Die Durchführung des Tests erfolgt dabei schrittweise wie folgt:
1. Man wähle zunächst eine bestimmte Signifikanzzahl (Irrtumswahrscheinlichkeit) a
(in der Praxis meist a ¼ 0;05 ¼ 5 % oder a ¼ 0;01 ¼ 1 %Þ.
2. Test- oder Prüfvariable ist die Zufallsvariable
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n1 n2 ðn1 þ n2 / 2Þ
X /Y
T ¼
. qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n1 þ n2
2
ðn1 / 1Þ S 21 þ ðn2 / 1Þ S 2
die der t-Verteilung von Student mit f ¼ n1 þ n2 / 2 Freiheitsgraden genügt.
Dabei bedeuten:
X; Y :
Schätzfunktionen für die unbekannten Mittelwerte m1 und m2 der
beiden normalverteilen Grundgesamtheiten (siehe hierzu Abschnitt 3.2.2)
S 21 ; S 22 : Schätzfunktionen für die zwar gleichen, jedoch unbekannten Varianzen s 21 und s 22 der beiden normalverteilten Grundgesamtheiten
(siehe hierzu Abschnitt 3.2.2)
n1 ; n2 : Umfänge der verwendeten unabhängigen Stichproben
/c
Die Berechnung des kritischen Wertes c und damit der kritischen Grenzen þ
erfolgt aus der Bedingung
P ð/ c ) T ) cÞH0 ¼ 1 / a
unter Verwendung von Tabelle 4 im Anhang, Teil B. Der nichtkritische Bereich
(Annahmebereich) lautet dann:
/c ) t ) c
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“)
465
3. Berechnung der Mittelwerte x! und y! und der Varianzen s 21 und s 22 der beiden
vorgegebenen unabhängigen Stichproben sowie des Hilfsparameters
s2 ¼
ðn1 / 1Þ s 21 þ ðn2 / 1Þ s 22
n1 þ n2 / 2
Daraus wird dann der Test- oder Prüfwert
rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x! / y!
n1 n2
^t ¼
.
s
n1 þ n2
der Testvariablen T bestimmt.
4. Testentscheidung: Fällt der Test- oder Prüfwert ^t in den nichtkritischen Bereich
(Annahmebereich), d. h. gilt
/ c ) ^t ) c
so wird die Nullhypothese H0 : m1 ¼ m2 beibehalten, anderenfalls zugunsten der
Alternativhypothese H1 : m1 6¼ m2 verworfen (siehe Bild). „Beibehalten“ bedeutet
in diesem Zusammenhang lediglich, dass man die Nullhypothese H0 aufgrund der
verwendeten Stichprobe nicht ablehnen kann.
1– a
H 0 beibehalten
H 0 ablehnen
a/ 2
^
t
Ablehnung
(kritischer
Bereich)
–c
a/ 2
0
^
t
Annahmebereich
(nichtkritischer Bereich)
c
t
Ablehnung
(kritischer
Bereich)
Anmerkungen
(1)
Bei gleichem Stichprobenumfang ðn1 ¼ n2 ¼ nÞ vereinfacht sich die Formel zur
Ermittlung des Test- oder Prüfwertes wie folgt:
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
x! / y!
n
^t ¼ n . qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
. ð!
x / y!Þ
2
2
s 1 þ s 22
s 21 þ s 2
(2)
Dieser Differenzentest lässt sich in ähnlicher Weise auch für einseitige Fragestellungen durchführen. In diesem Fall gibt es nur eine kritische Grenze.
(3)
Wird die Nullhypothese H0 : m1 ¼ m2 beibehalten (d. h. nicht abgelehnt), so ist
m1 ¼ m2 und s 21 ¼ s 22 . Die beiden unabhängigen Stichproben stammen somit aus
der gleichen Grundgesamtheit.
Hinweis: Musterbeispiel für einen Parametertest ! Abschnitt 4.2.6
466
XVI Grundlagen der mathematischen Statistik
4.2.4 Tests für die unbekannte Varianz s 2 einer Normalverteilung
Zweiseitiger Test
X sei eine normalverteilte Zufallsvariable. Es soll geprüft werden, ob die unbekannte Varianz s 2 (wie vermutet) einen bestimmten Wert s 20 besitzt. Auf der Basis einer Zufallsstichprobe x1 ; x2 ; . . . ; xn vom Umfang n wird daher die
Nullhypothese H0 : s 2 ¼ s 20
gegen die
Alternativhypothese H1 : s 2 6¼ s 20
getestet. Die Durchführung des Tests erfolgt dabei schrittweise wie folgt:
1. Man wähle zunächst eine bestimmte Signifikanzzahl (Irrtumswahrscheinlichkeit) a
(in der Praxis meist a ¼ 0;05 ¼ 5 % oder a ¼ 0;01 ¼ 1 %Þ.
2. Test- oder Prüfvariable ist die Zufallsvariable
Z ¼ ðn / 1Þ
S2
s 20
Dabei bedeuten:
S 2 : Schätzfunktion für die unbekannte Varianz s 2 der normalverteilen Grundgesamtheit (siehe hierzu Abschnitt 3.2.2)
2
s 0 : Vermuteter Wert der unbekannten Varianz s 2
n: Umfang der verwendeten Stichprobe
Die Testvariable Z genügt der Chi-Quadrat-Verteilung mit f ¼ n / 1 Freiheitsgraden. Die Berechnung der beiden kritischen Grenzen c1 und c2 erfolgt dabei
aus der Bedingung
P ðc1 ) Z ) c2 ÞH0 ¼ 1 / a
oder aus den beiden gleichwertigen Bestimmungsgleichungen
a
a
und
F ðc2 Þ ¼ 1 /
F ðc1 Þ ¼
2
2
mit Hilfe der tabellierten Verteilungsfunktion F ðzÞ der Chi-Quadrat-Verteilung mit
f ¼ n / 1 Freiheitsgraden (Tabelle 3 im Anhang, Teil B). Der nichtkritische Bereich (Annahmebereich) lautet dann:
c1 ) z ) c2
3. Berechnung der Varianz s 2 der vorgegebenen konkreten Stichprobe und des Testoder Prüfwertes
z ¼ ðn / 1Þ
^
s2
s 20
der Testvariablen Z.
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“)
467
4. Testentscheidung: Fällt der Prüf- oder Testwert ^z in den nichtkritischen Bereich
(Annahmebereich), d. h. gilt
c1 ) ^
z ) c2
so wird die Nullhypothese H0 : s 2 ¼ s 20 beibehalten, anderenfalls zugunsten der
Alternativhypothese H1 : s 2 6¼ s 20 verworfen (siehe Bild). „Beibehalten“ bedeutet
in diesem Zusammenhang lediglich, dass man aufgrund der verwendeten Stichprobe
die Nullhypothese H0 nicht ablehnen kann.
1– a
H 0 beibehalten
H 0 ablehnen
a/ 2
a/ 2
0
z^
c1
Ablehnung
(kritischer
Bereich)
c 2 z^
Annahmebereich
(nichtkritischer Bereich)
z
Ablehnung
(kritischer
Bereich)
Anmerkung
Der beschriebene Test ist zugleich auch ein Test für die (ebenfalls unbekannte) Standardabweichung s. Getestet wird dabei die Nullhypothese H0 : s ¼ s 0 gegen die Alternativhypothese H1 : s 6¼ s0 .
Hinweis: Musterbeispiel für einen Parametertest ! Abschnitt 4.2.6
Einseitige Tests
Analog verlaufen die einseitigen Tests, bei denen es jeweils nur eine kritische Grenze gibt.
Abgrenzung nach oben
1–α
H0 : s 2 ) s 20
H1 : s 2 > s 20
α
P ðZ ) cÞH0 ¼ 1 / a
Annahmebereich: z ) c
c
0
Annahmebereich
z
Ablehnung
kritische Grenze
468
XVI Grundlagen der mathematischen Statistik
Abgrenzung nach unten
1–α
H0 : s 2 ( s 20
H1 : s 2 < s 20
α
P ðZ < cÞH0 ¼ a
Annahmebereich: z ( c
0
c
Ablehnung
z
Annahmebereich
kritische Grenze
4.2.5 Tests für den unbekannten Anteilswert p ( Parameter p einer Binomialverteilung)
Es soll geprüft werden, ob ein unbekannter Anteilswert p ( Parameter p einer Binomialverteilung) einen bestimmten Wert p0 besitzt. Zu diesem Zweck wird der binomialverteilten Grundgesamtheit eine umfangreiche Stichprobe, d. h. eine Stichprobe, deren Umfang n
der Bedingung
n p0 ð1 / p0 Þ > 9
genügt, entnommen. Die Stichprobe selbst besteht dann darin, dass das Bernoulli-Experiment n-mal nacheinander ausgeführt und dabei die Anzahl k der „Erfolge“ festgestellt
wird. Als „Erfolg“ wertet man das Eintreten des Ereignisses A, „Misserfolg“ bedeutet
demnach, dass das komplementäre Ereignis A! eintritt. Die beobachtete relative Häufigkeit
für das Ereignis A („Erfolg“) beträgt somit hðAÞ ¼ k=n. Unter Verwendung dieser Stichprobe wird dann die
Nullhypothese H0 : p ¼ p0
gegen die
Alternativhypothese H1 : p 6¼ p0
getestet.
4 Statistische Prüfverfahren für unbekannte Parameter („Parametertests“)
469
Die Durchführung des Tests erfolgt schrittweise wie folgt:
1. Man wähle zunächst eine bestimmte Signifikanzzahl (Irrtumswahrscheinlichkeit) a
(in der Praxis meist a ¼ 0;05 ¼ 5 % oder a ¼ 0;01 ¼ 1 %Þ.
2. Test- oder Prüfvariable ist die näherungsweise standardnormalverteilte Zufallsvariable
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
U ¼
. ðP^ / p0 Þ
p0 ð1 / p0 Þ
Dabei bedeuten:
P^ : Schätzfunktion für den unbekannten Parameter p der binomialverteilten
Grundgesamtheit (siehe hierzu Abschnitt 3.2.3)
p0 : Vermuteter Wert des unbekannten Parameters p
n: Umfang der verwendeten Stichprobe (Anzahl der Ausführungen des
Bernoulli-Experiments)
/c
Die Berechnung des kritischen Wertes c und damit der kritischen Grenzen þ
erfolgt dabei aus der Bedingung
P ð/ c ) U ) cÞH0 ¼ 1 / a
unter Verwendung von Tabelle 2 im Anhang, Teil B. Der nichtkritische Bereich
(Annahmebereich) lautet dann:
/c ) u ) c
3. Berechnung des Schätzwertes p^ ¼ hðAÞ ¼ k=n für den Parameter p aus der vorgegebenen konkreten Stichprobe (n-fache Ausführung des Bernoulli-Experimentes,
dabei k-mal „Erfolg“) sowie des Test- oder Prüfwertes
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
n
u^ ¼
. ð^
p / p0 Þ
p0 ð1 / p0 Þ
der Testvariablen U.
4. Testentscheidung: Fällt der Test- oder Prüfwert u^ in den nichtkritischen Bereich
(Annahmebereich), d. h. gilt
/ c ) u^ ) c
so wird die Nullhypothese H0 : p ¼ p0 beibehalten, anderenfalls zugunsten der
Alternativhypothese H1 : p 6¼ p0 verworfen (siehe Bild). „Beibehalten“ bedeutet
in diesem Zusammenhang lediglich, dass man aufgrund der verwendeten Stichprobe
die Nullhypothese H0 nicht ablehnen kann.
H 0 beibehalten
1– a
H 0 ablehnen
a/ 2
a/ 2
–c
Ablehnung
(kritischer
Bereich)
0
u^
Annahmebereich
(nichtkritischer
Bereich)
c
u^
Ablehnung
(kritischer
Bereich)
u
470
XVI Grundlagen der mathematischen Statistik
Anmerkungen
(1)
(2)
Man beachte, dass dieser Parametertest nur für umfangreiche Stichproben gilt, d. h.
für solche, die der Bedingung n p0 ð1 / p0 Þ > 9 genügen. Bei kleinem Stichprobenumfang ist diese Bedingung jedoch nicht erfüllt und das angegebene Prüfverfahren
daher nicht anwendbar. Wir müssen in diesem Fall auf die Spezialliteratur verweisen
(siehe Literaturverzeichnis).
Analog verlaufen die einseitigen Parametertests. In diesen Fällen gibt es jeweils nur
eine kritische Grenze c.
Hinweis: Musterbeispiel für einen Parametertest ! Abschnitt 4.2.6
4.2.6 Musterbeispiel für einen Parametertest
Serienproduktion von Schrauben mit vorgegebener Länge
In einem Werk werden Schrauben produziert, deren Länge X eine normalverteilte Zufallsgröße mit dem Sollwert (Mittelwert) m0 ¼ 21 mm ist. Eine Stichprobenuntersuchung vom
Umfang n ¼ 25 führte zu dem folgenden Ergebnis:
Mittelwert: x! ¼ 20,5 mm,
Standardabweichung: s ¼ 1,5 mm
Es soll mit einer Irrtumswahrscheinlichkeit von a ¼ 1 % geprüft werden, ob die Abweichung des beobachteten Stichprobenmittelwertes x! ¼ 20,5 mm vom Sollwert
m0 ¼ 21 mm signifikant oder zufallsbedingt ist. Wir verwenden den in Abschnitt 4.2.2
ausführlich beschriebenen Test.
Zunächst werden Nullhypothese H0 und Alternativhypothese H1 formuliert:
Nullhypothese H0 : m ¼ m0 ¼ 21 mm
Alternativhypothese H1 : m 6¼ m0 ¼ 21 mm
Signifikanzzahl (Irrtumswahrscheinlichkeit): a ¼ 1 % ¼ 0,01
Testvariable:
T ¼
X / m0
X / 21 mm
X / 21 mm
pffiffiffiffiffi
pffiffiffi ¼
¼
S=5
S= n
S= 25
T genügt der t-Verteilung mit f ¼ n / 1 ¼ 25 / 1 ¼ 24 Freiheitsgraden.
Bestimmung des kritischen Wertes c:
P ð/ c ) T ) cÞH0 ¼ 1 / a ¼ 1 / 0;01 ¼ 0;99
P ð/ c ) T ) cÞH0 ¼ 2 . FðcÞ / 1 ¼ 0;99
FðcÞ ¼ 0;995
f ¼ 24
!
)
c ¼ tð0;995; 24Þ ¼ 2;797
(aus der Tabelle 4 im Anhang, Teil B entnommen)
)
FðcÞ ¼ 0;995
5 Chi-Quadrat-Test
471
Nichtkritischer Bereich („Annahmebereich“):
/c ) t ) c
)
/ 2;797 ) t ) 2;797
Berechnung des Testwertes ^t :
^t ¼
x! / m0
ð20;5 / 21Þ mm
/ 0;5
2;5
5
pffiffiffi ¼
pffiffiffiffiffi ¼
¼ /
¼ /
¼ / 1;667
1;5=5
1;5
3
s= n
1;5 mm= 25
Testentscheidung:
Der Testwert ^t ¼ / 1;667 fällt in den nichtkritischen Bereich (Annahmebereich).
Testwert ^t = –1,667
0,99
0,005
–2,797
0,005
0
2,797
t
Die Nullhypothese H0 : m ¼ m0 ¼ 21 mm wird daher beibehalten, d. h. nicht abgelehnt.
Die Abweichung des Stichprobenmittelwertes x! ¼ 20;5 mm vom Sollwert m0 ¼ 21 mm
ist zufallsbedingt, die Stichprobe liefert keinen Anlass, daran zu zweifeln, dass die normalverteilte Grundgesamtheit den Mittelwert m0 ¼ 21 mm besitzt.
5 Chi-Quadrat-Test
Der Chi-Quadrat-Test („ c 2 -Test“) ist ein Anpassungs- oder Verteilungstest und dient der
!berprüfung einer Hypothese über die Art einer unbekannten Wahrscheinlichkeitsverteilung. Es wird der Versuch unternommen, einer Grundgesamtheit mit der unbekannten Verteilungsfunktion FðxÞ eine bekannte Verteilungsfunktion F0 ðxÞ „anzupassen“.
X sei eine Zufallsvariable mit der unbekannten Verteilungsfunktion FðxÞ. Auf der Basis
einer Zufallsstichprobe x1 ; x2 ; . . . ; xn soll geprüft werden, ob (wie vermutet) F0 ðxÞ die
Verteilungsfunktion der Grundgesamtheit ist, aus der diese Stichprobe entnommen wurde.
Unter der Voraussetzung, dass sämtliche Parameter der als wahr angenommenen Verteilungsfunktion F0 ðxÞ bekannt sind, wird die
Nullhypothese H0 : FðxÞ ¼ F0 ðxÞ
(„die Zufallsvariable X genügt einer Wahrscheinlichkeitsverteilung mit der Verteilungsfunktion F0 ðxÞ“) gegen die
Alternativhypothese H1 : FðxÞ ¼
6 F0 ðxÞ
(„F0 ðxÞ ist nicht die Verteilungsfunktion der Zufallsvariablen X “) getestet.
472
XVI Grundlagen der mathematischen Statistik
Die Durchführung des Tests erfolgt schrittweise wie folgt:
1. Unterteilung der n Stichprobenwerte in k Klassen (Intervalle) I1 ; I2 ; . . . ; Ik und
Feststellung der absoluten Klassenhäufigkeiten (Besetzungszahlen) n1 ; n2 ; . . . ; nk .
Erfahrungsgemäß sollte dabei jede Klasse mindestens 5 Werte der vorgegebenen
konkreten Stichprobe enthalten 1Þ .
2. Für jede Klasse Ii wird unter Verwendung der als wahr angenommenen Verteilungsfunktion F0 ðxÞ zunächst die Wahrscheinlichkeit pi und daraus die Anzahl
n *i ¼ n pi der theoretisch erwarteten Stichprobenwerte berechnet (hypothetische absolute Häufigkeit; i ¼ 1; 2; . . . ; kÞ.
3. Test- oder Prüfvariable ist die Zufallsvariable
Z ¼
c2
¼
k
P
ðNi / n*i Þ 2
¼
n*i
i¼1
k
P
ðNi / n pi Þ 2
i¼1
n pi
die der Chi-Quadrat-Verteilung mit f ¼ k / 1 Freiheitsgraden genügt. Dabei bedeuten:
Ni : Zufallsvariable, die die empirische absolute Häufigkeit in der i-ten Klasse
beschreibt
n*i : Theoretisch erwartete absolute Klassenhäufigkeit, berechnet unter Verwendung der als wahr angenommenen Verteilungsfunktion F0 ðxÞ der Grundgesamtheit ðn*i ¼ n pi Þ
pi : Hypothetische Wahrscheinlichkeit dafür, dass die Zufallsvariable X einen
Wert aus der i-ten Klasse annimmt (berechnet mit der als wahr angenommenen Verteilungsfunktion F0 ðxÞÞ
n: Umfang der verwendeten Stichprobe
Dann wird anhand der vorgegebenen (und in k Klassen unterteilten) konkreten
Stichprobe x1 ; x2 ; . . . ; xn der Test- oder Prüfwert
z ¼ c^ 2 ¼
^
k
P
i¼1
ðni / n*i Þ 2
¼
n*i
der Testvariablen Z ¼
c2
k
P
i¼1
ðni / n pi Þ 2
n pi
berechnet.
4. Jetzt wähle man eine kleine Signifikanzzahl (Irrtumswahrscheinlichkeit) a (in der
Praxis meist a ¼ 0;05 ¼ 5 % oder a ¼ 0;01 ¼ 1 %) und bestimme die kritische Grenze c aus der Bedingung
P ðZ ) cÞH0 ¼ 1 / a
unter Verwendung von Tabelle 3 im Anhang, Teil B. Der nichtkritische Bereich
(Annahmebereich) lautet dann:
z ¼ c2 ) c
1Þ
Gegebenenfalls müssen nachträglich Klassen zusammengelegt werden.
5 Chi-Quadrat-Test
473
5. Testentscheidung: Fällt der Test- oder Prüfwert ^z ¼ c^ 2 in den nichtkritischen
Bereich (Annahmebereich), d. h. gilt
z ¼ c^ 2 ) c
^
so wird die Nullhypothese H0 : FðxÞ ¼ F0 ðxÞ beibehalten, d. h. nicht abgelehnt
und wir dürfen davon ausgehen, dass die untersuchte Grundgesamtheit einer Wahrscheinlichkeitsverteilung mit der Verteilungsfunktion F0 ðxÞ genügt (die Stichprobe
steht in keinem Widerspruch zur Nullhypothese). Anderenfalls muss die Nullhypothese H0 zugunsten der Alternativhypothese H1 : FðxÞ ¼
6 F0 ðxÞ abgelehnt werden (siehe Bild).
H 0 beibehalten
1– a
H 0 ablehnen
a
z^
0
c z^
Annahmebereich
(nichtkritischer Bereich)
z
Ablehnung
(kritischer
Bereich)
Anmerkungen
(1)
(2)
Sind ein oder mehrere Parameter der als wahr angenommenen Verteilungsfunktion
F0 ðxÞ unbekannt, so muss man zunächst für diese Parameter unter Verwendung der
vorgegebenen konkreten Stichprobe Näherungs- oder Schätzwerte bestimmen. Die
Anzahl der Freiheitsgrade vermindert sich dabei um die Anzahl der zu schätzenden
Parameter.
Bei einer diskreten Zufallsvariablen X sind die Klassen die möglichen Werte selbst.
&
Beispiel
Ein Würfel wurde 300-mal geworfen. Dabei ergab sich die folgende Häufigkeitsverteilung für die 6 möglichen Augenzahlen:
Augenzahl i
1
2
3
4
5
6
absolute Häufigkeit ni
35
39
62
56
70
38
Durch einen Chi-Quadrat-Test soll auf dem Signifikanzniveau a ¼ 1 % geprüft werden, ob die Zufallsstichprobe gegen eine Gleichverteilung der Augenzahlen spricht.
)
Nullhypothese H0 : pi ¼ 1=6
ði ¼ 1; 2; . . . ; 6Þ
Alternativhypothese H1 : pi 6¼ 1=6
1. Schritt: Klasseneinteilung
k ¼ 6 Klassen (sie entsprechen den 6 Augenzahlen, Spalte 1 der nachfolgenden Tabelle)
474
XVI Grundlagen der mathematischen Statistik
2. Schritt: Theoretische Häufigkeitsverteilung
Es wird vorausgesetzt, dass die Nullhypothese H0 zutrifft:
n*i ¼ n pi ¼ 300 .
1
¼ 50
6
ðSpalte 4 der nachfolgenden TabelleÞ
Klasse
(Augenzahl i)
ni
pi
n *i ¼ n pi
Dni ¼ ni / n*i
ðDni Þ 2
n *i
1
35
1/6
50
/15
225/50
2
39
1/6
50
/11
121/50
3
62
1/6
50
12
144/50
4
56
1/6
50
6
36/50
5
70
1/6
50
20
400/50
6
38
1/6
50
/12
144/50
S
300
1
300
0
1070/50
3. Schritt: Berechnung des Testwertes
Spalte 5 enthält die Differenzen D ni ¼ ni / n *i (Abweichungen zwischen den beobachteten und den theoretischen absoluten Häufigkeiten), Spalte 6 die daraus berechneten „Abweichungsmaße“ ðDni Þ 2 =n *i . Aufsummieren der letzten Spalte ergibt den gesuchten Testwert:
^z ¼ c^ 2 ¼
6
6
X
X
ðni / n *i Þ 2
ðDni Þ 2
1070
¼
¼
¼ 21;4
*
50
ni
n *i
i¼1
i¼1
4. Schritt: Berechnung der kritischen Grenze und des nichtkritischen Bereiches
P ðZ ) cÞH0 ¼ Pðc 2 ) cÞH0 ¼ 1 / a ¼ 1 / 0;01 ¼ 0;99
Die Testvariable Z ¼ c 2 genügt der Chi-Quadrat-Verteilung mit f ¼ k / 1 ¼ 6 / 1 ¼ 5 Freiheitsgraden. Aus Tabelle 3 im Anhang, Teil B erhält man:
P ðZ ) cÞH0 ¼ FðcÞ ¼ 0;99
f ¼5
!
Nichtkritischer Bereich: z ¼ c 2 ) c
c ¼ zð0;99; 5Þ ¼ 15;09
)
z ¼ c 2 ) 15;09
5. Schritt: Testentscheidung
Der Testwert ^z ¼ c^ 2 ¼ 21,4 fällt in den kritischen Bereich z ¼ c 2 > 15,09. Die Nullhypothese H0
wird daher abgelehnt. Wir dürfen davon ausgehen, dass der Würfel in irgendeiner Weise „verfälscht“ ist.
0,99
Testwert z^ = 21,4
0,01
0
15,09
z
&
476
Anhang Teil A
Integraltafel
Diese Integraltafel enthält über 400 ausgewählte in den naturwissenschaftlich-technischen
Anwendungen besonders häufig auftretende unbestimmte Integrale. Die Integrationskonstante wurde dabei aus Platzgründen stets weggelassen, muss also stets ergänzt werden.
!bersicht
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
Integrale
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
mit
ax þ b . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a x þ b und p x þ q . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a2 þ x2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a2 / x2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ax2 þ bx þ c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a3 + x3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a4 þ x4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
a4 / x4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x þ b und p x þ q . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x þ b und p x þ q . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 þ x2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
paffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 / x2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 / a2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax2 þ bx þ c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sin ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cos ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sin ða xÞ und cos ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
tan ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cot ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
einer Arkusfunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e ax . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ln x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sinh ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
cosh ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
sinh ða xÞ und cosh ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
tanh ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
coth ða xÞ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
einer Areafunktion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
© Springer Fachmedien Wiesbaden GmbH 2017
L. Papula, Mathematische Formelsammlung, DOI 10.1007/978-3-658-16195-8
477
478
479
480
482
484
484
484
485
486
487
488
490
492
494
496
498
500
503
503
504
505
506
508
509
510
511
511
512
Integraltafel
477
1 Integrale mit
ax þ b
ða 6¼ 0Þ
Hinweis: Im Sonderfall b ¼ 0 erhält man Integrale von Potenzen, die mit Hilfe der Potenzregel der
Integralrechnung elementar lösbar sind.
ð
ð1Þ
ða x þ bÞ n dx ¼
ða x þ bÞ n þ 1
ðn þ 1Þ a
ðn 6¼ / 1Þ
Fall n ¼ / 1: siehe Integral (2)
ð
dx
1
ð2Þ
¼
. ln j a x þ b j
ax þ b
a
ð
ða x þ bÞ n þ 2
bða x þ bÞ n þ 1
ð3Þ
x ða x þ bÞ n dx ¼
/
2
ðn þ 2Þ a
ðn þ 1Þ a 2
ðn 6¼ / 1; / 2Þ
Fall n ¼ / 1; / 2: siehe Integral (4) bzw. (5)
ð
x dx
x
b
ð4Þ
¼
/ 2 . ln j a x þ b j
ax þ b
a
a
ð
x dx
b
1
¼ 2
þ 2 . ln j a x þ b j
ð5Þ
ða x þ bÞ 2
a ða x þ bÞ
a
ð
x dx
1
b
ð6Þ
¼ /
þ
ða x þ bÞ n
ðn / 2Þ a 2 ða x þ bÞ n / 2
ðn / 1Þ a 2 ða x þ bÞ n / 1
ðn 6¼ 1; 2Þ
Fall n ¼ 1; 2: siehe Integral (4) bzw. (5)
ð
ð7Þ
x 2 ða x þ bÞ n dx ¼
ðax þ bÞ n þ 3
2 bðax þ bÞ n þ 2
b 2 ðax þ bÞ n þ 1
/
þ
3
3
ðn þ 3Þ a
ðn þ 2Þ a
ðn þ 1Þ a 3
ðn 6¼ /1; /2; /3Þ
Fall n ¼ / 1; / 2; /3: siehe Integral (8), (9) bzw. (10)
ð
ð8Þ
ð
ð9Þ
ð
ð10Þ
ð
ð11Þ
x 2 dx
ða x þ bÞ 2
2 bða x þ bÞ
b2
¼
/
þ 3 . ln j a x þ b j
3
3
ax þ b
2a
a
a
x 2 dx
ax þ b
b2
2b
¼
/ 3
/ 3 . ln j a x þ b j
2
3
a ða x þ bÞ
ða x þ bÞ
a
a
x 2 dx
2b
b2
1
¼ 3
/
þ 3 . ln j a x þ b j
3
3
ða x þ bÞ
a ða x þ bÞ
2 a ða x þ bÞ 2
a
x 2 dx
1
2b
b2
¼/
þ
/
n
3
n
/
3
3
n
/
2
3
ðax þ bÞ
ðn / 3Þ a ða x þ bÞ
ðn / 2Þ a ða x þ bÞ
ðn / 1Þ a ðax þ bÞ n / 1
ðn 6¼ 1; 2; 3Þ: Fall n ¼ 1; 2; 3: siehe Integral (8), (9) bzw. (10)
"
"
"ax þ b"
dx
1
"
¼ /
. ln ""
ð12Þ
"
x ða x þ bÞ
b
x
"
"
ð
"ax þ b"
dx
1
1
"
"
ð13Þ
¼
/
.
ln
"
"
x ða x þ bÞ 2
bða x þ bÞ
b2
x
ð
478
Integraltafel
ð
"
"
"ax þ b"
dx
a2 x2
2ax
1
"
"
¼
/
/
.
ln
"
"
x ða x þ bÞ 3
2 b 3 ða x þ bÞ 2
b 3 ða x þ bÞ
b3
x
ð
"
"
"ax þ b"
dx
1
a
"
"
¼
/
þ
.
ln
"
"
x 2 ða x þ bÞ
bx
b2
x
ð
"
"
"ax þ b"
dx
a
1
2a
"
"
/ 2 þ 3 . ln "
¼ / 2
"
x 2 ða x þ bÞ 2
b ða x þ bÞ
b x
b
x
ð
"
"
"ax þ b"
dx
ða x þ bÞ 2
2 aða x þ bÞ
a2
"
"
/
.
ln
¼
/
þ
"
"
x 3 ða x þ bÞ
2b3 x2
b3 x
b3
x
ð
"
"
"ax þ b"
dx
ða x þ bÞ 2
3 aða x þ bÞ
a3 x
3a2
"
"
¼
/
þ
/
/
.
ln
"
"
x 3 ða x þ bÞ 2
2b4 x2
b4 x
b 4 ða x þ bÞ
b4
x
ð14Þ
ð15Þ
ð16Þ
ð17Þ
ð18Þ
ð
8 mþ1
x
ðax þ bÞ n
nb
>
>
þ
.
x m ðax þ bÞ n / 1 dx ðm þ n 6¼ /1Þ
> mþnþ1
>
m
þ
n
þ
1
>
>
>
>
>
>
ð
ð
< x m ðax þ bÞ n þ 1
mb
m
n
x ða x þ bÞ dx ¼
/
. x m / 1 ðax þ bÞ n dx ðm þ n 6¼ /1Þ
ð19Þ
> ðm þ n þ 1Þ a
ðm þ n þ 1Þ a
>
>
>
>
>
ð
>
>
mþ1
>
ðax þ bÞ n þ 1
mþnþ2
>
:/ x
þ
. x m ðax þ bÞ n þ 1 dx ðn ¼
6 /1Þ
ðn þ 1Þ b
ðn þ 1Þ b
2 Integrale mit
Abkürzung:
Hinweis:
ð
ð20Þ
ð
ð21Þ
ð
ð22Þ
und
px þ q
ða; p 6¼ 0Þ
D ¼ bp / aq
q
Es wird stets D 6¼ 0 vorausgesetzt. Für D ¼ 0 ist p x þ q ¼
ða x þ bÞ.
Die Integrale entsprechen dann dem Integraltyp aus Abschnitt 1. b
ax þ b
ax
D
dx ¼
þ 2 . ln j p x þ q j
px þ q
p
p
"
"
"px þ q"
dx
1
"
¼
. ln ""
ða x þ bÞ ðp x þ qÞ
D
ax þ b"
dx
1
¼
ða x þ bÞ 2 ðp x þ qÞ
D
ð
ð23Þ
ax þ b
ða x þ
+
"
")
"px þ q"
1
p
"
þ
. ln ""
ax þ b
D
ax þ b"
+
dx
1
1
¼ /
þ
n
ðp x þ qÞ
ðn / 1Þ D ða x þ bÞ m / 1 ðp x þ qÞ n / 1
)
ð
dx
þ ðm þ n / 2Þ a .
ða x þ bÞ m ðp x þ qÞ n / 1
bÞ m
Fall n ¼ 1: siehe Integral (24)
ðn 6¼ 1Þ
Integraltafel
ð
ð24Þ
479
ða x þ bÞ m
ða x þ bÞ m
D
dx ¼
þ .
px þ q
mp
p
ð
ða x þ bÞ m / 1
dx
px þ q
ðm 6¼ 0Þ
Fall m ¼ 0: siehe Integral (2)
ð
ð25Þ
+
)
ð
ða x þ bÞ m
1
ða x þ bÞ m
ða x þ bÞ m / 1
dx
¼
/
/
m
a
.
dx
ðn / 1Þ p ð p x þ qÞ n / 1
ð p x þ qÞ n
ð p x þ qÞ n / 1
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (24)
ð
ð26Þ
ð
ð27Þ
ð
ð28Þ
x dx
1
¼
ða x þ bÞ ð p x þ qÞ
D
x 2 dx
b2
1
¼ 2
þ 2
2
ða x þ bÞ ð p x þ qÞ
a D ða x þ bÞ
D
ð
a2
ð
ð30Þ
ð
ð31Þ
b
q
. ln j a x þ b j /
. ln j p x þ q j
a
p
a2 þ x2
+
q2
b ðb p / 2 a qÞ
. ln j p x þ q j þ
. ln j a x þ b j
p
a2
ða > 0Þ
!x4
dx
1
¼
. arctan
2
þx
a
a
!x4
dx
x
1
¼
þ
.
arctan
ða 2 þ x 2 Þ 2
2 a 2 ða 2 þ x 2 Þ
2a3
a
dx
x
2n / 3
¼
þ
.
2
2
n
2
2
2
n
/
1Þ
ða þ x Þ
2 ðn / 1Þ a 2
2 ðn / 1Þ a ða þ x Þ
Fall n ¼ 1: siehe Integral (29)
ð
ð32Þ
ð
ð33Þ
ð
ð34Þ
x dx
1
¼
. ln ða 2 þ x 2 Þ
a2 þ x2
2
x dx
1
¼ /
ða 2 þ x 2 Þ 2
2 ða 2 þ x 2 Þ
x dx
1
¼ /
ða 2 þ x 2 Þ n
2 ðn / 1Þ ða 2 þ x 2 Þ n / 1
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (32)
ð
ð35Þ
!x4
x 2 dx
¼ x / a . arctan
2
þx
a
a2
ð
ð36Þ
)
"
")
+
"ax þ b"
x dx
1
b
q
"
"
¼
/
þ
. ln "
ða x þ bÞ 2 ð p x þ qÞ
D
a ða x þ bÞ
D
px þ q"
3 Integrale mit
ð29Þ
+
!x4
x 2 dx
x
1
¼ /
þ
. arctan
2
2
2
2
þx Þ
2 ða þ x Þ
2a
a
ða 2
ð
ða 2
dx
þ x 2Þ n / 1
ðn 6¼ 1Þ
)
480
Integraltafel
ð
ð37Þ
x 2 dx
x
1
þ
¼ /
.
2
ða þ x 2 Þ n
2 ðn / 1Þ ðx 2 þ a 2 Þ n / 1
2 ðn / 1Þ
Fall n ¼ 1: siehe Integral (35)
ð
ð38Þ
ð
ð39Þ
ð
ð40Þ
dx
1
¼ /
. ln
x ða 2 þ x 2 Þ
2a2
ð
ð
ð43Þ
ð
ð44Þ
ð
ð45Þ
ðn 6¼ 1Þ
3 2
2
a þ x2
x2
!x4
dx
1
1
¼
/
/
.
arctan
x 2 ða 2 þ x 2 Þ
a2 x
a3
a
x2
ð42Þ
dx
ða 2 þ x 2 Þ n / 1
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (31)
3 2
2
a þ x2
x2
dx
1
1
¼
/
. ln
x ða 2 þ x 2 Þ 2
2 a 2 ða 2 þ x 2 Þ
2a4
ð
ð41Þ
ð
ða 2
!x4
dx
1
x
3
/
. arctan
¼ / 4 /
4
2
2
5
2
2
a x
2 a ða þ x Þ
2a
a
þx Þ
x m dx
¼
ða 2 þ x 2 Þ n
ð
x m / 2 dx
/ a2 .
ða 2 þ x 2 Þ n / 1
dx
1
¼ 2 .
x m ða 2 þ x 2 Þ n
a
ð
x m / 2 dx
ða 2 þ x 2 Þ n
dx
1
/ 2 .
x m ða 2 þ x 2 Þ n / 1
a
dx
1
¼ 2 2
ð p x þ qÞ ða 2 þ x 2 Þ
a p þ q2
+
a2 / x2
ð
dx
x m / 2 ða 2 þ x 2 Þ n
3
2
!x4)
p
ð p x þ qÞ 2
q
. ln
þ
.
arctan
2
a2 þ x2
a
a
x dx
1
¼
ð p x þ qÞ ða 2 þ x 2 Þ
2 ða 2 p 2 þ q 2 Þ
4 Integrale mit
ð
+
3
a2 þ x2
q . ln
ð p x þ qÞ 2
2
þ 2 a p . arctan
ð p 6¼ 0Þ
!x4)
a
ð p 6¼ 0Þ
ða > 0Þ
"a þ x"
"
"
Die in den nachfolgenden Integralformeln auftretende logarithmische Funktion ln "
"
a
/
x
kann auch wie folgt durch Areafunktionen ersetzt werden:
8 !
!x4
a þ x4
>
fur
€ jxj < a
>
"a þ x"
< ln a / x ¼ 2 . artanh a
"
"
ln "
" ¼
!
4
! 4
>
a/x
>
: ln x þ a ¼ 2 . arcoth x
fur
€ jxj > a
x /a
a
8
!x4
1
>
>
.
artanh
fur
€ jxj < a
>
ð
"a þ x"
<a
a
dx
1
"
"
ð46Þ
¼
.
ln
¼
"
"
! 4
>
a2 / x2
2a
a/x
>
>
: 1 . arcoth x
fur
€ jxj > a
a
a
ð
"a þ x"
dx
x
1
"
"
¼
þ
. ln "
ð47Þ
"
2
2
2
2
2
2
3
ða / x Þ
2 a ða / x Þ
4a
a/x
Hinweis:
Integraltafel
ð
ð48Þ
481
dx
x
2n / 3
¼
þ
.
ða 2 / x 2 Þ n
2 ðn / 1Þ a 2 ða 2 / x 2 Þ n / 1
2 ðn / 1Þ a 2
ð
dx
ða 2 / x 2 Þ n / 1
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (46)
ð
ð49Þ
ð
ð50Þ
x dx
1
¼ /
. ln j a 2 / x 2 j
a2 / x2
2
x dx
1
¼
ða 2 / x 2 Þ 2
2 ða 2 / x 2 Þ
ð
ð51Þ
x dx
1
¼
ða 2 / x 2 Þ n
2 ðn / 1Þ ða 2 / x 2 Þ n / 1
Fall n ¼ 1: siehe Integral (49)
ð
ð52Þ
ðn 6¼ 1Þ
"a þ x"
x 2 dx
a
"
"
¼ /x þ
. ln "
"
2
/x
2
a/x
a2
ð
ð53Þ
"a þ x"
x 2 dx
x
1
"
"
¼
/
. ln "
"
2
2
2
2
/x Þ
2 ða / x Þ
4a
a/x
ða 2
ð
ð54Þ
x 2 dx
x
1
¼
/
.
2
ða / x 2 Þ n
2 ðn / 1Þ ða 2 / x 2 Þ n / 1
2 ðn / 1Þ
Fall n ¼ 1: siehe Integral (52)
dx
ða 2 / x 2 Þ n / 1
|fflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (48)
ð
" 2
"
"a / x2 "
dx
1
"
"
¼
/
.
ln
" x2
"
x ða 2 / x 2 Þ
2a2
ð
" 2
"
"a / x2 "
dx
1
1
"
"
¼
/
.
ln
" x2
"
x ða 2 / x 2 Þ 2
2 a 2 ða 2 / x 2 Þ
2a4
ð55Þ
ð56Þ
ð
ð57Þ
ð
ð59Þ
ð
ð60Þ
ð
ð61Þ
ð
ðn 6¼ 1Þ
"a þ x"
dx
1
1
"
"
¼ / 2 þ
. ln "
"
2
3
/x Þ
a x
2a
a/x
x2
ða 2
x2
ða 2
ð
ð58Þ
ð62Þ
ð
"a þ x"
dx
1
x
3
"
"
¼ / 4 þ
þ
. ln "
"
2
2
4
2
2
5
/x Þ
a x
2 a ða / x Þ
4a
a/x
x m dx
¼ a2 .
2
ða / x 2 Þ n
ð
x m / 2 dx
/
ða 2 / x 2 Þ n
dx
1
¼ 2 .
x m ða 2 / x 2 Þ n
a
ð
ð
x m / 2 dx
/ x 2Þ n / 1
ða 2
dx
1
þ 2 .
x m ða 2 / x 2 Þ n / 1
a
dx
1
¼ 2 2
ð p x þ qÞ ða 2 / x 2 Þ
a p / q2
+
ð
dx
x m / 2 ða 2 / x 2 Þ n
"
"
"a þ x ")
" ð p x þ qÞ 2 "
p
q
"
"
"
"
. ln " 2
. ln "
ðp 6¼ 0Þ
/
"
2
a / x2 "
2a
a/x
x dx
1
¼
ð p x þ qÞ ða 2 / x 2 Þ
2 ða 2 p 2 / q 2 Þ
+
" 2
"
"
")
" a / x2 "
" þ a p . ln "" a þ x ""
"
q . ln "
"
ð p x þ qÞ 2
a/x
ðp 6¼ 0Þ
482
Integraltafel
5 Integrale mit
Abkürzung:
Hinweis:
ax2 þ bx þ c
D ¼ 4ac / b2
3
2
b 2
Es wird stets D 6¼ 0 vorausgesetzt. Für D ¼ 0 ist a x 2 þ b x þ c ¼ a x þ
.
2a
Die Integrale entsprechen dann dem Integraltyp aus Abschnitt 1.
8
3
2
2ax þ
>
>
pffiffiffiffi . arctan
pffiffiffiffi
>
>
ð
<
D
D
dx
"
ð63Þ
¼
2
"
>
ax þ bx þ c
1
"2ax þ b
>
>
. ln "
>
: pffiffiffiffiffiffiffiffi
"2ax þ b
jDj
ð
ð64Þ
ð
ð65Þ
ða 6¼ 0Þ
2
b
pffiffiffiffiffiffiffiffi
jDj
pffiffiffiffiffiffiffiffi
þ jDj
/
dx
2ax þ b
2a
¼
.
þ
ða x 2 þ b x þ cÞ 2
D ða x 2 þ b x þ cÞ
D
"
"
"
"
"
fur
€
D > 0
fur
€
D < 0
ð
dx
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (63)
dx
2ax þ b
2 ð2 n / 3Þ a
¼
.
þ
ða x 2 þ b x þ cÞ n ðn / 1Þ D ða x 2 þ b x þ cÞ n / 1
ðn / 1Þ D
ð
dx
ða x 2 þ b x þ cÞ n / 1
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (63)
ð
ð66Þ
ð
ð67Þ
ð
ð68Þ
x dx
1
b
¼
. ln j a x 2 þ b x þ c j /
.
ax2 þ bx þ c
2a
2a
x dx
bx þ 2c
b
/ .
¼ /
ða x 2 þ b x þ cÞ 2
D ða x 2 þ b x þ cÞ
D
ð
dx
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (63)
ð
dx
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (63)
x dx
bx þ 2c
ð2 n / 3Þ b
¼/
/
.
ða x 2 þ b x þ cÞ n
ðn / 1Þ D ða x 2 þ b x þ cÞ n / 1 ðn / 1Þ D
Fall n ¼ 1: siehe Integral (66)
ð
ð69Þ
ð
ð70Þ
px þ q
p
2aq / bp
dx ¼
. ln j a x 2 þ b x þ c j þ
.
þ bx þ c
2a
2a
ax2
ð
dx
ðn 6¼ 1Þ
ða x 2 þ b x þ cÞ n / 1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (65)
ð
dx
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (63)
px þ q
ð2 a q / b pÞ x þ b q / 2 c p
dx ¼
þ
ða x 2 þ b x þ cÞ n
ðn / 1Þ D ða x 2 þ b x þ cÞ n / 1
þ
Fall n ¼ 1: siehe Integral (69)
ð2 n / 3Þ ð2 a q / b pÞ
.
ðn / 1Þ D
ð
dx
ða x 2 þ b x þ cÞ n / 1
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (65)
ðn 6¼ 1Þ
Integraltafel
ð
ð71Þ
x 2 dx
x
b
b2 / 2ac
¼
/
. ln j a x 2 þ b x þ c j þ
.
2
2
ax þ bx þ c
a
2a
2a2
ð
ð72Þ
483
ða x 2
ð
ðn / 2Þ b
.
ð2 n / 3Þ a
ð
x dx
ða x 2 þ b x þ cÞ n
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (68)
ð
dx
/
ða x 2 þ b x þ cÞ n
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (65)
" 2
"
ð
"ax þ bx þ c"
dx
1
dx
"
"/ b .
¼
/
.
ln
"
"
x ða x 2 þ b x þ cÞ
2c
x2
2c
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (63)
ð
ð74Þ
dx
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (63)
x 2 dx
x
c
.
¼/
þ
þ b x þ cÞ n
ð2 n / 3Þ a ða x 2 þ b x þ cÞ n / 1
ð2 n / 3Þ a
/
ð73Þ
ð
x ða x 2
dx
1
b
¼
/
.
þ b x þ cÞ n
2 ðn / 1Þ c ða x 2 þ b x þ cÞ n / 1 2 c
þ
1
.
c
ð
dx
x ða x 2 þ b x þ cÞ n / 1
ðc 6¼ 0Þ
ð
dx
þ
ða x 2 þ b x þ cÞ n
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (65)
ðn 6¼ 1; c 6¼ 0Þ
Fall n ¼ 1: siehe Integral (73)
ð
ð75Þ
x m dx
x m/1
¼ /
þ
n
þ b x þ cÞ
ð2 n / m / 1Þ a ða x 2 þ b x þ cÞ n / 1
ð
ð
ðm / 1Þ c
x m / 2 dx
ðm / nÞ b
x m / 1 dx
þ
.
þ
.
2
n
2
ð2 n / m / 1Þ a
ða x þ b x þ cÞ
ð2 n / m / 1Þ a
ða x þ b x þ cÞ n
ða x 2
ðm 6¼ 2 n / 1Þ
Fall m ¼ 2 n / 1: siehe Integral (76)
ð
ð76Þ
ð
ð77Þ
x 2 n / 1 dx
1
¼
.
ða x 2 þ b x þ cÞ n
a
ð
x 2 n / 3 dx
/
ða x 2 þ b x þ cÞ n / 1
ð
ð
c
x 2 n / 3 dx
b
x 2 n / 2 dx
/
.
/
.
a
ða x 2 þ b x þ cÞ n
a
ða x 2 þ b x þ cÞ n
dx
1
¼ /
/
x m ða x 2 þ b x þ cÞ n
ðm / 1Þ c x m / 1 ða x 2 þ b x þ cÞ n / 1
ð
ðm þ 2 n / 3Þ a
dx
.
/
/
ðm / 1Þ c
x m / 2 ða x 2 þ b x þ cÞ n
ð
ðm þ n / 2Þ b
dx
/
.
ðm / 1Þ c
x m / 1 ða x 2 þ b x þ cÞ n
ðm 6¼ 1; c 6¼ 0Þ Fall m ¼ 1: siehe Integral (74)
484
Integraltafel
ð
ð78Þ
dx
1
¼
ð p x þ qÞ ða x 2 þ b x þ cÞ
2 ða q 2 / b p q þ c p 2 Þ
"
ð
"
" ð p x þ qÞ 2
p . ln "" 2
ax þ bx þ
dx
þ ð2 a q / b pÞ .
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (63)
6 Integrale mit
Hinweis:
ð
ð79Þ
ð
ð80Þ
ð
ð81Þ
ð
ð82Þ
ð
ð83Þ
a3 + x3
"
"
"þ
c"
#
ð p 6¼ 0Þ
ða > 0Þ
Das obere Vorzeichen gilt für a 3 þ x 3, das untere Vorzeichen für a 3 / x 3.
"
"
3
2
" ða + xÞ 2 "
dx
1
1
2x * a
"
"þ
p
ffiffi
ffi
p
ffiffi
ffi
¼
+
.
ln
.
arctan
"a2 * ax þ x2 "
a3 + x3
6a2
a2 3
a 3
"
"
3
2
" ða + xÞ 2 "
dx
x
1
2
2x * a
"
"þ
ffiffi
p
ffiffi
ffi
p
ffi
¼
+
.
ln
.
arctan
"a2 * ax þ x2 "
ða 3 + x 3 Þ 2
3 a 3 ða 3 + x 3 Þ
9a5
3a5 3
a 3
" 2
"
3
2
2
"a * ax þ x "
x dx
1
1
2x * a
"+
pffiffiffi
pffiffiffi . arctan
¼
. ln ""
"
a3 + x3
6a
ða + xÞ 2
a2 3
a 3
" 2
"
3
2
"a * ax þ x2 "
x dx
x2
1
1
2x * a
"
"
p
ffiffi
ffi
p
ffi
ffiffi
. arctan
¼
þ
. ln "
+
ða 3 + x 3 Þ 2
3 a 3 ða 3 + x 3 Þ
18 a 4
ða + xÞ 2 "
3a4 3
a 3
"
"
" x3 "
dx
1
"
¼
. ln "" 3
3
3
3
x ða + x Þ
3a
a + x3"
7 Integrale mit
a4 þ x4
ða > 0Þ
pffiffiffi
" 2
"
3 pffiffiffi 2
"x þ a 2 x þ a2 "
dx
1
a 2x
"
" / p1ffiffiffi
p
ffiffi
ffi
p
ffiffi
ffi
¼
.
ln
.
arctan
"x2 / a 2 x þ a2 "
a4 þ x4
x2 / a2
4 2a3
2 2 a3
3 22
ð
x dx
1
x
ð85Þ
¼
.
arctan
a2
a4 þ x4
2a2
3
2
ð
dx
1
x4
ð86Þ
¼
.
ln
x ða 4 þ x 4 Þ
4a4
a4 þ x4
ð
ð84Þ
8 Integrale mit
ð
ð87Þ
a4 / x4
ða > 0Þ
"a þ x"
!x4
dx
1
1
"
"
¼
.
ln
þ
.
arctan
"
"
a4 / x4
4a3
a/x
2a3
a
Integraltafel
ð
" 2
"
"a þ x2 "
x dx
1
"
"
¼
.
ln
"a2 / x2 "
a4 / x4
4a2
ð
" 4
"
"a / x4 "
dx
1
"
"
¼
/
.
ln
"
"
x ða 4 / x 4 Þ
4a4
x4
ð88Þ
ð89Þ
9 Integrale mit
ð
ð90Þ
x
ð
ð92Þ
ð94Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b
ða 6¼ 0Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
ða x þ bÞ 3
a x þ b dx ¼
3a
ð
ð91Þ
ð93Þ
485
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 ð3 a x / 2 bÞ
a x þ b dx ¼
ða x þ bÞ 3
15 a 2
xn
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x þ b dx ¼
2xn
ð2 n þ 3Þ a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ 3 /
2nb
.
ð2 n þ 3Þ a
ð
x n/1
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼ 2 a x þ b þ b .
x
x ax þ b
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral (99)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ax þ b
ax þ b
a
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
.
dx
¼
/
þ
2
x2
x
x ax þ b
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral (99)
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ 3
ax þ b
ð2 n / 5Þ a
ax þ b
/
.
ð95Þ
dx
¼
/
dx
ðn / 1Þ b x n / 1
2 ðn / 1Þ b
xn
x n/1
Fall n ¼ 1: siehe Integral (93)
ð
ð96Þ
ð
ð97Þ
ð
ð98Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x þ b dx
dx
2 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
. ax þ b
a
ax þ b
x dx
2 ða x / 2 bÞ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
. ax þ b
3a2
ax þ b
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
x n dx
2xn ax þ b
2nb
x n / 1 dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
/
. pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð2 n þ 1Þ a
ð2 n þ 1Þ a
ax þ b
ax þ b
8
" pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi pffiffiffi "
" ax þ b / b "
>
1
>
> pffiffiffi . ln "" pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi ""
fur
€
>
>
ð
<
b
a
x
þ
b
þ
b
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
ð99Þ
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi !
>
x ax þ b
>
2
ax þ b
> pffiffiffiffiffiffiffi
>
fur
€
>
: j b j . arctan
jbj
b > 0
b < 0
ðn 6¼ 1; b 6¼ 0Þ
486
Integraltafel
ð
ð100Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
dx
ð2 n / 3Þ a
dx
ax þ b
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
.
/
2 ðn / 1Þ b
ðn / 1Þ b x n / 1
xn ax þ b
x n/1 a x þ b
ðn 6¼ 1; b 6¼ 0Þ
Fall n ¼ 1: siehe Integral (99)
ð101Þ
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
ða x þ bÞ 3 dx ¼
. ða x þ bÞ 5
5a
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
ð102Þ
ða x þ bÞ n dx ¼
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ n þ 2
ðn 6¼ / 2Þ
ðn þ 2Þ a
Fall n ¼ /2: siehe Integral (2)
ð
ð103Þ
x
ð
ð104Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ 3 dx ¼
2
35 a 2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
x ða x þ bÞ n dx ¼
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi )
5 ða x þ bÞ 7 / 7 b ða x þ bÞ 5
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ n þ 4
ðn þ 4Þ a 2
/
2b
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ n þ 2
ðn þ 2Þ a 2
ðn 6¼ / 2; / 4Þ
Fall n ¼ / 2; / 4: siehe Integral (4) bzw. (5)
ð
ð105Þ
ð
ð106Þ
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ 3
2
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x þ bÞ 3 þ 2 b a x þ b þ b 2 .
dx ¼
x
3
x ax þ b
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral (99)
x
2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx ¼ 2
a
3
ða x þ bÞ
10 Integrale mit
Abkürzung:
Hinweis:
+
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
b
a x þ b þ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b
)
und
¼
2 ða x þ 2 bÞ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 ax þ b
px þ q
D ¼ bp / aq
q
Es wird stets D 6¼ 0 vorausgesetzt. Für D ¼ 0 ist p x þ q ¼
ða x þ bÞ.
Die Integrale entsprechen dann dem Integraltyp aus Abschnitt 9. b
8 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
" pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi "
pffiffiffiffi
" p ða x þ bÞ / pffiffiffi
>
D ""
D
"
>2 ax þ b þ p
>
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
p
ffiffiffi
ffi "
.
ln
"
ffiffiffi
>
>
" p ða x þ bÞ þ D "
p
p p
>
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
<
ax þ b
0sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 1
ð107Þ
dx ¼
pffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
>
px þ q
>
2
j
D
j
2
a
x
þ
b
p ða x þ bÞ A
>
>
/
>
pffiffiffi . arctan @
>
:
p
p p
jDj
ð108Þ
fur
€
p > 0; D > 0
fur
€
p > 0; D < 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b
ax þ b
a
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx
¼
/
þ
.
ð p x þ qÞ n
ðn / 1Þ p ð p x þ qÞ n / 1
2 ðn / 1Þ p
ð p x þ qÞ n / 1 a x þ b
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (111)
Fall n ¼ 1: siehe Integral (107)
ðn 6¼ 1Þ
Integraltafel
ð
ð109Þ
487
px þ q
2 ða p x þ 3 a q / 2 b pÞ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi dx ¼
3a2
ax þ b
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b
8
" pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi pffiffiffiffi "
" p ða x þ bÞ / D "
>
1
"
"
>
>
pffiffiffiffiffiffiffiffi . ln " pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffi "
fur
€
>
>
"
"
>
p
D
ð
p
ða
x
þ
bÞ
þ
D
<
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
ð110Þ
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi !
>
ð p x þ qÞ a x þ b
>
>
2
p ða x þ bÞ
>
>
. arctan
fur
€
>
: pffiffiffiffiffiffiffiffiffiffiffiffi
jDj
pjDj
ð
ð111Þ
D > 0; p > 0
D < 0; p > 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax þ b
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
/
ðn / 1Þ D ð p x þ qÞ n / 1
ð p x þ qÞ n a x þ b
ð
ð2 n / 3Þ a
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
/
.
n
2 ðn / 1Þ D
ð p x þ qÞ / 1 a x þ b
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (110)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
11 Integrale mit
a x þ b und
Abkürzung:
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p x þ q ða; p 6¼ 0Þ
D ¼ bp / aq
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
½ 2 a ð p x þ qÞ þ D % ða x þ bÞ ð p x þ qÞ
ð112Þ
ða x þ bÞ ð p x þ qÞ dx ¼
/
4ap
ð
D2
dx
. pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
/
8ap
ða x þ bÞ ð p x þ qÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (114)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð rffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ða x þ bÞ ð p x þ qÞ
px þ q
D
dx
dx ¼
/
. pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð113Þ
ax þ b
a
2a
ða x þ bÞ ð p x þ qÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (114)
8
" pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ""
2
"
>
>
pffiffiffiffiffiffi . ln " a ð p x þ qÞ þ
p ða x þ bÞ " fur
€
>
>
ð
< ap
dx
sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi !
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
ð114Þ
>
ða x þ bÞ ð p x þ qÞ
2
p ða x þ bÞ
>
>
p
ffiffiffiffiffiffiffiffiffiffi
/
fur
€
>
: / j a p j . arctan
a ð p x þ qÞ
ð
ð115Þ
x dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
ða x þ bÞ ðp x þ qÞ
ap > 0
ap < 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ða x þ bÞ ð p x þ qÞ
aq þ bp
dx
/
. pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ap
2ap
ða x þ bÞ ð p x þ qÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (114)
488
Integraltafel
12 Integrale mit
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 þ x 2 ða > 0Þ
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4i
1 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 þ x 2 dx ¼
x a 2 þ x 2 þ a 2 . ln x þ a 2 þ x 2
¼
2
! x 4i
1 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼
x a 2 þ x 2 þ a 2 . arsinh
2
a
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
ða 2 þ x 2 Þ 3
ð117Þ
x a 2 þ x 2 dx ¼
3
ð116Þ
ð
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4i
1
a 2 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 þ x 2 dx ¼
x ða 2 þ x 2 Þ 3 /
x a 2 þ x 2 þ a 2 . ln x þ a 2 þ x 2
¼
4
8
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! x 4i
1
a 2 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼
x ða 2 þ x 2 Þ 3 /
x a 2 þ x 2 þ a 2 . arsinh
4
8
a
ð
q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
q
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a2
ð119Þ
x 3 a 2 þ x 2 dx ¼
ða 2 þ x 2 Þ 5 /
ða 2 þ x 2 Þ 3
5
3
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 þ x2 "
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x2
"
"
2
2
ð120Þ
dx ¼ a þ x / a . ln "
"
"
"
x
x
ð118Þ
x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
a2 þ x2
a2 þ x2
dx
¼
/
þ ln x þ a 2 þ x 2 ¼
2
x
x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!x4
a2 þ x2
¼ /
þ arsinh
x
a
"
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
"a þ a2 þ x2
a2 þ x2
a2 þ x2
1
"
ð122Þ
dx ¼ /
/
. ln "
"
x3
2x2
2a
x
ð121Þ
ð
!x4
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ ln x þ a 2 þ x 2 ¼ arsinh
a
a2 þ x2
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ a 2 þ x 2
a2 þ x2
ð
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
x 2 dx
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
x a2 þ x2 /
. ln x þ a 2 þ x 2 ¼
2
2
a2 þ x2
!x4
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a2
¼
x a2 þ x2 /
. arsinh
2
2
a
ð123Þ
ð124Þ
ð125Þ
ð
ð126Þ
ð
ð127Þ
"
"
"
"
"
x 3 dx
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
3
2
2
a þx
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 þ x 2 Þ 3 / a 2 a 2 þ x 2
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 þ x2
dx
1
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
. ln "
"
x
a
x a2 þ x2
"
"
"
"
"
Integraltafel
ð
ð128Þ
ð
ð129Þ
ð130Þ
489
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
x2 a2 þ x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 þ x2
a2 x
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
3
x
a2 þ x2
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 þ x2
1
a2 þ x2
"
. ln "
þ
"
2a3
x
2a2 x2
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4)
1
3
3 4
ða 2 þ x 2 Þ 3 dx ¼
x ða 2 þ x 2 Þ 3 þ a 2 x a 2 þ x 2 þ
a . ln x þ a 2 þ x 2
¼
4
2
2
¼
ð
ð131Þ
x
ð
ð132Þ
1
4
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! x 4)
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
3 4
x ða 2 þ x 2 Þ 3 þ a 2 x a 2 þ x 2 þ
a . arsinh
2
2
a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
ða 2 þ x 2 Þ 3 dx ¼
ða 2 þ x 2 Þ 5
5
x2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a2
a 4 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x ða 2 þ x 2 Þ 5 /
x ða 2 þ x 2 Þ 3 /
x a2 þ x2 /
ða 2 þ x 2 Þ 3 dx ¼
6
24
16
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
a6
. ln x þ a 2 þ x 2 ¼
16
/
¼
ð
ð133Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 þ x 2 Þ 3
x
ð
ð134Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 þ x 2 Þ 3
x2
1
dx ¼
3
dx ¼ /
¼ /
ð
ð135Þ
ð
ð136Þ
ð
ð137Þ
"
"
"
"
"
1
x
6
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2
a 4 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 þ x 2 Þ 5 /
x ða 2 þ x 2 Þ 3 /
x a2 þ x2 /
24
16
!x4
a6
/
. arsinh
16
a
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 þ x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
3
3
2
2
2
2
2
ða þ x Þ þ a
a þ x / a . ln "
"
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 þ x 2 Þ 3
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 þ x 2 Þ 3
x
"
"
"
"
"
þ
!
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
3 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 2
x a2 þ x2 þ
a . ln x þ a 2 þ x 2 ¼
2
2
þ
!x4
3 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 2
x a2 þ x2 þ
a . arsinh
2
2
a
dx
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
3
2
2
a
a2 þ x2
ða þ x Þ
x dx
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
3
a þ x2
ða 2 þ x 2 Þ
!
!x4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 4
x 2 dx
x
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi þ ln x þ a 2 þ x 2 ¼ / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi þ arsinh
a
a2 þ x2
a2 þ x2
ða 2 þ x 2 Þ 3
490
Integraltafel
ð
ð138Þ
ð
ð139Þ
ð
ð140Þ
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 þ x2
dx
1
1
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi / 3 . ln "
"
a
x
a2 a2 þ x2
x ða 2 þ x 2 Þ 3
"
"
"
"
"
dx
2x2 þ a2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a4 x a2 þ x2
x 2 ða 2 þ x 2 Þ 3
" qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"
"
" a2 p2 þ q2 . a2 þ x2 / qx þ a2 p"
dx
1
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi . ln ""
"
px þ q
"
"
ð p x þ qÞ a 2 þ x 2
a2 p2 þ q2
ð p 6¼ 0Þ
13 Integrale mit
ð141Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 / x 2 ða > 0; j x j < aÞ
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! x 4i
1 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 / x 2 dx ¼
x a 2 / x 2 þ a 2 . arcsin
2
a
ð
ð142Þ
x
ð
ð143Þ
ð
ð144Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
ða 2 / x 2 Þ 3
a 2 / x 2 dx ¼ /
3
x2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! x 4i
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a 2 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a 2 / x 2 dx ¼ /
x ða 2 / x 2 Þ 3 þ
x a 2 / x 2 þ a 2 . arcsin
4
8
a
x3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a2
ða 2 / x 2 Þ 3
a 2 / x 2 dx ¼
ða 2 / x 2 Þ 5 /
5
3
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 / x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 / x2
"
2
2
ð145Þ
dx ¼ a / x / a . ln "
"
x
x
"
"
"
"
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
!x4
a2 / x2
a2 / x2
dx ¼ /
/ arcsin
ð146Þ
2
x
x
a
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 / x2
a2 / x2
a2 / x2
1
"
ð147Þ
dx ¼ /
þ
. ln "
"
x3
2x2
x
2a
ð
!x4
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ arcsin
a
a2 / x2
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / a 2 / x 2
a2 / x2
ð
!x4
x 2 dx
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
x a2 / x2 þ
. arcsin
2
2
a
a2 / x2
ð148Þ
ð149Þ
ð150Þ
"
"
"
"
"
Integraltafel
ð
ð151Þ
ð
ð152Þ
ð
ð153Þ
ð
ð154Þ
ð155Þ
x 3 dx
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
3
2
2
a /x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 / x 2 Þ 3 / a 2 a 2 / x 2
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 / x2
dx
1
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
. ln "
"
x
a
x a2 / x2
"
"
"
"
"
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
2
x
a2 / x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2 / x2
a2 x
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
3
x
a2 / x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"a þ a2 / x2
1
a2 / x2
"
.
ln
/
"
"
2a3
x
2a2 x2
"
"
"
"
"
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! x 4)
1
3 2 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 4
x ða 2 / x 2 Þ 3 þ
a x a2 / x2 þ
a . arcsin
ða 2 / x 2 Þ 3 dx ¼
4
2
2
a
ð
ð156Þ
x
ð
ð157Þ
ð
ð158Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
ða 2 / x 2 Þ 3 dx ¼ /
ða 2 / x 2 Þ 5
5
x2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a2
a 4 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 / x 2 Þ 3 dx ¼ /
x ða 2 / x 2 Þ 5 þ
x ða 2 / x 2 Þ 3 þ
x a2 / x2 þ
6
24
16
!x4
a6
. arcsin
þ
16
a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 / x 2 Þ 3
x
ð
ð159Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 / x 2 Þ 3
x2
ð
ð160Þ
ð
ð161Þ
1
dx ¼
3
dx ¼ /
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a þ a2 / x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
3
2
3
2
2
2
2
ða / x Þ þ a
a / x / a . ln "
"
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða 2 / x 2 Þ 3
x
/
!x4
3 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 2
x a2 / x2 /
a . arcsin
2
2
a
dx
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
2
2
2
a
a2 / x2
ða / x Þ
x dx
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
2 / x2
2
2
a
ða / x Þ
ð
!x4
x 2 dx
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi / arcsin
a
a2 / x2
ða 2 / x 2 Þ 3
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"a þ a2 / x2
dx
1
1
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi / 3 . ln "
"
a
x
a2 a2 / x2
x ða 2 / x 2 Þ 3
ð162Þ
ð163Þ
491
"
"
"
"
"
"
"
"
"
"
492
Integraltafel
ð
ð164Þ
dx
2x2 / a2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a4 x a2 / x2
x 2 ða 2 / x 2 Þ 3
14 Integrale mit
ð165Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 2 / a 2 ða > 0; j x j > aÞ
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "" i
1 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
x 2 / a 2 dx ¼
x x 2 / a 2 / a 2 . ln " x þ x 2 / a 2 "
2
ð
ð166Þ
x
ð
ð167Þ
ð
ð168Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
ðx 2 / a 2 Þ 3
x 2 / a 2 dx ¼
3
x2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi " i
1
a 2 h pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"
x 2 / a 2 dx ¼
x ðx 2 / a 2 Þ 3 þ
x x 2 / a 2 / a 2 . ln " x þ x 2 / a 2 "
4
8
x3
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a2
x 2 / a 2 dx ¼
ðx 2 / a 2 Þ 5 þ
ðx 2 / a 2 Þ 3
5
3
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a "
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 / a2
" "
ð169Þ
dx ¼ x 2 / a 2 / a . arccos " "
x
x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
x2 / a2
x2 / a2
"
"
ð170Þ
dx ¼ /
þ ln " x þ x 2 / a 2 "
2
x
x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a "
1
x2 / a2
x2 / a2
" "
.
arccos
ð171Þ
dx
¼
/
þ
" "
2a
x
x3
2x2
ð
"
"x"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ""
dx
"
" "
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ ln " x þ x 2 / a 2 " ¼ sgn ðxÞ . arcosh " "
a
2
2
x /a
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ x 2 / a 2
x2 / a2
ð
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
x 2 dx
1 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a2
"
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
. ln " x þ x 2 / a 2 "
x x2 / a2 þ
2
2
2
2
x /a
ð172Þ
ð173Þ
ð174Þ
ð
ð175Þ
ð
ð176Þ
x 3 dx
1
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
3
2
2
x /a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx 2 / a 2 Þ 3 þ a 2 x 2 / a 2
"a "
dx
1
" "
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
. arccos " "
a
x
2
2
x x /a
Integraltafel
ð
ð177Þ
ð
ð178Þ
ð179Þ
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
x2 x2 / a2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x2 / a2
a2 x
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
x3 x2 / a2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a "
x2 / a2
1
" "
þ
.
arccos
" "
2a2 x2
2a3
x
+ qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi " )
1
3 2 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 4
"
"
x ðx 2 / a 2 Þ 3 /
a x x2 / a2 þ
a . ln " x þ x 2 / a 2 "
ðx 2 / a 2 Þ 3 dx ¼
4
2
2
ð
ð180Þ
x
ð
ð181Þ
ð
ð182Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
ðx 2 / a 2 Þ 5
ðx 2 / a 2 Þ 3 dx ¼
5
x2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
a2
a 4 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx 2 / a 2 Þ 3 dx ¼ x ðx 2 / a 2 Þ 5 þ
x ðx 2 / a 2 Þ 3 /
x x2 / a2 þ
6
24
16
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
a6
"
"
þ
. ln " x þ x 2 / a 2 "
16
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx 2 / a 2 Þ 3
x
ð
ð183Þ
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx 2 / a 2 Þ 3
x2
ð
ð184Þ
ð
ð185Þ
dx ¼
1
3
dx ¼ /
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"a "
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
" "
ðx 2 / a 2 Þ 3 / a 2 x 2 / a 2 þ a 3 . arccos " "
x
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ðx 2 / a 2 Þ 3
x
þ
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
3 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3 2
"
"
x x2 / a2 /
a . ln " x þ x 2 / a 2 "
2
2
dx
x
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
a2 x2 / a2
ðx 2 / a 2 Þ 3
x dx
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
2
2
2
x / a2
ðx / a Þ
ð
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi "
x 2 dx
x
"
"
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi þ ln " x þ x 2 / a 2 "
3
2
2
2
2
x /a
ðx / a Þ
ð
"a "
dx
1
1
" "
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi / 3 . arccos " "
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
a
x
3
2
2 / a2
2
2
x
a
x ðx / a Þ
ð186Þ
ð187Þ
ð
ð188Þ
493
dx
a2 / 2x2
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a4 x x2 / a2
x 2 ðx 2 / a 2 Þ 3
494
Integraltafel
15 Integrale mit
Abkürzung:
Hinweis:
ð189Þ
ð
x
ð
D ¼ 4ac / b2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffi
Es wird stets D 6¼ 0 vorausgesetzt. Für D ¼ 0 ist a x 2 þ b x þ c ¼ a
Die Integrale entsprechen dann dem Integraltyp aus Abschnitt 1.
3
x þ
2
b
.
2a
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
b ð2 a x þ bÞ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax2 þ bx þ c /
a x 2 þ b x þ c dx ¼
. ða x 2 þ b x þ cÞ 3 /
3a
8a2
ð
bD
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
/
.
16 a 2
2
ax þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (194)
x2
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x 2 þ b x þ c dx ¼
1
ð6 a x / 5 bÞ
24 a 2
þ
ð192Þ
ða 6¼ 0Þ
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
2 a x þ b pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
D
dx
a x 2 þ b x þ c dx ¼
ax2 þ bx þ c þ
. pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
4a
8a
2
ax þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (194)
ð190Þ
ð191Þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ax2 þ bx þ c
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ða x 2 þ b x þ cÞ 3 þ
5b2 / 4ac
.
16 a 2
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x 2 þ b x þ c dx
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (189)
ffi
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ð
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x 2 þ bx þ c
b
dx
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼ a x 2 þ b x þ c þ
. pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi þ c .
x
2
2
2
ax þ bx þ c
x ax þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (194)
Integral (197)
ffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ð
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a x 2 þ bx þ c
ax2 þ bx þ c
dx
b
dx
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
ffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx
¼
/
þ
a
.
þ
.
ð193Þ
x2
x
2
2
2
ax þ bx þ c
x ax þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (194)
Integral (197)
8
" pffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
1
"
"
>
>
pffiffiffi . ln " 2 a a x 2 þ b x þ c þ 2 a x þ b " fur
€
>
>
>
a
>
>
>
>
3
2
>
ð
>
< 1
2ax þ b
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffi . arsinh
pffiffiffiffi
fur
€
ð194Þ
a
D
>
ax2 þ bx þ c
>
>
>
!
>
>
>
>
1
2ax þ b
>
>
pffiffiffiffiffiffiffiffi
fur
€
> / pffiffiffiffiffiffiffi . arcsin
:
jaj
jDj
a > 0
a > 0; D > 0
a < 0; D < 0
Integraltafel
ð
ð195Þ
ð
ð196Þ
x dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
a x 2 þ bx þ c
495
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
b
dx
ax2 þ bx þ c
/
. pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a
2a
ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (194)
ð
x 2 dx
2 a x / 3 b pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3b2 / 4ac
dx
2 þ bx þ c þ
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
a
x
.
2
2
4
a
8
a
2
2
a x þ bx þ c
ax þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (194)
8
" pffiffiffi pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
"
"2 c ax2 þ bx þ c þ bx þ 2c"
>
1
>
"
"
>
> / pffiffiffi . ln "
"
>
>
"
"
x
c
>
>
>
>
>
>
3
2
ð
<
dx
1
bx þ 2c
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / pffiffiffi . arsinh
ð197Þ
pffiffiffiffi
>
c
Dx
>
x ax2 þ bx þ c
>
>
>
!
>
>
>
>
1
b
x
þ
2
c
>
>
ffi . arcsin pffiffiffiffiffiffiffiffi
>
: pffiffiffiffiffiffi
jcj
jDj x
ð
ð198Þ
ð199Þ
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ /
x2 ax2 þ bx þ c
c > 0
fur
€
c > 0; D > 0
fur
€
c < 0; D < 0
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð
ax2 þ bx þ c
b
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
/
.
cx
2c
x ax2 þ bx þ c
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (197)
ð pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2ax þ b
3D
ða x 2 þ b x þ cÞ 3 þ
.
a x 2 þ b x þ c dx
ða x 2 þ b x þ cÞ 3 dx ¼
8a
16 a
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (189)
ð
ð200Þ
x
ð
ð201Þ
ð
ð202Þ
ð
ð203Þ
fur
€
ð qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
1
b
ða x 2 þ b x þ cÞ 3 dx
ða x 2 þ b x þ cÞ 3 dx ¼
ða x 2 þ b x þ cÞ 5 /
.
5a
2a
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (199)
dx
4ax þ 2b
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
D ax2 þ bx þ c
ða x 2 þ b x þ cÞ 3
x dx
2bx þ 4c
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
3
D ax2 þ bx þ c
ða x 2 þ b x þ cÞ
dx
1
1
qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi þ .
c
2 þ bx þ c
3
2
c
a
x
x ðax þ b x þ cÞ
ðc 6¼ 0Þ
ð
ð
dx
b
dx
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi /
. qffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
x ax 2 þ bx þ c 2 c
ða x þ b x þ cÞ 3
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (197)
Integral (201)
496
Integraltafel
16 Integrale mit
Hinweis:
sin ða xÞ dx ¼ /
ð
ð205Þ
ð
ð206Þ
ð
ð207Þ
sin 2 ða xÞ dx ¼
ð
ð209Þ
ð
ð210Þ
cos ða xÞ
a
x
sin ð2 a xÞ
x
sin ða xÞ . cos ða xÞ
/
¼
/
2
4a
2
2a
sin 3 ða xÞ dx ¼ /
cos ða xÞ
cos 3 ða xÞ
þ
a
3a
sin n ða xÞ dx ¼ /
sin n / 1 ða xÞ . cos ða xÞ
n/1
þ
.
na
n
x . sin ða xÞ dx ¼
sin ða xÞ
x . cos ða xÞ
/
a2
a
ð
ð208Þ
ða 6¼ 0Þ
Integrale mit einer Sinusfunktion und einer
–– Kosinusfunktion: siehe Abschnitt 18
–– Exponentialfunktion: siehe Abschnitt 22
–– Hyperbelfunktion: siehe Abschnitt 24 und 25
ð
ð204Þ
sin ða xÞ
x 2 . sin ða xÞ dx ¼
ð
sin n / 2 ða xÞ dx
2 x . sin ða xÞ
ða 2 x 2 / 2Þ . cos ða xÞ
/
2
a
a3
x n . sin ða xÞ dx ¼ /
x n . cos ða xÞ
n . x n / 1 . sin ða xÞ
nðn / 1Þ
þ
/
.
a
a2
a2
ðn ( 2Þ
ð
ð211Þ
sin ða xÞ
ða xÞ 3
ða xÞ 5
dx ¼ a x /
þ
/ þ ...
3 . 3!
5 . 5!
x
(Potenzreihenentwicklung: Konvergenz für j x j < 1Þ
ð
ð212Þ
ð
ð213Þ
sin ða xÞ
sin ða xÞ
dx ¼ /
þa.
x2
x
ð
ð
cos ða xÞ
dx
x
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral (235)
sin ða xÞ
sin ða xÞ
a
dx ¼ /
þ
.
xn
ðn / 1Þ x n / 1
n/1
Fall n ¼ 1: siehe Integral (211)
ð214Þ
ðn 6¼ 0Þ
"
!ax4"
dx
1
"
"
¼
. ln " tan
"
sin ða xÞ
a
2
ð
cos ða xÞ
dx
x n/1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral (237)
ðn 6¼ 1Þ
ð
x n / 2 . sin ða xÞ dx
Integraltafel
ð
ð215Þ
ð
ð216Þ
497
dx
cot ða xÞ
¼ /
sin 2 ða xÞ
a
dx
cos ða xÞ
n/2
¼ /
þ
.
sin n ða xÞ
a ðn / 1Þ . sin n / 1 ða xÞ
n/1
ð
dx
sin n / 2 ða xÞ
ðn > 1Þ
Fall n ¼ 1: siehe Integral (214)
ð
ð217Þ
ð
ð218Þ
x . sin 2 ða xÞ dx ¼
x2
x . sin ð2 a xÞ
cos ð2 a xÞ
/
/
4a
8a2
4
x dx
x . cot ða xÞ
1
¼ /
þ 2 . ln j sin ða xÞ j
sin 2 ða xÞ
a
a
ð
!p
dx
1
ax4
¼ *
. tan
*
1 + sin ða xÞ
a
4
2
8
!
>
2
p . tan ða x=2Þ þ q
>
>
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
>
p
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
.
arctan
>
>
ð
<a p2 / q2
p2 / q2
dx
ð220Þ
¼
"
p þ q . sin ða xÞ >
" p . tan ða x=2Þ þ q / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
>
>
1
q2 / p2
"
>
>
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
p
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
.
ln
"
>
:
" p . tan ða x=2Þ þ q þ q 2 / p 2
a q2 / p2
ð219Þ
"
"
"
"
"
fur
€
p2 > q2
fur
€
p2 < q2
Fall p 2 ¼ q 2 : siehe Integral (219)
ð
"
!p
!p
x dx
x
ax4
2
a x 4""
"
¼ /
. tan
/
þ 2 . ln " cos
/
"
1 þ sin ða xÞ
a
4
2
a
4
2
ð
" !p
!p
x dx
x
ax4
2
a x 4""
"
¼
. cot
/
þ 2 . ln " sin
/
"
1 / sin ða xÞ
a
4
2
a
4
2
ð
!p
sin ða xÞ dx
1
ax4
¼ + x þ
. tan
*
1 + sin ða xÞ
a
4
2
ð221Þ
ð222Þ
ð223Þ
ð
ð224Þ
ð
ð225Þ
sin ða xÞ dx
x
p
¼
/
.
p þ q . sin ða xÞ
q
q
dx
p þ q . sin ða xÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (220)
ðq 6¼ 0Þ
"
!a x 4"
dx
1
q
"
"
¼
. ln " tan
.
"/
sin ða xÞ ½ p þ q . sin ða xÞ %
ap
2
p
ð
ð226Þ
ð
sin ða xÞ . sin ðb xÞ dx ¼
ð
dx
p þ q . sin ða xÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (220)
sin ðða / bÞ xÞ
sin ðða þ bÞ xÞ
/
2 ða / bÞ
2 ða þ bÞ
ða 2 6¼ b 2 Þ
Fall a 2 ¼ b 2 : siehe Integral (205)
ð
ð227Þ
sin ða xÞ . sin ða x þ bÞ dx ¼ /
1
ðcos bÞ
. sin ð2 a x þ bÞ þ
x
4a
2
ð p 6¼ 0Þ
498
Integraltafel
17 Integrale mit
Hinweis:
cos ða xÞ dx ¼
ð
ð229Þ
ð
ð230Þ
ð
ð231Þ
sin ða xÞ
a
cos 2 ða xÞ dx ¼
x
sin ð2 a xÞ
x
sin ða xÞ . cos ða xÞ
þ
¼
þ
2
4a
2
2a
cos 3 ða xÞ dx ¼
sin ða xÞ
sin 3 ða xÞ
/
a
3a
cos n ða xÞ dx ¼
cos n / 1 ða xÞ . sin ða xÞ
n/1
þ
.
na
n
ð
ð232Þ
x . cos ða xÞ dx ¼
ð
ð233Þ
ð
ð234Þ
ða 6¼ 0Þ
Integrale mit einer Kosinusfunktion und einer
–– Sinusfunktion: siehe Abschnitt 18
–– Exponentialfunktion: siehe Abschnitt 22
–– Hyperbelfunktion: siehe Abschnitt 24 und 25
ð
ð228Þ
cos ða xÞ
ð
cos n / 2 ða xÞ dx
cos ða xÞ
x . sin ða xÞ
þ
a2
a
x 2 . cos ða xÞ dx ¼
2 x . cos ða xÞ
ða 2 x 2 / 2Þ . sin ða xÞ
þ
2
a
a3
x n . cos ða xÞ dx ¼
x n . sin ða xÞ
n . x n / 1 . cos ða xÞ
nðn / 1Þ
þ
/
.
a
a2
a2
ðn ( 2Þ
ð
ð235Þ
cos ða xÞ
ða xÞ 2
ða xÞ 4
ða xÞ 6
dx ¼ ln j a x j /
þ
/
þ / ...
x
2 . 2!
4 . 4!
6 . 6!
(Potenzreihenentwicklung: Konvergenz für j x j > 0Þ
ð
ð236Þ
ð
ð237Þ
cos ða xÞ
cos ða xÞ
dx ¼ /
/a.
x2
x
ð
sin ða xÞ
dx
x
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral (211)
cos ða xÞ
cos ða xÞ
a
dx ¼ /
/
.
xn
ðn / 1Þ x n / 1
n/1
Fall n ¼ 1: siehe Integral (235)
ð
ð238Þ
ð
ð239Þ
ðn 6¼ 0Þ
"
!a x
dx
1
p 4""
"
¼
. ln " tan
þ
"
cos ða xÞ
a
2
4
dx
tan ða xÞ
¼
cos 2 ða xÞ
a
ð
sin ða xÞ
dx
x n/1
|fflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflffl}
Integral (213)
ðn 6¼ 1Þ
ð
x n / 2 . cos ða xÞ dx
Integraltafel
ð
ð240Þ
499
dx
sin ða xÞ
n/2
¼
þ
.
cos n ða xÞ
a ðn / 1Þ . cos n / 1 ða xÞ
n/1
ð
dx
cos n / 2 ða xÞ
ðn > 1Þ
Fall n ¼ 1: siehe Integral (238)
ð
ð241Þ
ð
ð242Þ
ð
ð243Þ
ð
x . cos 2 ða xÞ dx ¼
x2
x . sin ð2 a xÞ
cos ð2 a xÞ
þ
þ
4
4a
8a2
x dx
x . tan ða xÞ
1
¼
þ 2 . ln j cos ða xÞ j
cos 2 ða xÞ
a
a
!a x 4
dx
1
¼
. tan
1 þ cos ða xÞ
a
2
!a x 4
dx
1
¼ /
. cot
1 / cos ða xÞ
a
2
8
!
>
2
ð p / qÞ . tan ða x=2Þ
>
>
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi . arctan
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
>
>
>
ð
p2 / q2
<a p2 / q2
dx
¼
ð245Þ
"
p þ q . cos ða xÞ >
" ðq / pÞ . tan ða x=2Þ þ pqffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
>
2 / p2
>
1
"
>
>
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
. ln "
>
: pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
2
"
a q /p
ðq / pÞ . tan ða x=2Þ / q 2 / p 2
ð244Þ
"
"
"
"
"
fur
€
p2 > q2
fur
€
p2 < q2
Fall p 2 ¼ q 2 : siehe Integral (243) bzw. Integral (244)
ð
"
!a x 4
! a x 4"
x dx
x
2
"
"
¼
. tan
þ 2 . ln " cos
"
1 þ cos ða xÞ
a
2
a
2
ð
" ! a x 4"
!ax4
x dx
x
2
"
"
¼ /
. cot
þ 2 . ln " sin
"
1 / cos ða xÞ
a
2
a
2
ð
!a x 4
cos ða xÞ dx
1
¼ x /
. tan
1 þ cos ða xÞ
a
2
ð246Þ
ð247Þ
ð248Þ
ð
!a x 4
cos ða xÞ dx
1
¼ /x /
. cot
1 / cos ða xÞ
a
2
ð
ð
cos ða xÞ dx
x
p
dx
ð250Þ
¼
/
.
ðq 6¼ 0Þ
p þ q . cos ða xÞ
q
q
p þ q . cos ða xÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (245)
ð
ð
"
!a x
dx
1
p 4""
q
dx
"
ð251Þ
¼
. ln " tan
þ
.
"/
cos ða xÞ ½ p þ q . cos ða xÞ%
ap
2
4
p
p þ q . cos ða xÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (245)
ð
sin ðða / bÞ xÞ
sin ðða þ bÞ xÞ
ð252Þ
cos ða xÞ . cos ðb xÞ dx ¼
þ
ða 2 6¼ b 2 Þ
2 ða / bÞ
2 ða þ bÞ
ð249Þ
Fall a 2 ¼ b 2 : siehe Integral (229)
ð
ð253Þ
cos ða xÞ . cos ða x þ bÞ dx ¼
1
ðcos bÞ
. sin ð2 a x þ bÞ þ
x
4a
2
ð p 6¼ 0Þ
500
Integraltafel
18 Integrale mit
sin ða xÞ
ð
ð254Þ
sin ða xÞ . cos ða xÞ dx ¼
ð
ð255Þ
und
cos ða xÞ
ða 6¼ 0Þ
sin 2 ða xÞ
1
¼ /
. cos ð2 a xÞ
2a
4a
sin n ða xÞ . cos ða xÞ dx ¼
sin n þ 1 ða xÞ
ðn þ 1Þ a
ðn 6¼ / 1Þ
Fall n ¼ / 1: siehe Integral (293)
ð
ð256Þ
sin ða xÞ . cos n ða xÞ dx ¼ /
cos n þ 1 ða xÞ
ðn þ 1Þ a
ðn 6¼ / 1Þ
Fall n ¼ / 1: siehe Integral (286)
ð
ð257Þ
ð
ð258Þ
sin 2 ða xÞ . cos 2 ða xÞ dx ¼
x
sin ð4 a xÞ
/
8
32 a
sin m ða xÞ . cos n ða xÞ dx ¼
8
ð
sin m / 1 ða xÞ . cos ðn þ 1Þ ða xÞ
m/1
>
>
>
/
þ
.
sin m / 2 ða xÞ . cos n ða xÞ dx
>
>
ðm þ nÞ a
mþn
<
¼
>
ð
>
>
sin m þ 1 ða xÞ . cos ðn / 1Þ ða xÞ
n/1
>
>
þ
. sin m ða xÞ . cos n / 2 ða xÞ dx
:
ðm þ nÞ a
mþn
Beide Formeln gelten nur für m 6¼ / n. Fall m ¼ / n: siehe Integral (289) bzw. (296)
ð
ð259Þ
ð
ð260Þ
dx
1
¼
. ln j tan ða xÞ j
sin ða xÞ . cos ða xÞ
a
dx
1
¼
sin 2 ða xÞ . cos ða xÞ
a
ð
ð261Þ
sin m
+ "
)
!ax
p 4""
1
"
ln " tan
þ
"/
2
4
sin ða xÞ
dx
1
¼ /
þ
ða xÞ . cos ða xÞ
ðm / 1Þ a . sin m / 1 ða xÞ
ð
dx
sin m / 2 ða xÞ . cos ða xÞ
ðm 6¼ 1Þ
Fall m ¼ 1: siehe Integral (259)
ð
ð262Þ
ð
ð263Þ
dx
1
¼
sin ða xÞ . cos 2 ða xÞ
a
+ "
)
! a x 4"
1
"
"
ln " tan
"þ
2
cos ða xÞ
dx
1
¼
þ
sin ða xÞ . cos n ða xÞ
ðn / 1Þ a . cos n / 1 ða xÞ
Fall n ¼ 1: siehe Integral (259)
ð
dx
sin ða xÞ . cos n / 2 ða xÞ
ðn 6¼ 1Þ
Integraltafel
ð
ð264Þ
501
dx
¼
sin m ðaxÞ . cos n ða xÞ
8
ð
1
mþn/2
dx
>
>
þ
.
>
>
< ðn / 1Þ a . sin m / 1 ða xÞ . cos n / 1 ða xÞ
n/1
sin m ða xÞ . cos n / 2 ða xÞ
¼
ð
>
>
1
mþn/2
dx
>
>
þ
.
:/
ðm / 1Þ a . sin m / 1 ða xÞ . cos n / 1 ða xÞ
m/1
sin m / 2 ða xÞ . cos n ða xÞ
Obere Formel für n 6¼ 1, untere Formel für m 6¼ 1.
Fall n ¼ 1: siehe Integral (261); Fall m ¼ 1: siehe Integral (263)
ð
ð265Þ
ð
ð266Þ
ð
ð267Þ
sin ða xÞ
dx ¼
cos ða xÞ
ð
tan ða xÞ dx ¼ /
1
. ln j cos ða xÞ j
a
"
!ax
sin 2 ða xÞ
sin ða xÞ
1
p 4""
"
dx ¼ /
þ
. ln " tan
þ
"
cos ða xÞ
a
a
2
4
sin m ða xÞ
sin m / 1 ða xÞ
dx ¼ /
þ
cos ða xÞ
ðm / 1Þ a
ð
sin m / 2 ða xÞ
dx
cos ða xÞ
ðm 6¼ 1Þ
Fall m ¼ 1: siehe Integral (265)
ð
ð268Þ
ð
ð269Þ
sin ða xÞ
1
dx ¼
cos 2 ða xÞ
a . cos ða xÞ
sin ða xÞ
1
dx ¼
cos n ða xÞ
ðn / 1Þ a . cos n / 1 ða xÞ
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (265)
ð
ð270Þ
sin 2 ða xÞ
dx ¼
cos 2 ða xÞ
ð
tan 2 ða xÞ dx ¼
tan ða xÞ
/x
a
8
ð
sin m / 1 ða xÞ
m/1
sin m / 2 ða xÞ
>
>
/
.
dx
>
>
n
/
1
>
ðn / 1Þ a . cos
ða xÞ
n/1
cos n / 2 ða xÞ
>
>
>
>
>
ð
ð
<
sin m ða xÞ
sin m þ 1 ða xÞ
m/nþ2
sin m ða xÞ
ð271Þ
dx
¼
/
.
dx
n
n
/
1
>
cos ða xÞ
ðn / 1Þ a . cos
ða xÞ
n/1
cos n / 2 ða xÞ
>
>
>
>
>
ð
>
>
sin m / 1 ða xÞ
m/1
sin m / 2 ða xÞ
>
>
þ
.
:/
ðm / nÞ a . cos n / 1 ða xÞ
m/n
cos n ða xÞ
Fall n ¼ 1: siehe Integral (267); Fall m ¼ n: siehe Integral (289)
ð
ð272Þ
ð
ð273Þ
cos ða xÞ
dx ¼
sin ða xÞ
ð
cot ða xÞ dx ¼
cos ða xÞ
1
dx ¼ /
sin 2 ða xÞ
a . sin ða xÞ
1
. ln j sin ða xÞ j
a
ðn 6¼ 1Þ
ðn 6¼ 1Þ
ðm 6¼ nÞ
502
Integraltafel
ð
ð274Þ
cos ða xÞ
1
dx ¼ /
sin n ða xÞ
ðn / 1Þ a . sin n / 1 ða xÞ
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (272) und (293)
ð
ð275Þ
ð
ð276Þ
"
! a x 4" i
cos 2 ða xÞ
1 h
"
"
dx ¼
cos ða xÞ þ ln " tan
"
sin ða xÞ
a
2
cos m ða xÞ
cos m / 1 ða xÞ
dx ¼
þ
sin ða xÞ
ðm / 1Þ a
ð
cos m / 2 ða xÞ
dx
sin ða xÞ
ðm 6¼ 1Þ
Fall m ¼ 1: siehe Integral (272) und (293)
8
ð
cos m / 1 ða xÞ
m/1
cos m / 2 ða xÞ
>
>
>
/
/
.
dx
>
n
/
1
>
ðn / 1Þ a . sin
ða xÞ
n/1
sin n / 2 ða xÞ
>
>
>
>
>
ð
ð
<
cos m ðaxÞ
cos m þ 1 ða xÞ
m/nþ2
cos m ða xÞ
ð277Þ
dx
¼
/
.
dx
/
n
/
1
>
sin n ða xÞ
ðn / 1Þ a . sin
ða xÞ
n/1
sin n / 2 ða xÞ
>
>
>
>
>
ð
>
>
cos m / 1 ða xÞ
m/1
cos m / 2 ða xÞ
>
>
þ
.
:
n
/
1
ðm / nÞ a . sin
ða xÞ
m/n
sin n ða xÞ
Fall n ¼ 1: siehe Integral (276); Fall m ¼ n: siehe Integral (296)
ð
ð278Þ
ð
ð279Þ
ð
ð280Þ
"
!ax
dx
1
p 4""
"
¼ pffiffiffi . ln " tan
+
"
sin ða xÞ + cos ða xÞ
2
8
a 2
sin ða xÞ dx
x
1
¼
*
. ln j sin ða xÞ + cos ða xÞ j
sin ða xÞ + cos ða xÞ
2
2a
cos ða xÞ dx
x
1
¼ +
þ
. ln j sin ða xÞ + cos ða xÞ j
sin ða xÞ + cos ða xÞ
2
2a
ð
"
! a x 4"
dx
1
1
"
"
¼ +
þ
. ln " tan
"
sin ða xÞ ½1 + cos ða xÞ%
2 a ½1 + cos ða xÞ%
2a
2
ð
"
!ax
dx
1
1
p 4""
"
¼ *
þ
. ln " tan
þ
"
cos ða xÞ ½1 + sin ða xÞ%
2 a ½1 + sin ða xÞ%
2a
2
4
ð
"
"
" 1 + cos ða xÞ "
sin ða xÞ dx
1
"
¼
. ln ""
cos ða xÞ ½1 + cos ða xÞ%
a
cos ða xÞ "
ð
"
"
" 1 + sin ða xÞ "
cos ða xÞ dx
1
"
¼ /
. ln ""
sin ða xÞ ½1 + sin ða xÞ%
a
sin ða xÞ "
ð281Þ
ð282Þ
ð283Þ
ð284Þ
ð
ð285Þ
sin ða xÞ . cos ðb xÞ dx ¼ /
cos ðða þ bÞ xÞ
cos ðða / bÞ xÞ
/
2 ða þ bÞ
2 ða / bÞ
Fall a 2 ¼ b 2 : siehe Integral (254)
ða 2 6¼ b 2 Þ
ðn 6¼ 1Þ
ðn 6¼ 1Þ
ðm 6¼ nÞ
Integraltafel
503
19 Integrale mit
ð
ð286Þ
tan ða xÞ dx ¼ /
ð
ð287Þ
ð
ð288Þ
ð
ð289Þ
tan ða xÞ
ða 6¼ 0Þ
1
. ln j cos ða xÞ j
a
tan 2 ða xÞ dx ¼
tan ða xÞ
/x
a
tan 3 ða xÞ dx ¼
tan 2 ða xÞ
1
þ
. ln j cos ða xÞ j
2a
a
tan n ða xÞ dx ¼
tan n / 1 ða xÞ
/
ðn / 1Þ a
ð
tan n / 2 ða xÞ dx
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (286)
ð
ð290Þ
ð
ð291Þ
dx
¼
tan ða xÞ
ð
cot ða xÞ dx ¼
1
. ln j sin ða xÞ j
a
tan n ða xÞ
tan n þ 1 ða xÞ
dx ¼
2
cos ða xÞ
ðn þ 1Þ a
ðn 6¼ / 1Þ
Fall n ¼ / 1: siehe Integral (259)
ð
ð292Þ
dx
a p x þ q . ln j q . sin ða xÞ þ p . cos ða xÞ j
¼
p þ q . tan ða xÞ
a ð p 2 þ q 2Þ
20 Integrale mit
ð
ð293Þ
cot ða xÞ dx ¼
ð
ð294Þ
ð
ð295Þ
ð
ð296Þ
cot ða xÞ
ða 6¼ 0Þ
1
. ln j sin ða xÞ j
a
cot 2 ða xÞ dx ¼ /
cot ða xÞ
/x
a
cot 3 ða xÞ dx ¼ /
cot 2 ða xÞ
1
/
. ln j sin ða xÞ j
2a
a
cot n ða xÞ dx ¼ /
cot n / 1 ða xÞ
/
ðn / 1Þ a
Fall n ¼ 1: siehe Integral (293)
ð
cot n / 2 ða xÞ dx
ðn 6¼ 1Þ
ðq 6¼ 0Þ
504
Integraltafel
ð
ð297Þ
ð
ð298Þ
dx
¼
cot ða xÞ
ð
tan ða xÞ dx ¼ /
1
. ln j cos ða xÞ j
a
cot n ða xÞ
cot n þ 1 ða xÞ
dx ¼ /
2
sin ða xÞ
ðn þ 1Þ a
ðn 6¼ / 1Þ
Fall n ¼ / 1: siehe Integral (259)
ð
ð299Þ
dx
a p x / q . ln j p . sin ða xÞ þ q . cos ða xÞ j
¼
p þ q . cot ða xÞ
a ð p 2 þ q 2Þ
21 Integrale mit einer Arkusfunktion
ð
ð300Þ
arcsin
x . arcsin
ð
ð302Þ
arccos
x . arccos
ð
ð305Þ
arctan
x . arctan
ð
ð308Þ
arccot
x . arccot
ð
ð311Þ
! x4
! x4
x3
ax2
a3
dx ¼
. arctan
/
þ
. ln ðx 2 þ a 2 Þ
a
3
a
6
6
! x4
! x4
a
dx ¼ x . arccot
þ
. ln ðx 2 þ a 2 Þ
a
a
2
ð
ð310Þ
! x4
! x4
1
ax
dx ¼
ðx 2 þ a 2 Þ . arctan
/
a
2
a
2
x 2 . arctan
ð
ð309Þ
3 2
2 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! x4
! x4
x3
x þ 2a2
dx ¼
. arccos
/
. a2 / x2
a
3
a
9
! x4
! x4
a
dx ¼ x . arctan
/
. ln ðx 2 þ a 2 Þ
a
a
2
ð
ð307Þ
3 2
2
! x4
! x4
2x / a2
x pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼
. arccos
/
. a2 / x2
a
4
a
4
x 2 . arccos
ð
ð306Þ
3 2
2 pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
! x4
! x4
x3
x þ 2a2
dx ¼
. arcsin
þ
. a2 / x2
a
3
a
9
! x4
! x4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼ x . arccos
/ a2 / x2
a
a
ð
ð304Þ
3 2
2
! x4
! x4
2x / a2
x pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼
. arcsin
þ
. a2 / x2
a
4
a
4
x 2 . arcsin
ð
ð303Þ
ða 6¼ 0Þ
! x4
! x4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼ x . arcsin
þ a2 / x2
a
a
ð
ð301Þ
ðq 6¼ 0Þ
! x4
! x4
1
ax
dx ¼
ðx 2 þ a 2 Þ . arccot
þ
a
2
a
2
x 2 . arccot
! x4
! x4
x3
ax2
a3
dx ¼
. arccot
þ
/
. ln ðx 2 þ a 2 Þ
a
3
a
6
6
Integraltafel
505
e ax
22 Integrale mit
ð
ð312Þ
ð
ð313Þ
ð
ð314Þ
ð
ð315Þ
ð
ð316Þ
e a x dx ¼
ða 6¼ 0Þ
1
. e ax
a
x . e a x dx ¼
3
2
ax / 1
. e ax
a2
x 2 . e a x dx ¼
3 2 2
2
a x / 2ax þ 2
. e ax
a3
x n . e a x dx ¼
x n . e ax
n
/
.
a
a
ð
x n / 1 . e a x dx
e ax
ax
ða xÞ 2
ða xÞ 3
dx ¼ ln j a x j þ
þ
þ
þ ...
x
1 . 1!
2 . 2!
3 . 3!
(Potenzreihenentwicklung; Konvergenz für j x j > 0)
ð
ð317Þ
e ax
e ax
a
.
dx ¼ /
þ
n
x
ðn / 1Þ x n / 1
n/1
ð
e ax
dx
x n/1
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (316)
ð
ð318Þ
ð
ð319Þ
ð
ð320Þ
ð
ð321Þ
ð
ð322Þ
ð
ð323Þ
dx
x
1
¼
/
. ln j p þ q . e a x j
p þ q . e ax
p
ap
e a x dx
1
¼
. ln j p þ q . e a x j
p þ q . e ax
aq
dx
p . e ax þ q . e /ax
e a x . ln x dx ¼
ðq 6¼ 0Þ
8
3rffiffiffiffi
2
1
p
>
ax
>
.
e
.
arctan
fur
€
>
p
ffiffiffiffiffiffi
ffi
>
>
q
<a pq
¼
"
"
" q þ pffiffiffiffiffiffiffiffiffiffi
>
>
j p q j . e a x ""
1
"
>
>
pffiffiffiffiffiffiffiffiffiffi
€
" fur
> pffiffiffiffiffiffiffiffiffiffi . ln "
:
" q / j p q j . e ax "
2a jpqj
e a x . ln j x j
1
/
.
a
a
e a x . sin ðb xÞ dx ¼
ð p 6¼ 0Þ
pq > 0
pq < 0
ð
e ax
dx
x
|fflfflfflfflffl{zfflfflfflfflffl}
Integral (316)
e ax
½ a . sin ðb xÞ / b . cos ðb xÞ%
a2 þ b2
e a x . sin n ðb xÞ dx ¼
e a x . sin n / 1 ðb xÞ
½ a . sin ðb xÞ / n b . cos ðb xÞ% þ
a2 þ n2 b2
ð
n ðn / 1Þ b 2
þ 2
. e a x . sin n / 2 ðb xÞ dx
2
2
a þn b
506
Integraltafel
ð
e a x . cos ðb xÞ dx ¼
ð324Þ
ð
e ax
½ a . cos ðb xÞ þ b . sin ðb xÞ%
a2 þ b2
e a x . cos n ðb xÞ dx ¼
ð325Þ
ð
ð326Þ
ð
ð327Þ
e a x . cos n / 1 ðb xÞ
½ a . cos ðb xÞ þ n b . sin ðb xÞ% þ
a2 þ n2 b2
ð
n ðn / 1Þ b 2
þ 2
.
e a x . cos n / 2 ðb xÞ dx
a þ n2 b2
e a x . sinh ða xÞ dx ¼
e 2ax
x
/
2
4a
e a x . sinh ðb xÞ dx ¼
e ax
½ a . sinh ðb xÞ / b . cosh ðb xÞ%
a2 / b2
ða 2 6¼ b 2 Þ
Fall a 2 ¼ b 2 : siehe Integral (326)
ð
ð328Þ
ð
ð329Þ
e a x . cosh ða xÞ dx ¼
e 2ax
x
þ
2
4a
e a x . cosh ðb xÞ dx ¼
e ax
½ a . cosh ð b xÞ / b . sinh ðb xÞ%
a2 / b2
ða 2 6¼ b 2 Þ
Fall a 2 ¼ b 2 : siehe Integral (328)
ð
x . e a x . sin ðb xÞ dx ¼
ð330Þ
x . e ax
½ a . sin ðb xÞ / b . cos ðb xÞ% /
a2 þ b2
/
ð
x . e a x . cos ðb xÞ dx ¼
ð331Þ
Hinweis:
ða 2 þ b 2 Þ 2
½ða 2 / b 2 Þ . sin ðb xÞ / 2 a b . cos ðb xÞ%
x . e ax
½ a . cos ðb xÞ þ b . sin ðb xÞ% /
a2 þ b2
/
23 Integrale mit
e ax
ln x
e ax
ða 2
þ b 2Þ 2
½ða 2 / b 2 Þ . cos ðb xÞ þ 2 a b . sin ðb xÞ%
ðx > 0Þ
Integrale mit einer Logarithmus- und einer Exponentialfunktion: siehe Abschnitt 22.
ð
ð332Þ
ln x dx ¼ x . ln x / x ¼ x ðln x / 1Þ
ð
ð333Þ
ð
ð334Þ
ðln xÞ 2 dx ¼ x ðln xÞ 2 / 2 x . ln x þ 2 x ¼ x ½ðln xÞ 2 / 2 . ln x þ 2Þ%
ðln xÞ 3 dx ¼ x ðln xÞ 3 / 3 x ðln xÞ 2 þ 6 x . ln x / 6 x ¼ x ½ðln xÞ 3 / 3 ðln xÞ 2 þ 6 . ln x / 6%
Integraltafel
ð
ð335Þ
507
ðln xÞ n dx ¼ x ðln xÞ n / n .
ð
ðln xÞ n / 1 dx
ðn 6¼ / 1Þ
Fall n ¼ / 1: siehe Integral (336)
ð
ð336Þ
dx
ln x
ðln xÞ 2
ðln xÞ 3
¼ ln j ln x j þ
þ
þ
þ ...
ln x
1 . 1!
2 . 2!
3 . 3!
ð
ð337Þ
x . ln x dx ¼
ð
ð338Þ
ð
ð339Þ
ðx 6¼ 1Þ
3
2
1 2
1
x
ln x /
2
2
x 2 . ln x dx ¼
3
2
1 3
1
x
ln x /
3
3
x m . ln x dx ¼
x mþ1
mþ1
3
ln x /
1
mþ1
2
ðm 6¼ / 1Þ
Fall m ¼ / 1: siehe Integral (340)
ð
ð340Þ
ð
ð341Þ
ln x
1
dx ¼
ðln xÞ 2
x
2
ln x
ln x
1
dx ¼ /
/
xm
ðm / 1Þ x m / 1
ðm / 1Þ 2 x m / 1
ðm 6¼ 1Þ
Fall m ¼ 1: siehe Integral (340)
ð
ð342Þ
ðln xÞ n
ðln xÞ n þ 1
dx ¼
x
nþ1
ðn 6¼ / 1Þ
Fall n ¼ / 1: siehe Integral (343)
ð
ð343Þ
ð
ð344Þ
ð
ð345Þ
dx
¼ ln j ln x j
x . ln x
ðx 6¼ 1Þ
xm
ðm þ 1Þ 2
ðm þ 1Þ 3
dx ¼ ln j ln x j þ ðm þ 1Þ ln x þ
ðln xÞ 2 þ
ðln xÞ 3 þ . . .
ln x
2 . 2!
3 . 3!
x m . ðln xÞ n dx ¼
x m þ 1 . ðln xÞ n
n
/
.
mþ1
mþ1
ð
x m . ðln xÞ n / 1 dx
ðm 6¼ / 1Þ
Fall m ¼ / 1: siehe Integral (342)
ð
ð346Þ
xm
x mþ1
mþ1
dx ¼ /
þ
.
ðln xÞ n
ðn / 1Þ ðln xÞ n / 1
n/1
ð
xm
dx
ðln xÞ n / 1
ðn 6¼ 1; x 6¼ 1Þ
Fall n ¼ 1: siehe Integral (344)
ð
ð347Þ
ð
ð348Þ
ln ðx 2 þ a 2 Þ dx ¼ x . ln ðx 2 þ a 2 Þ / 2 x þ 2 a . arctan
ln ðx 2 / a 2 Þ dx ¼ x . ln ðx 2 / a 2 Þ / 2 x þ a . ln
!x4
a
!x þ a4
x /a
ða 6¼ 0Þ
ðx 2 > a 2 Þ
ðx 6¼ 1Þ
508
Integraltafel
24 Integrale mit
Hinweis:
sinh ða xÞ dx ¼
ð
ð350Þ
ð
ð351Þ
cosh ða xÞ
a
sinh 2 ða xÞ dx ¼
sinh ð2 a xÞ
x
/
4a
2
sinh n ða xÞ dx ¼
sinh n / 1 ða xÞ . cosh ða xÞ
n/1
/
.
na
n
ð
ð352Þ
x . sinh ða xÞ dx ¼
ð
ð353Þ
ð
ð354Þ
ða 6¼ 0Þ
Integrale mit einer hyperbolischen Sinusfunktion und einer
–– hyperbolischen Kosinusfunktion: siehe Abschnitt 26
–– Exponentialfunktion: siehe Abschnitt 22
ð
ð349Þ
sinh ða xÞ
ð
sinh n / 2 ða xÞ dx
ðn 6¼ 0Þ
x . cosh ða xÞ
sinh ða xÞ
/
a
a2
x n . sinh ða xÞ dx ¼
x n . cosh ða xÞ
n . x n / 1 . sinh ða xÞ
/
þ
a
a2
ð
nðn / 1Þ
þ
. x n / 2 . sinh ða xÞ dx
2
a
ðn ( 2Þ
sinh ða xÞ
ða xÞ 3
ða xÞ 5
dx ¼ a x þ
þ
þ ...
x
3 . 3!
5 . 5!
(Potenzreihenentwicklung; Konvergenz für j x j < 1Þ
ð
ð355Þ
sinh ða xÞ
sinh ða xÞ
a
dx ¼ /
þ
.
xn
ðn / 1Þ x n / 1
n/1
Fall n ¼ 1: siehe Integral (354)
ð
ð356Þ
ð
ð357Þ
ð
cosh ða xÞ
dx
x n/1
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
Integral (369)
ðn 6¼ 1Þ
"
! a x 4"
dx
1
"
"
¼
. ln " tanh
"
sinh ða xÞ
a
2
dx
cosh ða xÞ
n/2
¼ /
/
.
sinh n ða xÞ
ðn / 1Þ a . sinh n / 1 ða xÞ
n/1
ð
dx
sinh n / 2 ða xÞ
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (356)
ð
ð358Þ
ð
ð359Þ
"
" q . e a x þ p / ppffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 þ q2
dx
1
"
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
¼ pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi . ln "
" q . e ax þ p þ p 2 þ q 2
p þ q . sinh ða xÞ
a p2 þ q2
sinh ða xÞ dx
x
p
¼
/
.
p þ q . sinh ða xÞ
q
q
ð
dx
p þ q . sinh ða xÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (358)
ðq 6¼ 0Þ
"
"
"
"
"
ðq 6¼ 0Þ
Integraltafel
509
ð
ð360Þ
sinh ða xÞ . sinh ðb xÞ dx ¼
sinh ðða þ bÞ xÞ
sinh ðða / bÞ xÞ
/
2 ða þ bÞ
2 ða / bÞ
ða 2 6¼ b 2 Þ
Fall a 2 ¼ b 2 : siehe Integral (350)
ð
ð361Þ
sinh ða xÞ . sin ðb xÞ dx ¼
a . cosh ða xÞ . sin ðb xÞ / b . sinh ða xÞ . cos ðb xÞ
a2 þ b2
sinh ða xÞ . cos ðb xÞ dx ¼
a . cosh ða xÞ . cos ðb xÞ þ b . sinh ða xÞ . sin ðb xÞ
a2 þ b2
ð
ð362Þ
25 Integrale mit
Hinweis:
cosh ða xÞ dx ¼
ð
ð364Þ
ð
ð365Þ
sinh ða xÞ
a
cosh 2 ða xÞ dx ¼
sinh ð2 a xÞ
x
þ
4a
2
cosh n ða xÞ dx ¼
cosh n / 1 ða xÞ . sinh ða xÞ
n/1
þ
.
na
n
ð
ð366Þ
x . cosh ða xÞ dx ¼
ð
ð367Þ
ð
ð368Þ
ða 6¼ 0Þ
Integrale mit einer hyperbolischen Kosinusfunktion und einer
–– hyperbolischen Sinusfunktion: siehe Abschnitt 26
–– Exponentialfunktion: siehe Abschnitt 22
ð
ð363Þ
cosh ða xÞ
ð
cosh n / 2 ða xÞ dx
x . sinh ða xÞ
cosh ða xÞ
/
a
a2
x n . cosh ða xÞ dx ¼
x n . sinh ða xÞ
n . x n / 1 . cosh ða xÞ
/
þ
a
a2
ð
nðn / 1Þ
.
x n / 2 . cosh ða xÞ dx
þ
a2
ðn ( 2Þ
cosh ða xÞ
ða xÞ 2
ða xÞ 4
ða xÞ 6
dx ¼ ln j a x j þ
þ
þ
þ ...
x
2 . 2!
4 . 4!
6 . 6!
(Potenzreihenentwicklung; Konvergenz für j x j > 0Þ
ð
ð369Þ
cosh ða xÞ
cosh ða xÞ
a
dx ¼ /
þ
.
xn
ðn / 1Þ x n / 1
n/1
Fall n ¼ 1: siehe Integral (368)
ð
ð370Þ
ðn 6¼ 0Þ
dx
2
¼
. arctan ðe a x Þ
cosh ða xÞ
a
ð
sinh ða xÞ
dx
x n/1
|fflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflffl}
Integral (355)
ðn 6¼ 1Þ
510
Integraltafel
ð
ð371Þ
dx
sinh ða xÞ
n/2
¼
þ
.
cosh n ða xÞ
ðn / 1Þ a . cosh n / 1 ða xÞ
n/1
ð
dx
cosh n / 2 ða xÞ
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (370)
ð
ð372Þ
ð
ð373Þ
8
"
" q . e a x þ p / pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
>
1
p2 / q2
"
>
>
p
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
.
ln
"
>
>
" q . e ax þ p þ p 2 / q 2
>
a p2 / q2
>
>
>
>
>
<
/2
dx
¼
a ð p þ q . e a xÞ
p þ q . cosh ða xÞ >
>
>
>
>
>
>
>
2
>
>
. arctan
>
: pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2
a q / p2
cosh ða xÞ dx
x
p
¼
/
.
p þ q . cosh ða xÞ
q
q
ð
ð374Þ
cosh ða xÞ . cosh ðb xÞ dx ¼
p þ q . e ax
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
q2 / p2
"
"
"
"
"
fur
€
q > 0; p 2 > q 2
fur
€
p 2 ¼ q 2 6¼ 0
fur
€
p2 < q2
!
ð
dx
p þ q . cosh ða xÞ
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
Integral (372)
ðq 6¼ 0Þ
sinh ðða þ bÞ xÞ
sinh ðða / bÞ xÞ
þ
2 ða þ bÞ
2 ða / bÞ
ða 2 6¼ b 2 Þ
Fall a 2 ¼ b 2 : siehe Integral (364)
ð
ð375Þ
cosh ða xÞ . sin ðb xÞ dx ¼
a . sinh ða xÞ . sin ðb xÞ / b . cosh ða xÞ . cos ðb xÞ
a2 þ b2
cosh ða xÞ . cos ðb xÞ dx ¼
a . sinh ða xÞ . cos ðb xÞ þ b . cosh ða xÞ . sin ðb xÞ
a2 þ b2
ð
ð376Þ
26 Integrale mit
sinh ða xÞ
ð
ð377Þ
cosh ða xÞ
sinh ða xÞ . cosh ða xÞ dx ¼
sinh 2 ða xÞ
1
¼
. cosh ð2 a xÞ
2a
4a
sinh ða xÞ . cosh ðb xÞ dx ¼
cosh ðða þ bÞ xÞ
cosh ðða / bÞ xÞ
þ
2 ða þ bÞ
2 ða / bÞ
ð
ð378Þ
und
Fall a 2 ¼ b 2 : siehe Integral (377)
ð
sinh n þ 1 ða xÞ
ð379Þ
sinh n ða xÞ . cosh ða xÞ dx ¼
ðn þ 1Þ a
Fall n ¼ / 1: siehe Integral (384)
ð
cosh n þ 1 ða xÞ
ð380Þ
sinh ða xÞ . cosh n ða xÞ dx ¼
ðn þ 1Þ a
Fall n ¼ / 1: siehe Integral (382)
ðn 6¼ / 1Þ
ðn 6¼ / 1Þ
ða 6¼ 0Þ
ða 2 6¼ b 2 Þ
Integraltafel
ð
ð381Þ
ð
ð382Þ
ð
ð383Þ
ð
ð384Þ
ð
ð385Þ
ð
ð386Þ
511
sinh 2 ða xÞ . cosh 2 ða xÞ dx ¼
sinh ða xÞ
dx ¼
cosh ða xÞ
ð
tanh ða xÞ dx ¼
cosh ða xÞ
dx ¼
sinh ða xÞ
ð
coth ða xÞ dx ¼
dx
1
¼
. ln j tanh ða xÞ j
sinh ða xÞ . cosh ða xÞ
a
tanh ða xÞ dx ¼
ð
ð
ð389Þ
1
. ln j sinh ða xÞ j
a
"
! a x 4"
cosh 2 ða xÞ
cosh ða xÞ
1
"
"
dx ¼
þ
. ln " tanh
"
sinh ða xÞ
a
a
2
ð
ð388Þ
1
. ln ðcosh ða xÞÞ
a
sinh 2 ða xÞ
sinh ða xÞ
1
dx ¼
/
. arctan ðsinh ða xÞÞ
cosh ða xÞ
a
a
27 Integrale mit
ð387Þ
sinh ð4 a xÞ
x
/
32 a
8
tanh ða xÞ
ða 6¼ 0Þ
1
. ln ðcosh ða xÞÞ
a
tanh 2 ða xÞ dx ¼ x /
tanh n ða xÞ dx ¼ /
tanh ða xÞ
a
tanh n / 1 ða xÞ
þ
ðn / 1Þ a
ð
tanh n / 2 ða xÞ dx
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (387)
ð
ð390Þ
ð
ð391Þ
dx
¼
tanh ða xÞ
ð
coth ða xÞ dx ¼
x . tanh 2 ða xÞ dx ¼
x2
x . tanh ða xÞ
1
/
þ 2 . ln ðcosh ða xÞÞ
2
a
a
28 Integrale mit
ð
ð392Þ
coth ða xÞ dx ¼
ð
ð393Þ
1
. ln j sinh ða xÞ j
a
coth ða xÞ
1
. ln j sinh ða xÞ j
a
coth 2 ða xÞ dx ¼ x /
coth ða xÞ
a
ða 6¼ 0Þ
512
Integraltafel
ð
ð394Þ
coth n ða xÞ dx ¼ /
coth n / 1 ða xÞ
þ
ðn / 1Þ a
ð
coth n / 2 ða xÞ dx
ðn 6¼ 1Þ
Fall n ¼ 1: siehe Integral (392)
ð
ð395Þ
ð
ð396Þ
dx
¼
coth ða xÞ
ð
tanh ða xÞ dx ¼
x . coth 2 ða xÞ dx ¼
1
. ln ðcosh ða xÞÞ
a
x2
x . coth ða xÞ
1
/
þ 2 . ln j sinh ða xÞ j
2
a
a
29 Integrale mit einer Areafunktion
ð
ð397Þ
arsinh
!x4
!x4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼ x . arsinh
/ x2 þ a2
a
a
ð
ð398Þ
x . arsinh
ð
ð399Þ
arcosh
x . arcosh
ð
ð401Þ
artanh
x . artanh
ð
ð403Þ
arcoth
3 2
2
!x4
!x4
ax
x / a2
dx ¼
þ
. artanh
a
2
2
a
!x4
!x4
a
dx ¼ x . arcoth
þ
. ln j x 2 / a 2 j
a
a
2
ð
ð404Þ
3 2
2
!x4
!x4
2x / a2
x pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼
. arcosh
/
. x2 / a2
a
4
a
4
!x4
!x4
a
dx ¼ x . artanh
þ
. ln j a 2 / x 2 j
a
a
2
ð
ð402Þ
3 2
2
!x4
!x4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2x þ a2
x
dx ¼
. arsinh
/
.
x2 þ a2
a
4
a
4
!x4
!x4
pffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
dx ¼ x . arcosh
/ x2 / a2
a
a
ð
ð400Þ
ða 6¼ 0Þ
x . arcoth
3 2
2
!x4
!x4
ax
x / a2
. arcoth
dx ¼
þ
a
2
a
2
513
Anhang Teil B
Tabellen zur Wahrscheinlichkeitsrechnung und Statistik
!bersicht
Tabelle 1:
Verteilungsfunktion fðuÞ der Standardnormalverteilung . . . . . . . . . . . .
514
Tabelle 2:
Quantile der Standardnormalverteilung . . . . . . . . . . . . . . . . . . . . . . . . . .
516
Tabelle 3:
Quantile der Chi-Quadrat-Verteilung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
518
Tabelle 4:
Quantile der t-Verteilung von „Student“ . . . . . . . . . . . . . . . . . . . . . . . . . .
520
514
Tabelle 1: Verteilungsfunktion fðuÞ der Standardnormalverteilung
Tabelle 1: Verteilungsfunktion fðuÞ der Standardnormalverteilung
Schrittweite: Du ¼ 0;01
f(u)
Für negative Argumente verwende man die
Formel
o(u)
fð/ uÞ ¼ 1 / fðuÞ
u
ðu > 0Þ
Für u ( 4 ist fðuÞ ' 1.
u
u
0
1
2
3
4
5
6
7
8
9
0,0
0,1
0,2
0,3
0,4
0,5000
0,5398
0,5793
0,6179
0,6554
0,5040
0,5438
0,5832
0,6217
0,6591
0,5080
0,5478
0,5871
0,6255
0,6628
0,5120
0,5517
0,5910
0,6293
0,6664
0,5160
0,5557
0,5948
0,6331
0,6700
0,5199
0,5596
0,5987
0,6368
0,6736
0,5239
0,5639
0,6026
0,6406
0,6772
0,5279
0,5675
0,6064
0,6443
0,6808
0,5319
0,5714
0,6103
0,6480
0,6844
0,5359
0,5754
0,6141
0,6517
0,6879
0,5
0,6
0,7
0,8
0,9
0,6915
0,7258
0,7580
0,7881
0,8159
0,6950
0,7291
0,7612
0,7910
0,8186
0,6985
0,7324
0,7642
0,7939
0,8212
0,7019
0,7357
0,7673
0,7967
0,8238
0,7054
0,7389
0,7704
0,7996
0,8264
0,7088
0,7422
0,7734
0,8023
0,8289
0,7123
0,7454
0,7764
0,8051
0,8315
0,7157
0,7486
0,7794
0,8078
0,8340
0,7190
0,7518
0,7823
0,8106
0,8365
0,7224
0,7549
0,7852
0,8133
0,8398
1,0
1,1
1,2
1,3
1,4
0,8413
0,8643
0,8849
0,9032
0,9192
0,8438
0,8665
0,8869
0,9049
0,9207
0,8461
0,8686
0,8888
0,9066
0,9222
0,8485
0,8708
0,8907
0,9082
0,9236
0,8508
0,8729
0,8925
0,9099
0,9251
0,8531
0,8749
0,8944
0,9115
0,9265
0,8554
0,8770
0,8962
0,9131
0,9279
0,8577
0,8790
0,8980
0,9147
0,9292
0,8599
0,8810
0,8997
0,9162
0,9306
0,8621
0,8830
0,9015
0,9177
0,9319
1,5
1,6
1,7
1,8
1,9
0,9332
0,9452
0,9554
0,9641
0,9713
0,9345
0,9463
0,9564
0,9649
0,9719
0,9357
0,9474
0,9573
0,9656
0,9726
0,9370
0,9484
0,9582
0,9664
0,9732
0,9382
0,9495
0,9591
0,9671
0,9738
0,9394
0,9505
0,9599
0,9678
0,9744
0,9406
0,9515
0,9608
0,9686
0,9750
0,9418
0,9525
0,9616
0,9693
0,9756
0,9429
0,9535
0,9625
0,9699
0,9761
0,9441
0,9545
0,9633
0,9706
0,9767
2,0
2,1
2,2
2,3
2,4
0,9772
0,9821
0,9861
0,9893
0,9918
0,9778
0,9826
0,9864
0,9896
0,9920
0,9783
0,9830
0,9868
0,9898
0,9922
0,9788
0,9834
0,9871
0,9901
0,9925
0,9793
0,9838
0,9875
0,9904
0,9927
0,9798
0,9842
0,9878
0,9906
0,9929
0,9803
0,9846
0,9881
0,9909
0,9931
0,9808
0,9850
0,9884
0,9911
0,9932
0,9812
0,9854
0,9887
0,9913
0,9934
0,9817
0,9857
0,9890
0,9916
0,9936
2,5
2,6
2,7
2,8
2,9
0,9938
0,9953
0,9965
0,9974
0,9981
0,9940
0,9955
0,9966
0,9975
0,9982
0,9941
0,9956
0,9967
0,9976
0,9982
0,9943
0,9957
0,9968
0,9977
0,9983
0,9945
0,9959
0,9969
0,9977
0,9984
0,9946
0,9960
0,9970
0,9978
9,9984
0,9948
0,9961
0,9971
0,9979
0,9985
0,9949
0,9962
0,9972
0,9979
0,9985
0,9951
0,9963
0,9973
0,9980
0,9986
0,9952
0,9964
0,9974
0,9981
0,9986
3,0
3,1
3,2
3,3
3,4
0,9987
0,9990
0,9993
0,9995
0,9997
0,9987
0,9991
0,9993
0,9995
0,9997
0,9987
0,9991
0,9994
0,9995
0,9997
0,9988
0,9991
0,9994
0,9996
0,9997
0,9988
0,9992
0,9994
0,9996
0,9997
0,9989
0,9992
0,9994
0,9996
0,9997
0,9989
0,9992
0,9994
0,9996
0,9997
0,9989
0,9992
0,9995
0,9996
0,9997
0,9990
0,9993
0,9995
0,9996
0,9997
0,9990
0,9993
0,9995
0,9997
0,9998
3,5
3,6
3,7
3,8
3,9
0,9998
0,9998
0,9999
0,9999
1,0000
0,9998
0,9998
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
0,9998
0,9999
0,9999
0,9999
1,0000
Standardnormalverteilung
515
Zahlenbeispiele
(1)
fð1;32Þ ¼ 0;9066
(2)
fð1;855Þ ¼ 0;9682
(3)
fð/ 2;36Þ ¼ 1 / fð2;36Þ ¼ 1 / 0;9909 ¼ 0;0091
(durch lineare Interpolation)
Formeln zur Berechnung von Wahrscheinlichkeiten
(1)
Einseitige Abgrenzung nach oben
f(u)
P(U ≤ c)
PðU ) cÞ ¼ f ðcÞ
c
(2)
u
Einseitige Abgrenzung nach unten
f(u)
P(U ≥ c)
c
(3)
PðU ( cÞ ¼ 1 / PðU ) cÞ ¼ 1 / fðcÞ
u
Zweiseitige (unsymmetrische) Abgrenzung
f(u)
P(a ≤ U ≤ b)
Pða ) U ) bÞ ¼ fðbÞ / fðaÞ
a
(4)
b
u
Zweiseitige (symmetrische) Abgrenzung
f(u)
P(–c ≤ U ≤ c)
Pð/ c ) U ) cÞ ¼ Pðj U j ) cÞ ¼
–c
c
u
¼ 2 . fðcÞ / 1
516
Tabelle 2: Quantile der Standardnormalverteilung
Tabelle 2: Quantile der Standardnormalverteilung
f(u)
p: Vorgegebene Wahrscheinlichkeit
ð0 < p < 1Þ
o(u p ) = p
up : Zur Wahrscheinlichkeit p
gehöriges Quantil
(obere Schranke)
up
u
Die Tabelle enthält für spezielle Werte von p das jeweils zugehörige Quantil up (einseitige
Abgrenzung nach oben).
p
up
p
up
0,90
1,282
0,1
/1,282
0,95
1,645
0,05
/1,645
0,975
1,960
0,025
/1,960
0,99
2,326
0,01
/2,326
0,995
2,576
0,005
/2,576
0,999
3,090
0,001
/3,090
Formeln:
u1 / p ¼ / u p
u p ¼ / u1 / p
Standardnormalverteilung (Quantile)
517
Formeln zur Berechnung von Quantilen
(1)
Einseitige Abgrenzung nach oben
f(u)
P(U ≤ c) = p
PðU ) cÞ ¼ fðcÞ ¼ p
fðcÞ ¼ p ! c ¼ u p
c
u
Zahlenbeispiel:
PðU ) cÞ ¼ fðcÞ ¼ 0;90 ! c ¼ u 0;90 ¼ 1;282
(2)
Einseitige Abgrenzung nach unten
f(u)
PðU ( cÞ ¼ 1 / PðU ) cÞ ¼
P(U ≥ c) = p
c
¼ 1 / fðcÞ ¼ p
fðcÞ ¼ 1 / p ! c ¼ u 1 / p
u
Zahlenbeispiel:
PðU ( cÞ ¼ 1 / PðU ) cÞ ¼ 1 / fðcÞ ¼ 0;90
fðcÞ ¼ 1 / 0;90 ¼ 0;10 ! c ¼ u 0;1 ¼ / 1;282
(3)
Zweiseitige (symmetrische) Abgrenzung
f(u)
P(–c ≤ U ≤ c) = p
Pð/ c ) U ) cÞ ¼ 2 . fðcÞ / 1 ¼ p
fðcÞ ¼
–c
c
1
ð1 þ pÞ ! c ¼ u ð1 þ pÞ=2
2
u
Zahlenbeispiel:
Pð/ c ) U ) cÞ ¼ 2 . fðcÞ / 1 ¼ 0;90
fðcÞ ¼
1
ð1 þ 0;90Þ ¼ 0;95 ! c ¼ u 0;95 ¼ 1;645
2
518
Tabelle 3: Quantile der Chi-Quadrat-Verteilung
Tabelle 3: Quantile der Chi-Quadrat-Verteilung
f(z)
F(z (p;f) ) = p
z (p;f)
z
p:
Vorgegebene Wahrscheinlichkeit
ð0 < p < 1Þ
f:
Anzahl der Freiheitsgrade
zðp; f Þ : Zur Wahrscheinlichkeit p
gehöriges Quantil bei f Freiheitsgraden (obere Schranke)
Die Tabelle enthält für spezielle Werte von p das jeweils zugehörige Quantil zðp; f Þ in
Abhängigkeit vom Freiheitsgrad f (einseitige Abgrenzung nach oben).
p
f
0,005
0,01
0,025
0,05
0,10
0,90
0,95
0,975
0,99
0,995
1
2
3
4
5
0,000
0,01
0,07
0,21
0,41
0,000
0,020
0,115
0,297
0,554
0,001
0,051
0,216
0,484
0,831
0,004
0,103
0,352
0,711
1,15
0,016
0,211
0,584
1,064
1,16
2,71
4,61
6,25
7,78
9,24
3,84
5,99
7,81
9,49
11,07
5,02
7,38
9,35
11,14
12,83
6,63
9,21
11,35
13,28
15,09
7,88
10,60
12,84
14,86
16,75
6
7
8
9
10
0,68
0,99
1,34
1,73
2,16
0,872
1,24
1,65
2,09
2,56
1,24
1,69
2,18
2,70
3,25
1,64
2,17
2,73
3,33
3,94
2,20
2,83
3,49
4,17
4,87
10,64
12,02
13,36
14,68
15,99
12,59
14,06
15,51
16,92
18,31
14,45
16,01
17,53
19,02
20,48
16,81
18,48
20,09
21,67
23,21
18,55
20,28
21,96
23,59
25,19
11
12
13
14
15
2,60
3,07
3,57
4,07
4,60
3,05
3,57
4,11
4,66
5,23
3,82
4,40
5,01
5,63
6,26
4,57
5,23
5,89
6,57
7,26
5,58
6,30
7,04
7,79
8,55
17,28
18,55
19,81
21,06
22,31
19,67
21,03
22,36
23,68
25,00
21,92
23,34
24,74
26,12
27,49
24,73
26,22
27,69
29,14
30,58
26,76
28,30
29,82
31,32
32,80
16
17
18
19
20
5,14
5,70
6,26
6,84
7,43
5,81
6,41
7,01
7,63
8,26
6,91
7,56
8,23
8,91
9,59
7,96
8,67
9,39
10,12
10,85
9,31
10,09
10,86
11,65
12,44
23,54
24,77
25,99
27,20
28,41
26,30
27,59
28,87
30,14
31,41
28,85
30,19
31,53
32,85
34,17
32,00
33,41
34,81
36,19
37,57
34,27
35,72
37,16
38,58
40,00
22
24
26
28
30
8,6
9,9
11,2
12,5
13,8
9,5
10,9
12,2
13,6
15,0
11,0
12,4
13,8
15,3
16,8
12,3
13,8
15,4
16,9
18,5
14,0
15,7
17,3
18,9
20,6
30,8
33,2
35,6
37,9
40,3
33,9
36,4
38,9
41,3
43,8
36,8
39,4
41,9
44,5
47,0
40,3
43,0
45,6
48,3
50,9
42,8
45,6
48,3
51,0
53,7
40
50
60
70
80
20,7
28,0
35,5
43,3
51,2
22,2
29,7
37,5
45,4
53,5
24,4
32,4
40,5
48,8
57,2
26,5
34,8
43,2
51,7
60,4
29,1
37,7
46,5
55,3
64,3
51,8
63,2
74,4
85,5
96,6
55,8
67,5
79,1
90,5
101,9
59,3
71,4
83,3
95,0
106,6
63,7
76,2
88,4
100,4
112,3
66,8
79,5
92,0
104,2
116,3
90
100
59,2
67,3
61,8
70,1
65,6
74,2
69,1
77,9
73,3
82,4
107,6
118,5
113,1
124,3
118,1
129,6
124,1
135,8
128,3
140,2
Chi-Quadrat-Verteilung (Quantile)
519
Formeln zur Berechnung von Quantilen
(1)
Einseitige Abgrenzung nach oben
f(z)
P(Z ≤ c) = p
PðZ ) cÞ ¼ FðcÞ ¼ p
FðcÞ ¼ p ! c ¼ zð p; f Þ
c
z
Zahlenbeispiel ( bei f ¼ 10 Freiheitsgraden):
PðZ ) cÞ ¼ FðcÞ ¼ 0;90
(2)
f ¼ 10
! c ¼ z ð0;9; 10Þ ¼ 15;99
Zweiseitige (symmetrische) Abgrenzung
f(z)
1
2
(1–p)
P(c 1 ≤ Z ≤ c 2 ) = p
1
2
z
c1
c2
PðZ ) c1 Þ ¼ Fðc1 Þ ¼
1
ð1 / pÞ
2
Fðc1 Þ ¼
(1–p)
1
ð1 / pÞ ! c1 ¼ zðð1 / pÞ=2; f Þ
2
PðZ ( c2 Þ ¼ 1 / PðZ ) c2 Þ ¼ 1 / Fðc2 Þ ¼
Fðc2 Þ ¼
Pðc1 ) Z ) c2 Þ ¼ p
1
ð1 þ pÞ ! c2 ¼ zðð1 þ pÞ=2; f Þ
2
1
ð1 / pÞ
2
Zahlenbeispiel ( bei f ¼ 10 Freiheitsgraden):
Pðc1 ) Z ) c2 Þ ¼ 0;90
1
PðZ ) c1 Þ ¼ Fðc1 Þ ¼ ð1 / 0;90Þ ¼ 0;05
2
f ¼ 10
Fðc1 Þ ¼ 0;05
! c1 ¼ z ð0;05; 10Þ ¼ 3;94
PðZ ( c2 Þ ¼ 1 / PðZ ) c2 Þ ¼ 1 / Fðc2 Þ ¼
Fðc2 Þ ¼
1
ð1 þ 0;90Þ ¼ 0;95
2
f ¼ 10
1
ð1 / 0;90Þ ¼ 0;05
2
! c2 ¼ zð0;95; 10Þ ¼ 18;31
520
Tabelle 4: Quantile der t-Verteilung von „Student“
Tabelle 4: Quantile der t-Verteilung von „Student“
f(t)
F(t (p;f) ) = p
t (p;f)
t
p:
Vorgegebene Wahrscheinlichkeit
ð0 < p < 1Þ
f:
Anzahl der Freiheitsgrade
tðp; f Þ : Zur Wahrscheinlichkeit p
gehöriges Quantil bei f Freiheitsgraden (obere Schranke)
Die Tabelle enthält für spezielle Werte von p das jeweils zugehörige Quantil tðp; f Þ in
Abhängigkeit vom Freiheitsgrad f (einseitige Abgrenzung nach oben).
p
f
0,90
0,95
0,975
0,99
0,995
1
2
3
4
5
3,078
1,886
1,638
1,533
1,476
6,314
2,920
2,353
2,132
2,015
12,707
4,303
3,182
2,776
2,571
31,820
6,965
4,541
3,747
3,365
63,654
9,925
5,841
4,604
4,032
6
7
8
9
10
1,440
1,415
1,397
1,383
1,372
1,943
1,895
1,860
1,833
1,812
2,447
2,365
2,306
2,262
2,228
3,143
2,998
2,896
2,821
2,764
3,707
3,499
3,355
3,250
3,169
11
12
13
14
15
1,363
1,356
1,350
1,345
1,341
1,796
1,782
1,771
1,761
1,753
2,201
2,179
2,160
2,145
2,131
2,718
2,681
2,650
2,624
2,602
3,106
3,055
3,012
2,977
2,947
16
17
18
19
20
1,337
1,333
1,330
1,328
1,325
1,746
1,740
1,734
1,729
1,725
2,120
2,110
2,101
2,093
2,086
2,583
2,567
2,552
2,539
2,528
2,921
2,898
2,878
2,861
2,845
22
24
26
28
30
1,321
1,318
1,315
1,313
1,310
1,717
1,711
1,706
1,701
1,697
2,074
2,064
2,056
2,048
2,042
2,508
2,492
2,479
2,467
2,457
2,819
2,797
2,779
2,763
2,750
40
50
60
1,303
1,299
1,296
1,684
1,676
1,671
2,021
2,009
2,000
2,423
2,403
2,390
2,704
2,678
2,660
100
200
500
.
1,290
1,286
1,283
..
.
1,282
1,660
1,653
1,648
..
.
1,645
1,984
1,972
1,965
..
.
1,960
2,364
2,345
2,334
..
.
2,326
2,626
2,601
2,586
..
.
2,576
..
1
Formeln:
tð1 / p; f Þ ¼ / tð p; f Þ
tð p; f Þ ¼ / tð1 / p; f Þ
t-Verteilung von „Student“ (Quantile)
521
Formeln zur Berechnung von Quantilen
(1)
Einseitige Abgrenzung nach oben
f(t)
PðT ) cÞ ¼ FðcÞ ¼ p
P(T ≤ c) = p
FðcÞ ¼ p ! c ¼ tð p; f Þ
c
t
Zahlenbeispiel (bei f ¼ 10 Freiheitsgraden):
f ¼ 10
! c ¼ t ð0;90; 10Þ ¼ 1;372
PðT ) cÞ ¼ FðcÞ ¼ 0;90
(2)
Einseitige Abgrenzung nach unten
f(t)
PðT ( cÞ ¼ 1 / PðT ) cÞ ¼
P(T ≥ c) = p
c
¼ 1 / FðcÞ ¼ p
FðcÞ ¼ 1 / p ! c ¼ tð1 / p; f Þ
t
Zahlenbeispiel (bei f ¼ 10 Freiheitsgraden):
PðT ( cÞ ¼ 1 / PðT ) cÞ ¼ 1 / FðcÞ ¼ 0;90
FðcÞ ¼ 1 / 0;90 ¼ 0;10
(3)
f ¼ 10
! c ¼ t ð0;10; 10Þ ¼ / t ð0;90; 10Þ ¼ / 1;372
Zweiseitige (symmetrische) Abgrenzung
f(t)
P(–c ≤ T ≤ c) = p
Pð/ c ) T ) cÞ ¼ 2 . FðcÞ / 1 ¼ p
FðcÞ ¼
–c
c
1
ð1 þ pÞ ! c ¼ tðð1 þ pÞ=2; f Þ
2
t
Zahlenbeispiel (bei f ¼ 10 Freiheitsgraden):
Pð/ c ) T ) cÞ ¼ 2 . FðcÞ / 1 ¼ 0;90
FðcÞ ¼
1
ð1 þ 0;90Þ ¼ 0;95
2
f ¼ 10
! c ¼ t ð0;95; 10Þ ¼ 1;812
Index
A
abgeschlossenes Intervall 8
abhängige Stichproben 460
–– Variable 67, 243
–– Veränderliche 67, 243
Abklingfunktion 105
Abklingkonstante 292, 294 f.
Ableitung 130
––, äußere 134
––, höhere 131
––, implizite 137
––, innere 134
––, logarithmische 136
––, partielle 247 ff.
––, verallgemeinerte 328, 349
Ableitung der elementaren Funktionen
(Tabelle) 132
–– der Umkehrfunktion 136
–– einer in der Parameterform
dargestellten Funktion (Kurve) 137
–– einer in Polarkoordinaten dargestellten
Kurve 138
–– einer Vektorfunktion 369
Ableitungsfunktion 130
Ableitungsregeln 133 ff.
–– für Vektorfunktionen 369 f.
Ableitungssätze der Fourier-Transformation
332 f.
–– der Laplace-Transformation 348 ff.
absolute Häufigkeit 407
–– –– eines Stichprobenwertes 437
absolut konvergente Reihe 178, 181
Abspaltung eines Linearfaktores 79
Abstand einer Geraden von einer Ebene 63
–– eines Punktes von einer Ebene 62
–– eines Punktes von einer Geraden 58, 77
–– zweier paralleler Ebenen 64
–– zweier paralleler Geraden 58
–– zweier windschiefer Geraden 59
Abszisse eines Punktes 41
Achsenabschnitte 76 f.
Achsenabschnittsform einer Geraden 77
Addition komplexer Zahlen 231
–– von Brüchen 9
–– von Matrizen 203
–– von Vektoren 50, 198
–– von Zahlen 6
Additionssatz für beliebige Ereignisse 408
–– für Mittelwerte 430 f.
–– für sich gegenseitig ausschließende
Ereignisse 408
–– für Varianzen 430 f.
Additionssätze für Linearkombinationen
von Zufallsvariablen 430
Additionstheoreme der Areafunktionen 115
–– der Hyperbelfunktionen 239
–– der trigonometrischen Funktionen 95, 239
Adjunkte 206, 211
#hnlichkeitssatz der Fourier-Transformation
329 f.
–– der Laplace-Transformation 346
#hnlichkeitstransformation 329, 346
Algebra, Fundamentalsatz 234
––, lineare 198 ff.
algebraische Form einer komplexen Zahl
228
–– Gleichungen n-ten Grades 17 ff.
algebraisches Komplement 206, 211
Algorithmus, Gaußscher 218 f.
allgemeine Binomische Reihe 186
–– Exponentialfunktion 104
–– Kosinusfunktion 98
–– Logarithmusfunktion 107
–– Lösung der homogenen linearen Differentialgleichung 1. Ordnung 274
–– Lösung der homogenen linearen Differentialgleichung 2. Ordnung 284f.
–– Lösung der homogenen linearen Differentialgleichung n-ter Ordnung 297
–– Lösung einer Differentialgleichung 270
–– Sinusfunktion 98
allgemeines Kriterium für einen relativen
Extremwert 143
Alternativhypothese 456
Amplitude 99
Amplitudendichte, spektrale 319
analytische Darstellung einer Funktion 67,
243
Sachwortververzeichnis
Anfangsbedingungen 270
Anfangsglied einer Reihe 16
Anfangswerte 270
Anfangswertproblem 270
––, lineares 360 ff.
Anpassungstest 471
antiparallele Vektoren 47
Anwendungen der Differentialrechnung
138 ff.
–– der Integralrechnung 168 ff.
–– der Vektorrechnung 56 ff.
aperiodischer Grenzfall 293
aperiodisches Verhalten 293
äquatoriales Flächenmoment 172
#quipotentialflächen 378
äquivalente Umformungen einer Gleichung
21
–– –– einer Ungleichung 25
–– –– eines linearen Gleichungssystems
218
Arbeit einer konstanten Kraft 56
–– einer ortsabhängigen Kraft 169
–– eines Kraftfeldes 396
Arbeitsintegral 169, 396
Arbeitspunkt 139
Archimedische Spirale 129
Areafunktionen 113 ff.
–– mit imaginärem Argument 240
Areakosinus hyperbolicus 113
Areakotangens hyperbolicus 113 f.
Areasinus hyperbolicus 113
Areatangens hyperbolicus 113 f.
arithmetische Reihe 16
arithmetischer Mittelwert 305
arithmetisches Mittel 305
Arkusfunktionen 101 ff.
–– mit imaginärem Argument 240
Arkuskosinusfunktion 102
Arkuskotangensfunktion 102
Arkussinusfunktion 101
Arkustangensfunktion 102
Astroide 126
Asymptoten einer gebrochenrationalen
Funktion 88
–– einer Hyperbel 119, 121
Aufsuchen einer partikulären Lösung 275
Ausblenden einer Funktion 323 ff.
Ausgleichsgerade 313 f.
Ausgleichskurven 312 ff.
523
Ausgleichsparabel 315
Ausgleichsrechnung 312 ff.
äußere Ableitung 134
–– Funktion 134
–– Integration 258
äußeres Integral 258, 260
–– Produkt 53 ff.
Auswertung einer Messreihe 305 ff.
axiales Flächenmoment 172
axialsymmetrisches Vektorfeld 379
B
Basis 10, 12, 199
Basisfunktionen einer Differentialgleichung
284, 296
Basislösungen einer Differentialgleichung
284, 296
Basisvektoren 48, 199
Baumdiagramm 410
Bayes’sche Formel 411
bedingte Wahrscheinlichkeit 409
Beobachtungsfehler 304
Berechnung der Fourier-Koeffizienten 190,
192, 194
–– eines bestimmten Integrals 148
Bereich, einfachzusammenhängender
395 f.
Bereichsintegral, 2-dimensionales 257
––, 3-dimensionales 263
Bernoulli-de l’Hospitalsche Regel 73
Bernoulli-Experiment 417
Beschleunigung einer geradlinigen
Bewegung 138
Beschleunigungsvektor 370
bestimmt divergente Reihe 178
bestimmtes Integral 147ff.
Betrag einer komplexen Zahl 228
–– einer reellen Zahl 6
–– eines Vektors 49, 199
Beziehungen zwischen den Areafunktionen
114 f.
–– zwischen den Arkusfunktionen 103
–– zwischen den Hyperbelfunktionen
109 ff.
–– zwischen den trigonometrischen
Funktionen 94 ff.
Bildbereich 317, 344
Bildfunktion 316, 344
Bildungsgesetz einer Reihe 16
524
binärer Logarithmus 13
binäres System 7
Binärlogarithmus 108
Binomialkoeffizient 14
Binomialverteilung 417 ff.
binomische Formeln 15
binomischer Lehrsatz 14 f.
bi-quadratische Gleichungen 20
Bogenlänge einer ebenen Kurve 173, 371
–– einer Kurve 371
–– einer Raumkurve 371
Bogenmaß 91
Breitenkoordinate 45, 390
Brennpunkt einer Parabel 122
Brennpunkte einer Ellipse 117
–– einer Hyperbel 119
Brennweite einer Ellipse 117
–– einer Hyperbel 119
–– einer Parabel 122
Briggscher Logarithmus 13, 108
Bruch 8
Bruchrechnung 8 ff.
C
Cardanische Lösungsformel 19
cartesisches Blatt 128
charakteristische Gleichung einer Differentialgleichung 285, 297
–– –– einer Matrix 226
charakteristische Matrix 225
charakteristisches Polynom einer Matrix 226
Chi-Quadrat-Test 471 ff.
Chi-Quadrat-Verteilung 432 f.
Cramersche Regel 221
D
Dämpfungsfaktor 292, 294 f.
Dämpfungssatz der Fourier-Transformation
331
–– der Laplace-Transformation 348
Darstellung einer Funktion als Fläche im
Raum 244
Darstellungsformen einer Funktion 67 f.,
243 f.
–– einer komplexen Zahl 228 ff.
Definitionsbereich einer Funktion 67, 243
Definitionslücke 87
Sachwortverzeichnis
dekadischer Logarithmus 13, 108
dekadisches System 7
Deltafunktion 326f.
de Morgansche Regeln 407
Determinante, dreireihige 210
––, gestürzte 212
––, n-reihige 211
––, Wronski-Determinante 284, 296
––, zweireihige 209
Determinante einer komplexen Matrix 223
–– einer reellen Matrix 209, 211
Determinanten 209 ff.
––, elementare Umformungen 214
––, Multiplikationstheorem 213
––, Rechenregeln 212 f.
Dezimalbruch 4
Dezimalsystem 7
Dezimalzahl 4
d-Funktion 326 f.
Diagonalmatrix 202, 227
Dichtefunktion 414
–– der Standardnormalverteilung 424
–– einer Chi-Quadrat-Verteilung 432
–– einer Exponentialverteilung 427
–– einer Normalverteilung 423
–– einer t-Verteilung 434
Differential einer Funktion 131
––, totales 251 f.
––, vollständiges 251 f.
Differentialgleichung 270
––, allgemeine Lösung 270
––, Lösung 270
––, partikuläre Lösung 270
––, singuläre Lösung 270
––, spezielle Lösung 270
Differentialgleichung einer elektrischen
Schwingung 295
–– einer erzwungenen Schwingung 294
–– einer freien gedämpften Schwingung
292
–– einer freien ungedämpften Schwingung
291
Differentialgleichungen 270 ff.
–– 1. Ordnung 271 ff.
–– 1. Ordnung mit trennbaren Variablen 271
–– 2. Ordnung 283 ff.
–– n-ter Ordnung 270, 296 ff.
Differentialoperator 131
––, partieller 248
Sachwortververzeichnis
Differentialquotient 130 f.
––, partieller 248
Differentialrechnung 130 ff.
––, Anwendungen 138 ff.
Differentiation, gewöhnliche 130 f.
––, implizite 137
––, logarithmische 136
––, partielle 247 f.
Differentiation einer Vektorfunktion 369
–– eines Vektors nach einem Parameter
369 f.
–– nach einem Parameter 250
Differentiationssätze der Fourier-Transformation 332 f.
–– der Laplace-Transformation 348 ff.
Differenzenquotient 130
Differenzenschema 84
Differenzentest 460 ff.
–– bei bekannten Varianzen 462 ff.
–– bei gleicher (aber unbekannter) Varianz
464 f.
–– für Mittelwerte bei abhängigen
Stichproben 461 f.
–– für Mittelwerte bei unabhängigen
Stichproben 462 ff.
Differenzierbarkeit einer Funktion 130 f.
Differenzmenge 2
Differenzvektor 50
Diracsche Deltafunktion 326 f.
Dirac-Stoß 326 f.
diskrete Verteilung 413
diskrete Wahrscheinlichkeitsverteilungen
417 ff.
–– ––, Approximationen 422
diskrete Zufallsvariable 412
Diskriminante 18
divergente Folge 71
–– Reihe 178
Divergenz eines Vektorfeldes 382
–– –– ––, Rechenregeln 382
Divergenz in kartesischen Koordinaten 382
–– in Kugelkoordinaten 392
–– in Polarkoordinaten 387
–– in Zylinderkoordinaten 389
Dividend 6
dividierte Differenzen 85
Division komplexer Zahlen 232 f.
–– von Brüchen 10
–– von Zahlen 6
525
Divisor 6
Doppelbruch 10
Doppelintegral 257
–– in kartesischen Koordinaten 258 f.
–– in Polarkoordinaten 260
Doppelintegrale 257 ff.
doppelte Nullstelle 68
Drehsinn eines Winkels 92
Drehstreckung 232
Drehung eines kartesischen Koordinatensystems 43
dreidimensionales Bereichsintegral 263
Dreieck 28 ff.
––, gleichschenkliges 29
––, gleichseitiges 30
––, Inkreis 29
––, rechtwinkliges 29
––, Umkreis 29
Dreiecksimpuls 357
Dreieckskurve 195 f., 356
Dreiecksmatrix 202, 227
Dreiecksungleichung 6
Dreifachintegral 263
–– in kartesischen Koordinaten 264 f.
–– in Kugelkoordinaten 266 f.
–– in Zylinderkoordinaten 266
Dreifachintegrale 263 ff.
Drei-Punkte-Form einer Ebene 61
dreireihige Determinante 210
dreiseitige Pyramide 35
Dualitätsprinzip der Fourier-Transformation
335
Dualsystem 7
Durchschnitt von Ereignissen 406
–– von Mengen 2
E
ebene Kurven 368 ff.
Ebene 245
––, Abstand paralleler Ebenen 64
––, Abstand von einem Punkt 62
––, Abstand von einer Geraden 63
––, Determinantenschreibweise 62
––, Drei-Punkte-Form 61
––, Koordinatendarstellung 62
––, Normalenvektor 62
––, Parameterdarstellung 60 f.
––, Punkt-Richtungs-Form 60
––, Richtungsvektoren 60
526
––, Schnittgerade zweier Ebenen 66
––, Schnittpunkt mit einer Geraden 65
––, Schnittwinkel mit einer Geraden 65
––, Schnittwinkel zweier Ebenen 66
––, vektorielle Darstellung 60 ff.
Ebene senkrecht zu einem Vektor 62
ebenes Koordinatensystem 41 f.
–– Vektorfeld 378
echt gebrochenrationale Funktion 86
e-Funktion 104, 239
Eigenkreisfrequenz 292, 294 f.
Eigenvektoren einer quadratischen Matrix
225 f.
–– spezieller n-reihiger Matrizen 227
Eigenwerte einer quadratischen Matrix
225 f.
–– spezieller n-reihiger Matrizen 227
Eigenwertproblem 225 f.
einfachzusammenhängender Bereich 395
Einheitskreis 92
Einheitsmatrix 202
Einheitssprung 323
Einheitsvektor 46, 48, 199
Einheitswurzeln 235
Einschwingphase 294
Einweggleichrichtung 197, 358
elektrische Schwingungen in einem
Reihenschwingkreis 295 f.
elementare Umformungen einer Matrix 207
–– –– einer n-reihigen Determinante 214
Elementarereignis 405
Elemente einer Determinante 209
–– einer Matrix 200
–– einer Menge 1
Ellipse 33, 117 f.
––, Brennpunkte 117
––, Gleichung in Polarkoordinaten 118
––, große Achse 117
––, Hauptachse 117
––, Hauptform 117
––, kleine Achse 117
––, Mittelpunktsgleichung 117
––, Nebenachse 117
––, Parameterdarstellung 118
––, Ursprungsgleichung 117
Ellipsoid 38, 247
elliptische Krümmung 39
empirische Varianz 443
Sachwortverzeichnis
empirischer Wahrscheinlichkeitswert 408
Endglied einer Reihe 16
endliche Intervalle 8
–– Menge 1
–– Reihe 16
Epizykloide 124 f.
Ereignis 405
––, komplementäres 406
––, sicheres 407
––, zusammengesetztes 406
Ereignisbaum 410
Ereignisfeld 405
Ereignisraum 405
Ereignisse, Additionssatz 408
––, Durchschnitt 406
––, Multplikationssatz 409
––, Produkt 406
––, stochastisch unabhängige 410
––, Summe 406
––, Vereinigung 406
––, Verknüpfungen 406
Ergebnismenge eines Zufallsexperiments 405
Ergiebigkeit des Feldvektors 397
Erwartungswert 304
–– einer Funktion 416
–– einer Zufallsvariablen 415
Erweitern eines Bruches 9
erweiterte Koeffizientenmatrix 215
erzwungene Schwingung 294 f.
Euklid, Satz des Euklid 27
Euler, Streckenzugverfahren 277 f.
Eulersche Formeln 230, 239
–– Zahl 104
Euler-Venn-Diagramm 406
Evolute 142
Evolvente 142
exakte Differentialgleichung 1. Ordnung 273
explizite Funktion 67, 243
Exponent 10
Exponentialansatz 297
Exponentialform einer komplexen Zahl 229
Exponentialfunktionen 104 ff., 239
Exponentialverteilung 427 f.
exponentielle Fourier-Transformation 317
–– ––, Tabelle 338 f.
Extremwertaufgabe mit Nebenbedingungen
255 f.
Extremwerte, relative 142 f., 254 f.
Sachwortververzeichnis
F
Faktor 6
––, integrierender 273
Faktorregel der Differentialrechnung 133
–– der Integralrechnung 149
Falk-Schema 204
Faltung 334, 352
––, einseitige 352
––, zweiseitige 334
Faltungsintegral der Fourier-Transformation
334
–– der Laplace-Transformation 352
Faltungsprodukt der Fourier-Transformation
334
–– der Laplace-Transformation 352
Faltungssatz der Fourier-Transformation
334 f.
–– der Laplace-Transformation 352
Fass 39
Feder-Masse-Schwinger 291
Federpendel 291
Fehler 1. Art 449
––, größtmöglicher 310
––, maximaler 310
Fehlerintegral, Gaußsches 425
Fehlerfortpflanzungsgesetz, Gaußsches
308 ff.
––, lineares 310 f.
Fehlerrechnung 304 ff.
Feldlinien 379
Flächen im Raum 374 ff.
Flächendifferential 258
Flächenelement 258, 376
––, orientiertes 397
Flächenelement auf dem Zylindermantel
388
–– auf der Kugeloberfläche 391
Flächenfunktion 150
flächenhafter Integrationsbereich 258
Flächeninhalt 170 f., 261
Flächenintegral eines Vektorfeldes 397
Flächenkurve 375
Flächenmoment, äquatoriales 172
––, axiales 172
––, polares 172
Flächenmoment 2. Grades 172, 262 f.
Flächennormale 375
Flächenparameter 374
Flächenträgheitsmomente 172, 262 f.
527
Fluss eines Feldvektors 397
–– eines homogenen Vektorfeldes 398
–– eines Vektorfeldes durch eine orientierte
Fläche 397
–– eines Zentralfeldes 398
–– eines zylindersymmetrischen Vektorfeldes 398
Flussintegral des Vektorfeldes 397
Folge, divergente 71
––, Grenzwert 71
––, konvergente 71
––, Zahlenfolge 71
Formel von Moivre 112, 234
Formeln für Mehrfachprodukte von Vektoren
56
Fourier-Integral 316
Fourier-Koeffizienten 190, 192, 194
Fourier-Kosinus-Transformation 321
––, Tabelle 342 f.
Fourier-Kosinus-Transformierte 321
Fourier-Reihen 190 ff.
––, Tabelle 195 ff.
Fourier-Sinus-Transformation 321
––, Tabelle 340 f.
Fourier-Sinus-Transformierte 321
Fourier-Transformationen 316 ff.
––, exponentielle 317
––, exponentielle (Tabelle) 338 ff.
––, Fourier-Kosinus-Transformation 321
––, Fourier-Kosinus-Transformation
(Tabelle) 342 f.
––, Fourier-Sinus-Transformation 321
––, Fourier-Sinus-Transformation
(Tabelle) 340 f.
––, inverse 317
––, spezielle 321 f.
––, Tabellen 338 ff.
Fourier-Transformationsoperator 316
Fourier-Transformierte 316
––, inverse 317
––, Polardarstellung 319
––, verallgemeinerte 328
Fourier-Transformierte des Faltungsproduktes 335
–– einer Linearkombination 329
Fourier-Zerlegung einer nichtsinusförmigen
Schwingung 193 f.
freie gedämpfte Schwingung 292 f.
–– ungedämpfte Schwingung 291
528
freier Vektor 46
Freiheitsgrad 432, 434
Frequenz 99
Frequenzgang 294
Frequenzspektrum 319
Frequenzverschiebungssatz der FourierTransformation 331
Fundamentalbasis einer Differentialgleichung
284, 296
Fundamentalsatz der Algebra 234
–– der Differential- und Integralrechnung 150
Funktion 67, 243
––, Abklingfunktion 105
––, analytische Darstellung 67, 243
––, Areafunktionen 113 ff.
––, Areakosinus hyperbolicus 113
––, Areakotangens hyperbolicus 113 f.
––, Areasinus hyperbolicus 113
––, Areatangens hyperbolicus 113 f.
––, Arkusfunktionen 101 ff.
––, Arkuskosinusfunktion 102
––, Arkuskotangensfunktion 102 f.
––, Arkussinusfunktion 101 f.
––, Arkustangensfunktion 102 f.
––, äußere 134
––, Darstellung als Fläche im Raum 244
––, Darstellungsformen 67 f., 243 f.
––, Definitionsbereich 67, 243
––, Deltafunktion 326 f.
––, d-Funktion 326 f.
––, differenzierbare 130 f.
––, Diracsche Deltafunktion 326 f.
––, e-Funktion 104
––, echt gebrochenrationale 86
––, explizite 67, 243
––, Exponentialfunktionen 104 ff.
––, Flächenfunktion 150
––, Gammafunktion 433
––, ganzrationale 76 ff.
––, Gaußfunktion 106
––, gebrochenrationale 86 ff.
––, gerade 69
––, Graph 68
––, graphische Darstellung 68, 244
––, Grenzwert 72
––, Heaviside-Funktion 323
––, Hyperbelfunktionen 108 ff.
––, implizite 67, 243
––, Impulsfunktion 326 f.
Sachwortverzeichnis
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
––,
innere 134
Integrandfunktion 150
inverse 70
komplexwertige 236
konstante 76
Kosinusfunktion 93
Kosinus hyperbolicus 108
Kotangensfunktion 94
Kotangens hyperbolicus 109
lineare 76 ff.
linearisierte 139, 253 f.
Linearisierung 139, 253 f.
Logarithmusfunktionen 107 f.
Mittelwerte 169
monotone 69
Näherungspolynome 188 f.
Nullstellen 68
Parameterdarstellung 67
periodische 70
Polynomfunktionen 76 ff.
Potenzfunktionen 88 ff.
punktsymmetrische 69
quadratische 78 ff.
Sättigungsfunktion 105 f.
Schaubild 68
Sigmafunktion 323
Sinusfunktion 93
Sinus hyperbolicus 108
s-Funktion 323
spiegelsymmetrische 69
Sprungfunktion 323
Stammfunktion 148, 150
stetig differenzierbare 130
stetige 74
Stetigkeit 74
Symmetrie 69
Tangensfunktion 94
Tangens hyperbolicus 109
trigonometrische 91 ff.
Umkehrfunktion 70
unecht gebrochenrationale 86
ungerade 69
verallgemeinerte 326, 349
verkettete 134
Wachstumsfunktion 106
Wertebereich 67, 243
Wertevorrat 67, 243
Wurzelfunktionen 90
zusammengesetzte 134
Sachwortververzeichnis
Funktionen 67 ff., 243 ff.
Funktionsgraph 68
Funktionskurve 68
Funktionswert 67, 243
G
Gamma-Funktion 433
ganze Zahlen 4
ganzrationale Funktionen 76 ff.
Gauß-Funktion 106
Gauß-Jordan-Verfahren 206
Gaußsche Glockenkurve 106, 423 f.
–– Normalverteilung 304 f., 423 ff.
–– Zahlenebene 228
Gaußscher Algorithmus 218 f.
Gaußscher Integralsatz 400 f.
–– –– im Raum 400
–– –– in der Ebene 401
Gaußsches Fehlerfortpflanzungsgesetz
308 ff.
–– Fehlerintegral 425
–– Prinzip der kleinsten Quadrate 312
gebrochenrationale Funktionen 86 ff.
–– ––, Asymptote im Unendlichen 88
–– ––, Nullstellen 87
–– ––, Pole 87
–– ––, Unendlichkeitsstellen 87
gebundener Vektor 46
gedämpfte Kosinusschwingung 359
–– Sinusschwingung 358
Gegenvektor 47
gekoppelte Differentialgleichungen 300
gemeinsame Verteilung zweier Zufallsvariablen 428
gemischtes Produkt 55
geometrische Reihe 16, 181
gerade Funktion 69
Gerade 76
––, Abstand paralleler Geraden 58
––, Abstand von einem Punkt 58, 77
––, Abstand von einer Ebene 63
––, Abstand windschiefer Geraden 59
––, Achsenabschnitte 76 f.
––, Achsenabschnittsform 77
––, Determinantenschreibweise 57
––, Hauptform 76
––, Hessesche Normalform 77
––, Parameterdarstellung 57
529
––, Punkt-Richtungs-Form 57
––, Punkt-Steigungs-Form 76
––, Richtungsvektor 57
––, Schnittpunkt mit einer Ebene 65
––, Schnittpunkt zweier Geraden 60
––, Schnittwinkel mit einer Ebene 65
––, Schnittwinkel zweier Geraden 60, 78
––, Steigung 76
––, Steigungswinkel 76
––, vektorielle Darstellung 57 ff.
––, Zwei-Punkte-Form 57, 77
Geraden 57 ff., 76 ff.
––, parallele 58
––, windschiefe 59
gerader Kreiskegel 36
–– Kreiskegelstumpf 37
–– Kreiszylinder 36
gerades Prisma 34
Geschwindigkeit einer geradlinigen
Bewegung 138
Geschwindigkeitsvektor 370
gestaffeltes lineares Gleichungssystem 218
gewöhnliche Zykloide 124
Gleichheit von Mengen 1
–– von Vektoren 47
–– zweier komplexer Zahlen 229
gleichschenkliges Dreieck 29
gleichseitige Hyperbel 121
–– Pyramide 34
gleichseitiges Dreieck 30
Gleichung, algebraische 17 ff.
––, bi-quadratische 20
––, kubische 18 ff.
––, lineare 18
––, quadratische 18
––, trigonometrische 22
––, Wurzelgleichung 21
Gleichung einer Ellipse in Polarkoordinaten
118
–– einer gedrehten Hyperbel 121
–– einer Hyperbel in Polarkoordinaten 120
–– einer Parabel in Polarkoordinaten 123
–– eines Kegelschnittes 115
–– eines Kreises in Polarkoordinaten 116
Gleichungen mit einer Unbekannten 17 ff.
Gleichungssysteme, lineare 215 ff.
Glockenkurve, Gaußsche 423 f.
Gradient eines Skalarfeldes 380
–– –– ––, Rechenregeln 381
530
Gradient in kartesischen Koordinaten 380
–– in Kugelkoordinaten 392
–– in Polarkoordinaten 386
–– in Zylinderkoordinaten 389
Gradientenfeld 384
Gradmaß 91
graphische Darstellung einer Funktion 68,
244
graphisches Lösungsverfahren für
Gleichungen 22
Grenzwert einer Folge 71
Grenzwert einer Funktion 72
–– –– ––, Rechenregeln 72 f.
Grenzwertregel von Bernoulli und l’Hospital
73
Grenzwertsätze der Laplace-Transformation
353
große Achse einer Ellipse 117
–– –– einer Hyperbel 119
größter gemeinsamer Teiler 3
größtmöglicher Fehler 310
Grundgesamtheit 436
Grundintegrale (Tabelle) 152
Grundrechenarten 6
–– für komplexe Zahlen 231 ff.
Grundzahl 10
gruppierte Stichprobe 439
–– ––, Häufigkeitsfunktion 440
–– ––, Histogramm 440
–– ––, Kennwerte 445
–– ––, Stabdiagramm 440
–– ––, Staffelbild 440
–– ––, Treppenfunktion 441
–– ––, Verteilungsfunktion 441
–– ––, Verteilungstabelle 440
Guldinsche Regeln 40 f.
H
halboffenes Intervall 8
harmonische Schwingung 99 f., 240
Häufigkeit, absolute 407, 437
––, relative 407, 437
Häufigkeitsfunktion einer gruppierten
Stichprobe 440
–– einer Stichprobe 437
Häufigkeitsverteilung einer Stichprobe 437
Hauptachse einer Ellipse 117
Hauptdiagonale einer Determinante 209
–– einer Matrix 201
Sachwortverzeichnis
Hauptdiagonalprodukt 210
Hauptform einer Ellipse 117
–– einer Geraden 76
–– einer Hyperbel 119
–– einer Parabel 78, 122
–– eines Kreises 116
Hauptnenner 9
Hauptnormaleneinheitsvektor 372
Hauptwert des natürlichen Logarithmus
236
–– eines Winkels 42, 229
Heaviside-Funktion 323
hebbare Lücke 75
hermitesche Matrix 224, 227
Herzkurve 126
Hessesche Normalform einer Geraden 77
Histogramm 440
Hochpunkt 142
Hochzahl 10
Höhenkoordinate 44, 387
Höhenliniendiagramm 244
Höhensatz 26
höhere Ableitungen 131
–– ––, partielle 249
homogenes lineares Gleichungssystem 215
–– Vektorfeld 379
Horner-Schema 80
Hüllenintegral 397
Hyperbel 121 ff.
––, Asymptoten 119, 121
––, Brennpunkte 119
––, gedrehte 121
––, gleichseitige 121
––, Gleichung in Polarkoordinaten 120
––, große Achse 119
––, Hauptform 119
––, imaginäre Achse 119
––, kleine Achse 119
––, Mittelpunktsgleichung 119
––, Parameterdarstellung 121
––, rechtwinklige 121
––, reelle Achse 119
––, Scheitelpunkte 119
––, Ursprungsgleichung 119
Hyperbelfunktionen 108 ff., 233, 238
hyperbolischer Pythagoras 109
hypergeometrische Verteilung 419 f.
Hypothese 456
––, Alternativhypothese 456
Sachwortververzeichnis
––, Nullhypothese 456
––, statistische 456
Hypozykloide 125
I
imaginäre Achse 228
–– –– einer Hyperbel 119
imaginäre Einheit 228
–– Zahl 228
Imaginärteil einer komplexen Matrix 222
–– einer komplexen Zahl 228
implizite Differentiation 137
–– –– unter Verwendung der Kettenregel 137
–– –– unter Verwendung partieller Ableitungen 137
implizite Funktion 67, 243
Impulsfunktion 326 f.
inhomogenes lineares Gleichungssystem 215
Inkreis eines Dreiecks 29
innere Ableitung 134
–– Funktion 134
–– Integration 258
inneres Integral 258, 260
–– Produkt 51 f.
Integrabilitätsbedingung 273
–– für ein ebenes Vektorfeld 394
–– für ein räumliches Vektorfeld 395
Integral 147 ff.
––, Arbeitsintegral 169, 396
––, äußeres 258, 260
––, bestimmtes 147 ff.
––, Doppelintegral 257
––, Dreifachintegral 263
––, Flächenintegral 397
––, Fourier-Integral 316
––, Hüllenintegral 397
––, inneres 258, 260
––, Laplace-Integral 344
––, Mehrfachintegral 257 ff.
––, Oberflächenintegral 397
––, unbestimmtes 150 ff.
––, uneigentliches 167 f.
Integralrechnung 147 ff.
Integralsatz, Gaußscher 400 f.
––, Stokes’scher 401
Integrationssätze der Fourier-Transformation
334
–– der Laplace-Transformation 350 f.
531
Integraltafel 476
Integrand 148, 258, 264
Integrandfunktion 148, 258, 264
Integration, bestimmte 147 ff.
––, partielle 156
––, Produktintegration 156
––, unbestimmte 151
Integration der Bewegungsgleichung 168
–– durch Potenzreihenentwicklung des
Integranden 161
–– durch Substitution 153 ff.
–– einer gebrochenrationalen Funktion
durch Partialbruchzerlegung des
Integranden 157 ff.
–– einer homogenen linearen Differentialgleichung 1. Ordnung 274
–– einer homogenen linearen Differentialgleichung 2. Ordnung 284 f.
–– einer homogenen linearen Differentialgleichung n-ter Ordnung 296 f.
–– einer inhomogenen linearen Differentialgleichung 1. Ordnung 274 f.
–– einer inhomogenen linearen Differentialgleichung 2. Ordnung 285 f.
–– einer inhomogenen linearen Differentialgleichung n-ter Ordnung 298
Integrationsgrenzen 148
Integrationsmethoden 153 ff.
Integrationsregeln 149
Integrationsvariable 148, 258, 264
integrierender Faktor 273
Interpolationsformel von Lagrange 82 f.
–– von Newton 84 f.
Interpolationspolynome 82 ff.
Intervall 8
––, abgeschlossenes 8
––, endliches 8
––, halboffenes 8
––, offenes 8
––, unendliches 8
Intervallschätzungen 446, 449 ff.
inverse Fourier-Tranformation 317
–– Fourier-Transformierte 317
–– Funktion 70
–– Laplace-Transformation 345
–– Laplace-Transformierte 345
–– Matrix 205 f.
inverser Vektor 47
Inversion einer komplexen Zahl 237
532
–– einer Ortskurve 237
Inversionsregeln für Ortskurven 237
irrationale Zahl 4
Irrtumswahrscheinlichkeit 449
K
Kalotte 38
Kardioide 126
kartesische Form einer komplexen Zahl 228
–– Koordinaten 41, 44
kartesischer Normalbereich 258, 264
Kathetensatz 27
Kegelschnitte 115 ff.
Kehrmatrix 205
Kehrwert einer Zahl 8
Keil 36
Kennkreisfrequenz 292, 295
Kennwerte der Standardnormalverteilung
424
–– einer Binomialverteilung 418
–– einer Chi-Quadrat-Verteilung 432
–– einer Exponentialverteilung 427
–– einer hypergeometrischen Verteilung
420
–– einer Normalverteilung 423
–– einer Poisson-Verteilung 421
–– einer Stichprobe 442 f.
–– einer t-Verteilung 434
–– einer Verteilung 415 ff.
Kettenlinie 106
Kettenregel 134 f.
––, verallgemeinerte 250
Kippschwingung 196, 357
Klasse 439
Klassenhäufigkeit 439
Klassenmitte 439
Kleeblatt 128
kleine Achse einer Ellipse 117
–– –– einer Hyperbel 119
kleinstes gemeinsames Vielfaches 3
Koeffizientenmatrix 215, 300
kollineare Vektoren 47, 55
Kombinationen 404
–– mit Wiederholung 404
–– ohne Wiederholung 404
Kombinatorik 403 ff.
komplanare Vektoren 56
komplementäres Ereignis 406
Sachwortverzeichnis
komplexe Amplitude 240
–– Funktionen 238 ff.
komplexe Matrix 222
–– ––, Determinante 223
–– ––, Imaginärteil 222
–– ––, Realteil 222
–– ––, Rechenregeln 223
komplexe Zahlen 228 ff.
–– ––, algebraische Form 228
–– ––, Betrag 228
–– ––, Darstellungsformen 228 ff.
–– ––, Exponentialform 229
–– ––, Grundrechenarten 231 ff.
–– ––, Imaginärteil 228
–– ––, Inversion 237
–– ––, kartesische Form 228
–– ––, Phase 229
–– ––, Polarformen 229
–– ––, Realteil 228
–– ––, Rechenregeln 231 f.
–– ––, trigonometrische Form 229
komplexer Zeiger 240
komplexwertige Funktion 236
Komponentendarstellung eines Vektors 48,
199
Konfidenzgrenzen 449
Konfidenzintervalle 449 ff.
Konfidenzniveau 449
Konjugation 223
konjugiert komplexe Matrix 223
–– komplexe Zahl 229
–– transponierte Matrix 224
konkave Krümmung 140
konservatives Vektorfeld 395 f.
konstante Funktion 76
kontinuierliches Spektrum 318
konvergente Folge 71
–– Reihe 178, 181
Konvergenzbereich einer Potenzreihe 183
Konvergrenzkriterien für unendliche Reihen
179 ff.
Konvergenzradius einer Potenzreihe 183
konvexe Krümmung 140
Koordinaten, kartesische 41, 44
––, Kugelkoordinaten 45
––, orthogonale 386, 388, 390
––, Polarkoordinaten 42
––, rechtwinklige 41, 44
––, Zylinderkoordinaten 44
Sachwortververzeichnis
Koordinatendarstellung einer Ebene 62
Koordinatenebenen 245
Koordinatenflächen in Kugelkoordinaten 390
–– in Zylinderkoordinaten 388
Koordinatenlinien einer Fläche 374
–– in einem Polarkoordinatensystem 386
–– in Kugelkoordinaten 390
–– in Zylinderkoordinaten 388
Koordinatensysteme 41 ff.
––, ebene 41 f.
––, krummlinige 386
––, räumliche 44 f.
Koordinatentransformationen 42 f.
Korrelationskoeffizient 314
korrelierte Stichproben 460
Korrespondenz 316, 344
Kosinus hyperbolicus 108
Kosinusfunktion 93, 359
––, allgemeine 98
Kosinussatz 28
Kosinusschwingung 99, 359
––, gedämpfte 359
Kotangens hyperbolicus 109
Kotangensfunktion 94
Kreis 32, 115 f.
––, Gleichung in Polarkoordinaten 116
––, Hauptform 116
––, Mittelpunktsgleichung 116
––, Parameterdarstellung 116
––, Ursprungsgleichung 116
Kreisabschnitt 32
Kreisausschnitt 32
Kreisfrequenz 99
Kreiskegel 246
––, gerader 36
Kreiskegelstumpf, gerader 37
Kreisring 33
Kreissegment 32
Kreissektor 32
Kreiszylinder 247
––, gerader 36
Kreuzprodukt 53
Kriechfall 293
Kronecker-Symbol 199
krummliniges Koordinatensystem 386
Krümmung, elliptische 39
––, konkave 140
––, konvexe 140
––, Linkskrümmung 140 f.
533
––, parabolische 39
––, Rechtskrümmung 140 f.
––, sphärische 39
Krümmung einer Kurve 140 ff., 372 f.
–– einer Raumkurve 372
Krümmungskreis 141
Krümmungsmittelpunkt 141
Krümmungsradius 141, 372
Kubikwurzel 11
kubische Gleichung 18 ff.
Kugel 37, 246
Kugelabschnitt 38
Kugelausschnitt 37
Kugelkappe 38
Kugelkoordinaten 45, 390
Kugelschicht 38
Kugelsegment 38
Kugelsektor 37
kugelsymmetrisches Vektorfeld 379
Kugelzone 38
Kurve 67 ff., 368 ff.
––, Bogenlänge 173
––, ebene 368 ff.
––, räumliche 368 ff.
––, vektorielle Darstellung 368
Kurvendiskussion 145 f.
Kurvengleichung in Polarkoordinaten 68
Kurvenintegral 392 ff.
–– eines räumlichen Vektorfeldes 394
–– längs einer geschlossenen Linie 393
Kurvenkrümmung 140 f.
Kürzen eines Bruches 9
L
Lagrange, Interpolationsformel 82 f.
––, Koeffizientenfunktionen 82
––, Restglied 184
Lagrangesche Koeffizientenfunktion 82
Lagrangescher Multiplikator 255
Lagrangesches Multiplikatorverfahren 255 f.
Längenkoordinate 45, 390
Laplace-Experiment 408
Laplace-Integral 344
Laplace-Operator 385
–– in Kugelkoordinaten 392
–– in Polarkoordinaten 386
–– in Zylinderkoordinaten 389
Laplacesche Differentialgleichung 385
Laplacescher Entwicklungssatz 212
534
Laplace-Transformationen 344 ff.
Laplace-Transformationsoperator 344
Laplace-Transformierte 344
–– des Faltungsproduktes 352
–– einer Linearkombination 345
–– einer periodischen Funktion 354
–– spezieller Funktionen (Impulse) 355 ff.
leere Menge 1
Leibnizsche Sektorformel 171
Leibnizsches Konvergenzkriterium für alternierende Reihen 181
Leitlinie einer Parabel 122
Lemniskate 127
Linearkombinationen von Zufallsvariablen
430
linear abhängige Vektoren 221 f.
–– unabhängige Vektoren 221 f.
lineare Algebra 198 ff.
lineare Differentialgleichungen 1. Ordnung
274 ff.
–– –– 1. Ordnung mit konstanten Koeffizienten 275 f., 336, 361
–– –– 2. Ordnung mit konstanten Koeffizienten 284 ff., 337, 362
–– –– n-ter Ordnung mit konstanten Koeffizienten 296 ff.
lineare Funktionen 76 f.
–– Gleichungen 18
–– Gleichungssysteme 215 ff.
–– Unabhängigkeit von Vektoren 221 f.
linearer Mittelwert einer Funktion 169
lineares Anfangswertproblem 360 ff.
–– Fehlerfortpflanzungsgesetz 310 f.
lineares Gleichungssystem 215
–– ––, äquivalente Umformungen 218
–– ––, homogenes 215
–– ––, inhomogenes 215
–– ––, quadratisches 215
Linearfaktoren 79 f.
Linearisierung einer Funktion 139, 253 f.
Linearitätssatz der Fourier-Transformation
329
–– der Laplace-Transformation 345
Linien gleicher Höhe 244
Linienelement in Kugelkoordinaten 391
–– in Zylinderkoordinaten 388
linienflüchtiger Vektor 46
Linienintegrale 392 ff.
–– im Raum 394 f.
Sachwortverzeichnis
–– in der Ebene 392 f.
Linienspektrum 318
Linkskrümmung 140 f., 373
Logarithmen 12 f.
––, Rechenregeln 13
logarithmische Ableitung 136
–– Differentiation 136
–– Spirale 129
Logarithmus 12
––, binärer 13, 108
––, Briggscher 13, 108
––, dekadischer 13, 108
––, natürlicher 13, 107
––, Zehnerlogarithmus 13, 108
––, Zweierlogarithmus 13, 108
Logarithmus naturalis 13
Logarithmusfunktionen 107 ff.
Lösungen einer Differentialgleichung 270
Lösungsverhalten eines linearen
Gleichungssystems 216
–– eines quadratischen linearen
Gleichungssystems 217
Lücke, hebbare 75
M
Mac Laurinsche Formel 184
–– –– Reihe 185
Mac Laurinsches Polynom 184
Majorante 180
Majorantenkriterium 180
Mantelfläche eines Rotationskörpers 175
Massenträgheitsmoment eines homogenen
Körpers 176 f., 269
–– eines Rotationskörper 176 f., 269
Maßzahlen der Standardnormalverteilung
424
–– einer Binomialverteilung 418
–– einer Chi-Quadrat-Verteilung 432
–– einer Exponentialverteilung 427
–– einer hypergeometrischen Verteilung 420
–– einer Normalverteilung 423
–– einer Poisson-Verteilung 421
–– einer Stichprobe 442 f.
–– einer t-Verteilung 434
–– einer Verteilung 415 ff.
Matrix 200
––, charakteristische 225
––, Diagonalmatrix 202
––, Dreiecksmatrix 202
Sachwortververzeichnis
––, Eigenvektoren 225 f.
––, Eigenwerte 225 f.
––, Einheitsmatrix 202
––, elementare Umformungen 207
––, Elemente 200
––, hermitesche 224
––, inverse 205 f.
––, Kehrmatrix 205
––, Koeffizientenmatrix 215, 300
––, komplexe 222
––, konjugiert komplexe 223
––, konjugiert transponierte 224
––, n-reihige 201
––, Nullmatrix 201
––, orthogonale 203
––, quadratische 201
––, Rang 207
––, reelle 200
––, reguläre 205
––, schiefhermitesche 224
––, schiefsymmetrische 202
––, singuläre 205
––, Spaltenmatrix 201
––, Spur 202
––, symmetrische 202
––, transponierte 201
––, Umkehrmatrix 205
––, unitäre 225
––, Unterdeterminante 207
––, Zeilenmatrix 201
Matrixelement 200
Matrizen, Addition 203
––, komplexe 222 ff.
––, Multiplikation 203 f.
––, Rechenregeln 203 f.
––, reelle 200 ff.
––, Subtraktion 203
maximale Messunsicherheit 310
maximaler Fehler 310
Maximum, relatives 142 f., 254 f.
mechanische Schwingungen 291 ff.
mehrdimensionale Zufallsvariable 428
Mehrfachintegrale 257 ff.
mehrstufiges Zufallsexperiment 410 f.
Menge 1 f.
––, Differenzmenge 2
––, Durchschnitt 2
––, Elemente 1
––, endliche 1
535
––, leere 1
––, Obermenge 1
––, Restmenge 2
––, Schnittmenge 2
––, Teilmenge 1
––, unendliche 1
––, Untermenge 1
––, Vereinigungsmenge 2
Menge der ganzen Zahlen 4
–– der komplexen Zahlen 228
–– der natürlichen Zahlen 2
–– der positiven ganzen Zahlen 2
–– der rationalen Zahlen 4
–– der reellen Zahlen 4
Mengenoperationen 2
Messergebnis 307
Messfehler 304
Messreihe 305
––, Auswertung 305 ff.
––, Mittelwert 305
Messunsicherheit 307
––, maximale 310
Messwert 304
––, wahrscheinlichster 304
Methode der kleinsten Quadrate 312
Minimum, relatives 142 f., 254 f.
Minorante 180
Minorantenkriterium 180
Minuend 6
Mittelpunktsgleichung einer Ellipse 117
–– einer Hyperbel 119
–– eines Kreises 116
Mittelwert 304
––, arithmetischer 305
Mittelwert der Standardnormalverteilung
424
–– einer Binomialverteilung 418
–– einer Chi-Quadrat-Verteilung 432
–– einer Exponentialverteilung 427
–– einer Funktion 169
–– einer hypergeometrischen Verteilung 420
–– einer Messreihe 305
–– einer Normalverteilung 423
–– einer Poisson-Verteilung 421
–– einer Stichprobe 442
–– einer t-Verteilung 434
–– einer Zufallsvariablen 416
mittlerer Fehler der Einzelmessung 306
–– –– des Mittelwertes 306
536
Modulation 331
Moivre, Formel von Moivre 112, 234
monoton fallende Funktion 69
–– wachsende Funktion 69
Monotonie 69, 140
Multiplikation einer Matrix mit einem
Skalar 203
–– eines Vektors mit einem Skalar 51, 199
–– komplexer Zahlen 231 f.
–– von Brüchen 10
–– von Matrizen 204
–– von Zahlen 6
Multiplikationssatz für Ereignisse 409
–– für Fourier-Transformationen 333
–– für Mittelwerte 431
Multiplikationstheorem für Determinanten
213
N
n-dimensionale Zufallsvariable 429
n-dimensionaler Raum 199
n-dimensionaler Vektor 198
Nabla-Operator 380
Näherungspolynome einer Funktion 188
–– spezieller Funktionen (Tabelle) 188 f.
natürliche Zahlen 2
natürlicher Logarithmus 13, 107
–– –– einer komplexen Zahl 235 f.
Nebenachse einer Ellipse 117
Nebendiagonale einer Determinante 209
–– einer Matrix 201
Nebendiagonalprodukt 210
n-Eck, reguläres 32
Newton, Interpolationsformel 84 f.
––, Tangentenverfahren 24
n-Fakultät 14
nichtäquivalente Umformungen einer
Gleichung 21
Niveauflächen 378
Niveaulinien 378
Normalbereich in kartesischen Koordinaten
258, 264
–– in Polarkoordinaten 260
Normale 139
Normalenvektor einer Ebene 62
Normalgleichungen 312, 315
Normalparabel 78
Normalverteilung, Gaußsche 304 f., 423 ff.
––, standardisierte 305, 424 ff.
Normierung eines Vektors 51, 199
Sachwortverzeichnis
n-reihige Determinante 211
–– Matrix 201
Nullhypothese 456
Nullmatrix 201
Nullphasenwinkel 99
Nullstelle 68
–– einer gebrochenrationalen Funktion 87
–– einer Polynomfunktion 79
Nullstellenberechnung einer Polynomfunktion 81
Nullvektor 46, 199
numerische Exzentrität einer Ellipse 117
–– –– einer Hyperbel 119
numerische Integration 161 ff.
–– ––, Romberg-Verfahren 164 f.
–– ––, Simpsonsche Formel 162 f.
–– ––, Trapezformel 161 f.
numerische Integration einer Differentialgleichung 1. Ordnung 277 ff.
–– –– einer Differentialgleichung 2. Ordnung
288 f.
Numerus 12
O
obere Dreiecksmatrix 202
–– Integrationsgrenze 148
Oberflächenintegral 397 ff.
–– über eine geschlossene Fläche 397
Oberfunktion 344
Obermenge 1
Oberreihe 180
offenes Intervall 8
"ffnungsparameter 78, 122
Ordinate 41
orientiertes Flächenelement 397
Originalbereich 317, 344
Originalfunktion 316, 344
orthogonale ebene Koordinaten 386
–– Matrix 203
–– räumliche Koordinaten 388, 390
–– Vektoren 53, 199
orthonormierte Basis 52
Ortskurve 236 ff.
–– einer parameterabhängigen komplexen
Zahl 236
Ortsvektor 46
–– einer ebenen Kurve 368
–– einer Fläche 374
–– einer Raumkurve 368
Sachwortververzeichnis
P
p, q-Formel 18
Parabel 78 f., 122 f.
––, Brennpunkt 122
––, Gleichung in Polarkoordinaten 123
––, Hauptform 78, 122
––, Leitlinie 122
––, Normalparabel 78
––, "ffnungsparameter 78, 122
––, Parameterdarstellung 123
––, Produktform 79
––, Scheitelgleichung 122
––, Scheitelpunkt 122
––, Scheitelpunktsform 79
parabolische Krümmung 39
parallele Vektoren 47
Parallelebenen 245
Parallelepiped 34
Parallelogramm 31
Parallelogrammregel für komplexe Zahlen
231
Parallelverschiebung eines kartesischen
Koordinatensystems 42
Parameter 67
–– der Standardnormalverteilung 424
–– einer Binomialverteilung 418
–– einer Chi-Quadrat-Verteilung 432
–– einer Exponentialverteilung 427
–– einer hypergeometrischen Verteilung 419
–– einer Normalverteilung 423
–– einer Poisson-Verteilung 421
–– einer t-Verteilung 434
parameterabhängiger Ortsvektor 368
Parameterdarstellung einer Ebene 60 f.
–– einer Ellipse 118
–– einer Funktion 67
–– einer Geraden 57
–– einer Hyperbel 121
–– einer Parabel 123
–– eines Kreises 116
Parameterlinien einer Fläche 374
Parameterschätzungen 446 ff.
Parametertest 456
––, Musterbeispiel 470 f.
Parametertests 456 ff.
––, spezielle 457 ff.
Parsevalsche Gleichung 334
Partialbruch 157
Partialbruchzerlegung 157 ff.
537
Partialsumme 178
Partialsummenfolge 178
partielle Ableitungen 247 ff.
–– –– 1. Ordnung 247 f.
–– –– höherer Ordnung 249 f.
partielle Differentialoperatoren 248 f.
–– Differentialquotienten 248
–– Differentiation 247 ff.
–– Integration 156
partikuläre Lösung einer Differentialgleichung 270
Pascalsches Dreieck 15
Periode 70, 99
––, primitive 70
periodische Funktion 70
–– ––, Laplace-Transformierte 354
Periodizität 70
Permutationen 403
Pfad 410
Pfadregeln 411
Phase 99
–– einer komplexen Zahl 229
Phasendichte, spektrale 319
Phasenspektrum 319
Phasenverschiebung 294
Phasenwinkel 99
Pivotelement 219
Planimetrie 28 ff.
Poisson-Gleichung 385
Poisson-Verteilung 421
Pol 68, 75, 87
–– k-ter Ordnung 87
Polarachse 68
Polardarstellung der Fourier-Transformierten
319
polares Flächenmoment 172
Polarformen einer komplexen Zahl 229
Polarkoordinaten 42, 385
Polarwinkel 68
Polynom, charakteristisches 226
––, Interpolationspolynom 82 ff.
––, Mac Laurinsches 184
––, reduziertes 79
––, Taylorsches 184
Polynomfunktionen 76 ff.
––, Nullstellen 79
––, Produktdarstellung 79 f.
––, Reduzierung 81
––, Zerlegung in Linearfaktoren 80
538
Positionssystem 7
Potentialgleichung 385
Potenzen 10 f.
––, Rechenregeln 11
Potenzfunktionen 88 ff.
Potenzieren einer komplexen Zahl 233 f.
Potenzregeln 11
Potenzreihen 182 ff.
––, Konvergenzbereich 183
––, Konvergenzradius 183
––, Tabelle 186 ff.
p-reihige Unterdeterminante 207
Primfaktoren 3
primitive Periode 70
Primzahl 3
Prisma 33 f.
––, gerades 34
––, reguläres 34
––, schiefes 33
Produkt von Ereignissen 406
–– von Zufallsvariablen 431 f.
Produktdarstellung einer Polynomfunktion
79 f.
Produktform einer Parabel 79
Produktintegration 156
Produktregel der Differentialrechnung 133
–– der Vektoranalysis 370
Projektion eines Vektors 53
Prüfverfahren, statistische 456 ff.
Prüfverteilungen 432 ff.
Punktschätzungen 446
Punkt-Richtungs-Form einer Ebene 60
–– einer Geraden 57
Punkt-Steigungs-Form einer Geraden 76
punktsymmetrische Funktion 69
Punktwolke 314
Pyramide 34
––, dreiseitige 35
––, gleichseitige 34
––, reguläre 34
Pyramidenstumpf 35
Pythagoras, hyperbolischer 109
––, Satz des Pythagoras 26
––, trigonometrischer 95
Q
Quader 34
Quadrantenregel für trigonometrische
Funktionen 93
Sachwortverzeichnis
Quadrat 30
quadratische Funktionen 78 f.
–– Gleichungen 18
–– Matrix 201
quadratischer Mittelwert einer Funktion 169
quadratisches lineares Gleichungssystem 215
Quadratwurzel 11
Quantile der Chi-Quadrat-Verteilung
(Tabelle) 518
–– der Standardnormalverteilung 426 f.
–– der Standardnormalverteilung (Tabelle)
516
–– der t-Verteilung (Tabelle) 520
Quelldichte 382
Quelle 382
quellenfreies Vektorfeld 382, 384
Quellstärke pro Volumeneinheit 382
Quotientenkriterium 179
Quotientenregel der Differentialrechnung
134
R
radialsymmetrisches Vektorfeld 379
Radikand 11
Radizieren 11
–– einer komplexen Zahl 234
Rampenfunktion 359
Randbedingungen 271
Randverteilungen 429
Randwerte 271
Randwertproblem 271
Rang einer Matrix 207
rationale Zahlen 4
räumliche Kurven 368 ff.
räumlicher Integrationsbereich 264
räumliches Koordinatensystem 44 f.
–– Vektorfeld 379
Raute 31
Realteil einer komplexen Matrix 222
–– einer komplexen Zahl 228
Rechenregeln für Beträge 6
–– für Divergenzen 382
–– für Erwartungswerte 416 f.
–– für Faltungsprodukte 334, 352
–– für Gradienten 381
–– für Grenzwerte 72 f.
–– für komplexe Matrizen 223
–– für komplexe Zahlen 231 ff.
–– für Logarithmen 13
Sachwortververzeichnis
–– für Matrizen 203 f.
–– für n-reihige Determinanten 212 f.
–– für Potenzen 11
–– für relative Häufigkeiten 407
–– für Rotationen 384
–– für Vektoren 50 f., 55 f.
–– für Wahrscheinlichkeiten 408
–– für Wurzeln 12
Rechteck 30
Rechteckimpuls 195, 325, 356
Rechteckskurve 195, 355
rechtshändiges System 48
Rechtskrümmung 140 f., 373
Rechtssystem 48, 53
rechtwinklige Hyperbel 121
–– Koordinaten 41, 44
rechtwinkliges Dreieck 29
reduziertes Polynom 79
Reduzierung einer Polynomfunktion 81
reelle Achse 228
–– –– einer Hyperbel 119
reelle Matrizen 198 ff.
–– Zahlen 2 ff.
Regel von Sarrus 210
Regressionsgerade 313 f.
Regressionsparabel 315
regula falsi 23
reguläre Matrix 205
–– Pyramide 34
reguläres n-Eck 32
–– Prisma 34
–– Tetraeder 35
Reihe 16
––, absolut konvergente 178, 181
––, arithmetische 16
––, bestimmt divergente 178
––, Bildungsgesetz 16
––, binomische 186
––, divergente 178
––, Eigenschaften 181
––, endliche 16
––, Fourier-Reihe 190 ff.
––, geometrische 16, 181
––, konvergente 178, 181
––, Konvergenzkriterien 179 ff.
––, Mac Laurinsche 185
––, Potenzreihe 182 ff.
––, Taylorsche 185
––, unendliche 178 ff.
539
Reihen der Areafunktionen 188
–– der Arkusfunktionen 187
–– der Exponentialfunktionen 186
–– der Hyperbelfunktionen 187 f.
–– der logarithmischen Funktionen 187
–– der trigonometrischen Funktionen 187
relative Extremwerte 142 f., 254 f.
–– ––, allgemeines Kriterium 143
relative Häufigkeit 407
–– –– eines Stichprobenwertes 437
relatives Maximum 142 f., 254 f.
–– Minimum 142 f., 254 f.
Resonanzfall 295
Resonanzkreisfrequenz 295
Restglied 184
–– nach Lagrange 184
Restmenge 2
Rhombus 31
Richtungsableitung 381
Richtungskosinus 49
Richtungsvektor einer Geraden 57
Richtungsvektoren einer Ebene 60
Richtungswinkel eines Vektors 49
Rollkurve 124
Romberg-Verfahren 164 f.
Rotation eines Vektorfeldes 383 f.
–– –– ––, Determinantenschreibweise 383
–– –– ––, Rechenregeln 384
Rotation in kartesischen Koordinaten 383
–– in Kugelkoordinaten 392
–– in Polarkoordinaten 387
–– in Zylinderkoordinaten 389
Rotationsellipsoid 39
Rotationsfläche 175 f., 245 f.
Rotationskörper, Mantelfläche 175
––, Massenträgheitsmoment 176 f., 269
––, Schwerpunkt 165 f., 268
––, Volumen 173 f., 267
Rotationsparaboloid 39
Rotationsvolumen 173 f.
rotierender Zeiger 99
Rundungsregeln für reelle Zahlen 5
Runge-Kutta-Verfahren 2. Ordnung 279 f.
–– 4. Ordnung 280 ff., 288 f.
S
Sägezahnfunktion 357
Sägezahnimpuls 196
Sarrus, Regel von Sarrus 210
540
Sattelpunkt 144
Sättigungsfunktion 105 f.
Satz des Euklid 27
–– des Pythagoras 26
–– des Thales 27
–– über Linearkombinationen 329, 345
–– von Schwarz 249
–– von Steiner 172, 176
Schachbrettregel 211
Schätzfunktion 446
––, effiziente 447
––, erwartungstreue 446
––, konsistente 447
Schätzfunktionen für unbekannte Parameter
446 ff.
Schätzmethoden, statistische 446 ff.
Schätzungen für den Anteilswert 448
–– für den Erwartungswert 447
–– für den Mittelwert 447
–– für die Varianz 447
Schätzwerte für den Parameter einer
Binomialverteilung 448
–– –– –– –– einer Exponentialverteilung
448
–– –– –– –– einer Gaußschen Normalverteilung 448
–– –– –– –– einer Poisson-Verteilung 448
Schätzwerte für unbekannte Parameter 446 ff.
Schaubild 68
Scheitelgleichung einer Parabel 122
Scheitelpunkt einer Parabel 78, 122
Scheitelpunkte einer Hyperbel 119
Scheitelpunktsform einer Parabel 79
schiefes Prisma 33
schiefhermitesche Matrix 224
schiefsymmetrische Matrix 202
Schleifenkurve 127
Schnittgerade zweier Ebenen 66
Schnittkurvendiagramm 244
Schnittmenge 2
Schnittpunkt einer Geraden mit einer Ebene
65
–– zweier Geraden 60
Schnittwinkel einer Geraden mit einer Ebene
65
–– zweier Ebenen 66
–– zweier Geraden 60, 78
–– zweier Vektoren 52
schwache Dämpfung 292
Sachwortverzeichnis
Schwarz, Satz von Schwarz 249
Schwerpunkt einer homogenen ebenen Fläche
171 f., 261 f.
–– eines homogenen Körpers 268
–– eines homogenen Rotationskörpers
175 f., 268
Schwerpunktachse 172, 176
Schwingung, aperiodischer Grenzfall 293
––, aperiodisches Verhalten 293
––, erzwungene 294 f.
––, freie gedämpfte 292 f.
––, freie ungedämpfte 291
––, harmonische 99, 240
––, Kosinusschwingung 99
––, mechanische 291 ff.
––, Sinusschwingung 99
––, Superpositionsprinzip 100
Schwingungsamplitude 294
Schwingungsdauer 99
Schwingungsfall 292
Schwingungsgleichung der Mechanik 291
Schwingungslehre 98 ff.
sicheres Ereignis 407
Sicherheit, statistische 449
Sigmafunktion 323
Signum einer reellen Zahl 6
Simpsonsche Formel 162 f.
singuläre Lösung einer Differentialgleichung
270
–– Matrix 205
Sinus hyperbolicus 108
Sinusfunktion 93, 357
––, allgemeine 98
Sinusimpuls 197, 358
Sinussatz 28
Sinusschwingung 99, 357
––, gedämpfte 358
s-Funktion 323
Skalar 46
skalare Vektorkomponente 48
Skalarfeld 378
–– in Kugelkoordinaten 392
–– in Polarkoordinaten 386
–– in Zylinderkoordinaten 389
Skalarprodukt 51 f., 199
Spaltenindex einer Matrix 200
Spaltenmatrix 201
Spaltenvektor 48, 198
–– einer Matrix 200 f.
Sachwortververzeichnis
Spaltenzahl einer Matrix 200
Spannweite einer Stichprobe 437
Spat 34
Spatprodukt 55 f.
Spektraldichte 316, 319
spektrale Amplitudendichte 319
–– Phasendichte 319
Spektralfunktion 319
Spektrum 319
spezielle binomische Reihen 186
–– Dreiecke 29 f.
–– Exponentialfunktionen 105
–– Fourier-Reihen (Tabelle) 195 ff.
–– Fourier-Transformationen (Tabellen)
338 ff.
–– Integrale (Integraltafel) 476 ff.
–– Integralsubstitutionen (Tabelle) 154 f.
–– komplexe Matrizen 224 f.
–– konvergente Reihen 181 f.
–– Kurven 124 ff.
–– Laplace-Transformationen (Tabelle)
355 ff., 363 ff.
–– Logarithmusfunktionen 107 f.
–– Lösung einer Differentialgleichung 270
–– Potenzreihenentwicklungen (Tabelle)
186 ff.
–– quadratische Matrizen 201 ff.
–– Vektorfelder 379, 384 f.
–– Zahlenreihen 16 f.
sphärische Krümmung 39
spiegelsymmetrische Funktion 69
Spirale 129
––, archimedische 129
––, logarithmische 129
Sprungfunktion 323, 355
Sprungunstetigkeit 75
Spur einer Matrix 202
Stabdiagramm 413, 437, 440
Staffelbild 440
Stammfunktion 148, 150
Stammintegrale (Tabelle) 152
Standardabweichung 304
–– der Einzelmessung 305
–– der Standardnormalverteilung 424
–– des Mittelwertes 306
–– einer Binomialverteilung 418
–– einer Chi-Quadrat-Verteilung 432
–– einer Exponentialverteilung 427
–– einer hypergeometrischen Verteilung 420
541
–– einer Normalverteilung 423
–– einer Poisson-Verteilung 421
–– einer Stichprobe 442
–– einer t-Verteilung 434
–– einer Zufallsvariablen 416
Standardeinheiten 424
standardisierte Normalverteilung 305,
424 ff.
Standardisierung der Gaußschen Normalverteilung 424
Standardnormalverteilung 424 ff.
––, Tabelle 514 ff.
stationäres Skalarfeld 378
statisches Moment 171
Statistik 436 ff.
statistische Hypothese 456
–– Prüfverfahren für unbekannte Parameter
456 ff.
–– Schätzmethoden 446 ff.
–– Sicherheit 306, 449
statistischer Wahrscheinlichkeitswert 408
Steigung einer Geraden 76
Steigungsschema 84
Steigungswinkel einer Geraden 76
Steiner, Satz von Steiner 172, 176
Stellenwertsystem 7
Stereometrie 33 ff.
Sternkurve 126
stetig differenzierbare Funktion 130
stetige Funktion 74
–– Verteilung 414
–– Wahrscheinlichkeitsverteilungen
423 ff.
–– Zufallsvariable 412
Stetigkeit einer Funktion 74
Stichprobe 436
––, geordnete 437, 439
––, gruppierte 439
––, Häufigkeitsfunktion 437, 440
––, Häufigkeitsverteilung 437
––, Kennwerte 442 f.
––, Maßzahlen 442 f.
––, Mittelwert 442
––, Spannweite 437
––, Standardabweichung 442
––, Summenhäufigkeitsfunktion 438
––, umfangreiche 439
––, Urliste 437
––, Varianz 442
542
––, Verteilungsfunktion 438, 441
––, Verteilungstabelle 437, 440
Stichproben, abhängige 460
––, korrelierte 460
––, unabhängige 460
––, verbundene 460
Stichprobenfunktion 446
Stichprobenvarianz 443
Stichprobenwerte 446
stochastisch unabhängige Ereignisse 410
–– –– Zufallsvariable 429
Summe von Ereignissen 406
–– von Zufallsvariablen 430 f.
Summenhäufigkeitsfunktion einer Stichprobe
438
Stokes’scher Integralsatz 401
Störfunktion 274, 284, 296
Störglied 274, 284, 296
Störvektor 300
Strahlensätze 27
Streckenzugverfahren von Euler 277 f.
streng monoton fallende Funktion 69
–– –– wachsende Funktion 69
Streuung 305
Strophoide 127
Stürzen einer Determinante 212
Stützpunkte 82, 163
Stützstellen 82, 162
Stützwerte 82, 162
Subtrahend 6
Subtraktion komplexer Zahlen 231
–– von Brüchen 9
–– von Matrizen 203
–– von Vektoren 50, 198
–– von Zahlen 6
Summand 6
Summenregel der Differentialrechnung
133
–– der Integralrechnung 149
–– der Vektoranalysis 370
Summenvektor 50
Superposition gleichfrequenter harmonischer Schwingungen 100
Superpositionsprinzip der Physik 100, 241
Symmetrie einer Funktion 69
symmetrische Matrix 202, 227
Systeme linearer Differentialgleichungen
1. Ordnung mit konstanten Koeffizienten
300 ff.
Sachwortverzeichnis
T
Tangens hyperbolicus 109
Tangensfunktion 94
Tangente 139
Tangenteneinheitsvektor 371
Tangentenvektor 369
–– an eine Flächenkurve 375
–– an eine Koordinatenlinie 374
–– einer ebenen Kurve 369
–– einer Raumkurve 369
Tangentenverfahren von Newton 24
Tangentialebene 251, 376 f.
Taylor-Reihen 184 ff.
Taylorsche Formel 184
–– Reihe 185
Taylorsches Polynom 184
Teilbarkeitsregeln für ganze Zahlen 4
Teilmenge 1
Teilschwerpunktsatz 172
Teilsumme 178
Terrassenpunkt 144
Test für den unbekannten Mittelwert einer
Normalverteilung bei bekannter Varianz
457 f.
–– für den unbekannten Mittelwert einer
Normalverteilung bei unbekannter
Varianz 459f.
–– für die Gleichheit der unbekannten
Mittelwerte zweier Normalverteilungen
460 ff.
–– für die unbekannte Varianz einer
Normalverteilung 466 ff.
–– für einen unbekannten Anteilswert
468 ff.
Testverteilungen 432 ff.
Tetraeder 35
––, reguläres 35
Thales, Satz des Thales 27
Tiefpunkt 143
Tonne 39
Torus 40
totales Differential einer Funktion 250 f.
totale Wahrscheinlichkeit 411
Transformationssätze der Fourier-Transformation 329 ff.
–– der Laplace-Transformation 345 ff.
Transponieren einer Matrix 201
Sachwortververzeichnis
transponierte Matrix 201
Trapez 31
Trapezformel 161 f.
Trennung der Variablen 271
Treppenfunktion 359, 413, 438, 441
trigonometrische Form einer komplexen
Zahl 229
–– Formeln 95 ff.
trigonometrische Funktionen 91 ff., 238
–– ––, Additionstheoreme 95, 239
–– ––, Reihen 187
trigonometrische Gleichung 22
trigonometrischer Pythagoras 95
triviale Lösung 216
t-Verteilung von Student 434
U
!berlagerung gleichfrequenter harmonischer
Schwingungen 241
umfangreiche Stichprobe 439
–– ––, Einteilung in Klassen 439
Umkehrfunktion 70
Umkehrmatrix 205
Umkreis eines Dreiecks 29
Umrechnungen zwischen den Areafunktionen
114
–– zwischen den Hyperbelfunktionen 110
–– zwischen den trigonometrischen Funktionen 95
unabhängige Stichproben 460
–– Variable 67, 243
–– Veränderliche 67, 243
unbestimmte Integration 151
unbestimmtes Integral 150 ff.
unecht gebrochenrationale Funktionen 86, 88
uneigentliche Integrale 167 f.
unendliche Intervalle 8
–– Mengen 1
–– Reihen 178 ff.
Unendlichkeitsstelle 74 f., 87
ungerade Funktion 69
Ungleichungen mit einer Unbekannten 25
unitäre Matrix 225
Unstetigkeiten 75
Unterdeterminante 206, 211
–– einer Matrix 207
–– p-ter Ordnung 207
untere Dreiecksmatrix 202
543
–– Integrationsgrenze 148
Unterfunktion 344
Untermenge 1
Unterreihe 180
Untersumme 147
Urliste 437
Urnenmodell 417, 419
Ursprungsgleichung einer Ellipse 117
–– einer Hyperbel 119
–– eines Kreises 116
V
Variable 67, 243
––, abhängige 67, 243
––, unabhängige 67, 243
Varianz 304
––, empirische 443
Varianz der Standardnormalverteilung 424
–– einer Binomialverteilung 418
–– einer Chi-Quadrat-Verteilung 432
–– einer Exponentialverteilung 427
–– einer hypergeometrischen Verteilung
420
–– einer Normalverteilung 423
–– einer Poisson-Verteilung 421
–– einer Stichprobe 442
–– einer t-Verteilung 434
–– einer Zufallsvariablen 416
Variation der Konstanten 274 f.
Variationen 404
–– mit Wiederholung 404
–– ohne Wiederholung 404
Vektor 46, 198
––, Betrag 49, 199
––, Differenzvektor 50
––, Einheitsvektor 46, 199
––, freier 46
––, gebundener 46
––, Gegenvektor 47
––, inverser 47
––, Komponenten 48, 198
––, Komponentendarstellung 48, 199
––, Koordinaten 48, 198
––, linienflüchtiger 46
––, n-dimensionaler 198
––, Normierung 51, 199
––, Nullvektor 46, 199
––, Ortsvektor 46
544
––, Richtungswinkel 49
––, Spaltenvektor 48, 198
––, Summenvektor 50
––, Verschiebungsvektor 56
––, Zeilenvektor 48, 198
Vektoranalysis 368 ff.
Vektordarstellung in Kugelkoordinaten 391
–– in Polarkoordinaten 386
–– in Zylinderkoordinaten 389
Vektoren, Addition 50, 198
––, antiparallele 47
––, äußeres Produkt 53 ff.
––, Basisvektoren 48, 199
––, gemischtes Produkt 55 f.
––, inneres Produkt 51 f., 199
––, kollineare 47
––, komplanare 56
––, Kreuzprodukt 53
––, linear abhängige 221 f.
––, Linearkombination 199
––, linear unabhängige 221 f.
––, Mehrfachprodukte 56
––, orthogonale 53, 199
––, parallele 47
––, Rechenregeln 50 f., 55 f., 198 f.
––, Skalarprodukt 51 f., 199
––, Spatprodukt 55 f.
––, Subtraktion 50, 198
––, Vektorprodukt 53 ff.
Vektorfeld 378 f.
––, axialsymmetrisches 379
––, ebenes 378
––, homogenes 379
––, konservatives 395
––, kugelsymmetrisches 379
––, quellenfreies 384
––, radialsymmetrisches 379
––, räumliches 379
––, wirbelfreies 384
––, zylindersymmetrisches 379
Vektorfeld in Kugelkoordinaten 392
–– in Polarkoordinaten 386
–– in Zylinderkoordinaten 389
Vektorfunktion 368
vektorielle Darstellung einer Ebene 60 ff.
–– –– einer Fläche 374
–– –– einer Geraden 57 ff.
–– –– einer Kurve 368
Vektorkomponenten 48
Sachwortverzeichnis
Vektorkoordinaten 48
Vektorpolygon 50
Vektorpotential 384
Vektorprodukt 53 ff.
Vektorrechnung 46 ff.
Veränderliche 67, 243
––, abhängige 67, 243
––, unabhängige 67, 243
verallgemeinerte Ableitung 328, 349
–– Fourier-Transformierte 328, 349
–– Funktion 326, 349
–– Kettenregel 250
verbundene Stichproben 460
Vereinigung von Ereignissen 406
–– von Mengen 2
Vereinigungsmenge 2
Vergleichskriterien für Reihen 180
Vergleichsreihe 180
verkettete Funktion 134
Verschiebungssätze der Fourier-Transformation 330 f.
–– –– ––, Frequenzverschiebungssatz 331
–– –– ––, Zeitverschiebungssatz 330
Verschiebungssätze der Laplace-Transformation 347 f.
Verschiebungsvektor 56
Vertauschungsregel der Integralrechnung
149
Vertauschungssatz der Fourier-Transformation 335
Verteilung, diskrete 413
––, stetige 414
Verteilungsdichtefunktion 304
Verteilungsfunktion der Standardnormalverteilung 424
–– der Standardnormalverteilung (Tabelle)
514
–– einer Binominalverteilung 418
–– einer Chi-Quadrat-Verteilung 432
–– einer diskreten Zufallsvariablen 413
–– einer Exponentialverteilung 427
–– einer gruppierten Stichprobe 441
–– einer hypergeometrischen Verteilung
419
–– einer mehrdimensionalen Zufallsvariablen 428
–– einer Normalverteilung 423
–– einer Poisson-Verteilung 421
–– einer stetigen Zufallsvariablen 414
Sachwortververzeichnis
–– einer Stichprobe 438
–– einer t-Verteilung 434
–– einer Zufallsvariablen 413 f.
Verteilungstabelle einer gruppierten Stichprobe 440
–– einer Stichprobe 437
Verteilungstest 471
Vertrauensbereich 306
Vertrauensgrenzen 306, 449
Vertrauensintervall 306
––, Musterbeispiel 455
Vertrauensintervalle 449 ff.
–– für den unbekannten Mittelwert einer
beliebigen Verteilung 452
–– für den unbekannten Mittelwert einer
Normalverteilung bei bekannter Varianz
450
–– für den unbekannten Mittelwert einer
Normalverteilung bei unbekannter
Varianz 451 f.
–– für die unbekannte Varianz einer
Normalverteilung 453
–– für einen unbekannten Anteilswert 454 f.
Vertrauensniveau 306, 449
Verzweigungspunkt 410
Vietascher Wurzelsatz 18 f.
vollständiges Differential einer Funktion
251 f.
–– –– einer Potentialfunktion 396
Volumen eines Rotationskörpers 173 f.
–– eines zylindrischen Körpers 267
Volumendifferential 264
Volumenelement 264
–– in Kugelkoordinaten 391
–– in Zylinderkoordinaten 389
W
Wachstumsfunktion 106
Wachstumsrate 106
wahrscheinlichster Messwert 304
Wahrscheinlichkeit 407 ff.
––, bedingte 409
––, Berechnung mit der Verteilungsfunktion
der Standardnormalverteilung 425 ff.
––, totale 411
Wahrscheinlichkeiten, Rechenregeln 408
Wahrscheinlichkeitsaxiome von Kolmogoroff 408
545
Wahrscheinlichkeitsdichtefunktion 414
Wahrscheinlichkeitsfunktion 413
–– einer Binomialverteilung 418
–– einer hypergeometrischen Verteilung
419
–– einer Poisson-Verteilung 421
Wahrscheinlichkeitsrechnung 403 ff.
Wahrscheinlichkeitsverteilung einer Summe
von Zufallsvariablen 431
–– einer Zufallsvariablen 412 ff.
–– von mehreren Zufallsvariablen 428
Wahrscheinlichkeitsverteilungen, diskrete
417 ff.
––, stetige 423 ff.
Wahrscheinlichkeitswert, empirischer 408
––, statistischer 408
Wälzwinkel 124
Wegunabängigkeit eines Kurvenintegrals
394 f.
–– eines Linienintegrals 394 f.
Wendepunkt 144
Wendetangente 144
Wertebereich einer Funktion 67, 243
Wertevorrat einer Funktion 67, 243
windschiefe Geraden 59
Winkelmaße 91
Wirbel 383
Wirbeldichte 383
Wirbelfeld 383
Wirbelfluss 402
wirbelfreies Vektorfeld 383 f.
Wronski-Determinante 284, 296
Würfel 34
Wurzel 11 f.
––, Rechenregeln 12
Wurzelexponent 11
Wurzelfunktionen 90
Wurzelgleichung 21
Wurzelkriterium 180
Wurzelziehen 11
Z
Zahl, Eulersche 104
––, ganze 4
––, imaginäre 228
––, irrationale 4
––, komplexe 228
––, natürliche 2
546
––, Primzahl 3
––, rationale 4
––, reelle 4
Zahlenfolge 71
Zahlengerade 5
Zahlensysteme 7
Zehnerlogarithmus 13, 108
Zehnersystem 7
Zeiger 99 f.
––, komplexer 240
Zeigerdiagramm 99 f., 240
Zeilenindex einer Matrix 200
Zeilenmatrix 201
Zeilenumformungen einer Matrix 219
Zeilenvektor 48, 198
–– einer Matrix 200 f.
Zeilenzahl einer Matrix 200
Zeitfunktion 240
zeitliche Mittelwerte einer periodischen
Funktion 169
Zeitverschiebungssatz der FourierTransformation 330
Zentralfeld 379
Zerlegung einer Polynomfunktion in
Linearfaktoren 80
–– in Primfaktoren 3
Zirkulation des Vektorfeldes 393
Zufallsexperiment 405
––, mehrstufiges 410f.
Zufallsgröße 412
Zufallsstichprobe 436
Zufallsvariable 304, 412
––, Dichtefunktion 414
Sachwortverzeichnis
––, diskrete 412
––, Erwartungswert 415
––, Kennwerte 415 ff.
––, Linearkombinationen 430
––, Maßzahlen 415 ff.
––, mehrdimensionale 428
––, Mittelwert 416
––, n-dimensionale 429
––, Produkte 430 f.
––, Standardabweichung 416
––, stetige 412
––, stochastisch unabhängige 429
––, Summen 430 f.
––, Varianz 416
––, Verteilung 413 f.
––, Verteilungsfunktion 413 f.
––, Wahrscheinlichkeitsdichtefunktion 414
––, Wahrscheinlichkeitsfunktion 413
––, zweidimensionale 428
Zufallsvektor 428 f.
zusammengesetzte Funktion 134
zusammengesetztes Ereignis 406
zweidimensionale Zufallsvariable 428
zweidimensionales Bereichsintegral 257
Zweierlogarithmus 13, 108
Zweiersystem 7
Zweig 410
Zwei-Punkte-Form einer Geraden 57, 77
zweireihige Determinante 209
Zweiweggleichrichtung 197, 358
Zykloide, gewöhnliche 124
Zylinderkoordinaten 44, 387
zylindersymmetrisches Vektorfeld 379