Text
ЖУКОВСКИЙ, Н. Ем проф.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ВОЗДУХОПЛАВАНИЯ.
ИЗДАНИЕ ВТОРОЕ (ПЕРВОЕ ПОСМЕРТНОЕ).
ПОД РЕДАКЦИЕЙ
Мяж.-мех. В. П. ВЕТЧИНКИНА я Н. Г. ЧЕНЦОВА.
С 354 ФИГ. В ТЕКСТЕ.
ГОСУДАРСТВЕННОЕ ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО.
Ч1Н/ J । | | J
"“'I мо7 й!11.
“"hcuh hoi H fyfy
«4 T5W О _N ,
< к“Я
ПРОВЕРЕНО 19Ш г.
Пролетарии всех стран, соединяйтесь!
Р. С. Ф. С. Р.
Научно-Технический Отдел В. С. Н. X.
В. Серия I Научно-Техническпя Библиотека. №> XIII—2
333-60/
ЖУКОВСКИЙ, Н. Е., проф.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ВОЗДУХОПЛАВАНИЯ.
С 354 ФИГ. В ТЕКСТЕ.
МЩЕНИЕ ВТОРОЕ (ПЕРВОЕ ПОСМЕРТНОЕ).
ПОД РЕДАКЦИЕЙ
ИНЖ. МЕХ. В. П. ВЕТЧИНКИНА и Н. Erf1 ЕНЦОВА.
Москва — 1925 г.
Без разрешения Гостехиздата перепечатка не допускается.
Ленинградский Г^блнт V 11547. Зак. Ч 131R. 5000 акз. [9*
Типо-Литографня .Красный Печатник41, Ленинград, Между народны Л, 75.
ПРЕДИСЛОВИЕ РЕДАКТОРОВ.
Первое издание настоящего курса бы го составлено но лекциям Н. Е. Жуковского, читанным в 1011—12 г.г. в Высшем Техническом Училище. Лекции записывались И Г. Ченцовым и стенографировались В. П. Ветчинкины.м, затем обрабатывались и подвергались окончательному редактированию совместно е Н. Е. При этом нередко делались добавления против прочитанного иа лекциях.
В начале 1011 г. книга была даиа для перевода иа французский язык, что и было вынолнсно С. К. Джевецким в Париже. При этом были добавлены выдержки из разных статей Н. Е., а именно: теория определения места центра парусности, вихревая теория лобового сопротивления, данная проф. Карманом, и глава о подобии (специально написанная для франц, издания). Отдел винтов вовсе не попал в перевод, так как Н. Е. призпал § 37 этого отдела (теория винта, опирающаяся иа общие теоремы динамики) ошибочным и по (лежащим переделке на основании новейших данных (теории идеального пропеллера и вихревой теории гребного винта). Открывшаяся мировая воПна не позволила, однако, Н Е. осуществить эти переделки, и отдел винтов ие был издав на франц, языке.
Настоящее посмертное издание представляет собою соединение ру <-ского первого и французских) изданий, немного пополненное как иозд-иейшимп работами Н. Е. в той же области, так и примечаниями редакции. Из работ Н. Е. вошлн сюда: признак установившегося вихревого движения в конце § 17 на стр. 118—120 (по лекциям Н. Е. 1918 г., записанным Б. С Стечкиным); вихревая теория лобового сопротивления для движения жидкости в трех измерениях (но работе Н. Е. 191R г., литогр. в трудах Ц. А. Г. И.).
Из добавлений и примечаний редакции важнейшими являются: новая кривая (фиг. 35 bis) сопротивления воздуха прн больших скоростях по баллистическим опытам Крапца и пояснение к ней (стр. 41 и 45); построение по точкам сети фиг. 162 и 163 и примечание об изотермических сетях (стр. 126—130); спектры обтекания крылообразного контура по испытаниям Гёттингенской Лаборатории в 1913 г (стр. 166 —168); фиг. 230* . 231“ и 231“ в теории Кармана (стр. 177—1781; добавление к теории идеальной мельницы и о 16 режимах лопастного винта (стр. 251 — 256); окончательные выражения для к. и. д. винтов Джевецкого (етр. 291—292) и Сабц-иина-Юры ва (етр. 298).
В теории винтов, согласно воле Н. Е„ был значительно изменен § 39, при чем изложение было дано, по возможности, словами И. Е. из его II’ статьи по Вихревой теории гребного винта (1918 г.). В £ 40 добавлена теория идеальной мельницы (по статье Н. Е. 1920 г.). Вее внесенные изменения и дополнения либо отмечены словами, либо поставлены в квадратные скобки (вводные фразы для связи между старыми и новыми частями текста, мелкие редакционные изменения, и т. п.). Кроме упомянутых в тексте тип. большую помощь в этом чрезвычайно трудном издании оказала В. В. Пантелеева, которой выражаем свою искреннюю признательность.
В заключение считаем своим долгом выразить глубокую благодарность Гоотехиздату, шедшему иам навстречу во всех наших пожеланиях, как папр., переделка клише, изменения и добавления в тексте даже посте второй корректуры, и т. н.
В. Ветчинки».
Москва, 5 мая 1925 г. д Чениов.
ОТ АВТОРА.
_Es liegt In der That, so ueit icb erhe, *ur Ze’t к “in Grund vor. die hydrodlnamL-schen Glolcnungen nicht liir den genaven Anedruck der uirklicb die Beuegungen der biusslgkeilen regie rende n Gh -etzezv balton*
H. Uelmholtg.
Я помещаю здегь яти • лова Гельмгольца, так как в курсе лекции, читанном мною в Мое., в i.< м Высшем Техническом Училище, я стараюсь связать богатый опытный материал, накопленный аэро ютам и чески ми лабораториями, с теоретическим иссле ганием рассматриваемых за 1ач г помощью основных уравнений гидро щнамшси и теорип вязкости жидкостей.
В прежнее время уравнения гидро л и нам и кп имели успешное приложение толы» к полно'брачному движению жидкости, к теории планетных форм и к истечению из со» у (ов- В настоящее время, после блестящих исследовании Ге тьмгольца вихрях и Кирхгоффа о струях жидкости, область гнчродинамич. еких >п лений. охкатнпемых точным' анализом, вег более и более расширяется.
Объяснение опытных зак нов сопротивления движущейся жп шости па погруженные в нее тела, которое в теориях Понгсле и Ген-Венана опиралось е приближением на теорему Борда, можем быть теперь дано более рациона шным спсмч»боч • !..• мощью анализа Ранкина для хороших форм моделей и г помощью ио»•тгдоваштй лорда Рэлея и профессоров Кутта и (’ А. Чаплыгина для пластинок Факторами, объясняющими ситу сопротивления и подъемную силу аэропланов, выступают действие срывающихся струп и образование около планов так называемой циркуляции скорости. Результаты исследований профессоров Кутта и Чап ш-гина проверяются теперь в аэродинамической лаборатории Московского Высшего Технического Училшпн, и наблюдения дают хорошее по гтвер-ж ,oniie грорпп.
Курс моих лекции ра •ля«т<,я на части: теоретическую и при-। чнуЮ. В теоретическую -iai ю включается весь лабораторный маге рь «л н.п •‘опротив 1енпем жидкостей и теории пропеллеров. Практиче екая чисть шключает в сеА» описание конструкций различных типов аэропланов и дирижаблей кмг.етп п теорией их у прав тения и уггой-Ч1ГВОСТЛ.
Профадсор И. 'JiijKoecKNii.
UWna пн* гЛ
ОГЛАВЛЕНИЕ
СТР.
Предисловие ко второму вздавню . - . . а
От автора. . . 4
Оглавление .
Основные уравнения гидродинамики н теоремы, нз ннх вытекающие.
I. Выаод основных уравиепнй гидродинамики в форме зйлсра 7
; 2. Теорема Зйлора......................................................... U
, 3. Теорема Бернутдв. щ
4 Теорема Борда . «4
Приближенная теория прямого в косого ударв.
5- Теория Salnt-\ enanta ц РопсеМ .5
$ 6. Теории Weilner'a 11 Soreau 25
7. Опыты над прямым ударом потока воздуха
Невнхревое движение жидкости к фрикционная теория сопротивления.
§ 3. Невнхревое движение жидкости 45
§ 9 Сопротивление шара 49
10. Сопротивление моделей . 56
§11. Аэродинамические спектры 64
- 12. Давление воздуха на решеткя 72
Опыты над косым ударом потока воздуха
• 13. Сопротивление пластинок при косом ударе ... . .... 74
14. Опытные исследования относительно положения центра парусности пластивок
Теория вихрей.
§ 15. Движение жидкой частицы (I теорема Гетьмго □> . 106
§ 16. Вихревые нити (11 теорема Гельмгольца) . цо
6 17. Теорема Tbomson°a ........ И5
! 18. Ill н IV теоремы Гельмгольца о ввхрях. . . 121
О поддерживающих планах аэроплана.
< 19. Плоскопараллельный поток воздуха ..... .123
2(). Основная теорема о поддерживающей снл> потока. . 135
- 21. Поток, обтекающий руль....................................... . 139
* 22. Поток, обтекающий дугообразные контуры . . 142
СТР
Опытные исследовании иаХ поддерживающими пяянами аэропланов.
а 23. Опвсанне плоской трубы В. Т 1. а ее рабочее формулы . 146
: 24. Теорема проф. С. Л- Чаплыгина................ . . . .............149
а 25. Исследование подъемной свлы н лобовогосопротивления для теоретических форм. 153
& 26. О центре давления поддерживающих пл анон . . . . ........ 156
. 27. Лобовое слпротивлевие поддерживающих планов.............. - - . . 164
э 28. Опытные исследования поддерживающих планов аэропланов: Бреге, Антуанетт, Райта. Блерио. Фирмана Анрно и Нью пора ... ......... ..... 1ь8
Вихревая теория лобового сопротивления
29. Вихревая теория лобового сопротивления, данная профессором Карманом . . . 176 30. Ввхргвая теория лобового сопротивления для движения жидкости в трех изме-
рениях . . 190
Вязкость воздухя.
31. Свлы вязкости. ................................................... .193
. 32. Уравнения движения вязкой жядкости. - 199
Теория нннта гелнкоптерного и гребного
. 33. Лабораторные приспособления для исследования воздушных винтов 203
§34 Общий обзор теоретических исследований винта . ... 214
§ 35. Теория Эйфеля, приложимая к подобным винтам . . . 21(1
3 Ь Понятие о шаге и о скольжевнн винта 220
? 37. Поверхность тнгп внвта . .................................... . . 221
; HI. Теория Фербера, основанная на принципе однородности формул механики . 225
Ч 33. Теории винта опирающаяся на общие теоремы динамики................ . 229
, 40. Эмпирически формулы выражающие тягу впита н секундную работу, потребную для его вращении н теории идеальной мельницы 249
Расчет аннтв для аэроплана или дирижабля.
41. Способ Проф. Жуковского для определения действия данного винта на данном летательном аппарате . ........ .... . 260
42. Задача Фербера . . . 262
• 43. Задача кап. А И. Шабе кого 263
44 Опыты Dorand'a. .... 266
• 45. Задача Dorand'a...................................... . 268
46. Исследование винтомоторной группы по способу капитана Duchtaea . . . 269
47 Построение характеристики винтомоторной группы но способу В. С. Маргулиса . 271 4к. Теория Вапкшо а. . ................................................. 27 i
49. Теория проф. Д. П. Рузского. ........ ... . - . 279
: 50. Теория С. К Джевецкого...................................... . . 283
I 51. Попытка построить вввт с постояв вой скоростью за винтом, принимая во вни-
мание подсасывающий эффект топастей (теория Г. X. Сабинина н Б. Н. Юрьева). 293 - 52. О подсасывающем действии винта прв большом числе лопастей - . . 209
§ М. О подобии 302
Основные уравнения гидродинамики и теоремы, из них вытекающие.
§ 1. Вывод основных уравнений гидродинамики в форме Эйлера.
Основная задача гидродинамики ставптея Эйлером следующим образом: он рассматривает текущий поток во всякой точке внутри жидкой массы и исследует, как изменяются величины, характеризующие движение жид-
кости, в различных точках пространства.
Пу отв проекции скорости на прямоугольные оси координат в какой либо точке пространства (х, у, г) будут и, г\ w в момент времени Л Эти скорости явятся, вообще говоря, функциями четырех переменных х, у, г и t\
для случая же движения установившегося и рискнин скорости н, г,
вполне определятся некоторыми функциями трех координат (г, у, г) рассматриваемой точки пространства.
Выделим мысленно частицу жидкости в виде элементарного прямоугольного параллелепипеда с бесконечно-малыми ребрами dx, dy, dz, параллельными осям координат (фиг. 1), и составим для нее уравнения движения, опираясь иа принцип д’Аламбера, что су мма проекций всех сил, действу ющих на какую-либо движу -щу юся систему, вместе с проекциями силы
w
инерции, равна нулю.
Кроме массовых сил, действующих на частицу, иа нее действуют еще силы гидродинамического давления па гранях параллелепипеда, ее ограничивающего. Если в центре параллелепипеда С (х, у, Z) давление будет р, то иа правой грани ЪЬ'с'с, находящейся вправо от центра на расстоянии давление будет
. др Дг
р + Х- у
а на юной грани aa'd'd, находящейся влево от центра на раетоянии давление будет др dx
2-
Рассуждая точно так же и относительно остальных граней параллете-пипеда, получим давления на граны abed, a'b'c'd', adb'b, dd’e’e соответственно равными
Л'. 1 оу 2 _ др dy йу 2 *
др dz
Р~Ь 2-
Тогда сумма проекций иа ось х сил гидродинамических давлений, действующих на поверхность элементарного параллелепипеда, будет
(р-& d« • d*~(p+ * t) & dx d‘J- d~
Точно так же, сумма проекций на ось у будет равна
— дР - dx • dy • dz, оу °
и сумма проекции иа ось г:
- -р dx • dy - dz. dz *
Если проекции силы, действующей на единицу массы, будут X, Y и Z (в случае действия одной силы тяжести, при вертикальном положении оси г-ов, А' — Y = 0; Z = — у, при чем g = 9,81 “1/.вс»), то проекции сил, действующих на Macej данного параллелепипеда, будут равны:
X у dx dy dz, Y • q - dx dy - dz, Z q • dx • dy - dz, где p —плотность жидкости, dx-dy-dz—объем рассматриваемого парал-ле лепит* ia, а р dx • dy - dz—масса жидкости, заполняющей этот объем. Ускорения частицы жидкости (х, у, г) в момепт времени t будут выражаться вторыми производными от координат данной частицы жидкости по времени, т.-е. полными производными:
tPx dPy tPz d&’ dfl ’ dfi-
Проекции сил инерции всего параллелепипеда по осям коордпнат 6yjjT равны:
— р • dx dy dz
— edxdy-dz-^,
» j j
-e-dx dy - dz
Теперь, согласно принципу д’Аламбера» напигпем, что суммы проекций сил гидродинамического давления, взятые о обратным знаком:
длр dx dy • dz,
OX V >
dy V *
• dx dy • dz
or 3
должны равняться сумме проекций всех сил. действующих па Macej параллелепипеда (включая и силы инерции». Тогда получим:
• dx dy • dz - A' g dx - dy • dz—y-dc-dy dz fy dx dy dzr—Y g dx . dy dz — g -dx-dy-dz ^-dx-dy dz Z • q - dx • dy • dz— о -dx-dy-dz
Сокращая эти уравнения па dx-dy-dz и юля затем на у. получим:
1 1
в ах at»’
1 ! <>
е d</ аР’ [
1 aP_ 7___л I
p dr dt’’ |
Эйлерово преобразование этого уравнения состоит в том, что оивыражает вторые произво щые от координат по времени через скорости и, т, w и первые их производные по координатам и по времени:
<Ря?_du___ди .ди dx . ди dy .ди dz____ди . д" дм ди
dP~dt ~ it 'to dt + oy at ~'u< dt~at~T~" dx ' iy Wiz'
Здесь d“t есть потная производная по времени от скорости определенной частицы жидкости; поэтому, составляя ее. надо было принять во внимание, что в выражении и изменяется как время t, явно в него входящее, так и координаты х, у, г (вследствие передвижения частицы жи (кости
Таким же образом получаем:
-Гу . Эр . Эе . Эг
АР ot дх Оу * dh * . d» . d<r дк ар= «4-"^ + “-^-: к Эг-гдг и. г. w отнесены к одной и топ же точке пространства (х, у, г) н ко времени /, а и = г =^, w = Вставив в уравнения (I) соответствующие значения и получим три Эйлеровых уравнения движения жидкости:
₽ 1
Q 1
V
. ap
' dx
ip.
iy
. & dg
ди dt
dt dw dt
du
-- «2
OX
dr
--и 2
dx
8w
—
dx
du du
oy dz
dv dv
V x----IC .
ду о»
дю dtc
dy cU
Из уравнений (31 мы должны определить проекции скорости и, г, w в давление р; все эти величины рассматриваем, как функции х, у, г и t.
Что касается до цтотности е, то, в зависимости от потачи теплоты, устанавливается связь
е = <f <РУ
Для определения «, г, w и р, как функций от х, у, г и t, у нас найдено только три уравнения (2). Для получения же недостающего четвертого пользуются условием неразрывности жидкости.
Уравнение неразрывности получится, если выразить аналитически, что разница в количестве жидкости, входящей в элементарный параллелепипед и выходящей из него, вызывает в нем соответственное изменение плотности, при чем весь объем параллелепипеда остается заполненным жидкостью. Если же этого нет, если жидкость разрывается так, что в параллелепипеде образуется пустота, то изменения плотности по количеству вышедшей из параллелепипеда жидкости и вошедшей в него нельзя будет определить, и уравнение неразрывности ие будет иметь места. В случае несжимаемой жидкости плотность постоянна, и пустота должна образоваться всегда, когда количество вышедшей из данного объема жидкости больше количества вошедшей в него.
Обратимся снова к нашему элементарному параллелепипеду (фиг 1) е ребрами dx, dy и dz, параллельными осям координат, и с центром х, у, г. Еелн провести через точку (к, у, г) (где и, с, ir—проекции скорости по осям кординат, а р — плотность) площадки, параллельные граням, отнесенные к единице площади, то массы жидкости, протекшие в единицу времени в сторону положительного направления осей координат, были бы равны сответствснно ри, pc, pw. Для граней же безкоиечно - малого параллелепипеда, находящихся от его средины соответственно иа расстояниях dx dy tfc «
— "2 ’ — 2 ’ ~ F’
эти массы должны измениться соответственно иа величины: dx_ dy d(pw) dx
d® 2 ’ dy 2 ’ dr ' 2 ’
Поэтому для левой грани параллелепипеда, находящейся на расстоянии— от центра, количество втекающей жидкости через единицу площади будет равно:
еи -?£“». *
а через всю грань, измеряему ю площадью dy dz, будет равно:
Количество жидкости, вытекающей через правую грань, середина которой отстоит от центра параллелепипеда иа расстоянии будет соответственно равняться:
dz.
Вычитая нз последнего уравнения предыдущее, узнаем, насколько количество жидкости, вытекшей через правую грань, превышает количество жидкости, вошедшей через лев\ю. Находим:
[₽« Г] dy dz - [₽„ -Ц₽“». dy . dz = a,g> -dx dy dz.
Подобные ж»* выражения получатся при рассмотрении количеств житкости протекающих через остальные грани:
dx dy dz.
dx dydz.
Гуммируя их, получим, что
p(₽«) + ^)+^₽r)| ,dj. d d [ дх 1 ду * dr ] *’ ’
есть количество жидкости, вытекшей из данного параллелепипеда, отнесенное к единице времени, пли вернее, уменьшение количества жидкости в данном параллелепипеде за единицу времени. Количество же жидкости, вытекшей из данного пара дле лепил еда за время dt, будет равно:
[^+в<‘+Т]13)
Это изменение количества жидкости внутри параллелепипеда отразится на изменении плотности внутри его Еста в начале элемента времени dt плотность была р, то в конце этого элемента плотность будет р -р ~ dt\ отсюда количество жидкости в пара 1Л«-депипеде в начале элемента времени dt было gdx, dy, dz, а в конце этого элемента будет + dx dy dz
Поэтом), вычитая на первого выражения второе, получим количество жи 1КОСТИ, вытекшей из элементарного пара ьлелепипеда за время dt, равным:
р dx dy dz — (р dx dy dz =— dx dy dz dt . . . . (t)
Приравнивая выражение (3) выражению (4), будем иметь:
[ + д-(° *'> - Э-4^] dx dy dzdt-% dx dy dz dt.
| ox dy dz J " dt *
Сокращая обе части на dx dy dz dt, получим:
Ъ t d M | » <4»») t Д n /к»
• «)
Это и есть j равнение неразрывности для общего случая движения упругой жидкости.
В случае жидкости несжимаемой плотность будет иметь постоянную величину для всех точек жидкости и для всякого" времени, так что
р= const; ^- = 0.
Тогда в уравнении неразрывности первый член отпадает, а в осталь) них р можно вынести из пот знаков дифференциала и иа него сократить. Окончательно, уравнение неразрывности для несжимаемой жидкости примет вид:
Для частного случая движения упругой жидкости — движения уста-повишегося, где плотность и проекции скорости и, г, г в данной точке не
меняются со временем, частные производные равны нулю:
Пи времени от этих величин
й₽ = 0- 0“=-о- 01 = о-
dt • dt ’ dt и’
£-0. ot
Поэтому, для установившегося движения уравнение неразрывности и уравнения Эйлера напишутся в таком ви le:
d(pw) , .Hptu 3z dy
dlqw)
IУ)
U)
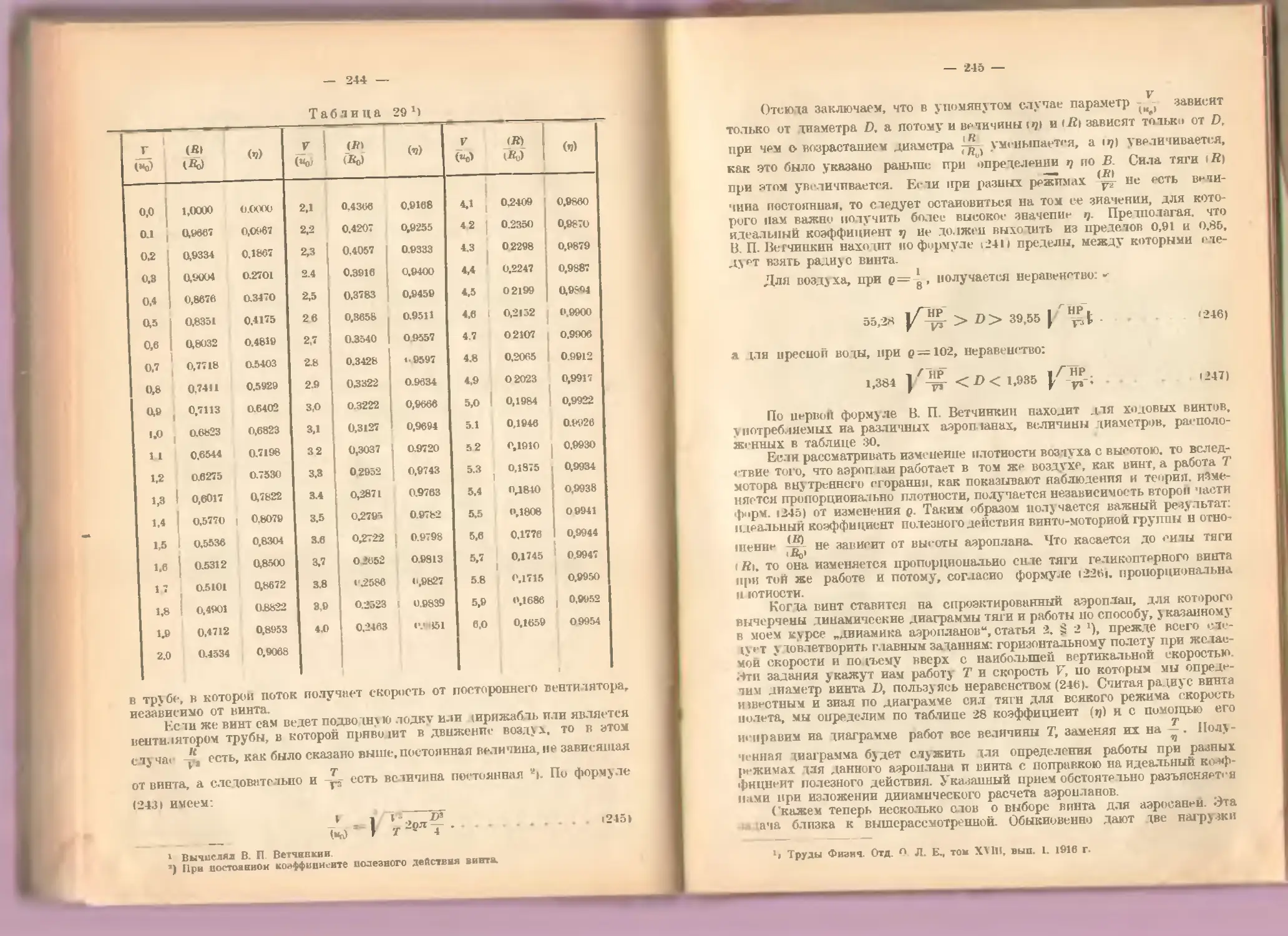
1 dp dx
1 dp
v dy
1 dp
₽ d:
du du
dy
Od i»T
M’
dy i .
В большинстве задач аэродинамики движение можно считать установившимся. Аэроплан летит с постоянною скоростью, и < корость частпц воздуха относительно аэроплана остается неизменной. Мы увидим впос ie i-ствни, что с большою степенью приближения можно в задачах г iiyj •»-плавания считать воздух несжимаемым и пользоваться уравнением неразрывности в виде (5’). Если бы мы хотели считаться со сжимаемостью воздуха, то нам пришлось бы нах лить 5 неизвестных: р, р. и, г и tr как функции х, у, г и t. при чем на лицо нме |ись бы только 4 у равнения: 3 уравнения Эйлера и четвертое — уравнение неразрывно-тн.
Для установления связи меж iy q и р считают p,i<-i чатриваглыи процесс изменения состояния воздуха, как происходящий при больших скоростях, адиабатическим, благодаря чему можно написать новое уравнение. выражающее зависимость между р и р.
Для адиабатического процесса — процесса, при котором тело не отдает наружу тепла и не получает сгм извне, зависимость между р н р будет такова:
я , .................... (в)
Р, Pol ’
где р и д, р0 и qo относятся к двум различным состояниям газа а постоянное у = —есть отношение уде юных, теп тот рассматриваемого газа: cf—удельной теплоты при постоянном (авлешш, е, удтьиой теплоты при постоянном объеме1).
Адиабатический процесс с >цр< нож дается ептьпым охлаждением при возрастании скорости. Вот почему при быстром полете аэроплана, при котором в окружающей его среде проис ходит адиабатический процесс, струя воздуха, окружающая аэроплан, оказывается несколько 2) хододне*-истального воздуха.
Все выведенные уравнения суть уравнения с частными производными. Инте1 рлрованне их представляет большие трудности.
Для разрешения вопросов вид :ухо л давания обыкновенно прибегают к некоторым гипотезам о потоке жидкости, оправдывающимся на опыте, и к общим теоремам, вытекающим пз дифференциальных уравнений аэродинамики. Такими теоремами являются: теорема Эйлера, теоремы Бернулли и Борда и теоремы Гетьмгольда о вихрях.
*) Для воздуха н некоторых других газов звачявне у= 1 40а
’) На 1сС нрв скорости 45 mt вес н на 5° при скорости * При и. ре '
- 2. Теорема Эйлера.
Теорема Эйлера, ик и вес Исследующие, относится к отучаю установившегося (внження. Бу дем принимать в дальнейшем изложении, что силы, юпствующие па массу частицы, равны нулю. По отношению к летящему аэроплану, все точки которого остаются приблизительно на одной высоте, те явления, которые вызываются силою тяжести, действующей на массу частицы, в частности — изменение давления, очень незна-чите 1ьны ice ли ограничиться сравнительно небольшими вертикальными перемещениями). Поэтому, при выводе уравнения Эйлера примем, что проекции но осям координат сил, действующих на единицу массы, равны нулю:
Л'=У=7=0.
Жпдкиоть при своем движении будет обтекать данную массу, образуя отдельные струи. Вес ьма тонкая струя получается так: вообразим в жид-кми некоторый малый замкнутый контур (фиг. 2, и проведем через его точки траектории частиц жидкости: тогда эти траектории образуют некоторую поверхность, которая называется поверх-ностью тока, она имеет форму трубки. Эту трубку, запол- и непную жидкостью, называют струей жидкости. VI
Выделим мысленно внутри текущей жидкости струю • (фиг. 3) и обрежем ее дву мя ортогональными к линиям тока сече- • ниями. Жидкость втекает через одно сечение и вытекает через ipyroe. Теорема Эйлера даст возможность найти равнодействую- »-щую всех енл гидродинамического .давления, действующих * на : различные точки поверхности етрупки нормально к поверхно- • / сти тока н к крайним ортогональным сечениям трубки. /
Представим все гидродинамические давления в виде сил; Ц// складывая этн силы, получим некоторую равнодействующую силу и пару. Теорема Эйлера дает возможность выразить их . 9
при ромощи ко.шчметв [вижепия жидкости, входящей в рассматриваемую трубку и выходящей из но** Именно, все силы гиipoдинамнческих давлений па поверхность струйки эквивалентны двум силам, из которых одна равна М1\ и приложена к точке В, в конце отру йки, а другая равна ИГ и приложена к точке J, в начале отру пки. Здесь V и —скорости, жидкости в сечениях В и Л, а М— масса жидкости, прохо [ялыя в единицу времени (секунду i через сечение трубки. В случае установившегося движения, М есть вс личина постоянная для (анной етруйкн п не зависит от времени.
Нерв.।я сила J/Г, сеть не что иное, как еекун шое количество дви-жрния жидкости в < • ченин В и принимается направленной по скорости, вторая же си. ы равна еекун хному количеству' движения жи (когти в сечении А и принимается направленной противоположно скорости. Гели эти силы пересекаются, т они имеют равнодействующую; если же не пересекаютс я, то силы изменяются < дн<»п силой и парой.
Д in вывода формулы Эйлера мы приложим к поверхности выделенной п обрезанной тру бочки жидкости — элементарной струйки — все силы гидродинамического давлеиия от окружающей среды и мысленно удалим вею жидкость, окружающую данную трубочку; то[да, если к массе "всякой точки жидкости, заключенной в трубочке, мы прибавим силы инерции, предварительно остановив жидкость, т<», по началу д‘Аламбера, получим равновесие данной системы.
Так как массовыми силами мы здесь пренебрегаем, то силы, эквивалентные всем силам гидродинамических давлений на трубку, должны быть эквивалентны силам, обратным силам инерции (ускорениям, умноженным на массы и направленным в сторону ускорений, т.-е. Smj). На основании этого, вместо того, чтобы искать равнодействующую ситу и пару для сил гидродинамического давления, будем искать их для сил mj.
Составим для этого суммы проекций сил mj на оси коорщнат
Sm • np,j; Im - upfJ; - m пр, J
Проекция пр,; есть производная проекции скорости Г, по времени, т.-е.
d Г, пр.7= Л ; поэтому
v v dl,
Z?«np,/ = 2m
Так как масса ие зависит от времени, то знак дифференцирования можно выиести за знак суммы, так что будем иметь:
2’ т пр, j = 2 т 1 - (т Г.) = ~ 2 т Г, . . (7|
Рассмотрим изменение количества движения I т V* в промежуток времени dt.
В момент t жидкость занимает часть трубочки от 4 до В, в момент t-\-dt жидкость передвинется вперед и займет новое положение от А' до В' (фиг. 3). Так как движение установившееся, т.-е. во всякой точке трубочки скорость не меняется со временем, то количество движения жидкости, заключающейся
*7» между А' и В для обоих моментов времени t и t-^-dt будет одинаково. Разница в количестве «Я движения {d 2 т У,) будет вызываться тем
/у обстоятельством, что во второй момент про-
/CZ падет некоторое количество движения жпдко-
Ууу рти от сечения А до сечения Л' и появится
новое количество движения жидкости от В до В1.
Пусть « ек^ндная масса протекающей жид-
А—-------------i кости равна jf; тогда за время dt протечет
/ масса Mdt. Эго будет масса жидкости, заклю-
/ чающейся между сечеипями А и А' или В и В1.
ФНГ. з. Если скорость в сечении А равна У, а в сечении
В равна Ц, то количество движения жидкости между сечениями А и А' равно MVdt, а количество движения жидкости между сечениями В и В' равно MVydt. Проекции количеств движений иа ось гг будут соответственно МУЙ/cos а и dt cos а, где а и аг — углы между направлениями скоростей и осью х. Разность количеств движения масс жидкости, находящихся между сечениями А и Л', и В и В',
MVX dt eos а, — W dt cos а, должна равняться изменению количества движения dim У, выделенной части струи АВ за время dt Поэтому,
dim У, = MVX dt cos а, — MV dt eos a и производная
2 m "P./= eosa,— MV cots a (8)
Такие же равенства получим для осей оу и ог:
2 т пр,> = М V, cos ft — MV cos ft )
2 m np.J — MV, cos y,—AfVcosy, j 11
где p и ft, у и у1 — углы скоростей V it V, с осями у и г
Подученные формулы доказывают, что, по приведении всех сил гидродинамических давлений иа CTpjftKy к сите и к паре мы получим силу, слагающуюся по правилу параллелограмма из сил W, и JfV.
Докажем теперь, что пара, полученная от сложения всех гидродинамических давлений при перенесении пх в точку О, равна паре, полученной от перенесения сил -VI' и .1/V, в эту точку.
Дтя этого обнаружим, что проекция моментов количеств движения относительно каждой из осей координат равна моменту гн (родпнампческих давлений относительно тех же осей.
Так как в рассматриваемом случае силы гидродинамического давления эквивалентны силам mJ, то моменты их будут равны моментам сил mj. Поэтому, моменты сил гидродинамического давления относительно осей координат будут
2 т (у пр,_/ — г пр,у),
2 т (г пр,/ — х пр.Д,
2 т (xnp.J— у пр,;).
Заменяя величины ускорения частиц равными им иодными производными но времени от проекции V,, V,, V. скоростей тех же частиц, получим для момента относительно оси х.
2 m (у пр.; — г пр,;) = 2 т I У jf - г л J.
Это выражение тождественно равно
л 2 т ly V, — г V,).
В самом деле, производя дифференцирование написанной суммы получим:
4 2 т (у V, - г V,) = S т ( у V. * - г -- V, .
а так как
то постедиее тождество примет вид:
й „ , л v d V- \
“2m (у V.-г и.) = 2т(,у'4ч V, V.-г *’- V, V.) =
v / d V Л У у - ,
что и требовалось доказать.
Итак, момент сил гидродинамического давления относительно осн х равен:
(v к—® v,>- (*°)
т.-е. производной по времени (отиостительно той же оси) момента количеств движения всей рассматриваемой жидкости, заключенной в трубке.
Рассмотрим теперь изменение момента количеств движения за бес-конечио-малыц промежуток времени dt. Разобьем для этого жидкость, 1аключенную в трубке, на две части: от А то .4' и от А' до В для начального момента, и от ,4 до В и от В до If для конечного.
Количества движения жидкости, заключенной между сечениями А и В, бу дут один и те же в оба момента, так как мы считаем движение установившимся. Разница d - т (у V, — г V,) между моментами количеств движения в тот п другой момент времени будет равна разности между моментом количеств движения жидкости, заключенной между А и .4, и моментом количеств движения жидкости между В и В'.
Масса жидкости, находящаяся между сечениями Л и Л и В и В равна, по предыдущему, Mdt. Количество движения жидкости между А и А', по предыдущему, равно MVdt, а между В и В' — M\\dt.
Момент количеств движения жидкости, заключенной между сечениями .4 и А', относительно оси х будет:
MVdt (у cosy—г rosft),
где a, ft у —углы скорости V с осями х, у, г.
Момент количества движения жидкости, заключенной между В и В’ относительно той же осп, будет равен
MVydt (у, cosyj — et cos ft,»,
где o„ ft и д— углы скорости V, с осями х, у, г.
Разность моментов бу дет равна.
MdttylVl L -7,— Vt < -ft) Mdt (у Vet sy — г Vcosft = d - m (у V,— г V >.
Отсюда:
* 2’m iy V,—z P,» =
= M iy, Vt cosy,— с, V, cosft) W(y V— г I/cos ft . . (Jl) Следовательно, и момент относите 1ьио оси х сил гидродинамического давления, равный
£ 2т\у V.-г V,),
равен разности моментов относительно той же оси секундных количеств движения входящей и выходящей жидкости.
То же самое получится и для осей у и z.
Таким образом, мы, доказали, во-первых, что проекция равнодействующей гидродинамических дав тений на элементарную струйку равна разности проекций количеств движения жидкости выходящей и входящей, и, во-вторых, что проекция момента гитродинамических давлений равна разности проекций моментов количеств движения вытекающей и втекающей жидкости. Отсюда, все силы гидродинамических давлений иа поверхность трубки эквивалентны силам и AfV, из которых последняя направлена в сторонобратную скорости. Если существует равнодействующая всех гидродинамических дав пений на стр$ йку, то опа вполне совпадает по величине, направлению и положению е равнодействующей количеств движения вытекающей и втекающей жидкости.
В этом и состоит теорема Эйлера.
Мы доказали теорему Эйлера д «я слу чая струнки с весьма малым поперечным сечением, так как считали скорость жидкости во всем ортогональном сечении одинаковой. Легко распространить это доказательство н на струю конечных размеров.
Предположим, что внутри беспредельной жидкой массы летит дирижабль D (фиг. 4) Тогда, приложив как к дирижаблю, так и к частицам окружающей opt in скорость, равпую и противоположна ю скорости дирижабля, можно будет рассматривать дирижабль как бы иеподвижным, а поток окружающей среды (воздуха) натекающим на него. Охватим поток, натекающий иа дирижабль, поверхностью тока. ___________—
Для этого возьмем большой кон- / \ Mv
ту р и проведем через все его точки tt
траектории жидкости; получим етрую большого размера, окру- ___________
жепнуто поверхностью тока. Обре- .
жем эту струю двумя сечениями.
л
Н.
ортогональными к траекториям
струек; эти ортогональные сечения будут местом входа Vn выхода жидкости Разобьем одно из этих ортогональных сечений на весьма малые •лемснтарные площадки и, проведя через их контур траектории жидкости, разобьем рассматриваемый поток па весьма тонкие стру нки, которые н другое ортогональное сечение разделят на элементарные площадки. Вдали от дирижабля стройки будут прямолинейны, вблизи же его будут инеибаться.
Ко всякой такой тонкой струйке можно применить теорему .Эйлера дродинамическом давлении. Весь эффект гидродинамического давления тр\ ю конечных размеров можно заменить суммой гидро щнамнческих [епий на тонкие струйки, из которых она состоит
, В самом деле, так как гидродинамические давления на поверхностях.
их рассматриваемым тонким струйкам, будут равны по величин-противоположны по направлению, то при суммировании они сократятся; ^останутся лишь гидродинамические давления: па внешнюю боковую /поверхность струн конечных размеров, иа крайние сечения этой струи на поверхность жидкости, совпадающую с поверхностью дирижабля.
i Отсюда вытекает, что все эти силы гидродинамических давлений бУдГт эквивалентны силам, представленным количествами движения вытекающей и втекающей жидкости через крайние еечеиия иашеп «труи конечных размеров. Так как на далеком расстоянии от дирижабля давление равно атмосферному, то от сил гидродинамических давлений у нас останутся только силы давления дирижабля иа окружающий его воздух. Отсюда следует, что сопротивление воздуха движению дирижабля будет эквивалентно силам, которые равны секундным количествам движения жидкости, натекающей на дирижабль и оттекающей от него, при чем первые беру тся в направлении движения жидкости, а последние — в направлении, противоположном движению жидкости.
Только что изложенная теорема Эйлера может служить для определения полного давления движущейся жидкости иа погруженное
в нее тело.
Если можно измерить скорости жидкости (напр., анемометром) вокруг погруженного в нее тела и по ним вычислить количества движения, то можно определить и давление жидкости на это тело. При этом может получиться или одна равнодействующая сила, или сила и пара.
Было бы ошибочно полагать, что силы, действующие иа летящим аэроплан, еводятся только к одной равнодействующей; в общем случае, кроме иее, может существовать и некоторая пара сил. Это же замечание iipat •• тиво и для вогнутых пластинок.
Теорема Эйлера оказалась очень полезной при исследовании винт >в в аэродинамическом институте Д. П. Рябушяйского. При первоначальных
Теорегвческве всвовы Воиухоолвввавя.
опытах в этом институте сила тяги горизонтального винта, подсчитанная по сумме количеств движения в струе, отбрасываемой им вниз, совпадала очень близко с непосредственно измеренной.
§ 3. Теорема Бернулли.
С точки зрения общей механики теорема Берпулли есть теорема о живых силах. Применить теорему о живых силах к данному случаю мы можем потому, что рассматриваем лвижеипе жидкости, обтекающей неподвижные те ia, установившимся, так что связи ие зависят от времени.
Выде1им в масс жидкости отдельную струйку (фиг. 5), проведя через какой-.шбо бесконечно-малый зам-*S кн.\ тый конту р в<*е линин тока, и обрежем
лХЛ струйку двумя ортогональными к ним сечениями Л и В.
В течение элемента времени dt масса жи цсосгн 1В перейдет в новое поюжение А'В. При этом количество р жидкости, заключенное в каждом из за-
~штрихованных концов струи между з ' сечениями Л п Л', В и Я, будет равно
Фжг 5 М dt, где М — секундная масса жидкости,
прохотящая через всякое сечение выделенной струи.
Изменение всей живой силы ма«-сы выделенной жидкости равно работе всех внешних сит; в данном случае—только сил гядродинамического давления, так как силой тяжести мы пренебрегаем. Изменение живой силы выделенной части струйки за время dt будет равно разности живых сил этой струйки в конечном положении А'В' и начальном АВ, Кинетическую энергию (живую сиду) в конечный момент можно разделить иа две части: во-первых, между сечениями Л' и В и, во-вторых, между В и В , а в начальный момент — на части А 4' п А'В.
Кинетическая энергия жидкости, заключенной между сечсннямн Л' и В, остается без изменения в течение всего элемента времени dt; поэтому изменение ее для данной стройки жидкости будет равно разности кинетических энергий в заштрих ванных концах струйки ВВ' и Л 4’.
Обозначая скорость жи xki сти в точке Л через V, а в точке В через получим приращение живой силы стройки за времи dt равным ^(7-7).
Напншем теперь су мяу работ всех сил гидродинамического давления, действующих на выделенную часть струйки за время dt.
Пусть р и pt — давления на единицу площади в сечениях .-1 и В, а и С] — соответственные тиощатн сечений струйки. Тогда силы гидродинамического давления на площадки Л к В выразятся через ра в р^,. Так как давление р направлено по движению жидкости, а р, — против него, то работы этих си г соответственно будут:
\-paVdt и —p,at V, dt,
где V dt и V,dt — пути, пройденные сечениями Л и 73 за время dt. Работа сил гидродинамического давления, действующих на боковые поверхности струйки, равна ну лю, так как силы направ щны нормально к перемещениям жидкости. Следовательно, искомая работа равна
pa V dt—р^ V, dt.
Приравнивая изменение живой силы crpjH работе сит гидродинамического давления, получим:
Mdt (Ь: — -£) = — ЛА V,d« + po Vdt (12)
Такое уравнение получается для несжимаемой жидкости.
Если же жидкость сжимаема, то нужно принять во внимание, кроме работы сил гидродинамического (авления, еще работу расширении упругой жидкости: последняя получается за счет внутренней (тепловой) энергии газа. Работа расширения равна произведению давления на изменение объема; для подсчета этой работы разобьем выделенную струю на беско-нечпо-матые части. Применяя к этим элементарным частям рас,суждения, аналогичные тем, которые делались при рассмотрении изменения кинетической энергии и количеств движения, мы должны заключить, что за время dt элементарная масса (1 — 2) (см. фиг. 5), перейдя в положение (Г — 2'), изменит свой объем иа величину, равную разности объемов жидкости (2—2'), протекшей за время dt через сечение 2, и (1 — 1'), протекшей за то же время через сечение 1. Так как объем жидкости, протекающей через какое-либо сечение стру и. равен , где р — плотность жидкости, отнесенная к массе, то изменение элементарного обт,сма струи между сечениями П — 21 будет равно работа расширения данного
элемента объема будет pd ), работа же расширения за время dt всей
выделенном струн 4В будет равна:
.4
Тогда для сжимаемой жидкости получится уравнение-
^.pjdt^ — Pla, V,dt poVdt-rf pd{-“] ИЗ) A
В этой формуле можно сделать преобразования: aV п о V, — объемы жидкости, протекающей черев сечения J и В в единицу времени, можно выразить через секундную массу’ жидкости и плотность ее:
oV=-f и 0,^ = ", О Р|
где р м <>, — плотность жидкости в сечениях А и В. Тогда
v v
Pi®, Iю V = Pi 91— Р v
Замечая, что опрсде |енный интеграл, распространенный иа всю выделенную часть ЛВ струйки, равен
находим, что s
ЛА V, ро V I
Поэтому правую часть уравнения (13) можно написать в таком виде:
— dt [pjOx Vj — ро V]
или, вынося dt из под знака интеграла и интегрируя но частям, получим:
Отсю (а уравнение (13) примет такой вид:
. ИГ.» УГ8\ .. Г if .
I aL— j )«=—<» J a dp, и in, no сокращения на Mdt.
Наменян марсовую imothoitb р через где 7 — вееовая плотность или у le.ii.HHii вес (вес 1 тР жидкости), а д -ускорение сиды тяжести и деля обе части уравнения <±7) иа д, получим:
/*в
f * «о,
2д '-я J i А
Это н есть самое общее выражение теоремы Берну л.ш тля установившегося движения. В нем только нс принята во внимание разность высот сечений А и В.
Таким образом, разность скоростных высот (скоростною высотою называется высота, с которой те то должно упасть, чтобы приобрести данную скорость» в конце и начале струи выражается черед интеграл
Ф>
распространенный на всю струйку.
Значение этого интеграла для несжимаемой жидкости, ня которой 7= const, будет:
_ .............................................(16(
а для сжимаемой (газа) зависит от того теплового процесса, который происходит в струг жи (кости при се течении. Если жидкость течет, сохраняя одну и ту же температуру ‘бу дучп подогреваема в тех местах, где имеет большую скорость». т.-е. изменяется изотермически, то у пр<»~ порционатъно давлению р. Тогда при интчрироватш получаем 1«>гариф-мичеекую функцию давления
Для аэродинамики интересен процесс адиабатический, при котором жидкости не пхбщают и от пее не ошимают тепла. Этот процесс имеет место, когда жидкость (газ) течет очень быстро. В этом случае 1аз, приобретая большую скорость, выделяет из себя много теплоты п охлаждается: например, из кодла компрессора, из под большого манора, воздух выходит совершенно юло (ным.
Для воздуха, движущегося при работ, винтов, и при струях, обте-киющнх аэрон таны. нужно принять адиабитпчсекий процесс. Если бы •тп явления происходили медленно. то воз ух (например, за винтом) брат он тепло из окружающей среды, и процесс нриб шла тся бы к изотермическому; но, в виду больших скоростей, с которыми воздух выходит из иод винта, обмен тепля с окружающим в< <у\«лм нр будет иметь места, и процесс будет адиабатическим (да- гным с и-м политропных процессов;.
Дтя л 1н«1б«1ти*11 ckoio проц* л : изменю я по закону Пуассона:
.• а/ ;
ГДН
/< ;• ел.
В политропных процессах, выражаемых таким же уравнением, локауте 1ь полкгроиности д может иметь различное значение Например, в изотермическом процессе /* = I.
Пользуясь этою зависимостью удельного веса от давления, иайдем значение интеграла
А
зя сжимаемой жидкости при адпабатичсеком процесс /Л /1 Pi 1
* -ft:
Давление р очень велико, оно измеряется-в килограммах на кв. метр и для нижних слоев атмосферы будет равно 10300 leg mt1. Когда аэрон, тан летит, он держит под крыльями избыточное давление Др 20 — 25 кд wifJ ’). Следовательно, относительные изменения давления, « которыми имеют дело в аэродинамике, будут весьма малы | — - .Д*
Если теперь в ф-ле 17; вместо pt под< твить р Jp, то получим:
Л» 14 1 1 . 1-
I dP ____Pt “£L_ =______— р
J - 1 fT—/•' fr (Т — «л
til н|
Разлагая двучлеи [{1 — 1] ш бишоп Ньютона, будем иметь:
[(‘+Z '“‘1 ’ "-“'р+ -1 = 11 /.)-*/,
при чем внешпми степенями пренебрегаем. Ты да
=_| а₽ = _ '₽ . .(16)
./ 4U-W Р * ‘Р"
Таким образом, при малых - j" vui упругой жидкости можно
9 Теперь 40, 50 м до 70 kg тР.
Цри-н. ред.
выразить так же, как н для несжимаемой:
/dp _____J]? — P—Pi
7 7 7 ’
независимо от величины показателя полптроппоети д. Поэтому в аэродинамике (для упругой жидкости при малом формула Бернулли пишется так же, как и для несжимаемой жидкости 1), в виде
или чаще в вп ie
П I Р гл I р.
2S+;=#+F=eonsl....... •i,si
которое можно прочесть так: сумма скоростной и пьезометрической высот есть величина постоянная для данной струйки I пьезо метрической высотой в данной точке называется высота столба жидкости или газа с площадью основания, равной единице, вес которого равняется давлению в рассматриваемой точке). Нивеллпрная высота не входит в формулу, так как влиянием силы тяжести мы пренебрегаем.
Это уравнение выражает не что иное, как закон сохранения энергии для частицы жидкости, так как и пропорциональны кинетической энергии, а ? и — потенциальной энергии одной и той же частицы жидкости в два различные момента времени, когда она проходит через сечения А и В.
Из уравнения (18х) находйм, что разность давлений в двух точках одной и тон же струи равна
Ai>='3 fFS- гл= (19>-
так как '/=9,81 mt:sec2, а удельный вес для воздуха при температуре 15'С и 760 тт давления равен /=1,1225 leg mt\ то
7 [ кд вес* _ д 8 nit1 * отсюда
dp=Ie(F2^F‘2) • (10'>-
Это — форму та практического характера; в ней давлением выражено в килограммах иа кв. метр. Определяя избыток давления Др в какой-либо точке, мы должны под Г, потразумевать скорость воздуха в этой точке, а под Г — скорость воздуха на той же линии тока, в той точке ее, где давление р нам известно.
Из уравнения (18) следует, что в тех местах, где поток замедляется (напр., перед нилотом, летящим иа аэроплане), давление будет повышенным.
Формулы Эйлера н Бернулли можно вывести также из общих уравнений гидродинамики; при этом вывод формулы Эйлера будет несколько сложнее, нежели из уравнений количеств движения, и мы его ие приводим, а теоремы Берн\ лли — проще, чем из уравнения живых сил.
‘) Это справедливо при иыиешвнх скоростях полета.
Прил. ptd.
Общие ур<\вненля гидродинамики в форме Эйлера напишутся для установившегося движения (ести пренебречь внешними (объемными) силами, т.-с. принять X=Y= Z~ 0) следующим образом:
Составим полный дифференциал давления, умножая первое уравнение на dx, второе—на dy, третье—на dz и затем складывая их. При суммировании будем собирать вместе члены, в которые входит одна и та же скорость; тогда получим:
Лг 4- * р р лг р Зу р
= ; <1,1 ^dx+'^dy^ ’;dz)~
-w^dx+~d,j+ dz] ..(20)
Желая получить изменение давления по линии тока, ми не можем г же дать произвольных значении перемещениям <lr, dy, dz; они будут являться функциями дуги ds и бу тут пропорциональны проекциям скорости в данной точке, так что
dx =ndt. dy—rdt, dz = wdt ... . (21)
Вставляя эти значения в уравнения (20), получим: d;=-«b<i+v* <|Л-
,г j*if=
—к:^+7+п^=
=-<v)dI+v(* '?)*]....(“’
где Г= j/«-—г*Ци*-’ Рсть абсолютная скорость жидкой частицы по ее траектории. Выражение в квадратных скобках есть полный дифференциал от , взятый по линии тока. Поэтому сравнение (22) можно переписать так:
-*=<?);......(аз)
интегрируя уравнение (23) между пре (елами А и В (соответственно скорости V и ГД имеем:
т.-е. выражение, полученное ранее другим путем.
§ 4. Теорема Борда.
Переходя к теореме Борда отметим, что она имеет приближенный характер, таная лишь суммарное выражение ьтя явлений разрыва н так называемого удара в жи (кости.
При движении воздуха часто можно наблюдать в нем струи, врывающиеся с большой скоростью в области застоя (где воздух движется с меньшей скоростью, пли остается неподвижным); при этом на границах струи образуется поверхность разрыва.
Примером может служить струя воздуха, отбрасываемая со страшной скоростью пропеллером. На границе потока от гстиконтерпого винта, висящего в воздухе, можно наблюдать даже струп, направленные вверх, хотя сам винт отбрасывает воздудс вниз.
Благодаря разности скоростей, на поверхности разрыва получается тренне воздуха о воздух, вследствие чего образуются на ней вихри.
Явления трения воздуха представляют большую важность н необходимо было бы исследовать их обстоятельнее. В "капельных жидкостях они превосходно псследованы опытным путем; опытов же относительно трения воздуха чрезвычайно мало. Имеются только общие < )обряжения, которые дал Борда иа основании теоремы Карно об уг (аре:
Есди в какую-либо систему, движущуюся с опре (елейной скоростью, врывается другая, и скорость последней, затухая, принимает скорость первой, то потеря живой силы равна живой силе потерянных скоростей.
Эта теорема Карно, выведенная сначала ыя случая удара шаров, оказалась вполне применимой для всех с iy чаев у (ара.
Свою задачу' мы поставим следующим образом.
В трубе большого размера (фиг. 6) течет жи (кость с определенной скоростью Г,. Положим, что в этуйкмдкость врывается струя иод напором и <• большой скоростью Г. thkJito F > Г,. Тогда ворвавшаяся струя не сметается с главной, не разойдется ма юнъкнми струйками, а пойдет отдельной колонной, которая завихри-вастся по краям, расширяется и постепенно принимает скорость потока; при этом кинетическая энергия струи итчастп сохраняется в виде скоростной энергии, отчасти переходит в потенциальную, характеризуемую повышением гидродинамического давления, и некоторая часть ее расходуется на работу трения и на образование вихрей.
Не вдаваясь в рассмотрение промежуточных состояний врывающейся струи, воаьмем на ней два сечения Л и В: А — при выходе пз на-адка, где давление р и скорость Г; В—там, где уже установились давление р1 и скорость главного потока. В промежутке между этими сечениями произошло и закончилось явление удара. Поэтому, прилагая иа участке АВ теорему’ Бернулли, мы должны дополнить ее членом, выражающим потерю на удар, т.-е. написать ее в виде Борда:
Фнг. 6
ИЛИ
_ц£ = Pl _l (У т ПУ
^7 ‘ 7 2д у ' 2д
.(24)
р,__р = V1 _ Г,2 _(7—7,)»
7 7 27 Й 2д
(24').
( Г — Г )’
Тут Г— 1' пре югавляет потерянную скорость, а *' —потерянный на удар напор. Для практических подсчетов переписываем уравнение (2 Г) так:
^(-’гг.-ггг) -
‘ I.)....................(’5),
Потеря иа удар может достигать значите явной величины. Напр., у ннверситетская труба гонит возду х из вентилятора со скоростью 20 mt see. скорость же воздуха в помещении трубы (вестибюль университета) равна 5 mt все. Потеря напора на удар равпа <20^—’* £*11,5 mt воздушного столба, в то время как скоростная высота выбрасываемого воздуха равна к 20,5 mt. Следовательно, относительная потеря = = 0,56.
Теорему Борда следует употреблять там, где образуются поверхности раздела.
Когда воздух врывается из под большого напора в пространство е малым давлением, то он, по большей части, образует поверхности раздела. Когда же воздух подсасывается в отверстие, то струи, подходящие к отверстию, имеют непрерывное распределение. Напр., когда воздух всасывается с помощью вентилятора в трубу (галерею), то воздух из помещения устремляется в отверстие трубы в виде целого ряда мелких, непрерывно распределенных струек. Поверхности разрыва нигде не получится, удара не будет, и теорему Борда прилагать нс следует.
Равным образом, если иа фиг. 6 нижняя трубка открыта в комнату и воздух подсасывается потоком, идущим по большой трубе, то струя будет выходить из колена .4 со скоростью потока в трубе, н удара не будет.
Приближенная теория прямого и косого удара.
£ 5. Теория Saint Venant а и Poncelet.
Перейдем к применению теорем, выведенных из общих уравнений гидродинамики, к решению вопроса о давлении, которое оказывает текущая жидкость на тела, поставленные в потоке.
Вопрос этот по существу’ очень труден. Решение его может быть облегчено при помощи некоторых гипотез, которые мы делаем, исходя из непосредственных наблюдений иад явлениями.
Сначала Poncelet, а потом Saint-Venant стали иа ту точку зрения, что если тело находится в потоке жидкости, то оно заметно возмущает не весь поток, а только часть его.
Ести тело движется в неподвижной жидкости, то на некотором расстоянии от него, как можно наблюдать, жидкость почти совершений спокойна; около же тела частицы жидкости находятся в движении, и скорость их тем больше, чем ближе они к телу. Движущееся тело как бы увлекает за собою цилиндр жидкости.
Если же тело неподвижно, а жидкость течет, то. отсту пая от тела на некоторое расстояние, мы получаем скорости жидкости равными и параллельными скорости потока, а око до тела начинается заметное изменение скоростей.
Вследствие всего этого Poncelet предлагает задачу о беспредельном потоке заменить задачей о цилиндрическом потоке около тела и считать, что жидкость течет как бы в трубе. Так можно сделать потому, что
скорости вис ци.тпн ipa равны и параллельны. Размеры этой тру бы меняются в зависимости от тела; их можно найти из опыта.
Опыты над телами в широких бассейнах и озерах дают совершенно одинаковые результаты е опытами в каналах, если размеры последних достаточно велики по отношению к размерам теза.
Этот взгляд сначала был высказан I’oncelet в его классическом курсе практической механики, а потом в специальной статье Saint-Venant'a, которая была пометена в работах Парижской Академии На) к. Теория Saint-Venant a основана на итеях Poneelet.
Saint-Venant рассматривал вопрос о давлении потока, движущегося со скоростью F, на неподвижную пластинку.
На практике большее значение имеет случаи движения тела в неподвижной жидкости. К нему мы легко можем перейти от случая Saint-Venant’a, придавши как потоку, так и пластинке скорость V в обратном направлении; тогда сама пластинка будет двигаться со скоростью Г, а поток вдали от все будет неподвижен.
Для нас безразлично, рассматривать ли тот, или другой случай, так как с теоретической точки зрения давление иа пластинку, движущуюся в неподвижной жидкости, и давление иа неподвижную пластинку в движу щемся потоке буду т равны *).
Сделавши это замечание, изложим по Saint-Venant у вопрос о давлении потока на пластинку.
Согласно его воззрениям, вообразим, что пластинка с площадью F (фиг 7) находится в трубе с постоянной площадью поперечного сечения F, в которой течет жидкость слева г - г направо со скоростью Г.
; ; Выделим мысленно массу
__________ i v жидкости, окружающую данное
----------------;-------------- =3 I -р- тело и ограничениу ю стенками
: ’ : трубы и понеречными сечениями
: : к и F. настолько удаленными от
............ " 1,1 п тастинки, что изменения, которые.
<ь>г j внесла она в распределение ско-
ростей на сечениях, утратились. Применим к ней теорему Эйлера. На основании постоянства расхода, скорости на обоих сечениях, Г и Г, равны между собою и равны скорости потока, так как эффект изменения плотностей очень ничтожен.
Тогда секундные количества движения жидкости на левом и на правом сечениях будут одни и те же, и силы, нм соответствующие, взаимно уравновесятся. Поэтому и все гидродинамические давления должны сами между собой уравновеситься.
Обращаясь к последним, заметим, что, на основании теоремы Борда (уравнение 24), давление на левом сечении будет больше, чем на правом
Р> Pi.
так как при движении жидкости около пластинки произойдет некоторая потеря напора, потеря на удар.
Следовательно, иа выде генную массу жидкости извне действу ет слева направо разность гидродинамических давлений, равная
(Р Pi) F.
’) Практически хе между итямн случаями замечается разница (парадокс Du boat). См в иже.
С другой стороны, на нее действует справа налево давление R самой пластинки, которое и должно уравновесить внешние гидродинамические давления.
Поэтому искомая сила сопротивления пластинки равна
Я — (р — A) F ..................(а)
Как сила сопротивления жидкости, она направлена слева направо, а как сила давления пластинки на жидкость — справа налево.
Для установления зависимости между р и р} рассмотрим подробнее, как отдельные струйки, одна из которых представлена на фиг. 7, обтекают пластинку.
Фотографии спектров потока, полученные для воды, показывают, что в передней части потока (перед пластинкой) струи распределены непрерывно; дойдя до нластники, они огибают ее; около краев пластннкн получается наибольшее сжатие «'труп, и жидкость здесь будет течь с наибольшей скоростью U. За пластинкой эти струйки устремятся в текущий со скоростью Vt поток и еамн примут эту скорость, при чем произойдет удар, вызывающий потерю напора, равную — •
Напишем теперь уравнение Борда между сечениями F и F:
_£__Р1„ = г? _ и' (P-JiP
7 2д 2д ‘ 2д
Отсюда, так как V= разность гидродинамических давлений па крайних сечениях выделенной части потока
p-A=;i(i'-H=27,n(v-ir (6)
Что касается значения скорости U в наиболее сжатом месте стру и, то ее можно выразить через скорость V самого потока, пользуясь условием постоянства расхода (т.-е. количества протекающей через данное сечение жидкости) во всех сечениях трубы (при этом берем средние значения скоростей U и V).
Объем жидкости, протекающей через сечение F't равен VF’. В месте наибольшего сжатия (недалеко за пластинкой, по направлению течения) объем протекающей жидкости нельзя выразить через U(F'—F), так как площадь сечения потока в этом месте не будет равна площади кольцевого сечения F'—F, а будет меньше ее, потому что жидкость протекает около пластинки не параллельно трубе, а под некоторым углом (кроме того, скорости в этом сечении будут различны по величине). Поэтому на практике выражают этот объем таким образом: берут среднюю скорость U, множат ее иа F* — F и еще на некоторый опытный коэффициент расхода v. Тогда условно постоянства расхода будет:
VF'=vU(F'—F). . .(е)
откуда
Л=.. ...................«и
Из уравнений (о), (Ъ), (с') находим, что давление потока на пластинку пли
Д = Г2Г1н/--П- ‘]’^ = *ГГ2’..............(26)
Для получения числовой величины к мы должны из оныгл определить две величины: отношение и к для определения надо из наблюдений над обтекаемыми телами найти место, где жнлкость почти покоится и определить, как велика та площадь, которую те тахкатынает в своем движении. Отношение (ля пластинок Poncelet принимает на основании опытов Dubuat, равным 6.
Что касается коэффициента г, то он будет меняться в ави<*нмостн от формы тела. Poncelet полагал, что в данной задаче v можно принять равным 0.8.
Для тел под F нужно подразумевать площадь его миделевого ссче-ння Ч-
Вычисляя коэффициент к для воздуха, мы юлжны принять
2д 10 ’
тогда получим:
4=О,Об(-=/ г -11* 11=0.06 4 =0.09.
Таким образом, оказывается, что коэффициент к для воздуха получается очень хороший. Современный коэффициент для во?духа, найденный из очень большого числа точных опытов, равен о,он».
Если бы мы взятн трубу ие кру глупо. а какой-нибудь иной формы, в зависимости от формы испытуемой пластинки, то вывод был бы один и тот же, потому что он опирается только па теорему Борка.
Poncelet дает величину к только для воды. Мы видим, что,подчитывая его для воздуха, мы получим близкое к действительности число. Значение коффнцнента сопротивления 0,09 не согласовалось с прежними наб поденнями, из которых коэффициент получался с i шиком большим. Напр., Лилиенталь принимал его, согласно опытам Марся, равным о,13.
Saint-Venant свои рассуждения проводит очень широко; при рассмотрении сопротивления цилиндрических тел ои дважды прилагает теорему Ьорда, предполагая, что стру я срывается и производит у tap как при стейках, так и позади цилиндрических тел.
При определении сопротивления JE по изложенному способу возмо-F'
жен некоторый произвол в выборе отпошеиия F , так как очень трудно определить из наблюдении iv границы, за которыми жидкость уже не захватывается движением тела; теоретически эта граница лежит и 'еско-нечности, практически же — близко к телу.
Впоследствии мы рассмотрим это явление о iee полно с гидро шна-мической точки зрения. Теперь же перейдем к другому фу н ^ментальному вопросу.
6. Теория Wellner а и Soreau.
Теория Poncelet и Saint-Venanta относилась к случат• прямого удара на пластинку; но где речь идет о косом ударе, или об у аре для очень наклонных пластинок, который особеино важен в авиации, гам надо воли
*) Площадью мидолевого сечения называется площадь перпендикулярного сечения, описанного около тела цилиндра, образующие которого параллельны скорости тела относительно жидвостя. Это определение относится к телам всякой формы-
иные рассуждения. Эти рассуждения, которые выставляются на вид г ктышшствр теорий сопротивления, были сфпрму тированы Wellner’oM
и Sorcau. Korean в 1910 г. провел эти рассуждения еще дальше, опираясь иа данные современных опытов.
Wellner рассматривает явление, принимая, что пластинка изогнута • iy гс кру га и что воз iyx у щряет по направлению касательной к переднему краю пластинки (фиг. 8). Примем, что хорда наклонена под углом i к скорости потока вдали '-т пластинки, (’летательно, центральный угол, стягивающий |
лгу, равен 2/. V '
Вы ie 1мм некоторый < лон но i пластинкой «г*—”---------‘Д*
и на I ней. вне которого движение прлнехо- ' Я-
щт со скоростями, почти неизменными. / •
Wellner считает этот стон заключенным .-.fr
между двумя дугами и Для под- V | /
счета давления на пластинку он проводит (ве \ ' /
крайние радиальные н юскоети Л,Л2 и BLB.> \ i J _
(через начало п конец пластинки) и прнме- j j*
ияет теорему Эи iepa. \
Вес дав icunc пластинки па поток опрс- у Г /
ютится но количествам движения, так как у [ /
площади сечений А1А2 и В^ п средние ско- у|/
р(-**ти в нпх равны, а потому и in (родинами- V/
'«•••кие давления буду! одинаковы. ’
Чтобы найти давление пластинки на поток, Фиг 8.
нужно выходящие количества движения брать по направлению потока, а входящие—в сторону противоположную потоку.
Чтобы найти (авленпе потока на пластинку, нужно входящие количества движения брать но направ юпию потока, а выходящие — в нротиво-шиэжную сторону.
Так как скорости в каждом из крайних сечений предполагаются параллельными между гобою, то секундное количество движения на том и другом равно 1мГ, и приближенно можно положить его равным
Ml , га’
где Тш есть ер1' шяя скорость в данном тении, a ceKjnunaa масса
Г . 9 “
Тогда
V т р = ’ pv = 1) где F—площадь поперечного сечения выделенного стоя, приходящаяся на единицу длины пластинки. считая длину по направлению, перпендикулярному скорости потока. Обе эти силы действуют под углом i к хорде и дают равнодействующую, направленную вверх по среднему радиусу (фиг. 9); она будет равна
P=2F ? F2 sin/.
9
В эту формулу входит величина F’. Но нам интересно ввести в форму iy не Fl, a F, т,-е. площадь поддерживающей поверхности. Для этого, подобно тому, как при выводе формулы Saint-Venanta, делаем гипо-
Ч Soreau предлагает поправку к этой форму зе, вводя скорость каждой отдезьной струйки на основан пн своего гипотетического закона распределения скоростей.
тезу, что отношение площади поперечного ссчепия выделенного слоя к площади пластпнкп, равное отношению точщины слоя к глубине пластинки (но хорде), есть величина
Фиг- 9.
постоянная для данной пластинки и ие очень больших углов 7, т.-е. полагаем:
2/’* 24.Д.
~F= АВ ’=">= c°nst.
Тогда
Р — т — FV* star. я
Д <я воздуха - — ', ат, по опыт-9 В
ним данпым, для различных пластинок колеблется между 1,5 и 3,5, Обозначая т | = (при чем 0,2 < kt < 0,4), будем иметь следующее.
Потная сила давления на пластинку
Р=Л1Г48 sin 7; . . (28)
Подъемная сила
R кх FF® sin 7 cos 7;
.(29)
Сила сопротивления движению
Q = kxFV* sin® 7 ................(30)
Wellner распространяет форм. (28), (29) и (30) и на случай плоских пластинок и вогн$тых не по дуге кр^га. Разница будет только в величине коэффициента к}.
На основания рассуждений нац опытными данными и иад теорией этого вопроса Soreau вводит новый гипотетический закон убывания скорости по мерс удаления от пластинки, близкий к действительности. Для коэффициента klt Soreau брал сначала величину 0,33, а теперь, иа основании опытов Rateau, взял 0,24.
Наука обладает полным теоретическим решением задачи о давлении потока иа пластинку. Анализ профессора Kutta и проф. С. А. Чаплыгина, вместе с указанной мною общей теоремой о подъемной силе, дают возможность чисто теоретическим п^тем найти коэффициент кг для всех форм пластинок и углов наклонения их, а также отыскать формы пластинок, дающие большую подъемную силу. (В этих иесле юваниях пластинки считаются бесконечно длинными и трение жидкости не принимается во вниманпе).
Любопытно, что чистая теория дает для дуги кр^га Aj —0,39, т.-е. величину, лежащую внутри пределов, найденных опытом.
§ 7. Опыты иад прямым ударом потока воздуха.
Исходя из того положения, что площадь потока, оказывающего действие иа пластинку, приблизительно в 6 раз больше площади самой пластинки, мы получили коэффициент сопротивления пластинки в воздухе к = 0,09. Этот коэффициент не согласовался с результатами первоначальных опытов с воздухом, которые даЪалн значительно больший коэффициет (0,13).
— 31 —
Между тем, если перечислить для воздуха (принимая гипотезу Ньютона) самые первые опыты иад сопротивлением — опыты Dubuat и Duchemin'a с водою,— то они дают коаффицнепт, близкий к современному, полученному путем совершенных методов наблюдения.
Dubuat, а затем Duchemin работали самостоятельно и произвели довольно тщательно два ряда опытов: один — с доскою, движущейся в спокойной воде (на озере), другой — с неподвижною доскою в канате, прн чем последний был настолько широк, что стенки его не оказывали непосредственного влиянии на форму струй, обтекающих пластинку.
Для опытов они брали доску Л в форме квадратного узкого ящнка сделаны небольшие
(фиг. 10), в одной из широких стенок которого были отверстия (три по диагонали н три по стороне). Такая доска прикреплялась к стержню В, опускавшемуся с плота, который при опытах в канале укрепляли неподвижно, а при опытах на озере тащили равномерно на буксире (иа двух лодках с берега). В полость ящика вставлялась трубка С, в которой находился поплавок D, отмечавший уровень воды в ней.
Если заткнуть пробками все отверстия в доске, кроме одного, то уровень воты в трубке определит давление на поверхности доски около открытого отверстия. Если это давленые будет выше гидростатического, то поплавок поднимется выше свободного уровня воды, и наоборот.
Открывая поочередно разные отверстия, наблюдатели определяли давления в различных точках доски, устанавливая доску отверстиями вперед (по движению», а затем, поворачивая ее отверстиями назад, они определяли давление на передней и задней стороне е**.
По их опытам, в которых они пришли к одинаковым числовым результатам, оказалось, что иа передней стороне движущейся пластинки давление выше гидростатического, а на задней — ниже.
Dubuat первый указал, что давление иа пластинк} можно рассматривать слагающимся из двух сил: одной, соответствующей избытку давления на передней стороне пластинки, и другой, соответствующей v меньшеяию давления иа за шей стороне ее. Первую силу Dubuat предложил назвать „давлением*4, вторую — „недавлением44.
Что касается до распределения давлений на пластинке, то „давление44 в середине ее самое большое, а затем уменьшается, медленно падая около середины и резко — у самых краев. „Недавление1* остается почти постоянным на всей доске (на фиг. 11 представлены результаты опытов Stanton’а над прямым ударом в потоке воздуха).
Dubuat и Duchemin писали формулу давления в виде:
теперь же ми пишем прямо:
Следовательно, вместо равно '/1В, а для воды — 51).
нашего к онн писали д’" IJ дли воздуха
Остановимся сначала на первой гр\ пне опытов (1виж$ щаяся пластинка в неподвижной жидкости».
Коэффициент к „давтения* равным 1,
формулы Dubuat п Duchemina получился для откуда вытекает очень любопытное соотношение'
Фнг. п.
т.-е. „дав тонне** равно весу столба воды с площадью, равной площади пластинки, и высотою, равной скоростной высоте
„Подавление- Q равно весу того же столба воды, помноженному иа 0,433, т.-е.
Q = 0,433 ?F^.
Тогда полное давление на пластинку, движущуюся в озере, будет
K=P+Q=l,l3yF^1 т.-е. равно весу столба воды с площадью пластинки и вы-сотой , умноженному па 1,13.
Принимая гипотезу Ньютона, что давления различных жидкостей, при прочих равных условиях, пропорциональны плотностям их, мы получим давление на пластинку, ДВИЖУЩЕЮСЯ в воз-ду хе, в таком виде:
= 0,089 F\~*.
Отсюда коэффициент со-противтения и частники в воздухе.
к = 0,089.
Современный коэффициент к, полученный из многочисленных новых наблюдений, равен 0,055 при не очень больших скоростях (до 10 mt/sec). При больших же скоростях он уменьшается до 0,07.
Опыты второго типа (с неподвижном пластинкой в потоке воды; дали силу давления на пластинку
«, = 4,86-/F-Ц.
Таким образом, по опытам Dubnat и Duchemin’a, удар текущей жидкости на неподвижною пэастпнку больше сопротивления пластпнки, движущейся в спокойной жпдкостн, н их отношение
R, И
1,3.
— 83 —
В этом и состоит парадокс Dubuat.
С точки зрения теоретической механики, явления, имеющие место в том и другом случае, вполне обратимы (если ие принимать во внимание трения», и Ry должно быть равно R.
Но явления в природе нельзя считать обратимыми. Поток в канале ие соответствует тому, набегающему на пластинку, теоретическому иевихревому потоку (небольшие вихри будут только непосредственно за пластинкой), который мы получим, обращая движение пластинки в озере, т.-е. придавая всей системе (пластинке, воде, дну и берегам озера) скорость пластинкп в обратном направлении. В природе наблюдается вихревое движение потока: установившийся поток в канале весь заполнен вихрями, которые непрерывно образуются иа стенках вследствие трения о них жидкости, и, распространяясь в потоке» очень долго сохра
няются, пока не затухнут от внутреннего трения.
Непосредственные наблюдения показывают, что струи около пластинки при опытах первого и второго типа имеют различный характер.
Poncelet указывает, что если пластинка движется в спокойной * ____________
жи дкости, то стру и имеют вид, как иа фиг. 12. Позади пластинки наблюдается вихревое кольцо, которое следует за пластинкой, а струн огибают это кольцо и за ним смыкаются.
Когда же завихренный поток у харяет на пластинку, то струи приобретают вид, как на фиг. 13. Струи срываются с краев пластинки н за ией идут довольно длинным рядом вихрей и воронок.
Так как течение в этих двух случаях различно, то. попятно* н силы зывдется, что завихренный поток действует сильнее.
В том случае, когда движутся и воздух, и пластинка, сила будет
Фиг 12.
сопротив хення буду т разные. Ока-
Фиг 13
пропорциональна квадрату относите хьной скорости пластинки и воз.хуха, а коэффициент сопротивления, зависящий от степени завихренности воздуха, будет больше 0,085 (для спокойного воздуха).
Этим объясняется, почему Лилиенталь (Hlienthal), производивший все свои опыты на ветру, получил коэффициент сопротивления для пластинки столь высоким (0,13).
Полезно было бы провести параллельно ряд чистых и аккуратных опытов иа ветру и в спокойном воздухе.
Покойный проф. Ф. Е. Орлов много занимался парадоксом Dubuat, полагая, что он и теоретически законен в виду его несомненного существования в действительности. Чтобы доказать, что парадокс Dubuat исчезает, если осуществить иезавихрениый поток (напр., привести в .движение все озеро вместе с его дним и берегами), я построил вместе с моим учеником В. В. Кузнецовым прибор Ч схематически изображенный на фиг. 14.
’) Ои стоит теверь в фазическом отдела Политехнического музея.
ТаорАтвчвскме оежовы «aajieua ввоеж.
3
и стенками канала, когча, вследствие трения частиц жидкости о стенки, в ией должны образоваться вихри.
Завихренностью потока в природе и нужно объяснить парадокс Dubuat.
Обратимся теперь к приборам для определения коэффициента сопротивления пластинок при прямом ударе потока воздуха.
Прибор Магеу я (фит. 16) представляет собою маленьку ю ротативную машину, иа которой можно было вращать диски с большими скоростями (до 10 mt'sec}.
Магеу определял давление в разных точках лиска спереди и сзади, поднося к различным точкам его коленчатую трубку т, вращавшуюся вместе с диском и передававшую давление неполвижному манометру при помощи с «едующего ирнспособ-тсння (фиг. 17): трубка т входила в пустотелую ось к. Внутрь этой оси входил трубчатый же шпиль и. который служил пятою для ’ Я прибора. В шпиле п были еде- . '
таны отверстия гх. Наблюдаемое II
.автеиие передавалось через ырки v и г, н трубку и
фиг. Т8.
в камеру’ L, а оттуда по трубкам р и q (каучгковая) к очень чувстви-тетьному манометру. Чтобы отделить полость между трубками к и п от внешнего воздуха, трубка к погружалась в ртутную ванну Q.
Общее расположение прибора Магеу’я во время опыта проставлено на фиг. 18.
При помогай своего прибора Магеу опред* лял для разных точек шока величины „давления" спереди и „недавления" сзади и установил из <гих опытов очень высокий коэффициент еопротивтения, равный 0.13. За Маге у’ем и остальные авторы и исследователи стали принимать это число, и оно долго держалось в научной литературе.
Причина, почему у Магеу’я потупился коэффициент сопротивления ci ть высоким, была та, что он производил опыты на короткоплечей
ротативной машине, и у него не было чистого нормального удара иа пластинку: вследствие центробежной силы у Матеу я получался поток, отчасти скользящий по самой пластинке, и сопро-
тивление воздуха, благодаря этому, сильно увеличивалось. На фиг. 19 указано направление струй этого скользящего потока.
Colardeau и Eiffel определяли коэффициент со противления на прямолинейном пути, для чего воспользовались башней Эйфеля (фиг. 2Oi, заставляя испытуемые тела падать со второго этажа ее (около 120 mt на i землею).
Colardeau первый нашел, что коэффициент 0,13 очень велик н что на самом деле он значительно ниже
Фиг 21.
Фнг. 19.
Фяг 20.
В его опытах испытуемые тела (гирю падали свободно, при чем увлекали за собою шелковинку, сматы-вавшу юси без ео-протйв. ишия с веретен особого типа (фиг. 21). Шелковинка была намотана на несколько (шесты веретен по 20 mt на каждом. При переходе с одного веретена на другое она размыкала контакт и этим отмечала соответствующие моменты на равномерно вращающемся барабане, иа котором каммер-тои чертил непрерывную. синусоиду (диаграмма его опытов изображена на фиг. 22). Наблюдалось время,
в которое модель проходила пространство, равное длине смотавшейся шелковинки.
Опыты Colardeau до известной степени являлись несовершенными; во-первых, потому, что испытуемая модель могла раскачиваться
ш
«ев» j
Фиг. 22.
при своем падении, а во-вторых, потому, что общее время пробега, и неравномерная часть движения могла быть принята во внимание только по формуле тел, падающих в сопротивляющейся среде.
Эйфель производил свои опыты иначе.
Со второго этажа башни был вертикально протянут направляющий проволочный канат, утолщающийся у самой земли. Но канату свободно могли скользить (фиг. 23) сильные рессоры Ra, с которыми была сое [инена испытуемая модель S со всеми приспособлениями для измерений: пружинами г, каммертономй (100 колебаний в секунду) и барабаном С, на который навертывалась закопченная бумага для записи. Во время опыта весь прибор падал вниз. При этом барабан С (сложивший и противовесом! вращался при помощи кол сика G и винта Rh со скоростью, пропорциональной скорости модели. Каммертон d, соединенный с пружинами г, записывал иа барабане сопротивление модели (уравновешиваемое пружинами > и, в то же время, длину пройденного ею пути за любой промежуток времени (иаприм.. за 20 колебаний, как на фиг. 24». При конце падения рессоры Ra набегали на утолщение направляющей проволоки и без удара останавливали прибор (припомощи трения).
Впос хедствип Эйфель изменил свой прибор, пристроив к нему, во избежание перекашивания, симметричную часть (прибор этот виден на фиг. 20). Однако, можно думать, что прежний прибор лучше,так как в нем нет лпшних частей, могущих внести изменения в поток, обтекающий исслед5 емыс модели. На нрм было произвр ipho и большинство опытов.
определялось только
Фпг. 23.
Эйфель onpt юлил зависимость силы сопротивления от формы и раз мрров пластинки.
Приводим таблицу полученных им коэффициентов к
Из этой таблицы можно установить, что коэффициент сопротивления несколько растет с увеличением модели и почти вовсе не зависит от формы.
Малые значения коэффи-
Фвг 25-
циента «0,085) получились потому, что Эйфель производил опыты с большими скоростями (20—40 mt'sPf'Y а коэффициент сопротивления падает с возрастанием скорости.
Над большими моде итми производил опыты Canovetu. Модели прикрепля гись к тележке (фиг. 25), которая катилась ио наклонно иа тянутому троссу.
Время, в которое модель проходила расстояние между двумя известными точками, определялось электрическими сигналами, подававшимися в момент, когда
модель проходила через этн точки, в особую будочку (фиг. 26) с измерительными приборами.
Вследствие больших размеров пластинок ои мог исслетовать сопротивления лишь при малых скоростях (5—10 тИзрс\.
Лилиенталь определял коэффициент сопротивления ^дя неподвижных пластинок на ветру Фиг. 27 представляет его прибор для определения силы давления ветра при известной его скорости, который может служить также и анемометром, если его предварительно нрогра iy кровать. (Лилиенталь употреблял такой анемометр при ско)-илях до 10 mt,*** i.
Интересно было бы прегради кровать этот прибор по коэффициенту 0,085 I ТЛЯ СПОКОЙНОГО воздуха) и проверить эту шкалу иа ветру.
Приведем теперь числовые результаты (см. табл. 2), полученные различным и экспериментаторам и, давая 1 величину коэффициента к для формулы: R=kPl
Фвг. 26 Фиг- 27
Таблица 2.
Экспсри мента тор
Магеу
Eiffel
Langley
CanovetU
Ch. Renard
ШЗ Для круглой и квадр. пласт. F= t mf
О.ОМ
0,08—0,09 В зависимости от величины пластинок
'»,<*• 5 Классвческое число.
Теперь принято считать Л = 0,085.
Это значит, что ветер при скорости V = 1 mt sec давит ла пластинку с площадью F=l mt- с силой R = 0,085 кд = 85 дг.
Важно отметить, что величина прямого удара потока от формы пластинок почти не зависит. Опыты в этом направлении были произведены Eiffel’eM, Colardeau, Canovetti и I’abbe Dantec и дали согласные результаты (см. табл. 3).
Таблица 3.
Е 1 Р F Е L.
CAX0VETTI
Цифры внутри пластинок обозначают площадь их mt2.
Colardeau для квадратной, круглой и треугольной пластинок (малых размеров, получил одинаково к = 6,07.
Сопротивление моделей.
На фиг. 28 изображен прибор Renarda для определения момента сопротивления вращающегося винта, а также моделей (иа рисунке изображен шар).
Сопротивление моделей определялось по моменту, необхо гимому для их вращения. Сравнивая сопротивление моделей различных форм и пластинок, Renard установил понятие о коэффициенте модели
Коэффициентом модели он называет отношение сопротивления модели к сопротивлению пластинки площадь которой равна площади миделевого сечения испытуемом модели.
Формулу силы сопротивления Renard писал в виде
R — knaFI'2, где ^ = 0,085, а с—коэффициент модели.
На таблице 4 приведены полученные Renard ом значения коэффициента о для симметричных сигарообразных моделей прн различном отношении ~ (фиг. 29). Эти числа показывают, что о сначала уменьшается.
Таблица 4.
2 3 4 5 в 7
о 0,073 '0,032 4 0,089 1 0,100 0,110 0,120
проходит через minimum, и затем возрастает. Объясняется это тем, что иа величине коэффициентов модели оказывается влияние двух факторов: с одной стороны, влияние струй, которые более правильно обтекают длинные тела, с другой — влияние трения. Благодаря первому фактору сопротивление модели уменьшается с увеличением длины ее, благодаря же второму—растет с длиной. Весьма длинные модели оказываются невыгодными. ЙерреПп’овская модель хуже модели Lebaudy. Наименьший коэффициент модели получается прн отношении
I
Фиг. 28
По Ренару для таких форм с = 0,03. У нас, при расчете дирижабля Комиссионного, и брали равным 0,3.
Фиг. 29. Фвг. 30.
Очень выгодной представляется форма итальянских дирнжабдей — е тупым передним концом и заостренным задним 'фиг. 30). Итальянцы принимают * =3 и о = 0,0б3.
Итальянский дирижабль Leonardo-da-Vinci, при одинаковой мощности машин, дает большую скорость, нежели другие дирижабли.
По способу Renard’a, так же, как и по способу Магеу’я, коэффициент сопротивления опредедяется иа довольно короткоплечен ротативной машине. Поэтому числа, полученные Renard’oM, ненадежны и могут быть ^спариваемы.
11 Вероятно, опечатка оервоясточвиЕЛ, разыскать н проверять которого ве удаюсь Скорее всего должно стоять число 0.082. Прим. р->
Опыты Canovetti и Eiffeln не подтверди тн очень низких коэффициентов модели, найденных RenardoM.
Приводим таблицу 5 коэффициентов сопротивления по их опытам.
Таблица 5.
Перейдем теперь к вопросу о зависимости коэффициента сопротивления от скорости.
На фиг. 31 представлена коловратная машина Langley я больших размеров. Благо таря большому радиусу (10 метров) можно считать путь
Фиг 31-
моцети почти прямолинейным. Машина эта была установлена во дворе „The Smithsonian Institution1* в Вашингтоне и приводилась в движение помощью паровой машины1).
На своей машине Langley уже при малых скоростях обнаружил факт Убывания коэффициента сопротивления с возрастанием скорости.
Все с нои опыты Langley
производит над квадратными
пластинками со стороной, равной 0,395 mt, и получил следующие цифры:
Таблица б.
Г 4,47»' •»43в**.ж 9.85»* 10,50**.,
К 0097 о.овв 0,075 0,078
J Одной из гравднозвейганх современных коловратных машин явхяетея машина, построенная фирмой Vickers Sons Л Maxim, радиус которой равен 1!(> футам i33 метрам).
Эйфель, на основании своих опытов. приходит к иным выводам, чем Langley. По опытам Эйфе тя minimum коэффициента сопротнв тения получается при гораздо больших скоростях, чем у Langley*я и, таким образом, результаты опытов по* ютнего вызывают некоторое сомнение.
Фиг. .
Приведем теперь pt у штаты опытов над шаром (маленький глобус
диаметром О,1(»о mt с площадью ми [елевого сечения F= 0,0222 mt2), произведенных н старой трубе Московского Университета (фиг. 32 и 33) студентом Г. И. Лукьяно
вым. Она быта небольших размеров и данала в< >мож-ность изменять скор< м тн В' чдуха, измерявшиеся анемометром в пре толах от I до 9 mt sec.
Прп определении коэффициента сопротнв тения принималось во внимание и небольшое изменение пт»»т-ности воздуха. Оказалось, что коэффициент к доволыю резко меняется с изменением скорости, все время пазая. Обычная ве шчина к 'O."’4i получалась между скор< >етямн 1 н м»-тра. а при скоростях в 9 метров к становилось равным 0.011. Я полагаю, что для шара эти ргзультаты могут быть объяснены схождением <*тру й с разных мест п верх н< нти шара при разных
Фиг аз.
скоростях.
Результаты опытов сту 1ента Лукьянова приведены на таблице 7.
При больших скоростях коэффициент превзойдет величину 0.024, как это подтверждается много численными наблюдениями над артнтле-рийскими енаря [ами.
Таблица 7.
Шар днам 0,168 т/. 1,44 3.23 4,66 хм 6,31 7,10 8,17 9,3₽
F= 0,0222 mt- к 0,027 ЦО22 0.019 0/317 и,015 0,014 ш 4011
Эйфель проиэво шл очень тщательные опыты в огом направлении над пластинками. На фиг. 31 представлена его кривая сопротивления воздуха в зависимости от скорости. На иец ои откладывал коэффициенты, полеченные не для одной какой-либо формы пластинки, Т а средине из наблютений над многими формами—ти-
сками, треугольниками, прямоугольниками и т. д. Средний коэффициент Эйфель получил равным 0,074 и провел для него горизонтальную прямую. Прямую эту он принял за ось абсцисс и ио ней откладывал квадраты скоростей, а по оси ординат—соответствующие эна-
Фнг. 34. чення fc. Из его наблюдений
оказалось, что minimum коэффициента получается при скоростях около 33 mt'sec. Так как в предетах его опытов (18->38 mt sec) коэффициент меняется очень маю, то мы можем считать закон сопротивления законом квадратов скоростей. При меньших скоростях коэффициент довольио быстро падает с возрастанием скорости, и потому при этих скоростях, ио мнеиию Эйфеля, закон квадратов иод-лежит сомнению, и лучше пользоваться какоп-ниоудь иной формулой сопротивления, иапример.
R=F\aV^~bV\ или R = kFV^,
Все указанные опыты относитесь к скоростям сравнитетьио малым (до 50 mti^c
При больших скоростях, с которыми имеет дело баллистика, коэффициент сопротивления
*=т£ -V(')
уже нельзя считать постоянным даже приблизительно. На основании многочисленных баллистических опытов Soreau составил приблизительную кривую представленную на фиг. 35 bis. Из нее видно, что мри подходе к скорости звука i33O коэффициент сопротивления
резко возрастает, проходит через maximum вскоре за звуковой скоростью (близ 360 wf/гес), затем довольно быстро натает и, наконец, снова медленно возрастает при скоростях, превышающих 500 nit/sfc 1i.
Невихревое движение жидкости и фрикционная теория сопротивления.
§ 8. Невихревое движение жидкости.
Изложивши опытные данные, мы перейдем к более глубокому анализу прямого удара потока воздуха на тела.
Прежде мы изложили теорию сопротивления в форме Коши, который определял сопротивление разрывом и \ таром стру й за моделью и прилагал теорему Борда.
Теперь изложим теорию Rankine а |
Rankine установил так называемую „фрикционную теорию1*, где главным источником сопротивления считает трение воздуха о модель, и ввел новое понятие о „приращенной поверхности-.
Теория эта при дожима только к хорошим моде тям, с которых струи почти не срываются, и нспридожима к дурным моделям, с которых струи срываются.
Точка зрения Rankine’a является основной при построении дирижаблей.
Надо заметить, что немногие, в 5енности из шп. занимающихся практикой воздухоплавания и морского дета, ясно представляют себе те теоретические соображения, иа основании которых Rankine к ней приходит.
Покойный Д. 11. Менделеев считал выводы Rankine'a теоретически несообразными и возражал против введенного им понятия о приращенной поверхности. Между тем, Rankine, как блестящий теоретик, ие мог допустить каких-либо несообразностей: теория его является строго научной и дает вполне верные заключения относительно величины и характера сопротивления хороших, правильно выработанных форм моделей, например, дли хороших форм дирижаблей и морских судов.
Теория Rankine а заставит нас войти в несколько сложный анализ, так как только благодаря ему мы будем иметь правильный способ определения хороших моде юй.
Ког ia ферма хороша, то сопротив теине почти все сводится к силам трения; чтобы определить последние, нужно знать скорости, с которыми жидкость течет в разных точках мод» ти. Поэтому, как введение в теорию Rankine’a,
Новейшие более точные опыты показывают несколько иную картав}, функция / (I / сначала несколько надает (до 200 mt кс), затем резко возрастает, как показано на фиг. 35 Ь|е. имеет шах. около 400 mt нее, а поел • этого более плавно, во непрерывно падает.
Возрастание коэффициента около звуковой скорости можно объяснить: аюбратованнем волн у носовой части модели (артиллерийскою сичр is): и (образованием пустоты за кормой; уменьшение же коэффициента при за-звуковых скорое ях объясняет» я тем. что носовая часть даст сопротивление почти пропорциональное ква 1рлгу скорости (но при и иаитетьно в I1-, раза, бдлыпее, чем при малых скоростях), а хвостовая — постоянное, равное атмосферному давлению X площадь миделя. Разделяя хвостовое сопротивление иа квадрат все возрастающей скорости, получаем непрерывное уменьшение коэффициента хвостовой части.
Прим реЗ
необходимо изложить способы н<-с о 1 иния погона жидкости, обтекающего данное тело без всяких срывов и ударов струй (явления Борда) и вихрей. Этот поток является частным случаем невнхревого движения жидкости, теорию которого мн сейчас и изложим.
Припомним уравнения гидродинамики дли установившегося движения
_1 if р дх
I др
о ду
р dz
•< дн Эи
= A -U - — V , — № ду 02
= 1 — и - — г дх ihc dx~~L
Г)
ду Л
ЧС |)м
;------W
оу ffl
— Z — u
Здесь X. Y и Z представляют слагающие по осям координат силы тяжести и каких-либо других сил природы «например, центробежных, если речь идет п вращающейся массе жидкости и расемаривается относительное твижение!. которые всег ia пмеют ситовую функцию Г, так что
i=’J. Г=ЭГ, Z='<! ...... 31
Л ду' oz
Введем обозначение:
р f
Если известен тепловой процесс, при котором совершается изменение состояния газа iнапример. какоп-ниб\дь политропный процесс!, то Рбу |ет некоторой определенной функцией от р или о.
Если жидкость несжимаема, то
Р=” ...... .... ЗУ.
Частная производная от интеграла
б по х будет
ЭР _ 1 !ф
ОХ € ОХ
Fx-ли выразить X и 11 первого из уравнений (2'> через V и Р и сое динить их в одной части уравнения, а остальные члены его — в другой, то оно перепишется так:
д >т г, ди ' ди
й IV—Pl-~=U —-+-Г -I-IT .... 33i
OX nf у i Jf • ’
Обозначим полную скорость частицы черн i Г, прн чем
Г=>/м> -4-м’а.
Тот ia, прибавляя и отнимая в правой части уравнения (33) члены
получим:
' / г- о ЭЛ» dw (dt дх(1-р- =U -.^-vl х-а\ . . (34)
Введем обозначения:
1____/дю fa 5= tU-S’-_____ I Ju Эи
2_____4 dz дх)* ,_____ 1 /Зг _ За''
' 2 Зх Зу/’
при которых уравнение (34) и ему соответствующие примут вид:
Д (и—р— ?) = 2 (уи-—:г llu-P^^^-^.
(85)
. ।»«)
(Лесь вторые части напоминают нам удвоенные выражения скоростей в известных формулах Эйлера:
u—qz—ry.
г =rx — pz, u—py—qx.
Be шипиы 4. q, С пграют весьма важную роль в гидродинамике. Они игиываются компонентами вихря и представляют проекции ио осям координат угловой скорости вращения частиц им. ниже теорию вихрен).
Уравнения (36) были впервые предложены покойным профессором Казанского университета И. С. Громеко. Теперь они известны под названием уравнений Л амба
Для любого момента мы можем назначить произвольные скорости всех частиц жидкости; но для того, чтобы эти скорости сохранялись, т.-е., чтобы поток был установившимся, необходимо удовлетворить исч вторым условиям.
X равнения гидродинамики в форме Ламба наказывают, что все условие сохранения потока состоит в том, чтобы вторые части >тих уравнений были частными производными от некоторой функции координат.
Одним из важнейших случаев, когда упомянутый признак у ювле-творяется. является случай движения жидкости без вращения чаетиц. т.-е. когда жидкая масса не завихрена, и
г=Ч='= О .
• • (Зч)
Рассмотрим подробнее этот случаи.
Условие (37) налагает на скорости и, г, № математические стеснения: dw dt dy dz* du____________________________dw
dz~~ dr* dt__du
Ox dy' J
Уравнения (38) аналогичны уравнениям, необходимым для существования силовой функции:
dz _ dY dy dz ’ dX _ OZ ie ox ’ 9Y_ 3X Ox dy
и показывают, что существует некоторая фу нкция Ф, названная Helmholtz’eM потенциалом скоростей, которая обладает тем свойством, что частные производные ее по координатам равны проекциям на оси координат скорости частицы жидкости, т.-е.
дх дФ ................................. (39)
4Ф=«’ 02
Важно заметить, что в нсзавихренном потоке, хотя частицы и трутся друг о друга, но потеря напора от вязкости совершенно отсутствует. Поэтому такой поток и устанавливается на некотором расстоянии от дирижабля.
В дальнейшем изложении мы будем предполагать, что потенциал скоростей Ф существует, т.-е. существует семейство эквинотенциальпых поверхностей, выраженных уравнением Ф = const.
Рассуждая таким же образом, как при рассмотрении поверхностей уровня, легко убедиться, что скорость во всякой точке жидкости нормальна к эквипотенциальной поверхности, через нее прове (ениой. И вообще все, что сказано в курсе механики о силовой функции, может быть отнесено и к потенциалу скоростей Helmholtz а, с тою только разницей, что роль силы в последнем случае будет играть скорость.
Итак, для случая невихревого движения вторые части уравнений Громеко cjTb нули и, следовательно,
V—P—= Const.. . . (40)
где const есть постоянная величина для всех точек потока. Это выражение называется интегралом Лагранжа.
Для случая несжимаемой жидкости
Р=>* ........... (32')
Если речь идет о движении жидкости, занимающей большое пространство (по высоте), например, в случае движения дирижабля — то нужно считатьсн и с действием силы тяжести. Силовую функцию для последней можно писать в виде
{7=—gz . (41)
Тогда интеграл Лагранжа представится в такой форме:
г+ '+% = const (40')
Теорема Лагранжа, как видно, есть та же теорема Бернулли, с тою разницей, что последняя относится к одной струйке, а первая —ко всему потоку (понятно, при условии существования в нем потенциала скоростей).
По уравнению (40) можно определить давление во всякой точке потока по скорости в этой точке и величине const.; что касается до const., то его находят, зная в какой-нибудь точке потока давление и скорость.
Если высота z мало меняется, то уравнение Лагранжа можно напнсать в виде:
„ = const — Г . . . •..............(40")
как пишет С. А. Чаплыгин и другие авторы.
ОIMH простенький опыт, показанный на воздухоплавательном конгресс в Париже в 1ь9о г. довольно ясно иллюстрирует эту теорему. Брали легкий шарпк нз тонкий резины, надул ати его воздухом и подвешивали па нитке, а сбоку дули чере трубочку. Как только через трубочку начинали (уть на шарик, последний подходил к струе I сбоку) и подтягивался к трубочке. Причина этого явления следующая. Если поток жидкости образуется нз состояния покоя, то, установившись, он б\ дет веема незавнхрен. Поэтому. согласно уравнении» Лагранжа (в котором const, имеет одну и ту же величину (ля всего потока), наименьшее давление молу чается там, i де скорость имеет наибольшую величину,т.-е. в середине струи; в стороне же от осп стру и давление больше. Шарик, передвигаясь н сторону меныпего [авлеипя, приблизится к оси < тру и, а затем несколько подтянется к отверстию трубочкп.
Идея о потенциале скоростей и незавпхренностн ноток а очень важна. Рассмотрение подобных движении позволило сблизить многие опытные ги ipo щнамические явления с теорией и дать их надлежащее объяснение.
Рассмотрим теперь, какие стеснения налагает на потенциал скоростей условие неразрывности в случае Несжимаемой жидкости:
<?« , да । dw
• • • • • (о)
Заменяя в этом уравнении скорости производными от потенциала скорострй Ф, получим:
дх^' д^~^~ ............ l J
Это уравнение называется уравнением Лапласа. Ему должен дов [створять потенциал скоростей Ф для несжимаемой жидкости.
Сумма вторых произво щых какой-либо фу пкции по координатам • •позначетея через Д и называется ее вторым дифференциальным параметром.
Если бы мы вообразили ишжение жидкости е потенциалом скоростей, не удовлетворяющим уравнению Лапласа, то жи (Кисть двигалась бы с образованием сжатия н расширения. Для воздуха при очень больших скоростях, как было указано выше, сжимаемость мала, так что его можно считать несжимаемым; следовательно, для незавихренного потока воздуха уравнение Лапласа »лжно у .овлртворяться
Для иссле ювапия движения тет в спокойном воздухе выгоднее обратить 1виженис, придавши как телу, так и окружающему его возду ху скорость, равную и противоположную скорости тела. Тогда тело остано внтся, а воздух будет набегать на него. При этом, если те до двигалось в положите дону ю сторону осн х, то, обративши движение, мы будем иметь следующие проекции скорости (ля бесконечно у деленных точек потока:
дФ __ дф_ I
ду f)z ’I
оф -т, ( •
fa----Т° I
где Г( есть скорость полета те да.
* 9 Сопротивление шара.
Поясним наши выводы на простом примере, рассматривая движение шара, 1ля которого функцию Ф определить довольно легко.
Для исследования течеиия жидкости около тара рассмотрим предварительно такую функцию потенциала скоростей:
Ф
V = W =
(43)
(44 b
i »op«ni4ecne «свевы вп । тин мш»
гдр г есть расстояние жидкой частицы от начала координат, а п — некоторый постоянный коэффициент. В теории притяжения эта функция выражает потенциал сил ньютонианского притяжения к данному центру (началу координат).
В рассматриваемом случае ньютониаискнм ситам будут соответствовать скорости жидкости. На опыте течение жидкости, заданное потенциалом скорости Ф= г можно воспроизвести следующим образом: беру т шарик с большим числом мелких отверстий (фиг. 36), ставят его в комнату со спокойным воздухом и вытягивают возду х из шарика при помощи тр\бочки и вентилятора. Тогда окружающий воздух будет устремляться к шару со всех сторон по радиусам и входить в отверстия. Так как воздух можно считать несжимаемым, то через всякую сферическую поверхность, коицентрическу ю с нашим шаром, будет проходить одно и то ж« количество во духа, и, следовательно, скорости его будут обратно пропорциомальиы квадратам расстоянии от центра сферы. В этом можно убедиться, всасывая в шар запыленный * воздух и фотографируя летящие пылинки малой выдержкой; при этом сфотографированные длины пу теи частиц будут пропорциональны скоростям воздуха.
Составим теперь выражение второго дифференциального параметра ДФ и убедимся, что он равен нулю. Заметим, что
= (^4-^-L
dr tr dr у чг
г г * иу г * ds
Частныя пронзво шые от потенциала скоростей (44) будут: дФ > / я \ п dr nr dx dx \ г J г> дх г® ’
дФ пу дФ пг.
ду г® ’ dt rg
б*Ф п 4пг дг п Зжх3
<Лх® г3 т* дх г® - г® '
д2Ф п I 3 пу*_
if 7S+-7S--
&Ф______я . 3 пг*
d? “ г®+ г5
Отсюда
.ф_ . О’Ф , <₽Ф__Зп^_Лк (.гг-.-,Ч.р)_
аг’ ' ду* “г де-
Итак, действительно, потенциал скоростей (44) дает исток, удовлетворяющий устовию несжимаемости.
Переходя к слу чаю обтекания жидкостью шара, возьмем более сложную функцию потенциала скоростей:
(45)
или, в раскрытом виде.
Ф—£-ГЛ .
(45)
где Ио должно равняться скорости потока в бесконечности; направление потока противоположно оси х.
Покажем, чти поток, даваемый этой ф-ией, удовлетворяет ур-ию
Лапласа. В самом деле, так как операции Д в переместительны, то
=„х:)-j'
Мы видели выше, что Л j = 0: с другой стороны, очевидно, что Д (Г’ох) = О. Следовательно, ДФ—о, что и требовалось (оказать.
Определим скорости потока в бесконечности м иа поверхности обтекаемого шара.
Для бесконечности:
•)Ф д* [ п \ т,
" = = (-г)- L = ->0-
.ф= aj (ЛЛ = 0.
“ = ь=^Г~) = °-
• - dxiiz г }
так как ^ (-=-) Д ( и (-£-) при г = со будут бескоиечно-малыми величинами второго порядка. Ур-ия эти показывают, что поток течет в бесконечности со скоростью Го в сторону, обратную оси х.
Покажем теперь, что рассматриваемый поток обтекает сферу. Для этого удобно перейти к полярным координатам. Тог ia
Ф = —Гх = -аье(Д +гоп, ... .145'1
так как х — г соя© (фиг. 371.
Было доказано в общей механике, что проекция силы иа касатель-
ную к данной кривой равна произво шой от силовой функции по элементу этой кривой. Аналогично, (ля определения проекции скорости на данное направление нужно взять производную от потенциала скоростей по элементу длины, соответствующему рассматриваемому направлению.
Поэтому скорость по направлению ра шуеа-вектора равна
Г ='*ф = — cose (— 3"-I .
Для того, чтобы иоток обтекал шар ра-лиуса а, необходимо, чтобы при г = а скорость Vr равиялась иулю, т.-е. необходимо подобрать параметр п так, чтобы
откуда
W =
При этом условии все частицы будут скользить по сфере радиуса г». Гогда соответствующий потенциал скоростей бу <ет:
ф = _ I’cosfl (£ + г) . . ... .147,"»
•Ф
шару, равиа - , где d&—шффе-ренциал дуги — берется по направлению скорости частиц па поверхности шара. Вследствие симметрии шара относительно осн потока |фиг. 38» всякая отде льная липиятокабу’Дет лежать в соответ-< твующей меридиональной плоскости ; тогда ds = ad О, и
( Н“1)= F0sin6 . . .I4t>i
Скорость, с которой жидкость течет по
Фнг. 38.
I’ '<*’ I Оф п
I. = ,л= 1W- = 10 sw е
• а иЬ v
Итак, получается необычайно простой закон распределения скоростей ио меридиану обтекаемого шара: скорость равиа скорости потока в бесконечности умноженной на j и иа sin угла между ра шусом-векто-ром и осью х.
Там, где жидкость встречает шар. 6 = 0 и И, = 0. На акваторе О = и г.==Ло-
точка потока, в которой полная скорость равна нулю, иазывается критической точкой.
Если струи не срываются, то распределение скоростей (по величине) будет симметричио относительно экваториальной плоскости, нормальной к оси иотока.
Зная скорости, определим по теореме Лагранжа давления в различных точках шара:
= const— = const — y ro8sinxe =
= L T ^(1- 4 -'«>
где consi выражено через давление p u скорость Го в бескоиечнистп.
Форм. (47) показывает, что иа шаре распределение давлений, также как и скоростей, должно быть симметрично относительно экваториальной плоскости.
Вследствие симметрия потока относительно оси, полное давление иа шаре должно направиться по осн потока. Но, так как для двух симметричных относительно экваториальной плоскости элементов площади 1.4 и В на фиг. 39) проекции {явлении иа ось иотока равны и противоположны, то все давление на шар райпо нулю.
Этот вывод можно распространить и на тела произвольной формы, если струи аккуратно их
обтекают и нигде но срываются. Фиг. за
Положение, что равномерно движущийся поток несжимаемой жидкости не оказывает никакого (явления на погруженные в него тела, носит название парадокса Эйлера.
Па опытах парадокс Эйлера не подтверждается. Объясняется это тем, что при выводе его не принимаются во внимание два важных фактора: схождение егру й с поверхности тела и трение жидкости о его поверхность.
Поэтому сфера не тотько имеет некоторое сопротивление при движении в жидкости, но еще и коэффициент этого сопротивления меняется со скоростью жидкости. Это изменение, которое Г. II. Лу кьянов установил еще в 1905 г. на опытах, произведенных в старой трубе Мпсковского Уни-
верситета и в его вестибюле (опыты с палением шаров । быт в дальнейшем п< утвержден опытами Эйфеля и Морена (Maurain). Фиг. 40 показывает результаты поздпейших опытов 1911—13 г.г., про-изве юнных Г. И. Лу кья-новым на7 4 шарами раз-i очных размеров. По оси абсцисс отложены произволения V JR 1), где I сеть скорость потока в mt spc и К радиус шара в mt и ио оси ординат соответственные значения коэффициентов сопротивления К= Эти
опыты были произведены в круглой трубе быв. Императорского Технического Училища в Москве при скоростях от 5—29 mt »с‘ для шара диамет-___ ром и,076 nit опыты
были продолжены в малой трубе типа «Эйфеля (диаметр рабочего сечения 0,30 mt) при скоростях от 13—43 mt
Опыты покат ли, что коэффициент сопротивления шара падает е у велпче-нирм скоростей потока -к Это изменение происходит от топ», что место срыва струй с поверхности шара меняется со скоростью потока. Фиг. 41 представляет аэродинамический спектр обтекания воздуха *!••-
— круг шара дпамет-
JK 4 0.24 Vlt СтреЛКН фнг 41 - представляют по ве-
тчине и направлению с?:ор< ти rivx' в экваториальной плоскости шара. Ма юнькн»? кружочки показывают ipannuy, ио которой отд» шет' я
I Как это сделано лордом Редеем для опытов Эйфеля.
•j ла ятом же cxoTDt ть ниже, в главе о иод'-бнн. число Рейвозьдса
непрерывный поток воздуха от вихревой области, образующей за шаром нечто вроде удлиненной кормы дирижабля. Точка пересечения этой раздельной линии с экватором шара определяет точку срыва струй с поверхности шара. Вследствие симметричности шара эти данные могут быть распространены и на весь шар. Вблизи шара на расстоянии до одного диаметра вихревая область представляет почти цилиндр, радиус которого мы назовем радиусом вихревой области и будем обозначать через Н'. Обозначим через Л угол срыва струй, представленный на фиг. 41. Опыт показывает, что этот угол возрастает с увеличением скорости, а также и радиуса сферы. Следовательно, радиус области вихревых колец при этом уменьшается, как то видно на фиг. 42.
Фиг. 42-
Фиг. 43.
Фнг. 43 показывает изменение у i ла срыва Л и ра туса вихревой области R 1в отношеиип к радиусу шара, в функции скорости для шара 0,12 mf. днам. Эти же значения представлены в табл. 8. В таблице 9 даны углы срыва с поверхности и радиусы вихревой области для различных шаров прп скорости 10 <. В обоих этих таблицах
таны так же коэффициенты сопротивления Кш и отношения нх к корням квадратным из радиуса вихревой области. Последние отношения остаются приблизительно постоянными тля каждой таблицы; таким образом в изменении угла срыва струй можно видеть причину уменьшения коэффициента сопротивления « фсры с возрастанием скорости.
В приведенных выше аналитических формулах для распределения лав тений по поверхности сферы мы не принимали во внимание ни трения жпткости, ни срыва струи; поэтому неудиви
тельно, что теоретические выводы не совпадают в точности с результатами опытов пад распределением давлений в различных точках поверхности шара, произведенных Г. И. Лукьяновым сначала в квадратной трубе Московского Университета, а затем в двух круглых трубах Аэродинамической Лаборатории В. Т. У. над шаром диаметром 0,057 mt.
Прибор, с которым производились эти опыты, изображен схематически на фпг. 41. Работы велись по способу Dubuat п Duchemln’a. Во всасывающую трубу ставили полый шар С <• олпим отверстием х. Шар можно было поворачивать около вертикальной «си z~ и тем самым поме
Фиг 44.
тать отверстие иод любым углом к горизонтальной оси потока. Благодаря такому устройству можно было, соединяя полость шара трубкой В с манометром А, определить давление во всякой точке горизонтального меридиана, а следовательно, вс те тствпе симметричности потока, ина всей поверхности шара.
Оказалось, что при угле в=0 давление на поверхности шара равно комнатному, в то время как в трубе давление было меньше комнатного, так как воздух про текал в ней с некоторою скоростью Лрн возрастании в давление уменьшалось, сначала действительно по закону
const— Го*sin-в, . . («I
а при больших углах в замечалось отклонение от него. В выражении iaj
Const - 'j . где р0 есть давление в трубе вдалеке от модели. V -
Т V Б .1 И Ц А 8-я.
Таблица углов >. и г' для шара d^-0,12 mt. при скоростях потока от 5 до 16,3 mt sec ua расстоянии г от поверхности шара.
г mt лес г' wit Кш К-
5 125е 0.0647 0.0247 0,098
7,7 129.5° 0,0606 0,0227 0093
138.7° 0,0522 0,0214 0,094
12,4 145° 0,0453 0.0202 0,096
145 149,5 0.0404 0.0200 0,099
16.3 152.5 0.0368 0.0201 0.104
Т А Б Л II Ц V 9-я.
Таблица углов лиг1 для различных шаров
на разстоянни г от поверхности шара при скорости потока v =• 10 mt'sec
Ради}с шара г mt г* mt К» Kw 1 г
О.О*й 144° 0,0334 0.0288 0,0052
0.06 151° 0.0334 00212 00044
0084 15в".а 0.50 0 Л1пч 0,0045
0.12 158 0,068 0,0174 0,0044
Л.) наблюдении оказалось, что наименьшее давление на поверхности шара будет нр прн в =90, как вытекает из теоретической формулы, а приблизительно при 0 = 75. При больших углах 0 давление снова несколько возрастает, но не так много, как бы следовало в формуле 147».
и имеет второй, более слабый, min ири 6=130’ Распределение галлеин и приблизительно представлено иа фиг. 45: па иен во внешнюю сторону круга, представлявшая • обтекаемый шар, отложены на еоответетвеиихы ра диусах-векторах понижения гав тении по отио шеиию к давлению в комнате. Из [награммы видно, что впереди сферы это понижение ра шо О. как то и следует ио теореме Борну л ш. На этой же фигуре пунктирными тин ними показано теоретическое понижение га влення, ВЫЧИС 1РНП0Р пл формуле 47 для тех скоростей, при которых производи шов испытания «от 1 — 20 mt sec в круг-юп трубе 1 mt диаме тра и от 13 - 42 mt st с в малой трубе Эйфеля щаметра 0,32 mt.i.
Диаграммы указывают на расхождения между теоретическими и опытными кривыми: это расхож iphhp показывает чти действительное о«7-
текание шара не тождественно с обтекаппем тео-
ретическим.
Рассмотренное в этом § теоретически»- течение (без срыва струй i так же возможно, но оно менее устойчиво, тем те тейпе со срывающимися струями; в приро je же всегда образуется 1внжсннс наиболее устойчивое.
Вопрос о сопротивлении шара требует очень внимате шного исследования, чтобы теоретически раз(»бу®ться в результатах опытов и составить заключение о месте схождения сгруй в зависимости от скорости потока К»
: 10. Сопротивление моделей.
Вопрос о наиболее выгодных формах корабля и дирижабля имеет грома шое практическое значение. Поэтому- многие Несте юватечп занимались т еретическим решением этого вопрос*. ш*Х'> 1я из правильной мысли, что затраты, проквве ленные па это, равно как и на прсдварптель-
нне ТеорСТНЧСРКИе опыты, юлжны п избытком окупиться впоследствии, при самой поетртйке
Rankine установи i цилин фичгкую форму для корабля, причем потенциал скоростей опр» делается с помощью двух полюсов н движение относится к плоско-параллельному потоку.
Если его прием распространить на дирижабль, имеющий фирму тела вращения, и рассматривать поток в трех измерениях, то надо положить
Ф = Гох-ь ' — г‘ . . («•
г г и гх уть расстояния точек жидкости от двух основных точек и В. которые будут играть роль пи 1юсов Rankine а 1фпг. 4<>).
Течение,' вира
4
жаемос функцией I ie>). у ювяетворяст уело-вию Лапласа и имеет в бесконечности скорость Го. иаправлеи-ну ю по оси л\
Хнгличане при-
<1»иг
держнваются закрут
ЮННОЙ формы днри
жабля, опираясь на форму, предложенную Rankine'HM ыя корабля. Можно придумать еще много дру гих теоретических форм чля дирижабля, которые будут удов, отворять всем свойствам потока, текущего без вращения частиц и имеющего вдали постоянную скорость. Несомненно, можно тео-
ретически подобрать форму, подобную той, которую имеет дирижабль Leonkrlo-da-Vinci: с тупым концом спереди и заостренным г «ди.
Есть очень простой способ вычерчивания лшпш
Фнг. 47
тока при помоши не двух.
а целого ряда полюсов, рае-П040ЖСННЫХ па оси дирижабля. Пусть .4, В, С, I), Е (фиг. 471 будут такие полюсы, а г. rlt г2........— расстояния от них какой-нибудь
точки AL Примем за потенциал скоростей функцию:
Ф = — Глот — V ”
(41* •
где дли правых полюсов w положительно, а для левых отрицательно, прп чем Sn = 0. Для каждой точки .V мы можем определить Ф. Сое циняя все точки, для которых Ф одинаково, получим эквипотенциальные линии, а проводя ортогональные к ним линии, найдем линии токов в меридиональном сечении дирижабля. Когда шнии тока, соответствующие данному потенциалу скоростей, уже вычерчены, то между ними окажете и такая, которая имеет 2 критические точки: в первой она расходится, а ю второй снова сходится. Тогда замкнутую часть линии тока между двумя критическими точками и можно примять .за меридиональное очертание модели.
В *воей работе „О наивыго дне ищем форме су юв“ *) я пока-за л, > го можно делать такие формы, что жидкость бу h i «шере щ всходить иа
Tpj чы Физ Отд. о ДЕ, т Ш, в I
острие, а сзади сходить с острия; но моя статья осносится к плоскопараллельному потоку и неприменима для дирижаблей.
Если форма теоретически определена, т.-е. найдена функция потенциала скоростей, то можно теоретически определить все скорости на поверхности модели.
Rankine дал способ определить ио этим скоростям сопротивление модели от трения. Ои полагает, что на данном элементе плошади модели спла трения равна произведению коэффициента треиия жидкости о модель z на элемент площади и иа квадрат скорости. Сумма проекций этих сил трения на ось мотели дает полное сопротивление моде ш.
Prandtl для потенциала скоростей взял функцию.
ф= <60>
Модель, обтекаемая таким потоком, очень близка к форме дирижабля Раг-сегаГя (задний конец острен иоредне го). Исследуя модель в трубе (скорость потока можно было получать в ней до 10 mt sec), Prandtl получил на поверхности модели давления, очень близкие к теоретическим, везде, кроме заднего конца модели. При этом теоретические давления определялись но теореме Лагранжа, зная по формуле (50) скорости в разных
точках модели.
Для определения давлении на поверхности модели Prandtl делал в пей много отверстий, которые все, кроме одного, заклеивались бумагой. Внутри модели получалось лавление, равное давлению в искомой точке поверхности; это давление и передавалось при помощи трубки к мано-
метру.
Результаты исследования Prandtl я изображены на фнг. 18 Пн П). По ординатам отложены давления. Ось модели соответствует давлению в трубе. На фиг. 48, I верхняя пунктирная черта соответствует кавлению в критической точке, которое равно комнатному; избыток давления в ней над давлением в трубе равен
V 8
у Пунктирная кривая представляет теоретическое давление. Сплошная кривая—наблюденное давление Из диаграммы видно.
что давление за критнче свой точкой быстро падает, становится ниже давления в трубе, потом енова возрастает, на значительном протяжении почти равно давлению в трубе, а к концу модели снова уменьшается. Подсчитывая теоретически, мы должны были бы получить изменения давления по пунктирной кривой, при чем давление в конце модели должно было бы превышать давление в трубе на величину, соответствующую скоростному напору.
Сравнивая теоретическое давление с наблюденным, видим, что они совпадают везде, кроме заднего конца модели, где лавление, хотя и выше давления в трубе, но гораздо меньше, чем в случае, если бы жидкость в конце имела скорость О.
Проекцию на ось модели всех сил гидродинамического давления, действующих на нее, Prandtl определяет графически следующим образом: он разбивает поверхность модели плоскостями, нормальными к ее оси, на ряд весьма узких колец (фиг. 49), па которых давления можно считать постоянными, и проектирует эти кольца на плоскость, перпендикулярную
осп модели. Топа проекция на ось модели элементарной силы давления на какое-либо кольцо получится, если умножить наблюденное с помощью дырочек давление иа проекцию соответствующего кольца. Для суммирования этих произведений Prandtl
перестраивает свою диаграмму х<тТП1 I I 11 1ПТПТг^
хавлений, откладывая по осн /J] |11 7 gg |
абсцисс одну за другой проек- Ча ! ’ ' |||>^ \ Vta//
ции площадей колец, а по оси —1—L.,.. IILL-—V.
Фиг. 49.
ординат — соответствующие давления. Получается диаграмма, как на фиг. 48, II. Площадь ее обойденная планиметром в направлении стрелок, дает в соответствующем масштабе равнодействующую всех сил гидродинамического давления на модель. На этой фигуре, как и на фиг. 48 I, сплошная черта представляет кривую, преобразованную из наблюденной, а пунктирная—из теоретической. В последней снланиметрированная площадь равна нулю. Подобные диаграммы^ для различных моделей представлены на фиг. 50 (I, II, П1).
С фугой стороны, непосредственно из опыта Prandtl определяет всю силу сопротивления модели, подвешивая ее в трубе и удерживая динамометром. Разность между этой силой и равнодействующей сил гидродинамического давления, подсчитанной на основании показаний манометра, дает равнодействующую сил трения воздуха о модель.
Выгодно коэффициент к обычной форму лы сопротивления R = kFV-\F— площадь миделя) разбить на две части: к = Лг где соответствует сопротивлению, определяемому по нормальным к поверхности гидродинамическим дав тениям, а к* соответствует силе сопротивления от трения — того
именно фактора, который, главным образом, принимался во внимание Rankine'HM в его расчетах.
Для формы модели, наследованной PrandtFeM, общий коэффициент опротивления оказывается очень низким: к ~ 0,0076, при чем fcj == 0,0033
и А*а = 0,0043 (в то время как для шара к -=0,024, а для плоский пластинки к — 0,085), так что большая часть сопротивления здесь вызвана грением. Если где 1ать мо 1ель длиннее, то может несколько уменьшиться, ио А*.? должно возрасти.
Опыты показывают, что сети однообразный поток течет по плоскости, напр. по д-ске, то сила трения возрастает почти по закону квадрата скорости. Англичане, которые ирспмд щес i ценно пользуются степенными формулами, находят, что сила трення пропорциональна Г1*®8; но подобная зависимость ие соответствует законам приро гы. Здесь, я думаю, существует бинарная формула вида а Г ЬГ2 прн чем первый член соответствует вязкости жидкости, а второй — непосредственно трению о пластинку. Для практических подсчетов совершенно достаточно писать, что сила тренпя
..................... (51)
гд-‘ f—площадь-трущемся поверхности, а I—скорость потока. Величина коэффициента / весьма важна для дирижаблей, так как для них коэффициент A't мал сравнительно с /£.2, зависящим от 7. К сожалению, опытов для определения этого коэффициента сделано очень мал*..
Американский исследователь—проф. Zahm де дат опыты еде сующим образом (фиг. 51» Узкая доска АВ (это может быть рамочка, оклеенная картоном, в зависимости <»т свойств in.,!...., ,... I гттр которого немного меняется коэффи-
’ и_________Цв | Щцент подвешивалась в трубе, через
; которую прогонялся воздух. Д. 1Я х стра-|1 "* пения юб<»вого п кормового еппротпвле-
• । ннй Zahm прикрывал теку медиымн
trTi.i .ГЭт,» .I-н iiij.u..&hiu=j скобочками, не связанными с доской,
_ а прнкррпленными к самой трубе, весьма
Ф|1Г- Jl близко от доски (на расстоянии около
0,5 тт\. Тогда, хотя поток и давит на уюлки, но это давление не оказывает влияния па испытуемую доску. Все же действие на нее сводится к силе треиия. Преследуя большую точность, Zahm определял с помощью манометров давление внутри упомянутых скобочек п принимал его во внимание. Если не принять этих прел осторожностей, то лобовое сопротивление—удар воздуха о кран доски и подсасывающий эффект кормы—окажет значительно* действие на пластинку (в зависимости от коэффициента kJ.
Из своих опытов Zahm нашел, что / = 0,0002.
Чтобы найтн силу тренпя, нужно к< »ффиииент у умножить на пло-шадь доски в mt2 и на квадрат скорости в mt sec.
Кроме Zahm‘a. опрс юлением коэффициента трения занимались также Prandtl, Canovetti, Frank, Eiffel п у пас А. И. Морпгпкин и Г. В. ('орокох мовский.
(anovetti, Морошкин п Сорокоу мовский получили числа, близкие к числам Zahm'a. Frandtl и; опытов с неподвижной моделью в трубе получил / == 0.0003.
Такое же число получи i Frank, производивший опыты на i моделями, качающимися, как маятники, по дуге крхга; но опыты его не отличаются точностью, так как движение, им рассматриваемое, было неравномерно.
Морошкин расположил опыты так. В трубу больших размеров фиг. 52» он вставлял трубы картинные, диаметром ю о.З mt и длиною ^6 mt. Эта труба подвешивалась горизонтально на нитях, притом так, что нс прикасалась к краям отверстия большой трх бы. Когда нз последней высасывался воздух, то на участке АВ ее никакого потока не получалось; весь в< ихх проходил по внутренней трубе при v м скорости в иен можно было изменять от 1 до 20 mt sec Действие потока в« к х ха на малую
трубу состояли только из трения и внутренние стенки ее. Скорости потока очень точно определялись анемометром и микроманометром. Одновременно е ними опредетялась сита, с которой поток увлекал трубу.
Сначала Морошкин получил для/ числа меньше ZahnroBCKHx, так как перед передним краем малой трубы у него получалось разреженно воздуха. Чтобы устранить последнее. Морошкин поставил пере нею напра-
ляюшую воронку
iid тонкого картона, благодаря чему все стру и вхо шли в тру -бу не изгибаясь, н подсасывания на краях трубы не по-iy-чалось. При лом
диаметр воронки в I
крайнем сечении ab фяг .„
был чу ть-чуть меньше диаметра трубы.
Много затру (нений пр» иставляла задача устранить нрогагывание воздуха меж iy трубами, не ст-сияя передвижений подвешенной трубы Окончательно Морошкин остановился на устройстве лабирпнта из бу ма-жек е зазубренны мп рифлеными краями (фпг. 52 11), на не юбне таби-рннга в сальниках паровых турбин; оказалось, что воздух через такие бумажки ие проходит. Числа, подученные Морошкиным, в среднем дают / = 0,0002 и близко подходят к числам Zahm'a и Canovetti. В круглой аэродинамической трубе В. Т. У. студент Г. В. Сорокоумовскип производи! опыты над трением воздуха о стенки модели (Деревянной лакированной доски, пустой внутри, размерами 292'<19 > 4 ст, с заостренными пере шим и задним кинцим и покрытой (ыркамн по стенкам» по способу Prandtl-я н получил / = 0,00018.
Разъясним теперь, что Rankine понимает под выражением ^прира-
щенная поверхность-.
Если форма хороша, т.-е. струи не покидают ее — не срываются — и теку т I как показывают наблюдения, так, что скорости говна (ают с теоретическими, то в формуле общего сопротивления
Rlt
где есть сопротивлении от давления вследствие срывания струй, a К* сопротив 1енпе от трения, можно величиною пренебречь вследствие ее сравнительной малостп (примером этого могут служить дирижабли Zeppelin’а и Leonardo-da Vinci). Тогда, по Rankine у.
J* I V'cos a df—x Го J f fjz ) cosadf, (52)
i де а есть угол между осью дирижабля, по направлению которой он перемещается. п направлением струй, совпадающим с направлением касательной к меридпану, Г—скорость потока на поверхности дирижабля, меняющаяся для различных его точек, а Го -скорость дирижабля (фиг. 53). Вводя обозначение-
cusidf=F, 153)
находим, что
K2 = 7.FVl
- (54/
Фиг.
Площадь F Rankine называет „приведенной" нти „приращенной* поверхностью. Умножая последнюю на коэффициент трения / и на квадрат скорости дирижабля Го2, получаем силл сопротивления дирижабля хорошей формы.
Иначе, приведенная поверхность Rankine'а есть поверхность той доски, которая, двигаясь вдоль своей длины, имеет то же самое сопротивление от трения, что и рассматриваемый дирижабль.
Приведенная поверхность больше поверхности самой формы, так как на середине модели жидкость течет гораздо скорое потока
Для шара, поверхность которого Г = 4 л а2, приведенная поверхность
*’=4°
sin4 8d8d ф === -А а2? л / sin4 GdG = —
4 J 16
так что
Из ур-ия
F 27
F = uT’'“t325.
ft = AF7==z FT,
получим для шара
Z P = I6 Л X = 5,3 0,000-2 = 0.0011.
Из наблюдений получаем к близкое к 0,02 (различно при разных скоростях и диаметрах!.
Это резкое несовпадение объясняется тем, что шар является дурною формою; струи с него срываются, и величиною сопротивления Я, в этом случае пренебрегать нельзя.
Итак, если форма дурная, то теория Rankinea к ней неприменима. Оставляя в стороне величину коаффициента сопротивления, нужно отметить, что и самый закон квадратов скоростей, как показывает опыт, не совсем верен. Это объясняется тем, что струи схотят с шара ие в одном п том же месте, а в разных, в зависимости от скорости (ем. выше, стр. 63—во.
Фиг. 54.
Фиг
Рассмотрим теперь другие формы моделей.
Prandtl у называет, что если взять тпек и пи шндры с одним и тем же диаметром, но различной длины (фиг. 54 н 55|, то коэффициенты сопротивления будут различны. То же самое установит Eiffel, бросая диски различной толщины с бапшн со скоростями 20 — 30 mt'тс. Он получил -летующие коэффициенты сопротнвтения.
Таблица 10.
* о а d 3 а
к 0.070 0,071 0,06» 0,051
Таблица эта показывает, что с увеличением длины цилиндра коэффициент падает, несмотря на увеличение трущейся поверхности; это
объясняется тем, что по мере того, как цилиндр становится длиннее, модель становится лучше. Prandtl говорит, что коэффициент уменьшается потому, что при тонком диске сзади образуется вихревое кольцо, которое сосет жидкость и образует „недавление** (ср. опыт Дюшемена», а при более толстых дисках это „недавление" меньше. „Давление* же спереди почти такое, как будто на диске стоит столб жидкости, равный скоростной высоте. Уменьшение сопротивления с возрастанием длины цишндра можно объяснить на основании теории Saint-Venanta, если разобрать условия образования вихрей около цилиндра. В зависимости от того, что струи с большой скоростью врываются в массу жидкости, текущей с малой скоростью, происходит потеря нанора п образуется сильное вихревое кольцо позади шска: поэтому эффект кормового сопротивления для диска велик. По мере удлинения цилиндра заднее вихревое кольцо ослабевает, п эффект кормового сопротивления у меныпается; образу ющпеся же сбоку цилиндра слабые вихревые кольца не оказывают никакого влияния иа сопротивление, так как давление сбоку перпен щкулярно оси цилиндра.
С очень длинными формами опыты в воздухе не производились, но можно думать, что для них коэффициент сопротивления будет возрастать
с длиною, вследствие того, что площадь, трения, а, следовательно, и сила трения, возрастают с длиною цилиндра, а коэффициент к подсчитывается по миде левому сечению, которое остается постоянным для данного диаметра.
Действительно, опыты с водою показывают, что коэффициент сопротивления, пройдя через некоторый minimum для опрг деленной длины цилиндра, затем снова
4>НГ. оо
возрастает.
Eiffel производил также опыты с двумя дисками, расставленными иа разные расстояния друг от друга (фиг. 36). Оказалось (табл. 11), что чем дальше диски друг от друга, тем коэффициент сопротивления бу ют меньше.
Таблица 11.
* о \ a d yd
к 0.070 0,069 0,061 0.053
I
Что касается вопроса о наиболее выгодных формах моделей, то опыт показывает, что для воздуха являются выгодными рыбообразные формы. Они, имея большой объем, имеют сравните льни малу ю приведенную иовер-нисть и принадлежат к типу хорошо обтекаемых форм.
Вопрос и том, где будут срываться струн, пока мало исследован. Для воды Thomson полагает, что струи будут срываться там, rie давление р, определяемо*1 по формуле Бернулли
Р~Ро =
становится отрицательным. Для воздуха, по мнению проф. С. \. Чаплыгина, схождение струй сделается необходимым, когда скорость будет подходить к скорости звука (33-т u/t swi. Может быть, этим объясняется то обстоятельство, что для дирижаб ы предпочтите 1ьнее рыбообразная форма, а тля корабля—форма аостреннымн концами, так как в после шей I — Го2 не велико.
Было бы очень важно поставить такой опыт: заставить пл»«скопарат-летьный поток воздуха сначала прохотпть между двумя парад ieдьиыми топкими слепками АВ, А’К |фиг. 57», а затем расходиться гю дугам ВС, ffC, которые можно изгибать. При малых скоростях потока н малой кривизне дут частицы жидкости будут двигаться ио луговым стенкам: при увеличивающейся же скорости потока н кривизне дуг струи будут срываться со стеиок. Посредством флажков if можно будет опре юлить точки г. j . г ie । >вершается срывание струй. Таким образом установилась бы связь между’ скоростью и радиусом кривизны обте
каемой поверхности, при которой (связи) начинается схождение струй.
Аналогичные наблюдения следовало бы сделать и для воды.
§ 11. Аэродинамические спектры.
Для исследования условий обтечення различных тел получают так называемые гидро- и аэродинамические ецентры, т.-е. фотографии линий тока около этих тел. Из различных способов получать гидро 1инамические спектры остановимся на мето ie гамбу ргского исследователя Ahlborna.
Модель опускается внутрь канала или большого продолговатого резервуара (2 X 0,5 X 0,5 mt5) так, что свободная поверхность жидкости разделяет ее пополам. Опа закрепляется на платформе, которая движется равномерно (со скоростью 0,25 mtsu-} на колесиках во краям канала На топ же платформе, прямо над моделью, поставлен фотографический аппарат, делающий снимки при помощи вспышки магния (выдержка около аегь Вес пространство жи ikoCTh наполнено взвешенными в ней мелкими частицами, иапрнмер, кофейной гущей. Если сделать моментальный снимок, то всякая частица на фотографической пластинке изобразилась быв виде точки. При фотографировании же с выдержкой всякая частица изобразится на снимке черточкой. Ряд черточек образует линии тока.
Описанный способ есть одни из наиболее точных методов получать спектры. Метод Д. П. Рябушинского, о котором будем говорить ниже, хотя и гает очень красивые спектры, но имеет тот недостаток, что около самой модели получаются фигуры, которые не суть линии тока и которые можно смешать с последними.
Фиг. 5ь изображает спектр, подученный Ahlborn'ow для модели сигарообразной формы. Спектр показывает, что эта форма очень выгодна, стру и обтекают се весьма стройно п аккуратно: нигде нет нн внхрей, ни схождения струн о модели.
На фиг. 59 изображен прекрасно удавшийся спектр от круглой пластинки (в жи шесть погружена была лишь половина се).
Очень важным для ги цюдинамики является вопрос, образуется ли впереди пластинки конус иепо шижноп жидкости? Обыкновенно теоретически у станавлн-вают, что спереди модели су шествует стройный
фнг. 58.
поток без разрыва и без
вихрей, п частицы жидкости доходят до самой модели, на которой в определенном месте нолучается критическая точка со скоростью, равной нулю. К потоку, натекающему
Фиг. 59.
на пластинку, за пластинкой присоединяется другой поток, совсем иного характера, с направлением струй, несоответствующим направлению г явного потока: частицы в нем но отно
Фиг. 60.
шению к пластинке движутся по замкнутым линиям, веде тствне чего сзади пластинки образуется вихревое кольцо из одних и тех же частиц. В опытах Ahlborn’a вихревая нить образует только полукольцо (фиг. 60), обрываясь на поверхности жидкости. Сзади этих вихрей главный поток снова смыкается. Если внимательно всмотреться в рнсу иок спектра, который схематически изображен иа фиг. 61, то можно заметить, что пласгннка вместе с образующимся за ней вихревым кольцом имеет приблизительно форму шара, который обтекается потоком. Ес та вообразить, что пространство, 1ннятое вихрем, зак.почено в твердые стенки, то для определения сопро-
Теорвтжчаскае осаааы аоэдххоплааашя.
тивления полученной таким обратим формы модели мы должны взять fc —0,024 — коэффициент сопротивления шара. Отнеся же найденное сопротивление к площади пластинки, которая выйдет меньше мпделев<го сечения шара, получим больший коэффициент А- = и.085.
В работ*.* Ahlborn а. помешено также нс»? <• ц. ванне относительно распределения лав юння вио-
Фнг. 62.
Тике, которое определялось по высоте различных точек свободной поверхности жидкости: углубления на поверхности потока соответствуют местам
Фяг. 63.
низкого давления, п наоборот.
Прн косом ударе (фиг. 62» явление принимает иной характер. Поток, натекаюшпи на п ластинку справа, разделяется несимметрично, и критическая точка приближается к переднему । верхнему на рисунке» краю пластинки. Вихри сзади пластинки располагаются также несимметрично: вихрь переднего края пластинки (верхний» сдвину !ся назад (влево), заднего края (нижппй)—вперед | вправо). Интенсивность вихрей будет также раз
лична. При очень малых углах наклона к направлению потока вихревые массы вовсе пропадают.
Фиг. 63 тает спектр в случае двух наклонных п завов, поставленных один за другим на разной высоте. Из рисунка видно, что вихри за передним планом слабее, чем в случае одного плана, за задним же интенсивность вихрей не уменьшается. Этим объясняется, почему уменьшается нормальный удар прн раз (ВШ'ании планов.
По отношению к подл>емноп силе по юбная комбинация 1вух наклонных планов представляет выгодную форму. Кроме того, то обстоятельство.
что поток прорывается между планами, значите «ьно увеличивает их устойчивость, чем объясняется, между прочим, успех змеев Hargrave а. (’тою же целью аэропланы (стали сначала в форме коробок и вертикальными перегородками. Получающееся прн этом течение с вполне выдо (енпыми отдельными струями обладает большою устойчивостью и нелегко псре-хо шт в другом тип течения.
На фиг. 6i изображена обыкновенная би-н тайная форма. Поток, проходя между двумя планами, вызывает вихри сладп на : планами. Над выпуклой стороной верхнего плана “бразу ются вихри более энергичные н опре (• юнныс. чем над нижним планом. Благо-
Фи г. 64.
„хря этому, верхний план
держит несколько большую нагрузку на о шинку поверхности, чем нижний.
Теперь опишем не которые пз епо« • -бов иг.лучения аэро t и н а м и ч е-
взаа
р к и х спектров, именно способы фотографирования (ымных струек и способ Д. П. Рябу ши некого.
Прибор Wei! пега для получения дымных спектров изображен на фиг. 05. Он пре ютавтяет из себя п.тоеку ю трубу, стенкп которой в ере (ней части аппарата - 'стоят из юркальных стекол, прп чем расстояние между широкими стенками равно 15тт. В-, пух в этот аппарат вдувается снизу. Для направления струп нижняя (Ш и верхняя iddi часть прибора разделена жестяными листами на 16 отдельных камер (15 X 15 тп^- Днм входит юрт боковую трубу R пол тем же напором, что и во ух, и входит в каждую камеру чере-з круг, toe отверстие в средние ее с диаметром d=l тт. Прп отсутствии исследуемой пластинки, дым идет в приборе параллельными вертикаль-пыми струйками. Если же поместить чероз отверстие S, закрываемое притертым зеркальным стеклом, к которому приклеивается мо
Фиг. 66.
дель, в среднюю часть аппарата пластинку, и ли каку ю - нибудь
модель, то струп дыма отклонятся и дадут спектр линий тока, который можно наблюдать через стеклянные стенки. Па фнг. 66 помещен маленький
— 68 —
На последнем можно части пластинки что воздух течет
цилиндрик круглого сечения, иа фиг. 67 дута крута, видеть, чт«» струи расширяются со стороны вогнутой и суживаются со стороны выпуклой. Отсюда заключаем, медленнее с вогнутой стороны и быстрее с выпуклой. Поэтому давление иа вогнутой сто- ? роне пластинки" больше, чем на выпуклой, что и вызывает некоторую подъемную ситу при сов- в падении хорды птастинки с направлением потока.
Аппарат Wellner’a был значительно упрощен и приспособлен к дсмонстри-ровапию спектров данцигским проф. WaRener’oM. Ящик Я (фиг. 68/, составленный двумя параллельными зеркальными стеклами и боковыми стенками, с сверху имеет сужение В, из которого всасывается воздух маленьким вентилятором через тру бку F. Комнат ный возду х устремляется в нижнее отверстие ящика С. Перед этим отверстием стоит трубка D с дырочками, в которую посредством трубки Е полается табачный дым. Стру п возду ха вместе с (ымнымн струйками проходят через ящик в трубку F вентилятора. Между стеклами ставится модель. Явления при постановке различных моделей получаются такие же, как в приборе Wellner’a.
На фиг. 69, 1 слева имеем спектр сжатой струи, вытекающей нз отверстия. Направо (69, 2) представ тс но плавное обтекание хорошей формы моде та. Струи дыма прекрасно изображают лнини тока. Но сбоку от модели струйки смешиваются; это показывает, что в его приборе образуются мелкие добавочные вихри от трения. Сзади на рисунке заметен маленький хвостик; он получается, несмотря на хорошую форму модели. В местах, где имеются вихри, на рисунке получаются чистые места, так как вихри нечем питать. Очертание же струй очень отчетливо.
Фиг. 70, з относится к прямому удару потока на пластинку. фнГ 69 К сожалению, на самую модель не
попало ин одной струйки. Поэтому рассматриваемый спектр не даст о пре деленного ответа ня спорный вопрос относительно существования конуса неподвижной жидкости перед моделью. Спектры же Ahldom’a ие подтверждают существования этого конуса.
На фиг. 70,7, представляющем собою крыло аэроплана Фербера, изображено приспособление для поворота пластинки во время опыта. На этом рисунке, равно как и на фнг 70, 8, сверху заметны завихренные места (без дыма). При малых же углах, иаиримср, на фнг. 70, 4, мест без
lit
Фиг. 67.
Фяг. I
дыма нет, т.-е. вихрен нс образуется. Пластинка эта, с расширением спереди, представляет собою хорошую форму аэропланного крыла. Обративши внимание на пластинку сзади крыла — руль глубины,— видим, что сверху нал нею струн ближе между собою, чем снизу. Получающаяся при этом разность давлений снизу и сверху пластинки вызовет некоторую подъемную силу, которая будет получаться даже в том случае, когда пластннка нагнута своим передним краем вниз под небольшим углом, не превышающим некоторого предельного.
Иа спектрах Wagener'а струн имеют очень простую форму, но не нужно переоценивать этой простоты, так как иначе можно впасть в ту же ошибку, в какую впадает Гилыпау, исследуя водяные спектры. Дело в том, что сети поставить отек-ляные стенки прибора очень близко между собою, то задерживающая си ла трения не позволит образоваться тем круговращательным щпжениям и срыву струи, которые полу чндись бы в свободном воздухе. Поэтому, ставя стекла очень близко друг к другу, мы замаскировываем очень важную сторону
рассматриваемого яв тения.
Этот недостаток имеет прибор Гнлыпау, находящийся в университет**, вследствие чего трение о стенки значительно искажает спектры. В его приборе не образуется вихрей сзади моделей. В тех случаях, когда в свободном пространстве струи обыкновенно срываются с поверхности.
например, с пластинки, в его приборе струи нс сорвутся, а обтекут п частнику очень аккуратно, подобно тому, как вода в водоносных песчаных слоях обтекает встречающиеся препятствия. Поэтому, прибор Гильшау мало пригоден для аэродинамических демонстраций.
Тру ба аэродинамической лаборатории В. М. Т. У., расположенная горизонтально, имеет расстояние между стенками в 30 ст, и измерения далп »динакову ю скорость по всей ее высоте; это показывает, что трение о стенки
трубы оказывает малое; влияние на исследуемые явления; это происходит оттого, что стенки трубы весьма гладкие (зеркальное стекло) и наблю-
еение производится недалеко от начала трубы (1 mt).
Статью об аэродинамических спектрах закончим рассмотрением работ, произведенных в аэродинамическом институте Д. П. Рябушинского в Ку чине
Метод исследования Д. П. Рябушинского зак почастся в следующем.
Фиг. 71.
половина (фиг. 71), в случае сферы —1
На горизонтальный железный лист, помещенный в средине трубы и предварительно посыпанный порошком плауна, который располагался на нем. вследствие сил сцеп |ення [ в виде маленьких капелек, \ ставилась половина иссле-дуемой модели, разрезанной ио плоскости симметрии. Например, в случае цилиндра — его ту сфера, и т. д. Когда приведут
и действие вентилятор и движение воздуха в трубе установится, постуки-
вают молоточком по листу; топа частицы подпрыгивают вверх и несутся в струе, а затем падают обратно на лист. При отсутствии потока частицы упали бы на прежнее место (фиг. 721. Поток воздуха, идущий в определенном направлен пи, заставит частицы разбрасываться веером в вертикальной плоскости (фиг. 73), направленной по скорости потока, так как различные частицы получают различные вертикальные скорости. Салясь на железный лист, частицы расположатся
в виде черточки, иаправ генной но скорости, существующей в данном месте потока. Например, на спектре, изображенном на фиг. 74, для потока, у 1аряюшегося иа плоскую пластинку ьО 80 тт нормально к ней, мы видим спереди, на некотором расстоянии от пластинки, очень хорошо расположенные черточки, которые дают направление скорости.
Д. П- Рябушииекпй предполагал, что черточки плауна дают нам всегда направление линий тока; но тогда являлось непонятным, почему
ii I
фвг ф 73 в спектре недалеко перед пластинкой
образуется вал нз плауна, н на нем незаметно никаких черточек: образование такого вала должно указывать как бы на застой жидкости пере л пластинкой, допустить су щ< етвование которого было бы странно. Теперь выяснилось, что причина образования на спектре
вата из плауна та же, что и образования" перед какими-либо препятствиями снежных заносов: оба эти явления очень близки между собою.
В своем докладе о снежных заносах, сделанном в Математическом Обществе, я исходил из того предположения, что на лет ку ю частицу, подброшенную в Воздух, действует сила тяжести и сила сопротивления воздуха, при чем после дням получается, главным образом, от вязкости
воздуха.
По теории Stokes'a еопро- Фиг '*•
тивтонне от вязкости пропорционально перво» степени скорости. Поэтому 1ля ничтожно малых, увлекаемых воздухом, частиц, скорость которых, всле дствие их малой инерции, может тппп» мало отличаться от скорости воздуха, сопротивление от вязкости получится в неско.гько сот раз больше. сопротив ления, подсчитанного по закону квадратов скорости, так что после шим можно пренебречь. Наоборот, при больших телах, обладающих большой инерцией и большой скоростью относительно воздуха, можно пренебречь членами с первой сте-ненью скорости пере i членами с квадратами ее.
С помощью математического анализа можно доказать такую теорему:
если частицы движутся в пространстве далеко от того места, где имеются препятствия, то они, действительно, идут в направлении ш тока; перед ирепят-
ствием же, где поток поворачивает и образует критические точки нулевой скорости, частицы отступают от движения потока н садятся, образуя бугры.
Можно вычертить те кривые, по которым лягут частицы в зависимости от характера движения потока, веса частиц и, вообще, от условий задачи. Оказывается, что снежный бугор должен подниматься перед
препятствием, немного впереди от него |фиг. 75): перед самым препятствием образуется вихрь, который отметает частицы и заставляет их осесть немного впереди. Если, согласно этой теории, вычертить те кривые, по которцы должны сесть частнцы, то получится несколько колец: одно, ближайшее к препятствию, очень резкое, другие — более слабые.
Имеется много исследований п
наблюдений относительно снежных
заносов. Рисунки киевского проф. Червинского, изображающие снежные
заносы около Киевского политехнического института, вполне подтверждают правильность предложенной мною теории. Снежные заносы дали кольца перед флигелями института и большое кольцо у главного здания (фиг. 76». Спектры Д. П. Рябушинского очень напоминают все эти явления снежных заносов, что и понятно, так как в Кучинском институте фотографировались не
пу ти летящих в потоке возду ха (скорость 5- б mtlsec) частиц, как дрлал Ahlbom с водяными струями, а те места, где частицы легли.
На спектре, изображенном на фиг. 74, для квадратной пластинки ьо X 80 тп/я, ближайший к пластинке
_ бугор представляет тин снежного
фиг' /6' запоса, второй бу гор—впереди него—
то-же, только более слабый. Между этими буграми замечаются линии тока, о происхождении которых скажем после. Второй бугор прорывается струйками. Черное же место перед самой моделью указывает, что здесь появляется крутящий вихрь, который действует в направлении, обратном скорости, н выметает частицы от модели (см. стрелку на фиг. 751. Он как бы стоит один в ямочке, а бугор уж поднимается пере lhhm. Поэтому около модели фотография дает пе линии тока, а подобие снежных бугров.
На фиг. 77, дающей спектр для квадратной пластинки 160 X 160 тт, моя мысль еще резче выражена. Здесь замечаем три бугра, из которых третий прорван линиями тока. Когда частицы
Фиг. 77.
плауна уже сели, продолжаю-
щийся поток воздуха сорвал их с третьего бугра и дал линии тока. Боковые бугры на спектре произошли оттого, что ветер срывает частицы
с заносов и шест их довольно длинною лентой. Если вдали от модели частицы располагаются более или менее близко к линиям тока, то около
нее линии тока смешаны с кривыми, по
которым располагаются частицы вследствие заноса, и нужно разобраться, какое явление преобладает.
Па фиг. 78 изображен спектр от шара с радиусом R=8O тт, где спереди резко выделяется тип снежного заноса. Все же остальные линии очень напоминают линии тока Ahlborna.
£12. Давление воздуха иа решетки.
В прежнее время надеялись
фпг. 7р получить хорошую подъемную
силу, делая поддерживающие планы регпетчатаго типа
Phlipps [1893 г.) построил летательную машину, у которой поддерживающие планы представляли вертикальною решетку с большим числом перьев, поставленных под малым углом к горизонту |фиг. 79).
Hiram Maxim (1893 г.) сделал свою летательную машину многопланного типа (фиг. 80).
Математик Painlevc недавно представил в Парижскую Академию Наук мо [ель Ч аэроплана (фиг. 81), у которого поддерживающие планы представляют решетку на подобие решетки Philippsa.
Фиг.
Те рпя решетки очень проста К ней с точностью можно приложить теорему Эйлера, потому что решетка на1 равтяет все стрти определенным и известным для нас образом.
’) Сдезаивую другим изобретателем. Прим. реЗ.
Студенты Московского Университета Эгесс н Загортан проделали аккуратно опыты С решеткой в трубе прямоугольного сечения. Пластинкн
Фиг. во.
(фиг. 82), чистом я, укреплялись с помощью барашков на рамочке под одинаковым у г том а, который проверялся по ватерпасу. Струи горизонтального потока ударялись п пластинки и отклонялись ими вниз. Получающаяся при этом подъемная сила измерялась при помощи весов, к которым была потвешена рамочка.
Обозначим (фиг. 83); п—число щелей, о—площадь одной из щелей меж (у двумя соседними пластинками при горизонтальном положении пластинок, Fv = an — площадь всех щелей, о = 7 —плотность воз-9 духа, V—скорость натекающего на
пластинки потока, U—скорость воздуха при выходе из решетки. М— секундная масса воздуха, проходящего через одну щель. Тогда
Кроме того, на основании уравнения неразрывности, для каждой струи, протекающей через одну щель, можно написать:
Г’о = Г<1 cos а.
отку ia
Фнг. 82.
Фнг. 83.
Если применить к струям, протекающим через решетку, теорему Эйлера, то подъемная сила будет равна проекции па вертикаль силы давления, которое оказывает поток на плаотинкн; так как горизонтальная сила, равная секундному ко шчеству движения входящей жидкости проекции на вертикаль не дает, а сила, равная секун шому количеству выходящей жидкости SMU, должна быть направлена в сторону, обратною скорости U, состав тающей с горизонталью у гол а, то подъемная сила будет равна
J?= 2? J/i’sina = w — оГ- sine = F 1 V'-tga.........<55)
g cos a 9 ъ '
Опыты Эгесса н Загор 1ана дали результаты, очень хорошо совпадающие с этой теоретической формулой.
В случае одной иластннки воспользоваться формулой Эйлера невозможно, так как мы ие знаем, насколько ве шка та масса жидкости, которая изменяет свою скорость благодаря ирисе тствию в потоке пластинки, и какую величину и направтенпе имеют скорости этих масс, удаляясь от пластинки. Поэтому, в формулу Wellner’a и входит некоторый опытный коэффициент 1).
Теоретически решетка вовсе не оказывает лобового сопротивления.
Опыты над косым ударом потока воздуха.
§ 13. Сопротивление пластинок при косом ударе.
Явления косого удара лежат в основе построения всех нынешних аэропланов и винтов. Поэтому они тщательно изучаются теоретически и в лабораториях. Остановимся на них по цюбно.
Косой удар на плоские пластинки довольно точно был исследован Langley см, впервые (1888 гл построившим ротативную машину (см. фиг. 31 на стр. 12) с длинными плечами (В = 9/25 mix. Все исследования, производившиеся на ротативных машинах до него, были неточны, так как прежние ротативные машины были короткоплечими, и эффект центробежных сил, вызывающих скользящий ноток, был значителен (ем. стр. 35). Окружные скорости в машине Langley я доходили до 30 mt sec.
Для определения вертикальной и горизонтальной составляющих Langley употреблял прибор, представленный на фиг. 84. Легкая рама может вращаться около горизонта льной оси АВ и около вертикальной CD. Вертикальная ось укреплена на Диске, которая j крспляется на конце плеча ротативной машины по направлению S.S вдоль плеча. Пластинка иа правом конце рамы может быть поставлена по i желаемым углом к горизонту. Поворот около “Си CD, удерживаемый горизонтальной пружиной, измеряет силу сопротивления воздуха по потоку, а поворот около оси АВ, удерживаемый вертикальными прхжииами Н и Я, определяет составляющую давления воздуха перпендикулярно к потоку. Эти повороты записываются ня хронографах.
Другой способ определения подъемной силы при косом у таре был довольно своеобразен. Пластинка помещалась на ротативной машине горизонтально и удерживалась электромагнитом (фиг. 85). Когда ток прерывался, пластинка падала в вертикальных направляющих, соединенных с ротативной машиной, так что в относительном движении получалось как бы падение пластинки в сильном горизонтальном потоке. Относительная скорость слагалась из скорости скольжения, или скорости потока, и скорости падения пластинки. Падение црн этом значительно замедлялось. Бремя падения можно было довольно точно определять. Зная вес пластинки и скорости скольжения и падения, можно определить коэффициент подъемной силы пластинки. В формулу, выражающею эту силу, будет входить
*1 В настоящее время со против зев не бесконечных решеток теоретически обстоятельно разработано проф- С. А Чаплыгиным н Kutta.
— 1Ъ —
уже ие квадрат скорости падения, а произведение двух скоростей—скольжения и падения (ом. уравнение 29. в котором Feos/ есть скорость сколь-
ткрния, а Vsin i — скорость падения . Гак как скорость скольжения велика то и подъемная сила получится большая.
Свои опыты Langley производил как с квадратными, так и с продолговатыми пластинками, и установил преимущество последних. Это видно из его диаграммы (фиг. 86), где по абсциссам оттожены углы, а по прш-натам отношение полной силы Л* при угле наклона г к силе прямого удара Nqq. Пластинка 15,2 X 61 ст, поставленная узким концом вперед.
дает почти правильный закон прямой линпн. Кривая, выражающая закон изменения подъемной силы квадратной пластинки (30.5 v 30,5 ст), идет несколько выше, чем кривая пластинок, поставленных узким концом вперед. Пластинка 76 X 12,2 ст, идущая широкой стороной вперед, при малых углах является наиболее выго той из разобранных.
Кроме опытов Langley я на ротативной машине, отноеитетъно косого
удара имеется целый ряд последований, произведенные в аэродинамиче-
ских трубах н галлереях. Русские исследователи являются одними из первых, начавших изучать сопротивление моделей в иску сствснном потоке воздуха при неподвижных моделях.
Впервые у казал па возможность работать в трубах со всасыванием воздуха проф. Wellner. Па фиг. S7 изображена его аэродинамическая труба. По причине се малых р. меров результаты, полученные в ней, представляли мало интереса и mine не были опубликованы. По идее Well-
Фиг. 87.
пег а были устроены аэродинамнческнструбывМосковскомУ ниверситете Старая труба была представлена на фиг. 32 и 33,(стр.43), а фиг. 88 представляет
Фиг. *8
новую университетскую трубу. Пости устройства малой университетской трубы была построена большая труба в аэро динамическом институте
Фиг. 8 1
Д. II. Рябушииского в К} чине. В этих трубах было произведено много опытов над прямым и косым у даром и центром парусности. На фиг. 89 изображен наружный вид Кучинской лаборатории, на фиг. 90 — общий вид большого за fa главного здания, на фиг. 91 — аэродинамическая труба.
Фнг. 92 показывает прибор Д. И. Рябушииского для определения силы действия потока воздуха на пластинку и ее центра парусности. Прибор качается на двух ножах, которые могут быть поставлены пли ио направлению потока, нли перпендикулярно к нему. В нервом случае весы измеряют силу, нормальную к потоку, во втором—силу по направлению потока »<ч»ирогивлснпе1.
Прибор, аналогичный описанному, построен теперь для всасывающей круглой трубы аэродинамической лаборатории В. Т. У
Фиг sil
Различные исследователи давали свои эмпирпческия формулы, выражающие зависимость сиды полного давления иа пластинку от у гла i наклона пластинки к потоку. Некоторые нз этих формул для плоских пластинок приведены в таблице 12 п, мя сравнения, изображены на диаграмме фиг. 93.
Несовпадение приве юштых в таблице формул обт>яенястся как различием в методах и условиях наблюдений, так п тем. что они относятся к пластппкам различной формы fc разными удлинениями) п разных размеров.
Формула Duchcmin a Ш» считается очннь хорошей и прекрасно совпадает с результатами опытов на ( квадратными йлаетинками.
Формулы Soreau (Ш и IV) получены ну тем интерполирования данных Langley я, приведенных на фиг. 86. Приближенная (ПГ) годна для малых углов, встречающихся в аэропланах. Его формулы являются единствен-
иыми, в которых принята во внимание продолговатость пластинки; остальные авторы этого не делали. В формулах Screen вхотит коэффициент
где I выражает ширину (размах) пластинки, a h—глубину ее, под которой мы, по примеру французов, всегда будем подразумевать размер пластинки по направлению потока. При очень длинных пластинках
1-:
m =-----J. 1,
и формула (Ш) ирнмет вит
Л’, = 5 iVso'sin i = 0,42 FV? sin i.
Коэффициент этой формулы в 5 раз ботьще коэффициента сопротивления для нормального удара.
Таблица t2
1. Renard =2 sin*--sin8* -•so Получена на корот-коплечей рогат виной маш иве.
П. Duchemln V, _ sin » А’ю ’ 1 + an*» При малых углах АГ. 2 А» sin i.
ПТ. Soreau Д’=11- 11 + sin i; l * Пряближеввая, для малых углов.
IV. Soreau -V, , 1 -mtgi -V>0 1J_)1 Для любого угла ». m имеет то же значение что в в III
V. Eiffel x- =_‘ л» so Для углов, и севших 30 , а дальше А'( = Ада
VI. РябуШЕЕСЕВЙ у 4=Bm2' Для УГЛОВ, М'-ЕЬ-п!Нх 45э, а дальше А, =- Ада.
УП. Rayleigh V, (4 4- Я) sin » Л ю 4 -г л sin » Теоретическая, для бесконечно ддиввоА пластинки, в предположении разрыввого течения.
Формула НПеГя (V) составлена на основании опытов над пластинками, падающими с башни, и пригодна ыя углов, меньших 30 (см. примечание к формуле V).
Формула лорда Rayleigh (VII) чисто теоретическая; она выведена для бесконечно длинной пластинки в предположении, что струи с пся сры-
каются, образуя за пластинкой завихренную область, и и ijt затем в беспредельную даль, не смыкаясь.
По теории Kutta и С. А. Чаплыгина (эта теория будет изложена ниже», относящейся к изогнутым пластинкам, подъемная сила получается гораздо 1ьше, чем по теории Rayleigh’n. Для случая действительной жидкости трением и вязкостью) пи явления С. А. Чаплыгина, ни явления itaylcigh’fl ие получается в чистом • н ie. 11ри малых углах закон об-i-кания пластинки ближе к замшу Kutta и Чаплыгина, а при олыпих — к закону Rayleigh я, хотя в действительности струи • мыкаются недалеко за пластинкой. Это изменение законов обтекания н является причиной того скачка, который наблю-ается в законе давления на пластинку при некотором, опре-।еденном для панной формы и скорости, угле. Зависимость итого угла от формы пластинки и скорости потока для случая идеальной жидкости указала (’ А. Чаплыгиным в статье:
» давлении плоскопараллельного потока на преграждающие тела".
Одним из первых исследователей, нзу чавших действие щижущегося потока воздуха иа кривые пластинки, является • шлиенталь (Otto Lilienthalk С юн пинты он производил как прямо на ветру, так и на коловратном машине. Дли определения давления ветра на н 1астинкн он пользовался приборами, представленными на фиг. 94 (I и ]1|. На первом приборе с помощью шнамометра г определялась горизонтальная с шгающая давления ветра на пластинку, на втором приборе с помощью такого же динамометра / определялась нертикатьная слагающая—подъ-• мная сила.
Кроме этих двух приборов, Лилиенталь пользовался при своих опытах также коловратной машиной Сдпаметр 7 mt, высота над землею 4,5 mt}, изображенной на фиг. 95. Па этой машине он одновременно мог onpe.iv-тять и горизонтальную, н вертикальную слагающие давлении потока на пластинку. Пластинки можно было устанавливать под различными углами к паправ тению потока. Вращение прибора (скорость пластинок изменялась "Т 1 то 12 mt агг) производитесь при помощи двух (чтобы уменьшить ывтение на ось) грjзов, привешенных к концам шнура, намотанного на
Фиг °2.
рстжческвс ос м воаэухоп.таааныя.
горизонтальный блок, н юпствовавших в одну сторону. Относя действие грузов к центрам сопротивления пластинок, можно было ле!ко подсчиты-
S d 3 g
вать гори jo нтаяьные составляющие. Вертикальные же <*остав.ипощ|п опре (елялись при помощи грузов, устанавш-ваемых па чашке, подвешенной к вертнка ibuou оси прибора.
Несмотря на ошибочное допущение, что центр парусности всегда • овладеет с центром пластинки. полученные Лилиенталем розу тътаты. как показывают более точный наблюдения других исслс ювателей, мож-
но считать _ овотьно пра
вильными. Это объясняется как малой глубиной пластинок (нс более 0,1 mt}. так и пх формой |фиг. 96». Обрез пластинок был с де таи в одной плоскости, так что они были ложкообразны.
ФМ1. 96.
Фиг. 97.
Диаграмма фиг. 97, построенная Лилиенталем на основании его опытов, дает дрн различных углах нактома i величину полной силы давления воздуха Д на пластинки различной вогнутости. Вогнутостью нс» । тастинки называется отношение стрелки дуги к длине хорды. Кривые вычерчены для пластинок с вогнутостью 1'№, 1 35, 1 *1Л и для плоском 11 1СТПНКИ
Что касается давленпя на плоскую пластинку, то Лилиенталь полу-
чи I для иее при всех углах закон синусов.
Сравнивая кривые между собою, видим, что при одном и том же угле наклона полное давление иа вогнутую пластинку гораздо больше, чем
На фиг. 98 изображена векторная диаграмма давлений на пластипкн. при чем направление потока принимается горизонтальным. Угол наклона пластинок обозначен при концах соответствующих векторов. Сами ж-векторы 1ают полну ю силу давления Л, как по величине, так и по направлению. Кривая I относится к опытам с вогнутой пластинкой (w = 1/12i, произведенным на ветру, кривая II—к опытам с тою же пластинкой на ротативной машине. Кривая III нанесена для сравнения и дает силы давления на плоскую пластинку нри опытах на ротативной машине.
Диаграмма показывает, что полное давление на вогнутую пластинку не только будет больше, чем на плоскую, но будет иметь и другое направление. Благодаря изменению после чисто, возрастание полной силы ывле-нпя, главным образом, вызывает увеличение подъемной силы и мало изменяет силу сопротивления по направлению потока.
Честь установления тою факта, что вогнутая пластинка обладает гораздо большей подъемной силой, чем плоская, принадлежит всецело Лилиенталю и составляет его важную заслугу, так как открытие это легло в основание устройства современных аэропланов. При малых углах наклона, напр., при 5е, вогнутая пластинка дает огромную подъемную силу по сравнению с плоскими. Подъемная сила получается даже при горизонтальном положении хорды пластинки (/=0) и даже при отрицательных углах наклона (например, при —5°).
Фиг. 99 дает векторную диаграмму сил давления при горизонтальном положении хорды пдастиики и различных направлениях потока *).
На основании опытов Лилиенталя, Soreau дает для пластинки с вогнутостью 11S при небольших углах i (до 10°—15°) формулу подъемной силы:
72 = 0,33 Г 74 . . . - (&«>
гда Г—скорость потока, F—площадь пластинки, а угол а° = Г+8'43', п формулу силы сопротивления (по направлению потока):
Q = 0,33FF2(ra2+s),...................(&*>
где г и s — опытные коэффициенты. Пользуясь данными Лилиенталя, Soreau нашел, что т=1 , s = — 0,0315 (при w = 1/la); таким образом, при а = 0 сила сопротивления Q получается у него отрицательной. Проф. Фан-дер-Флит, сверявший формулу Soreau с диаграммой Лилиенталя, показал, что получение отрицательного значения для величины s невозможно; как впдно из диаграммы фиг. 98, направление полной силы давления составляет с направлением потока угол, всегда меньший 90J. Неправильное значение для s Soreau получил благодаря имеющейся у него в таблице ошибке в знаке слагающих давления, направленных по хорде. Сам Soreau допускает существование отрицательной силы Q, как бы подсасывающей пластинку по направлению движения. Но это неверно. На основании теоретических соображений, с которыми согласны и вес наблюдения, никак нельзя допустить подсасывающего эффекта навстречу ветру. Теоретически, равнодействующая сил давления иа тело, погруженное в идеальную жидкость, со всех сторон аккуратно его обтекающую, перпендикулярна к направлению потока. Сила же Q, наблюдаемая при опытах, вызывается трением жидкости о поверхность тела и образованием вихрей, и не может быть отрицательной. Что касается угла 845', входящего в формулу Soreau, то он очень близок к Чаплыгинскому углу/*. Если мы обозначим нейтральный j гол, стягивающий хорду, через 26, то д почти равно , что для вогну -тости «? = 1/12 дает угол около 9°. Таким образом, чисто теоретические исследования Kutta и С. А. Чаплыгина близко совпадают с результатами опытов.
Фиг. 100 представляет результаты измерений, произведенных в трубе Кучинского Пиститута Д. П. Ряб^чпинского (прибор на фиг. 92). Кривые С£ тают коэффициенты сил, действующих по хорде пластинок, а кривые сил к ним перпендикулярных (множитель^ в коэффициенты С не включен». Углы наклона считались положительными, когда поток ударял иавогнутую сторону пластинки, и отрицательными, когда поток ударял на выпуклую.
Из диаграммы видно, что слагающие давления, направленные по хорде, при увеличении положительного угла наклона до некоторого значения, зависящего от вогнутости, становятся отрицательными (ср. фиг. 99). Marcel Deprey объясняет этим парение птиц и перемещение их против ветра при распростертых кры.гьях. По его мнению, в атмосфере всегда существует
’) Такую же диаграмму Лилиенталя для плоской пластинки см. $ 40, стр. 257. фиг. 304
DLJ8JL19 №
небольшой восходящий поток воздуха, который и прп горизонтальном положении крыльев птицы ударяет на пих под некоторым нотожителъиым
углом (фиг. 101 j. Горизонтальная слагающая давления при соответствующем угле наклона крыла к ветру бу 1ет равна пулю или отрицательна и тает итнце возможность парить и даже лететь против ветра. Однако, несмотря иа существование отрицательной силы по хорде пластинки, слагающая гавленпя по направлению ветра всегда будет положительна.
На диаграмме Д. П. Рябушинского налгаьжже. гомта 2 , ,
—•— ------ нанесена также кривая коэффициентов
/,S1D ”—, соответствующая теоретиче-4 + з sin а
ской формуле Rayleigh. Эта кривая идет на диаграмме ниже всех опытных кривых, в том чис ле и кривой для плоской пластинки, с которою она должна бы
совпадать.
Фпг. Ю1. Но опытам Рябушинского, maximum
кривой для плоской пластннки получается около 30°, при больших же хтлах кривая идет почти парал
лельно оси абсцисс вплоть до 90\ каждой пластинки остается почти постоянной.
В вопросе о влиянии вогнутости на величину подъемной силы пластинок следует хорошо разо-ораться, сравнивши меж iy собою все опыты, относящиеся к этой области. Наибольшего доверия за стуживают опыты, поставленные с большою тщательностью в Гет-
В пределах 20 —30е подъемная сита
Фяг. 102.
тишенской лаборатории проф.
PrandU’H. Там была произведена серия опытов с пластинками (фнг. 102), ширина которых (размах) и глубина оставались постоянными (Rox^ 20cznj, стрелка же дуги сечеиня — Да, следовательно, и вогнутость пластинки №* менялись:
Таблица 13.
г 2.49 2.04 1,65 1,42 1,00 0 81 0,33 | О
- ч 10 | 12 16 20 I 25 ( 60 <х
Из диаграммы |фиг. 103» видно, как значительно растет подъемная сила пластинки с увеличением ее вогнутости. Угол наклонения кривых к оси абсцисс с возрастанием стрелки становится вес больше. На фиг. 1< >4 изображена диаграмма сил сопротивления 1ЛЯ рассматриваемых пт истине к.
В университете И. П. Соколов делает теперь вместе со мной опыты с пластинками разных хорд, но с одинаковой строчкой, и получаются результаты, вполне подтверждающие теорему С. А. Чаплыгина, что цчастники <• различными хордамп, но с одинаковыми строчками, имеют одну и ту же подъемную силу. Однако, в случае очень выпуклых дуг силы трения могут изменить самый характер явления, например, вызвать вихри, и тогда подъемная сила может резко у пасть.
Сделавши общий обзор явлений косого удара, остановимся теперь подробнее иа розу тьтатах и обстановке опытов в аэро шнамическпх лабораториях Е1П‘еГя,‘Rateau и Prandtl’H.
решетки которые хорошо
охва-модсть, они образовать нею ско-
Фиг. 105 и 106 дают план и вертикальный разрез лаборатории ЕШеГя (20 12 mt\. Камерой для опыта с ел} жит просто часть комнаты (ем. также
фиг. 107). В d ставится испытуемая модель. Возду х высасывается из камеры центробежным вентилятором „Сирокко** tg (через воронк\ f, обходит кругом здания по корри-юрам j и i и воз-, вращается в камеру с через комнату а и насадок Ь. Для направления потока, в насадок Ь ставится решетка из квадратиков, которая разбивает поток
на от де 1ьные параллельные стр^ пки. При квадратных отверстиях поток можег нести с собою только маленькие вихревые кольца, на модели разбегаются в разные стороны. Если же устроить в насадке только про-шлъиыс перегородки, то в потоке будут существовать вихревые шнуры, которые обл «дают свойством «охраняться; тывая могут перед птение вихрей. Эйфель полагает, что врывающийся в камеру с поток не за-кнхривается об окружающий воздх х, т.-е. полагает, что поток проходит че-окр\ жающнй воздух
роз камеру с как ь трубе, сплошною массою, остается совершенно спокойным. Лица, которые утверждают, что, действительно, никакого щается. Возможно, что это и в рн ; j скорости, поток меньше з«хватывает окружающий воздух. Например, при «пытах в университете над истечением воздуха из котла компрессора, где скорость сходила до 200 mt депствитетьп » получалась резкая разница, если поставить руку в струю или около нее; щако н к этом случае было заметно, что стр\я расширяется конусом. Эйфель же утверждает, что
а < ... • л. •
ви ie ш аппарат Эйфеля, ветра в комнате не ощу-может быть, при очень большой
— JyS —
поток j пего не расширяется. Что касается малых скоростей, то при скоростях около 8 mt sec, с которыми [производились опыты в трубе М. У., ясно видно бы.и> закручивание во-гдуха.
Фнг. 105.
Фнг. 106,
Фиг. 108 представляет старую университетскую трубу. Буквы на фигуре поставлены соответственно с чертежом лаборатории Энфетя. с пред-
ставляет камеру со стеклянными стенками, присоединенную к верхнему краю трубы. На задней стенке камеры, идущей вдоль тру бы, ставится картонный лист с флажками на булавках. Расположение флажков, как показано на фиг. Ю9 *), cBMieTevfbCTByeT о вращении воздуха в камере.
Для измерения силы давления потока иа пластинку у Эйфеля на особом помосте поставлены весы Е, схема которых изображена на ||>нг. 108. Испытуемая пластинка S при помощп стержня С закрепляется в суппорте F ломаного рычага DE. Рычаг ЕЕ можно, по желанию, заставить качаться на ножах или около точки А, ИЛИ ОКОЛО точки В. От рычага DE идет тягаЯ к одному плечу коромысла весов, а к другому плечу по цвешена чашка для гру -зов Р н пру жнна Т (до 50 у/», которая натягивается рукою закотьцо К и заменяет мелкие грузы, которые пришлось бы перекладывать при всяком колебании скорости в трубе.
Фиг. 107.
Фиг. Ю8
Чтобы поток воздуха не давил на вертикальный стержень D томаного рычага н ие оказывал влияния иа точность измерения, стержень D прохо-шт внутри неподвижного цилиндра (фиг. 107).
Определение силы давления на пластинку прп данном угле наклона Эйфель производит, измеряя моменты этой силы относительно трех различных центров: В, Л и Л* симметричного с А относительно стержня С Для получения первых двух моментов ои заставляет рычаг вместе с укрепленной'на нем пластинкой качаться на ножах сначала око то точки В, затем около А и определяет грузы, уравновешивающие давление на пластинку. Чтобы иолу чить третий момент (относительно центра Л i, Эйфель поворачивает в суппорте Р стержень С с закрепленной на нем пластинкой па 180' и уравновешивает давление на пластинку, заставляя ее качаться околоJ
См стр. 90.
Конечно, предварительно определяют грузы, уравновешивающие рычаг с пластинкой, когда вентилятор не пушен в ход, п воздух в камере спокоен.
Из трех уравнений моментов, полу -ченннх на основании такого уравновешивания, легко определить давление R движущегося потока во. духа иа пластинку по величине, направлению и точке приложения
(взятой, наир., на хорде лластицкн). Для этого можно применить графическое построение. Но, по избежание кропотливой работы вычерчивания и для большей точности, вместо него обыкновенно пользуются соответствующими форму ламн.
Рассмотрим теперь результаты исследований Эйфеля. Па его дна-1 рам мах коэффициент подъемной силы обозначается через силы сопротивления через А> и полной силы давдения через А;.
Из диаграммы фиг. по видно, что подъемная сила плоской пластинки (*5X15 пп\ получает наибольшее значение при угле наклона в 30э, а затем падает и обращается в нудь, когда пластинка расположится перпендикулярно к потоку (i = 90 I. (’ила же сопротивления изменяется с углом наклона почти но закону прямой линии. Что касается полной
силы давления на пластинку (кривая А,), то опа вес время возрастает, сначала очень быстро, а затем Me i юн-нее. Впрочем, так Меняется полная сила только для пластинок длинных—с большим размахом; t ш квадратных же оца изменяется несколько иначе: сначала (до 30 } идет почти по прямой липни, а затем почти уже не меняется и постепенно переходит в силу прямого удара. Для длин них вогну тых пластинок (обозначения А',., к*в, к'я), как полу чп I Зифе ль для п ia-< тинки 90 X 1» ст и w = ‘
(фнг. ПО), потная сила сначала (до 16) возрастает довольно быстро, а затем мало меняется. Подъемная
Фиг. 110.
сита и силы сопротивления
при угле око.ю 45э почти равны, так что общая равнодействующая их приблизительно перпендикулярна к хорде пластинки и направлена по
ср« (Нему радиусу.
Вопрос о сите сопротивления по направ 1енпю движения является наиболее с 1абым местом теории Kutta и С. А. Чаплыгина. Теорстичс-' кп, если пластинка аккуратно обтекается, полная сила давления
должна быть перпендикулярна к потоку, так что слагающая в направлении движения равна нулю. Таким образом, теория, давая близ-
Фиг. 111.
кие к показаниям опыта результаты относительно подъемной силы совершенно ие объясняет возникновения силы сопротивлении. Полагать же.
что вся сила сопротивления возникает от одного трения о пластинку,
нельзя, так как сила трения неветика и никогда не может вызвать такого большого сопротивления. Kutta в своей постоянен работе дает некоторые соображения относительно возниковения сопротивления движению, о которых я буду говорить позднее *).
Как показывают опыты Рябушииского (фиг. 111), сила сопротивления прн углах наклона пластинок до 10° почти равна нулю, а при дальнейшем
возра< гании угла она постепенно переходит в силу прямого удара. Это можно объяснить тем, что при больших углах явление непрерывного обтекания по закону Kutta и Чаплыгина становится невозможным и переходит при углах в 15J — 40° (в зависимости от вогнутости) в разрывное течение по закона лорда Rayleigh.
В вопросе о подъемной силе между исследованиями Eiffel я и Ряб\-шинского замечается разница. По опытам Е1ПеГя наибольшая подъемная
сила для изогнутой пластинки получается при 16 , а затем начинает падать. По опытам же Рябуптинского подъемная сила проходит через максимум при угле наклона около 30\
Рисунки 112 и 113 представляют прибор Rateau. Ои устроил свой прибор несколько раньше лаборатории Эйфеля. Разница между ними та. что у Rateau наблюдения ведутся в нагнетаемой, а у Эйфе ля—во всасываемой струе воздуха. Поток у Rateau создастся крыльчатым вентилятором Г, диаметром 1,2 mt. Ои нагнетает воздух в квадратную со стороной 1,6 mt. камеру С, разделенную решетками для сохранения параллельности струй. К камере приставлен пирамидальный насадок В, через который воздух выбрасывается наружу с большой скоростью (свыше 20 mt sect Выходное отверстие насадка также квадратное, со стороной 0,7 mt. Против центра насадка устанавливается на специальной раме нспы-
Фнг 112.
Фиг. ИЗ.
дуемая модель (обыкновенно испытывались пластинки). Рама поддерживается на двух цилиндрических поплавках D из листового железа, погружен ных в стоящие по бокам сосуды с водой (они также обозначены буквами П). Вертикальные силы, действующие на раму, уравновешиваются грузами на чашках J, а горизонтальные— более сложным приспособлением: по обе стороны от рамки (симметрично) расположены две соединенные с ней балочки F. Они шарнирно соединяются с ломаными рычагами GK, качающимися па ножах If. К наклонным частям К ломаных рычагов подвешены чашки весов J.
При спокойном воздухе рамка с пластинкой стоит в определенном по гожении. Ког ха вентилятор пущен в ход и поток установился, на пластинку действует сила давления возду ха, стремящаяся поднять рамку и передвину ть ее поступательно. Нагружая тс н другие весы, приводят рамку в'прежиее положение п по величине нагрузок опреде ляют компоненты силы.
’) В дальней шеи бу лет изложена теория Karman’а, объясняющая лобовое сопротивление у бега ющ и мн вихрями.
Ratean исследовал пластинки с различными профилями сечения, изображенными на фиг. 114, и с одним и тем же размахом (50 ст). Полученные им 1ля различных углов наклона отношения подъемной силы к силе сопротивления, равные отношению приведены на диаграмме фиг. 115. Эти отношения являются наиболее важными ггри построении летательных машин, так как характеризуют коэффициент полезного действия данной пластинки и дают силу тяги, необходимою для поддержания данного гроза.
Фиг. 114. Фиг. 115.
k Для плоской пластинки (1) наибольшее отношение полечилось при угле около 2Э (сама подъемная сила при малых углах изменялась почти по закону прямой линии). На этом основании Джевепкий расчитывает своп
Фег, 117.
винты так, чтобы встречный воздух ударял на рабоче ю сторону впнта под углом в 1°57'. При таком угле он считает винт наиболее выгодным в отношении затраты энергии на данною силе' тяги.
Для второй пластинки (дуга типа Kutta с весьма малой толщиной) наивыгоднепшие условия получаются при угле около 3°, ; ля третьей (плоско-выпуклая пластинка, у которой рабочая поверхность совпадает с хордой) при угле около 4 . Кривые этих пластинок показывают что (прн дайной глубине) наиболее целесообразно давать сечениям поддерживающих планов (или лопастей винта) плоско-выпуклую форму, а не форму тонкой дуги.
Из всех пластинок наиболее выгодной оказалось шестая: сечение ее представляет тонкую лугу, подобную дуге второй пластинки, но вдвое-
меньших размеров. 'Гак как размах всех иласгинок один и тот ле, то это показывает выгодность употребления узких и длинных пластинок.
Фиг. 1J6 и 117 представляют шаграммы Rateau (ля плоской И на Фиг. 1141 и вогнутой (2 на фпг. 114, вогнутость И’ = ^ > млаетинок. Размах пластинок 50 cw, глубина 30 ст. На диаграммах нанесены по R кривых;
А,. А. и kt.
Они интересны тем, что при углах 23—36э кривые имеют разрыв: при этих углах невозможно определить силы, действующие на пластинку. так как пластпнка все время дрожит. Законы пзмененения этих кривых до разрыва и после разрыва совершенно различны. По этому повои у Rateau с Д. П. Рябу шниским (получившим непрерывно кривые) возник ••пор, о котором ем ниже.
Теперь опишем ла •ораторию Prandtffl в Геттингенском университете. Она представляет сбою одноэтажно iданис 11,5 9,5 mt |фиг. ll«i.
в котором находится кольцевая гадлерея в виде замкнутого четреугольника. Сечение се квадратное со стороною около 2 mt. так что человек может свободно проходить по ней во весь роет
Фиг- 118. Фег. 119.
(ем. фиг. 119ь В одном нз глинных (9 mt) коррпдормв галлереи—на черт, правый — ставится испытуемая модель, а в другом находится вентилятор. Два коротких (3 mt) боковых коррндора с лужат для соединения первых двух. Справа от галлереи находится комната для наблюдателя, в которой помещаются все приборы лаборатории (фнг. 120).
Для получения равномерного потока в корридоре испытания Prandtl поставил в галлерес целый ряд решеток При постановке их он руководился как иепосредственным опытом, так н теоретическими соображениями. Благи 1аря решеткам в галлерес Л получается поток весьма равномерный, в чем удостоверяются при помощи анемометра и .микроманометра. Вентилятор прнво штся в (виженис электромотором В 10 UP, который, для получения одииаковои скорости потока, регулиру ется автоматически при помощи особого приспособления: изменение разности давлений за вентилятором и пере i ним, при иомоши жидкого манометра и сервомотора, действует иа сопротивление шунтовой обмотки я ц-ктромотора, прпво-водяшего в движение вентилятор. Такое регулирование необходимо как вследствие изменения напряжения в электрической сети п нагревания обмоток, так и вследствие нагревания воздуха в зависимости от трения и вязкости. Это нагревание в маленькой трубе может быть очень значительно (наир., у В. А. Слесарева). У Prandtl’H нагревание невелико
так как помещение j него большое п скоростей больше ю mt s-. он ие полу чает. Модели подвешиваются в трубе при помощи различных спетом нитя-
ных провесов, через которые и силы, действующие иа модель.
Наблю дения, произве денные в Институте, относились, главным образом, к косому \ (ару, и чис ia, полеченные здесь, нужно считать одними из лучших.
Надо шмегпть, что } РгапйИ'я «как н \ Рябушинского) ко»м|>фицнент сопротивления £ опрс кутается для формулы: £
Р -и -FI 9 так • го £есть отвлеченное чис to. не .«висящее ни от выбора единиц для измерення величин, входящих в форм} I}, ни от давления, постольку, носкодькх «•но меняет плотность воздуха и щенение коэффициентов вязко
псре даются измерительным приборам
Фнг *,2Э
стп п трепня воз 1} ха о д<\в опием и температх рои, конечно, едино г на О. Употребление такой формулы совершенно накопи», ио при подсчетах юбпее иметь потный ко-м}к])пцмснт к £ —» в который уже включена
плотность ₽ = —. п который для давления в 760 тт и температуры 15 I бу (ет равен ^£«например. коэффициент РгашНГя £=0,2 соответствует
обычному коэффициент} сопротивления к = 0,025 |.
Прпве (ем сначала результаты опытов над плоскими и цетипкамп «фиг. 121с Глубина всех пластинок была одинаковая и равнялась 33 ст. \(линеипя же (отношение глубины к размаху)
были различны: 1 а. ’ х 1 «а 1 1»96« 1 1 п М» так _- °' ———
что размах пластинок изменялся от 105 до 17,5 см. ...
Все пластинки имели одинаковую толщину и края ----*
их были заострены.
На диаграмме (фиг. 1221 представлено изме-
пение коэффициента полной силы давления на пла- фиг |21.
етпнки в зависимости от изменения угла наклона
их к потоку. Диаграмма показывает, какое большое влияние оказывает на вид кривых величина удлинения пластинки. Для квадратной пластинки 1} (л. ' п давлении изменяется почти точно по линейному закон} (до 40 ь что вполне согласуется е опытами FiffelH. Также до 10° изменяется однообразно и нижняя кривая для пластинки. поставленной длинной стороной по направлению ветра (удл.1 «j.r = 2». Кривые для ipyrnx п щетинок, имеющих размах больше гл} бины, бодее пли менее прямолинейны дпшь (ля небо льших углов и достигают maximum'а приблизительно при угле в 20е. После toio, как по дъемная сила достигла своего maximum а, закон изменения ее как та ква тратноп. такн (ля продолговатой пластинки резко меняется: давление сначала стремите 1Ьно падаег, а затем снова начинает возрастать, но уже очень медленно (кривые на диаграмме ид}т лишь с ма ihm наклоном к оси абсцисс!.
Др}гой ряд опытов в институте РгапсНГя был произведен с пластинками, изогнутыми по д}ге крхга (фиг. 123». Все пластинки имели о шна-
ковую глубину в 20 ст и одинаковую стрелу прогиба 1,5 ст, так что вогнутость их была
1,5 _ 1
20 — 13,3’
Размах же пластинок был разный.
20, 30, 40, 55, 70, 80, 90 и 105 ст.
Толщина всех птастинок была одинаковая (0,26 ст), края были закруглены. Вопрос о форме закругтеиия краев очень важен, так как она оказывает
существенно*' втиянне на течение. В рассматриваемом случае оба края были закруглены по полуокружности.
На диаграмме фиг. 124 дается коэффициент подъемной силы пластинок на фиг. 125 коэффициент их силы сопротивления по иаправ тению потока (движения) а на
фиг. 126 — отношение этих
, _ Л. Фаг 123.
коэффициентов *.
Рассмотрим сначала изменение по съемной силы. Для квадратной пластинки (удл. х/1) «иа меняется в зависимости от углов наклона по закону' прямой линии и ири угле со40э получает максимальное значение. Затем величина подъемной силы резко падает. Для углов наклона око то 40°
для нес на опыте получалось два различных значения—одно почти в два раза больше другого (например, =0,8 и £*=0,4i.
По этому повод 5 Rateau с Д. П. Рябутпинскпм возник спор. Rateau, на основании «чюих опытов, первый указал, что при одном и том же
Фег. 124.
наклоне 1» гастннки к направлению потока могут существовать около нее 1ва различных течения. Соответственно о этим, центр парусности пластинки
1ет иметь два различных положения, и подъемный силы будут разные. Но опытам же Д. I]. Рябушинского, при которых он употреблял амортн-
затор, получилась для центра парусности непрерывная кривая с вполне определенным положением его на пластинке. Поэтому он был несогласен с мнением Rateau. Теперь, на основании опытов в институте Prandtl’a,
Фиг. 126-
этот спор нежно решить в пользу Rateau.
Если брать пластинки с все более и более увеличивающимся размахом, то maximum подъемной силы будет получаться при все более и более острых углах» так что прн очень большом размахе он должен получиться при угле сс 10".
Непосредственных опытов над пластинкой с чрезвычайно большим размахом ие было произведено. Изо
браженная на диаграмме фиг. 124 пунктирная кривая для нее построена не на основании наблюдений.
а путем экстраполяции, иа правильность которой нельзя вполне положиться.
Вычерчивая кривые для различных размахов (20... 105 cm), Prandtl усматривает, что с увеличением размаха кривые коэффициента подъемной силы стремятся слиться, приближаясь к определенному пределу. Этот
предел он и наносит на диаграмму.
Опыты с бесконечно-длинной пластинкой бу iy т произве (ены в аэродинамической лаборатории В. М. Т. У. Поставивши во всю вышину плоской трубы с горизонтальными широкими стенками узепьку ю пластинку, мы должны получить поток с параллельными струями, как будто п тастинка имеет бесконечно-большой размах. Prandtl полагает, что в таком опыте трение воздуха о стенки бу дет оказывать влияние на течение, при чем струпкн воздуха будут немного выгибаться, приближаясь к середине пластники. Но наблюдения с анемометром в нашей трубе, которая имеет высоту 30 ст, показывают, что во всех точках но высоте трубы скорость воздуха почти одинакова; это обстоятельство свидетельству ет, что тренне о стенки трубы очень мало.
Возвращаясь к опытам Prandtl’fl, мы из диаграммы фнг. 125 должны заключить, что изменение (коэффициента силы сопротивления по направлению потока) на большом протяжении выражается почти одной и той же кривой для пластинок различных размахов. Насколько сильно зависит от размаха закон изменения подъемной енты, настолько мало зависит от него закон изменения силы сопротивления.
На фиг. 126 изображена диаграмма отношений С*: характеризующих коэффициент полезного действия данной пластинки. Диаграмма показывает, что, независимо от размаха, отношение это полу чает наибольшую величину при угле наклона лэ 5°, и что величина отношения тем выше, чем больше размах. Отсюда и вытекает целесообразность употребления планов с большим размахом.
§14. Опытные нсследовання относительно положения центра парусности пластинок.
Закончим статью о косом ударе, изложивши отдел о центре давления или центре парусности.
На фнг. 127 представлен флюгерный прибор, которым в Московском Университете давно уже определяли центр парусности пластинок. Прежде
прибор выставляли прямо па ветер; теперь его ставят на трубу. Устройство прибора следующее. На общей вертикальной осн вращаются свободно н независимо друг от дру га флюгер с указателем z и вертикальная витка ЬЪ, сое пшенная неизменно с горизонтальным лимбом с.
В вилке ЬЪ закрепляют исследуемую пластинку так, чтобы направление пластинки проходило через нулевое деление лимба н ставят прибор на ветер ити в трубу. Когда установится равновесие, то указатель z отсчитает на лнмбе угол между плоскостью неследуемой пластиикн и направлением ветра, совпадающим с плоскостью флюгера, а расстояние S средины пластникн от ео осн вращения дает расстояние центра парусности от середины пластинки, так как при равновесии последней центр парусности должен совпадать с осью вращения. Закрепляя исследуемую пластинку в различных положениях, найдем соот-ветству ющие им у глы i между' пластинкой и направленном ветра и, наоборот, соответствующие положения центра парусности для различных углов i наклона пластинки к направлению ветра.
Закон перемещения центра парусности выражается для прямоу гольной плоской пластинки
Фиг. 127.
форму’ЛОЙ:
£ = О,з£(1 — sinz),......................
где S— расстояние центра парусности от середины пластинки, a L глу бина пластинки. Центр парусности нахолится в середине пластинки прп угле г —90°. Ио мере уменьшения угла г центр парусности приилм-жается к краю атаки. В пределе, когда угол i близок к нулю, центр парусности отстоит от переднего края пластинки на расстоянии равном 0,3 £ — 0,3 £ — 0,2 £, т.-е ее глубины.
Первые опыты в этом направлении были сделаны Avanzini н Ioessel'« я над воюю. Они получили результаты, вполне согласные с теми, которые найдены [.ля воздуха. Оба получили одну и ту’ же формулу, хотя работали каждый самостояте 1ьно.
По опытам A\anzini:
g
-j- = о,з (I — sin /)г
а по опытам loessel’fl.
-^- = 0,305(1—sin i).
Опыты Avanzini и loessel’n иад водой вполне подтвер цили, что для квадратной пластинки при / = 0° расстояние центра парусности от края атаки близко к 1!bL. При значительном же размахе пластинки расстояние •то увеличивается и доходит до 1/AL. По теории Kutta центр парусности бесконечно-длинной плоской пластпнки для любого угла i должен лежать па глубины пластинки от края атаки.
Формула, найденная Soreau для воды:
пнет для 1 = 0 расстояние от края атаки (равно как и от середины! равным глубины пластинки (£) и хорошо совпа (ает с данными опыта и о числами Langley’fl и Кнтшег’а для воздуха.
Обстояте.чьные исследования о центре парусности иронии денн моим учеником П. П. Соколовым, который устроил ьля этой цели деликатный аппарат. На нем можно было устанавливать иа (вух центрах а в с пластинки, как показано па фиг. 128, и наблюдать углы i, соответствующие данному положению центра парусности. Для этой цели в пластинку вставлялся еще штифт о, передававший при помощи полоски м п му фты т вращение пластинки
на ось а и соединенный с нею лимб.
(‘о ко лова при чем отло
к рае-
Фнг. 129 представляет дна1раммы наблюдений II. П. над прямоугольными пластинками различной продолговатости, диаграммы составлены по способу Ilagen’a: по оси абсцисс отношения расстояния центра парусности от края атаки стоянию его от заднего края пластинки, а по оси ординат—углы пластинки
с ветром. На кривых написаны величины продолговатости. За меру про долговатости П. II. Соколов считает отношение длины (глубины) п игтинки к ширине (размаху). Размеры пластинок быти от 18 30 ап д.« 20 3 ст.
Фиг. 130 представляет полярные диаграммы наблюдений II. П. Соколова. За полюс О взят центр пластинки, за полярную ось —направление ветра, за полярный угол — угол наклонения пластинки к ветру и >а радиус вектор — расстояние центра пару сност п от центра пластинки. Па кривых, так же, как и на фнг. 130, нанесены величины продолговатости.
Кривые фиг. 129 и 130 показывают, что по мере уменьшения угла i центр парусности перемещается от сре шны к краю атаки н при / = О для всех пластинок находится от него на расстоянии 16 длины. По шрнпя кривая ц.чя квадратной пластинки (>дл. 1) имеет седлообразную выемку. Д1Я длинной
пластинки, иду щей узкой стороной вперед (у дл. 4), кривая , 1ает«я бож •» выпуклой. Для пластинки, идущей широкий стороной вперед (удл. 0,4) седлообразная часть все более и более вытягивается и идет на полярной диаграмме почти параллельно полярной оси. При малых же углах все кривые для разных пластинок схо штся.
Опыты «'околов* принадлежат к исследованиям первой очереди Но еще бопее ранние исследования относительно положения центра парус пости дела I Kummer на коловратной машине, изображенной на фиг. 131 Ци шндрнчес «ая мидеть вставля-
лась в узкую рамочку, вращавшуюся около горизонтальной оси и помещавшуюся па конце и леча коловратной машины, которая приводы ысь в движение от руки, но довольно равномерно вследствие ее бо льшого момента инерции. На осн рамки, перпендикулярно к ней, прикреплялся каргонный лимб с двумя указателями, которые можно было переставлять от руки. С испытуемой же моделью неизменно соединялся третий у казатс п>. Всле дствие невозможности произвести отсчет на лимбе, вращающемся
вместе с моделью, наблюдатель
предварительно устанавливал два первых указателя таким образом, чтобы третий указатель, г»•единенный с моделью, находился между ними при движении машины. Сближая постепенно указатели и убеждаясь каждый р; । непосредственной пробой, что указатель, соединенный с моделью, действительно находится между ними, можно довольно точно отметить ука-
зателями угол наклона пластннкн к горизонтальному направлению движения. а затем и отсчитать его на лимбе (при остановленной машине).
Kummer производил исследования, главным образом, в интересах баллистики, поэтому и модели брал, по большей части, в форме ядер и пуль.
В исследованиях о квадратных пластинках (18 X 18 ст) его чанные совершенно сходятся с результатами опытов П. П. Соколова, равно как и с результатами, полученными в университете при помощи флюгерного прибора.
Более наглядно картину явления дают весьма тщательно н с большим искусством произведенные опыты Rateau и ЕШеГя. Они принадлежат уже к типу
новых—сделанных в 1909 году.
Фпг. 132 npt вставляет диаграмму Rateau для плоской пластинки 50 30 ст). На оси абсцисс отложены расстояния центра парусности пластинки от се края, выраженные в долях всей длины (глубины) пла-
стинки, а иа оси ординат—углы наклона пластинки к направлению потока. Из диаграммы видно, что прн г — 90°, центр парусности находится в середине пчастинки F. По мере уменьшения утла i центр парусностн приближается к краю атаки. Для углов от 90° до 40° закон выражается почти прямой линией, а между углами 40°—30 происходит изменение закона вследствие того что меняется самый характер обтекания пластинок (можно думать
что здесь течение с разрывом переходит в непрерывное). Rateau J тверждаст, по между углами 40 —30° ыя одного п того же положения центра парусности существует два положения равновесия—два различных у г.ынаь лона г— соответственно двум различным законам обтекания пластинки. II в атом Rateau можно верить, так как он хороший экспериментатор н теоретик.
При углах меньше 30 кривая имеет совершенно другой вид и приближается к краю атаки гораздо быстрее. При /==о° центр парусности находится от края атаки на расстоянии се »/4 (0,23) глубины пластинки. Возможно, что при очень длинной пластинке кривая пересечет ось обецнес на расстоянии 1/4 от края атаки.
Наблюдения Д. П. Рябушинского в Кучине очень близко подхотят к результатам Rateau. Разница лишь в том, что кривая, полу ченная в Кучине, непрерывна между углами наклона / = 30 — 40э. С теоретической точки зрения можно скорее принять выводы Rateau, потому что при этих углах происходит переход от одного типа потока к другому. Rateau полагает, что положение равновесия для промежутка 30° — 403 получены Рябушинским вследствие употребления масляного амортизатора, который, допуская только малые колебания около положения равновесия, те лает возможным существование установившегося потока воздуха. При отсутствии ж<- амортизатора, поток быт бы неустойчив.
Переходим теперь к опытам над изогнутыми пластинками.
Ими занимались еще бр. Райт (Wright) перед своими знаменитыми полетами. Более аккуратные опыты были произведены Spratt'oM на приборе (фиг 133), очснт. похожем иа прибор П. П. Соколова. Результаты своих опытов Spratt изображал на полярных диаграммах, где длина радиусов векторов дает расстояние центра парусности от середины пластинки, а полярный угол—угол стягивающей пластинку хорды с направлением потока.
Для пластинки с вогнутостью (см.
фиг. 134) центр парусности при угле г = 0® находится в середине пластннкп, а не ближе к краю
атаки, как для плоских пластинок. При небольшом увеличении у г,та i центр парусности перескакивает на значительное расстояние к заднему краю пластинки, при дальнейшем же его увеличении пере щигается снова к краю атаки, проходя через середину пластинки при г = 17°. Наибольшее удаление центра парусности от середины к переднему краю равно се 0,41 половины глубины и получается при угле i = 50°. Рели далее у величивать угол г, то центр парусности будет опять приближаться к средние и совпадет с нею при i = 90э 1 >.
Аналогичные результаты были получены (фиг. 135) Spratt’oM и для пластики с вогнутостью \24. Характер
Spratt
Фнг. 134-
явления остался неизменным, а чис ювые значения получились иные, вместо углов 17° и 50° Spratt иашел соответственно 10' н 30е, а для наибольшего расстояния от середины число 0,37 вместо 0,41.
*) Гудя по диаграммам главная часть опытов Spratt’а относилась к удару ветра иавыпуклую сторону пластннкп. что может паЯтн собе объяснение в способе определении ц. пар. (прнб. фиг- 133), при котором пластинка сама устанавливалась такам образом. Прим, ред.
Опыты с кривыми пластинками, произведенные в Московски Универ-ситете студентами Соколовым, Шу ваевым и Крюковым, дали числа, совпадающие с данными Spratt’a; но характер
найденного ими движения центра парусности казался в то время очень странным, и потому их работы не опубликованы.
Soreau, на основании своих опытов, дал такую формулу для расстояния центра пару сноети от середины пластинки:
2S_ tgi—igP__________
1 ~2(«tgfl+Mgi + 21g*i) ’
Фпг 135.
где L длила пластинки, а — у гол между хордой пластинки и касательной
проведенной к краю пдастинкн, равный половине центрального угла для пластинки, изогнутой но дуге крута.
Хорошо можно проследить движение центра парусности по диаграммам, построенным Эйфелем, на основании его прекрасных опытов. Эйфель изображает на диа-граммах самую исследуемую пластинку в различных положениях относи-
И7--1. тельно потока, направле-ние которого принимается эо х <5 ст постоянным (горизонталь-ным на фиг. 136), и от-д... ur= мечает положение центра °° пару сиости прямо на ней, 85 > is ст а не на хорде, как у Spratt’a. Ну нктирнаядуга окружности представляет геометрическое место середин пластинки при различных ее положениях.
—----- Из диаграммы видно, что
когда пластинка накло-] иена иод углом в 90°, то
центр парусности находится прямо посередине. При уменьшении утла центр парусности приближается к краю атаки и подходит к нему ближе
Фяг. 136. всего при угле в 15°.
При углах меньше 15
центр парусности снова передвигается к средине пластинки и при 0°
с нею совпадает.
Мы видим, что диаграмма тщательно проведенных опытов Эйфеля ие совпадает с диаграмой Spratt’a, На первой центр парусности пе пере-
— 104 —
[вигаетея от середины к заднему концу пластинки. При о он почти совпадает с серединой пластинки. Что касается отрицат. льных углов наклона (когда пластинка обращена к потоку выпуклой сториний), то для углов до—7е у Эйфеля пет наблюдений. При угле же—7 центр парусности уже пере [вииулся на значите »ьиос расстояние к краю атаки, а затем, прн большем наклоне, медленно переходит к середине пластинки, е которой и совпав дет при чо.
На Той же двшрамме изображена кривая (пунктирная» перемещения центров парусности для плоской пластинки. Предельное рае. оянпс центра парусности от края атаки равно ’ 4—1 . длины пластинки.
ния центра парусноети от переднего 90J ю 30 совершенно прямолинейны1
Фнг. 137 представляет наблюдения Rateau на [ кривыми пластинками, при чем они не совпадают <• наблю [епиямн Eiffel‘H. У Rateau центр пару сности нахо штся в середине пластинки при некотором положите »ьном у глс, при уменьшении же его центр парусности отходит к заднему краю, как у Spratt а Можно ду мать, что наблю [синя Rateau заслуживают большего доверия, чем иаблю !.ения ЕИТеГя, хотя здесь может быть сказывается влияние различной вогнут ети (у Rateau 1 „ у Fiffel я Откладывая на оси ординат углы наклона, а па осн абсцисс расстоя-края, Rateau получает гш углов от и закон. Между 35 — 25 происходит
разрыв, а затем уже получается иной закон. Центр парусности идлт очень быстро к краю атаки, йтом, приблизившись к нему па минимальное расстояние в 0,33 длины пластинки, идет назад к центру, проходит через него прн 4е, а затем удаляется в противоположную сторону, так что при 0э
находится на расстоянии о •, . в< ... i »ины и » .янки от края а гаки. Кот ta угол наклона сделается <яриц«»,т**льным. по *,ущс/*тву ет подъемная сила, центр пархсностп • пю больше i тядястсл от переднего края. Когда пластинка нагнут ня i-тре , т кич . » п i > никы.ш i . u СМИОЙ СИЛЫ нет, Т.-< П- уг 1 I, 11| I I I р .l По I • 'ШИ сила меня-т своп знак, то на пластинку деп> ti . г пара, которая л мит я нс выправить ее, а, наоборот, еще боле» нагну гь. Это указывает на бп тьшую опасность пак н»-нения планов пщ отрицательным у’’ ,. м. По исследованиям профессора С-А. Чаплыгина, для вогнуто* гя 1 гот продольный угод равен —9.
На фиг. 13ч изображ<ла <и ча, по» иная FopplcMB институте РгашШ’я для пластинок дина п» размера < , 2U rm, ио с различной
вогнутостью. На», и ибе» м. г-»ы углы иавлон.% на ven ординат расстоянии от края атаки. Диаграмму ма п шчаеуя от диаграммы Rateau. Ирм О шштр парусности нах». штся ш вогнутых
\L 25 ’ 1 -- !!’ Г л. Ш/
пластинок не В гредтк- I ЦД р 1<*< Г" ЗИП! К) К шиит. 1ЬШ» 4 глубины пластинки в стпрпму, и[. • ыш» ни лцжиую и-ib лаки. Прн увеличении угла центр паруси ети пр пт 1 q . р i । , ига. иагв ныпего ра стояния от края ат кп, а тем сни1 । при .•••» .» и ере шне.
ЛюбОПЫТНО i.TM'THT , ЧТ М 1 >С И О’ НИе 1"И и » I .’ли с нь <*ильно изменяет характер кривых и. шхчотря на то, |"ггн;<то» рассматриваемых иластннок чата, закон шпженпя цепра парусности для них резко отличается от закона движения центра парусности цлоеком пластинки
Многочисленный наблюдения относительно нотоження центра парусности, разобранный нами, производят очень сметное впечатление, но диаграммы Rateau, невидимому, лучше других.
Приведем здесь еще теоретическую формулу Rayleigh*я дли весьма длинных пластинок, выведенную в предположении разрывного течения за пластинкой:
........... -<6’>
где 8 обозначает расстояние центра парусности от средины пластинки н L ее глубину.
На диагра ме фиг. 139 собраны вместе кривые, поту 1енные различными исследователями из их наблюдений над движением центра парусности в зависимости от изменения угла наклона.
Кривые эти изображают:
1 -и бчюдения ЕИГеГя над пластинкой 90X15 ст; 1,7 = I
И— „ Joessel'fl (1870 г.) над квадратной плоской п частник >й
в воде, выражающиеся формулой 8 = 0,з£(1 — sin т);
Ш— „ Kummer'a (1875—70 г.) над плоской стеклянной пла-
стинкой 9 X 18 ст;
IV—наблюдения Kummer'a (1875—76 г.) вад плоской стеклянной пластинкой 9X8 ст ;
V — наблюдения Langley'n над плоской металлической пластинкой 30,5X30,5 ст;
VI — наблюдения Rateau (1909 г.) над плоской металлической пластинкой 50 х 30 ст;
VII — наблюдения Rateau (1909 г I над круговой дужкбй 50 X 30 cm, w = ;
VIII — те ретическую формулу Rayleigh’n: 8 = -’- L I
IX — наблюденияРябушинского (1908 г.) над пластинкой ЗОХ10 ст, и>=^);
Первый из размеров пластинок дает ее размах, второй ее глубину, w (Wolbung) обозначает вогнутость пластинки.
Теория вихрей.
Вихри играют весьма важну ю роль в случае вижения неустановивше-гося и с тужат основой для объяснения установившегося движения. Например, махание птиц крыльями является источником образовапня вихревых uihj -ров и колец, которые сбегают с крыльев н дают поддерживающую силу.
Ознакомившись с вихрями н циркуляцией скорости, мы перейдем затем к теоретическому вопросу о поддерживании планов аэроплана и покажем, как теория подтверждается действительными наблюдениями, которые сейчас ведутся.
Чтобы изложить статью о вихрях, нужно разъяснить механическое значение величин 17 и С, которые введены Helmholtz ем и называются компонентам вихря.
§ 15. Движение жидкой частицы.
Рассмотрим первый вопрос—движение жидкой частицы. Этот вопрос с большой подробностью ис< ч девай в моей магистер; кой диссертации: „Кинематика жидкого тела"1) и занимает е* первую главу.
1) Математический сборник, т. 7III. 1876 г. Сочинения Н. Е. Жуковского. т. I. Юбилейное падание Московского Математического Общества. 1911 г.
Вообразим себе частицу жидкости (фиг. 110), весьма малую, какой угодно формы. Обыкновенно берут ее в форме шарика. Внутри этой частицы берут какую-нибудь точку х, у, z, которая называется центром частицы (если это шар, то за центр частицы принимают центр шара), и в ней располагают начало СУ подвижных осей коортпнат (Ух у г', параллельных неподвижным осям Oxyz.
Координаты точек частицы относительно подвижных осей будут бесконечно-малыми порядка малости самой частицы.
Рассмотрим, из каких элементов слагается движение частицы. Все преобразования будем выполнять только для величин, относящихся к осн х. Формулы для остальных осей будем получать из формул для оси х круговой перестановкой.
Обозначим компоненты скорости точке через и, v, tv, скорости в центре ча-ip.- Последние
в какой-либо и компоненты стицы через представляются некоторыми функциями координат центра частниы х, у, г:
tx, у, г).
Скорость других точек частицы (координаты х^-х', у-{-у', z-j-z') будет:
“ = / у+iA ®+г')
Разложим эту скорость в ряд Тейлора, при чем, в вид} малости координат af, у' z', мы ограничимся здесь только первыми степенями их. Тогда
w_.
Выражение и упрощается, благодаря введению трех величии Helm-holtz’a: £, 17, С и еще трех других величин, обозначаемых через в„ в.„ 05.
Первые величины t, у, '— суть: t_______________________ 1 /ди> dr \ 1
? —^2 ” dlj* I
4 =
(351
плюс:
1 /ди
2 'г, I . Зи
Величины 0lf 0в, 03 составлены так же, как и |, q, ", только вместо минуса у ннх поставлен
01 =
0.=
dv дё' ди дх/
0.
Величины д, у, Z суть не что иное, как проекции по осям координат угловой скорости вращения частицы *) и называются компонентами внхря.
•) Они входят в ур-ия движения частицы кндкоств совершенно так же, иак компоненты угловой скорости р, q, г в формулы Эйчера для вращения тверд го тела: np*v=j«—ту, нт. д. Прим. рей.
юн —
Величины 6lt 08, 03 носят название ск«нинпп к.ор шпат них углов. Подробнее об этих величинах мы будем говорить при рассмотрении вязкости жидкости; теперь же заметим только, что 2 0, есть отношение полного бесконечно-малого изменения угла у и. ко времени, в течение которого это изменение происходит. Другими сл- илми, величина 2 01 является мерой быстроты, с которой этот угол скашивается.
Если рассматривать идеальною жидкость, то величины 0г, 02, 0Ч не играют роли в ее движении. Когда жидкость вязкая, они играют существенную роль.
Пользуясь формулами 135) и (o2i, можно выразить через £. у, 0,, 0.>, 03 все производные от скоростей по координатам, кр«»ме , °-, J' ; так.
J* 0 '
ду э
аг
Подставим их в выражение и; тогда
и г х -J- 0J/' + 0-Х -4- цг' — ty .
Введем теперь вспомогательную функцию Ф'
ф=4-(-йr^’+-v»,s+ £ ®'3+26iyV+2&,zx' зе,*/) .-63)
Тогда легко усмотреть, что
« = “.+а?+ —’-у.
v=”.+^-
, ЗФ' . , , .
«-' = w.+-j? -Lsm’ — ЧХ-
(64t
Если рассмотреть эти формулы, то они нам («дут полно» пр« и-га-вленис от том, как движется весьма малая частица жи хкогтн.
Движение весьма малой частицы жидкости слагается: во-первых, из поступательного движения го скоростью центра частицы, составляющие которой пи осям координат суть к,. г„ tr,; во-вторых, из некоторого другого движения, которое имеет потенциал скоростей Ф; это другое движение носит название деформации, так как только от него частица меняет свой внд; наконец, третье движение есть простое вращение с угловыми скоростями S, *)•
Это разложение движения весьма малой частицы жи >cih vruHo-влеио Гельмгольцем и составляет его'н е р в \ ю теорему и вихрях
В несколько иной форме разложение шпження частицы было дано Кошн. Последний не выделял движения с потенциалом скоростей, и потому у него не было отчетливого определения, что таю и < и роеть вращения частицы; если же выделить движение с потенциалом свор*, ей. то тем самым вполне определится и вращате^шиое движение частицы
По этому вопросу существует большой литературным спор м*-.». и Гельмгольцем и знаменитым французским академиком BerirandoM. Движение жидкой частицы можно представлять на разные ла 1ы, относя часть врашения к движению деформации. Задача об отделении движения
дефирм ции чт вращения допускает множество различных решений до тех пор. пока мы не станем на точку зрения Ге 1ьм гольца, что вращение есть то. чк) является лишним в движении с потенциалом скоростей.
Деформация характеризуется функцией Ф', которая представляет некоторый однородный многочлен второй степени относительно координат х‘, у, г*. Как известно из аналитической геометрии, такой многочлен выражает центральную поверхность второго порядка с центром в начале координат. Если направить оси координат по главным осям поверхности, то 1 юны с проига деннем разноименных коор шнат уничтожаются. Отсюда вытекает, что мы можем всегда выбрать оси координат так, чтобы многочлен выражения (63) получи i простейший вид:
При таком выборе осей величины
= О ............(«5)
Вообразим себе радиусы-векторы, исходящие из центра частицы, как бы покрытыми жидкостью (никакая частица жидкости при своей деформации не гх ппт со своего раднуса-вектора).
> р-ие го»| показывает, что такие радиусы, направленные по главным осям поверхности второго порядка Ф' = const., остаются под прямыми углами друг к другу (в течение малого элемента времепн) Осн этой поверхности называются осями деформации.
Предположим, что частица до деформации имела форму шарика, выражаемого относите дык» центра его ур-ием:
* а- Ч у'2 H’2=«2-
Назовем через of, у", 2* те координаты (относительно центра частицы) которые бу су т иметь точки частицы через бесконечно-малый промежуток времени dt. Тогда, ограничиваясь рассмотрением только движения дефер-v щнн, мы. на основании выражений (63') и (64), будем иметь:
» . дФ , ди ,
а -гг - -r-y at =х -• -, х al, ^^4,м. дФ' Л Г , д™ • М z - - dt — г! -+- 5- - г dt, dz 1 dz ’
И
Если при помощи последних уравнений исключим а/, у', а' из первоначального ур-ия шарика, то найдем:
по
Это будет уже ур-ие эллипсоида; полуоси его будут: 1 о (1 + dt),
« (1 + £- dt], о U+^-dt).
Таким образом, бесконечно-малый ша-( ( —j—ч-----------j-, рик, деформируясь, обращается в бесконечно-
малый эллипсоид, при чем оси его иапра-влены по осям деформации (фнг. 141).
/ Вследствие деформации, объем частицы,
А вообще говоря, изменится. Чтобы найти это
у изменение, нужно будет вычесть объем ша-
Фнг. 141. рнка из объема эллипсоида:
4-ЯЯ’а+-£ dt)(i4-^-dt)(i + ^<K)_A„eS = « яа»(*+ * + 3 \ дх * ду • dz
Еста объем ие меняется (для несжимаемой жидкости и для газа при не очень больших скоростях), то написанное выражение равно нулю, и мы придем к знакомому уже нам уравнению несжимаемости в форме Эйлера: -£- + 4 + ^ = 0-- <5'»
Итак, общее движение частицы состоит в следующем: частица продвигается вперед, вращается около некоторой оси и меняет свою форму, переходя от формы шарика к форме трехосного эллипсоида.
§ 16. Вихревые нити.
Теперь рассмотрим вращение частицы. Компоненты вращения суть £, т), С. Полная угловая скорость вращения есть со, при чем
- - • - • . (661
Если жидкость не завихрена, то частицы совсем не вращаются, и
t = i) = V=O ....... (37>
При рассмотрении вихревого движения Гельмгольц предлагает строить так называемые вихревые линии. Если мы в определенной точке жидкости найдем направление мгновенной оси вращения частицы, по ней продвинемся на бесконечно-малую длину, найдем новое положение мгновенной оси вращения, во ней снова продвинемся и т. д., то полученная линия и будет вихревой линией; короче говоря, вихревой тннней называется такая линия, касательные к которой направлены по осям вращения соответственных частиц жидкости.
Если взять какой-нибудь очень маленький kohtjp da и на нем построить линии вихрей, то получим поверхность в форме весьма тонком вихревой трубки. Helmholtz рассматривает массу жидкости, заключенную в этой трубке, в называет ее вихревой нитью (фиг. 142).
Произведение угловой скорости вращения жидкости иа площадь сечсння вихревом нити—aide—Гельмгольц называет напряжением вихревой нити.
— Ill —
Между вихревой нитью и струйкой жидкости есть геометрическое сродство Действительно, если бы мы вообразили, что жидкость течет со скоростями 5, г), данными формулами:
. _ 1 [ dw___Эс \
* “ ~2 \ду~дТ] • ___ 1 / di dw \ 57/ ’ - _ 1 (dv____ди \
’ 2 \ дх ду I *
и для этого течения жидкости стали бы строить линии тока и струйки жидкости, то усмотрели бы, что линии тока суть линии вихрей, а струйки этого воображаемого течения суть вихревые нити действительного течения.
Покажем, что взятое нами фиктивное течение жидкости удовлетворяет условию несжимаемости.
Составляем трехчлен:
I 1
дх ' ду ' dz
Если взять от ; производную no х, то в нее войдет - а*»
изводную от 1) по у войдет член — —и они сократятся; также и все остальные члены сократятся, и будет:
£+£+£=<>•
что н требовалось доказать.
Таким образом объем жидкости, протекающей но струнке воображаемого потока в единицу времени, — coda—будет равен постоянной величине.
Отсюда получается вторая теорема Гельмгольца о вихрях: вдоль всей вихревом нити напряжение вихря постоянно.
Эта замечательная теорема характеризует вихревые нити: из нее заключаем, что вихревая пить пе может внутри жидкой массы оканчиваться острием при непрерывном распределении скоростей. Действительно, если бы вихревая нить закапчивалась острием, как на фиг. 143. то do обратилась бы в О, и о в со. р»з это невозможно, то могут быть только два случая: или вихревые нптн сами в себе замыкаются, или концы их лежат на границах рассматриваемой жилкой массы: на свободной поверхности, или на стенках сосуда (фиг. 144).
Для доказательства третьей и четвертой теорем Гельмгольца о вихрях необхолимо предварительно ознакомиться с новым понятием о циркуляции скорости.
Циркуляцией скорости по какому-нибудь контуру называется выражение:
Г=| rcos'6ds,......................
т.-е. rvvvft пр-п-’T- upn. i.iu.i । । стп на касательную
к в»нт\р\ нас- ющп й ........ цгн. Это выражение
похоже па вира .и» ню •• ш ни I - Il Кбыь гилоп, t<i работа
ягой сты при rii |- .и ц**пнп ки и i. npj выразилась бы той же формулой.
В частном ।•. не. koi 1 > суще« г г. ‘Т^пциал скоростей Ф, проекция г м*р 1н па к •• .1'Р.тыг. ю вырад. i •< частной производной ст потенции тыши функции П1 печентд Qia и
/= ^*^ а» =Ф,—.. . . . (со)
где Ф1 п Ф, суть значения и >nminw ш . р •• теп в начале и в конце контура. Ес in кон ур ..и минутым, ти н
I ф{ фв О .....................(70)
Во ц»М1 и н<. i.itk-tih //_ контур ОаЬе, пр* *та ляюпцш б< лонрчно-малый прям уг-' н ник плопуцью do фнг. 1Г>» и и«•• тараемея опре-»МНТЬ <ЛЯ -Т" нрямоук. -IbHRKa цирку*
.1МИИЮ. и я По н<1 • на»Iнению часовой стрелки, in о - тр п. т ио с мнительной части осп х.
Е и и пн л.в»м через м. v и w функции гифT4ii.il, выражающие компоненты ско]пй ги, п пер* • »*»М от точки () к точке а, I*. (Я по* Л-Jlien гудем иметь скорость по .‘И 5 ровной
« Г-<>!/
Дд».....гажюния циркуляции 110 эле-
нту чЬ >1» и Помножить эту скорость на нн- ..и .| ".та <?’. •''егаьлян цирку шцпю Но .-к и «н должны 'коро- гь «> помножить н - г.ч лк • сь прнх тптея
п-ро ЦПГ.1П 1 1 рипат, тьноч направлении
1.0 и
Что каоа-п-и горн итальни! н.ън.лп' Н контур», то на эюменте Ъс скорость будет.
Ф« F 1 Ь»
а длин) жи мента его ф/ н)жн> г ,ять > • ikom—(минус;, так как для ,...давления цирку шипи п Ж1 ) шти , трицнд льном направлении осн у. На a 1СМСПТО Оо цирк шцип С г- к1ц.
Е< 1и в. IH’ гны пирсу ляпни по .п тьнцм ’1а<тям контура соединить вмеск. то ’с ин ’ u rrfv noHapiM, „кратятся, и останется
•lydz ' 2: tic,
где S ш пр-жие. 1 Kovl ,, нт впхря ио направлении* <н x, a do ,равно< dydt пощад* контура.
Таким оора.’ом. .ми видим, лго иирв- шя скорости, взятая по замкнутому контуру с птощадью da, г , -и а равна п ющади контура,
помноженной ня пмйи.» up,-кит в, и короетп вихря на ось х. Отсюда, в'Л“ дтвпе при,. । "П1нат, вытекает, что нпр, у-
1.1ШЯ • г I ГН ' • .1, .11.1UM. , ому дт-монту pal'll.. tMifiu<<n
проекции угловой скорости вращения частицы па норма ль к этому элементу, помноженной на площадь его:
/ = 2w cos a do
.(71)
Направление копту ра берется по часовой стрелке ьдя наб. ш дателя, глядящего с конца норма ш на контур.
Теперь перейдем к теореме Стокса fbtoke4 Докажем ее, опираясь на д р.п приш (71).
Зта । |- иа имеет место для контуров, обращающихся в точку не вы .а п -г । тн.
Hi ли пр страт тво односвязи о, то таким свойством обла тает ?-икни I «штур. Напр., если бы представить себе иапо шепнуло та юп пустую клмпату. то какой бы контур в ией ни взять, он мог бы. уменьшаясь, бра-тпты а в точку, оставаясь все время внутри жидкости.
Ее ш ясе ь комнате оставить стулья, то можно было бы вмобрШшть ь««игур, oxi тывающип перекладину стула; такой контур не 1ьзя было бы обратить в точку (пространств» называлось бы много'-вязным).
Если контур обладает свойством обратимости в точку, то мы можем
чер>- । него привести поверхность, которая вся лежит Иа »той поверхности построим две системы взаимно ортогональных кривых ।фнг. 146), которые рассекают 1-тощадьос на отдельные элементарные прямоугольники. I in-«и що. что циркуляция по внешнему кон-I . РУ Р I » сумме цирку 1ЯЦПЙ ПО отдельным ирпмо-ни ам:
Г=1/,
1лс как на венкой внутренней стороне прямого льникоь будем иметь по две циркуляции в иронии- к ложных направлениях, которые взаимно
вну три жидкости
Фиг. 146.
уппч -жа »л я, и станутся только несдвоснные циркуляции, которые
и j • по внешв । му Заменяем каж
контуру.
V" i через
2ы cos ado.
Тогд i
7 = 2ywcosadG «= 21 J wcosado.
(72)
Если принять условия скорости вращения частиц жидкости за скорости некоторой» течения, то выражение (72) представит объем жидкости, п|и текшей чер<‘ рассматриваемый контур. Как мы ужт видели, такой
-1 •• мый поток будет несжимаемым, п объем протекающей жи I-
тп Г но бу (ст <1авпссть от выбора поверхности, Прове ценной через |. )гту р. Количество жидкости, протекающей по каждой струйке этого ♦ Сражаемого потока, представляет не чти иное, как напряжение соответ-Т1ИННЫХ вихревых интси действительного потока.
Отсюда вытекает следующая теорема Стокса:
Циркуляция скорости по всякому замкнутому кон-iypy, обращающемуся в точку нс выходя из жидкости, р вна удвоенной сумме напряжений всех вихревых iniT-ей, проходящих через контур.
Из теоремы Стокса получается доказательство теоремы, обратной приведенной на предыдущей странице (формула 70) и заключающейся том, что е< лн цирку лпция скорости ио каждому замкнутому конгу ру есть Гяорвтяче«.гл« 8
нуль, то существует потенциал скоростей. Действительно, в рассматриваемом случае напряжение всех вихревых нитеп должно равняться нулю, т.-е.
со2 — ;2 4" Ч2 — — О,
а, следовательно, и
£==ij = C = O.
(37).
Приложим теорему Стокса к определению скоростей, которые развивает внутри жидкости находящийся в ней бесконечно длинный вихревой
шву р.
Пусть на фиг. 147 представлен такой шнур аЬ. Он отмечается тем.
что циркуляция скорости, взятая вокруг него, есть величина конечная. Она выражает двойное напряжение этого вихря. Можно рассматривать такой вихревон шнур или весьма тонким с очень большой скоростью вращения, или как цитнн ip конечной п тоща ди сечения, вращающийся с конечною же скоростью. В остальной части жидкости, вне шнура, вихрей нет, так что подсчитывая :, ч и С, мы получаем компоненты скорости вихря только внутри этого цилиндра. В результате, линии токов будут
симметричны относительно оси вихря и представят окружности; центры
постедних лежат на оси вихря, и плоскости их ем перпендикулярны. Цирку ляция скорости но каждой такой окружности равна
7= 2 пт F,
где F—скорость жидкости, а г — радиус окружности. Эта циркуляция должна иметь одну и ту же ве шчнну для всех окружностей, потому что каждую из них пронизывает один и тот же вихревой шнур. Эта величина равна
° т г Г.
-'о*о,
гдегои Ро—радиус вихревого шнура н скорость на его поверхности. Отсюда скорость каждой точки
т.-е. обратно пропорциональна радиусу. Давление
p=ponst— -= const — °2г/ ,
т.-е. уменьшается с у менынением г. Поэтому, внхревой шнур, вследствие пониженного давления, притягивает к 'ебе остальные массы; всякое твердое тело, находящееся вне вихревого столба, стремясь двигаться в сторону меньшего давления, будет приближаться к оси вихря.
Если рассматриваемый вихревон шнур заключен между двумя стенками, перпендикулярными его оси, те иа концах его будет пониженное давление, и потому он своими концами присасывается к стенкам.
Рассматриваемые вихревые шнуры в природе представляются в виде смерчей, которые опираются нижними своими концами на землю и ли воду’, а верхними на тучу.
Интересный опыт искусственного воспроизведения вихря демонстрировал Вейер на Парижской выставке в 1898 г. Прибор Вейера (фиг. 148) состоит из полого шкива с несколькими перегородками, расположенными
Фнг. 148.
в радиальных плоскостях и не доходящими до осн. Диаметр шкива 1 ml Шкив приводится во вращение сильной машиной. Переюро щи совершенно плоские, так что винтового эффекта прн вращении шкива не получается. Шкив ставится над большим чаном с водой, на расстоянии 3 mt над ее уровнем. Чтобы опыт лучше удался, воду следует несколько подогреть. Шкив прн своем вращении закру чивает столб воздуха, под ним находящийся. Вследствие пониженного дав 1ения в середине образовавшегося вихря, вода начинает подниматься, и сама приходит во вращательное движение от трения о крутящийся воздух. Через некоторое время образуется высокий водяной столб, внизу сплошной, а вверху образованный как бы нз капелек.
вихревой столб состоит из совсем ме <кнх капе тек,
Под самым шкивом которые разбрасываются перегородками. Опыт получается необыкновенно эффектный.
Аппарат, представленный на фнг. 149, показывает песочные впхрн. Сначала устанавливается воздушный внхро]-»й столб, который все более и более заполняется песком.
В этом приборе можно те тать и опыты сводов. При лтом тут получается любопытное явление (фиг. 150к подымается столб, а в середине получается утолщение, как бы шишка х. Перед самой крылаткой вода размывается. Для опыта в стеклянный сосуд наливается намыленная, несколько подогретая вода
Фнг. 150.
§ 17. Теорема Thomson's.
Теорему Thomson'a обыкновенно выводят из уравнений гидродинамики в форме Лагранжа. Но здесь мы докажем ее геометрическим способом, который мне удалось найтн н который в первый раз появляется в печати.
Этот способ изложения довольно прост и хорошо характеризует сущность теоремы.
Теорема Thomson'a относится к производной по времени от циркуляции скорости по контуру, проходящему через 1дни и те же материальные точки жидкости; когда жидкость движется, она уносит за собой и контур.
Пусть в момент t контур занимает положение Л В, а в момент t dt— положение АВ1 (фиг. 151). Для нахождения производной от циркуляции по времени нам надо бу'дет составить разность циркуляций скорости по контуру А* В’ и по контуру АВ и разделить ее на элемент времени dt. Таким образом найдем:
dt
СО» 6 (k>
ФН1. 152.
Фнг. 131.
При выводе удобно рассматривать отд, и.но каждый ктемент ab — ds контура АВ. Рассматриваемый элемент (фиг. 1521 занимал п >твягснне ^Л, а по истечении времени dt стал кшямить нол<-ЖепИС ft'b'. При ЭТОМ Перемещении МеЮ-ИТа И1Уе-няются: длина d-s, угол в н скорость Г
Чтобы установить тля дайн > го момента полное изменение элементарной циркуляции F cos 0 ds, мы рассмотрим ее изменения от разных причин, от каждой в от де лыки’ти, а затем эти изменения сложим. Одна причина есть перемещение элемента ab и его деформация, а другая — изменение скоростей элемента (происходящее оттого, что частицы коитура передвигаются, и поток меняется).
Сначала будем предполагать» что «лемепт аЪ hi ы «el пеп<». ДНИ - HU 4, • . кор<«'71[ пклу чп н • |»1 е пил-ши* и .пл н» нпе, н посмотрим. КПК изменив. 4 I rus© Вектор. виража юший
скорость, из Я< ю-ПО.ЮЖ'НПС Г' IB момент
ежеиия V (в момент t) перешел в новое J-l-dZi. Вместо разности
v cose' - г --е
можно взять прямо проекпню на касатс 1ьн> ю к элемент} ds бесконечн малого элемента, соединяющего концы этих векторов. Так как этот вектор, разделенный на dt, есть полное ускорение, то в рассматриваемое выражение войдет проекция полного ускорения частицы жидкости на направление ab. Назовем ее через j cos Л. Тогда изменение цирку тяцпи от первой причины будет
/ cos Л ds dt - . •-!>
Далее посмотрим, насколько будет изменяться цирку чяцни от другой причины, т.-е. оттого, что сам контур изменился, а скорости его точек остались прежние.
Составим изменение величины ab c»s 0. Кети мы ab и а'Ь' будем проектировать на аа', то получим:
d . . .. а’Ь' соэЯ " — ab cos в , ‘V аа ,,
м (ab cos 0) dt =----.. dt = ,, dt.
at ai
Точное выражение проекции бу хет bb‘ с&ьа—аа*, где а — бесконечно-малый угол между элементами аа н ЬЪ'. Принимая cos а равным единице, мы делаем ошибку второго поря [ка а ши ому i i> мы можем принебречь. Точка b пришла в Ь*, прямо продвинувшись i . с соответствующей частицей жидкости. Поэтом} будет ие что иное, как скорость точки Ь, т.-е. т- ,
1 - л d’-
Совершенно также аа' т.
i Иск» да
bb7, (v ™
. изменение циркуляции от второй причины равно
г4г*Л- .........................Ф)
Состав тян потное измепонпе элементарной циркуляции и деля его на dt, заметим, что член
д I .
г „
OS
Может быть представлен в виде
ю *
Следовательно, полная производная по времени от циркуляции скорм» ти равна <•$ мме двух интегралов, взятых но данному контуру Один
J*j соя (j, ds» ds
**'*ть цирку тяцпя ускорения по (анному контуру, а другой
пре итавтяет полу разность квадратов скоростей в конце н в начале контура. Таким обра
' 1 J J 1 и. Л> ris j s (’j ) *=j3 (Л <&) ds 4- ----,(73)
(\ есть скорость на конце контура, а — скорость в его начале.
На основ.цши основных ур-ин гидродинамики в форме Эйлера (1) проекция полного ускорения на ось j- есть не что иное, как разность
V— 1 *
р дх ‘
Е« чп су шествует силовая функция С, то
Тогда, пользуясь, как ранее, обозначением
J‘v=p-........................................... ™
получим, 1ТО
пр>> = X (V—Р);
' полное ускорение представляет вектор, проекции торогч ио осям координат cjTb частные производные координатам от функции II/—Р).
След кате 1Ы1о ) со» I;, <is। = (U—Р),
Па основании всего сказанного можем написать:
>-р> 7)-(5-Ро+Т) .............
— 11К —
Так выражается полная производная во времени от циркуляции скорости по какому-нибудь разомкнутому контуру.
Если контур замкнутый /фиг. 15Я), то правая часть
Л уравнения (71) обращается в нуль:
а к А
Отсюда:
1 = COIlSt.................. (7ti|
. Полученные равенства справедливы как для уста-
новившегося, так и для иеу становившегося движения, и представляют теорему Thomson'a:
Циркуляция скорости по замкнутому контуру, проводимому через одни и те ж₽ частицы жидкости, но все время движения есть величина постоянная.
Из теоремы Thomson’a вытекает, как частный случай, теорема Лагранжа, что если в начальный момент движения существовал потенциал скоростей, то он и всегда будет существовать.
Поэтому, если движение получается из состояния покоя, то вихрей не должно быть во все время движения. В действительности же они образуются, возникая около граничных стенок и распространяясь затем ио всей жидкой массе.
Доказательство теоремы Лагранжа дается таким образом: циркуляция скорости ио какому-нибудь замкнутому контуру, состоящему из о (них и тех же частиц, будет оставаться всегда одной и топ же; в начальный момент, по теореме Стокса, она была равна нулю, так как никаких вихревых нитей через контур ие проходило; следовательно, и во всякий момент никаких вихревых нитей через контур проходить не будет. Это рас гуж (ение можно приложить к любому контуру. Отсюда заключаем, что нигде в жидкой массе вихри ие могут образоваться: движение всегда будет иевихревое, т.-е. будет иметь потенциал скоростей.
Доказательство упомянутой теоремы было дано Лагранжом с помощью разложения в ряды. Теперь оио очень просто получается из теоремы Thomson’a.
Приложим теорему Thomson’a к установившемуся движению жидкости.
Пусть АВ (фиг. 154) есть линия тока; тогда» рассматривая изменение циркуляции по контуру АВ, найдем:
Д _ (ВВ | - [АЛ] _Г1Г1 dtdt f 'dt ~ dt ~~ dt ~ 1 1 1 ° ’
гак как промежуточные значения циркуляции останутся тс же По Thomson'y имеем:
Г,»- Г0-=(и—Р-1
отку да
~г ।— t t— I } — const. . (1“/)
Заменяя для несжимаемой жидкости р через J в выражении Р, получим уравнение Бернулли в обычном для гидравлики виде
— = const. 9
. . (IB )
Если все течение совершается под действием ситы тяжести, то
U= — дг, и следовательно,
₽ + ^-|-г = const . . (is")
Докажем, что теорема Берн} лли верна как для линии тока, так и для вихревон нити На фиг. 155 даны линии тока АВ и CD и вихревая нить АС. которая переходит в положение А'С, так как частицы жидкости,
Фиг. 151
Фнг. 166.
Фиг. 155.
лежащие иа ией, останутся одни и те же. Отсюда следует, что в установившемся движении всегда существуют поверхности вихря. Докажем, что трехчлен Берну пи постоянен иа линии вихря. Для линии АС по Thomson'y имеем
<1< /г Г,
АС
по, по прошествии временил dt, АС переходит в А'С., и следовательно
rfi —[СА]
dt dt
а так как контур Д'ЧТ'Л’ лежит иа поверхности вихря, то по Стоксу
[СЛ] + [ 4Я'] -I- [Л'С] + [СС] = О, или
[С А'] — [СА] = [ЛЛ'] — [СС], т.-е.
'di _ИГ|-[(ЧУ| _ пл- г.’л , dt ~~ dt----------dt ’
и, следовательно, иа основании теоремы Thomson’a
и р-ь т' г- = С„-Ро+ - 10‘, откуда
-ГЧ-Р-4- 7 -Р01 7 -1/о.
Таким образом, трехчлен Бернулли постоянен для А и С, а так как он постоянен для А и В, то трехчлен неизменен на всей поверхности вихря. Отсюда получаем 11 р и з и а к установившегося движения, по которому трехчлен Бернулли должен быть постоянен иа поверхности вихря и тока, которые совпадают.
Чтобы узнать, есть ли такая поверхность, выведем условие ее существования. Пусть (фиг. 156) dx, dy, dz будут проекции на оси координат элемента д>гп ds при переход- по этой поверхности. Вообразим
вектор „ч“ перпендикулярный к v и о», тогда »inus'u утлой его г осямп координат будут пропорциональны ветчинам
I и ш
(ijii'—Jr); (Jh —iw); <=r— 41/),
что можно проверить непосредственным вычислением. Взятый нами вектор лжеп совпадать с норма (ыо к поверхности тока и вихря т.-е. выраженп
1 dx j-И dy ф- III dz
должно быть потным дифференциалом при умножения его на интегрирующий множшель д; следовательно.
ц [I dx - II dy 1(1 dz] = dF.
Па поверхности вихря и тока F = const, а смцествование множителя /1 показывает, что поверхности вихря и тока совпадают. В уравнении F= const, справедливом для общей поверхности, плстояиным будет как раз трехчлен Берну тли, что непосредственно видно из уравнения it.С. Громекс (36), стр 47.
Из теоремы Tbomsona (.ля разомкнутого контура легко вывести гак называемый интеграл Лагранжа для нсустаиовшппогоея движения.
Прп существовании потенциала скоростей Ф имеем:
1= J"Г cos0ds= J ds = Ф, — Ф„ (»>•
Подставляя это в формулу у74), получим:
Преобразуем
лф. дФ, . дф. . d'F. . а®,
<и ~ л + ах <>у 11 ai
И"
ЭФ. d<f>. дф,
‘ = И„ aL=ri- а " дх * оу 1 ог
Поэтому полная производная ЯФ. дф, , аг = ’ г-
гту _
То же получим и для .
Подставляя, пай (ем:
-t'.-Lp.-L Y =^-Uo-Pn - Г = const,
.(77)
где const может зависеть только от времени.
Это уравнение отличается от ранее выведенного (40) тем, что в нем оф __
имеется член , т.-е. принимается во внимание изменени» потенциала скоростей с временем.
Давление во всякой точке жидкости определится из выраж иня
ТУ Г ОФ , гх
Р=Ъ - — ennsi . . (|<)
18. Ill и IV теоремы Гельмгольца о вихрях.
Первые две теоремы Гельмгольца мы уж «,'1тан"ви.тл ранее Именно-I. Первая теорема:
Частица жидкости двига тся т сим образом, что все ее хвижепие слагается из движоний поступательиого, вра-щательного и движения деформации. Движение ь формации имеет потенциал скоростей.
В этой теореме дается понятие о ве шчнпах с. »/. £ и fi вращении частицы
II. Вторая теорема:
Напряжение вихря вдоль всем нихреп--п нити остается постоянным.
Она устанавливает понятие о вихревых нитях и показывает, что они должны или быть замкнутыми, или ок.шчнглтьея на границах жидкости.
(II. Третья теорема II г 1 mho 1 tza.
Впхревая пить всег i«i оста^т* я вихревой нитью
Доказательство ,-е дя» д таким образом. Пу« п. фиг 157 предо га-г «лет вихревую нить, б чно т ю н ш конечных р «ер* Если на поверхности этой ппти мять клюш-нибу ц> замкнутый контур а, то тогда цирку ляция склр. стм по атому контуру в начальный МОМсНТ бу и г ну тем, так как через него не проходит вихревых нитей. По георе Thomson а, циркуляция скорости по этому контуру, при передвижении ОГЛ вместе е ЖП IK .ТЬЮ не пзм-няется И будец WF.lHr 1ЬВ >, Bert L , . ГЬС|[ нулем Отсюда очевидно, что вихревой шнур итчимся вихревым шпуром, так как во все время лижения пи о ша из бесконечно тонких внхргвых нитей не пересечет его границу.
IV. Четвертая теорема Helmholtza:
Напряжение вихревом инти во все вр«»мя Фиг. iflj.
I в и же и ия <*д п п ак он о.
Предположим, что нарпс'тайная па фиг. 157 вихревая нить бесконечно тонка, и охгатим с? контур ч Ь. Тогда, по ъорею Стокса, циркуляция по этому контуру равна июйному напряжению вихревой нити. Так как циркуляция скорости по контуру b не меняетсн при передвижении рассматриваемой жидком ма^сы, т*» не м^нягтеч я напряжение вихревой ннтм, что и требовалось дока «ать.
Хотя площадь 11 ченмя внхре юн нити и угловая скорость могут вихрений нити бу т < дно и т же Она не может ни радрватюя, ни n<*4i.\«ay гь.
Один из самых лучших примеров таких стойких вихревых нитей представляют вихревые кольца. Если вихрь ы .ими концами оом-киут и распо 1»'ж»*и в вп кильиа то врлще-НИ ГНЦ ЖП I -ТИ бу ТС у ЩС’ТВ, «пять п * 1ЬКО внутри польца Ча тины жн дкостгп, нахидя-ЩИС< :1 вну Грп КО.ТЫ1К, ВОС вр. М И ОС Г ЮТСЯ ВНУ-трп егл Boi I*.х б1, [ет крутиться около кольца, как пред юно на фиг 15S. Вихревое кольцо имеет • б^ .КйГЬ ЩП’р ИМЕННО В TJ
1-1 |и»ц бр- ют-я 1 ', х п середин,
К .Ullft.
Таким движущимся вихревым I I мн.КИИ TVHIHli- • ’ечку.
меняться, но напряжение
Фиг. 1бо.
Теоретически, чем тоньше кольцо, тем оно быстрее бежит. Бесконечно тонкое кольцо имеет бесконечно большую скорость поря ша 1g где D — диаметр кольца, a d— толщина его.
Движение вихревых колец демонстрируется на известном приборе Thomson'a для пускания дымных колец, представленном на фиг. 159.
Если образовать два вихревых кольца, то можно усмотреть, что диаметр переднего кольца увеличивается, при чем скорость его уменьшается; диаметр заднего кольца уменьшается, скорость увеличивается. Поэтому в некоторый момент заднее кольцо реднее. После няются своими повторится в <Это называется
Фиг. 159.
Фиг. 160.
пройдет сквозь пе-этого кольца поме-ролями, и явление прежнем порядке. ______________игрою колец.
Если кольцо набегает на нож, лезвие которого направлено перпендикулярно к плоскости кольца, то оио, разрезаясь, сейчас же опять восста-иовляется по прохождении через иож. Если кольцо встречает плоскость, то оно, расширяясь, беспредельно расстилается по плоскости.
Кроме дымных колец, можно пускать кольца в воде. Для этого служит прибор, который был мною построен во время празднования юбилея Гельмгольца в Москве. Он состоит (фиг. 160) из продолговатого стеклянного ящика М, наполненного водой, в который поставлена Г— образная стеклянная трубка L. На коиие этой трубки надет гуттаперчевый шарикN. При помощи его (сжимая шарик, а затем давая ему расширяться) заставляют небольшой пузырек воздуха остаться в конце Г-образной трубки. После того, быстро сжимают шарик и выталкивают из Г-образной трубки воду вместе с воздушным пузырьком.
в вихревое кольцо, а воздух разобьется в мелкие пузырьки, которые расположатся по окружности, лежащей внутри вихревого кольца. Получается кольцо, образованное как бы светящимися бисеринками, которое с большой скоростью бежит вдоль всего сосуда и ударяется в его переднюю стенку.
Прибавим еще некоторые указания относительно движения прямолинейных вихревых шнуров (им в природе соответствуют смерчи).
При теоретических исследованиях предполагают, что паралле >ьиые вихревые шнуры заключены между двумя перпендикулярными к ним плоскостями, и тем сводят задачу’ к задаче в двух измерениях, рассматривая движение жидкости только в какой-нибудь из плоскостей, параллельных вышеупомянутым. Если за массу шнура принять напряжение вихря и расположить эти массы в точках пересечения соответственных вихрей с плоскостью течения, то можно отыскать центр тяжести всех этих масс. Если рассматривать плоскопараллельное движение содержащей вихри жидкости в безграничном пространстве, при чем в бесконечности жидкость покоится, то имеет место следу ющий принцип сохранения центра тяжести
Выбегающая масса воды завернется
всех вихрей: он или стоит неподвижно, или движется прямолинейно и равномерно. ( ами же шн) ры движутся друг около друга и около своего центра тяжести. Если мн имеем два шнура, крутящихся в одну сторону, то они движутся по окружностям около своего центра тяжести. Если вихри вращаются в разные стороны, то они движутся вместе с их центром тяжести (лежащим в бесконечности) прямолинейно, и сохраняют между собой неизменное расстояние. Подробнее об этом см. магистерскую диссертацию Д. II. Горячева „О движении вихревых столбов”.
Проф. Н. П Кастерии осуществляет вихревые шпуры и их движение между двумя зеркалами.
О поддерживающих планах аэроплана.
g 19. Плоскопараллельный поток воздуха.
Плоскопараллельным потоком называется такой поток, у которого все частицы движутся параллельно некоторой плоскости, называемой напра-в л я ющ ей плоскостью потока.
Такой поток можно получить, ес.ги взять две близких между собою плоскости с малым трением воздуха о них, например, два зеркальных стекла, и между ними просасывать воздух. Если жидкость течет параллельно .плоскости, то слагающая скоростп ее по направлению, перпендикулярному к этой плоскости, равна нулю. Если, кроме того, поток не вихревой, и, следовательно, частицы ие имеют вращения (возможного, в данном случае, около осей, перпендикулярных направляющей плоскости), то будет существовать потенциал скоростей.
Обыкновенно за направляющую плоскость потока принимают плоскость ху.
Потенциал скоростей для плоскопараллельного потока обозначают буквой <р. Тогда для компонентов скорости по осям координат будем иметь формулы:
Условие несжимаемости для плоскопараллельного потока будет:
£+£ = 0 . (79)
Ох 1 оу
Вставляя в это ур-ие вместо скоростей их выражения через производные от потенциала ф, получим:
д? = ^£+^ = О, .SO.
у 5-г3 1 by*
т. е. ур-ие Лапласа для функции двух переменных.
Найдем теперь ур-ие линий тока.
Так как скорости направлены по касательным к линиям тока, то проекции скорости на оси координат, и и г, пропорциональны соответствующим проекциям элемента ds линии тока, dx и dy, т. е.
dx _ dy
и V
Это ур-ие есть диффереициа тьнос ур-ие липни тока. Из него получаем:
udу—rdx = O . .......... 811
124 —
Это дифференциальное ур-ис для с ту чая несжимаемой жидкости всегда интегрируется, так как признак того, что левая часть его есть потный шффереициал:
Эк _ 9J- г)
дх ду *
тождествен с условием несжимаемости (79). Положение эт« носит теоремы Клебша (Clebschi. Обозначая левую часть ур-ия 01 j через у, будем иметь для линии тока у р-ие
dy = O;
отсюда у р-пе:
чр = Const.
представляет ур-ие линий тока в конечном виде Функция «р называется функцией тока. Скорости « и v выразятся через нее следу ющимобразом:
Посмотрим теперь, какой смысл имеет выражение ip.
Покажем, что величина »/; представляет количество жидкости, протекающей между двумя линиями тока (фиг. 1Ы/. Проедем в гиюсдМити течения две бесконрчно-б тзкне линии i :а
и CD и пересечем струн между ними ломаний линией аЪс, состоящей из прямолинейных и параллельных осям координат стрелков dx и dy. Количество жидкости, протекающей с 1сва направо через отре «ок dy, есть udy, а протекающей сверху вниз через отрезок dx есть — rdx. так как « корпеть v считается положит льноц вверх. Поэтому величина
d ip = udy — vdx = dQ . . 434
есть не что иное, как ко шчество жидкости, протекшей между линиями тока ЛЯ и CD. Отсюда ясно, что,
г [е липин тока расположены iy ще, там скорости течения больше, и наоборот. Если взять расстояние между линиями тока не бегжонгчно-ма шм.
а конечным, то, суммируя эти выражения, получим, что количество жидкости, протекающей между ними, равно разности значений чр на той и другой линии тока;
V=v2—Vi «в»
Угловая скорость вращения ’ частицы жидкости
1 /Эс__*А
2 \дх ду/
О
841
г» Эю
Если подставить сюда значения _ и ох
(из jp-ий S2i:
ди
. выраженные через у»
дг
Ох
dx-
Эк____<Г-у
dy “ Э^* 1
то получим:
<
Следовательно, функция у> также, как и функция у, у ювлетворяету р-пю Лапласа.
’) Угзовая скорость считается положительной при вращении от оси -f--r к оси -I- *. т-о. иа фиг. 161 против часовой crpeiKi. fJftiM ped
Итак. в iiiwhocTH течения мы можем рассматривать два семейства линий. Одно, ff -Const, будет представлять эквипотенциальные линии, другое, (/•=-Const—пинии тока
Из у р-ИИ i78) и (82) имеем:
дф dt i. dg- dv
dz ~ dy ’ dy dx '
Отею ia находим. что
dv । дф dy dx *r ’ у dy
. (86)
(87)
Ур-ие зто показывает, что рассматриваемые семейства линий взаимно ортогональны. В самом деле, так как и ’ пропорциональны косинусам dv dv углов с о< 1ми х н у норма ген к эквипотенциальным линиям, а и— косинусам углов нормалей к линиям тока, то левая часть ур-ия (87) пронорцпонатьна косинупу угла между атими нормалями. Равенство его ну по (оказывает ортогональность систем у = const и у = const.
Линий, обладающих указанным здесь свойством ортогональности, можно начертить сколько угодно, но не все они могут быть выражены такими функциями у и »/•, которые у довлетворяют у равнению Лапласа. Последним свойством обладают только особые сети взаимно-ортогональпых кривых, так называемые изотермические сетн.
Е<- in мы возьмем однородную плоскую пластинку* постоянной тол
щины, ограниченную четырьмя произвольными, но взаимно-ортогональными, кривыми |фиг. ib2i, и два противоположных ее края будем поддерживать
при постоянных температурах н /°!, (наиример, в водяных баняхI, а два других оградим от потери тепла, то на ней можно бу тет провести две сети кривых: ЛИНИИ постоянной температуры и линии, к ним ортогональные |по направлению их по пластинке распространяется тепло, как показано стрелками на фиг. И|'2‘. Соответственно числу
<>ЖНЫХ контуров, огра Hit-Ill КАЮЩИХ пластинку, таких • • гей mi «жет быть бесконечное множество, и все они будут у ”. влгтворять ур-ию Лапласа
С геометрической точки «рения изотермическая сеть • еть так называемая квадратная сеть: ее можно вычер
тить так, что вся плоскость фнг 162
рл юбьется иа бсскоиечно-ма-п jc квадратики (фиг. 162).
Всякая другая (не изотермическая) ортогональная сеть не обладает такпм опством: здесь можно разбить иа квадратики только две бесконечно-узкнх 1<>СЫ (между соседними линиями с = const и у = const), которые на
фнг. юз заштрихованы; вся же остальная плоскость разобьется тогда совершенно определенным образом иа прямоугольники (см. фиг. 163).
Чтобы разбить плоскость изотермической сетью иа квадратики, надо фу нкциям у и у давать ния. В через между ниями
(фиг. 164 (, и выразим скорость в какой-либо точке через потенциал скоростей:
(78'(
и через функцию тока:
одинаковые прираще-самом деле, обозначим dn н dn' расстояние двумя соседними ли-каждого семейства
ап •
Фиг. ;
Фиг. 164.
Отсюда заключаем, что:
__ «V ап д»''
Если принять. ЧТО df£ = (Гу, то dn~du' т. е.. действительно, вся плоскость разбивается эквипотенциальными .шниями и линиями тока на квадратики.
Из ур (78') следует, что где скорости жидкости бо.1ьше, там и эквипотенциальные линии располагаются более густо.
Что касается абсолютной величины скорости, то ина выражается совершенно одинаково через потенциал скоростей у и через функцию тока у; именно:
'£г+(£)’=^)’+(£Т - les,
Поэтому, если изменить движение таким образом, чтобы функция у была потенциалом скоростей, а функция ?— функцией тока, то, несмотря иа различие движений, абсолютные скорости потока во всех точках будут одинаковы для обоих случаев; направления же будут различны; в первом случае скорости будут направлены по линиям у const, а во втором — по линиям 9 = const
Примечание реиакиии. Дополняем замечание проф. Н. Е. Жуковского об изотермических сетях.
Если мы будем какое-нибудь решение у (х»у) уравнения Лапласа:
J»=^+^=° (°’
приравнивать произвольному постоянному С, то мы получим изотермическое семейство кривых:
<f(x,V) = C,
— 127 —
т.-е. такое семейство кривых, которое вместе с семейством своих ортогональных кривых чает изотермическую сеть. Условие [«) достаточно для того, чтобы семейство кривых
у lx, у} = С
было изотермическим. Но, будучи достаточно, условие (а} ие является необходимым условием изотермнчиости.
Действительно, возьмем семейства кривых
t(x,y] = C и /(<r(x,pi) = f(C).
Очевидно, что оба эти семейства тожд-ственны, потому, что оба состоят из одних и тех же кривых. Однако, если функция <р (х,у\ удовлетворяет ур-ию Лапласа, то, вообще говоря, функция f[g> (х,р)] может и ие удовлетворять ему.
В самом дезе, обозначив
Р(х.У> = f[<f(x,y>].
после дифференцирования имеем:
зи» , _ <FP , dp l&r , ЗМ _ d’p [W
Ле1 • 3^ dif* 1\3х) л \Э, / |*d, \3х* • dyv d& |_ дх
принимая во внимание, что на основании условия (о) скобка (з^ + $ = 0-
Так как правая часть, вообще говоря, ие равна нулю, то функция Р{х,у) может не удовлетворять ур-ию Лапласа, хотя ур-ие
Р(Ы)=Ю и будет представлять изотермическое семейство.
Найдем необходимый признак изотермнчиости семейства кривых.
Пусть у нас имеется некоторое семейство кривых
U(x,y) = C,. причем AU ф О, так же, как и ДР в ур-ии (fe).
Чтобы семейство U=C было изотермическим, должна существовать такая функция
• <C)
^’[t'(z,y)J = 4 (x,y), которая удовлетворяла бы ур-ию Лапласа А<р = 0. Продифференцировав, мы будем иметь:
а*г । Уф
Отсюда
.0.
<рр
dr1_____
№ h
dr \dr) ' \ty I
(di
Левая часть этого выражения является фу нкцией только U; следовательно, правая часть, которую обозначим ‘ через—к, должна зависеть также только от Г Итак условие
34' . &V к— - дх“ ‘ ау!
(W)'
и является признаком изотермнчиости семенства кривых
Щх,У) = С.
= ftL)
(d)
Fean этот признак соблю рн, то функцию F мн найдем из ур-ия (d).
При наших обозначениях yp-ut это примет вид:
rfF , . dF
+ / dt? ~ °
Интегрируя, ne.iyia-tt ОКЛНЧаТв ЛЬН
r -fM
F~ 4 / di B. . if]
где l и В произво.тьные постоянны»*.
Семействе кривых, выраж «*мое функцией с/, удовдатвдряьщей ур-ию Лапласа, отличает»-я от хрупа тождественных семейств тем, что, если К Такому семейств црн» нднипть рто» шальное семейство
где функция ip тоже удовлетворяет ур-яю Лапласа (это елгдуег иа рас-суждений при нахож'“нии функции тока, см. стр. 124). то, давая этим функциям равномерные и равные приращения d? и dy:
#Ьэ — d</f const, мн получим квадратную есть, как »то гкозаио на стр. 126.
Очевидно,что,ес nt мы бу дем такую же кг.сдраипю е« ть образовывать и-1 хвух тождественных первоначальным изотермических семейств кривых:
U(x,y)^Ct и Vix,y)=CJr
г к» Г[ <,у] н Г। г.уj не у ко 1 |1яют уравнению Лапласа in этим функциям при и гея данагь нер «номерпне и неравный Между <•«и приращения, чтобы получить квадратную оть.
Если же ортогональные семейства кривых ио изотермичны, то-есть <|>\ нкцню, у довлетворяющд к» у равнению < laiuaca, по дыскать • ля инк не льзя, то, очевидно, уровню (*м. ртр. из—Г26‘
которое является н< обходимым для кзг :ратп'«п ег-гн, можно у овлетворить ТИШЬ прп частном значении ф\НКППЙ Ч и у, и в с»*тн будут лишь две потеки из квадратик Другие • по |<юки будут с остоять из прямоугольников с переменным огношением сторон
П рн мер 1. Возьмем дна ортогонатьных с меислва кривых—концентрические окружности и ратиуеы. Уравнения их соответственно будут:
а1 ?/-=Г. " Г,
ди , д1___у дЧт _2>J
Как ВИДИМ, УСЛОВИИ И горчично ТИ Cofi.Hf JPHO. По форму it- If) по.1 uix функ-ипи:
F, И
Так как Г -R', 1\ 2.1, gfl- £ Берем 2.1, = 1: £, <г Подучим: 1\ — lg К,
F.J -- .4, arc tg ГЦ-£2;
’ tge.
F.2- А,е-^-В„, t,= 1:‘ В., =0, Л - е.
Условие dy — dip дает ~ = dti = const, или
dR = RdO.
Очевидно, получается квадратная сеть (черт. I). Если бы мы взяли функции
С = Rr и Г= tg 0, и дали бы им равномерные и равные приращения dU— dV— const, то имели бы
2KtfB= tf® =const, т -е 6
dR= ; iW= const, cos’©. £ П
Чорт. I. Черт. 11.
Сеть получилась ве квадратная (черт II). Чтобы получить квадратную сеть, нужно было бы дать параметрам U в Г неравномерные и неравные приращении.
Пример 2. Семейства кругов с радиусом Г и общей хордой 2а: r = I’ + s5z”s
Признак нзотермичности семейств удовлетворен.
Ортогональным семейством будет семейство кругов
• fr + aP + y*
(а — о)2 +1/''
Присоединяя его и разделив две заштрихованных полоски (фнг. 162) да дс
на квадраты, получим квадратную сеть, так как условие =^7 удовлетворяется во всей плоскости. У казанная сеть носит название Неймановых бипо-тярных координат. Небольшой участок такой сети изображен на фиг. 162.
Теоретачаскн» осв»ы >»алзхо1ъ»*авиа S
Пример 3. Семейство парабол с общей осью, одинаковым параметром р и переменными абсциссами вершин 17:
y2 = 2p[x-\-Ul, или
д1 = —1- 34 =о- З-’Г _ £.
дх * Эх- * ду р ' Эу2 р ’
к = _й__ =______1___
1*+^ г+2(»+Г)
Семейство не изотермично.
Присоединяя ортогональное семейство
у = Ге ’,
получим не квадратную сеть, частично изображенную иа фиг. 163 *).
Перейдем теперь к применению теории ком 2 плексного Переменного к решению задач гидро-
динамики. Пользуясь этой теорией, можно вычерчивать на плоскости сколько угодно зквйпотен-М|ЧГ| пиальных линий и линий тока.
Вообразим плоскость комплексного переменного z=x-\-yi. = V—1; возьмем па ней
точку Л/ (фиг. 1631. определяемую координатами С___________________’ х, у, и будем считать точку W изооражснием ком-
Фвг. 163. плексного переменного г.
Возьмем какую пибу дь функцию от г. Ее можно разбить на две части—действительную и мнимую, так что
р<г) = е-|-ф1, . . . .(89)
где а и v действительные фу пкциии х п у. Заметив, что х ъ у входят в F(z) в виде г = х-1-у/, возьмем частные производные от тождества (89) по х и у. Тогда получим:
’ Ffc)*-FU)-.||+£/.
'ду ' ' ду 1 ду ’J
или, умножая последнее равенство иа —1‘
= + (90')
Отсюда заключаем, что
dtp _Зу
дх ду * - А • ,3в>
dtp_ dtp
ду дх
Таким образом, между ф$ нкциями у и у существует такая же связь, как и между функцией потенциала скоростей. Это свойство функций комплексного переменного дает простой прием строить сколько угодно потоков несжимаемой жидкости. Для этого и^жно брать разные функции от г и разбивать их на две части — действительную (©) и мнимую (уЛ Одну из функций (обыкновенно можно принять за потенциал скоростей: тогта другая будет функцией тока.
*) Написано сотрудником Ц. А. Г. И, М. Н. Весел он с к им Рвдакхмл
Рассмотрим теперь два примера на построение плоскопараллельных потоков. Хотя эти примеры весьма просты, ио даваемые ими потоки можно преобразовать в тс сложные потоки, которые обтекают пластинки и дужки.
Пример 1. Поток обтекает круглый цилиндр, ось которого перпендикулярна направляющей плоскости потока. Постараемся определить теоретически, как распределяются скорости в этом потоке.
Для этого возьмем такую функцию комплексного переменного:
F= — Г г — ‘ , ... <911
или
Р= - rjx + s/г)-^— = - I .z+j,/) - -
Заменяя x^-f-j/1 через г’ и отделяя чтены с i, получим: Р = -Г*-£-(
Отсюда:
9=—. .191
V=— + (91")
Пусть ур-ие:
у = const
представляет семейство линий тока. Const можно приписывать всевозможные значения. Полагая const — 0, получим ур-ие одной из линий тока:
v(l -*) = ’> -,в2>
•Это ур-ие удовлетворяется, если положить:
И = 0, или же
При втором предположении получаем:
г® = Ь_ = 0“ = const, * о
Фиг 166.
1 -е. ур-ие окружности радиуса « = у у-.
Итак, линия тока, выражаемая у р-ием (92i, сначала совпадает с осью -г, а потом переходит в окру жность. Эта окру ясность и будет основанием обтекаемого цилиндра. Для бескоиечио-\даленной точки потока получим __________ т- <><р_______п ду *
т.-е. поток в бесконечности движется параллельно оси х со скоростью V , направленной в отрицательную сторону оси х. Когда поток подходит к цилиндру радиуса а— то струйка, идущая по оси х, разделяется, обтекает цилиндр и снова смыкается за ипм, чтобы опять итти по оси х. При этом получаются две критические точки Л и В в которых скорости равны нулю (фиг. 166).
Для определения скоростей жидкости на поверхности цилиндра, представим функцию ? в полярных координатах:
где в—угол радиуса вектора с осью х. Скорость по направлению радиуса вектора .
’•=* = -К <**
Для точек на поверхности цилиндра шрн r = ai имеем Г, = 0.
Что касаеся скорости Г,, перпен (икутярной радиусу вектору. То она будет:
При г== а
. .193
У,== К sin в 1
>;=2 rQsme.
Итак, для точек, лежащих ’на поверхности цилиндра, скорость равна двойной скорости потока в бесконечности, умноженной на sin полярного угла. Этот простой результат от ш-чается от того, который мы полу чили для обтекаемого шара (ур-ие 46) только коэффициентом ( 2 вместо -у-).
Фиг. 167.
Фиг. 168.
Давление определяется по известной формуле:
= const—Ч, . . . (40")
что дает для точек на поверхности цилиндра:
1> = const 2 l’2sin’6=—+ ^—(j — 4sin?ft( . . (94|
₽ е Л
•Это ур-ие показывает, что давление будет самое низкое наверху и внизу цилиндра, где & — ±~.
Опыты показывают, что эта формула оправдывается довольно точно на передней стороне цилиндра. На задней же стороне давление, начиная
— i за —
л- некоторого места, выходит ниже теоретического и в точке В значительно ниже, нежели в точке А.
В плоской трубе В. Т. У. произведены студ. Г. И. Лукьяновым опыты над швленпем потока воздуха иа цнлиидр. Обстановка опытов была такая же, как в ранее описанных опытах с шаром )стр. 77). Цилиндр своими основаниями прикасался к параллельным зорка дам трубы. На середине цилиндра имелась дырочка, соединенная посредством гуттаперчевой трубки с манометром. Поворачивая цилиндр, ставили дырочку по i различными углами к оси трубы и записывали показания манометра. Манометр показывал уменьшение давления при дырочке против комнатного. Так как струйки в трубу подсасывались от спокойного воздуха, то формулу 194 j следует писать в виде:
Л = = 2 yo2sln2H
Off ff
Получились результаты, изображенные на шаграммах фиг. 167 и 168: на диаграммах откладывалась указанная высота Л. Пунктиром нанесены теоретические кривые. Отступление от теоретического распределения давлений показывают, что поток не такой, как предполагается теоретически: сзади питиндра образуются вихри (фиг. I69j.
Пример 2. Дру гая простая за-
йма получается, ее ш раегматривать фу икцию:
F=-lgz *>. . . . (9d)
я а
Если представить z в яке пене н-циальном виде:
Фиг. 169.
z = г (cos в i sin О) = re01,
то функция F разобьется на действительную и мнимую части
V = -£ lg“- ,a5’1
В этой задаче все линии тока суть круги, имеющие центром точку О,
Фиг. 170.
а эквипотенциальные поверхности—прямые, исходящие из той же точки О (фиг. 170). Еоли взять производную от у по дуге з, то найдем скорость г-Ц—ДД.................................(вв(
Легко видеть, что это есть поток, вызываемый вихревым шнуром, проходящим через начало координат (см. стр. 114i. Знак минус в формуле (96) показывает, что скорость направлена не в ту сторону, куда угол О возрастает, т.-е. что вихрь крутится по часовой стрелке.
Если брать циркуляцию скорости по тииин
гока, то I нужно помножить на 2.тг; тогда получим, что циркуляция 1=2к.
1) Натуральный логарифм.
Итак, мы рассмотрели два потока: один — бесконечный поток, ударяющий иа цилиндр (фиг. 171 к другой — вызываемый вихрем — поток, который около этого цилиндра крутится и скорость которого убывает но мере
удаления от цитпидра (фиг. 170а.
Примерз. Еслиэти два потока геометрически сложить, т.-е. сложить функ-
ции у из ур-ип (91') и (95 ) и функции у из j р-ий |91"> и i 95% то налу чцч новый поток |фиг. 172к конформные цреобразованпя которого дают различные потоки, обтекающие пластинки и дужки. Для этого сложного потока имеем
г0«- .* +*‘ig ; . от.
,г Гор1 т к
у=—----------;s---— &.................(97)
V~- Го» + Г‘“Л+ * '9<"1
Критические точки нулевой скорости, лежавшие в первом примере иа оси х и определяемые ур-иями: r = a, sin 8 = 0, переходят на новые места. Чтобы найти новые положения критических точек, приравняем нулю скорость иа поверхности цилиндра:
Г = 2 r0sin8— -^- = 0.
откуда
Если вихрь очень силен, то может случиться, что об₽ критические точки сольются в одну (sin8=1), или их на цилиндре совсем нет • sintf>l). Если циркуляция не очень велика ( д < 1), то критические точки всегда найдутся, и их будет две.
У же в злой задаче, в которой поток слагается из течения, вызываемого вихревым шнуром, и другого, представляющего поток, обтекающий цилиндр получается сила, перпендикулярная к скорости потока в бесконечности.
В верхней части цилиндра скорости будут сравнительно малые, а в нижней—большие. Поэтому, давление вверху будет больше, а внизу меньше, так что появится некоторая сила 1\ действующая на цилиндр сверху вниз (фиг. 172). Сила эта выражается ур-ием:
l*= / psinb add;
по интегралом берется давление р, множится иа площадь элемента айО'\ и проектируется на ось у. Как всегда,
Иодъинтегральная фушспия будет содержать члени с четными н нечетными степенями sin О. При интеграции в пределах от О до 2л нечетные степеии sine дадут О, так что такие члены мы прямо отбросим и будем обращать внимание только иа член с sin-6.
Следовательно, сила будет:
2л
Р= j р 2F0sin26 — udG, так как
j* sin2eJO — д. то
Р Р-2А-Г
Замечая, что 2 А есть циркуляция потока около цилиндра, представим «•илу в виде:
Р=АеГи. ..... . (99)
Мы видим, что сила перпендикулярна потоку и равна плотности жидкости, помноженной на циркуляцию скорости около обтекаемого цилиндра и на скорость потока в бесконечности.
Чтобы получить направление этой силы, надо взять вектор, представляющим скорость потока в бесконечности, и повернуть его на прямой угол в сторону, обратную циркуляции.
В рассматриваемой задаче о потоке, обтекающем цилиндр, мы можем при одной и Toil ще скорости Го брать различные цирку тяции А и соответственно с этим получать различные силы Р. В случае же обтекания гужск. можно взять, как увидим ниже, только одну определенную циркуляцию; поэтому для них и получается только одна, вполне определенная сила Р.
$ 20. Основная теорема о поддерживающей силе потока.
Дадим теперь общее доказательство теоремы, с которой мы встретились в только что рассмотренной частной задаче.
Теорема. Еслп поток, имеющий в бесконечности скорость Го, обтекает контур, и циркуляция скорости по этому контуру равна /, то "равнодействующую сил давления жидкости на коит\р полечим, если умножим вектор, представляющий скорость потока в бесконечности, на циркуляцию скорости и на плотность жидкости, и поверием полученный век гор на прямой угол в сторону, обратную циркуляции.
*) Длину цилиндра по направлению его образующих (перпеидикулнрио иапра вляюшеВ плоскости потока) принимаем за единицу, и потому она в формулы ие входит <.-*то относится ко всем исследованиям о плоскопараллельных потоквх.
Положим, что контор АВС »фиг. 173) обтекается установившимся невихревым потоком, который в бесконечности имеет скорость Го, напра-
Фиг. 173.
вленную в отрицательную сторону оси j Возьмем функцию потенциала скоростей в следующей форме:
<Г =—Vox~rf.
где функция / удовлетворяет jp-ию Лапласа
Jf=O
и условию, что на круто бесконечно большого радиуса В
< = а °'
<лг dt/
при чем порядок этих бесконечно малых ветичин будет д
Приложим ко всей массе жидкости, ограниченной контуром АВС и кругом радиуса R, принцип сохранения количеств движения i теорему Эйлера): силы, действующие на данную жидкую массу, уравновешиваются силами количеств движения жидкости; прн этом количества движения входящей жидкости надо брать по направлению потока, а выходящей — в обратную сторону.
Назовем через -Y и Y компоненты силы давления потока на тело (компоненты давления тела на жидкость будут — А' и—F>, через я и Д углы внутренних нормалей круга радиуса* R с осями х и у и через р гидродинамическое давление. Секундная масса жидкости, втекающей через данный элемент ds контура круга, будет:
giHcos«-|-ecos^)ds = nK— У,cos яcos;j]ds;
при этом знак ее (плюс для втекающей и минус для вытекающей жидкости) включен в формулу. Помножая секундную массу на компоненты скорости, прямо получаем проекции количеств движения жидкости с надлежащими знаками. Следовательно, имеем формулы:
005 « *+?/*(— го+ Й)[(~Г”+ ta)cos“+^cos^| ds=°;
-У-|-/рсояД<1т + оу^[( - F0+-^'coSa+^cos^ds = 0.
Интеграция производится по всему кругу радиуса R Гидродинамическое давление р выражается известной форму той (40"):
Р^с_1[(_Го + <Г + (^].
Когда будем делать подстановку, то прямо отбросим члены порядка 3.1
малости и члены вида: const, cos a ds, так как f cos ads —О.
Тогда получим:
А' = О 4’( I'cos ads — о 4'0 J'cos a ds
₽ ’ ’./*[Г° J?)cos n + cos rfs = °-
так как последний интеграл представляет полное количество жидкости, вошедшей в кр\г радиуса R, которое равно и} Лю.
Сита
l'= S «'о f cos 3 ds — о 1г0 У cos ads —
₽ 1'/[1£cos“~ дг cos^jds.
^ыма— c'u’sjS сеть проекция той части скорости, которая функции f, на направление касательной к кругу, считаемое ’” — -------л Действительно, проекция ско-
Здесь зависит от положителъным по часовой стре ше. рости на произвольное направление I есть к cos (Л x)4-t cos(/, у). В нашем случае (см. фиг. 174. на которой указано направление касательной и обозначены углы) роль ^£(7. л) играет^ (т—Д), а роль zd(7. у) играет^а. Следовательно, проекция скорости будет:
— и С >« 1 4-г COS п— „-(-««а— 5 cos.?. 1 dy дх '
Отсюда ви 1нм, что интеграл представляет циркуляцию скорости ио кругу радиуса R, взятую в направлении часовой стре лки. Эта цирку шция есть циркуляция I по произвольному замкнутому контуру, окружающему тело АВС, так как нигде в потоке вихрей нет.
Итак:
х=о, к=
(КТО)
Направление силы получается согласно фиг. 175.
Таким образом, же лаемая теорема доказана.
Применим эту общую теорему к определению подъемной си лы в с л> чае потока, обтекающего пластинку, и в случае потока, обтекающего дужку.
। Рассматриваемые потоки получаются с помощью
X конформных преобразовании вышеописанного (§ 19) *v; (— потока, обтекающего цилиндр.
\ Конформным преобразованием истока жидкости
мы будем называть следующую операцию. Представляя потенциал скоростей и фрикцию тока у с порт мощью комплексного переменного z = x+yi в форме:
:Фиг. 175. F(Z) = ...........(^9)
мы будем брать новое комплексное переменное = которое связано с переменным z соотношениями:
?=^С). :=zC?);. ..........-• (юр
функции ф будем подбирать так, чтобы всякой точке (х, у) прежнего потока соответствовала одна определенная точка (;, у) нового потока и чтобы в бесконечности было
.... . . (юг»
1 де л есть величина действительная, конечная и опре ютенвая. Тогда новый поток будет определяться формулой:
v + V'=F[^(:)] .
(103)
Всякой эквипотенциальной линии у — const и линии тока i/> = const в новом потоке будет соответствовать одна эквипотенциальная линия и одна танин тока, которые получаются через замену точек (х.у) прежней линии точками (;, rj).
При этом значения д и у на прежней линии будут те же, что и пгт преобразованной новой линии. Если эти линии основного потока представляют в бесконечности прямолинейную ортогональную сеть, то и в преобразованном потоке они будут представлять такую же и так же
направленную сеть.
Скорости и и г данного, а также «’ и г' преобразованного потока
непосредственно находятся, если взять произво шые соответственных функций комплексногб переменного н разбить ну на рйствительнуло и мнимую части:
d di dF
=«
Хиалогично
ду
dF dz dz dj.
l — lt
(Ю4)
Отсюда находим, что скорость в бесконечности в преобразованном потоке будет иметь то же направление, что и в данном, но величина скорости будет И0А, если данный поток имеет в бесконечности скорость Го.
Критические точки нулевой скорости преобразование! j потока будут соответствовать критическим точкам основного потока. Это следу г ин уравнения (104), которое при F (г) —0 обращается в
= 0 ___?»=0
д! и’ dij '
Исключение представляют точки, в которых ф' (*) — хи, следовательно, ф- = 0. ’ dz
В этих точках
f* (г) ф' (X) - m -t- nr,
где m и п конечны. Тогда точки преобразованного потока, соответствующие критическим точкам данного потока, ие будут критическими точками нулевой скорости, а будут иметь конечную скорость }/т'Д-п'-
Покажем теперь, что в преобразованном потоке циркуляция скорости по замкнутому контуру, охватывающему обте-
каемое тело, остается та же, что
п в данном потоке.
Можно поток, обтекающий контур ABCD (фиг. 176), преобразовать в поток, обтекающий контур в котором критическая точка А
* прежнего потока изображается
критической же точкой А в ионом потоке, а критическая точка С—точкой О' с конечной скоростью.
Согласно сделанным здесь замечаниям, потенциал скоростей в точках А и .4' будет иметь одно и то же значение у. Когда мы пройдем пи контуру АВС от точки
Фиг. 176.
А до точки С, то получим в данном потоке для потенциала скоростей значение дд. То же значение получим, когда пройдем по преобразованному контуру А'В'С из точки А в точку С. Но когда мы пройдем из точки 4 в точку С ио конту ру АВС или из точки А'
в точку С по контуру А ГУС, то получим непрерывное изменение потенциала скоростей от значения до значения <р,. Циркуляция скорости I, взятая по часовой стрелке по контуру ADCB, и циркуляция скорости Г ьзятая в том же направлении по преобразованному контуру А'Л'С'В', будут выражаться следующими формулами:
откуда следует, что
1—Г.
При этом переход е одной стороны тинип тока СЕ или С'Е' на другую сопровождается отним п тем же скачком q.,— qL в значении потеппиала скоростей
£ 21. Поток, обтекающий руль.
Конформное преобразование, соответствующее этой задаче, характе-ризуется такой функцией z й):
'= ’.-(*+-?•)............... <»«>
Полагая
* — г (ciв-)- i sin 8) получим:
Z=*z-\-qi— ’ [(^ г —^)cos6 г— *’ sin61 »
Отсюда
F.ctm плоскость переменного z была разбита радиусами и концентрическими кругами, то легко найти соответственную ортогональную сеть на плоскости С.
Чтобы узнать, во что обратятся круги, примем г = г0 и исключим 8
Тогда найдем:
Следовательно, все круги преобразуются в сифонусные эллипсы <- фокусным расстоянием 2 а, которое найдем из выражения:
1 hFFT^T-
На фиг» 177, на которой осп хОу и ;Оу совмещены, эти фокусы обозначены буквами С п Я. Круг АВС радиуса а в преобразованном потоке сжимается в прямую СА.
Уравнение преобразованных радиусов найдем, исключая т из уравнении (105х). Для этого разделим первое из них на cose, второе на sin8 возведем в квадрат и вычтем второе из первого.
Тогда квадраты сократятся, а в удвоенных пронзят тениях г сократится, и мы получим: „ '
‘ ___________9 — = 1
си сое1 С* л* sin2 в
i.-c. уравнение софокусных гипербол с тем же фокусным расстоянием 2 ч и теми же фокусами С и Я. Па совмещенных плоскостях г и С радиусы плоскости z служат асимптотами соответственных гипербол плоскости * (фиг. 177).
Итак, точки, лежавшие в плоскости z на кругах н радиусах (ДГ>. будут лежать в плоскости Z на софокусных эыипсах и гиперболах (if'). В бесконечной дали С = Д-г. что дает:
/. = 2; 5 = -^ /cos в— jj=-^-rsin6 = ~ . (а).
I Ж = «О X —.4Г>
Отсюда находим, что
10 = Л I 0 = 2 Т 0
Геометрически это поясняется тем, что разность значений у и у пл двух соседних линиях осталась прежняя, расстояния же dn и dn между
Ч 1
Фиг. 177.
ними уменьшились вдвое (форму та «).
Область, занятая жидкостью в плоскости z (т.-е., вне круга ралнуса а), занимает всю плоскость 7 от отрезка прямой С 4 до бесконечности Точки
плоскости г, лежащие внутри круга радиуса а, к потоку нс относятся и мы их рассматривать не будем.
Если в плоскости г вне круга радиуса а вообразить какой-нибудь замкнутый контур, то в плоскости Z он преобразуется в замкнутый 'же контур, охватывающий прямую СА-
Возьмем в плоскости z круг радиуса Ь, прикасающийся к основному кругу радиуса « в точке С (фнг. 178). Koria мы его преобразуем по формуле (105), то получится форма, представленная на фиг. 178: рыбообразная, с заостренным концом. Чтобы показать, что в точке С форма, - dn
действительно, заостряется, возьмем производную и покажем, что при т = а и 6 = я она обращается в нуль.
За независимое переменное примем 6; тогда
dr, = Л, . dj °1пе(1+ -*)<”*
л <ге • л - собе^- 4) " _(г+л£)8шв
Так как в точке С величина г для круга радиуса Ъ проходит через minimum, то ^L = o, и правая часть этого выражения при г—а и 6 = л обратится в (‘ Для раскрытия неопределенности надо взять от числите тя и знаменателя производные но переменному и потом положить:
Сделав это, увидим, что числитель обращается в пучь, а знаменатель будет 2а. Таким образом, и точке С имеем =0, и касательные к верхней и нижней ветвям контура идут по осн
Найдем силу давления потока на этот конту р. приложивши к нему общую теорему. Предположим, что прикасающийся круг радиуса б обтекается потоком, иду щим в бесконечности параллельно хор (с NC, под углом ₽ к оси х, как показано на фиг. 17«. Пусть .этот поток образует на круге радиуса b критические точки Л’ и С. Положение этих точек характеризует циркуляцию. Легко видеть, что угол 0 равен углу Я определяемому из уравнения так что
2 = 4 л b rosin/?.
Когда 7=0, то критическая точка X попадает в точку D, и тогда 3 = 0 Отступление критической точки X вниз от диаметра DC при общем направлении потока справа показывает, что круговой поток направлен против часовой стрелки.
Подставляя выражение циркуляции в общую формулу (100) и заметив, что Гп' = 2 Го, найдем:
Р=2 лоб l0’sin/? . (106)
Когда б = а, контур обращается в линию АС и вся форма — в пластинку. При Ъ близком к и, за площадь пластинки можно считать величину F— 2а. Тогда найдем, что
Р= лрРГ/ЯпД, ... . .(107)
т.-е. подъемная сида равна некоторому коэффициенту Л, умноженному на цлоща ц> пластинки, на квадрат скорости потока и на sinus угла.
Коэффициент подъемной силы
Л = яр = 0,39, . ..................(108>
при 15 С н 760 пин давлении, когда о = •
Soreau, на основании опытов Лилиенталя и Langley я, давал для пластинки
к = 0,33,
так что теоретический коэффициент несколько больше опытного, но немного. Мы увидим, что такой же коэффициент ло получается и для дужек, только в них вместо угла /? фигурирует некоторый угод (2 + ^)
Примечание редакции.
С / । в® А
Пользуясь свойствами конформного преобразования: z= -Ls-|- * . можно легко показать, как получается функция комплексного переменного
— 14-2
F = — Vq2—k хля плоскопараллельного потока, обтекающего цилиндр
I стр. 1311-
Будем преобразовывать поток, обтекающий плоску ю пластинку длиной 2а, лежащую на осп ОХ’ и имеющую середину в начале координат.
Постоянную скорость потока, направленную в отрицатетьную сторону осн ОХ, обозначим через 2F0.
Очевидно, что функция комплексного переменного для этого потока будет
F=-2F,21
Сделаем теперь преобразование
Тогда, по свойств) этого преобразования, отрезок прямой длиною 2я превратится в окружность радиуса 2а и прямолинейный поток в поток, обтекающий цплиндр.
Функция примет вид
р_____I' -_
г— 1С. г
Заменяя
o!F0 = fc,
получим формул) (41) стр. 131:
F= - Гоз - 4 )
> 22. Поток, обтекающий дугообразные контуры.
Дуга круга впервые была разобрана проф. Kutta. Он два раза делал конформное преобразование и после довольно с южного вывода получил поток, обтекающий дугу круга.
Рассматриваемое здесь преобразование принадлежит проф. С. А. Чап-тыгину и очень просто
Примем
;=z (л) |109>
где а, е и д суть действительные положительные величины, прп чем с>д и
а9— ед. ..... . (11U)
При бесконечно большом г получим:
откуда
i==i н ’«=?<-
Воякой точке М(х,у) будет сооответствовать вполне определенная точка Я'при зтом первая система точек занимает всю плоскость х О у. кроме круга радиуса а, оппсанного из начала координат, а вторая — всю плоскость ЬОу.
1) Примечание написано М. Н. Веселовским
Редакция.
Найдем связь между координатами точек Sf и АГ 'фиг. 179). Дтя
-этого перейдем к полярным обозначениям. Тогда координатами будут радиус-вектор г и полярный угол у, а точки М'— г и у. в отрицательную сторону оси расстояния OG — д и ОЁ = ег ссм линия точку V с точками О и Е и обозначим: MG— rlf ME=r„, ^.EMG =v, а соответствующие векторам MG и WE комплексные величины—z н z2. По правилам действии над комплексными величинами ’) найдем, что
~i=«+<Z. г. = г+*
Тогда моду ль (длина вектора) величины , ИО9) будет:
точки М Отложим
Фиг. 179
. (Ill)
а аргумент (полярный угол
7=/4 ЛМЕО- мао =
Всякая точка X, лежащая на круге рддну са а, изобразится точкой -Г, лежащей на том же круге.
В самом деле, из подобия треу голышков £Х0 и G-VO >у них ^.ЕОЛ общий, а с гороны, содержащие этот у го л, пропорциональны “ — — согласно формуле 110) можно для точки .V написать:
9
Тогда на основании ур-ия (111) получим:
= а.
Из подобия тех же треугольников имеем:
_ XEO = ^G\TO.
1) Комплексные велячпиы складываются ио правилу параллеюграма
, 4- ,, = Z + х, ч-1 (D+у,);
□рн умножении модули иг перемножаются а аргументы кладываются.
при деловая модули делится, а аргументы вычитаются:
<e-ej-
Принимая xlENG = v, ^.ХЕО — и, и замечая, что
Z. NG О = /я- г. ^2 NOB = / = 2 м 4- у,
находим
NOB = у = у —v = 2 ц.
Кети мы проведем из точки Е к кругу радиуса а двр касательных ЕЕ н ED «хорда FD пройдет через точку G) и обозначим угол между ними и осью х через то усмотрим, что, когда точка N и лет от В до F
п далее до М, (угол у возрастает от 0 до п шльше до лд, точка N'
идет от В до Л и затем возвращается в В (угол / сначала возрастает
до о, затем уменьшается до нуля к
Отсюда следует, что при указанном преобразовании весь круг радиуса а, изображается на tyre АВС того же круга с центральным у глом АОС, равным 2 а. При этом точки круга, лежащие справа от хорды FD. изображаются па внешней стороне дуги АВС, а «ежащие слева от хорды — иа внутренней стороне дуги.
Теперь прпсту пим к преобразованию указанным способом какой нибудь формы. За эту форму мы примем круг DLN радиуса b (фнг. 180),
Фиг. 180.
немного большего, неже ли а, при-касающийся к основному кругу в точке D. На этом круге начертим хорду ND, которая образует угол /3 с DP. Примем, что круг NDL обтекается потоком жидкости, который течет в бесконечности со скоростью Го по направлению ND и имеет такую циркуляцию что точки .V и D круга радиуса Ъ являются критическими точками нулевой скорости. Этот круг но ур-ию (111) «егко преобразуется в форму ('ST, окружающую дугу СВ А и напоминающую поперечный разрез крыла. Когда Ъ приближается к а, этот контур приближается к дуге СВА. Контур CST, представляющий конформное изображение круга NDL, будет в новом потоке представлять линию тока и может быть принят за контур обтекаемого тела.
Критическая точка N в новом потоке заменяется критической точкой Г. Что же касается критической точки D, то она в новом потоке заменяется точкой С, в которой скорость конечна и ветви обтекаемого контура касаются между собой. Это следует из того, что в точке D выражение
Р(г)* = Г1г>:«
конечно, несмотря на то, что F (г) в этой точке равно нулю, так как ур-ие
Лг а («+,)•
у iobt отвернете я корнем:
г = — д—i |/ — д~, представляющим точку D.
Сила, действующая на обтекаемое те по TSCb преобразованном потоке, на основании общей теоремы (ур-пе 100), будет нерпеп щкулярна хорде ND и равна:
Р= qI .............................(112)
где Гр есть скорость преобразованного потока в бесконечности.
Если мы обозначим через I циркуляцию по контур} TSC тгреобра-аованного потока, то она, по доказанному, будет та же, что п циркуляция скорости по кругу радиуса Ь в основном потоке. После шяя. по ф-ле (98j, будет
1= inb 10 ^п О, где
Что касается угла 0, то заметим, что хорда DN круга радиуса Ъ стягивает дугу л—2 0. Такую же дугу стягивает хорда DM на круге радиуса а. Вследствие этого имеем:
п — 20 л а л
Когда мы найденную величину подставим в выражение циркуляции ив ф-лу (112) для силы Р, то найдем для рассматриваемой формы крыла
следующую формулу:
Р= l.igb т;- sin “ sin (“ +fi). . (113)
Еста вместо Ъ подставить весьма близкую к нему величину а, то можно эту формулу представить в с де дующем виде:
Р = 4.юр Fj2 sin ° sin (y+£) ..(1141
Эта формула совпадает с формулой, полученной проф. ('. А. Чаплыгиным; при ,4=0 она обращается к формул} проф. Kutta:
P=2.t₽s Г02.
г tr- я—стрелка основной дуги, равная _ а . а s=2asm sin .
Хорда осиовпой дуги
г - 2 a sin а — 4 a sin ® соь *
При малых дугах можно также положить, что площадь пластинки
F=4/7.sin ° -
Тогда найдем, что
P~--jiqF Vv~ sin (® +/?) (115)
10
Теоретически ооокы воадуюилаваквж.
При (7 =— “ имеем Р=о.
Угол Д видный на фиг. ixf), может изменяться от ’ —~ до О и vT о ДО - (’ + °
Опытные исследования над поддерживающими планами аэропланов.
§ 23. Описание плоской трубы В. Т. У. и ее рабочие формулы.
Чтобы поставить исследования над к бесконечно тлипиым, я, по идее стюеги
плас гинками, приближающимися ученика П. II. Соколина, построит
Фиг. Ifi
для аэродинамической лаборатории Императоре!. »г»О Технического > чилпща прямоугольна ю трубу, сечепис которой но горизонтальному направлению имеет 150 ст, а пи вертикальному 30 ст Фотография ее предогавлена на фиг. 181. Труба выполнена ггудсн-и>м A. II. Туполевым.
Вентилятор (’прокко, приводимый в движение электромотором постоянного тока в 23 силы (он работает е не югрузком, потребляя при
14,0 Л. С., что лает качество тру бы Z=0. через • м |нпп цилиндрический конец, прп чем скорость в 1рубе может быть доведена (о 25 да/аег3). Нафиг. 182представлена (иаграмма 4), показывающая распределение скоростей в прямиуго1Ь-нпм сечении трубы.
Испытуемая пластинка DDEE (фиг. 183 к обыкновенно представ ляю-
скороетн 21,7 mt всего
10 *) высасывает из трубы возду х
щая часть аэроплана, нырезанну ю двуыя параллельными плоскостямп, перпенли- • j°?loz У У . z ку лирными планам и параллельными • ;
осн аэриилала, ставится в трубу, копа 4---------’— -----*—•—
переднее стекли ее поднято. Стержень
F, скрепленный с пластинкой, проходит Фиг 1«2
через отверстие Сдпамчтр которого не-
много больше диаметре! стержня! в средней сюйке трубы и укреплен
Ч Ныне Высшего Московского. Прим. ред.
!> Качеством аэродинамической трубы называется отношение живой силы струи воздуха в рабочем сечения. ™ . где m есть секундная масса протекающего чере-з трубу воздуха к мощности на валу вентилятора Прим. р^А.
Д В ВИВ । вентмаятор Сирокко был заменен крыльчатым вентилятором типа mt
Н. Е Жуковского, после чего скорость войду та в трубе повысилась до Зо при том же моторе. Прим pi
Ц Построена В. 'тесаревым в 1010 г
трубочке Н, которая прочно связана с рамочкой АВС. В эту рамочку
" трех шариках по горнзон-
Фнг 183.
пи се проекциям: Р—на
гавлено зеркальное стекло, которое катается па и.ному стеклу плоской трубы. Таким образом метлика и рамочка составляют одно твердое । X которое может перемещаться только гори-штально. Рамочка может по желанию у крепиться к любой нз точек .4. В или С.
При испытании опреде »яют моменты сплы •противления воздуха относительно этих трех • нтров, пользуясь разновесками, положенным п • чашки весов М п Д' (они вишы нафиг 181 >. : 1ля моменты силы сонротпв гения воздуха отно-« птельно трех центров моментов, мы легко опре-• (им се величин.), направление н положение.
Выве (ем теперь рабочие формулы для и юской трубы В. Т. У. Все размеры даны и* фиг. 1st 1).
Полная сила R сопротивления воздуха иа-праилена по прямой Ь'Х; положим, для у добства, и । она приложена в точке О, лежащей также н на прямой НВ. Be титану и направление этой силы В будем определять ..... ”Г *.----- г> _л нанравлеппе, перпендику iяркое потоку, и Q—на направление потока; точку же приложения бу (ем определять расстоянием л = 110 от точки Н по направлению потока.
Д1Я опреде >ения этих трех величин бу (ем писать ур-ия моментов около центров А, В л С. при чем силы натяжения нити (в граммам обозначим соответственно через А,В и С.
Величины Р, Q, х на фиг. 181 нарисованы положите юными. Гр\ ты А, В и С будем считать положительными, если они лежат на чашке .V (с»т стороны трубы, обращенной к ротативной машннер Тогда
Е
во
В SO = В 030 —
Г116)
Фиг
1*4
С . 25 = Р (25 —X) — Q 62,5.
11тсюда
(117)
(118)
< Обозначим для сокращения __ а \
н третье из уравнении (116) н вычтя из них удво-
С юливши второе • ин •• перрон, нап (ем:
Р
16 В — эу 16 ,, -----;. — = . к ~
(119)
Ч В настоящее время рамса, катающаяся ио трубе, заменена потолочным подвесом, чтп ла»т значительно большую точность измерений Принцип же измерения (по трем м lie*'гам) оставлен прежним /7/ми. рг>
KJ*
х определяем по первому из ур-им (116) и заменяем в его выражении В ПО ур-ю (119) через Р и qt тогда
................. (120)
So (I* В}
Непосредственно мы получаем х = —' р- -> но пользуемся преобразованным уравнением (120). как лаюпшм меныпую погрешность при вычислен пн.
Формулы (117), (ПН), <119) п(120)суть рабочие формулы нашей плоской трубы.
Прп испытаниях, кроме величин .1. В я С, необходимо знать угол /?, иод которым хорда испытуемой пластинки наклонена к потоку, п скорость Fo в трубе. Угол определяется просто ио лимбу, а скорость — по звонкам: через каждые 100 оборотов вентилятора подастся электрический звонок. По секундомеру определяют обыкновенно продолжительность 500 оборотов (в секундах), которая обознается через 1^,. Затем определяется скорость Го потока по специально построенной диаграмме, в которой по оси абсцнос отложены Т50О, а по осп ординат — соответственные скорости Fo. Следовательно, прп работах полу чаем таблицу 11.
Таблица 14.
№ набд. г '* 2 В С
Посте по течется получают нову ю таблицу 15.
Таблица 13.
»абт. V, <? <? Р ; | t, 4Г | а- | •
Коэффициенты А-, и определяется из формул:
S = у р. кя - ... (121)
где F площадь пластинки в mt'2.
Понятно, что в _ *, <? ~ *;
Последнее отношение является наиболее важным для практики: об этом см. стр. 9 '. настоящего курса.
По в- 1ПЧИНС х определяют положение центра парусности пластинки. Для этого надо направление сплы перенести на xopiy пластинки, что чрезвычайно просто делается графически. Пр< дставпм себе пластинку.
укрепленную в точке Н и стоящею в трубе (фиг. 1*5). Ясно, что наттра-в юние равнодействующей пройдет через точку G, прн чем FG = S будет
расстояние центра парусности от середины хорды, — в данном случае отрицательное. Когда модель ис-
следуется под разными углами, построение величин S быстрее всего делать так (фиг. 186): па горизонтальной оси отмечаем точку
Фиг. 186.
укрепления модели II. Из пег, как из центра, описываем две окружности: дну радиусом Hi, равным расстоянию хорты от точки укрепления, а тру гую радпусом HF't она дает геометрическое место сере ihh хорты. Касательно к первой окружности проводим прямую iF иод углом /? к горизонтали *). Откладываем НО =» х и От = 1 ст (всегда вправо, так как Q всегда положительно), из т восстав 1яем перпендикуляр тп и откладываем на прм тп = (вниз, если Р<0). Тогда прямая On даст нам направление равно явствующей и точка G — положение центра парусности иа хорте. Теперь откладываем Я от точки на хорде, принятой за нулевую, до точки G. За ну левую точку обыкновенно принимается середина хорды F, прн чем Я считается положительным по направлению к краю С, противоположному краю атаки. Так сделано и на фиг. 183 и 186. Когда подсчеты кончены, то строются для каждой дужки две диаграммы: иа первой стри-ются кривые 7г, п **, на второй—кривая центра парусности пластинки; последняя строится ио способу проф. РгапйН’я, а именно: вычерчивается испытуемая фирма; середина ее хорды принимается за начало коор щнат; за ось ординат, по которой откладываются расстояния S, принимается сама хорда; углы откпадываются по оси абсцисс, положите 1ьные в сторону вогнутости формы (см. ниже фиг. 196, 197. 198, 199).
? 24. Теорема проф. С. А. Чаплыгина.
Первые наблюдения в плоской тр\бе В. Т. У. относи тин. к проверке форму лы:
Р = 4 /rosin-* • ...........(1*4)
которую можно иодсгавить выражение стрелки изгиба
f = -П sin"-” .
Она даст положение хорды пластинки
loO •—
От этой подстановки форму та получает ви и
Р = 2Jiof Го’ .
(114)
и чает интересную теорему проф. С А. Чаплыгина:
Подъемная сила туговых кланов при хорде, направленной по скорости, не зависит от глубины их и одинакова для всех планов, имеющих одну и ту же стрелку’ изгиба.
Для проверки се были сделаны из цинкового листа в 3 мт толщины четыре плана (фиг. 183) глубиной DE = 120, 210, 3(50 и 480 ют мри общей стрелке изгиба /“=10 тт и ширине 7)7) = 290 тт. Пластинки пометца-лись в нашу трубу так, что точки 2), I) отстоя in от верхнего и нижнего зеркального стекла на 5 тт. Скорость в трубе изменялась от 11 до 20 метров в секунду. Наблюдения показали, что подъемная сила С возрастанием глубины пластинок увеличивается незначительно. Ниже приве (ены таблицы (16, 17, 18, 19) результатов наблюдений; коэффициент 2 к определяется в них путем деления подъемной силы Р (в килограммах) на квадрат скорости и на и ющадьми 1е левого сечения 0,29 f (в ква (ратных метрах).
Таблица 16
13.70 Г. «Г. 17JD0 18.7<| 21.10
0.249 ЦШ 0.42»» “"'20
Таблица 17.
Вогнутость 1
РЛу ц ОДЬ.- НДХТ 0.281 0,416 0.4&G
2 Л I 0..V2 0 44 0,42 0 39 0,41
) См. стр. 77 курса.
Таблица 1*
Вогнутость
ПВО 14.30 15.25 16.1.1 18,60 1 JOIS
OJ43 I • 1.314 и,371 Ц4И Л.5К' 0,614
— —
2* 0,62 | O5J ! ПЛ2 0,50 «|,х*
Таблица
Н о,г н у т О С т ь
1 ll.flb 12 Ю 14.5Л» 1»Д1
— — ... —. • — ——
0 347
0,60
0,45» • 1,Ь:.И
Pkg О 240
O.ol 0,71
о.ъо -цпа
Мы видим, что коэффициент тем как теоретически оп должен
•к в среднем выхо шт равным 0,5, меж ту бы равняться 2ло = 2 л ' = 0.78.
Чтобы показать, что на результат мало влияет ширина прямоугольной трубы. 1ишь бы модель упиралась концами в et нижнюю н верхнюю стенки, бы.in произведены аналогичные наблю ценим в ква [ратной Tpj6e аэродинамической лаборатории Московского Университета, имеющей отверстие 0,63 X 0.63 тГ-. В этой тр\бо прн скоростях, изменявшихся <»т 3 до 7 метров и секунду, испытывались пластинки (• те танные из такого же цинкового листа, как и прежние, при стрелке тт. но г i.vбинт ЗОЛ тт Ширина была что они
Фиг. 188
той же изгиба Ю имевшие 160. 200 и (фнг. 187). пластинок «О ст, так отстояли от краев трубы на 15 тт. 11а фиг 1»8 изображено расположе-
Фиг. 187.
ние опыта прн ирипо щятой крышке, на которой укреплены В'ч-ы, поддерживающие нластннк$ После установки крышка опускалась
вниз, и всасываю!цпй вентилятор пускался в ход о желаемой скоростью.
Результаты наблюдений даны в нижеследующих таблицах 20, 21 И 22.
Таблица 20.
Вогнутость 1/1в.
3.2 4,1 4,6 5,3 5>, 1 6,6
Pty 0.02" 0.04S 0,047 0.ОЭ.-1 0075 0,100 0,130
2к । 0.44 0,46 0,47 0.44 0-45 0.48 0,49
Таблица 21
Таблица 22.
В этих опытах коэффициент 2 к получается немного менее найденного в плоской Tpj6e: может быть, это происходило от того, что края пла< гинки были бо iee удалены ит стенок трубы, чем в опытах Технического > чнлища.
§ 25. Исследование подъемной силы и лобового сопротивления для теоретических форм.
Далее были исезедованы две формы планов, построения которых указаны в §§ 21 и 22. Точные конторы, соответствующие этим формам.
. 240
Ь> 160 тл.
Фиг. 189.
изображены на фиг. 189. Первая крылообразная форма имеет параметры а = 750 ?»7«, Ь = 702,5 тт, а=20°,
а вторая, которую, по моему мнению, удобно принять за контур корабельных рулей, имеет в одной модели параметры л= 250 тт, 5 = 260 тт, а в другой— а =-. -250 тт, 5 = 270 тт.
На фиг. 190 и 191 даны диаграммы коэффициентов (согласно обозначу
ченню Эйфеля) к,, кж, к для этих форм, а также коэффициенты к*. к, .
-* тля дуги круга п плоской пластпнкн, посл\живших базисами этим *.
фирмам (для дуги круга при а = 750 тт, 2 а = 40° и Хирде d=512 mm, а для пластинки при глубине d^5Q0mm. Сравнение этих шаграмм, состав тонн их по средним коэффициентам из наблюдений при скорости от 11 । • 20 метров в секунду. шдграммами Эйфеля, взятыми тля евмого большого удлинения 6 (90 i5 ст), показывает, что подъемная сида в трубе В.Т.У. получается несколько больше, что п следовало ожидать, так как наблюдения в этой Грубе при6.1ижаются к наблюдениям над бесконечно длинными пластинками. Па диаграммах 190 и 191 так же, как у Эйфеля, наибольший коэффициент к9 получается для пластинки п тля дуги круга при /?= 13', только он имеет для пластинки значение 0,08 вместо 0,05 у Эйфеля и для угн круга 0,10 вместо 0,08 у Эйфеля (при несколько большей вогну тоети, которая в нашей модели , а у Эйфеля . Равным образом, значение к9 при /? = 0 i-чя нашей дуги круга получилось 0,04 и для крылообразной формы 0.05; между тем, для дуги, исследованной Эйфелем, получилось только 0,02.
Сравнение диаграмм крылообразной фирмы н формы руля с шаграм-мамп их базпеов приводит к заключению, что при ма.шх углах ft подъемная сила ин первых более, иеже in для вторых, что согласно с форм. (107) и (114). Отрицательный угол, при котором Р = 0, выходпт на диаграмме 190 1ля дуги круга равным — 4,35 и для крылиобрпзпого контура — 6, топа как теоретический угол был бы— °-= — 10 . Если будем определять коэффициент к ьля крылообразного контура по значению кг = 0,053 для случая /? = 0, то надо воспользоваться уравнением:
0,053 -= к sin £ .
Здесь надо положить, согласно теории, = ю, и тогда получнтся.
Л =
0.053
sin 1G
= 0,31.
Если же будем оиреде шсь коэффициент к из значения к, при 10 для дужкп п тля крылообразного контура, то, замечая, что на диаграмме 190 прп р 10 Af' = 0,094, Л, = 0,101, опытный угол ^определяемыйпоР= о. для 1ужки равен — 4°,3, а для крылообразного контура — 6е,0, найдем для дужки
к “ sin (4°,3 -+- 10) — °’ЗЬ’
для крылообразного контура
к =
—5- = 0.37.
sin lb -♦10°)
Таким же образом для руля нз шаграмм фш. 191 при/?= 10\ найдем Л, = — 0,052, откуда
к= = 0,30. sin 10° *
В моем сочин. поддерживающих Планах типа Антуанетт" х) (1911 г.) шна формула, выражающая поддерживающею снл^ контуров, ограниченных [вумя пересекающимися дугами кругов, которые приняты за очертание крыл в аэрон дане Антуанетт. Такая же формула выведена в новом (втором) сочинении профессора Kutta: ,Uber ebene Zirkiilationsstromungen nebst flugtechnischen Anwendimgen ®i. Формула эта аналогична формуле [аннон в начале этой работы для [угн круга, п имеет вид:
при чем
Р= 4 лря sin sin ' 5-4-3 i Г-, . . . < Г22>
' 123»
гд<’ 2flt и ±а2 суть выраженные в долях радиуса углы, соответствующие более выпхктой и менее выпуклой дуге, а а радикс, ввответствующий lyre 2 а прн топ же стягивающей хорде d. Ш формулы (123) видно, что (уга 2 а зактючена между дугами 2 а, и а,-|-ао.
Фнг 193.
Ьказпнып тпп контура принят для поддерживающих планов в аэроплане \ нт Ланетт, прн чем частный случаи, при котором о. — 0. ыл псстедован Rateau и прет южен им для очертания сечения пропеллеров. В нашей плоский тр\бе были исследованы две модели при орде d = 500 тт. Первая модель имела jriu а, -22,3, а., = 7’.Ь. а вторая а,= l*i .2. а. = 0, т.-е принадлежала к типу Rateau. Диаграммы ля этих Mo.ie.ieii, с ответ< их тише скорости lJ.7«d»c, представ кны на фиг. 192 и 193. Согласно формуле(123) для первой мод ди надо положит!
“=Tus =1о.и;
- = 1,04.
_______ л
’) Труды Фпзич. Отд. о-ва Любят. Естествознания в Москве, т. XV. вып. 11.
2‘ Muunggberichle der Komgllch Bayerischen Xkaderme der Wbs^n^chaften, i ll
Тогда угол атаки, при котором Р = 0, получится по формуле U22i равным
= — 'X
между тем, как по диаграмме он равен — 6°. При /3 — 11° ио.т}чаем по диаграмме
к —0,095
Топа пз jp-ия
0,095—~пк sin (О’ -|- и )=—fcsinl7:
найдем, что
fc= °-™’5 —0,31.
1,01 sin 1<
Что касается второго контура — типа Rateau, для которого по формуле (122) имеем:
п
-1,89,
2 = 1,06,
то диаграмма фпг. 193 дает как подъемную силу, так н отрицательный угол, при котором Р = О, менее теоретических. Именно, вместо критического угла
“ =—5,07
диаграмма дает только — 1 30'; коэффициент же к*, соответствующий наибольшей подъемной сите, получающейся но диаграмме при угле в 10°, равен 0,066, что нужно признать несколько малым, так как, вычисляя по нему к, иахо щм:
0,068
1,06 Sin 1Г:«/ -
§ 26. О центре давления поддерживающих планов.
Мы приступаем к выводу обгпеп формулы момента (по отношению к произвольной точке) сил давления потока J жи IK0CTH, обтекающей uoi руженлое в нес твер-
дое тело.
Пусть имеем (фиг. 194) плоскопараллельный поток жидкости, текущей в бесконечности со скоростью То и "бтекаюшеп некоторый контур, при чем циркуляция скорости но этому контуру имеет конечную величину J. Назовем через lf0 сумму моментов относительно центра О сил давления жидкости на рассматриваемый контур М <на часть цилиндрической поверхности тела, имеющую длину, равную единице но направлению, перпендикулярному чертежу! и проведем из центра О окружность
весьма большим радиусом 7?. Напишем, что момент равен сумме моментов количеств шпженпя жидкости, протекающей в единицу времени
через все элементы начертанной окружности (массы втекающей жидкости надо брать со знаком (—))- Получим:
л2я
Ч = „У
и
— vj [их \-rij){uy -IJC} de, . (124)
n
где и н v компоненты скорости, а 0 угол радиуса-вектора R с осью Ох, отсчитываемый против стрелки часов.
Предположим, что поток жидкости характеризуется функцнею мнимого переменного z — x-^-yi следующего вида:
l’(2j у у/.
где tp потенциал скоростей, а у фу нкцня тока.
Мы имеем (по основной теореме о функциях комплексного переменного):
Составляем произведение:
dF
Z-^- = их 1'у-\-\иу — VXM
и возводим еги в квадрат:
22 = [(их-|- ту)- — (иу — wi2J 4- 2((их -ту) (иу-- VX).
Отсюда видно, что *
*<мг-*-г$л(пу —гх)=д. ч?>[^ г2! *£-)(126)
С другой стороны, для всякой точки С окружности радиуса К имеем:
z = R (cos 0 / sin в).
dz =* R (— sin 0-г- i cos 0) <f0,
rfe=R(^rnH + .Ss®F=a <127>
Иодотановка выражений (127) n (12fi) в форм) iy (124) дает нам
(12Н>
г (е интеграция распространяется на окружность весьма большого радиу са R' Если рассматриваемый плоскопараллельный поток получается с помощью конформного преобразования
: = ...................(129)
из другого более простого потока, при чем в бесконечности
г=(Л+рО:..........................
’) Сокращенное обозначение: (ействительпая часть
и скорость Г’м новою потока по скорости старого выражается формулою:
10=1„Ул< + ^, (130)
то удобно формулу (128) приложить сначала к плоскости мнимого переменного С и напирать:
где интеграция ведется по окружности весьма большого кр.\га, провс ten-ного из точки О на плоское ги мнимого переменного Z. Потом следует перейти к плоскости мнимого переменного г, прп чем оси хОу считать совмещенными с осями с()у. Бесконечному кругу на плоскости переменного Z будет, в силу соотношения (129). соответствовать тоже бесконечно большой круг. Мы получим формулу:
<”•’
формулы (128) и (131) сводятся к формулам, выведенным неско.шко иным способом профессором С. А. Чаплыгиным1), только у него интеграция в* тется не по окружи сти бесконечно-большого круга, а по конгу р\ обтекаемого те ы, что, разумеется, 1ает один и тот же результат, когда в потоке жидкости нет точек с бесконечно-билыпими скоростями.
Приложим полученную формулу (131) к частному случаю потока, обтекающего ру 1ь (фнг. 178). Мы можем положить для этого потока
dF (z-A-allz— m) . , . . ,
« — д----(i-osy- -sin3). .(132)
в котором и есть комплексная ве щчипа. •'•чответ'твуюиыя точке Л’.
В бесконечности имеем:
а
м —1осоьЗ, i - КмпД
а в точках Л’ и С, при г = м и - а имеем:
н = г — 0.
Переходим к определению точки при п>ж<‘нпя найденной силы. Для этого пользуемся форму ними (131) н (132), из которых найдем:
dF Г ’(cos2 ? —/е1п2Ду£ -г<0(г—nyir--{-G2)
’ dz I —a)
Vu2(cos2fl -!П_\У)*г 2(«—n) ’ I. .(133)
где ненаписанные члены порядка малости выше — могу т быть отброшены.
Подстановка формулы (133) в выражение (131) приводит нас к следующей величине момента Ц. сид давления на пластинку СИТ относите тьно центра моментов О:
ЗГ„ = д. ч|" и)(з« —»)(co-.2.i -sin2,.?) i Qj =
=д. ч. [.тоГ0\(н—И)(з«- H)(cos2,< fsin23)]. -(134)
Ч Математический Сборник т. 2s, 1910 i .О ;авленип плоскопараллельного потока на преграждающие тела*, форм 52. ЛЗ.
Сюда следует на основании фиг. 195 подставить такие величины:
а-—п -.V.4
. Л’П ’-И—ЛЛ
Зя—n = sFt
1 <>
COS 2/?4-/1*102,7—С
Произволение этих величин дает нам:
Л’Л-Л'Р
Если Ъ близок к а и точка Лг и приблпжаскя к Л, то у приближается к ’ . и мы получаем:
2.т—(у-I /)=л—д, Фиг. 195.
где /л=^. INF. Величина в формул» (131) но в чает такое значение:
Vo=—лр J0-2nsin^ - .VP 5>in/*=—;roF0-’4rt2sin/?cos/?
Но так как Vc,' 2Г0, то
lf0== -о I .2«5мп |9cosj9 (1351
Преобразуя это выражение по форму ле (1о7), находим
(136).
Фиг. 196.
Эта формула показывает (фнг. 17S). что точкою !грпложения силы Р иа оец симметрии Ос рассматриваемого контура является точка S, не а-внеящая от угла /? н отстоящая от А па рас< гоянин одной четверти всей i-шны CJ- Этот результат совпадает с тем, который указывает Кутта1).
Наблюдения ио тверж (ают его только ыя малых углов, не превосходящих л°, прн которых мы имеем па диаграмме (фиг. 190) скопление |'н»'1ков(х), указывающих положение центров парусности для тонкого руля, (ля плоской пластинки, служащей ему базисом, кривая центров давления (значки (о)) плавно приближаются к оси абсцисс-
hutia. „ЪЬег eine mit den Grundlagen des Flugproblems in Bezlebungstehende zwcidi in(>r«uionale StromuDg**. Nunchen. 1910
Заметим здесь, что в ваблю «.-ниях Эйфеля кривая центров давления пластинки с удлинением 6 начинается тоже на расетоянпн длины, пластинки от края атаки, а не на как получается для удлинения 1,т.-е. для квадрата.
Причину значительного разногласия между теорией н практикой в рассматриваемом явлении надо искать в образовании около пластинок вихрей движущихся и < гоячих.
Так как указанная нами форма для руля ирн небольших отклонениях от /7 = 0 дает неподвижный центр давления, то эту форму, ио нашему мнению, удобно употреблять в корабельном деле, помещая ось вращения руля на расстоянии немного меньшем 1, длины от края атаки (ыя поддержания руля в устойчивом положении).
В упомяну том в преды дущем параграфе моем сочинении1) выведена общая формула момента сил гидродинамических тавденни на крылообразный контур относительно центра, помещенного (фиг. 1R0) в иача ie С дуги базиса С А, противоположном краю атаки Я2), а равно и формула момента для контура типа Антуанетт.
Первая формула такова:
X. = 1.10 Г; b-sin2 J | sin (4- Э) cos +
t , cos “ cos ft sin ( “ 4- /7) 4- cos2 ° sin ft cos ft |. . (137)
и момент Mr считается положительным uo стрелке часов.
Принимая теоретически сп iy Р нерпен щкулярной направлению потока, получим расстояние „ —.S' (S есть расстояние центра парусности от середины хорды, считая его положительным по направлению к краю, противоположному краю атакп) точки приложения этой ен.ты на хорде <’A = tl. считая от С, ио формуле:
-L~s
2 1* соз $
(13«)
Па и'тавляем сюда значения Р н V не формулы (111), и формулы (137):
f-s= f
cos " sin 3 |
cos cos ,i
Легко усмотреть, что, принимай fi за абсциссы, a S за ординаты3), мы выразим уравнением (139) диаграмму центров давления, вычерченную ио способу профессора Prandthi. Она предо гавтсна на фиг. 197.
Такая же шаграмма, построенная ио наблюдениям над вышеописанным кры юибразиым контурам н дугою круга, соответствующем его базису, пре ставлена на фиг. 198. Наблюдения над дугой обозначены знаком (J, а над крылообразным контуром знаком (" ).
При /?=— подучаем у- -t-oc. Это показывает, что рассматриваемая кривая имеет асимптоту, параллельную стягивающей хорде
’) О поддерживающих планах типа Антуанетт, ф-ла (35), полагая в ней я = 2.
") Ута формула прежде была дана профессором Г. А. Чаплыгиным в его сочинения .0 давлевин плоскопараллельного потока иа npei раждающие тела"- Математический сборник Т.
А) На Фибрах, изображающих эт i кривые, обыкновенно ось абспвсс расположена вертикально, а ось ординат (** горизонтально
и отстоящую от нее на расстоянии " в сторону выпуклости контура. На практике вместо углав случае крылообразного контура фигурирует угол в 6 , а в случае соответственной дуги кру га угол в 4 ,3.
Фнг. 197.
оооо л*'»**’'»
fi( MxaecifiJb
Фиг. 198.
При 0 —— “ е теоретической приводятся к паре, момент которой.
точки зрения все ей ты давления по формуле (137), имеет величину:
Jfe = — 4ггр Г d‘ sinа cos8 . (140)
при чем знак (—) показывает, что эта пара вращает против стрелки часов. Таким образом, когда поддерживающие планы аэроплана теряют подъемную силу, они подвержены действию нары, стремящейся нагнуть переднюю част? аэроплана внпз.
Замечая, что хорда основной дули крыла с = 2а sin а = Iosin ® cos
стрелка ее /= £ tg-J- = 2«sin® * и вогнутость ir = — = * tg
и, принимая приближенно cos* за единицу, иолу чнм из формулы (140):
4/ =— Л.!‘ ГЛ-сое* “ <— 7 Гс*1г. (1409.
Теор*т>чвеки« освовы оэдтхьвлвлжвв*
11
Сделаем анализ нашей теоретиче^койчсривой, данной уравнением (139). При /?-=0 пол \ чаем:
О £<*
Производная S но £ при 0 = 0 будет: ds d Г/, । ЛГ = -4 L(1 + £)tg
eotg * ]:
при малом угле а она имеет ботылую отрицательную величину. При значении 0 = ’ — “ , которое, как это следует из фиг. 180, является крайним возможным углом в рассматриваемом анализе, получаем:
Эта величина положительна.
Вид кривой представляется нам нижеследующим: при/? = “ ордината S = -|-co и, с возрастанием абсцисс fi, J меныпается до нуля, которого достигает приблизительно при /? = 0; в этой точке тангенс угла наклонения касательной к оси обсцнсс имеет большую отрицательную величину, и кривая переходит на сторону отрицательных <8. Так как при fi— Jордината S должна бы'ть опять положительна, то на стороне отрицательных ор 1инат имеется minimum для S, после которого кривая поворачивает опять к оси абсцисс. Когда абсцисса Д начиная от значения---и ют уменьшаясь, тогда ордината S, начиная от зна-
чения — со, идет возрастая. Получается вторая ветвь кривой, соответствующая отрицате льному значению Р.
Действите льная кривая центров давления, изображенная на диаграмме (фиг. 108), по виду очень близка к теоретической (фиг 197); она получается как бы путем передвижения теоретической кривой вниз приблизительно на пространство /? = о .
В вышецитнроваивом моем сочинении выведена также формула для момента сил давления иа контур типа Антуанетт:
= 4лео‘> Го2(?) sin»|[sin /+|)+
+ (П — 11 сот “cos^btn^-j-^)-;—-1 cos “sm0c<s/?|. (141)
где момент берется относительно края контура, противоположного краю атаки и считается положительным по направлению часовой строчки, п и а определяются по формуле (123), а а есть радиус, соответству ющий дуге 2а при стягивающей хорде d. Подставляя это значение №е, а также значение Р из формулы (122) в формулу (138), найдем для крпвой центров давления пластинки типа Хптуанетт формулу:
ein/?
2 й 2п
-— —+ (я — 1)+ —cos в-----------— I.
СОЗ ^-СОЗ 0 3 2 61П (?+ у)|
- (142)
Кривая, выраженная этой формулой, представлена на фиг. 199. Вид ее довольно близок к виту кривой центров парусности крылообразного контура фиг. 197). Она имеет асимптоту, соответству ющу ю углу /9 = — ~. Прн /9 = 0 получается S = О, т.-е. кривая пересекает ось абсцисс в средине хорды. Тангенс угла наклонения касательной к оси абсцисс выражается формулой!
d s _ d Г 8ip 2 n»-i С03 г Bip j~ d^ 2n|^ CO8 £ CO3? P 3 Slns( j-f-“)
При /9 — 0 про из so тая
.1143)
и имеет при небольшом а большую отрицательную величину. Угол атаки, соответству ющий наименьшему значению S, находим, приравнивая иу ию вторую часть формулы (143), откуда получаем:
Если а мал и п близок к 2, то вторая часть формулы будет немного менее 1 и угол fl, при котором S minimum немного менее 45 . Прн этом значении кривая повернет к оси ординат.
Разумеется, можно ожидать подтверждения теории наблюдениями только для углов, изменяющихся в небольших пределах (между—15° и 4- 15е), так как при бо 1ьших углах, как показывают аэродинамические спектры, за пластинками образуются стоячие вихри.
На фш. 200 представлена диаграмма центров давления для вышерассмотренного контура типа Rateau.
Мы видим, что здесь так же, как иа фиг. 198. опытная диаграмма против теоретической сдвинута внпз, в данном случае приблизительи она у гол 3°. 5.
При Р — 0 имеем подобно предыдущему:
Я = — Г„® cf = — 7 V (141)
1Г
$ 27- Лобовое сопротивление поддерживающих планов.
Самою трутною частью в теирпи поддерживающих планов аэропланов является оире деление силы сопротивления, действующей по направлению потока. На диаграмме (фиг. 190) видно, что прп £ = 0
А\ = 0,0025 — 7гп.
Ес ли отнести этот коэффициент к трению влзду ха о стенки модели, то его надо еще разделить иа 2, так как иа наших диаграммах коэффициенты ка получались, дети си.(у сопротивления по направлению потока жидкости на квадрат скорости и на площа п> мо ie-ти, взятую с одной стороны, а трение происходит на верхней н нижней сторонах модели.
Тогда потучаем:
-= 0.0012.
Этот коэффициент в пять раз более наблюденного профессором Prnndtl ем коэффициента трения о твердый стенки С возрастанием yr la /? величина к возрастает, при чем кривая имеет при небольших углах
форму параболы, обращенной выпуклостью вниз и имеющей осью — ось орлннат наших шаграмм.
Разложим fcx иа тве части Ао и Л, и соотвествснио с этим всю силу сопротивления Q разобьем на две части, Qo н Qt. Сила <?0 определяется, как проекция иа направление потока силы Т, указанной в форм. 16) моей статьи, помешенной Zeitschrift file Flugieehnik imd Moiorluftschiffahrt. 1910, Heft 22.
Qt = Teas (a —/?)
1 л p I 2 a sin “ cos (a — ₽) coss " sin2 =
= .tp )'2Fcos" " cos a cossin2/?-|-я о l"Fcoss ° sinosin5^. . (144)
Из этой формулы видно. что правая ветвь кривой к'х будет несколько приподнята сравнительно с левой ветвью, что согласно с диаграммой фнг 190. Если бутем пренебрегать членами третьего порядка относительно малых величии а и Д то выражение всей силы Q можем представить в виде:
Q = .TpFjsin2/? + ^] F2 (145)
Наблюдения дают для коэффициента к этой формулы значение, меньшее теоретического я о = 0,39.
Возьмем на датаграмме (фиг. 1901 £=10. При этом найдем:
= =0,01,
откуда следует, что
А' = —1 -0,0012 = sin1 10
Причину возникиовеипя силы Т нс и>зя видеть в образовании на краю атаки А вследствие трения жи цсостп (фиг. 2О| | нсподвнж ной жидкой массы, закругляющей линию тока, так как при всяком таком закруглении равнодействующая сил щвленпя жи ikocth 6j дет иернен (нкулярна к напра-
вдсншо скорости потока. Эта причина, по моему мнению, заключается в убегании вихрей, образующихся при крае атаки. Охваченная линиею тока, жидкая масса прихотит в движение и образует вихревую площадку R, заштрихованную на фиг. 2<И, с напряжением вихря где Г
есть циркуляция по контуру AR, охватывающему вихревую площадку. Центр вихря R пе будет оставаться вено ишжным, а полу чит некоторую скорость и.
В вышеупомянутом сочинении: „О поддерживающих планах типа Антуанетт** я показал, что при помещении точки R на касательной к дуге СА, проведенной из се конца А, скорость и центра вихря бу дет направлена нерпендикутярио к ИЛ. Кроме того, при выборе Г под условием, что скорость жидкости в то малом КА стремится к пределу:
Фиг. 201.
'1ке Л кснечиа, мы находим, чти Гн при
Г»==Г= ЬтрсГ’Чн “ .. Jsin’ft........П*'1'
при чем Г становится очень мал, а и очень велик.
Если построить замкнутую линию тока, окружающую вихрь К, и вообразить, что эта линия отвердела (заштрихованная площадка), то можно, на основании изложенного в моем сочинении „О присос щнеиных вихрях"1) правила, выразить силу давления иа этот отвердевший контур выше-паинсанною силою 7*, направление которой получим, повернув вектор и па прямой угол в сторону, обратную циркуляции Г. Мы найдем, таким образом, силу Т, изображенную на фиг. 201, которая бы действовала на вихревую площадку К, если бы она отвердела и оставалась неподвижной. Рассматривая эту в тощадку и дугу С.4, как одно тело, бу дем иметь общу ю действующую на них силу, периендику лирную к скорости потока и выражаемую ф-лой (1Н) (вследствие малости циркуляции Гь Из этих раз-суждений еле сует, что па нашу дугу будет действовать направленная перпендикулярно потоку сила Р, выраженная ф-лом (П4), и направленная по касательной к краю атаки в сторону потока сила Т—7*.
С такой точки зрения оправдывается заключение проф. Kutta. По бу дучи ничем удерживаема, вихревая площадка К убегает от края атаки в направлении м, а на ее место зарождается новая вихревая площадка, и т. д. Таким образом, острие является причиной образования вихрей, которые, убегая, образуют силу сопротивления жидкости, направленную по потоку.
Так как вихрь К уничтожает бесконечные скорости при крае атаки .4, то равнодействующая Р я Г для прямой пластинки будет перпендикулярна к пластинке, а для дуги круга пройдет через его центр, как это показано в первом сочинении профессора Kutta.
Разумеется, вихри могут сбегать с края атаки и при резком закруглении этого края. Они могут сбегать и с кормы, н я думаю, что в этих убегающих вихрях < лсду ет искать причину всяких лобовых сопротивлений.
’) Труды Физия. Отд., т. XIII, вып. II. 1906 г.
[На фиг. 202—208] представлены спектры течения *) для дужки Жуковского, полу ченные по способу Альборна (ликоподий иа поверхности воды).
^ = 0°
Дужка двигалась равномерно в воде при различных углах наклона средней своей хорды к направлению движения. Спектры 202—206 снимались
Фиг. 203.
фотытрафичсекой камерой, двигавшейся вместе с дужкой. Углы наклона были О', 8°, 13, 17е и 19.
Фиг 204.
На первых трех снимках можно приближенно считать стр.\ я жидкости прилегающими к поверхности дужки. На последних двух они отхо-
х) Иа статьи др ф Prandl я: „Bericht iiber die Gottinger Modellversnchanstalt“, поме-щевноП в Jahrbuch der Luft—Fahrzeug-Gesellschaft, Band VI, [912—1913 r. Berlin.
дят от нее все более н более. Этому соответствует убывание подъемной силы, возраставшей сначала с увеличением угла нак лона. Спектры пока-
Фиг. 205
зывают подъем струй спереди и опускание их сзади (ужки, что, как известно, связало с появлением подъемной си ты. Завпхрнвание возни-
Фиг. 206-
кает на верхней поверхности дужки н около заднего ее края, и увелн-
фяг. 207.
чивастся вместе с углом наклона дужки. Спектры фиг. 207 и 20« получены при неподвижной фотографической камере. Углы наклона 0° и 10г
Спереди ij жки струйки как бы выходят из источника; поза, до дужки замечается полоса от потока, вызванного сбегающими с дужки кармаи-скими вихрями (ем. ниже, § 29)].
Фнг. 208.
§ 28. Опытные исследования поддерживающих планов аэропланов: Бреге Антуанетт, Райта, Блерио, Фармана, Анрно и Ньюпора.
В плоской трубе В. Т. У. были произведены также опытные исследования над формами контуров ио сдерживающих планов в различных системах аэропланов. Эти исследования производит Г. И. Лукьянов ’) весной 1911 года. Исследуемые модели представляли вырезки поддерживающих планов шириной 0,295 mt, который помещались между зеркальными горизонтальными стенками трубы так, что между краями модели, и этими стенками оставался промежуток 2,5 тт; глубина всех моделей бралась 0,5 mt, что <• оставляет от | до | действительной величины; угол атаки изменятся от — 1а до 15', считая от стягивающей мо * ль хорды, при чем знак-}-берется, когда ветер дует на вогнутою часть модели, скорость же изменялась от 10 до 20 метров.
Сравнение полученных результатов с результатами наблюдений Эйфеля2) показали, что коэффициенты подъемной силы к9 получились в наших опытах большие, нежели у Эйфе ш, что и следовали ожидать, так как плоская труба дает результаты, приближающиеся к бесконечно длинным планам, а у Эйфеля брались планы с у щинением 6.
Что же касается до коэффициентов fc, силы сопротивления, действующей по направлению потока, то они получились почти такие же. как у Эйфе ля.
На фиг. 209 представлены кривые, выражающие зависимость этих коэффициентов от угла атаки для поддерживающего плана Бтерно XI по наблюдениям Эйфеля ik9stk,s] и по нашим наблюдениям (к9, кж), а на фиг. 211 даны такие же кривые ря модели поддерживающего плана Райта.
Отношение кг:к9 для очень длинных планов выходит меньше, нежели для моделей Эйфеля. Кривые, выражающие это отношение в опытах Эйфеля ( I п в наших опытах (*-), даны на фиг. 210 для но цдерживаю-
1) Труды Отделения Фазических наук О. Л Е , т. 1э, выл », ЦЦ2 г.
2) В лаборатории Champ-de-Mars.
-
щих планов Блерио, а па фиг. 212 для поддерживающих планов Ранта Так как поддерживающие планы тем выгоднее, чем менее, то отсюда следует заключить, что с удлинением плана его качество увеличивается.
Фнг. 212.
Иа фиг. 213 и 213 bis лани точные контуры испытанных моделей: (1П) Бреге, (I) Антганетт. (VI) Райт, -ill) Блерио XI, (IV) Фарма н. (V) Лнрно, фиг. 213 bls Ньюпор IV.
Все эти планы испытывались сначала при потоке воздуха с 1ева направо, как они употребляются в практике. При этом мы сочли практичным произвести все испытания прн одной и той же скорости, соответ-
Фиг. 213.
1 о
ствующей действительной скорости полета аэропланов, так как коэффициенты kt и кх немного изменяются со скоростью.
HuDBOp IV.
Фиг. 213 bls.
Па фнг. 214 отложены по оси ординат к и кг для мотели плана Блерно XI J) при угле атаки в 0° для различных скоростей от 12 до 20 метров. Этот результат наших опытов показывает небольшое возрастание коэффициентов со скоростью.
За скорость испытания всех планов мы приняли 17 mt /sec, что соответствует G1 километру в час и довольно близко к действительной скорости аэропланов.
1) На фигуре ошибочно поставлено: Блерно IX.
На нижепомещенных фигурах для этой скорости даются при разных углах атаки между —15° и -|-15° коэффициенты подъемной силы кч и лобового сопротивления кж.
Фиг. 215 соответствует аэроплану Бреге, фиг. 216 аэроплану Антуанетт, фиг. 217 аэроплану Райта, фиг. 218 аэроплану Блерио XI, фиг. 21» аэроплану Фармана. фиг. 220 аэроплащ Лнриои фиг. 221 аэроплану Ньюпор.
На тех же фигурах даны кривые *' 1). Кроме того, на диаграммах (фиг. 222—228) даны кривые S, абсциссы которых выражают в долях хорды
х) На фнг. ’15—221 левые масштабы дают а кг а правые - Pi Q в Э при сно-роств 17 —, н также %- — **
•« V
крыла расстояния .S’ центра давления ва стягивающей хорде, считая от края атаки (на фигурах край атаки слева).
Рассматривая приведенные диаграммы, видим, что наибольшая всти-
а наибольшие отрицательные уг1Ы, при которых Р= о, в планах Бреге (—4’1, Блерио (—3,"5| и Фармана (—3,’5).
Что касается до кривых S, то они характеризуют планы но отношению к устойчивости. Для всех положении, при которых кривая S с возра-
станисм угла атаки приближается к переднему краю i на тиаграммах втсво), положение равновесия планов неустойчиво и тем более неустойчиво, чем больше по абсолютной величине тангенс угла касательной с осью абцисс.
равновесия. Для того, чтобы планы могли быть с выгодою употребляемы без больших стабилизаторов, нужно, чтобы S получал minimum прн небольших углах, когда — имеет довольно зиачите.хьную вс шчпну. Фиг. 225 и 227
Ап* с ->еПе
Фвг 223
показывают, что аэропланы Блерио и Анри о имеют minimum тля <S при 12°,5 .. г
и при этом ординаты кривой , которая в этих типах медленно и з м с. н лете я, имеют emo довольно хорошую величину 10. Летание при изменении угла от 7Г до 15 на таких планах может быть совершаемо с выго дою бы сильного стаби.1изатора. Довольно хорош в том же отношении тип Бреге; но контуры планов Фармана н Райта едва ли можно у по треблять для мииоплаион.
Кроме изложенных наблюдений, все модели, представленные на фнг 213
и 213 bis, быта еще испытаны, направляя на них поток воздуха в обратную
фиг. 225.
сторону, т.-е. справа налево (за исключением симметричного относительно
Фнг. 226-перпендикуляра к хорде крыла Антуанетт). При этом оказалось, что
наибольшие величины и абсолютные значения отрицательных углов, при которых Р = 0, по большей части увеличились, ио за то устойчивость значительно уменьшилась.
Фиг. 227.
Кривые испытания обращенных крыльев нанесены ну нктирнымн линиями на соответственных графиках (215—228) для тех же нормально поставленных крыльев.
Мы видим, что в обращенных формах Maximum для , кроме Бреге, везде получил большие значения, прн чем для планов Райта это значение дошло до 18,3. Абсолютные значения отрицательных углов, при которых Р=0, то же все возросли, кроме планов Фармана, при чем 1ля оберну того Блерио угод дошел до—6. Но вместе с~уветичепнем Maximums £ получилось, особенно в типах Блерио и Анрмо, быстрое падение после Maximum^- Все
кривые S резко приближаются к неродному краю с возрастанием угла атаки и в пределах наблюдений не имеют minimums для £». Для угла, дающего
этот minimum, значение должно получиться весьма незначительное. Это
показывает, что обернутые планы по своей неустойчивости едва ли могут употребляться, как главные планы аэропланов.
Приводим сравните 1ьпую таблицу (23) величин, полученных из наших наблюдений тля различных планов, подобную таблицу Эйфеля 1|, при чем отношепне S к длине стягивающей хорды мы будем означать через с, а тангенс утла касательной к кривой S с осью абсцисс через tggc. Эта ве шчина, которая во всех наших наблюдениях отрицате шная, до 1жна быть введена, как характеристика степени допускаемой неустойчивости
Таблица 23.
Угол атаки при F*-O. Бреге. Ahtj- p-v Ьаерао Фар-аяетг. XI. май. л.р.о, Ь«’ г ойращ. оФращ.( Riepao Фаражи Анрио (Яращ. оЬращ. о&ращ.
-4° -ГЛ -3°,5 —з°.я| - т Л -2° 5 —Ь'Л —-гд. -6 -1 ;л -5 ,2
Угол атаки при Мах +’• 4-4°, +5° 4-6 + ГЛ +1 +з“/. +4° +4» 4-4с,5
Мах 7 V 17,3 le.o .2 15 12.6 15.3 1М 12,3 16,2 16
Значение k* при £ Мах Значение при у Мах 0.045 -0,0 > 0,054 । 0,057 0.066 -о.о» —о.ое — см* 1 0042 —0,09 0,009 —0,11 0,040 0,061 4-одЪ рощ 0066 0,05 4‘ +0,0э| -|-0,09 0,071 4-0.07
Значение tgy при £ Мах —1,30—0.7 Г, — 120 -9 SO -0,44 —2,10 —1.7; -1,00 —2,00 —1,00
Принимая в<» внимание как степень неустойчивости, таки подъемную силу, приходим к заключению, что для однопланов иаивыгоднейш ими формами являются типы Блерио и Анрно. Тин Антганетт, который дает самую большую подъемную силу 2ЬЛ Ад при угле 4 ,5. дает прн этом угле степень неустойчивости tg</= - о,77 сшшком большую, что лишает возможности пользоваться этим углом аттакн.
Что касается до обращенных форм планов, то онн, не будучи годными для главных поддерживающих планов вс тедствне больших отрицательных значений tgy п малой устойчивости, удобны для устройства рулей высоты, так как при малом сопротивлении они дают хорошую подъемную силу; неустойчивость же при вращении их будет только способствовать манипуляциям над ними, преодолевая силу трения в органах управления.
Вихревая теория лобового сопротивления.
§ 29. Вихревая теория лобового сопротивления, данная профессором Карманом 2 3).
1е. Про(|»ессора Prandtl ®) и Karman 4 * *| предложили определять лобовое сопротивление цилиндрических те I, движущихся в жидкости по
r L'Aerophlle. 1911, Аё 12.
Сообщено в от1₽теинн фввнкн О. Л. Е. в 1913 г ноября 16. Напечатано в .Трудах Физнч. Отт О. Л. Е., т. XVII. вып. 1, 1914 г.
3) Prandtl Abries d»T Lehre von der Fliisslgkeits- und Gasbewegung. lena IMJ. S- 33.
4) harman. Uber den Mechanismcs des Wlderslandes, den ein bewegter Kvrper in ciner
Fliisslgkeit erfabrt. X'achrichten von der KonigHcIirn Gesellschaft der Wissruschafteo zu
Gottingen. 191], Helt \ S Л(К».
направлению, перпендикулярному образующей, с помощью рассмотрения количества движения, сообщаемого телом возникающим за ним вихревым шнурам.
Па фиг. (229) изображен профессор Прандтль перед устроенным им в Геттингентском Университете водяным бассейном, ио верхней части которого катится тележка с фотографиче-
ским аппаратом н с прикрепленным к пей погруженным в воду вертикаль ным цилиндрическим ити призматическим телом. На фиг. 230 [о], Ь, изображен такой вертикальный цилиндр при взгляде сверху и дана фотография вихрей, возникающих при начале движения.
Цилиндр доспи ает почти до та бассейна, и вихревые шнуры опираются на дно и свободную поверх-ностьжидкостн, на которой образуют воронки.
При дальнейшем движении вихревые шнуры [увеличиваются в размерах (фиг. 231 рф, становятся неравными (фиг. 231), Ь], отбегают от цилиндра, и постепенно образуют 1ва ряда внхреи, расположенных так, как это представлено на фиг. (2321
Расположение вихрер всегда такое, что перпендикуляр, опущенный из центра вихря одного ряда на направление движения тела, проходит на
равном расстоянии между7 вихрями другого параллельного ряда, при чем и
вращения вихрей в том н другом
ряду совершаются в противоположные стороны: на фиг. (2321 верхние вихри вращаются по часовой стре ikc, а нижние—против часовой стрелки. Профессор Karman дока ил. что только такое расположение вихрей может быть устойчивым, прн чем воздействующие друг иа друга вихри получают обшуюскорость и по направлению к телу, которая меньше скорости движения I самого тела, вследствие чего вихри в относительном движении отходятот Те га со скоростью Г—и.
Мы наложим здесь теорию harman а в несколько упрошенном виде. Начнем с вывода величины силы лобочиго сопротивления. Пусть |фнг. 233j Л и В будут два параллельные вихревые шнура, вращающиеся в противоположные стороны с одинаковыми циркуляциями J. Количество движения, сообщаемое вихргм Л массе жидь ти, заключенной в бесконечно длинной полоске мп, верней шкулирнин 1В, которой по направлению АВ соответствует ширина #7.г, <* по направлению, перпендикулярному плоскости чертежа, высота, равная единице, будет выражаться интегралом:
*) За стойкой у 1лкнеивой обтекаемой фермы вихри занимают значительно бол е узкую область, чем за пилиндром. как ато видно из сраввецпя фиг -Д с фиг 221g и h, представляющих обтекание цилиндра. ^тим о< меняется е • тьшее сопротивление сравнительно с цилиндром.
Нрнм jrd.
12
dxe l i'-
Jedx
, /> ?’ Jn . . у J0
= А'^/ •_' = ->!* arctg£=Yjx.
T- J l+'
ГД° 9 ПЛОТНОСТЬ ЖИДКОСТИ.
Эта величина ив зависит от значении л и имеет дтя всех полосок с левой стороны от -4 одно и то же потожителъное значение, а с правой такое же отрицательное значение «считая количества движения положительными снизу вверхI. Слагая количество 1ви-жения, сообщаемое вихрем А, е количеством движения, сообщаемым вихрем В, придем к заключению, что количества движения по всем полоскам inn, расположенным вправо от А и влево от В, сократятся, и все количество движения, сообщаемое жидкости парок»
(Фиг. 231-е].
Фнг. 231-Ь.
в противоположные стороны вращающих вихрей, будет:
Jq j* dr —Лю. . (247)
где Ъ расстояние между вихрями. Что касается до количества 1вижения, направленного по полоскам т'п, параллельным АВ, то оно будет нулем, так как в дв\ ч симметричных точках п' и т' количества .изижения в указанном направлении имеют противоположные знаки. Таким образом вектор, получаемый от сложения всех количеств движения жидкости, заключенной между двумя плоскостями, перпендику «ярннми ОСЯМ ВИХ-рей и отстоящими па единицу расстояния друг от ipyra, бу дет направлен вверх перпендику лярно к АВ и будет иметь величину Jb о. Для вихрей, имеющих устойчивое расположение, как изображенное на фиг. 1234), мы
— 179 —
можем циркуляцию J каждого вихря разложить на две циркуляциин и рассматривать с этими циркуляциями пары вихрей 'АВ. ABt,..
Булем иметь от пары вихрей J и В проекцию вектора количеств движения М на направление ЛЛд
М cos а —
= ^JbQCQsa = ~JhQ.
Фиг, 232.
Вектор М', пре летав пято- (Фиг. 23i-c|.
щий равно действующую коли-
честв (вижения от пары вихрей ЛД, даст по направлению АА' такую же проекцию; что же касается до проекций векторов М и М на направление перпендикулярное Л.4’, то они будут равны и противоположны по знаку; поэтому все вносимое парами вихрей количество движения будет направляться иа фиг. <234) по линии вихревых рядов в направлении к обтекаемом} телу, которое ца фиг. <234) расположено с левой стороны. Мы увидим ниже, что для устойчивости двух рядов вихрей, представленных нафиг. 1234),
между расстоянием Л этих рядив и расстоянием / Двух смежных
вращающих в одну сторону вихрей необходимо должно существовать соотношение:
cosh = у'Т, .(14*i
причем скорость движения вихрей выражается простою формулою:
,,4в)
Эта скорость направлена на фиг. 1234 j по направ лению к телу, зарождающему вихри. В относительном лвижении, как было сказано, вихри удаляются от
тела со скоростью V—и. Число тивоио.чожнне стороны, которые тела, бу дет У~’—
пар вихрей, вращающих в про-зарождаются в одну секунд} действием Это соответствует, иа основании фиг. <234), гскуплному
количеству движения R, развиваемому телом в сторону его движения
(1501
которое в выражает силу лобового сопротивления на единицу длины тела.
Что касается до циркуляции J, то, так как ,ша вихря образовались оттого, что струи жидкости в движении относительно тела, сорвавшись с поверхности тела, охватывают сначала почти неподвижную в относительном движении жидкость на протяжении Z, то можно с приближением принять:
J= VII......... fl51>
На основании форм. (151) и (149) выражение (150) получает следующий вид
Л = Т * е№=0,Б92 -- ₽FF-, . . (ISO')
ye • в
где « есть площадь миделя на единицу длины обтекаемого тела. Если назовем через к теоретический коэффициент сопротивления, который дает теория Кагшап'а, и положим (для воздуха е — *-)
i=^R.S±p’A =0,074 А , ... . (152)
1 в * •
то увидим, что ои зависит от отношения ширины омываемого тета к расстоянию между рядами вихрей. С возрастанием этого отношения возрастает и коэффициент сопротивления.
3е Перейдем теперь к выводу форм. (148) и (149) и к исследованию вопроса об устойчивости вихревых цепочек.
Вместе с устойчивым расположением вихревых шнуров, данным па фиг (234), мы будем рассматривать неустойчивое, представленное на фиг. (235).
Легко усмотреть на обоих фигурах, что вихрь А от верхнего ряда вихрей не получает скорости, а от вихрей нижнего ряда получает скорость, наиравленну ю по прямой AAlt так как все симметричные вихри В и Bt •ебщают ему одинаковые скорости
J т 2я г’ направленные под равными углами к липни AAV Составляя сумму проекций всех этих скоростей на направление AAlf мы найдем скорость «, получаемую вихрем J:
дта скорость тля расположений вихрей иа фиг. (231) и на фиг. (235) выражается формулой (153) и «154 к
м = —V А
— " ~(24- 1Я ,+*•’
j/x? * I ' " =я\ — w+»'a
. I15.il
. . . . /154)
Су ммирование распространяется на все целые и положите чьные значения к от I до оо. Найденная здесь величина и удобно выражается <• помощью гиперболических функций.
Мы воспользуемся здесь формулами, приведенными в курсе дифференциального исчисления Бертрана1)- Разложение sins в бесконечный ряд производителей ио его корням приводит к формуле:
япг = гП (1-т^з)-
Для разложения косинуса получим:
Изменяем в паи 1енных формулах г на г V— 1, вследствие чего тригонометрические функции обращаются в гиперболические:
cosh (г) = 77 1 + Гг*—• ,15г>|
sinhlzi —г/7 **56
Для получения из этих формул рядов, фигурирующих в формулах 115-4) и 1154 ь возьмем от обоих частей их логарифмы и от обоих частей полученных равенств возьмем производные по г:
tgh(z)
—' (24-1)»
cotgh(г) = у + 2 V
. (157)
1158)
Если в эти формулы подставим
яЛ г=
Ч Bertrand Traite de calcul differontie). Paris. (864. p. 415. (Ж Бертран Дифферев цвальвое исчисление Русса перев. М В. Пирожкова. 19П г. §§ 4(4—405, стр 40В—411|
182 —
то найдем:
tgh(^'l = -V —* t (160)
' I / -ч — (jA ip J+*’
cotgh ft)=2; + у _ j. (I60,
Подстановка найденных сумм в выражения (153) и (151) позволяет выразить скорость и для расположений, данных на фш (234) и фиг. Г235>, след! юшнми простыми формулами, содержащими 1 иперболические ф\ нкпнн:
J. . <т*\ . (161)
и = 21‘вЧт)-
«=^ cotgh . . (162)
Мн видим, что нри расположении вихрей как на фиг. (234) скорость их поступательного движения м возрастаете увеличением у, а при расположении вихрей, данном на фиг. (235), скорость их поступательного движения и убывает с возрастанием -
Покажем теперь, что расположение вихрен на фиг. (234| устойчиво, а расположение вихрей на фиг. (235( есть неустойчивое.
Вообразим прямоугольные оси координат хоу, расположенные так, что ось ох параллельна нижним и верхним ря iav вихрей, ось оу щюходит через вихрь А, и предио-тожим, что эти оси движутся < соответственной' скоростью ti справа налево. Относительно этих
осей наши вихри в данном расположении будут неподвижны, но прн малом перемещении их центров они прядут в движение. Допустим сначала, что все вихри закреплены, кроме вихря .4; координаты же этого вихря получили малые приращения £, у. Так как скорости, сообщаемые вихрю -1 всеми другими вихрями имеют, как известно, функцию скоростей, то, называя эту функцию прн отброшенной скорости и через Fix, у), можем написать:
dj_ д
dt дх \ дх/ ' • ду \дх / dt) д idF\t 1 д [dF\ di-дх ajjc+dylч’
(163)
В виду того, что при иевозм> щеипом расположении все вихри на наших движущихся осях неподвижны,
дх ду ’
далее вследствие того, что смешение вихря А параллельно оси оу может развить только скорость по оси ох, имеем:
= 0
а так кнк
то и
3>F_c^F_ дх7 ~ ду* “°
^=0
dz3 °’
Из всех вторых производных остается только
<гт _ дхду °
Составляем эту производную, принимая во внимание, что с измене* ином ординаты уточки Л, изменяется с одной стороны скорость —«, получаемая от вихрей нижнего ряда, а с другой стороны развивается, как
иго видно на фиг. (236), скорость, параллельная ори от от действия на вихрь Л вихрен верхнего ряда. Эта поететняя скорость будет для обоих расположений вихрей:
J ч □ —1
г де rj расстояние смешенного центра Л от Л'Л, Вследствие сказанного найдем:
<164)
Входящая сюда сумма может быть определена по формуле из которой имеем:
• cosh(x) — sinh U) о
z1 smh (г) "
Положив десь r обоих частях г = 0 и определив предел. к которому стремится дробь в левой части равенства (удобно развернуть sinh и) и cosh ic) в рядыц найдем, что
. <16б)
Подставляя значение этой суммы в формулу <164) и приписывая для и значения (161) и (162), получим для расположения вихрей, данного на фиг. <234» и на фиг. (235), следующие значения а:
(К«
Формулы (163), на основании сказанного, приведут нас к следующим уравнениям движения точки А:
dt
(168)
Эти уравнения приветят к выражениям ускорений:
dr
dt*
..........................(169)
Фиг. 237.
которые показывают, что точка А, будучи смещена от своего первоначального положения, отталкивается от этого положения независимо от знака коэффициента а.
Движение точки А может быть устойчивым только при предположении, что а = о, которое невыполнимо ио формуле (167) и выполняется по формуле (166) под условием
cosh (yj = Уз х).
*) Автор теории, проф- h Arman, дает несколько иное условие устойчивости вихревой цепочки, а именно, cosh (’*) = V2. откуда у =0,281, что с наблюдениями не так хорошо сходится. Причина разногласия заключается в различной постановке задачи о смещениях вихрей, причем постановку Н. Е. следует призвать более правильной. Прим. р«д.
Это совпадает с вышеприведенною формулою (148) и дает нам *=0,3«5=,^; ............470)
отсюда же по формуле (1Ы j следует формула (149».
Нафиг. (2371 представлен полученный в Аэродинамической Лаборатории В. Т. У. снимок с вихрей, идущих за прямоугольной пластинкой 15 ХЗ тт сечением при скорости около J mt sec. На верхней половине представлена просто фотография вихрей, на нижней — та же фотография с промерными линиями. Эти промеры показывают, что теоретическое отношение* = 2,74 почти строго соблюдается в действите льном движении: именно у = 3,12: 2,77; •2,73; 2,75, как это и записано на соответственных местах рисунка. Первое чисто получено вблизи тела, где расстояние между вихрями еще не установилось; последнее получено, как 2 ~:Л.
Мы видим, таким образом, что расположение вихрей, данное на фнг. (235), неустойчиво; распо ложение же вихрей, j казанное иа фнг. (234) при закреплении всех вихрен, кроме одного вихря А, дает для этого последнего безразличное положение равновесия. Если же, кроме вихря А, мы будем считать свободным еще \
вихрь Д то без труда'усмотрим, что оба вихря прн ХХ'?
расположении фиг. (234) будут в устойчивом по- ___________£
ложении равновесия. X/
Будем (фиг. 238) называть через р и q проск-или смещения вихря Л на прямую АВ —г и на s'f's перпендикуляр к этой прямой; подобные же проек-цин 1ля смещения вихря В обозначим через /и q' ft**---------------
Так как вихри А и В от собственных смещений при выполнении условия (148) ие нолу- ,1>иг 238
чают скоростей, а эти носледние для вихря А являются только от смещения вихря В и для вихря В — от смещения вихря А, то согласно фиг. (238) имеем:
dp__J I 9^_ J д'
*“2»г г~*2.1^’
dq____ J р
dt
dp'___ J д
dt 2 л г®’
dt 2»г»*
< оотвественные ускорения будут:
d*g______Ji 1
dP~ 4л»г*Я’
.'fro показывает нам. что оба вихря будут притягиваться к своим первоначальным положениям, и 1вижение их при закреп <рннн всех других вихрей будет безусловно устойчиво.
4 . Переходим теперь к действительному явлению н предполагаем, что все вихри могут свободно передвигаться, ири чем имеется расположение вихрей, соответствующее фиг. (234) прн выполнении условия я = о. Относим нашу систему вихрей фиг. 1239» к подвижным осям хоу, ука»ан-ным выше, и называем через с, ij смешение точки Л, через |ш. i]t приращение координат точек Л2.... через i/f смещения точек Blt В^,..., при чем смещения tj , будем считать полижите.шными в направлении вниз. Компоненты скорости^ и точки Л выразятся формулами:
dz __ J —у,______
dt ~ Ji r',* •
di)_ J x - x, , J x—x/
dt~~~2x^~T» ’
<рмг. 239.
где первые суммы вторых частей распространяются на все верхние вихри, кроме А, а вторые — иа все нижние вихри. Эти скорости равны нулю тля несмещенных вихрей. При весьма малом смещении вихрей в силу dn
условия в = о в скоростях и не полу чится членов, зависящих от изме ___________________ . dz dn ~
нений (J, ч) координат вихря А, так чтом и d(будет линейно зависеть от смещений j,. ч , Мы получим:
<Е Jyix-z,? JK е, ,г у (I — х.' — *’ ,•
dt 2.тг,1 4i т XJ <* ’ * Ч‘ ’
Лч Л’УЧ’-’ЛТ У О»—[ J УЧ* — — ** f
at --£ JL ‘ V ~ - > Д. “V? “ 41 ’“2л — <• a‘
Так как все вихри J„ Bv В.,,.. симметричны, то написанные уравнения могут быть применены к любому нз вихрей, которому можно приписать роль вихря Л.
Покажем, что сравнения (171) н им подобные для других вихрей допускают частные интегралы:
5 = .V cos г~ (х 4-zh,
.................. (I7S)
при чем такие же формулы (с тем же коэффициентом ЛЛ выражают все смешения 3., i?P т)\г и разница заключается только в том, что абсциссам х надо приписывать значения, соответствующие вихрям Aj, Л2,..., Bj..
При подстановке формулы 11751в у равнении 1174) все члеиыприсоа ( в первом уравнении )174i и все члены при sin (^/.11 во втором уравнении 1174) обретаются в нуль, так как
V Д,- yin (~r х,| = о
V~-«—pi"' =
V >in
потому что при о шиаковых потожитетьных и отрицательных значениях а* или Z; члены сумм сокращаются.
Вследствие этого первое у равнение 1174) можно сократить иа sin ("£ at), второе иа eos("< **/> п >’ ,|аг получится для определения скорости Z распространения волны и длины полны L уравнения:
J«V -са-о ,п ’ — (131-1У, +*?)*
[.2А—11Я П +
лР
(2* — 1)й * -А2
— ~~v V COs
(176)
1- sin Г(2Л —Пл
-В=.тГ) I
j v lat-ifj-*’
— £+**)’
Эти уравнения заменяются следующиыи двумя:
(24-1)’7-* ,
,-----------,,cos (<2fc — 1) я . —
((М-1)*4+*’)' L>
(<2*- О5
^^sinf'-JA—ПжА),
[<>*— i>.-rA]
V j cos(2ft.4-tj = o. . . .1177)
Корни -£ последнего из этих уравнений определяют ллины воли, а подстановка этих корней в первое уравнение дает соответственные скорж ти
распространения волн. Наименьший корень второго уравнения (17<> будет *):
а следовательно ему удовлетворяют также кирни:
/=£+«•
где п произвольное целое число. Различные длины волн даются формулою:
L=^1
при чем при п — О получается самая длинная волна. Так как вторая часть первой формулы (177) будет для всех шачении п иметь одинаковую величину положительную или отрицательную, то скорость а будет убывать с уменьшением L. Всякое расположение отклоненных вихрей может • 2 быть разложено на ряд указанных
_ \ 7 - волн, которые побегут с разлпч-
ными скпростямп а, сохраняя свои амплитуды. Таким образом рас-' положение вихрей, данное на
* • фиг. i234j, следует считать устои
' 7 ~ - : : : чивым.
. ------ 5. На фнг (2101 дана диа-
, грамма скоростей воздуха, опре ш-
Z - " , ’ д • ’ ленных микроманометром и флюг-
ерком Сабинина в круглой трубе J J ~ ~~~ " - Аэродинамический Лаборатории В.
- Z - - Т. 5. для потока, обтекающего
7 - вертикально поставленный круг-
7 л ни цилиндр диаметром 57 л/ж
- - - и длиною 740 шт, упирающийся
фвг. 240. киицами своими в стенки
трубы.
Направления стрелок дают направления скоростей, а длина стрелок в принятом масштабе даст величины скоростей. На фиг. 1240» принято: 1 щт = 5,2 шт длины, а на стрелках 1 жж = 4,2—. Измерения производились на средине высоты цилиндра. За величину h расстояния между вихревыми рядами можно принять расстояние меж iy двумя линиями, на которых флюгерок приходил во вращательное движение; эти линии на фиг (240) представлены кружками, при чем стрелки на кружках дают направление вращения флюгерка. На нашей фигх ре это расстояние равно 70 шт. Принимая h равным 70 шт, находим: *=£=1.25; это дает по формуле (1521
А* = 0,0925.
Определение силы сопротивления о помощью динамометра приводят нас к меньшему числу.
’) Riemann- „Die partiellen Diffierential-GleichungenBd. 1., S. 76. i910.
На прилагаемой таблице воздуха от 3,4 до 17,6 метров
тля различных скоростей
1ано это число в секунду:
V к Г к
3,4 0.0500 12,2 0,0511
5,5 0,0513 13,1 0.0504
6,7 0,0505 13,9 0,0500
8,0 0,0500 14.1 0,0513
9,8 0,0505 16.1 0,0301
11,3 0,0500 17,к 0,0507
В ерегнем получаем:
к = 0,0505.
Если принимать во внимание ие только уменьшение количества движения, которое происходит за моделью от уменьшения скорости потока., как это делает Karman, но и увеличение давления от этой причины. то получается коэффициент сопротивления к0, близко подходящий к наблю-1еииям. Вообразим, что тело охвачено прямоугольным параллстепипе н»м. высота которого параллельна осям вихрей и равна единице, а ширина настолько значительна, что на боковых стенках, параллельных скорости потока, можно считать скорость равной I. Что касается до длины параллелепипеда, то ее вообразим настолько большой, что на стенке, черед Котору ю жидкость входит, можно считать скорость равной Г, а на стенке, через которую жидкость выходит, обозначим скорость по направлению потока через Г', а скорость, перпендикулярную этому направ лению, через w. На основании теоремы Эйлера можно написать:
7? ff «ГУа +
ff'"10 ffsr2da-ffp'da'
где двойные интегралы распространяются иа элементы do плошадей сторон параллелепипеда, перпендикулярных скорости потока, &р и р суть гидравлические явления, определяемые по формулам:
т> = с- 4(-s
dF У'* »е-
где С одно и то же постоянное, а в ере гнем значении обращается в ну.ль. По тставляя получим:
Я = ff v^da-ff e^^do+ J'fe'^do. (itsi
Первый член представляет в сре тем потерянное количество (виження, которое вычисляет harman по формуле (150'к что касается до второго члена, то ои представляет по. и.вину первого члена: наконец, третий член I рассматриваемой адаче есть малая величина, если предположить, что вихри продета! 1яют жидкие цилип 1ры конечных размеров, вращающиеся, как твердо- тело. Для всех точек на фиг. <234>. леж нннх на прямой, проходящей через точки J и В перпен гнкулярно шнип 4 1, скорости г суть нули; тля всех остальных линии, перпендикулярных к .1J,, эти скорости приближаются к нулю на пекогором расстоянии от прямых Л 4t и ВВХ.
вблизи же этих прямых они, вообще, не вс тки. На основании этого можно написать
R= .7(1 ’" = ”,296 Н -|-д| о * аГ2. . . (179)
у в
где ц — малая величина, учитывающая третий член формулы Ц78» Отою та получаем коэффициент сопротивления
*-0 = у (14-Д| = О,29в,1+/Л8-£- = 0,037 (1+д)-, I1SO)
где к определяется по формуле И52) и после шее числовое значение взято для воздуха.
Для вышепривр генного наблюдения над цилиндром имеем
р = 0,09.
На фиг. (237) ыя пластинки 15X3 мм было найдепо — = 3,6, отку ла
к0 = 1,05 (1 - и) р.
По опытам над той же пластинкой в воздухе было найдено
к = 0.145 = 1.16 о, откуда
р = о.ю.
По опытам над вихрями за цилин (ром d = 38 тт в воде, фотографии которых ие приведены, подучено
ft = 0.10
Таким образом, получаются довольно близкие к действительности результаты, если к формуле Karman а прибавить множитель 4 -
§ 30. Вихревая теория лобового сопротивления для движения жидкости в трех измерениях 1).
1 . Эта статья представляет продолжение моей работы, напечатанной под тем же названием в 1-м вып. XV! 1-го тома Трудов Физического Отделения О. Л. Е. в 1914 г. [и здесь в £ 29]. Мне удалось теперь распространить теорию Кармана на движение жидкости в 3-х измерениях. В основу изложения кладу определение количества движения жилкой массы, внутри которой помещен замкнутый плоский вихревой шнур. Мы имеем следующую нристую теорему.
Количество движения безпредельной жидкой массы, внутри которой находится замкнутый плоский вихревой шнур, равно циркуляции скоростп, умноженной на площадь шнура я плотность жидкости.
Вообразим (фиг. 241) замкнутый вихрь АВ и на элементе df его площади построим бесконечно тонкий цилиндр гг. Количество (внжения в направлении оси z'z, сообщаемое элементу массы Qdfdz при точке G элементом вихря BC = ds будет
d^dt - — 2idsolidf I - —
(»2 + Л)у / lp+0’ /
где i величина, аналогичная силе тока. Так как из подобия ABCD^AEBG следует, что
hds=r2d<p
то
2i nd =2i{}dfd<f.
Совершая интеграцию по всему замкнутому контуру вихря и нотом по всей пло-шз in его, будем иметь для суммы количеств движения всех призм, пересекающих площадь f, величину
4л»р/’..........(141)
и для всех призм, ее не пересекающих, величину нуль. Таким образом, все опреде-<яемос количество движения выразится форм.
< 181». Но если замкнем концы прямой сс* некоторым контуром, бесконечно учаленным от внхря, то получим для циркуляции J по контуру, охватывающему внхрь, выражение
вследствие чего искомое количество движения
4.T?pf=±:Jfo, .....................1182)
что и требовалось доказать.
2°. Определим теперь лобовое сопротивление тонкой птастинки. Предположим, что она равномерно покрыта массами плотности Г и отталкивает по закону Ньютона внешнюю точку силою, проекция которой на нормаль к н застилке выражается формулою
/40),
где со телесный угол, под которым видна пластинка из притягиваемой точки, a ju некоторый коэффициент. При вступлении притягиваемой точки на плоскость пластинки ю = 2л для точек, лежащих внутри контура р
пластинки, и со —о чля всех внешних точек. Если положим ц = и силу отталкивания пластинки будем считать за скорость жидкости, то получим распределение скоростей несжимаемой жидкости в пре (положении, что поток вытекает из площади пластинки в ту и другую сторону с нормальною скоростью V. Построим теперь (фиг. 242) на контуре рассматриваемой пластинки АВ прямой ци шндр AB<'D, имеющий площадку АВ своим основанием, и прибавим к жидкости во всех точках внутри цилиндра скорость Г, направленную вверх, а во всех точках вне цитиндра скорость Г. направленную вниз. От этого прибавления получится поток жидкости, теку щий н бесконечности во всех точках вне цилиндра вниз со скоростью I. а во всех точках внутри цилиндра со скоростью Г вверх. Па плоскости же пластинки мы будем иметь внутри ее контура с обоих ее сторон скорость нуль, а вне ее контура скорость Г вниз.
В моем сочинении „Насадки и диффузоры аэродинамических труб'*') показано, что полученный поток жидкости может быть образован из равио-
*) Труды Авиационного Расчетно-Испытательного Бюро, вып. 6—7, 1918 г
мерного потока и потока, вызванного соленоидальным вихрем, образован ным из вихревых колец, равномерно расположенных по боковой поверх ности цилиндра ABCD, при чем на
каждое ко льцо ширины dz приходятся циркуляция скорости Vdz. Па фиг. 242 с правой стороны представлены линии токов жидкости, вызванные таким соленоидальным вихрем. Самые вихревые ленты, расположенные но цилиндру, будут иметь некоторую толщину" и будут двигаться вниз со скоростью равной у. Кроме того, они будут иметь ешс радиальную скорость, направленную от оси цилиндра. Эта скорость вызовет расширение вихревых колец но мере удаления от пластинки. Но для нас для определения зарождающегося количества движения важна только скорость,
Фиг. 242.
с которою вихревые кольца цо мере зарождения отбегают от пластинки.
зарождающимися вих-которое должно быть
Секундное количество движения, вносимое вверх рями. равно силе лобового сопротивления R, направленной вниз, согласно формуле (182), будит
Zi = Vdz fen, где п число вихрей, отбегающих от
пластинки в 1’. Но
«=4
R = 0,0625 К V*f.
Это IК — 0,0625 есть
значение коэффициента, к которому он устремляется при возрастании скорости Г. На фиг. 243-а н фиг. 243-6 таны графики изменения коэффициента Л с изменением скорости по опытам в аэродинамической трубе Московского Университета для квадратной и круглой пластинки, при чем но и абсцисс отлагается
поэтому
п = 2 dz.
скорость Г в метрах в секунду, а по оси ординат коэффициент К.
Что касается до возрастания коэффициента К с уменьшением корости. то оно иа мой взгтя 1 объясняется влиянием вязкости жидкости.
Вязкость воздуха.
Выведем теперь ур-ия движения жидкости, принимая во внимания ее вязкость, и выясним, почему движение с потенциалом скоростей имеет такой большой практический интерес и отчего всегда говорят о движении «• потенциалом скоростей, хотя мыслимо много различных движений жидкости, обтекающей данные контуры.
£ 31. Силы вязкости.
Припомним сначала то, что уже известно о деформации весьма малой частицы жидкости По первой теореме Гельмгольца (стр. 108) движение весьма малой частицы жидкости состоит из поступательного движения со • коростью ее центра, вращательного с угловыми скоростями с. jj. С, равными компонентам вихря, и, наконец, внутреннего движения ^формации, обладающего потенциалом скоростей. (Относительно определенности разложения движения на вращательное и внутреннее движение деформации см. стр. 108).
Если через центр (х, у, г) рассматриваемой частицы жидкости провести подвижные оси координат О'х!у's', параллельные неподвижным Oxyz, то функция потенциала скоростей для движения деформации, как известно, будет:
Ф= 2 [йаГ', + |»Ч + Йг'’+2в-»'г' + 2в*г'а< + 2в’а: ‘»' ] • -(63>
где
(62)
называются ко орд и-
Ветичцян в.,, е3 (стр. 1081 с коше ния ми натных углов. Покажем здесь нх кинематическое значение.
Для этого рассмотрим скошение угла afo'y*. Полагая, что ось г' перпендикулярна плоскости чертежа (фиг. 244) и что оси у' и af при деформации повернулись
около & на утлы z и найдем, что посте деформации
угол между ними будет 2 —л—/<, т.-е. уменьшится во время деформация иа величину л-|~д. Если скорости и и v при переходе соответ-(твенно иа dy и dx получают приращенияdy н^ dx, то
оу О-Т
у dxdt:dx = ^dt,
дх дх ’
л = &* dydt:dy = ?* dt, ду * * ду ’
Яdt Ц- ?“ dt: г 1 ду 1 дх
» р«тичв*и« оевсаы вождухоцаланаа
18
отношение же величины /л-f-л к элементу времени равно
Д —/- _ 0« । __
dt ду'дх ~ *
и дает скорость изменения прямого угла х'о'у' в плоскости, перпендикулярной оси г, за элемент времени dt.
Укажем теперь на некоторые свойства тех добавочных енл, которые развиваются Ъ жпдкогтн вследствие вязкости—сит внутреннего трения.
Возьмем в жидкости бесконечно-малый прямоугольным параллелепипед ребрамп <Zr, dy, dz, пара (дельными осям коортпнат (фиг. 245) и разложим добавочиу ю си чу, действу ющую на какую-либо его грань вследствие вязкости, на слагающие, пара тельные осям координат; топа одна из них будет нормальна к грани, а две другие будут лежать в ее плоскости. Относя все силы к единице площади, введем такие обозначения. Силы, действующие на грани y’z'. z'x', х'у' нормально к ним. будем обозначать через Д’]. А'з, Л* и будем считать положительными, если онп направ 1еиы внутрь параллелепипеда |на чертеже в положительную сторону х, у, г). Компоненты же, лежащие в плоскости тех гранен, к которым они приложены, будем обозначать через Tlt Т2, Тэ, соблюдая правиле», чтобы сила, действующая на грань, иерпендикулярную одной осн, н сама параллельная другой оси
. Таким образом, наир., Тх будет сила, действующая на грань xz, перпендикулярную оси у, и параллельная оси з; и ш сила, действующая на грань Zу, и паралле 1ьная оси у. Одинаковое обозначение для этих двух сил мы в праве ввести потому, что оин по абсолютной величине равны между собой. В самом деле, силы
'т,-^ 11 -17.+ \ 1 ду 2 1 1 1 ду 2 '
на двух противоположных гранях, иерпендп-ку тярных оси у, дают (фнг. 216) пару Tldxdydz, . («I
стремящуюся вращать параллелепипед около осн х (соответствующей индексу Тр против часовой стрелки. См ш
и -(т.'+^^.
Фиг 245 отмечалась индексом третьей оси
приложенные иа гранях, перпендику 1ярных к осн z. даю г пару
Г; dx dy dz. .................... I In
стремящу юся вращать параллеленшк* i также около л/, и<» у же по часовой стрелке Так как обе пары (а) и (bt должны уравновешиваться, то отсюда вытекает, чт силы Tt для «беих пар граней имеют одинаковую ве шчииу.
Такое же рассу ждеине можно применить и к силам Т2 и Т3.
Отсюда следует, что различных по величине тангенцна.1ьных сил имеется всего трш Ту, Т2, Тг
Вообразим теперь в жидкости бесконечно малый тетраэдр (фиг. 217) <• боковыми гранями, пара где щнымн плоскостям координат, и основа-пи нм АВС и назовем через R, Bv, Rt равно действующую п ее проекции
на оси коор шпат сил вязкости, действующих на единицу нтощади грани АВС с той стороны, где лежит начало координат (изнутри тетраэдра). Так как проекции равно <ей-ствующей всех упругих сил, действующих на площадку АВС изнутри тетраэдра, будут равны сумме проекций на соответствующие осн всех сил, действующих на грани тетраэдра, параллельные плоскостям координат.
снаружи тетраэдра, то можно написать:
Rxo = Л 1 ох —|— Тд Т^ |
J?,e=Xcf + Tj ©,4-TsO,, , (183»
Я, о — .V3 о, + Т? 0,-1- Ti о9, )
где о, ож, о. площади граней 4ВС, ВО С, СО’А, АО В. Называя через а, /?, у углы нормали к площадке ЛВС с осями координат х, у, г, и замечая, что
or = acosfi. 0,=00087,
можем переписать уравнения (183) в таком виде
Я,=Д’ 1 cos а г Т3 cos i? -f- Т2 cos у, Я, = jV2 cos р 4- Ту cos 7 Г3 cos а. Я. = cos / 4- Т.> cos a -J- Tt cos Д.
. <183 i
Если обозначить i ищу перпендикуляра, опущенного из начала координат на площадку о через Я, а коор шиаты его основания через У, у', то най »ем:
х 1 V7
cos а = - . cos-j ', cosy = п.
Тогда
- Тз!1' + Т.^, ; = ^.
B, = ,X2y-Tt 7?. = (.V3a 4-r,x+ri!/')i = l . (1S4)
где
F= ‘ (A'1a:,sJ-.V.//',-L.Vsy ’Г,//’ 4-2 Т,г'х-\-2 Т,ху\ .(185)
Зная шесть коэффициентов, входящих в выражение F', можно определить все три слагающих Я,, Яи Яж силы Я, действующей на площадке а в зависимости от вязкости, при любом направлении площадки. Очевидно, что си ты внутреннего трения, появляющиеся в жи ikocth вследствие ее вязкости-ра-звпваются только в зависимости от внутреннего движения частиц— внження деформации—и не зависят от вращения н посту нательного двн-
I9t>
жеиия, так как при пос четких различные точки всякой выделенной бесконечно - малой массы жидкости ^относительно друг друга не передвигаются.
Если приравняем постоянным величинам функции Ф' и F't то полученные уравнения
Ф' = const и F' = const
будут выражать некоторые центральные поверхности второго порядка; первая характеризует деформацию жидкой частицы и называется поверхностью деформации1); вторая характеризует силы внутреннего |рения, развивающиеся от вязкости, и носит название поверхности сил вязкости1). II для той, и тля другой поверхности можно выбрать оси координат так, чтобы в выражения функций Ф' и F' входили только квадраты координат. Это будет иметь место, когда за координатные оси будут приняты главные оси упомянутых поверхностей второго порядка. Так как вязкость, согласно сказанному, зависит только от деформации частиц, то главные оси для обоих поверхностен будут один н те же: оси деформации совпадают с осями вязкости. Поэтому, когда оси координат выбраны так, что в функции деформации Ф' величины
^ = 62 = 03^=0,
то п в функции F', характеризующей силы упругости, величины
7't = Т2 = Т9 = 0.
Обозначим для направленных таким образом осей координат величины
ди дт dw дх* ду* dt
соответственно через «х, е2, е3, а величины Л’8, Лт3 через их, \п.>, п$, т.-е. положим, что
(£)=«.. (»)=*». (£)=d
\М0 w0 <ч0 (18в>
(-Vl)c=»l- №)о=Я«- (-V»)o=«s.
где значки (0) показывают, что величины
2. £ и Л., .V„ .V,
дх* ду* dt 1 * ’ 3
взяты (ля главных осей деформации. Тогда
фо = 2~ («1 -Ra У ’ + «в 2,а),
/’о =~2~(П1Ж )•
Силы вязкости зависят от первых степеней производных от скоростей, так что величины nt, nit являются некоторыми функциями первой степени относительно трех величин е2, с8, которыми характеризуется деформация. При этом зависимость п1 от е4 и е3 симметрична, а от ег
’) Приведенный анализ применим и к случаю сил. развивающихся и упругом теле при его деформации: указанные поверхности будут носить там названия: поверхность деформации и поверхность сит упругости.
является обособленной, вследствие чего эти функции мы можем представить в виде
«1 = 7.^, f-»'(*.- гз). |
п2 = 7.^ Н('.»-Hi), j (188)
«s = ^e8 + v(<l+c.j). |
Прибавляя и вычитая в этих выражениях соответственно »»/,, vt, и замечая, что для несжимаемой жидкости
, &м Л Эи-
-г “Г **ч =---Г - . =0.
11313 дх 1 -1у дх ’
получим для последней:
rti = Р- —v) — — - fl ci» |
н., = (л »•)' =— -Д'1,,! (139)
и,=(Л—»)^ = —’де,, I
г I»* ц, как у видим далее, есть величина положительная.
Но, если nl9 и.„ м8 пропорциональны ер са, «3, то и между функ-
циями Fe' и Фо' существует такая же пропорциональная зависпмость/т.-е.
РО = -2ДФ’О.
Если перейти теперь к произвольным осям координат, то вид функций изменится, но связь между ними остается прежняя:
F =— 2иФ,. (190)
или в раскрытой форме:
* (xV1Z,+.V,J/!-| 2Т,гл2 \ гТ,/у) =
T2wi.'/^' 2ft,z'af+ie3xy' (190)
Из этого тождества находим, что
л'1 = — У’ = —*»= — •;<*; (191)
фиг. 24S-
ь=-4£+^), *i=-< з-
• ОМ
Пз этих формул мы видим, что в однородной, изотропной во всех направлениях и несжимаемой жидкости силы, появляющиеся в п^й вследствие вязкости, характеризуются одним только коэффициентом «.
Покажем теперь, что коэффициент /* есть величина положительная.
Для этого возьмем один нз простейших слу чаев течения (фиг. 248), именно, когда жидкость движется слоями параллельно оси х со скоростью п, пропорциональною координатам z частиц, так что u = a2z, v = w — О.
Так как в выражениях (191) и (192) все производные от компонентов скорости, кроме п‘, дтя рассматриваемого течения будут равны нулю.
— И»8 —
то полная сила внутреннего трении, действующая на всякий слой житкостп, параллельный плоскости ху, со стороны прилежащего к нему стоя будет равна
Т2 = —= —... (f)
Так как Т,, как сила, у герживающая верхний слой и препятствующая его движению, должна быть направлена в отрицательную сторону осп х— быть отрицате льной согласно обозначению фиг. 245 — то и правая часть выражения (с) должна быть отрицательной, следовательно, у должно быть величиною положительной, что и требовалось показать Величина у носит название коэффициента вязкости.
На основании весьма тонких опытов найдено, что ьтя воздуха при 0° и 760 mm 1ав ления
у = 0,00017 lpr.-масеа1, cm~\ sec-1],
пли в принятых намп единицах,
р = 0,0000017 (рг.-вес1, wJ-1, я/с1].
Обычно в практике пользуются другим коэффициентам »», который называется кинематическим коэффициентом вязкости. Он представляет коэффициент вязкости, разделенный на плотность жидкости, а именно:
он имеет размер
[»*] = [jnZ2 хм-1],
т.-е. одинаковый с размером цирк\ тяцпн скорости.
этот коэффициент равен:
для воздуха v — 0,0000133 mt2 м>с при О и 760 тт давления 143 „ 13е _ 760 _
0,0000245 . „ 100е 760 .
0,00133 О _ .7,6.
ДЛЯ ВОДЫ V — 0,00000178 „ „ О' С
0,00000100 „ 20’
0,00000056 „ 50е „
0,00000030 „ 100 „
ДЛЯ ртути v = 0,000000125 „ О .
0,000000091 „ _ 100 w
тля глицерина v 0,00068 _ . 20' „
Кривая вязкости воды в зависимости от температуры представлена на фиг. 249. Мы видпм, что вода прн оэ С оказывается в 7,5 раз менее вязкой Iотнося вязкость к единице массы), нежели воздух, и разница эта еще увеличивается с повышением температуры.
§ 32. Уравнения движения вязкой жидкости.
Выведем теперь основные уравнения движения несжимаемой ’) жидкости, принимая во внимание ее вязкость. Для этого при рассмотрении движения жидкого параллелепипеда (фиг. 1,стр. 7) ну жно к обычным поверхностным силам — силам гидродинамического давления — присоединить «нлы, развивающиеся на гранях параллелепипеда в зависимости от вязкости.
Добавочные су ммы проекции этих сил иа оси коор шнат буду т равны <на фиг. 250 показаны миль компоненты, параллельные оси х):
— dr dy - dz — dy - dz - dr - dz dx - dn.
ix &У J CZ **
vX, л j j •>/.., , •»T. , , j
--— dy dz - dx — dz dx • dy — ' dx dn dz, Jy " jz v дх я у
*v >T T
— J dz dx - dy — dx • dy dz — dy dz dx
(193)
Заменяя здесь силы А и Г их выражениями из уравнений (191) и (192) н замечая, что коэффициент
расширения du dv . спо дх 1 dy' dz
для несжимаемой жидкости равен нулю, получаем вместо первой < трокн:
ох3 1 ду2 дхоу
+ эХ + а’“]^4Иг =
= y.Audxdydz, . . (193'»
«1 вместо второй и третьей:
yAvdxdydz, | /г J wdxdydz, /
(193)
’) В вопросах авнациа воздух можем считать несжимаемым в силу соображеввА, наложенных на стр. 2] 22.
где символы Ju, Jv, Ju’ —вторые дифференциальные параметры от «, г. w -равны:
. __З2» । д^и
дуз • •
. дч . аь у.
Jr=ta»+a?+•
. (Pw । Pic . Э’ш
Jw==a^ + v+&a’-
Добавляя к правой части уравнений («) (на стр. 9 курса) выражения (193) и деля уравнения иа Qdxdydz, получим дифференциальные \ равнения движения вязкой несжимаемой жи щостп:
Q дх Q dt
,g=r-L''jl. "
*^ = Z+"JH - £
Q dz ' (> dt
8w du
U -Д-----Г a ------
dx dy
8u
dr dv fa-
ll Г “a------W ’
ox dy we
dtr die die
dx dy dz
(194)
Эти уравнения называются уравнениями Stokesa1).
Для движения с потенциалом скоростей Ф вторые дифференциальны»* параметры от скоростей будут равны:
J«= i8'1' = 4- (J<z>i=o. dx ox
Jr=J—= 8 (J<Z>)=o,
Лн =4 8* — .-(J<Z>) = 0, dz dz v ’ ’
так как операции J и переместительны, а АФ — о для всех точек несжимаемой жидкости.
Таким образом, при существовании потенциала скоростей члены уравнений (194), содержащие коэффициент вязкости /1, пропадут и уравнения (191) будут пметь такой жр вит, что н уравнения движения идеальной жн (кости:
1 Эр ,, Эи Зм 8м du d дх dt dx оу dz
1 др _у___ dr Or dv Or
Q dy dt U дх ду dz '
1 др „ дю дю дю дю
Р = И Эх ~Т „ ~№^
(21
Отсюда заключаем, что при сущеетвованпп потенциала скоростей вязкость не оказывает влияния на движение внхтри жилкоети, а также не влияет иа распределение давлении внутри ее. Влияние вязкости при существовании потенциала скоростей может проявляться только при стенках сосуда, на которых должны быть соблюдены граничные условия.
Относительно степени прилипанпя текущей жидкости к стенкам слще ctbjiot различные мнения. Некоторые исследователи думают, что жидкость около стенок совсем не движется, фугпе полагают, что она скользит по ним
О Уравнения двпхеиня упругого тела будут иметь такой же внт. что и уравнения (194), с тою только разницей, что они ие содержат членов, в которые входит давление р. н кроме того, вместо одного коэффициента («» в ннх будут фигурировать два: второй коэффициент зависит от ежнмаомоств тела
Так как вязкость пропорциональна первой степени производной от скорости, а трение о стенки, согласно опытам, получается пропорции нальным квадрату скорости, то в этом вопрос** между данными наблюдениями и теорией было большое разногласие. Причины его теперь во** более и более выясняются. Больше всех в этом направлении сделал английский исследователь Osborne Reynolds.
Течение жидкости в трубе, при котором жидкость на стенках неподвижна, а по мере отступления от них изменяет скорость по параболическому закону, называется движением типа Poiseuillen. Это движение весьма устойчиво, но в трубах значительного шаметра оно сохраняется только при скорости нс превосходящей известного предела. Этой было обнаружено Osborne Reynolds ом.
Если в такую текущую по трубе жидкость впустить струнку окрашенной жидкости, то прп малых скоростях эта струйка течет совершенно прямо; прн увеличении же скорости наглупит момент, когда окрашенная струйка начнет колебаться, а затем затушуется и разобьется: движение сделается несколько спутанным. Если ирп этом движении наблюдать скорости. то можно усмотреть, что средняя скорость потока будет уже иная, чем прежде; вместе с тем скорое tn в каким- либо сечении трубы буду т изменяться уже не по закону параболы, а по эллипсу, при чем постепшй прн боть-1ИИХ скоростях будет иметь очень короткую ось по наврав тению потока. Этот эллипс в плоской трубе В.Т.У. почти переходит в прямую.
Для течения типа Poiseuille'ii уравнения Stokes а хорошо оправдываются. Но когда жидкость (воздух) движется с громадною скоростью, то 1авление на обтекаемом теле вполне совпадает с тем давлением, которое получается в предположении существования потенциала скоростей. Отступления получаются лишь в том случае, когда сопротивление обтекаемой поверхности движению воздуха очень велико, например, если в поток* имеется шар, оклеенный пробкой.
Я предлагаю считать (это ие очень точно подтверждено опытами, но все же довольно близко к действительности), что при стенках скорость жидкости равна нулю, ио чту затем она очень быстро возрастает и становится равной топ теоретической, которая получается в предположении существования потенциала скоростей *).
Слой жидкости около стенок, не имеющий потенциала скоростей, а следовательно завихренный, весьма тонок. Его толщина Л зависит от скорости иотока: если скорость мата, то толщина довольно велика; а если скорость велика, то толщина мала.
Если ввести гипотезу, что толщина завихренного слоя обратно пропорциональна скорости, то можно примирить закон пропорциональности сил внешнего трения (жидкости о иоверхноети тел) квадратам скоростей— г законом пропорциональности сил внутреннего трения (вязкости) первым степеням производных от скоростей но координатам.
В самом де к. пусть в потоке жидкости, движущейся в бесконечности го скоростью Го, помещено неподвижное тело вращения, окруженное завихренным слоем переменной толщины h (фиг. 251). Разобьем мысленно этот стой на ряд еще более топких. Тангенциальные силы (отнесенные к единице плогпади), препятствующие частицам внешних слоев свободно продвигаться относительно внутренних, будут даны для всякой точки А1 поверхности выражением:
I dw | ди , аг+-st)-
* ) Опыты последних зет вполне подтверждают *то предположение Н Е.
Ifyu.K pt '
it in за ось £ принимать касательную к меридиональному сечению тела к точке ЛЛ а за ось г—нормаль к его по верхноети в тон же точке.
Вследствие медленности изменения w с пзмрненпем £ можно принять, что
=0-дх
а вследствие малой то.тщпны завихренного слоя и обращения в ну ib скорости и на поверхности тела можно положить, что
ди _ «п dt h •
где п0 скорость иа внешней поверхности завихренного слоя
Вставляя эти значения в выражение Т.2, получим:
Т.
h ’
а. полагая но нреддиткс.нной гипотезе
будем иметь-
Т,
(195)
К
Так как Г, т.-е. скорости течения жидкости на поверхности тела в предположении существования потенцпа ia скоростей во всем пространстве, занятом жидкостью, то формула (195) будет находиться в согласии с опытным законом внешнего трения жидкости о поверхности
...............................................................Qi) приведенном на стр. оО курса.
Сравнивая формулы (195) н (51), заключаем, что по нашей гипотезе
На основанпп опытных данных относительно коэффициентов /« и получается, что
* • г. М 0.0С«Юи2 „ _
Л = — = п = 0,01 fflt- sec.
а толщина завихренного слоя
. 0.01 .
h г mt.
Для примера приводим
(табл. 24) толщину завихренною стоя при различных скоростях, вычисленную па основании предложенной гипотезы:
Таблица 24.
Изложенные рассуждения относятся к случаю [впжения тел в жидкости е большой скоростью; при весьма же медленном движении, как показывают исследования движения маятника в воздухе, явление вполне удовлетворяется уравнениями Stokes а н предположением, что на поверхности тела скорость равна нулю.
Теория винта геликоптерного и гребного.
Литература о пинтах так богата, что требуется большое внимание,, чтобы охватить все исследования н привести их в стройную систему Пр говоря уже о многочистемных исследованиях над винтом, пропзво [я-щихся за границей (в научных воз.(ухойлаватстьных журналах: „La Technique Aeronautique4*, /Zeitschrift fur Flugtechnik und Motorinftbchiffartr и других можно встретить статью о винтах почти через 2-3 номера), напомним, что в России псстедованпя винтов (главным образом, геометрических, т.-е. винтов с постоянным шагом) j же швно производились в Ку пинском Институте Д. П. Рябушинского, который являет* и одним из пионеров в этой области. В нестояще время нссл* . займе винтов производится в Политехническом Институте в Ленинград-П. Наконец, в нашей аэродинамической лаборатории подготовляются самое юяге шные исследования над винтами.
В -этом отделе мы будем держаться такого плана:
( начала укажем на те приспособления, с помощью которых исследуются впиты, сперва <• неподвижною осью — м о покойном воздухе и в потоке, — затем винты двигающиеся.
Потом изложим те теории, которые, нс вдаваясь в подробности, дают характеристику вннта Па общие формулы, даваемые этими теориями, стали обращать внимание тишь очень недавно.
Затем предложим некоторые гипотезы, которые приноровлены к той нти иной форме винта. В зависимости от того, какого характера вннт рассматривается и какие гипотезы кладутся в снование теории, мепятся и теоретическое развитие самой задачи о силах, действующих на винт
Наконец, в заключение этого отдела, сделаем некоторые попытки применения гидродинамической теории к исследованию винта и. в частности, разберем вопрос о том, как изменяется работа винта и форма потока г у вс диче нис м чис ia лопастей. Вопрос этот можно решить только войдя обстоятельно в гидродинамическую теорию винта Приближенно же этот вопрос различными авторами реша лея различно: одни считали тягу вннта пропорциональною числу лопастей, а другие полагали, что двухлопастным вннт при бо iMnoft скорости действует совершенно так же, как н винт со многими лопастями.
о 33. Лабораторные приспособления для исследования воздушных винтов.
Переходим теперь к описанию приборов для исследования винтов.
Вслльиер иронзво шл исследования над винтом с неподвижною осью Но впнт (фиг. 2521 имел 5 mt в дпамстре и приводился в движенш паровою машиною (локомобилем) при помощи ре.мешшн передачи. Ось винта
*) Слова относятся к несин iOJ2 г.
Прим
могла свободно подниматься вверх и вниз внутри патрона, который охватывал ее; при этом передвижении оси трение было очень мало.
При помощи динамометра, расположенного внизу, определялась сила тяги винта 1ля различного числа оборотов. Затрачиваемая же на вращение винта работа определялась по
работе локомобиля.
Фиг. 253 представляет основной прибор Ренара, который послужил прототипом большинства аппаратов дли исследования винта с неподвижною осью. Мотор, па горизонтальную ось которого насажен винт, подвешен в виде маятника на горизонтальных нрпзмах, расположенных вверху, прн чем эти призмы могут быть поставлены истрпямн или перпендикулярно оси или вдоль ее; при первом положении призм измеряется сила тяги, при втором— момент пары, вращающей винт. 11ротивовесы, изображенные на рису ике, позволяют цептр тяжести всего аппарата поставить довольно близко к опор
Фнг. 252.
ной осн и этим сделать аппарат
чу вствптетьным.
Фиг. 254 пре вставляет неравно помещенное в печати гетикоптерное приспособление Ренара— е двумя параллельными впнтамп и с мотором
Фиг. 251
Фиг. 293.
в 5 лош. сил. Опыты с этим прибором ограничились ТОЛЬКО опр( 1CHHPM силы тяги. Результаты их легли в основание теоретических с- обряжений Ренара о наибольшем грузе, поднимаемом геликоптером.
Фиг. 255 изображает аппарат азролинамнческоп лаборатории Московского Университета для определения как подъемной силы, так и момента пары сил, которая развивается от сопротивления воз iy ха вращению винт а Умножая этот момент на угловую скорость, полу чпм работу, затрачиваемую
на вращение винта. Подобный в отдельной комнате для пс-пытанпя винтов >).
Фиг. 256 дает схему устройства этого аппарата. Рамка а имеет возможность поворачиваться около дву х взаимно перпендику лирных исей хх и уу. Винт Н приводится во вращение круглым ремнем ЬЪ, бегущим но роликам с, <*’, с" и еще по двум, помещенным в рамке. Ролики в рамке расположены так, что ремень не дает пары сил, стремящейся вращать рамку.
Когда впнт будет вращаться, тогда он потянет рамку вверх или вниз — в зависимости от направления вращения. Эту силу тяги измеряют изменением груза q. Одновременно с этим рамка в силу действия горизонтальных составляющих енл давления воздуха будет поворачиваться околооси у у в сторону, обратную вращению винта. Измеряя момент пары, вызывающей ато вращение, грузом р, умноженным на плечо длиною во
аппарат будет поставлен и в В. жТ. У
Фнг. 255.
всю рамку, и помножая этот момент на
Фиг.
угловую скорость винта, определяем работу, потраченную на его вращение; вредные сопротивления внутри рамки не оказывают при этом влияния на измерение.
На фиг. 257 представлен первый аппарат Д. II. Рябушинского для иссле хования вивтов. Вращение от электромотора передается через четыре шкива иа горизонтальный шкив, сидящий на осп випта и связанный с нею помощью пружины. К этой оси с помощью пе вращающегося шарпковш» подшишшка привешивалась чашка весов для измерения силы тяги вннта. (’ила сопротивления для передвижения оси винта сверху вниз в этом приборе весьма мала. Это объясняется тем, что при быстром вращении п медленном щиженип вдоль оси силы трения располагаются почти перпси (икулярно к оси вращения и почти не влияют на силу, действу ющую по оси 1». Пру жина, связывающая горизонтальный шкив с осью, с помощью особого присно-соблення определяет момент пары, вращающей винт.
Новый аппарат Д. П. Рябу пншекого, представленный па фнг. 256 построен по принципу Ренара (фиг. 253|—с мотором внутри подвижной системы. Благо (аря такому устройству все силы, действующие на качаю-щгюся на ножах рамку. на которой закреплен винт, кроме еп л
сопротивления воздуха движению впита и натяжения нитей, уравновешивающих рамку, будут силами внутренними и из рассмотрения исключаются.
Отличие аппарата Д. П. Рябушинского от динамометрических весов Ренара состоит в том, что в последних впит ендпт на осн мотора, в нервом же электромотор сидит внизу качающейся рамки на расстоянии 2 mt от вала впнта. расположенного сверху, и передает ему движение при помощи бесконечного ремня. Ножи, на которых качается рамка с винтом и мотором.
•) В качество примера такого же явлении можно привести хорошо известный факт, что якорь влектромотора во время движения может быть совершенно свободно передни «ут пальцем вдоль оси.
Фиг. 25»1
опираются на стальные опоры, за крепленые в особой чу гушюй рамке неподвижной полставки прибора и расположены: одна пара- перпендикулярно оеп винта, фугая— параллельно ей. Заставляя рамку качаться на первых ножах и определяя натяжение нитей, уравновешивающих рамку, гру зами, находят силу тяги винта; заставляя же рамку качаться на второй паре ножей, определяют момент пары от сопротнв. гения воздуха вращению винта, а. следовательно, и затрачиваемую па его вращение работу.
Такой аппарат вместе г прибором, изображенным на фиг. 255, поставлен в Ио-гитехническом Инстпту те в Ленинграде.
Перейдем теперь к недавно построенному ио поводу юбплея Общества Немецких Инженеров институту для исследования винтов, директором которого в настоящее время является Бендеманн (Веп-demann *).
Здание институ та (фиг. 259) специально приспособлено для исследования винтов. В сере [ине его имеется высокое помещение, в котором можно в летнее время открывать окна, благодаря чему поток воздуха, бросаемый винтом, может прямо уходит!» наружу, вто время как обычно, в* том числе н в нашей лаборатории, устанав ш вается круговращение воздуха. К этому помещению примыкают две пристройки. в одной из кото-
рых, левой, гтонт другой специальный прибор для нссле гования винтов.
Главный аппарат представляет из себя башню, представленную на фпг. 260. Вертикальная ось винта, помешенног» сверху, проходит череч полый вал, на который передается вращение от электромотора, и опирается иа подпятник, устроенный в горизонта ibhom рычаге, оттягиваемом вверх особою пружиной. Сила тягп винта определяется с помощью гру зов. действующих на* упомянутый рычаг. Передвижения осн впита вверх н внп .
конечно, очень ма ih.
В настоящее время эго г институт нер»'весен в Adler-4 оГ около Берлина и значительно расширен
Что касается ипре ic.iviiH» затрачиваемой на вращение винта работы, то оно совершается с помощью обыкновенного Подшильдеровского динамометра тля трансмиссий, состоящего из двух горизонтальных и двух вертикальных конических зубчатых колее. Верхнее колесо заклинено на <>си винта и полу чает вращение от нижнего горизонтального, сидящего на полом валу, с помощью упомянутых вертикальных колес, вращающихся вольно иа горизонтальном рычаге. Этот рычаг в средине между колесами
Фиг. 259.
имеет втулочку, через которую прохотнт ось вннта, и имеет стремление поворачиваться около последней. Определяя с помощью нитей и грузов момент пары сил, необходимый тля удержания вертикальных ко тес на месте, находят передаваемую через динамометр работу.
Лопасти винта с помощью показанного на рисунке приспособления могут быть поставлены под разными углами к горизонтальной оси впнта Перейдем теперь к способам исследования винта подвижного.
Между условиями работы винта подвижного и винта неподвижного существует очень большая разница. Один и тот же винт может давать очень хорошие результаты (большую силу тяги, малую затрату работы
на крашение» при неподвижной оси и очень малый коэффициент полезного
действия при его движении в воздухе. Между тем, главный интерес дляпрактики возду хо плавания представляют впнты подвижные. Отсюда и вытекает необхо щмость отдельного пселе овання винтов при нх движении относительно воздуха.
Существует два метода для такого после ювания: по первому сами винты передвигаются в пространстве, по второму — впит с неподвижною осью вращается в набегающем на него потоке воздуха. Прп последнем способе можно считать, что вннт как бы движется в воздухе со скоростью, равной и противоположной скорости потока.
Фиг. 261 представляет один из старых аэродинамических ипетн-т\тов (построен около 10 лет тому назад» — институт Сгоссо, основанный Finci и Soldatti. Сильный вентилятор сгущает воздух и бросает его через трубу на вращающийся винт, придвинутый по рельсам к отвер стию трубы. Определяя скорость вращения винта н силы, на него действующие, можно сделать заключения относительно свойств вннта в потоке воздуха.
Более подробно аппарат Сгоссо изображен на фиг. 262. Динамоме трическис весы позволяют при по-южении впита, представленном на рисунке, определить силу тяги; поставивши же их нерпендику лярно к указанному положению, можно
определить пару, вращающую винт. Фиг. 260.
На фиг. 263 пре (ставлены опыты
Сгоссо, аналогичные тем. которые делал в В. Т. У стул. А. В. Духовецкий
ФНГ 261-
и результаты которых он докладывал на первом Воздухоплавательном Съезде: кольцо с бумажками поставлено в поток воздуха, отбрасывав мни винтом; направление бу мажек показывает направление стру й потока Поток полу чается приблизительно цилиндрический, несколько закр* ни ный в сторону вращения вннта Бол- • внимательное ясспедование, как • было с делано Духовецким, н кап л ни. ’ что поток за винтом сна'жяа • \ вается. а потом сноьд расширь •• •
Многие прежде ставили на вннт ребра, чтобы не давать жии wubm
Теоретячггка» оггоаы вмзухоплааввия
К
воздуха удаляться от осн вннта 1под влиянием центробежных сил, как они полагали». -Это оказывается совершенно излишним: частицы потока, отбрасываемого винтом, сами стремятся приблизиться к оси. Явление
Фиг- 262.
Фнг. 263.
происходит так, как будто поток воз iyxa устремляется черед отверстие: стр\ я за винтом получает- я суживающаяся, а линии тока перед винтом похожи на те. которые получаются прп пстсченнп жидкости через отверстие
1аборатория Эйфеля была
уже описана ранее на стр. ч8— 89. ФПГ. 105. 106, {07. Здееь \ Ш»МЯ-нем 1ишь о Гом, что непог р»- v етвецио ОТНОСИТСЯ К ИСеЛ»« ЮВЛ-нию винтов.
Для iwc.ie юванмя вннт «•<>-единился «фиг. 2611 в одно цело° с дв\ хенльным мотором и ИОДВе-птпвалгя на двух тягах в ци.лин-(рп,1“ск«»м потоке воздуха, нр<>-1 екающем через камеру испита ння. Винт мог {вигаться нли вперед и назад, оставаясь парал-лельным себе, или мог-поворачиваться в стороны — направо ц налево.
Методы иге. о г гания винтов у Эйфеля и \ Ггоссо одинаковы. Разница заключает пыько в т< м, чт«» Эйфель пссчедовал винты в хорошо очерченной цилиндрической стрх*-. идущей нз одною тверстия комнаты в другое, а Сгоссе—в рассеивающейся струе. подобной струе, выходящей из трубы Рато. Способ Эйфеля более совершенный и имеет еще то удобство, что наблюдатели стоят в разреженной комнате.
Ко второй группе нссле даваний подвижного вппта относятся такие, прн которых сам вннт может перемещаться г ж* iae мой скоростью. Исследования этого типа будут поставлены \ наг в лаборатории иа ротативном
<1 аг _
приборе, построенном В. А. Слесаревым (фиг. 2«5 >). При после юванин винтов, поставленных на тележки, цшамомстры у потребляют^ по большей ча**ти гидростатические.
На <|>иг_ 26«». 207 и 268 изображена те южка. которая приготовлялась к*последней воздухоплавательной выставке в Берлине, но не поспела. Винт у нем — громадного размера. мотор в 100 л. с. От горизонтального вала мотора пере лап а идет сначала к вертикальному валу. а от него снова к горизонтальному, на котором сидит винт. Зубчаты'• г леса (для нпх устроены ушпренпя вве рху п внизу вертикального ва fa. вп [Ные иа риг. 2661 позволяют менять скорость вращения впита.
Движение тг,л°жк( сообщается от мотора прн помощи v Лой пере дачи к к< л» • дм, а не г upon ллера. Б. иг- )аря -тому < корость .вяления поводеи 1 п чпс.ли оборотов винта н '’свершение не зависят тру г от тру га.
i ила тяги и момент вра» щающеп пары определяются масляными динамометрами: чпею оборотов винта и скорость тете жкп определяются тахометрами; все показания перс даются на ряд циферблатов, помещенных в перечней части тележкп.
Сначала тележка была \с;ано кла в Гейл льберге. i . г । некоторым еиняч. она работала плох »; потом т- южка была перенесена в 11а; здесь if icj -вания винтов производил на нем Bejeuhr. которому удалось полу-ШТЬ прн атом ценные рсз\ ЛЬТаТЫ.
К]юме описанной, подобная же тележка с впитом устроена в новой Французской лаборатории в Saint-Syr’e около Медона. Здесь тележка двп-жетгя но рельсам, проложенным по горе и движущей силой является сила тяжести. На ггом аппарате произве юны былп -ммечатсльные исследования Дорана (Dorand)
Вместо того, чтобы ставить исследуемый пропс шер иа тележку, можно поставить его на лодку ити гидроплан, как это ° далал Eomarini на Lago Maggidre |фиг. 269). Наконец, в последнее время, пошли еще дальпю в этом направлении и стали устраивать лаборатории уже прямо на лея.(тельных аппаратах — как на дирижаблях, так и иа аэропланах.
Фиг 270 и 271 npi .-‘тавляют лабораторию Legrand а, устроенную на мр« ине. Гребпои винт (фиг. 270) приводится в движение мотором „Гном", прн чем сила тяш пере (ается легалетьному аппарату прн помощи ( ,лста-
Для полу ч< вия сравнимых между сь.юю результатов испытания рал 1Я лных м< •'Дей винтов необходимо получать для них Ео<4фицнвгг полезного действия с погрешностью, не превосходящей 3 ,. След, входящие выражение ь п. д величины силу тяги, работу и--тора н скорость ~ необходимо измерять с еще меньшей погрешностью порядна 1 , Такой точности намерений нельзя получить па ротативном пр»л"ре. в присутствия центробежных сил, во много (до ДО) раз превосходящих вес. п сп*тВ> .i «тока вызванного вращением всей фермы (фиг. 2( >1. Поэтому на ирнГ »ре щ изн итись • >«гы лишь качественного характера в ли по испытанию винтов на месте(0ез вращении фермы). 3 и гальиейшеи .ч>т ротатпвный прибор (ил спят. /7ри.и. г—*
точно сильной । пружины, позволяющей пропеллеру несколько передви-
Фнг. 2Ьб.
Фиг. 267-
1аться вдоль оси в своих по (шипникаж С помощью тру бок силы давления передаются измерительным прмб«>-______ _______________. рам — масляным динамометрам <на рис. трубки, ведущие к динамометрам.
i переплетены с трубками, подающими / I в мотор бензин и мае тор Маслянан ' колонка прнво щт в движение неко-
торый поршенек, который штифтом чертит на вращающемся небольшом хронографе, подобном тем. которые ставятся на зондах, нли силу тяги, или момент вращающей пары.
На фиг. 271 дано несколько другое расположение: видно, как подве-юны трубки, как расположен хроно граф и т. н.
Фиг. 272 представляет примерную шаграмму силы тяги за время одного полета. Левая часть кривой относится к началу полета, правая
часть — к спуску, средняя — горизонтальная- к нормальному полету
помощи описанного апиа-
Зная скорость движения и измеряя при
Фиг.
• 11 i « и iy тяги п чисто оборотив винта, получим ве< элементы, характери-• •щие винт при его работе на практике.
Несмотря на то, что опытное исследование винтов еше далеко не закончено, уже теперь наметились те величины, на основании которых можно делать заключения о качествах данного винта.
Эмпирические формулы Soreau характеризовали вннт тремя коэффициентами. Теперь Эйфель показал, что всякий винтхарактеризуется некоторыми двумя кривыми.
Фиг. 27U.
фиг. 2C-.-
; 34. Общий обзор теоретических исследований винта.
Все работы но теории винта можно разделить на 4 группы.
К первой группе относятся после овапия винта, основанные иа принципе подобия ц на принципе однородности формул механики.
В работах этом группы ра«*< матри-ваются серии подобных винтов и для тих серии выводятся некоторые • бшне шклю-пення. которые >атем проверяются на опыте п относятся к определенной серии.
Фш 271.
Фиг. 272
Представителями этой группы исследовании являются Eiffel, Renard Dorand и Ferber. Из них Эйфель работает в своей лаборатории, а Доран состоит руководителем института в Saint-Syr с, где имеется рельсовый путь <ля испытания винтов. Принцип однородности формул позволил капитану
Ферберу сделать замечательные выводы по теории винтов, которые, к сожалению. мало были известны; теперь, когда лабораторные работы так широко развернулись, выводы Фербера получают все большую и большую цену. На Всероссийском съезде Воздухоплавания присутствующие имели удовольствие слушать прекрасный [оклад капитана Шабского, как выбирать винт для дирижабля па основании графиков Фербера.
Вторую группу составляют последования пропеллеров на основании обшпх формул механики, а именно: теоремы количеств движения и теоремы живых спл; здесь особенно хорошо поддается исследованию геометрический винт. «Это направление впервые было установлено Мюнхенским профессором Финетсрвальдером (Finsterwaklen Ч. Он п Bendemann, а из русских Д. П. Рябу шинскпй очень много занимались определением количества движения п живой силы массы потока, отбрасываемой винтом. С опытном стороны исследования Рябушинского являются главными для суждения о плодотворности по (обной теории. Еще раньше Рябушинского в атом же направлении работай! Патпцк Александер.
Этот метод все: * . плодотворен и с помощью его теория винта может быть хорошо разработана
Третья группа работ заключается в рассмотрении набегающего на винт потока как бы состоящим из отдельных летящих частиц: в нссле-"ованпи материального удара этих частиц о крылья впита, на которые они вступают под некоторым углом, н определении потери энергии вследствие этого удара. Этот способ рассмотрения работы винта аналогичен теории епцротивдеиия Ньютона для поступательных движений нластпнки.
Главным представителем этой теории является Rankine. Можно указать п лруми авторов—среди русских ученых проф. Д. II. Рузского, который эту тему выбрал для своей диссертации иа звание адъюнкта в Киевском Политехникуме.
Четвертая группа работ зактючаетея в разбитии впита на отдельные ♦тементы цилиндрами, ось которых с овпадает с осью впита, рассмотрении всякого отдельного элемента как пластинки н распространения ua нет формул, bhbi денных из наблюдений над ударом потока воздуха на пластинку. Это есть метода, которая была положена в основание прекрасно разработанной теорип впнта Джевецкого. а также теории Рато.
Из четырех указанных направлений одни га и» оплот войти глубже в теорию впнта с одной стороны, а другие — другой. Например, теория ударная (Rankine, Рузский! со ершенно упускает из виду число лоцаетей винта (по существу, она больше ••оответствует винту со многими топа-етямп|, а теория Джевецкого слишком высоко оценивает влияние увеличения числа тог детей винта п их и тощадн. По носледенеп теории tai а впнта пропорциональна числу лопзетси, между тем как эта пропорциональность опытом опровергается. Если п есть разница между трех- и дву лопастным винтом отношение пх тягп будет все же меньше, чем 3:2), то нрп уветичеяии числа лопастей сверх шести сила тяги нс возрастает.
Все указанные теории страдают одним недостатком: в иих ие рассма-трш .ется п< гок жи [кости в радиальном направлении, а предполагает» я. it [вижущаяся воздушная масса как бы течет в цилиндре, соосном винту, •♦то предположение особенно неверно [ля геликоптерного впнта. потому • то там эффект подсасывания оч^нь резок и частицы, как показывают [иаграммы студента В. Т. У. Духовенкою н других наблюдателен, идут а гиба ясь, как будто жидкость вливается в отверстие винта. Если сколь-
Ч Его лекции ие напечатаны, а известны по литографированным выпискам: иаи вошли в статью Bendcmaon’a. помещ» иную в .Журнале немецких инженеров' и--ре еденною в Бюллетенях Политехническою общества (1УН> г. .V 7).
женпе винта близко к ну лю, тогда, действию ilho. радиальное лвиженне неве тико.
Слетавши эти общие заключения, перейдем к рассмотрению тсорпи. на которой основывались иестедования первой группы.
§ 35. Теория Эйфеля, приложимая к подобным винтам.
Эйфель ставит ту же задачу, «по и Ренар, ио рассматривает ре подробнее, чем последний; поэтому при изложении теории Эйфеля мы получим, как частный случай, и формулу Ренара.
Предположим, что мы имеем винт какого-либо вида с диаметром, равным единице. Тогда, изменяя этот винт подобно во всех частях, получим целую серию подобных винтов.
* Вообразим, что винт с диаметром I) движется поступательно слева направо параллельно своем оси со скоростью V и вращается с числом оборотов А’ в секунду, по часовой Ч стрелке — для наблюдателя, смотрящего сзади и сверху. На фигуре 273 винт изображен в тот момент, когда лопасть А стоит горизонтально.
Скорость посту нательного движения 1ля всех точек винта будет выражаться одним я тем же вектором Г. скорость же вращения, а следовательно и абсолютная скорость, будут для разных точек разные. Для какой-либо точки М скорость вращения будет выражаться вектором Мп — 2 -т Ат > О V, а абсолют t а ная скорость — вектором Мт. Скорость с вращения точки А, лежащей на окру ж-фиг- 2|3- пости винта, выражается вектором 4с =₽
— л DX, а абсолютная скорость ее — вектором „4«. при чем тангенс угла нактонеппя последнего к осп винта (горизонтальном на фиг. 273) равен отношению Для любом же точки 5/
этот тангенс будет равен --.
Если изменить в одно и то же число раз как поступательную скорость И, так и скорость но окружности .~iDX, то углы встречи отдельных струн с элементами вннта хх и утлы этих гтру п с осью винта не изменятся; следовательно, нс изменяется н направление сил давления на каждый элемент винта, а вместе с ними и всей равнодействующем силы. Другими словами, какова бы ни была скорость V. равноденствующ.1 я имеет одно и то же направление. если только ие менпетея отношение — или проще
Силу удара ветра, как показывает опыт, во всех явлениях опроти-в.ления можно считать пропорциональной квадрату скорости.
На этом основании Эйфель полагает, что общая равнодействующая 1ля лопасти вннта с диаметром, равным единице, будет равна
г 1де коэффициент А должен зависеть лишь от отношения скоростей
или проще от отношения . .Перехо 1я теперь от винта с диаметр» »м. равным единице, к винту, подобному ему. но с диаметром D. мы увели-
jyt
чим площади соответствующих элементов в отношении . Тогда, при том же отношении скоростей, направление полной силы, действующей па лопасть, не изменится, величина же ее. которую Эйфель обозначает через Ф. бу 1ет не J Г2, а в D1 раз больше:
Ф = К'-’р’
Вво 1Я обозначение:
находим, что
0 = Ax№D‘^B5 = №D‘f(^ =V’D‘flZi. . 1197)
так как Л есть фу икпия . Итак, равнодействующая Ф (авлеппй на каждд ю лопасть пропорциональна произведению №£>* н. кроме того, зависит от величины К: направление же равнодействующей зависит только г д. Чтобы найти тягу винта R, нужно г множить силу Ф на когпиус утла наклона ее к оси винта iHa функцию м п на чпе ю лопастей. Сделавши это, получим, что сита тяги
й-вП)*,. . . П98)
1д*- коэффициент а должен зависеть лишь от величины
Если бы мы стали определять момент пары сопротивления, то гсть умму моментов впех спл давления относительно иси винта, то пришлось ы равнодействующую Ф спроектировать на направление, перпендикулярное к потоку (помножая на синус угла наклона силы к оси винта), а питом к-множить величину проекции*па расстояние равнодействующей от -си вннта и на чисто лопастей. Упомянутое расстояние в группе подобных винтов пропорционально диаметру D, поэтому в формулу момента диаметр 1) будет входить уже не в 4-ой степени, а в 5-ой.
Для полу чения же секу ндной работы на (о номнижнть момент пары противления иа угловую скорость 2лЛГ. Поэтому, секундная работа
T=JN9IF,........................(199»
• (е коэффициент ,? будет зависеть также только от л. Формулы (198) и (199i \ть формулы Ренара, который считал в них коэффициенты а п j постоян-пы.мп для данной гру ппы подобных винтов. По изложенной же здесь теории Чпфедя, эти величины суть функции К, как это и подтверждается наб лю-•нмямн.
Напомним, что в основание теории Эйфеля легли две гипотезы: ^-первых, закон ква (ратов скоростей, и, во-вторых. цопу щение. что закон распределения струй зависит только от величины Л = нисколько не 1ВПСПТ от абсолютной величины скорости Г, подобно тому, как. например, направление равно [ействующеп (авленцп на пластинку завпент только от ji (а наклона плаетникп к потоку и не завпент от самой скорости. Но эго тушение — только гипотеза, приблизительно верная прп ие очець больших скоростях. При больших же скоростях могут развиваться вихри и может ш тучаться новое распределение скоростей в потоке, а вме- ге «тпм изменяться и самый вид функций а и Д.
*3 Величину можно рассматривать, как отношение пути, пройденного bibtom киль оси за одни оборот, к диаметр) винта
— 21Ь —
Из уравнений (196» и <199) следует, что
° = ;т^>. = Л </>. ..........'2М>'
Э= Г^=/,1Л1......................'2011
Если найти функции Д и f?, т<> нее в данной группе подобных винтов будет известно, потому что все свойства их вытекали бы из свойств этих двух фрикций.
Здесь будет полезно отметить, что размерность величин а и ft, равно как и коэффициента к известной формулы сопротивления Q — kFV2, одинакова с размерностью плотности р =
В самом лете, из выражений i200i и <201 вытекает, что
'“1 -= [*’ “ii ‘
Точно так же !*]=[£ = »'Г‘ ~<=].
Для массовой же плотности ‘ имеем:
9
Ы=[^- ~*J ‘ -2|
Итак, величины а, 3 и к имеют тот же самый размер. что и плотность
Из коэффициентов а и £ так же, как из А*. можно выделить плотность н виде множителя, потому что сила iai лени я т гущей жи »сти на те.и. как прекрасно доказано разнообразными опытами, пронорпиональпа и’ни ности. п написать*
а я 9
Тогда величины —, — будут
нулевого
и ?м»р. НИЯ.
р
= [Ат/ т(
9
— ,п^
<\
Посмотрим теперь, насколько опыт оправдывает теорию Эйфеля.
За независимое переменное при определении функции а и ,3 Эйфель принимал величину к Изменять же последнюю можно пли изменяя скорость Г потока при постоянном числе оборотов винта, или изменяя его число оборотов 2V при hoi гоянной скорости потока.
При опытах, результаты которых представлены на фиг. 274. 275 и 276. произведение ND оставалось [ля каждой кривой приблизительно одним и тем же, так что каждая кривая на шаграммах соответствует постояв-
ному числу оборотов Л; величина же /. менялась лишь путем изменения скорости в 'трубе Г, доходя до значения К=1, соответствующего скорости Г=Л7). Пунктирные продолжения кривых доходят до осн ординат, где они отмечают точки, соответствующие ге. шкоптерному винту.
Фиг. 27-1-
Фнг. 275.
Пунктирная кривая i VD='24.I построена Дораном ио его опытам в Saint-Cyre на колясках. Эйфель д»лал опыт с винтом, m лобным винту Дорана, но в 3 рала меньшим. при чем окружную скорость к»я почти ту же ( VD = 24.1 mt & с).
Оказывается, что кривые, полученные в том н другом случае, очень олпзки друг к другу.
Вообще ио опытам оказалось, то течение кривых а ця подобных винтов от размеров их мало л висит. Скорость же на окружности винта оказывает на них •••лыпес влияние. При у меньше пни ее и а несколько ууменьшается По в сущности вс*1 эти кривые »ГНЬ близки Друг К другу И I" гпто чно хорошо опрашивают теорию. согласно которой все они лжны совпадать друг с другом.
Ренаровский коэффициент а. определенный им для геликоптержн винта, равняется 0,020. Опыты Эйфеля показали неправильность пр и •-
шжения, что силу тяги винта г< лпкоптернлго можно считать динм». i й силой тя!н винта in движного.
Что касается коэффициента секундной работы — /?, то значения ег нанесены на диаграмме фиг. 275, при чем за независимое переменное принято снять X.
Верхняя (пунктирная। кривая—Дорана, а остальные Эйфеля. пи кривые ,3 ичут еше ближе ipyr к ’ругу, чем кривые а иа фиг. 274.
Когда сила (коэффициент at обращается в нуль, работа iкоэффициент /?| в нуль еще не обращается. Диаграммы показывают, что вблизи точки, где сила обращается в нуль, можно приближенно считать работ} и силу тяги изменяющимися по закону прямой линии. При этом сила тяги представилась бы прямой, пересекающей ось абсцисс прн к 7^1. а работа представлялась бы линией, пересекающей ось абсцисс при большем значении к. Поэтом}, если начало координат поместить в точку, где а = 0. то сила тяги определялась бы одним коэффициентом— углом наклона указанной прямой к оси абсцисс, а работа— двумя коэффициентами. Эти прямые понадобятся впоследствии, когда будет излагаться теория Фербера.
По кривым а и j? Можно определить и коэффициент полезного действия впита г). Он выражается отношением ееку и шых работ: полученной .RJ’ и затраченной Т:
R1 aXWV ai.
Ч=-у-= .д-да =-, . <202!
Если кривые для а и/?уже вычерчены, то па основании выражения (202 > без тру ia можно построить и кривую для rj (фиг. 276>. Из диаграммы видно, что ij обращается в нуль (ва рала: когда Г = 0 (впит геликоптер-пый| и когда /»’ = о. Кривые ij для различных SD сначала (при малых Л» очень близки к слиянию, а дальше несколько расхо (ятея. Верхняя iпунктирная! Дорана, остальные—Эйфеля Паивы годнейшему действию винта соответствует значение параметра к, близкие к “ топ», при котором R — 0.
Если считать, чти для каждого типа винта существует только одна • mpt де лепная пара кривых а и независимо от скорости на окружности винта ,tDV. то опыты для построения этих кривых при разных типах винтив делать будет очень просто Можно поставить мотор с винтом в трубу я луть в нее. Измеряя число оборотов винта и скорость ветра в трубе, р
>тк (адывасм по оси абсцисс величину к-= а по оси ординат вели-
чины а = у2/>4и уу>- основании сделанного юпущенпя, при гру-
бых опытах можно и не стремиться к тому, чтобы подогнать на окружности винта одну и ту Же скорость
£ 36. Понятие о шаге и скольжении впита.
В геометрическом винте шаюм называется тот п}ть, который бы винт прошел параллельно своей оси в соответствующей ему гайке за о шн оборот. Если такой винт (представляющий очень топку ю винтовую поверхность). вращаясь в воздухе, бу дет двигаться поступательно так, как <я лвигалея бы в неподвижной гайке, то он не бу д< г в'озму щать во/духа и не разовьет силы тяги. Поэтому можно сказать, что шаг геометрического винта равен тому пути, который пробегает винт за время одного оборота при отсутствии силы тяги.
Если обозначить через Г—скорость поступательного движения винта, •дерел А’—число его оборотов в секунду, а через Н шаг впнта. то для Геометрического винта бу ют справедливо такое соотношение:
Н— £ при /? = О. . 1203,
В винте, (ля которого Нельзя указать соответствующей гайки, принято шаг винта характеризован, динамически, именно: по аналогии с геоме-
трическпм винтом, шагом винта произвольной формы называют и5 ть, который проходит он яри одном обороте, когда ого сила тяги равна ну 1ю Ч
При таком опрегелеиин шага уравнение 1203» будет иметь силу’ уж< ие только тля геометрического винта, но и тля винта любой формы.
В. А. Слесарев для определения величины приложил такой прием к винту, находящемуся на ротативной машине, пристроить маленькое перышко н параллельно пути винта поставить круговую дужку из закон-ченой бу Mai и. Тогда винт, вращаясь около своей оси я двигаясь вместе С ротативной машиной, вычертит на закопченой бумаге перышком ряд черточек, но которым можно определить путь, пром тонный винтом при одном обороте. Если тяга впнта В бу ict равна нулю, то расстояние между шумя смежными черточками и будет проставлять шаг винта.
П1аг можно определить и но Эйфслевеким кривым, ес ш знать тиаметр винта D и то значение К, при котором сила тяги В равна нулю ш —0| так как нз выражении П%| и <2O3i еле (ует, что при Я = 0
г я ' XD ~~ D
Величина отношения шага винта к диаметру называется пропорциональным шагом: обозначим его через Л. Тогта будем иметь такое соотношение:
h = ” (2041
Еста винт движется в воз. iy хе не со скоростью УН, а с иною (Г), то говорят, что он скользит в воздухе. Абсолютное скольжение (за “Динину времени) будет равно УН Г, а относительное
_ №—Г Г,______1
' ~ ХИ — 1 ГВ 1 *
Величина г полу чается отрицательной, когда 1 > УН, то есть когда впнт работает, как мельница. Решая уравнение <170» относительно л, найдем:
X = —И. 1206)
1205»
г 37. Поверхность тяги винта.
Скажем теперь несколько слов, как собрать весь опытный материал < винтах в одно целое. Очень удобно это е делать, как нре длагает Dipl-Ing. В. С. Маргулис ’>, рассматривая поверхность, соединяющую вес, что дают различные * опыты над ним. Представление об этой поверхности очень важно.
Сила тяги R является для данного винта функцией только поступательной скорости F п числа его оборотов -V. Эту функцию на основании уравнений (198) в (200) можно написать в виде:
ff=fi.V. l'i №/, (£| . - '1W
>) По многочисленный опытам (Д. П. Рябушинского, Дораиа и др.) оказалось, чт итвошеиие \ прн не меняется при изменении скоростей.
*) Был в то время (ШН г.) экстерном в В. Т. У и членом Воздухоплавательного Кружка
Будем по оси х откладывать числа оборотов V, по оси у — скорости Г, по осп г—силу тяги R и посмотрим, какая поверхность получится при этом п|шг. 277).
Перетекая поверхность плоскостями, проходящими через ось К бу тем получать в с» ченпях параболы второй степени, так как для таких плоскостей
J = /g BUN=const, и
It — № • const.
Вершины парабол лежат в начале координат, а оси совпадают с >сыо R. Па фит. 277 эти паработы представ Тены сплошными линиями Ор1 и Oqt-
Парабола (ОрЪ. по которой пересекается поверхность с плоскостью Г = 0. соответствует геликоптерному винту. Когда ^,=Н. где Н шаг впита, парабола обращается в прямую линию. лежащую в тонкости АТ) Г, так как тг
при ^~Н сила тяти _R = 0. Отсюда заключаем, что рассматриваемая поверхность пересекает плоскость Л’ОГ по прямой линии 10.41. Вся часть поверхности внутри угла АОЛ', для которого tg АОХ— Н. расположена выше плоскости VOF и (ает положительны»- значения гля тяги. При больших ж» углах точки поверхности расположены ниже плоскости УОГ 1фуяк-ция f\ переменит свой знаю; тогда для силы тяги получаются значения отрицательные, и винт будет работать как мельница ветер настолько вели к, что сила тяги винта направлена назад.
Для построения линпй пересечения поверхности с плоскостями, парал-юлЬиыми плоскости R0X (одна из них — O'bd' —показана иа чертеже», нужно пользоваться опытами, при которых К держалось по<-гоянным, сила же тяги менялась путем изменения числа оборотов -V. Будем эти шипи называть кривыми Рябу ппшекого. так как он произьг т в этом напра? гении многочисленные исслн звания, и у неги имеется полная таблица таких кривых 1тя разных винтов и скоростей. Эти кривые пересекают плоскость I ОА’ конечно, в тех точках i/п, где их плоскости п<*р»*р«'нают прямую £ = Н. Направо от этих точек кривые юнду т вверх, что бу ют соответ-рцювать положительной тяге. Эта часть кривых имеет приблизительно впт парабол, смещенных вершинами вниз и вправо. Для точек кривых, лежащих нтево от точкп а. соответствующих случаю, когда число ибиио-п»в настолько мало, что скорость ветра Р превпехо шт произведение УН, сила R будет направлена в обратную сторону. В этой части кривые имеют minimum (точка /т.
Что касается плоскости НОГ, то ее кривые пересекают ниже оси ОV. лтн показывает, что кома число оборотов равно ну по, существует оцре-•• ленная сила (О/), действующая на винт по направлению ветра.
Плоскости (наир., O"bdh, параллельные R0V, для которых А’= o©nsf. • ддут рассекать рассматриваемую поверхность тягн но некоторым кривым» kn(j\, имеющим выпукло ть вверх. Кривые эти выражают силу тяги инта при постоянном числе юротлв и суть кривые Эш> гевекого коэффициента а.
В самом нл.-, при постоянном *V и D, величины
торыс откладывает «Эйфель по оси абсцисс и оси ординат, гоответственно пропорциональны V и R, которые откладываем мы при построении нашей поверхности. Поэтому вид кривых будет одинаков, масштабы же будут разные. Чтобы найти, например, а для геликоитерного впита i нужно {резок 0"д (фиг. 277» разделить на произведение V2/?.
-Зная для данного вннта пли кривую Эйфеля, или кривую Рябупшн-«•кого, мы бу м знать и вс- поверхность тяги, потому что все сечения и ?»скостямн. проходящими iepc3 OR, будут параболы. Для постр> ни я u-н -рхпостп на •) будет через ось OR проводить различные и !•••• ги и строить на них параболы, проходящие через точку персе» чения i i - к <тгн с кривой Рясу hi инс кого шли Эйфеля). Имея гл я занною впита ря
кривых Рябушииского шли Эйфеля» или нронлво (я наблюдение при постоянном у , можно исследовать н самые параболы.
Так как исследования не доводятся ю очень больших V и Л. то на практике тля построения той части поверхности тяги, которая <<»«»т-ветствует малым надо пользоваться кривыми Эйфеля, а той, которая соответствует ^>Н. кривыми Рябушииского.
На фиг. 278 *1 279 приставлены кривые Рябушииского. По оси ординат отложены силы тяги винта К, по оси абсцисс чиста оборо-
Фжг. 278.
Фиг- 279 О-
тов Л; каждая кривая построена тля определенной скорости ветра К которая доходила до в mt sec. Чисчи оборотов винта менялось в пределах от N — — 30 до # = 30 обор сек.
Те части кривых, на которых винт работает, как мельинца, для воз-ду хоплавания не интересны. Отметим только ту их замечательна ю особенность, что они имеют minimum прп положительном N: этот minimum исчезает при большом шаге. Точки пересечения Kpiniwx Рябушииского с осью абсцисс (7?=0) даду т точки пересечения поверхности тяги с плоскостью NO V.
Рассматривая кривые, мы можем убедиться, что формула (203». данная 1ля определения шага винта, довольно хорошо совпадает с наблюдениями. В самом деле, умножая шаг винта Н (он известен, так как у Д. П. Рябу-
Ч На фнг. 279 следует читать А= = 1,0 (вместо 0.51
шивского нес ie девались впиты геометрические» на число оборотов Лт в той точке кривой, где /?=О, мы получаем (табл. 25 и 26) числа, очень близкие к действптс п>ным скоростям, при которых испытывался внпт.
Таблица 26.
Средние величины УН п иогрешность в •' 0 для винтов таблицы 26.
Л’Я 2,00 4.31 ’•.68
—- .
1 ?/• 45 ftP
. 1 —1 i —
Погрешность в п 3 3 4.2 .43
Кривые Рябушииского можно перестроить на кривые Эйфеля, изменяя соответственно масштабы абсцисс и ор шнат. Число точек какой-либо кривой а (про-изне деппе ND для нес постоянно) равно числу кривых Рябушпн-екого, построенных для постоянных скоростей V. На фиг. 280
и 2S1 изображены построенные но кривым Рябушпнскоги кривые а для двух винтов: с шагом H = 0,3D и шагом H=\&D. Рассматривая их. вишм, что они и по характеру.
и по величине ординат довольно близко но (ходят к кривым, полученным Эйфелем.
Фнг. 281.
д 38. Теория Фербера, основанная иа принципе однородности формул механики.
Самые выдающиеся исследования в области теории винта и практические выводы нз нея принадлежат капитан.) Ферберу.
Иа основании идеи однородности формул механики Фербер ио дходит к почти оконченным формулам тля винта. Вее силы, действующие на .--.па . саоаы аоадуховаваалва. 15
винт, зависят: во-первых, от коэффициента сопротнв теиия к„ в разных жидкостях в зависимости от их плитноети и коэффициент сопротивления будет разный (тля простоты его можно взять из опытов с прямым у даром на пластинку >; во-вторых, от геометрических размеров винта: диаметра D и пропорционального шага h; в-третьих, от кинематических элементов: числа оборотов V и от скольжения г. Поэтому, в самом общем виде можно написать, что тяга
R — ф1 (к, г, Л, V, D)......... . <207)
при чем шаг надо полагать в смысле уравнений (203) и (204). Точно также и секу ндцая работа винта будет зависеть от тех же элементов, т -е.
Т = ф.> (к, г, h, \, I))...............(20s)
Замечая, что коэффициент к имеет размер плотности:
[А] = [ftp1, mt~*t sec ’],
Фербер рассуждает далее так: слева в уравнении (207) стоит сила R; в правой части зависит от си ты только коэффициент к, н притом зависит линейно; сл-довате 1ьно, он должен войти в праву ю часть выражения (207) простым множителем. Тог та вся остальная часть формулы относительно силы должна быть нулевого измерения. Далее, так как время входит в коэффициент к во второй стспенп, а из остальных ве шчин только одно А зависит от пего, имея размер [see-1], то N должно входить в правую часть формулы (207) во второй степени. Только в таком случае зависимость второй части формулы от времени уничтожится. (3 другой стороны, к относительно длины имеет размер (—4). Значит, D должно входить в четвертой сгепеии, так как остальные элементы от длины не зависят.
На основании приведенных рассуждений Фербер заключает, что в формулу (207) должен войги множитеть kN^D*. Что касается остальной части функции, то она должна зависеть только от отвлеченных величин, которыми могут быть только h н г; следовательно, выражение для тягн должно иметь такой вид:
R— АЛ(й, г) . , . (207*)
Что касается секундной работы, то для получения ее надо помножить си iy на скорость, так что размер ее будет [A;/1 mt1 sec-1]. Поэтому, но сравнению с выражением для силы тяги в формуле для работы прибавятся еще множители .V и D, так что бу [ем иметь:
Т=кХЧРъ, (h, г), . . (208'
где —некоторая функция отвлеченных величин Л и г. Воя задача ево-дптся теперь к определению ви ia фу нкций о?! и для разных винтов. В основе рассуждений Фербера лежит общая идея измерения— измерение к—и предположение, что формула не меняет своего строения от абсолютного значения входящих в нее величин; этим предположением пользуется и Эйфеть при изложении своей теории. Дальнейшие рассуждения Фербера, которые идут дальше, чем рассуждения Эйфеля, опираются на то, что формулы рассматриваются им для малого скольжения г (при этом условии винт работает наиболее выгодно). Последнее предположение дает дальнейшее развитие формулам Фербера. Если г мало, то функции и ф.2 можно развернуть в ря i по степеням г и ограничиться первыми степенями. Тогда можно написать:
|Л, п А' 4г.
Ъ ih, r) = ir-t-Rr.
где величины Л. 4, В и В суть функции ишигоЛ. Тогда формулы (207') и (208) перепишутся так:
R=k№D* (4'4-Jr . (207")
T=kNsI^ (B'-^-Br) . . (208'9
Положив
a = k (A'+Ar),
0 = k (ZT+Br),
и подставив их в (207*) и (208 ), получим формулы Эйфеля (iOS) и (199).
Найдем теперь зависимость величин Л, А, В’, В от й. Если скольжение будет равно нулю, то винт будет вращаться как в гапк» и силы тяги никакой пе бу (ет (эго следует из определения шага винта). Другими словами, когда г = 0, то и с ю. !жно обратиться в нуль, гак что
АЛ' = О.
Отсюда зактючаем, что А' очень мало иди прями равно пулю. Далее. е«- in h меняет знак, то и R меняет знак. Следовательно, й должно входить в Л в нечетной степени; Фербер допускает, что
кА = ah.
Что касается коэффициента работы (S. ю разделим его, как в формулах Ренара и Эйфеля, иа две части. Часть его кВ' зависит от трения и принимается о иг каковой при всяком й. Обозначим се кВ' [Г. Эта величина очень важная, хотя и бо 1ьшпнстве теорий винта она принимается равн«»п нулю. В рассуждениях Ранкина она называется коэффициентом вытеснения. Коэффициент кВ должеп о- iep/кать множителем Л, так как ирп h 0, т.-е. при обращении винта в диск, г становится бесконечно велико, а работа должна быть конечна. С другой стороны, h не может входить в выражение работы в первой степени, а должен входить в четной степени, так как, если величина Л изменяется в—й, то работа не изменится. Фербер принимает, что й входит в выражение работы во второй степени и полагает:
кВ=?№.
Па основании всех этих рассуждений получаем формулы:
/? = «Лг№1>. . (209)
Т=(/?'й2г+^") A’»7F.................(210)
а кроме того, на основании ур-ий(19б) и (206):
Г=й\7)(1— г).....................(211)
Это основные формулы Ферй-ра
Подобный же формулы с тремя коэффициентами подучает Soreau на основании эмпирических данных.
Энфслевские коэффициенты « н но теории Фербера выразятся таким образом:
a = ahr . . . (212)
0 = /Г+?к’г . (213)
геди в эти формулы подставить выражение- г через Л (ур-не 2«»5). то ио. гучим:
а а (й —А). . (212)
Д = /'+£й ГЛ—А) ...................(213)
Поэтому, если провести иа фиг. 274 н 275 прямые линии, близкие к Эмфетевскям кривым ан? около того места, где 1?=0, а. следовательно, и г=0, то это и будут кривые а п по Ферберу. Если кривою а Продолжить до пересечения о осью абсцисс (для Эйфедсвского винта лто бу дет при а = 1), то абсцисса точки пересечения Ло по форму ie (2оо) 6} дет равна проворциоиальному шагу винта ft. Если изменить на фигурах 274 и 275 масштаб осп абсцисс через умножение на а начало
координат перенести в ту точку, где а = 0, то кривые Эйфеля вблизи начала координат н представят приблизительно те прямые Фербера, кото-f'He даны форму шми (212) и (213). 1рныая а пройдет через начало координат, а прямая /? через него не проходит. Фербер определи.! прямые а и для винтов Левассера (фиг. 282). Да-хьнейшие исследования Фербера состоят в следующем. Он принимает за независимые переменные скольжение г и коэффициент полезного действия винта ч = (ем. теорию Эйфеля) н выражает через них все оста, тьные элементы, характеризу ю-пше винт и его работу. Затем он строит графики этих элементов для
Фнг. 282. каждого типа винтов с одинаковыми
а‘, У и /Г и на основании этих графиков подсчитывает вннт но заданным условиям его работы. Выразим через г н ij те эхемепты винта, которыми Фербер пользуется для расчета. На основании ур-нн (209), (210) и (211) имеем:
Ь‘ F __ a 'hr V2Z>* • XhD (1 — г) _ а'Л’г (1 — г)
" Т ~ (£№г + 3 ~~ Th*r + ,гг ’
.(2Н>
отку да
л’ =---------
a'r (1 — г — Д ч)
Это есть первая расчетная формула Фербера.
Вторая расчетная величина Фербера есть й, определяемая выражением:
DV
1 R
Для нахождения ее разделим R на Г2. Тогда получим:
R ____ a'hrN'-D1_______a'r
Г2 ~ №Л’Лг (l^rf "" (I—ry-h 1’
где ft, по ур-пю (215), есть функция только г и ij. Отсюда уже легко найти:
л
Й= VR
(1 -
I аг
.(’Hi)
1И теперь из основных формул Фербера — (209) и (211)— исключить D, гавить Лт, для чеГи надо В разделить на Г4, то будем иметь:
К ___ a'hrX'D1 ____ a'r I
тг (1 —гр — 7Г— гр Л3 V* *
Из этого выражения получаем третью расчетнуювеличину Ферберау,
которая является тоже функцией то.1Ько и и г и служит 1ля определения Аг:
V*
1 а'г
(I-ГРЛ1 2
(217)
На основании трех указанных рирмул можно, задаваясь ве-ичинами г} н г, определить мгличпны h, 6 н у, а по ним Н, I) и N.
> помяну тын I рафик Фер-• ра строится с теду ющим об-р1мом. Откладывая по оси <гннес г (от О до 1), а по " и ординат т] (тоже от 0 до 1), отмечают точки, дтя которых одна из вспомогательных в&шчии (ft, 0 или >') имеет одинаковое значение. < М* линяя их друг с другом.
Получают кривые, для кото-пых Л, й или V ПОСТОЯННЫ. ФиГ- 283’
11а фиг. 283 кривые этн представ дены: ft — сплошными линиями, й — большим пунктиром с точками.
Л е -коротким пунктиром.
Пользование графиком Фербера при выборе винта будет показано
Ниже, в 42 и 13.
39. Теория винта, опирающаяся иа общие теоремы динамики.
Теперь перейдем к теории випта, опирающейся иа общие соображения механики: на теоремы количеств движения и живых сил. В ней. главным образом, рассматривается, как втияет суммарное количество дви-ынпя на подъемную силу геликоитерного винта н на еиту тяги винта пж\ щегося.
Прежде всего остановимся на условиях возникновения силы тяги при вращении винта.
Па первый взгляд кажется, что струи в гедикоптерном винте обра-• ют замкну тые линии, которые вес пересекают винт 1) н симметричны относительно его птискости; жидкость движется по ним сначала к винту, '«•том из-под винта, кругом, снова к винту, и т. д. (фиг. 284). Решая \ю задачу, мы никакой подъемной силы по.iy чить не можем. Эту мы ль • hi. ясно отмечает Бендеман в своих общих рассуждепиях 1 б уетрой-
*) На подобна ситовых линий магнитного поля, образующегося около кольца, по которому течет электрический ток.
стве винта, которые он ве ют на основании ненапечатанных лекций профессора Финстервальдера.
Но такая задача не соответствует тому, что происходит в тействи-те.тьности при вращении винта: струи, его обтекающие, имеют ту замечательную особенность, что лпнни тока перед винтом и за винтом несимметричны. За винтом получается струя, которая движется со скоростью, значите 1ьио превосходящей скорость окру жаюпюй жидкости н образует разрыв жидкости.
Около струн, отбрасываемой геликоптерным винтом, воздух спокоен, и можно даже иабдю шть движение в обратную сторону
В винте гребном этого обратного движения не будет, ио будет скачок скорости: за винтом жидкость, текущая со скоростью, соответствующей скорости всего потока, и жидкость, текущая с большей скоростью, будут находиться в непо-ерс д'твенной близости одна от ipy гой.
Струя, образуемая винтом, шрает роль, аналогичную той, которую играет струя, вытекающая через отверстие — из сосуда с водой тоже в воду. Это-то обстоятельство—образование «за вингом разрыва жидкости и отдельной струи—и дает силу тяги винта. Если мы будем исследовать эту струю, то пай тем, что она развивает трение об окружающий ее медленно текущий ii<i3iyx, па (остаточно большом расстоянпп от вннта замаскировывается и, наконец, сливается с общим потоком воздуха.
Все силы трепня, образующиеся вследствие разрыва жидкости, направлены в одну стиролу и, с тагаясь, дают ту силу, которая то щает винт против потока
Хотя трение и является истинным источником силы действия винта, ио решать задачу с трением мы отказываемся- вследствие ее трудности— и заменяем ее иной задачей.
Охватим винт (фиг. 285) сферой, описанной из центра винта, боль-” —---------- ------— " ------- “ сравнительно с безграничным про-
Фиг 285.
шой сравнительно с винтом, но малой С] страиством. Вну трп этой сферы трение играет незначительную роль, и здесь мы можем, не принимая его во внимание, рассматривать задачу чисто динамически, считаясь только о тем, что струи образуют разрыв: это дает нам возможность считать, что мы под винт как бы подставили трубку, ограничивающую крайние стру н, протекающие через внлт. Внутри этой трубки будет течь отдельная струя, а со всех сторон жидкость будет подсасываться к ней и вливаться в нес. Тогда мы получим возможность опре юлить силу тяги винта по количествам движения. Для этого придадим всеп системе iвинту и жидкости! скорость винта в обратную сторону так, чтобы винт не имел поступательной скорости, и рассмотрим распределение около него линий тока. За винтом имеется отдельная струя, имеющая основанием площадку CD на поверхности сферы, а в»» всех 1ру гих точках поверхности сферы жидкость
при гребном впнте течет со скоростью V, а прн геликоптерном винте со скоростью, близкой к нулю. В случаи винта гребного только та часть линий тока, которая вступает внутрь сферической поверхности через площадку АВ, проходит через випт. Все же остальные линии прохо дет, изгибаясь, мимо впита.
Ее.ш винт будет геликоптериый, то линии тока будут направлены как показало на фиг. 280 Ч-
Рассматриваемая теория охватывает, таким образом, общим анализом и гезикоптернын впит, и пропеллер, и является для пих общей.
В действите шности подсасывающий
аффект существует как в геликоптерном, так и в гребном випте; н в тех теориях, где ои не принимается во внимание, как, например, в теории Джевецкого, мы имеем некотору ю неточность.
Для опре деления сизы действия жидкости на винт надо, ио теореме Эйлера, подсчитать приращенпе секундного количества движения жидких масс.
Жидкость, которая течет мимо граничного конту ра АаС, ВЪТ), вся бу дет течь ио струйкам, которые немножко изогну тея около винта, а потом выпрямятся и пойдут параллельно, так что массы, скорости и количества движения на концах струек, обрезанных нашей сферой, будут одни и тс же. Поэтому надо считать массы и скорости только на площадках АВ и CD.
Фнг. 286.
Чтобы получить силу, действующую на винт, надо количество движения выходящей струн считать направдениым в сторону, обратную потоку, а количество движения входящей струи—но потоку.
Обозначив через М секундную массу жидкости, протекающей через и лошадь действия винта. через V—скорость потока за винтом, через V— скорость потока до винта, получим, что MU направлено вверх, а АП’—
вниз, и сила
(Г— Г|
(21*)
лто можно доказать со всей строгостью, если взять очень большую сферу и интегрировать количества движения по всей ее поверхности, приняв во внимание, что для всех точек сферы скорости, добавочные к постоянным скоростям, будут порядка .
Если внутри жидкости существуют трення, то они в формулу Эндера не войдут.
Что касается секундной работы Г, то, применяй для ее определения ур-ие живых сил (ур-ие Бернулли» к струе ABCD, мы увидетн бы. что работа сил гидродинамического лав тения па боковой поверхности струи и на ее сеченпях АВ п CD в ур-ие не войдет. В самом деле, работа на боковой поверхности, вследствие того, что струя ограничена лилиями т«»ка. равна пулю; а работы на площа щах АВ и СВ противоположны, так как гидродинамические дав тения на них, бтагодаря большому радиусу сферы, одинаковы, а секундные объемы протекающей жидкости равны.
I На подобие сшовых лилий магнитного ноля образ' юшегооя около соленоида
Поэтому, в ур-не войдет то гъко работа Т от действия винта, которая и идет на приращение живой силы, и мы получим:
Т= ~ (IP— Г).........................(216)
Но, кроме живой си ты, энергия может проявляться в других формах: на счет ее может происходить трение, могут получаться у iapu на впит, может закручиваться прошедшая черед винт струя (см. стр. 210, фиг. 2ЬЗ»; наконец, могут образоваться вихрп. живая сила которых при определении скоростей анемометрами не может быть измерена. Со всеми этими потерями в действительности приходится считаться; поэтому теоретическая работа винта, даваемая ур. (219), всегда меньше действительной работы двигателя.
(Так же и сила тяги А на самом деле бывает несколько меньше определенной по ур. (205) вследствие трення воздуха о лопасти и пониженного давления в струе за винтом вследствие ее вращения.
По бу ieM пока пренебрегать указанными потерями и определять „идеальную тягу (А') по ур. (218) и „идеальную мощность" (Т) по ур. (219). заключая их в скобки 1.ля отличия от действительных тяги R н секундной работы Т, которые будем писать без скобок.
Заметим тут же, что в случае хороших пропеллеров тяга на 2—.г’, меньше идеальной, а работа мотора приблизительно на 20° с больше идеальном.
Кроме того, (ля случая „идеального пропеллера- мы должны считать скорость U в отброшенной им струе постоянной по всему сечению струи: для действительного пропеллера под U надо подразумевать среднюю скорость потока за винтом г) ].
Будем пока пренебрегать указанными потерями и определять Т по ур-ию (219).
Если мы разделим формулу (219) на (218|, то получим отношение работы к силе, т.-е. число килограммометров работы в секунду, которое соответствует килограмму силы тяги:
Это ур-ие было нервом попыткой на основании общих соображении механики осветить задачу о винтах; она принадлежит профессору' Ве.лль-неру. Он считал для геликон те рного впнта (где Г=-0)
т _ и
R ~ 2
(22ОЭ
Это отношение он называл „фиктивной скоростью" п определял эту фиктивную скорость для геликоптерных винтов и разных пропеллеров, висящих в воздухе. (Определения Велльнера относились, конечно, к действительным тяге и работе, а нс к идеальным).
(Будем теперь рассматривать затраченную (идеальную) мощность, как произведение из силы тяги на скорость в месте ее приложения, т.-е. в плоскости вращения винта:
(2) = (Л)Г„ $ = . .(221)
отсюда, на основании j р. (220), находим:
J) 1ля этого, как увидим ниже, надо строить препеллер специальной формы.
При н pei*
т.-е. скорость в плоскости идеального пропеллера равна средней арифметической из скоростей набегающего потока и отхо (ятей стр} и. На основании этого мы можем написать:
Г, = F-f- к, С= Г-,-2и . . (223)
По у равнениям (220) и (223) сейчас же можно определить скорость подсасывания к винту:
« = -&— *' <224>1
Зная скорость и, легко получаем секхищую массу ЛА если известна величина площадки F, через которую протекает воздух, проходящий через винт, т.-е. ab; практически за ату п гощадку следует брать площадь, ометаему ю винтом, т.-с, ’ xD2; к ней же относится и скорость
тогда
\f=F1 V.^eF Ч -и>. s
Составим теперь выражения для силы тяги н работы мотора через скорость подсасывания «:
(К) = 5Р(У-(-и)-2и . . . . (218')
(П - Л(Г4-н) = оГ(Г-)-и)8- 2 и . (221')
Подставив сюда значение и из у равнения (224), ноту чим теоретическую формулу, выражающую силу тяги винта через отношение работы к сите:
............. •«»»
Ниже мы \ кажем, насколько эта формула отступает от опытных данных.
В несколько ином виде она была приведена Д. П. Рябушянским в Bull. II, § 4, стр. 75, jp. (7j.
Если положим в формуле (225) Г = 0 и перенесем из второй части в первую Т1 делителем, a R2 множителем, то получим такую формулу для геликоптериого винта:
......................
к, орая показывает, что не зависит от скорости вращения винта. При-
7 1
ннмая с приближением, что (ля воатуха f- = -g- получим:
В (ей, твптельиости отношение у., дает ве шчину меньшую чем <t так •ио можно написать:
Г 4 —
Этот коэффициент, которым отличается постоянным множите.* м : • • •ответственного Ренаровского коэффициента */• мы будем называть к а ством геликоптериого винта.
») Ренар пишет: &=Е *, так как полагает, что струя за винтом не шпмрга сжатию, а идет спюшвой цилиндрической колонной ///* г
Ренар установил на своих наблюденпях. что остается постоянным. Что касается отношения , которое, согласно Ведльнеру, равно
j- , где U—скорость потока за виигим, то оно с возрастанием U 65 дет
убывать; поэтому, чем медленнее гонит воздух гетикоптерный впит, чем он больше, тем он при той же работе больше поднимает. Отсюда вытекает, что прямой расчет делать ге.шкоитерный винт очень большим.
Ренар это покашы на опыте, для чего
пользовался прибором, схематически представленным на фиг. 287.
В таблице 27 в первом столбце стоит число оборотов Л\ ви-втором столбце отио-
В *
шение т силы тяги к работе; оно все время падает с \вг шчением числа оборота
тов. Что касается отношения-^, которое
Фиг. J67. выражает Рснаровское качество винта, то
оно для данного винта одно н то же. Вообще, при испытании винта как геликоптерного, надо искать отношение куба силы к квадрату работы. Но эта величина характеризует ситу тяги винта при (аннон работе, независимо от его шаметра. Чтобы включить эту зависимость, Таблица 27. *
» £ = Е> Л “ 4 Ь Величина EJ говеем не представляет коэффи-цИента полезного цпетвия, так как центр винта не перемещается и полезной работы не производит. Wellner предлагает для апреле leinifl И брать формулу B=lnNDi3,. i22b где а—некоторый коэффициент, Л'= чисто лошадиных сил, а I) диаметр пинта. Если отсюда определить R. то работа войдет О в степени “ . Сравнивая формилу Ренара: Я3 _ poF. П.2Я5 yj Е Е j., , 1~ь7 ) 1
о,_* O.7G 24 0214 0,f"> 32 0,173 O.TJ 35 0,145 074
40 01211 0,78 48 О 104
с формулой Велльнера, найдем связь .меж iy и и Е.
а=1э 1 я Е=47,0 Е. >-•
(Коэффициент а может быть определен и чисто теоретическим путем, на основании уравнения (2261.
7? = ( 2е F Т2 = | 7 - 1>- N = 20,BS | 0 ) £>“№, 1229)
огкуда _
а = 75 J л | ® ;
для воздуха, ври Р= ь . это сает
« = 33,2 pty 2 тГ 2 дат1) ].
Д. П. Гябушинскии непосредственно из очень многих опытов определят и он никогда не подучал больше половины, а всегда меньше; наибольшая величина Е, которую он находил, была 0,4; она у него колеблется от 0,14 до 0,41. Если принять это значение для Е, то выходит, что а изменяется от 7 до 19, а Велдьиер дает тля а числа 9, 10 и 11.
Таким образом, формулы Ренара и Велльиера довольно близко подходят одна к другой.
Рябуплшскнй доказывает теорему, что Е всегда меньше половины и распространяет ее па всякие винты, но опыт показал, что можно строить хорошие винты, которые дают Е немножко больше половины.
По моему мнению, эту теорему можно доказать только для геометрического винта, [так как из теоретических соображений выходит, что Е нс может быть больше единицы: следовательно, Е не может быть больше
— = 0,707,
V- ’ eV ,
но может быть больше половины]. _
В основание док£лательства Д. И. Рябу- 7г _______*
шинского ложится формула ; 1
T=RNH, w “
приблизительно справедливая для хорошо Z
сделанного очень узкого геометрического фиг 288.
винта (этой формулой пользуется Pninlc\e>_
Положим, что мы имеем две лопасти, выр«. анные из геометрического винта |фпг. 288i. Это будет два сечения винта иа некотором расстоянии г от осп. При этом силы давления на переднюю и заднюю части элемента лопасти da идут в одном н том же направлении, перпендикулярно к этому элементу, так что
dR—pdaccsa, . и/)
где а угол между направлением нормали к элементу винта и направлением его оси, т.-е. у гол поклона винтовой .шип к плоскости перпендикулярного сечения винта.
Он ре селим теперь dT, т.-е. ту работу, которую надо преодолеть, чтобы вертеть винт. Составляющая силы, перпендикулярная радиусу, будет pda sin а, скорость элемента бу дет 2.тгДт, так что
dT=pda sin а • 2.xrV; . (б)
исключая отсюда pda при помощи уравнения («/, пай сем:
dT= dR tg a 2лгХ.
Другими словами, чтобы получить dT. нал dR помножить на tgo и на 2лгХ. Но так как шаг вннта H=2wtga, то
dT=dR-UN.
При интегрировании этого выражения по всему контуру винта замечаем, что Л и л одни и те же для всех точек контура, а потому
T=RHN ........ . .12:10»
Еста мы из этой формулы определим
к? в _ /м« 9
ПЛ)1
н сравним ею с подобным же выражением Ренара:
Я5 — IF 7 F* г- ~ ъ ’
то найдем:
123П
Чтобы закончить доказате «ьствл теоремы, нужно обнаружить, что и будет всегда меньше ИХ. Для «этой» надо стать иа точку зрения у тарной теории.
Ести элемент геометрического винта имеет скорость IF по направлению, церпен тику тарному к радиусу’ в правую стороиу н впнт вращается, как в гайке, то в сек унту он продвигается вперед иа NH
(фиг. 289). Если бы частица воздуха подошла к вниту со скоростью подсасывания Nil, прямопротився «сложной ско-
Фнг. 289.
ростп движения винта в гайке, то в движении относительно винта она имела бы скорость .11), слагающуюся из скорости АС=ХН, взятой в сторону, обратную скорости движения винта в гайке, и скорости IF. обратной скорости движения элемента впнта do перпендикулярно радиусу. Эта скорость AD была бы направлена по лопасти винта, и винт не получал бы никакого давления от воздуха.
В действительности частицы воздуха
ио шаенваются к винту со скоростью ВМ, меньшей N1I. гак что вся скорость частицы относительно винта будет представлена некоторым вектором J.V. Разложим эту скорость на скорость Я У. направленную по лопасти, и скорость MN препендику-лярно лопасти; последняя скорость потеряется на удар. При схождении с винта частица сохранит относительную скорость A.V, к которой для получения абсолютной скорости частицы надо прибавить скорость ТГ
в сторону движения элемента винта do, при чем осевая скорость бу дет м =AQ. Эта скорость, как видно на чертеже.
всегда меньше AC=NH. Таким образом, теорема
доказана Ч- -Ч
Струи за винтом раньше всех исследовал Патрик Александер, затем Д. П. Рябушпнекнй. Последний произвел обширный ря I опытов, измеряя скорости струп на i винтом и под ним (на расстоянии 0.1 mt от крыла» прп разных числах оборотов. Винт был геометрический. D=2tnt, Н—1,5 тЛцрнтра.тьнын угол 18й; »= 100, 200 и 300 оборотов в минуту. Скорости определились
Фиг. 290.
по трем направлениям (фпг. 290):
Г,—по радиусу, положите «ьная к центру;
1) Ошибка итого доказательства заключается в том. что п ударной теории не принимается во внныание сжатия струй, вследствие которого скорость жидкости, уходящей от винта, еще продолжает возрастать до некоторого upt вела Прим. реч.
Ft—в плоскости винта, перпендикулярно радиусу’, положительная
в сторону вращения винта;
Г — по оси винта, положительная вниз
Распределение скоростей под винтом прп п 100 оборотов в мпнуту показано на фиг. 291. Из нее видно. что поток движется но ион н по направлению к центру и. кроме того, еще вращается. Г. дает наибольшие
ординаты почти на самом конце лопасти. I ’корость движения по радиусу на всем протяжении впнта по южительиа. Что касается направления, перпендикулярного винту, то под винтом жи (кость вращается в сторону впнта; над винтом же жидкость иног щ вращается в обратную сторону, так что Гг над винтом может иметь отрицательное значение, но только в некоторых случаях.
В опытах Рябушииского сначала возбуждало сомнения то обстоятельство, что над концом в нита скорость I , переходит в отрицательную; ио впоследствии что обстоятельство получило очень просте объяснение. Дето в том, что измерения пре»изводились п i винтом, недалеко от места наибольшего
сжатия струп, а потом были перенесены на самый винт; поэтому на винте оказались точки, нс принадлежащие главной струе. Сравнение графиков для w= 100. 200 и 800 оборотов в минуту (последние два в нашем курсе пе помещены) показывает, что соответственные скорости почти пропорциональны числу оборотов.
Для определения количества движения жидкости Рябу щпнекип помножал элементы площадей на квадраты соответствующих скоростей и иа
• , и затем складывал графически эти произведения ыя всего винта. Сравнивая определенное таким образом количество движения с действительной силой тяги К, он наще I, что получается почти полное равенство; » среднем:
л = »
Мн 1.03'
Живую силу ои определял также графически, нын секундные массы на
помножая элемеитар-
2
Прн этом оказалось, что работа, затраченная на вращение винта, случалась почти вдвое больше, чем живая сила струи. Именно, как • роднее из многих наблюдений, подучаюсь, что
Г = 1
' о, -
Главным источником этого несоответствия можно считать образование* и\реп, потому что они ие могут быть измерены анемометрами, н жиыя и ia. на них потраченная, не учитывается.
Укажем теперь соображения, которые выставляет Парсеваль, и » • »ые подтверждают мысль, что затраченная работа не соответствуй г ...» и ie. On онредетяет из опыта силу тягп Н и работу мотора Т (Я ио вннта и затем вычисляет те скорости, которые соотвеп-тн ь• ш ьы 1учаемым вели чинам согласно теоретическим формулам. Обози»ч-«я < *
рость, получсннjю из формулы для тяги впнта. через У, а полученную из формулы работы мотора— через Г, он для мягкого винта своего дирижабля нашел:
Я= J F. 1 •*=. 2S0 ку.
Т .= i- F Г— 5250 kq. mt *ес.
2д
Из этих формул получаем:
Г — 12,7 mt -ес; V— 14,5 mt w
V приблизительно совпадает с истинной скоростью потока ла винтом, а скорость 14,5 mt sec стишком велика: это есть та скорость, которая получилась бы при условия равенства между живой сплои струи п затраченной работой, т.-е. если бы нс было потерь. Парсеваль предлагает характеризовать качество винта отношением этих скоростей:
m = J H.s8 . i232i
Для хорошею винта это отношение должно быть, по возможности, ближе к единице.
Между коэффициентами качества випта, по Парсевалю т, по Ренару Е2 и по Рябу шнискому просто Е [и действительным Е] су ществу ет весьма простая связь. Чтобы получить ее, (- вставим выражение -у.,. Обыкновенно в нем F8 сокращается, но здесь, так как I" не равно V, в числитель войдет множитель F”, а в знаменате ib Г6, так что будем иметь:
• ®’=2F,^ ..227"
Отсюда находим, что Рсцаровскип коэффициент
2fr = me, . 1233»
а коэффициент Рябушинского
E|/’2 = ms (-233'1
и действительный коэффициент
Е - т\ 233'* i
На основании этих формул, для мягкого впнта, и<*следоваиного Пар севалем, получим
2£r = in6=0,45: Е У 2 о,ь7[ — Е].
Ес.ти бы мы хотели написать формулу работы так, чтобы в и«*с вошла скорость, которая определяется непосредственно из подъемной силы, то пришлось бы обе частп равенства помножить на
(Ь ,’ = „,3[=E|.
так что получилось бы:
TE = ^-FKb: . >234»
— -9
отсюда видпм, что [ленствптельныи| коэфффициент (качества, выраженный в форме] Рябушинского, Е как раз равен отношению работы теоретиче-
свой, которую мы затратили бы при идеальном винте, к действительной работе мотора.
Составляя формулу Ренара с его коэфицпептом качества и Эйфелев-< кими коэффициентами а и Д находим, что
-- £'• — Г? я
Т1 7s 77 — 2 —8 *
откуда s
£ = 2} ? -=1,60 <2351
[действительный коэффициент качества
Е= 4 “/2-2,2бП-|.
- 1 п
Если взять а и р hi опытов Эйфеля, то можно непосредственно определять Е Что же касается до а н то они являются функциями самого впнта и в данной группе подобных винтов зависят только от отношения шага к диаметру, не меняясь с изменением абсолютных величин скоростей. Меняя отношение шага к диаметру, можно выбирать Е. Такие опыты впервые были сделаны Рябуншнсктгм. Вся суть выбораЧеликоптерного винта состоит в том, чтобы Е было возможно больше. У некоторых авторов в хороших винтах получалось [качество ио Рябушинскому] Е > 4-. но вообще Е< * , а для геометрического винта это обязательно. Величина Е, как [это следует из опытов Рябушинского (фнг. 292), начиная от очень маленькой при малом отношении mai а к диаметру, довольно быстро возрастает, затем, пройдя через максимум прн 0.75—1,0, снова
падает. Пз этих опытов видно, что, во-первых, делать геликоитерныс винты очень малого inaia невыгодно, а во-вторых, что тс винты, с которыми производил опыты Рябушинекий для по-троения кривой (чисто геометрические, очень широкие, с центральным углом 144 ), довольно плохи. Е для них ие превосходит 0,18. В других виптах Ря-буппшекин получал Е до 0,4, Парсеваль де 0,47.
2=2 Закончив описание ге шкоптер-ных винтов, вернемся снова к теории идеального гребного винта х) и определим идеальный коэффициент полезного действия его, исходя одни раз из силы тяги, скорости и диаметра, а другой раз— из мощности, скорости
и диаметра.
Так как полезная пению (221 I равна (Д) видпо, будет
работа винта равна (R) V, а затраченная, по урав-{V и}, то коэффициент полезного 'ействня, оче-
|»7» =
(В) г _ V
(7) - Г+
23.
’) Закиоченное между знаками = стр. 23ч—24В) заимствовано из „Вихреве! Теории Гребного Винга“ Н. Е. Жуковского сгатья 4. S 6. Труды Авиационного Гасчетио-Исцыгатальпиго Бюро прн В. М.Т. У. вып. 3, 1918 г Прим, рел
(аже н в пц-а |ьяом слу час ои оказывается меныпс е (иницы. Это объясняется подвижностью среды, на которую винт опирается, чтобы развить силу тягн. Мы видим, что коэффициент полезного действия повышается с уменьшением скорости «, т.-е. с у мсиьшспшм силы тягп. Ког 1л сила тяги обращается в нуль, тогда идеальный коэффициент полезною действия обращается в единицу, но тогда и полезная работа пропеллера равна нулю.
Обращаясь к формуле (225) и разделив обе части ее на оГГ*2, получим К1'1Дратное уравнение
-(р', ^В=2 I -1)Уг- 1237)
pFVJ > (ч> I (ч)
Отв 1ечснпую величину
в = (238>
В. II. Ветчпнкин называет коэффициентом нагрузки па ометае-м у ю винтом площадь.
Решая квадратное уравнение (237), найдем идеальный коэффициент полезного действия
6?) = - ~~ -
Ц-Г1+2В
/14-2В —1
в
(239)
скорость подсасывания
„1Т+2 7?-
W == I - ,--
(240)
2 + В(п)
Приводим таблицу 2Ь значений (ц) и -£• по аргументу В.
Если по осн абсцисс будем откладывать В, а по оси ординат ~ ==£• то получим параболу, уравнение которой будет
2В = * il-l).
Эта парабола представлена на фиг. 293. Взяв пнверсию ее ординат, мы полу чим крпву ю JC,выражаюшу ю у по В, согласии формуле (239). Эта кривая пересекает ось ор шнат на рас» гоянии С А — 1 н расстилается по оси ОВ, как по асенчптоте, при чем с возрастанием абсциссы В ор шпата ее (j?i постоянно уменьшается до ну ля. В. П. Ветчинкии рядом с упомянутой кривой чертит семейство линий, которые полу чинись из наблюдений Эйфеля для равяичных винтов, располагая действительные коэффициенты полезного действия (?» по параметру В; как мы видим иа фиг. (293), все эти линии идут довольно близко одна к тру го ft, немного ниже кривой JC, дающей идеальный коэффициент полезного действия. Прн чем понижение коэффициента против идеального прп значении В, несколько отличном от нуля, ие более 15°/q. Таким образом оказывается, что главная величина действительного коэффициента полезного действия зависит от идеального коэффициента.
Этот коэффициент возрастает с уменьшением В, поэтому выгодно увеличивать радиус вннта. Заметим, что выражении 1238) для В только D характеризуется винтом, величина же зависит от сопротив 1еиия дирижабля или судна, если речь идет о гребном винте. н от гидродинамических потерь в трубопроводе, если речь идет об веигиляторе.
Таблица 28 *)
1 В 1 |«) В 1 +1 (Ч) в Г (о)
ООО 1.00 0 100СО О.<И1 1,3366 0.7481 3.8 1,9663 0.5086
0,02 1,0099 0.9902 0,95 1,3515 0,7399 4.0 2,<00С 0,5000
0,04 1,0196 0.9418 1,00 1.звво <1.7321 4.5 2.0811 0,4805
0.06 1.0292 0,0717 1,1 1 3944 0,7172 5,0 2,1583 0,4633
0.08 1,0385 0,9629 1,2 1,4220 0,7032 5,5 2,2321 0,4520
0.10 1.0477 0,9545 1,3 1.4487 0,6903 6,0 23028 0,4343
1 0,15 । 1,0701 0,9343 1.4 1.4747 0,6781 6,5 2,3708 0.4218
0,20 1.0916 0,9161 1.5 1,5000 0.6667 7,0 2,4365 0,4103
0,25 1,1124 0,8990 1,6 1.5247 0,6559 7,5 2,5000 0,4000
0,30 1,1325 0,8830 1.7 1,5488 0,6457 8,0 2,5616 0.3904
0,35 1,1519 0.8680 1,8 1,5724 0,6360 9,0 2,6794 0,3732
0,40 1,1708 0.8540 1.9 1,5954 О,Ь268 10,0 2,7913 0.3583
0.45 1,1892 0,8410 2.0 1,6180 0,6180 12,0 3,0000 0,3333
0.50 1.3071 0.8284 2.2 1,6619 0.6017 17,5 3.5000 0,2857
0,55 1,2246 0.8166 £4 1.7042 0.5868 24,0 4,0060 0.2500
0,60 1,2416 0,8055 2.6 1,7450 ',5730 31,5 4.5000 0,2222
0,65 1,2583 0.7947 2.8 1,7845 <•5604 40 5,0000 0,2(НЮ
ото 1,2746 0,7646 3,0 1 8229 9,5486 60 6.W00 0,1667
0,75 1,2906 0.7748 3,2 1,8601 0,5376 112 S.OOUO 0,1250
0.80 1,3062 0,7655 3,4 1.8946 0,5273 180 10.00ПО 0,1000
0,85 2.3216 0,7567 3.6 1,9318 0,5177 ас СО 0.0000
Мы показали, как определяете!! идеальный коэффициент по силе тяги; ио па практике обыкиопенно лается работа мотора и скорость полета аэроплана. Поэтому покажем как по этим тайным определить i Ж) и 141. Назовем через iB„i силу тяги рассматриваемого винта, когда он вращается при за кшиой работе Т, как геликоптерпып винт. Подставляем знамение 2t>F из формулы 1226| в формулу 122Ы; получаем
(Л,.1) , т т (Вд _ V
Г! \(Л) 1 (Л> ЫО <в> г
) Вычислял В II Ветчинкии.
Тевретяческле ясаовы оэдуюи-авввяяи
Таблица 29 1)
Г (*$)) (в) (Йо) (ч) - 1 (ч> 1 да flw (ч) V (Я) (ч)
0,0 1 1,0000 Cl.fXXX) 2,1 0.4366 0.9168 1 4.1 0,2409 0.9860
0.1 0,9667 0,0967 2,2 0.4207 0,9255 42 0.235О 0,9870
0,2 0,9334 0,1867 2,3 0,4057 0.9333 4.3 0 2298 0,9879
0,3 0,9004 0.2701 2.4 0.3916 0,9400 4,4 0,2247 0,9887
0,4 0,8876 0.3470 2,5 0,3783 0,9459 4,5 02199 0,9894
0,5 0,8351 0.4175 26 0,3658 0.9511 4,6 1 0,2152 0.9900
0,6 0,8032 O.48W 2,7 0.3540 09557 4.7 02107 0.9906
0.7 0,7718 0.5403 2.8 0.3428 *9597 4.8 0,2065 0.9912
аз 0,?411 0.5929 2.9 03322 0.9634 4,9 02023 0,9917
о,» 0,7113 0.6402 3,0 0.3222 0,9666 5,0 1 0,1984 0,9922
1.0 0,6823 0,6823 3,1 0,3127 0.9694 5.1 0,1946 0.9926
и 0.6544 0.7198 32 0,3037 0.9720 52 0,1910 0.9930
1.2 0.6275 0.7530 3,3 02952 0,9743 5.3 0,1875 0,9934
1,3 0,6017 0,7822 3.4 0,2871 0.9763 5,4 ОД840 0,9938
1.4 0,5770 0.8079 3,5 0,2795 0.9782 5.5 <«,1808 0 9941
1,5 1 0,5536 0,8304 3.6 0,2722 | 0.9798 5,6 0.1776 0,9944
1.6 | 0.5312 0,8500 3,7 0.2652 0.9813 5,7 0,1745 0.9947
1 7 0.5101 0,8672 3.8 <^586 «,9827 5.8 0.1715 0,9950
1.8 I 0,4901 0.8822 3,9 0.3523 1 0.9839 5,9 0,1686 , 0,9952
1.0 0,4712 0,8953 4.0 0.2463 <.’451 6,0 0,1659 09954
2.0 0.4534 0,9068
в трубе, в которой поток получает скорость от постороннего вентилятора, независимо от винта.
Еста же винт сам ведет подволну Ю лодку или (ирижабть пли является вентилятором трубы, в которой прнво iht в движение воздух, то в атом случае у, есть, как было сказано выше, постоянная величина, не зависящая от винта, а следовательно и есть величина постоянная По формуле (2431 имеем:
...................|2«’
1 Вычислял В. П Ветчннкии.
2 ) При постоянной коаффиписите полезного действия винта.
у
Отсюда заключаем, что в упомянутом случае параметр - - зависит только от тиаметра D, а потому и величины ы?» и tR\ зависят только от D, при чем о возрастанием диаметра уменьшается, a iq) увеличивается, как это было указано раньше при определении q по Б- Сила тяги iR) при этом увеличивается. Е<ти при разных режимах не есть величина постоянная, то следует остановиться на том ее значении, для которого нам важно получить более высокое значение q. Претполагая. что идеальный коэффициент q не должен выходить из пределов 0,91 и 0,85, В. П. Вегчинкин находит но формуле i24D пределы, между которыми следу ст взять радикс винта.
Для воздуха, при получается неравенство:
__ 1/^ ОР . Гк ЕЕ I Л HP |
оэ,28 у -уу > D> 39,55 |
1246)
1ля пресной воды, при
6 = 102, неравенство:
1,384 ]'-!£ <D< 1,035
1247)
По цервой формуле В. П. Ветчинкин находит дтя ходовых винтов, употребляемых иа различных аэропланах, величины диаметров, расположенных в таблице 30.
Если рассматривать изменение плотности воздуха с высотою, то вследствие того, что аэроплан работает в том же воздухе, как винт, а работа Т мотора внутреннего сгорания, как показывают наблюдения и теория, изменяется пропорционально плотности, получается независимость второй части фирм. 1245) от изменения р. Таким образом получается важный результат: идеальный коэффициент полезного действия винто-моториой группы н отношение не зависит от высоты аэроплана. Что касается до силы тяги <fti. то она изменяется пропорционально сите тяги геликоптерного винта при тон же работе и потому, согласно формуле i226i. пропорциональна и ютиости.
Когда винт ставится на спроэктированный аэроплан, для которого вычерчены динамические диаграммы тяги и работы по способу, указанному в моем курсе „динамика аэро планов “, статья 2, § 2 Ч, прежде всего сле-1У«*т удовлетворить главным заданиям: горизонтальному полету при желаемой скорости и по гьему вверх с наибольшей вертикальной скоростью. Зти задания укажут нам работу Т и скорость V, по которым мы определим диаметр винта D, пользуясь неравенством (246). Считая радиус винта известным и зная по диаграмме сил тягн для всякого режима скорость полета, мы определим по таблице 28 коэффициент (q} и с помощью его исправим иа диаграмме работ все величины Т, заменяя ихна-J. Полученная диаграмма будет с ту жить для определения работы при разных режимах для данного аэроплана и винта с поправкою на идеальный коэффициент полезного действия. Указанный прием обстоятельно разъясняется нами при изложении динамического расчета аэропланов.
( кажем теперь несколько слов о выборе впнта для аэросаней. Эта 1ача близка к вышерассмотренной. Обыкновенно дают две нагрузки
1» Труды Физия. Отд. о л. Е., том XV 111, вып. 1. 1916 г.
Таблица во1).
\ а р о и л. Фарм. Фарм. учеби. 7 Фарм. 16 Фарм. 22 Фарм. 27 Вуазен. Моран. Парас. Биль Ньмпор XI. ,
Мощность мотора Не лош. сил. 50 60 яо 107 150 132 80 ьо
1Г font h 72 90 108 115 145 108 126 155
Г mt вес. 20 25 30 32 37,5 30 ж 43
- 3.12 2,44 ЗДЗ( 2.26 2,11 2,76 1,7! 1.25
D 4,37 3,42 2.01 3,17 2,95 3,86 2,39 1,75
Действительный диаметр D . . 2,6 2.6 25 2.5 2.75 2,83 2.5
мотира: усиленную работу е перегрузкой мотора для плохого пути при малой скорости и нормальную работу для большой скорости и желают построить впит, чтобы он давал хороший коэффициент полезного действия 1ля обоих случаев движения и надлежащую силу тяги, чтобы с (вниуть сани с места 1на снегу особенно заметна разница между коэффициентом трения для сдвигания с места и коэффициентом трения иа ходу,.
Если в формуле 1245) мы возьмем ^ = 1,0 и определим отсюда при за (анных Т и V величину D, то с одной стороны най щм довольно хороший идеальный коэффициент 0,68 и хорошую силу тяги ля гелпкоптерного винта, которая найдется по формуле:
С другой стороны для меньшей Iнормальной) работы 7^ и большей скорости Гп которые соответствуют хорошей юроге, мы найдем при принятом радиусе вннта более высокий коэффициент полезного действия, нежели о,68, как это следует из формулы (244) и графики (294). =
Было упомянуто, что одна из причин, вследствие которых наблюденная живая сила струи меньше работы, потраченной мотором, заключается в образовании вихрей за винтом. Это вполне доказал профессор Высшей Технической Шко гы в Шарлоттенбурге Oswald Flamm -), который задался целью выяснить явления, происходящие в воде около винта. Д1Я этого он построил бассейн со стенками и дном из зеркального стекла, пиною Ю mt, шириною 0,8 mt и с глубиною воды в нем 0,6 mt. Над этим бассейном могла двигаться по рельсам легкая тележка, снабженная электромотором, от которого приводился во вращение винт, находящийся по i тележкой в воде и у кретонный на аппарате, напоминающем по своей форме мину Уайтхеда Этот винт при своем вращении двигал и всю тележку. Для изменения скоростей поступательного движения к тележке сзади подвешивался груз, перекинутый через блок. У конца бассейна, где тетежка развивала наибольшую скорость и винт—наибольшее число оборотов, помещался большой электрический прожектор в 24000 свечей,
1) Вычислял В- П. Ветчпикни.
2» Oswald Flamm .Судовый 1ребиой винт н его действие в воде" Перевод с немецкого. В. М. Каменского. Москва 1910.
а напротив него, по другую сторону бассейна, стереоскопический фото-i рафическпй аппарат, который автоматически производи.! снимок в момент, когда винт пробегал между обьективом аппарата и прожектором; вы юржка для всех снимков была -екущы. В момент съемки автоматически нроизво отлись измерения поступательной скорости тележки п числа оборотов винта. Кроме тоги, следовало бы измерять осевое давление впита (измерялся только груз, подвешенный к тс.южк*-» и величину крутящего момента. Но, ио недостатку средств для построения соответствующих приборов, этн измерения ие произво. цтлпсь.
Винты Flamm испытывал водяные, корабельного типа, диаметром около юо тт. Фотография «иного из них ирпведена на фиг. 295.
Из этих снимков можно
вывести важные заключения:
11 Окою винта, как сиерс in, так и сзади, ia-вленне пониженное; наибольшее понижение проис ходит у самого винта. На фотщ рафиях это и «называется понижением у ровня свободной поверхности воды •коло впита и образованием в ней корытообразного у глу-блеиия, в котором отражают-
Фиг 2“5.
Фиг. 296. Р. 5. Пробный снимок без измерений.
гя ви? душные пузырьки.
2j Вода отбрасываете л винтом, независимо от его формы, правильной цилин ipuческой струги, и только довольно далеке от винта эта правильность теряется. На фотографиях видим почти цилширнчсский столб воздушных пузырьков и винтовые линии, навитые иа цилин ip, чего не могло бы быть при иной форме отбрасываемой струи.
3) За винтом образуются, по иашему мнению. две системы вихре! о шн большой вихрь с осью, составляющей про (олжеипе осн винта, и вихри, расиоложспные по винтовым линиям, отходящим от края каждой лопасти.0< i -гих винтовых лпиип’также совиа гает с осью вращения винта, а шаг и\ равен ну ти, пройденному во юй в движении относительно винта за один оборот п«»-С 1ГДИСГО.
На фото! рафия < мы вместо центрального ши ря наблюдаем в< мт: ную тру бку.в ви те Ж1 > • * иног ia в несколько м«» ров д 1ИНОЮ, а вмест • •<* рей за лопастями •••• пшные винтовые »И1ШИ 1фИГ. 29Н. 297. 'Ml На этих рису нк- \ г и 4ч • W после буквы Г 'ми-чают нумер игпмпмм*
миге» винта, V — поступательную скорость тележки в mt «ч. и оборотов виита в минуту, д— груз в кд, подвешенный к те»"
Известно, что находящийся в вою воздушный пузырек • ««»•*»»« • торону, в Котору ю давление понижается, и не выхо шт и< t
давление minimum; известно также, что на осях вихревых нитей имеется minimum давления; на пих. следовательно, и должен екоптяться находя-
щийся в воде воздух. .Эти доказывается на приборе, построенном мною в Московском Универси-
Фиг. .9;. Р. 10 Г=У п — 2' . О ку.
Фиг, 299. Р 10 1'=- 2,7 mt кг. п = 2^д — 2 кд
Фнг. 299. Р. 10. Г = 2,0 mt af, п = 2100, д~ 4 кд
ПТОНКОСТИ
тете ко даю чествования памяти Гельмгольца и описанном в конце $ I s настоящего курса (стр. 122). Кроме того, на осях вихрей может нс только собираться воз-iyx, введении ii в воду извне, ил также и выделяться волду х, растворенный в воде, если только понижение давления и количество растворенного воздуха юстаточны для этого. II то, и другое явление наблюдаются иа фотографиях Flamm’a. По большей части жгут и винтовые тиннн образуются из воздуха, всосавшегося с поверхности воды (фиг. 29«, 297. 298); иногда же такого всасывания совершенно нет. а жгут юн. вообше, сохраняется дольше винтовых тпнии, идущих от лопастей», хотяитонкнй. все-таки существует: с ослабленном вихря он исчезает, как это ясно вн дао на фнг. 299. Центральный вихрь, следствием которого является воздушный жгут, вызывается быстрым вращением винта и закручиванием и.(ушего за ним столба воды.
Образование спиральных вихрей объясняется следующим образом. Пусть лопасть вннта (фнг. 300) вращается, как показано, против часовой стрелки (ля наблюдателя, глядящего сверху, н отбрасывает струю воды вниз. Движение лопасти можно разложить на два: иа двн-
женне, перпендикулярное
лопасти; от движения по
к плоскости, и движение вдоль
направлению, перпендикулярному лопасти, от ге краев стр^и отбрасываются назад и образуют замкнутые линнн токов, опирающиеся концами
на лопасть, а от движения вдоль лопасти эти линии токов соскальзывают и замыкаются, образуя последовательно винтовой вихревой шиур, ось которого пройдет через средины этих замкнутых линий токов.
Частицы воздуха, расположенные на вихревых нитях, движ\тся по кругам и образуют на конце винта болыпнь скорости, которые анемометром и микроманометром отме- [ пены быть не могут, потому что в одной и той же точке чзх——----ч
пространства направлены то в одну, то в другую у
сторону; анемометр определяет среднюю арифметиче-скую скорость потока, а микроманометр колеблется около своего положения равновесия, соответствующего -"7' ' средней квадратичной скорости струи. Эти то вихри, фяг д(>> распространяющиеся также и внутрь струи, и служат, по моему мнению, причиной, почему истинная живая сила по существу совсем ие та, котирую определяем по средним скоростям Чтобы получить всю живую силу, надо полученную по средним скоростям живую силу 1 помножить на
S 40. Эмпирические формулы, выражающие силу тяги вннта и секундную работу, потребную для его вращения |и теория идеальной мельницы).
Для силы тяги разные авторы дают разные формулы. При постоянной скорости F и переменном числе оборотов Л' все оии дают для тяги закон изменения но параболам, различно расположенным относительно осей координат. При постоянном N и переменной скорости V одни формулы тают параболу, другие—прямую.
На основании теоремы количеств движения мы получили для силы тяги вннта такую форму ту:
й=й^((й-г) S
Кроме того, при вывело теоремы Рябушинского мы нашли, что для очень узкого геометрического винта «нкушшая работа
T=RNH. . . . ... <230)
Исключая Т из формулы <225) при помоши выражения (230) и вводя поправочный коэффициент, no.ij чпм:
F> VH, . . . . <225'1
где
5 = 8^-
Ь 9
При постоянном У эта формула дает изменение тяги в зависимости от V по линейному закону.
Д. П. Рябупшискнй принимает \ что
B=a(.V-—^ ...............12481
R в зависимости от К параболу.
Rene Amoux на основании своих опытов находит несколько иной »кон изменеиия силы тяги со скоростью, шагом и числом оборотов, именно:
Я = .................(249)
*) Bull. 11, стр. 95, ф-ла (в)
Пр*м ред
Эта формула, так же, как и формула (225'», даст иля тяги винта тоже линейный закон изменения со скоростью F. Выражение 1 — есть скольжение впнта г. Поэтому формула Арну вполне совпадает с формулой Фербера:
R= a'hr №!)*,. ..... 1209)
если принимать, что В = a'hD*; но формула Фербера более подробная, так как в ней указана зависимость R не только от N и Г, но и от параметров Л н D, постоянных тля данного впита.
Соро предлагает для силы тяги формулу, представляющую тоже однородный многочлен второй степени отн<м итс.1ьно F и Лг, и упоминает, что эта формула найдена им для геометрического винта теоретическим путем.
Как любитель составлять эмпирические формулы на все хорошие опыты, Соро составил формулы п для после (них опытов Дорана в Saint-Суг*е над винтом Джевецкого:^
R = о,94 Л™—0,20 .V 4 — 0,14 F-, I
Т=0,015б№ — 0,0023 VP’ — О.ООПЛ’Г" ( • '-оО>
Форму та Соро для работы а) похожа на выражение для силы тяги, помиоженное иа ХН (как обыкновенно и бывает в теоретических формулах), но несколько отличается ит него коэффициентами: к коэффициенту при прибавлена некоторая положительная величина, у чптывающая влияние трения воз iyxa.
Формулы Соро дают отклонение от наблютений, не превышающее о* Горо очень иску сен в составлении эмпирических формул; коэффициенты их он определяет, вероятно, но способу наименьших квадратов. Д. П. Рябу-шинскнй тоже составлял формулы для Дорановскнх опытов, определяя коэффициенты их графическим способом; чиста, которые он получил, несколько разнятся от чисел Соро.
В последнее время Соро остановился на степенных формулах, которые для практического применения удобнее многочленных, но имеют тот недостаток, что уже утрачивают механический смысл. Степенная форму ла Соро тля силы тяги является как бы сретней между формулами Д. П Рябушииского и Арну; имеино, для силы тягн Соро пишет.
Л=С№[1-(^|, ... ... <251)
где р= 1,162; а (ля работы:
T=D.V’[l+K-(^/], ... . . <251 >
1 ie q = 1,21, т.-е. довольно близко к р. Член е, вхо (Я1ций в формулу, учитывает работу трения Ч. Коэффициенты С, D и « зависят от формы н размеров винта, а р и д постоянны для всех винтов.
На фиг. 301 нанесены кривые, выражающие закон изменения тяги Я в зависимости от числа оборотов -V <при постоянной скорости Г) по различным эмпирическим формулам. Размеры впита взяты следующие:
D = 0,30 mt;
Н= 0,5 D = O,15ml:
P= 3 mt sec.
I Коэффициент при .VV* восстановлен uo нанята, так как в первом изданий стоит опечатка- О.(Х)7/. При. и
-) Момент трения нронорциона-эен №, а работа тр<-нвя—.V1.
L.3K
На той же диаграмме нанесены п теоретическая кривая, даваемая уравнением i225'i, и опытная кривая, полученная Д. П. Рябушинокнм для винта тех же размеров. Коэффициенты эмпирических формул по юбраны так, чтобы кривые проходили через точки С и Z>, общие с опытной кривой.
ви шо из чертежа, все кривые при
.¥> ~ довольно близки к опытной: при Аг>-^ все кривые расходятся. Ближе всех к опытной кривая Соро (Hi, которая сливается с ией иа всем протяжении, кроме маленького кусочка между О и 5 обор сек.; в этом месте она начерчена пу нктнром. Ось N кривая (’про пересекает в точках О и ~
Затем следует кривая Кепё Arnoux «IV), сливающаяся с опытной при ,V>15. Она представляет параболу, смешенную вершиной вправо от начала координат на величину X кривая Арну пересекает, как i в точках О н
'ТПеолетрвинт I
VtKTWl <A_t- ы =n
I -О-0ЛЫТКАЯ(Л0ПЧЧ
Фнг. 301
- rwwwMTfl
Ап-_ РЯБУИИНСК । ^JV—Яепе 2-*-. Л/ьполих.
^Зк-иЬех 1 ТЮРЕТИЧЕС
, ,я и вниз. Ось ir кривая Соро,
Кривая Рябушииского till । пересекает опыт-ну ю кривую прн .V = , при чем прп xV>
Фиг 302.
идет выше ее, а при Ат<^ниже. Она представляет парвболу, смешенную вершиной вниз от начала координат.
Кривая теоретическая в соединении с геометрическим винтом пре (етавтяет параболу, елпваюшу к>ся с параболой Rene Arnoux. Ось Ат она нсрессдагт в точках ~ и О. Второе пересечение соответствует случаю, когда *V=0.
При А’ отрицательном ни о ша из формул не выражает закона нзмеиенпя силы тяги даже приблизительно: это и понятно, так как там происходит совершенно другое явление: винт бросает воз ух против потока, подсасывая его снизу, а перед винтом образуется закругленная 1 оловка. как это пре (ставлено на фнг. 302. Распределение линий тока около винта получается совсем иное, чем при положительном А’. Поэтому. весь анализ, основанный на том, что пот винтом есть струя, станет искрило жимым.
При реоакиии. Позднейшие вз1 ля
ды на теорию винта, к которым Н. Е. прнше. i за период 1912- 1914 г. г., дают более по. «рчбиый
ответ на случай отрицательного V, а именно:
Пока число оборотов невелико, поток проходит сквозь винт .ам-ляясь обратным вращением его лопастей. При повышении числа
ротов замедление потока все усиливается, пока, наконец, винт не погонит поток назад, согласно фнг. 302.
Переменив знак в форму те (22-7, стр. 219), подучим ветвь параболы IV, направленную на фиг. 301 вниз н притом расположенную несколько ниже опытной кривой силы тяги. Это показывает, что отрицательная сила тяги по опытам выходят меньше теоретической, как и следует согласно пояснению И. Е. к фиг. 302 н при подходе к царисованпоц там картине яв лення.
Приводим здесь также теорию идеальной мельницы впервые полученную нами в 1914 г. и написанную Н. Е. Жуковским в 1920 г. *> § 1 статьи: Ветряная мельница типа _Н. Е. Ж.-.
Идеальный коэффициент использования энергии
ветра Когда поток
Фиг. 285'.
приводит во вращение мельницу, то скорость его уменьшается и из Г (фиг. 285'>3» обращается в плоскости мельницы 4В в Г— м, а за мельницею в Г— к,.
Легко доказать, что wx = 2 и. Действительно, мы можем нанимать
откуда
Если
•w Vs т(Г — к.)2 .j. ,
->---------—И- = ?п(1 — u)ult
будет п юшадь, [ометаемая мельницей), то живая сила (ветра), которою мы располагаем (каждую секунду), будет
ной скорости (т.-е., будет
а потребная на вращение под сопротивляющимся моментом работа, к идеальном случае, когда работа не тратится ни на образование окруж-имеется спрямляющий аппарат), ни на тренне,
Коэффициент использования энергии ветра в этом случае есть
-2 В*^-“ = 2 В9,......... (II)
1итографировано в Трудах Центрального Adpoi идродмнамнческого Института в 1920 г.; напечатано на франц, языке, в Билл. Моск Института Космической Физики вып. 1. 1923 г.
’> Расширение струи н длины стрелок скоростей на фигуре соответствуют наибольшему а с пользованию энергии ветра. Прим. ред.
где в=₽«г2............................................. (Ш)
Мы имеем для работы, выделенной мельницею, формулу
7=7? (Г—и), откуда
и = V--т
“ Л •
Но
P=2m« = 2eF(F-«)« = 2gF(F- .
IqFV* 2 ' *Г RV ‘
Здесь
_г — ftLr“ м ~ RV ~~ *'
посему ®=(1 -ч)ч- (1X1
Определяя отсюда
1 , , Л В I I т I 1—2В В I
Ч=2-±У4--г [=----------2------=7^,, гВ]»- ПО
находим для коэффициента использования энергии ветра выражение
Таким образом, в мельницах коэффициент испотьзования эиергин ветра определяется через нагрузку.
Формулы (V) и (VI) дают нам законы изменения и | в зависимости от В (фиг. 293'). Наибольшая возможная величина В есть * . Но это не есть величина, дающая Мах. для с. Чтобы найти это последнее значение, надо приравнять нулю производную от формулы (Vi). Получаем уравнение
1—1 1 — 2 /1 — = о
pi--'в
тку да
в=-’ [,= ;] ли.
*) В оригвнале Н Е стоит - = но тогда •/ быта бы велнчнноа. <*| - • ко •ффвцненту полезного действия мельвнцы, и потом) мы перешли к обычным o6<j ч*. ИЯМ. 7/ркж f
Мы пришли к интересному заключению, что все мельницы, дающие максимальное использование действия ветра, должны иметь [коэффициент] нагрузки иа квадратный метр ]ометаемой площади].
и
Фиг. 293'.
Подставляя это значение в /VI), находим идеальное значение
S Мм= 4=- = 0,5926.
Так кратко изложил Н. К. теорию идеальной мельницы, отметив в ней номером лишь одну формулу (Л’1). Это следует объяснить крайне тяжелыми условиями того времени (напр., 2Э тепла в квартир»* Н. Е., так как статья писалась в феврале 1920 г.).
Исходя из соображения, что ветер имеет неограниченный запас энергии. Н. Е. ие обращает внимания на коэффициент полезного 1ействпя ветрянки. По, когда ветрянка стоит на самолете и крутит либо помпу, лпбо динамо от радио-станции, ее коэффициент полезного действия.
начннает играть важную родь, так как работу RV приходится брать ие у природы, а от мотора.
Пользуясь верхними ветвями кривых ?; и £ иа фиг. 293, что соответствует верхний знакам урр. (V) и (VI), найдем, что ч=1 при В = О. Это показывает, что для ветрянок на самолетах следует брать довольно большие диаметры, соответствующие малым В и большим ц.
Что касается до нижних ветвей кривых и то они соответствуют чрезмерно заторможенным ветрянкам, очень медленно вращающимся.
Приводим таблицу 28' коэффициентов и расположенных по В.
На фиг. 301 область ветряка лежит межд$ точками О и С, т.-е. между о и -|-20 обор. сек. При этом верхние ветви кривых >/ и с получаются при числе оборотов в секунду больше 10, а нижние — меньше 10.
В связи с довольно подробным анализом кривых Рябушинского заметим, что проф. Г. А. Ботезат в своей статье: „Исследование явления работы лопастного винта*4 (Ленинград, 1917 г.) рассматривает 16 режимов лопастного винта в случае, еелп поток 1ует вдоль его осн. Из них 7 режимов соответствуют потоку, дующему на винт спереди, 7 — потоку езади и 2 - - гелнкоптерпому винту.
Эти режимы следующие:
А) Поток дупп спереди (крпвые Рябт шннского, фиг. 278 п 279 прн I ф 0, фиг. 301 и 303).
1) Гребной винт (участок CD на фиг. 301).
Обороты Л’, тяга В и работа Т положительны.
2» Особая точка (С на фиг. 301).
Тяга В = О, работа Т " о. У > О.
Таблица 28
Идеальная мельница.
Верхняя ветвь. В Нижняя ветвь.
। Ч Ч «•
о.ооо 1.00 0.000 0.W 0.000
0,180 0.95 0,095 0.05 0.010
0,324 0.90 0.1 Ю 0.10 0036
0.434 0.35 0.255 0.15 0.076
0.51*2 0,80 О.бЭО 0,20 0.128
0.75 ОДЛ 0,25 0.188
О.5ъ8 0 70 О.420 0.30 0,252
0.3926 0.667 0.4444 U 333 0,2963
0.591 065 0.455 035 0,319
0 576 0,80 0.480 0.40 0.М4
0.545 0,55 0.495 0 45 0,445
0.500 0.50 0.500 0.50 0500
3) Промежуточный режим
В<п 7 > О, А > о.
4) Особая точка темного левее С па фиг. 301»: ветряк, вертящийся в холостою, как анемометр.
7? < О, Х>0, 7=0.
5) Ветряная мельница (иа фиг. 301 участок от О почти до Ci. т.-е от О до 16—18 об./сек.).
У >0, Н < О, Т <
6) Стоячий ветряк
Л =0. К < <». 7=0.
71 Винт, вертящийся в обратную ц. <трсч.\ потоку
У < О. к < о.
сторону и стремящийся уть
7 > 0.
В j lP>nv>p отсутствует, в и нт верт и т с я ни месте> как м апк on т- рн ы «-М» Вращение положительное.
V > О, R > 0. 7 О.
Правы»' участки кривых I (соотв. Т — О на фиг. 273 и 279.
91 Вращение отрицательное.
X < О, R < О, Т > о.
Левые участки тех же кривых.
При винте, отличном от вполне симметричного геометрического, как испытанные у Д. П. Рябушииского, и кривые Г=О в правых и левых ветвях отличались бы между собою.
Ci Поток дует сзади.
10—16) Повторяются режимы (1—7) группы А. Для вполне симметричного геометрического винта кривые были бы те же, что и (1 — 7); для несимметричных винтов и кривые различны.
В. Ветчинки».
Фнг. :<
растать.
Отметим здесь же тот интересный факт, что винт малого шага, вращающийся в поло-жительную сторону, при числе оборотов N <2 , дает отрицательную силу’ тяги бо ть-
шую (по абсолютной величине), нежели неподвижный винт в том же потоке, как будто, вращаясь, он покрывает площадь, большую, нежели действительная площадь проекции винта на плоскость, нормальную к его оси. На кривых Рябушииского это явление отмечено существованием minimum'а ординат при у
0<N<-gr. При большом шаге этот minimum исчезает (фиг. 3031.
Когда винт может Брататься в потоке воздуха свободно, как анемометр (т.-е. когда работа, потраченная иа его вращение, равна нулю), то ои, при малом шаге, дает большее сопротивление потоку, нежели виит невра-щающийся. Для элемента лопасти весьма узкого геометрического впита (фиг. 22ь) результат этот мы получаем теоретически, взявши векторную диаграмму Лилиенталя для плоской пластинки. Диаграмма эта, подобно изображенной иа фиг. 99, построена таким образом, что пластинка сохраняет постоянно горизонтальное положение, направленно же потока меняется.
Пусть АС (фнг. 304) — пластинка, изображающая элементарную лопасть винта,
О—ее центр, хОх—направление оси впита. Ветер, дуюший по направлению этой оси, разовьет силу 0i‘. соответствующую на диаграмме Лилиенталя углу г' ветра с пластинкой. Составляющая Ос этой силы погонит пластинку АС по направлению, нерпен (икулярному хх, т.-с. начнет врашать винт. Вследствие этого вращения направление ветра будет делать все меньшие и меньшие углы с лижущейся пластинкой. Наконец, угол дойдет до значения i, при котором сила сопротивления воз iyxa Oi направится по оси вмпта, а уповая скорость перестанет воз-
Па кривой Лилиенталя все векторы Oi, Oi <qt О д<> 9(i) взяты ня некоторой постоянной скорости V. Если скоро ть будет иная, то векторы диаграммы пал») б\ ет умножить на отношение квадратов скоростей.
Положив Z — / = «, найдем, что новая скорость будет:
Ое _ Od_______У.
cos eOd Cusn
Отсюда следует, что сила, действующая но осп впнта, вра сматри-ваемом случае будет:
n. Oi
Oj = , .
J сов2а
Построение этой силы очень просто. Надо из i восставить перпендикуляр к Oi до пересечения с продолжением прямой Ое в точке f, потом из f восставить перпендикуляр к Of до пересечения с вектором Oi в точке j. Таким образом, для каждой точки i шаграммы Лплпенталя можно построить соответственную точку j и получить диаграмму, дающую силы давления потока иа вращающийся винт ирн различных углах i' наклонения лопасти к оси впита. Эта диаграмма изображена на фнг 304 На иен же построена диаграмма, дающая сп ты давтепия потока на винт невращающппся, также в зависимости от углов i’. Она представляет геометрическое место векторов Ок, т.-е. проекций на ось винта векторов Oi’.
На фиг. 305 изображена кривая давлений па элемент винта, вращающегося как анемометр, в Декартовых
Фнг. 304.
За единицу принято давлс-
кривая авленпй на целый состоял из двух плоских а ширину 4 ст; они могли
_ ж координатах: по осн абсцисс
отложены угты а наклона лопасти к плоскости, перпендикулярной оси винта, а ио оси ординат—давления на впит. ~ ние иа винт неподвижный.
На той же фиг. 3<»5 построена опытная винт, вращающийся, как анемометр. Вннт дощечек, имеющих инну по радиусу 15 ст, ставиться под разными углами к плоскости вращения виита. Скорость V равнялась 1,1 mt (sec. Опыты эти производил студент В. Т. У., I’. В. Соро-коу мовский.
Разница между кривой теоретической и опытной довольно незначительна, и ее нужно- было ожи ать, так как теоретическая кривая пс тро> па 1ля одного только элемента впнта.
’) Построена В. П Ветчиикнным в доложена на I Всероссийском Воздухоплаватель ном съезде е Москве в 1*11 г. Прим. ред.
Теор«тачесие ссвоаы воадухоилав&Вмж.
Рассмотрим теперь зависимость силы тяги винта от скорости потока Г (прн Лт постоянном). Все формулы за исключением формулы \риу, дающей • линейный закон, представляют
3
2
i
Формула Рябушинского прн Г = О
параболы. Кривые, выражающие силу тягн R и работу мотора t в зависимости от скорости потока, суть ио что иное, как Эйфелевские кривые сир, преобразованные через помножение абсцисс и ординат на постоянные числа. Оин идут, все время понижаясь с возрастанием F; поэтому ЭВ х-
производная ду должна быть все время отрицательной при Гий положительных, а у гол О (фиг. 306) касательной к кривой с осью ординат должен быть острым, что и соответствует наблюдениям.
. дН
дает 0 = 90 , потому что д
обращается в нуль вместе с V. Степенная формула Соро также дает 6 = 90е. Все эти формулы представлены на фиг. 306.
Дальнейший ход кривых до Г = NH не представляет никаких особенностей. При Г > NH винт работает, как мельница; он перестает гнать воздух вниз, и последним ударяет на заднюю сторону лопастей. *
абсцисс отложены эти скорости, а по оспординат — сила тяги в Ат/. Число оборотов X держится постоянным иа каждой кривой. Углы в получились довольно резко острые.
На фиг. Зоя представлены наблюдения Гебера (Geber) того же типа.
Углы 6 тоже дово.льно острые, а не прямые.
Здесь можно у казать на близкое совпадение .этих кривых с кривыми Фербера и \рнj: они весьма близки к прямым. Legrand полагает, ’гго это
получается всегда, когда число оборотов довольно большое, а скорость невелика—до 6 mt sec.
На фиг. 309 представлены результаты дальнейших опытов Гобера1). Он работал с геометрическими винтами в воде и обратил особенное внимание иа неразработанный еще вопрос — работу мотора и коэффициент полезного действия винта. Его опыты заслуживают большого внимания и могут примкнуть к опытам над винтами в воздухе, как это экспериментально показал проф. Wagener аналогичными опытами с воздухом. Гебер определят коэффициент полезного действия винта прн разных скоростях (до 3,5 mlsec.) и постоянном числе оборотов и строил отдельные кривые для каждого числа оборотов (фиг. 309).
Как видно из диаграммы, коэффициент потезного действия идет почти по закону прямой линии, пока скорость пе достигнет вс шчины, близкой к ЛЯ, когда коэффициент полезного действия круто падает вниз и обращается в нуль (при V=NH}, потому что обращаются в нуль скольжение и сила тяги вннта. При значениях же у меньше максимального можно ••читать, что коэффициент полезного действия пропорционален скорости Г. Так как
то, если приняты T=^RNH, получим:
п = . дг_= у (952)
’ КУН ХН*
при чем это выражение становится неверным, ког ia мы подходим к малым величинам силы тяги.
Если же принять, что T=RXH-\-KN*.......................................... .(253)
то получим:
<2&4'
J) Заимствованы из статья Legrand'a в Bull de la societe d'encouragement d'industrl Hgtlonale; 1911, № 4
При большой силе тяги R влияние члена К№, зависящего от трения, невелико; когда же мн подходим к скорости V, при которой 7?=О, то чиститель обращается в нуль, а знаменатель летается конечным, почему у и обращается в нуль, как показывают опытные диаграммы.
Расчет винта для аэроплана или дирижабля.
§ 41. Способ проф. Н. Е. Жуковского для определения действия данного виита иа данном летательном аппарате.
Заканчивая анализ действия винта, основанный на общих теоремах механики, обратим внимание иа поверхности, с помощью которых можно представить как силу, так и работу винта.
При построении поверхности тяги впита можно пользоваться как формулой (225х, стр. 251), выведенной приближенным теоретическим анализом, так и более точной зависимостью, взятой пз опытов пли более тонкой теории. Как формула (225), так и эмпирическая формула Соро, составленная на основании опытов Дорана, обе представляют однородный многочлен второго порядка относительно Л” и V. Поэтому поверхность, построенная выше иа фиг. 277, в той ее части, которая важна длн воздухоплавания, представляет из себя гиперболический параболоид: сечения ее плоскостями, перпендикулярными осям Дг и Г, пре (став, илот параболы (соответственно кривые Эйфеля и Рябушинского!, а сечения, перпендикулярные оси 7?— гиперболы (член J52— 4АС>0 и для нашей теоретической кривой, и для формулы Соро). Поверхность эта (• ьтообразная и имеет две системы прямолинейных образующих, наклоненных под некоторым углом друг к другу и, в нашем случае, юризонтальных. Ее можно получить, если между двумя прямыми, не параллельными и нспересекающпмисл, двигать третью прямую так, чтобы она все время была параллельна некоторой плоскости. Эта третья прямая п образует так называемую косую плоскость или поверхность гиперболического параболоида.
Что касается работы, потребной для вращения винта, то ее, пока мы не подойдем близко к месту, где скольжение равно ну тю, можно представлять в виде произведения
Т= RNH.
Вставляя сюда значение Л из формулы (225), получим однородный многочлен третьей степени относительно N и Г (неполный, так как зависимость от V первой степени):
T=R.\'H=$ f (А’Я)г1А'Я— Г). (255)
Если бы мы захоте in его построить в виде поверхности, то, полагая
ХН—х, V=y, Т=г',
получили бы поверхность третьего порядка, пмеюпы ю вид, аналогичный поверхности для силы тя1 п. Уравнение ее бу де г:
г = Jz’(j — у) . 1256)
Она пересечет плоскоеь АУ по оси А', потому что Т=о, при Л’ = 0 и еще по прямой, наклоненной к оси А под углом в 45 , так как прп Т — О при х = у.
Для решения задачи и расчете винта (ля тетатетыюго аппарата надо, кроме этой поверхности, характеризующей секундную работу, потребну ю для вращения винта, построить те другу ю поверхность третьего порядка—поверхность полезной работы:
Т, KV^- * Г(УН— I)(A’W) . (257)
Поверхность эту можно получить, умь»жая ко .р пшаты г поверхности, выражающей силу тя! и к, на Г; она также бу 1ет иметь седлообразный вид и перес» ет плоскость Л1 по той же прямой, наклоненной к осн Л под углом в 15 , чт л сита тяги.
При помощи этих двух поверхностей, представляющих полезную работу впнта RI и работу " Т, потребну ю для его вращения, можно, зная характеристику мотора и работу сопротивления всего чета тельного аппарата, определить iritcTBue вннта на тапнич летательном аппарате.
Фиг 310
Характеристика мотора дает мощность мотора в виде фу нкции числа
••г» оборотов в минуту и:
НЕ — /‘(и),
при чем легкие моторы обладают тем свойством, что работа их с возрастанием числа оборотов у ве тичнвастся почти по прямом липли, а затем • разу падает и приближается к нулю.
Что касается работы сопротивления летательного аппарата QV, то характеристика ее будет кубической параболой, так как снта сопротивления движению Q пропорциональна Г-.
Рассмотрим, для примера, вопрос о скорости» с которой полетит фонтан ити дирижабль при данных винте и моторе, и о числе оборотов последнего.
*) Вычислен* и яостроева В. И Ветчпяжиным.
Прим. рсд.
Будем (фиг. 310) по осп X (направленной назад) откладывать числа оборотов в минуту я, (слева стоят соответствующие ветичнны NH) по оси Y (влево) — скорости полета в mt sec, а по оси Z — мощность в лошадиных силах ПР.
Строим сначала (пользуясь опытами Дорана, описанными ниже в § 44) поверхность (OFREO) полезной мощности вннта (ур-ие: z=RV) и поверхность (OUSTXO) мощности, потребной для вращения винта (ур-ие: 2 = Т).
Затем, в плоскости ZX вычерчиваем характеристику мотора OF, а в плоскости 5Z—характеристику работы сопротивления данного летательного аппарата (OQj и проводим две цилиндрические поверхности: одну (ODHPO)—г характеристикой мотора, как основанием, и образующими, параллельными оси Г, а другую (OQLEO)— с характеристикой работы сопротивления, как основанием, и образующими, параллельными оси А. Ординаты первой цилиндрической поверхности представляют работу мотора, ординаты второй — работу сопротивления летательного аппарата QV.
Опредстяем линии пересечения цилиндрической поверхности 0DHP0, характеризующей мощность мотора, с поверхностью OUSTNO, характсри-зу ющей мощность, потребную для вращения винта (линия АВ), и цилиндрической поверхности OQLEO, для работы сопротивления летательного аппарата с поверхностью OFREO полезной мощности винта (линия CD), и вычерчиваем проекции этих линий пересечения (аЬ) и (cd) на плоскости XY; они пересекутся друг с другом в точке т, координата х которой даст нам число оборотов п винта, а координата у даст скорость V всего летательного аппарата. Отношение же координат г точек той и другой седлообразной поверхности, лежащих на вертикали точки т, даст нам коэффициент полезного действия данной винтомоторной группы. При этом выясиптся также, насколько выгодно работает мотор, т.-е. насколько близко к тому числу оборотов, при котором он выделяет наибольшую мощность.
Из предыдущих рассуждений и построения вытекает довольно важное заключение: у дирнжаб тя или аэроплана, имеющего опре деленные мотор и винт, сама собою устанавливается определенная скорость полета и число оборотов мотора, так как существует только одна пара значений V и п (только одна точка т), для которой одновременно и мощность, развиваемая мотором, равна мощности, воспринимаемой винтом, и полезная работа вннта равна работе сопротивления всего тетательного аппарата.
Если при построении поверхностей для работы винта во осн X откладывать величины NH, а не п, то они остаются одними и теми же для всех шагов впита данного типа, и будет меняться только масштаб.
8 42. Задача Фербера
Рассчитаем виит для аэроплана или дирижабля на основании графиков Фербера. Обыкновенно дается скорость полета V и подъемная сила летательного аппарата; ио последней соображают форму’ и размеры аппарата в при данной скорости определяют силу тяги винта R. Итак, Г н R известны. Помножая R на V, получают полезну ю работу, сообразно с которой и строится мотор. Зная характеристику мотора и задаваясь его скоростью вращения так, чтобы коэффициент полезного действия его был возможно большим, определяют затрачиваемую работу Т и коэффициент полезного действия. Если, как это обыкновенно бывает, виит насажен прямо на валу мотора, то и число оборотов винта N будет также задано числом оборотов мотора. Неизвестными являются лишь шаг виита Н и диаметр винта D.
Так ставит задачу об определении размеров винта Фербер.
Для примера он решает такую задачу. Скорость полета V = 12 mt «ее, сила тяги R= 100 кд. Мотор в 40 HP, так что развиваемая им мощность Т = 40 75 кд mt/sec = 3000 кд mt/sec. Число оборотов Л = 1ч 6 в секунду. Требуется найти Н и D.
По имеющимся данным находим коэффициент полезного юпствия вннта д: ЛГ 12.100
4= Г “ зооо =0-4
и ветчину v\ ___
Я У It 18.6 *100 - оо
V = --- s= 1.-»-
на шаграмме Фербера (фиг. зш горизонта, гь д—0,1 а через точку их исрео“че11ИЯ .V (1“вую, потому что большему скольжению, менее выгодной работе
Затем провотим н крнву ю v = 1,29 ), правая соответствует а, следовательно, и винта), проводим, интерполируя на г та с линии б и Л. Находим, что точке If соответствует скольжение винта г=0,41 и значения 6=2,7, Л=О,52 Пользуясь последними величинами, определяем из выражения (2П>) диаметр винта:
л 2,7 V100 .... .
D= —_ = — — = 2,2о mt
и, наконец, шаг винта:
Я = ЛД = 0,52 2,25 = 1,17 mt.
Таким образом, прн помощи графиков Фербера легко рассчитать размеры винта, не обременяя себя сложными вычислениями.
Если бы задача решалась бате.- точно, то нежио было бы принять во внимание и характеристику мотора. При этом выяснилось бы. иа<-к<пьк<> нужно отступить от числа оборотов, соответствующего наивыгодиейшей работе мотора, для получения иаивыгодпейгаей работы всей винтомоторной группы. Эту задачу решил капитан Шабский, и в особой форме член Воздухоплавательного Кружка при Высшем Техническом Училище В С. Маргулис. Статья капитана Шабского напечатана в трудах I Всероссийского Воздухоплавательного Съезда.
§ 43. Задача кап. А. И. Шабского
Требуется лететь со скоростью 12 mt sec, при чем сила тягл винта Л = 100 кд. Мотор дан в 40 сил при 1120 оборотах в минуту. Отсюда находим: Г,= 3000 кд-mt/sec и Л'=18,6. Дана также и характеристика мотора. По большей частп она очень близка к прямой линии (враща н.пый момент на коренном валу мотора довольно близок к постоянству е е ‘кундная работа равна моменту, помноженному па угловую скорость а потом сразу падает, когда мотор переходит известно» число оборот в На фнг. 312 представлена характеристика одпого из легких мол ров ’), подтверждающая сказанное. По оси абсцисс отложено число оборо в, а но оси ординат — мощность.
') 11* чертеже ошибочно поставлено / вместо в, *) Гвом 50 лошадиных свл.
Прим. ред.
Если принять приближенно, что
T=AN
и воспользоваться соотношениями
RV г==л'п
то можно вывести, что
В Г X\R Ri
VV ХА F2 ” .41
В нашем случае
Л
»/ =
nr
ЗООО 18,0 100 12
IttiA кто
I6l.12
Iftl, 7,45 -V
Фиг. 313.
Выражая величину tp через основные переменные у и г, можно вычертить кривою 4г=0,52 на графике Фербера. Но проще сделать это иначе. Бу чем проводить горизонтали, соответствующие разным у, п вычерчивать кривые тля v, равных 0.52 : 4. Тогда точки пересечения горизонталей 1) г соответственными кривыми v будут точками кривой 4г = 0.52.
Из графика Фербера видим, что кривая v=l, соответству юшая 4=0,52, имеет maximum нри ^=0,48; следовательно, пересечения еще не получится. Прн больших 4 кривые е проходят еще дальше от соответственных горизонталей. Отсюда заключаем, что 4 < 0,5, v > 1,04.
Определив предельные условия, составляем таблицу: Таблпца 31.
ч o,52*)j 0,4 о,3 <1.116 I 0.2 0,104
Вычерчиваем кривые v (Интерпол и р.\ я на глаз) и по точкам строим кривую ^i’=o,52 |фнг 313) Взятыми значениями у верхняя часть кривой не определена. Поэтому возьмем еще i?=0,45 и */=0,18; соответственные г будут: 1,15 и 1,08. Вычерчивая и эти кривые*1, нахрднм всю кривую JKL; она выражает на графике Фербера закон, который да» гея характеристикой мотора н устанавливает связь между <•<» льженисм винта л коэффициентом полезного действия прн ганним моюрс и дайной скорости V. Затем отыскиваем, где на этой кривой будет коэффициент полезного действия наибольшим; это будет, конечно, в верхней точке К кривой, соответствующей значениям ??—0.48, г=0.51, г = 1,08. Через точку К прово гим кривые Л и <5; получается Л.=0,85. д=2.5.
Теперь определяем размеры винта, чисто оборотив и мощность. с какой будет работать мотор.
г, A'R V» Ю ,
D =* , - = —— 2,08 mt:
И = 1,77 nit:
vV* rv
2V=V = Л = 15Л. и=60A =930;
\r Лч
7=2500 kg^jnt sec = 3-3,3 HP.
Как внднм. получился результат, ювольно апачи reлыш отличающийся от того, который мы приближенно получаем с «гласно Ферберу.
У нас вышло довотьно глинное построение, потому что мы наносили на график Фербера вею характеристику мотора. Для действительного же расчета винта надо иметь только ее верхнюю часть, так что достаточно построить только кривые
1) = 0,40; 0.45; 0,48;
г =1,30; 1,15; 1,08,
определить точк^ К и нровсстл кривые h = 0,85 и <5=2.5. Кроме того, от всех этих кривых надо проводить только нужные нам части, ймк на фнг. 311. Весь расчет про-штся на прозрачной кальке, нс вычерчивая ничего лишнего,а прямо мп.южив ее иа графпк Фербера. Основной квадрат следует начер
тить как для установки кальки, так и для того. чт«"5ы впосл»-итвии ризу определить положение вс к точек расчетного чертежа относительно • дмого графика.
*) Отмеченные звездочкой * значения v уже имеются на графике Ферберв.
Можно было бы решить задачу и для более сложной характеристики
Т=!» (Л’), а именно: из выражения
Т=Ф (ЛЭ
И форм}лы
’=¥
определить у и установить связь между » и у. Затем из трех формул можно исключить Т и JV и получить одно ур-ие, связывающее у и v и данные величины Л и Г. Но мы этого не делаем, так как указанное решение довольно сложно, а результат будет очень немного отличаться от полученного в предположении
T=AN.
S 44. Опыты Dorand’a.
Самыми важными для расчета воздушных винтов в настоящее время1) являются опыты Дорана (Dorand), произведенные в Военной Воздухоплавательной Лаборатории в Chalais-Meudoii. Эти опыты производились иа тележке, движущейся по рельсам, в безветренную погоду. Определялась сила тяги винта н потребная мощность мотора в зависимости от скорости поступательного движения V и числа оборотов N. Опыты производились прн переменной скорости V и постоянном JV, и на графиках наносились семейства кривых, каждая для постоянного числа оборотов. У пас (фиг. 315 и 316) представлены графики Дорана для
Фиг. 315. Фиг. 316-
скорость V при опытах изменялась от О до 12 nit sec.
С помощью графиков 7? и Т можно для любой скорости н любого числа оборотов определить коэффициент полезного действия випта q, как
!) Начало 1012 года.
Прил. ред.
отношение RV к Т. Кривые т) нанесены у нас на одной диаграмме, с сплои тяги R (фиг. 315), при чем одна из них доходит до Г—А7/=19,7 mttsec.
Конечно, пунктирные части кривых R и экстраполированы; у обра щается в нуль дважды: при
Г=О
и при
V=NH,
т.-е. когда
Г=0.
Кривая ц имеет здесь приблизительно такой же вид, как и ыотвст-ствующая кривая Gebcr’a для водяного вннта. Па таких графиках
Мах
остается для всех подобных внитов (несмотря па различные диаметры) почти одинаковым и мало зависит от числа оборотов. Приво цгч дтя сравнения таблицы 32 и 33.
Таблица 32. Таблица 33.
Ввит А=0,75; D=2t5 mt Ввит Л=0.7Г»; 0=4.3 mt
V » 10 10,5 N | 3.45 | 4
Мах г; 0,73 0,74 0.73 Maxij 0,71 0.75
Следующая серия опытов Дорана относится к опреде <еиию наибольшего коэффициента полезного действия, достижимого в группе винтов одного типа, но с различным пропорциональным шагом Л = .
Для определения этого Maximum Maximoruni коэффициента полезного; действия были изготовлены пять винтов с различными Л: 0,625: 0,75; О.«74
1.0; 1,29; для каждого из них определяюсь Pi и Zp соответствующие
Max Ч=ЧМ.
Затем, откладывая но осн абсцисс71, а по оси ординат сц, Д, zlt по пяти найденным точкам строили кривые со* ответствующнх величин:
“1= Д^у.=/1<Л>.......I25S>
А =&»>.- (259J
.1:2001
. .(261)
Очевидно, что кривая (2611 должна иметь Мах., так как i]=0 при Л=0 (диск» и прн 7»=оэ (крылатка,; на фиг. 317 он наблюдается при Л = 1,2. Это и • -ть искомый Maximum Maximorum дан-
ного типа винтов, равный 0,84. Его довольно легко определить с точностью, потому что изменения у весьма малы при h, близком к 1.
26b —
§ 45. Задача Do rand a.
Пользуясь экспериментальными кривыми uj»nr. 3171, можно ыя каждого данного случая подобрать винт, который работал бы с Мах. коэффициента полезного юйствпя. Чтобы винт с данным пропорциональным шагом работал при он должен иметь те значения а„ Д и Л1э которые даются дтя него на фиг. 317. Следоваюлъпи, (ля воякой скорости V мы находим единственное значение
\1). Г
Z.J
Это дает возможность выбрать Д' ври данном £)„ и наоборот; но прн атом поглощаемая винтом мощность ia, еле вшательно, и тяга вин raj будет различна. Если же поставить условие, что мощность мотора нам дана, то получим единственные и вполне опред» теннис значения L) и Л. Их выражения легко получить из ур-нй г’Зй) совместно с (2t*0):
‘ м j’ • О«2)
'-Л7‘=7 л^ ••(**>
Таким образом, тля каж. torn Л при {энных
Фяг. 3i8.
Гы Г ил\ дим тс значения D и У. при которых rj будет иметь Maximum.
Для непосредственного их опре {едения, Доран, пользуясь формулами (262) и (263), построил особи п график, изображенный на фиг. 318. На нем по оси абсцисс отложены величины h (от 0,6 до 1,3), а по осн ординат ветчины чМаж, D и X, прн ч_ем точки, соответствующие о щой и той же скорости, «--дпиены друг с другом кривыми. Таким образом, на диаграмме, кроме кривой т/Мах, имеется два оменетва попарно сопряженных кривых D и V, каждая пара для онредс Юнной скорости I (от 17 до 24 mt «ее). При построении предполагалось, что секундная работа Т, поглощаемая винтом. постоянна и равна 48 HP.
Чтобы построить потчбнып график (ля гругого значения Т' мощности, нужно множить диаметры, полученные для Г=48 IIP па J' w , а чиста оборотов — иа j/” Но можно пользоваться одним и тем же графиком
и для различных мощностей мотора. Для >гоь* паю только придавать другие значения тем скоростям, для которых построены кривые. Именно, если кривые А’ и D построены тля СКОрС.1 ти V при Т—48 ПР, то прн мощности Г эти же кривые будут f «ответствовать скоростям
Г= 1 I I» на КРИВО° N
и
l’-=l J 7 на кривой D.
Значения 1?м от этого ие меняются, так как нр зависят от абсолютных величин скоростей. Пам выгодно держаться больших величин ijm, лежащих в правой части графика; следовательно, выго (но по возможности увеличивать (иаметр винта и уменьшать чисто его оборотов. Вопрос же о том, нужно ли ставить от мотора к винту перс шчу для уменьшения числа оборотов последнего, решается в каждом частном слу чае особо, так как добавочный вег от передачи и потерн на трение в ней могут поглотить вся выгоды, достав темне увеличением коэффициента полезного действия винта.
Разрешим при помошп этого графика две затачп.
1) Требуется подобрать вин гы (ля мотора в 48 НР, дающего 20 оборотов в секунду при скоростях 17, !*, 19, ... 24 mt я*с. Провидим горизонта lb, проходящую через А’=20. Из точек перессченпя ее с кривыми N прово (им ординаты, отрезки которых от оси абсцисс до соответственных кривых В дадут нам диаметры винтов, ш кривой — коэффициенты полезного действия, а абсциссы—величины ft. Нанрпмер, получаем (Табл. 34):
Таблица 31.
F : ! so 22 24
D 2 30 S.io 2.20 ' 2,14
h <>.614 0,754 081
0.53 0,60 0- - 0,71
2) Распотагаемая мощность на осп винта 48 ПР, а диаметр внпта по конструктивным < лображениям не дочжен превосходить определенной величины D. Скорость полета И дана. Опре де шть ft, V и г/м . Горизонталь, проведенная на высоте (анного диаметра, пересекает кривую D, соответствующую данной скорости Г, в определенной точке: ордината, проведенная через эту точку, дает значения и V, абсцисса же ее — величину нронорциона гьногл гаага ft. На основания вышесказанного получаем решение единственное и определенное, так как В выгодно брать возможно больше.
§ 46. Исследование винтомоторной группы по способу Duchfcne'a.
Несколько, иначе разрешает задачу о выборе вннта для аэроплана к титан Duchene 1‘.
П Опубликовано в ж}риале .La Technique Aeronautique." 1911. .V 37.
Чтобы выяснить полную характеристику работы винто-моториой группы, надо иметь отдельно характеристику собственно мотора (ио оси абсцисс откладываются числа оборотов, а по осн ординат — мощности в HP) if отдельно характеристики винта, как нх строит Доран: по оси абсцисс отложены скорости поступательного движения К, а по оси ординат иа одной диаграмме мощность, поглощаемая винтом, выраженная в ИР, а на другой — сила тяги в кд; при этом каждая кривая соответствует определенному числу оборотов.
На фиг. 319 и 320 представлены такие диаграммы новых опытов Дорана. Диаграмма мотора ставится рядом с диаграммой мощности винта, а над последней ставится диаграмма силы тяги винта, как иа фиг. 320.
Фиг 319.
Фиг. 320.
Каждой точке, наир. РП(Х> первой диаграммы, представляющей мощность мотора при поо обор! чин, соответствует одна кривая 1100 (пунктирная) из диаграммы мощности винта, и иа этой кривой точка 41100 с той же ординатой («иаИиоо— РиооЛюД Абсцисса Оо11<к>, очевидно, представляет ту скорость поступательного движения, при которой винт, делая 1100 обор/мин, как раз поглотит мощность, выделяемую мотором при том же числе оборотов. Когда точка Р пройдет по диаграмме мотора, точка А опишет на диаграмме винта кривую (сплошную), вершина которой соответствует вершине Ри диаграммы мотора. Эта кривая представляет диаграмму мощностей, с которой может работать вннто-моторная группа при различных скоростях поступательного движения и соответственных числах оборотов. Точка Л1СЙ0, с абсциссой нуль, соответствует винту с неподвижной осью. Продолжая ординаты до пересечения с соответственной кривой К, полу чим диаграмму силы тяги винто-моторной группы в зависимости от скорости поступательного движения (сплошная кривая R). Произведение сизы тяги иа скорость дает полезную работу, выделенную винтом (сплошная толстая кривая). Мах. ее соответствует вершине кривой В*. Обыкновенно она не лежит на одной ординате с вершиной Ат диаграммы затраченной мощности. Отношение дает нам коэффициент полезного действия винто-моторной группы (кривая у).
Из прпве (енных рассуждений и диаграмм Duchene’a вполне выясняется юйствие винто-моторной группы.
§ 47. Построение характеристики винто-моторной группы по способу Маргулиса.
В. С. Маргулис предлагает строить характеристики вппто-моторноп группы, пользуясь логарифмической сеткой *) Для этого он строит сна-чкла поверхность тяги вннта подобно тому, как было изложено в § 37, только ось п он считает ио направлению от наблюдателя, а ось Г вл-по оси R вверх, как л прежде, откладывается сила тягл. Поверхность, вычерченная на фнг. 322, построена по опытам Дорана для винта D = 2.5 mt, If —1,875 mt. Вычертив линии пересечения поверхности с плоскостью
») Доложено яа 1 Всероссийском Воздухоплавательном Съезде в апреле 1011 года
п = 1500 oofMUH, он вычерчивает вертикальные параболы, которые проходят через начало координат и различные точки этой кривой, представляя линии пересечения поверхности с вертикальными плоскостями, проходящими через ось 11.
Вместо этой поверхности, для практического пользования Маргулис предлагает вычерчивать на логарифмической бумаге соответственную номограмму по следующему способу.
Возьмем на фиг. 323 диаграмму Дорана, в которой по оси абсцисс откладываются скорости поступательного движения, а по оси ординат — сила тяги для указанного винта при п — 600 обор/мин, изображенная кривой аЪ.
На логарифмической бумаге (фиг. 324) по оси абсцисс откладываются логарифмы сотен числа оборотов от правой руки к левой, а по оси ординат— логарифмы метров скорости и килограммов силы тяги, так что начало координат соответствует 100 oSJmuh, 1 mt]sec и 1 кд силы тяги. Числу оборотов 600 соответствует ордината, начерченная толстой линией. На ней откладываем силы тяги, соответствующие различным скоростям. Через каждую полученную таким образом точку проводим прямую линию, ординаты которой представляют логарифмы силы тяги при различных числах оборотов и различных скоростях, соответствующих одному и тому же отношению —; при этом полученная линия представляет изображение
у
параболы, представленной на фиг. 322 для того же отношения —, т.-е. для одного и того же коэффициента полезного действия. Эта линия будет на логарифмической бумаге прямою, образующей с осью абсцисс угол у, при чем tgy = 2 (вследствие того, что парабола второй степени). Через все точки ординаты, представленной толстой линией, будут проводиться такие прямые, которых на фиг. 324 представлено пять, соответственно пяти взятым точкам кривой аЪ. Они соответствуют различным отно-г
шениям —. п
Кроме того, строятся еще прямые линии, ординаты которых представляют логарифмы скорости при данном числе оборотов. Эти прямые линии даны для постоянных отношений ~ и потому образуют с осью
абсцисс углы /9=45° (tg/9=l). Отрезки этих линий на оси ординат дают постоянное отношение — (на нашем рис. умноженное на 100), кото-V V
рому соответствуют линии ( — = A; lg7= Ig^i). При — малом эти отрезки отрицательны и обращаются в — со для — = о, т.-е. для гелико-птерного винта. На нижней диаграмме вычерчены прямые мощности, поглощаемой винтом, построенные с помощью кривой Дорана тп (фиг. 323) для того же числа оборотов 600. Для всякой ординаты точки, взятой на утолщенной вертикали, мы строим прямую линию, выражающую связь между логарифмом мощности и логарифмом числа оборотов при соответствующем постоянном отношении . Эти прямые будут пересекать ось абсцисс под углом а, тангенс которого равен 3, так как они представляют кубические параболы.
С помощью трех начерченных семейств прямых линий (всего 14) можно по данному числу оборотов и скорости определить силу тяги винта и поглощаемую им мощность. Для этого по 1д числа оборотов и 1д ско-V рости определяем точку и смотрим, какому отношению ~ соответствует прямая скоростей, проходящая через эту точку. По этому отношению берем прямые, соответствующие силе тяги и мощности и определяем их пересечения с прямой, параллельной оси ординат и проходящей через взятую точку.
Переходим к винтомоторной группе, Для этого вычертим на диаграмме мощности винта логарифмическую кривую характеристики мотора, т.-е. откладываем по оси абсцисс 1g числа оборотов мотора, а по оси ординат 1g выделяемой им мощности; получится кривая ef. Для каждой точки этой кривой смотрим нумер проходящей через нее прямой мощности винта и, проведя через эту точку параллель оси ординат, определим точки ее пересечения с прямыми скорости поступательного движения и силы тяги, обозначенных тем же нумером. Каждый такой нумер соответствует определенному коэффициенту полезного действия винта. Эти две группы точек пересечения соединяем непрерывными линиями и получаем кривые поступательных скоростей (cd) и сил тяги [e'f), соответствующих различным числам оборотов данной винтомоторной группы. Кривая e'f, перенесена (пунктиром) и на диаграмму Дорана для силы тяги, изображенную на фиг. 323.
§ 48- Теория Ранкина.
Ранкина (Rankine) можно считать основателем теорий винта, основанных на рассмотрении удара. Здесь дано изложение теории Ранкина по Буслеют), с некоторыми изменениями, облегчающими вывод основной формулы Ранкина.
Пусть линия АС (фиг. 325) представляет направление элемента лопасти винта, а линия АВ лежит в плоскости, перпендикулярной оси винта, которая параллельна плоскости чертежа и направлена вертикально. Лопасть движется горизонтально слева направо, как показывает большая стрелка, со скоростью ВА. Предполагается, что винт вступает в совершенно спокойный воздух со скоростью V. Как всегда, мы обращаем движение и рассматриваем винт, вращающийся в набегающем на него со скоростью V потоке. Угол наклона лопасти к направлению ее движения обозначим через д>. Если бы частицы воздуха прямо скользили по лопасти
*) Буслей. Гребной винт. Перевод Креницкого. Москва. 1892 г. Теоретические основы воздухоплавания.
винта, то скорость потока должна -бы быть ВС. Эту скорость, которую мы обыкновенно обозначаем через УН, Ранкин называет через V,. Сложив ее со скоростью движения тонаотн, взятой в обратную сторону, по правилу треугольника, получили бы АС- Но
воздух подходит с меньшей скоростью V=BB. Воздушные частицы вступают на толасть с относительной скоростью AD, а так как лопасть направлена ио АС, то происходит улар. При ударе составляющая относительной скорости ED, перпендикулярная лопасти, уничтожится, и останется только составляющая АЕ, направленная по лопасти С этой последней скоростью частицы и сой-
Фвг зг.
тут с лопасти, при чем в абсолютном дви-
жении к скорости АЕ прибавится скорость движения лопасти ВА. Эту абсолютную скорость, BE, мы разложим на вертикальную ХЕ, которая будет представлять скорость уходящего от винта потока по направлению
осн винта, и горизонтальную LE, которая показывает, что поток за винтом
вращается в ту же сторону, куда и винт.
Для определения силы тяги внита надо, прежде всего, определить количество протекающего через винт воздуха. Это очень легко делается из чертежа, тогда как Ранкин пишет довольно длинные, формулы. Опре-В'тим, прежде всего, ЕС. Из чертежа ясно, что
В свою очередь,
ЕС = DC sin <р = (V,—И sin <f.
LC=ЕС sin <f = (Г.—I') sin2 f.
Отсюда вертикальная составляющая скорости уходящего от винта воздуха.
NE = BC—LC= V — (V,—Fisitfy-— К,(1 —rsin’yj = и, . i-’iili
К.^_Г_ЯУ Г r — V. ~ АН
(’OS')
представляет ветнчину скольжения, определенную уже ранее.
Полное количество М протекающей через винт жидкости (секундная мюса) получится, ести взять площадь 2nxdx того кольца, которое опи-ыпает адемент винтовой линии, помножить его иа скорость и и проинте-|рнровать все такие произведения, изменяя а: от о до а. т.-е.
• <1
M—2n—J^ujcdx = 2n^-V,J^(l — .(265)
Здесь а = есть радиус винта. Интеграл этот очень просто берется, («•йствитсльно, мы всегда имеем для геометрического впита:
'К!Г = 2^ • s‘n<f = 2"х 1 1
1 hi это значение синуса возвести в квадрат и по (ставить в (265), а затем помножить числителя и знаменателя на I—j , тэ получим:
А/=2я-^1', / /1—
9 J 1 * + (»'/
Второй член подъиитегральноц функции д.,1- логарифм, так что окончательно количество протекающей жидкости
У л д Г./т-’ »1 Д jg i[i .1261»)
х /7 -
Здесь пришлось прибавить мн, житель 2 , а Двойка сократилась при
интеграции. В дальнейшем Ранкин обозначает ля окрчщення:
- cotgp,, ................... .1267)
где у, угол наклонения крайнего элемента лопасти к птоскоети, перпендикулярной оеи винта. Прн обычных наших обозначениях q= ц
Т0Г'1а У = FV. (1 - ' '«V £ ),................(266')
9 9* J
гдр F—площадь, описываемая винтом. Это, конечно, всегда меньше, чем
Чтобы определить cm\ тяги, нужно взять приращение количества движения, т.-p. разность МРЖ1у количествами движения ухотящеп струи
J.T f[n‘].rdr
и подходящей 2П, то есть
В=2я д f[u8] zilr - .(26IS)
Этот интеграл легко берется на основании тех же преобразовании. При этом Ранкин находит выгодным подставлять УI ие в окончательной форме, а в вн ie ннт трала (уравнение 2Ь5' и затем подвергнуть вее выражение небольшому преобразованию:
= 2л- J |\!(1 — rsin-'yi-’ — Г,Г(1 — rs-ln2»-)] -г<?х =
= 2л~У* 1,(1—гчп*у;(Г,— P.jsin’'/—Г) idx.
Заменяя, по уравнению (205), \',т черт, Г,— Г, выводим эту величину за скобку: „
й=2.т Гг.П, - Г| 11 —rsin8gi) (1- sin’9>)zrfa = .7
= 2.1 : ГГ.(К—Г)[1—(1-г) sin”?-f-TsinM xdx.
*) Натуральней логарифм.
Заменяя, как и предел*1. sin’г/ через
получим:
1
Первый интеграл мы уже взяли, л второй совершенно такой же, только знаменатель у него в ива трате; первый приводится к логарифму, а второй .просто к дроби. Подставляя пределы интеграции О ц о, находим:
R = FF.iF. гф — (1 г; 1вО+’г,_ гф^,]. • - <2«е)
г ie q имеет указанное значение iyp. 267). Эго и есть формула, которую дает Ранкин (ля силы тяги винт .
Секундная работа, поглощаемая винтом, равна
T = -RXH. 1230)
Это справь 1ЛИВ0, кот ia мы ставим -тлвпе. что сила давления ветра в егда нормальна к поверхности пластинки. Следовательно, во всех у iap-ных теориях эта формула совершенно верпа.
Если мы остановимся на Геликонтерном винте, то должны будем положить для скорости притекающего ветра н скольжения:
Г=О, г I.
Тогда формула подъемной силы примет вид
F = F 1,’|1 2 '1J '<1 - * . (270)
9 в2 1 + <Г '
( оглаено с нашпмп обозначениями и фг,рму Лой У. = Д7/ = р.
подставляя это в уравнение (27U) и заменяя через -J-, получим:
9 °
= » । ,П)
Л I а 5’ 14-<г ’
Сравнивая эту формулу с формулой Ренара 227), увидим, что к-.зффнцнент качества £-равен
272)
.*кнм образом, дано теоретич» «. выражг ши* для Е, которое и юсь не мч лет быть <• ibiue половины, как это видно на фиг. 32«
1ак как q = ~, то q — -~ при Л = 0 и q- о
при Л = .В первом случае, когда шаг очень мал, качество винта самое • (ьшое. так как третий член стремится к нулю, так же, как и второй.
в числителе которого входит логарифм бесконечности, а в знаменателе прямо бесконечность, т.-е. величины несравнимые между собой. Опыт же (фиг. 292, кривая E = f(h), полученная Рябу тип неким) показывает, что при чалом шаге и качество впнта низко.
Причина разногласия теории с опытом заключается в неправильности предположения, что секундная работа выражается формулой:
Г = яхн.
о чем мы неоднократно уже упоминали. Когда сила тяги вннта обращается в нуль, работа на его вращение все-таки затрачивается; она зависит от трения.
Когда шаг винта очень велик и q стремится к нулю, тогда и Е стремится к нулю чрезвычайно быстро. Доказать это очень просто, разлагая выражение в ряд ио степеням д. Известно, что
г^7=1 - а"+ .
Отсюда находим, что
£3=т|,-2(’- 2 + Г-’Г + ) + + )] =
т.-е. обращается Подставим
в нуль значительно бистрее <j.
в формул) (269) для сили тяги винта
тогда иолу ним:
« = j-F^. V) [г.-(2Г.-гЛ"+’’>+(Г.-Г)1^] =
|г. (1_^л + ^ + г(>ва+Л__^_ф(273,
это есть одноро ший многочлен второй степени относительно Г и относительно X (так как Г, = Л"Я), т.-е, гиперболический параболоид. Наблюдения должны показать, насколько гиперболический параболоид Ранкина отступает от действительной поверхности тяги винта, о которой ми много говорили више.
Если принять форму ку Т= КХН, которая очень хороша для геометрического винта и оправдывается на опыте, пока скольжение не подходит близко к нулю, и подставить J вместо F„ то формула Ранкина получает вид формулы, выведенной из общих соображений механики:
Строение формулы то же самое те же общие множители -- F и R — V, а. во вт-1рой rs. так же и Г, помноженные иа не. горне г-. «ффи-циенты; ип । к, .ффицпентн получают л и окончат тъной фирме. Вен т.-ория по ipocua б. того тушения, которое было сделано при выводе иа пен .лпн общих си бра^енпп механики, когда нр дполагд -»гь, '<ю вея cKupoi ть направлена по вертикали.
форму ia Рапкина перестает быть точной. к<» RXH ш ко к нулю. Поправка дтя этого сличая на так пазывн i „выт* гноило- бы ia с “тана Бу с чс“ч.
49. Теория проф. Д. П. Рузского ‘)-
Профессор Дмитрий Павлович Р\ ’кни р«<[*....> г <-. кующую практическую ш .v о суд ( м винте: какой мпжно j- лучить наибь [ыпии коэффициент uni. ш< , . действия гребне»! » винта, t- i .д даны скорость судна и ер- сопротивление, а машину можно ставить какую угодно, сообразуясь тишь с в доизмешспнем судив.
Рассмотрим сначала элементарный винт, лоцае-ти которого эктючены между двумя б шзкими соосными пплип рами Пусть д-н < ш ц.пог впнта даны: сила тягл А’, площадь /’основания кольцевой по юстн, в которой он движется, и чироеть Г иог.-ко. н»>гающеп- на винт.
При этих у- ювиях и составляющая м скорости потока, шбраеы-Bi лого вши I и*. наир] ленпю его оси, будет вполне определенная. В гамом д. . гита тяги
К .......I2IM
а Секундная масса
11-1 Fu.
9
гд* прмнитьшч* было »5ы за F считать кольцевую площадь нормального «-«* тення струи, выбегающей из-под элементарного винта. Исключая из *гих двух уравнений М, найдем связь между V и и.
Падача состоит в том, чтобы подобрать число обор i >в так чн -ы при даином радпу'Ч’ #лгм» нтарною винта коэффициент и- миноги • I: твия был найду чпшм.
Рузский ра- «атривв т ев а 6^ ударное вхождение струи на винт, а ногой исг.1 у г у .ар.
Пусть на фнг. 327 (чтооы получить более кратко*» я т»«.енпг, фигура им килько видоизменена против взятой Рузским) ОВ пр<* и-тавляетскорость
частиц ВОДЫ (| гноентельно <1~меит»1рногп вннта; она раскладывается на две: на пернгндику. шрну ю р.«-дпуч у ОС «». представляющую скорость движения ЛоПи- ти, направленную в обратную стороне, и на вертикальну к» СА= V. которая пред стаи лягте кл-роеть всего шпика отио-«Н1 льн< инт.
Ь лн чнетицн «ды пегупаег на лопасть бел у лра, -к на фиг на пр. -лит Пи ней, не меняя величины ы.лро'тн < ор. . ь в
ф£П >.
Фиг. J37
•) 1.с<ерта:;ня. iat евная иа степень адъюнкта Киевского Политехни- tct.- г Чнституга под назаапвеы; В1 ория гребпых вянюв“. Ки- в. 1010 г.
только сбывает вследствие трения), и еюдпт по направлению конечного элемента юпасти е относительной скоростью ОА, равной ОВ. Ее вертикальная 1-о1тавляю1цая ВА — и представляет скорость уходящей струи по оси винта л горизонтальная составляющая ОВ, кинематически сложенная I* ci ;лелыо «. ваятой в ттрямом направлении, дает скорость потока по ш-рпепдикуляру к радиусу винта. На фигуре 327 для получения ее надо ОВ вычесть из скорости C0--W. Отрезок CD-=y будет представлять скорость, с которой ноток вертится, выйдя из лиц винта. Абсолютная скорость частицы, уходящей т винта, есть С Л.
Так как, по у 1 вши, винт врезывается в воду бед удара, то потери живой силы никакой иет (если нс считать потери на трение), и полное приращение се будет Mlu- -if - I'2) (так как квадрат скорости отходящее । потока СА1 = и-рif, а квадрат скорости подходящего потока СВ‘ = 1~-| Поэтому коэффициент иолсипого действия элементар-пого винта будет равен
„_вг_ M(»-pF 2(« 1)Г
Ур. (275) справедливо, ели считать, что горизонтальная скорость жидкости перпендикулярна радиусу лопасти, когда струя вышла из под впита. Так как я вполне определяется по Г, В и F, то написанный коэффициент laBUeUT только от у и будет иметь maximum, ког да у пме. т наименьше' значеипе
Посмотрим, каков будет у. Так как мы скалили что в раеематри-ваемом случае безударного вхождения струи относительная скорость входящей и выходящей жидкости одна и та же, то
n-f-w2 = u2 (w—yf;
здесь И’2 сокращается, и получается уравнение:
if — 2«’!/-)-(«“ — V‘) = u. . .(276)
Это уравиенпе связывает нейтральную величину в работе Ру зек го, у, с величиной w. Если откладывать по оси м /. обсцисс w, а по оси ординат у, то получим
/ ату связь в вп д кривой. Оиа пре дста-
/ вляет гиперболу (фиг. 320) с центром
J / в начале коор шпат, так как выражение
/ В-— 4 о и отсутствуют члены с пер-
/ I выми степенями if И у. . [₽гк > найти се
/ \ аесимптоты. О дну из них найдем, решив
в ' уравнение <276) относите.1ЫЮ и
1 м2 — Г 3
Фиг 329. ,Г = j У in
Полагая в пем у = , получим ю = -| у (так как второй член обра-
щается в пулы. Это п будет уравнение одной пз асеимптот. Тангенс угла наклона ее к оси у равен ., . Для нахождения другой аесимптоты решим уравнение (276) относительно у, при чем сохраняем только знак минус, т к как верхняп ветвь гиперболы прилежит к найденной уже ассимптоте и в теории винта роли Не играет; выражение ля у разлагаем
по биному Ньютона п. потагая w очень большим. шраничпваемся нервны членом разложения; топа
у W + Vи’—(и3 F'i = и. 11 11— '| 12'в,)
это дает р = о при w и показывает, чт второй а. симитотой гиперболы служит ось Ow. Когда ir довольно велико, можно для вычисления у ограничиваться одним этим членом.
Чтобы получить коэффициент ii6iejUt.ru действия элементарного винта т] возможно больше, надо, гласно ск&ганниму. брать у возможно меньше; ири этом скоро ть w получается очень большой iвследствие уве личения числа оборотов!, а панрав тения скоростей ОВ и ОА в начале и конце элемента лопасти сливаются между ••..бой. Величина у может получиться малой ие только ч/pei учстпченце w, по и через приближение н к К, ири чем сила тяги < гит- т постоянной вследствие увеличения площади. Коэффициент п • зиого действия ири этом приближается к единице. По, так как мы должны о -тановмться на оиределенные числе оборотов и площади вин га. то ноту чаем и определенное максима ibnot значение коэффициента полезного действия, превзойти которое пи в каком случае не удастся. Именно, полагая у достаточно малым и пренебрегая ям, получим этот наивысший прется:
что согласуется вполне с формулой <220р
Перейдем теперь к элементарному впнту. действующему е ударом жидкости о лопасть (фиг. 330) зависящим от шага и скольжения. Как и прежде, лопасть движется слева направо со скоростью СО = «’ (фиг. 331 к скорость потока Г, направленная вниз, равна СВ; относительная скорость входящей на юпасть стру й-ки выражается вектором ОВ; относительная скорость уходящем струйки направлена ио лопасти; у го т ВО 4 равен углу атаки в. Разложим скорость О В на напра
вление лопасти и па перпендикулярное к нему; последняя скорость, 1/7, уничтожится при ударе, и струйка сойдет с лопасти со скоростью 0.4, меньшей, нежели ОВ. Ра.доживши ее на составляющие по оси впита и по перпендикуляру' к радиусу, Найдем, что абсолютная скорость уходящей струйки выражается вектором СА1) и имеет оставляющие по указанным направлениям DA*=u и CD —у.
Теперь идача состоит в определении коэффициента полезного действия винта. Приложить теорему живых сил, как в первом случи*, здесь нельзя, так как часть живой силы теряется на удар. П» • иыу Ру <ский пользу ется теоремой о монеитс количеств движения, горня всегда верна, независимо от присутствия трения, удара и пр., т.н г • зависит только от внешних сил. Ес можно приложить и к первому случаю, когда явление происходит б»?з у тара.
’) Линия ГА ошибочно пропущена на чертеже. Л>м.« ро1
Так как при своей работе винт сообщает жилкой масс** известии! вращате ibhoc движение, а жи (кость, подходя к винту, этот движения не имела, то для сообщения его на осп винта должен развиться вращательный момент. По теореме механики, он равен приращению момента количеств движения всех движущихся масс около этой оси. ра деленному на время, так что момент сил, вращаюпшх винт; равен секундному приращению момента количеств движения всех масс около его оси. Работа, (дтрачиваемая на вращение вннта, равна произведению этого момепга па угловую скорость, т.-е. равна произведению секундной массы V на скорость //, перпендикуляр ну ю радиусу данного элементарного винта, расстояние х этого элемента от оси вйита и угловую скорость ш.
Т =- xVi/x ю = Mytc, так как x<a—w. Полезная работа винта равна нроизл* хеппю силы тяги на скорость судна, так что коэффициент полезного [епшвпя лнного элемента
— м iu ~ Fj v — <“ ~_D г
Г* Mt/ic tfW
Это выражение коэффициента полезного действия виц га все! ха верно; прн помощи уравнения i276) его легко привести к виду (273». Для рассматриваемого же случая имеем следующие соотношения, видные из фнг. 331:
Г-Д- w® — ОД2ВЛ- = «2-{-1 ic — [« — гг.
откуда, по сокращении, находим:
у2—icy-j-ши — Г) = О .
(279)
Это тоже гипербола с центром в начале координат [фиг. 332). Одна
Фпг. 332.
ее аесимптота — прямая, наклоненная под углом в 45е к осям координат; действите ibuo, уравнение (279) можно представить в ви (е
ic
у
Рассуждая совершенно так же. как и при исследовании уравнения 1276). найдем:
отсюда видим, что у приближается к нулю при возрастании и; •.»• ц>ва-тельно, другая аесимптота будет ось w.
Подставляя icy из урГ (279) в выражение коэффициента полезного хеиствия элементарного винта (ур. 27ы, получим
_ — —Iм ~ n v »Н(п
* «(«—V)4-j/a
Здесь опять tj будет Maximum, когда у бу ют иметь наименьшую величину; поэтому, согласно формуле (2791. выгодно увеличивать w При очень большой скорости w шаг випта, угол атаки 0 н вс птчина у приближаются к нулю; направления скоростей ОВ и ОД сливаются между собой, и коэффициент полезного действия достигает наибольшего возможного значения
. I-’bd
в действпте лыкягти же ecei ла меньше и, кроме того, меньше коэффициента полезного действия. опре едяемоги по уравнению 12771 дтя элементарного винта, работающего без удара. Если мн бу лем увеличивать радиус элементарного винта и его площадь, а разность «— Г уменьшать, то у будет приближаться к нулю несмотря на то, что ге конечна. Коэффициент полезного действия при этом будет стремиться к единице.
Изложивши теорию элементарных внитов, Ру зский от них с помощью интегрирования переходит к цельным винтам. Но мы этого вопроса здесь затрагивать не будем, так как идея его рассуждений уже здесь достаточно выяснена на основании вышесказанного об элементарных винтах.
§ .>0. Теория С. К. Джевецкого ’).
Фпг
Теория С. К. Джевецкого принадлежит к теориям виита четвертой группы (СМ. выше), основанным на рассмотрении винта как бы состоящим из бесконечного множества отдельных элементов и применении к каждому из них результатов наблюдений у дара ветра па пластинку. Она опирается на следующие допущения: что действующие силы пропорциональны площади и квадрату скорости, что винт всту паст в невозму шенныи воздух и что поверхиости тока струй являются цилиндрами, е, „гепыми винту
Теория Джевецкого (овольио обширна; но здесь она несколько переработана, резу льтатом чего является краткость изложения и форму л; основная идея при этом хорошо отмечается. Изменение манеры Джевецкого состоит в том, что мы рассматриваем не коэффициент полезного дейетвия, а „коэффициент вре щого действия"; нужно лишь вычесть его из единицы, чтобы получить коэффициент полезного действия.
Положим, что на фиг. 333 представлен цилиндр радиуса е, соосный с винтом; на цилиндре взята некоторая точка О, которая описывает от движения винта винтовую линию АВ со скоростью «, направленной по касательной к этой тииип, при чем эта скорость слагается из скорости Г посту нательного движения винта, направленной вверх, и скорости вращения ы₽, наврав генной по окру ж-иости CD. Встречный воздух идет относительно лопасти в направлении, обратном движению точки О, 6 с той же скоростью иг Пусть направление лопасти будет EF и образу ет с направлением винтовой липни АВ угол 0; тогда, на основании сказанного выше, воздух встречает лопасть под тем же углом р (если винт широкий, то он значительно возмущает возду х, и тогда нельзя считать, что угол встречи лопасти с воздухом есть Р).
Так как Джевецкнй делает для воздуха винты довольно узкие, то к ним можно применить результаты иаблюдеиий над пластинками. Именно, рассматривается как пластинка небольшая часть ef лопасти, вырезанная двумя цилиндрами сносными винту (фиг. 331). Так как наклон лопасти к оси винта меняется пе резко, то можно считать, что на i,*utihv большом протяжении идет одна пластипка, и применить к элементу результаты у лара на пластинку Джевецкнй предлагает брать л лппепи
’) С. IL ДжевсцкпЛ Теория воздушных внитов и способ их вычисления Киев IBIU г.
Потом} что тля таких именно пластинок имеются опиты; но т}т лучше считал!, пластинки бесконечно - (.чинными, раз мы станем па ту точку
Фаг. 334.
зрения, что несь протекающий в< здух зак точен между шумя цп титрами, соосными винту. Bel cn (у действия потока на пластинку ра дожим иа тве состав ляющих: насилу А нормальную к винтовой линии, и на силу Q, направлена} ю ио ней. Это суть силы, которые мы возьмем прямо из наблюдении иад пластинками той формы, которую имеет сечение винта. В винтах Джезецкого употребляется
дужка Рато с нлоекой рабочей поверхностью icm. фиг. 199 н 200); поэтому и данные надо брать с диаграммы этой (ужки 1фиг. 198).
Если рассматривать пластинку,двигаютцу юся по направ лению винтовой
линии, то у видим, что < и та Р нс произво (пт никакой работы, а вею работ} производит одна сида Q, гак что вся секундная работа вредного сопротивления получится, если мы Q помножим"иа скорость и. Эта величина, разделенная на секундную работу мотора, нет коэффициент вредного действия, который мы будем обозначать буквой секундную же работу мотора получим, если спроектируем силы Р и Q на окружность CD и алгебраическую сумму проекций помножим иа скорость вращательного движения лопасти oip = wsin«, где а есть угол между осью винта и винтовой линией АВ. Следовательно, коэффицист вредного действия
е
у _ 9"___________= _ J- _ Ц8Й
(/'соя., eosine) wsln a sinacosn . * .ш"а
обозначая отношение J, 6j кили /х и вво (я в формулу угол 2а, получим:
Очевидно, что 5 —° при Q -О, т.м /х = 0, и будет тем меньше, чем меньше /х, так как уменьшением /х знаменатель в после дней формуле растет.
Рассмотрим диаграмму дужки Рато (фиг. 193). Па ней представлены в виде коэффициентов: подъемная сида Р, которая возрастает почти пи прямой линии, лобовое сопротивление Q (кривая в виде параболы), которое
Р 1
вызывает потерю работы, и отношение ; последнее отношение быстро возрастает, достигает Maximum а, равного 14, при 3 = 4°,5, и затем снова падает. Ясно, что винт будет иметь самый высокий ке «ффицпеНт полезного действия, когда отношение (ля каждого его элемента будет наибольшим, или /г нанмеиьшнм; для выполнения этого по нашим опытам (фиг. 193), со теним с опытами Рато (фиг. 115). отошью бы брать угол атаки в 4’,5; Джевецкий, на основании опытов Ланглея и Рато, предлагает брать/л = 0,07, 3 = 2, и считай н\ по.-тояннычц для всех элементов винта. Собственно, из оиыт в Джевецкий берет только величину (с и (оказывает на еиовашш теоремы Ueno-Ренара, что а— Формула Пеио и Ренара получается из ваших формул (115) и (145); если в них бу (ем ‘‘читать углы о и Р малыми и заменим приближенно синусы малых дуг через дуги, то, прпилмая
получим:
Р .то Fl ’.,
' - 4| = .ipFT < i-a =Pli fl-' I), . (263)
ПС
отношение
продифференцировав это уравнение, при £=«=
М»» «=
найдем, что minimum д получается
откуда
/. :-4 =х, -- *
отсюда паивыголнейшип угол атаки
Для плоской пластинки, iyrn круга и крылообразной формы Н. Е. Жуковского это таключение оправдывается; для других же форм ио большей частп выходит п Для форм поддерживающих планов, испытанных Г. И. Лукьяновым, Мах получается при
Обозначим наименьшую величину /< через tg-/ и включим его в выражение коэффициента вредного , -йствия; тогда фирму та еще более упростится и получится
„ 2 tg , __2 sin
' , n _ *- tg / cm . а ч - tg { sin ^2 a — у) 4- sin ; ’
I ip
te? j4.
По мере возрастания угла а при у постоянном величина £ сначала весьма быстро уменьшается, проходит через minimum при а = 45 4~-у » и затем «•нова возрастает. Заменяя в последнем уравнении сумму синусов >гтов (2a—yi и у чрре удвоенное произведение синуса их полусуммы на косинус полу разности, получим форму ту, удобную для логарифмирования
11п_< .(2851
sin a cos (а— у)
В дальнейшем мы встретимся с величиной, играющей весьма важную р<» и. в предлагаемой теории, — отношением скорости Г поступательного виженпя винта к его угловой скорости со. Отношение это, посюяин -апного впнта. Джев^цкий называет Mui у л е м и обозначает бу етюй Л/:
V=- г ...............................ГЛ»в>
а J Л А
.V пргдетавдяет число оборотов винта в секунду). Модуль есть величина линейная, и потому ею можно воспользоваться, как единицей длины при
пш'трнеини диаграмм и определении размеров винта. Выбор этой е щницы пр* •’тавтярт ту выгоду, что формулы и тнаграммы, в которых за ш-.ивиеимое переменно принят мо уль, строются раз навсегда и пригодны дтя всех винтов; в зависимости от соотношения между V и <о меняется ветичина модуля, а вместе с нею подобно изменяется и весь винт; винты же, размеры которых выражены различным числом модулей, различаются по своей форме, пропорциональному шагу, и т. д. Число модулей, заключающихся в радиус*3, будем обозначать через г:
Q = ZM.
5 / 74 / 05ео
1 0560
I 0.586
/ 0609
1 0635 /- - 0669
- ОЬ9Ь
- -0730. /---0,767 /- - 0807- -/-- -0896.
[----0869.-
Вернемся снова к коэффициенту’ вредного действия £ элемента винта. Зависимость его от угла а мы уже рассмотрели. Прибавим только, что наименьшее значение, какое можно приписать углу а в действительном винте, есть у, потому что тогда £= 1, и вся работа поглащается иа вредное действие; если взять элемент еще ближе к оси, где «</, то ои будет (авать отрицательную тягу. Так как между углом а и радиусом р существует связь:
tg«= = г, P = Jtftge, . (287)
то для каждого радиуса р ветчина £ при данном у иолу 1ается вполне определенной. Зависимость между J и о при р= 0,07 = ^-,т-е. у=4",0, представлена на фиг. 335. На ней ио оси абсцисс отложены величины г |т.-е. величины р, выраженные числом модулей), а по оси ердииат слева направо (от О' к О) коэффициенты вредного
2 действия, а справа налево, ют О к О ) — коэффициенты полезного действия •>) (ОО' = 1,
•2 р = 1 — Z). Вычис деиие удобнее всего произ-
ц водить по формуле (235). Minimum f нри-
ю ходится при п = 45°= 47°, чему соответ-9 ствует г =1,07 а далее f возрастает вместе 6 с г. Диаграмма показывает, что наивыгоднейшее действие производят близкие к оси винта элементы, находящиеся от нее на рас-6 стоянии от 0,5 до 5 модулей. На практике же 5 оказывается, что при этих условиях площадь лопастей недостаточна для развития потребной силы тяги, и приходится делать винты с лопа-
5 стями в 7 и бо iee модулей (во ие более 12).
2 Чтобы по коэффициентам полезного дей-
7 ствия ч отдельных элементов подсчитать коэф-₽/оо7 фициепт полезного действия р0 всего вицта, j---- Джевецкии сначала брал средний коэффициент
‘ полезного действия между данными пределами, а потом стал коэффициенты полезного действия отдельных элементов лопасти помножать иа квадраты соответствующих радиусов и сумму их делить иа сумму квадратов радиусов:
У О'
Фиг. 335.
Ширина «лсментов допасти I в эту формулу не входит, так как Джевец-кий обыкновенно принимает ее для всего виита постоянной и-равной
-D, г •.* f) диаметр винта. Полученная величина коэффицие нта поw ног., действия пыясгея все-таки прпближепнон.
Дтя п< пчення 1 «чиоп величины коэффициента вредного действия 1О всего вит а, на основании сказанного в начале параграфа, надо взять вира ггипс
I Quid о » _ о. _
I fPcoso Q чп a) w sin а Ido
J -£ . Р wld Q
(2881
I* (sin а соча— £ sin2 а» PwldQ V.
где ни[ Р иХ/ тепер] надо понимать силы, отнесенные к единице пто-1ца [и. Прет*.ты интегрирования определяются начальным радиусом лопасти q,. который всегда берется равным половине модуля, и конечным е2. Подвергая это выражение тому же самому преобразованию, которое было сдетано выше, получим
₽•
I sinyPtcIdn
- _______£i_
j -unacosfa—yjPtcldQ.
Так как I = (> (?,. то на I сокращаем; дифференцируя второе из уравнений (287) находим do — da, ио условию, w = ; что касагтся до
силы Р, ти она равна A'fws к9 величина как одинаковая, по пррднол*>жсшпо, для всех дужек, сокращается, и мы получаем величину мвпеящен тотт.к от у п пределов « (от ар с ответствующего началу пасти, д «о, . иответств}ющсго концу лопасти):
а» i’ da ^nr I -^a
',= J,— --------- • l2eyJ-
Г sinn cos (a — 7Э da
J *a*5c
Преобра.|у«*м знаменатель этого выражения:
Г sin a cos (a — 7) d« /* sip a (enwg COST sjd a &io t) da cos-41 ~~ J ~ co*
/* sin a da - Г sin* «И _ J co8*n M cot?a
= 1 ’Уг -slnz/
Вхоцпипе ею (И интегралы pi (решаются по ил стиым форм} лам:
/Д Ч^МЗ .
Л& Г[.с ?
Если бы составить хля этих формул шплпцы, то можно ими пользоваться для определения точною значения ‘_.
Джсвсикпй, пользуясь приближенной формулой: % составит
подобною таблипу «ко (ля винтов • различной длиной лопастей от 5 ™ 12 модулей:
Таблица Л5.
Ра 1 - ем 7Af OV 1OV I1.V • °*? l2Jf
Ъ 1 *• o.tw П«4 OAW 0.61Я
Перейдем теперь к построению винта пи по > -бу Джевецкого. Для этого возьмем 1фиг. З3(я оси координат JW К, так. чтобы ось Л была
Фиг. 336.
еще, что лопасть винта
параллельна оси винта и направлена по скорости; по ven Л отложим расстояние ОМ, равное одному модулю, и па оси Г отмстим точки Я, A,. 1-U • 44, отстоящие от начала
координат на ~2, 1, 2, 3, 4 модуля. Расстояния О А, ОАХ соответственно равны радиусам впита р. Если соединим точки А с точкой М прямыми «на фиг. 336 -пунктирные!, то их углы е -сью X будут представлять углы а (см. фиг. ззз) винтовых типпп с осью винта, а отрезки AJf, Ajlf, 4.,V - • -направления и величины скоростей элементов лонасти относительно воздуха. Повернувши все эти направления АМ,АгМ на угол Р, при котором хостигаст Maxi-mum’a, получим нужные нам направлении лонасти в различных точках винта. Задавшись ве шчиной, формой и расположением сеченый лопасти отпейте л ьио главного радиуса OY. получим полную графику винта; ну жпо только приставить к ней лекала и приступить к его постройке. Заметим Джевецкого представляет лопасть геометриче
ского винта, шаг которого равен д 2л М, только повернутого около
своего главного радиус* нгз угол р в сторону увеличения шага.
Желая отстоять спою теорию, Джевецкпй доказывает, что геометрический винт должен работать хуже его винта, потому что угол атаки $ нельзя иметь наивыгелнейшим на всей лопасти.
Доказывается это очень просто. Пусть иа фиг. 337 длина O.V равна модулю , а длина ОН равна где Н — шаг геометрического
винта. Тогда углы МА„Н, МА,Н, . . . будут представлять углы встречи лопасти с воздухом тя разных радиусов СЦ, OAt, . . Проведя через точки М и Н окружность, касательную к оси О Г (в точке Ло), увидим, что наибольший угол атаки есть МА^Н = р все остальные 1лы как измеряемые полуразиостью дуг МН и mh (или других, еще меньших) будут меньше у гла МАСН. " Следовательно, в геометрическом винте угол атаки $ сначала идет возрастая, недалеко от оси (на расстоянии от 1 до 1,5 мо-’V THi достигает Maximum а, а затем снова \ бывает.
У
Фнг. 337.
Если мы за наибольший угол в геометрическом виите примем угол.
р
«ггветствующий Мах то получим винт с плохим коэффициентом полезного действия, потому что отношение £ весьма быстро падает удалением от наивыгоднейшего угла атаки, особенно если итти в сторону его уменьшения. Но это рассуждение не совсем убедительно.
|ело в том, что приравнять наивыгоднейшему можно ие наибольший ч • л атаки геометрического винта, а какой-нибудь другой, например,
1 2
। и ты и на расстоянии от оси равным или -у- длины лопасти. В сторону увеличения угла атаки отношение /х падает не так быстро, и коэффициент полезного действия всего винта может быть лишь немного меньше коэффициента полезного действия винта Джевецкого.
Приведем теперь расчет винта, предложенный Джевецким. Коэффициент полезного действия винта устанавливается числом модулей Z и вели-ппюй отношения /х. Способ вычерчивания и построения винта опреде-• 4»*тся формой сечения лопасти, наивыгоднейпгим углом атаки р и (истом модулей Z в лопасти (ширина лопасти I всегда делается постоянной и равной или % , если ширину выражать в модулях).
Размер модуля определяется по скорости н числу оборотов. Для м ««лучения потребной силы тяги остается произвол в выборе числа оборотов .V, числа лопастей а и числа модулей в лопасти Z; при этом Джевец-ки! предлагает никогда ие делать лопасти длиннее 12 модулей. Если ила тяги все-таки выходит недостаточной, то нужно увеличивать число «•«•lacTfft до трех или четырех; более четырех лопастей в воздушных винтах никогда не делают.
J (есь мы встречаемся с общим недостатком всех, до сих пор опубликованных, теории вннта: в них предполагается, что сила тяги и поглощаемая мощность пропорциональны числу лопастей, тогда как на опыте •го предположение не оправдывается; при большом же числе лопастей, а < iy чае дальнейшего его увеличения, сила тяги почти ие меняется
При проектировании винта задается сита тяги R и скорость и<«« ту
«иного движения F. Надо определить диаметр винта 2Z.V. и« •• --ролов N и число лопастей а. Для определения их поступим • •• <>> щмм образом. В знаменателе уравнения (288) стоит поглощаемая «> tii«»t топастью винта мощность Т", в числителе—потерянная мощность Т К V рааиость этих двух величин, умноженная иа число лопастей а, щи и • биую нам полезную мощность RV. Производя указанные imurra
кцкчкие осасвы веадуховлалавва.
новки и преобразования и вынося общих постоянных множите лей нз-по i знака интеграла (теперь они не сокращаются), иан 1ем:
РУ ktV3 Ml а Г lint! cos (а — у) da к.Г 1 Jf/а sinт Г da
cost J cos'a. cosy J cos’/i •
сокращая на I, заменяя ширинv лопасти l через - и раскрывая выражение модуля, потупим:
п k_V*Za I Г elno COS (a — l da (* da ]
R=irfx^\J -аи'Ч^а |-
Поглощаемая винтом мощность
«1
f — 75 ]{p___ S1 C sin« cos (a — /) da
34т’5-С08/ J coe^c
= 7Sn Zif \Z), . . . 1291,
где HP представляет мощность в лошадиных силах, а
у ____________kf.Z /* BiDK соя la — r)da
! 75.24 л’-cosr J cos’a
Пределы нитрирования определяются по уравнению (287); так как всегда берется Pi = " , то нижний предел остается постоянный:
р] = аге tg -i- — 20" .13';
верхний же предел определяется ио уравнению:
о4 = аге tg jj} = аге tg Z.
где длина лопасти р берется от 5 до 12 модулей Величина Zy \Zt для к, = 0,015 и 7 = 4,0 вычислена Джевсцким. В указанных пределах (между 5 и 12 модулями, она ювольно точно может быть выражена уравнением:
v зоиоооо ’
Приводим также таблицу 30 значений обратной ей величины, заимствованную из сочинепия Джевецкого:
Таблица .!«.
Z 5 б Г и 9 10 11 1 12
\:Zy(Z) 3953 3024 1058 । 549 | 302 ' 230 14 | 104
Рели подставить приближенную величину ZyiZ) в уравнение (291), то получим так называемое уравнение сов.ипmuwстн.
НР =
п
300X1110
(295)
но которому в на ю подсчитывать все элементы винта. Для практического пользования это уравнение весьма удобно.
Джевецкин приходит к уравнению совместимости несколько отличным от указанного путем. Именно, он за (ается ие полезной мощностью RV, как бы следовало, а затраченной на валу мотора; последнюю же uiipe-чрляет приближенно по коэффициенту полезного действия винта (приближенно, потому что коэффициент полезного действия винта неизвестен, пока не опредетсн параметр Z». Закон изменения ширины лопасти с радиусом сначала предполагается произвольным, так что под знаком интеграла входит неопределенная функция у (tgai, которая впоследствии определяется условием, что ширина лопасти I постоянна и равна в ; интеграция ведется по tga, принятому за независимое переменное. Наш путь является более коротким и, кроме того, более точным, так как элементы винта определяются по входящим в условие задачи силе тяги и «-корости1).
Примечание редакции. Окончательное интегрирование уравнений С. К Джевецкого при постоянной ширине топасти, равной и постоянном р дает следующий результат:
<’п.ла тяги всего винта
4-e(i-7>=bSi i|l,+ai'* И2» ‘ + 2*^
А 1
1 * * I *
+lg(2-| 1+^)] • 1290)
* ъ
Это в случае. если мотор строится под аэроплан. Если же дай мотор как это чаще бывает, и под него проектируют аэроплан, то надо иттк путем Джевепкого, исхода л мощности иа валу мотора. Прнл. ред.
Поглощаемая винтом мощность
Г=75НР = *^ i ’ | (»+«*>’ +
+ 1 V (1 + IР [* 1+?+1g (*+1 1 + ^)] р=
= ^H|<1+*)l+'*n£ <291')
Коэффициент полезного действия винта Джевецкого удобно представить в виде
. . . . (289')
Для удобства подсчетов нами вычислена таблица 37 значении (1-1-г1)2 С, D, с и d ио параметру от 3 до 10:
Таблица 37.
Z, «Л . С 05 % d
D ofi С
3 30.2 15.5 60,5 0.512 2,20
4 68.6 26.3 203 0.384 2.96
5 131.1 40,2 486 0,307 3,7!
6 223,6 57,0 998 0,255 4,47
7 352,1 76,; 1836 0,218 5,21
8 522,6 99,5 3119 0.190 5,98
9 731,1 125,1 4981 0Д71 6.80
10 1013,6 153,7 7590 0.152 7,50
Нижний предел интегрирования Z, принят ним 0,5. Коэффициенты end вычислены в том
здесь постоянным и равнее предположенииг).
*} Взято иа статьи В. П. Ветчннкпна. Расчет гребного вивта (статья первая). Бюллетени Политехнического Общества 1913 г., № 5. Реоакцня.
В заключение приведем результаты испытания винта Джевецкого. Испытания производились в аэродинамической лаборатории В. Т. У., Г. И. Лукьяновым. Винт, диаметром в 2,6 mt с лопастью в 30 ст ширины, был распилен иа части, длиною каждая
н । 29,5 ст ширины каждая и испытаны в плоской трубе. Как известно-розу льтаты этих испытаний относятся к бесконечно длинным пластинкам 1); опытные данные о таких именно пластинках положены в основание всей ь
. >рии. Па фиг. 338 представлена шаграмма коэффициентов к,, к, и л
я выреза, лежащего недалеко от края лопасти; при этом малая вели-iHiia к. на чертеже увеличена в 10 раз. На фиг. 339 представлен ход и । «<-иеция по длине лопасти элементов, характеризующих пластинку: маю ималыюго значения и’наивыгоднейшего угла р, при котором это ми -пне получается; кроме того, на этой же фигуре нанесены кривые • I) пктирпыс) значений-^- и к, при /? = 2", принятом у Джевецкого за .и. 1ТШИЙ угол. Как видим, нн один из элементов ие остается < иным на всей длине лопасти. Кроме того, и углы Р. и й, более, м прево ходят значения, принятые при проектировании винта; ...... я близко к 0,07 при Д = 2“, minimum же его доходит и 0.06
81 IIiiiimikx построить винт с постоянной скоростью за винтом, принимая во внимание подсасывающий эффект лопастей.
, I. и Н Т. > . Г. X. Сабинин и Б. Н. Юрьев задались вопросом ; । , к и >рый бы давал равномерный йотой по всей площади.
Их и >• I ..»|ия примыкают к теории Джевецкого, которую оии соединяют Лщими Т' чргмамн о количестве движения
< грог гета .того положения заметно нарушается влиянием аааора между грубо! ваастявиоВ, яая ято яыясннтось за последнее время. Прил. реЗ
Рассуждения и чертеж 1фиг. 340) здесь совершенно такие, как у Джевецкого (фиг. 333). Обозначения тоже сохраним прежние. Под скоростью Г надо подразумевать скорость поступательного движения винта, или скорость потока вдали от випта. так как авторы теории считают, что воздух приходит в движение еще перед винтом, когда после ший только подходит к данному месту—считают, что воздух подсасывается к винту и подходит к нему с некоторой скоростью Г-.-«, = Г1Г пока ।анной па чертеже. Пройдя через винт, воздух еще ускоряется и уходит уже со скоростью V - и2= Г9. Абсолютная траектория элемента винта (точки О) изобразилась бы винтовой линией АП, образующей с осью винта угол о; эта линия на фнг. ЗЮ не изображена. Траектория этого элемента относительно подходящего во.дхха изображается винтовой линией .1ХД. образующей с осью винта угол а,. Абсолютная скорость точки О изображается вектором «*, слагающимся из I' и сор и па чертеже не изобра-
женном. Относительная скорость лопасти и подходящею воздуха изображается ректором 1гь слагающимся из Г, и о>о:
Фнг 340.
воздухом обозначим через /?, при чем, ио (бирается так, чтобы отношение берется из опытов над
трубе. Таких опытов в настоящее Полная сила, действующая на
бе конечно
it— ' = -
СО*;, 8100]
Угол встречи лопасти е пь хх« щпшм как и в теории Джевецкого, он и было наименьшим. А гол 9 длинными пластинками в плоской время имеется достаточное количество, элемент лопасти ld$ (I — ширина лопасти на (ашюм ридиусе» и отнесенная к единице площади, разлагается иа составляющие Р по нормали к винтовой линии Bt и Q—по ней. Спроектировав эти силы на ось вннта и на касательную к цнлнп ipy CD, получим формулы для силы тяги-------- ——
шия __ а.
и затраченной мощности элементарного винта, совершенно совпадаю-с формулами Джевецкого; to.ti.ko в них вместо угла а фигурирует и вместо скорости Г — скорость Гр
dH (Pxjnaj Q cosaj Ido -- Pco^a, Itgcq — pl Wp, dT = (I*cosa, —t— Q Unaj) \\tvaildo = Рчпа, Il -г Wo Ft,
i к
Обозначим сип-
< другой стороны, сила тяги винта равна секундному приращению количества движения по осп винта жидкости, 1фошедшей через виит.
гак что
dR = | Г8 — Г) dM.
Секундную мае, у следует определять по скорости Г2 в сечении ab,
• иответству ющем
♦•Г 541
наибольшему сжатию |фиг. В41), прн чем площадь этого сечения равна площади, омстаемой винтом, помножен-ной на коэффициент сжатия $ Его следовало бы определять иа ппблю [опий струи воздуха за винтом, но пока приближенно можно брать коэффициент сжатия струй жидкости, истекающих из сосудов.
При гелпкоптерном винте можно считать, что
г\ в нлаются в отвори!не винта как бы иа очень широкого сосуда IM внутрь (фпг. 3421 и Принять : — 0.55.
I • । кипы 1 р(*быо! можно провести аналогию о истечением жидко-’t и •• । аоретие в дне трубы (фиг. 343).
।. н 1меп> нии отношения площадей сечения трубы и отверстия • и । сжатия : меняется, при чем опытами установлено. что
Fs — V с ~~ «. ~ к, — г
................чти постоянным: величина его меняется от 1,6 до 1,8. |(г“ -’W 1 < тношенпях между I и Г, в гребных винтах отношение J «ЧИН» принять равным 1,7s. Тогда для коэффициента сжатия с~' £- = °.5в + 0.44 р-.
Itjna,.......... .pm th надо считать равным разности V, и Г. так как
wt, tibil* • '» 'ШТ к винту со скоростью Г 4- прирашенп ско-
। »ч« • . тки эффектом винта.
ТЫ** м 11«>счим:
•IM = Е 2 л о <?о Г„
rfft 2.4orfpl'2w5 - .(247)
, .'II выражения (266) И (297), найдем, ЧТО
!•», J 1 , * -о| = 2.т р<?еЕКаи, 2PS)
Это уравнение позволяет подобрать ширину лопасти так, чтобы поток за винтом был равномерным и, вследствие этого, наплучшим образом использовать площадь, ометасмую винтом.
При определении ширины лопасти заметим, что по уравнению расхода
Тогда из формулы (298) находим:
tu
ТС Ч
+
jq,
1299) ‘)
Вторая форма этого уравнения позволяет построить кривую, ординаты которой, умноженные на Л/, “3, тают очертания лопастей винтов
I 1
с постоянной скоростью потока за винтом (фиг. 3-11).
Скорость подсасывания мг (а вместе с нею и скорость перед винтом) должна быть определена из опыта. Если принять, что при постоянной, скорости Г2 скорость Г, тоже постоянна для всей лопасти, что следовало бы из формулы F, = $Г>, то получим следующую простую формулу для силы тяги:
R = £ it У Р2 и2 f Qdo = Г, — pj3), (ЗОО)
01
Числитель этого выражения
где обозначает радиус втулки. По данным К и V, задаваясь диаметром винта, определяем = F9 — V. Переходя затем к уравнению (299) и задаваясь угловой скоростью со, иайдеы величину модуля Мг, ширину лопасти I на каждом радиусе и коэффициент полезного действия всего вннта; угловую скорость о придется брать согласно характеристике мотора. Определим коэффициент полезного действия винта
RV
Vo f
rv= сл j- F г. И, - е,3) = s-л - - м* г г, и, (Z,2 z,»i.
Циркуляция скорости вокруг лопасти с длиной do равна
7 ।
при ц — О, J= const.
Прим. p’d.
Для того, чтобы полу чпть знаменатель, надо объиитегрировать выражение мощности, затраченной иа вращение элементарного винта. Преобразуя иодъинтегра.тьную функцию, представим ее в таком виде:
dT=/’sinn1 (l-f-ptga,) l\/dp =
Замечая, что
= 1f/'ga, я)
» COSO, ' 1 " *
0 Ле
Г I + Ч1 («. — и)
= )/1 -j- tg'<il — ]/1 + г,-
и заменяя р, de и tgc, их выражениями через г,, получаем:
dT = Г- 2 я £ М^и.,
В выражении коэффициента полезного действия винта общие постоянные множите ли сокращаются, так что получается:
г
4° —
. . - (301)
Входящий сюда интеграл легко берется:
= |!',(S1,) + <1 + U’) A(31-|-W»+,ts(1+JK?) г'1В(г,-м1 =
ж«-* 3 Zt •“ z, Iz,
•; (7!-’_Z,’l + 1 +^)(Z,-Z,) +
+ (!+?’)
II »'ЫШП радиус о, -MjZ,. как и у Джевецкого, следует брать црибчи-«» "Ио в потовину модуля. Если пренебречь малым членом
«•< рык в» я > не превосходит 0.02, то получим для коэффициента полеа-u" irt' tiMM рассматриваемого винта выражение:
•__________________2,+ Z,_____
[уд4К1+й]% + [,‘ n^+a+в») (^-r2B)J
=^6(Z2).....................(3021
Приводим здесь таблицу Зъ ве.шчин 0(Z.>), принимая Zx- 0,5; 0,075:
ТЧЬЛИЦА зн
2 i * t “ I « I 10 1 11 I 12
W(Z). 0.77g ОД 51 0,727. П.701 О.67Я 0,656 0.615
Как и в винтах С, К. Джевецкого, убывает <• удлинением допасти винта (возрастанием ZJ.
Примечание редакции. ( погрешностью, никогда не превосходящей 1°’о, можно отбросить в раскрытом виде знаменателя формулы (301) все члены со степенями р выше первой. Тогда получается удобное пя по шчетов прибдиженное выражение коэффициента полезного действия винта Сабинина-Юрь«ва при мобом (но постоянномi значении р\
при чем значения а при Z,=o,5 даются следующей таблицей:
Таблица 69.
Z-2 4 5 6 7 ” 8 1 10
п 2 62 7,15 4,73 4,3з 4,95 5.5S ( бДн 6£7
('равнение величины а с величиной d из табл. 37 (стр. 292) показывает, что механический (зависящий от трения возду ха о лопасти) коэффициент полезного действия винта ('абпнцна-Юрьева выше такого же для винта Джевецкого, т.-е. что форма лопасти винта Джевецкого менее рациональна ’).
При построении винта углы лопасти с осью его определяются так же, как и у Джевецкого, с той лишь разницей, что за скорость перед винтом берется ие скорость Г всего потока, а скорость I р сообразно с этим, к наших формулах к величинам а, М и Z. встречающимся у Джевецкого, в прибавлены значки (1). Если приближенно положим Г, Т, то перейдем к винту Джевецкого. лающему равномерный поток.
По достатком изложенной здесь теории яв ляется (опущение. что ноток иод винтом на всем кольцевом элементе имеет постоянна ю скорость, между тем как в действительности скорость в каж щй точке изменяется со временем, делаясь больше при прохождении лопасти через эту точку2). Это явление будет особенно резким ири очень \зких частях лопасти.
*) Взято нз вышеукяз&ннов статьн В. П Ветчинкима (см. прим, п стр 292).
Редакция.
) Практика построения подобных винтов показала, что погрешность указанного допущения пе сильно отражается на окончательных результатах силы тяги н работы винта Ирим. pfd.
52. О подсасывающем действии винта при большом числе лопастей.
В моей заметке ..Теория гребного вннта с большим числом лонастеп*') я применяю способ Неппера. изложенный в его теории турбин, для опре-етения скорости, с которой воздух вступает на топатки виита. при чем предполагается, что скорость по радиусу винта равна нулю. Эта теория имеет тот недостаток, что она не сказывается с хорошо исследованными и росами о влиянии фирмы дужек на силы сопротивления, а должна аимствовать свои коэффициенты из опытов над турбинами и вентиляторами: правильно поставленными опытами можно определить эти коэффициенты и непосредственно ыя винта.
В основу теорпи ставится пре (положение. что над винтом образу стоя >засть пониженного давления р, в которую притекает во.и\х из под > м .сферного дав синя р(. Рассекая внешнюю поверхность, ометаемуто • пнтом, cwn-нымц цилиндрами на б сконечно-тонкие кольца, мы можем •.. идный объе j воздуха dQ. протекающий через кольцо с радиусами о к q -de (фиг. 315) для геликоитерного винта представить формулой:
dQ - 2.Todoa J - “
*2 ло(1() и ,
. .(303)
। а » сть некоторый коэффициент истечения, он должен быть определен ..... и приближенно. на основании данных 1И(равпики. может быть ложей равным 0.62. При движении жидкости между (вумя смежными
лопаггямп можно воспользоваться теоремой Бернулли гая относительного движения (к абс«. потному видению теорему Бернулли прилагать неяыя, так как ш-паткп движутся, и мы будем иметь связи, «висящие от времени2), принимая на основании опытов, что в выходящей из-под впита струе давление близко к атмосферному. Относительная <*к<>р<»гть вхедяшей жи (ко-ти подучит»-я через с южгнне скорости и сп скоростью вращательного 1ви-женпя од, взятой в обратную сторону, и направится под углом 6 к плоскости, перпендикулярной леи винта. Называя у гол конечного элемента винта с этой пло-
Фиг if.
скостью через /. определим относит^ 1ьные
\ । щей н выходящей етру п; дзя этого надо dQ разделить иа
• . । и .'jrodosini: вследствие этого теорема Бернулли напи-
*—1’2 =*•+(_ -f L
’ iprfpsiney 'ig --rpdpsIniJ 2д *
»V > 'ГО
~ 1____1 1=1 /1 1 ______ 1 (ЗОН
• in"® sin 2-rpdp I 1 tg-® tg* 1 '
. TtjJW । ' Фи Па) a <». Л. E.. г \1И, вып. 2, 1907 г.
Ь Джимам глучж» струи рассекаются лопатками ввита, чег нет в отвесите:ьиом 'Ним. йр«.м ре
Здесь
tg/ =
н
ZZIQ
tg0 = —, toQ ’
где H есть шаг вннта, расчитанный по направлению выходящего элемента. Исключая из формул (303j и (304) величину * , находим:
откуда
1 ___о’р3 ____4nV
а2
. (305)
. (306)
Из формулы (305) видно, что при постоянном Н осевая скорость и вытекающей из-под винта жидкости возрастает при передвижении к концу лопасти, как это представ тено на фиг. 346. Если лопасти винта сделать
Фиг. 347.
закру пленными, как на фигуре 347, то угол 6 будет устанавливаться сам собой, согласно формуле (Зов), прн заданном Н. Формула (305), которую можно преобразовать перенесением Н в знаменатель:
позволяет надлежащим подбором Н построить винт с большим числом лопастей, дающий произвольный закон распределения скорости и в разных точках лопасти. Если желаем получить пот винтом поток постоянной скорости, то следует положить
Ауу + А? = const;
4л’с’р2 1 й2 *
если здесь, для простоты, сделаем подстановки
1 о 1 ->
е2 =а-, ^=»-,
то найдем, что х и у предстанляют координаты эллипса:
-^а. + У = const.
— 301 —
Переходим к гребному винту, который можно рассматривать, как винт без поступательной скорости в потоке, набегающем на него со скоростью V. В этом случае секундное количество жидкости dQ, протекающее через элементарное кольцевое сечение винта, можно выразить формулой __________________________________________
й<2=2яейоо | уг.
где рид, имеют прежние значения. Что касается формулы (304), то она .станется без перемены, и мы полу чим:
1 соV 4- У* 4тр2
ткуда
п На ] о2 +
............... (307)
(.••л того, чтобы винт греб воздух, необходимо, чтобы и было больше V, пк как воздух, выходя со скоростью V из-под атмосферного давления, itpiixo 1ИТ в область пониженного давления со скоростью и; тогда, по пер-• • формуле (307), имеем:
г (А. -1) < - % Г) е2 ........................(308)
11.. чи'ая . еь а = 1, получаем:
V>°-
NH— Г>0 .
1»г< .» |.а* > «и>тпо показывает, что скольжение винта во всех частях лопасти авмнн»< быть положительным, чтобы над этими частями сохранялось дав.че-м- w ..... атмосферного. Это же неравенство (308) дает величину иаи-
ш»ммн> р* м«< а по i условием, чтобы все части лопасти развивали полота* • Мы имеем
....... ...... ам*||иая сь теория предполагает, что струи вступают на м01.................। 1 ипж» • I •• осн, что было бы совершенно точно, если бы
• MMfainii к небольшую цилиндрическую трубу.
53. О подобии.
Чтобы иметь возможность применять результаты лабораторных опытов пад малыми моделями, подвергнутыми действию потока, к телам подобным, но больших размеров, с которыми мы имеем дело в действительности, прибегают к так называемой теории подобия в задачах гидродинамики.
В § 32 были уже выведены уравнения гн фодпнампки для установившегося движения:
дх
др
О*
ди
дх
дг
дх
>w
дх
/и - ди
ду * дг
dt ог
Ле
— А 4 ' J»i
= У+-£- j< 1 Q
. . (194
при чем за основные е щницы измерения были приняты килограмм-сила, метр и секунда, так что размерность обоих частей > равнений есть
[Ay'. m‘, s ’|.
Размерность входящих в уравнения величин р, р. X. Г такова:
9 = [kff‘, ml-*, sec"] р = 1*<А mt-1, sec | X = Ikg3, mt1, srr-3| Р = [Лр\ mt1, sec 4
. . (309)
Наконец, размерность кинематического коэффициента вязкости.
— v — [leg , mt-, sec-1].
Пусть наряду е рассмотренным движением происходит другое движение, с линиями тока, подобными первым, так, что каждой точке в первом движении с коор (инатами (х, у, г) соответствует во втором точка с координатами:
х' — 1х, у' — 1у, г' = 1г.
и пусть, кроме того, времени t первого движении соответствует время tt = rt во втором и. наконец, пусть каждый килограмм силы в первом случае заменяется qkg во втором. Это новое движение удовлетворяет дифференциальным уравнениям (194'), потому что. если написать эти самые уравнения для величин, отмеченных ян (иксом ( ), и разделить иа
, то получим уравнения (194').
Величины, вхо (ящпе в формулу 194', будут/ для нового движения таковы:
Р =9«/
Р =рч‘-А = Х(га
Г=Пг 1 v=rPr->
Отсюда получается
ы 1И
р _ у _
4» Г» оР
. (3111
I hi (опустить, что вязкость и сита тяжести, действующая на жидкость < швают ппчтожно малое влияние на давление, зависящее главным
. 1|».МОЧ »>т скорости, то можно будет положить
Л== K=z = o, р = 0,
и tn* 1с1шя I, г. г/ не будут по (чинены никаким ограничениям.
Форму та 13111 покалывает, что при сделанном выше приближении, mi • но считать, что коэффициенты сопр'лпив гения, полученные из опытов • и' • 1ью, могут быть распространены без изменения так лее и на тела • ь а чительныл размеров.
♦т условие справедливо и в случае образования поверхности разящ модечи, потому, что по теории Кирхгоффа, граничные условия • I- »>»т. чтобы квадрат скорости жидкости относительно тела на поверх-..» гн pai (ела был бы такой же, как и в бесконечности. Если выразить • к пне дли факторов, отмеченных индексом (' », то ати уравнения мчшя Z2 представят то же самое условие, выраженное для । 11,1,1" ibiioro потока.
। in опыты в лаборатории делаются над маленькой моделью, то -и м-n-ти стоя жидкости, прилегающего к модс.ш, играет заметную I • »п|>«»тив. юнин движению и. чтобы сравнивать опыты над моделями । .«м.. й иг-шчпны. нужно по формуле (310/ иметь
♦ а м •отнетствующие коэффициенты вязкости в сравниваемых пото-•. It......чер« » Л и Л' соответствующие размеры обоих моделей, можно
• »- ... -с it формуле заменить I его значением 1= j- . Подучаем:
= Г»........................(312.
I» I»
мвии н<н‘нт название чисел Р'йюльоса.
Н «»• ••»<>« ».реходят от одной модели к другой и когда размеры « .« Л м ш обоих незначительны, надо производить опыты
«М» * » лих опытов чис м Рейнольдса были одинаковы.
ь .* .'Ы «аются в о (ной и той же жидкости, то (олжно быть:
Г/Г = ГЛ ......................(312’1
</₽ ..__ вГ
» •
к единице массы, и перенесем их
« н у I*», hi ипн (IU4): тогда поете типе можно написать в вив
- : ч- Z и-r-
tax (19 Г>:
отштенная
н в уравнениях (311) члены — (Г и р- — U могут быть подставлены вместо р. и .
т- 0 0
Если, например лабораторные опыты были произведены над малой моделью дирижабля, то. если пренебречь в таянием силы тяжести на результаты опытов с моделью, давление на поверхность самого дирижабля может быть выражено формулой:
. г* / ₽т»
р f ₽ = рП-Р.
откуда, полагая р = р’ и U' = —gz’, найдем
. V'»
Р = P~Q9Z, ... . - -(313)
т.-е. давление на дирижабль можно вычислить, умножая давление, найденное на модели, на отношение квадратов скоростей и присоединяя гидростатическое давление.
До сих пор мы предполагали, что в потоке жидкости нет свободной поверхности, на которую действует постоянное давление атмосферы. В последнем случае, согласно уравнению (194')» должны иметь для всей свободной поверхности
............(314)
где UD п с}ть значения силовой функции н скорости в точке, весьма удаленной от погруженного тела.
Формула (314) 1ает
Г—С, —Р„’) = О
илв, иначе
_ v -v«L
---V- с0 •
Дтя силы тяжести значения силовой функции можно написать в вид»:
U = — gz, 1„ =-- gz0.
Тогда будем нмсть:
Переходя к подобном.) движению, находим, что I и г связаны с условием: 1т »=1, откуда получается, что
или иначе
т.-е. отношение линейных размеров равно отношению квадратов скоростей. Это закон Фру да, применяемый при опытах над моделями судов в опытовом бассейне.
неразрывности (51. которое для установившегося движения npiiiiiiM.il т форму
1 (е*) । <> (рс> । д (с«) _ 0 Xr I" ву ‘ >s ’
уш однородным, хотжно существовать для второго потока, если оно 1 мщчтнует в первом. Для несжимаемой жидкости это уравнение не нала-гвет никакой зависимости между /, т и Q.
Ио. если жидкость 'ж и маема, следуя закону, выраженному- ура iiiiriiiK ы (в):
Р Iq', р' s'®
гл» с и с'—коэффициенты, определяемые температурой н (явлением. « к ще» т у ющими на значительном расстоянии от тела, то ветичииы I, т п q будут подчиняться зависимости, выраженной Соотношением:
ql * =
пли иначе
£ =(фГ*
Если предположить. что тепловой пронес.- есть процесс адпабатпч! скин, е показателем адиабаты у равным 1.4 и принять во внимание, что скорость звука выражается форм) той
* = )
то из формулы (316) получим:
V л'
V — д ’ ............13141
Отсюда следует, что для возможности сравнения опытов вроде шнны в газе при разных давлениях и темп ратурах, нужно, чтобы скорости обоих потоков относи, шеь друг к другу, как CKOpot ти звуки, опр> де темы*' этими температурами и давления ми.
При опытах с большой скоростью необходимо принимать в сообр.-ж иве это правило, указанное Hairston u Booth.
Когда процесс изотермический и копа температуры и (авленил в точке, весьма удаленной от точки тела, равны в обоих* потоках, бу (ет
у = I и $ — *;
форм\та 13171 дает тогда
Г Г .
«Это показывает, что оба опыта надо производить прп одинаковой скоро ти.
Скажем, наконец, несколько слов об осуществлении условия положи тельности (явлений в обоих рассматриваемых потоках.
Пренебрегая изменением высоты, можем написать
р + ₽ =Ро + » V-
где Го есть скорость тела, или, лучше, скорость обтекающей непс (внясп тело жи (костя в бесконечности, а рс атмосферное давление
Т«ор*твчес«яа оснааы возауховлаагжая
Если давления положительны, то
р=р<,-е >"•
Предполагая, что это неравенство удовлетворяется для первого движения, мы можем однако допустить, что оно не у ювлетвиритсл для второго вследствие возрастания члена
Н4 ¥)
«Это налагает ограниченно на q. I и т. Прилагая написанное выше неравенство ко второму движению, мы Должны будем получить
Обозначая максимальное разреженно в первом движении через Лр0, имеем
;-р< =₽ (Л- — -xj-
откуда можно написать, что
I о V*’ л р\-
Это неравенство указывает на затру шительность использования результатов опытов над воздушными винтамп для винтов водяных. В самим деле, так как отношение плотностей воды и воздуха равно приблизительно 800. то, чтобы перейти ит воздушных винтов к винтам водяным, надо было бы произвести опыты над первыми с разреженном л весьма незначительным, т.-е. со скоростью вращения очень малой. Этн условия, к сожалению, очень не выгодны для действия воздушных виитов.
Замеченные опечатки.
Стр. Строка. Напечатано. Должно быть.
S 14 сверху . . 30
129 П снизу Семейства Семейство
178 26 сверху (2471 (147)
203 17 снизу мевятся меняется
Ju7 2i сверху Общества Общества
ЭЛ институту Институту
313 сбоку фиг. 286 фиг. 2нн
ш 12 сверху * Л;
Т2§ (1 — г) V А (1-г) /а
I снизу
Уа'г У а'г
форм (225) Е (R)
«зш 12 снизу Т3 (3V
233 12 . Е1 (£)2
форм 1 R* (₽
2и Л Г
233 9 снизу R (Л)а
7» (Г)’
форм (22 . R? (RF
233 Т* (7?
„ 2 R9 2 И»
234 6 снизу F Л 3^
239 J сверху коэфнциентом коэффициентом
254 24 . 2113 1’"?